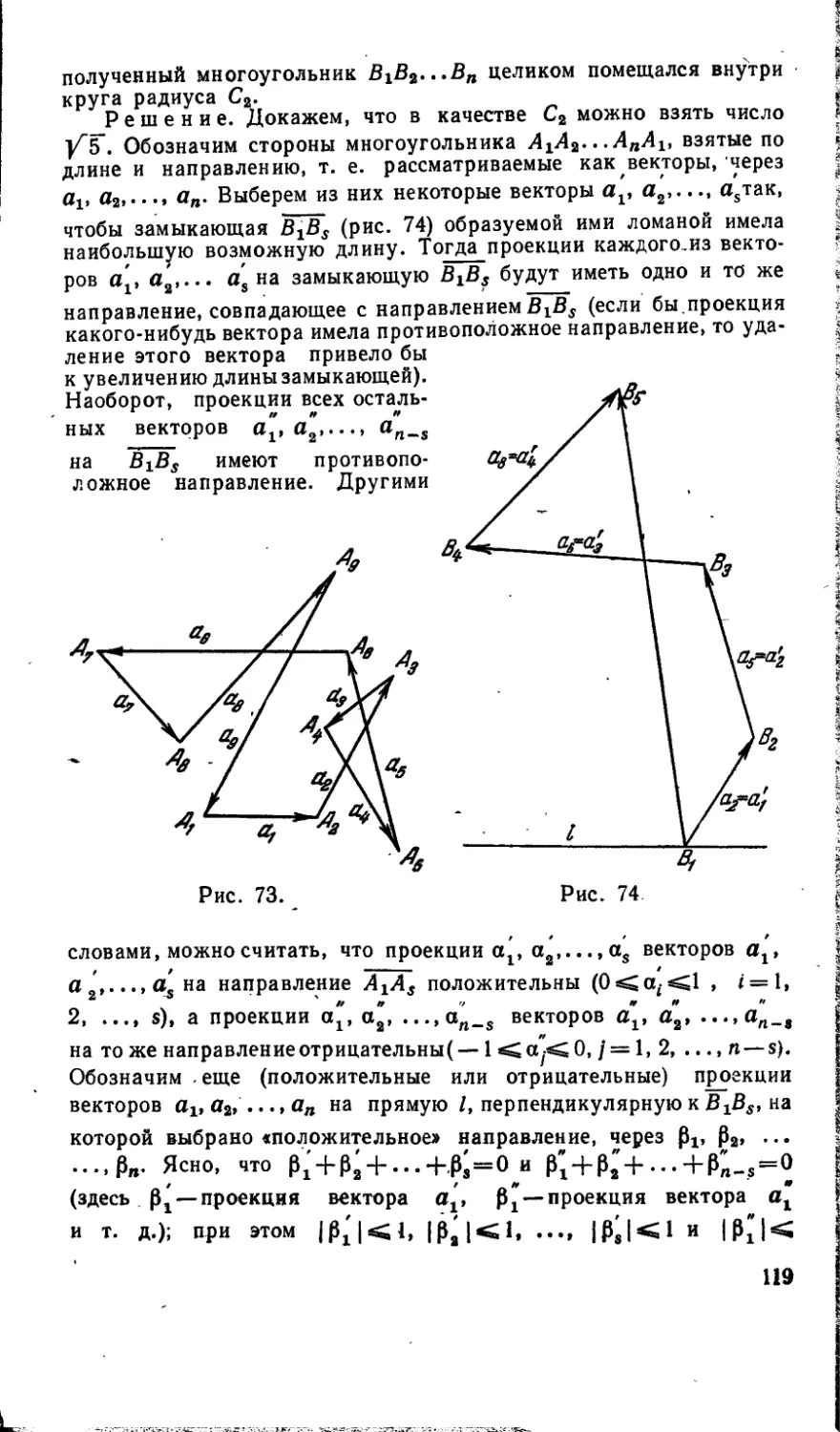
Текст
О МАТЕМАТИЧЕСКОЙ
ИНДУКЦИИ
И. С. СОМИНСКИЙ, л. И. ГОЛОВИНА,
и. м. яглом
О МАТЕМАТИЧЕСКОЙ
ИНДУКЦИИ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1967
5124513
С 61
УДК 512.0+513.0
Илья Самойлович Соминский, Лидия Ивановна Головина,
Исаак Моисеевич Я г лом
О математической индукции
М., 1967 г., 144 стр. с илл.
Редакторы А. П, Баева, Ю. А, Гастев
Техн, редактор А. Л. Благовещенская Корректор Л. С. Баку лова
Сдано в набор 30/XI 1966 г. Подписано к печати 2/Ш 1967 г. Бумага 84х108/32.
Физ. печ. л. 4,5. Условн. печ. л. 7,56. Уч.-изд. л. 8. Тираж 75 000 экз.
Т-01803. Цена книги 24 коп. Заказ № 1075.
Издательство «Наука»
Главная редакция физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени
Первая Образцовая типография имени А. А. Жданова
Главполиграфпрома Комитета по печати при Совете Министров СССР
Москва, Ж-54, Валовая, 28.
2-2-2
169-67
ПРЕДИСЛОВИЕ
В 1950 г. в издаваемой Гостехиздатом—Физматгизом —
издательством «Наука» серии небольших книжек «Популяр-
ные лекции по математике», рассчитанных в первую очередь
на учащихся средней школы, появилась брошюра И. С. Со-
минского «Метод математической индукции».
Эта брошюра доступно излагала содержание метода ин-
дукции, широко применяющегося в самых разнообразных
разделах математики, начиная от вопросов, входящих в курс
средней школы, и до самых продвинутых ее частей.
Книжка такого рода была очень нужна, и брошюра
И. С. Соминского заслуженно пользовалась большим успе-
хом; в последующие годы она выдержала несколько пере-
изданий и была переведена на многие иностранные языки.
Некоторым недостатком брошюры И. С. Соминского
можно было считать почти полное отсутствие в ней приме-
ров и задач геометрического содержания.
Конечно, метод математической индукции, по самому
существу своему связанный с понятием числа, имеет наи-
большие применения в арифметике, алгебре и теории чисел.
Но понятие целого числа является основным не только
в теории чисел, специально занимающейся изучением его
свойств, но и вообще во всей математике. Поэтому метод
математической индукции применяется в самых разнообраз-
ных областях математики.
В частности, применения этого метода в геометрии осо-
бенно интересны и эффектны; они легко могут заинтересо-
вать начинающего математика.
В 1956 г. в той же серии «Популярные лекции цо
математике» вышла в свет книжка Л. И. Головиной
и И. М. Яглома «Индукция в геометрии».
Выпуская эту книгу, мы имели в виду дополнить содер-
жание брошюры И. С. Соминского геометрическими примерами.
1* 3
Нашу книгу мы рассматривали как естественное продолжение
брошюры И. С. Соминского; в предисловии к этой книге
указывалось, что она будет особенно интересна читателям,
знакомым с книжкой «Метод математической индукции».
Ныне издательство «Наука» сочло целесообразным объе-
динить книги «Метод математической индукции» и «Индукция
в геометрии» в одну.
Так как настоящая книга выпускается после смерти Ильи
Самойловича Соминского, скончавшегося 25 июля 1962 г.,
то подготовку ее, естественно, нам пришлось взять на себя.
Введение и первая часть настоящей книги довольно точно
воспроизводят брошюру «Метод математической индукции»;
лишь содержание Введения несколько расширено за счет
примеров, заимствованных из книги «Индукция в геометрии».
. Вторая часть книги в основном совпадает с последним
изданием брошюры «Индукция в геометрии»; добавлено
лишь несколько новых задач.
Работа над обеими частями книги в первую очередь
преследовала цель большей их унификации.
Так, например, мы отнесли в конец книги все указания
к решению геометрических задач в соответствии с тем, как
это было принято в брошюре И. С. Соминского.
От книги «Индукция в геометрии» идет разделение всего
материала на «примеры», сопровождаемые подробными реше-
ниями, и «задачи», доставляющие читателкг материал для
самостоятельной работы.
Книга рассчитана на учащихся старших классов средней
школы, студентов младших курсов педагогических институ-
тов, университетов и других вузов, а также на учителей
математики; она может быть использована в работе школь-
ных математических кружков.
Введение к книге и § 1 первой части вполне доступны
учащимся неполной вредней школы; остальные части требуют
несколько большей подготовки.
Много интересных задач на метод математической индук-
ции читатель может найти в книге В. А. Кречмара, Задач-
ник по алгебре, изд-во «Наука», М., 1964. Широкое обсуж-
дение принципа индукции содержится в статье выдающегося
польского математика В. Серпинского «О математиче-
ской индукции», «Математика в школе», 1936, № 3.
1966 г.
Л. И. Головина,
И. М. Яг лом
ВВЕДЕНИЕ
Утверждения подразделяются на общие и частные.
Приведем примеры общих утверждений.
Все граждане СССР имеют право на образование.
Во всяком параллелограмме диагонали в точке пере-
сечения делятся пополам.
Все числа, оканчивающиеся нулем, делятся на 5.
Соответствующими примерами частных утверждений
являются следующие:
Петров имеет право на образование.
В параллелограмме ABCD диагонали в точке пересечения
делятся пополам.
140 делится на 5.
Переход от общих утверждений к частным называется
дедукцией. Рассмотрим пример.
Все граждане СССР имеют право на образование. (1)
Петров — гражданин СССР. (2)
Петров имеет право на образование. (3)
Из общего утверждения (1) при помощи утверждения (2)
получено частное утверждение (3).
Переход от частных утверждений к общим называется
индукцией. Индукция может привести как к верным, так и
к неверным выводам. Поясним это двумя примерами.
140 делится на 5. (1)
Все числа, оканчивающиеся нулем, делятся на 5. (2)
Из частного утверждения (1) получено общее утвержде-
ние (2). Утверждение (2) верно.
140 делится на 5. (1)
Все трехзначные числа делятся на 5. (2)
5
Из частного утверждения (1) получено общее утвержде-
ние (2). Утверждение (2) неверно.
Спрашивается, как пользоваться в математике индукцией *),
чтобы получать только верные выводы? Ответ на этот
вопрос и дается в этой книжке.
1. Рассмотрим сначала два примера индукции, недопу-
стимой в математике.
Пример 1. Пусть
1.2^2-3 ‘
Легко проверить, что
е _ 1 _ 1 о 1 , 1__ 2
г>1“ 1-2~~ 2 ’ 1-2 * 2-з ~ 1Г *
с +
8 1-2 '2-3 ‘3*4 4*
На основании полученных результатов утверждаем, что
п
при всяком натуральном п Sn = ,
Пример 2. Рассмотрим трехчлен х24-х + 41, на кото-
рый обратил внимание еще Л. Эйлер, Подставив в этот
Трехчлен вместо х нуль, получим простое число 41. Под-
ставив теперь в этот же трехчлен вместо х единицу, получим
опять простое число 43. Продолжая подставлять в трех-
член вместо х последовательно 2, 3, 4, 5, 6, 7, 8, 9, 10,
получаем всякий раз простое число 47, 53, 61, 71,
83, 97, ИЗ, 131, 151. На основании полученных результа-
тов утверждаем, что при подстановке в рассматриваемый
трехчлен вместо х любого целого неотрицательного числа
всегда в результате получается простое число.
Почему рассуждения, приведенные в этих примерах, не-
допустимы в математике? В чем порочность выводов,
которые нами сделаны?
Дело в том, что в обоих этих рассуждениях мы высказали
общее утверждение относительно л ю б о г о п (во вто-
ром примере относительно любого х) только на основании
того, что это утверждение оказалось справедливым для
некоторых значений п (или х).
♦) См. Послесловие. Немногочисленное подстрочные примеча-
ния редактора всюду отмечаются звездочками; сноски, принадлежа-
щие авторам, нумеруются»
6
Индукция широко применяется в математике, но при-
менять ее надо умело *). При легкомысленном же отношении
к индукции можно получить неверные выводы.
Так, если в примере 1 сделанное нами общее утвержде-
ние случайно оказывается верным, как это доказано ниже
в примере 10, то в примере 2 наше общее утверждение
является неверным.
В самом деле, при более внимательном изучении трех-
члена х2 4-х 4-41 обнаружили, что он равен простому числу
при х = 0, 1, 2, ..., 39, но при х = 40 этот трехчлен
равен 41а, т. е. числу составному**).
2. В примере 2 мы встретились с утверждением, .спра-
ведливым в 40 частных случаях и все же вообще оказав-
шимся несправедливым.
Приведем еще несколько примеров утверждений, которые
справедливы в нескольких частных случаях, а вообще не-
справедливы.
Пример 3. Двучлен хп — 1, где я —натуральное число,
представляет для математиков большой интерес. Достаточно
сказать, что он тесно связан с геометрической задачей о
делении окружности на п равных частей. Не удивительно по-
этому, что двучлен этот всесторонне изучается в математике.
Математиков, в частности, интересовал вопрос о разложении
этого двучлена на множители с целыми коэффициентами.
Рассматривая эти разложения при многих частных значе-
ниях л, математики наблюдали, что все коэффициенты раз-
ложения по абсолютной величине своей не превосходят
единицы. В самом деле,
х—1=х—1,
х2--1=(х~-1)(х+1),
х8— 1 = (х— 1) (х2 + *+ 1),
х^1 = (х^1)(х+1).(х2+1),
хб — 1 = (х— 1)(х4 + х8 + х2 + х+1),
х6-1 = (х— 1) (х+1) (х*4-х+1)(х2-х+
Были составлены таблицы, в пределах которых коэффи-
циенты этим свойством обладали. Попытки доказать этот
факт для всякого п успеха не имели.
*) См. Послесловие.
**) И уж совсем сразу бросается в глаза, что при я = 41
х2+х+41=41а4-41 + 41 делится на 41.
7
В 1938 г. в журнале «Успехи математических наук»
(вып. IV) была опубликована заметка выдающегося совет-
ского математика Н. Г. Чеботарева, в которой он
предложил нашим математикам выяснить этот вопрос.
Эту задачу решил В. К. И в а н о в т). Оказалось, что указан^
ным свойством обладают все двучлены хп — 1, степень кото-
рых меньше 105. Одним же из множителей х105— 1 является
многочлен
х48 4- х47 + х4в — х43 — х42 — 2х41 — х40 х39 +
хзв + х36 + х34 + х33 + х32 + х31 — х28 — х2в — х24 —
— X22 — X20 + X17 + Х1в + X15 + X14 + X13 +
+ х12 — х9 — х8 — 2х7 — хв — х5 + х2 + х + 1,
уже не обладающий этим свойством.
Пример 4. Рассмотрим числа вида 22” + 1. При
/1 = 0, 1, 2, 3, 4 числа 2а’+ 1 = 3, 2а* + 1 =5, 2а*+1 = 17,
2а’+1 = 257, 2а’+1 = 65 537 —простые. Замечательный
французский математик XVII в. П. Ферма предполагал, что
все числа такого вида — простые. В XVIII в. Л. Эйлер
нашел, что 225-}-1 =4 294 967 297 = 641 «6 700417 —состав-
ное число.
Пример 5. Знаменитый немецкий математик XVII в., один
из создателей так называемой «высшей математики»,
Г. В. Лейбниц доказал, что при всяком целом положи-
тельном п число л3 —/г делится на 3, число пь — п делится
на 5, число д7 — п делится на 7*). На основании этого он
предположил было, что при всяком нечетном k и любом
натуральном п число пк — п делится на А, но скоро сам
заметил, что 29 —2 = 510 не делится на 9.
Пример 6. В ошибку такого же рода впал однажды
известный советский математик Д. А. Г р а в е, предположив,
что для всех простых чисел р число 2/?~1—1 не делится
на р2. Непосредственная проверка подтвердила это пред-
положение для всех простых чисел р, меньших тысячи.
Вскоре, однако, было установлено, что 21092— 1 делится
на 10932 (1093 — простое число), т. е. предположение Граве
оказалось ошибочным.
х) «Успехи математических наук», 1941, вып. IV, стр. 313—317.
•) См., например, книгу: Д. О. Шклярский, Н. Н. Чен-
цов, И. М. Яг л ом, Избранные задачи и теоремы элементарной
математики, ч. 1, Физматгиз, М., 1959 (задачи 27а), б), в)).
8
Пример 7. Поставим задачу о нахождении наибольшего
возможного числа частей, на которое могут разбить пло-
скость п окружностей. Ясно, что при л = 1 это число равно
двум (рис. 1, л); при л == 2 — четырем (рис. 1, б); при п = 3 —
восьми (рис. 1, в). Естественно
ожидать, что и в дальнейшем ___
удастся каждый раз проводить { Л
окружность так, чтобы она раз- V ) ( (/ )
бивала на две части каждую У
из имевшихся ранее частей; в Ф 'Х х
таком случае число частей при ( \ 0
добавлении новой окружности J
будет удваиваться и для п
окружностей окажется рав- ( \
ным 2". Однако это заключение J
неправильно: на самом деле
наибольшее число частей, на &
которое можно разбить плоскость
четырьмя окружностями, рав- Рис. 1.
но 14, а не 16; для п окружно-
стей это число равно л2—л + 22 *).
Пример 8. На сколько частей делят пространство л пло-
скостей, проходящих через одну точку, если никакие три
из них не проходят через одну прямую?
рассмотрим простейшие частные случаи этой задачи. Одна
плоскость делит пространство на две части. Две плоскости,
Проходящие через одну точку, делят пространство на четыре
части. Три плоскости, проходящие через одну точку, но не
проходящие через одну прямую, делят пространство на во-
семь частей.
На первый взгляд может показаться, что с увеличением
числа плоскостей на единицу количество частей, на которые
разбивается пространство, увеличивается вдвое, и, таким об-
разом. четыре плоскости разобьют пространство на 16 частей,
пять — на 32 части, а вообще л плоскостей разобьют про-
странство на 2П частей.
В действительности это не так, а именно: четыре Пло-
скости разбивают пространство на 14 частей, пять плоско-
стей— на 22 части. Можно доказать, что л плоскостей
разбивают пространство на л (л—1) + 2 частей**).
*) См. решение задачи 33 (п. Б) части II, стр. 142.
♦♦) Решение см. ниже, на стр. 24, пример 13.
9
Пример 9. Приведем еще один весьма убедительный при-
мер. Подставляя в выражение 991л2+1 вместо п последо-
вательно целые числа 1, 2, 3, ,мы никогда не получим
числа, являющегося полным квадратом, сколько бы дней или
даже лет мы ни посвятили этим вычислениям. Однако если
мы сделаем отсюда вывод, что все числа такого вида не
являются квадратами, то мы ошибемся. На самом деле ока-
зывается, что среди чисел вида 991л2+ 1 имеются и квад-
раты, только наименьшее значение л, при котором число
991л2 + 1 есть полный квадрат, очень велико. Вот это число:
л = 12 055 735 790 331 359 447 442 538 767.
Рассмотренные примеры позволяют сделать простой и
в то же время важный вывод.
Утверждение может быть справедливым в целом ряде
частных случаев и в то же время несправедливым вообще,
3. Теперь возникает такой вопрос. Имеется утверждение,
справедливое в нескольких частных случаях; Все частные
случаи рассмотреть невозможно. Как же узнать, справедливо
ли это утверждение вообще?
Этот вопрос иногда удается решить посредством приме-
нения особого метода рассуждений, называемого методом
математической индукции (полной индукции, совершенной
индукции).
В основе этого метода лежит принцип математи-
ческой индукции, заключающийся в следующем:
Утверждение справедливо для всякого натурального п,
если: 1) оно справедливо для л=1 и 2) из справедливости
утверждения для какого-либо произвольного натурального
n = k следует его справедливость для п = k + 1.
Доказательство*). Предположим противное, т. е.
предположим, что утверждение справедливо не для всякого
*) Начинающийся здесь текст до п. 4 читатель может опустить
без ущерба для понимания дальнейшего. Дело в том, что упоми-
наемый ниже принцип наименьшего числа, с помощью
которого здесь доказывается принцип математической индукции,
ничуть не более (хотя и не менее) очевиден, чем сам принцип
математической индукции. С другой стороны, эти два предложения,
как показывает более глубокий их анализ, оказываются эквива-
лентными только после принятия дополнительных допущений.
Ограничимся поэтому принятием принципа математической индук-
ции как интуитивно чрезвычайно убедительного допущения и за-
помним, что он является одной из аксиом, определяющих на-
туральный ряд чисел. Подробнее по этому поводу см. Послесловие
и указанную там литературу.
10
натурального п. Тогда существует такое натуральное т, что
1) утверждение для п — т несправедливо, 2) для всякого л,
меньшего т, утверждение справедливо (иными словами, т
есть первое натуральное число, для которого утверждение
несправедливо).
Очевидно, что т>1, так как для /2=1 утверждение
справедливо (условие 1). Следовательно, т—1—натураль-
ное число. Выходит, что для натурального числа/л—1
утверждение справедливо, а для следующего натурального
числа т оно несправедливо. Это противоречит условию 2.
Конечно, при доказательстве принципа математической
индукции мы пользовались тем, что в любой совокупности
натуральных чисел содержится наименьшее число. Легко
видеть, что это свойство в свою очередь можно вывести
как следствие из принципа математической индукции. Таким
образом, оба эти предложения равносильны. Любое из них
можно принять за одну из аксиом, определяющих натуральный
ряд, — тогда другое будет теоремой. Обычно за аксиому при-
нимают как раз сам принцип математической индукции.
4. Доказательство, основанное на принципе математиче-
ской индукции, называется доказательством методом мате-
матической индукции. Такое доказательство должно со-
стоять из двух частей, из доказательства двух самостоя-
тельных теорем:
Теорема L Утверждение справедливо для л=1.
Теорема 2, Утверждение справедливо для л = &4-1,
если оно справедливо для n = еде k—произвольное
натуральное число.
Если обе эти теоремы доказаны, то на основании прин-
ципа математической индукции утверждение справедливо для
всякого натурального п.
Пример 10. Вычислить сумму (см. пример 1)
С -5- _1_I_J_I 1 1
°" 1.2^2-3^ • • • ^л(п-Н)’
12 3
Мы знаем, что ^=2 — , 53 = ~. Теперь мы не
повторим ошибку, допущенную в примере 1, и не станем
сразу утверждать, что 5л=—т при всяком натураль-
П -у- 1
ном п.
Будем осторожны и скажем, что рассмотрение сумм
*?2, 53, позволяет высказать' гипотезу (предположение),
о П
что =: jj-pj при всяком натуральном л. При этом мы
11
знаем, что гипотеза эта верна при л=1,2, 3, 4. Для про-
верки гипотезы воспользуемся методом математической
индукции.
Теорема 1. Для л = 1 гипотеза верна, так как^! = у.
Теорема 2. Предположим, что гипотеза верна для
n = k, т. е. что S*ef^ + 2qj+ • • • = ’ где
k—некоторое натуральное число. Докажем, что тогда ги-
потеза обязана быть верной и для л = £4-1, т. е. что
о -*±1
d*+i~fc+2-
Действительно, 5^+1 = Sfe 4- (&+2) ’ слелователь“
но, по условию теоремы,
~ _ k , 1 _ £24~2Л4-1 _£4-1
d*+i““£4-l + (fc4-l)(64-2) (£4-1)(^4-2) £4-2’
Обе теоремы доказаны. Теперь на основании принципа
п
п+Т
математической индукции мы утверждаем, чтоЗл =
при всяком натуральном л.
Замечание 1. Необходимо подчеркнуть, что доказа-
тельство методом математической индукции безусловно тре-
бует доказательства обеих теорем, 1 и 2.
Мы уже видели, к чему привело пренебрежительное от-
ношение к теореме 2 (пример 2).
Сейчас мы покажем, что нельзя опускать и теорему 1.
Рассмотрим пример.
Пример 11. Теорема. Всякое натуральное число равно
следующему за ним натуральному числу.
Доказательство проведем методом математической индук-
ции. Предположим, что
£f=£4~1> (1)
Докажем, что
k+ 1 = k 4- 2. (2)
Действительно, прибавив к каждой части равенства (1)
по 1, получим равенство (2). Выходит, что если утверждение
справедливо для л = £, то оно справедливо и для л = £-^1.
Теорема доказана. и
Следствие. Все натуральные числа равны.
Где же здесь ошибка? Ошибка заключается в том, что
первая теорема, необходимая для применения принципа ма-
12
тематической индукции, не доказана и не верна, а доказана
только одна вторая теорема.
Теоремы 1 и 2 имеют свое особое значение. Теорема 1
создает, так сказать, базу для проведения индукции. Тео-
рема 2 дает право неограниченного автоматического рас-
ширения этой базы, право перехода от данного
частного случая к следующему, от л к л + 1.
Если не доказана теорема 1, а доказана теорема 2 (см.
пример И), то, следовательно, не создана база для прове-
дения индукции, и тогда бессмысленно применять теорему 2,
так как и расширять-то, собственно, нечего.
Если не доказана теорема 2, а доказана только теорема 1
(см. примеры 1 и 2), то, хотя база для проведения индукции
и создана, право расширения этой базы отсутствует.
Замечание 2. Метод математической индукции разо-
бран выше для простейшего случая. В более сложных слу-
чаях формулировки теорем 1 и 2 должны быть соответст-
венно изменены. .
Иногда вторая часть доказательства опирается на спра-
ведливость утверждения не только для л = А, но и для
п = k— 1. В этом случае утверждение в первой части должно
быть проверено для двух последовательных значений л.
Иногда также вторая часть доказательства состоит в уста-
новлении справедливости требуемого рассуждения для ка-
кого-то значения п в предположении справедливости его для
всех натуральных чисел меньших л. Ниже читатель
найдет примеры такого рода (см. пример 3 на стр. 42).
Иногда утверждение доказывается не для всякого нату-
рального л, а для всякого целого л, превосходящего неко-
торое целое т1). В этом случае в первой части доказатель-
ства утверждение проверяется для n = z»+l, а если это
требуется, то и для нескольких последующих значений л.
5. Вернемся еще раз к примеру 1 для выяснения одной
существенной стороны метода математической индукции.
Изучая, сумму 5п=+ + 2Тз + . .. При разных
12 3
значениях л, мы подсчитали, что S, = —,
а 2 о 8 4
и это навело нас на гипотезу, что и при всяком л.
х) Так, например, любое утверждение, касающееся свойств
произвольных n-угольников, имеет смысл лишь при п^З.
13
Для проверки гипотезы мы использовали метод математи-
ческой индукции.
Нам повезло, мы высказали гипотезу, которая подтвер-
дилась. Если бы мы высказали гипотезу неудачно, то
порочность гипотезы обнаружилась бы при попытке дока-
зательства теоремы 2.
Пример 12. Рассмотрим суммы
С __ 1__I ___1 I 1 •
°«Т2 > 2-3 ' ’
Допустим, что, изучая мы высказали гипотезу
При п= 1 формула (1) верна, так как <Si = v Предполо-
А
£ 1
жим, что формула (1) верна при n = k, т. е. «
Попытаемся доказать, что формула (1) верна и при л = ^+ 1,
т. е. что >$*+1 = 3^4. Имеем,
5Л + 1 = Sk + =
*4-1 1 **4-4*а4-5*4-2
“ 3*4-1+ (*+1) (ft+2) “ (*4-1) (*4-2) (3*4-1) ’
т. e. результат получился иной.
Выходит, что из справедливости формулы (1) прил = А
не следует ее справедливость при я = Мы обна-
ружили, что формула (1) неверна.
Таким образом, метод математической индукции позво-
ляет в поисках общего закона испытывать возникающие при
этом гипотезы, отбрасывать ложные и утверждать истинные.
Чтобы научиться применять метод математической ин-
дукции, надо рассмотреть достаточное количество задач.
Чтобы не повторять без конца слова «Теорема 1» и
«Теорема 2», мы условимся в дальнейшем помечать первую
и вторую части доказательства по индукции (эти части и
составляют содержание двух теорем, доказательство ко-
торых равносильно пользованию методом индукции) зна-
ками 1° и 2°. Кроме того, мы будем различать примеры,
снабженные подробными решениями, и задачи, предназна-
ченные для самостоятельной работы читателя. В конце книги
приведены указания, относящиеся к решению всех приве-
денных в тексте задач. Иногда эти указания представляют со-
бой лишь ссылку на иную, доступную читателям литературу;
в других случаях они содержат полное решение задачи*
ЧАСТЬ I
ИНДУКЦИЯ В АРИФМЕТИКЕ И В АЛГЕБРЕ
§ 1. Доказательства тождеств; задачи
арифметического характера
Пример 1. Выпишем в порядке возрастания нечетные
положительные числа 1, 3, 5, 7, Обозначим первое из
них «ь второе «2, третье и3 и т. д., т. е. «х=1, «2 = 3,
«3 = 5, «4 = 7,... Поставим перед собой такую задачу:
составить формулу, выражающую нечетное число ип через
его номер п.
Решение. Первое нечетное число можно записать
так:
^ = 2.1 — 1; (1)
второе нечетное число «2 можно записать так:
«2 = 2.2-1; (2)
третье нечетное число и3 можно записать так:
«3 = 2.3-1. (3)
Внимательно рассматривая равенства (1), (2), (3), можно
высказать гипотезу, что для получения любого нечетного
числа достаточно от удвоенного номера его отнять 1, т. е.
для л-го нечетного числа имеем формулу
«п = 2л-1. (4)
Докажем, что формула эта справедлива.
1°. Равенство (1) показывает, чтодлял=1 формула (4)
справедлива.
15
2°. Предположим, что формула (4) справедлива для n — k,
т. е. *-е нечетное число имеет вид uk~2k—1. Докажем,
что тогда формула (4) обязана быть справедливой и для
(*4~ 1)-го нечетного числа, т. е. что (*4“ 1)-е нечетное число
имеет вид uk+1 = 2(*+U—1, или, что все равно,
^+i = 2^+ !•
Для получения (&4-1)-го нечетного числа достаточно
к *-му нечетному числу прибавить 2, т. е. иЛ+1 = «й4-2.
Но, по условию, «Л = 2*—1. Значит, н^+1 = (2*—1) +
+ 2 ==2&+1, что и требовалось доказать.
Ответ. ип — 2п—1.
Пример 2. Вычислить сумму первых п нечетных чисел.
Решение. Обозначим искомую сумму Sni т. е.
5„=1 + 3 + 5+...+(2л-1).
Для решения таких задач в математике существуют
готовые формулы. Нам интересно решить эту задачу, не при-
бегая к готовой формуле, а пользуясь методом математи-
ческой индукции. Для этого прежде всего надо построить
гипотезу, т. е. просто постараться угадать ответ.
Придаем л последовательно значения 1, 2, 3, ... до тех
пор, пока у нас не накопится достаточно материала, чтобы
на основе его построить более или менее надежную гипотезу.
После этого останется только эту гипотезу проверить
методом математической индукции.
Имеем 1, 52 = 4, 53 = 9, S4=16, S5= 25, S6 = 36.
Теперь все зависит от наблюдательности решающего задачу,
от его способности по частным результатам угадать общий.
Полагаем, что в данном случае легко заметить, что 5Х=12,
52 = 22, 53 = За, 54 = 42. На основе этого можно предполо-
жить, что вообще £п = л2.
Докажем, что гипотеза эта справедлива.
I6. При п=\ сумма представляется одним слагаемым,
равным 1. Выражение л2 при л=1 также равно 1. Значит,
при л=1 гипотеза верна.
2°. Допустим, что гипотеза верна для л = *, т. е. Sk=*k2.
Докажем, что тогда гипотеза должна быть верной и для
л = *4-1, т- е. = (*4- I)2- Действительно, = +
+ (2*4-1), Но 5Л = *2 и потому 5л+1 = *24-(2^4-1)==
е=(*4-1)2, что и требовалось доказать.
Ответ. Sn~n2.
Задача 1. Найти ип, если известно, что = 1 и что
при всяком натуральном *> 1
16
Указание. «1==:3-1— 2, и2 = 3-2— 2.
Задача 2. Найти сумму Sn = 1 + 2 + 22+ ... +2""1.
Указание. 51 = 2—1, 52 = 22—1, 53 = 23—1.
Пример 3. Доказать, что сумма п первых чисел нату-
п(п+1)
рального ряда равна —
Решение. Эта задача отличается от предыдущих тем,
что гипотезу здесь строить не надо, она дана. Нужно только
доказать, что гипотеза верна.
Обозначим искомую сумму Sn, т. е. Sn = 1 + 2+ ,..
1°. При /2=1 гипотеза верна.
2°. Пусть 5ft=l+2 + 3-H...+A = ^±^-. Покажем,
„ е (*+1)(* + 2) D
что ол+1 = -—:—В самом деле,
^l-51 + (4+l) = ^ + (4+l) = !J±№+2>.
Задача решена.
Пример 4. Доказать, что сумма квадратов п первых чисел
~ л (п+1) (2n+1)
натурального ряда равна !.
Решение. Пусть 52 (п) = I2 + 22 + З2 + ... + /22.
г. 52(1)=Р = Н1±1ф±Ь1).
2°. Предположим, что S2 (л) = —. Тогда
52 (л4-1) = 12 + 224-32+...+л2 + (л+1)2 =
= ».(п + 1)(2п+1) + (я + !)»
и окончательно
S2 (п +1) = <п+1) [(п+1) + 1Ц2(п-Ь1)Ч-11 .
Пример 5. Доказать, что
•$„= 1—22 + 32—42+ ... +(— 1)"-1л2 =
Решение. 1°. При п—1 гипотеза, очевидно, верна
2°. Пусть
S* = 1 — 22 + З2— ... + (— I)*"1 = (— I)*-2 .
17
Докажем, что
5л+1 = 1-22 + Зг—...+(—l)ft-1*2 + (—l)ft(*+l)2 =
= (_l)*(i±W±2) #
2
Действительно,
= $* +(-!)*(*+1)2 =
' + (-!)* (Л 4- D2 =
— (— D* Г(*4-1)-Ц =
Задача 3. Доказать, что
I2 + З2 + 52 + ... + (2л — I)2 = .
и
Задача 4. Доказать, что сумма кубов п первых чисел
Гп (и+1)12
натурального ряда равна —-I .
Задача 5. Доказать, что
уПЧ-1_ 1
1+Х + х2+ -_+хп = Х 1 (Х=/=1).
Л •“ 1
Пример 6. Доказать, что
1 -24-2-34- ... 4-(л —1)« = ,1)п(д+1)ф
О
Решение. 1°. 1 • 2 => .
о
2°. Если
1-24-2-34-...4-(л—1)и=.11Г.1)”(п+1) t
О
то
1.24-2-3 4-... 4-(л—1) л 4-л (л 4-1) =
= (п—1)п(п+1) + л п (п + 1) (п + 2)
3
з
Пример 6 можно также вывести из результатов при-
меров 3 и 4, если заметить, что
1-2 + 2- 3+...+(л-1)л =
= 1(1 + 1) + 2(2+1) + 3(3 + 1) + ...
• • • 4* (л—1) [(л—1)+1] = [12 + 22+... + (я—I)2] +
+ [1 + 2+...+(л-1)].
18
Задача 6. Доказать, что
1 -2-3 + 2-3-4+ ... + л (л+ 1) (л 4-2)==
_п(п4-1)(п + 2)(п4-3)
4
п*
1
Задача 7. Доказать, что
1-ЗтЗ-5т ' ’ ‘ (2л— 1)(2п+1) 2л-р1 *
Задача 8. Доказать, что
Р4- —4- 4- "2 _п(п+1)
1-3-Г‘3-5ф ’ ’ * + (2л —1) (2л+1)~2 (2n+1) *
Задача 9. Доказать, что
Ь4 ' 4-7 ' 740 ‘ (Зл —2) (Зл-|-1) Зп+1 *
Задача 10. Доказать, что
_L+_L._L+ .. 1___________«_
1 -5 ' 5-9 ' 9-13“ “ (4л —3) (4л +1) 4n-f-l ’
Задача 11. Доказать, что
_+___________1_____+ . = _2_
а (а+1) (а+1) (а+2) ' ' (a-f-n— 1)(а+л) а(а+п)'
Пример 7. Доказать, что если v0 = 2, vt = 3 и для
всякого натурального А'имеет место соотношение vk+1 = 3vk —•
— 2^-1, то f„ = 2"+l.
Решение. 1°. Для п = 0 и п—\ утверждение спра-
ведливо по условию.
2°. Предположим, что »fc_1 = 2*!-1-]-1; vft = 2*-f-1. Тогда
®*+i = 3 (2* +1)—2 (2*-14-1) = 2fe+1 +1.
1
а2—еа
что если вх = , «2 =
всякого натурального k > 2
«* = (а + ₽)«л-1—ор«*-а, то
Задача 12. Доказать,
а3-₽8 .
= -£=jr («¥=₽) и для
имеет место соотношение
рл+1
а=р •
Пример 8. Произведение
ком «! и читается так: «п факториал». Полезно запомнить,
что 11 = 1, 21 = 2, 31 «б, 41 = 24, 51 = 120.
1«2*3...л обозначается зна-
19
Вычислить S„= Ы ! + 2• 2 ! + ... -j-n-n!
Решение.
S1=ll! = l, S2 = 1-1 1 + 2-21 = 5,
S8=l-1 I + 2-2 !+ 3-3! = 23.
Присматриваясь к этим результатам, можно заметить, что
$1 = 2! —1, S2 = 3! —1, S3 = 4! — l.
Это дает возможность высказать гипотезу, что
$„ = (л+1)!-1.
Проверим эту гипотезу.
1°. Для п = 1 гипотеза верна, так как $х = 1-11 = 2! — 1.
2°. Пусть
$*=1-1 1 + 2-21 + ... + ft-ft I = (&+1)! — 1.
Покажем, что
$й+1 = 1-1 1 + 2-2 ! + ...+ft-ftl + (ft+l) (ft + 1)! =
= (ft + 2)l — 1.
Действительно,
S*+i = Sft + (A+l)(A+l)! = [(ft+l)!-l] +
+ (ft+l)(ft+l)l = (ft+l)![l+(ft+l)]-l =
= (ft+l)!(ft + 2) —l = (ft + 2)l—1.
Задача 13. Доказать тождество
1_______ 2 2" _ 1 , 2n+!
l+x ' l+x2 ‘ 1+^2“ X— 1"*” l_x2"+l *
Пример 9. Дано:
а + р = да, ар = а (а#=₽), А,^т-
А а Л а
Az=*m--------— ’ А^ = т--------------- и т. д.,
т------- т---------
т — 1 а
т------т
т—1
т. е. для k > 1
Л+1 = да—т;
Доказать, что
20
Решение. 1°. Докажем сначала, что формула (1) верна
для /2 = 2. По условию,
« _ ,„ , оч _ «Р _ «2+Р2+«Р—а—Р
m_ i - (а -Г Р) (а+р)-1 а+р-1 •
(а3_АЗ)_/а2_R2)
По формуле (1) Л2 = уа2р^)Z7(a~g) • Сократив последнюю
х ft л + бф —-СС—• |3
дробь на а—р, имеем Л2 =— a+frJLi—“Г> чт0 и требо-
е.
валось доказать.
2°. Пусть формула (1) справедлива для п = т.
л -
к (а*—₽*) —(а4-1—р*"1) *
Докажем, что тогда она должна быть справедлива
я_ь.1 т е А _ (а*+2-₽*+2)-(а*+1-0‘+1)
*+i (a*+i_p*+i)_(a*_ р*)
Действительно, ДА+1 = «—или Дй+1 = (а+Р)—
Пользуясь равенством (2), имеем
А+1 I ТР/ (а*+1_,р*+1)_(а*_р*)
(сс**8 —Р*+*) —(ct*+i —P*+i)
— р*+1)_(а*_р*)
(2)
и для
Теорема доказана.
Задача 14. Упростить многочлен
1 _ * - I * I / Л\пх(х 1) ••• (х—-Л-Ь1)
1 1!+ 2! •••+< 1) .
Пример 10. Доказать, что любое целое число рублей,
большее 7, можно уплатить без сдачи денежными билетами
достоинством в 3 и 5 рублей.
Решение. 1°. Для 8 рублей утверждение справедливо
(ибо 8 = 3 + 5).
2°. Пусть утверждение верно для k рублей, где k—целое
число, большее или равное 8.
Возможны два случая: 1) k рублей уплачивается одними
трехрублевыми билетами и 2) k рублей уплачивается денеж-
21
ными билетами, среди которых есть хоть один билет пяти-
рублевого достоинства.
В первом случае трехрублевых биЛетов должно быть
де менее трех, так как в этом случае k > 8. Для того чтобы
уплатить & + 1 рубль, заменим три трехрублевых билета
двумя пятирублевыми.
Во втором случае для уплаты &+1 рубля заменим один
пятирублевый билет двумя трехрублевыми.
Пример 11. Доказать, что ёумма кубов трех последова-
тельных натуральных чисел делится на 9.
Решение. 1°. Сумма 13 4-23 4-З3 делится на 9. Значит,
утверждение справедливо, когда первым из трех последова-
тельных натуральных чисел является 1.
2°. Пусть сумма £3 + (Л4-1)3-}-(&4-2)8, где k—неко-
торое натуральное число, делится на 9, Сумма
<Л+1)3+(^ + 2)8 + (^ + 3)3 =
z=:(^+l)8 + ^ + 2)3 + *3 + 9Jfe2 + 27A + 27 =
= [*3 + (^ + 1)8 + (^ + 2)8] + 9^2 + З^Ч-3)
представляет собой сумму двух слагаемых, каждое из ко-
торых делится на 9, а потому тоже делится на 9.
Задача 15. Доказать, что при любом целом л^О
Ля=11п+24- 122л+1
делится на 133.
Пример 12. Из 2л чисел 1, 2, 2п произвольно
выбрали п 4-1 число. Доказать, что среди выбранных чисел
найдутся хотя бы два числа, из которых одно делится на
другое.
Решение1). 1°. Для двух чисел 1, 2 утверждение
справедливо.
2°. Допустим, что из 2п чисел 1, 2, , 2л, где л^2,
удалось выбрать так л 4-1 число, что ни одно из них не
делится на другое, Совокупность всех этих чисел обозна-
чим для краткости 2ИЛ+1. Докажем, что тогда из 2л — 2
чйсел 1, 2, , м> 2л—2 можно выбрать л чисел таких, что
опять ни Одно из них не будет делиться на другое.
Возможны четыре случая:
1) ^n+i не содержит ни 2л—1, ни 2л.
^n+i содержит 2л—1 и не содержит 2л. 4
4 Это решение принадлежит М. А. Ф р и д м а н у.
22
3) Л4п+1 содержит 2л и не содержит 2л—1,
4) Мп+1 содержит и 2л—1, и 2л.
Случай 1. Исключим из ЛГя+1 какое-нибудь число,
Останется л чисел, каждое из которых не больше, чем
2л—2. Ни одно из этих чисел не делится на другое.
Случай 2. Исключим из Мп+1 число 2л—1. Оста-
нется л чисел, каждое из которых не больше, чем 2л—2.
Ни одно из этих л чисел не делится на другое.
Случай 3. Исключим из Мп+1 число 2л и опять по-
лучим тот же результат.
Случай 4. Прежде всего заметим, что в Мп+1 не со-
держится число л, так как иначе в Мп+1 нашлось бы два
числа (2л и л), из которых одно делится на другое.
Исключим из М„+1 числа 2л—1 и 2л. Совокупность
оставшихся л—1 чисел обозначим 2Ия-1. Присоединим к
/Ип_1 число л. Получим л чисел, каждое из которых не
превосходит 2л—2. Остается показать, что среди этих
л чисел ни одно не делится на другое.
В Afn+1 не было двух чисел, из которых одно делится
на другое. Значит, таких чисел не было и в Оста-
ется только убедиться в том, что таких чисел не появи-
лось и тогда, когда мы к присоединили число л.
Для этого достаточно убедиться в том, что: 1) ни одно
число, входящее в не делится на л и 2) число л не
делится ни на одно из чисел, входящих в Л4п_1.
Первое вытекает из того, что все числа, входящие в
не превосходят 2л—2.
Второе вытекает из того, что число 2л не делится ни
на одно из чисел, входящих в Мп_1.
Итак, если допустить, что утверждение неверно для 2л
чисел 1, 2, ..., 2л, то оно неверно и для 2 (л—1) чисел
1, 2, ..., 2л—2. Значит, если утверждение верно для
2 (л—1) чисел 1, 2, ..., 2л—2, то оно верно и для 2л
чисел 1,2, ..2л.
Отсюда и из пункта 1° следует, что наше утверждение
справедливо для 2л чисел 1, 2, 2л, где л—любое
натуральное число.
Заметим, что эта задача имеет следующее простое ре-
шение.
Выберем из 2л чисел 1, 2, ..., 2л произвольное
л-j-1 число. Совокупность этих чисел обозначим 7Ия+1.
Каждое четное число, входящее в Мп+1, разделим
на такую степень двойки, чтобы частное было нечетным.
23
Совокупность этих частных и всех нечетных чисел, вхо-
дящих в Л/л+1, обозначим через 7Ия+1. В 2Ип+1 содержится
л + 1 нечетное число, каждое из которых меньше 2п.
Так как всех положительных нечетных чисел, меньших 2л,
имеется всего л, то в Mrt+l найдутся хотя бы два равных
числа. Каждое из этих чисел пусть равно k.
Полученный результат означает, что в Мп+1 было два
числа 2sk и 2lk (где одно из чисел s и t может равняться
нулю). Но одно из чисел 2sk и 2*k делится на другое.
Задача 16. Доказать, что п различных прямых, про-
веденных на плоскости через одну точку, делят плоскость
на 2п частей.
Пример 13. Доказать, что п плоскостей, проходящих
через одну точку так, что никакие три из них не проходят
через одну прямую, делят пространство на Ап = п(п—1)4-2
частей.
Решение. 1 °. Одна плоскость делит пространство на
две части, и Дх = 2. Для л=1 утверждение справедливо.
2°. Предположим, что утверждение справедливо для
п = &, т. е. k ялоскостей делят пространство на k(k—1)4-2
частей. Докажем, что тогда k +1 плоскостей делят про-
странство на &(&+1)4-2 частей.
Действительно, пусть Р есть (k 4- 1)-я плоскость. С каж-
дой из первых k плоскостей плоскость Р пересекается по
некоторой прямой и, таким образом, плоскость Р разбита
на части посредством k различных прямых, проходящих
через одну точку. На основании задачи 16 утверждаем,
что плоскость Р разбита на 2k частей, каждая из которых
представляет собой плоский угол с вершиной в данной
точке.
Первые k плоскостей делят пространство на некоторые
многогранные углы. Некоторые из этих многогранных углов
делятся посредством плоскости Р на две части.
Общей гранью двух таких частей служит часть пло-
скости, ограниченная двумя лучами, по которым Р пересека-
ется с гранями данного многогранного угла, т. е. один из
2k плоских углов, на которые плоскость Р разбита.
Это означает, что число многогранных углов, разбивае-
мых на две части плоскостью Р, не может быть больше,
чем 2k.
С другой стороны, каждая из 2k частей, на которые
разбивается плоскость Р, в результате пересечения ее с
24
первыми k плоскостями, является общей гранью двух мно-
гогранных углов и таким образом делит многогранный угол,
образованный первыми k плоскостями, на две части.
Это означает, что число многогранных углов, которые
разбиваются на две части плоскостью Р, не может быть
меньше, чем 2А.
Итак, плоскость Р разбивает на две части точно 2k
частей пространства, образованных первыми k плоскостями.
Поэтому если k плоскостей разбивают пространство на
k(k—1)Ч~2 частей, k 4-1 плоскость разбивает простран-
ство на [й(£—1)4-2]4~2& = &(&4-1) + 2 частей. Утверж-
дение доказано.
§ 2. Тригонометрические и алгебраические задачи
Пример 14. Доказать тождество
Л sin 2"+1 а
cos а cos 2а ... cos 2” а = .— ♦
2я+1sin а
Решение. 1°. При /г —О тождество справедливо, так
как
sin 2а
COS а = 7Г-: .
2 sin а
2°. Пусть тождество справедливо при л = &, т. е.
cos а cos 2а ... cos 2*а = - +-*-- .
2*+* sin а
Тогда оно справедливо и при л==Л4-1* Действительно,
cosacos2a... cos2*a cos 2*+*a=esbi_^a.
2*+*sina 2ft+2sina
Пример 15. Доказать, что Ло=со5д0, если известно,
что Ах = cos 0; А2 = cos 20 и для всякого натурального
£>2 имеет место соотношение Ak = 2 соз0ЛЛв1—ЛА_2.
Решение. 1°. Утверждение справедливо при л=1 и
л = 2.
2°. Пусть ЛЛ_2 = cos(£—2)0, ЛЛ-1 = сб5(Л—1)0. Тог-
Д4 Л^ = 2 cos0 cos(k—1)0—cos(Zj—2)0»=cos&0, ибо
cos k 0 4- cos {k — 2) 0 = 2cos 0 cos (k— 1)0.
25
Пример 16. Доказать, что
п *4" 1
Sin g— X
sin х + sin 2х +... + sin nx=--------— sin ™.
sin |
Решение. 1°. При n—1 утверждение справедливо.
2°. Пусть
. Л+1
sin х
sin х 4- sin 2х -|- ... + sin kx —-------sin 4?.
. X &
s,n т
Тогда
sin х 4- sin 2x + ... + + sin (k 4- 1) x =
. /г +1
sm x b
=-----— sin у + sin (A4- l)x =
sinT
. fe+1
Sin—
X
smy
. kx , o . /г + 1 ~ /г+1
sm у + 2sin -у- x cos -y- x =»
. /г + 2
fc + 1
-----------sin xx
. x--------2 ’
siny
ибо
o Й4-1 . x . k4-2 ~ . kx
2cos—5— x sin -s- = sin—x—sin -5-.
At At JL Z
Задача 17. Доказать, что
. 2n+l
1 sin ~x
у + cos x + cos 2x + ... + cos nx -------r
2siny
Задача 18. Доказать, что
sin x + 2sin 2x + ... + n sin nx =
— (n~b 0 s*n sin (a+1) jg
4 sin2 y
26
Задача 19. Доказать, что
cosx +2cos2х-|-.,. +л cosnx —
__(п4~1)с°8 —ncos(n + |)x — 1
4sin2 -i-
А
Задача 20. Доказать, что
+ +itg^=^ctgj—cig* (х^тп).
Задача 21. Доказать, что
arc etg 3 + аге etg 5 + ... + аге etg (2п + 1) =
= arctg2 4-arctg-2.-|- .., -J-arctg^il—narctg 1.
А П
Пример 17. Доказать, что
п , .
(1+Z)“ = 2a (cos ™ + /sin™) К
Решение. 1°. При п=*\ утверждение справедливо,
так как 1 4- i = 2 2 ( cos у -f- i sin—j .
2°. Пусть (1-H)* = 22 cos-^-j-Zsin^^ . Тогда
(1 + i)k^ = 2T ( cos^+/ sin2T ( COS + i sini) =
в2^(СО5(Щ)«+/8|п(±н)«).
Задача 22. Доказать, что
(j/з— t)" = 2B (cos ™ — fsin^) »
Пример 18. Доказать теорему:
Если в результате конечного числа рациональных дейст-
вий (т. е. сложения, вычитания, умножения и деления) над
комплексными числами х1, х2, ..., хп получается число и9
*) По определению, Р= — 1.
27
то в результате тех же действий над сопряженными комп-
лексными числами xlf x2i хп получится число ut со-
пряженное си.
Решение. 1°. Прежде всего покажем, что утверж-
дение верно для каждого из четырех действий над
двумя комплексными числами. Пусть = а + Ы, x2 = c-}-di.
Тогда
хг + х2 = (а—Ы) + (с—di) = (а + с) — (b + d) i = о?
Точно так же утверждение проверяется для вычитания, ум-
ножения и деления.
2°. Пусть теперь дано некоторое рациональное выраже-
ние от комплексных чисел х±, х2, •••> хп- Вычисление та-
кого выражения сводится, как известно, к последователь-
ному выполнению одного из четырех действий над двумя
комплексными числами, причем действия эти могут быть за-
нумерованы.
Например, пусть и = -*1*2А*^ . Для вычисления и до-
*1“г*2—хз
статочно произвести действия:
1) Х1х2 = и1> 2) х8х4 = а2, 3) Л1 + *2 = ы8,
4) us—х8 = а4, 5) «1 + «2 = «в, 6) а6:«4 = и.
Предположим, что утверждение верно для всех выраже-
ний, которые вычисляются посредством не более k дей-
ствий. Термин «действие» здесь означает сложение, либо
вычитание, либо умножение, либо деление двух комплекс-
ных чисел. Покажем, что тогда утверждение должно быть
верно и для выражений, требующих k 4-1 действий.
Действительно, последнее (&4~1)"е действие мы вы-
полняем над числами ut и «у, которые сами вычислялись
посредством не более чем k действий.
В результате замены чисел х2, хп сопряжен-
ными, числа Ui и Uj заменяются сопряженными ut и «у, а
тогда и результат (&4-1)"г0 действия над ними, т. е.
число и, также заменится сопряженным числом и.
Задача 23. Доказать, что йри любом натуральном п
(cos х 4- i sin х)п == cos nx 4- i sin nx.
28
§ 3. Задачи на доказательство неравенств
Пример 19. Доказать, что при любом натуральном п > 1
L + ...+_L>13
п + 1 ^п+2т т 2п ' 24 •
Решение. Обозначим левую часть неравенства через
Г. S2 = T75==n7, следовательно, при л = 2 неравенство
справедливо.
13
2°. Пусть Sfe > 24 при некотором А. Докажем, что тогда
и ^*+i>24- Имеем Sfe = + ••• +~2F> ^*+1 =
=_L+_L+ +_L+_L__-_L_
fe+2^fe.+3^ • 2fe ’ 2fe+l ^2k+2 ’
Сравнивая5йи5А+1,имеем5А+1—,
T" e‘ 5*+i~sfe = 2(/t+l)(2fe+l) •
При любом натуральном k правая часть последнего ра-
13
венства положительна. Поэтому 5Л+1> Sk. Но^>-^-,
е 13
значит, и 5Л+1>^.
Задача 24. Найти ошибку в рассуждении.
Утверждение. При любом натуральном п справедливо
неравенство 2" > 2л +1.
Доказательство. Пусть неравенство справедливо при
л = А, где k—некоторое натуральное число, т. е.
2ft>2* + l. (1)
Докажем, что тогда неравенство справедливо и при л »=&-}-1»
т. е.
2*+1> 2(&+1) + 1. (2)
Действительно, 2к не меньше 2 при любом натураль-
ном k. Прибавим к левой части неравенства (1) 2*, а к
правой 2. Получим справедливое неравенство 2*-}-2л>
> 2&4-1+2, или 2*+1 > 2 (&+ 1)+ 1. Утверждение до-
казано.
Задача 25. При каких натуральных л справедливо не-
равенство 2">2л+1?
29
Пример 20. При каких натуральных п справедливо не-
равенство 2" > л2?
Решение.
При л=1 неравенство справедливо, так как 21 > I2.
При л = 2 неравенство несправедливо, так как 22 = 22.
При л = 3 неравенство несправедливо, так как 23 < З2.
При л = 4 неравенство несправедливо, так как 24 = 42.
При л = 5 неравенство справедливо, так как 25 > 52.
При л = 6 неравенство справедливо, так как 2е > 62.
По-видимому, неравенство справедливо при л=1 и при
любом п > 4. Докажем это.
1°. При л = 5 неравенство справедливо.
2°. Пусть
2й > Л2, (1)
где k—некоторое натуральное число, большее 4.
Докажем, что
2*+1>(А+1)2. (2)
Мы знаем, что 2й>2^4-1 при Л>4 (задача 25). По-
этому если мы к левой части неравенства (1) прибавим 2*,
а к правой 2&-J-1, получим справедливое неравенство (2).
Ответ. 2п > л2, когда л = 1 и когда л > 4.
Пример 21. Доказать, что (1 -}-а)л > 14-ла, где а>
> — 1, а =0=0, л—натуральное число, большее 1*).
Решение. 1°.При л==2 неравенство справедливо, так
как а2 > 0.
2°. Пусть неравенство справедливо при л = &, где k—
некоторое натуральное число, т. е.
(1 + а)й > 1 +Аа. (1)
Покажем, что тогда неравенство справедливо и при
« = &+!> т. е*
(1 + а)й+1> 1 +(А 4-1) а. (2)
Действительно, по условию, 1 + а > 0, поэтому справедливо
неравенство
(1 4-а)й+1 > (1 4-Ла)(14-а), (3)
полученное из неравенства (1) умножением каждой части
его на 14-ос. Перепишем неравенство (3) так: (1 + «)л+1>
*) Это неравенство часто называю! неравенством
Бернулли.
30
> 1 + (&+1) a 4-Ла2. Отбросив в правой части последнего
неравенства положительное слагаемое Ла2, получим спра^
ведливое неравенство (2).
Задача 26. Доказать, что при любом натуральном п > 1
Задача 27. Доказать, что при любом натуральном п > 1
4" (2п)!
л+1 (л!)2 •
Пример 22. Доказать, что
+ (a + b)\ (1)
где а + 6>0, п — натуральное число, большее 1.
Решение. 1°. При л = 2 неравенство (1) принимает
вид
2(а24-Л2)> (я + й)2. (2)
Так как а ^Ь9 то справедливо неравенство
(a — £)2>0. (3)
Прибавив к каждой части неравенства (3) по (а4-Л)2, полу-
чим неравенство (2).
Этим доказано, что при л = 2 неравенство (1) справедливо.
2°. Пусть неравенство (1) справедливо при л = Л, где
k—некоторое натуральное число, т. е.
2*"1 (0*4-^*) > (« + *)*. (4)
Докажем, что тогда неравенство (1) должно быть спра-
ведливо и при л = Л4-1, т. е.
(а + &)*+1. (5)
Умножим обе части неравенства (4) на а-\-Ь. Так как,
по условию, т0 получаем следующее справед-
ливое неравенство:
> (а + Ь)к*1. (6)
Для того чтобы доказать справедливость неравенства (5),
достаточно показать, что
2й (<?+14- йй+1) > 2*-1 (а* 4- Ьк) (а + Ь), (7)
31
или, что то же самое,
а*+1
akb 4-
(в)
Неравенство (8) равносильно неравенству
(ak—bk)(a—b)>0. (9)
Если а > Ь9 то ak > Ьк9 и в левой части неравенства (9)
имеем произведение двух положительных чисел. Если а < Ь,
то ак < Ьк, и в левой части неравенства (9) имеем произве-
дение двух отрицательных чисел. В обоих случаях нера-
венство (9) справедливо.
Этим доказано, что из справедливости неравенства (1)
при zz — & следует его справедливость при л = &4-1.
Пример 23. Доказать, что при любом х > 0 и при
любом натуральном п справедливо неравенство
х» + хп-« + х'’-<+.-.+рт+^+4->"+1’ <4
Решение. 1°. а) При л=1 неравенство (1) прини-
мает вид
(2)
Неравенство (2) вытекает из неравенства (х—1)22>О.
б) При л = 2 неравенство (1) принимает вид
х2+1+4г>3- (3)
Неравенство (2) справедливо при любом х > 0; значит, оно
справедливо и при замене х на х2, т. е. х2 + 2. Прибавив
к каждой части последнего неравенства по 1, получим
неравенство (3).
2°. Предположим, что неравенство (1) справедливо при
n = k, где k—некоторое натуральное число, т. е.
x*+x*-«+,,.+_l_4.J_>A+l, (4)
Докажем, что тогда неравенство (1) справедливо и при
л = Л + 2, т. е.
х*+в+х*+**-» + ... + ^ + Ц_+ ’ >Л+3. (5)
X* 2 х«+2
32
Заменив в неравенстве (2) х на xk+2, получаем
xk+2 + -^—^2. (6)
Сложив почленно неравенства (4) и (6), получим неравен-
ство (5).
Подведем теперь итог.
В пп. 1° а) и б) мы доказали, что неравенство (^спра-
ведливо при л=1 и при 72 = 2.
В п. 2° мы доказали, что из справедливости неравен-
ства (1) при n = k вытекает его справедливость и при
72 = /? 4*2. Иными словами, п. 2° дает нам право перехода
от 72 = 6 К 72 = ^4-2.
Результаты пп. 1° а) и 2° дают нам право утверждать,
что неравенство (1) справедливо при любом нечетном п.
Точно так же результаты пп. 1° б) и 2° дают нам право
утверждать, что неравенство (1) справедливо при любом
четном 72.
В целом мы имеем право утверждать, что неравенство (1)
справедливо при любом натуральном 72.
Пример 24. Доказать теорему:
Среднее геометрическое нескольких положительных чисел
не больше их среднего арифметическое о, т. е, если а19
a2i ап положительны, то
< -+»»+...+«„. (1)
Решение. 1°. При 72 = 2 неравенство (1) принимает вид
(2)
Это неравенство легко получить из справедливого при лю-
бых положительных и а2 неравенства
Неравенство (2) имеет простой геометрический смысл. На пря-
мой АВ отложим последовательно отрезки ах и а2- На сумме их
как на диаметре опишем окружность. Тогда + _ радиус этой
окружности, а р4— половина хорды, перпендикулярной к диа-
метру в общей точке и а2 (рис. 2), из чего и усматривается
справедливость неравенства (2).
2°. Предположим, что неравенство (1) справедливо при
72 = Л. Докажем, что тогда оно справедливо и при п = 2£. 2
2 И. С. Соминский и др.
Действительно,
2k__________
]/аха2... a2k = . ~£/aft+1... a2k <
у/"aiaa* • .. ,а%ь
^1 + ^2+ • - + afe . ak + 1 + • • • + a2k
k ' k
- __
а1 + а2 ~Н • • • + а^Ч~ ♦ • • + a2fe
2k
Неравенство (1) проверено при п = 2 и, таким образом,
можем утверждать, что оно
справедливо при д = 4, 8, 16
и т. д., т. е. вообще при
n = 2s, где 5—натураль-
ное число.
3°. Для того чтобы
доказать справедливость
неравенства (1) при вся-
ком натуральном /г, пока-
жем, что из справедли-
вости неравенства при
л = & следует его спра-
ведливость при п =ss k — 1.
Итак, пусть ах, а2,
«й-i — некоторые положительные числа. Пусть X—не-
которое, пока не определенное, положительное число.
Тогда
у/"аха2... ak_гХ<^Д1 + а2+ - •»+flfe-i+^
Выберем X так, чтобы
ах+д2+ • • • ~~Fafe i-bX ai+a2~h * ••
k k—1
т. е. положим X = . Имеем
k — 1
или
7. ^ai+а2 + • • •+ak-l
у аха2... ам .
Пусть теперь/га—произвольное натуральное число. Если
я* = 2*, то, согласно 2°, для него неравенство справедливо.
Если же «^2^, то найдем такое в, чтобы т было мень-
ше 2J, и тогда на основании 2° и 3° утверждаем, что не-
равенство верно для п = т.
§ 4. Доказательство некоторых теорем
элементарной алгебры
методом математической индукции
Теорема 1. Квадрат многочлена равен сумме квад-
ратов всех его членов, сложенной со всевозможными их
удвоенными попарными произведениями, т. е.
(а1 + 02 4* • ♦ • + ап)2 “ ai + 4" • • • + ап +
+ 2 (Л102 + а1аз+ • • • U)
1°. Для п = 2 формула (1) может быть доказана непо-
средственным умножением.
2°. Допустим, что формула (1) верна для n — k— 1, т. е.
(0г + 02 + . .и + = я* + я2 + • • • +^l-i + 2S,
где S — сумма всевозможных попарных произведений, со-
ставленных из а19 а2, ... , ak_v Докажем, что
(«! + «2 + • • • + ak- 1 + ak^ ~
= а2 + а14“ • • • 4- 4“ ak4"
где Sx—сумма всевозможных попарных произведений, со-
ставленных из а19 а2, ... , ak_l9 ak, т. е.
•S1 = S + (014-«а 4- • • • 4-6Zai-i) ak*
Действительно,
(ai4- • • • 4-^-i + afe)2 = [(ai+ • • • 4-^-i)4-^]2==
= (ai + ... 4-^-i)24“2 (0i + ... + ^-i)
= 0i + ... 4- #£-i + 2S + 2(0j+ ... ^ + #1 =
= 0i + a* + .. . + + 2SV
Теорема 2. л-й член арифметической прогрессии
может быть вычислен по формуле
6Zn = ai4-^(^—l), (1)
где ах—первый член, d—разность прогрессии.
2* 8Е
1°. Для л=*1 формула (1) верна.
2°. Предположим, что формула (1) верна для л==А, т. е.
аЛ = a^d (k— 1). Тогда ak+1 = ak + d= al-\-d(k—\) -f-
+ d—a1 + dk1 т. e. формула (1) оказывается справедли-
вой и для п = k -j-1.
Теорема 3. л-й член геометрической прогрессии
может быть вычислен по формуле
®п=в19"-1, (1)
где аг—первый член, q—знаменатель прогрессии.
1°. Для п=1 формула (1) верна.
2°. Пусть aJfe==a1^~1. Тогда akq^axqk.
Теорема 4. Число перестановок из m элементов
может быть вычислено по формуле
(1)
1°. Прежде всего заметим, что Рх=1 и, таким образом,
при /»=1 формула (1) верна.
2°. Пусть Pk = k\. Докажем, что Pk+1 = (k + 1)!.
Из данных &4-1 элементов av а2, ... , ak, ak+1 возь-
мем только первые k и составим из них всевозможные пе-
рестановки. По условию, таких перестановок будет k\.
В каждой из этих перестановок поставим элемент ak+1
последовательно перед 1-м элементом, перед 2-м, ... , перед
&-м, после &-го. Этим путем мы из одной перестановки из k
элементов получим й-pi перестановок из элементов.
Всего имеем k\ (&+ 1) — (&+ 1)! перестановок из &-|-1
элементов.
Необходимо выяснить:
1) нет ли среди этих перестановок двух оди-
наковых;
2) все ли перестановки из k -|~ 1 элементов нами получены.
1) Допустим, что среди (£-|-1)! перестановок имеются
две одинаковые. Назовем их рх и р2. Пусть в перестановке
рг элемент аЛ+1 занимает s-е место, считая слева. Тогда
и в элемент ak+1 занимает 5-е место, считая слева.
Удалим из рх и р2 элемент Получим две одина-
ковые перестановки из k элементов: рх и р2.
Выходит, что для получения рх и р2 в одну и ту же
перестановку из элементов ах, л2, ... , ak д в а р а з а
на одно и то же место был поставлен элемент ofe+1.
Это противоречит правилу, по которому построены пере-
становки.
36
2) Допустим, что некоторая перестановка р из k 4-1
элементов нами не получена. Пусть в р элемент зани-
мает 5-е место слева. Удалим из р элемент ak+1. Получим
перестановку р из первых k элементов. Значит, для полу-
чения р достаточно было взять перестановку р и поставить
в нее элемент аЛ+1 так, чтобы он занял s-е место слева.
Мы не могли не взять перестановку р, так как брали
всевозможные перестановки из первых k элементов.
Мы не могли не поставить элемент ak+1 на указанное место,
так как ставили его и первым, и вторым, ... , и (А4~1)‘м
слева.
Итак, составленные нами перестановки все различны
и всякая перестановка из элементов нами получена.
Из сказанного вытекает, что /\+1 = (А+1)Ь
Теорема 5. Число размещений из m элементов по п
может быть вычислено по формуле
Anm = m(m—1) ... (m — л4-1). (1)
1°. Прежде всего заметим, что = и, таким обра-
зом, формула (1) верна при п=1.
2°. Предположим, что Akm = m(m—1) ... (tn—&4-1),
где k < tn. Докажем, что Akn^1 = tn(m—1) ... (tn—k).
Для получения всех размещений из m элементов по Л 4-1
достаточно взять все размещения из m элементов по k и
к каждому из них приписать в конце каждый из ос-
тавшихся тп—k элементов. Нетрудно убедиться, что со-
ставленные таким образом размещения из m элементов
по & 4-1 все различны и, кроме того, всякое размещение
из m элементов по k 4-1 содержится среди полученных.
Выходит, что Д^+1=Л^(т—k}~m(m—1) ... (m—k).
Теорема 6. Число сочетаний из m элементов по п
может быть вычислено по формуле
(Z
_т(т — 1) ... (/и —п+1)
1*2 ... п
(1)
1°. Прежде всего заметим, что Ст = т и, таким обра-
зом, при л=1 формула (1) верна.
2°. Допустим, что + дока.
же., что
37
Для получения всех сочетаний из т элементов по &4-1
выпишем все сочетания из т элементов по Лик каждому
из них в качестве (&4-1)-го элемента присоединим каждый
из т—k оставшихся элементов. Ясно, что таким путем
будут получены все сочетания из т элементов по Л 4-1,
но каждое из них получится k 4-1 раз.
Действительно, сочетание а19 .,, , ak, ak+1 полу-
чится, когда к сочетанию а2, аз» ak+i присое-
динится элемент аг, когда к сочетанию аг, а3, ... , ak9 ak+1
присоединится элемент а2 и т. д., когда, наконец, к
сочетанию а19 а2, . > ak присоединится элемент ak+1.
Таким образом,
w—& т (т— 1) ... (m—Л)
m -Cm^+1 - b2 k(k+l) •
Теорема 7. Каковы бы ни были числа а и b и каково
бы ни было натуральное число п, имеет место формула
(a + b)n^an + C1nan-1b+ ,. t + C'nan~sbs + ...
^+Cn-1abn-'+bn (1)
(формула бинома Ньютона).
1°. При л = 1 имеем а-\-Ь~ а-\-Ь и, таким образом,
для этого случая формула (1) верна.
2°. Пусть (а4-й)*= akCkak~xbС*а*“262-)- ... -}-bk.
Тогда
(а+ *)*+1 = («+*)*(« + *) = '
= (а* + <^а*-^+,,,+**)(« + *) =
= а*+1 + (1 + &) akb + (Ci + C2k) ak~^ + ...
«i» +(C* + C*+1) ak~sbs+1+ . . .+bk+1.
Имея в виду, что С*4-С^+1 = С*Х1, получаем
(fl + ^+ia=a»+i + ci+1akb+ C^+1aft-^2 + ...
... + Cl++\ak-sbs+1 + • • • + bk+1.
ЧАСТЬ II
ИНДУКЦИЯ В ГЕОМЕТРИИ
§ 1. Вычисление по индукции
Наиболее естественное применение метода математиче-
ской индукции в геометрии, близкое к использованию этого
метода в теории чисел и в алгебре,— это применение к ре-
шению геометрических задач на вычисление. Рассмотрим
несколько примеров.
Пример 1. Вычислить сторону а2п правильного 2"-уголь-
ника, вписанного в круг радиуса /?.
Решение. 1°. При п = 2 правильный 2п-угольник есть
квадрат; его сторона = /?]/ 2 . Далее, согласно формуле
удвоения
находим, что сторона правильного восьмиугольника ав =»
==/?]/'2—Y 2 , сторона правильного шестнадцатиугольника
й1в = /?}/' 2-/2 + /Т, сторона правильного тридцати-
двухугольника а32 = /? 2—2 +V2 + Y 2. Можно
предположить поэтому, что сторона правильного вписанного
2/г-угольника при любом п 2 равна
at» = RY 2-/2+/'2+-..+/2. . (1)
л-2 двойки
39
2*. Допустим, что сторона правильного вписанного
2"-угольника выражается формулой (1). В таком случае по
формуле удвоения
п — 1 двойка
откуда следует, что формула (1) справедлива для всех п.
Из формулы (1) вытекает, что длина С —2 л/? окружности ра-
диуса R равна пределу выражения
п-2 двойки
при неограниченном возрастании п и, следовательно,
л== lim 2-/2+... + К2 =
П -* со 4 ! — V— — '
п — 2 двойки
lim 2» У 2—V2+... + V 2 .
«-►СО Ч, , ' ✓
п — 1 двой ка
Задача 1. Пользуясь формулой (1), доказать, что л
равно пределу, к которому стремится выражение
2
V гО+уЧ’) tG+]/4(i+УЧ))---
когда число множителей (квадратных корней) в знаменателе
неограниченно возрастает (формула Виета). Закон со-
ставления множителей определяется первыми тремя, которые
уже написаны.
Пример 2. Указать правило вычисления радиусов гп и Rn
вписанной и описанной окружностей правильного 2"-уголь-
ника, имеющего данный периметр Р.
40
описанной окруж-
и
Рис. 3.
Решение. Г. г2 = у , = ~ 2
2°. Зная радиусы гп и Rn вписанной
ностей правильного 2"-
угольника периметра Р,
вычислим радиусы гп+1и
Т?/2+1 вписанной и опи-
санной окружностей 2”+1-
угольника того же пе-
риметра. Пусть ЛВ(рис.З)
— сторона правильно-
го 2"-угольника пери-
метра Р, О—его центр,
С—середина дуги АВн
D—середина хорды АВ;
далее, пусть EF—сред-
няя линия треугольника
АВСиО—ее середина. Так как / EOF = ЕОС + £FOC=
= 4- АОС+ 4- у/ ВОС=4- // АОВ* то EF равно стороне
правильного 2"+1-угольника, вписанного в круг радиуса ОЕ,
причем периметр этого 2"+1-угольника равен 2n+1EF =
АВ
= 2n+1-у = 2"ЛВ, т. е. тоже равен Р. Таким образом,
Г„+1 = 00 И Rn+1=OE-
Далее, ясно, что ОС—00—00—OD, т. е. Rn—rn+1 =
= ги+1—г„, откуда rn+1 = -—. Наконец, из прямо-
угольного треугольника ОЕС имеем Of2 — ОС-OG, т. е.
/?п+1 = /?„г„+1 и Rn+l = VRn-rn+l. Итак, окончательно:
rn+i = ;?4LL и ^ = У^п-гп+1
Рассмотрим последовательность г2, /?2, r3, , гП9 Rn,,..
Члены этой последовательности стремятся к радиусу окружности
Р 1
длины Р, т. е. к т-. В частности, при Р=2 имеем г2=— и
4&JT 4
1/”2" 1
Р2 = . Полагая еще гх = 0 и рх = —, получаем следующую
теорему:
Если составить последовательность чисел
1 1 /7 V"2+l /2 /2+4 /2 /2"+4+/7+1
’ 2 * 4 ’ 4 ’ 8 * 8 ’ 16 ’ •••’
41
первые два члена которой равны 0 и > а каждый из остальных
попеременно равен среднему арифметическому и среднему геометриче-
скому двух предшествующих, то члены этой последовательности
стремятся к —.
Пример 3. Определить сумму внутренних углов л-уголь-
ника (не обязательно выпуклого!).
Решение. 1°. Сумма внутренних углов треугольника
равна 2d. Сумма внутренних углов четырехугольника равна
так как каждый че-
тырехугольник можно
разбить на два треуголь-
ника (рис. 4).
2°. Предположим уже
доказанным, что сумма
внутренних углов любого
^-угольника, где k < л,
равна 2d (k — 2), и рас-
смотрим л-угольник
^1^2 • • •Ап*
Прежде всего дока-
В
жем, что во всяком мно-
гоугольнике можно найти диагональ 2), разбивающую его
на два многоугольника с меньшим числом сторон (для вы-
пуклого многоугольника это ясно). Пусть Л, В, С—любые
три смежные вершины многоугольника. Через вершину В
проведем всевозможные лучи, заполняющие внутренний угол
АВС многоугольника до пересечения их с контуром много-
угольника.
Возможны два случая:
А. Все лучи упираются в одну и ту же сторону много-
угольника (рис. 5, а). В этом случае диагональ АС разби-
вает наш л-угольник на (л—1)-угольник и треу-
гольник.
Б. Не все лучи упираются в одну и ту же сторону
(рис. 5,6). В этом случае один из лучей будет проходить
через некоторую вершину М многоугольника, и диагональ
ВМ будет разбивать многоугольник на два многоугольника
с меньшим числом сторон.
Ч Заметим, что диагональ невыпуклого многоугольника может
пересекать его или целиком лежать вне его (как диагональ BD на
рис. 4, б).
42
Вернемся теперь к доказательству нашего основного
утверждения. В л-угольнике A^2.. .Ап проведем диагональ
A^Afa разбивающую его на Л-угольник A1A2..,Ak и (л—
—Л-|-2)-угольник АхАкАк+1.. .Ап. Согласно сделанному пред-
положению, суммы внутренних углов Л-угольника и (л—k + 2)-
угольника соответственно равны 2d (k — 2) и 2d[(n—Л-j-
+ 2) — 2] = 2яЦл— k)\ поэтому сумма углов л-угольника
Рис. 5.
АХА2. ..Ап будет равна 2d(k—2)-\-2d(n—k) = 2d(n — 2),
откуда следует справедливость нашего утверждения для
всех л.
Как мы видели в примере 3, во всяком многоугольнике
можно найти диагональ, разбивающую его на два много-
угольника с меньшим числом сторон. Каждый из этих
многоугольников, не являющийся треугольником, мо^но
снова разбить на два многоугольника с меньшим числом
сторон и т. д. Следовательно, каждый многоугольник мо-
жно непересекающимися диагоналями разбить на тре-
угольники.
Пример 4. На сколько треугольников л-угольник (не обя-
зательно выпуклый) может быть разбит своими непересекаю-
щимися диагоналями?
Решение. 1°. Для треугольника это число равно еди-
нице (в треугольнике нельзя провести ни одной диагрнали);
для четырехугольника ато число равно, очевидно, двум (см.
рис. 4, а и б).
2°. Предположим, что мы уже знаем, что каждый Л-уголь-
ник, где k < л, разбивается непересекающимися диагона-
лями на Л—2 треугольника (независимо от способа разбие-
ния). Рассмотрим одно из разбиений л-угольника . ,Ап
на треугольники. Пусть АгАк—одна из диагоналей этого
разбиения; она делит л-угольник A1Ai.ttAn на Л-угольник
43
A1A2...Ak и (/z —&-(-2)-угольник A1AkAk^1.. .Ап. В силу
сделанного предположения, общее число треугольников раз-
биения будет равно
(Аг — 2) + [(л—k + 2) — 2\=п — 2;
тем самым наше утверждение доказано для всех п.
Задача 2. Определить число W непересекающихся диа-
гоналей, используемых при разбиении л-угольника на тре-
угольники.
Пример 5. Указать правило вычисления числа Р (л) спо-
собов, которыми выпуклый л-угольник может быть разбит
на треугольники непересекаю-
щимися диагоналями.
Решение. 1°. Для тре-
угольника это число равно,
очевидно, единице: Р(3) = 1.
2°. Предположим, что мы
уже определили числа P(k)
для всех k < л; найдем, чему
равно в таком случае Р(л).
Для этого рассмотрим выпук-
лый л-угольник ДХД2...ДЛ
(рис. 6). При всяком разбиении
его на треугольники сторона
AtA2 будет стороной одного
тре-
из треугольников разбиения, третья вершина этого
угольника может совпасть с каждой из точек А3) Д4 ,... ,Дд.
Число способов разбиения л-угольника, при которых эта
вершина совпадает с точкой А3) равно числу способов раз-
биения на треугольники (л—1)-угольника ДХД8Д4.. .Ап, т. е.
равно Р(п—1). Число способов разбиения, при которых
эта вершина совпадает с Д4, равно числу способов раз-
биения (л—2)-угольникаД1Д4Дб. .. Ani т. е. равноР(п—2)=*
= Р(п—2)^(3); число способов разбиения, при которых
она совпадает с А5, равно Р(п—3)-Р(4), так как каждое
из разбиений (л—3) -угольника Д^.. .Ап можно комби-
нировать при этом с каждым из разбиений четырехугольника
Д2Д3Д4Д5, и т. д. Таким образом, мы приходим к следующе-
му соотношению:
Р(л) = Р(л— 1) + ^(л—2)Р(3) + Р(л~3)Р(4)+ ...
...+Р(3)Р(л-2) + Р(л-1). (2)
44
С помощью этой формулы последова!ельно получаем:
Р(4) =Р(3)+Р(3) = 2,
Р(5) = Р(4) + Р(3)Р(3) + Р(4) = 5,
Р(6) = Р (5) + Р(4) Р (3) + Р (3) Р(4) + Р(5) = 14,
р(7) = Р (6) + Р (5) Р (3) + Л4)Р(4) + Р (3) Р (5) + Р (6) - 42
и т. д.
Примечание. С помощью формулы (7) можно доказать, что
х 2(2гг—5)! г
Р = (п—1)! (л—3)! ^СМ” напРимеР» КНИГУ
при всяком п имеем
А. М. Я г л о м и И. М. Я г л о м, Неэлементарные задачи в эле-
ментарном изложении, М., Гостехиздат, 1954 (серия «Библиотека
математического кружка», вып. 5), решение задачи 51 б)].
Задача 3. На сколько частей выпуклый л-угольник раз-
бивается всеми своими диагоналями, если никакие три из
них не пересекаются в одной точке.
§ 2. Доказательство по индукции
Уже некоторые предложения предыдущего параграфа
можно рассматривать как примеры использования метода ма-
тематической индукции для доказательства геометрических
теорем.
Например, предложение примера 3 можно сформули-
ровать так: доказать, что сумма углов л-угольника равна
2d(n— 2); в примере 4 было доказано, что непересекающие-
ся диагонали разбивают л-угольник на л—2 треугольника.
В этом параграфе мы рассмотрим дальнейшие примеры та-
кого же рода.
Пример 6. Дано л произвольных квадратов. Доказать,
что их можно разрезать на части так, что из полученных
частей можно сложить новый квадрат.
Решение. 1°. При л=1 наше утверждение не нуж-
дается в доказательстве. Докажем, что и при п » 2 оно также
справедливо. Обозначим стороны заданных квадратов ABCD
и abed соответственно через х и у; пусть х^у. На сторонах
квадрата ABCD со стороной х (рис. 7, а) отложим отрезки
AM = BN=CP= = разрежем этот квадратно пря-
мым МР и NQ, которые, как легко видеть, пересекаются в
центре О квадрата и образуют между собой прямой угол,
разбивая квадрат на четыре равные части. Эти куски при-
45
ложим ко второму квадрату, как показано иа рие. 7, б.
Порученная фигура тоже будет квадратом, так как углы при
точках Л4', V, Р', Q' — развернутые, углы Л', B't С', Df —
прямые и А1В' = В'Cf — С'D'«= Df Af.
В*
Рис. 7.
2°. Допустим, что наше утверждение уже доказано
для п квадратов, и пусть дано 1 квадратов Л?3, /<2,.<.,/<п,
Выберем любые два из этих квадратов, скажем Кп и
Как показано в п. 1°, разрезая один из этих квадратов и
прикладывая полученные куски ко второму, можно получить
новый квадрат К'.
Далее, согласно сделанному нами предположению квадра-
ты /Сх, • • •» К' можно так разрезать на части, что
из этих частей можно сложить новый квадрат, что и требова-
лось доказать.
Пример 7. Дан треугольник АВС. Через его вершину С
проведено п— 1 прямых CMlf СМ2, «,., СМп~х, разбивающих
треугольник на п меньших треугольников АСМЪ .
..., ХС£. Обозначим через гь г2, ..., тп и рх, ,р2, ..., ря
соответственно радиусы вписанных и вневписанных окруж-
ностей этих треугольников (все вневписанные окружности
вписаны в угол С треугольника; см. рис. 8, а), и пусть
г и р — радиусы вписанной и вневписанной окружностей са-
мого треугольника АВС.
Доказать, что
Pi Ра ’ ’ ’ ’ * рл Р ’
46
Решение. Обозначим через S площадь треугольника
АВС и через /? — его полупериметр; тогда, как известно,
S=pr. С другой стороны, если О—центр вневписанной ок-
ружности этого треугольника (рис. 8, б), то
•£ = 5а(олс + 5досв—<£долв =
= т&р+тар—4ср = г (ь+а~с)р= (/>—Ор;
следовательно, рг = (р—с)р и —
47
Далее, по известным формулам тригонометрии
, А
tg2
(р—Ь) (р—с)
р(р—а)
В (р—а) (р—с)
2 V Р(Р—Ь)
и
откуда
f Л. -в / (Р—Ь) (р—с) (р—а) (р —с) р—с г
*2 V р(р — а) Р(Р-Ь) р р‘
(3)
После этих предварительных замечаний обратимся к до-
казательству теоремы.
1°. При п=1 наше утверждение не нуждается в дока-
зательстве. Докажем его справедливость для п = 2. В этом
случае треугольник АВС прямой СМ разбит на два мень-
ших треугольника АСМ и СМВ. В силу формулы (3)
ri г2 а А 4. СМ А . СМВ, В
. А , СМ А. ШГ-£СМА. В . А . В г
= tgTtg— tg-------tgT = tg1-tgy = ?-.
2°. Предположим, что наше утверждение уже доказано
для п—1 прямых, и пусть дано п прямых СМг, СМ2, ...,
СМп, разбивающих треугольник АВС на л 4-1 мень-
ших треугольников ACMr, MtCM2, ...,МпСВ. Рассмотрим
два из этих треугольников, скажем АСМг и МгСМ2. Как
мы видели в п. 1°, ~ • ~=— , гдег12 и р12—радиусы вписан-
Р1 Ра Pia
ной и вневписанной окружностей треугольника ЛСЛГ2.Нодля
п треугольников АСМ2, М2СМ3, ..., МпСВ в силу сделанного
предположения имеет место равенство — • — •
Р12 Рз Рп Рл4-1
= —и, следовательно, — • — • ... . —.
Р Р1 Р2 Рп Рп + 1 Р
Задача 4. Пусть прямые СМ и СМ' двумя способами
разбивают треугольник АВС на два треугольника АСМ, СМВ
и ACM', СМ'В; rlf r2nrt,r2— соответственно радиусы ок-
ружностей, вписанных в эти треугольники. Доказать, что
если г1 = г1, то г2 = гя, и что аналогичное свойство имеет
место также и для радиусов вневписанных окружностей.
Задача 5. В обозначениях примера 7 доказать, что
rt+Pi I гй+р2 । । Гл4-Рк f+p
*1 "Г ’ ‘ Ял /? ’
48
где /?!, /?2,.. .,Rn vlR—соответственно радиусы описанных
окружностей треугольников ACMV Л^СМ^, ..., МпСВ, АВС.
Задача в. Дано п окружностей Сх, С2, ..., Сй, прохо-
дящих через точку О; вторые точки пересечения окружнос-
тей и С2, С2 и С3, ..., Сп и Сх обозначим, соответст-
венно, через Дх, Л2, ..., Ап (рис. 9). Пусть В1 — произ-
вольная точка окруж-
ности Сх, отличная от
О и от Av Проведем
секущую пере-
секающую окружность
С2 в точке В2, затем
секущую В2Д2, пере-
секающую окружность
С3 в точке В3, и т. д.
(в случае, если; на-
пример, точка В2 сов-
падает с Д2, вместо
секущей через точку
А2 проводим каса-
тельную к окружности С2). Доказать, что полученная в
конце концов на окружности Сх точка Вп+1 совпадает с Bt.
Пусть на плоскости задана сеть линий, соединяющих меж-
ду собой какие-то точки А19 Л2, .
Рис. 10.
.., Ар и не имеющих других
общих точек; мы будем
считать еще, что эта сеть ли-
ний «состоит из одного кус-
ка», т. е. что из каждой
из точек А19 Д2, ..., Ар
можно попасть в любую
другую, двигаясь только
вдоль линий сети (свойство
связности). Такую сеть
линий мы будем называть
картой, заданные точки—
ее вершинами, отрезки
кривых между двумя смеж-
ными вершинами — грани-
цами карты, части плос-
кости, на которые она раз-
бивается границами (в том числе .и бесконечную внешнюю
область),— странами карты. Так, на рис. 10 точки Дх,
49
А2у Д3, Д4, Д5, Дв, Д7, А3 являются вершинами карты, кривые
^1^2> ^2^7» АвА7, АдА^, А^А31 Д3Л6, ^вА5, А5А7,
Л4Д8—ее границами, области ах, а3, а3 и бесконечная внеш-
няя область а—ее странами.
Пример 8. Теорема Э й л е р а. Обозначим число стран
произвольной карты через число ее границ—через I и число
вершин—через р. Тогда s-]-p = l + 2.
Доказательство. Проведем индукцию по числу I
границ карты.
1°. Пусть Z = О, тогда s=l, р=1; в этом случае
s р = Z -р 2.
2°. Предположим, что теорема справедлива для любой
карты, имеющей п границ, и рассмотрим карту, содержащую
/ = границ, стран и р вершин. Возможны два случая.
Рис. 11.
а) Для любых двух вершин карты существует един-
ственный соединяющий их путь вдоль границ карты (хотя
бы один такой путь существует ввиду связности карты). В этом
случае карта не содержит ни одного замкнутого контура и, сле-
довательно, имеет вид, изображенный на рис. И; при этом
$ = 1. Покажем, что на такой карте найдется хотя бы одна вер-
50
шина,принадлежащая только одной границе (как вершина Аг на
рис. 11; такую вершину мы будем называть крайней).
Действительно, возьмем произвольную вершину карты. Если
она—не крайняя, то она служит концом по крайней мере
двух границ. Пройдем по одной из этих границ до второй
ее вершины. Если и эта вершина—не крайняя, то она служит
концом какой-то другой границы; пройдем по этой границе
до второго ее конца и т. д. Так как карта по условию не
содержит замкнутых контуров, мы не вернемся ни к одной из
ранее пройденных вершин и ввиду конечности числа вершин
карты в конце концов придем к такой вершине, которая уже
будет крайней. Удалив эту вершину вместе с единственной
границей, имеющей ее своим концом, мы получим новую карту,
в которой Г —1==л, ^ = 5=1, р'~Р—1, причем эта
новая карта останется, конечно, связной. В силу индуктив-
ного предположения s'+р' = /'4~2, откуда и $4-р = /4-2.
б) Существуют две вершины, соединимые более чем одним
путем (рис. 10). В таком случае на карте имеется некоторый
замкнутый контур, проходящий через эти вершины. Удалив
одну из границ этого контура (без вершин), мы получим
новую связную карту, в которой Г = 1—1=л, р' =р, s' =
—1. По предположению $'-[-// = /'4-2, откуда и
s 4-Р = /4~ 2.
Пример 9. Доказать, что если в каждой вершине карты
сходится не менее трех границ (т. е. если карта не содержит
таких вершин, как Д2, Д3, Лб, Л8, и таких границ, как А^А3
на рис. 10), то найдется страна карты, имеющая не более
пяти границ.
Решение. Так как в каждой из р вершин карты схо-
дится не менее трех границ, то Зр не превосходит удвоен-
ного числа границ 2/ (удвоенного, ибо каждая граница соеди-
няет две вершины); отсюда
(4)
Предположим теперь, что каждая из s стран карты имеет
не менее шести границ; тогда 6s не превосходит удвоенного
числа границ 2/ (удвоенного, ибо каждая граница разделяет
две страны), откуда
(5)
1 2
Неравенства (4) и (5) дают: / = А что
противоречит теореме Эйлера. Следовательно, наше пред-
51
положение о том, что каждая страна имеет не меньше шести
границ, неверно.
Задача 7. На плоскости даны пять точек. Доказать, что
нельзя соединить каждую из этих точек с каждой другой
попарно не пересекающимися линиями
(РИС’ 12)-
______\ \ Другие примеры применения тео-
/_____\ । ремы Эйлера о картах читатель смо-
I / / жет найти в книге: Е. Б. Дынкин и
I / / В. А. У с п е н с к и й, Математические
ч / беседы, М.—Л., Гостехиздат, 1952
(серия «Библиотека математического
* * кружка», вып. 6).
Рис. 12. Задача 8. Доказать, что еслир —
число вершин, I—число ребер и $—
число граней выпуклого многогранника, то s-|-p = / + 2
(теорема Эйлера о многогранниках).
Задача 9. Доказать, что всякий многогранник имеет либо
треугольную, либо четырехугольную, либо пятиугольную
грань.
Задача 10. Доказать, что не существует многогранника
с семью ребрами.
Другие примеры применения теоремы Эйлера о многогран-
никах читатель может найти, например, в книге: Д. О. Ш к л я р-
ский, Н. Н. Ченцов.и И. М. Яг л ом, Избранные задачи
и теоремы элементарной математики, ч. Ill, М., Гостехиздат,
1954 (серия «Библиотека математического кружка», вып. 3).
Задачи о раскраске карт
Пусть на плоскости задана некоторая карта. Мы будем
говорить, что она правильно раскрашена, если каж-
дая ее страна закрашена определенной краской, причем
любые две страны, имеющие между собой общую границу,
закрашены в разные цвета. Примером правильно раскрашенной
карты может служить любая географическая карта. Всякую
карту можно правильно раскрасить, например, закрасив
каждую ее страну в особый цвет, однако такая раскраска
неэкономна. Естественно, возникает вопрос, каково то наи-
меньшее число красок, которым можно правильно раскра-
сить заданную карту. Ясно, что, например, карту, изобра-
женную на рис. 13, а, можно правильно раскрасить двумя
красками; для правильной раскраски карты, изображенной
52
на рис. 13, б, необходимы уже три краски; карту же,
изображенную на рис. 13, в, можно правильно раскрасить
только четырьмя красками. До сих пор не найдено н и о д н о й
карты, которую не удалось бы правильно раскрасить четырьмя
Рис. 13.
красками. Впервые, по-видимому, обратил внимание на это
обстоятельство известный немецкий математик Мёбиус более
ста лет назад. С тех пор многие крупные ученые пытались
решить эту проблему четырех красок, т. е. либо
доказать, что четырех красок
достаточно для раскраски лю-
бой карты, либо найти при-
мер карты, которую четырьмя
красками раскрасить нельзя,
однако до сих пор этого нико-
му не удалось сделать. Уста-
новлено только, что для пра-
вильной раскраски любой кар-
Рис. 14.
ты, во всяком случае, доста-
точно пяти красок (см. ниже пример 13). Нетрудно найти
также условия, при которых карта может быть раскрашена
двумя (пример 11) или тремя (пример 12) красками. Мы
укажем, кроме того, некоторое условие, необходимое и до-
статочное для того, чтобы карта могла быть правильно
раскрашена четырьмя красками (пример 14); вопрос же о
том, выполняется ли это условие для любой карты или
имеются ли карты, ему не удовлетворяющие, остается, по-
нятно, открытым.
Любопытно отметить, что для некоторых поверхностей,
устроенных, казалось бы, более сложно, чем плоскость, про-
блема раскраски карт решена полностью. Так, например,
69
доказано, что на поверхности «баранки», или тора (рис. 14),
для Арайильной раскраски любой карты достаточно семи
красок, причем существую! карты, которые нельзя правильно
раскрасить шестью красками1).
В дальнейшем мы будем предполагать, что карта не со-
держит неразделяющих границ, т. е. границ, по обе стороны
от которых лежит одна и та же страна (как граница Д4Л8
на рис. 10, стр. 49), потому что в противном случае поста-
новка задачи о правильной раскраске не имеет смысла. Мы
будем также предполагать, что карта не содержит вершин,
в которых сходятся лишь две границы (как вершина А2 на
рис. 10), ибо такая вершина была бы лишней. Другими
словами, мы будем рассматривать лишь такие карты, в каж-
дой вершине которых сходится не менее трех границ, т. е.
карты, удовлетворяющие условию примера 9; результат
этого примера в дальнейшем будет неоднократно использо-
ваться.
Нам будет удобно еще считать, что на карте имеется
только одна бесконечная область, т. е. что карта не имеет
границ, «уходящих в бесконечность»; можно показать, что
отказ от этого последнего условия не изменил бы ни одного
из дальнейших выводов.
Карту, в каждой вершине которой сходится ровно три
границы, мы будем называть нормальной. Пусть дана
х) Сравнительно недавно немецкий геометр Г. Рингель по-
лучил результаты, близкие к окончательному решению проблемы
раскраски карт, начерчёйных на любой поверхности, отличной от
плоскости (или от сферы). Наименьшее
число красок, необходимое для правиль-
ной раскраски поверхности, устроен-
ной как «сфера с сквозными дырами»,
согласно Рингелю, видимо, выража-
ется следующей довольно сложной фор-
мулой:
где квадратные скобки чобозначают целую часть числа; так
для тора (рис. 14), имеющего одну «дыру», это число равно
"74.1^491 Г141
—— HI'ol ags^t а для кренделя» (рис. 15) оно имеет вид
J L 2 J
"7+ /1 + 48-21 Г7+/971 Г 16,8 ...1 о ,г
—Г J---- =» ... ЦЕ I =«8. (См. изложение
х л _ l 2 J
результатов Рингеля в сборнике «Математическое просвещение»,
вып. 3, Физматгиз, М., 1958, стр. 205—266.)
54
произвольная карта 5 (рис. 16, а). Выделив около каждой
413 вершин этой карты, в которой сходится более трех
границ, достаточно малый кружок и присоединив его к одной
из стран, окружающих эту вершину, мы получим нормальную
карту S' с тем же числом стран (рис. 16, б); при этом
из всякой правильной раскраски карты S' легко получается
правильная раскраска карты 5 тем же числом красок и
наоборот. Поэтому в вопросе о правильной раскраске карт
мы часто будем ограничиваться рассмотрением нормальных
карт.
Выясним теперь, как устроены простейшие нормальные
карты1). Пусть р—число вершин, /—число границ и 5—
число стран нормальной карты; тогда 2/ = Зр (ср. выше
стр. 51), откуда р ='у/. Кроме того, по теореме Эйлера
$_|_р = /-|_2; значит, 5 = (Z—р)-|~2==4-4-2 и, следователь-
о
но, 5^2. Но при 5 = 2 находим, что /=0; такой карты,
очевидно, не существует. Полагая 5 = 3, получим / = 3 и
/> = 2; эта простейшая нормальная карта имеет вид, изобра-
женный на рис. 17, а. При 5 = 4 получаем / = 6 и р = 4.
Покажем, что в этом случае карта имеет вид, изображен-
ный на рис. 17, б или в. Действительно, обозначим через k2
число двуугольников карты, через k3—число ее треуголь-
ников и через k±— число четырехугольников (так как р = 4,
карта не может иметь стран, число вершин которых больше
2) Здесь и в дальнейшем не различаются «одинаково устроен-
ные» карты (как изображенные на рис. 13» в и 26, а), страны и
границы которых можно перенумеровать так, что на обеих картах
одинаково занумерованные страны разделяются одинаково зану-
мерованными границами.
55
четырех). Тогда Ла + ^э + ^4 = 5'“4 и 2^2 + 3&3 + 4&4
==2/ = 12 (ср выше стр. 51); из последнего равенства видно,
что ka четно*. Сумма Л2 + ^з + Л4> равная 4, с точностью
до порядка слагаемых может иметь вид 2 + 2 + 0, 2+1 +
^1,34-1+0,4 + 0 + 0. Рассмотрим каждый из этих случаев.
Если два из значений k равны 2 и одно—нулю, то при
Л2 = 2, £3 = 2, Л4 = 0 сумма 2А?2 + ЗЛг3 + 4Л4 = 10 < 12; при
А2 = 2, ^з = 0, &4 = 2 сумма 2&2 + 3&3 + 4£4 = 2/= 12—
этому случаю отвечает карта, изображенная на рис. 17, б;
при &2 = 0, Л3 = 2, /г4 = 2 сумма 2&2 + 3&8 + 4&4 = 14 > 12.
Если одно из значений k равно 2 и два—единице, то
лишь при &2 — 1, &3 —2, &4= 1 сумма 2&2 + З&з + 4А4 = 12—
такая карта существует, но она не является нормальной
(рис. 18).
Если одно из значений k равно 3 и одно—единице, то
должно быть &8 = 0, так как k3 четно; при этом 2&2 +
+ 4Л4#=12.
Наконец, если одно из значений k равно 4 и остальные —
нулю, то лишь при А2 = &4 = 0, &з = 4 сумма 2А?2+ЗЛг3 +
+4&4 равна 21 = 12—соответствующая карта имеет вид,
изображенный на рис. 17, в.
Иногда мы будем раскрашивать не только страны, но и
границы карты; при этом цвета, в которые закрашены
границы, мы будем обозначать цифрами 1, 2, 3, ... Если
все границы, сходящиеся в одной и той же вершине, по-
лучают при такой нумерации границ разные номера, то мы
будем называть соответствующую нумерацию границ карты
правильной (см., например, . рис. 19). Отметим, что
задача о такой нумерации вершин карты, при которой
«соседние» вершины, т. е. вершины? соединенные одной гра-
ницей, получают разные номера, тоже связана с задачей
66
о правильной раскраске стран карты; см. по этому по-
воду, например, книгу Е. Б. Дынкина и В. А. Успенского,
указанную на стр. 52, в которой читатель сможет также найти
другие доказательства многих из приводимых ниже теорем.
Пример 10. На плоскости дано п окружностей. Доказать,
что при любом расположении этих окружностей образуемую
ими карту можно правильно раскрасить двумя красками.
Решение. 1°. При /2—1 утверждение очевидно.
2°. Предположим, что наше утверждение справедливо для
любой карты, образованной п окружностями, и пусть на
плоскости задано л+1 окружностей. Удалив одну из этих
окружностей, мы получим карту, которую в силу сделанного
предположения можно правильно раскрасить двумя красками,
например черной и белой (рис. 20, а). Восстановим затем
отброшенную окружность и по одну сторону от нее (напри-
мер, внутри) изменим цвет каждой области на противопо-
67
ложный (т. е. черный — на белый и наоборот); легко видеть,
что при этом мы получим карту, правильно раскрашенную
двумя красками (рис. 20, б).
Л
РисЛ 2L
Рис. 22.
Задача И. На плоскости задано п окружностей, в каж-
дой из которых проведено по хорде. Доказать, что обра-
зуемую ими карту можно правильно раскрасить тремя крас-
ками (рис. 21).
Пример 11. (Теорема о двух красках.) Для того
чтобы карту можно было правильно раскрасить двумя крас-
ками, необходимо и достаточно, чтобы в каждой ее вершине
сходилось четное число границ.
Решение. Необходимость этого условия очевидна,
так как если в какой-нибудь вершине карты сходится нечет-
ное число границ, то уже страны,
окружающие эту вершину, нельзя
правильно раскрасить двумя крас-
ками (рис. 22).
Для доказательства достаточ-
н о с т и условия проведем индукцию
по числу границ карты.
Рис- 23- 1°. Для карты с двумя граница-
ми утверждение очевидно (рис. 23).
2°. Предположим, что теорема справедлива для любой
карты, в каждой вершине которой сходится четное число гра-
ниц и общее число границ которой не превосходит п, и пусть
дана карта 5, имеющая п +1 границ и удовлетворяющая
тому же условию." Начиная с произвольной вершины А
карты станем двигаться в произвольном направлении вдоль
58
границ карты. Ввиду конечности числа вершин карты мы
вернемся в конце концов в Одну из уже пройденных
вершин (карта не имеет крайних вершин, потому что на ней
нет неразделяющих границ) и сможем выделить некоторый
не имеющйй самопересечений замкнутый контур, состоящий
из границ карты. Удалив этот контур, мы получим карту S'
с меньшим числом границ, в каждой вершине которой также
сходится четное число границ (потому что в каждой вершине
карты £ отбрасывалось четное число границ’—0 или 2). В
силу индуктивного предположения карту S' можно пра-
вильно раскрасить двумя красками.
Восстановив отброшенный контур и изменив все цвета с
одной стороны от него (например, внутри), мы и полу-
чим правильную раскраску карты 5.
Пример 12. (Теорема о трех красках.) Для того
чтобы нормальная карта могла быть правильно раскрашена
тремя красками, необходимо и достаточно, чтобы каждая ее
страна имела четное число границ.
Доказательство. Необходимость сформулиро-
ванного условия очевидна, так как если на карте имеется
страна а с нечетным числом
границ, то уже а и страны, х /
пограничные с ней, невозмож- /
но правильно раскрасить тремя \-----—/
красками (рис. 24). Р / \ У
Для доказательства до- / Л
статочности условия про- ' .s
ведем индукцию по числу п
стран карты. у | fi
1°. Для нормальной карты, ' I
состоящей из трех стран (см. |
рис. 17, а на стр. 56), наше^ рис 24.
утверждение очевидно. Нор-'
мальную карту, состоящую из четырех стран и изображен-
ную на рис. 17, б, тоже можно, очевидно, раскрасить тремя
красками (для этого достаточно закрасить «внутреннюю»
страну той же краской, что и внешнюю область); нормальная
карта, изображенная на рис. 17, в, не удовлетворяет усло-
вию о четности числа границ каждой страны.
Таким образом, каждая нормальная карта, число стран
которой равно 3 или 4 и каждая страна которой имеет чет-
ное число границ, может быть правильно раскрашена тремя
красками.
59
9» Ппедположим, что теорема верна для любой нормаль-
z страна которой имеет четное число границ
Н°обпхееТч1<сло стран которой равно п—1 или л, и рассмотрим
нормальную карту S, удовлетворяющую тому же условию и
имеющую п 4-1 стран. Как вытекает из примера 9, на
карте S найдется страна а, имеющая не более пяти границ.
В нашем случае а будет иметь либо две, либо четыре гра-
ницы. Рассмотрим каждый из этих случаев.
А. а имеет две границы. Пусть А и В—вершины
этой страны, ох и о2 — соседние с ней страны (рис. 25).
Удалив границу между страна-
ми а и ах, мы получим карту S',
которая также будет нормаль-
ной, так как точки Ап В просто
перестанут быть вершинами
(мы условились, что карта не
имеет лишних вершин), а в
остальных вершинах будет схо-
Рис. 25.
диться прежнее число границ.
Каждая страна карты S' также имеет четное число границ, так
как число границ каждой из стран ог и о2 уменьшится на 2,
а число границ каждой из остальных стран не изменится.
Так как число стран карты S' равно л, то в силу индуктив-
ного предположения ее можно правильно раскрасить тремя
красками а, |3, у. Пусть страны а' = о14-а и^ = а2 по-
лучат при этом соответственно цвета аир. Восстановив
страну а и закрасив ее цветом у, мы получим правильную
раскраску карты S.
Б. а имеет четыре границы. Может случиться, что
какие-либо две из прилегающих кос противоположных
сторон стран граничат между собой или даже совпадают
(рис. 26, а или 17,6); однако в этом слу,чае две другие
граничащие с о страны уже не могут ни иметь между собой
общих границ, ни совпадать. Пусть такими будут страны о2
и о4 (рис. 26, 6). Присоединим страны а2 и о4 к о, удалив
границы АВ и CD. Мы получим карту S', которая будет так-
же, очевидно, нормальной, причем и на этой карте каждая
страна будет иметь четное число границ. Действительно, если
число границ страны ох было равно 2Аг, число границ страныо2
равно 2k2i число границ страны о3 равно 2£3 и число границ
страны а4 равно 2£4, то страна о' = о4-о24-о4 будет иметь
2k2 + 2k^—4 границ, страна будет иметь 2kx — 2
60
границ и страна о'=о8 будет иметь 2£3 — 2 границ, в то
время как число границ каждой из остальных стран не
изменится. (В том случае, когда страны ох и о8 совпадают,
эта страна на карте S' будет иметь на четыре границе меньше,
чем на карте S.)
Так как карта 5' имеет п—1 стран, то ее в силу индук-
тивного предположения можно правильно раскрасить тремя
Рис. 26.
красками а, 0, у. Покажем, что при этом страны о* и а'з бу-
дут закрашены в один и тот же цвет (это утверждение оче-
видно, если а'3 совпадает с о'). Действительно, пусть страна о'
окрашена цветом а, страна а'—цветом 0. Так как на участке
MV к а' прилегает нечетное число стран (2&2— 3) и цвета
этих стран должны, очевидно, чередоваться в последователь-
ности у, 0, у, 0, ...,у, то страна о3 будет закрашена цве-
том 0. Восстановив страну о и закрасив ее цветом у, мы по-
лучим правильную раскраску карты S.
Пример 13. (Теоремаопятикрасках.) Любую нор-
мальную карту можно правильно раскрасить пятью красками.
Доказательство. 1°. Для карты, число стран кото-
рой не превосходит пяти, утверждение очевидно.
2°. Предположим, что теорема справедлива для любой
нормальной карты, число стран которой равно п—1 или л,
и рассмотрим карту S, состоящую из лг-j-1 стран. Как было
показано в примере 9, карта S содержит по крайней мере
одну страну о, число границ которой не превосходит пяти.
Рассмотрим все случаи, которые при этом могут иметь место.
61
а) а имеет две границы (см. рис. 25 на стр. 60).
Пусть 04 и а2 будут соседние с о страны. Присоединив страну
<4 к а, мы получим нормальную карту 3', число стран кото-
рой равно tt.
В силу индуктивного предположения карту 5' можно пра-
вильно раскрасить пятью красками. Страны а'=04-04 и
а'=а2 будут при этом окрашены какими-то двумя из этих
красок. Восстановив страну о, мы сможем закрасить ее одной
из трех оставшихся красок.
б) о имеет три границы (рис. 27, а). Присоединим
04 к а. Закрасив полученную карту 3' пятью красками, мы
Рис. 27.
сможем затем закрасить страну а одним из двух цветов, не
использованных при закраске стран a' = <74-04, a* = a2,
в) о имеет четыре границы (рис. 27,6). Найдутся
две из прилегающих к а стран, которые между собой не сов-
падают (см. пример 12). Присоединив к о одну из этих
стран, например о2, мы получим карту 3' из п стран, кото-
рую в силу индуктивного предположения можно правильно
раскрасить пятью красками. При этом страны a'=an a' =
= o2 + or, a3 = a3 и a4 = a4 получат какие-то четыре из пяти
возможных цветов (или меньше, если о' и а' совпадают или<
закрашены одним цветом). Восстановив страну о, мы сможем
закрасить ее в пятый цвет.
г) о имеет пять границ (рис. 27, в). Как в приме-
ре 16, найдутся две соседние с о страны, не граничащие между
собой и не совпадающие; пусть это будут 04 и о3. Присоеди-
нив обе эти страны к о, мы получим нормальную карту 3',
имеющую п—1 стран. В силу индуктивного предположения
карту 3' можно правильно раскрасить пятью красками. При
62
этом страны a'=ai + tf + a3> аа==:а2» а4 = а4 и а5г=сгв по’
лучат какие-то четыре из этих пяти цветов. Восстановив
страну а, мы сможем закрасить ее в пятый цвет.
Пример 14. (Теорема Волынского 1).) Нормальную карту
в том и только в том случае можно правильно раскрасить четырьмя
красками, если ее границы можно правильно занумеровать тремя
цифрами.
Решение. А. Если нормальную карту можно правильно рас-
красить четырьмя красками, то ее границы можно правильно зану-
меровать тремя цифрами.
Пусть нормальная карта S правильно раскрашена четырьмя
красками а, 0, у, 6. Обозначим цифрой 1 границы между странами,
закрашенными в цвета аир или в цвета
у и 6, цифрой 2—границы между стра- к
нами, закрашенными в цвета а и у или в
цвета р и 6, и цифрой 3—границы X. %
между странами, закрашенными в цвета \
а и 6 или в цвета р и у. Полученная б/ ’
нумерация границ будет правильной: д
действительно, если в какой-либо верши- X7 ^3
не А сходятся две границы, отмеченные <
одной и той же цифрой (например, цифрой
1, рис. 28), то страны о2 и о3, отделяемые *°-
от страны Gi границами с одинаковым но-
мером, должны были бы иметь один и тот же цвет (так, если в
нашем примере имеет цвет а, то а2 и а3 закрашены цветом Р), но
это не может иметь места, так как о2 и о3 граничат между собой.
Б. Если границы нормальной карты можно правильно зануме-
ровать тремя цифрами, то ее страны можно правильно раскрасить
Рис. 29.
четырьмя красками. Доказательство этого утверждения мы про-
ведем индукцией по числу п стран карты.
1°. Границы простейшей нормальной карты, состоящей из трех
стран (см. рис. 17, а на стр. 56), можно единственным образом
занумеровать цифрами 1, 2, 3 (с точностью до перестановки этих
цифр). Раскрасим эту карту, как указано на рис. 29< а. При этом
граница между странами, окрашенными в цвета аир, будет иметь
номер 1, граница между странами, окрашенными в цвета Р и 6,—
г)В. В. Волынский (1923—1943), советский математик,
погиб на фронте Великой Отечественной войны.
63
номер 2 и граница между странами, окрашенными в цвета а и 6,—
номер 3. <
Правильную раскраску карты £ четырьмя красками а, 0, у»
при которой границы между цветами а и (3 и между цветами у и б
имеют номер 1, границы между цветами а и у и между цветами 0
и 6—номер 2 и границы между цветами а и б и между цветами 0
и у—номер 3, мы будем называть допустимой. Мы показали,
что простейшую нормальную карту, состоящую из трех стран, можно
допустимым образом правильно раскрасить четырьмя красками.
Покажем, что это же верно и для нормальной карты, состоящей
из четырех стран (рис. 17, б и в). Границы карты, изображенной
на рис. 17, в, можно единственным образом (с точностью до пере-
становки цифр) правильно занумеровать цифрами 1, 2, 3 (рис. 29, б).
Раскраска этой карты, указанная на рис. 29, б, будет допустимой.
Карта, изображенная на рис. 17, б, допускает две существенно
7 7
Рис. 30.
различные нумерации границ (рис. 30, а и б). Раскраски этих карт,
указанные на рис. 30, а и б, также будут допустимыми.
2°. Предположим, что всякую нормальную карту, границы кото-
рой правильно занумерованы тремя цифрами и число стран которой
равно л—1 или л, можно допустимым образом раскрасить четырьмя
красками, и рассмотрим нормальную карту S, имеющую л+1 стран,
границы которой также правильно занумерованы тремя цифрами.
Как мы видели в примере 9, на карте S найдется страна о, число
границ которой не превосходит пяти. Рассмотрим различные част-
ные случаи, которые при этом могут иметь место.
а) о имеет две границы. Единственная (с точностью до
перестановки цифр) возможная нумерация границ в окрестности а
изображена на рис. 31, а. Присоединим страну к а; новой границе
MN, разделяющей страны а’ = ах + а и а2 = а2 (рис. 31, б), отнесем
номер 1, номера остальных границ оставим без изменения. Получен-
ная карта S' будет нормальной; ее границы будут правильно зану-
мерованы тремя цифрами. Так как число стран карты S' равно л, ее
можно правильно раскрасить четырьмя красками, причем, если
страна 0^ имеет цвет а, то страна о2 будет цвета 0. Восстановив
страну о и закрасив ее цветом у, мы получим допустимую рас-
краску карты £ четырьмя красками.
64
б) <г имеет три границы. Единственно возможная нумера-
ция границ в окрестности а указана на рис. 32, а. Представим себе,
что карта S начерчена на резиновой пленке, и стянем страну а
в точку; при этом границы ЛВ, ВС и АС пропадут, а вершины А, В
и С сольются в одну А — В = С = А' (рис. 32, б). Не меняя нумера-
ции границ МА', NA', РА' (бывших МА, NB, PC) и всех осталь-
ных, мы получим нормальную карту S' с правильно занумерован-
ными границами. Так как число стран карты S' равно п, ее можно
правильно .раскрасить четырьмя красками; при этом, если страна а*
окрашена цветом а, то страна а2 будет цвета 6 и страна а3 — цвета у.
Восстановив страну а и закрасив ее цветом р, мы получим допу-
стимую раскраску карты S.
в) о имеет четыре границы. В этом случае возможны
две существенно различные нумерации границ в окрестности стра-
3 И. С. Соминский и др. 65
ны о (рис. 33, а и 34, а). Рассмотрим первый случай (рис. 33, а),
Найдутся две соседние с а схраны, не имеющие между собой общих
границ (см. пример 12). Так как обе пары противоположных
Рис. 33.
стран <гх> о3 и о2, в смысле нумерации границ равноправны, мы
можем предположить, что не имеют общих границ страны и о3.
Присоединим к о обе страны и о3; новым границам NP и MQ
отнесем номер 3 (рис. 33,6). Полученная карта S' будет нормальной
с правильно занумерованными границами. Так как число стран
карты S' равно n—1, ее можно правильно раскрасить четырьмя
красками, причем если страна о' = 01+^3+^ закрашена цветом а,
то страны а2=а2 и о4 = о4 будут цвета б. Восстановив страну ст,
мы закрасим ее цветом р.
Во втором случае (рие. 34, а), если не имеющими общих границ
странами являются 01 и а3, то можно рассуждать аналогично; только
в этом случае новая граница NP получит по-прежнему номер 3, а гра-
ница MQ —номер 2 (рис. 34, б); страна о4 = о4 будет закрашена цве-
том у* Восстановив страну о, мы по-прежнему закрасим ее цветом р.
Рис. 35.
Наконец, предположим, что не имеют общих границ страны оа
и о4. Стянем четырехугольник ABCD в отрезок так, чтобы точка А
совпала с точкой В, а точка С—с точкой D; при этом граница ВС
сольется с AD. Нумерацию границ MAtNB, PC и QD оставим преж-
ней, а новой границе BC==AD отнесем номер 1 (рис. 34, в). Полу-
ченная карта S' будет нормальной с правильно занумерованными
границами. Так как число стран карты S' равно п, ее можно пра-
вильно раскрасить четырьмя красками, причем если страна а' имеет
цвет а, то страна <у'’будет цвета 6, страна о'— цвета а и страна о4 —
цвета у. Восстановив страну о, мы закрасим ее цветом р.
3*
67
г) и имеет пять границ. В этом случае, с точностью
до перестановки цифр 1, 2, 3, возможен только один способ ну-
мерации границ в окрестности страны о (рис. 35, а). Рассмотрим
сначала случай, когда страна о6 не совпадает и не имеет общих
границ ни с о2, ни с о3. Присоединим страну о5 к а, новой границе
МВ отнесем номер 2, новой границе RD—номер 1; границу ВС
переименуем в 1, границу CD—в 2. Мы получим нормальную
карту S' (рис. 35, б) с правильно занумерованными границами. Так
как число стран карты S' равно п, ее можно правильно раскра-
сить четырьмя красками, причем если страна о' = а+аб закрашена
цветом а, то страны о2 и о4 будут цвета р, а страны а* ио' —
цвета у- Восстановив страну о, мы закрасим ее цветом 5.
В том случае, когда страна о5 граничит или совпадает с о2,
то страны Oi и о3 не граничат между собой и не совпадают, если
же страна о5 совпадает или граничит с о3, то не могут ни совпа-
дать, ни граничить между собой страны о2 и о4. Так как оба
последних случая в смысле нумерации границ равноправны, до-
статочно рассмотреть случай, когда страны а-х и о3 не имеют общих
границ и не совпадают. Присоединим обе эти страны к о, новой
границе NP отнесем номер 3, новой границе ME — номер 2 и но-
вой границе EQ — номер 3. Мы получим нормальную карту S'
(рис. 35, в) с правильно занумерованными границами. Так как
число стран карты S' равно п—1, ее можно правильно раскрасить
четырьмя красками, причем если страна о' = о + а14~а8 закрашена
цветом а, то страны а2 = а2 и о4==о4 будут цвета 6, а страна
а^ = сгб —цвета у. Восстановив страну о, мы закрасим ее цветом £.
Так как не известно, всякую ли нормальную карту можно пра-
вильно раскрасить четырьмя красками, то не известно также,
границы всякой ли нормальной карты можно правильно зануме-
ровать тремя цифрами. Можно доказать лишь следующее более
слабое утверждение.
Пример 15. Границы всякой нормальной карты можно пра-
вильно занумеровать четырьмя цифрами.
Доказательство. Мы докажем это утверждение для лю-
бой (даже не обязательно связной; см; выше стр. 49) карты, в каж-
дой вершине которой сходится не более трех границ. Доказа-
тельство проведем индукцией по числу п вершин карты.
Г. При п — 2 утверждение очевидно.
2°. Предположим, что наше утверждение справедливо для любой
карты, в каждой вершине которой сходится не более трех границ
и число вершин которой равно и, и рассмотрим карту S, удовлет-
воряющую тому же условию и имеющую л-(-1 вершин. Удалив
одну из этих вершин, скажем Ло» вместе с принадлежащими ей
границами, мы получим карту S', в каждой вершине которой схо-
дится не более трех границ и число вершин которой равно п.
В силу индуктивного предположения границы карты S' можно
правильно занумеровать четырьмя цифрами 1, 2, 3, 4. Восстано-
вим вершину До с ее границами. При этом возможны три случая:
а) Вершина До соединена (одной, двумя или тремя границами)
лишь с одной вершиной карты S' (рис. 36, а, б, в). В этом
случае нумерация границ карты S' легко продолжается в пра-
вильную нумерацию границ карты S.
68.
б) Вершина Ло соединена с двумя вершинами Лх и Л2 карты S',
причем с одной из них она может быть соединена двумя границами
(рис. 37, а и б). Легко
1
нумерацию* границ карты S.
в) Вершина Ло соединена с тремя верши-
нами Alf Л2, Л3 карты S' (рис. 38). Наименее
благоприятным случаем будет тот, когда через
каждую из вершин Лр Л2, Л3 карты S' про-
ходит по две границы. Для каждой из границ
A(iAli Л0Л2, Л0Л3 мы будем иметь в этом
случае по два возможных номера, из кото-
рых не удастся выбрать трех различных но-
меров лишь в тол? случае, если эти три пары
> проверить, что при этом во всех
мерация границ карты S' может быть продолжена в
случаях ну-
правильную
одинаковы, т. е. если три пары границ карты
S', проходящих через вершины Лх, Л2, Л3, р
получили одинаковые номера, скажем 1 и 2. ^ис*
Выделим тогда на карте S' контур макси-
мальной длины, начинающийся в вершине Л! и состоящий попе-
ременно из границ с номерами 1 и 3 (такой контур может состоять
лишь из одной границы и может заканчиваться и в одной из
69
вершин Д2 и Дз)- Этот контур не может иметь самопересечении,
так как, по предположению, границы карты S' занумерованы пра-
вильно. Переменим номера границ этого контура, заменяя единицу
тройкой и наоборот.
При этом нумерация границ карты S' останется, очевидно,
правильной, причем в новой нумерации три пары границ, прохо-
дящих через вершины А1Г Д2 и А3 карты S', уже не будут зану-
мерованы одинаково; а в этом случае правильная нумерация границ
карты S' легко может быть продолжена в правильную нумерацию
границ карты S.
§ 3. Построение по индукции
Применение метода математической индукции к решению
задач на построение может иметь место в том случае, если
в условии задачи фигурирует некоторое целое положитель-
ное число п (например, в зада-
а чах на построение л-угольников).
A Ниже мы рассмотрим ряд приме-
I ров такого рода. При этом в
| настоящем параграфе мы будем
I рассматривать и самопересекаю-
7*** I щиеся многоугольники (рис. 39);
д\ другими словами, под многоу-
\ | гольником в большинстве задач
\ I понимается какая угодно
\ I замкнутая ломаная А^А^.А^
Ч Пример 16. На плоскости да-
#з ны 2п +1 точек. Построить
(2л1)-угольник, для которого
Рис* эти точки являются серединами
сторон.
Решение. 1°. При п = 1 задача сводится к построению
треугольника по заданным серединам его сторон и решается !
легко (достаточно провести через каждую из трех заданных
точек прямую, параллельную прямой, соединяющей две дру-
гие точки).
2°. Предположим, что мы умеем строить (2л — ^-уголь-
ник по заданным серединам его сторон, и пусть даны 2л+1
точек Дх, Д2, .,. , Д2й+1, являющиеся серединами сторон
искомого (2л + 1)-угольника xtx2.. .х2п+1.
Рассмотрим четырехугольник х1х2п^1х2пх2п+1 (рис. 40).
Точки Д2п_ь An+i служат серединами трех его сторон
Х2п-1Х2п> Х2пХ2п + 1> Х2п + 1Х1*
70
Пусть А — середина четвертой стороны XjX^^. Четырех-
угольник Л2„_1Л2пЛ2п+1Л —параллелограмм (для доказа-
тельства достаточно провести прямую ххх2„ и рассмотреть
треугольники х1х2п+1х2„ и x1x2n_lxin, для которых от-
резки Л2,Ав+1 И А2п-1А
так как точки Л2га.1, А2п и
Л2„+1 нам известны, то чет-
вертая вершина А паралле-
лограмма легко может быть
построена. Точки Аи Д2,. .. ,
Л2п_2, являются середи-
нами сторон (2п — 1 )-угольника
хгх2.. .а:2п_1, который со-
гласно сделанному предполо-
жению мы можем построить.
Далее, остается только постро-
ить отрезких1х2и+1 и х2п_гх2п
(точки хг и х2й-1 уже оп-
ределены), делящиеся попо-
лам в известных точках
А%п+1 и
В случае многоугольника, не имеющего самопересечений,
ясно, что понимать под внешними и внутренними (по отно-
шению к этому многоугольнику) точками. В общем случае
это понятие теряет смысл; так, например, нельзя сказать,
расположена ли точка А на рис. 39 внутри или вне много-
угольника.
Вместо этого мы введем следующее определение. Пусть
дан произвольный многоугольник А1А2...Ап. Установим
для этого многоугольника определенное направле-
ние обхода его вершин (скажем, в порядке А19 Л2,..., Ап).
Пусть на одной из сторон, например ЛХД2,^многоугольника
построен треугольник АгВА2. Если направление обхода вер-
шин треугольника в порядке Al9 А2, В противоположно
направлению обхода вершин многоугольника (одно — по?
а другое — против часовой стрелки), то мы будем говорить,
что треугольник обращен во внешнюю сторону по
отношению к многоугольнику; если же направления обхода
вершин треугольника и многоугольника совпадают,—будем
говорить, что он обращен во внутреннюю сторону
по отношению к многоугольнику.
Пример 17. На плоскости даны п точек. Построить
n-угольник, стороны которого являются основаниями равно-
71
бедренных треугольников с вершинами в данных п точках
и углами ах, а2, .. , при вершинах1).
Решение. Мы будем считать, что некоторые из углов
ах> а2, ... , ап могут быть и больше 180°, условившись, что
при а< 180° соответствующий равнобедренный треугольник
обращен во внешнюю сторону по отношению к многоуголь-
нику, а при а> 180° —во внутреннюю сторону (причем угол
при вершине в этом случае равен 360° — а).
1°. Пусть л = 3. Допустим, что задача решена, хъ х2,
х8 —вершины искомого треугольника, Дх, Л2, А3— заданные
вершины построенных на его сторонах равнобедренных тре-
угольников с углами ах, а2, а3 при вершинах (рис. 41, а).
При повороте плоскости вокруг точки Дх на угол ах (мы ус-
ловимся считать, что все повороты производятся против часо-
вой стрелки) вершина х± перейдет в х2, при повороте вокруг
точки А2 на угол а2 вершина х2 перейдет в х3. Оба эти по-
ворота, последовательно выполненные один за другим, рав-
носильны одному повороту на угол ах + а2 вокруг некоторой
точки А, которую можно построить по точкам Лх и А2 и уг-
лам ах и а2 следующим образом: на отрезке А±А2 при точках
лл «1 а2 Л
Ах и А2 строим углы и точка А пересечения вторых
сторон этих углов и будет центром результирующего пово-
J) Предыдущий пример можно считать частным случаем при-
мера 17 при а1=а2 = ...==аяж 180°.
72
рота на угол сс1-|-сс2 [см., например, И. М. Яг л ом, Геомет-
рические преобразования, 1, § 2 гл. I части первой, М.,
Гостехиздат, 1955 (серия «Библиотека математического круж-
ка», вып. 7)]. При этом результирующем повороте вершина
хг переходит в х3. Следовательно, вершина х3 переходит
в хг при повороте вокруг точки А на угол 360°—(а1 + «2) и,
значит, точка А является вершиной равнобедренного тре-
угольника с основанием xtx3 и углом 360°—(ах + а2) при
вершине.
По точкам А и А3, если они не совпадают (что может иметь
место, лишь если а14-а2 + а3 = 360°«Л), можно построить
сторону хгх3. Для этого на отрезке АА3 по обе стороны от то-
чек А и А3 строим соответственно углы —° и с*з .
Точки пересечения сторон этих углов и будут вершинами
хх и х3 искомого треугольника. После этого нетрудно по-
строить и вершину х2. При ах + а2 4~а3 = 360°-й (когда
точка А совпадает с Л3) решений задачи является неопре-
деленным.
2°. Предположим, что мы умеем строить л-угольник по
вершинам построенных на его сторонах равнобедренных тре-
угольников с заданными угламй при вершинах, и пусть тре-
буется построить (л + 1)-угольник по вершинам Лх, Л2, ... Ля,
Лл+1 построенных на его сторонах равнобедренных треуголь-
ников с углами ах, а2, ... , ал, ая+1 при вершинах.
Пусть х±х2 .. - хпхп+1 — искомый (л 4- 1)-угольник
(рис. 41, б). Рассмотрим треугольник х1хпхп+1. Как в п. 1°,
по известным вершинам Ап и Ап+1 равнобедренных треуголь-
ников хпАпхп+1 и хп+1Ап+1х1У построенных на сторонах
хпхп+1 и хп+1х1ч можно найти вершину А равнобедренного
треугольника хгАхп, построенного на диагонали х±хп и име-
ющего угол при вершине, равный 360°—(ал4-ап+1). Этим
наша задача сводится к задаче о построении л-угольника
х^х2 .. . хп по вершинам АгА2 ... Ап_±А построенных на его
сторонах равнобедренных треугольников с известными углами
ах, а2, ... , а„-1, 360° — (ал + «л+1) при вершинах. В силу
индуктивного предположения л-угольник хгх2 ... хп может
быть построен, после чего уже нетрудно построить и иско-
мый (л + 1)-угольник х±х2 ... хпхп+1.
При 04 + а2 + ... + ап = 360° • k решение задачи является
невозможным или неопределенным (почему?).
Задача 12. На плоскости дано л точек. Построить л-уголь-
ник, для которого эти точки являются вершинами построен-
73
ных на его сторонах треугольников, имеющих заданные углы
при вершинах и заданные -отношения боковых сторон.
Пример 18. На плоскости даны окружность и п точек.
Вписать в окружность л-угольник, стороны которого прохо-
дят через заданные точки.
Решение. Эта задача —трудная; для ее решения надо
применить метод математической индукции совсем неожи-
данным образом. А именно, здесь не удается воспользо-
ваться индукцией по числу п сторон многоугольника; вместо
Рис. 42.
этого приходится рассматривать более общую задачу о по-
строении п-угольника, k соседних сторон которого проходят
через k заданных точек, а остальные л — k сторон парал-
лельны заданным прямым (эта задача переходит в рассматри-
ваемую при k = n) и проводить индукцию по
ч и с л у k.
1°. При k=\ имеем такую задачу: вписать в окружность
л-угольник, сторона А±Ап которого проходит через заданную
точку Р, а остальные л—1 сторон AtA2i Л2Л3, ... , Ап__1Ап
параллельны заданным прямым
Допустим, что задача решена и искомый многоугольник
построен (рис. 42, а, б). Возьмем на окружности произволь-
ную точку и построим вписанный многоугольник В±В2 ...
стороны ВгВ^ В2В3, ... , Вп_гВп которого параллельны со-
ответственно прямым /х, /2, ... , ln~v Тогда дуги А-^В^
74
А2В2, ... , АпВп будут равны между собой, причем дуги А±Вг
и Л2В2, Л2В2 и А3В3 и т. д. будут иметь противоположные
направления на окружности. Следовательно, при четном п
дуги AxBt и АпВп направлены в противоположные стороны,
и четырехугольник А1В1ВпАп является равнобедренной тра-
пецией с основаниями А±Ап и ВгВп (рис. 42, а). Поэтому
сторона АхАп искомого многоугольника параллельна стороне
ВгВп л-угольника ВХВ2 ... Вп\ следовательно, в этом слу-
чае через точку Р надо провести прямую, параллельную ВгВпУ
после чего уже без труда определяются и остальные верши-
ны л-угольника ^AtA2 . . .Ап д
(провести исследование). р>
При нечетном л дуги АгВг —fyf —
и АпВп имеют одинаковые на-
правления и четырехугольник д ~ \Z
является равнобед- и/ \
ренной трапецией с основани- А/
ями АгВп и ВгАп (рис. 42, б). /
Так как диагонали А±Ап и \Х /
В1Вп трапеции равны, то . в /
этом случае нужно провести
через точку Р прямую, на -----
которой заданная окружность Рис. 43.
отсекает хорду А^, равную
известной хорде BtBn, т. е. прямую, касательную к окруж-
ности, концентрической с заданной и касающейся ВгВп (ис-
следование!).
2°. Предположим, что мы уже умеем решать задачу о по-
строении вписанного в окружность л-угольника, k последо-
вательных сторон которого проходят через k заданных то-
чек, а остальные л — k сторон параллельны заданным прямым,
и пусть требуется вписать в окружность л-угольник, у ко-
торого &4-1 соседних сторон АгА2, А2А3, . .. , ДА+1Дй+2
проходят через &+1 заданных точек Р1, Р2, ... , РЛ+1,
а остальные n — k—1 сторон параллельны’заданным прямым.
Допустим, что задача решена и искомый л-угольник по-
строен (рис. 43). Рассмотрим стороны АгА2 и А2А3 этого
многоугольника. Проведем через вершину Дг прямую AjA29
параллельную РгР^ обозначим через Л2 точку пересечения
этой прямой с окружностью и через Р2 — точку пересечения
прямой Х/Ц с РхРг. Треугольники РХА2Р2 и Р\Р2А3 подобны,
так как / А2Р±Р2 ~ Д^Л', = 2^ АИ/а и / АъР^Рг =
75
, P P A P
= ^/Р2Р2Д3. Следовательно, , откуда
*3? 2 ^2^2
п'п __ -^3^2'^2^2
2 2“ *
Так как произведение A3P2-A2P2 зависит лишь от данной
точки Р2 и от окружности (но не от выбора точек А2 и Д3!),
то оно может быть определено; поэтому величина отрезка
может быть найдена последовательно, точка Р2 может
быть построена. Таким образом, нам известны k точек
Р2, Р3, .. • , ^4+1’ чеРез которые проходят k соседних сторон
ЛИз, лзл4, ... , ЛА+1Л^+2 л-угольника XH2A3 ... Л„,
остальные же п — k сторон его Ak+zAk+& , ЛлЛ1, Л1Л2
параллельны известным прямым. В силу индуктивного пред-
положения мы можем построить «-угольник АГА2А3 . .. Ап,
после чего уже нетрудно построить и искомый «-угольник
Д1Л2 ... Ап.
Задача 13. В заданную окружность вписать «-угольник,
k сторон которого (не обязательно соседних!) проходят
через k заданных точек, а остальные «— k сторон парал-
лельны заданным прямым.
Пример 19. Даны две параллельные прямые Z и Zr С по-
мощью одной линейки разделить отрезок АВ прямой Z на «
равных частей.
Решение. 1°. Пусть « = 2. Произвольную точку 5
плоскости, не лежащую на прямых I и 119 соединим с точ-
ками А и В (рис. 44, а) и обозначим через С и D точки
пересечения прямых AS и BS с прямой 1Х. Точку пересе-
чения прямых AD и ВС обозначим через Т2, точку пересе-
чения прямых ST2 и I—через Р2. Докажем, что точка Р2 —
искомая, т. е. что АР2 — ~- АВ.
Обозначим через Q2 точку пересечения прямых ST2 и Zx.
Легко видеть, что А Т2Р2Вс/эД T2Q2C, Д ДВТ2с/эД DCT^,
ДВЛР2сл ДВС(?2 и Д ВДВ слД BCD, откуда =
Т.В АВ Р^А SA АВ г л л Р2В Р.А
~ TtC ~ CD И Q2C SC CD • ледовательно, ,
а поэтому Р2А — Р2В и АР2 = — АВ.
2°. Предположим, что мы уже умеем, пользуясь одной
линейкой, строить такую точку Рп отрезка АВ, что АРп =
76
= ~Л7?. Выберем вне I и 1г произвольную точку S, и обо-
значим через Тп и Qn точки пересечения прямой SPn соот-
ветственно с AD и (рис. 44, б). Точку Тп+1 пересечения
Рис. 44.
прямых AD и СРп соединим с 5 и обозначим точки пере-
сечения с прямыми и I через Qw+1 и Рп+1.
Докажем, что Prt+1— искомая точка, т. е. что ДРп+1==
= —к АВ.
Действительно, из подобия треугольников CQrt+1Tn+1
и рпРп+1Тп+1> CT„+1D и Рпта+1А имеем:
Рп+1?п ^пТп+1 АРп \
CQn+1 СТп+1 CD ’ w
из подобия треугольников SAPn+1 n,SCQn+1, SAB и SCD
имеем:
АР n+i ^4 АВ / У»
CQ„+1“~5C~'CD’ л '
р р др
Из равенств (6) и (7) следует ==-д~£ или» так
Лгга + 1 Ad
как Рп+1Р„ = АР„—АР„+1 и АРп = ±АВ,
1ав-арп+1- ±ав
п п
APn-ki АВ
1 АВ—АРп+1 = - АРп.,,
п и + 1 п - «+1’
откуда окончательно АРп+1 = АВ.
77
Для того чтобы найти последующие точки Р^+1> • • •
деления, достаточно тем же приемом построить отрезки
^n + l^n + i = + Pn + iPn+i — д_ j Pn+i йит.д,
Замечание. Для построения точек Рп+1, Р"п+1, ... мож-
но также поступить следующим образом. Используя точку Р2,
можно провести через точку В прямую /2 || I (см. рис. 45, а, где
Рис. 45.
точка Т выбрана на BS произвольно). Пусть Kj—точка пересече-
ния прямой РП + 1С с /2 и Pw+1—точка пересечения прямой KiQn+i
с I (рис. 45, б). Тогда легко проверить, что Рл+1Рп+1 == ЛРп+1 =
ЛВ. Построение следующих точек P"n+V ...—ана-
логично.
Задача 14. Пользуясь циркулем данного раствора а и
линейкой, построить отрезок, равный а[п.
78
§ 4. Нахождение геометрических мест
по индукции
Рассмотрим несколько задач на нахождение геометриче-
ских мест с помощью метода математической индукции.
Пример 20. На сторонах выпуклого д-угольника Ах., .Ап
отложены отрезки В2С2, ВпСп. Найти гео-
метрическое место внутренних точек М этого многоуголь-
ника, для которых сумма площадей треугольников МВХС13
Рис. 46
ЖВ2С2, ..., МВпСп постоянна (равна сумме 5дл<ов1с1 +
+ 5дм0в2с2+ ... +*$дл40впсп, где Мо — определенная точка
внутри многоугольника).
Решение. 1°. Пусть л = 3 (рис. 46). На сторонах
Д8Д2 и А3АХ треугольника АХА2А3 отложим отрезки Л3Р=«
= В2С2 и A3Q = B3C3.
Тогда х)
*$ДЛ10В2С2 + $ДМ0В3С9 = S&M 0РЛ8 + S^M0QAt =
= ВдРрЛ8 +S&MCPQ
1) Здесь мы считаем, что точка Л1о лежит внутри четырехуголь-
ника AxA2PQ‘t рассуждение мало изменилось бы и в ином случае.
79
и, следовательно,
+ 5дМ 0В2С2 + 5 дм 0В8С3 “
= S^pQAi + (^ДМоВА + 5дморр)-
Аналогично
5дмв1с1 + 5дмв2с2+5дмв8с8 = 5дррл8+(5дмв1с1+5дмрр)-
Мы видим, что искомое геометрическое место определяется
условием
5дмв1с1 + 5дмр<? =5дм0в1с1 +5дморр«
Пусть теперь 7V—точка пересечения прямых AjA2 и PQ
(если эти прямые параллельны, искомое геометрическое
место будет отрезком параллельной им прямой). Отложим
на сторонах угла A2NP отрезки NR = PQ и Х5 = В1С1;
тогда 5дм0В1С1+5дм0Рр = 5дМ(Л8 + S^MoNR +
+ 5дм0Я8 и аналогично 5дмв1с1+‘5дмрр =5длгяв+5дмя8.
Следовательно, искомое геометрическое место состоит из
тех точек Л, лежащих внутри треугольника, для которых
5дмя8 = 5дм0К8, т. е. представляет собой отрезок XY
прямой, проходящей через точку Л40 (и параллельной пря-
мой ^S1)).
2°. Пусть мы уже знаем, что для л-угольника искомое
геометрическое место представляет собой отрезок прямой
(проходящей, разумеется, через точку 2Й0). Рассмотрим
теперь (л-f- 1)-угольник АгА2.. .АпАп+1; пусть В^С^ В2С2,
..., BnCni Вп+1Сп+1 — заданные отрезки, отложенные на
его сторонах, и Мо—точка внутри (л+1)-угольника (рис.
47). На сторонах угла А1Ап+1Ап от вершины Ап+1 отло-
жим отрезки Ап+1Р*=„ф и An+1Q = Bn+1C„+1. Тогда
•$дмвяс„4- 5дмвя+1ся+1 =‘5длглп+1/> + 5дл1Лп+1<2 =
= 5ДЛп+1/’<? Н-^дмрс-
Следовательно, для точек М искомого геометрического места
5дмв1с1 + 5дмв2с.+ . .. +5дмвп_1сп_1 + 5дмрр =
= 5дм0В1С1 + 5дл10в2С2+ • . . +5дл10Вп«1Сп-1 + 5дл10Р(?.
В силу индуктивного предположения искомое геометри-
ческое место представляет собой отрезок прямой, прохо-
дящей через точку /Ио.
х) Индукцию можно было бы начинать со случая п=2, когда
«n-угольник» представляет собой угол, имеющий лишь две стороны.
80
Из решения задачи нетрудно усмотреть также метод
построения этого геометрического места.
Задача 15. Даны п прямых /г, /2, /и, на каждой
из которых задано по от-
резку В^С^, В2С21 • • •,
ВпСп и точка 7И0. Найти
геометрическое место точек
7И, для которых алгебраи-
ческая сумма площадей тре-
угольников МВ2С2,
.. ., МВпСп, где площадь
треугольника MBfif (/ = 1,
2, ..., п) берется со зна-
ком плюс, если точка М
лежит с той же стороны
от прямой 1Ь что и точка
Л40, и со знаком минус—в
противном случае, равна
соответствующей сумме для
точки Л40.
Задача 16. Доказать,
что в четырехугольнике,
который можно описать около
Рис. 47.
круга, середины диагоналей
лежат на одной прямой с центром круга (рис. 48).
Задача 17. Доказать, что1 прямая, соединяющая сере-
дины диагоналей выпуклого четырехугольника (не парал-
лелограмма и не трапеции), делит пополам отрезок, соеди-
няющий точки пересечения противоположных сторон (рис. 49).
Пример 21. Даны п точек Alf А2) ..., Ап и п (поло-
жительных или отрицательных!) чисел а21 ..., ап.
Найти геометрическое место точек Л/, для которых сум-
ма аг • МА 1 + а2 • МА2 + ... + апМАп постоянна.
81
Решение. 1°. Пусть п = 2. Для определенности будем
сначала предполагать, что оба числа ах и а2 положительны.
Возьмем на отрезке точку О, делящую его в от-
#2
а1 + а2
ношении т. е. такую точку О, что
^1^2
перпендикуляра, опущенного из М на прямую АгА2 (рис. 50).
Тогда имеем:
-М41 = ЛЮ24-Д1О2 ± 2АХО -НО,
ЛМ22« ЛЮ2 + А2О* Т 2А2О.НО.
Умножая первое из этих равенств на А2О, второе—на
АгО и складывая их почленно, получим:
МА* • А2О + MAl -AjP^ МО* (А2О + ДХО) +
+ А1О*.А2О + А2О*.А1О = МО*.А1А2+А1О.А2О-А1А2.
Подставим теперь вместо А±О и А2О их значения; по-
лучим:
+.MAf - МО* • ЛхЛа + 5-Ь- а-Ь- AiA* ’
ИЛИ
aiMAl + a2MAl = (ах + аа) Л4О2 + А^.
82
Следовательно, если агМА1 + а^МА* = R3, то
МО2 = Лзг — /тТа» AiA* = const.
+ (ai + a2)* 1
Отсюда вытекает, что если —~---------—а^2 чо A, Al > 0.
«1 + ^2 («1+я2)2 1 2 ’
то искомым геометрическим местом будет окружность с цен-
тром в точке О радиуса 1/ --------------.- АД2; если
' «1+^2 (Я1 + «2)2 1
_ __ alq2 Л /2 _ П
«1+*2 (а^)2*1*2^’
то искомое геометрическое место состоит из единственной
точки О; наконец, если —-------< 0, то это
^+«2 («1 + ^2)2 1
геометрическое место не содержит ни одной точки.
Случай,, когда аг и а2 оба отрицательны, очевидным
образом сводится к предыдущему. В случае, когда > 0,
а2 < 0 и a14-a2s/= 0 (например, ^х + а2>^)» точку О сле-
дует выбрать на продолжении .отрезка AjA2 правее точки
А2 так, чтобы было
Л 0= _fil_ И А,0
2 |ai + aa| 1
дальнейшие рассуждения не будут отличаться от вышеизло-
женных. Наконец, если ai + a8 = 0, то —а2, и наша за-
дача сводится к следующей: найти геометрическое место
точек УИ, для которых разность квадратов расстояний от
двух заданных точек Аг и А2 постоянна. Пусть Н—осно-
вание перпендикуляра, опущенного из точки М на прямую
ЛгД2 (рис. 50), тогда МА2 — МН2 + , MA2t^=MH2 +
A-A2tP и, следовательно, МА2—MA^Ajfi2—А^Н2. Если
МА2, — МА2 =- R2, то A Ji—A Ji = -Д- ,
1 2 ’ 12 Л1Л> ,
чем полностью определяется точка Н\ отсюда следует, что
искомым геометрическим местом будет в этом случае прямая,
проходящая через точку Н и перпендикулярная к Ax?l2.
2°. Предположим, что мы уже доказали, что при п за-
данных точках соответствующее геометрическое место пред-
ставляет собой окружность, если Дх + а2 + • • • + и
83
прямую, если ^ + ^4- ... +^ = 0. Рассмотрим теперь
лн- 1 точек Лъ Л2, . .., X-м и п+ 1 чисел аг, а2, ...,
an+i* Предположим, что ап 4- fln + i =Н= 0 (если бы было ^„ +
+ #„+1 = 0, то мы заменили бы эту пару чисел числами
и а +1 или числами лп-1 и ап\ если одновременно
йп + ^+1 = °> ап-1 + ал + 1 = 0 И аИ-1 + ап=0» Т0 ^-1 =
= ап~ ал + 1 = 0, и мы можем непосредственно воспользо-
ваться индуктивным предположением, так как при этом за-
дача сводится к случаю п — 2 точек Лх, Л2, ..., ЛЛ_2 и
п — 2 чисел а19 а2, ..., ап_2).
Как в п. 1°, покажем, что на отрезке АпАп+1 можно
найти такую точку О, что для любой точки Ж плоскости
аЛ^п + вв+1«+1 = (ап + а +1) МОЧ--^1 АпА*+1-
ип~Гип + 1
Тём самым наша задача сведется к нахождению геомет-
рического места точек Ж, для которых постоянна сумма
ахЖЛ1 4~ л2ЖЛз + ... + + (#rt + #„+i) МО2.
В силу индуктивного предположения это геометрическое
место будет окружностью при а± 4- а2 + . .. + ап 4- лп+1=/=0
и прямой при ax4-a24- ... + #„ + #w+i = 0.
Задача 18. Найти геометрическое место точек, сумма
квадратов расстояний которых от п заданных точек по-
стоянна.
Задача 19. Найти точку, сумма квадратов расстояний
которой от п заданных точек минимальна.
Задача 20. Найти геометрическое место точек, отноше-
ние расстояний которых от двух заданных точек постоянно.
Задача 21. Дан л-угольник АгА2.. .Ап. Найти геомет-
рическое место таких точек Ж, что многоугольник, верши-
нами которого являются проекции точки Ж на стороны за-
данного многоугольника, имеет данную площадь 5.
§ 5. Определение по индукции
Интересные примеры применения метода математической
индукции в геометрии доставляют задачи, содержащие по-
нятия, само определение которых использует переход
«от л к л 4-1». Задачам такого рода и посвящен настоя-
щий параграф.
Пример 22. Определение медиан и центра тя-
жести л-угольника.
84
1°. Центром тяжести отрезка мы будем назы-
вать его середину (рис. 51, а).
В таком случае медианы треугольника А1А2А3
можно определить как отрезки, соединяющие вершины тре-
угольника с центрами тяжести противоположных сторон
Рис. 51.
(рис. 51, б). Как известно, медианы треугольника пересе-
каются в одной точке и делятся в ней в отношении 2:1, счи-
тая от вершины. Точку, в которой пересекаются все медианы
треугольника, называют центром тяжести треуголь-
ника.
Условимся теперь называть медианами четырех-
угольника Л1Л2Л3Д4 отрезки, соединяющие его вершины
Л2, Л3, ^4 с центрами тяжести Оь О2, ®8» ^4 тРе‘
угольников, образованных остальными тремя вершинами
(рис. 51, в). Докажем, что медианы четырехугольника пере-
секаются в одной точке и делятся в ней в отношении 3:1,
считая от вершины. Действительно, обозначим через 5 центр
тяжести (середину) стороны AjA2, а через О4 и О3 — центры
85
тяжести треугольников ЛХЛ2Л3 и пусть еще О—
точка непесечения меДиан А3О3 и Л4О4 четырехугольника.
Так как-₽<Лз и ^4—медианы треугольников А]А2А3 и
л , , SA3 3 ЗД4 3 S4s $Л4
то = у и —г, и, следовательно, .
Отсюда вытекает, что О8О4||Л3Д4 и ^ = |^ = т-
Далее, Из подобия треугольников ОО3О4 и ОЛ3Л4 имеем:
0А4 ОА3 _А3А4 3
004 ОО3 О3О4 1
Таким образом, любые две соседние (т. е. выходящие из
смежных вершин) медианы четырехугольника в точке пере-
сечения делятся в отношении 3:1. Отсюда следует, что все
.Рис. 52.
четыре медианы четырехугольника проходят чергз одну
точку О, в которой все они делятся в отношении 3:1.
Точку О пересечения медиан четырехугольника называют
центром тяжести четырехугольника.
2°. Предположим, что для всех k < п мы уже определили
медианы ^-угольника как отрезки, соединяющие вершины
^-угольника с центрами тяжести (k—1)-угольников, рбразо-
ванных остальными k—1 вершинами, и для всех k < п опре-
делили центр тяжести ^-угольника как точку пересечения
86
его медиан. Мы будем также предполагать уже доказанным,
что медианы /г-угольника при k < п делятся в точке пере-
сечения (центре тяжести ^-угольника) в отношении (k—1): 1
(считая от вершины).
Определим теперь медианы л-угольника как отрезки,
соединяющие вершины л-угольника с центрами тяжести
(л—1)-угольников, образованных остальными л—1 верши-
нами. Докажем что все. медианы п-угольника А1А2»-.Ап
пересекаются в одной точке и делятся ею в отношении
(п—1): 1 (считая от вершины). Действительно, пусть 5 —
центр тяжести (л—2)-угольника А±А2.. -Ап~2; тогда прямые
SAn_ х и SAn будут медианами (л—1)-угольников^41А2...А/1.1
и АгА2..-Ап_2Ап (рис. 52). Если Оп и Оя.1 — центры тя-
жести этих (л—1)-угольников, то в силу индуктивного
х /г —1 „
предположения —= --л * = -—:— . Следовательно,
O„_iOn и ^)”~1d” = nT1 • Обозначим через О точку
пересечения медиан Оп^1Ап^г и ОпАп л-угольника А±А2 ...Ап.
Из подобия треугольников OOn_tOn и ОАп^1Ап следует,
что ~ тг"1 л” = ~~т~^ - Таким образом, любые
иип-1 иип ип-1ип 1
две смежные медианы л-угольника в точке пересечения
делятся в отношении (л—1): 1. Отсюда и следует, что все
медианы л-угольника пересекаются в одной точке (и де-
лятся в ней в отношении (л—1):1).
Теперь мы можем определить центр тяжести л-уголь-
ника как точку пересечения его медиан, а затем и меди-
аны (л+1)-у го л ь ника как отрезки, соединяющие вер-
шины (л-{- 1)-угольника с центрами тяжести л-угольннков,
образованных остальными л вершинами. Метод математиче-
ской индукции позволяет утверждать, что наши определения
медиан и центра тяжести л-угольника имеют смысл при
любом л.
Задача 22. В л-угольнике АгА2.. .Ап обозначим через Ог
центр тяжести (л—1)-угольника А2А3.. .Ап,ч через О2—
центр тяжести (л—1)-угольника А1А8...АП и т. д., через
Оп — центр тяжести (л—1)-угольника АгА2...Ап_г. Дока-
зать, что л-угольник О1О2.,.Оп подобен данному л-уголь-
нику AjA^.A*.
Медианой fe-ro п о р я д к а л-угольника (k < л) назы-
вается отрезок, соединяющий центр тяжести ^-угольника,
образованного любыми k вершинами л-угольника, с центром
87
тяжести (п — &)-угольника, образованного остальными п—k
вершинами. Таким образом, медиана А-го порядка является
одновременно и медианой (п — k)-ro порядка. Медианы
л-угольника, определенные в примере 22, можно было бы
назвать медианами первого порядка.
Задача 23. Доказать, что все медианы &-го порядка
л-угольника пересекаются в одной точке и делятся в ней
в отношении (л—k):k.
Задача 24. Сформулировать утверждение задачи 23 при
л = 4, k = 2.
Окружность, проходящая через середины трех сторон
треугольника (рис. 53), называется окружностью Эй-
лера этого треугольника; она обладает рядом интересных
свойств (так, например, окружность Эйлера треугольника
АВС, кроме середин £>, Е, F сторон, проходит еще через
основания Р, Q, R высот АР, BQ и CR и через три точки
К, L, А4, делящие пополам отрезки Д/У, ВН, СН высот
между точкой Н их пересечения и вершинами1); поэтому
окружность Эйлера часто называют еще окружностью
девяти точек треугольника). Так как окружность Эйлера
треугольника АВС описана вокруг треугольника DEF, по-
добного АВС с коэффициентом подобия ~, то радиус ее
1) Так как четырехугольник KFDM (рис. 53) —прямоугольник
(ибо FK || ВН || DM, так как KF и DM —средние линии треуголь-
ников АВН и СВН с общим ос-
нованием ВН; FD ]] АС [| КМ, так
как FD и КМ —средние линии
треугольников АВС и АИС с об-
щим основанием АС; ВН АС),
то отрезки FM и DK равны и
имеют общую середину. Так же
доказывается, что и отрезок EL
равен им и середина EL совпада-
ет с общей серединой FM й KD.
Отсюда следует, что окружность
Эйлера, проходящая через точки
D, Е и F, проходит также через
К, L и М (центр этой окруж-
ности совпадает с общей сере-
диной DK, EL и FM, а диаметр
равен общей длине этих отрезков).
Далее, так как по доказанному К и D —диаметрально противо-
положные точки окружности Эйлера и KPD = 90°, то окруж-
ность Эйлера проходит через точку Р; так же доказывается, что
она проходит и через точки Q и R.
88
равен /?/2, где R—радиус описанной окружности исход-
ного треугольника АВС. Понятие окружности Эйлера может
быть следующим образом распространено на любой впи-
санный в окружность многоугольник.
в)
Рис. 54.
Задача 25. 1°. Окружностью Эйлера хорды
АгА2 окружности 5 радиуса R называется окружность ради-
уса /?/2, центром которой служит середина хорды
(рис* 54, а). Три окружности Эйлера сторон вписан-
ного в окружность S треугольника АгА2А3 пересека-
ются в одной точке' О, которая является центром ок-
ружности радиуса /?/2, проходящей через центры трех
окружностей Эйлера; эта окружность называется
89
окружностью Эйлера треугольника А1А2А8
(рис. 54, б).
2°. Предположим, что нами уже определена окружность
Эйлера вписанного в окружность *9 л-угольника и известно,
что ее радиус равен 7?/2 (/?—радиус окружности S). Рас-
смотрим теперь (л 4- 1)-угольник А1А2А3 . .. Ап+1, вписанный
в окружность 5. В таком случае п 4-1 окружностей Эйлера
л-угольников Л2Л3.. .Лп+1, АгА3. . ,Ап+1> . . А]А2 . .. Ап
пересекаются в одной точке, которая является центром
окружности радиуса /?/2, проходящей через центры всех
л 4-1 окружностей Эйлера;
эта окружность называется
окружностью Эйле-
ра (л4-1)-угольника
А]А2.. .Лл+1(см. рис. 54, в,
где ' изображена окруж-
ность Эйлера четырехуголь-
ника).
Задача 26. Пусть
А1А2.. .Ап— произвольный
л-угольник, вписанный в ок-
ружность <5. Доказать, что
центр тяжести л-угольника
(см. пример 22) лежит на
отрезке, соединяющем центр
5 с центром окружности Эй-
лера л-угольника, и делит этот отрезок в отношении (л—2): 2.
Задача 27. 1°. Пусть треугольник АВС вписан в окруж-
ность S и Р—произвольная точка этой окружности. Дока-
зать, что основания перпендикуляров, опущенных из точки
Р на стороны треугольника АВС, лежат на одной прямой
(рис. 55; эта прямая называется прямой Симпсона
точки Р относительно треугольника АВС).
2°. Предположим, что мы уже определили прямую Симп-
сона точки Р окружности 5 относительно любого вписан-
ного в нее л-угольника; пусть АгА2. . .Ап+1—вписанный
в окружность 5 (л4- 1)-угольник. Доказать, что основания
перпендикуляров, опущенных из точки Р на л 4-1 прямых
Симпсона этой точки относительно всевозможных л-уголь-
ников, образованных л вершинами (л 4- 1)-угольника
АгА2.. .An+V лежат на одной прямой. Эту прямую мы бу-
дем называть прямой Симпсона точки Р относительно
(л 4- 1)-угольника . .Лл+1.
90
Рис. 56.
Пример 23. Г. Пусть Zx, Z2, Z3, Z4 —четыре прямые общего поло-
жения, т. е. такие, что никакие две из них не параллельны и никакие
три не проходят через одну точку; Ох —центр окружности, опи-
санной вокруг треугольника, образованного прямыми Z2, Z3, Z4;
О2 —центр окружности, описан-
ной вокруг треугольника, обра-
зованного прямыми /х, Z3, Z4, и
т. д. Тогда четыре точки О19 О2,
03 и 04 лежат на одной окружнос-
ти, называемой окружностью
центровчетырех прямых
/1, /2. h (рис- 56).
2°. Пусть уже определена
окружность центров п прямых и
пусть даны п+1 прямых об-
щего положения Zx, Z2, ...,Zn+1.
Обозначим центр окружно-
сти центров п прямых Z2, Z3,
..., Zn+1 через Ох, центр окруж-
ности центров п прямых /х, Z3,
..., Zn+1 — через О2 и т. д. Тогда
п+1 точек Ох, Оа, О3, Оп+1 лежат
_ _ - на одной окружности,
называемой окружностью центров п+1 прямых Zv /2,
/з» • • •» ^п + 1*
Доказательство. 1°. Пусть llt Z2, Z3, Z4—четыре прямые
общего положения (рис. 57), Л12 — точка пересечения Z3 и Z4, А13—
точка пересечения Z2 и Z4 и т. д.; — центр окружности С19 опи-
санной вокруг треугольника, образованного прямыми /2> Z3 и Z4,
91
и т. д. Докажем, прежде всего, что окружности Сх, С2, С3 и С4
пересекаются в одной точке М. Действительно, если М есть точка
пересечения и С2, отличная от Л12, то
£ Л13Л4Л12=« £ А13АиА12 = между Z2 и *з’>
Z Л12Л4Л2з=^ Л12Л24Л23 = между Z3 и 1^.
Отсюда следует, что £ А13МА23= £ между 12 и Zx = Z ^1з^з4^2з>
т. е. что окружность С3 проходит через М; точно так же доказы-
вается, что и С4 проходит через Л4.
Теперь мы уже можем доказать, что точки 0г, 02i 03 и О4
лежат на одной окружности. Рассмотрим три окружности Clt С2
и С3, проходящие через одну точку Л4; и С3 пересекаются еще
в точке Л13, С2 й С3 —в точке Л23. Отсюда следует1):
Z O1O3O2 = Z 41зЛ4Л2з= Z A13A34A23=Z между 12 и Zx.
Точно так же доказывается, что и </ О1О4О2= £ между Z2 и
^\O3O2i откуда и вытекает требуемое утверждение.
2°. Предположим, что для п прямых наши утверждения уже
доказаны; при этом мы можем также считать уже доказанным,
что дуга окружности центров п прямых Zx, 12...1п между цент-
рами Ох и О2 окружностей центров л —1 прямых l2t Z3, ..., 1п и
п — 1 прямых llt Z3, ...» 1п равна удвоенному углу между прямыми
/х и 12 (см. конец п. Г). Рассмотрим теперь п+1 прямых Zx, Z2,... ,ln+i
общего положения; пусть Oj—- центр окружности Ci центров п
прямых Z2, Z3, . ..,Zw+1 и т. д., О12~центр окружности С12 цент-
ров л —1 прямых Z3, Z4, . ..,Zn+1 и т. д. Докажем, что окружности
Ci, С2, ..., Си+1 пересекаются в одной точке Л4. Действительно,
пусть М—отличная от Oi2 точка пересечения окружностей Сх и
С3. В таком случае имеем1):
Z О13Л1О12=у ^Oi3C12 = Z между Z2 и Z3;
L О12МО23 = у ^O12O23=Z между Z3 и Zr.
Отсюда следует, что Z ^13^1023 = Z между /2 и Zi = Z ^13О34°23»
т. е. что окружность С3 проходит через Л4. Точно так же доказы-
вается и то, что каждая из остальных окружностей С4, Сб, ..., С„+1
проходит через Л4.
Рассмотрим теперь три окружности Clt С2 и С3, проходящие
через одну точку М; Сг и С3 пересекаются еще в точке О13, С2
и С3—в точке О23. Мы имеем1):
Z ^1^3^2= Z ^13^^23= Z ^13^43^23 =Z МвЖДу /2 И Zp
г) Точнее, эти углы равны или составляют в сумме 180°. Вообще,
чтобы сделать нижеследующие рассуждения независимыми от чер-
тежа, надо воспользоваться понятием направленных углов
(см., например, написанные Д. И. Перепелкиным решения
задач в книге Ж. Адама р, Элементарная геометрия, ч. 1, М.,
х Учпедгиз, 1948, стр. 488—489).
92
Точно так. же показывается, что и для любой из точек Oz(/=4,
5, ...» п+1) / ОХО^О2 = ^ между /2 и /ь откуда и следует, что
все точки О19 О2, 03, 04, .Оп+1 лежат на одной окружности.
В формулировке примера 23 можно также заменить всюду
описанные окружности вписанными. Однако здесь появляется одно
Рис. 58.
дополнительное затруднение, связанное с тем, что, в то время
как описанная окружность треугольника (окружность, проходя-
щая через все вершины треугольника) определяется однозначно,
за его вписанную окружность (окружность, касающуюся всех
сторон треугольника) можно принять одну из четырех окружно-
стей (всех трех сторон касаются одна вписанная и три вневпи-
санные окружности). Чтобы устранить это затруднение, можно
поступить следующим образом. Введем в рассмотрение направ-
ленные прямые и окружности, указав стрелкой на каждой
линии направление движения по ней; далее будем считать направ-
ленные прямую и окружность касающимися лишь в том
случае, если направления их в точке касания, совпадают. При
этом будет существовать уже одна-единственная направ-
ленная окружность, касающаяся трех данных направленных пря-
мых llt 12 и /3, не пересекающихся в одной точке (рис. 58, а, б),—
93
центры направленных вписанных
образованных /2, /3 и /4; l19 13 и
Рис. 60.
О2, О3, ..., Ол+1 лежат на одной
направленная вписанная окружность образованного /1, /2 и к
треугольника.
Задача 28. Г. Пусть 119 12, 13 и /4—четыре направленные пря-
мые общего положения, т. е. такие, что каждые две из них пересека-
ются и никакие три не имеют общей точки; О2, и
окружностей треугольников,
/4 и т. д. Тогда четыре точки
Оц 03 и 04 лежат на одной
окружности, называемой о к-
ружностью центров
четырех направлен-
ных прямых и /4
(рис. 59).
2°. Пусть уже определена
окружность центров п направ-
ленных прямых и пусть даны
п+1 направленных прямых
общего положения llt 12, ...,
Zn, 1п+1> Обозначим через О19
О2, ..., Оп, Оп+r центры ок-
ружностей центров п+1 сово-
купностей по п направленных
прямых, которые можно вы-
делить из наших п + 1 прямых.
В таком случае п+1 точек О19
окружности — о к ружности
центров п+1 направленных прямых.
Задача 29. Определение ортоцентра вписанного в ок-
ружность многоугольника. Г. Ортоцентром тре-
угольника, как известно, называется точка пересечения его
высот.
2°. Пусть уже определен ортоцентр n-угольника ЛГЛ2...Л„,
вписанного в окружность S, и пусть имеем вписанный в S
(п + 1)-угольник Л1Л2.. .AnAn+t. Обозначим через Н19 H2i ...,
Яп+1 ортоцентры п + 1 многоугольников Л2Л3... Л„+1, Л1Л3Л4...
Л*+1, ...» Л1Л2...Л„. В таком случае равные S окружности с
центрами в точках Яр Я2, ..., Нп+1 пересекаются в одной точ-
ке Я; эта точка и называется ортоцентром (п+1)-угольника
Л1Л2...Л„+1 (так, на рис. 60 изображен ортоцентр четырехугольника
Л1Л2Л3Л4).
Задача 30. Г. Центральной точкой двух (пересекаю-
щихся) прямых называется точка их пересечения (рис. 61, а).
Центральной окружностью трех прямых общего
положения (см. пример 23) называется окружность, проходящая
через центральные точки каждой пары из этих прямых (рис. 61,6).
Пусть теперь даны четыре прямые общего положения /х, /2, /3, /4.
Обозначим через центральную окружность трех прямых /2,/3, /4,
через ^—центральную окружность трех прямых /ь /3, /4 и т. д.
Тогда четыре окружности $з> S* пересекаются в одной точ-
ке О, которая называется центральной точкой четырех
прямых l19 l2t 13, 14 (рис. 61, в).
2°. Предположим, что уже определена центральная окружность
2n—-1 прямых и центральная точка 2п прямой, и пусть даны 2п+1
94
прямых общего положения Zlt Z2, ...» Z2n) Z2n+1. Обозначим через
центральную точку 2п прямых /2, Z3, ...»Z2rt, Z2w+1, через Л2—цент-
ральную точку 2л прямых llt l3t ..., Z^, Z2rt+1 и т. д., через Л2„+1 —
центральную точку 2л прямых l19 12, 12п. Тогда точки Ах, Л2,...
..., A2n+i лежат на одной окружности, которую мы будем назы-
вать центральной окружностью 2л -j-1 п р я м о й /ь Z2,...
• • • » _
Пусть, наконец, задано 2л+2 прямых llt l2i ...» Z2n+1, l2n+2
общего положения. Обозначим через Sx центральную окружность
Л
Рис. 61.
2л+ 1 прямых /2, /3, Z2l+1, /2я+2, через S2 — центральную ок-
ружность 2л4-1 прямых l19 Z3, ..., /2„+1, 12п+2 и т. д., через S2/2+2 —
центральную окружность 2л4-1 прямых llt l2t ..., 12п+1. Тогда
окружности Sx, S2, ...» S2rt+1, S2n+2 пересекаются в одной точке,
которую мы и будем называть центральной точкой 2л4-2
прЯМЫХ Zi, Z2, ..., l2n+li Ьп+Ъ’
Задача 31. Г. Даны три прямые llt /2, /3 общего положения.
Центр окружности, описанной вокруг образованного ими треуголь-
ника, называется центральной-точкой трех прямых.
Рассмотрим теперь четыре прямые lt, Z2, Z3, /4 общего положе-
ния. Обозначим через Ах центральную точку трех прямых Z2, Z3, Z4,
через А2 — центральную точку трех прямых Zx, l3i Z4 и т. д. Тогда
четыре точки Alf А2, А3, Д4 лежат на одной окружности (см. выше
пример 23), которая называется центральной окружно-
ст ь ю ч е т ы р е х прямых Zi, Z2, Z3, Z4.
2°. Пусть уже определены центральная точка 2л—1 прямых и
центральная окружность 2л прямых и пусть даны 2л 4-1 прямая
общего положения llt 12, ..., Z2n, Z2rz+1. Обозначим через Si цент-
ральную окружность 2л прямых Z2, Z3, ...» Z2rt, Z2n+1, через S2 —
центральную окружность 2л прямых lv 13, ..., Z2rt, Z2rt+1 и т. д.,
95
через S2rt+i — центральную окружность 2*г прямых llt Z2, ...,
Тогда окружности Sx, S2, •••, + 1 пересекаются в одной точке,
которую мы будем называть центральной точкой 2п4~ 1
ПрЯМЫХ Zt, Z2, ^2/Р ^2л + 1-
Пусть, наконец', дано 2п4-2 прямых общего положения llt Z2, ...
..., ^2/i+2* Центральную т’оуку 2м4-1 прямых Z2, Z3, /2и+2 обо-
значим через Д1, центральную точку 2n-]-l прямых llt Z3, ...
..., Z2rt+2 —через А2 ит.д., центральную точку 2п4-1 прямых
/1, /2» ••» Z2„+1 —через А2я+2. Тогда точки Ар А2, ..., А2п+2
лежат на одной окружности, которую мы и назовем централь-
ной окружностью 2п4"2 прямых Z1? Z2, ..., Z2rt+2.
Линейным элементом называется совокупность точки А
и заданного в ней направления, определяемого прямой а, прохо-
дящей через А. Линейный элемент обозначается символом (А, а).
п линейных элементов (Аь а^), (А2, а2), ..., (Ап, ап) мы будем
называть конциклическими (от слова «цикл»—окружность),
если прямые ах, а2, ..., ап—прямые общего положения (см. выше
пример 23) и п точек Аь А2, ...» Ап лежат на одной окружности.
Задача 32. 1°. Направляющей окружностью двух
линейных элементов (Ai, и (А2, а2) (таких, что точки
Ах и А2 различны, а прямые и- а2 пересекаются) называется
окружность, проходящая через точки Аь А2 и через точку пере-
сечения аг и а2 (рис. 62, а). Направляющие окружности трех пар
линейных элементов (Ах, аг) и (А2к о2), (Аь аг) и (А3, а3), (А2, а2)
и (А3, о3) (таких, что точки Alf А2, А3 все различны, а прямые
ах, 0з—общего положения) пересекаются в одной точке, назы-
ваемой направляющей точкой трех линейных эле-
ментов (Ах, ai), (А2, а2) и (А3, о3) (рис. 62, б).
Рис. 62.
2°. Пусть нами уже определены направляющая окружность 2л—2
конциклических линейных элементов и направляющая точка 2n —1
конциклических линейных элементов. Рассмотрим 2п концикличе-
ских линейных элементов. В таком случае 2п направляющих точек
всевозможных совокупностей по 2п—1 из них лежат на одной
окружности, называемой направляющей окружностью 2л
96
конциклически х линейных элементов. Далее, если
рассмотреть 2п+1 конциклических линейных элементов, то всевоз-
можные совокупности по 2п из них определят 2n+1 направляющих
окружностей, которые все пересекаются в одной точке —н а п р а в-
ляющей точке 2«+1 конциклических линейных
элементов.
§ в. Индукция по числу измерений*)
При изучении курса стереометрии бросается в глаза из-
вестная аналогия между стереометрическими и планиметри-
ческими теоремами. Так, свойства параллелепипеда во многом
подобны свойствам параллелограмма (ср.,.например, теоремы:
«В параллелепипеде противоположные грани равны и диаго-
нали пересекаются в одной точке и делятся в ней пополам»
и «В параллелограмме противоположные стороны равны и
диагонали в точке пересечения делятся пополам»), свойства
шара подобны свойствам круга (ср., например, теоремы: «Ка-
сательная плоскость шара перпендикулярна к радиусу, про-
веденному в точку касания» и «Касательная к окружности
перпендикулярна к радиусу, проведенному в точку касания»).
Однако наряду с этим имеет место и существенная разница
между свойствами плоских и пространственных фигур. Главное
различие здесь состоит в том, что фигуры на плоскости имеют
два измерения («длина» и «ширина»), в то время как про-
странственные тела имеют три измерения («длина», «ширина»
и «высота>>). Соответственно этому положение точки на пло-
скости полностью определяется двумя координатами х и у
(рис. 63, б), в то время как для определения положения
точки в пространстве надо знать три ее координаты х, у и z
(рис. 63, в). Поэтому наше обычное пространство часто
называют трехмерным пространством («простран-
ством трех измерений»), в то время как про плоскость говорят,
что она представляет собой двумерное'пространство
(«пространство двух измерений»).
Эту терминологию можно распространить еще дальше.
Положение точки на прямой полностью определяется одной
единственной координатой х (рис. 63, а); это связано с тем,
что на прямой линии все фигуры (отрезки) имеют лишь одно из-
мерение («длину»). Поэтому прямую называют одномерным
пространством; это позволяет считать, что число измере-
ний пространства может быть равно единице, двум или трем.
*) См. Послесловие.
4 И. С. Сом и некий и др. 97
Стереометрические теоремы обычно бывают сложнее
соответствующих планиметрических предложений; в свою
очередь свойства плоских фигур, разумеется, много сложнее
свойств фигур на прямой (отрезков). При этом доказательства
«трехмерных» (т. е. стереометрических) теорем часто суще-
ственно опираются на знание соответствующих «двумерных»
Рис. 63.
(т. е. планиметрических) предложений; так, например, дока-
зательство того, что диагонали параллелепипеда делятся
в точке пересечения пополам, использует соответствующее
свойству, диагоналей параллелограмма. В свою очередь до-
казательства «двумерных» теорем иногда основываются на
аналогичных «одномерных». -Это обстоятельство делает воз-
можным использование в некоторых геометрических задачах
индукции по числу измерений, заключающейся
в последовательном переходе*) от одномерного к двумер-
ному, а затем к трехмерному пространству; примеры такого
рода и собраны в настоящем параграфе.
В современной математике и физике большую роль играет
понятие n-мерного пространства, в котором поло-
жение точки определяется п координатами; здесь п—произ-
вольное целое положительное число, возможно, большее
трех1). Свойства фигур в д-мерном пространстве часто до-
*) См. стр. 124.
Э См., например, § 7 статьи «Векторы и их применения в гео-
метрии», Энциклопедия элементарной-математики, кн. IV, Физмат-
гиз, М., 1963 или специальную статью «Многомерные простран-
ства», ЭЭМ, жн. V, «Наука», 1966.
98
называются с помощью математической индукции по числу
измерений пространства; при этом, строго говоря, лишь при
доказательстве «л-мерных» теорем, где п—л ю б о е, мы можем
с полным правом говорить о «методе индукции» (ибо лишь
здесь у нас полностью работает «теорема 2» из описания
этого метода, утверждающая возможность перехода от
произвольного значения п = k к следующему значению
см. выше, стр. И). Метод математической индук-
ции позволяет перенести на д-мерное пространство, где п—
любое, все результаты этого параграфа. Однако, поскольку
понятие о многомерных пространствах выходит за рамки
математической подготовки, предполагаемой у читателя
настоящей книги, мы- ниже всюду ограничиваемся лишь
случаями л=1, 2 или 3 (т. е. случаями прямой, плоскости
и обычного пространства)*).
При разборе примеров и решении задач этого параграфа
следует иметь в виду, что окружности на плоскости (т. е.
геометрическому месту точек, равноудаленных от данной
точки О, рис. 64, б) в пространстве соответствует сфера
(поверхность шара, .рис. 64, в), а на прямой линии—пара
точек, равноудаленных от данной точки О (рис. 64, а); кругу
- *) Подробнее об этом см. стр. 124.
4* 99
на плоскости в пространстве соответствует шар, а на пря-
мой—отрезок, наконец, треугольнику АВС на плоскости
(рис. 65, б) в пространстве соответствует тетраэдр (т. е.
произвольная треугольная пирамида, имеющая четыре вер-,,
шины Д, В, С, D, рис. 65, в), а на плоскости — отрезок АВ,
имеющий две «вершины» А и В (рис. 65, а).
Следует отметить, что вопрос о том, какое стереометрическое
предложение соответствует данной планиметрической теореме,
вообще говоря, не решается однозначно. Иногда удобно считать,
что треугольнику на плоскости отвечает не тетраэдр (фигура,
имеющая на одно измерение больше), а такой же треугольник,
только расположенный в пространстве; аналогично этому можно
а)
В
Рис. 65.
считать, что прямой на плоскости в пространстве соответствуют и
прямая, и плоскость. При этом можно получать разные «стерео-
метрические аналоги» одной и той же планиметрической теоремы.
Так, например, теореме «сумма квадратов расстояний от точки М
плоскости до всех вершин правильного л-угольника с центром О,
вписанного в окружность радиуса /?, равна п (Т?2-)-ОЛ42)» (см.,
. например, указанную на стр. 139 книгу Д. О. Шклярского и др.,
задача 234) отвечают следующие две стереометрические теоремы:
«сумма квадратов расстояний от точки М пространства до всех
вершин правильного n-угольника с центром О, вписанного в ок-
ружность радиуса 7?, равна п(/?2+ОМ2)» и «сумма квадратов
расстояний от точки М пространства до всех вершин правильного
многогранника с п вершинами, вписанного в сферу с центром О
и радиусом /?, равна.п (/?2-рОМ2)»; обе эти теоремы верны и обе
выводятся из соответствующей «двумерной» теоремы, так что при
выводе обеих используется индукция по числу измерений. Мы не
останавливаемся подробнее на этом вопросе, предоставив читателю
самостоятельно сравнить переход от «одномерной» к «двумерной» и
к «трехмерной» теоремам, например, в нижеследующих примерах 26
и 33 с одной стороны и 25 и 32 с другой стороны.
Во всех примерах и задачах настоящего параграфа основным
считается «трехмерное» (стереометрическое) предложение, хотя
часто наибольший интерес представляет соответствующий резуль-
тат, относящийся к «двумерному» (плоскому) случаю и переход от
двумерного к трехмерному случаю лишь намечается, а не прово-
дится со всей полнотой.
100
1. Вычисление и нахождение геометрических мест с помощью
индукции по числу измерений
Пример 24. На сколько частей разбивают пространство
п плоскостей, каждые три из которых пересекаются и никакие
четыре не имеют общей точки (такие плоскости мы будеп
называть «плоскостями общего положения»)?
Рассмотрим последовательно следующие задачи.
А. Определить, на сколько частей разбивают прямую
п точек.
Решение. Обозначим это число через F1(n); очевидно,
что Ft (п) = п + 1.
Б. На сколько частей разбивают плоскость п прямых,
каждые две из которых пересекаются и никакие три не имеют
общей точки (л прямых «общего положения»)?
Решение. 1°. Одна прямая разбивает плоскость на
две части.
2°. Предположим, что нам известно число F2 (л) частей,
на которые разбивают плоскость п прямых общего положе-
ния, и рассмотрим /г 4-1 прямых общего положения. Первые
п из них разбивают плоскость на F2 (п) частей; (/z-J- 1)-я
прямая /, по условию, пересекается с каждой из остальных
п прямых в п различных точках; эти точки разбивают пря-
мую .1 на Fv (п) = п 4- 1 частей (см. пункт А).
Следовательно, прямая I пересекает п 4-1 из ранее по-
лученных частей плоскости, и значит, добавляет к F2 (п)
частям
Fi (л)=л-Н
новых частей.
Таким образом,
F2 (п 4- 1) = F2 (л) + Fr (л) = Г2 (л) + (п 4-1). (8)
Подставляя в равенство (8) вместо п значения л—1,
л—2, ..., 2, 1, получим:
Л(«) =F8(n—1) + л,
F2 (п—1) = F2 (п—2)+ (л—1),
f2(3) =F2(2) + 3,
/%(2) =F2(l)-|-2.
101
Сложим все-эти равенства; так как F3 (1) = 2, мы будем иметь;
F, (л) ==Г2 (1) +[" + («-1) + • • • + 2] =
= 1+[л + (л—1)+... +2+1],
и окончательно: F2 (п) = 1 ~^2 .
В. Задача, сформулированная в начале настоящего примера.
Решение. 1°. Одна плоскость разбивает пространство
на две части.
2°. Предположим, что нам известно число F3(n) частей,
на которые разбивают пространство п плоскостей общего
положения, и рассмотрим л-р 1 плоскостей общего положения.
Первые п из них разбивают пространство на F3 (л) частей;
(«+1)-ю плоскость л эти-л плоскостей пересекают по л
прямым общего положения и, следовательно, разбивают ее
п24-л+2
на/72(л) =---частей (см. пункт Б). Таким, образом,
получаем соотношение
F3 (п + 1) = F3 (п) + F8 (п) = F3 (л) +. (9)
Заменив в равенстве (9) п на п—1, п—2, 2, 1, будем
иметь:
F3, (л) = F3 (п-1) + ("-l)a+^-D+2 i
F3 (л—1) = F3 (п -2) + (
F8(3) = F3(2) + 2^±2,
Л. (2)=F3(1) + H±1±2 .
Складывая все эти равенства, получим:
Л(«) = Л>и)+у[(л-1)а + («-2)2+... + 12]+
+ 4 [(«-1) + (я-2) + ... + 1] +1 [2 + 2+ ... +2],
„ ' п ^Т^раз
102
или окончательно, учитывая, что F3 (1) = 2:
fs (Л) = 2 + Мп-1И2п-1) _|_ (л-1) =ж
_(п+1)(п2-п + 6)
6
Задача 33. На сколько частей разбивают пространство
п сфер, каждые две из которых пересекаются между собой?
Пример 25. Найти геометрическое место точек простран-
ства, сумма квадратов расстояний которых от п заданных
точек Лх, Л2, ..., Ап постоянна (равна d2).
Рассмотрим последовательно следующие задачи.
А. На прямой даны п точек 4Х, Д2, ..., Ап, Найти точки М
прямой такие, что МА% + МА% -|- ... +М4* = d2, где d—
заданное число.
Решение. Примем нашу прямую за числовую ось; пусть
точкам Alf А2, ..., Ап соответствуют числа ах, a2i .. ., ап,
а искомой точке 2И—число х. В таком случае длины от-
резков 2ИЛ1, MA2t . . ., МАп будут равны (х—ах), (х—а2),...
..., (х—ап) и, следовательно, МА* + МА2 + ... -]-МА* =
= (х—а1)г + (х—а2)2+ ... '+(х—а„)а. Но
(х—а1)2 + (х—а2)24- . >. 4-(х—а„)2 =
= х2—2а1х-[-а2 4-х2—2а2х-|-о2 4- • • • 4-*2—
—2а„х4-а2 =
= лх2--2(а14-а24-... 4-«„)* +(л2 4-4- • • • 4-«2) =
= „ (x-ai+a*+-±£»)2 4- (а* 4- al 4- • • 4-
(Д1 + Оа+ - -+ап)2
п
или, если обозначить через А точку, соответствующую
а2 4** •- • • И- ап
числу -i-!—!,
МА\ 4- М42 4- ... 4- МА* = пМА2 4- (а? 4-4- • • • + «п) —
Таким образом,
лМ42 = 4Р-(а2 4-а2 4- • • • 4-
103
и, значит,
мл- /Гр-(<.; + <.;+..•+<;) +<-a-+“.±-.+°.g].
Это равенство, вообще говоря (если подкоренное выра-
жение положительно), определяет две точки 2И, удовлетво-
ряющие условию задачи (они расположены по разные
стороны от точки Д).
Б. Найти геометрическое место точек плоскости, сумма
квадратов расстояний которых от п заданных точек Дх,
А2, Ап постоянна (и равна d2).
Решение1). Выберем на плоскости какую-нибудь (без-
различно какую) прямоугольную систему координат и обо-
значим проекции точек Дх, Д2, ..., Ап на ось х и на ось у
соответственно через Al9 А2, .. ., Ап и Дх, А2, ..., Ап'> про-
екции точки М на оси координат обозначим через ЛГ и М"
В таком случае
МАЛАГА?
МА^М'А? +m"a*,
MAl^M’An +М"А’п
и, следовательно,
МА\ + МА1 + • • • + = (М'А'х + М'А'г 4- ... 4- М'А'п ) 4-
+ (МпА” + M№aZ + ... + ЛГА*).
Но, в силу формулы (10),
М'Л' + ЛГЛ^ + ... +М'А‘ =
= пМ'Л'2 4- (а2 4- о2 4- . . . 4- а2) — -<?.( + ?2-+ • • • +а„)2
' ' 1 ’ 2 1 1 П' д >
//£ .. *2 "2
М’А^ + ЛГ'Л2 + • • • + М"Ап =
= /МГЛ"2 + (df 4-df 4-... 4- d2) _^i+.b2+^--+^)2 t
где at, a2, an и ..., bn — абсциссы и ордина-
ты точек Alf А2, ..., Ап, А' и Д" —точки осей х и у с
х) Иное решение этой задачи было намечено выше (см. при-
мер 21 и задачу 18 на стр. 81—84).
104
координатами
^1+^2 + • • • ~Van ы &1+&2+ •••+&«
и о
п-----------------------п
Таким образом
AlAj^ 4~ УИЛ 2 -|~ ... -|~ Л1Ап = лМА? 4_(^i4_^2_F • • • ~h “И
+ (6° + +•••+**) - (а1+а2+^-:+а”)2 -
(&1+»2+-..+<>п)2 (П)
(Л—точка плоскости, проектирующаяся на оси координат
в точки Л' и Л"), откуда
пУИЛ2 = d2 — (#1+02 + • • • + Яд) — (^1 + + • • • + &п) +
[ (^1 + ^2+ • • • +Лп)2 (^1 + ^2+- » >+^га)2
* П ‘ _ П
и, значит,
УИЛ =
^\Г 4.^)4. (fll+a2 + .-+fln)f (61 + &2+... + г>п)2|
J nL n nJ
т. е. искомое геометрическое место представляет собой
окружность радиуса
т/Lp2~(flg+gg+..^^)-(^+dj+...+^)+(ai+ag+••+gw)\^tAt.:.r.+6n)tl
у П L tj nJ
если подкоренное выражение положительно; состоит из
одной точки Л, если оно равно нулю, и не содержит ни
одной точки, если оно отрицательно.
В. Предложение, сформулированное в начале примера.
Указание. Рассмотреть прямоугольную систему коорди-
нат х, у, z в пространстве, спроектировать все точки на пло-
скость хОу и на ось Oz; далее воспользоваться формулами (10)
и (П).
2. Определение и доказательство с помощью индукции
по числу измерений
Пример 26. Тетраэдр, четыре вершины которого зануме-
рованы цифрами 1, 2, 3 и 4, разбит на меньшие тетраэдры
так, что каждые два из тетраэдров разбиения либо совсем
не имеют общих точек, либо имеют общую вершину, либо
105
имеют общее ребро (но не часть ребра), либо имеют общую
грань (но не часть грани). Все вершины полученных малых
тетраэдров занумерованы теми же цифрами 1,2, 3 и 4, при-
чем все вершины, лежащие на грани большого тетраэдра,
w нумеруются тремя цифрами, которыми занумерованы вершины
этой грани, а все вершины, лежащие на каком-либо ребре
большого тетраэдра, нумеруются двумя цифрами, которыми
занумерованы концы ребра. Доказать, что найдется по крайней
мере один малый тетраэдр, все четыре вершины которого
занумерованы разными цифрами.
Рассмотрим последовательно следующие задачи.
А. Отрезок, концы которого обозначены цифрами 1 и 2,
разбит на несколько непересекающихся меньших отрезков и
все точки деления занумерованы цифрами 1 или 2 (рис. 66, а).
6)
Рис. 66.
Доказать, что найдется по крайней мере один отрезок
разбиения, концы . которого занумерованы разными
цифрами.
Решение. Покажем, что число отрезков, обозначен-
ных цифрами 1, 2, нечетно; отсюда и будет следовать
существование хотя бы одного такого отрезка (ибо нуль есть
число четное). Обозначим через А число концов отрезков
разбиения, занумерованных цифрой 1. Это число, очевидно,
будет нечетным, ибо каждая цифра 1, стоящая внутри боль-
шого отрезка (число таких цифр 1 обозначим через fe),
является концом двух отрезков разбиения, и лишь единст-
венная цифра 1, которой занумерован конец большого от-
106
резка, принадлежит одному отрезку разбиения; следова-
тельно, Д = 2&+1.- С другой стороны, пусть р будет число
отрезков И среди всех наших отрезков разбиения и q—
число отрезков 12. Тогда число А вершин 1 будет равно
A — 2p-}-q. Из равенства 2&+1 = 2p-\-q следует, что q
нечетно.
Б. Треугольник, вершины которого занумерованы цифра-
ми 1, 2 и 3, разбит на меньшие треугольники так, что два
треугольника разбиения либо Товеем не имеют общих точек,
либо имеют общую вершину, либо имеют общую сторону
(но не часть стороны)-. Все вершины треугольников разбиения
нумеруются цифрами 1, 2 и 3, причем вершины, лежащие на
стороне большого треугольника, нумеруются одной из цифр,
которой занумерованы концы этой стороны (рис. 66, б).
Доказать, что найдется по крайней мере один треугольник
разбиения, все вершины которого занумерованы разными
цифрами.
Решение. Покажем, что число треугольников 12 3
нечетно. Для этого сосчитаем общее число А сторон тре-
угольников разбиения, занумерованных цифрами 1, 2. Число
отрезков 1 2, лежащих внутри основного треугольника,
обозначим через /г, а число таких отрезков, лежащих на
стороне 1 2 большого треугольника,—через I (на других
сторонах основного треугольника вообще не может быть
отрезков 1 2). Так как каждый из первых k отрезков раз-
биения принадлежит двум треугольникам разбиения, а каж-
дый из / последних отрезков — одному, то A = 2k-\-l.
С другой стороны, пусть р—число треугольников разбие-
ния, вершины которых занумерованы цифрами 1, 2, 2 или
1, 2, 1, и q—число треугольников 1 2 3. Так как каждый
из первых р треугольников имеет-две стороны 1 2, а каж-
дый из q последних — одну такую сторону, то Л = 2р-|-^.
Из равенства 2k-\-l — 2p-\-q следует, что число q четно
или нечетно одновременно с числом /. Но число I нечетно
в силу предложения А, а следовательно, и q нечетно.
В. Предложение, сформулированное в начале этого при-
мера.
Решение. Пусть А будет число граней тетраэдров раз-
биения, обозначенных цифрами 1, 2, 3. Если А? таких граней
лежат внутри основного тетраэдра и I—на его грани 12 3,
то A=*2k + l.
С другой стороны, если р — число тетраэдров разбиения,
обозначенных цифрами 1, 1, 2, 3; 1, 2, 2, 3 или 1, 2,
107
3, 3, a q—число тетраэдров разбиения, обозначенных циф-
рами 1, 2, 3, 4, то, очевидно, А=2р + ^. Из равенства
2^ + 7= 2р + ^ следует, что числами / одновременно четны
или нечетны.
Но число I в силу предложения Б нечетно, и следова-
тельно, и q нечетно.
Во введении к этому параграфу мы указывали, что «индук-
ция по числу измерений иногда может быть заменена обык-
новенной индукцией». Приведем здесь соответствующие
примеры.
Пример 27. Доказать сформулированное в примере 26 А
предложение индукцией по числу п отрезков разбиения.
Решение. 1°. При п = 1 утверждение очевидно.
2°. Предположим, что наше утверждение уже доказано
для любого разбиения отрезка на п меньших отрезков, и
пусть дано разбиение отрезка 1 2 на д +1 меньших отрез-
ков. Если не все из этих отрезков обозначены цифрами 1, 2,
то найдется отрезок, концы которого обозначены одинако-
выми цифрами, например 1 1. Стянем этот отрезок в точку,
тогда мы получим разбиение отрезка 1 2 на п меньших
отрезков. В силу индуктивного предположения в этом раз-
биении, а значит,, и в первоначальном разбиении найдется
по крайней мере один отрезок, обозначенный цифрами 1, 2,
что и требовалось доказать.
Пример 28. Доказать сформулированное в примере
26 Б предложение индукцией по числу п треугольников раз-
биения.
Решение. 1°. При д=1 утверждение очевидно; при
д = 2 оно легко проверяется.
2°. Предположим, что наше утверждение уже доказано
для любого разбиения треугольника 1 2 3 на п или меньше
треугольников, и пусть мы имеем разбиение треугольника на
д+1 треугольников. Если не все из этих треугольников
обозначены цифрами 1, 2, 3, то найдется треугольник, у кото-
рого две вершины имеют одинаковые номера, например 1.
К стороне 11 прилегают либо два треугольника разбиения
(если эта сторона лежит внутри основного треугольника,
рис. 67/а), либо один треугольник (если эта сторона лежит
на стороне основного треугольника, рис. 67,6). Стянем от-
резок 1 1 в точку; мы получим новое разбиение треуголь-
ника 1 2 3 на п—1 (в первом случае, рис. 67, в) или над
(во втором случае, рис. 67, г) треугольников. В силу индук-
тивного предположения в этом разбиении (а значит, и в пер-
108
воначальном разбиении) найдется по крайней мере один тре-
угольник, вершины которого обозначены цифрами 1, 2, 3.
Ю - *)
Рис. 67.
Задача 34. Доказать теорему примера 26 В индукцией
по числу п тетраэдров разбиения.
Предложение примера 26 можно еще уточнить. Введем
понятие «ориентировки» тетраэдра, вершины которого зану-
мерованы цифрами 1, 2, 3, 4, различая тетраэдры, для ко-
торых обход вдоль грани 1 2 3 от вершины 1 к вершине 2
и затем к вершине 3 представляется из вершины 4 совер-
шаемым по часовой стрелке, и такие, для которых этот
обход наблюдается из вершины 4 происходящим против
часовой стрелки. В таком случае имеет место следующее
предложение.
Задача 35. Доказать, что в условиях примера 26 число
тетраэдров разбиения, занумерованных цифрами 1, 2, 3, 4 и
ориентированных так же, как и основной тетраэдр, будет
109
ровно на единицу больше числй тетраэдров 1 2 3 4, ориен-
тированных противоположным образом.
Пример 29. В пространстве задано п шаров, каждые че-
тыре из которых пересекаются. Доказать, что все эти шары
пересекаются, т. е. что существует точка, принадлежащая
всем шарам.
Рассмотрим последовательно следующие задачи.
А. На прямой задано п отрезков, каждые два из которых
пересекаются. Доказать, что все отрезки пересекаются, т. е.
что существует точка, принадлежащая всем отрезкам.
Решение. 1°. Для п = 2 утверждение очевидно.
2°. Предположим, что наше утверждение уже доказано
для любых п отрезков, и пусть на прямой задан л 4-1 по- *
парно пересекающихся отрезков /г, /2, .. ., /я, /я+1. В силу |
Л <
индуктивного предположения п отрезков /х, /2, ..., 1п пере-
секаются. Обозначим их общую часть (которая будет, оче-
видно, точкой или отрезком) через /.Докажем, что отрезок
/я+1 пересекается с /. Допустим, что это не так; тогда су-
ществует точка А, разделяющая /я+1 и I (рис. 68, а). Но
каждый из отрезков /х, /2, ..., 1п содержит I и, по усло-
вию, пересекается с отрезком /я+1, следовательно, каждый
из этих отрезков содержит точку А, а значит, точка А при-
надлежит Г. Полученное противоречие доказывает, что /я+1
ПО
.—-------------------------------------------------———
и I пересекаются; их общая часть принадлежит всем задан-
ным отрезкам /2, •••>
Б. На плоскости задано п кругов, каждые три из кото-
рых пересекаются. Доказать, что существует хотя бы одна
точка, принадлежащая всем этим кругам.
Решение. 1°. При л = 3 утверждение очевидно.
2°. Предположим, что наше утверждение уже доказано
для. любых п кругов, и пусть на плоскости задано
кругов Сх, С2, .. ., Сп, Сд+1. В силу индуктивного предположе-
ния п кругов Сь С2, . ..,С„ пересекаются; обозначим их
общую часть через С (рис. 68,6) («круговой многоугольник»
С может представлять собой целый круг или состоять из
одной лишь точки). Нам надо доказать, что фигура С и круг
Сл + 1 пересекаются. Предположим, что это не так; в таком
случае можно провести прямую /, разделяющую фигуры Сга+1
и С: такой прямой будет, например, перпендикуляр / к пря-
мой, соединяющей центр О круга Сп + 1 с самой близкой к О
точкой А фигуры С, восставленный в середине отрезка АВ,
где В—точка пересечения отрезка ОА с окружностью круга
С„+1 (рис. 68, в)1).
Так как каждый из кругов Сх, С2, ..., Сп содержит
фигуру С и, по условию, пересекается с кругом Сп+1, то
он пересекает и прямую /. Обозначим отрезок, по которому
круг Сг пересекает прямую /, через аъ отрезок, по которому
КРУГ С2 пересекает эту прямую,—через а2и т. д. На прямой I
мы будем иметь тогда п отрезков а2, ..., ап. Любые
два из этих отрезков пересекаются. Действительно, рассмот-
рим два из них, например ах_и я2. Пусть М—произвольная
точка фигуры С (тогда точка М принадлежит обоим кругам
Сх и С2). Далее, так как любые три из заданных кругов
пересекаются, то существует точка N, принадлежащая одно-
временно кругам Сх, С2 и Сп+1. Тогда отрезок MN целиком
принадлежит кругам Сх и С2, а, значит, точка его пересече-
ния с прямой I будет общей точкой отрезков и а2.
1) Действительно, если прямая / не разделяет фигур Сп+1 и С,
то на ней найдется точка /С, принадлежащая фигуре С. В треуголь-
нике ОАК угол ОАК — острый; кроме того, по определению точки А
ОА^ОК. Следовательно, основание L перпендикуляра, опущен-
ного из О на прямую ЛК, будет лежать между точками А и К.
Так как обе точки Л и К принадлежат всем кругам Сх, С2, ..., Сп,
то и весь отрезок ЛК, а следовательно, и его точка L принадлежат
каждому из кругов Clt С2, ..., Сп и, значит, L принадлежит С.
Поэтому должно быть OL^OA, Полученное противоречие(«пер-
пендикуляр больше наклонной») доказывает наше утверждение.
111
Как следует из предложения А, на прямой I существует
точка, принадлежащая всем отрезкам а19 a2i ..., ап. Эта
точка должна принадлежать всем кругам Clt С2, . . ., Сп и,
значит, фигуре С, что противоречит построению прямой /.
Следовательно, фигуры Cw+1 и С должны иметь хотя бы одну
общую точку, которая и будет общей точкой всех кругов
С\, С2, ..., Сл, с„+1.
В. Предложение, сформулированное в начале примера.
Решение. 1°. Для л = 4 утверждение очевидно.
2°. Предположим, что наше утверждение уже доказано
для любых п шаров, и пусть дано п + 1 шаров Фх, Ф2, ..., Фп,
Фп+1. Обозначим через Ф пересечение п шаров ФХ,Ф2, .. .,ФИ
(существующее в силу индуктивного предположения). Тогда
точно так же, как в примере 29 Б, можно показать, что
если шар Ф„+1 не пересекается с Ф, то существует разде-
ляющая их плоскость л. Фигуры, по которым каждый из шаров
Фх, Ф2, .. ., Фд пересекает плоскость л, являются кругами,
любые три из которых пересекаются; следовательно, на пло-
скости л существует точка, принадлежащая всем этим кру-
гам и, значит, принадлежащая Ф, что противоречит опреде-
лению плоскости л.
Предложение примера 29 тоже може^ быть доказано
индукцией не по числу измерений, а прямо по числу фигур.
Пример 30. Доказать предложение примера 29 Б индук-
цией по числу кругов.
Решение. Мы докажем соответствующее предложение
для круговых многоугольников, т. е. для фигур, каждая из
которых является пересечением конечного числа кругов; от-
сюда, в частности, будет следовать и наше первоначальное
утверждение.
1°. Для д = 3 утверждение очевидно.
Пусть даны четыре круговых многоугольника Сх, С2, С3,
С4, каждые три из которых пересекаются. Обозначим через
Лх общую точку фигур С2, С3 и С4, через Л2 —общую
точку фигур Сх, С3 и С4 и т. п. Возможны два случая:
а) Одна из точек А19 Л2, Л3, Л4, например Л4, принадле-
жит треугольнику, образованному остальными тремя точками
(рис. 69, а). Тогда, так как весь треугольник ЛХЛ2Л3 при-
надлежит С4, точка Л4 тоже принадлежит С4 и, следовательно,
Л4 будет общей точкой всех четырех фигур С19 С2, С3, С4.
б) Ни одна из точек А19 Л2, Л3, Л4 не принадлежит тре-
угольнику, образованному остальными точками. В этом слу-
чае точка А пересечения диагоналей (выпуклого) четырех-
112
угольника Д1Л2Л8Л4 (рис. 69, б) как общая точка треуголь-
ников A1A2A8j ДхД2Д4, AjA8A4 и Л2Д8Л4 будет общей точкой
всех четырех фигур Сх, С2, С8, С4.
2°. Пусть наше утверждение уже доказано для п круго-
вых многоугольников. Рассмотрим п + 1 круговых многоуголь-
ников С19 С2, . .., Сп, Сп+1. Обозначим через С пересечение
фигур Сп и Cw+1 (ясно, .что С тоже будет круговым много-
угольником) и докажем, что любые три из п фигур Сх,
С2, . .., ^*„-1, С пересекаются. Действительно, если среди
этих трех фигур нет С, то они пересекаются по условию.
Рис. 69.
Рассмотрим теперь любую тройку этих фигур, содержащую С,
например Сх, С2, С. Так как из четырех фигур Сх, С2, Cw, Сп+1
любые три пересекаются, то в силу п. 1° эти четыре фигуры
имеют общую точку, которая и будет общей точкой фигур Сх,
С2 и С.
Так как любые три из п фигур .Сх, С2, ..., Ся_х, С
пересекаются, то в силу индуктивного предположения все
эти фигуры имеют общую точку, которая и будет общей
точкой л 4-1 фигур Сх, С2, ..., Си, Сп+1.
Задача 36. Доказать предложение примера 29 В индук-
цией по числу п шаров.
• Задача 37. На плоскости дано п точек Лх, Л2, ..., Ап,
расстояние между каждыми двумя из которых не превосходит
единицы. Доказать, что все эти точки можно заключить в круг
радиуса —(теор ема Юн га)!).
!) Дж. Юнг —английский математик XIX в.
113
Задача 38. В пространстве дано п точек Ах, А2, ..., Ал,
расстояние между каждыми двумя из которых не превосходит
единицы. Доказать, что все эти точки можно заключить в
Кб
шар радиуса —.
Обобщение предложения примера 29 и ряд приложений
более общей теоремы можно найти в книге: И. М. Я г дом
и В. Г. Болтянский, Выпуклые фигуры, § 2, М.— Л., Гос-
техиздат, 1951 (серия «Библиотека математического кружка»,
вып. 4).
Пример 31. Рассмотрим какое-то конечное'число полу-
пространств1), заполняющих все пространство. Доказать,
что из них можно выбрать четыре (или меньше) полупрост-
ранства, уже заполняющих все пространство.
Рассмотрим последовательно следующие задачи^
А. Вся прямая покрыта каким-то конечным числом лучей.
Доказать, что из них можно выбрать два луча, уже покры-
вающих всю прямую.
Решение. Пусть А будет самая правая вершина всех
лучей, направленных влево, а В—самая левая вершина всех
лучей, направленных вправо. Так как лучи, по условию, по-
крывают всю прямую, то точка. В лежит не правее А, и два
луча с вершинами в точках А и В полностью покрывают всю
прямую.
Б. Вся плоскость покрыта каким-то конечным числом п
полуплоскостей2). Доказать, что из них можно выбрать две
или три полуплоскости, уже покрывающие всю плоскость.
Решение. Доказательство проведем индукцией по числу
п полуплоскостей.
Г. При л = 3 утверждение очевидно.
2°. Предположим, что наше утверждение справедливо
для п полуплоскостей, и пусть дано п4- 1 полуплоскостей
Fj,‘ В2, . .., Fn, F„+1, покрывающих всю плоскость. Границы
этих полуплоскостей обозначим соответственно через
Zx, Z2, ...,Zrt, Zn+1. Возможны два случая.
1-й случай. Прямая 1п+1 целиком содержится в одной
из заданных полуплоскостей, скажем в Fn. Тогда прямые 1п
и 1п + 1 параллельны. Если полуплоскости Fn и Fn+1 распо-
ложены по разные стороны от своих границ (рис. 70, а), то
1) Полупространством называется часть пространства,
лежащая по одну сторону от некоторой плоскости.
2) Полуплоскостью называется часть плоскости, лежащая
по одну сторону от некоторой прямой.
114
две полуплоскости Fn и Fn+1 уже покрывают всю плоскость.
В противном случае одна из этих двух полуплоскостей цели-
ком содержится в другой (например, Fn+1 содержится в Fe;
а)
6)
Рис. 70.
рис. 70, б), и теорема следует из индуктивного предполо-
жения, так как в этом случае уже п полуплоскостей (в нашем
случае—Fu F2, Fn) покрывают всю плоскость.
2-й случай. Прямая /д+1 не содержится ни в одной из
полуплоскостей F19 F2t . .., Fn. Тогда она полностью по-
крывается этими полуплоскостями, которые высекают на ней
т^п лучей, покрывающих всю прямую. Как мы видели в А,
из этих лучей можно выбрать два, также покрывающих
всю прямую. Соответствующие полуплоскости пусть будут
7'\_1 и К- Рассмотрим теперь отдельно два возможных
случая взаимного расположения полуплоскостей Fn~u F
И ^+V
а) Полуплоскость Fn+1 содержит точку пересечения пря-
мых и[ 1п (рис. 71, а). В этом случае три полуплоскости
?п И ^п + 1 Уже покрывают всю плоскость.
б) Полуплоскость Fn+1 не содержит точки пересечения
прямых /я_х и 1п (рис. 71,6). В этом случае плоскость по-
115
крывается п полуплоскостями F19 F2, • • •> Z7», и теорема сле-
дует из индуктивного предположения.
В..Предложение, сформулированное в условии задачи.
Решение. Доказательство проведем индукцией по числу
п заданных полупространств.
1°. При л = 4 утверждение очевидно.
2°. Предположим, что наше утверждение справедливо
для п полупространств, и пусть задано п+ 1 полупространств
Рис 72.
V2i Vn, У„+1. Границы этих полупространств обо-
значим соответственно через л., л2, ..л х1. Возможны
два случая.
1-й случай. Плоскость лп+1 целиком содержится в од-
ном из полупространств V,, 1/2, .. ., Vn, например в Vn.
В этом случае плоскости пп+1 и п„ параллельны. Если
полупространства Vn+1 и V„ расположены по разные стороны
от своих границ, то эти два полупространства уже заполняют
все пространство. В противном случае одно из двух полупро-
странств Vn+1 и Vn целиком содержится в другом, и теорема
следует из индуктивного предположения.
116
2-й случай. Плоскость яп+1 не содержится ни в одном
из-полупространств Vx, V2, Vn. Тогда она полностью
покрывается этими полупространствами, которые высекают
на ней т^п полуплоскостей F2, ...,Fm.
В силу результата Б из этих полуплоскостей можно вы-
брать две или три, также покрывающие всю плоскость
(рис. 70, а и 71, а). Рассмотрим отдельно каждый из воз-
можных здесь случаев.
а) Плоскость зтл+1 покрывается двумя полуплоскостями
(рис. 70, а), скажем, Ft и F2, причем соответствующие
плоскости зтг и л2 параллельны (рис. 72, а). В этом случае
все пространство заполняется двумя полупространствами
Vi И V2. .
б) Плоскость' ял+1 покрывается двумя полуплоскостями
Fr и F2, но соответствующие плоскости и л2 пересекаются
(рис. 72, б). Если полупространство содержит линию
пересечения плоскостей jq и л2, то три полупространства
У2 и Ул+1 заполняют все пространство. В противном случае
полупространство Vn+1 покрывается полупространствами
и V2, и теорема следует из индуктивного предположения.
в) Плоскость лп+1 покрывается тремя полуплоскостями
(рис. 71, а), скажем Fu F2 и F3, причем плоскость л3 па-
раллельна линии пересечения плоскостей и зт2 (соответ-
ствующие плоскости образуют «призму»; см. рис. 72, в).
В этом случае три полупространства V\, V2 и V3 заполняют
все пространство.
г) Плоскость зтл+1 покрывается тремя полуплоскостями Fv
F2 и F3i и плоскость я3 не параллельна линии пересечения
яг и л2 (соответствующие плоскости образуют «пирамиду»;
см. рис. 72, г). Если полупространство Vn+1 содержит точку
пересечения плоскостей F19 F2 и F3, то четыре полупрост-
ранства V19 V2, V3 и Vn+1 заполняют все пространство;
в противном случае полупространство Vn+1 покрывается
полупространствами Vlt V2i V3, и теорема следует из индук-
тивного предположения.
Задача 39. Доказать, что в пространстве не может су-
ществовать более четырех лучей, попарно образующих между
собой тупые углы.
Пример 32. Доказать существование числа С3, такого, что сто-
роны каждого пространственного многоугольника А19 А..,Ап,
длина каждой из сторон которого не превосходит 1, можно пере-
ставить (не меняя их величин и направлений) таким образом, чтобы
полученный в результате этой перестановки многоугольник можно
было заключить в шар радиуса С3.
117
Как и всюду в этом параграфе, рассмотрим сначала соответст-
вующие> «одномерную/ и «двумерную» задачи.
у д На прямой задано п точек Лх, Л2, Лп, причем длина
каждого из отрезков АхА2, Л2Л3, •••» АпА} не превос-
ходит 1. Доказать существование такого числа Сг (не зависящего
от положения точек и от числа п!), что отрезки А4А2, Л2Л3,
Ап-Мл» AnAi можно переставить на прямой таким образом, чтобы
полученная «ломаная» В1В2.. .BnBv каждое звено которой совпадает
по величине и направлению с одним из звеньев «ломаной» А1А2...
• • -An-iAnAv целиком лежала внутри отрезка длины 2СХ.
Решение. Условимся считать длину а; звена Az-A/+x(i = 1,2,...
..., п; за Ли+1- принимается точка Ах) нашей «ломаной» АХА2... А„АХ
положительной, если точка Az + 1 расположена правее Л, (мы считаем
прямую, на которой лежат все точки, горизонтальной), и отрица-
тельной в противном случае. Очевидно, ях + я2 есть длина от-
резка АгА3 (которая может быть согласно нашему условию поло-
жительной или отрицательной), а1 + я2 + а3—длина отрезка А^4
и т. д?, ях + я2+... 4-ял_х— длина отрезка Л1Л„, ях+я2+...
• • • +^«_1+^я = 0 (это есть длина «отрезка АХАХ»). Так как каждое
«звено» ломаной BtB2.. .ВпВг равно какому-то звену первоначаль-
ной ломаной А±А2., .АпА1У то наше предложение можно сформу-
лировать так:
Даны п положительных и отрицательных чисел alf а2, ...,
ап _lt ап> каждое из которых по абсолютной величине не превосхо-
дит единицы и сумма которых равна нулю; доказать, что эти
числа можно расположить в туком порядке ai , ai , ..., az , я;
(здесь ix, r2,. ..,in_x, in суть те же номера 1, 2Т..., п— 1, л, но как-то
переставленные), чгпо все суммы а^, а^ + а^, а^ + а^ + а^, ..., aZj+
+ af-2+... ио абсолютной величине не превосходят
некоторого числа Сг (не зависящего от последовательности ях, я2,
..., ап и даже от числа и).
Докажем, что в качестве Сх можно взять число 1. Пусть
a j, я2, ..., ар — все положительные числа из последовательности
ях, я2, ...,яя, аяр я2, . ..,я^—все отрицательные числа (р + ^ = л).
Возьмем столько первых положительных чисел a’v а'2, ..a'k(k^p),
чтобы их сумма не превзошла единицы (например, одно числа а' ),
затем добавим столько отрицательных чисел я„, я2, ...,aj
чтобы сумма всех выписанных чисел стала отрицательной, но по
абсолютной величине была не больше единицы. Потом снова обратим-
ся к положительным числам и т. д., пока не исчерпаем всех заданных
чисел. Полученная при этом последовательность я* =Яр я* = я',...,
я^ = ял; я^ + 1 = ях, &k + 2 =sa2i • • •» aZ+Z^a/» • • • обладает, очевидно,
требуемым свойством.
Б. На плоскости дан многоугольник Л1Д2... Ап (который может
быть невыпуклым или даже самопересекающимся), причем длина
каждой из сторон этого многоугольника не превосходит единицы
(рис. 73). Доказать существование такого (не зависящего от много-
угольника) числа С2, что стороны многоугольника можно переста-
вить, не меняя их величин и направлений, таким образом, чтобы
118
полученный многоугольник ВгВ2..9Вп целиком помещался внутри
круга радиуса С2.
Решение. Докажем, что в качестве С2 можно взять число
Обозначим стороны многоугольника AiA2. . .AnAlf взятые по
длине и направлению, т. е. рассматриваемые как векторы, через
alt a2i..ай. Выберем из них некоторые векторы av а2,..., а5так,
чтобы замыкающая ВгВ3 (рис. 74) образуемой ими ломаной имела
наибольшую возможную длину. Тогда проекции каждого.из векто-
ров av as на замыкающую В^В? будут иметь одно и то же
направление, совпадающее с направлением BYBS (если бы.проекция
какого-нибудь вектора имела противоположное направление, то уда-
ление этого вектора привело бы
словами, можно считать, что проекции otp а2,..., as векторов а*,
а 2,..., as на направление A}AS положительны (0«Caz^l , / = 1,
2, ..., s), а проекции a'', а”, ...,art_s векторов а*, а2, ...,ап~9
на то же направление отрицательны( — 1 «С О, /= 1, 2, ..., n—s).
Обозначим еще (положительные или отрицательные) проекции
векторов alt а2, ап на прямую /, перпендикулярную к В±В3, на
которой выбрано «положительное» направление, через р2, •••
Ясно, что p1 + P2 + ...+,ps=0 и Рг + Р2+ ... +РП_$—О
(здесь р1 —проекция вектора а', р* —проекция вектора а*
и т. д.); при этом [р' |р2|<1, ...» |р'|<1 и |Р"|<
119
I 0* I 1»* • •» I 0« s |<1. В силу п. А можно так расположить
числа 0*. 02..₽'5 и числа 0", 02..-.. 0n-s. чтобы при любом V
выполнялись неравенства 0, + 0, + • • •+ 0V< 1 и 0,4-0,+ ...
... + ₽;<1. Если теперь все числа 0', 02.₽' и 0', 02.0"_s
объединить в одну общую последовательность так, чтобы у станов -•
ленный выше порядок следования чисел 0р 0a»...,0s и порядок
следования чисел 01, 02,..., 0n_s не нарушались, то сумма любого
числа первых членов полученной последовательности не превзой-
дет 2.
Расположим теперь числа a*, as и a*, d an_s в
одну общую последовательность так, чтобы сумма любого числа
первых членов этой последовательности по абсолютной величине
не превзошла единицы. Как видно из рассуждения, проведенного
в п. А, это можно сделать, не нарушая порядка следо-
вания чисел ах, da>..d' и чисел а", а”.......a”_s между
собой. Пусть соответствующее расположение наших векторов
будет а*, а*, . .. . а*.
Тогда для любого v будем иметь: а* + а* + ... + а* 1, 0* +
+ 0*+...+0*^2, где a*k и 0^-—проекции ak (/? = !, 2, ..., п)
на BXBS и на Z. Так как проекции замыкающей ломаной, образован-
ной векторами a*, а*..a* (v=l, 2, ..., п) на прямые B^BS и
I равны соответственно а*+ а*+...+<х* и 0^ + 0* + ... + 0*, то
если длина этой замыкающей равна cv, tocJ =(a*+<х* +... +<х*)2 +
+ (Р1+0,+ ---+₽С)2. т-е. с*<5, с,< Кб?
Мы нашли, что расстояние любой вершины полученной вектор-
ной ломаной от фиксированной точки Ах не превосходит
отсюда следует, что весь полученный многоугольник помещается
в круге радиуса Y 5.
В. Предложение, сформулированное в начале примера.
Указание. Доказать, что в качестве С3 можно взять }^2Т.
Рассуждение в этом случае аналогично проведенному в п. Б; 0Р
02,..., 0П будут проекции векторов ab а2..ап на плоскость л,
перпендикулярную к замыкающей BXBS.
Пример 33. Определение медиан и центра тяжести те-
траэдра.
А. Центром тя жести отрезка называется его се-
редина.
Б. Медианой треугольника называется отрезок,
соединяющий любую из его вершин с центром тяжести про-
тивоположной стороны. Известно, что.медианы треугольника
пересекаются в одной точке; эта точка называется центром
тяжести треугольника.
120
В. Медианой тетраэдра называется отрезок, со-
единяющий любую из его вершин с центром тяжести противо-
положной грани.
Докажем, что медианы тетраэдра пересекаются в одной
точке.
Рассмотрим тетраэдр ABCD (рис. 75), и пусть Ох, О2,
О3 и О4—центры тяжести треугольников DBC, ACD, ABD
и АВС. Так как прямые
и АО2 пересекаются л.
в серединеРотрезка CD,
то прямые и ВО2 . , / /|\\\
также пересекаются в / / I \\^\
некоторой точке О12; /
аналогично АОг и СО3, X----V р
АО± и DO4, ВО2 и СО3, /
ВО2 и Z)O4, СО3 и DO4 / \/
пересекаются в’ точках /
^13> ®14» ^23» ^24 И ^34* — у ®2 Чч\/
Докажем, что все эти jJ=---------— >———
точки совпадают (на чер-
теже— точка О). Дейст- Рис. 75.
вительно, если бы, на-
пример, О12 и О13 не совпадали, то прямые AOlf ВО2 и СО3
лежали бы в. одной плоскости л (в плоскости О12О18О23), но
тогда и прямая Z)O4, пересекающая ДО1? ВО2 и СО3, лежала
бы в той же самой плоскости, т. е. все четыре вершины тетра-
эдра должны были бы лежать в одной плоскости л. Так как
это неверно, то точки О12 и О13 должны совпадать; с этой
точкой совпадают и все остальные точки О14, О23, О24, О34.
Точка пересечения медиан тетраэдра называется цент-
ром тяжести тетраэдра.
' Задача 40. Доказать, что центр тяжести делит каждую
из медиан тетраэдра в отношении 3:1, считая от вершины.
ПОСЛЕСЛОВИЕ
Ю. А. Гастев
Индукция (лат. inductio —наведение)— переход от частного
к общему; дедукция (лат. deductio—вывод)—-переход от общего
к частному. Всем известна роль процессов обобщения результатов
отдельных наблюдений и опытов (т. е. индукции) для эмпириче-
ских, экспериментальных наук. Математика же издавна считается
классическим образцом осуществления чисто дедуктивных методов,
т. к.явно или неявно всегда подразумевается, что все математические
предложения (кроме принятых за исходные—аксиом) доказыва-
ются, а конкретные применения этих предложений выводятся
из доказательств, пригодных для общих случаев (дедукция).
Но вот мы читаем: «Индукция широко применяется в матема-
тике, но применять ее надо умело» (стр. 7 настоящей книги);
«... как пользоваться в математике индукцией, чтобы получать
только верные выводы?» *) (стр. 6). Что же все это, собственно, зна-
чит? Не следует ли понимать дело так» что среди математических
методов есть «достоверные», действующие, так сказать, безотказно
(дедуктивные), и «не вполне надежные», дающие подчас, особенно
в неумелых руках (как выражаются авторы, «при легкомысленном
отношений»), осечку (индуктивные)? Если бы это было действи-
тельно так, то где же искать критерии надежности таких «индуктив-
ных» методов? Как вернуть себе уверенность в непреложной обя-
зательности математических выводов? Или это безнадежная затея,
и достоверность математических заключений— той же природы, что
и опытные обобщения экспериментальных наук, так что любой
доказанный факт неплохо было бы еще «проверить» (подобно тому
как школьникам часто рекомендуется «проверять» правильность вы-
полнения арифметических действий или решения уравнений ц&общей
формуле)? В действительности дело обстоит не так. Индукц и я,
т. е. «наведение» (на мысль, на догадку, на гипотезу) играет в
математике, безусловно, очень большую, но чисто эври-
стическую роль: она позволяет догадываться о том,
каким, по всей видимости, должно быть решение.
Устанавливаются же математические предложе-
ния только дедуктивно. Ни один математический результат
не может претендовать на достоверность, истинность, коль скоро
он не выведен из исходных посылок.
*) Такого рода трактовка «индукции в математике» стала почти
традиционной для школьных учебников—-вплоть до самых новых
(см., например, §§ 62—63 учебника алгебры Е. С. Кочеткова
и Е. С. Кочетковой).
122
Ну, а как же «метод математической индукции»? Дело все в
том, что «математическая индукция» есть дедукт ивный метод.
В самом деле, разберемся детальнее в структуре математических
умозаключений, выглядящих как «переход от частного к об-
щему». Легко убедиться, что так называемая математическая индук-
ция на самом деле вовсе не есть индукция —это чисто дедук-
тивный метод рассуждения! Доказательство, проводимое этим
методом, состоит из двух частей: 1) так называемый базис-
доказательство (дедуктивное!) искомого предложения для одного
(или нескольких) натурального числа (например, для 0 или 1;
это то, что на стр. И именуется «Теоремой 1»); 2) индукцион-
ный шаг («Теорема 2»^, состоящий в доказательстве (опять-таки
дедуктивном) общего утверждения: для всех п верно, что из
того, что искомое утверждение справедливо для и, вытекает, что
оно справедливо и для п + 1. «Принцип математической индукции»
(стр. 12)—точно формулируемое предложение (интуитивная убеди-
тельность которого признается многими математиками как неоспори-
мая; при аксиоматическом же построении арифметики он фигурирует
в качестве аксиомы), позволяющее извлечь из базиса и индукцион-
ного шага чисто дедуктивное доказательство рассматриваемого пред-
ложения для всех натуральных Чисел п. Таким образом, никаких «не
учтенных в посылках» случаев, на которые затем («по индукции»)
надо было бы еще «распространять» заключение, не остается —
теорема именно доказывается для. всех натуральных чисел:
из базиса, доказанного, скажем, для числа 0, мы получаем, по ин-
дукционному шагу, доказательство для числа 1, затем таким же
образом для 2, затем для 3 ... —и так утверждение может быть
обосновано для любого натурального числа *).
Иначе говоря, название «математическая индукция» обусловлено
тем, что этот метод просто ассоциируете яв нашем сознании
с традиционными «индуктивными» умозаключениями (ведь базис
действительно доказывается только для-частного случая); индук-
ционный шаг, в отличие от основанных на опыте критериев правдо-
подобности индуктивных умозаключений в естественных (и обще-
ственных) науках, есть общее утверждение, не нуждающееся
ни в какой частной посылке и доказываемое по строгим
канонам дедуктивных рассуждений. Потому-то и называют матема-
тическую «индукцию» «полной», или «совершенной», что она (в про-
тивоположность обычной, «несовершенной» индукции, не обеспечива-
ющей нам полного знания) есть дедуктивный («стопроцентно
надежный») метод доказательства. .
Итак, в качестве метода доказательства индук-
ция в математике не применяется, что, разумеется,
никак не исключает широкого применения в ней дедуктивного ме-
тода «математической индукции» **).
*) О встающих в связи с такого рода обоснованием метода
проблемах см. указанную ниже литературу.
**) О чрезвычайно плодотворной роли «обычной» («неполной»)
индукции в формировании математических догадок, ведущих затем
и к открытиям новых фактов, и о связи «обычной» индукции с методом
математической индукции см. в Книге Д. Пой а, Математика и
правдоподобные рассуждения, М., ИЛ, 1957, т. I (особенно глава?).
123
Условившись отныне в таком понимании термина, мы можем,
конечно, позволить себе теперь и вольные перефразировки вроде
«индукции в геометрии» (как названа вторая часть этой книжки)
или «индукции в математике». Но при этом всегда надо помнить,
что первое выражение, строго говоря, имеет совсем не тот смысл,
что громоздкое (но точное!) выражение «употребление дедуктивного
метода математической индукции для доказательства теорем гео-
метрического содержания» (хотя, для облегчения речи, и употреб-
ляется как его синоним), а второе — отнюдь не то же самое
(вопреки чисто грамматическим признакам), что «математическая
индукция»; последний термин следует восцринимать целиком,
а вовсе не в смысле «индукция в математике».
Особого внимания в этом отношении требует § 6 второй части
«Индукция по числу измерений». Приведенные в этом параграфе
доказательства теорем планиметрии, опирающиеся на доказатель-
ства аналогичных утверждений для прямой, и доказательства
стереометрических теорем, опирающиеся на соответствующие пла-
ниметрические результаты, сами по себе не являются, конечно, не
только «обычной» индукцией, но и применением принципа матема-
тической индукции: в них не доказывается никаких утвер-
ждений, справедливых для всех п (в данном случае—-числа изме-
рений пространства); это — просто переходы от одного частного
случая (и = 1 или п = 2) к другому частному случаю (п = 2 или
п = 3). Верно, однако, и то, что аналогия, усматриваемая в при-
водимых доказательствах, позволяет извлечь из них ц подлин-
ный индукционный шаг («теорему 2»), нужный для доказательства
рассматриваемого предложения для общего случая *).
Метод математической индукции (в той форме, в какой он рас-
сматривается в этой книжке) есть метод доказательства арифме-
тических теорем, точнее, теорем, выражающих общие свойства
натуральных чисел (0, 1, 2, ... ; иногда, как в этой книге, нату-
ральный 'ряд уславливаются начинать с единицы, что абсолютно
не принципиально). И для арифметики натуральных чисел этот
метод, в известном (достаточно разумном и сильном) смысле, яв-
ляется универсальным (а часто и единственным) орудием дока-
зательств.
Дело в том, что при аксиоматическом (дедуктивном) построении
арифметики все ее здание опирается на определения операций
над натуральными числами по математической индук-
ции**) (например, при определении сложения прежде всего
определяется, — в качестве базиса индукции, — что значит при-
бавить единицу или нуль; затем—индукционный шаг определе-
ния— определение прибавления произвольного натурального числа
сводится к определению прибавления предшествующего чи-
сла). И вполне понятно потому, что «добираться» до общих свойств
натуральных чисел, связанных, скажем, с операциями сложе-
ния или умножения, нам приходится (если уж мы хотим обосно-
вывать их аксиоматически) по той же «лестнице» (на нижней
«ступени» которой находится соответствующее свойство для наимень-
шего натурального числа), по которой мы «совершаем восхождение»
*) См. стр. 97 и далее.
♦*) Называемые также рекурсивными определениями.
124
к интересующему нас общему понятию; грубо говоря, иначе просто
не видно, как за нужное нам доказательство «ухватиться» *).
И так обстоит дело с доказательством любого общего арифметиче-
ского утверждения! И если, это не видно из школьного курса
арифметики и алгебры, то лишь потому, что он (совершенно резонно)
опирается не столько на аксиоматический метод, сколько на опыт
и интуицию ** ***)). В конце концов самый придирчивый и критически
настроенный читатель часто довольствуется знанием того, что, ска-
жем, дистрибутивность умножения относительно сложения можно
доказать, и уже не требует самого доказательства. (Но такая,
пусть вполне обоснованная, уверенность так же отличается от
подлинного доказательства, как, скажем, газетная информация от
подлинного знания очевидца, причем эта аналогия простирается
весьма далеко.) Поэтому-то метод математической индукции и по-
является в школьном курсе математики гораздо позже интуитивно
прозрачных и легко постигаемых свойств арифметических действий,
например, в связи с формулой бинома Ньютона, которая уже отнюдь
не такова, чтобы справедливость ее «бросалась в глаза».
В той мере, в какой другие разделы математики опираются на
арифметическую основу, они нуждаются в методе математической
индукции. Потребность эта бывает двоякого рода. Прежде всего
многие разделы математики просто строятся на базе арифметики
натуральных'чисел (скажем, теория рациональных чисел, приводя-
щая в свою очередь к теории действительных чисел); другие же
могут быть интерп р етированы в арифметических терминах
(например, любой факт евклидовой геометрии можно выразить на
«координатном языке» действительных чисел). В этих случаях утвер-
ждения, предположим, геометрического содержания могут быть
доказаны именно для такой арифметической интерпретации с помо-
щью математической индукции. Можно сказать, что геометрическая
или какая-либо иная «специфика» подобных предложений не более
существенна для самого доказательства, чем, например, природа
рассматриваемых объектов в задаче о сложении трех огурцов с
пятью огурцами или трех пароходов с пятью пароходами.
Но бывает так, что базис индукции доказывается существенно
неарифметическими методами ♦♦♦). Ив этом случае, однако, индук-
ционный шаг (даже если он опирается на геометрические или ка-
кие-нибудь другие аксиомы) представляет собой некоторое обш ее
утверждение о натуральных числах, поскольку в нем
*) Точно так же, как любая теорема о свойствах «ортоцент-
ров многоугольников», определяемых по математиче-
ской индукции (стр. 94 настоящей книжки), по необходимо-
сти должна доказываться этим методом.
**) В тех же случаях, когда в школьном курсе доказываются
какие-либо общие свойства натуральных чисел, то доказательство,
если и не проводится по индукции, то лишь благодаря тому, что
в качестве посылок (часто неявных) используются предложения,
для строгого обоснования которых индукция все же необходима
(подобно тому как употребление постулата о параллельных в евкли-
довой геометрии можно «здмаскировавь», пользуясь вместо него
каким-нибудь из его следствий).
***) Примеры такого рода читатель найдет во второй части
этой книжки.
125
идет речь о выполнении некоторого свойства для любого натураль-
ного числа п *).
Отметим еще, что метод, оказавшийся столь плодотворным для
проведения доказательств, следующих процессу построения нату-
рального ряда 0, 1, 2, ... , может, быть обобщен и на процессы
совершенно другого вида. Например, в исчислениях математической
логики, оперирующих с формулами («высказываниями»), построен-
ными из «элементарных формул» («элементарных высказываний»)
вида 4, В, С ... с помощью, допустим, знаков & («и»), V («или»),
ZD («если ... , то ...») и ~J («не»), общие свойства формул доказы-
ваются путем так называемой индукции по построению
формулы: доказывается, что 1) искомым свойством обладает
любая элементарная формула (базис), и 2) из того, что этим свой-
ством обладают формулы X и У, следует, что им обладают фор-
мулы (X & У), (X V У), (ХгэУ) и “] X (индукционный шаг); из этого
делается вывод о справедливости доказываемого предложения для
всех формул указанного вида. Аналогия с рассматриваемой' в на-
стоящей книге математической индукцией настолько прозрачна, что
бросается в глаза и неподготовленному читателю.
Вообще, любая математическая (или логическая) конструкция,
состоящая в переходе от одного или нескольких исходных объек-
тов к новым объектам с помощью одной или нескольких операций
перехода, может служить основой соответствующего «индуктив-
ного» (являющегося, как мы уже видели, чисто дедуктивным)
метода определения и доказательства. (Относительно подчиненная
роль метода математической индукции в математическом анализе,
кстати, объясняется именно тем обстоятельством, что действитель-
ные числа, в отличие от натуральных, не являются продуктом
такой развертывающейся четко очерченной конструкции, так что
различного рода «индукции по'действительным числам» далеко не
обладают той универсальностью, как метод математической индук-
ции в арифметике и его модификации в математической логике.)
Для разрешения тех вопросов обще логического и обще-
математического характера, которые могли бы возникнуть теперь
у читателя, отсылаем его к специальной литературе •♦). Задачу же
первоначального ознакомления с конкретными применениями
метода математической индукции в элементарной математике может
с успехом выполнить эта книжка. * **)
♦) То есть сам переход «от п к п+1» доказывается для
любого п. “
**) См., например, Л. Генкин, О математической индукции,
М., Физматгиз, 1962; Э. Ландау, Основы анализа, М., ИЛ, 1948;
И. В. Арнольд, Теоретическая арифметика, М., Учпедгиз, 1939,
§ 13, 14, 17, 19; С. К. Клини, Введение в метаматематику, М.,
ИЛ, 1957, § 7, 13, 21, 38 и др.г «Математическая индукция»—Фи-
лософская энциклопедия, М., 1964 (т. 3).
УКАЗАНИЯ И РЕШЕНИЯ*)
ЧАСТЬ ПЕРВАЯ
Индукция в арифметике и в алгебре
1. Гипотеза: —Зп —2.
Г. Для п = 1 гипотеза верна.
2°. Пусть иА = 36—2. Тогда
uk+1 = uk + 3 = 3k--2 + 3 = 3 (fc-j- 1)—2.
2. Гипотеза: Sn=2n —1.
Г. Для п=1 гипотеза верна.
2° Пусть Sk = 2k— 1. Тогда Sft+i = S* + 2ft=2ft+i — 1.
[Можно также сразу образовать разность 2S„ — S„ и показать,
что она равна 2Л — 1.] —
3. Г. При n—1 утверждение справедливо.
2°. Пусть 12 + 32+ ... +(2& — l)2 = fe.(2-^~.P (2fe+ V .
Тогда
I2 + З2 + ... + (26— 1 )2 + (2k + 1)2 =
__6 (26-1) (26+1) [ (2/? +1)2(6+1) (26+1) (26+3) .
3 , 3
4. Г. При п=1 утверждение справедливо.
2’. Пусть l8+284-... + fes= 4J2.
Тогда
12+2®+... +#>+(*+1)3 =
^2(Н-1)2 ) (h , i)?= pfe+lHfe+2)J2 .
5. Г. При п=1 утверждение справедливо. ’
2°. Пусть 1+л+х2+...+х* = ^--------J-.
*) Ниже указываются номера задач. Решения примеров
приводятся в тексте.
127
Тогда
, . у^ 4-1___1 , у^ + 2_1
l+x + x2+ ...H-xfe+x*+i = i--Д + х*+1 = 2---‘
X—1 . X—1
6. Г. При п=1 утверждение справедливо.
2°. Пусть
1.2- 3 + 2-3-4+ ... + k (*4-1) (fe+2) = -.<*+ ^-±2) <*+?).
Тогда
Ь2.3 + 2.3.4+,..+£ (k+ 1) (k + 2) + (k+1) (k + 2) (Н-3) =
J^+iHH-.2.)..^+3)+(fe+n (fe+2) (fe+3)=
(*-Ц)(*4-2) (*4-3)(*+4)
4
7. Г. При м—1 утверждение справедливо.
2°. Пусть Пз + з^+"- + (2*—I) (2*4-1) =2*4-1 *
Тогда
J_+J_4. | 1 I 1
1-3^3-5^ ” ’ ' (2*—I) (2*4-1) 42*4-1) (2*4-3)
_ k 1 ’ _*-)-l
.2*4-1 '"(2*4-1)(2*4-3) —2*4-3 *
8. 1°. При n—1 утверждение справедливо.
о» п 1а , 22 , , *а *(* + 1)
2. Пусть 1.3-r3.5+--.+(2ft_1)(2ft+1) ~2 (2*4-1)*
Тогда
Р , 22 , , *2 , (Л+1)а
1.3 + 3-5"Г ” • ^(2k-1) (2fe+1) + (2й+1) (2*4-3) “
_*(*+!) (*+1)2 _ *(2*+3)+2(* + 1)
~2(2k + l)'r(2k+l)(2k + 3) ' ' 2 (2*4-1)(2*4-3) =
_(*4-1)(2*24-5*4-2)_(*+1) (2*4-1) (*4-2)_(*4-l)(fe4-2)
“ 2 (2*4-1) (2*4-3) 2 (2*4-1) (2*4-3) 2 (2*4-3) *
9. Г. При п = 1 утверждение справедливо.
2°. Пусть —4-—4-... 4-(3fe_2) (3fe+i)=aqTf ’
Тогда
J_ 4-2-4- 1 1
1.4'r4"7 ' 43*—2) (3*4-1)"1"(3*4-1) (3*4-4)
k , 1 *4-1
=3*-Н43*4-1) (5*4-4)=ЗГм •
128
10. Г. При п=1 утверждение справедливо.
2, Пусть Р5 + 5^+’-’+(4А_з)(4/г+1) = 4^р1-
Тогда
, 1 Г 1
1-5~5*9 ‘ ’ ~(4&—3) (4&+1Г (4fc+1) (4^ + 5)
__ k 1 _/А>+1
4fe+1 +(4fc+ 1) (4&Ч-5) 4fe + 5 °
11. 1®. При /г = 1 утверждение справедливо.
2°. Пусть
. -L-+_____-J__...+ i 1 k .
a(a+l)T(a+l)(a + 2)T T(a + fe —l)(a+fe) a (a+4) ’
Тогда-
__L_+_________!___+
а(а+1Г (a + l)(a + 2)^ ‘
...+_______!______ । i
T(a + fe— 1) (a+fe)T(a + fe) (a + H-1)
fe 1 _ *+l
а(а + Л) + (а-Н)(а+й + 1) a(a+*+l)’
12. 1°. При n = l и n = 2 утверждение справедливо.
о. г, a*-1—a*-PA
2 . Пусть «й-2=—;--- --------—
. । a\ a*—
w*=(a+₽)-—£-
Ct—p
13. 1®. При n = 0 имеем
^₽—’ Тогда
’ a*"1—B*~l (?+! —fi*+i
-»> a_g
1 1.2
— ^4-y-—. Следовательно,
утверждение справедливо.
2°. Пусть
1,2,4, 2k _ 1 2^+1
1+-»+1+-«8+1+х4+*” + 1 + х2*_а:—1+1_X2*+1’
Тогда
1 , 2 , 4 । 2fe 2*+1 .
i+x l + № i H-x4 l-f-x2* 14-x2*+1
1 2^+1 2ft+1 1 2^+2
x—1 — ха^+1 1x2^+1 —l"^l — x2^+2
14. При n = l имеем 1—^s=—2—1.
При n=2 имеем
1 x 1)__ x—1 x (x— 1) _(x—1) (x—2)
1 1! “Г 2! ~ 1 + 2 2!
5 И. С. Соминский и др.
129
При п = 3 имеем
х х(х—1) х(х—1) (г—2) __
1 ~ ТР 2! 3! ~ •
__(х—1)(х—2) х(х—1) (х — 2)_ (х—1) (х—2) (х—3)
“2 6 “ 3!
Это наводит на гипотезу:
1___х I х (* 0 t/ t\nx(x——л + 0д
1! + 2! ~
___(_(х D (* 2)...(х п)
п!
Г. При п = 1 гипотеза верна.
2°. Пусть
__х х(х—1)_ . х(х—1) ... (х —& + !)_
ц-h 2| -
. (х— 1) (х—2)... (х—fe)
' й!
kl
Тогда
, х,х(х-1) , , пЛ(х— 1)(х—2) ... (х—k + \) ,
ir 2! ...-t-i Ч ±
j (___l)^f+1 % 1) *' * _(___1)^ 2) * * * (х ty
(/г+1)! ,
t /_+1 х (х ^) ••• k)
4 (/г+1)! ““
__/__1 \&+i (х О (х 2) »». (х k) Г х
{ } /г! [л+1
__/___1 \Л+1 (х 1) (х 2) .. - (х /г) (х k 1)
4 (*+1)1
15. 1°. При п = 0 утверждение справедливо.
2°. Предположим, что утверждение справедливо при п = /г,
т. е. что А^— 11^+2 +122**1 делится на 133. Тогда
Ак+1= 11*+3+122 ^+1)+!= ц^+з+ 122*+з =
= lbllfe+2 + 144.122fe+1 =
= 1Ы 1*+а +133- 122^+i+ 1Ь122*+1 =
= 11 (1Р+2+ 12^+х)+133-122*+! = И Ak+ 133.122^+i.
Мы представили Ак+1 в виде суммы двух слагаемых, каждое
из которых делится на 133. Значит, Ак+1 делится на 133.
16. 1°. При п = 1 утверждение задачи, очевидно, справедливо.
2°. Предположим, что при п = утверждение справедливо,
т. е. что k прямых делят плоскость на 2k углов. Так как (/г + 1)-я
прямая рассекает на части сразу два вертикальных угла, то она
увеличивает число частей, на которые делится плоскость, на
два. Поэтому (/г+1)-я прямая делит плоскость на 2/г + 2 = 2(&+1)
частей.
130
17. Iе. При п = 1 утверждение справедливо, так как
. Зх . х , ( . Зх . х\
sinT sin 2"+(sinT~~sin *2/ 1 ’
— ---=—- 4- cos x.
o . x--------------------------n . x-2
2 sin--- 2sin-~-
Z Z
2°. Пусть
. 2£-f-l
1 Sln x
-g- + cosA:+cos 2*+ ... +cos kx =------—.
2 sin 4
Тогда
i + cosx+cos 2x+. ..-{-cos £x+cos (£ + 1) x«
sin —^7 x sin x4-2 sin ~ cos (k +1) x
=------4- cos (k +1) x =---------—-----------±---------------
2 sin — 2sin~
z z
. 2fe+l , /. 2Л + 3 . 2*+l \ . 2*4-3
sin —4— x+ I sin ——X —sin ——X ) Sin —5— X
Z \ Z Z / **
Л • X . x
2 sin-5- 2sin —
z z
18. Г. При n=l утверждение справедливо, так как
2sinx —sin2x 2 sin x (1 — cosx)
— i= sin x.
. . 9 x----------------------A . 9 x
4 sin2— 4 sin2 —
2°. Пусть
•- . . o . o , . . . . (£4-1) sin kx—k sin (fc 4-1) x
sin x 4- 2 sin 2x -J-... + £ sin £x = —5—----------—!<
4 sin2 —
Тогда
sinx4-2sin2x-f-...+£sin £x-|-(£+l) sin (£-|-1) x=«
= (fe+l) sinfex-fesin(fe+l)x + (fe + 1)s.n (ft+1}x =
4 sin2 4
_(£4~ 1) sin £x —£ sin (£4-l)x-|-2(£ + l)sin (£4~ 1) x (1—cosx)
4 sin2 у
_(£ + 2) sin (£4-1) x + (^+1) sin £x 2 (£-}-1) cosx sin (£+1) x_
4 sin2 4- 4 sin2
A A
5*
131
(Z?4~2) sin (Z?4-1)x + (fe+ 1) sin kx (fe+1) [sin (fe + 2)x4-sin
4 sin2 4 sin2
m (fe + 2) sin (fe 4- 1) x—(fe +1) sin (fe + 2) x
4 sin2 -2-
19. Г. При n — 1 утверждение справедливо, так как
4 sin2 4-
2 cos л:—cos2x—1 2cosx—2cos2x cosx(l—cosx)
--------------------------i== cos x.
4sin2~ 2sin2-^-
Л £
2°. Пусть
Л o , o n 7 , , . . (fc-4- l)cos kx—k cos (k + l)x— 1
cos 2x + 2 cos 2x 4- ... + k cos kx = -—!—------------—!—i------
4sin2y
Тогда
cos*4-2 cos 2*+ cos £*+(& +1) cos (&+1) x —
= + (Л+ D cos (*+1) x =
4 sin® у
(&4-1) cos Zjx —/? cos (&4-1) x— 1
----------------------------------+
4sin2y
2 (fe+1) cos (&+1) * (1—CQsx)__ ,
4sin2y
__(Zg-|-2) cos (fe+ l)x + (fe+ 1) coskx
4sin2r|-
2 (fe-|-1) cos x cos (Ze 4~ 0 x +1 _
4 sin2 -g-
__(Z?4-2) cos (Zz4~ i) x4~(Z?4~ 1) cos fex
4sin2y
(^4-1) [cos (Z?4~2) x + cosZsx] + l _
A . 9 X
4sm2 —
__(k + 2) cos (fe4~ 1) x—(fe4~ 1) cos(Z?4~2) x— 1
4sin2y
132
20. Iе. При л«=1 утверждение справедливо, так как
2®. Пусть
1 . х । 1 . х , ,1.x 1 . х
2 tg 2 2а tg 2а 2^ t§ "2^~ 2fe Ctg 2k
Тогда
2 tg 2 + 2а tg 2а + ... + 2<! tg 2к +2U1tS2S+I-
1 , х . ,1.x
еа — Ctg— — Ctg X Н---tg ~-=
2k 2k 2*+1 2*+1
1 2*+» , 1 ’ . 1.x,
=—-----------------------—ctg X=— ctg ———ctg X.
2*+1 cte_L_ 2fe+1ctg— 2+1 2*+1 8
62*+1
2__1 1
21. 1®. Имеем tg (arc tg 2—arc.tg 1) = ^—7—^=—. Поэтому
1 "т* Z • 1 о
arc tg 2—arc tg 1 ^arc tg y—'arc ctg 3. Значит, при n —1 утверж-
дение справедливо.
2°. Покажем сначала, что
arc ctg (2/г + 3) = агс tg гФт—arc tg 1. (1)
Л 1
Действительно,4g
arc tg
k + 2
/г+1
k+2 .
* 1\ *+1 1
arc g 1 J- ^ + 2 -2fe + 3
Значит,
1 k + 2
arc tg arcctg(2^ + 3) = arc tg^-i-j—arc tg 1.
Предположим, что утверждение справедливо при л==/г, т. е.
arc ctg 3+arc ctg 5+ ... +arc ctg (2/? +1)==
' =arctg2+arc tg-| + ...+arctg^il—Aarctgl. (2)
Докажем, что тогда оно справедливо и при п==/г + 1, т. е.
arc ctg 3+arc ctg 5 + ... + arc ctg (2k + 3) —
';=arc tg 2+ ... +arc tg|i^— (*+l)arctg 1. (3)
Сложив почленно равенства (1) и (2_), получим равенство (3).
133
22. Iе. При п=1 утверждение справедливо, так как
ж X*' о • с\ I t \
У 3 — i = 2 cos-?—i sin — .
\ 6 6 J
2°. Пусть С/”3—z)fe = 2ft ^cos-~r—/sin —.
Тогда
(Y 3—г)^+1 —2^ f cos— i sin 2 fcos-^—i sin=
\O о / \ о о j
rcos(tHii_isln!5±!>_"l.
L о о J
23, Г. При n=J утверждение справедливо.
2е. Пусть (cosx-J-zsin x)fe = cos/ex + isin kx. Тогда
(cos х + i sin x)*+1 = (cos kx + i sin kx) (cos x + i sin x) —
— (cvskx cosx—sin kxsin x)4~/ (cos &x sin x4-sin kx cosx) =
= cos (& + l)x + /sin (fc+l)x.
24. Ошибочна самая последняя фраза: «Утверждение доказано».
В действительности доказано, что неравенство 2я > 2п + 1 справед-
ливо при nx=/f + l, если оно справедливо при n = fc, где £ —любое
натуральное число.
Отсюда еще не следует, что неравенство это справедливо
хотя бы при одном значении п и тем более п р и любом
натуральном п.
Короче говоря, ошибка заключается в том, что доказана только
теорема 2, а теорема 1 не рассматривалась и база для индукции
не создана.
25. Легко видеть, что 3—наименьшее натуральное значение л,
при котором неравенство 2я > 2л 4-1 справедливо.
Учитывая, что из справедливости неравенства при л — fe следует
его справедливость при n = k-\-\ (задача 24), утверждаем, что
неравенство справедливо при любом натуральном л^З.
26. 1°. При л = 2 неравенство справедливо, так как
+ т?>/г
2°. Пусть
(1)
Докажем, что
(2)
При любом k 0 имеет место неравенство
1
> fk + l—y k.
(3)
134
Действительно, неравенство (3) равносильно неравенству
1+ 1/ > Ь полученному из него умножением обеих частей
F К “г 1
на Vfc +1 + У k. Сложив почленно неравенства (1) и (3), получим
неравенство (2).
27. Г. При п=2 неравенство принимает вид -х-< 6 и, следо-
о
вательно, справедливо.
4k (2k}\
2°. Пусть r-j—г < 7ттт2, где &$*2. Нетрудно проверить, что
К 1 у/? 1 I
4(6+1) (2fe-J-1) (2*4-2) _ п „
-ТТ2 < (6+в* 'приk > °- Поэтому
4й 4(6+1) (26)! (26+1) (26+2)
6+1* 6+2 <(6!)2* (6+1)а ’
4*+* (26+2)!
6+2 < [(6+1)!р‘
ЧАСТЬ ВТОРАЯ
Индукция в геометрии
1. Обозначим через S2n площадь правильного 2”-угольника,
вписанного в круг радиуса /?, а через й2п —его апофему. Тогда
, из формулы (1) следует, что
т. е.
6а»=1/
л-i двоек
и
S2n=y (2”о2п) Л2п
n-з двойки
«$2п
S2n + 1
c=2w-2/?a2n-i
(здесь предполагается, что п^З). Далее, имеем:
2/,“1а nh2n h п 180°
= on^i^““~p"=C0s"9^ ’ откуда следует, что
Z */\u2n t i\ *
s. S. Sa S2«-‘ 180’ 180°
$7“Ss’ Ss„ ~cos 4 COS 8
9
Так как S4 = 2R2 и lim S n = jiR2, то — равно пределу выражения
П-ыхз * 2Т
45° 45°
cos 45° cos —х— cos • • • Затем остается только воспользоваться
2 4
л. „а
формулой cos -у
180°
cos а
2
135
L
2. Из того, что N диагоналей и п сторон л-угольника явля-
ются сторонами л —2 треугольников (см. пример 4), следует, что
27V + п = 3 (п — 2), N = п—3.
3. Выпуклый (л+ 1)-угольник ЛхЛ2.. .АпАп+1 диагональю АгАп
ёазбивается на л-угольник А2Аа...Ап и треугольник AiAnAn+1.
читая известным число F (л) частей, на которые разбивается
своими диагоналями л-угольник АгА2.. .Ап, сосчитаем, сколько час-
тей добавляется от присоединения вершины Ля+1 (это число на
единицу больше числа частей, на которые диагонали, выходящие .
из вершины Лд+i, разбиваются остальными диагоналями). Так мы
найдем соотношение
Г(л+1) = Г(л) + (л —1) + 1 (л —2)4-2 (л-3) + .,.
...4-(л-3)24-(п~2)1,
которое с помощью примеров 3 и 6 части I можно переписать
в виде
F (п+1) = f (n) + (n-1) + -” (-2—V2-}-
Г / \ I л3 л2 , 4л
₽F(n)+_„+_
1.
Суммируя аначения F (л), F (п— 1), .F (4) и используя резуль-
таты примеров 3 и 4 и задачи 4 из части I, получим:
/„ч —(«—0 (п —2) (л2-Зл + 12)
г {п) 24
4. . В обозначениях примера 7 доказать сначала, что
г - 2г р , 2р . , -
~= 1---и -^- = 14--~ (где h—высота, проведенная из вер-
шины С), откуда вытекают равенства
5. Как известно, S —рг = (р —с) р = —,
4/\
откуда, применяя
теорему косинусов, получаем:
£+_А_
г + р р ^Р—С = (a+b) [c*-(a-b)t]
2R abc 2abc
2S
Ь2+с2—а2 , а24-с2 —Ь2
2Ьс
2йс
cosCAB+cosCBA.
136
в. Предварительно доказать следующую лемму. Пусть и О2—
центры окружностей и С2, пересекающихся в точке О, и ВгВ2 —
секущая, проведенная через вторую точку пересечения этих
окружностей (рис. 76); тогда отрезки ВГВ2 и ОгО2 видны из точки О
под одним и тем же углом. Затем доказать предложенную теорему
для трех окружностей. После этого, предполагая, что теорема
справедлива для п—1 окружностей, рассмотреть п окружностей
Ср С2, ...» С„. Провести секущую через точку Вп_1 и точку пере-
сечения окружностей и Сг\ к n— 1 окружностям Сх, С2,..Сп~х
применить индуктивное предположение.
7. Предположив, что все эти точки соединены с соблюдением
условий задачи, мы придем к карте,
имеющей 5 вершин, — = 10
границ и, следовательно, 7 стран (теорема Эйлера!). Невозможность
такой карты вытекает из рассуж-
дений, близких к тем, которые
привели к неравенству (5).
8. Поместим многогранник
внутрь шара достаточно большого
радиуса и из центра шара (кото-
рый можно считать находящимся
внутри многогранника) спроекти-
руем все точки многогранника на
сферу (поверхность шара). Полу-
ченную на сфере карту спроекти-
руем из произвольной ее точки, не
Рис: 76.
принадлежащей никакой границе, на плоскость, касающуюся сферы в
диаметрально противоположной точке (стереографическая
проекция). К полученной плоской картеприменим теорему Эйлера.
9. См. пример 9.
10. Применить теорему Эйлера.
11. Пусть карта, образованная п окружностями с хордами,
правильно раскрашенная тремя красками а, р, у.
Проведем (п + 1)-ю окружность и цвета стран, расположенных
внутри этой окружности по одну сторону от соответствующей хорды,
изменим по схеме а~>р, Р~^у, a нвета стран, расположенных
внутри окружности по другую сторону от хорды, — по схеме ау»
12. Задача может быть решена аналогично примеру 17 (пред-
ставляющему собой ее частный случай), только вместо поворота
вокруг заданной точки Ах на известный уголо^ здесь следует рас-
сматривать преобразование подобия, состоящее из поворота на
угол ах и центрально-подобного преобразования (гомотетии) с тем
же центром и коэффициентом подобия, равным отношению сто-
рон соответствующего треугольника (и аналогично для других
заданных точек). Последовательное выполнение двух таких пре-
образований равносильно некоторому третьему преобразованию того
же типа (см., например, § 2 гл. I части второй указанной выше
книги И. М. Яглома). Следовательно, в обозначениях, аналогичных
принятым в решении предыдущего примера, по вершинам и А2
треугольников хгх2Аг и х2х3Я2 можно найти вершину А треуголь-
ника хгх3А, построенного на отрезке х±х3 и имеющего известный
угол при вершине и известное отношение боковых сторон.
137
Построение стороны хгх3 треугольника хххгх9 по точкам А и А3
можно выполнить, например, следующим образом. Последователь-
ность двух известных преобразований подобия с центрами А и А3
переводит Хх в себя (сначала хг
переходит в х3, затем х3—в хг). Но
последовательность этих преоб-
разований равносильна одному
преобразованию подобия с центром
в некоторой точке В, которую
можно построить. Так как точка
В переходит в себя, то она сов-
падает С ИСКОМОЙ ТОЧКОЙ Хх. Если
сумма заданных углов при вер-
шинах кратна 360°, а произведе-
ние отношений сторон равно еди-
нице, то решение задачи невоз-
можно или неопределенно.
13. Пусть сторона AtA3 ис-
комого многоугольника проходит
через точку Р, а сторона Л2Л3
параллельна прямой I (рис. 77).
Обозначим через Р' точку, сим-
метричную с точкой Р относитель-
но диаметра окружности, перпен-
дикулярного к прямой /, и через
4'
Рис. 77.
А2 —точку пересечения прямой Р'А3 с окружностью. В п-уголь-
нике Лх4243...Ап сторона А}А* параллельна заданной прямой/,
а сторона А2А3 проходит через известную точку Р'. Выполнив
такое построение соответствующее число раз, мы сведем эту задачу
к построению n-угольника, у которого k соседних сторон про-
ходят через известные точки, а остальные n—k сторон параллельны
заданным прямым.
14. На окружности радиуса а отметим точки Л2, Л8, Л4,
А3, являющиеся вершинами правильного шестиугольника.
“....... i ОАп такая,
что ОВп=~ ОАп = ~ (здесь считается A3jn+k = Ak при любом/пи
fe = l, 2, 3, 4, 5,
сечения прямых
^5’ .
Предположим, что нам уже известна точка Вп радиуса
а . .
п ---- ~ -
6; Вх==Лх)» и обозначим через Вп+1 точку пере-
ОАп+1 и BnAn+i; тогда ОВ„+1 = ^-^ .
геометрическим местом является прямая линия;
15. Искомым .............................
доказательство аналогично решению примера 20.
16. В обозначениях рис. 48 имеем:
S£BCE + 5 ДЛЯ Е — 5ДВСг + 5&ADF = 5ДВСО + 5Д ADO 5’
где S—площадь четырехугольника. Отсюда в силу результата
примера 20 (или задачи 15) следует, что точки £, F и О лежат
на одной прямой.
138
17. В обозначениях рис. 49 (где точки М и ЛГ—середины диа-
гоналей АС и BD, а Р —середина отрезка ЕР) имеем:
5ДЛВЛ1 + 5ДС£Ш == 5 Д A BN + 5&CDN ==S^ABP^‘S&CDP = у S >
где S—-площадь четырехугольника. Отсюда в силу результата
задачи 15 следует, что точки М, N и Р лежат на одной прямой.
18. Достаточно в условии примера 21 положить а1 = а2=...=
19. Центр окружности, которая является искомым геометри-
ческим местом в задаче 18.
20. Если М—точка искомого геометрического места, то
AM
и, следовательно, ДМ2 —с2-ЕМ2 = 0; поэтому настоящая
задача сводится к примеру 21.
21. Можно показать, что площадь треугольника, вершинами
которого являются проекции точки М на стороны треугольника
1 I 42 I
Л1Л2Л3, равна 5ДЛ1Л2л8» где # —радиус описанной
окружности 2 треугольника Д1Д2Дз, d — расстояние точки М от
центра окружности 2. Отсюда вытекает, что при п = 3 искомое
геометрическое место представляет собой окружность, концентри-
ческую 2 (или пару таких окружностей). Далее, при помощи ин-
дукции по числу сторон многоугольника показывается, что и при
любом п искомое геометрическое место, вообще говоря, будет
представлять собой окружность (или пару концентрических
139
окружностей). [См. решение задачи 90 из книги: Д. О. Ш к л я р-
с к и й, Н. Н. Ченцов й И. М. Я г л о м, Избранные задачи
и теоремы элементарной математики, ч. 2, М., Гостехиздат, 1952
(серия «Библиотека математического кружка», вып. 2).]
' 22. Как доказано в примере 22, и -//-==----? .
Аналогично О2О3||А2А3 и -/-/==-—г и т. д.
Л2 А3 ** ““ *
23. Пусть Sx и 52 — центры тяжести (/г—1)-угольника
А2А3. • - Ah и (л—k — 1)-угольника Ak+2Ak+3- --Ап> О± и О2 —центры
тяжести fc-угольников А^... Ад и А2А3... А*+1, О3 и О4—центры
тяжести (л— £)-угольников Ад+1...АЯ и A^+g.-.A^Ai (рис. 78).
гт. ^1’^1 O2S4 1 г\ и л я O3S2 О4 S2
Тогда t о^Го2лк+ГП и °А1И1л*+1’ о^7“бм]=
_____д__[ и <WAxA*+1. Если теперь О—точка пересечения
медиан fc-го порядка О2О4 и OjOg, то из подобия треугольников
OOtO2 и ОО3О4 имеем:
1 А А
00 _ООа_О1Оа_ k Л1Л»+1 n—k
00$ ОО4 O3O4 1 « . k
и=кА1А*+1
Можно также доказать, что при любом k точка пересече-
ния медиан fc-го порядка л-угольника совпадает с его центром
тяжести.
24. Отрезки, соединяющие середины противоположных сторон
и середины диагоналей произвольного четырехугольника, пересе-
каются в одной точке и делятся в ней пополам.
25. Пусть ЛхДгАзДд—произвольный четырехугольник, вписан-
ный в окружность S. Из того, что, например, окружность Эйлера
треугольника 4142А3 проходит через три середины отрезков
ЯИр Я4А2, Я4А3, где Я4—точка пересечения высот А^АзАз (см.
выше), вытекает, что она центрально-подобна (гомотетична) ок-
ружности S с центром подобия в точке Н4 и коэффициентом подо-
бия ~; поэтому середина отрезка Я4А4 принадлежит этой
окружности. Теперь остается только заметить, что середины
отрезков HjAi, Я2А2, Н3А3 и Я4А4 (где Нх, Яа и Я8—-точки
пересечения высот соответствующих треугольников) совпадают; это
вытекает из того, что, например, четырехугольник А1НяЯ1Аа
является параллелограммом (ибо А1Я2||А2Я1ХАзА4 и А]Я2==
= А2Я1 = удвоенному расстоянию от центра S до А3А4).
Предположим теперь, что для всех /г-угольников, число стороц
k которых не превосходит л ^4, существование окружности
Эйлера уже доказано, и рассмотрим (л+1)-угольник Ar...An Ая+1,
вписанный в окружность S. Нам надо доказать, что окруж-
ности Эйлера Slt S2........Sn+1 л-угольников А2А3. ..Ая+1,
А1А3А4.. .Ая+1,.. .'AiA^'An пересекаются в одной точке; для
этого достаточно доказать, что пересекаются в одной точке каж-
дые три из них, например Sx, $я и$8.
140
[Ибо если каждые три из п^5 окружностей (никакие две из
которых не совпадают) пересекаются в одной точке, то и все
окружности пересекаются в одной точке (для п = 4 это уже не-
верно).]
Обозначим через S12, S13, S23 окружности Эйлера (л— 1)-
угольников Д3А4...Д„+1, А2А4Аь. .. Ап+1, A1A4A5... Ап+1 и через
О12, 013» 023—их центры; пусть еще 019 02, 03—центры окруж-
ностей Sx, S2, S3 и 0123—центр окружности Эйлера S123
(п—2)-угольника А4А5...А„+1. В таком случае мы придем к
рис. 79, из которого нетрудно усмотреть равенство треугольников
010203 и O23O13O12. [Для доказательства равенства сторон 0±09
и 023013 этих треугольников достаточно рассмотреть треугольники
OiO2O12 и О23О13О123, в которых
D
01201^«5 012^2 = 0123^23 = 0123^13 = "у >
Z ^1^12^2 в £» ^1^12^123 4“ ^123^12^2 в
“2 01301201234*2 01гз01202з = 2 Ох3О12^2з
и Z ^23^123^132 О13О12О2з, как вписанный и центральный
угол описанной вокруг 0120хз^23 окружности, опирающиеся
на одну дугу; также доказывается, что ОхО3 = О23Ох2 и 080з=>
*=О1зО121- Из того, что
ДОГО2О3 и Д о23о13о12
и окружности S23, &1Я и
S12 пересекаются в одной
точке 0x23» Уже следует,
что и окружности Sx’
S2 и S3 пересекаются в
одной точке.
26. Решение этой
задачи можно найти в
книге И. М. Яглома,
указанной выше (см.
решение задачи 52 в)).
27. Теорема о пря-
мой Симпсона точки Р
относительно треуголь-
ника АхА243 широко
известна; доказательство
ее вытекает, например,
из того, что в обозначе-
ниях рис. 55 четырех-
угольники PAiMK,
PLA2K и PMA3L впи-
сываются в окружность,
в силу чего AiKM =
= /41РМ, £A2KL =
A2PL и Z MPL =
= 180°—^ А3=£ АгРА2> откуда вытекает, что £ АгКМ = £ A2KL.
Полное решение задачи 27, а также другие решения задач
22—26 можно найти в § 8 книги И. М. Яглома «Комплексные
числа», Физматгиз, М., 1963.
141
28. Решение этой задачи близко к решению примера 23.
29. См., например, указанную на стр. 141 книгу И. М. Я г-
лома, стр. 53 — 65. Заметим, что ортоцентры вписанных в окруж-
ность многоугольников обладают рядом свойств, близких к свой-
ствам ортоцентров треугольников; ряд таких свойств, доказывать
которые по необходимости приходится методом математи-
ческой индукции (ибо ортоцентр многоугольника определяется
по индукции), указан в названной книге И. М. Я гл ома.
30. Доказательства сформулированных здесь предложений
можно найти в книге Д. О. Шкл яре кого и др., указанной
на стр. 140 (см. решение задачи 125), и в книге И. М. Я г л о м,
Геометрические преобразования, II, М., Гостехиздат, 1956 (серия
«Библиотека математического кружка», вып. 8) (см. решение за-
дачи 218 а)).
31. Доказательства сформулированных здесь предложений
совершенно аналогичны доказательствам предложений, составля-
ющих содержание задачи 30.
32. Доказательства предложений, составляющих содержание
этой задачи, можно найти в указанной в ответе к задаче 30 книге
И. М. Яглома (см. решение задачи 218 6)).
33. Рассмотрим последовательно следующие задачи.
А. На сколько частей делят прямую п «одномерных окруж-
ностей», т. е. п пар точек (см. введение к этому параграфу).
Ответ. 2п точек делят прямую на 2п+1 частей.
А*. Найти число Фх (п) частей, на которое делят окружность
п пар точек, расположенных на этой окружности.
Ответ. Фх(п) = 2п.
Б. Найти число Ф2 (п) частей, на которые делят плоскость п
попарно пересекающихся окружностей.
Решение. Так как п окружностей пересекают (п+1)-ю ок-
ружность в п парах точек и, следовательно, делят ее на Фх(п) =
==2п частей (см. п. А'), то (п+1)-я окружность пересекает
ф1(п) = 2п из тех Ф2(п) частей, на которые делят плоскость п
окружностей. Отсюда получаем равенство Ф2 (п+1) = Ф2 (п) +
-|-Ф1 (п) = Ф2(п) + 2п. Используя это равенство и то, что Ф2(1) =
= 2, будем иметь: Ф2 (п) = п2—п + 2.
Б'. На сколько частей делят сферу п попарно пересекающихся
окружностей, расположенных на этой сфере?
Ответ. На Ф2(п) = п2 — п + 2 частей.
В. Исходная задача.'
Решение. Так как п сфер пересекают (п+1)-ю сферу по
п окружностям и, следовательно, разбивают ее поверхность на
Ф2(п) = п2 —п + 2 частей (см. пункт Б'), то если п попарно пере-
секающихся сфер разбивают пространство на Ф3(п) частей, то
п + 1 сфер разобьют пространство на Ф3 (п+ 1)==Ф3 (п) + Ф2 (п) =
= Ф3(п)+(м2 — « + 2) частей. Отсюда и из того, что Ф3(1) = 2»
« лч / \ п (п2 Зп + 8)
можно наити Ф3(п) = —1.
34. Доказательство аналогично доказательству утверждения
примера 28.
35. Рассмотреть последовательно следующие задачи.
А. В условиях примера 26 А будем различать отрезки 1 2,
для которых направление от вершины 1 к вершине 2 совпадает с
142
направлением от 1 к 2 для основного отрезка, и отрезки 1 2, для
которых направление от 1 к 2 противоположно направлению
основного отрезка. Доказать, что число первых отрезков на еди-
ницу больше, чем число вторых.
Б. Будем говорить, что треугольник 12 3 (см. пример 26 Б)
ориентирован по часовой стрелке (или против часовой стрелки),
если обход его вершин от вершины 1 к вершине 2 и затем к вер-
шине 3 происходит по часовой стрелке (или против часовой
стрелки). Доказать, что число треугольников разбиения, зануме-
рованных цифрами 1, 2, 3 и ориентированных так же, как и
основной треугольник, ровно на единицу больше числа остальных
треугольников разбиения, занумерованных цифрами 1, 2, 3.
В. Предложение, сформулированное в начале условия задачи.
36. Доказать соответствующее предложение для «шаровых
многогранников», т. е. тел, каждое из которых является пересече-
нием конечного числа шаров. Доказательство этого предложения
проводится аналогично доказательству утверждения примера 30.
37. Показать прежде всего, что любые три из этих точек
можно заключить в круг радиуса -4=. Затем построить круг
У 3
радиуса с центром в каждой из заданных точек и показать,
У
что любые три из этих кругов пересекаются. Общая точка всех
этих кругов, существующая в силу результата примера 29 Б,' и будет
центром круга радиуса , содержащего все заданные то^кй.
38. Доказательство аналогично решению задачи 37.
39. Пусть в пространстве задана некоторая конечная система
лучей, попарно образующих между собой тупые углы, причем
предположим, что эта система является максимальной в том
смысле, что не существует ни одного луча, который с каждым из
заданных лучей образует тупой угол. Отнесем каждому лучу по-
лупространство, ограниченное плоскостью, перпендикулярной к
этому лучу, и расположенное от нее по ту же сторону, что и луч.
Ввиду максимальности нашей системы лучей эти полупространства
заполняют все пространство, и наше утверждение следует из
результата примера 31.
40. Воспользоваться тем, что центр тяжести треугольника
делит медианы в отношении 2:1 (ср. пример 22).
СОДЕРЖАНИЕ
Предисловие .............................................. 3
Введение ................................................. 5
Часть I. Индукция в арифметике и в алгебре................15
§ 1. Доказательства тождеств; задачи арифметического ха-
рактера (примеры 1—13; задачи 1 — 16).................15
§ 2. Тригонометрические и алгебраические задачи (приме-
ры 14—18; задачи 17—23)............................. 25
§ 3. Задачи на доказательство неравенств (примеры 19—24;
задачи 24—27) ....................................... 29
§ 4. Доказательство некоторых теорем элементарной ал-
гебры методом математической индукции (теоремы
Часть П. Индукция в геометрии .......................... 39
§ 1. Вычисление по индукции (примеры 1—5; задачи 1—3) 39
§ 2. Доказательство по индукции (примеры 6—15; зада-
чи 4—11)..............................................45
§ 3. Построение по индукции (примеры 16—19; задачи
12-14)............................................... 70
§ 4. Нахождение геометрических мест по индукции (при-
меры 20—21; задачи 15—21).............................79
§ 5. Определение по индукции (примеры 22—23; задачи
22-32)............................................... 84
§ 6. Индукция по числу измерений (примеры 24—33; зада-
чи 33—40)............................................ 97
1. Вычисление и нахождение геометрических мест с по-
мощью индукции по числу измерений (примеры 24—25;
задача 33) ........................................101
2. Определение и доказательство с помощью индукции по
числу измерений (примеры 26—33; задачи 34—40) . . 105
Ю, Л. Гастев. Послесловие................................122
Указания и решения . . . ............................... 127