Гусеничные тягачи. Теория - Антонов А.С.

Автор: Антонов А.С.

Теги: машиностроение военная техника

Год: 1959

Похожие

Гусеничные транспортеры-тягачи

Танк

Многоцелевые гусеничные и колесные машины.

Руководство по эвакуации бронетанковой техники

Текст

ГУСЕНИЧНЫЕ
ТЯГАЧИ
ЧАСТЬ ПЕРВАЯ
ВОЕННОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ОБОРОИЫ СОЮЗА ССР
МОСКВА —1959
PosjaGTSM
ПЕРЕД ПОЛЬЗОВАНИЕМ КНИГОЙ ВНЕСТИ СЛЕДУЮЩИЕ
ИСПРАВЛЕНИЯ
Стра- ница Строка Напечатано Следует читать
dF dF г dF ,,, dF
9 1 снизу dF = ^,dP' + dy. дР 1 dF = 7dP 4- -д— d<p. dP dy 10
68 14 снизу rfPc = 2Д = °’4’ rfPc ~ 2,5 ~
69 8 снизу Ат ? 'n> 7
70 9 снизу не должен должен
105 3 сверху Q c
155 5 снизу cg = 1 п Сд = 1 n
162 10 сверху S ““ шр) 4- S = °’ 0 0
163 12 снизу • - • + Ukr^n = О’ 59) • • + ъьЛ = °- <159>
164 18 снизу Мо + Mi + /П2 + ... + + Мп = 0. Mq 4- + гИ2 4- . .. 4- + M„=0. (16Г)
164 11 снизу (162). (161).
168 16 сверху “19 = “19 = Г’ “19 = “3‘ = ’
170 21 снизу -4- ” 0, 44, + i’^M? = 0;
198 2 снизу - { 2(1 + 1) + 2-2 + ... - { 2 (1 + 1) + 1 -2 + ...
224 19 снизу <7 = , (223) q = f223)
225 9 сверху = 4 370 000 кг!см?. = 4 370 000 кгсм.
238 2 снизу яг, = 70 000 кгм-. mi = 70 000 кг/л;
283 2 снизу Gx 4 0. G, = 0.
313 1 снизу Мс = xcG = (hz sin a + 4- m cos a) G. Mc = xcG = (hz sin a. + 4- m cos a) G.
314 10 снизу hz = 0,9 m\ hz = 0,9 л;
315 4 сверху hz
317 11 снизу hz = 0,9 m\ hz = 0,9 л;
324 15 сверху ускорение ускорение земного тяготения
324 16 сверху Кроме модельных испыта- ний земного тяготения, Кроме модельных испытаний,
Все вышеперечисленные опечатки изменены & соответствии с таблицей.
Изменения Ьнес PosjoGTSM 01.04.2015.
Изд. № 8/825. Зак. Ли 2469
АВТОТРАКТОРНОЕ УПРАВЛЕНИЕ
МИНИСТЕРСТВА ОБОРОНЫ СОЮЗА ССР
ГУСЕНИЧНЫЕ
ТЯГАЧИ
ЧАСТЬ ПЕРВАЯ
ТЕОРИЯ
ВОЕННОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ОБОРОНЫ СОЮЗА ССР
Москва —1959
Профессор, доктор технических наук
А. С. АНТОНОВ
ГУСЕНИЧНЫЕ ТЯГАЧИ
Часть первая. Теория
Книга предназначена для подготовки
инженеров автотракторной специальности,
а также для инженеров, интересующихся
вопросами теории гусеничных тягачей.
ПРЕДИСЛОВИЕ
Гусеничные машины находят широкое применение как в армии,
так и в народном хозяйстве. К ним относятся танки, транспортеры,
тракторы, различные инженерные и дорожные машины.
Во время Великой Отечественной войны появился еще один тип
гусеничных машин — это гусеничный артиллерийский
тягач. Эта машина как по своему назначению, так и по своим
техническим данным отличается от всех других типов гусеничных
машин.
Основное назначение тягача — буксировка прицепа (орудия)
и перевозка людей (расчета) и грузов (боекомплекта).
Тягач является транспортной машиной. Он обладает высокими
скоростями движения (равными скоростям движения танков),
большой грузоподъемностью и не уступает танкам и тракторам
в проходимости на местности. Кроме того, тягач должен обла-
дать и другими качествами, например, износостойкость его ходовой
части не должна намного отличаться от износостойкости ходовой
части колесных тягачей; подвижность на дорогах должна быть та-
кой же, как у колесных машин; он не должен портить дорог своим
гусеничным движителем. Только в этом случае он будет удовлетво-
рять требованиям, предъявляемым к транспортной машине.
Все это накладывает на конструкцию быстроходных гусеничных
тягачей, как на определенный тип самоходных машин, специфиче-
ский отпечаток.
В настоящей книге обобщается накопленный за послевоенные
годы опыт конструирования тягачей, а также освещаются вопросы
теории и расчета тягачей.
Следует, конечно, иметь в виду, что, несмотря на свою специ-
фику, гусеничные тягачи, являются лишь одним из типов самоход-
ных машин и поэтому имеют много общего с автомобилями, тан-
ками, тракторами, транспортерами. Много общих вопросов также
и в теории и расчете этих машин. Поэтому в данной книге рас-
сматриваются не только вопросы, относящиеся к конструкции тя-
гачей, но и общие вопросы, относящиеся к конструкции колесных
и гусеничных самоходных машин вообще.
Во всякой книге, рассматривающей конструкции механизмов
или машин в целом, прежде всего должны изучаться предъявляе-
I* 3
мые к конструкции требования. Выполнение этих требований
должно быть показано на конкретных примерах. При этом
интерес представляют не только современные (действующие) кон-
струкции, но и уже устаревшие, в которых, однако, оригинально
решен тот или иной вопрос, показано удовлетворительное решение
того или иного требования, которое может быть полезным для раз-
работки новых конструкций.
Особенно важно, чтобы в книге, посвященной изучению кон-
струкций, были рассмотрены проблемные вопросы.
Следует иметь в виду, что правильно сформулированная и свое-
временно поставленная проблема уже является шагом вперед
в развитии техники.
Примером этого может служить развитие конструкций совре-
менных силовых передач, к которым предъявляется основное тре-
бование непрерывности и автоматичности регулирования их пере-
даточного числа. За последние годы эта проблема привлекала вни-
мание многих изобретателей, конструкторов и ученых.
Книга предназначается для подготовки инженеров автотрактор-
ной специальности, а также для инженеров, интересующихся раз-
витием современной автотракторной (главным образом гусеничной)
техники.
Книга выпускается двумя отдельными частями: часть пер-
вая — теория и часть вторая — конструкция и расчет.
Автор приносит благодарность преподавателям и адъюнктам
кафедры гусеничных машин Военной академии тыла и транспорта
доцентам Е. И. Магидовичу, Г. А. Иванову, М. М. Запрягаеву,
кандидатам технических наук Л. К. Крылову и И. С. Новохатько,
инженерам П. Я. Волчку, А. Е. Маркову, Ю. А. Кононовичу,
Л. В. Григоренко, А. Е. Ржонжевскому, А. Н. Сковородникову,
Б. А. Ляпунову, В. И. Белокоскову, А. И. Неженцеву, взявшим на
себя труд просмотреть рукопись книги и сделавшим по ней ряд
ценных замечаний.
ГЛАВА Г
ОСНОВЫ ТЕОРИИ ГУСЕНИЧНОГО ДВИЖИТЕЛЯ
1. КИНЕМАТИКА И ДИНАМИКА ГУСЕНИЧНОГО ОБВОДА
Гусеничным движителем называется рабо-
чий механизм гусеничной машины, с помощью
которого осуществляется ее движение.
Гусеничный движитель, как правило, состоит из двух гусениц 1
(рис. 1), двух ведущих колес 2, двух направляющих колес 3 с ме-
ханизмами натяжения 4 гусениц, опорных 5 и поддерживающих 6
катков.
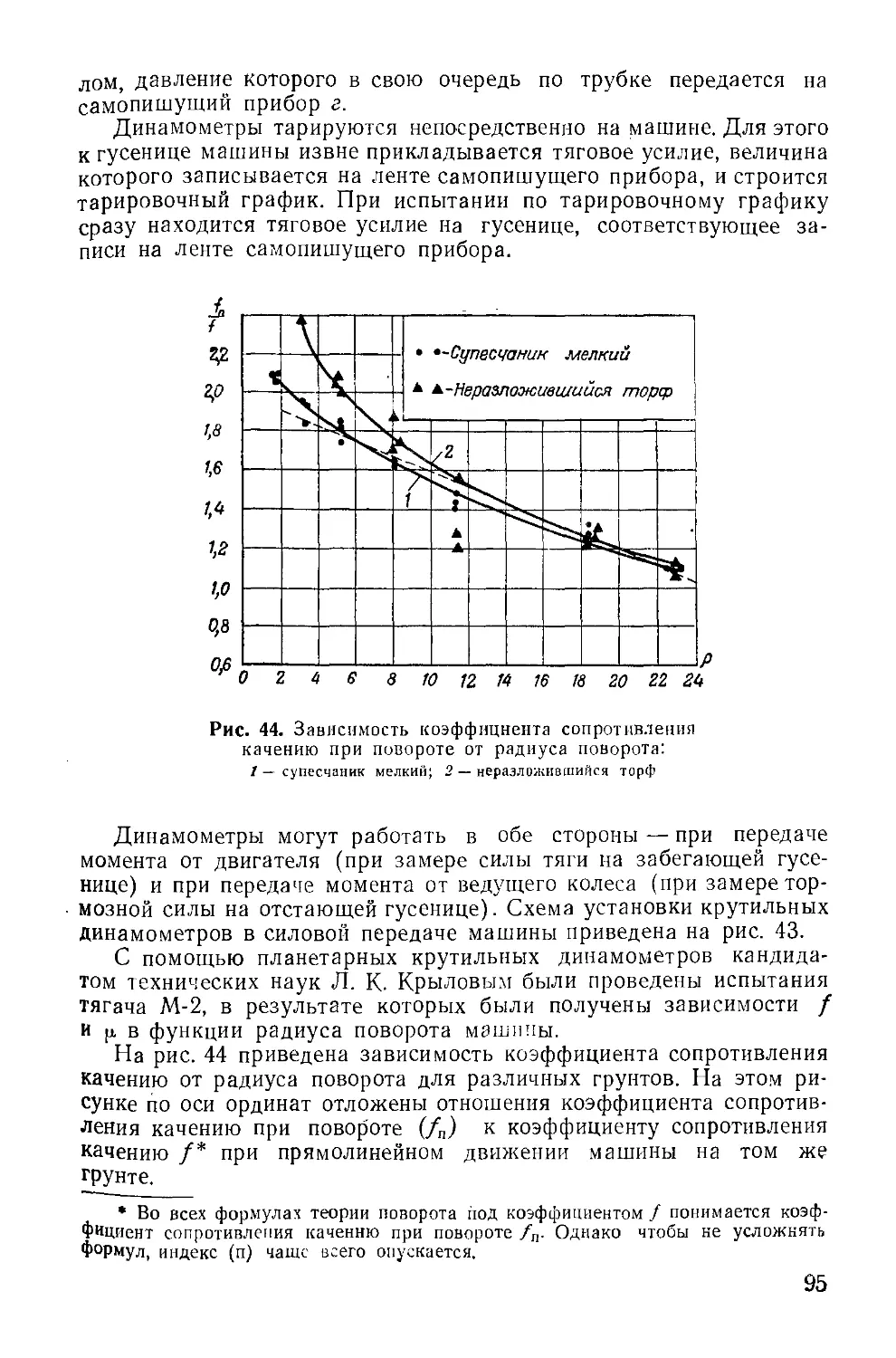
Рис. 1. Гусеничный движитель:
а — с поддерживающими катками; б — без поддерживающих катков; 1 — гусе-
ница; 2 — ведущее колесо; 3 — направляющее колесо; 4 — механизм натяжения;
5 — опорный каток; 6 — поддерживающий каток
Если применяются опорные катки большого диаметра, то под-
держивающие катки могут отсутствовать, так как их роль выпол-
няют опорные катки (рис. 1,6).
Основным элементом гусеничного движителя являются гусе-
ницы, которые могут быть выполнены или в виде замкнутых пло-
5
скозвенчатых цепей, или в виде резиновых или резино-металличе-
ских (с тросовой основой) лент.
Гусеницы состоят из дуговых ветвей, огибающих дуги колес и
катков, свободно провисающих или просто свободных ветвей, рас-
положенных между дуговыми ветвями, и опорных ветвей, лежа-
щих на грунте.
кинематика гусеничного обвода
Представим себе гусеницу в виде замкнутого геометрического
обвода, лежащего в вертикальной плоскости и имеющего нуле-
вую толщину и по форме копирующего гусеницу. Рассмотрим дви-
жение этого обвода.
Рис. 2. Определение скоростей движения гусеничного обвода
Свяжем неподвижные оси координат ху (рис. 2) с дорогой, по
которой движется машина (обвод). Подвижные оси коорди-
нат хоуо свяжем с плоскостью, в которой лежит обвод. Движение
осей х0уо характеризует поступательное движение машины в целом,
а следовательно, и обвода гусениц. Обозначим скорость этого' дви-
жения буквой V.
Кроме того, гусеничный обвод совершает относительное дви-
жение по отношению к реям координат хоуо. Это движение будем
характеризовать относительной скоростью оо.
Возьмем на обводе какую-нибудь произвольную точку а. Эта
точка будет участвовать в двух движениях — в относительном дви-
жении по отношению к осям хоуо и в переносном движении вместе
с осями хоуо по отношению к неподвижным осям ху.
Скорость относительного движения оо можно представить как
скорость перематывания гусеницы по отношению к корпусу ма-
шины. Скорость же переносного движения v есть скорость движе-
ния корпуса мащины по отношению к дороге. Абсолютная ско-
рость будет равна геометрической сумме относительной и перенос-
ной скоростей
V = + v.
6
Спроектируем скорости Vo и v на оси х и у. Получим
Vx — v + v0 cos <р;
Vy = v0 sin <p,
где Vx и Vy—проекции абсолютной скорости V на оси хну;
<р — угол, под которым расположена касательная
к обводу, проведенная в точке а.
Величина абсолютной скорости будет равна
V — V Vx + = V v2 -f-v2 + 2w0 cos <p . (1)
По этой формуле можно определить абсолютную скорость лю-
бой точки обвода. Практический интерес для нас представляют
точки, лежащие на опорной ветви.
Примем для опорной ветви (точка в) угол ? = 180°. Тогда из
формулы (1) получим
V = v — v0,
где V—абсолютная скорость скольжения опорной ветви
по отношению к доро'ге.
Если скорость движения машины v больше скорости перематы-
вания гусениц 0о, то скорость скольжения V есть величина поло-
жительная. Положительное скольжение опорной ветви называется
юзом; отрицательное скольжение (при v0^>v)—буксова-
нием.
При равенстве относительной и переносной скоростей скорость
скольжения равна нулю; в этом случае в каждый данный момент
опорная ветвь гусениц лежит на грунте неподвижно.
Проскальзывание опорной ветви по грунту будем характеризо-
вать коэффициентом а, который назовем коэффициентом
in роскальзы вания гусениц.
Коэффициент проскальзывания есть отношение переносной ско-
рости (скорости корпуса машины) к относительной скорости (ско-
рости перематывания гусениц), т. е.
Если коэффициент проскальзывания и скорость перематывания
гусениц известны, то из формулы (2) определяется скорость дви-
жения корпуса машины
v == w0.
Коэффициент проскальзывания может иметь следующие значе-
ния: при юзе 1, при буксовании а < 1 и при отсутствии про-
скальзывания а — 1.
В реальных условиях движения юз появляется при торможении
Машины, буксование — при разгоне или при движении по мягкому
7
грунту, обладающему значительным сопротивлением движению,
а также при движении на подъем или при движении с тяжелым
прицепом.
При повороте машины обычно одна из гусениц движется с бук-
сованием, а другая — с юзом, т. е. одновременно происходит юз и
буксование гусениц.
В теории гусеничных машин пользуются еще одним коэффици-
ентом, характеризующим проскальзывание гусениц по грунту.
Этот коэффициент определяется как отношение абсолютной ско-
рости скольжения опорной ветви при буксовании к относи-
тельной скорости:
Где а' — коэффициент буксования.
Хотя явление проскальзывания всегда наблюдается при движе-
нии машины, однако в большинстве практических расчетов им
пренебрегают, как величиной незначительной. При рассмотрении
же некоторых специальных вопросов, например поворота машины,
им пренебрегать нельзя, так как проскальзывание гусениц в этом
случае имеет большое принципиальное значение.
ДИНАМИКА ГУСЕНИЧНОГО ОБВОДА
Выделим на какой-нибудь свободной ветви обвода элементар-
ную дугу dS (рис. 3) и рассмотрим ее равновесие.
На дугу действуют следующие силы:
Р' + dP'—натяжение со стороны отброшенной верхней части
ветви;
Р'— натяжение со стороны отброшенной нижней части
ветви;
dQ — вес элементарной дуги, где dQ = qdS, a q — вес еди-
ницы длины обвода,
или отношение веса трака к его
шагу;
dK — центробежная сила, дей-
ствующая на дугу. Центро-
бежную силу выразим сле-
дующей формулой:
g р ’
где р — радиус кривизны обвода;
dS ,
Окончательно для элементарной
центробежной силы получим вы-
ражение
dK=-g~-d<f.
8
Спроектируем все силы, приложенные к элементарной дуге,
на ось Хо- Пренебрегая бесконечно малыми второго порядка, по-
лучим
— Р' sin d<? + dP' cos H—— sin d<? = 0.
Это выражение есть полный дифференциал функции *
Р = (Р‘---cos
' о
тогда dF = 0.
Интегрируя это выражение, находим
(Р' — т/2 ) cos ? = с,
(4)
где с — постоянная интегрирования.
Если свободную ветвь рассматривать как абсолютно гибкую
нить, то она будет провисать по цепной линии. Достаточно точно
цепная линия заменяется параболой, которую можно выразить
следующей формулой:
2c1Xq Xq
----2с----
где х0 и у0 — координаты точки, лежащей на параболе;
с и с, — постоянные интегрирования.
Для симметрично провисающей ветви, например для одной из
свободных верхних ветвей обвода, постоянные интегрирования бу-
дут (рис. 4):
где а —длина пролета ветви;
/0— относительный провис ветви, или отношение абсолютного
; провиса f к длине пролета а.
Подставляя постоянную интегрирования с в формулу (4), по-
ручим выражение динамического натяжения в произвольном сече-
нии ветви обвода:
Р’ =_________L -L.^2
8/о cos у ' g о ’
* Полный дифференциал равен сумме частных дифференциалов по всем пе-
ременным;
р dF dF
dF — —— dP + —— do.
de' d<f T
9
Из формулы следует, что натяжение зависит от угла ?. Наиболь-
шее натяжение будет в точках подвеса, где |? = '?п1ах- Наименьшее
натяжение — в нижней точке, где ? = 0.
Расчет показывает, что для реальных обводов при нормальном
натяжении гусеницы Ртах отличается от Pmin не более чем
на 2%. Поэтому приближенно можно принять в предыдущей фор-
муле ? = 0, т. е. считать, что натяжение в обводе не зависит от
положения сечения обвода, или во всех сечениях обвода натяже-
ние одинаковое. Тогда величина натяжения будет определяться по
формуле
P--W + T-"o- (5)
В этом уравнении первый член выражает статическое натяже-
ние в обводе, второй член — динамическое натяжение в обводе.
Статическое, или, как его иначе называют, предваритель-
ное натяжение (так как оно создается предварительным на-
тягом гусениц водителем), характеризуется величиной относи-
тельного провиса /0. Предварительное натяжение считают силь-
ным, если /0 — 0,01—0,02, средним, если /=0,02—0,03, и
слабым, если /0 = 0,03—0,05.
Динамическое натяжение в обводе вызывается действием цен-
тробежных сил и зависит от скорости движения обвода.
При скорости движения обвода примерно 20 км/час динамиче-
ское натяжение равно среднему статическому натяжению, а при
скорости 50 км/час превышает его почти в 5 раз.
Таким образом, в быстроходных гусеничных машинах на натя-
жение обвода большое влияние оказывает динамическое натяже-
ние. При высокой скорости движения машины величина динамиче-
ского натяжения может быть очень значительной. Поэтому гусе-
ницы быстроходных машин должны быть максимально облегчены.
Облегчение гусениц достигается созданием решетчатых или
«ажурных» траков. Были попытки изготовлять траки из легких
металлов, однако эти попытки положительных результатов пока
не дали, так как при этом значительно снижалась механическая
прочность гусениц.
10
Гусеницы быстроходных машин имеют вес на единицу длины
обвода д = 40—120 кг/м в зависимости от веса машины. Чем тя-
желее машина, тем выше q. Для тягачей максимальный вес погон-
ного метра гусеницы составляет 80 кг/м.
2. НЕРАВНОМЕРНОСТЬ ДВИЖЕНИЯ ГУСЕНИЧНОГО
ДВИЖИТЕЛЯ
Гусеницы состоят из траков, которые при перематывании со-
здают неравномерность движения гусеничного движителя и вызы-
вают в нем динамические нагрузки. Эти нагрузки носят периоди-
ческий характер и в свою очередь могут вызывать резонансные
явления в силовой передаче и в двигателе машины.
Пусть гусеница движется по ровному несминаемому грунту без
проскальзывания. Обозначим геометрические размеры движителя,
как указано на рис. 5. Спроектируем на ось х— х отрезки х, с,
г и а, тогда
х = с + sin ? — a cos а.
Из рис. 5 определим
асоза = И«2 — (Ь — rcosc?)2 (6)
и возьмем производную по времени от координаты х и угла <₽.
Получим выражение скорости движения оси заднего опорного
катка, или скорости корпуса машины,
dx г , (Ь — г cos ср) sin <₽ “I dv>
dt L )/ аг — (Ь — г cos ср)2 J dt
где г—радиус заднего колеса движителя;
dv
=— угловая скорость заднего колеса движителя.
Учитывая равенство (6)
и преобразуя полученное
выражение, находим
t'=(cos f+tg«• sin f) ru>, (7)
откуда следует, что скорость
движения машины есть
функция углов <р, а, и угло-
вой скорости ш.
Допустим, что заднее ко-
лесо является ведущим,
связанным с силовой переда-
чей машины. Пусть это ко-
лесо имеет со = const. Тогда
v будет функцией углов
и а. Так как угол а в равен-
Рис. 5. Определение кинематики гусе-
ничной цепи
11
Рис. 6. График изменения скорости дви-
жения машины
стве (6) зависит от <р, то и
в конечном итоге будет толь-
ко функцией ф.
Угол ф периодически из-
меняется от некоторого на-
чального значения до неко-
торого максимального значе-
ния, после чего цикл повто-
ряется. При этом верхний
трак наклонной ветви сопри-
касается с ободом колеса и,
следовательно, выключается
из наклонной ветви, переходя
в дуговую ветвь, а крайний трак опорной ветви переходит в наклон-
ную ветвь.
На рис. 6 приведен примерный график изменения скорости и
движения машины в функции угла ф. Из графика видно, что дви-
жение машины происходит неравномерно.
Неравномерность движения зависит в первую очередь от мелко-
звенчатости или крупнозвенчатости гусеницы. Чем более мелко-
звенчата гусеница, тем выше равномерность движения машины.
Если вместо гусеничной цепи будет гусеничная лента, то неравно-
мерности движения обвода не будет.
Проанализируем формулу (7) более подробно.
Так как выражение р скобке есть величина переменная, то при
oj = const будет переменной и скорость движения машины, а при
v = const — скорость вращения ведущего колеса ею. При больших
скоростях движения машины и, следовательно, при большой ча-
стоте изменения угла ф скорость v вследствие инерции машины
заметно изменяться не будет, но периодически будет изменяться
скорость ведущего колеса, а следовательно, скорости всех шесте-
рен и валов силовой передачи и скорость вала двигателя, -т. е.
в силовой передаче и двигателе возникнут колебательные явления.
Эти явления будут несколько сглаживаться проскальзыванием
имеющихся в силовой передаче фрикционных муфт, но все же
они могут вызвать чрезвычайно вредные резонансные явления.
Как показывают опыты, эти явления создают значительные на-
грузки в силовой передаче машины, иногда превосходящие в не-
сколько раз расчетные нагрузки.
Если машина движется на низшей передаче, т. е. с малой ско-
ростью, то время одного цикла изменения угла ф увеличивается.
За это время скорость движения машины v может заметно изме-
ниться. Скорость же ведущего колеса в этом случае можно счи-
тать величиной постоянной, так как изменение выражения в скобке
будет компенсироваться изменением скорости v. -
Неравномерность движения можно наблюдать у машин, имею-
щих крупнозвенчатые гусеницы, как, например, в сельскохозяй-
ственных тракторах, если трактор медленно движется по твердому
несминаемому грунту,
12
В действительности же при любых скоростях движения машины
скорости v и сю — величины переменные, причем при движении на
высших скоростях больше изменяется скорость ш, а на низших —
скорость V.
Рассматривая неравномерность движения гусеничного движи-
теля, мы предполагали, что машина движется по недеформирую-
щемуся грунту. Кроме того, предполагалось, что последний трак
опорной ветви не может выворачиваться, пока на нем находится
опорный каток.
Если машина движется по мягкому грунту и задний опорный
каток подрессорен (у быстроходных гусеничных машин), то край-
ний трак опорной ветви, когда по нему катится опорный каток,
не лежит неподвижно на грунте, а частично выворачивается.
Вследствие этого неравномерность движения обвода сглаживается.
Таким образом, действительная неравномерность движения обвода
будет несколько -ниже теоретической.
УДАР В ОБВОДЕ
При движении обвода траки ударяются об ободы' колес и кат-
ков. Удар вызывает шум в движителе и снижает к. п. д. дви-
жителя.
На рис. 7 представлена дуговая ветвь обвода и часть верхней
свободной ветви. Допустим, что дуговая ветвь вращается с некото-
рой постоянной угловой скоростью сю. При этом свободная ветвь
перемещается поступательно, т. е. параллельно самой себе. В мо-
Чгент соприкосновения крайнего трака свободной ветви с ободом
колеса поступательная скорость всех точек трака будет равна
,v' = ги>. После того как трак, придя в соприкосновение с ободом
.колеса, начнет вращаться вместе с колесом как одно целое, ско-
рость его средней точки будет равна v'' — г'ш. Таким образом,
в момент соприкосновения трака с ободом колеса его средняя
точка имеет скорость v', а после соприкосновения — v". Скорость
трака изменяется на величину До, при этом мгновенно в обводе
возникает явление удара.
Как и неравномерность движения, величина удара зависит от
шага траков гусеницы. Чем
ближе цепной обвод к ленточ-
ному, тем меньше в нем удары.
Неравномерность движения
и удары создают динамические
нагрузки в гусеницах движи-
теля. Эти нагрузки несколько
сглаживаются вследствие упру-
гости обвода, способной по-
глощать (амортизировать) ди-
намические нагрузки. Упру-
гость обвода объясняется нали-
чием в обводе свободно прови-
сающих ветвей.
Рис. 7. Удар в цепном обводе
13
С уменьшением предварительным натягом провиса свободных
ветвей обвод делается более жестким, а следовательно, увеличи-
ваются в нем динамические нагрузки, величина которых при силь-
ном натяге может стать критической. Поэтому, например, в крупно-
звенчатых гусеницах сельскохозяйственных тракторов в обводе
иногда делают дополнительную пружинную амортизацию, которая
предохраняет гусеницы от разрыва.
ОПРЕДЕЛЕНИЕ СКОРОСТИ ДВИЖЕНИЯ ГУСЕНИЧНОЙ МАШИНЫ
Вследствие неравномерного движения гусеничной машины ее
скорость может быть определена только как некоторая средняя
скорость.
Допустим, что за один оборот ведущего колеса перематывается
и расстилается перед машиной z траков; если шаг трака I, то за п
оборотов в секунду ведущее колесо перематывает длину гусени-
цы zln, т. е. на такое расстояние за одну секунду машина продви-
гается вперед. Это и будет ее средняя секундная скорость движе-
ния. При отсутствии проскальзывания опорной ветви
v = v0 — zln. (8)
Заменив цепной обвод ленточным обводом, скорость которого
равна средней скорости цепного обвода, получим
= = (9)
где (ик — угловая скорость ведущего колеса;
гх—приведенный радиус дуговой ветви ведущего колеса.
Величину приведенного радиуса определим следующим обра-
зом. Приравняем в формулах (8) и (9) v — v0, тогда получим
г. = 4. (10)
Как показывает теория гусеничного движителя *, приведенный
радиус приближенно равен радиусу окружности, проведенной че-
рез центры шарниров дуговой ветви цепного обвода, лежащей на
ведущем колесе. Этот радиус больше радиуса, определенного по
формуле (10), на 1 — 1,5%.
3. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
ГУСЕНИЧНОГО ОБВОДА
При вращении ленточного гусеничного обвода часть энергии
в нем теряется на внутреннее трение. Потеря энергии происходит
во всех сечениях обвода, в которых изменяется его кривизна. Дей-
ствительно, при изменении кривизны происходит относительное
* А. С. Антонов Теория гусеничного движителя. Машгиз, 1949.
14
Смещение двух Соседних сечении, в результате чего й возникают
внутренние потери.
Ленточный обвод имеет ветви с постоянной и переменной кри-
визной. Так, все дуговые ветви и спрямленная опорная ветвь (если
она лежит на ровном участке дороги) имеют постоянную кри-
визну. Свободные ветви, провисающие по цепной линии, имеют
переменную кривизну. Таким образом, потери в ленточном обводе
происходят только в свободных ветвях.
Так как кривизна меняется вдоль всей свободной ветви, то по-
тери будут происходить также вдоль всей ветви. Потери будут
больше в тех сечениях ветви, где больше изменяется кривизна.
В теории гусеничного движителя доказывается, что наибольшие
потери происходят в точке а перегиба свободной и дуговой ветвей
(рис. 8) (в точке их. сопряжения), так как в этом месте кривизна
изменяется наиболее сильно. В остальных сечениях свободной
ветви изменение кривизны незначительно, и потери в этих сечениях
Рис. 8. Изменение кри- Рис. 9. Работа шар-
бизны Б точках сопря- нира сопряжения дви-
жения свободных и дуго- ного обвода
вых ветвей
по сравнению с потерями в точках сопряжения также будут незна-
чительны. Поэтому этими потерями можно пренебречь и свободные
ветви считать спрямленными, т. е. имеющими постоянную нулевую
кривизну. Тогда по;ери в обводе будут определяться только поте-
рями в точках сопряжения.
Это положение с некоторым приближением можно отнести и
к цепному обводу, т. е. к гусеничной цепи.
Рассмотрим работу шарнира сопряжения цепного обвода.
Допустим, что траки а и b (рис. 9) вначале принадлежат сво-
бодной ветви (это положение звеньев обозначено на рисунке пунк-
.тиром). В какой-то момент трак b соприкоснется с ободом колеса;
в следующий момент трак b будет принадлежать дуговой ветви и
, начнет вращаться с угловой скоростью <u. С этой же скоростью
.будет происходить и относительное угловое перемещение трака b
.Ло отношению к траку а, находящемуся в свободной ветви.
5». Обозначим момент сил трения в шарнире через Mt, тогда мощ-
.Ность трения будет
Nt = • ш.
15
Суммируя эту мощность по всем шарнирам сопряжения, получим
мощность, затрачиваемую на трение в одном обводе,
1=п 1=п
^тр ~ = S
i=l ;=1
В гусеничных цепях применяются шарниры трех типов: про-
стой шарнир, или шарнир скольжения с плавающим паль-
цем; шарнир качения, или игольчатый шарнир; упругий
шарнир, или сайлент-блок.
Приближенно можно считать, что силы трения в шарнирах
первых двух типов подчиняются закону Кулона, т. е. пропорцио-
нальны нормальной силе, сжимающей трущиеся поверхности шар-
ниров. Тогда момент трения в шарнире может быть выражен сле-
дующей формулой:
где р- — коэффициент трения;
Ро — натяжение цепи;
dm — диаметр пальца шарнира (для простого шарнира) или
диаметр окружности, проходящей через оси иголок (для
игольчатого шарнира).
Если к обводу приложена сила Р, идущая на преодоление со-
противления движению обвода, то к. п. д. обвода будет равен
т) — Pv° -
,0 Рио+^тр’
Угловую скорость какой-нибудь дуговой ветви можно выразить
через относительную скорость и соответствующий приведенный ра-
диус дуговой ветви, тогда
После преобразования получим формулу к. п. д. цепного гусе-
ничного обвода
*1о =--------~п-------- (11)
, . Pai
+ чр г,-
1
где Р 01—натяжение в соответствующих ветвях обвода, в которых
находится рассматриваемый шарнир сопряжения.
Следует различать свободные ветви, в которых действует толь-
ко натяжение Р', определяемое по формуле (4), и ветви, в кото-
рых, кроме натяжения Р', действует еще рабочее натяже-
ние, создаваемое двигателем и передающееся от ведущего колеса
к опорной ветви, где оно проявляется в виде реакции грунта, кото-
рая называется с и л о й тяги (Р),
16
Рассмотрим влияние на к. п. д. обвода различных факторов.
Согласно формуле (11) к. п. д. зависит от коэффициента трения
(р), диаметра шарнира (</ш) трака, силы тяги (Р), натяжения, дей-
ствующего в обводе (Ро), и от радиусов дуговых ветвей обвода (г).
Коэффициент трения р. определяется опытным путем. При по-
мощи этого коэффициента учитываются потери не только на куло-
ново трение, но и другие: на удар, на абразивное трение. Поэтому
коэффициент р. точнее называется коэффициентом потерь.
Согласно опытным данным коэффициент р имеет значение
0,4—0,6; при этом меньшее значение соответствует большим ско-
ростям обвода.
Для закрытого шарнира, защищенного от попадания в него
абразива, коэффициент р уменьшается. Для шарниров с игольча-
тыми подшипниками, работающими в смазке, этот коэффициент
почти в 10 раз меньше, чем для открытых шарниров.
Формула (11) показывает, что чем меньше диаметр шарнира,
тем выше к. п. д. обвода. В сельскохозяйственных тракторах иног-
да применяют трубчатые пальцы шарниров. Это приводит к увели-
чению (1Ш> а следовательно, и к снижению к. п. д. обвода. В бы-
строходных гусеничных машинах пальцы стремятся делать воз-
можно меньшего диаметра, чтобы повысить к. п. д. обвода.
К. п. д. увеличивается с увеличением радиуса дуговых ветвей
обвода. Радиус дуговых ветвей зависит от радиуса колес (веду-
щего и направляющего) и радиуса крайних опорных катков.
В быстроходных гусеничных машинах делают опорные катки
большого и малого диаметра. Для повышения к. п. д. обвода катки
большого диаметра имеют преимущество по сравнению с катками
малого диаметра.
К. п. д. зависит от натяжения в обводе. С повышением скоро-
сти движения обвода динамическая составляющая натяжения уве-
личивается в квадратичной зависимости. При высоких скоростях
движения динамическая составляющая оказывает наибольшее
влияние на силу Ро и в основном определяет к. п. д. обвода.
Для повышения к. п. д. желательно, чтобы между трением
в шарнирах и натяжением в гусеницах не было линейной зави-
симости, определяемой законом Кулона. Такой зависимости может
и не быть, если применить шарниры качения, так как в них трение
увеличивается медленнее, чем натяжение, или упругие шарниры,
работающие на принципе скручивания резиновой втулки. Хотя
в упругих шарнирах имеются потери на внутреннее трение в ре-
зине (на гистерезис), но эти потери непропорциональны натяже-
нию гусеницы. С увеличением натяжения их относительная вели-
чина уменьшается.
К- п. д. увеличивается с увеличением силы тяги, т. е. силы,
движущей машину и представляющей собой реакцию грунта, при-
ложенную к опорным ветвям гусениц. Если бы обвод работал вхо-
лостую, то к. п. д. равнялся бы .нулю, так как сила тяги в этом
случае равна также нулщ.'"^а^1^г^^а§§м, энергия двигателя
2—2469 17
шла бы на перематывание гусениц и не совершала бы полезной
работы.
Заметим, что при движении машины на высших передачах,
т. е. в хороших условиях движения, к. п. д. падает не только
вследствие увеличения потерь в шарнирах (за счет увеличения
динамического натяжения обвода), но и вследствие уменьшения
силы тяги. Чем меньше сила тяги, тем менее рационально исполь-
зуется энергия в движителе, тем ниже его к. п. д.
Пример. Определим к. п. д. обвода гусеничного тягача, движущегося по хо-
рошей дороге с максимальной скоростью (рис. 10).
Рис. 10. Определение к. п. д. гусеничного обвода
Вес тягача G = 15 т; скорость обвода г?о = 50 км/час-, ведущие колеса — пе-
редние; радиус ведущих и направляющих колес и = 0,25 м; радиус передних
и задних опорных катков /2 = 0,12 м; вес трака гусеницы Q = 8 кг; шаг трака
/ = 0,14 м; длина пролета верхней свободной ветви а = 0,8 м; диаметр пальца
шарнира цепи = 0,02 м. Принимаем нормальный провис цепи fo = O,O3,
коэффициент потерь в шарнире ц = 0,4, коэффициент сопротивления качению
обвода на хорошей дороге с твердым покрытием f = 0,06, дорогу — горизон-
тальной.
Находим силу тяги одного обвода при равномерном движении машины по
горизонтальному участку пути. Сила тяги определяется произведением коэффи-
циента сопротивления качению на вес, приходящийся на одну гусеницу:
л fG 0,06-15000
Р = = —§--------= 450 кг'
Определяем натяжение в обводе. Так как ведущее колесо — переднее, то под ра-
бочим натяжением (Ро = Р' + Р) находятся пять шарниров сопряжения (на
рис. 10 обозначены черными точками). В трех шарнирах действует только натя-
жение Ро = Р'-
Определим величину натяжения Р'. Вес единицы длины обвода можно опреде-
лить как отношение веса трака к его шагу, т. е.
Q 8
? = 0J4=57 Кг/М-
Тогда согласно формуле (5)
2
Рабочее натяжение будет
Ро = Р1 + Р = 1330 + 450 = 1780 кг.
18
Определяем величину под знаком S в формуле (11):
8
х1 Рч1 2-1780 2-1780 1 780 1330 2-1330 _вепп ,
2.Т " ПХ25- + ^Т2- + W + W + = 78500 кг/м-
1
Подставляя полученные данные в формулу (11), получим
Отсюда следует, что в шарнирах сопряжения гусеничного обвода тратится
не менее 41% мощности, подводимой к обводу.
Рассмотрим, как влияет на к. п.д. обвода расположение ведущего колеса.
При заднем расположении ведущего колеса число шарниров сопряжения, ра-
ботающих под'рабочей нагрузкой, уменьшается до трех, тогда
8
2 ~ = 74970 кг/м.
1 1
Отсюда -г;о = 0,60.
Из рассмотренного примера следует, что в гусеничном обводе
при движении на высоких скоростях происходят значительные по-
тери энергии в шарнирах сопряжения. Так, при скорости движе-
ния машины 50 км/час к. п. д. обвода примерно равен 0,6. При
этом, как показывает расчет, на высоких скоростях движения,
когда обвод в основном растянут центробежными силами, к. п. д.
почти не зависит от расположения ведущего колеса.
4. ВЗАИМОДЕЙСТВИЕ ОПОРНЫХ ВЕТВЕЙ ГУСЕНИЦ
С ГРУНТОМ
Под действием крутящего момента, приложенного к ведущему
колесу со стороны силовой передачи, в задней наклонной ветви
обвода создается рабочее натяжение Р (рис. 11). Это натяжение
стремится выдернуть опорную ветвь из-под опорных катков. Но
так как вес машины прижимает опорную ветвь через катки
к грунту, то под действием натяжения Р на опорной ветви возни-
кает касательная реакция грунта, направленная в сторону движе-
ния машины, которая и удерживает опорную ветвь на месте. Эта
реакция называется силой тяги. Вследствие того что опор-
ная ветвь лежит на грунте неподвижно, при перематывании гусе-
ницы ведущим колесом корпус машины получает движение вперед.
При этом толкающие корпус силы Рт и Р" будут приложены
к оси заднего колеса и к оси заднего опорного катка.
Если пренебречь потерями в гусенице и на осях заднего колеса
и опорного катка, то равнодействующая толкающих сил Р? и Р'т
2* 19
будет равна силе тяги Р. Действительно, из схемы сил, приведен-
ной на рис. 11, имеем
Рт = Pcosa;
Р”=Р— Pcos а,
откуда
р; + р;=л
Нетрудно доказать, что сумма толкающих сил равна силе тяги
и при переднем расположении ведущего колеса.
Рис. И. Определение сил, толкающих корпус
машины
Таким образом, силу тяги можно условно представить как силу,
вызывающую движение корпуса, а следовательно, и машины в це-
лом. В этом случае нет необходимости определять внутренние
силы, толкающие корпус.
---------------------------------—
Рис. 12. Реакции грунта, действующие на опорную ветвь гусеницы
Рассмотрим подробнее взаимодействие опорных ветвей гусениц
с грунтом.
При движении машины на опорную ветвь действуют касатель-
ные М и нормальные Ли реакции грунта, приложенные к опорной
ветви, как показано на рис. 12.
Касательные реакции возникают вследствие натяжения опор-
ных ветвей, которое является результатом перематывания или тор-
можения гусениц, а также вследствие местного проскальзывания
20
участков опорной ветви по грунту. В общем случае касательные
реакции могут иметь как положительное, так и отрицательное зна-
чение, т. е. быть направлены вперед (по движению машины) или
назад.
Если опорная ветвь имеет положительное проскальзывание
(юз), то все касательные реакции получают только отрицательное
значение, т. е. направлены против движения машины.
Если проскальзывание опорной ветви отрицательное (буксова-
ние), то все касательные реакции получают положительное значе-
ние, т. е. направлены по движению машины.
Спроектируем касательные и нормальные реакции на ось х — х,
лежащую в плоскости дороги. При этом положительные проекции
обозначим штрихом, а отрицательные — двумя штрихами, т. е.
№'х > 0, &t"x < 0, Ьп'х >0 и Дл" 0.
Сумма положительных проекций касательных реакций и яв-
ляется силой тяги, возникающей на гусеницах:
Р = 24-
Сумма всех остальных проекций является силой сопро-
тивления качению; обозначим ее буквой R, тогда
#=24 + 24 + 24-
Рассмотрим два частных случая движения машины.
Допустим, что тягач тянет в гору тяжелый прицеп по гладкой
дороге с твердым недеформирующимся покрытием; при этом гусе-
ницы частично пробуксовывают.
Так как грунт под гусеницами не деформируется, то все нор-
мальные реакции направлены перпендикулярно к плоскости до-
роги и, следовательно, S ^пх + 2 ^пх ~ 0- При буксовании гу-
сениц касательные реакции положительны и, следовательно,
2Д^ = 0, а сила сопротивления качению равна нулю (# = 0). На
Опорных ветвях гусениц будет реализоваться только сила тяги (Р).
, Рассмотренный случай движения является идеализированным,
так как нельзя представить абсолютно ровный и абсолютно неде-
формирующийся грунт. Фактически сопротивление качению имеется,
во оно настолько мало по сравнению с силой тяги, что им можно
пренебречь.
, . Допустим, что одиночный тягач тормозится на ровном недефор-
мирующемся грунте (асфальте). Тогда опорные ветви будут дви-
гаться, юзом. Отсюда S 4 = 2 ^пх + 2 ^п'х = 0- На опорных
ветвях будет реализоваться только сила сопротивления ка-
чению
# = 24-
внешняя касательная сила внутри машины уравновешивается
’Нательной силой на тормозах.
21
При движении машины по мягкому (деформирующемуся) грун-
ту всегда появляется сопротивление от проекций нормальных ре-
акций (S^nr)- Это сопротивление назовем лобовым со-
противлением в отличие от касательного сопро-
тивления, которое возникает вследствие действия проекций
касательных реакций (2
Касательные реакции появляются в результате действия раз-
личных тормозных сил, возникающих внутри машины, например
сил сопротивления на осях катков, в шарнирах гусениц, в силовой
передаче и т. д.
Касательное сопротивление может иметь место только в ведо-
мом движителе, когда толкающее корпус машины усилие
приложено извне, а не создается внутри машины (например, дви-
гателем) .
Если на опорных ветвях гусениц возникают силы тяги как ре-
зультат работы двигателя, то такой движитель называется ве-
дущим.
Примером ведомого движителя является движитель прицепа.
Ведомый движитель может иметься и у тягача, если тягач дви-
жется по инерции при отключенном двигателе или под гору под
действием силы тяжести.
При повороте машины к одной из гусениц обычно приклады-
вается сила тяги, создаваемая двигателем, а к другой — тормозная
сила, создаваемая тормозом механизма поворота. В этом случае
гусеничный движитель является одновременно и ведущим и ве-
домым.
Ведущий движитель при работе всегда частично пробуксовы-
вает, а ведомый — частично движется юзом.
5. МЕТОДЫ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ
СИЛЫ СОПРОТИВЛЕНИЯ КАЧЕНИЮ И СИЛЫ ТЯГИ
ПО СЦЕПЛЕНИЮ
Для тяговых расчетов необходимо знать сопротивление каче-
нию машины и предельное значение силы тяги, которую можно
реализовать на данном грунте по сцеплению гусениц с грунтом.
Обе эти силы могут быть определены экспериментально или вы-
числены по формулам, если будут известны соответствующие опыт-
ные коэффициенты. Рассмотрим методы экспериментального опре-
деления силы сопротивления качению, силы тяги по сцеплению и
коэффициенты, характеризующие эти силы.
СИЛА СОПРОТИВЛЕНИЯ КАЧЕНИЮ И КОЭФФИЦИЕНТ
СОПРОТИВЛЕНИЯ качению
Отношение силы сопротивления качению R, определенной экспе-
риментально на горизонтальном участке пути, к весу машины G
называется коэффициентом сопротивления каче-
нию f, т. е. __ н
'~~G'
22
Сила R может быть определена одним из следующих методов
методом буксировки, методом затухания движения или мето ом
замера силы тяги, равной силе сопротивления качению при равно
мерном движении машины.
Метод буксировки
Испытуемая машина буксируется тягачом или при помощи
какого-нибудь другого тягового средства (например, с помощью
лебедки); при этом между буксируемой машиной и тягачом поме-
щен динамометр (рис. 13).
Рис. 13. Определение силы сопротивления качению
методом буксировки
Показание динамометра дает значение- силы сопротивления
качению R = Рл.
При испытании должны соблюдаться следующие условия.
Движитель испытуемой машины должен быть отключен от си-
ловой передачи, так как сопротивление в силовой передаче вызы-
вает дополнительные касательные сопротивления грунта и, следо-
вательно, увеличивает силу сопротивления качению ведомого дви-
жителя по сравнению с силой сопротивления качению ведущего
движителя. Полностью избавиться от касательных сопротивлений
нельзя, так как даже при полностью отключенной силовой пере-
даче в движителе остаются внутренние силы сопротивления, кото-
рые влияют на величину силы R.
Участок, на котором производятся испытания, должен быть
строго горизонтальным, т. е. не иметь подъемов и спусков. Если
горизонтальный участок подобрать нельзя, то испытания следует
проводить по двум взаимно противоположным направлениям и
определять среднее арифметическое значение полученных сил.
В этом случае влияние подъема и спуска на силу R исключается.
При испытаниях движение машины должно быть равномерным,
так. как силы инерции могут значительно исказить результаты
испытаний.
Если испытуемая машина буксируется тягачом, то она не дол-
жна двигаться по его следу, так как лобовое сопротивление на
23
уплотненном гусеницами тягача грунте будет меньше, чем на
обычном грунте. Чтобы избежать движения по следу, применяют
буксировку испытуемой машины с помощью длинного троса.
Метод затухания движения
Машина разгоняется до определенной скорости v, после чего
силовая передача отключается и машина движется по инерции до
остановки.
™ 8G ->
Кинетическая энергия движения машины Jo— ~2gV должна
равняться работе силы R на пути 5Т:
Т'о = RS-r,
откуда
= (12)
где 8 — коэффициент, учитывающий кинетическую энергию вра-
щающихся масс машины, так называемый коэффициент
вращающихся масс. Приближенно этот коэффициент мож-
но принять равным 1,2.
Метод замера силы тяги
При равномерном движении машины на горизонтальном уча-
стке пути сила тяги равняется силе сопротивления качению. Заме-
ряя силу тяги, можно определить и силу сопротивления качению.
Для замера силы тяги применяются динамометры различных
типов: электрические или механические крутильные динамометры,
устанавливаемые в силовую передачу, с помощью которых заме-
ряется передаваемый крутящий момент.
Из рассмотренных трех методов определения сопротивления
качению последний метод является хотя и сложным, но наиболее
точным. Этот метод, в частности, позволяет определять сопротивле-
ние качению как функцию скорости движения машины.
Опыты показывают, что сопротивление качению зависит от
многих факторов, например: от характера и состояния грунта, от
удельного давления гусениц на грунт, от конструкции движителя
(от диаметра и числа опорных катков, от формы траков гусениц),
от скорости движения машины и т. д. Учесть влияние всех этих
факторов на сопротивление качению невозможно. В расчетах при-
ближенно принимают, что сопротивление качению зависит только
от характера грунта и от сцепного веса машины и не зависит от
устройства ее ходовой части и скорости движения. В этом случае
оценивают сопротивление качению по следующей формуле:
(13)
24
где R—расчетная сила сопротивления качению;
f— коэффициент сопротивления качению;
(7С — сцепной вес машины.
Сцепным весом называют равнодействующую всех внеш-
них сил, действующих на машину и прижимающих машину к грун-
ту, т. е. проекцию внешних сил на ось, перпендикулярную к пло-
скости опорных ветвей гусениц (к плоскости дороги). Сцепной вес
зависит в первую очередь от веса машины, а также от угла подъ-
ема дороги, от веса прицепа и расположения упряжного крюка
тягача и прицепа.
При движении одиночной машины по горизонтальному участку
пути сцепной вес равен весу машины:

дри движении одиночной машины на подъем
= Geos а, (14)
Рис. 14. Определение сцепного веса тягача:
а — тягач с многоосным прицепом; б — тягач с одноосным прицепом
25
Если тягач движется с многоосным прицепом, как показано на
рис. 14, а, то сила на упряжном крюке направлена по стяжке
под углом 7 к силе сопротивления на крюке /?„. Сцепной вес тя(
гача будет выражаться следующей формулой:
(7С = Geos а + 7?к tg у, (15)
а сцепной вес прицепа
GC1 = Gx cos а — R, tg 7. (16)
В выражениях (15) и (16) угол 7 определяется из геометрических
размеров сцепки:
tgT = A^K£. (17)
Если прицеп одноосный (рис. 14,6), то угол 7 можно опреде-
лить по формуле
tgY = ^-, (18)
где Qx6—хоботовое давление прицепа.
Хоботовое давление в свою очередь определяется из условий
равновесия прицепа:
Qx6 = Gx cos а + RK------y-Gjsina. (19)
*2 12 *2
Кроме сцепного веса, для определения силы сопротивления ка-
чению надо знать коэффициент сопротивления качению. Значение
коэффициента сопротивления качению приведено в табл. 1.
Таблица 1
Коэффициенты сопротивления качению (для гусеничного движителя)
Дорога /
Асфальтовое шоссе ...... Булыжно-щебеночное шоссе Проселочная дорога . Каменисто-песчаное дно брода Снежная целина (погружение гусениц на 300—700 мм) Укатанная снежная дорога Заболоченная местность (погружение гусениц до 200 мм) Свежевспаханное поле Глубокая грязь Сухое болото Грунт суглинистый с травяным покровом 0,04—0,05 0,06—0,07 0,07—0,10 0,15—0,20 0,15—0,25 0,06 0,20—0,25 0,10—0,12 0,10—0,13 0,10—0,12 0,07—0,09
Для сравнения в табл. 2 приведены коэффициенты сопротив-
ления качению для колесного движителя.
26
Таблица 2
Коэффициенты сопротивления качению (для колесного движителя)
Дорога / для стальных ободов / для баллонов
Асфальтовое шоссе 0,02 0,02
Сухая укатанная дорога 0,06—0,08 0,03—0,05
Свежевспаханное поле 0,20 0,18
Болото 0,40 0,25
Укатанная снежная дорога 0,05 0,03
Из сравнения данных табл. 1 и 2 видно, что гусеничный дви-
житель имеет меньшее сопротивление качению на мягких грунтах
и большее — на твердых грунтах.
Следует иметь в виду, что значения коэффициентов сопротивле-
ния качению гусеничных машин всегда несколько завышены, так
как в них учитываются внутренние потери в ходовой части ма-
шины, от которых при испытании нельзя освободиться. Потери эти
на твердых грунтах могут быть очень значительными и вполне со-
измеримыми с потерями, идущими на деформацию грунта, т. е.
с истинными внешними потерями сопротивления качению машины
(все внутренние потери должны учитываться к. п. д. машины).
СИЛА ТЯГИ ПО СЦЕПЛЕНИЮ И КОЭФФИЦИЕНТ СЦЕПЛЕНИЯ
Силой тяги по сцеплению называется предельное зна-
чение силы тяги, которое можно реализовать на данном грунте.
Силы сцепления опорных ветвей гусениц с грунтом склады-
ваются из двух видов сил: сил кулонова трения, возникающих
между наружной поверхностью гусениц и грунтом Д/Тр, и сил за-
цепления шпор траков с грунтом Д/3 (рис. 15).
Рис. 15. Зацепление шпор с грунтом
Силы зацепления могут возникнуть только после того, как сила
натяжения гусеницы Р, стремящаяся сдвинуть опорную ветвь
с места, будет больше сил кулонова трения 2S А^тр- В этом случае
произойдет сдвиг гусеницы и шпоры упрутся в грунт (перед шпо-
рой возникнет лунка, что является признаком частичного проскаль-
зывания опорной ветви). На шпорах возникнут реакции зацепле-
ния S Д/8.
27
При частичном проскальзы-
вании опорной ветви сила тяги,
равная по абсолютной величи-
не силе натяжения Р задней
наклонной ветви, будет равна
В этой формуле наличие
второго члена указывает на ра-
боту шпор и, следовательно,
на явление частичного про-
скальзывания опорной ветви
гусеницы по грунту.
Отношение силы тяги к весу
машины называется удель-
ной силой тяги:
Рис. 16. График зависимости удельной — = <рг.
силы тяги от коэффициента буксования G
(характеристика гусеницы по сцепле- тт ,« ,
НиЮ) На рис. 16 приведен график
зависимости удельной силы
тяги от коэффициента буксования а', полученный опытным путем
на горизонтальном участке пути.
Из этой зависимости следует, что при некотором определенном
значении коэффициента буксования а' удельная сила тяги дости-
гает своего максимального значения (<ртах = >р), после чего про-
исходит срыв грунта гусеницами, или 100% буксование гусениц.
Предельное по сцеплению значение удельной силы тяги <р на-
зывается коэффициентом сцепления.
График на рис. 16 характеризует сцепные качества гусениц.
Так, для гусениц, имеющих различную форму опорной поверхно-
сти (большие или малые шпоры, наружные шпоры или впадины),
график будет иметь различный вид. Лучшим сцеплением обладают
гусеницы при наибольшем значении коэффициента сцепления. <р и
наименьшем значении коэффициента буксования а'. Кривая
изображенная на рис. 16, называется характеристикой
гусеницы по сцеплению. Очевидно, что, чем круче ха-
рактеристика, тем лучше сцепные качества гусениц.
Рис. 17. Экспериментальное определение коэффициента сцепления:
Z — испытуемый тягач; 2 — динамометр; 3 — тормозная тележка; 4 — счетчик оборотов
28
Экспериментально характеристика определяется следующим
образом.
Испытуемый тягач 1 (рис. 17) буксирует тормозную тележку 3.
Между тягачом и тележкой помещен динамометр 2. Сила тяги на
гусеницах тягача будет равна
Р=/? + /?«,
где Rx— сопротивление на крюке, замеряемое динамометром;
R— сила сопротивления качению, которую можно определить
по формуле (13), если задаться значением коэффициента
сопротивления качению f для данного грунта.
Отсюда находим Р и, следовательно,
Далее опытным путем определяется коэффициент буксования
,__ V _ v0 — v _ So — S'
Q — 1 "" Q
Vo Vo <Sq
где б),— теоретический путь, проходимый машиной при равномер-
ном движении;
5—фактический путь, проходимый машиной.
Теоретический путь замеряется счетчиком 4 оборотов гусеницы,
фактический путь — непосредственно на дороге.
После определения коэффициентов <р' и а' можно построить
графическую зависимость <р' от о', или характеристику гусеницы.
; Силу тяги по сцеплению, а следовательно, и коэффициент
«цепления можно определить и без замера буксования гусениц.
Для этого тягач так загружается динамометрической тележкой,
чтобы его гусеницы полностью буксовали. Тогда динамометром за-
меряют силу тяги по сцеплению.
В табл. 3 приведены значения коэффициентов сцепления для
Гусеничного движителя.
Таблица 3
Коэффициент сцепления (для гусеничного движителя)
Дорога т
Асфальт летом Твердый грунт с дерновым покровом (целина) .... Уплотненный суглинистый грунт (грунтовые дороги) Слег плотный глубиной 300 мм Песок «ОДото . 0,3—0,5 0,7-0,9 0,6—0,8 0,4—0,6 0,5—0,6 0,3—0,5
29
Приведенные в табл. 3 данные относятся к гусеницам быстро-
ходных гусеничных машин, не имеющих высоких шпор.
Установка дополнительных (съемных) шпор может повысить
коэффициент сцепления в 1,3—1,5 раза в зависимости от харак-
тера грунта. На несвязанных, например песчаных, грунтах шпоры
незначительно влияют на коэффициент <р. Наоборот, на слежав-
шихся, плотных грунтах, особенно покрытых дерном, это влияние
может быть очень значительным. Так, для гусениц сельскохозяй-
ственных тракторов, имеющих высокие шпоры, коэффициент ? на
влажном скошенном лугу достигает 1,2; на сухом же песке он
составляет всего 0,4—0,5.
Если известен коэффициент сцепления, то можно определить
силу тяги по сцеплению Рс по формуле
Рс = <?Gc,
(20)
где (7С —сцепной вес машины.
Сила тяги по сцеплению определяет возможности движения ма-
шины по сцеплению гусениц с грунтом. Эта величина имеет боль-
шое значение в тяговых расчетах гусеничных машин.
Влияние конструктивных параметров гусеницы на ее сцепные
качества
В теории гусеничного движителя рассматривается вопрос
о влиянии конструктивных параметров гусениц на коэффициент
буксования а' и на коэффициент сцепления ? *. Приведем здесь
без вывода основные формулы, характеризующие эти зависимости:
максимальное значение коэффициента буксования
а
max
(22)
коэффициент сцепления
где <р0—коэффициент трения гусениц о грунт;
р-—коэффициент внутреннего трения грунта;
(7С — сцепной вес машины;
с — коэффициент пропорциональности между напряжением
в грунте и его деформацией;
F—упорная площадь шпоры;
i — число шпор на опорной ветви гусеницы;
L—длина опорной ветви.
* Карельских Д. К-, Кристи М. К. Теория, конструкция и расчет трак-
торов. Машгиз, 1940.
30
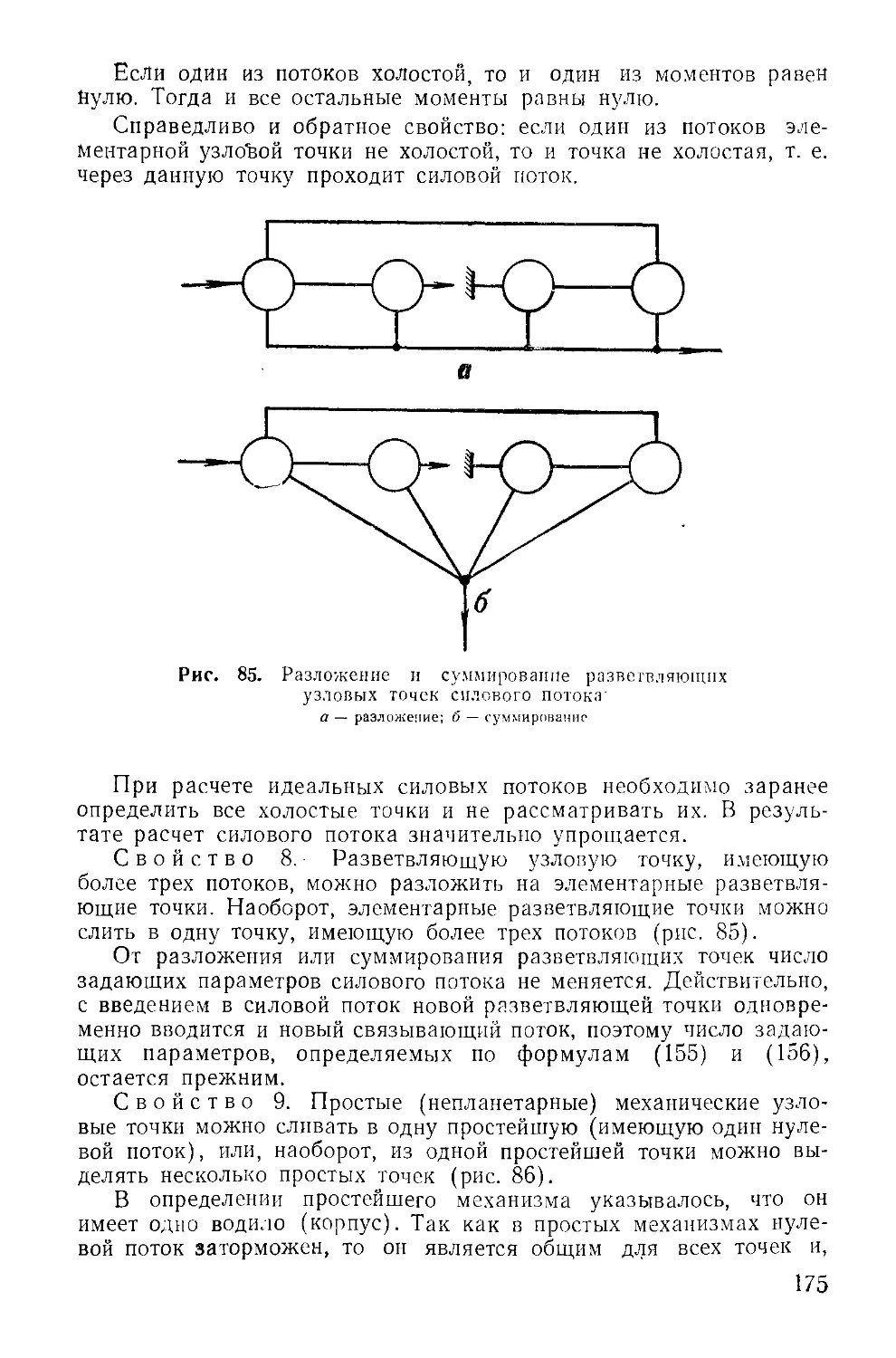
Из формул (21) и (22) следует, что чем больше шпор имеют
'опорные ветви гусениц, тем меньше при равной силе тяги буксова-
ние гусениц. Максимальное значение коэффициента буксования за-
висит от длины опорной ветви. Чем длиннее опорная ветвь, тем
меньше коэффициент атах.
Коэффициенты буксования а' и атах зависят также от упорной
площади шпор F. Чем больше упорная площадь, тем меньше бук-
сование.
Из формулы (23) следует, что коэффициент сцепления ? зави-
сит от числа шпор, от упорной площади шпор и от длины опорных
ветвей гусениц.
Большого влияния на коэффициент сцепления число шпор не
оказывает. Действительно, если приближенно принять 1 + i I,
то коэффициент сцепления вообще не будет зависеть от числа
шпор.
Коэффициент сцепления увеличивается с увеличением упорной
площади шпор и длины опорной ветви гусениц.
На коэффициент сцепления влияет также сцепной вес. Чем
больше сцепной вес, тем меньше коэффициент сцепления. Однако
следует заметить, что в формуле (23) член ~~ — величина ма-
Лая, которой можно пренебречь. Учитывая приближенное равен-
ство 1 получим после подстановки в формулу (23)
। р
? = ?о + -2-'
, Отсюда следует, что коэффициент сцепления в основном зави-
сит от коэффициента трения гусениц о грунт (?о) и от коэффи-
циента внутреннего трения грунта (р). Влияние шпор на сцепные
качества гусениц проявляется через коэффициент р. Например,
для уплотненного песчаного грунта <р0 = 0,35; р = 0,65; тогда <р —
^0,35 + 0,32 = 0,67.
В данном случае влияние шпор на коэффициент сцепленйя
очень значительное.
ГЛАВА II
ДИНАМИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
ГУСЕНИЧНОГО ПОЕЗДА
1. УРАВНЕНИЯ ДВИЖЕНИЯ ГУСЕНИЧНОГО ПОЕЗДА
ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ, ОПИСЫВАЮЩИЕ
ДВИЖЕНИЕ ГУСЕНИЧНОГО ПОЕЗДА
Гусеничный поезд, состоящий из тягача и одного или несколь-
ких прицепов, представляет собой механическую систему, движе-
ние которой описывается двумя законами механики: принципом
Даламбера и теоремой живых сил.
Согласно принципу Даламбера всякую неравномерно
движущуюся систему можно рассматривать
как находящуюся в статическом равновесии,
если к внешним силам, действующим на си-
стему, добавитьсилы инерции.
Теорема живых сил может быть сформулирована следующим
образом.
Производная по времени от полной кинетиче-
ской энергии системы равна сумме мощностей
внешних и внутренних сил, действующих в си-
стеме.
Математически теорема живых сил запишется в таком виде:
= + (24)
где То— полная кинетическая энергия системы, или кинетиче-
ская энергия в переносном и относительном дви-
жении;
S Мвш — сумма мощностей внешних сил, приложенных к си-
стеме;
~S — сумма мощностей внутренних сил, действующих в си-
стеме.
В качестве механической системы можно рассматривать от-
дельно тягач и прицеп или поезд в целом. В дальнейшем при вы-
воде уравнений движения под системой будем понимать одиночную
машину — тягач или прицеп.
32
ВНЕШНИЕ СИЛЫ, ДЕЙСТВУЮЩИЕ НА ГУСЕНИЧНЫЙ ТЯГАЧ
И НА ПРИЦЕП
В общем случае неравномерного прямолинейного движения на
подъем (или спуск) на гусеничный тягач действуют следующие
внешние сиды (рис. 18):
G — сила веса, приложенная в центре тяжести тягача;
Р — сила тяги, действующая в плоскости опорных ветвей гу-
сениц; -
R — сила сопротивления качению; в дальнейшем будем счи-
тать, что опорные ветви гусениц имеют частичное буксова-
ние, поэтому сила R будет являться лобовым сопротивле-
нием качению гусениц;
/—сила инерции поступательного движения тягача, прило-
женная к его центру тяжести;
— сила тяги на крюке;
N—равнодействующая нормальных реакций грунта, прило-
женная в центре давления опорных ветвей гусениц.
Рис. 18. Внешние силы, действующие на тягач
в общем случае неравномерного прямолинейного
движения
Задачу рассматриваем как плоскостную, поэтому силы Р, R и JV
есть равнодействущие сил, приложенных к отдельным гусеницам.
На рис. 19 представлена схема внешних сил, действующих на
гусеничный прицеп. На схеме Rt представляет собой лобовую со-
ставляющую силы сопротивления качению; Pt — касательную со-
ставляющую силы сопротивления качению. Остальные силы имеют
то же значение, что и для тягача.
Разделение силы сопротивления качению на две составляю-
щие— касательную и нормальную (лобовую) — позволяет сопо-
ставлять эти силы с соответствующими силами, действующими на
тягач (силы Р и R). Природа сил R и Ri одинакова: это лобовые
‘(нормальные) реакции грунта, представляющие собой лобовое со-
противление движению тягача и прицепа. Природа сил Р и Pi
.также одинакова: это касательные реакции грунта, вызванные дей-
3—2469 33
стВием внутренних сил, развивающихся в тягаче й прицепе. Раз-
ница между Р и Pi заключается только в направлении их действия.
Реакция Р, вызванная рабочим натяжением гусениц, положительна;
реакция Р\, вызванная действием внутренних сопротивлений в при-
цепе, отрицательна.
• Внутренние сопротивления в прицепе могут быть различны.
Прежде всего это силы трения в движителе.
Рис. 19. Внешние силы, действующие на гу-
сеничный прицеп в общем случае неравно-
мерного прямолинейного движения
Если в качестве прицепа буксируется какая-нибудь аварийная
машина, причем для общности рассматриваемых явлений можем до-
пустить, что ее силовая передача не отключена ни от двигателя, ни
от движителя, то к силам трения в движителе прибавятся еще силы
трения в силовой передаче и тормозные силы, создаваемые прово-
рачиваемым вхолостую двигателем. Так же будут действовать силы
и в прицепе, если на нем установлен тормоз.
Рис. 20. Внешние силы, действующие на колесный прицеп
в общем случае неравномерного прямолинейного движения
При неравномерном прямолинейном движении, кроме перечис-
ленных сил, будут еще действовать инерционные силы вращаю-
щихся деталей машины, которые также создают сопротивление
34
проворачиванию движителя и вызывают на грунте отрицательную
касательную реакцию.
На рис. 20 представлена схема внешних сил, действующих на
колесный прицеп.
В этом случае внешние силы имеют ту же природу, что и
внешние силы, действующие на гусеничный прицеп. Разница заклю-
чается только в том, что на колесный прицеп действуют реакции
грунта (нормальные и касательные), приложенные к каждому ко-
лесу в отдельности.
ПЕРВОЕ УРАВНЕНИЕ ДИНАМИКИ ТЯГАЧА И ПРИЦЕПА
Спроектируем все внешние силы, действующие на тягач, на
ось х — х (см. рис. 18).
Получим
Р— (R + G sin а) — Рк cos у — / = 0.
Обозначим выражение в скобке через /?0 и назовем эту вели-
чину силой сопротивления движению (не смешивать
с силой сопротивления качению /?); тогда
Ro = R + G sin а — f Gc + G sin а. (25)
Сила сопротивления движению может быть выражена через
коэффициент сопротивления движению /0:
Ro —/(ХЛ
Где
/o = sina+/-^.
Если угол а <10°, то приближенно можно принять sin а =
= tg а = I, где I—подъем дороги, a cos а ==1. При угле сцепки
тягача и прицепа т, близком или равном нулю, будем иметь
Gc = G. Окончательно получим
fo=f + i- (26)
Кроме того, обозначим Pkcosy через /?к; эта величина назы-
вается сопротивлением на крюке.
Выражая силу инерции через ускорение, из уравнения проекций
сил на продольную ось машины получим согласно Даламберу
первое уравнение динамики гусеничного тягача
(27)
Уравнение внешних сил для прицепа (см. рис. 19) может быть
получено из уравнения (27), если ввести для соответствующих ве-
личин индекс 1 и изменить знак сил Р и RK. Получим первое
Уравнение динамики гусеничного прицепа в та-
ком виде:
£L-^- = -Pi-Roi+Rv (28)
3« 35
Заметим, что в уравнении (28)
RK1 = R*-
Сила сопротивления движению Z?o i может быть определена по'
формуле (25), если входящим в формулу величинам приписать
индекс 1.
Для колесного прицепа согласно схеме сил, представленной на
рис. 20, будем иметь первое уравнение динамики
~ sin “ + <29)
Если обозначить
Ri= Rx + R,,
то первое уравнение динамики колесного прицепа выразится в та-
ком же виде, как и для гусеничного прицепа (см. формулу 28).
ВТОРОЕ УРАВНЕНИЕ ДИНАМИКИ ТЯГАЧА И ПРИЦЕПА
Применим теорему живых сил к выводу второго уравнения ди-
намики тягача.
Определим вначале полную кинетическую энергию тягача То.
Кинетическая энергия будет равна кинетической энергии тягача
в его поступательном движении с корпусом (Т) и кинетической
энергии масс, участвующих в относительном движении по отноше-
нию к корпусу (Т'). В относительном движении участвуют эле-
менты движителя (гусеницы, колеса, катки), силовой передачи
(валы, шестерни, муфты, тормозные барабаны) и двигателя (махо-
вик, коленчатый вал, шатуны, поршни).
Полная кинетическая энергия будет равна
Обозначим величину в скобке через 8 и назовем ее коэффи-
циентом вращающихся масс.
Тогда
7’0 = 87’,
где
т— Gv2
2g •
Коэффициент вращающихся масс является величиной, не завися-
щей от времени. Поэтому производная по времени от полной кине-
тической энергии может быть выражена как
dT0 6G dv <i6G dv
dt g dt g dt *
(30)
36
Вычислим теперь мощности внешних и внутренних сил, дей-
ствующих на тягач.
Внешние силы, которые могут выполнять работу, а следова-
тельно, давать мощность,— это сила тяги (Р), сила сопротивления
качению (7?), сила сопротивления подъему (Gsina) и сила сопро-
тивления на крюке (/?к). Соответственно этим силам будем иметь
мощности, как произведение силы на скорость перемещения той
части машин, к которой приложена данная сила.
Условимся приписывать мощностям знак плюс, если сила и ско-
рость направлены в одну сторону, и знак минус, если они направ-
лены в разные стороны.
Мощность силы тяги равна произведению силы тяги Р на абсо-
лютную скорость скольжения опорной ветви гусеницы по грунту.
Так как скорость скольжения при буксовании направлена в про-
тивоположную по сравнению с силой тяги сторону, то мощность
должна иметь знак минус. Учитывая формулу (2), получим
Np = PV= — (l—c)Pv0.
Определим теперь мощность сопротивления качению.
Выше было установлено, что если тягач движется с частичным
^уксованием гусениц,то сопротивление качению является лобовым
Сопротивлением, т. е. сила сопротивления действует по нормали
М обводу (рис. 21). В поступательном движении обвод переме-
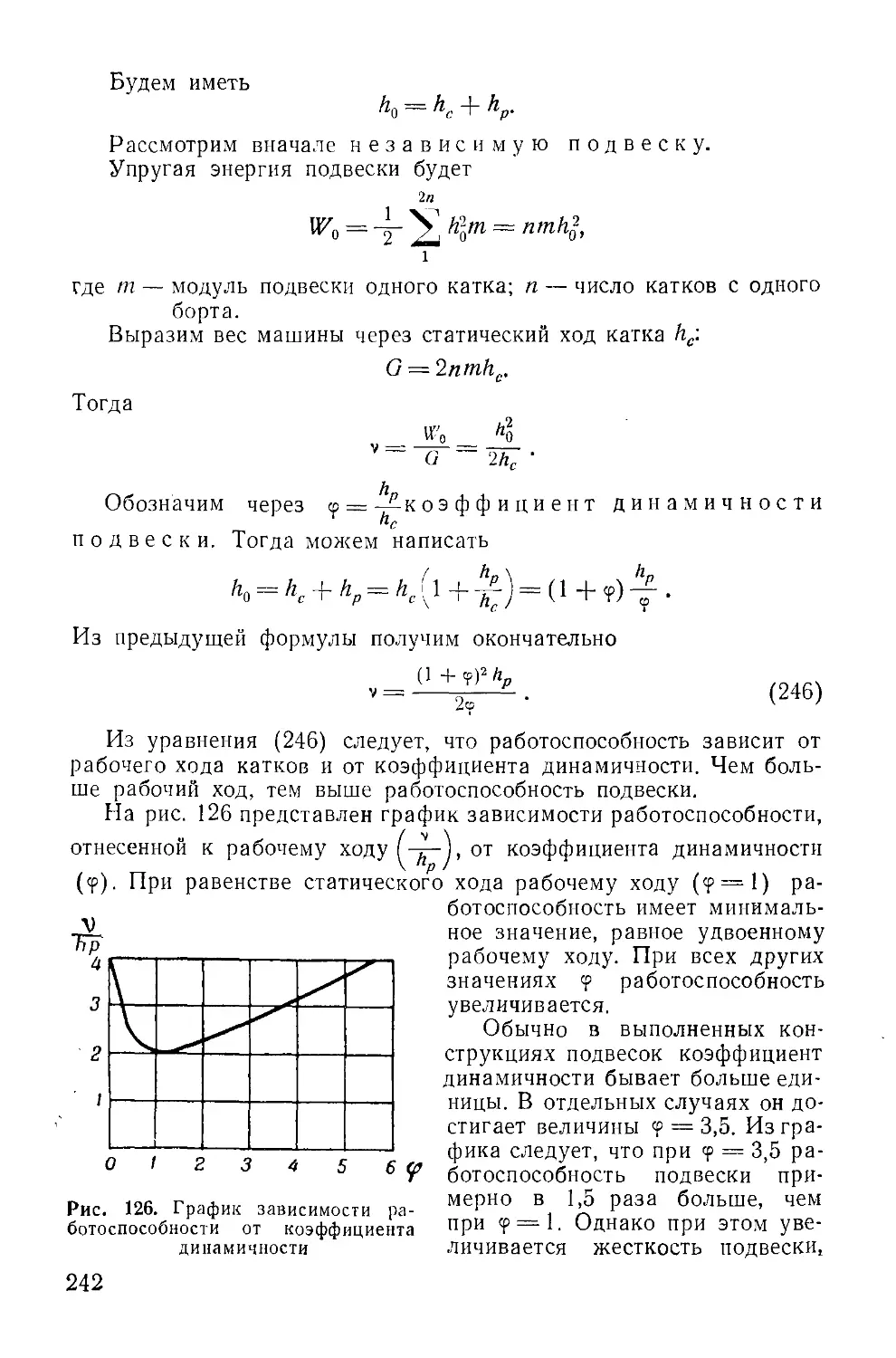
шается со скоростью v, тогда
М? = — vR = — av0R.
Так же находим мощности и остальных внешних сил;
= — vG sin a = — °v0G sin a;
= — vRK = — cvaRx.
37
Суммируя найденные мощности, получим
S AZBIU = - [(1 - а) Р + а (/? + Gsin а) + а/?и] Vo.
Из первого уравнения динамики можем написать
+ Ъ +
По уравнению (25)
Ro = R + G sin а.
Подставим Р и Ro в формулу 2 7V„UI. Приведя подобные члены,
получим
+ (31)
Определим теперь
К мощности внутренних сил относятся: мощность, которую дает
двигатель Л7Д, и мощность внутренних потерь в силовой передаче
и движителе тягача Л\р. Первая мощность положительна, вторая
отрицательна.
Выразим это следующим уравнением:
= (32)
Выражая Л/Тр через к. п. д. машины, будем иметь
МР = (1-’1)^д.
Окончательно получим
S Чн = ^д-
Определив из • уравнений (30), (31) и (32) значения ,
SAU и S Nvli и подставив эти величины в формулу (24), найдем
troG dv Г/. ч G dv , n . n *] ,
“•^0-57- = —1_(!—°)y-5r + /?o + ^J Я'о + ^д-
Это выражение можно переписать в таком виде:
Обозначим
7=1 + (8—1) а,
р - -
д~ v0 •
(33)
(34)
Величину 7 назовем коэффициентом приведенной
м а с с ы машины, а величину Рл— силой тяги по двига-
телю, тогда второе уравнение динамики тягача за-
пишется в таком виде:
= (35)
Второе уравнение динамики по своей форме аналогично пер-
вому уравнению (27). Разница заключается только в том, что здесь
вместо массы тягача подставлена приведенная масса 7 —, а вместо
о
силы тяги — сила тяги по двигателю Рл.
Коэффициент 7 представляет собой некоторую величину, харак-
теризующую условное приращение массы тягача. В действительно-
сти, конечно, никакого приращения массы тягача нет. Приращение
массы рассматривается только как влияние 7 на величину ускоре-
ния . Чем больше величина 7, тем медленнее будет разгоняться
тягач при одном и том же значении действующих на него внешних
сил и силы тяги по двигателю. Разгон замедляется как бы вслед-
ствие увеличения массы тягача в 7 раз. В действительности
ускорение уменьшается вследствие того, что часть энергии двига-
теля идет на разгон вращающихся деталей, и вследствие того, что
гусеницы при движении тягача частично проскальзывают, что и учи-
тывается в выражении (33) коэффициентами 8 и о.
Сила тяги по двигателю также является условной силой. Эта
сила нигде не приложена, и если она называется силой, то только
потому, что согласно формуле (34) имеет размерность силы.
Силу тяги по двигателю можно представить как такую силу
тяги, которую можно было бы получить на гусеницах, если бы тягач
двигался равномерно. В общем случае тягач движется неравно-
мерно, и поэтому сила тяги по двигателю Рл не равна действи-
тельной силе тяги Р, приложенной к гусеницам. При равномерном
движении обе силы по величине будут равны (Р, =Р), хотя по
физическому смыслу и в этом случае они будут различны, так как
Р есть реакция грунта на опорные ветви гусениц, т. е. сила, а Рд —
удельная мощность, приходящаяся на единицу скорости обвода, т. е.
величина, имеющая только размерность силы.
Второе уравнение динамики для гусеничного прицепа можно
написать аналогично уравнению (35).
Допустим, что в качестве прицепа буксируется гусеничная ма-
шина, у которой не работает двигатель. Будем считать, что двига-
тель не отключен от гусениц и при их проворачивании в нем тра-
тится некоторая тормозная мощность 7VT1.
В прицепе мощность идет не от двигателя к гусеницам, как
b тягаче, а от гусениц к двигателю, работающему в качестве
Тормоза.
39
Тормозная сила, которую создает двигатель, работающий в ка-
честве тормоза, по аналогии с силой тяги по двигателю может быть
выражена следующей формулой:
р __
T1 llVoi
Сила эта имеет знак, обратный знаку силы тяги (Р).
Повторив все приведенные выше рассуждения для прицепа, по-
лучим второе уравнение динамики прицепа в таком виде:
= + (37)
Здесь Рт1 — сила, аналогичная силе тяги по двигателю. Эту
силу назовем тормозной силой. Она имеет то же физическое
значение удельной мощности, что и сила тяги Рд.
В уравнение (37) входит коэффициент 71, который определяется
по формуле, аналогичной формуле (33):
П = 1 + («1- 1)°., (38)
где 8]—коэффициент вращающихся масс прицепа;
<3j — коэффициент скольжения движителя прицепа при юзе.
Из формулы (37) можно получить также второе уравнение ди-
намики колесного прицепа. При этом должно быть известно устрой-
ство прицепа (одноосный или многоосный).
В дальнейшем в качестве прицепа будем рассматривать колес-
ный прицеп. Примем следующие допущения: колеса прицепа испы-
тывают одинаковое сопротивление качению; колеса вращаются сво-
бодно; трение в подшипниках колес отсутствует. Кроме того, пре-
небрежем проскальзыванием колес по грунту. Тогда РТ1 = О,
«Ji = 1, 7i = 81.
Получим силу сопротивления движению прицепа
R0l = Я] + sin я> )
где I (39)
Ri 1
Для колесного прицепа из формулы (37) получим
+ (40)
Определение коэффициента вращающихся
масс
Пусть какая-нибудь деталь силовой передачи (например, вал
или шестерня), вращается с угловой скоростью ™z, где t — индекс
данной детали. Момент инерции детали пусть будет О/. Тогда ки-
нетическая энергия или живая сила детали будет равна 0^.
Выразим угловую скорость детали через угловую скорость ведущего
40
колеса <ок. Для этого введем передаточное число it между рассма-
триваемой деталью и ведущим колесом.
Тогда
. . Vo
z = Zz<oK — lt • .
' к
Определим общую кинетическую энергию всех вращающихся
деталей:
В этой формуле могут быть учтены не только детали силовой пере-
дачи, но и вращающиеся детали движителя — ведущие и направ-
ляющие колеса, опорные и поддерживающие катки. Каждая из этих
деталей входит в формулу со своим передаточным числом.
Кроме вращающихся деталей, в относительном движении уча-
ствуют также гусеницы и детали кривошипно-шатунного механизма
двигателя, т. е. детали, совершающие сложное вращательно-посту-
пательное движение.
Детали кривошипно-шатунного механизма можно учесть, если
момент инерции маховика двигателя увеличить на 20—30%, т. е.
если этот момент инерции умножить на коэффициент 1,2—1,3.
Кинетическая энергия гусениц может быть выражена формулой
GpVg
где Ог — вес двух гусениц.
Согласно определению коэффициента вращающихся масс 8 по-
лучим
Выразим v через <w0. Тогда окончательно получим выражение
коэффициента вращающихся масс
8 = 1
, _Gr. 4- g -
&G rffi
(41)
Если пренебречь проскальзыванием гусениц по грунту, т. е. при-
вить а = 1, то формула (41) примет такой вид;
й=1+^ + £1Т^- (42)
Из формулы (41) следует, что коэффициент вращающихся масс
зависит от а и в общем случае не является величиной постоянной.
41
Коэффициент 8 можно принять на данной передаче величиной по-
стоянной, если пренебречь проскальзыванием гусениц.
Из формул (41) и (42) следует, что коэффициент 8 есть квадра-
тичная функция передаточных чисел it. С увеличением передаточ-
ных чисел 8 возрастает.
Определять коэффициент 8 по формуле (41) или даже по упро-
щенной формуле (42) трудно, так как для определения моментов
инерции вращающихся деталей требуется большая вычислительная
работа. В ориентировочных расчетах, главным образом учебных,
можно пользоваться следующей приближенной формулой:
8= 1,2 + 0,0015 /о, (43)
где /о — общее передаточное число силовой передачи от двигателя
до ведущих колес.
При исследовании динамики гусеничных машин приходится
пользоваться тремя различными значениями коэффициента 8:
8 — полный коэффициент вращающихся масс (включены все
фрикционные элементы силовой передачи);
8'—коэффициент при отключенном двигателе (выключен глав-
ный фрикцион);
8" — коэффициент при отключенной силовой передаче.
Полный коэффициент 8 определяется по формуле (42) или (43).
При отключенном двигателе 8'=1,3—1,5 (меньшая величина
соответствует более высокой передаче в коробке передач).
Наибольшее влияние на коэффициент вращающихся масс ока-
зывает маховик двигателя. Действительно, при 1о = 50 определен-
ный по формуле (43) коэффициент 6 = 4,95, а при отключенном
двигателе 8'= 1,3—1,5, т. е. в 3—4 раза меньше.
Коэффициент 8 значительно возрастает с увеличением общего
передаточного числа силовой передачи io- Так, в некоторых довоен-
ных гусеничных машинах (танках) общее передаточное число со-
ставляло io = 90. В этом случае 8 = 13. В современных быстро-
ходных машинах (тягачах) io обычно не превышает 45. Только
у сельскохозяйственных тракторов оно достигает 60.
Для прицепов коэффициент 8i можно ориентировочно прини-
мать для колесного прицепа 1,1 и для гусеничного—1,2.
Уравнения равномерного движения гусеничного поезда
Равномерное движение есть частный случай неравномерного
движения, которое мы рассматривали выше и для которого вывели
общие формулы. Поэтому из этих формул можно получить и фор-
мулы равномерного движения.
Примем в общих уравнениях динамики поезда [уравнения (27),
(28), (35) и (37)] = 0, тогда получим
Р-/?0-Я = О,
+ Roi — Rm ~ 0;
42
Рд-/?о-/?к=О;
Рп + Rm — Rki = О,
где /?к = Яр
Для колесного прицепа примем РТ1 = 0, тогда из приведенных
уравнений будем иметь
P=P. = R0 + R.-,
Rk — Rm : = Rm !
р^о.
Из первого и второго уравнений следует, что сила тяги Р равна
силе тяги по двигателю Рл и силе сопротивления движению поезда.
Сила сопротивления движению поезда складывается из сопротивле-
ния тягача (Ro) и сопротивления прицепа (/?и = /?01).
Из третьего уравнения следует, что касательная, составляющая
сопротивления качению прицепа равна нулю.
Чтобы движение поезда было обеспечено по сцеплению,
должно соблюдаться следующее неравенство:
Р<РС = ?<Л>
“г. е. сила тяги должна быть меньше силы тяги по сцеплению.
2. ТРОГАНИЕ МАШИНЫ С МЕСТА И ПЕРЕКЛЮЧЕНИЕ
ПЕРЕДАЧ
Для гусеничных машин, особенно работающих с прицепом, тро-
гание с места и переключение передач являются вопросами, важ-
ными как в теоретическом, так и в практическом отношении. Тро-
гание машины с места и переключение передач сопровождается
буксованием главного фрикциона (сцепления) и падением числа
оборотов вала двигателя. Длительное буксование фрикциона мо-
жет привести к его перегреву, а падение оборотов ниже допусти-
мых — к остановке (заглоханию) двигателя.
За время переключения передачи гусеничная машина, работаю-
щая в тяжелых дорожных условиях, быстро теряет скорость. Паде-
ние скорости ниже определенной величины вызывает остановку дви-
гателя, для предотвращения которой нужно быстро переключать
передачи. Поэтому. при конструировании гусеничных машин уде-
ляется большое внимание вопросам облегчения переключения пе-
редач.
Для упрощения рассмотрения явлений, происходящих при пере-
ключении передач, заменим вращательно-поступательно движу-
щуюся динамическую систему гусеничного поезда более простой
Приведенной вращательной динамической системой, схема которой
Представлена на рис. 22. Здесь в приведенной массе 1 двигателя
учитываются все массы, связанные с валом двигателя и располо-
женные до главного фрикциона, а также ведущие детали главного
43
фрикциона. Масса 2, имитирующая массу поезда, приведена к ве-
дущему колесу движителя. Зубчатый механизм 3 имитирует сило-
вую передачу тягача (коробку передач, главную передачу и борто-
вые передачи); механизм считаем идеальным. Фрикционная муфта 4
имитирует главный фрикцион тягача.
Рис. 22. Приведенная схема динамической системы гусеничного
поезда;
/—приведенная масса двигателя; 2 — приведенная масса, имитирующая массу
поезда; 3 — зубчатый механизм; 4 — фрикционная муфта
Допустим, что в начальный момент фрикционная муфта 4 вы-
ключена и ведущий вал муфты вращается с угловой скоростью o>i,
а ведомый — с угловой скоростью <02.
Включим мгновенно фрикционную муфту. Так как скорости «м
и а>2 не равны между собой, то в муфте будет пройсходить сколь-
жение ведомых и ведущих дисков или их буксование.
Под действием момента трения, величина которого всегда
больше момента двигателя и имеющего противоположное моменту
двигателя направление, маховая масса 1 начнет снижать свои
обороты. Одновременно момент трения в муфте, воздействуя на ве-
дущий вал зубчатого механизма (вал силовой передачи), будет
разгонять маховую массу 2 или эквивалентную ей массу поезда.
Представим торможение массы 1 и разгон массы 2 в виде гра-
фика (рис. 23). Допустим, что в момент времени £ = 0 фрикцион-
Рис. 23. График буксования главного фрикциона
ная муфта мгновенно включается. С этого момента масса 1 будет
приобретать скорость о>' < o>f, которая за период времени t0 будет
падать. Если приближенно принять, что моменты, действующие на
массу / (момент двигателя и момент трения муфты),— величины
44
постоянные, то закон изменения ш' будет линейный. На графике
скорость ш' изобразится прямой линией, наклонной к оси абсцисс.
С момента включения фрикционной муфты масса 2 начнет оаз-
гоняться. Обозначим скорость ведомого вала муфты через ш2- Если •
принять, что сопротивление движению поезда есть величина по-
стоянная, то скорость й)2' будет изменяться также по закону пря-
мой линии. За время 0 < t < t0 скорости и с«2 не равны между
собой. Следовательно, между ведущими и ведомыми деталями
фрикционной муфты происходит буксование (см. заштрихованный
участок графика). В момент to буксование муфты прекращается,
так как скорости to,' и а>2' уравниваются и делаются равными неко-
торой скорости <1>о- После этого вся система начинает разгоняться
как одно целое (без буксования муфты) до нормальных оборотов
двигателя (до угловой скорости спи).
Составим дифференциальные уравнения движения рассматри-
ваемой динамической системы и определим время буксования фрик-
ционной муфты (главного фрикциона) to и скорость ш0, до которой
за время to падает скорость вала двигателя.
Рассмотрим равновесие массы 1 и массы 2.
На массу 1 действуют два момента: момент двигателя 7ИД и мо-
мент трения буксующей фрикционной муфты 7Иф. Кроме того, со-
гласно принципу Даламбера к массе 1 должен быть приложен инер-
ционный момент Мр. Направление моментов указано на рис. 22:
моменты Мл и М.х направлены в одну сторону, а момент Л7ф —
в противоположную.
На массу 2 действуют следующие моменты: приведенный к ма-
ховику 2 момент 1ъМф, момент сопротивления движению MR и инер-
ционный момент М)2. Моменты MR и Mj2 направлены в одну сто-
рону, момент ZoMj, — в противоположную.
Согласно принципу Даламбера можем написать следующие
уравнения равновесия маховых масс 1 и 2:
Л/д + Л/?1-Л1ф = 0;
г0^ф j2 MR = 0.
Инерционные моменты будут равны:
где 0] и @2 — приведенные моменты инерции маховых масс 1 и 2;
ю” — угловая скорость вращения массы 2.
Заменив скорость через скорость ведомого вала муфты <о2',
ДОЛучим
• 1 ’
<1>2 = —----------Ч>2 ,
г0
45
или
J * *
do>2 1 d2
dt i0 dt ‘
Тогда
Подставляя М.х и Mj2 в уравнения равновесия, определим уско-
рения:
dw\ — м,
dt 0! ’
du'i __ (»ОМФ - ЛГд) t0
dt 02
Примем приближенно, что 7Иф, Л4Д и — величины постоянные,
тогда
do>}
—тт~ = const;
at
—-тт = COnst.
at
Следовательно, масса 1 движется равнозамедленно, а масса 2 —
равноускоренно.
Скорости будут равны согласно закону равнозамедленного и
равноускоренного движения
21 ©2 •
где t — текущее время.
При t = t0 скорость <»j = 2 ~ <»0. Подставив эти величины
в предыдущие уравнения и решив их относительно t0 и 0, по-
лучим
а =__________~ °-'5_________• (44';
01 02
46
Подставив в уравнение (45) значение to из формулы (44), по-
лучим
(о0 = <й1
____~~ ___________
(М4ф-Мя)го 01
Мф — МЦ ®2
(46)
Так как <и0 <С «и, то скорость соц характеризует падение числа
оборотов вала двигателя. Для дизелей допустимое значение отно-
шения «>о : > 0,5, для карбюраторных двигателей это значе-
ние меньше 0,4.
Как было отмечено выше, величины to и ш0 (особенно с«о) имеют
большое значение для тяговых расчетов гусеничных машин, так как
позволяют судить о возможности трогания машины с места и воз-
можности переключения передач в различных условиях движения
машины.
В формулы (44) и (46) входят моменты инерции приведенных
масс 0, и 02.
Момент инерции 0] определяется по эмпирической формуле
01 = т®т, (47)
где т—опытный коэффициент (1,2—1,3), учитывающий вращаю-
щиеся и движущиеся возвратно-поступательно массы дви-
гателя;
0ОТ—момент инерции маховика двигателя.
Момент инерции маховой массы 2 определяется из следующих
условий. Кинетическая энергия приведенной массы 2, равная
-у- 02<л2, должна равняться кинетической энергии поезда, равной
-^-/Ипг»2, где Л4П—приведенная масса поезда с учетом вращаю-
щихся деталей, v — скорость поезда.
Масса поезда и его скорость определяются по формулам:
М8^+8А
п g
V =
где г*— радиус ведущего колеса.
Тогда получим выражение момента инерции
(48)
АНАЛИЗ ЯВЛЕНИЯ БУКСОВАНИЯ ГЛАВНОГО ФРИКЦИОНА
1. Из формул (44) и (46) следует, что чем меньше <о2, т. е.
ниже скорость движения машины в момент включения глав-
Jforo фрикциона2 тем больше время буксования t0 и меньше ско-
рость шо.
47
С увеличением to и уменьшением <л0 увеличивается вероятность
перегрева фрикциона и вероятность остановки двигателя.
2. На величину скорости <о2 значительно влияет время переклю-
чения передач ДЛ Чем меньше Д?, тем меньше падение скорости ею?.
В свою очередь на Д/ влияет конструкция коробки передач и ее
привода управления. Так, например, для переключения передач
в планетарных коробках передач, а также в коробках с избирате-
лем (см. ч. II) требуется меньше времени, чем в обычных коробках
(непланетарны.х), имеющих простое управление.
На время Д/ влияют также и такие факторы, как квалифика-
ция водителя, степень его утомленности и др.
3. При одном и том же времени переключения передач Д? паде-
ние скорости юг зависит от условий движения поезда. Чем больше
сопротивление движению, тем сильнее за время переключения
передачи падает скорость <о2.
4. Наличие прицепа увеличивает момент инерции приведенной
массы ©г, а следовательно, увеличивает и время буксования фрик-
циона tQ.
5. С увеличением момента инерции 01 увеличивается время бук-
сования i0, а также увеличивается скорость <оо, т, е. возрастает ве-
роятность перегрева фрикциона; вероятность же остановки двига-
теля уменьшается.
6. С увеличением момента трения фрикциона 7ИФ уменьшается
время t0 и скорость <о0.
В эксплуатации на момент трения могут влиять различные фак-
торы, как-то: замасливание поверхностей трения фрикционных дис-
ков, ослабление или поломка нажимных пружин, разрегулировка
механизма выключения. Во всех этих случаях момент трения умень-
шается.
Момент трения будет уменьшаться также в том случае, если
водитель будет нажимать на педаль фрикциона, не выключая его
полностью.
При трогании поезда на подъемах или вообще в тяжелых усло-
виях движения возможна остановка двигателя. Поэтому для трога-
ния с места следует медленно включать фрикцион, вследствие чего
уменьшается 7ИФ и увеличивается с«о (время to при этом возрас-
тает) .
7. На to и wo влияет момент двигателя Мя и момент сопротив-
ления движению MR. С увеличением Мя и MR время буксования
фрикциона возрастает. На скорость <ло моменты и MR влияют
по-разному. С увеличением скорость о>о возрастает, а с увели-
чением Л4Р— падает.
8. Время буксования главного фрикциона и вероятность оста-
новки двигателя зависят от передаточного числа силовой передачи.
С уменьшением передаточного числа, т. е. с повышением передачи,
вероятность перегрева фрикциона и вероятность остановки двига-
теля увеличиваются.
48
Пример. Определим время буксования главного фрикциона тягача и падение
угловой скорости вала двигателя при переключении передач со второй на третью.
Для расчета примем следующие данные:
G = 6 т\ Gi = 1,5 т; гк=0,25 м; 0т=О,14 кгм сек2-, Л4Д = 40 кгм\
= 48 кгм; гг( = 2200 об/мин-, гп = 12,84; =6,65. Передачи переключают
на горизонтальном участке грунтовой дороги.
Определим 61 и ва по формулам (47) и (48). Задаемся т= 1,3; S'= Si =1,2;
тогда
= 1,3-0,14 = 0,18 кгм сек2\
п 1,2 (6000 + 1500) 0,252
02 = -4—>----g-gj--------= 57,3 кгм сек2.
Находим момент сопротивления движению MR.
MR = (Ro + 7?oi) rhi
где Ro = fG и Roi=fiGt. Пусть f = 0,08 и ft = 0,05, тогда
MR = (0,08 -6000 + 0,05-1500) 0,25 = 138,5 кгм.
Определяем угловые скорости ы, и <лз:
<>! = ^- = 231 1/сек.
Скорость а>2 определяется из следующих условий.
До переключения передачи скорость поезда была
о»! 231-0,25 — ,
= = ~П/&Г = 4’5 м/сек-
За время переключения передачи поезд двигался с отключенной силовой
передачей равнозамедленно. Ускорение поезда составит
=-------$ +-01г- = - “ 0,605 м/сек2.
dt 9„ G * G\ 1,2 (6000 4- 1500)
о------1» о, —
g g
Примем время переключения передачи Д/ = 3 сек. Тогда за время Д/ паде-
ние скорости поезда будет
Дг = — U = — 0,605-3 = — 1,81 м/сек.
В момент включения фрикциона скорость поезда на третьей передаче равна
+ Дг = 4,5 — 1,81 = 2,69 м/сек,
откуда
rIII . 2,69 fi д
«г = — = 025 '6’65 = 71,5 7
Из формул (44) и (45) получим
231—71,5
‘°= 48—40 (6,65-48 — 138,5)6,65 ’
0,18 + 57,3
48___40
Wo = 231 — • J -2,4 = 124 1/сек
0,1о
30
Или nQ = G)o — 1180 об/мин.
4—2469 49
Отсюда следует, что несмотря на то, что время буксования главного фрик-
циона невелико, за этот период угловая скорость вала двигателя падает почти
в два раза, что может вызвать остановку двигателя.
3. ГРАФИК РАЗГОНА ГУСЕНИЧНОГО ПОЕЗДА
Параметрами, характеризующими маневренные качества одиноч-
ной гусеничной машины или гусеничного поезда, являются время
путь разгона, при которых в заданных дорожных условиях
и
поезд достигает определен-
ной скорости движения. Эти
параметры определяются из
графика разгона.
На рис. 24 представлен
примерный график разгона
двух машин, полученный
опытным путем. На графике
по оси абсцисс отложено
время разгона, а по оси орди-
нат — скорость разгона.
На графике видны участ-
ки, на которых переключа-
ются передачи. За время пе-
реключения Д/ скорость ма-
шины падает на величи-
ну Дп. Для машин с обыч-
ным переключающим устрой-
ством (кулисой) время
переключения составляет
примерно 2—3 сек., а для
отдельных машин может до-
ходить и до 5 сек.
График разгона позво-
Рис. 24. график разгона гусеничного поезда ляет также сравнивать ма-
шины и в отношении их при-
емистости. Так, одна машина (кривая /) обладает лучшей приеми-
стостью, чем другая машина (кривая 2), так как скорости, напри-
мер v — 25 км/час (средней скорости движения по грунтовым до-
рогам), одна машина достигает за 10 сек., а другая машина —
за 27 сек.
График разгона может быть получен опытным путем с помощью
соответствующей аппаратуры или построен по формулам.
Рассмотрим построение графика разгона по фор-
мулам.
Для практических расчетов допустимо принять, что момент дви-
гателя есть величина постоянная, равная среднему моменту в диа-
пазоне рабочих оборотов. Под рабочими оборотами будем понимать
обороты двигателя, находящиеся между максимальной мощностью
и максимальным крутящим моментом при работе двигателя на
внешней характеристике.
50
Обозначим через коэффициент приспособляемости двигателя,
MN — крутящий момент, соответствующий максимальной мощности
(рис. 25), Мс—средний крутящий момент. Примем
Крутящий момент двигателя пропорционален силе тяги по дви-
гателю. Согласно формуле (34) сила тяги по двигателю равна
Р __
д VO
Примем NJl = Ne, где Ne— максимальная мощность двигателя
при работе двигателя на внешней характеристике; ^0= — рас-
Рис. 25. Внешняя характеристика двигателя
четная скорость движения машины на Z-ой передаче. Эта скорость
соответствует nN оборотам двигателя. Примем Рл как среднюю ве-
личину, тогда
п ^д + 1
Выберем следующие условия разгона поезда. Будем считать,
что внутреннее трение в прицепе мало и им можно пренебречь.
Кроме того, пренебрегаем проскальзыванием в движителе тягача и
прицепа. Тогда
(49)
^т1 = 0; Т = й; Y1 = й1-
Согласно второму уравнению динамики гусеничного поезда
[формулы (35) и (37)] будем иметь
8f
^T'^ = ~R°i + R-
4*
51
Отсюда находим
dv Рд —/?о —/?oi
dt , G ..
о----р 8,-
g g
Так как Рд, Ro и 7?01—величины постоянные, то и —величина
постоянная. Движение поезда будет равноускоренным. Поэтому
время разгона на t-ой передаче будет выражаться формулой
/ -5^» (51)
dt
где vu — скорость, с которой начинается разгон поезда на Z-ой пе-
редаче;
— скорость, до которой разгоняется поезд на /-ой передаче.
Для построения графика разгона необходимо знать падение ско-
рости поезда Ду за время переключения передач Д/.
При переключении передачи силовая передача отключается от
двигателя и тягач движется по инерции. Тогда Рд=0, 8 = 8". Из
формулы (50) получим
dv __ Rq + Rqi /сох
dt ~ b"G 8tGi ’ ' }
g g
тогда падение скорости Ду выразится формулой
Дт/ = 5-Д/. (53)
dt . \ /
В момент перехода на / + 1 передачу скорость поезда будет
vi ((+j) . Эта скорость равна v2t + kv, где Дг/<0. Тогда напишем

По формулам (49—54) строится график разгона.
Пример. Построим график разгона гусеничного поезда. Для построения гра-
фика примем следующие данные: G = 12 т\ Gi = 1,5 т; = 234 л. с., = 1,2-
Расчетные скорости на передачах I—IV будут: vt = 8 км/час, V], = 13 км/час,
VH1 = 22 км/час, vlv = 35 км/час, а передаточные числа силовой передачи:
= 37,4; 101[ = 23; /оп1 = 13,6; i0IV = 8,57.
Прицеп колесный; дорога, на которой происходит разгон, грунтовая; участок
дороги горизонтальный.
Определяем по формуле (49) величину Принимаем •»; = 0,85 для всех
передач, тогда
Рд1 = 7375 кс, Рд11 — 4540 кс, РдШ = 2680 кг\ РлП = 1685 кг.
52
Определяем по формуле (43) значения коэффициентов вращающихся масс
8, = 1,2 + 0,0015-37,42 = 3,3; 8П = 1,2 + 0.0015-232 = 2;
8И1 = 1,2 + 0,0015-13,62 = 1,48; 8,у = 1,2 + 0,0015-8,57» = 1,31.
Кроме того, принимаем 8" = 81 = 1,2.
Пусть коэффициент сопротивления качению для тягача и прицепа f = 0,08
и fi = 0,05. Тогда Ro = 960 кг-, RM = 75 кг.
dv
По формуле (50) находим :
I = 1,50 м/сек* =1,33 м/сек* = 0,825; (=0,365.
\dt h kdt п к at ;П1 к / iv
Определяем теперь по формуле (52) ускорение равнозамедленного движения
dv
= — 0,61 м/сек?.
Допустим, что разгон поезда происходит с места на первой передаче. Тогда
V1I — V2I — ® км/час = 2,22 м/сек.
Из формулы (51) находим
2 22
'> = Т50 = М8 СеК'
Принимаем время переключения на всех передачах Д1=2 сек. Тогда по фор-
муле (54) находим
V111 = V2I + '~ТГ М — 2,22 — 0,61 -2 = 1,00 м/сек = 3,6 км/час.
Рис. 26. Построение графика разгона
53
Для остальных передач определим аналогично
tn = 1,97 сек.; и1Я1 = 8,65 км/час.
Построение графика разгона приведено на рис. 26.
Из графика может быть определено время разгона
п+1
/р = + пД/
I
и путь разгона
п+1 и
Sp = s + S д^>
1 1
где tj, — время разгона на каждой передаче;
п — число переключений;
М—время переключения, одинаковое на всех передачах;
Si — площадь, заключенная между осью абсцисс и линией разгона на дайной
передаче;
A5j — площадь, заключенная между осью абсцисс и линией замедления движе-
ния для участков переключения передач.
В качестве примера определяем
^21 + ^111 (2,22 + 1)2
ASj =-----2----- 3-----------2-----= 3,22 М И Т’ Д‘
Здесь был рассмотрен разгон поезда с первой передачи. Обычно разгон на-
чинают со второй передачи, а для одиночной машины — даже с третьей; время и
путь разгона в этом случае значительно уменьшаются.
ГЛАВА III
ТЯГОВЫЕ РАСЧЕТЫ
1. ЗАДАЧИ ТЯГОВЫХ РАСЧЕТОВ. ПОРЯДОК ТЯГОВОГО
РАСЧЕТА ПРОЕКТИРУЕМОЙ МАШИНЫ
Тяговым называется расчет, согласно которому определяются
скоростные и тяговые качества существующей машины (поезда)
или по заданным скоростным и тяговым качествам опреде-
ляются расчетные параметры проектируемой машины, например
мощность двигателя, передаточные числа силовой передачи и т. д.
Первый вид тягового расчета называется поверочным
расчетом существующей машины, второй вид—рас-
четомпроектируемой машины.
В настоящей главе рассматривается тяговый расчет проекти-
руемой машины. Поверочные же расчеты приводятся в тексте книги
при решении тех или иных конкретных задач.
Тяговый расчет проектируемого гусеничного тягача (или оди-
ночного транспортера) основывается на заданных технических
условиях на проектирование.
В технических условиях должны быть отражены основные тре-
бования, предъявляемые к проектируемой машине, и заданы
следующие расчетные величины, являющиеся исходными данными
для тягового расчета.
Для расчета транспортера должны быть заданы: вес транспор-
тера G, максимальная скорость движения на хорошей дороге т/тах;
максимальный угол преодолеваемого подъема атах.
Для расчета тягача необходимо знать вес G{ и тип прицепа (ко-
лесный или гусеничный), максимальную скорость движения поезда
г'.' , максимальный угол преодолеваемого поездом подъема a'mgx/
максимальную скорость движения одиночной машины (с грузом на
платформе) т/тах.
В качестве исходных данных для расчета могут быть приняты
и другие величины, например: мощность двигателя (когда известен
двигатель, который будет поставлен на проектируемую машину),
максимальная скорость движения, диапазон скоростей, т. е. отноше-
ние максимальной скорости к минимальной, и др. Выбор тех или
иных величин определяется техническими условиями на проектиро-
вание машины.
Тяговый расчет транспортера производится в та-
кой последовательности.
55
1. По заданному весу G транспортера и его максимальной ско-
рости движения г»тах находим мощность двигателя.
2. По заданному максимальному углу преодолеваемого подъема
дороги атах находим минимальную скорость движения z>min транс-
портера. Зная максимальную и минимальную скорости, определяем
v
„ j max
диапазон скоростей а — ——-.
vmin
3. Разбиваем диапазон скоростей по передачам и находим рас-
четные скорости на передачах vp.
4: По расчетным скоростям определяем передаточные числа си-
ловой передачи io.
Расчет тягача.
1. По весу прицепа Gt определяем вес тягача G.
2. Зная вес поезда G-j-Gt и его максимальную скорость дви-
жения находим мощность двигателя Ne.
3. Определяем максимальную и минимальную скорости движе-
ния одиночного тягача ^maX) откуда находим диапазон ско-
ростей.
Диапазоном скоростей можно также задаться. Тогда по диапа-
зону и максимальной скорости определится минимальная скорость.
4. Определяем число передач в диапазоне скоростей и находим
расчетные скорости на передачах ^р.
5. Зная расчетные скорости, находим передаточные числа сило-
вой передачи.
Рассмотрим более подробно тяговый расчет транспортера и оста-
новимся кратко на особенностях тягового расчета тягача,
работающего с прицепом.
2. ТЯГОВЫЙ РАСЧЕТ ТРАНСПОРТЕРА
Как указывалось выше, исходными данными для тягового рас-
чета транспортера являются: вес транспортера G, максимальная
скорость движения ^1пах, максимальный угол подъема дороги атах
Под максимальной скоростью транспортера будем' понимать
скорость движения в наиболее благоприятных условиях. Эти усло-
вия определяются выбранными значениями коэффициента сопротив-
ления качению f и тангенсом угла подъема дороги I = tg а. Чем
большими в расчете будут приняты значения величин f и Z, тем
легче будет обеспечиваться максимальная скорость движения транс-
портера. Однако при этом следует иметь в виду, что с увеличением f
и I возрастает мощность двигателя. Таким образом, величины f и i
надо выбирать осторожно. Эти величины обычно задаются в неко-
торых пределах.
Согласно табл. 1 минимальный коэффициент сопротивления ка-
чению гусеничной машины по хорошим дорогам находится в преде-
лах 0,04—0,05. Максимальный подъем, который обычно имеют до-
роги, определяется следующими данными: на равнинной местности
56
I = 4% (0,04), на холмистой местности / = 5% (0,05), на гористой
местности i = 6% (0,06).
Если транспортер предназначается для работы на равнинной
местности, то максимальный подъем дороги будет около 4%. Рас-
считывать максимальную скорость на этот подъем, однако, нецеле-
сообразно, так как такой подъем встречается редко. В качестве
расчетного можно принять / = 1 — 1,5%.
Современные транспортеры имеют z>ma]l порядка 50—60 км/час.
Превышать в расчете эти скорости нецелесообразно, так как скоро-
сти сверх 50—60 км/час практически трудно реализовать. Завыше-
ние же ^тах поведет к завышению мощности двигателя Ne.
Так как гусеничная машина значительное время работает на
местности, где по условиям работы подвески скорость движения
не превосходит 25—30 км/час, то машина будет иметь лишнюю
мощность, которую не сможет использовать. Поэтому она будет
работать неэкономично. Таким образом, завышение максимальной
скорости неизбежно вызовет снижение топливной экономичности
машины.
Между т/тах и удельной мощностью (Л7у), т. е. мощностью, при-
ходящейся на 1 т веса машины, существует следующая эмпириче-
ская зависимость:
^тах = 3,2Л/у, (55)
где г'п,.,,. выражено в км/час, a N? — вл. с./г.
Из формулы (55) следует, что для современных транспортеров,
имеющих = 50—60 км/час, удельная мощность должна состав-
лять примерно 16—19 л.с./т.
Максимальный угол подъема, который может преодолеть гусе-
ничная машина на местности, определяется коэффициентом сцепле-
ния гусениц с грунтом <р.
Допустим, что одиночная машина движется на подъем, угол ко-
торого равен а1Пах. Сопротивление движению машины будет
/?0 = R + Gsin amax = (/cos amax + sin amax) G.
Предельное значение силы тяги по сцеплению определится по фор-
муле
Л C0S Я,пах-
Приравняв при равномерном движении машины Рс к Ro, полу-
чим после сокращения на О cos amax
tgCtmax = 'P— /• (56)
Расчетное значение ? следует брать для гусениц без шпор не
выше 0,8. Если машина имеет съемные шпоры, то значение у
можно выбирать до единицы.
. Кроме того, примем /==0,1, тогда атах = 35— 40°.
Таким образом, максимальный угол подъема в тяговом расчете
одиночной машины следует выбирать около 35° (и не выше 40°).
57
ОПРЕДЕЛЕНИЕ МОЩНОСТИ ДВИГАТЕЛЯ
Мощность двигателя определяется из условия обеспечения мак-
симальной скорости движения машины по хорошим дорогам.
Допустим, что машина движется равномерно, тогда
Р=Л = /?о-
Согласно формуле (34) сила тяги по двигателю будет равна
р __
* VO •
Подставим в эту формулу вместо v0 максимальную скорость
^max, Кроме ТОГО, примем . /?o=^0min И А/д = Ne, ТОГДЭ
^0 minimax /С'7'v
где Ne — паспортная, или номинальная, мощность двигателя, т. е.
мощность, определяемая в условиях заводских испытаний
и указанная в паспорте двигателя.
В двигателе, установленном в машине, эффективная мощность
обычно ниже паспортной, так как при снятии характеристики на
заводе двигатель не оборудуется системой охлаждения, воздухо-
очистителем и глушителем, которые поглощают часть его мощно-
сти. Все эти потери можно учесть в общем к. п. д. машины ц.
Однако точное численное значение к. п. д. определить трудно.
Воспользуемся некоторыми опытными данными и по ним опре-
делим значение т] на максимальной скорости движения машины.
В табл. 4 приведены значения максимальных скоростей несколь-
ких гусеничных машин, полученные при испытании на горизонталь-
ном асфальтированном шоссе, а также данные по удельным мощно-
стям одиночной машины и значения отношения
Таблица 4
Значения максимальных скоростей, удельных мощностей
и отношения vraax : 1Уу гусеничных машин
G, т °тах’ км1час ЛГу, л. с./т ®max :
45 50 15,6 3,2
40 28 8,8 3,2
31 55 16,2 3,4
23 45 13,9 3,2
20 32 9,7 3,3
13 61 19,7 3,1
9 47 15,2 3,1
6 €4 20,6 3,1
58
Несмотря на то что в табл. 4 вес машин, максимальная ско-
рость и удельная мощность изменяются в очень широких пределах
(вес изменяется в 7 раз, скорость — в 2,2 раза, удельная мощ-
ность— в 2,4 раза), отношение максимальной скорости к удель-
ной мощности остается почти постоянным. Поэтому этим отноше-
нием можно пользоваться при расчетах. Определим т;, воспользо-
вавшись данными табл. 4. Примем среднее значение величины
^тах’-^у равным 3,2 и составим следующее уравнение мощностей
при движении машины по участку пути с подъемом I, равным 1 —1,5%
270^ =f0Gvmax 1000, где /0 =/ + I,
откуда
27(М„ __f
1000G '° max •
Ho^ = 7Vy. Тогда, учитывая, что -= 3,2, окончательно будем
иметь
^ = 11,81/0.
Для асфальтированного шоссе примем/0= 0,04—0,05. Тогда по-
лучим т] = 0,47—0,59.
Итак, общий к. п. д. при движении машин с максимальной ско-
ростью находится в пределах 0,5—0,6. Этим к. п. д. и можно поль-
зоваться в тяговом расчете при определении мощности двигателя.
Заметим, что в коэффициент сопротивления качению /0 входят
потери в движителе при его буксировке (см. выше). Строго говоря,
эти потери следовало бы отнести к внутренним потерям, тогда
коэффициент/0 уменьшился бы, а с ним уменьшился бы и к. п. д.
Последний на максимальной скорости движения машины составит
величину меньше 0,5. Отсюда следует, что внутри машины на вред-
ные сопротивления тратится больше половины мощности двигателя.
С этими потерями следует бороться. Особенно большую мощность
поглощают гусеницы с простыми шарнирами (данные
табл. 4 относятся к гусеницам с простыми шарнирами).
Для определения к. п. д. на любых скоростях машины, имею-
щей обычную зубчатую силовую передачу, можно пользоваться
следующей эмпирической формулой:
= 0,85 — 0,00551/, (58)
где v — скорость движения машины в км/час.
ОПРЕДЕЛЕНИЕ ДИАПАЗОНА СКОРОСТЕЙ
При расчетах пользуются кинематическим и силовым диапазо-
нами скоростей.
Кинематическим диапазоном скоростей назы-
вается отношение максимальной расчетной скорости vpn к мини-
59
мальной расчетной скорости ^pl. Обозначим кинематический диапа-
зон буквой dx, тогда
dx = ~^-. (59)
Vpi
Кинематическим диапазоном удобно пользоваться при расчете
зубчатых силовых передач, так как он представляет собой отноше-
ние передаточных чисел на низшей и высшей передачах. В гидро-
механических и в электромеханических силовых передачах, имею-
щих при движении машины две степени свободы, удобнее поль-
зоваться силовым диапазоном. Силовым диапазоном
называется отношение силы тяги по двигателю на расчетной низ-
шей передаче к силе тяги по двигателю на расчетной высшей
передаче. Обозначим силовой диапазон dc. Тогда
= (60)
Расчетную силу тяги по двигателю можно определить из форму-
лы (34). Подставив вместо мощность и вместо Ко расчетную
скорость vp, получим
р ____ .
'д! — „ •
vpl
р __
JX.fl fl •
Тогда
Отсюда следует, что между силовым и кинематическим диапа-
зонами имеется зависимость. Эта зависимость’ характеризуется от-
ношением к. п. д. машины на низшей и высшей передачах. Для
определения зависимости между dK и примем в формуле (58)
01 = 5 км/час п vn — 50 км/час. Получим т]1=0,82 и fi„~0,57.
Тогда
<4^1,44<4.
Таким образом, с и л о в о й диапазон почти в полтора
раза больше кинематического диапазона.
Определим теперь, какой диапазон скоростей должна иметь
транспортная гусеничная машина.
Примем следующие условия движения одиночной машины: ма-
шина развивает наибольшую расчетную скорость по хорошим до-
рогам, характеризуемым коэффициентом сопротивления качению
/=0,05 и подъемом дороги 4 = 0,02 (2%); машина должна пре-
одолевать подъемы до 35°.
60
Сопротивление движению машины Согласно формуле (25) бу-
дет равно
Ro = fGc 4- G sin a.,
тогда для одиночной машины
Ro — (f cos a 4- sin a) G,
или
$0=f0G.
Для углов подъема дороги a.< 10°
/о ~ f i-
Расчетная величина /0 для выполнения первого условия прини-
мается равной /0 = 0,07. При равномерном движении машины со-
противление движению равно силе тяги по двигателю, т. е. Rn = Рд,
тогда Рдл = 0,07 G. Движение на максимальный подъем a = 35°
должно совершаться также равномерно, причем на низшей расчет-
ной скорости, тогда
/?0 = (/cos 35° + sin 35°) G = Рд1.
Примем/= 0,1, тогда РД1 = 0,65 G, откуда получим силовой диа-
пазон
Кинематический диапазон машины, имеющей обычную зубчатую
силовую передачу, будет равен
d = -^- = — — 7
к 1,44 1,44 •
Таким образом, транспортная гусеничная машина
должна иметь силовой диапазон порядка 10. Ма-
шина с обычной зубчатой силовой передачей при этом должна
иметь кинематический диапазон порядка 7. Так
как кинематический диапазон зависит от отношения коэффициентов
полезного действия на низшей и высшей передачах, то для машин,
имеющих гидромеханическую или электромеханическую силовую
передачу, кинематический диапазон должен определяться с учетом
к. п. д. гидро- или электропередачи. В данном случае формула (58)
для определения к. п. д. не подходит.
Современные гусеничные машины с механической (зубчатой)
силовой передачей имеют кинематический диапазон порядка 6—10
и силовой диапазон порядка 9—14; чем выше диапазон, тем шире
.скоростные и тяговые возможности машины. Однако при большом
Диапазоне увеличивается необходимое число передач, усложняется
конструкция коробки передач и затрудняется управление машиной.
Поэтому расширять диапазон следует только в том случае, если на
машине предполагается установить многоскоростную коробку пере-
дач с облегченным управлением.
В отечественных тягачах кинематический диапазон равен: в тя-
гаче АТ-Т — 6,6, в тягаче АТ-С — 5 и в тягаче АТ-Л — 9,2.
ОПРЕДЕЛЕНИЕ МИНИМАЛЬНОЙ СКОРОСТИ
Минимальная расчетная скорость определяется по максимальной
расчетной скорости и выбранному кинематическому диапазону
Минимальная скорость тягачей и транспортеров обычно лежит
в пределах 4—7 км/час. Так, тягач АТ-Т имеет скорость 5,5 км/час,
АТ-С — 6,8 км/час, АТ-Л — 4,5 км/час.
ОПРЕДЕЛЕНИЕ РАСЧЕТНЫХ СКОРОСТЕЙ (РАЗБИВКА ПЕРЕДАЧ
ПО КОЭФФИЦИЕНТУ ИСПОЛЬЗОВАНИЯ МОЩНОСТИ)
Внутри заданного диапазона скоростей разбивку передач можно
выполнить различными способами: по геометрической прогрессии,
по арифметической прогрессии, методом типовых сопротивлений.
При разбивке передач по геометрической прогрес-
сии предполагается, что за время переключения передачи скорость
машины не изменяется. Это допущение, в какой-то мере приемлемое
для расчета автомобилей, совершенно неприемлемо для расчета гу-
сеничных машин, так как за время переключения передач скорость
гусеничной машины быстро падает.
Кроме того, при разбивке передач по геометрической прогрессии
низшие передачи слишком близко сдвигаются одна к другой, в то
время как между высшими передачами получается большой разрыв.
В результате этого средняя скорость движения машины, которая
для транспортной машины определяется в первую очередь работой
на высших передачах, снижается. Для сближения верхних передач
и, следовательно, повышения средней скорости движения машины
разбивку передач можно выполнять по арифметической
прогрессии.
Для геометрической прогрессии соотношение между соседними
скоростями
— q = const,
vt
а для арифметической прогрессии
vt+i— vt = а = const.
На рис. 27 приведен график разбивки передач по геометрической
и арифметической прогрессии. Из графика видно, что при арифме-
62
тической прогрессии передачи сдвинуты в сторону высших передач.
Так, при одном и том же диапазоне скоростей (dK = 42 : 4) и од-
ном и том же числе передач (п = 5) при арифметической прогрес-
сии между скоростью 42 км/час и 23 км/час имеется передача со
скоростью 32,5 км/час, которой нет при геометрической прогрессии.
Машина с промежуточной передачей 32,5 км/час будет, очевидно,
иметь более высокую среднюю скорость движения и будет лучше
использовать свою мощность.
Разбивка передач по закону арифметической прогрессии яв-
ляется несколько произвольной, так как сдвигать передачи в сто-
рону высших передач можно и по любому другому закону, а не
только по закону арифметической прогрессии.
Рис. 27. График разбивки передач:
а—по геометрической прогрессии; б — по арифметической
прогрессии
Можно делать разбивку передач по типовым сопротив-
лениям. Из опыта эксплуатации машин устанавливают, какие
дорожные условия можно считать типовыми для машин данного
класса, после чего определяют типовые сопротивления движению
и по ним находят расчетные скорости. Однако и этот метод недо-
статочно определенен.
Наиболее правильным, с нашей точки зрения, является метод
разбивки передач по коэффициенту использования
мощности*. В основе этого метода лежит следующее положе-
ние. Чем больше снимаемая с двигателя мощность, тем выше сред-
няя скорость движения машины. Для гусеничных машин, движу-
щихся не только по дорогам, но и вне дорог, средняя скорость
является основным показателем их подвижности и маневренности.
Назовем отношение фактически снимаемой с двигателя мощ-
ности к номинальной (паспортной) мощности Ne коэффи-
циентом использования мощности f\N, тогда
Коэффициент i\N показывает, какая часть номинальной мощ-
ности затрачивается двигателем на совершение фактической работы
при движении машины.
* Метод разбивки передач по коэффициенту исполь.ования мощности был
предложен Е. И. Магидовичем.
63
В эксплуатации возможны два случая работы двигателя: дви-
гатель работает с неполной нагрузкой и двигатель работает на
внешней характеристике. В первом случае водитель машины может
поддерживать постоянными обороты двигателя за счет изменения
подачи горючего (при наличии всережимного регулятора обороты
автоматически поддерживаются постоянными), во втором случае
с увеличением нагрузки обороты двигателя будут падать.
Так как длительное время на внешней характеристике двига-
тель работать не может, а на величину средней скорости влияет
главным образом длительный режим работы двигателя, то при раз-
бивке передач следует учитывать только работу двигателя на ча-
стичной нагрузке, т. е. когда обороты nN остаются примерно по-
стоянными, а меняется момент и мощность двигателя.
Обозначим через /0 коэффициент сопротивления движению:
f _ Rq
Jo— Q •
Равномерное движение машины характеризуется следующим ра-
венством:
Rov = 'r\N^
где v — фактическая скорость движения машины;
N* — фактическая мощность, идущая на преодоление сопротив-
ления движению машины.
Тогда
f _
'° vG'
Примем, что двигатель работает на постоянных расчетных обо-
ротах, тогда v—vp будет расчетной скоростью движения машины
на данной передаче, откуда
, _
7о VpG •
Допустим, что Л^ = Л^, тогда /0 =/р, где /р назовем
расчетным коэффициентом сопротивления дви-
жению:
/р = ^- (62)
Взяв отношение /0 к /р, получим
fo=f^N, (63)
откуда следует, что между коэффициентом сопротивления движе-
нию fo и коэффициентом использования мощности т)^ существует
линейная зависимость (/р = const).
Выразим зависимость (63) в виде графика, представленного на
рис. 28.
На графике по оси абсцисс отложены значения коэффициента
использования мощности а по оси ординат — значения коэффи-
64
циента сопротивления движению f0 и расчетного коэффициента /р
на различных передачах.
Допустим, что известны расчетные скорости на передачах vpl,
vp2 и т. д. Тогда по формуле (62) определяем расчетные коэффи-
циенты сопротивления движению /р1, /р2 и т. д. Отложим в произ-
вольно выбранном масштабе величины этих коэффициентов на пра-
вой оси графика и соединим полученные точки с началом осей ко-
ординат. Получим семейство прямых. Каждая прямая характери-
зует движение машины на данной передаче.
Рис. 28. График разбивки передач по коэффициенту исполь-
зования мощности
В зависимости от сопротивления движению, которое преодоле-
вает машина на данной передаче, коэффициент использования мощ-
ности будет иметь различные значения. Чем больше/0, тем больше
i)w. При /о = /р коэффициент использования мощности становится
равным единице (100%), т. е. мощность двигателя используется
полностью.
Дальнейшее увеличение сопротивления движению (увеличе-
ние /0) потребует перехода на следующую пониженную передачу.
При этом коэффициент использования мощности получит меньшее
значение. Так, при переходе с четвертой передачи на третью коэф-
фициент использования мощности падает примерно до тгщз 71 % ;
при переходе с третьей передачи на вторую — до 7]!)2 68 % и со
5—2469 65
второй на первую — до три ~ 58%. Здесь и ниже через -(]0/ обозна-
чается минимальное значение коэффициента использования мощно-
сти на передачах.
Если задаться значением коэффициентов tqoi> tqo2 ит. д., то можно
определить расчетные коэффициенты /р1, /р2 и т. д., а следова-
тельно, и расчетные скорости на передачах, т. е. произвести раз-
бивку передач.
Из графика (рис. 28) напишем следующую пропорцию:
/рЗ :/р2 = ’’Пог • 1>
но из формулы (62) можем написать
/рз :/р2 = ('Пэ • (&р2 ’• ^>з)-
Тогда в общем виде для 7-ой передачи получим
vpt — -По/’ (м-ц , (64)
где т]0/—коэффициент использования мощности в момент переклю-
чения Лой передачи;
---отношение к. п. д. на Лой и (/4~1)"°й расчетных скоро-
стях (определяются из формулы 58);
v р —расчетная скорость на (/4~1)-ой передаче.
Для последовательного ряда передач можем написать:
v =71 .1!^».^ •
Р (л-1) "О (л-1) Р"’
^(л—2)
<77 --«Л , —--. <77 •
р (л-2) *10 (п—2) Р (л—О ’
Z'pf ’lol Vp2 •
Перемножим левую и правую части равенств. После сокращения
одноименных членов получим
-Qoi • ^02 • -Поз • • •. -Go ,„_,) = , (65)
где и —кинематический и силовой диапазоны.
Формула (65) позволяет подбирать коэффициенты Для
этого задаемся силовым диапазоном dc и выбираем значения ве-
личин т)0< так, чтобы их произведение равнялось -г- . При этом
ис
следует выбирать большие значения коэффициентов на ходо-
вых передачах и меньшие — на неходовых передачах.
Зададимся теперь расчетной скоростью на высшей передаче кр„.
Ее можно принять или равной заданной скорости или не-
66
сколько меньшей. Если максимальные обороты двигателя равны
д , а расчетные—nN, то можно взять
v ——— •'О . (66)
РЛ «max maX V ’
Зная t'o,,, находим по формуле (64) все остальные расчетные ско-
рости. При этом в формулу (64) подставляются значения к. п. д.
из формулы (58).
При определении коэффициентов нужно задаться числом
передач или определить его следующим способом.
Примем в формуле (65) = const. Кроме того, приближенно
можно считать, что к. п. д. на передачах одинаков. Тогда из фор-
мулы (64) получим
= const.
Vpf
Но это есть условие разбивки передач по закону геометрической
прогрессии. Из формулы (65) получим
л=1 —|SA. (67)
1g lo v
Задаваясь некоторым «редким значением т)Оср, определяем в пер-
вом приближении число передач п, после чего по формуле (65)
уточняем истинные значения коэффициентов на передачах t.
Если взять в качестве примера iOcp = 0,75 и rfc = 8, то со-
гласно формуле (67) получим
1 °’9 о о
п~ 1 -0,125 ~ 8’2-
Из этого примера следует, что геометрическая прогрессия тре-
бует большого числа передач. Для уменьшения числа передач
следует брать переменные значения not.
В табл. 5 приведены значения для некоторых транспортных
М- сельскохозяйственных тракторов.
Таблица 5
Значения коэффициентов использования мощности
Передачи ijo тягачей и тракторов
АТ-Т AT-C М-2 С-80 ДТ-54 КД-35
Яервая — вторая . . 0,45 0,54 0,55 0,71 0,77 0,82
Вторая — третья . . 0,68 0,78 0,53 0,70 0,85 0,89
Третья — четвертая 0,69 0,59 0,56 0,70 0,87 0,85
Ягетвертая — пятая 0,57 0,61 0,78 0,77 0,80 0,67
5*
67
Из таблицы следует, что максимальное значение коэффициента
использования мощности в гусеничных тягачах не превосходит 0,78,
в сельскохозяйственных же тракторах оно увеличивается до 0,89.
Это объясняется тем, что диапазон скоростей сельскохозяйственных
тракторов уже, чем диапазон скоростей гусеничных тягачей, вслед-
ствие чего при одном и том же числе передач последние распола-
гаются ближе друг к другу.
Проанализировав разбивку передач в гусеничных тягачах, можно
сделать следующие выводы. Наилучшую разбивку передач имеет
тягач АТ-Т, так как у него наибольший коэффициент использования
мощности (0,68—0,69) приходится на наиболее ходовые передачи.
В тягаче АТ-С наибольший коэффициент приходится на вторую пе-
редачу, а в тягаче М-2 — на четвертую. Обе эти передачи для тя-
гача не являются ходовыми. Можно считать, что при прочих рав-
ных условиях тягач АТ-Т должен иметь большую среднюю скорость
движения.
При разбивке передач наибольшие значения коэффициентов ис-
пользования мощности следует принимать на ходовых передачах:
для транспортеров ходовыми передачами являются две высшие пе-
редачи, для тягачей — две средние. Для первой передачи, как нехо-
довой, можно брать Цо порядка 0,4—0,5. В этом случае остальные
передачи получат большее значение тр.
В целях повышения коэффициента цо в гусеничных машинах вы-
деляют из общего диапазона первую передачу, которую называют
в этом случае замедленной. Следующую за ней передачу на-
зывают первой ит. д. Отношение первой передачи к замедленной
составляет примерно 2,5, что соответствует т)о = 0,4.
Рабочий диапазон скоростей при общем диапазоне rfc = 10
в этом случае будет б/рс = = 4. В рабочем диапазоне машина
фактически и работает большую часть своего времени. Общий диа-
пазон используется сравнительно редко.
ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ЧИСЕЛ СИЛОВОЙ ПЕРЕДАЧИ
Зная расчетные скорости на передачах, можно определить пе-
редаточные числа силовой передачи.
Расчетная скорость машины выражается формулой
где гк—приведенный радиус ведущих колес в м;
nN—расчетное число оборотов вала двигателя в минуту;
i0—общее передаточное число силовой передачи;
т/р—расчетная скорость машины в м/сек.
Передаточное число i0 равняется произведению постоянного пе-
редаточного числа in на переменное передаточное число коробки
68
(69)
(70)
(71)
(72)
передач 4- Постоянное передаточное число дают главная пере-
дача и бортовая передача *, тогда
4 ~ 44 •
Из формул (68) и (69) получим
. _ ~rxnN -
30fnWp •
Для определения ix следует задаться приведенным радиусом
ведущего колеса гь. и постоянным передаточным числом 1а.
Радиус ведущего колеса выбирается в зависимости от конструк-
ции машины, Обычно гк = 0,2—0,3 м. Чем тяжелее машина, тем
больший радиус ведущих колес она имеет.
Постоянное передаточное число определяется следующим обра-
зом. Допустим, что в коробке передач имеется прямая передача. На
прямой передаче 4 = 1. Из формулы 70 определяем
. _^rxtiN
1а~ '30^7
Если прямая передача является высшей, то — Учи-
тывая формулу (66), напишем
= —— • V
р n max
'‘max
В коробках с поперечным расположением валов нет прямой пе-
редачи. Обычно передаточное число в этих коробках на высшей
передаче меньше единицы и составляет 0,7—0,8.
Подставив в формулу (71) 4 на высшей передаче и &р из
формулы (72), получим значение 4- При этом следует иметь
в виду, что вторичный вал коробки передач будет вращаться с чис-
лом оборотов, большим числа оборотов вала двигателя. Эти обо-
роты ограничиваются условиями работы подшипников и обычно не
должны превосходить 4000—4500 в минуту.
Чем больше будет 4> тем меньше будут габариты коробки пе-
редач, так как через нее будет передаваться меньший момент.
' Для тягачей 4 обычно находится в пределах 6—7, для тан-
ков —7—12.
; Заметим, что 4 > 7 получить в механизме, имеющем пару
Шестерен, нельзя. Поэтому, например, бортовые передачи с 4>7
бывают двухрядные или планетарные (см. ч. 2).
3. ОСОБЕННОСТИ ТЯГОВОГО РАСЧЕТА ТЯГАЧА
Тяговый расчет гусеничного тягача в отличие от тягового
расчета транспортера имеет некоторые специфические особенности,
t Как указывалось выше, при расчете тягача в качестве одной из
* Постоянное и переменное передаточное число может также давать плане-
тарный механизм поворота.
69
расчетных величин должен быть задан вес прицепа Gi. Тогда вес
тягача G будет являться величиной определяемой. Рассмотрим вна-
чале в общем случае определение отношения Gi : G, исходя из
заданных условий движения поезда по сцеплению.
Чтобы обеспечить движение поезда по сцеплению, должно со-
блюдаться следующее неравенство между силой тяги по сцепле-
нию Рс и силами сопротивления тягача Ro и прицепа Roit
где
Рс > ^0 + ^01>
(73)
Рс =
Ro — + Gsina;
Ai=/iGci + sin a.
Из формул (15) и (16) определяем значение сцепного веса:
Gc = G cos a + /?„ tg у;
GCI = Gj cos a — RK tg y.
Здесь /?K=/1GC1. Подставив Gc и GC1 в неравенство (73), по-
лучим после преобразования
Gi
G
<p—f — tga
fi + tg a
_ (?—/ +A)/itgT
' 1 + fi tg 7
(74)
Из полученной формулы следует, что соотношение между ве-
сами Gi и G зависит от угла у: чем больше угол у, тем больше от-
ношение Gi : G, или чем больше хоботовое давление, тем больше
можно принимать вес прицепа по сравнению с весом тягача.
В практических расчетах принимают угол у = 0. Тогда из фор-
мулы (74) получим
Gi —
G fl + tg a
(75)
Примем в формуле (75) <р —0,8; /=0,1; /=0,05; a = 20°.
После подстановки получим < 0,83, т. е. вес тягача при приня-
тых дорожных условиях должен быть больше веса прицепа.
Из формулы (75) следует, что чем большим будет принят вес
тягача, тем при заданном весе прицепа будет выше проходимость
гусеничного поезда, так как дорожные условия могут быть при этом
приняты' более тяжелыми. Увеличение веса тягача влияет также и
на маневренность поезда, повышая его поворотливость и разгон.
Однако значительно увеличивать вес тягача по сравнению с весом
прицепа все же нежелательно, так как это будет ухудшать топлив-
ную экономичность поезда.
70
Gi
Топливная экономичность улучшается, если отношение -q- при-
ближается к единице.
Для тягачей различной весовой категории отношение весов
О- принимают различное. Чем тяжелее тягач, тем больше отно-
шение ут- приближается к единице. Для тяжелых тягачей —
= 0,8—1.
Легкие тягачи более маневренны. В выполненных конструкциях
легких тягачей отношение весов тягача и прицепа находится в пре-
делах -^- = 0,4—0,5, т. е. значительно меньше единицы.
ОПРЕДЕЛЕНИЕ МОЩНОСТИ ДВИГАТЕЛЯ ТЯГАЧА
Мощность двигателя тягача определяется по формуле
^0n minimax
Ne =----------- > - (7°)
где /?01| т1п — сопротивление движению поезда на хороших грунто-
вых дорогах;
т/'гаах—максимальная скорость поезда на хороших грунтовых
дорогах.
Сопротивление движению можно определить по следующей
формуле:
^On min fon min ^0 >
где /Оп min—коэффициент сопротивления движению поезда;
Go — общий вес поезда.
Поверочные расчеты показывают, что скорость т/тах обычно
^Оставляет
S'max = (0.5-0,6) , (77)
Где т/тах—максимальная скорость одиночного тягача при движе-
нии его по хорошей дороге с твердым покрытием и с
грузом на платформе.
Коэффициент сопротивления движению поезда, состоящего из
гусеничного тягача и колесного прицепа, находится в пределах
An min =0,07-0,09.
71
Так как v ах задается в технических условиях на проектирова-
ние, то согласно формуле (77) можно определить г/тах (если ^тах
не задано условиями на проектирование). Задаваясь /Оп т1п, нахо-
дим /?Оп т1п. Тогда по формуле (76) определится номинальная (пас-
портная) мощность двигателя Ne. После того как мощность Ne
определена, необходимо проверить, достаточно ли этой мощности
для обеспечения заданной по техническим условиям максимальной
скорости движения одиночной машины г'тах. Если мощности ока-
жется недостаточно, то следует произвести перерасчет. Мощ-
ность Ne в этом случае определяется по скорости движения оди-
ночной машины, движущейся с грузом на платформе. Расчет ве-
дется так же, как для транспортера.
Если в результате расчета окажется, что скорость одиночной
машины значительно превосходит заданную техническими усло-
виями скорость ^п1ах, то это означает, что слишком завышена ско-
рость поезда v'm!a или приняты слишком тяжелые условия движе-
ния поезда (взят слишком большой расчетный коэффициент /Опт1п).
Пример. Определим мощность двигателя тягача. Примем вес тягача 7000 кг\
вес колесного прицепа 6000 кг\ на платформе тягача' имеется груз 2000 кг. Ма-
ксимальная скорость одиночного тягача wmax = 35 км/час.
Определяем вес поезда: Go = 7000 + 2000 + 6000 = 15 000 кг. Примем
vmax — Q'5vrnax, или wmax = 0,5-35 = 17,5 км/час. Задаемся коэффициентом
сопротивления движению /0|1 min = 0,075. Определяем по формуле (58) к. п. д.
тягача при движении со скоростью 17,5 км/час. Будем иметь к; =
= 0,85 — 0,0055 • 17,5 = 0,75, тогда по формуле (76) находим
0,075-15000-17,5 п_
Ne = —--------------= 97 л. с.
Проверим, обеспечивается
шины vmax.
Воспользуемся формулой
=/о min G = 0,05 (7000 + 2000) = 450 кг. Из формулы (58) находим =
= 0,85 — 0,0055 • 35 = 0,66 и окончательно получим
0,75-75-3,6
ли данной мощностью скорость одиночной ма-
(57). Примем fn -0,05, тогда R
Так как Ne < Ne< то максимальная скорость одиночной машины вполне
обеспечивается мощностью двигателя 97 л. с.
Далее тяговый расчет тягача ведется в такой же последователь-
ности, которая указывалась выше для транспортера.
В заключение тягового расчета транспортера или тягача строятся
основные характеристики машины. К числу основ-
ных характеристик относятся график удельной силы тяги, график
разбивки передач по коэффициенту использования мощности, гра-
фик разгона.
72
Построение второго и третьего графиков было рассмотрено
выше. Рассмотрим здесь построение графика удельной силы тяги.
График удельной силы тяги строится по внешней характери-
стике двигателя.
Имея внешнюю характеристику, определяем мощность двига-
теля Л\ и соответствующее этой мощности число оборотов вала
двигателя zza.
Определяем скорость движения машины по следующей формуле:
v = , (78)
где v— скорость движения машины в км/час-,
пк— число оборотов вала двигателя в минуту;
гк— радиус ведущих колес в м;
iot—общее передаточное число силовой передачи на передачах.
Удельная сила тяги <рд определится по формуле
_ f\ _ 270^д
тд (] VQ >
(79)
где т]— к. п. д. машины;
G— вес машины в кг;
Л7Д— мощность двигателя в л. с.;
v— скорость движения машины в км/час.
<рд строится в функции v, причем по оси абсцисс откладывается
скорость v (в км/час), а по оси ординат — удельная сила тяги <рд.
На рис. 29 представлен примерный график удельной силы тяги,
построенный по внешней характеристике двигателя.

Рис. 29. График удельной силы тяги:
а — внешняя характеристика двигателя
73
График удельной силы тяги характеризует тяговые качества
машины, а также ее способность преодолевать те или иные сопро-
тивления; график коэффициентов использования мощности харак-
теризует экономичность машины и ее скоростные данные; график
разгона характеризует приемистость или динамику машины.
Если тяговый расчет ведется для тягача, то желательно основ-
ные графики построить как для одиночного тягача, так и для
поезда.
ГЛАВА IV
ТЕОРИЯ ПОВОРОТА ГУСЕНИЧНЫХ МАШИН
1. КИНЕМАТИКА И СТАТИКА ПОВОРОТА
ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
Гусеничная машина поворачивается вследствие изменения ско-
ростей перематывания ее гусениц.
Условимся гусеницу с меньшей скоростью называть отстаю-
щей и приписывать ей индекс 1 и гусеницу с большей скоростью
называть забегающей и приписывать ей индекс 2 (рис. 30).
Машина поворачивается вокруг некоторой точки О,‘ которая на-
зывается центром поворота. Центр поворота есть мгновен-
ный центр вращения корпуса машины.
Центр поворота лежит на оси, параллельной поперечной оси ма-
шины и в общем случае смещенной от нее на величину X, которую
назовем смещением центра поворота.
Рис. 30. Поворачивающаяся гусеничная машина
В плане
75
Вращение корпуса машины вокруг центра поворота сообщает
опорным ветвям гусениц переносное движение со скоростями vt и
v2 в точках «1 и п2. Кроме того, точки «1 и п2, принадлежащие
опорным ветвям гусениц, участвуют в относительном движении по
отношению к корпусу со скоростями Уо| и Уо2. Относительные и
переносные скорости имеют противоположные знаки. Если бы ско-
рости Уо1 и У1, Уо2 и v2 были бы по абсолютной величине попарно
равны, то абсолютная скорость точек rii и п2 равнялась бы нулю
(Vi = 0, 1/2 = 0) и эти точки были бы мгновенными центрами пово-
рота опорных ветвей гусениц. При повороте гусеничной машины
обычно имеется следующее неравенство скоростей: | z/Oi КI I
и | ^021> I ^21. т- е- опорная ветвь отстающей гусеницы движется
юзом, а забегающей гусеницы — частично буксует (> 0, V2 0).
Точки О, гь и п2 лежат на одной прямой, перпендикулярной про-
дольной оси машины. Эта прямая называется линией центров
поворота.
Поворот машины характеризуется угловой скоростью 8
и радиусом поворота R. Радиус поворота равен расстоя-
нию от центра поворота до продольной оси машины. Обычно удоб-
нее пользоваться относительным радиусом поворота
р =/? : В, где В — ширина колеи машины, или расстояние
между продольными осями опорных ветвей гусениц.
Длину опорной ветви, равную расстоянию между осями край-
них опорных катков, будем обозначать буквой L. Эта величина яв-
ляется опорной базой машины.
Отношение опорной базы к ширине колеи машины назы-
вается относительной опорной базой.
Относительная опорная база является важным геометрическим
параметром, характеризующим поворот гусеничной машины.
ХАРАКТЕР ПОВОРОТА ГУСЕНИЧНОЙ МАШИНЫ
Поворот гусеничной машины условно можно разбить на три
этапа: вход в поворот, совершающийся в общем случае с пе-
ременным радиусом (р = var) и переменной угловой скоростью
(2 = var) по некоторой дуге аб (рис. 31), равномерный по-
ворот, совершающийся с постоянным радиусом (р = const) и по-
стоянной угловой скоростью (2 —const) по дуге окружности бв, и
выход из поворота, совершающийся с переменным радиу-
сом и переменной угловой скоростью по некоторой дуге вг. Таким
образом, поворот гусеничной машины имеет характер равно-
мерного и неравномерного поворота. Равномерный поворот, однако,
может отсутствовать. Так, если машина движется по дороге и со-
вершает повороты на сравнительно небольшой угол, то она не успе-
вает войти в поворот, как уже выходит из него. Таким образом,
участок равномерного поворота фактически отсутствует. Несмотря
на это, в дальнейшем рассматривается главным образом равномер-
ный поворот с постоянной скоростью и постоянным радиусом,
76
Это объясняется тем, что в практических расчетах чаще всего при-
ходится решать вопросы равномерного поворота, так как эти во-
просы непосредственно относятся к тяговому расчету машины при
повороте, а также к выбору механизма поворота. Рассмотрение
вопросов неравномерного поворота является специальной задачей,
имеющей лишь частное значение в теории и расчете гусеничных
машин.
Рис. 31. Характер поворота гусеничной машины
(вход в поворот, равномерный поворот и выход
нз поворота)
ОПРЕДЕЛЕНИЕ РАДИУСА И УГЛОВОЙ СКОРОСТИ ПОВОРОТА
Согласно рис. 30 для скоростей точек, принадлежащих корпусу
и расположенных на продольных осях гусениц, можем написать
следующее равенство:
у, я+g ?+4~
*’ р-4-'
Кроме того,
^ = й.
D
Выразим переносные скорости и через относительные ско-
рости Пог и пог и коэффициенты проскальзывания опорных ветвей
По грунту Oi и а2:
^2 = •
п
Подставляем сц и v2 в предыдущие формулы, после преобразования
получим
_____<*1У01 + стэ^'ов . / 80)
? ~~ 2(a2v02 — (JjVoi) ’ '
й =
<%Ург — <ЦУр1
В
(81)
где р и £2 — действительный радиус поворота и действительная
угловая скорость поворота машины.
Теоретическим радиусом рт называется радиус по-
ворота при отсутствии проскальзывания гусениц.
Приняв в формуле (80) в! = а2 = 1, получим теоретический ра-
диус
__ Ург + Vqi
т 2 (v02 — Voi)
(82)
Выразим р через рт. Из формулы (82)
Уог
Vol
1
Рт + ~
г •
Рт 2
Подставив это выражение в формулу (80), после преобразова-
ния получим
п= 2Рт - С
р 2 (1 — 2сРт) >
где
с==Е1П2?>о.
4“ ^2
Величина с обычно значительно меньше 2рт; тогда в числителе
ее можно принять равной нулю. Окончательно будем иметь
1
р = т------------
-2-----2с
(83)
Допустим, что при повороте машины отстающая гусеница имеет
юз (б! 1), а забегающая — буксование (e2 < 1), тогда с 0. При
с = 0 (проскальзывание опорных ветвей отсутствует) и р = рт, т. е,
действительный радиус равен теоретическому. Чем больше про-
скальзывание опорных ветвей, тем больше с и, следовательно, тем
больше действительный радиус отличается от теоретического.
Как показывают опыты, между действительным и теоретическим
радиусом поворота существует зависимость, близкая к линейной
/2Е±3. (84)
78
где коэффициент k можно принять величиной постоянной, завися-
щей только от грунта. Так, для суглинистого грунта с травянистым
покровом этот коэффициент равен примерно 1,5. Для других грун-
тов k изменяется и находится в пределах 1,3—1,6.
ПРОСКАЛЬЗЫВАНИЕ ОПОРНЫХ ВЕТВЕЙ ГУСЕНИЦ ПРИ ПОВОРОТЕ
Покажем, что при повороте гусеничной машины всегда происхо-
дит продольное проскальзывание опорных ветвей гусениц по грунту.
Допустим вначале противное, а именно: опорная ветвь гусеницы
Рис. 32. Поворот опорной ветви гусеницы:
а — поворот без смешения центра поворота; б — поворот со смещением
центра поворота
не имеет продольного проскальзывания, т. е. она только поворачи-
бается в плоскости дороги. Полюсом поворота опорной ветви в этом
Случае является точка, расположенная на средней оси ветви. Эта
^очка есть мгновенный центр поворота опорной
Ветви (точка п, рис. 32, а). Кроме того, гусеница имеет еще пере-
катывание, т. е. она вращается в плоскости, перпендикулярной
к плоскости дороги. Это движение гусеницы нас здесь, однако, не
Интересует.
Допустим, что между опорной ветвью и грунтом действуют силы
Кулонова трения (эти силы являются основной составляющей сил
взаимодействия гусеницы с грунтом). Согласно законам трения
79
Как видно, взаимодействие гусениц с грунтом — чрезвычайно
сложное явление. В этом случае действуют четыре вида сил:
силы лобового сопротивления, силы трения, силы
среза и силы нагребания грунта.
Отнесем лобовое сопротивление к числу заданных сил, так как
его можно определить через коэффициент сопротивления качению.
Неизвестными реакциями будут силы трения, среза и нагребания
грунта. Между этими силами имеется следующая, принципиальная
разница: силы трения можно считать зависящими только от нор-
мальных сил, прижимающих опорную ветвь к грунту и практиче-
ски не зависящими от перемещения и скорости опорной ветви; силы
же среза и нагребания грунта, наоборот, зависят от перемещения и
скорости ветви.
Срез грунта также зависит от радиуса поворота машины. Грунт
срезается не сразу: вначале (на больших радиусах поворота, когда
угол поворота гусениц мал) грунт уплотняется и только потом сре-
зается.
Нагребание грунта также зависит от радиуса поворота и на ма-
лых радиусах заметно влияет на сопротивление повороту.
Следовательно, силы среза и нагребания являются функцией ра-
диуса поворота машины: чем круче поворачивается машина, тем
больше эти силы. Кроме того, они являются также и функцией ско-
рости поворота машины.
Математически учесть все явления, сопровождающие взаимо-
действие гусениц с грунтом при повороте, не представляется воз-
можным.
Поэтому в теории поворота принимается ряд упрощающих за-
дачу допущений.
Рассмотрим эти допущения.
1. Элементарные силы взаимодействия опорных ветвей с грун-
том (Д0 принимают зависящими от элементарной нормальной на-
грузки (Д/г) и от коэффициента сопротивления повороту р, а также
направленными в сторону, противоположную скольжению их точек
приложения.
При этом коэффициент сопротивления повороту р. принимают
зависящим от радиуса поворота р.
2. Нормальные силы, прижимающие опорные ветви гусениц
к грунту, считают рассредоточенными. При этом эпюру нормаль-
ных сил принимают прямоугольной.
3. В опорных ветвях гусениц учитывают только длину, шири-
ной гусениц пренебрегают.
4. Принимают также, что полюсы поворота опорных ветвей ле-
жат на продольных осях гусениц.
5. Сопротивление повороту принимают не зависящим от скоро-
сти поворота.
Принятые допущения несколько искажают действительную кар-
тину поворота. Так, например, четвертое допущение не соответ-
ствует физической сущности явления, происходящего при повороте,
82
так как известно, что при расположении полюсов поворота на про-
дольных осях гусениц нельзя получить на гусеницах продольных
реакций.
Второе допущение также упрощает физическую сущность
явления: нормальные нагрузки на грунт на твердых грунтах явля-
ются скорее сосредоточенными, чем рассредоточенными. Только на
мягких грунтах, когда опорная ветвь погружается в грунт, нагрузка
на грунт передается всей поверхностью опорной ветви и выравни-
вается, приближаясь к рассредоточенной. Но даже и в этом случае
считать эпюру прямоугольной можно только условно, так как фак-
тически она будет пикообразной формы.
Однако принятые допущения значительно упрощают расчетные
формулы. Некоторая же неточность результатов расчета компенси-
руется опытным значением коэффициента р, который подставляется
в расчетные формулы.
ОПРЕДЕЛЕНИЕ РЕАКЦИИ ГРУНТА, ДЕЙСТВУЮЩИХ
НА ОПОРНЫЕ ВЕТВИ ГУСЕНИЦ
Обозначим элементарную силу трения, действующую на опор-
ную ветвь гусеницы, через At Согласно первому допущению
М — рАл,
где Ал—элементарная нормальная сила;
Р— коэффициент сопротивления повороту.
Так как полюс поворота лежит на продольной оси гусеницы (по
четвертому допущению), то силы А/ будут перпендикулярны к этой
оси (рис. 35).
6*
Рис, 35. Взаимодействие опорной ветви гусеницы с грунтом
при повороте
83
сила трения направлена противоположно абсо-
лютной скорости скольжения (У). Так как при указан-
ном расположении мгновенного центра вектор скорости скольжения
точки а, лежащей на продольной оси гусениц, направлен пер-
пендикулярно этой оси, то и сила трения t будет направлена пер-
пендикулярно продольной оси. Тогда сила трения проектируется на
про-дольную ось в точку и, следовательно, не дает продольной со-
ставляющей.
Если точка а смещена с продольной оси, то сила трения будет
давать продольную составляющую. Однако всегда можно найти на
опорной ветви симметричную точку, которая дает такую же по ве-
личине составляющую силы трения, но противоположно ей направ-
ленную. В результате сумма проекций этих сил будет равна нулю.
Таким образом, при расположении полюса поворота (мгновен-
ного центра поворота) на продольной оси опорной ветви нельзя
получить продольную силу трения.
Однако при повороте машины продольная сила всегда суще-
ствует: это или сила тяги, создаваемая двигателем на забегающей
гусенице, или тормозная сила, создаваемая тормозом на отстающей
гусенице.
Допустим теперь, что полюс поворота смещен от продольной оси
на некоторую величину Я (рис. 32,6). Тогда опорная ветвь полу-
чает, кроме поперечного скольжения (ЕД также и продольное
скольжение (ЕД. Вследствие продольного скольжения на опорной
ветви возникает продольная реакция грунта (tx).
Таким образом, продольная сила (реакция) может возникать
на опорной ветви только при наличии продольного проскальзывания
этой ветви. Скорость продольного проскальзывания равна
ЕЛ = ХЙ,
где X—координата полюса поворота;
Q—угловая скорость поворота машины (а следовательно, и
Рис. 33. Расположение полюсов по-
ворота
опорной ветви, так как опорная
ветвь вращается с той же скоро-
стью, что и машина).
В зависимости от расположе-
ния полюса поворота проскальзы-
вание о-порной ветви может быть
положительным или отрицатель-
ным. Соответственно этому и про-
дольная сила будет направлена
вперед или назад.
На рис. 33 показано располо-
жение полюсов поворота опорных
ветвей отстающей и забегающей
гусениц. Так как на забегающей
гусенице создается положительная
сила (сила тяги), а на отстаю-
80
Рис. 34. Смещение полюса поворота гусеничной машины
щей — отрицательная сила (тормозная сила), то полюсы поворота
«1 и л2 в этом случае располагаются вне машины. Следовательно,
Забегающая гусеница имеет буксование (отрицательное скольжение,
так как V2CO), а отстающая — юз (положительное скольжение,
так как Vi>0).
Это явление будет происходить всегда в тех случаях, когда на
гусеницах создаются противоположно направленные продольные
силы (сила тяги и тормозная сила).
,, На рис. 34 показан поворот гусеничной машины при полностью
Заторможенной отстающей гусенице. Поворот отстающей гусеницы
Совершается вокруг точки п\, смещенной с опорной ветви гусеницы.
|Это и есть полюс поворота данной гусеницы. Таким образом, опыт
Подтверждает наличие смещения полюсов поворота гусениц.
2. ВЗАИМОДЕЙСТВИЕ ОПОРНЫХ ВЕТВЕЙ ГУСЕНИЦ
С ГРУНТОМ ПРИ ПОВОРОТЕ МАШИНЫ
ОСНОВНЫЕ ДОПУЩЕНИЯ ТЕОРИИ ПОВОРОТА
При повороте гусеничной машины на ее ходовую часть дей-
ствуют реакции грунта, создающие сопротивление повороту машины.
L Эти реакции имеют различную природу. Так, в плоскости опор-
fcx ветвей действуют силы трения, силы деформации грунта, воз-
никающие вследствие среза грунта шпорами и кромками гусениц, и
Й^1Ы лобового сопротивления перекатыванию гусениц. При крутом
Ц>вороте на мягком грунте гусеницы нагребают грунт, при этом
|р5акции грунта передаются на корпус машины через опорные ветви
«Усениц, а также и непосредственно через опорные катки (см. рис. 34).
6—2469 81
Кроме поперечных касательных реакций М, на опорную ветвь
должны действовать также и продольные касательные реакции,
равнодействующая которых дает силу тяги или тормозную силу Р.
Заменим правую и левую часть эпюры поперечных сил равно-
действующими Т' и Т" (рис. 36, а). Приложим к точке п две рав-
ные и противоположно направленные силы Т' и Т”. Получим пару
сил, момент которой равен
Л7С = Гд, + Т"а2,
и поперечную силу
у __ 'Р’________________________Т"
Рис. 36. Равнодействующие реакций грунта, приложенные
к опорной ветви гусеницы при повороте
Таким образом, реакции грунта, действующие на опорную ветвь
гусеницы, приводятся к силе тяги Р, поперечной реакции грунта Т и
моменту сопротивления повороту(рис. 36,6).
Положительная сила Р, или сида тяги, возникает в результате
работы двигателя, т. е. в результате натяжения забегающей гусе-
ницы ведущим колесом.
84
Отрицательная, или тормозная, сила возникает вследствие тор-
можения (с помощью тормоза) ведущего колеса отстающей гусе-
ницы.
Возможно и такое положение, когда при повороте машины на
обеих гусеницах возникают только положительные (но не равные
по величине) силы тяги. Это может происходить при повороте тя-
гача с прицепом или при повороте машины на подъеме.
Поперечная реакция грунта Т возникает вследствие действия на
машину какой-нибудь внешне приложенной к корпусу поперечной
силы или равнодействующей поперечных сил.
Так, поперечной силой может являться составляющая центро-
бежной силы, составляющая силы тяги на крюке или составляю-
щая веса машины при повороте тягача на косогоре.
Реакция грунта уравновешивает внешнюю поперечную силу.
Под действием центробежной силы (вернее, ее поперечной состав-
ляющей) машина стремится перемещаться в радиальном направ-
лении. Реакция же Т удерживает машину от радиального переме-
щения, т. е. от заноса.
Поперечная реакция Т может быть направлена к центру пово-
рота машины или от центра поворота в зависимости от того, в ка-
ком направлении действует внешняя поперечная сила (по отноше-
нию к которой поперечная реакция всегда действует в противопо-
ложном направлении).
Определим реакцию Т и момент Л7С.
Согласно схеме сил на рис. 37 можем написать
4+z 4~z 4+z 4-z
т= Г — Т" = У М — 5' м = и (— 2 Дл)-
О о 0 0
Будем рассматривать Ап как силу, приходящуюся на
длины опорной ветви. Пусть на опорную ветвь действует
тогда при прямоугольной эпюре
л N
откуда
4+х
Г = дл = !лд/г(4 + х} = !л4(4+^;
единицу
сила N,
Тогда
т_ 2p.XJV
1 ~ L *
Согласно предыдущему
(85)
+ Т"а2,
85
где
«1 — 2 ( 2 + ,
тогда
_ 1 / L у\
а2— 2 2 )’
(86)
Рис. 37. Определение момента сопротивления повороту при
прямоугольной эпюре давлений:
а — нормальная эпюра давлений; б — касательная эпюра давлений
Формулы (85) и (86) выведены для одной гусеницы. В этом
случае реакция N равна половине сцепного веса машины ('Д^с)-
Для двух гусениц получим выражение суммарной силы Т и суммар-
ного момента 7ИС:
у 2 p-XGc
(87)

(88)
В формулу (87) входит смещение центра поворота X. Вели-
чина X может иметь как положительное, так и отрицательное зна-
чений;' В зависимости от этого и поперечная реакция Т будет поло-
жительной или отрицательной. Примем в качестве положительного
86
значения X смещение центра поворота назад в сторону кормы ма-
шины, тогда при повороте машины по часовой стрелке положитель-
ная реакция Т будет направлена от центра поворота, а следова-
тельно, поперечная сила должна быть направлена к центру пово-
рота. Отсюда следует, что под действием центробежной силы центр
поворота смещается вперед, т. е. имеет отрицательное смещение.
Под действием силы тяги на крюке центр поворота может сме-
щаться как назад, так и вперед в зависимости от направления силы
тяги на крюке; чаще всего он смещается назад, так как попереч-
Рис. 38. Определение момента сопротивления повороту при
треугольной эпюре давлений:
а — нормальная эпюра давлений; б — касательная эпюра давлений
ная составляющая силы тяги на крюке обычно направлена к центру
поворота поезда.
В формулу (88) величина X входит в квадрате, следовательно,
ее знак не влияет на величину момента /Ис. С увеличением X как
реакция Т, так и момент Л7С увеличиваются.
При отсутствии поперечной силы момент сопротивления пово-
роту будет выражаться следующей формулой:
М = (89)
Эта формула получена для прямоугольной эпюры нормальных
Давлений гусениц на грунт (см. второе допущение).
Допустим теперь, что эпюра нормальных давлений имеет какую-
нибудь другую-форму, например треугольную (рис. 38). По анало-
87
гии с предыдущим получим для треугольной эпюры следующее вы-
ражение момента сопротивления повороту:
Отсюда следует, что при треугольной эпюре давлений момент Л7С
примерно на 30% меньше момента /Ис при прямоугольной эпюре.
Таким образом, изменение эпюры нормальных давлений дает
уменьшение момента сопротивления повороту и тем самым облег-
чение поворота гусеничной машины.
Однако изменять эпюру нормальных давлений для облегчения
поворота все же не следует, так как треугольная (или трапецие-
видная) эпюра давлений ухудшает проходимость машины по мяг-
ким грунтам вследствие получающегося неравномерного давления
на грунт под опорными катками. Кроме того, неравномерное рас-
пределение нагрузок по опорным каткам приводит к неравномер-
ному износу резиновых бандажей катков. Ухудшается также и
плавность хода машины, так как машина в этом случае сильнее
раскачивается на неровностях дороги.
3. ОПРЕДЕЛЕНИЕ СИЛ ТЯГИ НА ОТСТАЮЩЕЙ
И ЗАБЕГАЮЩЕЙ ГУСЕНИЦАХ
ОБЩИЕ УРАВНЕНИЯ ПОВОРОТА ГУСЕНИЧНОЙ МАШИНЫ
На рис. 39 приведена схема внешних сил, действующих на ма-
шину в общем случае поворота.
На схеме Ри Р2, Т и Afc — касательные реакции грунта, дей-
ствующие на опорные ветви гусениц; Qx, Qy — проекции на оси х
и у равнодействующей всех внешних сил, приложенных к корпусу
машины, в том числе и лобового сопротивления качению гусениц.
В число внешних сил могут входить согласно принципу Далам-
бера и силы инерции: сила инерции поступательного движения и
инерционный момент вращательного движения. Силу инерции
можно включить в силы Qr и Q а инерционный момент прибавить
к моменту сопротивления А4С. Тогда представленная на рис. 39
схема сил будет описывать общий случай поворота гусеничной
машины.
Составим уравнение моментов внешних сил относительно то-
чек П2 и п}. Получим выражение сил тяги на отстающей и забе-
гающей гусеницах:
P2 = + ^ + ^Qx + a-^Qr (90)
Эти уравнения назовем общими уравнениями по-
ворота гусеничной машины, так как они описывают как
88
равномерный, так и неравномерный поворот (в по-следнем случае
в -/Ис, Qx и Qy должны входить инерционные члены).
В формулы (90) входят координаты точки /га: ат и Ьт. Эти
координаты определяются из уравнения моментов внешних сил,
приложенных к корпусу машины:
где Pxi и Р . — проекции внешних сил на оси х — х и у — у,
xt и у t — координаты точек приложения сил, отсчитывае-
мые от оси отстающей гусеницы и от поперечной
оси у —у.
Рис. 39. Внешние силы, действующие на гусенич-
ную машину при повороте
РАВНОМЕРНЫЙ ПОВОРОТ ОДИНОЧНОЙ МАШИНЫ
НА ГОРИЗОНТАЛЬНОМ УЧАСТКЕ ПУТИ
Определим силы тяги на отстающей и забегающей гусеницах
при равномерном повороте одиночной машины на горизонтальном
Участке пути.
Пренебрежем центробежной силой; тогда поперечная сила Qv
будет равна нулю. Продольной силой Qx является сила сопротивле-
ния качению fG, действующая вдоль оси х — х.
89
Тогда bm = 0,5 В. Из формулы (89) имеем
Л4С = ^,
с 4 >
где G — сцепной вес машины, равный ее полному весу.
Подставив Qv = 0 и Or = fG в формулы (90), получим
> V-GL . fG
1 4В т 2 1
р ___?GL . fG
G~ ’lB г 2 •
(92)
Обычно первый член в этих формулах по абсолютной величине
больше второго члена. Тогда Рх будет величиной отрицательной,
т. е. продольная реакция грунта на отстающей гусенице будет тор-
мозной силой.
ВЛИЯНИЕ ОТНОСИТЕЛЬНОЙ ОПОРНОЙ БАЗЫ
НА ПОВОРОТЛИВОСТЬ МАШИНЫ
В формулы (92) входит отношение -^-,или относительная
опорная база машины.
Из формул (92) следует, что чем больше отношение , тем
больше (по абсолютной величине) тормозная сила Pt. Так как тор-
мозная сила создается усилием водителя (при отсутствии серво-
механизмов), то с увеличением -g- управление машиной затруд-
няется.
Величина -g" влияет также и на силу тяги Р2. С увеличением g-
увеличивается сила тяги, а следовательно, возрастает нагрузка на
двигатель, так как силу тяги Р2 создает двигатель.
Для обеспечения поворота машины по сцеплению необходимо,
чтобы сила тяги Р2 была меньше силы тяги по сцеплению РС) т. е.
чтобы выполнялось следующее неравенство
\>.GL fG___ 1
Тв+^<-2^
откуда
(93)
Формула (93) позволяет определить предельное значение вели-
чины Для этого необходимо подставить в формулу (93) зна-
чения коэффициентов, соответствующих наиболее тяжелым усло-
90
виям поворота машины. Примем: <р =0,6;/—0,12; р = 0,7; тогда
получим
L 2 (0,6—0,12) ~ .
В < 0,7 ~ 1>4-
d i
В современных гусеничных машинах величина -g- находится
в пределах 1,2—1,8.
Чем меньше тем машина будет легче пово-
рачиваться.
,, L
У некоторых тяжелых танков довоенного времени -g- равня-
лось 2,5 и выше. Эти машины обладали плохой поворотливостью,
особенно на подъемах, где они часто теряли управление.
Для тягачей, работающих с прицепом, не должно превосхо-
дить 1,5, так как тягач с точки зрения поворота работает в более
тяжелых условиях, чем одиночная машина (для тягача сила тяги
на забегающей гусенице А требуется большая, чем для одиночной
машины).
4. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ КАЧЕНИЮ
И СОПРОТИВЛЕНИЯ ПОВОРОТУ
ОПРЕДЕЛЕНИЕ МАКСИМАЛЬНОЙ ВЕЛИЧИНЫ
КОЭФФИЦИЕНТА СОПРОТИВЛЕНИЯ ПОВОРОТУ
Поворот гусеничной машины характеризуется двумя опытными
коэффициентами — коэффициентом сопротивления качению f и
коэффициентом сопротивления повороту ц. Как показывают много-
численные опыты, оба эти коэффициента зависят от радиуса пово-
рота и с уменьшением радиуса увеличиваются.
Опытным путем определить f и р в функции радиуса поворота р
весьма трудно. Для этого требуется специальная аппаратура, при
помощи которой можно было бы замерять силы тяги на отстающей
и забегающей гусеницах в функции радиуса поворота и по ним вы-
числять f и р.
” Значительно проще (с помощью одного динамометра) опреде-
/ляется максимальная величина коэффициента сопротивления пово-
роту ртах на одном минимальном радиусе поворота.
Для этого отстающую гусеницу испытуемой машины связывают
через динамометр с корпусом, как показано на рис. 40. Машина
Поворачивается вокруг заторможенной таким способом гусеницы
с минимальным радиусом рт = -^-. При повороте на отстающую
гусеницу действуют две силы: касательная реакция грунта Д, рав-
ная тормозной силе, замеряемой динамометром, и реакция лобового
сопротивления грунта Ri.
91
Сила Р\ есть сила тяги на отстающей гусенице, которую можно
определить по формуле (92). Если под Pt понимать положительную
величину силы, замеряемую динамометром, то можем написать
р I Р-GA , fG I pGL fG
1 I 4U + 2 | 4 В 2 ’
откуда
+ <94>
В выражении (94) величина f есть коэффициент сопротивления
качению полностью заторможенной гусеницы. Приближенно его
можно принять равным обычному коэффициенту качения.
Рис. 40. Экспериментальное определение макси-
мального коэффициента сопротивления повороту
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ СОПРОТИВЛЕНИЯ КАЧЕНИЮ
И СОПРОТИВЛЕНИЯ ПОВОРОТУ В ФУНКЦИИ РАДИУСА ПОВОРОТА
ПРИ ПОМОЩИ КРУТИЛЬНЫХ ДИНАМОМЕТРОВ
Рассмотрев выражения для сил тяги Рри Р2 в формулах (92)
как два уравнения с двумя неизвестными f и р и решив эти уравне-
ния совместно, находим
J G
где и Р2 — абсолютные значения сил тяги на отстающей и забе-
гающей гусеницах; если эти силы каким-либо спосо-
бом будут определены, то по формулам (95) опреде-
лятся и значения коэффициентов f и р.
Заметим, что предлагаемый здесь метод определения коэффи-
циентов |i и / решением двух уравнений отличается от общеприня-
того метода, когда в качестве неизвестного рассматривается только
один коэффициент р, а коэффициент f принимается величиной за-
данной. В этом случае р определяется по значению одной силы
тяги, значение другой силы тяги делается заданным, что, конечно,
неверно, так как обе силы тяги определяются экспериментально и,
следовательно, ни одна из них не может быть задана произвольно.
92
/
Рис. 41. Общий вид
планетарного кру-
тильного динамо-
метра:
1 — планетарный механизм;
2 — рыча1, 3 — мессдоза
Рассмотрим определение сил Pi и Р2.
Для определения сил Pi и Р2 может приме-
няться различная измерительная аппаратура.
Главное требование, предъявляемое к этой
аппаратуре, заключается в том, чтобы силы Pi
и Pi могли быть измерены на любом радиусе
поворота машины.
В качестве измерительной аппаратуры при
определении сил тяги Pi и Pi могут приме-
няться планетарные крутильные динамометры
(рис. 41).
Принципиальная схема такого динамометра
представлена на рис. 42.
Динамометр состоит из двухрядного плане-
тарного механизма, имеющего две , солнечные
шестерни. Солнечная шестерня одного ряда
связана с ведомым валом 1 механизма пово-
рота; солнечная шестерня другого ряда свя-
зана с ведущим валом 2 бортовой передачи ма-
шины; водило а механизма через мессдозу в
заторможено на корпус машины.
Для планетарного механизма можно составить два уравнения
статики:
Мо + Л/11 Л4, = 0;
+ Л42 = 0,
откуда
Рис. 42. Принципиальная схема планетарного крутильного динамометра:
I — ведомый вал; 2 — ведущий вал; а — водило; б — рычаг; в — мессдоза, г — самопи-
шущий прибор
93
где М>— момент на ведомом валу динамометра;
/]— к. п.д. полюса зацепления пары шестерен (для всех
шестерен к. п. д. принимаем одинаковым — 0,98);
г’12 — передаточное число между валом 1 и 2;
— момент на водиле динамометра.
Момент Мо замеряется с помощью мессдозы. Для этого на во-
диле имеется выступ, который опирается на рычаг б; усилие от ры-
чага передается через шарик на мессдозу. Мессдоза заполнена мае-
Рис. 43. Установка крутильных динамометров в сило-
вой передаче гусеничной машины:
/ — двигатель; 2 —коробка передач; 3 —бортовые фрикционы; 4 и
5 — крутильные динамометры; 6 и 7 — бортовые передачи
94
лом, давление которого в свою очередь по трубке передается на
самопишущий прибор г.
Динамометры тарируются непосредственно на машине. Для этого
к гусенице машины извне прикладывается тяговое усилие, величина
которого записывается на ленте самопишущего прибора, и строится
тарировочный график. При испытании по тарировочному графику
сразу находится тяговое усилие на гусенице, соответствующее за-
писи на ленте самопишущего прибора.
Рис. 44. Зависимость коэффициента сопротивления
качению при повороте от радиуса поворота:
1 — супесчаник мелкий; 2 — неразложившийся торф
Динамометры могут работать в обе стороны — при передаче
момента от двигателя (при замере силы тяги на забегающей гусе-
нице) и при передаче момента от ведущего колеса (при замере тор-
мозной силы на отстающей гусенице). Схема установки крутильных
динамометров в силовой передаче машины приведена на рис. 43.
С помощью планетарных крутильных динамометров кандида-
том технических наук Л. К. Крыловым были проведены испытания
тягача М-2, в результате которых были получены зависимости f
и р. в функции радиуса поворота машины.
На рис. 44 приведена зависимость коэффициента сопротивления
качению от радиуса поворота для различных грунтов. На этом ри-
сунке по оси ординат отложены отношения коэффициента сопротив-
ления качению при повороте (/п) к коэффициенту сопротивления
качению /* при прямолинейном движении машины на том же
грунте.
* Во всех формулах теории поворота под коэффициентом f понимается коэф-
фициент сопротивления качению при повороте /п. Однако чтобы не усложнять
Формул, индекс (п) чаше всего опускается.
95
Из графика следует, что коэффициент сопротивления качению
при повороте резко изменяется с уменьшением радиуса поворота.
На рис. 45 приведена зависимость коэффициента ц от радиуса
поворота р на различных грунтах. Как и коэффициент /п, коэффи-
циент р. увеличивается с уменьшением радиуса.
Рис. 45. Зависимость коэффициента сопротивления повороту
от радиуса поворота на различных грунтах:
I — рыхлый снег (слой И см, /° = 9 — 11° С); 2— суглинок (пылевидный)*
3 — суглинок (с включением гравия); 4 — сухая грунтовая дорога; 5 — супесча-
ник мелкий; 6— болото (неразложившийся торф)
В тяговых расчетах гусеничной машины при повороте следует
учитывать переменное значение обоих коэффициентов. Для этого
можно предложить следующие эмпирические формулы, полученные
на основании опытов Л. К- Крылова:
А=(1 + тД)/:
н = ^з +
(97)
. (98)
где f— коэффициент сопротивления качению при прямолинейном
движении машины (берется из табл. 1);
Нтах — коэффициент сопротивления повороту при минимальном
радиусе (берется из графика, рис. 45);
р — действительный радиус поворота.
96
5. ПОВОРОТ ТЯГАЧА С ГУСЕНИЧНЫМ ПРИЦЕПОМ
ОСНОВНЫЕ ЗАВИСИМОСТИ, ОПРЕДЕЛЯЮЩИЕ ПОВОРОТ
ГУСЕНИЧНОГО ПРИЦЕПА
При повороте гусеничного поезда на прицеп действуют следую-
щие внешние силы и моменты (рис. 46):
PKi — сила тяги на крюке, приложенная под углом Tj к про-
дольной оси прицепа;
A- f\Gx — сила сопротивления качению на одной из гусениц, где
Gi — вес прицепа, f\ — коэффициент сопротивления ка-
чению прицепа;
Тг — поперечная реакция грунта;
Л7С] — момент сопротивления повороту.
Допустим, что поезд поворачивается на горизонтальном участке
пути. Внутренними потерями в прицепе пренебрегаем, поэтому тор-
мозные силы прицепа отсутствуют.
Так как сила тяги на крюке дает поперечную составляющую, то
при повороте прицепа будет смещаться центр поворота.’.
Рис. 46. Внешние силы, действующие на гусеничный прицеп при повороте
Составим следующую систему уравнений:
1. Уравнение проекций сил на ось х—х
PK1cos Т1 (99)
2. Уравнение моментов относительно точки п
(аи + 'А) Я» sin Т] = Л4С1. (ЮО)
7—2469 97
Момент сопротивления повороту определяется по формуле (88),
в которой примем сцепной вес Gc равным весу прицепа Gi (счи-
таем, что сила тяги на крюке действует в горизонтальной плоскости
и, следовательно, сила РК1 не дает вертикальной составляющей).
Тогда
ЛГс1=^[1+(2^2]. (101)
Приравняв поперечную силу Pxl sin yj к реакции Т из формулы (85),
получим
у _ рк1 sin Ti Ц
1 Sp-iGi
Решая систему уравнений (99), (100), (101) и (102), находим
РК1 = G, Vfi + tf с20 ; (ЮЗ)
tg-O = (104)
где
= + (105)
Рассмотрим теперь совместное движение тягача и прицепа.
Прицеп может соединяться с тягачом непосредственной шарнир-
ной сцепкой (рис. 47, а) или через промежуточное звено (рис. 47, б).
В качестве промежуточного звена может применяться трос или ка-
кое-нибудь жесткое устройство. Сцепка без промежуточного звена,
очевидно, является частным случаем сцепки с промежуточным зве-
ном, когда длина звена равна нулю. В данном труде рассматри-
вается поворот тягача, имеющего промежуточное звено.
При равномерном повороте поезда тягач и прицеп должны по-
ворачиваться вокруг одного центра (точка О на рис. 47,6). Так как
стяжка а, б представляет собой жесткую (одностороннюю или дву-
стороннюю) связь между тягачом и прицепом, то проекции скоро-
стей движения точек а и б на направление стяжки должны рав-
няться между собой:
г/а cos а = t'e cos ₽,
где аир —углы между векторами скоростей va и v6 и осью стяжки.
После соответствующих геометрических преобразований на осно-
вании равенства скоростей получим *
Rcos у — R cos ft = («к1 + sin ft — (aK — X) sin y.
* А. С. Антонов. Теория и расчет гусеничного трактора. ВТА, Ленин-
град, 1950.
98
Кроме того, из геометрического построения (рис. 47, б) будем иметь
/?! — /? cos (7, + у) = I sin Т1 + (ак — у.) sin (Т1 + т).
Из этих уравнений находим
/? =
__ (Ящ + Xi) sin Ti — (дк — X) sin у + Z sin у, cos у, + (ак — X) sin (у, +у) cos у, .
~ cos у — cos Yi cos (fi + y) ’ '
/?i = Zsiny! + (aK — X) sin (T1 +7) + /?cos(tj + 7). (107)

Рис. 47. Соединение прицепа с тягачом:
а — непосредственная шарнирная сцепка; б — сцепка с помощью промежуточного
звена
7*
99
Входящие в формулы (106) и (107) величины X и опреде-
ляются по формулам:
(108)

(109)
у PKL sin 7
Z ~ 2pG ’
_ Рщ Lj sin Ti
2pi Gi
Получив систему уравнений (103.—109) с семью неизвестными
7, 71, \ А, Р. = Л1, Ъ
и решив эту систему, получим значения всех неизвестных величин.
При этом радиусом поворота тягача R = ?В следует задаться.
Определив указанные величины, можем найти силы тяги на от-
стающей и забегающей гусеницах тягача. Далее производится тя-
говый расчет поезда при повороте, т. е. определяются по силам
тяги все необходимые расчетные параметры.
Пример. Определим радиус поворота гусеничного прицепа и силы тяги на
отстающей и забегающей гусеницах тягача.
Дано:
L = 2,2 л; В = 1,37 м; ак = 1,32 л; G = 8000 кг-,
= 1,76 м\ Вх = 1,47 м-, ак1 = 1,23 м\ Gt = 4000 кг-,
I — 0,75 м\ R = 4 м.
Поезд совершает поворот на горизонтальном участке сухой грунтовой дороги.
Определяем относительный радиус поворота тягача:
р = — - =29
р В 1,37 ’
Задаемся коэффициентом сопротивления качению на грунтовой дороге
/ = 0,075 и коэффициентом сопротивления повороту р111ах =0,73. Тогда по фор-
мулам (97) и (98) найдем
0,14;
=
0,53.
15
15 + 2,9
3
4 + 2,9.
Принимаем, что коэффициенты /п и р для тягача и прицепа равны (/п = /ni и
Р- = Pi)-
Из
формулы (105) находим
с0
-2Нг=«да
Из
Из
формул (103) и (104) находим
Рк = РК1 = 4000/0,142 + 0,532.0,322 = 870 кг\
tg 71 = о 14’0,32 ~ 1,2; отсюДа 71 = 50,5°.
формулы (109)
870-sin 50,5°. 1,76 п о„0
— 2-0,53-4000 = 0'278 *-
100
В дальнейшем задаемся произвольно
значениями угла у. Например, у'= —10°;
у" = 0; у"'= +10°. Соответственно этим
углам находим смещение центра пово-
рота тягача:
870-0,174-2,2 _
х“ 2-0,53-8000 ~ 0,04 м' х -°’
Х'" = 0,04 м.
По формуле (106) находим радиус по-
ворота /?:
R' = 6,07 м; R” = 4,57 л; R”’ = 3,66 м.
Строим графическую зависимость
(рис. 48) R = F(у) и из нее определяем
угол у, соответствующий заданному ра-
диусу R = 4 м. Получаем у ~ 5°. Этому
углу соответствует
X =
870-sin 5°-2,2
2-0,53-8000
= 0,020 м.
По формуле (107) находим значение радиуса поворота прицепа
/?! = 0,75-0,772 + (1,32 — 0,02) 0,824 + 4-0,566 = 3,91 м.
Определим теперь силы тяги на отстающей и забегающей гусеницах.
На рис. 49 представлена схема сил, действующих на тягач. Составив урав-
нение моментов относительно точек гц и пг [можно было бы воспользоваться
и общими формулами (90)], получим
Pi =
_ COS у
В + 2 + 2
аК -- X П •
Рк sin у;
Рис. 49. Схема внешних сил, действующих на тягач при
повороте
101
где
Afc p-GZ, Г / 2/\ 2-1 0,53-8000-2,2 Г 72-0,02\2П_
В ~ 4В L1+ '\ L ) J _ 4-1,37 L + \ 2.2 / J
fG 0,14-8000
-----= эбО кг-,
PKcos7 870-0,996 ло_
—1 f-----------------= 430 кг\
PK sin т = 1’32_-(L02-870-0,087 = 72 кг.
D 1,0/
Тогда Pi = —782 кг и Pj = + 2762 кг.
Полученное значение тяги Ра следует проверить по сцеплению. Будем иметь
ср' =
2Р,
G
2-2762
8000
= 0,69.
Действительный коэффициент сцепления ср на твердых грунтах обычно больше
полученного расчетом ср'. Однако на мягких грунтах ср' может оказаться
больше ср, тогда поворот поезда с радиусом R = 4 м окажется невозможным.
ПРИБЛИЖЕННОЕ ОПРЕДЕЛЕНИЕ СИЛ ТЯГИ
НА ОТСТАЮЩЕЙ И ЗАБЕГАЮЩЕЙ ГУСЕНИЦАХ
ПРИ ПОВОРОТЕ ТЯГАЧА С ГУСЕНИЧНЫМ ПРИЦЕПОМ
Для упрощения расчета поворота тягача с гусеничным прицепом
в первом приближении можно принять угол 7 = 0. Тогда силы тяги
на отстающей и забегающей гусеницах будут определяться следую-
щими формулами:
> ?GL fG . Рк
1 4В 2 2 >
р _ -i.GL fG । /',<
^2 — 4 в -Г 2 + 2
(ИО)
В формулах (110) Рк = Рк1. Величина Рк] определяется по фор-
муле (103). Из формулы (НО) следует, что сила Р, может иметь
как положительное, так и отрицательное значение. Величина Pi бу-
дет меньше нуля, если ,
/G ,
2 2 4В •
Чаще всего Pi является тормозной силой, т. е. имеет отрицатель-
ное значение. В этом случае наличие прицепа облегчает управ-
ление машиной, так как уменьшает величину тормозной силы.,
102
Однако прицеп затрудняет поворот тягача, так как увеличивает
силу тяги на забегающей гусенице Pi, а следовательно, увеличи-
вает нагрузку на двигатель.
Таким образом, наличие прицепа облегчает управление маши-
ной, но создает дополнительную нагрузку на двигатель.
6. ПОВОРОТ ТЯГАЧА С КОЛЕСНЫМ ПРИЦЕПОМ
В качестве прицепа будем рассматривать двухосный прицеп,
представленный на рис. 50.
Передняя ось прицепа имеет шарнирное устройство, позволяю-
щее поворачиваться передним управляемым колесам.
Рис. 50. Кинематика поворота гусеничного тягача с колесным
прицепом
Пусть'поезд поворачивается на горизонтальном участке пути без
поперечного скольжения. Тогда при установившемся повороте и тя-
гач и прицеп будут иметь общий центр поворота О.
Рассмотрим реакции грунта и силы, действующие на прицеп.
"а прицеп действуют следующие реакции грунта:
°1( /?,' — реакции сопротивления качению колес;
Л> —поперечные реакции грунта, препятствующие боко-
вому смещению прицепа;
103
— моменты сопротивления повороту колес, возникаю-
щие вследствие того, что упругое колесо опирается
на упругий грунт некоторой площадкой, а не точ-
кой, как это могло бы быть, если бы колесо и дорога
были абсолютно жесткими.
Кроме того, на прицеп действует сила тяги на крюке Рк1.
Если пренебречь трением в шарнирах прицепа (точки а и б) и
моментом сопротивления повороту М'сХ, то сила РК1 должна пройти
вдоль стяжки прицепа. Достаточно точно можно принять силу Рк]
равной силе сопротивления качению прицепа
P^=AGb (111)
где Д — коэффициент сопротивления качению при прямолинейном
движении;
Ог — вес прицепа.
Кроме того, приближенно будем считать, что радиус поворота
передней оси прицепа равен радиусу поворота тягача /?б — Я-
В действительности радиус поворота прицепа R6 может быть и
больше радиуса поворота тягача R. Это следует учитывать при
вождении поездов, так как прицеп в этом случае не будет вписы-
ваться в колею тягача.
Как показывают исследования, все принятые здесь допущения
дают погрешность в расчете, не превышающую 10%.
Определим угол наклона стяжки (а следовательно, и силы тяги
на крюке) к продольной оси тягача 7.
Смещением центра поворота тягача пренебрежем. Тогда можем
написать следующие равенства:
R cos у + ак sin 7 = R6 = /?;
/?sin 7 — aKcosy = l1
откуда
sin 7 =
(дк + Г) R
rt + R2 ’
R2 — aKl
cos 7 = —5------—
«I + R2
(H2)
Зная угол 7, найдем составляющие сил тяги на крюке тягача:
poshly =/.^4^
(из)
Далее, составляя уравнения моментов внешних сил, действую-
щих на тягач, найдем силы тяги на отстающей и забегающей гусе-
ницах тягача (Pi и Рг).
104
7. ЗАНОС ГУСЕНИЧНОЙ МАШИНЫ ПРИ ПОВОРОТЕ
При повороте гусеничной машины на нее действует центробеж-
ная сила С, которая стремится вызвать поперечное скольжение ма-
шины, или ее занос. Заносу препятствует реакция грунта Т.
Рассмотрим здесь занос одиночной машины.
На рис. 51, а показано действие на машину поперечной силы Qy,
являющейся проекцией на ось у — у центробежной силы С.
Сила Qy, равная поперечной реакции Т, вызывает смещение центра
поворота на величину X. При этом, как следует из рисунка, попе-
Рис. 51. Реакции грунта, действующие на гусеничную машину:
а — при отсутствии заноса; б — прн заносе
речные реакции будут направлены в противоположные стороны *.
Чем больше центробежная сила, т. е. чем круче поворот машины
при постоянной угловой скорости Q, тем больше смещается центр
поворота.
• Если центр поворота выходит на край опорных ветвей гусениц,
как это показано на рис. 51, б, то поперечные реакции будут на-
правлены в одну сторону. С этого момента наступает занос машины.
* Здесь условно эпюра реакций построена не на гусеницах, а на продольной
°си Машины.
105
Установим математическую зависимость между скоростью дви-
жения машины и радиусом ее поворота при заносе. Центробежная
сила выражается формулой
gRc gB?c
Согласно рис. 51,6 можем записать следующие равенства:
Q
С=—;
COS а ’
V
=----;
и с COS а ’
Ре
Р
COS а *
Подставив С, vc и ргв формулу центробежной силы, получим
Q=A.^ (114)
-v g Bp ’ v ’
где v — продольная скорость движения машины;
р — относительный радиус поворота машины.
Согласно формуле (87) имеем на горизонтальном участке пути
У _ LT _LQy
2р. Gc 2pG ’
где сила Qv имеет отрицательное значение, следовательно, и смеще-
ние X будет отрицательным, т. е. центр поворота машины сместится
вперед.
Так как при заносе Х = -у,
то
Qy = т о.
Принимаем р = рс, где рс —коэффициент поперечного скольжения
гусениц.
В первом приближении можно считать рс = ргаах, т. е. макси-
мальному значению коэффициента сопротивления при повороте.
Подставив Qy в формулу (114), получим выражение крити-
ческой скорости поворота машины по заносу
(115)
или значение критического радиуса по заносу:
^=^в- (116>
Пример. Определим критическую скорость по заносу транспортера, движу-
щегося по снежной дороге, имеющей минимальный радиус закругления R = 6 м.
Примем рс = ртах = 0,5.
Из формулы (115) находим
гкр = У 0,5-9,81-6 = 5,4 м/сек, или 19,5 км/час.
106
Из рассмотрения заноса одиночной машины следует, что ее кри-
тическая скорость по заносу ниже критической скорости тягача,
работающего с прицепом. Это объясняется тем, что на тягач, кроме
центробежной силы, действует противоположно ей направленная
составляющая силы тяги на крюкеРк sin у. Поэтому суммарная по-
перечная сила, вызывающая занос, меньше одной центробежной
составляющей. Следовательно, при равных условиях смещение
центра поворота тягача будет меньше, чем смещение центра пово-
рота одиночной машины, и занос тягача наступает при большей
критической скорости.
Аналогичное явление имеет место и в прицепе: на сцепку при-
цепа при повороте действует поперечная сила, направленная про-
тивоположно центробежной силе и уменьшающая поперечную
реакцию, действующую на прицеп (7’1).
Заметим, что при повороте гусеничного поезда может наблю-
даться явление наката прицепа на тягач, вызванное сниже-
нием при повороте средней скорости тягача. Снижение средней ско-
рости зависит от устройства механизма поворота. Некоторые меха-
низмы поворота не вызывают снижения средней скорости (диффе-
ренциальные механизмы), другие, наоборот, могут значительно
снижать эту скорость. Чем больше снижается средняя скорость, тем
сильнее проявляется явление наката. В результате наката тягач
может потерять управление, что в свою очередь может вызвать
аварию машины.
Явление наката не следует смешивать с явлением заноса, так
как причины этих явлений различные.
8. БАЛАНС МОЩНОСТИ ПРИ ПОВОРОТЕ ГУСЕНИЧНОГО
ПОЕЗДА. ВЫВОД ОСНОВНОГО УРАВНЕНИЯ БАЛАНСА
При повороте одиночной гусеничной машины или поезда мощ-
ность двигателя, затрачиваемая на поворот, расходуется на преодо-
ление внешних и внутренних (тормозных) сопротивлений. Баланс
мощностей в этом случае запишется в таком виде:
na = n» + nt,
где Мд—необходимая для поворота мощность;
No—-мощность, затрачиваемая на преодоление внешних сопро-
тивлений или сопротивлений грунта: прессование грунта
гусеницами, срез грунта в поперечном направлении, сопро-
тивление движению прицепа, потери на проскальзывание
опорных ветвей по грунту и т. д.;
Мт—мощность, затрачиваемая в тормозе отстающей гу-
сеницы, управляющем поворотом машины. Л,гт — есть
мощность регулирования поворота. В эту
мощность не входят потери, оцениваемые коэффициентами
полезного действия механизмов силовой передачи, в том
числе и механизмов поворота. Эти потери учитываются об-
щим к. п. д. машины.
107
Определим вначале мощность внешних сопротивлений No.
Если не учитывать влияние гусениц, то мощность сопротивления
движению машины может быть вычислена как произведение тол-
кающих корпус машины сил на скорости переносного движения
корпуса. В теории гусеничного движителя было показано, что тол-
кающие корпус силы можно приближенно заменить силами тяги.
Тогда на отстающей и забегающей гусеницах получим мощности
PiOi и P2V2. Эти мощности идут на преодоление внешних сопро-
тивлений.
Кроме того, при повороте происходит проскальзывание опорных
ветвей гусениц по грунту, на что также затрачивается определен-
ная мощность. Эта мощность будет равна Р\К и P2V2, где Kt и
V2 — скорости скольжения опорных ветвей гусениц.
Суммируя полученные мощности, найдем мощность внешних
сопротивлений
+ P2V2 + Р] Ц + Р2^2-
Согласно теории гусеничного движителя абсолютные скорости
можно выразить через относительные и переносные:
Ц = - Vf,
V2 ~ ^02 К'
После приведения подобных членов окончательно получим
No = Р^01 + Р2^02- (И7)
Таким образом, мощность, идущая на преодоление
внешних сопротивлений, определяется суммой
произведений сил тяги на относительные ско-
рости вращения гусениц. Иначе говоря, при определении
мощности внешних сопротивлений проскальзывание гусениц можно
не учитывать, или, что то же самое, рассматривать поворот машины
не на действительном, а на теоретическом радиусе.
Заменим силы тяги Pi и Р2 их равнодействующей
P0 = Pt + P2.
Допустим, что при повороте равнодействующая сил тяги Ро при-
ложена на некотором расстоянии от продольной оси машины
(рис. 52). Выразим это расстояние в частях ширины колеи В и обо-
значим через ял. Чтобы найти мощность силы Ро, необходимо умно-
жить силу Ро на скорость ее точки приложения.
Обозначим эту скорость через и0, тогда
Ч = Ро^о-
108
Скорость Wo можно выразить через угловую скорость поворота ма-
шины
= (рт + ?д) Щ
где рт — теоретический радиус поворота.
Тогда
Ч = Ро (рт + ?д) 5Q.
(П8)
Величина qa называется динамическим фактором
поворота.
Скорость корпуса машины при повороте изменяется по закону
прямой линии. Очевидно, всегда можно найти такую точку на оси
центров поворота, скорость которой будет равна скорости прямоли-
нейного движения машины до поворота.
Рис. 52. Определение динамического и кинематиче-
ского факторов поворота
При этом предполагается, что прямолинейное движение проис-
ходит на той же передаче, что и поворот.
Обозначим эту скорость через vn. Расстояние от продольной оси
машины до точки корпуса, движущейся со скоростью wn, выразим
в частях В и обозначим через qK. Величина qK называется кине-
матическим фактором поворота. Скорость vn можно
также выразить через угловую скорость 2:
== (Рт + ^к) BQ.
109
Если скорость прямолинейного движения умножить на силу
тяги при прямолинейном движении Р, то можно получить мощность
прямолинейного движения
Nn = P^n = P(pT + ^)5Q. (119)
Исключив из уравнений (118) и (119) 2, окончательно получим
ЛГ„ = 46 + Nn. (120)
0 Р Рт + qK п р \ Рт + qj п v 7
Формула (120) является основной формулой баланса мощности
при повороте.
ОПРЕДЕЛЕНИЕ ДИНАМИЧЕСКОГО И КИНЕМАТИЧЕСКОГО
ФАКТОРОВ ПОВОРОТА
Для определения составим уравнение моментов сил Pi и Р2
относительно центра симметрии машины (точка с). Сумма этих мо-
ментов должна равняться моменту равнодействующей Ро = Pi -ф Р2:
откуда
= <121)
Определив силы тяги на отстающей и забегающей гусеницах, по
формуле (121) можем найти значение динамического фактора пово-
рота ?д.
Так, например, при повороте одиночной машины на горизонталь-
ном участке пути силы тяги равны:
р _ pGL fG .
“ 4В ' 2 ’
р _। fG
О — 4В + 2 >
откуда
<7д = ;г4- (122)
Следовательно, динамический фактор поворота зависит от до-
рожных условий (/ и р.) и от относительной опорной базы ма-
шины
Формула (122) справедлива только для равномерного поворота,
когда силы тяги равны силам сопротивления движению. Формула
же (121) является общей формулой.
ПО
Определим теперь кинематический фактор пово-
рота qK. Согласно рис. 52 можем написать
vn Рт + Як .
t'oj , 1
Рт + -у-
у.. р,+4
Исключив из этих уравнений радиус рт, после преобразования по-
лучим
1
2
Ура - Уп
VO2 — VO( •
Здесь Уо1 и с?о2 — скорости перематывания гусениц при полно-
стью затянутом тормозе механизма поворота, т. е. при отсутствии
тормозных потерь в механизме поворота (А'т^=0). Назовем эти ско-
рости расчетными скоростями и обозначим’ через р и
^р. Тогда предыдущая формула перепишется в таком виде:
__ 1 г?2р
2 щр — vlp
Из этой формулы следует, что кинематический фактор зависит
только от отношения скоростей vn; v2p и vlp: v2p, т. е. от передаточ-
ных чисел силовой передачи: гп2 и г12.
(123)
РАСЧЕТНЫЙ РАДИУС ПОВОРОТА И ЕГО ОПРЕДЕЛЕНИЕ
Как было указано выше, расчетным радиусом
рота называется такой радиус, при
ные потери. Соответствующие этому
четными скоростями. Обозначим
через рр относительный расчетный
радиус. Тогда из скоростных тре-
угольников рис. 53 получим
_ У1р + УЭр
р₽— 2 (v2p — vIp)‘
Расчетный радиус наравне с
кинематическим и динамическим
факторами поворота является ве-
личиной, характеризующей пово-
рот гусеничной машины. Кроме
того, как и кинематический фак-
тор, расчетный радиус характери-
3Ует принципиальное устройство
механизма поворота.
П О В 0-
котором отсутствуют тормоз-
радиусу скорости будут рас-
(124)
Рис.
53. Определение расчетных
скоростей при повороте
111
На рис. 54 представлена кинематическая схема силовой Пере-
дачи гусеничной машины, имеющей в качестве механизма поворота
бортовые фрикционы.
Если при прямолинейном движении и при повороте число обо-
ротов вала двигателя остается постоянным, то — ^п- При полном
торможении отстающей гусеницы vtp = 0. Из формулы (123) полу-
чим значение кинематического фактора поворота
п _ J_____Уп — _ _1_
2 vn— 0 2 •
При полном торможении отстающей гусеницы тормозные потери
равны нулю. Следовательно, машина поворачивается на расчетном
радиусе, тогда ^ = 0. Из формулы (124) находим рр = .
Рассмотрим теперь в качестве механизма поворота простой
(автомобильный) дифференциал. Согласно свойству дифференциала
скорость средней точки машины при повороте будет равняться ско-
Рис. 54. Кинематическая схема силовой передачи гусе-
ничной машины, имеющей в качестве механизма по-
ворота бортовые фрикционы
рости прямолинейного движения машины. Тогда vlp + v2p = 2^n-
При повороте на расчетном радиусе -<7lp 0 и v2p = 2t'n. Из формул
(123) и (124) получим = 0, рр ===-.'-
Соответствующим подбором передаточных чисел можно создать
механизм поворота с любым расчетным радиусом и с любым значе-
нием кинематического фактора.
МОЩНОСТЬ, НЕОБХОДИМАЯ ДЛЯ ПОВОРОТА
Согласно балансу мощности, на расчетном радиусе мощность
внешних сопротивлений No равняется мощности необходимой
для поворота, так как тормозная мощность NT в этом случае равна
нулю. Мощность А'д назовем мощностью, потребной на поворот.
112
Подставив в формулу (120) вместо текущего радиуса р расчет-
ный радиус рр, получим формулу мощности, потребной на , по-
ворот:
д Р Рр + qK " Р \ Рр + <7к 1 п v 7
Из формулы (125) следует, что потребная на поворот мощность
зависит от двух факторов, которые определяются устройством
механизма поворота: от расчетного радиуса, зависящего в свою оче-
редь от передаточных чисел механизма поворота (^p^ip)» и от
кинематического фактора, также зависящего от передаточных чи-
сел механизма поворота (^р •' ^ip и vn : vip). Чем больше рас-
четный радиус, тем меньше мощность двигателя,
потребная на поворот.
Так как расчетный радиус одновременно определяет и мини-
мальный радиус поворота машины, то при проектировании меха-
низма поворота выбирать его слишком большим нельзя, так как это
отразится на маневренности машины. Можно, однако, создать ме-
ханизм с двумя расчетными радиусами. Один (малый) расчетный
радиус будет обеспечивать машине высокую маневренность (способ-
ность круто разворачиваться), а другой (большой) — поворот с ма-
лой затратой мощности. Механизм с двумя расчетными радиусами
называется двухступенчатым механизмом поворота.
С точки зрения уменьшения величины потребной мощности Л'д
кинематический фактор следует брать возможно большим, однако
чем больше кинематический фактор, тем средняя скорость дви-
жения машины при повороте падает больше по сравнению со ско-
ростью прямолинейного движения. Увеличивая кинематический фак-
тор, вводят передаточное число в силовую передачу, причем чем
больше величина qK, тем больше это передаточное число. Если пере-
даточное число будет слишком большим, то машина, войдя в пово-
рот, не сможет выйти из него, так как при этом будет останавли-
ваться двигатель. Такое же явление наблюдается в случае прямо-
линейного движения при переходе с низшей передачи на высшую,
если разрыв между передачами будет слишком большой.
Увеличение кинематического фактора, кроме того, снижает при
повороте среднюю скорость движения машины, что может вызвать
накат на тягач прицепа.
Если в формулу (125) подставить <7К = <7Д, то получим
N N
* JL р 1 vn-
р
Для одиночной машины можно считать -р- = 1. Тогда мощность,
потребная на поворот, будет равняться мощности, необходимой для
осуществления прямолинейного движения.
При мощность, потребная на поворот, может быть
меньше мощности для прямолинейного движения.
8—2469 113
ГРАФИК БАЛАНСА МОЩНОСТИ
Наглядное представление о расходе мощности двигателя при по-
вороте дает график баланса мощности. Г рафик уста-
навливает зависимость между мощностями NA, No и и радиусом
поворота рт.
Примерный график приведен на-рис. 55.
Рис. 55. График баланса мощности при механизме поворота,
имеющем один расчетный радиус
На графике мощности No и NT выражены в частях мощно-
сти прямолинейного движения Afn.
График строится в такой последовательности.
Для конкретного тягача имеем в качестве заданных величин
Ne, Q, Qb В, L, I, а„ рр и qk.
Согласно формуле (84)
Р = Лгрт.
Принимаем величину k равной 1,4—1,5.
Зададимся несколькими значениями радиуса рт и по формулам
(97) и (98) найдем
f __(1 । 15 к г
/п + 15 + pJ/,
и = (о,з + -Л—') И
г . к ’ 1 4 + р J ‘
114
В этих уравнениях коэффициентами / и ртах задаемся в зависи-
мости от выбранного грунта.
Для построения графика надо определить по формулам (125)
и (120)
= A рр+ .
Л^п Р Рр + <7к ’
. Рт +
Р Рт + Як
Входящие сюда величины выражаются следующими расчетными
формулами, полученными из формул (90), (121), (ИЗ);
Л = — — + — + -к со— — Р sin Y
1 В ' 2 ' 2 В к ьш ’’
п Мс , fG , Рк cos у . ак гу
Ро = Pl + Pi = fG + Рк cos т;
P = fG + f^,
a — p~~pi — Mc + gt/yiiiT .
Уд 2(Л + Д) (fG + PK cos T) В ’
Р.созу=/,О,-^,
P,sinT-/lO1(<1*i+')R.
Смещением центра поворота пренебрегаем, тогда при повороте
на горизонтальном участке пути по формуле (89) имеем
М = !ф.
На основе полученных величин строится график.
Представленный на рис. 55 график построен для тягача М-2 ве-
сом 7 т, поворачивающегося с колесным прицепом весом 5 т. На
графике заштрихована область тормозной мощности. При этом при-
нято, что минимальный радиус поворота, допускаемый сцепкой
тягача, равен 2.
Из графика следует, что значительная часть мощности двига-
теля (почти 50%) тратится в тормозе отстающей гусеницы. Расход
тормозной мощности можно значительно уменьшить, если заменить
механизм поворота с одним расчетным радиусом (бортовые фрик-
ционы) двухступенчатым механизмом поворота, имеющим два рас-
четных радиуса Рр1 = 4~ и ррз > ~ .
Так как при любом расчетном радиусе тормозные потери равны
нулю, то график баланса мощности на втором расчетном радиусе
8* . 115
строится так же, как и на первом. На рис. 56 представлен график
баланса мощности при механизме поворота с двумя расчетными ра-
диусами. Из графика следует, что на второй ступени ^рр3>-4~)
потеря мощности в тормозе значительно меньше, чем на первой
ступени (Ppi = '2~^- Таким образом, механизм поворота с двумя
расчетными радиусами по расходу мощности более экономичен,
чем механизм с одним расчетным радиусом.
Рис. 56. График баланса мощности при механизме поворота,
имеющем два расчетных радиуса
Можно было бы создать механизм поворота с тремя и больше
расчетными радиусами. Это, однако, делать нецелесообразно, так
как механизм поворота при этом сильно усложняется. Экономич-
ность же механизма при трех и более расчетных радиусах возра-
стает незначительно *.
По графику баланса мощности можно определять возможности
машины в отношении ее поворота на разных радиусах в зависи-
мости от мощности, которой располагает двигатель машины.
Нанесем на график (см. рис. 55) максимальную мощность дви-
гателя, приведенную к гусеницам, fiiNe и отнесенную к мощности
прямолинейного движения:
М? __ 1
Nn Pvni •/] дг ’
1 Ниже будут рассмотрены специальные механизмы поворота с двойным
подводом мощности, имеющие несколько расчетных радиусов.
116
где V/— к. п. д. силовой передачи и ходовой части машины при
движении ее на данной передаче;
vni — расчетные скорости на передачах при Прямолинейном
движении;
''l.vz — коэффициент использования мощности на передачах.
Величина— характеризует запас мощности двигателя, кото-
‘N
рый может быть использован при повороте машины. Эта величина
называется коэффициентом запаса мощности. На-
несем значения коэффициента запаса на график баланса мощности.
Тогда можем определить, на каких передачах возможен поворот
машины ис какими минимальными радиусами он будет происхо-
дить.
Из графика видно, что по мощности двигателя поворот на пер-
вой и второй передачах возможен на всех радиусах, на четвертой и
пятой передачах совсем невозможен, а на третьей передаче воз-
можен только с радиусом рт > 8.
ГЛАВА V
ТЕОРИЯ СИЛОВОЙ ПЕРЕДАЧИ
(ТЕОРИЯ СИЛОВОГО ПОТОКА)
Силовая передача гусеничных машин по своему устройству и
по принципу своего действия может иногда представлять чрезвы-
чайно сложную передающую энергию систему. Силовые передачи
бывают зубчатые простого типа, планетарного типа, гидромехани-
ческие, электромеханические, фрикционные, инерционные. Передача
энергии от двигателя к движителю может совершаться в них по-
следовательными или параллельными (замкнутыми) потоками мощ-
ности. В замкнутых потоках может быть разветвление потока или
его циркуляция. Наконец, силовая передача может представлять
как статическую, так и динамическую передающую систему. Ра-
бота последней обычно сопровождается крутильными колебаниями.
Сложность силовой передачи обусловливается прежде всего
теми требованиями, которые к ней предъявляются.
Гусеничной машине приходится работать в очень тяжелых и
разнообразных дорожных условиях с широким диапазоном измене-
ния сопротивлений движению (почти в 10 раз). Поворот гусенич-
ной машины совершается не так, как поворот колесной машины,
вследствие чего в гусеничной машине применяются специальные
и часто очень сложные механизмы поворота. Все это отражается на
устройстве силовой передачи.
Современная силовая передача по преимуществу ступенча-
тая и неавтоматическая. Между тем условия эксплуата-
ции быстроходных гусеничных машин, особенно военного типа, ра-
ботающих в тяжелых дорожных условиях, требуют установки на гу-
сеничных машинах непрерывной (прогрессивной) и
автоматической силовой передачи. Непрерывная си-
ловая передача, в которой передаточное число меняется непрерыв-
но, позволяет точно приспосабливать работу двигателя к постоянно
меняющимся дорожным условиям, вследствие чего повышаются
средние скорости движения машины и улучшается ее топливная
экономичность. При непрерывной силовой передаче можно решить
и такую важную проблему гусеничной техники, как проблему
создания рационального механизма поворота,
не имеющего тормозных потерь и дающего кинематическое регу-
лирование поворотом.
Силовая передача, кроме непрерывности, должна также обла-
дать автоматичностью, так как только при автоматической силовой
передаче при прямолинейном движении машины можно точно и не-
118
прерывно регулировать передаточное число соответственно непре-
рывно меняющимся дорожным сопротивлениям. Если силовая пере-
дача будет непрерывной, но не автоматической, водителю придется
постоянно самому регулировать ее передаточное число, что будет
утомлять его и отвлекать от выполнения основной задачи — наблю-
дения за дорогой и регулирования движения машины.
Проблема непрерывности и автоматичности силовой передачи
выходит далеко за пределы теории гусеничных машин. Это обще-
научная и общетехническая проблема, решение которой имеет важ-
ное значение во всех случаях преобразования мощностного потока
первичного двигателя: в автомобилях, в кораблях, в тепловозах,
в станках и т. д. Особенно большое значение приобретает эта про-
блема в настоящее время в связи с развитием современной авто-
матики.
До сих пор различные проблемы силовой передачи рассматри-
вались как частные задачи и решались главным образом в порядке
изобретательства. Между тем эти вопросы требуют систематиче-
ского изучения й глубокого научного исследования.
Изучение проблемы силовых передач в целом потребовало со-
здания единого метода исследования. В любой передающей энергию
системе, в том числе и в силовой передаче самоходной машины,
передача энергии описывается некоторыми общими принципами.
Один из таких принципов известен в науке как закон сохранения
энергии, другой общий принцип — это закон равновесия. На осно-
вании этих двух принципов разработана общая теория передающих
энергию систем, которая названа теорией силового потока.
Теория силового потока дает общий метод расчета любой пере-
дающей системы — механической, гидравлической, электрической
или смешанной. Следует заметить, что до настоящего времени во
всякой передающей системе, как правило, был свой метод расчета,
основанный на своей научной дисциплине — на механике, на гид-
равлике или на электротехнике. Для инженера-механика, занимаю-
щегося конструированием, а следовательно, и расчетом силовых
передач гусеничных машин, такое разнообразие методов расчета
создавало большие трудности. Инженер-механик должен был обла-
дать почти универсальными знаниями, чтобы уметь рассчитать
сложную планетарную зубчатую силовую передачу, передачу с па-
раллельными потоками мощности, гидромеханическую или электро-
механическую силовую передачу, а также силовую передачу, в ко-
торой совершаются сложные динамические процессы.
Теория силового потока позволяет инженеру-механику произво-
дить не только механические расчеты силовых передач, но и рас-
четы комплексные — гидромеханические и электромеханические,—
а также статические и динамические.
На основе теории силового потока разработан новый метод рас-
чета гидромеханических передач, созданы основы синтеза передаю-
щих систем, метод моделирования динамических нагрузок в сило-
вых передачах гусеничных машин, разработаны вопросы теории
импульсных передач и др. Теория силового потока позволила со-
119
здать новые испытательные стенды, позволила исследовать новый
тип непрерывно-автоматической многопоточной силовой передачи.
В настоящей главе излагаются лишь основы теории си-
лового потока. Во второй части книги приводится приложе-
ние теории к расчету различных типов передач, применяющихся в
гусеничных машинах.
Специальные вопросы теории силового потока —вопросы син-
теза передающих систем, вопросы колебаний и др.— в данной ра-
боте не рассматриваются или рассматриваются только в общих
чертах. С этими вопросами можно ознакомиться в специальной ли-
тературе.
1. ОПРЕДЕЛЕНИЯ И ПРИНЦИПЫ ТЕОРИИ СИЛОВОГО
ПОТОКА
Всякую передачу энергии в силовой передаче или в какой-либо
другой передающей системе можно рассматривать' как некоторый
поток мощности, идущий от источника к потребителю или от двига-
теля к движителю машины. При этом передачу мощности можно
расчленить на два явления: на явление собственно передачи мощ-
ности без преобразования мощностного потока и на явление пре-
образования мощностного потока. Потоки, которые передают энер-
гию без преобразования, называются направленными или
силовыми потоками (СП), а места в передаче, где преоб-
разуется поток, называются узловыми точками (УТ). Та-
ким образом, передача энергии может рассматриваться как пере-
дача мощности через систему узловых точек, связанных между со-
бой направленными потоками. Такая передача называется сило-
вым потоком передающей системы или силовой
передачи.
Кроме направленных потоков, в передающей системе могут
быть рассеянные потоки, характеризующие рассеивание энер-
гии в узловой точке (например, через тепло, звук, вибрации и т. д.)
и подвод энергии к точке извне, а также аккумулирующие
потоки, характеризующие накопление энергии в узловой точке.
Физически узловые точки представляют собой механизмы или
устройства в передаче, в которых происходит какое-либо преобра-
зование силового потока. Так, в механическом силовом потоке вся-
кий зубчатый механизм изменяет скорости и моменты. Этот меха-
низм в силовом потоке силовой передачи будет представлять узло-
вую точку. Узловую точку дают фрикционные муфты, подшипники,
электрические сопротивления, т. е. любое преобразующее поток
устройство.
Направленный поток представляет собой поток энергии, пере-
дающийся по валам силовой передачи, по трубам гидропередачи
или по проводам электропередачи. При этом условно принимаем,
что потери в валах, трубах и проводах происходят в узловых точ-
ках, а передача энергии по валу, трубе или электропроводу яв-
ляется идеальной, т. е. не имеющей потерь.
120
Если узловым точкам и силовым потокам дать геометрическое
обозначение, то любую передающую энергию систему можно пред-
ставить в виде схемы силового потока.
Схема силового потока позволяет обобщенно, (независимо от
устройства) рассматривать передачу и трансформацию мощности
в" передающей системе и устанавливать общие расчетные зависи-
мости, характеризующие эту систему, а также позволяет наглядно
представлять процессы преобразования энергии в системе.
КИНЕТИЧЕСКИЙ, ДИНАМИЧЕСКИЙ И МОЩНОСТНОЙ
ФАКТОРЫ СИЛОВОГО потока
Мощность механического, гидравлического и электрического по-
тока энергии выражается следующими аналогичными зависимо-
стями;
N = <»/И,
N--HQ,
N=PI,
(127)
где ш — угловая скорость потока;
М — момент потока (здесь и ниже рассматривается передача
механической энергии только вращательным движением);
Н—напор гидравлического потока;
Q — весовой расход рабочей жидкости, протекающей через
трубопровод;
Р—напряжение электрического потока;
/ — величина тока.
Аналогичное выражение мощности можно получить и д л я д р у-
гих форм энергии.
Заметим, что в приведенных формулах величины ш, Н и Р яв-
ляются относительными величинами и математически выражаются
следующими разностями:
о) = Ш1 — о>2;
uj — ш, -
Н = Н,—Н2-
Р=Ру—Р2,
где (Oj — <и3—разность скоростей валов — подводящего и отводя-
щего поток механической энергии от данного устрой-
ства, в котором затрачивается мощность N;
— Н2—разность напоров гидравлических потоков — подводи-
мого и отводимого от данного гидравлического
устройства;
Р\ — Р2 —разность потенциалов на зажимах электрического
потребителя энергии.
Подставив эти разности в формулы (127), получим
N = ш1 Л/ — о>2 Л/;
N = H1Q — H.,Q;
N^PJ — pJ.
121
Выражения оцМ, <u2M, HiQ, H2Q и т. д. по форме аналогичны
выражениям мощности (127), и их можно обозначить через Л/i и Л/2.
Разница заключается только в том, что величины со, Н и Р в фор-
мулах (127) имеют относительное значение, т. е. один поток рас-
сматривается по отношению к другому потоку (например, первый
по отношению ко второму), а величины ом, ш2, Hi, Н2 и т. д. в вы-
ражениях Л\ и Л/2 имеют «абсолютное значение», т. е. потоки Mi
и М2 рассматриваются относительно какого-либо третьего потока,
условно принятого за нулевой поток (имеющего нулевую угловую
скорость, нулевой напор или нулевой потенциал). В качестве ну-
левого потока обычно принимается поток, связанный с землей.
В этом случае считаем, что угловая скорость этого потока, а также
напор и потенциал равны нулю.
Заметим, что величины ЛА и Н2 не являются мощностями в об-
щепринятом значении этого слова; эти величины — произведение
абсолютной скорости на крутящий момент, абсолютного напора на
весовой расход и потенциала («абсолютного напряжения») на ве-
личину тока.
Эти величины в отличие от мощности назовем мощностными
факторами силового потока.
Если мощностной фактор характеризует силовой поток, то
мощность характеризует рассеянный поток энергии.
Обозначим мощностной фактор силового потока той же бук-
вой, что и мощность, но с индексом I (I = 0; 1; 2; 3...). Мощности же
припишем индекс I. Тогда будем иметь соответственно и Nt
для силовых и рассеянных потоков.
Мощностной фактор есть произведение двух величин, одну из
которых назовем кинетическим фактором силового
потока и обозначим через и„ а другую — динамическим
фактором силового потока и обозначим через <?г. Под
кинетическим фактором будем понимать скорости, напор и
потенциал, под динамическим — крутящий момент, весовой расход,
величину тока.
Эти величины могут быть векторными (скорость, момент)
или скалярными (напор, расход, потенциал, величина тока).
Мощностной фактор — всегда величина скалярная.
В общем виде можем записать выражение мощностного фак-
тора как скалярное произведение кинетического фактора на дина-
мический фактор
(128)
Если м; и qi— величины скалярные, то они имеют алгебраиче-
ское значение.
Алгебраическое значение имеет и мощностной фактор.
Если кинетический и динамический факторы — величины век-
торные, то они изображаются параллельными векторами.
Условимся считать мощностной фактор положительным, если
кинетический и динамический факторы имеют одинаковые знаки
или если их векторы направлены в одну сторону. Если кинетиче-
122
ский и динамический факторы имеют разные знаки или их век-
торы направлены в разные стороны, то мощностной фактор имеет
отрицательное значение.
Силовой или рассеянный поток будем считать положительным,
если он подводится к узловой точке, и отрицательным, если он от
нее отводится.
Итак, силовой поток характеризуется тремя величинами: мощ-
ностным, кинетическим и динамическим факторами. ЛАощн ост-
ной поток характеризуется только одной величи-
ной — мощностью.
Передача энергии в различных передающих системах заклю-
чается в преобразовании силовых потоков, т. е. в изменении их
мощностных, кинетических и динамических факторов. Преобразо-
вание силовых потоков сопровождается рассеиванием энергии, т. е.
переходом ее из одной формы в другую. Этот процесс может быть
как положительным, так и отрицательным: энергия в виде поло-
жительных рассеянных потоков может подводиться к узловым точ-
кам или отводиться от них отрицательными потоками. Отрицатель-
ный рассеянный поток назовем диссипативным потоком.
Диссипативный поток характеризует внутренние потери в преобра-
зующем энергию устройстве или в его узловой точке.
Силовые потоки могут быть постоянными и перемен-
ны м и. Постоянные силовые потоки не зависят от времени и опи-
сывают статические явления. Переменные силовые потоки зависят
от времени и описывают'динамические явления. В узловых точках
переменных силовых потоков происходит накопление, или аккуму-
ляция, энергии.
Аккумулирующий поток является направленным, или силовым.
Он характеризуется тремя факторами: мощностным, кинетическим
и динамическим.
Условимся аккумулирующему потоку приписывать индекс /,
тогда
ДВА ПРИНЦИПА ТЕОРИИ СИЛОВОГО ПОТОКА
Пользуясь приведенными выше определениями, сформулируем
основные принципы теории силового потока. Примем эти принципы
без доказательства как некоторые общие законы передачи энер-
гии в передающих системах.
Первый принцип. Сумма мощностных факторов и мощностей
всех подводимых и отводимых от узловой точки силовых и рас-
сеянных потоков энергии равна нулю.
Математически этот принцип может быть записан следующим
равенством
SM + S^=0, (129)
где Nt—мощностные факторы направленных потоков узловой
точки;
Nt— мощности рассеянных потоков узловой точки.
123
Аккумулирующие потоки, если таковые имеются в узловой
точке, входят в сумму направленных потоков, т. е. в первый член
равенства (129).
Второй принцип. Сумма динамических факторов всех внешних
подводимых и отводимых от узловой точки силовых потоков одной
формы энергии равна нулю.
Здесь под «формой энергии» понимается форма силового по-
тока, динамический фактор которого характеризуется какой-либо
одной размерностью. Так, например, механические силовые потоки
вращательного и поступательного движения имеют различную
форму, так как их динамические факторы различны по размерно-
сти (динамический фактор вращательного потока имеет размер-
ность момента, а динамический фактор поступательного потока —
размерность силы).
Математически второй принцип запишется следующей вектор-
ной суммой, если динамические факторы силовых потоков — вели-
чины векторные:
= (130)
Если динамические факторы — величины скалярные, то второй
принцип запишется алгебраической суммой
S^ = o. (131)
К узловой точке могут подводиться потоки различной формы
энергии. Например, в электрических машинах имеются потоки ме-
ханические и электрические. Согласно второму принципу, равен-
ства (130) и (131) следует применять в отдельности для каждого
вида энергии.
Первый принцип характеризует мощностные явления в узловой
точке, а второй — равновесные явления. В соответствии с этим
уравнение (129) назовем уравнением мощностных фак-
торов, а уравнение (130) или (131)—уравнением рав-
новесия.
Согласно второму принципу на равновесие точки влияют только
внешние направленные потоки, внутренние же и рассеянные потоки
на равновесие точки не влияют.
Аккумулирующие потоки могут быть внешними или внутрен-
ними, и в зависимости от этого они входят или не входят в уравне-
ние равновесия узловой точки.
Если узловая точка описывается скалярным уравнением равно-
весия, то такая точка называется скалярной узловой точ-
кой, если же векторным уравнением — то векторной узловой
точкой.
КИНЕТИЧЕСКАЯ, РАЗВЕТВЛЯЮЩАЯ И ДИНАМИЧЕСКАЯ
УЗЛОВЫЕ ТОЧКИ СИЛОВОГО ПОТОКА
Всякий силовой поток можно представить состоящим из трех
типов узловых точек: кинетической, разветвляющей и динамической.
124
Кинетическая узловая точка преобразует только
кинетические факторы направленных потоков, абсолютная же ве-
личина динамических факторов при этом не изменяется.
Это может быть, если узловая точка имеет парные направлен-
ные потоки одной формы энергии. Согласно второму принципу по-
лучим
+ <?2 —
или
I <71! = I <72 [•
В узловой точке одной формы энергии, имеющей два потока,
обязательно должен быть рассеянный поток. Действительно,
согласно первому принципу
^i<7i “Ь «г<7г = О,
отсюда, учитывая, что <72 = —получим
(и,— и,) = °-
Если щ — и2^ 0 и д,=р 0, то и 2 N/ ¥= 0. Но это означает, что в уз-
ловой точке имеются рассеянные потоки (или рассеянный поток).
Если точка принадлежит переменному силовому потоку, то в
число двух направленных потоков могут входить внешние аккуму-
лирующие потоки. Кроме того, точка может иметь и внутренний
аккумулирующий поток, который, однако, на равновесие точки не
влияет (см. второй принцип).
Разветвляющая узловая точка преобразует только
динамические факторы направленных потоков. При этом кинетиче-
ские факторы не изменяются.
Согласно уравнению (129) можем написать
«i<7> + и2д2 -Ь ... + ипдп + 2 <4 == 0.
Так как по определению разветвляющей точки ее кинетический фак-
тор не меняется, то
И] — «2 = ... = ип.
Тогда из уравнения мощностных факторов получим
Мл (<71 + <?2 + • • + <7,г) + S М 0’
где 2 4i = 0, отсюда 2 М — 0-
Если под Nt понимать только диссипативные потоки (т. е. потоки
одного отрицательного знака), то в разветвляющей узловой точке
не может быть диссипации энергии, а следовательно, не будет и
внутренних потерь.
При = уравнение мощностных факторов переходит в
•Уравнение равновесия. Следовательно, разветвляющая узло-
вая точка описывается только одним уравне-
нием— уравнением равновесия.
125
Рис. 57. Условное
обозначение узло-
вых точек:
а -* динамическая ска-
лярная; б — динамиче-
ская векторная; в — ки-
нетическая со сколь-
жением; г — кинетиче-
ская холостая; д — ки-
нетическая полностью
включенная; е — тор-
мозная си скольжением;
ж — разветвляющая
Динамическая уз-
ловая точка преобразо-
вывает как кинетические, так
и динамические факторы на-
правленных потоков.
Кинетическая и разветв-
ляющая узловые точки яв-
ляются элементарными
точками силового потока,
так как их нельзя разложить
на более простые точки.
Динамическая же точка есть
составная точка, так
как она всегда может
быть представлена в виде
силового потока, состоящего
из более простых кинети-
ческих и разветвляющих
точек.
а
6
Обозначение узловых
точек и потоков
На рис. 57 и 58 приве-
дено условное обозначение
узловых точек и подводимых
к ним потоков.
Узловые точки динамиче-
ского типа обозначаются
кружками, Кинетические точ-
ки — параллельными линия-
ми с перекрестием и развет-
вляющие — точками.
Рис. 58. У словное обо-
значение потоков:
а — направленный внешний:
б — направленный внут-
ренний (относительный);
в — рассеянный положи-
тельный; г — рассеянный
отрицательный (диссипа-
тивный); д — направленный
немеханический (электри-
ческий и др.); е— аккуму-
лирующий кинетический;
ж — аккумулирующий по-
тенциальный; 3 и и — холо-
стой сквозной и конечный;
к — временно заторможен-
ный (со скольжением); л —
постоянно заторможенный

126
Потоки обозначаются линиями. Направление потока мощности
или мощностного фактора определяется стрелкой. Если стрелк. на-
правлена к узловой точке, мощность или мощностной фактор о
тока положительны (поток подводится к узловой точке), если же
стрелка направлена от узловой точки, то отрицательны (поток
отводится от узловой точки). Если динамический фактор потока
равен нулю, то поток холостой, если равен нулю кинетический
фактор, то заторможенный.
2. ХАРАКТЕРИСТИКИ УЗЛОВЫХ ТОЧЕК
Изложенные выше два принципа теории силового потока устана-
вливают общие закономерности для узловых точек независимо от
того, как устроена та или иная точка и какой по форм, энергии по-
ток она преобразовывает. Однако для полного изучения вопросов
передачи энергии и ее преобразования важно также знать внутрен-
ние процессы, протекающие в узловых точках.
Эти процессы зависят от внутренних силовых потоков, которые
имеются в узловой точке,, или от внутренних связей.
Система уравнений, описывающая эти связи,' называется харак-
теристикой узловой точки. В зависимости от вида свя-
зей характеристика может быть кинетической или динамической.
Определим характеристики узловых точек, описывающих раз-
личные преобразующие устройства силовых передач.
Заметим, что если в соответствии с двумя принципами теории
силового потока узловых точек может быть только три (по числу
факторов силового потока), то в зависимости от характеристик их
может быть бесчисленное множество, так как в природе нет двух
преобразующих устройств, которые по внутреннему устройству были
бы совершенно одинаковы.
Рассмотрим здесь только основные узловые точки, встречаю-
щиеся в передающих системах механического, гидравлического и
электрического типа.
МЕХАНИЧЕСКАЯ УЗЛОВАЯ ТОЧКА
Под механической узловой точкой будем понимать точку, описы-
вающую какой-либо механизм.
Рассмотрим узловые точки зубчатых механизмов.
На рис. 59 представлена коробка передач с параллельными ва-
лами. В схеме силового потока эта коробка дает динамическую уз-
ловую точку скалярного типа.
Действительно, коробка имеет три внешних звена: ведущий
вал /, ведомый вал 2 и корпус коробки 0. Каждое звено соответст-
вует одному направленному потоку. Следовательно, узловая точка
Имеет более двух направленных потоков и не может быть кинети-
ческой. Не может быть она и разветвляющей точкой, так как по-
токи 1, 2 и 0 имеют разные кинетические факторы (угловые ско-
рости). Следовательно, коробка может описываться только дина-
мической узловой точкой.
127
Рис. 59. Коробка передач с па-
раллельными валами:
а — скалярная узловая точка коробки
передач; б — коробка передач; О —
корпус коробки передач; I — ведущий
вал; 2 — ведомый вал
Рис. 60. Коробка передач с поперечными валами:
а — векторная узловая точка; б — коробка передач; 0 — корпус
коробкн передач; 1 — ведущий вал; 2, 3 — ведомый вал
128
Точка имеет один заторможенный поток 0 и диссипативный по-
ток внутренних потерь t.
Так как валы коробки параллельны, то векторы динамических
факторов направленных потоков (моменты) также будут парал-
лельны. В этом случае уравнение равновесия запишется в скаляр-
ной форме
м. + м^м^о,
тогда и узловая точка, описывающая данную коробку, будет ска-
лярной точкой.
На рис. 60 представлена коробка передач с поперечными ва-
лами. Так как эта коробка будет описываться векторной у з-
ловойточкой, то и уравнение равновесия запишется для нее в
векторной форме
— 0.
Заметим, что векторная точка всегда имеет заторможенный поток
корпуса, так как при непараллельных валах невозможно вращение
картера коробки. Затормо-
женный поток корпуса имеют
и узловые точки, описываю-
щие механизмы с парал-
лельными, но не соосными
валами.
Рассмотрим теперь диф-
ференциальный зуб-
чатый механизм, схе-
ма которого представлена на
рис. 61.
Дифференциальный
ханизм является соосным
ханизмом, причем все
валы могут вращаться. Сле-
довательно, он будет описы-
ваться скалярной узловой
точкой с незаторможенными
потоками.
Если в этой точке затор-
мозить один из потоков 1
или 2, то узловая точка бу-
дет описывать планетар-
ный механизм. Если бу-
дет заторможен поток 0 (по-
ток водила), то точка будет
описывать простой
Осн ы й механизм.
Дифференциальный
ханизм называется
ме-
ме-
его
с
Рис.
61. Дифференциальный зубчатый ме-
ханизм:
а _ узловая точка дифференциального механизма;
б — дифференциальный механизм; 0 — водило; с —
сателлит; Z — солнечная шестерня; 2— эпицикл
129
с о-
ме-
Р °’
п
9—24G9
стейшим, если ои имеет одно водило. Если же в механизме,
кроме того, имеются три вала, то такой механизм будет элемен-
тарным.
Соответственно и узловая точка, имеющая один нулевой по-
ток 0, называется простейшей механической, а имеющая, кроме
того, три направленных потока,— элементарной.
На рис. 62 представлены различные типы простейших дифферен-
циальных механизмов, применяющихся в силовых передачах гусе-
ничных машин.
Из простейших механизмов могут создаваться сложные ме-
ханизмы, имеющие больше одного водила. Сложные механизмы,
как и простейшие, применяются в силовых передачах гусеничных
машин в качестве коробок передач, механизмов поворота, борто-
вых передач.
Механическая узловая точка, которая здесь рассматривается,
может описывать или один простейший механизм, или группу свя-
занных между собой простейших механизмов. Например, плане-
тарная коробка передач может состоять из одного или нескольких
простейших механизмов. В этом случае она также будет описы-
ваться механической точкой, но имеющей несколько нулевых по-
токов (потоков водила. 0).
Заметим, кроме того, что механическая точка описывает не
только зубчатые механизмы, но и механизмы других типов, напри-
мер червячные, карданные, фрикционные, кривошипно-шатунные
и т. д. Таким образом, механическая узловая точка описывает
много различных типов механизмов.
Определим характеристику узловой точки про-
стейшего дифференциального механизма.
Характеристика должна состоять из двух видов математических
зависимостей: из уравнений кинематики механизма (кинематиче-
Рис. 62. Типы простейших планетарных механизмов:
а — однорядный эпицикл; б — двухрядный эпицикл; в — механизм
с внешним зацеплением шестерен; г — простой дифференциал; д —
двойной дифференциал
130
скйя характеристика) и из
уравнения, описывающего
диссипативный поток ме-
ханизма, т. е. потери, про-
исходящие в механизме
(диссипативная характе-
ристика).
Рассмотрим вначале
кинематическую ха-
рактеристику уз-
ловой точки.
Условимся обозначать
кинематическую схему ме-
ханизма, как указано на
рис. 63. Ось А—А назы-
вается главной осью,
ось В—В — осью с а-
Рис. 63. Обозначение кинематической схемы
простейшего дифференциального механизма
т е л л и т а. Все зубчатые
колеса или шестерни, вращающиеся только вокруг главной оси, на-
зываются центральными шестернями. Шестерни, вра-
щающиеся вокруг оси В—В (в относительном движении) и одно-
временно вокруг оси А—А (в переносном движении), называются
шестернями сателлита. Радиусы центральных шестерен и
шестерен сателлита обозначим соответственно буквами А и В с ин-
дексом того ряда, в котором находится данная шестерня.
Рассмотрим вращение каких-нибудь главных валов механизма,
например k и т, по отношению к главному валу р. Относительная
скорость вала k будет
ЧР) = Ш4 —“р-
Индекс р в скобке показывает, по отношению к какому валу
рассматривается вращение вала k.
Для вала т соответственно получим
(0^) = (°т —V
Отношение скоростей и
передаточным отношен
(о^) называется обобщенным
и ем; обозначим его через
№
<°т—шр
шк —
=
mk
(132)
Первый индекс при I (т) показывает, что скорость входит в чис-
литель, а второй индекс (&),— что скорость входит в знаменатель.
Если в качестве звена р взять водило 0, то
ДО) 1' = U'm — Мт — ы0
mk mk <4 — “О
(133)
9*
131
гдеi'mk называется внутренним передаточным отноше-
нием механизма (или простейшей механической узловой
точки).
Между обобщенным и внутренним передаточным отношением
можно установить следующую зависимость. Из формулы (132) на-
пишем
Цр) = Шт шр.
mk — top
— ш0) — (мр— шо) _ ют~~юр
(“й — %) — (“р — “о) u>k — ш
откуда
mk ] •'
1 l!‘P
(134)
Внутреннее передаточное отношение может быть выражено че-
рез отношение радиусов соответствующих шестерен или их чисел
зубьев. Так, если условно считать водило неподвижным (а это воз-
можно, так как мы рассматриваем движение по отношению к во-
дилу), то внутреннее передаточное отношение между какими-нибудь
двумя главными валами определяется, как и в простом механизме,
по формуле
где т и k — индексы двух произвольно взятых главных валов цент-
ральных шестерен.
Отношение следует выбирать со знаком плюс, если валы т и k
в относительном движении (при неподвижном водиле) вращаются
в одну сторону, и со знаком минус, если они вращаются в разные
стороны.
Если кинематическая схема механизма известна и известны раз-
меры его шестерен, то может быть определено внутреннее, а сле-
довательно, и обобщенное передаточное отношение механизма.
Согласно формуле (132) имеем
цр) = .Ют~Юр.
mk «k-up '
Из этого выражения получим уравнение кинематики простей-
шего дифференциального механизма
“т-^Ь + ®-1)“р = о- (136)
Формула (136), описывающая геометрически определенный ме-
ханизм, заданный внутренними передаточными отношениями iml!,
является кинематической характеристикой про-
стейшей механической узловой точки. Из этой фор-
мулы можно получить п—1 независимых уравнений кинематики,
132
которые связывают абсолютные скорости главных валов централь-
ных шестерен и скорость вала водила или соответствующие кине-
тические факторы направленных потоков узловой точки.
Величина п—число ненулевых потоков (1, 2,... п).
Так как механизм имеет п -ф- 1 главных валов, то скорости ка-
ких-нибудь двух валов должны быть заданы. Следовательно, меха-
низм (или узловая точка) имеет две степени свободы.
Если в качестве звена р принять водило, то характеристика уз-
ловой точки перепишется в таком виде:
— + ^mk~~ 1)(u0 = °- (137)
Этой характеристикой будем пользоваться в тех случаях, когда из-
вестна кинематическая схема механизма. При синтезе механизмов,
когда кинематическая схема еще только определяется, при-
ходится пользоваться обобщенной характеристикой по уравнению
(136).
Определим теперь диссипативную характеристику
узловой точки.
Потери мощности в зубчатом механизме могут определяться
различными формулами. Они могут зависеть от устройства меха-
низма, от передаваемой через механизм мощности, от скоростей
вращения шестерен и от других факторов. Эти зависимости носят
эмпирический характер и устанавливаются только на основании
опытных данных. Обычно потери мощности в зубчатых механизмах
определяются через коэффициенты полезного действия полюсов за-
цепления шестерен. При этом к. п. д. чаще всего принимается ве-
личиной постоянной. Тогда потери мощности будут пропорциональны
величине относительной мощности (по отношению к водилу), пере-
даваемой через полюс зацепления пары шестерен. Такой способ
определения потерь является неточным. Он учитывает влияние
только одного из факторов — передаваемой мощности. Устройство
же механизма (его расчетные размеры), скорость вращения ше-
стерен и подшипников не учитываются. В действительности ско-
рость вращающихся шестерен оказывает на потери иногда даже
большее влияние, чем передаваемая мощность. Поэтому пренебре-
гать влиянием этого фактора нельзя. Нельзя также пренебрегать
и влиянием размеров механизма. Действительно, механизм, рассчи-
танный на передачу малой мощности, будет иметь меньшие потери,
чем механизм, рассчитанный на передачу большой мощности. Ве-
личиной, Характеризующей размеры механизма, является модуль
его шестерен. Чем крупнее модуль, тем обычно выше потери.
Наконец, потери зависят от числа находящихся в зацеплении ше-
стерен, в том числе и шестерен, вращающихся вхолостую. Так, в
простом механизме вращение с одного вала на другой передается
одной парой шестерен. В планетарном же механизме таких пар
Несколько. Очевидно, и потери в обоих механизмах будут различны.
Заметим также, что в планетарном механизме шестерни сателли-
тов участвуют в двух движениях: в относительном (по отноше-
133
нию к водилу) и в переносном. В этом случае потери зависят от
относительных скоростей шестерен и от относительных мощностей,
передаваемых через полюса зацепления шестерен сателлитов и
центральных шестерен.
Инженером И. Н. Корнелаевым была предложена следующая
эмпирическая формула потерь в полюсе зацепления шестерен:
Nlp = -(Am^ + BNp),
(138)
где N/p— мощность, теряемая в полюсе, в л. с.;
т—модуль шестерен в мм\
vp—относительная окружная скорость шестерни при враще-
нии по отношению к водилу в м!сек\
Np — относительная мощность, проходящая через полюс за-
цепления шестерен, в л. с.\
А, В, k — опытные коэффициенты.
Для простых (непланетарных) механизмов скорость vp и мощ-
ность Np имеют абсолютное значение. В планетарных и дифферен-
циальных механизмах это величины относительные.
При определении потерь в планетарном (или дифференциаль-
ном) механизме условно принимается, что механизм имеет один
сателлит, через полюса зацепления шестерен которого проходит
вся относительная мощность.
Опытные коэффициенты, входящие в формулу (138), имеют сле-
дующие значения: Л = 0,005, k = 1,5 (для механизма, в котором
применяется смазка поливом), k—\,7 (для механизма, в котором
применяется смазка разбрызгиванием), В = 0,02 (для конических
шестерен), В = 0,015 (для цилиндрических шестерен внешнего за-
цепления простого механизма), В = 0,01 (для цилиндрических ше-
стерен внешнего зацепления планетарного механизма), В = 0,005
(для цилиндрических шестерен внутреннего зацепления планетар-
ного механизма).
Относительная скорость и относительная мощность опреде-
ляются следующими зависимостями:
= шо) А;
= К — шо) М{,
где wz—абсолютная угловая скорость шестерни /;
<о0 — скорость водила;
At— радиус шестерни г;
Мг— момент, приложенный к i-му валу механизма.
В формулу (138) подставляется абсолютное (положительное)
значение скорости vpi и мощности Npl.
134
Заметим, что при передаче относительного потока Np от полюса
к полюсу его величина уменьшается за счет потерь в полюсе.
Однако этим уменьшением можно пренебречь и считать, что отно-
сительный поток, проходящий через последовательно расположен-
ные полюса зацепления, не изменяется.
Если узловая точка элементарная (трехпоточная), то через по-
люса зацепления проходит один относительный поток, который
подводится к узловой точке. Этот поток и требуется определить.
Относительные угловые скорости, а следовательно, и окружные
скорости полюсов зацепления определяются из кинематической ха-
рактеристики узловой точки.
Учитывая формулу (138), можно определить к. п. д. полюса за-
цепления
Np + Ntp
’I N
"p
Подставляя в полученное выражение Ntp, получим
,р=1-В-Л-^-.
Из формулы следует, что к. п. д. зависит от относительной окруж-
ной скорости вращения шестерен и от передаваемой через полюс
мощности. Чем меньше передаваемая мощность, тем ниже к. п. д.
Если узловая точка холостая, то потери в полюсах опре-
делятся по формуле (138), в которой следует принять Ntp = — Np.
Получим
Amvp
N‘p — 1 — В
Полученные характеристики справедливы как для скалярных,
так и для векторных узловых точек.
Если по ходу задачи можно пренебречь потерями в механизме,
т. е. рассматривать механизм как идеальный, то соответствую-
щая узловая точка будет описываться только кинематической ха-
рактеристикой, без диссипативной функции. В этом случае на схеме
силового потока узловая точка изображается без диссипативного
потока t.
Кинематическая характеристика позволяет определять по двум
заданным абсолютным скоростям все остальные абсолютные ско-
рости главных валов механизма, а также внешние передаточные
числа , где т и k — произвольные числа из ряда 0, 1, 2...
Зная абсолютные скорости центральных шестерен и водила,
можно найти относительные скорости сателлита.
Рассматривая водило как неподвижное звено механизма, напи-
шем следующее равенство окружных скоростей двух шестерен са-
теллита и центральной шестерни, находящихся в ряду г:
± со'Л,,
135
или
“с = ± 4; (mi ~ шо)>
где Аг—радиус центральной шестерни Z;
— радиус шестерни сателлита, находящейся в зацеплении
с центральной шестерней;
< oz— абсолютная скорость вала Z;
< о0— скорость водила.
Знак плюс (+) берется при внутреннем зацеплении шестерен,
знак минус (—) —при внешнем зацеплении шестерен.
ГИДРОДИНАМИЧЕСКАЯ УЗЛОВАЯ ТОЧКА
Гидродинамическая передача — гидромуфта или гидротранс-
форматор— состоит из системы лопастных колес, связанных между
собой циркулирующей в передаче рабочей жидкостью.
Колеса бывают трех типов: колеса насоса, турбины и направля-
ющего аппарата. Каждое из колес преобразует поток мощности, иду-
щий от двигателя. Следовательно, лопастное колесо можно рас-
сматривать как некоторую динамическую узловую точку.
К колесу подводятся три потока: механический, идущий по валу
колеса, гидравлический на входе в колесо и гидравлический поток
на выходе из колеса. Таким образом, рассматриваемая точка будет
Рис. 64. Гидродинамическая узловая точка,
описывающая лопастное колесо гидродинами-
ческой передачи:
а — гидродинамическая узловая точка; б — узловая точка
насоса; в— узловая точка направляющего аппарата; г —
узловая точка турбины
трехпоточной гидроди-
намической узловой
точкой (рис. 64, а).
Условимся обозначать
подводимый к точке ги-
дравлический поток ин-
дексом I, отводимый —
индексом 2 и механиче-
ский поток, идущий по ва-
лу,—буквой, которой обо-
значена сама точка (а).
На рис. 64 (б, в, г)
приведены узловые точки
насоса Я, направляюще-
го аппарата А и турби-
ны Т. Как видим, разница
между этими точками за-
ключается только в зна-
чении механического по-
тока: поток насоса поло-
жительный (мощность от
двигателя подводится по
валу к колесу насоса),
поток турбины отрица-
136
тельный (мощность снимает-
ся с колеса турбины), поток
направляющего аппарата за-
торможен (колесо направ-
ляющего аппарата непо-
движно) .
Определим характе-
ристику узловой точ-
ки лопастного колеса.
Пусть лопастное колесо
вращается с некоторой угло-
вой СКОрОСТЬЮ О) (рис. 65)
(в частном случае, напри-
мер для колеса направляю-
щего аппарата, скорость
<о = 0). Рабочая жидкость
поступает во внутреннюю по-
лость колеса и движется по
его каналам от сечения ка-
нала 1 к сечению канала 2.
Рассмотрим движение
средней струйки жидкости
вдоль оси канала,образован-
ного лопатками колеса.
Жидкость участвует в
двух движениях: в перенос-
ном — вместе с колесом и в
Рис. 65. Параллелограмм скоростей рабо-
чей жидкости лопастного колеса гидроди-
намической передачи:
1 — сеченне канала на входе; 2— сечение канала на
выходе
относительном — по отношению к ко-
лесу.
Переносную скорость жидкости обозначим буквой U, относи-
тельную — буквой W и абсолютную— буквой V. Тогда будем иметь
следующее равенство векторов скоростей потока жидкости:
V=U+ W.
Разложим абсолютную скорость V по двум направлениям: по
направлению окружной скорости колеса и перпендикулярно ей.
Первая составляющая называется окружной скоростью
потока и обозначается буквой и, вторая составляющая назы-
вается меридиональной скоростью потока и обозна-
чается буквой
Из параллелограмма скоростей получим
v = U — W cos [Т,
где U — гш.
Выразим относительную скорость W через весовой расход жид-
кости, проходящей через живое сечение каналов. Пусть площадь
живого сечения будет F. Тогда весовой расход Q определится по
формуле
Q=l/4»
где 7 — объемный вес жидкости.
137
Так как
то
W = PQ^r,
T^sin Р' ’
откуда
г, = гш —(139)
T^tgP' v 7
При входе в колесо и выходе из него поток жидкости оказывает
на колесо динамическое действие. Это действие выражается неко-
торым моментом, который уравновешивается внешним моментом,
приложенным к валу колеса.
Если воспользоваться теоремой моментов количества движения,
то можно получить известное турбинное уравнение
Эйлера
Q Q
М= —
Перенесем члены из правой части этого равенства в левую и при-
мем следующие обозначения:
= Y
после чего получим
М + М1 + М2 = 0. (141)
Если величину М рассматривать как динамический фактор ме-
ханического потока, а величины и М2—как динамические фак-
торы гидравлических потоков, то полученное уравнение (141) бу-
дет уравнением равновесия узловой точки, т. е. будет выражать
второй принцип теории силового потока.
Подставим в формулы (140) скорости v\ и v2 из формулы (139),
После преобразования получим
/И, = a,o>Q— &iQ2,
M2 = — a2ioQ + ^2Q2,
где
(142)
(143)
1, 4
£7^1,2^ ₽1,г’
138
Выражения динамических факторов гидравлических потоков (ко-
торые назовем гидравлическими моментами), представ-
ленные в форме уравнений (142), дают уравнения характе-
ристики гидродинамической узловой точки.
Входящие в эти уравнения величины 2 и Z'b 2 называются п а-
раметрами гидродинамической узловой точки.
Уравнениями характеристики гидродинамической узловой точки
устанавливается зависимость между гидравлическими моментами,
угловой скоростью колеса и весовым расходом рабочей жидкости.
Эта зависимость определяется параметрами узловой точки.
Заметим, что уравнениями (142) можно пользоваться, т. е. рас-
сматривать их как уравнения характеристики узловой точки, если
параметры а и b будут известны. Но в параметр b входят гидравли-
ческие углы Pj и Если вход жидкости в колесо происходит без
гидравлического удара, то гидравлический угол равен геометриче-
скому углу наклона лопаток При геометрически определенной
узловой точке угол рх известен, а следовательно, будет известен и
угол
Гидравлический удар может отсутствовать только-на каком-ни-
будь одном режиме работы гидропередачи. Поэтому первым урав-
нением характеристики можно пользоваться только на этом (без-
ударном) режиме.
Как показали опыты Кухарского и Новохатько, при выходе по-
тока из лопастного колеса происходит его отклонение от профиля
лопаток, следовательно, и в этом случае гидравлический угол ?2
не равен геометрическому углу $•>:, однако если ввести соответству-
ющую поправку, то угол может быть определен через угол Рг-
В этом случае будет известен параметр Ь2 и, следовательно, можно
будет пользоваться вторым уравнением характеристики.
Уравнения (142) были выведены из струйной теории, однако с
точки зрения теории силового потока безразлично, на каких осно-
ваниях составлены уравнения характеристики. Важно только,
чтобы они достаточно точно отражали физическую сущность явле-
ний. Не исключено, что в будущем будут найдены более точные ха-
рактеристические зависимости, описывающие гидродинамическую
узловую точку. На метод расчета гидравлического силового потока
это, однако, не повлияет.
Кроме уравнений (142), в характеристику узловой точки должна
входить еще диссипативная функция гидравличе-
ских потерь. Определение диссипативной функции является
специальной задачей гидродинамики. Выразим эту функцию здесь
пока в самом общем виде как мощность гидравлических потерь:
М = <р (ч Q).
Функция эта зависит от угловой скорости колеса и от весового рас-
хода жидкости. Определение диссипативной функции приводится
в ч. 2 книги.
139
ФРИКЦИОННАЯ, ТОРМОЗНАЯ И РАЗВЕТВЛЯЮЩАЯ УЗЛОВЫЕ ТОЧКИ
МЕХАНИЧЕСКОГО СИЛОВОГО ПОТОКА
В силовых передачах гусеничных машин наравне с зубчатыми
механизмами широко применяются фрикционные муфты и тор-
моза. Каждое из этих устройств в схеме силового потока описы-
вается своей узловой точкой.
Так как у фрикционной муфты имеется два вала, т. е. два ме-
ханических потока мощности, то в силовом потоке муфта будет
описываться кинетической узловой точкой, которую иногда назы-
вают фрикционной узловой точкой. На схеме силового
потока она будет обозначаться как обычная кинетическая точка
(см. рис. 57, в, г, д).
Фрикционная муфта в работе имеет три положения: частично
включенное, выключенное и полностью включенное. Соответственно
этому и фрикционная точка будет работать со скольжением, т. е.
будет частично включенной (будет иметь диссипативный поток),
холостой или полностью включенной.
Если в фрикционной точке один поток постоянно затормозить, то
фрикционная точка превратится в тормозную точку, которая
в силовой передаче будет описывать тормоз (см. рис. 57, е).
Тормозная точка, как и фрикционная, может быть холостой, ча-
стично включенной или полностью включенной. В последнем слу-
чае ее направленный поток будет заторможен (см. рис. 58, и, к, л).
Характеристикой фрикционной, а следовательно, и тормозной
точки является момент трения Mt муфты или тормоза. Момент
этот может быть задан как функция скорости скольжения, удель-
ного давления или согласно закону Кулона принят величиной по-
стоянной.
В любом механизме или в каком-нибудь механическом преоб-
разующем устройстве всегда встречаются узлы, в которых преоб-
разуются только моменты без преобразования скоростей. Так, на
рис. 66 представлены два таких устройства: одно устройство — вал
с жестко посаженными на нем шестернями (рис. 66, а), с которых
снимаются потоки мощности, другое—тормоз, посаженный на
сквозном валу (рис. 66,6). Оба эти устройства описываются раз-
ветвляющей узловой точкой.
Согласно определению разветвляющая точка не изменяет кине-
тического фактора силового потока (в данном случае — угловой
скорости), а меняет лишь его динамический фактор (момент).
Разветвляющая точка вала с посаженными на нем шестернями
имеет четыре направленных потока, из которых два (У и 4} идут
по валу и два (2 и 3) — по шестерням.
Это устройство изображается в схеме силового потока одной
разветвляющей точкой с четырьмя внешними потоками (внутрен-
ний поток, идущий от точки К к точке М, в узловой точке не изоб-
ражается).
Тормоз, сидящий на сквозном валу, дает разветвляющую точку
с тремя потоками, из них потоки 1 и 2 идут по валу и поток 3 (тор-
140
мозной) идет в тормоз (в тормозную точку), в которой он рассеи-
вается в виде диссипативного потока t.
Характеристикой разветвляющей узловойточ-
к и является система уравнений, устанавливающая зависимость
между кинетическими факторами потоков
О)] = о>2 . = ш
(144)
Число уравнений характеристики, очевидно, будет п—1,
Рис. 66. Механические устройства, дающие разветвляющие
узловые точки:
а — вал с зубчатыми шестернями; б — тормоз иа сквозном валу
УЗЛОВЫЕ ТОЧКИ ЦЕПИ ПОСТОЯННОГО ЭЛЕКТРИЧЕСКОГО ТОКА
Все явления передачи и преобразование энергии в цепях по-
стоянного электрического тока можно описать с помощью электри-
ческих узловых точек силового потока. Электрические узловые
точки могут быть трех типов: электрокинетическая, электроразвет-
вляющая и электромеханическая.
Рассмотрим эти точки и определим их характеристики.
Электрокинет и ческой точкой называется точка, опи-
сывающая потребитель и источник энергии электрической цепи по-
стоянного тока.
Допустим, что имеется проводник, по которому течет электриче-
ский ток. Проводник обладает некоторым омическим сопротивле-
нием. Можно условно считать, что сопротивление проводника со-
средоточено в одной его точке, а остальные участки не обладают
сопротивлением. Тогда в схеме силового потока омическое сопроти-
вление может быть представлено в виде электрокинетической узло-
вой точки, диссипативный поток которой характеризует электриче-
ские потери в проводнике (рис. 67).
141
а
6
Рис. 67. Омическое сопротивление цепи
постоянного электрического тока:
а — омическое сопротивление; б — электрокиие-
тическая узловая точка омического сопротивления
Характеристикой э л е к т р о к и н е т и ч е с к о й точки
является зависимость, устанавливаемая зако-
ном Ома:
1= Р1~Р\ (145)
где /— величина тока, протекающего через проводник;
Рх и Р2—потенциалы на концах проводника;
г— электрическое сопротивление проводника.
' Применим к узловой точке
первый и второй принципы
теории силового потока, т. е.
составим для нее уравнение
мощностных факторов и урав-
нение равновесия:
Р^+РЛ+Л^О;
4 + 4 = 0,
откуда
Nt = -(P>-P2)I,
где. I — абсолютное значение
тока.
Здесь и дальше принимаем,
что ток подводимого потока 1
является всегда величиной положительной, ток же отводимого по-
тока 2 будет величиной отрицательной:
4 = -Л = -/. (146)
Подставив в полученное выражение величину Р}—Р2 — г1 из
характеристики (145), получим окончательно
Nt = — гР. (147)
Уравнение (147) есть закон Джоуля-Ленца.
Заметим, что уравнение (147) можно рассматривать вместо
уравнения (145) как характеристику узловой точки. Тогда из урав-
нения мощностных факторов и уравнения равновесия получим з а-
к о н Ома.
Обозначим I = q — динамический фактор, Pi — Р2 = и'—отно-
сительный кинетический фактор и -у=Х = const.
Из уравнения (145) будем иметь
д = Хм',
следовательно, между динамическим и относительным кинетическим
факторами узловой точки существует линейная зависимость
(рис. 68,а), т. е. узловая точка имеет линейную ха-
рактеристику,
142
Есть электрические приборы, которые дают электрокинетиче-
скую узловую точку с нелинейной характеристикой
(рис. 68,6). К таким приборам, например, относится двухэлектрод-
ная лампа (диод), бареттер (железная проволока, работающая
в атмосфере водорода) и др.
Заметим, что фрикционная точка, в которой трение подчиняется
закону Кулона (Afz = const), имеет линейную характеристику, а
кинетическая точка гидромуфты имеет нелинейную характеристику,
Рис. 68. Характеристики электрокинеТических узловых
точек:
а — характеристика узловой точки омического сопротивления; би-
характеристика узловой точки электронной лампы
подобную характеристике узловой точки электронной лампы
(диода).
Узловые точки с подобными характеристиками позволяют полу-
чать подобные механические, гидравлические и
электрические силовые потоки. Подобие силовых пото-
ков позволяет с помощью одних потоков (например, электриче-
ских) описывать явления, происходящие в других потоках (напри-
мер, в механических или в гидравлических).
В экспериментальной технике этот вопрос представляет боль-
шой практический интерес (см. ниже моделирование сило-
вых потоков).
Рассмотрим теперь электрокинетическую точку
источника электрического тока.
Эта точка отличается от точки электрического сопротивления
наличием в ней, кроме диссипативного, еще и положительного рас-
сеянного потока.
Возьмем в качестве источника электрического тока аккумуля-
торную батарею (рис. 69, а). В схеме силового потока она будет
описываться электрокинетической точкой с двумя рассеянными по-
токами, как представлено на рис. 69,6.
На рисунке t\ — положительный рассеянный поток, характери-
зующий преобразование химической энергии электролита и элек-
143

Рис. 69. Источник постоянного
электрического тока:
а — источник тока; б — электронике-
тическая узловая точка источника
a
тродов в электрический ток, a t2—
диссипативный поток, характеризующий
внутреннее сопротивление источника.
Характеристикой точки будут сле-
дующие зависимости:
Na=EI, 1
Nt2 = -rl\\
(148)
где Е— ЭДС источника;
I— ток, проходящий через источ-
ник;
г— внутреннее сопротивление
источника.
В цепях постоянного электрическо-
го тока имеются узлы, которые соглас-
но первому закону Кирхгофа разветв-
ляют токи. Аналогичные узлы имеются
и в силовом потоке. Эти узлы явля-
ются электроразветвляющими узловыми точками
силового потока.
Характеристикой электроразветвляющей точ-
ки является равенство кинетических факторов всех подводимых
и отводимых от точки потоков, или, иначе говоря, равенство их по-
тенциалов:
Р, = Р2 = Р, = ... = Рп.
(149)
Мы рассмотрели чисто электрические явления, происходящие
в цепях постоянного электрического тока. В электросиловых пере-
дачах большое значение имеют смешанные электромеханические
явления, происходящие в электрических машинах, в которых меха-
нический силовой поток превращается в электрический и наоборот.
Чтобы описать эти явления, надо рассмотреть узловые точки
электрических машин — электродвигателя и электрогенератора.
Обе эти машины в теории силового потока описываются одной
электромеханической узловой точкой.
Электромеханическая точка принадлежит к типу кинетических
узловых точек, так как опа имеет по два направленных потока
одной формы энергии: электрический подводимый 1 и отводимый 2
потоки, механический поток якоря и заторможенный механический
поток статора (рис. 70).
В зависимости от знака механического потока якоря электроме-
ханическая точка описывает или электродвигатель электрического
тока, или генератор.
Характеристикой узловой точки является следую-
щая зависимость между динамическими факторами механического
и электрического силовых потоков, т. е. между моментом М и то-
ком I:

(150)
144
Рис. 70. Электродвигатель и генератор электрического тока:
а — электродвигатель; б — генератор; в — электромеханическая узловая точка
электродвигателя; г — электромеханическая узловая точка генератора
где М— момент механического потока;
I—ток, проходящий через обмотку якоря;
Ф—магнитный поток обмотки возбуждения;
ст—коэффициент машины.
3. ПОСТОЯННЫЕ СИЛОВЫЕ потоки
типы постоянных силовых потоков
Выше были рассмотрены отдельные узловые точки преобразую-
щих устройств. В силовой передаче эти устройства связаны между
собой в единую передающую систему. Если соединить направлен-
ными потоками отдельные узловые точки, то можно получить сило-
вой поток передающей системы.
Силовые потоки бывают двух видов: постоянные, т. е. не за-
висящие от времени, и п е р е м е н н ы е, т. е. зависящие от времени.
Рассмотрим в качестве примера постоянный механический сило-
вой поток силовой передачи гусеничной машины,
‘Схема которой представлена на рис. 71.
10—2469
145
Каждое передающее устройство силовой передачи описывается
узловой точкой. Связывая эти узловые точки направленными (свя-
зывающими) потоками, получим силовой поток передачи (рис. 71, а).
В данном случае силовой поток описывает прямолиней-
ное движение машины, так как точки г бортовых фрик-
6
Рис. 71. Схема силовой передачи гусеничной ма-
шины:
а—схема силовой передачи; б—схема силовою потока при
прямолинейном движении машины; на схеме а; а — главный
фрикцион; б — коробка передач; в — главная передача; г — бор-
товые фрикционы; <9—тормоза; е — бортовые передачи; иа
схеме б\ а — узловая точка главного фрикциона; б — узловая
точка коробки передач; в — узловая точка главной передачи;
г— узловая точка бортового фрикциона; д — разветвляющая узло-
вая точка тормоза; е— узловая точка бортовой передачи
пионов (механизма поворота) полностью сблокированы, а точки д
тормоза полностью выключены.
На рис. 72 представлен силовой поток той же передачи при по-
вороте машины. Здесь узловая точка г правого фрикциона полно-
стью выключенаг а узловая точка з правого тормоза частично
146
включена, и в ней энергия рассеивается вследствие пробуксовки
тормоза (машина поворачивается с радиусом больше расчетного, а
следовательно, имеет тормозные потери в механизме поворота).
На схеме силового потока наглядно показана так называемая
рекуперация мощности, т. е. явление возвращения мощ-
ности с забегающей гусеницы на отстающую, всегда сопровождаю-
щее поворот гусеничной машины.
Рис. 72. Схема силового потока при повороте гусе-
ничной машины:
а — узловая точка главного фрикциона; б — узловая точка ко-
робки передач; в — узловая точка главной передачи; г — узловая
точка бортового фрикциона; 0 — разветвляющая узловая точка
тормоза; е — узловая точка бортовой передачи; ж и з — тормоз-
ные узловые точки
Действительно, в узловой точке з правого тормоза происходит
диссипация энергии тормозным потоком t. Так как узловая точка г
правого фрикциона полностью выключена, то диссипативный поток
мог возникнуть только вследствие того, что к тормозу подводится
энергия со стороны отстающей гусеницы. Так как отстающая гусе-
ница не может являться источником энергии, то энергия, очевидно,
подводится от двигателя через забегающую гусеницу и через грунт
на отстающую гусеницу.
Это явление и называется рекуперацией мощности.
Заметим, что мощность от забегающей гусеницы на отстающую
условно передается через землю, где часть мощности No затрачи-
вается на внешние сопротивления при повороте. Поток, связываю-
щий обе гусеницы, здесь не рассматривается. Поэтому на схеме
силового потока он обозначен как условный пунктирной линией.
На этот поток не следует смотреть как на направленный, так как
10*
147
Рис. 73. Схема силового потока гидроди-
намического трансформатора:
А — узловая точка направляющего аппарата; Н —
узловая точка насоса; Т — узловая точка турбины
в нем в скрытом виде име-
ются преобразующие энер-
гию узловые точки.
Из схемы силового пото-
ка следует, что если бы ме-
ханизм поворота позволял
направить основную часть
потока мощности, идущего
от отстающей гусеницы, на
забегающую гусеницу, то
от двигателя на поворот по-
требовалась бы меньшая
мощность. Поворот машины
совершался бы более эконо-
мично, а тормоза меньше из-
нашивались.
При бортовых фрикционах этого сделать нельзя, так как фрик-
цион отстающей гусеницы размыкает поток, идущий к забегающей
гусенице.
Все механизмы поворота с расчетными радиусами больше поло-
вины позволяют передавать силовой поток от отстающей
на забегающую гусеницу. В этом случае между гусеницами со-
здается замкнутый циркулирующий силовой по-
ток, идущий по контуру: забегающая гусеница — грунт — отстаю-
щая гусеница — механизм поворота — забегающая гусеница.
Явление циркуляции силового потока объясняет причину, в ре-
зультате которой в графике баланса мощности при повороте ма-
шины на втором расчетном радиусе (рр2 > ) падает потребная
на поворот мощность двигателя и уменьшаются тормозные потери
(см. рис. 56). Причина этого явления состоит в том, что силовой
поток, идущий от отстающей гусеницы, вместо того чтобы полно-
стью превратиться в рассеянный поток в узловой точке правого
тормоза, частично возвращается через механизм поворота к забе-
гающей гусенице.
Рассмотрим другие типы постоянных силовых потоков.
На рис. 73 представлен силовой поток одноступенчатого (трех-
колесного) гидродинамического трансформатора.
Устройство трансформатора показано на рис. 74. Трансформатор
состоит из насоса Н, турбины Т и направляющего аппарата А,
между которыми циркулирует рабочая жидкость (показано замкну-
той линией).
Принцип работы трансформатора заключается в следующем: при
вращении колеса насоса рабочая жидкость под действием центро-
бежных сил отбрасывается от центра колеса к периферии. Рядом
с колесом насоса находится колесо направляющего аппарата. Ра-
бочая жидкость от колеса насоса попадает на лопатки колеса на-
правляющего аппарата. В аппарате силовой поток преобразуется
148
Рис. 74. Гидродинамический трансформатор:
Н — насос; А — направляющий аппарат; Т — турбина
(изменяются его кинетический и динамический факторы), после чего
жидкость поступает на лопатки колеса турбины, отдавая ему свою
энергию. Потеряв часть энергии, гидравлический поток возвра-
щается к колесу насоса.
Соответственно числу колес силовой поток состоит из трех
гидродинамических узловых точек (Я, А и Г) (см. рис. 73), связан-
ных между собой направленными гидравлическими потоками
(7 и 2) *. Энергия к трансформатору подводится механическим по-
током Я и отводится механическим потоком Т. Механический по-
ток направляющего аппарата А при этом заторможен.
На рис. 75 представлена схема силового потока гидродина-
мической муфты, применяющейся иногда в качестве сцепления
автомобилей.
Силовой поток состоит из двух гидродинамических узловых то-
чек: узловой точки Я колеса насоса и узловой точки Т колеса тур-
бины. Колесо направляющего аппарата, а следовательно, и соответ-
ствующая ему узловая точка в силовом потоке отсутствует.
На рис. 76 представлена схема цепи постоянного электрического
тока. Цепь состоит из двух источников тока (а и в) и двух потре-
бителей тока (сопротивлений) б и г. Один потребитель г включен
во внешний контур цепи, а другой б —
во внутренний контур цепи. Цепь
имеет, кроме того, два узла е и д, в ко-
торых ток разветвляется.
Согласно схеме цепи построена
схема электрического сило-
вого потока (рис. 76, б).
Силовой поток состоит из четырех
электрокинетических и двух электро-
разветвляющих узловых точек; каждая
точка соответствует своему преобразую-
щему устройству цепи.
Рис. 75. Схема силового пото-
ка гидромуфты:
Н — узловая точка насоса; Т — узло-
вая точка турбины
* Так как iндравдические потоки передают
аначаем их, так же как и обычные механические
механическую энергию, то обо-
потоки, сплошными ЛИНИЯМИ.
149
Рис. 76. Схема цепи постоянного электрического тока:
а — схема цепи; б — схема силового потока цепи; а и в — узловые
точки источников электрического тока; б и г — узловые точки омиче-
ских сопротивлений; е и д — разветвляющие узловые точки
3
Рис. 77. Принципиальная схема электросиловой пе-
редачи гусеничной машины:
а _ генератор; б — двигатель внутреннего сгорания; я и г - ио
тор-генераторы; д и е— регулирующие сопротивления
150
На рис. 77 представлена принципиальная схема электросиловой
передачи гусеничной машины.
Силовая передача состоит из генератора а электрического тока,
приводимого во вращение двигателем внутреннего сгорания б, двух
мотор-генераторов виги регу-
лирующих сопротивлений д и е.
Силовая передача описы-
вается схемой электроме-
ханического силового
потока (рис. 78).
Силовой поток состоит из
трех электромеханических а, в
и г и двух электрокинетических
д и е точек. Кроме того, на
схему силового потока нанесе-
на узловая точка б двигателя
внутреннего сгорания. Эта точ-
ка принадлежит к типу кине-
тических точек с одним затор-
моженным, одним механиче-
ским и одним положительным
рассеянным потоком t, характе-
ризующим подвод тепловой
энергии к двигателю (диссипа-
тивные потоки на схеме не обо-
значены) .
На схеме рис. 78, а пред-
ставлен силовой поток при пря-
молинейном движении машины,
а на схеме рис. 78,6 — поток
при повороте машины.
При прямолинейном движе-
нии оба регулирующих сопро-
тивления (см. рис. 77) полно-
стью выключены — точки д и е
(рис. 78) полностью включе-
ны, а при повороте одно из
сопротивлений полностью вы-
ключено, а другое е частично
включено.
В первом случае механиче-
ские потоки точек виг оба
отрицательные, а во втором
случае один поток (точки в)
отрицательный (на забегающей
положительный
Рис. 78. Схемы силовых потоков элек-
тросиловой передачи:
а — при прямолинейном движении машины; б —
при повороте; а — узловая точка генератора;
б _ узловая точка двигателя внутреннего сгора-
ния; в и г — узловые точки мотор-геиераторов;
д и е — узловые точки регулирующих сопротив-
лений; ж и з— разветвляющие узловые точки
гусенице), а другой поток (точки г)
(на отстающей гусенице).
Из схемы силового потока видно, что электрические потоки яв-
ляются замкнутыми, вследствие чего при повороте имеется циркуля-
ция силового потока.
151
Таким образом, электросиловая передача обеспечивает поворот
машины с циркуляцией.
Мы рассмотрели лишь некоторые типы силовых потоков. Не-
трудно себе представить, что любое передающее энергию устройство
или система передающих устройств может быть описана схемой си-
лового потока.
ОБЩИЕ УРАВНЕНИЯ СИЛОВОГО ПОТОКА
Всякий силовой поток описывается уравнениями узловых точек
и уравнениями связывающих потоков.
Уравнениями узловых точек называются уравнения
мощностных факторов (129), уравнения равновесия (130) или (131)
и уравнения характеристик узловых точек.
Эти уравнения могут быть записаны в следующем виде:
S 4t = О,
(«, Я), = О-
(151)
В этих уравнениях i — номер потока; / — номер уравнения ха-
рактеристики данной точки; с? — функция (уравнение) характери-
стики.
Узловая точка может иметь несколько уравнений характери-
стики. Каждое из этих уравнений дает зависимость между кинети-
ческими и динамическими факторами внешних направленных пото-
ков данной точки.
Связывающий поток представляет собой некоторый направлен-
ный поток, связывающий две узловые точки. Введем условно в этот
поток полностью включенную кинетическую узловую точку. Оче-
видно, на передачу энергии эта точка никакого влияния не окажет,
так как полностью включенная кинетическая точка силовой поток
не преобразует.
Для этой точки напишем два основных уравнения:
«1аДа 4“ «26 Я26
Да “Ь Дб = О,
где а и б — узловые точки, которые связываются потоком.
Отсюда получим
«1а «26 = О-
Окончательно можем написать уравнения связываю-
щих потоков:
Дп —«ут = 0-
Д» + Ярп = °>
(152)
152
где п и т— буквенные обозначения узловых точек;
i и j— номера потоков узловых точек.
Систему уравнений (151) и (152) назовем общими урав-
нениями силового потока.
Решив эти уравнения, найдем все кинетические, динамические и
мощностные факторы, а также рассеянные потоки и к. п. д. сило-
вого потока, т. е. произведем полный расчет его.
ЗАДАЮЩИЕ ПАРАМЕТРЫ СИЛОВОГО ПОТОКА
Во всяком расчете имеются величины, которые задаются, и вели-
чины, которые определяются.
Определяемыми величинами в расчете силового потока являются
его кинетические, динамические, мощностные факторы и мощности
рассеянных потоков.
Если число уравнений силового потока (151 и 152) меньше
числа определяемых величин, то остальные величины должны быть
заданы. Эти величины назовем задающими параметрами
силового потока.
Определим, какое число задающих параметров следует принять,
чтобы рассчитать силовой поток.
Для этого подсчитаем все неизвестные величины, подлежащие
определению, и вычтем из их числа число уравнений, которое можно
составить для силового потока.
Основными величинами, которые необходимо определить, яв-
ляются кинетические и динамические факторы направленных пото-
ков, а также мощности рассеянных потоков.
Если кинетические и динамические факторы будут определены,
то по формуле W = uq определятся и все мощностные факторы
силовых потоков.
Допустим, что узловая точка имеет число направленных по-
токов. Тогда для т точек число неизвестных кинетических и дина-
т
мических факторов составит 2 2 пы> где/— индекс точки.
1
Обозначим через b общее число всех рассеянных потоков узло-
вых точек. Тогда число неизвестных (определяемых) величин будет
2 S пы + Ь.
1
Определим число уравнений, которое можно составить для си-
лового потока.
Кинетическая и динамическая узловые точки, с которыми мы
в дальнейшем будем встречаться, могут иметь направленные по-
токи одной или двух форм энергии. Обозначим число кинетических
и динамических точек, преобразующих одну форму энергии, соот-
ветственно через ск и са и две формы энергии — через ск и с'л.
Разветвляющая точка имеет направленные потоки только одной
формы энергии. Обозначим число разветвляющих точек через ср.
153
Кинетическая и динамическая узловые точки описываются двумя
уравнениями: уравнением мощностных факторов и уравнением
равновесия. Число уравнений мощностных факторов, которое можно
составить для этих точек, будет
+ Сл + Ск + Сд.
Точки сх> сд и ср описываются одним уравнением равновесия,
а точки с'к и сд —двумя уравнениями равновесия. Число урав-
нений равновесия будет
с* + сд + Ср + 2 (ск + сд).
Общее число уравнений мощностных факторов и равновесия для
всех точек будет
2 (ск + сд) + 3 (ск + сд) -ф ср.
Каждая точка, кроме того, задана уравнениями характеристики.
Обозначим число уравнений характеристики данной точки через с.
Тогда общее число уравнений характеристик для числа точек т бу-
т
дет 2) С-
I
Связывающий поток описывается согласно формуле (152) двумя
уравнениями. Если силовой поток имеет k связывающих потоков, то
число уравнений будет 2k.
Наконец, некоторые величины или зависимости между величи-
нами мо^ут быть заранее известны или определены по схеме сило-
вого потока. Так, все тормозные точки дают нулевое значение кине-
тического фактора постоянно заторможенного потока. Следова-
тельно, эти величины являются известными.
Число заранее известных величин или зависимостей будем учи-
тывать коэффициентом р.
Вычитая из числа неизвестных число уравнений, находим о б-
щее число задающих параметров силового
потока:
т г-
= 2 S noi + — ^_2 (ск + сд) + 3 (ск + сд)-(-Ср-(-
+ ^ct + 2k+p], (153)
где X— общее число кинетических и динамических задающих
параметров силового потока;
т — общее число узловых точек;
п01 — число направленных потоков узловой точки:
b—число рассеянных потоков;
ск, с, и Ср — число кинетических, динамических и разветвляющих
узловых точек;
154
С/—число уравнений характеристики данной узловой
точки г;
k — число связывающих потоков;
р— число уравнений кинетических или динамических
факторов, которое можно составить непосредственно
по схеме силового потока или которое задано за-
ранее.
Задающие параметры могут быть кинетическимии дина-
мическими. Число задающих кинетических параметров опреде-
ляет число степеней свободы силового потока или той системы, ко-
торую он описывает.
Обозначим число задающих кинетических параметров через Хи.
Тогда число динамических задающих параметров будет
\ = Х-ХИ. ‘ (154)
При определении числа задающих параметров следует иметь
в виду:
1. В число определяемых неизвестных величин кинетической
(в том числе и тормозной) точки всегда должен включаться рас-
сеянный поток, даже если точка полностью включена или полностью
выключена. Следовательно, при определении коэффициента b
должны учитываться все кинетические точки.
2. Равный нулю динамический фактор холостой кинетической
т
точки учитывается в выражении SC как заданная характеристика
, I
точки и, следовательно, не должен учитываться в величине р.
3. Тормозная точка механического силового потока имеет один
постоянно заторможенный поток, который должен быть учтен при
определении величины р.
4. Разветвляющая точка дает п — 1 уравнений характеристики
(и, = и2 = .., = ид), которые должны учитываться в величине
т
^с1-
1
Формула (153) справедлива для любого силового потока, со-
стоящего из любого числа узловых точек. Следовательно, она спра-
ведлива и для одной точки.
Определим число задающих параметров основных узловых точек,
входящих в рассмотренные выше силовые потоки.
Точка а (рис. 79) — механическая узловая точка
с диссипативным потоком (t).
т
Число направленных потоков п + 1. Тогда 2 » nOi = 2(« + 1),
где п — число ненулевых потоков узловой точки; 6=1; са = 1.
Точка описывается кинематической характеристикой, состоящей из
п — 1 уравнений кинематики и одного уравнения потерь, т. е.
т
2 с. = п. Из схемы узловой точки следует, что один поток по-
стоянно заторможен = 0), тогда р — 1.
155
Из формулы (153) получим
X = 2 (/г -ф- 1)4- 1 —- (2-1 4- п 4- 1) = п.
Следовательно, общее число задающих параметров равно числу
ненулевых потоков п.
Точка имеет одну степень свободы (Хи=1). Тогда на основа-
нии формулы (154) число задающих динамических параметров
будет
\ = п— 1.
Следовательно, чтобы рассчитать точку, надо задать одну ско-
рость (о>) и п— 1 момент (Л4). Остальные величины определятся
из уравнений силового потока.
Рис. 79. Определение задающих параметров узловых точек:
а — механическая узловая точка с диссипативным потоком; б — гидродинамическая точка
лопастного колеса; в — разветвляющая узловая точка; г — холостая кинетическая узловая
точка; д—полностью включениая кинетическая точка; е — кинетическая точка с диссипа-
тивным потоком; ж — холостая тормозная точка; з — полн .стью включенная тормозная
точка; и — тормозная точка с диссипативным потоком; к — кинетическая точка с подводом
энергии рассеянным потоком и с внутренним сопротивлением; л — кинетическая точка
с направленными потоками двух форм энергии, один из которых заторможен
Точка б — гидродинамическая точка лопаст-
ного колеса.
т
Имеем 2 2 пш = 2-3; b = 1; сд = 1. Остальные величины в фор-
муле (163) равны нулю. Тогда получим
Х = 2-Зф- 1 —2-1=5.
Следовательно, точка должна быть задана пятью задающими
параметрами. В этом случае определятся все кинетические и дина-
мические факторы направленных потоков.
156
Точка в — разветвляющая узловая точка.
т
Имеем 2 2 noi = 2/z; b = 0; гр = 1. Для данной точки можем со-
ставить п — 1 уравнений кинематической характеристики. Тогда
т
~^Jcl = n — 1. Остальные величины формулы (153) равны нулю,
I
Следовательно,
X = 2п — (1 + /г — 1) = п.
Точка имеет одну степень свободы. Поэтому
Точка г — холостая кинетическая узловая
точка.
т
Имеем 2 S noi = 2-2 = 4; ск = 1. Уравнение характе-
т
ристик будет одно (^ = 0), или = b тогда
1
Х = 4 + 1 — (2-1 + 1) = 2.
Точка имеет две степени свободы. Следовательно,
\-о,
т. е. динамические параметры в данном случае не задаются.
Точка д — полностью включенная кинетиче-
ская точка.
т
Имеем 2 2 ,го/= 2 • 2 = 4; Z»=l; ск = 1. Уравнений характери-
стики для этой точки нет, так как величина qt нам неизвестна.
Точка полностью включена. Следовательно, ti\ = и2, тогда р = 1.
Окончательно получим
Х = 4 + 1 — (2-1 + 1)== 2.
Точка имеет одну степень свободы. Тогда
Х? = 2-1=1.
Точка е — кинетическая точка с диссипатив-
ным потоком.
т
Имеем 2 S noi = 2-2 — 4; 1; ск = 1. Остальные величины
I
равны нулю. Тогда
X = 4 + 1 — (2-1) = 3.
Так как Хв = 2, то Х?=1.
Точка ж — холостая тормозная точха.
157
т
Имеем 2 2 noi — 2-2 == 4; b = 1; ск = 1. Кроме того, имеем одно
уравнение характеристики ((^=0) и один заданный кинетический
т
параметр заторможенного потока (п = 0), т. е. 2 ci — I и Р=1>
I
откуда
Х = 4 + 1 — (2-1 + 1 + 1)’= 1.
Число степеней свободы Ха = 1. Тогда
\ = 0.
Точка з — полностью включенная тормозная
точка.
т
Имеем 2 2 п<а = 2-2 = 4- b=\\ ск=1. Кроме того, задан ки-
1
нетический фактор «2 = 0 и равенство кинетических факторов
«1 = «2, тогда р = 2.
Из формулы (153) получим
Х = 4 + 1 —(2-1 +2)=1.
Так как Ха==0, то ^=1.
Точка и — тормозная точка с диссипативным
потоком.
Имеем 2 2 ,го/= 2-2 = 4; £=!; ск = 1; р = 1
I
(известна скорость постоянно заторможенного потока), тогда
Х = 4 + 1 — (2-1 + 1)=2.
Так как \,= 1, то \=1.
Точка к—кинетическая точка с подводом энер-
гии рассеянным потоком и с внутренним сопро-
тивлением.
т
Имеем 2 2 ,го/= 2-2 = 4; Ь = 2; ск = 1; тогда
Х = 4 + 2 — (2-1) == 4.
Так как = 2, то — 2. Следовательно, должны быть заданы
два характеристических уравнения рассеянных потоков (см. элек-
трокинетическую точку источника).
Точка л — кинетическая точка с направлен-
ными потоками двух форм энергии.
т
Имеем 2 2 ,го/= 2• 4 = 8; с'к = 1; /?=1; тогда
I
Х = 8—(3-1 + 1)=4.
Так как Ха= 1, то 3. Следовательно, должны быть заданы
три динамических параметра.
158
Для электромеханической точки это будут следующие величины:
момент, величина тока и уравнение характеристики, связывающее
момент с величиной тока [см. формулу (150)].
Так же определяются задающие параметры и для других типов
узловых точек.
Пример. Определим число задающих параметров силовых потоков, представ-
ленных на рис. 72, 73, 76, 78, а.
Определяем число задающих параметров силового потока силовой
передачи при повороте (см. рис. 72).
т т
Имеем 2 2 noi = 58, b = 5; ск =5; сд = 4; ср = 2; 2е' = П; £ = Ю;
I 1
р = 8; тогда
X = 4.
Определяем число задающих параметров силового потока гидроди-
намического трансформатора (см. рис. 73).
Имеем 2 noi = 18; b = 3; сд = 3; = 3; & = 3; р = 1;
I 1
тогда К = 5.
Заметим, что в качестве характеристик гидродинамических точек можно брать
только второе уравнение гидравлического момента Л42 [формула (142)]. Первое
уравнение (Л41) брать нельзя, так как в общем случае работы трансформатора
неизвестен угол входа потока Р/.
Если заданы три диссипативных потока, то число задающих параметров
будет два. Обычно в качестве задающих параметров принимают скорости на-
соса (ын) и турбины (ыт).
Определяем число задающих параметров силового потока цепи
постоянного электрического тока (см. рис. 76),
т т
Имеем 2 noi = 28; b = 6; ск = 4; ср = 2; С1 = Ю; fc = 7;
1 1
тогда К = 0.
Силовой поток полностью задан характеристиками кинетических узловых
точек и дополнительных задающих параметров не требует.
Определяем число задающих параметров силового потока электро-
силовой передачи при прямолинейном движении машины
(см. рис. 78).
т
Имеем 2 2 noi = 44; b=2 (кинетические точки регулирующих сопротивле-
1
т
ний); = 2; ск = 3; ср = 2; Q = 7; k = 8; р = 5, тогда
1
К = 3.
Здесь при определении X узловая точка б не учитывалась, так как она
не принадлежит к силовому потоку силовой передачи.
4. РАСЧЕТ МЕХАНИЧЕСКОЙ СИЛОВОЙ ПЕРЕДАЧИ
Под расчетом механической силовой передачи понимается опре-
деление кинетических, динамических и мощностных факторов ее си-
лового потока, а также передаточных чисел и к. п. д.
159
Механическая силовая передача состоит из зубчатых механиз-
мов и фрикционных элементов — фрикционных муфт и тормозов.
Силовой поток механической силовой передачи соответственно
будет состоять из механических, фрикционных, тормозных и раз-
ветвляющих узловых точек.
Составляя уравнения силового потока и решая их совместно,
найдем скорости, моменты и к. п. д. силовой передачи.
Таким образом, расчет силовой передачи сводится к расчету ме-
ханического силового потока.
Здесь и ниже мы рассматриваем постоянный механиче-
ский силовой поток, т. е. равномерно вращающуюся пере-
дачу. Явления, происходящие в этом силовом потоке, носят стати-
ческий характер.
ЧИСЛО ЗАДАЮЩИХ ПАРАМЕТРОВ МЕХАНИЧЕСКОГО
СИЛОВОГО ПОТОКА
Для механического силового потока число задающих параме-
тров определяется по следующим формулам:
\, = 2(си-|-Сф)-|-ср —/г —(155)
4 = S(« — 1),+ ]£(«— + — k — ф. (156)
Здесь —число кинематических (кинетических) задающих па-
раметров, или число степеней свободы силового по-
тока;
Хм—число статических задающих параметров;
стм, сф и ср—число механических, фрикционных и разветвляющих
узловых точек (тормозные точки включаются в сф);
k—число связывающих потоков;
ср—число заранее известных скоростей или каких-либо
заданных кинематических зависимостей;
ф— число заранее известных моментов (в том числе и
нулевых моментов холостых кинетических точек);
п— число ненулевых направленных потоков узловой точки.
Формулы (155) и (156) являются частным случаем более общих
формул (153) и (154).
При определении числа задающих параметров следует иметь
в виду:
1. Механическая точка принимается здесь простейшая, т. е. име-
ющая один нулевой поток.
Если в силовой передаче имеются сложные планетарные пере-
дачи, то их всегда можно представить в виде системы простейших
передач, а следовательно, сложную механическую точку можно
всегда представить в виде системы простейших узловых точек.
2. Механическая точка имеет п ненулевых потоков и один нуле-
вой поток (поток водила).
160
Разветвляющая точка и фрикционная точка нулевых потоков
не имеют.
3. Под <р следует понимать число заторможенных потоков и
число сблокированных кинетических (фрикционных и тормозных)
точек. Под ф следует понимать число холостых кинетических точек.
Кроме того, в <р и ф могут входить и заданные величины или
соотношения величин в зависимости от характера задачи.
Пример. Определим число задающих параметров силового потока силовой
передачи гусеничной машины при повороте (см. рис. 72).
Имеем: см = 4; Сф = 5; ср = 2; k = 10.
Определим величины tp и ф.
Из схемы силового потока известны скорости заторможенных потоков узло-
вых точек б, ж, з, е (правая), е (левая) и в. Всего известно 6 скоростей. Кроме
того, сблокированы точки а и г, а следовательно, известны два соотношения
между скоростями. Тогда будем иметь ср = 8. Из схемы силового потока имеем
два равных нулю момента холостых узловых точек жиг. Отсюда ф = 2.
Находим
ф - Ч = <2 - Ч + Ч + 2 (2 - 1), = 5;
ср
2 («- 1), = 2(3- 1)^ = 4.
Подставив в формулы (155) и (156) полученные величины, найдем
Хш = 2(4 + 5) + 2 — 10 —8 = 2;
Хи = 5 + 4 + 5— 10 — 2 = 2.
Таким образом, при повороте машины число степеней свободы равно двум.
Следовательно, должны быть заданы два кинематических параметра.
Кроме того, должны быть заданы два статических параметра, т. е. какие-
нибудь два момента.
Так как в узловой точке з имеется проскальзывание, то поворот машины
совершается на действительном радиусе.
При повороте на расчетном радиусе узловая точка з блокируется полностью.
Тогда ср = 8+1 =9. Силовой поток будет иметь одну степень свободы.
Заметим, что задающие параметры — величины независимые.
Поэтому нельзя принимать в качестве задающих параметров ско-
рости и моменты, связанные каким-нибудь уравнением силового
потока и определяемые из этого уравнения.
Для упрощения расчета следует отбрасывать в схеме силового
Потока все полностью включенные фрикционные узловые точки, так
Хак они вырождаются в направленные потоки, а также все холо-
Етые потоки. Число задающих параметров от этого не меняется, а
расчет силового потока значительно упрощается.
[ Формулы (155) и (156) могут применяться как к силовому по-
иску в целом, так и к его части, т. е. к какому-нибудь узлу, вклю-
чающему в себя часть узловых точек. Эти узлы могут изобра-
жаться одной узловой точкой, имеющей внешние потоки узла (на-
правленные и рассеянные).
161
11—2469
УРАВНЕНИЕ МОМЕНТОВ МЕХАНИЧЕСКОЙ УЗЛОВОЙ ТОЧКИ
Составим для механической узловой точки согласно первому
и второму принципам уравнение мощностных факторов и уравне-
ние равновесия.
Будем иметь
S + S Nt = °;
О
S ЛД = 0.
о
Умножим последнее равенство на «>р, где р — индекс произ-
вольно взятого потока, и вычтем его из первого равенства. Получим
S (“z + S М — о,
где <о;—= <о(р) —относительная угловая скорость потока I по
отношению к потоку р.
Тогда будем иметь
2 + S Nt = 0. (157)
о
Рассмотрим теперь диссипативный поток.
Пусть через полюс зацепления пары шестерен протекает относи-
тельный поток Nft Передача этого потока сопровождается поте-
рями энергии. Выразим эти потери через к. п. д. полюса следую-
щей формулой:
^z=-(l-^zW
где гр — к. п. д. полюса зацепления шестерен, через которые про-
текает относительный поток Л''0’.
Если относительный поток отрицательный, то
М/=—fi — — W>.
1 \ V- / 1
Для общности примем
Zz = 7lz ПРИ ^0)>0,
Zz =-7- при NJ0’ <0.
(158)
Тогда мощность, теряемая в полюсе зацепления, выразится
формулой
= — (1 — Z/)AZ<0).
162
Уравнение (157) перепишется в таком виде:
S<»r,7Wz-S(i-ZzX'=0.
о о
Отсюда находим
2 (шН — (0(0)) Mt + S = О,
о о
где
ш(р) _ ш(0) = Ш/ _ Шр _ ш. _|_ Шо = _ (Шр _ Юо) = _ ш(0)г
Тогда
— <»<0) S м, + s у ,о><0)м. = о.
р о о '
Но согласно второму принципу
S7Wz = 0.
о
Отсюда получим
» Z/<oj°Wz = 0.
о
Подедим левую и правую части равенства на какую-нибудь отно-
сительную скорость <о<.°), где г —произвольно взятый индекс из
ряда чисел 1, 2, 3... п. Тогда окончательно получим следующее
уравнение, описывающее механическую узловую точку:
хЛг'Ч + /2г2г^2 + • + 'Lni'nrMn = °> (159)
где i'r, i'r ит. д. — внутреннее передаточное отношение между
потоками 1 и г, 2 и г и т. д.
Коэффициент потерь X —т. или 1 : nq, где д определяется по фор-
муле Корнелаева
mr'f
= = —(159')
Для расчетов, имеющих ориентировочное и главным образом
сравнительное значение, можно принять iq = const. В этом случае
к. п. д. полюсов принимают: для пары цилиндрических шестерен
с внешним зацеплением -rj = 0,975, для пары цилиндрических шесте-
Рен с внутренним зацеплением д = 0,985, для пары конических
Шестерен д = 0,955.
11*
163
Уравнение (159) назовем уравнением моментов ме-
ханической узловой точки.
Это уравнение не является новым уравнением силового потока,
описывающим механическую точку. Это всего лишь преобразован-
ное для более удобного пользования уравнение мощностных фак-
торов, вытекающее из первого принципа теории силового потока.
Поэтому, если в дальнейшем будем пользоваться уравнением мо-
ментов, то одновременно нельзя пользоваться уравнением мощност-
ных факторов, и наоборот.
Если узловая точка идеальная, то, приняв Х=1, уравнение
моментов можно записать в таком виде:
+ ... + i$Mn = О,
(160)
где индексы р, т, г и т. д. — произвольные числа из ряда 0, 1, 2
и т. д.
Кроме уравнения моментов, узловая точка описывается еще
уравнением равновесия. Если точка скалярная, то
м0 + + М2 +... + Мп — 0.
(161)
Если точка векторная, те
(161')
Уравнение моментов и уравнение равновесия полностью описы-
вают действительную (реальную) механическую узловую точку.
Заметим, что в уравнение равновесия векторной точки входит
реактивный момент Л40. Этот момент требуется определять только
при прочностном расчете корпуса механизма. Если по ходу задачи
нет необходимости в определении момента Л40, то нет необходи-
мости и в пользовании векторным уравнением (161). Тогда вектор-
ная точка будет описываться одним скалярным уравнением момен-
тов (159).
Допустим, что мы имеем элементарную (трехпоточ-
ную) точку. Для этой точки можем написать
Х/12 "Ь Хгг22 ^2 — 0;
+ ЛД + М2 = 0,
где г22 = 1.
Решая эти уравнения, получим
^0 = г21 1 ) М2.
164
В общем же виде будем иметь
Mi?--1)*!
Момент произвольного потока трехпоточной идеальной точки
можно выразить общей формулой.
Возьмем три потока т, k и р. На основании формулы (160)
можем написать
где
/(Р) = 0.
Тогда получим
Mn = -i^Mk, (163)
где n, k и р — произвольные числа из ряда 0, 1, 2.
Обобщенное передаточное отношение, входящее в формулу (163),
может быть выражено согласно формуле (134) через внутренние
передаточные отношения.
Формула (163) позволяет сразу определить.значение момента
любого потока элементарной узловой точки, если известен один из
моментов этой точки.
Чтобы определить X/ действительной точки, следует предвари-
тельно определить направление относительных потоков jV<°>, после
чего по формулам (158) определить значения х; = или 1:
Направление относительных потоков можно найти, если вместо
действительной точки вначале рассмотреть идеальную точку. Так
как потери в узловой точке не могут изменить направление отно-
сительных потоков, то в действительной точке относительные потоки
будут иметь то же направление, что и в идеальной.
УРАВНЕНИЯ МЕХАНИЧЕСКОГО СИЛОВОГО ПОТОКА
Механический силовой поток, как и силовой поток вообще, опи-
сывается системой уравнений узловых точек и связывающих
потоков.
Так как в силовой поток входят только точки трех типов: меха-
йическая, фрикционная и разветвляющая, то для них можем напи-
сать следующие уравнения мощностных факторов, равновесия и
характеристики.
165
(164)
Механическая узловая точка описывается в общем
виде уравнениями кинематики и статики:
—1) шР = °;
S ’f.k =
fe=l
k=n
2Ж = о.
fe=0
Для фрикционной точки можем написать уравнение мощ-
ностных факторов и равновесия
ш.Л4. 4- <.>„+, + М = 0, 1
I <1б5>
Для разветвляющей точки можем написать
О), = О>2 = . . . = (!)„,
1г=п
^=о.
Й=1 I
Кроме того, согласно формулам (152) получим уравнения свя-
зывающих потоков
()>,„ - <0 „ = О, 1
иг jtn >1
Min + Mjm = °- ’
ПРИМЕРНЫЙ РАСЧЕТ МЕХАНИЧЕСКОГО СИЛОВОГО ПОТОКА
Рассмотрим в качестве примера расчет силового потока плане-
тарной передачи (рис. 80), являющейся частью механической сило-
вой передачи машины.
Силовой поток состоит из трех механических а, б, в и одной
разветвляющей г узловых точек.
Определим вначале число задающих параметров силового потока.
Согласно формулам (155) и (156) будем иметь
= 2 (3 + 0)+ 1-5-1 = 1;
Хи = (2 - 1)а + (2 - 1)б + (2 - 1)а + (4 - 1)г - 5 = 1.
Отсюда следует, что силовой поток определяется одним кине-
матическим и одним статическим задающим параметром или одной
скоростью и одним моментом. Передача имеет одну степень свободы.
Пусть заданными величинами будут <о0(, = 100 1/сек и Л40о =
= 30 кгм. Кроме того, заданы внутренние передаточные отношения
механических точек: +a = —1,4; z'26 = — 1,66; г)2а =— 1,95.
Для определения всех скоростей и моментов, а также мощностей
необходимо составить уравнения силового потока. Решая эти урав-
нения, найдем все искомые величины.
166
Следует, однако, заметить, что при большом числе узловых
точек такой способ решения задачи является чрезвычайно громозд-
ким, так как приходится решать систему линейных уравнений
с большим числом неизвестных.
В большинстве случаев решение задачи можно значительно
упростить, если применить способ последовательного
решения узловых точек.
Способ этот заключается в следующем.
Рис. 80. Кинематическая схема планетарной пе-
редачи:
а — кинематическая схема планетарной передачи; б — схема
силового потока передачи; а, б, в — механические узловые
точки; г — разветвляющая узловая точка
Вначале производим кинематический расчет силового потока.
Выбираем на схеме силового потока такую узловую точку, в кото-
рой, если задать скорость одного потока, определятся по уравне-
ниям кинематики скорости остальных потоков. Эту скорость примем
равной единице. Учитывая уравнения связей, переходим от точки
к точке, выражая их скорости через заданную единичную скорость.
Таким образом находим все скорости силового потока.
Заметим, что так как задающий параметр нами выбран
(w = l), то заданная условиями работы передачи скорость (в на-
шем примере о>о<> = 100 11сек) теперь уже должна рассматри-
ваться как величина неизвестная.
167
Согласно схеме силового потока выгоднее всего задаться ско-
ростью потока 1а = Оа, так как в этом случае легко определяются
скорость потока I и потоков узловой разветвляющей точки г.
Будем иметь
(О0а = 0),2 = <1>1г <1>4S 1.
Из характеристики точки а, учитывая, что о>2а = 0, получим
ш1а + (г12а 0 “оа = О,
откуда <о1а = 2,4.
Для точки б имеем
ш2б = “1а = 2,4;
ш1б = и)1г= 1-
Из характеристики узловой точки б имеем
Ш16 ’ ^'126 Ш2б “Ь (г'12б 0 “’об = О,
откуда <о0б=1,87.
Для точки в имеем
“1Я = «Ъг= 1;
ш2в = “об = 1,87.
Из характеристики точки в
„ ш1в г'12а ш2б Т (^"12в " 1) Ш0в ~ 0>
отсюда os=l,58.
Таким образом, нами определены все скорости потоков.
Результаты вычислений вносим в табл. 6.
Таблица 6
Расчетные данные к числовому примеру
Точка а Точка б Точка в Точка г
0 1 2 0 I 2 0 1 2 I 2 3 4
1 2,4 0 1,87 1 2,4 1,58 1 1,87 1 1 1 1
м — 1,71 0,71 1 1,И —0,43 —0,71 1,73 -0,59 -1,14 —2,73 1,71 0,59 0,43
N -1,71 1,71 ° 2,14 —0,43 -1,7! 2,73 -0,59 —2,14 —2,73 1,71 0,59| 0,43
Согласно полученным данным скорость <о0в=1,58. Выше эта
скорость была задана: <о08 = 100 \jceK. Тогда переходный множи-
тель находим из следующего равенства:
1,58/п = 100 \jceK,
168
откуда
т = 63,3 1 /сек.
Умножая на множитель т все приведенные в таблице скорости,
получим действительные скорости потоков с размерностью Мсек.
Определим моменты силового потока. Узловые точки вначале
примем идеальными. Зададимся моментом какого-нибудь потока.
Желательно выбирать ненулевой поток и несвязывающий поток.
В данной схеме силового потока целесообразно принять /И2я 1.
Тогда согласно формуле (159) при /, = 1, получим
^1а 4“ г2!а^2а ~
откуда
^„=-^•1=0,71.
Из уравнения равновесия будем иметь
Л40а = — Ма — Л42а = —0,71 —1 = — 1,71'.
Согласно уравнению связывающего потока имеем
ТИ2б = —М1а = —0,71;
^16 + г2!б^26 — 0.
Отсюда
7И16 = г’2167И26 — 0,43;
7Иоб = Л416 Л42б = 1,14.
Аналогично определяются моменты точек виг.
Умножая скорости на моменты, получим мощностные факторы.
Результаты вычислений проверяем на сумму моментов и мощност-
ных факторов:
£ Д = 0; 2^ = 0-
Определим переходный множитель моментов
/Иоа = 1,73/г = 30 кгм,
откуда
п = 17,3 кгм.
Рассмотрим действительный силовой поток, т; е. будем считать,
что входящие в силовой поток узловые точки действительные.
Чтобы определить коэффициенты потерь X, необходимо знать
направление относительных потоков мощности
А') = = (и, — <о0) Mt.
169
Для этого вычисляем вначале скорости «> и заносим их в таб-
лицу (табл. 7).
Таблица 7
Расчетные данные к числовому примеру
Точка а Точка б Точка в Точка г
0 1 2 0 1 2 0 1 2 i 2 3 4
СО 1 2,-1 0 1,87 1 2,4 1,58 1 1,87 1 1 1 1
со' 0 1,4 —1 0 —0,87 0,53 0 -0,58 0,29 0 0 0 0
Знак Л1 — — + + — + + + — — —
Знак N' — + — + — +
X 1 '<1 ’I ч
Затем определяем знаки моментов.
Если силовой поток состоит из элементарных узловых точек,
описывающих однорядные эпициклы, то внутренние передаточные
отношения таких точек — величины отрицательные. Из уравнения
моментов и равновесия получим
+ г21ТИ2 = 0;
ЛД + ЛД + М2 = 0.
Находим, что моменты ненулевых потоков (1,2) имеют
один знак, а момент нулевого потока (0) — обрат-
ный знак.
Таким образом, если нами определен знак какого-нибудь одного
момента узловой точки, то становятся известны и знаки остальных
моментов.
Так, согласно табл. 7 скорость потока Он имеет знак плюс. Но
сам поток отводимый; следовательно, мощностной фактор имеет
знак минус. Отсюда момент Мов имеет знак минус, а моменты М1д
и М2в — знак плюс *. Согласно уравнениям связи /Иоб = — М2д. От-
сюда момент /Иоб имеет знак минус и моменты /И1б и ЛТ2б — знак
плюс. Аналогично определяются знаки остальных моментов. Далее
определяются знаки относительных мощностей и коэффициенты
потерь X. Полученные данные заносятся в табл. 7.
Если узловые точки имеют внутреннее передаточное отноше-
ние i‘n > 0, то знаки моментов ЛД и М2 в этом случае противо-
* Одноименные по знаку кинетический и динамический факторы дают поло-
жительный мощностной фактор, а разноименные—отрицательный мощностной
фактор.
170
положим, а знак момента Л40 зависит от величины передаточного
отношения. При < 1 знаки Л40 и М2 противоположны, при
г'21 > 1 — одинаковы.
При расчете может оказаться, что указанным выше способом
знаки моментов в разветвляющих точках не определяются. Чтобы
их все же найти, надо произвольно задаться знаком одного из
моментов. После того как таким способом определится знак задаю-
щего момента (потока на входе или выходе), определяют, правиль-
но ли был принят знак момента. Если знак задающего момента
получится противоположным тому, который был задан условиями
работы механизма, то исходный знак следует изменить на обрат-
ный, что, в частности, и сделано нами в данном расчете.
Определив коэффициенты потерь Xz, из уравнений (159) и
(161) находим значение моментов действительной узловой точки.
В рассмотренном здесь расчете было принято допущение, что
т] = const. Это допущение однако весьма приближенно и часто
приводит к большим неточностям в определении потерь в механиз-
ме, особенно если шестерни механизма вращаются с большими
окружными скоростями. Кроме того, это допущение не учитывает
потери в холостых узловых точках, т. е. в точках, не передающих
силовой поток. Во всякой сложной зубчатой передаче (например,
в коробке передач) такие точки всегда имеются. Поэтому в уравне-
ние (159) лучше подставлять т) — -гц,, полученное на основании
формулы (159').
Если учитывать потери по формуле (138), то согласно данным
табл. 6 следует определить относительные окружные скорости
шестерен и относительные мощности. Так, для узловой точки а
будем иметь
<о]а = (<о1а — <иоа) т = (2,4 — 1) 63,3 = 88,5 1/сшс;
Ш2а = (ш2а -<1>0а) ,п = (0- 1) 63,3 = — 63,3 ЦсеК.
Допустим, что шестерни имеют модуль 4 мм и радиусы
А =0,1 м\ А2а = г' А. = 1,4-0,1 = 0,14 м..
Тогда
Л1а = 88,5 -0,1 = 8,85 м/сек-,
~ ш2а^2а “ 63,3 -0,14 = 8,85 М/свК,
Относительная мощность будет равна
кт ' лл 88,5-0,71-17,3 , . -
yVla = (Ta^ia^=—---------=14,5 Л. С.
Подставляем в формулу (159') скорости vp = vx 2а и мощность
Np — N', а также т = 4; Д = 0,01; В2 = 0,005; А = 0,005; k— 1,5;
получим tqi = 0,954; тр = 0,959,
171
Отсюда коэффициенты потерь будут равны
Zi — = 1,048; Х2 = 1,042.
Заметим, что потери в узловых точках все же проще находить
непосредственно по формуле (138), а не через к. п. д. Поэтому для
действительных силовых потоков целесообразнее пользоваться пер-
вым принципом теории силового потока в форме уравнения мощ-
ностей, а не уравнения моментов (159). Уравнение (159) следует
применять тогда, когда к. п. д. полюсов зацепления принимается
величиной постоянной или когда узловые точки считаются идеаль-
ными.
СВОЙСТВА УЗЛОВЫХ ТОЧЕК МЕХАНИЧЕСКОГО
СИЛОВОГО ПОТОКА
При расчете силовых потоков необходимо знать основные свой-
ства входящих в силовой поток узловых точек. Некоторые из этих
свойств были рассмотрены, и здесь их только напомним. Остальные
свойства определим.
Свойство 1. При заторможенном нулевом потоке внешние
передаточные Отношения механической узловой точки равны вну-
Рис. 81. Блокирование потоков меха-
нической узловой точки:
а — механическая узловая точка; б—разветвля-
ющая узловая точка
ческой узловой точки, имеющей не
тренним передаточным отноше-
ниям.
Из характеристики узловой
точки имеем:
— 1) “о = °-
Примем о>о = 0. Тогда
-1 = /'
ю* тк тк'
Свойство 2. Если сбло-
кировать два потока механи-
равные единице внутренние пе-
редаточные отношения, то механическая точка превращается в раз-
ветвляющую (рис. 81).
Примем в обобщенной характеристике
Шт — Ш — 1) “р = 0.
Получим
О— ^)<Dm = (1— ^)“р-
Отсюда o>m = wj, = (ор. Таким образом, скорости всех потоков
равны между собой. Но в этом случае узловая точка превращается
в разветвляющую точку.
172
г
Рис. 82. Узловая точка со сквозным потоком:
а—узловая точка; б — кинематическая схема механизма
Свойство 3. Если внутреннее передаточное отношение ка-
ких-нибудь двух произвольно взятых потоков механической точки
равно единице, то и внешнее передаточное отношение этих потоков
равно единице. В этом случае оба потока можно рассматривать как
один сквозной поток, проходящий через узловую точку.
Сквозной поток условимся обозначать двумя индексами (1, 3),
как показано на рис. 82.
Из характеристики узловой точки имеем
шт — 1',п№ + — 1) “о = О-
Примем ^й=1. Тогда = Следовательно, два вала
механизма т и k вращаются как один сквозной вал. При этом чи-
сло внешних валов механизма не меняется. Поэтому сквозной
поток имеет два индекса: на входе и выходе.
Свойство 4. Механическая узловая точка со сквозным по-
током может быть представлена в виде узловой точки без сквоз-
ного потока, если из нее выделить разветвляющую узловую точку
(рис. 83).
Чтобы доказать это свойство, необходимо составить уравнения
силовых потоков, представленных на рис. 83, а и б. Оба потока
описываются одними и теми же уравнениями. Следовательно, узло-
вые точки идентичны.
Справедливо и обратное
свойство: разветвляющую
точку можно ввести в меха-
ническую точку, тогда полу-
чим одну механическую точ-
ку со сквозным потоком.
Свойство 5. Если вну-
треннее передаточное отно-
шение двух потоков механи-
ческой узловой точки равно
—1, то средняя арифметиче-
Рис. 83. Выделение из узловой точки со
сквозным потоком разветвляющей точки:
а — узловая точка со сквозным потоком; б — выле
леиие из узловой точки разветвляющей точки
173
ская скорость этих потоков равна скорости нулевого потока (потока
водила).
Из характеристики узловой точки имеем:
Ш1 г12 “з + (z'i2 — 0 шо — О-
Подставляем сюда г]2 = — 1. Получим
Y (Ш1 + <о3) = «О-
Этим свойством обладает простой (автомобильный) диффе-
ренциал.
Свойство 6. Элементарная узловая точка, имеющая вну-
треннее передаточное отношение, равное —1, и одинаковые по
знаку скорости ненулевых потоков, разветвляет нулевой поток или
суммирует ненулевые потоки (рис. 84).
Рис. 84. Элементарная механическая узловая
точка, разветвляющая и суммирующая силовой
поток:
а — узловая точка, разветвляющая силовой поток; б — узло-
вая точка, суммирующая силовой поток
Так как при г]2 =— 1 моменты Mi и Л42 имеют всегда одина-
ковые знаки и противоположны по знаку моменту Л40, то при оди-
наковых по знаку скоростях оц и о>2 потоки Ni и N2 будут также
одинаковы по знаку и противоположны по знаку потоку No-
Простом дифференциал в настоящее время не применяется в гу-
сеничных машинах как механизм поворота, так как он обладает
свойством 6: при подводе к нему нулевым потоком (0) от двига-
теля мощности часть ее идет на забегающую гусеницу, а часть —
непосредственно в тормоз отстающей гусеницы, установленный на
одном из ненулевых валов. Вследствие этого механизм поворота
получается крайне неэкономичным.
Свойство 7. Идеальная элементарная узловая точка, имею-
щая внутреннее передаточное отношение, не равное единице яв-
ляется холостой точкой, если один из ее направленных потоков яв-
ляется холостым.
Действительно, для элементарной точки имеем
Д + г21 М2 = 0;
Л10 + ф- М2 — 0.
174
Если один из потоков холостой, то и один из моментов равен
Нулю. Тогда и все остальные моменты равны нулю.
Справедливо и обратное свойство: если один из потоков эле-
ментарной узловой точки не холостой, то и точка не холостая, т. е.
через данную точку проходит силовой поток.
Рис. 85. Разложение и суммирование разветвляющих
узловых точек силового потока'
а — разложение; б — суммирование
При расчете идеальных силовых потоков необходимо заранее
определить все холостые точки и не рассматривать их. В резуль-
тате расчет силового потока значительно упрощается.
Свойство 8. Разветвляющую узловую точку, имеющую
более трех потоков, можно разложить на элементарные разветвля-
ющие точки. Наоборот, элементарные разветвляющие точки можно
слить в одну точку, имеющую более трех потоков (рис. 85).
От разложения или суммирования разветвляющих точек число
задающих параметров силового потока не меняется. Действительно,
с введением в силовой поток новой разветвляющей точки одновре-
менно вводится и новый связывающий поток, поэтому число задаю-
щих параметров, определяемых по формулам (155) и (156),
остается прежним.
Свойство 9. Простые (непланетарные) механические узло-
вые точки можно сливать в одну простейшую (имеющую один нуле-
вой поток), или, наоборот, из одной простейшей точки можно вы-
делять несколько простых точек (рис. 86).
В определении простейшего механизма указывалось, что он
имеет одно водило (корпус). Так как в простых механизмах нуле-
вой поток заторможен, то он является общим для всех точек и,
175
Рис. 86. Слияние нескольких простых механических точек в одну
простую механическую точку:
а — три простые механические точки; б — одна простая механическая точка
следовательно, механизм имеет кинематически один общий корпус.
Но в этом случае механизм описывается одной узловой точкой.
Справедливо и обратное положение. Узловая точка с одним
заторможенным нулевым потоком может быть разложена на ряд
простых узловых точек.
На основании свойства 9 можно значительно упрощать схемы
силовых потоков.
Свойство 10. Фрикционная узловая точка не изменяет
момента силового потока, а разветвляющая узловая точка не из-
меняет его скорости.
Это свойство вытекает из определения кинетической и разветвля-
ющей узловых точек и не требует доказательства.
5. ЗАМКНУТЫЕ СИЛОВЫЕ ПОТОКИ
Замкнутым силовым потоком называется такой
поток, который имеет замкнутый контур направленных потоков.
Замкнутые силовые потоки могут быть разветвленными и
циркулирующими.
На рис. 87, а представлен разветвленный замкнутый поток.
Подводимая к потоку мощность разветвляется в точке а и подво-
дится к точке б двумя параллельными потоками. В точке б оба
потока суммируются (поэтому эта точка называется суммирую-
щей) в один отводимый поток.
На рис. 87, б представлен циркулирующий силовой поток. От
точки а поток подводится к точке б и возвращается к точке а. Таким
образом, имеется замкнутый круг циркуляции силового потока.
Заметим, что циркулировать может только силовой поток,
характеризуемый мощностным фактором, мощностной же поток,
характеризуемый мощностью, циркулировать не может, ибо он
всегда в конечном итоге является рассеянным потоком.
Если допустить, что внутри контура циркулирует мощностной
поток, то мощность одного из параллельных потоков будет больше
подводимой извне мощности, но это противоречит закону сохране-
ния энергии.
Замкнутые потоки энергии широко применяются в гидродина-
мических и в электрических передачах. С механическими замкну-
176
1ЫМи потоками, в частности с циркулирующими потоками, инже-
неры встретились сравнительно недавно при решении задач передачи
энергии в планетарных механизмах. На явление циркуляции впер-
вые обратил внимание, вероятно, Бакингэм в своей книге по зубча-
тым передачам. С 30-х годов явление циркуляции учитывается при
расчете планетарных коробок передач в гусеничных машинах.
Однако этому явлению в то время еще не придавалось большого
значения и оно не связывалось с явлением циркуляции в гидрав-
лических и электрических системах, т. е. не обобщалось.
Теория силового потока показала, что все потоки энергии яв-
ляются замкнутыми, т. е. уравновешенными, потоками и явление
циркуляции в механических передачах не является каким-то исклю-
чительным явлением,— оно обще всем передающим системам как
механическим, так и немеханическим. Всякий силовой поток можно
представить в виде замкнутого силового потока.
Допустим, что мы имеем «разомкнутый» силовой поток, пред-
ставленный на рис. 87, в. Он состоит из двух кинетических точек,
одна из которых является источником энергии, а другая — потреби-
телем, и одной динамической узловой точки, являющейся преобра-
зователем силового потока.
Приведем всю систему в движение со скоростью и0, равной
скорости одного из потоков (например, потока 0 узловой точки а),
но противоположно ей направленной. Тогда этот поток «затормо-
зится», а ранее заторможенные потоки будут теперь передавать
энергию (рис. 87, г).
г
Рис. 87. Замкнутые силовые потоки:
а — разветвленный поток; б — циркулирующий поток; в — абсолютный поток;
г — относительный поток
12—2469
177
Так как ранее заторможенные потоки имеют теперь одинаковую
скорость ио, то их можно соединить в разветвляющую узловую
точку, как показано на рис. 87, г. Полученный силовой поток яв-
ляется замкнутым потоком, в котором может происходить явление
циркуляции. Если силовой поток, представленный на рис. 87, в, счи-
тать абсолютным, то силовой поток на рис. 87, г будет отно-
сительным. Относительный силовой поток условимся обозна-
чать пунктирными линиями.
Допустим, что рассматриваемый силовой поток является меха-
ническим потоком и его динамическая точка является узловой точ-
кой какого-нибудь зубчатого механизма. Если относительный поток
циркулирующий, то через механическую узловую точку будет про-
ходить относительная мощность, большая мощности источника. Но
тогда в узловой точке возникнут большие потери энергии и ее к. п. д.
может оказаться очень низким.
Рассмотренное нами явление физически объясняет причину
больших потерь энергии в некоторых типах зубчатых механизмов,
через которые циркулирует большая -относительная
мощность.
ЗАМКНУТЫЙ МЕХАНИЧЕСКИЙ ПОТОК
С РЕГУЛИРУЮЩЕЙ УЗЛОВОЙ ТОЧКОЙ
Введем в одну .из параллельных ветвей замкнутого силового
потока механическую узловую точку R (рис. 88) с регулируемым
передаточным отношением (значок сс здесь и ниже означает, что
передаточное отношение узловой
—величина переменная).
Назовем отношение
мощности (или мощност-
ного фактора), проходя-
щей через параллельную
ветвь, к мощности, подво-
димой к силовому потоку,
коэффициентом цир-
куляции
его буквой
ТОЧКИ
Рис. 88. Замкнутый поток с регулирующей
узловой точкой
и обозначим
е. Получим
для двух параллельных
ветвей:
__ ТДб . __ Мрб
Составляя уравнения кинематики узловых точек и связывающих
потоков замкнутого силового потока, можем установить связь
между внешним передаточным числом силового потока в целом и
внутренними передаточными отношениями входящих в силовой
поток узловых точек.
Будем иметь
. __________________________1__________________
г12 ,(р) ,-(р) ,(р) ,(р) .(7г)
mka mkb т" nka ‘ mkR трй
178
Обозначим
а — № * b -— № • i — i№
U l'nikal'mk6* U t'nkalmp& . v
Тогда
. _ 1
г12 — a + bi ’
e = aZ12;
£д> =rz= bitj2 .
Из этих формул следует, что сумма коэффициентов циркуляции
равна единице:
е + ^=1. (171)
(168)
(169)
(170)
Рис. 89. График коэффициентов циркуляции
Коэффициенты циркуляции могут быть величинами как поло-
жительными, так и отрицательными, причем при положитель-
ных значениях ей силовой поток будет развет-
вленным, при отрицательном значении одного из
коэффициентов — циркулирующим.
Представим изменение коэффициентов циркуляции в виде гра-
фика (рис. 89). Из графика следует, что в области положительных
значений величины — силовой поток разветвленный, в области
отрицательных — циркулирующий.
12*
179
Исследуем влияние коэффициентов циркуляции на диапазон из-
менения передаточных отношений силового потока.
Пусть в регулирующей узловой точке устанавливаются два
крайних передаточных числа 1\ и Z2, причем величина всегда
больше величины Z2. Отношение этих передаточных чисел назовем
диапазоном регулирования точки R или внутренним диапа-
зоном замкнутого силового потока.
Обозначим внутренний диапазон буквой d. .
При передаточных числах регулирующей точки 1\ и t2 внешнее
передаточное отношение силового потока получает значения zI2 (1)
и г12 2). Отношение этих величин назовем внешним диапазо-
ном силового потока; обозначим его буквой D.
Из приведенных выше формул можно получить следующую за-
висимость между внешним и внутренним диапазоном и коэффици-
ентами циркуляции:
= (172)
“ R!
где ега и —два значения коэффициентов циркуляции, соот-
ветствующие крайним значениям передаточного отношения регу-
лирующей точки 1 = 1} и I = Z2.
Коэффициент циркуляции в общем виде определяется по
формуле
=(173)
1 + -г~:
—i
а
Исследуя формулу (172) с помощью графика, приведенного на
рис. 89, придем к следующим выводам:
1. Если силовой поток разветвленный, то внешний диапазон
всегда меньше внутреннего диапазона. При этом через регулирую-
щий механизм (точка /?) протекает мощность, меньшая, чем мощ-
ность, которая подводится к передаче (к силовому потоку).
2. Если силовой поток циркулирующий, то внешний диапазон
всегда больше внутреннего диапазона. При этом через регулирую-
щий механизм протекает поток, мощность которого больше мощ-
ности подводимого к передаче потока.
Таким образом, за счет циркуляции силового потока можно
расширять диапазон передачи, делая его больше диапазона регу-
лирующего механизма. При этом через регулирующий механизм
будет протекать силовой поток, больший, чем подводимая от дви-
гателя мощность.
Разветвленный поток, наоборот, позволяет пропускать через
регулирующий механизм только часть мощности двигателя, но
при этом сокращается диапазон передачи.
В механических силовых потоках трудно получить значитель-
ное расширение диапазона передачи за счет циркуляции мощности
180
или значительное уменьшение потока, проходящего через регули-
рующий механизм, так как в первом случае увеличивается на-
грузка, а во втором — скорости передачи. И то и другое будет вы-
зывать повышенный износ передачи.
Замкнутые силовые потоки могут быть не только в механиче-
ских силовых передачах, но и в гидравлических, и в электри-
ческих. В случае применения замкнутых силовых потоков в указан-
ных передачах расширение внешнего диапазона будет достигаться
соответственно за счет увеличения весового расхода жидкости или
силы электрического тока, а уменьшение разветвленного потока,
проходящего через регулирующую точку,— за счет увеличения ги-
дравлического напора или напряжения электрического тока.
ИСПОЛЬЗОВАНИЕ ЯВЛЕНИЯ ЦИРКУЛЯЦИИ СИЛОВОГО ПОТОКА
В ИСПЫТАТЕЛЬНЫХ СТЕНДАХ (СТЕНД ЦИРКУЛЯЦИИ)
Возможность получения в замкнутых силовых потоках при
сравнительно небольшой затрате мощности первичного • двигателя
больших статических нагрузок в виде циркулирующих потоков
позволяет использовать это явление для испытания на износ или
для обкатки различных механизмов силовой передачи: коробок
передач, бортовых передач, карданных механизмов и т. д.
Особенно большое значение это имеет при испытании механиз-
мов силовой передачи гусеничных машин, когда передаваемая
через механизм мощность составляет иногда сотни лошадиных
сил, что при испытании разомкнутым (последовательным) потоком
потребовало бы от первичного двигателя еще большую мощность.
В циркулирующем силовом потоке первичный двигатель компенси-
рует лишь потери в испытуемом механизме и в редукторах стенда.
Основной же нагрузочный поток создается в результате цирку-
ляции.
На рис. 90 показан стенд циркуляции, применяющийся для
испытания на износ и для обкатки автомобильных коробок пе-
редач *.
Стенд состоит из передвижной станины 1, двух зубчатых ре-
дукторов 2 и 3, червячного нагружателя 4 и торсионного вала 5.
На стенде зеркально одна к другой установлены две испытуе-
мые коробки передач 6 н 7.
Коробки устанавливаются зеркально для того, чтобы на всех
передачах общее передаточное число обеих коробок равнялось
единице, иначе стенд не сможет работать.
Принципиальная схема стенда приведена на рис. 91. На нем
же показано устройство основного элемента стенда — нагружа-
теля.
* В. И. Мухин. Диссертация. Ленинград, 1954,
181
7
Рис. 90. Стенд циркуляции для испытания на износ автомобильных коробок
передач:
1 — станина; 2 и 3 — зубчатые редукторы; 4 — червячный нагружатель; 5 — торсионный аал; 6 и
7 — испытуемые коробки передач
Рис. 91. Схема стенда циркуляции:
а — схема стенда; б — схема силового потока стенда; а — механи-
ческая узловая точка; б — кинетическая узловая точка; / — червяч-
ное колесо; 2—торсионный вал; 3 — червяк; 4 — корпус нагружа-
теля; 5 и 6 — зубчатые редукторы; 7 и 8 — коробки передач; 9 —
электродвигатель
182
Нагружатель состоит из червячного колеса 1, посаженного на
торсионный вал 2, червяка 3, установленного на подшипниках
в корпусе 4 нагружателя, который жестко связан с зубчатым ре-
дуктором 5.
При вращении червяка червячное колесо и корпус нагружателя
вращаются в различные стороны, закручивая торсионный вал и
создавая статическую нагрузку в замкнутом контуре стенда. Так
как нагружатель самотормозящийся, то созданная нагрузка сохра-
няется и после того, как будет прекращено закручивание торсион-
ного вала.
Нагрузка производится при неподвижном стенде. После того
как стенд нагружен, он запускается, и в его замкнутом контуре
возникает статический циркулирующий силовой поток (рис. 91,6),
который и нагружает установленные на стенде испытуемые меха-
низмы (в данном случае коробки передач).
На рис. 91,6 представлена схема силового потока стенда.
Здесь механическая узловая точка а описывает зубчатые меха-
низмы стенда — редуктор и коробки передач (так как все эти
механизмы простые, то согласно свойству 9 механической узло-
вой точки их можно на схеме силового потока изображать одной
узловой точкой).
Червячный нагружатель в схеме силового потока описывается
кинетической узловой точкой 5. Эта точка постоянно замкнута и,
следовательно, не имеет потерь. Потери в стенде происходят в зуб-
чатых механизмах, т. е. в механической точке а.
Кинематический и статический расчет стенда циркуляции
Согласно формуле (156) число статических задающих параме-
тров силового потока стенда равно
Хи = (3-1)а + (1)6-2 = 1.
Отсюда следует, что внутренний поток задается одним мо-
ментом.
В качестве задающего момента следует принять расчетный мо-
мент на валу испытуемого механизма, который создается нагружа-
телем.
Расчетный момент примем равным некоторому среднему эксплуа-
тационному моменту, с которым обычно работает механизм.
Так как передаточное число точки а равно единице, то замкну-
тый поток имеет одну степень свободы (если бы передаточное
число не равнялось единице, то согласно формуле (155) силовой
поток имел бы нуль степеней свободы, т. е. он был бы заторможен).
Примем в качестве задающих параметров расчетную мощность
Np, подводимую к коробке 8 (рис. 91) со стороны электромотора,
и угловую скорость ведущего вала коробки (wp).
Составляя развернутую схему силового потока стенда, состоя-
щую из четырех механических точек: две точки коробок передач
(к8 и к7) и две точки редукторов (р5 и рб), и решая уравнения си-
183
лового потока, получим следующие выражения мощностей на ве-
домых валах (2) механизмов:
Мк8 (^р + Л/,к8), АТ>к7 = A7jk8 А/ук,, ATjpj = А^2к7 N^N.+ N^-N^, (174) (175)
и момент нагружателя
.. ^2рб (176)
Ш2р5
Здесь Nt — потери в узловых точках, определяемые по фор-
муле (138), — мощность электромотора, <»2р5 — угловая ско-
рость торсионного вала, определяемая через скорость ч>р и переда-
точное число редуктора гр6. Этим передаточным числом следует
задаться. При этом должно соблюдаться равенство
Zp6-*p5 = l- (177)
По формуле (175) определяется мощность по которой под-
бирается электромотор, а по формуле (176) определяется расчет-
ный момент нагружателя Л4Н.
6. РАСЧЕТ ГИДРОДИНАМИЧЕСКОГО ТРАНСФОРМАТОРА
РАСЧЕТ СИЛОВОГО ПОТОКА ОДНОСТУПЕНЧАТОГО
ТРАНСФОРМАТОРА
При расчете гидродинамического трансформатора следует иметь
в виду следующее,
С одной стороны, трансформатор является механической систе-
мой, работа которой вполне точно описывается уравнениями рав-
новесия (в пределах точности струйной теории). С другой стороны,
это система диссипативная, т. е. имеющая внутренние и внешние
потери, которая может описываться лишь приближенно, эмпириче-
скими зависимостями.
Таким образом, расчет гидротрансформатора, с одной стороны,
математически точен, с другой стороны, он приближен, поскольку
приближенна диссипативная функция. Степень приближения опре-
деляется точностью определения диссипативной функции гидрав-
лических и механических потерь, имеющих место в трансформа-
торе. Чем точнее будет определена диссипативная функция, тем
точнее будет и расчет трансформатора.
Пользуясь вторым принципом теории силового потока, можем
составить точные уравнения равновесия гидромеханической си-
стемы трансформатора. К этим уравнениям необходимо добавить
приближенные уравнения мощностных факторов, в которые вхо-
дят диссипативные функции потерь.
184
Заметим, что высказанные здесь соображения относятся не
только к расчету гидротрансформаторов, а справедливы для всякого
расчета, если, конечно, расчет реален, т. е. учитывает диссипатив-
ные явления. Особенность расчета гидродинамических передач
заключается лишь в том, что если в других передачах можно хотя
бы в первом приближении пренебречь диссипативными явлениями,
то в гидропередачах этого делать нельзя.
Рассмотрим расчет силового потока трансформатора, т. е. точ-
ную часть общего расчета. При этом диссипативную функцию
гидравлических потерь трансформатора считаем заданной и пока
определять ее не будем (определение диссипативной функции при-
водится в полном расчете трансформатора, см. ч. 2).
Трансформатор может быть одноступенчатым или многосту-
пенчатым.
Одноступенчатый трансформатор в свою очередь может иметь
два направления гидравлического потока: насос — турбина — на-
правляющий аппарат — насос или насос — направляющий аппа-
рат— турбина — насос. Условимся направление потока обозначать
следующей формулой: Н Т > А Н или Н > А-^ Т -> Н, кото-
рую назовем структурной формулой силового потока.
Чаще всего одноступенчатые трансформаторы выполняются по
структурной формуле Н Т А -> Н.
Произведем расчет одноступенчатого трансформа-
тора этого типа.
Составим уравнение внешних мощностей трансформатора:
ДГ = —и>иЛ4и —о>тЛ4т. (178)
Из уравнения равновесия узловых точек, учитывая связываю-
щие потоки, получим
Л4т = Л42н-М2 1 (179)
М. = Л72т — М„..
А "1 2А '
Эти моменты могут быть определены по формуле (142):
/И2к = ^-2k0)kQ ^2к^3>
где/И2к—гидравлические моменты потоков на выходе;
k—индекс гидродинамической узловой точки (k = Я, Т
или Д).
В параметры узловой точки а2к и Ь'2к входят согласно форму-
ле (143) геометрические размеры трансформатора и угол на вы-
ходе гидравлического потока |32к. Все эти величины должны быть
заданы. Угол Р'к принимается равным углу наклона лопаток
с учетом некоторого отклонения потока (см. расчет трансформа-
тора, ч. 2),
185
Подставив моменты Л4„, Л4Г и Л7Д в равенство (178), получим
после преобразования значение диссипативного потока
трансформатора
= [(^н — А2А) Q — a2HwH] “hQ +
+ [(^т — ^2н) Q + — д2т"\] "\Q. (180)
Допустим, что суммарные гидравлические потери в колесах
трансформатора определяются некоторой диссипативной
функцией (а>„, о)г, Q).
Приравняв эту функцию к Nt и задавшись значениями угловых
скоростей и)н и <ог, получим из уравнения (180) значение весового
расхода Q в функции скоростей <»и и <»т. Тогда из формул (179)
можно определить моменты механических потоков ЛТН, /Ит и ЛТА.
Далее может быть определен гидравлический к. п. д. трансфор-
матора по следующей формуле:
<1а|)
Величина Nt определяется из уравнения (180) со знаком минус.
Если принять <»и = const, тогда все величины выразятся в функ-
ции одной угловой скорости вала турбины (<от) или его числа обо-
ротов (лт).
Рис. S2. Каноническая характеристика одноступенчатого
гидротрансформатора и его узловая точка:
а — характеристика; б — узловая точка
186
Графическая зависимость моментов /Ии, 7ИТ и к. и. д. при
<1>н = const называется канонической характеристикой
трансформатора.
На рис. 92 приведена примерная каноническая характеристика
одноступенчатого трансформатора.
Получение канонической характеристики является конечным ре-
зультатом расчета силового потока трансформатора.
Каноническая характеристика есть паспорт трансфор-
матора. По этой характеристике производится расчет гидромеха-
нических передач.
Если каноническая характеристика определена, то в дальней-
шем нет необходимости рассматривать гидротрансформатор как си-
стему узловых точек, т. е. представлять его в виде силового потока.
Все внутренние потоки, не влияющие на равновесие трансформа-
тора в целом, могут быть отброшены, а осе гидродинамические
узловые точки слиты в одну узловую точку гидротранс-
форматора, имеющую только механические по-
токи и диссипативный поток. Обозначение этой точки
приведено на рис. 92, б. В общем случае узловая точка гидро-
трансформатора имеет три степени свободы, а при затор-
моженном направляющем аппарате — две степени свободы; отме-
чается она двумя черточками.
Заметим, что узловая точка гидротрансформатора вполне опи-
сывается канонической характеристикой, если заданы две скорости
% и о)т. Так как каноническая характеристика определяется при
заданной скорости <ои, то достаточно задать еще скорость о>т или
. сот
передаточное число гтн — — .
мн
Рассмотрим теперь, расчет силового потока многоступен-
чатого трансформатора.
На рис. 93 приведена кинематическая схема многоступенчатого
трансформатора и схема его силового потока. Трансформатор со-
стоит из одного колеса насоса, двух колес турбины и двух колес на-
правляющего аппарата.
Колеса турбины жестко связаны между собой механической
связью. Колеса направляющего аппарата заторможены.
Силовой поток состоит из пяти гидродинамических узловых то-
чек и одной разветвляющей точки, к которой подводятся механиче-
ские потоки от турбинных колес.
Число ступеней трансформатора определяется числом его тур-
бинных колес.
Данный трансформатор является двухступенчатым со структур-
ной формулой Н 7”1 А1 -> Т2 -> А2 -> Н.
Составим уравнение внешних мощностей трансформатора;
Nt = -а>нЛ1н- <от/Ит,
где ЛД — момент на ведомом валу трансформатора.
187
6
Рис. 93. Кинематическая схема многоступенчатого ги-
дродинамического трансформатора:
а — схема трансформатора; б — схема силового потока трансфор-
матора
Из уравнения равновесия разветвляющей механической точки
получим
/И, = /Ит1 /ИТ2.
Кроме того,
^2А2 ^2И>
/ИТ1 = ^2н ^2т1>
= ^2т| ^2А1>
/ИТ2 = ^2А1 ^2т2 ">
^А2 = ^2т2 ^2А2 •
Из характеристики гидродинамической точки определяем М2к и,
подставляя в предыдущие формулы, находим моменты всех механи-
ческих потоков, в том числе и моменты /ИТ| и /Ит2, по которым най-
дем момент Мт. После этого строится каноническая характеристика
трансформатора.
7. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
И ЭЛЕКТРОМЕХАНИЧЕСКИХ ПЕРЕДАЧ
Теория силового потока позволяет рассчитывать не только меха-
нические и гидравлические передачи, но и цепи постоянного и пере-
менного электрического тока, а также электромеханические пере-
дачи, применяющиеся в колесных и гусеничных машинах в качестве
силовых передач.
188
РАСЧЕТ СИЛОВОГО ПОТОКА ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
ПОСТОЯННОГО ТОКА
Рассмотрим вначале силовой поток электроцепи постоянного
тока и покажем, что первый и второй принципы теории силового
потока применимы и к передачам этих типов.
Воспользуемся силовым потоком электроцепи постоянного тока,
приведенным на рис. 76. Выделим в этом потоке какой-нибудь замк-
нутый контур, например а—е—в—д—г—а.
Составим для кинетических узловых точек, входящих в этот
контур, уравнения мощностей и уравнения равновесия.
Для точки а будем иметь
Р1аЛа + Р2а4а + NЦа + Мга = 0>
Д>а Ла А >
где /а — абсолютное значение величины тока, проходящего через
точку а.
Отсюда находим
р ___________________ р ______ ^tta +
~1а '28 I
‘й
Для остальных точек по аналогии с предыдущим получим
р ___Р __ Pfle + Nt2e .
П» 1в
Складывая левые и правые части равенств, найдем
^а-^а+^1в-^в + ^-^ =
__________ / Л'на + Nlsa | Nf;. \
~~ - 4 + 1° ' Л Г
Из схемы силового потока следует, что потенциалы Р попарно
сокращаются.
Тогда получим
Лфа + Мга । । ^1г _о
/ ' I ' I
'а 'в г
Подставив в это выражение значения рассеянных потоков (из
формулы 148), получим
S£\ = Sc-A-
Это есть второй закон Кирхгофа.
Первый закон Кирхгофа, а также закон Ома вы-
водятся непосредственно из определения электроразветвляющей и
электрокинетической узловых точек силового потока.
189
Выше было показано, что из первого и второго принципов теории
силового потока вытекает также и закон Джоуля-Ленца.
Таким образом, основные закономерности цепей постоянного
электрического тока могут быть получены из основных принципов
теории силового потока. Отсюда следует, что и все остальные зако-
номерности, получающиеся как следствие из законов Ома и Кирх-
гофа, должны получаться и из теории силового потока.
Расчет электрического силового потока, а следовательно, и рас-
чет цепей постоянного электрического тока производятся так же,
как и расчет механического или гидравлического силового потока.
Для этого составляются уравнения мощностей и уравнения равнове-
сия узловых точек и связывающих потоков. Решая совместно эти
уравнения, находим все кинетические и динамические факторы си-
лового потока, т. е. потенциалы и величины токов.
Следует иметь в виду, что электрический силовой поток, как и
всякий другой силовой поток, может иметь холостые и за-
торможенные потоки. Холостым поток будет тогда, когда
динамический фактор (величина тока) равен нулю:
^ = / = 0;
поток будет заторможенным, когда кинетический фактор (потен-
циал) равен нулю:
U=P = 0.
Холостой поток соответствует разомкнутой цепи, заторможенный —
заземленной цепи.
РАСЧЕТ СИЛОВОГО ПОТОКА ЭЛЕКТРОСИЛОВОЙ ПЕРЕДАЧИ
Рассмотрим расчет силового потока электросиловой передачи,
принципиальная схема которой приведена на рис. 77, а силовой по-
ток — на рис. 78, а и б.
Проследим вначале по схемам силового потока передачу энер-
гии в силовой передаче при прямолинейном движении и при пово-
роте машины.
Соответствующие обозначения к схемам силовых потоков были
даны выше, в разделе 3 «Постоянные силовые потоки».
1. Прямолинейное движение. Механический поток
от точки б (рис. 78, а) подводится к точке а. Здесь он преобразуется
в электрический поток, который идет к разветвляющей точке ж.
Если регулирующие сопротивления выключены (узловые точки д и
е полностью включены) и сопротивления движению машины на
обеих гусеницах одинаковы, то в точке ж поток разветвляется по-
ровну. Один поток направляется к точке в, другой — к точке г.
В этих точках электрические потоки преобразуются в механические.
Обе точки работают в режиме моторов. Гусеничная машина дви-
жется прямолинейно.
190
Электрический силовой поток, пройдя через точки в и г, скла-
дывается в точке з и возвращается в точку а, образуя замкнутый
циркулирующий поток.
2. Поворот. Включим сопротивление е, тогда в точке е бу-
дет происходить скольжение и появится диссипативный поток. При-
мем вначале как допущение, что при этом скольжении машина по-
ворачивается; тогда к отстающей гусенице от забегающей (левой)
подводится через землю механический поток. Узловая точка г бу-
дет работать в режиме генератора, а электрический поток, прохо-
дящий через эту точку, изменит свое направление (по сравнению
с потоком при прямолинейном движении). В результате в точке ж
будут складываться потоки генераторов а иг. К точке в подводится
поток больший, чем поток, вырабатываемый основным генерато-
ром а. Так как согласно характеристике электромеханической точки
момент пропорционален току (при постоянном потоке возбужде-
ния), то момент механического потока точки в будет больше, чем
при прямолинейном движении. Одновременно механический поток
точки г меньше потока точки в, так как через эту точку проходит
лишь часть тока, идущего через точку в. В результате на левой и
правой гусеницах создадутся различные по величине и направлению
силы тяги, что и явится условием поворота гусеничной машины.
Произведем теперь расчет силового потока.
Рассмотрим из двух случаев движения наиболее общий—пово-
рот машины.
Из уравнения равновесия узловой точки ж можем написать
4 = Л-4.
где I — абсолютное значение тока.
Согласно характеристике электромеханической узловой точки
имеем выражения динамических факторов электри-
ческого силового потока:
г __
стяФа ’
в cme&e
г
г С Ф '
тг г
(182)
Примем в качестве задающих параметров моменты на ведущих
колесах машины. Эти моменты пропорциональны моментам Mg и Мг\
следовательно, Мь и Мг можно рассматривать как величины за-
данные.
Кроме того, заданными величинами являются потоки возбужде-
ния Ф и коэффициенты машин ст.
Из предыдущих формул определяются токи /а, 1д, 1г и мо-
мент Мл.
Таким образом, находим все динамические факторы силового по-
тока электрической передачи.
191
Определим теперь кинетические факторы.
Составляем уравнения мощностей для точек а, в, г и е‘.
= 0;
ДЛ + ^Л+%<=°;
ЛеЛе+^еЛе-^ = 0.
Для разветвляющих точек ж и з имеем
^2а = Рщ ~ Р-1г’ Р\л = Р1а — ^1е
и для связывающего потока е — г величину Р2е — Р1г.
Кроме того, из равновесия точек а, в, г и е получим
*2а — 21а — 'а,
/„ = — Л = — I;
2g 18 8’
^ = -Аг = -4;
Де Ле ' Д ' Д
Решая полученную систему уравнений, находим
П ____ Р _ .
г2а Ча / >
'а
<&аМа
D р — 8 6 .
г2а *]а — I >
‘в
P^-Px^-Y'-rJ,,
* ?
где Р2в— P\a = VB — напряжение генератора а.
Окончательно получаем выражения кинетических фак-
торов электрического силового потока:
т г _ ыа^а
иа J >
'а
“8 = -^Г> <183)
(К1 + Ге/г) 4 I
(О = ----. I
г Мг 1
Скорость <оа определяется числом оборотов двигателя и, следова-
тельно, задана. Кроме того, должно быть задано сопротивление ре-
гулирующей точки е. Тогда из полученных формул определится
напряжение генератора Ка и скорость ведущих колес машины
% и %•
Заметим, что моменты Мд и Мг имеют противоположные знаки,
так как механический поток точки в отрицательный, а точки г —
положительный. Поэтому скорости <«в и <ог должны иметь одинако-
вые знаки.
192
Регулируй сопротивление ге, можно изменять скорость шг,
а следовательно, регулировать поворот машины.
Примем ге = 0. Получим % = %, т. е. машина в этом случае
будет двигаться прямолинейно. При этом ток /г становится равным
по величине и направлению току 1д, так как при прямолинейном
движении моменты Мв и Мг равны.
8. ПЕРЕМЕННЫЕ СИЛОВЫЕ ПОТОКИ
ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
Особенностью переменных силовых потоков является то, что
узловые точки этих потоков могут накапливать или, наоборот, отда-
вать ранее накопленную в них энергию. Потоки, принадлежащие
узловым точкам, через которые совершается аккумуляция или от-
дача энергии, называются аккумулирующими, и обозна-
Рис. 94. Узловые точки с аккумулирующими пото-
ками:
а — с положительным аккумулирующим потоком; б — с отрицав
тельным аккумулирующим потоком
Аккумулирующий поток считается положительным, если
энергия подводится к узловой точке, и отрицательным, если она
отводится от узловой точки.
Аккумулируемая в узловой точке энергия может иметь две
формы: кинетическую (Г) и потенциальную (/7).
Кинетическая энергия есть квадратичная функция кинетиче-
ского фактора и. Потенциальные потоки, которые здесь рассматри-
ваются, также являются квадратичной функцией, но только ди-
намического фактора q. Поэтому можем написать
П=^-. (185)
В этих формулах m и п — некоторые постоянные положительные
величины.
13—2469 1 93
Определим мощности аккумулирующих потоков. Для этого про-
дифференцируем величины Т и П по времени. При этом мощност-
ному фактору аккумулирующего потока условимся приписывать
знак минус, если в узловой точке происходит накопление энергии.
Будем иметь
Т=-"'“Д <186>
<18?)
Знак минус показывает, что при возрастании кинетического и
, f du ~ n dq ~
динамического факторов (-^>0 и в узловой точке на-
капливается энергия (Л\<0 и 2Vn<0), т. е. точка является со-
противлением при прохождении через нее силового потока.
Рассмотрим различные примеры переменных силовых потоков,
которые представляют интерес с точки зрения исследования и рас-
чета переменных режимов работы силовых передач самоходных
машин.
РАЗВЕТВЛЯЮЩАЯ ИНЕРЦИОННАЯ ТОЧКА
Представим себе некоторую неравномерно вращающуюся ма-
ховую массу, посаженную на сквозном валу (рис. 95). Масса имеет
три потока: два механических 1 и 2, идущих по валу, и один акку-
мулирующий, или инерционный, <3.
Так как скорости всех трех потоков равны (масса жестко поса-
жена на вал), то
U)] = (1)2 — 0)3 = ш
и, следовательно, неравномерно вращающаяся маховая масса опи-
сывается разветвляющей узловой точкой.
Составим для этой точки уравнение равновесия:
Д + м2 + Д = о,
где М3 — динамический фактор
инерционного потока.
Динамический фактор можно
определить из формулы (186),
если представить аккумулирую»
щий поток в следующем виде:
А'г = ид.
В этом уравнении
Рис. 95. Неравномерно вращающаяся
маховая масса:
а — неравномерно вращающаяся масса; б —
ра язетвляющая инерционная узловая точка
маховой массы

194
Выразим q через Л43, а и через <о и обозначим коэффициент т.
через 9, придав ему значение момента инерции маховой массы.
Тогда будем иметь
Л7 = _ 9 .
J dt
Но это есть инерционный момент маховой массы.
Итак, неравномерно вращающаяся на валу маховая масса
в схеме силового потока описывается разветвляющей инерционной
узловой точкой с одним инерционным потоком, в котором накапли-
вается кинетическая энергия.
Определим число задающих параметров инерцион-
ной узловой точки.
Число задающих параметров определяется по общей формуле
(153), причем в число п0 добавляется один направленный инер-
ционный поток.
Заметим, что в инерционной точке появляется новое неизвест-
ное— время t. Кроме того, добавляется и новое уравнение аккуму-
.. dT „ ,,
лирующего потока 7VT = —. 1аким образом, число задающих
параметров узловой точки с введением времени не меняется и фор-
мула (153) остается без изменения.
Для трехпоточной точки будем иметь согласно формуле (153)
т т
2 S«o/=2-3; ср= 1;S^ = 2. Тогда Х= 2-3 —(1 + 2)= 3. За-
дающими параметрами являются: скорость (со), время (/) и один
из моментов механического потока (2И),
ИНЕРЦИОННАЯ ТОЧКА ПРОСТЕЙШЕГО
ДИФФЕРЕНЦИАЛЬНОГО МЕХАНИЗМА
Рассмотрим теперь более сложную инерционную систему — диф-
ференциальный инерционный механизм (рис. 96). Допустим, что
звенья механизма имеют массу и, следовательно, обладают инер-
цией.
Подсчитаем по теореме Кёнига кинетическую энергию меха-
низма:
т=4 м+4- м+4 w+
+4 +4 9с< •
В уравнении первые три члена выражают кинетическую энергию
двух центральных шестерен и водила, а четвертый и пятый члены —
кинетическую энергию сателлита в переносном и относительном
движении. В переносном движении сателлит рассматривается как
материальная точка, расположенная на оси сателлита и имеющая
13» 195
массу т, равную-у , где Q — вес сателлита. Радиус оси сателлита
выразим через До.
В относительном движении сателлит вращается вокруг собствен-
ной оси с относительной скоростью о>с. Моменты инерции 91, 92 и
90, а также момент инерции точечной массы т, расположенной на
оси сателлита, берутся относительно главной оси механизма, а мо-
мент инерции сателлита 9С — относительно оси сателлита.
Рис. 96. Дифференциальный инерционный меха-
низм:
а — схема инерционного механизма; б —схема силового по-
тока инерционного механизма
Объединим третий и четвертый члены уравнения. Вынесем за
скобку «>о и обозначим выражение в скобке
90с = 90 + тА20.
Тогда получим
+ 4- «+4 •
Дифференцируя величину Т по времени, находим суммарный
инерционный поток механизма
Nr~ — ^!<»! + 02<»2 + 0с’°0 ~ai + 9сшс ~dt) •
Этот поток можно рассматривать как сумму инерционных пото-
ков разветвляющих точек, расположенных на главных потоках 0, 1
и 2, а также инерционного относительного потока сателлита с.
Не примем пока во внимание разветвляющие точки и рассмо-
трим только механическую точку с относительным потоком.
196
Составим для механической точки уравнение мощностей и урав-
нение равновесия. При этом уравнение мощностей напишем в форме
уравнения относительных мощностей:
С1и>.
4- о)' М' — 0 о>' -г?- = 0;
11'22 с С (It
< + /и; + м2 = о.
В этих уравнениях через М[ обозначен момент потока без учета
инерционной массы этого потока, так как разветвляющие точки
пока не рассматриваются.
Заметим, что в уравнение равновесия момент относительного по-
тока не входит, так как этот поток является внутренним и, следо-
вательно, не может влиять на равновесие узловой точки.
Поделим уравнение мощностей на какую-нибудь относительную
скорость, например на скорость <»' и представим отношения скоро-
стей как внутренние передаточные отношения. Получим
/ \
где выражение в скобках есть момент инерционного потока. Обо-
значим его через /И' .
Тогда окончательно получим
М'+121М2 + ^Мс = 0, (188)
где
Мо + /и; + /и2 = 0. (189)
Уравнение (188) есть уравнение моментов инерционной точки, ко-
торое можно было бы сразу получить из уравнения (159), подставив
в него инерционный член ^ЛМ'С и приняв коэффициент потерь
Х/= 1 (здесь потери не учитываются).
Таким образом, инерционный дифференциальный механизм опи-
сывается уравнениями, по форме аналогичными уравнениям ста-
тики.
Число задающих параметров данной узловой точки, так же как
и разветвляющей инерционной точки, определяется по формуле
(153). Нужно только иметь в виду, что относительный инерцион-
ный поток входит в число направленных потоков и, следовательно,
учитывается в величине «о. Кроме того, следует учитывать, что от-
носительный поток сателлита дает дополнительное уравнение кине-
матической связи.
197
Так, для трехпоточной точки с четвертым относительным потоком
будем иметь 2S/z0Z = 2-4; Sct = 2. Тогда по формуле (153)
1 1
получим X = 4. Механизм имеет две степени свободы, и время за-
дано. Таким образом, должен быть задан еще один момент механи-
ческого потока.
Определим теперь внешние моменты, приложенные к валам
механизма.
Входящие в формулы (188) и (189) моменты принадлежат пото-
кам, расположенным между разветвляющими и механической точ-
ками. Нас же интересуют моменты потоков, подводимых извне
к разветвляющим точкам. Для определения этих моментов следует
рассмотреть равновесие инерционных разветвляющих точек, кото-
рые ранее не были учтены. После соответствующих вычислений по-
лучим общую формулу внешнего момента простейшего инерцион-
ного механизма
Л4к=Л4к + 0к^, (190)
где k—общее обозначение потоков 0, 1, 2;
9„—момент инерции маховой массы потока k\
<ок — скорость потока k.
Следует иметь в виду, что для водила
9ос = 9о + тА20,
где т — масса сателлита;
Ло — радиус оси сателлита.
СИЛОВОЙ ПОТОК НЕРАВНОМЕРНО ДВИЖУЩЕЙСЯ
ГУСЕНИЧНОЙ МАШИНЫ
Теория силового потока рассматривает не только работу
различных передач, но и движение машины в целом, в частности
неравномерное или инерционное движение гусеничной или колесной
машины.
Рассмотрим в качестве примера инерционный силовой поток
прямолинейно движущейся машины.
Силовой поток будет состоять из четырех узловых точек: а, б, в
и г (рис. 97).
Для упрощения считаем, что зубчатые механизмы силовой пере-
дачи простые и безынерционные.
Определим вначале по формуле (153) число задающих параме-
тров силового потока:
Х = 2 [(3)а + (2)б + (3)e + (3)J + 1 -
-{ 2(1 + 1)4- 1-2 + [(2)а +(0)6 + (1)в + (2)J + 2-3 + 1 } = 5.
Так как число степеней свободы = 2, то ХЛ1 = 3.
198
Примем в качестве задающих скоростей скорость подводимого
и отводимого потоков (о>1 и <о2); в качестве задающих моментов —
момент двигателя (Mi), момент сопротивления движению машины
(М2) и момент трения главного фрик-
циона (Мб — М1б).
Составим теперь уравнения силово-
го потока.
Учитывая связывающие потоки, мо-
жем написать
Мб -ф- /21 М2д — 0;
М] + Л1Яа — = 0;
-м2в + м3г +< = 0.
тока неравномерно движу-
щейся машины:
а — разветвляющая узловая точка с
инерционным потоком маховых масс,
связанных с ведущим валом главного
фрикциона; б — узловая точка глав-
ного, фрикциона; 'в — механическая
точка описывающая все зубчатые меха-
низмы силовой передачи; г — разветв-
ляющая узловая точка с инерционным
потоком масс, связанных с ведущими
колесами машины
Здесь Д = М]а и Л12 = Кроме
того, инерционные моменты равны
М —_____а .
Подставив значения инерционных моментов в приведенные урав-
нения, получим следующую систему дифференциальных уравнений
движения машины:
~~dT т----ё; - О,
(йгЛТб + '12 о
dt' е2 ~
Аналогичные уравнения были выведены в гл. II при рассмотре-
нии вопросов переключения передач. Сравнивая обе системы урав-
нений, следует иметь в виду, что и М2 <0.
СИЛОВОЙ ПОТОК, ОПИСЫВАЮЩИЙ УПРУГИЕ ЯВЛЕНИЯ
В ПЕРЕДАЮЩЕЙ СИСТЕМЕ
До сих пор мы считали механические передачи абсолютно жест-
кими. В действительности звенья передач имеют упругость, которую
в некоторых задачах приходится учитывать. Так, колебательные яв-
ления в механизмах силовой передачи, часто вызывающие поломку
валов, зависят от упругости деталей. В некоторых передачах, на-
пример в импульсных, специально вводятся упругие торсионные
валы, без которых передача работать не может.
Рассмотрим явление упругости деталей силовой передачи с точ-
ки зрения теории силового потока.
Условно разрежем упругий вал и в разрез поместим некоторую
упругую муфту. Разрезанные части вала теперь можно рассматри-
199
вать как абсолютно жесткие, так как упру-
Чрх гость вала будет сосредоточена в муфте.
I В силовом потоке упругая муфта представ-
ляет собой кинетическую узловую точку сакку-
Г мулирующим потоком потенциальной формы
I энергии.
, \/ г Эта точка называется упругой у з л о-
— "* X *'' вой точкой силового потока. Обо-
f \| значим ее, как показано на рис. 98, где
Ту-—поток потенциальной энергии /7;
t — диссипативный поток потерь на гисте-
6 резне.
Рис. 98. Упругая узло- Определим для этой точки число задающих
вая точка параметров. Учитывая, что аккумулирую-
щий поток является направленным, будем
т т
иметь 2 2 пы = 2 ‘ 3 = 6. Кроме того, b = 1; си = 1; S ci = 1 (ха-
1 1
рактеристика потерь на гистерезис). Тогда из формулы (153) по-
лучим
Х = 6 + 1 —(2+ 1) = 4.
Заданными величинами можно считать две скорости («>), время
(О и один момент (М).
Составим теперь для упругой точ-
ки уравнение мощностных факторов
и уравнение равновесия:
М + N2 + N.. + Nt = 0;
М, + /И, = 0.
Подставим в формулу (187) вме-
сто. п коэффициент эластичности X,
вместо q — момент потока М. ~
получим
2
Тогда
2V = — Х/И —
1 у dt ’
Отсюда, решив уравнения
вого потока, находим его кинетиче-
ские и динамические факторы. При
этом должен быть задан коэффи-
циент эластичности X и диссипатив-
ный поток t.
Рассмотрим в качестве примера
применения упругой точки силовой
поток колебательной системы, пред-
ставленной на рис. 99.
(191)
сило-
Рис. 99. Механическая колеба-
тельная система:
а — схема колебательной системы; 6 —
схема силового потока колебательной си-
стемы
а
200
Силовой поток состоит из одной упругой узловой точки с тремя
аккумулирующими потоками: двумя инерционными и одним упру-
гим. Потерями на гистерезис пренебрегаем.
Составим дифференциальные уравнения движения системы:
-Г- "F Ч0;
+ /и, = О,
откуда
Ш1 — “г ’
2 Ш; — Ш2 ’
В этих уравнениях
уИ2
На основании закона Гука можем выразить момент упруго-
сти через угол закрутки вала:
ПГ ~~ ?2>-
Подставив эти величины в уравнения силового потока, подучим
дифференциальные уравнения движения колеба-
тельной системы:
Аналогично составляются дифференциальные уравнения и более
сложных колебательных систем.
СИЛОВОЙ ПОТОК ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрение явлений, происходящих в электроцепях перемен-
ного тока, показывает, что эти явления полностью описываются
основными принципами теории силового потока. Цепи переменного
электрического тока широко применяются при исследовании раз-
личных колебательных процессов, происходящих в механических
передачах (например, в силовой передаче машины, в упругой
201
подвеске, в импульсных передачах и т. д.). Кроме того, цепи пере-
менного электрического тока могут применяться в электромехани-
ческих силовых передачах самоходных машин.
Электрическая цепь переменного тока в общем случае характе-
ризуется тремя видами сопротивлений: активным г, емкостным с и
индуктивным L.
Подставим в формулу (186) вместо кинетического фактора и
напряжение V, а вместо коэффициента т— емкость конденсатора с.
Получим
N^-cV^. (192)
Эта формула выражает мощность емкостного сопро-
тивления конденсатора, установленного в цепи переменного
электрического тока и имеющего на обкладках разность потенциа-
лов Pi — Р2 — V.
Емкостное сопротивление можно представить в виде кинетиче-
ской узловой точки с аккумулирующим потоком формы энергии Т
(рис. 100).
Рис. 100. Узловая точка
емкостного сопротивления
цепи переменного э. ектри-
ческого тока
Рис. 101. Узловая точка
индуктивного сопротивле-
ния цепи переменного элек-
трического тока
Так как в формуле (192) принят относительный кинетический
фактор V, то аккумулирующий поток будет относительным.
Подставим в формулу (187) вместо динамического фактора q
величину тока I *, а вместо коэффициента п — индуктивность L про-
водника. Получим
NL — ~Li^~. (193)
Эта формула выражает мощность индуктивного со-
противления цепи переменного электрического
тока.
* В электротехнике переменный ток обозначается малой буквой I.
202
Индуктивное сопротивление можно представить в виде кинети-
ческой узловой точки с аккумулирующим индуктивным потоком
(рис. 101).
Составим теперь силовой поток цепи переменного электрического
тока (рис. 102). ~
Узловую точку а генератора v ?
переменного напряжения можно
описать следующей характеристи-
кой:
М = Vi, 1
I/ I/ • / (194)
V = Vm sin <>>t, ]
где Vт — максимальное значе-
ние напряжения;
<о — частота колебаний на-
пряжения;
t — время.
Составим дифферен-
циальные уравнения си-
лового потока цепи пере-
менного электрического
тока.
Согласно первому принципу
для силового потока можем напи-
сать уравнение внешних мощно-
стей узловых точек:
Ч + М + Ч + ^ = о.
Так как поток замкнутый и состоит
только из кинетических.точек, то
Рис. 102. Цепь переменного элек-
трического тока и ее силовой поток:
а — цепь тока; б — силовой поток; а — узло-
вая точка генератора; б — узловая точка оми-
ческого сопротивления; в — узловая точка
индуктивности; г — узловая точка емкости
цепи
4 = 4 = ia = i,
где I — абсолютное значение тока.
Узловые точки а, б и т. д.
имеют следующиехарактеристики:

N6 = — /72;
N = — ;
в dt ’
n. — cV,7F-
Тогда получим
dt d К,
203
Выражаем Уг через I. Для этого составляем уравнения мощно-
стей и равновесия точки г:
dV,
РХг11г + Р^2г~сУг-а(=()>
Чг = — г’1г = — 1-
Учитывая, что Р1г—Ргг—Уг> после сокращения на Уг получаем
Тогда
У— ri — L — К = 0.
dt г
Дифференцируем это выражение по времени. После замены выра-
dVs i
жения -^-выражением — находим
dV dl , d'4 I r.
th--г w — L —• — == 0.
dt dt dt? c
Подставив в это уравнение
rfiz ., ,
— = УтШ cos ut,
получим окончательно дифференциальное уравнение переменного
электрического силового потока
d4 , г di , i 2, /, с* \
ДД + Т ~dt + ~cL = ~Д cos U95)
МОДЕЛИРОВАНИЕ СИЛОВЫХ ПОТОКОВ
Две передающие и преобразующие энергию
системы подобны, если они описываются одним
силовым потоком.
Допустим, что имеется механическая инерционная система
(рис. 103, а) и цепь переменного электрического тока (рис. 103,6).
Инерционная система состоит из импульсатора а, вызывающего
знакопеременные импульсы, двух маховых масс б и в, между кото-
рыми установлена упругая связь г (например, скручивающаяся пру-
жина), и некоторого переменного сопротивления д.
Электрическая цепь состоит из электрического импульсатора а,
двух заземленных конденсаторов б и в, индуктивности г и элек-
тронной лампы д, представляющей собой в электроцепи перемен-
ное сопротивление.
Нетрудно убедиться, что механическая система и цепь электри-
ческого тока описываются одним и тем же силовым потоком, схема
которого представлена рис. 103, в.
204
a
Рис. 103. Моделирование механической и электрической пере-
дающих систем:
а — механическая передающая система; — электрическая передающая си-
стема; в — силовой поток передающих систем. На схеме а: а — импуль-
сатор механических колебаний; б и в — инерционные массы; г — скручиваю-
щаяся пружина; д — механическое сопротивление. На схеме б\ а — импуль-
сатор электрических колебаний; б и в — конденсаторы; г — индуктивность;
О — электрическое сопротивление. На схеме в: а — узловая точка импуль-
сатора механических и электрических колебаний; бив — узловые точки инер-
ционных масс и конденсаторов; г — узловая точка скручивающейся пружины и
индуктивности; д — узловая точка механического и электрического сопро-
тивлений
205
На этой схеме точка а описывает механический и электриче-
ский импульсаторы, точки бив — инерционные массы и емкости,
точка г — упругую связь и индуктивность; точка д — сопротивление
механической системы и электрической цепи.
Чтобы соблюдалось подобие систем, узловые точки а (импуль-
сатора) и д (сопротивления) должны иметь одинаковые характе-
ристики в обеих системах, т. е. должны описываться однотипными
уравнениями.
Действительно, точки б, в и г аналогичны в обеих системах, так
как их аккумулирующие потоки определяются по одним и тем же
формулам (186) и (187). Если к тому же будут аналогичны и точ-
ки а и ф той передающие системы будут аналогичными или подоб-
ными, т. е. будут описываться одной системой уравнений.
Таким образом, одна передающая система описывает работу дру-
гой передающей системы, или одна система является мо-
делью другой системы.
Моделирование передающих систем в настоящее время широко
применяется в испытательной технике. Особенно удобно при испы-
таниях применение электрических моделей, построение которых не
представляет труда и значительно дешевле, чем построение меха-
нических моделей и тем более проведение натурных испытаний.
Моделировать можно не только системы различного типа (элек-
трические и механические), но и однотипные системы (например,
механические), если одна система проще другой системы.
Так, имеются стенды (например, в Военной академии тыла и
транспорта), которые моделируют в лабораторных условиях движе-
ние гусеничной машины и работу агрегатов ее силовой передачи
и двигателя (см. ч. 2).
Механическое моделирование находит также применение при
исследовании крутильных колебаний, происходящих в силовых пе-
редачах гусеничных машин.
ГЛАВА VI
ТЕОРИЯ ПОДРЕССОРИВАНИЯ И ПЛАВНОСТЬ ХОДА
ГУСЕНИЧНЫХ МАШИН
1. ПОДВЕСКА ГУСЕНИЧНЫХ МАШИН
Подвеской называется устройство, предназначенное для погло-
щения и рассеивания энергии динамических нагрузок, приходящихся
на гусеничный движитель машины при движении по неровностям
дороги, и обеспечивающее плавность хода машины.
Подвеска состоит из упругих и жестких элементов,
расположенных между опорными катками и корпусом, машины.
Совместно с движителем подвеска образует ходовую часть
машины.
Рассмотрим здесь в самом общем виде работу подвески.
При движении машины по неровностям дороги на ее ходовую
часть действуют динамические нагрузки. Энергия динамических на-
грузок передается через опорные катки и подвеску на корпус ма-
шины и на все установленные в нем агрегаты, а также и на нахо-
дящийся в корпусе экипаж.
Если эту энергию не поглощать и не рассеивать, она будет вы-
зывать разрушение подшипников ходовой части, ослабление креп-
лений агрегатов в корпусе, утомление экипажа.
Процесс накопления и рассеивания энергии в подвеске происхо-
дит следующим образом.
При наезде машины на препятствия упругие элементы деформи-
руются, поглощая энергию динамических нагрузок; в следующий
момент, распрямляясь, они выделяют ранее накопленную энергию,
часть которой переходит в кинетическую энергию движения кор-
пуса, вызывая его колебания, а другая часть рассеивается на тре-
ние в упругих элементах, в сочленениях жестких элементов подвески
или в специальных устройствах — амортизаторах.
Чем выше скорость машины, тем больше подводится энергии
к подвеске, тем больше ее будет поглощено упругими элементами и
больше рассеяно.
При определенной скорости движения машины и при определен-
ных высотах неровностей на дороге наступает баланс, когда энер-
гия, подводимая к ходовой части, уравнивается с энергией рассеи-
ваемой. В этом случае устанавливается колебательное движение
корпуса с постоянной амплитудой. Если скорость будет повышена,
то энергия подводимая станет больше энергии рассеиваемой, ампли-
207
туда колебаний начнет возрастать, пока не произойдет жесткий
удар в подвеске. Подвеску будет пробивать.
Так как пробивание подвески — явление недопустимое (в конеч-
ном итоге оно приведет к разрушению ходовой части), то водитель
снижает скорость машины, количество подводимой к подвеске энер-
гии уменьшается, и пробивание подвески прекращается.
Отсюда следует, что подвеска ограничивает скорость движения
машины по дорогам с местными неровностями.
Так, по наезженным автотранспортом осенним дорогам скорость
гусеничных поездов иногда снижается в два раза по сравнению со
скоростью, которую при данных дорожных сопротивлениях мог бы
обеспечить двигатель.
Чем совершеннее будет подвеска, т. е. чем она больше сможет
поглощать своими упругими элементами энергию динамических на-
грузок и быстрее ее рассеивать, тем выше будет маневренность и
подвижность гусеничных машин.
В настоящей главе рассматриваются общие вопросы теории
подрессоривания, а также вопросы плавности хода гусеничных ма-
шин. Во второй части книги дополнительно будут рассмотрены кон-
струкции и расчет подвесок.
2. ПРИВЕДЕННАЯ СХЕМА ПОДВЕСКИ
Упругие и жесткие элементы подвески, соединенные между со-
бой, а также с корпусом и опорными катками машины обра-
зуют ту или иную схему подвески. Основным различием схем яв-
ляется способ подрессоривания опорных катков. С этой точки зре-
ния все схемы подвесок можно свести к трем основным видам:
независимой, балансирной и смешанной под-
вески.
Рис. 104. Независимая торсионная подвеска:
7—опорный каток; 2 — балансир; 3 — ось балансира; 4 — опора оси балансира;
5— торсион; 6 — шлицованный конец торсиона; 7 — неподвижный кронштейн тор-
сиона; 8 — крышке
208
Независимой называется
подвеска, в которой каждый опор-
ный каток подрессорен незави-
симо от других катков. На
рис. 104 представлена широко рас-
пространенная в настоящее время
независимая торсионная подвеска.
В качестве упругого элемента
этой подвески применяется сталь-
ной стержень (торсион), который
при перемещении опорного катка
закручивается, поглощая энергию,
подводимую к катку.
Балансирной называется
подвеска, в которой опорные кат-
ки связаны между собой жестки-
ми или упругими элементами в
тележки.
Балансирные подвески могут
быть парно-балансирные или
сложно-балансирные. Последние
в настоящее время в гусеничных
Рис. 105. Парно-балансирная под-
веска: •
/—балансир тележки; 2—ось балансира;
3 — направляющий стакан; 4 — кронштейн
подвески
машинах не применяются.
На рис. 105 представлена парно-балансирная подвеска. Она
имеет два опорных катка, связанных между собой балансиром в те-
лежку. Таких тележек машина имеет несколько.
Примером смешанной подвески является подвеска, пред-
ставленная на рис. 106. В этой подвеске один каток подрессорен
независимо, а остальные сбалансированы в тележки.
Кроме различия по основным схемам, подвески могут также
различаться между собой и по конструктивным признакам, по типу
упругого элемента и т. д.
Чтобы упростить исследование и расчет подвески, все многооб-
разие схем подвесок можно свести к одной, так называемой приве-
денной, или расчетной, схеме.
Рис. 108. Смешанная подвеска:
1 — резиновый упругий элемент; 2 — балансиры тележек; 3 — оси балансиров
14—2469
209
ПРИВЕДЕНИЕ ПОДВЕСКИ К РАСЧЕТНОЙ СХЕМЕ
Приведенной называется такая схема подвески, в которой
отсутствуют жесткие кинематические звенья и которая, несмотря
на это, эквивалентна с точки зрения подрессоривания действитель-
ной схеме. В качестве приведенной (расчетной) схемы принимают
наиболее простую схему независимой подвески, в которой условные
рессоры опираются непосредственно на оси опорных катков без про-
межуточных жестких звеньев. К этой схеме подвески и приводится
действительная схема.
На рис. 107 показана действительная и приведенная схемы неза-
висимой торсионной подвески. Оси опорных катков приведенной
Рис. 107. Действительная и приведенная схемы независимой
подвески:
а — действительная схема подвески; б — приведенная схема подвески
схемы располагаются на корпусе в том же месте, где и оси опор-
ных катков действительной схемы.
Такой способ приведения называется приведением под-
вески к катку.
В балансирной подвеске приведение можно сделать к катку или
к тележке, т. е. к точке крепления тележки на корпусе машины.
На рис. 108 показано приведение парной балансирной подвески
к катку и к тележке. Как видим, в случае приведения к катку
условная спиральная рессора располагается над осью катка, в слу-
чае приведения к тележке — над осью тележки.
Чтобы привести действительную схему к расчетной схеме, необ-
ходимо выполнить условия приведения, на которых мы остано-
вимся ниже.
210
в
Рис. 108. Приведение парно-балансирной подвески к катку
и к тележке:
а — парно-балансирная подвеска; б —приведение подвески к катку; в —
приведение подвески к тележке
3. ПРИВЕДЕНИЕ К РАСЧЕТНОЙ СХЕМЕ НЕЗАВИСИМОЙ
ПОДВЕСКИ
Рассмотрим вначале приведение к расчетной схеме независимой
подвески.
Чтобы действительная и приведенная схемы были эквивалентны
с точки зрения подрессоривания, они должны иметь одинаковую
зависимость между силой Р, приложенной к оси катка и направлен-
ной перпендикулярно плоскости дороги, и вертикальным перемеще-
нием h катка.
Эта зависимость называется характеристикой под-
вески катка.
14* 211
Две подвески эквивалентны, если они имеют
одина ков нехарактеристик и.
Это и является условием приведения подвески к расчетной
схеме.
ХАРАКТЕРИСТИКА ПОДВЕСКИ И ЕЕ МОДУЛЬ ЖЕСТКОСТИ
Характеристику подвески можно представить в виде графиче-
ской зависимости в осях координат Р и h, как показано на рис. 109.
Здесь в качестве оси абсцисс принята ось перемещений h катка,
в качестве оси ординат — ось нагрузок Р на каток.
Характеристика подвески
определяется модулем же-
сткости, т. е. производной
от силы Р, приложенной к кат-
ку, по вертикальному переме-
щению h катка:
т = (196)
Характеристика будет л и-
н е й н о й, если пг — const, или
нелинейной, если т ~ var.
Как известно, производная
всякой графически выражен-
ной функции пропорциональна
тангенсу угла наклона каса-
тельной, проведенной в данной
Рис. 109. Характеристики подвески тоцке кривой> изображающей
функцию, к ее оси абсцисс. Для
линейной характеристики наклон самой характеристики к оси
абсцисс определяет и величину ее модуля:
т = (197)
где т — модуль характеристики;
а — угол наклона касательной;
тр и tnh — масштабы силы Р и перемещения h.
Для нелинейной характеристики в каждой ее точке будет свой
модуль.
Модуль является величиной, позволяющей оценивать протека-
ние характеристики, т. е. изменение ее жесткости с изменением
хода h катка. Для подвесок с линейной характеристикой модуль
заменяет характеристику, так как дает полное и исчерпывающее
представление об упругих свойствах подвески.
Характеристика подвески определяется или аналитическим, или
графоаналитическим методом.
При аналитическом определении характеристики требуется уста-
новить математические связи между силой Р, приложенной
212
к катку, и перемещением h катка. Для некоторых подвесок эти
связи устанавливаются легко. Но в общем случае аналитическое
определение характеристики — задача чрезвычайно сложная.
Значительно проще определяется характеристика графоаналити-
ческим методом. Метод этот, кроме своей простоты, позволяет опре-
делять характеристику подвески любого типа.
Рассмотрим вначале аналитический метод определения характе-
ристики.
Аналитический метод определения характеристики подвески
Составим для подвески, представленной на рис. НО, уравнение
моментов сил, приложенных к рычагу (балансиру) подвески.
На рычаг действует сила Р, приложенная к оси катка, сила Q —
в точке закрепления рессоры и реакция R шарнира.
Будем считать в первом приближении, что рессора (спиральная
пружина) всегда расположена вертикально и, следовательно, сила Q
параллельна силе Р (а следовательно, и реакции R).
Из уравнения моментов бу-
дем иметь
Ра cos а — Q6 cos а = О,
откуда после сокращения на
cos а находим
P=~Q, (198)
где а и b— плечи рычага;
Q— сила сжатия пру-
жины.
Допустим, что пружина
имеет линейную характери-
стику
Рис. ПО. Силы, приложенные к балан-
сиру подвески
Q = mPf,
где тр—модуль рессоры (mp = const);
/ — стрела прогиба рессоры.
Выразим / через h — перемещение катка. Из рис. ПО можем на-
писать следующее приближенное равенство
h _ а
Т~~ь
Q = пг„ — h.
Ра
или
Тогда
213
Подставляя Q в формулу (197), получим характеристику подвески
(199)
-г / Ь \2
Так как величины ( —I и тр постоянные, то характеристика яв-
ляется линейной. Модуль характеристики будет
т = тР = const. (200)
Рассматривая формулу модуля, видим, что его величина зави-
сит от жесткости рессоры (/ир) и от геометрических параметров
/ Ь \
подвески I — ) Отсюда следует, что на жесткость подвески можно
влиять не только модулем упругого элемента, но и размерами жест-
ких звеньев подвески.
b < а, следовательно, т тр, т. е. жест-
кость приведенной подвески
Так, в данном случае
Рис. 111. Определение характеристики
торсионной подвески
к меньше жесткости рессоры.
Мы получили довольно
простое выражение характе-
ристики подвески потому,
что выше были приняты не-
которые допущения. Если бы
мы эти допущения не прини-
мали, то характер зависимо-
сти Р, h был бы довольно
сложный и модуль жестко-
сти не имел бы постоянного
значения.
Определим теперь х а-
р а ктеристи ку тор-
сионной подвески
(рис. 111).
Момент, скручивающий
торсион, будет равен
Pasin(ao4-a). Согласно закону Гука этот момент равен т.рл, где
тр—модуль жесткости . торсиона или момент, закручивающий
торсион на один радиан; a — угол закрутки торсиона в радианах,
а—длина рычага (балансира). Тогда
Ра sin (a0 + a) = трл. (201)
Кроме того, согласно рис. 111 имеем
h = a cos % — a cos (a0 a). (202)
Из формул (201) и (202) получим характеристику торсионной под'
вески в виде двух математических зависимостей:
М „а
Р=_______Р____
a sin (a0 4- a) ’
h~a [cos % — cos (% + a)].
(203)
214
Для графического построения
характеристики подвески следует
задаться значением углов а. Тогда
по формулам (203) определится
сила Р и перемещение Л. Зная Р
и h, строим по точкам характе-
ристику подвески.
В качестве примера на рис. 112
приведены две характеристики
торсионной подвески, имеющей
различные начальные углы (ао)
наклона балансира. Характери-
стика 1 имеет больший угол, чем
характеристика 2.
Из сравнения характеристик
видно, что при достаточно боль-
ших начальных углах наклона ба-
лансира характеристику торсион-
ной подвески можно считать ли-
нейной.
Графоаналитический метод
построения характеристики
подвески
Пусть задана характеристика
упругого элемента (рессоры) и ки-
нематическая схема действитель-
1 — с большим начальным углом; 2 — с мень-
шим начальным углом балансира
ной подвески. Для общности возьмем характеристику упругого
элемента криволинейной (рис. 113).
Разобьем характеристику упругого элемента на несколько эле-
ментарных участков, внутри которых отрезок характеристики можно
Характеристика
упругого элемента
Рис. 113. Построение характеристики подвески
215
считать прямой линией. Приращение потенциальной энергии упру-
гого элемента на элементарном участке характеристики будет
где I—номер участка характеристики.
Аналогично приведенному уравнению напишем выражение эле-
ментарной работы силы Р:
bWp = -P-l-lf-1- Д/г;..
Если пренебречь трением в подвеске, то работа силы Р должна
равняться работе силы Q, или A Wp = Д WQ, тогда
(Qz-, + QJ Д/(. = (Рм + Дй;.
Откуда
+ (204)
Примем в этой формуле Z—1. Тогда Qz_j = Qo = 0; =
= Р(> = 0.
Из формулы (204) получим
₽, = <?,<• (205)
Отсюда находим начальное (первое) значение силы Р±. В даль-
нейшем пользуемся общей формулой (204).
В формулы (204) и (205) входит отношение величин Д/ к ДА
Эти величины определяются из кинематической характеристики под-
вески.
Рис. 114. Построение кинематической характеристики
подвески
216
Допустим, что нам известно
из чертежа начальное положение
рычага подвески и положение ры-
чага при упоре в ограничитель
(положения 0 и п на рис. 113).
Разобьем угол поворота рычага
на h положений и для каждого
положения графически найдем от-
резки Дй(- и Д/(-. По этим отрез-
кам строим кинематическую ха-
рактеристику подвески, как функ-
цию / по h (рис. 114).
Теперь мы можем по форму-
лам (204) и (205) построить ха-
рактеристику подвески. Для этого
Рис. 115. Графическое построение
характеристики подвески по отрез-
кам
берем из кинематической харак-
теристики отрезки Д/j и Д/ii и по
характеристике упругого элемента
находим силу Qb Подставляя в
формулу (205) Q], Д/1 и Д7?1, по-
лучим Pi. Далее из кинематической характеристики определяем
Д/2 и Д/г2 и из характеристики упругого элемента находим Q2- При-
мем в формуле (204) I — 2. Будем иметь

Из этого выражения определяется сила Pi.
На рис. 115 приведена характеристика подвески, построенная по
отрезкам Дй, и Pt указанным выше способом.
Если характеристика упругого элемента линейная, то
Qi = mPfi
и
Qi-i = mpft-v
где tnp— модуль жесткости упругого элемента.
Тогда формула (204) перепишется в таком аиде:
(206)
где
Л = S Д/. (207)
1
При этом модуль упругого элемента тр и кинематическая ха-
рактеристика подвески должны быть заданы.
217
1. ПРИВЕДЕНИЕ К РАСЧЕТНОЙ СХЕМЕ БАЛАНСИРНОЙ
ПОДВЕСКИ
Балансирная подвеска приводится к схеме независимой приве-
денной подвески при выполнении следующих условий: I) переме-
щается только один каток, а остальные катки тележки остаются
на месте; 2) все' катки тележки перемещаются вертикально одно-
временно и на одинаковую высоту.
Первый случай приведения соответствует наезду одним катком
на единичную неровность дороги, второй — наезду на неровность
(или неровности одинаковой высоты) одновременно всеми катками
тележки (рис. П6).
Рис. 116. Наезд на неровность:
а — катком; б — тележкой
Возможен и третий, промежуточный случай, когда катки одно-
временно наезжают на различные по высоте неровности. Этот слу-
чай однако здесь не рассматривается.
Первый случай приведения балансирной подвески является
приведением к катку, второй — приведением к те-
лежке.
Задача приведения балансирной подвески состоит в том, чтобы
найти характеристику подвески при перемещении одного катка или
при параллельном перемещении всех катков тележки.
Определим характеристику парной подвески.
Дадим одному из катков перемещение h\ (рис. 117, а). Соста-
вим уравнение моментов относительно оси неподвижного катка
(точка п):
(а + д') cos <р—Q^cos<f> = 0. (208)
Кроме того, имеем
hi ______________________ (а + b) cos <р
/ b cos <р ’
218
Допустим, что характеристика упругого элемента линейная.
Тогда
Ьт„
Q = mJ hv
а + Ь 1
Подставив значение Q в уравнение (208), после преобразований
получим характеристику балансирной подвески по катку
р.ЧтттРЛ (209)
Отсюда следует, что характери-
стика линейная. Модуль жестко-
сти будет равен
(2Ю)
Для второго катка
Из полученных формул сле-
дует, что если подвеска несимме-
трична (а Ь), то жесткость ха-
рактеристик обоих катков будет
различной.
Определим характеристику
подвески по тележке.
Дадим обоим каткам парал-
лельное перемещение (рис. 117,6).
Тогда, составив уравнение момен-
тов относительно оси одного из
катков, получим для первого
катка
P^a-^b) — Qb = 0,
Рис. 117. Приведение к расчетной
схеме балансирной подвески:
а — приведение к катку; б —приведение
к тележке
для второго катка
Р2 (а + Ь) — Qa — 0.
Из условия перемещёния катков имеем
А1=А2=/-
По-прежнему считаем характеристику упругого элемента линейной.
Тогда
Qz= tnpf = mphx = mph2.
219
Подставив значение Q в уравнение моментов, получим
(211)
Р» = —7-7- т h,
J а + b Р '
где h = h} = h2.
Как видим, характеристики являются линейными. Модуль будет
равен ' b i m, = —г~г тп, 1 а + b Р’ . а <212) тп- 2 а + b Р 1
Возьмем отношение модуля характеристики катка (формула 210)
к модулю характеристики тележки (формула 212):
тг _ Ь
пк а + b
Для симметричной подвески имеем а — Ь. Тогда = ]/2. От-
ZWj
сюда следует, что модуль жесткости по катку меньше
модуля жесткости по тележке. Это значит, что если
машина наезжает на местное препятствие поочередно отдельными
катками, то подвеска будет мягче, чем при наезде на местное пре-
пятствие одновременно всеми катками тележки (т. е. при парал-
лельном перемещении катков).
Таким образом, жесткость балансирной подвески определяется
не только ее устройством, но и характером препятствий, которые
встречает машина при своем движении.
Если характеристику балансирной подвески нельзя определить
аналитическим методом, то следует воспользоваться изложенным
выше графоаналитическим методом. Для этого, как и при незави-
симой подвеске, вначале графически строим кинематическую ха-
рактеристику подвески, а затем по кинематической характеристи-
ке— характеристику подвески.
5. ОБЩИЕ УРАВНЕНИЯ УПРУГОСТИ ПОДВЕСКИ
С ЛИНЕЙНЫМИ ХАРАКТЕРИСТИКАМИ УПРУГИХ
ЭЛЕМЕНТОВ
Так как всякую схему подвески можно представить в виде при-
веденной схемы, то это позволяет установить общие математические
зависимости, описывающие любую схему подвески.
Эти зависимости называются общими уравнениями
упругости подвески.
Примем вначале, что подвеска имеет линейные характеристики
приведенных упругих элементов. Составим для этого случая урав-
нения, описывающие работу подвески.
220
При заданной жесткости свободная длина спиральной рессоры
может быть выбрана произвольной. Это позволяет принять, что все
рессоры приведенной подвески в свободном (ненагруженном) со-
стоянии имеют одинаковую длину и закреплены на корпусе машины
на одной высоте. Тогда получим расположение рессор приведенной
подвески, как показано на рис. 118. Линия аб определяет началь-
ную длину /о приведенных рессор.
Рис. 118. Приведенная схема подвески
Задачу рассматриваем как плоскостную.
Примем следующие обозначения:
Q — проекция на вертикальную ось машины равнодействующей
внешних сил, приложенных к корпусу;
q — плечо приложения силы Q, замеряемое от оси наиболее
нагруженного опорного катка;
0 — угол продольного наклона корпуса или угол дифферента;
2PZ— суммарная нагрузка на два симметричных опорных катка,
расположенных по разным бортам машины;
ht — перемещение опорных катков относительно корпуса или
деформация приведенных упругих элементов;
2mz — модуль жесткости пары симметрично расположенных упру-
гих элементов;
lt — расстояние оси Z-ro опорного катка от оси наиболее на-
груженного «-го катка.
Составляем следующую систему уравнений:
1. Уравнение проекций внешних сил, действующих на корпус
машины:
Л 1
(214>
221
Здесь и ниже знак £ означает суммирование по одному борту
от / = 1 до I — п. Пределы суммирования в дальнейшем опускаем.
Сила Pi— нагрузка на один каток.
2. Уравнение моментов внешних сил относительно оси наиболее
нагруженного катка:
= (215)
Так как уравнений два, а число неизвестных сил Pt больше двух,
то задача является статически неопределимой. Чтобы решить ее,
надо составить еще дополнительные уравнения.
3. Уравнение упругих сил:
pt^=.tnlhl. (216)
4. Уравнение связей между деформациями:
h^hn-clb (217)
где Z = 1, 2 . . . (« — 1);
с — дифферент корпуса, равный tg 9, где 9 — угол наклона кор-
пуса.
Дифферент принимаем положительным, если корпус имеет на-
клон в сторону наиболее нагруженного катка.
Из формул (214—217) получаем 2п Д- 1 уравнение, решив кото-
рое находим 2п Д- 1 неизвестное: «-неизвестных сил (2/Д), «-неиз-
вестных деформаций (АД и дифферент (с).
Полученная система уравнений будет общими уравне-
ние ми упругости подвески единенными характе-
ристиками упругих элементов.
Решим эти уравнения относительно величин с и hn.
Из формул (216) и (217) имеем
Pl = mAhn — cli)-
Подставив Pt в формулу (214), получим
S mi (hn — cli)=^Q.
Это равенство можно переписать в таком виде:
hn^mi-c^mili=-^Q. (218)
Из формулы (215) находим
S nil = д- Я0.>
или
К S ^li - с S tnfi = 4- qQ. (219)
222
Решив уравнения (218) и (219) относительно с и получим окон-
чательно
с = ? S — S m-ilt _ Q .
( /И,/, )2 — ZW,- СТ,-/? 2
q S — S m^i q
(S«^)2-S«/S^'2
(220)
(221)
Определив по формулам (220) и (221) дифферент с и перемещение
катка hnt находим по формулам (216) и (217) силы Pt и переме-
щения ht для всех катков.
ОПРЕДЕЛЕНИЕ ПРОЕКЦИИ РАВНОДЕЙСТВУЮЩЕЙ ВНЕШНИХ СИЛ,
ПРИЛОЖЕННЫХ К КОРПУСУ МАШИНЫ И КООРДИНАТЫ
ТОЧКИ ЕЕ ПРИЛОЖЕНИЯ
В расчетные формулы (220) и (221) входят неизвестные вели-
чины Q и q.
Определим эти величины для общего случая движения машины.
Пусть машина движется ускоренно на подъем, имея на крюке не-
которую силу тяги (рис. 119). Считаем, что ведущее колесо ма-
шины заднее. Тогда на корпус машины будут действовать следую-
щие внешние силы и моменты:
О'—вес подрессоренной массы машины;
/—сила инерции в поступательном движении машины;
Рис. 119. Внешние силы, приложенные к корпусу машины
223
Рк— сила тяги на крюке;
Р—сила тяги машины, приведенная к оси заднего колеса;
,44 = гкР— момент, полученный вследствие переноса силы тяги Р
с окружности ведущего колеса на его ось.
Если ведущее колесо переднее, то силу тяги Р приходится при-
водить к оси заднего и переднего колес, как показано на рис. 120.
Рис. 120. Приведенные силы тяги к переднему и заднему колесам
Составляем уравнение проекций сил, действующих на корпус, на
вертикальную ось машины г. Получим в общем виде
Q-^Р^г, (222)
где Р„р, — проекция силы на ось z.
Составляем уравнение моментов относительно оси наиболее на-
груженного опорного катка (см. рис. 119):
V/1 -х
q = ^прг , (223)
где х — плечо силы Рпрг от оси катка.
Принимая согласно рис. 119 наиболее нагруженным передний
каток (если в действительности окажется наиболее нагруженным
задний каток, то в расчете дифферент с получит отрицательное зна-
чение), будем иметь
S Рирг = О' cos а + Р sin ₽ + RK tg у;
S Р„ргх = aG' cos а + (/ + G sin a) b + +
+«K#KtgT — bpP cos $ + apPsinp + Prx.
Из этого выражения находим Q и q.
При составлении уравнений проекций и моментов можно пре-
небрегать изменением координат точек приложения сил вследствие
изменения дифферента, так как в расчете это существенного зна-
чения не имеет.
Пример. Определим нагрузки на опорные катки Pt, перемещения кат-
ков hj и дифферент корпуса с тягача, стоящего неподвижно на горизонтальном
участке дороги.
Даны модули рессор приведенной схемы подвески: mi = 50 кг/см',
т2 = 65 кг/см', т3 = 75 кг/см-, — 65 кг1см.\ ms = 50 кг1см-
224
Расстояния осей опорных катков от оси переднего катка h = 200 с.п;
/2 = 150 см; l3 = 100 см; Ц = 50 см.
Вес подрессоренной массы тягача принимаем равным весу машины
G' = G = 6000 кг.
Продольная координата центра тяжести а = 120 см.
Для неподвижного тягача, стоящего на горизонтальном участке пути, имеем
Q = G' « G, q — а.
Находим 2= 305 кг[см; mih — 30 500 кг; mtl2i =
= 1 370 000 кгсм .
Подставив эти величины в формулы (220) и (221), получим с = —0,0453 и
йз = 5,3 см.
Так как с<0, то корпус имеет дифферент на корму. Определяем теперь по
формулам (216) и (217) нагрузки на катки Pi и перемещения Л/;
Й! = 5,3 + 0,0453-200 = 14,4 см, = 50-14,4 = 720 кг;
й2 = 5,3 + 0,0453-150 = 12,1 см, Р2 = 65• 12,1 = 790 кг;
h3 = 5,3 + 0,0453-100 = 9,8 см, Р3 = 75- 9,8 = 735 кг;
й4 = 5,3 + 0,0453- 50 = 7,6 см, Р4 = 65- 7,6 = 495 кг;
Л5 = 5,3 см. Р6 = 50 • 5,3 = 265 кг.
Проверяем результат вычислений на сумму сил Р,: Pl = 3005 кг.
Должно быть 2 Pl = б = 3000 кг. Как видим, точность вычислений
вполне удовлетворительная.
Заметим, что если при решении задачи какая-нибудь из сил по-
лучит отрицательное значение, то соответствующую этой силе рес-
сору не следует рассматривать и расчет произвести снова без нее,
так как согласно устройству подвески все рессоры могут работать
только на сжатие, т. е. иметь только положительные силы Pt.
6. РАСЧЕТ ПОДВЕСКИ С НЕЛИНЕЙНЫМИ
ХАРАКТЕРИСТИКАМИ УПРУГИХ ЭЛЕМЕНТОВ
Задача расчета заключается в определении нагрузок Pt на опор-
ные катки, деформаций ht упругих элементов и дифферента с кор-
пуса при заданных нелинейных характеристиках приведенных упру-
гих элементов.
Задачу эту можно решить только приближенно.
Воспользуемся для этого методом последовательного прибли-
жения.
Обозначим на чертеже в масштабе положение днища корпуса
(линия аб) и положение осей катков 1, 2, 3, 4, 5 (рис. 121, а) в сво-
бодном (разгруженном) состоянии.
15—2469
225
Допустим, что заданы также сила Q, приложенная к корпусу,
ее плечо приложения q и характеристики упругих элементов
(рис. 121,6).
Рис. 121. Расчет подвески с нелинейными характери-
стиками:
а ~ схема деформаций упругих элементов; б — характеристики
приведенных упругих элементов
Необходимо так сдеформировать упругие элементы, чтобы сумма
усилий(S^z), приходящихся на катки, равнялась бы величине-2 Q,
а сумма моментов (S^z) этих сил равнялась бы моменту qQ.
Заметим, что при деформации упругих элементов оси катков
должны расположиться на некоторой прямой линии, параллельной
226
опорной ветви Гусениц, а следовательно, и грунту, на который гу-
сеница опирается (предполагаем, что грунт представляет собой ров-
ную площадку). Обозначим эту линию буквами тп и найдем поло-
жение ее относительно днища корпуса (относительно линии аб).
Проведем линию тп вначале параллельно линии аб на неко-
торой произвольной высоте. Получим деформации упругих элемен-
тов йь hi, h3 и т. д.
Зная деформации /Т, по характеристикам находим нагрузки на
катки Рг Суммируем эти нагрузки. Если 2 Pi~ Q> то положе-
ние линии тп в первом приближении считаем найденным. Если
S Pt =# "2“ Q, то линию тп поднимем или опустим так, чтобы ве-
чина стала равной Q.
Составляем теперь уравнение моментов 2 Сравниваем эту
величину с величиной -^-qQ. Допустим, что мы получили
S'tP( < qQ. Повернем линию тп вокруг точки k на некоторый
небольшой угол 0. Оси катков займут новое положение на ли-
нии т'п', а деформации получат новое значение и т. д.
Определяем снова по характеристикам нагрузки 2/ Pt на катки
и вычисляем моменты 2 hPi-
Так как точка k лежит на линии действия силы Q, то вели-
чина 2/ЛТмало изменяется по сравнению с величиной2 Pf Вели-
чина же S'z'3/, быстро увеличиваясь, приближается к 4^ qQ. После
одного — двух приближений находим ^^Р^ ~qQ. Если при этом
Z3; все же значительно изменяется, то придется также смещать
точку k влево или вправо. После нескольких последовательных при-
ближений получим
SZ,p,«4-?q.
Определенный из чертежа угол 0 дает значение дифферента кор-
пуса.
Таким образом определяются нагрузки на опорные катки, де-
формации приведенных упругих элементов и дифферент корпуса
Машины.
Мы рассмотрели расчет приведенной схемы подвески с линей-
ными и нелинейными характеристиками. При этом определялись де-
формации не действительных упругих элементов, а приведенных,
т. е. условных. Однако от приведенных деформаций перейти к де-
формациям действительных упругих элементов нетрудно. Для этого
следует иметь в виду, что деформация приведенной
15* 227
рессоры hi есть перемещение оси опорного катка
относительно корпуса машины. Если схема действи-
тельной подвески известна, то по перемещению оси опорного катка
определяется и деформация упругого элемента Зная деформа-
цию fi и модуль упругого элемента tnpi, находим усилие, деформи-
рующее упругий элемент Q, и, следовательно, определяем все дан-
ные, необходимые для расчета элементов подвески на прочность.
7. ПЛАВНОСТЬ ХОДА ГУСЕНИЧНЫХ МАШИН
И ПАРАМЕТРЫ ПЛАВНОСТИ ХОДА
Под плавностью хода понимается плавное (без резких колеба-
ний и толчков) движение корпуса гусеничной машины при движе-
нии ее по неровным дорогам или местности.
На рис. 122 приведены графики угловых колебаний корпуса
двух машин, двигавшихся по одной и той же дороге примерно
с одной и той же скоростью.
е
' бt
Рис. 122. Угловые колебания корпуса машины:
а — плавные колебания; б — резкие колебания с пробива-
нием подвески
На графиках по оси абсцисс отложено время t, а по оси орди-
нат — угол поворота корпуса или угловая амплитуда его колеба-
ний 0. Сравнив оба графика, можно сделать вывод, что -одна из
машин (рис. 122, а) обладает более высокой плавностью хода, чем
другая (рис. 122,6). Действительно, на нижнем графике (см.
рис. 122,6) показаны резкие изменения угловых перемещений 0
корпуса по времени t, т. е. большие ускорения. Острые «пики» на
кривых показывают, что происходило пробивание подвески вслед-
ствие большой амплитуды колебаний (©! и 02).
228
На стандартной трассе с различными видами неровностей легко
можно по записи колебаний корпуса оценивать плавность хода гу-
сеничных машин и гусеничных поездов и давать оценку качеству
их подрессоривания.
Параметрами плавности хода машины могут служить следую-
щие величины:
— частота К и период Т собственных колебаний корпуса;
— размах продольных угловых колебаний, т. е. сумма угловых
амплитуд (©i-j-02);
— максимальное ускорение корпуса (утах);
— критическая скорость &кр движения машины, при которой на-
ступает пробивание подвески.
Рассмотрим эти параметры подробно.
Рис. 123. Основные виды колебания корпуса:
а— вертикальные колебания; б — продольные угловые колебания; в —поперечные угловые
колебания
При движении машины ее корпус совершает три основных вида
колебаний: вертикальные (рис. 123, а), продольные угловые
(рис. 123,6) и поперечные угловые (рис. 123, в).
Вертикальные колебания происходят относительно вертикальной
оси машины и представляют собой поступательное знакоперемен-
ное перемещение корпуса; продольные угловые колебания происхо-
дят относительно поперечной оси машины и представляют собой
знакопеременное угловое перемещение корпуса с кормы на нос и
обратно (иногда такие колебания называют «галопированием»);
229
поперечные угловые колебания являются угловыми колебаниями во-
круг продольной оси машины.
Все эти три вида колебаний совершаются одновременно, скла-
дываются и создают .сложный колебательный процесс корпуса ма-
шины.
Сложность колебаний обусловливается прежде всего наличием
на машине гусениц, которые накладывают на корпус дополнитель-
ные упругие связи, а также неопределенностью неровностей дороги,
по которой движется машина. Эти неровности создают импульсы
сил, передающихся от ходовой части машины на корпус и вызы-
вающих его вынужденные колебания. Кроме того, в ходовой части
имеется трение в механизмах, Которое также влияет на характер
колебаний корпуса.
Учесть все эти явления" можно только экспериментально. По-
этому параметры плавности хода — это в основном эмпирические
величины. Однако как бы ни были сложны действительные колеба-
тельные процессы корпуса машины, в основе их лежат собствен-
н ы е, или свободные, колебания. Эти колебания поддаются
математическому анализу и расчету и поэтому представляют для
нас особый практический и теоретический . интерес. Следует иметь
в виду, что расчет машины на собственные колебания пока является
единственно достоверным и теоретически обоснованным.
Собственные колебания характеризуются частотой и пе-
риодом, которые при расчете подвески можно принять в качестве
основных параметров плавности хода машины. Те же дополнитель-
ные колебания, которые накладываются на собственные колебания
вследствие движения машины по неровностям дороги, а также
вследствие влияния гусениц и внутреннего трения в ходовой части,
должны учитываться дополнительными оценочными параметрами
(размахом, максимальным ускорением и главным образом критиче-
ской скоростью), полученными на основании эксперимента.
Ниже рассматриваются только два вида собственных колеба-
ний: вертикальные и продольные угловые. Эти колебания имеют
наибольшее значение в оценке плавности хода гусеничной машины.
Размах продольных угловых колебаний харак-
теризует раскачивание корпуса машины при движении ее по неров-
ной дороге. Чем больше при прочих равных условиях размах коле-
баний, тем больше вероятность пробивания подвески- и тем ниже
плавность хода машины.
Плавность хода машины по размаху колебаний должна сравни-
ваться при одинаковых скоростях движения машин и на одной' и
той же дороге.
Как показывают опыты, на колебание корпуса машины суще-
ственно влияет наличие или отсутствие у машины прицепа. Наличие
прицепа значительно уменьшает размах колебаний и повышает
плавность хода гусеничного поезда.
Максимальное ускорение характеризует динамические
нагрузки, которые испытывает ходовая часть машины, ее корпус,
крепления агрегатов, а также грузы и экипаж, находящиеся в ма-
230
шине. Чем больше ускорение, тем выше динамические нагрузки.
При значительных динамических нагрузках могут разрушаться ба-
лансиры катков и ограничители, появляться трещины в сварных
швах корпуса или рамы и т. д. Большие ускорения вредно влияют
на экипаж, вызывая его быструю утомляемость. Заметим, что
утомляемость экипажа объясняется не столько непосредственным
воздействием динамических нагрузок на организм человека, сколько
главным образом мышечным напряжением, которое приходится со-
здавать человеку против резких толчков. Так, человек, сидящий
в кузове, при сильной тряске вынужден крепче держаться за борта
машины, упираться ногами в пол и прижиматься спиной к бортам
кузова.
В качестве оценочного параметра принимают также линейное
ускорение крайних точек корпуса, в которых склады-
ваются наибольшие линейные перемещения, возникающие вслед-
ствие продольных угловых колебаний, с вертикальными перемеще-
ниями, возникающими вследствие вертикальных колебаний.
Кроме того, следует учитывать также ускорения при
пробивании подвески. Эти ускорения создают наиболее
опасные динамические нагрузки па машину, приводящие к ее из-
носу, а следовательно, и к сокращению срока ее службы.
Из всех параметров плавности хода наиболее важным является
критическая скорость движения машины по про-
биванию подвески. Эта скорость характеризует маневрен-
ные качества машины, повышение которых и должна обеспечивать
подвеска.
Первые английские гусеничные танки 1916 г. имели критические
скорости на местности порядка 2—3 км/час (при максимальной
расчетной скорости 6 км/час). Современные быстроходные гусенич-
ные машины имеют критическую скорость на местности до 25 км/час
(при максимальной расчетной скорости 40—50 км/час), т. е. в де-
сять раз большую. Прогресс этот достигнут в результате примене-
ния в современных машинах упругой (мягкой) подвески. Старые
же английские танки имели безрессорную жесткую подвеску.
8. ОПРЕДЕЛЕНИЕ ЧАСТОТЫ И ПЕРИОДА СОБСТВЕННЫХ
КОЛЕБАНИЙ КОРПУСА МАШИНЫ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КОЛЕБАНИИ КОРПУСА
При составлении дифференциальных уравнений колебаний кор-
пуса примем следующие допущения:
— задачу рассматриваем как плоскостную;
- — подвеску считаем приведенной с линейными характеристи-
ками упругих элементов;
— пренебрегаем влиянием на колебания корпуса: гусеничного
обвода, трения в ходовой части, начального (статического) диффе-
рента корпуса, а также вращающихся внутри его маховых масс;
23J
— машину считаем неподвижно стоящей на горизонтальном
участке пути.
Допустим, что корпус под действием веса занимает начальное
положение аб (рис. 124). Центр тяжести его подрессоренных масс
лежит в точке с. Приложим к корпусу какую-нибудь вертикальную
Рис. 124. Составление дифференциальных уравнений собственных коле-
баний корпуса машины
силу, под действием которой рессоры сожмутся и корпус получит
некоторый дифферент с углом 9. Центр тяжести в этом случае пе-
реместится из точки с в точку с' на величину z. Пока действует
приложенная сила, корпус находится в равновесии. При этом рес-
соры поджаты на величину
Дй, = z -ф «,-9. (224)
Перемещение корпуса вниз и поворот его по ходу часовой стрелки
считаем положительными. Тогда согласно рис. 124 величину at сле-
дует принимать положительной, когда рессора находится справа от
центра тяжести, и отрицательной, когда рессора находится слева от
центра тяжести. Будем иметь
Дй4 = z— (ZjS;
ДЛ4 = z ф а40 и т. д.
Дополнительная нагрузка, которую получили рессоры, равна
ДР,=—tn^h^ (225)
В уравнении (225) принят знак минус (—), так как сила упру-
гости направлена всегда противоположно деформации Дй7 рес-
соры.
232
Уберем теперь силу, приложенную к корпусу. Корпус под дей-
ствием упругих сил ДР, придет в колебательное движение.
Составим дифференциальные уравнения этого движения.
Согласно принципу Даламбера можем написать следующие
уравнения равновесия системы:
-^Mz^^Pt- (226)
(227)
где Mz — сила инерции, приложенная в центре тяжести машины;
7И— подрессоренная масса машины;
z — ускорение центра тяжести;
/у0 — инерционный момент;
/у—момент инерции подрессоренных масс, взятый относи-
тельно оси, проходящей через центр тяжести, перпенди-
кулярно к плоскости чертежа;
ft — угловое ускорение корпуса;
ДР,— дополнительная нагрузка рессоры.
Подставляя в уравнения (226) и (227) силы ДР, из фор-
мулы (225) и учитывая формулу (224), получаем
_1_/Иг = —S "Ъ (z + ^°);
4- =—s aimi (z+«/9)>
или
4- Mz 4- z 2 mt + 9 S aimi — 0; (228)
4-/? + zS«z/nz + 0S«1X- = O. (229)
Уравнения (228) и (229) есть дифференциальные
уравнения собственных колебаний корпуса.
В каждое из этих уравнений входят две координаты: коорди-
ната вертикального перемещения z корпуса и координата углового
перемещения 0 корпуса. Таким образом, вертикальные и угловые
колебания связаны между собой и взаимно влияют одни на другие.
ОПРЕДЕЛЕНИЕ ПЕРИОДА И ЧАСТОТЫ
СОБСТВЕННЫХ КОЛЕБАНИИ
Из теории дифференциальных уравнений известно, что уравне-
ния вида (228) и (229) имеют следующее решение:
z = A cos {kt + <р0); (230)
0 = 5 cos (£/ + %), (231)
233
где А и В— амплитуды колебаний;
k— круговая частота колебаний, рад /сек-,
<f>0—начальная фаза;
t—текущее время.
Определим из этих уравнений частоту k. Для этого из фор-
мул (230) и (231) определяем z и 9:
z = —Ak'‘ cos (kt -ф <р0);
0 = —Bk2 cos (kt -ф <p0).
Подставляем?) 0, % и 0 в уравнения (228) и (229). После сокра-
щения на cos (kt -ф <р0) получим
---ЛЬ4&2 ф Л 2 aimi = 0;
— i IyBk2 + А 2 aiml + В S арп1 = 0.
Поделив первое уравнение на А, а второе на В, будем иметь
--Mk2 + tnt + ~ S atmi = 0;
z /1
— -ip V3 + 4' = °-
Перепишем эти уравнения в таком виде:
-i- Mk2 — в
S aimi А
А
aiml В
Перемножаем равенства (232) и (233):
- V S + М S af/nj k2 +
+ S //?7 S — (S арП^2 = 0.
Пусть
(232)
(233)
(234)
борта
1уМ
где tni — модули жесткости приведенной рессоры с
машины.
234
Тогда предыдущее уравнение перепишется в таком виде:
/г4 — а/г2 + b = 0.
Решив это биквадратное уравнение, получим частоту
<235)
4= = |/ т-/(т)’-4- <236>
Из уравнений (235) и (236) следует, что корпус машины совер-
шает два вида колебаний: одно—с частотой ki и другое — с часто-
той k-i.
Частоту можно приближенно считать частотой вертикальных
колебаний, а частоту /г2 — частотой угловых колебаний.
Если известна частота колебаний, то период колебаний
определяется по общей формуле
7-=^, ’ (237)
где тг = 3,14;
k = ki или ki.
Частоту можно выразить в другой размерности, более удобной
для практического пользования, в кол/сек.:
(238)
МОМЕНТ ИНЕРЦИИ КОРПУСА
Для определения численного значения частоты и периода ко-
лебаний необходимо, кроме геометрических параметров подвески,
модулей жесткости ее ’упругих элементов и подрессоренной массы
корпуса, знать еще момент инерции/у.
Геометрические параметры и модули жесткости известны из рас-
чета подвески, подрессоренную массу можно приближенно принять
равной 0,85—0,9 от общей массы машины . Остается опреде-
лить момент инерции.
Определить момент инерции сравнительно трудно. Его прихо-
дится или подсчитывать (что требует много времени), или опреде-
лять экспериментально. Для этого необходимо привести кор-
пус машины в колебательное движение и замерить частоту его соб-
ственных колебаний, после чего по приведенным выше формулам
обратным подсчетом определить момент инерции / .
Воспользуемся данными, полученными Г. А. Ивановым для тя-
гачей.
235
Эти данные приведены в табл. 8. Они относятся к машинам,
имеющим груз на платформе, и к машинам без груза на плат-
форме.
Таблица 8
Значение моментов инерции /у для тягачей
(данные Г. А. Иванова)
Наименование Марка тягача
АТ-Л Я-12 М-2 АТ-С AT-T
Вес без груза на платформе, т 5,8 6,5 7,2 12 20
Вес с грузом на платформе, т 7,8 8,5 9,2 15 25
Момент инерции без груза, кгм сек2 1605 1740 2730 4540 10 250
Момент инерции с грузом, кгм сек2 2280 2400 3280 5320 12 800
По данным табл. 8 можно составить эмпирическую формулу для
определения момента инерции:
/у = AGL2, (239)
где I— момент инерции в кгм сек2;
G—вес машины в кг;
L — опорная база машины в м;
А — коэффициент, равный 0,04.
Из уравнения (239) следует, что момент инерции есть линейная
функция веса машины (G) и квадратичная функция ее опорной
базы (L).
Пример. Определим частоту и период собственных колебаний гусеничной
машины.
Дано:
G = 7000 «г; = — 1,7 м\ а2 = — 1,2 м\
а3 = — 0,2 м\ ai = + 1,0 м\ а6 =? + 1,5 м;
L = 3,2 а/; т = 70 кг/см = 7000
м
Определяем массу М и момент инерции (у.
Примем подрессоренную массу равной 0,85 от общей массы машины.
Тогда
.. 0,85-7000
М — —------------= 606 кг.\Г‘
У,о1
сек2.
Момент инерции определяется по формуле (239):
/у = 0,04 0,85 • 7000 • 3,22 — 2440 кгм сек1.
Находим теперь
2 = 2-5-7000 = 70 000
м
= 2 (1,72 4- 1,22 + 0,22 + ]>02 + 1>52).7Ооо = 107 000 кгм;
2 = 2(— 1,7 — 1,2 —0,2 + 1 + 1,5)-7000 = — 8400 кг.
236
Из формул (234) определяются:
_ 70 000 107 000
а 606“ + 2440 “ 139
1 сек',
b =
70 000-107000 —(-8 400)2
2440-606
= 5010 1/селА
Из формул (235) и (236) находим частоты
К = р/ ^ + |/ - 5010 = 10,75 1/сс/с;
= - |/ (?)2 ~ 5010 = 616 }/ceK'
или согласно формуле (238)
Ю.75
«1 = ~.v < 1 , = 1,72 кол сек, '
1 2-3,14
~ 1,05 кол)сек.
Период колебаний определяется по формуле (237):
Л = Y075- = О.584 сек>
т 2-3,14 ппс
Г. = ——— = 0,95 сек.
6,6
ПРИБЛИЖЕННЫЕ ФОРМУЛЫ ЧАСТОТЫ КОЛЕБАНИЙ
Из рассмотренного выше числового примера следует, что вели-
чина2аг//г/—относительно малая и ею можно пренебречь. Тогда
уравнения (232) и (233) перепишутся в таком виде:
1т, = 0;
Отсюда находим приближенные формулы частоты собственных
колебаний:
т5- • (240)
(241)
Частота k{ есть частота вертикальных колебаний; она зависит
от суммарной жесткости рессор и веса (массы) машины. Чем
Жестче подвеска, тем больше частота колебаний: чем больше вес
машины, тем частота колебаний меньше.
237
Частота k2 есть частота угловых колебаний. Она зависит от
жесткости рессор (mz) и их взаимного расположения ('e/j. Чем
ближе к краям разнесены жесткости рессор, тем больше частота
угловых колебаний.
Частота колебаний уменьшается с увеличением момента инер-
ции машины (/ ).
Если подставить в дифференциальные уравнения (228) и (229)
= 0, то уравнения перепишутся в таком виде;
-i- Mz + г S mt = 0;
4 ° = 0-
Из этих уравнений следует, что при принятом допущении
z/nz = 0) вертикальные и угловые колебания не зависят одни
от других.
Допустим, что все рессоры имеют одинаковую жесткость и оди-
наковый статический ход катков. Получим
Р
'У' т, --= пт — п ,
hc
где Рс—статическая нагрузка на рессору приведенной схемы;
hc— статическое перемещение катка;
п—число рессор одного борта машины.
Кроме того, можем написать
где G'— вес подрессоренной массы машины;
g— ускорение земного тяготения.
Тогда из формулы (240) получим
4,= /^. (242)
Отсюда следует, что частота вертикальных колебаний корпуса
машины зависит только от статического поджатия рессор. Чем
больше статическое поджатие, т. е. чем мягче подвеска, тем меньше
частота колебаний.
Пример. Определим частоты колебаний гусеничной машины, взяв данные
из предыдущего примера.
Имеем
М = 606 кгм~г сек-’,
Zv = 2440 кгм сек2’,
2 = 70 000 кг/м\
ajmt = 107 000 кгм.
238
Подставляя эти данные в формулы (240) и (241), находим
. , /107 000 ,,
= У ~244Г = 6,63 1/сеК-
Как видим, разница в частотах, полученных по точным и приближенным фор-
мулам, весьма незначительна.
9. ВЛИЯНИЕ КОНСТРУКТИВНЫХ ФАКТОРОВ
НА ПЛАВНОСТЬ ХОДА МАШИНЫ
На плавность хода машины влияют два вида факторов: кон-
структивные и дорожные.
К конструктивным факторам относятся: вес машины, ее момент
инерции, статическое поджатие рессор, расположение опорных кат-
ков относительно центра тяжести машины, работоспособность
(удельная потенциальная энергия) подвески и характеристики упру-
гих элементов;
К дорожным факторам относятся характер дороги, по которой
движется машина, высота и взаимное расположение неровностей
дороги.
Наибольший интерес представляют для нас конструктивные
факторы, так как на них можно в той или иной мере влиять и тем
самым оказывать влияние и на плавность хода машины.
ВЛИЯНИЕ НА ПЛАВНОСТЬ ХОДА ЖЕСТКОСТИ
УПРУГИХ ЭЛЕМЕНТОВ ПОДВЕСКИ
Из формулы (240) следует, что.на частоту вертикальных коле-
баний влияет суммарная жесткость рессор и вес машины. Если жест-
кость всех, рессор одинакова и также одинаковы статические хода
катков, то на частоту вертикальных колебаний будет влиять только
статический ход катков. Чем больше будет статический ход, тем
мягче подвеска, тем меньше частота вертикальных колебаний и
выше плавность хода машины [формула (242)].
Это положение справедливо только для подвесок с линейными
характеристиками. Однако большинство современных подвесок
имеет характеристики, близкие к линейным.
Согласно формуле (241) на частоту продольных угловых коле-
баний влияет распределение суммарной жесткости (V afmt) вдоль
опорной базы машины.
Чем больше будет жесткость сосредоточена к центру тяжести
машины, тем меньше будет величина 2и меньше частота угло-
вых колебаний. Однако при этом следует иметь в виду, что при дви-
жении на местности машину может сильно раскачивать, и это при-
ведет к пробиванию подвесок крайних опорных катков. Поэтому
иногда приходится, наоборот, рассредоточивать жесткость к краям
239
опорной базы машины. В этом случае хотя частота угловых коле-
баний и увеличивается (вследствие увеличения величины» д,/?;,),
но уменьшается размах колебаний корпуса, а следовательно, и ве-
роятность пробивания подвески.
На величину 2 можно влиять двояко: или расстановкой
средних опорных катков (положение крайних катков задано .вели-
чиной опорной базы машины), или изменением жесткости mt.
Обычно положение средних опорных катков определяется не из
условия плавности хода машины, а из условия необходимости полу-
чения заданной эпюры нагрузок на грунт. Тогда на плавность хода
можно влиять только изменением жесткости (mJ.
На частоту угловых колебаний влияет момент инерции /у. Чем
больше момент инерции, тем меньше частота колебаний и выше
плавность хода. Момент инерции в свою очередь зависит от массы
машины и ее распределения по длине машины. Чем дальше от
центра тяжести машины разнесены ее тяжелые массы (двигатель,
агрегаты силовой передачи, груз на платформе), тем больше ее мо-
мент инерции.
Заметим, что на колебания корпуса влияют вращающиеся махо-
вые массы двигателя и силовой передачи, оси которых совпадают
с продольной осью машины. Эти массы создают гироскопический
эффект, который влияет на колебания корпуса так же, как и мо-
мент инерции 1у.
РАБОТОСПОСОБНОСТЬ ПОДВЕСКИ
Работоспособностью подвески называется отношение полной
упругой энергии рессор 1Рц к весу машины G.
Обозначим работоспособность буквой v. Тогда согласно опреде-
лению
v = (243)
Работоспособность имеет размерность длины и представляет со-
бой удельную потенциальную энергию.
Работоспособность в физическом смысле можно рассматривать
как некоторую высоту падения машины, при которой (высоте) вся
работа падения переходит в упругую энергию рессор.
Действительно, если машина падает с высоты h, то работа па-
дения будет равна hG. Допустим, что эта работа идет на полное
поджатие рессор опорных катков (приведенных рессор). Пусть ра-
бота поджатия будет VPo. Тогда hG = 1Р0, или
Отсюда h = v.
Работоспособность подвески характеризует ее запас потенциаль-
ной энергии на одну тонну веса машины. Че.м выше работоспособ-
240
ность, тем больше энергии внешних динамических нагрузок может
поглотить подвеска, тем меньше вероятность ее пробивания.
Пусть имеется характеристика действительного упругого эле-
мента. В общем случае будем считать, что эта характеристика не-
линейная (рис. 125). Тогда можем написать
dW=Qdf,
где dW—дифференциал упругой энергии;
df—дифференциал деформации рессоры;
Q— нагрузка на рессору.
Отсюда
/max
W= f Qdf, (244)
о
где /тах — максимальная деформация рессоры до упора балансира
подвески в ограничитель.
Для всех упругих элементов подвески получим
При нелинейной характеристике интеграл может быть вычислен
аналитически, если известна функция Q =/•'(/), или графически —
по площади, заключенной между кри-
вой характеристики и осью абс-
цисс.
Если характеристика линейная
(а большинство стальных рессор
имеет линейную характеристику), то
Тогда получим для одной рессоры
Лпах л
:: w = (/npfdf=. (245)
, о
Рис. 125. Определение упругой
энергии рессоры
- При этом характеристика приве-
денной рессоры (характеристика по
Катку) может и не быть линейной.
Рассмотрим, от каких факторов зависит работоспособность под-
1вески.
J Будем считать, что все рессоры имеют одинаковые линейные ха-
рактеристики.
< Обозначим через Ао, hc и hp соответственно общий ход катка
Дот разгруженного положения до упора подвески в ограничитель),
’Статический ход (под статической нагрузкой от веса машины) и ра-
бочий ход (от статического положения до упора подвески в ограни-
читель) .
16—2469
241
Будем иметь
Ао = hc + hp-
Рассмотрим вначале независимую подвеску.
Упругая энергия подвески будет
2л
= = nmh0’
где т — модуль подвески одного катка; п — число катков с одного
борта.
Выразим вес машины через статический ход катка hc:
G = 2nmhc.
Тогда
_ Го __ %
v ~ а ~ ис •
Обозначим через ср = —к. о э ф ф и ц и е н т динамичности
подвески. Тогда можем написать
/ h„ \ h„
h0 = hc + hp=hc[\+-1^=V+'?)^-.
Из предыдущей формулы получим окончательно
(1 +^hp
v =
(246)
2?
Из уравнения (246) следует, что работоспособность зависит от
рабочего хода катков и от коэффициента динамичности. Чем боль-
ше рабочий ход, тем выше работоспособность подвески.
На рис. 126 представлен график зависимости работоспособности,
отнесенной к рабочему ходу от коэффициента динамичности
(ср). При равенстве статического хода рабочему ходу (ср = 1) ра-
Рис. 126. График зависимости ра-
ботоспособности от коэффициента
динамичности
ботоспособность имеет минималь-
ное значение, равное удвоенному
рабочему ходу. При всех других
значениях ср работоспособность
увеличивается.
Обычно в выполненных кон-
струкциях подвесок коэффициент
динамичности бывает больше еди-
ницы. В отдельных случаях он до-
стигает величины ср = 3,5. Из гра-
фика следует, что при ср = 3,5 ра-
ботоспособность подвески при-
мерно в 1,5 раза больше, чем
при ср = 1. Однако при этом уве-
личивается жесткость подвески,
242
так как при заданном значении hp (рабочий ход ограничивается
конструктивными пределами подвески) должен уменьшаться
статический ход hc и, следовательно, должна повышаться жест-
кость подвески.
В современных гусеничных машинах работоспособность нахо-
дится в пределах 300—500 мм и редко имеет большую величину
даже при больших значениях коэффициента динамичности. Так, на-
пример, для артиллерийского тягача М-2 при <р — 3,5 работоспособ-
ность v = 400 мм.
Выше было указано, что работоспособность можно представить
как некоторую условную высоту падения машины, при которой
подвеска полностью поглощает энергию падения.
Допустим, что падение машины совершается с высоты одного
метра. Тогда подвески современных машин могут поглощать от
30 до 50% энергии падения. От 50 до 70% энергии идет на удар
гусениц о грунт и балансиров об ограничители.
Таким образом, запас потенциальной энергии современной под-
вески невелик. Этим и объясняется, что на местности, имеющей
неровности около 100—150 мм, скорость машин, как- правило, не
превышает 15 км/час.
Работоспособность можно поднять, повышая жесткость подвески
(повышая коэффициент динамичности), а также увеличивая рабо-
чий ход опорных катков.
Теоретически рабочий ход может равняться дорожному про-
свету (клиренсу) машины (в действительности он всегда меньше
•дорожного просвета), т. е. быть около 400 мм.
Если принять коэффициент динамичности <р = 3,5, то предель-
ное значение работоспособности согласно графику (рис. 126) будет
Vmax = 3 400 = 1200 мм.
Следовательно, современная подвеска использует около ‘/з своей
предельной работоспособности.
Определим теперь работоспособность балансирной
подвески и сравним ее с работоспособностью независимой под-
вески.
Выше было указано, что жесткость балансирной подвески зави-
сит от того, как работают опорные катки. Если катки тележки по-
лучают независимое перемещение, т. е. работают поочередно, то
жесткость подвески меньше жесткости при одновременной работе
катков. При движении машины по неровностям дороги могут рабо-
тать как отдельные катки, так и тележка в целом.
При расчете подвески, т. е. при выборе жесткости ее упругих
элементов, следует исходить из работы отдельных катков, а не всей
тележки в целом, в противном случае подвеска окажется слишком
мягкой и при наезде отдельными катками на местные препятствия
ее будет часто пробивать.
Модуль жесткости по катку балансирной подвески примем рав-
ным модулю жесткости по катку независимой подвески.
В этом случае при движении машины по единичным неровно-
стям обе подвески будут обладать одинаковой жесткостью (при
16* 243
Рис. 127. Сравнительная характери-
стика балансирной и независимой
одновременном наезде на препят-
ствия одинаковой высоты несколь-
кими катками балансирная под-
веска будет обладать большей
жесткостью, чем независимая).
Под статической нагрузкой
жесткость независимой и балан-
сирной подвесок будет различ-
ной. Действительно, под статиче-
ской нагрузкой все катки подвес-
ки относительно корпуса полу-
чают примерно одинаковые пере-
мещения, т. е. работают не один,
а все катки тележки. В этом слу-
чае жесткость балансирной под-
вески будет больше жесткости
независимой.
подвесок На рис. 127 представлен гра-
фик сравнительной характеристи-
ки балансирной и независимой подвесок. На этом графике индексн
относится к независимой и индекс б к балансирной подвеске. При-
мем для сравнения, что рабочий ход обеих подвесок одинаковый
(/грн = /грб). Так как в области статического хода катков балансир-
ная подвеска жестче независимой, то статические хода обеих под-
весок будут разными (hcK > hc6). В области рабочих ходов обе
подвески имеют одинаковую жесткость (mH = m6).
Упругая энергия независимой подвески определяется площадью
треугольника обе, а балансирный — площадью фигуры габв. Сле-
довательно, упругая энергия балансирной подвески меньше незави-
симой на величину площади заштрихованного треугольника оаг.
Если выразить работоспособность балансирной подвески через
работоспособность независимой подвески, то можно получить сле-
дующую формулу:
1 т«
т6
(1 + ?)2
VH>
(247)
где vfl— работоспособность балансирной подвески;
vH— работоспособность независимой подвески;
т„ и тб— модули жесткости независимой подвески по катку и
балансирной подвески по тележке;
<р— коэффициент динамичности независимой подвески.
Из формулы (247) следует, что работоспособность балансирной
подвески зависит от отношения модулей жесткости и от коэффи-
циента динамичности независимой подвески <р.
При большом значении <р (независимая подвеска жесткая)
v6 мало отличается от %. Так, при <р = 2 и -^- = 0,5 (парная
подвеска) v6 = 0,95va.
244
При <р, близком к единице, работоспособность балансирной под-
вески будет значительно меньше работоспособности независимой.
Таким образом, по работоспособности балансирная подвеска не
только не имеет преимуществ по сравнению с независимой, но,
наоборот, при значениях коэффициента динамичности, близких
к единице, значительно ей уступает.
Однако балансирная подвеска по сравнению с независимой
имеет меньшую угловую амплитуду колебания корпуса. Действи-
тельно, при переезде единичной неровности корпус машины с неза-
висимой подвеской перемещается больше, чем корпус машины с ба-
лансирной подвеской (рис. 128). Так, для независимой подвески,
считая ее абсолютно жесткой (для сравнения), имеем
• в Л
sin 9 = -j- .
Для парной, тоже абсолютно жесткой балансирной подвески имеем
• й г
sinO = ^,
где '/а есть передаточное число парной балансирной подвески. В об-
щем случае для сложно-балансирной подвески получим
sin 9' = ^-. (248)
Чем больше опорных катков объединяет тележка, тем меньше
передаточное число 1\ при двух катках I — 0,5, при четырех I —
= 0,25 и т. д. Из формулы (248) следует, что угловое перемещение
корпуса 9' при балансирной подвеске меньше, чем при независимой.
Таким образом, только за счет выбора схемы подвески, не учи-
Рис. 128. Перемещение корпуса машины при наезде
на единичную неровность:
а — при независимой подвеске; б — при балансирной подаеске
245
тывая ее жесткости, можно получить уменьшение амплитуды коле-
бания корпуса.
Это и послужило причиной появления в гусеничной технике ба-
лансирных подвесок.
В настоящее время балансирная подвеска почти не применяется.
Это объясняется главным образом тем, что независимая подвеска,
особенно торсионного типа, значительно проще балансирной. Кроме
того, наличие в балансирной подвеске двух жесткостей (по катку и
по тележке) неблагоприятно отражается на плавности хода ма-
шины. Так, если машина движется по мелким, но близко располо-
женным одна к другой неровностям (например, по булыжной мосто-
вой), то на неровности наезжают одновременно все катки тележки.
В этом случае машину будет сильно трясти, так как работают не
отдельные катки, а тележки в целом, жесткость которых больше
жесткости отдельных катков.
Ранее балансирные подвески применяли широко. Количество
балансиров, связывающих опорные катки, стремились увеличивать.
Для этого в тележки объединяли большое число опорных катков.
В настоящее время такие подвески уже не применяют. Если балан-
сирные подвески еще и встречаются в гусеничных машинах, то
лишь как парные подвески.
ХАРАКТЕРИСТИКИ УПРУГИХ ЭЛЕМЕНТОВ И ИХ ВЛИЯНИЕ
НА ПЛАВНОСТЬ ХОДА МАШИНЫ
Характеристики упругих элементов могут быть линейными и
нелинейными. Последние бывают: выпуклые, вогнутые, выпукло-
вогнутые (рис. 129).
Проанализируем влияние характеристик на плавность хода
машины.
Чтобы можно было сравнивать характеристики, необходимо
прежде всего задаться условиями сравнения.
Условимся, что для всех сравниваемых подвесок рабочий
ход (hp) и общая потенциальная энергия (1У0) — величины одина-
ковые.
Кроме того, примем, что все катки имеют одинаковые характе-
ристики упругих элементов.
Будем рассматривать только вертикальные колебания корпуса.
Тогда по характеристике одного катка можно судить о поведении
всей подвески машины в целом.
Нелинейные характеристики будем сравнивать с линейной ха-
рактеристикой.
На рис. 130 приведены две характеристики: линейная 1 и выпу-
клая 2. Обе характеристики имеют общую точку пересечения под
статической нагрузкой. В этой точке выпуклая характеристика
обладает большей жесткостью, чем линейная (угол наклона каса-
тельной, проведенной к выпуклой характеристике, больше угла на-
клона линейной характеристики). Так как колебания корпуса со-
вершаются вокруг точки статического равновесия, то при движении
машины по неровностям дороги амплитуда, или размах колебаний,
246
Рис. 129. Различные виды характеристик приведенных
подвесок:
а —линейная; б — выпуклая; в — вогнутая; г — выпукло-вогнутая
при подвеске с характеристикой 1 будет больше, чем при подвеске
с характеристикой 2. При этом подвеска с характеристикой 1 будет
давать меньшую частоту колебаний, т. е. большую плавность хода.
При движении по относительно хорошим дорогам, где высота
неровностей меньше 50 мм, пробивание подвески исключено. В этом
случае не амплитуда, а частота
определяет плавность хода ма-
шины.
Подвеска с характеристикой 1
будет обладать лучшей плавно-
стью хода по сравнению с подве-
ской, имеющей характеристику 2.
При динамическом увеличении
хода катка жесткость выпуклой
характеристики уменьшается и
при hp делается меньше жестко-
сти линейной характеристики. Для
того чтобы не пробивало подвес-
ку на больших неровностях, необ-
ходимо увеличивать жесткость с
увеличением хода катка. Таким
Рис. 130. Сравнение выпуклой харак
теристики с линейной:
Z — линейная характеристика; 2 — выпуклая
247
образом, как при движении по хорошим дорогам (малые неровно-
сти), так и при движении на местности (большие неровности) вы-
пуклая характеристика является неудовлетворительной.
На рис. 131 представлена линейная 1 и вогнутая 2 характери-
стики. Под статической нагрузкой подвеска с вогнутой характери-
стикой работает мягче подвески с линейной характеристикой;
с увеличением хода катка жесткость нелинейной характеристики
повышается и при hp может быть значительно больше жесткости
линейной характеристики.
Рис. 131. Сравнение вогнутой характеристики
с линейной:
Z — линейная характеристика; 2—вогнутая характеристика
При движении по ровным дорогам машина будет обладать хо-
рошей плавностью хода; при движении по местности подвеску
с вогнутой характеристикой будет пробивать реже, чем подвеску
с линейной характеристикой.
Таким образом, вогнутая характеристика имеет преимуществе
перед линейной характеристикой.
На рис. 132 представлена линейная 1 и выпукло-вогнутая 2 ха-
рактеристики.
Под статической нагрузкой подвеска с выпукло-вогнутой харак-
теристикой обладает малой жесткостью, с увеличением же хода
катка жесткость характеристики будет увеличиваться.
По сравнению с другими характеристиками (линейной, выпу-
клой и вогнутой) выпукло-вогнутая характеристика обладает явным
преимуществом. Она может обеспечить машине наилучшую плав.-
ность хода как при движении по хорошим дорогам, так и на
местности.
К сожалению, практически получить эту характеристику трудно,
так как требуется значительное усложнение подвески (введение
дополнительного упругого элемента или усложнение жестких
звеньев подвески).
248
В настоящее время стремятся получить вогнутую характери-
стику. Для этого применяют специальные упругие элементы, напри-
мер спиральные конические рессоры, резиновые или гидравличе-
ские упругие элементы. Вогнутую характеристику получают также
при использовании пневматических упругих элементов (надутые
воздухом резиновые подушки).
Рис. 132. Сравнение выпукло-вогнутой характе-
ристики с линейной:
/ — линейная характеристика; 2— выпукло-вогнутая харак-
теристика
Можно считать, что фактически все подвески имеют вогнутую
или, точнее, приближающуюся к ней ломаную характеристику, так
как на всех подвесках применяются упругие, обычно резиновые,
ограничители хода. После соприкосновения с ограничите-
лем жесткость подвески резко возрастает.
В тягачах в качестве ограничителей иногда применяют так назы-
ваемые подрессорники — упругие элементы с конической
рпиральной пружиной переменной жесткости.
10. ВЛИЯНИЕ ДОРОЖНЫХ ФАКТОРОВ НА ПЛАВНОСТЬ
ХОДА МАШИНЫ
Как уже отмечалось выше, на плавность хода машины влияет
высота неровностей и их взаимное расположение на дороге. Форма
Неровности практически не влияет на плавность хода.
Взаимное расположение неровностей на дороге является чрез-
вычайно неопределенным фактором. Неровности, особенно на мест-
ности, располагаются хаотически, и подчинить их какому-либо
закону невозможно.
249
Хотя на наезженных автотранспортом грунтовых дорогах выяв-
ляется некоторое волнообразное чередование неровностей, однако и
здесь нет закономерности: интервал между отдельными волнами
может меняться даже на одной и той же дороге в очень широких
пределах.
Определенное чередование неровностей может, конечно, создать
неблагоприятные резонансные условия движения машины, при ко-
торых наступит пробивание подвески даже на небольших неров-
ностях. Однако учесть это в практических расчетах подвески не-
возможно.
Поэтому рассмотрим влияние на плавность хода только одного
дорожного фактора —-высоты единичной неровности.
ИСПЫТАНИЕ ГУСЕНИЧНОГО ТЯГАЧА
НА ЕДИНИЧНЫХ НЕРОВНОСТЯХ
Наиболее полные исследования гусеничных тягачей на плавность
хода были проведены в 1953 г. Г. А. Ивановым. Испытывались
как одиночные машины, так и машины с прицепом.
Задачей испытаний было определение размаха продольных угло-
вых колебаний, максимального ускорения, критической скорости по
пробиванию подвески, частоты колебаний, а также влияния колес-
ного прицепа на колебания корпуса тягача.
Полученные в результате испытаний данные позволяют судить
о плавности хода одиночной машины или поезда при переезде через
единичные неровности.
Рассмотрим кратко методику испытаний и основные выводы,
полученные на основании этих испытаний.
При испытаниях применялась следующая методика.
Машина разгонялась до определенной скорости и проходила на
этой скорости единичную трапециевидную неровность (рис. 133).
С помощью специальной измерительной аппаратуры записывались
продольные угловые колебания и ускорения корпуса машины.
В качестве измерительной аппаратуры применялись два прибора:
гироскопический прибор угловых колебаний корпуса машины кон-
струкции Г. А. Иванова (рис. 134 и
135) и акселерограф ускорений СП-11.
Гироскопический прибор состоит из
трех основных узлов: гироскопа 1, пи-
шущего устройства 2 с электроискро-
вой системой записи и лентопротяжно-
го механизма 3 с электромагнитным
отметчиком времени.
Гироскопический прибор работает
следующим образом. Когда корпус ма-
шины поворачивается, вместе с ним
поворачивается вокруг продольной оси
и корпус прибора. Так как ось гироскопа остается в пространстве
неподвижной, то кольцо 4 поворачивается относительно корпуса
Рис. 133. Тягач, переезжающий
через единичную неровность
250
Рис. 134. Гироскопический прибор угло-
вых колебаний корпуса машины
Рис. 135. Принципиальная схема гироскопического прибора угловых колеба-
ний корпуса машины:
/ — гироскоп; 2 — пишущее устройство; 3 — лентопротяжный механизм; 4 — кольцо; 5 — диск
251
прибора. С ним поворачивается и диск 5, который передает дви-
жение через систему блочков на ползун электроискрового пишу-
щего устройства.
На рис. 136 показан образец записи угловых колебаний корпуса
одиночной машины при переезде ее через неровность высотой
150 мм со скоростью И км/час. По оси абсцисс отложено время,
по оси ординат — угловое перемещение.
Колебания имеют явно выраженный периодический характер и
являются быстрозатухающими.
На рис. 137 представлен другой прибор, применявшийся при
испытаниях,— акселерограф СП-11.
Прибор — инерционного типа, имеет в качестве чувствительного
элемента инерционную массу весом 500 г, подвешенную на четырех
консольных плоских пружинах. К массе с помощью рычажного
Рис. 136. Примерная запись угловых колебаний корпуса ма-
шины при переезде единичной неровности
механизма прикреплена стрелка, имеющая на конце специальный
штифт, с помощью которого ускорения записываются на бумажной
ленте.
Прибор работает следующим образом. Когда корпус машины
получает ускорение, с ним вместе перемещается и корпус прибора.
Так как барабанчик, на который надета бумажная лента, соединен
с корпусом прибора, то при перемещении корпуса перемещается и
барабанчик с бумагой. Инерционная масса и соединенное с ней
перо вследствие инерции остаются на месте; таким образом, непо-
движное перо на движущейся ленте записывает, соответствующие
ускорения.
Для замера максимальных ускорений акселерограф помещал-
ся в носовую или кормовую часть машины, где ускорения являются
наибольшими.
Испытания проводились на неровностях различной высоты. Под
гусеницы машины укладывались две трапециевидные деревянные
призмы высотой Н = 50, 100, 150, 200 мм.
Из записи колебаний были определены угловые амплитуды 9, и
02 и по ним размах колебаний 0! +02 в функции скорости движения
машины.
252
Рис. 137. Акселерограф СП-11
Результаты испытаний одиночной машины (тягача М-2) пред-
ставлены на графике рис. 138. Каждая кривая соответствует опре-
деленной высоте неровности Н.
Из графика следует, что размах колебаний имеет максимум,
причем чем выше неровность, тем этот максимум больше сдвигает-
ся влево, в сторону меньших значений скоростей движения машины.
Так, при неровности высотой 50 мм максимум лежит на скорости
Рис. 138. Результаты испытаний тягача на размах колебаний
253
около 22,5 км/час, при неровности высотой 100 мм — на скорости
17,5 км/час, при неровности высотой 150 мм — на скорости
13,5 км/час и при неровности 200 мм—на скорости 8,5 км/час.
Явление максимума размаха колебаний условно называется
резонансом, а соответствующая ему скорость резонанс-
нойскоростью.
При движении одиночного тягача ио неровностям высотой по-
рядка 100—150 мм резонансные скорости лежат в пределах 13—•
Рис. 139. Зависимость между высотой неровности и критической
скоростью по пробиваемости
Опыты показывают, что на неровностях высотой 50—100 мм
удара в ограничитель не наблюдается. Подвеску начинает пробивать
на неровностях высотой 150—200 мм.
Скорость движения машины при этом соответствует резонансной
скорости.
На основании проведенных испытаний установлена зависимость
между высотой неровности и критической скоростью по
пробиваемости подвески. Эта зависимость приведена на
рис. 139.
Из рисунка следует, что при движении по неровностям высотой
порядка 150 мм, которые можно считать средними неровностями на
местности, критическая скорость для данной машины (М-2) со-
ставляет примерно 12 км/час. На неровностях высотой 200 мм кри-
тическая скорость падает до 8 км/час.
254
На рис. 140 приведены результаты испытаний на размах коле-
баний корпуса гусеничного тягача, движущегося с колесным при-
цепом (сплошные кривые). Для сравнения здесь же приведены дан-
ные для одиночного тягача (пунктирные кривые).
Из сравнения результатов испытаний видно, что прицеп гасит
колебания тягача. Так, при движении по неровности высотой
150 мм со скоростью 13 км/час одиночная машина имеет размах
колебаний около 12°, а тягач с прицепом — около 9°.
На основании записи колебаний удалось получить частоты
и периоды затухающих колебаний. Для разных ма-
шин они имеют разное значение и лежат в пределах:
частота и период вертикальных колебаний
k\ = 0,95 — 3,2 — ; Т = 0,3 — 1,0 сек-,
1 ’ ’ сек ’ ’ ’
— без прищ с прицеп HQ

Н= 150мм

H-100MJ f
———
Н-50ММ
5 1 9 И 13 15
Рис. 140. Результаты испытаний на размах колебаний гусеничного поезда и
одиночного тягача
частота и период угловых колебаний
^ = 0,6-2,!^-; Т = 0,5 — 1,7 сек.
Отсюда следует, что частота вертикальных колебаний выше частоты
угловых колебаний.
Полученные частоты затухающих колебаний приближенно можно
сопоставлять с расчетными частотами собственных колебаний, опре-
деляемых по формулам (240) и (241).
На рис. 141 приведены записи ускорений, полученные с помощью
акселерографа, для двух машин, имеющих различную схему под-
вески и различную жесткость рессор. Подвеска, имеющая большую
жесткость, при движении по дороге показала максимальное ускоре-
ние порядка 10 м/сек2 (верхний график), а имеющая меньшую
жесткость — ускорение порядка 5 м/сек2.
255
При наезде на неровность высотой Н = 200 мм происходил жест-
кий удар в ограничитель и ускорение в первой подвеске повыша-
лось до 5g, а во второй — до 2,5g, где g — ускорение 9,81 м/сек?.
Рис. 141. Результаты испытаний на величину максимального уско-
рения
На рис. 142 приведены зависимости максимальных ускорений от
скорости движения машины и высоты неровности.
Из рисунка следует, что с увеличением высоты неровности уско-
рение возрастает, однако при неровностях высотой 50 и 100 мм
удара в ограничитель не происходит. Удар происходит при движе-
нии по неровностям высотой 150—200 мм.
256
На основании проведенных опытов можно сделать вывод, что
при наезде на единичное препятствие в пределах упругого хода
катков максимальное ускорение доходит до 1,5 g, или до 15 м/сек2.
При ударе в ограничитель ускорение возрастает до 5—-6 g, или до
50—60 м/сек2.
шины п высоты неровности
Следует иметь в виду, что ускорения порядка 5—6 g создают
значительные динамические нагрузки как на корпус машины, так и
на расположенные в нем агрегаты и грузы. Так, при весе двигателя
тяжелого тягача примерно в 800 кг динамическая нагрузка на дви-
гатель составит при ускорении в 6 g около 5 т. Эта нагрузка будет
действовать на крепления двигателя к корпусу, ослабляя их и на-
рушая центровку двигателя. Кроме того, большие динамические
нагрузки могут вызвать и поломку деталей ходовой части машины.
Поэтому при эксплуатации машины следует предохранять подвеску
от пробивания, т. е. двигаться по неровным дорогам со скоростями
ниже критической.
I7-24G9
ГЛАВА VII
ПРОХОДИМОСТЬ ГУСЕНИЧНЫХ МАШИН
1. ОПРЕДЕЛЕНИЕ. ПАРАМЕТРЫ ПРОХОДИМОСТИ
Проходимость является одним из основных качеств гусе-
ничной машины. Высокая проходимость вместе с высокой манев-
ренностью делает гусеничную машину самой вездеходной из всех
существующих самоходных машин.
Под проходимостью следует понимать способность гусеничной
машины преодолевать своим ходом без вспомогательных средств
встречающиеся на ее пути местные препятствия.
Эти препятствия бывают самыми различными. Каждое из них
по-своему воздействует на машину, препятствуя ее движению.
В зависимости от воздействия на машину все препятствия мож-
но разбить на три группы.
1. Препятствия, создающие большое сопротивление движению
и требующие на свое преодоление силу тяги, близкую к силе тяги
по сцеплению.
2. Препятствия, способные вызвать опрокидывание машины.
3. Препятствия, способные вызвать затопление машины.
К первой группе относятся мягкие грунты * (болото, сыпучие
пески, рыхлый снег); крутые подъемы; пороговые препятствия;
броды.
Ко второй группе относятся рвы, крутые спуски.
К третьей группе относятся топкие болота, водоемы (водные
препятствия), замерзшие водоемы (ледяные препятствия).
В данной главе рассматриваются все виды препятствий, кроме
водных, и возможности их преодоления гусеничными машинами..
Преодоление водных препятствий рассматривается в следующей
главе.
ПАРАМЕТРЫ ПРОХОДИМОСТИ
Для объективной сравнительной оценки проходимости гусенич-
ных машин служат параметры проходимости.
К параметрам проходимости относятся следующие величины:
— вес машины (G);
— удельная мощность одиночной машины (Ny) и гусеничного
поезда (АГ);
* Здесь и ниже под грунтом понимается естественное основание, по кото-
рому движется гусеничная машина.
258
— Максимальная удельная сила тяги по двигателю f<pl 111ах);
— среднее и действительное удельное давление гусениц на
грунт [q и <7тах);
— дорожный просвет (£);
— углы проходимости (у1п и у2п);
— опорная-база (Л);
— относительная координата центра давления гусениц на грунт
и вертикальная координата центра тяжести (йг);
— углы бокового крена по опрокидыванию (рк) и по сцепле-
нию (|3С);
— высота точки затопляемости машины (Лзт).
Рассмотрим эти параметры в отдельности и определим их чис-
ловое значение для современных гусеничных машин.
Вес машины
Чем меньше вес машины, тем выше ее проходимость по мяг-
ким грунтам, особенно если грунт имеет сверху коркообразный
покров (например, травяной покров на болотах).
Влияние веса на проходимость по мягким грунтам проявляется
как непосредственно, так и через удельное давление гусениц на
грунт. Чем тяжелее машина, тем труднее получить малое удельное
давление на грунт, тем хуже будет проходимость машины.
Вес влияет также и на проходимость машины по льду.
Удельная мощность одиночной машины и гусеничного поезда
Преодоление препятствий часто зависит от скорости движения
машины, от ее приемистости и динамичности. Чем скорее машина
проходит препятствие, тем успешнее будет преодоление его.
'С ходу могут преодолеваться короткие крутые подъемы, заболо-
ченные участки, рвы, небольшие, но глубокие водоемы, непроходи-
мые при движении машины на низкой скорости, и другие препят-
ствия.
Динамика машины прежде всего зависит от удельной мощно-
сти. Удельная мощность влияет также и на статическое преодоле-
ние препятствий, увеличивая силу тяги по двигателю.
Следует различать удельную мощность одиночной маши-
ЦЫ (2Vy) и удельную мощность гусеничного поезда |WJ. В первом
Случае удельная мощность есть отношение номинальной мощности
Двигателя к полному весу машины (с грузом на платформе), во
втором — отношение номинальной мощности к полному весу
поезда.
В табл. 9 приведены значения удельной мощности одиночной
Шашины (2Vy) и гусеничного поезда для современных тягачей
® сельскохозяйственных тракторов.
17*
259
Таблица 9
Удельная мощность одиночной машины ;Vy и гусеничного поезда /Vy
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П СТЗ-З С-60 С-65 С-80 ДТ-54
Ny, л.с./m 12 16,6 16,6 14,1 17,2 10,2 6 5,8 7,9 10
N , л.с./m 7,5 8,3 8,6 8,6 10,9 м 3 3,1 4,3 5,5
Из табл. 9 следует, что одиночные тягачи имеют удельную мощ-
ность порядка 12—18 л.с./т, тягачи с прицепом — 7—10 л.с./т.
Значительно меньшей удельной мощностью обладают сельскохозяй-
ственные тракторы. Их удельная мощность составляет 6—10 л. с./т
для одиночной машины и 3—5 л.с./т для машины с прицепом *,
Максимальная удельная сила тяги по двигателю
Сила тяги по двигателю определяется по формуле
р 270^
д WP
Поделим левую и правую части этого равенства на полный вес
р
машины G. Обозначим = ю Величина уд называется у д е л ь-
G ‘д
ной силой тяги по двигателю. Кроме того, = Ny.
Тогда получим формулу удельной силы тяги по двигателю
^ = 0,27^. (249)
Если в этой формуле принять ^p = ^min,то будем иметь макси-
мальное значение удельной силы тяги тах. Эта величина характе-
ризует проходимость машины по тяжелым дорогам. Чем больше
?дтах, тем выше проходимость машины и тем большие подъемы
(и другие препятствия) может преодолевать машина.
Заметим, что удельная сила тяги ?дтахдолжна быть меньше или
равна некоторому среднему коэффициенту сцепления <р, характе-
ризующему средние дорожные условия движения машины. Реко-
мендуется принимать ср = 0,8. Очевидно, ?д П1ах не должно быть зна-
чительно меньше ср, так как при малом <рд тах будет не полностью
использоваться сила тяги двигателя по сцеплению. Желательно
иметь <рд тах 0,8, т. е. равной коэффициенту сцепления ?.
* Вес прицепа для сельскохозяйственного трактора условно принимался
равным 0,8 от веса трактора.
260
В табл. 10 приведены значения ?д П1ах
Таблица 10
Максимальное значение удельной силы тяги по двигателю <рд тах
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П ДТ-54 С-65 С-80
max 0,61 0,72 0,56 0,72 0,66 0,64 0,36 0,73
Из табл. 10 следует, что<рдт11х значительно меньше 0,8. Это
можно объяснить тем, что либо конструктор в тяговом расчете за-
высил минимальную расчетную скорость, не желая расширять диа-
пазон скоростей коробки передач, или в расчете был принят не
полный, а номинальный вес тягача, т. е. вес без груза на плат-
форме (для артиллерийских тягачей). Однако это неверно, так как
машина работает обычно с полной нагрузкой, и, следовательно,
в расчете должен учитываться не номинальный, а полный вес ма-
шины.
Среднее и действительное удельное давление гусениц на грунт
Удельное давление характеризует проходимость машины по
мягким грунтам. С уменьшением удельного давления проходи-
мость повышается.
Следует различать среднее удельное давление, как
отношение полного веса машины к опорной площади гусениц, и
действительное удельное давление.
Среднее удельное давление определяется по формуле
(250)
где G— полный вес машины в кг;
b—ширина одной гусеницы в см;
L—длина опорной базы машины в см.
Иногда среднее удельное давление определяют также и при по-
гружении гусениц в грунт. Погружение условно принимают на
глубину 100 мм. Для этого в формуле (250) следует увеличить
Длину опорной базы L на ДА, где ДА — проекция на плоскость до-
роги частично погруженных в грунт наклонных ветвей гусениц,
Величину ДА можно определить по формуле
AZ,= 10(V- + -M, (251)
UgTi tgTs/’ v 7
где li и — углы наклона передней и задней ветвей гусениц. Если
Принять 7, = -[г = 25°, то ДА. = 43 см, что для существующих тяга-
чей на 10—15% увеличит длину опорной базы и тем самым умень-
шит на ту же величину среднее удельное давление.
261
В табл. 11 приведены значения среднего удельного давления гу-
сениц на грунт для тягачей и сельскохозяйственных тракторов,
определенного по формуле (250).
Таблица 11
Среднее удельное давление гусениц на грунт (без погружения
гусениц)
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П СТЗ-З С-60 С-65 С-80 ДТ-54
q, кг/см'1 0,55 0,65 0,56 0,49 0,45 0,33 0,47 0,53 0,48 0,40
Рис. 143. Эпюра действительного
удельного давления гусениц на
грунт (опытные данные):
а — машина с опорными катками малого
диаметра; б~ машина с опорными кат-
ками большого диаметра
Из табл. 11 следует, что удельное давление тягачей и сельско-
хозяйственных тракторов находится в пределах 0,4—0,6 кг!см2.
Для танков оно составляет
0,8—0,9 кг/см2.
Машины высокой проходимо-
сти имеют удельное давление
0,15 — 0,20 ~.
’ с.и2
Снегоходы имеют удельное
давление 0,035 — 0,05 .
Среднее удельное давление
лишь примерно характеризует
проходимость гусеничных машин
по мягким грунтам, так как про-
ходимость зависит в первую оче-
редь от действительного, а не
среднего удельного давления.
На рис. 143 представлены две
машины, под гусеницами которых
на глубине 200 мм с помощью ги-
дравлических мессдоз были заме-
рены удельные давления.
Как видно из полученных
эпюр, удельное давление состав-
ляет <7п1ах — 1,5 — 2 кг)см2, среднее же удельное давление для этих
машин было порядка 0,7—0,8 кг/см2, т. е. в 2,5 раза меньше макси-
мального.
Дорожный просвет
Дорожный просвет, или клиренс, есть расстояние от полотна до-
роги до низших частей корпуса машины (обычно до ее днища).
Дорожный просвет k характеризует проходимость по мягким
262
грунтам, а также по местности с выступающими неровностями
(кочки, пни, большие камни и т. д.).
Чем больше дорожный просвет, тем выше проходимость ма-
шины.
Значения дорожного просвета приведены в табл. 12.
Таблица 12
Дорожный просвет
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П стз-з С-60 С-65 С-80 ДТ-54
k, мм 370 425 400 350 325 337 405 405 382 280
Из табл. 12 следует, что дорожный просвет k составляет 300—
400 мм.
Углы проходимости
Углом проходимости уп называется угол наклона прямой, про-
веденной через две точки: касательно к гусеницам и к выступаю-
щим частям корпуса машины в передней или задней части машины
(рис. 144),
Угол проходимости уп может быть меньше (рис. 145, а) или
больше (рис. 145, б) угла наклонной ветви гусеницы -р Если угол
проходимости меньше угла наклонной ветви, то в корпусе машины
имеются выступающие части, которые, задевая за местные неров-
ности грунта, могут препятствовать движению машины.
В табл. 13 приведены значения углов наклона передних и
задних Т2 ветвей гусениц и углов проходимости у1п и ?зп.
263
Таблица 13
Углы проходимости
Параметр Марка машины
АТ-Т АТ-Л АТ-С М-2
Т1> град. 20 30 20 22
Та> град. 35 20 25 30
Tin- град. 35 58 25 30
Т2п. град. 30 40 35 35
Из табл. 13 следует, что почти все тягачи (за исключением тя-
гача АТ-Т) имеют углы уп, большие углов 7.
Рис. 145. Преодоление местного препятствия при разных
углах проходимости:
а — угол проходимости меньше угла наклонной аетви гусеницы; б — угол
проходимости больше угла наклонной ветви гусеницы
264
Опорная база
Чем больше опорная база машины (Л), тем более широкие рвы
и более высокие пороги она может преодолеть.
Машина, имеющая более длинную опорную базу, под меньшим
углом преодолевает местные неровности дороги, вследствие чего
корпус машины получает меньший наклон а. Составляющая веса
Gsin а, препятствующая движению машины, при этом будет меньше.
Таким образом, проходимость тяжелых гусеничных машин, имею-
щих большую базу, выше проходимости средних и легких машин.
Как известно из теории поворота, увеличение опорной базы
приводит к ухудшению поворотливости машины. Поэтому увели-
чение опорной базы L должно сопровождаться одновременным
увеличением ширины колеи машины В для того, чтобы относитель-
ная опорная база L = находилась в допустимых (с точки зре-
ния поворота) пределах.
В табл. 14 приведены значения опорной базы L и относительной
опорной базы L' для тягачей и сельскохозяйственных тракторов.
Опорная база и т относительная опорная база а б л и ц а 14
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П СТЗ-3 С-60 С-65 С-80 ДТ-54
L, см 275 , 388 281 277 267 197 202 213 237 180
и 1,31 I 1,17 г19 1,16 1,32 1,37 1,17 1,25 1,25
Из табл. 14 следует, что для тягачей опорная база находится
в пределах 267—388 см, а относительная база — в пределах 1,3—
1,5.
Относительная координата центра давления гусениц на грунт
и вертикальная координата центра тяжести
Продольная устойчивость гусеничной машины зависит от по-
ложения центра давления гусениц на грунт и от положения по вы-
соте центра тяжести машины.
Центром давления называется точка приложения рав-
нодействующей всех нормальных реакций грунта, действующих на
опорные ветви гусениц.
Положение центра давления может быть определено графиче-
ским или аналитическим способом.
Графическим способом центр давления определяется как
.точка пересечения равнодействующей всех внешних сил, приложен-
ных к корпусу машины, с плоскостью дороги.
265
Для этого наносим на чертеж в масштабе все действующие на
машину силы. Складываем эти силы графически и определяем их
равнодействующую. Продолжая линию действия равнодействующей
до пересечения с плоскостью дороги, находим точку пересечения,
которая и будет являться центром давления.
Рассмотрим теперь аналитическое определение положе-
ния центра давления.
Линия горизонта
Рис. 146. Определение координаты центра давления
На машину действуют следующие внешние силы и реакции
грунта (рис. 146):
W— нормальная реакция грунта, приложенная в центре дав-
ления;
G— вес машины;
/—сила инерции поступательного движения;
7?к—сопротивление на крюке;
Р— сила тяги;
R— сила сопротивления качению.
Составим уравнение моментов всех сил относительно центра
давления (точки /г).
После преобразования получим
__ aG cos а — (/ + G sin a) hz — hKRK - aKRK tg T (
G cos a + Ru tg T •
Параметром проходимости является относительная коор-
дината равная отношению абсолютной координаты хк к по-
ловине опорной базы машины:
= (253)
266
Эта координата позволяет сравнивать машины между собой
в отношении их проходимости (абсолютная координата такого
сравнения не дает).
Машина устойчива до тех пор, пока центр давления лежит
внутри опорной базы машины, и теряет устойчивость, когда центр
давления смещается к оси заднего или переднего опорного катка.
В первом случае относительная координата получает значение
хк — 0, во втором — х'к = 2.
Машина обладает наибольшей устойчивостью, если центр дав-
ления лежит посредине опорной базы или если хк = 1.
Так, тягач АТ-Т, стоящий на горизонтальном участке пути,
имеет относительную координату х’к— 1,17 (центр давления ма-
шины смещен несколько вперед), а тягач АТ-П имеет х’к = 1.21
(здесь смещение центра давления вперед еще больше).
Заметим, что потеря устойчивости еще не означает опрокиды-
вания машины. Машина может двигаться с частично приподня-
тыми опорными ветвями гусениц (реакция грунта N в этом случае
будет находиться в крайней опорной точке гусениц). .
Обычно принято оценивать устойчивость машины по располо-
жению по высоте (по вертикальной координате hz) центра тя-
жести. Чем выше расположен центр тяжести, тем меньше устой-
чивость машины.
Определение устойчивости по координате Л, является частным
случаем определения устойчивости по расположению центра давле-
ния. Действительно, приняв / = 0 и RK = 0, получим из формулы
(252)
хк = а — (254)
где обычно hz = (0,35 — 0,40) Н\
Н— высота машины.
Углы бокового крена по опрокидыванию и по сцеплению
Углы бокового крена характеризуют движение машины на
подъеме параллельно основанию подъема.
Различают углы бокового крена по опрокидыванию машины
(Рк) и по сцеплению (ft.).
Определим угол Рк.
На рис. 147 показано движение машины параллельно основа-
нию подъема. В общем случае центр давления машины находится
в точке k, расположенной между гусеницами. Если центр давле-
ния сместится на осевую линию правой гусеницы, то возможно
опрокидывание машины. Угол и будет углом, характеризующим
^предельное положение центра давления. Этот угол определится
по формуле
(255)
267
где В—ширина колеи машины;
hz— вертикальная координата
Рис. 147. Движение машины с боковым
креном
tg Рс = Рс-
В
2hz >[Лс>
центра тяжести машины.
Определим угол бокового
крена по сцеплению.
Сцепление машины будет
обеспечено, если составляю-
щая веса G sin р станет
меньше равнодействующей
поперечной реакции грунта
рс О cos 0:
Osin р <pc(7cos Р,
где рс— коэффициент попе-
речного скольже-
ния гусениц.
Предельное значение угла
= |3С определится из ра-
венства
(256)
Так как обычно
то угол Рс < Рк, т. е. сползание машины к основанию подъема бо-
лее вероятно, чем ее опрокидывание.
В табл. 15 приведены значения углов и |3С.
Таблица 15
Углы бокового крена
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П
Рк, град. 43 51 41 48 57
₽с. гРаД- 20 25 25 25 25
Из табл. 15 следует, что углырс значительно меньше углов Рк.
Высота точки затопляемости машины
Гусеничная машина может двигаться не только на суше, но и
вброд или вплавь. Способность к преодолению водных препятствий
определяется расположением точки затопляемости машины (Азт).
Под точкой затопляемости понимается такая точка (отверстие)
в машине, через которую вода может проникать в корпус и затоп-
268
лять его. Точкой затопляемости может быть наиболее низко рас-
положенное отверстие в корпусе или отверстие выпускной трубы
двигателя.
От положения точки затопляемости зависит глубина брода,
преодолеваемого машиной. Глубина преодолеваемого брода должна
быть меньше высоты Азт.
Значения глубины преодолеваемого брода приведены в табл. 16.
Таблица 16
Глубина брода
Параметр Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П СТЗ-3 С-60 С-65 С-80
Лбр, см 60 100 100 100 НО 60 70 60 80
Из табл. 16 следует, что точка затопляемости для сухопутных
машин должна находиться выше 60—100 см от грунта.
Мы рассмотрели основные параметры проходимости и дали их
численное значение для современных гусеничных машин.
Следует иметь в виду, что проходимость машины определяется
не каким-нибудь отдельно взятым параметром, а совокупностью
их. Только при высоком значении всех или по крайней мере наи-
более важных параметров машина будет обладать высокой прохо-
димостью.
2. ПРЕОДОЛЕНИЕ МЯГКИХ ГРУНТОВ
При движении машины по мягкому грунту, например по бо-
лоту, глубокому снегу или сыпучим пескам, гусеницы погружаются
в грунт, вследствие чего возрастает лобовое сопротивление движе-
нию машины. Увеличение сопротивления требует повышения силы
тяги. Так как мягкий грунт обладает плохими сцепными качест-
вами, то сила тяги может быстро достичь предельного значения по
сцеплению. В этом случае гусеницы машины забуксуют и машина
остановится. В дальнейшем попытка преодолеть препятствие при-
ведет лишь к тому, что гусеницы, буксуя, будут углублять колею
до тех пор, пока машина окончательно не сядет днищем на грунт.
В этом случае сразу возрастет сопротивление вследствие упора
корпуса в грунт и возникновения сил трения скольжения между
днищем и грунтом. Одновременно уменьшится сцепной вес ма-
шины, так как сила тяжести теперь будет передаваться на грунт
не только через гусеницы, но и частично через днище корпуса.
Уменьшение сцепного веса снизит силу тяги по сцеплению, вслед-
ствие чего машина застрянет в грунте и не сможет выбраться из
269
Него без посторонней помощи или без применения вспомогатель-
ных средств.
Следует различать два вида мягких грунтов: с глубоким и не-
глубоким залеганием. Если глубина залегания мягкого грунта до
твердого основания меньше 1,5—2 дорожных просветов машины, то
такой грунт считается грунтом неглубокого залегания. Если глу-
бина залегания больше 2 дорожных просветов, то такой грунт счи-
тается грунтом глубокого залегания.
Так как дорожный просвет гусеничных машин равен примерно
400 мм (см. табл. 12), то мягкий грунт неглубокого залегания дол-
жен иметь толщину слоя 600—800 мм.
Процесс преодоления грунтов неглубокого и глубокого залега-
ния принципиально различен.
Если глубина залегания грунта невелика, то гусеницы, углуб-
ляясь в грунт, будут уплотнять его, сцепные качества уплотнен-
ного грунта улучшатся и сила тяги по сцеплению возрастет. Ма-
шина сможет преодолеть препятствие даже при частичной потере
сцепного веса вследствие соприкосновения днища машины с грун-
том. На грунтах неглубокого залегания величина удельного давле-
ния почти не влияет на проходимость машины. Иногда машина
с большим удельным давлением даже легче преодолевает мягкие
грунты, чем машина с меньшим удельным давлением. Это объяс-
няется тем, что гусеницы с большим удельным давлением сильнее
уплотняют грунт или углубляются настолько, что получается сцеп-
ление гусениц с твердым основанием. И в том и в другом случае
сила тяги по сцеплению резко возрастает.
На грунтах глубокого залегания гусеницы не достигают твер-
дого основания и не могут заметно уплотнить грунт.
Если на грунтах неглубокого залегания основным фактором
преодоления препятствия является сила тяги по сцеплению, то на
грунтах глубокого залегания этим фактором является лобовое со-
противление. Чем меньше погрузится машина гусеницами в грунт,
тем меньше будет лобовое сопротивление и тем больше вероят-
ность преодоления препятствия.
Так как при преодолении грунта глубокого залегания корпус
машины также частично погружается в грунт, то преодоление пре-
пятствия напоминает преодоление водных преград: машина как бы
плывет по мягкому грунту.
Преодоление болот с глубоким залеганием и с жидкой конси-
стенцией грунта часто переходит в обычное плавание, т. е. на ма-
шину согласно закону Архимеда начинает действовать подъемная
сила.
Мягкие грунты сухой консистенции и обладающие большим
внутренним сцеплением в отношении проходимости по ним гусе-
ничных машин характеризуются следующими качествами: плот-
ностью и несущей способностью.
Плотность есть вес одного кубического сантиметра грунта, вы-
раженный в граммах (г/см3).
В табл, 17 приведены значения плотности снега.
270
Плотность снега
Таблица 17
Характеристика снега
Пушистый сухой...............................
Оседающий....................................
Осенний .....................................
Талый весенний ..............................
Зимняя автомобильная дорога .................
Снеговой наст, верхний слой..................
Снеговой наст на всю толщину.................
Плотность, г!см*
0,01—0,03
0,07—0,19
0,20-0,50
0,60—0,70
0,63
0,46
0,24
Из табл. 17 следует, что плотность снега может находиться в
широких пределах от 0,01 до 0,7 г/см9.
Плотность снега зависит от многих факторов: от времени ле-
жания, от температуры окружающего воздуха, от удельного давле-
ния, которым снег уплотняется.
За длительное время, особенно если морозы сменяла оттепель,
снег может настолько слежаться, что приобретет плотность и не-
сущую способность грунтовой дороги.
Рис. 148. Зависимость плотности снега от удель-
ного давления штампа и температуры окружаю-
щего воздуха
На рис. 148 приведена примерная зависимость плотности снега
от удельного давления штампа, с помощью которого осуществля-
лась нагрузка на снег, и температуры окружающего воздуха.
С увеличением удельного давления от 0 до плотность
снега резко повышается. От удельного давления 0,2 и выше она
271
возрастает уже медленно. Отсюда следует, что проходимость по
снегу будет сильно зависеть от удельного давления, если оно из-
меняется в пределах до 0,2 , и почти не зависит, если удельное
давление изменяется в более высоких пределах.
Кривая зависимости плотности от удельного давления, харак-
теризующая болотистый грунт и пески, носит более пологий ха-
рактер. В этом случае проходимость будет зависеть от изменения
удельного давления во всем диапазоне допускаемых в гусеничных
машинах удельных давлений (см. табл. 11).
Из рис. 148 следует также, что плотность снега повышается
с увеличением температуры окружающего воздуха.
Под несущей способностью грунта понимается сопро-
тивление грунта внедрению в него с помощью штампа рассредото-
ченной нагрузки, характеризуемой удельным давлением, выражен-
ным в кг/см2.
Обозначим через h глубину залегания мягкого грунта
(рис. 149), а через S и я соответственно осадку грунта и некоторый
Рис. 149. Глубина залегания мягкого грунта

коэффициент, называемый коэффициентом несущей спо-
собности грунта.
При одной и той же плотности грунта или при одном и том же
удельном давлении на грунт осадка грунта S зависит от глубины
залегания грунта h. Чем больше h, тем больше будет и осадка
грунта. Связь между глубиной залегания и осадкой выражается
коэффициентом несущей способности грунта
S = ah. (257)
Коэффициент а зависит от тех же факторов, что и плотность
грунта.
На рис. 150 приведена примерная зависимость коэффициента а
от удельного давления для рыхлого снега при температуре окру-
жающего воздуха t ——10,8° С.
Чем больше осадка грунта, тем больше лобовое сопротивление
движению машины. Выразим величину допустимой осадки через
272
ak, где a — некоторый опытный коэффициент, k — дорожный про-
свет. Тогда из формулы (257) можно получить предельную
глубину допустимого залегания мягкого грунта:
Примем ориентировочно а = 1,5; k = 400 мм. Допустим, что
среднее удельное давление гусениц на грунт составляет 0,4—
0,8 к.г!см2. Из графика (рис. 150) находим а = 0,6. По формуле
получим предельную глубину залегания рыхлого снега h = 1000 мм.
Коэффициент несущей способности а можно рассматривать как
£
относительную осадку -у . Из графика (рис. 150) следует, что од-
ного давления
носительная осадка резко возрастает с увеличением удельного
давления до 0,2 кг/см2. При дальнейшем его увеличении осадка
становится величиной почти постоянной. Таким образом, заметное
влияние на проходимость по рыхлому снегу при данной характери-
стике снега удельное давление оказывает только до q <Z 0,2 кг/см2.
Если q >0,2 кг/см2, то практически безразлично, будет ли удель-
ное давление равно 0,3 кг/см2 или 0,8 кг/см2. Так, согласно преды-
дущей формуле при а =1,5, если удельное давление равно
0,3 кг/ся2, допустимая глубина залегания снега будет h ~ 2,5 k,
если же 0,8 кг/ся2, то h — 2,4 k.
По рыхлому снегу могут двигаться только специальные гусе-
ничные снегоходы. Среднее удельное давление гусениц этих снего-
ходов должно быть очень низким.
А. А. Крживицкий в книге «Тяговые свойства трактора на транс-
порте» указывал, что наиболее желательным надо считать такой
Трактор-снегоход и такие колесные или гусеничные прицепки и
18—2469
273
сани, которые могли бы двигаться по снегу, как передвигается по
нему человек на лыжах, поэтому наивыгоднейшее удельное давле-
ние на снег от трактора и прицепок не должно превышать удель-
ного давления лыжника.
Удельное давление лыжника среднего веса (75 кг), идущего на
лыжах марки «raqutte», около 0,1 кг/см2. На этих лыжах можно
двигаться главным образом по снегу, покрытому легкой коркой.
Чтобы двигаться по рыхлому снегу, удельное давление должно
быть еще меньше. Так, аэросани имеют удельное давление по-
рядка 0,04—0,06 кг/см2. Этому удельному давлению соответствует
резкое падение коэффициента несущей способности а (см. рис. 150).
В США несколько лет назад испытывались гусеничные снего-
ходы с средним удельным давлением гусениц q = 0,035 кг!см2. Это
были специальные машины, предназначенные для связной и раз-
ведывательной службы в северных районах страны.
Машины этого типа чаще всего имеют резиновые гусеницы, хотя
бывают машины и с металлическими гусеницами обычного типа.
В снегоходах общего пользования с металлическими гусени-
цами удельное давление обычно находится в пределах 0,15—
0,20 кг!см2.
Движение гусеничной машины по болоту в основном анало-
гично движению ее по снегу, однако имеются здесь и некоторые
особенности. Болото иногда может быть покрыто довольно проч-
ным травяным покровом, обладающим несущей способностью, до-
статочной, чтобы выдержать вес легкой гусеничной машины. В этом
случае проходимость определяется уже не только удельным давле-
нием гусениц на грунт, но и непосредственно весом машины.
Если на болоте травяного покрова нет, то болото преодоле-
вается так же, как и рыхлый снег, и проходимость машины опреде-
ляется только удельным давлением.
Для определения проходимости гусеничных машин по болоту
трудно дать какие-либо количественные зависимости, так как под
понятием «болото» подразумеваются самые разнообразные грунты
с различной несущей способностью. Практически применяется сле-
дующее правило преодоления болот. Если под ногой чело-
века не выступает вода, то такое болото для гу-
сеничной машины преодолимо.
Так как удельное давление ноги человека составляет 0,5—
0,6 кг/см2, то указанное правило определяет проходимость болот
при таком же среднем удельном давлении гусениц.
Следует, конечно, иметь в виду, что это правило весьма условно.
Однако точнее проходимость по болоту определяется в каждом
конкретном случае только опытным путем.
Проходимость по мягким грунтам зависит от конструкции
гусеничного движителя. Как уже отмечалось выше, сред-
нее удельное давление в гусеничных машинах может значительно
отличаться от действительного. Чем ближе действительное удель-
ное давление будет к среднему, тем выше будет проходимость ма-
шины.
274
Действительное удельное давление зависит от ширины и шага
траков, от диаметра и числа опорных катков машины, а также от
эпюры нагрузок на катки.
Чем больше ширина и шаг траков, а также число опорных кат-
ков (см. рис. 143), тем ближе действительное удельное давление
к среднему удельному давлению.
На проходимость оказывает влияние эпюра нормальных нагру-
зок на грунт. Чем ближе эпюра к прямоугольной, тем ближе дей-
ствительное удельное давление к среднему. Опыт показывает, что
некоторая перегрузка задних опорных катков не ухудшает прохо-
димость машины по мягким грунтам. Наоборот, перегрузка перед-
них опорных катков приводит к зарыванию их в грунт и тем самым
к ухудшению проходимости машины.
Действительное удельное давление зависит также от натяжения
гусениц. С увеличением натяжения гусениц нагрузка на грунт не-
сколько уменьшается и удельное давление выравнивается.
Гусеничный тягач работает обычно с колесным прицепом. Чтобы
проходимость прицепа и тягача были одинаковы, прицеп должен
быть поставлен на полозья.
Движение полозьев по мягким грунтам характеризуется двумя
величинами: удельным давлением полозьев на грунт (<?) и коэф-
фициентом сопротивления скольжению их по грунту (р.).
В табл. 18 приведено значение удельного давления q и коэффи-
циента р. для деревянных ошипованных полозьев.
Таблица 18
Удельное давление и коэффициент сопротивления скольжению
ошинованных полозьев по снегу
Состояние снега Глубина залегания, мм Наружная температура, ° С Удельное давление полозьев, кг!см2 и*
Свежий 450 + 1 0,13 0,13
Свежий 220 4-1 0,15 0,11
Старый 140 4-2 0,16 0,09
Твердая дорога 400 — 1 0,18 0,04
Из табл. 18 следует, что коэффициент сопротивления скольже-
нию по рыхлому снегу составляет примерно 0,1, по твердой до-
роге — 0,04.
Удельное давление полозьев на мягком неслежавшемся снег}
составляет 0,13—0,15 кг/см2.
Если бы гусеницы передавали на снег равномерно распреде-
ленное давление, то при расчете машины удельное давление гусе-
ниц можно было бы принимать таким же, как и для полозьев. Так
как действительное удельное давление выше среднего удельного
давления, то для гусениц среднее удельное давление следует при-
нимать ниже удельного давления полозьев.
* В коэффициент (1 входит и лобовое сопротивление движению полозьев.
18* 275
3. ПРЕОДОЛЕНИЕ КРУТЫХ ПОДЪЕМОВ
При движении на подъем гусеничного поезда или одиночной
машины к сопротивлению качения добавляется составляющая веса
машины, параллельная плоскости дороги. Сила же тяги по сцеп-
лению, которая должна обеспечивать движение машины, при этом
падает, так как на подъеме уменьшается сцепной вес машины
(Gc=Gcosa вместо Ос = G на горизонтальном участке пути).
Таким образом, крутые подъемы могут являться значительным
препятствием на пути движения гусеничной машины.
Определим предельные углы подъема, которые может преодо-
левать гусеничный поезд по условиям сцепления и по двигателю.
Угол подъема по сцеплению обозначим через ас, а угол подъ-
ема по двигателю — через ад.
Определяем силу сопротивления равномерному движению
поезда на подъеме
7?оп = (О + GJ sin а + (/G + /Д) cos а.
Приравниваем это сопротивление силе тяги по сцеплению
Рс = <f>Ocosa.
После преобразования получим
tg«c =-------(258)
1 +
Приравняем теперь сопротивление ROn силе тяги по двигателю
Ря =
где ?д—удельная сила тяги по двигателю, определяемая по фор-
муле (249).
После преобразования получим
COS а. 7 71 G
tg “д =---------G------• (259)
' + ~б~
Подставляя в формулу (249) расчетные скорости на передачам
1>р получим значение на передачах удельной силы тяги. Тогда по
формуле (259) находим значения углов подъема по двигателю.
Формула (259) внешне похожа на формулу (258). В ней только
вместо коэффициента сцепления <р подставлена величина
Угол ац из формулы (259) определяется методом последователь-
ного приближения *. Для этого принимаем вначале cos % = 1, после
чего по формуле (259) определяем в первом приближении tga;i и,
276
следовательно, угол ад. Далее по этому углу вычисляем cos ад
и подставляем его значение в формулу (259). Из формулы нахо-
дим новое значение tgafl и новое значение угла ад и т. д.
Обычно при решении задачи бывает достаточно сделать одно —
два приближения.
Пример. Определим максимальный угол подъема гусеничного поезда для
следующих данных: Ne =112 л.с.; G = 9000 кг; vmin = 4,5 км/час; G,=
= 5000 кг; = 0,7; / = 0,08; Л = 0,04.
Задаемся »] = 0,8.
Из формулы (258) определяем угол подъема по сцеплению:
tg а<
0,7-0,08-0,04™
5000
1 + 9000
= 0,39,
откуда ас = 21°20'.
Определим угол подъема по двигателю.
Сначала по формуле (249) находим
АС 112
П max = 0,27-9 —= 0,27-0,8 = 0,596.
*д max ’ • at ’ ’ п,д 5 ’
vmin v
Принимаем в формуле (259) в первом приближении соьад = 1 и получаем
_ 0.596-0,«8-0.04™
tg - 5000 ~ О-32-
1 + 9000
Тогда ад = 18,5°, откуда cos 18,5° = 0,948.
Подставим в формулу (259) величину cos 18,5; получим
tg“a =
0,596 . А. ... 5000
W - °’08 - °’04 9000
5000
1 + 9000
= 0,34,
|>ткуда ад = 19°.
£ Таким образом, при решении задачи можно было бы ограничиться первым
Приближением, так как уточнение угла дало всего 0,5°.
| Из сравнения углов «с и яд следует, что предельный подъем определяется
|Глом подъема по двигателю, равным 19°.
ПРЕОДОЛЕНИЕ ПОДЪЕМА ПО КОСОГОРУ
Крутой подъем обычно преодолевается перпендикулярно к его
Снованию, или, как говорят, в лоб.
В том случае, когда сцепления гусениц с грунтом недостаточно
|ля преодоления подъема в лоб, этот подъем можно попытаться
Преодолеть наискось к основанию, т. е. покосогору.
* Угол ад можно определить также, решив квадратное уравнение. Однако
^Роще пользоваться методом последовательного приближения.
277
Рассмотрим движение одиночной машины на подъем с курсо-
вым углом ₽<90° к основанию подъема (рис. 151, а).
Разложим по правилу параллелепипеда силу веса G по осям
координат х, у и z (рис. 151,6). Будем иметь
Gx — О' sin [3 = О sin а sin [3;
Оу — О cos 3 = G sin а • cos [3;
Gz — Geos a.
При движении на машину действует поперечная сила Оу. Эта
сила вызывает поперечные реакции грунта (см. рис. 151, а). Будем
Рис. 151. Движение машины по косогору:
а — вид сверху; б — аид сбоку; в — разложение силы веса
по правилу параллелепипеда
считать, что между гусеницами и грунтом действуют только силы
кулонова трения, величина которых характеризуется некоторым
коэффициентом трения скольжения рс.
Условие несползания машины в поперечном направлении запи-
шется следующим неравенством:
Gy ^cGz,
где Gz—сцепной вес машины.
Предельное значение Gy = ycG2'. Подставляя в это уравнение
Gy и Gz, после преобразования получим
COS р = .
г tg«
(260)
278
Из этой формулы следует, что чем больше угол подъема дороги
(рис. 151,6), тем большим должен быть и курсовой угол 0.
Вторым условием движения машины на подъем должно быть
обеспечение силы тяги по сцеплению:
РсЖо,
где
Рс = ср Gz;
R0 = Gx + fGz.
После преобразования получим
tg a- sin [3 < ? —f.
Предельное выражение этого неравенства будет
tga-sin р = ср— /,
откуда
sin?=ni^- . (26D
Сравнивая эту формулу с формулой (260), видим, что для обе-
спечения продольного сцепления гусениц с грунтом при увеличении
угла подъема а курсовой угол 0 должен уменьшаться, а для обе-
спечения поперечного сцепления, наоборот, увеличиваться.
Возведем в квадрат sin [3 и cos 0 в формулах (260) и (261) и
сложим левые и правые части равенств.
Получим после преобразования
tg «с = + (?—/)2. (262)
где ас — предельный угол подъема по продольному и поперечному
сцеплению.
Действительный угол а должен быть меньше углаас.
Пример. Определим предельный угол подъема, который сможет преодо-
леть машина при движении с курсовым углом ₽ = 90° и ₽ < 90° (по косо-
гору).
Дано: рс = 0,5; = 0,7; /=0,08.
Определим вначале угол а при курсовом угле ₽ = 90°.
-Из формулы (261) получим
tg а = tp — / = 0,7 — 0,08 = 0,62, или а = 32°.
Из формулы (262) определяем угол ас при 3 < 90° (движение по косо-
гору) :
tgac = J/0,52 + 0,622 = 0,63, или ас = 39°.
Из полученных данных следует, что при движении по косогору машина
может преодолеть подъем на 7° больше, чем при движении с курсовым углом
₽ = 90°, т. е. в лоб.
Из формулы (260) определяем, с каким курсовым углом должна при этом
Двигаться машина:
cos ₽ = =. JL5 = или = 52„
tg a tg 39° 1 1 г
279
Таким образом, видим, что преодолевать крутой подъем, дви-
гаясь по косогору, иногда бывает выгоднее, чем двигаясь перпен-
дикулярно к его основанию.
Все эти выводы относятся к одиночному тягачу. Гусеничный
поезд должен преодолевать подъем всегда в лоб.
ОПЫТНЫЕ ДАННЫЕ ПО ПРЕОДОЛЕВАЕМЫМ
ГУСЕНИЧНЫМИ МАШИНАМИ УГЛАМ ПОДЪЕМА
Ниже приводятся некоторые опытные данные по углам подъ-
ема, которые могут преодолевать одиночные гусеничные машины
и тягачи с колесным прицепом.
В табл. 19 приведены предельные углы подъема для одиноч-
ных машин, движущихся в различных дорожных условиях.
Таблица 19
Предельные углы подъема, преодолеваемые одиночными
гусеничными машинами
Характер грунта
Предельный угол подъема
в градусах
Плотный грунт, покрытый дерном...........
Плотный песчаный грунт....................
Грунт, покрытый травой (после дождя) . . . .
Снег плотный глубиной 250—300 мм..........
Обледенелый снежный покров глубиной 50—
100 мм..................................
Обледенелый грунт. Машина с дополнитель-
ными шпорами .............................
30—35
25—30
20—25
20—25
10—15
До 20
В табл. 20 приведены предельные углы подъема для современ-
ных тягачей и сельскохозяйственных тракторов, где атах — угол
подъема одиночной машины с полной нагрузкой, атах —угол подъ-
ема тягача с штатным прицепом.
Таблица 20
Предельные подъемы, преодолеваемые одиночной машиной и тягачом
с штатным прицепом
Угол подъема Марка машины
М-2 АТ-Т АТ-С АТ-Л АТ-П СТ 3-3 С-65 ДТ-54
“тах> град- 30 30 30 35 35 30 30 30
“max. град- 18 25 17 25 25 15 15 17
Из табл. 20 следует, что тягачи и сельскохозяйственные трак-
торы преодолевают подъемы порядка 30—35°. Выше указывалось,
280
что в этих машинах сила тяги по сцеплению полностью не реали-
зуется; следовательно, приведенные в таблице углы являются
углами подъема по двигателю, а не по сцеплению.
Если на машине имеется лебедка, то она может быть использо-
вана как вспомогательное средство для преодоления крутых подъ-
емов. Для этого следует закрепить трос лебедки за анкер, уста-
новленный на верхней горизонтальной площадке подъема.
Если подъем преодолевается отдельным тягачом, но не преодо-
левается поездом, то следует отсоединить прицеп и после того, как
Рис. 152. 3 атягивание машины на подъем с помощью блока и
тягача
тягач преодолеет подъем, подтянуть прицеп с помощью лебедки или
самого же тягача. Так как тягач движется в этом случае по гори-
зонтальному участку пути, его сцепного веса может оказаться до-
статочно для создания силы тяги, необходимой для вытягивания
прицепа.
На рис. 152 показано преодоление крутого подъема с помощью
второго тягача и блока.
Машина 1 движется на подъем, развивая силу тяги. Кроме того,
ей помогает машина 2. После того как машина 1 поднимется на
верхнюю горизонтальную площадку подъема, она может вытянуть
на подъем и машину 2. В этом случае блок уже не потребуется.
4. ПРЕОДОЛЕНИЕ ПОРОГОВЫХ ПРЕПЯТСТВИЙ
На рис. 153 показано преодоление гусеничной машиной поро-
гового препятствия.
Преодоление порогового препятствия можно разбить на сле-
дующие четыре этапа.
Машина подходит к препятствию и упирается передней дуго-
вой ветвью гусениц в ребро препятствия (1-й этап, рис. 153, а). На
281

Рис. 153. Преодоление одиночной машиной
порогового препятствия:
а — первый этап преодоления препятствия; б — вто-
рой этап преодоления препятствия; в — третий этап
преодоления препятствия; г —четвертый этап прео-
доления препятствия
дуговой ветви создается сила
зацепа Р3, и одновременно
на опорную ветвь действует
сила тяги Р. Под действием
этих двух сил передняя
часть машины приподнимает-
ся и машина продвигается
вперед (2-й этап, рис. 153,6).
Если препятствие такой
высоты, что центр тяжести с
машины при движении ее
вперед окажется в плоскости
вертикальной стенки порога
(3-й этап, рис. 153, в), то
препятствие будет преодо-
лено (4-й этап, рис. 153, г).
Может, однако, оказаться,
что прежде чем точка с дой-
дет до вертикальной стенки,
заглохнет двигатель или за-
буксуют гусеницы. В этом
случае препятствие окажет-
ся непреодолимым.
Определим наибольшую
высоту преодолеваемого гу-
сеничной машиной порого-
вого препятствия. Допустим,
что гусеничный обвод и реб-
ро порога не деформиру-
ются.
При преодолении порога,
расположенного на горизон-
тальном участке пути, маши-
на становится под некото-
рым углом к горизонталь-
ной плоскости дороги. Чем
выше порог, тем этот угол
будет больше. В третьем
этапе преодоления порога
каждой высоте порога соот-
ветствует определенный угол
наклона машины, под кото-
рым этот порог преодоле-
вается, и, наоборот, каждому
углу наклона машины соот-
ветствует определенная высота преодолеваемого порога. Это по-
зволяет определить высоту порога графически.
Изобразим в масштабе часть гусеничного обвода: опорную
ветвь, заднюю наклонную и заднюю дуговую ветвь (рис. 154). На-
282
несем на график центр тяжести машины (точка с). Из центра тяже-
сти проведем несколько лучей 1, 2, 3 и т. д. Перпендикулярно этим
лучам проведем касательные к обводу Г, 2', 3' и т. д.
Отрезки Я161, а2б2 и т. д. будут изображать в масштабе вы-
соту порога, который может преодолеваться машиной при соответ-
ствующих углах наклона оц, «2 и т. д.
Для определения максимальной высоты преодолеваемого по-
рога повернем отрезки aidi, а2б2 и т. д. вертикально и соединим
их концы плавной кривой. Максимальная ордината этой кривой и
будет максимальной высотой порога, преодолеваемого машиной
по расположению центра тяжести (Ап).
Высоте порога Ап соответствует определенный угол наклона
машины. Машина может преодолеть этот порог, если угол наклона
будет меньше угла наклона по сцеплению и по двигателю. Действи-
тельно, в третьем этапе преодоления порога на машину действуют
те же силы, что и при преодолении соответствующего подъема. Раз-
ница заключается только в том, что при движении на подъем ма-
шина опирается на грунт всей опорной поверхностью своих гусе-
ниц, а при преодолении порога — лишь на ребро порога. Это, ко-
нечно, как-то влияет на величину коэффициента сопротивления ка-
чению и на коэффициент сцепления. В основном действуют те же
силы, что и при преодолении подъема. Поэтому в данном случае
могут быть применены формулы (258) и (259), по которым опре-
деляются углы подъема машины по сцеплению и по двигателю.
Следует только принять в них G± = 0.
Рис, 154. Графическое определение высоты преодолеваемого порога
283
Тогда получим
tg»c = ?—/;
(263)
tga_A^__/ (264)
Отсюда можем найти углы ас и ац. Откладываем величину этих
углов на графике (рис. 154) и находим соответствующие высоты
преодолеваемого порога /гпс и Апд. Из трех полученных величин Лп,
Лпс и Апд выбираем меньшую. Это и будет высота преодолеваемого
порога по положению центра тяжести, по сцеплению или по дви-
гателю.
Так как при преодолении порога гусеница опирается на грунт
только частью своей опорной поверхности, то коэффициент сцепле-
Рис. 155. Определение
графическим способом
высоты преодолеваемого
порога по сцеплению
ния <р в формуле (263) следует принимать несколько меньшим, чем
в обычных тяговых расчетах. Ориентировочно можно рекомендо-
вать ас = 25 — 30°. Этот угол, как правило, меньше ад и меньше
угла по положению центра тяжести. Тогда расчетной высотой пре-
одолеваемого порога будет высота Апс.
Величина Апс определяется простым геометрическим построе-
нием, как показано на рис. 155.
Для этого из центра тяжести проводится наклонный луч под
утлом ас к вертикали. Перпендикулярно этому лучу проводятся две
прямые: одна в точке пересечения луча с опорной ветвью гусеницы,
другая — касательно к обводу. Отрезок между этими линиями и
будет высотой преодолеваемого порога по сцеплению Апс.
Рассмотрим влияние на высоту преодолеваемого порога положе-
ния центра тяжести.
На рис. 156 показаны четыре смещенных положения центра тя-
жести: с — нормальное положение центра тяжести, 1 — смещение
вперед, 2 — смещение назад, 3 — смещение вверх и 4 — смещение
вниз.
284
Определяем построением для этих четырех положений высоту
порога по сцеплению ЛГ], > hni > ЛГ1Я > Лп2. Следовательно, высота
преодолеваемого порога тем больше, чем больше вперед вынесен
центр тяжести машины и чем ниже он расположен.
Рис. 156. Влияние на высоту преодолеваемого
порога положения центра тяжести
На высоту преодолеваемого порога влияет наклон задней ветви
обвода. Чем меньше угол наклона задней ветви, тем выше будет
преодолеваемый порог. На рис. 156 пунктиром показан обвод с не-
Рис. 157. Графическое определение высоты преодолеваемого
порога, расположенного на подъеме дороги
сущим направляющим колесом, опирающимся на землю. Из ри-
сунка видно, что высота порога резко возрастает при неизменном
положении центра тяжести.
285
На высоту преодолеваемого порога влияет также угол местно-
сти. Если порог расположен на подъеме, то высота преодолеваемого
порога уменьшается, если порог расположен на спуске, наоборот,—
увеличивается.
На рис. 157 показано определение высоты преодолеваемого по-
рога, расположенного на подъеме а.
Мы рассмотрели преодоление порогового препятствия одиноч-
ной гусеничной машиной. Если препятствие преодолевается тяга-
чом, имеющим коле'сный прицеп, то предельная высота порога
определяется проходимостью колесного прицепа. Колесный прицеп
может преодолевать порог, равный примерно 2/3 радиуса его ко-
лес. Даже при довольно больших колесах, равных в диаметре од-
ному метру, высота преодолеваемого порога составит всего 300 мм.
Это почти в три раза меньше высоты порога, преодолеваемого гу-
сеничной машиной.
Основным вспомогательным средством преодоления порога слу-
жат аппарели. Для получения аппарели срывают ребро порога, как
указано на рис. 158. При срытии ребра порог превращается в
----------
30-35°
Рис. 158. Аппарель
подъем. Угол подъема следует делать 30—35°. При меньшем угле
увеличиваются земляные работы, при большем — машина может
не преодолеть подъем по двигателю или по сцеплению.
Кроме аппарели, как вспомогательное средство могут приме-
няться колейные мосты или фашины.
5. ПРЕОДОЛЕНИЕ РВОВ
Ров одиночная гусеничная машина преодолевает следующим об-
разом. Продвигаясь вперед, машина вывешивается своей передней
частью над рвом (рис. 159). Когда центр давления й, лежащий на
одной вертикали с центром тяжести машины, переместится за край
рва, машина начнет опрокидываться в ров. Если ширина рва будет
такова, что при опрокидывании гусеницы перекроют ров, то центр
давления окажется снова внутри опорной базы машины и равнове-
сие восстановится. Машина сможет продолжать движение. Ров бу-
дет преодолен, если центр давления окажется за передним краем
рва раньше, чем задняя часть гусениц оторвется от грунта.
Ширина преодолеваемого рва теоретически определяется наи-
меньшим расстоянием от центра давления до крайней точки перед-
286
ней или задней дуговой ветви гусеничного обвода (Zmin). Практи-
чески эта величина должна быть уменьшена, чтобы гарантировать
перекрытие рва гусеницами.
Обозначим через Zp ширину преодолеваемого рва. Тогда можно
принять
Zp = 0,8Zmin. (265)
Если корпус машины выступает за габариты гусеничного об-
вода, то величину Zmin следует определять от центра давления до
выступающей части корпуса.
выступающая часть корпу-
са не должна быть распо-
ложена слишком высоко
над грунтом, так как ма-
шина будет сильно накре-
няться вперед (или назад)
и может застрять на пре-
пятствии.
Для преодоления наи-
большей ширины рва
центр тяжести машины
должен располагаться по-
средине ее опорной базы.
Для тягачей это усло-
вие обычно не выполняет-
При этом необходимо учитывать, что
ся, так как центр тяжести Рис. 159. Преодоление рва одиночной машиной
их бывает смещен не-
сколько вперед для того, чтобы при работе тягача с прицепом (при
наличии силы тяги на крюке) получить равномерную нагрузку на
опорные катки.
При преодолении рва одиночной машиной может быть исполь-
зована сила инерции поступательного движения.
При подходе тягача ко рву резко увеличивают подачу горючего,
вследствие чего появляется сила инерции /, которая смещает центр
давления k назад (рис. 160).
После того как передние ветви
Рис. 160. Использование силы инерции
при преодолении рва
гусениц окажутся на противо-
положной стороне рва, маши-
на сможет двигаться равно-
мерно, центр давления в этом
случае снова займет прежнее
положение, совпадающее по
вертикали с положением центра
тяжести с.
Если ров преодолевается
тягачом с одноосным колесным
прицепом, то проходимость
поезда определяется проходи-
мостью колесного прицепа.
287
Предельная ширина рва, которую сможет преодолеть колесный
прицеп, примерно равна радиусу колеса прицепа. Проходимость гу-
сеничного поезда при наличии колесного прицепа резко снижается.
Вспомогательными средствами преодоления рвов являются за-
сыпка рва, колейные мосты или аппарели.
Эти средства позволяют преодолевать ров как одиночной маши-
ной, так и поездом.
6. ПРЕОДОЛЕНИЕ КРУТЫХ СПУСКОВ
Крутой спуск — опасное препятствие. Неосторожное движение
на крутом спуске легко может вызвать аварию машины.
КРИТИЧЕСКАЯ СКОРОСТЬ ПО ОПРОКИДЫВАНИЮ
При движении на спуске центр давления опорных ветвей гусениц
на грунт смещается вперед,' уменьшая устойчивость машины
(рис. 161, а). Если по какой-либо причине изменится сопротивление
движению машины (например, машина наедет на препятствие), то
возникнет сила инерции /,
Рис. 161. Преодоление крутого
спуска:
а — равномерное движение, б — на-
езд на препятствие
направленная вперед (рис. 161,6).
Центр давления в этом случае вы-
ходит за опорную поверхность гусе-
ниц и машина теряет устойчивость.
Если машина благополучно про-
шла спуск, то в месте перехода
Рис. 162. Опрокидывание машины
в конце спуска
наклонной плоскости дороги в горизонтальную она все же может
опрокинуться. Сопротивление движению в этом случае резко воз-
растает, так же как при переходе с горизонтального участка пути
на подъем. Увеличение сопротивления вызывает появление силы
инерции и возможность потери устойчивости или даже опрокиды-
вание.
288
Выше уже отмечалось, что потеря устойчивости и опрокидыва-
ние — это не одно и то же. Чтобы машина опрокинулась, она
должна обладать достаточным запасом кинетической энергии, спо-
собным поднять центр тяжести машины в вертикальное положение,
после чего центр тяжести перейдет за точку опоры п и машина
опрокинется (рис. 162).
Рассмотрим опрокидывание машины в конце спуска (где опро-
кидывание наиболее вероятно). Примем некоторые допущения.
Допустим, что подвеска машины жесткая, грунт недеформи-
руется и точка п не перемещается по грунту. Тогда вся кинетиче-
ская энергия поступательного движения машины затратится на
подъем ее центра тяжести. Машина опрокинется, если центр тяже-
сти займет наивысшее положение, т. е. расположится по вертикали
над точкой п.
Работа, которая затрачивается на подъем центра тяжести, бу-
дет равна hG. Приравняем эту работу кинетической энергии ма-
шины. Тогда получим критическую скорость движения
машины по опрокидыванию
г^р = V 2gh, (266)
где h — высота подъема центра тяжести.
Величина h может быть определена из геометрического построе-
ния (см. рис. 162):
h = Vai + b'1 — a cos а — ^sina. (267)
Полученная по формуле (266) величина критической скорости
несколько уменьшена, так как часть кинетической энергии расхо-
дуется на деформацию грунта при ударе, а часть — на скольжение
точки п по грунту. Этими потерями, однако, пренебрегаем и ведем
.расчет с некоторым запасом устойчивости.
Пример. Определим критическую скорость движения машины на спуске,
если а = 0,5 м\ 6 = 1,5 м\ a = 30°.
Из формулы (267) находим
Л = J/0)52 + 1,52 — 0,5-0,87 — 1,5-0,5 = 0,4 м.
Тогда
vKp = 1/2-9,81-0,4 =2,8 м/сек, или .10 км/час.
Отсюда следует, что если скорость в конце спуска будет равна или больше
10 км/час, то машина может опрокинуться.
ТОРМОЖЕНИЕ МАШИНЫ НА СПУСКЕ
Чтобы машина не опрокинулась на спуске, она должна дви-
гаться равномерно и со скоростью, меньшей критической.
Равномерное движение обеспечивается торможением ма-
шины. Рассмотрим различные способы торможения.
19—2469 2 89
Допустим, что движители тягача и прицепа полностью затормо-
жены. Если поезд равномерно скользит под уклон, то сила сопро-
тивления движению будет
Яоп = (?+/) Geos a+ (<f>! +/i)GjCosa,
где <f>(7cosa —касательное сопротивление тягача;
fG cos a—лобовое сопротивление тягача;
^(/jCosa —касательное сопротивление прицепа;
/jC/jCosa —лобовое сопротивление прицепа.
Сила, которая движет поезд, есть сумма составляющих веса
тягача и прицепа, параллельных дороге, т. е.
Osin а -|- sin a.
Приравняем эту силу силе сопротивления движению. После пре-
образования получим угол наклона дороги, при котором возможен
равномерный спуск поезда с полностью заторможенным движите-
лем тягача и прицепа:
¥ + f + (?i +/i)
tga =----,---- -----(268)
1 +
Из этой формулы можно получить некоторые частные формулы
движения поезда под уклон.
1. Движение поезда под уклон без торможе-
ния тягача и прицепа.
Принимаем ® = 0; 'fi='O. Получаем
Примем Gi = G; f — 0,08; /j = 0,04. Получим a = 3,5°. Для оди-
ночного тягача будем иметь a = 4,5°. В первом случае тягач подтал-
кивается колесным прицепом, так как сопротивление качению при-
цепа меньше сопротивления качению гусеничного тягача.
На уклоне примерно в 4° и более поезд или одиночный тягач
нужно притормаживать, чтобы он двигался равномерно.
2. Оба движителя полностью заторможены.
Примем ® = 0,8; ?i = 0,5.
Из формулы (268) получим для поезда a = 35,5° и для одиноч-
ной машины a = 41,5°.
3. Если прицеп не имеет тормозов, то при <pi = 0
a = 25°.
Следовательно, при торможении прицепа значительно увеличи-
вается угол равномерного спуска поезда.
Равномерный спуск поезда с прицепом, имеющим торможение,
290
возможен при углах Наклона дороги примерно 4—35°. Равномерный
спуск одиночной машины возможен при углах 5—-40°.
Если спуск затяжной, то торможение поезда с помощью тормо-
зов может вызвать их перегрев. Поэтому на затяжных спусках
поезд следует тормозить двигателем.
Определим предельный угол равномерного спуска при торможе-
нии двигателем.
Обозначим тормозную мощность двигателя, т. е. мощность, иду-
щую на проворачивание коленчатого вала неработающего двига-
теля со стороны силовой передачи, через NT. Пусть NT = &Ne, где
Ne—паспортная мощность двигателя; е — эмпирический коэффи-
циент тормозной мощности.
На гусеницах тягача будет создаваться тормозная сила
Р =
Т ’ll'p ’IVp ’
где г'р — расчетная скорость на передаче.
Подставим во второе уравнение динамики тягача [формула (35)]
вместо силы тяги по двигателю (Рд) тормозную силу (— Рт) и при-
dv _
равняем ускорение нулю. Получим
— RT — Ro — RK = 0.
Для прицепа будем иметь
— — Rot + Rki = 0.
Сложив оба равенства и учтя, что RK = RKl, получим
Pt + Ro "Е Рц + Roi=
Ro= /Geos а — Gsina;
Rot — ftPt cos a — sin a-
Отсюда находим угол равномерного спуска поезда при тормо-
жении тягача двигателем:
Рт + Pfi . f f <?1
. G cos ct/p G
tg aT =-------1------------. (269)
1 + 7Г
Угол aT находится методом последовательного приближения
(см. раздел 3 «Преодоление крутых подъемов»).
Из формулы (269) следует, что чем ниже включена передача
(меньше скорость г'р), тем больше угол равномерного спуска ма-
шины.
Заметим, что расчетной скорости vf соответствуют вполне опре-
19* 291
деленные расчетные обороты двигателя, при которых двигатель бу-
дет давать расчетную тормозную силу Рт.
Поэтому, чтобы получить полное торможение двигателем, спуск
надо производить на расчетной или близкой к расчетной скорости.
Так как низшая передача имеет очень малую расчетную ско-
рость— 4—5 км/час, то при спуске эту скорость легко можно пре-
высить, причем водитель может и не заметить это превышение. Обо-
роты двигателя превысят расчетные, а это может привести к его
аварии. Поэтому спуск следует производить не на низшей передаче,
а на следующей за ней, причем скорость на этой передаче должна
быть меньше критической по опрокидыванию.
Для определения угла ат необходимо знать коэффициент тор-
мозной мощности е и тормозную силу прицепа Рп.
Ориентировочно коэффициент е находится в пределах 0,3—0,5.
Тормозная сила Рт] зависит от устройства тормозов прицепа. При
полном торможении прицепа Рт] = %ОС1, где ®i — коэффициент
сцепления движителя прицепа с грунтом, <7с1 — сцепной вес при-
цепа. Если прицеп не притормаживается, то Рп — 0.
Заметим, что коэффициент тормозной мощности г зависит от
тормозных потерь, происходящих в двигателе. Потери эти зависят
от механического трения и главным образом от термодинамических
потерь сжимаемого и выбрасываемого из цилиндров двигателя воз-
духа. Термодинамические потери увеличиваются, если перекрыть
выпускную трубу двигателя заслонкой и тем увеличить сопротивле-
ние выбросу воздуха.
Пример. Определим угол равномерного спуска при торможении тягача
двигателем.
Примем: е = 0,3; Ые = 112 л. с.; т; = 0,8; vp = 15 км/час, РТ1 = 0; G —
= 9000 кг; G. = 5000 кг. Задаемся f = 0,08 и Л = 0,04.
В первом приближении считаем cos ат = 1.
Тогда
tgaT
5000
9000
= 0,12.
Из этого выражения а = Т. Так как cos 7° = 0,9925, т. е. величине, близкой
к единице, то вторую подстановку можно не делать.
Проверим на критическую скорость возможность движения одиночного тя-
гача со скоростью 15 км/час на спуске при а = 7°.
Примем а = 0,5 л; 6 = 1,5 м. Тогда по формуле (267) находим
h = J/6?52 + 1,52 — 0,5-0,99 — 1,5-0,12 = 0,9 м.
Из формулы (266) получим
vKp — J/2-9,81 -0,9 = 4,2 м/сек, или vKp = 15 км/час.
Таким образом, критическая скорость равна скорости спуска. Учитывая,
что при 7-градусном спуске дорога не может резко перейти с уклона на горизон-
тальный участок, а также учитывая, что формула (266) была выведена с неко-
торым запасом, можно допустить спуск машины со скоростью, равной крити-
ческой. - -
292
Чтобы не потерять управление машиной, на спуске не рекомен-
дуется останавливать двигатель. Двигатель должен работать, но с
минимальной подачей горючего. В этом' случае машина всегда смо-
жет продолжить движение после преодоления спуска.
Кроме торможения машины механическими тормозами или дви-
гателем, возможно и комбинированное торможение — и тормозами
и двигателем. Это наиболее эффективный способ торможения ма-
шины, при котором тормоза имеют наименьший износ.
Комбинированное торможение, однако, возможно не на всех ма-
шинах. Например, оно невозможно на машинах, у которых, прежде
чем затормозить гусеницы, нужно предварительно отключить их от
двигателя.
Заметим, что при крутом спуске особенно опасен поворот ма-
шины, так как поперечная устойчивость машины значительно
меньше продольной. Поэтому необходимо следить, чтобы спуск ма-
шины происходил строго перпендикулярно к основанию спуска.
7. ПРЕОДОЛЕНИЕ ЛЕДЯНЫХ ПРЕПЯТСТВИЙ
Для движущейся машины лед на реке или озере представляет
мост, опирающийся на воду (плавающий мост). Если бы воды
подо льдом не было, то одни береговые припаи не смогли бы удер-
жать тяжелую массу льда. Лед в виде висячего моста, не опираю-
щегося на воду, встречается только на узких речках шириной в не-
сколько метров. Переправа по такому льду опасна независимо от
его толщины.
В начале весны, когда вода спадает и уходит из-под льда, следует
особенно осторожно преодолеватьзамерзшиеводоемы. Перед въездом
на лед, необходимо тщательно разведать, опирается ли лед на воду.
Следует иметь в виду, что трещины на льду у берегов не яв-
ляются препятствием для переправы. Наоборот, наличие трещин
показывает, что вследствие убыли воды из-подо льда он не выдер-
жал собственной тяжести и осел на воду.
Лед трескается и зимой в сильные морозы вследствие большой
разности температур между льдом и окружающим воздухом. На
Байкале, например, трещины зимой иногда доходят до двух метров.
Наличие трещин и в этом случае не является препятствием для пе-
реправы. Трещины следует перекрыть прочным деревянным настилом.
Для выяснения возможности переправы необходимо рассчитать
грузоподъемность льда.
Грузоподъемность в первом приближении может быть
определена по следующим формулам*:
(27°)
_________ (271>
* Более точные формулы приводятся в соответствующих специальных спра-
вочниках и руководствах.
293
где Gr — грузоподъемность льда в тоннах при движении по льду
гусеничной машины;
GK — грузоподъемность льда в тоннах при движении по льду
колесной машины;
h — толщина прозрачного слоя льда в сантиметрах.
Если гусеничным тягачом буксируется гусеничный прицеп, то в
формулу (270) следует подставить сумму весов тягача и прицепа.
При буксировке гусеничным тягачом колесного прицепа в расчет
необходимо ввести суммарный вес поезда, определяя грузоподъем-
ность льда по формуле (271). При этом расчет будет произведен со
значительным запасом.
Формулы (270) и (271) справедливы только для льда пресно-
водных водоемов. Грузоподъемность льда соленых водоемов при-
мерно в три раза меньше.
Если пр льду переправляется колонна машин, то между двумя
соседними машинами должны выдерживаться следующие дистан-
ция и интервал:
для гусеничных машин
(272)
для колесных машин
= % + 6, (273)
где dr — расстояние между двумя соседними гусеничными маши-
нами в метрах;
dK — расстояние между двумя соседними колесными маши-
нами в метрах;
Gr — вес гусеничной машины в тоннах;
GK — вес колесной машины в тоннах..
При выполнении указанного условия напряжения, возникающие
в толще льда от двух соседних машин, не складываются и не дают
повышенного суммарного напряжения. Если расстояния между ма-
шинами выдерживаются согласно формуле (272) или (273), то не
имеет значения, идет ли по льду одиночная машина или колонна
машин.
Для расчета ледяной переправы следует знать толщину льда на
трассе. Для этого по обе стороны трассы делают проруби на рас-
стоянии примерно 25 м одна от другой, очищают лед от слежавше-
гося слоя снега и замеряют толщину h прозрачного льда (рис. 163).
Вспомогательным средством для преодоления ледяных препят-
ствий служит намораживание льда.
На рис. 164 приведены кривые образования льда на пресновод-
ных водоемах. На графике по оси абсцисс отложено время в сут-
ках, а по оси ординат — толщина образовавшегося льда в санти-
метрах.
294
По кривым можно определить время, которое потребуется для
увеличения толщины льда до величины h, если известна среднесу-
точная температура воздуха.
Рис. 163. Определение толщины льда
Пример. Определим, за сколько суток толщина льда достигнет 40 см, если
в момент замера она составляет 20 см, а среднесуточная температура воздуха
равна —20° С.
По кривой, соответствующей —20° С, находим, что увеличение толщины
льда от 20 до 40 см требует 6 суток (9—3 = 6). Таким образом, если средне-
суточная температура будет равна —20°, то за 6 суток толщина льда достиг-
нет 40 см.
Рис. 164. Кривые времени, образования льда на
пресноводных водоемах
Для усиления ледяной переправы, когда нет времени ждать
естественного увеличения толщины льда, создают деревянный на-
стил или намораживают искусственный слой.
Для намораживания льда огораживают трассу снежными ва-
лами и заливают ее водой. .Чтобы намораживание происходило
295
быстрее, а прочность намороженного слоя была больше, на трассу
накладывают хворост.
На рис. 165 приведен график намораживания льда на толщину
5 см. Так, при температуре воздуха —-10° С для намораживания
слоя льда в 5 см требуется 7 часов, а при температуре —25° С
только 3 часа.
Следует иметь в виду, что искусственно намороженный слой
Рис. 165. Кривая намораживания льда
льда долго держаться не может (если не произойдет заметного
похолодания), так как вследствие увеличенной толщины льда теп-
лоотдача воды ухудшается и лед начинает подтаивать изнутри.
Через некоторое время лед приобретает естественную толщину,
соответствующую данной температуре окружающего воздуха.
Намораживать лед имеет смысл только в сильные морозы.
ГЛАВА VIII
ПЛАВАНИЕ ГУСЕНИЧНЫХ МАШИН
1. ПЛАВАЮЩИЕ МАШИНЫ
Всякая гусеничная машина, если она имеет достаточное водоиз-
мещение, способна своим ходом преодолевать водные препятствия,
т. е. способна плавать. Для этого на машину не требуется
устанавливать специальный водяной движитель. Ее гусеничный дви-
житель может обеспечить достаточную силу тяги для преодоления
на плаву сопротивления воды. Кроме того, раздельное вращение
гусениц может использоваться для поворота машины не только на
суше, но и на воде.
Таким образом, гусеничный движитель действительно является
универсальным движителем, обеспечивающим гусеничным машинам
подвижность, проходимость и маневренность как на суше, так и на
воде.
Примером плавающей гусеничной машины, у которой в качестве
водяного движителя используются гусеницы, является отечествен-
ный плавающий транспортер ГТ-С (рис. 166).
Кроме плавающих машин, использующих для движения на воде
свой сухопутный движитель, применяются также гусеничные ма-
Рис. 166. Гусеничный плавающий транспортер ГТ-С
297
Рис. 167. Гусеничный плавающий транспортер К-61
шины со специальным водяным движителем — с гребным винтом
или с водометным движителем, например отечественный плаваю-
щий транспортер К-61 (рис. 167),имеющий в качестве водяного дви-
жителя гребные винты.
Плавающие гусеничные машины, имеющие в качестве водяного
движителя гребные винты или водометный движитель, являются
специальными машинами.
Если такая машина используется преимущественно на суше, то
ее водяной движитель в этом случае не нужен и является вредным
балластом, ухудшающим подвижность и проходимость машины на
суше. Действительно, винт обычно открыто располагают в кормо-
вой части машины. При движении по резко пересеченной местности,
по каменистым дорогам, в лесу, при преодолении местных препят-
ствий — рвов, порогов и т. д.— винт легко может быть поврежден.
Поэтому водитель будет вести машину осторожно, будет снижать
скорость движения и обходить препятствия, вместо того чтобы их
преодолевать.
Кроме того, как гребной винт, так и водометный движитель со
своим приводом сложны по конструкции, занимают много места в
машине, требуют дополнительного оборудования в виде рулевого
управления и т. д. Наконец, плавающая машина должна иметь
специальный корпус, приспособленный к условиям скоростного пла-
вания.
Все это усложняет и удорожает гусеничную машину.
В транспортных машинах, имеющих общее, а не специальное
назначение, нецелесообразно применять в качестве водяного дви-
жителя какой-нибудь другой движитель, кроме гусеничного. Однако
этот движитель все же следует приспособить к условиям плавания.
Только в этом случае он сможет обеспечить машине нужную ско-
рость на плаву.
В настоящей главе рассматривается теория плавания гусенич-
ных машин специального и общего назначения,
299
2. ПЛАВУЧЕСТЬ И ОСТОЙЧИВОСТЬ
ОСНОВНЫЕ понятия
Плавающая машина должна обладать следующими основными
свойствами: плавучестью, остойчивостью, способностью к входу и
выходу из воды, подвижностью и маневренностью на воде.
Пл авучестью называется способность тела держаться на
поверхности воды.
При погружении тела в воду на его подводную часть действуют
реакции воды. Равнодействующая этих реакций называется
подъемной силой и обозначается буквой Q. Она приложена
в центре тяжести вытесненного объема воды. Этот центр назы-
вается центром водоизмещения (точка р на рис. 168). Чтобы
тело, находилось в равновесии, центр тяжести тела (точка с) и
точка р должны лежать на одной вертикальной прямой, а подъем-
ная сила при этом должна равняться весу тела (Q = G).
При плавании тела граница его погруженной части опреде-
ляется так называемой ватерлинией (ВЛ).
Если тело имеет нормальный (расчетный) вес и плавает в спо-
койной воде, то его ватерлиния будет называться грузовой ва-
терлинией (ГВЛ).
Приложим к телу некоторую пару сил, момент которой обозна-
чим буквой М (рис. 169). Под действием этой пары тело повернется
и займет новое положение (чтобы на чертеже не вращать тело, мы
можем, поворачивать его ватерлинию).
При повороте тела центр водоизмещения уже не будет лежать
на одной прямой с центром тяжести, а несколько сместится на ве-
личину г.
Для равновесия тела необходимо, чтобы момент М равнялся мо-
менту пары сил G и Q, или
Рис. 168. Силы, действующие
ца свободно плавающее тело
Рис. 169. Поворот плавающего тела
под действием приложенного момента
299
Если убрать пару сил, то тело будет стремиться под действием
момента Qr занять свое первоначальное положение.
Способность плавающего тела восстанавливать свое первона-
чальное положение после прекращения действия внешних сил, при-
ложенных к телу, называют его остойчивостью. Остойчивость
характеризуется величиной плеча г, которое называется плечом
остойчивости. Чем больше при одном и том же крене тела
плечо остойчивости, тем больше восстанавливающий момент и
остойчивость плавающего тела.
В зависимости от того, вокруг какой оси поворачивается тело,
остойчивость может быть продольной или поперечной.
В общем же случае тело может поворачиваться вокруг произволь-
ной оси.
Кроме плеча г, остойчивость характеризуется положением
точки т, лежащей на пересечении вертикальной оси тела и линии
действия подъемной силы при малом угле поворота тела. Эта точка
называется метацентром.
Тело обладает остойчивостью, т. е. способно восстанавливать
свое первоначальное положение, пока метацентр лежит выше центра
тяжести тела.
Таким образом, положение метацентра характеризует свойство
плавающего тела сопротивляться опрокидыванию.
ФОРМУЛА МЕТАЦЕНТРИЧЕСКОЙ ОСТОЙЧИВОСТИ
Положение метацентра определяется положением центра водо-
измещения. В свою очередь положение центра водоизмещения
может быть вычислено по клиновидным объемам, входящим
в воду и выходящим из воды при повороте тела (рис. 170).
Из механики известно, что если часть массы какого-нибудь тела
переместить из одного положения в другое, то вместе с этим пере-
местится и общий центр тяжести тела параллельно перемеще-
нию массы. При этом путь перемещения общего центра тяже-
Рис. 170. Положение метацентра при
повороте плавающего тела
сти будет относиться к пу-
ти центра тяжести переме-
щаемой массы, как эта мас-
са относится к массе всего
тела.
Согласно рис. 170 можно
считать, что левый клин пе-
ремещен направо. Тогда бу-
дем иметь
рр’ = д
пп' Q ’
где q — подъемная сила
клина;
Q — общая подъемная
сила плавающего
тела.
300
Из схемы сил на рис. 170 приближенно можем написать
рр' _____________________ р sin а
пп' 2а ’
откуда
- Q sin а
Величина р называется метацентрическим радиусом.
Выразим силы q и Q через объемы v и V согласно формулам
q = yv и Q = уК,
где v—объем клина;
V—водоизмещение плавающего тела;
у — удельный вес воды.
Тогда получим
___ 2av
Р V sin а ’
Если допустить, что плавающее тело имеет ящикообразную
форму, то для малых углов наклона а будет справедлива следую-
щая формула:
LB3
р “ 12И»
где L — длина тела;
В — ширина тела.
LB3
Величина -уу есть момент инерции площади грузовой ватер-
линии, взятый относительно оси, проходящей через центр тяжести
этой площади.
Обозначим момент инерции буквой I. Тогда получим формулу
метацентрической остойчивости
р-4- <274>
Определив р и зная положение центра тяжести тела, найдем
расстояние от центра тяжести до метацентра. Это расстояние на-
зывается метацентрической высотой. Метацентрическая
высота характеризует остойчивость тела при малых углах его на-
клона. Академик А. Н. Крылов образно определяет метацентриче-
скую высоту как рычаг, за который волна раскачивает корабль.
Сравнивая метацентрическую высоту вновь проектируемой плаваю-
щей машины с метацентрической высотой уже выполненной ма-
шины, можно определить остойчивость новой машины. Знание ме-
тацентрической высоты позволяет судить об остойчивости машины
на плаву.
Более наглядное представление об остойчивости дает, однако,
не метацентрическая высота, а восстанавливающий момент.
301
Обозначим расстояние от центра тяжести до центра водоизме-
щения через Л. Тогда метацентрическая высота будет'равна
р + h — у +
Знак минус берется, если центр тяжести лежит выше центра
водоизмещения, а знак плюс, если этот центр расположен ниже
центра водоизмещения.
Момент статической остойчивости определяется формулой
М = Q + h\ sin а.
Учитывая, что Q — G и, кроме того, при у=1 V = G, получаем
М= (/ + GA) sin а. (275)
Из формулы (275) следует, что остойчивость плавающего тела
будет тем выше, чем больше момент инерции площади ватерлинии,
чем ниже лежит центр тяжести тела и выше его центр водоизме-
щения (при положении центра тяжести выше центра водоизмеще-
ния) и чем меньше вес тела.
Пример. Определим поперечную остойчивость плавающего гусеничного
транспортера, представленного на рис. 171. Дапо: вес транспортера 4,5 т, длина
корпуса по грузовой ватерлинии £ = 4,37 м, ширина корпуса В =1,86 м, рас-
стояние между центром тяжести и центром водоизмещения h = 0,13 м.
Определяем момент инерции площади ватерлинии, считая эту площадь
прямоугольной:
/ = ^ = ^^ = 2,34№.
Водоизмещение машины V = 4,5 №. Метацентрический радиус поперечной
/ 2,34
остойчивости будет р = -у = -2-у = 0,52 м*.
Согласно формуле (275) получим момент поперечной остойчивости
Л-1 = (2,34-4,5-0,13) sin а,
или
М = 1,75 sin а.
При а =10° момент поперечной остойчивости М будет равен 0,3 тм. или
300 кгм.
Выведенная формула метацентрической остойчивости справед-
лива только для малых углов наклона плавающего тела. Кроме
того, при выводе этой формулы предполагалось, что наклон телу
дает пара сил. В плавающих гусеничных машинах дифферент
или боковой крен машины* ** может быть большим и вы-
♦ Для моторного катера, имеющего длину 11,5 м, ширину 2,3 м и осадку
на корме 0,69 м, метацентрический радиус равен 1 м.
** Дифферентом называется поворот машины относительно поперечной оси
(с кормы на нос,.и наоборот), а боковым креном—поворот вокруг продольной
оси (с борта на борт).
302
зываться не только парой сил, но и одной силой. Например, при
форсировании водных препятствий на борту машины могут нахо-
диться люди. Машина под их весом осядет и накренится. Или, на-
пример, при движении по воде в корпусе может открыться течь.
В результате этого к весу машины прибавится вес воды, что вызо-
вет осадку и дифферент машины. К машине может быть приложена
Рис. 171. Определение поперечной остойчивости
плавающего гусеничного транспортера:
«•—вид транспортера сбоку; 6 — вид транспортера сверху
и пара сил. Это произойдет тогда, когда внутри машины будут пе-
ремещаться какие-нибудь грузы, в результате чего начнет переме-
щаться и центр тяжести машины, но вес машины при этом оста-
нется прежним.
Определение остойчивости при больших углах крена и при при-
ложении к машине пары сил или одной силы является практически
важной задачей. Конструктор, проектируя плавающую машину, дол-
жен знать, какую дополнительную нагрузку может выдержать ма-
шина, не затонув, или каким запасом плавучести она должна обла-
дать. Важно знать также запас плавучести и лицам, использующим
машину на плаву, т. е. эксплуатирующим ее.
303
В теории корабля остойчивость при больших углах крена й за-
пас плавучести определяются по так называемой диаграмме
Рида. Диаграмма Рида устанавливает связь между восстанавли-
вающим моментом, приложенным к корпусу корабля, и дифферен-
том или боковым креном корабля.
На рис. 172 в качестве примера приведена диаграмма Рида для
продольной и поперечной остойчивости плавающей гусеничной ма-
шины водоизмещением в 3 т. По оси абсцисс отложен угол пово-
Рис. 172. Диаграмма Рида:
а — для продольной остойчивости; б — для поперечной отстойчивости
угол наклона, который получит машина, если к ней приложить
внешний момент М'. Например, при приложении в поперечной пло-
скости момента М' = 650 кгм машина получит крен 0Л = 30°.
На построении диаграммы Рида мы здесь останавливаться не
будем. В расчете плавающих машин она не находит широкого при-
менения. Вместо диаграммы Рида рассмотрим другую диаграмму —
диаграмму затопля-емости. Как и диаграмма Рида, диа-
грамма затопляемости характеризует остойчивость машины на
плаву, но остойчивость рассматривается здесь на границе затопляе-
мости, т. е.— предельная остойчивость.
Заметим, что здесь рассматривается только остойчивость н а
спокойной воде. Большое практическое значение имело бы
рассмотрение вопроса остойчивости машины на волнах (плавание
гусеничных машин на море). Однако пока этот вопрос теоретически
не разработан. Заметим только, что при плавании на волнах ма-
шина может потерять свои водоходные качества, которыми она
в полной мере обладает на спокойной воде.
3. ДИАГРАММА ЗАТОПЛЯЕМОСТИ
Определим на корпусе плавающей на воде машины точку за-
топляемости а (рис. 173). Обозначим, кроме того, следующие ха-
рактерные точки: с — центр тяжести машины,/? — начальный центр
304
водоизмещения, соответствующий плаванию машины с грузовой
ватерлинией.
Приложим к машине некоторую силу q, под действием которой
машина дополнительно погрузится в воду, а точка затопляемости
переместится в плоскость ватерлинии. В этом случае машина будет
находиться на границе затопляемости.
Пусть условно точка а находится неподвижно на поверхности
воды. Будем изменять как величину силы q, так и ее координату/.
Тогда машина получит наклон под различными углами 9. При этом
центр водоизмещения из положения р переместится в положение р',
определяемое некоторой координатой xpt отсчитываемой от на-
чального положения центра водоизмещения р.
В центре водоизмещения р' будет приложена подъемная сила Q.
Заметим, что при неподвижном состоянии точки а величины Q, хр
и 9 могут быть определены геометрически. Действительно, задавая
наклон корпуса машины, т. е. задавая угол 9, можно найти соот-
ветствующее этому углу водоизмещение, а зная удельный вес
воды, можно подсчитать подъемную силу Q. Она будет равна
объему погруженной в воду части машины, умноженному на удель-
ный вес воды.
Определив центр тяжести вытесненного объема воды, найдем и
координату хр. Таким образом, будут известны величины Q, хр
и 9, Эти величины можно выразить двумя графическими зависимо-
стями. Например, Q = f(x/J) и 0 = <р(Л'р). Так как при переме-
щении грузов машина может получать дифферент на корму или на
нос, то функции Q = F (хр) и 0 = <р (хр) следует построить для
задней и передней точек затопляемости и объединить их в одном
графике. Этот график назовем диаграммой затопляемо-
сти (рис. 174).
Диаграмма затопляемости устанавливает связь между подъем-
ной силой Q, углом наклона машины 9 и координатой центра водо-
измещения х при нахождении машины на границе затопляемости.
20—2169 305
Рассмотрим условие равновесия плавающей машины, находя-
щейся на границе затопляемости.
Составим согласно рис. 173 уравнение моментов сил, действую-
щих на машину, относительно начального положения центра водо-
измещения (относительно точки р) и уравнение проекций сил на
вертикальную ось.
Получим
q + G = Q.
Кроме того, из рис. 173 имеем
lc = h sin в.
Тогда окончательно получим следующее уравнение равно-
весия на границе затопляемости:
—l-Q- + h sin 0 — хр — 0. (276)
1+ Т
Следовательно, величины Q(Q=<?-|-G), 0 и хр, кроме зави-
симости, определяемой диаграммой затопляемости, подчиняются
также еще и зависимости, определяемой уравнением равнове-
сия (276).
Покажем на примерах, как пользоваться диаграммой затопляе-
мости.
Пример 1. Определим запас плавучести машины, имеющей нормальную за-
грузку.
Дано: q = 0; 0=0. Из уравнения (276) находим хр = 0.
Запас плавучести определится как разность подъемной силы на границе
затопляемости Q и веса машины G при хр = 0.
Из диаграммы (рис. 174) имеем
Q — G = 5000 — 3250 = 1750 кг.
306
Следовательно, если в центре тяжести машины приложить силу, равную
1750 кг, то машина погрузится в воду так, что ее точка затопляемости пере-
местится в плоскость грузовой ватерлинии.
Пример 2. На машину положим дополнительный груз весом q на расстоя-
нии Z от ее центра тяжести. Требуется определить запас плавучести машины.
Под запасом плавучести здесь понимается величина дополнительного
груза /, который необходимо поместить в центр тяжести машины, чтобы ма-
шина погрузилась до границы затопляемости.
Дано: G = 3250 кг; Л = 15 см; q = 350 кг; Z = 20 см.
Зададимся произвольно грузом / = 400 кг. Тогда подъемная сила будет
равна Q = G + q + q' = 3250 -f- 350 -j- 400 = 4000 кг. По диаграмме затопляе-
мости находим хр = 7,8 см и в = 13°. Из уравнения (276) определяем
Z 20
ХР = -—+ A Sin е = - 32507W + 15 sin 130 = 5’21 СМ-
+ + 350
Но по диаграмме затопляемости хр — 7,8 см. Следовательно, необходимо взять
новое значение силы q'. Примем /=1075 кг. Тогда Q = 3250 + 350 + 1075 =
= 4675 кг. Из диаграммы затопляемости находим хр = 2,4 см и в = 2,8°.
Из уравнения (276) определяем хр = 2,2 см. Эта величина близка к получен-
ной из диаграммы (2,4 см).
Таким образом, мы определили запас плавучести /=1075 кг. Значит, ма-
шину можно дополнительно загрузить до границы затопляемости на 1075 кг.
4. РАСЧЕТ ПЛАВАЮЩЕЙ МАШИНЫ НА ПЛАВУЧЕСТЬ
И ОСТОЙЧИВОСТЬ
Расчет на плавучесть и остойчивость заключается в определе-
нии начального водоизмещения машины и построении для нее диа-
граммы затопляемости при дифференте и крене.
Будем считать, что корпус машины, как это обычно и бывает,
в подводной части имеет постоянную ширину b (рис. 175). Про-
ведем на боковой проекции корпуса ориентировочно грузовую ва-
терлинию. Пусть площадь смачиваемой поверхности одного борта
будет S. Тогда подъемная сила корпуса определится по формуле
где у — объемный вес воды.
Для пресной воды принимаем 7 = 1, для морской воды
7= 1,025.
Одновременно с корпусом в воду погружается и ходовая часть
машины: ее движитель и подвеска. Обозначим вес ходовой части
Рис. 175. Расчет корпуса плавающей машины на плавучесть и остойчивость
20*
307
через GX4, а ее объемный вес — Через yi. Тогда объем вытесненной
ходовой частью воды будет Gx4:y*. Вес воды в объеме ходовой ча-
сти составит
О = -^-G
Ч:хч — '“'хи-
Суммируя подъемную силу корпуса и ходовой части, получим
окончательно
Q=y^5 + ^l). (277)
Определим входящий в эту формулу объемный вес ходовой
части ух.
В ходовую часть входят: металлические (стальные) детали,
объемный вес которых обозначим через ус, резина бандажей опор-
ных и поддерживающих катков, объемный вес которой ур.
Иногда для увеличения водоизмещения применяют поплавки.
Будем считать, что поплавки полностью погружаются в воду. Обо-
значим объемный вес поплавков через уп.
Кроме того, примем следующее обозначение величин:
qc — вес всех металлических деталей ходовой части;
<7Р — вес резины в ходовой части;
qn — вес поплавков.
Тогда объем ходовой части будет равен
а вес ее
^хч == + <7р + tftl-
Окончательно получим объемный вес ходовой части
у =2™. = + 7р + ?п . (278)
1 9с , 9р <Jn
-— т---т----
7с Тр Тп
Можно принять: ус = 7,8 т'м2-, ур = 2 уп = 0,5 mjM? (дерево),
уп = 0,25 иг/ж3 (пробка).
Чтобы машина плавала, подъемная сила Q должна равняться
весу машины G. Тогда по формуле (277) можно определить пло
щадь боковой проекции корпуса машины. Обозначим ее через
S.=-&-%?• <279’
Уточняем теперь положение ватерлинии, которой мы задались
выше произвольно.
* Принимаем, что ходовая часть полностью погружается в воду.
308
Если, например, при расчете окажется, что 50у>5, то намечен-
ную нами ватерлинию следует передвинуть вверх. Для этого па-
раллельно первоначально намеченной ватерлинии проводим на
небольшом расстоянии одну от другой новые ватерлинии, которые
образуют поправочные слои. Поправочных слоев берем столько,
сколько необходимо для того, чтобы площадь S стала точно равна
площади So-
Для определения площади боковой проекции So ее разбивают
на простейшие геометрические фигуры (обычно треугольники и
прямоугольники) и вычисляют их площади.
Тогда
= + (280)
где У) 6*,— сумма площадей простейших фигур;
2^ — сумма площадей поправочных слоев.
Определив площадь So, находим продольную координату ее
центра тяжести. Если боковая проекция разбита на треугольники,
то центр тяжести треугольника лежит в точке пересечения его ме-
диан. Поэтому положение центра тяжести каждого треугольника
легко определяется при геометрическом построении.
Продольная координата центра тяжести боковой проекции, ко-
торая одновременно является и координатой центра водоизмеще-
ния, определяется по формуле
S Si*i
хР=~^г
где X; — координаты центра тяжести отдельных треугольников;
St—площади треугольников.
Начало осей координат выбирается произвольно.
Для обеспечения плавучести машины с принятым углом диф-
ферента центр тяжести ее должен находиться на одной вертикаль-
ной прямой с центром водоизмещения. Перемещая при компоновке
машины основные агрегаты машины, добиваются выполнения
этого условия.
При выборе положения ватерлинии следует иметь в виду, что
машина на плаву изменяет свой дифферент в ту или другую сто-
рону. Поэтому начальную или статическую ватерлинию проводят
с учетом ходового дифферента. В плавающих автомобилях с вин-
товым движителем угол начального дифферента принимают по-
рядка 5—8° на корму. Гусеничный водяной движитель дает ходо-
вой дифферент на корму. Поэтому начальный дифферент в этом
случае следует давать на переднюю часть (2—3°).
Необходимо определить также запас плавучести.
Для плавающих автомобилей высоту надводной части борта
принимают порядка 300—600 мм, что соответствует примерно 80%
запаса плавучести. Более точно запас плавучести определится по-
сле построения диаграммы затопляемости.
30^
Рис. 176. Определение с помощью калек площадей боковых проекций
и центров тяжести площадей
310
Диаграмма затопляемости строится так же, как указывалось
в предыдущем разделе.
Определяем вначале точку затопляемости. На рис. 175 на бо-
ковой проекции корпуса обозначены открытые жалюзи, через ко-
торые вода может проникнуть в корпус. Поэтому точкой затопляе-
мости явится точка а, находящаяся на уровне жалюзи.
Проводим на листе бумаги горизонтальную линию и наклады-
ваем на лист кальку так, чтобы точка а оказалась на горизонталь-
ной линии. Повернем кальку относительно точки а на некоторый
небольшой произвольный угол. Получим на кальке площадь боко-
вой проекции корпуса, ограниченную сверху проведенной на бу-
маге прямой линией, а снизу — контуром корпуса. Переносим пря-
мую линию на кальку. Окончательно получаем на кальке боковую
проекцию корпуса, соответствующую данному углу дифферента (или
крена при построении диаграммы на крен) 91. Затем снимаем но-
вую кальку, соответствующую новому углу дифферента 92, и т. д.
Контуры боковых проекций корпуса, полученные на отдельных
кальках, разбиваем на треугольники и вычисляем их площади и
координаты центра тяжести площадей.
На рис. 176 приведено несколько калек, последовательно сня-
тых с боковой проекции корпуса. На кальке 1 показано определе-
ние площадей проекции и координат центра тяжести треугольни-
ков. Проекция на кальке 2 получена поворотом кальки на некото-
рый произвольно взятый угол против хода часовой стрелки и т. д.
Подставив в формулу (277) значения площадей боковых проек-
ций корпуса St, получим значения подъемной силы Qz, соответ-
ствующие этим площадям. Из построения одновременно опреде-
ляются углы дифферента 9.
Таким образом, мы определили для различных углов наклона
машины величины подъемной силы Q, углы 9 и координаты хр.
По этим данным строим диаграмму затопляемости.
Сложнее определить водоизмещение и центр водоизмещения,
если вторая (поперечная) проекция корпуса не прямоугольна.
В этом случае вместо площадей надо вычислять объемы и находить
центры тяжести этих объемов, а затем определять общий объем
водоизмещения и его центр тяжести, а следовательно, и центр
водоизмещения.
5. ВХОД МАШИНЫ В ВОДУ и выход ИЗ ВОДЫ
Так как плавающая машина одновременно является и сухо-
путной машиной, она в отличие от корабля должна обладать спо-
собностью входить своим ходом в воду и выходить из воды.
Эти свойства плавающей машины не менее важны, чем рассмо-
тренные выше свойства плавучести и остойчивости.
Вход в воду и выход из воды в основном зависят от крутизны
берега: чем круче берег, тем труднее вход и особенно выход ма-
шины. При большой крутизне берега машина при входе в воду
может слишком накрениться вперед и ее передняя точка затопляе-
311
мости может оказаться под водой. В этом случае произойдет
затопление машины. При выходе из воды машина накреняется на
корму и также может затонуть, если ее задняя точка затопляемо-
сти окажется под водой. Кроме того, при выходе машины гусеницы
могут потерять сцепление с грунтом и забуксовать.
ВХОД В ВОДУ
При входе машины в воду передняя часть корпуса и частично
ходовая часть погружаются в воду (рис. 177). Вследствие этого на
машину начинает действовать подъемная сила Q, приложенная
в центре водоизмещения р. Действие подъемной силы выразится
в том, что центр давления опорных ветвей гусениц сместится из
точки kx к задним опорным каткам. При продвижении машины впе-
ред сила Q будет возрастать, так как увеличится водоизмещение
входящего в воду объема корпуса. С увеличением силы Q центр дав-
ления будет смещаться назад до тех пор, пока не придет в точку &г;
после чего машина частично всплывет, т. е. ее корпус повернется
относительно точки k2. При дальнейшем движении машины реак-
ция грунта в точке k2 исчезнет и машина всплывет полностью.
Возможность или невозможность входа машины в воду зависит
от того, достигнет ли раньше центр давления задней крайней точки
опорных ветвей (точки k2) или точка затопляемости а окажется
в плоскости ватерлинии. В первом случае машина всплывет и,
следовательно, вход в воду будет возможен. Во втором случае ма-
шина начнет затопляться, т. е. вход в воду окажется невозможным.
Изобразим в масштабе корпус машины и нанесем на него пе-
реднюю точку затопляемости а (рис. 178).
Примем теперь, как и при построении диаграммы затопляемо-
сти, что точка а лежит всегда в плоскости ватерлинии, т. е. машина
находится на границе затопляемости.
Проведем через точку а под произвольными углами а несколько
ватерлиний ВЛ1, ВЛ2, ВЛЗ и т. д.
312
Угол а будем отсчи-
тывать от днища корпу-
са, считая, что днище
параллельно плоскости
дороги. Тогда углы а
будут характеризовать
углы входа машины в
воду на границе затоп-
ляемости (см. рис. 177).
Ватерлинии отсекают
на боковой проекции
корпуса смачиваемые
поверхности. Определим
центры тяжести площа-
дей этих проекций. По-
лучим точки р{, pi, р3
и т. д. Если допустить,
что вторая проекция
Рис. 178. Построение диаграммы входа
корпуса прямоугольная,
то точки pi, pi и т. д. будут центрами водоизмещения погруженной
в воду части корпуса. В этих точках приложена подъемная сила Qi,
Qi и т. д. Чтобы не усложнять задачу, водоизмещением ходовой ча-
сти машины пренебрегаем (это пойдет на увеличение запаса плаву-
чести машины).
Нанесем на чертеж точку k—крайнюю заднюю точку опорной
поверхности гусениц (рис. 178) — и произведем следующее по-
строение.
Из точки k опустим перпендикуляры на ватерлинии, которые
определят направление подъемных сил Q (см. рис. 177). Опустим
затем на эти перпендикуляры новые перпендикуляры из точек
pi и т. д. Получим плечи моментов подъемных сил хр1, хр2 и т. д.
Зная величину подъемной силы Q и плечо этой силы хр, найдем
момент, который стремится повернуть машину вокруг точки k:
Mf = xpQ
(282)
На рис. 179 дан график, на котором момент выражен в функ-
ции угла а.
Этот график называется диаграммой входа, а кривая
на графике — кривой всплытия.
Диаграмма входа, как и диаграмма затопляемости, не зависит
от действующих на машину сил, а определяется только геометри-
ческой формой машины — формой подводной части ее корпуса при
нахождении машины на границе затопляемости.
Кроме диаграммы входа положение машины определяется так-
же условиями равновесия.
Из рис. 177 определим момент действия силы веса, взятый от-
носительно точки ki.
Мс = xcG== (h- sin а + rn cos a) G. (283)
313
Если Л1с^>Мр, то машина не может войти в воду при задан-
ном угле входа а, так как ее точка затопляемости окажется под
водой.
Если Л4с^.Мр, то при данном угле входа машина всплывет,
т. е. вход ее в воду будет возможен.
Кривая всплытия делит поле диаграммы на верхнюю и нижнюю
части. Если точка, определяемая координатами Мс и а, лежит на
кривой всплытия или ниже этой кривой, то при данном угле а или
даже большем угле машина всплывет. Если точка лежит выше
кривой всплытия, то машина при данном угле а всплыть не сможет.
Мр
Мы рассмотрели статический вход машины в воду, т. е. вход
при движении машины на малой скорости. Однако машина может
входить в воду и с ходу, т. е. на большой скорости. В этом случае
угол спуска берега на вход машины не влияет. Он может быть
равен 90°. Расчет все же рекомендуется вести на статический вход
в воду, как это было рассмотрено выше.
Пример. Допустим, что G = 5000 кг; hz =0,9 м; т =1,5 м; угол спуска
а = 20°.
По формуле (283) получим Мс = 8600 кгм. На диаграмме входа отклады-
ваем точку с координатами Мс — 8600 кгм и а = 20°. Как видим, эта точка
лежит ниже кривой всплытия. Следовательно, вход в воду под углом в 20°
вполне возможен.
Если точка с координатами Мс, а лежит на кривой всплытия, то это озна-
чает, что машина находится на границе затопляемости. Для безопасного входа
машины в воду эта точка должна лежать ниже кривой всплытия, как в настоя-
щем примере.
314
Следует иметь в виду, что формула (283) является общей.
В этой формуле могут меняться как вес G, так и координаты цен-
тра тяжести машины. Допустим, что на машину погружен допол-
нительный груз. Этот груз изменит величину G, Лг и т, вследствие
чего изменится и момент Мс. Диаграмма же входа останется преж-
ней, так как момент всплытия Mp = xpQ не зависит от веса ма-
шины и координаты ее центра тяжести.
При построении диаграммы входа мы пренебрегли водоизме-
щением ходовой части машины. Если бы это водоизмещение было
учтено, то кривая всплытия сместилась бы несколько вверх, т. е.
всплытие машины наступало бы раньше. Следовательно, в рассмо-
тренном выше примере момент Мр, поворачивающий машину, по-
лучен с некоторым запасом, что облегчает всплытие машины.
ВЫХОД из воды
При выходе из воды (рис. 180, а) машина вначале соприка-
сается передними точками гусениц с грунтом. Цепляясь гусени-
цами за грунт, она начинает поворачиваться, одновременно про-
двигаясь вперед. Водоизмещение корпуса при этом ' изменяется —
корпус кормой все больше погружается в воду, пока задняя точка
затопляемости а, расположенная в кормовой части машины, не
опустится до уровня воды (рис. 180,6); после чего опускаться
дальше корпус не сможет. Если в момент, когда точка а опустится
до уровня воды, опорные ветви гусениц соприкоснутся с грунтом,
машина выйдет из воды (рис. 180, в). Если угол грунта будет
больше угла наклона опорных ветвей гусениц, то выход на берег
окажется невозможным.
Подобно диаграмме входа может быть построена диаграмма
выхода.
Для этого через заднюю точку затопляемости а проводим не-
сколько ватерлиний и определяем площади смачиваемых поверх-
ностей корпуса. По этим площадям определяется водоизмещение.
По водоизмещению находится подъемная сила Q и центр водо-
измещения р.
Координаты центра водоизмещения хр, а следовательно, и мо-
мент подъемной силы, взятый относительно точки k, определяются
так же, как было показано на рис. 178:
Наносим на график кривую момента (кривую выхода) и кривую
подъемной силы в функции угла а, в результате чего получаем
диаграмму выхода (рис. 181).
Определяем момент силы веса машины Мс = xcG по формуле
(283). Если при выходе из воды работает винт (водомет), то мо-
мент Мс уменьшается на величину момента от тяги винта. Прене-
брегать этим моментом нельзя.
Чтобы машина могла выйти из воды на подъем а, должны со-
блюдаться следующие два условия:
315
I. Момент подъемной силы Мр должен быть больше момента
веса машины Мс, или, иначе говоря, точка с координатами Мс и а
должна лежать под кривой выхода.
2. Должно обеспечиваться сцепление гусениц с грунтом.
Рассмотрим последнее условие.
Направление движения
в
Рис. 180. Выход машины из воды:
а — машина подходит к берегу; б — машина выходит на берег; в — полное
соприкосновение гусениц с грунтом при выходе машины на берег
316
Вследствие Частичного погружения машины в воду ее сцепной
вес уменьшается и на подъеме становится равным (G— Q)cosa.
Сила тяги по сцеплению при этом будет 'f(G— Q)cosa. Сила со-
противления движению равна G sin a+/(G— Q)cos а — Q sin а.
Приравняем силу тяги по сцеплению к силе сопротивления дви-
жению.
После преобразования получим формулу, из которой опреде-
ляется угол выхода по сцеплению:
tgac = ?—/•
(284)
Из формулы (284) следует, что угол ас не зависит от величины
подъемной силы Q.
Чтобы машина могла выйти из воды, угол ас должен быть
больше угла а по затопляемости.
Рис. 181. Диаграмма выхода
Пример. Определить, сможет ли машина выйти из воды, если подъем бе-
рега составляет а — 20°.
Дано: G = 5000 кг; hz = 0,9 м\ т, = 1,5 м. Диаграмма выхода машины
представлена на рис. 181.
По формуле (283) определяем Мс = 8600 кгм. Точка с координатами
Мс — 8600 кгм, a = 20° лежит ниже кривой выхода. Следовательно, по затоп-
ляемости выход возможен.
Определим теперь угол подъема по сцеплению. Зададимся ср = 0,7 и
/==0,1. Тогда по формуле (284) находим
tg ac ==.0,7 — 0,1 — 0,6,
откуда ac=31°. Следовательно, сцепление на выходе обеспечено (ac > а).
Для плавающих машин максимальный угол входа около 25°,
а угол выхода несколько меньше — около 20°.
317.
6. ПОДВИЖНОСТЬ И МАНЕВРЕННОСТЬ НА ПЛАВУ
Под подвижностью на плаву понимается способность машины
к прямолинейному движению на воде, а под маневренностью —
способность менять заданный курс движения, т. е. способность
к повороту машины.
Подвижность обеспечивается водяным движителем—гусени-
цами, гребным винтом или водометным движителем. Маневрен-
ность обеспечивается или движителем, или специальными пово-
ротными устройствами (при гребных винтах), например рулем по-
ворота.
Высокая подвижность и маневренность машины на плаву опре-
деляются двумя факторами: сопротивлением движению машины
на плаву и силой тяги, создаваемой водяным движителем.
Сопротивление движению в свою очередь зависит от формы
подводной части корпуса машины, а сила тяги — от мощности дви-
гателя машины и от ее водяного движителя (от его к. п. д.).
СОПРОТИВЛЕНИЕ ВОДЫ ДВИЖЕНИЮ ПЛАВАЮЩЕЙ МАШИНЫ
Всякое плавающее тело, в том числе и плавающая гусеничная
машина, испытывает при движении на воде три вида сопротив-
лений:
— сопротивление трения смоченной поверхности о воду;
— сопротивление формы, или вихревое сопротивление;
— волновое сопротивление.
При движении плавающего тела в воде в пограничном слое,
примыкающем к смоченной поверхности тела, развиваются силы
сопротивления движению, которые можно разложить на нормаль-
ные и касательные. Касательные, или силы трения, есть силы,
возникающие вследствие вязкости жидкости в пограничном слое.
Нормальные силы являются результатом вихревых явлений, также
вызванных вязкостью жидкости, и волнообразования. Эти силы на-
зываются силами сопротивления формы и волнового сопротивления.
Волновое сопротивление есть сопротивление образованию волн,
т. е. сопротивление колебательному движению воды, совершаю-
щемуся под действием силы веса и импульсов, получаемых от дви-
жущегося на поверхности воды тела (тела, плавающие под водой,
например подводные лодки, волнового сопротивления не испыты-
вают) .
Известный английский ученый Вильям Фруд установил сле-
дующую эмпирическую формулу сопротивления трения:
Rs=fSvn,
где Rs —сопротивление трения в ка;
S—смоченная поверхность в м2;
v—скорость движения тела в м/сек\
п—показатель степени;
/—коэффициент сопротивления трения,
318
Согласно опытам Фруда показатель степени для тел различной
шероховатости находится в пределах 1,43—1,99, а коэффициент
сопротивления в пределах 0,148—0,202. Обе эти величины зависят
также и от длины смоченной поверхности.
Для плавающей машины, имеющей S = 25 м2; v = 3 м/сек
можно принять /==0,17 и п = 1,85, тогда
= 0,17-25-31,85 = 32,4 кг.
Мощность, затрачиваемая на преодоление сопротивления тре-
ния, при скорости движения машины на плаву 3 м/сек, или
И км/час (максимальная скорость на воде плавающих гусеничных
машин) будет равна
ЛА = 32,4-3 = 97 — , или 1,3 л. с.
° ’ сек ’ ’
По сравнению с мощностями, которыми располагают двигатели
плавающих машин, эта мощность очень мала. Следовательно, не
сопротивление трения является главной составляющей сопротивле-
ния движению на воде плавающих гусеничных машин,-
Автором была получена зависимость, представленная на
рис. 182, между сопротивлением движению и скоростью буксировки
для гусеничной машины весом 3 т. Как видим, при скорости букси-
ровки машины 10 км/час общее сопротивление равно 470 кг.
Сравнивая эту величину с величиной сопротивления трения, опре-
деленной по формуле Фруда, находим, что для плавающих машин
сопротивление трения составляет менее 10% от общего сопротив-
ления. Следовательно, основными видами сопротивления будут со-
противление формы и волновое сопротивление.
Заметим, что даже в плавающих судах, имеющих неудачную
с точки зрения обтекаемости форму, например в баржах, сопротив-
ление трения при скорости 3 м/сек составляет около 60% от об-
щего сопротивления дви-
жению. На остальные со-
противления приходится
40% *.
Гусеничная машина
имеет плохо обтекаемую
ящикообразную форму
корпуса, создающую боль-
шое вихревое и волновое
сопротивление движению
машины. На вихревое
и волновое сопротивле-
ние влияют лобовая и кор-
мовая оконечности кор-
пуса, а также ходовая
часть машины. ным автора)

Рис. 182. График зависимости между силой
сопротивления движению и скоростью букси-
ровки гусеничной машины на воде (по дан-
В. В. Звонков. Тяга речных судов. Речиздат, 1946.
319
Рис. 183. Очертания кормовых и носо-
вых частей барж по данным проф. Сад-
лера
Интересные опыты были по-
ставлены проф. Садлером по
исследованию влияния формы
носовых и кормовых очертаний
судна на его общее сопроти-
вление движению (рис. 183).
На рис. 184 приведена диа-
грамма сопротивления движе-
ншо, приходящегося на одну
тонну водоизмещения судна
(баржи) при скорости его дви-
жения 9,6 км/час.
Из диаграммы видно, что
в зависимости от формы бар-
жи сопротивление может изме-
няться больше чем в два раза.
Самое большое сопротивление
испытывает баржа с ящико-
образной формой, т. е. как раз
той формы, которую имеет кор-
пус плавающей гусеничной ма-
шины.
Следует иметь в виду, что
по сравнению с сопротивле-
нием барж сопротивление
машины должно быть еще больше, так как ходовая часть
гусеничных машин является источником сильных вихреобразо-
ваний.
Вихревое сопротивление зависит в первую очередь от формы
кормовой части плаваю-
щего тела.
Классический опыт
был в свое время постав-
лен Хил-Шоу. В бассей-
не протаскивалось тело,
имеющее зубчатую фор-
му (рис. 185, а). Вначале
тело протаскивали тупым
концом вперед, а потом —
заостренным.
Опыт Хил-Шоу пока-
зал, что при движении те-
ла в направлении стрел-
ки, т. е. тупым концом
вперед, сопротивление
меньше, чем при движе-
нии против стрелки, т. е.
в противоположном на- рис# 184. Диаграмма сопротивлений по даи-
правлении. ным проф. Садлера
320
Этот несколько неожиданный результат объясняется тем, что
заостренная кормовая часть создает меньшее разрежение, так как
поток воды имеет возможность обтекать тело.
Как известно, идеальным с точки зрения обтекаемости является
каплеобразное тело (рис. 185,6). Жидкость обтекает это тело
почти без образования вихрей, а следовательно, и без вихревых
потерь. Каплеобразное тело имеет сопротивление, в 16 раз меньшее,
чем сопротивление диска, полученного поперечным сечением тела
в его наиболее широком месте.
----- J
Рис. 185. Сопротивление формы:
а — зу.бчатое тело; б — каплеобразное тело
ФОРМУЛЫ ОБЩЕГО СОПРОТИВЛЕНИЯ ДВИЖЕНИЮ
ГУСЕНИЧНЫХ МАШИН
Определить сопротивление движению гусеничной машины в воде
по формулам сопротивления трения, вихревого и волнового сопро-
тивления невозможно, так как каждая плавающая машина имеет
свои особенности в отношении сопротивления движению, которые
нельзя учесть этими формулами. Поэтому сопротивление движе-
нию гусеничной машины на воде определяется формулами общего
сопротивления.
Как показывают проведенные нами исследования, получить уни-
версальную формулу общего сопротивления для машин всех клас-
сов очень трудно. Наиболее точным методом определения сопро-
тивления является метод моделирования.
21 —'2469
321
Этот метод заключается в следующем.
Изготовляется деревянная или металлическая модель машины
и буксируется в бассейне. В результате испытаний находят
функцию
Rm = <Р (^м),
где — сопротивление движению модели;
— скорость буксировки модели.
Пользуясь законами подобия между силой сопротивления мо-
дели (RJ и силой сопротивления натуры (/?„) можно приближенно
принять (для гусеничных машин) следующую зависимость:
RH = 68RM, (285)
где & = р —геометрический масштаб. В этом выражении Ан—
линейный размер натуры по ватерлинии, а Ам —
линейный размер модели по ватерлинии.
Рис. 186. Буксировка модели в бассейне
Кроме того, при моделировании (по Фруду) имеется зависи-
мость между скоростями модели и натуры:
Т'В = Т',К*. (286)
Если функция <p(^M) будет найдена, то можно определить со-
противление натуры. Для этого, используя формулы (285) и (286)
и учитывая RM = <р (£*„), получим
(287)
Здесь индексы н опущены.
322
Инженером Ю. А. Кононовичем была построена и испытыва-
лась в бассейне модель гусеничного транспортера ГТ-С (рис. 186).
Модель имела ’Л линейной величины натуры (6 = 4). В качестве
линейного размера принималась длина по ватерлинии. Длина мо-
дели составляла А„ = 1,16 м.
В результате испытаний была получена функция сопротивления
движению (рис. 187)
Rm = <Р (^м) = <Р •
Рис. 187. Кривая сопротивления движению модели:
1 — опытная кривая; 2 — расчетная кривая
На графике рис. 187 по оси абсцисс отложена скорость букси-
ровки модели, а по оси ординат — сопротивление движению мо-
дели.
Функцию (vM) можно выразить следующей приближенной
параболической зависимостью:
где а — опытный коэффициент.
Согласно кривой рис. 187 принимаем коэффициент а = 4,6. На
рис. 187 пунктиром показана парабола при а — 4,6. Она несколько
22-2469 323
отличается от опытней кривой, но это отличие лежит в допустимых
пределах.
Заменим /?,, и через R и v согласно формулам подобия.
Получим
R = 4,66М. (288)
Более точное значение общего сопротивления дает следующая
формула, полученная инж. Ю. А. Кононовичем:
R = 0,016Gp1,7+1,5f;
где G— вес машины в кг,
v— скорость в м/сек,
Fr— число Фруда.
Число Фруда определяется по формуле
где L — линейный размер, вычисленный по ватерлинии, в м\
g—ускорение земного тяготения в м/сек2.
Кроме модельных испытаний, Ю. А. Кононовичем были прове-
дены буксирные испытания транспортера ГТ-С.
На графике рис. 188 приведены две кривые сопротивления дви-
жению транспортера ГТ-С: 1 — опытная кривая и 2— кривая, по-
лученная на основании формулы (288) при й = 4.
Из графика видно, что обе кривые близко подходят одна к дру-
гой. Следовательно, формула (288) достаточно точна.
Рис. 188. График буксировочного сопротивления плавающего
транспортера (ГТ-С):
I — опытная кривая; 2 — расчетная кривая
324
Так как все гусеничные машины в основном похожи одна на
другую, то формула (288) может быть применима для гусеничных
машин различных типов.
Следует, однако, иметь в виду, что сравнивать машины по со-
противлению движению можно только в том случае, если испы-
тания проводятся в совершенно одинаковых условиях. Так, на со-
противление движению влияет дифферент машины (с увеличением
дифферента сопротивление возрастает), а также глубина водоема.
На мелководье сопротивление больше, чем в глубоком водоеме.
ВОДЯНОЙ ДВИЖИТЕЛЬ (ПРИНЦИП РАБОТЫ)
Как мы уже отмечали выше, в плавающих гусеничных маши-
нах могут применяться три типа водяных движителей: винтовой
движитель, водометный и гусеничный.
Водяные движители всех типов, несмотря на их значительное
конструктивное различие, по существу работают одинаково.
При работе движитель отбрасывает назад поток воды, вслед-
ствие чего на самом движителе создается реакция воды или сила
тяги, направленная вперед, под действием которой и происходит
движение машины.
Рассмотрим этот вопрос в общем виде.
Допустим, что через движитель проходит поток воды, скорость
которого до движителя равна щ, а после движителя Движитель
создает ускорение потоку, вследствие чего скорость и2 всегда
больше скорости щ.
Как известно, изменение количества движения по времени ка-
кой-либо массы равно силе, действующей на эту массу. Для потока
воды, создаваемого работающим движителем, можно написать
<289)
где Р— сила тяги движителя;
М
-щ- — т —секундная масса воды, т. е. масса воды, проходящая
через движитель за одну секунду.
Скорость приближенно можно считать равной скорости дви-
жения машины. Обозначим эту скорость через и. Скорость и2 есть
скорость потока в осевом направлении, которую создает движитель.
Эта скорость зависит от формы движителя и скорости его рабочих
элементов. Обозначим эту скорость через W и в дальнейшем бу-
дем называть ее скоростью движителя.
Секундную массу можно выразить следующей формулой:
g
где Д —удельный вес. воды (Д — 1000 кг/.и3);
g—ускорение 9,81 м/сек2-,
А — упорная площадь движителя, или площадь проекции ра-
бочих элементов движителя на плоскостьг перпендику-
лярную к оси движения машины.
22*
325
Подставив указанные величины в формулу (289), получим
р = — z>). (290)
Обозначим отношение приращения скорости W—v к скоро-
сти W через So. Эта величина называется скольжением дви-
жителя. Тогда предыдущую формулу можно переписать в та-
ком виде:
Р=АЛ11725о. (291)
Из формулы следует, что сила тяги движителя зависит от его
скорости W и от скольжения So. Чем больше скорость W
и чем больше скольжение, тем больше и сила
тяги. Кроме того, сила тяги зависит от упорной площади дви-
жителя А.
Определим теперь коэффициент полезного дей-
ствия движителя.
Мощность, которую отдает движитель на преодоление сопро-
тивления движению машины, равна произведению силы тяги на
скорость движения машины, или Ри. Мощность, которая подводится
к движителю со стороны двигателя, равна произведению силы
тяги на скорость движителя, или PW. Тогда коэффициент полез-
ного действия движителя будет
V
’I = V’ (292)
т. е. он равен отношению скорости движения машины к скорости
движения рабочих элементов движителя.
Заметим, что даже в первом приближении нельзя при-
нять скорость v равной скорости W, так как всегда имеется сколь-
жение в движителе, то коэффициент полезного действия даже
условно нельзя принимать равным единице.
Формула (292) была выведена без учета некоторых дополни-
тельных явлений, которые сопровождают работу движителя. В ча-
стности, не учитывались попутные потоки воды, которые всегда
возникают при работе движителя, а также потери на трение воды
о рабочие элементы движителя и др. Поэтому коэффициент по-
лезного действия, определенный по формуле (292), называется
условным коэффициентом полезного действия.
Обычно условный к. п. д. несколько больше действительного (на
5—10%).
Выведенные формулы силы тяги (291) и к. п. д. (292) являются
основными для расчета работы водяного движителя любого типа.
ВИНТОВОЙ ДВИЖИТЕЛЬ
Винтовой движитель работает по тому же принципу, который
был рассмотрен в предыдущем разделе. Лопасти винта отбрасы-
вают подтекающий к винту поток воды, вследствие чего на винге
создается толкающая машину сила тяги.
326
Рис. 189. Гребные винты:
а — трехлопастный винт; б — четырехлопаст-
ный винт
Рис. 190. Расположение гребных винтов:
а — открытый винт; б — винт в направляющем
коиусе
На машине могут быть уста-
новлены один или два гребных
винта.
Два винта устанавливаются,
во-первых, для получения большей
силы тяги и, во-вторых, для того,
чтобы не применять руля как
средства поворота машины на
воде, так как рулем в этом слу-
чае служат вращающиеся с раз-
ным числом оборотов гребные
винты, которые и создают поворачивающий момент машине.
Движитель с двумя винтами обычно имеет более высокий к. п. д.,
чем движитель с одним винтом.
Винты бывают трех- и четырехлопастные в одновинтовом дви-
жителе и трехлопастные в двухвинтовом движителе (рис. 189).
Г ребные винты могут
быть цельными и с повора-
чивающимися лопастями. По-
ворот лопастей позволяет, не
меняя скорости вала винта,
регулировать скорость дви-
жения машины, а также со-
общать машине задний ход.
Однако винты с поворачи-
вающимися лопастями очень
сложны и требуют специаль-
ного привода к лопастям.
Диаметр ступицы в этих
винтах иногда достигает
одной трети от внешнего
диаметра лопастей, что
влияет на к. п. д. винта.
Винты могут располагаться открыто (рис. 190, а), в нише или
в направляющем конусе (рис. 190,6). Направляющий конус улуч-
шает условия работы винта, повышая на 20—30% его тягу. Кроме
того, конус предохраняет винт от попадания в него посторонних
предметов при движении машины на суше и может служить рулем
поворота машины на плаву.
б
ВОДОМЕТНЫЙ ДВИЖИТЕЛЬ
В водометном движителе имеется лопастной насос, который
заключен в кожух и помещен внутри машины. К кожуху насоса
присоединены три трубы: центральная, или подводящая, и две бо-
ковые, или отводящие, как это показано на рис. 191. По централь-
ной трубе вода подается к насосу, а по боковым выбрасывается
наружу в сторону, противоположную движению машины. Под дей-
ствием выбрасываемой воды создается сила тяги, толкающая ма-
шину вперед,
327
Рис, 191. Принципиальная схема водо-
метного движителя:
а — вид сбоку; б — вид сверху
Для поворота машины на воде перекрывается одна из отводя-
щих труб. Поток, выбрасываемый через другую отводящую трубу,
будет создавать момент, поворачивающий машину. На рис. 192
представлена конструкция водометного движителя с одной трубой
и поворачивающимся насадком 5, служащим для поворота машины.
Водометный движитель в
судах начал применяться
с 1866 г. В 1882 г. были про-
ведены сравнительные испыта-
ния движителей двух типов:
винтового и водометного. Коэф-
фициент полезного действия
водометного движителя оказал-
ся ниже коэффициента полез-
ного действия гребного винта.
Это объясняется тем, что при
движении воды по трубам до-
полнительно терялась энергия
на трение воды о стенки труб.
Преимущество водометного
движителя перед винтовым за-
ключается в том, что он защи-
щен от повреждений. Кроме
того, машина с водометным дви-
жителем легко изменяет на-
правление движения. Насос во-
дометного движителя в случае
открывшейся в корпусе маши-
использован и как откачивающий.
Применяющиеся на отечественных речных судах водометные
движители используются также как гидромониторы для очистки
мелководных участков рек.
ны течи может быть
Рис. 192. Конструкция водометного движителя:
I — подводящая труба; 2— вал насоса; 3 — лопастный насос; 4 — отводящая тр}гба; 5— повора-
чивающийся насадок; 6— поворотный валик привода управления машиной
328
ГУСЕНИЧНЫЙ ДВИЖИТЕЛЬ
Гусеничный водоходный движитель может работать при частич-
ном или полном погружении его в воду. В последнем случае верх-
ние ветви гусениц гонят воду по направлению движения машины,
а нижние — в противоположном направлении. На нижних ветвях
создается положительная тяга, толкающая корпус машины вперед,
а на верхних ветвях — сила сопротивления, препятствующая дви-
жению машины. Если бы обе ветви гусеничного обвода находились
в совершенно одинаковых условиях работы, т. е. имели одинаковую
длину, форму и были бы погружены в воду на одинаковую глу-
бину, то они производили бы взаимно противоположное действие
на корпус машины, и последний при работающем движителе оста-
вался бы неподвижным. В действительности верхняя и нижняя
ветви обвода работают в различных условиях. Верхняя ветвь ко-
роче, она ближе расположена к поверхности воды. При вращении
гусеницы верхняя ветвь гонит не только воду, но и захватывает
пузырьки воздуха (вследствие того, что она расположена близко
к поверхности воды). Нижняя ветвь гонит чистую . воду. Кроме
этого, нижняя ветвь длиннее, на ней работает большее число шпор,
которые захватывают воду. Поэтому создаваемая нижней ветвью
тяга больше сопротивления, вызываемого работой верхней ветви.
Благодаря этому машина и движется. Заметим, что если верхнюю
ветвь изолировать от поверхности воды крылом, а в передней части
обвода сделать изогнутые кожухи, которые направляли бы поток,
создаваемый верхней ветвью, назад, то тяга машины увеличится,
а с нею повысится и скорость движения машины. Иногда вместо
изогнутых кожухов впереди гусениц устанавливают наклонные под-
крылки (отражательные козырьки), которые выполняют ту же роль,
что и изогнутые кожухи: они направляют поток воды назад (или
по крайней мере не позволяют создаваться потоку, направленному
вперед).
Кожухи или подкрылки являются основным средством повыше-
ния скоростей движения плавающих машин. Скорость движения
также можно повысить за счет установки на гусеницах гребных ло-
паток. Однако установка высоких лопаток на наружной поверхно-
сти гусениц снижает ходовые качества машины при движении ее
на суше. Установка же внутренних лопаток, как показывают
опыты, не дает большого тягового эффекта.
Гусеничный движитель как водоходный неоднократно исполь-
зовался в опытных конструкциях судов, а также и в плавающих
гусеничных машинах.
В 1937 г. на Северной Двине проводились испытания парохода
«Зюйд», оборудованного по бортам гусеницами.
Каждая гусеница длиной около 14 м имела по 14 плиц длиной
1,6 м и шириной 0,35 м. Скорость движения при испытании дохо-
дила почти до 14 км/час. Коэффициент полезного действия этого
движителя приближался к к. п. д. гребного винта — 0,46—0,57.
329
В отдельных случаях к. п. д. гусеничного движителя достигал 0,75 *.
Однако используемый на плавающей машине гусеничный движи-
тель будет иметь значительно меньший к. п. д., так как на гусени-
цах нельзя создать достаточно большие гребные лопатки.
Тип водяного движителя выбирается в зависимости от назна-
чения машины. Если машина специальная, предназначенная для
длительного плавания с большой скоростью, то на такую машину
следует устанавливать гребной винт или водометный движитель.
Если машина сухопутная, но должна обладать водоходными каче-
ствами, то в качестве водяного движителя целесообразнее исполь-
зовать гусеничный движитель самой машины.
7. ОПРЕДЕЛЕНИЕ СКОРОСТИ ДВИЖЕНИЯ МАШИНЫ
НА ПЛАВУ
Основным параметром, характеризующим подвижность и ма-
невренность машины на воде, является с к о р о с т ь ее движе-
ния. Скорость зависит от формы и размеров корпуса машины,
от устройства движителя, а главное, от мощности двигателя. Если
машина не специальная, то мощность двигателя выбирается в за-
висимости от условий движения машины на суше. Если же машина
специальная плавающая, то мощность двигателя должна рассчи-
тываться по заданной скорости движения машины на плаву. Эту
мощность берут выше, чем это требуется для движения машины
на суше.
Определим скорость движения машины на плаву по заданной
мощности двигателя.
Из формулы (291) находим силу тяги:
P = (293)
Составим баланс мощностей — подводимой от движителя и
реализуемой на плаву:
где Ne— номинальная мощность двигателя;
т)м— механический коэффициент полезного действия машины,
учитывающий потери в моторной установке и в приводе
к водяному движителю (а также механические потери
в самом водяном движителе);
т;— условный коэффициент полезного действия водяного дви-
жителя.
* Наиболее высокий к. п. д. винта составляет 0,78. А. Брике. Мелкое судо-
строение. ОНТИ, 1936, стр. 192—196.
330
Подставив в уравнение баланса выражение -q из формулы (292),
получим

(294)
Подставим значение W в формулу (293). После преобразова-
ния будем иметь
Р, = |‘ЧЛ':(1-^). (295)
При установившемся движении сила тяги Р должна равняться
силе сопротивления движению R, или P = R.
Из-формулы (288) определяем R и подставляем его значение
в формулу (294) вместо величины Р. Получим
(W* = А (1 - .
Обозначим
д__
4,&k4g ’
С 4/&№g •
(296)
(297)
Тогда предыдущее уравнение перепишется в таком виде:
г»6 bv^— с — 0. (298)
Решая это уравнение, находим скорость движения машины на
плаву:
<2")
где v выражено в м/сек.
Из анализа формул (294) и (296—297) следует, что скорость
движения машины на плаву зависит от мощности двигателя
(.Ди-Ч-), от упорной площади (Д) движителя и от линейного раз-
мера машины (А).
При этом считаем, что коэффициент а, как и в формуле (288)
равняется 4,6.
Упорную площадь гребного винта можно определить по сле-
дующей формуле:
Л = (300)
В этом уравнении а —Х-, где F—площадь проекции лопастей
Л) г
винта на плоскость, перпендикулярную к его оси; го—площадь
331
диска винта, т. е. площадь круга, который описывается крайними
точками лопастей винта.
Величину а обычно принимают равной 0,3—0,5 в зависимости
от числа лопастей (при большем числе лопастей величина а
больше).
В уравнении (300) X — число гребных винтов на машине.
Для водометного движителя упорная площадь может быть при-
ближенно определена по формуле (300), если в нее подставить
значение диаметра лопастного колеса насоса.
Значительно сложнее определяется упорная площадь гусенич-
ного движителя. Как мы отмечали выше, силу тяги создает нижняя
ветвь гусеницы; кроме того, на величину толкающей корпус силы
влияет и верхняя ветвь, которая частично нейтрализует действие
нижней ветви. Упорная площадь в первом приближении будет
равна разности упорной площади нижней и верхней ветвей. Про-
цесс создания толкающей корпус силы, однако, осложняется еще
целым рядом дополнительных явлений, полностью учесть которые
в настоящее время не представляется возможным. Поэтому условно
упорная площадь гусеничного движителя нами определяется по
следующей формуле:
А = ?ЬЬ, (301)
где (л—некоторый опытный коэффициент—коэффициент движи-
теля;
b — ширина гусеницы в л;
L— опорная база машины в м.
Коэффициент движителя должен быть определен на основании
опытов, проводимых с машинами различных типов. Он зависит от
многих факторов: от формы траков, от погружения в воду верхних
ветвей гусениц, от наличия отражательных козырьков и т. д.
Для гусеничного транспортера ГТ-С, имеющего ширину гусениц
6 = 0,36 м и опорную базу £ = 3,33 м, коэффициент р = 3,6 • 10~4.
Вернемся теперь к гребному винту и рассмотрим способ его под-
бора для машины, т. е. определения его размеров по заданной ско-
рости движения машины на плаву и по числу оборотов винта.
Если задана скорость машины и и известны все величины, вхо-
дящие в формулы (296) и (297), кроме величины упорной пло-
щади А, то эта площадь определяется из уравнений (296—298).
Определив упорную площадь А, по формуле (300) находим диа-
метр винта. При этом задаемся для трехлопастного винта коэффи-
циентом а, равным 0,3—0,4, а для четырехлопастного — коэффициен-
том 0,5.
Определим шаг винта.
Допустим, что мы имеем винт и гайку, причем винт отождествим
с гребным винтом, а гайку — с затвердевшей и неподвижной водя-
ной средой. Тогда за один оборот винт получит осевое перемеще-
ние на величину шага h. За п оборотов перемещение будет равно nh.
332
Это есть скорость IF, определяемая по формуле (294). Тогда мо-
жем написать
h = , (302)
где W— скорость движителя в м!сек\
п — обороты винта в минуту;
h — шаг винта в м.
Как показывают экспериментальные исследования, к. п. д. винта
зависит от шагового отношения h : D.
Наиболее рациональное шаговое отношение должно находиться
в пределах
0,8<4< 1.5- (303)
Желательно, чтобы оно было близко или даже равно 1,5.
При расчете винта следует учитывать возможность появления
кавитации, т. е. разрыва сплошности потока воды. Кавитация
зависит от удельного давления, которое оказывает-поток на ло-
пасти винта.
Обозначим удельное давление буквой q. Тогда
Р 4Р
q — -т- = —. (304)
Удельное давление не должно превышать 1 кг/см2. Обычно
в расчетах его принимают равным 0,5—0,8 кг/см2.
Кавитация зависит также от скорости крайних точек лопастей:
где V не должно быть более 45—55 м!сек.
Выполняя условия, выраженные формулами (303), (304) и
(305), мы можем определить геометрию винта, т. е. его диаметр
(/)) и шаг (Л). При этом числом оборотов винта (л) задаемся.
Заметим, что число оборотов винта лимитируется шаговым от-
ношением и кавитационными явлениями. Поэтому обороты винта
имеют предел.
Чтобы наиболее полно использовать мощность двигателя и, сле-
довательно, получить максимально высокую скорость движения
машины на плаву, надо иметь в силовой передаче машины спе-
циальную водоходную передачу. При этом эта передача должна
реверсироваться, чтобы обеспечить машине задний ход на плаву.
Обычная сухопутная передача заднего хода имеет слишком низкую
скорость и поэтому не создает достаточную тягу на плаву, т. е. не
обеспечивает машине задний ход.
Зная скорость движения машины и и скорость движителя IF,
по формуле (304) можно определить условный к. п. д. дви-
жителя 7].
333
Пример. Определить, как изменится скорость движения машины на плаву,
если на ией поставить гребной винт.
Дано: Ne = 74 л. с.\ k = 4; L = 3,33 я; b = 0,36 я; D =0,3 м; X. = 1.
Задаемся: т;м = 0,75; а = 0,3.
Определяем по формулам (300) и (301) упорную площадь винта Двн 11
гусениц ДГн:
3-14-0,32
4ВИ = 0,3 — — = 0,021 л/2-
4ГИ = 3,6• 10~4• 0,36 3,33 = 0,00043 м\
Из формул (296—297) находим:
1000-0,021-0,75-74-75 _
™ “ 4,62-44-9,81 ’ -
_ 1000-0,021-0,752-742.752
Свн “ 4,63-4е-9,81 ~94’
. 1000-0,00043-0,75-74-75
=---------4,62--44-9,-81-----= °-034;
_ 1000-0,00043-0,752-742-752 _
Сги “ 4,63-4е-9,81 ~ '
Из формулы (299) находим скорость машины при винтовом и при гусеничном
движителе:
3 / /j 552 j g5
vBH = у у ----------1- 94---= 2,09 м/сек, или 7,5 км/час,
I/ /0,0342 о,О34 , ,, ,
г>гн = У у —-------1" 1,91----— = 1,11 м/сек, или 4 км/час.
Таким образом, вследствие применения гребного винта скорость движе-
ния машины может повыситься примерно на 87%. Это объясняется тем, что
упорная площадь винта (ДВн) значительно больше упорной площади гусениц
(^гн)-
Определим силу тяги винта.
Будем иметь
Р = R = 4,6-W* = 4,6-42.2,0942 = 322 кг.
Удельное давление на винт будет
Р 322
4 = ~А = 0,021-10000' = 1,53 кг!смг'
Это превышает указанную выше норму. Чтобы снизить удельное давле-
ние, надо увеличить диаметр винта, при этом окружная скорость виита V не
должна превышать 45—55 м/сек.
Определяем по формуле (294)
№ = -
0,75-74-75 .. ,
----зло--- ~ 13 м!сек-
334
Тогда к. п. д. виита будет
Ч =
у 2,09
W ~ 13
= 0,16.
Как видим, к. п. д. гребного винта, установленного на гусеничной ма-
шине,— величина очень низкая. Это объясняется большим скольжением винта.
Так, в данном случае скольжение составляет
у 13 — 2,09
•$о = —=------------X----0,84, или 84%.
W 10
ГЛАВА IX
ТОПЛИВНАЯ экономичность ГУСЕНИЧНОГО
ПОЕЗДА
1. ПАРАМЕТРЫ ТОПЛИВНОЙ ЭКОНОМИЧНОСТИ
Топливная экономичность зависит от различных конструктив-
ных и эксплуатационных факторов.
К конструктивным факторам, влияющим на топливную эконо-
мичность, относятся: тип машины — тягач или транспортер; тип
двигателя — дизель или бензиновый двигатель; тип силовой пере-
дачи — фрикционно-зубчатая, гидромеханическая, электромехани-
ческая; разбивка передач в ступенчатой силовой передаче, диапа-
зон передач; тип механизма поворота; тип привода управления дви-
гателем и механизмами силовой передачи — ручной непосредствен-
ного действия или сервопривод, автоматизированная силовая пе-
редача и др.
К эксплуатационным факторам относятся: условия движения
машины — величины дорожных сопротивлений, движение одиноч-
ной машины или движение в колонне; состояние машины — сте-
пень ее изношенности, особенно изношенности двигателя; отре-
гулированность или неотрегулированность топливной аппаратуры
в дизелях или карбюратора в бензиновых двигателях; степень
засорения воздухоочистителя; тип и вес прицепа; квалификация
водителя и др.
Топливная экономичность оценивается расходом горючего, от-
несенным к той или иной единице измерения, например к мощ-
ности двигателя, к пути, проходимому машиной, или ко времени
работы двигателя. Величина расхода является параметром
топливной экономичности машины.
Примем в качестве параметров топливной экономичности сле-
дующие величины:
— удельный расход горючего в граммах на одну эффективную
лошадиную силу за час, работы двигателя (gejl ^час)'’
— километровый расход горючего в литрах на один (или на
сто) километр пути движения машины
— часовой расход горючего в литрах за один час работы дви-
гателя ;
336
— рабочий расход горючего в килограммах на тоннокилометр
( Кг \
полезной работы машины ( qv -—(Н)
Рассмотрим каждый из этих параметров в отдельности.
УДЕЛЬНЫЙ РАСХОД ГОРЮЧЕГО
Удельный расход горючего характеризует топливную экономич-
ность двигателя в зависимости от числа оборотов его вала и за-
грузки двигателя.
На рис. 193 показаны внешняя характеристика двигателя (7VJ
и характеристика удельного расхода горючего (gj в функции обо-
ротов вала двигателя.
Из рисунка следует, что при оборотах nge, несколько смещенных
влево от оборотов, соответствующих максимальной мощности Пу,
расход горючего наименьший. Это значит, что при определенных
оборотах двигатель работает наиболее экономично. Обороты nge
по топливной экономичности являются эксплуатационными оборо-
тами двигателя.
Рис. 193. Внешняя характеристика
двигателя (характеристика мощности
и удельного расхода горючего)
Рис. 194. Зависимость удельного
расхода горючего от загрузки дви-
гателя
На рис. 194 представлена зависимость удельного расхода го-
рючего (ge) от загрузки двигателя, т. е. от снимаемой с двигателя
эффективной мощности. Из рисунка следует, что с изменением за-
грузки удельный расход сильно меняется. Так, при полной загрузке
двигателя расход горючего составляет примерно 240 г/л. с. час
(бензиновый двигатель), а при 20% загрузки—600 г/л. с. час, т. е.
почти в три раза больше.
Удельный расход зависит также от типа двигателя; в дизеле
удельный расход горючего меньше, чем в бензиновом двигателе,
примерно на 30—40%.
337
КИЛОМЕТРОВЫЙ РАСХОД ГОРЮЧЕГО
Расход горючего в литрах на единицу пути движения машины
определяется по формуле
1000-р ’
гДе Як — расход горючего в л/км\
ge—удельный расход горючего в г/л.с.час,
— фактическая мощность, снимаемая с двигателя, в л.с.\
у — объемный вес горючего в г/см*-,
v — скорость движения машины в км/час.
Приведем эту формулу к несколько иному виду. Напишем сле-
дующее равенство:
270т]77д = ROnv, (307)
где ROa— общее сопротивление движению поезда;
v—скорость поезда;
г; — к. п. д. тягача;
77д—фактическая мощность, расходуемая на преодоление
сопротивления /?Оп.
Подставляя в формулу (306) 7УД из равенства (307), получим
формулу километрового расхода горючего:
9. = fife. (308)
где /?Оп в тоннах.
Из этой формулы следует, что километровый расход зависит
от удельного расхода ge и от общего сопротивления движению
поезда /?Оп-
На величину ge влияет загрузка двигателя и число оборотов
вала двигателя.
Общее сопротивление движению поезда можно представить
в таком виде: ^0п Уоп^О» (309)
где /о + fol (ЗЮ)
1+£ . (j
G0 = G + Gi- (ЗП)
В этих равенствах /Оп—общий коэффициент сопротивления
движению поезда; <70 — общий вес поезда; /0 — коэффициент со-
противления движению тягача; /01 — коэффициент сопротивления
движению прицепа.
338
Отсюда следует, что расход qK зависит от соотношения веса
тягача и веса прицепа, от общего веса поезда, от к. п.д. тягача и
сопротивлений дороги.
Для сравнения топливной экономичности гусеничных поездов
необходимо испытывать их в одинаковых дорожных условиях (т. е.
при одинаковых коэффициентах сопротивления движению /0 и /01)
и при одинаковом отношении весов прицепа и тягача (Gi : G).
В табл. 21 приведены опытные данные по километровому рас-
ходу горючего для тягачей, работающих со штатным колесным
прицепом на грунтовых дорогах.
Таблиц а 21
Километровый расход горючего
Параметр Марка машины
М-2 АТ-Л АТ-С АТ-Т АТ-П
дк, л)км 1Д 0,9 1,6 1,95 1,0
Из табл. 21 следует, что тягач АТ-П, имеющий бензиновый дви-
гатель, расходует на 1 км пути больше горючего, чем тягач АТ-Л,
имеющий двигатель дизель, хотя вес тягача АТ-Л с прицепом на
15% больше веса тягача АТ-П с прицепом.
В табл. 22 приведены опытные данные по километровому рас-
ходу горючего для двух одиночных машин, на одной из которых
установлен двигатель дизель, а на другой — бензиновый двигатеть.
Машины испытывались в различных дорожных условиях.
Таблица 22
Километровый расход горючего
Дорога Для машины с двига- телем дизель, вес 20 tn, расход горючего, л!км Для машины с бензи- новым двигателем, вес 22 т, расход горючего, л[км
Булыжно-щебенчатое шоссе 1,69 2,15
Тяжелая проселочная дорога 2,01 2,80
Местность 2,2-1 3,35
Из табл. 22, как и из табл. 21, следует, что расход гОРЮчего
зависит от типа двигателя. Кроме того, на расход влияет х^Рактер
дороги. Чем тяжелее дорога, тем больше расходуется горю116' ^
339
ЧАСОВОЙ РАСХОД ГОРЮЧЕГО
Расход горючего за 1 час работы двигателя определяется по
формуле
_ gerlNNe
У* ~ юооу ’
где </ч—часовой расход горючего в л/час,
ge—удельный расход горючего в г/л. с. час,
f\N—коэффициент использования мощности;
Ne — номинальная (паспортная) мощность двигателя в л. ел,
у — объемный вес горючего в г/см3.
Из формулы (312) следует, что часовой расход зависит от удель-
ного расхода, от коэффициента использования мощности и от но-
минальной мощности двигателя; С увеличением этих величин ча-
совой расход возрастает.
В табл. 23 приведены опытные данные по часовому расходу для
тягачей, работавших с штатным колесным прицепом.
Испытания тягачей проводились на грунтовых дорогах.
Таблица 23
Часовой расход горючего
Параметр Марка машины
М-2 АТ-Л АТ-С АТ-Т АТ-П
q4, л/час 16 19 34 50 22
Из табл. 23 следует, что тягач АТ-П с бензиновым двигателем
расходует горючего на 15—30% больше, чем тягачи АТ-Л и М-2,
приближающиеся к нему по весу, но имеющие двигатель дизель.
Заметим, что часовой расход горючего у тягача АТ-Л несколько
выше, чем у тягача М-2, что объясняется более высокими скоро-
стями движения тягача АТ-Л.
Часовой расход горючего как оценочный параметр топливной
экономичности был введен для быстроходных гусеничных машин
из сельскохозяйственных тракторов. Однако условия работы сель-
скохозяйственного трактора и транспортной гусеничной машины
различны. Сельскохозяйственный трактор работает почти при по-
стоянной загрузке двигателя, а транспортная машина — обычно
при переменной загрузке. Поэтому часовой расход в применении
к транспортным машинам не характеризует полностью топливную
экономичность машины. Для транспортных машин более харак-
терным параметром является километровый расход.
РАБОЧИЙ РАСХОД ГОРЮЧЕГО
Рассмотренные нами параметры ge, qK и qv характеризуя рас-
ход горючего машины, не позволяют, однако, судить о том, какую
полезную работу при данном расходе совершила машина, т. е. ка-
340
кой полезный груз она перевезла. Между тем именно это является
особенно важным при оценке топливной экономичности транспорт-
ных машин, вследствие чего и введен дополнительный параметр —
рабочий расход горючего.
Определим рабочий расход горючего как производную от ве-
сового расхода по совершенной гусеничным поездом полезной ра-
боте:
__ dQ
dWn ’
Согласно формуле (308) километровый расход, выраженный
в килограммах, равен
____ ёе^оп _ ёг/otiGo
Ч* ~ 270-/] “ 270т] ’
тогда элементарный весовой расход
tZQ = q'KdS,
где dS — элементарный путь, проходимый машиной.
Обозначим через Gr и Grl вес в тоннах полезного груза, пере-
возимого на тягаче и на прицепе (если тягач буксирует артилле-
рийскую систему, то Gr] —полный вес системы).
Тогда элементарная работа, которая будет затрачена на пере-
возку грузов, будет равна
dWa = (faG?+fmGJdS.
Подставляя dQ и dW в приведенное выше выражение qpt оконча-
тельно получим
= 270т] (/Й+/oiGr i)' • (313)
Примем приближенно /о ~/м ~/ои- Тогда формулу (313)
можно переписать в более простом виде:
= "270^ ‘ ~G^ ’ (314)
где
Go = G + G15
Qo = + Grl.
Из формулы (314) следует, что рабочий расход горючего зави-
сит от его удельного расхода, от к. п. д. тягача и отношения веса
поезда к общему весу перевозимого груза.
Выразим рабочий расход qp через километровый расход qK.
23 -2469 341
Из формулы (308) можем написать
ge Wk = Wk
270т] ROn f0uG0
Подставив это выражение в формулу (314), окончательно по-
лучим
Qp^Y^q-Як- (315)
г Уоп^го
Из этой формулы следует, что рабочий расход зависит от кило-
метрового расхода, от характера дороги и веса перевозимого груза.
В табл. 24 приведены значения рабочего расхода горючего. При
определении qp принималось: у = 0,86 а/с.и3; /Оп = 0,08; вес полез-
ного груза определялся как сумма груза на платформе и полного
веса прицепа. Значения qK взяты из табл. 21.
Таблица 24
Рабочий расход горючего
Параметр Марка машины
АТ-П М-2 АТ-Л АТ-С АТ-Т
qp, кг/ткм 2,18 1,47 1,40 1,0 0,7
Со Gro 2,06 1,90 1,83 1,71 1,66
Д, г/л. с. час 1,05 0,77 0,77 0,59 0,42
Из табл. 24 следует, что из всех тягачей наилучшей топливной
экономичностью обладает тягач АТ-Т, а наихудшей — тягач АТ-П.
Это объясняется тем, что тягач АТ-П имеет бензиновый двигатель,
а тягач АТ-Т — дизель. Кроме того, полезный груз тягача АТ-Т
выше полезного груза тягача АТ-П.
Сравнивая тягачи АТ-Т и АТ-С, видим, что, несмотря на одно-
типные двигатели этих машин, их топливная экономичность раз-
лична: тягач АТ-Т имеет более высокую экономичность, чем тя-
гач АТ-С. Это объясняется тем, что у тягача АТ-Т величины 4^-
До
и 27q- меньше. На топливную экономичность повлияла также ме-
нее рациональная разбивка передач в тягаче АТ-С и дросселировка
его двигателя: задросселированный двигатель имеет больший
удельный расход.
Рассмотренные параметры топливной экономичности гусенич-
ного поезда могут являться одновременно и параметрами оценки
топливной экономичности одиночной машины. Для этого в приве-
денных выше формулах следует принять вес прицепа Gi = 0.
342
2. ВЫБОР РАЦИОНАЛЬНОГО ОТНОШЕНИЯ МЕЖДУ ВЕСОМ
ПРИЦЕПА И ВЕСОМ ТЯГАЧА И РАЦИОНАЛЬНОЙ ПЕРЕДАЧИ
ПРИ ДВИЖЕНИИ ГУСЕНИЧНОГО ПОЕЗДА ПО ТОПЛИВНОЙ
экономичности
n / Gi \
Рациональное отношение веса прицепа к весу тягача 1 мо-
жет определяться двумя факторами: во-первых, проходимостью
поезда и, во-вторых, его топливной экономичностью. Выше, в
главе .III, было установлено, что для лучшей проходимости поезда
отношение -т=г должно быть не больше единицы.
Q
Рассмотрим теперь, какое отношение целесообразно иметь
с точки зрения топливной экономичности*.
Обозначим вес перевозимого на тягаче груза через aG, где G —
полный вес тягача. Вес груза в прицепе примем равным весу при-
цепа, т. е. Gtl= Gi. Тогда Go = G ф- Gi, О,й = aG ф- Gb
Из формулы (316) получим
(316)
Отсюда следует, что чем больше величина и а, тем меньше
рабочий расход горючего и выше экономичность поезда.
Представим формулу (316) в виде графика. Примем величину
условно равной единице и а = 0,25, что будет соответство-
вать некоторому среднему соотношению между весом груза на
платформе и весом тягача.
Q
Тогда можем построить зависимость qp в функции
(рис. 195).
Из полученного графика следует, что с увеличением веса при-
цепа рабочий расход горючего вначале резко падает, примерно до
G G
-т~ = 0,75, а потом, начиная с величины -/г — 1,25, делается почти
и <1
постоянным.
На графике (рис. 196) приведены опытные и расчетные даннце
по рабочему расходу qp, выраженному в функции Как ви-
дим, кривая по расчету и кривая, полученная опытным путем, почти
совпадают.
Таким образом, можно сделать вывод, что для улучшения топ-
ливной экономичности при сохранении удовлетворительной прохо-
димости должно находиться в пределах 0,75—1,25.
♦ Г. А. Иванов и Е. И. Магидович. Труды ВТА № 62. 1955.
23*
343
Рис. 195. График зависимости рабочего
расхода горючего от отношения веса при-
цепа к весу тягача
Рис. 196. График рабочего расхода горючего:
I — кривая расхода, полученная расчетом; 2 — кривая
расхода, полученная опытным путем
344
Рассмотрим вопрос о выборе рациональной передачи, на кото-
рой должно совершаться движение поезда.
Пусть груз перебрасывается из одного пункта в другой. При
этом можно двигаться или на высших передачах, имея относительно
небольшой вес прицепа, или на низших — с большим весом при-
цепа. Определим, какой режим движения является наилучшим в
отношении топливной экономичности.
Сопротивление движению поезда равно
R^foG + f^. (317)
На данной передаче тягач развивает максимальную силу тяги
по двигателю fpG, где /р — расчетный коэффициент сопротивления
движению [см. формулу (62)]. Так как при равномерном движе-
нии /?Оп — fpG, то из равенства (317) определим вес прицепа
G1—fp~f°G, (318)
Joi
по-прежнему считая, что вес прицепа равен весу- перевозимого
груза.
Для определения величины (71 необходимо знать значения рас-
четных коэффициентов сопротивления движению на передачах. Так,
например, для тягача М-2 имеем: /р1 = 0,55; /рй = 0,31; /р3=0,16;
/Р4 —0,09;/р-= 0,07. Зададимся средними дорожными условиями:
// = 0,08 и /о1 = 0,05 (для колесного прицепа).
Из формулы (318) находим вес прицепа при движении поезда
на различных передачах: G1(1) = 9,4G; G1(2) = 4,6G; G](3)=1,6G;
G|(4) = 0,2G.
Определим рабочий и километровый расход горючего при дви-
жении поезда на второй и третьей передачах. В формуле (316) при-
мем 275— = 1 и а = 0,25. Формулу (308) перепишем в таком виде:
_ Se^on _ Sefoxfi /1 , Ci \
™ 270гд 270т]| G ) '
Здесь примем
§efоп<? ___ <
270тц
Тогда получим qp (2) = 1,16; qp (3) = 1,4; qK (2) = 5,6; qK (3) = 2,6.
Из этих равенств следует, что если поезд будет двигаться на
второй передаче, то рабочий расход горючего будет примерно на
17% ниже расхода при движении поезда на третьей передаче. Од-
нако при этом километровый расход на второй передаче более чем
в 2 раза выше километрового расхода на третьей передаче, а ско-
рость поезда на второй передаче в 2 раза меньше скорости поезда
на третьей передаче. Таким образом, движение на второй передаче
нецелесообразно. Нецелесообразно и движение на первой и четвер-
345
той передачах (на пятой передаче движение невозможно), так как
на первой передаче поезд будет двигаться с очень малой скоростью
(почти в 6 раз меньше, чем на третьей передаче), а на четвертой
передаче буксируется слишком малый груз; кроме того, для четвер-
той передачи получим <7р(4) = 2,б7, <7 4)= 1,2. По рабочему рас-
ходу эта передача по сравнению с третьей неэкономична.
Отсюда можно сделать вывод, что наиболее целесообразной пе-
редачей является третья. Эта передача ближе всего подходит и к
рациональному (близкому к единице) значению Таким обра-
зом, рабочей передачей для тягача является передача, обеспечи-
Gt ~
вающая отношение д-, близкое к единице.
3. ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ МОЩНОСТИ ДВИГАТЕЛЯ
Как уже отмечалось выше, удельная мощность двигателя, или
отношение номинальной мощности к весу тягача, характеризует
подвижность как отдельной машины, так и гусеничного поезда.
Чем выше удельная мощность, тем выше подвижность. Однако
чрезмерное увеличение удельной мощности приводит к тому, что
двигатель начинает работать со значительной недогрузкой, а это
снижает его экономичность, а следовательно, и экономичность ма-
шины.
Определим удельную мощность, которой должен располагать
тягач, работающий с колесным прицепом в средних дорожных ус-
ловиях.
Из определения удельной мощности тягача можем написать
следующее равенство:
N = ^G°vma*_ ,31g,
yvy G 0,27t]G ’
где /Оп — общий коэффициент сопротивления движению поезда, со-
ответствующий максимальной скорости Z/niax.
Согласно формуле (310) имеем
/о +/ol
/йа=' 1 + ^1
+ G
Чтобы правильно выбрать удельную мощность, надо правильно
задать коэффициент сопротивления движению поезда.
Гусеничный поезд должен развивать максимальную скорость на
хороших грунтовых дорогах. Эти дороги характеризуются следую-
щими коэффициентами: f — 0,06; /j = 0,03; подъем дороги примем
i = 3%.
Тогда
/0 = 0,06 +0,03 =0,09;
/01 = 0,03 + 0,03 = 0,06.
346
Для определения общего коэффициента сопротивления движе-
нию поезда /Оп необходимо знать отношение Примем ориен-
тировочно это отношение равным единице. Тогда получим
1 + 1 = 0,075.
Выше указывалось, что наилучшее отношение равно
0,75—1,25. Тогда вес поезда будет Go = G -ф- Gi равно (1,75—2,26) G.
Зададимся к. п. д. тягача на скорости z/maxv] = 0,7, Тогда из фор-
мулы (319) после преобразования получим
7Vy = (0,7 — 0,9)г/тах. (320)
Таким образом, удельная мощность тягача, выраженная в ло-
шадиных силах на тонну веса машины, должна равняться 0,7—0,9
от максимальной скорости поезда, выраженной в км/час.
Примем = 25 км/час. Тогда удельная мощность будет
равна 17—22 л. с./т.
Согласно формуле (55) максимальная скорость одиночной ма-
шины равна

При Ny— 17—22 л. с./т получим ^тах = 54—70 км/час. Совре-
менные тягачи имеют скорость ^шах, лежащую близко к нижнему
пределу.
Если принятьг'шах > 25 км/час, то получим завышенное значение
удельной мощности, так как скорость г'шах > 25 км/час для поезда,
движущегося по дороге с коэффициентом сопротивления /0 = 0,09,
маловероятна.
4. ВЛИЯНИЕ НА ТОПЛИВНУЮ ЭКОНОМИЧНОСТЬ
РАЗБИВКИ ПЕРЕДАЧ
Разбивка передач значительно влияет на топливную экономич-
ность машины.
Мы условились оценивать разбивку передач по коэффициенту
использования мощности +v. Чем полнее используется мощность
двигателя, т. е. чем ближе -qN к единице, тем выше экономичность
машины. При расчете нельзя точно определить, как в эксплуатации
будет использоваться мощность двигателя. Однако, если принять,
что водитель стремится получить высокие средние скорости движе-
ния машины (поезда), он должен полнее использовать мощность
двигателя. В этом случае график использования мощности может
характеризовать топливную экономичность машины.
347
На рис. 197 приведены графики использования мощности тяга-
чей АТ-Л, АТ-П, АТ-С и АТ-Т, а в табл. 25 — сводные данные по
расчетным скоростям (^р), расчетным коэффициентам сопротивле-
ния движению (/р и /рп) и минимальным значениям коэффициента
использования мощности (т)0) для тех же машин.
Таблица 25
Сводные данные по скоростным, тяговым и экономическим
показателям артиллерийских тягачей
Передача Тягач АТ-Л Тшач АТ-П
V Р’ км) час fv ^рп ’Ь V Р’ км! час 4 •^рп ^0
I 4,51 0,70 0,43 0,38 5,30 0,72 0,42 0,51
II 11,26 0,27 0,16 0,55 10,10 0,36 0,21 0,54
III 19,21 0,15 0,09 0,65 17,70 0,20 0,11 0,45
IV 27,9 0,10 0,06 0,59 33,71 0,09 0,05 0,67
V 41,92 0,06 0,04 0,62 среднее значение 45,00 0,06 0,04 0,56 среднее значение
Передача Тягач АТ-С Тягач АТ-Т
км/час 4 f рп ^0 Р’ км/час ^рп ^0
I 6,38 0,58 0,30 0,53 5,50 0,67 0,34 0,45
II 11,64 0,30 0,16 0,77 11,70 0,30 0,15 0,69
III 14,65 0,24 0,12 0,59 16,45 0,21 0,11 0,68
IV 23,25 0,14 0,07 0,69 23,00 0,14 0,07 0,57
V 32,00 0,10 0,05 0,64 среднее значение 36,20 0,08 0,04 0,62 среднее значение
Проанализируем на основании графиков (рис. 197) и сводной
табл. 25 разбивку передач тягачей.
Тягач АТ-Л имеет на третьей — четвертой передачах расчетные
коэффициенты сопротивления движению /рп = 0,06—0,09. Эти ко-
эффициенты соответствуют хорошим грунтовым дорогам (/рп =
= 0,06) и местности среднего качества (/рп = 0,09). Эти коэффи-
циенты можно считать типовыми, т. е. наиболее часто встречаю-
щимися в эксплуатации. Тогда третья и четвертая будут рабочими
передачами поезда. Большую часть времени тягач будет работать
на этих передачах. Следовательно, топливная экономичность поезда
будет определяться движением на третьей и четвертой передачах.
348
Рис. 197. График коэффициентов использования мощности тягачей
Согласно сводной табл. 25 минимальный коэффициент исполь-
зования мощности т|о на третьей — четвертой передачах составляет
0,59—0,65, а в среднем 0,62. Этот коэффициент можно считать
вполне удовлетворительным.
В тягаче АТ-Л правильно принято трз > k)o-i, так как поезд чаще
будет работать не на третьей, а на четвертой передаче.
б целом разбивка передач тягача АТ-Л вполне удовлетвори-
тельна.
Иную разбивку передач имеет тягач АТ-П.
На четвертой передаче трм = 0,67, а на третьей 7p.3j= 0,45. На
первой и второй передачах тр выше, чем тр на третьей передаче.
349
Разбивка передач сделана неверно, так как третья и четвертая пе-
редачи чаще используются, чем первая и вторая, а следовательно,
они должны иметь и более высокий коэффициент тр. Среднее зна-
чение к)о на третьей и четвертой передачах для тягача АТ-П состав-
ляет 0,56, а для тягача АТ-Л — 0,62.
В тягачах АТ-С и АТ-Т средний коэффициент тр на третьей и
четвертой передачах выше, чем средний коэффициент тягача АТ-П,
и примерно равен среднему коэффициенту тягача АТ-Л.
Из табл. 25 можно сделать выводы. В тягаче АТ-1' неудачно
выбран коэффициент к)02. Он слишком высок для второй передачи.
Для лучшей экономичности целесообразнее повысить коэффициент
т]оз, несколько снизив коэффициент трг. В этом отношении коэффи-
циенты т|о для тягача АТ-Л выбраны правильнее.
В основном в тягаче АТ-Т разбивка передач произведена вполне
удовлетворительно. Наиболее ходовая третья передача имеет вы-
сокий коэффициент использования мощности т|оз = 0,68, который
выше, чем тот же коэффициент на той же передаче у других машин.
Тягач АТ-С имеет самое высокое значение тр на второй пере-
даче. Для быстроходного тягача это иметь нецелесообразно. Тягач
имеет очень высокий средний коэффициент тр. Этот коэффициент
получен за счет высокого значения коэффициента тр на четвертой
передаче. Было бы целесообразнее несколько снизить тр4 и повы-
сить т|оз, который у тягача АТ-С слишком низок.
Общая разбивка передач в тягаче АТ-С в отношении средних
скоростей по топливной экономичности произведена менее удачно,
чем в тягачах АТ-Т и АТ-Л.
Высокое среднее значение коэффициента использования мощно-
сти (по всем передачам) зависит от диапазона скоростей и числа
передач в этом диапазоне. Чем уже диапазон и больше число пе-
редач, тем легче получить высокое среднее значение т]Оср. Так как
все рассматриваемые здесь тягачи имеют пять передач, то т]Оср за-
висит только от диапазона скоростей.
В табл. 26 приведены значения кинематического и силового диа-
пазонов для четырех основных тягачей: АТ-Л, АТ-П, АТ-С и АТ-Т.
Таблица 26
Значение диапазонов скоростей dK и dc
Тягач Диапазон скоростей

АТ-Л 9,3 12,5
АТ-П 8,5 11,6
АТ-С 5,0 6,0
АТ-Т 6,6 8,3
Из табл. 26 следует, что наибольший диапазон скоростей имеет
тягач АТ-Л, затем тягач АТ-П. Значительно меньше диапазон у
тягачей АТ-С и АТ-Т, что и позволило в этих тягачах получить вы-
сокие значения коэффициентов использования мощности,
350
5. ТЯГОВО-ЭКОНОМИЧЕСКАЯ ХАРАКТЕРИСТИКА
ГУСЕНИЧНОГО ПОЕЗДА
ПОСТРОЕНИЕ ТЯГОВО-ЭКОНОМИЧЕСКОЙ ХАРАКТЕРИСТИКИ
Для общей оценки тягово-экономических показателей гусенич-
ного тягача или гусеничного поезда служит тягово-экономи-
ческая характеристика (рис. 198).
Для построения этой характеристики в правом верхнем углу
наносится график использования мощности для одиночного тягача
и для поезда (соответствующим изменением масштабной линейки
коэффициента /0). По формуле (62) определяются расчетные коэф-
фициенты сопротивления движению
, _ nGrltNe ,
Jpl ~ VptG
где Ne— мощность тягача в л. с.;
vpt— расчетные скорости в км/час-,
— к. п. д. тягача;
t— передача.
К- п. д. тягача определяется по формуле (58)
(321)
Рис. 198. Тягово-экономическая характеристика гусеничного поезда
351
В правом нижнем углу графика проводится переходная прямая.
В левом нижнем углу строится кривая удельного расхода ge в
г)л. с. час как функция коэффициента использования мощности.
Кривая эта должна определяться опытным путем.
Так как график использования мощности строится для постоян-
ных расчетных оборотов вала двигателя (п.у), то и кривая удель-
ного расхода должна строиться для постоянных оборотов.
В верхнем левом углу строится график расхода горючего в лит-
рах на километр пути по формуле
= 270tiZy /о^о-
При построении графика задаемся значением коэффициента со-
противления движению. Примем этот коэффициент для примера
равным 0,1. Подставим в предыдущую формулу у и ?),. Чтобы опре-
делить необходимо задаться скоростью движения тягача. Ско-
рость определяется ориентировочно по значению принятого коэф-
фициента сопротивления движению.
Примем, кроме того, для одиночного тягача Go = G. Тогда по-
лучим qK как линейную функцию ge. Эта функция характеризует
километровый расход для одиночного тягача.
Задаемся/о = 0,2; 0,3 и т. д. Получим семейство прямых, выхо-
дящих из начала осей координат. Эти прямые будут характеризо-
вать расход qK в функции сопротивления дороги.
Покажем теперь, как пользоваться тягово-экономической харак-
теристикой.
Допустим, что одиночный тягач, для которого построена харак-
теристика, движется по дороге со средним значением коэффициента
сопротивления движению /0—0,1. Движение происходит на третьей
передаче.
Проводим пунктирную прямую, параллельную оси абсцисс, до
пересечения с лучом /pS (в правом верхнем углу). Из точки пере-
сечения опускаем прямую. Получаем коэффициент использования
мощности Ti v?-0,57. Далее, проводя пунктирную линию через пере-
ходную прямую (правый нижний график) до пересечения с кривой
удельного расхода, находим на оси абсцисс величину ge~
270 г/л. с. час. Пунктирная прямая пересекает луч /0= 0,1. Проек-
тируем точку пересечения на ось ординат. Найдем q* 1,43 л/км.
Допустим, что нужно определить те же величины для поезда,
движущегося по дороге с коэффициентом сопротивления /оп = 0,08.
Расчет проводится так же. Только в левом верхнем графике вер-
тикальную пунктирную линию проводим не до пересечения с лучом
/0 = 0,1, а до пересечения с дополнительным лучом /Оп = 0,08 (по-
казан пунктирной линией). Расход q„ определяется величиной, по-
лученной пересечением пунктирной горизонтальной прямой с этим
лучом.
При помощи тягово-экономической характеристики можно
решать различные задачи: определять возможные передачи, на
которых будет двигаться тягач (или поезд) при заданных сопротив-
352
лепиях; определять наиболее экономичные передачи в данных до-
рожных условиях (при данных сопротивлениях); оценивать исполь-
зование мощности двигателя; определять запас хода тягача и др.
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО
РАСХОДА ГОРЮЧЕГО
со-
ма-
ха-
Основу построения тягово-экономической характеристики
ставляют две опытные величины: удельный расход ge и к. п. д.
шины ц, На основании этих величин дальнейшее построение
рактеристики проводится расчетом.
Коэффициент полезного действия машины посредством опытов
определить трудно. Поэтому им можно задаться по формуле (322).
Таким образом, для построения тягово-экономической характери-
стики должна быть определена лишь одна опытная величина —
удельный расходу. Эту величину необходимо получить в функции
коэффициента использования мощности (функцию ge от оборо-
тов вала двигателя не рассматриваем, так как принимаем nN =
== const).
Для определения функции ge = ‘Р ("Пат) можно воспользоваться
одним из двух методов. Испытать двигатель в лаборатории и снять
с него соответствующие характеристики или эти характеристики
снять непосредственно в машине методом ходовых испытаний.
Рассмотрим второй метод как более простой.
Согласно формуле (308) напишем для одиночной машины
270^^ (323)
ёе foG
Выразим теперь коэффициент использования мощности
3,7/0GvpZ
<324)
где ge — удельный расход в г/л. с. час,
у — объемный вес горючего в г/см?\
qt.— километровый расход горючего в л/км-,
G — вес машины в т;
vpt — расчетная скорость в км/час,
Ne — номинальная мощность в л. с.
В формулах (323) и (324) величины ^z, qK и /0 неизвестны.
В первом приближении величинами и /0 можно задаться.
Тогда в результате опытов должна определяться только величина
расхода qK.
Для этого испытываемая машина движется равномерно по вы-
бранному участку пути. Водитель поддерживает постоянными обо-
роты вала двигателя, причем эти обороты должны соответствовать
расчетной скорости движения машины на данной передаче. С по-
мощью специальной аппаратуры замеряется расход горючего. Зная
длину мерного участка, находят километровый расход в л/км.
Скорость движения машины известна, так как она является рас-
четной. Испытания проводятся на всех расчетных скоростях по не-
скольку раз на каждой передаче.
353
Результаты испытаний и расчетов по формулам (323) и (324)
заносятся в таблицу (табл. 27).
Таблица 27
Примерная таблица результатов испытаний на топливную экономичность
опыта № замера Up, км!час ?к, л/км g г/л.с. час
1 2,16 481 0,32
1 2 5,50 2,18 478 0,33
3 2,17 484 0,31
Результат 5,50 2,17 481 0,32
среднего замера
1 1,81 351 0,41
2 2 11,62 1,79 356 0,40
3 1,83 352 0,42
Результат 11,62 1,81 353 0,41
среднего замера
Р, с. 199. Схема прибора для опре-
деления расхода горючего:
I — мерная колба; 2 — трехходовой кран;
3 — топливный бак
На основании данных табл. 27
в левом нижнем углу тягово-
экономической характеристики
строится зависимость ge = <р (т^).
На рис. 199 показана схема
прибора для определения расхода
горючего при испытаниях. При-
бор состоит из стеклянной колбы 1
с несколькими мерными шарами и
трехходового крана 2. Колба при-
соединяется к топливному баку 3
и к топливоподкачивающему на-
сосу двигателя (или к карбюра-
тору).
При испытании колба, запол-
ненная горючим, с помощью кра-
на отсоединяется от топливного
бака. С началом испытаний кран
открывается и двигатель получает
питание горючим из колбы. Испы-
тания ведутся до тех пор, пока из
мерного шара не будет израсхо-
довано все горючее.
Имеются и другие приборы для определения расхода горючего.
Однако данный прибор является наиболее простым, и поэтому он
чаще всего применяется при испытаниях машин.
, л
ОГЛАВЛЕНИЕ
Стр.
Предисловие ............................................................ 3
Глава I. Основы теории гусеничного движителя 5
1. Кинематика и динамика гусеничного обвода....................... —
2. Неравномерность движения гусеничного движителя................ 11
3. Коэффициент полезного действия гусеничного обвода............. 14
4. Взаимодействие опорных ветвей гусениц с грунтом............... 19
5. Методы экспериментального определения силы сопротивления ка-
чению и силы тяги по сцеплению................................... 22
Глава II. Динамика прямолинейного движения гусеничного поезда 32
1. Уравнения движения гусеничного поезда.......................... —
2. Трогание машины с места и переключение передач ..... 4.3
3. График разгона гусеничного поезда............................. 50
Глава III. Тяговые расчеты 55
1. Задачи тяговых расчетов. Порядок тягового расчета проектируе-
мой машины......................................................... —
2. Тяговый расчет транспортера................................... 56
3 Особенности тягового расчета тягача .............. 69
Глава IV. Теория поворота гусеничных машин 75
1. Кинематика и статика поворота.................................. —
2. Взаимодействие опорных ветвей гусениц с грунтом при повороте
машины............................................................ 81
3. Определение сил тяги на отстающей и забегающей гусеницах . . 88
4. Экспериментальное определение коэффициентов сопротивления ка-
чению и сопротивления повороту ................................... 91
5. Поворот тягача с гусеничным прицепом.......................... 97
6. Поворот тягача с колесным прицепом............................ ЮЗ
7. Занос гусеничной машины при повороте......................... 105
8. Баланс мощности при повороте гусеничного поезда. Вывод основ-
ного уравнения баланса .......................................... 107
Глава V. Теория силовой передачи (теория силового потока) 118
1. Определения и принципы теории силового потока................ 120
2. Характеристики узловых точек................................. 127
3. Постоянные силовые потоки.................................... 145
4. Расчет механической силовой передачи ........................ 159
5. Замкнутые силовые потоки..................................... 176
6. Расчет гидродинамического трансформатора.................... 184
7. Расчет электрических цепей постоянного тока и электро.механпче-
• ских передач...................................................... 188
8. Переменные силовые потоки ............................. .... 193
Глава VI. Теория подрессоривания и плавность хода гусеничных машин 207
1. Подвеска гусеничных машин................................• —
2. Приведенная схема подвески............................. • • 203
3. Приведение к расчетной схеме независимой подвески.............211
355
Стр.
4. Приведение к расчетной схеме балансирной подвески.............218
5. Общие уравнения упругости подвески с линейными характери-
стиками упругих элементов ........................' ............ 220
6. Расчет подвески с нелинейными характеристиками упругих эле-
ментов ..........................................................225
7. Плавность хода гусеничных машин и параметры плавности хода 228
8. Определение частоты и периода собственных колебаний корпуса
машины...........................................................231
9. Влияние конструктивных факторов на плавность хода машины 239
10. Влияние дорожных факторов на плавность хода машины . . . 249
Глава VII. Проходимость гусеничных машин 258
1. Определение. Параметры проходимости............................ —
2. Преодоление мягких грунтов...................................269
3. Преодоление крутых подъемов..................................276
4. Преодоление пороговых препятствий............................281
5. Преодоление рвов.............................................286
6. Преодоление крутых спусков...................................288
7. Преодоление ледяных препятствий..............................293
Глава VIII.Плавание гусеничных машин 297
1. Плавающие машины ............................................ —
2. Плавучесть и остойчивость.....................................299
3. Диаграмма затопляемости.......................................304
4. Расчет плавающей машины на плавучесть и остойчивость . . . 307
5. Вход машины в воду и выход из воды........................ 311
6. Подвижность и маневренность на плаву........................318
7. Определение скорости движения машины на плаву................330
Глава IX. Топливная экономичность гусеничного поезда 336
1. Параметры топливной экономичности.............................. —
2. Выбор рационального отношения между весом прицепа и весом
тягача и рациональной передачи при движении гусеничного поезда
по топливной экономичности ..................................... 343
3. Определение удельной мощности двигателя.......................346
4. Влияние на топливную экономичность разбивки передач . . . 347
5. Тягово-экономическая характеристика гусеничного поезда ... 351
Антонов Александр Сергеевич
ГУСЕНИЧНЫЕ ТЯГАЧИ. ЧАСТЬ I
Под наблюдением редактора инженер-полковника Косоротова Б. В.
Технический редактор Срибнис Н. В. Корректор Ларин В. В.
Сдано в набор 30.8.58 г. Г-53770 Подписано к печати 18.6.59 г.
Формат бумаги бОХЭЗ1/^ — 22*/4 печ. л, 22,25 усл. печ. ж 22,03 уч.-изд. л.
Военное издательство Министерства обороны Союза ССР
Москва, К-9, Тверской бульвар, 18
Изд, № 8/825 Зак. № 2469
2-я типография Военного издательства Министерства обороны Союза ССР
Ленинград, Д-65, Дворцовая пл., 10
PnsjaGTSM