Автор: Кузнецов Ю.В. Тронин Ю.В.
Теги: электротехника электроника радиоэлектроника учебное пособие
ISBN: 5-7035-0260-8
Год: 1992
Текст
Министерство науки, высшей школы и технической политики
Российской Федерации
КОМИТЕТ ПО ВЫСШЕЙ ШКОЛЕ
МОСКОВСКИЙ ОРДЕНА ЛЕНИНА И ОРДЕНА ОКТЯБРЬСКОЙ РЕВОЛЮЦИИ
АВИАЦИОННЫЙ ИНСТИТУТ имени СЕРГО 0РДК0НИКИДЗЕ
Ю.В. КУЗНЕЦОВ, Ю.В. ТРОНИН
ОСНОВЫ АНАЛИЗА ЛИНЕЙНЫХ РАДИОЭЛЕКТРОННЫХ
ЦЕПЕЙ
(Частотный анализ)
Учебное пособие
Утверждено
на заседании редсовета
24 октября 1991 г.
Москва
Издательство МАИ
1992
621.396 (075)
К- 891
УЖ: 621.372.011.71 (075.8)
Кузнецов Ь.В., Тронич D.B. Основы анализа линейных радиоэлектрон-
ных цепей (Частотный анализ): Учебное пособие. - М.: Изд-во МАИ,
1992. - 64 с., ил.
Рассмотрены некоторые вопросы теории линейных радиоэлектрон-
ных цепей, дающие необходимую основу для частотного анализа и рас-
чета типичных радиоэлектронных устройств.
Теоретические методы иллюстрируются примерами практических •
приемов анализа и расчета воздействия сигналов на радиоэлектрон-
ные цепи.
Для студентов факультета радиоэлектроники ЛА дневной и ве-
черней формы обучения, изучающих дисциплины "Основы радиоэлектро-
ники", "Радиотехнические цепи и сигналы".
Рецензенты: И.И. Литвак, О.Е. Антонов
7031 0гб0’8'© Московский авиационный институт, 1992
4. АНАЛИЗ ЦЕПЕЙ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ
4.1. Постановка вопроса
Анализ цепи при гармоническом воздействии играет особую роль
как в теории, так и в инженерной практике. Отметим некоторые при-
чины этого.
I. Гармонические сигналы, а также сигналы, близкие к ним,
чрезвычайно широко используются в радиоэлектронике.
2. Теоретический анализ линёйных цепей при гармоническом
воздействии значительно проще, чем для общего случая - произволь-
ного сигнала. Вйесте с тем, получаемые в результате анализа ха-
рактеристики цепи - так называемые частотные характеристики -
очень информативны. Часто само назначение той или иной цепи или
устройства дается в терминах именно их частотных характеристик
(усилитель нижних частот, усилитель промежуточных частот, частот-
ный корректор, полосовой фильтр и т.п.).
3. По известным частотным характеристикам цепи можно проана-
лизировать ее работу и при других воздействующих сигналах, резко
отличных от гармонических (например одиночных импульсов). Этой
цели служит спектральный анализ.
4. Частотные характеристики цепей легко контролировать экс-
периментально. Радиоэлектронные лаборатории оснащены генераторами
гармонических сигналов и другой измерительной аппаратурой, пред-
назначенной как раз для снятия частотных характеристик цепей.
Простота и удобство теоретического анализа линейных цепей
при гармоническом воздействии являются следствием того, что функ-
ции вида
(tit**) (4.1)
Sin
есть собственные функции любой линейной цепи. Это означает, что
при воздействии на цепь сигнала (4.1) частнъш решением динамичес-
ких уравнений для любого напряжения или тока в цепи будет функция
3
того же вида, с той же частотой й) и лишь другими амплитудами
и начальными фазами <PWX :
#вьн sin (wI+Vsm) . (4.2)
В силу линейности цепи амплитуда ^wjr пропорциональна /1$х,
а вследствие инвариантности цепи во времени изменение фазы вход-
ного сигнала вызывает такое же изменение фазы выходного гармони-
ческого сигнала, поэтому разность фаз - <PSX , определяемая
цепью, остается неизменной.
Итак, отыскание реакции цепи на входной гармонический сигнал
сводится к определению двух величин: коэффициента передачи цепи
по амплитуде и сдвига фазы в цепи:
л
<4.3>
Как правило, оба эти параметра цепи зависят от частоты гармони-
ческого воздействия. Это и есть частотные характеристики цепи:
амплитудно-частотная (АЧХ) и фазо-частотная (ФЧХ):
ЛЧХ -К„ (ti>) = i (4.4)
. (4.5)
Следует еще раз подчеркнуть, что частотные характеристики описы-
вают реакцию цепи только на гармоническое воздействие и только
частное решение динамических уравнений. Предполагается, что
вклкхгение сигнала произошло давно (теоретически при-со ) и соб-
ственная реакция на включение (т.е. решение однородного динами-
ческого уравнения) давным-давно закончилась. В цепи наблюдается
установившийся режим.
Для нахождения частотных характеристик цепи нет необходимости
описывать связь между токами и напряжениями в форме динамических
интегродифференциальных уравнений. Можно воспользоваться специаль-
но разработанным для этой цели методом комплексных амплитуд, поз-
воляющим описывать законы токораспределения в цепях, содержащих Я
L , С элементы, так же как для чисто резистивных цепей, т.е. си-
стемой алгебраических уравнений.
4
4.2. Некоторые сведения из алгебры
комплексных чисел
Напомним некоторые положения алгебры комплексных чисел.
Комплексное число Z = x+/y мыслится как точка комплексной плос
кости (рис. 4.1), заданная декар-
товыми координатами (#,,у). х -
называется действительной (вещест-
венной) частью % , у - мнимой,
X у у -ImZ . Та же точка
(конец вектора Z ) может быть за-
дана в полярных координатах - мо-
дулем I Z I и аргументом <р . Оче-
видны выражения:
Рис. 4.1
I Z I =- У + у2*, (f = arctcr , (4.6)
a~lZlcosip, у=12\&п<? . (4.7)
Известная формула Эйлера устанавливает связь между тригонометри-
ческими функциями и экспонентой с мнимым показателем:
е. ~ COsf -к jStnf . (4.8)
Вцражая X и у из (4,7), имеем
Z = #t/y - I ZKcvsy + jStn<p)^iZ\е. (4.9)
Итак, имеются две основные формы записи комплексного числа: алге-
браическая (через проекции # и У ) и показательная (через модуль
и аргумент):
Z-л?+/у-I Z! £ . (4.10)
/V
.Множитель В представляет собой вектор единичной длины,
расположенный под углом . При выполнении операций с комплексны-
ми числами могут быть использованы обе формы записи, однако удоб-
нее операции сложения и вычитания выполнять в проекциях
, (4.II)
а операция умножения, деления, возведения в степень - в показатель-
ной форме:
5
i, iz<l нъ-ъ)
7 f
(4.12)
Действия (4.II) и (4.12) иллюстрируются рис. 4.2. Обратим
внимание на то, что умножение Z на € есть не что иное, как
поворот вектора Z на угол *. Полезно
запомнить следующие
•л J
J0 1 J £ :
г -I, е -J,
частные случаи:
-/J чл
е. --i. е
т.е. умножения на у , -у ,
операции поворота вектора на
это тоже
— — + 1
Z 9 “ л
Я
2 >
В практических приложениях к расчету
цепей часто результат получается в форме
А 0+7^
дроби z — --— , а желательно иметь его
C+jd
в показательной форме или форме действи-
тельной и мнимой частей. Можно рекомендо-
вать действия, проиллюстрированные следу-
ющим примером:
Пример 4.1.
Рис. 4.2
7-J2
хВо избежание ошибок заметим, что речь идет об умножении на
экспоненту именно с мнимым показателем. Умножение на экспоненту
с действительным показателем - это изменение модуля. Например:
6
Приведем числитель и знаменатель к показательной форме:
2, = 5+j5 = I Z,) e,<f,r I Zt I - У 52 + jz'=5,83, -arete -34,4 °;
Z.,-7-j2-lZjeT^ \'lz\^7z^ -7,28, Rarefy'j--<7,7°.
Отсюда
Z =
J 38.4°
5.85 e j52,/°
.J? yO = 0,8 €
7, 28 8 }'
Z - 0,8 cos 52,7°* j0,8sin 52,1° =0,5475) 0,583.
Другой путь приведения к форме в проекциях - дрмножение числителя
и знаменателя на число, комплексно-сопряженное со знаменателем:
5^1Ъ _ (^)( ?+ jZ) ~
7-j2 ~ (7-]2)(7+J2) “ 7г+2г
—0,547j 0,585
4.3. Комплексный сигнал, комплексная амплитуда
Сопоставим две функции времени
fl(t) = flcos(wt + (p) (4.13)
и
<(wt+4>)
&t)~fle (4.14)
Это разные математические объекты: Sit) описывает периоди-
ческое изменение некоторой величины во времени; fl(t) - изменение
во времени положения точки (или вектора) в комплексной плоскости
(рис. 4.3).
Вектор S(t) длиной fl вращается с угловой скоростью СО ,
так что время его оборота равно Т~ , т.е. - период/ S(t). В
момент времени t = 0 угол вектора равен начальной фазе (р сигна-
ла Sit) .Из рассмотрения проекции вращающегося вектора Sit) на
вещественную ось х получаем
Xi t) « Не Sit) fl cos ( t (p)- S(t) .
7
Итак, в поведении функции 6(t) и S(t) много общего. Можно дей-
ствительному сигналу S(t) сопоставить комплексный сигнал
причем такое сопоставление взаимно однозначно:
S(t) ~ fiws(U)t + V) S(t) =fle . (4.14,a)
При расчете цепей можно мысленно заменить реальный воздействующий
сигнал 5р (t) его символом £> (^) с заданной амплитудой, час-
од ' 6Х .
jU)t
тотой и фазой. При этом, поскольку В - также собственная функ-
ция линейной цепи, оцень легко найти реакцию цепи - комплексный
сигнал на выходе
Очевидно*, (t) - это символ реального выходного сигнала S(t)
в котором в явной форме присутствуют амплитуда и фаза искомой ре-
акции. Сначала этот метод так и назывался - символический. Запись
перехода от действительного сигнала к комплексному и обратно, а
^Приведем более строгое обоснование: сигнал S(t) cos cot
, J №
можно рассматривать как сумму двух сигналов = и
(используя формулу Эйлера). Поскольку S^t) и $z(t)
комплексно-сопряженные, то и реакции цепи на эти воздействия также
комплексно, сопряжены. Реакция на сигнал 3(t) является суммой ре-
акций на 3(t) и sz(t) .
8
также и все действия в процессе анализа цепи можно сделать еще
более компактными, если ввести понятие комплексной амплитуда /?
сигнала s(t) :
j(o)t+<p) yV j&t . ju)t
S(t)-Ae. - He e = Ae . (4.16)
Комплексная амплитуда - неподвижный во времени вектор, со-
держащий информацию и об амплитуде действительного сигнала и о
jwt
его начальной фазе. Множитель вращения £ опущен. Реальный
сигнал S(t) сопоставляется сразу с комплексной амплитудой:
stf) - A cos ( cot + -Ле (4.17)
4.4. Комплексные сопротивления, проводимости
Между напряжениями и токами в элементах L и С цепи сущест-
вуют следующие связи:
. diAb . . r duc(t)
L lit C dZ
Для случая комплексных сигналов
jUit
ur(t)-l[e ;
С- с
(4.18)
у’ (e>t
йАЬ = V. е
L
4 «) - Кe
t
дифференцирование дает след/ицие соотношения:
- jCllt •
Те1 =ju)CUcei .
С 4 с
(4.19)
jcot
Сокращая на £ , получим для комплексных амплитуд:
K-iwLiL > • (4-го>
Отношение комплексной амплитуда напряжения на элементе к ком-
плексной амплитуде тока через него можно трактовать как некоторое
сопротивление, а обратное отношение - как проводимость. По опреде-
9
лению, это-комплексные сопротивления и проводимости ("импеданс"
и "адиитанс").
Все три основные элемента цепи Л , L , С становятся рав-
ноправными : напряжение на элементе равно произведению тока на
сопротивление (подразумеваются комплексные амплитуды напряжения
Здесь комплексные сопротивления
и, соответственно, комплексные проводимости
У ^-L- --i-L- , Y^jwC. (4.22)
R Я 4 . J b)l £ J
Все правила расчета цепей, эквивалентные преобразования, основан-
ные на законах Ома и Кирхгофа применительно к резистивным цепям,
теперь оказываются справедливыми для любых соединений резисторов,
конденсаторов, индуктивностей при условии гармонического воздей-
ствия. В- этом и состоит метод комплексных амплитуд.
Этот метод оказался очень удобным и получил широкое распро-
странение. Часто в технической речи не делается различия между
сопротивлением и комплексным сопротивлением. Так, например, можно
услышать:’"ток через индуктивность равен напряжению, деленному
на ja)L ". Однако это вовсе не означает, что . Надо
всегда помнить, что речь идет о комплексных амплитудах - символах
гармонических сигналов.
Пример 4.2. Найти комплексные сопротивления и проводи-
мости последовательного и параллельного соединений И к С
(рис. 4.4). Имеем:
7 „ У . у= J_= _L___________/шС согигсг . д>С
rt z R + ^-z ~ '/+cvzRzCe JUuVl2i
1шС
„ /
Ж R _ R . wRC у
4“ л, / / 4-/<уйГ " 7+<у2«2С2 У+й)2^2 ’ yz = ^+JaC-
jb>c
Заметим, что комплексное сопротивление резистора - чисто ве-
щественное (или, как говорят, активное), а емкости и индуктивнос-
ти -'чисто мнимое (реактивное). Комплексное сопротивление некото-
рого соединения активного и реактивного сопротивлений содержит и
10
вещественную, и мнимую части. При этом может оказаться, что обе
части зависят как от активного, *гак и от реактивного сопротивле-
ний. Таковы в рассмотренном примере X 1 •
Рис. 4.5
Рис. 4.4.
Пример 4.3. Определить теки -^(6, 9 и
напряжение u(t) в цепи рис. 4.5,а гри воздействии e(i) =
- I cos со f . при следующих данных: со - I03 1/с, С = 2 мкФ,
L = 200 мГн, Л - 100 Ом. Перейдем к схеме рис. 4.5,6, в кото-
рой элементы схемы заменены комплексными сопротивлениями
2Ж = 100 ом , ZL= jcoL= f 105- 0,2 = J200 Ом ;
Z - -rAr = ~ f —. 1 'K = ~i5OO 0м .
c JtoC 1 10s-Z 106 J
Все переменные - комплексные амплитуды.
Уравнения для определения искомых переменных очевидны:
Выполняя действия с комплексными числами, получим:
J2 в- I-
й.
II
Проверка результатов(if-Iz + )• ) удовлетворяется.Теперь
нужно привести запись комплексных амплитуд к показательной фор-
ме: .ж
/2 2е* 1*>ае
V~l^> ’ В '>
i. ,1л
J' Viog z>1t,e мЯ,
Ji,К . iO,Z9
I - 1.3 г мА L- 0,96& мА .
Z 9 .3
Окончательный результат
ti(f) - 0,19 as (103t + 1,86) ,
и аналогично для токов.
4.5. Комплексный коэффициент передачи,
комплексная частотная характеристика
Заменив элементы цепи R , L , С их комплексными сопротив-
лениями и используя любой из методов расчета цепи (законы Ома и
Кирхгофа, эквивалентные преобразования, метод узловых напряжений
и пр.), можно получить связь между воздействием и реакцией в фор-
ме .
£ “ZSL (4.23)
Л/г «х
Здесь комплексные амплитуды; К - комплексное чис-
ло, определяемое цепью, ее структурой и параметрами, а также час-
тотой воздействующего сигнала о> . Очевидно, л имеет смысл коэф-
фициента передачи цепи. В зависимости от того, что конкретно по-
нимается под воздействием и реакцией (ток, напряжение), коэффици-
* ент К может быть безразмерным либо иметь размерность сопротивле-
ния или проводимости.
Удобно записать К в показательной форме:
к ^\К\е^к . (4.24)
Тогда из (4.23) получим
14,-1 *"1141.
12
Таким образом, модуль коэффициента передачи - это коэффициент
пропорциональности между амплитудами, а аргумент дает значение
сдвига фазы выходного гармонического сигнала относительно
но го. Так, в рассмотренном выше примере 4.3 было найдено,
при воздействующем сигнале e(t) « Cos 1D5t или при Е = I
вход-
ЧТО
ком-
i2
Это
репи-
плексная амплитуда выходного напряжения V равна •
число и есть комплексный коэффициент передачи Е . Пе
сав К в показательной форме, получили K^0J9e . При воз-
действии
e(i) - fl cosUoH + q)
выходной сигнал
U(t) - O,19flcos(lO3t + (f + ^8G) .
Комплексные сопротивления ветвей, содержащих L или £ , за-
висят от частоты воздействия со . Поэтому и комплексный коэффици-
ент передачи является функцией частоты. Эту функцию называют ком-
плексной частотной характеристикой цепи и обозначают 1С( (О) (или
Итак, комплексная частотная характеристика есть отношение
комплексных амплитуд сигналов на выходе и входе как функция час-
тоты воздействующего гармонич еского сигнала:
К(со) ~ -"f**- (4.25)
при условии, что iS$x - гармонический сигнал частоты ц}.
Модуль iXYeo)! называют амплитудно-частотной характеристикой, ар-
гумент - фазочастотной характеристикой цепи.
Пример 4.4. ^fiTOTjigpgiOEOjifipgflsa^
На рис. 4.6 приведены простейшие частотно-зависимые цепи, содер-
жащие один реактивный элемент. Определим их комплексные частотные
характеристики.
Для схемы а
к(к) _ i. _ ---------1—
13
Идя схемы б
Рис. 4.6
от
хе:
К((л)) = 4-
Для . схемы в
и
K(ti) = т
$ ]й)С
Нетрудно заметить, что зависимость
частоты в этих трех схемах одна и та
Jte) =
(4.26)
Запишем комплексную
форме:
Здесь Т - постоянная времени цепи, при-
чем т = ЛС или некоторый
безразмерный или размерный коэффициент,
частотную характеристику в показательной
nir,iir,
П
+ <аМ
У 4+(l*)t)z
-jarctyw't
е
(4.27)
АЧХ и ФЧХ цепи имеют следующий вид:
I к(ы)\- — , q> (tt)) -arctqмт . (4.28)
1 У /+(^г)г * ’ .
Характерные черты АЧХ (рис. 4.7): при низких частотах коэффициент
передачи близок к I, с увеличением со коэффициент передачи моно-
тонно падает, стремясь к нулю. Граничной точкой "полосы пропуска-
ния" чаото считают частоту, при которой коэффициент передачи умень-
шается до -Х=^0,7 от максимума. Из (4.28) видно, что
УГ
tz У 2
Асимптотика АЧХ (характер спада АЧХ при
"хвост”) имеет вид
Ct)
0,1
больших частотах, или
14
т.е. коэффициент передачи обратно пропорционален первой степени
частоты. Рассмотренные простейшие схемы, пропускающие низкие час-
тоты и не пропускающие высокие, являются фильтрами нижних час-
тот (ФНЧ).
Рис. 4.7
Рис. 4.8
Пример 4.5. Angpgoj^neci^tj?£или£ель. Простейшая схема
усилителя на транзисторе, предназначенного для усиления звуковых
и видео-сигналов, приведена на рис. 4.8,а. Разделительный конден-
сатор С препятствует воздействию постоянного напряжения ("закры-
тый" вход). КонденсаторСк ограничивает прохождение излишне высо-
ких частот. На рис. 4.8,6 дана схема замещения по переменным на-
пряжениям и токам, в которой транзистор представлен идеальным ис-
точником коллекторного тока = Sи^. Поскольку потенциал эмиттера
фиксирован, управляющее напряжение база-змиттер . Коэффи-
циент S -крутизна характеристики коллекторного тока в рабочей
точке.
Комплексная частотная характеристика левой части схемы
Йг Я № ~ , ’ (4.29)
t— яг - постоянная времени входной цепи.
Правая часть схемы - рассмотренный выше ФНЧ, его характеристика:
15
к _ м*
КЛО)) =
Gt
T«=V* •
(4.30)
Общая частотная характеристика
К (и) - K (a>) /C>(ct)).
Е 7 л
Определим АЧХ и ФЧХ первого звена ( CR -цепочки), для
ставим (4.29) в показательной форме:
. ТС
i
а)Т 8
"* 4/ у <> г ' jarctq 61)Т
V / 4- соЧ* eJ
чего пред-
(4.31)
Отсюда
|Я^)|
О) т
ty(W) -
— arc tq со т .
(4.32)'
£
г
На рис. 4.9 приведены АЧХ и ФЧХ обоих звеньев, при этом учтено ус-
ловие тг » Tfe, обычно выполняемое в схеме апериодического усилите-
ля. Общая АЧХ определяется перемножением и lJQ(co)l а общая
ФЧХ - сложением Щ(£0) и <f%(CO). Общая АЧХ дана на рис. 4.9 . При
Т в ней имеется плоский средний участок, на котором гармони-
ческие сигналы вне зависимости от частоты усиливаются одинаково:
KD -SR^/Ккяеив и верхние границы этого участка определяются по-
стоянными времени:
Пример 4.6. Фильтр нижних частот второго порядка ис-
пользует два реактивных элемента разного вида - L и f . Одна из
возможных схем дана на рис. 4.10. Выражения для комплексной частот
ной характеристики можно записать из рассмотрения делителя Z£
16
Рис. 4.9
После несложных алгебраических преобразований получим
ж---------------— .« =— е ,(4.зз)
( /- weLC)+jco к + wk
fv ft
Конкретный вид АЧХ и ФЧХ зависит от соотношения параметров .
Часто их выбирают так, чтобы АЧХ имела вид рис. 4.10,в. На том же
рисунке пунктиром дана АЧХ фильтра первого порядка. Как видим, АЧХ
фильтра второго порядка имеет лучшую форму - здесь более резкий
переход от полосы пропускания к полосе непропускания. Асимптотика
Рассмотренные примеры использования метода получения комплекс-
ной частотной характеристики - простейшие. Здесь было достаточно
применить свойотво делителя напряжения. В более сложных разветв-
ленных схемах приходится составлять систему уравнений относительно
нескольких комплексных амплитуд напряжений или токов. Удобно,
17
в частности, воспользоваться методом узловых потенциалов в форме,
которая была введена для резистивных цепей [3] :
напряжение некоторого Л -того узла равно взвешенной
сумме всех остальных узловых напряжений U* , имеющих с £ -м уз-
лом общие ветви:
к - Z к.. к
к k t
Веоовой коэффициент - отношение проводимости ветви i,k к.соб-
ственной проводимости рассматриваемого узла А' .
Пример 4.7. Акхи^н^_®Ч_второго_пор2Д5а (рис. 4.П).
В схеме отмечены узловые напряжения . Проводимости
ветвей:
2
Собственные проводимости узлов I и 2:
Хг ~ + + + /
Запишем систему из трех уравнений:
V - -%- г
vi у с
72Е
г
з *
Последнее уравнение отражает тот факт, что ОУ включен как идеаль-
ный повторитель (выходное напряжение подано непосредственно
на инвертирующий вход).
18
Из системы уравнений имеем
После простых преобразоцвний получим
ад- й- -_________
(4.34)
О
где постоянные времени
„ £а
2 &г
тэ^
Сравнив (4.34) с (4.33), обнаружим точное совпадение струк-
туры формулы. Разница лишь в параметрах: вместо LC - ^Д2»вмвс-
то я" " * Применение активного элемента схемы ОУ позволило по-
дучить фильтр второго порядка без индуктивности. Проектирование
так называемых ЛИС -фильтров (активных фильтров наЯС -элемен-
тах) - одно из важных приложений современной радиоэлектроники.
4.6. Резод§а5|еы&:ц§дд
В цепях с L и С элементами при определенных значениях
частоты воздействующего сигнала проявляется эффект резонанса -
резкое возрастание тока пли напряжения. Этот эффект широко ис-
пользуется в радиотехнических устройствах.
Анализ и расчет резонансных цепей особенно нагляден к прост
при использовании метода комплексных амплитуд. Комплексные сопро-
тивления индуктивности и емкости являются чисто мнимши:
(4.35)
Величины
\-ш1’ (4-36)
называются реактивнши сопротивлениями индуктивности и емкости.
Как видим, реактивные сопротивления L и С имеют разные знаки
и обратную зависимость от частоты.
19
При
/
и -
(4.37)
имеем
При такой частоте происходит взаимная компенсация реактивных со-
противлений, общее сопротивление последовательно соединенных L
и Г становится равным нулю и происходит резкое возрастание тска.
В этом и состоит эффект резонанса с позиций метода комплексных
амплитуд.
Простейшие резонансные цепи - последовательный и параллель-
ный контур из L и С (рис. 4.12) - различаются подачей воздейст-
вия: в последовательном контуре сигнал вводится в форме источника
напряжения, включенного "внутрь" контура /Г, а в параллельном -
в форме источника тска, включаемого "вне" контура.
Для схемы б
При резонансной частоте (4.37) сопротивление последовательно-
го контура Z и проводимость параллельного У становятся равными
X» 2*
дулю.
Ток в последовательном контуре, а значит, и напряжения lfL f
и Vc делаются бесконечно большими. В параллельном контуре беско-
нечно большим становится напряжение на контуре. При отходе от. ре-
зонансной частоты равенство модулей реактивных сопротивления нару-
шается, токи и напряжения резко падают. Частотная характеристика
резонансного контура дана на рис. 4.13.
Рассмотренный случай является идеализированным, т.к. в схеме
не учитываются активные сопротивления, всегда так или иначе при-
сутствующие в реальных схемах (либо в виде резисторов, либо в виде
•выходных сопротивлений источников, сопротивлений потерь и т.п.).
Тем не менее модель идеального резонансного контура чрезвычайно
полезна.
20
Рио. 4.12
Рис. 4.13
Основное правило: на резонансной частоте последовательный
контур - это короткое замыкание, параллельш^ контур - это разрыв.
В реальных резонансных цепях необходимо учитывать активные
сопротивления, шунтирующие контур, а так-
же включенные в контур последовательно
("сопротивление потерь”); Наиболее прос-
тые выражения получаются, если в после-
довательном контуре активное сопротивле-
ние г включено "внутрь" контура, а в
параллельном - сопротивление В включено
щунтом (рис. 4.14,а и б).
Вводятся в рассмотрение два парамет-
ра контура - характеристическое (волно-
вое) сопротивление J и добротность Q :.
9-^ , 9-у <«.«>
^уактеристическое српрот^тение - это модуль реактивного со-
противления индуктивности и емкости на резонансной частоте (без
учета знака). Добротность - соотношение мевду реактивным и актив-
ным сопротивлением. Чем выше добротность, тем ближе реальный кон-
тур к идеальному, для которого Q = оо ( R = оо ? /*•-= 0 ).
21
Резонансная частота cd? и добротность Q - два основных па-
раметра, определяющих вид комплексной частотной характеристики
резонансного контура.
Определим эту характеристику для параллельного контура
(рис. 4.14,6):
К(ъ» -
Здесь суммарная проводимость
(4.43)
Преобразуем (4.43) с тем, чтобы ввести в формулу параметры й)р и
Q (4.41), (4.42):
г ш 2
Z /?
(4.44)
В этом выражении зависимость от частоты сосредоточена в члене
уравнения, который принято называть нормированной расстройкой
~ О) шр
S “ 7Т----71 ‘ (4.45)
5 Ct)D Си
Г "
При J = О .
Таким образом, комплексная частотная характеристика парал-
лельного контура
К(а>)- - - . (4.46)
Аналогичные выкладки для пос ле дева тельного контура дают
77^- • <4'47)
Для высокодобротных контуров (/?»/) формулы (4.46) и (4.47) мож-
но переписать так, чтобы аргументом была не нормированная расстрой-
ка £ , нелинейно зависящая ст частоты, а более простые абсолютная
расстройка А или относительная расстройка :
Л О) = СО — (f)p ; (4.48)
Sa) - 4? • (4.49)
22
При Q»f уже малые расстройки приводят к резкому спа-
ду АЧХ. Учитывая это, произведем замену:
Г _ ж Ч _ /
3 а>р СО ti)p tiJptrtd) vw '
]
Используя приближение ‘yT'F ~ /-дополучим
I = / + 610-/ + -2бь) ~2-Щ- • (4.50)
Тогда
р v
Kfao)~---------—--------- „Тм • (4.51)
' UjZQfa) 4+'/2Q±?
f 1
Огсцда запишем вццаженкя для АЧХ и ФЧХ:
I Х(АЮ) | - -==^==- (4.52)
wp
СРК (лш)^ -Zarcty 2Q . (4.53)
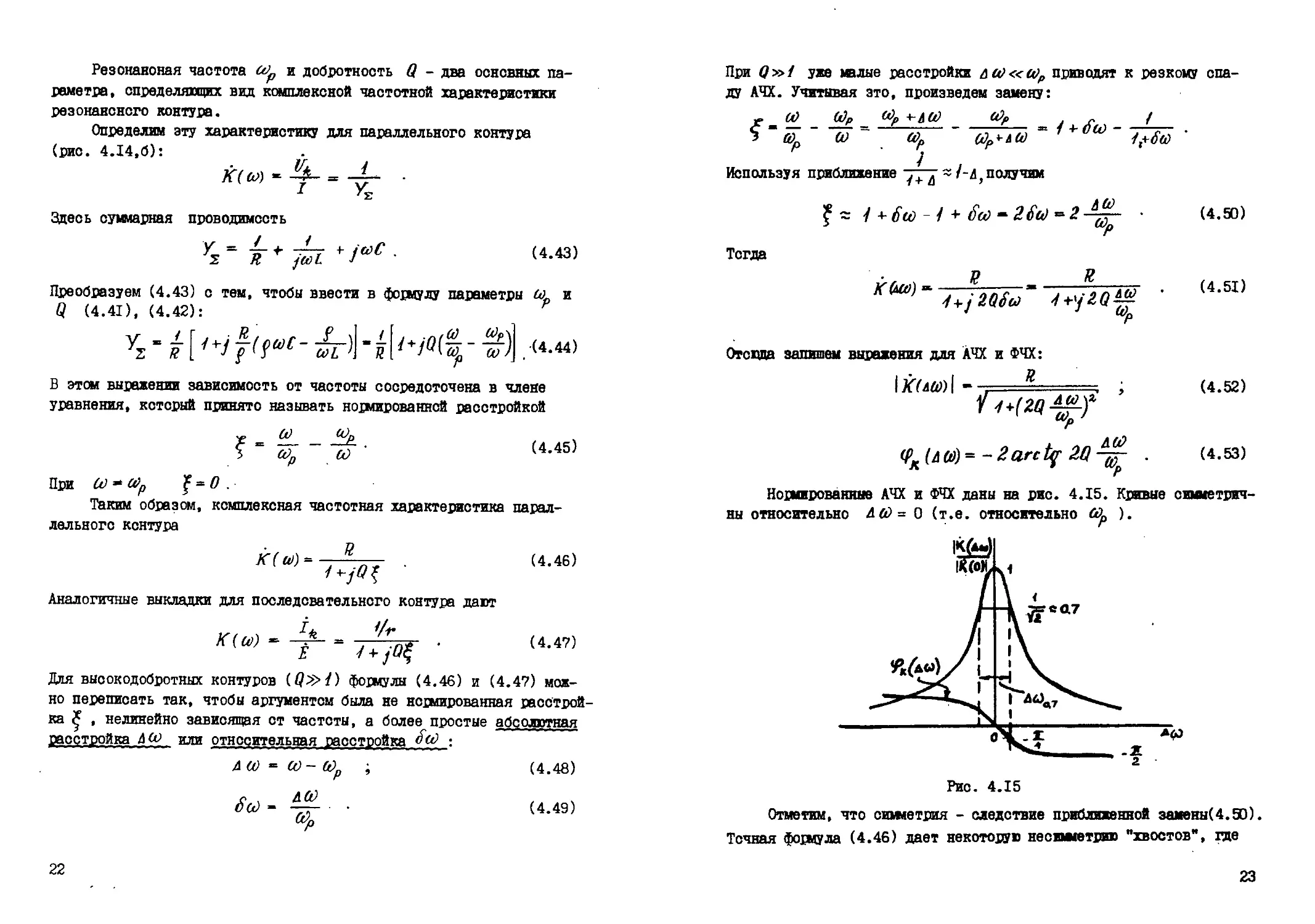
Ногмированине АЧХ и ФЧХ даны на рис. 4.15. Кривые симметрич-
ны относительно Лб)= 0 (т.е. относительно ).
Рис. 4.15
Отметим, что симметрия - следствие приближенной замены(4.90).
Точная формула (4.46) дает некоторую несимгетрию "хвостов", где
23
неравенство Мй)1« не выполняется. Резонансную кривую часто
характеризуют полосой пропускания по уровню s 0,7.
Из (4.52)
Л (^0,7
~2~ .2
lt)p
откуда
~Q
(4.54)
Эта формула используется для удобного экспериментального опреде-
ления добротности по снятой резонансной кривой: добротность гавна
отношению резонансной частоты к полосе пропускания:
Q - ----И—
4 ^4^7
На рис. 4.16,а и б показано влияние добротности на вид резонанс-
ной кривей. Рис. 4.16,а дает нормированные кривые. Чем выше доб-
ротность, тем уже резонансная кривая, меньше полоса пропускания.
(4.55)
24
На рис. 4.16,6 приведены ненормированные кривые, построенные
с учетом того, что добротность Q регулируется изменением сопро-
тивления R , при* этом чем больше # (а следовательно, и Q ), тем
выше вдет резонансная кривая - пс любому абсолютному уровню кри-
вые расширяются.
Связь мевду добротностью и полосой пропускания (4.55) дает
еще одну запись АЧХ, часто используемую:
4# ч*
(4.56)
При анализе переходных процессов в резонансных контурах
удобно ввести параметр, определяющий инерционность системы - по-
стоянную времени контура . Этот параметр аналогичен пс смыслу
постоянной времени М или в простейших ФНЧ (см. пример 4.4).
i
Постоянная времени резонансного контура
т. = 2UC .
К
Связь мевду и полосой пропускания А (я) следующая:
ГУ Vf/
Г 91>Г 110 - 2
ь £Kl ’ G>p = % ЛО)О7
(4.57)
(4.58)
Подставляя в (4.51), получим еще одну формулу комплексной частот-
ной характеристики:'
«(&<•» “ -учттг (4-59)
25
Из сравнения с (4.26) видна аналогия частотных характеристик ре-
зонансного контура и фильтра нижних частот первого порядка (см.
рис. 4.17).
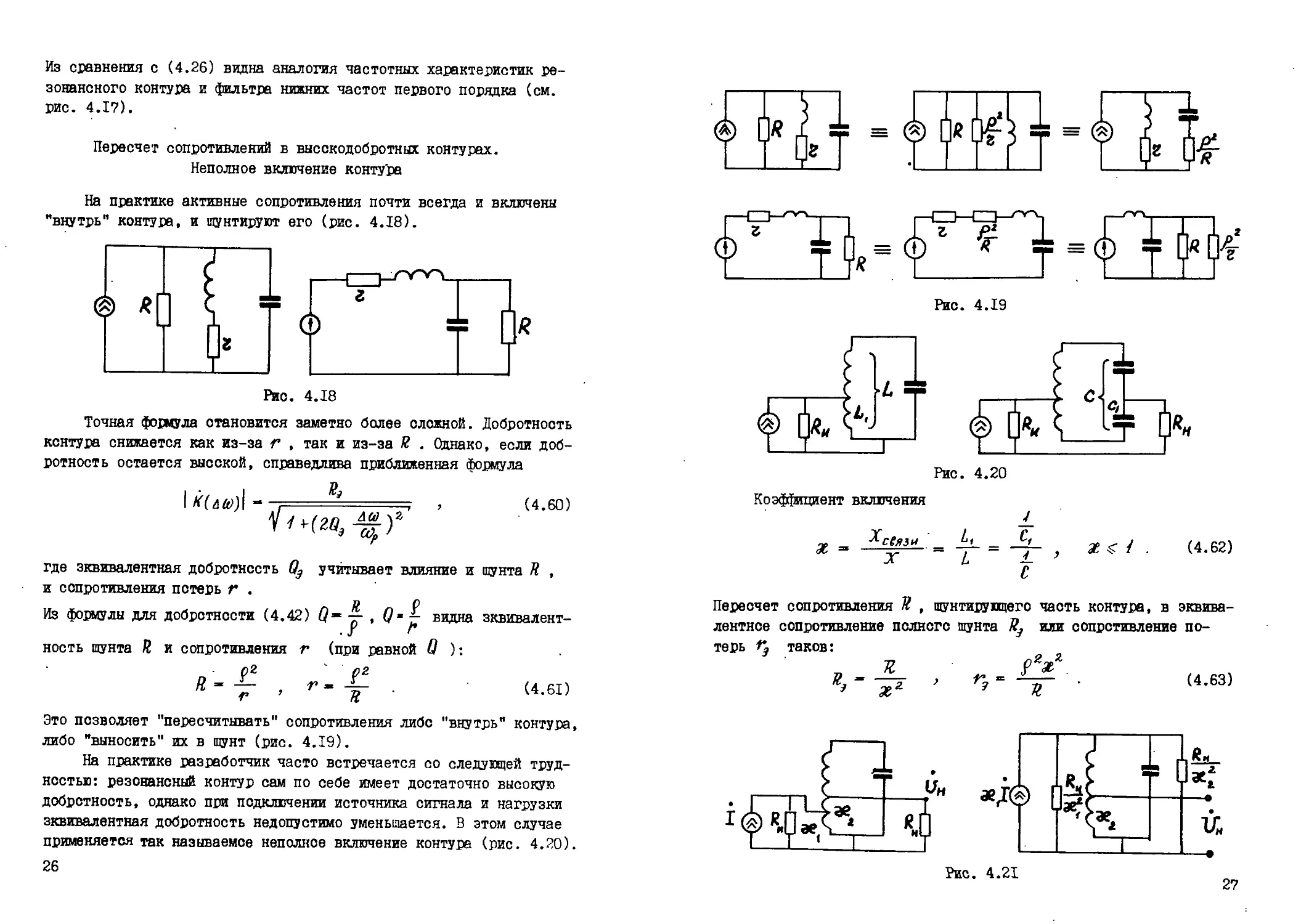
Пересчет сопротивлений в высскодобротных контурах.
Неполное включение контура
На практике активные сопротивления почти всегда и включены
"внутрь" контура, и шунтируют его (рис. 4.18).
Рйс. 4.18
Точная формула становится заметно более сложной. Добротность
контура снижается как из-за г , так и из-за Л? . Однако, если доб-
ротность остается высокой, справедлива приближенная формула
р
I , (4.60)
где эквивалентная добротность учитывает влияние и шунта И ,
и сопротивления потерь г .
Из формулы для добротности (4.42) цж — , Q* £• видна зквивалент-
.f г
ность шунта Й и сопротивления г (при равной Q ):
fl-jr , г-±_ . (4.61)
Это позволяет "пересчитывать" сопротивления либо "внутрь” контура,
либо "выносить" их в шунт (рис. 4.19).
На практике разработчик часто встречается со следующей труд-
ностью: резонансный контур сам по себе имеет достаточно высокую
добротность, однако при подключении источника сигнала и нагрузки
эквивалентная добротность недопустимо уменьшается. В этом случае
применяется так называемое неполное включение контура (рис. 4.20).
26
Рис. 4.19
Рис. 4.20
Коэффициент включения
У
Z , Ху3-= -Т- = -V" , (4.62)
Пересчет сопротивления Н , шунтирующего часть контура, в эквива-
лентное сопротивление полного шунта или сопротивление по-
терь Ъ таков:
я pV
г - А- > . (4.63)
3 X 3 и
Рис. 4.21
27
При расчете удобно также вводить эквивалентный источник,
включенный на весь контур (рис* 4,21)
11 - XI . (4.64)
Пример 4.9. Высскодобротный контур ( Q =100, f =
= 500 Ом) должен быть подключен к источнику с Ли = I кОм и на-
грузке Кн = 2 кОм (см. рис. 4.21). Желательно, чтобы добротность
нагруженного контура была не менее Q? Ъ §0.
Определим эквивалентную добротность при полном включении ис-
точника и нагрузки. Собственное сопротивление потерь контура
-^-= 5 ОМ. Пересчет шунтов Ли и
х -» о- ,
Общее сопротивление
потерь Г- = 380
И* дает
Р2
Н. “ *=• 125 Ом .
н Р
кн
Ol что соответствует зквива-
лентнсй добротности
дачи при
Пересчитав
резонансу:
в единый шунт #
определим коэффициент пере-
Г — — Р
/>« т '
— = 658 Ом •
я
Применим
КИ #£ =
неполное включение: для источника 0,1, для нагруз-
0,15. Вносимые в контур сопротивления потерь
гн - 2,8 Ом .
j = ргжг_
2,5 Ом
= 2,5 + 2,8 + 5 = 10,3 Ом, что дает
Q3 = 48,5 и резонансное сопротивление
передачи Крсз ,
Общее сопротивление потерь
эквивалентную добротность
= 24,3*103 Ом.
Определим коэффициент передачи ff , для чего введем эквива-
лентный источник тока, включенный на весь контур: - 0,1. Напря-
жение на контуре
к
Напряжение на нагрузке
Как
364
28
JHU'.Ur,
> ut х •
видим, коэффициент передачи несколько уменьшился (с 658 до
См), однако требования по добротности выполнены-
5. АНАЛИЗ ЦЕПЕЙ С ПРИМЕНЕНИЕМ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
5.1. Постановка вопроса
Интегральное преобразование Лапласа, изучаемое в курсе мате-
матики, устанавливает взаимно-однозначное соотношение между сиг-
налом £ (t) и комплексной функцией комплексной переменной р S(p)
(как говорят в математике, "оригиналом" и его "изображением").
Связи между воздействующими сигналами и реакциями в линей-
ной цепи, получаемые по законам токопрохождения, можно легко пере-
вести в такие же или более простые связи между изображениями воз-
действий и реакций. Так, суммирование токов или напряжений пере-
ходит в суммирование их изображений, система динамических интегро-
дифференциальных уравнений - в подобную по форме систему алгебраи-
ческих уравнений. Определив в результате решения системы уравнений
изображение реакции» можно с помощью обратного преобразования Лап-
ласа найти выходной сигнал. Этет подход схематично показан
на рис. 5.1.
Рйс. 5.1
Как известно, преобразование Лапласа применимо к функциям
времени, тождественно равным нулю при t < 0*. Таким образом, рас-
сматриваемый метод применим для анализа цепей под воздействием
сигналов, имеющих четкий момент начала, который можно принять
за t - 0. Это могут быть: одиночный импульс произвольного вида
^Ииеется в виду одностороннее преобразование Лапласа. Исполь-
зование более сложного двустороннего преобразования Лапласа снимает
зте ограничение.
29
(нс с определенным началом); сигнал включения типа ступеньки S(t),
включение гармонического сигнала или любого периодического сиг-
нала (периодического только при 1>О)Л Есть математическое огра-
ничение и на скорость нарастания сигнала при Однако это
ограничение настолько слабое*» что практически не учитывается.
Таким образом» аппарат использования преобразования Лапласа
очень хорошо дополняет метод комплексных амплитуд» который пред-
назначен для анализа установившегося режима. Методом преобразова-
ния Лапласа анализируют переходной режим ст момента включения
к установившемуся состоянию» а также прохождение одиночных им-
пульсов и специальных тестевых сигналов (например, линейно нара-
стающего сигнала).
Решение системы уравнений относительно изображений токов или
напряжений приводит к следующему выражению:
функция К(р ), определяемая структурой и параметрами цепи, имеет
тот же смысл, что и коэффициент передачи ст входа к выходу для ре-
зистивных цепей или комплексная частотная характеристика в методе
комплексных амплитуд. Но здесь это передача не сигнала, а. его изо-
бражения.
По определению, передаточная Функция пени есть отношение изо-
боажения выходного сигнала к изображению входного;
К(р) - (5.1)
% (р)
В зависимости от конкретного содержания сигналов $^(1) >
fyb/x( ) передаточная функция может быть безразмерной или раз-
мерной (сопротивление, проводимость). Если передаточная функция*
цепи найдена, тс анализ прохождения любогс сигнала
сводится к следующей цепочке:
4,W >
(5-2>
Для практического использования зтей методики нужно уметь:
а) по заданному сигналу находить его изображение,
кНарастание должно быть не быстрее экспоненты с любым пока-
зателем.
30
б) пс заданному изображению находить сигнал»
в) пс заданной структуре цепи находить ее передаточную
функцию.
В цепочке действий (5.2) не фигурируют начальные условия
(состояние цепи в момент подачи сигнала). В такой форме предпола-
гается, что исходное состояние - "нулевое" (в цепи нет токов че-
рез индуктивности, а емкости разряжены). В терминах, введенных
ранее[31в связи с решением динамических уравнений, это - реакция
при нулевом состоянии (РЯС). Однако использование преобразования
Лапласа позволяет найти также реакцию при нулевом воздействии,
т.е. вызванную ненулевыми начальными условиями (РНВ).
Преобразование Лапласа может быть использовано как метод ре-
шения динамических уравнений цепи; передаточная функция цепи при
этом не вычисляется. Исходными для анализа являются сами динами-
ческие уравнения и заданные начальные условия.
Наконец, списание сигналов с помощью их изображений как
функций комплексной переменной р , а также описание цепей по их
передаточным функциям К (р) открывает еще один путь анализа сиг-
налов и цепей. Это так называемая диаграмма полюсов - нулей
в р -плоскости. При некоторых ограничениях на класс цепей указа-
ние координат полюсов и нулей передаточной функции дает очень на-
глядную информацию с частотных и временных характеристиках цепи.
Все эти вопросы рассматриваются в данной главе.
5.2. Определение изображения по заданному сигналу
Из математики известны определения прямого и обратного преоб-
разований Лапласа S(t) S(p) -
QO .
$(р) = \ s(t) eat , $(p) = > (5.3)
0
$(/)=-^-7 ( S(p)edp, S(t) - L* (tip)] . (5.4)
ft-joo
Справа даны условные записи прямого L [ • } и обратного L [ *) пре-
образований*.
хВыбор пути интегрирования в (5.4) (параметр о ) определяется'
областью сходимости. В рамках данной книги прсблемысходимости ин-
теграла Лапласа не обсуждаются. При необходимости читатель может
воспользоваться обширной литературой пс преобразованию Лапласа и
его приложениям.
31
На практике редко приходится находить изображение с помощью
интеграла (5.3). Почти всегда можно обойтись табличными парами
j(t) применением небольшого числа основных свойств пре-
образования Лапласа.
Таблица 5.1
Основные свойства преобразования Лапласа
Основные операции Сигнал Изображение
I. Линейная комбинация $(р)-ц(р)1&г(р)
2. Дифференцирование sib - S(p)~ pX(p)-x(D)
3. Интегрирование S(i)~\x(P)di’+S(D)
4. Сдвиг вс времени S(i) - X(t-T) . ~PT S(p) =X(p)e
5. Изменение масштаба 4(i) = x(a-t) $(p) “tax
6. Умножение на t S(i) - tx(i) ' dp
-st . ~<£i
7. Умножение на 8 s(t) = e л (I) ^(fi) ~ X ( р+<ь)
8. Умножение сигналов s(t) ~st(b £,(t) Pfpi-fypyfyp)
9. Свертка сигналов S(t) -Stli)*s£(t) ~ '^(p)
10. Периодическое продол- k
жение одиночного им- и £т(1>) ~ / - e.pl
пульса ST С*)
KKJkA 1 T ZT 3T I
32
Таблица 5.2
33
Окончание табл. 5.2
Пользуясь основными свойствами (табл. 5.1), можно получить все
формулы табл. 5.2.
Приведем примеры получения изображений сигналов, не указанных
в табл. 5.2.
Пример 5.1. Сигнал на рис. 5.2 нетрудно представить се-
бе как cywy двух сигналов:
£ V t) • и0 в О $ t < j
s'? i) = - Ur e • / (t - г) , Ur = u0 елг.
Обувтмь внимание на запись второго сигнала! Сомножитель / (£-Т)не-
обхсдим, иначе второй сигнал начнется не при t^T , а при / = О
и при суммировании с s'( t ) получим нуль.
Соответствующие изображения:
Пример 5.2. Рассмотрим сигнал, изображенный на рис.5.3,
В данном случае можно пойти двумя путями.
I. Представить S’ (t) как сумму трех сигналов s'(t),
изображения которых - табличные.
34
2. Получить вспомогательный сигнал Sz(~t), продифференциро-
вав $ (t ). Изображение $е (t ) состоит из двух табличных. Исполь-
зуя операцию интегрирования (в изображении это умножение на ,
придем к 8(р).
. Рис. 5.2 РИс. 5.3
В первом варианте
<-, > A -L _ £ ± »pr- JL ,~рТ
£(р) т fl* т р*е р е
Во втором варианте
После интегрирования сигнала (t)
• Пример 5.3. Сигнал вида "меандр" (рис. 5.4). Изображе-
ние одиночного импульса
35
s<(p> Ly—
Введя периодическое продолжение (IL 10, табл. 5.1)
ST(V- р
и добавив отрицательную ступеньку/ГУ получим
-pf -рт -р? it
„ у (1-е Л f 2-2 -1*е? { (1~е )
lf>p\i-ePT 2J 2р j_e-pr ‘ 2р 1 - e~fi\
Рис. 5.4 Рис. 5.5
Пример 5.4. Линейно нарастающий’гармонический” сигнал
(рис. 5.5).
Удобно воспользоваться изображением П. 10, табл. 5.2 и прави-
лом умножения на t :
d
dp [ р2 t
’ог
*2
(ft2 *
Приведенные примеры показывают, как найти изображение сигнала, ст- .
сутствупцего в таблице, не прибегая к вычислению интеграла (5.3).
36
В общем случае можно найти оригинал (т.е. сигнал) по изобра-
жению, используя формулу вычетов для взятия интеграла (5.4):
(5.5)
2j[j J ' t
где resi - вычет подынтегральной функции F(р} в ее полюсе .
Если Г(р ) записать в виде дроби
ГО» =
f Р Я(р) ’
то полюса корни уравнения И(р) =0 .
Вычет в простом полюсе
Вычет в полюсе
res, =
t
Приме
res. -
t
О(Р)
dH(p)
dp
P*Pi
' Q(p)(p-fii)
Пр)
(5.6)
(5.7)
Р 5.5.
P*Pi
кратности п
</*•'
Найти сигнал пс изображению:
~ (р+Ыр+г)* ' fit
Вычислим вычеты подынтегральной функции S(p)e
и двукратном полюсе рг = -2:
- 2peft
(р+2)(Зр+4) д
Zfl+pi+fjtfc'L
в простом полю-
res
--2f*
~2t -21
- 2е +4te
р-2
d F
dp . (p+O(p+2)z\p^2
•Ответ: S(t) * - 2е~^+ 2e
Пользование методом вычетов (5.5) предполагает соблюдение ос-
торожности, т.к. применение формул (5.6), (5.7) без анализа пове-
дения функции Г (р) на плоскости р может привести к ошибочным
результатам. Наиболее частая ошибка этого типа происходит в том
случае, когда изображение $ (р ) не является правильной дробью, а
содержит целую часть.
се р,= -I
=
2
37
л
Пусть, например, дано изображение S (р ) = . Степени чис-
' р+/
лителя и знаменателя одинаковы, а значит, дробь содержит целую
часть. Выделим ее:
<?/ )- А 1 *
fl) р+-1 р+1 1 р + 1 ’
Обращение изображения о помощью таблицы (ПП. I и 3 табл. 5.2)
дает . r , -t
S(i) - е .
Определение вычета по
(5.6) дает другой результат:
ре А*
res =. —----------
(fl+i)
ар г
-t
= -е
Содержащаяся в сигнале S-функция утеряна.
Необходимо было сначала выделить целую часть дроби, а затем
уже брать вычет.
Неверный результат получится и в том случае, когда в изобра-
женин есть члены вида £ (что говорит о наличии запаздывающих
составляющих в сигнале). Так, формальнее вычисление выче<а для
случая изображения прямоугольного импульса (П. 16 тИбл. 5.2) дает
ошибочный результат S (t) - О:
» (&е°)е°-0 .
рч>
res
Up
Практичный и удобный метод определения сигнала по изображе-
нию - разложение рациональной функции f>(p ) на простые дроби. Ме-
тод удобно пояснить на примере.
Пример 5.6.
Определяем корни знаменателя: /7, = О, Д = -I, =
Тогда р) можно разложить на три простые дроби:
= w+llp+iL. = J_ + + J_
р(р+1)(р+2) Р р*1 P*Z
38
Коэффициенты fl , В , С пока что не определены. Их можно найти не-
сколькими способами, порекомендуем два из этих способов.
I) Приведение правой части к общему знаменателю:
Вр(р+г)+ Ср(ри)
)(?<-£)
Раскрывая числитель и приравнивая коэффициенты при одинаковых сте-
пенях р справа и слева,, получим систему уравнений относительно
П т ZJ ~ С Т ’
ЗА +2В + С - 11 ,
Решение системы дает значения коэффициентов: й = 2, 5=3,
2) Искусственный прием: домножение правой и левой частей
на двучлены (p-pt) с последующим переходов р р^ .
В нашем случае
4 рг + 41 р ^4
Подставив р = -I, получим
=
в=з .
-//
9
Аналогично
р _ 4/>г+ Ир <-
р(р+1}
д^р + пр г
(ф+1)(р+2)
р=о
Найдя неопределенные коэффициенты, испсльзуем табличные пары:
—т*~ 8(1) = 1(1).
Несколько сложнее найти разложение, если схади корней зна -
менателя есть кратные. Тогда в разложении должны быть дроби со зна-
менателями вида ^p Pi Покажем на примере методику искусственно-
го приема для нахождения неопределенных коэффициентов.
Пример 5.7.
яр) =
А
г п .
г
Коэффициенты й и С можно найти, как и в
примере 5.6:
39
Коэффициент В таким способом найти нельзя - мешает член с С .
Вычтем справа и слева дробь —£—
(р+2)г
2рг + 4р+1 1 _J_ + В
(р +1)(p + 2)z (p+2)z р+1 Р+2
Проведя выражение слева к общему знаменателю, получим
2рг + 5р + 2 _ й В
(р+1)(р+2)г ~ р+1 р+?
Дробь слева не может содержать двукратного полюса р^ = -2, т.к.
соответствующего члена справа теперь нет. Это значит, что числи-
тель должен делиться на р+2 наделе.
Разделив:
имеем и
(р+2)(2р+1) _ 2р+1 _ * + В
(р+1)(р + 2)г “ (р+1)(р+2) Р+1 Р+%
Теперь легко определить В :
Разложение найдено:
. У 5 / . / -t ~2t -2t
'S(p)------1— + -+2— —т——г +5e -te
' r p+2 (p+2)
Остановимся на важном в приложениях случае ксмплексно-о спря-
женных корней. Можно решать задачу обычным методом разложения
на простые дроби - в результате получим экспоненты с комплексными
показателями. Иопользуя формулы Эйлера
+ j>~J*
--------3--------=
2 ’ 2j
(5.8)
40
получим окончательный результат в виде колебательного сигнала
(10-15. табл. 5.2).
Однако можно пойти и другим путем - "подгонкой” под подходя-
щую табличную пару из числа 10-15, табл. 5.2.
Пример 5.8.
df ч _ Зр+30 .
" p* + 5f>+100
О
Детерминант знаменателя J = 3 - 4*100< 0, что говорит о комп-
лексно-сопряженных корнях. Следовательно, сигнал должен иметь
вид зкспоненциально-гармоническсгс колебания вида (ПП. 13-15,
табл. 5.2).
Возьмем наиболее общий случай (П. 15, табл. 5.2):
t х х . л COSty fl +(<£§tn<P -(0WS<!>)
М-*' ,л,
Сопоставляя коэффициенты при степенях О в знаменателе, определим
частоту СО и затухание </ :
2оС - 3 — X - 1,5 ;
й)2 + аСг » 100 — СО - / 100-2,25 “ 9,887 .
Сопоставляя коэффициенты при степенях f> в числителе, найдем ос-
тальные параметры: амплитуду й я начальную фазу <р :
flees (f> - 3 ;
fldCCostf - fl(t)S<n(f -30 .
Зная «С и со , получим
л . fldccosff-so 1,5-3 -30
Далее:
432+2,579* ~ 3,956 ;
(f = arc tq = 0,71 .
fl cos tp
Итак, искомый сигнал
S(t) - 3,956 О*'5 cos ( 9,887t -6,71) .
б заключение рассмотрим случай, когда в изображении есть чле-
ны с сомножителем вида & , что говорит о наличии запаздывающих
слагаемых. При обращении такие члены нужно выделить и рассматри-
вать отдельно.
41
Пример 5.9.
fZ( 1-eSf>)
без
S(p) - %(p) + Sz (p)
। £ и с этим множителем:
/г________/г -f>f>
р(р+5) р(р^5)
Изображению 3>,(р) соответствует сигнал (П. 5, табл. 5.2)
. .. -Л.
Изображению 5г(р) соответствует такой же сигнал, нс включаемый
в момент t = 6:
ег(Ь--4(/-е**'6))Ш-6) .
5.4. оздкдадзта .аамдаттАЛдяяи.чмд
Рассмотрим соотношения между изображениями напряжений и то-
ков в элементах R,L,C.
Резистор И . Соотношение для временных функций
ий(Ь-2^(1)
соответствует такой же связи изображений:
Vgfpi-KIgfp) . (5.9)
Имцеость С . Соотношение
‘ Г f + ие(О)
о
по свойству 3 табл. 5.1 переходит в
Ч</» - Ч <f” < <5-“>
ность L . Дифференциальная связь временных функций
U It)- L
La
diL(t)
dt
дает в изображениях (П. 3, табл. 5.1):
UL(p) - plljp) ~LiL(O) ,
ВИИ
(5.II)
42
г UL (р) Ч (О)
- ir * — •
(5.12)
При нулевых начальных условиях формулы особенно просты:
lfalp) -ZIK(f>) ,
UL(p) = plIL(p) , (5.13)
“ ~рС '
Ъвыясся понятия операторного сопротивления I и операторной про-
ШДИ2СДЯ-У^,СДВР1МДВД,ВД9С>И1еВДЙ BOTPJjWfflflj.TQSQB*-
Для элементов R, L ,С соответственно имеем:
ZH ZL"pL > zc~ pt. ’
l-fr- y-fc
(5.14)
Любую схему, содержащую Л , L , С элементы, а также независимые
и зависимые источники напряжений и токов можно заменить точно
таким же соединением операторных сопротивлений и источников изо-
бражений напряжений и токов. При анализе полученной цепи можно
использовать все законы тскораспределения, как для чисто резистив-
ной цепи. Получив выражение для выходного изображения, тем оамш
определяем передаточную функцию цепи.
Пример 5.10. Найти передаточную функцию цепи рис.5.6,а.
На рис. 5.6,6 дана операторная_схема. Рассматривая делитель напря-
жения, верхнее сопротивление которого Я , а нижнее - параллельное
соединение pL и , имеем
f^W 4с _ pL________________.
1t+pL\\-b H+pz1llC+pL g*
* fjlj
Отсюда передаточная функция
pl;
K(fl) " p2UC*pl
^Название "операторное сопротивление” можно связать с тем
фактом, что умножение на сопротивление Z соответствует некоторой
операции над сигналом /(t ); умножению ? на константу ( Zp ), инте-
грированию \1Г ) или дифференцированию ( Z. ).
с д*
43
1C W fr) R
Рис. 5.6
Рис. 5.7
Пример 5.II (рио. 5.7,а). Теперь рассчитаем схему ме- '
точке А слева,
соответственно
тодом эквивалентного генератора, подключенного к
Эквивалентное выходное сопротивление и ЭДС равны
(рис. 5.7,6)
1 1
3
pc,
Рс,
Е;(р) = I(p) Zj .
Изображение выходного напряжения
1*РТ1 ’
Проведя несложные алгебраические выкладки, получим
/ffp\ = = л______________________________
? Г(р) 1
Сравнивая методик} составления операторных схем и нахождения
передаточной функции с методикой комплексных сопротивлений и полу-
аналогию: простой заменой переменной А
чения комплексной частотной характеристики, можно видеть полную
можно перейти от комп-
лексных сопротивлений к операторным и от комплексной частотной ха-
рактеристики к передаточной функции. Следует, однако, отдавать се-
бе отчет в том, что это - разные понятия.
Стоит отметить, что нет единой терминологии как в литературе
пс одной и той же дисциплине, так и (особенно) в смежных дисципли-
44
нах. Например, иногда авторы используют термин "передаточная
функция", имея в виду комплексную частотную характеристику.
В работах по кибернетике, автоматическому регулированию и некото-
рых других (в том числе и по радиоэлектронике) вместо "передаточ-
ная фикция" часто употребляется термин "системная функция".
Терминами "передаточная функция" или "системная функция"
определяется отношение изображений двух сигналов (воздействия и
реакции). При конкретизации в этом же смысле могут применяться
и другие термины. Так, если вход-
ные и выходные токи и напряжения, тс
те^Р)
Z (р)~ ^gb-~.
ТР„(Р)
- функция входного сопротивления;
- функция передаточного сопротивления,
- функция выходной проводимости и т.д.
Все зтс - "передаточные функции" ("системные функции").
5.5. Учет .начальных условий
При анализе реакции цепи при ненулевых начальных условиях
необходимо иметь в виду "полные" формулы связи между токами и на-
пряжениями в индуктивности и емкости (5.10)-(5.12).
При переходе к операторным схемам емкость следует заменить
не просто операторным сопротивлением -у? , но и включить последо-
ис(0) д
вательно независимый источник напряжения —. Аналогично индук-
Р
тивность при учете начального тока iL(0) заменяется операторная
7 ^(0)f ко'
сопротивлением pL и параллельным источником тока —(рис. 5.8).
Для нахождения реакции нужно учесть воздействия всех источни-
ков и входного сигнала и независимых источников, изображающих как
Uc(0) . iL(0) . t .
бы скачки напряжения —^ue(0) l(t) и тока .
По ’принципу суперпозиции можно их рассматривать по отдельности.
45
Рис. 5.8
Пример 5.II (рис. 5.9). Реакция ) на воздейст-
вие e{t ) црн заданных начальном напряжении на конденсаторе #/69
ж токе в индуктивности iL ( 0 ) складывается из трех составляющих,
которые можно найти, анализируя три операторные схемы ( £ , £ ,д ),
подученные из общей схемы б исключением двух источников.
Рис. 5.9
46
Длясхемы в
>г'/ ' - ЯгЛР1
Va (р) = -------—
' + -rhz
? Kg+pL
Для схемы г
pl
яг*Р1
рС и,(0)
H^pl р
В этих выражениях использованы правила параллельного и последова-
тельного соединения сопротивлений (проводимостей) и правиле дели-
теля напряжения.
После алгебраических преобразований получим
vz(p)^ ** °) ,
рг+ р ( y + т-) r^F + )
Г ' ' Т* Тя / Ту Т^ лл ?
Замечание. Цри составлении операторных выражений вс избежание сши-
бок рекомендуется проверять размерности отдельных членов (размер-
ность изображений ж токов ТГ(р),Ъ/С ; 1(р), й/С ; размерность р ,
Ус ; размерности типичных сочетаний pl , Ом; рС, I/Cht; НС , с;
| , о; Ом2; U , о2).
Л С
¥1
5.6. Операторный метод решенияgager;
уравнений g ацяляза структурных схем
При разработке радиоустройств или сложных радиоэлектронных
схем часто бывает так, что задается не принципиальная схема уст-
ройства, а система интегродифференциальннх уравнений, которые раз-
рабатываемая схема призвана реализовывать. Другой формой задания
может быть структурная схема, состоящая не из элементов, а из ук-
рупненных блоков, выполняхцих те или иные операции.
Применение операторного метода (т.е. преобразования Лапласа)
для анализа в таких случаях тоже чрезвычайно полезно.
Пример 5.12. Задана система интегродифференциальных
уравнений относительно V1 (t) и V& (t) при воздействии е (t) и
начальных условиях ^(0)**% и :
V,(t) - e(t) р dtftt) . '
Ж, С dt IL ~ ’
t г
цау-w <_ Н jg(fidt: + i(0)-0
kz L }
о
Переходя к изображениям (используя ПП. 2 и 3, табл» 5.1), имеем
- 4- t рСК(р)-Щ ^-^.ц
n-i 1*1 ^Z
№z nz * pl P u •
Решив систему алгебраических уравнений, найдем изображения ^(р} и
Vz(p) > а затем перейдем к самим сигналам (t) и Vz (t).
Пример 5.13. Задана структурная схема рис. 5.10,а, в ко-
торой использованы блоки сушатора ( © ), умножителя на пара-
метр () и интегратора с принудительной установкой начального
значения. Можно составить для нее систему динамических уравнений
в той или иной форме, например
t
y(t) = ( аД xtt')-4' ytt')-iz x(^)] <# + Уо ;
о
i
Z (£) “ yf Z ) dt + Zp •
Перепишем эту систему нв изображениях” Х(р), Y(p), Z(p) :
48
У(р) = %\X(p)-bY(p)-kZ(p)] + * ;
г' * '
Г '
Решение системы (подстановка Z (р) в первое уравнение, группиров-
ка членов при УЛр ))дает
В(Р) р} В(р)У* *?)
(5.15)
В(р) - f)* *atfyp + а.( аг 1г .
Рис. 5.IO
Коэффициент при Z( р ) - передаточная функция цепи, второй и
третий члены описывают переходный процесс РНВ; коэффициенты при уо
и - передаточные функции от точек подачи и £о дс выхода.
Структурная схема может быть задана (или перерисована) в опе-
раторной форме (рио. 5.10,6), где блок интегратора заменен опера-
/ Уо
тором — с добавлением суиватора, подключающего источник — , Для
р
49
простоты записи изображения часто обозначают одной буквой (вмес-*
то X (р ) - просто X ).
Пс операторной схеме можно сразу составить систему оператор-
уравнений. Из рис. 5.10,6 видно, что в сумматоре складываются три
изображения: X , . и -^У. Сумма умножается на коэффициент а,
и поступает на вход блока о передаточной функцией На выходе
имеем
V
Складывая о изображением , получим У . Итак,
Рассматривая передачу Y-^Z, запишем
%-Y > = Z .
Это те же уравнения, что и полученные из динамических уравне-
ний (5.15).
Структурные схемы метут содержать блоки с некоторой заданной
передаточной функцией. Составление операторных уравнений и в этом
случае не представляет труда.
Пример 5.14. Для структурной схемы рис. 5.II имеем оче-
Рис. 5.II
видное уравнение
откуда
(p+f -l)(p+<t)
5.7. йстльсэдя и переходная характеиотаст _,педд
Помимо комплексной частотной характеристики цепи К (),
включающей АЧХ и ФЧХ, очень важными являются импульсная и переход-
ная характеристики.
По определению, шщудьсная характеристика пепд У_( I ) есть ре-
яхттия на яхп^нпй ситуял 6 (t ). т.е. отклик на чрезвычайно корот-
50
кий импульс, как бы дающий исходный "удар"» после которого цепь
предоставлена самой себе.
Пегеходвдя характеристика цепи 4£ )_ - реакция на входной
сигнал У(t . т.е. переходный процесс, вызванный скачком на входе.
В совокупности частотная и импульсная (или переходная) характерис-
тики дают всестороннее описание цепи - как в частотной области,
так и во временной.
Все три характеристики цепи ТС (/ ), £ (f ), h(t ) относи-
тельно просто связаны с передаточной функцией цепи К (р).
Связь К (р ) с К {jto ) уже была отмечена выше:
К(р) =
(5.16)
fu) = p
Установим связь g'kt ) и k{t) с /Г(р ).
Найдем изображения
& (р) - L [ %(t)} , Н(р)-Ь[Ш>} .
По общим правилам
К(р)5е,,(р) .
Учитывая, что L { = l, L{f(t)}~ ^ получим
G(.p) - К(р) ,
(5.17)
(5.18)
Другими словами, импульсная характеристика цепи есть сигнал, изо-
Сражения которого - передаточная йгнкция цепи:
f(£) *4— Л?р) . (5.19)
Заметим, что переходная характеристика цепи является интегралом
от импульсной характеристики (5.17):
t
(5:20)
о
Пример 5.14. При работе источника тока i (t ) (рис. 5.12,а)
на резистор й. форма напряжения на нем и ( t ) реально не повторяет
форму тока из-за наличия "паразитной" емкости С , шунтирующей ре-,
зистрр. В цепи проявляется инерционность, особенно сказывающаяся
на форме выходных сигналов при резких изменениях тока.
51
Рис. 5.12
С целью ускорения передачи пиков ж скачков последовательно
с резистором вводят некоторую "ускоряющую" индуктивность L
(рис. 5.12,6). Однако при неудачном выборе L в цепи может возник-
нуть колебательный процесс установления (т.к. образовался резо-
нансный контур). Проанализируем работу схемы с точки зрения ее им-
пульсной и переходной характеристик. Передаточная функция цепи
без L ' j
»?;* *.iig
K(f>) - Л
ей соответствуют импульсная характеристика
R
т
и переходная
h(t) - И( /-г
экспоненциально
нарастание.
тока соответствует реакция с
а скачку тока - "затянутое"
Передаточная функция цепи с "ускоряющей" индуктивностью
„ . Ж
Как видим, импульсу
убывающим "хвостом"
К(р)
2.
52
Корни полинома - знаменателя
р - - — ± V —f- ' - _ (/ ± V /_ х -kJ)
Г*'г 2L V tfl* LC 2L( f | • сцг ) •
Выбор L пазлшяч на вид К(р ) и, значит, на импульсную и пере-
ходную характеристики.
При L “ -г- корень действительный кратности 2:. л •
Это так называемый типический режим установления. Если выбрать
Z >£„. корни будут комплексно-сопряженные, что означает наличие
колебаний.
Возьмем для сравнения L =2L при этом .
Я. - F «
Изображения импульсной характеристики и переходной запишем в виде
/ ^+Г 7 Р + Т
L (P+f) с Р
л+ к.
Ю ~ Т -Чтг » W ~ г ~г~9-----ё~2\ •
*Р г с p(p + j-) С Р(рг+р^{»)
Используя один из методов перехода ст изображения к сигналу, опи-
санных в разд. 5.3, получим
2t Л
St -11.
А>/ v ** u
Графики этих сигналов приведены на рис. 5.12,в и г. Разработчик мо-г
жет выбрать желательный характер реакции на импульсы и скачки.
5.8. /1иягпямма полюсов-нулей
• Читатель, по-ввдимому, уже заметил, что передаточная функция
цепи К(р ) - очень информативная характеристика, через нее можно
получить как частотные свойства цепи (АЧХ, ФЧХ), так и временные
53
(импульсная и переходная). Однакр^непосредственно из записиК(р )
трудно увидеть какие-либо характерные черты АЧХ, ФСС, % (t ),
4(f). Но QCTb способ такого представления К (р ), что связь
с АЧХ и (t ) становится почти наглядней. Это - диаграмма полю-
сов-нулей в р -плоскости.
Комплексная переменная р в преобразовании Лапласа имеет раз-
/ /Г
мерность , ту же, что и частота СО и затухание о в экопонен-
циэльно-гарыоническом колебании вида
$(t) = е cm cot .
Имеет смысл (и вскоре это выяснится) мнимую и вещественную сои
комплексной р -плоскости отождествить соответственно с частотой
и затуханием б :
р ~ б ¥ .
Передаточная функция К (р ) образует как бы некоторый рельеф над
плоскостью ((Г, /й) ), Комплексная частотная характеристика, поду-
чаемая из К(Р) заменой p*jco теперь может трактоваться как се-
чение всего "рельефа" К(р ) вертикальней плоскостью, проходящей
- через ерь мнимых величин /а). Передаточная функция любой цепи, со-
держащей сосредоточенные элементы И , L , С , имеет обязательно
вид дробно-рациональной функции р о действительными коэффициента-
ми:
fC(p)
р + а,р л ат
й(р)
Ъ(р)
(5.21)
где //(/>) и 5 (р ) - нормированные полиномы (т.е. с коэффициента-
ми I при старших степенях р ).
Корни числителя p6i называются нулями функции К(р ), а корни
знаменателя pni - полюсами. Эти течки, представленные на р -плос-
кости, и образуют диаграмму полюсов-нулей (рис.- 5.13). Полюсы отме-
чены крестиками, нули - кружками. Дополнительным кружком отмечают
'кратные полюсы и нули. Так, на рис. 5.13 крестик в кружке оз-
начает двукратный полюс. 5,4
Количество полюсов п определяет порядок цепи, количество ну-
лей tn - не больше п (может быть и отсутствие нулей). И нули, и
полюса могут располагаться либо на действительной оси, либо комп-
лексно-сопряженными парами (как и рп* на рис. 5.13).
Для устойчивых цепей (а только такие цепи и имеют смысл как
линейные) все полюсы расположены в левой полуплоскости (т.е. бп<0)
54
Идеализированные цепи без потерь име-
ют полюсы строго на мнимой оси
как, например, идеальный контур, рас-
смотренный в гл. 4. Нули в общем слу-
чае могут быть расположены как слева,
так и справа.
Если заданы координаты полюсов
и нулей, то можно по ним записать по-
линомы Я (р ) и В( р) hl саму переда-
точную функцию с точностью до произ-
вольного коэффициента k :
Рис.
. k <р р„хр-р^...
(р-Pa, УР-Рп,)-
Пусть, нацример, дано р0* = 0, рп* = -2
ух, 1 0-0
д = -
0
5.13
(5.22)
Тогда
/
п (р + 2)(р+1-])(р + 1*/) п р3 + 4рг + 6р+4
Итак, поведение функции К( р ) на всей /> -плоскости полностью
определяется тем, как расположены точки полюсов и нулей.
Наглядна такая аналогия: рельеф К{р) - это как бы, эластич-
ная "палатка”, натянутая на высокие шесты, поставленные в точках
полюсов, и притянутая гвоздями в точках нулей.
Рассмотрим связь между комплексной частотной характеристик
кой К (jo) ) и положением полюсов и нулей К(р ). При замене
в (5.22) (5.16) имеем
К (/ (я)/ К / (5.23)
Каждый двучлен в (5.23) представляет собой вектор, проведен-
ный из фиксированной точки (нуля или полюса) в точку мнимой оси
с "текущей" координатой ju) , скользящую по оси при изменении ар-
гумента частотной характеристики (см. рис. 5.13). При этом как дли-
на вектора, так и его угол будет изменяться с изменением й) . Имен-
но это изменение и формирует частотную характеристику цепи.
Обозначим через и Qi векторы, проведенные из полюсов и
нулей (см. рис. 5.13):
55
1й - Pn~ ni(ш) ;
— n Ш(a>)
ia - Poi* Qt ~Qi(a»e
Пда таком обозначают К ( jti) ) может быть представлена как произ-
ведение : . . .
1Ги)^Гш) - -
(5-24)
То есть общая частотная характеристика формируется как произведе-
ние отдельных, "парциальных" частотных характеристик, каждая из
которых связана о отдельшш нулем, или полюсом. При этом результи- ‘
рупцая АЧХ определяется изменениями длин векторов О<-( ) и Rt(&).
а ФЧХ - суммированием аргументов Щ ( & ) и вычитанием аргумен-
тов </£ ( ^ )» Рассмотрим парциальные АЧХ, связанные с одним ну-
лем й) ) и с одним полюсом £п( (V ):
ig(&))-Q(a) , kn(u) - •
Из рис. 5.14 видно, что
"Вклад" нуля в общую АЧХ - создание "провала" на частоте, равней
координате % нуля, и возрастание (асимптотически пропорциональ-
но частоте (**й> )) при увеличении частоты. "Вслед” полюса в общую
АЧХ - создание подъема на частоте, равной координате полюса.
Асимптотика при возрастании частоты ~ . Глубина провала и высота
подъема определяются действительной координатой нуля или полюса
( % или ). Чем ближе полюс к оси /ТУ , тем острее "резонанс-
ная" кривая АЧХ.
Зная характер парциальных АЧХ, можно по диаграмме полюсов -
нулей даже на глаз приблизительно проанализировать вид результи-
рующей АЧХ цепи. Приведем примеры такого анализа по заданным ди-
аграммам полюсов - нулей (рис. 5.15).
Диаграмма рис. 5.15,а. Это цепь третьего порядка. Все три
парциальные АЧХ имеют форму "резонансных" кривых, причем.централь-
ная (на0) более низкая и широкая, а две другие, связанные с.
комплексно-сопряженными полюсами, более узкие и )Высокие, т.к". эти
56
Рис. 5.15
57
полюса расположены ближе к мнимой оси. Перемножение трех кривых
должно дать более широкую и выровненную результирующую АЧХ. Об-
ласть пропускаемых частот - от нуля до некоторой частоты, прибли-
зительно равной мнимой координате верхнего полюса. При cJ бу-
дет наблюдаться резкий спад (асимптотически Это - фильтр
нижних частот.
Диаграмма рис. 5.15,6. Это цепь второго порядка. Вклад комп-
лексно-сопряженных полюсов - две симметричные резонансные кривые,
. вклад двукратного нуля р0 = 0 - нарастающая парабола Пере-
множение их дает типичную АЧХ фильтра верхних частот: малый коэф-
фициент передачи для области низких частот -для высо-
ких.
Диаграмма рис» 5.15,в. Это цепь четвертого порядка, т.к., кро-
ме двух указанных на рисунке полюсов,обязательно должны быть еще
два комплексно-сопряженных с ними. Нуль Pq = 0 свидетельствует
о непропускании прий? — О* На частотах в районе расположения полю-
сов наблюдается "горб”, формируемый в результате пе-
ремножения двух узких резонансных кривых, немного разнесенных по
частоте. Это - полосовой фильтр.
Расположение полюсов на р -плоскости дает наглядную информа-
цию и о временных характеристиках цепи, поскольку передаточная
функция К(р ) является одновременно лапласовским изображением им-
пульсной характеристики y(f ) (5.19).
Вспомнив метод обратного преобразования путем разложения
на простые дроби, перепишем К{р ) (5.21):
--------ISS1--------------
Знаменатель каждой дроби определяется одним из полюсов. Таким об-
разом, соответствующий этой дроби сигнал ff(,t ) можно считать
"вкладом" данного полюса в общую импульсную характеристику:
/?(/) = У. ff. (h . (5.26)
(5.25)
Коэффициенты fl , В , С ... зависят не только от полюсов, но и от
числителя p)t т.е. ст нулей. К сожалению, здесь нет простого
соотношения: каждый коэффициент завиоит ст всех нулей (и всех по-
люсов).
Тем не менее информация о "вкладах" каждого полюса является
полезней: по расположению полюсов можно сразу увидеть характерные
черты "элементарных" сигналов, из которых складывается импульсная
характеристика цепи.
Связь между диаграммой полюсов и видом сигнала можно распро-
странить на произвольные сигналы, не обязательно являющиеся им-
пульсными характеристиками*
Ра смотрим некоторые примеры связей между расположением полю-
сов и видом элементарного'сигнала, что, по сути дела, является
просто иллюстрацией пар сигнал-изображение табл. 5.2.
I. Простой полюс на действительной оси (рис. 5.16,а). Коор-
дината полюса соответствует постоянной затухания экопоненциально-
Gnt
го сигнала $(£)=£ . Расположение полюсов в левей полуплоскос-
ти говорит о опадающей экспоненте, в правой - с возрастающей.
Рис. 5.16
59
2. Пара комплеконо-орпряженных полюсов (рис. 5.16,6). Мнимая
координата полюса соответствует частоте заполнение радиосигнала.
Характер спада или нарастания определяется вещественней координа-
той полюса.
3. Двукратный или трехкратный полюс (рис. 5.16,в) соответст-
вует сигналам вида • Такой же является "огибающая"
радиосигнала в случае кратных комплексно-сопряженных полюсов.
Отметим еще один аспект диаграммы полюсов. Если сопоставить
классический метод решения динамических уравнений цепи с оператор-
ным методом, можно увидеть, что характеристическое уравнение
$(/?) = 0, определяющее возможные решения однородного дифферен-
циального уравнения, в точности совпадает с полиномом-знаменате-
лем передаточной функции К (р )
Корни характеристического
уравнения - это собственные частоты цепи, а соответствующие им
временные функции - собственные моды, т.е. те колебания, которые
возможны в цепи без внешнего воздействия (из-за ненулевых началь-
ных условий). Отсюда следует, что диаграмма полюсов - это не что
иное как диаграмма собственных частот цепи, а соответствующие ей
элементарные сигналы - перечень собственных мед.
Любой переходный процесс в цепи обязательно будет складывать-
ся из этих собственных иод, однако - в каком именно сочетании -
зависит от начальных условий.
В частности, свободные колебания в цепи после "мгновенного
удара" на входе (т.е. подачи 6 -функции) - это импульсная харак-
теристика, включающая все мсды, о коэффициентами, зависящими ст
полинома-числителя /?(р ) или от диаграммы нулей.
Выше (с. 54) было отмечено ограничение: число нулей W не
больше числа полюсов И . Теперь виден физический смысл этого огра-
ничения: если/л то частотная характеристика оказывается без-
гранично нарастающей
Um\ X М - 00,
а импульсная содержит дублетО. В пассивных цепях, а также в ре-
альных активных' цепях это невозможно. Однако цля идеализированных
моделей активных цепей это ограничение следует снять.
60
ilWWl
№ надеемся, что внимательный читатель заметил: все методы
анализа цепей - и метод динамических уравнений, и метод комп-
лексных амплитуд, и метод преобразования Лапласа - родственны,
тесно взаимосвязаны. Описание цепей и сигналов во временной об-
ласти (дифференциальные уравнения, переходный режим, импульсная
и переходная характеристика) и в частотной области (изображения
сигналов в плоскости комплексной переменной р'6+ja) передаточ-
ная функция цепи, комплексная частотная характеристика) суть
картины одного и того же объекта в разных ракурсах. При решении
той или иной задачи исследователь может с равным основанием вос-
пользоваться как "временно языком", так и "частотным”. В ряде
случаев целесообразно переходить о одного языка на другой - так
задача будет реиена наиболее просто. Но для этого нужно овладеть
обоими языками.
61
ЛИТЕРАТУРА
I. Матханов П.Н. Основы аналгаа электркчеокжх ца-
пав. Линейные цепи. - М.: Выси, школа, 1990.
2. С к б е р т У.М. Цепи, снгналы, системы: В 2-х я. Ч.1.-
М.: Мкр» 1988.
3. Кузнецов D.B., Т р о н и н D.B. Основы анализа
линейных радиоэлектронных цепей (Временной анализ). - М.: Изд-во
МАИ, 1992.
отлай
4. Анализ цепей при гармоническом воздействии.........3
4.1. Постановка вопроса................................3
4.2. Некоторые сведения из алгебры комплексных чисел .. 5
4.3. Комплексный сигнал, комплексная амплитуда ....... 7
4.4. Комплексные сопротивления, проводимости...........9
4.5. Комплексный коэффициент передачи, комплексная
• частотная характеристика.............................12
4.6. Резонансные цепи.................................19
5. Анализ цепей о применением преобразования Лапласа .....29
5.1. Постановка вопроса ..............................29
5.2. Определение изображения по заданному сигналу ....31
5.3. Определение сигнала по изображению ..............37
5.4. Определение передаточной функции цепи ...........42
5.5. Учет начальных условий......................... 45
5.6. Операторный метод решения интегродифференци-
альных уравнений и анализа структурных схем............48
5.7. Ишульоная и переходная характеристики цепи.......50
5.8. Диаграмма полюсов-нулей .........................53
Заключение...............................................61
Литература ............................................ 62
63
Тем. план 1992, доп.
Кузнецов Юрай Владимирович
Тронин Юрий Владимирович
ОСНОВЫ АНАЛИЗА ЛИНЙЖХ
РАДООЭЛЖТРОННЫХ ЦЕПЕЙ
(ЧАСТОТНЫЙ АНАЛИЗ)
Редактор М.С. Винниченко
Техн, редактор Н.Б. Карякина
Подписано в печать6.06.92
Бум. офсетная. Формат 60x84 I/I6. Печать офсетная
Уел. печ. л. 47^. Уч.-изд. л. 3,?7. Тираж 1000
Зак. гЗЬУ/441. Цена 45 к.
Типография издательства МАИ
I2587I, Москва, Волоколамское шосое, 4