X. ФРЕИДЕНТАЛЬ
ЯЗЫК ЛОГИКИ
Перевод с английского
Ю. А. ПЕТРОВА
Под редакцией
Ю. А. ГАСТЕВА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1969

517
Ф 86
УДК 164
THE LANGUAGE
OF LOGIC
by
HANS FREUDENTHAL
PROFESSOR OF PURE
AND APPLIED MATHEMATICS,
UTRECHT UNIVERSITY,
UTRECHT, THE NETHERLANDS
ELSEVIER PUBLISHING COMPANY
AMSTERDAM — LONDON — NEW YORK
1966
2-2-3

Оглавление
ОТ РЕДАКТОРА ПЕРЕВОДА
Глава 1
МНОЖЕСТВА И ОТОБРАЖЕНИЯ -
Глава 2
ВЫСКАЗЫВАНИЯ 35
Глава 3
СУБЪЕКТ И ПРЕДИКАТ ¦ 57
Глава 4
ФОРМАЛЬНАЯ ЛОГИКА 89
Глава 5
ЯЗЫК И МЕТАЯЗЫК ¦ Ц6
ОТВЕТЫ = 132

От редактора перевода
В 1961 г. в Хаарлеме (Нидерланды) вышла небольшая
книжка «Exacte logica» («Точная логика»"). Автор ее про-
профессор Х.Фрейденталь—известный голландский математик
с весьма широкими интересами; развивая традиции оте-
отечественной школы интуиционистов, он еще в 30-е годы
внес существенный вклад в построение интуиционистской
топологии; в последние годы большую популярность за-
завоевала книга Фрейденталя «Lincos» («Lingua cosmica»),
описывающая предложенный им «космический язык».
«Exacte logica», впрочем, рассчитана на читателей, в
большинстве своем не только ничего не слышавших ни про
интуиционизм, ни про топологию,ни про математическую
лингвистику (о космосе, правда, в наши дни говорят
с детства...), но и о логике знающих лишь то, что это
что-то средневековое... Но за последнее время слово
«логика» (да еще с эпитетом «математическая») неожи-
неожиданно вошло в моду; журналисты, физики и лирики
приучили своих читателей ассоциировать его cb всяческой
кибернетикой. Совсем ничего не знать о логике в совре-
современном смысле этого слова становится уже как-то непри-
неприлично, старомодно, что ли. Но в школе логику не про-
проходят. Специальные книги очень трудны, во всяком слу-
случае слишком трудны, чтобы читать их просто «для общего
образования».
В таких случаях интеллигентная публика обращается
обычно к популярной литературе. В конце концов, геоло-
геологию и минералогию тоже почему-то не проходят в школе,
но есть же прекрасные книги В. А. Обручева и А. Е.
Ферсмана — не учебники, а именно хорошие книги, по-
понятные и интересные каждому культурному человеку.
Книг такого уровня по логике,на русском языке пока,
к сожалению, нет. Правда, есть выходящий большим ти-
тиражом журнал «Наука и жизнь», с успехом ликвидирую-
4

щий пробелы в наших знаниях по космогонии, химии и
проблеме снежного человека. Но логики в этом журнале
практически нет — по крайней мере логики как таковой,
хотя есть много интересных и полезных вещей, близких
к логике, вроде комбинаторных задач и «психологичес-
«психологического практикума». Говоря об отсутствии хороших массо-
массовых изданий по логике, я имею в виду не элементарные
учебники (они-то как раз стали появляться, и среди них
есть совсем не плохие), а именно книги, посвященные самым
началам этой науки, не предназначаемые для какого-
либо «специального назначения»: не «логика для учите-
учителей», или «для философов», «для инженеров» и т.п., а
просто-таки «логика для любознательного читателя».
Подозреваю, что с такими книгами не густо не только у нас.
Быть может, в этом одна из причин явного и безусловного
успеха книжки Фрейденталя, за короткий срок
выдержавшей несколько переизданий на разных языках
(настоящее русское издание следует авторизованному
английскому переводу, вышедшему под названием
«Language of logic», которое и воспроизводится на титуль-
титульном листе; по-видимому, и автор счел его более ясно пере-
передающим дух и замысел книги).
«Язык логики» не есть то,?что принято^называть «ув-
«увлекательной» книгой; вернее, увлекает в ней"не-
ней"неискушенного читателя не форма изложения, предельно
простая и скромная, а сам процесс приобщения к серьез-
серьезному знанию. Автор не заигрывает с читателем, не соб-
соблазняет его «красочными» примерами, но относится к не-
нему с уважением и доверием: Не подавляет его обилием
«ученых» терминов, но и не «успокаивает» тем, что в ло-
логике «все просто». Задачу свою автор видит не в сообщении
как можно большего количества сведений, а в том, чтобы
обучить самим основам именно «языка логики» — того
самого языка, на котором читатель мог бы и говорить за-
затем, не рискуя быть смешным, как всякий полузнайка
(«запас слов» сознательно ограничен, но зато теперь чи-
читатель сможет, если захочет, смело пользоваться и более
трудными «словарями» и «грамматиками»), и читать книги,
написанные на этом языке. X. Фрейденталь не внушает
читателю, что «языку» этому можно научиться похо-
походя, но с редкостным тактом и вниманием демонстрирует
подстерегающие его трудности, делая его, так сказать,
полноправным соучастником в процессе рассуждения.

(Замечу в скобках, что термин «язык», имеющий в логике
обычно точный испециальный смысл, автор упот-
употребляет несколько расширительным образом; оговаривая
это обстоятельство в подстрочных примечаниях, я ста-
старался свести их к минимуму; псевдопроблемами «унифи-
«унификации» — и, тем более, «обоснования» — терминологии
автор предпочитает не заниматься, стараясь лишь, чтобы
она не была слишком вычурной и не слишком отклоня-
отклонялась от разговорной интуиции; во всяком случае пере-
переучиваться после этой книжки внимательному чита-
читателю не придется.)
Комментировать книгу по существу здесь нет нуж-
нужды — предоставляя слово автору, позволю себе выразить
уверенность, что читатель по достоинству оценит й эле-
элегантность и точность изложения, и являющийся, по-ви-
по-видимому, привилегией настоящих ученых «аромат под-
подлинности», столь явственно ощутимый в этой небольшой
книжке.
В заключение, как один из первых признательных чи-
читателей русского перевода книги профессора Фрейден-
таля, с удовольствием выполняю приятную обязанность
поблагодарить его за любезно указанные им неточности
английского издания.
Ю. А. Гастев

t л й в а 1
Множества и отображения
1.1. Примеры множеств. Множество всех людей (жи-
(живущих в настоящее время). — Множество всех атомов
водорода.— Множество всех положительных целых чи-
чисел (т. е. 1, 2, 3, ...).— Множество всех целых чисел
(т. е. ..., —3, —2, —1, 0, 1, 2, 3, ...).— Множество всех
рациональных чисел (т. е. целых чисел и дробей, напри-
7 26 , ц^-
мер, т-, 77- и т. п.;.— Множество всех действительных
чисел (т. .е., кроме рациональных, также таких чисел,
как ^2, log 7, я, бесконечные десятичные дроби);
это множество может быть также представлено в виде
так называемой числовой шкалы, т. е. горизонтальной
прямой линии, на которой положительные числа рас-
располагаются вправо, а отрицательные — влево от точки 0.
Гг
-@123
Множество всех комплексных чисел (имеющих вид
а + Ы, где а и Ъ — действительные числа, а символом i
обозначен корень квадратный из—1, не являющийся
действительным числом).— Множество всех точек X,
находящихся на равном расстоянии от двух фиксирован-
фиксированных точек А и В (в геометрии вместо «множество» обыч-
обычно говорят «геометрическое место»).— Множество всех
действительных! чисел х, удовлетворяют^ условию
— 3 «^а: «^ 5.— Множество всех действительных чисел хг
удовлетворяющих уравнению хг-\-1 =0 (в это множест-
множество на самом деле не входит ни одно число; это так

называемое «пустое» множество).— Множество пар чйсеД
(ж> #)> удовлетворяющих условию Зж + 2у =6.— И так
далее.
Мы не будем определять, что такое множество, а огра-
ограничимся примерами.
1.2. В основе теории множеств лежит отношение
«принадлежности». Число 3 принадлежит множеству на-
натуральных чисел (а также множеству целых чисел,
ч тт 26
рациональных чисел и т.д.); Число ^- принадлежит
множеству рациональных чисел (является элементом, или
членом, этого множества')), но не множеству целых чисел
и не множеству действительных чисел х, удовлетворяющих
условию — 3<i> <^ 5. Никакой предмет не является эле-
элементом пустого множества. Множество полностью опре-
определено, если мы можем сказать относительно любого
предмета, является или не является он элементом этого
множества. Вместо «а является элементом А » мы будем пи-
писать «aGE-4», вместо «а не является элементом А»—«aZjEA».
ЕЕ — это так называемый знак принадлежности.
Пусть А — множество целых чисел, В — множество
действительных чисел, С — множество английских дра-
драматургов. Тогда
Шекспир
Пустое множество — это такое множество X, для кото-
которого не существует такого а, что оёХ, или, иными сло-
словами, а ф X для произвольного а.
Пустое множество обозначается цосредством Q.
Когда два множества А и В равны? — Тогда, когда
для произвольного а, если он является элементом А, то
он является также элементом В, и обратно. Иными слова-
словами, когда для произвольного а если утверждение аЕ^
верно, то верно и утверждение а ЕЕ В, и когда для произ-
произвольного а из истинности а ЕЕ В следует истинность
а ЕЕ А.
При соблюдении этих условий мы будем писать «А =В».
Если А и В не равны, то мы пишем «А =)= Вь.
х) Выражения «г принадлежит X» и «г является элементом X»,
в равной мере служащие переводом английского «г is a member of
X*, имеют, по определению, один и тот же смысл и употребляются
ниже как совершенно равнозначные.-^ Прим. ред.

1.3. Быть частью. Содержаться в. Другим важным
отношением является отношение «быть включенным в»,
или «содержаться в», или «быть подмножеством». Мно-
Множество всех английских драматургов содержится в мно-
множестве (или включено в множество, или является подмно-
подмножеством множества) всех драматургов. Множество всех
целых чисел содержится в множестве всех действитель-
действительных чисел.
«А содержится в Вь (синонимы: «А включено в В»,
«В содержит А») обозначается через А а В или В zd A.
Знак с: называется знаком включения.
<<А не содержится в В» обозначается через А ф В
или В ф А.
. Точное определение отношения cz: А а В означает,
что каждый предмет а, принадлежащий А, принадлежит
и В. Иными словами: для каждого а из а ?Е А следует
а(=В.
Если А а В, но не А = В, то А называют собствен-
собственным подмножеством В. Согласно нашему определению
само В также является (несобственным) подмножеством В.
Таким образом, В а В. Кроме того: если А а В а А1),
то А = В; если А а В и В а С, то А а С.
1.4. Рассмотрим множество А, состоящее из трех
элементов: Аргентины, Бразилии, Чили, обозначаемых
соответственно буквами а, Ь, с. Таким образом, х GE А ис-
истинно тогда и только тогда, когда х — а или х = Ъ или
х = с. Это обстоятельство принято выражать записью
А = (а, Ъ, с). Сколько всего подмножеств у множества At
— Восемь (= 23):
О — пустое множество;
(а) — множество, имеющее а в качестве единственного
элемента, и аналогично (Ь) и (с);
(а, Ь) — множество, состоящее лишь из двух элемен-
элементов а и Ъ, и аналогично (а, с) и (Ь, с);
(а, Ь, с) — само множество А.
Рассмотрим теперь множество В, имеющее четыре эле-
элемента а, Ь, с, d. **' h^i Щ
Оно имеет ровно в два раза больше подмножеств, чем
множество А. В самом деле, новый элемент d можно при-
присоединить к произвольному подмножеству множества А,
х) A d В d A — естественное сокращение защси двух вклю-
включений; ЛС-ВиВС-4-— Прим. перев,
9

а можно и не присоединять. При этом, очевидно, получа-
получаются все подмножества множества В. Каждое подмноже-
подмножество множества А дает два подмножества множества В,
так что В действительно имеет 24 подмножеств.
Обобщая сказанное, мы получим, что множество, со-
состоящее из п элементов, имеет 2п подмножеств. Это спра-
справедливо и для п = 0: пустое множество имеет 2° = 1
подмножество, а именно, само пустое множество, (хотя
элементов пустое множество и.не имеет).
1.5. Множество всех английских семей — это не то
же самое, что множество всех англичан. Обозначим пер-
первое множество через А, а второе — через В. Элементами
множества В являются отдельные англичане и англичан-
англичанки. В то же время никакой человек не является элемен-
элементом множества А, так как элементами этого множества
являются не люди, а именно семьи. Не является исключе-
исключением и семья, состоящая из одного человека. «Семья»,
единственным членом которой является мисс Джонс, и
сама мисс Джонс — не одно и то же. Семья эта есть мно-
множество, состоящее ровно из одного человека; что же ка-
касается самой мисс Джонс, то она вообще не является мно-
множеством. Множество В всех англичан имеет примерно в
четыре раза больше элементов, чем множество А всех
английских семей. Каждый элемент множества А являет-
является подмножеством множества В: если сё4, то с а В.
Но не каждое подмножество множества В является эле-
элементом множества А, а лишь такое, которое является
семьей.
Пусть множество С есть объединение трех клубов а,
Ь, с, причем а состоит из членов а, Р, у, б и е, Ъ состоит
из членов а, у, ц и v, a с состоит из членов б, р, о и т:
С = (а, Ь, с),
а = (а, Р, У, б, е), Ъ = (а, у, ц, v), с = (б, р, а, т).
Тогда а ЕЕ а, Р ЕЕ а, у ЕЕ а и т. д., а ЕЕ Ъ, у ЕЕ Ъ и т. д.,
бес, рее и т.д. Кроме того, а ЕЕ С, Ъ еС, с ЕЕ С.
Но а <? С, р ф С, у ф С, ц ф С, р ф С и т. д.
1.6. Подчеркнем еще раз: элемент а и множество (а),
единственным элементом которого является этот а,—
это разные вещи: (а) имеет в точности один элемент, а
именно, а; что же касается самого а, то оно вообще может
и не быть множеством, а если все же а есть множество, то
10

оно может как вовсе не иметь элементов, так и иметь один
элемент или более.
Из того, что аЕ^аиаЕЕА, отнюдь не вытекает
а ЕЕ А. (Хотя такой случай и возможен — пусть, напри-
например, А является объединением, состоящим как из индивиду-
индивидуальных членов, так и из клубов, а является одним из
этих клубов, а а является как членом клуба а, так и ин-
индивидуальным членом объединения А.)
Не путайте ЕЕ и с. В примере из п. 1.4
но не о с 4, b cz А, с а А. Кроме того,
(а) с А, (Ъ)^А, (с) с: А,
но не (а) 6Е А, (Ь) (ЕА, (с) 6Е А и т. д. Наконец,
(а) с= (а, Ь),
но не (а) 6Е (а, Ь).
1.7. Операции над множествами. К множествам мо-
могут быть применены определенные операции. Из двух дан-
данных множеств А и В можно образовать
1) их объединение А [} В,
2) пересечение А (] В,
3) разность А \ В.
A U В есть результат совместного рассмотрения обоих
данных множеств в качестве одного множества. А П В есть
общая часть данных множеств.
А \В есть результат удаления из множества А эле-
элементов, принадлежащих множеству В. Более точно:
с 6Е A U В означает с 6= А или J) с ?=2?.
с 6Е А П В означает с ЕЕ Л и с е= В.
с ее А \В означает с ЕЕ А и с ф В.
Пример. Пусть А — множество всех людей муж-
мужского пола, В — множество всех взрослых людей; тогда
A U В — множество всех людей, за исключением дево-
девочек, А П В — множество всех мужчин, А \ В — мно-
множество всех мальчиков, В \ А — множество всех (взрос-
(взрослых) женщин.
х) Здесь «или» понимается в том смысле, что с может быть эле-
элементом обоих данных множеств.
11

Если А |"| В = 5, то А жЁ называют непере6екаюЩи~
мися (или дизъюнктными) множествами.
Чтобы не путать знаки U и П > заметим, что U по-
похож на букву U из слова Union x).
Рис. 1.
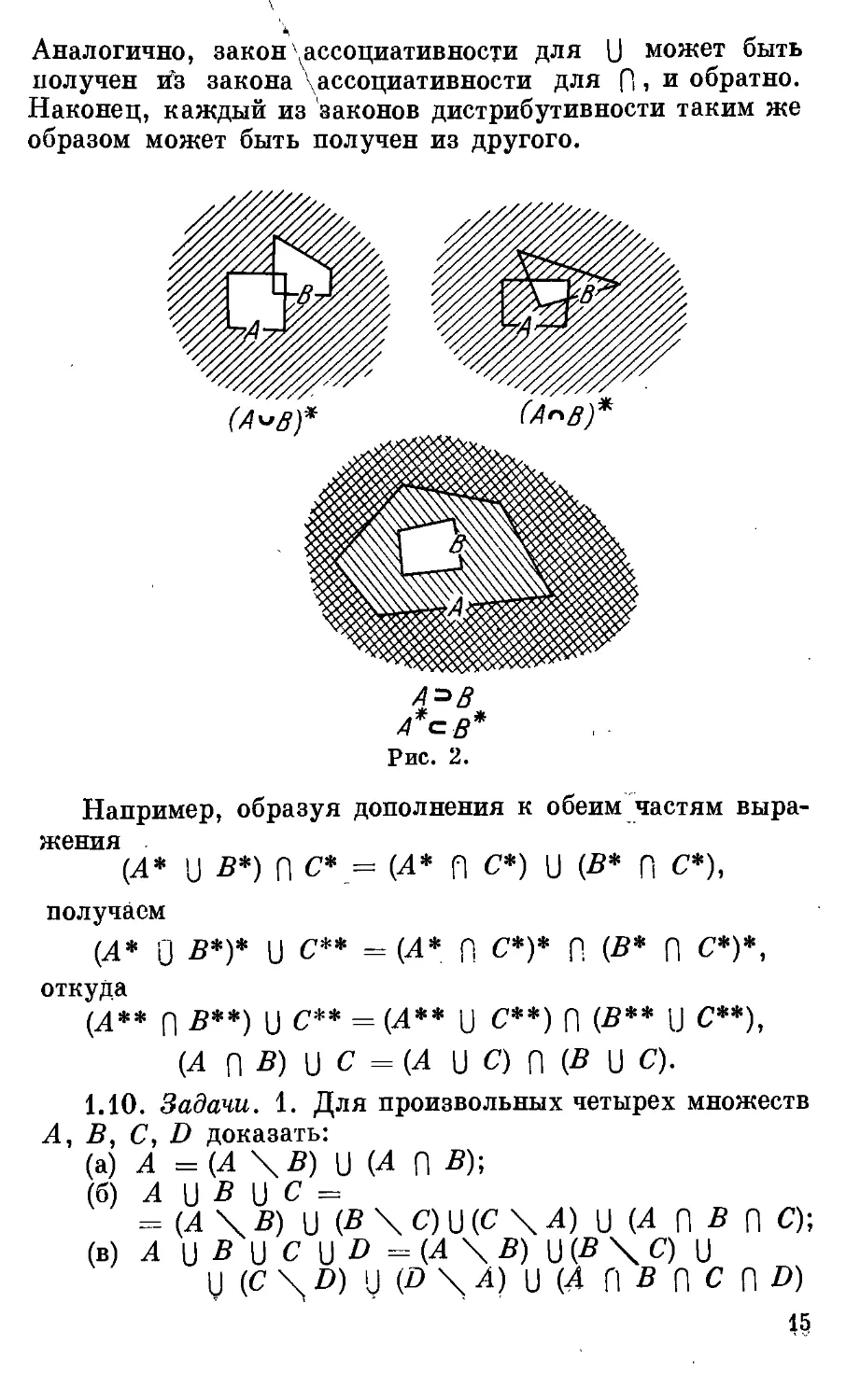
1.8. Законы для операций \}и {\. Операции U и П
подчиняются определенным тконам:
A U Б = В U А
(A U В) U С = A U (В U С)
А П В =В П А
(А (]В) (] С =А [\ (В [] С)
(коммутативность U)
(ассоциативность U)
(коммутативность П)
(ассоциативность П)
(A U В) П С = (А П С) U (В П С) 1 . й ' '
(Л П В) О С =0 U С) П (Д U С) I (Дистрибутивности)
Законы ассоциативности гласят, что в выражениях вида
А {] В {] С и А (] В (] С расположение скобок не игра-
играет роли, так что их можно вообще опускать. Напротив,
в таких выражениях, как
(A U В) П С или A U (В, П С),
расположение скобок играет существенную роль.
Пример. Пусть А — множество всех мужчин, В —
множество всех женщин, С — множество всех людей
старше пятидесяти лет; тогда А {] В — множество всех
людей, (A U В) fl С — множество всех людей старше
Объединение.— Прим. персе.
12

пятидесяти лет; В.[]С — множество Ёсех женщин старте
пятидесяти лет, A \j (В[\С) — множество всех людей,
за исключением женщин не старше пятидесяти лет.
Перечисленные законы очень похожи на обычные за-
законы арифметики, относящиеся к операциям сложения
(в их формулировках вместо U пишется + ) и умноже-
умножения (вместо П — знак умножения • или X). Лишь
для последнего из перечисленных выше законов нет соот-
соответствующего арифметического закона.
Первые четыре закона доказать легко. Докажем шестой
закон (пятый закон доказывается аналогично).
Нам надо доказать, что множества
D = (Л П В) U С
Е = (Л U С) П (В U О
совпадают, т. е. что
1) если гЕЙ, то х ?; Е;
2) если х ЕЕ Е, то х ЕЕ D.
Доказательство 1). Пусть х ЕЕ {А [\ В) [} С.
Тогда
либо (а): х ЕЕ А П В,
либо (Р): ж ЕЕ С.
В случае (а) х ЕЕ А, так что х EiA [} С, ижЕЕ-В,
так что х ЕЕ В IJ С. Из х ЕЕ А [} С и х ЕЕ В [} С
следует а; ЕЕ (Л [} С) П (В [) С). Следовательно, а; ЕЕ Я.
В случае ([3) а; ЕЕ С, так что жЕЕЛ \] С ъ х^.В \] С,
откуда х ЕЕ (Л U С) П (¦# U С); следовательно, жЕЕ-Е.
Доказательство 2). Пусть а; ЕЕ (Л \]С) П E U С).
Тогда а; ЕЕ Л U С. Следовательно, (т): а; ЕЕ Л или а: ЕЕ С.
Кроме того, а; ЕЕ В [} С. Следовательно, (б): х ЕЕ В
или а; Е: С.
Если а; ЕЕ С, то х ЕЕ (Л П В) J С; следовательно,
х EEZ).
Если хфС, то ввиду G), х е=А, а ввиду (б), х ЕЕ 5;
следовательно, а; ЕЕ Л A 5, откуда а; ЕЕ (Л П В) [} С, и,
наконец, х EiD.
Другие законы:
А и О =4, ^ П О =О.
Л с- Л U В, А о Л П #•
Если А а В, то Л U' С с: В U С и Л ПСсВ AС
13

Если i с С и ? с С, то А {] В cz?.
Если А<^ВжАсС,тоАсВ[\С
1.9. Законы обратимости. Мы будем предполагать, чтй
все множества, рассматриваемые в этом разделе, содержатся
в некотором фиксированном множестве Т (от «Total») *).
Пусть A cz Т. Множество
А* = Т\А
называется дополнением А (До множества Т). Таким об-
образом, а ЕЪ А* тогда и только тогда, когда а ф. А.
О* = т, т* = о-
Легко доказать, что
(А*)* =А
(т. е. что дополнение дополнения А есть само А).
Если А а В, то A* Z5 В* A-й закон обратимости).
В самом деле, если с ее В*, то с(?В; но тогда с(?А,
и, следовательно, с ее А*
(A U В)* = А* {] В* B-й закон обратимости).
Действительно, с ЕЕ (A IJ 5)* тогда и только тогда,
когда с ф А [} В. Но с не является элементом объеди-
объединения А и В тогда и только тогда, когда с не принадле-
принадлежит ни А, ни 5, т. е. когда с ЕЕ А*, а также с ЕЕ В*.
Аналогично,
(А П #)* =^4* U В* C-й закон обратимостиJ).
Эти три закона обратимости могут быть также сфор-
сформулированы следующим образом:
При переходе к дополнениям множеств («применении
звездочки») символы сиз,а также U и П > взаимно за-
заменяются.
Это свойство позволяет вывести закон коммутативно-
коммутативности для IJ из закона коммутативности для (~|, и обратно.
х) Такое фиксированное в пределах некоторого контекста
(«рассуждения») множество называют обычно «универсумом рас-
рассуждения», или «универсальным множеством» (последний термин
выражает то обстоятельство, что Т является «универсальным источ-
источником» элементов всех рассматриваемых множеств).— Прим. ред.
2) 2-й и 3-й законы обратимости более известны под именем
«законов Де Моргана».— Прим. ред. ¦
14

Аналогично, закон ассоциативности для U может быть
получен иЪ закона \ассоциативности для П i и обратно.
Наконец, каждый из законов дистрибутивности таким же
образом может быть получен из другого.
Например, образуя дополнения к обеим частям выра-
выражения
(A* U В*) П С* = {А* П С*) U (В* Г, С*),
получаем
(А* О В*)* U С** = (А* П С*)* И (В* П С*)*,
откуда
(Л** П В**) U С** = (A** U С**) П (^** U С**),
(Л П 5) U С = (A U С) П (^ U С).
1.10. Задачи. 1. Для произвольных четырех множеств
А, В, С, D доказать:
(а) А =(А\В) [j (А {] В);
(б) А \) В {) С =
= {А\В) [} (В\С)[)(С\А) [j (А П В П С);
(в) Л U5UCU^=D\B)U(?\C) U
y(cy)[j(fl\i)UD П 5 П С П ?>)
15

Доказать, что:
(а') множества А \ В и А (] В из/(а) не пересекаются;
(б') множества А \ В, В \ С, С\ А и А (] В (] С
из (б) попарно не пересекаются;
(в') не всякая пара множеств А \В, В \С, С \D,
D \А, А (} В {] С f\ D из (в) непременно является
непересекающейся (укажите пример, противоречащий про-
противоположному утверждению).
2. Для любых трех подмножеств А, В и С множества
Т доказать:
(а) A U В = A U (В \ (А Л В) );
(б) А \В =А П В*;
(в) А* О (В и С)* = {А Л В)* ЛИЛ С)*;
(г) если А с С, то A U (В Л О = (А [) В) {] С
(закон Дедекинда);
(д) (А \В)\С =(А\С)\(В\С);
(е) (В \ С) \ (В \А) оЛ \CdD\B)U
U (В\С).
3. Для любого натурального числа п и для любых п
множеств Ах, А%,..,, Ап-^ Ап доказать:
Ах U Az U ••• U ^«-1 U ^п =
= (^4^) U (A2\A3) U Из\^4) U -
... U (Ап-г \Ап) U (Л„\Л) О {Аг ПЛП -Л Ап).
1.11. Отображения. Под отображением f множества.
Л в множество В понимается некоторое правило, посред-
посредством которого каждому элементу х множества А сопо-
сопоставляется некоторый (единственный для данного х)
элемент у множества В. Это отношение между х из А
в. у аз В обозначается посредством
Здесь х есть переменная, значения которой пробегают
все множество А, каждое у является «образом» со-
соответствующего х, а / есть знак, обозначающий данное
конкретное отображение. Необходимо" отметить, что тер-
термин «отображение» мы здесь относим к самому правилу
отображения; результат же применения отображения к
некоторому прообразу х называют образом этого х.
(Иногда рассматриваются отображения, сопоставляющие
одному х несколько у, но в этой книге такие отображения
нам щ понадобятся.)
16

\
Понятие «отображение» является обобщением поня-
понятия функции. Пусть, например, функция / определяется
равенством
A) f(x) = Зж2 - 6х — 9.
Здесь А и В — множества действительных чисел. Отобра-
Отображение (функция) / сопоставляет каждому действитель-
действительному числу х его образ
у = Зх2 — Ъх — 9;
например, сопоставляются
числам х — — 1, 0, 7з. 3,...
соответственно числа у = 0, —9, —32/3, О,...
В случае
B) ' В(Х) = Т=2 (для
определяется функция g, отображающая множество А
действительных чисел, отличных от 2, в множество В дей-
действительных чисел.
Другие примеры:
C) А — множество всех велосипедов, В — множество
всех людей; / сопоставляет каждому велосипеду его вла-
владельца.
D) А — множество всех людей (живых или умер-
умерших), В — то же самое множество; / сопоставляет каждо-
каждому человеку его мать.
E) А — множество всех людей, В — множество всех
человеческих голов; / сопоставляет каждому человеку
его голову.
1.12. Отображение / множества А в множество В
называется отображением множества А на множество В
(или накрывающим отображением, или, короче, накрытием);
если каждый элемент множества В является образом не-
некоторого элемента из А.
Отображение / множества А в множество В называет-
называется взаимно-однозначным (или одно-однозначным, или,
короче, просто 1 — 1-) отображением, если различным
элементам множества А сопоставляются различные об-
образы множества В.
Таким образом, / является накрытием, если каж-
каждый элемент множества В имеет по крайней мере один

прообраз в множестве A; f взаимнооднозначно, если
каждый элемент множества В имеет не' более одного про-
прообраза в множестве А.
Рассмотрим еще раз отображения, описанные в
примерах из п. 1.11.
Отображение A) не является ни накрывающим, ни
взаимно-однозначным. В самом деле,
За;* — 6х — 9 = 3(х* — 2х — 3) =*= 3(х - IJ - 12
всегда «С —12, так как (х — IJ всегда > 0; —12 яв-
является минимумом (достигаемым при х = 1); f(x) не мо-
может принимать меньшие значения, следовательно, не
каждый элемент множества В является образом, а / не
является отображением множества А на множество В.
(Но если бы в качестве В мы взяли множество всех дей-
действительных чисел !> —12, то / оказалось бы накрыти-
накрытием). / не взаимно-однозначно, так как, например, 0 име-
имеет два прообраза: —1 и 3.
Отображение B) взаимно-однозначно, но не является
накрытием: 1/(ж—2) заведомо не примет значение 0. Если,
однако, a =f= 0, то существует ровно одно х Ф 2, образом
которого является а, а именно, определяемое равенством
^- = а, или х = 2 Н .
Отображение C) не является ни накрытием, ни взаимно-
взаимнооднозначным: есть люди, не имеющие велосипеда, и есть
люди, имеющие более чем один велосипед.
Отображение D) не является ни накрытием, ни взаим-
взаимно-однозначным.
Отображение E) является накрытием и взаимно-одно-
взаимно-однозначным отображением.
1.13. Пусть даны три множества А, В, С, отображение
/ множества А*ъ множество В и отображение g множества
В в множество С. Беря для произвольного элемента х из
А его /-образ у, являющийся элементом В, а для этого у
в свою очередь его g-образ z, являющийся элементом С,
' = ё{у) = *(/(*)),
мы получим некоторое отображение h множества А в мно-
множество С:
Цх) = g(f(x)).
Это h называется композицией, или произведением, данных

отображений и обозначается посредством gf:
П р и м е р. Пусть каждое из множеств А, Б, С есть
Множество всех людей (живых или умерших), / сопостав-
сопоставляет каждому человеку его мать, a g сопоставляет каждо-
каждому человеку его отца. Найти gf. Найти fg. Совпадают ли
эти отображения?
Пусть каждое из множеств А, В, С есть множество
действительных чисел, / определено равенством f(x) =
= х — 2, a g — равенством g(x) = Ъх.
g(f(z)) = Щх) = 3(х - 2) = Зх - 6;
) = /C*) =3*-2.
Предостережение: Нельзя образовать композицию
произвольных отображений. Если мы возьмем в качестве
/ отображение из 1.11C), а в качестве g — отображение
из 1.11D), то gf(x) будет означать мать владельца велоси-
велосипеда х. С другой стороны, fg(x) (т. е. владелец матери ве-
велосипеда х) является бессмыслицей. Чтобы иметь возмож-
возможность образовать из отображений / и g новое отображение
gf, мы должны потребовать, чтобы / было отображением
в такое множество, на котором было бы определено g.
1.14. Особо важны отображения, являющиеся одно-
одновременно взаимно-однозначными и' накрывающими. Если
/ есть 1 — 1-отображение множества А на множество В,
то для каждого элемента у ЕЕ В существует ровно один
элемент х ЕЕА такой, что у =f(x). Сопоставляя каждо-
каждому элемеату у ЕЕ В тот элемент х ЕЕА, для которого
у =f(x), мы получим 1 — 1-отображение g множества В
на множество А, обратное данному отображению f.
Иными словами, отображение g, обратное 1—1-отоб-
ражению / множества А на множество В, определяется
так:
х = g(y) тогда и только тогда, когда у = f(x),
т. е.
gf(x) = х для всех х Е: А
и
}g(lf) = У Для всех у ЕЕ В.
Частным случаем 1 — 1-отображения множества А на
19

самб себя является тождёстЁённое отображение ф, ойрё*
деляемое следующим образом: '¦
ф(ж) = х для всех ге4.
Если отображение g обратно отображению /, то gf и fg
совпадают с тождественным отображением ф.
Примеры. Пусть каждое из множеств А, В есть
множество действительных чисел, а / определено равенст-
равенством f(x) = Зх 4- 5. Тогда отображение g, обратное отобра-
отображению /, задается равенством f(g(x)) = х, откуда 3g(x) +
+ 5 = х, а значит, g (х) = — (ж — 5).
О
Пусть / — отображение из 1.11E). Обратное / отобра-
отображение сопоставляет каждой человеческой голове своего
хозяина.
1.15. Кардинальные числа. Когда мы говорим о двух
множествах А и В, что они имеют равное число элементов
или что одно из них имеет больше или меньше элементов,
чем другое? На каком основании мы утверждаем, что в
комнате имеется столько же людей, сколько стульев?
Мы просим присутствующих сесть на стулья. Если оста-
останутся незанятые стулья, то стульев больше, чем людей;
если все стулья будут заняты, но некоторым нехватит
стульев, то людей больше, чем стульев; если же каждый
человек будет сидеть, а свободных стульев не останется, то
количества людей и стульев равны. Такое рассаживание
соответствует эффективному (или попытке прийти к эф-
эффективному) 1 — 1-отображению множества людей на мно-
множество стульев.
Определение кардинальной экви-
эквивалентности. Два множества А и В называются
кардинально эквивалентными, если существует 1—1-ото-
бражение множества А на множество В.
(В высказывании «А и В кардинально эквивалентны»
А и В совершенно равноправны: в определении мы по-
потребовали существования 1—1-отображения множества А
на множество В, но тогда, как мы .знаем, существует и
1—1-отображение множества В на множество А, обрат-
обратное первому.)
1.16. Множество натуральных чисел 1, 2, 3,... карди-
кардинально эквивалентно множеству четных чисел
2, 4, 6,...;
требуемое отображение / имеет вид f(x) = 2х.
20

Аналогично, Множество натуральных чисел карди-
кардинально эквивалентно множеству этих же чисел, тысяче-
тысячекратно увеличенных, а также множеству чисел ^> 3000
(в последнем случаз определим / посредством
f(x) = х + 3000).
Множество N натуральных чисел бесконечно. Каждое
множество А, кардинально эквивалентное N, называют
счетно бесконечным: мы можем пересчитывать (пере-
(перенумеровывать) элементы такого множества А с помощью
натуральных чисел, располагая их в последователь-
последовательность.
Конечные и счетно бесконечные множества называют
счетными 4) множествами.
Множество А всех целых чисел счетно бесконечно — мы
можем расположить элементы множества А в последова-
последовательность:
N-A, 2, 3, 4, 5, 6, 7,...
А:0, 1, -1, 2, -2, 3, -3,...
Множество А всех рациональных чисел счетно бесконеч-
бесконечно:
N: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, И, 12, 13, 14,
А: 0,1,-1,2, -2, V.,-1/.. 3, -3, 7з, -Ч„ 2/з, ~7з, 72,
N: 15, 16, 17, 18, 19, 20, 21, 22, 23, ...
А:-*/*, 4, -4, V*, -V., 74, -3А, 7з, ~7з,-
(Как это продолжить?)
Бесконечное множество может быть кардинально
эквивалентно своему собственному2) подмножеству. Для
конечных множеств это невозможно.
1.17. Существуют ли несчетные бесконечные множества?
Рассмотрим множество А — множество точек некото-
некоторого отрезка (например, множество действительных чи-
чисел х, для которых 0 <^ х «^ 1).
Множество А не может быть счетным. Предполо-
Предположим, что А счетно. Тогда точки множества А можно
г) Автор здесь придерживается терминологии, принятой, на-
например, Н. Бурбаки. В отечественной литературе счетными чаще
называют множества, которые автор именует счетно бесконечны-
бесконечными.— Прим. ред.
2) В смысле определения из п. 1.3 (стр. 9).— Прим. ред.
21

На множестве А можно выбрать ыодотрезок А1 такой, что
<НфАг- A)
(По нашей терминологии отрезок — это интервал,
включающий свои крайние точки.) На Аг выберем под-
отрезок А% такой, что а% (?Аг, и так далее. Вообще (для всех
натуральных п): наЛп выберем ыодотрезок Ап+1 такой, что
an+i<?An+i- ' B)
Длины отрезков Аг, А2,... составляют убывающую после-
последовательность (такие отрезки называют стягивающими-
стягивающимися): Аг ^> А2 ^> А3 гэ ... Пусть с — точка, общая для
всех этих отрезков:
с GE Ап для всех п. C)
Так как с ее А, то точка с должна получить какой-то но-
номер. Пусть этот номер есть число р:
с = av. D)
Но ap?jEAp, хотя из C) и D) следует, чго ар е=Ар.
Мы пришли к противоречию. Поэтому наше предполо-
предположение должно быть неверным. Отсюда следует, что не су-
существует никакого пересчета множества А. Множест-
Множество А явдяется бесконечным, но не счетно бесконечным.
Заметим, что наше доказательство использовало
«интуитивное» представление, согласно которому каждая
стягивающаяся система отрезков имеет общую точку *).
*) В принадлежащем Г. Кантору доказательстве этой теоре-
теоремы никакие интуитивные геометрические представления не исполь-
используются. Это доказательство (цослуждвшее образцом для многочис-
многочисленных «диагональных» рассуждений, в том числе для доказывае-
доказываемой ниже в п. 1.19 теоремы) состоит в приведении к противоречию
предположения о существовании пересчета всех бесконечных де-
десятичных дробей из отрезка [О, 1J: для любой последовательности
вида
0,«ц «и ... а1п ...
0,а21 ап ... ам ...
0,а
п1
(ац = 0, 1,..., 8, 9 — ;'-й десятичный знак j-й дроби) строится «диа-
22

1.18. Когда мы можем сказать, что множество А усту-
уступает в количественном отношении множеству В («карди-
(«кардинально мажорируется» 1) множеством В)? В приведенном
выше примере относительно людей и стульев мы говорили,
что людей имеется меньше, чем стульев, если остаются не-
незанятые стулья, в то время как все люди сидят. Когда
мы имеем дело с бесконечными множествами, то такой спо-
способ проверки заведомо недостаточен. Например, множест-
множество натуральных чисел может быть отображено с помощью
1—1-отображения само в себя не только таким способом,
что ничего оставаться не будет, но и таким способом, что
получится некоторый остаток (примеры: отображение
/, определяемое формулой f(x) = х, и отображение g,
определяемое соотношением g(x) = 2х). Имея в виду это
обстоятельство, дадим следующее определение: множество
А кардинально мажорируется множеством В, если суще-
существует 1 — 1-отображение А в В, но не существует 1—1-
отображения В в А. Будем говорить также, что в этом
случае множество В кардинально минорируется множе-
множеством А 2).
Другими словами, множество А кардинально мажо-
мажорируется множеством В, если А кардинально эквивалент-
эквивалентно части В, но В не является кардинально эквивалентным
части А.
Пример. Множество А точек отрезка (см. п. 1.17)
кардинально минорируется множеством N точек, прону-
пронумерованных натуральными числами. Действительно, по-
последовательно нумеруя бесконечное количество точек av
а,,... множества А, мы получим часть множества А, кар-
кардинально эквивалентную N, в то время как из п. 1.17
непосредственно очевидно, что множество А не может быть
кардинально эквивалентным никакой части множества N.
тональная дробь» O.bjbj ... Ъп... (bn=f=ann), не принадлежащая
этой последовательности,— Прим. ред.
J) По-английски здесь просто «A cardinally majorized by В»,
т. е. речь идет лишь о некотором уточнении естественного слово-
словоупотребления. В переводе пришлось один раз сказать «усту-
«уступает в количественном отношении», а второй — «кардинально ма-
мажорируется» (аналогично: «превосходит» и «минорируется»), т. е.
ввести специальным определением точный термин, соответствую-
соответствующий (но не совпадающий) понятному, но не точному.— Прим. ред.
2) Или «В (кардинально) мажорирует А», или «.4 минорирует
В», причем ниже чаще употребляется как раз такая терминоло-
терминология.— Прим. ред.
зз-

1.19. В п. 1.4 было показано, что множество- из п
элементов имеет 2П подмножеств, следовательно, более
чем п подмножеств.
Возьмем теперь произвольное (быть может, бесконеч-
бесконечное) множество А и построим множество Q всех подмно-
подмножеств множества А: х ?Е ?2 тогда и только тогда, когда
х cz А.
Покажем, что множество Q кардинально мажорирует
множество А.
Теорема. Множество подмножеств множества
А кардинально мажорирует множество А.
Доказательство1). Соотнесем каждому эле-
элементу а ЕЕ А подмножество (а) множества А, состоящее
только из одного элемента а; это будет 1—1-отображение
множества А на часть множества Q. Нам надо теперь по-
показать, что не существует 1—1-отображения множества
Q на часть множества А. Другими словами: не существу-
существует 1—1-отображения части Ао множества А на множество
Q. Верным оказывается даже более сильное утверждение:
Не существует отображения части Ао множества А на
множество Q.
Чтобы доказать его, допустим, что / есть отображение
части Ап cz А на множество Я, и выведем из этого допу-
допущения противоречие.
Для каждого элемента х его образ f(x) является эле-
элементом Q, а следовательно, частью множества А. Тогда
можно задать вопрос, что истинно:
х ЕЕ f(x) или х ф. /(ж)?
Обозначим через U множество элементов х ЕЕ Ао таких,
что х €jEf(x), т. е.
х ЕЕ U тогда и только тогда, когда ХЕЕАотахф f(x). A)
Естественно, что U а А, поэтому U €Е й. Так как / ото-
отображает Ао на Q, то существует и такое, что
и ЕЕ Ао B)
"U =f{u). C)
*) Это доказательство, предъявляющее более высокие требо-
требования к навыкам читателя к абстрактному мышлению, при первом
чтении книги может быть опущено,
34

Так что же верно!
и ?Е U или и ф V'}
Мы должны ответить на этот вопрос с помощью выраЖе-
ния A). Подставим в A) и вместо х. Тогда A) будет гласить:
и ЕЕ U тогда и только тогда, когда «Е^имЁ f(u).
D)
Согласно соотношению B) и ?Е Аь в любом случае, так
что мы можем опустить в выражении D) это излишнее
условие:
и ЕЕ U тогда и только тогда, когда и ^Ё f(u). E),
Принимая во внимание C), получим:
и ЕЕ / (и) тогда и только тогда, когда и (?f (и). F),
Это и является требующимся противоречием; следова-
следовательно, теорема доказана. Из этой теоремы следует, что
для каждого множества А существует множество В такое,
что А кардинально минорирует В.
1.20. Для двух произвольных множеств А и В должна
быть справедлива одна из альтернатив:
(а) А кардинально эквивалентно некоторой части
множества В
или
(а') А не является кардинально эквивалентным ника-
никакой части множества В.
Кроме того, может иметь место одна из следующих
альтернатив:
(Р) В кардинально эквивалентно некоторой части мно-
множества А
или
(р") В не является кардинально эквивалентным ника-
никакой части множества А.
Из этих альтернатив можно образовать четыре комби-
комбинации:
(а) и (Р'); в этом случае, по определению, А кардиналь-
кардинально минорирует В.
25

(а') и (Р); в этом случае, flo определению, В кардинала
ёо минорирует А.
(а) и (р); в этом случае А и В оказываются кардиналь-
кардинально эквивалентными. (Это известно из так называемой тео-
теоремы эквивалентности, доказанной Ф. Бернштейном.
Доказательство это довольно-таки трудно, так что мы
его опустим.)
(а') и ({Г); а этого случая вообще не может быть. Дока-
Доказательство этого факта, основанное на так называемой
аксиоме выбора (аксиоме Цермело), нам также придется
опустить.
Если принять оба эти утверждения, то из них будет
следовать, что
Два произвольных множества А и В всегда находятся
в одном из трех отношений: А и В кардинально эквива-
эквивалентны, А кардинально мажорирует В или В кардиналь-
ао мажорирует А.
1.21. Мы определили, что значит, что два множества
кардинально эквивалентны (что значит, что одно из них
кардинально мажорирует другое), но не говорили еще
о кардинальном числе *) множества. Для конечных множеств
мы можем определить кардинальное число множества А
просто как число элементов множества А. Для бесконеч-
бесконечных множеств это, естественно, не является удовлетвори-
удовлетворительным определением.
На ранних стадиях развития теории множеств опреде-
определение кардинального числа было следующим: кардиналь-
кардинальное число множества А есть то общее, что есть у всех мно-
множеств, кардинально эквивалентных множеству А.
Оборот «то общее, что есть...» довольно-таки туманен.
В настоящее время для таких определений даются впол-
вполне удовлетворительные способы. Чтобы понять, как это
делается, рассмотрим еще один пример.
Если мы хотим узнать, весит ли какое-нибудь тело А
один фунт, то мы сравниваем его со стандартным весом в
один фунт при помощи весов. В более общих терминах
можно сказать, что если мы хотим узнать вес тела А, то
мы сравниваем это тело со стандартными эталонами веса.
Мы пытаемся найти какой-нибудь стандартный вес — и
это как раз и есть самое трудное. Но если эта задача уже
*) И здесь (ср. примечание *) на стр. 23) «cardinal number» мож-
можно было перевести как «количественное число» или просто «коли-
«количество».» Прим. ред.

решена, то мы соотносим с А тот стандартный вес, кото-
который является его весом.
Но совершенно независимо от какого бы то ни было мно-
множества стандартных весов мы можем в каждом конкрет-
конкретном случае узнавать с помощью взвешивания, являются
или нет два тела А и В одинаково тяжелыми. Всем телам,
которые столь же тяжелы, как и тело А, мы соотносили
один и тот же вес. Мы можем объединить все эти тела в
один класс *), который будет обозначен посредством {А }.
Все X GE {А } столь же тяжелы, как и А. Они составляют
один весовой класс, который отличается от других весо-
весовых классов. Всем телам, принадлежащим одному и то-
тому же весовому классу, мы хотим соотнести один и тот
же вес. Вес тела А, таким образом, зависит только от
класса {А}, элементом которого тело А является. Для
элементов различных классов соответственно и веса долж-
должны быть различными.
Итак, простейшей отличительной чертой тел, завися-
зависящей только от их весового класса и специфичной для каж-
каждого весового класса, являются как раз сами эти весовые
классы, которым принадлежат тела. Поэтому вес тела
можно определить через весовой класс, элементом кото-
которого оно является. Иначе: под весом тела А мы понимаем
класс всех тел, которые являются столь же тяжелыми,
что и тело А.
Аналогично: кардинальное число множества А есть
класс всех множеств, кардинально эквивалентных А.
1.22. В предшествующем изложении все еще остается
пробел. Будем писать А ~ В вместо «А столь же тяжело,
как и В».
Весовой класс {А} тела А мы определили так:
@) Хе{^} тогда и только тогда, когда X —А.
*) Слово «класс» — синоним слова «множество», используемый
для того, чтобы избежать частых повторений последнего. [Тем не
менее существуют некоторые устойчивые традиции выбора этих
синонимов; скажем, вместо «класс эквивалентности» (см. п. 1.22)
не принято говорить «множество эквивалентности», хотя это, ко-
конечно, столь же «верно». Это своего рода «математическая стили-
стилистика», и гибкость ее вовсе не свидетельствует о потере точности
(точно так же, как красноречивость адвоката не дает оснований го-
говорить о его неуважении к закону).— Прим. ред.]
27

Конечно, мы хотим, чтобы каждое тело было элементом
весового класса, и, в частности, чтобы тело А было
элементом класса {А}; следовательно,
A) A ЕЕ {А}. '
Кроме того, мы хотим, чтобы весовой класс характеризо-j
вался каждым из его элементов, т. е. чтобы всегда имело'
место
B) если В ge {А}\ то {А} = {В}.
Заметим, что если в дополнение к A) мы потребуем лишь
выполнения условия
B') если В GE {А}, то {A} cz {В},
то будет автоматически выполняться и B). Это можно
обосновать следующим образом. Если В GE {А}, то
{A} cz {В} (в силу 2')); отсюда в силу A) *) получим
А ?Е{#}; теперь, ввиду B') (заменив А на В и В на А),
будем иметь {В} cz {А} и, следовательно, {А} = {В}.
Итак, при наших предположениях выполняется ус-
условие
если В ЕЕ {А}, то {А} = {В},
т. е. не что иное, как B) 2).
Далее, согласно определению @) утверждение A)
есть не что иное, как
A*) А^А,
а B') — не что иное, как
B*) если В — А и С — А, то С ~ В.
Из A*) и B*) следует также
C*) если А ^.В, то В ~ А,
в чем можно убедиться, заменив в B*) В на А, А на В
С на Я.
A*), B*), C*), очевидно, выполняются, если знак
читать как «одинаково тяжело». Но они будут также в
*) И связи между отношениями принадлежности и включе
ния (см. пп. 1.2 и 1.3).— Прим. перев.
2) Последняя фраза добавлена '(для ясности) к тексту автор
при переводе.— Прим. перев.
28

подняться, если мы знаку — придадим значения «одина-
«одинаковой длины», «одинакового возраста», «равноценно»,
«так же красиво», «конгруэнтно», «подобно», «равно»,
«одновременно». В каком-то смысле более нейтрально
знак — читается как «эквивалентно».
Тогда три закона A*), B*), C*) будут звучать так:
A") Каждый объект эквивалентен самому себе (реф-
(рефлексивность).
B") Если два объекта эквивалентны третьему, то они
эквиваленты друг другу (транзитивность).
C") Если какой-нибудь объект эквивалентен другому
объекту, то этот другой объект также эквивалентен пер-
первому (симметричность).
Отношения (такие, как «быть одинаково тяжелым»,
«быть конгруэнтным» и т. п.), характеризующиеся свой-
свойствами A"), B") и C"), — причем для их характеристики
на самом деле достаточно лишь первых двух свойств,—
называются отношениями эквивалентности.
Если на множестве Q определено отношение эквива-
эквивалентности, т. е. если нам известно о каждой паре элемен-
элементов А и В множества Q, является или нет истинным пред-
предложение А ~- В, то мы можем разбить все множество Q на
классы, эквивалентные между собой элементы мно-
множества Q в один и тот же класс. Класс эквивалентности
{А} тогда определяется как множество всех XehQ таких,
что X — А.
Понятие «кардинальной эквивалентности» как раз
является примером такого рода понятия эквивалентности.
Действительно, во-первых, каждое множество карди-
кардинально эквивалентно самому себе в силу тождественного
отображения. Во-вторых, если множества В и С карди-
кардинально эквивалентны множеству A, to существуют 1—1-
отображение^ множества В на множество А и 1—1-ото-
бражение g множества С на множество А; если h есть ото-
отображение, обратное к /, то kg, будучи произведением 1—1-
накрытий, так же будет 1—1-накрытием. Следовательно,
множество С кардинально эквивалентно множеству В.
Класс кардинальной эквивалентности множества А на-
называют также кардинальным числом множества А.
1.23. Между парами тел существует, кроме того, отно-
отношение «быть менее тяжелым» (или «быть более тяжелым»).
Это отношение можно также перенести на пары весовых
классов, исходя из следующих соображений:
29

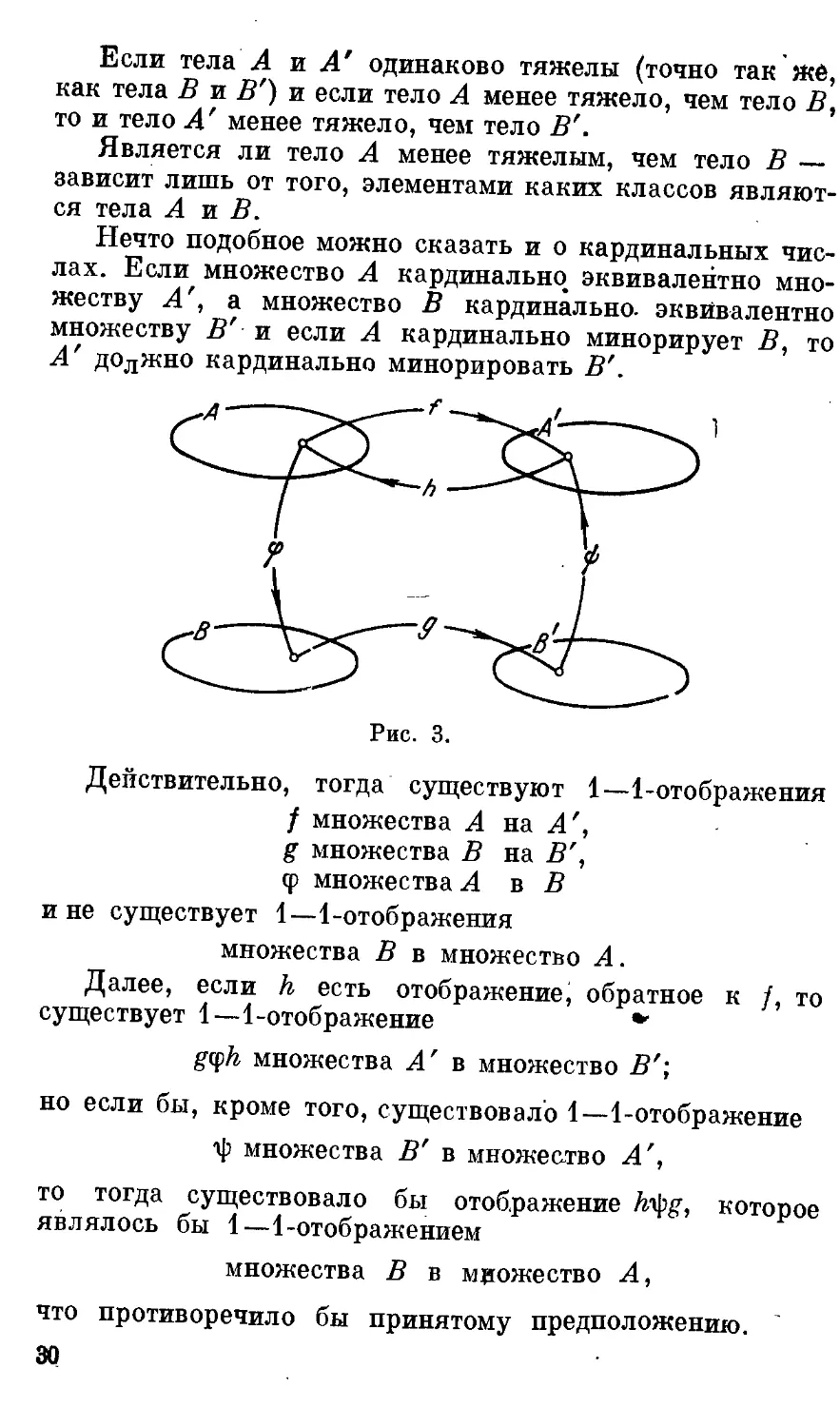
Если тела А и А' одинаково тяжелы (точно так же,
как тела В и В') и если тело А менее тяжело, чем тело В,
то и тело А' менее тяжело, чем тело В'.
Является ли тело А менее тяжелым, чем тело В —
зависит лишь от того, элементами каких классов являют-
являются тела А и В.
Нечто подобное можно сказать и о кардинальных чис-
числах. Если множество А кардинально эквивалентно мно-
множеству А', а множество В кардинально, эквивалентно
множеству В' и если А кардинально минорирует В, то
А' должно кардинально минорировать В'.
Рис. 3.
Действительно, тогда существуют 1—1-отображения
/ множества А на А',
g множества В на В',
Ф множества А в В
и не существует 1—1-отображения
множества В в множество А.
Далее, если h есть отображение, обратное к /, то
существует 1—1-отображение *¦
gq>h множества А' в множество В';
но если бы, кроме того, существовало 1—1-отображение
•ф множества В' в множество А',
то тогда существовало бы отображение htyg, которое
являлось бы 1—1-отображением
множества В в множество А,
что противоречило бы принятому предположению.
30

Следовательно, мы можем дать ойределение: если мне)*
жество А кардинально минорирует множество В, то мы
будем говорить, что кардинальное число множества А
меньше кардинального числа множества В.
1.24. Благодаря этому отношению «меньше» совокуп-
совокупность кардинальных чисел можно рассматривать как упо-
упорядоченное множество (подобно, скажем, натуральным
или действительным числам).
Будем говорить, что множество Z упорядочено посред-
посредством отношения < (читается «меньше чем»), если для
каждых двух различных элементов а, Ъ множества Z име-
имеет место одна и только одна из двух возможностей:
а •< Ъ или Ъ < а,
и если для любых трех различных элементов а, Ъ, с мно-
множества Z
иза<йиЬ<^с следует а <с
(транзитивность отношения <).
Вместо а < Ъ можно также писать Ъ^> а, вместо
«а < Ъ или а = Ь» можно писать a <J b, вместо а ^ b
можно писать — Ъ > а.
1.25. Пары. Образование классов с Помощью понятия
эквивалентности является одним из наиболее общих ме-
методов формирования математических понятий. Приведем
несколько примеров.
Отправляясь от целых чисел, рациональные числа
можно определять как дроби с целыми числителями и
знаменателями. При этом очевидно, что, например, 8/10
и 12/15 должны представлять одно и то же рациональное
число. Более точно это формулируется так. Через
{а, Ь}
мы обозначаем пару, образованную из а и Ъ, точнее, упо-
упорядоченную пару, т. е. такую, что <а, by отлична от
<Ь, а> (во всяком случае, если a =f= b). (Таким образом,
{a, by — это не просто множество с элементами а и Ь.)
Из двух данных множеств А, В мы можем образовать
множество всех пар <а, by таких, что o?i и b ее В. Мы
обозначим это множество через уА, В{. Таким образом,
с?L, В{ тогда и только тогда, когда с = {a, by для
каких-то ибА и Ь^В.
91

Пусть G — множество всех целых чисел, а Я — мно-
множество всех целых чисел =j= 0. Образуем ) G, Н <, т. е.
множество всех пар <а, Ь> таких, что s ? б и i E Я,
и будем помнить, что пару {a, by мы хотим ввести для пред-
представления дроби а/b. Имея это в виду, мы введем следую-
следующее отношение эквивалентности:
для пары <а, &> е= > G, Н < и пары <а', Ь'> g= >G, H <
положим, по определению, что
тогда и только тогда, когда
аЪ' =а'Ь.
(Вспомните о дробях 8/10 и 12/15; они представляют одно
и то же рациональное число, так как 8 X 15 = 12 X 10.)
Проверив, что это отношение является отношением экви-
эквивалентности, подобным рассмотренным в п. 1.22 и удов-
удовлетворяющим свойствам A*) — B*), произведем посред-
посредством этой эквивалентности разбиение на классы.
Класс, элементом которого является пара <а, Ь),
т. е. класс
«а, 6»,
назовем рациональным числом. (Так, например, <4, 5>,.
<— 4, —5>, <—8, —10>, <80,100> принадлежат одному и
тому же классу — рациональному числу, нормальное
представление которого есть дробь 4/б-)
Мы можем теперь определить сложение рациональных
чисел исходя из сложения упорядоченных пар, которое
мы определим так:
если
<о, &>S>G, H< и <с, d>EE)G, Ж,
то
(а, Ь> + <с, d), = {ad + be, bd}.
Последняя пара.опять-таки ЕЕ> G, Н(, Потому что b=f=Ot
d =j= 0, а следовательно, bd =j= 0. (Удостоверьтесь, что это
соответствует обычному правилу сложения для дробей.)
Если каждое слагаемое замедено эквивалентным,
то сумма также заменится на эквивалентную. Пусть,
32

например,
<о, Ь> — <а', Ь'>, <с, d)-<c', d'>;
тогда
об' =о'Ь, ed' = e'd. (*)
Мы должны показать, что
<ad + be, bd) ~ <o'd' + Ь'с', b'd'>
и, следовательно, что
(ad + bc)Vd' = (a'd' + b'c')bd. (**)
Левый член равенства (**) равен
„ adb'd' + beb'd' = ab'dd' + Wed',
а в силу (*) он равен
a'bdd' + We'd = {a'd' + b'c')bd,
где последний член равен правому члену равенства (**).
Теперь для двух рациональных чисел мы можем одно-
однозначно определить их сумму
«а, Ь» + «с, d» = {{ad + be, bdy},
так как мы уже показали, что класс суммы двух пар не
зависит от выбора этих пар в их классе.
Аналогично можно определить другие операции с ра-
рациональными числами и доказать все известные ариф-
арифметические законы.
1.26. Вот еще один пример образования классов по-
посредством отношения эквивалентности:
Пусть G снова есть множество целых чисел. Пусть т —
фиксированное целое число, а Н — множество целых чи-
чисел, кратных т, т. е. с ЕЕ Н тогда и только тогда, когда
с =md для некоторого d ЕЕ G. Легко видеть, что если
Ъ ЕЕ Н и с ЕЕ Н, то ис — b EEH. Теперь условимся, что
a — b тогда и только тогда, когда а — Ъ ЕЕ Н,
т. е. если разность a — b кратна т. Введенное таким об-
образом отношение есть отношение эквивалентности. В самом
деле, a — а, поскольку a — a = О ЕЕ Н;
если b — а и с ~ а, то Ь — а ЕЕ Н ис — а ЕЕ Н, так
что
(Ь — а) — (с — а) е Н.
откуда с — b ЕЕ Н, а значит, с — Ь.
2 X. Фрейдентапь 33

Класс {а} состоит из всех целых чисел, которые отли-
отличаются от а разве лишь на слагаемое, кратное т. Пере-
Переход от а к {а} означает, что мы игнорируем эти кратные
т слагаемые.
Именно так, например, мы пользуемся часами (то =
= 12), отождествляя 12 часов, 13 часов и т. д. соответствен-
соответственно с О часов, 1 часом и т. д. Аналогичная ситуация —
в вычислительной машине с шестиразрядным сумматором
(то = 1 000 000), которая для 334 896 -f 884 391 дает от-
ответ 219 287.
Определенные таким образом классы {а} называют
обычно целочисленными вычетами по модулю т. Для та-
таких классов можно определить операции сложения, вы-
вычитания и умножения:
{а}+ {Ъ} = {а+.Ь},
{а} - {Ь} = {а- Ъ},
{a}.{b} ={a.b}.
Здесь, конечно, надо доказать, что если а' — а, Ь'— Ъ, то
а' + V — а + Ъ и т. п.
Читатель сможет проделать это самостоятельно.
Пример.' По модулю 12: {7} + {8} = {3}, {7}—
-{8} ={11}, {7},{8} = {8}, {3}.{4} = {0}.
Последняя формула показывает, что произведением
по модулю 12 может быть {0}, даже если ни один из со-
сомножителей не есть {0}. Поэтому определить деление по
модулю 12 не удается. По модулю же 7 мы можем делить
так же, как это делается в множестве рациональных чи-
чисел. Там каждый {a} =f= {0} имеет обратный: {1} =
= {1}.{1} = {2}-{4}={3}.{5} ={6}.{6}; отсюда, напри-
мер, {4} есть класс, обратный к {2}.
То же справедливо для каждого простого модуля т,
т. е. для чисел =f= 0 и =f= 1, не имеющих других делителей,
кроме 1, —1, т, —т).
1.27. Теория множеств — сравнительно новая об-
область математики. Ее основатель — Георг Кантор
A845-1918).

Глава 2
Высказывания
2.1. В логике под «высказыванием» понимают то, что
выражается, как говорят в лингвистике, посредством
осмысленного утвердительного предложения 4).
Примеры.
Все люди смертны.
Сократ — человек.
Если а < Ъ, то Ъ ^> а.
Все негры — белые.
Все белые люди белы.
Если снег горит, то остается зола.
Высказывания не обязательно должны быть истин-
истинными утверждениями.
«Высказывание» — это не то же самое, что «предложе-
«предложение». «Предложение» — чисто лингвистическое понятие,
а «высказывание» есть термин логики. Предложения «Со-
«Сократ — человек» и «Socrates is a man», выражают одно и то
же высказывание, хотя и в различных языках. «Который
час?» и «Остановитесь!» не выражают высказывания.
Напротив, следующие утверждения — высказывания:
«Джон спросил Питера, который час» и «Джон сказал
Питеру: „Остановитесь!"».
2.2. В третьей главе мы подвергнем простые предложе-
предложения (вроде «Сократ — человек») дальнейшему анализу,
напоминающему обычный грамматический разбор. В на-
настоящей же главе мы будем расчленять высказывания
*) То есть повествовательного предложения, о котором можно
(по крайней мере в пределах определенного контекста) говорить,
что оно истинно или ложно.— Прим. ред.
2* 35

только до тех пор, пока их составляющие также будут вы-
высказываниями.
Чтобы соединять предложения в более сложные пред-
предложения, мы используем связки.
Соединение посредством связки «и»:
Швеция выиграла у Германии и Бразилия выиграла у
Швеции.
Соединение посредством связки «или»:
Звонок испорчен или дома никого нет.
Соединение посредством связки «если..., то...»:
Если поезд прибывает, то подается сигнал, что путь
закрыт.
Соединение посредством связки «тогда и только тогда,
когда»:
Поезд прибывает тогда и только тогда, когда по-
подается сигнал, что путь закрыт.
Многократное соединение встречается в предложении:
Если А выиграет у В, и С выиграет у D, то А будет
играть против С, и В будет играть против D.
Имеются, конечно, и многие другие связки, но те,
которые мы здесь упомянули, представляют особый инте-
интерес из-за их специфически логического характера *).
Для того чтобы установить, является ли истинным
сложное высказывание ар и q», нам надо лишь знать,
истинны ли обе его компоненты р и q. Если это так, то
«р и q» истинно. Нам незачем для этого знать что-либо о
содержании высказывания р или высказывания q. Точно
так же мы можем сделать заключение об истинности вы-
высказывания «р или <7», если мы знаем, что по крайней мере
одно из составляющих высказываний истинно,* причем
смысловое содержание высказываний р и q не играет
здесь никакой роли. Заметим 2), что «р или q» считается
истинным и тогда, когда р и q оба истинны.
г) Часть этой фразы, начинающаяся после слова «связки», не
имеет никакого точного смысла; подробнее о различных связках
см. ниже, п. 2.11.— Прим. ред.
2) Конечно, здесь мы не столько «замечаем» это обстоятельство,
сколько условливаемся о его выполнении, так что последние две
fpsbt, по существу, являются определением связки «или».
о же в еще большей степени относится к последующему рассуж-
рассуждению о связке «если..., то...», хотя сказанное, конечно, не мешает
нам по мере возможностей заботиться о том, чтобы подобные опре-
определения не слишком расходились с привычным словоупотреб-
словоупотреблением.— Прим. ред,
30

Нечто аналогичное имеет место и относительно выска-
высказывания «если р, то qy>. Когда такое высказывание истин-
истинно? Для ответа на этот вопрос рассмотрим подробнее один
из примеров, приведенных выше.
Имеются четыре возможности, представленные четырь-
четырьмя случаями в следующей схеме:
^^^-^поезд
сигнал ¦~--^
путь закрыт
путь свободен
прибывает
не прибывает
Какие из этих четырех возможностей подтверждают
высказывание
«если поезд прибывает, то подается сигнал, что путь
закрыт» и какие из них противоречат ему? Если мы обна-
обнаружим, что поезд прибывает и что подан сигнал «путь
закрыт» (левый столбец, верхняя строка), то высказыва-
высказывание подтверждается. Оно также подтверждается, если
поезда нет и подан сигнал «путь открыт» (правый столбец,
нижняя строка). Это высказывание все еще истинно, если
поезда нет, но сигнал «путь закрыт» все же подается (пра-
(правый столбец, верхняя строка), так как наше высказывание
ничего не говорит о том, что произойдет в том случае, когда
поезда нет,— ведь тогда может быть подан любой сигнал:
«путь закрыт» или «путь свободен». Но если мы обнару-
обнаружим, что поезд прибывает, и в то же время увидим, что по-
подан сигнал «путь свободен» (левый столбец, нижняя строка),
то тут уж высказывание нельзя считать подтвержденным.
Таким образом, мы находим, что высказывание «если
р, то д» не является истинным только в том случае,
когда р истинно, a q тем не менее не истинно; во
всех других случаях это высказывание истинно. Иными
словами, оно истинно как в случае, когда р ложно, a q
имеет произвольное значение, так и в случае, когда q ис-
истинно, а р произвольно. В дальнейшем мы будем писать
р /\q вместо «р и q»,
р \/ q вместо «р или ф>,
р -> q вместо «если р, то ф>,
р *-* q вместо «р тогда и только тогда, когда q».
3?

тое \/ ~*4wo «или»;, /\ — это переверну
не 3SE^2SSTи "столь наглядно- ™
Каждая связка имеет специальное наименование:
Р А д - конъюнкция (высказываний р ж q)
PVg- дизъюнкция (высказываний р и q)
Р-+Я- импликация (от высказывания р к о)
Р - 9 9Квмвал (высказываний р и ?).
к связкам
ния, например, 3°К СТроить новые высказыва-
ности построения°ТН^ УДелить внимание последователь-
r и ?V(«A>)
. - —г случае мы
связываем с г поспелей™ У 9 И ПЛолУченный результат
мы вначале образуеТП г A= B° ВТ°Р°М СЛуЧае
38

Относительно связки | мы примем следующее согла-
соглашение: если за связкой | непосредственно следует буква,
то связка относится к этой букве; если же сразу после
связки | открываются скобки, то связка относится ко
всему заключенному в скобки выражению. Например, в
мы вначале образуем отрицание высказывания р, а затем
объединяем его с г посредством дизъюнкции, в то время
как в
1 (р V г)
вначале образовано р V г, а затем его отрицание.
В высказывании нас прежде всего интересует его
истинностное значение, т. е. является оно истинным или
ложным. Чтобы ответить на этот вопрос, нам ничего не
надо знать о составляющих высказываниях, кроме
их истинностных значений. Эта информация полностью
определяет истинностное значение сложного выска-
высказывания.
Для обозначения лжи мы будем использовать символ
О, а для обозначения истины — символ 1.
Истинностное значение высказывания р мы будем обо-
обозначать через |р|. Таким образом, для любого конкрет-
конкретного р справедливо либо \р\ = О, либо \р\ —1.
Для каждой связки мы можем составить так называе-
называемую истинностную таблицу, показывающую, когда
высказывание, образованное посредством этой связки,
истинно, а когда ложно:
p
0
0
1
1
я
0
1
0
1
IP
1
1
0
0
рЛя
0
0
0
1
p\/v
0
1
1
1
р-*я
1
1
0
1
p~{
1
0
0
1
I P/Z
1
0
0
0
Слева от вертикальной черты выписаны все четыре воз-
возможные комбинации значений пары высказываний р,
q (т. е. комбинации «р ложно» и «р истинно» с щ ложно»
39

и «<? истинно»). Справа выписаны значения полученных вы-
высказываний в каждой из возможных комбинаций. Напри-
MePi \РЛя\ — 1 тогда и только тогда, когда \р\ ~i
и \я\ = 1; Р -*¦ Я ложно тогда и только тогда, когда р
истинно, a q ложно, и т. п.
В приведенной выше схеме есть одна новая связка,
играющая важную теоретическую роль — это «черта»
в высказывании р / д, которое следует читать как
ни р ни q (т. е. не р и не q).
Действительно, это высказывание истинно только тогда,
когда оба высказывания р и q ложны.
Теперь мы можем определять истинностные значения
более сложных комбинаций высказываний и строить для
них истинностные таблицы. Когда, например, истинно вы-
высказывание ~~\ р \/ <7? Или, напротив, когда оно ложно?
Оно ложно только тогда, когда "~| р ложно и q также
ложно. Это же самое можно выразить иным образом: оно
ложно только тогда, когда р истинно, a q ложно. Отсюда
видно, что ~~| р V <? истинно и ложно в точности при тех
же условиях, что р -*¦ q. Значит, ~~\р\/яяР~^Я рав-
равносильны (эквивалентны), т. е.
I 1 Р V Я\ = I P -* Я I Для всех р, q. ¦
Еще один пример: ~](~~\р Д ~~\ q) ложно тогда и только
тогда, когда ~~\р Д ~] q истинно. Последнее же означает
не что иное, как то, что ~~\р истинно и ~1 q также истин-
истинно, а это имеет место тогда, когда р ложно и q ложно. Но
р \/ q также ложно только при этих же условиях. Таким
образом, ~~| (~~\р Д ~~I q) и р V q равносильны.
Следовательно,
I ~1 П Р А ~1 Я) I = I Р V Я I Для всех р, я-
Другие очевидные примеры равносильности высказы-
высказываний:
I ~~1 С\Р) I = \Р\ Для всех р,
\Р Л Я\ = \Я Л Р\ Для всех р, я-
Мы можем решить вопрос о равносильности двух вы-
высказываний, подставив во всех возможных комбинациях
О и 1 вместо букв, входящих в эти высказывания, и находя
истинностные значения результатов таких подстановок
согласно истинностным таблицам.
40

Прим
р q r
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

ер.
1(р\/я)Аг] г-
1
1
1
0
1
0
1
0
»CIpA~~U
1
1
1
0
1
0
1
0
1)(г-+~1р)А~1я
1
1
0
0
1
0
0
0
2.4. Сложные высказывания
р-^р,р V~lp, (р-»-?)-»- П q--*~\p),
И (Р V Я) «- П РЛ ~| ?). Р -* (Я -* Р).
(р -*• д) -* ((? -»¦ 0 -* (р -> »¦ ))
имеют ту характерную особенность, что они тождествен-
тождественно истинны, т. е. истинны всегда, независимо от того, яв-
являются ли составляющие их высказывания р, q, r, ...
истинными или ложными1). (Проверьте это.)
Напротив, высказывания
р /\~\р, (р-*?)ЛП
являются тождественно ложными, т. е. ложными неза-
независимо от того, являются ли р, q, г,... истинными или
ложными. (Проверьте это.)
Высказывания
p. p Vp. p Лр
иногда принимают значение «истина», а иногда — значе-
значение «ложь» («истина», если р истинно, и «ложь», если р
ложно).
Высказывание
(р -*¦ я) -*¦ (я -*¦ р)
х) Тождественно истинные высказывания принято также на-
называть тавтологиями.¦—Прим. ред.
41

также иногда истинно, а иногда ложно (ложно, если р
ложно, a q истинно, и истинно во всех других случаях).
Высказывание
(р ->• д) -»- (г -> д)
тоже иногда истинно, а иногда ложно.
Если нам дано какое-нибудь высказывание А, состоя-
состоящее из высказываний/), q, r,..., то мы можем попытаться
придать р, q, r,... такие истинностные значения, чтобы А
стало истинным. Такая ситуация называется «выполне-
«выполнением» высказывания А. Если мы сможем осуществить
такую операцию, то высказывание А будем называть вы-
выполнимым. (Если выполнение высказывания А невозмож-
невозможно, то А является тождественно ложным.)
Подобную операцию можно попытаться осуществить
и с любым данным множеством Q высказываний А. Если
мы сможем придать р, q, r,... такие истинностные значе-
значения, что все высказывания А ЕЕ® одновременно окажут-
окажутся истинными, то Q называется выполнимым.
Мы можем также попытаться придать р, q, r,... такие
истинностные значения, чтобы А стало ложным. Если
такая операция осуществима, то А называется оспоримым.
(В противном случае А оказывается истинным для любого
набора значений р, q, r,..., т. е. тождественно истинным.)
Будем говорить, что множество Q высказываний оспо-
оспоримо, если при некотором наборе значений р, q, r, ...
хотя бы одно j4 ей оказывается ложным.
Из изложенного выше следует, что «невыполнимость»—
это то же самое, что и «тождественная ложность».
Аналогично, «неоспоримость» — синоним «тождественной
истинности». Если какое-нибудь высказывание А тождест-
тождественно истинно, то А, конечно, является также и выполни-
выполнимым. Если А тождественно ложно, то А также оспоримо.
Если А тождественно истинно, то \ А тождественно лож-
ложно. Если А тождественно ложно, то \ А тождественно
истинно. Если А выполнимо, то \А оспоримо. Если А
оспоримо, то \А выполнимо.
2.5. Принцип эквивалентности. В п. 2.3 нам уже при-
приходилось рассматривать равносильные (эквивалентные)
высказывания, например,
Р-+Я к ~~\р\/ q,
ППрАП?) и руд,
1Пр) и р.
42

Из этих пар мы можем получить высказывания, являю-
являющиеся тождественно истинными:
(р-+я)+*(Лр V я)>
Дело в том, что высказывание
А <->?
истинно тогда и только тогда, когда А и В одновременно
истинны или ложны, а если это имеет место всегда, то
это как раз и значит, что эти высказывания равносильны.
На основании этого мы можем сформулировать следую-
следующий общий принцип.
Принцип эквивалентности. Если А и В
состоят из р, q, r,... и если они равносильны, т. е. если
\А\ = \В\ для всех р, q, r,...,
то
А *->В
тождественно истинно, и наоборот, если Л <-» В тождествен-
тождественно истинно, то А и В равносильны.
2.6. Принцип дедукции. Другой метод получения тож-
тождественно истинных высказываний основан на принципе
дедукции.
Высказывание р -v q, очевидно, не является тождест-
тождественно истинным (оно ложно, если р истинно, a q ложно).
Однако если мы будем считать q истинным, то р -»- q
также будет истинным, ибо случай, когда р -*- q ложно,
нашим предположением исключается. Поэтому при до-
допущении Щ является истинным» р —*¦ q также оказывается
истинным. Но из сказанного вытекает тождественная ис-
истинность высказывания
Ч -*¦ (Р -*¦ Я)-
Обобщение этого метода получения тождественно истин-
истинных импликаций формулируется в виде следующего прин-
принципа.
Принцип дедукции. Пусть А1г..., Ап, А, В —
высказывания, состоящие из р, q, r,..., и пусть В ис-
истинно для всех тех наборов значений р, q, r,..., для кото-
которых высказывания А1}..., .Ап, А одновременно истинны.
43

Тогда
истинно для всех тех наборов значенийр, q,r, ..., для кото-
которых А!,..., Ап одновременно истинны.
В самом деле, допустим, что существует набор значе-
значений р, q, г, ..., при котором Аг,...,Ап, истинны, но А-уВ
ложно. Тогда для этого же набора значений высказывания
Аг,...,Ап, А были бы истинными, а В тем не менее было
бы ложным, что противоречит нашему предположению.
Более кратко принцип дедукции может быть сформу-
сформулирован так:
Если в предположении, что Ах,..., Ап, А истинны, В
истинно, то в предположении, что Аи..., Ап истинны,
импликация А ->• В тождественно истинна.
В частности, если в предположении, что А истинно,
В истинно, то А ->• В тождественно истинно.
Пример. Высказывание
тождественно истинно.
Это можно показать следующим образом. Предполо-
Предположим, что (р ->• q) Д (<7 -*¦ г). Мы хотим доказать р -*¦ г.
(Если мы с этим доказательством успешно справимся, то
согласно принципу дедукций поставленная нами задача
будет выполнена.) Из предположения следует, что р —*- q,
а также q-*~ r истинны (так как конъюнкция этих выска-
высказываний истинна лишь в этом случае). Теперь предполо-
предположим также, что р истинно. Тогда, в силу того, что р -*- q
истинно, q также должно быть истинным (см. истинностную
таблицу для импликации). Из того, что q истинно аналогич-
аналогичным образом следует, что г истинно, так как q-y r истин-
истинно. Следовательно, предположив, что (р ->- q) /\ (q->- г)
истинно и р истинно, мы находим, что г истинно. Тогда,
согласно принципу дедукции
р ->- г истинно в предположении, что (р ->- q) /\ (q ->• г)
истинно,
а из этого следует (как уже было показано), что
тождественно истинно.
44

Используя принцип дедукции, докажите, что выска-
высказывания
(р-*?)-*[(?-* г)-*(р-г)],
1(Р -+ q) Л (г -> s)] -> [(р Д>) -> (q Д «)],
[(р -+ ?) у (Г _> в) 1 ^ [(р д Г) -> (q \/ в)]
тождественно истинны.
Используя принципы эквивалентности и дедукции,
докажите, что высказывание
тождественно истинно, т. е. докажите посредством прин-
принципа дедукции тождественную истинность высказываний
[р-+ (я->г)] ->» [(р Л?)^Н
Вариантом принципа дедукции является принцип дизъ-
дизъюнкции, который читатель неосознанно мог уже приме-
применять при изучении ранее изложенных проблем.
В ходе какого-либо доказательства нам иногда прихо-
приходится рассматривать различные возможные случаи а и
Р; если нам удается прийти к некоторому заключению D
как в случае а, так и в случае р, то мы в конечном итоге
заключаем, что D справедливо в любом из этих случаев.
В этом и состоит формулируемый ниже принцип.
Принцип дизъюнкции. Пусть Alt..., An,
В, С, D суть высказывания, состоящие из высказываний
р, q, г,... Пусть для любого набора значений р, q,r,...,
для которого Alt..., An истинны, либо В, либо С является
истинным. Пусть, кроме того, D истинно как в предполо-
предположении «А^..., Ап, В истинны», так и в предположении
«Alt..., An,C истинны». Тогда D истинно в предположении
«Ац..., Ап истинны».
Принципы дедукции и дизъюнкции могут также быть
сформулированы для бесконечной системы высказываний,
а не только для системы из п высказываний Alt..., An.
2.7. Принцип отрицания.
Принцип отрицания. Если высказывание
А тождественно истинно, то \А тождественно ложно.
Это следует из сказанного в конце п. 2.4.
45

Высказывание р /\~] р, как видно из соответствую-
соответствующей истинностной таблицы, тождественно ложно (выска-
(высказывания р и не р не могут выполняться одновременно, они
взаимно исключают друг друга — так гласит закон про-
противоречия). Поэтому высказывание
1(рЛ~\р)
тождественно истинно.
^ Можно привести и дальнейшие примеры принципов по-
подобного рода.
2.8. Принцип подстановки.
Принцип подстановки. Пусть А есть
тождественно истинное высказывание, состоящее из вы-
высказываний р, q, r,... Любое высказывание, выводимое
из А посредством подстановки каких-либо высказываний
вместо высказываний р, q, r,..., также является тождест-
тождественно истинным.
Справедливость этого принципа очевидна 4).
Пример. Тождественная истинность высказыва-
высказывания (<7 ->¦ (р -*¦ q )) нам уже известна. Подставив в него
высказывание р -> q вместо высказывания q и ~~] (г \/ р)
вместо р, мы получим новое высказывание:
(Р -*¦ Я) -*- {I ~1 (г V РI -*- (Р -* «)},
также являющееся тождественно истинным.
2.9. Modus ponens. Все изложенные принципы слу-
служили цели выведения новых высказываний из некоторых
тождественно истинных высказываний. С ях] помощью
мы получаем все более длинные тождественно истинные
высказывания. Теперь мы рассмотрим принцип, посредст-
посредством которого из некоторых тождественно истинных вы-
высказываний можно получить более короткие тождественно
истинные высказывания.
Modus ponens. Если А и А -*¦ В суть тождест-
тождественно истинные высказывания, то В также тождественно
истинно.
Символически сказанное записывают так:
л
А~*В
.J) Тем естественнее для читателя воспользоваться представив-
представившимся случаем проверить себя и не приступать к чтению п. 2.9,
не доказав этого утверждения.— Прим. ред.
46

Действительно, если высказываниям р, q, г,..., из ко-
которых состоят А и В, приданы некоторые значения, то
согласно истинностной таблице для импликации и в си-
силу того, что А -*¦ В истинно, могут иметь место только
следующие случаи:
А ложно и В истинно, А ложно и В ложно,
А истинно и В истинно.
Однако все случаи с «А ложно» исключаются (так как А
всегда истинно), так что остается только третий случай,
а в этом случае В истинно.
Пример. Мы уже знаем, что высказывание
тождественно истинно. Заменим в нем р на какое-нибудь
конкретное тождественно истинное высказывание А (по
принципу подстановки). Полученное высказывание
также будет тогда тождественно истинным. Но в силу того,
что А тождественно истинно, высказывание
является также тождественно истинным согласно modus
ponens. Так, например, тождественно истинным является
высказывание
g-Ир-»- (g->-p)L
2.10. Сводка тавтологий. Приведем здесь некоторую
сводку тождественно истинных высказываний. Удостоверь-
Удостоверьтесь в их истинности при помощи истинностных таблиц
или применяя изложенные выше принципы.
A)
B)
C)
D)
E)
(p ¦-> q) *¦
(p ¦-> q) *¦
(p «->¦ q) -»
Л —>- D.
1(рЛ"
+ l(p -*¦ ?',
->(<?«-»¦ p)
- (p -^ g).
1' P 1 •
(См. п. 2,7; закон противоречия.)
F) (рЛ1р)-*я-
(Из противоречия- следует все, что угодно.)
47

G) ~]-]P"P. I -
(Закон двойного отрицания.)
(8) pVIp-
(Закон исключенного третьего: р или не р — третьей воз-
возможности нет.)
(9) (рЛр)<-»Р-
A0) (Р\/Р)'*->Р.
(И) p^{q^p).
(См. д. 2.6; если р истинно, то р истинно при любом пред-
предположении.)
A2) [p-+(q-+T)]
(См. п. 2.6.)
A3) -]р -> (р -> q).
(Может быть получено из A2) подстановкой высказыва-
высказывания \р вместо р, высказывания р вместо ^высказыва-
^высказывания q вместо г и с использованием F).)
A4) (p-»q)V(9-*'P)-
(Замечательная формула. Следует непосредственно из
истинностной таблицы для импликации. Если р истинно,
то второй член дизъюнкции истинен; если р ложно, то
первый член дизъюнкции истинен; следовательно, по
крайней мере один член дизъюнкции истинен.)
A5) (р-+я) » П Р V Я)-
¦ A6) (р-+д)
(Закон контрапозиции. На нем основано косвенное дока-
доказательство, или reductio ad absurdum. Мы хотим доказать,
что q истинно в предположении р. Согласно принципу
дедукции это приведет к доказательству истинности вы-
высказывания р -> q. Вместо этого мы можем согласно A6)
доказать ~] q-*-"^p. В таком случае предположим | q,
т. е.что # ложно, и из этого предположения выведем ~]р.
Таким образом, мы получим/? -> # с помощью ~\ q—>- \ p.)
A7) 1(р -*¦ я) А (Я -* г)] ->(р -+ г).
48

(См. п.\2.6; транзитивность импликации.)
A8)' (p-+q)-+l(q-+r)-+(p-+r)].
A9) (р V q)~(q \/ р):
(Коммутативность связки \/.)
B0) (р Л ?) «-> to Л р)-
(Коммутативность связки Д.)
B1) [(р V ?) V Н «-> [р V (? V О!-
B2) [(р /\q) /\r\^[p /\(q/\ r)\.
(Ассоциативность связок \/ и Д соответственно. В силу
этих законов мы можем отныне писать
Р V ? Vг вместо (p\J q)\/ г и р V (q V г)
и
р /\q /\r вместо (р Д q) Д г и р Д (? Л г).
так как расстановка скобок не влияет здесь на истинност-
истинностные значения.)
B3) [(р V д) Д г] «-> [(р Д г) V (? Л г)].
B4) [(р Д д) V Н - 1(Р V О Д (д V О.
(Законы дистрибутивности.)
B5) П (рУ?I-ПМП Я)-
B6) [-| (
(Законы обратимости.)
Законы A9) — B4) весьма похожи на аналогичные
законы для операций над множествами. Этой связи мы
еще коснемся позднее.
B7) [(р -v г) Д (q -» г)} «-> [(р V ?) -* Н.
B8) [(р -v ?) Д (р -v г)] «-> [р -v (q Д г)].
(Эти два закона могут быть доказаны непосредственно
или могут быть выведены из законов дистрибутивности
посредством закона A5).)
B9) П (р -v q) ~ (р Д -| q).
49

(Следует из A5) и B5).) j
C0) [(р -+ д) А (г -> s)} -* {(р Д г) -+ (д /\ *)]'.
C1) Цр-+д)\/(г-+ s)] -+[(р Лг)-* (д V *)Ь
(Доказать эти законы предлагалось в п. 2.6.)
2.11. Все пропозициональные функции. В таблице,
приведенной в п. 2.3, кроме описанных ранее связок,
имеется еще связка, обозначенная знаком /. Но этими
связками отнюдь не исчерпываются все возможные связ-
связки. До сих пор мы имели дело со связками, при помощи
которых из одного или из двух данных высказываний об-
образуется новое высказывание. В более общем случае мы
можем поставить задачу обозреть все возможные опера-
операции, посредством которых из п данных высказываний
образуется новое высказывание. Другими словами, мы
рассматриваем plf..., pn как переменные, принимающие
лишь значения 0 (ложь) и 1 (истина), и отыскиваем все
функции F от этих переменных, значениями которых
также могут быть только 0 и 1. Сколько таких функций
существует?
Для ответа на этот вопрос мы прежде всего определим
число различных наборов значений системы рг,..., рп.
Такой набор полностью определен, если мы знаем, какие
из pi имеют значение 1. Следовательно, число таких на-
наборов равно числу различных подмножеств множества
из п элементов, т. е. 2™ (см. п. 1.4). F полностью определе-
определена, если мы знаем, для какого набора значений перемен-
переменных /?!,..., рп функция F(p1,..., pn) будет иметь значение 1.
Следовательно, число различных функций F равно числу
подмножеств множества из 2П элементов, т. е.
22П функций F
от переменныхplf..., pn. Эквивалентные между собой функ-
функции F (т. е. принимающие одинаковые значения для оди-
одинаковых наборов значений аргументов) мы считаем совпа-
совпадающими.
50

Функция F от одной переменной р полностью извест-
известна, если мы знаем таблицу
р
0
1
Р{р)
Обозначим такую функцию через CatCtl. Функция Соо,
тождественно равная 0, может быть представлена в виде
р Д \ р (так как она никогда не принимает значения
«истина»).
Функцию Сп, тождественно равную 1, можно предста-
представить в виде р \/ \ р (так как она всегда принимает значе-
значения «истина»),
С01(р): р *).
Функция F от переменных рх, р2 полностью определяется
таблицей
Pi
0
0
1
1
Pi
0
1
0
1
F(Pi, ft)
a3
4
Обозначим такую функцию через COlO2Oaa,. Существует
всего шестнадцать таких функций; из них значение 1 при-
принимают:
0 раз — 1 функция,
1 раз — 4 функции,
2 раза — 6 функций,
3 раза — 4 функции,
4 раза — 1 функция.
*) «Тождественная» функция, переводящая истину в истину,
а ложь — в ложь.— Прим. перев.
51

Первая и последняя функции в этом списке вообще не за-
зависят ни от р1( ни от р%. Из остальных две функции зави-
зависят только от р1; а две — только от р„ (первые две — это
СОоп и С1100, эквивалентные соответственно рх и ~~\ рх,
а вторые две — это С0101 и Сюк» эквивалентные соответ-
соответственно р2 и ~~]р2).
Далее, значение 1 дважды принимают функции
Pi *^Pi и рх
Наконец, имеются функции
Pi А Pa, IPiA Pi, Pi A "I Pi, I Pi V 1 Pi,
принимающие значение 1 только однажды, и функции
Pi V Pi, H Pi V Pi, PiV1Pi,1PiV1Pi,
которые принимают значение 1 по три раза.
Рассмотрим теперь функцию
F(Pl,~; Pn).
Положим
F{Pl,-~, Pn-U 0) =
F(plt..., pn_lf 1) =
Тогда
---, Pn-l)] А ГРп-
Следовательно, функция .F может быть выражена через
функции от менее чем и переменных с помощью связок
^ин ^ош и ^oooi (т- е- связок *~1, \/, Д). Повторяя этот
редукционный процесс, мы приходим к следующему вы-
выводу.
Каждая функция F(p1,..., pn) (эквивалентные функции
отождествляются) может быть представлена с помощью
связок "~1 > V> Л-
Равносильности
(р V я) <-  Пр V П¦?)
позволяют ограничиться только одной из связок \/ или Д.
А так как
52

то возможно обойтись только лишь связками | и -к
Необходимое количество связок может быть даже све-
сведено к одной связке, например, к связке «черта», которая
определяется истинностной таблицей, приведенной
в п. 2.3.
Так как
(Р / Я) ~ Г\Р А 1 ч),
'ГО
~]р <-> 0> / р);
кроме того,
р Л я «-» (( ~1р) / П ?))
Все связки могут быть также получены посредством функ-
функции | р V ~~I ?• Можно показать, что, кроме этих двух
связок, не существует других функций от двух перемен-
переменных, обладающих этим свойством.
2.12. Двоичная система счисления. Обычно мы запи-
записываем число в десятичной системе счисления — посред-
посредством символов 0, 1, 2,..., 9. Самый правый числовой
разряд представляет единицы, следующий разряд —
десятки, затем идет разряд сотен и т. д. Вообще, и-й
числовой разряд—это кратное числа Ю". Иначе говоря,
запись пппп-х.-.а^по означает an>10n + «n-i'10"+_•••
... + «!• 10 + «О-
В электронных вычислительных машинах обычно ис-
используется двоичная система счисления, единственными
цифровыми символами которой служат 0 и 1. Значение
каждого числового разряда удваивается по сравнению
со значением соседнего справа разряда, т. е. запись
аЛап-1... а1 а0 означает здесь
ап . 2П + ап-х • 2" + ... + ах . 2 + а„.
В двоичной системе вычисление соотношений
37 + 30 = 67, 67 - 30 = 37, 13x5= 65, 65 : 5 = 13
принимает следующий вид:
, 100101
+ 11110
1000011
1000011
-" иио
100101
1101
Х 101
UOi
0000
1101
1000001
1000001
101
110
101
101
101
| 101
1101
53

Арифметические операции здесь те же, «тто и в десятичной
системе, только сложение и умножение намного проще:
a
0
0
1
1
b
0
1
0
1
ab
0
0
0
i
a + b
00
01
01
10
Это напоминает таблицы, используемые в логике вы-
высказываний:
ab соответствует а/\Ь,
левая цифра в столбце под формулой а + Ъ соответ-
соответствует а /\Ь,
а правая цифра в этом же столбце — формуле
~] (а <-> Ь) (а и Ь несовместимы).
2.13. Переменные, которые могут принимать в точ-
точности два значения, можно интерпретировать как про-
пропозициональные переменные (переменные, обозначающие
высказывания). Например,
выключатель (включен — выключен),
свет (горит — не горит),
электрический проводник (под напряжением — не
под напряжением),
дверь (открыта — закрыта).
Эти значения можно понимать как соответствующие
«истине» или «лжи» A или 0).
На рис. 4 приведен план внутренней части дома. Раз-
Различные цифры соответствуют дверям. Выражение «г-я
дверь открыта» («закрыта») понимается как аналог вы-
высказывания «pi истинно» (соответственно «ложно»). Тог-
Тогда возможность пройти из нижней левой части дома в
верхнюю правую в плане выражена посредством
l(Pi ЛР2Л Ре) V рМр? V (р8 А Р»I Л Рп) V
V {Up* A />8) VpsI A pu A Pv А р»»-
В телефонных коммутаторах, вычислительных машинах,
релейных устройствах, электронных трубках и элект-
электронных лампах используются различные переключатели.
На рис. 5 схематически представлены контакты, верх-
верхний из которых в нормальном положении открыт, а ниж-
54

ний — закрыт. В первом случае контакт в цепи q закрыт
тогда и только тогда, когда ток проходит по цепи р и,
следовательно, электромагнит возбужден. Во втором же
ш ¦¦—
J
[
t
!
i
9
—1
1
/3
1
г
о
... И -
Рис. 4.
Рис. 5.
случае контакт в цепи q закрыт тогда и только тогда, ког-
когда ток не проходит по цепи р и, следовательно, электро-
электромагнит не возбужден. Если мы подключим цепь q к ис-
источнику напряжения (например, к батарее), то действие
выключателя в цепи q может быть представлено посред-
посредством р и \ р соответственно.
На рис. 6изображены диаграммы цепей для г = р /\q
(открытые в нормальном состоянии контакты, соединен-
соединенные последовательно), р V q (открытые в нормальном
55

состоянии контакты, соединенные параллельно),;
~1 (р <-» q) (двусторонний переключатель). i
В вычислительных машинах приходится решать зада-;
чи реализации сложных функций от большого числа про-
пропозициональных переменных. Мы уже показывали,
как они могут быть образованы из функций двух типов
Рис. 6.
(и даже только одного типа). Конечно, очень важно де-
делать это по возможности наиболее простым путем.
Человеческий мозг состоит из биллионов элементов
(нейронов), которые находятся в двух состояниях («воз-
(«возбужденном» и «невозбужденном») и соединены в громад-
громадное множество путей. Вполне возможно,, что здесь имеются
аналоги всех шестнадцати пропозициональных функций
от двух переменных. При изучении функций мозга широ-
широко пользуются далеко идущей аналогией между его рабо-.
той и работой вычислительных мащин.

Глава 3
Субъект и предикат
3.1. «Все» и «существует». В главе 2 мы имели дело с
образованием высказываний из более простых высказыва-
высказываний или с расчленением высказываний на менее сложные.
Простейшие (атомарные) высказывания далее анализи-
анализируемы не были. Однако при грамматическом анализе пред-
предложений они подразделяются на части, среди которых
имеются подлежащее (subject) ') и.сказуемое (predicateJ).
В логике термины «субъект» и «предикат» используются
для обозначения соответствующих понятий при анализе
высказываний.
Математические высказывания могут содержать так
называемые переменные. Высказывание
(а + Ь) (а — Ь) ¦ = а2 — б2
истинно для всех чисел а, Ь; высказывание
ж2 — Зх + 2 = О
истинно только для некоторых х, а именно, для г =1 и
х = 2; высказывание
Bх + у = 3) Д (Ах + 2у = 5)
никогда не является истинным (эти равенства несов-
несовместимы) .
*) Английский термин «subject» переводится и как «подлежа-
«подлежащее» (термин лингвистики), и как «субъект» (логический термин).—
Прим. ред.
2) Аналогично, английскому «predicate» соответствуют два
русских термина: «сказуемое» и «предикат».— Прим. ред.
57

Приведем другие примеры (в которых переменные про-
пробегают множество всех людей):
Pi=
Рг-
Рз-
Pi-
Рь-
Pt-
Pi-
Ps-
P9:
X
X
X
X
У
X
У
У
X
живет в Лондоне.
живет в Англии.
есть лорд-мэр Лондона.
есть отец у.
есть сын х.
моложе, чем у.
старше, чем х.
моложе, чем z.
моложе, чем z.
Все эти высказывания иногда оказываются истинными, а
иногда ложными. Например, высказывание р3 верно лишь
для одного х; р1 верно приблизительно для 8 000 000 х;
р2 верно приблизительно для 50 000 000 х.
В то же время высказывания
Рз~>
«Рз~>
Pi «-»•
¦Pi.
Pi)
Рь,
Pi-»-
Л (Pi
Ре <-*
Рг,
-»-J
Р7.
Рз
>гI
Ре
-»-Pi,
->-(Рз
->(Рв
являются тождественно истинными, а высказывания
Pi А Ре, Рь Л Ре '
никогда не принимают значения «истина».
(Высказывание
[(Рз -»¦ Pi) Л (Pi -»¦ PiI -»¦ (Рз -»¦ Рг)
останется истинным высказыванием при замене рх,
/>2, Рз любым другим высказыванием. В других же при-
примерах под рг, р2, р.л подразумеваются именно указанные
выше их значения.)
Поскольку нам приходится иметь дело с высказывани-
высказываниями, содержащими переменные, нам понадобятся специ-
специальные символы, указывающие, является ли высказыва-
высказывание тождественно истинным, истинным в некоторых слу-
случаях или не является истинным никогда.
58

3.2. Высказывание вида F(x),. содержащее перемен-
переменную х, представляет на самом деле целую систему выска-
высказываний в том смысле, в каком этот термин употребляет-
употребляется в главе. 2. Мы получаем эту систему, подставляя вместо
переменной х всевозможные конкретные примеры а, Ь,
с,..., служащие значениями этой переменной х:
F(a), F(b), F(c),...
Например, мы можем поочередно подставлять вместо х
в высказывание pL(x) имена разных людей, получая при
этом уже высказывания в смысле главы 2; например,
Чемпион мира по джиу-джитсу живет в Лондоне,
Брижит Бардо живет в Лондоне,
Лорд-мэр Лондона живет в Лондоне;
некоторые из этих высказываний оказываются истинными,
а некоторые — нет.
Для любого постоянного высказывания р (т. е. вы-
высказывания в смысле главы 2) имеются две возможности:
либо оно истинно, либо оно ложно. Можно было бы обой-
обойтись и одним истинностным значением (например, «ис-
«истина»), так как ложность высказывания р можно выра-
выразить через истинность высказывания | р. Так как же
обстоит дело теперь? Понадобится ли нам новое понятие
истинности, специально приспособленное, для рассматри-
рассматриваемых здесь «высказываний», зависящих от некоторых
переменных, или достаточно будет комбинировать с уже
имеющимся термином «истинно» новые термины «всегда»
(«тождественно»), «иногда», «никогда» (подобно тому, как
вместо «р ложно» мы говорим « | р истинно»)?
Что значит, что высказывание F(x), скажем, высказы-
высказывание
х живет в Лондоне —v x живет в Англии
тождественно истинно? — Это означает, что истинны все
высказывания
F(a), F(b), F(c),...
или, иными словами, что истинна конъюнкция высказы-
высказываний
F(a)/\F{b)/\F{c)/\...
59

Но это очень громоздкая запись, особенно если перемен-
переменная х в F(x) пробегает бесконечную предметную область.
Поэтому мы предпочитаем писать
AxF(x),
читая эту формулу как
для всех х F(x).
То, что F(x) всегда (тождественно) истинно, т. е. истин-
истинно для всех х, выражается теперь посредством утвержде-
утверждения, что
AxF(x) истинно.
Таким образом, употребление термина «всегда» наря-
наряду с термином «истинно» позволяет нам утверждать истин-
истинность общего высказывания. Аналогичным образом вводит-
вводится и термин «иногда». Если высказывание F(x) — скажем,
высказывание
х живет в Лондоне —
является иногда истинным, то это означает, что истинно
по крайней мере одно из высказываний
F(a), F(e), F(c),...
или, иными словами, что истинна дизъюнкция высказыва-
высказываний
V-
И эту запись мы упростим с помощью обозначения
что читается как
существует х такой, что F(x).
Истинность F(x) для некоторого х теперь будет выра-
выражаться с помощью утверждения
VxF(x) истинно.
Так мы вводим термин «иногда» наряду с «истинно»
для формулировки высказываний. (Заметим, что «сущест-
«существует х такой, что...» вовсе не означает, что существует
только один такой х -• их может быть и больше. Более
того, даже все х могут быть такими — «все» есть частный

случай «некоторые».) Ясно, что <iF(x) никогда не истинно»
означает то же самое, что «не существует х, для которого
F(x) было бы истинно», т. е. VxF(x) не истинно, или, ины-
иными словами, истинно
3.3. Знаки Л и V называют кванторами — они ука-
указывают «количество» ') значений переменной, для которых
данное высказывание истинно. В выражениях
VxF(x) и ДЛх)
х уже не является переменной в прежнем смысле, а иг-
играет роль связанной переменной.
Имеются и другие способы связывания переменных.
Один из них мы уже знаем — это подстановка вместо пере-
переменной некоторого предмета; примером может служить
подстановка слова «Марс» или «Сириус» вместо перемен-
переменной х в высказывание
х есть планета
(в первом случае получающееся ё результате подстановки
высказывание истинно, во втором — ложно).
Заметим, что высказывания
(Л^(х)) + F(a)
и
F(a) -* VxF(x)
истинны.
3.4. В одном и том же высказывании различные пере-
переменные могут быть связаны различными способами. Возь-
Возьмем, например, высказывание
х есть мать у
или, сокращенно, хМу.
Тогда
Уу(хМу)
можно прочесть как «ж есть мать».
Здесь одна переменная была исключена связыва-
связыванием, другая пока свободна. Мы можем связать и эту
х) Quantum, quantity — количество, quantify — определять
количество, quantifier (квантор) — соответствующее отглагольное
существительное,— Прим. ред.

переменную х:
что можно прочесть как «существует мать». Высказыва-
Высказывание
будет означать, что каждый (человек) есть мать. Конечно,
это высказывание ложно. Однако следующее высказыва-
высказывание уже истинно:
Мы могли, конечно, начать также и с переменной х:
Vx№y),
что читается «г/ есть ребенок» 4);
означает: «существует ребенок»;
означает: «каждый (человек) есть чей-то ребенок». Это вы-
высказывание истинно.
Мы можем вообще начать с квантора всеобщности:
Л„ (хМу)
означает: «ж есть мать каждого (человека)»;
Л*\ (хМу)
означает: «любой человек является матерью каждого (че-
(человека)»;
(**)
означает: «существует мать всех (людей)».
Или начнем опять с х:
означает: «у есть ребенок каждого (человека)»;
х) Здесь всегда подразумевается дополнение «некоторой
матери».

означает: «любой человек есть ребенок каждого (чело-
(человека)»;
УуКх(хМу)
означает: «существует некто, кто является ребенком каж-
каждого (человека)».
Обращаем внимание читателя на то, что высказывания
(*) и (**), различающиеся только порядком вхождения
кванторов, имеют различные истинностные значения.
3.5. В то же время, если в какое-нибудь выражение
входят одноименные кванторы, порядок их вхождения не
играет роли. Высказывания
УхУу(хМу) (существует мать),
WyWx(xMy) (существует ребенок),
Ух,у (хМу) (существует пара «мать —
ребенок»)
равносильны. Вообще, попарно равносильны любые вы-
высказывания вида
VsV/X*, у), VyVx F(x, у), Vx,y F(x, у).
(Мы условились ранее обозначать упорядоченную пару
х и у через (х, у}; однако всюду, где это не чревато недо-
недоразумениями, мы будем пользоваться более простыми обо-
обозначениями.) Как можно удостовериться в равносиль-
равносильности приведенных высказываний? Для этого вместо
переменных подставим все возможные предметы а, Ь, с,... и
запишем
F(a,
F(b,
F(c,
VxF(x,
a),
a),
a),
a),
F(a,
F(b,
F(c,
VxF(x,
b),
b),
b),
b),
F(a,
F(b,
F(c,
VxF(x,
с),-
с),-
с),-. ^
c),...
Vv^(a, У)
V,/(b, y)
V/(c, y)
В конце г'-й строки написана дизъюнкция высказываний
из этой строки, а под у'-м столбцом написана дизъюнкция
высказываний из этого столбца. Дизъюнкцией высказыва-
высказываний из правого столбца является высказывание
V,VvJP(*, у).
63

Чтобы удостовериться в истинности этого высказыва-
высказывания, мы должны в последнем столбце найти истинное вы-
высказывание, а чтобы удостовериться в истинности такого
высказывания из последнего столбца, мы в свою очередь
должны в строке, в которой оно расположено, найти ис-
истинное высказывание. Таким образом, наша задача сво-
сводится к нахождению пары (х, у}, для которой истинно
F(x, у), т. е.
v*,yF(x, у). ;
Но в точности то же самое можно сказать и о проверке на
истинность высказывания
VvVxF(x, у).
В этом случае нам пришлось бы следовать по схеме в об-
обратном порядке, отыскивая вначале нужный столбец, а за-
затем уже строку.
3.6. Посредством аналогичного рассуждения можно
показать и равносильность высказываний
K\F(x, у), ЛуЛх F(x, у), Ах<у F(x, у).
В точности так же рассматриваются и выражения,
содержащие более чем две переменные.
3.7. Если р не зависит от х, то, конечно, высказывания
Vxp *^р
и
Лхр<-+р
истинны.
3.8. Законы дистрибутивности B3), B4) (см. п. 2.10)
приводят нас к аналогичным законам для V и Л.
Пусть р не зависит от х. Тогда
[р A VxF(x)] «[V^A F{x))\,
lp V W(*)\ ~ IK(P V F (x)].
Доказательство видно из соотношений
[р A (F(a) V F(b) V F(c) V-)W
«-» (р Л *"(*)) V (р Л f (Ъ)) V (р A F(c)) V ...)
и т. д.
3.9. Такая же аналогия имеется с формулами B7) и
B8) из п. 2.10 — высказывания
64

[Лх(р-+F(x))] „{p-+AxF(x)}
истинны.
3.10. Какое высказывание является отрицанием вы-
высказывания
«все люди смертны»?
Конечно, это не высказывание
«все люди не смертны»,
— ведь первое высказывание опровергается уже тогда,
когда можно найти хотя бы одного человека, не являюще-
являющегося смертным. Поэтому отрицанием первого из приве-
приведенных высказываний является высказывание
«существует человек, который не смертен».
Вообще, если мы хотим найти высказывание, равно-
равносильное высказыванию
 KF(x),
мы должны мысленно представить его в виде
П (F(a) /\F(b) Д F(e) Д ...);
тогда, вспомнив соотношение B6) (см. п. 2. 10), получим
откуда искомым высказыванием'будет
Отрицанием высказывания «F(x) верно для всех а*»
является, таким образом, высказывание «существует х,
для которого неверно F(x)i>; следовательно,
Если мы возьмем, например, в качестве F(x) высказыва-
высказывание
(х человек) -*¦ (х смертен),
то получим истинное высказывание:
{ ~~| Л,, [(х человек) ->¦ (х смертен)]} *-*
<->{\^, | [(г человек) -*¦ (х смертен)]},
3 X. Фрейденталь 65

или, применяя B9) (см. п. 2.10):
•*-» {ЧкЦ* человек) Д "~j (х смертен)!}.
3.11. Истинным является и высказывание
Левая часть этой эквиваленции читается как «не суще-
существует такого х, для которого F(x)», а правая — как «для
всех х не F(x)».
Законы, полученные нами в пп. 3.10—3.11, можно
кратко сформулировать так: отрицание и квантор можно
менять местами, перевертывая при этом квантор. Это на-
напоминает законы обратимости B5) — B6), описанные в
п. 2.10, и аналогичные законы, относящиеся к операциям
над множествами.
3.12. Задачи. Предполагая, что переменные пробегают
множество людей, примем следующие обозначения:
М(х): х есть мужчина,
V(x): х есть женщина,
xJy: х моложе, чем у,
хКу: х есть ребенок у,
xGy: х состоит в браке с у,
U(x): х живет в Утрехте,
А(х): х живет в Амстердаме.
Представьте в символической форме следующие высказы-
высказывания:
1. Каждый человек имеет отца и мать.
2. Каждый, кто имеет отца, имеет и мать.
3. Каждый человек моложе своих родителей.
4. Каждый человек моложе родителей своих родителей.
5. х состоит в браке.
6. Существует мужчина, жена сына которого старше
его самого.
7. х и у братья (т. е. имеют общих родителей).
8. Если в Утрехте есть женщина, имеющая брата в
Амстердаме, то в Амстердаме есть мужчина, имеющий сест-
сестру в Утрехте.
9. Не всякий женатый мужчина живет в Утрехте.
66

10. Не каждая женщина в Утрехте не имеет сына в
Амстердаме.
11. Все дети человека х состоят в браке.
12. Существует человек, все дети которого состоят
в браке.
13. Каждый ребенок человека х состоит в браке с ре-
ребенком человека у.
14. У человека у существует ребенок, который не сос-
состоит в браке с ребенком человека х.
15. Существуют два человека такие, что каждый ребе-
ребенок одного из них состоит в браке с ребенком другого.
16. Существуют два человека такие, что ни один ребенок
одного из них не состоит в браке с ребенком другого.
17. Если у является ребенком человека х, то каждый
ребенок человека у является внуком человека х.
18. Какова связь выражения
\Ш*КУ » U(y))] ~ [(У^Ку) - Щу)\)
с выражениями из п. 3.9?
Укажите, на основании каких законов истинны (не-
(независимо от значений К, G, U и т. д.) следующие высказы-
высказывания:
Г ' 19. П Л, {[Vy (xGy)] -> Щх)} ~ V* (VH (xGy) Д И ^ (*)).
20. П \УХ (хКу)] «-> [VA И (хКу) ].
21. Ух\(yKx-+Vz(zKy)) ++ П\Vy[yKxДЛг(~](гКу))].
Введем следующие обозначения:
Z(x, t): я вижу предмет х в момент времени t;
Р(х, t): я беру предмет х в момент времени t;
t' <C t: момент времени t' предшествует моменту t.
Напишите с их использованием символические выра-
выражения для высказываний:
22. Я всегда что-то вижу.
23. Иногда я ничего не вижу.
24. Существуют предметы, которые я никогда не вижу.
25. Я вижу каждую вещь в некоторый момент
времени.
26. Если я вижу предмет, то я тут же его беру.
27. Если я вижу предмет, то я беру его спустя некото-
некоторое время.
28. Перед тем как я беру предмет, я вижу его.
3* 67

29. Если я беру предмет, не видя его до этого, то че-
через некоторое время я вижу его, но не беру.
30. Не существует предметов, которые я никогда не
беру.
31. Я никогда не беру того, что я всегда вижу.
32. Всегда существуют вещи, которые я не вижу и
не беру.
33. Я беру всякую вещь, которую я никогда не вижу.
34. Я беру всякий предмет, который я еще не взял до
этого.
35. Я всегда вижу либо все, либо ничего.
36. Если я беру некоторый предмет, который до этого
уже видел, то я ранее видел предмет, который взял позд-
позднее.
37. Некоторые вещи, которые я видел ранее, я всегда
вижу вновь спустя определенное время.
38. Если я когда-либо видел две вещи одновременно,
то в будущем я также увижу их только одновременно.
39. Если я когда-либо видел и взял предмет одновре-
одновременно, то и впоследствии я либо делаю и то и другое, ли-
либо не делаю ни того, ни другого.
Пусть переменные в нижеследующих выражениях про-
пробегают множество действительных чисел, а алгебраиче-
алгебраические знаки имеют свои обычные значения; прочтите эти
выражения и определите, истинны ли они.
40. Лх,у{х + у = у + х).
41. AxVv(x + y = 3).
42. VyAx(x + y =3).
43. VXVV (x + у = 3).
44. Лх,у(х + у =3).
45. (Ax,v(x + у = ЗЪ-*О. - *
46.
47.
48. ..,, ^ , vy-^ч ' ^-\^Л/-
49. Л„, ь, с {[Ух {ах* + Ьх + с = 0)] «-> (Ьа - 4яс > 0)}.
50. Ла,ь,с{1 Лх(ах* + Ьх + с>0)]^
52. Ля{[«
68

53. M[(*:>i)v(*< 2)] <-»(*=*)].
54. Ла
55. К
56.
57.
58. Ль {[ЛаУж(ж2 + ах + Ъ =
59.
60.
3.13, Один из приведенных выше вопросов следовало
бы сопроводить предостережением.
Является ли истинным высказывание
«Если из ж2 -+- ах + Ь = 0 следует х ==. 1 или ж = 2,
то a = — Зи Ь = 2 (где ж, а, Ь принимают значения из
множества действительных чисел)»?
Нет, не является!
Дело в том, что, например, «ж2 + 1 =0» также импли-
имплицирует «ж = 1 или ж= 2» (для любых ж), так как ж2 + 1 =
= 0 ложно (для любого ж), а мы знаем, что когда р ложно.
р —>- q всегда истинно. Отсюда высказывание
Лж{(ж2 + ах + Ъ = 0) -* [(ж = 1) V (* = 2I} (*)
является истинным, скажем, и при а =0, Ъ =1. Следо-
Следовательно, мы не можем вывести из (*) того, что (а =
= — 3)Д (Ь = 2), как это утверждается в п. 3.12 E5).
Вместо выражения ж2 + .1 =0 мы могли бы взять (в ка-
качестве еще одного контрпримера) любое другое квадрат-
квадратное уравнение, не имеющее (действительных) корней. Но
подошли бы и выражения ж2 — 2ж + 1 =0 или ж2 — 4ж+
+4 = 0, так как
- 2ж + 1 = 0) -> (ж = 1)],
откуда ясно, что
Ах [(ж2 - 2ж + 1 = 0) -> (ж = 1 V * = 2I
(и аналогично с другим примером). Мы можем достовер-
достоверно утверждать, что
Ла,ь(Л.{(*« + аж + Ь = 0) -> [(ж - 1) V (* = 2)]) ->
= 2)] VI V«.B [(
69

или
Ло,ь (V*. „ [(х ф у) Д (я2 + ах + Ъ = у2 + ay + b = 0)]
~* (Л* {(я2 + ах + Ъ = 0) -> [(ж = 1) -> (* = 2)]}) -
Для тех, кто никак не склонен согласиться, что для
всех х
(«• + 1 = 0) -»- [(я = 1) V (* = 2I ¦
истинно, приведем следующее рассуждение.
Пусть х2 + 1 =0. Тогда
0 < я2 = - 1 < 0.
Следовательно, 0 = х" = — 1=0. Отсюда а: = 0, а
так как 0 = — 1, то и 0 = 1, а потому х = 1, откуда и
следует (ж = 1) \/ (х = 2).
3.14. Множество всех... Те предметы ж, для которых
высказывание
х есть человек
истинно, составляют некоторое множество, а именно, мно-
множество людей. Те х, для которых истинно высказывание
х* — Зх + 2 = 0,
образуют множество, состоящее из чисел 1 и 2.
i^j Пусть F(x) есть некоторое высказывание, зависящее
от х. Тогда те х, для которых F(x) истинно, образуют
некоторое множество, которое мы будем обозначать через
№(*)•
Например,
\х (х есть человек) — это множество всех людей,
U(**-3x + 2 =0) =A, 2).
Вообще,
Предмет z принадлежит |ж F(x) тогда и только тогда,
когда высказывание F(z) истинно. Пусть х принимает зна-
значения из некоторого «универсального множества» Т (на-
(например, из множества всех людей или множества всех
действительных чисел).
Если F(x) тождественно истинно, то \SF (х) равно Т.
7Р

Если Р(х) никогда не бывает истинным, то fx F(x)
есть пустое множество. к..
Множества |х F(x) и |я j F(x) являются дополнения-
дополнениями друг к другу.
Докажем теперь, что
[AJF(x) -+ G(x))\ <-> [(t, F(x)) с (fx G(x))l
Доказательство. Допустим, что
Ax(F(x)-^G(x)) A)
истинно.
Пусть
а €= (tx ВД- B)
Мы должны показать, что тогда а е= (fxG(a;)). Из A)
следует, в частности, что
F(a) -+ G(a)',
из B) в силу определения оператора \ следует, что F (а).
Следовательно (по modus ponens), G(a). Отсюда (по опре-
определению оператора f)
а е (\xG(x)).
Мы доказали одну из импликаций, составляющих дока-
доказываемую эквиваленцию.
Вторую импликацию читателю предлагается доказать
самостоятельно.
Докажите также следующие утверждения:
ЫП*) Л <*(*)) =(Т**Х*)) П (fxGW),
!.№)\/ад) =(t*^(*)) о (ug(x)).
В п. 2.10 мы обращали внимание на сходство законов
A9) — B4) для у и П, с одной стороны, и законов для \/
и Д — с другой. Как видно из двух последних формул, это
не случайное сходство. Эта аналогия распространяется
и на операцию "~1 и операцию * (взятия дополнения) со-
согласно п. 2.10 B5)—B6). (Укажите, где мы только что стал-
сталкивалась с этой аналогией.)
3.15. Задачи. Используя обозначения, введенные в
п. 3.12, дайте символические обозначения для следующих
множеств:
1. Множество жителей Амстердама.
2. Множество жителей Амстердама, состоящих в бракв.
71

3. Множество детей человека у.
4. Множество пар, состоящих в браке.
5. Множество всех моментов времени, в которые я ви-
вижу предметы, но не беру их.
6. Множество всех предметов, которые я беру, пред-
предварительно их не видя.
7. Проверьте, совпадают ли множества |<ж у>хКу,
yy, \y\*y
Проверьте, истинны ли (в области действительных чи-
чисел) следующие высказывания:
8. 11<а,ь,с>Ух(ах* + Ъх + с = 0)] =
>0)] Л !<О)Ь,с> ((а = 6= Q) -> (с = 0)]}.
9. Us8+ 1 =0):=|*(*2 + 2:=0).
»- (у= 0)) = t«vb (а*= 1).
И. |*[(ж - 1) (х - 2) (z - 3)(х - 4) > 0] =
= {ft«(*<l)J U ftiB<*<3)] U [t*(*>4)]>.
12- A,,b,etd ({f* [(^2 + ах + 6)(х2 + еж + d) = 0]} =
= Ш*2 + ее + 6 = 0)] U tfx(a:2 + сх + d = 0)]}).
13.. WaK № + ах + 6 > 0) = |ьуо (а2 < 6).
Пусть А — множество.
14. Что такое \х(Х сг Л)?
Пусть В — множество, отличное от А. Проверьте, яв-
являются ли истинными следующие высказывания.
15. tx(X а А) П U (X с В) = U (X с А П 5).
16. U(X с il) U Ы* сЛ)= fx(X c4U^).
17. U(XczA
Пусть малые буквы пробегают множество натураль-
натуральных чисел, а х Div у обозначает высказывание <sx являет-
является делителем у», т.е.
К,у[х Div у *-> Vz(xz = г/)].
18. Что такое f^a: Div г/?
19. Что такое f^a; Div г/?
20. Что такое f^a; Div г/ П Тж« Div z?
21. Что такое \гх Div z (] |гг/ Div z?
72

При ответах на последние три вопроса используйте
термины «кратное», «общий делитель (множитель)», «об-
«общее кратное».
22. Что такое f^Div а [\\яа Div ж?
23. Что такое ^ ((х Div а) Д Лу{(у Div x)
[fo l)
fo )V (У )»
В п. 1.22 мы разбивали некоторое множество ?2 на
классы эквивалентности. Пусть на множестве Q задано
отношение эквивалентности; элементы множества ?2 обо-
обозначим малыми буквами; х — у будет означать «а; экви-
эквивалентно г/».
24. Что означает |ж (х — у )?
25. Истинно ли высказывание
а»„ ([г е t« (* ~ г/I -> It* (*-*/) = t* (* - г)])?
26. Докажите, что
tx{VB [А =Ъ(х~у)]}
есть множество всех классов эквивалентности (в Q).
27. Проверьте справедливость равенства (обратитесь
в случае надобности к п. 1.25):
>А, В{ = \УХ,У [(х Е4)Л(У?5)ЛB=A, у»].
3.16. В первой главе мы ввели понятия объединения
и пересечения лишь для конечного числа множеств. Но
нам уже приходилось встречаться с различными примера-
примерами «множеств множеств».
Пусть N — множество натуральных чисел, a R —
множество действительных чисел.
Пусть, далее, Мп есть множество чисел <^— , т. е.
Пересечение всех Мп есть тогда множество
t*U* €= Д)Л(*<0)].
Это пересечение мы обозначим через
Пусть Ра — множество действительных чисел < а.
Рассмотрим все множества Ра такие, что а ? R \Р0.
73

Их пересечением служит Ро:
Вообще, пусть имеется система множеств Мп; различаю-
различающихся с помощью индекса га (принимающего значения из
некоторого множества N). Тогда пересечение этих мно-
множеств будет обозначаться через
т. е.
п *-* А„ [(га е N) -> (с е AfJ].
Обратите внимание на связь между Ли А. Мы можем
аналогично определить объединение множеств Мп (га EzN) '¦
с eur,ew мп«. vn [(и <= #) -> (с е ад.
Мы видим, что между U и V тоже существует связь.
Если по вопросу о том, какому множеству принадле-
принадлежит индекс га, не возникает неопределенности, то введен-
введенные выше обозначения упрощаются: UnMn и П„Мп.
Остановимся теперь на связи введенных здесь понятий
и содержания п. 3.14.
Пусть F(x, у) — высказывание, зависящее только от х
и у (здесь снова х пробегает некоторое универсальное мно-
множество Т, а у — некоторое множество N, не связанное
непосредственно с Т). Для каждого п Е: N мы рассмотрим
множество Мп всех таких х, для которых F(x, га) истинно,
и возьмем их пересечение:
») = UKF{x, га).
Рассмотрите случай, когда N состоит только из "двух эле-
элементов, и сравните его с предпоследней формулой из п.3.14.
Аналогично,
\in\xF(x, n) =WnF(x, л).
Сравните это соотношение с последней формулой из п.3.14.
3.17. Задачи. Будем употреблять обозначения, вве-
введенные в п. 3.15.
1. Что такое t\Y\x (X a Y с А)?
2. Что такое Urfx (X с Y с А)?
Пусть малые буквы: обозначают натуральные числа.
3. Что такое f^f» xDivy? '
74

4. Что такое 0„|х a;Div г/?
5. Что такое Un f, Vx Л„ ((z = хп)Д
AfoDi[(
Afo(y )VO/
6. Что такое По |XVV (х = ау + 1)?
3.18. Определенный артикль *). Мы можем говорить
о некоем вполне определенном Решенииа) уравнения За; =
= 2, но нельзя говорить о Решении уравнения Ох = 38)
или уравнения а;а — Ъх + 6 = О4). Мы говорим о (един-
(единственном) вполне определенном х со свойством Е> если
имеется одно и только одно х, которое обладает этим свой-
свойством Е. Если F есть такое свойство, что F(x) может
оказаться истинным высказыванием, то говорить о (един-
(единственном) вполне определенном х можно при выполнении
следующего условия:
VxF(x) Д A,,, [(F(x) Д F(y)) -+(х= у)].
(Заметьте, что для формулировки этого условия нам необ-
необходимо иметь в своем распоряжении отношение = .)
Единственное вполне определенное х, обладающее свой-
свойством F(x), обозначается через
Пусть предметная область, которую пробегают пере-
переменные, состоит из действительных чисел. Как тогда, на-
например, обозначить самое большое х, для которого
х2 — х ^ 5? Ответ:
|х {(Xs - х < 5) Л К Ю/а - У < 5) -»¦ (У < х)]}.
Как обозначить наименьшее множество, элементами
которого являются числа 288 и 120, а также и разность
а—Ъ любых двух чисел а и Ъ, являющихся элементами
х) См. следующее примечание.— Прим.. ред.
а) В английском языке (как и в большинстве других европей-
европейских языков) существительное, выражающее имя вполне опреде-
определенного (единственного) предмета (т. е. в некотором обобщен-
обобщенном смысле «имя собственное»), снабжается определенным ар-
артиклем the, грамматической функции которого и посвящен
данный пункт. В переводе существительные, снабженные в ори-
оригинале определенным артиклем, пишутся (если это обстоятельство
надо как-то подчеркнуть) с прописной буквы («Решение» — пере-
перевод «the solution», в отличие от «решение» — «a solution»), или снаб-
снабжаются эпитетом «вполне определенный».— Прим. ред.
3) Вообще не имеющего решений.— Прим. перев.
4) Имеющего два решения: г= 2 и х= 3.— Прим. перев.
75

этого множества? — Определим высказывание F(X) о
множествах X следующим образом:
F(X) <-> {A20 е X) Л B88 е!)Л Лв,ь([(а ЕЕ X) Л
А F ЕЕ Z)] -> (а - 6 ЕЕ X))}.
Существуют ли множества X, удовлетворяющие усло-
условию F(X)? Конечно; ему удовлетворяет, например, мно-
множество всех чисел. Если X есть такое множество, то
288 ЕЕ X и 120 е X. Следовательно, 168 = 288—120 ЕЕХ,
откуда 168-120 = 48 ЕЕ X, так что 120 - 48 = 72 ее X,
значит, 72-48 = 24 ЕЕ X. Кроме того, 0 = 24 - 24 ЕЕ X,
— 24 =0 — 24 ЕЕ X. Все произведения вида 24та (где
т есть целое число), т. е. кратные числа 24, являются
элементами множества X (объясните, почему). Пусть
А есть множество всех этих произведений. Тогда верно
F(A) (почему?). Таким образом, мы доказали
AX[F(X)-+(X => А)].
Следовательно, F(A) истинно, и всякое X, для которого
F(X) истинно, включает множество А. Поэтому А яв-
является наименьшим множеством X, обладающим свойст-
свойством F(X).
Мы можем поставить следующий общий вопрос. Пусть
М — множество множеств X, определенных высказыва-
высказыванием F(X) о множествах X, т. е.
ЛХ1(Х е М)++F(X)];
имеется ли в Ж наименьшее множество А, т. е. такое А,
что высказывание
(ЛеЖ)ДЛх[Aе^-^Aэ А)]
является истинным? Надо сказать, что в общем случае
такого множества может и не существовать. (Пример —
множество М, являющееся множеством всех непустых
подмножеств некоторого множества (а, Ь), т. е. М состоит
из множеств (а), (Ь) и (а, Ъ).)
Согласно требованию, предъявляемому к А, оно долж-
должно содержаться в каждом множестве X ее М, а следова-
следовательно, и
А а Пх<=м X.
Но так как А также должно содержаться среди X Е5 М,
76

то истинным должно быть и высказывание
откуда
А =
Из этого немедленно следует, как мы уже знаем, что су-
существует не более одного такого множества.
(Пх<=мХ) ЕЕ М, вообще говоря, не обязано быть ис-
истинным (см. пример). Но если оно все-таки истинно, то
есть наименьшее множество, принадлежащее множеству
М, потому что
)с У для всякого
Доказанный критерий позволяет показать существо-
существование наименьшего множества, элементами которого явля-
являются числа 288 и 120, а также и разность а — Ъ любых
двух чисел а и Ъ, являющихся элементами этого же мно-
множества. Это очевидно из нижеследующего. Пусть М —
множество всех таких множеств. Для каждого X Ei M
справедливо, что 120 6Е X; следовательно, 120 ЕЕПхемХ.
То же самое можно сказать и о числе 288. Кроме того,
если а €Е ПхемХ и&? ПхемХ, тоа?Х для всех ХёМи
Ъ ?Е X для всех X €Е М, а потому и a — Ь ЕЕ X для всех
X ЕЕ М и, значит, а — b^ ПХеМХ. Таким образом, Пх^мХ
удовлетворяет всем требованиям, предъявляемым к мно-
множествам, принадлежащим к М. Следовательно, ПхемХ
есть наименьшее множество, являющееся элементом мно-
множества М.
(В последнем абзаце неоднократно повторялось слово
«все». Попробуйте переписать этот абзац, пользуясь
логическими символами.)
3.19. Предикаты, отношения. В этой главе мы часто
пользовались схемами вроде
... смертен,
... живет в Амстердаме,
... является ребенком...
... эквивалентно...
В каждом из этих примеров предполагается, что вместо
точек будет • что-то подставляться (элементы определен-
определенного множества, скажем, имена людей, и т. п.). При
77

этом мы получаем некоторые высказывания, которые мо-
могут оказаться ложными или истинными.
Выражения такого рода с одним свободным местом на-
называют свойствами, или предикатами; такие же выраже-
выражения с двумя или более свободными местами называют
отношениями. То, что мы подставляем на эти свободные
места, называют субъектами.
Отношения, впрочем, также можно считать предиката-
предикатами: предикатами пар субъектов, троек субъектов и т. д.
«... живет в Амстердаме» есть свойство индивидуальных
людей, а «... является ребенком...» есть свойство пары
индивидуумов (точнее, упорядоченной пары), «х является
ребенком у» есть высказывание, которое может быть для
некоторых пар х, у истинным, а для других пар — лож-
ложным (если оно истинно для пары (х, г/>, то оно, очевидно,
ложно для пары (у, ж>).
Предикат «... живет в Амстердаме» мне известен пол-
полностью, если я знаю множество всех тех х, которые, будучи
поставленными вместо точек, обращают этот предикат в
истинное высказывание; обратно, это множество полно-
полностью определяет соответствующий предикат.
Аналогично, отношение «... является ребенком...»
полностью определяется множеством всех тех пар <аг, г/>,
подстановка которых на свободные места этого отношения
обращает его в истинное высказывание.
Пусть /'(..., ...) — некоторое отношение с двумя сво-
свободными местами. Пусть на первое его пустое место мож-
можно подставлять элементы некоторого множества М, а на
второе пустое место — элементы некоторого множества
N. Скажем, в предикат Z(..., ...) из п. 3.12 на первое место
можно подставлять предметы, а на второе место — момен-
моменты времени. Рассмотрим множество
Р = >M,N(,
состоящее из всех тех пар (х, г/>, для которых х EzM,
у ? N (см. п. 1.25).
Мы можем тогда понимать отношение F(..., ....) как
предикат (?(...), на единственное свободное место которого
можно подставлять элементы множества Р и для которого
верно следующее:
Лх,уЩ<х, у)) <-> F(x, у)].
В п. 1.24 мы ввели определение: «Множество упорядо-
упорядочено посредством отношения <;, если...». Мы можем те-
78

перь переформулировать это определение, не прибегая
к термину «отношение». Заменим для этого отношение
«... меньше, чем...» таким множеством Y пар, что подста-
подстановка элементов любой из них (в нужном порядке) на
свободные места этого отношения обращает его в истин-
истинное высказывание. Новое определение будет тогда зву-
звучать так:
Множество Z упорядочено посредством множества
У с: >Z, Z< , если
Ла,ъ{[(а ZEZ) АФ SEZ) МаЧ=Ь)\~*[«а, Ь> е Г) *-*
^ «Ь, а) $ У)]} /\ Ла, ь, с {!(« Е Z) Д (Ь G Z) Д
3.20. Определение отображения, данное выше (см.
п. 1.12), также можно переформулировать. Отображение
/ множества А в множество В нам полностью известно,
если мы знаем все элементы {а, Ь> множества )А, В{,
обладающие тем свойством, что элемент Ъ есть /-образ
элемента а. Более того, мы просто можем рассматривать /
как множество этих пар <а, by, так что / с; у А, В{. Те-
Теперь встает вопрос, какие части множества У А, В{
являются отображениями множества А в множество В!
Обозначим множество отображений множества А в мно-
множество В через
Тогда
>(Vb«a, 6>е=/)]Л
Л А«.ь.е{[<в,ь>е/)Л«в.с>е/)]-*(& = с)}].
/-образ элемента а получит тогда следующее выраже-
выражение:
fa =|Ь «а, 6>е/).
3.21. Пользуясь введенными здесь обозначениями,
запишем в символической форме доказательство теоремы
из п. 1.19.
A) Q =U (ХсЛ).
B) Ао с А.
C) /е=(Л^П).
79

D)
E).
F)
G)
(8)
(9)
A0)
A1)
A2)
A3)
A4)
A5)
A6)
A7)
Л*{(-'
U = f
М(*
(и е
/(И) :
(и е
(и е
(«е
[(«6
(we
(»<?
(м е
* К*
ее/)
^о) /
'о-
= г/.
?0<-
Ао)-
= А0)
U) <-
U) <-
U) <-
ел0)
<->[(«
в) А (Л
\ (/(")
>[(м е
-> [(м е
А (и 5
¦* (М §Ё
¦ ~] (и
> П (м
с((же^0) А(/(ж):
А (* ф. /(«))!•
еЛ0) А (ж ^/(ж)
» = и)\.
= г/).
Uo) А (« ^/("))]•
:"^0) Д (М ^ U)].
е^0) А(и^гтI
5 ?01 <-> (и ^ ?0-
?0-
е?0-
е?О.
Разъяснение:
A) Определение множества ?2 как множества подмно-
подмножеств.
B) Допущение множества Ао и
C) функции /, которая отображает множество Ао в
множество Q и даже
D) на множество ?2.
E) Определение множества U.
F) То же, но иными словами.
G) U имеет прообраз при отображении /, обозначаемый
через
(8) и.
(9)—A0) Следует из (8).
A1) Получается подстановкой и вместо х в F).
A2) Получается из (И) посредством замены f(u) на U
согласно A0).
A3) Высказывание
тождественно истинно.

A4) Получается из A3) и (9) по modus ponens.
A5) Получается из A4) и A2) с использованием тож-
тождественной истинности высказывания
1(Р ++ Я) А (Я ++ гI <-> (Р ++ г).
A6) Определение символа Ф.
A7) Противоречие : р <-* | р тождественно ложно.
Предлагаем читателю в качестве упражнения изложить
символически теорию эквивалентности (см. п. 1.22).
3.22. Функции. В п. 1.11 мы ввели ряд терминов,
связанных с понятиями отображения и функции.
Такие обозначения, как
A) функция f(x),
B) функция у = f(x),
C) функция х2 — За; + 2,
D) функция у = х2 — За; + 2,
E) функция ах2 + Ъх + с,
вызывают ряд возражений, из-за которых мы будем избе-
избегать ими пользоваться. Поясним эти возражения на не-
нескольких примерах.
A) В предложении «Функция f(x) принимает значение
f(a) для х = a» f(x), очевидно, должно означать функцию,
a f(a) — число. Почему? Ведь буква а ничем не лучше и
не хуже буквы х.
B) Если у = f(x) есть функция, то выражение
у — f(x) = 0 в согласии с обычными правилами алгебры
также должно быть функцией. Пусть теперь, например,
f(x) — 2а;. Тогда г/ — 2а; =0 тоже следует считать функ-
функцией. Но какой именно функцией? Из чего, собственно,
следует, что х надо считать «независимой», а у — «зави-
«зависимой» переменной?
C) Обозначение, приведенное выше под этим номером,
по меньшей мере спорно. Оно не сможет нас удовлетво-
удовлетворить. Возьмем, например, вместо упоминаемого там много-
многочлена второй степени просто х или 7. Нам придется тогда
говорить о функции х и функции 7, что уже само по себе
не особенно приятно.
Кроме того, приняв терминологию C), мы неизбежно
придем к терминологии E), неудовлетворительной и по
другим причинам.
D) Это обозначение подвержено тем же возражениям,
что и обозначение ('$).

E) Предполагается, что это есть функция от х. Но
почему? Почему не функция от а? от Ь? от с? или от всех
их вместе?
В физике функцию, полученную из «функции /(#)>>
подстановкой вместо х «функции ф(ф, очень часто назы-
называют «функцией /(?)>>. Это ведет к многочисленным недо-
недоразумениям.
Корректная терминология может быть проиллюстри-
проиллюстрирована на следующих примерах:
Уравнение
f(x) = За;2 — 6а; — 9 (для всех а;)
определяет функцию (отображение) /.
Уравнение
f(x) = За;2 — 6а; — 9 (для всех х, О <а; <; 1)
определяет функцию /, которая отображает множество
таких х, что 0 < х < 1, на множество таких х, что
— 12 <х < — 9.
Уравнение
ж» . ж*
sin* =х-ж + --..,
определяет функцию sin (функцию «синус»).
За;2 — 6а; — 9 как функция от х является непрерывной.
Если под / мы понимаем выражение За;? — 6а; — 9 как
функцию от х, то f(x) = За;2 — 6а; — 9.
яа;2 -\- Ьх -\- с как функция от х является квадратичной
функцией от х для всех a =/= 0.
Точная терминология для функций (отображений)
особенно необходима, если рассматриваются множества
функций. Как мы записали бы, что функция является
элементом множества А? Если мы обозначим функцию
через f(x), то эту принадлежность функции множеству
можно было бы записать как-то вроде f(x) ЕЕ А. Но вы-
выражение f(x) EL А имеет совсем другой смысл, а именно
тот, что значение, которое / соотносит х, является элемен-
элементом А. В то же время обозначение / ЕЕ А не вызывает
никаких возражений. Близкая ситуация возникает тогда,
когда мы рассматриваем отображение какого-нибудь мно-
множества функций в другое (или в то же самое) множество.
Например, пусть K(s, t) есть непрерывная функция па-
пары (s, О @ < s < 1, 0 < t < {).
83

Уравнение
определяет отображение А такое, что
А отображает множество непрерывных функций (опре-
(определенных на отрезке [0, 1]) в себя. А может быть также
определено посредством соотношения
(для всех s, 0 <^ s <^ 1, и функции /, определенной и не-
непрерывной на отрезке [0, 1]). Но говорить, что
Af(t) = q(s),
не имеет никакого смысла.
Переменные s и t вообще не должны быть связанными
с /, g и А. Отображение А имеет своим аргументом / как
таковое, и в результате его применения получается g —
образ при этом отображении. (Надо сказать, что бессмыс-
бессмысленные обозначения только что упомянутого вида все еще
часто встречаются в литературе.)
Лишь для немногих функций, например, для sin,
cos, log, — употребляются постоянные обозначения. Для
За;2 — 6а; — 9 как функции от х никакого специально
«закрепленного» за ней функционального символа нет.
Мы можем, конечно, ввести для этой функции «собст-
«собственное имя» /, положив, по определению,
ЛхЩх) = За? — 6а; — 9].
Однако язык неимоверно усложнится, если мы для каждо-
каждого конкретного предмета будем придумывать специальное
имя. Язык математики замечателен тем, что для большин-
большинства объектов в нем имеются алгоритмические имена,
т. е. имена, образованные согласно некоторым вполне
определенным правилам. (Вспомните натуральные числа
с их именами, образованными с помощью подобных
83

правил J).)
Зж2 — 6^ — 9 как функция от х
есть алгоритмическое имя для рассматриваемой функции,
однако это имя слишком громоздко. Мы его сделаем не-
немного короче и будем писать
%х (Зг2 - бх - 9).
Таким образом, эта запись означает: За:2 — 6а;.— 9 как
функция от а;.
Если мы хотим рассматривать такую функцию не для
всех значений х, а лишь для значений из некоторого мно-
множества А, то мы будем писать это .4 позади выражения,
определяющего значение функции, и отделять его верти-
вертикальной чертой. Например,
К (Зх* - 6х - 91 |, (- 3 <аг < 5))
обозначает функцию, которая определена только в интер-
интервале (—3, 5).
Выражение %х (ах2 + Ъх + с) для каждого значения
а, Ъ, с обозначает различные функции.
Напротив, выражение \х, а, ь, с> (ах2 + Ъх + с) есть
функция четверки переменных х, а, Ъ, с. Конечно,
(a) =/(a).
Если х пробегает некоторое множество А, а у — мно-
множество В, т. е. пара (х, у) принадлежит множеству пар
)A,B<, то
(я, У),
(x, У),
вообще говоря, являются различными объектами. Дейст-
Действительно, для а?4
(KKf(x> У)) (а) = hf(a' У)'
а) Хорошо известные примеры «алгоритмических имен» — но-
номера домов (вместо принятых в прошлом веке «дом Михеева» или
«что напротив Сенного рынка») или отражающие химический со-
состав названия органических соединений (скажем, «гексаметилен-
тетрамин» вместо «специально придуманного» слова «уротропин»).—
Прим. ред.
84

в то время как
f( ))() и
в общем случае просто не определены.
В самом деле, ведь в этих функциях вместо перемен-
переменных можно подставлять только элементы множеств В и
соответственно }А, В{. Аналогично для bEzB:
(ьЛ/(*. у)) (*) = М*. ъ),
в то время как обозначения
(W(*. у)) (Ь) и (W/(*. у)) Ф),
вообще говоря, не имеют смысла.
3.23. Точно так же, как и выражение
х* _ ба; — 9,
выражение
х есть человек
мы можем понимать как функцию от х. В первом случае
множество образов (или, как говорят, область значений)
состоит из чисел, а во втором случае — из высказываний.
Вторая функция может быть обозначена посредством
... есть человек.
Если мы сделаем подстановку вместо точек, то получим
высказывание. Таким образом, эта функция отображает
множество предметов в множество высказываний. Такие
функции называют пропозициональными (или высказыва-
телъными) функциями. Пользуясь введенным выше сокра-
сокращением, мы можем обозначить эту функцию как
%х(х есть человек).
Отношение
... меньше, чем...
также можно обозначить через
3.24. Задачи. Дайте символические выражения для
следующих функций (предикатов):
1. Квадрат...
2. Корень квадратный...
3. Множество подмножеств...
4. Мать...
85

5. То, что я вижу (как функция времени).
6. Отношение «состоять в браке».
7. Отношение дяди к племяннику.
8. Что означает запись
[V. ь. о U (а** + Ьх + с = 0)] «1, - 3, 2»?
9. Объясните разницу между %х (х ^> 0) и ^ (ж ,> 0).
10. Что означает запись
И. Что означает запись
12. Напишите символическое выражение для функции,
которая принимает значение 0 для всех моментов времени
t, в которые я ничего не вижу, и значение 1 для всех мо-
моментов t, в которые я что-то вижу.
3.25. Способы связывания. В отличие от старой логи-
логики, изучавшейся со времен Аристотеля, современную ло-
логику часто называют «логистикой». Ее основателями при-
принято считать Дж. Пеано A858—1932), А. Н. Уайтхеда
A861—1947) и Бертрана Рассела (род. 1872) *). Главное
отличие языка логистики от обычного разговорного языка
состоит в употреблении переменных. В предложениях
Там идет собака
и
Собака есть млекопитающее
переменной является «собака».
В первом предложении эта переменная связана экзи-
экзистенциально (существует собака, которая где-то
«там» идет). Во втором предложении переменная связана
универсально (каждая собака есть млекопитающее).
Но эти способы связывания переменной никоим образом
не усматриваются из самой формы этих предложений —
они выявляются из их содержания.
В разговорном языке переменные крайне специализи-
специализированы. Переменную «собака» можно использовать толь-
*) Во главе этого ряда (при всей условности такого рода
списков), конечно, следует поставить Г. Фреге A848—1920).—
Прим. ред.
86

ко для собак, переменную «кошка» — только для кошек,
переменную «что-то» — только для вещей, переменную
«кто-то» — только для людей (иногда, правда, и для жи-
животных), переменная «где-то» — только для мест и т. д.
По отношению ко всем этим переменным часто не делается
формального различия между экзистенциальным связы-
связыванием и универсальным связыванием. Это видно из сле-
следующих примеров:
Я что-то съел
и
Что-то лучше, чем ничего.
В обычной речи часто возникают трудности, когда требу-
требуется употреблять большое число переменных одного и то-
того же рода. Поэтому мы и говорим «собака», «другая со-
собака», «эта собака». Уже в древности геометры ощущали
необходимость в большом числе переменных для обозна-
обозначения точек. Поскольку геометрии учили устно, можно
было обходиться такими переменными, как «эта точка»
и «та точка»; для того же, чтобы обеспечить этой науке
большую точность в записи, переменные для точек обоз-
обозначали как «точка At>, «точка В», «точка С» и т. д. От-
Отсюда и пошла наша практика обозначения переменных
буквами. В логистическом языке переменные, как прави-
правило, свободно взаимозаменяемы. Зато способ связывания
переменной всегда точно определен. Выше мы уже гово-
говорили о следующих видах связывания:
связывание путем подстановки (см. п. 3.3),
экзистенциальное связывание (V),
универсальное связывание (Л),
связывание определенным артиклем (],),
образование множества (|),
образование функции (к).
Назначение всех этих операций — устранение неопре-
неопределенности при употреблении переменных.
В обычной речи существует еще одна очень важная
форма связывания, а именно,
демонстративное (указательное) связывание.
«Здесь» есть переменная для частей пространства.
В результате ее произнесения она связывается тем местом,
где она произносится. «Теперь» есть временная перемен-
переменная. В результате ее произнесения она связывается
87

моментом времени, в который она произносится. «Я»- свя-
связывается самой личностью говорящего. То же относится
к словам «там», «вчера», «вы», «это», «то» и т. п. Эти
переменные связываются «указательно» *).
Последний вид связывания, который мы упомянем,
это
вопросительное связывание,
обозначаемое посредством знака вопроса.
3.26. «Найдите х, удовлетворяющее уравнению Зх =
= 4» записывается символически как
?* (Зх = 4).
В выражении ?х (х2 — Зх + 2 = 0) мы спрашиваем о
всех решениях этого уравнения.
3.27. Задачи. 1. Запишите в символической форме:
«для какого Ъ существуют значения а такие, что — х2 -f-
-f- ax + а + Ъ имеет отрицательные значения для всех х?».
Пусть F(x, у, t, p) обозначает: «х произносит высказы-
высказывание р, обращенное к у в момент Ц. Дайте символиче-
символическую запись следующих вопросов.
2. Когда х говорит нечто самому себе?
3. Какое высказывание, будучи кому-то сказанным,
никогда не будет им никому больше повторено?
4. Насколько позже то, что некто сказал, возврати-
возвратилось к нему?
J) Отсюда и термин «указательное местоимение».»- Прим.
перев.

Глава 4
Формальная логика
4.1. Мы познакомились в предыдущих главах с эф-
эффективным логическим символизмом. Мы описали неко-
некоторый язык— логистический язык. Иногда нам приходи-
приходилось и работать в этом языке — получать символические
заключения и строить цепи заключений и доказательств.
Но мы делали это лишь от случая к случаю. Конечно,
всегда полезно узнать, что какое-то предложение можно
вывести из некоторого другого предложения. Но если мы
хотим систематизировать такого рода знания, то нам надо
исходить из некоторой системы утверждений и вывести
затем, прямо или косвенным путем, все остальные утвер-
утверждения из этих исходных.
Такие исходные утверждения называют аксиомами.
^Аксиоматический метод состоит в такой организации
какого-нибудь раздела математики (или какой-либо
другой науки), когда из всех его истинных утверждений
выбрано некоторое подмножество, из которого можно
вывести все остальные истинные утверждения данного раз-
раздела науки. Классический пример аксиоматического мето-
метода представляет аксиоматическое построение геометрии.
Изучая окружающее нас пространство, мы узнаем некото-
некоторые свойства объектов, которые мы называем точками,
прямыми, плоскостями, кругами и т. д. Несколько таких
установленных утверждений об этих объектах и выбирает-
выбирается в качестве аксиом. Если мы выбрали достаточное коли-
количество таких верных утверждений, то из них удается
вывести все нужные геометрические утверждения, не об-
обращаясь вновь к изучению реального физического про-
пространства и не вспоминая относящихся к нему значений
таких слов, как «точка», «прямая» и т. п.

4.2. Пример. Йусть Р есть некоторое множество
объектов, называемых точками. Подмножества множест-
множества Р некоторого специального вида именуются прямыми.
Множество всех прямых обозначим через R. Некоторые
подмножества множества Р называются плоскостями. Мно-
Множество всех плоскостей обозначим через V. Возьмем в ка-
качестве исходных утверждений следующие:
2.
р>„,г,
Р)A
5.
6. ptt{
A (P S ^ П го)] -+ Vr [(r ?ER) A (r с » Г) ю)]} •
Из этих аксиом удается вывести значительную часть
геометрии. И для этого совершенно незачем знать, «что яз
себя представляют» точки, прямые, плоскости.
Выведите в качестве упражнения следующие утверж-
утверждения: через прямую и точку, расположенную вне этой
прямой, проходит одна и только одна плоскость; две раз-
различные пло.скости либо вообще не имеют общих точек,
либо имеют общую прямую.
Совокупность трех множеств Р, R, V, для которых вы-
выполняются условия
и аксиомы 1—6, мы будем называть геометрией инцидент-
инцидентности (принадлежности).
4.3. Нам уже приходилось встречать аксиоматические
системы такого рода в предыдущих главах. Например, из'
90

аксиом для понятия эквивалентности, т. е. из
Л„(а ~- а)
\,ь,с {1Ф ~ а) А (с ~ а)] -* (с - Ь)},
можно вывести утверждения, относящиеся к этому поня-
понятию, которые обычно считаются истинными.
Точно так же из аксиом для отношения порядка
К,ь {(а Ч=Ь)^ {{a <b)\/(b
Ла,ь1(а <6)-»-~1 (Ь <а)],
К,ъ,с {К* < Ь) А (Ь < с) -* (а <с)]}
мы можем вывести все общие свойства этого понятия.
Если понадобится, мы можем затем добавить определе-
определения
>W(a >&)¦*(&< а)],
Ло,ь {а < Ъ) ~ [(а <6) V (а = Ъ)]}
и т. п.
Когда мы выбираем какую-нибудь систему аксиом, нам
следует позаботиться, чтобы из этих аксиом не следовало
слишком много (в частности, чтобы из них не следовали
ложные утверждения) или слишком мало.
4.4. Наша ближайшая цель — формулировка системы
аксиом для исчисления высказываний. Здесь нам придется
пойти дальше, чем в предыдущих примерах. Мы не только
точно перечислим исходные высказывания (аксиомы),
но и точно укажем допустимые способы выведения из
этих аксиом новых утверждений, которые в результате
также могут считаться истинными. До сих пор молчали-
молчаливо подразумевалось, что новые утверждения можно вы-
выводить с помощью известных методов логики. Но что это
за «известные методы логики» — точно не оговаривалось.
Теперь же мы точно укажем, какие именно операции мож-
но.прямо или косвенно, применить к аксиомам, чтобы по-
получить из них утверждения, которые можно и должно
рассматривать как истинные, т. е. как теоремы. Мы точно
укажем также, как должны выглядеть правильно пост-
построенные формулы. (Скажем, знакосочетание « ->- р ->- »
не является правильно построенной формулой.)
91

Мы не будем связывать с формулами никакого значе-
значения (смысла); никакого значения мы не будем связывать и с
входящими в них буквами и стрелками. Формула — это
просто множество знаков определенного вида на бумаге.
Предполагается, что читатель умеет различать и отождест-
отождествлять эти знаки. Если две стрелки по каким-либо при-
причинам немного отличаются на вид, то их все равно сле-
следует отождествлять и считать одним и тем же. символом.
Все операции будут формализованы, так что выполнять
их могла бы и машина.
Впоследствии мы, впрочем, опять будем интерпрети-
интерпретировать эти написанные на бумаге знаки, причем теоремы
тогда должны будут истолковываться как тождественно
истинные высказывания.
В дальнейшем основную роль будут играть два сим-
символа:
Для стрелки ->¦ мы будем иметь в виду ее прежнее значе-
значение. Знак ® будет впоследствии интерпретирован как
кождественно ложное высказывание. Два этих символа
твляются «постоянными» — в противоположность симво-
яам р, q, г,..., которые служат «переменными», т. е. та-
лими, вместо которых можно подставлять что-то другое.
4.5. Аксиомы для высказываний. Пропозициональный
язык (или язык для высказываний, propositional language)
строится из
простых формул х) ((§), р, q, r, ...)
и
связок: ->¦ (стрелка), ( , ) (скобки).
Формулы:
(а) каждая простая формула есть формула,
(б) если А и В — формулы, то (А ->¦ В) также есть фор-
формула,
(в) все формулы выводимы из простых формул посред-
посредством повторного применения принципа (б).
Пояснение. Написанные здесь буквы А и В
не являются сами объектами пропозиционального языка,
который мы здесь рассматриваем. Их следует понимать
как сокращенные обозначения для формул этого языка,
имеющих более или менее сложное строение.
J) «Простых» в том смысле,' что из них строятся сложные
формулы.
92

Вместо А ->- (g) мы будем также писать ~~\ А. Связки
V и А нам здесь не нужны, так как их, оказывается, мож-
можно выразить через связки ->¦ и |.
Для удобства самые крайние скобки в формулах мы
будем опускать, а для большей наглядности будем поль-
пользоваться также фигурными и квадратными скобками г).
Аксиомы. Если А, В, С — формулы, то
1. С->(Л->С),
2. (А -> В) -> {[А -> (В -> С)] -> (Л -> С)},
3.
являются аксиомами.
Modus ponens есть операция, посредством которой из
двух формул
А
и
А ->В
получается формула 5.
Если Г есть множество формул, & D — формула, то
вывод D из V есть цепочка формул, последней форму-
формулой которой является D и такая, что каждый член этой це-
цепочки
(а) либо есть аксиома,
(б) либо есть член Г,
*) То есть, например, вторая из написанных ниже аксиом ста-
становится формулой пропозиционального языка (в смысле данного
выше определения) лишь после замены всех фигурных и квадрат-
квадратных скобок на круглые, добавления пары внешних скобок и под-
подстановки вместо входящих в получившееся в результате выраже-
выражение
((А _¦!»)- ((А - (В - О) -* (А - С)))
букв А, В и С произвольных формул этого языка, причем вместо
одной и той же буквы следует подставлять одну и ту же формулу,
но вместо различных букв необязательно подставлять различные
формулы. Можно, скажем, вместо каждой из букв А и В подста-
подставить одну и ту же переменную р, а вместо С — постоянную <g),
в результате чего мы придем к формуле
((Р ->Р)-^((Р -* (Р - ® )) -* (Р - ® ))),
лишь к которой, собственно (как и к любому другому результату
подобного рода подстановки, конечно), и применим в буквальном
смысле термин «аксиома». (Те же оговорки относятся и к употреб-
употреблению этого термина в дальнейшем изложении.) — Прим. ред.
93

(в) либо получается по modus ponens из некоторой пары
более ранних членов этой цепочки.
Говорят, что формула D выводима из Г, если существу-
существует вывод D из Г. В этом случае пишут
T\-D.
Г-теорема — это любая формула, выводимая из Г.
Y-теорией называется совокупность всех формул, вы-
выводимых из Г.
Если множество Г пусто, то говорят просто «выводима»,
или «доказуема», и соответственно «теорема», «теория».
Доказуемость D символически обозначается так:
\-D.
4.6. Теорема о дедукции. Если
г, л ья.
то
T\-A-+D.
Доказательство1). В условии теоремы гово-
говорится, что имеется некоторый вывод D из Г, А. Этот
вывод есть некоторая последовательность формул 2.
Заменим каждый член С этой цепочки 2 на А -> С. В ре-
результате мы получим новую цепочку 2', последним чле-
членом которой будет формула A ->.D, т. е, та самая форму-
формула, которая согласно утверждению теоремы должна быть
выводима из Г. Но 2' еще не есть вывод. Нам придется
вставить в 2' некоторые дополнительные звенья. Соглас-
Согласно определению понятия вывода из F, мы должны раз-
различать следующие случаи для звеньев цепочки 2 (см.
и. 4.5):
(а) С есть аксиома;
(б) С принадлежит цепочке Г, А;
(б') СеГ;
(б") С =А;
*) Здесь слово «доказательство» имеет значение, отличное от
того, что было введено в конце предыдущего пункта. Там оно озна-
означало некоторую формальную операцию в рамках пропозициональ-
пропозиционального языка, здесь же мы употребляем его в обычном содержатель-
содержательном смысле.
94

(в) С выведено из пары предыдущих звеньев цепочки
2 посредством modus ponens. r i
(а) Перед звеном А -*- С в цепочке 2' мы вставим ак-
аксиомы
С и С-*(А-*С)
(т. е. аксиому 1). А -> С выводится отсюда по modus
ponens.
(б') Перед А -> С в цепочке 2' вставим звенья
С, С-**(А-* С),
первое из которых принадлежит Г, а второе есть аксиома.
Отсюда по modus ponens получим А -> С.
(б") Подставляя А вместо С в аксиому 2, мы получим
аксиому
(А -> В) -> {[А -> (В -> А)] -> (А -
Подставляя 4 -> 4 вместо 5, мы получим из этой аксио-
аксиомы аксиому
(А -> (А -> 4)) -> {U -> (( А -> 4) -> 4)] -> D -> 4)}.
A)
Перед 4 -> 4 мы теперь вставим в цепочку 2' эту аксио-
аксиому, а кроме того, аксиому
А-+{А-+А), B)
полученную из аксиомы 1 подстановкой А вместо С, и
[А -> ((А -> А)-+ А)] -> (А -> 4), C)
получающуюся из A) и B) по modus ponens, и, наконец,
аксиому
А -> ((А -> 4) -> Л), D)
также получающуюся из аксиомы 1 подстановкой 4 вместо
Си4->4 вместо 4.
Из C) и D) по modus ponens получим А -> А.
(в) Пусть С получено по modus ponens из формул
В, E)
В-* С, F)
95

входящих в цепочку 2 перед С. В цепочке 2' соответст-
соответствующими формулами являются
А-»В, E')
А -> (В -> С), F')
которые, следовательно, входят в 2' перед рассматривае-
рассматриваемой нами формулой А -> С. Перед этой формулой А -> С
вставим аксиому 2
(А -> В) -> {№ -> E -> С)] -> D -> С)}, G)
а также формулу
[А -> E -> С)] -> D -> С), (8)
получающуюся из E') и G) по modus ponens. Тогда
А-+С
выводится по modus ponens из F') и (8).
После всех этих вставок цепочка 2' превратилась в вы-
вывод А -> D из Г, что и требовалось.
4.7. Еще несколько теорем.
Доказательство. Из аксиомы 1 получаем
(беря (х) вместо С)
(х) _> (А -> <g>)
или, в других обозначениях,
® -> П А).
Поэтому верно также (подставляя | С вместо А)
&-+ППС))- ¦
Следовательно, (х) (— ~~| (~]С). Формула (~~\(~}С)) -> С
есть аксиома вида 3 *).
*) Напоминаем, что 1.— 3. из п. 4.5, не являющиеся формула-
формулами пропозиционального языка, указывают вид (форму), который
должны иметь конкретные аксиомы, получающиеся из этих выра-
выражений подстановкой произвольных формул вместо входящих в
них букв А, В, С. Поэтому выражения вида 1.— 3. называют обыч-
обычно схемами аксиом (аксиомными схемами), или формами аксиом.
В дальнейшем мы не оговариваем э4ого обстоятельства, в нужных
случаях слегка варьируя терминологию.« Прим. ред.
96

есть вывод формулы С из (g). Следовательно,
®\-С,
т. е. из лжи следует все, что угодно. Следовательно (по
теореме о дедукции),
Таким образом, для (§).->- С существует доказательство.
Поэтому мы можем вставлять ®->-С в цепочки доказа-
доказательств, так как, если потребуется, вывод (g) ->¦ С может
быть вставлен заблаговременно. Присоединив таким об-
образом к цепочке В -*-(§), В цепочку
мы получим вывод С из В ->• (g), В. Следовательно,
Отсюда (по теореме о дедукции)
так что (повторное применение теоремы о дедукции)
|_ (Я-Kg) _>(?_> С),
что и требовалось доказать.
Доказательство. В, | С, В -+ С, \— С, С
-*¦ (8)> (§)• Следовательно (по теореме о дедукции),
в, п
откуда
и окончательно
4.8. По ходу доказательства первой теоремы из п. 4.7
мы установили, что <?)}— С и |— (g) —>- С
Значит, если (§) входит в Г, то Г-теория содержит
все формулы. Больше того, если (§) выводима из Г, то
из Г выводима любая формула. Такая теория не представ-
представляет никакого интереса. Мы предпочитаем теории, в кото-
которых не каждая формула доказуема.
V» 4 X, Фрейденталь 97

Назовем множество формул Г непротиворечивым, если
из Г не выводима ®, или (что то же самое) если не каждая
формула выводима из Г. Если Г непротиворечиво, то А и
| А не могут быть одновременно выводимы из Г, потому
что вместе с А и А -> (х) должно было бы быть доказуе-
доказуемым также и (х), так что Г было бы противоречивым.
Если Г непротиворечиво и Г |— А, то Г, А также не-
непротиворечиво, так как иначе было бы Г, А |— ®.
откуда (по теореме о дедукции) Г|—А -> (х)', так что и
А, и \ А были бы одновременно выводимы из Г.
Если Г непротиворечиво, то либо Г, А, либо Г, \А
непротиворечиво. В противном случае было бы Г, А |— ®,
равно как и Г,~~| А |— (Я), откуда мы получили бы Т\— \А
и Г|— ~~| (~~| А), а следовательно, и V \— А.
Непротиворечивое множество формул Г можно рас-
расширить до максимально непротиворечивого множества
А, т. е. до такого множества формул, которое при лю-
любом дальнейшем расширении становится противоре-
противоречивым.
Мы будем мыслить все формулы расположенными в не-
некоторой последовательности согласно некоторому под-
подходящему принципу упорядочения ').
Пойдем вдоль этой последовательности, пока не дойдрм
до формулы, которой еще нет в Г и которую можно до-
добавить к Г без нарушения непротиворечивости. Добавим
эту формулу к Г. Продолжая этот процесс, мы получим
множество А формул, которое включает Гик которому
без нарушения непротиворечивости нельзя добавить ни
одной формулы. Из сказанного следует:
Если А максимально непротиворечиво, то в точности
одна из формул А,~~]А принадлежит А и каждая формула,
выводимая из А, принадлежит А.
4.9. Оценка пропозиционального языка. Мы уже гово-
говорили выше, что собираемся интерпретировать пропозицио-
пропозициональный язык. Этим мы теперь и займемся. Мы будем
«оценивать формулы».
х) Это непосредственно возможно, если в рассматриваемом язы-
языке имеется только счетное множество простых формул и, следова-
следовательно, только счетное множество формул. Вообще читатель мо-
может иметь в виду именно этот случай. В общем случае нужную
последовательность можно получить с помощью так называемого
вполне упорядочения формул; но мы этих вопросов касаться здесь
не будем.
98

Оценка пропозиционального языка состоит в припи-
приписывании каждой его формуле одного из «значений» О
(ложь) или 1 (истина) таким образом, что (g) получает
значение 0, а для каждой пары формул В, С значение В -> С
определяется посредством следующей таблицы:
В
0
0
1
1
с
0
1
0
1
1
1
0
1
При оценке все аксиомы (см. п. 4.5) автоматически при-
принимают значение 1.
Доказательство. Аксиомы вида A) могут
иметь значение 0 только в том случае, когда А -> С имеет
значение 0, а С имеет значение 1. Но эти два условия про-
противоречат друг другу. Аксиомы вида B) могут иметь зна-
значение 0 только в том случае, когда значения приписаны
следующим образом:
В 1
А
(А
А
А
А
С
В
В
А
(В
{А -> С) О
1
О
1
О
1 (следует из 1-й и 5-й строк)
О (следует из 6-й и 7-й строк)
О (следует из 3-й и 8-й строк).
Но тогда между оценками для 5-й и 9-й строк возникает
противоречие.
Аксиомы вида C) могут иметь значение 0 только в том
случае, когда А имеет значение 0, а (А ->(§))-> ® имеет
значение 1. Но тогда А -> (g) должна была бы получить,
с одной стороны, значение 0, а с другой стороны — зна-
значение 1.
00

При оценке все теоремы получают значение 1.
Пусть D есть теорема, а С — формула из доказатель-
доказательства формулы D. Допустим теперь, что все звенья дока-
доказательства, предшествующие С, имеют значение 1. Надо
показать, что в таком случае и С получит значение 1.
Если С аксиома, то С имеет значение 1 (это было доказано
ранее). Если С получена по modus ponens из каких-то более
ранних звеньев В и В —>• С, имеющих значение 1, то сог-
согласно приведенной выше таблице значений С также полу-
получит значение 1.
В соответствии с п. 2.4 мы назовем множество формул
Г выполнимым, если существует оценка, при которой
все формулы из Г принимают значение 1. Такая оценка
называется выполнением множества формул Г. Если же
такой оценки не существует, то мы будем говорить, чго
Г невыполнимо, или ложно.
Назовем формулу А
Y-истинной,
если для каждой оценки, которая выполняет Г, фор-
формула А принимает значение 1.
А называется
истинной (просто истинной),
если А принимает значение 1 для каждой оценки.
Если для некоторых оценок А принимает значение О,
т. е. А не является истинной, то мы будем говорить, что
А оспорима.
Таким образом, «истинность» и «неоспоримость» —
это одно и то же.
Для каждой оценки формулы А и ~~| А должны иметь
различные значения, так как в противном случае (соглас-
(согласно таблице значений для А -+¦ В) (g) получила бы значе-
значение 1 (при одинаковых значениях А и А -> (g) формула
0 получает значение 1 '), а это противоречит определению
понятия оценки.
х) См. первую и последнюю строкд таблицы зпачении.— Прим.
перев.
100

Таким образом, если А истинно, то \ А ложно; если
А ложно, то "^ А истинно.
4.10. Каждый язык имеет синтаксический и семанти-
семантический аспекты. Если мы переведем английскую фразу
«it is raining» как «идем дождь» или как «идут дождь»,
то сделаем синтаксическую ошибку. Если мы переведем
ее как «идет снег», то это будет семантическая ошибка
(хотя с синтаксической точки зрения такой перевод пра-
правилен). В синтаксисе мы интересуемся формальным аспек-
аспектом языка, а в семантике — значениями. Понятия «гла-
«глагол», «окончание», «предложение», «знак препинания»
относятся к синтаксису; понятия «синоним», «мета-
«метафора», «истинно», «удачно сказанная фраза» — к
семантике.
В пп. 4.5—8 мы занимались синтаксическим аспектом
языка. В п. 4.9 мы вступили в область семантики. Оце-
Оценивая формулы, мы придаем им значения. Значения 0, 1
не принадлежат к словарю пропозиционального языка.
Правда, и такие понятия, как «формула», «доказательство»,
«доказуемая формула», «непротиворечивость» не принад-
принадлежат пропозициональному языку, но они тесно связаны
с ним. Их роль по отношению к пропозициональному язы-
языку примерно та же, что у понятий «глагол», «окончание»,
«предложение», «знак препинания» для обычного разго-
разговорного языка. Понятия же «выполнимо», «ложно», «ис-
«истинно», «оспоримо» соответствуют (по своему отношению
к языку) понятиям типа «синоним». Ради предосторожно-
предосторожности мы даже будем иногда говорить семантически истин-
истинно или семантически ложно. Синтаксический аналог ис-
истинности — это доказуемость.
4.11. Пусть Г — выполнимое множество формул.
Пусть D выводима из Г. Тогда для каждого выполнения
Г формула D принимает значение 1.
Это можно показать следующим образом. Для любого
звена С доказательства формулы D имеется три возмож-
возможности: С есть либо
(а) аксиома, либо
(б) принадлежит Г, либо
(в) получается по modus ponens из двух более ранних
звеньев доказательства:
В, В->С.
В случае (а) мы знаем из п. 4,9, что С имеет значение 1,
101

а в случае (б) С получит значение 1 в силу определения
оценки и выполнимости множества Г. Если мы уже знаем,
что все звенья доказательства, предшествующие звену С,
имеют значение 1, то это, в частности, относится и к В и
В -у С. Таблица значений для В -у С показывает, что С
тогда также получит значение 1. Поэтому каждое звено
доказательства есть формула, имеющая значение 1. Сле-
Следовательно, D, будучи последним звеном, также получит
значение 1.
4.12. Каждое выполнимое множество формул Г непро-
непротиворечиво.
В самом деле, согласно п. 4.11 всякая формула, вы-
выводимая из Г, имеет значение 1. ® имеет значение 0 и,
следовательно, не выводима из Г. Значит, Г непротиворе-
непротиворечиво. Верна и обратная теорема:
Каждое непротиворечивое множество формул Г выпол-
выполнимо.
Доказательство. В соответствии с п. 4.8 мы
строим для Г максимально непротиворечивое А,
которое включает Г. Кроме того, согласно п. 4.8 из каж-
каждой пары формул А, \ А одна и только одна принадле-
принадлежит А.
Всем элементам А мы придадим значение 1, а всем
формулам, не являющимся элементами А, — значение 0.
Удостоверимся, что мы произвели оценку А.
® имеет значение 0 и ввиду непротиворечивости А не
принадлежит А.
Теперь обратимся к таблице значений (п. 4.9). В слу-
случаях, соответствующих ее первым двум строкам, | В
принадлежит Д. Но А принадлежит и формула | В ->¦
-* {В-*- С) (первая теорема из п. 4.7), так что А (— (В -*¦ С);
следовательно, В ->¦ С принадлежит, А и потому В -у С
действительно имеет значение 1. В случае, отраженном в
третьей строке < таблицы, В принадлежит Аи \ С при-
принадлежит А. Поскольку А принадлежит формула В -*¦
-*-((~\С)-*-( | (В-*¦ С))) (вторая т,еорема из п. 4.7), то
Д |—~~] (В -*¦ С); следовательно, | (В -*¦ С) принадлежит
А и, значит, В -»- С не принадлежит А; поэтому В -у С
имеет значение 0. В случаях, соответствующих второй
и четвертой строкам таблицы, С принадлежит А, а так
как С —*¦ (В—*¦ С) есть частный случай аксиомы 1, то
\\~ В -*¦ С; поэтому В -*¦ С принадлежит А. Таким
'"пазом, В ->¦ С действительно имеет значение 1. Поэто-

му Г выполняется, ибо Д включает Г, а каждая форму-
формула из А принимает значение 1.
4.13. По контрапозиции 1) из предыдущей' теоремы
получаем:
Каждое невыполнимое (ложное) множество формул Г
противоречиво.
Теперь мы подошли к главной нашей цели:
Теорема о полноте. Каждая истинная фор-
формула пропозициональные языка доказуема.
Доказательство! Пусть А — истинная фор-
формула. Тогда ~~| А ложна (см. окончание п. 4.9); следова-
следовательно, она невыполнима и (по предыдущей теореме) про-
противоречива.
Следовательно,
и, значит,
Теперь мы можем последовательно выписать:
доказательство для ~~|(~|Л), аксиому 'А и, наконец, А.
Эта цепочка формул и будет доказательством для А.
Следовательно, А доказуема.
Данная теорема показывает, что предложенный нам
список аксиом достаточно полон для доказательства лю-
любой истинной формулы. Поэтому ее и называют «теоремой
о полноте».
4.14. Аксиомы субъектно-предикатного языка. Рассмот-
Рассмотренный до сих пор пропозициональный язык — доволь-
довольно-таки бедный язык. В третьей главе мы пользовались
гораздо более сильными лингвистическими средствами.
Теперь мы эти средства подвергаем аксиоматизации.
Субъектно-предикатный язык
состоит из
субъектов, в числе которых имеется бесконечное коли-
количество переменных, а также (быть может, но не обязатель-
обязательно) постоянные субъекты;
элементарных (исходных) 0-местных, 1-местных, 2-мест-
2-местных,... предикатов, среди которых непременно должен
быть 0-местный предикат ® (нульместный предикат —
*) См. п. 2.10, формула A6) и пояснения к ней.*= Прим. ред.
*) См. п. 4.8.— Прим. ред.
103

это то, что мы раньше называли элементарными формула-
формулами — высказываниями);
связок: ->, ( , ), Л.
Субъекты и предикаты вместе составляют так называ-
называемый словарь языка.
Формулы:
(а) Если / есть элементарный га-местный предикат
(га ~^> 0), аж1г..,а;п— субъекты, то f(xlt...,xn) есть формула.
Каждый нульместный элементарный предикат есть фор-
формула.
(б) Если А и В — формулы, то (А -*¦ В) — формула.
(в) Если А — формула, а х —переменный субъект,
то ЛХА — формула.
(г) Любая формула получается повторным примене-
применением принципов (а), (б), (в).
Вместо «переменный субъект» мы можем говорить бо-
более кратко — «переменная».
Свободные и связанные переменные.
В соответствии со способами а), б), в) построения фор-
формул мы определим «свободное» и «связанное» вхождения
переменной в формулу.
а) В / (#!,...; хп) переменная х{ входит свободно.
б) Любое свободное (связанное) вхождение перемен-
переменной х в А (и аналогично, в В) является также свободным
(соответственно связанным) вхождением в А -*¦ В ').
в) Любое свободное (связанное) вхождение перемен-
переменной у в А является также свободным (соответственно свя-
связанным) вхождением в Л,. А, если переменная у отличает-
отличается от переменной х. Любое вхождение переменной х в ЛХА
называется связанным (переменная х, являющаяся индек-
индексом при Л в записи Л,., вообще не рассматривается при
такой терминологии как «вхождение» 2).
Посредством этих соглашений дйя любого вхождения
переменной в произвольную формулу определено, долж-
должно ли оно рассматриваться как свободное или как свя-
связанное.
х) Таким образом, одна и та же переменная может входить
п одну и ту же формулу как свободно, так и связанно (пример —•
и хождения в импликацию А -» В переменной х, входящей в А сво-
оодно, а в В — связанно).— Прим. ред.
2) Этот индекс указывает лишь,, какую переменную в подкван-
горном выражении связывает квантор.— Прим. перев.
104

Формулу с п различными свободными переменными
называют формулой степени п. Формулы степени 0 назы-
называют также высказываниями.
Вместо А ->¦ 0 мы будем в дальнейшем писать \А.
Аксиомы: Если А, В, С — формулы, то аксиомами яв-
являются выражения следующих видов:
1. — 3. (см. п. 4.5);
4. Л,. (А -> В) -v (A -»- Л,. В), если переменная не вхо-
входит свободно в А;
5. \А -у А', если А' получена из А подстановкой
субъекта у вместо каждого вхождения х; при этом пред-
предполагается, что х не входит свободно ни в какую подфор-
подформулу формулы А вида \С.
Кроме modus ponens, мы примем еще одно средство по-
построения доказательства, а именно,
связывание: операцию, посредством которой формула
В заменяется формулой AJB.
Вывод формулы D из множества формул Г определяет-
определяется как в п. 4.5, с добавлением случая
(г): или получено связыванием с помощью \ из пре-
предыдущей формулы этой цепочки, при условии, что х не
входит свободно ни в какую формулу из Г.
Формула, выводимая из множества формул Г, опреде-
определяется тогда так же, как и в п. 4.5. Аналогично определяют-
определяются понятия:
Т-теорема, Т-теория, доказуемая формула (теорема),
теория.
Доказательство теоремы о дедукции потребуется те-
теперь дополнить в соответствии с новым случаем (г) в опре-
определении вывода:
Если
суть формулы из вывода из Г, А, то в этот вывод между
формулами
А-+В и А -+ АХВ
нам надо будет теперь вставить новые звенья, а именно:
формулу
Л*(-А + В),
получающуюся с помощью связывания из А -»- В, и ак-
аксиому
АХ(А -+В)-+(А-+ ЛХВ).
S X. Фрейденталь 105

(Отметим, что х здесь не должно свободно входить в Г, А.)
Из этих двух формул мы тогда по modus ponens получим
А -*¦ ЛХВ. В дальнейшем мы будем пользоваться сокра-
сокращением
вместо ~~1 Лх(~~] А).
Доказательства формул
полученные в п. 4.7, остаются в силе. Легко доказать так-
также, что
Непротиворечивость определяется так же, как в п. 4.8.
4.15. Формулы без свободных переменных мы будем
называть высказываниями; этот термин оправдан тем, что
с такими формулами мы можем оперировать, как с выска-
высказываниями в смысле пп. 4.5—4.13. В частности, мы можем
расширить каждое непротиворечивое множество высказы-
высказываний до максимально непротиворечивого множества вы-
высказываний, которому принадлежит ровно одно высказы-
высказывание из любой пары высказываний А, \ А. Но мы хо-
хотим добится большего.
В нашем словаре может не быть никаких конкретных
постоянных субъектов. Предикаты, как и раньше, не за-
закреплены ни за какими определенными субъектами. Мо-
Может случиться, что Vjj/l доказуема и тем не менее в на-
нашем словаре не найдется «примера»,- подтверждающего
высказывание «существует х такое, что А», т. е. в нем не
существует никакого фиксированного субъекта, который,
будучи подставленным вместо х, обращал бы А в доказу-
доказуемую формулу. Теперь мы расширим, во-первых, словарь
(добавлением постоянных субъектов) и, во-вторых, дан-
данное непротиворечивое множество Го высказываний (до-
(добавлением некоторых новых высказываний), чтобы полу-
полученное в конечном итоге множество высказываний Q было
максимально непротиворечивым и чтобы для каждого вы-
высказывания VaA из Q в словаре можно было бы найти не-
некоторый постоянный субъект а, так что формула А',
106

Получаемая из А подстановкой (согласно аксиоме 5) а
вместо х, также принадлежала бы Q.
Мы будем строить такое Q последовательно. Будем ис-
исходить из того, что у нас имеется неограниченный «запас»
объектов, которые мы можем в случае надобности добав-
добавлять к словарю в качестве постоянных субъектов. Для
начала мы расширим данное множество формул Го до
максимально непротиворечивого множества До (см. п. 4.8).
Мы можем считать, что высказывания из До расположены
в последовательность; возьмем из этой последовательнос-
последовательности первое высказывание вида УхА (где х — переменная,
А — формула). Возьмем тогда объект а из имеющегося
в нашем распоряжении запаса, добавим его к словарю
в качестве постоянного субъекта и добавим к До вы-
высказывание А', полученное из А подставкой а вместо х
(во всех тех вхождениях, где х свободно). Легко показать,
что непротиворечивость До в этом случае не нарушится.
В самом деле, пусть До, А' образуют противоречие,
т. е.
тогда (по теореме о дедукции)
В выводе Е формулы \ А' из До мы заменим а во всех
его вхождениях на переменную у, которая не встречалась
в этом выводе (здесь используется бесконечность числа
переменных). Мы утверждаем, что получившаяся в ре-
результате цепочка формул Е* также является выводом.
Чтобы удостовериться в этом, рассмотрим каждое звено С
первоначального вывода (результат подстановки у вместо
а в формулу С обозначим через С*). Перебирая возмож-
возможные способы вывода, мы видим, что надо учесть четыре
случая:
(а) С есть аксиома;
(б) С принадлежит До;
(в) С получено из некоторой пары предшествующих
формул посредством modus ponens;
(г) С имеет вид hJB и получено из некоторой предше-
предшествующей формулы В посредством связывания.
Случай (б) можно сразу исключить: дело в том, что а
вообще не входит в До. В случае (а) очевидно, что и С*
будет аксиомой. Точно так же в случаях (в) и (г) мы сраву

видим, что С* получено из предшествующих формул це-
цепочки 2* посредством той же процедуры, посредством ко-
которой получено С из соответствующих формул цепочки 2.
Следовательно,
где А" выведена из А' посредством подстановки у вместо
а, т. е. выведена из А подстановкой у вместо х во всех сво-
свободных вхождениях х.
Связывая у, мы получим также
откуда (аксиома 5) имеем
отсюда связыванием х получаем
или
что совместно с данным
означало бы противоречивость Ао.
Эта противоречивость является следствием допущения
о противоречивости Ао, А'. Отсюда следует, что Ао ос-
остается непротиворечивым после добавления А'. Теперь
мы можем вставить А' в последовательность высказыва-
высказываний Ао сразу же за УХА. После этого мы ищем следую-
следующее высказывание такого же вида — назовем его V^,—
берем объект Ъ из имеющегося у нас запаса, добавляем его
к словарю в качестве постоянного субъекта и добавляем
к Ао, А' высказывание В', получающееся из В подста-
подстановкой Ъ вместо у. При этом, как мы уже знаем, не-
непротиворечивость сохраняется. Продолжая так и дальше,
мы получаем, таким образом, метод порождения нового
словаря и непротиворечивого множества 1\, обладающих
тем свойством, что для каждой формулы вида У2.йГ|из 1\
в^этом словаре найдется постоянный субъект к такой,
что К' (полученное подстановкой к вместо каждого сво-
свободного вхождения z в К) принадлежит Гх.
108

1\ снова расширяется до максимально непротиворе-
непротиворечивого множества Аг высказываний. С Ах мы поступа-
поступаем так же, как с Ао, получая некоторое Г2 со свойствами,
аналогичными свойствам 1\, и так далее.
За конечное число шагов описанного типа мы получа-
получаем искомое расширение словаря и расширение множества
Г до множества й с требуемыми свойствами:
й является максимально непротиворечивым множест
вом высказываний;
для каждого высказывания УХА из й найдется «при-
«пример» а, подтверждающий высказывание «существует х
такое, что Аь.
Это свойство множества Q можно сформулировать по-
другому:
й является максимально непротиворечивым множест-
множеством высказываний;
если все высказывания, полученные из формулы А
подстановкой вместо х любого конкретного постоянного
субъекта, принадлежат й, то и ЛХА принадлежит й.
Докажем выполнение этого нового условия при выпол-
выполнении первоначального условия. Предположим против-
противное. Тогда множеству й будет принадлежать формула
| ЛХА (ведь й максимально непротиворечиво!), т. е. попро-
попросту Vj.( \A). Но тогда нашелся бы постоянный субъект
а такой, что | А' принадлежало бы й (где А' получено
из А подстановкой а вместо х). Тогда А', очевидно, не
принадлежало бы й (й непротиворечиво!), что противоре-
противоречит предположению. Обратное утверждение доказывает-
доказывается так же.
4.16. Проблема интерпретации субъектно-предикат-
ного языка, аксиоматически введенного в п. 4.14, в прин-
принципе решается построением й.
Что мы имеем в виду, говоря об «интерпретации»?
Мы хотим, чтобы «субъекты», «предикаты» и знаки —>, Л
данного субъектно-предикатного языка соответствовали
интуитивным представлениям, изложенным в главе 3.
С субъектами дело ясно. Вспомним теперь, что мы в главе 3
понимали под предикатом? Предикат, скажем «...есть
человек», полностью определен, если после подстановки
на место точек в этой фразе наименования какого-либо
предмета мы знаем, истинно или ложно получившеес'я
высказывание. Предикат «...меньше, чем...» определен,
если известно, для каких пар предметов он истинен, а для
109

каких ложен, «-местный предикат определен, если для
каждой п-ки объектов alf ...» ап известно, истинно или
ложно высказывание, полученное подстановкой каждого
aj на г-е аргументное место F.
«-местный предикат, таким образом, отображает мно-
множество и-ок предметов в множество, состоящее из двух
высказываний: «истинного» и «ложного» (мы будем их также
обозначать соответственно через 1 и 0). Если нам дано
какое,-нибудь множество предметов /, то через Г1 мы будем
обозначать множество >/,..., /< n-ок предметов из /.
В этих терминах интерпретация нашего субъектно-преди~
катного языка может быть охарактеризована следующим
образом:
каждому постоянному субъекту а сопоставляется неко-
некоторый элемент множества / (обозначаемый через Ra);
каждому «-местному предикату F сопоставляется ото-
отображение (обозначаемое через RF) множества 1п в мно-
множество {0, 1}.
Таким образом, каждой формуле F(xv...,xn) сопостав-
сопоставляется выражение (RF)(x1,..., ?„), которое при подстанов-
подстановке элементов множества / вместо хъ..., хп принимает зна-
значение 0 или 1.
Заполняя места субъектов . субъектно-предикатного
языка элементами множества /, т. е. производя отображе-
отображение множества субъектов в множество /, мы интерпретиру-
интерпретируем каждый из этих субъектов. Но фактически нам надо
зафиксировать значения (т. е. образы при этом отображе-
нии)*лишь постоянных субъектов *), так что, строго гово-
говоря, интерпретация есть класс (эквивалентных в опреде-
определенном смысле) отображений.
Но мы наложим на интерпретацию еще дополнительные
требования. Как и раньше, мы потребуем, чтобы (нуль-
местный предикат) (g) всегда принимал значение 0. Мы
потребуем, далее, чтобы при интерпретации сохраняла
силу таблица значений для импликации (->-) из п. 4.9.
*) Что касается переменных, то для них фиксируется лишь
область изменения, т. е. как раз то самое множество /, элементы
которого служат интерпретациями констант (все I как бы «дер-
«держатся наготове» целиком, а подстановка — в языке — постоян-
постоянного субъекта вместо переменной есть «сигнал», указывающий,
какой конкретный предмет будет использован на этот раз для ин-
интерпретации). Редакция данного абзаца сильно отличается от тек-
текста оригинала,— Прим. ред,
НО

И, наконец, мы наложим дополнительное условие на интер-
интерпретацию знака Л. В главе 3 мы истолковывали запись
Л^ так, что А истинно, что бы мы ни подставили вместо
х. В соответствии с прежним истолкованием мы потребуем
теперь, чтобы в случае, когда интерпретация некоторой
формулы А имеет значение 1 для любой подстановки в А
постоянных субъектов, интерпретация АХА также долж-
должна иметь значение 1. Если все эти требования выполнены,
то мы будем говорить, что интерпретация «поддается
оценке». На основе этих предварительных рассмотрений
мы можем теперь дать точное определение.
4.17. Рассмотрим некоторый субъектно-предикатный
язык. Пусть / — некоторое множество, 7П — множество
>/,...,/< элементов из / G° есть, по определению, множе-
множество, состоящее из одного элемента г0).
Отображение со, сопоставляющее каждому субъекту
некоторый элемент множества 7, называется заполнением.
Интерпретацией над 7 называется такое отображе-
отображение R, что
каждому постоянному субъекту соответствует элемент
множества 7;
каждому элементарному n-MecTHOMyJ предикату со-
соответствует отображение множества 7П в множество {0,1}.
Пусть R — интерпретация.
Заполнение со, по определению, согласуется с интерпре-
интерпретацией R, если со и R совпадают для каждого постоянного
субъекта.
Мы будем говорить, что R поддается оценке, если для
каждого заполнения со интерпретация R порождает оцен-
оценку, т. е. каждой формуле С приписывает значение |С)Ш =
= 0 или 1 (в зависимости от со) так, что выполняются
следующие требования:
(а) Если С имеет вид /(х^..., х„) (/ есть n-местный эле-
элементарный предикат, а хх,..., хп — субъекты), то
),..., со(хж)>) для п > О,
{Rf){i0) Для п = О,
(б) Если С имеет вид (А -> В), то |С|т зависит от
\А |ш и \В\а согласно таблице значений для импликации
из п. 4.9.
Ш

в) Если С имеет вид \А, то \С\Ш = 1 тогда и только
тогда, когда \А \а> = 1 для каждого заполнения
со', которое отличается от со разве лишь значением
ДЛЯ Z.
' Принимая во внимание способ порождения формул
(см. п, 4.14), мы видим, что такая оценка, если она во-
вообще возможна, единственна (при данной интерпрета-
интерпретации R).
Проверяя случаи (а), (б), (в), мы видим, что:
Значение С при заполнении со зависит только от того,
какие значения со поставляет переменным, свободно вхо-
входящим в С В частности, значение высказывания не за-
зависит от со.
Но оно, конечно, зависит от интерпретации R.
Пусть Г есть некоторое множество высказываний.
Поддающаяся оценке интерпретация над /, в которой
каждое высказывание из Г принимает значение 1, назы-
называется
выполнением множества Г над /. Если Г имеет такое
выполнение, то мы будем говорить, что Г выполнимо
над /; в противном случае мы будем говорить, что оно
невыполнимо, или ложно, над /.
Будем говорить, что высказывание А
Т-истинно над I, если для каждого выполнения мно-
множества Г над / оно принимает значение 1;
Т-истинно, если оно Г-истинно над/ для каждого /;
истинно над I, если для каждой поддающейся оценке
интерпретации над /оно принимает значение 1;
истинно, если для каждого / оно истинно над /.
Аналогично можно определить понятия «.оспоримо»
и т. п.
4.18. Пусть Г есть некоторое множество высказыва-
высказываний, выполнимых над /. Пусть D —' формула, выводимая
из Г. Тогда для каждого выполнения Г над / формула
D принимает значение 1.
Это утверждение аналогично теореме из п. 4.11 и дока-
доказывается аналогично. Только мы должны здесь принять
во внимание еще ту возможность, что звено С было полу-
получено из предшествующего звена посредством связывания,
т. е. что оно имеет вид АХВ. Если о звеньях, предшествую-
предшествующих С, известно, что они имеют значение 1 для поддаю-
поддающейся оценке интерпретации R и каждого заполнения
со, согласующегося с R, то, в'частности, это верно и для
112

В. Согласно определению поддающейся оценке интерпре-
интерпретации (см. 4.17 (в)), ЛХВ будет тогда также иметь значе-
значение 1 для каждого заполнения.
4.19. Отсюда следует (см. также п. 4.12):
Каждое множество высказываний, выполнимое над
каким-нибудь множеством I, непротиворечиво.
¦ Верно и обратное утверждение:
Каждое непротиворечивое множество высказываний вы-
выполнимо над некоторым множеством I.
Доказательство. Расширим согласно п. 4.15
множество постоянных субъектов и данную непротиворе-
непротиворечивую систему высказываний Г. Мы получим максималь-
максимально непротиворечивую систему высказываний Q, включаю-
включающую Г и такую, что в ней для каждого высказывания
УХА найдется такой постоянный субъект а обогащенно-
обогащенного языка, что формула А', полученная из А подстанов-
подстановкой а вместо х, также принадлежит Q. Возьмем в ка-
качестве / множество постоянных субъектов обогащенно-
обогащенного языка. Определим интерпретацию R следующим
образом:
для каждого постоянного субъекта а положим
Ra = a;
для каждого элементарного n-местного предиката /
и каждой n-ки (а!,..., а„> из 1п положим
(Д/Жв!,..., а„» = 1,
если высказывание, получающееся из f(x1,..., xn) подста-
подстановкой at вместо х-% (i = 1,..., п), принадлежит Q, и 0 в
противном случае.
R поддается оценке и |С [т определено для каждой фор-
формулы С и для каждого согласующегося с R заполнения со
посредством следующего соглашения:
|С|Ш = 1 или О
в зависимости от того, принадлежит ли Q высказывание,
полученное из С подстановкой со(а;) вместо каждой пере-
переменной х, свободно входящей в С, или нет. Чтобы убедить-
убедиться в этом, нам надо лишь проверить выполнение требова-
требований (а), (б) и (в) из п. 4.17.
(а) Пусть С имеет вид f(x1,..., хп) (см. п. 4.17), п ^> 0.
Согласно определению (Rf)«со (а^),..., со(а;п)» вычисляется
113

посредством подстановки cofo) вместо xt в f(xl,.:., xn),
после чего надо проверить, принадлежит этот результат
Q или нет. Согласно определению это равносильно вы-
вычислению !/(#!,..., Х„)|т.
Для п = 0 это также очевидно. |®|т =0 следует из
непротиворечивости множества Q (т. е. из того, что ® не
принадлежит Q).
б) См. доказательство в п. 4.11.
в) Пусть С имеет вид Лг А (см. п. 4.17). Пусть |С|Ш =1.
Пусть со' — заполнение, отличающееся от со разве лишь
значением для аргумента г. Пусть С — результат под-
подстановки со (ж) в С вместо каждой свободной переменной х;
пусть А' — результат подстановки со'(ж) в А вместо каж-
каждой свободной переменной х, отличной от г; наконец, пусть
А" есть результат подс1ановки со'бс) в А вместо каждой
свободной переменной х.
Если А" получено из А' подстановкой со' (г) вместо
г, то С имеет вид \А', а любая такая формула принад-
принадлежит Q, так как \С\и, = 1. Из аксиомы 5 (см. п. 4.14) мы
видим, что результат подстановки co'(z) вместо z принад-
принадлежит Q. Таким образом, А" принадлежит Q, откуда
ий- =1.
Пусть \С\и, =0, а С ж А' определены, как выше.
Тогда С, а значит, и ЛгА' не принадлежит Q. Поэтому
"~| AZA' принадлежит Q, а тогда и Vt(~~]Ar) принадле-
принадлежит Q. Таким образом, существует (см. начало доказа-
доказательства) такой постоянный субъект а, что для каждой
формулы А", полученной из А' подстановкой а вместо z,
| А" принадлежит Q, а следовательно, А" не принадле-
принадлежит Q. Пусть со' есть такое заполнение, что co'(z) = а,
а в остальном совпадающее с со. Тогда А" оказывается
результатом подстановки со'(ж) в А вместо каждой свобод-
свободной переменной х. Следовательно, \А |т. = 0.
4.20. Как и в п. 4.13, из последней теоремы следует
Теорема о полноте. В субъектно-предикат-
ном языке каждое истинное высказывание доказуемо.
Теорема эта впервые доказана К. Гёделем A930).
Приведенное здесь доказательство принадлежит (с точ-
точностью до деталей) Л. Генкину A949).
4.21. Теорему п. 4.19 можно несколько усилить. Вспом-
Вспомним, как мы получали Q (см. п. 4.15).
Предположим, что наш словарь счетно бесконечен.
Тогда имеется лишь счетное множество формул, так что
114

й Ао обстоит Только из счетного множества формул. Та-
Таким образом, для получения Г\ нам достаточно добавить
счетное число формул, причем словарь при этом также рас-
расширится не более чем на счетное множество символов, и
так далее. Счетным оказывается и расширенный сло-
словарь. Следовательно, / также счетно. Итак:
Если словарь счетен, то каждое непротиворечивое мно-
множество вжказываний выполнимо над счетным I.
Вообще, оказывается, что в качестве / можно всегда
выбрать множество той же мощности, что и данный
словарь.
Как мы увидим в следующей главе, последнее заклю-
заключение носит парадоксальный характер.

Г л fa] в а б
Язык л метаязык
5.1. Хотя субъектно-предикатный язык богаче, чем
пропозициональный язык, он также может оказаться
недостаточным для некоторых целей. Дело в том, что в
естественном языке встречаются не только предикаты от
субъектов, но и предикаты от предикатов. Рассмотрим
предложения:
Этот дом — красный.
Красный — это цвет.
Цвет — это оптическое явление.
Если мы будем считать субъектом «этот дом», то «крас-
«красный» следует рассматривать как предикат. Но в следую-
следующем предложении этот предикат уже сам выступает как
субъект высказывания, в котором «цвет» (или «...это
цвет») выступает в качестве предиката (второй ступени).
В третьем же предложении этот предикат второй ступени
является субъектом высказывания, образованного с по-
помощью нового предиката (третьей ступени).
Употребляя такого рода предикаты различных ступе-
ступеней, надо соблюдать известную осторожность. В разго-
разговорной речи предикаты второй ступени не применяются
непосредственно к субъектам: предложение «этот дом есть
цвет» считается не ложным, а бессмысленным.
В логике, как правило, предпочитают обходиться пре-
предикатами лишь первой ступени. Но тогда «красный» во
втором из приведенных выше предложений надо понимать
не так, как «красный» в первом предложении. «Красный»
(точнее — «...есть красный») из первого предложения
есть настоящий предикат, во 'втором же этот термин
является на самом деле субъектом. Но в таком случае
116

следует установить четкую связь между двумя этими трак-
трактовками.
Вспомним, какова связь между предикатами и субъек-
субъектами в логистическом языке. Предикату F (первой ступе-
ступени) сопоставляется некоторое вполне определенное мно-
множество, а именно, множество всех тех х, для которых
справедливо F(x), т. е.
причем это множество мы можем затем уже рассматривать
как некоторый субъект. Иными словами, множества мож-
можно рассматривать и как субъекты. Скажем, слово «крас-
«красный» из второго предложения следует теперь понимать
как множество всех красных объектов. Аналогично, «зеле-
«зеленый» следует понимать как множество всех зеленых объек-
объектов. «Цвет» из третьего предложения есть в таком слу-.
чае множество, состоящее из всех конкретных цветов,
т. е. некоторое множество множеств.
Но если мы хотим рассматривать множества как субъек-
субъекты, то нам понадобится не только предикат, понимаемый
как «... есть множество», но и специальное отношение
между субъектами, которое можно было бы понимать как
... есть элемент ...
или
Однако и этого самого по себе недостаточно. Если мы,
например, хотим в качестве основы геометрии сформули-
сформулировать свойства точек, прямых и т. п., то нам понадобят-
понадобятся некоторые аксиомы, относящиеся к множествам. Эти
аксиомы можно сформулировать по-разному. Но в любом
случае в этих аксиомах должны быть зафиксированы
обычные теоретико-множественные операции, посредством
которых конструируются новые множества; надо, в част-
частности, чтобы в нашей теории было пустое множество, что-
чтобы объединение произвольного множества множеств са-
само было множеством, чтобы для каждого множества су-
существовало множество всех его подмножеств и т. п.
Так мы получим некоторую систему Г высказываний,
в которые входят предикаты «... есть множество» и
«...есть элемент...», а также отношение равенства ... = ... .
Такая система называется системой аксиом для теории
117

МйожёСтв. Теория множеств при таком подходе есть Г-тео-
рия, т. е. совокупность высказываний, выводимых из Г.
5.2. Но и этого еще недостаточно для математики, по-
скольку вся она основана на понятии натурального числа').
Натуральные числа можно ввести обычным образом,
Введем специальный предикат
... есть натуральное число,
обозначаемый буквой Z. Тогда имеет место:
Z(l), Z{2), ZC),...
Теперь нам надо аксиоматически выразить известные свя-
связи между натуральными числами. Это достигается вве-
введением отношения
...(непосредственно) следует за ...,
что сокращенно записывается как
V(... , ...);
например, высказывания
7B,1), V C,2), V D,3),...
истинны.
Система аксиом для натуральных чисел была предло-
предложена Пеано:
2) Л*{Z(х)->IVV(Z(у) Д V (ух))]}.
3) -\VxV(l,x).
4) K,x>,v{lZ(x)/\Z(x')/\Z(y)]-+
5)AXtX,,v{lZ(x)/\Z(x')/\Z(y)]
6)
Особенно важную роль играет последнее утверждение,
выражающее так называемый
х) Следует отметить, что в достаточно сильных системах аксио-
аксиоматической теории множеств арифметика натуральных чисел
строится без привлечения каких-либо дополнительных средств.
Построения эти, однако, далеко выходят за рамки настоящей кни-
книги.— Прим. ред.
Щ

Принцип полной индукции. Пусть F
есть некоторое свойство натуральных чисел, причем 1 об-
обладает свойством F и если какое-либо натуральное число
обладает свойством F, то (непосредственно) следующее
за ним число также обладает этим свойством; тогда все
натуральные числа обладают свойством F.
С помощью этого принципа можно определить сло-
сложение и умножение натуральных чисел:
х + 1 следует за х;
х + (у + 1) следует за х + у;
1-У =У,
(х + 1)-у =х-у + у. ¦
5.3. В качестве аксиом для множеств и для натураль-
натуральных чисел мы выбрали утверждения, рассматриваемые в
обычной математике как истинные. Образуемая ими си-
система Г удовлетворяется множествами и натуральными
числами в их обычном интуитивном понимании. Можно
поэтому считать, что Г непротиворечива. При построе-
построении системы Г мы можем обойтись счетной совокупно-
совокупностью субъектов. Согласно п. 4.21 Г должна быть, таким
образом, выполнима уже над некоторой счетной областью /.
Это очень странно: ведь в теории Г имеются объекты,
интерпретируемые обычно как несчетные множества.
Например, множество всех подмножеств множества нату-
натуральных чисел является, очевидно, несчетным (см. п. 1.19).
Это заключение известно под именем парадокса Лёвенгей-
ма — Сколема. Как объяснить это явное противоречие?
Существование такого несчетного множества М долж-
должно быть выведено из Г средствами субъектно-предикат-
ного языка. Но, с другой стороны, эти средства не позво-
позволяют вывести из Г взаимно-однозначное отображение /
множества М в множество натуральных чисел. Г выпол-
выполнимо над некоторой счетной областью /. Следовательно,
в некоторой поддающейся оценке интерпретации М долж-
должно быть интерпретировано посредством некоторого счет-
счетного множества.
Что из этого следует? — Не что иное, как то, что вза-
взаимно-однозначное отображение множества М, существо-
существование которого мы можем установить, говоря о субъектно-
предикатном языке, не выводимо из Г средствами самого
этого субъектно-предикатного языка.
5.4. Сказанное позволяет усвоить тот факт, что когда
мы говорим о субъектно-предикатном языке, нам часто
119

приходится выходить далеко за пределы самого этого
языка. Действия в определенном выше субъектно-преди-
катном языке вполне могут быть передоверены машине.
В соответствии с очень простыми приведенными выше
правилами машина может успешно выписывать формулы.
Машина может также последовательно применять прави-
правила вывода и получать таким образом одну теорему за дру-
другой. Сможет ли машина получить любое Г-истинное вы-
высказывание?
Какую бы последовательность знаков мы ни ввели в
машину, машина сможет проверить, является ли она фор-
формулой. Но сможет ли машина также удостовериться
в истинности или ложности произвольного данного вы-
высказывания каким-либо образом, кроме как последо-
последовательно применяя правила вывода, в ожидании, что рано
или поздно появится это высказывание или его отри-
отрицание?
Мы показали выше, что каждое Г-истинное высказы-
высказывание субъектно-предикатного языка выводимо из Г (во
всяком случае, если Г непротиворечиво). Но при этом
мы пользовались некоторыми средствами, для машины
недоступными. Эти средства мы заимствовали не только
из субъектно-предикатного языка, но и из обычного рус-
русского языка. Чтобы убедиться в доказуемости формулы,
нам приходилось, например, проводить рассуждение сле-
следующего вида: допустим, что для А не существует доказа-
доказательства; возникнет некоторое противоречие. Здесь мы
убеждаемся в искомой доказуемости косвенными средства-
средствами (приведением к абсурду). Но, опровергнув допущение,
что для А не существует доказательства, мы отнюдь не
воспроизвели доказательства для А! А единственный спо-
способ, с помощью которого машина может убедиться в до-
доказуемости какой-нибудь формулы А, состоит в прямом
построении доказательства для этой А.
Значит, нет ничего невероятного в том, что некоторые
высказывания, которые мы должны признать истинными,
говоря о субъектно-предикатном языке, не удается дока-
доказать (и не удается опровергнуть) с помощью машины, ра-
работающей в этом языке. Согласно знаменитой теореме
К. Гёделя A931) в каждом языке, средствами которого
можно построить последовательность натуральных чи-
чисел, действительно имеются такиег-неразрешимые предло-
предложения. Теорема эта известна поц именем теоремы о непол-

ноте. Позднее мы опишем в общих чертах идею доказа-
доказательства этой теоремы.
Надо заметить, что все эти трудности не возникают,
если мы ограничиваемся пропозициональным языком.
Теорему о полноте для пропозиционального языка можно
доказать совсем элементарными средствами, а именно,
средствами, доступными для машины '). Что же касается
субъектно-предикатного языка, то для него аналогичная
задача, вообще говоря, непосильна для машины.
5.5. В доказательстве полноты субъектно-предикат-
субъектно-предикатного языка мы использовали для обсуждения свойств
этого языка русский язык. Можно ли рассчитывать, что-
чтобы машина, владеющая лишь субъектно-предикатным
языком, могла говорить об этом языке так, чтобы, напри-
например, установить доказуемость какой-либо формулы?
Ответ на этот вопрос мы рассмотрим несколько позднее.
Пока же я хочу обратить внимание читателя на одну
опасность, подстерегающую всякого, кто хочет обсуждать
свойства какого-либо языка на самом этом языке. Сущест-
Существует знаменитый парадокс о критянине, утверждающем,
что все критяне лжецы. Спрашивается, лжет он сам или
говорит правду, произнося это утверждение. Уточним
формулировку парадокса. Спрашиваем: если некто гово-
говорит «Я лгу», то лжет он или говорит правду? Если он
лжет, то он лжет, что он лжет, и, следовательно, говорит
правду. Если же он говорит правду, то верно, что он лжет,
так что он лжет.
Трудности, в которые лжец завлек нас и самого себя,
могут быть объяснены тем, что мы стали говорить о свой-
свойствах некоторого языка на этом же самом языке. Если
человек, родным языком которого является русский язык,
говоря о свойствах русского языка, пользуется только
английским языком, то этот человек никогда не придет к
подобному парадоксу. Такой человек не скажет «собака»
есть существительное», а скажет «„собака" is a noun»; вме-
вместо «утверждение „Авель убил Каина" ложно» он скажет
«the assertion „Авель убил Каина" is] false». Он никогда
J) Говоря здесь о «машине», автор отнюдь не претендует на ос-
освещение достаточно сложных и спорных проблем типа «может ли
машина мыслить», понимая под «машиной» некоторое устройство,
«владеющее» выразительными и дедуктивными средствами неко-
некоторого данного (скажем, пропозиционального или субъектно-пре-
субъектно-предикатного) языка.— Прим. ред.
121

не скажет «Я лгу», так как это утверждение само" го-
говорит о ложности его прямых утверждений, сделанных на
русском языке. Поэтому вместо «я лгу», он сделает анало-
аналогичное утверждение об утверждениях, воспользовав-
воспользовавшись не русским, а английским языком: «Everything I
speak in Russian is false», и в этом утверждении уже не
заключено ничего относящегося к нему самому, так как
оно высказано на английском (а не на русском) языке.
Конечно, наш лингвист может захотеть высказаться по
поводу каких-либо обстоятельств, относящихся к англий-
английскому языку. Но для этого он может, например, восполь-
воспользоваться немецким языком, т. е. вместо «Everything I
speak in Russian is false» сказать «Alles, was ich auf eng-
lisch sage, ist falsch». Эти два утверждения формально не
противоречат друг другу (независимо от того, истинны ли
они).
Более точная формулировка парадокса лжеца выгля-
выглядит так:
То, что написано на 19-й и 20-й строках 122-й страни-
страницы этой книги, ложно.
(Читателю предлагается дополнительно обдумать этот
вопрос самостоятельно.)
Следующее «определение» известно под именем пара-
парадокса Ришара:
Наименьшее число, которое нельзя определить в рус-
русском языке при помощи менее чем сотни букв.
Если вы подсчитаете количество букв в этой фразе,
то обнаружите, что «это число» было «определено» посред-
посредством менее чем одной сотни букв. (И здесь советуем об-
обдумать этот вопрос детальнее.)
Все, что говорилось выше, в начале этой главы, и рас-
расшифровывает ее название «язык и метаязык». Язык, на
котором говорят о некотором данном языке, и называет-
называется его метаязыком.
5.6. Каким же образом мы можем все-таки научить
машину говорить о субъектно-предикатном языке на этом
же субъектно-предикатном языке?
Начиная с этого места, мы будем предполагать, что
наш (счетный) субъектно-предикатный язык содержит
понятия множества, равенства и натурального числа. Си-
Система Г состоит, таким образом, из аксиом для этих по-
понятий. Всюду ниже мы будем опускать знак Г в выраже-
выражениях «Г-истинно», «вывод из Г» и Т. Ц.
т

Дли разговора о субъектно-предикатном языке мы
предложим некоторый код, построенный на основе само-
самого субъектно-предикатного языка. Элементам субъектно-
предикатного языка мы припишем некоторые кодовые
числа (номера). При этом мы воспользуемся некоторыми
общеизвестными свойствами натуральных чисел.
Натуральное число р называется, как известно, про-
простым, если р =/= 1 и р не имеет делителей, отличных от 1 и р.
Простые числа 2, 3, 5, 7, И, 13, 17,... мы обозначим (в их
естественном порядке) через
Pi. Рг, Рз. Р4> Рб. Ре, Ръ--.
Теперь мы придадим в качестве кодовых номеров
числам 1, 2, 3,..., п — числа 21, 22, 23,..., 2П; другим
постоянным субъектам — числа За, З2, З3,...,; переменным
хг, хг, х3 — числа 51, 52, 53,... ; элементарным га-мест-
12 3
ным предикатам — числа 7", 7 п, 7 ™,. ..
Далее, если / есть элементарный га-местный предикат
с кодовым номером [/], a Zi,..., zn суть субъекты, имеющие
соответственно кодовые номера [г^,..., [zj, то формуле
-.jZn) мы припишем кодовый номер
если А и В — формулы (с кодовыми номерами [А]
и [В]), то формуле (А-+В) мы припишем кодовый номер
наконец, если А — формула (с кодовым номером
Ы1), а. х — переменная (с кодовым номером [х\), то фор-
формуле АХА мы припишем номер
Таким образом, каждой формуле в качестве кодового
номера приписано (по крайней мере) одно натуральное
число. Чтобы проверить, является ли данное натураль-
натуральное число кодовым номером, а если да — то к какой фор-
формуле оно относится, нам достаточно разложить это число
на простые множители и последовательно проделать все
123

шаги «обратного перевода». Для машины это не состав-
составляет никакого труда. Если, например, среди простых сом-
сомножителей какого-нибудь числа оказалось число 23, то
это число — если оно является кодовым номером — долж-
. но иметь вид 23а • 29Ь. В этом случае оно должно быть
кодовым номером некоторой формулы, имеющей вид АХА,
где А я х имеют соответственно кодовые номера а и Ь.
Эти числа а и Ь исследуются точно так же — и так вплоть
до субъектов и элементарных предикатов. Утверждение
«х входит в качестве свободной переменной в формулу А» в
результате кодирования переходит в арифметическое со-
соотношение, связывающее [х] и [А], и машина способна
«понять» это соотношение. Свойству формулы быть аксио-
аксиомой соответствует некоторое арифметическое свойство ее
числового кода, наличие или отсутствие которого также
может быть установлено машиной. Тот факт, что формулы
А\, А2,..., Ат
образуют цепочку вывода, выражается после кодирова-
кодирования посредством некоторого числового соотношения меж-
между [А)], [А2],..., [Ат], которое опять-таки может быть про-
проверено машиной.
Подобной последовательности формул 2 мы припишем
в качестве кодового номера число
То обстоятельство, что такая 2 является выводом
(из Г) некоторой формулы С, выражается посредством
арифметического соотношения между [2] и [С], которое мы
обозначим через
[2] Рг [С).
Мы можем запустить машину и велеть ей производить
одну за другой цепочки выводов. Мы можем ждать и смот-
смотреть, что из этого выйдет, но мы не можем дать машине
конкретную формулу и дать команду искать доказатель-
доказательство для этой формулы (или ее отрицанияI). Однако име-
J) И дело здесь не только в том, что описанные до сих пор
в этой книге методы не позволяют полностью автоматизировать
(или, как говорят, алгоритмизировать) .задачу отыскания доказа-
доказательства (или опровержения) произвольной формулы субъектно-
124

ющиеся у нас средства позволяют сформулировать в аб-
абстрактных терминах тот факт, что некоторая формула до-
доказуема. Доказуемость формулы о кодовым номером а
мы будем обозначать через
или, короче,
Ерг а.
Средства, с помощью которых мы здесь говорили о субъ-
ектно-предикатном языке, принадлежат этому же субъект-
но-предикатному языку. Мы можем, следовательно, сде-
сделать так, чтобы машина говорила о своем собственном
языке (в соответствии с описанным кодом). По данной
формуле машина может вычислить ее кодовый номер, а
по данному кодовому числу может построить формулу,
номером которой является это число. Машина может ре-
решить, является ли данное число п кодовым номером неко-
некоторого высказывания, является ли п кодовым номером
некоторой формулы с единственной свободной перемен-
переменной х-± и т. п.
Когда машина произвела доказательство, она может
определить кодовые номера этого доказательства и
предикатного языка (по более общепринятой терминологии —
исчисления предикатов): как доказал в 1936 г. А. Чёрч, такая
автоматизация (алгоритмизация) вообще невозможна. Однако
для некоторых фрагментов субъектно-предикатного языка такая
алгоритмизация поиска доказательства (или вывода) оказывает-
оказывается возможной (не говоря уже о пропозициональном языке, для
которого она достигается весьма просто), и проблематика, свя-
связанная с выделением таких «разрешимых» фрагментов языка (клас-
(классов формул), отысканием и упрощением соответствующих алгорит-
алгоритмов, а также алгоритмов более ограниченного типа (например,
строящих доказательство для доказуемых формул, но оставляю-
оставляющих открытым вопрос о доказуемости недоказуемых, и т. п.), в
настоящее время интенсивно развивается как за рубежом, так и в
нашей стране. Главные усилия здесь направлены на сокращение
процедур поиска вывода, так как теоретические разрешающие
алгоритмы (даже для случая пропозиционального языка), в прин-
принципе решающие проблему, на практике оказываются слишком гро-
громоздкими даже для машины. (Сходная ситуация, которую мы пре-
предоставляем обдумать читателю, возникает в шахматах, где теорети-
теоретически «тривиальная» наилучшая стратегия, состоящая, скажем
в полном переборе вариантов на десять ходов вперед, оказывается
абсолютно бесполезной не только для шахматиста-человека, но
и для машины.)— Прим. ред.
125

Доказанной формулы (скажем, Ь и а соответственно) и yr-f
верждать
b Рг а,
а также
Е рга.
5.7. И тем не менее имеющиеся у нас средства не по-|
эволяют рассчитывать на то, чтобы в непротиворечивом!
языке можно было дать определение: что такое истина.]
Это можно показать, следуя А. Тарскому A933), следую-1
щим образом.
Будем записывать то обстоятельство, что формула с
кодовым номером п является истинным (точнее, Г-ис-
тинным) высказыванием, с помощью формулы Т(п). Ины-
Иными словами,
Т(п) тогда и только тогда, когда формула
с кодовым номером я истинна. A)
Покажем теперь, что предикат Т не является предика-
предикатом нашего субъектно-предикатного языка (т. е. не мо-
может быть воспроизведен машиной), во всяком случае,
если этот язык Г-непротиворечив.
Мы рассмотрим формулы, в которые хх входит в качест-
качестве единственной свободной переменной. Записью F(n)
будем обозначать то обстоятельство, что я является кодо-
кодовым номером такой формулы. Предикат F может быть по-
построен машиной. Пусть я есть кодовый номер некоторой
формулы с единственной свободной переменной хх. Если
подставить в эту формулу вместо свободной переменной
хх число а, то получится формула, кодовый номер которой
мы будем обозначать через
S(a, я).
(Это обозначение имеет смысл только для тех я, для кото-
которых имеет место F(n).) Чтобы вычислить S(a, я), необхо-
необходимо лишь разложить на множители кодовый номер я и
заменить в этом разложении множитель 5 (кодовый но-
номер переменной хг) на 2° (кодовый номер формулы а).
Это, очевидно, может делать машина. Машина также спо-
способна образовать число S(n, n).
Рассмотрим теперь это число как арифметичес-
арифметическую функцию, которую мы обозначим через R. Иначе
126

говоря,
R(n) есть кодовый номер формулы, получающейся
в результате подстановки в формулу с кодовым
номером п числа п вместо каждого вхождения
ее единственной свободной переменной хг. B)
Функция R определена для всех таких кодовых чисел п
(т. е. для всех п, для которых справедливо F(n )). Машина
может образовать функцию R и вычислить R(n) для каж-
каждого п, для которого эта функция определена.
Допустим теперь, что машина может также построить
предикат Т, т. е. формулу Т(хг). Тогда для каждого числа
п она сможет образовать формулу
Что касается этой формулы, то машина может построить
предикат Р (т. е. PiXj) ) такой, что для каждого п формула
(~\T(R(n) ) *-* Р(п)) доказуема. C)
Положим теперь, что
р есть кодовый номер предиката Р(хг). D)
Но тогда справедливо F(p).
Заменив теперь п в B) и C) на р, получим, что
R(p) равно кодовому номеру формулы, получающейся
в результате подстановки в формулу с кодовым номером
р (содержащую единственную свободную переменную
хг) числа р вместо переменной хг. E)
Тогда
r\T(R(p)) <-> Р(р)) доказуема. F)
Если подставить теперь в E) явное выражение форму-
формулы с кодовым номером р согласно D), то получим, что
R(p) равно кодовому числу формулы Р{р). G)
Подставив теперь в A) R(p) вместо п, получим, что
T(R(p)) истинно тогда и только тогда, когда формула
с кодовым номером R(p) истинна, откуда ввиду G)
T(R{p)) истинно тогда и только тогда,
когда Р (р) истинна, (8)
137

В результате мы получили противоречие между F) и (8)
(во всяком случае, если мы требуем, чтобы никакое лож-
ложное утверждение не было доказуемым). Значит, мы дока-
доказали ложность предположения о том, что предикат истин-
истинности может быть порожден машиной.
Если предъявить вместо A) более сильное требование
к Г, а именно,
Т(п) <-> N доказуема (Г)
(где jV есть высказывание с кодовым номером и), то в ре-
результате получим
Т(В(р)) <-> Р(р) доказуемо. (8')
Таким образом, в этом случае машина даже способна вы-
вывести противоречие.
5.8. Мы знаем, что предикат Ерг может быть образо-
образован машиной. Заменим теперь в тексте п. 5.7 предикат Т
на Ерг. Тогда a priori условия, аналогичные A) и (Г),
не должны выполняться.
Но мы знаем, что
машина может преобразовать доказательство В
для А в доказательство для Ъ Рг а и обратно A")
(здесь а и Ъ — кодовые номера А и В).
Будем теперь вместо В(р) писать q. Иными словами, q
есть кодовый номер формулы Р(р), которую мы обозначим
через Q. Поскольку Т заменено на Ерг, мы получим
"~]Ерг(<7) -+¦ Q доказуема, F')
q = кодовому номеру формулы Q. (!')
В процессе обращения доказательств машина никогда не
придет к формуле
[Ь Pr q,
так как в противном случае эту формулу можно было бы
согласно A") сразу преобразовать в доказательство для Q,
а значит (в силу F')),— и в доказательство для формулы
~~1 Ерг (q), которая противоречит Ь Pr q.
С другой стороны, машина может проверить для каж-
каждой цепочки формул (если она является доказательством
128

Q), а следовательно, и для каждого Ь, какая из двух воз-
возможностей имеет место:
Ъ Рг д или " )(Ь Рг д).
Но мы только что видели, что первую формулу машина
выдать не может. Следовательно, машина получит все
формулы вида
1 Ф Рг <?)•
Поэтому можно было бы ожидать получить и обобщение их,
т. е. формулу
АГ\ (* Рг д) 1),
ИЛИ
-]VX(X Pr д).
Но это есть не что иное, как
~1 Ерг д,
а тогда в силу F') машина должна была бы доказать Q.
Доказательство В формулы Q машина могла бы тогда
преобразовать согласно A") в доказательство выражения
Ь Рг д,
где Ь есть кодовый номер доказательства В, но это, как по-
показано выше, невозможно.
Таким образом, в предположении непротиворечивости
нашего языка мы нашли такой (выразимый в машине)
предикат Ф от натуральных чисел, что машина может
доказать
Ф (а) для каждого а,
но не
Л*Ф(*).
(Ф(х) есть не что иное, как сокращение для | (a:Prq).)
Это и является основным содержанием гёделевской теоре-
теоремы о неполноте, о которой мы уже упоминали в п. 5.4.
Высказывание Лжф(а:) не доказуемо машиной, хотя
для каждого а машина сможет доказать высказыва-
высказывание Ф(а).
Тот факт, что это недоказуемое высказывание в из-
известном смысле утверждает свою собственную недока-
недоказуемость, заставляет нас считать его истинным.
Здесь мы для краткости опускаем требование Z(x).
129

В таком случае напрашивается идея добавить ЛжФ(а;)
к Г в качестве новой аксиомы. Останется ли в таком
случае система непротиворечивой? Казалось бы, что да.
Ведь ЛжФ(а:) -*- (g) означает также V,. | ф(х). А если от-
отсюда мы сможем получить (для некоторого числа а) фор-
формулу ~] Ф (а), это будет противоречить тому, что Ф(а)
для всех а. Но такое заключение было бы слишком по-
поспешным: из п. 4.15 мы знаем, что для доказуемой форму-
формулы V^ может и не найтись «примера» А (а). Однако Ф
можно изменить (мы этого здесь делать не будем) таким
образом, что высказывание Лд.Ф(а;) действительно может
быть добавлено к Г без нарушения непротиворечивости
(хотя с высказыванием Ерг ЛЯФ (х) дело обстоит не так).
Но и в обогащенном таким путем языке снова можно
будет найти высказывания, подобные Ф.
5.9. Что же касается формулы |Л,,.ф(а:), то ее-то во
всяком случае можно добавить к нашему языку без нару-
нарушения непротиворечивости (ибо вывод (g) из ~~] Лжф (х)
являлся бы доказательством недоказуемости Ляф (х)).
В языке, обогащенном новыми аксиомами, как раз и ока
жется, что
высказывание УХА доказуемо, но нельзя доказать
никакого конкретного «примера» А (а) (*)
(в качестве А надо взять ~~| Ф (х)).
Согласно теореме о полноте мы можем добавить к тако-
такому языку такое количество новых постоянных субъектов,
что (*) уже больше не будет иметь места. В нашем случае
этими новыми константами оказались бы, конечно, новые
натуральные числа. Но какие? Ведь в нашем языке уже
имеются все натуральные числа. Разумеется, системы
Пеано способствовали представлению (совершенно ошибоч-
ошибочному!), что они совершенно адекватным образом уточняют
интуитивное понятие натурального числа. Но мы только
что пришли здесь к понятию «числа», удовлетворяющему
этим аксиомам и в то же время совершенно не согласую-
согласующемуся с привычным интуитивным понятием.
5.10. Но почему бы нам просто не запретить языки, для
которых имеет место (*)? Добавим, например, в качестве
правила вывода к каждому субъектно-предикатному
языку|
если F(a) для каждого постоянного субъекта a, roAxF(x)
130

или
если VxG(x), то существует постоянный субъект а
такой, что G (а).
Все дело в том, что такое «правило вывода» было бы со-
совершенно бесполезно для машины, так как если коли-
количество постоянных субъектов бесконечно, то машина
никогда не сможет завершить задание по провер-
проверке F{a)\
5.11. Мораль всего сказанного такова: формализуя
словесный оборот «все» посредством квантора Л, мы пы-
пытаемся заключить бесконечное в конечные рамки. Но
при зтом мы можем рассчитывать лишь на частичный
успех.

(б)
=
А
(А
= (А\В) U
4 \ В) U {А
\ В) U [А П
И п
(Я4
В) =
3\С)
\С)[[}
U (J
(Л
5 П
п ^
Ответы
1.10
1(а) Для х Ei существуют ровно две взаимно ис-
исключающие возможности: либо х Ez В, т. е. х ЕЕ А П В,
либо х §Ё В, т. е. х ^ А \ В.
С)
здесь соотношение 1 (а) было использовано дважды, а
дистрибутивность была использована один раз. Анало-
Аналогичный анализ для В ж С показывает:' (левая часть
соотношения 1F)) сг (правая часть 1F)). Обратное оче-
очевидно, (в) Аналогично 1F). (а') См. задачу 1 (а), (б') Ана-
Аналогично, (в') А = С, В = D = О-
2 (а) Следует из задач 1(а),(а')- F) То же. (в) См.-
п. 1.9. (г) Примените дистрибутивность.
(д) (А\С)\(В\С)=]
= (А П С*) \ (В П С*) = {А П С*) П E П С*)* =
= (Л ПС*) П E* U О = Л ПС* П5* = (А П 5*) ПС* =
(е) Следует из задачи 2 (д).
3. См. задачи 1F) — (в).
3.12
2.
3.
132

4 • Аж, „, г [{хКу A yKz) -* xJz ].
5. Vy{xGy).
6. V», „, z (M (x) A yKx /\yGz/\V (z) A xJz).
7. Vu, „(M (x) A ^B/) A xKu A */#« A «JP» A
/\yKv /\uGv).
8. V,, VtZ(V(x)/\U(x)/\M (у) АА(У)Л *KzA yKz) -
9.
10.
11. Av(yKx-+Vz(yGz)).
12.
13.
14.
15. V», vAUt v [(uKx -+ Vp (pKy A uGp)) A {vKy
16. Vx<v-]Vu>v(uKxAvKyA^Gv).
17. yKx->{Az[zKy-±Vu(uKxAzKu)]}.
18. Истинно независимо от значений К и U.
19 — 21. См. п. 3.10 (а также п. 2.10).
22. AtVxZ(x,t).
23.
24.
25. AxVtZ(x,t).
26. At,x{Z(x,t)-*P(x,t)).
27. \,[2(г,0-*У|'(К'
28. Л(, x [P (x, t) -> V(, ((/' < t) A Z (x, <'))] •
29.
30. -|V*-|V,i>(M).
31. Ax[AtZ(x,t)-+-}Vt,P(x,t')].
32. ^x("lZ(z, t)/\~\P(x, t)).
133

33. A
34.
35. At(AxZ(x,t)\/-]VxZ(x,t)).
36. V
37. л^ж, r,r [Z(x,«')/\(f <t)A%(*. ПA(t<П].
38. Ax, Vt t {[Z(x, t)AZ(У, t)] -*/r [(t< t')->'
39. Ax{Vt[(Z(x, t)/\P{x,
40. Истинно.
41. Истинно.
42. Ложно.
43. Истинно.
44. Ложно.
45. Истинно.
46. Ложно.
3.15
1. \хА{х).
3. \х(хКу).
47. Истинно.
48. Истинно.
49. Ложно.
50. Ложно.
51. Истинно.
52. Истинно.
53. Истинно.
54. Истинно.
55. Ложно.
56. Истинно.
57. Ложно.
58. Истинно.
59. Истинно.
60. Ложно.
5. \tVx[Z{x, t) /
6. t*V, {P(x, t) А  Vr[(«' <t) A Z(x, t')]}.
7. Второе и третье выражения бессмысленны. Мы мо-
можем поставить \х лишь перед высказыванием (зависящим
от х), но не перед обозначением множества.
8. Истинно. 10. Истинно. . 12. Истинно.
9. Истинно. И. Истинно. 13. Ложно.
14. Множество всех подмножеств множества А.
15. Истинно. 16. Ложно.
17. Ложно. 18. Множество делителей у.
19. Множество кратных х.
20. Множество общих делителей у и z.
21. Множество общих кратных х и у. 22. (а).
134

23. Множество простых делителей а.
24. Класс эквивалентности, которому принадлежит у.
25. Истинно.
3.17
1. О* 2. Множество подмножеств множества А.
3. О- 4. Множество натуральных чисел.
5. Множество степеней простых чисел. 6. О-
3.24
I. Х^. 2. XsYx. 3. М* (* ci). 4.
5. M*Z(*. О- 6. K,yxGy.
7. Ьж,у[ад Л ^(У) A Vu,v(*Ku /\vKu A
8. A, 2).
9. Предикат «быть положительным»; множество поло-
положительных чисел.
10. Функция, сопоставляющая некоторым функциям
их значения от аргумента 1.
II. Множество функций, сохраняющих операцию сло-
сложения.
12. M
3.27
2. ?tVpF(x,x, t,p).
3. ?рЛ(.
4. JhAr.K.pVyl^z, г/, t\ p)/\VzF(z, x,

Ханс фрейденталь
Язык логики
М., 1969 г., 136 стр. с илл.
Редакторы В. В. Донченка, К. А. Михайлова
Техн. редактор И. Ш. Аксельров
Корректор Л. С. Сомова
Сдано в набор 16/VI 1969 г. Подписано к печати
24/XI 1969 г. Бумага 84Х108'/12. Физ. печ. л. 4,25.
Условн. печ. л. 7,14. Уч.-изд. л. 6,75.
Тираж 16 000 экз. Цена книги 49 к.
Заказ JVj 2598.
Издательство «Наука»
Главная редакция
физико-математической литературы.
Москва В-71, Ленинский проспект, 15
2-я типография издательства «Наука».
Москва, Шубинский пер., 10