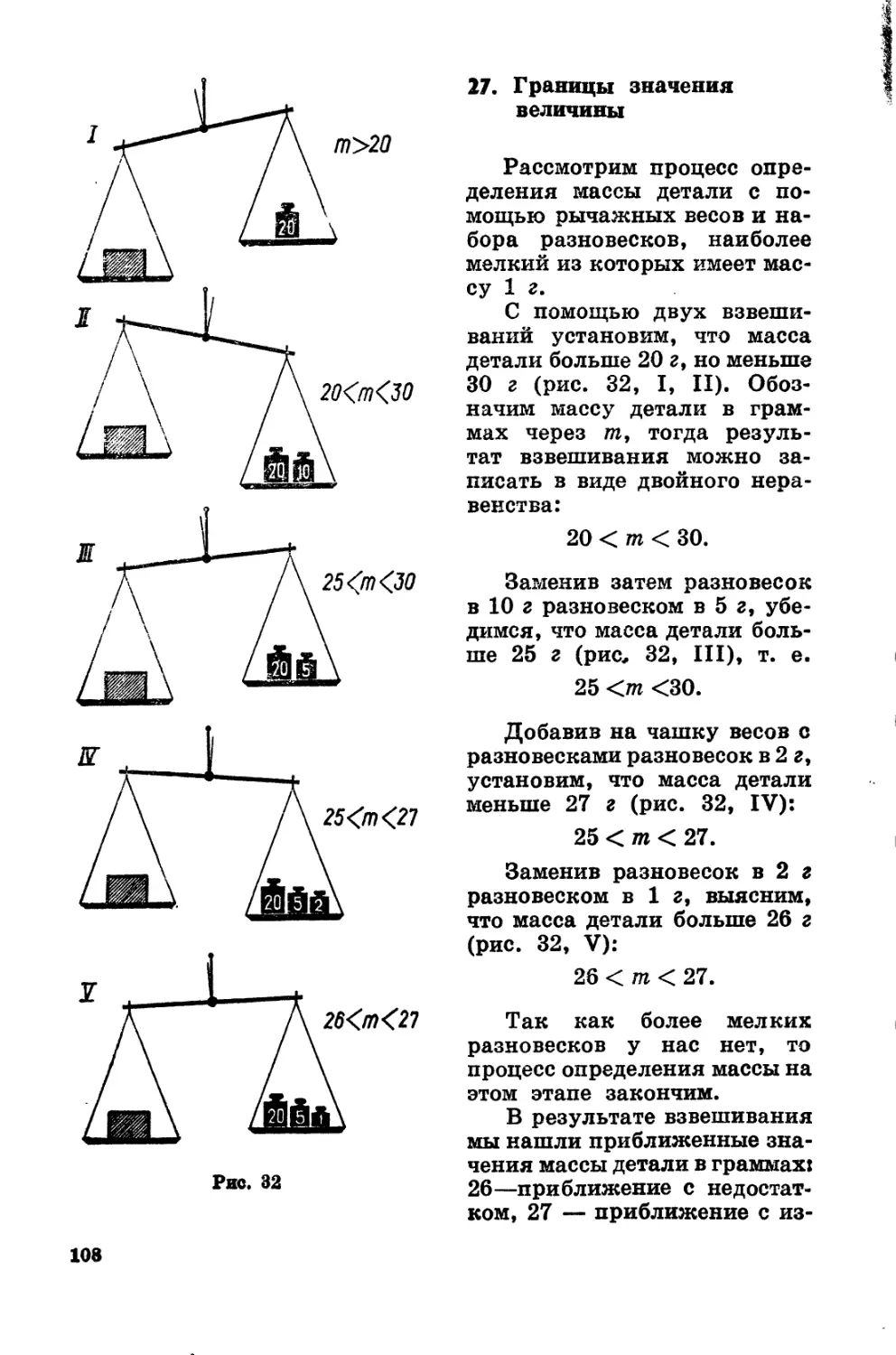
Текст
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ
И УСЛОВИЕ РАВЕНСТВА ДРОБИ
НУЛЮ
1
1 !
2
з
4
А
2х-2
5х-20
2а-0,6
0,3а+6
Зх+1
х(х-З)
2у+1
у2-100
В
25
8х+2^
0,12а+2,4
1,5а-45
(х+10)(х-5)
5х-1
4у2-1
у2+4
С
20х-5
12
60
0,01а+4
(5х-1)2
х(2х+3)
25у2+0,1
9у2-4
D
12х-8 1
9х+12
1 1
1
| 1
1
1
1 ЮОа-0,5
! 72^
| 1
1 1
! 1
; (5х+2)3 1
(5х-1)(х+5)
2у*+у
у2-0,25
ГРАФИЧЕСКОЕ РЕШЕНИЕ
НЕРАВЕНСТВА
К*>9(х)
и
1
It
1
1
Г Я^ь
I
[
[
1
[
кишмтилшшт
j\
1 1
1
1
•6т
•\jm
V
4*
h>
п
ъ
п
0
1
i
I t
1
3
1
1
-Л
W
>^te
X
АЛГЕБРА
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ 1-го КЛАССА
СРЕДНЕЙ ШКОЛЫ
Под редакцией А. И. МАРКУШЕВИЧА
Утверждено Министерством просвещения СССР
ИЗДАНИЕ 6-е
МОСКВА «ПРОСВЕЩЕНИЕ» 1977
612 (075)
A 45
Ю. Н.МАКАРЫЧЕВ, Н. Г. МИНДЮК,
К. С. МУРАВИН, С. Б. СУВОРОВА
60601—178
103<03)_77 М,Ф' Ш,СЬМ°
Глава I
ДРОБИ
§ 1. ПОНЯТИЕ ДРОБИ
1. Целые выражения
Числовые выражения, а также выражения с переменными,
в которых используются операции сложения, вычитания,
умножения, деления и возведения в степень, называются
рациональными.
В VI классе мы изучали целые рациональные выражения —
это все числовые выражения, а также такие рациональные
выражения с переменными, которые не содержат операции деления
на выражение с переменными.
Было показано, что всякое целое выражение можно
преобразовать в тождественный ему многочлен стандартного вида.
Например, выполнив преобразование а (а2 + 4а — 12) —
— (2а — З)2 = а3 + 4а2 — 12а — 4а2 + 12а — 9 - а3 — 9, мы
целое выражение а (а2 + 4а — 12) — (2а — З)2 представили
в виде многочлена а3 — 9 стандартного вида.
Было показано также, что некоторые многочлены можно
преобразовать в произведение, т. е. разложить на множители.
При этом использовались различные способы.
Например, многочлен х3 — 5я2 + 30* можно разложить на
множители путем вынесения общего множителя за скобки:
х* _ 5х2 + 30* = х (х2 — Ъх + 30).
Многочлен аЪ — 2Ь + Ъа — 10 можно разложить на
множители, применяя способ группировки:
аЪ — 2Ъ + Ъа — 10 = (аЪ — 26) + (5а — 10) =
= Ъ (а — 2) + 5(а— 2) = (а — 2) (Ь + 5).
При разложении на множители двучлена у3 — 64
используется тождество сокращенного умножения (разность кубов двух
выражений):
уз _ 64 = уз _ 4з в (у _ 4) (уа.+ 4у + 16).
8
При разложении некоторых многочленов на множители
используется несколько способов:
Зг/5 - 243у = Зу (у* - 81) = Зу (у2 - 9) (у2 + 9) -
= 3i/(i/ — 3) (у + 3) (у2 + 9).
Существуют многочлены, которые нельзя представить в
виде произведения двух многочленов не нулевой степени.
К числу таких многочленов относится, например, двучлен
х2 + 1.
Бели бы такое разложение было возможно, то многочлен дс2 + 1 можно
было бы представить в виде произведения двух многочленов первой степени,
каждый аз которых при некотором значении х обращался бы в нуль. Но тогда при
том же значении х обратился бы в нуль и тождественно равный произведению
двучлен *2+1, а это невозможно, так как при всех х значение х3 неотрицательно,
а значение ж2 + 1 положительно.
1. Преобразуйте выражение в многочлен стандартного вида:
а) х (х + 3); д) 2р2 (Зра - д2) + 2р У;
б) 2у (у - 5); е) 6д3 - g (4р2 - Зд);
в) За (о2 — 2а — б); ж) 2 (то — Зл) + 3 (то — 2л);
г) ЪЬ (1 — 36 — 6*); з) о2 (о2 + б2) — б2 (а2 — б2).
2. Представьте в виде многочлена стандартного вида:
а) (х - 2) (х+5); в) (с+4) (а - 4); д) (р +1) (р +1);
б) (у+8)(у—7); г) (6-3)(6+3); е) (9 -?)(? -9).
3. Замените выражение тождественно равным многочленом
стандартного вида:
а) {у-ЬЪ)(у+ЬЪ)\ г) (р2-1)(1-р2); ж) (-у + Ь)2;
б) (2с+3)(3 —2о); д) (*+7)2; з) (-Зр-д)2.
в) (36 — 1) (36—1); е) (а — 2х)2;
4. Решите уравнение:
а) — 5* = 16; д) 2(х—5)— 3(8 — *)=1;
б) 2х = А. е) 18 -15 (у -3)=5 (9- у);
' б' ж) х(х — 8)—х(х— 9) =25;
1 8 ' и) (х+ 3) (х— 5) = (*+1) (.г + 6);
г) 0,01у = -1; к) (у + 3) (у-4) = (у- 2)(у + 6).
5. Представьте выражение в виде произведения:
а) ах + ау; е) 8а6 + 126с;
б) 56—5с; ж) хг—ху,
в) бто —18; з) ху — у2;
г) Юл+ 15; и) 8ху'+ бху2—18ху;
д) 15а*— 20ау; , к) 15а36 + 10а26 — 20а262.
в. Разложите на множители:
а) Ь(у — 3) — х(у — 3); д) рд_4р + 12 —Зд;
б) ту — тх+пу — пх; е) а2+ аЬ +ах + Ьх\
в) а6+8а+9Ь + 72; ж) х2— ху—5х+ Ьу\
г) 6т — 12 — 2п+гпп; з)а + Ь—а2—аЬ.
7. Представьте многочлен в виде произведения:
а) а2—9; в) х2— 4у2; д) я3— 4л:; ж) а2—6а+9;
б) 16—с2; г) 25а2— б2; е) 49р3—р; з) 16*2+8ж+1.
8. Решите уравнение:
а) (*_2)(*+5) = 0; г) х2—12*=0; ж) *2+9=0;
б) (у+8)(2у—3) = 0; д) *2+21*=0; з) 25л;2— 4=0.
в) 4 (х — 3) =0; е) у2— 64 = 0;
9. Представьте в виде произведения:
а) а3-8; в) 1-8у3; д) me-l;
б) 27bs+l; г) у3— 64fr3; e) p8—q*.
10. Постройте график функции:
а) у = ^-х; б)у = 2х — 3; в) у = — ^-х+2; г)у=0-*+4.
2 4
Укажите множество значений х, при которых:
у=0; у>0; #<0.
11. Постройте графики функций у=х и у = |#|.
Пользуясь графиком функции y = \x\f решите уравнение:
а) |х| = 2; б) \х\ = 0; в) |*| =* —3.
12. Проходит ли график функции у=5х2 через точку А (2; 20),
В (-2; 20), С (2; -20), £>(|; 1,2б1 J5?f-|;-1,2б)?
13. Длина прямоугольника втрое больше его ширины. Если
длину и ширину этого прямоугольника увеличить на
5 еле, то его площадь увеличится на 140 см2. Найдите
длины сторон данного прямоугольника.
14. Длина прямоугольника на 10 см больше его ширины.
Если длину уменьшить на 15 см, а ширину увеличить
5
на 5 см, то площадь прямоугольника уменьшится на 105 еле2.
Найдите площадь данного прямоугольника.
15. Из двух городов, расстояние между которыми 180 км,
навстречу друг другу выехали одновременно мотоциклист
и велосипедист и встретились через 2 часа. Найдите
скорость велосипедиста, если известно, что мотоциклист
проезжает за час на 60 км больше, чем велосипедист.
16. Из натурального ряда выбрали три последовательных
числа так, что произведение второго и третьего числа
оказалось больше произведения первого и второго числа на 80.
Найдите среднее число.
2. Дробь. Область определения дроби
Выражение вида —, где буквами а и Ь обозначены выраже-
ь
ния числовые или содержащие переменные, называют дробью.
Выражение а называют числителем дроби, выражение Ъ —
ее знаменателем.
1 1.
3 16 -1-3*7 7 3
Дроби —, , являются числовыми выражения-
5 0,02 22
1 1
8 х2 — Ьх + 7 а Ъ
ми, а дроби —, !—, выражениями, содержа-
а у — 2 10
щими переменные.
Для отыскания значения числового выражения,
представленного в виде дроби, обычно находят значение ее числителя и
знаменателя и первый результат делят на второй. Если
знаменатель дроби равен нулю, то такая дробь не имеет значения,
так как делить на нуль нельзя. В таких случаях говорят, что
дробь не имеет смысла.
Значение дроби, содержащей переменные, зависит от
значений входящих в нее переменных. Например, дробь ^-i— при
а — 5
2
а = 8 принимает значение, равное 3—, при а — 4 ее значение
з
равно —7.
При а = 5 дробь а не имеет смысла. Число 5 —
единых — 5
ственное значение переменной а, при котором рассматриваемая
дробь не имеет смысла. При всех остальных значениях а эта
дробь имеет смысл.
6
Говорят, что область определения выражения ° есть
а —5
множество всех чисел, кроме 5.
Определение. Областью определения выражения с
одной переменной называется множество значений переменной,
при которых это выражение имеет смысл.
Целое выражение имеет смысл при всех значениях
входящих в него переменных. Например, многочлен уъ—8у2 + 3у — 17
имеет числовое значение при любом значении у, так как для
нахождения значения этого многочлена придется над числами
выполнять действия: возведение в степень, умножение,
сложение и вычитание, которые всегда возможны. Поэтому область
определения целого выражения есть множество всех чисел.
Чтобы найти область определения дроби, числитель и
знаменатель которой—целые выражения, причем знаменатель —
выражение с переменной, нужно найти значения переменной,
обращающие знаменатель этой дроби в нуль, и исключить их из
множества всех чисел.
Приведем примеры.
х 4
1. Найдем область определения дроби .
АХ —J— О
Числитель и знаменатель этой дроби имеют смысл при
любых значениях х.
Выясним, при каких значениях х знаменатель дроби
обращается в нуль. Для этого решим уравнение:
2x-f6=0,
2х = —6,
х = —3.
х 4
Дробь имеет смысл при x=h—3, т. е. область
определения данной дроби (обозначим ее буквой X) состоит из всех
чисел, кроме —3.
Это можно записать так: Х=] — оо; —3[|J]—3; +°°[.
2. Знаменатель дроби при любых значениях а от-
а2 + 1
личен от нуля (уравнение а2+ 1 = 0 не имеет корней). Поэтому
область определения этой дроби есть множество всех чисел:
] —оо; +оо[.
3. Знаменатель дроби при любом х равен нулю. По-
л: — д:
этому область определения выражения есть пустое
х — х
множество. Такие дроби мы в дальнейшем рассматривать не
будем.
7
Область определения дроби, содержащей две переменные,
например дроби , состоит из множества пар чисел вида
х — У
(х; у), которые не обращают знаменатель х—у в нуль (т. е.
не являются решением уравнения х—у=0). Пары чисел (2; 2),
(—2,3; —2,3), (31—; 31—) и вообще все те, у которых
значение х равно значению у, не входят в область определения
дроби . Если же значение х не равно значению {/, то х — у не
х-у
равно нулю и в этом случае дробь имеет смысл.
х — У
Условие, при котором дробь имеет смысл, можно за-
х — у
писать кратко: х—у ф 0 или хфу.
17. Какие выражения являются дробями:
£, ±ъ, -A-f iL + i, L9 2l, £.1?
6* б х-у 2с 1 7 5 Ъ
18. Составьте дробь:
а) числитель которой — произведение переменных х и у,
а знаменатель — их сумма;
б) числитель которой — разность переменных а и bf a
знаменатель — их произведение;
в) числитель которой — разность квадратов переменных
х и у9 а знаменатель — сумма квадратов этих
переменных;
г) числитель — удвоенное произведение переменных а и
6, а знаменатель — сумма кубов этих переменных.
19. Найдите значение дроби:
0,75 - 0,4 — 5,7 ч 1292 — 712
а) ; в) ;
1,86 : 0,31 58
-ч 1,95 : 1,3 + 2,5 ч 2532 — 472
5) ; г) •
3,4 • 0,8 + 3,28 300
20. Найдите значение дроби ^=L- при у = 3; 1; —5; —; —1,6.
У 2
х 4- 5
21. Найдите множество значений дроби ——, зная множест-
л: — 3
во значений переменной х:
J7; 1; 0; -5; б|; -13; -0,2; I}.
8
22. Найдите значение дроби *а~*~ ' при:
а2 4- Ь2
а) с = — 3, Ъ = —1; б) а = 1-; 6 = —0,5.
23. При каком значении переменной значение дроби:
v х — з - v р — 7 с
а) равно 1; в) равно 5;
б) равно —1; г) равно 9?
24. Найдите область определения дроби:
.)JLS B)fi-4; д)-^: «)*=»;
х — 2 1 — 2х 3 (4г/ — 1) 10
б) -*!-; Г) -JL-; е) —^—; в) *2-2*-3.
* + 6 7f/ + 2 ' Ь(9 + 10у) 25
25. Найдите область определения выражения:
б) i/3-2j/2 + 3j/-6; з) •
е)—^—;
в) 16 . уа + 1
—+ 7
г) —— ; ж) - ; к)
а(а-4) х — 2' |Я + 2
26. Функция / задана формулой. Найдите область
определения функции f:
ч 1 _ч 12 ч 9 ч б
а) у--; 6),/ = —; в) у = -^ г) у - _.
27. Напишите дробь, которая не имеет смысла при:
а) х =7; в) у =6 или у=13;
б) а = —9; г) 6=0 или & = —2.
28. При каком условии дробь не имеет смысла:
а)-£-; 6)-£-; в) -JL-* г) -j-*—; д)-Ь е)-^-?
а — Ь а + Ь а2 + Ъ2 a2 — b2 ab а (Ь— 2)
8
f/
1*
9
— 4
a
|-5
41
§ 2. СВОЙСТВА ДРОБЕЙ
3. Условие равенства дроби нулю
Если числитель дроби равен нулю, то дробь либо равна
нулю, либо не имеет смысла.
Например, дроби —, , —г- равны нулю, а дробь — не
~~ ' 2—
11
имеет смысла.
Если дробь равна нулю, то ее числитель равен нулю,
а знаменатель отличен от нуля (иначе дробь не имела бы
смысла).
Итак:
Дробь —равна нулю тогда и только тогда,когда а = ОиЬфОш
ь
Покажем, как условие равенства дроби нулю можно
использовать при решении уравнений.
Рассмотрим примеры.
2х 5
1. Решить уравнение = 0.
2% 5
Дробь обращается в нуль при тех и только тех зна-
3 + х
чениях х, при которых 2х — 5 = 0 и 3+хф0, т. е. при тех
значениях х> которые являются решениями системы:
\2х— 5 = 0,
\Ъ+хфО.
Уравнение 2х—5=0 имеет корень, равный 2,5. При этом
значении х выражение 3+х отлично от нуля: высказывание
3+2,5=7^=0 истинно. Следовательно, число 2,5—корень уравне-
ния = 0.
3 + *
Решение можно записать так:
2х — 5
-0;
з + *
2х — 5 = 0,
3 + х ф 0;
2х — 5 = 0,
2х = 5,
х = 2,5.
Высказывание 3 + 2,5 ф 0 истинно.
Ответ: 2,5.
10
~2 K«
2. Решить уравнение - — = 0.
10 — 2*
х2 5*
Дробь обращается в нуль тогда и только тогда, когда
10 — 2х
х2 — Ъх = 0 и 10 — 2х ф 0, т. е.
(Х* — Ъх = О,
IЮ — 2х Ф 0.
Решим уравнение
х2 — 5х = 0;
х (х — 5) = О,
х = 0 или я = 5.
Проверим, обращается ли при этих значениях лс
предложение 10 — 2х ф 0 в истинное высказывание.
Пусть х = 0. Высказывание 10 — 2 • 0 =^= 0 истинно.
Пусть я = 5. Высказывание 10 — 2 • 5 =^= 0 ложно. .
Данное уравнение имеет единственный корень 0.
Ответ: 0.
29. Известно, что числитель дроби равен нулю. Следует ли
отсюда, что дробь равна нулю?
30. Известно, что дробь равна нулю. Следует ли отсюда, что
ее числитель равен нулю?
31. Докажите, что значение дроби равно нулю:
1 5\ 1 / 2 1 1\
-_- .8 — — И— : 7— — — • 0,23
ч \4 24/ 3 ^ч \ 9 3 6/
а) - -; б) .
1,85—1,62 1
2— + 1,2
8
32. Какая из дробей не имеет смысла:
8,3 • 1,2+4,2 5,6 • 2,1 — 11,76 9
ИЛИ
(3— — 2—) .5 — 7— (б — 3—| -6 — 7,9
\ 5 15/ 3 V 3/
33. Какая из дробей равна нулю:
11 2 2
3,6: 1--2.5 _8:- + 2-9
или ?
27 3 15 3 4 5
- : 9 — — : 1— 1— • — — 1 : —
31 4 16 4 5 7
11
34. Докажите, что значение дроби равно нулю:
ч х (х —- 5) — 0,5* (2* — Ю) , 0
а) — - - при всех х ф 2;
X —— <2
б) -—■— при всех хф— 2 и хф2.
*2— 4
35. Напишите дробь, которая содержит переменную у и
обращается в нуль при:
а) у = 8; б) у = —1.
36. При каких значениях у значение дроби равно нулю:
а) 1; в) t^f; д) ^^L;
5 У2 + 1 8
б) !L=!; Г) 1±1; е) 0г-тнц-ц?
3 у—1 у
37. Существуют ли значения переменной х> при которых
дробь равна нулю:
а) ; б) ; в) ^ ; г) —1—?
*— 2 7 * + 5 *2 + 1
38. Решите уравнение:
al'-^Oi г)^ = 0; ж)^=^^0;
125 ' х — 2 ' 2х
^ч 5* —12 Л ч х — 5 л ч л:2 + 16 л
б) ——— = 0; д) ; = 0; з) —Г— = 0.
37 5 — * х
в) = 0; е) —С— = 0;
39. Функция задана формулой. При каком значении х
значение функции равно нулю:
ч х tf4 л:—4 ч х + 9 ч (л: -f 5) (ж—7)«
а) г/ = —; б) г/ = ; в) г/ = —2—; г) у = —-—— '?
40. Функция / задана формулой у = - + '**—■-*-
х-2
Найдите: а) / (0), / (—3), / (3), / (12); б) область
определения X функции; в) множество значений переменной х,
при которых / (х) = 0; г) координаты точки пересечения
графика функции с осью у. Проходит ли график функции
через точку А (7; 2), В (—6; 9)?
12
4. Основное свойство дроби. Сокращение дробей
Сравним соответственные значения дробей -^- и —.
ох 8
З*2
При х = 0 дробь — не имеет значения (не имеет смысла\
8х
Поэтому в этом случае нельзя указать пару соответственньп
3#2 Зж
значений выражений и —. Для всех остальных значений д
8* 8 ^
соответственные значения этих выражений существуют.
При х = 2 соответственные значения этих дробей равны:
3*а 3. 2* 8
■ __ ■ гт: .
8х' ~~ 82 4
3* 3-2 3
— — ■ —— —
8 8 4
Соответственные значения рассматриваемых дробей равны
и при любых других значениях переменной х, где х ф 0. Это
следует из свойства частного: если делимое и делитель
умножить или разделить на одно и то же число, отличное от нуля,
то значение частного не изменится. Следовательно, можно
утверждать, что все соответственные значения рассматривае-
3#2 Зх
мых дробей равны. Это значит, что дроби и — являются
8х 8
тождественно равными, а равенство
3*а __3*_
8* "~~ 8
тождеством.
Рассмотрим дроби — и —. На основании свойства ча-
Ьс Ъ
стного при Ь ф Оке ф 0 все соответственные значения этих
дробей равны. (При 6 = 0 или с = 0 одна дробь или обе дроби не
имеют значений.)
Поэтому дроби — и — являются тождественно равными, а
Ьс Ь
равенство
тг-т- (1)
be Ь
тождеством.
Тождество (1) выражает основное свойство дроби. Оно
позволяет заменять дробь вида — тождественно равной
Ьс
дробью — или, как говорят в таких случаях, сокращать дробь
b
— на общий множитель с числителя и знаменателя.
be
13
Рассмотрим примеры сокращения дробей,
2х(х 2)
Пример 1. Числитель и знаменатель дроби —- -
5(* — 2)
содержат общий множитель х — 2. Сократив данную дробь на
общий множитель, мы выполним тождественное
преобразование:
2х (х — 2) __ 2*
5(* —2) ~~ б"
Заметим, что области определения дробей — - и —
5 (х — 2) 5
различны. Область определения первой дроби есть множество
всех чисел, отличных от 2, а область определения второй
дроби — множество всех чисел. В результате сокращения мы
получили дробь, область определения которой шире, чем область
определения исходной дроби.
а2 9
Пример 2. Для упрощения дроби разложим на
аЪ-\- ЪЬ
множители ее числитель и знаменатель и выполним
сокращение:
а2 — 9 _ (а — 3) (а + 3) _ а — 3
ab + гЪ Ъ (а + 3) Ь
п р и м е р 3» Пусть требуется сократить дробь
Выполнив преобразование, получим:
а*&*
а*Ь4 а5Ь4 Ъ
Выражение — тождественно выражению . Действи-
ь ь
тельно, при любых значениях а и Ъ (Ь ф 0) значение каждого из
этих выражений есть число, противоположное значению дроби
—. Поэтому все соответственные значения выражений и
ь ь
— равны и равенство
т—j (2)
есть тождество.
Если числитель и знаменатель дроби — умножить на —1,
ь
то получим дробь, тождественно равную первой:
—а —а • (—1) а
~Т ~ Ь • (—1) ~~ —&'
Поэтому равенство
также является тождеством.
14
Тождества (2) и (3) применяются в тождественных
преобразованиях выражений, содержащих дроби. В частности, когда
выполняют сокращение дробей, то дроби вида — или —
ь —ь
принято представлять так: . Поэтому, выполнив преобра-
ь
зование дроби —, окончательный ответ следует записать
в виде ——.
ъ
Мы знаем, что деление можно заменить умножением делимого на число,
а
обратное делителю. Поэтому все соответственные значения выражений —
Ъ
1
и а • ■— равны и равенство
о
aL_ £
Ъ~°" Ь
есть тождество.
Из этого тождества следует:
1. — • Ъ — \а • —I . 6 = а • [— . Ъ) — а • 1 = а.
Ь \ Ъ) \Ъ )
—а 1 1 / 1\ а
Мы показали, что равенства
а —а а
— • Ь = а и — =— —
Ъ Ь Ъ
являются тождествами.
41. Какими числами (равными, противоположными,
обратными) являются соответственные значения выражений:
а) х и -; в) £- и —Ц д) -£ и -*-.
х 5 5 5 —5
б)±и 1; Г) У. И_*.; e)JLK =*?
Ь а 5 5 5 —5
42. Сравните соответственные значения дробей ~* с и — при:
ъ -\-с ь
а) а = 3, Ь = 5, с = 7; б) а = -, & = —, с = — К
2 3 6
15
43. Сравните соответственные значения выражений — и —
be Ь
при:
а)а=3, Ь = 5, с = 7; б) а = i-, & =-, с = — i.
2 3 6
44. Найдите общий множитель числителя и знаменателя и
сократите дробь:
а)!-; б) £; в) «^ г) „4; д) -=?=; в) -51и
3* 24у а2 7&2 —Юр2 —17/п»-
45. Сократите дробь:
ч 10* ч 2а ч аЪ ч ад;2
а) —; в) —; д) ; ж) ;
1Ъу —Ау —ас ху
-v 6а ч —6р ч —ab ч тпп
б) —; г) —-; е) ; з) .
46. Упростите выражение:
ч За* v 4а2 ч а^Ь3 7р2*3
а) —; в) —; д) ; ж) ——;
bay вас а*Ь* 23р3*«
б)5^; p)J?gL; e)*j^ в) 63,V
15а&' 48**/2' *V ' 42*V "
47- Представьте выражение в виде дроби со знаменателем Юя:
ч —a w4 а ч а ч —а
а) ; б) ; в) ; г) .
—10* —Юле ' —10* 10*
48. Упростите выражение:
а)-2^. B)Z^M. rtJ-W.
За3 ' (—8Ь3)2' (—6oV)*'
—20*2 15* V (—4а3)*
49. Найдите значение выражения:
ч 81* Лч 8126
а) ; б) .
1612 2733
50. Сократите дробь:
а) а(Ь-2). б) 3(* + 4). в) 15a*(a-&). , 3%(*+2у)
5 (Ь — 2) * с (а: + 4)' 10Ь (а — Ь) ' 42* (* +2у)"
51. На рисунках 1 и 2 изображены графики функций
(* + 2) (* — 2) (* — 1) (* — 2) _
w = _ь—\—П L и у = J l^ l. Почему точка
" х+2 V *-1
Р (—2; —4) не принадлежит графику первой функции, а
точка Q (1; —1) — графику второй функции?
16
г
■Ч
^
Л
г
F
,
у
-J
V-
J\
\
Т
J
0
L
1
/
0
;-/
4
7
J
Л
'
"У
ч
V.
►
^
^
X
-£
-2
А
!
и\
Jl
i
7
J
2
/
^
7
/
4
7
J
l-£
;*
i
Г
3
4
X
Рис. 1
Рис. 2
52. Докажите, что следующие дроби не являются
тождественно равными:
а) —>— и —;
6 2
б) —— и —.
а а
53. Разложите на множители числитель или знаменатель
дроби и выполните ее сокращение:
а)
б)
За+12Ь
Gab
15& — 20с
в) т
3*
9х — 6у
г)
Д)
е)
1т
1т + 21п
а2—6а
ж)
2а —4
3(а — 2)
к)
8х*+15*у"
За»
5л: (у+ 3)
6у +18
И)
а — ЗЬ
8*у —Зу2' ' а* —За&*
54. Напишите выражение, противоположное данному:
а) х\ в) а—Ь;
б) —2р; г) 2л: —у; е) — ^; з)
A)f;
е)-т;
ч а —Ь
ж) ;
7 з
12
Я — Р
55. Известно, что при некоторых значениях а и 6 значение
дроби равно 5. Найдите при тех же значениях а и Ъ
а—Ъ
значение выражения
1
а)
Ь —а
б) а — Ъ\ в) Ъ — а; г)
&-а
17
56. Докажите тождество:
а) = —1; б) *—— = z.
о —а л: + У х + У
57. Упростите выражение:
a) 5(g-6); г)22'—*>; ж) ^"»; к) ^=i*_*.
8(Ь—а) 33а(3с —а) а (3 — х) ' 30 —Юс
б о (дс — 2у), . -45Ь(2&-7). -6pg + ЗОр .
}Ъ(2у-х)9 Ш2(7-2Ь)' Зе-10 '
в)5*(*~у); е) 8(fl^12) ; и) 2а~8Ь-
*3(У — «)' 126 — аЬ ' 126—За'
58. Сократите дробь:
а) *>2-*2 . б) х+гу- в) 4fl2-962- г) 55лса^66^
Р (Р — Q) ' л2 — ty2' 2а2 + Заб' 25*2 — 36&2 "
59. Упростите выражение:
а) е-1 ■ б) (Ь-2)3- в) <2*~2^2. г) 25fl2~25b2
(1 —а)2' 2 —& ' 4л:2— 4#2 ' (5а —5Ь)2
60. Найдите область определения дроби и сократите дробь:
ч i/2 — 16 ч а2 + 10а + 25
а) -£ j в) ! г .
3i/ + 12 а2 — 25
Лч 15г2 — 92 ч i/2 — 9
б) -^—г; г)
25г2 —9 у2_6^ + 9
61. Преобразуйте дробь в целое выражение:
ч 25 — а2 .хв + х* ч Ь7 — fr™
а) ; в) ■ ; д) ;
' а —5 ' х* + х*' ' &б-Ь2'
Лч *2 —2*+1 ч а«—а* ч с6 — с4
б) -£—; г) ; е) .
1 — х ' а4-а2' сз + с2
62. Упростите выражение:
. ах + Ьх—ау — Ьул . а2 + 2дс + с2 жч У6 — 1 .
7х — 7у ' а2 + ас — а* — с*' i/4 + i/2+ l'
-ч 8а + 4Ь ч а» + Ь3 * 1 + *6
б) — ; д) ; з) —■—.
2ас + be — 2ad—bd a*—ab + b* 1 + **
В) ХУ — Х + У-У2. е) У2 + 2У + 4 .
*2—у2 * ' уз_8 '
18
63. Найдите значение выражения:
оЧ 15а2 —10аЬ 0 . Л1
а) 3afr-2b2 при а = -2, Ь = -0,1;
-ч 9с2— Ы2 2 .1
б) при с = —, а = —.
18c2d — 12cd2 3 2
64. Докажите, что значение выражения не зависит от с (сф2):
. ср2 — 2р2. g. сх — 2х + су—2у
2рс — 4р сх — су — 2х-{-2у'
65. Решите уравнение:
х2 — 4 у2 — 7у
б) ^-2,2 + .-2 = у-у =()>
7 *з + * 15i/+ 5
§ 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ В ДРОБЬ
ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ
5. Произведение дробей
Рассмотрим выражения а^\—, ?—У-, 2 : р, а • (1 -\ ). При
Ъ х + у \ с]
составлении каждого из них использована операция деления
на выражение, содержащее переменные. Такие рациональные
выражения называют дробными.
Одна из основных задач тождественных преобразований
дробных выражений состоит в том, чтобы данное выражение
представить в виде дроби, числитель и знаменатель которой —
целые выражения. Мы увидим в дальнейшем, что такое
преобразование всегда возможно.
В этом параграфе мы рассмотрим преобразование в дробь
произведения и частного двух дробей, а также натуральной
степени дроби.
Рассмотрим произведение двух дробей — —.
Ь d
Если переменные а, &, с и d принимают натуральные
значения, то по определению умножения обыкновенных дробей
имеем верное равенство:
*-.L = SL. (1)
Ь d bd v
19
Например, при а = 3, Ь = 7, с = 15, d = 13 получим:
7 ' 13 ~~ 7 13 "
Равенство (1) будет верным и при любых других значениях
о
переменных а, Ь, с и d, где б^Оий^О. Например, если а = —,
2
7
6 = —, с = 5,1 и б? = 1,2, то
8
12 51 __ 51 -j^#
7 ' 12 ~~ 7 ~ 7 '
а с
Т ' 7
ас
ML
3
—
__ 2
~~ 7
■~—
8
3
—
_ 2
7
— .
8
5Д
1,2
•5,1
1,2
3
_ 2 '
~ 7
—— .
8
3
—
_ 2
""" 7
8
8
5,1 10
о г>2 ' 10
8
5,1 • 8 • 10
. 1,2 • 8 . 10
12- 51 _ -2_
7 • 12 ~" 7 "
Поэтому все соответственные значения выражении — • — и
b d
— равны и равенство (1) есть тождество.
bd *
Доказать это можно следующим образом.
а?
Дробь — можно рассматривать как частное, где ас — делимое, bd —
bd
ас ас
делитель. В таком случае выражение — • — есть значение частного —. Мы
b d bd
внаем, что делимое равно делителю, умноженному на частное. Поэтому равенстьо
ас _ а с
bd ~ b ' d
будет верным в том и только в том случае, когда верно равенство
а с \
— • — bd = ас.
U ' d)
Проверка показывает, что при b Ф 0 и d Ф 0 это равенство верно:
Г7МН(И —
В преобразовании мы воспользовались ранее доказанным тождеством
— . Ь = а.
Ъ
ас ас
Следовательно, равенство — = — • — верное.
bd b d
20
Произведение двух дробей тождественно равно дроби, у
которой числитель равен произведению числителей данных
дробей, а знаменатель — произведению их знаменателей.
Приведем примеры преобразования в дробь произведения
дробей.
1 6а*_ 10у3 6о2 • 10у3 _ 4а
" byi " 21ab ~~ 5i/3 • 21аЬ ~~ 1Ь
2 х* — 2ху ^ У __ ^ (* — 2у) • у __ жу
3 * *2 —4у2 3(* —2у)(* + 2у) 3* + 6у#
66. Представьте произведение в виде дроби и сократите ее,
если это возможно:
ч 2
а)г
в)*
' 4
в) — •
' 10
л:
8
"i"5
5
а
2я
е) — •
' 3
Т5
Зп.
>
т.
>
а
ч Ь Ь2
ж) ;•»
ч Р2 g2
з) — • —;
ч За2 а3
и) — ;
' *2 1в*3
Л3
2л2
25.71»
67. Представьте одночленный множитель в виде дроби со
знаменателем 1 и выполните преобразование:
а)*.£; в) е-!; д) -1 • ^; »)**•£;
5 2d у —и*
68. Упростите выражение:
' 8д3 25р3 ' * \ 10*V>/
* 14л:2 * \ 18а2]* W 3fr * 7Ь2 * а3*
ч гт 2 4 л*3 ч 15л:а 12и3 х
Р4?4 8^а 25** 9у
69. Замените выражение тождественно равной дробью:
ч л:2 — ах а ч а — b 8&4
а) ; в) ;
' а2 *2 ' 4Ь3 а2 —а&'
б) pg + g2 . £р. г) ю2--9ц2 . _2и» .
27 «2 m2n2 m+Зл
21
. ж3 — х2у х*у + ху\ . 4и" — О2 а — Ъ
д) . ; з) • :
х2 + у2 х*у а2 — аЪ 2аЬ + Ь2
лч (а + Ь)2 2ЬаЬ а3 __ 8 7а + 21
50а2 а2 —Ь2 5а+15 а2 + 2а + 4
х2 - 4у2 28*2 . *3 + 27 12* + 9
»v —— • -т—:—г"т~г> к/
Sbxy х2 — 4ху + 4у2 8* + 6 *2 —3* + 9
70. Упростите выражение:
а* + ау + 2* + 2у 8а — 16
а)
б)
2а + 4 а* + а# — 2* — 2у
а& — 5Ь* + За — 15* а — 2Ь
4Ь3 — а2Ь а — 5*
—*—\ г)-
а& — 2Ь ' 4*3 — 36*
в) (2 - а)2. —~; г) —Ц— • (х2 - 9).
71. Решите уравнение:
ч 4*2 — 25 4 л v , _ч 2*4-1
а) = 0; в) (х — 5) ^— = 0;
8*+ 24 2*+ 5 ' v *2 —25
*1-2*6*±18== r)(x + 3).f!ziii = 0.
30 * ' V ' 9 — *2
72. Докажите, что соответственные значения выражений— и
d
— являются взаимно обратными числами.
с
6. Частное двух дробей
Мы знаем, что деление одного числа на другое можно
заменить умножением делимого на число, обратное делителю. Так
как соответственные значения дробей — и — являются взаим-
d с
но обратными числами, то частное — : — равно произведению
Ь d
— • — при любых значениях а, Ь, с и d, кроме Ь9 с и d, равных
Ъ с
нулю:
а # с a jd
~b ' d ~~ Ъ ' с'
22
Это тождество дает возможность представить частное двух
дробей в виде произведения, а следовательно, и в виде дроби.
Частное двух дробей тождественно равно произведению
делимого на дробь, обратную делителю.
Приведем примеры преобразования в дробь частного двух
дробей.
t 5*з . 15*
ба " 2а2
5*з 2а^_
6а 15*
5*3 ■ 2а2 о*2
6а 15* 9 "
а —ЗЬ
(а + 2Ь) (а — ЗЬ)
2 а + 2Ь # а* + 2аЬ _ а + 2Ъ
" fl2 _ 9&2 ' а _ ЗЬ ~~ а2 — 9Ь2 ' а2 + 2аЬ (а + ЗЬ) (а — ЗЬ) • а (а+2Ь)
1 1
а (а + ЗЬ)
а2 + ЗаЬ
73. Представьте частное в виде дроби:
ч * 2
а) - : т;
у з
ч лг Ьтп
в) - : —;
2л n
б)
р . г.
г)
6а
12а
74. Упростите выражение:
а) Ъ : -;
а
б) - : У,
X
ч а2 а3
е) ^ : *;
7 В» у»
в) За:
12а
г) £? : 5*;
д) 3J*E1 : 14m»,»»;
е) 15о3Ь*
35а4Ь2
12р . 8£
35ва ' 21«"
81^/_18^N
7р3 V 35p*j
3)
45m3 4 27m4
28л3 ' 42n6'
75. Замените выражение дробью:
а)
б)
в)
г)
Д)
* — 2 # 3* —6,
10а4
У3
15а3Ь
а2 — ЗаЬ а — ЗЬ
т2 — 4/г2 . (яг + 2тг)2.
Зтл " 9т2 '
1 „ 4а + 4а2 ш 4а* —lt
15а2 " 5а3 '
а2 — За* З*2 — а*
е)
5*2 — Ьх Ь2 — 5Ь*
ЗОЬу
ж) (2х — у) :
21Ь — 7а
60*2/
2*2 — *у
3)
:(а —3&);
12*
36а
Ь — а
и) (а + 5&) :(а2 —25&2);
к) (*2 — 6zi/ + 9у2) : (я2 — 9у2).
23
76. Найдите значение выражения:
а> "ТТ" : —^П ПРИ *= —0,25;
2х3 Ьх2
-ч а2 —9 а + 3 2
б) — : ■ при а = —.
а2 — 2а + 4 9а* + 72 * 3
7. Степень дроби
Выражение (—) является степенью дроби —. Покажем,
что это выражение можно представить в виде дроби.
По определению степени имеем:
\ь) ~ ъ
а а а а
Ь Ь ' Т Ь'
По свойству произведения дробей:
а а а а а ааааа
Ь Ъ Ь Ъ Ь ЬЪЬЪЬ
По определению степени с натуральным показателем:
ааааа а5
ЪЪЪЪЪ ~~ № *
Итак, \-А =з —.
Вообще, для любого натурального п9 большего 1, и Ъ ф О
имеем:
(а\Л__ а а а _
Ъ) Ъ Ъ Ь
п раз
Степень дроби тождественно равна дроби, у которой числи-
тель есть степень числителя, а знаменатель — степень
знаменателя.
Рассмотрим пример преобразования степени дроби в дробь:
2а2Ь\4__ (2а2Ь)4 _ 16а8Ь4
/2а2Ь\
\3*У J
\Ъху J (Ъху)* 81*ty
24
77. Представьте степень в виде дроби:
78. Представьте дробь в виде степени:
ч 4а2Ь6 -ч 64а6 ч — 8а6 ч — (л: — 4)*
а) ; б) ; в) ; г) —* —.
' хю > &12С24» ' (а— б)3 ' 32л:10
79. Упростите выражение:
Ъ2 \з ж2 + 10* + 25
ч /2а8\5 / с9 \* ч / Ь2 V
*ч / 3*7\4 /9лб\з
3*7\* /9лб\з /а —2\2 2а —а2
3 — Ь/ 9 — Ь2
& — а
' \9&2 / \ 16aV V ab2 — б? ) \а2 + 2а6 + б2
80. Докажите тождество:
(*2 — 10s + 25)3 -• (х + 5)3 _ j
(5 — *)3 . (25 — *2)3 ~
81. Решите уравнение:
I ж + 2 I
§ 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ В ДРОБЬ
СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ
8. Сумма и разность дробей» имеющих равные знаменатели
Выражение 1— есть сумма двух дробей с равными
знает с
менателями. Покажем, что эту сумму можно представить в
а 0, + Ъ
виде дроби ——.
е
Если переменные а, Ь и с принимают натуральные значения,
то равенство
± + ±„-±Ь (1)
С С С
25
верно на основании правила сложения обыкновенных дробей
с одинаковыми знаменателями. . Например, если а =2, &=3 и
с=7, то
JL-L— — 2 + 3
7 7""" 7
Это равенство будет верным и при любых целых и дробных
значениях а, & и с, где с ф 0.
2
Например, если а = 1,5, & = —5, с = -, то
з
£±1-Ь5 + 1? ?_ 4- — _ iL _.15 ?! 5--
с с ~ Ц !L~~ 2. А ~~ 4 2~~ 4 ~~ 4'
3 3 3 3
-зА
а + Ь __ 1,5—5 2_ 7_ д_ 21 _ _ _1_
с ~ JL ~ А ~~ 22~~ 4 ~" 4*
3 3
Все соответственные значения выражений — -\— и а—£—
ее с
равны, и равенство (1) есть тождество.
Докажем это.
а 1 Ь , 1
Воспользовавшись тождествами — = а • — и — =&. —, получим:
с ее с
a b 1 11 а+Ъ
— + — =а . — + Ь • — = — (а + Ь) = —— .
с с с с с с
Разность дробей с равными знаменателями можно заменить
суммой и представить в виде дроби:
aba —Ь а — Ь
с с с с с
Сумму дробей можно представить в виде дроби и в том
случае, когда число слагаемых больше двух.
Например:
а . b d /fl I Mi ^ _ fl + & I ^ _fl'
j I — I Ы —= 1 —
с с с \c с J с с с
__ _ _ _ __ = j + b + d
с с с \с с j с с с
26
Сумма дробей с равными знаменателями тождественно
роена дроби с тем же знаменателем и числителем, равным сумме
числителей данных дробей.
Приведем примеры преобразования суммы и разности
дробей.
а2&_б 2 + ЬаЪ _4_ __ а2Ь — 6 + 2 + ЪаЬ + 4 _ а2Ъ + ЬаЬ _
ab2 ab2 ab2 db2 ab2
аЪ (а + 5) а + 5
2.
ab2 &
бас —у х + 4у __ б* — у — (х + Ау) __ 6* •— у — х — 4у _ бх — 5у
5у 5у 5у Ъу by
5(х — у) х — у
Ьу у
в За , 2л За , 2х • (—1) За , — 2х За — 2*
о. 1 = 1 = Н = .
х — а а — х х — а (а—х) • (—1) х — а х — а х — а
В примере 3 знаменатели х — а и a — х — противоположные
выражения. В подобных случаях, чтобы знаменатели дробей
сделать равными, умножают числитель и знаменатель одной
из дробей на —1.
82. Представьте сумму или разность дробей в виде дроби:
ч а , Ь
а)7+Г'
' 3 3
ч a . 2a#
в) ——;
' 7 7
ч 5ь2 гь2
г) ;
8 8
д)*-±!_£;
А; 9 9'
е)Г2 + ~1Г;
ч* + 3,2-я
У У
з)*1±1_1.
a a
83. Преобразуйте выражение в дробь:
у + 5 * + 2. 5Ь + 2с-7 & + 3.
9 9 ' 2Ь 2Ь '
*ч 8* — 3 . 24 — х ч a — 2 , 2а + 5 3 — а
б)-1Г + -1Г; д)— + 1 Г;
ч 5 ч -f 2л 5-п—Зл, . 3* — 2у 5* — Зу * — 4у
в) ^ е) -J ■
8п 8л 2* 2* 2*
27
84. Являются ли толсдественно равными выражения:
ч 5 5 ч 8 8
а) -и— ; в) -и
а — Ь b — а (х — у)2 (у — дг)а
б) и —:—; г) — -
к хг — у2 уг — яа
85. Представьте выражение в виде дроби:
а) -^ + -*-; г) -&. _ J*L; ж) fc=» + «_±».
у —1 1 —у р —g д_р у—7 7 —z/
б) _« 5L. д) fl + 1 г <*-2. з)fr —12 _ 8 + 2fe
7 с— з 3-е' W2a-1 l-2a' 'lO = fr fr =-Ю"
ч w . 2л ч * + 9 8 — 2*
в) 1 ; е) —- ;
m — л л — m 1 — дх Зле — 1
86. Упростите выралсение:
а)-^ — +—-; г)
р —2 2 —р р —2 а3—1 1—а3 а3—1
~ 2а . а & ч Зс + 2 4с —2,2с—5
б) • д) ! ;
а — Ь Ь — а а — Ъ (с — I)2 (1-е)3 (1-е)8
в)£±_2_?^ + 4а--1; е) 2* + 1
а — 3 3 — а а — 3 (л: — I)5* (1 — л:)3 (1 — *)»
87. Докажите, что множество значений выражения содержит
лишь один элемент:
а) (х+У)2 (*-У)\ б) (а-Ъ? (а + Ь)*
ху ху * а2 + &2 а8 + Ь* #
88. Найдите значение выражения:
Р2<? - g3 2pg2 - g3 й п 9-
Е-Л ПрИ р —- у g = О ^5.
p-2g р-2</
89. Постройте график функции, заданной формулой:
ч *2 + 1 2 лч л:2 , 4
а) у = —-1- ; б) у = .
' * *-1 л: —1 * л: —2 2 — л;
90. Решите уравнение:
17 17 J/ + 3 У + 3
11У + 29_8У-24 _** 6*_ = Q
7 41 41 *-6 6 — 1:
28
9. Сумма и разность дробей, имеющих различные знаменатели
Пусть поставлена задача: сумму дробей — и - представить
Ъ d
в виде дроби.
Умножим числитель и знаменатель первой дроби на d9 a
числитель и знаменатель второй дроби на &. Получим:
а . с __ ad , be
~bd ~bd bd
Выражение d называют дополнительным множителем к
числителю и знаменателю дроби —, выражение Ъ — дополнитель-
ъ
ным множителем к числителю и знаменателю дроби —. Мы
d
- а с -. ad
заменили дроби — и — тол^дественно равными им дробями —
Ь d bd
и —, имеющими равные знаменатели. Говорят, что дроби —
bd Ь
и -- привели к общему знаменателю. Выражение bd — их об-
d
щий знаменатель.
Теперь можно сумму дробей — и — представить в виде
b d
дроби:
а . с ad be ad-{-be
~b ~d ~~"bd bd~ bd
Выполняя преобразование суммы или разности дробей в
дробь, часто удается найти более простой общий знаменатель
дробей слагаемых, чем произведение их знаменателей.
Рассмотрим примеры.
г а+Х а~-1 __ 3(о+1)т2(а- 1) __ За + 3 + 2а — 2 _ 5а+1
4 6 ~~ 12 "" 12 "~ 12
0 а + 3 b — 3 а + 3 6 — 3 & (а + 3) — а(Ь — 3)
а2 + db ab + Ь2 a(a + b) b (а + b) ab (а + b)
_ аЬ + ЗЬ ~ аЬ + 3fl _ 3 (а + &) __ 3
ab (а + b) ab (а + b) ab
91. Представьте сумму или разность дробей в виде дроби:
a)± + V в)-—*■; в) £ + ■*-; г) «--А;
7 2 3 4 б ' 12 ^ 18 7 21 6
29
ч 3 . 5 ч 2 , 3 ч8* 3*
Д) —Ь —; ж) ; и) ;
a b9 За 2а ' 15 10
лч 8 7 ч 5 3 ч Ъу , 7у
е) ; з) ; к) — + —.
х у Ъх 4х 12 10
92. Представьте выражение в виде дроби:
\ Х 1 3
а) ——;
Ъу ' 2у'
*ч Ь 5
б) ;
За 2а
ч 1 , 1
В) Ь — 5
15а* 9а
ч 3 5
г) ;
1т 28тп
ч а 3
4рЗ Зр
Ж) ^3 + _JLZL2;
3 5
ч 2х —5 ж —4
з) ;
6 5
ч 4а2 + ЗЬ2
и) ——
10
с2 —3d2
К)
12
2а2 —&3
15
2с2 — d2
•
8
93. Преобразуйте сумму или разность дробей в дробь:
ч 2а — ЗЬ , 4а — ЪЬ
Д) —тг- -I иг-»
*)
б)
в)
г)
а2
* —у
4р2 — 5в2
Ь + 2с
аЬ
"»
х — т
________ •
>
- +
с —
2р-
Р
2Ьш
3?
е)
а2Ь а&2
х — 2у 2х — у%
ху2 х2у
За2 — 5а + 1 , 5а —3
з)
а'у ау
W—b + l х2 — :
be с2 ' ~' ЬН Ъх*
94. Представьте выражение в виде дроби:
Л , 1 . 1
а) - + - + -;
ао ос ас
6)± + I—L;
6л: Ъх 15*
ч 5 1,1
g л _i_ •
14*з 21х2у 4jci/2 '
ч 2 , 3 5
г) .
За2& 5аЬ2 4Ь3
95. Преобразуйте выражение в дробь:
у—2 2* + 3 Ъх — 3 . у2 —2 З*2—7 , х2 +1
*ч2а — b a— 46 , 2a — 15Ь ч 5a2—12a&+4b2 , a-f2b a—5&
6) ; r) • !
' 6 2 8 2a& a &
80
96. Замените сумму иди разность тождественно равной
дробью:
а-\-Ь Ь х — у у 2а a + 3 5 с*^ 1
97. Целое выражение х — Ъу представьте в виде дроби со
знаменателем, равным:
а) 1; б) 2; в) а; г) х + Ъу.
98. Представьте выражение в виде отношения двух
многочленов:
a)* + i; г)А+4; ж)(-^ + а-Ь;
а х — 2у ЪаЪ
с 2а Ъху
В)"_±2Ь_3; e)^±M.-2y;
Ь 4л;
99. Решите уравнение:
а) — =0; г) л: = 0;
_5л:—6 5л: + 6 Л ч 5л: —8 . 2л: —7 л
б) — -~- = 0; д) — 1 х = 0;
3 12 6 9
> — У л ч л: —9 8 — 3
—- — У = 0; е)
9 * ' ' 14 28
100. Замените дробью сумму или разность дробей:
ч1.3 ч1,1 ч , &2 , t
а) —— + i ; д) —- Н ; и) а -\ + Ь;
1 + х 1 — х х + У У — х а>—Ь
в) — —; е) -* а-; к) X-*l±W+2
'2а — 1 2а + 1 р — q р + q' х + 2у *
ч Зл: 4- 2 2 — Зх ч m , п
2 — Зл: Зл: + 2 т — п т-\- п
"-Т-В + —з' в>-Ь-Г^
*/ Ь 3 у — 3 a -f & & — а
31
101. Упростите выражение:
.,_!_..___*__. в)_^ £+!—+ *
6(6+1) 6(6 — 1)* х+1 (ж —1)(х+1) г — Г
--v 5 3 . т — 3 , m + 3 2т
б' ~~; ^г ;—r~zr> г)
* (х — 2) л: (л: + 2) /и + 3 т — 3 (го + 3) (/и — 3)
102. Решите уравнение:
а) -2 L^O; в) !=* + i±-9 = 0;
* + 1 ж—1 ж—4 л: -1-4
3* + 1 * + 3 *+5 *+2
103. Знаменатель каждой дроби разложите на множители и
полученное выражение представьте в виде дроби:
ч 3 . 5 ч 1— 3* , 8
2х — 2у 3* — Зу *2 — Зх Зх — 9
б) r~r + iATZ> ж)-1—+ *
4а + 46 6а + 66' ' & — ху ху + у2 '
в) _i^ iJU. з) ? —.
4у—2 6# — 3' а2 + а& об—б2'
ч 36 6 ч m , 1
г) ^гт-^ — ^7—-=; и) «—о +
56+15 26 4 б' 1 — in» 1 + ш*
а — 1 б ч 4л 2
а2 + 2а 6а + 12 л2 — 9 л — 3
104. Упростите выражение и найдите его значение:
ч а + 1 а + 2 0
б> -Йг + ^ при у =1А
I/2 4- 3z/ j/2 — 9
105. Докажите, что выражение принимает положительные
значения при всех значениях а, при которых выражение
имеет смысл:
•Ч^в. в) *' + * + ! _1,
3 аг -\- а а
*ч 1 ч д3 За*+ 81
б) ; Г) ■ .
а* + а2 + 1 а—3 а2—9
82
106. Упростите выражение:
4
а)
х + 2 х—2
3 , 12
•-4*
б) 1 + : +
„*_9 j,_3 J/ + 3
в)
т4 + -
о —б о + 6 36 —а2'
r)_ai_ + _J ______
7 2& + 3 3 — 2b 4fc2 — 9
9
3 — х х2 — 3* '
е)
ж)
з)
и)
к)
3 2х — 1 _ £#
2л:2 + 2л л:2 — 1 х '
а —1 , о + 1 , 5а — 1
2а+ 2 3 —За За2 —3'
4m 2m + l , 2/R-1
__________ ■ _L_ ■
4m2 —1 6m —3 4да + 2*
2а+ b 16а , 2а — Ь
2а2 — аЬ 4а*—Ъ* 2a* + db
Ю , у б
! —25и2
25у2
+
5i/2 — *i/ x*+bxy
107. Замените выражение дробью:
х + 2 х — 2
а)
в)
г)
Д)
е)
з)
х2 + 2х + 1 *2 — 1*
1
-ч а + 3& , а —3&
б) . 7, , T^-
tt2—2а£+&* а2 — Ь2 *
2 + '
(а — З)2 а2 — 9 (а +
л: — у
2х
2а2 + 7а + 3
+
х + у
х2 — 2ху-\-у2
1 —2а 3
1 3pQ v дс — 2
Р —5
оз
Ж)
+
6*
*2 + 2*; + 4 *3 — 8 ж —2*
За2
6а3 + 48а
а3 +64 а2 — 4а + 1б"
108. Между двумя пристанями А и В, расположенными по реке
на расстоянии а км (рис. 3), курсирует катер, имеющий
собственную скорость Ъ км/ч. Сколько времени
потребуется катеру на путь от А до В и обратно, если известно,
что скорость течения реки
равна 5 км/ч?
Составьте выражение и
найдите его значение при:
1) а = 50, Ь = 25;
2) а = 105, Ъ -= 40.
Объясните физический
смысл значения скорости
при Ъ = 5. Рис. 3
2 Алгебра, 7 кл.
Si
109. Чтобы купить т кг слив, нужно заплатить с руб., а на
покупку (т — 5) кг апельсинов необходимо затратить на
3 руб. больше. На сколько выше цена 1 кг апельсинов По
сравнению с ценой 1 кг слив?
Составьте выражение и найдите его значение при т = 10,
с - 4.
10с Представление дроби в виде суммы нескольких слагаемых
Мы знаем, что сумму дробей всегда можно представить в виде дроби.
Например:
* — 5 2 3*(* — 5) 2 З*2 — 15.Г-1-2
х З*2 Вх2 ' З*2 Ъхл
дх2 — 15* + 2
Чтобы решить обратную задачу — представить дробь —
3*"
в виде суммы двух дробей, можно все преобразования выполнить в обратном
порядке:
З*2 — 15*+ 2 3*(* — 5) , 2 * — 5 2
З*2 З*2 З*2 * ' Ъх2
w „ З*2 — 15*+ 2
Дробь можно представить в виде суммы нескольких сла-
З*2
гаемых иначе:
З*2 —15* + 2 З*2 15* _2 Ъ_ ( J2__
З*2 = З*2 ~~ З*2 З*2 = "" * ^ З*2 "
Некоторые задачи удается решить проще, если данную дробь представить
в виде суммы нескольких слагаемых. Приведем пример.
Ъп2 + 20
3 а д а ч а. При каких натуральных значениях п дробь принимает
п
натуральные значения?
Решение. Представим данную дробь в виде суммы двух слагаемых
(целого выражения и дроби):
5л2+ 20 Ъп2 20 20
= + — = Ъп + —.
п п п п
Целое выражение Ъп при любом п £ N принимает натуральные значения.
20
Дробь — обращается в натуральное число при тех и только тех значениях /г,
п
которые являются натуральными делителями 20, т. е. при я, равном 1, 2, 4, 5,
10, 20.
34
Нам удалось решить задачу довольно просто, представив дробь в виде
суммы целого выражения и некоторой правильной дроби, т. е. дроби, у которой
степень числителя меньше степени знаменателя. Такое преобразование дроби
всегда возможно, если только степень многочлена числителя не меньше степени
многочлена знаменателя.
110. Представьте дробь в виде суммы двух дробей:
а) £±1; б) «(—2) + Г
' х* • ' а2-4
111. Представьте дробь в виде суммы трех слагаемых:
*» + ta+l. о»-1 + 8а
я2 а + 1
112. Представьте дробь в виде суммы целого выражения и дроби:
ч У+1 ч Ра-2р + 7
а) ; в) ;
У Р — 2
2а2 — а — 3 *2 -f 5* — 9
Ъ) —+—; г) —*тг~-
#2_|_ 7# 25
113. Учащимся была поставлена задача: «Представить дробь
х — 5
в виде суммы целого выражения и дроби». Были получены четыре ответа:
7х „ 2* — 25
3) х2 — ж "
х; л
2) X
Все
-г
+
ли
о -г
12*
*-5*
— 25
-5 '
ответы верные?
4)*+ 12 +
*-5 '
35
ж — 5
114. При каких натуральных значениях /г дробь принимает натуральные
значения:
5п2 + 8п + 12 (тг-3)2^
а) ; б) ?
п п
115. Докажите тождество:
баг л 18 ах аЬ
а) —— = 6 — ——-; б) —— = а -
* + з х + г х + ъ х + ь
35
116. При каком значении а тождественно равны выражения:
2х а 2х а
х + Ь х + 3 3-х 3-х
х а * + 2 «о
б) - и 1 + -; г) —±— и - 1 + ?
х — 5 х — 5 5 — х 5 — х
117. Представьте дробь в виде суммы целого выражения и дроби:
5х —2х 2х х — 3
а) ——; б) -; в) ; г) .
х + 2 ас —1 5 — х 2-х
118. При каком целом п значение дроби есть целое число:
дп 7п 0
■> 1ГГ*' б) 1Г=7?
119. Найдите такие значения а и Ь, чтобы выполнялось тождество:
5* а Ь
б)
(* —2)(* + 3) х — 2 х + 3
5л: + 31 а Ъ
(х — 5) (х + 2) * — 5 * + 2
11. Тождественные преобразования дробных выражений
Мы выяснили, что сумму, разность, произведение и частное
дробей всегда можно представить в виде дроби, числитель и
знаменатель которой — целые выражения. Следовательно, любое
дробное выражение также можно представить в виде дроби.
Если при этом нужно выполнить несколько преобразований, то
предварительно следует определить порядок их выполнения.
Приведем пример.
Пусть нужно представить в виде дроби выражение
1 х2 4
. 1_ 2х. Это выражение представляет собой сумму
х + 2 Зх
I х2 4
произведения дробей и и целого выражения 2х. По-
х + 2 Зх
этому сначала нужно произведение указанных дробей заменить
дробью, а затем сумму представить в виде дроби:
-.1 *2 — 4 __ (х+2)(* — 2) _ х — 2в
х + 2 Зх (х + 2) . Зх Зх
m x — 2 ,0 * — 2 , 2* • 3* б*2 + * — 2
2) f- 2х = = ! .
з* а* з* зх
тт - б*2 + X — 2
Данное выражение мы представили в виде дроби .
Зх
36
120. Определите порядок вьшолнения преобразований и
упростите выражение:
'\ж+1п / 4ж»—1* w\o* —ва о» + 6а/ а» +1
б) р у): y-y + ^i e) («_ «Lt*\.(A + _L.Y
3 6?^ 6 ' \2 —а j V ^ а-2/
4у *» —*у ж2 (л: —2)а 3(* + 6)
121. Упростите выражение:
\а —6 а-|-&/ \ а а/
.) (р -« + ^=А: (тЧ + — + -Ь>
\ Р + 9 / \Р*—«* в —Р Р+Я)
'\2* + у 2* —у z/2~4*2/ \ 8*2 2/
W \я*—Ьху х* + Ъху ) х* + у2 '
\ 9Д2 — 16Ь2 т I ЗЬ — 4а _ ЗЬ + 4а \
в' 7а "\4Ь2 — ЗаЬ 4&3 + Зад ]*
У2-*2 \У2-х* ^ х2+2ху+у*)'
а-2 / а а2 + 4 j \
а2+2а " \ а2 — 2а а3 ~4а а2 + 2а ;
122. Найдите значение выражения:
/ * + 5 х — 5 50 \ ж — б 1
'\2x-10 2* + 10 25-**2/ 5* F 4
б) *2-^+*а =(т^ + -т Ч
* + у \г/2—*2 * + у у—*/
ал 3
при дг = 8,4, у =в — —.
5
37
123. Используя основное свойство дроби, упростите
выражение:
а
а) хг; б)
а с у а*
124. Докажите, что множество значений выражения состоит из
одного элемента:
2 /o + 2N
а — Ь
+з
С
а+Ь '
2х— 5
—1
Е> 2х 4- 5
—L- + i
а2 + 1 1
. в2 о
г) —
а — —
i +3
v а а2 + 1 fi4 \а —2 / а* —8 __ 2а
U /' U + 2/
125. Выполните подстановку и упростите полученное
выражение:
а
— —х
. х — а ао ^ч Ь и
а) -, где х = ——-; б) -г , где х
х — Ь a + b' ' Ь . " а +- 6'
— —I— дг '
а
126. а) Смешали 6 кг кофе по цене 4 руб. 50 коп. за килограмм
и х кг кофе по цене 4 руб. за килограмм. Какова цена
1 кг смеси?
Составьте выражение и найдите его значение при х = 4,
я: = 19.
б) Имеется чай двух сортов: первый сорт по цене 10 руб.
за килограмм и второй сорт по цене 8 руб. за килограмм.
Сколько килограммов чая первого сорта нужно взять,
чтобы его смесь с 20 кг чая второго сорта стоила 8 руб.
75 коп. за 1 кг?
в) Для изготовления сдобы идет мука двух сортов:
первого сорта по цене 45 коп. за килограмм и второго
сорта по цене 36 коп. за килограмм. Муки первого сорта
взяли 100 кг. Сколько нужно взять килограммов муки
второго сорта, чтобы 1 кг смеси стоил 42 коп.?
§ 5. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
12. Определение степени с отрицательным целым показателем
В технических книгах и справочниках можно встретить
записи вида 6-1023 или 10~4. Мы знаем, что выражение 1023
означает произведение двадцати трех множителей, каждый из
которых раЕен десяти. А какой смысл приписывается записи 10~4?
S3
Чтобы разобраться в этом, рассмотрим последовательность
натуральных степеней десяти:
10\ 102, 103, ... (1)
Эту последовательность можно представить в другом виде:
10, 100, 1000, ... (2)
Попробуем последовательность (2) продолжить влево. Так
как каждый ее член меньше последующего в 10 раз, то перед
числом 10 следует поставить 1, перед числом 1 — число —,
1 1
перед числом число и т. д.:
Г 10 1С0
... , —, —, 1, 10, 100,... (3)
100 10 V
В последовательности (1) показатель каждого члена на 1
больше показателя степени предыдущего члена. Продолжая
по этому закону последовательность (1) влево, мы должны перед
членом 101 записать член 10°, перед членом 10° — член 10""1,
перед членом 10"1 — член 10~2 и т. д.:
..., 10~2, Ю-1, 10°, 101, 102, ... (4)
Сопоставляя последовательности (3) и (4), естественно
принять, что 10"1 равно —, 10~2 равно —. Такое соглашение и
ю юо
принято в математике не только для степени числа 10, но и для
степени любого, не равного нулю числа.
Определение. агп = —, где а Ф 0 и п £ N.
ап
Выражение О""3 (и вообще нуль в отрицательной степени)
считается выражением, не имеющим смысла.
После того как мы определили степень с целым
отрицательным показателем, такие выражения, как 10~4, ( ) , З""8,
приобрели вполне определенный смысл:
ю-* = J-, /_ ±)~*= —* з-8 = -!.
10* V *1 (-.-) 3*
127. Представьте выражение в виде дроби:
а) Ю-3; б) 2-3; в) 5~2; г) 7"1; д) а~4; е) Ь~5.
128. Представьте выражение в виде степени с отрицательным
показателем:
а) "^ б) Т^ в> "IT* г) —; д)
1
81;
ж) ;
89
129. Каждое из чисел 16, 8, 4, 2, 1, —, —, — представьте
2 4 8
в виде степени с основанием 2.
130. Дана последовательность:
—, —, —, 1, 5, 25, 125, 625.
126 25 5
Запишите эту последовательность, представив каждый ее
член в виде степени с основанием 5.
131. Докажите, что значения следующих выражений являются
взаимно обратными числами:
а) -^ и 28; в) 5* и 5~«; ' д) (|)* и (|)\
б) 3-а и З2; г) Ю-20 и 10м; е) (-Y* и (-\~\
132. Докажите, что:
133. Используя отрицательный показатель, запишите
выражение, значение которого обратно значению выражения:
а) 87; б) 1510; в) (—2,7)6; г) 2525.
134. Найдите значение выражения:
а) 5~2; в) (-25)"1; д) (|р; ж)3-г + 4"1;
б) (0,34)«; г)(_о,5)-*; е> (^р з)2-3-2-*.
135. Узнайте, какое из чисел больше:
а) 2-8 или З-5; в) 5~7- или 5"5; д) (—2)3 или 2~3;
б) (0,2)"8 или (0,5Г3; г) (0,4)"3 или (0.4)-4; е) 3~4 или (—З)4.
136. Сравните с нулей:
а)(-1)6; б)(-2)"3; в) (-0,1)*; г> (~1р
137. Представьте выражение:
а) — в виде степени с основанием 3;
7 27
*ш
1 \3
в виде степени с основанием 7;
в) 25~2 в виде степени с основанием 5;
г) 8~3 в виде степени с основанием 2.
13. Свойства степени с целым показателем
Нам известны следующие свойства степени с натуральным
показателем:
1. атап = ат+п.
2. ат : ап = ат~п, где т > п.
3. (ат)Л = атп.
4. (а&)" = a"&".
Буквами тип здесь обозначены натуральные числа.
Покажем на отдельных примерах, что эти свойства,
установленные для степеней с натуральными показателями,
справедливы и для степеней с любыми целыми показателями. При этом
основание степени будем считать отличным от нуля.
Пример 1. Докажем, что 5~3 • 55 = 5~3+5.
По определению степени с отрицательным целым
показателем 5-3 = —. Поэтому 5-3 • 55 = — . 55- — = 55~3 = б~3Ч
5? 53 53
Основное свойство степени распространяется и на степени
с целым показателем: произведение степеней с одинаковыми
основаниями равно степени с тем же основанием и показателем,
равным сумме показателей этих степеней.
Для того чтобы свойство атап = ат+п выполнялось для любого целого
показателя степени, мы обязательно должны были принять, что а~п = —
(а ф 0, n$N).
Действительно, потребовав, чтобы сохранялось основное свойство степени,
получим для любого п £ N и а Ф 0:
апа-п _ ап-.п = ао _. 1#
Отсюда а~п необходимо должно быть равным —-.
41
Пример 2. Докажем, что 3° : З2 = 3°~2:
3°: З2 = — _ з9 • — = 3° • 3~2 = 3°-2.
32 — ° З2
Свойство частного степеней с равными основаниями
сохраняет силу и для целых показателей, но при этом снимается
ограничение, согласно которому показатель степени делимого
должен быть больше показателя степени делителя.
Пример 3. Покажем, что равенство (абУ"в=аб(~в)
является тождеством:
(а5)-б = J_ = _L = а-зо = ав<-в)
(fl5)3 fl30
Выполняя преобразование, мы дважды опирались на
определение степени с отрицательным целым показателем.
138. Найдите значение выражения двумя способами (первый —
с использованием определений степени с целым
показателем, второй — с использованием свойств степени):
а) 8°.82; в) (2"3)2; д) (34)"2;
б) 23 : 25; г) (З"1)"2; е) (|) 3.
139. Найдите значение выражения:
а) З-4 • З3; в) 2" : 212; д) (2'Г1; ж) (|р I;
б) 16 • 2-3; г) 5-3 : 5"'; е) (±р з) (|р. ±.
140. Вычислите:
ч о-2 аз ч 2 ч (—5)~5 251в
«кг-шч^ип
2_22
3_10 gj /JV_5 , jv4 /1\Ю /1\-3
„«,:^ ж>^; K,(i)-».(i)*-(i)".
г) 125-4:25~5;
81
42
141. Используя отрицательный показатель, представьте дробь
в виде произведения:
а)
б)
з в
1 О >
Ь2
У
в)
г)
2а.
с
8fl5
&3
Д)
е)
1
*2г/3
1
Ь*с2
ж)
з)
а + 2
(а-2)2'
(Ь — 5)3
Ь + б '
142. Представьте произведение в виде дроби:
а) Заг5; в) о°6-2; д) с (а + Ь)"1;
б) 2у-3; г) 5а-3&3; е) 2х (х — ЗуГ2.
143. Представьте степень в виде произведения:
a) (a-'ir1)-2; в) (0,5а-3&6Г8 5
б) (*y-x)2; г) (—2т5»-3)2; е) (— 0,5ягУ)8.
д)(|р-2в2'"3
144. Найдите значение выражения:
а) 0,2а-26*-5о3Ь-3 при а = —0,125, 6=8;
б)
■*~\
»..-, ПРИ * = 7'У = -8-
—2х~° у~
145. Представьте выражение в виде дроби:
а) а-2 + б-2; д) (а + Ь"1) (а"1 -&);
б) 2х-1-ху-г\ е) (ж— 21/-1) (ж"1+2*/);
в) с3ж~5+а-2х3—2а-4д;-3; ж) (a^ + fe-1) (а + Ь)~1;
г) 5&-вс4—ЗЬс~3—2&2с; з) (а— Ъ)~\а-%— Zr2).
146. Заполните таблицу:
п
2п
—8
—7
—6
—5
1-4 1
—з|
о! 1
0
1 1
2
3
4
5
п
2"
6
7 |
8
9
10
1 П
12
1
13
14
15
16
-13
147. С помощью таблицы (см. № 146) выполните умножение.
Сначала по таблице представьте каждый множитель в
виде степени с основанием 2, затем замените произведение
степеней степенью и снова воспользуйтесь таблицей:
а) 32 .1024; в) 8192 . —; д) 4096 • —;
' 512 ' 64
б) JL. Ю24; г) 512 -8; е) — . I.
' 256 16 8
14. Стандартный вид числа
В технике, в физике, астрономии имеют дело с очень
большими и очень малыми (положительными) числами. Например,
расстояние от Земли до Солнца 149 000 000 км\ свет проходит
через оконное стекло за 0,00000000001 сек. Гораздо удобнее
как для запоминания, так и для выполнения некоторых
вычислений такие числа записывать иначе:
149 000 000 = 1,49-108;
0,00000000001 = Ю-11.
Любое положительное число представляют в виде
произведения числа а, где 1 ^ а < 10, и целой степени 10:
а-10я.
При этом если число а дробное, то его представляют в виде
десятичной дроби, выполняя, если это необходимо,
округление.
Такую запись называют стандартным видом числа. Число
п называют порядком числа.
Например, время продолжительности урока (в секундах)
в стандартном виде запишется так: 2,7 Ю3. В этой записи
а =2,7; п = 3.
Масса одного атома водорода 0,0000000000000000000000017 г.
Запишем это число в стандартном виде: 1,7-10""24. Здесь а = 1,7;
п = —24.
Числа, записанные в стандартном виде, легко умножать
и делить, так как легко умножать и делить целые степени
десяти. В результате может получиться число нестандартного
вида. При необходимости его легко привести к стандартному
виду.
44
Приведем примеры:
1) (3,1 • 103). (2,3-104) =(ЗД- 2,3) 107 =7,13 107;
2) 4'8 ' 10* = ^ • Ю-6 = 3,2 • 10-в;
1,6 • 108 ij5
3) (8 • 103) • (4,5 • 104) ==36 • 107 =3,6 ■ 108.
148. Записано ли число в стандартном виде? Если нет, то
запишите его в стандартном виде и назовите его порядок:
• а) 3,4-108; в) 10,6-109; д) 19Ю~6;
б) 7,51 Ю5; г) 5,2-Ю-4; е) 410"8.
149. Запишите в стандартном виде число:
а) 7 000 000 000; г) 1 001 000; ж) 0,00000572;
б) 2 860 000 000; д) 0,02; з) 0,01006.
в) 30 920 000 000; е) 0,0013;
150. Между какими последовательными целыми степенями
числа 10 расположено число (запишите в виде двойного
неравенства):
а) 365; б) 24,08; в) 0,0057; г) 0,0001002?
151. Выразите время в секундах и запишите полученное число
в стандартном виде:
а) 1 час; б) 1 сутки; в) 30 суток; г) 1 год.
152. Выразите массу в граммах и полученное число запишите
в стандартном виде:
а) 37 ц; б) 78 мг; в) 43,2 т; г) 969,54 кг.
153. Число, о котором говорится в предложении, запишите в
стандартном виде:
а) масса Земли равна 6 000 000 000 000 000 000 000 г,
б) в одном грамме водорода содержится
600 000 000 000 000 000 000 000 атомов;
в) радиус атома водорода равен 0,0000000001 см;
г) расстояние 1 км свет проходит за сек.
154. Сколько секунд длится один футбольный матч? Ответ
запишите в виде числа в стандартном виде.
155. Выполните действия:
а) (1,2510в).(4101а); в) (4,2 Ю-2)-(4,2-107);
б) (6,21O-2):(3,1104); г) 10б:(8Ю~2).
45
156. Свет проходит 3-108л* в секунду. Какое расстояние (в
метрах) пройдет свет за 1000 сек? за 0,01 сек? за 1 ч?
157. Колесо делает один оборот за 3-10-2 сек. Сколько
оборотов сделает колесо за 1 ч?
158. Расстояние от Земли до звезды Альфа Центавра
составляет приблизительно 2,06 105 астрономических единиц
(астрономической единицей называется расстояние от
Земли до Солнца). Сколько километров от Земли до
звезды Альфа Центавра, если известно, что от Земли до
Солнца 1,5-108 км?
15. Степенная функция с целым показателем
В курсе алгебры VI класса мы рассматривали функции,
которые задавались формулами у = ах9 у = ах2, у — ах3, где х и
у — переменные, а — число, не равное нулю. Такие функции
называют степенными функциями с целым показателем.
Функция, которую можно задать формулой вида у = ах h, где
х и У — переменные, а и п — заданные числа, причем а =£ 0 и
п £ Z, называется степенной с целым показателем.
Здесь мы познакомимся со степенной функцией с
отрицательным показателем, равным —1 и —2.
Функция у = ах^1 представляет собой обратную
пропорциональность, так как по определению степени с отрицательным
показателем ах"1——, где афО. Следовательно, графиком функ-
х
ции у = ах"1 является гипербола, которая при а > 0
расположена в первом и третьем координатных углах (рис. 4), при а < 0 —
во втором и четвертом координатных углах (рис. 5),
г3
J-*
"".
\и\
\ Т
Ч1л
У
1\
\
*ч i*
-J 11- i- Y
пУ-2£х
1 1 1
н
V
|Ч+-
0 \ 1 \ I
7 1
° '
1 1
1
U. |
1
-f
Hi Их
Рис. 4 Рис. 5
46
-3
?
1
-1
\ч\
\ '
J-7-
r
0
\
1
1
\o
' 1
I /
' ?
i z
-J-7
IJ
\
1
>
I
•■ л
у=-4х~1
X
Рассмотрим функцию, заданную -формулой у = ах~2 (афО).
( При а=1 формула у=ах~2 принимает вид у=х~2. Построим
график функции у=х~2.
При х=0 выражение х~2 не имеет смысла. Значит, число О
не принадлежит области определения функции. При любых
других значениях х выражение х~2 имеет смысл. Значит, область
; определения функции есть множество: ] — оо; 0[U]0; + <*>[.
Переменную х, значения которой составляют область
определения функции, обычно называют аргументом функции.
Для рассматриваемой функции только число 0 не является
значением аргумента.
Составим таблицу:
X
У
— 3
0,11
—2,5
0,16
—2
0,25
—1,5
0,44
—1
1
—0,5
4
0,5
4
1
1
1,5
0,44
2
0,25
2,5
0,16
3
0,11
Построим точки, координаты которых помещены в таблицу
(рис. 6). Можно предположить, что график функции
расположен выше оси х. Действительно, значение выражения х~2 при
всех значениях аргумента (х ф 0) положительно.
Следовательно, график функции не содержит ни одной точки с
неположительной ординатой.
Противоположным значениям аргумента х соответствуют
равные значения функции. Значит, график функции
симметричен относительно оси у.
Так как функция не определена при х = 0, то график функции
не пересекает оси у.
График функции у = х~2 состоит из двух ветвей (рис. 7).
Рассмотрим функцию у=х~2 на множестве отрицательных
чисел. Если х = —2, то #=0,25; если х==—0,5, то у =4; если
х = —0,1, то у = 100. Мы замечаем, что с возрастанием значений
аргумента х значения функции возрастают. Говорят, что
функция у=х~2 является возрастающей на множестве ] — оо; 0[.
Вообще, функция f называется возрастающей на множестве А, если
любому большему значению аргумента, принадлежащему
множеству А, соответствует большее значение функции, т. е.
если х2 >хг и хи х2 € А, то / (х2) >/ (хх).
Рассмотрим функцию у=х~2 на множестве положительных
чисел. Если х=0,5, то у =4; если х=29 то у =0,25; если я = 10,
то у =0,01. Мы видим, что с возрастанием значений аргумента х
значения функции убывают. Говорят, что функция у=х~2
является убывающей на множестве ]0; +оо[.
Вообще, функция f называется убывающей на множестве В,
если любому большему значению аргумента, принадлежащему
47
Тж
Ш
Трг
чЗ
Ш
tjjiiitl
ж
[ixtx
fj+|+
ЕР^щяР?
[ЩЩ$
Рис. 6
вваавгавававйавааввааввваbbbbbbbbbiвв
, >aaaaававвавяававвававяаааавяавваншаа
аааааавввааваа!аавававвавbbbbbbbbbi ii
вваававяявваяваввваааяавававаававвааа
ававвааааВввваавввввваввваавввваваааа
! ааваа ааввааввав вввааааввааавававввиа
аавав ваввваввва вввввааваа аавваввавив
аавававвввввввваввв1аввавввввввввв1ва
авяяяаяававвсааавааввавааавааваавасва
аавааваааввавявввааввававааваававяааа
«авва«ваявквявааавааааряввааяаавяаавв
аааааавввааяававаававвввв ааваа вааваав
::...::::..:... ::.............-!.^:.
ввввваввааввааавяааааааваававаававаав
ааваа ввваваааав-ваваааааав ваяя в ааааваа
яаававаавввввваававввавввавввававвавв
вавяввввавававвавввавааввааавввввявав
iаававваававвааваааааааававааааbbbbiав
вваяв•■■■■ааваавявавявяаааввяваввааав
1 *"" вввяя ааваа вв)ааав_ааяа аяваваявяяаа
авввввввяавявввяввввваввваваааяаяа!»
авалеваввавввааааввааввваввввааввв!ва
авввававввавввваввваваааааааааааавааа
ммама авщавмаваа вааиааагяяв аваааваааааа
1вваавававаbbbbbbbbbiававвавввававвввв
вааввввввВввааввяявваааавваявааваяава
ававваааааааававаававвваааваававаааав
:ававвааававвааваявваавааввавааааааава
аавааввввв1авв1вавв|вввв1ааввваавв11в
ававв ааваа ваавааваа*ааваа аавваввавив
ввааваавававвававававваааввааааваавав
ававваааааавававаавввваааваавваваааав
«•■яяввваяаааавв аааааааава аввваваяааав
авава авяяааяяввяяяяааваа!ваяякввввааа
вваавваваавввваяааввааававвваввавваав
авваввавваааваавввввввявавааааввааааа
«■bwSвваавааваааяаяавввааваааявввааав
аавяввввававввввваввв
аавааваавквяваввавааа
аавваавваваавааааввяв
аааавваавВВВВИВМН!
ввввввввввааавввваааа
ваавааавааввааввааваа
»•«•«■шяваввввв■■.■«■
ававааваа*ааававааваа
аавааввааавааавававва
ваава вввавававв вавваа
«аваааввавваааавввааа
ааваааавааваававваавв
ваваавввввЕвааавваваа
■ авва ввввв в/'"В-СД aaai
вввввававвваававааваа
ввваа вааааваааввввввв
-ававввааяввваааавааа
ааваа ввааааавва авааав
■■вав вааааваава ааваав
вввааавааввввв!вааваа
BBBI
авв
aaai
BBBI
aaai
BBBI
BBBI
вва<
III
вва
аав<
■ ва
IBI
■В)
вв
BB il
II 1
ВТ.II
в аа
«II
Г IBI
аввиввввавявив ви
ввввавававвваввв ви
в!иавввавЗЗВ!аг iSS!
вввааввававввак. aaai
BiBiaaaiiBBBBii шввв
авваавававввввгibbib
:::;::::;::::• ::s.i
вава ввавааав"*ааваа!
аааавввяаав'^ааааваа
aaaiвввааа^ дав ааввяа
авв1вввв>'^аааааввва
авааавв' ^вавааааааа
вввг-~ ^вааааааввваа
■"" • .аввававваавваи
Г^ШД
аваавааваааааa laaaai
вававаааааававававаi
авввававвввваиваав!
■вааавваавваааавввв!
ававаававвввааававва
F^TnTP~ftffl
iff Ii
i
Ё
BBBI
■■»■
Ё
0
ваа!
BBBI
aaai
aaai
аваа
88»
У^яааявааав
квввввввав
аВваваВаяя.
■ввввваааа-
аваа.ваава
аваа ~ввввв
•в!а ввввв
1 вав,, ававв
«вав ввваа
■авв вваав
■вва авава
■ BBBI IBBBB
ibbbi швав
•вава bbbi
IBBBB BBBI
-•авва,; авва
iBBaaiiaai
■ваааа aai
Яш
Tf^tffT
■ваааававв
laaaaiaaaa
■ваваlaaaa
raaaaiaraaa
ааанввав
iBeaaiaaaa
aSSSiaaSi
■ваваававв
naiaiaaai
■BBBBIBBBB
[яяавнвав
ввввааваа
гвваваяявя
IHMIIII
aaauaai
a< uaaai
eas 0»aaa
aasaia^;-
:::::::
BBBBBBI
IBBBBBl
BBBBBBI
■вваав
IBBBBBl
laaain
fsssiSi
::5s:::
ааааваа
IBBBBII
ааааваа
■aaaaai
вявввва
BBBBBBI
BBBBBBB
аввввва
BBBBBBB
ВВЯВВВВ
IBBBIBI
ssssii!
:::::::
ввваааа
IBBBBBB
«Saba.
Raaiiaala
bbbbibbbb
BBBBiaaaa
TfTPfFfW^fff
llWWUiUfff
ааа ававвааваа вав
■авв ibbbbbbbbi вав
вва ааваав авва ааа
laBaiBBBBB bBbbbbi
BiBiBiaiiaBii bbi
аааibbbbвввввaai
вваав ааавааваааа
ававвввваявва ааа
аааававаавааава!
гвва ввавявавва Вва
аввввааваааавава
авв ававвавввв-вва
аВаааавааввваВва
авававвааввав ваа
ааа аавававвав ваа
ввваввваввввавяа
■ав авввмавяаавв
ваа вввввааввв вва
авв аавввавааавав
гавввВвВв1авааввв
ввав авва1вяаавва
ава.ввяавааваа вва
ававваававвавава
авв ааавваавав ваа
ввваавяямавама
5:::кк::-с::::
ааа ааввааввав SSS
ааааввявibbbbавв
аввавава i«aaiавв
вва аавав аавааааа
ааа вввввааваавав
аввавввавввавав!
ваа вввввааввв"в"
вввааввваваавваа
вававаагввввааввв
аваавваааааааваа
ввавваавibbbbааа
ввааавававваввав
вк,-...ма». -— в
аавуЗавааавая вМ
вваааШаав iaaaa ваяв
■ТТ 1 1 1 I 1 1 1 1 1 II 1~Г
ч\
щ
м
Рис. 7
множеству В, соответствует
I меньшее значение функции, т. е.
если х2>хх и х19 х2 € В9 то
/(*2)</(*i)-
Функцию, возрастающую
на данном множестве или
* убывающую на нем,
называют монотонной функцией на
этом множестве.
На рисунке 8 построен
график функции у=ах~2 при
а»—1. График этой функции
симметричен графику
функции у=х~2 относительно оси
х> так как при одинаковых
значениях аргумента" х зна- Рис. 8
чения этих функций
являются противоположными числами.
График функции у=ах~2 при а>0 расположен в верхней
полуплоскости, при а < 0 — в нижней полуплоскости.
159. Используя график функции у=х~2 (см. рис. 7), найдите:
а) значения функции, соответствующие следующим
значениям аргумента: 0,7; —0,7; 1,4;
б) значения аргумента х, которым соответствует значение
функции, равное 3.
160. Используя график функции у = — х~2 (см. рис. 8),
выясните, возрастает или убывает функция у = —х~2 на
множестве:
а) ] — оо;0[; б) ]05 +оо[.
161. Постройте график функции # = — 4лг2 и, пользуясь им,
выясните, на какое множество отображается
промежуток:
а) [_4; -2]; б) [2; 4]; в) [1; 2]; г) [-2; -1].
162. Принадлежит ли графику функции #=0,01ага точка:
а) А (ОД; 1); в) с(—±; 1); д) Е (-0,01; 100);
б) В (10; 1); г) D (0,5; 0,04); е) J? (0,01; —100)?
163. Найдите значение а, при котором график функции у=адг2
проходит через точку:
а) В (—0,1; 1000); б) С (50; 0,05).
49
8ч
-1
\
\
Г
'/,
Т1^
J
\
|
О
•2
i
1
0
А
1
О
L
1
f
/
I
f
^
х
164. Функция задана формулой у=3,88х~2. Не выполняя
построения графика этой функции, ответьте на вопросы:
а) При каких значениях х функция принимает
положительные значения?
б) Существует ли значение аргумента х, при котором
значение функции равно 0? равно —5?
в) На каком множестве функция возрастает?
г) На каком множестве функция убывает?
165. Функция задана формулой у = —4,51лг~2. Выясните:
а) При каких значениях х функция принимает
отрицательные значения?
б) Существует ли значение х9 при котором функция
принимает значение, равное 1; 0; —100 000?
в) На каком множестве функция убывает?
г) На каком множестве функция возрастает?
166. Используя графики функций у — — х~1 и у == —4л:""1 (см.
4
рис. 4 и 5), найдите множество значений аргумента, на
котором каждая из функций монотонна, и укажите
характер монотонности (возрастание или убывание).
167. Постройте график функции у = бяг1. Выясните, возрастает
или убывает функция: а) на множестве положительных
чисел; б) на множестве отрицательных чисел.
§ 6. УРАВНЕНИЯ, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ
В ЗНАМЕНАТЕЛЕ
16. Решение уравнений с переменной в знаменателе
(1)
^0 (2)
Пусть требуется решить уравнение
бх _ 2х + 1
3* — 1 х
Представим уравнение (1) в виде
б* 2х +1
з* — 1
/ 2х + 1 „ ,_
(перенесли выражение —— из правой части уравнения (I)
X
в левую с противоположным знаком).
Решим уравнение (2). Для этого выражение в левой его
части представим в виде дроби:
бх2 — (2х + 1) (З.г — 1)
0.
х (3.t — 1)
50
Используя условие равенства дроби нулю, имеем:
/ б*2— (2*+1)(3*—1)=0,
\х(3х—1)=^0,
6л:2— 6л:2 — х+1 = 0,
х = 1.
Высказывание 1 • (3 • 1—1) Ф О истинно.
Ответ: 1.
Уравнение (1) можно решить иначе.
Приведем выражения в левой и правой частях его к общему
знаменателю:
б*2 (2* + 1)(3*— 1)
х (3* — 1) х (3* — 1)
(3)
Так как знаменатели этих дробей равны, то дроби будут
равны при тех и только тех значениях х> при которых равны
числители и знаменатель отличен от нуля, т. е. равенство (3)
верно тогда и только тогда, когда выполняется условие:
/6*2=(2* + 1)(3*— 1),
\х(3х—1)=^0.
Решая уравнение, получим:
6х*=6х2+х—1,
х—1=0,
х=1.
Высказывание 1(3 1—1)=И=0 истинно.
Ответ: 1.
Рассмотрим другие примеры.
1. Решить уравнение:
За + 1 х — 5 __ .
х — 3 х
Решение. Представим уравнение в виде
^±1 + £=* __4=0
х — г х
и заменим выражение в левой части дробью:
(3* + 1) х + (х — 5) (х — 3) — Ах (х — 3)
= 0.
х (х — 3)
Воспользовавшись условием равенства дроби нулю, имеем:
51
((Зх + 1)х+(х— 5)(*— 3)— 4л: (л:—3) = 0,
1 л: (ж — 3)=^= О,
3*2+л:+л:2— &С + 15- 4*2+12* = О,
5л:+ 15=0,
л: = —3.
Высказывание —3(—3—3)^0 истинно.
Ответ: —3.
2. Решить уравнение:
14 4
У-3 у + 1 (у-8)(у+1)
Решение. Приведем выражение в левой и правой
частях данного уравнения к общему знаменателю:
У + 1 + 4<0_3) _ 4
<¥-8)(0 + 1) (У-3)(а + 1)
Гу + 1+4у-12=4,
1(у-8) (у+1)^=0,
У=3.
Высказывание (3—3) (3 + 1)^0 ложно.
Ответ: уравнение не имеет корней.
168. Решите уравнение:
ч * — 2 * + 5 л х ч 2ж + 3 х — 5
a)"i г--1; ^srr-i-rn5
5 2 1 — 3* 1 + 2х
B)x!_4=3 + 2f. ж) 1 1 .
х 2 1Су — 1 2 —5г/
ч *а + 5 Зх + 10 ч 3 5
Г) _Х_ = у ; 3) -
2л: 6 8 — Ъу 7у — 2
169. Найдите корни уравнения:
a)_i i-=i. p) 8 I у =*~2°У2.
У —2 у—3 у9 2у — 1 2у + 1 1 —4у2 '
ф JL + _1_ = !£. т) У + Ь -^5 ^-+-Г-5
( — 2 у+ 2 у У2 — Ьу 2у2—10у 2у* — 50
52
170. Решите уравнение:
а) = ; в) = х;
х + о х + 5 Zx — 5
-ч 2х2 3* ч 1 +ж —6*а
б) = ; г) —— = #.
7 2* — 3 2* — 3 3* + 1
171. Числитель дроби на 2 меньше знаменателя. Если
числитель этой дроби уменьшить на 1, а знаменатель
увеличить на 3, то значение дроби будет равно 0,25. Найдите
дробь.
172. Знаменатель дроби на 5 больше ее числителя. Если
числитель этой дроби увеличить на 1, а знаменатель оставить
без изменения, то значение дроби будет равно —. Найдите
з
дробь.
173. Моторная лодка прошла против течения реки 16 км и
вернулась обратно, затратив на обратный путь на
40 мин меньше, чем на путь против течения. Найдите
собственную скорость лодки, зная, что скорость течения
реки 2 км/ч.
174. Турист проплыл на байдарке по течению реки 24 км и
затем вернулся обратно. На весь путь он затратил 7 ч.
Какова скорость течения реки, если собственная скорость
байдарки была 7 км/ч?
175. Две землечерпалки могут при совместной работе углубить
дно реки за 12 дней. За сколько дней выполнила бы ту же
работу каждая землечерпалка, работая одна, если
известно, что производительность одной из них в 1,5 раза выше
производительности другой?
176. Производительность самоходной косилки в 5 раз выше, чем
производительность бригады косцов. Сколько дней
потребуется бригаде косцов, чтобы скосить луг, если известно,
что самоходная косилка и бригада косцов, работая
совместно, смогут закончить сенокос за 3 дня?
177. Из города А в город В вышел поезд. Первые 450 км из-за
задержки в пути он шел медленнее, чем требовалось по
расписанию, на 10 км/ч. На оставшемся участке пути
протяженностью 750 км поезд увеличил скорость, с которой
должен был идти по расписанию, на 8 км/ч, в результате
чего он в город В прибыл вовремя. Какую скорость
должен был иметь поезд по расписанию?
178. От деревни Дубки до села Боровково а км. Мальчик на
путь в Боровково обычно тратил столько же времени,
сколько и на обратный путь. На этот раз туда он шел со
53
скоростью, на 1,5 км/ч большей, чем обычно, а обратно со
скоростью, на 1 км/ч меньшей обычного. В результате
время, затраченное на путь туда и обратно, оказалось
такое же, как и всегда. С какой скоростью ходил обычно
мальчик от деревни Дубки до села Боровково и обратно?
Покажите, что ответ задачи не зависит от расстояния а
между деревнями.
179. На перелет от Москвы до Новосибирска самолет тратит по
расписанию столько же времени, сколько и на обратный
путь. Из-за встречного ветра в Новосибирск самолет летел
со скоростью, на 60 км/ч меньшей, чем полагалось. В
Москву же он летел со скоростью, на 70 км/ч большей, чегл
обычно. В результате на оба рейса он затратил столько
времени, сколько требовалось по расписанию. Какова
скорость самолета по расписанию?
17. Уравнение с параметром
Рассмотрим задачу: «Теплоход, имевший собственную
скорость 26 км/ч, отошел от пристани и проплыл против течения
реки 80 км. Сколько времени затратил теплоход на весь путь,
если известно, что скорость течения реки равна Ъ км/ч?»
Обозначим время (в часах), затраченное теплоходом на весь
путь, буквой х.
Скорость (в км/ч) теплохода против течения реки равна 26 — Ь.
Имеем уравнение:
(26— Ь) х =80. (1)
В это уравнение относительно х входит переменная 6,
обозначающая скорость течения реки в км/ч. Такую переменную,
которая в пределах рассматриваемой задачи сохраняет одно и
то же значение, называют параметром.
По смыслу задачи параметр Ъ может принимать значения,
меньшие 26 и большие 0, т. е. 0 < Ъ < 26.
Если Ь = 6, то уравнение (1) примет вид: 20х = 80.
Если &=10, то уравнение (1) примет вид: 16л: = 80. Каждому
значению параметра &, где 0<&<26, соответствует определенное
уравнение. Эти уравнения одно от другого отличаются лишь
коэффициентом при х. В выражении (26 — Ъ)х — левой
части уравнения (1) — множитель (26 — Ь) выполняет роль
коэффициента.
Выразим переменную х через параметр Ь:
54
Так как 0<&<26, то уравнение (1) имеет корень, который
может быть найден по формуле х = .
26 — Ъ
Итак, время, затраченное теплоходом на весь путь, равно
26 — Ъ
С понятием параметра мы встречались и раньше, не
употребляя этого термина. Например, когда определяли линейную
функцию как функцию, которую можно задать формулой вида
y=kx+b, буквами к и Ъ обозначались параметры. При
рассмотрении линейного уравнения с двумя переменными как
уравнения вида ах + Ьу = с буквами а, & и с обозначались
параметры — коэффициенты линейного уравнения.
Рассмотрим примеры решения уравнения с одним
параметром.
Пример 1. Дано уравнение относительно х:
тх— 8 = х.
Решить его.
Решение. Приведем данное уравнение к виду ах=Ь:
тх—х== 8,
(т — 1)х =8.
Если т —1=0, то уравнение примет вид: 0#=8. Очевидно,
что это уравнение не имеет корней.
Если т—1^0, то мы можем переменную х выразить через тх
т — 1
Ответ: уравнение имеет единственный корень ,
т — 1
если тф\\ уравнение не имеет корней, если т= 1.
Пример 2. Дано уравнение относительно х:
пх= 5п.
Решить его.
Ъп
Решение. Если п ф0> то х= —, х = 5.
п
Если п=0, то уравнение примет вид: 0#=0. Очевидно, что
этому уравнению удовлетворяет любое значение х.
Ответ: уравнение имеет единственный корень 5, если
пфО; уравнение имеет бесконечное множество корней (любое
число — корень уравнения), если п = 0.
55
Пример 3. Решить уравнение с параметром а:
2-у
Р
Решение. Приведем данное уравнение к виду — = 0:
Я
-— — 3 = 0,
2 —у
a-Z(2-y) n
2-у
Sy+a-6 n
■ — и»
2-у
jdy + a— 6 = 0,
\2-уф0,
Zy = 6 — а,
6 —а
3
Мы выразили переменную у через а. Теперь нам нужно проверить, при
6—а
каких значениях а предложение 2 — Ф 0 обращается в истинное высказы-
3
ванне, говоря иначе, нужно выяснить, при каких значениях а предложение
Л 6—а
2 — —-— = 0 обращается в ложное высказывание.
Решим уравнение:
6-
6-
— а
-6 + а
3 ~~
а
1=°'
а = 0.
<*= О лбпятт
0
ТЯ*
3
при всех значениях параметра а, не равных нулю.
6— а
Ответ: уравнение имеет единственный корень —-—, если а ф 0; уравне-
3
ние не имеет корней, если а = 0.
180. Дано уравнение с параметром а:
ах=2а+3.
Напишите уравнение, которое получится при указанном
значении а, и решите его:
а) а=10; б) а = 1; в) а = —1,5; г) а=0.
181. При каких значениях параметра а уравнение ах =5 не
имеет решений? При каких значениях а данное уравнение
имеет корень, равный:
а) 1; б) I; в) -2; г) -3,5?
э
182. Существуют ли такие значения параметра &, при которых
уравнение Зх — b не имеет решений?
183. Решите уравнение с параметром а:
а) ах = 8; б) 5х = а; в) (а — 2) #= 20; г) х = 1 — с*
184. Уравнение относительно х приведите к виду ах = Ь и реши»
те его:
а) ся+2=5; б) 6я—ся = 1; в) сх—5 = *; г) сх+7х=0.
185. Выразите переменную я через а:
а)х+2=ах, аф\\ в) 1—=2, а=£0, аф—\
х а 2
*ч* + 3., у - ч 2*4-3 /0
б) -Х- =1, афЬ\ г) а = —Х-, а=^2.
а — 5 * — 4
186. Выразите переменную г/ через а и Ь:
а) а = ^-±-^; в) - = - + -, а Ф О и Ь=#=0, а + ЬфО;
2 у а Ь
в)*±1=*9 rjl^l+l, а^=0 и &=^0, а — &^©0
2—у b а у Ъ
ЪфО, а + Ъ Ф 0;
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ I
К пункту 1
187. Преобразуйте выражение в многочлен стандартного вида:
а) 5х2 (х2—2х+3); е) (3&—2) (Ь2—7Ь—5);
б) -&у2 (у2-5у-1); ж) (у-1Ку3+у2+9+1);
в) Зх2(—Ъх2+Ах—1) + 16*4; з) (х+1)(х*—хь+х*—х+1);
г) 8i/e-2y3(l-5y-i/2+4i/8); и) (а2+7а+3)(а2-4в+2);
д) (а2—5а+4)(2а+3); к) (Ь2—ЗЪ—5){Ь2+ЪЪ—5).
57
188. Представьте выражение в виде многочлена стандартного
вида:
а) (—4х+7а)(7а+4х); е) (*+1)3;
б) -(а—76) (7Ь+а); ж) (у — 2)3;
в) (Зс2- 8) (Зс2 + 8); з) (х + у)3- (х+у) (ж2- ху + у2);
г) (2х—Ъу)2\ и) (го—п)3—(го—п) (тй+тп+п2);
д) -2(у-If+(2-у)'; к) xiy-xf-y (y-xf+iy-xf.
189. Найдите значение выражения:
а) х2— (х— у)2 при х = — 3, у=—1;
б) 9ж2— (Зх+у)2 при * = —3, у = —1;
в) (x-4jJ-{y-6^J при л;=10, у =9;
г) (х+у)2—(х—yf при*=—, у = — 5.
4
190. Разложите на множители:
а) а2Ъ+аЬ2\ в) тъп2+т2пъ; д) 2с8—250с2;
б) х3у— ху3; г) pV—PV; е) 81г9+3г3.
191. Представьте в виде произведения:
а) 7х—Uxy + 21ах; е) 16ck + 6k— 40c—15;
б) 9ху—дху + 15ау; ж) хх—х3+х2—х;
в) — 48а56+Збс6Ь5—12а6Ьв; з) с4—2с3—с2+2с;
г) 8ао2—ба2&2—2с&+2а362; и) 36 (о—2)2—25а2;
д) 35аж—49&*—5а+7&; к) 100 (2у2 + 1)2—121у\
192. Решите уравнение:
а) 8* — 5 (ж+2)=1; г) 15у2+25у = 0;
б) 6(*— 9)+25 = 4*— 31; д) 36у2 — 25 = 0;
в) 15у2— 25у=0; е) 36i/2-f25=0.
198. Докажите тождество:
(х+а) (х+Ъ)=х2+(а+Ъ)х+аЪ.
194. Приведите многочлен к виду (х+а) (х+Ь):
а) *2+5х+6; б) х2— 5*+6; в) ж2+7л:4-12; г) x2+Zx+2.
195. Приведите уравнение к виду (х+а) (х+Ь) = 0 и найдите
его корни:
а) x2+8x+15=0; в) х2—6х+8=0;
б) х2— 8*+15=0; г) *2-f6* + 8=0.
58
193. Докажите тождество:
а4+я2 + 1=(а2+а + 1)(а2 — а + 1).
Почему при любом значении а верно неравенство:
а) а4+а2+1>0; б) а2+а + 1>0; в) а2—а + 1 > О?
197. Разложите на множители:
а) Xs—1; г) р8+р4 + 1; ж) б6—Ь4+2&3 + 1.
б) у« + 1; дХ&12-1;
в) а8—1; е) ав+2а8—а2+1;
198. Постройте график функции:
&) у =—0,5лН-3; г) у =—1,5л: — 2; ж) у=х3;
б) у=0,5х+2\ д) у=095х2; з) у = — х*.
в) у = 195х—1; е) у = — 0,5л:2;
Используя график, выясните, при каких значениях х:
1) У ==0» */ > 0> ^/ < 0; 2) переменная [/ возрастает с
возрастанием х; убывает с возрастанием х.
199. Решите уравнение:
а) |х|=3; в) |х—2|=1; д) \х\=х;
б) |*| = — 5; г) |*+2|=5; е) |х| = — х.
200. Сумма двух чисел равна 25, а их разность равна 1. Найдите
эти числа.
201. Одно число в 5 раз больше другого. Сумма этих чисел
равна 54. Найдите меньшее число.
202. Одно число на 1 больше другого, а квадрат первого числа
больше квадрата другого на 21. Найдите эти числа.
К пункту 2
203. Найдите значение дроби:
2
2,25 : 1,5 + 3 : 1
а)
«Д
' ' 3
1,1 ;
-4—) . 22,5
15/
з—
7
ч 15
(5,56 — 4,06): 3*
г) ;
' 3 1
14— • — + 2,17
20 5 ^
ч 372 + 111
ч 395 -f 7Q2
е) ———
' 84
59
£04. Найдите значение выражения при:
3-я
а)х=— 1; б) х = 0,5; в)* =24; г) х = 3-.
4 8
205. Найдите область определения дроби:
ал *-3 .
"' 10* + 50'
б) ;
' 16* — 64'
ч а + 5
в) ———;
2а2 - 98
D—1—;
*3 — 4*
л) 5 •
™ 16»'-1'
X
2
— —8
9——
а
ч Ю
з) ;
1*1-2*
ч 30
и) ;
1^1 + 3
ч а2 + 1
к), , -
\а\ — а
206. При каком условии дробь не имеет смысла:
*s + j/a ' (ж-У)2' (* + 1)а + (у - 1)* '
-ч 1 ч аЪ ч 8 о
б) ; г) ; е) ?
' *у* (а — &)2—1 |а + Ь|—1
207. Составьте дробь, которая не имеет смысла при:
а) у = 0 или у=2; в) а= 0 или 6=0;
б) j/ = 2 или у= —; г) а = 0 и & = 0.
о
208. Какие натуральные значения х и у удовлетворяют
уравнению:
в)*±1?=1; б) —? 1?
7 7 7 * + 2#
209. Запишите в виде дроби частное от деления числа 273 на
двузначное число вида 10а+1. Укажите множество
значений переменной а. При каких значениях а составленное
выражение принимает целые значения?
210. В бассейн объемом 400 м3 проведены три трубы. Через
одну из них вода поступает, через две другие вытекает.
60
Через первую трубу поступает 15 м3 в час, а через каждую
из двух других вытекает х м3 в час. Если открыть все
три трубы, то пустой бассейн через некоторое время
наполнится. Через сколько времени наполнится водой
пустой бассейн, если открыть все трубы? Составьте
выражение. Найдите множество значений переменной яг.
211. Первый поезд вышел из А в В и проходил в час по 60 км.
Второй поезд вышел из В в А на 3 часа позже, чем первый
из А. Поезда встретились через у часов после выхода
первого поезда. Расстояние от А до Б равно 700 км. На каком
расстоянии от В произошла их встреча? Какова скорость
второго поезда?
Составьте выражения и найдите их значения, если:
а)у=8; б) у =6.
212. Найдите область определения функции:
а) у = -; г) у = --—-; ж) у =
* — 2 " *2—4 ' " \х \—х
б) У = ЧЧ; Д) У = т—i—Т; 3> У = , *
я2 —- 5* | # | + 3
К пункту 3
213. Какая из дробей равна нулю:
2 б \ 1
— — — . 5— — 2
ч \3 18/ 7
а) - - ; в)
1 7
2 : — — — . 120
_1в_24 ^-тд.^.,.т^, ?
4 3\ 7,32—2,72
214. Придумайте дробь, которая содержит переменную х и
обращается в нуль при:
а) х = 1,5; в) х=0 или х=2;
2
б) # = - ; г) * = —5 или х=5*
о
61
2-i
3
(о,75 +
1,22 + 2
— 21
7,32
1
' 9
2
1,8 + 1,8» — 9
-2,72
215. При каких значениях а значение дроби равно нулю:
(2а + 1)*-81.
а)
б)
в)
(а+Ра.
17 '
aa(g + 5),
о2 — 5а '
Г)
Д)
е)
о» + 125
(а-2)(а-1)(а' + 1).
а
(2а + 5) (а-0,1) (а2+ 1).
а+ 10 *
ж)
з)
\а
1«
1-
10
1-
3.
9
«9
25
216. Решите уравнение
N 15* + 45
а) —
х
б)Ш-21=0:
14л: + 21
в) У(^81 = 0
. 9х — х* Л
г) — = 0
Д)
ж —9
4у2-У
У
= 0:
V-25=0
2J/ + 5
*»—49
У2+4
217. Найдите множество значений х, при которых / (х) =0,
если:
а) /(*) =
б) / (ж) =
х — 3.
*2 — 9
в) /(x) = -l^L; д) /(*) =
6 + х
г) /(*) = |я| + 3; е) /(*) =
5 6 + аг
К пункту 4
218. Сократите дробь:
405ах
ч 99*
а) ;
22у
б)
2166с
180ас
в)
г)
4:5ау
18аЬс t
Шас '
Д)
е)
35gSy4
28a4i/8
7*7у*
14*V
ж) iz^L
3)
219. Упростите выражение:
1ху + 14 т _ч б*2 — 6а2.
а)
б) 8(Д""12>;
8а— 12
(За — Зс)2#
В)
9а2 — 9с2
г)
Д)
е)
(6х— ба)2
(2а — 2&)2
2Ь2 — 2а2
(4х —4у)»,
(2у — 2*)* '
ж)
з)
и)
(ga _ 9)2 ^
(3-а)» '
(5g-2p)* .
(4р2 — 25а2)3'
х2 — 100.
*з. + ДОХ)'
К)
8уЗ — 1
У — 4у*
62
220. Докажите тождество:
10ab —15Ь2 10Ь2 — 15а!?
а)
б)
в)
г)
4а2 — 6аЬ 4лЬ — 6а2
2л:2 + 10*1/ 2*2 — Юху
— 2оу2 *2 — 10*1/ + 25i/2
а2 — 4а 4- 4 а2 — аЪ + 26 — 4
С2 + оь — 2а — 2Ь а2 + 2а + 2Ь — Ь2
(2х — Ву)* + 2х—ду __ 4*2 — 12ху + 9у2
4*2 — 9z/2 + 2* + 3// 4*2 — 9у2
221. Сократите дробь:
fc21 + 1 * (у - 2)i; ~ г/ (х - г)2
узз _ ! а (Ь -J- Рг — Ь (а + 1)^
*зз -j- л:22 + я11 ' а2 (6 + 1) — &2 (а + 1) *
222. 1) Если у дроби ^— переменные хну заменить
ду2 — Ьху
соответственно через kx и ky (k — не равное нулю число),
то получится дробь, тождественно равная
первоначальной. Докажите это.
2) Проверьте, какие из следующих дробей обладают
указанным выше свойством:
2*»-у». б *2-5j/, (*2-у2)2 . Г) (*2 + У2)*
4ху*+7у*' х + Ъу2* (х+2у) (3* — у)*' (* — dyf "
2х2 4- и2 2 3
223. Докажите, что значение дроби ±-2— при х = — иу=-
равно значению зтой дроби при х =2 и у=3.
224. Найдите значение дроби:
ч a2 + Zab 1,1
а) J при а = - и Ь = -;
а2 — аЬ 6 б
^ч а2 — аЪ 3 7 1
б) при а = — и 6 = —.
а2 + ^2 4 2
225. Докажите, что при всех значениях переменных а и х> при
которых дробь имеет смысл, ее значение не зависит от х:
ч а2 — 2ах -f б* — 9 гч (а + З*)2 — (3* — I)2
а) —;—; 7~» б)
(а -|- 3)- — lax — 6* 6* — 6а* — (а — I)2
63
22/6. Докажите, что если вместо переменной х подставить нату-
2х
ральное число, то получится несократимая дробь -.
2х+ 1
К пункту 5
227. Представьте произведение в виде дроби:
. 54*V 22q5*5 ^ 5а* — 5fr3 18а2 — 18&2 л
Па* ' 81г/в ' 12а + 126 ' а2 + аЬ + Ь* '
_ 8&«вв 55с2*5 ч х2—2ху ж4 — 16i/4
б) . ; г) — . —.
33*1 12Ь4 *2 + 4у2 (* — 2у)2
228. Решите уравнение:
а) (* + 5)—=0; Г)^=Ц.^ = 0;
х —2 ж+1 2*
х Л ч л:2 — 4* 3*
= 0; д)
* + 3 5 *2 -4
Lz2?e0; e)5!+i,
5s +10 х4 — 1
* w 1 \ * л ч аг2 — 4* 3* 4- 1 Л
в) (л;+ 2).^^ =0; е) £±i . (* — 1) = 0.
К пункту 6
129. Представьте частное в виде дроби:
144a1Qy8 . 60oV ч 25а« 10а*&
65Ь4г3 ШМ 6а8 — 6&8 9аа + 9аЪ + 952
*ч 192твл9 36ттгв7г8 ч Ьх*у 10х10у2
б) ——— : ———; г) * •
77р 55р3 ' а2 — 2аЬ + 4Ь2 а3 + 8Ь«
230. Упростите выражение:
ч а2 — Юса; + 10ах —ас а2 — 100*2
а) -^ : — ;
х2 — ах а2 — ах
б. тг2 — lOpft — 2pn + 5fen р2--6р4 .
в)
Г)
Д)
е)
б&тг — рп п2 — 25 V2
я4 — i/4 2я + у
4х2 — 2х — у — у2 х* + х2у + ху*-\- уз
а9 — Ь6 а — ЗЬ
а2 + а__зЬ — 9&2 ' (а2 + Ъ2)2 — а2Ь2 '
6^у + в — 4^~9у т 9у2 — 12у + 4
ж2 — 12*+ 36 " 3*и/ — 18у — 2* + 12 '
15аЬ —15 + 9а — 25& . 9а2 — 30а + 25
9а2 — 30а!> + 25ba 15а — 25Ь + 9а2— 25Ь2
64
К пункту 9
231. Замените выражение дробью:
аИ + 3 * 1
X X — 3 X2
б) 8 +gL=i_
2л:2 + 2л: л:2 — 1
8 , Ь«—8&
в) ^гтт + от;—г»*
10
-Зл:
2 #
>
X
г) 2*2+* + 10 + _«
4л:2 — 25 5 — 2л;
. 4а2 + За+2 1— 2а .
W аз — 1 а2+а +1*
ЗЬ + 6 ЗЬ2 — 12 л:2 + л# + у2 ж?— у* х*-у
232. Упростите выражение:
1,1.1
а)
(а —&)(&—с) (с —а)(а —Ь) (Ь — с) (с — а)
б) , 1 + „ * + ■ *
а (а — Ь)(а — с) Ъ(Ь — с) (Ь — а) с(с — а) (с — Ь)
233. Докажите, что множество значений выражения состоит из
одного элемента:
.Ъ+1 , е+1 Ь + с ч be —а2 . ас — Ъ2 , аЪ — с2
а) -~]— + — -1—; в) 1 1 ;
Ь с be ab be ae
g. х у (х + у)2 . у л: . х + у х(х+-у)
У х ху у л: — у у(х — у)ш
234. Докажите тождество:
. ах -f- by bx — ay a2 -\-b* л
Е) (а-Ь)(х+у)~ (а + Ь)(х + у) ~а2-&2'
Ь2+&у + дс2 &2_Ьу + х2 ^ (Ь> + ^
(&4~л:)2 (Ь — л:)2 (&2 —л:2)2'
В) * + Й + * = 1.
(л: — у)(х — г) (у — х)(у — г) (г — х)(г—у)
235. Решите уравнение:
a)_J !_ = 0; т)*=1+ !=* = *
2л: — 1 5л: — 6 ' Зу + 1 У + 3
6)-i ^=0; д)^-9 + _^ = 2;
Зл: + 5 4* + 8 2* — 5 Зл: — 2
У — 1 У — 3 ' 3* — 2 2л: — 3
3 Алгебра» 7 ал. од
236. При каких значениях а и Ь тождественно равны
выражения:
v ах + 6
Я 1
UI
х + 10
3*-9
К пункту
* — 5 3* — 5
2х + 20 2(* + Ю)'
ах + Ь 4х2 + 45* + 50<
5* + 2 15л2 — 39* — 18
10
237. Представьте дробь в виде суммы двух дробей:
а)£±^ б)-А_; в) 3* + 1 ; г) 7* + 14-.
а2 — 9 б2—1 х(х + 1) (*-2)(* + 5)
238. При каком целом п значение дроби есть целое число:
а) *±±. б) -5L.?
3—тг 2 — п
239. Написанные равенства — тождества. В них буквами а, Ь
и с обозначены некоторые числа. Найдите их:
а) 4** + 3*-25 =в_о_ + _1_ + , с .
(ж — 1) (х + 2) (х — 3) я: — 1 ж + 2 я — 3
(л:—I)3 х — 1 (* — I)2 (л: — I)3
ч Юл:2 — 1 ах—31 Ь . с
(х — 1) (х + 2)2 (* + 2)2 * + 2 л: —1
240. Представьте дробь ———, если это возможно, в виде
х2 — 9^
суммы двух дробей и , где а и Ъ — целые числа.
х + з х — 3
К пункту 11
241. Представьте выражение в виде дроби:
■> (■+!)'• "(f+'Hf-1)"
"(i-7)' "(i+'Hf-1)"
€6
242. Докажите, что при любых натуральных значениях п
значение выражения
(£+т):(^~;г+т)~натуральяое число-
243. Докажите, что при любом целом а и дробном х значение
выражения
/ а2 -\-х*\ / 2а , 4а \
[а ——)•( 1 —четное число,
V а + х ) \ х а — х)
244. Докажите, что при любом значении х, большем 2, значение
выражения
/i±i + JL- _ 2): *±±- х2~Ьх + * - отрицательное
V 2х * +3 / х + 3 2х
число.
245. Упростите выражение:
\ / а — 3 6а — 18 \ # 5а — 15 .
\ а2 — 8а + 9 а3 + 27 / " 4а3 + 108'
Qt*±!L + ab+!A- 5а b ■
' \5а2 — 5аЬ /
а + Ь а — Ь
12а* + 12а& + &»
16а
B)/_JL_+_i_ + _L_\
' \(2а — Ь)2 4а3 — Ь2 (2а + Ь)2 /
v 4с2 . / 1 1_ _ J* \
(с-2)« " \ (с + 2)2 (с —2)2+ с2-4 /
. у'2 (4х* — Ах2у , х — у
2* + у \ багу + 3z/2 Z J х — у
ч а+26 /0 . 2, а — 2&\ 1 —баб2
е) ,^" ь ■ 2а& —а2+; *
а2 — 2а& V Зад + 6Ь2/ ЪаЪ
246. Предстазьте в виде целого выражения:
а)( * 2о__аз + 25аМ /Q_ _15о_у
\а2 + 5а + 25 5 — а а3 —125 / \ а — 5 /
б) /(!-*)(!-*) _ ! \2« (1-а2)(1-62)
\ 1 + аЬ / (1+аЬ)2
247 • Преобразуйте выражение в дробь:
* 1 / a . 4а3Ь— аЬ2 , Ь2 \ За*
а) 1 : --;
' \а — Ъ Ъ* — а3 а2 + а& + Ь2 / (а — &)*
б) / °~* _ * \ . /2* + а , 2а_+х\
' \а2 + а* + *2 a — */ * \ а х I
3* 67;
248. Докажите тождество:
ч Ь2 "" Ь + а2 "" а ,
а) = аЬ;
1 +2 '
б) (a — W_ а? -Ъ* (fl+&)a
(а + Ь)2 + 2 (а3 — Ь2) + (а — &)2 (а2 — Ь2)2
249. Выполните подстановку и упростите полученное
выражение:
ч ах . Ь* оЬ
а) —■ 1 -, где л:
х -\- а х —Ь а — Ъ
~ х2у2 2аЬ 2аЬ
.у2' а2—Ъ2 " а* + Ь2
К пункту 12
250. Представьте выражение в виде степени с целым
показателем:
ч 1 ч 1 ч 4 ч 1
а) ^ г) —;; ж) —г; к)
Ю4 —8 а"2 (0,0001)"
*ч 1 ч 1 „ч 9а2
б) 1^555; д) й; 3) ^;
ч ! ч ! ч 1
(__5)в ' *8 ' ' 125а»'
251. Докажите, что следующие выражения взаимно обратны:
а)1 и №Х\ в) 1000-2 и (0,001)"2;
б) (|)4 и (0,6)-4; г) 2,5-' и (|)"
'2\-4
252. Сравните выражения:
а) 5-8 и 7-3; в) (2,9)-10 и (ЗД)"10;
б) (|)~3 и (|)~3; г) (0,43Г10 и (0,52)
68
-ю
К пункту 13
253. Найдите значение выражения:
254. Представьте выражение в виде дроби:
а)~а-18Ь"6 — -а-6&-12;
24 18
'28 * 35 * '
в) (х2+ху) (х2—у2)^1 (ху—у2))
г) (а+1) (а2—1Гга3;
д) ит (п—т)~2—п (т—п)~1\
е) (2а+1) (2а—I)-1—(2а—1) (2а+1)
k-i
255. Представьте дробь в виде целого выражения:
а) ! • в) » ! •
7 яг»+ ж"12 а"б -{- а"8 + а"7
у20_у21 ^ Ь3 + &2 + &+1
' „-21 „29 ' '
у-21 — у29 ' &-3 + Ь-2 _|_ &-1 + !
256. Упростите выражение:
а) (x-i+y-^iix+y)-*;
б) {<ггЪ2— а2&~х) : (а-3— гг3);
в) {аг1 + Ъ-1)аЪ(Ъ*— а2)"1;
г) (6 + &-2)-((&2 + 1)&-2— Ь-1)-1;
д) (ar*-а-8)-(а"1—зг1)-1;
е) (аЬ-1—а-^Ивг1—Ь-1)-1.
257. Решите уравнение:
а) 5*-1— 6 = 0; г) 6 (у—З)-1— 4 (г/— 2)~1 = 0;
б) 3 + 10ж-1= 0; д) (5—л:"1)"1- 2~2;
в) Эх"1— 8 (2х + 1Г1= 0; е) (9—я-1)-1^-2.
К пункту 14
258. Запишите в стандартном виде число, о котором говорится
в предложении:
а) один карат равен 0,0002 кг;
69
i 1 и 111 И111111111
У~1 и 1TP Im
i-j-j Н~ГП~ГР /
mm \W\\
11x11111 г! 117111 LH
M -i - Щ /) Lffi
MMM
Д^Ущ]Д
б) скорость электрона
равна 59 450 000 см/сек;
в) одна миллисекунда
(м/сек) равна 0,000278 ч;
г) одна верста равна
1066,8 м.
259. Выполните действия над
числами, записанными
в стандартном виде:
а) 3,44-1016-7-Ю-12;
б) 8,1Ю~23-2-1021;
в) 4,2 10й-5,1 -Ю-7;
г) 9,6-1О-|2:(8,2-10-1в).
К пункту 15
260. Постройте график
функции у = 12х~1. Найдите:
рис# g а) область определения
функции; б) множество
значений функции; в)
множество значений аргумента, на котором функция принимает
положительные значения; отрицательные значения; г)
промежутки, на которых функция возрастает.
-
р
«. i
<
„1
(
1
/
{
-2
/
/
/
/
"ч
-1
У-
г
о
У.
4'
3
о
L
1
/
■О
4
[L
i
3
7
\
и
5
6
Л
70
Рис. 10
261. Функция f задана графиком (рис. 9) на отрезке [—4; 8].
Пользуясь графиком, найдите:
а) множество значений функции /; б) множество значений
х, при которых / (яг) = 0, / (х) < 0, / (х) > О; в) множество
значений аргумента, на котором функция f возрастает,
убывает.
262. Функция g задана графиком (рис. 10) на отрезке [—3; б].
Укажите промежуток, на котором функция g:
а) возрастает; б) убывает.
263. В одной и той же системе координат постройте графики
о
функций / (х) = — х2 и g (х) = 12дг2.
4
Используя построенные графики, решите уравнение или
неравенство:
а) f(x) = g (х); в) f(x)>g (х); д) / (х) < 1;
б) f(x) <g (х); г) / (х) =у; е) g (х) > 3.
4
264* Известно, что точка (а; 6) принадлежит графику
функции f. Принадлежит ли этому графику точка (—а; &),
если:
а) / (х) - 81х2; в) / (х) = 2х3; д) / (х) = 5х;
б) / (х) = 46х"2; г) / (*) = - Зх-4; е) / (х)=5 |xj?
265. Симметричен ли относительно оси у график функции,
заданной формулой:
а) у = —37х~2; б) у-16х"3; в) у= х3; г) у= |х|3?
266. Чем отличаются друг от друга графики функций f и g9
ч если:
а) /(х) = х, *<*) = |*|; г) f(x)=x~\ g(x) = \x\'i;
б) /(х) = х2, g(x) = \x\2; д) /(*) = *-*, g(x) = |x|"2;
в) /(х)-х3, g(x) = |x|3; e) f(x)=xr\ g(x) = \x\-*1
К пункту 16
267. Решите уравнение:
1 — X 1 + * 1-Х*
^ 5 3 20
о) = ;
' ж—2 х + 2 ха—4
х+2 __ х + 1 = 4
х + 3 х — 1 ~~ (х+ 3) (х—1)'
?L±2 + _3 1 з
x-fl х —2 жа_х_2*
71
268. Турист проехал на велосипеде 28 км по шоссе и 25 км по
проселочной дороге, затратив на весь путь 3 ч 36 мин. С
какой скоростью ехал турист по шоссе, если известно, что
по шоссе он ехал в 1,4 раза быстрее, чем по проселочной
дороге?
269. Мотоциклист рассчитывал проехать 120 км за
определенное время. Через час после отправления ему пришлось
сделать пятнадцатиминутную остановку. Чтобы прибыть
на место назначения вовремя, мотоциклист увеличил
первоначальную скорость в 1,2 раза. С какой скоростью
ехал мотоциклист в начале пути?
270. Мотоциклист выехал из города А в город Б. Если он
будет ехать со скоростью 50 км/ч, то опоздает на 1 ч, если
же он будет ехать со скоростью 70 км/ч, то приедет в В
на час раньше срока. Каково расстояние между городами
А и В?
271. Турист выехал на мотороллере из А в Б со скоростью
50 км/ч. Через 24 мин после отправления из А он снизил
скорость на 10 км/ч и поэтому прибыл в Б на 18 мин
позже, чем предполагал. Сколько километров от А до Б?
272. Моторная лодка, имевшая собственную скорость 16 км/ч,
отошла от пристани А одновременно с плотом вниз по
течению. У пристани Б лодка развернулась и на обратном
пути встретила плот в 20 км от пристани А. Каково
расстояние между пристанями А и В, если известно, что
скорость течения реки равна 4 км/ч?
273. Поезд должен был пройти расстояние АВ со скоростью
56 км/ч. Однако через полтора часа после выхода из А он
был задержан на 30 мин и, чтобы прийти в Б по
расписанию, должен был остальной путь проходить со скоростью
63 км/ч. Чему равно расстояние АВ?
274. Пройдя путь из М в К, равный 360 км, автомобиль
повернул назад и через час после выхода из К увеличил
скорость на — первоначальной. В результате на обратный
путь он затратил на 1 ч 15 мин меньше, чем на путь из М
в К. Какова первоначальная скорость автомобиля?
275. В хоккейном матче команда «А» в каждом периоде
забросила одинаковое количество шайб, а команда «В»
в каждом следующем забивала на одну шайбу больше,
чем в предыдущем. В чью пользу и с каким счетом
закончился матч,, если известно, что третий период
закончился вничью и одна из команд забросила шайб в 2 раза
больше другой?
276. Два подъемных крана, из которых второй начинает работу
на 5 ч позже первого, разгрузили баржу за 11 ч. За
сколько часов может разгрузить баржу каждый кран, если
производительность второго крана на 10% больше, чем
производительность первого крана?
277. Из М в N вышел товарный поезд, а через 10 мин навстречу
ему из N в М отправился пассажирский поезд, который
шел со скоростью, в 1,5 раза большей, чем скорость
товарного поезда. Пассажирский поезд, пройдя 210 км,
встретился с товарным поездом. Найдите скорость
каждого поезда, зная, что расстояние MN равно 360 км.
278. От станции А к станции В отправился поезд. Пройдя 48 км,
поезд был задержан у семафора на 15 мин и поэтому,
чтобы прийти в Б по расписанию, последующий путь
проходил со скоростью, в 1,2 раза большей. Зная, что
расстояние АВ равно 168 км9 найдите первоначальную скорость
поезда.
279. Числитель правильной дроби на 2 меньше знаменателя.
Если числитель дроби увеличить на 2, а знаменатель
увеличить в 2 раза, то получится —. Найдите дробь.
К пункту 17
280. Равенство = а2 — а — уравнение относительно х. На-
х — 1
пишите уравнение, которое получится при указанном
значении параметра а, и решите его:
а) а=—5; б) а— 0; в) а = 1; г) а = —2.
281. Дано уравнение относительно х:
х+1
Покажите, что:
а) уравнение не имеет корней, если Ь= 0;
б) уравнение имеет единственный корень ~~ , если Ъф 0.
282. Покажите, что уравнение
а —з а —3
при любом значении параметра а, где а Ф 3,имеет
бесконечное множество корней.
73
283* Дано уравнение относительно х. Решите его:
а Л- 5
а) Ъх —Zb=2x— Ь\ в) —— = а;
х — 3
б) ах— 42=7*— 6а; г) i±f = а.
1 —ж
284. Дано уравнение относительно х. Решите его:
a> T ^Г" = 2; г) - + 8 = -;
6 10 ж ж
6)2o£-3L+7^=35e; rtl±fe£;
ж х а + 2
jp2 49
285. При каком значении параметра а уравнение = О
х + а
имеет:
а) два корня; б) один корень?
Зя 4
286. Зная, что q(x) = , найдите:
5
а) q (2); в) q (а); д) q Щ;
б) q (— |); г) q (-а); е) q (а + 2).
287. Известно, что f (х) = . Докажите, что:
a) f(a) = /(-а); б) /(-а) + /^ = 1.
288. Пусть f(x) = . Докажите, что:
х + 1
а) /(*)•/ <-*) = 1; в) / (-1 ] • / (х) = -1;
б) / (|) = -/ (х); г) / (|) • / (-*) = -1.
289. Известно, что равенство
JL_l. JL — -1 —
ж р(дс) х р(х)
есть тождество (р(х) — выражение, содержащее
переменную х). Найдите р (jc).
Т4
290. Выясните условие, при котором равны дроби:
а) —— и —; б) — и —; в) — и —; г) — и —.
8 + а 8 а 4 Ь а Ь d
291. Докажите, что:
а) если (х—у)2 =4 и (у+2) (2у—х) ф 0, то дроби
х у — 2
и равны;
у + 2 2у — ж
б) если | я—i/|=2 и (Здс+2) (2x + i/) ^ 0, то дроби
4х —• у Ъх — 2
£ и равны.
3* + 2 2х л- у
292. Докажите, что равенство:
ч a2-fb2 a2 a Ь
а) —!— = — верно при условии, что — = —;
- а2 + 2Ьс + 2ас + Ь2 1 1,11
б) —! л !— -. — верно при условии, что —1— = —;
а262 с2 a b с
в) 1 1 = верно при условии, что
а Ь с а-\~Ъ +с
(а + &)(& + е) = 0 и аЬс ф 0.
Глава II
НЕРАВЕНСТВА И ИХ ПРИМЕНЕНИЕ
К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
§ 7. НЕРАВЕНСТВА И ИХ СВОЙСТВА
18. Понятия «меньше» и «больше»
По известному нам определению из двух чисел а и Ъ
меньшим считается то, которому соответствует на координатной
прямой точка, лежащая левее, и большим считается то, которому
соответствует на координатной прямой точка, лежащая правее
(рис. 11).
да a b
a>b a<b
Рис. 11
Например: —16 меньше 0 (неравенство —16 <0 верно), так
как точка с координатой —16 лежит на координатной прямой
левее точки с координатой 0.
— больше — (неравенство — > — верно], так как точка с ко-
ординатой — лежит на координатной прямой правее точки с
координатой —.
Пусть а и & — некоторые числа, причем а больше Ь. Тогда
точка с координатой а лежит на координатной прямой правее
точки с координатой Ь. Перемещению по координатной прямой
вправо от точки Ь соответствует прибавление к числу Ъ
положительного числа (рис. 12).
у/шятм*
Рис. 12
Значит, а=Ь + с, где с — положительное число. Отсюда
следует, что а — Ь = с. Итак, если а больше Ь, то разность а — Ь
есть число положительное.
Допустим теперь обратное: разность а—Ь равна
положительному числу с. Какое из чисел больше: а или Ь? Так как
а — 6 = с, то а = Ъ + с. Но прибавление к Ъ положительного числа
соответствует передвижению от точки с координатой Ъ вправо
по координатной прямой.
Значит, точка с координатой а лежит правее точки с
координатой Ь, т. е. а больше Ъ.
Аналогично можно показать, что если а меньше &, то
разность а—Ъ отрицательна, и, наоборот, если разность а—Ъ
отрицательна, то а меньше Ъ.
Итак, справедлива теорема:
а>Ъ тогда и только тогда, когда разность а — 6 положительна;
а< Ь тогда и только тогда, когда разность а —Ь отрицательна*
Очевидно, что а=Ь в том и только в том случае, если
разность а—Ъ равна нулю.
Замечание, а ^ Ь (а не меньше Ь, т. е. а больше Ъ или
а равно 6) тогда и только тогда, когда разность а — Ъ равна
положительному числу или нулю (неотрицательна).
а ^ Ъ (а не больше Ь, т. е. а меньше Ъ или а равно Ь) тогда
и только тогда, когда разность а — Ь равна отрицательному
числу или нулю (неположительна).
Неравенства, составленные с помощью знаков > или <,
называют строгими; неравенства, составленные с помощью
знаков !> или ^, называют нестрогими.
Покажем, как сформулированную выше теорему можно
использовать при решении задач.
1. Сравнить числа — и 0,33.
з
Нам известны различные способы сравнения дробей.
Рассмотрим еще один. Вычислим разность дробей:
i— 0 33 = - — — = 100~99 = JL
3 ' ~ 3 100 ~" 300 300'
Так как разность чисел — и 0,33 положительна, то — больше
3 3
0f33, т. е. неравенство — > 0,33 верно.
о
2. Доказать, что при любом значении переменной а верно
неравенство
а2+7а — 34<а(а + 7).
77
Составим разность левой и правой частей неравенства к
преобразуем ее:
а2+7а — 34 — а (а+7) =а2+7а — 34 —а2 — 1а = —34.
При любом значении а эта разность отрицательна.
Следовательно, при любом значении а верно неравенство
а2+7а — 34 < а (а+7).
3. Доказать, что при любом значении переменной 6 верно
неравенство
6(6—1)>6—1.
Как и в предыдущем случае, составим разность левой и
правой частей неравенства и преобразуем ее:
6 (6—1) — (6 —1) =(6—1) (6—1) =(6—I)2.
Преобразовав разность, мы получили не число, как в
примере 2, а выражение с переменной 6. Особенность этого
выражения состоит в том, что при любом значении 6 его значение
неотрицательно: при 6 = 1 оно равно нулю, а при
6^1—положительно. Значит, при любых значениях 6 рассматриваемая
разность неотрицательна (положительна или равна нулю). Отсюда
можно сделать вывод, что при любых значениях 6 верно
неравенство, причем 6(6—!)=»&—1 при 6 = 1 и 6 (6—1)>6—1 при
Ьф1.
293. Верно ли неравенство:
а) —5 <0; г) 15 < 15; ж) - < 0,35;
б) ll< 1; Д) ° < ~1; 3) ~й >-°'075?
в)-7>-11; е)^>0,17;
294. Поставьте знак >, < или = так, чтобы получившееся
высказывание было истинным:
а) - ... -; г) 3,0001 . .. 3,001;
8 16
б) —3- ...—-; д) —0,0018 . . . —0,0016;
7 7
в) 0,04 . . . i; е) —Щ . . . —0,0256.
53 626
295. Сравните числа а и 6, если разность а—6 равна:
а) -2,7; б) 8; в) 0; г) <-1)17; д) 5~а.
78
296. Пусть а, Ь и с — некоторые числа. Сравните числа а и Ь,
если разность а—Ь равна:
а) |с|; в) (-с)2; д) с2+1;
б) —с2; г) 4+|с|; е) —5—с2.
297. Известно, что а <Ь. Может ли разность а—Ь выражаться
числом 3,7; —5; (—ОД)5; |—0,71; 2~7; — |—3|?
298. Как расположены на координатной прямой точки,
изображающие числа а и Ь, если известно, что:
а) а—Ь = —7; в) Ь—а = —1,3;
б) а—Ь=30,6; г) Ь—а=0?
299. Объясните, почему можно утверждать, что неравенство
верно при всех значениях переменной:
а) *2+5 > 0; в) (а—З)2 > 0;
б) 1+а2>0; г) —р2—2<0.
300. Существует ли такое значение х, при котором неверно
неравенство:
а).2*2+7>0; б) *2>0; в) 3x+l<*+l; г) (х—4)2>0?
801. Докажите, что при любом значении а верно неравенство:
а) 3 (а+1)+а—4 (2+а)<0; б) (а—2)2— а (а—4)>0.
302. Докажите, что при любом значении т верно неравенство:
а) m2 + 15m+56>m(ro+15);
б) (7т—1)(7го+1)<49т2;
в) (2т+3) (2ти+1)>4/ю (т+2);
г) Зт (т+6)<(3?ю+6) (т+4).
303. Докажите, что при любых значениях переменных верно
неравенство:
а) а (а + Ь)^ аЬ\ в) 2Ъс < Ь2+с2;
б) т2—тп+п2 ^ тп; г) а (а—ЪУ J> Ъ (а—Ь).
304. Докажите, что при любом значении переменной а верно
неравенство
Ji±i>l>2a.
2
79
305. Сравните сумму квадратов двух неравных чисел а и 6
с их удвоенным произведением.
306. К каждому из чисел 0, 1, 2, 3 прибавили одно и то же
число k. Сравните произведение крайних членов
получившейся последовательности с произведением средних ее
членов.
19. Свойства неравенств
Рассмотрим некоторые свойства неравенств.
1. Если а>Ь, тоЬ<.а, и, наоборот, если а<.Ь9 тоЬ>а.
Геометрически это очевидно: если точка с координатой а
лежит на координатной прямой правее точки с координатой &,
то точка с координатой Ъ лежит левее точки с координатой а,
и наоборот (рис. 13);
да а Ь
Рис. 13
2. Если а> Ъ и Ь >с, то а>с.
В самом деле, если точка с координатой а лежит правее точки
с координатой &, а точка с координатой Ъ лежит правее точки
с координатой с, то точка с координатой а лежит правее точки
с координатой с (рис. 14).
с b a
Рис. 14
Это свойство неравенств называют транзитивностью
соотношения неравенства.
3. Каково бы ни было число с, если а>Ь, то a-f-c>6+c.
На координатной прямой хорошо видно, что это свойство
справедливо для положительного с (рис. 15) и для
отрицательного с (рис. 16), для с = 0 оно очевидно.
80
b b+c a Q+c
Рис. 15
b + c b q+c a
Рис. 18
Докажем это свойство, не обращаясь к координатной прямой.
Рассмотрим разность
(а+с) — (Ь +с) =а—Ь.
Так как а>Ъ, то разность а—Ъ положительна, значит, и
разность (а+с) — (Ь+с) положительна. Следовательно,
а+с> Ь+с.
Итак, если к обеим частям верного неравенства прибавить
одно и то же число, то получится верное неравенство.
Используя это свойство, получаем, что если а + Ъ>с, то
а+Ь+(—Ь)>с + (—Ъ), т. е. а>с—Ь.
Если из одной части верного неравенства перенести в другую
какое-либо слагаемое, изменив его знак на противоположный*
то получится верное неравенство.
4. Каково бы ни было положительное число с, если а>Ъ, то
ас>Ьс. Каково бы ни было отрицательное число с, если а>Ь9
то ас <СЬс.
Для доказательства преобразуем разность ас—Ъс в
произведение:
ас—Ьс=с (а—Ъ).
Так как а > Ъ, то а — Ъ — положительное число. При
положительном с произведение с (а—Ъ) положительно, а
следовательно, положительна и разность ас—Ъс, т. е. ас>Ьс. При
отрицательном с произведение с (а—Ъ) отрицательно, а значит,
отрицательна и разность ас — Ъс, т. е. ас < Ъс.
Итак, если обе части верного неравенства умножить на одно
и то же положительное число, то получится верное неравенство.
Если обе части верного неравенства умножить на одно и то
же отрицательное число и заменить знак неравенства на
противоположный, то получится верное неравенство.
При с = —1 получаем, что если а>Ъ, то а (—1) < Ъ (—1), т. е.
—а <—Ъ.
Если у обеих частей верного неравенства изменить знак на
противоположный и знак неравенства также изменить на про*
тивоположный, то получится верное неравенство.
Например, из верного неравенства —103 <—87 получаем
верное неравенство 103 > 87.
Так как деление можно заменить умножением на число,
обратное делителю, то очевидно, что если обе части верного
81
неравенства разделить на одно и то же положительное число,
то получится верное неравенство, а если разделить на
отрицательное число и поменять знак неравенства на
противоположный, то также получится верное неравенство.
Например, разделив обе части неравенства 120 > 80 на 10,
получим верное неравенство 12 > 8. Разделив обе части
неравенства 120 > 80 на —40 и поменяв знак неравенства на
противоположный, также получим верное неравенство —3<—2.
307. Запишите верное неравенство, которое получится, если
к обеим частям неравенства 18>—7 прибавить по:
а) —5; б) 2,7; в) —18; г) 7.
308. Запишите верное неравенство, которое получится, если
обе части неравенства —9 < 21 умножить на:
_1
3
а) 2; б) — 1; в)
г)<-3)-
309. Запишите верное неравенство, которое получится, если
из обеих частей неравенства 5>—3 вычесть по:
а) 2; б) 12; в) -5; г) (-j) \
310. Зашипите верное неравенство, которое получится, если
обе части неравенства —15 <—3 разделить на:
а) 3; б) -3; в) -1; г) -А.
311. Покажите на координатной прямой, что если а<Ь, то
—а>—Ъ. Рассмотрите случаи, когда числа а и 6 оба
положительны; оба отрицательны; Ъ положительно и а
отрицательно; а~0 и Ь положительно; а отрицательно и 6=0.
312. Каков знак числа а, если:
а) 5а<2а; г) — 12а >— 2а; ж) —а<—0,01?
б) 7а>3а; д) 7а=2а;
в) —За<8а; е) —а>3;
313. Известно, что а >&. Объясните, на основании каких свойств
неравенств можно утверждать, что верно неравенство:
а) —7а<—7Ь; г) 0,01а—0,7 >0,01&—0,7;
82
3 3
в) 2а + 11>2Ь + И;
Д)1-
е)2-
-а<1 — Ъ;
а, Л Ь
-- <2 — -.
2 2
314* Докажите, что:
1) если а О» то 6>а;
2) если а О и Ъ ^с, то а ^с;
3) если а^Ъ и с — произвольное число, то а+е^.Ь+с;
4) если а^Ь и с — положительное число, то ас^Ьс;
5) если а^Ь и с — отрицательное число, то ае^Ьс.
315. Какие из неравенств верны при любых значениях
переменной XI
а) х (х+5)>5х—3; в) Зх (* + 1)>Зг*;
6) х (х—2) >— 2дг— 4; г) (1+х)%> 4дг?
316. Известно, что а <Ь. Сравните полусумму чисел а и & с
числом а; с числом 6.
317. а) Как изменится дробь—,если к ее числителю и
знаменателю прибавить одно и то же положительное число?
13
б) Как изменится дробь —, если к ее числителю и зна-
4
менателю прибавить одно и то же положительное число?
318. Докажите, что с -\— J> 2 при с > 0. Сформулируйте свой-
с
стзо суммы двух взаимно обратных положительных чисел.
Проиллюстрируйте его числовыми примерами.
319. Докажите, что верно неравенство:
а) 9а + — >6 при а >0; в) & + 2 < — - при k<0;
к
а г " ' 5 ' х
б) 25а + - < 10 при а < 0; г) - + - < — 2 при х<0.
20. Понятие логического следования
Рассмотрим два предложения с переменной а:
«сумма цифр числа а делится на 9» и «число а кратно 3».
Каждое из них при одних значениях а обращается в истин*
ное высказывание, а при других — в ложное. Например, при
а =39 первое предложение выражает ложь, а второе — истину;
при а =72 каждое из предложений истинно; при а =67 оба
предложения ложны.
Из свойств делимости чисел вытекает: если при некотором
значении а первое из предложений истинно, то истинно и
второе. В таких случаях говорят, что второе предложение следует
из первого. Эту мысль записывают с помощью знака логического
следования =>:
(сумма цифр числа а делится на 9)=> (число а кратно 3).
83
Приведенную запись можно прочитать по-разному,
например:
а) если сумма цифр числа а делится на 9, то число а
кратно 3;
б) из того, что сумма цифр числа а делится на 9, следует,
что число а кратно 3.
Эту запись можно прочитать также, используя понятия необходимое условие
и достаточное условие;
в) условие, что сумма цифр числа а делится на 9, достаточно длл того, чтобы
число а было кратно 3;
г) условие, что число а кратно 3, необходимо для того, чтобы сумма цифр
числа а делилась на 9.
Из предложения «число а кратно 3» не следует
предложение «сумма цифр числа а делится на 9». В самом деле, можно
указать такое значение а, например 12, при котором
предложение «число а кратно 3» обращается в истинное высказывание, а
предложение «сумма цифр числа а делится на 9» — в ложное.
Приведем еще примеры следования одного предложения из
другого.
Пример 1. Каждое из уравнений
*2_8л.= 0 и (х2—8х) (* + 5) = 0
представляет собой предложение с переменной х. Из первого
предложения следует второе:
(х2—8х = 0)=>((х2—8х) (х + 5) = 0).
В самом деле, еели при некотором значении х множитель
х2—8х равен нулю, то и произведение (х2—8х) (дс+5) равно
нулю. Значит, если при некотором значении х первое уравнение
обращается в истинное высказывание, т. е. в верное равенство,
то и второе обращается в истинное высказывание.
Пример 2. Неравенства
у>8 и у>4
представляют собой предложения с переменной у. Из первого
неравенства следует второе:
(y>8)=>(i/>4).
В самом деле, каждое значение у, обращающее в истинное
высказывание (в верное числовое неравенство) предложение
у > 8, обращает в истинное высказывание и предложение у > 4.
Пример 3. Из неравенства 17* > 3,4 следует
неравенство х > 0,2:
(17х>ЗА)=$(х>0,2).
84
Действительно, если обе части верного неравенства
разделить на одно и то же положительное число, то получится
верное неравенство. Значит, если при некотором значении х
неравенство 17х > 3,4 обращается в истинное высказывание, то и
неравенство х >0,2 обращается в истинное высказывание.
320. Прочитайте запись:
а) (/-А и Z.B — вертикальные углы) => (Z-A ^ ^-В);
•S ХЧ XS
б) (/-A, Z_jB, Z_C — углы треугольника) ==ф (А+В+С =
=180°);
в) ([АС] и [ДО] — диагонали прямоугольника) с=>(|АС | =
= IadI);
г) ([АС] и [BD] — диагонали ромба) :=> ((AC) ± (BD)).
321. Докажите, что из предложения «число а кратно 5» следует
предложение «сумма а+15 кратна 5». Запишем вывод,
пользуясь знаком логического следования.
322. Докажите, что:
а) из того, что \а\ >3, не следует, что а>3;
б) из того, что а2 = 16, не следует, что а =4.
323. Приведите пример предложения, которое следует из
предложения «четырехугольник ABCD — квадрат».
324. Следует ли второе уравнение из первого:
а) 3*=12, х =4; в) х+у=129 Ъх+5у=60;
б) Ъх—17=0, Ьх=17; г) 14х+7у=4,9, 2х+у=0,7?
325. Следует ли второе неравенство из первого (при
положительном ответе используйте в записи знак логического
следования):
а) а>12, а>5; в)а>3, а>6; д) а<4, |а|<12;
б) Ъ <17, Ъ <2; г) Ъ <—4, Ъ <—1; е) \Ь |< 8, Ь < 8?
326. Среди данных неравенств укажите такое, из которого
следуют все остальные:
а) х>9, *>4, х>1, х>11;
б) у<10, у<5, у<2, у<12;
в) х>1- , х>1,2, х>1- , х>1;
г) а<—2,5, а<—3,5, а<—3, а<—2.
327. Докажите, что второе неравенство следует из первого:
а) 3*>24, х>8; в) 5х—1>0, 5х>1;
б) — 7х<—28, #>4; г) 4*—3<5, 4х<8.
85
328. Следует ли первое предложение из второго, следует ли
второе предложение из первого:
а) число а кратно 8; число а четное;
б) число т меньше 1; число т отрицательное;
в) 1,3 (х—1) = 0; х—1=0;
г) 6>12; 6<5?
329. Прочитайте запись, пользуясь словами «если ..., то ...».
Докажите:
а) (а и & — положительные числа и а > Ь) г=> (— < — ];
\а Ъ)
б) (а и 6 — положительные числа и а < &):=£>[—> -Л
330. Докажите, что:
а) (а > ft) =ф (5а—4 > 56—4);
б) (а >&)=>(—6а+2<—6ft+2).
331. Следует ли второе предложение из первого:
а) ^^?-0; х —12 = 0; в) ?^1*<0; 2.т — 5 < 0;
б) х2 — 4 = 0; ^^ = 0; г) 33 — х > 0; Z^-=^ > 0?
' 17 ' Ю
332. Приведите пример уравнения, которое следует из
уравнения —Ъх =—12. Приведите пример неравенства, которое
следует из неравенства —1Ъх <—26.
21. Равносильные предложения
Рассмотрим два предложения:
«ft — положительное число» и «—& — отрицательное число».
Из первого предложения следует второе и, наоборот, из второго
предложения следует первое:
(& — положительное число) =>(—ft — отрицательное число);
(—ь — отрицательное число) =>(6 — положительное число).
Если из первого предложения следует второе и из второго
следует первое, то эти предложения называются равносильными.
Предложения «ft — положительное число» и *—& —
отрицательное число» равносильны. Эту мысль записывают с помощью
знака <=>:
(& — положительное число) «=» (—& — отрицательное число).
Приведенную запись можно прочитать по-разному:
а) если 6 — положительное число, то —ft — отрицательное
число, и, наоборот, если —Ъ — отрицательное число, то & —
положительное число;
б) предложение «ft — положительное число» равносильно
предложению «—Ъ — отрицательное число»;
86
в) —Ь является отрицательным числом тогда и только тогда,
когда Ь — положительное число;
г) для того чтобы число Ь было положительным, необходимо и достаточно,
чтобы число — Ь было отрицательным.
Предложения «сумма цифр числа а делится на 9» и «число а
кратно 3» не являются равносильными, так как из второго
предложения не следует первое.
Приведем примеры равносильных предложений.
Пример 1. Уравнения 27* =0,81 и *=0,03,
представляющие собой предложения с переменной *, равносильны:
(27* =0,81) & (* =0,03).
Докажем это. Если обе части верного равенства разделить на
одно и то же число, то получится верное равенство. Значит,
если при некотором * первое уравнение обращается в верное
равенство, то и второе обращается в верное равенство, т. е.
из первого уравнения следует второе. Если обе части верного
равенства умножить на одно и то же число, то получится
верное равенство, поэтому из второго уравнения следует первое.
Пример 2. Неравенства 12*—25 <0 и 12* <25
представляют собой предложения с переменной *.
Если из одной части верного неравенства перенести
слагаемое с противоположным знаком в другую часть, то получится
верное неравенство. Значит, из первого неравенства следует
второе и из второго — первое, т. е. рассматриваемые
неравенства равносильны:
(12*—25 < 0) <& (12* < 25).
Нам известно, что значение переменной, обращающее
уравнение (неравенство) с одной переменной в истинное
высказывание, называется его решением. Очевидно, что из одного
уравнения следует другое, если каждое решение первого является
решением второго. Аналогично из одного неравенства следует
другое, если каждое решение первого является решением
второго. Подобным же образом формулируется условие следования
для уравнений (неравенств) с двумя переменными и для систем
уравнений (неравенств).
Нетрудно понять, что равносильны те и только те уравнения
или неравенства, множества решений которых совпадают.
Замечание. Уравнения или неравенства, содержащие
одни и те же переменные и не имеющие решений, также
считаются равносильными.
833. Прочитайте запись:
а) (а >&)«=> (а—Ь — положительное число);
б) (а<Ь)<?=>(а—& — отрицательное число);
87
в) (аЬ==0)<=Ка=0 или 6 = 0);
Г) /1=оЫа=ОиМО).
334. Докажите, что предложения *=3 и |*|=3 не являются
равносильными.
335. Докажите, что если число а четное, то число а+1
нечетное, и, наоборот, если число а+1 нечетное, то число а
четное. Запишите вывод, пользуясь знаком
равносильности.
836. Равносильны ли предложения:
а) а и 6 — четные числа, сумма а+Ь —, четное число;
б) число а кратно 3, сумма а+6 кратна 3;
в) натуральное число а оканчивается цифрой 0;
натуральное число а кратно 10?
337. Равносильны ли уравнения:
а) 8*=24 и (* — 3)(х —15) = 0; в) 2х — 7 = 0и~—-' =0;
х + 5
б) 10* = 50 и (*2+ !)(* — 5) = 0; г) х2 —16= 0 и^-=^ =0?
я — 4
338. Составьте уравнение, равносильное данному:
а) 2*+3=5; б) Зу—1=8.
339. Докажите, что равносильны неравенства:
а) 26* > 52 и х > 2; в) 2* +16 < 0 и 2х <—16;
б) х—14>0и*>14; г) — 3*<3 и *>—1.
340. Составьте неравенство, равносильное данному:
а) 14л: < 28; б) х>3.
§ 8. НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
22. Графическое решение неравенств с одной переменной
Пусть требуется решить неравенство 0,5*—1,5>0, т. е.
найти множество значений переменной *, при которых это
неравенство верно. Сделаем это с помощью графика функции #=0,5*—
—1,5 (рис. 17). Мы видим, что график расположен выше оси х
при значениях *, принадлежащих промежутку ]3; +оо[.
Значит, при указанных значениях *, и только при них, значение
выражения 0,5*—1,5 положительно, т. е. неравенство 0,5*—
—1,5 > 0 обращается в верное числовое неравенство. Числовой
промежуток ]3; + оо[ — множество решений неравенства 0,5*—
—1,5 >0.
88
-5
-и
-Л
-г
t
и
у —-
_1\
•f
7
0
f
/
^
т
2L*T"J
Г"Т~
й
,0^
"4
г
&
5
<
г
7
в
3
If
1 \
\х\
Рис. 17
У
-f
\
>
л
-11
V
п
?
\
>
V
N
Чо
L
ч
-а\
-t
-JL
7
V
i
/
н
2
0
Z*
А
\
ft
?
и
\
10
12
х\
Рис. 18
На рисунке 18 построен график функции y=f(x). С помощью
графика можно решить неравенство f(x) < 0. Из рисунка видно,
что график расположен ниже оси х при значениях х,
принадлежащих промежутку ]—8; 2[ или промежутку ]6; + оо[. Значит,
множество решений неравенства
f(x) < 0 есть объединение двух
множеств: ]—8; 2[(J]6; + <*>[.
Рассмотрим еще пример.
Пусть требуется решить
неравенство х2>2х. Для этого
построим в одной системе
координат графики функций у=х2 и
у=2х (рис. 19). Неравенство
х2>2х верно при тех и только
тех значениях х, при которых
график функции у=х2
расположен выше графика функции
у=2х, т. е. при значениях х,
принадлежащих множеству
]— оо; 0[ или множеству]2; + оо[.
Множество решений
неравенства Х2>2х: ]— оо; 0[LI]2; + оо[. Рис. 19
> \ u/i! и i / у i м
1 1 1 \ 1 1 1 1 t 1 \и-х21 \/и-2х 1
i 1 У"л I )/У*' , 1
ч\ 11U1
\ к //
\ г и
М \ L л
1 \ П /
1 \ т N км и
: \\\\\ Ш/ч
i \ N // • М ч
их // 1
: \ \i //
N \ \\лА
I v^W\ MMl
\"\-3 \-2 \-1 \Лр\ * \ 2 \3 \Т\х\
I f III
МММ \/Ц II 1 1 II 1 II1
89
1 1 1 t 1 1 1 1 1 1 1 1 1 1 M 1 1 1 1 1 1 1 1 1 1 I 1 II 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 И 1 1 1 1 1 1 l^rTH 1 1 1 1 1 1 1 1 1 1 1
VS/!W Ul Л1 1 1 1
" "I ' J——J j C71 У'/ J—J—r—j——T—J -1 | II 'jf j I 1 1 \ I I] II 1 | Г I I
1 JHtTTHJ 1111111 Hi MM N111111J11
\12\-10 -a \-6 kkU \a г]Л\ б\ в \т\ щ k\ w\\\ x
/Mill l^-U^n I | Г I Pkl f
Ум ГгГм MtJ
У\ U Nisi
ГИ rl I I I I I I I I I I I I I I rkl I I I I
Рис. 20
841. Решите графически неравенство:
а) х—2<0; б) 7—2х>0. , >
842. На рисунке 20 построен график функции y=g(x).
С помощью графика решите уравнение g(#)=0 и
неравенство g(x) >0.
В одной системе координат построены графики фзгнкций
12
у = — и у = х + 1 (рис. 21). Найдите с помощью графиков,
при каких значених х обращается в' истинное
высказывание предложение:
343.
a) i£ = х + 1; б)
X
12
>* + 1;
в) — < х + 1.
X
-tfu
а
?ш
ч
^
-б
-
5
-^
-2
/
\
ж
т
7Л1
1
Я
1
/?|
1
^
?|
Ч
d
я
?|
l\
l\
Г
л
01
я\
\
"У
г
л
1
\
\
\
\\
у
л
у--
\
\
/
}
т
.12
/
Ч
У
Ч
4
/
к
/
^
5
\
/
*н
t
к,
■»*
с
z/
**
3
*ча
;
^у
мм
0
MB
f
7
2
«
"г
f
Рис. 21
90
344. Решите графически уравнение я2 =4 и неравенства **<4;
х1 >4.
345. Покажите с помощью графиков, что неравенство х2>х—1
верно при любом значении х.
346. Покажите с помощью графиков, что множество решений
неравенства х2 < х—2 пусто.
23. Решение линейных неравенств с одной переменной
Рассмотрим решение неравенств вида аде+6 >0 или а#+Ь <0,
где а и Ь — некоторые числа. Такие неравенства называются
линейными.
Начнем с примера. Решим неравенство
12 — Зх > 0. (1)
Нам известно, что если из одной части верного неравенства
перенести слагаемое в другую часть с противоположным
знаком, то получится верное неравенство. Поэтому из неравенства
(1) следует неравенство
—Зх > —12. (2)
Если обе части верного неравенства разделить на одно и то
же отрицательное число и поменять знак неравенства на
противоположный, то получится верное неравенство. Значит, из
неравенства (2) следует неравенство
х <4. (3)
Из свойств неравенств вытекает справедливость обратного:
из неравенства (3) следует неравенство (2), а из неравенства (2)
следует неравенство (1).
Итак, мы можем сделать вывод, что
(12—3х>0) :=>(*< 4)
и (*<4)=»(12—3х>0),
т. е. что неравенства (1) и (3) равносильны:
(12—3*>0)<^(х<4).
Множество решений неравенства #<4, а значит, и
равносильного ему неравенства 12—Зх > 0 есть числовой промежуток
]—оо; 4[ (рис. 22).
Рис. 22
§1
Таким образом, решая неравенство вида ах+Ь > 0 или ах +
+Ъ <0 при а=^0,мы находим равносильное ему простейшее
неравенство вида х>с или х<с (с —некоторое число), множество
решений которого очевидно.
Приведем еще примеры решения линейных неравенств.
Пример 1. Решить неравенство 4(6—#)<3(*—13).
24—4*<3*—39,
—4#—3*<— 39—24,
—7*<— 63,
#>9.
Ответ: [9; + оо[.
Множество решений неравенства показано на координатной
прямой на рисунке 23.
jm^mmws/mw*
Рис. 23
При решении линейных неравенств могут представиться
особые случаи, когда множество решений неравенства пусто или
когда решением неравенства служит любое число. Рассмотрим
примеры.
Пример 2. Решить неравенство 2(х+8)—5* <4—Зх.
2х+16—5х<4—3*,
2х—Ъх+3х<—12,
0-*<—12.
Неравенство 0х<—12 не имеет решений, так как ни при
каких значениях х оно не обращается в верное числовое
неравенство^ Значит, и неравенство 2(*+8)—Ъх <4—Зх не имеет
решений, т. е. множество его решений пусто.
Ответ: 0.
Пример 3. Решить неравенство 5 (х—12) < 12(х—1)—7х.
Ъх—60 < 12*—12—7х,
Ъх—12* +7х < —12 +60,
0-*<48.
Неравенство 0-х <48 верно при любом значении х. Значит,
и неравенство 5(х—12)< Щх—1)—7х верно при любом значении
х, т. е. множеством его решений служит множество всех чисел.
Ответ: ]—оо; +<х>[.
92
347. Найдите множество решений неравенства и покажите его
на координатной прямой:
а) *<3; б) *>5; в) *<0; г) х>— 1.
348. Найдите множество решений неравенства 5я+1>11.
Назовите несколько значений переменной х,
принадлежащих этому множеству.
349. Решите неравенство Зх—2 < 6. Принадлежит ли множест-
4 4
ву решений неравенства число 4; 2—; 2—?
350. Решите неравенство и покажите на координатной прямой
множество его решений:
а) 12*>18; д) 7х—24 < 4; и) 0>12+5х;
б) 6*<15; е) 18—5х < 12; к) 17—х>6—6х;
в) — Зх<108; ж) 14>6—х\ л) 12*+0,5<13х — 1;
г) — 5*>6,4; з) 17<3+4х; м) 8х>5+12*.
351. Решите неравенство:
а) 5 (х—1)+7< 1—3 (х+2); г) 1,7—3(1—т) <—(т—1,9);
б) 4 (а+8)—7(а—1) < 12; д) а (а—4)—а2 >12—6а;
в) 4 (6—1,6)—1,2>6ft—1; е) (2х—1) 2х — 5х<4х2—х;
ж) (а—I)2—(а—7)(а—3)<2а+0,8;
з) (Зх—I)2—3*(1,2+3*) > 8л;+177.
352. Решите неравенство:
а)-^±-^<<>; г)!^-5*>0;
18 б
б) > 0; д) дс < 4;
42 б 10
ч 3 + * , 2 — ж . Л 2ж — 1 . * + 3 ^ .,
в) -~— Н — < 0; е) —- h —±— > 1.
353. При каких значениях yv
а) значения дроби больше соответствующих значений
б
дроби •
12
*ч £ 4,5 — 2у
б) значения дроби — меньше соответствующих зна-
5
чений дроби ~ у ?
93
Рис. 24
854. Найдите, при каких значениях х значения функции /
положительны (ответ проверьте графически):
a) f(x)=3x—6; б) f(x) = — 2*—5.
855. Найдите, при каких значениях х значения функции /
отрицательны (ответ проверьте графически):
a) f(x)=x—8; б) f (х) = 3—1,5*.
856. Постройте график функции у = — х + 2 и найдите, при
о
каких значениях х значения функции больше 4.
Проверьте ответ, решив соответствующее неравенство
алгебраически.
857. Найдите множество значений переменной х, при которых
значения функции, заданной формулой у = —#+2,
больше —3. Ответ проверьте графически.
858. Пользуясь графиками функций у=х+1 и у =0,5* +2
(рис. 24), найдите, при каких значениях х верно
неравенство х+1 >0,5я+2. Проверьте правильность ответа,
решив это неравенство алгебраически.
859. Найдите множество решений неравенства:
а) 15(х+4)—5*<10лг; в) Зх+7 >(x+2)+(2*+l);
б) 31 (2х + 1)—12*>50х; г) 12х—КЗ (4х—3).
94
Звв. При каких значениях х значения дроби —^— больше
х 4-1
соответствующего значения дроби ? Ответ проиллю-
«Зж -4- S
стрируйге с помощью графиков функций у = —^— и
361. Найдите наибольшее целое число, удовлетворяющее
неравенству
1,6—(3,2-0,2^X5,1.
362. Найдите наименьшее целое число, удовлетворяющее
неравенству
8 (0,6—г/) < 24,2-7i/.
363. При каких натуральных значениях п разность
(2—1,2и)—(0,5л—6,5} положительна?
364. При каких натуральных значениях п сумма
(—27,1 +Зл)+(7,1 +5п) отрицательна?
365. При каких положительных значениях х верно
неравенство
0,75—х< 1,5—0,5*?
366. Найдите множество отрицательных значений у,
удовлетворяющих неравенству
1,2(у—5><0,бу+0,1.
367. Выделите из числового промежутка 1—1; 5[
подмножество значений переменной х, при которых значения
выражения х—4 меньше соответствующих значений
выражения 2—2х.
368. Выделите из числового промежутка [—1; 6] подмножество
значений переменной х, при которых значения
выражения 12+3* больше соответствующих значений выражения
32—2х.
369. При каких значениях а верно равенство:
а) |а|=а; в) \а—2\=а—2; д) |3а—1|=3а—1;
б) |а|=—а; г) \а—5|=5—а\ е) [2а+5|=—2а — 5?
370. Сторона прямоугольника 6 см. Какой должна быть другая
сторона, чтобы периметр прямоугольника был меньше
периметра квадрата со стороной 4 см?
911
371. Длина прямоугольного параллелепипеда 12 дм, ширина
5 дм. Какой должна быть высота параллелепипеда, чтобы
его объем был меньше объема куба с ребром 9 дм?
372. На соревнованиях каждый стрелок делал 10 выстрелов.
За каждое попадание он получал 5 очков, а за каждый
промах снималось 1 очко. Победителем считался тот, кто
наберет не меньше 30 очков. Сколько раз стрелок должен
был попасть в мишень, чтобы оказаться в числе
победителей?
373. Туристы отправились на моторной лодке по течению реки
и должны возвратиться обратно к стоянке. Скорость
течения реки 2 км/ч, а собственная скорость лодки 18 км/ч.
На какое расстояние могут отъехать туристы, чтобы
прогулка продолжалась не более 3 ч?
§ 9. СИСТЕМЫ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ
24. Решение систем линейных неравенств с одной переменной
На рисунке 25 построены графики функций у=х + 1 и
У = —2л:+8. С помощью графиков нетрудно решить задачу:
♦Найти множество значений переменной х, при которых обе
функции принимают положительные значения».
Искомое множество —
числовой промежуток ]—1; 4[.
Решим ту же задачу, не
обращаясь к графикам.
Найдем множество значений х,
при которых верно как
неравенство я + 1>0, так и
неравенство —2х+8>0, т. е.
найдем множество общих
решений этих неравенств.
Если ставится задача найти
множество общих решений двух
или нескольких неравенств,
то говорят, что надо решить
систему неравенств.
Значение переменной, при
котором каждое из
неравенств системы обращается в
верное числовое неравенство,
называется решением системы.
Множество решений
системы есть пересечение множеств
решений входящих в нее нера-
Рис. 25 венете.
ГП 1 М ''/1 М 1 II 1 1 1 ! 1 !
1 II 1 \ i т 1 1 1 1 II II 1 1 1
1 I V Ч
Mill \fl| Ч N
i \\\\ к ч i И
А 1
1 1 И я\ II
1 1 1 1 i 1 ы\к' 1
1 1 7 \ь 1
I И я \* чИ
М И iH 1\Ич
М \ №/]\
1 \ yf
ч /1 \ 1/|
ч 1 М и iVrf
J -И 1/С
11 ij j/f \
ч ч о J/f \
Mill г\ X
и 1 и 1 ^j/f \
| j/Г 1 \
II 1/Г 1 Ч | \
-J -2 ]А 10 \\ 1 | 2 3 ЛГХ
I I i j/f | U I | I |\
| [/] Ч I Ч Ч \
]/\ i I I I о! I I I I I \
\/\ I I I 4 II I I II I I I I \ I
96
Шт^чш\\ч^
Рис. 26
Итак, надо решить систему неравенств
х + 1 > 0, (1)
—2х + 8 > 0.
Заменив каждое неравенство простейшим, ему
равносильным, получим систему, равносильную данной:
х > —1, (2)
х <4.
Множество решений неравенства х >—1 — числовой
промежуток ]—1; + оо[э неравенства х < 4 — числовой промежуток
]—оо; 4[. С помощью координатной прямой найдем пересечение
этих множеств (рис. 26). Получаем, что числовой промежуток
]—1; 4[ — множество решений системы (2), а значит, и
равносильной ей системы (1).
Мы получили тот же ответ, что и при графическом способе
решения системы неравенств.
Приведем еще примеры решения систем линейных неравенств.
Пример 1. Решить систему неравенств:
(3*>27,
14—х < 0.
Получаем:
{*
Зх > 27, [х > 9,
х < —4; \х > 4.
Множество решений неравенства х > 9 — числовой
промежуток ]9; +оо[, неравенства х >4 — числовой промежуток
]4; +оо[. Пользуясь координатной прямой, находим, что
пересечением этих множеств служит числовой промежуток ]9;
+ оо[ (рис. 27).
Ответ: ]9; +оо[.
Рис. 27
Пример 2. Решить систему неравенств:
(7 >*,
\2х — 1 < 0.
4 Алгебра, 7 кл. 97
к^ччччччччч^
2
Рис. 28
Получаем:
(х < 7, \х < 7,
|2*<1; |ж<£.
Найдем пересечение множеств решений неравенств х ^ 7
и я ^ — , т. е. найдем пересечение числовых промежутков
]— оо; 7] и 1— оо; -1 {рис. 28).
Числовой промежуток — оо; — I — множество решений
заданной системы неравенств.
Ответ: — °°; — .
Пример 3. Решить систему неравенств:
12* — 9 < О,
\—3* < —18.
Получаем: (х < 4,5,
\х > 6.
Множество решений неравенства х < 4,5 — числовой
промежуток ]—оо; 4,5,[, а множество решений неравенства х > 6 —
числовой промежуток ]6; +оо[. Пересечение этих множеств
пусто (рис. 29).
Ответ: 0.
Рис. 29
Пример 4. Решить двойное неравенство:
—КЗ—2*<3.
Данное двойное неравенство представляет собой иную запись
системы неравенств:
/3 — 2х > —1,
\3 — 2х < 8.
98
e
Заменяя каждое из неравенств системы равносильным, получим:
\х <2,
\х >0.
Пересечение множеств решений неравенств # < 2 и # > О —
числовой промежуток ]0; 2[.
Запись решения двойного неравенства можно вести иначе:
—1< 3 — 2х < 3,
—4 < —2х < О,
2 > л: > 0.
Ответ: ]0; 2[.
Пример 5. Решить систему неравенств:
Зх — 6 > О,
18 < 5х,
1,7* — 13,6 < 0.
Получаем:
[3*>6, (*>2,
*>3,6, х>3,6,
11,7л: < 13,6; U< 8.
Так как неравенство х>2 следует из неравенства дг>3,6, то
решение полученной системы сводится к решению системы двух
неравенств:
(х > 3,6,
\х <8.
Числовой промежуток ]3,6; 8[ — пересечение множеств реше*
ний неравенств х> 3,6 и х< 8.
Ответ: ]3,6; 8[.
374. Решите систему неравенств:
а) f*>17, в) {х>0, д) fx>—1,
\*>12; \*<в; 1«<3;
б) /*<1, г) (х<—3,5, е) /*>8,
\х < б; 1*>8; |*<20.
375. Найдите множество решений системы неравенств:
а) (2х—12 >0, в) /3*—10 <0,
б) f
[3* > 9; \2х > 0;
4*<—4, г) /6х>42,
5—jc > 0; \4*+12<0.
99
376. Найдите множество решений системы неравенств и
укажите несколько чисел, принадлежащих этому множеству:
а) (х — 0,8 > 0,
\—5х < 10;
б) {:
*<о,
4<0;
в) /1 > 3*.
15*—1 > 0;
г) /10* < 2,
1*>0,1.
377. Решите систему неравенств:
(5 (ж—2) — х > 2, в) /7* +3 > 5*—19,
" {!.
-3 (х — 1)< —2;
14*+1< 22—3*;
б) (2х—(* — 4)< 6,
г) /3 (2—3*)—2 (3— 2*) >х,
я: > 3 (2л: — 1)+18; \6 < *2—л; (л:—8).
378. Найдите целые решения системы неравенств:
fy>0, в) /6-4&>0,
У>4; \36 —1>0;
г) /3 — 18л: < О,
,2 — 0,1л; > 0.
а) (у$
17,2
б) /12а — 37 > О,
16с< 42;
10,5
379. Объясните, почему данная система неравенств не имеет
решения:
а) /*+7<*+1, в) [х — 3>0,
12 — х > 0; 13 — х > 0;
б) /(*-2)2<0, г) /|*|<3,
1*>12.
К* - 2,
1*<1;
380. Найдите множество значений переменной а,
удовлетворяющих системе неравенств:
а) /2,5а— 0,5 (8 — а)< с +1,6,
U.5 (2а—1)—2а< а+2,9;
б) /0,7(5а+1) —0,5(1
12а—(а — 1,7) > 6,7
+а) < За,
381. Найдите целые решения системы неравенств:
а)
2х—^±>х,
б)
х—1<3—
* + 1.
х — 1
2* —
> 2л: — 1,
>* — 3;
в) /17*—5(*+0,6)<3*,
12 (3,5 — *)+5 (2*—2,4) > * — 26;
г) /х < 39+3,6 (5*—1)—2 (2* —1,8),
\6* (2,5*—1) — 3* > * (15*+2) —11.
100
882. а) На рисунке 30
построены графики функций
у =х +3 и у
=0,5*—1.Пользуясь графиками,
найдите множество значений
переменной ху при которых
обе функции принимают
положительные значения.
Проверьте правильность
ответа, составив систему
неравенств и решив ее
алгебраически.
б) Составив систему
неравенств, найдите, при каких
значениях переменной х
обе функции у=—дс+6 и
у=3х—9 принимают
положительные значения.
Проверьте правильность ответа
НО -8 Н
5 \7
\и\
Р
я
с
U
у г
. Jo
jRL
-2 |0
*£э
l/i
—Л
ТО
11 1 11
' U
•1*;
-Ци
- ■■ 1- * с
/^ 1
\ У&п
%^
гГ2 И
щ
Рис. 30
с помощью графиков.
883. Решите двойное неравенство:
а) —3<2ж—КЗ; б) —12<5—*<12.
384. С помощью координатной прямой найдите множество ре*
шений системы неравенств:
б) f—1 <* < 3,
а) /3<*<5, б) Г-
\ж< 4,2; [х > 2,5.
385. Решите систему неравенств:
a) ix > 8, б) [у < —1,
\х>7, \у< — 5,
U > —4; (у<4;
в)
т>9,
т>10,
/и<12;
г) f«<6,
g<5,
Iff >И.
386. Решите систему неравенств:
а)
б)
ж—4 < 8,
2л:+5 < 13,
3—х >1;
(3—2у < 7,
7у>7,
12у>144,
И—У < 1;
в)
г)
2х—1<х+д,
5х—1 > 6 — 2х,
х—3 < 0;
(5х— 4 < 4ж—2,
1—2* > 2—4*.
За: — 3 < Ьх—5,
117* >0.
387. а) Найдите все двузначные числа, большие 40, но мень*
шие 80, у которых цифра единиц на 4 меньше цифры
десятков.
101
6) В двузначном числе цифра единиц на 1 меньше цифры
десятков. Если к этому числу прибавить 7, то полученная
сумма будет больше 19, но меньше 51. Найдите это
двузначное число.
388. Если турист увеличит скорость на 1 км1чу то за 4 ч он
пройдет расстояние, большее 20 км. Если же он уменьшит
скорость на 1 км/ч, то за 5 ч он пройдет расстояние»
меньшее 20 км. Какова скорость туриста?
25. Примеры решения нелинейных неравенств
Решение некоторых нелинейных неравенств сводится к
решению линейных неравенств и их систем. Приведем примеры.
Пример 1. Решить неравенство (х—2)(3—х) > 0.
Значение произведения двух множителей положительно в
том и только в том случае, когда значения множителей одного
енака, т. е. оба положительны или оба отрицательны. Значит,
данное неравенство обращается в верное числовое неравенство
при тех и только тех значениях переменной х9 которые
удовлетворяют хотя бы одной из систем неравенств
х—2 > 0, (х—2 < 0,
3-х > 0 или [3-х < 0.
Так как каждое решение первой системы является
решением заданного неравенства и каждое решение второй является
решением заданного неравенства, причем других решений
неравенство не имеет, то множество решений неравенства
(х—2)(3—х) > 0 есть объединение множеств решений этих
систем неравенств.
Заменяя каждую систему неравенств равносильной, получим:
х >2, (х < 2,
х < 3 или [х > 3.
Множество решений первой системы — числовой промежуток
32; 3[.
Множество решений второй системы пусто.
Множеством решений заданного неравенства служит
объединение числового промежутка ]2; 3[ и пустого множества, т. е.
числовой промежуток ]2; 3[.
Ответ: ]2; 8[.
На рисунке 31 построены графики функции у=х—2 и у =3—х.
Нетрудно заметить, что при значениях х, принадлежащих про-
102
межутку ]2; 3[, и только при
этих значениях, функции
принимают значения
одинакового знака (обе
положительны), а значит, положительно
и произведение (х—2)(3— х).
Пример 2. Решить не-
равенство <0.
1 — х
Значение дроби
отрицательно, если числитель и
знаменатель имеют значения
противоположных знаков.
Значит, данное неравенство
верно в том и только в том
случае, когда верна хотя бы
одна из систем неравенств
/2х — 3 > О,
-х < О или
S
-2
Z
S
ч
-/
/
/
V
Ji\
71
и
'$
L
•*
7
0
'/
f
■з
л
i
К
s>
f
3
^
А
£
и
.V
X
[I
Отсюда
[х>1,5,
х>1
или
Рис. 31
/2х—3 < О,
[1— х>0.
(*<1,5,
|х<1.
^Множество решений первой системы неравенства —
числовой промежуток ]1,5; +оо[, второй — числовой промежуток
] — оо; 1[. Множество решений заданного неравенства —
объединение этих двух множеств.
Ответ: ] — оо; 1[11]1,5; +оо[.
Пример 3. Решить неравенство
5*— 4
2-х
>0.
Значение дроби положительно, если числитель и
знаменатель имеют значения одинаковых знаков. Значение дроби равно
нулю, если числитель равен нулю, а знаменатель отличен от
нуля. Значит, данное неравенство верно при тех и только тех
значениях х, при которых верна хотя бы одна из систем нера*
венств
Отсюда
Г5х-4>0,
[2—х>0
[х<2
или
или
(5х—4< Of
12 — х<0.
(*< 0,8t
ix>2.
108
Множество решений первой системы — числовой промежуток
[0,8; 2[, множество решений второй системы пусто.
Объединение этих двух множеств — числовой промежуток [0,8; 2[.
Ответ: [0,8; 2[.
3* — 2
Пример 4. Решить неравенство > 3.
х — 2
Данное неравенство легко свести к неравенству такого вида, который
рассмотрен в примере 2. Для этого перенесем 3 в левую часть неравенства и
преобразуем полученную разность в дробь:
3* — 2
3>0,
-1
х — 2
Sx — 2 — 3* + 6
ж —2
4
>0,
>0.
х — 2
Так как числитель дроби положителен, то значение дроби будет
положительно при положительных значениях знаменателя, т. е. тогда и только тогда,
когда верно неравенство
х — 2 > 0.
Множество решений неравенства х — 2 > 0, а значит, и заданного
неравенства — числовой промежуток ]2; +оо[.
Ответ: ]2; +оо[.
389. Найдите множество решений неравенства (х—2) (х—5) < 0.
Укажите несколько значений переменной х,
принадлежащих этому множеству. Вычислите соответствующие им
значения произведения (х—2) (х—5) и сравните их с нулем.
390. Найдите множество решений неравенства
(у-Ъ) (2у-3) > 0.
Принадлежит ли этому множеству число —8; 0; 1,5; 10;
1000?
391. При каких значениях переменной у:
а) значение произведения (у—1) (у—3) отрицательно;
б) значение произведения у (у—1) положительно?
392. Решите неравенство:
а) х(х—5) > 0; в) (2х—1) (х+1) > 0;
б) (х—1) (х—2) < 0; г) (6+х)х < 0.
393. Решите неравенство, разложив на множители многочлен,
записанный в левой части:
а) а2+6а > 0; в) х2—64 > 0;
б) б2—7,5Ь < 0; г) у2—0,25 < 0.
104
394. При каких значениях у верно неравенство:
а) (у - 8) Q/2 +6) > 0; в) (у - 2)2(у-3) > 0;
б) (12 - Зу) (1 +7у2) < 0; г) (г/ - 2,7)(5-у)2 > 0?
О
395. а) При каких значениях переменной а дробь поло-
а + 4
жительна?
2 5
б) При каких значениях переменной Ъ дробь — отри-
15 — Ь
цательна?
396. При каких значениях переменной верно неравенство:
1
— 7 —
а)—^—>0; б) -<0; в) -^- > 0; г) (-=1>12 < 0?
*-7,2 ' ' 5-а Ь-37 у -13
397. Найдите множество решений неравенства
* —з
*—8
>0.
Укажите несколько значений переменной х>
принадлежащих этому множеству. Вычислите соответствующие им
значения дроби и сравните их с нулем.
398. Найдите множество решений неравенства
9 — з*
Ъх +10
<0.
Выбрав произвольное значение переменной х, не
принадлежащее найденному множеству, покажите, что
соответствующее ему значение дроби неотрицательно.
399. Решите неравенство:
&)1=1>0. б)^^<0; B)f±l>0; г) -£- < 0.
9—х х Зяа+6 х—1
400. При каких значениях переменной х значения функции
у = положительны; отрицательны?
X —— а
401. Найдите целые решения неравенства:
ч Зле — Ю . л ч х . л
а) — < 0; в) — < 0;
х + 4 Ъх — 11
7 3-2*^ 4*-1 ^
105
402. Найдите множество решений неравенства:
а) х2 > 0,7х; б) 2у < у2; в) хг < 16; г) л:3 > 25.
403. Решите неравенство сначала графически, а затем
алгебраически:
а) х2>3х; б) х2<3х.
404. Решите неравенство:
а)—— >0; г) >0; ж)—±-<0;
1 + Х X X
б)^^<0; д)_!_<0; 3)1—^^о.
х х — 2 х
в)^-1<0; е)-^->0;
4х 1-х
§ 10. ПРИМЕНЕНИЕ НЕРАВЕНСТВ К ОЦЕНКЕ ТОЧНОСТИ
ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ
16. Точные и приближенные значения величин
В практической деятельности люди постоянно имеют дело
со значениями различных величин: длин, площадей, объемов,
касс, температур и др.
Истинное значение величины удается определить лишь в
некоторых случаях. Можно, например, точно указать число
вагонов железнодорожного состава, точно подсчитать, сколько
учеников находится одновременно в классе. Но в большинстве
случаев приходится иметь дело лишь о приближенными
значениями величин.
Приближенные значения нередко получаются в результате
счета большого числа предметов. Лишь приблизительно
оценивают количество зрителей телепередачи, число перелетных
птиц, число деревьев в лесу.
Приближенные значения получаются в результате
измерений. Невозможно, например, точно измерить длину стержня.
Ведь измерения мы ведем с помощью какого-либо прибора
(линейки, штангенциркуля, микрометра, оптиметра* и др.), а точ-
* Оптиметр — оптико-механический измерительный прибор.
ность измерения прибором всегда ограничена. Кроме того,
изготовляя прибор в заводских условиях, гарантируют лишь ту
или иную степень точности его изготовления. Наконец,
производя измерения, мы вносим ошибки, связанные с нашим опытом
работы и с нашими личными качествами.
Невозможно точно измерить площадь земельного участка,
температуру воздуха, скорость полета самолета и т. д.
Приближенные значения получаются при округлении
истинных значений величин. Так, число 2,19563 в расчете, не
требующем высокой точности, молено округлить, заменив его числом
2,196 или даже 2,20, которые являются приближенными
значениями числа 2,19563 с избытком.
405. Укажите, какие числа являются точными значениями
величин, а какие приближенными:
а) число жителей города составляет 7061 тыс. человек;
б) станок состоит из 82 деталей;
в) масса станка 1230 кг\
г) пассалшрекий самолет находился в полете 2 ч;
д) в самолете 86 пассажиров;
е) скорость звука 332 —;
сек
ж) отношение длины окружности к диаметру равно 3,14;
з) время конькобежца на дистанции 500 м9 установленное
с помощью фотофиниша, равно 40,21 сек.
406. Округлите число до десятых и укажите характер
полученного приближения (является ли оно приближением
данного числа с недостатком или с избытком):
а) 12,41; в) 3,45; д) 121,03;
б) 8,493; г) 11,75; е) 1,98.
407. Округлите до сотых число:
а) 6,113; в) 1,407; д) 2,5013;
б) 0,318; г) 10,275; е) 11,096.
408. Округлите число 1976,102 до сотых, до десятых, до
единиц, до десятков, до сотен. Какие из полученных чисел
являются приближениями данного числа с недостатком?
409. Округлите число л = 3,14159... до десятитысячных, до
тысячных, до сотых. В каждом случае укажите характер
приближения.
107
m>20
20<m<30
25<m<30
25<m<27
26<m<27
27. Границы значения
величины
Рассмотрим процесс
определения массы детали с
помощью рычажных весов и
набора разновесков, наиболее
мелкий из которых имеет
массу 1 г.
С помощью двух
взвешиваний установим, что масса
детали больше 20 г, но меньше
30 г (рис. 32, I, II).
Обозначим массу детали в
граммах через т, тогда
результат взвешивания можно
записать в виде двойного
неравенства:
20 < т < 30.
Заменив затем разновесок
в 10 г разновеском в 5 г,
убедимся, что масса детали
больше 25 г (рис, 32, III), т. е.
25 <т <30.
Добавив на чашку весов с
разновесками разновесок в 2 г,
установим, что масса детали
меньше 27 г (рис. 32, IV):
25 < т < 27.
Заменив разновесок в 2 г
разновеском в 1 г, выясним,
что масса детали больше 26 г
(рис. 32, V):
28 < т < 27.
Так как более мелких
разновесков у нас нет, то
процесс определения массы на
этом этапе закончим.
В результате взвешивания
мы нашли приближенные
значения массы детали в граммах:
26—приближение с
недостатком, 27 — приближение с из-
бытком. Другими словами, мы установили границы значения
массы в граммах. Число 26 — нижняя граница, число 27 —
верхняя граница.
Заметим, что если бы наиболее мелким был разновесок в 2 г,
то границами значения массы детали в граммах были бы числа
25 и 27, т. е. масса была бы определена менее точно. Еще более
грубую оценку массы мы получили бы, ограничившись
результатами 3-го или 2-го взвешивания (см. рис. 32).
Зная границы значения некоторой величины, можно
оценить значение другой величины, зависящей от первой. Пусть,
например, известны приближенные значения (в см) с
недостатком и с избытком длины а стороны равностороннего
треугольника:
5,4<[ а ^ 5,5.
Нужно найти границы периметра Р.
Периметр равностороннего треугольника вычисляется по
формуле Р=3а. Из условия а^ 5,4 следует, что За!> 16,2; из
условия а<; 5,5 следует, что За^ 16,5. Числа 16,2 и
16,5—приближенные значения периметра треугольника (в см) с
недостатком и с избытком:
16,2 < Р < 16,5.
Заметим, что запись решения можно вести с помощью
двойного неравенства:
5,4 <J a <; 5,5;
5,4 • 3 < За < 5,5 • 3, т. е.
16,2<Р<16,5.
Рассмотрим еще один пример. Пусть известны границы
некоторого числа х:
3 < х < 6.
Требуется оценить значение выражения —.
X
Из условия задачи следует, что х — число положительное.
Так как х > 3, то — < —; так как х < 6, то — > -. Значит.
х з х б
7<I<V
6x3
Заменим границы значения выражения — десятичными дро-
X
бями. При этом число — можно заменить только меньшим числом
6
(любым приближением с недостатком), а число только ббль-
3
шим числом (любым приближением с избытком). Так как
- = 0,166... и - = 0,333...,
6 3
юэ
'! I i м i ы i i ( i i r i i ' i i i i i i i i i i i i i i i i i i i i l i i I ' i i i i м i i 1
0 0,1 ^\ 0,2Q3 } Q4 Of5
6 J
Рис. 33
то в качестве границ значения выражения — можно взять деся-
х
тячные дроби 0,1 и 0,4:
0,l<i<0,4.
х
Заменив нижнюю границу числом 0,1, а верхнюю — числом
0,4, мы расширили промежуток, которому принадлежит
значение выражения — (рис. 33). Если бы мы поступили иначе, округ-
X
лив бесконечные десятичные дроби 0,166... и 0,333... по
известным правилам округления, то получили бы, что 0,2 <— <0,3.
Но тогда неизвестное нам истинное значение выражения — мог-
х
ло оказаться за пределами полученных границ (см. рис. 33).
410. Укажите границы:
а) средней скорости пешехода;
б) роста учащегося вашего класса;
в) температуры воздуха в вашей области.
411. Можно ли из куска ткани длиной I м9 где 2,6^/^2,8,
сшить платье, на которое при данной ширине требуется
не менее:
а) 2,4 м\ б) 2,7 м; в) 2,9 м?
412. Можно ли из квадратной пластины со стороной а мм
вырезать круг диаметром d мм, если:
а) 53 < а < 55, б) 53 < а < 55,
49<d<51; 52 < d< 54?
413. а) Найдите границы периметра квадрата со стороной
а см, где 5,1 ^ а ^ 5,2.
б) Определите границы длины стороны квадрата, зная,
что периметр квадрата равен Р еле, где 15,6^Р^15,8.
414. Дано, что 3 ^ а ^ 4. Оцените значение выражения:
а) 5 а; г) а; ж) 5—а; к) —.
5 л
б) 0,3 а\ д) а+2; з) 2а +5;
в) —а; е) а—3; и) 0,1а—0,1;
но
415. Известно, что 8,4 < 6 < 9,2.
Верно ли, что:
а) 8,1< Ъ < 9,4; в) 8 < 6 < 9;
б) 8,6 < 6 < 9,3; г) 7 < 6 < 10?
416. Пусть 11,39 < у < 11,53. Укажите другие границы числа
у так, чтобы соответствующее двойное неравенство было
верным. Приведите несколько примеров.
417. Укажите два последовательных целых числа, две после*
довательные десятичные дроби с одним знаком после
запятой, две последовательные десятичные дроби с двумя
знаками после запятой, между которыми заключено число:
а) 18,243; б) 1-; в) —0,591.
Ответы запишите в виде двойных неравенств.
418. Известно, что 7 < Ъ < 8. Оцените значение выражения —.
ь
Замените найденные границы десятичными дробями с
двумя знаками после запятой.
28. Теоремы о почленном сложении и умножении верных
числовых неравенств
Зная границы некоторого числа а, мы можем, используя
известные свойства неравенств, оценить значения таких
выражений, как За, —5а, а+10, 2а—4 и т. д.
А как оценить сумму чисел а+&, разность а—6,
произведение а&, частное —, если известны границы а и &? Для того чтобы
ь
решить эту задачу, нам придется рассмотреть некоторые новые
свойства неравенств.
Сложим почленно левые и правые части верных неравенств
6 >—3 и 12 > 5, каждое из которых составлено с помощью
знака >. Легко видеть, что сумма 6+12 больше суммы —3+5,
т. е. верно неравенство 6+12 >—3+5.
Если сложить почленно левые и правые части неравенств
2<6 и —12 <—4, то сумма 2+(—12) будет меньше суммы
6+(—4), т. е. верным является неравенство 2+(—12) <6+(—4).
Теорема 1. Если а>Ь и с >d, то а + с >b + d (a, b, с и d—
любые числа).
Доказательство. Так как а>Ъ% то а+с > Ь+е.
Аналогично, так как c>d, то Ь+с> b+d. По свойству
транзитивности из неравенств а +с >Ь +с и &+с> 6+d следует
неравенство а+с> b +d.
ill
Таким образом, при почленном сложении верных неравенств
одного знака верным будет неравенство того же знака.
Теорема верна и в том случае, если число рассматриваемых
неравенств больше двух. Например, складывая почленно
левые и правые части неравенств 3 < 5, —1 < 7, —10 <—9,
получим верное неравенство 3+(—1)+(—10)<5+7+(—9), т. е.
—8< 3.
Если а > Ъ и с < dj то нельзя заранее сказать, в каком
соотношении будут находиться суммы а+с и b+d. Например,
складывая почленно верные неравенства 12 > 8 и —10 <—5,
мы будем иметь верное неравенство 2 < 3, составленное с
помощью знака <. А при почленном сложении неравенств 6 > 1
и —8 <—7 верным оказывается неравенство —2 >—6,
составленное с помощью знака >.
Рассмотрим вопрос о почленном умножении неравенств.
Теорема 2. Еслиa>buc>d,гдеа,Ь,сиd—положительные
числа, то ac>bd.
Доказательство. Так как а>Ъ та. с —
положительное число, то ас >Ъс. Так как с >d и b — положительное число,
то bc>bd. По свойству транзитивности из неравенств ас>Ьс и
bc>bd следует неравенство ac>bd.
Итак, при почленном умножении верных неравенств одного
знака с положительными членами верным будет неравенство
того же знака.
Например, при почленном умножении неравенств 4 > 3 и
1^1 vll^O1 i^1
— > — получим верное неравенство 4 • — > 3 • —, т. е. 1 > —.
Из верных неравенств 0,1 < 0,5 и 9 < 10 следует неравенство
0,1 • 9<0,б • 10, т. е. 0,9 < 5.
Теорема верна и в том случае, если число рассматриваемых
неравенств больше двух.
Следствие. Если числа а и b положительны и а> &, то
а* > Ь\
Действительно, перемножив почленно два верных
неравенства а>Ъ и а>Ъ с положительными членами, получим верное
неравенство а2 > Ь2.
Верно и обратное: если а2 > &2, причем а и b — числа
положительные, то а> Ь.
Действительно, из неравенства а2 > &2, где а > 0 и 6 > 0, не
могут следовать соотношения а<Ь или а—Ь.
Если бы было верно неравенство а < Ъ (а и b — числа
положительные), то было бы верно и неравенство а2 < Ь2, что
противоречит условию теоремы.
112
Из равенства а=Ь следовало бы, что аъ=:Ь%% что также
противоречит условию теоремы.
Значит, из неравенства а2>&2, где а>0 и Ь >0, следует
неравенство а>Ь.
Справедливы и более общие утверждения: если а>Ь>0 и
п € N, то ап> Ьп\ обратно, если ап > Ья, где а > О, Ь > 0 и п € JV,
то а>Ь.
419. Примените к данным неравенствам теорему о почленном
сложении неравенств:
а) 12 >— 5, 9>7; в) —2,5 <—0,7, — 6,5 <—1,3;
б) — 28 < 0, —10 <— 6; г) 11 > 7,4, 0 > —8.
420. Примените к данным неравенствам теорему о почленном
умножении неравенств:
а) 5>2, 4>3; в) 3 > 1, | > |;
о 5
б) 1< 7, 10 < 15; г) 8 < 10 i < i.
4 2
421. Покажите на примерах, что при почленном умножении
неравенств одного знака с отрицательными членами
неравенство, составленное с помощью того же знака, может
быть неверным.
422. Примените к двум данным неравенствам теорему о
почленном сложении неравенств:
а) а>—10, 6>2; в) /гс>7, п>—7;
б) х<5, у<—8; г) с<12, d<—4.
423. Примените к двум данным неравенствам теорему о
почленном умножении неравенств:
а) а > 12, 6 > -J-; б) 0 < а < 0,5, 0 < 6 < 2.
о
424. Верно ли, что:
а) (т>2 и п>5)=ф(т+п>7);
б) (т>2 и л >5)=ф(т+и>6);
в) (т>2 и п>5)=ф(т+л>10);
г) (т>4 и п >3):=>(/7т>12);
д) (т>4 и л>3)=ф(ти>9);
е) (т>4 и п >3)=> (тп >22)?
425. Верно ли, что:
а) (а < Ъ) =-> (а2 < б2); б) (а3 < б2) ==-> (а < Ъ)1
на
29. Применение метода границ для оценки значения суммы,
разности, произведения и частного
Пусть известны приближенные значения чисел а и 6 с
недостатком и с избытком: 2,8 < а < 3 и 1,5 < Ь < 1,7. Каковы
границы суммы а+ 6, разности а — Ь, произведения аЪ и частного — ?
ь
Решить поставленную задачу мы можем с помощью теорем,
рассмотренных в предыдущем пункте.
Для оцешси суммы воспользуемся теоремой о почленном
сложении числовых неравенств. По условию а > 2,8 и Ь>1,5.
Сложив почленно неравенства а>2,8 и 6>1,5, каждое из
которых составлено с помощью знака >, получим:
а+Ь>4,3.
Аналогично, применяя теорему о почленном сложении
неравенств к неравенствам с<3и &<1,7, получим:
a+b<4J.
Итак, мы нашли границы суммы чисел а и Ь:
4,3<а+Ь<4,7.
Заметим, что запись решения удобнее вести с помощью
двойных неравенств:
2,8< а <3,
1,5 < Ъ <1,7
4,3<а+Ь<4,7.
А как найти приближения с недостатком и с избытком
разности а — &?
Так как а — Ь = а+(—Ь), то, для того чтобы найти границы
разности а — 6, следует сначала оценить выражение —&, а
затем, воспользовавшись теоремой о почленном сложении
неравенств, оценить сумму а+(—&).
Известно, что 1,5<&<1,7. Значит, —1,5>—Ъ>—1,7.
Запишем последнее соотношение с помощью знака <:
—1,7 <—Ъ<—1,5.
Применим к двойным неравенствам
2,8<а<3 и —1,7 <—Ь<—1,5
теорему о почленном сложении неравенств:
2,8 < а <3,
—1,7 < — Ъ <-1,5
2,8+(—1,7)<а+(—Ь)<3+(—1,5).
Таким образом, 1, К а — Ь < 1,5«
114
Для того чтобы найти границы произведения ab,
воспользуемся теоремой о почленном умножении неравенств (все члены
неравенств — числа положительные):
2,8 <а <3,
1,5<6 <1,7
2,81,5<а&<31,7, т. е. 4,2<а&<5,1.
Для нахождения границ частного чисел а и Ь представим
дробь — в виде произведения: — = а • —.
ь ь ь
Найдем сначала границы значения выражения — . Так как
ь
1,5 < Ъ < 1,7, то _ > - > -L, или, иначе, — < 1 < J-. Теперь
1,5 Ь 1,7 1,7 Ь 1,5
к неравенствам 2,8<а<3и — < — < — можно применить
теорему о почленном умножении неравенств:
2,8 < а < 3,
±< ± <±
1,7 Ь 1,5
2,8 • —- < а • — < 3 , т. е. — < — < —.
1,7 ь 1,5 1,7 ъ 1,5
Верхняя граница частного — равна 2. Заменим нижнюю гра-
ь
2 8
ницу -1— десятичной дробью с одним знаком после запятой. Раз-
делив числитель на знаменатель, получим бесконечную
десятичную дробь 1,64... . Значение нижней границы необходимо взять
2 8 а
с недостатком. Так как 1,6 < —, то 1,6 < — < 2.
1,7 Ь
Для оценки значения выражения мы воспользовались
методом, который заключается в том, что приближенное значение
выражения находится дважды: один раз получается число,
заведомо меньшее искомого результата, другой раз — заведомо
большее. Этот метод называют методом границ.
426. Пусть 3<а<4 и 4<Ь<5. Найдите границы значения
выражения:
а) а+Ь; б) а—Ь\ в) аЬ\ г) — •
ь
115
427. Пусть 6^ дс^ 7 и 10^ у ^ 12. Оцените значение выражения:
а) х + у; б) х—у\ в) у—х; г) ху\ д) —; е) ^-.
у х
428. Пусть 5<т<6и1<л<2. Докажите, что 11 < 2т + п < 14
и Km — 2л <4.
429. Пусть 6< с< 7 и 2< d< 3. Докажите, что 24< с (d+2)< 35
и 0<- —2<1,5.
d
430. Найдите границы значения выражения:
а) За+7&, если 1,2<а<1,4 и 0,2<Ь<0,4;
б) - + 0,66, если — 3 < а < — 2 и 0,5 < Ь < 1;
в) Ь2 — а&, если 3<а<4 и 5 < Ь < 6;
г) — + —. если 0,1< а < 0,2 и 0,4 < Ь < 0,5.
а &
431. Известны длины а и Ъ основания и боковой стороны
равнобедренного треугольника, выраженные в мм: 26^ а^ 28
и 41^&^43. Оцените периметр треугольника.
432. Найдите границы длины средней линии трапеции, если
известны приближенные значения (в сантиметрах) с
недостатком и с избытком длин а и с ее оснований:
3,4<а<3,5 и 6,2<с<6,3.
433. Можно ли перевезти на трехтонном грузовике за один
рейс 14 плит, каждая массой m яг, где
260 < т < 270,
если не допускается перегрузка свыше 500 кг?
434. Можно ли за один рейс перевезти на пятитонном
грузовике 3 плиты, каждая массой тх кг, и 8 плит, каждая массой
т2 кг 9 где
970 < тг < 1030, 245 < т2 < 255,
если не допускается перегрузка свыше 800 кг?
435. У подножия Останкинской телевизионной башни и
вблизи ее вершины расположены барометры. Показание
нижнего барометра в мм рт. ст. равно ри где 755 ^рх ^756,
а показание верхнего барометра в мм рт. ст. равно р2»
где 713 ^р2^ 714. Определите, на какой высоте
расположен второй барометр. (Считайте, что на каждые 12 м
высоты давление понижается на 1 мм рт. ст.)
436. В треугольнике ABC известны величины двух углов:
58°<^ВС<59° и 102°<ЖМ<103°.
Определите границы величины угла CAB.
lie
30, Погрешность приближения
Имея некоторое приближенное значение величины, полезно
знать, на сколько оно отличается от истинного значения, т. е.
какова его погрешность.
Определение. Погрешностью приближенного значения
величины называется разность между истинным и приближенным
значениями этой величины.
Например, заменяя число х = 3,283 приближенным
значением а = 3,2 с недостатком, мы допускаем погрешность х — а =
= 0,083. Если в качестве приближенного значения числа х взять
приближение Ъ = 3,3 с избытком, то погрешность этого
приближения будет х — Ъ =—0,017. Легко понять, что погрешность
приближения с недостатком всегда положительна, а погрешность
приближения с избытком отрицательна.
Однако, как правило, важнее знать не характер
приближения, а то, как близко оно к истинному значению.
Выясним, к примеру, какое из двух приближений числа х
является лучшим. Для этого сравним модули погрешностей.
Модуль погрешности приближения с избытком (\х—&| =0,017)
меньше, чем модуль погрешности приближения с недостатком
(\х—а\ =0,083). Следовательно, приближенное значение с
избытком, равное 3,3, лучше, оно меньше отличается от заданного
числа х =3,283.
0,081 0,017
ас , . , ^7-TTltfih.b
3,2 $3
Рис. 34
Если мы изобразим на координатной прямой точки с
координатами х> а и &, то расстояние между точками с координатами
х и Ъ будет меньше, чем расстояние между точками с
координатами х и а (рис. 34).
437. Пусть х — некоторое число и а — его приближенное
значение. Найдите погрешность приближения и модуль
погрешности, если:
а) х=9,7 и а =10; в) х=0,84 и а =0,8;
б) л: =0,8 и а = 1; г) х=3,62 и а =3,6.
438. Известны приближенное значение а некоторого числа х
и погрешность приближения. Найдите х, если:
а) а=12 и х— а=0,3; в) а=21 и х—а =—0,2;
б) а=3,2 и х— а =0,07; г) а =0,4 и х— а=—0,03.
117
439. Пусть а — приближенное значение числа х и |х — а\ —
модуль погрешности. Найдите дг, если:
а) а = 10 и \х— а|=1; в) а=7,5 и \х— а|=0,1;
б) а=2 и |др_а|=0,3; г) а = 3,6 и |х— а|=0,02.
440. Обратите число у в десятичную дробь и округлите эту
дробь последовательно до десятых, до сотых, до
тысячных. Найдите в каждом случае погрешность приближения
числа десятичной дробью, если:
441. Проверьте, что число 0,66 является приближенным зна-
2
чением числа — с недостатком, а число 0,67 — с избытком.
з
Какое из этих двух приближений лучше?
442. Какое из двух приближений числа — лучше: 0,16 или 0,17?
6
443. Известны границы длины а и ширины Ъ (в метрах)
комнаты прямоугольной формы: 7,5 ^ а ^ 7,6 и 5,4 ^ b ^ 5,5.
Подойдет ли это помещение для школьной библиотеки,
если для этого требуется комната площадью не менее
40 м2?
444. Вычислите границы длины окружности, диаметр которой
равен d сму где 4,5 < d < 4,6. Считайте, что 3,14 < л < 3,15.
445. Длина воздушной трассы между двумя пунктами равна
s км. Самолет преодолевает ее за время t ч. Определите
границы средней скорости самолета, если
4950 < s < 5050, 5,9 < % < 6,1.
31. Точность приближения
Рассмотрим пример. Пусть известны границы массы т
(в граммах) металлической пластинки:
4 t^m <; 5.
Приближенным значением массы (в граммах) может служить
и число 4, и число 5, а также любое другое число между
ними, например 4,1; 4,3; 4,5; 4,65; 4,85; 4,9.
Возьмем в качестве приближенного значения массы число 4.
Не зная точного значения массы т, мы не можем определить
и погрешность приближения. Однако легко понять, что модуль
118
погрешности не может превосхо- Ю
дить 1. Действительно, рассмот- дц ( . ■ . . ■ ■ ■ . Тч t
рев рисунок 35, а, мы видим, 4 5
что, где бы в промежутке [4; 5] т
ни находилась точка с коорди- - i ..^ ,,,,,, >t t
натой т, она удалена от точки с ч/ А ^2 ' 5
координатой 4 не более чем на 1. '
Значит, \т— 4|< 1. J
Говорят, что число 4 явля- ^ Г i i . л i
ется приближенным значением 4 4,5 5
массы т в граммах с точностью
до 1. Рис- 35
Выберем теперь в качестве
приближенного значения массы
в граммах число 4,2 и оценим значение выражения \т—4,21.
Из рисунка 35,6 видно, что, где бы ни находилась точка с
координатой т в промежутке [4; 5], она удалена от точки с
координатой 4,2 не более чем на 0,8, т. е. \т—4,21^ 0,8.
Число 4,2—приближенное значение массы т в граммах с
точностью до 0,8.
Аналогично, число 4,7 — приближенное значение массы т
в граммах с точностью до 0,7.
Возьмем в качестве приближенного значения массы т в
граммах среднее арифметическое границ, т. е. число 4,5. С
помощью рисунка 35,6 легко увидеть, что значение выражения
\т—4,51 не превышает половины расстояния между точками
с координатами 4 и 5, т. е. не превышает 0,5. Число
4,5—приближенное значение массы пластинки в граммах с точностью
до 0,5.
Последнее приближение оказалось наиболее выгодным, так
как модуль погрешности мы оценили меньшим числом, чем в
предыдущих случаях.
Вообще, если в качестве приближенного значения числа х
взято число а и известно, что модуль погрешности такого
приближения не превосходит некоторого числа А, т. е. \х—а|^й,
то говорят9 что число а является приближением числа х с
точностью до h.
Записывают это так:
х = а ± й.
Приведем примеры.
1. Известно, что 2,6 ^ х ^ 2,9. Вычислить приближенное
значение ху равное среднему арифметическому границ, и
определить точность этого приближения.
2,9 + 2,6 = 5J> = 2 75
2 2 *
119
Модуль погрешности приближения числа х числом 2,75 не
о о ост 2,9 — 2,6 0,3
превышает полуразности чисел 2,9 и 2,6. Так как =—=
*=0,15, то х=2,75±0,15.
2. Найти границы, в которых заключено число у, если
у = 12,7±0,5.
Так как 12,7 есть приближенное значение числа у с
точностью до 0,5, то у отличается от 12,7 не более чем на 0,5. Значит,
12,7— 0,5<у< 12,7+ 0,5, т. е.
12,2 <у< 13,2.
3. Доказать, что число 0,14 является приближенным
значением числа — с точностью до 0,01.
7
Найдем модуль погрешности приближения числа — числом
0,14:
- — 0,14
7
14
———
100
=
1
—
7
7
_— —
50
~~*
50—49
350
350"
Так как — меньше 0,01, то верно неравенство 0,14
<
^0,01. Значит, число 0,14 является приближенным значением
числа — с точностью до 0,01.
7
Эту задачу можно решить и другим способом.
Разделив числитель дроби — на знаменатель, получим
бесконечную десятичную дробь:
- = 0,14 ... .
7
Значит, 0,14 < — < 0,15. Отсюда ясно, что модуль
погрешности приближения числа — числом 0,14 не превышает 0,01.
Действительно,
11 _ 0,141 < 10,15 — 0,141, но 0,15 — 0,14 = 0,01,
следовательно, верно неравенство
- — 0,14
I 7
< 0,01.
4. Найти множество приближенных значений числа 3,7 с точностью до 0,1.
В качестве приближенного значения числа 3,7 с точностью до 0,1 можно
вэять любое число а, отличающееся от числа 3,7 не более чем на ОД. Значит,
120
приближенным значением числа 3,7 с точностью до 0,1 является любое число,
принадлежащее промежутку [3,7 — 0,1; 3,7 + 0,1], т. е. промежутку [3,6; 3,8].
В частности, приближенным значением числа 3,7 с точностью до 0,1 является
и само число 3,7. Вообще, всякое число является своим приближением с
любой степенью точности.
5. Электроплитка рассчитана на напряжение 220±10в.
Найти сопротивление спирали электроплитки, если известно,
что через нее должен идти ток 5 ± 0,1а.
Известны приближенные значения с недостатком и с
избытком напряжения U (в вольтах) и силы тока / (в амперах):
210<[/<230 и 4,9</<5,1.
Для определения сопротивления R спирали плитки (в омах)
воспользуемся законом Ома: R =—.
Оценим вначале значение выражения —, а затем произве-
тт 1
дения и- —.
Так как 4,9</<5,1, то -1>I>-L, т. е. i-<i<-L.
Применим к неравенствам
210<J7<230 и
5,1^ / ^4,9
теорему о почленном умножении неравенств:
210 — < U • - < 230 • —, т. е.
5,1 ^ / ^ 4,9'
210 ^ JL ^23°
5,1^ / ^4,9'
Значение нижней границы следует взять с недостатком, а
верхней — с избытком.
Так как
210 лл л 230 лаа
— == 41,1 ... и — = 46,9 ..., то
5,1 4,9
41 < R < 47.
В качестве приближенного значения сопротивления R возь-
41 4- 47
мем среднее арифметическое границ: ——— = 44. Модуль
погрешности этого приближения не превышает полуразности
границ: 47~~41 = 3. Итак, R == 44 ± 3.
Ответ: 44±3 ом*
121
446. Вычислите приближенное значение х, равное среднему
арифметическому границ, и укажите точность этого
приближения:
а) 6< х< 8; в) 4,5 < х < 4,8;
б) 2<х<3; г) 2,81<*<2,83.
447. В каких границах заключено число у, если:
а) у=3±1; в) у=6,5±0,6;
б) у=3,9±0,2; г) у=0,4±0,15?
448. а) Докажите, что число 1,4 является приближенным
значением числа 1,361 с точностью до 0,05.
б) Докажите, что число 0,3 является приближенным зна-
2
чением числа — с точностью до 0,05.
7
449. а) Округлите до десятых дроби: 1,487; 0,35; 2,714.
Убедитесь в каждом случае, ,что модуль погрешности
приближения, полученного в результате округления, не
превосходит половины от 0,1, т. е. 0,05.
б) Приведите несколько примеров округления
десятичных дробей до сотых. Убедитесь в каждом случае, что
полученный результат является приближением с
точностью до половины от 0,01, т. е. до 0,005.
450. Является ли число 0,2 приближенным значением числа
0,1981 с точностью до 0,5; 0,1; 0,01; 0,001?
451. Пусть — <# < —. Докажите, что числа — и — являются
31 ^ ^ 30 ^ 31 30
приближенными значениями числа х с точностью до 0,01.
452. Известно, что — <#< — • Являются ли числа — и —
100 ^ ^99 100 9Э
приближенными значениями числа х с точностью до 0,05;
0,01; 0,001?
453. При измерении длины а и ширины Ь прямоугольника
получили, что а=5,4±0,1 см и Ъ = 3,7 ± 0,1 см. Найдите
приближенные значения периметра и площади
прямоугольника.
454. Найдите приближенное значение площади фигуры,
изображенной на рисунке 36, если
а=1,2±0,1 см, с=2,2±0,1 см,
&=2,4±0,1 см, d=l,4±0,l см.
455. Вычислите приближенное значение площади
заштрихованной части фигуры, изображенной на рисунке 37, если
а=8,2±0,2 см, с=2,6±0Д см,
Ь=6,4±0,2 см, d=l,7±0,l см.
с
456.
457.
Рис. 86
Требуется уложить 1000±20 м* бетона. В кузов
самосвала заливают 2,25±0,02 мг бетона. Сколько рейсов
самосвала потребуется для этой работы?
Брусок имеет объем V м* и массу т кг. Вычислите
плотность материала, если 0,0064< F< 0,0065 и 17,3<т<17,5.
Определите по таблице плотностей, из какого материала
сделан брусок.
Наименование
медь
сталь
чугун
алюминий
Плотность / — |
U8/
8900
7800
7000
2700
458. Можно ли включить в цепь прибор, имеющий
сопротивление 44±0,5 ом, чтобы при напряжении 215±15 в сила
тока не превысила 6 а?
459. Требуется оклеить обоями стены комнаты общей площадью
30±0,2 м2. Сколько необходимо иметь рулонов обоев,
если в одном рулоне содержится 7 ±0,03 м обоев при
ширине 0,75±0,03 м!
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К ГЛАВЕ П
К пункту 18
460. Докажите, что при любых значениях у:
а) значение выражения (6у—1) (у +2) меньше
соответствующего значения выражения (Зу+4) (2у+1);
128
б) значение выражения (Зу—1) (2у+1) больше
соответствующего значения выражения (2у—1) (2+Зу).
461. Составьте двучлен с переменной х:
а) принимающий положительные значения при любых
значениях х;
б) принимающий отрицательные значения при любых
значениях х\
в) принимающий при одних значениях х положительные
значения, при других — отрицательные и
обращающийся в нуль при х9 равном 5.
462. Какие из неравенств верны при любом значении
переменной а:
а) (а— 8)2>0; в) 4— а2<0; д) (а—9)2+26>0;
б) (5—2а)2 > 0; г) —18— а2 < 0; е) (а—5)2+(а—З)2 > 0?
463. Докажите, что при любом значении Ь верно неравенство:
а) (Ь +4) (Ь— 4)— &2 < 0; в) (&—7) (Ь +6) +(Ь +50) > 0;
б) (2&+1)2—2(2&—1)>0; г) 5(Ь—2)—(Ь—1)(Ь+6)<0.
464. Докажите, что при всех значениях переменной а
выражение принимает положительные значения:
а) (а2+2а+1)+8; в) а2+2а+6;
бМа2—2а+1)+4а2; г) а2— 4а +12.
465. Докажите, что при любых значениях переменной а
значение дроби неотрицательно:
(а-1)а, . 9а2-6а+1. g2 + 6a+10>
а)_1Г""' В) а* + 1 ' Д) й *
g. a2 + 4a + 4. . 49a2 + 14a + 1, . 4a2 — 4a + 8
' 7 * ^ a2+ 9 * 5
466. Какие из неравенств верны при любых значениях
переменной х:
а) 4х (х +4) > (2х +3) (2х—3)—16х;
б) х2<(3х—1) (Зх+1)—4 (2л;2—1);
в) (5х—1)(5х+1)<25х2— (х+1);
г) (х +4) (х— 4) +12 <х(х + 4)— 4х?
467. Как изменяется произведение чисел а и 6 при увеличении
множителя Ъ на 1?
468. Выясните, при каком условии значения произведения
(a+1) (&+1) больше соответствующих значений
произведения аЪ. Проиллюстрируйте ответ примерами.
124
. Докажите, что полупериметр треугольника больше длины
каждой из его сторон.
470. Катер прошел 20 км по течению реки и 20 км против
течения реки. Затратит ли он на весь путь больше времени,
чем ему требуется на прохождение 40 км в стоячей воде,
меньше или столько же?
471. Сравните площадь квадрата со стороной 10 см с площадью
произвольного прямоугольника, имеющего тот же
периметр.
К пункту 19
472. Запишите верное неравенство, которое получится, если:
а) к обеим частям неравенства прибавить число,
записанное в скобках:
18> -5(104); |> 1(0.1).. }>j(-})
б) обе части неравенства умножить на число, записанное
в скобках:
47 > 47(6); °'34 < °'37 (~2); 7 < 7(_1);
в) обе части неравенства разделить на число, записанное
в скобках:
! > 7 (1); 0,°6 < 0'21 (-°'03); 10'2 > 8Д (-1)'
473. Какое из соотношений «а больше 6», «а меньше 6», «а
равно 6» имеет место, если верно неравенство:
а) 0,3а > 0,36; в) 17а < 176; д) 0,25а >! 6;
4
б) — 5а<—56; г) —1,2а >—1,26; е) — 0,02а < —- 6?
50
474. При каких значениях а и 6 верно неравенство:
а)а6>0; г) - < 0; ж)-<0;
ъ ъ
б) аЪ < 0; д) а?Ъ > 0; з) — > 0;
ъ%
в) - > 0; е) аЪ* < 0; и) - < 0?
ъ ь
475. Докажите, что если а>6, то:
^ а) а+5>6+3; б) 1—а<2—6.
126
476. Докажите, что если а>&>0, то:
а) 5а>46; в) — 4а < — 2Ь;
б) 17а>12&; г) — 5а < —1,2&.
477. Верно ли, что если а>Ь, то:
а) а+1>Ь+1; в) 1— а<1— Ь;
б) а-1>&— 1; г) ->-?
3 3
478. Верно ли, что если а>Ь, то:
а) (а+1)Ь<а& + а; в) а2>Ь2;
б) {а+1)(6—1)<а&; г) a2+b2>2ab?
479. а) Как изменяется правильная дробь--/а> О, 6>0, — < 1)
при прибавлении к ее числителю и знаменателю одного
и того же положительного числа?
б) Как изменяется неправильная дробь — (а>0, 6>0,
ь
— > 1) при прибавлении к ее числителю и знаменателю
одного и того же положительного числа?
480. Докажите, что при всех значениях переменной с верно
неравенство:
а) —-1— > с; б) < —.
' 2 ^ с2 + 1 ^ 2
481. Докажите, что при всех значениях переменных а, & и с
верно неравенство
а2+&2+с2+3>2(а+Ь+с).
482. Докажите, что при любых значениях а, Ь и с верно
неравенство < ^
а2+ b* + c2^ab + ac + be.
Указание. Умножьте обе части неравенства на 2.
483. Докажите, что при всех значениях а и Ъ верно неравенство
аа+аЬ+&2>0.
Указание. Используйте тождество ab =2 -а- ■— Ь.
2
484. Докажите, что при любых положительных значениях х
и у верно неравенство:
а) хь + уъ^х*у+ху*\ б) *4+y*>*V + *ys,
126
485. Докажите, что при указанных значениях переменных
верно неравенство:
а) п3+1>п2+п при тг>1;
б) пг+1<п2+п при п<—1.
486. У продавца были весы с различными по длине плечами.
Один килограмм товара он взвесил на левой чашке, а
другой тому же покупателю — на правой. Получил ли
покупатель 2 кг товара, больше 2 кг или меньше?
487. Докажите, что при а > О и 6 > О верно неравенство:
а)£ + £>7 + Г «> (• + *>(! + })>*•
488. Докажите, что если а>|Ь|, то а>Ь.
К пункту 20
489. При каких значениях а из неравенства 17 > 14 следует
неравенство 17а >14а? из неравенства 4 < 10 следует
неравенство 4а >10а?
490. Докажите, что:
а) из того, что ас— be, не следует, что а=Ь;
б) из того, что а — отрицательное число, не следует, что
а+0,1 — отрицательное число.
491. Найдите среди неравенств такое, из которого следуют все
остальные:
а) л:>8, *>5, х> 1, *>12;
б) #<4, х<2, Ж 1,5, *<18;
в) *>1,2, *>1—, х>1-, *>1~;
5 2 3
г) *<1,2, х < 1,02, х< 1,002, х<1.
492. а) При каких значениях а из неравенства х > а следует
неравенство лс>12?
б) При каких значениях Ъ из неравенства х < Ь следует
неравенство х < 9?
493. а) Следует ли из предложения х > 3 предложение
х(х*+1)>3(х2+1)?
б) Следует ли из предложения у < б предложение
y(-i/2-2)>5(-i/2-2)?
494. При каких значениях а:
8
а) из неравенства ах>3 следует неравенство дс>—;
а
б) из неравенства ах<2 следует неравенство *>~?
о
127
495. Пусть С — пересечение множеств A is. В. Верно ли:
а) (а 6 А)*=ф (а £ С); б) (а £С)=ф(а £ А)?
496. Докажите, что:
а) функция, заданная формулой f(x)=3x + 0,5,
возрастает на всей области определения;
б) функция, заданная формулой /(#) = —2х — 2, убывает на
всей области определения.
497. Докажите, что функция, заданная формулой f(x) = — , убы-
х
вает на множестве положительных чисел, убывает на
множестве отрицательных чисел. Проиллюстрируйте вывод на
графике.
j2
498. Докажите, что функция, заданная формулой /(#)= ,
X
возрастает на множестве положительных чисел,
возрастает на множестве отрицательных чисел. Проиллюстрируйте
вывод на графике.
К пункту 21
499. Равносильны ли предложения:
а) число а кратно 5; число 7а кратно 5;
б) число Ъ кратно 7; число 35& кратно 7;
в) число а кратно 4 и 6; число а кратно 12;
г) натуральное число а оканчивается цифрой 5;
натуральное число а кратно 5;
д) а и Ъ — нечетные числа; сумма a + b — нечетное число?
500. Равносильны ли предложения:
а) х > 3; х + 1 > 3 + -;
X X
б) х > —3; х + - > — 3 + -?
X X
501. Равносильны ли предложения:
а) «множество А есть подмножество множества В* и
«пересечение множеств А л В есть множество А»;
б) «множество А есть подмножество множества В» и
«объединение множеств А к В есть множество В»?
502. Равносильны ли уравнения:
а) х=1 и х2=х; г) х2=4х и х2—4=4* — 4;
б) х2 = х и х9 = х2; д) *2~25 = 0 и х2 — 25 = 0;
ж —ю
в) х2 = 4х и х = 4; е) я = 2 и —^Ц- = -?
2 ж —2
128
503. а) При каком значении а уравнение ах + 1 =11 равносильно
уравнению Ъх — 4 = 21?
б) При каком значении b уравнение Ъх — 24 = О
равносильно уравнению 8 — Зх = —10?
504. а) При каких значениях р уравнение
х — р
равносильно уравнению х2 — 16 = 0?
б) При каких значениях Ъ уравнение
^=^1=0
Ь — х
равносильно уравнению 25 — х2 = 0?
505. Докажите, что:
а) (х > 17) <^> (х + 2 > 19); в) (х > 2) фф (12,5л: > 25);
б) (х + 2 < 11) <=> (х < 11 — 2); г) (х < —3) <=ф (—7х > 21).
506. Равносильны ли неравенства:
а) 25* < 125 иК5; в) |*|<10 и * <10;
б) х2 < 25 и л: < 5; г) — * > — 1,4 и х < 1,4?
К пункту 22
507. Найдите с помощью графиков:
а) множество значений переменной х9 при которых
функция у =3х — 6 принимает положительные значения,
отрицательные значения;
б) множество значений переменной х> при которых
функция у = х + 4 принимает значения, большие 1.
508. Построив в одной системе координат графики функций
у = х3 и у = х29 решите, используя их, уравнение я3=л:2
и неравенства х3 > х2 и хг < х2.
509. Решите графически неравенство:
а) х + К 3; в) Зх — 4 > 2х;
б) 0,6 — 2х>3,6; г) Ъх — 1<х — 3.
510. а) Решите графически уравнение я2 =1,5* и неравенства
я:2>1,5дс, х2 <1,5*.
б) Решите графически уравнение 0,5x3=2jc и неравенства
0,5л;3 > 2х, 0,5jc3<2*.
5 Алгебра, 7 кл. J29
511. а) С помощью графиков функций у = — и у = 3 решите
х
неравенство — < 3.
о
б) С помощью графиков функций у = *2 и у = — решите
неравенство *^ > —.
х
К пункту 23
512. Найдите множество решений неравенства и покажите его
на координатной прямой:
а) *>4; в) *^5; д) *>0;
б) *<3; г) *> — 1; е) х<7.
513. Решите неравенство:
а) 0,01 (1 — 3*) > 0,02л: + 3,01;
б) 12 (1 — 12*) + ЮОх > 36 — 49*;
в) (0,6* — 1)— 0,2(3*+1)<5* — 4;
г) - (6* + 4) — - (12* — 5)<4 — 6*;
з 6
д) (3* + 1) (х — 1) — З*2 > 6*+ 7;
е) 15*2-,(5* — 2) (3* + 1)<7х— 8.
514. Найдите множество решений неравенства:
a)a^=i_i>?il + 8; в)!^а-2<!^-а;
4 3 4 8
-ч За — 1 а — 1 л ч 5а За — 1 , 2а — 1 . л
б) > 0; г) < 1.
2 4 6 3*2
515. Решите неравенство:
а)«Г^+*-0.25 «-0Д25 6)^^f_lzL->l.
4 4 8 3 2
616. Найдите множество натуральных значений *,
удовлетворяющих неравенству:
а) 3(5—4*)+(28+2*) >0; б) (*+1)(*—1)—(*2—3*)< 14.
617. Составьте неравенство с одной переменной, множеством
решений которого служит:
а) множество положительных чисел;
б) множество отрицательных чисел.
130
518. Составьте какой-либо двучлен с переменной х:
а) принимающий отрицательные значения тогда и только
тогда, когда значение х меньше 17;
б) принимающий положительные значения тогда и
только тогда, когда значение х больше 1,2.
519. Составьте какой-либо двучлен с переменной у:
а) принимающий отрицательные значения тогда и только
тогда, когда у больше 6;
б) принимающий положительные значения тогда и только
1
тогда, когда у меньше —.
з
520. Существует ли такое значение ft, при котором верно
неравенство:
a)0ft<—1,7; r)|ft|>—1; ж) (ft — l)2 +(ft — 2)2<0;
б) ft—8>ft; д) |ft|<—1; з) (ft — l)2 —ft(ft — 2)<0?
в) |ft|<0; e) (ft-7)2<0;
521. При каких значениях х:
а) значение дроби *~ больше соответствующего значе-
ния дроби ;
4
12
б) значение дроби больше соответствующего значе-
6
ния дроби £±-?
522. Решите неравенство:
а) 2(4i/-l)-5i/<3i/+5;
б) 6(1— у) — 8(Зу + 1)+30у>-5.
523. Сравните квадрат числа а с квадратом числа, на 1
меньшего, чем а.
524. Найдите, при каких значениях а уравнение имеет
положительный корень:
а) Зх = 9а; в) х — 8 = За + 1;
б) х +2 = а; г) 2х — 3 = а + 4.
525. Найдите, при каких значениях Ъ уравнение имеет
отрицательный корень:
а) 10* = 3&; в) 2х — 1 = 6 + 2;
б) х — 4 =Ь; г) Зх — 3 = 5& — 2.
526. При каких значениях т верно равенство:
а) \2т — 16| =2/п — 16; в) |ш +6 | = — лг — 6;
|12-6ж| _^ь . |Ю**-35| = _1?
12 — 6/л ' ; 10/я — 35
5* 131
ложительные значения при значениях х, больших —, и
527. а) При каком значении а множеством решений неравен-
з 1
ства х>— служит числовой промежуток ]—; +<х>[?
а 6
б) При каком значении Ъ множеством решений неравен-
о
ства х<— служит числовой промежуток ]—оо; —2[?
ь
528. При каких значениях а равносильны неравенства:
а) 5х — а > 0 и х > —; в) ах — 4 > 0 и х > —;
5 а
б) Зх + а < 0 и х < — —; г) а* — 4 > 0 и * < -?
3 а
529. При каких значениях k функция y = kx — 2 принимает по
ложительные значения при
только при этих значениях?
530. При каких значениях Ъ функция у — — х + Ъ принимает от-
рицательные значения при значениях х, меньших 4, и
только при этих значениях?
531. Для премирования 12 пионеров надо купить краски и
карандаши. Набор красок стоит 50 коп., а набор карандашей
стоит 20 коп. Сколько наборов красок следует купить,
чтобы стоимость покупки не превышала 4 руб.?
532. С турбазы в город, отстоящий на расстоянии 24 км> вышел
турист со скоростью 4 км/ч. Спустя 2 ч вслед за ним
отправился второй турист. С какой скоростью должен идти
второй турист, чтобы догнать первого до его прихода в
город?
533. От деревни до совхоза 20 км, а от совхоза до станции
40 км (рис. 38). Из совхоза по направлению к станции
выехал велосипедист со скоростью 12 км/ч. Одновременно
из деревни на станцию через совхоз по той же дороге
отправился мотоциклист. С какой скоростью должен ехать
мотоциклист, чтобы догнать велосипедиста до его приезда
на станцию?
534. Расстояние между пунктами А и В равно 28 км. Из пункта
А в пункт В вышел турист со скоростью 4 км/ч. Спустя
30 мин навстречу ему из пункта В вышел другой турист.
С какой скоростью должен идти второй турист, чтобы
встреча произошла в точке, расположенной ближе к
пункту А 9 чем к пункту В?
20 км 40 км
/ Y \
Деревня Совхоз Станция
Рис. 38
132
535. Между поселками А и В, расположенными на расстоянии
62 км, находится станция С, удаленная от А на 30 км.
Из А в С выехал велосипедист со скоростью 12 км/ч.
Спустя 30 мин из В в С выехал мотоциклист. С какой
скоростью должен ехать мотоциклист, чтобы успеть приехать
в С раньше велосипедиста?
К пункту 24
536. Решите систему неравенств:
а)
х > 8, б)
х>2;
У<5,
у<3;
в)
х> 6,5,
х > 6,05;
г)
У<Ь±*
У<Ъ-
537. Найдите множество решений системы неравенств:
а) /*>6, б) (х<—1,7, в) /*<—5,7, г) (х>—2,1,
|х<9,3; (*>—2,8; 1*>4; |х<—2,01.
538. При каких значениях а система неравенств
fx>3,
\х<а
не имеет решения?
539. Решите систему неравенств:
х>4,
х>8,
х>9,
х>3;
б)
х<1, в)
*<5,
х<2.
*<0;
*>3,5,
*>6,
*<1,
*<0;
г)
*<—3,
*<—2,
Ж—5,
х>8.
540. Объясните, почему не имеет решения система неравенств:
а) /л:2 + 1<0, в) (6* <0,
(Зх —1>0; \3а:>0;
б) /2ж — 4 >2* — 1,
\5х >0;
541. Решите систему неравенств:
г) (3*+5<0,
\3.т2+5<0.
а) (0,3* —К л:+ 0,4,
\2 — Зх<5х + 1;
б) /2,5* — 0,12 > 0,6* Н
[ 1 — 2х > —х — 4;
0,07,
в)
2х + 1,4 <
Зж— 7
2* >3 —-;
5
133
г) (3(х — 2)(х + 2) — Зх?<х,
[5х — 4 > 4 — 5дс;
д) <(х-4)(5х-1)-5х*>х + 1,
\3х — 0,4 < 2л: — 0,6;
е)
1 + 1±5>2-
з t
Зх-±>4.
4
2,
542. Найдите целые решения системы неравенств:
а) (6х (х — 1) — (2х — 1) Зх < х,
\0,5х — 3,7 < 0,2л: — 0,7;
б) /0,7* — 3(0,2л: + 1)<0,5л: +1,
[0,3 (1 — л;) + 0,8л: > х + 5,3;
в) (1(3дс_2) + 1(12л: + 1)>0,
О О
-i (14* - 21) + | (9л: - 6)< 0;
г> 10,2 (5л:—1) + - (Зл: + 1)< л; + 5,8,
3
8х — 7—- (6х — 2) > х.
543. Решите двойное неравенство:
а) — 9<3х<18;
б) К
2х-
<2;
в) 3 < 5* — 1 < 4;
Г) о < Ц^£ < 1.
544. а) При каких значениях х значения выражения 2х — 4
принадлежат числовому промежутку ]—1; 5[?
б) При каких значениях х значения дроби
жат числовому промежутку [0; 5]?
принадле-
545. Найдите множество положительных значений
переменной у, удовлетворяющих системе неравенств:
а) (Зу-(у+6)<5у + 9, б) (v_v^zl<1_L
{12у-2(3-у)<2(у-2у, \у з ^Х 6*
[2у*+уа-2у) + 5 + у>0.
546. Найдите множество отрицательных значений
переменной у9 удовлетворяющих системе неравенств:
а) (5у — 1 2у — 1
6 2
У + 4
>о,
б) ((У+6)(5-у)+у(у-1)>0,
{ 0,3у (10J/+20) - ЗуЧЗО >0.
<0;
134
547. Смешали 12 кг ириса и 10 кг карамели. Килограмм ириса
стоит 1 руб. 60 коп., а стоимость 1 кг смеси больше 1 руб.
40 коп., но меньше 1 руб. 80 коп. Какова стоимость 1 кг
карамели?
548. Если туристы будут проходить в день на 5 км больше, то
они пройдут за 6 дней расстояние, большее 90 км. Если же
они будут проходить в день на 5 км меньше, то за 8 дней
они пройдут расстояние, меньшее 90 км. Сколько
километров в день проходят туристы?
549. Числитель и знаменатель дроби — целые положительные
числа, причем числитель на 3 меньше знаменателя. Если
к числителю и знаменателю прибавить по 1, то получится
дробь, меньшая —; если же из числителя и знаменателя
5
вычесть по 1, то получится дробь, большая—. Найдите
5
все такие дроби.
К пункту 25
550. Решите неравенство:
а) (Зх — 4) (х — 1) < 0; г) (х+1) (5 +2х) > 0;
б) (22 — х)х > 0; д) (1,8 — х) (3 +х2) > 0;
в) (1 — 3*) (1 — 2х) > 0; е) (15 —2х) (4л;2+1) <0.
551. Найдите множество решений неравенства:
а) (х+5) (х — 1)>х — 1; б) (х — 2)х>2(х — 2).
552. При каких значениях у верно неравенство:
а) (у + Ъ)\2у -12)< 0; в) (у2- 6у+9)(15-у)< 0;
б) (у - 3,5) (у - 5)2 > 0; г) (у + б)2 (у - 2)2 (Зу - 15) > 0?
553. а) При каких значениях и произведение
(и — 2) (и — 5) (и — 7) положительно?
б) При каких значениях г произведение
г (г — 3) (г — 4) отрицательно?
554. Решите неравенство:
а) 0,5л:2 > х\ в) х2 + 11<0;
б) 0,5л:2 < х; г) (л: + 2)л: > 2л: — 9.
555. Равносильны ли неравенства х > 1 и л:2 > л:?
556. Решите неравенство:
а) > 0; в) —— > 0; д) < 0;
х Ах + 4 {х + 5)2
-ч 3 — 4* . Пт ч 17,3 — х ^ л ч 14 — 2х ^ л
б) < 0; г) — < 0; е) > 0.
' х + 1 ' 1 + х ^ ' (8 - х?
135
557. Найдите целые решения неравенства:
а) < 0; 6) > 0; в) < 0; г) > 0.
х — 2 *-7 ' 5*-1^ ' 6*
558. Решите неравенство:
а)^-2>2; в)-^>Б; д)2-^-4>2;
ж ж ж
б)1<1; r)fLTT<15 е)^=-2<5.
Ж «+ 1 JC + 1
о
559. При каких значениях х значения функции у = — больше 4?
х
Решите задачу графически и алгебраически.
560. При каких значениях переменной а верно неравенство:
a)<i^>0; б)^^<0?
а — 5 а — 2
К пункту 26
561. Округлите число:
а) 0,478 до сотых; в) 141,28 до единиц;
б) 12,05 до десятых; г) 1253,41 до десятков.
562. Округлите до сотых число:
а) 1,205; б) 13,096; в) 24,997; г) 49,995.
563. Округлите число 69,9998 до тысячных, до сотых, до
десятых, до единиц, до десятков.
К пункту 27
564. Укажите границы:
а) температуры воздуха на территории СССР;
б) барометрического давления в вашей местности;
в) роста взрослого мужчины;
г) скорости легкового автомобиля.
565. В доме 60 квартир. Все квартиры заселены, причем число
жителей в одной квартире не превышает 5 человек.
Укажите границы числа жителей дома.
566. Чтобы изготовить деталь, нужно а кг металла. Имеется
р кг металла. Можно ли сделать деталь, если:
а) 23,9 <а<24,7, б) 23,9 <а<24,7, в) 23,9 <а< 24,7,
24,8 <р < 25,4; 23,4 <р<23,9; 24,3 <р < 24,9?
567. Можно ли из прямоугольной пластины длиной а мм и
шириной Ъ мм вырезать круг диаметром d мм, если:
а) 84<а<86, б) 84<а<86, в) 84<а<86,
65<6<67, 65<&<67, 65<&<67,
62<d<64; 71<d<73; 66<d<68?
136
568. Масса алюминиевой пластины, определенная на
аналитических весах с ценой деления 0,0002 г, составляет 2,9062 г.
Какие приближенные значения массы с недостатком и с
избытком были бы получены при взвешивании пластины
на школьных весах с набором разновесков, где масса
самого мелкого разновеска 10 мгЧ 100 лег? 1 г?
569. Часы с секундной стрелкой показывают 8 ч 28 мин 15 сек.
Какие приближенные значения времени с недостатком и с
избытком можно прочитать по циферблатам часов, не
имеющих секундной стрелки, при цене деления, равной:
а) 1 мин; б) 5 мин?
570. Оцените длину средней линии треугольника ABC,
параллельной стороне АВ, если 10,4 см< \АВ|< 10,5 см.
571. Дано, что 5 ^ х ^ 6. Найдите границы значения выражения:
а) 0,2*; в) х + 3; д) Зх + 4; ж) - + 2;
« X
б)—0,5*; г) 10 —г, е) 2х — 5; з) —Ц-.
572. В каких границах заключено число с, если:
а) —1,6<4с<0,4; в) 0,4<2с + 1<1,2;
б) —9< —Зс<1,8; г) 1,8>0,3 —с>1,6?
573. С позующью графика функции у = Zx + 2 найдите множество
значений выражения Зя + 2, если х £ [0,5; 1]. Ответ
проверьте вычислением.
574. С помощью графика функции у= 1 — х найдите множество
значений выражения 1 —#, если х £ ]—1,5; 0[. Ответ
проверьте вычислением.
К пункту 28
575. Примените к данным неравенствам теорему о почленном
сложении неравенств:
а) 13,4 > 12,3, б) —1,8 <— 0,5,
—11,6 >—11,9; 0,3<0,5.
576. Примените к данным неравенствам теорему о почленном
умножении неравенств:
а) 15<23, 0,1<0,2; б) 100 > 50, ->-.
2 5
577. Примените к трем данным неравенствам сначала теорему
о почленном сложении неравенств, а потом теорему о
почленном умножении:
а) 5>4, 3>2, ->~; б) 0,1<0,5, КЗ, 7<10.
3 4
13Т
578. Докажите, что если а > Ъ и с > d, где а, 6 и с —
положительные числа, ad — отрицательное, то ас > bd.
Проиллюстрируйте эту теорему на примере.
579. Докажите теоремы:
а) (а > Ъ и с > d) =Ф (а + с > Ъ + d);
б) (а>&>Оис>й>0)с=ф(ас>&й).
580. Докажите, что если а^2 и &^5, то:
а) 5а+2&>20; б) а&+4>14.
581. Докажите, что если с !> 3, то с2+6 !> 15.
582. Какой числовой промежуток образуют значения
выражения а + &, если:
а) а<Е[3; + <х>[ и Ь€[—3; + <х>[;
б) а^]—оо; 5[ и &£]—оо; —8[? w
583. Какой числовой промежуток образуют значения
выражения аЬ9 если:
а) а€[12; + оо[ и&£[1; +<х>[;
б) а€]0;0,5]и&€]0;2]?
584. Пусть л:€[2; +сх>[ и #€[4; +oo[. Найдите множество
значений выражения:
а) Ъх + 2у; б) -4 (*+у); в) х (у-1); г) А + 1.
К пункту 29
585. Найдите границы значения выражения:
а) а +2&, если 0<а<1 и —3<Ь<—2;
б) — а — Ь, если 7<а<10 и 14<&<15;
в) 5а + 7&, если 2,5<а<3,2 и — i <Ь<0;
35
г) -—5а, если 1,2<а<1,3 и 2<Ь<3.
4
586. Оцените значение выражения:
а) тп — 1, если 2 ^ т ^ 3 и 11 ^ п ^ 12;
б) т(п — 1), если 0,1 ^ т ^ 0,2 и 5,1 ^ п ^ 5,2;
в) h n, если 5 < т < 10 и 12 < л ^ 15;
m
г) , если 7 < m < 8 и 13 < п < 14.
m + n
587. Зная, что 3^а^10и1^х^4, найдите границы значения
разности ах — 2х и произведения я (а — 2). Сравните
результаты.
588. Пусть 3 <^# ^4и1 ^ у <^ 2. Определите границы значения
произведения (х+у)(х—у) и разности х2— у2. Сравните
результаты.
589. Найдите методом границ приближенные значения суммы
—Ь — и разности , обращая каждую из дробей
7 9 7 9
— и — в десятичную с тремя знаками после запятой.
тт 1,1 11
Для проверки выразите сумму —|— и разность ■— — ■—
в виде обыкновенных дробей и обратите их в десятичные
с четырьмя знаками после запятой.
590. Пусть А, В и С — три точки, не лежащие на одной прямой,
причем 29 мм < \ АВ | < 31 л^ле и 39 мм < \ВС |< 41 мм.
Может ли \АС\ быть равным:
а) 30 мм\ б) 60 мм?
591. Найдите границы значения выражения:
а) т +п — k, если 3,7<т<3,9, 2,6 <Ж2,7 и
l,2<fc<l,3;
б) - + &, если 3,25 < а < 3,26, 6,13 < Ъ < 6,14 и
с
2,51<с<2,52;
в) -^-, если 3,04 < а < 3,05, 1,15 < Ъ < 1,16 и
Ь — с
0,14 < с < 0,15.
К пункту 30
592. Найдите погрешность приближения числа у числом Ь,
если:
а) у=2,8иЬ= 3; в) у = —2,8 и Ь = —3;
б) у = 2,8 и Ъ = 2,5; г) у = —2,8 и Ь = —2,5.
593. Какое приближенное значение числа х = 35,84 имеет
погрешность, равную: а) 0,04; б) —0,16?
594. Пусть а — приближенное значение с недостатком
некоторого числа х и \х—а\ — модуль погрешности. Найдите х,
если:
а) а = 12 и |л: — а|= 0,3;
б)а = — 8 и |ж —а|=0,4.
595. Пусть Ъ — приближенное значение с избытком некоторого
числа х и \х—&| — модуль погрешности. Найдите дс, если:
а) Ь =6 и |* — Ь\ =0,1;
б) b = — 9 и \х — Ь\ =0,2.
5
596. Какое из двух приближений числа— лучше: 0,55 или 0,56?
9
139
597. Какое из четырех приближений числа я =3,14159... лучше:
3,141, 3,142, З-i или 3-?
7 71
598. В практике вычислений значение выражения (1+т)2
при значениях т, близких к нулю, находят по
приближенной формуле: (1 +т)а«1 +2т. Какова погрешность
этого приближения? Найдите этим способом приближенное
значение выражения (1 +т)2 и погрешность приближения,
если:
а) т = ОД; б) т = 0,05; в) т = —0,1; г) т = —0,01.
599. При вычислении значений выражения (1+т)3 при
значениях т, близких к нулю, пользуются приближенной
формулой (1 + т)3^1 +3т. Найдите приближённое
значение выражения (1 + ттг)3, если:
а) т = 0,001; б) т = —0,001.
600. Найдите приближенное значение выражения (1 + тгг)(1 + п)
при т=0,03 и п=0,01, пользуясь формулой (1+тя)(1+л)^
я^ 1 + т + п. Какова погрешность приближения? Каков
точный результат?
Решите эту же задачу, считая, что т = 0,02 и п = —0,01.
601. Вычислите значение выражения при т = 0,002.
Найдите приближенное значение этого же выражения,
пользуясь формулой « 1 — т.
1 + т
Решите задачу, считая, что т = —0,001.
К пункту 31
602. Пусть а <! х ^ &. Какова точность приближения числа х
а + &0
ЧИСЛОМ —:—?
2
603. Покажите на числовой прямой множество приближенных
значений числа:
а) 2,5 с точностью до 1; в) —2,4 с точностью до 1;
б) 0,7 с точностью до 0,5; г) —2,6 с точностью до 0,5.
2
604. Найдите множество приближенных значений числа —
с точностью до 0,01. Какие из чисел 0,14; 0,15; 0,16; 0,17;
1 7
0,162; 0,164; —; — принадлежат найденному интервалу?
6 45
Относительно какого из данных чисел можно утверждать,
что оно является приближенным значением числа — с
точностью до 0,01?
140
605. Какие из чисел 1,44; 1,45; 1,46;
1,47; 1,463; 1,468 являются прибли-
7
женными значениями числа 1— с
15
точностью до 0,01?
606. Можно ли на полке длиной 6 ± 0,01ж
и шириной 1,1 ± 0,01 м разместить в
один ряд 8 ящиков, длина которых
1 ± 0,005 м и ширина 0,75 ± 0,005 м?
607. Какова будет сила тока в гирлянде
из 18 последовательно соединенных
лампочек, если сопротивление
каждой лампочки 24±2,4 ом> а напряжение в сети 215±15 в?
608. Площадь большого поршня гидравлического пресса
S2 = 240 ± 1 см2, а малого Sx =* 12 ± 0,02 см2 (рис. 39).
Достаточно ли силы в 470 ±5ина малом поршне, чтобы
получить на большом не менее 9000 н? (Силу трения не
учитывать.)
609. Определите, какую мощность разовьет двигательная
установка первой ступени многоступенчатой ракеты в конце
ее работы, если скорость полета к этому моменту равна
3000 ± 10 м/сек при тяге двигателя 10* ± 104 н. (Ответ дать
в млн. киловатт.)
610. Достаточно ли 40 кафельных плиток, чтобы облицевать
прямоугольный участок стены длиной 1 ±0,005 м и
шириной 0,8 ± 0,005 лс, если кафельная плитка имеет форму
квадрата со стороной 15 ± 0,2 см?
611. Хватит ли одного рулона линолеума, чтобы покрыть пол
площадью 40 ± 0,2 лс2, если в рулоне 20 ± 0,05 м при
ширине полотнища 2 ± 0,01 м?
Ш
|Ш1 i^feAl
Глава III
КВАДРАТНЫЕ КОРНИ
§ 11. ПОНЯТИЕ КВАДРАТНОГО КОРНЯ
32. Рациональные числа
В курсе математики мы встречаемся с различными числами.
Натуральные числа (целые положительные числа)
используются при счете. В множестве N натуральных чисел есть
наименьшее число — число 1 и нет наибольшего.
Натуральные числа, числа, им противоположные, и нуль
составляют множество Z целых чисел. В множестве целых чисел
нет ни наименьшего числа, ни наибольшего.
Любое натуральное число является числом целым. Поэтому
множество натуральных чисел есть подмножество множества
целых чисел:
N с= Z.
Это можно проиллюстрировать с помощью специальных
схем, носящих название «кругов Эйлера».
На рисунке 40 большой круг изображает множество Z
целых чисел, а малый (заштрихованный) — множество N
натуральных чисел. Всякая точка малого круга принадлежит
большому кругу.
Незаштрихованной части большого круга соответствует
множество целых чисел, не являющихся натуральными, т. е.
множество целых неположительных чисел. Говорят, что множество
целых неположительных чисел является дополнением множества
натуральных чисел до множества целых чисел.
Вообще, пусть имеются два множества
А и 17, причем А является
подмножеством U.
Тогда множество, состоящее из всех
тех элементов 17, которые не
принадлежат -4, называется дополнением множества
А до множества U.
Кроме целых чисел, мы изучали
также дробные числа (положительные и
отрицательные).
Целые и дробные числа составляют
Рис. 40 множество рациональных чисел.
142
Рациональные числа — это все числа,
которые нам известны. Например,
29, —41,
О 1 -У
U' 5' 3'
27*-
5
рациональные числа.
Множество рациональных чисел
обозначают буквой Q.
Так как любое целое число является
в то же время числом рациональным, то
множество целых чисел есть подмножест- Рис. 41
во множества рациональных чисел:
ZczQ.
Это соотношение между множествами Z и Q показано с
помощью «кругов Эйлера» на рисунке 41. Дополнением множества
целых чисел до множества рациональных чисел служит
множество дробных чисел.
Термин «рациональное число» произошел от латинского
слова ratio, что в переводе на русский язык означает
отношение. Любое рациональное число может быть представлено в
т
виде отношения —, где т — целое число, а п — натураль-
п
ное, причем одно и то же число может быть представлено в
виде такого отношения многими способами. Например:
.1 _ А — JL — 19-
2 ~~ 4 " ю ~ 80'
3 _ — 3 _ — 6 __ —12 _ —30.
9
4
-1,8
4 8 . 24 40
- Zf — izi? — —180>
5 ~~ 10 "~ 100 '
_7_ 14 21 105.
1 ~~ 2 ~~ 3 ~~ 15*
^JD _^__0
"" 1 ~~ 8 ~~ 2Э'
Заметим, что среди дробей, изображающих данное
рациональное число, всегда имеется одна и только одна дробь,
являющаяся несократимой. Для целых чисел это дробь со
знаменателем, равным 1.
612. Какие элементы множества X, где
Х=\—ЮО; —14,5; —2; —-; 0; 10; 15; 20-],
являются:
а) натуральными числами; б) целыми числами;
143
в) дробными числами;
г) рациональными числами;
д) отрицательными числами;
е) неотрицательными числами?
613. Составьте такое подмножество множества С, где
С=|-4~; -3; 0; |; 6; 8,3; 9; 121,
элементами которого являются:
а) натуральные числа; г) четные числа;
б) целые числа; д) числа, кратные 3;
в) нецелые числа; е) положительные числа.
614. Назовите несколько значений дс, при которых истинно
высказывание:
а) х £ N; б) х i Z\ в) х £ Q.
615. Верно ли:
а) (x£N)^(x£Z); в) (х € £)=Ф (х £Q);
б) (^Z)^>(^N); г) (х g Q)=> (х £ Z)?
616. Даны множества А и U. Убедитесь в том, что A a U.
Выпишите множество, которое является дополнением
множества А до множества U:
а) А-{—30; —10; 10}, С7={0; 10; 20; —10; —20; —30};
б) А = {—3; 0; 1}, £/={—3; —2; —1; 0; 1; 2; 3}.
617. Пусть iV — множество натуральных чисел, a Q —
множество рациональных чисел.
а) Изобразите с помощью «кругов Эйлера» соотношение
включения для множеств N и Q.
б) Покажите на вашем рисунке штриховкой множество,
которое является дополнением множества N до
множества Q. Назовите несколько элементов этого множества.
в) Верно ли высказывание: всякое натуральное число
является рациональным?
г) Верно ли высказывание: всякое рациональное число
является натуральным?
618. Какое множество является дополнением:
а) множества четных чисел до множества целых чисел;
б) множества нечетных чисел до множества целых чисел;
в) множества дробных чисел до множества
рациональных чисел;
г) множества положительных чисел до множества
рациональных чисел;
д) множества неположительных чисел до множества,
рациональных чисел? ,
144
619. Найдите объединение и пересечение множеств:
а) N и Z; б) Z и Q; в) Q и N.
620. Представьте в виде отношения целого числа к
натуральному следующие числа:
а) 4; 25; 0; — 27; —100;
б) 0,3; -10,7;4;2|;-3i.
5 8 4
621. Представьте число в виде несократимой дроби —, где
п
т — целое число, а п — натуральное:
а) 36; в) 4,6; д) 15^; ж) ^;
О (О
б) -45; г) -10,2; е)-П^, з) --g-.
3 95
622. Пусть a£N и b£N. Верно ли, что:
a)a+b£iV; б) a — bgiV; в) ab£N; г) - € N?
ь
623. Пусть a£Z и b£Z. Верно ли, что:
a) a+b£Z; б) a — b£Z; в) ab£Z; r)-£Z?
ь
624. Пусть a£Q и b£Q. Верно ли, что:
а) a+b£Q; б) a — b£Q; в) ab£Q; г) -^Q (&=^=0)?
625. Выполните действия с рациональными числами:
а) (3,2-5,9): (_*JL :} + !);
б) (0,18 : (—0,3)—10,2) : (—0,01).
33. Арифметический квадратный корень
Пусть площадь некоторого квадрата 64 см2. Чему равна его
сторона?
Обозначим длину стороны квадрата в сантиметрах через дс.
Тогда площадь квадрата в квадратных сантиметрах будет х2.
По условию площадь равна 64 см2* Следовательно, для того
чтобы найти сторону квадрата, нужно решить уравнение
х2 = 64.
145
Существуют два числа, квадраты которых равны 64: это 8 и
—8. Так как длина стороны квадрата выражается
положительным числом, то она равна 8 см.
Числа 8 и —8 называют квадратными корнями (или
корнями второй степени) из числа 64.
Вообще, квадратным корнем из числа а называется число,
квадрат которого равен а.
Число — является квадратным корнем из —, так как ( —) =
= —. Число также квадратный корень из —, так как
(4r-f
Квадратный корень из 0 равен 0, так как 02=0. Этот корень
из 0 единственный.
Квадратный корень из —16 не существует, так как не
существует числа, квадрат которого был бы равен
отрицательному числу.
В рассмотренной задаче условию удовлетворял лишь один
квадратный корень из 64 — число 8. Положительный
квадратный корень из 64 называют арифметическим.
Точно так же число арифметический квадратный ко-
з
рень из —, число 0,1 — арифметический квадратный корень
у
из 0,01. Число 0 будем считать арифметическим квадратным
корнем из 0.
Определение. Арифметическим квадратным корнем из
числа а называется неотрицательное число, квадрат которого
равен а.
Для арифметического квадратного корня из числа а
принято обозначение: Уа. Знак У называется знаком корня9 а
число а — подкоренным числом.
Например, запись ]/"4 означает арифметический
квадратный корень из 4. Причем У 4=2, так как 22=4 и 2 —
неотрицательное число. Отрицательный квадратный корень из 4 есть
число, противоположное У 4. Его обозначают так: —]/4.
Очевидно, что —]/Л4~ =—2.
Запись j/1,21 означает арифметический квадратный корень
из 1,21; У 1,21=1,1, так как 1Д2 = 1,21 и 1,1
—неотрицательное число.
Запись У0 означает арифметический квадратный корень
из 0; У0=0, так как 02=0 и 0 — число неотрицательное.
146
Из определения арифметического квадратного корня
следует:
1) Выражение У~а при отрицательных значениях а не имеет
смысла. Например, не имеет смысла выражение ]/"—25, так
как не существует числа, квадрат которого был бы равен
отрицательному числу.
2) Если выражение У~а имеет смысл, то его значение
неотрицательно.
626. Проверьте, что:
а) числа —3 и 3 являются квадратными корнями из
числа 9;
о о
б) числа — и являются квадратными корнями из чис-
9
ла —;
49
в) числа 0,05 и —0,05 являются квадратными корнями
из числа 0,0025;
2 2
г) числа 1— и —1—являются квадратными корнями из
о о
Л
числа 2—.
9
627. Докажите, что:
а) число 5 есть арифметический корень из 25;
б) число —7 не является арифметическим корнем из 49;
в) число 0,3 — арифметический корень из 0,09;
г) число 2 арифметический корень из 5—;
4 16
д) число 0,6 не является арифметическим корнем из 3,6;
е) число —0,4 не является арифметическим корнем из 1,6.
628. Докажите, что верно равенство:
а) ^121 = 11; б) К400 = 20; в) )Л),25 = 0,5; г) 1^0,09 =0,3.
629. Какие из данных выражений имеют смысл:
а) УТ00, У —100, —1/100;
б)]/Т2, ]/^Т2, -]/Т2, -У~(=4Г<1
630. Найдите значение корня:
а) >^49; г) У~0М
б) У 10000; д) ]Л)Д6
в) /2500; . е) V^M
ж) у* .)/!«
147
631. Найдите значение выражения:
а) 3|/~9;
б) — 71/1Щ;
в) 0,1]/400;
PI : »
. V"900
д)—;
е) К3600 + уТбОО;
Ж) ]/16 + |/Т;
з)]/"| + К1оо;
и) VT-VT»
«)/4-/гв
632. Составьте таблицу квадратов натуральных чисел от 11
до 20. Пользуясь этой таблицей, найдите:
а) /289; в) /169; д) У144 + УШ;
б) |/225; г) УШ; е) /400 — ]/"324.
633. Решите уравнение:
а)|/х = 10; в) У у = 1; д)81/"&=8; ж) 31/^ = 1;
6)j/a = 9; T)Ym = l; e)5]/~c = 0; 3)2^0 = 5.
634. Почему уравнение не имеет корней:
а) }/"* = —5; в) — Ух = 2;
б) |/"^ + 1 = 0; г) 5Ух = —15?
34. Уравнение л;2=а
Рассмотрим решение уравнения #2=а, где а — некоторое
число. В зависимости от значения а возможны 3 случая.
1) При а < 0 уравнение х2 = а не имеет корней, так как не
существует числа, квадрат которого равен отрицательному
числу.
На рисунке 42 построены парабола у = х2 и прямая у = а.
Рассматривая графическое решение уравнения х2=а, где а<0,
мы видим, что парабола и прямая не имеют общих точек.
2) При а=0 уравнение имеет единственный корень,
равный 0.
На рисунке 43 показано графическое решение уравнения
х2 = а> где а=0. Парабола у—х2 и прямая у = а (при а=0она
совпадает с осью х) имеют одну общую точку, абсцисса
которой равна нулю.
3) Рассмотрим теперь случай, когда а>0.
Пусть а =9. Решениями уравнения х2=9 служат числа 3
и —3, которые являются квадратными корнями из 9. Исполь3-
148
1Г
\
JL
^г
г*
V
\
\
у
\
\
\
-2
И\
}
■8
р
и
А
t
0
L
Ч.
0
■ к
t=L
11
у=х
2
с
4"
'х\
~vw~
/
т
1 1
и м
и 1
\
\) i
TTi
?|
л
f\
1
01
*г
"т
1
j
и
у
/
/
fli
у-
2
¥ГП
V
/
/
\\\\
х,! \,7
1У=*
*а (а*0)
ИГ
~2
V/
л
о
0
г
0
Л
7
-2-
(7
1
/
/
!
i
/
/
/
7
_i_
7
У**'-:
X
у=а (а<0)
Рис. 42 Рис. 43 Рис. 44
зуя^ знак арифметического корня, их можно обозначить так:
V9 и —у&
На рисунке 44 построены парабола у=х2 и прямая у=9.
Прямая пересекает параболу в двух точках, абсциссы которых
3 и —3.
Рассмотрим уравнение я2=2.
Никакое целое число не является его решением.
Действительно, 1а = 1, т. е. I2 меньше 2; 22=4, т. е. 22 больше 2. А
между 1 и 2 целых чисел нет.
Не существует и дробного числа, квадрат которого равен 2.
Доказательство. Допустим, что существует такое дробное число,
квадрат которого равен 2. Тогда это число можно представить в виде несократи-
m
мой дроби —, где тп — целое число, а л — натуральное,
л
[ m \2 т2
Если — =2, то —- = 2 и т2 = 2л2.
\ л } л2
Так как число 2л2 четное, то и равное ему число лг2 тоже четное. Но если
четным является число т2, то и число т также четное.
Представим четное число т в виде 2k и подставим выражение 2k вместо т
в равенство т2 = 2п2. Получим:
(2k)2 = 2л2,
4&2 = 2л2,
2k2 = л2.
Число 2k2 четное, значит, и равное ему число л2 также четное. Но если четным
является число ла, то четное также и число л.
149
Рис. 45
Мы пришли к выводу, что числа тип четные. Но это противоречит пред-
т
положению о том, что дробь — несократима. Значит, не существует дробного
п
числа, квадрат которого равен 2.
Таким образом, уравнение х2=2 не имеет рациональных
корней.
Однако, построив график функции у = х2 и прямую у = 2,
мы видим, что, так же как и в предыдущем случае, прямая
пересекает параболу в двух точках (рис. 45). Поэтому
естественно считать, что уравнение х2=а и в этом случае имеет два
решения. Но эти решения не являются рациональными числами.
Корни уравнения я2 =2 — числа новой природы; их называют
иррациональными.
Обозначим корни уравнения я2 =2, являющиеся
иррациональными числами, так: У^2 и —у1Г(]/2Г— положительное
иррациональное число, квадрат которого равен 2; —Y% —
число, ему противоположное). С помощью графика (см. рис. 45)
150
числа У2 и —]/2 мы
можем приближенно выразить
рациональными числами:
У~2^1Л и —1/2"^—1,4.
Можно доказать, что
корни таких уравнений, как
*2=3, х2 = 5, х2= 6,5, также
не являются рациональными
числами. Их обозначают
соответственно УЗ и —1/3, УЪ
и —1/5, |/б75 и —1/1^5. Чис-
ла_}/3, -УЗ, |/5, —1/5,
1/6,5, —J/6,5 иррациональ- Рис. 46
ные. Заметим, что к
иррациональным числам относится
также число я, выражающее отношение длины окружности к
диаметру.
Итак, уравнение х2=а при а>0 имеет два решения: Ya
и —У а, которые могут быть рациональными или
иррациональными числами (рис. 46).
Мы знаем, что всякому рациональному числу соответствует
точка координатной прямой. Однако обратное предложение
неверно: не всякой точке координатной прямой можно поставить
в соответствие рациональное число.
Например, решая графически уравнение х2=2, мы указали
на оси х точки, абсциссы которых (1/2 и —1/2 ) не являются
рациональными числами. Вообще, на координатной прямой
бесконечно много точек, абсциссы которых — иррациональные
числа.
Рациональные числа и иррациональные составляют
множество действительных чисел. Каждому действительному числу
соответствует точка координатной прямой. Справедливо и
обратное: каждой точке координатной прямой соответствует
некоторое действительное число. Таким образом, введя в
рассмотрение множество действительных чисел, мы можем каждой точке
координатной прямой поставить в соответствие ее координату.
Множество действительных чисел принято обозначать
буквой R. Так как каждое рациональное число является
действительным, то множество рациональных чисел Q есть
подмножество множества действительных чисел R: Q cz R. Множество
иррациональных чисел является дополнением множества
рациональных чисел до множества действительных чисел.
Подробнее о понятии действительного числа будет
рассказано в старших классах.
т
л
V
\
V
\
i
!
!
L
V
\
-Уп
V
л
t/i
л
1
1
±
0
\
?
\
1
I
1
i
1
i
Г1
]У
W
~¥
-Д
у=а(а>'0)\
"*
Х\
151
635. Постройте на миллиметровой бумаге график функции
у=х2 и прямую у =7. Отметьте на оси х точки, абсциссы
которых равны V7 и —V7.
Найдите для каждого из чисел У 7 и —УТ:
а) два последовательных целых числа, между которыми
заключено это число;
б) две последовательные десятичные дроби с одним
знаком после запятой, между которыми заключено это число.
636. Используя график функции у=х2, отметьте на оси х
точки, абсциссы которых равны УЪ, —У 5, У4, — ]/^4, ]/3,5,
-УТ7б.
637. Запишите с помощью знака У корни уравнения и,
используя график функции у=х2, найдите приближенные
значения этих корней:
а) х2=3; б) х2 =6,5.
638. Решите уравнение:
а) х2 = 12; г) х2 — 0,04 = 0; ж) 2х2 = -;
о
б) *2 = 16; д) *2 =1; з) |*2- Ю = 0;
в)*2 + 8 = 0; е)- — *2 = 0; и) 5х2 — 23=0.
639. С помощью рисунка 45 найдите множество решений
неравенства:
а) *2<2; б) х2>2.
640. Имеет ли смысл выражение:
а) УП\ б) К"83Д; в) — yl86; г) К11^?
641. При каких значениях переменной имеет смысл
выражение:
а) Ух; в) j/"=^25*; д) VA
б) V~x; г) УШ; е) |^8Г2?
642. Найдите область определения выражения:
а) Ух^=Ъ; г) /8Т4?; ж) Y и-7п*
б) V^+2; д) /^П; з) /Щ.
в) У2*=Т; в) /^р;
35. Тождество 0/а)2 = а
Рассмотрим выражение ]/аГ, где а^О. По определению
арифметического квадратного корня значение этого
выражения есть число неотрицательное, и квадрат его равен а. Значит,
при любом неотрицательном а верно равенство
(Уа)* = а. (1)
Равенство (1) является тождеством. Действительно, при всех
значениях а, при которых каждое из выражений (V^)2 и а
имеет смысл, их соответственные значения равны.
Пользуясь тождеством (1), любое неотрицательное число
можно представить в виде квадрата некоторого числа. Например,
2 = (J/2)2, 5 = (V5)\ ± = {УЩ'
Приведем примеры применения тождества (1) в
преобразованиях.
Пример 1. Найти значение выражения (ОДуНПЗ)2.
По свойству степени произведения
(0ДК18)2 = (0Д)Ч1/"18)2.
Так как (У~Щ2 = 18, то
(ОД)2 • (j/l8)2= 0,01 • 18 = 0,18.
х2—3
Пример 2. Сократить дроб^
x+fS
х2 3
Представим числитель дроби —•—j=- в виде разности квад-
ратов:
х* — 3 = х2 — (Уз)2.
Тогда
*2-з = *2_(/з)2 = (х + Уг)(х-Уг) =х_ у^
x+Vs ~ x + yii x + уг
643. Найдите квадраты чисел:
]/25, К81, V29 КЗ, -VI. V5, -1/6, ]/1. -Vh3.
644. Найдите значение выражения:
а) (1/7)2; в)(-К26)2; д) 10]/2 . V*, ж) (0,5/в)2;
б) V? • Vb г) - 1/2в • К26; е) (3 У^)2; з) (- 21/Тб)2;
153
»>М" «т> л)(# '<-Ш
645. Представьте данное выражение в виде квадрата:
а) 9; в) 6; д) 2,5; ж) а, где а>0;
б) 64; г) 10; е) 0,25; з) 4&, где Ь>0.
646. Сократите дробь:
ч 2 лч 5 ч 10 ч а
а) -ля б) —тт^; в) гтт=; г) —
/2' yV З/ю' 3j/a
647. Разложите выражение на множители, вынося общий
множитель за скобки:
а) 3 + |^3; в)3/П—11; д) а — 5/а;
6)6 — 1/6; г) 21/7 + 7; е) & — 3)^6.
648. Сократите дробь:
а) jO±i. б) 2~^; в^ ^t12; г) с~^.
8 /2 7/12 5 Vc
649. Докажите, что значение выражения есть число
рациональное:
а) (1 + J/2)(1 - 1/2); г) (^3 +УЩ(l/в-1/3);
б) (1/5 - 2) (1/5 + 2); д) (2/3-1 )(2 /З + l);
в) (1/7 +1/2)(1/"7;-1/2); е) (^5 + 2/16)(у^-2l/lO).
650. Представьте выражение в виде разности квадратов двух
выражений и разложите его на множители:
651.
652.
154
а) х2— 9; в) 4а2 —7;
б) а2—3; г) 16&2 —11;
Сократите дробь:
а2 — 4 *ч с2 — б
а) ; б) т=-;
Решите неравенство:
а) *2—3<0; б) х2>7.
Д) с —4,
е) 5 — а,
v * —2
В)У~х+Г2;
где с>0;
где а > 0.
г) -7= т=
36. Приближенные значения квадратных корней из
положительных чисел
Мы знаем, что квадратный корень из положительного числа
может быть числом иррациональным, и в этом случае его
нельзя представить ни в виде целого, ни в виде дробного числа.
Примером могут служить такие числа, как У§, j/16, ]Л*б. На
практике иррациональные числа обычно заменяют их
приближенными значениями, выраженными десятичными дробями.
Рассмотрим прием, с помощью которого можно найти
приближения ]/{Гс любой степенью точности.
Так как
2^<5<32, то
2<|/"5<3(рис. 47, а).
Число 2 — приближенное значение 1^5 с недостатком, а
число 3 — с избытком, причем эти числа являются
приближенными значениями 1^5 с точностью до 1. Действительно,
\УЪ— 2|<3 — 2, т.е. |1/~5 — 2|<1, и
11/5—3|< 3 — 2, т. е. Ц/5 —3|<1.
Разделим отрезок [2; 3], длина которого равна 1, на 10
равных частей. Получим отрезки:
[2; 2,1], [2,1; 2,2], [2,2; 2,3], . . ., [2,9; 3].
Будем последовательно возводить в квадрат числа 2; 2,1; 2,2;
2,3; 2,4; ... , пока не получим числа, большего 5.
Из таблицы видно, что
2,22<5<2,32,
следовательно,
2,2<1/5<2,3 (рис. 47, б).
X
*2
2
4
2Д
4,41
2,2
4,84
2,3 "1
5,29
гы\ 1
и) 2
А) ■ *
С) 2 2,1
в) I MMMMlllll III
Т5
1 Г i
2,2 2,3
P*
i
2A
1
2,5
W5
inlifmii nil him mini ii i nihil
• »
2,6 2,7
111 ii ih i MiUUiLu 4t
i —
2,8
. . .»■■,! .
1
j
' '.
2,9 3
■un In in mil.
2,23 2,24-
Рис. 47
155
Число 2,2 — приближенное значение УЪ с недостатком,
число 2,3 — с избытком, причем каждое из этих чисел является
приближением УЪ с точностью до 0,1. Действительно,
||/"5 —2,21< 2,3 — 2,2, т. е. 11^5 —2,21 < 0,1, и
\УЪ — 2,31< 2,3 — 2,2, т. е. \УЪ — 2,3 | < ОД.
Чтобы найти приближенные значения У 5 с точностью до
0,01, нужно отрезок [2,2; 2,3] длиной 0,1 снова разделить на
10 равных частей и выделить отрезок длиной 0,01, который
содержит точку с координатой УЪ.
Из таблицы видно, что 2,232 < 5 < 2,242, следовательно,
2,23 <У~5<2,24 (рис. 47, в).
X
X2
2,2
4,84
2,21
4,8841
2,22
4,9284
2,23
4,9729
2,24
5,0176
Число 2,23 — приближенное значение У 5 с недостатком, а
число 2,24 — с избытком, причем каждое из этих чисел
является приближением УЪ с точностью до 0,01.
Аналогично найдем отрезок длиной 0,001, который содержит
точку с координатой У 5:
2,236 < УЪ < 2,237.
Числа 2,236 и 2,237 — приближенные значения УЪ с точностью
до 0,001; 2,236 — приближение с недостатком, а 2,237 —
приближение с избытком.
Точно так же находят приближенные значения УЪ с
недостатком и с избытком с точностью до 0,0001, до 0,00001 и т. д.
653. Докажите, что:
а) 3 < |/12 < 4; б) 7,1 < уТЙ < 7,2.
654. Сравните числа:
а) ]/7 и 3; в)]/5и 2,2; д) )/^25 и 2,5;
б) 7 и К50; г) 3,3 и ]/П; е) УТ&Г и 2,1.
655. Найдите два последовательных целых числа, между
которыми заключено число:
а) /27; б) Y&J; в) УОА; г) У~ЩМ Д) Kl20; e) ]/"148.
156
656. Найдите две последовательные десятичные дроби с одним
знаком после запятой, между которыми заключено число:
а) /"3; б) — J/1J; в) ^18; г) —/18.
657. С помощью рисунка 47 выясните, какое из двух чисел
является лучшим приближением )Л>:
а) 2 или 3; б) 2,2 или 2,3.
658. Найдите две последовательные десятичные дроби с одним
знаком после запятой, между которыми заключено число
У2. Какая из найденных дробей является лучшим
приближением Y^l
659. Что больше:
а) /29 или /16 + ]/l9; б) /27 или /20 + VI?
37. Нахождение приближенного значения корня методом
последовательных приближений
Пусть требуется вычислить 1^2 с точностью до 0,0001. Ясно, что 1 < ]Л*< 2.
Примем за первое приближение число 1.
Тогда
V2 = l + alt (1)
где а\ — погрешность первого приближения, причем
0 < ai < 1.
Возведем обе части равенства (1) в квадрат, получим:
2 = 1 + 2ai + а2г
Так как а\ меньше единицы, то число а\ меньше аи Отбрасывая это число, мы
получим приближенное равенство:
2^1 + 2аь
Из этого равенства найдем приближенное значение аи получим, что а\ tz, 0,5.
Тогда
V2 « 1 + 0,5 = 1,5.
За второе приближение примем найденное значение корня, т. е.
1/2"= 1,5 + а2,
где й2 — погрешность второго приближения.
Чтобы найти более точное значение корня, повторим описанный процесс.
Получим:
2 = 2,25 + За2 + а%
или
31 2 ^ 2,25 + За2,
157
откуда
а2 « —0,083.
Следовательно,
/2 w 1,5 — 0,083 = 1,417.
Приняв найденное приближенное значение корня за третье приближение, снова
получим:
^2 = 1,417+ а3,
где а3 —погрешность третьего приближения.
Повторив весь процесс еще раз, найдем:
а3 % —0,00278
и
Y2 = 1,417 — 0,00278 = 1,41422.
Аналогичным путем найдем погрешность четвертого приближения. Получим:
а4 « —0,000006 ...
Так как | ай | < 0,00001, то найденное приближение к }^2 дает значение
корня с требуемой точностью.
Если обозначить последовательные приближения к Yll через у19 у2, у3
и т. д., то можно заметить, что при нахождении каждого следующего
приближения использовалось предыдущее. Действительно, если
V2 = уг + а19
где уг — первое приближение и ах — его погрешность, то
2 = у\ + 2угаг + а2и
или
2 ку\ + 2у1а1.
Отсюда
2-У?
2у
2 — у\
У2 = У1 4
2-У? У?+2
2Ух 2^!
Если
где у: — второе приближение во, — его погрешность, то получше
2-jr|
в, =;
2уа
и
2 —у! у| + 2
*-* + 2у2
Вообще, если уп_г — приближение, полученное на (и — 1)-м шаге, то
fi-i +2 1/ , 2 \
Ул = ~~9^ ' или Уя = Т Уя-1+Т—Г ' где п = 2, 3, 4,
158
Эта формула позволяет находить каждое следующее приближение к V%*
если известно непосредственно предшествующее приближение. При этом
необходимая точность достигается при совпадении двух последовательных
приближений в пределах заданной точности. Проиллюстрируем это на примере.
Пусть требуется вычислить ]/"б с точностью до 0,001. Формула для
нахождения последовательных приближений к |/ТГ будет иметь вид:
1 / 5
где п = 2, 3, 4, ...
За у\ примем число 2, тогда
1 / 5
*2===2 ~
•К>
2,25,
у3 = | ^2,25 + -~А = ~ (2,25 + 2,2222) = 2,2361,
уй = | f 2,2861 + 2-^~) = | (2,2331 + 2,2360) = 2,23605.
Мы видим, что третье и четвертое приближения совпадают с точностью
до 0,001. Следовательно, уже на третьем шаге был получен ответ на вопрос
задачи.
Приведенные рассуждения можно распространить на случай получения
последовательных приближений к корням из любых положительных чисел.
Так, для Ух формула для получения последовательных приближений будет
иметь вид:
Уп
= ^(^_1+1^ТУ « = 2,3,4, ...
Замечание. За первое приближение, вообще говоря, можно принять
любое положительное число. Но если мы хотим получить нужный нам результат
быстрее, то следует по возможности выбирать yi точнее (с меньшей погрешностью).
660. Найдите методом последовательных приближений значение. корня с
точностью до 0,001:
a) ^20; б) /36^5; в) /525; г) /95\28.
38. Таблица квадратов
В «Четырехзначных математических таблицах» В. М. Бради-
са помещена таблица квадратов чисел. В этой таблице даны
квадраты чисел от 1 до 10 с шагом 0,001. Такие числа
записываются не более чем четырьмя цифрами.
В первом столбце таблицы помещены числа от 1 до 10 с
шагом 0,1, т. е. числа, записываемые не более чем двумя цифрами.
159
В соседнем столбце даны точные значения квадратов этих
чисел. Например,
2,22 = 4,840; 3,42 = 11,56; 6,02 = 36,00.
Кроме рассмотренных двух столбцов, таблица содержит еще
девять столбцов, помеченных сверху и снизу цифрами от 1 до 9.
Эти столбцы используются для нахождения квадратов чисел от
1 до 10 с шагом 0,01, т. е. чисел, записываемых не более чем
тремя цифрами.
Покажем на примере, как находятся квадраты таких чисел.
Пусть требуется найти 7,342. В первом столбце находим число 7,3
(первые две цифры числа 7,34). Квадрат числа 7,34 помещен
в той же строке, на пересечении этой строки и столбца под
номером 4. Он равен 53,88.
Полученный результат является приближенным. Какова
точность этого приближения?
Найдем значение выражения 7,342 обычным умножением:
7,342 = 7,34 • 7,34 = 53,8756.
Мы видим, что приближенное значение числа 7,342, равное
53,88, получено округлением до сотых числа 53,8756. Модуль
погрешности в этом случае не превышает половины единицы
разряда, до которого проводилось округление, т. е. половины
от 0,01. Таким образом, мы получили приближенное значение
с точностью до 0,005.
Вообще, приближенные значения квадратов чисел от 1 до 10
с шагом 0,01 получены в результате округления
соответствующих точных значений и отличаются от них не более чем на
половину единицы разряда, до которого проводилось округление.
Например, 7,632^ 58,22. Модуль погрешности полученного
приближенного значения не превышает половины от 0,01, т. е.
0,005. Значит, 58,22 — 0,005< 7,632< 58,22+0,005, т. е. 58,215<
<7,632< 58,225.
Для нахождения квадратов чисел от 1 до 10 с шагом 0,001
в таблице справа помещены еще 9 столбцов. Это так называемые
столбцы поправок.
Найдем, например, значение выражения 2,3422. На
пересечении строки «2,3» и столбца «4» помещен квадрат числа 2,34:
2,34^5,476. В столбце поправок под номером 2 находим на
пересечении с этой же строкой число 9, которое прибавляем к
последней цифре числа 5,476. Получаем: 2,3422^ 5,485.
Приведем еще пример. Пусть требуется найти 8,43722. Так
как в таблице даны квадраты чисел от 1 до 10, записанных с
помощью не более четырех цифр, то основание степени придется
округлить до тысячных. Получим: 8,43722^ 8,4372я^ 71,18.
Мы разобрали на примерах, как с помощью таблицы
находятся квадраты чисел от 1 до 10 с шагом 0,1, 0,01 или 0,001, Эта
же таблица может быть использована для нахождения квадра-
160
тов положительных чисел, меньших 1 или больших 10. Для
этого достаточно представить данное число в стандартном виде,
т. е. в виде а-10п9 где 1^ а < 10 и п — целое число.
Найдем, например, значение выражения 342. Число 34 в 10
раз больше числа 3,4. Квадрат числа 3,4 находим по таблице:
3,42=11,56. Тогда
342 = (3,4 • 10)2 = (3,4)2 • 102 = 11,56 • 100 = 1156.
Приведем еще примеры:
0,3572 - (3,57 • Ю-1)2 = 3,572 • Ю-2 « 12,74 • 10~2 = 0,1274;
432,72 = (4,327 • 102)2 = 4,3272 • 104 » 18,72 • 104 = 187 200.
661. Найдите с помощью таблицы квадраты чисел:
а) 1,3; 4,7; 2,8; 5,7; 8,3; 7,2; 9,6;
б) 2,34; 5,12; 8,37; 9,56; 3,04; 6,19;
в) 1,243; 4,325; 7,239; 8,127; 6,571; 9,044.
662. Найдите значение выражения 1,0122 по таблице и
вычислением. Определите модуль погрешности приближенного
значения, найденного по таблице.
663. Округлите число до тысячных и найдите его квадрат,
пользуясь таблицей:
а) 3,1238; б) 1,0058; в) 4,1405; г) 6,3752.
664. Найдите по таблице квадраты чисел:
а) 5,243; 52,43; 5243; 0,5243;
б) 1,315; 0,01315; 131,5; 13 150;
в) 345; 290; 1281;
г) 0,351; 0,00425; 0,012482.
39. Таблица квадратных корней
В «Четырехзначных математических таблицах» В. М. Бради-
са помещена таблица значений арифметических квадратных
корней. Устройство ее сходно с устройством таблицы квадратов.
Приближенные значения корней даны для чисел в
промежутке от 1 до 100. Причем числа от 1 до 10 берутся с шагом 0,001,
а от 10 до 100 — с шагом 0,01.
Покажем на примерах, как с помощью таблицы находятся
приближенные значения арифметических квадратных корней.
1. Найти значение выражения 1/5,6.
В первом столбце находим число 5,6, а в соседнем столбце
на той же строке читаем приближенное значение |/"5,6:
УЬ£ж 2,366.
б Алгебра, 7 кл.
151
2. Найти значение выражения ]^23,5.
В первом столбце находим число 23 и в этой же строке на
пересечении ее со столбцом под номером 5 читаем результат:
1^2^5^4,848.
3. Найти с помощью таблицы значение выражения 1/45,34.
В первом столбце находим число 45, затем на пересечении
этой строки и столбца под номером 3 находим приближенное
значение }^45,3:
1^4^3^6,731.
В столбце поправок под номером 4 в той же строке
находим число 3. Прибавляя поправку к последней цифре числа
6,731, получаем: |^45,34 « 6,734.
Заметим, что приближенные значения корней, приведенные
в таблице (без учета столбцов поправок), имеют модуль
погрешности, не превышающий половины единицы последнего
разряда в записи приближенного значения корня.
Например, число 2,796 является приближенным значением
|/7,82 с точностью до половины от 0,001, т. е. с точностью до
0,0005:
^7^2 =2,796 ± 0,0005.
С помощью этой же таблицы находят квадратные корни из
положительных чисел, меньших 1 или больших 100. Рассмотрим
примеры.
4. Найти значение выражения ]/245.
Число 245 в 100 раз больше числа 2,45, квадратный корень
из которого можно найти по таблице. Поэтому
J/245 = У"2,45 • 102.
Легко проверить, что
/2,45 • 102 = V2A5 • 10.
Действительно,
{V2A5 • Ю)2 = [V2A5)2 • 102 = 2,45 . 102,
т. е. 1^2,45-10 — неотрицательное число, квадрат которого
равен 2,45 102. Значит, ]/ 2,45-10 — арифметический
квадратный корень из 2,45 • 102, и равенство |/~2,45-102= 1^2,45 • 10 верно.
Значение выражения |/"2,45 находим по таблице:
V~2A5& 1,585.
Тогда
1/245 = j^45 .10 ~ 1,565 ■ 10 = 15,65.
162
5. Найти приближенное значение выражения 1/0,235.
Число 0,235 в 100 раз меньше числа 23,5. (Квадратный
корень из числа 23,5 можно найти по таблице.) Поэтому
1/0,235 = 1/23,5 • 10~2.
Легко убедиться, что
/23,5 • 10"2 = /23,5 . Ю-1.
Значит,
УоДЗЬ == У 23^5 • Ю-1 ~ 4,848 • 10"1 = 0,4848.
Вообще, чтобы найти корень из положительного числа,
меньшего 1 или большего 100, следует представить это число в виде
а-102*, где 1<^а<100ий—целое число, и воспользоваться
формулой УаЛ02к = Уа10К
665. Пользуясь таблицей, найдите арифметические квадратные
корни из следующих чисел:
а) 4,3; 6,2; 8,9; 10; 50; 75;
б) 1,25; 14,7; 20,8; 40,1; 83,2;
в) 1,143; 4,835; 60,37; 81,92;
г) 1,0058; 6,83251; 20,156.
С помощью таблицы найдите приближенное значение
выражения:
а) У"5Д; г) У2Ж; ж) ]/7Д53; к) |/37^21;
б) 1/6; д) 1/^3175; з) УЩ(Н; л) у153Д9;
в) 1/48; е) УЩ$; и) 1/6М8; м) 1/87\25.
667. Представьте в виде а-102*, где 1^а<100 и k£Z, число:
а) 115; в) 1230; д) 0,007;
б) 692; г) 0,03; е) 0,00059.
668. Пусть j/3"= а и У30 = р. Преде тавьте в виде 10* а или 10й (3,
где ftg Z, число:
а) 1/300; б) 1/3000; в) У0£; г) УоМ.
669. С помощью таблицы найдите приближенное значение
корня:
а) 1/бЖ; 1/652; 1/6520; 1/0^652;
б) 1/3,278; 1/3278; 1/0,03278; 1/327800.
6* 163
670. Найдите приближенное значение выражения:
а) У 345; в) |/I28l7 д) 1^25740; ж) ]/0,0724;
б) у'гЭО; г) ^3720; е) У&Щ\ з) ]/0,00425.
671. Найдите с помощью таблицы значение выражения и
докажите, что найденное значение является точным:
а) УЗЖ; в) >^676; д) 1^1521;
б) |/0,0256; г) 1/961; е) у12704.
672. Для каждого из чисел У~7 и Уз укажите с помощью
таблицы две последовательные десятичные дроби с одним
знаком после запятой, между которыми заключено это число.
Методом границ найдите приближенное значение
выражения:
а) )/7 —1,5; б) УЗ + 0,2; в) У1 + УЪ; г) У7 — УЗ.
673. Найдите приближенное значение выражения У 3,1 + У 15,7.
(В качестве границ чисел У3,1 и ^15,7 возьмите две
последовательные десятичные дроби с одним знаком после
запятой.)
40. График функции у = Ух
Каждому неотрицательному значению х соответствует
единственное значение выражения Ух. Формулой у =Ух задается
функция, областью определения которой служит числовой
промежуток [0; +оо[.
Если я=0, то у=0, следовательно, начало координат
принадлежит графику функции. При х > 0 значение выражения ]/~х
положительно. Поэтому график функции у = }/~х расположен в
I координатном углу.
Для построения графика функции у = У~х воспользуемся
таблицей:
X
In
0
0
0,5
0,71
1
1
2
1,41
3
1,73
4
2
5
2,24
б
2,45
7
2,65
8
2,83
9
з
Большему значению аргумента в этой таблице соответствует
большее значение функции. Можно доказать, что,_вообще, если
Xi и #2 — неотрицательные числа и х2>х1$ то Ухг>У1с^ т. ё.
функция у = У~х возрастает на всей области определения.
164
тшншмпниимшпмн >■■■■■•■■■ ■■■■•■■■■■■■■■■■■
«■^■■■■■■•■■■■•■■■■«■■■■■«■■««■■■■^■■«■■■■■.■■^«■■..■■■■■■■»iii>-E ^.uifiiiiiiiiiiiiii
Sim«li ••■■■■■Biiiiiiia(anluiiiuaiiiiai«natUiHilili»<- ^.auiMMtMiiliiiiiiiii
l3B
68
В
Tj 1111
$g§
jffis
Й
XlJ4]JJ|4:
Pfh
Щш
i ti-1
Рис. 43
Для доказательства составим разность выражений У~хг и ylcl и выполним
такие преобразования, в результате которых можно будет определить знак этой
разности:
(Уъ-У^ЛУъ + Уъ) = х2 - хг
Уъ+Уъ Уъ+Уъ'
Так как х2 > хх > О, то х2 — xt > 0 и У х2 + Ухх > 0. (Каждое из
выражений Ухх и У~х2 имеет смысл, причем Ухг> 0 и У х2 > 0.)
г, а вместе с ним и значение разности Ух2—
ут2-гъ =
Значит, значение дроби /—— ,—
— У^ положительно. Из неравенства Ух2—Ухх > 0 следует неравенство
Уч > угх.
Функцию, которая возрастает на всей области определения,
принято называть возрастающей. Итак, функция у = У^х
возрастающая.
Построив в координатной плоскости точки, координаты
которых занесены в таблицу, и соединив их плавной линией,
получим график функции у = Yx (рис. 48).
674. С помощью графика функции у = ]/гх найдите значение
выражения Ylc, если я:=2,5; 3; 5,5; 6; 8,4.
675. С помощью графика функции y = Yx найдите значение
переменной х, если ]/гх = 192; 1,7; 2,5.
676. Принадлежит ли графику функции y = Vx точка А (64; 8),
В (—81; 9), С (100; —10)?
1G5
677. С помощью графика функции у = Ух сравните числа:
а) ylj и У 2^3; в) У 2$ и 2;
б) 1^5 и |/^8; г) |/бД и 3.
678. Что больше:
а) У 68 или У72; б) 8 или ]/бб?
679. Оцените значение выражения ]/"#, если 0 ^ х ^ 4.
На какое множество функция у = ]/# отображает
промежуток:
а) [0; 9]; б) [100; 400]; в) ]0,01; 1[?
680. Найдите границы значения выражения:
а) V^f3, если 0,16 < х < 0,25;
б) Ух—1, если 0,25 < *< 2,56.
681. С помощью графика функции у=Ух выясните, при каких
значениях х обращается в истинное высказывание
предложение:
а) К* = 2; б)Ух>2; ъ)У1с<2.
682. Решите уравнение и неравенства:
а) УН = 10, Ух > 10, УН < 10;
б)Ух = у~7, Ух>у1, -\п<уч.
683. Решите неравенство:
а)К*>3; в)1<Ух<3; д)1/х<}/5;
б)Ух<3; г))/^>|/5; е) У2 < Ух </5.
684. Решите графически уравнение ]^я = 6 — я.
685. В какой координатной четверти расположен график
функции:
а) у = —Ух; б) у = |/^с?
§ 12. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ
КВАДРАТНЫЕ КОРНИ
41. Тождество Ух2 =\х\
Сравним соответственные значения выражений Ух2 и х.
Из определения арифметического квадратного корня следует,
что при х ^ 0 соответственные значения этих выражений равны.
Например,
при х =6 уТа = /б2 = 6,
при х = О Vx2 = VO2 = 0.
Таким образом, при х^О верно равенство
VI? =х.
Если я<0, то соответственные значения выражений Vх2 и
х — противоположные числа.
Например,
при х = — 5 Ух2 = VT1^)2 = 5,
при х = —0,3 К%2"== К(—0,3)2 = 0,3.
Значит, при х < 0 верно равенство
Можно_заметить, что при любых значениях х значение
выражения Vх2 совпадает со значением выражения \х\9 т. е. все
соответственные значения выражений Vх2 и 1*1 равны, значит,
равенство
K?=UI (1)
является тождеством.
Рассмотрим примеры преобразований выражений с
использованием тождества (1).
1. Найти значение выражения 0,2]Ал:2 при х = —24,5. Так
как }/~я2 = |л:|, то
0,2]/"?= 0,2 • | х | = 0,2 • |—24,51= 0,2- 24,5 = 4,9.
167
2. Упростить выражение У"0,09а2, если а^О.
Представим подкоренное выражение ]/4),09a2 в виде квадрата
одночлена и воспользуемся тождеством (1):
1/"0,09а2 = V(0,3a)2 = |0,3а | = 0.8-
При а^0 |а| = а, следовательно,|^0,09а2 = 0,3а.
3. Упростить выражение — j^a8.
Представим подкоренное выражение а8 в виде квадрата
одночлена: a8=(a4)2. Тогда
Значение выражения а4 неотрицательно при любом значении
переменной а. Значит, при любом а | а41 = а4 и — ]/а8 = — а4.
<& 2
686. а) При каких значениях переменной х из множества
{3; —4; 0; 10; —5} верно равенство Ух2=х?
б) При каких значениях переменной с из множества
{4; —2; 7; —7; 0; —9} неверно равенство }/гс2=с7
в) При каких значениях переменной а из множества
{2; 9; —6; 1; —8} верно равенство У~а2=—а?
г) Назовите несколько значений переменной у, при
которых неверно равенство Vy2 — —у.
687. Вычислите:
а) 1/"(0Др; г) VOW; ж) К(=23р;
б) /(-0,4)2; д) 1/"(-1,9)2; з) УЖ2\
в) К(-0,8)2; е) К(2Ж2; и) /(=W2.
688. Найдите значение выражения:
а) У*2 при * = 22; —35; —1-; 0;
з
б) 2Va? при a = —7; 12;
в) 0,1 Vy* при у = —15; 37.
689. Замените выражение тождественно равным:
а) 1/р; в) |/9&"2; д) V 0,01с2;
б) Vti г) КЗб*5; е) УШ*^
168
690. Преобразуйте выражение:
а) У?9 если с^О; г) У"4а2, если а^О;
б) У а2, если а > 0; д) ]/0,25&2, если Ъ < 0;
в) ]/Р, если х < 0; е) |/ ^, если л: < 0.
691. Замените выражение тождественно равным:
а) У (а — I)2; в) )/" х2 + 2* + 1;
б) У (с + 2)2; г) У4у2-4у + 1.
692. Преобразуйте выражение:
а) j/^a: — 4)2> если л: > 4; г) V (7 + у)2, если у < —7;
б) К(а — 2)2, если а < 2; д) /(10 + с)2, если с > —10;
в) У"(3 — т)29 если m ^ 3; е) У(п -\- 4)2, если я < —4.
693. При каких значениях переменной верно равенство:
а) Ух2— 2*+1 = * — 1; в) Ус2— 6с + 9 = 3 — с;
б) 1/4а2 + 4а + 1 = 1 + 2а; г) J/*4 + 2*2 + 1 = х2 + 1?
694. Представьте подкоренное выражение в виде квадрата
одночлена и найдите значение выражения:
а) У¥; в) Y(=W\ д) 3 Y(=W\ ж) 0Д/(=3)~8;
б) Y&; г) КРзр; е) -2 Ko^W; з) шУЩу\
695. Упростите выражение:
а) Ут*> если m ^ 0; в) Ух8, если я < 0;
б) У У6, если I/ < 0; г) ]/о^, если а ^ 0.
696. При каких значениях переменной верно равенство:
а) Уу2 = —у; в) Ух« = *3; д) /о14 = —а7; ж) ]/? - —х2;
б) J/7 = I/2; г) 1/?5"= —с5; е) /Р = Ь4; з) Уб5^ Ь6?
697. Упростите выражение:
а) V(y2-lf; в) ]ЛуП - ]/1б)2;
б) У (1 - )/3)2; г> V(Yl - У&)\
169
698. Решите уравнение:
а) Ух2 = 4; в) У(х — I)2 ^ 1;
б) УТ2 + 1 = 0; г) У(х + 7)2 =з 3.
699. Постройте график функции i/ = j/"*2". На каком множестве
эта функция возрастает?
42. Теорема о корне из произведения
Сравним значения выражений |/"81-4 и У81-У4.
Перемножив числа 81 и 4, получим, что]/Л81-4 = уЛ324. Так как 324 = 182,
то У 324 = 18. Таким образом,
|/"8Г4 = 18.
Найдем теперь значение выражения jAsi-j/^:
/81. j/4 = 1/92- У¥ = 9 • 2 - 18.
Значит, ]/"8]Т4 = J^Sl - ]/4.
Теорема. £сл я а > 0 я 6 > 0, го Ktfft = /а • У¥.
Для того чтобы доказать, что равенство УаЬ~Уа-УЬ, где
а^О и &!>0, ^зерно, достаточно убедиться в том, что значение
выражения Уа-УЪ неотрицательно и квадрат его равен ab.
Значение выражения Уа-УЪ неотрицательно, так как при
а^О и Ь^ 0 каждое из выражений У а иУЬ имеет смысл и
принимает неотрицательное значение.
Найдем квадрат произведения ]/"а •)/"&, получим:
{уъ.уъу={уъ)2-{уъу=аъ.
Итак, на основании определения арифметического
квадратного корня равенство УаЬ = Уа-УЬ, где а^О и &^0, верно.
Таким образом, корень из произведения неотрицательных
множителей равен произведению корней из этих множителей.
Теорема верна и в том случае, если число множителей под
знаком корня больше двух.
Приведем примеры применения этой теоремы.
1. Найти значение выражения У 64 0,04.
Воспользуемся доказанной теоремой:
У 64 . 0,04 = /64 • УОМ = 8 • 0,2 = 1,6.
2. Найти значение корня У"32-98.
Преобразуем подкоренное выражение:
32-98 =(16-2) (49-2) =16-49-4.
170
Для нахождения значения выражения /16-49-4
воспользуемся теоремой о корне из произведения неотрицательных
множителей:
/16 49-4 = /16 . /49 • /I = 4 . 7 - 2 = 56.
3. Представить в виде одночлена выражение ]/ 49а2Ьв, где
а<0 и &>0.
По теореме о корне из произведения неотрицательных
множителей
]/49а266 = /49 • Ко1. уТв = 7 - |а| • | Ь3|.
При а<0 и &>0 |а|=—а и |&3| = Ь3, следовательно,
/49а2&6=7(—а)-Ъ* = — 7аЬ\
4. Найти значение произведения |/^20-|/3.
Запишем формулу /a& = /a/&, где а^О и &^0, иначе
Va-Vb= V~ab.
Тогда
/20 . /5 = ]/10б = 10.
700. Найдите значение выражения:
а) /100 ■ 49; г) /81 • 400; ж)/ 0,36 . 169;
б) /i2iT64i д) VT^. з) /12Ь0Д9;
в) 1/9-64; в) Т/УЖ *> KMll^
е) К 81' 49' к) /2,25 • 0,04.
701. Найдите значение корня:
а) 1/810 • 40; в) У 75-48; д) /2,5 • 14,4;
б) /72 • 32; г) /4,9 • 360; е) /90 • 6,4.
702. Вычислите:
а) У132 —122; в) /172 — 82;
б) У 3132 — 3122; г) /117» —1082.
703. Сравните значения выражений:
а) /52 -{-122 и 5 + 12; б) /10» — б2 и 10 — 6.
171
704. а) Найдите катет прямоугольного треугольника, если
гипотенуза равна 41 см, а другой катет — 40 см.
б) Найдите площадь прямоугольника, если одна из его
сторон равна 56 см, а диагональ — 65 см.
705. Представьте выражение в виде произведения корней:
а) /15; б) ]/21; в) /7а; г) У^Зс.
706. Разложите выражение на множители, вынеся за скобки У 2:
а) /10 + /2; б) УЪ — /16; в) /18 + /22; г) 2 — /14.
707. Сократите дробь:
а) УЯ-У*. б) Уа + УЪ. В)У7-У1§. г) У1В-5
/5 VI Кб У 6 — /10
708. Вычислите:
а) 1/28 • З4; б) У 5~4 • 2~4; в) yV2 • 104; г) У11* • 10~6.
709. Вычислите значение выражения, разложив вначале
подкоренное выражение на множители:
a) /576; б) /Шб; в) /Ш; г) /19600.
710. Представьте выражение в виде одночлена:
а) У~9а2, где а >0; д) /а2?, где о > 0 и с> 0;
б) 1/25С4", где с> 0; е) 1/0,36Ь2с\ где & <0;
в) /0.36&2, где & < О; ж) ]/4ав&4» гДе а < 0;
г) У 81j/10, где у < 0; з) Ус14л10, где а > 0 и х < 0.
711. Используя формулу Уа-УЪ = УаЪ, где а>0 и&^0,
найдите значение произведения:
а) У2- /8|_ д) У21 • 1/2Т3; 3) l/^• l/I-
6)1/10.^40; e)>ag.m 3 *'
в)1Л2.1^; и)Г1Т2./з1.
г) /27 • /3; ж) /63 1/7; ' 3
712. Найдите область определения выражения и упростите его:
а) х Y~x - Ух; в) У а5 • Уа?;
У 5Ь2
713. Найдите область определения каждого из выражений и
выясните, какая из них является подмножеством другой:
а) ]/х(х — 2) и Ух- Ух — 2;
б)]/д2_1 и Ух + 1-Ух^Л.
43. Теорема о корне из дроби
Сравним значения выражении "i / — и ——•
У 81 |/ \9/ 9 |Л§1 ^ »
Значит, 1/ — == -—.
V 81 ^й
Теорема. £гл# а>0 а Ь>0, то л/ — = zJL.
У ъ уь __
Доказательство. Если а ^ О и & > О, то выражение ——
имеет смысл и принимает неотрицательное значение, так как
У а )0и )/^6 > 0. Докажем, что квадрат выражения —^
У^\2 (/^)2 а
а
равен —:
/ь"/ (VT)2
ь
У^ [V^2
Так как значение выражения —~ неотрицательно и ^—^_
Vb \Уь
= —, то на основании определения арифметического квадратного
ъ
корня равенство -i / — = L-ji, где а ^ 0 и & > 0, верно.
Итак, корень из дроби, числитель которой неотрицателен, а
знаменатель положителен, равен корню из числителя,
деленному на корень из знаменателя.
173
Приведем примеры.
- _ /"зб У~гь _ б
JL •
Лзё __
У 169 "~ /169 13
f~L — YA _ JL
У $ ~ ут ~ /т'
В результате преобразования выражения |/ -g- мы получили
дробь -г=., знаменатель которой ]/"5 не является рациональ-
V 5
ным числом. Такие выражения иногда бывает удобно
представлять в виде а]/^, где а — рациональное число, а & —
натуральное.
о
Для того чтобы выражение —— привести к виду a\fby вос-
пользуемся основным свойством дроби и умножим числитель
и знаменатель дроби -^= на )Л>:
JL = 2'^2^а 0.4^5.
В полученном выражении вида а]/& а= 0,4 и &= 5.
Итак, ]/у = 0,41^5.
Выполняя некоторые преобразования, удобно пользоваться
формулой 1 / — = ^4, где а ^ 0 и & > 0, записав ее иначе:
V ь уъ __ _
*— = л[ -
VT У *"
Пусть, например, требуется упростить выражение L— . До-
У12
лучим:
n5el/5el/*eA = 2f5.
/12 V 12 у 4 2
714. Найдите значение корня:
»i/§ *V% *УШ -»v^
•»^2? -»К$ «/S •»/»£•
174
I 715. Представьте в виде частного корней выражение:
i
■>У$ б,уЪ в,]/|; г)|/Г|.
716. Представьте в виде ci\fb^ где а — рациональное число и
Ъ — натуральное, выражение:
ч 2 ч 6 ч 3
а) —=л в) —=.; д)
*ч * ч 9 ч 21
б) —; г) ——; е)
У 2 2 /з 2 /14"
717. Представьте выражение в виде а]УЬ9 где а — рациональное
число и & — натуральное:
•>Vn* оУт* б)/^ *>У
2^
15'
718. Представьте в виде aj/^ft, где а — рациональное число
и & — натуральное, выражение:
а) 9 У J; в) 1 ]/|; д) 2 /б/Г; ж) 41/12Д;
б) 20 j/Ь г) | j/i_; e) 12 /1^"; з) ± /О^
719. Упростите выражение:
.)£!. в)^3; д)^; «) 1?°; и) Ш,
/18 У 111 У 45 У 30 /34
J^. Г) Vf. e)fX2; з)1?; к)*?.
/2300 /28 /65 /250 /65
720. Найдите области определения каждого из выражений и
выясните, какая из них является подмножеством другой:
а) /гг!
— 5 Vx — Ъ ,. /2ж — 4 |А2ж — 4
— И i——; 6) -i/ —— И у-
+ з /7+~з V 10* Vvix
175
44. Вынесение множителя из-под знака корня
Выражение У 16а имеет смысл, если а^О. Преобразуем это
выражение, используя теорему о корне из произведения
неотрицательных множителей. Получим:
yj6a =уИГ.уа = 4Уа.
Мы заменили корень из выражения 16а, где а ^0,
произведением чисел 4 и У а. В этом случае принято говорить, что
множитель 4 вынесен из-под знака корня.
Приведем примеры.
Пример 1. Сравнить числа ]/^50 и 41/2.
Преобразуем выражение У 50:
1/50 = /2572 = ]/25 • У 2 = 5]/2.
Ясно, что
5]/2>4]/2.
Поэтому
]/50>4/2.
Пример 2. Упростить выражение 2]/~8-f 31/2 — 2]/Т8.
Вынося в слагаемых 2J/8 и —2]/18 множитель из-под знака
корня, получим:
2УЪ + ЗУ2 — 2У^ = 2УТ^+8У^ — 2У9^2^
= 2Vr4- /2 + 31/2 — 2/9- 1/2 =
= 41/2 + 31/2 — 61/2 = (4 + 3— 6) 1/2 = 1/2.
Пример 3. Вынести мнолштель из-под знака корня в
выражении У9а1.
Выражение У 9а1 определено при а^О. Представим
подкоренное выражение 9а7 в виде такого произведения, в котором
один из множителей тождественно равен квадрату одночлена:
9а7 = 9а6-а = (3а3)2а. Тогда по теореме о корне из произведения
неотрицательных множителей
УШ* = УЩа*?а = 1/(ЗаУ • УЪ = |3а31. Уа = За3^а.
721. Вынести множитель из-под знака корня:
а) У12; г) 1/32; ж) 1/363; к) ОД 1/20000.
б) 1/18; д) 1/108; з) ]/845;
в) 1/50; е) /Ш; и) - 1^275;
176
722. Сравните числа:
а) 3/1$ и /12; г) З/Ш и 21/270;
б) /20 и 3]/"5; д) /72 и 0,5 /ЙЙГ;
в) -/54 и -/150; е) /24 и ^/216.
3 5 3
723. Упростите выражение и найдите с помощью таблицы его
приближенное значение:
а) У12-У27 + ±УТ8; б) А /18 + 1 /"8-1 /50.
Z О Z О
724. Упростите выражение:
^ , 1
а) 3 У~2 + К32 - 1^200; г) )^80 + -±-^20 + 3]/45;
б) 2/72 — /50 - 2 /~8; д) /75 — 0,1/300 - /27;
в) 5/"3 +-/27-/48; е) /98 — /72 — i/~8.
3 2
725. Вынесите множитель из-под знака корня:
а) /7а2, где с > 0; г) /0,01Ь5, где Ъ > 0;
б) ]/ 10у\ где у < 0; д) /№, где а > 0;
в) 1/1б*3, где ж > 0; е) /27с«, где с < 0.
726. Найдите область определения выражения и вынесите
множитель из-под знака корня:
а) /9ж; в) /"Ш2; д) /ИР; ж) /За1; и) /ioo7;
б) У^Ш; г) /Ь5; е) /— 18л;3; з) /^о5; к) ]/ — 45а7.
727. Упростите выражение:
а) /25а* + 4а/а3 — а*У~а;
б) 6а/~&— -/1бТ3 + УЬЬ.
728. Вынесите положительный множитель из-под знака корня:
а) Vx2y, если х >0, у >0 и если # <0, у >0;
б) Ухуъ, если х > 0, у > 0 и если х < 0, j/ < 0.
177
729. Вынесите множитель из-под знака корня в выражении:
а) У 9а?Ь, где а < О, Ь > 0;
б) V 25а2Ь3, где с> О, Ь > 0;
в) У 144с3&3, где а < 0, 6 < 0;
г) У 32с463, где а < 0, & > 0;
д) К 75W, где с> 0, & < 0;
е) У8аьЬ7, где а < 0, Ь < 0.
730. Представьте выражение в виде а/&, где о —
рациональное число и & — натуральное:
а)/~б/1; в)-/~5/Т0; д) 0,5 /1 ■ /24;
5
б) /15 • 1/30; г) 0,5/~2 • У12; е) - /12 0,5 /48.
4
731. Докажите, что равенство верно:
а) (3 У~Ъ — 2 ]/~3) ■ /"б + /60 = 15;
б) (/28— 2]/~3 +V!) ■ У~Ч + /84 = 21.
732. Упростите выражение:
а) (/12 + 2 /18) • /"2 — /150;
б) (/15 — /20) • 2 /~5 + /75;
в) (3 У~2 — УЪ + 1) • 2 /~2;
г) (4 /"3 — 2/"б — 1) • 2 /~3.
733. Преобразуйте выражение:
а) (У~2 + I)2; д) (/"6 + У~6)\
б) (/1 - 2)2; е) (2 /15 - / б)2;
в) (/1 - /I)2; ж) (/10 - 3 /~5)2;
г) (2 /"5 + y~2f; з) (/21 + 2 /П)2.
45. Внесение множителя под знак корня
Пусть требуется сравнить числа 3/5 и 2/7. Это легко будет
сделать, если мы сумеем каждое из этих чисел представить в
виде арифметического квадратного корня.
В выражении 3 /5 положительный множитель 3 можно
представить в виде арифметического квадратного корня из 9. Тогда
3/5 = /9/5 = /9-5 = /45.
178
Преобразуем аналогично выражение 2"|/"7:
2/~7 = /1. /7 = /ТТ = /28.
Ясно, что
/45 > /28.
Поэтому __
3/~5> 2/7.
Итак, для сравнения чисел 3/5 и 2]/7 мы каждое из них
представили в виде арифметического квадратного корня. В
таких случаях говорят, что в каждом из выражений 3/5 и 2/7
мы внесли множитель под знак корня.
Рассмотрим теперь выражение —4/3. Его значение
отрицательно. Поэтому это выражение нельзя представить в виде
арифметического квадратного корня. Однако выражение —4/3
можно преобразовать так:
_4 У~з = — /16 • /"3 = - /16^3 = — /48.
Внеся положительный множитель 4 под знак корня, мы
представили —4/3 в виде выражения, противоположного
арифметическому квадратному корню.
Приведем еще пример. В выражении а/2 множитель а
перед корнем может принимать любые значения. Поэтому для
преобразования этого выражения нужно рассмотреть два
случая: a J> 0 и а < 0.
Если а ^ 0, то а = /а2 и
а /"2 = /а2 . /"2 = /2а5.
Если а < 0, то а = — /а2 и
а /"2 = — /а2. /"2 = — /^а2.
734. Внесите множитель под знак корня:
а) 7/10; в) 5/"6; д) 6 ]/|;
б) 5/"3; г) 10Кб; е) 2 j/J.
735. Внесите положительный множитель под знак корня в
выражении:
а) 3/~5; в) 2/Т;
б) -5/^; г) -6/1;
179
е) -12/|;
ж) — ]/Ъе;
з)
•±v*
736. Сравните числа:
а) 2J/1 и 3|/~2; в) -Уб и бТ/1;
б) 51/1 и 41/"5; г) -1/72 и 7 "l/I.
3 г 3
737. а) При каких значениях переменной х из множества
{2; 3; —5; —10} верно равенство хУз=УЗх*7
б) При каких значениях переменной с из множества {—3;
1; 4; 10; —10} верно равенство сУИ=—У 5с2?
в) Назовите несколько значений переменной а, при
которых неверно равенство
г) Назовите несколько значений переменной Ь, при
которых верно равенство b}/r7 =—УЧЪ2.
738. Внесите множитель под знак корня:
а) aV% где а>0; д) х j/A;
б) аУ~3, где а < 0; е) х ]/_ 1;
в) — Ь]/"3, где 6>0; ж) у|/~3;
г) — Ъ У~Ъ, где Ъ < 0; з) — с ]/Та.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ III
К пункту 32
739. Пусть К — множество четных чисел и L — множество
чисел, кратных четырем.
Постройте «круги Эйлера» для множеств К и L. Покажите
на вашем рисунке штриховкой множество четных чисел,
не кратных четырем.
Является ли истинным высказывание:
а) для того чтобы число было четным, достаточно, чтобы
оно было кратно четырем;
б) для того чтобы число было четным, необходимо, чтобы
оно было кратно четырем;
180
в) для того чтобы число было кратно четырем,
достаточно, чтобы оно было четным;
г) для того чтобы число было кратно четырем, необходимо,
чтобы оно было четным?
740. Постройте «круги Эйлера» для множества В чисел,
кратных 6, и множества С чисел, кратных 3.
Является ли истинным высказывание:
а) для того чтобы число было кратно 6, достаточно, чтобы
оно было кратно 3;
б) для того чтобы число было кратно 6, необходимо, чтобы
оно было кратно 3?
741. Постройте «круги Эйлера» для множества В чисел,
кратных 6, множества С чисел, кратных 3, и множества Z
целых чисел.
742. Постройте «круги Эйлера» для множества рациональных
чисел Q, множества целых чисел Z и множества
натуральных чисел JY.
743. Пусть А — множество равносторонних треугольников, В—
множество равнобедренных треугольников. Какое из
множеств является подмножеством другЬго? Постройте
«круги Эйлера» для множеств А и В.
744. Постройте «круги Эйлера» для множества А
равносторонних треугольников, множества В равнобедренных
треугольников и множества С всех треугольников.
745. На рисунке 49 построены «круги Эйлера» для множества Z
целых чисел и множества Р положительных чисел. Какая
часть схемы соответствует множеству:
а) натуральных (целых положительных) чисел;
б) положительных, но не целых чисел;
в) целых, но не положительных чисел?
Назовите несколько элементов множества для каждого
из случаев а), б) и в).
746. Постройте «круги Эйлера» для множества С
прямоугольников и множества D ромбов. Заштрихуйте часть схемы,
которая соответствует множеству
квадратов.
747. Постройте «круги Эйлера» для
множеств А, В, С и F, где:
А — множество выпуклых
четырехугольников;
В — множество параллелограммов;
С — множество прямоугольников;
F — множество квадратов. Рис. 49
QD
181
748. Постройте «круги Эйлера» для множеств А, В, С, D и
F, где:
А — множество выпуклых четырехугольников;
В — множество параллелограммов;
С — множество прямоугольников;
D — множество ромбов;
F — множество квадратов.
749. Постройте «круги Эйлера» для множеств рациональных
чисел Q, целых чисел Z, положительных чисел Р и
четных чисел К.
750. Что является дополнением множества:
а) квадратов до множества прямоугольников;
б) равносторонних треугольников до множества всех
треугольников;
в) квадратов до множества ромбов;
г) чисел вида 3ft, где k — целое число, до множества целых
чисел?
751. Найдите дополнение до числового промежутка [3; 9]
числового промежутка:
а) [3; 6]; б) [5; 6]; в) ]3; 9[; г) [3; 9[.
752. Найдите значение выражения:
1_ (2- • — + 30,6 • 1-^ • 0,1.
V 7 15 г)
753. Вычислите:
7:/А .1,05 — 0,308:0,11].
К пункту 33
754. Найдите значение выражения:
/одб и
а) 0,31Л289; е)
2УоМ
б) _ 4 V 0,81; ж) /2500 — /625;
755. Докажите, что верно равенство:
а) 5-(з-|/| + ]/0^5) = 2,5;
б) 11 : (0,151/1600 — 0,29^400) = 55;
в) (]/225 -Ь 3 |/I2l) : (j У1Щ + 0,78 KlOo] = 6;
г) /_6 Y\ + ^ • ^р) : /26 = 3.
К пункту 34
756. Решите уравнение:
ajiLzii+^+i^S; б) *=± -£±* = _ 18.
757. Зная длины а и Ь катетов прямоугольного треугольника,
найдите длину его гипотенузы:
а) а=3 слс, Ь=4 ам; б) а =2 см> 6=3 слг.
758. На рисунке 50 показано построение прямоугольных
треугольников. Известно, что
\OA\=\AB\ = \BC\ = \CD\ = \DE\=l.
Докажите, что:
а) | ОБ |=]/2; в) |OZ>! = |/~4;
б) |ОС|=]/3; г) |ОЯ| = |/~5.
759. Используя теорему Пифагора, постройте отрезок, длина
которого:
а) /6; б) УЛ.
760. Найдите область определения выражения:
*>V\x\l
б) У \х | + 1;
в) V 1*1-1;
г) V я2 + 9;
е) V4 —л2;
ж) У —л2 —5;
Ух
v 1
и) .
}/*2—16
0 7 А
Рис. 50
183
761. При каких значениях переменной имеет смысл выражение:
1 ч 4
а)7^Т; B)TWfl д)1^+4 + |Л5^; .
б) Whr; г) тЬг; е) VVT^ - у^^7
762. При каких значениях переменных о и 6 имеет смысл
выражение:
a) Vrt>; в) yW; д) ]/(а + 5)2;
б) 1/ а26; г) К - а&2; е) l/__l_?
г (а — Ь)2
763. Решите уравнение:
а) У~х~+1 = 1; е) К*2 + 9 - 5;
б) ]/";*; — 2=5; ж) )/* х2 — Зх = лг;
В) ]/5д: —4 - 0; з) ]/" 2х2 - 10х + 25 - *;
г) 0,5 ]/ л: + 4 - 3; и) |/ х + 4 - * — 2;
д) УЗх + 4 - — 10; к) j/1 — 2* = * + 1.
К пункту 35
764. Сократите дробь:
а) -^5 6)ii;
/11 К 7
/3
21/5
765. Упростите выражение:
а) (К"3 - 1) • (1 + 1Л8); в) (/1 -1^6) (]Аб + /"2);
б) (3 V~5 — 2) (2 + 3 ]/"5); г) (3 ]/"2+2 Kl0)(2 )Л~0—3]/2).
766. Представьте выражение в виде разности квадратов и
разложите его на множители:
а) 9а2—с, где с > 0; б) а—46, где а > 0 и 6 > 0.
767. Сократите дробь:
а) —; б) —= —; в) —= г; г) ———.
а — уъ УЪ +Уд (Ух — 3 Г 1-{-2 у^+а
768. Решите уравнение:
v Ж—-25 с *ч * — 4 л
а) -т= = 5; б) ——= = 4.
9 V ж + 5 ' ]/ж — 2
184
К пункту 36
769. Докажите, что:
а)2</8<3; в) 3,8 <УТъ <3,9;
б) 5 </30 <6; г) 7,2 </52 < 7,3.
770. Сравните числа:
a) /7 и —2,4; б) —/7 и —2,4.
771* Что больше:
а) /13 или КЗ +1/"10; г) 7 — К"2 или 5 + У~2;
б) j/30 или |/20-]/5; Д) 2]Л8 или /15;
в) /15 — 2 или /~3 + 2; е) 0,5/24 или /14?
К пункту 40
772. Расположите числа в порядке возрастания:
а) /40, /52 и 7; б) /12, /79 и 10.
773. Расположите числа в порядке убывания:
а) /60, 8 и /56; б) /47, /93 и 7.
774. Найдите границы значения выражения:
а) 10/ я, если 1 < х < 1,44;
б) l^L, если 4^ х <;б,25.
775. Решите неравенство:
а) 2 У~х > 5; б) А /"* < 2; в) 0,5 < ОД /~х < 0,8.
з
776. Постройте график функции:
а) У=— Ух; б) у=-У^х.
777. Решите графически уравнение и неравенство:
а) /"* = х, У~~х > *; б) У~х = -х, У~х <-х.
2 2
778. Решите уравнение:
а)]/"* = 2*; в)-—|/~ж = 0;
б) 1^~ж + Ъх = 0; г)х = 5|/~*.
185
779. Решите графически уравнение:
a) Ух=х—2; б) У~х=х—6.
780. Найдите область определения функции:
а) у = —==—; б) у = А
/* + 1 — 5 1 + /х + 10
К пункту 41
781. Назовите выражение, противоположное:
а) 5; в) ]/3; д) с; ж) т—п;
б) —15; г) — У7; е) —а; з) c+k.
782. Вычислите значение выражения (если оно имеет сгдысл):
а) У (- 12)2; в) К=1б"2; д) j/ - (- 15)2;
б)-1^Ж2; г)-К(-П)2; e)-V (-20)2.
783. Найдите значение выражения:
а) У(—х)2 при х = 9; —13; 1,6; —2,8;
б) У (т—п)2 при ттг = 25 и л = 10; m = 15 и я = 20;
т=— 30 и /г =40.
784. Вычислите:
а) )/~106; в) К^; д) У (- 10)*;
б) ^(=^; г) ]Л(=^р; е) j/JT^.
785. Найдите значение выражения, предварительно представив
подкоренное выражение в виде квадрата:
а) 1/Т3; в) /16*; д) У^¥; ж) /25^9;
б) У¥; г) /253; е) У~2^§; з) /8^18.
786. Замените выражение тождественно равным:
а) Т^Р, если х > 10; г) |/ 16с2, если с < — 25;
б) ]/"а2, если а < — 5; д) V^Jn2, если т > — 7;
в) V 4у2, если г/ > 100; е) Уп2, если л < 8.
787. Преобразуйте выражение:
а) V (р + 0,5)2, если р > 0; г) у (3 —А)2, если h > 20;
б) У (с —I)2, если с < 0; д) V(x — 5)2, если х > 0;
в) У ф + 2)2, если 6 > 4; е) К(# — б)2, если у < 10.
788. Упростите выражение:
a) V(2-V^T+V(V2r-lY', B)V(Vf-2f+V(V7-5)\
6)V(V3-5f+V(l-V9)2i г)1/(/15-2)2-1/(К15-3)а.
789. Решите уравнение:
а) ОД |/лГ2 = 2; в) |/Т2 - — *; д) ]/> — 2)2= 2 — *|
б) б]/*2 = 4; г) /(я—Ю)2 = я — 10; е) Уф+х)2 = 5 + х.
790. Решите неравенство:
а) 1/"Р>1; б) V~x2<2.
791. Постройте график функции:
ч У^ ч 1/~2 ч l^+X
а) у = ■х^-; г) у = —хух2; ж) у = -—^Г—;
б) У- -2^*2; Д) у==1/]? + я; з) */ = 0,5(*-уТ2).
в) I/ = # Ух2; ©) У = "К*2 — *§
К пункту 42
792. Вычислите:
а) У 196 • 0,81 • 0,36; г) ]/1,44 . 1,21 — 1,44 . 0,4;
б) V ХТб ' 54 " °'01 ; д) У 146'52 ~~109'52 + 27 * 256;
в) У 0,87 . 49 + 0,82 . 49; е) У 117,6а — 26,52 — 1440.
793. а) Найдите катет прямоугольного треугольника, если
гипотенуза равна 234 сл&, а другой катет 90 см.
б) Найдите площадь прямоугольника, если одна из сторон
равна 72 дм, а диагональ 97 для.
794. Представьте выражение УаЬ, где а<0иЬ<0, в виде
произведения корней.
187
795. Упростите:
а) Уб4а10Ь\ где о > О, Ь > 0;
б) У 36хУ\ где х > 0, у > 0;
в) У 25а16*4, где с < 0, х > 0;
г) У 81с1вж10, где с> 0, * < 0;
д) У0,01а40Ь12, где а > О, & < 0;
е) -Уб,25*14д14, где л: < 0, 6 < 0.
5
К пункту 48
796. Найдите значение корня
а)|/
б)]/
1552 —1242
164
98
в)
г)
V
l/:
1492-
4572 —
145,52
-762
38±2 '
— 9б,52
1762 — 1122 '
797. Упростите выражение:
а) V&?9 где х<0; в) °'2 У~Ш9 где а > °' Ь> 0;
б) j/g, где а > 0, & < 0; г) 4 ]/-^, где х < 0, z/< 0.
798. Представьте выражение 1/~, где а<0и КО, в виде
частного корней.
К пункту 44
799. Вынесите множитель из-под знака корня:
а) 0,5 КбО; в) 0,01 К~300; д) ]Д g; ж) ]/2 1;
б) 2J/150; г) 0,2^375; е) ]Л g; з) ]Л
800. Сравните числа:
а) - 1^200 и 10 |А"8; в) 0,5]/108 и 9 ]/"3;
5
б) 7]/| и 0,8/50; г) |/63 и 4,5^28.
188
13
32"
801. Упростите выражение:
а) 3J/18 — УТБ+ -1/Т47;
б) - ^200 + 2 ^50 — 4 У~Ъ\
5
в) zY^i-vu-vm + uY1^
r)fi300- 2У~Ъ2 — 12]/Т| + 5 ]/з-|-.
802. При каких значениях а и & верно равенство:
а) У~а?Ъ = аУЪ\ в) V~aFb=a?Vb\
б) уИ*Ь=—аУЪ; г) 1/о56=а3КЬ?
803. Вынесите множитель из-под знака корня:
а) ]/а*&, где а > 0, Ь > 0;
б) )/ 8а3Ь, где с < 0, Ь < 0;
в) К 98&V, где & > О, с> 0;
г) У 108о17&13, где с < О, Ъ < 0.
804. Представьте выражение в виде с|/Т, где с —
рациональное число и Ъ — натуральное:
*Vb ч>УЪ *i*Vb г) 120 у*
805. Упростите выражение:
а) aV~a — a2Y^—V~№\
806. Решите уравнение:
а)||^_2^ = }^_6.
б) 2^3^—41/3* =2—3VlJc;
в) 3 V2x — 5 V8ic + 7 УШс = 28.
189
807. Найдите значение выражения:
а) х2 — Ах + 3 при х = 2 + V~%\
б) хг — Ьх + 5 при х = 3 — К"2;
в) 2л:2— 6л: — 2 при л: = 1 — У^З;
уТз —1
г) 5х2 + 2х — 5 при х
5
808. Докажите, что значение выражения есть число
рациональное:
а) (2 ]/1 +5)(5-2|/""3) + (4-К"5)2+8|/~В;
б) 60К"3 — (5 V~2 — 1) (1 + 5 К"2) + (3 /"3 —10)2;
■o(^f-l)(l+SKD.
К пункту 45
809. Внесите множитель под знак корня:
а){Г8; e)3aj/I^f;
б) -|уТ8; ж) аЬ ]/|, где с> 0 и 6 > 0;
в) — хгУ~3; з) 2а& |/^, где а < 0 и Ъ < 0;
г) а* V^4; и) а6 V^T + Т' гдз а < ° и Ь > °-
д) —Зс У\ а;
810. Расположите числа в порядке возрастания:
&)-У72> УШ) и 7 /"2;
3
6)5]/-^, /17 и i|/62;
в) 8 К 0^2, /41 и J-J/250;
г) 12j/~0^, ]Л89 и |^160.
190
811. Внесите положительный множитель под знак корня:
а) (х—1) у j^Tv где *> 1;
б) (х + 5)у ^-g, где х > — 5;
в) (*+2)]/^, где *<-2;
г) (х — 4) "J/734. где л: > 4.
812. Внесите множитель под знак корня:
а) (Ь-1)УЪ; в) (x + l)V^l
б) (а + 2)/~5;
г) {х — 2)Y—x\
где 0 < а < 1;
где — 2 < а < 0.
е) (2 - а) |/51^4-
813. Решите уравнение:
a)(*-10)/F=4 = 0; г) (ж + 2) ]/^=| = 0;
б) (* + 4)]/^-2 = 0
в) (*-1)/^ = 0:
V __ ft
Д) ~—1Vr*=2 = 0;
е)
2х — 4
6 — 2*
9 — х
Ух — 9 = 0.
Глава IV
КВАДРАТНЫЕ УРАВНЕНИЯ
§ 13. РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
46. Графический способ решения квадратных уравнений
Задача. Одна сторона прямоугольника на 2 м меньше
другой, а площадь прямоугольника равна 8 ж2. Найти стороны
прямоугольника.
Решение. Пусть меньшая сторона прямоугольника
равна х м\ тогда другая сторона равна (х+2) м, а площадь —
х (х+2) м2. По условию задачи площадь прямоугольника
равна 8 ж2.
Следовательно,
х (х +2) =8.
Раскрывая скобки, получим:
*2+2х=8.
Решим уравнение графически. Для этого представим его в
виде
д;2=8 —2л:.
В одной и той же системе координат построим графики
функций у=х2 и у =8 — 2х (рис. 51). Парабола и прямая
пересекаются в точках А (—4; 16) и В (2; 4). При х=—4 и при х=2
соответственные значения выражений я2 и 8 — 2х равны,
поэтому числа —4 и 2 являются корнями уравнения я2=8 — 2ху
а следовательно, и корнями равносильного ему уравнения
х(х+2)=8.
По смыслу задачи значения х и х+2 должны быть
выражены положительными числами, значит, условию задачи
удовлетворяет только поло лейте л ьный корень уравнения. Задача имеет
единственное решение: длины сторон прямоугольника равны
2 м и 4 м.
При решении задачи мы встретились с уравнением, которое
после переноса всех его членов в левую часть имеет вид:
х2+2х — 8=0.
Всякое уравнение вида ах2+Ьл+с=09 где а,Ь и
с—некоторые числа, причем аф0,ах — переменная, называется квадрат-
ным уравнением.
192
Nil ' • " " \ \ Ы I I 1 MM
\\А-4И6\ Lrt И 1 /
MLi 1 | > P 1
W I 1 ! U 1 i</=X2|
1 il\ 1 I 1 1 i PI 1 1 1 1 r /1 1
IV-1 1 M1 MM/
I 1 M\ w 1 I M
И Y* i h M v
' ' V- г MiF
\' 'VM и M7
INilr lllllll
l\ 1 i 4[ 1 U 1 1 1 Iji
'\ ' \ ' i м м i/
M\ M N \4 111 11/M •
1 M 1 m I tf 1 j
1 i 1 i\jj i | I I и
1 1 1 1 j V 1 i
1 1 1 4i! i i i i\i 1 1 1 1 1 /1 1 1 !
1 ч IV 1 M rk'l M/l
ими L \ и/ i
! и '\i 1 и!
1 \ Mf N / I
\ ' \ / M
l\M ' 4 ' М/ч М
\ I 1 M M'1 1
\ /. \StB(2-M
\ Al II 1
M\ i м N '/Pi И
\ M i i / W \\\
\' M / \
I I \\\\ г Мл M К И
И \ U У 4
i \i I/ К
МММ • тФгi И' v
-4 -J \-2 \-1 Щ I 1 \ 2 \3 UK
I M i I I 4 M I I IN
j /j I I j I | I I I I
I I Л
p. I
\ 1 I I I I | I |//j I j j I I | I 1 |
\ii i 1 A 1 i / i 1
1 nl 1 1 1 1 1 1 \i/ 1 1 1 1 1 I 1 i 11 I
|Ш(-Д7;75.7)Г ' И И |/Ч
\ \\ !i M 1 I
l\ \in\ ' // у 1 1
1\ 1 1 \ W\ J_ W I
M\ \ M iff M i /i M
i i \ \i 1 i l i 1 i /i 1
111 Vc* | \ \in 1 I l/
i 11VJ i L! 11
1 1 1 Vх I f I 1 1
'11 iVt-o \ q\ I i I1 !
M\ i\^' I M /i M
1 j 1 1 \ \ | 711 / I ' 1
i i 1 i \l 1 X i 1 1 1 1 1 1 1/ 1 1 1 i
I \\ \r 1 M / ! 1 И
Ui IN 1 M м/ М
N 1 \li M i i/i 1 I
M IV V5 /MM
и V M / ii
Ml m V i /1 И
1 ! M\ H M'M
\ \H i/i M
\ И Л / |
N I \ 1/
4 j \/i '''И
M 1 К МЩ7;п,я)
МММ lvM>№ \' и 11
1-4 -J -2 И \Щ V 1 2 3T IX
1 1 1 1 1 4 Mi 1 1
И Г \ M
1 1 И о \ 1
1 Г \ 1
M \
\
Рис. 51
Рис. 52
В уравнении х2 + 2х—Ъ = О а = 1; Ь== 2; с = —8.
Коэффициент а условились называть первым коэффициентом
квадратного уравнения, коэффициент Ъ — вторым, ас —
свободным членом.
Чтобы решить графически квадратное уравнение ах2+Ъх +
+с=0, целесообразно записать уравнение в виде
ах2 = —Ъх — с
и построить в одной и той же системе координат графики
функций у = ах2 и у =—Ъх — с.
Абсциссы точек пересечения графиков являются корнями
уравнения ах2+&хтс=0.
Если графики не имеют общих точек, то уравнение не имеет
корней.
7 Алгебра, 7 кл.
193
Приступая к графическому решению квадратного
уравнения, часто бывает удобно предварительно разделить все его
члены на первый коэффициент. Например, для графического
решения уравнения
2*2+6х — 5=0 (1)
заменим его равносильным уравнением:
х*+3х — 2,5 =0. (2)
Представив уравнение (2) в виде
*2=—Зх+2,5,
найдем абсциссы точек пересечения параболы у=х2 и прямой
у = — 3*+2,5 (рис. 52).
Приближенные значения корней: —3,7 и 0,7.
Квадратное уравнение, первый коэффициент которого равен
единице, называется приведенным. Графическое решение
приведенных квадратных уравнений имеет то преимущество, что,
используя одну и ту же параболу у=х2, можно решить большое
число уравнений.
814. Решите графически уравнение:
а) х* + гх — 4=0; д) 12л;2—6х+1 = 0;
б) х%— 2х — 3=0; е) 3*2+12*+10 = 0;
в) х2+3х—1=0; ж) — 4*2+Зх+7=0;
г) х2+2*+5=0; з) 9*2+6х+1 = 0.
815. Решите графически уравнение и неравенства:
а) ха=*+2; б) *2+х=12; в) х2—2= 0,4*;
х2>*+2; х2+х—12 >0; х2—2 > 0,4*;
х2 <х+2; х2 + х—12 <0; х2—2 <0,4*.
47. Решение квадратных уравнений выделением квадрата
двучлена
В предыдущем пункте при решении задачи мы получили
уравнение
*2 + 2*=8. (1)
Это уравнение было решено графически. Нельзя ли решить
его, не прибегая к построению графиков?
Уравнение (1) равносильно уравнению
х2+2х — 8=0. (2)
Трехчлен х2+2х— 8 лишь свободным членом отличается от
трехчлена *2+2х+1, тождественно равного квадрату двучлена
х+1. Прибавим к левой части уравнения (2) сумму
противоположных чисел 1 и —1.
194
Получим:
х2+2х — 8=(*2+2*+1) — 1— 8=(*+1)2— 9.
Мы выделили в левой части уравнения (2) квадрат
двучлена. Уравнение (2) равносильно уравнению
(* + 1)2— 9=0. (3)
Разложим левую часть уравнения (3) на множители как
разность квадратов:
(х+4)(х— 2)=0. (4)
Числа —4 и 2 — корни уравнения (4). Так как уравнение
(4) равносильно уравнению (1), то корни уравнения (1): —4 и 2.
Решим еще несколько уравнений вида ах2+Ьх+с=09
применяя способ выделения квадрата двучлена в левой части
уравнения.
Пример 1.
х2+13*+40=0. (5)
Из трехчлена я2+13я+40 выделим квадрат двучлена. Если
рассматривать х2 как квадрат первого члена двучлена, а 13*—
как удвоенное произведение первого члена на второй (13л: =»
= 2х • — , то вторым членом двучлена должно служить число
13
—. Прибавим к левой части уравнения (5) сумму
противоположных чисел { —) и —{ —) и преобразуем левую часть
уравнения в произведение:
х2 + 13*+40 = х2 + 2х • ^ + № i2- № + 40 =
/ ,13^2 169 . лг. I , 13\2 9 ' , ow , кч
= Г+ г"]-Т+ Г + "г) — 7 = ^ + 8)(^+5)-
Уравнение (5) примет вид:
(х+8)(х+5)=0.
Его корни: —8 и —5.
Пример 2.
Зх2—11* — 20-0. (6)
Выделив квадрат двучлена из выражения Зх2—Их — 20,
получим:
Зд:2—11л: — 20 = 3|> — -х — -) =
3 3
б " ' 36/ 36
= 8|^-2.S« + ^-^_f)-8((x-S)'_«)_
=3(('-$-m*-^1h3*-»hi}
195
Уравнение (6) равносильно уравнению
8(*-б)(* + -|) = о. ,:
Следовательно, уравнение (6) имеет корни и 5.
з
Пример 3.
4*2—4х+1 = 0. (7)
Трехчлен в левой части уравнения тождественно равен
квадрату двучлена 2х—1. Значит, уравнение (7) можно записать
в виде
(2х—1)2=0.
Очевидно, что левая часть уравнения обращается в нуль
1
только при х== —.
2
Уравнение (7) имеет единственный корень, равный —-.
Пример 4.
*2+10х+26=0. (8)
Так как *2+10*+26=(х2+2х-5+ 25)—25+26=(*+5)2 + 1, то
уравнение (8) примет вид:
(х+5)2+1=0.
Выражение (#+5)2+l при любом значении переменной х
положительно, следовательно, уравнение (8) не имеет корней.
816. Решите уравнение, выделяя квадрат двучлена:
а) х2— 2х — 35=0; д) х2+х — 2=0;
б) *2+8* —20=0; е) 4*2+12;с+9= 0;
В) X*+Q4=— 16x; ж) 5*2+3*—8=0;
г) 8+7х=х2; з) 2*2— 9* +10=0.
817. Докажите, что уравнение не имеет корней:
а) г2 +142 +50=0; в) Зх2— 7л:+5= 0;
б) у2—Ну +32 = 0; г) Юл:2— *+1 = 0.
48. Формула корней квадратного уравнения
Мы научились решать уравнения вида ах2+Ьх+с=0
графически и путем выделения квадрата двучлена в левой части
уравнения. Первый из этих способов не обеспечивает высокой
точности значений корней, второй — требует в каждом случае
196
выполнения громоздких преобразований. Поэтому удобнее,
решив квадратное уравнение в общем виде, вывести формулу
его корней.
Для решения уравнения
ax2+bx+c=09 где аФО, (1)
воспользуемся уже знакомым нам приемом выделения квадрата
двучлена:
ах2 + Ъх + с = а \ х2 -\— х + — ] =
\ а а ]
Ц 2а 4а2/ 4а2 а/ 1\ 2а) 4а2 j
Обозначим выражение Ъ2—4ас буквой D. Тогда
ах2 + Ъх + с = а ((х А )
Пусть значение D отрицательно. Тогда отрицательно и
значение дроби — (знаменатель дроби положителен, так как а
4а2
отлично от 0). В этом случае выражение (х-\ )
положительно при любом х> и уравнение (1) корней не имеет.
Пусть значение D равно 0. Тогда равно 0 и значение дроби
—. Уравнение (1) примет вид:
4а2
■(*+=)■-*
Так как афО, то
х + - - 0.
2а
Отсюда
_ __ j>_
2а
Уравнение (1) имеет единственный корень, равный .
2а
Пусть значение D положительно. Представим дробь — з
4а2
виде квадрата: — =(l1R) . Тогда уравнение (1) будет равно-
4а2 \ 2а )
сильно уравнению
197
Разлагая разность квадратов на множители, получим:
\ 2а 2а )\ 2а 2а )
Так как а=^9, то
Отсюда
2а 2а 2а 2а
_ь _ Yd — ь + Vd
х = ^— или х =
2а ~~ 2а
Принята следующая краткая запись:
—b±V~D
х = •
Х 2а
(А)
Мы видим, что наличие корней у квадратного уравнения и
их число зависят от выражения D=&2 — 4ас. Это выражение
называют дискриминантом квадратного уравнения
(«дискриминант» по-латыни — различите ль).
В зависимости от знака дискриминанта различают три
случая:
если D <0, то уравнение не имеет корней; если .0=0, то
уравнение имеет один корень ; если D >0, то уравнение
2а
имеет два корня, которые могут быть найдены по формуле (А).
Заметим, что формулой (А) можно пользоваться и в том
случае, когда D=0. Действительно, при jD=0 формула (А) примет
вид:
х = -ъ±Уо т< е> ж„±.
2а 2а
Таким образом, формула (А) применима к любому
квадратному уравнению, имеющему корни.
Рассмотрим примеры решения квадратных уравнений с
использованием выведенной формулы.
Пример 1. 12*2+7х+1 = 0.
В этом уравнении а = 129 &=7, с = 1.
Найдем дискриминант:
D=72— 4121=1.
Так как дискриминант положителен, то уравнение имеет
два корня, которые можно найти, воспользовавшись формулой
(А):
—7 + ^1 ^ 1 1
х = ^—• Корни уравнения: — -^ и — -^ •
198
Пример 2. х2—12*+36=0. Так как а=1, &=—12,
с=36, то Z) =(—12)2— 4-1-36 =0. Уравнение имеет единственный
корень: х = ~— = 6.
Пример 3. 7л;2—25* + 23 = 0.
Здесь а =7, Ь =—25, с =23.
Дискриминант JD=(—25)2—4-7-23=625 — 644. Так как
дискриминант отрицателен, что уравнение не имеет корней.
Если хотя бы один из коэффициентов Ъ или с квадратного
уравнения ax2+bx+c=0 равен нулю, то такое квадратное
уравнение называется неполным.
Приведем примеры неполных квадратных уравнений:
1) 3*2+17*=0. Здесь а=3, &=17, с=0.
2) 4*2—121=0. В этом уравнении а =4, Ь=0, с=—121.
Как мы знаем, неполные квадратные уравнения легко
решаются разложением на множители левой части уравнения:
1) 3*2 + 17*=0, *(3*+17)=0, х=0 или * = —-;
о
2) 4*2 — 121 = 0, (2х+ 11) (2х— 11) = 0, * = —5- или * = 5-.
Можно решать неполные квадратные уравнения и по
формуле (А), но это менее удобно, чем решение путем разложения
левой части уравнения на множители.
Решим, например, рассмотренное выше неполное
квадратное уравнение 4*2—121=0 по формуле (А).
Дискриминант D уравнения равен О2 + 4-4-121=16-121.
Применяя формулу (А), имеем:
0±VW7w_^±*1n Жв_5!Или*=5±
*— 8 8 2 2
Мы видим, что решение уравнения 4х2 —121 =0 путем
непосредственного разложения левой части на множители проще,
чем по формуле.
Уравнение 7я2=0, в котором а =7, Ь=0, с=0, также
является неполным квадратным уравнением. Очевидно, что это
уравнение имеет только один корень — число нуль.
818. В уравнении вида ax2+bx+c=0 назовите коэффициенты
а, & и с, вычислите дискриминант и укажите число корней
уравнения:
а) 2х2+Зх+1 = 0; в) 2*2 + х+1 = 0;
б) 3*2+7*+2 = 0; г) 5*2 — 2х — 3 = 0;
199
д) х2+5х — 6=0; ж) 9л:2— 6*+1 = 0;
е) л:2+2л:+2=0; з) 4л:2— 7х— 2- 0.
819. Решите уравнение по формуле (А):
а) 3*2+7*+4:=0; ж) 4х2+х— 3 = 0;
б) 5л:2— 8д:+3 = 0; з) 2л:2—Зл:— 9=0;
в) 2л:2— 7х+3=0; и) л:2—Зл:— 40= 0;
г) 2л:2 + 11л:+9=0; к) л:2+7х—60= 0;
д) 2л;2— 9л:+9=0; л) 12л:2+7* =0;
е) Зл:2—13л:+14=0; м) 81л:2—49=0.
820. Решите уравнение:
а) 5л:2 = 9л:+2; д) г— 5=22— 25;
б) — л:2+Зл:+40=0; е) 2+5=22+25;
в) 14=л:2+5л:; ж) 0,7х2 = 1,Зл:+2;
г) —Зл:2+8 = 10л:; з) 7=0,4i/+0,2i/2.
821. Приведите уравнение к виду ал;2+&л;+с=0 и найдите его
корни:
а) (л:+4)2=Зл:+40; в) (Зл:—1)2=4(л:+1)2;
б) (2х—3)2=11л:—19; г) 4(*+3)а=(*—5)2.
822. Найдите методом границ приближенные значения корней
уравнения:
а) 5л:2—х—1=0; б) 2*2+7*+4=0.
Указание. В качестве приближенных значений арифметического
квадратного корня с недостатком и с избытком возьмите две последовательные
десятичные дроби с двумя знаками после запятой.
49. Другой вид формулы корней квадратного уравнения
Корни квадратного уравнения ал:2+&л:+с=0 могут быть
найдены, как известно, по формуле
х=-Ъ~^В, где D = 62-4ac. (А)
Иногда при решении квадратных уравнений удобно
пользоваться формулой корней, записанной в другом виде.
Разделим числитель и знаменатель дроби ~"ь ± VD на 2 и
2а
внесем множитель — под знак корня. Получим:
л
— - + — YD — — ±y±L
-Ъ±УР = 2 - 2 = 2 V 4
2а а а
200
Так как D = Ъ1 — 4ac, то — = = ас, т. е.
4 4 4
D /Ь\2
— = — —ас.
4 \2)
Формула корней квадратного уравнения примет вид:
* = , где — = т —ас. (В)
а 4 \ 2 /
Формулой, записанной в таком виде, можно пользоваться
для решения любого квадратного уравнения, дискриминант
которого неотрицателен (очевидно, что если D^O, то и —^0).
4
Обычно на практике ее применяют в том случае, когда Ъ — чет-
ъ
ное число и, значит, целое число.
Пусть, например, требуется решить уравнение
9х2—14х+5 = 0.
Применим формулу (В). Здесь —=—7, а =9, с =5.
Л =(_7)2 —9-6 = 4.
4 v
7=fc]/*4
9
5 i
Я =: — ИЛИ X = 1.
9
5
Корни уравнения: — и 1.
Заметим, что использование формулы (А) привело бы к
более сложным вычислениям.
Приведем еще пример. Решим уравнение
5л:2 + 8х-г6=0.
h D
В этом уравнении — = 4, а = 5, с = 6. — = 42— 5 • 6 =—14.
Мы нашли, что отрицательное число. Знак — совпадает
4 4
со знаком D. Так как дискриминант отрицателен, то уравнение
не имеет корней.
201
823. Решите уравнение:
а) З*2—14*+ 16 = 0;
б) 5*2—6*+1 = 0;
в) *2+2*—80=0;
г) ж2—10*—24=0;
д) *2—22*—23=0;
824. Решите уравнение:
а) *2— 1,6*— 0,36=0;
б) *2—2*+0,91 = 0;
в) *2 +6*+19,7=0;
е) 4*2—36*+77=0;
ж) 15у2—22у— 37=0;
з) З*2+32*+80=0;
и) 7za—202+14=0;
к) у2—52^+576 = 0.
г) 8*2—4* +0,5=0;
д) 2*2—10*+12,5=0;
е) -i*2+2*—9 = 0.
825. При каких значениях * верно равенство:
а) (3*+1)2=3*+1;
б) (3*+1)2=3(*+1);
в) (3*+4)2=4(*+3);
г) 4(*+3)2=(4*+3)2;
д) 4(*+3)2=(2* + 6)2;
е) 9(*—4)2=4(*—9)2?
826. Существует ли такое значение с, при котором верно
равенство:
а) Зс+0,6=9а2+0,36; б) 0,4а+1,2=0,16а2+1,44?
827. Решите уравнение:
ж2 +1
а)
б)
в)
2
ж2 + 3
в
Зл + 4
— * = 2;
х + 4
3
ж2 — 4ж
= 5;
10
:--1;
г)
Д)
е)
ж2 — 4 2* + 3
8
(V + I)2
5
1-У
= 1;
_£.
12 4 2'
3 —у Jf —2 . (у—2)2
8
828. Найдите множество корней уравнения:
а)
б)
в)
г)
Д)
2жа
ж—2
ж2 —6ж
ж—5
2ж — 1
ж + 7 ~
бу_+1 =
У + 1
ж
7ж —6
ж-25
5
+
ж-5'
Зж + 4
У + 2.
У
5
ж—2 х+2 ж2 —4
е)
ж)
з)
и)
к)
Зх + 1 * — 1
-2
4
1;
г/
* + 2
4
9y2-l" Si/4-1 1-3#
4 5 1
-0;
1;
ж + З 3 —л: л: —3
2л:+1 3(2л: —1) 8л:
0;
2л:—1 7(2х + 1) 4л:2 —1
2У-5 У + 2 у-5 = ^
У2—By y2 + 3y
■9
202
829. а) Существуют ли такие значения переменной у, при
которых равны соответственные значения суммы дробей
У-JL- и и кх произведения?
б) Существуют ли такие значения переменной у, при
которых равны соответственные значения разности дробей
и __L_ и их произведения?
«Г — -* У + 2
830. Найдите множество значений £, при которых уравнение
не имеет корней:
а) Зх2—2x+t=0; в) 4х2 +tx+l = 0;
б) 5.т2+18лг+*=0; г) 48x2+tx— 5=0.
831. Найдите множество значений i>, при которых уравнение
имеет два корня:
а) 10*2+40*+i;=0; в) их2—6х + 1 = 0;
б) 2*2+1>*+18=0; г) 7x2+vx— 25 = 0.
832. При каких значениях k уравнение имеет один корень:
а) 16*2+й>*+9 = 0; в) kx2—100* +fe= 0;
б) 15*2—90*+й = 0; г) 25*2 +kx + 2 = 0?
50. Задачи, приводящие к решению квадратных уравнений
Многие задачи геометрии, физики, техники приводят к
квадратным уравнениям.
Рассмотрим, например, следующую задачу.
i Тело брошено вертикально вверх с начальной скоростью
40 м/сек. Через сколько секунд тело окажется на высоте 60 м?
Решение. В курсе физики доказывается, что если не
учитывать сопротивление воздуха, то высота, на которой
окажется тело, брошенное вертикально вверх, может быть найдена
по формуле
h = vJ—- l\
2
где h — высота в метрах, t — время в секундах и i>0 —
начальная скорость тела, выраженная в м/сек, g — ускорение
свободного падения в м/сек2. Подставим в формулу заданные значе-
( ния i>0 и А и будем считать, что — & 5*:
* Ускорение свободного падения в условиях Земли g ~ 9,8 м/сек2 здесь
округлено до 10 м/сек2.
203
60 =Ш—5t\ отсюда
t2—8*+12=0.
Решая квадратное
уравнение, находим его корни:
2 и 6.
На рисунке 53 дан
график зависимости h от t9 где
h = 40f — 5*2.
Рассматривая график, мы замечаем,
что тело, брошенное
вертикально вверх, в течение
первых 4 сек поднимается
на высоту 80 м, а затем
начинает снижаться и падает
на землю. На высоте 60 м
от земли тело оказывается
дважды: через 2 сек и через
6 сек после бросания.
Таким образом,
условию задачи удовлетворяет
любой из найденных
корней.
Рассмотрим другую
задачу.
Моторная лодка прошла 42 км по течению реки и 20 км
против течения за 5 ч.
Найти собственную скорость лодки, если известно, что
скорость течения реки на всем участке пути равна 2 км/ч.
Решение. Пусть х км/ч — скорость лодки в стоячей
воде, тогда скорость лодки по течению реки (х+2) км/ч, а
против течения (х—2) км/ч.
Время, затраченное на прохождение 42 км по течению реки,
ч, а время, за которое лодка прошла 20 км против тече-
W
т
L/7/l-L
гУОт
i 1
1
1
г/ит
1
1
гТт
m
; !
m
70
гсСгт
1
L-7/7-L
1 1
!
■
1 /
1/1
У1
/
1\
I
1
, 1
1
|У
2
5
1
г
i I \
\
1\г
\ Л NUI
51 6 | 7 | в цсёю
Рис. 53
х + 2
ния реки
20
* —2
Время, затраченное лодкой на весь путь, равно
Следовательно,
42
: + 2
+
20
Ч.
42
х + 2
+
20
(1)
По смыслу задачи собственная скорость лодки должна быть
больше скорости течения, значит, искомое значение х должно
удовлетворять неравенству
х>2.
204
Решение уравнения (1) сводится к решению системы:
\Ъх2— 62*+24 = О,
\(х+2) (Х — 2)Ф0.
Числа ~ и 12 — решения системы, из них только число
5
12 удовлетворяет условию х>2.
Следовательно, задача имеет единственное решение:
собственная скорость моторной лодки равна 12 км/ч.
833. а) Произведение двух натуральных чисел, одно из
которых на 6 больше другого, равно 187. Найдите эти числа,
б) Представьте число 120 в виде произведения двух чисел,
одно из которых на 2 меньше другого.
834. а) Найдите периметр прямоугольника, длина которого
на 4 см больше ширины, а площадь равна 60 см2.
б) Периметр прямоугольника равен 62 м. Найдите его
стороны, если площадь прямоугольника 210 м2.
835. а) Произведение двух последовательных натуральных
чисел больше их суммы на 109. Найдите эти натуральные
числа.
б) Квадрат суммы двух последовательных натуральных
чисел больше суммы их квадратов на 112. Найдите эти
натуральные числа.
836. а) Доска прямоугольной формы имеет площадь, равную
4500 см2. От нее отрезали часть прямоугольной формы
той же ширины и длиной 120 см. Оставшаяся часть доски
представляет собой квадрат. Найдите сторону этого
квадрата.
б) От листа оконного стекла квадратной формы отрезали
прямоугольную полосу шириной 40 см. Оставшаяся
прямоугольная часть стекла имеет площадь 3200 см2. Найдито
размеры куска стекла, от которого отрезали полосу.
837. а) Числитель некоторой обыкновенной дроби на 1 больше
знаменателя. Если к числителю дроби прибавить 3, а к
знаменателю 18, то полученная дробь будет меньше
исходной на 1. Найдите исходную дробь.
б) Числитель некоторой обыкновенной дроби на 4 меньше
знаменателя. Если числитель уменьшить на 3, то
полученная дробь будет вдвое меньше исходной. Найдите эту
дробь.
20 §
838. а) Спортивная площадка прямоугольной формы имеет
площадь, равную 840 м2. Если ширину площадки увеличить на
4 м, а длину уменьшить на 5 м, то ее площадь не
изменится. Найдите размеры спортивной площадки.
б) Площадь земельного участка прямоугольной формы
была равна 1200 м2. После увеличения длины участка на
8 м, а ширины на 6 м его площадь увеличилась на 528 м2.
Найдите первоначальные размеры участка.
839. а) В зрительном зале сельского клуба было 160 мест. При
расширении зала число мест в каждом ряду увеличили на
2, а число рядов увеличили на 1. В результате в зале
стало на 38 мест больше, чем было первоначально. Сколько
рядов в зрительном зале?
б) Для перевозки 150 туристов предполагалось выделить
несколько автобусов, но так как приехало на 18 туристов
больше, то добавили еще один автобус и в каждый
посадили на 2 человека меньше, чем предполагали
первоначально. Сколько автобусов было выделено для перевозки
туристов?
840. а) Катеты прямоугольного треугольника относятся как
8 : 15, а гипотенуза равна 6,8 м. Найдите площадь
треугольника.
б) Отношение гипотенузы прямоугольного треугольника
к его катету равно 13 : 12, а другой катет равен 15 см.
Найдите периметр треугольника.
841. а) Повысив скорость поезда на 10 км/ч, удалось
сократить на 1 ч время, затрачиваемое поездом на
прохождение пути в 720 км. Найдите первоначальную скорость
поезда.
б) Велосипедист проехал расстояние 67 км за 4 ч,
причем на последних 27 км пути его скорость была на 2 км/ч
больше, чем на предыдущем участке пути. Сколько
времени затратил велосипедист на последние 27 км пути?
842. а) Два автобуса отправились одновременно из города в
пионерлагерь, расстояние до которого 72 км. Первый
автобус двигался со скоростью, превышающей скорость
второго автобуса на 4 км/ч, и прибыл в пионерлагерь на
15 мин раньше, чем второй автобус. Найдите скорость
каждого автобуса.
б) Из пункта А в пункт В, расстояние до которого 33 км,
одновременно выехали два велосипедиста. Один из
велосипедистов, двигаясь со скоростью, превышающей
скорость второго велосипедиста на 4 км/ч, прибыл в пункт В
на 48 леи» раньше, чем второй. Сколько времени находился
в пути каждый велосипедист?
206
843. а) Теплоход прошел 9 км по озеру и 20 км по реке (по
течению) за 1 ч. Найдите скорость теплохода в стоячей воде,
если скорость течения реки равна 3 км/ч.
б) Турист проплыл по реке на лодке 6 км против течения
и 15 км по озеру, затратив на путь по озеру на 1 ч больше,
чем на путь по реке. Зная, что скорость течения реки
равна 2 км/ч, найдите скорость лодки в стоячей воде.
844. а) Моторная лодка прошла 45 км по течению реки и 22 км
против течения, затратив на весь путь 5 ч. Найдите
скорость лодки в стоячей воде, зная, что скорость течения
равна 2 км/ч.
б) Катер, развивающий в стоячей воде скорость 20 км/ч,
прошел 36 км против течения и 22 км по течению реки за
3 ч. Найдите скорость течения реки.
845. На расстоянии 80 м переднее колесо повозки сделало на
8 оборотов больше заднего. Найдите длину окружности
каждого колеса, если известно, что длина окружности
переднего колеса на 0,5 м меньше длины окружности
заднего колеса.
846. а) При уборке урожая с каждого из двух участков
собрано по 180 т картофеля. Площадь второго участка была
на 2 га меньше, чем площадь первого участка. Сколько
тонн картофеля собрано с одного гектара на каждом
участке, если урожай картофеля на втором участке был на
3 т с гектара больше, чем на первом участке?
б) При уборке урожая с каждого из двух участков
собрано по 210 ц пшеницы. Площадь первого участка была на
0,5 га меньше площади второго участка. Сколько
центнеров пшеницы собрано с одного гектара на каждом
участке, если урожай пшеницы на первом участке был на 1 ц
с гектара больше, чем на втором участке?
51. Квадратные уравнения с параметрами
Рассмотрим квадратное уравнение
З*2 — Ьах — 2а2 = 0.
Дискриминант этого уравнения:
D = 25а2 + 24а2 = 49а3
при всех значениях а неотрицателен, значит, уравнение имеет корни при любом
значении а.
Если а = 0, то D = 0; уравнение имеет единственный корень. Этот корень
можно найти, подставив значение а в уравнение. Получим: З*2 = 0, х = 0.
Если а Ф 0, то D > 0; уравнение имеет два корня.
207
По формуле (А) находим:
5с -+- ]/"49а3 5а ± \ la \
х —
6 6
При а > 0 | 7а | = 7а и корни уравнения вычисляются по формуле
5а ±7а
х = .
6
При а < 0 | 7а | = —7а и корни уравнения вычисляются по формуле
5а±7а
х = .
6
Таким образом, при любом а, отличном от нуля, уравнение имеет два
корня, которые вычисляются по формуле
5а ± 7а 1
х _ т> е# £ __ _ а или ^ _ 2а.
6 3
1
Ответ. При афО уравнение имеет два корня: — —а и 2а; при а = О
3
уравнение имеет единственный корень, равный 0.
Рассмотрим уравнение относительно х:
х (2* + 5) — Ъ (х + 3) = 3.
Чтобы решить его, представим это уравнение в стандартном виде. Получим
квадратное уравнение:
2*2 + (5 — Ь) х — 3 ф + 1) = 0.
Найдем дискриминант уравнения:
D = (5 — Ь)а + 24 (Ь + 1) = 25 — 10Ь + Ь2 + 245 + 24 = Ь2 + Ш + 49 = ф + 7)2.
При любом значении Ь дискриминант неотрицателен. Значит, при любом Ь
уравнение имеет корни.
Если Ь= —7, то D = 0 и уравнение имеет единственный корень. Подставив
в уравнение значение Ь, равное —7, найдем, что х = —3.
Если Ъ Ф —7, то D > 0 и уравнение имеет два корня. По формуле (А)
b-b±VW+W . &_5 + |Ь + 71
* 4 ' *~ 4
Так как | Ь+7 |= &+7 при Ь>— 7 и | Ь+7 | = — (Ь + 7) приЬ<— 7, то корни
уравнения можно найти по формуле
Ь — 5 ± ф + 7)
# = .
4
Ь+1
Корни уравнения: и —3.
2
Ответ. При Ъ——7 уравнение имеет единственный корень—3, при Ъф—7
уравнение имеет два корня: и —3.
2
847. Решите относительно х уравнение:
а) х2+2Ьх—Ш2=0; в) *2—2£*+4fe—4=0; д) 2л:2—(а+5)*+а+3=0;
б) 18*2—15а*+2а2=0; г) х2—6*+9—а2=0; е) З*2—(*—5)*—2*—2=0,
208
52. Теорема Виета
Уравнение
5*2_ 4х—12-0
имеет корни —1— и 2. Сумма корней равна —, а произведение
5 5
12
_ 5"
Нетрудно заметить, что сумма корней рассматриваемого
уравнения равна отношению второго коэффициента к первому,
взятому с противоположным знаком, а произведение корней
равно отношению свободного члена к первому коэффициенту.
У всякого ли квадратного уравнения, имеющего два корня,
сумма и произведение корней обладают теми же свойствами?
Известно, что квадратное уравнение ах2 + Ьх+с=0 имеет
два корня при D > 0. Обозначим их через хх и х2.
—Ъ — УТ> __ —ъ + УЪ
^и — 7TZ » ^2 —
2а ' 2 2а
Найдем сумму и произведение корней:
-Ъ — УЪ —ь + УЪ __ —2Ъ == _ А:
2а ' 2а ~' 2а а
- У~5 . —& + УТ) (—Ь)2 — (У1>)2
%i i Х% — ■
Итак,
2а 2а 4а2
Ь2 — D __ Ь2 — (Ь2 — 4ас) __ 4ас _ _с_
4а2 4а2 4а2 а'
а а
При D = 0 квадратное уравнение ax*+bx+c=0 имеет
единственный корень, который может быть найден по формуле
■Ь±У1)
X =
2а
Если условиться считать, что при D = 0 квадратное
уравнение имеет не один корень, а два равных корня, то вывод
распространяется на любое квадратное уравнение, имеющее корни.
Итак, справедлива теорема:
Сумма корней квадратного уравнения ах2-\-Ьх-{-с=0 равна
, а произведение корней равно —.
a a
Эта теорема называется теоремой Виета, по имени
знаменитого французского математика Франсуа Виета (1540—1603).
209
Виет — юрист по образованию, заинтересовавшись астрономией и
математикой, быстро добился известности благодаря найденным им общим методам
решения уравнений 2-й, 3-й и 4-й степени. Виет впервые стал использовать
буквенную символику для обозначения не только неизвестных величин, как делали
до него, но и для обозначения коэффициентов. Он внес большой вклад в
развитие математики, но сам из всех своих открытий больше всего ценил
установление зависимости между коэффициентами уравнения и его корнями.
В случае приведенного квадратного уравнения
соотношения между его корнями и коэффициентами принимают более
простой вид. В самом деле, если в уравнении ax2+bx+c=0,
имеющем корни, коэффициент а равен 1, то сумма корней
равна —Ъ, а произведение корней равно с, т. е. сумма корней
приведенного квадратного уравнения равна второму коэффициенту,
взятому с противоположным знаком, а произведение корней
равно свободному члену.
Рассмотрим, например, уравнение
х2—7х+10=0.
Так как дискриминант положителен (D=(—7)2—4-10=9), то
уравнение имеет два корня. Пусть ххл х2 — корни уравнения.
По теореме Виета ^i+x2=7, x1-x2=10.
В тех случаях, когда нужно составить квадратное уравнение
по его корням, применяют теорему, обратную теореме Виета.
Если числа тип таковы, что их сумма равна — р, а
произведение равно q, то эти числа являются корнями уравнения
x2+px+q=0. (1)
Докажем это.
По условию т + п = —р и тп = q. Заменив в уравнении (1)
коэффициенты р и q соответственно на т + п и тп, получим:
х2 —- (т + п) х + тп = 0. (2)
Преобразуем левую часть уравнения:
х2 — (т + п) х + тп = х2 — тх — пх + тп = х (х — т) — п (х — т) =
= (х — т) (х — /г).
Очевидно, что уравнение (х — т) (х — п) = 0, равносильное уравнению (2),
имеет корни типы никаких других.
Следовательно, числа т и п, и только они, являются корнями уравнения
х2 + рх + q = 0.
Пусть, например, нужно составить квадратное уравнение
с корнями —15 и 22.
Коэффициенты р и q приведенного уравнения x2+px-\-q=Q,
имеющего данные корни, можно найти из равенств:
р=— (—15+22); q=—15-22.
210
Получим: р=—7; q=—330.
Значит, приведенное уравнение, имеющее данные корни,
будет иметь вид:
*2_7x — 330=0. (3)
Очевидно, что можно составить сколько угодно квадратных
уравнений, имеющих данные корни —15 и 22. Для этого
достаточно умножить все члены уравнения (3) на любое, не равное
нулю число. Например, умножая уравнение (3) почленно на 2,
получим: 2л:2—14* — 660 =0.
848. Не решая уравнения, найдите сумму и произведение его
корней (если они существуют):
а) 2х2—9х—10 =0; д) i г2 + г — 7 = 0;
б) 5л;2 +12* +7 = 0; е) З*2— 8х+10=0;
в) *2_37д:+27 = 0; ж) 4у2—19=0;
г) у2 +41у—371 = 0; з) х2— 210л: =0.
849. а) В уравнении х2+рх—35=0 один из корней равен 7.
Найдите другой корень и коэффициент р.
б) В уравнении л;2—13x+q=0 один из корней равен 12,5.
Найдите другой корень и коэффициент q.
850. а) В уравнении 5л:2+&л:+24=0 один из корней равен 8.
Найдите другой корень и коэффициент Ь.
б) В уравнении Юл:2—33л:+с=0 один из корней равен 5,3.
Найдите другой корень и коэффициент с.
851. Почему уравнение не может иметь корни одинаковых
знаков:
а) Зл:2 + 113л:—7 = 0; в) 4л:2 + &л:—100=0;
б) 5л:2—291л:—16=0; г) л:2 + &л:—d2=0?
852. Не решая квадратных уравнений, определите, какие из
них имеют один положительный и один отрицательный
корень, два отрицательных корня, два положительных
корня:
а) л;2+7л:—1 = 0; г) 19л;2 — 23л; + 5=0;
б) л;2—7л: + 1-0; д) 2л;2 + 51/Зл: + 11=0;
в) 5л:2+17л: + 16=0; е) 11л:2—9л:+7 — 5]/2=0.
853. Решите уравнение и проверьте правильность решения на
основании теоремы, обратной теореме Виета:
а) л:2+19л:+88=0; в) Зл:2— 4л:— 4=0; д) л:2—2л: — 9=0;
б) л:2—Зл:—88=0; г) 2л:2+7л:+6=0; е) 2л:2+9*+8=0.
211
854. Составьте квадратное уравнение, имеющее:
а) два положительных корня;
б) два отрицательных корня;
в) корни разных знаков;
г) один положительный корень, а другой равный нулю.
855. Составьте квадратное уравнение по данным корням и для
проверки решите его:
а) 3; 10; д) 2-^3; 2 + У&9
б) -7; -4; е) - Vb \Ь\
в) —-; 3; ж)5 — 3 ]/2~; 5 + 3^2;
о
г) 1,5; 3,5; з) -7— 4]/1Г; —7 + 4|/з1
§ 14. КВАДРАТНЫЙ ТРЕХЧЛЕН
53. Корень многочлена
Каждому значению х соответствует одно и только одно
значение многочлена хъ—2х2+Ъх—Ю.
Найдем значения этого многочлена при некоторых
значениях х.
X
х3 — 2хг + 5х —10
—3
—70
—2
— 36
0
—10
1
—6
2
0
5
90
Мы видим, что среди взятых значений переменной х есть
такое (число 2), подстановка которого в многочлен обращает
этот многочлен в нуль. Говорят, что число 2 есть корень много-
члена хъ— 2х2+Ъх—10.
Вообще, корнем многочлена с одной переменной называется
значение переменной, при котором значение многочлена равно
нулю.
Мы нашли один корень многочлена х3—2#2+5л:—10. Имеет
ли этот многочлен другие корни, кроме 2? Чтобы ответить на
этот вопрос, нужно решить уравнение
Xs — 2х2-\-Ъх —10-0.
Разложим многочлен на множители:
х* — 2х2 + 5х — 10=х2(х — 2)+5(х — 2)=(х — 2)(х2 +5).
Так как множитель х2+5 положителен при всех значениях
х> то уравнение (х—2)(дг+5)=0, а следовательно, и многочлен
Xs—2я2+5л:—10 ивдеют только один корень: число 2.
212
Найдем множество корней многочлена x's+2x2—9х—18. Для
этого решим уравнение хг*+2х2—9х—18=0:
х2(х+2) — 9(*+2)=0,
(х+2)(х2—9)=0,
(х+2)(х+3)(х—3)=0\
х = —2, или х = —3, или х=3.
{—2; —3; 3} — множество корней многочлена х3+2х2—9х—18.
Многочлен л;4+5л:2+1 не имеет корней, так как при любом х
его значение положительно и, следовательно, ни при каком х
значение многочлена не равно нулю.
Иногда бывает нужно решить обратную задачу: найти
многочлен, корнями которого служат данные числа (и только они).
Пусть, например, нужно найти многочлен с корнями 2; 3
и —4.
Запишем произведение трех множителей: (х—2){х—3)(#+4),
где х — переменная.
Очевидно, что это произведение обращается в нуль при х9
равном 2, 3, —4, и только при этих значениях х.
Преобразуем произведение (х—2)(х—3)(#+4) в многочлен
стандартного вида:
(х — 2) (х—3) (х+4)=хд—х2—Ых+24.
Корнями этого многочлена являются числа 2; 3 и —4.
Очевидно, что существует сколько угодно многочленов с тем же
множеством корней {2; 3, —4}. Например, любой многочлен вида ах3 — ах2 — 14а*+
+ 24а, где а Ф 0, коэффициенты которого соответственно пропорциональны
коэффициентам многочлена х3 — я2 — 14я + 24, будет иметь своими корнями
числа 2; 3 и —4, и только эти числа. Это следует из тождества
ах3 — ах1 — Uax + 24а = а (х3 — х2 — 14* + 24).
856. Докажите, что многочлен не имеет корней:
а) **+1; в) —xQ— 2; д) 2х2— 4х+ 5;
б) 2л:4+3; г) *а+2*+2; е) — х2+3х — 11.
857. Найдите корпи многочлена:
а) хъ— 4*; г) Зу2 +Ъу— 2; ж) 4а3— 8а2 + а — 2;
б) 2х—3; д) х2— 4*+4; з) &3 + 5&2—4& — 20.
в) у4—1; е) х*+ 10**— х—10;
213
858. Не вычисляя корней трехчлена, найдите их сумму и
произведение:
а) 2х2—Ъх—8; б) З*2— -х — 12.
7
859. Найдите многочлен по множеству его корней:
а) {2; -3}; в) {0; 7}; д) {1; 2; 3};
б) {5; -5}; г) {4}; е) 0.
860. Почему число 3 не является корнем многочлена
х4 + Ъхъ + Ах2 + 18* + 11?
861. Почему число —5 не является корнем многочлена
х* _ Зх3 — 4*2 + 28* + 11?
54. Разложение квадратного трехчлена на множители
В предыдущем пункте были рассмотрены примеры
разложения многочленов на множители. Решение этой задачи для
произвольных многочленов третьей и четвертой степени достаточно
трудно.
Здесь мы ограничимся рассмотрением задачи разложения
на линейные множители квадратного трехчлена — многочлена*
второй степени с одной переменной.
Пусть известно, что квадратный трехчлен ах2+Ьх+с, где
х — переменная, а, & и с — числа, причем а Ф 0, имеет корни
Xi и х2. Покажем, что в этом случае он может быть представлен
в виде произведения:
ах2 +Ьх +с= а(х — хг)(х — х2). (1)
Для доказательства тождества (1) преобразуем его правую
часть:
а (х — хг) (х — х2) = а (х2 — ххх — х2х + ххх2) -=
=а (х2 — (*! + xj х + хгх2).
Корни хг и х2 трехчлена ах2+Ьх+с являются корнями
уравнения ax2+bx+c=0. По теореме Виета
i — ъ — с
Х-±-\-X2— И Х\Х2 •
а а
Выполнив подстановку, получим:
a (х2 — (хг + х2) х + х±х2) = а (х2 -\ х + —) = ах 2+ Ъх + с.
\ a a J
Тождество доказано.
Рассмотрим пример. Трехчлен 2х2— Ъх—3 имеет корни,
так как дискриминант квадратного уравнения 2х2—Ъх—3=0
положителен. Корни этого трехчлена — числа и 3.
214
Пользуясь тождеством (1), представим трехчлен в виде
произведения:
2r> _ 5*— 3 = 2 (х + —\ (* — 3).
Если множитель 2 внести в скобки, то полученное тождество
запишется так:
2х2—Ъх—3 =(2х+1)(х—3).
Тождество (1) может быть распространено и на квадратный
трехчлен, имеющий единственный корень. В этом случае х1==х%
и тождество (1) примет вид:
ах2 + Ьх + с= а(# — хг)(х— хг)9 т. е.
ах2 + Ьх + с = а{х — хх)2.
Например, трехчлен —2Ъх2+10х—1 имеет единственный
корень, равный —(в этом легко убедиться, решив уравнение
5
—25г*+10л:—1=0). Применяя тождество (1), получим:
— 25*2 + 10* — 1 = —25 (х — -^
Если квадратный трехчлен не имеет корней, то он не можеу
быть представлен в виде произведения двух многочленов первой
степени.
Действительно, пусть npiiD<0 ax2+bx+c=(kx+m)(px+q).
Очевидно, что в этом случае и корни трехчлена.
k p
Но это противоречит условию.
Рассмотрим примеры применения тождества (1).
х 5
Пример 1. Сократить дробь .
Решение. Попытаемся разложить на множители
знаменатель дроби — квадратный трехчлен Зх2—13*—10.
D =132 +4 -3-10 =289; D > 0. Следовательно, квадратный
трехчлен имеет два корня.
Применяя формулу корней квадратного уравнения,
найдем их:
_ 13 -17 _ 2 т 13+17 __ ~
1 6 3 2 6
Пользуясь тождеством (1), имеем:
З*2 —13х — 10 = з(х+ -)(* — 5).
Мы разложили на множители знаменатель дроби, и теперь
ее можно сократить:
З*2 —13* —10 / 2\ к 3*+2
215
Пример 2. Решить неравенство
х2 — х — 20 < 0.
Решение. Выяснив, что дискриминант трехчлена
х2—х—20 больше нуля, найдем его корни —4 и 5. Разложим
трехчлен на множители:
х2 — х — 20 = (х + 4)(х — 5).
Множеством решений неравенства (х+4)(х—5) < 0 служит
объединение множеств решений систем неравенств:
*+4>0, Г*+4<0,
х — 5<0 и \х — 5>0.
Оно представляет собой, числовой промежуток ]—4; 5[.
Пример 3. Разложить многочлен 4jc2 + 9bx + ЪЬ2 на множители.
Решение. Данный многочлен можно рассматривать как квадратный
трехчлен относительно х.
Выразим с помощью формулы корней квадратного уравнения переменную
х через Ъ:
В = (9Ь)2 — 4 • 4 . 5&2 = 81Ь2 — SOb2 = b2; D >0 при любых b.
Отсюда
—9b — b 5 —9> + b
Xl==-——^^-b; Х2 = ——=_ъ.
Пользуясь тождеством (1), имеем:
4*2 + ibx + ЪЬ2 = 4 (х + — b\ (х + Ъ) == (4л: + 5Ь) (* + Ь).
862. Найдите корни трехчлена и разложите его на множители:
а) 2а2 — 5а + 3; в) 2х* —5х — 7; д) —у2 + 6у— 5;
б) 5у2 +2у — 3; г) я2 — Их + 30; е) — г2 — 5г + 6.
863. Разложите трехчлен на множители, если это возможно:
а) 4х2 — 9х + 5; д) х2 — х — 3;
б) 4Ь2 — 9Ь + 7; е) 2у2 — 5у+ 8;
в) _3г/2 +8у + 11; ж) 3z2 — 122 + 12;
г) 16а2 — 24а + 9; з) —48а2 — 8а + 1.
884. Зная, что числа —3,8 и 4 — корни квадратного трехчлена
10у2—2у—152, разложите на множители выражение:
а) —Юг/2 +2у + 152; в) 100у2 — 20у -^ 1520;
б) Ъу2 — у — 76; г) -у2 + 0,2i/ + 15,2.
216
Докажите тождество:
а) 7х2 + 19л: — 6= (7л: — 2)(х+ 3);
б) (5а — 4) (3 — а) = —5а2 + 19а — 12.
При каком значении р выражение х2 +рх +36
тождественно равно произведению двучленов:
а) .г+4 и х+9; в) х+6 и я+6;
б) х—2 и я—18; г) я—1 и л:—36?
867. Сократите дробь:
7*2 + х — 8 ч б2 — 8Ь + 15 ч с2 — с — 110
а) ! ; в) ; д) ;
' 7*-7 fr2-25 '22+9с-с2
5а + Ю _ч У2 - 5у - 36, . 5а2 + 8а + 3
2а2 + 13а +18 81 — у2 14 + За — 11а2
868. Решите неравенство:
а) (л:+ 10) (х — 6)>0; г) За2 — 10а — 8<0;
б) 2 (у +3)(у — 9)<0; д) л:2 + 6л; —55<0;
в) 2у2 — 1у + 6 > 0; е) *а — 5л: > 0.
869. Найдите область определения функции:
а) у - V 81— л2; г) у = /х2 + 20л: + 100;
б) у = Vlte-x*; Д) J/ = К2*-л:2-2;
в) у = ]/7л2-10л:-33; е) у = -^ *
V 4t> — 4л: — х1
870. Постройте график функции:
*а — 5* + 6 -ч — 2*2 + 7* — 3
а) р = г—; б) у = -ь— .
х — 2 2х — 1
871. Докажите, что значение выражения не зависит от
значения переменной, принадлежащей области его определения:
e) (_JL + _Ц . *±± !_;
\jc — 5 * + 4/ * + 10 л: —5
«я £=ii +-±* .(_■_ +_ 6
2а —10 а + 6 \а — 5 25
в) / 22 10 \ у2-36 3.
U2 + У - 30 У2-Ьу] 48 2/
ч Ь —4 & / 10
г)т—I — т
Ь_6 3 \Ь2—2Ь —24 б2 + 46
872. Упростите выражение и найдите множество значений
переменной х9 при которых значение выражения
положительно:
ч Зх2— 4*4-1 . А , о *ч к , ^ б*2+13*+ 2
а) =^- + 4л: + 3; б) 5л:+ 4 ±—- .
1— х * + 2
217
1 i ' 1 1 1 j bi 1 ' M ! -Ч 1
i ■ т 1 kL й
! : L ^ »< <2п
\\ ' ' ' И Ч =4 Ч
\\ ' \ 1 1 л N ! Ч ' /
\ \И г м! ' /
IV \ * 7 И 1 1/ /
A v и : I ниМ/|'
ill \ It 1 i 1 1 ! ' ' /1 i 1 / И
1 \ Ч»! I5'1 ' I/I J /
\ Н ; г/| 1
1 \'\\ 1/ М ! $ ^ ' *
\i \ Л | ' l t i/M
\ Лl\ IJ |/|/| /
\1 \ \ !^ М/ / i 4 1
i M\i?l///I
:i'\\vl//X
1 |\\\L \jY/\ Mi
1 i |SAa[ [АЛ l
1 i 1 i i i^^^p^i МММ
1 1 -2 \ L^fSffcJ 2 1 1 1 \X\
1 1 1 | \//7 л V\W MM
M ' ' ' A /f\ \ \W 1
I ///1J W x i
' ' \ / I M \l \\ \ '
M 1/1 /1\ ' ? M\ \ x 1
i / / / pi 1 i\i\l \ 1 i
l/l / i/ 1/ i 1 yj \ |\ |
///MiMi^X
1 / / I i \ A i \ i\ \
1*- \'\ / /l I ! 1 "In \ 1
«w / #' / и ' i 'I' \ \\
1 г/ 1 I 111 1 i^1 1 1 \\! i 1 \ 1 1
ЭД-1 /1 l7 1 i Ц |U
l/h7 R 1 ! И \ v
/ k/ Ы U 1 I \
/ \ i I-l Is M i U
Л / Ir» s N\
Рис. 54
55. График функции
у = ах2 + Ьх + с
Мы уже неоднократно
встречались с графиком функции
у =ах2> являющейся частным
случаем функции у=ах2 + Ьх+с.
На рисунке 54 изображены
параболы — графики функции
у= ах2.
Напомним некоторые
свойства графика функции у — ах2:
1. График проходит через
начало координат.
2. График имеет ось
симметрии: это ось ординат.
3. При а>0 кривая
расположена в верхней
полуплоскости, причем ветви параболы
уходят вверх; при а <0
парабола расположена в нижней
полуплоскости, а ее ветви уходят
вниз.
4. От коэффициента а
зависит форма параболы: чем больше
\а\, тем «круче» ветви параболы.
Перейдем теперь к
построению графика функции у= ах2 +
+ Ьх+ с с любыми
коэффициентами а, Ъ и с (а Ф 0).
Пусть нужно построить
график функции
у=х2+4х—5.
Найдем значения функции для некоторых
промежутка [—6; 2]:
значении х из
X
\у
—6
7
—5,5
3,25
—5
0
-4,5
—2,75
—4
—5
—3
—8
—2
—9
—1
—8
0
—5
0,5
—2,75
1
0
1,5
3,25
2
7
Точки, координаты которых указаны в таблице,
изображены на рисунке 55, они намечают некоторую кривую. Если
приложить шаблон параболы у = х2 так, чтобы вершина параболы
совпала с точкой (—2; —9), ось симметрии была параллельна
218
\-6
-A
-4
-3
-2
-1
Ж
♦
I
7
г\
1
-d-
j|
/VI
1
-74-
J
-o-L.
4_l_
/l
0
7
-94-
1
-74-
"1
«
Л
ГА
y\
-74-
/
01
o|
o\
J\
m\
tU\~
in
n
1
1
1
/
/
/
/
f
i
/
/
/
/
I
1
\l
\
\l
у
/
/
L
-
X
-,
1
b'
►
5
<
-/
>
s
?
f
у
С/
7
д
о
5
л
ч
3
?
L
1
0
-1
■г
-3
-к
■5
•6
-7
■в
■9
10
[
<
i
i
I
X
Рис. 55 Рис. 56
оси ординат и ветви направлены вверх, то окажется, что все
построенные точки принадлежат параболе (рис. 56).
В последующих классах будет доказано, что графики
функций у = ах2 + Ъх + с и у = ах2, где а Ф О, при одном и том же
значении а конгруэнтны и существует параллельный перенос,
переводящий график функции у = ах2 в график функции
у=ах2+Ьх+с.
Так как график функции у=ах2— парабола, ось симметрии
которой перпендикулярна оси абсцисс, а ветви при а>0
направлены вверх, а при а <0 — вниз, то графиком функции
у=ах2 + bx+с также является парабола с осью симметрии,
перпендикулярной к оси абсцисс, и ветвями, направленными
вверх при а>0 и вниз при а <0.
ЗД
Для построения графика функции у = ах2 + Ъх + с при D > О
удобно найти точки пересечения графика с координатными
осями и определить положение вершины параболы. Эти точки
позволят начертить график функции у=ах2 + Ъх + с.
Рассмотрим пример.
Построить график функции
у=х2 — 2х — 8. (1)
Найдем точку пересечения графика с осью у.
При х=0 значение у равно —8, следовательно, кривая
пересекает ось у в точке А (0; —8).
Подставляя в уравнение (1) значение у, равное нулю,
определим точки пересечения параболы с осью х. Решая уравнение
х2— 2х— 8=0,
найдем его корни —2 и 4. Значит, точки пересечения графика
с осью абсцисс: В (—2; 0) и С (4; 0) (рис. 57).
Точки В и С принадлежат параболе и лежат на
перпендикуляре к ее оси симметрии, значит, точки В и С симметричны
относительно оси симметрии параболы.
Отсюда следует, что ось симметрии параболы пересекает
ось абсцисс в точке D, равноотстоящей от точек В и С Абсцисса
точки D равна полусумме абсцисс точек В и С:
-*±± = i.
2
Очевидно, что вершина параболы лежит на ее оси
симметрии. Поэтому абсцисса вершины параболы та же, что и у точки
D, т. е. равна 1.
Подставляя в формулу (1) значение х=19 найдем ординату
вершины параболы:
у = 12_2.1 — 8 = — 9.
Итак, вершина параболы Н имеет координаты (1; —9).
Наметив точки А, В, С и Н, строим график функции у =
=х2—2х—8 (рис. 57).
Если квадратный трехчлен ax2Jr bx+ с не имеет корней, то
график функции у = ахг + Ьх + с не пересекает оси х. Для
построения графика функции у = ах2 + Ъх + с в этом случае
целесообразно найти точки пересечения графика с какой-нибудь
прямой, параллельной оси абсцисс. За такую прямую удобно
принять прямую у=с. Дальнейшее построение выполняется
аналогично рассмотренному выше.
Пример. Построить график функции
у = 2*2 + 6х + 7. (2)
Парабола пересекает ось у в точке А (0; 7). Проведем
прямую у=7 и найдем точки пересечения параболы у=2х2+6х+7
220
1
1
1
I
I
1
г6
I
\
\r
lb
4
лr
i: *
-1
♦л
'/1
"1
-7-1-
/|
_£*!_
-cL
j
//
Г
-7J-
Ol
Г
■fl
^>УТ
u\
-1L.
/l
?
Z.I
.74-
J
41
"Г
M
J
Л1
Ol
ЛГ
Ol
Ol
J\
in\
1
T?
p
/i
U,UJ |
~F
4/ф-б>)
|r
3
V(/,-
-5)
1
j
ШЧ-ри^
Тр
X
IV 1 II II
\w(-3-j\
' 4 ' i^Wr
qr//r-fffXj-
U -3 -2 j-7
_J 1 l_J 1 l_i...
\i/\
la 1
Ш
/7f
7?»
7?!
1
ffl
1
7Л
lol
+
I
... ;...«•
«I
\0\
Ml
JO I
JUL
/1
' 71
PI
?
К
1\
r
' 1\
r/i
, LoJ_
li
T
f
I
I
Л
f
f
f
I.
/i
fi i
7A(0;7)
1
2 I
[ [ |
i I I
T x
Рис. 57
Рис. 58
с этой прямой. Для этого подставим в уравнение (2) значение у,
равное 7:
7 = 2х2 + 6х + 7.
Приведя уравнение к стандартному виду, получим:
х2 + 3х=0.
Корни этого уравнения —3 и 0, значит, парабола у=2х* +
+ 6х + 7 и прямая у = 7 пересекаются в точках -А (0; 7) и
В (—3; 7) (рис. 58).
Точки А и В симметричны относительно оси симметрии
параболы, поэтому абсцисса вершины параболы равна полусумме
абсцисс точек А и £, т. е. —1—.
221
Подставляя в уравнение (2) значение х=—1—, найдем ор-
динату вершины параболы:
Вершина Н параболы имеет координаты: /—1—; 2—).
Точки А, В и Н определяют параболу (рис. 58).
873. Используя график функции f(x) = х2 — 2х — В (см. рис. 57),
найдите:
а) значение функции, соответствующее х=—1,5; —8; 4;
б) значение аргумента, которому соответствует значение
функции, равное 7; —8; —27;
в) множество значений аргумента, на котором f (х) = О,
/ (х) < 0, / (х) > 0;
г) множество значений аргумента, на котором функция /
убывает, возрастает;
д) значение переменной х, при котором функция
принимает наименьшее значение.
874. Не выполняя построения графика, найдите координаты
точек пересечения графика фуцкции с осью х и с осью у:
а) у = х% — Ъх — 8; е) у — Вх х2;
б) у = —х2 + 2х + 3; ж) у = (х—5) (х + 3);
в) у = х1 — 6х; з) у = (2х + 1) (х — 2);
г) у = —2х2 + 1х\ и) у = х2 — 7х + 13;
д) у = Зх2 + 9х; к) у = —2л:2 — 5* — 7.
875. Постройте график функции у = х2 + 2х — 15.
Рассматривая построенный график, найдите:
а) множество значений х, на котором значения функции:
1) отрицательны, 2) положительны;
б) множество значений дг, на котором функция: 1)
возрастает, 2) убывает;
в) наибольшее или наименьшее значение функции;
г) множество значений функции.
876. Постройте график функции и проведите исследование
функции по схеме, предложенной в предыдущем упражнении:
а) у=х2+4х; в) у=х2+2х—3; д) у=— х2+6х — 10;
б) у=4*—х2; г) у=±х2— 4х+6; е)у=— 2*2—Ьх — 2.
2
222
877. а) Сколько общих точек с осью абсцисс имеет график
функции у = х2 + 6х + 9?
б) Докажите, что график этой функции расположен в
верхней координатной полуплоскости.
в) Постройте график функции у = х2 + 6х + 9 по
точкам, заполняя таблицу:
X
У
— 6
—5
—4
—3
—2
—1
1
0
Рассматривая построенный график, укажите
множество значений х, на котором функция: 1) убывает, 2)
возрастает.
878. Постройте график функции у = х2 — 2х + 1.
Рассматривая построенный график, найдите наименьшее
значение функции и укажите множество значений х, на
котором функция: 1) убывает, 2) возрастает.
879. Постройте график функции у = —х2 + 4х — 4 и укажите:
а) наибольшее значение функции;
б) множество значений функции;
в) множество значений х, на котором функция: 1)
возрастает, 2) убывает.
880. Постройте график функции у = (х + 2) (х — 4) и,
пользуясь им, решите неравенство:
а) (х + 2) (х — 4) > 0; б) (х + 2) (х — 4)< 0.
881. Укажите координаты вершины параболы:
а) у = (х + 5) (х + 3); б) у = 2 (х — 1)(х — 5).
882. Постройте график функции у = х2 — 6х + 10.
Рассматривая график, укажите множество значений х, на котором
функция: а) убывает, б) возрастает.
883. Постройте график функции:
а) у = х2 — 2х + 8; б) у = — -х2 + 2х — 3.
884. Докажите с помощью графика, что неравенство
выполняется при всех значениях х:
а) х2 — Зх + 8> 0; б) —х2 + 6х — 10 < 0.
885. Проходит ли график функции у = х2—7х—31 через точки
А (3; —43), В (—8; 89), С (—5; —29)?
223
886. а) При каком значении с график функции у =2х2 -f 7x + с
проходит через точку А (—10; 150)?
б) При каком значении Ъ график функции y=x2Jrbx—19
проходит через точку D (—11; —30)?
887. Известно, что график функции у = ах2 +Ьх — 48 проходит
через точки М (1; 2) и N (2; 10).
Найдите значения коэффициентов а и Ъ.
888. Известно, что график функции у = 2х2 + Ьх+ с проходит
через точки Р (3; 2) и Q (—2; 12). Найдите значения
коэффициентов & и с.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ
К ГЛАВЕ IV
К пункту 46
889. Решите графически систему уравнений:
а) (2* + у = 8, в) (.. 1 д)/(*-1)у = 0,
\у=х2; \у-~х' \у=2х2;
IУ = х2;
б) (5* — 2j/ = 0, r)fj/ = — x2, e) ((* — j/)(* + |/) = 0,
h/ = *2; »=-; U/ = -*2.
Г 8*
890. Решите графически уравнение:
а) *2 = 5ж — 8; r)i*2 = 7 —ж; ж) *2-Ь 6* — 16 = 0;
б) ж2 = - ж + 5; д) *2 — л: = —12; з) — i*2+* + 2 = 0.
2 3
в) 2*2=3*+10; е) Зж2 + 5* = —8;
891. Решите графически неравенство:
а) х2 > — х + 12; в) - ж2 < 2ж; д) .г3 - х + 4 > 0;
2
б) я2 < 5* + 6; г) - хг > — Зж; е) 2х2 + еж + 3 < 0.
К пункту 47
892. Решите уравнение, выделяя квадрат двучлена:
а) х2 — 16* + 48 = 0; д) ж2 + 7х — 18 = 0;
б) ж2 + 12* + 27 = 0; е) ж2 — 11* + 28 = 0;
в) *2 + 10* — 39 = 0; ж) 2*2 — 5* + 2 = 0;
г) *2 — 6* — 55 = 0; з) З*2 — * — 70 = 0.
224
К пунктам 43 и 49
893. Решите по формуле (А) уравнение:
а) 4х2 + 7х + 3 = 0; д) 8х2 + х — 75 = 0;
б) х* + х — 90 = 0; е) Зх2 — 11* — 14 = 0;
в) х2 — х — 90 = 0; ж) Зх2 + И* — 34 = 0;
г) 5х2 — 18* + 16 = 0; з) х2 — х — 1 = 0.
894. При каких значениях х справедливо равенство:
а) (5* + З)2 = 5 (х + 3); д) (5* + З)2 = Ъх + 3;
б) (Зх + 10)3 = 3 (х + 10); е) (5* + З)2 = (Зх + 5)2;
в) (Зх — 8)2 = Зх2 — 8х; ж) (4х + 5)2 = 4 (х + 5)2;
г) (4* + 5)2 = 5х2 + 4х; з) (2х + 10)2 = 4 (х + 5)*?
895. Решите уравнение, применяя формулу (В):
а) х2 — 18* + 80 = 0; г) 5х2 + 26* + 24 = 0;
б) х2 + Ux — 15 = 0; д) 9х2 — 78* + 25 = 0;
в) Зх2 — 22* — 25 = 0; е) х2 — 208х + 402 = 0.
896. Решите уравнение и выполните проверку:
а) х2 — 2х — 5 = 0; г) Ъу2 — 1у + 1 = 0;
б) х2 + 4х + 1 = 0; д) 2у2 + 11у + 10 = 0;
в) Зу2 — 4у — 2 = 0; е) 4*2 — 9г — 2 = 0.
897. Найдите приближенные значения корней уравнения:
а) х2 — 2* — 2 = 0; в) Зх2 — 7х + 3 = 0;
б) х2 + 5х + 3 = 0; г) 5х2 + 31х + 20 = 0.
898. Решите уравнение:
а)(х-1)8 = х(х + 2)2-9; fl)f±J + -^; = 4;
О X — 1
б) (х + 2У= х(х- 1)2+ 62; е) !±J*_ JL = 2;
4 X -f- A
в)(2У+1)*_4^-1 _22 8_
8 5 х—1 * + 1
(JL_3)!_i_,= 3)-*- + -*°- = 3.
7 20 2 * — 3 1 — *
8 Алгебра, 7 кл. 225
899. При каких значениях переменной у:
а) значение суммы дробей и —— равно значению
у+1 у—2
их произведения;
тюб ей
у-з у + г
б) значение суммы дробей —— и равно значению
их произведения;
в) значение разности дробей у "*" х* и —— равно значению
у—4 у-\-4
их произведения;
г) значение разности дробей —-— и равно значению
2у — 1 2у + 4
их произведения?
900. Решите уравнение:
а)-* L_+_JL_e0;
у2 — 9 у2 + гу Ьу+ 2у*
б) -у-1 -f 8 = 2у + 1-
14y2 + 7i/ 12у2~3 6уя~3/
ч 3 1 3
в)
*2__9 9 — Ьх+х* 2д:2 + 6л:
901. При каком значении а один из корней уравнения
ах2 — Зх — 5 =0 равен 1?
902. Докажите, что один из корней уравнения ах2—(а +с) х +с=0
равен 1.
903. Найдите соотношение между коэффициентами уравнения
ах2+ Ьх+ с=0 в том случае, когда один из корней его:
а) равен —1; б) равен —, где с Ф 0.
а
904. Найдите множество значений параметра а, при которых
уравнение имеет единственный корень:
а) 4х2 + 28* + а = 0; в) ах2 + 28* + 4 = 0;
б) 25л:2 + ах + 16 = 0; г) х2 + ах + 114 = 0.
905. Докажите, что корни уравнения сх2 + Ъх + а = 0 (сФО) об-
ратны корням уравнения ах2 + Ъх + с = 0 (а Ф 0).
К пункту 50
906. а) Найдите пять таких последовательных целых чисел,
чтобы сумма квадратов трех первых чисел равнялась
сумме квадратов двух последних.
б) Найдите три таких последовательных четных числа,
чтобы сумма квадратов первых двух равнялась квадрату
третьего числа.
226
907. Сад и огород имеют форму прямоугольника; площадь
каждого из них равна 1500 м2. Ширина сада на 5 м больше
ширины огорода, а длина сада на 10 м меньше длины
огорода. Найти размеры сада и огорода.
908. а) Один завод должен был изготовить 720 станков, а
другой за тот же срок — 660 станков. Первый завод,
изготовляя в день на 10 станков больше, чем второй, выполнил
заказ за 2 дня до срока, а второй завод, изготовив 22
станка сверх плана, закончил работу за 1 день до срока.
Сколько станков изготовлял ежедневно каждый завод?
б) Две соревнующиеся бригады рабочих должны были
изготовить к некоторому сроку по 240 деталей. Изготовляя
в день на 8 деталей больше, чем вторая бригада,
первая выполнила задание за 3 дня до срока, опередив
вторую бригаду на 1 день. Каков был срок выполнения
работы?
909. а) Одна тракторная бригада должна была вспахать 240 га,
а другая на 35 % больше, чем первая. Вспахивая
ежедневно на 3 га меньше второй бригады, первая все же
закончила работу на 2 дня раньше, чем вторая бригада. Сколько
гектаров вспахивала каждая бригада ежедневно?
б) С одного участка собрали 1440 ц пшеницы, а с другого,
площадь которого была на 12 га меньше,—1080 ц. Найти
площадь каждого участка, если известно, что на первом
участке собирали пшеницы с каждого гектара на 2 ц
больше, чем на втором.
910. а) При постройке здания требовалось вынуть 4500 м9
грунта в определенный срок. Перевыполняя дневную
норму на 45 лс3, строители уже за 4 дня до срока выполнили
96% задания. Определите срок работы.
б) Два звена должны были прополоть овощные культуры
на участке в 7200 м2. Пропалывая в час на 120 м2 больше
второго звена, первое звено закончило работу на 1 час
позже второго и при этом выполнило 60% всей работы.
Сколько часов работало каждое звено?
911. а) Бригада рабочих должна была к определенному сроку
изготовить 360 деталей. Перевыполняя дневную норму на
9 деталей, бригада уже за 1 день до срока перевыполнила
плановое задание на 5%. Сколько деталей изготовит
бригада к сроку, если будет продолжать работать с той
же производительностью труда?
б) По плану колхозная бригада должна была к
определенному сроку прополоть овощные культуры. Начав работать
на 2 дня позже, чем было намечено первоначально,
бригада перевыполняла дневную норму на 2 га и уже за 1 день
8*
227
до срока прополола 49 га, что составляло 93% задания.
Какой срок был установлен бригаде для выполнения
задания?
912. а) Бригаде рабочих было поручено изготовить в
определенный срок 270 деталей. Перевыполняя задание, она
ежедневно изготовляла на 6 деталей больше, чем
требовалось по заданию, а потому за 4 дня до срока бригада уже
сдала 264 готовые детали. Сколько деталей должна была
изготовлять бригада в один день по заданию и какой срок
ей был дан для его выполнения?
б) По плану бригада колхоза должна была убрать
урожай зерновых с 540 га к определенному сроку. После того
как убрали 30% урожая, бригада, получив дополнительно
комбайн, стала ежедневно убирать на 9 га больше, чем
первоначально, и закончила уборку на 1 день раньше
срока. Сколько дней продолжалась уборка урожая?
913. а) Отправляясь в путешествие, турист рассчитывал
истратить в дороге 72 руб. В течение первых 5 дней его расходы
совпадали с расчетными, затем он стал расходовать в
день в среднем на 1 руб. больше, чем предполагал, и,
задержавшись в пути на 1 день, вернулся домой, истратив
на все путешествие на 23 руб. больше, чем намечал.
Сколько дней продолжалось путешествие?
б) Бригада рабочих должна была в определенный срок
изготовить 272 детали. Через 10 дней после начала работы
бригада стала перевыполнять дневную норму на 4 детали
и уже за один день до срока изготовила 280 деталей.
Сколько деталей изготовит бригада к сроку?
914. а) Две машинистки получили для перепечатки рукопись.
После 2 ч совместной работы одна из машинисток
получила другое задание и вторая, оставшись одна,
закончила работу через 1 ч 20 мин. За сколько часов могла
бы перепечатать рукопись каждая машинистка, если
второй на это понадобилось бы на 1 ч 10 мин больше, чем
первой?
б) Уборку урожая с участка начал один комбайн. Через
2 ч к нему присоединился второй комбайн, и после 8 ч
совместной работы они убрали 80% урожая. За сколько
часов мог бы убрать урожай с участка каждый комбайн,
если известно, что первому на это понадобилось бы на 5 ч
больше, чем второму?
915. а) Цех завода получил заказ изготовить к определенному
сроку партию деталей. Если выполнение заказа поручить
первой бригаде, то она закончит работу на 3 дня позже
срока. Вторая бригада, работая одна, могла бы выпол-
228
нить заказ на 8 дней позже срока. Над выполнением
заказа работали совместно обе бригады и закончили работу
за день до срока. Сколько дней понадобилось бы каждой
бригаде, чтобы одной выполнить заказ?
б) Два трактора могут вспахать зябь на 18 ч быстрее, чем
один первый трактор, и на 32 ч быстрее, чем один второй
трактор. За сколько часов может вспахать зябь каждый
трактор, работая один?
916. а) Поезд вышел со станции А по направлению к станции В.
Пройдя 450 км, что составляло 75% всего пути, он был
задержан на полчаса, и машинист, увеличив скорость на
15 км/ч, привел его на станцию В без опоздания. Найти
первоначальную скорость поезда.
б) Мотоциклист предполагал проехать расстояние 90 км
за определенное время. Проехав 54 км, он должен был
остановиться у закрытого шлагбаума на 5 мин.
Продолжая движение, он увеличил скорость на 6 км/ч и прибыл
к месту назначения в намеченное время. Найти
первоначальную скорость мотоциклиста.
917. а) Расстояние между городами А л В 260 км. Через 2ч
после выхода автобуса из А в Б он был задержан на 30 мин,
поэтому, чтобы прийти в Б по расписанию, должен был
увеличить скорость на 5 км/ч. Найти первоначальную
скорость автобуса.
б) Велосипедист проехал 40 км от города до турбазы.
Возвращаясь обратно, он 2 ч ехал с той же скоростью, s
затем сделал остановку на 20 мин. Начав движение
снова, он увеличил скорость на 4 км/ч, а потому затратил на
обратный путь столько же времени, сколько на путь
из города до турбазы. Сколько времени затратил
велосипедист на путь из города до турбазы?
918. а) Катер, скорость которого в стоячей воде 15 км/ч,
отправился от речного причала вниз по течению реки и, пройдя
36 км, догнал плот, отправленный от того же причала за
10 ч до отправления катера. Найти скорость течения реки,
б) Турист проплыл по течению реки на плоту 12 км,
возвратился обратно на лодке, скорость которой в
стоячей воде 5 км/ч. Найти скорость течения реки, если
известно, что на все путешествие турист затратил 10 ч.
919. а) Моторная лодка прошла 39 км по течению реки и 28 км
против течения за то же время, за которое она могла в
стоячей воде пройти 70 км. Какую скорость имеет моторная
лодка в стоячей воде, если скорость течения реки 3 км/ч?
б) Турист проплыл на байдарке 25 км по озеру я 9 км
против течения реки за столько же времени, сколько ему
229
потребовалось бы для того, чтобы проплыть по течению
реки 56 км. Зная, что скорость течения реки равна 2 км/ч,
найти скорость лодки в стоячей воде.
920. а) Рыболов отправился на лодке от пункта N вверх по
течению реки. Проплыв 6 км, он бросил весла, и через
4 ч 30 мин после отправления из N течение снова отнесло
его к пункту N. Зная, что скорость лодки в стоячей воде
90 м/мин, найти скорость течения реки.
б) От пристани А в направлении пристани В, отстоящей
от А на 40 км, отправили плот. Через 3 ч 20 мин после
отправления плота навстречу ему от пристани В против
течения реки вышла моторная лодка, которая встретила
плот в 16 км от А. Найти скорость течения реки, если
известно, что скорость моторной лодки в стоячей воде
равна 15 км/ч.
921. а) Поезд должен был по расписанию пройти перегон, рав-
ный 420 теле, за определенное время. Пройдя — всего
расстояния, он был задержан в пути на 15 мин. Затем машинист
увеличил скорость на 10 км/ч, и перегон был пройден без
опоздания. Сколько времени затратил поезд на
прохождение перегона?
б) Мотоциклист проехал расстояние MN, равное 180 км,
с некоторой средней скоростью. Возвращаясь обратно,
2
он — расстояния от N до М ехал с той же скоростью,
3
а затем увеличил скорость на 5 км/ч и возвратился в М,
затратив на обратный путь на 8 мин меньше, чем на путь
из М и N. Сколько времени затратил мотоциклист на весь
путь в оба конца?
922. Автотурист проехал расстояние между пунктами A is. В,
равное 400 км, с некоторой средней скоростью.
Возвращаясь обратно, он 2 ч ехал с той же скоростью, а затем
увеличил скорость на 10 км/ч и возвратился в пункт А,
затратив на обратный путь на 40 мин меньше, чем на путь
us А и В. Сколько времени затратил автотурист на
обратный путь?
923. а) Расстояние между пунктами А и В велосипедист
проехал за 3 ч. Возвращаясь обратно, он первые 24 км ехал
с той же скоростью, а затем увеличил скорость на 2 км/ч
и прибыл в пункт А, затратив на обратный путь на 10 мин
меньше, чем на путь из А в В* Найти расстояние между
пунктами А и В.
б) Автобус проходит расстояние между городами М и N
по расписанию за 5 ч. Однажды, выйдя из Af в Л", авто-
£30
бус был задержан на 10 мин в 56 км от М и, чтобы
прибыть в город N по расписанию, должен был оставшуюся
большую часть пути проходить со скоростью,
превышающей первоначальную на 2 км/ч. Найти скорость автобуса
по расписанию.
924. а) Расстояние от пристани М до пристани N по течению
реки катер проходит за 6 ч. Однажды, не дойдя до
пристани N 40 км, катер повернул назад и возвратился к
пристани М, затратив на весь путь 9 ч. Найти скорость
катера в стоячей воде, если скорость течения реки равна
2 км/ч.
б) Велосипедист предполагал проехать расстояние от
турбазы А до турбазы В за 4 ч. Однако, проехав 30 км, он
вынужден был снизить скорость на 3 км/ч, так как
дорога пошла в гору, и прибыл на турбазу В на
полчаса позже, чем предполагал. Найти расстояние между
турбазами.
925. Из пункта А в пункт В, расстояние до которого 20 км,
выехал велосипедист, а через 15 мин вслед за ним со
скоростью 15 км/ч отправился другой велосипедист, который,
догнав первого, повернул назад и возвратился в пункт А
за 45 мин до прибытия первого велосипедиста в В. Найти
скорость первого велосипедиста.
926. Из А в В со скоростью 4 км/ч вышел турист. Спустя час
вслед за ним из А вышел второй турист, проходивший
в час 5 км9 а еще через час из А выехал велосипедист,
который, обогнав одного туриста, через 10 мин обогнал
и другого. Найти скорость велосипедиста.
927. а) На огороженном участке прямоугольной формы
длиной 150 м и шириной 110 м разбит прямоугольный газон,
одинаково отстоящий от ограды. Найти длину и ширину
4
газона, если известно, что площадь газона составляет —
площади участка.
б) Участок прямоугольной формы имел площадь 1200 м2.
После увеличения длины участка на 4 м, а ширины на
6 м его площадь увеличилась на 35%. Найти
первоначальную длину и ширину участка.
928. а) Коробка (без крышки) имеет форму прямоугольного
параллелепипеда с квадратным основанием. Площадь дна
коробки на 176 см* больше площади поверхности боковых
ее стенок. Высота коробки — 10 см. Найти площадь дна
коробки.
б) Из прямоугольного куска жести с измерениями 30 см
и 48 см нужно сделать открытую коробку. Для
этого по углам прямоугольника вырезают квадраты, а
231
46 см
оставшуюся часть сгибают
(рис. 59). Определить,
какую длину должна иметь
сторона вырезаемого
квадрата, чтобы площадь
основания коробки равнялась
ее боковой поверхности.
929. а) Длины сторон
прямоугольника 37 м и 6 м.
Прямая, параллельная его
стороне, делит прямоуголь-
Рис 59 ник на два подобных, но не
конгруэнтных
прямоугольника. Найти площадь
каждой части,
б) Прямая, параллельная стороне прямоугольника и
отстоящая от нее на 9 м, отсекает прямоугольник, подобный
данному. На какие части делит эта прямая площадь
прямоугольника, если его периметр равен 176 м?
930. Через вершину прямоугольника вне его проведена
прямая, отсекающая на продолжениях противоположных
сторон отрезки в 15 см и 40 см. Найти площадь
прямоугольника и его стороны, если известно, что периметр
прямоугольника равен 98 см.
931. а) Сплав меди с цинком, содержащий 5 кг цинка,
сплавлен с 15 кг цинка. В результате содержание меди в сплаве
; понизилось по сравнению с первоначальным на 30%.
Какова была первоначальная масса сплава?
б) Сплав золота с серебром, содержащий 80 г золота,
сплавлен со 100 г чистого золота. В результате
содержание золота в сплаве повысилось по сравнению с
первоначальным на 20%. Сколько серебра в сплаве?
К пункту 51
932. Дано уравнение относительно х. Решите его:
а) х2—13ах+42а2=0;
б) 2х2+7ах—9а2 =0;
в) 4х2—(5с+4)х+с2+с
-0;
г) 3x2—(4k—6)x+k2—2k = 0;
д) х(3х—1)—2п(х—2) =10;
е) ах(х+5)+х(х+2) =3 — 6а.
933. Найдите множество значений t, при которых уравнение
имеет по крайней мере один корень:
а) 9х2 — 12x + t = 0; в) tx2 + 6х — 1 = 0;
б) 4х2 + tx + 9 = 0;
г) х2 — (2* + 1)*+ t2 —1 = 0,
232
К пункту 52
934. Найдите значение Ъ и решите уравнение:
а) 2х2 + Ъх — 10 = 0, если оно имеет корень, равный 5;
б) Здс2 + Ъх + 24 = 0, если оно имеет корень, равный 3;
в) (Ъ — 1)х2+(6+1)дс=72,если оно имеет корень, равный 3;
г) (Ь — 5)х2 — (Ъ + 2)х + Ъ = 0, если оно имеет корень»
« 1
равный —.
935. Почему уравнение 7л:2 + Ъх — 23 = 0 при любых значениях
Ъ имеет один положительный и один отрицательный
корень?
936. Почему уравнение 12л:2 + 70л: + а2 + 1 =0 при любых
значениях а не имеет положительных корней?
937. В уравнении 6х2 + Ъх + 1 = 0 один из корней больше
другого на—. Чему равно значение Ъ?
6
938. а) Разность корней уравнения 25л:2—30я + с=0 равна 0,8.
Найдите коэффициент с.
б) Отношение корней уравнения 24л:2 + Ъх + 25 = 0
равно 1,5. Найдите коэффициент Ъ.
939. Разность квадратов корней уравнения 2л:2 + 7л: + с = 0
равна 1,75. Найдите с.
940. Один из корней уравнения Зл:2 + Ъх + с= 0 равен —1—,
з
а другой — второму коэффициенту уравнения. Найдите
коэффициенты Ъ и с.
941. Один из корней уравнения ах2— 5л: + с = 0, где а >0 и с Ф 0,
равен а, другой корень равен с. Найдите коэффициенты
а и с.
942. Составьте квадратное уравнение с корнями уг и у2» если:
а) ух = 10; у2 = 12; е) ух = —УЪ\ у2 = УЪ\
б) Уг = — 3; уг = 8; ж) уг = 2 — УЗ; у2 = 2 + У3\
в) Ух = — 7; jr2 = 0;
тЛ ,1 — *. 7/ — Я- ч 11 — 2/30 11+2^30
„ч „ _ 2. I/ — 0 1- ч —Ю—7]/2 —10 + 7/2"
943. Составьте уравнение по его корням ух и у2 и для проверки
решите составленное уравнение:
a) yi = а + 5, у2 = 3; б) ух = 2а + 1, у2 = —1.
233
944. Составьте квадратное уравнение, корни которого были
бы на 1 больше соответствующих корней уравнения
2х2 — 8х + 3 = 0.
945. Составьте квадратное уравнение, корни которого были
бы на 0,2 меньше соответствующих корней уравнения
5*2 _ х — 2 = 0.
946. Составьте квадратное уравнение, корни которого
равнялись бы квадратам соответствующих корней уравнения
Зх2 + 7х + 1 = 0.
947. Составьте квадратное уравнение, корни которого были бы
обратны соответствующим корням уравнения
4х2 — 13* + 7 = 0.
948. Пусть корни уравнения ах2+Ьх+с=0 равны хх и х2*
Выполнив необходимые вычисления, найдите значения
коэффициентов и корней уравнения, соответствующие пустым
клеткам таблицы:
№
1
2
3
4
1 5
1 6
7
а
5
2
6
9
Ъ
43
—100
—5
1
с
—132
180
12
—7
*i
1
2
—10
0,7
2
3
1
*2
6
—6
1,3
3
К пунктам 53 и 54
949. Найдите корни многочленов:
а) х3 — 9х2 + х — 9; в) Xs — Зх2 + Зх — 1;
б) Xs + 9х2 — 4х — 36; г) *4 — 100.
950. Докажите, что число 15 не является корнем многочлена
х* _ 13*3 — 207л:2 + 1681л: + 8.
951. Докажите, что чцсло —13 не является корнем многочлена
х* — 20л:3 + 919л:2 — 840л: + 26.
234
952. Напишите многочлен с целыми коэффициентами, зная
множество его корней:
а) X = {5; 10); г) X = /1; 3; -б);
2 Л 1)
б) Х = {-3; 0; 3}; д) *={-|; 0;
3J
};
в)А" = {1; 2; 3}; е)Х = {-|; -3; |; з).
953. Разложите, если возможно, на линейные множители:
а) х* — Зх — 21; д) о2 + о — 20; и) 3j/2 — 2&у — 5Ь2;
б) 5л:2 + 13л: + 8; е) 1Ьг — ЪЪ + 1; к) г2 — 2г — 1;
в) —4л:2+7л:—3; ж) с2 — аЪ — 6&2; л) 2с2 + cd + 4d2;
г) 10л:2+9л:—63; з) х2 + ах — 30а2; м) л:3 — 12л:2 + 20л:.
954. Разложите на множители:
а) б*3 — 31*2 — 31* + 6; в) 4ЪЪ — 4Ь* — 81 (Ь — I)3;
б) а2 (с — 5)3 — 36а + 180; г) 5л;3 — 19л:2 — 38л: + 40.
955. Сократите, если возможно, дробь:
_5о3 + 13а + 6 . Зс2 — 11с + 10
(fl__2)3—1 ' (5 — с)3 — 8с3 '
б) 27-(р + 1)3 ^ Га2 _ 5а - 4
7р2_9р —10 27а3 — (а — I)3
956. Докажите, что на всей области определения выражения
его значение не зависит от а:
а,(
4 а+1 \ 15а —12
5а2 + а — 4 9 (5а — 4)/ а + 7 а+1
б) -JL4- ^±i . Z9^-1) _ (2а-7)2
2 — а а — 1 " \ За + 4 За2 + а — 4
8 \ За + 4 1
в)( а- + 8 )
V За2 + а — 2 9а2 — 4 /
ч 21 , а2 —25 / 6 , а
9а2 — 4 а + 1
4а+6 а + 2 \25—а2 2а2 —7а —15/'
. 3 За + 12 . / 2а —1 а—5 \
а —2 25 —а2 \а2—25 "~ 2а2 + 9а —5 J'
/ 4 (а — 2) а — 3 \ а2 — 4
в) [ а* — а — "
6 4 —а2/ а —1 а —3
235
957. Решите уравнение:
35ж
а)
б)
_ «±I + fiLz? _ о;
44-lOJt—6r2 Зх + 1 'г —2
25* — 21 2* — 3 х + 4
2r* + 5jt — 12 *-М 3 — 2*
13 .1 б
0;
в) = ,
2£/2 + у _ 21 2у + 7 у2 — 9
958. Решите неравенство:
а) х2 — Ъх + 6 < 0;
б) — я2 — 7л: +6 > 0;
959. Найдите область определения функции
в) Зх2 + 4* — 7 > 0;
г) — Зх2 — 10* < 3.
а) jf = |/V - 49;
б) у = V144 -9л:2;
В) */ = }/*2 — 2* — 63Г
г) г, - К-*2 + х + 42;
Кх - 3
д; j/ - ^2 __ 2х - 8о;
Г2 _ 2Х — 80
Ж) J/ = -^ г»
7 ^ *2 — х — 2
е) у
3) 0 =
*2 _4_ * __ 5
К 9 — га
К пункту 55
960. Не выполняя построения графика, укажите, в каких
точках пересекает координатные оси график функции:
х2 + 2х
120
а) у
б) у = — *2 + * + 58;
в) у = 2*2 + 9jc + 11;
г) у = (х —3)(2* + 1);
д) г/ = (5 - 2х) (1 + х)\
е) у -= х3 — 2х2 — 99*;
ж) г/ = г3 + 10х2 — 4* — 40;
з) у = х* — 2х2 + 3.
961. Постройте график функции:
а) у = 2х2 — 5*; д) у = ха + 2*
15;
б) у = 6х — 2х2;
в) у = 4*2 - 9;
г)у = 4 — |х2;
е) У = -*а
3* + 4;
ж) у = (2* — 7) (ас + 1);
з) у = (2 — х)(* + 6).
982. Найдите множество значений х, при которых
переменная у возрастает с возрастанием дс, если:
а) у = 9 — х2;
б) у =1**-8;
в) у = х2 — Зх — 18;
г) у = —х2 — 4лг + 5
963. Решите графически неравенство:
а) ха
2 < 0; в) 2х2 + Зх — 5 < 0;
б) ж2 + 2* — 15 > 0; г) \х2 — 5х + 12 > 0.
964. Не выполняя построения графика, выясните, в каких
координатных четвертях расположена парабола, если:
а) у = 2*2 — х + 3;
б) у = х2 — 2х — 63;
в) у = х2 + 16* + 3;
г) у = —Зх2 + 2х
965. Постройте график функции:
7.
а) У = |*2 — * —12|;
б) у = I*2 + 2* — 8|;
в) у = х2
= -2
1*1 - 12;
г) у = *2 + 2 |х| — 8.
966. Напишите уравнение, соответствующее каждой из
парабол, изображенных на рисунке 60.
\\\\ш шш ш\\ш\ш
шШ\шш\Ш\\\\\\\\\\Ш
\ш\\\ \\\\\ш \\\\\\\\\\\\щ
\\\\\\ш\\\ш\\\\\\\\\\\\ \Ш
\\\\\\\\ \\\\\Ш \\\\\\\\\\\\\\Ш
| 1 || Д
—/? L_f: '/Л J "? О L. i \ni 1 \ жО 1 1 /\.\ к \ £ \ *7 \ п 1VI
\ 9 \ 1 1 \ 1 . 1 i i /1 i Jr i 1 i Л! 1 г ■ 1
11 1 1 1 1 1 1 111 1 1 1 1 ЧИ 1 1 1 1 11 1\1 1 мм Г 1
мУ^ш13[{ 1 1 1 1 1 1 1 111 1 1 1 1 1 1 1 1
ППй IN m
/J \-т(1) \ ГП
III I НШ 1111111 MTi I M 111111
Рис. 60
ОТВЕТЫ
Глава I
1. д) 6р4; е) 6з5 — 4p2q + Sq2; ж) Ът — 12п; з) а4 + б4. 2. б) у2 + j/ — 56:
е) —02+18$—81. 3. б) 9—4а2; ж) у2—2уЬ+Ь2; з) 9p2+6pq+q2. 4. a) —3 -
5
в) 12; г) —100; д) 7; з) любое число; и) —2 —. 5. б) Ь{Ъ — с); д) Ъа (Зх — 4#):
* 3
з) У (х — у); и) 3*# (у2 + 2у - 6); к) 5а2Ь (За — 4& + 2). 6. а) (5 — *) {у - 3)
в) (Ь + 8) (а + 9); д) (q - 4) (р - 3); ж) (* - у) (х - 5). 7. а) (а + 3) (а - 3)
в) (х + 2у) (х - 2у); д) * (* + 2) (* - 2); ж) (а - 3)(а-3). 8. а) {2; —5}
г) {0; 12}; е) {-8; 8}; ж) 0; з) |-|-; --}• 9. а) (а - 2) (а2 + 2а + 4)
г) (у — 4&) (у2 + 4&у + 16Ь2); д) (т — 1) (/тг+1)(т2 — т + 1) (т2 + лг + 1)
е) (р4 + З4) (р2 + q2) (р + 5) (р - 3). 11. а) {-2; 2}; б) {0}; в) 0
12. А — да; В — да; С — нет; D — да; Е — нет. 13. Длина 17,25 см,
а 2 у
ширина 5,75 см. 14. 144 см2. 15. 15 км/ч. 16. 40. 17. —, , —
6 х — у 1
2 Г 2 1 )
19. а) —0,9; б) —; в) 200; г) 206. 21. 3; —3; —1—; 0,4; —; —1,5; —1,72 .
3 (^ 3 2 J
22.а) 1,5; б)0.24. а)]-оо;2[ U ]2; + «>[; Д>]-оо; ~ CljA +оо[;ж)]-оо;+оо[.
4 4
25. а) ]— оо; + оо[; в) ] — оо; 1 [[}} 1; 4 [ |J ] 4; + оо[; ж)^0и^2;
в)у фОиу Ф2;и) хф—5 идг^=5; к) ]—оо; +оо[. 28. а) При а =6; б) при а=— Ь;
в) при а = 0 и Ь = 0; г) при \а\ = |Ь|; д) при а—О или &=0; е) при а=0 или &=2.
88. а) {8}; б) U |J; в) {3}; г) (~з|}; д) 0; е) {-8}; ж) {-4; 4}; з) 0.
40. в) {-3; 6}; г) (0; 9). 46. б) ~; г) j-\ е) -; з) —. 47. a) -J-;
За 4л# #2 2*4i/ 10*
—а а а 9с8 9*3 3 4
10* 10* 10* 8fr 5*/2 4а4 а7
а 4- 4& 36—4с х т а — 6 5у 2
б) 3. 53. а) ; б) ; в) ; г) ; д) ; е) —; ж) —;
' 2а& ' 26 ' Ъх—2у ' т+Ш f За Ъх—Ъу ' 3
5* 1 1 Ь —а 12 5
в) -т; и) —, к) --. 54. в) Ь—а; г) у—2х; ж) —-—; з) . 57. а) — —.
6а 3* 3 р — q 8
238
бЭ. а) -L; б) _{Ь_2), .) fjj; „ |±» 62. a) 2±*. 6) -*-; в) t-1, г) Щ
a — l * + У a—& 7 c—d *+у a—*
Д) a + &; ©)—g-. «) y2 — U з) 1+ я:4 — *2. 63. а) 100; б) 1,5. 65. а) (0}
б) {2}; в) 0; г) f 0; ±1 68. а) -&; б) -^; в) ^; г) ^ ?
I о J од 4 р2 2*
тЛ -• <л Х аа *ч Р (Р + g) ч 2(м-3л) Ь (о + Ь) ч 2а-&
д) Т; е) iTt:- 69- б> —Тп—; г) —~ 5 е> г~,—h з)
7 '10* dq mn ' ' 2а (а -Ь)' ' аЪ
ч 3(*+3) „ Ь + 3 5 (а—2) 7
., ___. 70. ., 4; б) -j^ptf в) —р-; г) -. 71. а) 2,5; б) {-3; 2}:
в)-{; г) <7;-7}. 73. а) £ б) £ в) А; г) 7f!; д) Л; ., 1
* *У «3 6 &2 а х
1 9 16 3 2 (2а — 1) а
w4 ,; з) —-. 74. а) ab; б) —; в) —; г) —. 75. б) —; г) 1 '
2а262 юрд Ху 4' 8у ' ЗЬ* 3(2а+1)
—2*2 * + у 7 1 * — 3i/
е> ~ТГ; ж> 5 3> V и> ^ к) ТГ- 76- а) 6>25; б) -56,
Ь2 х а — Ь а — ЪЬ х + Зу
*3 25а2 (х+у)3 (a—l)4 /2ab3 2 / 2а \6 /_2а2\3
77. а) —; б) ; и) l—^. к) * L# 78# а) / JL. . б) /J^i . в) / —±11 .
х /4— ж\5 (2—a)(3+b) а4 а + & * — у
ое % х — 5 a + 6 2л- лг 5р 3 х —17 6
85. а) ; б) -; в) ; г) ——; д) ; е) -; ж)
У — 1 с—3 п — т р — q 2а—1 дх — 1 7 — у
2Ь — 4 лл 2р + 5 7а 1 1 3* — 1
8) й=* 86- а> 7=Т' б) 1; в) ^г) rrVд) —i; e> S=v- «■ *
90. а) 2; б) - 17 }; в) 0; г) (-6; 0}. 91. а) *±»; б) 5-^; в, ^
ч 2с—7d 3&+5a Sy—7x 13 1 7* 67у 2*+15
г) ,ft ; Д) ; е) — ; ж) —; з) —; и) —; к) —. 92. а) !—;
42 аЪ ху ' ' 6а ' 12* ; 30 ; 60 10у
^ 2Ь-15 оо оЧ д2 + Ь2 лч w-y 4p2+2pg~-8g2 262 + 2с2
б) —г—. 93. а) ; б) ; в) ; г) ——;
oa a4o my pq be2
4а2 — ЗаЬ — 3&2 х2 — 4ху + У2 8а2 — 8а + 1 б2 + х2 — Ьх%
л ^ • е> ^i s «) —^ ; з) —^— .
а2 + 2аЬ — Ь2 лх2 + у2 — 2а2 + 9а + 9 Зс2—8с—5 м х—Ьу
96. а) — ; б) ; в) ! !—; г) . 97. а) ?;
Ь (а + Ь) ' у (х - у) ' 2а (а + 3) ' ; 5 (с - 1) ; 1 *
^ 2х — 10у ах —bay х2 —2Ьу2 ^ 2(* + 2) 4а2 + 1
б) ; в) -; г) —. 100. a) v ^ ; б) —;
2 a * + Ъу ' 1 - х2 ' ' 4а2 -1
ч 24* 2 (у2 + 9) 2у 2а$ /п2 + 2тп — п2 а2 + Ъ2
в> 4"=р; г) "Тзр д> ^—^2; е> -г^> ж> m,«n. •• 3> ^г^;
и) 7=7; к) *^Ь* 102' а) {3>; б) {~1; 1>; в) {~6; 6}; г) Ь27; °f
19 5 и Ъ а —6 1
103. а) ; б) ; в) —; г) ; д) ; е) — —;
6(* — у) 12(a-fb) ; 6{2у—1) ' 10 (Ь + 3) ; 6а (а + 2) ' Zx
х2-\~у2 3(а2 + &2) 12 1
ж) —; з) — —-1—~; и) ; к) . 104. а) — —; б) 0.
' ху (*2 — у2) ' аЪ (а2 — Ь2) ' 1 — т2 п + 3 9 6
239
1 6H-19 3 8 1 1 2*114-1
106. a) ; б) ——; в) ; г) ; д) 0; е) ; ж) — ;а) =!=—;
х+2 V-9 в—6 Z-2b ' '2* («--I)' ' 6 6(271-1)
2 5 — х 2х 2(а2 + 3д2)
и) — —; к) . 107. а) ; б) —— -
a *(* —5у) (x + DHx-D (a-6)2(a + 4
36 8ху* 1 р —<? 2 За
в> 7^ ^ г) ,3 ^ » I ,5 в) ————-; ж) -; з)
(а2-9)2 (*2-у2)2 а —1 р2 + pq + «2 *_2' а + ±
2аЬ 1 1 3.71 +5с
108- ГХ—Гг; 1) 4 - ч; 2) 5 - ч. 109. — -; на 1 руб. 114. а) При л=1, тг=2,
о4—zd о о т {т — о)
л = 3, л = 4, и = 6 или л — 12; б) при тг = 1, п = 3 или л = 9. 116. а) а^—6;
10 2 10
б) a = 5; в) a = 6; r) a = 7. 117. а) 5 — ——; б) — 2 — ; в) — 2 +
х + 2 *—Г 5 —jc
г) — Ц -. 118. а) При и£А, где А = {— 8; — 5; — 4; — 3; — 1; 0; 1; 4};
х — 2
б) при п£В, где В = {—24; —10; —3; 0; 2; 3; 5; 6; 8; 11; 18; 32}. 119. а) a = 2,
1-х /a-f-6,2 12
6 = 3; б) а = 8, 5 = 3. 120. а) -; б) 1 - у; в) -^H 5 Д) —. в) 1;
&х — 1 \ о J a
г —2 аЬ 1 10
з) -—. 121. а) -г-—\ б) - 2х\ в) q*~-pq; г) - —; д) -; е) 2; ж) 2л:2 + 2ху;
ж+ 6 а2—Ь2 4х х
2ах —а2 а — Ь 4- Zc 2х—и 5 1
з) а-2. 122. а) -8; б) 9. 123. а) ; б) —- ; в) У °; г) —.
2а*+х2 а + Ъ — с 2*+у+5 ' а—1
a2 a ^ 27 + 4*
1*5- а) —; б)—. 126. а) ——; 4,3 руб., 4,12 руб.; б) 12 кг; в) 50 кг.
о* о х + о
ш- а) i^; б) рд) ^; е) gr- ш- а) 8~7; б) 15~"; в) (-2-7)-'-
1 1 1 57 13 1 1
134. а) -; б) 1; в)- -; г) 16; д) 1-; е) 1-; ж) -; з) -. 139. а) 9; в)-;
Лэ ЛЬ о Ь4 со 1о 4
3 8
д) 16; ж) 0,5. 140. е) 8; ж) 1; з) —125; и) —; к) —8—. 141. а) 3&~2; б) ху~и,
4 9
ж) (а+2) (а-2)"2; з) (&—5)8(Ь+5Г1. 142. д) -—; е) —. 144. а) -1;
а + Ь (х—Зу)*
а2 + б2 Су2 —х2 а? + а2*8 — 2дг2 5с7— 357 — 26М
б) -4. 145. а) -—; б) ; в) ; г) — ;
а2аг *>y2 a4jc5 b9c*
1 — а2Ь2 2*V — Злг£/ — 2 1 а + 6 Л „ Л
д) ; е) —* 1 ; ж) -; з) / . 149. а) 7 . 10*
ab xy db a2&3 — агЪ1
б) 2,86 • 109; в) 3,092 • 1010; г) 1,001 • 10б; д) 2 • 10~2; е) 1,3 . 10~3
ж) 5,72 • 10 6; з) 1,006 • 10"2. 150. а) 102 < 365 < 103; в) 10"3 < 0,0057 < 10"2
153.г) 3,3-10 Л 155. а) 5- 10е; б) 2Ю"в; в) 1,764- 10б; г) 1,25-106.156. 3- 10й; 3 108
1,08 . 1012. 158. 3,09 • 1013. 160. а) Убывает; б) возрастает. 161. а) — 1; ——
240
б) — 1; —j ; в) [ — 4; — 1]; г) [ — 4; — 1]. 162. а) Да; б) нет; в> да; г) да;
2 2
д) да; е) нет. 168. а) 35; б) 11; в) — 2 -~; г) 1,5; д) —0,2; е) —; ж) 0,2;
о 11
з) 1. 169. а) —3; б) 5; в) {0; 1}; г) 15. 170. а) 5; б) 0; в) {0; 5}; г) -. 171. —.
3 5
172. —. 173. 10 км/я. 174. 1 км/ч. 175. 30 и 20 дней. 176. 18 дней. 177. 64 км/ч.
6
178. 6 км/ч. 179. 840 км/ч. 183. а) Уравнение имеет единственный
8
корень —, если а Ф 0, и не имеет корней, если а = 0; б) уравнение
а
а
имеет единственный корень — при любом а; в) уравнение имеет
5
20
единственный корень , если а Ф 2, и не имеет корней, если а = 2;
а — 2
г) уравнение имеет единственный корень 2а — 2 при любых значениях а.
5
184. в) Уравнение имеет единственный корень , если сф1, и не имеет корней,
с—1
если с=1; г) уравнение имеет единственный корень 0, если сф—7, и имеет
бесконечное множество корней (любое число — корень уравнения), если с = —7.
2 а 4а + 3
185. а) х = ; б) х = а — 8; в) х = ; г) х = . 186. а) у=2а —
а — 1 2а — 1 а — 2
2а—26 ab ab
— Ь; б) у = ——; в) у= ——; г) у = ~ . 189. a) 5; б) — 19; в) 22;
а + о а ■+ о b — а
г) —5. 195. а) —3 и —5; в) 2 и 4. 197. а) (х—1) (х+1) {х2-\-х+1) (*2—*—1);
г) (р2 4- р -Ы) (р2 — р + 1) (р4 — р2 + 1); е) (а? + а+ 1) (а3 - а -Ь 1);
ж) (б3 + Ь2 + 1) (б3 — Ь2 + 1). 199. д) Уравнение имеет бесконечное множество
корней. Любое неотрицательное число — его корень; е) уравнение имеет
бесконечное множество корней. Любое неположительное число — его
корень. 201. 9. 202. 10 и 11. 203. а) 3; б) 7; в) 30; г) 2; д) 37; е) 79. 205. к) ]—оо; 0[.
206. а) Если х = 0 и у = 0; б) если х = 0 или у = 0; в) если х = у;
г) если \а — Ь\ = 1; д) если х = —1 и у = 1; е) если |а+&| =1. 212. ж) ]—с»; 0[;
з)]0; +со[. 217. б) {-3; 3}; г) 0; д) {6}. 221. а) ^9 * : б) Г ;
о1 + 1 ж"
2 а (а —с) пр — 2р2 х—у а2 — Ъ2 2х — 3
в) . 230. а) — -; б) — —; в) —; г) ; д) ;
(5Ь+3)(За+5Ь+5) 1 1 б2 + 4 2
б) (За-56) (За-5)' Ш' а) 5=5? б) ^"=^; в) НГ; Г) ~ i^T*'
6а2 4-3 2х — 2у 1
Д) -~1Г-т; е) — *—. 232. а) 0; б) —. 249. а) а + Ъ. 253. а) 9;
а3 — 1 х2 -\-ху + у2 аЬс
241
б) 0. 255. а) *17; б) у50; в) а12; г) Ъ*. 256. а) х2у2; б) а2Ь2; в) —;
Ь—а,
г) Ь + 1. 268. 17,5 кле/ч. 272. 50 км. 283. а) Уравнение имеет единствен-
2Ь
ный корень , если Ъ Ф 2. Если Ь = 2, то уравнение не имеет корней;
О —— А
5 +4а
в) уравнение имеет единственный корень , если а^Ои аф—5. Урав-
а
нение не имеет корней, если а=0 или а——5; г) уравнение имеет единственный
а —1
корень , если а Ф — 1. При а = — 1 уравнение корней не имеет.
а+ 1
а —3
284. в) Уравнение имеет единственный корень , если а Ф 3. Если а = 3,
4
то уравнение корней не имеет. 290. г) ad = Ьс и bd Ф 0.
Глава II
293. в) Да; г) да; е) да; ж) да; з) да. 325. а) Да; б) нет; в) нет; г) да;
д) нет; е) да. 326. а) х > 11; б) у < 2; в) х > 1—; г) а < —3,5. 337. а) Нет; б) да;
3
в) да; г) нет. 343. в) ]—4; 0 [ |J ]3; +оо[. 350. а) ]1 -; + оо[; б) ]— оо; 2,5];
в) ]-36; + оо[; г) ]-оо; —1,28]; д) ]—оо; 4[; е) ]1,2; + оо [; ж) [-8; + оо[;
з) ]3,5; + оо[; и) ]—оо; -2,4[; к) ]-2,2; + оо[; л) [1,5; +оо[; м) ]—оо; -1,25].
351. а) 1—оо'; —-Д б) ]9; +оо[; в) ]-оо; -3,1[; г) ]—оо; 0,8[; д) ]6; +оо[;
7 2
е) ]0; + оо[; ж) ]-оо; 3-[; з) ]—оо; —10[. 352. а) ]—оо; —-[; б) ]—оо; 2,4];
15 о
в) ]17; +оо[; г) ]-со; —[; д) ]—оо; 3,5[; е) ]-0,25; +оо[. 353. а) ]—оо; 3[;
1о
б) ]7; +оо[. 354. а) ]2; +оо[; б) ]— оо; —2,5[. 355. а) ]—оо; 8[; б) ]2; + оо [.
356. ]6; + оо[. 357. ]— оо; 5[. 353. ]2; + «>[. 359. а) 0; б) ]— оо; + оо[5
в) ]_оо; +оо[; г) 0. 360. ]—оо; +оо[. 361. 33. 362. —19. 363. 1, 2, 3, 4.
364. 1, 2. 365. Неравенство верно при всех положительных значениях х,
366. Неравенство верно при всех отрицательных значениях х. 367. ]—1; 2[.
368. ]4; 6]. 369. в) [2; +оо[; г) ]—оо; 5]; д)
—; +оо ; е) ] — оо; —2,5].
370. Меньше 2 см. 371. Меньше 12,15 дм. 372. 7, 8, 9 или 10 раз. 373. Не более
26- км. 374. а) ]17; +оо[; б) ]-оо; 1[; в) ]0; 6[; г) 0; д) [-1; 3]; е) ]8; 20 ].
о
375. а) ]6; +оо[; б) ]—оо; -1[; в) ]0; 3-[; г) 0. 376. а) ]0,8; +оо[; б) [2; 4];
3
в) ]"=-; "к? г) ]0,1; 0,2[. 377. а) ]3; +оо[; б) ]-оо; -3[; в) [-11; 3]; г) 0.
О о
242
378. a) 0, 1, 2, 3; б) 4, 5, 6, 7; в) 1; г) 1. 380. а) ]— оо; 2,8[; б) 0,
381. а) 0, 1, 2; б) —6, —5, —4, —3, —2, —1, 0; в) —2; —1,0; г) —2, —1,0.
382. а) ]2; +оо[; б) ]3; 6[. 333. а) ]—1; 2[; б) [—7; 17]. 384. а) [3; 4,2];
б) ]2,5; 3[. 385. а) ]8; +оо[; б) ]—оо; —5[; в) ]10; 12[; г) 0. 388. а) ]—со; 2[;
б) ]12; +оо[; в) ]1; 3[; г) ]1; 2[. 387. а) 51, 62, 73; б) 21, 32 или 43.
388. Более 4 км/ч, но менее 5 км/ч. 389. ]2; 5[. 390. ]—оо; 1,5[[J] 5; +со[.
391. а)]1; 3[; б) ]-oo;0[|J]l; +оо[. 392. a) ]-oo;0[U]5; +co[; б) ]1; 2[;
в) ]-оэ; —l[Ui-r; +оо[; г) ]-6; 0[. 393. а) ]-оо; -6[L)]0; + со [;
б) ]0; 7,5[; в) ]—оо; — 8[L)]8; Ч-оо£; г) ]—0,5; 0,б[. 394. а) ]8; + оо [;
б) ]4; +оо[; в) ]3;+оо[; г) ]2,7; 5[[J]5; +00 [. 395. а) ]-4; +оо[;
б) ]-оо; 15[. 396. а)]7,2;+оо[; б) ]-оо; 5[; в) ]37; +оо[; г) ]—оо; 13[.
397. ]—оо; 3[L)]8; + со[. 398. ]—оо; —2[L)]3; +oo[. 399. а) ]7; 9[;
б) ]0; 2[; в) ]—5; +оо[; г) ]0; 1[. 401. а) —3, —2, —1, 0, 1, 2, 3; б) 2, 3, 4, 5;
в) 1, 2; г) 1. 402. а) ]-оо; OCU30.7; +оо[; б) ]-оо; 0[L)]2; +co[; в) ]-4; 4[;
г) ]-оэ; -5[t)]5; +оо[. 403. б) ]0; 3[. 404. а) ]-оо; -1[L)]0; + °о[;
б) ]0; 4[; в) ]0; -к; г) ]0; 1-к; д) ]-оо; 2[; е) ]-оо; 1[; ж) [- -£-; 0[; з)]0; -Ц-].
о 4 Ли
427. а) 16 < х + у < 19; б) — 6 < х — у < — 3; в) 3 <у — х < 6; г) 60 < ху < 84;
д) 0,5 < -< 0,7; е) - < - < 2. 430. а) 5<3а+76<7; б) —1,2<— +0,6& <—0,4;
у 7 х 2
в) 1 < Ь2 — аЬ < 21; г) 7 < — + — < 12,5. 433. Нельзя. 434. Можно.
а Ъ
436. 18°<СЛВ<20°. 439. а) 11; 9; в) 7,6; 7,4. 442. 0,17 — лучшее приближение.
443. Подойдет. 444. 14,1 < nd < 14,5. 445. 810 < — < 860.
450. Не является приближением с точностью до 0,001. 451. Являются.
452. Являются. 453. Р = 18,2± 0,4 см; S = 20 ± 1 см2. 455. 48±4 см2.
KB
456. 445 ± 15. 457. 2700 ± 40 —. Алюминий. 459. 7. 494. а) При положительных
мв
значениях; б) при отрицательных значениях. 495. а) Нет; б) да. 499. а) Да;
б) нет; в) да; г) нет; д) нет. 501. а) Да; б) да. 502. а) Нет; б) да;
в) нет; г) да; д) да; е) нет. 507. б) ]—3; +оо[. 509. а)]—оо; 2[;
б) ]-оо; ~1,5[; в) ]4; +оо[; г) ]-оэ; - -[. 511. а) ]-оэ; 0[U]2; +oo [;
б) ]—оо; 0 [[J] 2; +оо [.513. а)]—со; —60 [; б) [4,8; +оо[; в) ]0,5б;+оо[;
г) ]-со; ^]. 514. а) ]-оо; -115[; б) ]0,2; +со[; в) ]-оо; 15[;
10
г) ]—оо; 1,4[. 515. а) ]—оо; 0,325[; б) ]—1; +оо[. 516. а) {1; 2; 3; 4};
б) {1; 2; 3; 4; 5}. 520. а) Нет; б) нет; в) да; г) да; ж) нет; з) нет,
521. а) Таких значений нет; б) при любом значении х. 522. а) ]—оо; +со[;
б)]-оо;+оо[. 524. а) ]0; +оо[; б) ]2; +оо[; в) ]-3; +оо[; г) ]-7; +оо[.
243
626. a) 7—oo; 0[? 6) l—co; —4[; в) ]— oo; —S[; г)1—со; — —[.
5
526. a) [8; + oo[; 6) ]— 00; 2L; в) ]—oo, — 5]; r) J—00; 3,5[. 527. a) 18; 6) —1.
629. 4. 531. He более 5 наборов. 532. Более 6 км/ч. 533. Более 18 км/ч.
2 1
634. Более 4 —км/ч. 535. Более 16 км/ч. 538. в) ]6,5; foo[; г) J—оо; 5—[..
3 4
637. б) ]—2,8; —1,7[; г) ]—2,01; —2,1[. 539. a) J9; +оо[; б) J—оо; 0[;
в) 0; г) 0. 541. а) ]-; +оо[; б) ]0, 1; 5[; в) 0; г) ]0,8; + со[; д) ]-оо; -0,2[;
о
5
е) ]1~;+оо[. 542. б) —10; в) 1; г) 2, 3, 4, 5. 543. а) ]—3; 6[; б) ]1,5; 2,5[;
в) [0,8; 1]; г) [-2; 1]. 544. а) ]1,5; 4,5[; б) [5; 15]. 545. а) ]0; ~[;
в
б) ]0; 0,8[. 546. а) ]—1; 0[; б) ]—5; 0[. 547. Дороже 1 руб. 16 коп., но
дешевле 2 руб. 04 коп. 548. Более 10 км и менее 16 — км. 550. а) II; 1 — ; б) [0; 22];
в) ]—оо; jtUJ^S +»Ь г) ]-оо; _2,5[|J]-1; +oo [; д) ]-оо; 1,8[;
е) ]7,5; +оо[. 551. а) ]—оо; -4[L)]1; +со[; б) ]—со; 2[|J]2; +co[.
552. а) ]-со; _5[|J]-5; 6[; б) ]3,5; 5[U]5; + со[; в) ]—со; 3[U]3; 15[;
г) ]5; +оо[. 553. а) ]2; 5[L)]7; +«[; б) ]—оо; 0[[j]3; 4[.
654. а) ]-оо; 0[L)]2; +оо[; б) ]0; 2[; в) 0; г) ]—со; +оо[.
556. а) ]-оо; 0 [J]-; +оо[; б) ]-оо; -HLlA + »Ь »> 1-Ь Ч:
& 4
г) ]-оо; -1 CU[ 17,8; + со[; д) ]-оо; -5[U]-5; 8[; е) ]-оо; 7[.
557. а) 3; 4; б) 4; 5; 6; в) 1; 2; г) 1; 2. 553. а) ]—2; 0[;
б) ]—со; 0CU31; +оо[; в) ]0; 1,2[; г) ]-1; +со[; д) ]-оо; 0[; е> ]-1; +оо[.
659. ]0; 2[. 566. а) Можно; б) нельзя; в) неизвестно. 571. г) 4<10 — * < 5;
ж) 2 -- < - + 2 < 2 т; з) - < —— < ~. 572. а) -0,4< с <0,1; в) -0,3<
ОД? 5 о ДР -(- 2 7
<с<0,1. 584. а) [18; +оо[; б) ]—оо; —24]; в) [6; +оо[
; г) ]о; {].
Ъ 1
685. в) 12,3<5а+7&<16; г) — 6<—5а<—5,25. 586. в) 12,1< Ьл< 15,2;
4 л*
111 а
г) — < < —. 590. а) Может; б) может. 591. б) 7,41 < j- Ь < 7,44;
22 т+п 20 с
в) 2,98 < — < 3,05. 593. а) 35,8; б) 36. 594. а) 12,3; б) —7,6. 595. а) 5,9;
Ь—с
б) —9,2. 597. 3,142. 605. 1,46; 1,47; 1,493; 1,468. 607. 0,5 ± 0,1а. 6ЭЗ.
Достаточно. 611. Неизвестно.
244
Глава HI
625. а) 0,5: б) 1080 631 б) —0,7: в) 2; г) 0,2; к) 0,5. 633. ж) —; з) 6,25.
638. а) \ Г2; —/12; в) 0; г) 0,2; —0,2; з) /30; —/30. 639. а) [—/2; /2J;
б) J— оо; —/2[|J]K2» +<»[. 641. в) При х < 0; г) при г>0; д) при любых дс.
642. д) ]2; +оо[; е) [-2,5; +оо[; ж) [0; 2[; з) ]-оо; —1[U[9; + оо(..
644. ж) 2; з) 60; и) 0,13; л) 0,5. 668. а) 10а; б) 100; в) 0,10; г) 0,1а.
672. в) V 74- /3=4,4±0,1; г) /7— /3=0,9±0,1. 673./ЗД+/15Д=5,7±0,1.
680. a) 3,4<^jc+3<3,5; б) —0,5</*—1<0,6. 683. а) ]9; +оо[; в) ]1; 9[;
Д) [0; 5]; е) [2; б]. 694. б) 27; г) 16; е) —200; ж) 8,1; з) 0,001. 697. а) /2—1;
в) ^ П—J 10. 698. в) 2; 0; г) —10; —4. 700. з) 7,7; и) 0,48; к) 0,3.
701. а) 180; б) 48; в) 60; г) 42; д) 6; е) 24. 702. б) 25; г) 45. 704. а) 9 см;
б) 1848 см2. 708. а) 72; б) 0,01; в) 25; г) 0,121. 710. д) ас; е)—0,66с2;
а*Ь2 1 __
ж) — —-; з) —aV. 711. з) —; и) 2. 716. г) 1,5 /3; д) —0,15/5; е) —0,75 /14.
3 2
717. г) К??. 718. б) 4 /5; г) — \ И; е) 1,2 /130; з) 0,05 /10. 719 а) —;
15 11 3
в) /3; д) til; ж) tJL; и) £J . 722. д) /72>0,5/162; е) /24 = — ^216.
3 3 2 3
724. б) 3/2; г) 14/5; е) 0. 725. а) а /7; б) —у /10; в) 4* /*;
г) 0,1 б2/б; д) 5о3»/2о; е) — Зс3/§". 727. а) 8а2 /а; б) 0. 729. а) —За/б;
б) ЪаЬУЪ; в) Uabfab; г) 4а2Ь /26; д) — 5а63 /За; е) —2а263/2аК
730. г) /6; д) 3/2; е) 0,5 J/ 6. 732. а) 12 — 3/6; б) 15/3—20;
в) 12 — 4 } 3 + 2 )/2; г) 24 — 12 /2—2 /3". 733. б) 7 — 4 /3; г) 22+4/10;
е) 66—12/10; з) 77 + 28 } 6. 736. в) — /б"<б|/~-1; г) — /72<7]/*-?-.
2 г 2 3 г 3
751. а) ]6; 9]; б) [3; 5[IJ]6; 9]; в) {3; 9}; г) {9}. 752. —3,32. 753. —3 —.
3
4 1 _ _
754. а) 5,1; б) —3,6; в) ——; г) —; д) 10,22; е) 1. 756. а)/3, — У 3;
7 8
б) /20, -/20. 760. а) ]-оо; + оо[; б) ]-оо; +оо[; в) ]— оо; — 1]у[1; +оо[;
г) ]-оо; +оо[; д) ]-оэ; -3]U[3; +oo[; е) [-2; 2]; ж) 0; з) ]0; +оо[;
и) ]—оо; —4[у]4;+оо[. 761. а) При х>2; б) при х > Ои хф 4; в) при*>—2;
г) при х^О; д) при —2<л:<15; е) при *>3. 762. а) а>0, 6>0 или а<0, 6<0
или а = О, Ъ — любое или а — любое, Ъ = 0, б) а — любое, не равное 0, 6^0
или а = О, Ь — любое; в) a — любое, Ь — любое; г) а<0, Ь — любое, отличное
от 0, или а — любое, Ъ = 0; д) а — любое, b — любое; е) а — любое, Ъ — любое,
245
причем а ф Ь. 763. г) 32; д) 0; е) 4, —4; ж) 0; з) 5; и) 5; к) 0.
764. а) 2/И; б) 2/7; в) 2/3+1; г)3^5"1. 765.6) 41; г) 22.
768. а) 100; б) 0. 775. а) ]6,25; +ооГ; б) [0; 36[; в) ]25; 64[.
780. а) [0; 24 [|J]24; +оо[; б) [—10; 0]. 784. б) 8; г) 81; е) 81.
785. а) 8; б) 243; в) 1024; г) 125; д) 18; е) 24; ж) 15; з) 12. 788. а) 1;
б) 6; в) 3; г) 1. 789. г) [10; +оо[; д) ]—оо; 2]; е) [—5; + оо[. 792. а) 7,56;
б)-; в) 9,1; г) 1,08; д) 128; е) 108. 796. а) 8,5; б) --; в) -; г) —.
£А УО /£У 10Э
801. а) 8/3; 6)4/2; в) —/И; г) 4,5/13. 803. б) —2а/2аЬ; г) 6aW/ЗаЬТ
805. а) —2а /а; б) 6л: /ж. 806. а) 36; б) 1—; в) 2. 807. б)—2; г)—2,6.
3
809. в) —/3?; г) /о3"; д) —/За1; е) — /^За"3; ж) /а&*; з) уЪа?Ь;
и) -/аЬ(а+&). 812. в) /*<*+1)2; г) . -/_*(*_2)2; д) - |/За(1-Д).
г 1 + а
е) |/5gg(QT2)> 813. a) 10; 4; б) -4; 0; в) 0; г) 5; д) 6; е) 0.
Глава IV
819. а)--; -1; б) 0,6; 1; в) 0,5; 3; г) -4,5; -1; д) 1,5; 3;
13 7
е) 2; 2--; ж) —1; т; з) —1,5; 3; и) —5; 8; к) —12; 5; л) — --; 0;
«5 4 12
и)--;-. 820. а) -0,2; 2; б) -5; 8; в) -7; 2; г) -4; -; д) -4; 5;
е) 0; ж) —1; 2—; з) —7; 5. 821. а)—8; 3; б) 1т; 4; в) ——; 3; г) —И; — ~.
| 4 5 3
822. а) 0,558+0,0005 или — 0,358+0,0005; б) —2,781+0,005; —0,719 ± 0,005.
824. а) 1,8; —0,2; б) 0,7; 1,3; в) 0; г) 0,25; д) 2,5; е) —9; 3.
2 г 2
825. б) — -—; —-; в) —2; -—; г) —1,5; 1,5; д) любое число является корнем
о о 9
1 2
уравнения; е) —6; 6. 826. а) — —; —; б) 1; 1,5. 827. а) —1; 3; б) —5;
15 5
7; в) —2; 12; г) —2,8; 6; д) —4; 5; е) —2; 2,4. 828. а) 1,5;
2 1
В) _27; —1; д) —9; ж) 1; 2—; и) 0. 829. а) —11; б) 6. 830. а) ]—; +оо [;
3 3
б) ]16,2; +оо[; в) ]—4; 4[; г) 0. 831. а) ]-оо; 40[; б) ]—оо; —12 [lj]12; +оо[;
в) ]—оо; 0 [UJ0; 9[; г) ]—оо; +оо[. 832. а) £=+24; б) А?==135; в) £=+50;
г) £= + 10/2. 835. а) 11 и 12; б) 7 и 8. 837. а) —; б) —.
3 10
839. а) 8 рядов или 10 рядов; б) 6 автобусов. 840. а) 9,6 м2; б) 90 см.
246
841. a) 80 км/ч; б) 1 -- ч. 844. а) 13 км/ч; б) 2 км/ч. 845. 2 ле и 2,5 ле.
846. а) 15 г и 18 г; б) 21 ц и 20 ц. 847. а) — ЪЪ; ЗЬ; б) — а; —а; в) 2£—2; 2;
6 3
а + 3 * 4-1
г) 3 — а; 3 + а; д) 1; ——; е) —2; —^-. 850. а) 0,6; Ь =—43; б) —2;
л 3
с =—Юб. 853. д) 1 ± /16. 855. з) *2+14*+1=0. 867. г) — У—~;
У + 9
с + 10 5о + 3
Д) -^7+Т;е)14-11о'838' а)]—°°; —^CUjS; +oo[;b)]-co;1,5[U]2;+oo[;
г) ]—-; 4[; д) [-11; б]; е) ]—оо; 0]|J[5; +oo[. 869. а) [-9; 9]; б) [0; 16];
о
в) —оо; —1 "Z" (J [3; + оо[; г) ]—оо; +оо[; д) функция не определена ни при
каких значениях х; е) ]—9; 5[. 871. а) Так как при всех допустимых
значениях * данное выражение имеет только одно значение, равное 1, то оно не зависит
от х. б) Выражение имеет только одно значение, равное 1,5, следовательно,
оно не зависит от а. в) Значение выражения при любом (допустимом) у равно
—, значит, оно не зависит от у. г) Значение выражения при любых (допустимых)
4
значениях Ь равно 1, следовательно, оно не зависит от Ъ. 881. а) (—4; —1);
б) (3; —8). 885. Через А и В проходит, через С не проходит. 886. а) с = 20;
б) Ъ = 12. 887. а = —21; 6=71. 888. Ь= — 4; с=—4; 889. а) (—4; 16) и (2; 4);
б) (0; 0) и (2,5; 6,3); в) (2; 4); г) (-0,5; 0,3); д) (1; 2) и (0; С); е) (0; 0);
(—1; —1); (1; —1). 890. а) Корней нет; б) —2; 2,5; в) —1,6; 3,1;
г) —4,9 и 2,9; д) корней нет; е) корней нет; ж) —8; 2; з) —1,4; 4,4.
891. а) ]-оо; -4 [U]3; +оо[; б) ]-1; 6[; в) ]0; 4[; г) ]—со; -3 [ЩО; +оо[;
Д) ]_оо; +оо[; е) ]—1,5; —1[. 892. а) 4; 12; б) —9; —3; в) —13; 3;
2 3
г) 11; —5; д) —9,2; е) 4; 7; ж) 0,5; 2; з) -4—; 5. 893. а) —1; — —;
о 4
12 2
б) —10; 9; в) —9; 10; г) 2; 1,6; д) —3—; 3; е) — 4 ~; 1; ж) —5-; 2;
о о о
з) 1±У> б . 894. а)-1,2; 0,2; 6) —4—; -1-=-; в) 2^; 4; г) -2-; -1;
2 о 3 3 11
3 2
д) — —; ——; е)—1; 1; ж) —2,5; 2,5; з) любое число — корень уравне-
5 5
1 11
ния. 895. а) 8; 10; б) —15; 1; в) —1; 8—; г) —4; —1,2; д) —; 8-;
S о о
е) 200; 8. 898. а) 1 ±/б; е) 9±V П3 . 898. а) —1-; 1; б) -3-; 2;
8 7 о
1
в) —0,9; 1,5; г) —7; 3; д) 11; 13; е) —14; 5; ж) —3; 7; з) —5; 4-.
899. а) —4; 3; б) —6; в) 12; г) 5. 900. а) —1— или 1; б) корней нет; в) 9.
247
908. a) 72 станка и 62 станка; б) 8 дней. 909. а) 15 га и
18 га или 24 га и 27 га; б) 72 га и 60 га или 120 га и 108 га.
911. а) 432 детали; б) 10 дней. 912. а) 18 деталей; 15 дней; б) 9 дней .
913. а) 25 дней; б) 300 деталей. 914. а) 5 ч 50 мин; 4 ч 40 мин; б) 25 ч и
20 ч. 915. а) 10 дней; 15 дней; б) за 42 ч и 56 ч. 918. а) 3 км/ч; б) 2 kjk/ч
или 3 км/ч. 919. а) 10 км/ч; б) 5 кл*/ч. 920. а) 2,4 км/ч или 3 км/ч; б) 3 кж/ч.
921. а) 5 ч 15 мин; б) 7 ч 52 лшк. 922. 6 ч. 923. а) 48 км или 54 кж;
б) 42 км/ч. 924. а) 18 км/ч; б) 48 жж или 60 км. 925. 10 км/ч. 926. 20 км/ч,
win 7 км/ч, или =;6,5 ялг/ч. 927. а) 100 ж и 60 ж; б) 50 ж и 24 л или
16 л и 75 ж. 928. а) 1936 см2; б) 6 еж. 929. а) 6 л2 и 216 ж2; б) 1320 см2 и 216 еж2.
930. 600 см2; 24 еж; 25 ел. 931. а) 10 кг или 25 кг; б) 120 г. 932. б) —4,5а; а;
1 _ 1 2л — 5
в) ~-е; е+1; г) — k; k — 2; д) 2; —-—; е) если аф—1, то * =—3 или
4 3 3
2а —1
*=— ; есЛИ а=_1, то х=—3. 937. 6=—5 или 6=5. 939. с=6. 940. 6=1;
а + 1
с=— 4. 941. а=1; с=4. 942. е) i,2-_5=0; ж) i/2—4i/hl=0; з) 25у2—1Ш/+
+ 1 = 0; и) 9#2+60#+2=0. 944. 2у2 — 12у +13 =0. 943. 5у2+у—2=0.
946. 9z/2—43z/+l=0. 947. 7у2—13y+4=Q. 949. a) 9; б) —9; —2; 2;
в) 1; г) —/16; /10. 952. в) *3—6х2+11*—6=0; д) 9*3 + З*2 — 2х = 0:
е) 4*4 — 37*2 + 9 = 0. 953. ж) (а — 36) (а + 26); з) (х + 6а) (* — 5а)
и) (*/+6)(Зг/—56); к) (2—1+У%) (2—1—/2); л) не разлагается на линей
ные множители; м) х (х — 2) (х — 10). 954. a) (t + 1) (* — 6) (6Г — 1)
б) (а + 1) (а — 2) (а — 3) (а — 5) (а — 6); в) (6—1) (26—3) (6—3)(262+96—9)
5а + 2 р2 + 5р + 13 с — 2
г) (*+2)(5*-4)(*-5). 955. а) - о „ , ; б) - Т Т ^ в)
-За+З' 7р + 5 Зс2 + 23
За —4
г) —г— . 956. а) При всех значениях переменной а из области опре-
13а2— 5а + 1
1
деления значение данного выражения равно — —, следовательно,
3
3
оно не зависит от а; б) значение выражения равно — при любых
5
(допустимых) значениях а; в) значение выражения равно 1 при любых
(допустимых) значениях а; г) значение выражения равно — при любых (допус-
2
3 1
тимых) значениях а. 957. а) —; б) 2—. 959. а) ]— оо; —7] U [7; +оо[;
16 3
б) [-4; 4]; в) ]-оо; -7] U [9; +оо[; г) [-6; 7]; д) [0; 10[ U ]Ю; +оо[;
е) ]_оо; -8 [ U ]-8; 5]; ж) ]-оо; -2] [} ]2; +оо[; з) ]-3; 3[. 960. а) (-12; 0),
(10; 0), (0; —120); б) (—7; 0), (8; 0), (0; 56); е) (0; 0), (—9; 0), (11; 0);
ж) (—10; 0), (—2; 0) (2; 0), (0; —40); з) (**—2*2+1)+2=(*2—1)2+2,
следовательно, график пересекает только ось ординат в точке (0; 3). 9S4. а) В I и II;
б) в I, И, III и IV; в) I, II и III; г) в III и IV.
248
ПРИЛОЖЕНИЕ
НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ ЗНАКИ,
ВСТРЕЧАЮЩИЕСЯ В УЧЕБНИКЕ
€ — знак принадлежности множеству.
# — знак непринадлежности множеству.
0— знак пустого множества,
с:— знак включения одного множества в другое.
П — знак пересечения множеств.
(J — знак объединения множеств.
=£> — знак логического следования.
<=* — знак равносильности.
Y — знак арифметического квадратного корня.
[а; 6] — множество решений неравенства а ^ х ^ &.
]а; 6[ — множество решений неравенства а < х < 6.
]а; + оо[ — множество решений неравенства х > а.
[а; + оо[ — множество решений неравенства х ^ а.
]—оо; а[ — множество решений неравенства х < а.
]—оо; а] — множество решений неравенства х ^ а.
ТАБЛИЦА КВАДРАТОВ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 10 ДО 99
h\ единицы
^\
десятки \ч
1
2
3
4
5
6
7
8
9
1
0
100
400
900
1600
2500
3600
4900
6400
8100
1
121
441
961
1681
2601
3721
5041
6561
8281
2
144
484
1024
1764
2704
3844
5184
6724
8464
3
169
529
1089
1849
2809
3969
5329
6889
8649
4
196
576
1156
1936
2916
4096
5476
7056
8836
5
225
625
1225
2025
3025
4225
5625
7225
9025
6
256
676
1296
2116
3136
4356
5776
7396
9216
7
289
729
1369
2209
3249
4489
5929
7569
9409
8
324
784
1444
2304
3364
4624
6084
7744
9604
9
361
841
1521
2401
3481
4761
6241
7921
9801
ТАБЛИЦА КУБОВ НАТУРАЛЬНЫХ ЧИСЕЛ ОТ 1 ДО 10
И СТЕПЕНЕЙ ЧИСЕЛ 2 И 3
п
п*
2"
3»
1
1
2
3
2
8
4
9
3
27
8
27
4
64
16
81
5
125
32
243
6
216
64
729
7
343
128
2187
8
512
256
6561
9
729
512
19683
10
1000
1024
59049
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
Определение 1. ап = ааа ... а, где п £ N и п ф 1.
п раз
Определение 2. а1 = а.
Определение 3. а0 = 1, где а Ф 0.
Определение 4. агп = —, где п € N и а ф 0.
ап
СВОЙСТВА СТЕПЕНИ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
Если тип — целые числа, а ф 0 и Ъ ф 0, то:
1°. атап = a"*+";
2°. а™ : а* = ат'п\
3°. (а™)* = а™;
4°. (аЪ)п = алЬ*;
5°. (f )"=-£.
ОЦЕНКА СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО
1) а < * < 6 3) а < ж < 6 (а>0)
\ \ \ \
с < у < d с < у < d (с > 0)
a+c^.x+y^.b+d ас < ху < bd
2)о< ж О 4)а<*<Ь (с>0)
(с >0)
с < у <d с < у < d
а—d<^;c—j/ ^b—с £ < *_< _ь_
ТОЖДЕСТВА СОКРАЩЕННОГО УМНОЖЕНИЯ
1. (а — Ь) (о + Ь) = с2 — Ь2;
2. (с + б)2 = а2 + 2аЬ + Ь2;
3. (а + Ь)3 = а3 + Зс26 + ЗсЬ2 + Ь3;
4. (а + Ь) (а2 — аЬ + б2) = а3 + б3;
5. (о — Ь) (с2 + аЪ + б2) = а3 — б3.
ОГЛАВЛЕНИЕ
Глава I. ДРОБИ
§ 1. Понятие дроби 8
1. Целые выражения —
2. Дробь. Область определения дроби 6
§ 2. Свойства дробей 10
8. Условие равенства дроби нулю —
4. Основное свойство дроби. Сокращение дробей 13
§ 3. Тождественное преобразование в дробь произведения и частного
двух дробей 19
5. Произведение дробей —
6. Частное двух дробей 22
7. Степень дроби 24
$ 4* Тождественное преобразование в дробь суммы и разности двух дробей 25
8. Сумма и разность дробей, имеющих равные знаменатели ... —
9. Сумма и разность дробей, имеющих различные знаменатели 29
10. Представление дроби в виде суммы нескольких слагаемых ... 34
11. Тождественные преобразования дробных выражений 36
§ 5. Степень с целым показателем S3
12. Определение степени с отрицательным целым показателем . . —
13. Свойства степени с целым показателем 41
14. Стандартный вид числа 44
15. Степенная функция с целым показателем 46
§ 6. Уравнения, содержащие переменную в знаменателе 50
16. Решение уравнений с переменной в знаменателе —
17. Уравнение с параметром 54
Дополнительные упражнения к главе I 57
Глава II. НЕРАВЕНСТВА И ИХ ПРИМЕНЕНИЕ
К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
§ 7. Неравенства и их свойства 78
18. Понятия «меньше» и «больше» —
19. Свойства неравенств 80
253
20. Понятие логического следования 83
21. Равносильные предложения 86
§ 8* Неравенства с одной переменкой 88
22. Графическое решение неравенств с одной переменной —
23. Решение линейных неравенств с одной переменной 91
§ 9. Системы неравенств с одной переменной . • . . . 96
24. Решение систем линейных неравенств с одной переменной ... —
25. Примеры решения нелинейных неравенств 102
t 10. Применение неравенств к оценке точности приближенных
вычислений 106
26. Точные и приближенные значения величин —
27. Границы значения величины 108
28. Теоремы о почленном сложении и умножении верных числовых
неравенств 111
29. Применение метода границ для оценки значения суммы,
разности, произведения и частного 114
30. Погрешность приближения 117
31. Точность приближения 118
Дополнительные упражнения к главе II 123
Глава III. КВАДРАТНЫЕ КОРНИ
§ 11. Понятие квадратного корня 142
32. Рациональные числа —
33. Арифметический квадратный корень 145
34. Уравнение х2 = а 148
35. Тождество (]/а)2 = а 153
36. Приближенные значения квадратных корней из
положительных чисел 155
37. Нахождение приближенного значения корня методом
последовательных приближений 157
38. Таблица квадратов 159
39. Таблица квадратных корней 161
40. График функции у = У х 164
§ 12. Преобразование выражений, содержащих квадратные корни .... 167
41. Тождество ]/х2 = \х\ —
42. Теорема о корне из произведения 170
43. Теорема о корне из дроби 173
44. Вынесение множителя из-под знака корня 176
45. Внесение множителя под знак корня 178
Дополнительные упражнения к главе III 180
254
Глава IV. КВАДРАТНЫЕ УРАВНЕНИЯ
§ 13. Решение квадратных уравнений 192
46. Графический способ решения квадратных уравнений —
47. Решение квадратных уравнений выделением квадрата
двучлена 194
48. Формула корней квадратного уравнения 195
49. Другой вид формулы корней квадратного уравнения .... 200
50. Задачи, приводящие к решению квадратных уравнений . . 203
51. Квадратные уравнения с параметрами 207
52. Теорема Виета 209
§ 14. Квадратный трехчлен 212
53. Корень многочлена —
54. Разложение квадратного трехчлена на множители 214
55. График функции у = ах2 + Ьх + с 218
Дополнительные упражнения к главе IV 224
Ответы 238
Приложение 249
Юрий Николаевич Макарычев
Нора Григорьевна Миндюк
Константин Соломонович Муравин
Светлана Борисовна Суворова
АЛГЕБРА
Учебное пособие для 7-го класса
средней школы
Редактор Я. Я. Никитина
Художественный редактор Е. Я. Карасик
Технический редактор Е. В. Богданова
я М. И. Смирнова
Корректоры В. И. Громова
в Г. Я. Смирнова
Сдано в набор 14/IV 1976 г.
Подписано к печати 27/VII 1976 г.
60x90Vie. Бум. типогр. № 3. Печ. л. 16-f
-f-форз. 0,25. Уч.-изд. л. 13,30-(-форз. 0,30.
Тираж 2350 тыс. экз.
Ордена Трудового Красного Знамени
издательство «Просвещение»
Государственного комитета Совета Министров РСФСР
по делам издательств, полиграфии и
книжной торговли. Москва, 3-й проезд
Марьиной рощи, 41. Заказ 68.
Саратовский ордена Трудового Красного
Знамени полиграфический комбинат Рос-
главполиграфпрома Государственного
комитета Совета Министров РСФСР по
делам издательств, полиграфии и книжной
торговли, г. Саратов, ул.
Чернышевского, 59.
Цена 26 коп.
график функции у=ах2+Ьх+с
-
/ -(
j -;
\-b-i
Э —
\-i
* t
■ -c
i-l
1 -i
■■*■■> 1
yj
7
vr
5
л
.4
2
t
i
гдо
i -1
-2
ч
о
Л
■ 1
1
I
/
i/-1
-4
-5
I
I
f
i
i A i
» ^
I ^
:
[ l
Vc
к
) 6 -
» t
<8
> 7 8
^^^
X
X
1 ' '1
1
1
j
'
:
■
i
i
i
i
—-j
~ i
-i
i-a
i i
-^
{-2 -1
i i
i _]
V
>]
i
01
^5j
4
9
^1
l
-1
9
— C\
i/ -
\
>
1
У|Г^
г
0
L. 1 .
-2
"-4
ta
1
v
\
г
k^
^*
4
J 3 4
2 у
/
l/
/
r
"
1 II
L
i
f
'
—"*
с
kh
>
^
> (
V
\
■-' —1
/
|T
i /
L
V
\
i
/
f
f
i
/1
f
r
* 8 9 10 11
' £
\
J £
1 10 1
i
X
^»
X
—
1