Автор: Воробьев Е.И. Егоров О.Д. Попов С.А.
Теги: инженерное дело техника в целом кибернетика механика проектирование роботы промышленные
ISBN: 5-06-001134-8
Год: 1988
Текст
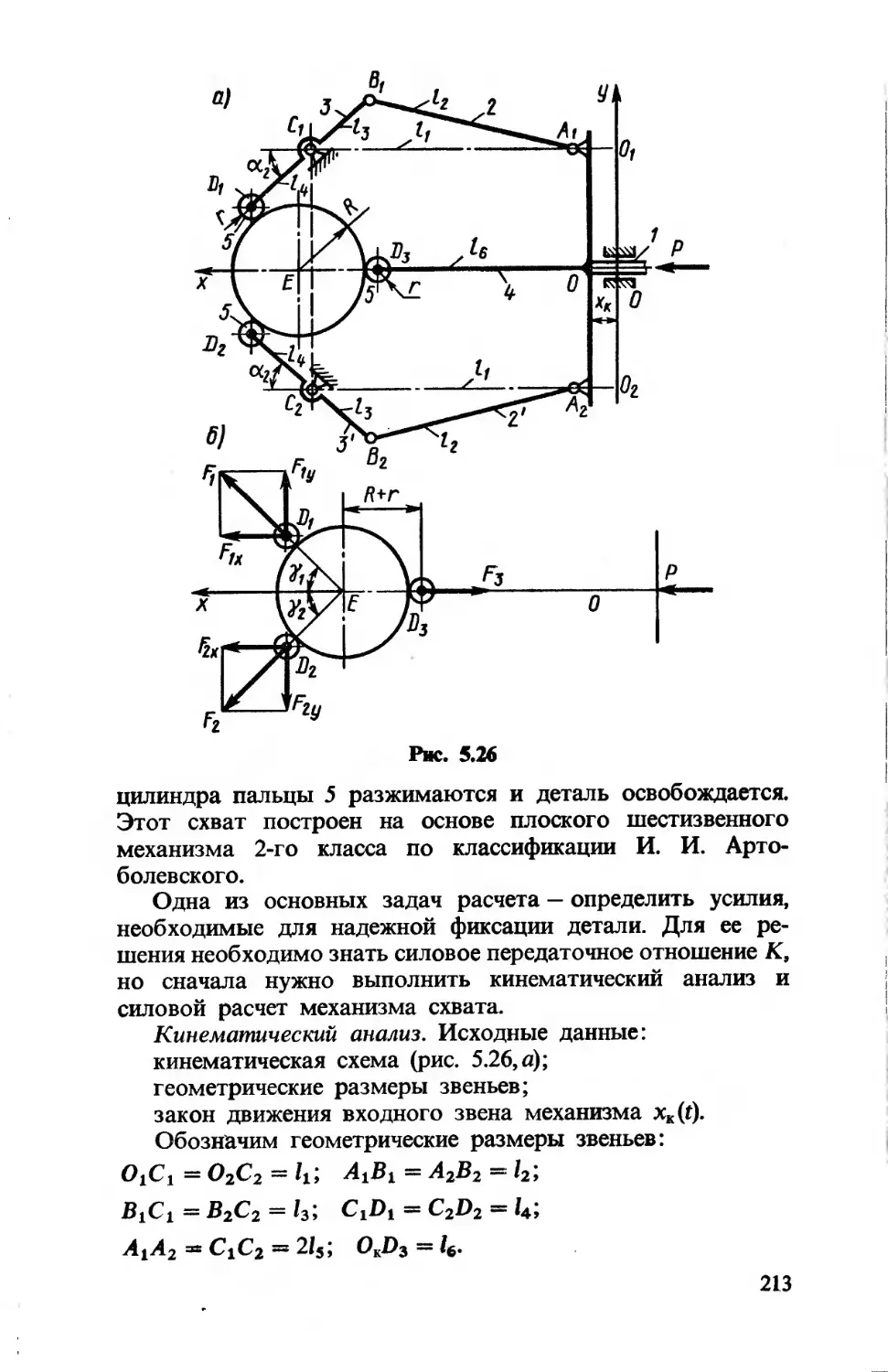
ПРОМЫШЛЕННЫХ
В трех книгах
Под редакцией К.В.Фролова, Е.И.Воробьева
Расчет
и проектирование
механизмов
Допущено Министерством
ысшего и среднего
специального образования СССР
в качестве учебного пособия для студентов
высших технических учебных заведений
Москва « Высшая школа »1988
ББК 32.816
М55
Авторы :
Е. И. ВОРОБЬЕВ, О. Д. ЕГОРОВ, С. А. ПОПОВ
Рецензенты: кафедра «Промышленные роботы и ро-
бототехнические системы» Московского станкоинстру-
ментального института (зав. кафедрой — д-р техн, наук,
проф. В. С. Кулешов); кафедра «Детали машин и теория
механизмов и машин» Московского авиационного технологи-
ческого института им. К. Э. Циолковского (зав. кафед-
рой — д-р техн, наук, проф. Е. И. Степанычев)
Механика промышленных роботов: Учеб, по-
М55 собие для втузов: В 3 кн./Под ред. К. В. Фро-
лова, Е. И. Воробьева. Кн. 2: Расчет и проектиро-
вание механизмов/Е. И. Воробьев, О. Д. Егоров,
С. А. Попов. — М.: Высш, шк., 1988.— 367 с.: ил.
ISBN 5-06-001134-8
В книге рассмотрены методы расчета и проектирования меха;
низмов промышленных роботов: основных, передаточных, меха-
низмов схватов, уравновешивания и развязки движений. Изложены
способы определения интегральных и дифференциальных характери-
стик манипуляторов. Описаны методы синтеза манипуляторов по
заданным положениям объекта. Даны примеры расчета и проекти-
рования механизмов манипуляторов.
2702000000(4309000000) — 029
М-------------------------------160—88
ББК 32.816
6Ф0.1
001(01)—88
ISBN 5-06-001134-8
© Издательство «Высшая школа», 1988
1
Предисловие
«Расчет и проектирование механизмов» — вторая книга
из серии «Механика промышленных роботов». В книге из-
ложены основные вопросы расчета и проектирования меха-
низмов, входящих в манипуляционную систему роботов.
К ним относятся основной механизм манипулятора, различ-
ные передаточные механизмы, механизмы схватов, уравно-
вешивания и развязки движений.
Для проектирования манипуляторов промышленных ро-
ботов универсального типа используются различные крите-
рии качества, а также дифференциальные и интегральные
характеристики, способы определения которых даны в книге.
Манипуляторы специальных роботов проектируются по
заданным перемещениям объекта, методы их проектирова-
ния основаны на условиях геометрических связей незамкну-
тых кинематических цепей.
Последовательно изложены методы расчета и проектиро-
вания механизмов схватов и в том числе теория удерживания
объекта. В заключительных главах книги рассмотрены воп-
росы, имеющие важное значение для повышения качествен-
ных показателей роботов: уравновешивание, аккумуляция
энергии, развязка движений и точность исполнительных
механизмов роботов.
Работа над книгой распределилась следующим образом:
Предисловие, Введение, гл. 1 — 5, § 8.2—8.4, 9.1, 9.3, 9.4 напи-
саны Е. И. Воробьевым; гл. 6 — С. А. Поповым; гл. 7,
§ 9.2 — О. Д. Егоровым.
Авторы выражают благодарность коллективам кафедр
«Промышленные роботы и робототехнические системы»
Московского станкоинструментального института и «Детали
машин и теория механизмов и машин» Московскою авиа-
ционного технологического института им. К. Э. Циолков-
ского за труд по рецензированию рукописи и ценные заме-
чания.
Авторы благодарят за помощь при подготовке книги
сотрудников кафедры «Теория механизмов и робототехни-
ка» Московского института химического машиностроения
В. А. Иванова, Н. И. Гданского, С. Д. Парадеева, Т. Н. Ба-
лакиреву, М. В. Онищенко.
Замечания и пожелания по улучшению содержания книги
просим присылать по адресу: 101430, Москва, ГСП-4,
Неглинная ул., д. 29/14, издательство «Высшая школа».
Авторы
Введение
Промышленный робот — это машина-автомат, состоящий
из исполнительного механизма — манипулятора и системы
управления.
Исполнительный механизм — манипулятор — представля-
ет собой пространственный механизм с несколькими сте-
пенями свободы, снабженный по каждой из них управляе-
мым приводом. Движения от приводов передаются звень-
ям манипулятора, которые будем называть основными.
Для захвата объектов манипуляторы оснащаются захват-
ными устройствами (схватами).
В состав манипулятора входят механизмы, выполняющие
различные функции: основной механизм, передаточные ме-
ханизмы, механизмы захватных устройств, механизмы урав-
новешивания и механизмы развязки движений.
Основной механизм содержит несущие звенья
и может быть схематично представлен как незамкнутый
пространственный механизм с несколькими степенями сво-
боды. Механизмы с несколькими степенями свободы типа
манипуляторов являются в технике сравнительно новыми
объектами проектирования. Методы их исследования и про-
ектирования в настоящее время интенсивно развиваются.
Анализ таких систем опирается на хорошо разработанные
методы аналитической механики, а методы проектирования
требуют еще своего развития.
Эганы проектирования основных механизмов следую-
щие: структурный, кинематический и динамический синтез
и оптимизационный синтез с учетом многих критериев.
Следует отметить, что на всех этапах синтез манипуляци-
онных механизмов имеет существенные особенности по
сравнению с синтезом механизмов с одной степенью сво-
боды.
На этапе структурного синтеза приходится учитывать
условия и возможности движения выходного звена в неко-
торой области пространства и большое многообразие струк-
тур незамкнутых кинематических цепей. Здесь необходимо
формулировать критерии, позволяющие решать задачу вы-
бора структуры манипулятора по различным условиям дви-
жения выходного звена. Одна из новых задач структурного
синтеза — выбор структуры (компоновки) промышленного
робота из отдельных модулей и агрегатов по условиям
выполнения заданных технологических движений.
1
На этапе кинематического синтеза манипуляторов реша-
ется задача выбора постоянных параметров кинематической
схемы механизма. Помимо известных задач кинематического
синтеза механизмов для осуществления заданной траектории
или передаточной функции возникает целый класс новых
задач синтеза по заданным условиям движения твердого
тела или его элементов (под условиями движения будем
понимать задание положений, скоростей, траекторий твердо-
го тела или его элемента — плоскости, прямой, точки).
Условия движения могут быть заданы значениями коорди-
нат и их производных в отдельные моменты времени или
уравнениями (или неравенствами), формализующими требо-
вания к движению выходного звена манипулятора.
На этапе динамического синтеза решается задача выбора
параметров динамической схемы механизма: масс, их распо-
ложения, жесткостей звеньев. Для механизмов манипулято-
ров эти задачи решаются на основе построения динамиче-
ских моделей и моделирования их движения на ЭВМ.
На этом этапе решаются задачи статического уравновеши-
вания сил тяжести звеньев и динамической развязки дви-
жений манипулятора.
Задача динамической развязки движений манипулятора
состоит в определении условий, при которых кинетическая
энергия системы не зависит от ее (системы) положения.
Решение этой задачи упрощает задачу построения опти-
мального управления и аккумуляции энергии.
Передаточные механизмы в манипуляторе пред-
назначены для передачи движения от двигателей к основ-
ным звеньям. В качестве передаточных используются раз-
личные виды механизмов и передач: рычажные, зубчатые,
мальтийские, шарико-винтовые, зубчато-ременные, волновые
и др. Степень сложности переда i очного механизма зависит
от расположения двигателей. Если двигатель расположен
на соседнем звене от звена, к которому передается дви-
жение, то передача получается весьма простой, однако
в этом случае двигатель находится на подвижном звене
и перемещается вместе с манипулятором. Если двигатель
расположен на основании, то передаточный механизм с иль
но усложняется: переда!очные кинематические цепи образу-
ют вместе с основными звеньями сложную многозвен-
ную механическую систему с несколькими степенями сво-
боды.
Анализ, а тем более синтез такой системы представляет
довольно сложную задачу. При ее проектировании основ-
ными являются задачи обеспечения управляемости системы,
1
кинематической развязки движений, выбор наиболее простой
структуры передач и места расположения приводов.
Под кинематической развязкой движений манипулятора
понимается независимость параметров движения по отдель-
ным степеням подвижности. Такая зависимость появляется
при использовании сложной структуры шарнирно-зубчатых
механизмов планетарного типа. Кинематическая взаимо-
связь движений является нежелательной для промышлен-
ного робота; она усложняет программирование и затрудня-
ет выполнение заданных операций.
Основные требования, предъявляемые к исполни-
тельным механизмам промышленных роботов,— обеспече-
ние заданной точности и быстродействия при повышении
относительной грузоподъемности (под относительной грузо-
подъемностью понимается отношение максимальной массы
переносимого груза к массе робота). Следовательно, пере-
даточные механизмы должны оцениваться и с точки зре-
ния точности передаваемых усилий. Поэтому важной зада-
чей при выборе передаточных механизмов и их проектиро-
вании является получение высокой точности, нагрузочной
способности и малых габаритов.
Для взаимодействия с объектом робот снабжается
захватным устройством. Наиболее широкое приме-
нение в промышленных роботах находят механические
захватные устройства, в которых объект захватывается
4
зажимается двумя или несколькими звеньями механизма.
В захватных устройствах нашли применение многие виды
механизмов: шарнирные, кулачковые, зубчатые и червячные,
винтовые и др. Основные требования к механизмам захват-
ных устройств — надежность удерживания объекта, компакт-
ность и легкость.
При проектировании механизмов захватных устройств
возникают новые задачи — выбор параметров из условия
обеспечения устойчивости и неизменности положения объек-
та в схвате, получение заданного закона изменения уси-
лия.
При проектировании механизмов роботов приходится
учитывать ряд требований, формулируемых обычно в тех-
нико-экономическом задании. Эти требования можно объ-
единить в несколько групп:
требования первой группы относятся к кинематике ме-
ханизма: они определяют характер движения выходного
звена механизма и точность заданного движения;
требования второй группы относятся к динамике меха-
низма, его габаритам;
1
требования третьей группы — к надежности и долговеч-
ности проектируемого механизма и его элементов;
требования четвертой группы — к энергетическим харак-
теристикам механизма.
Конечной целью проектирования механизмов манипуля-
торов является получение их оптимальной структуры
и параметров. Приведенный далеко не полный перечень
требований показывает, что сформулировать единый крите-
рий оптимизации затруднительно. Поэтому практически
процесс проектирования является итерационным.
На этапе структурного синтеза из набора кинемати-
ческих схем выбирается некоторая схема по некоторому
критерию. На этапе кинематического синтеза определяются
геометрические параметры механизма. При этом решая об-
ратные задачи о положениях и скоростях манипулятора,
определяют кинематические требования к приводам и пере-
даточным механизмам. Далее, исходя из опыта проектиро-
вания; выбирают массы и конструктивные параметры звень-
ев и, решая обратные задачи динамики, определяют тре-
бования к приводам по усилию.
После этого проектируют приводные и передаточные
механизмы.
Из решения задачи точности позиционирования робота
определяются требования к точности изготовления деталей
основного и передаточного механизмов.
После определения основных параметров приводов и
конструкции возможно провести моделирование или расчет
основных характеристик робота с учетом предполагаемой
системы управления. В поисках наилучшего варианта при-
ходится возвращаться к начальным этапам проектирования
и выбирать другую структуру или другие параметры меха-
низма. Следует, однако, отметить, что при выполнении
отдельных этапов синтеза весьма эффективно учитывать
требования более поздних этапов. Это достигается соот-
ветствующим выбором целевых функций — критериев опти-
мизации.
Вопросы синтеза манипуляторов разработаны значи-
тельно меньше, чем вопросы анализа: синтез манипулято-
ров опирается в основном на методы их анализа. Задачи
структурного синтеза планетарных механизмов роботов
с несколькими степенями свободы рассматривались в ра-
ботах А. Г. Овакимова, А. И. Корендясева, И. В. Калаби-
на, Б. А. Петрова, В. П. Степанова [27, 28, 29, 20, 21, 31].
Задачи синтеза незамкнутых кинематических цепей по задан-
ным положениям тела в пространстве впервые рассматри-
1
вались в работах Б. Роса, П. Чена. Ю, Л. Саркисяна,
Е. И. Воробьева [46, 47, 37, 10, 11].
Вопросы проектирования захватных устройств решались
в многочисленных работах, из которых следует отметить
работы В. Н. Данилевского, Ю. П. Боренштейна, С. Н. Кол-
пашникова, И. Б. Челпанова [6, 12, 19]. Расчет и проекти-
рование уравновешивающих механизмов рассмотрены в ра-
ботах М. В. Попова, Л. Н. Петрова, Б. А. Петрова [32, 33,
31]. Принципы построения манипуляторов с аккумулятора-
ми энергии резонансного типа разработаны в статьях
Л. М. Болотина, А. И. Корендясева, Л. И. Тывеса, Б. Л. Са-
ламандры [21, 22, 5].
Раздел
Проектирование
манипуляторов
Глава 1
Общие вопросы теории синтеза
и оптимизации механизмов промышлен-
ных роботов
Задача синтеза механизмов «состоит в определении постоян-
ных параметров по заданным условиям. Задача синтеза
механизма применительно к конкретным условиям обычно
ставится и решается как задача определения постоянных
параметров механизма, при которых некоторая функция,
выражающая основное условие проектирования механизма
и называемая целевой, получает экстремум. Постоянные
параметры, как правило, определяются при наличии неко-
торых ограничений на их шачения. Такие задачи называ-
ются задачами оптимизационно! о сип i е з а меха-
низмов или задачами оптимизации механизмов.
Целевые функции называют также иногда функциями
цели или критериями оптимизации. Целевая функция (обыч-
но математически) выражает основное требование к про-
ектируемому механизму. Другие требования называют до-
полнительными условиями синтеза. Следует отметить,
что не всегда удается выделить основное требование.
В таких случаях решается многокритериальная задача опти-
мизации.
Параметрами синтеза называются постоянные ве-
личины, определяющие кинематическую, динамическую схе-
му механизма или его конструкцию. Входными назы-
ваются параметры, определяемые в процессе решения за-
1
дачи синтеза. Выходными называются параметры, за-
данные уже при постановке задачи.
В зависимости от этапа, на котором решается задача
оптимизационного синтеза, смысл параметров синтеза, целе-
вой функции и ограничений может изменяться.
Например, на этапе кинематического синтеза передаточ-
ного механизма в качестве целевой может быть использо-
вана функция, характеризующая отклонение закона движе-
ния выходного звена механизма от заданного положения.
Ограничения могут быть наложены на относительные дли-
ны звеньев или на максимальную длину звена. При реше-
нии задачи кинематического синтеза шарнирного механизма
радиального хода сварочного промышленного робота тре-
буется спроектировать его кинематическую схему так, чтобы
точка шатуна совершала приближенное движение по прямо-
линейной горизонтальной траектории в радиальном на-
правлении. В этом случае целевой будет функция откло-
нения точки звена механизма от прямолинейной траек-
тории.
Сложность решения задачи синтеза зависит от числа
параметров, вида целевой функции и ограничений.
1.1. Методы оптимизационного синтеза
механизмов
Разработано большое число методов оптимизации; укажем
основные, нашедшие наиболее широкое применение в синте-
зе механизмов промышленных роботов.
Метод случайного поиска. Этот метод, называемый ме-
тодом Монте-Карло, состоит в начальном выборе случайных
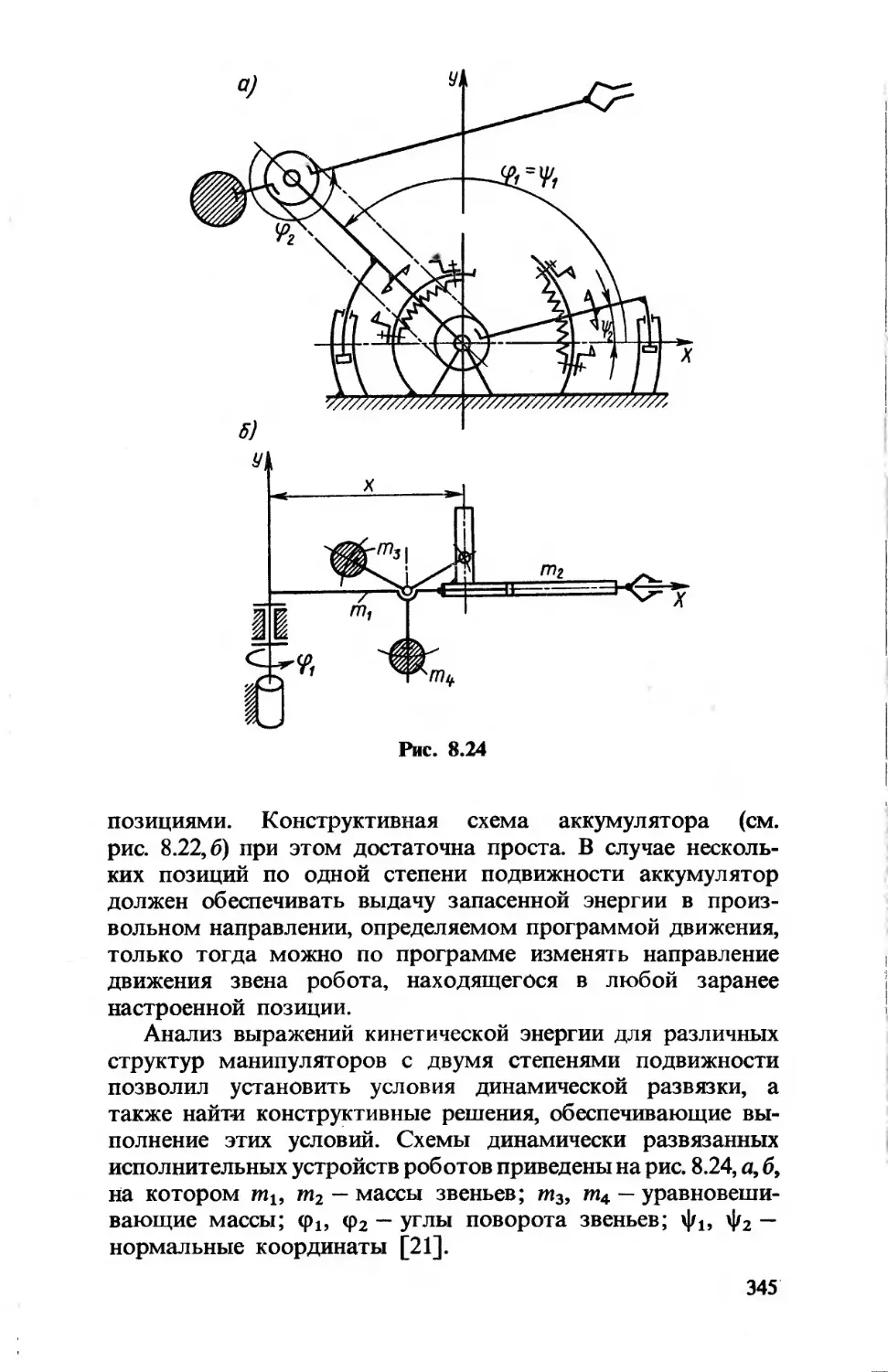
значений параметров, проверке ограничений, вычислении
целевой функции и выборе таких значений параметров, при
которых целевая функция имеет экстремальное значение из
всех вычисленных
Метод случайного поиска универсален, позволяет обсле-
довать всю область допустимых значений параметров; ос-
новным недостатком является очень большой объем вычис-
лений.
Метод направленного поиска.
ускорения вычислений
разработаны многочисленные способы перехода к новым
значениям параметров после вычисления предыдущих.
Если имеется аналитическое выражение целевой функции,
то направление движения в пространстве параметров опре-
деляется путем определения частных производных по пара-
10
1
метрам синтеза. Такой подход используется, например,
в методе наискорейшего спуска [42].
Следует отметить, что поиск экстремума целевой функ-
ции методом наискорейшего спуска носит локальный харак-
тер, значение найденного экстремума может зависеть от
начального приближения.
Пусть целевая функция явно задана в виде
F(Pi, . рт) = 0;
выбраны начальные значения параметров. Поиск экстремума
целевой функции методом наискорейшего спуска осуществля-
ется по итерационной формуле
где р' = [рь р2, • • •, pjr — вектор постоянных параметров
механизма на шаге г (т — знак транспонирования матрицы);
Лг — вектор приращений параметров в точке г; Хг — шаг
вдоль направления вектора sr; s' — вектор направления
наискорейшего спуска.
При движении вдоль вектора s' производная от целевой
функции имеет наибольшее значение.
При переходе от точки р' к точке локального минимума
для обеспечения сходимости поиска должно выполняться
условие
F (р' + 1) < F (П
это, во-первых, и, во-вторых, чтобы функция F (р) убывала
по направлению вектора производная от нее по X вдоль
этого направления должна быть отрицательной. Эти условия
выполняются, если век гор s' направлен в сторону, противо-
положную направлению градиента функции F (р), т. е.
где
l|VF,(p) ||
— норма градиента.
Если целевая функция F(p) является плохо обусловлен-
ной, т. е. в матрице вторых производных отклонение наи-
большего собственного значения от наименьшего в некото-
1
рых точках велико, то процесс поиска экстремума методом
наискорейшего спуска затруднен.
Если целевая функция F(p) в некоторой точке рг может
быть аппроксимирована рядом Тейлора с точностью до
производных 2-го порядка, то может быть применен метод
Ньютона.
В этом методе совмещены процедуры выбора шага и
направления вектора поиска sr путем решения задачи опти-
мизации min(VFJA) при наличии условия
d2F(p)
Spt Spj
— матрица размером т х т — гессиан функции F (р) в точке
г; к — постоянный коэффициент.
Решением этой задачи является вектор
Алгоритм Ньютона обладает квадратической скоростью
сходимости, т. е. дает возможность получить минимум це-
левой функции за т операций. Недостатками этого метода
являются трудность выбора хорошего начального приближе-
ния и необходимость вычислять матрицу вторых производ-
ных и обратную ей.
Целевую функцию не всегда удастся выразить аналити-
чески через параметры синтеза. Например, в случае синтеза
направляющего механизма робота по прямой линии в ка-
честве целевой функции может быть выбрано максимальное
отклонение точки схвата от прямой линии, измеренное по
оси у (рис. 1.1):
I У К “ У Imax’
Выразить эту функцию анали-
тически через параметры механиз-
ма не удается, однако можно ука-
зать алгоритм ее вычисления.
Поэтому можно рассчитать на
ЭВМ значение целевой функции
при любом значении параметров.
В данном случае для решения
задачи оптимизационного синтеза
можно использовать методы пря-
мого поиска без вычисления
12
производных. Одним из наиболее простых является метод
Гаусса — Зейделя — метод поиска локального мини-
мума. Алгоритм состоит в поочередном изменении пара-
метра по формуле
р'+1 = Pri + MX (i = 1, . • •, гп),
где lf — m-мерный вектор с компонентами
1, если i = j;
О, если i^j (7=1, ..., tn),
определяющий направление поиска; Ц — длина шага вдоль
направления 1, на r-й итерации.
Длина шага определяется решением задачи оптимизации
вида
Поиск заканчивается при выполнении условия
II РГ+1 “/Il
где е — выбранная малая величина.
Глобальный детерминированный метод оптимизации —
ЛП-поиск. ЛП-поиск является детерминированным аналогом
метода Монте-Карло. Метод позволяет решать задачи оп-
тимального проектирования механизмов и машин с учетом
самых различных требований и ограничений. Метод был
предложен И. М. Соболем и Р. Б. Статниковым [38].
При проектировании механизмов с учетом ограничений,
а также упругости и массы звеньев, наличия нескольких
критериев задача оптимизации значительно усложняется.
Можно отметить следующие основные особенности опти-
мального проектирования механизмов и машин:
целевая функция зависит от большого числа параметров,
часто не выражается аналитически через них, поэтому
характер рельефа r-мерной гиперповерхности, выражающей
целевую функцию, неизвестен;
оптимальные значения параметров могут оказаться на
границе области (область поиска часто оказывается много-
связной);
условия физической реализуемости конструкции приводят
к нелинейным ограничениям в виде неравенств;
задачи оптимизации связаны с учетом нескольких
критериев, поэтому методы линейного и нелинейного
1
программирования оказываются пригодными лишь для ре-
шения задач на отдельных этапах или локальной оптими-
зации.
Применение ЛП-поиска позволяет более или менее равно-
мерно просмотреть все пространство параметров. При этом
с ростом числа просмотренных вариантов возрастает ве-
роятность получения оптимального (глобального) решения
задачи.
При выборе вариантов применяется тактика р-точек.
Сущность этой тактики состоит в том, что оптимизация
целевых функционалов осуществляется путем перехода через
точки, равномерно распределенные в пространстве парамет-
ров. Задается квазиравномерная числовая последователь-
ность точек в m-мерном кубе, которая обладает тем свой-
ством, что для любой области U в этом кубе справедливо
соотношение
lim [SN (17)/N] = V(U),
где N — общее число испытаний; SN(U) — число пробных
точек с номерами 1 < i < N, принадлежащими 17; V(U) —
объем области U.
Метод ЛП-поиска позволяет решать задачи многокри-
териальной оптимизации механизмов, машин, конструкций;
является перспективным для применения к задачам опти-
мизации параметров роботов.
1.2. Методы приближения функций
в^синтезе механизмов
Методы теории приближения функций позволяют провести
качественный анализ отдельных решений, а также получить
основное условие синтеза механизма, которое можно при-
нять за целевую функцию. Впервые задачи синтеза меха-
низмов с применением теории приближения функций были
поставлены и решены П. Л. Чебышевым. Наибольшее при-
менение получили методы: интерполирования, квадратиче-
ского приближения и наилучшего приближения.
Интерполирование. В этом методе заданная функция
у = F (х) и приближающая функция у = FM (х), реализуемая
механизмом на отрезке х0, хт, совпадают в к точках, на-
зываемых узлами интерполирования. Условие совпадения
значений функций в узлах интерполирования имеет вид
F (xf) - FM (xf) = 0.
(LI)
Если приближающая функция механизма может быть
представлена в виде полинома
п
ем w = Е Pifi (*)>
»=1
где pi — постоянные коэффициенты, зависящие только от
искомых параметров;^ (а) — линейно независимые непрерыв-
ные функции аргумента, не содержащие постоянных неиз-
вестных параметров, то система уравнений получается ли-
нейной относительно коэффициентов р,. При числе узлов
интерполирования i, равном числу коэффициентов, эти коэф-
фициенты могут быть определены из данной системы, если
ранг расширенной матрицы не меньше п. После этого
могут быть найдены постоянные параметры, определяющие
схему механизма.
Этот метод может быть использован для решения раз-
личных задач кинематического синтеза механизмов. Напри-
мер, при синтезе механизма по заданным положениям
входного и выходного звеньев система (1.1) дает основное
условие синтеза. При числе параметров, большем чем число
заданных положений, оставшиеся параметры могут быть
использованы для удовлетворения ограничений.
Квадратическое приближение. Этот вид приближения
функций состоит в том, что параметры приближающей
функции механизма определяются из условия минимума
среднеквадратического отклонения от заданной функции
[25]
Дкв *о)>
где J = f [Fm(x) — F(x)]2; х^хт — значения аргумента в на-
Л'о
чале и конце отрезка приближения. Для минимума средне-
квадратического отклонения необходимо, чтобы интеграл J,
стоящий под корнем, получил минимум. Это может быть
достигнуто при условии dJ/dpk = 0 (к = 0, 1, ..., т).
Если приближающая функция механизма имеет вид
обобщенного полинома вида
т
Ем = Е Pifi (х) = 0,
i = O
то после Дифференцирования по параметрам получим
f Е Pi fi W - WJ h W dx = °-
*0
1
Систему (1.2) можно привести к виду
т).
(13)
Последняя система уравнений является линейной относи-
тельно постоянных коэффициентов функции механизма, за-
висящих только от его искомых постоянных параметров.
Метод квадратического приближения может использо-
ваться не только для решения задачи приближения задан-
ной функциональной зависимости механизма, но и для
решения задачи синтеза механизма по заданным положе-
ниям, когда число заданных положений превышает число
постоянных параметров. В этом случае можно решать за-
дачу приближенного воспроизведения заданного числа поло-
жений, а вместо интеграла J использовать сумму вида
*
s = £ - Г(л,)]2;
i = 0
коэффициенты ск1 и Ьк в системе (1.3) также вычисляются
как суммы
Ск1 ~ с1к —
т
ьк = Y F (xi)fk(xt) (к, 1 — 0, 1, ..., т).
«=о
Если приближающая функция не является обобщенным
полиномом, то система уравнений для вычисления неиз-
вестных коэффициентов будет уже нелинейной. В этом слу-
чае для ее решения можно применить метод итераций {2].
1.3. Общие вопросы синтеза механизмов
по заданным условиям движения
ведомого твердого тела
Одна из основных задач при проектировании манипулято-
ров — построение механизма, осуществляющего заданные
условия движения объекта в пространстве. Геометрически
объект можно представить как точку, прямую, плоскость,
твердое тело. Под условиями движения объекта будем по-
нимать уравнения, неравенства, связывающие обобщенные
координаты объекта или их производные по времени,
16
и также значения этих координат или их производных в не-
которые моменты времени.
Наиболее общим видом объекта будем считать твердое
тело. Задача синтеза механизма по заданным условиям дви-
жения твердого тела охватывает как частную задачу синтез
передаточных и направляющих механизмов, когда воспро-
изводится лишь закон движения тела по одной обобщен-
ной координате или заданная траектория точки тела.
Рассмотрим различные способы задания движения твер-
дого тела и его осуществления с помощью механизмов.
Задание закона движения твердого тела и его элементов.
Движение твердого тела полностью определено в простран-
стве, если задано изменение во времени его обобщенных
координат, число которых, как известно, равно шести. За
обобщенные координаты могут быть приняты различные
переменные параметры движения. Например, можно задать
движение произвольной точки С твердого тела и движение
тела вокруг этой точки тремя углами Эйлера v|z, 0, <р в функ-
ции времени. В этом случае закон движения твердого тела
будет представляться в виде:
V = Л (0;
Ус — fi (0 >
zc = А (0;
ф — f& (0>
0 -f5 (0;*
Ф = А (0-
Можно задать движение некоторой прямой линии, при-
надлежащей твердому телу, и движение относительно этой
прямой. Движение прямой линии можно задать четырьмя
независимыми параметрами или двумя дуальными углами
Л I- f /i. В = 0 + cb. В этом случае закон движения
твердою тела может быть представлен в виде:
а = А (0;
где Ь, р — смещение и поворот линии кратчайшего расстоя-
ния между прямой и осью z; h, а — кратчайшее расстояние
и угол между осью z и прямой; f ф — смещение и поворот
тела относительно прямой.
Закон движения можно записать более компактно с ис-
пользованием комплексных углов р — р (t), а = а (г), ф = Ф (0-
Можно также задать движение некоторой плоскости,
принадлежащей телу, и движение тела относительно плоско-
сти. Движение плоскости можно задать тремя независимы-
17
ми параметрами, например координатами ее точек пересе-
чения с осями координат а, Ь, с. Движение тела относительно
плоскости определяется также тремя независимыми парамет-
рами хс, ус, Ф (точка С — начало системы координат, свя-
занной с телом). В этом случае закон движения тела пред-
ставляется в виде:
а — fi (0>
Ь = f2 (0;
с = Л (0;
хс = Л (0;
Ус = Л (0;
ф = Л (0-
(1-4)
Требование осуществления закона движения твердого
тела является наиболее полным. В конкретных технических
задачах часто требуется осуществить не полностью закон
движения, а обеспечить лишь заданное движение какого-
либо элемента твердого тела: точки, плоскости, прямой или
их сочетаний.
Закон движения элемента тела задается несколькими из
уравнений (1.4). Движение тела в этом случае называют
не полностью определенным.
Задание программы движения твердого тела и его элемен-
тов. В некоторых случаях для выполнения технологических
операций задаются не обобщенные координаты твердого
тела или его элемента, а некоторая связь между этими
обобщенными координатами и их производными.
Например, требование обеспечения движения по задан-
ной траектории в пространстве математически сводится
к необходимости при движении тела выполнять условия:
fi (х, у, z) = 0; /2 (х, у, z) = 0, (1.5)
где х, у, z — координаты произвольной точки твердого тела.
Условие движения точки тела по какой-либо поверхности
может быть выражено одним уравнением вида
f (х, у, г) = 0.
(1.6)
На обобщенные координаты прямой линии могут быть
наложены соответственно одно, два или три условия.
В этих случаях твердое тело должно двигаться так,
чтобы прямая, принадлежащая телу, находилась соответ-
ственно на линейчатой поверхности, конгруэнции прямых
или линейчатом комплексе. Если за обобщенные координаты
прямой принять координаты х, у точки ее пересечения
с плоскостью Оху и два из трех независимых направляю-
щих косинусов I, т, п, то эти условия математически выра-
жаются так:
18
1
для трех условий связи между обобщенными координа-
тами прямой имеем линейчатую поверхность:
fi (х, у, I, т) = 0; /2 (х, У, К ™) = 0; /з (х, у, /, т) = 0; (1.7)
для двух условий связи — конгруэнцию прямых
fl (х, у, /, т) = 0; f2 (х, у, I, т) = 0; (1.8)
для одного условия связи — линейчатый комплекс
/(х, у, /, т) = 0.
Аналогично, между обобщенными координатами плоско-
сти могут быть установлены одно или два уравнения вида:
f(a, Ь, с) = 0 или Л (а, Ь, с) = 0; f2 {а, Ъ, с) = 0, (1.9)
определяющие соответственно одно- и двухпараметрическое
семейство плоскостей.
Между обобщенными координатами элементов твердого
тела, имеющих пять степеней свободы, могут быть уста-
новлены одно, два, три или четыре условия связи. Такими
элементами могут быть, например, сочетания прямой и ле-
жащей на ней точки (элемент вращательной пары), прямой
и проходящей через нее плоскости (элемент поступательной
пары). В этом случае получаем соответственно одно-, двух-,
трех- и четырехпараметрические семейства этих элементов.
Уравнения вида (1.5)—(1.9), связывающие обобщенные
координаты, будем называть геометрической, или
г о л о номной, программой.
В выражение программы могут входить не только
обобщенные координаты, но и их производные. Например,
если задана некоторая траектория движения точки тела
и скорость движения по траектории, то это условие можно
записать в виде:
fi (х, у, z) = 0; f2 (х, у, z) = 0; х2 + у2 + z2 - v2 = 0, (1.10)
где v = const.
Программу, в выражение которой входят как обобщен-
ные координаты, так и их производные, будем называть
дифференциальной.
Таким образом, программа в отличие от закона движе-
ния связана с неявной формой задания движения твердого
тела или некоторых свойств движения.
Помимо непрерывной формы движение тела можно за-
давать в дискретной форме, т.е. задавая значения
обобщенных координат и их производных в некоторые мо-
менты времени:
19
в случае закона движения имеем
Xik=fi(tk) (i = 1, ...» 6; fc = 1, ..., ти);
(L11)
в случае программы движения
г < 6; s 6).
s; к = 1, ...» т;
Приближенное задание движения твердого тела. Техниче-
ское устройство может реализовать движение лишь с не-
которой точностью, т. е. могут быть реализованы лишь
некоторые требуемые характеристики движения. В связи
с этим и движение целесообразно задавать приближенно.
Значения координат любой точки подвижного тела в не-
подвижной системе Oxyz могут быть найдены из уравнения
(1.12)
где [х] — столбец координат точки в неподвижной системе
Oxyz; [xj — столбец координат точки в системе OxjyjZj, свя-
занной с телом;
«13
«23 а2
«33 «3
О
— матрица 4-го порядка, в которой элементы (к = 1, 2, 3;
I = 1, 2, 3) — косинусы углов, образованных осями к и /;
at (i— 1, 2, 3) — координаты начала системы OxjyjZj в системе
Oxyz. При движении тела элементы матрицы MOj являются
функциями времени.
Раскладывая элементы матрицы в ряд Тейлора, получим
= + + + + ..., (1.13)
где М, Л}, М — производные от матрицы MOj по времени.
Выражение (1.13) позволяет задать движение твердого
тела в функции времени с точностью до и-го порядка,
например для описания движения с точностью до 1-го по-
рядка необходимо задать значения углов Эйлера и их первых
производных по времени, для описания движения с точ-
ностью до 2-го порядка достаточно задать вторые произ-
водные от углов Эйлера по времени и т, д.
Приближенное осуществление заданного движения твердо-
го тела с помощью механизма. Для реализации заданного
20
движения твердого тела существенное значение имеет не
только общая подвижность механизма, но и подвижность
его рабочего, или выходного, звена. Подвижность выход-
ного звена определяется числом его независимых обобщен-
ных координат.
Положение звена механизма как твердого тела в прост-
ранстве определяется шестью переменными, которые могут
быть зависимыми между собой. Число независимых пере-
менных, определяющих положение звена, будем называть
его числом степеней свободы, или подвижностью звена.
Очевидно, что число степеней свободы звена механизма
не всегда совпадает со степенью подвижности механизма,
так как число степеней свободы звена не может превосхо-
дить шести, а число степеней подвижности механизма
не ограничено.
Пользуясь матричным методом кинематического ана-
лиза, можно установить систему уравнений связи между
обобщенными координатами механизма qt (i — 1,..., и) и пе-
ременными параметрами Xj (j = 1, ..., 6), определяющими
положение звена:
Fк (^1» • • • » -^6> 01» • • • » Оп» ^1» • • • , ^s) Q (^ 1» • • • ,
где Ci, ..., cs — постоянные параметры механизма.
Переменные параметры хь ..., х6, определяющие поло-
жение звена, задаются обобщенными координатами меха-
низма, т. е. являются функциями обобщенных координат:
xi Ф1 (01» • • • > Оп)’»
х2 Фз (01» • • • > On)»
(115)
хб Фб (01» • • •» On)’
Интересно выяснить, имеет ли система (1.15) реше-
ние в некоторой области изменения переменных хх,...
..., х6 относительно qi9 ...» qn. Для этого необходимо,
чтобы эти шесть функций были независимыми. Согласно
известной теореме условием независимости функций явля-
ется отличие от нуля якобиана этих функций от каких-либо
шести переменных qt (i = 1, ..., и) в некоторой точке
Мо(«?, q°), т. е. условие
(ф1> • • • > Фе) , q
б (91, - - •, 9б)
(1.16)
где qt — какие-либо шесть из п обобщенных координат.
21
Если, кроме того, функции хь ..., х6 дифференцируемы
в окрестности точки Мо и все частные производные
1-го порядка непрерывны в самой точке Мо, то выполняются
все условия теоремы о существовании неявной функции.
Тогда система (1.15) всюду в некоторой окрестности
точки Мо имеет единственное решение:
41 = Vi (*ь • •, *б);
42 = Фг (хь . • •, х6);
(1.17)
4п = Фе (хь .. ., х6).
Таким образом, основным условием разрешимости урав-
нений (1.15) относительно обобщенных координат является
условие (1.16).
Так как связь между функциями qt (i — 1, и) и Xj
0 =1» • • •» 6) задана неявно в виде (1.14), то для составле-
ния якобиана (1.16) можно воспользоваться выражениями
частных производных в
виде
Итак, если ранг функциональной матрицы (1.16) равен
шести, то с помощью механизма можно осуществить про-
извольное пространственное движение твердого тела, зада-
вая функции qi (t) (i — 1, ..., 6) в зависимости от функции
X/ (0 (i — 1, ...» 6)1 Такие механизмы будем называть jwe-
ханизмами с полной подвижностью относительно твердого
тела. Если ранг функциональной матрицы системы (1.16)
меньше шести, то такие механизмы будем называть меха-
низмами с неполной подвижностью относительно твердого
тела. Если существует не единичное, а конечное множество
различных комбинаций qh при которых ранг матрицы
Якоби системы (1.16) равен шести, то такие механизмы
будем называть механизмами с избыточной подвижностью
относительно твердого тела.
Уравнения связей кинематических цепей. С одним из
звеньев механизма свяжем подвижную систему координат
O'x'tfz?. Задача состоит в том, чтобы определить постоян-
ные и переменные параметры механизма, такие, чтобы дви-
жение системы координат O'x'y'z' происходило заданным
образом. Возможность осуществления заданного движения
выходным, или рабочим, звеном зависит от свойств кине-
матических цепей, присоединяющих рабочее звено к непод-
вижному звену. Эти кинематические цепи могут наклады-
1
вать на его движение различные ограничения, которые
будем называть связями. Эти ограничения могут быть
выражены в наиболее общем случае для механизмов с твер-
дыми звеньями в виде:
ГДх, у, z; /, m(n); с19 ..., ск; ql9 ...» qn) = 0 (i = 1, г;
г и), (1.18)
где х, у, z — координаты некоторой точки твердого тела
в неподвижной системе координат; /, т, п — направляющие
косинусы прямой, принадлежащей телу, в неподвижной си-
стеме координат; cs — постоянные параметры механизма;
qj — обобщенные координаты системы — переменные пара-
метры цепи.
Уравнения связи, записанные в форме (1.18), называются
параметрическими, так как они содержат переменные пара-
метры.
Координаты точки х, у, z и направляющие косинусы /,
т, (и), входящие в уравнения связи (1.18) и отнесенные к си-
стеме Oxyz, могут быть выражены линейно через соответ-
ствующие величины в подвижной системе координат
O'x'y'z' и элементы матрицы MOj, задающей положение
системы в пространстве.
Имеем:
И = м0УМ; И = 1оЛП, (119)
где Мoj, Loj — матрицы перехода соответственно 4-го и 3-го
порядка, имеющие вид:
[«Ц «12 «13 I
«21 «22 «23 I»
«31 «32 «33-J
[«11 «12 «13 «1
«21 «22 «23 &2
«31 «32 «33 «3
О 0 0 1_
где а2, а3 — координаты начала системы O'x'y'z' в систе-
ме Oxyz; (к, 1 — 1, 2, 3) — направляющие косинусы оси к
системы Oxyz относительно оси I системы O'x'y'z'.
Следует отметить, что элементы этих матриц выража-
ются через обобщенные координаты твердого тела, напри-
мер через углы Эйлера. Таким образом, чтобы знать эти
матрицы, надо задать или закон движения твердого тела,
или его положение в некоторый момент времени.
Число точных положении твердого тела, осуществляемых
механизмом. При задании т конечных положений тела
уравнение связи должно удовлетворяться в этих положениях.
В этом случае уравнение связи (1.18) приводится к системе
нелинейных уравнений вида:
Ур %j9 ^j(^j)» ^1» • • • , ^k.t Qip ••• 9 Qnj) H
0=1, ..., m; i = 1, ..., r; r > n). (1.20)
Полученная система содержит к + 5 неизвестных постоянных
параметров и т • п неизвестных значений обобщенных коор-
динат qj кинематической цепи в этих положениях, т. е. об-
щее число неизвестных равно к 4- 5 4- т • и.
Число уравнений равно т • г, поэтому максимальное
число точных положений твердого тела, осуществляемых
рассматриваемой кинематической цепью, определяется из
условия
откуда
т < (к
5)/(г - и),
* где к — число постоянных параметров; г — число уравнений
связи.
В некоторых частных случаях удается исключить пере-
менные параметры qi9 , qn из уравнений связи, тогда
Fi(x, у, z; к сь ..., ск) = 0. (1.21)
Для т заданных конечных положений приходим к системе
нелинейных уравнений вида:
Zj, /у, Wly(My), Су, . .
которую надо решить относительно постоянных параметров
сь ..., ск. В этом случае максимальное число точных
положений определяется из условия
к 4- 5 > т • г,
откуда
т < (к 4- 5)/г.
(1.23)
(1.24)
Если связь наложена на координаты точки х, у, z, то
приходим к уравнению связи вида
(^> Уу ^9 Cj.9 * * . 9 ^к) И.
(1.25)
Координаты х, у, z выражаются через х', у', z' по форму-
лам (1.15). Для т заданных конечных положений приходим
к системе т • г уравнений с к 4- 3 неизвестными.
Максимальное число точных положений
т < (к 4- 3)/г.
(1.26)
1
Если связь накладывается только на координаты прямой,
принадлежащей твердому телу, то координаты х, у, z и
направляющие косинусы /, т (и) могут быть выражены через
четыре независимых параметра, определяющих положение
прямой в подвижной системе координат, например две коор-
динаты точки пересечения прямой с плоскостью Оху и две
независимых направляющих косинуса. В этом случае макси-
мальное число точных положений твердого тела, осуществ-
ляемых цепью,
т < (к + 4)/г.
(1.27)
Приведенные формулы позволяют проверить возмож-
ность реализации выбранной кинематической цепью задан-
ного числа положений объекта.
Глава 2
Геометрические и кинематические
характеристики манипуляторов
Рассмотрим вопросы определения геометрических и кинема-
тических характеристик, с помощью которых можно оцени-
вать качество манипуляторов универсального типа и решать
задачи оптимизационного синтеза.
2.1. Подвижность и структурный
синтез манипуляторов
Подвижность манипулятора определяет его способность
совершать различные независимые движения и является
одной из основных характеристик.
Подвижность манипулятора характеризуется его числом
степеней свободы, под которым понимают число независи-
мых возможных перемещений.
Для определения числа степеней свободы манипулятора
с голономными связями достаточно найти разность между
общим числом координат, определяющих положение его
звеньев, и числом независимых уравнений связей. Эта разность
представляет собой число независимых координат, опре-
деляющих положение системы и называемых обобщенными
координатами.
Общее число координат, определяющих положение твер-
дого тела, как известно, равно шести, тогда для и-звен-
ного манипулятора число таких координат равно би.
25
1
Если механизм содержит пар i-ro класса, то общее
число связей /, налагаемых на относительные движения
звеньев, равно сумме числа связей всех пар:
Если все уравнения связей независимы, приходим
вестной формуле Малышева
I
I
Подвижность незамкнутой кинематической цепи
(2.2)
В случае избыточных, или пассивных, связей, уравнения
которых могут быть получены как следствие других,
число уравнений связей уменьшается и равно [35]
5
где q — число избыточных связей, а число степеней свободы
механизма
(23)
При известном числе степеней свободы можно из
последней формулы найти число избыточных связей
(2.4)
t
i
(
Избыточные связи часто получаются при конструиро-
вании механизмов. Для плоского кривошипно-ползунного
механизма по формуле (2.4) получим
механизме имеют место три избыточные связи,
устранить избыточные связи в кривошипно-
механизме, можно уменьшить класс входящих
т. е. в этом
Чтобы
ползунном
в него кинематических пар: например, две любые враща-
тельные пары заменить на сферические или одну пару
1
заменить на сферическую, а другую — на цилиндрическую.
Легко проверить по формуле, что в обоих случаях будут
отсутствовать избыточные связи.
В манипуляторах избыточные связи могут появиться,
например, при проектировании передаточного механизма
для осуществления движения в шарнире основного ме-
ханизма.
О. Г. Озол предложил структурную формулу для опре-
деления числа избыточных связей для многоконтурных
механизмов вида
q — JV + 6/с — Л (2.5)
где к — число независимых контуров в механизме, отли-
чающихся от других контуров, по крайней мере, одним зве-
ном или кинематической парой; f — сумма подвижностей
кинематических пар.
В некоторых случаях механизм бывает построен таким
образом, что на все звенья наложено несколько общих
связей. Например, все звенья плоского механизма совершают
движение в одной плоскости, а все звенья сферического
механизма совершают движение вокруг одной неподвижной
точки.
Для определения числа степеней свободы плоских
механизмов используется формула Чебышева
W = Зи — — рд,.
(2.6)
Сферические механизмы в промышленных роботах ис-
пользуются в устройствах ориентации схвата, у которых оси
кинематических пар пересекаются в одной точке. Структур-
ная формула для сферических механизмов такая же, как
и для плоских механизмов.
Следует отметить, что построить точный плоский или
сферический механизм невозможно, так как невозможно
добиться точной параллельности осей или пересечения их в
одной точке, т. е. в действительности механизм оказывается
пространственным. Поэтому в нем появляются избыточные
связи. Движение механизма оказывается возможным лишь
при наличии зазоров или за счет деформаций звеньев,
что приводит к дополнительным реакциям в кинемати-
ческих парах и снижению надежности механизмов. В связи
с этим применение механизмов с избыточными связями
нежелательно.
Практическое определение числа степеней свободы по
структурным формулам оказывается затруднительным ввиду
того, что уравнения связей могут быть зависимыми.
1
В связи с этим для определения числа степеней свободы
необходим анализ системы возможных перемещений или
скоростей механизма.
Манипулятор в процессе его функционирования может
иметь различную структуру. Во время движения в про-
странстве он может быть рассмотрен как незамкнутая
кинематическая цепь с несколькими степенями свободы. При
выполнении технологической операции на движение манипу-
лятора накладываются дополнительные связи и он превра-
щается в замкнутый механизм.
Следует различать число степеней свободы манипулятора
и число степеней свободы схвата. Очевидно, что эти
понятия не совпадают. Схват манипулятора как твердое
тело не может иметь число степеней свободы больше
шести, в то время как число степеней свободы мани-
пулятора не ограничено. При движении манипулятора его
оси могут занимать различные положения, что может
изменить число степеней свободы схвата.
Поясним это более подробно. Рассмотрим незамкнутую
кинематическую цепь с п степенями свободы, содержащую
поступательные и вращательные пары.
Угловая скорость схвата и линейная скорость какой-
либо его точки могут быть выражены формулами
(2.7)
(2.8)
где — линейная скорость в поступательной паре i;
a)j — угловая скорость во вращательной паре j; rjn —
радиус-вектор, задающий положение точки звена п (схвата)
относительно центра вращательной пары j.
Проецируя векторные уравнения (2.7) и (2.8) на оси
декартовой системы координат, получим систему шести ли-
нейных уравнений относительно п неизвестных и со,. Если
ранг матрицы этой системы равен шести, то система
имеет решение, а схват имеет число степеней свободы,
равное шести. Если ранг системы меньше шести, то
оси манипулятора занимают особенное положение, а число
степеней свободы схвата меньше шести.
Элементы матрицы системы линейных уравнений яв-
ляются плюккеровыми координатами кинематических винтов
движения звеньев в кинематических парах. Поэтому
28
1
определение ранга матрицы линейной системы может быть
заменено определением ранга подмножества кинематических
винтов пар.
Укажем случаи, когда у манипулятора с п степенями
свободы число степеней свободы схвата становится меньше
шести.
Первый случай, когда ранг матрицы равен пяти, т. е.
определитель 6-го порядка равен нулю, а определители
5-го порядка не равны нулю. Это означает, что между
плюккеровыми координатами винтов кинематических пар
имеет место одно условие связи, что означает, что
эти оси принадлежат линейному комплексу.
Если ранг матрицы системы равен четырем, то равны
нулю все определители 5-го порядка, т. е. между плюк-
керовыми координатами винтов пар имеются два условия
связи, т. е. оси пар принадлежат одной конгруэнции.
И если ранг матрицы системы равен трем, то оси
манипулятора находятся на некоторой линейчатой поверх-
ности, например лежат в одной плоскости, пересекаются
в одной точке или параллельны.
Структурные формулы, приведенные выше, позволяют
решать задачу структурного синтеза механизмов. Согласно
терминологии по теории механизмов и машин под структур-
ным синтезом механизма понимается проектирование его
структурной схемы по заданным структурным условиям.
Под структурными условиями будем понимать условия
движения перемещаемого объекта: его тип, число степеней
свободы, вид движения. Тип перемещаемого объекта может
быть идеализирован точкой, отрезком прямой, плоскостью
с точкой на ней, твердым телом.
Число степеней свободы объекта определяется числом
его обобщенных координат. Так, при изменении одной
обобщенной координаты движение объекта может быть
вращательным, прямолинейным, поступательным, при изме-
нении двух обобщенных координат — цилиндрическим и
т. д. Очевидно, что для реализации заданного движения
объекта с числом степеней свободы Wo число степеней
свободы механизма WM не может быть меньше чем Wo:
WM Wo. (2.9)
В том случае, когда добавление некоторой подвиж-
ности механизму не добавляет новой подвижности пере-
мещаемому объекту, будем говорить, что введенная подвиж-
ность является пассивной по отношению к объекту.
При структурном синтезе механизма манипулятора всегда
29
следует иметь в виду возможность появления пассивных
подвижностей.
Условие (2.9) позволяет решить задачу отбора цепей,
имеющих минимальное число степеней свободы и обладаю-
щих полной подвижностью относительно заданного вида
движения объекта. Уравнение для простой незамкнутой
цепи раскрывается в виде
6п - 5р5 - 4р4 - Зр3 = Wo; р5 + р4 + р3 = и,
где Pi (i = 3, 4, 5) — число пар г-го класса; п — число звеньев.
Система представляет собой систему диафантовых урав-
нений, решаемую в целых числах. Решения этой системы,
определяют кинематические схемы манипуляторов с задан-
ным числом степеней подвижности, содержащих пары
третьего, четвертого и пятого классов (табл. 2.1).
Проверка условия для всех схем, имеющих заданную
подвижность, позволяет получить схемы, обладающие полной
подвижностью по отношению к пространственному движе-
нию точки. Аналогично могут быть составлены наборы
схем, обладающих полной подвижностью по отношению к
движению прямой, плоскости, твердого тела.
При проектировании промышленного робота задача
структурного синтеза манипулятора является одной из
основных: ее решение связано непосредственно с выпол-
нением функций робота. Так, число степеней свободы
манипулятора не является заданным, как это обычно
бывает при проектировании плоских и пространственных
механизмов с одной степенью свободы, а должно выбирать-
ся исходя из условий выполнения технологических опера-
ций и перемещений выходного звена.
Задачу выбора числа звеньев, числа, класса и порядка
расположения кинематических пар основной цепи будем
называть основной задачей структурного синтеза манипу-
лятора.
Кроме того, следует иметь в виду, что для всего
манипулятора приходится решать задачу структурного синте-
за механизма с несколькими степенями свободы, содержа-
щего как основную кинематическую цепь, так и кине-
матические цепи приводов.
При структурном синтезе следует стремиться получить
статически определимые системы, удовлетворяющие усло-
виям непринужденной сборки и индифферентности к де-
формациям звеньев.
Рабочий орган промышленного робота — механизм с
несколькими степенями свободы — может быть представлен
30
1
Число
степеней
свободы
Таблица 2.1
Число
звеньев
Структурная формула
кинематической цепи
Число
кинемати-
ческих пар
»4= 1
Р.Р Р.Р-: Р.Р.Р.Р.: Р.Р.Р.Р
Р.Р.Р-Р
Р t РрР; РзР4Р5Р5Р5;
р4=1
/>3=1
/>4=2
Р4=1
р5р5р5Р4; Р5Р5Р4Р5; Р5Р4Р5Р5;
Р4Р5Р5Р5
Р.Р_Р_Р_Р
31
Число
степеней
свободы
Продолжение табл. 2.1
Число
звеньев
Число
кинемати-
ческих пап
Структурная формула
кинематической цепи*
Р РР РРР
5 5 5 5 5 5
* Р5, Р4, Р3 — символы пар пятого, четвертого и третьего классов
соответственно.
как последовательное наслоение механизмов с одной сте-
пенью свободы. Отметим, что этот принцип образования
механизмов отличен от известного принципа Ассура
образования механизмов. Принцип Ассура предполагает
образование механизмов путем присоединения статически
определимых структурных групп, и при этом подвижность
механизма не изменяется. Принцип наслоения ме-
ханизмов предполагает построение на одном из подвижных
звеньев нового механизма, так что при этом число
степеней свободы всей системы возрастает.
Таким образом, принцип наслоения механизмов можно
считать общим принципом структурного синтеза механизмов
с несколькими степенями свободы.
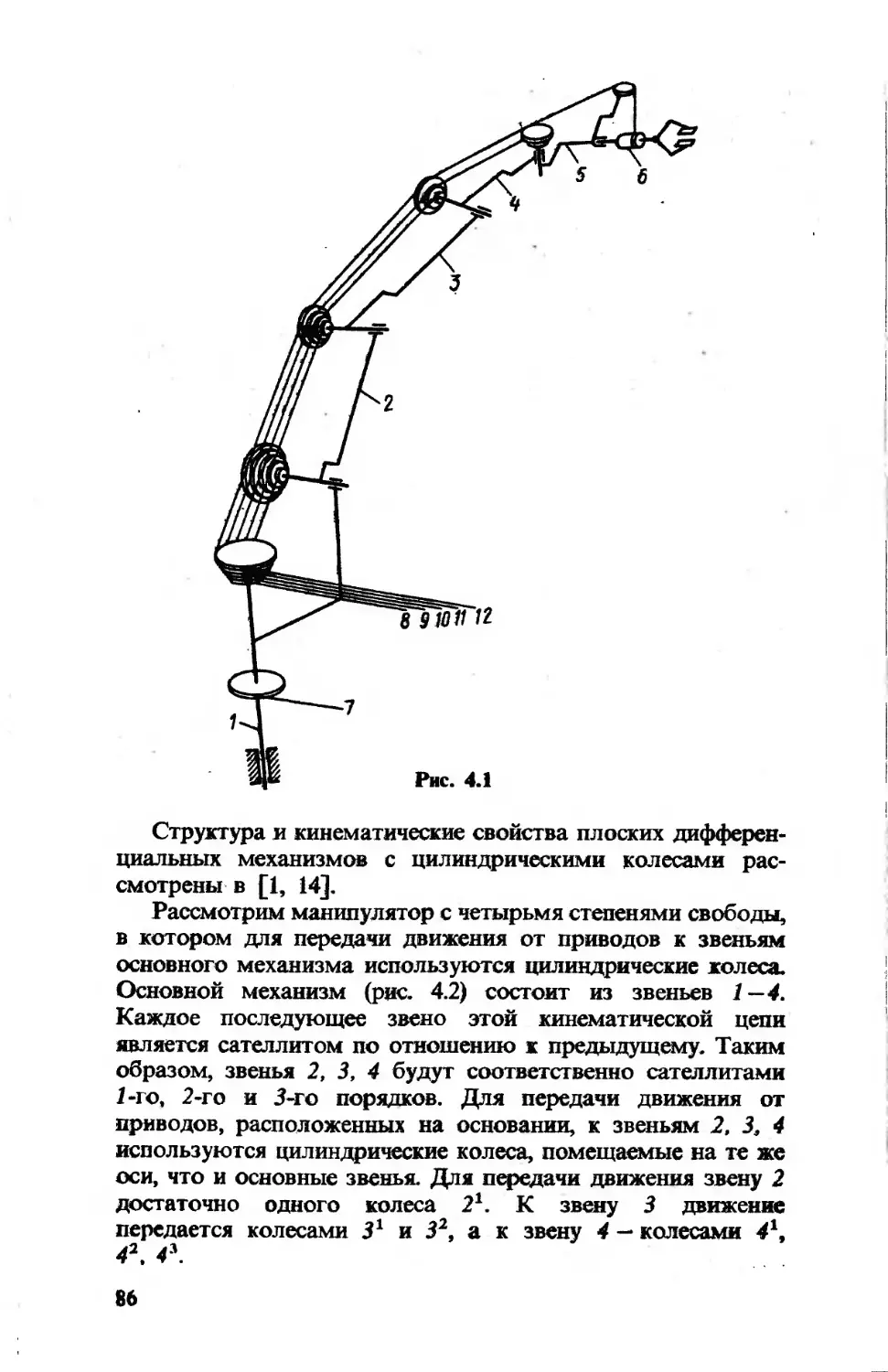
Например (рис. 2.1, а), звенья 1. 2. 3. 4 образуют
основную кинематическую цепь, а звенья 1, 2, Г, 2'
образуют механизм с одной степенью свободы, построен-
ный на подвижном звене 1. Таким образом, число
степеней свободы системы звеньев 1, 2, Г, 2' равно двум.
На подвижном звене 2 построен еще один механизм
с одной степенью свободы, включающий звенья 2, 3, 2", 3'.
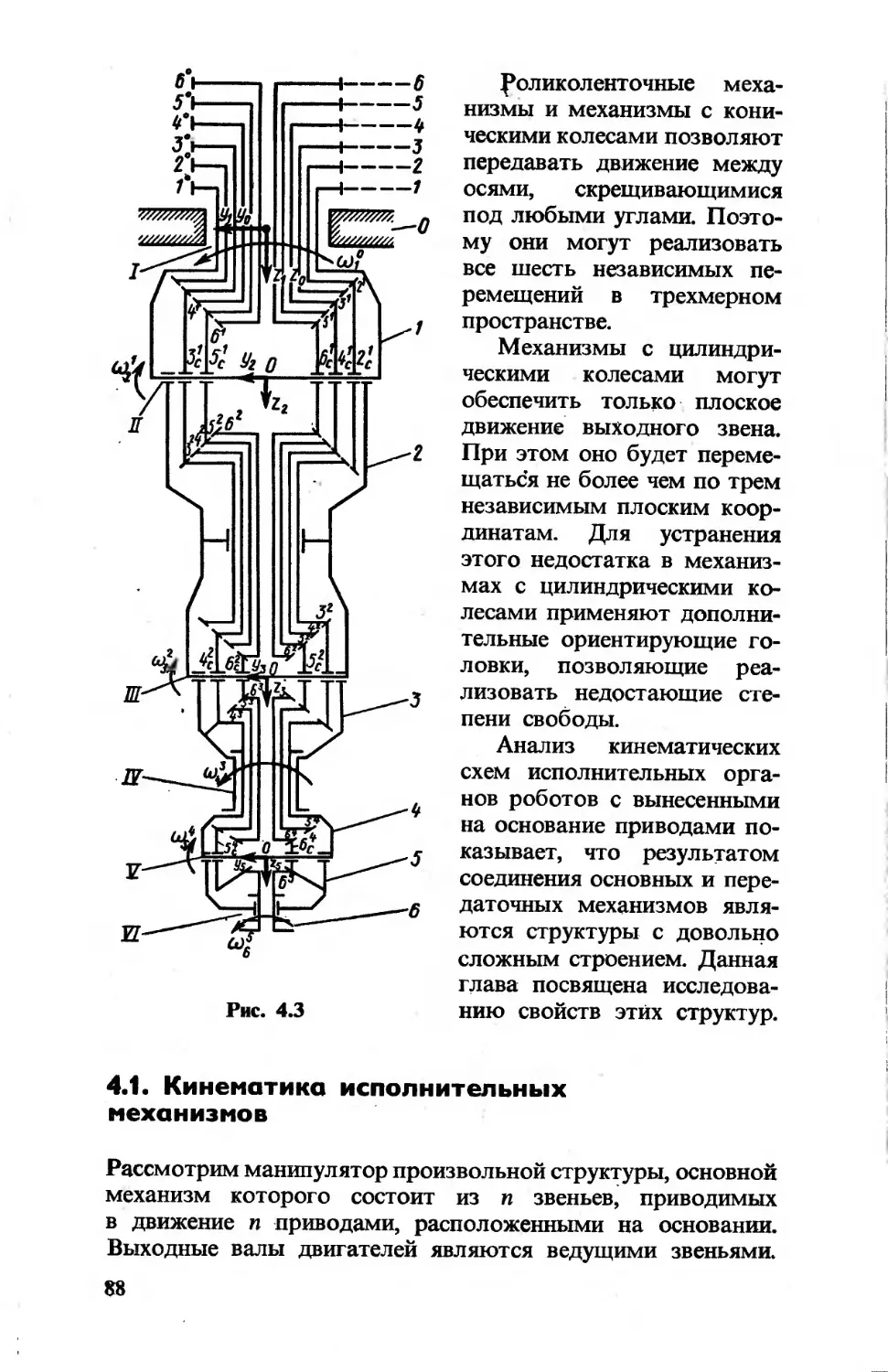
Рис. 2.1
1
Система звеньев 7, 2, 3, 7', 2', 2", 3' будет уже обладать
тремя степенями свободы.
Рассмотрение данного примера позволяет сделать вывод,
что для образования механизмов с несколькими степенями
свободы к основной кинематической цепи можно при-
соединять группы звеньев, обладающих числом степеней
свободы, равным нулю, с учетом числа степеней свободы
внешних кинематических пар.
Такие группы звеньев, как известно, называются
структурными группами или группами Ассура. Структурные
группы можно присоединять не только к соседним
звеньям, но и к любым звеньям основной кинемати-
ческой цепи, число степеней свободы при этом не из-
меняется.
На рис. 2.1,6 показан пример плоской кинематической
цепи с четырьмя степенями свободы, у которой привод-
ные структурные группы вводятся между различным
звеньями. От того, к каким звеньям присоединяются
структурные группы, содержащие привод, зависят все основ-
ные характеристики проектируемого манипулятора: усилия
в кинематических парах, расход энергии на перемещения,
быстродействие. *
В связи с этим задачу структурного синтеза в широком
смысле нельзя ограничивать геометрическим уровнем. Хотя
без перечисления полного набора структур нельзя решить
и задачу выбора оптимальной структуры.
На основании сочетаний приведенных в табл. 2.1 пар
различных классов можно получить структуры различных
кинематических цепей.
Например, для сочетания Р5р5Р5Р5р5Р5, содержащего
шесть пар пятого класса, можно получить различные
кинематические цепи с шестью степенями свободы, содер-
жащие вращательные и поступательные пары.
Если все пары считать вращательными, то получим
структуру вида ВВВВВВ, если три пары считать поступа-
тельными, то структуру вида ПППВВВ. В этих символи-
ческих представлениях кинематических цепей знак П озна-
чает поступательную, знак В — вращательную пару. Порядок
расположения букв в формуле соответствует порядку
расположения кинематических пар в цепи начиная от
неподвижного звена.
При построении структуры цепи с шестью степенями
свободы, предназначенной для перемещения и ориентации
объекта типа твердого тела, следует иметь в виду следую-
щее: перемещение объекта из одного положения в другое
2 Механика промышл. роботов, кн. 2
33
целесообразно разделить на операцию переноса, осуществляе-
мую переносными подвижностями, и операцию ориентиро-
вания, осуществляемую тремя вращательными движениями
схвата.
Таким образом, кинематическая цепь манипулятора
функционально может быть расчленена на две части:
механизм переносных движений и механизм ориентирую-
щих движении.
Механизм ориентирующих движений должен содержать
только вращательные пары: три — для ориентирования
твердого тела и меньше — в частных случаях: для плоскости
, или прямой.
Кинематическая цепь механизма переносных движении
может содержать как вращательные, так и поступательные
пары. Эта кинематическая цепь должна иметь не менее
трех степеней свободы и обеспечивать перемещение объекта
в рабочем пространстве робота. Возможно восемь различ-
ных сочетаний пар кинематической цепи с тремя степенями
свободы: ВВВ, ВВП, ВПВ, ВПП, ПВВ, ПВП, ППП, ППВ.
Важно при этом отметить, что не всякая кинемати-
ческая цепь с тремя степенями свободы обеспечивает
три степени свободы движения точки, т. е. ее движение
по трем независимым координатам. Для этого ранг
матрицы должен быть равен трем:
dx/c^ dx/dq2 dx/dq3
dy/dq2
dz/dq^ dz/dq2 dz/dq2
где x, у, z — координаты точки выходного звена; qi9 q2i
q3 — обобщенные координаты кинематической цепи.
В табл. 2.2 показаны структурные кинематические схемы
механизмов манипуляторов с тремя степенями свободы,
различающихся взаимным расположением осей и доставляю-
щих точке выходного звена объемное движение.
Однако следует отметить, что все многообразие схем
этим не ограничивается. Так как цепи манипуляторов, как
правило, имеют оси перпендикулярные, параллельные или
скрещивающиеся под прямым углом, то их можно получить
из трехзвенной кинематической цепи общего вида со скрещи-
вающимися осями (рис. 2.2). Оси пар А, В, С скрещи-
ваются под углами «i и а2, кратчайшие расстояния между
осями пар равны соответственно h3 и й2, смещения
центров пар вдоль их осей равны и Ь2. Для получения
различных вариантов трехзвенных цепей, достаточно полагать
34
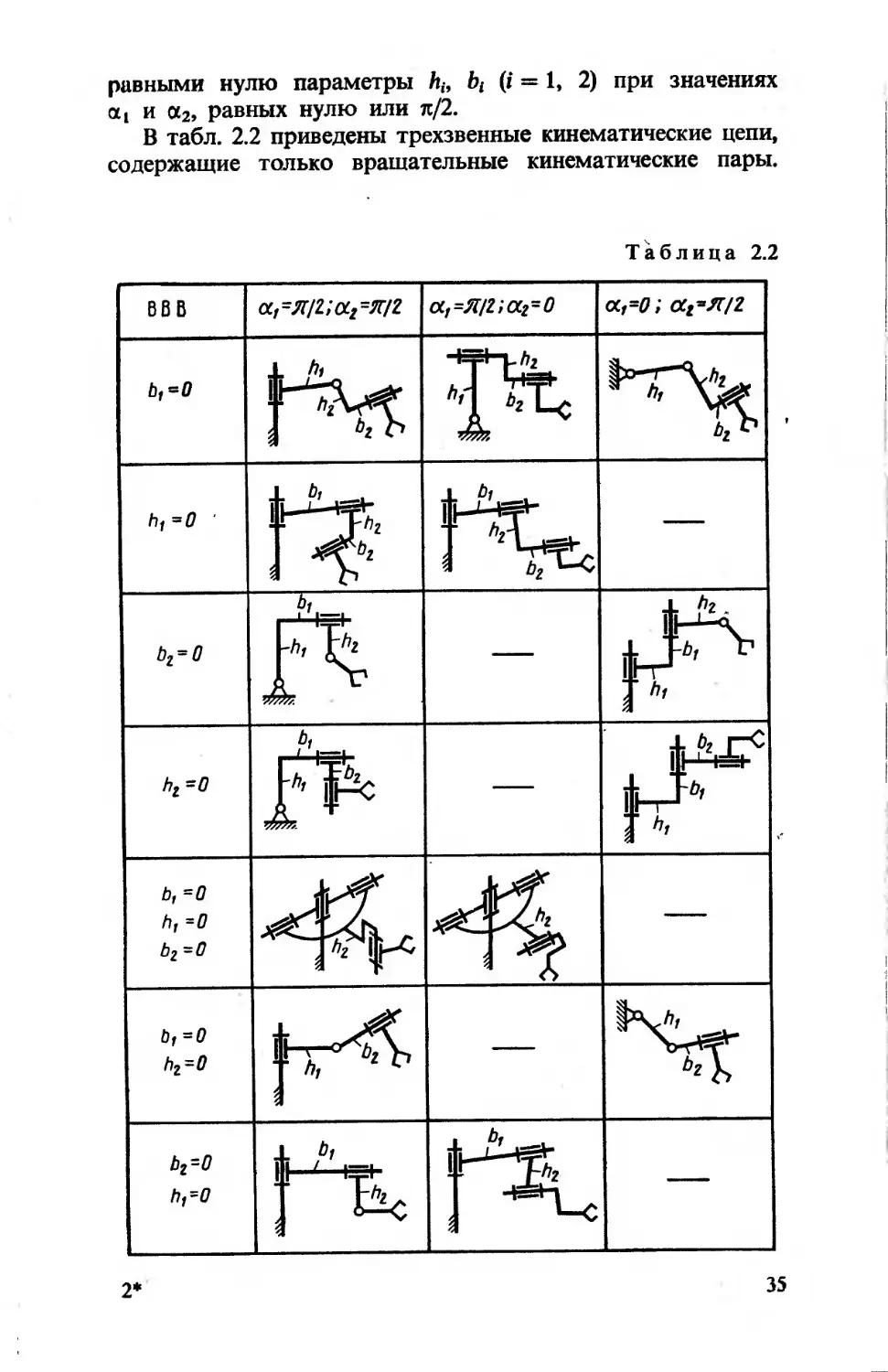
равными нулю параметры hi9 bt (i == 1, 2) при значениях
«| и а2, равных нулю или п/2.
В табл. 2.2 приведены трехзвенные кинематические цепи,
содержащие только вращательные кинематические пары.
Таблица 2.2
2*
35
Продолжение табл. 2.2
Аналогично могут быть получены и кинематические цепи,
содержащие как вращательные, так и поступательные пары.
Вопрос о выборе структуры кинематической цепи пере-
носных движений для конкретного робота является слож-
ным и определяется предъявляемыми к нему техническими
требованиями по точности и быстродействию и выпол-
няемым технологическим процессом.
В Частности, кинематические схемы, содержащие только
поступательные пары, обеспечивают независимость кинемати-
36
ческих ошибок от положения
объекта в рабочем простран-
стве.
Манипуляторы, исполь-
зующие кинематическую схе-
му с одной вращательной
и двумя поступательными
парами типа В ± П1 П,
удобно могут быть построе-
ны с применением пневмо-
привода или гидропривода,
но обладают малой жест-
костью в вертикальном направлении, а кинематическая
ошибка возрастает с удалением от оси вращения.
Роботы, построенные с использованием структуры
В1ВЦВ (например, ТУР-10), обладают большей компакт-
ностью, но имеют меньшую зависимость ошибки от положе-
ния в рабочей зоне.
Роботы, построенные по схеме В ± В1 П (например,
«Универсал-15»), имеют значительную жесткость в верти-
кальном направлении и приемлемую компактность конструк-
ции.
В производственных условиях движения роботов не
сводятся только к переносу и ориентированию объектов.
Роботы совершают движения вдоль автоматических линий,
около станков, загружают детали в станки. Поэтому их
движения более многообразны. Аналогично движениям
человека их можно разбить на три вида: глобальные,
региональные и локальные.
Глобальные — это движения робота на расстояния, пре-
вышающие размеры самого робота, например движения
транспортного робота вдоль цеха при обслуживании не-
скольких станков.
Региональные — это движения робота в пределах его
рабочего пространства, определяемого размерами звеньев
руки робота.
Локальные — это малые движения робота в отдельных
зонах рабочего пространства, соизмеримые с размерами
схвата, например локальное движение вставки штифта в
отверстие в зоне отверстия.
37
1,1. Рабочее пространство манипулятора.
Зона обслуживания
Рабочее пространство манипулятора ограничивается
поверхностью, огибающей все возможные положения схвата.
Однако не все части этого рабочего пространства
одинаково приспособлены для выполнения различных опера-
ций. В связи с этим в рабочем пространстве выде-
ляется его часть, в которой можно выполнять данную
операцию. Эта часть рабочего пространства называется
зоной обслуживания.
Количественно рабочее пространство манипулятора
оценивается его объемом. Форма и объем рабочего
пространства манипулятора определяются в значительной
мере его функциональными возможностями.
Определим границы рабочего пространства плоского
манипулятора с двумя степенями свободы с учетом ограни-
чений на углы относительного поворота <Pi <р2 (рис. 2.3, а)
[16]. Пусть ограничения на углы поворота в шарнирах
заданы в виде
Ф1н < Ф1 < Ф1вэ Ф2н < Ф2 Ф2в,
тогда графически построить рабочую зону можно следую-
щим образом (рис. 2.3, б). Проводим дугу радиусом /] 4-
с центром в точке А в пределах угла поворота звена 1
Ф1н < Ф1 < Ф1в- Полученная дуга К^К2 принадлежит границе
рабочей зоны, так как
находится на максимально возмож-
Рис. 2.3
1
ном удалении от шарнира А. Из центров в точках и В2,
соответствующих крайним положениям шарнира В, следует
радиусом 12 описать дуги окружностей в пределах
Ф2н Ф2 Ф2в- Участки K'iKi и.К2К2 дуг принадлежат
границе рабочего пространства. Дуги, описанные в направ-
лении к оси Ах, уходят внутрь рабочего пространства
и не принадлежат его границе.
Если дуги KiK'i и К2К2 пересекаются, процесс построе-
ния внешней границы рабочего пространства закончен. Если
дуги KiKi и К2К2 не пересекаются, следует внешнюю
границу заменить дугами внутренней границы.
Внутренняя граница строится следующим образом. Из
центра в точке А описываются дуги радиусами АК2 или АК\ в
пределах возможного поворота звена 1 — угла <pt. Если
эти дуги перекрываются, то на этом построение границы
рабочего пространства заканчивается.
В данном случае они не перекрываются, поэтому из
крайних точек К3 и К3
этих дуг следует провести
с центром в точке А дуги KZ3K4 и К3К4 радиусами
АК3 и АК3, соответствующими положению точки К при
другом предельном значении угла <р2, равном ф2н«
Описанное построение границ рабочего пространства
соответствует случаю, когда оно образует односвязную
область.
Если внешняя граница замкнута, то внутренняя гра-
ница рабочей зоны также образует обычно замкнутую кри-
вую.
Форма внутренней границы зависит от значения угла фд,
образуемого прямой АК'2 или АК2 с осью абсцисс.
J Если | 2<рд | > ф2в, то дуги перекрываются и внутренняя
граница является окружностью радиуса
г = 01 + /2 + 2/i/2 cos ф1д.
В том случае, когда условие не выполняется, внутрен-
няя граница включает еще две дуги, которые очерчиваются
при <рх = ±Ф1п и изменении ф2.
Аналогично можно построить границы рабочего про-
странства для и-звенных плоских манипуляторов с враща-
тельными парами.
В этом случае участок внешней границы
представляет собой дугу окружности с центром в точке А
п
радиуса Ri — £ с центральным углом ±Ф1П, когда изме-
i— 1
няется только угол
39
Соседние участки внешней границы строятся путем
последовательного поворота зйеньев, когда изменяются
последовательно углы <р7- (/ = 2,..., и) и радиусы окружностей
Л
соответственно равны Rj = £ 1к.
k=j
Внутренняя граница рабочего пространства также строится
путем последовательных поворотов звеньев, начиная с
первого. При этом, если внешняя граница не замкнута,
ее крайние точки служат исходными для построения
внутренней границы. Она может также и отсутствовать,
если все точки, охватываемые внешней границей, принадле-
жат рабочему пространству.
2.3. Угол и коэффициент сервиса
Для оценки возможности выполнения манипулятором опе-
рации ориентирования объекта в заданной точке рабочего
пространства используются понятия угла и коэффициента
сервиса [16].
Углом сервиса 0 называется телесный угол, кото-
рый описывает продольная ось схвата при движении
вокруг закрепленной точки (рис. 2.4).
Коэффициентом сервиса в данной точке
рабочей зоны называется отношение угла сервиса в этой точке
к телесному углу 4п:
Кв = 0/(4я). (2.10)
Угол сервиса и, следовательно, коэффициент сервиса в
каждой точке рабочей зоны зависят от постоянных
параметров манипулятора, ограничений на относительные
перемещения звеньев и координат точки в рабочей зоне.
Для оценки возможности манипулятора к ориентиро-
ванию объектов по всей рабочей зоне используется средний
коэффициент сервиса, который оп-
ределяется по формуле
А
(2.11)
Коэффициент сервиса может
быть использован при проекти-
ровании манипуляторов вследствие зависимости его от
постоянных параметров механизма. Кроме того, эту ха-
рактеристику можно использовать также для выделения
в рабочей зоне манипулятора наиболее удобных участков
с достаточно большим коэффициентом сервиса.
Для пояснения понятий угла и коэффициента сервиса
рассмотрим эти величины для манипулятора с двумя сфери-
ческими и одной вращательной парами (рис. 2.4).
При фиксированной точке D схвата 3 анализ углов
сервиса звена 3 оказывается связанным с известными
условиями Грассгофа проворачиваемости плоского шарнир-
ного четырехзвенника.
Считаем, что ограничений на относительные углы по-
ворота звеньев нет. Для данного механизма целесооб-
разно использовать понятие базовой плоскости — плоскости,
проходящей через точки ABCD. При фиксированном поло-
жении точки D весь манипулятор можно привести в базо-
вую плоскость вращением вокруг оси, проходящей через
шаровые шарниры А и С. В базовой плоскости ме-
ханизм может рассматриваться как плоский четырехзвенник.
Определение угла сервиса рассматриваемого манипулятора
можно свести к определению возможных положений звена
CD плоского четырехзвенника в базовой плоскости. Затем,
вращая весь механизм вокруг оси AD, найти все возмож-
ные положения звена CD.
Второе возможное вращение звеньев — совокупности
звеньев АВС вокруг оси АС — не оказывает влияния на
положение звена CD и может не приниматься во внима-
ние при определении угла и коэффициента сервиса.
ВьХцелим в рабочей зоне ее часть с коэффициентом
сервиса, равным единице. В этой части угол сервиса
должен быть равен 4л, т. е. звено CD должно двигаться
вокруг неподвижной точки £>, занимая любое положение.
Это условие будет выполняться, если в плоском четырех-
звенном механизме звено CD будет кривошипом. Чтобы
коэффициент сервиса был равен единице, угол сервиса
должен быть равен 4л, т. е. точка С должна иметь воз-
можность занять любое положение на сфере радиуса CD
с центром в точке D. Это условие выполняется, если
звено CD является кривошипом в плоском четырехзвеннике.
Поэтому для определения искомых соотношений долж-
но использоваться условие существования кривошипа в
плоском кривошипно-коромысловом механизме, так как
звено АВ в манипуляторе обычно не совершает полного
оборота.
41
В кривошипно-коромысловом механизме (рис. 2.5, а)
имеют место три условия существования кривошипа [25]:
G + + R — AD.
(2.12)
Эти условия приводят к выражениям для границ зоны
с коэффициентом сервиса, равным единице.
Из первого уравнения системы (2.12) следует
max
Из второго и третьего неравенств системы (2.12) получим
шах
Поэтому область полного сервиса находится между
окружностями с радиусами, равными Ктах и Rmin
(рис. 2.5, в). При R < Kmin (зона 3) коэффициент сервиса
Кв<1.
При увеличении расстояния от точки А, коэффициент
сервиса изменяется от 1 до 0, когда все звенья 1, 2 и 3
вытягиваются в одну линию до величины +12 + /3.
При нахождении точки D в этой зоне угол сервиса
0 может быть определен по формуле 0 = F/Z3, где F —
площадь поверхности сферического сектора, получаемого
тах вокруг AD.
при вращении плоского четырехзвенника в его предельном
положении вокруг оси AD (рис. 2.5,6).
Этот сферический сектор получается вращением дуги
радиуса 13 с углом раствора <р
Площадь сферической поверхности равна F = 2 л/3 (1 —
— COS Фтах), ПрИЧСМ
COS фтах
(»1 + /г)2]/(2Л/з).
С учетом этих зависимостей
зоне 2 находится по формуле
коэффициент сервиса в
Рис. 2.5
42
Ке = + l2)2
- (R - h)2 W3).
(2.13)
При уменьшении расстояния от точки D до точки А
коэффициент сервиса также уменьшается от единицы в зоне 1
и до некоторого значения на границе зоны (рис. 2.5, в).
В этом случае формула для коэффициента сервиса имеет
вид
Z1)2 + (R - 13)2]/(4W3).
(2.14)
I
Рассмотрим вопрос об определении коэффициента сер-
виса и зон его распределения для манипулятора с шестью
степенями свободы, содержащего шесть вращательных
кинематических пар (рис. 2.6, а). Ограничения на относитель-
ные углы поворота отсутствуют. Выявим зоны рабочего
пространства с коэффициентом сервиса, равным единице.
При отсутствии ограничений на углы поворота в
шарнирах манипулятора рабочее пространство его может
быть получено путем вращения плоской зоны обслужи-
вания, построенной в базовой плоскости ВСЕ, вокруг оси
пары А [1]. Поэтому анализ можно проводить, рас-
сматривая коэффициент сервиса плоского манипулятора
в базовой плоскости.
Если обозначить расстояние от точки В до точечного
объекта в рабочем пространстве через R, то максималь-
ное расстояние, при котором обеспечивается полный
коэффициент сервиса, равный единице,
Rt = L 4- L — L
•'Imax — »2 • *4. *6*
Эта величина определяет внешнюю границу зоны полного
коэффициента сервиса и соответствует вытянутому в одну
линию участку цепи манипулятора BCDEK.
При приближении положения объекта к центру пары А
он попадает на вторую граничную кривую, которая
соответствует второму предельному положению манипу-
лятора.
Максимальное расстояние от оси пары А К2тах =
= 12 — ^4 "Ь ^б*
Третья граничная кривая соответствует третьему пре-
дельному положению. В этом случае максимальное рас-
стояние от оси пары А R3max =• — /2 + U +
Возможны и другие предельные положения манипуля-
тора, определяющие граничные кривые в рабочей зоне
манипулятора (рис. 2.6,6):
1
Рис. 2.6
Объемы этих граничных зон зависят от конкретных зна-
чений I, (i = 2, 4, 6).
Рассмотрим, как изменяется коэффициент сервиса в раз-
личных зонах рабочего пространства для манипулятора с дву-
мя сферическими и одной вращательной парами при заданных
размерах звеньев. Примем для определенности Ц > /2 + 1з I
h > /з [18].
Зона полного сервиса ограничивается сферами радиуса
11 + h ~ h R 11 •” 1г + 1з«
В точках рабочего пространства, расположенных в зоне,
ограниченной сферами радиуса + l2 + l3 > R > Ц — 12 + Ц,
угол сервиса может быть найден из соотношения
cos 0 = [Z| + R2 - (h + /2)2]/(2К/3).
Углу 0 в базовой плоскости в пространстве соот-
ветствует шаровой сектор с площадью сферической по-
верхности s = 2nl2 (1 — cos0). Тогда коэффициент сервиса для
этой зоны
KQ — 0/(4я) = з/(4л/з) = (1 — cos0)/2. (2.15)
Подставляя значение cos0 в последнее выражение, получим
= [(/i + 12)2 -Ц- К2]/(4К/3). (2.16)
Рассмотрим зону рабочего пространства, ограниченную
сферами радиуса R согласно следующему неравенству:
11 — h + 1з > R > 11 — 1г — 1з- В этом случае имеем
cos0 — [(/i — /2)2 — 1з 1^2]/(2Л/з).
Подставляя это значение в формулу (2.15), получим выра-
жение для коэффициента сервиса для этой зоны в зави-
симости от К в следующем виде:
Кв = [(R + /3)2 - (h - l2Yl/(4Rl3).
1
Приведенные формулы получены без учета ограничений
па значения углов поворотов звеньев в шарнирах. Учет
ограничений уменьшает зоны с заданным значением коэф-
фициента сервиса.
2.4. Характеристики множества возможных
скоростей схвата манипулятора
Ввиду того что манипуляторы представляют собой си-
стемы с несколькими степенями свободы, скорость точки
выходного звена — схвата может изменяться как по вели-
чине, так и по направлению в зависимости от конфигура-
ции манипулятора и его обобщенных скоростей. С точки
зрения оценки скоростных качеств манипулятора представ-
ляет интерес изучение всего множества возможных скоростей
схвата.
Считаем, что обобщенные скорости манипулятора из-
меняются в некоторых пределах. Рассмотрим множество
возможных линейных скоростей точки схвата на примере
плоского манипулятора с двумя вращательными парами
(рис. 2.7). В любой момент времени линейная скорость
точки К схвата равна сумме векторов линейных скоростей
этой точки при движении только в шарнире А или в шар-
нире В:
v = Vi + v2,
где Vi — линейная скорость точки К, соответствующая
движению только в шарнире А с угловой скоростью
фх; v2 — линейная скорость точки
движению только в шарнире В
с угловой скоростью ф2, причем
= (р ^А.К —- ф1 (/j -J- 12 Ч”
+ cos ф2)1/2; v2 = ф/2.
Если считать, что обобщенные
скорости Ф1 и ф2 могут изме-
няться в некоторых пределах:
ф! С Ф1 < Ф1'; Ф'1 < Фг С фг, то все
возможные линейные скорости
точки К при заданной конфигура-
ции будут лежать внутри парал-
лелограмма, построенного на
векторах г'ь v2t v2, соот-
К, соответствующая
Рис. 2.7
1
ветствующих максимальным угловым скоростям ф'ь ф'[
С точки зрения оценки скоростных качеств манипуля-
тора представляют интерес возможность и скорость манипу-
лятора совершать движение объекта из заданной конфигу-
рации в различных направлениях.
Скоростные возможности плоского манипулятора в задан-
ной конфигурации будет характеризовать площадь парал-
лелограмма, построенного на векторах независимых возмож?
ных скоростей схвата. Эту величину называют мобиль-
ностью конфигурации манипулятора [16].
В общем случае под мобильностью конфигурации
манипулятора понимается величина
Mq = /Но dy dz/r3), (2.17)
I
г
где х, у, z — координаты характеристической точки схвата
манипулятора в момент времени t. Величина Mq определяет
объем множества точек х, у, z в момент времени t = 0.
Мобильность конфигурации характеризует скоростные
качества манипулятора в некоторой его конфигурации с
учетом ограничений, наложенных на обобщенные скорости
в шарнирах.
Для определения мобильности конфигурации манипуля-
тора можно использовать его функцию положения, т. е.
зависимости вида
дифференцируя которые по времени, получим
dr ,
v
Так как величина qj должна удовлетворять некоторым
ограничениям, то
(
I
1
1
v
где q'j, q” — ограничения на величину qf, 0 < 1.
Последняя формула показывает, что точки конца вектора
заполняют в пространстве некоторый многогранник, кото-
рый называется допустимым многогранником скоростей
конфигурации [16].
1
Мобильность конфигурации равна объему допустимого
многогранника скоростей; для плоского манипулятора пло-
щадь допустимого многогранника равна
S„ = | х г7-|, (2.18)
при этом
- q'i),
«)].
Тогда мобильность конфигурации плоского манипулятора
выражается так:
М q =
дх ду дх ду
Bq, 8q} 8q{ 8qt
(2.19)
ЙГ - ® (i’j ~
Для плоского двухзвенного манипулятора координаты
схвата выражаются так (рис. 2.7):
х = ZiCOSCPi +
Z2 cos (<р2 + Ф1); У = Zi simp! +/2sin((pi + <р2),
тогда мобильность конфигурации равна
Af, = ltl21 sin <р2 |(ф; - <p'i)(<j>2 - Vi).
(2.20)
Последнее выражение показывает, что мобильность этого
манипулятора не зависит от угла поворота первого звена,
а зависит лишь от угла поворота второго звена по
отношению к первому.
Рассмотрим мобильность конфигураций пространственно-
го манипулятора с тремя вращательными парами (рис. 2.8, а).
Рис. 2.8
47
Скорость точки схвата К в любой момент времени
равна векторной сумме скоростей (рис. 2.8,6):
гк = Vi + г2 + г3,
где — скорость точки К во вращательном движении
в шарнире 4,
= Ф1 p2cos(p2 + /3cos(<p2 + ф3)];
г2 — составляющая скорости точки К в плоском движении,
равная скорости полюса точки В в плоском движении,
Г2 — ф2/2^
г3 — составляющая скорости точки К в плоском движении,
скорость вращения этой точки вокруг шарнира В
f з = (Ф2 + Фз) ?з-
Векторы скоростей v2 и г3 составляют между собой
угол ф3. Тогда площадь параллелограмма, образованного
скоростями, равна
S2 = ф2/2 (ф2 + Фз) 1з I sin ф3 |.
При изменении ф2 и ф3 в пределах ф2 ф2 ф2;
Фз < Фз < Фз площадь допустимого параллелограмма ско-
ростей при движении лишь в парах В и С равна
^ф2<р., = ^3 I 81Пф3 I (ф2 — ф2)(ф2 — ф2 + ф'{ — Ф1).
При движении во всех парах мобильность конфигу-
рации манипулятора равна площади прямоугольного парал-
лелепипеда :
Mq = /2/31 sin ф3 | (ф2 - ф2) (ф2 - ф'2 + ф1 - ф1) [Z2 cos ф2 +
+ /3 cos (ф2 + ф3) (ф] - ф'О]. (2.21)
Последнее выражение показывает, что мобильность кон-
фигурации зависит лишь от двух обобщенных координат
ф2 и фз и не зависит от угла фх.
Представляет интерес определить конфигурацию манипу-
лятора, в которой мобильность достигает своего макси-
мального значения. Для решения этой задачи достаточно
исследовать на экстремум выражение, стоящее под знаком
модуля в формуле (2.21). Взяв частные производные
от этого выражения по ф2 и ф3 и приравняв их нулю,
получим следующие выражения:
tg ф2 =
h sin фз
12 + 1з cos фз
; совфз
cos 2ф3
СО8ф2
48
1
Последние выражения определяют четыре конфигурации
манипулятора с экстремальной мобильностью, из которых
выделяется одна конфигурация условиями
—л/2 < ф] < 0 < ф2 < я/2.
Исследование максимального значения мобильности в
зависимости от величин 12 и 13 показывает, что наиболее
выгодной по критерию мобильности является схема с одина-
ковой длиной звеньев 12 и 13.
Рассмотрим мобильность конфигурации манипулятора с
двумя вращательными и одной поступательной кинемати-
ческими парами (рис. 2.9).
Линейную скорость точки схвата К можно рассматри-
вать как векторную сумму скоростей г2, v3 движений по
каждой обобщенной координате:
t?i = ф|5зСО8ф2^ г2 — ф2$3; v3 = S3.
Векторы скоростей v2, v3 образуют прямоугольный
параллелепипед, объем которого
V = ФхФг&з^з cos ф2.
При изменении обобщенных скоростей фх, ф2, <53
заданных пределах:
• / А • А' А • О' С С”
Ф1 Ф1 Фг, Фг Фг Фг» ^з ^з ^з,
объем допустимого многогранника скоростей, представляю-
щий мобильность конфигурации, равен
Mq = s3 cos ф2 (ф; - фу (ф£ - ф'2) & - §у. (2.22)
Выражение мобильности этого манипулятора показывает,
что оно зависит только от угла ф2. При ф2 = 0 мобиль-
ность конфигурации имеет мак-
симум, при ф2 = я/2 мобиль-
ность обращается в нуль.
Помимо мобильности кон-
фигурации, характеризующей
скоростные качества манипуля-
тора в некоторой конфигура-
ции, рассматривают мобиль-
ность манипулятора, характе-
ризующую скоростные каче-
ства манипулятора во всем ра-
бочем пространстве.
Под мобильностью манипу-
лятора в рабочем простран-
Рис. 2.9
1
стве понимается среднее значение мобильности конфигу-
раций [16]:
V
К Qi
f - f M(q)Aq
Qi Qi
(2.23)
где V = q" — q'{ (i = 1,..., и) — объем и-мерного куба, обуслов-
ленного ограничениями по обобщенным координатам мани-
пулятора % ^qt^ q".
В частности, для плоского манипулятора с двумя вра-
щательными парами мобильность при симметричных огра-
ничениях в соответствии с формулой (2.23) равна
М
(2.24)
= hh (Ф1 ~ Ф1)(ф2 - Ф9(1 - COS<p2).
Последняя формула показывает, что мобильность плоско-
го манипулятора с двумя вращательными парами зависит
только от угла ф2 между звеньями 1 и 2.
Коэффициент передачи скорости. Механизм универсального
манипулятора должен обеспечивать перемещение схвата в
различных направлениях с некоторыми заданными скорос-
тями. Однако в различных точках рабочего пространства
могут возникать случаи, когда сообщение заданной скорости
схвату в заданном направлении требует очень большой
скорости в некотором приводе.
Рассмотрим простейший пример механизма манипуля-
тора (рис. 2.10, а), воспроизводящего движение схвата по
траектории со скоростью v. Как видим, в различных
положениях скорости Vi и v2, необходимые для получения
скорости v, весьма различны. Найдем эти скорости. Имеем
v2. Проецируя на на-
а)
—*
откуда
v sin а2
v sin dj
sin («! + а2) *
V = Vi
правление скорости v это урав-
нение, получим
v = v1 cos «i
На основании теоремы си-
нусов получим
Vi/r2 = sin a2/sin аь
v2 cos а2.
(2.25)
1
модуль заданной скорости; v2
a2
модули необ-
углы, образо-
«1,
v2 с вектором ско-
a sin0 и sin a2 0. Для оценки способности
Vi/v и k2 — v2/v. При изменении направления
где v
ходимых составляющих скоростей;
ванные векторами скоростей
роста v.
Выражения для Vj и v2 показывают, что эти скорости
стремятся к бесконечности, когда угол (oti + a2) стремится
к
манипулятора реализовать скорость объекта в заданном
направлении в некоторой точке рабочего пространства
можно использовать коэффициенты, которые назовем ко-
эффициентами возрастания скорости по заданному направле-
нию : к
заданной скорости схвата значения этих коэффициентов
изменяются и при
С точки зрения ограничения скоростей в кинемати-
ческих парах представляют интерес максимальные значения
этих коэффициентов:
{^1тах При к1тлк > ^2тах9
Г II
^2тах ПрИ ^1тах < К2тах.
it стремятся к бесконечности.
(2.26)
Как показывает анализ, максимальные значения коэф-
фициентов ki и к2 определяются максимальным значением
угла («!
этих коэффициентов должны быть ограничены.
Величину, обратную к, называем коэффициентом
передачи скорости в заданной точке. Максималь-
ным значениям к соответствуют минимальные коэф-
фициенты передачи скоростей
меняется от 0 до 1.
аг)тах- В рабочей зоне манипулятора значения
Этот коэффициент из-
Если какой-либо коэффициент
0, то в данной конфигурации манипулятора существует
направление, по которому передача скорости невозможна.
При проектировании манипулятора следует стремиться,
чтобы среднее значение коэффициента передачи скорости по
рабочей зоне было максимальным.
Коэффициент неравномерности пучка возможных скорос-
тей. Совокупность векторов независимых возможных скорос-
тей схвата в некоторой точке рабочего пространства
образует пучок независимых возможных скоростей.
Можно рассматривать пучок независимых линейных и
угловых скоростей. Коэффициент является функцией двух
переменных аь а2, его максимальное значение достигается
при at
пучка (рис. 2.10, б) с двумя лучами (и = 2). Отклонение угла
а2 от п/2 приводит к уменьшению значений
ос2 = л/2. Это соответствует оптимальной форме
OCi
I
1
/
i
г
!
I
1
1
Правильность формы пучка в некоторой точке рабочей зоны
можно оценить отношением
8 = лДифшаД
(2.27)
где 6 — коэффициент неравномерности пучка возможных ско-
ростей; <ртах — максимальный угол между лучами пучка;
п — число лучей пучка.
Величина 5 изменяется от 0 до 1 и так же, как и
величина коэффициента передачи скорости, может быть
использована в качестве целевой функции при синтезе
манипуляторов.
Глава 3
Синтез незамкнутых
кинематических цепей по заданным
положениям объекта в пространстве
При проектировании механизмов по заданным положениям
объекта (твердого тела) в пространстве всегда возникает
вопрос: какими простейшими механизмами можно реализо-
вать эти положения? Чтобы ответить на этот вопрос,
необходимо вначале рассмотреть синтез простейших не-
замкнутых цепей с двумя кинематическими парами и
определить их возможности по реализации заданных
положений тела в пространстве.
Более широкими кинематическими возможностями обла-
дают трехзвенные кинематические цепи, составляющие осно-
ву системы переносных движений роботов.
3.1. Синтез двухзвенных незамкнутых
кинематических цепей*
*
Рассмотрим вначале задачи кинематического синтеза прос-
тейших двухзвенных незамкнутых кинематических цепей по
заданным положениям объекта в пространстве. Под объектом
в самом общем случае будем понимать твердое тело,
перемещаемое с помощью механизма с незамкнутой
кинематической цепью. Как будет показано ниже, в
процессе решения задачи с помощью таких простейших
* Под двухзвенными понимаем незамкнутые кинематические
цепи с двумя подвижными звеньями.
52
т), задавая положение
манипуляторов возможно осуществление некоторого числа
заданных положений твердого тела в пространстве.
Кинематическая цепь с двумя сферическими парами
(рис. 3.1). Задача ставится следующим образом. Пусть
объект — твердое тело должен занимать т заданных поло-
жений в пространстве. Эти положения будем задавать
матрицей 4-го порядка Моj (j = 1
системы O'x'y'z', связанной с телом. Требуется определить
постоянные параметры механизма, выходное звено которого
может занимать заданные положения в пространстве.
Под постоянными параметрами механизма понимаются
независимые величины, однозначно определяющие геомет-
рию механизма. Для данного механизма это: координаты
точки А (хА, уА, zA) в системе Oxyz, координаты точки
В (хв, ув, zB) в системе O'x'y'z', связанной
звеном механизма, длина звена АВ = I
метров.
Для решения задачи используем условие связи, которое,
очевидно, состоит в том, что в любом заданном положе-
нии подвижной системы O'x'y'z' расстояние I между центра-
ми сферических пар остается постоянным во всех заданных
положениях. В аналитическом виде это условие можно
записать так:
с выходным
всего семь пара*
- *а)
(Ув, - Ул)
где т — число заданных положений объекта; xBj, Увр
zBj — абсолютные координаты точки В в j-м положении
объекта в системе Oxyz.
При произвольных координатах точки Bj выражение
(3.1) представляет собой систему уравнений относительно
четырех неизвестных -хА, уА, zA, I. Эта система после
преобразования может быть представлена в виде линейной
относительно некоторых новых
выражаемых нелинейно через
искомые:
переменных alt а2, а3, а4,
&lXBj
агУВ)
a3zBj
а4 — О,
где аг = -хл; а2 = -2ул; а3 =
== -2гл; а4 = х% + угА + z2A - /2;
/ = 1, ..., т.
Система (3.2) имеет един-
ственное решение, если ее
определитель не равен нулю.
После нахождения cij (j =
Рис. 3.1
1
= 1,..., 4) определяются постоянные параметры кинемати-
ческой цепи.
Решение задачи синтеза для четырех положений точки
Bj (/=1,...,4) означает, что координаты точки Bj на
выходном звене могут быть выбраны произвольно. Во
всех случаях в четырех заданных положениях системы
O'x'y'z' могут быть найдены координаты точки xBi, yBj9 zBj
в неподвижной системе координат.
Если координаты точки В в системе Oxyz считать
искомыми, то в уравнение связи войдут еще три неизвест-
ные величины х'в, у'в, z'B, через которые координаты
хВ9 Ув, zB выражаются линейно,
будет уже входить семь постоянных параметров. В этом
случае для семи заданных положений твердого тела получим
систему семи уравнений для определения семи постоянных
параметров.
В теории синтеза механизмов показано, в каких
случаях система (3.2) имеет решение для числа положений,
больших четырех [37, 47]. В частности, для пяти заданных
положений тела получаем систему пяти линейных уравне-
ний связи вида (3.2) относительно четырех неизвестных:
имеет, как известно,
решение лишь тогда, когда определитель расширенной
матрицы равен нулю:
det5 = | ед-zj/1 = 0.
: в уравнение связи
Эта система
У А,
(3.3)
Подставляя в (3.3) выражения абсолютных координат,
получим алгебраическую форму 4-го порядка относительно
хв, Ув, %в> которая будет определять поверхность 4-го
порядка в подвижной системе координат — геометрическое
место шарнира В — точек, которые в пяти положениях
остаются на сфере.
При шести заданных положениях твердого тела полу-
чаем систему шести линейных уравнений относительно
четырех неизвестных.
Для совместности этой системы необходимо, чтобы ранг
ее расширенной матрицы был равен четырем. Это возможно,
если равны нулю любые два минора 5-го порядка в
этой матрице, что приводит к двум уравнениям 4-го
порядка относительно координат шарнира В в подвижной
системе координат. А пересечение этих двух поверхностей
определяет геометрическое место шарнира В в подвижной
системе координат, которые в шести положениях лежат
на сфере. Этим геометрическим местом является кривая
10-го порядка [37].
Бели задано семь положений твердого тела, то расчет-
ная система уравнений связи является линейной систе-
мой семи неизвестных с четырьмя неизвестными. Для
совместности такой системы необходимо, чтобы ранг рас-
ширенной матрицы такой системы был равен четырем, что
сводится к системе трех алгебраических уравнений 4-го
порядка относительно координат точки В и величины I.
Показано, что число действительных решений такой
системы не более 20 [37]. Это означает, что существует
20 точек в подвижной системе, которые в семи поло-
жениях тела остаются на одной сфере, а следовательно,
эти семь положений тела могут быть реализованы с
помощью одной' кинематической цепи, содержащей два
сферических шарнира.
Кинематическая цепь с вращательной и сферической пара-
ми (рис. 3.2). Эта кинематическая цепь определяется девятью
независимыми постоянными параметрами: тремя координа-
тами точки В в подвижной системе — х'в, z'b', тремя
координатами точки А в неподвижной системе координат —
хл, Уа, za, двумя независимыми направляющими косину-
сами оси пары А и длиной звена АВ — I.
Как и выше, для кинематического синтеза этой цепи
используем условие связи, накладываемое этой цепью на
относительное движение соединяемых тел. Таким условием
является нахождение точки В подвижного тела на окруж-
ности радиуса I в любом положении тела в неподвиж-
ной системе координат.
Это условие связи запишем в виде уравнения окруж-
ности в неподвижной системе координат, которая является
линией пересечения сферы и плоскости, перпендикулярной
оси вращательной пары. Следует отметить, что сфера
может быть произвольного радиуса, но центр ее должен
лежать на оси вращательного шарнира А.
Так как число уравнений связи равно двум, а число
постоянных параметров цепи
равно девяти, то максимальное
число точно реализуемых поло-
жений твердого тела равно че-
тырем.
Если точка В имеет четыре
положения Bj 0=1, • • •, 4) на
одной окружности, то это оз-
начает, что система уравнений
для определения сферы, про-
веденной через четыре по-
Рис. 3.2
55
1
Рис. 3.3
ложения точки В, должна иметь бесконечно много ре-
шений.
Такое условие может быть выполнено, если ранг расши-
ренной матрицы расчетной системы и ранг ее матрицы
равны трем. Для этого необходимо, чтобы равнялись нулю
любые два минора 4-го порядка в расширенной матрице.
Эти условия приводят к системе двух уравнений 3-го по-
рядка относительно координат xBi ув, zB, определяющих
в подвижном теле геометрическое место точек, имеющих
четыре положения на одной окружности. Любую из этих
точек можно взять за центр В проектируемой цепи. Ось
вращательной пары определяется пересечением двух плос-
костей, перпендикулярных отрезкам BiB2, ВХВ3 и проходя-
щих через их середины.
Уравнение этих плоскостей имеет вид
(х - х;)х + (у - yj)y + (z - Zj) z = (Rl~ R])/2 (/=2,3). (3.4)
Координаты точки А определяются из условия пересече-
ния оси, задаваемой уравнением (3.4), и плоскости вращения,
определяемой заданными положениями точки Bf, Направ-
ляющие косинусы оси определяются как направляющие
косинусы нормали к плоскости вращения звена АВ,
Кинематическая цепь с плоскостной и сферической парами
(рис. 3.3). Данная кинематическая цепь определяется. шестью
постоянными параметрами: три параметра определяют
плоскость пары Л, например три отрезка а, Ь, с, отсекаемые
плоскостью на координатных осях; три координаты xBi yBi zB
точки В в подвижной системе координат O'x'y'z'.
Тело, связанное данной кинематической цепью с не-
подвижным звеном, обладает пятью степенями свободы, и
кинематическая цепь накладывает на его движение одну
связь, которая выражается ус-
ловием: точка В во всех поло-
жениях тела должна находиться
в одной плоскости.
Уравнение плоскости в не-
зависимых параметрах, записан-
ное для т положений, имеет
вид
aXi 4- byt 4- czt 4- 1 = О
(i = 1, ..., т)
и образует линейную систему
уравнений для определения по-
стоянных параметров.
56
1
4 воз-
При трех заданных положениях тела система имеет реше-
н ие относительно трех параметров а, Ь, с при произвольном
выборе координат точки В в подвижном теле.
При четырех заданных положениях тела i = 1, .
никает линейная система четырех уравнений с тремя неиз-
вестными Ь, с, для существования решения которой необ-
ходимо, чтобы определитель 4-го порядка был равен нулю.
Этот определитель представляет собой некоторую куби-
ческую форму относительно абсолютных координат точки
В (*в, У в, zb)- Абсолютные координаты точки В выражаются
линейно через координаты точки В в подвижной системе,
связанной с телом.
Подставляя выражение для координат в выражение опре-
делителя, приходим к поверхности 3-го порядка в системе
Oxyz. Эта поверхность является геометрическим местом
точек подвижного тела, остающихся на плоскости в четырех
произвольных положениях тела в пространстве, поэтому
любая из точек этой поверхности может быть выбрана за
центр шарнира В при синтезе кинематической цепи по
четырем заданным положениям тела.
В случае решения задачи синтеза кинематической цепи
по пяти заданным положениям тела приходим к системе
пяти линейных уравнений относительно трех неизвестных:
а, Ь, с. Для совместности системы необходимо, чтобы
ранг матрицы был равен трем. Это условие приведет к ра-
венству нулю двух определителей 4-го порядка. После под-
становки в них выражений координат точки В в системе
Oxyz через координаты этой же точки в системе O'x'y'z'
приходим к системе двух кубических уравнений, которые опре-
деляют геометрическое место точки В в подвижном теле.
Это геометрическое место есть кривая 6-го порядка.
При решении задачи синтеза кинематической цепи по
максимально возможному числу положений, равному шести,
получаем систему шести линейных уравнений с тремя не-
известными. Для совместности такой системы необходимо
равенство нулю трех миноров 4-го порядка, что приводит
к системе трех алгебраических уравнений 3-го
относительно координат точки В в подвижной
порядка
системе
цепи с
Эквивалентной рассмотренной кинематической
плоскостной и сферической парами является цепь, содер-
жащая две поступательные и одну сферическую кинемати-
ческие пары.
В этом случае две поступательные пары определяют
плоскость плоскостной пары.
1
сферической
Кинематическая цепь с поступательной
парами. Эта кинематическая цепь определяется следующими
параметрами: четырьмя параметрами, определяющими по-
ложение прямой, например это могут быть четыре коор-
динаты точек пересечения прямой с двумя координатными
плоскостями, и тремя координатами точки В в подвижной
системе координат. Всего число постоянных параметров
равно семи.
Условие связи состоит в том, что точка В подвижного
тела в любом его положении находится на прямой линии.
Уравнение прямой линии можно задать двумя уравне-
ниями плоскости в неподвижной системе координат. Таким
образом, для N заданных положений приходим к системе
2N уравнений вида
При трех заданных положениях получаем систему шести
уравнений с шестью неизвестными: alf a, blf b, cl9 с.
В этом случае положение точки В в подвижной системе
координат произвольно.
Кинематическая цепь с цилиндрической i
парами (рис. 3.4). Цилиндрическая пара в кинематическом
отношении эквивалентна совокупности вращательной и
поступательной пар, оси которых совпадают. Поэтому и
задачи синтеза для этих
выходного звена эквивалентны.
Кинематическая цепь с цилиндрической и сферической
кинематическими парами определяется следующими по-
стоянными параметрами: ось цилиндрической
тырьмя независимыми параметрами; точка В
Oxyz — тремя; h — расстояние от точки В до оси
ческой пары. Условие
лежать на цилиндре
выходного звена 3.
В векторной форме
Л = I (&Bi *А) Х I 9
i сферической
цепей по заданным положениям
пары — че-
в системе
цилиндри-
В должна
связи цепи одно: точка
радиуса г при любом положении
это уравнение связи запишется так:
где ё — орт оси цилиндрической пары.
Это уравнение, записанное для N положений, приводит
к системе N уравнений с семью неизвестными. Следова-
тельно, максимально возможное число положений тела
равно семи.
Для четырех заданных положений приходим к системе
четырех линейных уравнений относительно четырех неиз-
цилиндрическом
положение на оси вращательной пары ее
вестных: х, у, z, г. В этом случае направление оси цилинд-
рической пары считаем заранее выбранным.
Кинематическая цепь с вращательной
парами (рис. 3.5). Эта кинематическая цепь характеризуется
одиннадцатью независимыми постоянными параметрами:
четыре параметра определяют положение оси пары А
в системе Oxyz и четыре — положение оси пары В в системе
O'x'y'z', два параметра — взаимное расположение осей пар А
и В (кратчайшее расстояние h и угол скрещивания осей а)
и расстояние b
центра.
Число уравнений связи, накладываемых цепью на отно-
сительное движение связываемых ею тел, равно трем, так
как эта цепь является трехподвижной: одна степень подвиж-
ности обеспечивается вращательной парой А и две — ци-
линдрической парой В.
Эти три уравнения связи должны удовлетворяться во
всех N заданных положениях подвижного тела, что приво-
дит к системе 3N уравнений с 11 неизвестными. Следо-
вательно, максимальное число, при котором система может
иметь решение, N = 3, два параметра при этом могут быть
выбраны свободно.
Приведем уравнения связей, накладываемых цепью на
относительное движение соединяемых ею тел. Такими
уравнениями являются:
условие постоянства угла между осями пар А и В
где LA, Lb — направляющие векторы осей пар А и В;
а — угол между осями;
условие постоянства расстояния между осями пар А и В
(гв — гА) (Ьл х LB) = h = const,
1
X
где ?А> ?в -^радиусы-векторы точек, лежащих на осях пар
А и В; La, Lb — направляющие косинусы осей пар А и В;
условие невозможности сдвига точки выходного звена
вдоль оси вращательной пары А
(fB — rA) La — b — const.
Так как два постоянных параметра при заданных трех
положениях могут быть свободны, то можно, например,
задаться направлением оси пары А и из первого уравнения
найти угол а, а затем из двух других — остальные па-
раметры.
Отметим также, что рассмотренная кинематическая цепь
с вращательной и цилиндрической кинематическими парами
кинематически эквивалентна цепи с тремя парами: двумя
вращательными и одной поступательной. Причем ось одно]
из вращательных пар параллельна направлению поступа-
тельного движения в поступательной паре. Такие кинемати-
ческие цепи также могут быть использованы в манипуля-
торах промышленных роботов.
Кинематическая цепь с двумя цилиндрическими парами
(рис. 3.6). Эта кинематическая цепь доставляет четыре
степени свободы выходному звену.
Цепь определяется следующими постоянными парамет-
рами: восемь параметров определяют положение осей пар
Л и В в подвижной и неподвижной системах координат,
два определяют взаимное положение осей пар А и В,
С и D. Таким образом, число параметров равно десяти.
Число условий связи, накладываемых на относительное дви-
жение соединяемых тел, равно двум.
Для N заданных положений выходного звена приходим к
системе 2N уравнений с десятью неизвестными. Следова-
тельно, максимально возмож-
ное число положений, для ко-
торых система может иметь
решение, равно пяти.
Приведем уравнения связей,
накладываемых цепью на отно-
сительное движение тел:
условие постоянства рас-
стояния между осями пар А
и В
(гв - ?л) (La *LB) = h = const;
условие постоянства угла
между осями пар А и В
60
cos a = const.
При трех заданных положениях получаем линейную
систему уравнений для определения постоянных параметров.
3.2. Синтез трехзвенных незамкнутых
кинематических цепей со сферической
парой на выходном звене
Рассмотрим задачи построения незамкнутых кинематиче-
ских цепей с тремя подвижными звеньями по заданному
движению твердого тела в пространстве.
Пусть задан закон движения твердого тела в простран-
стве, например заданы движение полюса xc(t), yc(t), zc(t)
и законы изменения углов Эйлера ф (t), <р (t), 6 (t) в функции
времени. Задана структура кинематической цепи, с помошью
которой предполагается осуществить это движение.
Требуется определить постоянные и переменные пара-
метры кинематической цепи из условия, что некоторая систе-
ма координат, связанная с выходным звеном цепи, совершает
движение, близкое к заданному.
В этой главе будем рассматривать такие кинематические
цепи, число степеней подвижности которых меньше шести,
т. е. с неполной подвижностью по отношению к твердому
телу. Очевидно, что в этом случае речь может идти лишь
о приближенном осуществлении заданного движения или
о точном осуществлении некоторого числа конечных поло-
жений твердого тела.
Кинематическая цепь ВВС (рис. 3.7). Кинематическая цепь
содержит две вращательные и
и обеспечивает пять степеней
свободы присоединяемому твер-
дому телу, накладывая одно
условие связи на перемещение
точки звена 3.
Получим условие связи для
этой цепи [10]. Введем системы
координат Axiytz19 О^у^,
Вх2У2^29 связанные со звеньями
кинематической цепи следую-
щим образом. Система
О0х0у0г0 — неподвижная. Систе-
ма Oxyz — также неподвиж-
ная, ее ось z направлена по
одну сферическую пары
1
оси пары А, а ось х по линии кратчайшего расстояния
между осями z0 и z±, Система Axiyizt связана со звеном
1, ее ось направлена по оси пары А, а ось Xi по линии
кратчайшего расстояния между осями zt и z2. Система
О^у^ связана со звеном 1, ее ось zt совпадает с осью
пары В, а ось Xi направлена по линии кратчайшего рас-
стояния между осями пар А и В. Система Bx2y2z2 связана
со звеном 2.
Постоянные параметры кинематической цепи показаны
Ъ2 — поворот и смещение
поворот и смещение последую-
на рис. 3.7: р, <pt> ф2, b
последующей системы координат по оси z предыдущей
системы; а, аь h, hi9 h2
щей системы координат по оси х предыдущей.
В подвижной системе OiXiyiZi, связанной со звеном 2,
точка С описывает окружность, ее уравнение имеет вид
(3.5)
Выразим координаты хь yt, Zi через координаты х, у, z,
используя матрицы поворота:
[xj = Ма1Мф1 [х], (3.6)
где [xt] - столбец координат точки С в системе OiX^Zi;
[х] — столбец координат точки С в системе Oxyz; Мар
— матрицы 4-го порядка комплексного поворота соот-
ветственно на углы 0ц и ф! вокруг осей xt и zP
В развернутом виде уравнение (3.6) имеет вид
L0
О
COSOtj
— sin «i
О
О
sin at
cosai
О
COS (pi
—sintpi
0
0
sin <Pi 0
coscpj 0
0 1
0 0
Перемножая матрицы в правой части (3.7), получим:
xt s х cos (pi + у sin ф1 - hi;
Ух — cos ax (—х sin ф1 4- у cos ф1) + sin oti (z — bj;
zi — — sin eq (—xsin фд +ycos9i) + cosai (z — bi).
(3.8)
О
О
О
Подставив (3.8) в (3.5), получим:
(xcoscpi + ysintpi — h^2 + [cosa(—xsincpi + ycostpj +
+ sin a! (z — bt)]2 = h2; (3.9)
sin oti (x sin (pi — у cos (p J + (z — bi) cos cq = b2.
(3.10)
Уравнения (3.9), (3.10) содержат переменный параметр фр
Этот параметр можно исключить следующим образом:
возведя в квадрат (3.9) и сложив с (3.10), получим
х2 + у2 + (z — bi)2 — 2 (х cos (pi + у sin <рх) ht = h2 + b2,
откуда
Возводя в квадрат и складывая (3.10) и (3.11),
одно уравнение связи, не содержащее переменных
ров:
получим
парамет-
У
х
У
2h
sin a-t
Уравнение (3.12) представляет уравнение поверхности
4-го порядка в системе Oxyz и содержит пять постоянных
параметров: bl9 hif ab b2, h2. При Ъ2 = 0 и а = л/2 урав-
нение (3.12) превращается в уравнение тора
(3.13)
Уравнение (3.13) содержит три постоянных параметра: Ьъ
hi, h2. Чтобы перейти к системе координат OQxGyQzo,
произвольно расположенной относительно этой кинемати-
ческой цепи, выразим координаты х, у, z в формуле
(3.12) через координаты х0, уо, zo- Для преобразования
координат используем матричное уравнение
[х] = МаМэ [х0],
(3.14)
где [х0] — столбец координат точки С в системе П0х0Уо^о 5
Ма, — матрицы 4-го порядка комплексного поворота
вокруг осей х и z на углы аир.
63
1
развернутой форме уравнение (3.14) имеет вид
У
cos а
-sin а
О
О
О
sin а
cos а
О
О
О
cos р
-sin Р
О
О
sin Р
cos Р
О
О
Перемножая
получим:
х = х0 cos Р
матрицы в
х0
Уо
правой части уравнения
(3.15)
(3.15),
О
О
Уо sin 0 - h ;
У = (-*о sin Р 4- у0 cos Р) cos а 4- (z0 - b) sin а; (3.16)
z — (х0 sin Р + Уо cos Р) sin а 4- (z0 — b) cos а.
Подставляя (3.16) в уравнение связи (3.12), получаем
одно уравнение связи рассматриваемой цепи, которое содер-
жит девять постоянных параметров: Ь, р, h, a, bi9 hit b2t
h2i аР
Для девяти заданных положений подвижной системы,
связанной со звеном 2, уравнение связи (3.12) с учетом (3.16)
дает систему девяти уравнений с девятью неизвестными, из
которой могут быть найдены постоянные параметры цепи.
Это означает, что произвольная точка подвижного простран-
ства в любом из девяти заданных положений удовлетво-
ряет условиям связей этой кинематической цепи. Обозначим
координаты точки С подвижного пространства х', у', z'. Ее
координаты в неподвижной системе линейно выражаются
через координаты в подвижной и элементы матрицы Mqj,
задающей положение подвижной системы координат:
[х0] = MOj [х] (/ = 1,...,и), (3.17)
где [х0] — столбец координат точки подвижного простран-
ства в системе О0х0у0г0; [х'] — столбец координат этой же
точки в системе O'x'y'z'. Подставляя (3.17) в (3.12), получим
уравнение связи цепи, содержащее 12 постоянных пара-
метров.
Для десяти заданных положений условия связи (3.12)
дают систему десяти уравнений с девятью неизвестными.
Ранг функциональной матрицы этой системы не превышает
девяти, так как только девять уравнений могут быть незави-
симыми. В связи с этим координаты точки С в подвижной
системе должны быть связаны одним уравнением, т. е.
в системе O'x'y'z' в этом случае определена некоторая
поверхность, где может располагаться шарнир С.
Для 11 заданных положений между координатами шар-
нира С (х', У, z') в подвижной системе должно быть два
условия связи, т. е. геометрическое место решений есть не-
которая кривая, аналитические выражения которой дают
условия связи (3.12), записанные для 11 заданных положений.
Для 12 заданных положений получаем 12 уравнений с 12
независимыми параметрами: b, р, h, а, Ьъ h19 ах, b2, h2, х',
У, г'.
Следовательно, максимальное число точных положений
твердого тела, осуществляемых этой кинематической цепью,
не превосходит 12.
В тех случаях, когда число определяющих параметров
невелико, задача упрощается. Рассмотрим частные случаи.
В случае определения пяти постоянных параметров кине-
матической цепи, описываемой уравнением (3.12), это уравне-
ние можно представить в виде
(3.18)
где
Pi =hi;
Л(х, у, z)= —4(x2 + y2);
Рг = (bj -hi- bl)2
4hi
sin2 ax
x (bl + b2 cos2 ax)
Sbrb2hl ctg «i
sin
fit*, y, z) = 1;
Рз = (bi + hl ctg2 at); f3 (x, y, z) - 4z2;
p4 = bi; /4(*, У, z) = —4z(x2 + y2 + z2);
p5 = (b? - hj - bl); /5(x, y, z) = z(x2 + y2 + z2);
Рб = bi (bl - hl- Ы) -
? 2b2bictgoci . z .
-2h?bi ctg2 0Q--------:-------; f6 (x, y, z) = -4z;
sin «1
F (x, y, z) = — (x2 + y2 + z2)2.
Между шестью коэффициентами pt (ii — 1,..., 6) имеет место
одно условие связи. Найдем это условие связи следующим
3 Механика промышл. роботов, кн. 2 65
1
образом: из выражения для р6 найдем
Ьг/sina! = (-р6
р4р5 - 2prp4 ctg2 а1)/(2р1 ctg «О;
(3.19)
из выражения для р3 найдём
ctg2 «! = (р3 - pi)/pt.
(3.20)
Подставляя (3.19) с учетом (3.18) в выражение (3.20), после
преобразований получим условие связи между коэффициен-
тами следующего вида:
я „2 , [?4Р5 ~ Рб ~ Р4 (Рз ~ Р4)]
Р2 = Р5 + --------7----------------
\Рз — Р4-)
~ 4р4 [Р4₽5 ~ Рб ~ 2р4 (р3 — рд)].
+ 4pi(p3 -р4)
(3.21)
Записав уравнение (3.18) для пяти заданных положений и
используя уравнения связи, получим совместную систему
шести уравнений, из которой определим коэффициенты р,
(i — 1,..., 6). Затем найдем и пять постоянных параметров
механизма: hu blt h2, b2, aj.
В случае определения четырех постоянных параметров
кинематической цепи уравнение (3.12) представим в виде
(3.22)
Pi = h2 + b2 + 4Ь2 —
2 Sin2»!
р2 — h2 + b2 ;
Рз — 4А2,
= Л!
— b2 cos «!;
fi (х, у, z) == 1;
/г(х, у, z) = - 2[х2 4- у2 + (zb2)2];
7з(х, у, z)= -(х2 + у2);
f4(xfytz) = 2(z-bi);
р5 4hj ctg2 «!; f5 (х, у, z) = (z - bi)2;
F (x, y, z) = [x2 + y2 + (z - bi)2]2.
Между коэффициентами имеет место уравнение связи
|>4/(Р1 - Р2)]2 = Рз/(Рз + Рз) • (3.23)
Для четырех заданных положений тела в этом случае при-
ходим к системе четырех линейных уравнений вида (3.22).
Используя- эти уравнения и уравнение связи, найдем р4
66
(i = 1,..., 5), а затем и четыре постоянных параметра меха-
низма.
Для определения трех постоянных параметров восполь-
зуемся уравнением (3.13) кинематической цепи частного вида.
Это уравнение можно представить в виде
6
Е Pifi(x, у, z) = F(x, у, z),
i = i
(3.24)
где
Pi = hj;
fi (x, y, z) = x2 + y2;
Pi = (b2 - bl)2;
= (bl - hl);
Ps — bi;
Ре = (b? - hl) bi;
fi (*> y, z) = -1;
/з (*» У> z) = - 4z2;
/4(х, у, z) = -2(x2 + у2 + z2);
fs (x, y, z) = 4z(x2 + y2 + z2);
fe(x,y,z) = 4z;
F(x, y, z) = [x2 +y2 + z2].
Шесть коэффициентов pt (i = 1, ..., 6) связаны между собой
тремя условиями:
Рз = Ps ; Ре = PiPs ; РАг = Рз - Pi • (3.25)
Это значит, что из пяти уравнений вида (3.25) независи-
мыми могут быть только три уравнения, т. е. максимальный
ранг функциональной .матрицы этой системы равен трем.
Следовательно, максимальное число точных положений тела,
осуществляемых цепью вида (3.13), равно трем.
Кинематическая цепь ПВС
(рис. 3.8). Кинематическая цепь
ПВС содержит вращательную
и сферическую пары и обеспе-
чивает присоединяемому твер-
дому телу пять степеней сво-
боды.
Кинематическая цепь накла-
дывает одно условие связи на
движение звена 3,
накладывая
одно ограничение на коорди-
наты точки С. Постоянные
переменные параметры ме-
ханизма, а также системы
координат показаны на рис. 3.8.
Получим это условие связи.
Xi
о,
Рис. 3.8
3*
67
В подвижной системе координат OiXiyiZi, связанной со
звеном 7, траектория движения точки представляет собой
окружность радиуса h2 с уравнением
х2 4- У1 = hj; zY = b2. (3,26)
Выражая координаты х19 у19 ~z1 через координаты х, у, z
по формулам (3.5) и подставляя в (3.26), получим
(х cos 1 4- у sin ij/i — h^2 + [cos oil (—x sin ф1 4- у cos \|/i) +
4- sin a! (z - st)]2 = hl; (3.27)
sin «1 (x sin — у cos фх) + (z — si) cos «i = b2.
Последние два уравнения связаны через переменный пара-
метр si — перемещение в поступательной паре А. Исключим
этот параметр: возведем в квадрат второе уравнение (3.27)
и сложим с первым, после преобразований получим
х2+у2+ (z —Si)2 — z(xcosi|/i — у sin \]/i) 4- h2 = hl 4- bl.
(3.28)
Из уравнений (3.27) найдем
_ — sin «i (х sin — у cos ф1 — b2)
Z ~ Sj — ~— — "
cos at
Подставляя последнее выражение в (3.28), получим одно
уравнение связи, не содержащее переменных параметров:
х2 (1 4- tg2 eq sin2 ф) 4- у2 (1 4* tg2 at cos2 фх) —
2xy tg2 eq sin ф cos ф
2x I hi cos ф1
cos «1
cos eq
cos «1
(3.29)
Последнее уравнение представляет собой уравнение ци-
линдра с образующей, параллельной оси z, заданного в
системе xyz. Уравнение (3.29) можно представить в виде
Р1Х2 4- P2J2 + Рзху + PtX 4- р5У + р6 = 0, (3.30)
где
Pi = 1 4- tg2a/sin^i; р2 = 1 4- tg2ax совфд;
68
р4 = —2 hi cos фх
cos otx
cos «1
cos2 a!
Чтобы получить уравнение этого цилиндра в произволь-
ной системе xoyozo, надо в уравнении (3.29) координаты х,
у, z заменить на xoyozo по формулам (3.16).
Рассмотрим вопрос о построении данной кинематической
цепи по заданному движению твердого тела в простран-
стве. Движение твердого тела будем задавать серией конеч-
ных положений в моменты времени ti (i = 1,..., п). За вы-
ходное звено примем звено 3. Рассмотрим вначале задачу
построения цепи частного вида, у которой ось поступа-
тельной пары А совпадает с осью z. В этом случае условие
связи имеет вид (3.29). Представим это уравнение в виде
6
£ Pifi (х, У, z) = F (х, У> z) > (331)
1=1
где
Pi — 1 + tg2 at sin2 фх;
p2 — 1 + tg2 «1 cos фх;
fl (x, y, z) = x2;
ft (x, y, z) = y2 ;
Рз = hi cos фх
^2
cos oh
tg «x.COS фх
/з(х, у, г)= —2y;
p4 = hi sin фх
cos «x
tg CLi COS фх
p5 — tg2 ax sin фх cos фх;
fs = -2xy;
Рб
cos ax
(h2 + b2 — hi);
F (x, y, z)
Уравнение связи (3.31) содержит пять постоянных пара-
метров: ах, Фх, b2, h2i hi и шесть коэффициентов pf- Между
коэффициентами имеет место одно условие связи вида
pl =(Pi ~ 1)(Pi - О-
(3.32)
1
Для определения постоянных параметров цепи исполь-
зуем условие, что при движении твердого тела координаты
некоторой точки должны приближенно удовлетворять усло-
вию связи кинематической цепи ПВС на некотором интер-
вале времени или удовлетворять точно в некоторых поло-
жениях.
*
Для пяти заданных положений уравнение (3.30) приво-
(ится к системе пяти линейных уравнений с шестью не-
известными коэффициентами р{ (i = 1,..., 6), между которы-
ми имеет место еще условие связи (3.32). Таким образом,
в этом случае получаем систему шести уравнений с шестью
неизвестными. Решая эту систему уравнений, приходим к
Квадратному уравнению относительно р5, которое в общем
случае дает два значения коэффициента р5 и два множества
коэффициентов pg (i « 1,..., 6), удовлетворяющих условию
связи (3.30). При известных значениях коэффициентов р,
постоянные параметры кинематической цепи определяются
следующим образом: из выражения для и р2 имеем:
Pi 4- р2 = 2 4- tg2 осх; oq = arctg ± j/2 - (pt - p2);
*82 Ф1 = (Pi - l)/(Pi ~ 1); Ф1 = arctg ± ]/(p2 - l)/(pi - 1);
из выражений для p3 и p4 получим:
Рз sin ф1 — р4 cos i|/i =
—— tgotj;
COS
(3.33)
Рз COS \|/j + p4 sin ф! == ,
откуда
b
2
(—Рз sin + p4 cos ij/j) cos di/tg cq ;
hi = рз cos ф! 4- p4 sin i|/i;
= у bl/cos^i - b2 + hl - p6.
й2
(334)
Это означает, что пять положений твердого тела могут
быть осуществлены восемью кинематическими цепями вида
ПВС, различающимися значениями постоянных параметров^
Рассмотрим теперь построение кинематической цепи
общего вида, описываемой уравнением (3.29) с учетом (3.23),
по заданному движению твердого тела в пространстве.
Подставляя (3.16) в (3.29), после преобразований получим
Уравнение связи (индексы «0» при этом опущены)
AiX2 + А2у2 + Л322 4- А4ху 4- A5xz + A6yz
Л7х 4* Л8у 4- A9z 4- Л10 = 0,
(3.35)
70
p2 cos2 a sin2 р
p3 sin2 p cos a;
Л2 — Pi sin p + p2 cos2 P cos2 a — p3 sin p cos a;
Л3 — pi sin2 a;
+ p3 sin2 p cos a
Л4 = pi cos р sin р — р2 sin р cos р cos2 а
- рз cos2 р cos а;
Л6 = р3 sin р sin а
р2 sin а cos а cos р;
— 2(hpicosp + biPisinacosasin р+
p3h cos a sin р — p3b cos p sin a — p4 cos p
p2b2 sin2 a — 2p3hb sin a — 2p4h
6) определяются по форму-
Л8 = —2 (pih sin p — p2b sin a cos a cos p — p3h cos a cos P
+ p3b sin p sin a — p4 sin p — ps cos a cos p);
A9 — 2 (p3h sin a + ps sin a);
Л10 ~ Pih
+ 2psb sin a
Коэффициенты pt (i = 1
лам (3.30). Координаты шарнира С, входящие в условие связи
(3.35), выражаются линейно через координаты этого же
шарнира в системе O'x'y'z' и элементы матрицы по
формулам (3.17).
Условие связи (3.35) не содержит промежуточных пере-
менных параметров и является основой для синтеза рас-
сматриваемой кинематической цепи по заданному движению
выходного звена 3 в пространстве методом интерполиро-
вания, квадратического приближения или оптимизационным.
Следует отметить, что из десяти коэффициентов At
(i = 1, ..., 10) независимыми являются только восемь. Дей-
ствительно, первые шесть коэффициентов At содержат лишь
четыре параметра и поэтому связаны двумя условиями.
Это означает, что при произвольном выборе положения
шарнира С в подвижной системе число воспроизводимых
положений объекта не превосходит восьми. С учетом зави-
симостей (3.17) максимальное число точных положений
твердого тела, осуществляемых данной цепью, не превосхо-
дит И, так как лишь не более 11 коэффициентов в урав-
нении связи могут быть независимыми.
Кинематическая цепь ВПС (рис. 3.9). Кинематическая
цепь ВПС содержит вращательную, поступательную и сфе-
рическую пары и обеспечивает пять степеней свободы при-
71
I
I
f
I
г
1
I
1
1
Рис.
В системе
Oxyz
эти
соединяемому твердому телу.
Кинематическая цепь наклады-
вает одно условие связи
движение звена 3. Получим это
условие связи. Со звеньями
нематической цепи свяжем
стемы координат, как показано
на
ки-
си-
R — постоянные
пара-
_ системе координат
О1Х1У151 точка С движется по
некоторой прямой. Ее уравне-
ние можно представить в виде
пересечения двух плоскостей
Xi = R sin 6; ji = R cos 5, (3.36)
где 6,
метры,
уравнения получают вид
R cos 5;
(—х sin (pi + у cos (pi) cos cci + (z — bi) sin = R sin
где bi, oti — постоянные параметры.
В эти два уравнения входит переменный параметр <р1э
исключая который, получим одно уравнение связи между
постоянными параметрами цепи и координатами точки С
подвижного пространства. Возводя в квадрат и складывая
уравнения (3.37) и (3.38), получим условие связи в виде
R sin 5 — (z — bi) sin ai
(3.37)
(3.38)
у2 = (R cos 5
COS OCj
. (3.39)
В уравнение (3.39) входят пять постоянных параметров: R,
5, Ьь аъ bi.
Уравнение (3.39) можно представить в виде
Ро + Pi (х2 + у2) + p2z2 + p2z =
где p0 = R2sin26 + (RcosS + bi)2
cos2 oil + b2sin2ai
(3.40)
2RsinS^i х
2R sin 5 sin a.
где ро =
х sin a; pi = cos2 at; р2 = sin2 at; p3 —
Рассмотрим построение данной цепи по заданным поло-
жениям подвижной системы О'
нения связи (3.39). Это означает, что мы предполагаем зара-
нее, что цепь расположена относительно неподвижной
системы координат так, что ось z проходит через ось
вращательной пары А. Развернем выражение (3.39) и после
преобразования получим
x'y'z' с использованием урав-
1
(х2 + у2) cos2 «1 = (R cos 5 + hi)2 cos2 oci + R2 sin2 5
+ b2 sin2 an + z(—2bi sin ax + 2R sin 5 sin a£).
Z* sin2 ax+
(3.41)
Последнее выражение можно представить в виде
*
3
Е Pifi (*> y,z) = F (х, у, z) > (3.42)
J= 1
(KcosS + ^i^cos2»! + K2sin25 + b2sin2a1 +2Kfe1sin5sina1
Pi =
sin2 ai
2bj + 2R sin 5
cos2 at ’
Ji(x, y,z) = 1;
p3 = tg2 at;
/2 (*> У, z)
F(x, y9.z) = x2 + y2;
/3 (x, y, z) = z2.
Для трех данных положений получаем линейную систему
трех уравнений относительно трех постоянных коэффициен-
тов. Определяя коэффициенты из решений этой системы,
далее приходим к системе трех нелинейных уравнении с
пятью неизвестными параметрами. Очевидно, что двумя из
них можно задаваться произвольно. Важно отметить, что
для четырех положений не получаем решения относительно
коэффициентов р, (i = 1, ..., 4), так как ранг матрицы
системы все равно равен трем. Это означает, что синтез
для четырех положений при данном расположении цепи
невозможен, несмотря на наличие пяти параметров в
уравнении связи.
Для того чтобы построить кинематическую цепь для
осуществления большего числа заданных положений, нужно
использовать общий случай ее расположения относительно
неподвижной системы координат. В этом случае в уравнение
связи (3.39) будет входить большее число постоянных пара-
метров. Заменим координаты х, у, z, входящие в уравнение
связи (3.39), через координаты х0^ Уо> zo по формулам,
аналогичным (3.16). После преобразований представим это
выражение в виде
AiX2 + А2у2 + A3z2 + Лдху + Asxz + A6yz + Л7х
А3у + AgZ + Лю — 0,
где коэффициенты (i
стоянные параметры
образом:
(3.43)
= 1, ..., 10) выражаются через по-
кинематической цепи следующим
Ai = />! (cos2 P + sin2 p cos2 a) + p2 sin2 P sin2 or;
42 = Pi (sin2 p + cos2 P cos2 a) 4- p2 cos2 P sin2 a;
A3 — Pi sin2 a + p2 cos2 a;
A4 — —(pi + pi cos a — p2) sin 2P;
(3.44)
A$ — (—Pi sin j sin 2a + p2 sin p sin 2a);
A6 — (Pi — P2) cos p sin 2a;
A7 = —2/i cos Ppx
b sin p sin 2api —
—bp2 sin p sin 2a + p3 sin p sin a;
+ bp2 cos p sin 2a — p3 cos p sin a;
A9 — —2b (pi sin2 a + p2 cos2 a) + p3 cos a;
410 = p0 4- h2pi + b2pi sin2 a + b2p2 cos2 a — bp3 cos a;
p0 = R2 sin2 6 + (R cos 5 + hi)2 cos2 ax
b2 sin2 aj + 2Rbx sin 5 sin a,
определяющих
А
А
V
4
p; это означает, что между ними имеет место
х, у, z линейно выражаются через
где pi (i = О, 1, 2, 3) определяются формулами (3.40).
Полученное условие связи содержит девять постоянных
не содержит переменных параметров
относительные положения звеньев кинематической цепи,
является основой для ее синтеза известными методами
приближения функций.
Следует отметить, что условие связи (3.44) содержит де-
сять коэффициентов, из которых независимыми являются
лишь семь. Действительно, первые шесть коэффициентов 4,
(i ~ 1, ..., 6) содержат лишь три постоянных параметра
е
менее трех условий связи. Входящие в условие связи коор-
динаты шарнира С
координаты этого же шарнира в подвижной системе O'x'y'z'
и элементы матриц M0J. В этом случае условие связи будет
содержать уже 12 постоянных параметров: Ь, р, й, a, bi9 hi,
аь 5, R, х'с> у'с, z'c> однако число независимых коэффициентов
не будет превышать десяти и поэтому число точных поло-
жений твердого тела, осуществляемого этой цепью, не
превышает десяти.
Кинематическая цепь ППС (рис. Э.10). Кинематическая
цепь ППС содержит две последовательно расположенные
поступательные и одну сферическую пары и обеспечивает
пять степеней свободы присоединяемому твердому телу,
накладывая на его движение одно условие связи.
Получим условие связи
для этой цепи. Как и выше,
используем системы коорди-
нат, связанные со звеньями;
х расположение показано
на рис. 3.10.
Уравнение траектории
движения точки С в системе
OiXiyiZi имеет вид
Xi = r2cos^2;
У1 = г2 sin ф2.
Выразим координаты
через координаты хь
подставим в (3.45),
(3.45)
У1
Уь zi
полу-
чим:
х2 cos фх + yi sin = г2 cos ф2;
cos cq (—Xi sin фх + yi cos ф i) + sin at (zx — Si) =
(3.46)
= r2 sin ф1,
где «i — поступательное перемещение в паре А.
Второе уравнение системы (3.46) содержит переменный
параметр Si и может быть удовлетворено при произволь-
ных значениях постоянных параметров, поэтому лишь пер-
вое уравнение является условием связи.
Заменим входящие в него координаты xt, yr, zx через
координаты х, у, z, получим
(х cos р + у sin р — h) cos ф1 + sin ф1 [cos a (—х sin Р
— r2 cos\p2 — 0.
I t
4
Это уравнение связи можно использовать для синтеза
кинематической цепи.
3.3. Синтез трехзвенных незамкнутых
кинематических цепей с цилиндрической
порой но выходном эвене
Рассмотрим задачи построения кинематических цепей обще-
го вида с цилиндрическими парами по заданному движению
твердого тела в пространстве.
Движение твердого тела будем, как и выше, задавать
серией его конечных и бесконечно близких положений в не-
которые моменты времени ti9 определяемых матрицей Мц
1
и ее производными по времени. Одно из конечных звеньев
незамкнутой кинематической цепи будем считать связанным
с неподвижным звеном. Второе конечное звено будем счи-
тать выходным или рабочим.
Задача построения кинематической цепи состоит в опре-
делении ее постоянных параметров, таких, что движение
выходного звена мало отличается от заданного движения
твердого тела.
Кинематическая цепь ВВЦ (рис. 3.11). Кинематическая
цепь ВВЦ содержит две вращательные и одну цилиндри-
ческую кинематические пары и обеспечивает присоединя-
емому телу четыре степени свободы.
: Кинематическая цепь определяется следующими постоян-
ными параметрами: Ь, р, A, a, bb hlt ах, b2, а2, h2i где
b, bi, Ь2 — смещение звеньев соответственно по осям z, Zj, z2;
h, hu h2 — кратчайшие расстояния между осями соединенных
кинематических пар; р — угол поворота системы относитель-
но оси z; а, аь а2 — углы поворота систем относительно
осей х, Xi, х2. Углы <рь <р2 — переменные параметры.
Эта кинематическая цепь накладывает два условия связи
на движение некоторой прямой звена 3 — оси цилиндриче-
ской пары, которые определяют двухпараметрические се-
мейства прямых — нелинейную линейчатую конгруэнцию.
Составим уравнения этой конгруэнции. Для этого со
звеньями механизма свяжем системы координат, как пока-
зано на рис. 3.11. Уравнения оси цилиндрической пары в
системе Bx2y2z2, связанной со звеном 2, имеют вид
х2 = h2; у2 = — t sin ct2; z2 = г cos a2, (3.47)
где x2, y2, z2 — координаты
точки, принадлежащей оси
< пары в системе Bx2y2z2.
Л Чтобы получить уравне-
Уу ние прямой в неподвижной
системе координат Oxyz, сле-
дует в уравнениях (3.47) ко-
ординаты х2, у2, z2 заменить
на координаты х, у, z. Вос-
пользуемся для этого мат-
ричным уравнением преобра-
зования координат
[х] = [х2],
(3.48)
где [х] — столбец координат
76
точки звена 3 в системе Oxyz; Мр, Мл, Мф1, Л/ф2 —
матрицы 4-го порядка, определяющие взаимное располо-
жение систем координат, связанных со звеньями; [х2] —
столбец координат точки звена 3 в системе Bx2y2z2.
Умножая матричное уравнение (3.48) последовательно
слева на обратные матрицы Мр1, М~\
получим
и = м-^м-„1м
-;м; 1 [х].
(3.49)
Перемножая матрицы в правой части (3.49), получим
выражения координат [х2] через координаты [х]. Исклю-
чая переменный параметр t и сделав замену координат
х2, J2, z2 на координаты х1? yi, zlf получим первые
два уравнения конгруэнции:
Xi (cos <Pi cos cp2 4- sin <pi cos oti sin (p2) + yx (sin <px cos ф2 —
— cos cpi cos «t sin <p2) — Zi sin «i sin ф2 — hi cos ф2
4- bi sin «i — h2 — 0;
Xi (—cos ф1 sin ф2 — sin Ф1 cos ф2 cos at 4- tg a2 sin «i sin Ф1) 4-
4- yi (—sin Ф1 sin ф2 + cos ф1 cos ai cos ф2 — tg a2 sin at cos фх) 4-
4- Zi (sin »i cos ф2 4- tg a2 cps ax) 4- hi sin ф2 — sin otj cos ф2—
— tg a2 (bi cos ai 4- b2),
где Xi, yi, Zi — координаты точки прямой в
ЛХ1У121.
Координаты Xi, у19 zr выражаются, в свою
через координаты этой же точки в неподвижной
Oxyz следующим образом:
Xi = х cos р — у sin р — h;
У1 = х cos a sin р — у cos a cos p 4- (z — b) sin a;
Zi — x sin a sin P — у sin a cos p 4- (z — b) cos a.
(3.50)
системе
очередь,
системе
(3.51)
Получим следующие два уравнения конгруэнции — усло-
вие связи для угловых параметров оси цилиндрической
пары С.
Направляющие косинусы оси пары С можно записать
в виде
^ai^<p2
(3.52)
где [/] = [/, т, и]т; [/2] = [/2, ш2, и2]т (/2, т2, п2 - на-
правляющие косинусы оси пары С в системе Bx2y2z2); Lp, ...
..., Ьф2 — матрицы поворота 3-го порядка соответственно
на углы р, ф2:
77
cosp —sinp 0~| Г1 0 0
sinp cosp 0 I; La=| 0 cos a —sin a
_ 0 0 11 L.0 sin a cos a
0
COSOtj
sin
0
—sin «j
cos оц
(3.53)
Подставив выражения матриц (3.53) в (3.52), получим
уравнения связи. Следует, однако, заметить, что перемноже-
ние матриц в правой части (3.52) весьма громоздко. По-
этому умножим последовательно левую и правую части
уравнения (3.52) на обратные матрицы JL^1, АГ1,
получим
Ах,Ар2 [А
(3.54)
Входящие в выражение (3.54) матрицы АГ1» АГ1, Ьр 1
получаются соответственно из матриц Le, Lp путем транс-
понирования. Подставив в (3.53) значения этих матриц, по-
лучим уравнения связи для угловых параметров:
/ (cos <рх cos р — sin срi cos a sin Р) 4- т (cos срх sin Р 4-
4- sin фх cos a cos р) 4- п sin фх sin a — — sin ф2 cos a2;
— (sin фх cos p 4- cos фх cos a sin p) 4- m (sin фх sin p
4- cos фх cos a cos p) 4- n cos фх sin a =
— cos cos ф2 cos a2 — sin at sin a2;
/sin a sin p — m sin a cos p 4- n cos a =
= sin at cos ф2 cos a2 4- cos ax sin a2.
(3.55)
Из последних трех уравнений для направляющих косинусов
лишь два являются независимыми и могут быть использо-
ваны для синтеза.
Уравнения (3.50) и (3.55) представляют собой условия
связей, накладываемых кинематической цепью на положение
прямой линии
независимых уравнения содержат два переменных параметра
оси цилиндрической пары С. Эти четыре
78
1
они эквивалентны лишь двум
<Pi и <р2, следовательно
условиям между четырьмя независимыми параметрами
прямой, т. е. определяют нелинейную конгруэнцию прямых.
Положение прямой (оси цилиндрической пары) в по-
движной системе O'x'y'z' будем определять четырьмя па-
раметрами: координатами а', Ь' точки пересечения прямой
с плоскостью О'х'у' и двумя направляющими косинусами
Г, т' (ri).
Так как положение твердого тела в пространстве задано*
то для каждого положения j можно считать заданными
матрицы М оj и Lqj, определяющие положение и ориентацию
подвижной системы O'x'y'z' относительно неподвижной Oxyz.
Это позволяет выразить координаты х, у, z через а', Ь',
а направляющие косинусы а', Ь' через Г, т’(п') следующим
образом:
£хJ — MGJ [х ];
Loi И •
(3.56)
Формулы (3.56) позволяют линейно выразить величины х,
у, z через a', b', а I, т, п через Г, т', п':
х •= ссцД' + ос12Ь' + а0 ;
у = а21а' + а22Ь' + Ьо;
z = а31а' + и32Ь' + с0;
I = аХ1Г + аХ2т' + ахзи';
m = а21Г + а22ги' + а23м';
и = а31Г + а32т' 4- а33и'.
h2, а2, а',
С учетом (3.56) уравнения (3.50) и (3.55) дают условия
связи между 14 постоянными параметрами цепи: Ь, 0, й, а,
и элементами
матриц, определяющих заданные положения тела в про-
странстве.
Решение задачи синтеза в общем случае сводится к ре-
шению нелинейной системы уравнений (3.50), (3.55) [с учетом
(3.56)], записанной для п заданных положений твердого тела.
Это решение может быть получено известными методами
оптимизационного синтеза. При этом наряду с постоянными
параметрами приходится одновременно определять и 2п зна-
чений углов <plf, <p2i 0 = 1» ...» и) в заданных положениях
тела.
В случае синтеза по точным положениям для семи за-
данных точных положений тела получаем систему 28 неза-
висимых уравнений, из которой можно определить 14 по-
стоянных параметров кинематической цепи и 14 значений
1
переменных углов <рп и ф2/. Максимально возможное число
точно воспроизводимых положений твердого тела данной
цепью не может превосходить семи, так как при большем
числе заданных положений тела число уравнений превышает
число неизвестных.
В частных случаях, когда определяется неполное число
параметров, задача упрощается. Например, если задаться
угловыми параметрами кинематической цепи: р, ос, aj, a2,
Г, т\ входящими в уравнение связи угловых параметров (3.55),
то из этих уравнений можно определить значения углов
в заданных положениях. После этого постоянные линей-
ные параметры можно определить из уравнений связи (3.50);
¥
считая углы дь и <р2 в заданных положениях известными.
В этом случае получаем следующую систему линейных
уравнений:
(3.57)
1
X f ijPi ~ Fj >
(3.58)
где
Рз = К;
Pt = bi;
Р5 = ^2 »
= U \
Pi = b';
к6 — а';
k"j ~~ b ,
fij — f и(фи» <P2j) »
9iJ = ffij (ф1> Ф2>) »
^ = ^(Ф1> Ф2>);
Rj = Rj(q>ij, фгу).
Из этой системы линейных уравнений для четырех задан-
ных положений твердого тела можно найти восемь линей-
ных параметров.
Кинематическая цепь ВЦЦ (рис. 3.12). Эта кинематиче-
ская цепь содержит вращательную и две цилиндрические
пары и доставляет выходному звену 3 пять степеней
свободы.
Кинематическая схема цепи определяется 13 независи-
мыми параметрами: Ь, р, h, cl, bi9 hi, ab h2, a2, a', b', I', m'.
Условия связи, накладываемые этой кинематической цепью
на движение выходного звена 3, можно получить из
80
1
условий связей цепи ВВЦ,
заменяя постоянный пара-
метр Ь2 на переменный s2.
Второе уравнение системы
(3.50), которое будет теперь
содержать переменный пара-
метр s2> может быть удов-
летворено при любых зна-
чениях других параметров и
может быть отброшено. Сле-
довательно, три уравнения
связи, полученные из (3.50)
и (3.54), будут содержать два
переменных параметра <рх,
условию связи между пара-
ф2, что эквивалентно одному
метрами прямой — оси цилиндрической
пары.
Таким образом, все прямые подвижной системы коор-
динат O'x'y'z', удовлетворяющие этому условию связи,
должны принадлежать линейчатому комплексу. Решение за-
дачи, синтеза в общем случае сводится к решению системы
Зп уравнений, образованной из условий связи вида:
х (cos <р! cos ф2 4- sin фх cos sin ф2) 4- у2 (sin фх cos ф2 —
— cos ф! cos sin ф2) — zt sin ocx sin ф2 — hi cos ф2 4-
bi sin oti — h2 — 0;
I (cos фх cos p 4- sin фх cos a sin P) 4- m (cos фх sin p 4-
+ sin фх cos a cos P) 4- n sin фх sin a = — sin ф2 cos a2 ;
— I (sin фх cos p + cos фх cos a sin P) + m (sin фх sin p 4-
+ cos фх cos a cos p) 4- n cos фх sin a —
= cos ax cos ф2 cos a2 — sin sin a2.
(3.59)
(3.60)
Максимальное число точно воспроизводимых этой цепью
конечных положений твердого тела равно 13, так как в этом
случае получаем систему 3-13 = 39 независимых уравнений,
из которых можно определить 13 постоянных параметров
цепи и 26 значений переменных параметров ф1Ь фгг
(i = l, 2,..., 13).
В частных случаях задача упрощается. Например, если
задаться угловыми параметрами р, a, аь а2, Г, т', то из
уравнений связи для угловых параметров можно найти зна-
чения переменных углов ф1ь ф21- (i = 1, ..., и), соответствую-
щих заданным положениям системы O'x'y'z'.
1
При известных углах Ф1,-,. Фа» второе условие связи
[уравнение (3.60)] можно удовлетворить всегда за счет пере-
менного параметра s2. Таким образом, для обеспечения
заданных положений системы O'x'y'z' достаточно удовлетво-
рить в п заданных положениях первое условие
[уравнение (3.60)].
Для семи заданных положений задача сводится к реше-
нию системы семи линейных уравнений относительно семи
линейных параметров — h, b2, h2, hi9 a', bf: *
f
^fijPi ~ Fj О’ ~ U • • •» 7),
где
Pi = h; fij — cos фи cos ф2, + sin ф17- cos oti sin ф2,;
о
p2 = b\ f2j — sin a (sin ф1л- cos ф2, — cos ф1?- cos cq sin ip2j)
+ cos a sin at sin ф2; ;
Рз = ; f3j = sin «! sin <p2j; /4/ = cos ф2>; fSj = 1;
p4 = hi; = AjOiVA + + 6?i
Ps = h2\ fjj = Afi$2 + Bf^2 + Cj<x^3;
Рб = b';
P7 = «'; Fj = Ajdoj + BjbOj + CjCqj.
Кинематическая цепь ВПЦ. Рассмотрим вопрос о по-
строении кинематической цепи ВПЦ, содержащей враща-
тельную, поступательную и цилиндрическую пары, по задан-
ным движениям тела в пространстве. Кинематическая цепь
определяется постоянными параметрами: b, Р, h, a, bt, h19
«ь Фг, h2, a2, a’, b't I', m', (n').
Для синтеза используем полученную выше систему
уравнений (3.50) и (3.54), в которой параметр ф2 следует
считать постоянным, а Ь2 — переменным. Эта система четы-
рех независимых уравнений в данном случае содержит два
переменных параметра фь Ь2. В общем случае синтеза
цепи задача сводится к решению системы нелинейных
уравнений. Решение может быть выполнено известными
методами.’
Для семи заданных положений твердого тела уравнения
связи дают систему 3*7 = 21 уравнений, из которых можно
определить 14 постоянных параметров и 7 значений пере-
менных параметров фп (i = 1
7) в заданных положениях.
При большем числе заданных положений число неизвест-
ных будет меньше, чем число уравнений. Число угловых
1
параметров равно семи: р, а, ф2> аь а2, Г, т' и не меньше,
чем максимальное число положений. Следовательно, макси-
мальное число точных положении твердого тела, осуществ-
ляемых этой цепью, равно семи.
Последнее условие необходимо проверять, потому что
заданная ориентация тела в заданных положениях может
быть осуществлена лишь за счет угловых параметров
кинематической цепи, но не линейных.
Уравнения (3.54) для направляющих косинусов содержат
теперь уже один переменный параметр ф] и не зависят от
линейных постоянных параметров цепи и от линейного
переменного параметра Ь2-
Следовательно, эти уравнения можно отдельно использо-
вать для определения угловых параметров цепи. Из трех
уравнений связи для направляющих косинусов независи-
мыми являются лишь два. Особенностью системы уравне-
ний связи для направляющих косинусов является то, что
переменный угол ф1 входит лишь в два уравнения. Первое
уравнение может быть всегда удовлетворено за счет вхо-
дящего в него угла фР Если параметры выбрать так, чтобы
удовлетворялось третье уравнение, не содержащее фь то
второе уравнение будет также удовлетворяться.
Таким образом, для выбора угловых параметров кине-
матической цепи можно использовать лишь одно третье
уравнение системы (3.50), не содержащее переменных пара-
метров, или условие связи, полученное исключением угла
ф| из первых двух уравнений.
Раздел
bidJ
Построение
двигательных
систем роботов
Глава 4*
Планетарные механизмы
промышленных роботов
Важной конструктивной характеристикой манипуляторов
является способ расположения двигателей относительно
приводимых ими в движение звеньев. От выбранного
варианта компоновки во многом зависят технические
характеристики роботов, их быстродействие, управляемость
и возможные области применения.
Существуют три типа расположения приводов: непосред-
ственно в шарнирах механизма, на основании и комбини-
рованное на подвижных и неподвижных звеньях.
Создаются также конструкции и механизмы, в которых
все движения манипулятора осуществляются от одного
двигателя через муфты переключения.
Наиболее распространенным является тип исполнитель-
ного механизма с комбинированным расположением двига-
телей. При комбинированном расположении двигателей
часть двигателей расположена на основании, а часть на
подвижных звеньях, причем, как правило, на звеньях с
меньшим числом степеней свободы по сравнению со
звеньями, к которым передается движение.
Например, у промышленного робота Unimate-2600 фир-
мы Kawasaki (Япония) двигатели переносного и трех
* Глава написана совместно с Н. И. Гданским.
1
звеньям.
ориентирующих движении установлены на втором подвижном
звене, считая от неподвижного.
Расположение двигателей на подвижных звеньях (в
шарнирах) механизма является наиболее простым с точки
зрения передачи движения от двигателей
Протяженность кинематической цепи от двигателя к при-
водному звену в этом случае минимальна, что позволяет
уменьшить кинематические ошибки передачи движения. В то
же время такое расположение приводов значительно
увеличивает габариты и массу подвижных звеньев, что
приводит к уменьшению доли полезного груза. Этот
недостаток частично может быть устранен путем разработки
новых конструкций силовых электроприводов с уменьшен-
ной массой.
На некоторых производствах расположение приводов на
подвижных звеньях, так же как и комбинированное, не-
желательно с точки зрения технологии. В таких случаях
все двигатели необходимо выносить на основание.
Компоновка приводов на основании позволяет умень-
шить массу подвижных звеньев, но в то же время
требует применения многозвенных передаточных кине-
матических цепей. Это приводит к увеличению ошибок
передачи движения от двигателей: при передаче движения
через промежуточные подвижные звенья возникает так назы-
ваемый эффект кинематического взаимовлияния приводов,
который необходимо устранять путем введения особого
дифференциального привода, осуществляющего развязку
движений; в многозвенных кинематических цепях возникают
люфты, требующие специальных мер по их выборке.
При размещении приводов на основании, так же как и в
комбинированных схемах, передача движения через про-
межуточные звенья и кинематические пары может осу-
ществляться роликоленточным или зубчато-рычажным диф-
ференциальным механизмом, состоящим как из цилиндри-
ческих, так и из конических колес. Например, у манипу-
лятора с шестью степенями свободы (рис. 4.1) звенья
1—6 (основной механизм) приводятся в движение тросами
1—12 (передаточный механизм) от шести приводов. Переда-
ча движения осуществляется с помощью гибких звеньев —
проволочных тросов или стальных лент. Каждый трос
одним концом соединен с приводом, а другим — с ро-
ликом, жестко скрепленным с ведомым звеном. Транзит-
ная передача движения через промежуточные шарниры
происходит по свободно вращающимся роликам, усга нет-
ленным на одной оси с приводными.
I
г
I
I
4
f
4
I
r
!
I
1
85
1
Структура и кинематические свойства плоских дифферен-
циальных механизмов с цилиндрическими колесами рас-
смотрены в [1, 14].
Рассмотрим манипулятор с четырьмя степенями свободы,
в котором для передачи движения от приводо]
к звеньям
основного механизма используются цилиндрические колеса.
Основной механизм (рис. 4.2) состоит из звеньев 1—4.
звено этой кинематической цепи
Каждое последующее
является сателлитом по отношению к предыдущему. Таким
образом, звенья 2, 3, 4 будут соответственно сателлитами
2-го, 2-го и 3-го порядков. Для передачи движения от
приводов, расположенных на основании, к звеньям 2, 3, 4
используются цилиндрические колеса, помещаемые на те же
оси, что и основные звенья. Для передачи движения звену 2
достаточно
передается колесами З1 и З2
одного колеса
4
86
4
Шарнир 1
Рис. 4.2
Шарнир k
Шарнир
Шарнир I
со
от
и
Полученный механизм отличается от обычного диф-
ференциального тем, что у него отсутствуют колесо с
внутреннем зацеплением и цепь, соединяющая его
стойкой (на рис. 4.2 показаны штриховыми линиями). Их
можно выбросить по той причине, что движение
привода передается сателлиту 4, а колеса 5, 52
являются ведомыми и на кинематику основного механизма
не оказывают никакого влияния.
В манипуляторах с более высокой подвижностью обра-
зование основного и передаточного механизмов происходит
аналогично. При п степенях свободы выходное звено будет
сателлитом (и — 1)-го порядка.
Передача движения от приводов к звеньям основного
механизма в большинстве серийно выпускаемых роботов осу-
ществляется с помощью трубчатых валов, на концах
которых жестко закреплены конические колеса. Эти колеса
входят в состав трехзвенных дифференциальных механиз-
мов (ТДМ), которые являются составляющими элементами
кинематических цепей, передающих движение от приводов к
основным звеньям [31].
На рис. 4.3 приведена кинематическая схема манипуля-
тора МЭМ-10 с шестью степенями свободы. Манипулятор
установлен на стойке и содержит шесть основных звеньев
1—6. Внутри них движение передается с помощью ТДМ.
5-6 об-
Соединения звеньев 0-1,
разуют шарнйры 7, 77, 777, 7 К, V, VI основного меха-
низма.
87
1
Рис. 4.3
Роликоленточные меха-
низмы и механизмы с кони-
ческими колесами позволяют
передавать движение между
осями, скрещивающимися
под любыми углами. Поэто-
му они могут реализовать
все шесть независимых пе-
ремещений в трехмерном
пространстве.
Механизмы с цилиндри-
ческими колесами могут
обеспечить только плоское
движение выходного звена.
При этом оно будет переме-
щаться не более чем по трем
независимым плоским коор-
динатам. Для устранения
этого недостатка в механиз-
мах с цилиндрическими ко-
лесами применяют дополни-
тельные ориентирующие го-
ловки, позволяющие реа-
лизовать недостающие сте-
пени свободы.
Анализ кинематических
схем исполнительных орга-
нов роботов с вынесенными
на основание приводами по-
казывает, что результатом
соединения основных и пере-
даточных механизмов явля-
ются структуры с довольно
сложным строением. Данная
глава посвящена исследова-
нию свойств этих структур.
4.1. Кинематика исполнительных
механизмов
Рассмотрим манипулятор произвольной структуры, основной
п
механизм которого состоит из
звеньев,
приводимых
в движение п приводами, расположенными на основании.
Выходные валы двигателей являются ведущими звеньями.
98
1
Рис. 4.4
Их углы поворота обозначим <pt, ф2,..., Ф«, а относительные
углы поворота звеньев основного механизма* — qi9 q2->-”>4n
(рис. 4.4). Из-за взаимного влияния приводов углы отно-
сительного поворота звеньев qt в общем случае являются
функциями не одной, а нескольких обобщенных координат
Фу, т. е.
& = &(фь ф2?• • • >фи) (i =
Рассмотрим перемещение звеньев механизма в течение
малого промежутка времени At. Приращения углов поворота
ведущих валов Аф7- за этот промежуток обозначим Афь
Аф2,...,Афи. Приращения углов qt обозначим через
Ддь Ад2,..., А</„. Новое положение звеньев основного
механизма показано на рис. 4.4 штриховыми линиями.
Пренебрегая производными 2-го и выше порядков по
Аф?-, связь приращений А^ с Аф^- можно представить в виде
* В дальнейшем для краткости вместо терминов «звенья
основного механизма» и «звенья передаточного механизма»
используются термины «основные звенья» и «передаточные звенья»
соответственно.
89
4
= 1. • ")
(4.1)
ь..., Дд„]т — вектор приращений углов ф;
Дф„]т ~ вектор приращений углов фу; Т —
или в матричной форме
Д^ = Т Дф,
где Дд = [Д^
Дф = |^Дф^,...,
функциональная матрица Якоби, состоящая из частных
производных вида (it j
являются частными передаточными отношениями от звена i
и); эти производные
г
кинематической матрицей исполнительного
органа робота будем называть матрицу Г, задающую
зависимость (4.1) вектора Дд перемещений основных звеньев
от вектора Дф перемещений выходных звеньев приводов.
У рассмотренных выше роликоленточных и зубчато-
рычажных механизмов частные передаточные отношения не
зависят от <р, поэтому коэффициенты матрицы Т яв-
ляются постоянными величинами.
Для управления движением манипулятора необходимо
знать* обратную зависимость Дф от Дд.
Управляющей матрицей исполнительного органа
робота будем называть матрицу J, задающую обратную
зависимость вектора Дф перемещений выходных звеньев при-
водов от вектора Д(7 требуемых перемещений основных
звеньев:
г
Дф = J Д^. (4.2)
Матрицу J найдем, умножая обе части равенства (4.1)
слева на обратную матрицу
\ При этом получим
(4.3)
Управляемостью исполнительного органа робота
будем называть наличие взаимно однозначного соответ-
ствия между множеством векторов Д<?, описывающих
перемещения основных звеньев, и множеством векторов Дф,
описывающих перемещения выходных звеньев приводов.
Иными словами, каждому перемещению звеньев Д#
должно соответствовать строго определенное перемещение
Дф приводов и наоборот.
Поскольку зависимость Дф от Дд задается управляю-
щей матрицей J, математическая формулировка критерия
управляемости будет следующей:
I
4
f
ч
I
г
1
1
1
1
04>i
det J
г<р2
(4.4)
а<р
I
Неравенство нулю определителя матрицы J является
необходимым и достаточным условием существования и
единственности решений уравнения (4.2). Так как матрица J
является обратной по отношению к кинематической
матрице Т, то условие управляемости (4.4) можно заменить
эквивалентным:
1
(4.4а)
как по
если у
т. е. проверку управляемости можно проводить
управляющей, так и по кинематической матрице.
Условие (4.4), например, не будет выполнено,
манипулятора МЭМ-10 (см. рис. 4.3) все конические сателли-
ты в шарнирах II, III, V разместить по одну сторону от
осей основных звеньев. При этом det J = 0, т. е. система
неуправляема.
Условие управляемости в формулировке (4.4) впервые бы-
ло получено в работе [3]. Здесь же приведен пример меха-
низма, в котором это условие нарушается.
В дальнейшем будем рассматривать механизмы, обеспе-
чивающие взаимно однозначное соответствие Aq и Дф.
Управляющая матрица J для манипуляторов с приводами,
расположенными непосредственно в шарнирах, имеет диаго-
нальный вид
1
^22
(4.5)
л). Это озна-
Из (4.5) следует: А<р7
чает, что отработка* угла А^- производится пропорциональ-
ным поворотом выходного вала j-ro двигателя.
При размещении приводов на основании и в комбини-
рованных схемах матрица J является недиагональной,
1
в частности треугольной:
22
(4.6)
пп
Зависимости Дф; (Дд) имеют вид: Дф7 = £ Ддь т. е.
Л=1
поворот j-го привода вызывает смещение основных звеньев
1, Развязка движений состоит в приведении матрицы
J к диагональному виду (4.5) введением дополнительного
дифференциального привода [27, 20].
Задача кинематического анализа заключается в опреде-
лении кинематической матрицы Т, связывающей Дф с Дф
Матрицу J находим обращением матрицы Т. Для исполни-
тельных органов, удовлетворяющих условиям управляемости,
задачу можно решать вначале относительно J, а затем
находить матрицу Т.
Наряду с непосредственным определением вида матриц Т
можно применить метод, заключающийся в последователь-
ном анализе кинематики отдельных шарниров исполни-
тельного органа.
Рассмотрим в общем виде процесс передачи движения
в i-м шарнире манипулятора (рис. 4.5). Обычно для
осуществления независимых перемещений основных звеньев
i, i + 1, ..., п к шарниру i с помощью п — i + 1 ведущих
(передаточных) звеньев подводится п — i + 1 независимых
движений. Одно ведущее звено приводит в движение i-e
основное звено, а остальные п — i ведущих звеньев приводят
в движение п — i ведомых транзитных звеньев, выходящих
из шарнира i
звеньев ф, т (/ _ у,..., ф„ j _ у в скорости ведомых ф,
9(i+1)т<> • • •>Фи|» в шаРнире можно задать матрицей Tt
(рис. 4.5). Преобразование скоростей ведущих
П'
Рис. 4.5
1
частных передаточных отношений дфк j । *. Вид эле-
ментов матрицы 1\ зависит от устройства шарнира.
Поскольку в рассматриваемом i-м шарнире не происходит
преобразования относительных угловых скоростей qi,
q2, •••» Qi-i основных звеньев 1, ..., (i — 1), то матрицу 7}
размером (и — i + 1) х (и — i + 1) дополняем до матрицы Tt
размером п х п следующим образом:
I1 ° ъ
О Izl'—l
О 1 IJ (4.7)
q Ti I } п — i + 1
Искомую матрицу Т при этом находим как произведение
Т = ТкТк-iTfc-2.. • 7\, (4.8)
где 7\, Т2,..., Тк — матрицы вида (4.7), описывающие
кинематику шарниров 1,.,.,/с.
Отметим, что условие управляемости должно выполнять-
ся для всех матриц Tt в i-x шарнирах, иначе из
det — det Tf = 0 получим det Т = 0. Поскольку в каждом i-м
шарнире det Тг 0, для него существует управляющая
матрица Jt — IT1, задающая обратную зависимость
Ф/Т0-1>---»ФиТ0-1) от qh Ф(/+1)Тр...,Ф„Т{. Аналогично, доопре-
деляя матрицу до J,, можно найти управляющую
матрицу J всего исполнительного органа в виде произве-
дения
J = JiJ2 ...Jf <4-9)
Матрицы Ti и Ji будем по аналогии с Т и J назы-
вать кинематической и управляющей матрицами шарнира.
Отметим, что структура шарниров может отличаться
от описанной выше, например из шарнира i может при-
водиться в движение предыдущее звено i — 1 основного
механизма или из шарнира i + 1 — звено г. Однако общий
ход рассуждений при этом сохраняется.
Рассмотрим кинематику конкретных типов исполнитель-
ных органов.
* Здесь и в дальнейшем выражение । обозначает
угол поворота передаточного звена к, принадлежащего основному
звену i.
93
1
t
ным механизмом. Выделим из механизма
анного типа
свободы произвольный
(см. рис. 4.1) с п степеням;
шарнир (рис. 4.6, а). Ролики
передаточного
механизма
i + 1,...»и свободно вращаются на оси шарнира и служат для
транзитной передачи движения к звеньям i+l,...,n с по-
мощью тросов i + 1,..., п. Ролик i закреплен на оси шарни-
ра жестко и служит для передачи движения звену i с
помощью троса i. Радиусы роликов i, i п i-ro
шарнира обозначим rih ri{i+ i rin.
В качестве ведущих звеньев возьмем участки 1, 2,...,п
тросов (рис. 4.6, б) от приводов до точек их касания с роли-
ками первого шарнира, в котором звено 1 соединяется
со стойкой. Обобщенными координатами будут длины рас-
смотренных участков тросов sx, s2,...,s„. Ведомыми являют-
ся основные звенья. Их относительные углы поворота
обозначим q19
Зависимость вектора перемещений Ад от As носит
сложный характер, поскольку поворот каждого i-ro основ-
ного звена вызывает цепь взаимосвязанных дополнитель-
ных поворотов звеньев i+l,...,n. Поэтому вначале опре-
делим управляющую матрицу J, задающую обратную
зависимость As от Ад, а уже по ней найдем кинемати-
ческую матрицу Т = J “1.
Рис. 4.6
94
Условно считая ведущими
основные звенья, а ведомы-
ми — тросы, найдем выражения
для составляющих матрицу J
частных передаточных отноше-
ний от троса j к звену i (j и
i — номера троса и звена соот-
ветственно).
Очевидно, при j < i и
поскольку трос j не доходит
до i-ro звена и его перемещение
не зависит от угла поворота
этого звена.
При j i рассмотрим, как
связано угловое перемещение
Дф звена i
участке от привода j к ролику j первого шарнира) за малый
промежуток времени At. Положительное направление отсчета
задающего сгиб основного звена i, выбираем
= 0,
длины троса j (на
и приращение
угла qb
в сторону, противоположную подводу тросов к роликам
шарнира i (рис. 4.7).
В начальный момент движения угол обхвата тросом j
ролика j в
Длина /у части троса, лежащей на ролике, равна
ОуГу. После поворота звена i на угол Дд, получим следую-
щие выражения для угла обхвата ay и длины участка,
обхватываемого тросом j:
Новое положение звена i показано на рис. 4.7 штриховой
линией.
Так как при определении частного передаточного от-
ношения и
руется,
тросом j
i — 1. i — 2
шарнире i обозначим через ау (рис. 4.7).
части
У a
и длины участка
Qi 9 hj = hj “Ь ij
положение звеньев — 1,
то увеличение длины участка,
передастся
I- 1,...,и фикси*
охватываемого
по шарнирам
в шарнире
.,1 к ведомому участку (тросу) и уменьшит
его на такую же величину (Д^гу).
В результате получим, что
= - =
получим, что отношение Asj/Aqi
является константой. Так как
I
I
f
ч
I
[
!
1
1
и
= lim - Л.
д»-*о
то и а = - Гу.
Матрица J при этом (с учетом того, что при j < i
и« — 0) имеет вид
1
(4.10)
Л
det J = (— 1)" П г и
i = 1
/о,
следовательно, манипуляторы с ро-
ликоленточными передаточными механизмами всегда управ-
ляемы.
Кинематическая матрица Т, полученная обращением J,
Г1
I ^21 ^22 0 I
т = |............, (4.11)
I ^п2 • • • ^лл I
где tij = (- 1)*+Jdet Jj{/( (-1)" fl r**)> Ja ~ минор элемента
\ k=l /
Ьл матрицы J, получающийся из нее вычеркиванием строки
j и столбца i.
Найдем вид некоторых элементов матрицы Т и поясним
их смысл. Диагональные элементы tib связывающие по-
ворот i-ro звена с перемещением троса i, равны
tit=-l/rib откуда Agf = - А$£/гк. Элементы t(i+1)h распо-
ложенные под диагональю, задают поворот звена
i + 1 при перемещении Asf троса i. Они равны
l)/[riir(i+1) (<+!)]•
ъ а+
можно следующим образом: при
Объяснить вид t
перемещении i-ro троса на величину As, звено i повернется
на угол
лежащей на ролике i
и. При этом длина части троса i + 1,
1 шарнира i, изменится на величину
—&Siri{i+iy/гц. Это вызовет изменение Asfrf (i+1>/гь длины части
троса i +1, лежащей на ведущем ролике i +1 шар-
нира i + 1, что приведет к повороту его на угол
A#i+i —
ri (t + l)
ru ^(i+i)(i+i)
откуда и получим
ri(i + l)
rur(t+1) (i+1)
1
Элементы вида t(i+2>,, описывающие повороты (i + 2)-х
основных звеньев при перемещении i-x тросов, равны
. = + ---------Г,i+1)<. + 2> (4.12)
r iir (i + 2) (i + 2) Г iir(i + 1) (i + 1 )r(i + 2) (f + 2)
Первое слагаемое определяет поворот (i 4- 2)-го звена,
обусловленный поворотом i-ro звена, а второе слагаемое
описывает поворот, вызванный смещением (i -I- 1)-го звена.
Аналогичным образом можно объяснить вид и других
членов кинематической матрицы Т.
В простейшем случае, когда радиусы всех роликов
одинаковы — = r (i, j = 1,...»и), управляющая и кинемати-
ческая матрицы J и Т принимают вид:
(4.13)
Как видно из выражения матрицы Т, особенностью
кинематики данных механизмов является отсутствие влияния
перемещений тросов j на движение звеньев (/ 4- 2),
(/ + 3),..., п. Это следует из tu+ 2)j = Го+з) j = • • • = tnj = 0.
Кинематика манипулятора с передаточным механизмом,
состоящим из цилиндрических колес. Применим для кине-
матического анализа рассматриваемых механизмов предло-
женный выше метод, заключающийся в последовательном
анализе шарниров. Рассмотрим произвольно выбранный
i-й шарнир дифференциального механизма с п степенями
свободы (рис. 4.8).
Рис. 4.8
4 Механика промышл. роботов, кн. 2
97
1
Ведущими звеньями шарнира будут сателлит i — 1 основ-
ного механизма и передаточные сателлиты Г2, (i — 1)‘~2,...
...,и‘“2. Обобщенными координатами являются их углы
поворота на сателлите i — 2, принадлежащем основному
механизму.
Ведомыми звеньями являются сателлит i, являющийся
основным звеном, и передаточные сателлиты (i + 1)*“
Поскольку число ведомых звеньев на единицу меньше
числа ведущих звеньев, то условно к ведомым отнесем и
сателлит i — 1.
Найдем вид кинематической матрицы 1\ шарнира i,
размеры которой (п — i + 2) х (и — i + 2). Нумерацию строк
и столбцов установим от i — 1 до п так, чтобы номеру к
строки соответствовало ведущее звено к, а номеру столбца
j — ведущее звено у, расположенное на сателлите i — 2. Эле-
менты tkj являются частными передаточными отношениями
u*,j: t так как в роли ведомого
и ведущего выступает звено — сателлит i — 1.
При к > (i — 1) tkk = Мусtj_ 1)(/ф-_2) = —zk]i-2/zk]i-i> no’
скольку при остановленном сателлите i — 1 передача от
колеса к1-1 к колесу к*-2 превращается в обычную
передачу с внешним зацеплением. Для сокращения записи
такие передаточные отношения от колеса к1-1 к колесу
к* “ 2 будем обозначать ик, учитывая, что tkk = ик для
к > i — 1.
Поскольку движение ведомых звеньев к'"1 не зависит от
ведущих звеньев (к — 1)’- 2,..., и* ~ 2, лежаших справа от
колеса к1'1 (рис. 4.8), отсюда следует, что все элементы
tkj (j > к), лежащие над диагональю, равны нулю.
Движение ведомых звеньев к*-1
дущих колес (к — l)i-2, (к — 2)*“2,..
к'”1 (рис. 4.9). Поэтому под диагональю во всех столбцах,
кроме (i — 1)-го, также будут нули, т. е. при i
не зависит также от ве-
,i‘“2, лежащих слева от
к
tkj = 0.
Определим элементы tk(i-1} (к = 1,...,и — i + 2) столбца
i ~ 1, равные частным передаточным отношениям от ведо-
мого колеса к'~1 к сателлиту i — 1, который для этого
колеса является водилом.
Предварительно введем понятие расчетной схемы. В диф-
ференциальном механизме скорость ведомого звена является
* Здесь и в дальнейшем передаточные отношения от звена к
к звену j будем обозначать ukj.
функцией скоростей нескольких
ведущих звеньев.
Расчетной схемой для
определения частного передаточ-
ного отношения ujs от ведомого
звена j к ведущему $ назовем гра-
фическое изображение механизма,
который получается из первона-
чального после остановки всех ве-
дущих звеньев, кроме s.
Расчетная схема для опреде-
ления ик показана на
рис. 4.9. Используя формулу Виллиса для планетарных
механизмов [1], получим
^0-1)= Ukui-D,(f-1)= 1 ~ 1)лто-2)»
Рис. 4.9
где ик । а _ । )tk । (j _ 2) — передаточное отношение от колеса к* 1 1
к колесу к'~2 при остановленном сателлите i — 1, являющем-
ся водилом для колеса fc*"1, и отпущенном колесе
к*~2. Отсюда tfc(l-i) = 1 - (-4~2/4-1) “ 1 -
Таким образом, все элементы кинематической матрицы
Т, шарнира определены. Она имеет вид
В качестве примера рассмотрим манипулятор с четырьмя
степенями свободы (см. рис. 4.2). Основные звенья 1,2. 3
осуществляют перемещение схвата, связанного с колесом 4,
по трем независимым плоским координатам. Замыкающую
цепь 53, 52,
51*, показанную штриховыми линиями, при
анализе кинематики не учитываем.
В шарнире 7, где звено 1 соединяется со стойкой О,
кинематическая матрица будет единичной:
* Обозначения звеньев
звену к на основном звене
вида к' соответствуют передаточному
I.
поскольку
скоростей
колес (21,
о2 = —^2/
матрица шарнира 2
здесь не происходит преобразования угловых
звеньев. В шарнире 2 передаточные отношения
22), (З1, З2), (41, 42) обозначим, как и ранее,
2; 03 = — zj/z2; 04 = — zi/zi. Кинематическая
(1 - из)
(1 —1/4)
1/2 и
О 1/3
О 0 1/4
Передаточные отношения в шарнире 3 of = —Z3/Z3;
ui — — zi jzi. Кинематическая матрица шарнира
1 О
1 -ul ul
1 — ui О
l/д
шарнире 4
Аналогично в
т -Г 1 0
1 — 1/4 1/4
где ui = (- z4 /zi).
Дополняя матрицы Т
вательно перемножая матрицы Т15 Т2, Т3, Т4
полную кинематическую матрицу манипулятора:
4 ДО
последо-
получим
1 - о2
1 - of (1 - 03) - Ц3О3
[(1 — w2((l —1/3) +
4-04(1 —1/4)) —
__< 4 .4*1
—W4W4W4J
О
«2
i/l(i-wf)
[i/l(l~wl) +
4-02(1 —
— O4) — 04]
о
о
U3U3
oloi(l-oj)
О
О
з и
о
о
о
(4.14)
100
1
Полученная матрица Т определяет зависимость отно-
сительных угловых скоростей основных звеньев 1 — 4 [вектор
со0™ = (соь ф2> со3, со4)т] от угловых скоростей ведущих валов
2, 21, З1, 41 [вектор сЬвед = (<0i, <о2ц <o3i, <о41)]:ю°™ = Тсовед.
В случае, когда числа зубьев всех колес (k, I — 1,...,и)
одинаковы, получим = — 1, а матрица Tf имеет вид
О
(4.15)
Умножая матрицы Ти, получим выражение
для кинематической матрицы всего дифференциала:
(4.16)
Управляющая матрица рассмотренного дифференциала
Кинематика манипулятора с передаточным механизмом,
состоящим из конических колес. Структура шарниров
манипулятора, звенья которого приводятся в движение
коническими передачами (см. рис. 4.3), более сложная по
сравнению с предыдущими рассмотренными случаями и
допускает много вариантов компоновки.
Как и у предыдущих типов исполнительных органов,
шарнир выполняет две основные функции: обеспечивает
относительное перемещение звеньев основного механизма
и передачу движения к следующему шарниру. Транзитные
движения внутри шарнира передается, с помощью ТДМ.
Внутри основного звена I движение передается трубчаты-
ми валами, на которых со стороны шарнира i жестко
закреплены выходные колеса ТДМ, а со стороны шарни-
ра z-4-l установлены входные колеса последующих ТДМ
(рис. 4.10).
101
Рис. 4.10
Способ передачи движения от внутрен-
звеньев
основным определяется
устройством шарнира. В работе [31] рас-
смотрены три типа шарниров манипул я
торов, наиболее широко применяемых в
современных конструкциях. Поскольку дви-
жение транзитных ТДМ не влияет на пере-
дачу движения к основным звеньям, то
в схемах шарниров (рис. 4.11, а—в) они
не показаны. Как видно из приведенных
схем, ведомой вилке 2 сообщаются два
вращательных движения — вокруг оси z
и вокруг оси у. При этом полную
угловую скорость звена 2 можно представить как сумму:
С>2 = &2у 4- G>2Z.
Очевидно, во всех схемах co2z = Зависимость же еО2У
от угловых скоростей ведущих звеньев имеет более слож-
ный характер. В дальнейшем вращение вокруг оси у в
отличие от вращения вокруг оси z будем называть сгибом.
Разберем, как осуществляется сгиб в рассмотренных схе-
мах привода основных звеньев.
В шарнире (рис. 4.11, а) вилка 2 имеет зубчатый
сектор, входящий в зацепление с коническим колесом вала 21.
Изгиб вилки 2 вызывается вращением этого вала отно-
сительно вилки /.
В двух других схемах изгиб осуществляется от двух
передаточных валов 21 и З1 как через промежуточные
Рис. 4.11
сателлиты (рис. 4.11,6), так и непосредственно
звенья
через зубчатые секторы на ведомой вилке (рис. 4.11, в).
Схема привода (рис. 4.11, в) позволяет также с помощью
валов 21 и З1 сообщать вращательное движение вилке I
(а следовательно,
Вторую функцию шарниров — передачу движения — мож
вилке 2) вокруг оси z.
но осуществить, устанавливая внутрь основных звеньев
автономные ТДМ, служащие только для транзитной передачи
движения. Структура автономного ТДМ (звенья 21, 21с
и 22) и его положение относительно ведущего 1 и ведомого
2 основных звеньев рассматриваемого шарнира даны на
рис. 4.12. Ведущий вал ТДМ 21 находится внутри ведущей
вилки 1, сателлит 21с автономного ТДМ вращается на
оси шарнира, а ведомое звено 22 находится внутри
ведомой вилки 2.
Число автономных ТДМ в шарнире равно числу
передаваемых через него транзитных движений.
Рассматриваемые шарниры относятся к сферическим
механизмам, поскольку траектории точек, лежащих на звеньях
шарнира, располагаются на концентрических сферах с цент-
ром в средней точке шарнира. Число степеней свободы W
у сферических механизмов равно [1]:
W = Зп — 2р5 - р4 + q,
(4.17)
где п — число подвижных звеньев шарнира; р5 — число вра-
щательных пар; р4 — число зацеплений; q — число избыточ-
ных связей.
Для шарнира, показанного на рис.
п = 9, р5 — 10, р4 = 5, q = 2. Две избыточ-
ные связи вносит вращательная пара V
(см. рис. 4.3). По формуле (4.17) получим:
3.9 — 2 -10 — 5-2 = 4. Две степени
свободы вносят ведущая вилка 1 и вал 21,
связанный с ведомой вилкой 2, а осталь-
ные две степени свободы вносят автоном-
ные ТДМ (звенья З1, 31с, З2, 41, 4хс, 42).
В общем случае
всегда
складывается
W шарнира также
из числа степеней
свободы основных звеньев и передаточ-
ных, связанных с ними, а также из числа
автономных ТДМ. Подсчитывать обе со-
ставляющие можно независимо.
Задача кинематического анализа заклю-
чается в том, чтобы по заданным угловым
скоростям ведущих звеньев найти:
4.13, получим:
Рис. 4.12
103
Рис. 4.13
Рис. 4.14
угловые скорости ведомой вилки и
ных
вокруг оси у относительно
угловые скорости ведомых валов
ведомой вилки.
сателлитов автоном-
ведущей вилки;
ТДМ относительно
В частности, кинематическими характеристиками шарнира
(рис. 4.13) являются угловые скорости со^,
co<tlc, Ю4Т2, зависящие от угловых скоростей веду-
щих звеньев «4, co^i, (dffi, СО4Ц. Положительное направ-
ление отсчета угловых скоростей — против часовой стрелки.
Порядок кинематического анализа следующий: вначале
определяются угловые скорости основных и связанных с
ними передаточных звеньев (I группа звеньев), а затем —
угловые скорости ведомых звеньев автономных ТДМ (II груп-
па звеньев). При расчете угловых скоростей I группы
звеньев наличие автономных ТДМ можно не принимать во
внимание.
Поскольку рассматриваемые дифференциальные механиз-
мы являются сферическими, расчет передаточных отно-
шений в них имеет свои особенности. Кратко остановимся
на них.
Пусть у шарнира i ведущими являются основное звено
i — 1 и передаточные звенья (рис. 4.14). Обоб-
104
1
щенными координатами их будут углы поворота вокруг оси z:
(pf-i, <pfj(j(,-!)• Выходными звеньями являются:
основное звено i и передаточные (i\+1и*. В отли-
чие от дифференциалов, у которых входные и выходные
звенья вращаются вокруг параллельных осей, в рассматри-
ваемых шарнирах абсолютное движение выходных звеньев
состоит из вращений вокруг осей z и у. При этом
составляющие угловых скоростей вокруг оси у у выход-
ных звеньев равны между собой, а составляющие по оси
z — различны. Соответственно координатами, характеризую-
щими положения выходных звеньев, будут углы поворота
фм фо ф(|’+ 1)1 г» • • • > Фи| /•
Пусть звено приводится от ведущих звеньев а, Ь, с
(a, Ь, с — любые три звена из i — 1, Тогда,
применяя формулы для плоских дифференциалов, получаем
“mi = + (1 -
где u<fflb — частные передаточные отношения от звена
к1 к а и b при остановленных остальных ведущих
звеньях.
Однако формула плоских дифференциалов не учитывает
геометрический характер сложения относительных угловых
скоростей звеньев. Поэтому для получения правильного
результата используем следующий прием:
вначале по формуле для дифференциалов определяем
сумму со? и со? для ведомой вилки i: со,- = со? + со?. Так как
cof = of_ i, то отсюда находим: of — со,- — со?_ j;
для внутренних передаточных валов к1 (к = i + 1,..., и)
по формуле для дифференциалов находим ок j,- =
= co?Tf 4- co?t/; так как со?т,- = со?, то со?п = сом, - со?.
Рассмотрим расчет угловых скоростей основных звеньев
у наиболее употребительных типов шарниров (см.
рис. 4.11, а—в). В реальных шарнирах числа зубьев у
входных и выходных колес ТДМ равны, т. е. zif„ = z1|(n+i),
а отношение чисел зубьев сателлитов z,-cT„ к z,Tn в каждом
шарнире постоянно. В дальнейшем будем обозначать
ик = z{ где к — номер шарнира.
Поскольку силовой расчет требует учета инертности са-
теллитов, при наличии сателлитов в - шарнире кинемати-
ческий анализ будет проводиться раздельно. Вначале рас-
сматривается передача движения от ведущих звеньев шарнира
к сателлитам, а затем — передача движения от сателлитов
к ведомым звеньям шарнира. Кинематическую матрицу
в первом случае будем обозначать Т *, во втором —
105
Г**. Очевидно, Т**Т* = Т, где Т — кинематическая матрица
всего шарнира.
Найдем для первого типа шарнира (см.
рис. 4.11, а) зависимость угловых скоростей вращения и сгиба
6ВЫХ = (<01, от угловых скоростей входных звень-
ев <ввх = (а>1, col 11Л Поскольку сателлиты отсутствуют,
сразу определяем кинематическую матрицу шарнира Т.
Как было отмечено ранее, со2 = <х>1- Найдем зависимость
от 6ВХ.
По формуле для дифференциалов получим
со2 = + ю2 =
1,211Ш211 + (1 ~ м2с11,2Т1)ю1-
Расчетная схема для показана на рис. 4.15, а.
Из нее следует, что I wJcji.zti I = z2fi/z2cTi = Vм- Знак
i,2ti определим следующим образом: при со2р>О,
(со2| 1 направлена против часовой стелки вокруг оси z)
и левостороннем расположении сателлита (см. рис. 4.11, а)
®2с 11 > 0, а при правостороннем — со2с ц < 0. Следовательно,
MJcfi,2ti — ±l/w. Здесь и в дальнейшем верхний знак—
для левого расположения сателлита, нижний — для правого.
Подставляя значение w^ii.afi в формулу для со2 и
вычитая из нее col = ®I, получим
(4.18)
Кинематическая матрица шарнира принимает вид
(4.18а)
У шарниров второго типа (см. рис. 4.11,6) передача
движения осуществляется через сателлиты. Поэтому кине-
Рис. 4.15
106
магический анализ проводим раздельно. Вначале определяем
зависимость угловых скоростей ©* = [©*, ©5сТ1]т от
о>вх = L^i, ®2tb и •
Применяя, как и в предыдущем случае, формулу для
дифференциалов и вычисляя передаточные отношения
wS’t?,2ti И м&тЪт1 для левостороннего (2J) и правостороннего
(3J) сателлитов, получим:
®3ct 1
Поскольку 11 == созс т 1 = <^>15 зависимость ©* от ©вх
будет следующей:
©1 = ©1;
Матрица Т* имеет вид
[1 0 0 “1
-1/и 1/и О .
1/и 0 — 1/и J
(4.19а)
Найдем теперь независимость вектора ©вых = (©i, ©$,
©з|2)т от ©*. Так как ©£=©^2, то задача сводится к
определению кинематики вала З2. Поскольку на валу З2
суммируется движение от всех ведущих звеньев, для вывода
уравнений его кинематики разложим абсолютные скорости
ведущих звеньев на составляющие.
Первое движение:
= ©р ©2с11 = °>2ctl = <»Ь <®3СТ 1 = °>3с|1 =
оно представляет собой синхронное вращение входных
звеньев вокруг оси z со скоростью
Второе движение:
©Г = 0; ©2ст 1 = «hcti - горсть
здесь ведущая вилка неподвижна, а сателлиты вращаются
вокруг оси у. При этом ©, = ©* + ©** 0 = 1, 2хс, З1^).
Это же свойство в силу линейности зависимостей ©2
©1,
GJ2cti,
выполняется и для звеньев
107
1
В первом движении все ведущие звенья вращаются с
одинаковой угловой скоростью (01 вокруг оси z. Поэтому
®2 = со? = юз т 2 = = °>1- В° втором движении при (0? = 0
рассматриваемая часть шарнира превращается В дифферен-
циальный механизм с двумя степенями свободы (рис. 4.15,6).
Пипкя 2 является в нем водилом, звено З2 — сателлитом.
Вилка 2 является в нем водилом, звено З2
Поскольку вилка 2 вращается только вокруг оси у, то
по формуле для дифференциалов получим:
♦♦
У = М^2сГ,1ю2сТ1
iMcfb = V(i
(1
“ U^2c\ 1) Ю3с 11 ’
M2,2ct 1
Расчетная схема для определения дана на Рис* 4.15,6.
В результате имеем
♦♦ ♦♦
I
г
у = 1/2(02cf 1
Сателлит З2
вокруг осей у и z. Используя формулы для дифферен-
циалов, имеем
**v
б>з|2 “ ЮЗГ2
Л^зс fi-
совершает сложное вращательное движение
** *r
G>3f2
t2?2cTl) ®3cfl»
Для определения i можно использовать расчетную
схему на рис. 4.15, в. Вычитая из со**2 величину со3*?2 =<о2 \
получим
ЮЗТ 2 ~ Ч
Вычитая из суммы со?Т2
щую связь векторов со*
4- ®з скорость со!, получим следую
и йвых.
и
2Ю2с| 1
и
Л, 1-
(4.20)
3
f
ч
I
г
1
I
1
Г
Кинематическая матрица имеет вид
1 о
0 71
0 -и/2
О
w/2J
(4.20а)
Умножая матрицы Г** и Т*, находим кинематическую
матрицу всего шарнира
108
1
Т = Т'**Т'* =
о
о
1/(2и)
-1/2
О
— l/(2w)
-1/2
(4.21)
Рассмотрим третий тип шарнира (см. рис. 4.11, в).
Ведущими звеньями в нем являются передаточные валы
21 и З1, выходными — основные звенья 1 и 2. Вилки 1 и 2
совершают следующие движения: вилка 2 изгибается вокруг
оси у относительно вилки 1 с некоторой угловой
скоростью cof, а вместе они вращаются вокруг оси z
с угловой скоростью о! = (02. Поскольку движение в шар-
нире передается непосредственно от ведущих звеньев к ве-
домым, минуя сателлиты, кинематический анализ проводим
сразу для всего шарнира.
Анализируемый шарнир является дифференциальным
механизмом с числом степеней свободы W = 2. Вилка 1
является в нем водилом, а вилка 2 с зубчатыми
секторами 2хс и З1 с играет роль сдвоенного сателлита.
Поскольку звено 1 вращается только вокруг оси z, по
формуле для дифференциалов для него получим:
ico2f i + 0 ~ М^О^зть
В результате
(01 = (01 = 1 4" !•
Вилка 2 осуществляет сложное вращательное движение
вокруг осей у и z, поэтому для нее
со2 = (of + (о2 = i(o2t i + (1 — нЗД1)(озт t;
“S’ti = = v(l - 4jti) =
Вычитая из (o2 величину со2 = (0i, получим
и
(02 =
и
2
В итоге связь векторов (bBX
— [(of, (of]T будет следующей:
И ®вых
(j) -j WWW44
U
U
(4.22)
109
1
Кинематическая матрица шарнира
(4.22а)
Таким образом, кинематика основных и связанных с ними
передаточных звеньев у основных типов шарниров (см.
рис. 4.11, а—в) рассмотрена.
Определим кинематику автономных ТДМ, передаю-
щих транзитные движения через шарниры. Возможны два
варианта расположения сателлитов относительно центра
шарнира: левостороннее (рис. 4.16,а) и правостороннее
(рис. 4.16,6).
Выражения для угловых скоростей сателлитов получены
при анализе второго типа шарниров (см. рис. 4.11,6) и даны
формулой (4.19). Объединяя формулы для обоих вариантов
расположения сателлитов, получим
(4.23)
где со„ — угловая скорость ведущей вилки; п — угловая
скорость ведущего вала ТДМ; верхний знак — для лево-
стороннего расположения сателлита, нижний — для право-
стороннего.
Отметим, что формула (4.23) задает составляющую
со, ♦ „ по оси у — со*’ । п. Вокруг оси z сателлиты вращаются
вместе с вилкой и, поэтому со' ♦ „ = со„.
С
Найдем выражение для угловых скоростей ведомых
валов автономных ТДМ. В общем случае эти скорости
зависят от сои — угловой скорости ведущей вилки, coz-; „ —
угловой скорости ведущего вала ТДМ, а также от
скоростей передаточных звеньев, приводящих вилку и + 1.
ПО
Рис. 4.16
Для того чтобы полученные выражения были справедли-
вы для всех типов шарниров, в качестве ведущих звеньев
возьмем вилки и, п 4- 1 и вал in. Таким образом,
механизмы, показанные на рис. 4.16, а, б, являются диф-
ференциальными с W = 3.
Поскольку движение от ведущих звеньев к ведомым валам
ТДМ передается через сателлиты, вначале определим связь
скоростей со, । и с сои, <о/с । <оп +1, а затем — искомые зависи-
мости (0/Т„ (<0„, (0и+1, (0,|п).
Для этого разбиваем движение ведущих звеньев на два
составляющих движения:
1) о? = сой;
<о?+1 =<о«+1 =»«;
<*\Ди = =
2) со** = 0;
со**1 =<о&+1);
<0/с t«• = <°i£ t «♦
В первом движении получаем синхронное вращение всех
звеньев рассмотренной части механизма со скоростью со„
вокруг оси z. Следовательно, со‘Ти + ] = coff „ + j = <ои.
Во утором движении первоначальный дифференциаль-
ный механизм утрачивает одну степень свободы. В получен-
ных механизмах (рис. 4.16, в, г) W = 2, ведущими являются
вилка п + 1 и звено i", ведомым — звено Г+1. Поскольку
звено i"+1 вращается вокруг осей у и z, по формуле
для дифференциалов имеем:
(1
«”tHi.icf= +“
Вычитая из ю*|И + 1 составляющую
чим
1 ♦♦
= ц. WCOjc f и i UG)n + j.
полу-
Вычитая ИЗ суммы (О + ! + (О + j скорость <ой, получим
(0s... ., = т ио * + мео , ..
if п+1 ' ict» — и+Г
(4.24)
Подставляя в (4.24) зависимость coicTfJ (со„, <of|„) из (4.23),
получим требуемую связь (Oj|„ + i со скоростями соп,
<®i | и> + 1 ’
<0/1 „ +1 — <ои - «ли ± иоп + р (4.25)
Таким образом, рассмотрение кинематики автономных
ТДМ закончено.
В качестве примера рассмотрим шарнир, показанный на
рис. 4.13. Ранее было выявлено, что у шарнира W = 4.
Ведущими являются звенья 1, 21, З1, 41, ведомыми —
звенья 2, З2, 42. Поскольку в передаче движения участ-
вуют сателлиты, кинематический анализ проводим раздельно.
Вначале находим связь угловых скоростей со{1} = [оц, (Оггь
®3tb ®4t]T И С0{1с} = [соь COj, (O^cfb
Шарнир относится к первому типу (см. рис. 4.11, а)
с правосторонним расположением зубчатого сектора на ведо-
мой вилке. Поэтому по формуле (4.18) для получаем
€0*2 = (®1 ~ ®2f 1)/М‘
Угловые скорости сателлитов Згс и 4х с находим по
формуле (4.23):
©ЗсТ 1 = ”(«1 - С03| !>/«; ®4сГ1 = “ Ю4Т 1)/W-
В результате матрица, связывающая cb{lc} с со{1}, имеет вид
1 1 О О О 1
1/и — 1/и О О I
— 1/и 0 1/и О
1/и О 0 — 1/и I
Найдем зависимость угловых скоростей cb{2} = [<&ь
0>3t2, »4Т2]т от 00{1с}- По формуле (4.24)
(Оз|2 = + мсо& °>4|2 ~ wcoin —
В результате получим матрицу следующего вида:
О 1 U
О и —и
О —и 0 и
Умножая Т** на Т*, получим полную кинематическую
матрицу шарнира
1/и —1/и
О
О
112
det T — — 1/u 0, следовательно, условие управляемости вы-
полнено и существует управляющая матрица шарнира
J = Т~ 1 *
1
J = 1 —W о
1 и — 1
1 — и 0 — 1
При определении относительных скоростей основных
звеньев наряду с рассмотренным выше порядком кине-
матического анализа можно использовать принцип обраще-
ния движения. Это позволяет проводить исследование более
наглядно.
В кинематическом анализе всего манипулятора относи-
тельные скорости удобно выражать в системах координат,
жестко связанных с основными звеньями. Для каждого
такого звена, например звена i на рис. 4.17, введем две
системы координат.
Первую систему поместим в центре О, шарнира i.
Ось Zi направим по оси звена i, ось у, — по оси шарнира
г, а ось Xi дополняет оси yb до правой тройки;
вторую систему О1+1х\у% поместим в центре Oi+l шарнира
i + 1, ось z\ направим, как и zh по оси звена i, ось
у- — по оси шарнира i + 1, ось х[ дополняет оси у-, z- до
правой тройки. Поскольку в общем случае оси шарниров
i и /4-1 перекрещиваются под углом уь связь систем
OiXiy^i и Oi+1x-y-z- будет следующей:
x'i = Xi cos 4- у,- sin xt = x- cos Yi — yj sin y^
y'i = - Xi sin yt 4- y£ cos Yi; yt - x • sin y< 4- yj cos Yi ;
Z; = Zi — lii Zi = Zi + 4,
где Ц — длина звена i.
Рис. 4.17
113
Поскольку при пересчете угловых скоростей значение
имеют только повороты координатных осей, а сдвиги не
учитываются, введем матрицу В(_7л направляющих косину-
сов между осями (х-, y'h z-) и (xf, yb zf):
[<0x, (0y, <02]? = В (_ T.) [co*,
co’, co2]?;
cos
COS (yC Xi)
_cos(z-, Xi)
cos(x-, yj)
COS (уГу<)
cos (zC У i)
cos (х;Д)1
cos (у£\) I =
cos(z-, Z;)J
(4.26)
Обратной B(-7.) будет матрица B*t.
Отметим, что переход от системы 0<+рс!уИ к системе
Oi+iXi+iyt+iZi+i, связанной со звеном i 4-1 и повернутой на
угол qi+1 вокруг оси у-, задается матрицей В£.+ г При этом
[со*, со5’, о2]]+1
[со*, со3’, со2] р
Матрица имеет вид
О
1
О
cos qt +!
_ sin q,+1
- singi+1
О
COSC/i+i _
(4.27)
Обратный переход от системы Ol+1xl+1yi+1zf+1 к системе
Oi+ix'iy'iZ'i осуществляется матрицей Ву_д,+1.
Определим относительные скорости основных и переда-
точных звеньев манипулятора МЭМ-10 (см. рис. 4.3).
Звенья основного механизма 1—6 приводятся в движение
шестью приводами, расположенными на основании. Последо-
вательно рассмотрим шарниры I — V. Там, где передача
движения осуществляется через сателлиты, кинематический
анализ проводим раздельно.
В качестве обобщенных координат шарнира I и всего
исполнительного механизма выберем углы поворота отно-
сительно стойки 0 цилиндрических колес 1° — 6°, установ-
ленных на валах 7, 21—б1 (см. рис. 4.3). Скорости
множества звеньев {1} = 7, 21,...,б1 относительно стойки 0
114
задаем вектором (co^f{% = [col0, ь • • •»t]T в системе
OoX0yQZ0i жестко связанной со стойкой.
Определим относительные угловые скорости основных
звеньев i (i = 2, ...» 6) и принадлежащих им передаточных
звеньев в системах координат О^- iZ^. ъ жестко связан-
ных с основными звеньями i — 1.
Шарнир II. Ведущими в нем являются основное
звено 1 и передаточные 21—61, ведомыми — основное
звено 2 и передаточные З2 —62. Скорости их определяем
в системе координат O2x2y2z2. Шарнир относится к пер-
вому типу (см. рис. 4.11, а). Зубчатый сектор расположен
на вилке 2 справа. Поэтому скорость сгиба вилки 2
С0$ = (®1 - ®2Ti)/w2.
(4.28а)
Сателлиты 31с, расположены слева, сателлиты 41с,
б1 с — справа, поэтому для них по формуле (4.23) получим:
^Ctl =------(Ю1 “* ЮЗТ 1)’ 1 — — ~ (Ю1 “ Ю5Т 1)’
U2 и2
^Icti = —(°>i" <»4т i); <Ti= “ °М1)-
^^2
(4.286)
Откуда матрица Т*, связывающая вектор а>(|с) = [ю4, wi,
с входным вектором <о{1) =
= ®2fi> ®зf i» i» ^511» i] , будет следующей.
l/«2
-l/w2
l/«2
“l/«2
l/w2
— 1/^2
0 l/«2
0 0
0 0
о 0
— 1/l/j
0
0
V«2
0
Определим матрицу T$*, связывающую ректор со{2} в
= [(Of, (0£ (0f|2, <0ft2, cofT2, C0£T2]' с вектором (0{1с}.
Выражения для cof 12, * • •, <0612 берем из формулы (4.24)
с учетом расположения сателлитов:
«>3t2 = ®5|2 = -И2С0£сГ1 + W2°>^
(0^2 = “2°>iT1 “ «6|2 = w2^ct 1 - и2<^-
115
В результате матрица TJ* будет следующей:
«2
О
О
«2
и2
Умножая TJ* на Г*,
для всего шарнира 2:
1
l/u2 — l/t/2
2 — £ — 1
Тг = О 1 о
2 — 1 О
О 1 О
получим кинематическую матрицу
О
О
О
Найденные матрицы Т* и задают зависимость век-
торов относительных скоростей со{1с} и о{2} от угловых ско-
ростей ведущих валов соо = [юио> o>2fo> о, <°4to> ю5то, юбто]Т:
®{lc} = -^2^0 j ®{2} = TzWq.
Шарнир III. Ведущими в нем являются основное звено
2 и передаточные З2, 42, 52, б2, ведомыми — 3, 43, 53, б3.
Шарнир относится ко второму типу (см. рис. 4.11,6).
Используя формулы (4.19а), (4.20а), (4.23) и (4.24), получим
следующие уравнения связи между векторами cSp) =
= [<4 <12, <12, t2]T; <°{2с} = [< <42, <42, f2,
<ц]т и &{з} = [< <t3, <тз, ^бГзТ’-
1 1 ,
<|2 = “ — т 2: <42 = “ — °5Т2;
Из из
1 1 2
<t2=+— «>4t2; <f2=+—®6f2
11 w3 u3
M = ~2 <42 + ~2 <t2’ ®4t3 = -y <42 - -y<t2’
<|3 = «3<42 “ M3<; <f3 = -“3<42 + W3<
116
В результате матрицы Т* и
с <в{2} и ю{3} с со{2с}, будут следующими:
fj*, связывающие й{2<^
о
l/«3
1/Ыз
1/«з
1/|<з
I
О
1/2
“з/2
О —и3/2
О и3/2
1/2
~«з/2
~«з/2
"з/2
о
о
Из
* на
Умножая
Т3 всего шарнира:
Т$, получим
кинематическую матрицу
О — 1/(2м3)
О -1/2
О 1/2
О -1/2
О
1/(2«з)
—1/2
— 1/2
1/2
О
О
О
Для того чтобы
связь
относительных скоростей
Для того чтооы найти ______ _____ ____
°>{2с} и ®{3) со скоростями ведущих звеньев со0 = [(о1|0, •••
. . . , (Og | q] .
®{2c} = T5T2c&oJ cop} = T3T2g>o>
необходимо умножить матрицы TJ и T3 на T2:
4
/
i
।
I
1
1
ПТ2 =
l/w2
*2/u3
О
-2/и3
О
-1/и2
1/«з
1/Мз
1/«з
1/Из
1/и3
О
О
-1/“з
; (4.29)
1/«з
О 1/из
117
1
Т3Т2 =
1
l/u2
—1/1/3
-1
—
. -1
о
~1/«2
1/м3 1/(2м3) — 1/(2ы3)
О 1/2 1/2
О -1/2 1/2 1
О 1/2 -1/2 0 1-
(4.29а)
Шарнир IV. В шарнире IV не происходит преобразо-
вания угловых скоростей звеньев.
Шарнир V. Матрицы Т?, Т*5* и Т5 для шарнира V
берем из (4.19а), (4.20а) и (4.21):
Г I о
Л = 1 — 1/и3 1/а5
[ 1/и5 0 - 1/и5
'10 о
Т5= 0 1/(2н5) — 1/(2u3)
1-1/2 -1/2
Произведение Т5Т3Т2 ~
рица всего исполнительного
’ 1
1/U2 — 1/«2
—1/1/3 1/мз 1/(2мз)
Г= -1 0 1/2
0 0 - l/(2w
0 0 1/2
10 О
; Т** = 0 1/2 1/2
О -и5/2 и5/2
где Т — кинематическая мат-
механизма:
0
- 1/(2и3)
1/2
) 1/(2u5) 1/(2u5) -1/(2w5) I
1/2 -1/2 -1/2 J
(4.30)
Таким образом, кинематический анализ завершен.
Для силового расчета манипуляторов необходимо также
знать абсолютные угловые скорости основных и передаточ-
ных звеньев. Выясним, как можно охарактеризовать абсо-
лютные угловые скорости произвольного основного звена i
и принадлежащих ему передаточных звеньев в системах
координат OiX^iZi и Oi+iX-y-z-.
Рассмотрим множество звеньев {/} — вилку i с принадле-
жащими ей трубчатыми передаточными валами (i + 1)\ . • •
..., п* (рис. 4.18, а). Очевидно, у всех звеньев из множества
11В
1
(/} абсолютные скорости вокруг осей xf и yt будут одина-
ковыми, обозначим их (О^, cofft. Различными будут скорости
звеньев i, (i 4- I)1, ..., ri вокруг оси zh их обозначим cof,
(ojtВведем вектор абсолютных угловых ско-
ростей множества звеньев {/}:
<^ = [>ц.. <0?, e>f,+ 1)T,, 0^(1’.
(4.31)
Рассмотрим другое множество звеньев — {гс}, состоящее
из вилки i и принадлежащих ей сателлитов (i 4- 1)с', ...» пс‘
(рис. 4.18, б). Абсолютные скорости звеньев из множества
{ic} задаем в системе Of+1x-y-z-. Очевидно, угловые скорости
всех звеньев из {Ц вокруг осей х,- и равны, обозначим
их со*. р со*.Вокруг оси у- скорости различны, обозначим
их со?, оо+1) ...» <oj ti. Введем вектор абсолютных ско-
ростей множества звеньев {ic}:
= [®k)’ < “к}> “Ъ+М”
(4.32)
Поскольку все абсолютные скорости являются функция-
ми скоростей t,
векторы (о?Йс, (offs
..., ф„ ведущих валов манипулятора,
будем представлять следующим образом:
° (1 +1) t i
Я11Ф1 + Д12Ф2 +
Я12Ф1 + а22ф2 +
«13Ф1 + а32$2 +
С?14ф1 4- Я42Ф2 +
СО
z
/
Я(и-1+3)1Ф1"^ Л(и~1+3)2ф2
(4.33)
Рис. 4.18
119
абс
04
«21Ф1
«31Ф1
«41Ф1
«12Ф2
«22Ф2
«32Ф2
«42Ф2
$1лФл
$2лФл
^ЗлФл
^4иФл
^(и — i + 3) «Фи
(4.34)
Или в векторном виде:
I
1
(4.3 5)
(4.36)
Ф»]т;
«1И
• • • ^1и
Для того чтобы найти у всех звеньев i = 1, 2,
торы О)?6?, достаточно установить зависимости а>
* v)7 VCJ
п век-
'Л®®® ОТ
I
!
I
1
Найдем зависимость <Ь^С от c&jjfLnj. Вектор й){^пс}
дан в системе координат звена i — 1. Посколь-
ку система OiX^Zi повернута на угол qt вокруг оси у[-19
то проекции скоростей на ось у{ те же, что и на ось yj-i.
Проекции на оси хь zt задаются матрицей BJ.. В результате
имеем
за-
120
1
где
(4.37)
Вначале рас
Найдем зависимость (со^ от
смотрим шарниры первого типа (см. рис. 4.11, а). Для них
искомый вектор можно представить в виде следующей
суммы:
отн
где (Ь,абс = [со*, со?, cof, oof, ..., cof]т - расширенный вектор
абсолютных скоростей звена i; = [0, 0, 0, .
..., со* °J]T — вектор относительных скоростей трубчатых ва-
лов (i + 1)‘, ...» и1 относительно основного звена i.
Их можно представить в следующем виде:
й>,^ = С’ 1)с1)
где
(4.38)
отн _
W -
G)
где
(4.38а)
У матрицы 7?* взяты лишь те строки, которые задают
скорости трубчатых валов.
В итоге для шарниров первого типа
со,-
Т V) (й>Г- 1)с}),-
(4.39)
121
Для шарниров второго типа (рис. 4.11, б) вектор (б)*^)
разлагаем следующим образом:
(Й$с). = ^абс^ + 6о™
где (0(^1) — Е®(»_ 1)» ®(i—1), ®(j—i), •••, ®(i— i)J рас-
ширенный вектор абсолютных скоростей звена (i — 1);
= [0, соГт, G>fOT, • • •, “ вектоР относитель-
ных скоростей основного звена i и трубчатых валов
(i + 1)', ...» п\
Слагаемые вектора представляем в виде
где
(4.40)
1 0
0 1
(4.40а)
в матрице Т-** взяты строки, задающие относительные ско-
рости выходных звеньев.
В итоге
й?6е = (СП + (й?6с_ )..
(4.41)
В дальнейшем будем матрицы (С\с + f ft) и (С’’ + f ft)
обозначать соответственно IVft и Wft.
В итоге зависимости вектора (®шс), от (Ц(ь- 1)с})< й
(w^-dj^-d будут иметь следующий вид:
(<ф;= И?*(&^_ад)(; (4.42)
(<&$'),. = И7*^. iw)(i_!, (4.43)
от Вначале переходим
Найдем вид зависимости
к системе координат О^у^:
(4.44)
122
где
Затем раскладываем на составляющие
Й)?бс
где G)^ = [cof, cof, со?, cof, ..., соф - расширенный вектор
абсолютных скоростей звена i; со= [0,0, 0, co^J 1)с । h ...
..., cof;°t ,Т — вектор относительных скоростей звеньев из
множества {ic} относительно звена L
По аналогии с предыдущим выводом представляем эти
векторы в следующем виде:
где
1 О
1
О 1
о 1 о
о 1 о
• • •
О 1 о
(4.45)
где
(4.46)
В матрице t*i+i взяты только те
ют угловые скорости сателлитов.
строки, которые зада-
123
В итоге зависимости вектора («>{&) от (<5^)г и ((M-f),-
будут следующими:
((Ь$%; (4-47)
) ЙЦ (6^),. (4.48)
f * +,) (4.47), переводящую (S“f“),. в (S>(y)f,
Матрицу (С,
обозначим через ГУ*.
Определим, как связаны между собой векторы абсолют-
ных скоростей множеств звеньев вида {/} и {ic} у манипу-
лятора, показанного на рис. 4.3. Абсолютные скорости
звеньев {1} = 1, 21
тором = (cof, со{, of, <o2f 1» • • • >
(of в нем равны нулю.
В системе координтат O^x^y^z^
в системе OiX^y^z^ задаются век-
юб t i)T- Составляющие со*,
Переход к абсолютным скоростям звеньев {1с} = 1
21с, ..., 6*с (вектор (со{1С})1'= (<of, <о$, cof, со^сТ1, ..., со^ц
осуществляется матрицей
Из (4.47) получим
О О
О О
О 1 О
l/w2
l/w2
V«2 .
124
1/н2
О l/w2
О О
о о
I
I
4
f
ч
I
г
1
I
1
о
1/«2
1/м2
1/и2
l/w2
1/п2
1
I О 1 1/^2 I — VM2
=== I 0 1 — 1/^2 I 0 1/^2 Q
I О 1 1/^2 I О О — 1/^2
О 1 -l/l42 0 0 0 1/н2
О 1 l/u2 О О О О -1/и2
В системе координат O2x2y2z2
(Й(к}>2 = fy2 (&^)r.
Абсолютные угловые скорости звеньев множества {2} =
= 2, З2, ...» б2 в системе O2x2y2z2 задаются вектором
?2р2 = (®2» °>2> °>з 12’ • • • > Ю61 г)- Его находим, умножая
(®{1с})г на- ^1*-
Матрицу перехода W%* определяем из (4.42), учитывая,
что шарнир II относится к первому типу:
Аналогично строим переходные матрицы для абсолют-
ных скоростей остальных множеств звеньев вида {/} и {ic}:
(й>{2§})з = (б>Й)3 = и*3* («Ws;
1
11 0 0 0 0 0 0
О 1 0 0 0 0 0
ООО 1 000
0 0 0 0 1 0 0 Изрз!
0 0 0 0 0 1 о
0 0 0 0 0 0 1 J
(&$)4- = (®?4))з' = -В (- «.) (й (4))з;
(&$}), = iv*5 (<&$)<;
11
о 1 О
оо1 ;
0 1 — 1/ws 1/ws
О 1 1/wj о -1/«5
(w^))s = В5> (® {4с()4';
(«$р5 = w*s*
110 0 о о
ООО 1/2 1/2
0 0 10 о
0 0 1 — н5/2 W5/2
Таким образом, матрицы перехода между векторами
абсолютных скоростей найдены.
126
1
4.2. Силовой расчет дифференциальных
исполнительных механизмов
Допустим, для выполнения некоторой операции уже опре-
делена кинематика исполнительного органа, т. е. определены
законы изменения относительных углов поворота основных
звеньев руки во времени: qr (t), W, • • •, Qn (0> гДе 0 < f < T.
Проведя кинематический анализ исполнительного органа
и определив его управляющую матрицу J, мы можем по
известным qt (t) (i — 1, ..., п) найти законы изменения обоб-
щенных координат ср, (г) (j = 1,...» и), которые должны быть
отработаны приводами.
В процессе движения на исполнительный орган действуют
внешние силы (полезная нагрузка и силы тяжести звеньев),
а также силы инерции.
Для осуществления требуемого движения внешние и
инерционные нагрузки должны быть преодолены (уравнове-
шены) с помощью приводов. Определение приводных мо-
ментов сил М1 (г), М 2 (Г), • • •, (г) (0 < t Г), развиваемых
двигателями, является первой задачей силового расчета.
Второй задачей является определение реакций в кинемати-
ческих парах, вызываемых внешними, а также инерционны-
ми силами. Обе задачи решаются совместно, поскольку
и в том и в другом случае необходим анализ передачи
усилий в исполнительном органе.
Рассмотрим реакции, возникающие в кинематических
парах механизмов. На рис. 4.19 показана вращательная
пара, соединяющая звенья р и q. Ось z направлена по оси
вращения. Так как пара полностью исключает поступатель-
ное относительное движение звеньев и относительный по-
ворот вокруг осей х и _у, то со стороны звена р на q
действует^сила реакции Rpq = Ryq, и реактивный
момент Mpq — [Мpq, MyPq, 0]т. Всего пять неизвестных рецк-
цдш. Реакции со стороны звена q на р равны: Rqp = — Rpq;
Mqp — — Л/pg.
Реакция в коническом зацеплении является шестым
неизвестным при рассмотрении равновесия одного кониче-
ского колеса. Она может быть выражена через передавае-
мый окружной момент.
Допустим, на схеме зацепления двух конических колес р
и q (рис. 4.20) ведущим является колесо р и выходной
момент на нем равен Мр. Тогда окружная сила
F* = Мр/Гр,
где гр — средний радиус колеса р.
127
Рис. 4.20
Радиальная сила на колесе q
Fq = F'tg a cos 6i
= Mp tg a cos 61/Гр,
где а — нормальный угол зацепления передачи;
= arctg (rp/rq) — угол делительного конуса колеса р.
Осевая сила на колесе q
Fq = Ff tg a sin 5- = Mp tg a sin §<Jrp.
Соответственно радиальная и осевая силы на колесе
рг _ _ра. ра _ __рг
Р ~ 1 г Р ~ 1 <Г
Знаки и направление момента Мр и сил F\ Fa, Fr не-
обходимо выбирать в зависимости от положения колес от-
носительно системы координат шарнира.
Разбиение исполнительного механизма на статически оп-
ределимые части. Силовой расчет любого исполнительного
механизма можно провести целиком, т. е. записать уравне-
ние статического равновесия каждого звена, объединить эти
уравнения в одну систему и совместно решить их отно-
сительно реактивных и приводных сил и моментов. Не-
достатком такого подхода является быстрый рост числа
уравнений в системе с увеличением сложности исполнитель-
ного механизма. Равновесие каждого звена описывается
шестью уравнениями. Поэтому у руки, показанной на
рис. 4.3, например, система должна была бы иметь 6 • 28 =
= 168 уравнений. Очевидно, составление и решение такой
системы уравнений чрезвычайно затруднено.
Поэтому для упрощения силового расчета весь механизм
необходимо разбить на статически определимые части,
128
1
имеющие сходную структуру, соответственно и сходный
порядок силового расчета. Выясним, как это можно сделать
на примере части манипулятора МЭМ-10, содержащей схват
(рис. 4.21).
Допустим, мы выделили звено 6, Оно соединено враща-
тельной парой 6-5 со звеном 5 и находится в зацеплении
с сателлитами 54с и 64с. Во вращательной паре 6-5 имеем
пять неизвестных. Каждое зацепление дает по одному
неизвестному. Общее число неизвестных реакций равно семи.
Число же уравнений статического равновесия у звена 6
равно шести. Поэтому такая система не будет статически
определимой.
Если выделить звено 5, получим десять неизвестных
реакций (по пять в каждой из вращательных пар 4-5, 6-5).
Вторую вращательную пару на оси А —А, соединяющую
звенья 4 и 5, не учитываем, поскольку она дублирует пер-
вую. Число же уравнений статики по-прежнему равно шести.
Поэтому система сил звена 5 также статически неопреде-
лима.
Если выделить систему звеньев 5 и 6, то общее число
неизвестных реакций равно 12 (по пять во вращательных
парах 5-6, 5-4 и по одной в зацеплениях 5с-6, 6с-6). Число
уравнений статики для двух звеньев равно 6 • 2 = 12. Сле-
довательно, выделенная часть исполнительного механизма
статически определима.
Исходя из рассмотренного примера, можно предполо-
жить, что при последовательном отделении основных звень-
ев вместе с принадлежащими им передаточными, начиная
от конечного звена (схвата), будем всегда получать стати-
чески определимые системы.
Докажем справедливость этого утверждения в случае
когда произвольное i-e и (i — 1)-е
основные звенья соединены шар-
ниром первого типа (рис. 4.21).
Для других типов шарниров
доказательство аналогично. Ес-
ли манипулятор с п степенями
свободы, то в i-м основном
звене содержатся передаточные
звенья (i 4- 1)', ..., и‘, приводя-
щие в движение оставшиеся
основные звенья (i 4- 1), ..., п.
Все множество звеньев i,
(i 4-1)‘, ..., и* обозначим через
{/}. Через {ic} обозначим мно-
Рис. 4.21
129
5 Механика промышл. роботов, кн. 2
1
жество звеньев, содержащее вилку i и сателлиты
(i + 1«с, расположенные на вилке i, через {(i — 1)с} —
множество звеньев, содержащее вилку (i — 1), i и
сателлиты (i 4- 1)с,-1,...,ис,_1, расположенные на вилке
i — 1. Покажем, что если проводить силовой расчет
от {ic} к {!} и от {/} к {(i — 1)с}, то выделенные
множества звеньев будут статически определимы.
Допустим, силовой расчет множества звеньев {Ц уже
проведен. При этом определены реакции в парах, соединяю-
щих множества звеньев {/} и {Ц. Неизвестными у множества
{/} являются (и — i — 1) реакций в зацеплениях /‘-Г-1,
(i 4- l)‘-(i 4- 1)с-1,..., и’-Мс”1 и 5(и — i + 1) реакций во враща-
тельных парах i~i — 1, i-(i 4- 1)‘, (i 4- l)‘-(i 4- 2)*, ..., (и — I)1 и*.
Всего число неизвестных реакций равно 6 (и — i 4- 1). Оно
равно числу уравнений статики для множества звеньев {/},
поскольку в нем содержится (п — i 4- 1) звеньев. Множество
звеньев {i} является статически определимым.
У множества звеньев {(/ — 1)с} неизвестными являются
п — i реакций в зацеплениях (i 4- l)c-1-(i 4- I)'-1,..., иГ1-»'"1,
а также 5 (п — i) реакций во вращательных парах
(i 4- 1)с-1-0 ~ 1)> ~ 1)- Всего неизвестных реакций
6 (п — г).
В множестве звеньев {(/ — 1)с} может быть рассмотрено
только равновесие сателлитов (i 4- l)^”1, ..., nj-1, поскольку
вилка i рассмотрена при анализе множества звеньев {/},
а у вилки i — 1 не могут быть еще определены реакции
в парах (i — (i — l)-(ii — 2). Число сателлитов п — i.
Для них можно составить 6 (и — i) уравнений статики. Сле-
довательно, множество {ic} также статически определимо.
Таким образом, силовой анализ манипулятора МЭМ-10
(см. рис. 4.3) следует проводить по следующим множествам
звеньев: {5} =5, 6; {4с} = 4, 5cIV, 6cIV; {4} = 4, 5IV, 6IV
и т. д.
Передача усилий в шарнирах. После того как определена
структура статически определимых частей исполнительного
механизма, необходимо выяснить, как происходит передача
усилии между множествами звеньев в шарнирах.
Поскольку множества звеньев двух типов — {/} и {<с}, то
надо рассмотреть два случая передачи усилий: от {1} к {ic}
Исследуем передачу усилий в шарнире от множества
звеньев {?} к {ic}. Множество {i} (см. рис. 4.18, а) состоит
из основного звена i и принадлежащих ему передаточных
валов (i 4- 1)‘, ..., и‘, множество {Q (см. рис. 4.18, б)-- из
вилки i и сателлитов (i 4- 1)с£, ..., ис*.
130
1
Возьмем произвольное звено пе{/}. Его силовое взаимо-
действие с множеством {Ц в системе координат
можно представить в виде суммарной силы Fa[fc} и суммар-
ного момента Ma{i}, приложенных в центре 0,+1 шарнира
/4-1. Аналогично, все силы и моменты, действующие со сто-
роны {/} на звено bce{ic},^B системе О/+1Х/УЙ можно
свести к суммарной силе ь и суммарному моменту
приложенным в точке 0i+1.
Абсолютное движение звена а е {i} представим в виде
суммы поступательного движения точки Oi+1 со скоростью
и вращательного движения вокруг этой точки со ско-
ростью <bfl. Аналогично абсолютное движение звена Ьс е {/с}
представим в виде суммы v0 и &Ьс.
Суммарная мощность всех реактивных сил и моментов,
передаваемых множеством звеньев {/} к {/с},
N {<} = I [(А.»с) • Ч+1) + • ад]. (4.49)
Лб{0
Суммарная мощность, воспринимаемая множеством {ic}
от {/},
N{/c> = S • %+1) + • й>ьс)]. (4.50)
Ьс е
Пренебрегая потерями мощности на преодоление трения
в кинематических парах, связывающих {/} с {/с}, полагаем
= N{ic}. (4.51)
Подставляя в это равенство выражения для мощностей
и учитывая, что линейные скорости vo точек приложения
суммарных сил Fa{l-c} одинаковы, получим
£ i^a{ic} ' To/+i) 4" =
а е {£} а е {/}
= Z (^{оьс * ^о/+1) + X ьс' ®ьс)- (4-52)
е {ig} bg e {/g}
Так как при силовом расчете мы вводим силы инерции
и рассматриваем статическое равновесие {/} и {/с}, то сум-
марная сила У Fa[i}, действующая со стороны множества
в е {/}
{/’} на множеству {Ц, должна быть равна обратной суммар-
ной силе У F{i}b . Отсюда следует, что в (4.52) первые
ьс 6
слагаемые в обеих частях тождественно равны, и в резуль-
1
тате условие (4.51) равенства мощностей сводится к выра-
жению, связывающему моменты:
X (МЛ {1-с} • ша) = X (мюьс * ®ьс)- (4-53)
ее {i} i>ce{ic}
В (4.53) моменты Meyc}, A/y}f>c и абсолютные скорости
(оа, (Ьь заданы в системе Ot+1 х[у-z,-.
Так как вначале проводится силовой расчет множества
звеньев {ic}, а уже потом — расчет множества {/}, то равен-
ство (4.53) можно использовать для определения моментов
Ma[i} по уже найденным Му}Ьс. Рассмотрим решение этой
задачи более подробно.
-Каждый из моментов Ma{i}, M{i}bc имеет три составляю-
щие по осям х-, у-, z-. Поскольку при раздельном силовом
расчете для каждого звена находятся все три неизвестные,
число неизвестных в 3 раза больше числа звеньев. При
расчете рассматриваемых шарниров, являющихся многозвен-
ными механизмами, это приводит к быстрому увеличению
размерности задачи. Поэтому по аналогии с расчетом
абсолютных угловых скоростей расчет моментов необходи-
мо осуществлять в свернутом виде.
Подставим в (4.53) составляющие моментов и угловых
скоростей по осям у-, z-:
Е + м^а + =
ae{i)
= Е (м«ьМ
+ + Мт ьсЧ).
(4.54)
Так как у множества {/} равны составляющие абсолют-
ных угловых скоростей по осям х-, у'ь а у множества {ic} —
по осям х«, у-, то обозначая эти составляющие через (0у},
и (О у }, (Оу }, выражение (4.54) преобразуем к следующему
виду:
(Е+ (Е м<и.с1)°>« =
ae{i} ae{i} ee{i}
= ( Е л/«ьс)«>Ъ+( Е м«ь>(.с) + ( Е а/bc)<oge.
G {/q} fcg Е {i'q} Е {|q}
(4.55)
Правую часть в (4.5J) можно представить в виде ска-
лярного произведения М» л'абс
Ml
Mt MZ<
t,]
ncT,J
— вектор приводных моментов множества {Ц;
132
1
— вектор абсолютных угловых скоростей множества {Ц,
введенный ранее (4.32).
Левую ч^сть (4.55) представляем в виде скалярного про-
изведения Мх • (Ьмс, где
= [Л^/}> Mf(}, Mf1+1)t(, .... AfjJ1
— вектор выходных моментов множества {/};
= [со^, о?, <^i+1)T(, .... <oJrJT
— вектор абсолютных угловых скоростей множества {i} (4.31).
В итоге равенство (4.55) принимает вид
А?^х • =
(4.56)
Выясним, как можно выразить искомый вектор Мв$к че-
рез найденный при силовом расчете вектор приводных мо-
ментов и известные векторы и
Обозначим через р размерности векторов Мп^ и
через q — размерности векторов М®“х и cb;c.
Элементы матрицы IF*i+1, задающей связь векторов
абсолютных скоростей (ct рр
(cofg)f (4.47), обозначим
г »
через Соответственно к-е компоненты вектора
(1 к р) обозначим (А/ЪД, s-e компоненты вектора М-х
(1 < s q) — через (Af?nx)s. Преобразуем с учетом этих обо-
значений скалярное произведение, стоящее в правой части
(4.56):
абс
МЧ
• со
iks Иск
При выводе было использовано изменение порядка сум-
мирования. Через (Ж*+1)т и 1\к обозначена транспонирован-
ная матрица Ж*+1 и ее элементы. В результате получаем
(4.57)
133
Поскольку равенство (4.57) должно выполняться для лю-
бых вскюров (coVjjc)r, отсюда следует:
М= (ж*\+ J1 Mn{i(4.58)
4 J I C>
Еще раз отметим, что вектор определяемый по
(4.58), задан в системе Oi+1x£y-zJ. Для того чтобы получить
вектор моментов в системе Oi+1xiyfzl-, его надо умножить
на матрицу В*:
Й) = &71 (М-Х).„
где
(4.59)
Рассмотрим передачу усилий от множества звеньев {ic}
к {i + 1}.
Проведя аналогичное доказательство, получим, что век-
тор выходных моментов множества {ic} в системе
Oi+ixi+1yi+1zi+i можно найти из уравнения
(4.60)
Для того чтобы выходные моменты множества {ic} найти
в системе Ox+1x-y-z-, умножим вектор на матрицу
«1+1
(4.61)
Таким образом, связь выходных моментов множеств
звеньев {/} и {ic} с приводными моментами множеств {Ц,
{i + 1} задается формулами (4.58), (4.59) и (4.60), (4.61).
134
1
Силовой расчет множеств звеньев вида {/}. Выше были
рассмотрены задачи разбиения исполнительного механизма
на статически определимые множества звеньев {i}, {ic} и
передачи усилий между этими множествами.
Перейдем непосредственно к силовому расчету. В общем
случае для множества звеньев вида {i} исходными данными
явл яются:
1) инерционные и внешние силы и моменты, приложен-
ные к звеньям из множества {*};
2) реакции со стороны звеньев из множества {ic}.
Для сокращения записи инерционные и внешние зилы
и моменты заменим их суммами:
0 + 1) Г*
। гвн
+ г 0+ !)!'’
М. = + М?н;
^(i+l)ti = ^0+1)Т« + ^S-Dth
(4.62)
= + Mf}.
Через F{i}, М{1} обозначены суммарные внешние и инер-
ционные силы и моменты, приложенные к звеньям из {/}.
При силовом расчете предыдущего множества звеньев
{ic} в системе координат Ol+1x^z- определены:
1) вектор выходных моментов множества {/}
м^х = [м^1х х, м$хл м?ы
вых z АТ вых zIt .
(i+l)f/> •••» lvlnji J »
2) реакции в кинематических парах, соединяющих {ic}
с {г}:
а) силы реакции, действующие от колес к1 на сателлиты
к[ в зацеплениях к1-к[,
(ДГ = [*Г1)х, Rli+1}v, 1)х]? (bi+ 1, и);
135
б) суммарная сила реакции, действующая на вилку i
со стороны вилки i + 1 и сателлитов,
(Д)г = [Я*, ЯГ, Я?]т;
в) суммарный момент от сил реакции, действующих на
вилку i,
(М,)г = [МП 0, М?]т.
Определим, как выражается в системе координат
Oi+1x'y-z- сила реакции Я£+1, действующая на сателлит /с’
от колеса к', через момент сил М®“^, передаваемый колесом
/с* сателлиту к[.
Окружное усилие, действующее по оси х-,
К^Пх = +MlV/rkV,
здесь и дальше верхний знак — для левостороннего распо-
ложения сателлита, нижний — для правостороннего.
Составляющие по осям y'if z-:
«/'+'>>’ = ± I I tg a cos 61 = ± 1 1 t'i+ltg.°t_;
Г*Ф’ ]/w2i+i 4- 1
K/i+l>2 = I I tg a sin 8! = ШЙ'Я — tg * ;
rl<V ]/U2i+1 + l
следовательно,
Реакции (см. пп. 1, 2) показывают, как звенья из мно-
жества {/} действуют на звенья из множества {гс}. Для того
чтобы найти в системе О^^у^ обратные реакции, дей-
ствующие со стороны звеньев из {ic} на {/}, надо реакции,
указанные в пп. 1 и 2а, взять с обратными знаками и
умножить на матрицу В*., задающую переход от системы
координат O.+ iX-j/Zf к системе О{+iх{у^ь а реакцию п. 26
просто умножаем на В*..
В итоге получаем:
Г) вектор выходных моментов сил, приложенных к звень-
ям из множества {(} со стороны звеньев из множества {ic},
136
1
I
Л/И*
M(“2
MV+2»Ti
MB\Z
1ГЛ «fl
—M|JJX cos Yf 4- M™*y sin yf
— M®J},X sin Yi — M^fjxy cos Yi
— Mfblxz
-M(“w
о
—мвь^
fl
KM
(4.63)
2') реакции в парах, соединяющих звенья множеств {/}
и {Ц:
а) силы реакции в зацеплениях, действующие со стороны
сателлита к* на колесо к1:
V
, Л/г»? |tgawj+1 .
—cos у, ± -—“Т/ в 1+1 sin %
r*ti '•Mi|/“2i + l + 1
—-~LL- sin Yi 4--T- z •-=- cos Yf ;
+ 1
I MIT, I tg a
(4.64)
б) суммарная сила, действующая co стороны вилки i + 1
и сателлитов, принадлежащих ей, на вилку i:
(Ri)i
: cos Yi — R? sin Yi
sin Yi
Ry cos у»
(4.64a)
(JVT j)i —
Mf cos Yi
M* sin Yi
(4.646)
Внешние и инерционные силы и моменты (4.62), а также
реакции (4.64) — (4.646) являются исходными данными для
силового расчета.
В результате расчета необходимо определить:
приводные моменты, приложенные к звеньям из мно-
жества {i} со стороны множества звеньев {(i — 1)с};
реакции во внешних парах, соединяющих множества
звеньев {i} и {(i — 1)с};
реакции во внутренних парах, соединяющих звенья мно-
жества {i}.
1
Возможен следующий метод решения: для (п — i + 1)-го
звена, входящего в {i} (i, (i 4- I)1,..., л1), составить 6 (и — i + 1)
уравнений статического равновесия и, совместно решив их,
найти все неизвестные реакции во внешних и внутренних
кинематических парах множества звеньев {/}; по найденным
реакциям во внешних парах можно определить приводные
моменты.
Метод имеет следующие недостатки:
число уравнений в системе быстро растет с увеличением
числа звеньев в множестве {/}, например для одного звена
необходимо составить шесть уравнений, для двух — 12, для
трех — 18 и т. д.; составление и совместное решение таких
систем затруднены уже при наличии в множестве {/} двух
или трех звеньев;
в том случае, когда целью силового расчета является
определение только приводных моментов двигателей, расчет
реакций во внутренних парах множества {г} не нужен и,
следовательно, нет необходимости составлять и решать
полную систему уравнений.
Для устранения этих недостатков необходимо применять
специальную последовательность силового расчета, позво-
ляющую выделить отдельно расчет приводных моментов,
реакций во внешних кинематических парах и реакций во
внутренних парах.
Изложим, как можно реализовать описанную последо-
вательность расчета для множества {/} в общем случае»
Моменты сил в уравнениях статического равновесия будем
рассматривать относительно точки Ot — центра шарнира i,
в котором приводится в движение основное звено i (см.
рис. 4.18, а).
Вектор приводных моментов Mf = [AfЛ/ЭД, M?z, ...
..., Af°|JT находим из уравнений статического равновесия
всего множества звеньев {/} во вращательных движениях
вокруг осей xt и yf и каждого звера из множества {/} —
вокруг оси При это^ момент М, создаваемый относи-
тельно точки силой F = [Fx, F”, F’]T, приложенной в не-
которой точке А, будем обозначать через MA(F) и пред-
ставлять в виде:
I Мх
,Ф(Г) = | м>
1_М2
pV'-pV'
- Ро,л X F = I p2o.AFx - pfaF2
L pxOiAFy - pb.^
где р&.л, р£.л, pzOiA - проекции вектора р0.л на оси xh yb zt.
138
1
Найдем моменты, создаваемые силами реакций и
Д-. Вектор соединяющий точку О,- с точкой Ак контакта
колеса /с* с сателлитом /£, в системе Of+iX-y-z- имеет вид
(Ро^)/' — [0> + гк т i> 4 rkc t JT>
где lt — расстояние от Of до Oi+1; rk^if rk ।f — начальные
радиусы колеса к' и сателлита к^. В системе
ipo^i = ВУ. = [•+ гк Г. sin Yi> ± »•* t i cos у» /, - n t ,]T.
Момент от силы Rk+1
М(^+1) = ФоЛ)х («/+'),=
(4.65)
Момент от силы Л,-
(4.66)
Внешние и инерционные силы, приложенные к звену к1
(к — i, ..., и), будем обозначать Fkj (1 < j < jk), где jk —
число этих сил. Точки приложения сил обозначим Tkj.
Моменты, создаваемые этими силами, относительно точки
Г PbiTkflj ~
м (Fw) = (50Л. X = pb.7j.FJ; - • (4-67)
L - Р&|ТцД-«
Найдем вид уравнений статического равновесия звеньев
из множества {/} во вращательных движениях вокруг осей
139
1
I
xb yb zb Вначале рассмотрим вращение всего множества
вокруг оси хь В этом движении на звеньях {i} действуют:
приводной момент МЧ$ со стороны звеньев {(i — 1)с};
внешние и инерционные моменты Мхщ (4.62);
моменты Мх (Fkj) (4.67) (к — i 4- 1, ..., и), создаваемые
вокруг оси Xi внешними и инерционными силами;
входной момент (4.63), приложенный со стороны
вилки i 4- 1 и сателлитов {ic};
момент Мх (Ri) — — № (4.66), создаваемый реактивной
силой Rii
) (к = i 4- 1,..., и), создаваемые силами
моменты Мх (Rk +1
[+1 в зацеплениях шарнира i 4-1.
В итоге уравнение статического равновесия множества {/}
во вращательном движении вокруг оси xt будет следующим:
и п
M4V
Рассматривая аналогично статическое равновесие {i} во
врашательном движении вокруг оси yf и отдельных звеньев
{/} — вокруг оси zb получим остальные уравнения:
и п
М",?, + Y £ М (F+ w + Е M(R[+ >) = 0;
k-ij-1 k = i+l
• •
М"’- + Mf+ У Мг (FJ + = 0;
MJf+ M^, + f Мг (F„j) + = 0.
J— 1
Из составленной системы находим вектор приводных
моментов множества {i}:
140
1
п Jk
МУ®
п ^к
Е Wv)W+W
Ml
м;л:
Mi
М*г
1ТЛ. fl.
Mi
Мъ1-
1V1 nfl
п
(4.68)
Прежде чем перейти к определению реакций в кинема-
тических парах, соединяющих {/} с {(i — 1)с}, необходимо
найти выходные моменты звеньев из множества {(i — 1)с}.
Выражение для M^i}} в системе координат О.х.у.г,- нахо-
дим из (4.60):
Мвых = (4.69)
Вначале находим реакции в зацеплениях. У произволь-
ного fc-ro сателлита &с‘-1 в зацеплении с колесом к1 окруж-
ная сила
Яi ~ _ i)/rkc । (i-1)«
Составляющие по осям yh zc.
, , в I ЛС^-1) | ц tg а
Rl= + | R*k | tg a cos 8j = +----
U‘ +
R2 . IAC<,_.)Itg«X
Rf. = \Rl tg a sin Ot —-------. .
to-+1
KC I v r
Полная сила реакции в зацеплениях:
|tga/(r*+ 1)
(fc=(i+l),...»м).
(4.70)
141
I
Момент Л? (К*), создаваемый силой Rlk
точки О„
относительно
M (ДО =
(4.71)
Определим реакции во вращательной паре (i — l)-i со
стороны вилки i — 1 на вилку i:
к •• = ГД1_ Д/,—1W. RZii— 14
Реакцию находим, составляя уравнение статиче-
ского равновесия множества {г} в поступательном движе-
нии:
откуда
(4.72)
Составляющая реактивного момента
(4.73)
Составляющую Мх
менты, которые создаются силами Rk (4.70) в зацеплениях
сателлитов fcj"1
находим, вычитая из
с колесами к1:
Л
мх<
= МПЛ
t
I
г
1
I
1
(±|М^Р _„|) =
I
г
м
М5
п
щ
п
Л
о
М1^ мо-
г
(+|a^“tW)-
= Л/*?о — —
щ
(4.73а)
Таким образом, реакции во внешних кинематических
парах определены [формулы (4.71)—(4.73а)].
142
1
Если задачей силового расчета является определение
только приводных моментов, то на этом расчет множества
{/} завершается и переходим к следующему множеству
звеньев — {(i—1)с}. В случае полного силового расчета не-
обходимо также найти реакции во внутренних кинемати-
ческих парах множества {/}.
Между собой звенья из {/} соединены вращательными
парами вида к*-(к - 1)* (к = и, ..., i + 1). В каждой такой
паре неизвестными являются: сила реакции
= Pfy-iJtUt
Ry(k -1) Т i, к f i>
(*-DtutJT и момент М(Л_1)Т/ЛТ/
~ [ЛЛ* -1) j i, к ТI» Щк - 1) Т i,k Т i> 0]Т-
Реакции можно определить из системы урав-
нений, описывающей статическое равновесие внутренних
трубчатых валов п\ ..., (i*+ 1)‘ в поступательном движении.
С учетом = ~R(k-iyti,kv система принимает вид:
R -4-7?» 4-jR»+1 + F = О*
^(«-nt»,nti «Т»^ «V т «Т»
4
(и — 1) f i
Ri, (i +1) t i
R(i +1) T i + + t i + R(i +1) T i
(4.74)
где R'k । i9 R£ ft — реакции вала к* с сателлитами i-ro и
(i + 1)-го шарниров; Fk^ — сумма внешних и инерционных
сил, действующих на в<|л к'.
Обозначим суммы Fk^ + ^и» + Rkti1 через Д|,., введем
векторы R = 1)| jt j,..., jRj(/+ JT и F = [F„।F^+ j J1.
Система (4.74) примет вид
AR + F — О,
(4.74а)
— двухдиагональная матрица.
143
Решение (4.74) в векторном виде * следующее :
(4.75)
где А 1 — матрица, обратная матрице А:
или
(л- 1)Т i, nfi
(и—2)fi, (и—l)t ’ “
(4.75a)
• - ffi+Dti-
Составляющие ЛТ1, Щк-1уи,ки реактивных мо-
ментов (к = и, ..., i + 1) находим аналогично. Уравнения
равновесия произвольного к-го внутреннего вала во враща-
тельных движениях вокруг осей xi9 имеют следующий
вид:
~Щи,(к+1)и +
jk
+ ^Tl + EMW = 0;
J — 1
M* (К' T () + Mx (R$\I)
i, (k +1) t i + MVi.tut.- + + M'(Rtfl)
jk
+ M^j+ £M4^-) = o,
j= 1
где Му(Кк^9 My (КЩ)>- составляющие
по осям xi9 yt моментов сил реакций Kj^f, RttJ вала к*
с сателлитами i-ro и (i + 1)-го шарниров [см. (4./1), (4.65)];
М хк । f, М11 j — суммы проекций на оси xi9 внешних и инер-
ционных моментов, действующих на вал к1 [см. (4.62)];
Мх (Fkj), Му (Fkj) — моменты вокруг осей xi9 yif создаваемые
внешними и инерционными силами, действующими на к1.
Обозначив суммы
(RiTi) + М*(R^}) + £ ЛГ (Fy);
j=l
- Щи + My(R^J + My (Rtfl) + f Mf(Fk)
j=i
144
и, введя векторы
Мх —
MVl)U«Ti
MУ(п - 2) f i, (« -1) fi
Мх =
(п— l)fi,nfi
^«-2)ti,(«-l)|i
^i+Dti,(»+2)ti
L ^(i+l)ti. -
’ A^"Tf "
^\n— l)f i
^ii+2)ti
получим системы уравнений относительно Мх,
гичные (4.74а):
АМХ + Мх = 0;
АМУ + Му = 0.
М\ анало-
(4.76)
(4.77)
Матрица А имеет тот же двухдиагональный вид, что
и (4.74а). Следовательно, решения уравнений (4.76), (4.77)
также будут аналогичны решению (4.74а):
1) Т i, «fi -^nji’
^(«-2)ti,(«-l)fi = ~^nfi — MXy —
M1,(i+Dti = “-^iti ~ ^1«-i)ti - • • • -
^n-l)fi,«ti= “^«t»»
№(n_2)|i.(«— l)t» “”-^«ti ~ ^«-Dti»
(4.78)
(4.79)
^,(i + l)ti “ "^Jff ^«-l)|i “ ’ ’ ’ ^i+nti*
Таким образом, выражения (4.75a), (4.78), (4.79) опреде-
ляют реактивные силы и моменты во внутренних кинема-
тических парах множества {(}.
В качестве примера рассмотрим силовой расчет мно-
жества звеньев {5} = 5, 6 у манипулятора МЭМ-10 (рис. 4.21).
Внешними силами являются: сила тяжести звена 5, сила
тяжести звена 6, сила тяжести груза, удерживаемого захва-
том 6. Массы звеньев 5, 6 и груза обозначим через т5, тб9
тг. Центры масс звеньев 5, 6 и груза находятся на оси
Osz5 на расстояниях ls , ls , ls от центра Os шарнира 5.
о о п
145
1
Центральные моменты инерции звеньев 5, 6 и груза обозна-
чим через Л5 = [J?, л5, /г5]т; Л6 = Ut, Jy6, Л Г; 4 = [Л
jy9 J*]\ При этом JI = Jys> = J£.
Пусть для рассматриваемого момента движения в кине-
матическом анализе уже определены проекции на оси х5,
У5, z5-
ускорения свободного падения д\
абсолютных линейных ускорений центров тяжести звень-
ев 5, 6 и груза:
(4s5)s = Ей«5> ая515 > (as6)s = ^s6]s>
(<у5 = К, «?г, О?;
абсолютных угловых ускорений звеньев 5, 6:
@з)з = [ез> еДз; (6б)з = [ев> 6&JJ,
при этом 85 = 8g, 8$ = 8&.
Внешние силы, действующие на звенья 5 и 6, будут сле-
дующими:
F™ = "ЫЬ; F™ = (w6 + "U 05-
Внешние моменты отсутствуют.
Инерционные силы
= ~m5dSs; = -m6aS6 - тДг.
Инерционные моменты
Моменты от внешних сил относительно точки О5:
М (FH =
— Ц5т50У5
Ь5^505
О
- (46 Юб + Ьгтг) 0У5
(lS6m6 + д$
О
Моменты от сил инерции:
[h^5ays 1 Г lS6m6ay6 + lsmrayr
-lasmsc^5 I; M(F£) = | - lS6m6axS6 -
0 J L 0
146
t
Поскольку множество {5} — конечное и реакции со сто-
роны предыдущего множества звеньев {5с} отсутствуют, то
из (4.68) находим приводные моменты звеньев
{5} ~~
Г мм
ММ
- - (Jg+J^) eg - (т51,5 + т61
+тг1^) gl + + wigljgtZjg +
- J5eJ - (J>6 + JJ) eg + (m3/.5 + m6lS6
X 05+"«5^5
s6 '
mJ. ау.
m6L,ax — mJ. а
Перейдем к расчету реакций во внешних парах. По фор-
муле (4.69) находим выходные моменты на вилке 4 и сател-
литах 5cIV, 6cIV (матрица перехода W** определена ранее
в кинематическом анализе)
д/выхх
м {4с}
1 0
о о
[^♦]тЛ/^5)= о о
о 1/2
О 1/2
О о
о о
1 1 I х
О —W5/2 I
О «5/2
М"*
му + м%
Щг
му _
В итоге
5c|IV
(1/2) М^} - (Uj/2)
(1/2) + (Hs/2) JVf?2
о
M?z + Mg2
(1/2) М^} - (Us/2) W
(1/2) + («уг) Mg2
Л/^}
х
М^У
147
1
Реакции в зацеплениях 5cIV-6, 6cIV-6 находим из (4.70):
^6ctIV
^5сfIV /Г5с ТIV
-1 t IVI «5 tg а/(гм IV + 1)
I ^5c t IV I tg a/(r5cfIV ]/u5 + 1)
^6cfIV I I ^6c11VАбеfIV __________
^6cfIV I = I I M??frv I M5 tg a/(r6cfIV j/W5 + 1)
- ^6cf IV J L I ^6c|IV I tg a/(r6c|IV ]/M5 + 1)
Реактивную силу во вращательной паре 4-5 находим из
(4.72):
m6aSf. - тга
5cfIV
Ч + шг) 9 s -
^6ctiv]-
5
У реактивного момента М4,5 = [М4> 5, О М4) 5]т из (4.73а)
получим
= = - (Jz6 + J*) £g,
из (4.736) следует
5 = М%}
«5
(I I -
I д/вых
I 1V16ct\
Расчет реакций во внешних парах закончен.
Определим реакции во внутренней вращательной паре
5-6. Силу К5,6 определяем из (4.75а):
= -[(«6 + 1ИГ)05 - «16% - + K|ctIV + K|cTIV].
Составляющие М$г6, реактивного момента М5>6 =
= [М5,6, 6, б]т определим из (4.78), (4.79). При ^этом
ромеиты, создаваемые вокруг осей х5, у5 силами K|cjIV,
^6ctiv, находим из (4.71):
= -[М^ 4- MX(FIH) + ЛГ(Рб) +
+ M'(R55criv) + Af>(Klt,v)];
Щ, 6 = - Щ = - [М?> + МУ (FF) + МУ (Fg)
M>(R^n) + My(R^n)-].
Подставляя значения моментов, получим:
м;. о = - [-м + Ji) eS - (l,6m6 + ls mr) gi +
14K
у ul + 1 tga ,
lS6m6af,6 + + !-----—5—(I Mgftv I ~ IMgfa |)];
MJ. e = - [-(Л + J?) e£ + (l„6m6 + krnj g*s -
- ^6me°s6 - l.mrt' + Mgfy + M^y].
Таким образом, в результате силового расчета найдены:
приводные моменты множества {5}
М?
= Л^}, Mf, М^]Т;
выходные моменты множества {4с}
м$5 = [м$Г, мг", м^, м?ГтЪ]т;
реакции во внешних кинематических парах множества
6c|IV
[Л/4.5, 0> Ml.sT во вра-
в зацеплениях 5cIV-6, 6cIV-6;
б) сила Л4,5 и момент М4г 5 = [М4> 5, О, М4> 5]т во вра-
щательной паре 4-5;
реакции во внутренней кинематической паре 5-6: сила
Я5 6 и момент М5> 6 = [М£ б, М\ 6, 0]т.
Силовой расчет множества звеньев вида {Ц. Принципы
силового расчета те же, что и при расчете множества вида
{/}. Приводные и реактивные силы и моменты необходимо
определить в системе координат Ol+1x;yjz- (см. рис. 4.17).
Вместо всей вилки i условно рассматривается равновесие
ее части
Выше, при расчете множества {i
нат Of+iXi+iJi+i^i+i определены:
1) вектор выходных моментов множества {ic}
М= [М^х, М?ы*у,
2) реакции в кинематических парах, соединяющих {ic}
вала, содержащего сателлиты.
1} в системе коорди-
МПы1хг.....
а) в зацеплениях сателлитов к'с с колесами к1 (к = i
п) силы
б) во вращательной паре i-i
1 сила
и момент
+ О» ^Ц<+1)]Т’
149
1
Силы и моменты, описанные в пп. 1, 2, определяют,
как действуют звенья из множества {Ц на звенья множества
{i + 1}. Для того чтобы найти в системе обратные
реакции, действующие со стороны {i + 1} на {ic}, необходимо
силы и моменты пп. 1, 2 взять с обратными знаками
и умножить их на матрицу ,
системы Oi+1Xi+iyi+1zt+1 к системе
задающую переход от
Oi+iXtfizl.
В результате получим:
Г) вектор входных моментов, приложенных к {ic} со
стороны {i + 1}:
Mj-^cosg
WJzsingf+1
Йс)
— ЛЛН* cos ql+1
ШЧХ,
L J L
2') реакции co стороны {i + 1} на {ic} :
а) силы в зацеплениях kt+i-k‘c (к = i+ 1.и)
Mt™ cos д,ч. i
» , ! — l< I.. .....— —-
(4.80)
(4.81)
I | tg Qt COS ft .ц
б) силу, действующую co стороны вилки
1 на вилку i
R(i +1) i
~ ^i(i +1) C0S ^i + 1 ~~ ^i(i+ 1) S*n 9i+ 1
рУ
^F(i+1) s*n Qi+1 ^i(i+l) COS Qi + 1
(4.82)
и момент, действующий co стороны i
1 на i
-Mf(/+i)Cos^+i - Mf(i+1)sin&+1
0
singi+i -Mf(i+1)cos&+1
(4.82)
К звеньям из {ic} приложены также внешние и
инерцион-
ные силы и моменты, которые заменяем суммами:
-Л/?ых>’
М sin g,+!
150
I
М<+1)сТ< “ ^O + DcTi +
(4.84)
M(*+ De f«
M tf = .;
”c T1 nc T * »c T1 ’
M, j( = Ml. + mw,.
UCJ \lc} vci
Внешние и инерционные силы (4.84) вместе с реакциями,
действующими со стороны {i + 1} на {ic} [(4.80) — (4.83)],
являются исходными данными для силового расчета мно-
жества звеньев {ic}.
MBk(R[+l), M°i+i(Rk+1), создаваемые силами Rk+l относи-
тельно центров Вк вращательных пар k*c-i и точки Oj+1
(рис. 4.22).
Радиусы-векторы
POf+Hfc
системе координат
i+ixi+iyi+izi+i имеют вид
(pBkAi)i +1
— [0, 0, Гкс । {]т; (р0. + +!
i Гк t if rkc t i]T-
в системе
Умножая эти векторы на матрицу получим
векторы рВкАк, pOi+iAk
0
х K[+1], получим искомые выражения для моментов:
Рис. 4.22
1
T |Af^(|u(+1 tg a cos ф+!/!/«?+! + 1
l&k (R[+ *) = - Mffi,
L ± | | ut+! tg a sin ft+!/]/ft2+! + 1.
+1 (R ‘+1) =
; (4.85)
Ml™ . + ltgacosft+i
+ —c-sinft+, +----£----------------------
U/ +j Ц' +1
Ui+1
cos qt+1
- M ,
i I ]/“?+1 + 1 tg a sin -n
Щ+ 1
(4.86)
Как и в случае множества {г}, расчет начинаем с опреде-
ления приводных моментов
Ml X = [MV? Mfy, мк}
Vcj L Ver 1 Vcj
M"> t (]T.
V 1
Для определения их составляем уравнения статического
равновесия всего множества {ic} во вращательном движении
вокруг осей х-, z'i и каждого звена из {ic} — вокруг оси у-:
+ Wj + м^
Л
M°i+1X(K;+1)
(ЛГ (Гу)) = О; = 0;
+ м?у + МЬС} + Mv+ш + £ M°'+‘2(«i+1)
k~i+ 1
£ £ (ЛГ (Гу)) = 0;
it — i j — 1
(4.87)
WHm/ + WAm* + = 0;
jn
+ АРИХГ- + Ш tf + У (My(F„)) 0.
«cl1 ncT1 nc Г1 t—i v
J- 1
Система описывает статическое равновесие звеньев {ic}
под действием: а) приводных, б) входных (4.80), в) внешних
и инерционных (4.84), г) реактивных моментов сил (4.81) —
152
1
I
(4.83), а также д) моментов сил, создаваемых внешними
и инерционными силами. Из (4.87) получим
ис/
М^У
М
п ______
(<с) -
МК)
»с t,
М"У
MW + ЛЯ
+A1J
О
»
му,
М‘Ч
Mi
Z М” (Л,у)
(4.88)
Затем определяем выходные моменты М"'"
Из (4.58) получим
Wjx = [^+1]TM^c}.
звеньев
(4.89)
Теперь определяем реакции во внешних кинематических
парах, соединяющих {ic} с {/}. Эти пары являются за-
цеплениями.
У произвольного к-го колеса входящего в зацепление
с сателлитом /с*., окружная сила Rtf = + М™*/гк ।,. Составляю-
щие по осям yj, z\:
153
1
Rtf = ± |Kix|tgacos8i = ± ||ui+ttgot/(rMfуuj+1 + 1);
R* = l^ltgasinSj = |M|^|tga/(rktlJ?i4?+i + 1).
Полная сила реакции в зацеплении к1-к[ в системе
Oi+ ix'tytz'i
+ Ml^/rkU __________
I ^kfi I Ui+1 <*/(rkii]/ui+i + У
I| tg a/(r*Tf ]/u}+l 4- 1) .
(4.90)
где к = i + 1,..., n.
Таким образом, реакции во внешних кинематических
парах множества {ic} найдены.
Найдем моменты MBk(R})9 M°i+^(Rik)i которые создают
эти реакции относительно вращательных пар kl-i (точки
Вк) и в центре шарнира О|+1:
Мв“ (*Й = 1>вклк t, X Д; М°‘+> (Л0 = Pol+lAkv X R[.
Величину находим из (4.90). Векторы рВклк11, Pol+lAkv
в системе Ol+1xiy[z'i имеют вид:
= [0, 0, Дт; р0/+1ллр = [0, ±rk]i, -r*ct Дт;
умножая их на R0 получим:
М°<+ (J?0
МВк (R‘i) =
(4.91)
±|A/^ll/u?+1 + ltga
±M^ui+1
(4.92)
Найдем реакции во внутренних вращательных парах
Q-i, соединяющих сателлиты к10 с вилкой i. Силы реакции
Rifkc^ находим из уравнений статического равновесия са-
теллитов в поступательном движении:
^i,kc]i + + R-k + Fk^i ~
где \ R[ — силы реакций, действующие на сателлит к[ со
внешних
к*с (4.84).
стороны колес fc/+1 (4.81) и к1 (4.90); F
и инерционных сил, действующих на сателлит
В результате имеем
сумма
n).
(4.93)
154
1
Составляющие М[к реактивных моментов
= в паРах Q-i находим из урав-
нений статического равновесия сателлитов во вращатель-
ных движениях вокруг осей х[, Zti
Mfa, + М^,+ + M^R?') + £ M«(Fy) = 0;
J= 1
Л»
b ^kc]i
MB* (Rti
mb& (Ki+ x)
0,
где M^c |h Af|c|f — суммарные проекции на оси xj, zj внеш-
них и инерционных моментов,
действующих на сателлит
(4.84); Mx(Rk^t M2(Rk^, Мх - проекции
на оси xj, zj моментов от сил реакции Rk, Rk+1 относительно
центров пар Вк (4.85), (4.91); Мх (Fkj), М2 (Fkj) — составляющие
по осям х-, z- моментов внешних и инерционных сил
относительно Вк
В результате получаем:
M?kcV = - MxkJf + Мв*х(R‘k) + (Rj+i)
Jk 1
£ Mx (Fkj) ;
J
(4.94)
j
+ №**(/$ + M^(R>^) + £
j— 1
(4.95)
Таким образом, реакции во внутренних кинематических
парах найдены. Они определяются по формулам (4.93)—
(4.95).
Для дальнейшего силового расчета необходимо знать
суммарные реакции, действующие на вилку i со стороны
вилки i + 1 и сателлитов.
В системе координат О^+^у'^ суммарная сила реакции
V+1H
(4.96)
где F(l+1)i определяется по формуле (4.82); Ri k Ti
Сила Ri приложена в центре Oi+i шарнира i 4-
— по (4.93).
1.
Аналогично находим в системе координат Oi+1xjy;z;
составляющие по осям xj, z\ полного реактивного момента
Af(, действующего со стороны вилки i + 1 и сателлитов
155
на вилку i. Так как
-> -► « -> -►
^i = ^(i+l)i+ Z tPOi+iBk Х
к=< + 1
ф
Mkc]i,i = JT’ ^Oi+lBk ~ [0, irfct»» ЧТ»
то
= t М^сТ,Т £ rkURlkcU; (4.97)
k = i+l *=i+l
Mj = Щ+п, - t Mt^,± £ rkVR\kc1„ (4.98)
fc = i+l k=i+l
где Mz{i+i)t определяются из (4.83); Mftk |fi Mzitku - из
(4.94), (4.95); Я?м/, К?м, - из (4.93).
В качестве примера рассмотрим расчет множества
звеньев {4с} = 4, 5cIV, 6cIV манипулятора МЭМ-10 (см.
рис. 4.21).
Исходными данными являются: массы сателлитов 5cIv.
£ IV тт
ос — Tn5cfiV, wifotiv' Центральные моменты инерции сател-
литов: Jsjc = J£c, J5C]T; JS6c = /ут, причем J$G »
= *^5c J 6c — Jfc •
Для рассматриваемого момента движения в кинемати-
ческом анализе найдем проекции на ос
У4, 4:
ускорения свободного падения д
= [з« з,> зJ5-;
абсолютных линейных
ускорений центров тяжести сател-
литов :
(ass)4z = [л*5, as5> J
(^5б)4' Е^зб> ^s6> ^s6j|4' >
абсолютных угловых скоростей вилки 4 и сателлитов
5с’v, 6cIV:
(£4)4' Ге4, 4,
(^5с Т iv)4' — Le5cf IV, e5cfIV, e5ctiv]4' J
(^6cfiv) — [e6ctIV, e2cfIV, e6cjIv]T,
При ЭТОМ 64 — E5c|iv e6c|IV 9 e4 eic|IV “ e6cfIV*
156
Внешние силы, действующие на звенья 5c,v, 6c,v в системе
05x4yi4, будут следующими:
^5cfIV — w5c|iv^4'j
^6cfIV ~ W6c|IV^4'-
Внешние моменты отсутствуют.
Инерционные моменты и силы:
Я Л рЛ
•'Sc’M IV
ТУ Fy
J 5c 5c j IV
JLe5
Ma
JW6cfIV
/Л рЛ
•/6cb6cTIV
ТУ Fy
J 6c 6c t IV
Jz £z
*'6cfc6cfIV
5с j IV — ~ т5с | IV fee f I v)4’> 5
^6cflV
W6cfIV (4s6ctiv)4'
Моменты от внешних и инерционных сил равны нулю,
поскольку силы приложены в центрах тяжести В5, В6,
являющихся одновременно центрами вращательных пар
4-5 с™, 4-6ciN.
При силовом расчете множества {5} были определены
в системе координат O5x5y5z5:
1) AfB$^ — вектор выходных моментов множества {4с};
2) реакции в кинематических парах:
а) силы реакций K^C|IV, -Ricnv в зацеплениях 5cIV-6, 6cIV-6,
действующие eg стороны сателлитов 5 с1 v, 6с1 v на звено 6;
б) реакции Я4>5, M4t5 во вращательной паре 4-5.
Так как для силового расчета множества {4с} необходи-
мо знать реакции, действующие со стороны множества
звеньев {5} на {4с} в системе O5X4y4z4, то по формулам
(4.80) — (4.83), зная реакции пп. 1, 2, определяем:
Г) вектор входных моментов, приложенных к множеству
звеньев {4с} со стороны {5}:
М^У
- cos qs - Лфу sin q5
-ЬГГЛ*У
МЪ
м^2}
•M?cfiv
f
i
г
1
\
1
МЗДЛ sin qs - Мcos q5
~ мв5сыт7у
-
2') реакции co стороны {5} на звенья из {4с}:
а) силы, действующие в зацеплениях 5cIV-6, 6cIV-6 со
стороны звена 6 на сателлиты 5cIV, 6c,v:
157
1
(^6c j I v)4'
M^yCOSgg
r5cjIV
Д вых
M5cfIV -
Ox
r5ctIV
I л#вых
I м5cTi
I mmiv । tgacosg5
r5c f IV ]/M5 + 1
APffiiv cosg5 | M|cbITxiv | tg a sir
r6cfIV
I Л/ВЫХ
I 7W6c?
r6cfIV
Mg?IV .
— T sm a5
r6cfIV
6) реакции в паре 4-5, действующие со стороны звена 5
на звено 4:
I — R%, 5 COS <15 “ ^4. 5 8>п Qs I
(В 54)4/ = I — ^1.5 I»
L R4, 5 sin <15 - Rz4, 5 cos q5 J
5,4)4'
- Mit 5 cos q5 - 5 sin qs
0
M4,5 sin q5 - Mlt 5 cos q$
Реакции пп. Г, 2' вместе с внешними и инерционными
силами являются исходными данными для силового расчета
множества {4с}.
Прежде чем перейти к расчету, определим по формулам
(4.85), (4.86) моменты MB5(/?fcTIV), М^К^у), М^^цу),
M°s (#6cjiv)> создаваемые реакциями «5ctIV> R&tIV ОТНОСИ-
тельно точек В5, В6, Os:
(Blcf iv) —
158
I *Ov I
МВб (^6с t iv) ~
-\M
вых
6cfIV
us tg a cos g5/|/U5 +1
I u5 tg a sin q5/]/w| +1
rM5ctTv •
sm q5
“5
w5
-
cos qs
Wfiv
—££J— cos qs
w5
5c JIV I *©'
U5
sin qs
M&tiv •
—--Ц-- sm qs
«5
ACtiv
—cos o5
u5
w5
- у
1 t iv 1 tg«
COS ^5
sm qs
Силовой расчет начинаем с определения приводных мо-
ментов.
Для этого используем формулу (4.88):
Afnx
M{4c}
ъ =
{М
Мпу
lvl 5с t IV
М^У
1V16с j IV
5cfc5c t IV
A^{4c}
M{T} -
+ M^(K|ctIV)
e
MJ.
м^г} - J25c8|cTIV - j
+ M^(RlcVV)
A^5c?IV ” ^cflV^cfV
— ^fiv£^cjiv
z ez
6ce6cflV
0
+ (^5,4)4'
M°’-’(KLTiv)
Из (4.89) определяем выходные моменты множества
звеньев {4}. Матрица PF* была определена в кинемати-
ческом анализе:
159
М*$ =
М*$х
МВ$У
Л/|ЫХ2
Л/|^
Л/^ft _
о
О
о
о
о
о
-1/«5
1/«5
О
1/«5
1/«5
- л/% -
Л/%
Л/scfiv
- Л/П6*Т IV -
М$У
Л/% - (l/w5) Л/^
•" -^5cfiv
5с ТIV
(1/м5) AfJ^iiv
-^6ctIV
(l/u5)WTIV
Реакции в зацеплениях 5cIV-5l\ 6cIV-6IV определяем по
формуле (4.90):
[— Л/5 “ivA 5 f IV ”1
I Л/^iv I Us tg ot/(r5| jy |/н| +1) I;
I Afstiv I tg a/(r51 iv +1 J
Л/?| iv/r6|iv
- I Л/g^v I w5 tg a/(r6TIV
I Л/JTiv | tg a/(r61
Моменты от K5C|iV, K^v
по формуле (4.91):
~l I «s tg
(^6cfiv)4' “
в точках В
5, B6 определяем
л/в’(ПТ1У)
Л/Вб (^6c t iv) =
Л/?^и5
О
Реакции во внутренних кинематических парах 5cIV-4,
6c,v-4 множества {4с} находим из (4.93)—(4.95). Силы реакции
^4.5ctIV = ”(^5ctIV 4" ^5cfIV 4" l^cfiv)»
К «МнТIV ~ “ (^6с| IV 4" ^6cfIV + ^6c|iv)-
160
Составляющие по осям х'^, z'4. реактивного момента:
^4,5сТIV = ~(^5cfIV + MBsX (R 5cjiv) + MB-X (^5c||v)) J
MUtiv = + MB*X «.|IV));
^4,5c f IV = “(^5ctIV + MBsZ (^5cjiv) + (/?5c|iv)) C
^4,6cfIV = — (^6ctIV + MB*Z (i?6cfiv) + (^6cf!v))-
Таким образом, все приводные моменты и реакции во
внешних и внутренних кинематических парах множества
звеньев {4с} определены.
4.3. Кинематическая развязка движений
В схемах исполнительных механизмов с приводами, выне-
сенными на основание, транзитные движения к более уда-
ленным от приводов звеньям передаются внутри промежу-
точных звеньев. При этом движения промежуточных звеньев
накладываются на передаваемое транзитное. Это явление
называется кинематическим взаимовлиянием движений. Оно
существенно затрудняет управление исполнительным меха-
низмом, поскольку перемещение вала одного привода вызы-
вает перемещение сразу нескольких звеньев [20, 21].
Кинематика исполнительных механизмов описывается
кинематическими матрицами Т. Структура матриц определя-
ется видом шарниров, входящих в состав манипулятора,
независимо от вида передаточных механизмов (тросовые,
зубчатые и т. д.). Шарниры разделим на две группы [31].
К 1-й группе отнесем те, в которых выходное (основное)
звено приводится от одной переда! очной кинематической
цепи. К этой группе относятся, в частности, шарниры в ме-
ханизмах с тросовым приводом (см. рис. 4.6, п), а также
конические шарниры первого типа (см. рис. 4.11, и)
Ко 2-й группе отнесем шарниры, у которых выходное
основное звено приводится в движение от двух передаточ-
ных кинематических цепей. Примерами гаких шарниров
являются шарниры, показанные на рис. 4.П,н,«.
Если все шарниры манипулятора относятся к 1-й группе,
то кинематическая матрица будет треугольной:
22
£И2 • • •
о
t
ьлл
6 Механика промышл. роботов, кн. 2
(4.99)
161
В частности, у исполнительного механизма (рис. 4.23)
кинематическая матрица
I1 1
- \/и2 \/и2 О
1/и3 - l/i/?
-1 1 I (4.100)
— l/t/5 l/w5 I
0 1 — 1 I
1 — 1 □
где и2, и3, и5 — передаточные отношения в шарнирах П,
III, V
Такие исполнительные механизмы в дальнейшем будем
называть механизмами с треугольной кинематической мат-
рицей.
В случае, когда часть шарниров относится ко 2-й группе,
матрица Т уже не будет треугольной. Например, у испол-
нительного механизма (см. рис. 4.3) шарниры III и V
относятся ко 2-й группе, поэтому в его кинематической
матрице (4.28) есть элементы, лежащие над главной диа-
гональю.
Кинематическая матрица Т задает зависимость отно-
сительных угловых скоростей основных звеньев §2» • • • > Q»
от угловых скоростей входных валов Ot, co2ti» юзть •••
..., а>иц. Поскольку входные валы соединяют с валами
двигателей цилиндрическими зубчатыми передачами, в даль-
нейшем будем рассматривать кинематическую матрицу
(4.101)
задающую зависимость 4i> •••> от угловых скоростей
валов двигателей ф15 ф2, •••> Фи- Матрица
(4.102)
где г/J, и2, ..., и„ — передаточные отношения цилиндриче-
ских передач; w? = -zf/z?, где zf-колесо, насаженное на
вал двигателя i; z? — колесо на i-м входном валу мани-
пулятора.
Строки матрицы Т' получаются умножением тех же строк
матрицы Т на соответствующий диагональный элемент
162
матрицы Z. Структура матрицы Т'
та же, что и Т.
Элементы (i = 1, •. ♦,
щие на главной диагонал
и), лежа-
являются
4 ы
частными передаточными отношени-
ями от i-ro основного звена к i-му
Передаточные отношения г- (i # /),
диагонали, ха-
лежащие вне главной
* рактеризуют влияние j-го привода
на i-е звено. Такие связи будем на-
зывать перекрестными. Полностью
устранить перекрестные связи путем
выбора конструктивных параметров
нельзя, а можно лишь свести их
число к минимуму, тогда в матрице
Т' не равны нулю только элементы
лежащие под главной диаго-
налью. Число этих элементов равно
п — 1. Такой прием называется само-
компенсацией.
В качестве примера использования
самокомпенсации можно привести
исполнительный механизм с тросо-
вым приводом (см. рис. 4.1), у кото-
рого радиусы всех роликов одинако-
вы. В этом случае матрица Т (4.13),
а следовательно, и матрица Т' будут
Рис. 4.23
двухдиагональными.
Самокомпенса-
ция также есть у исполнительного
механизма, показанного на рис. 4.23.
Матрица
(4.100). Очевидно, самокомпен-
сация возможна у исполнительных механизмов
ными кинематическими матрицами. В общем
туру кинематической матрицы Т у механизма
пенсацией можно представить в виде
с треуголь-
виде струк-
с самоком-
’ 1
— 1/^2 1/^2 Н I
— 1/^3 1/Пз I
(4.103)
1/4-1
L о — i/^л
163
I
где й; — ± Ui (щ — передаточные отношения в шарни-
ре f).
Полностью кинематическое взаимовлияние может быть
устранено путем применения в управляющих ЭВМ специаль-
ных программ, осуществляющих о азвязку движений. Однако
этот путь в настоящее время считается нецелесообразным
из-за значительного усложнения программного обеспечения.
Развязку можно осуществить также за счет введения
дополнительных систем управления приводами.
Однако предпочтение отдается решению задачи, при
котором в состав кинематических цепей, связывающих
приводы с основными звеньями, вводятся дополнительные
зубчатые механизмы. Их расположение в передаточной цепи
и внутренняя структура могут быть различными. Поиск
оптимальных вариантов продолжается и в настоящее время.
В общем случае постановка задачи развязки движений
будет следующей: путем добавления к исполнительному
механизму дополнительных передаточных механизмов при-
вести результирующую кинематическую матрицу Т к диаго-
нальному виду [20, 21, 27, 28]:
(4.104)
Наиболее распространенной является развязка движений
путем установки системы дифференциальных приводов на
основании между двигателями и входными валами мани-
пулятора (рис. 4.24).
Будем, как и ранее, обозначать угловые скорости основ-
ных звеньев в относительном движении через q = [#i, q2,
..., 4п]\ а угловые скорости выходных валов двигателей
через ф = [Фь Ф> •••, Фл]т. Введем также вектор ф =
=[Фь Фг, •••» ФиГ угловых скоростей цилиндрических
колес, закрепленных на валах двигателей. Если механизм
развязки отсутствует, то ф = ф и связь векторов q и ф
следующая:
q — Т'ф.
Если же между выходными валами двигателей и цилинд-
рическими передачами установлен механизм развязки, то
угловые скорости выходных цилиндрических колес ф отличны
от скоростей валов двигателей ф. Кинематическую матрицу
164
I
механизма развязки обозначим
через 17. Тогда связь векторов
фиф можно представить в виде
ф = 1/ф. (4.105)
Зависимость же вектора q от
ф будет следующей:
| = Г 17ф. (4.106)
Поскольку в качестве кине-
матической матрицы всего ис-
полнительного механизма при
наличии механизма развязки
выступает произведение Т' U,
условие развязки (4.104) прини-
мает вид
T'U = Т. (4.107)
Возможны два подхода к
решению задачи о развязке.
Первый заключается в том, что
заранее задают матрицу Т, по
ней из (4.107) определяют мат-
рицу 17, а по U проектируют
сам механизм развязки. Второй
задают конструктив-
подход
более
предпочтитель-
ный, состоит
в том, что заранее
ную схему механизма развязки (по возможности наиболее
простую), и в процессе синтеза уточняют лишь параметры
схемы таким образом, чтобы произведение T'U давало
диагональную матрицу.
Рассмотрим решение задачи о развязке для исполнитель-
ных механизмов, у которых число перекрестных связей,
равное (и— 1), минимально, т. е. имеет место их самоком-
пенсация. Кинематические матрицы Т таких механизмов
являются двухдиагональными (4.103).
Синтез механизма развязки при втором подходе можно
провести по матрице Т, поскольку, умножив (4.107) на
Z-1, получим
TU = Z~1T= Т, (4.108)
где произведение Т диагональных матриц Z-1 и Т явля-
ется также диагональной матрицей.
Матрицу Т можно представить в виде
где
4
(4.109)
Здесь Ек_2, Еп-к~ единичные матрицы порядка /с —2,
п — к.
Это свойство матрицы Т показывает, что механизм
развязки может быть спроектирован путем последователь-
ного соединения однотипных двухстепенных дифференциа-
лов, каждый из которых осуществляет развязку движений
по двум координатам. В качестве элементов механизма
развязки (рис. 4.25) обычно используют суммирующий ко-
нический дифференциал (рис. 4.26, а). Входными звеньями
являются колеса к и к'9 выходным — водило Нк. Зависимость
угловых скоростей соя, (cok, сок,) находим по формуле для
плоских дифференциалов
где «К*
= 1/(1 — икк>ку) = J/2. Расчетная схема для
определения и$ркк показана на рис. 4.26,6. В итоге получаем
= W2 + ®я/2-
166
Опишем, как происхо-
дит присоединение диф-
ференциалов и как при
этом изменяется кинема-
тическая матрица всего
механизма развязки.
Пусть вначале вход-
ные валы двигателей к —
— 1 и к были соединены
напрямую через простые
цилиндрические зубчатые
передачи с входными ва-
лами (к — I)1 и к1
(рис. 4.27, а). При этом движения, передаваемые от двигате-
лей к — 1 и к, были не развязаны между собой.
После введения суммирующего дифференциала так, как
показано на рис. 4.27,6, выходная скорость вала (к — 1)-го
двигателя не изменилась, а скорость вала к-го двигателя
стала равной:
где и* — z*- Jz* — передаточное число рядовой передачи,
состоящей из колес z*_ls z**r, z* (рис. 4.27,6).
к
(к-1)
б)
Рис. 4.27
Кинематическую матрицу преобразования скоростей, ко-
торое осуществил введенный дифференциал, можно пред-
ставить в виде
(4.110)
где Ек_2, Еп~к — единичные матрицы порядка к — 2,
п — к.
Поскольку дифференциалы рассмотренного типа после-
довательно вводятся между валами двигателей 1 и 2, 2 и
3, ..., п — 1 и и, в результате получим следующее разло-
жение полной матрицы U:
и = ипип-х ...и3и2,
(4.111)
где Ui (i = и, и — 1, ..., 3, 2) — матрицы вида (4.110).
Из (4.111) индукцией по п несложно показать, что кине-
матическая матрица U механизма развязки будет сле-
дующей
(4.112)
п п п п
168
1
Умножив U на Т (4.103), получим
♦ Из общего вида матрицы Т следует, что она будет
диагональной, если передаточные отношения wf, wf, ...
..., и* рядовых передач в дифференциалах будут следую-
щими:
= 2, == 2, ..., w* = 2. (4.114)
При выполнении условий (4.114) итоговая кинематическая
матрица
и
иг/(2а2)
о3/(2а3)
(4.115)
п°/(2аи)
Если у манипулятора отсутствует самокомпенсация пере-
крестных связей, то механизм развязки можно построить с
помощью суммирующих дифференциалов аналогичным
образом. Число их в этом случае будет больше чем п—1.
169
1
4.4. Выборка зазоров в исполнительных
механизмах
вижение
В схемах с размещением приводов на основании
к основным звеньям манипулятора передается по много-
звенным кинематическим цепям, длина которых к тому же
возрастает в случае применения дополнительного механизма
развязки.
Для того чтобы обеспечить относительное движение
звеньев передаточной цепи, кинематические пары, соединяю-
щие эти звенья, должны иметь зазоры. В длинных цепях
суммарное действие зазоров может привести к значитель-
ным кинематическим ошибкам при перемещении исполни-
тельного органа по заданной программе. Зазоры в кине-
матических парах могут также стать причиной появления
неустойчивых режимов, вызвать повышенные вибрации,
большие динамические нагрузки и усталостные поломки.
Для устранения перечисленных негативных явлений не-
обходима принудительная выборка зазоров в передаточных
цепях исполнительных механизмов, которая также называ-
ется натяжением передаточных цепей [29, 30].
Наибольшее распространение получил выбор зазоров с
помощью замыкающих кинематических цепей, содержащих
упругий элемент.
Рассмотрим вначале простейший пример. Редуктор, со-
держащий два цилиндрических колеса 1 и 2, соединяет
двигатель
Если реактивный момент Л1р, прикладываемый со стороны
рабочего механизма, больше нуля, т. е. направлен против
часовой стрелки (рис. 4.28,6), то в зацеплении участвуют
левые участки рабочих профилей зубьев, выделенные жир-
ными линиями. Между правыми участками образуется зазор.
Если же Мр < 0 (рис. 4.28, в), то в зацепление будут
входить правые участки рабочих профилей зубьев, а зазор
с рабочим механизмом РМ (рис. 4.28, а).
170
Рис. 4.28
1
образуется между левыми.
РМ
Рис. 4.29
цепи,
цепь,
I
1
1
(рис. 4.29). Момент закрутки торсиона обозна-
Он будет постоянным, если будет сохра-
ныи момент меняет знак, при
прохождении его через нуль
кинематическая связь колес
1 и 2 разрывается до тех пор,
пока не входят в зацепление
рабочие профили с противо-
положной стороны.
Для принудительной выборки зазора в основной
содержащей колеса 7, 2, используется замыкающая
состоящая из колес 2' и предварительно закрученного
торсиона
чим через М
няться относительный угол закручивания концов а и b
торсиона (рис. 4.29). Концы торсиона будут двигаться оди-
наково, если круговое передаточное отношение пзк замкнуто-
го контура, состоящего из колес 2', Г9 1 и 2, будет равно
единице:
= 1^2'1'^12 = ( — ~ 1 »
и
отсюда
г1/гг) — М21
т. е. передаточное отношение замыкающей цепи должно
быть равно передаточному отношению основной цепи:
W'j п = Un if. (4.116)
о.ц •
Это условие должно выполняться для любых
цепей, содержащих торсионы.
Так как после введения замыкающей цепи
торсионом реактивный момент в зацеплении
ж = м
замыкающих
с взведенным
стал равен
М
то, выбрав Мг достаточно большим, можно всегда обеспе-
чить Мр > 0, т. е. зазор будет выбираться по левым
участкам рабочих профилей зубьев.
Рассмотрим более сложный пример. Пусть дифферен-
циальный механизм (рис. 4.30) приводится в движение от
двух независимых приводов Д1 и Д2. Двигатели сообщают
звеньям шарнира 2 следующие два движения:
совместное вращение вокруг оси z (угол gj;
сгиб звена 2 относительно оси у (угол цД.
171
1
м
берем из (4.22):
Зависимость угловых скоростей звеньев 1 и 2 от ско-
ростей валов 21 и З1
(о3, = 41 ~ 4г/м-
С02'
Если валы 2' и 3' соединены с валами двигателей Д1
и Д2 цилиндрическими передачами с передаточными отно-
шениями и\ = — zjz u$ = — z-Jz т то со2-, ®з' выражаются
через угловые скорости валов фх, ф2 двигателей так:
Ю2' = ^1^Р1 > ®3' = ^2ф2 •
Связь 41, 4г с фь ф2 следующая:
4i — Uifyi/2 + п2ф2/2; 4г = uu^i/2 — ш/2ф2/2.
Допустим, мы решили ввести замыкающую цепь от при-
водов к звену 1. Тогда по свойству (4.116) для переда-
точного отношения замыкающей цепи получим
Фе = «1Ф1/2 + ^2Фг/241-
Из общего вида и3 ц следует, что замыкающая цепь должна
соединять оба двигателя со звеном 1 через суммирующий
дифференциал. Структуру его возьмем такую же, как и в
случае развязки движения (см. рис. 4.26, а). Требуемое пере-
даточное отношение в цепи получим, например, если соеди-
ним валы двигателей 1 и 2 с входными валами 1в и 2В
дифференциала (рис. 4.31) передачами с передаточными
отношениями — w? — z^Jzio и — Uj = z^/z^ а выходное звено
172
г
г
(
!
1
1
1
Рис. 4.31
дифференциала Н с колесом 1° — передачей с и — — 1.
Вследствие наличия кинематической связи между обоими
движениями звеньев 1 и 2 введенная замыкающая цепь
образует два замкнутых контура. При этом дополнительные
реактивные моменты передаются не на два вала, как в
предыдущем случае, а на три — 2, 2', 3'. Найдем эти
моменты.
Здесь и в дальнейшем моменты и силы, создаваемые
торсионом, обозначим верхним индексом «н». Так, моменты,
передаваемые валам 2, 2', 3', обозначим М\, М1!, Л2". Для
их определения условно отсоединим входные валы 2, 2', 3'
от остальной части исполнительного механизма по сече-
нию А—А (рис. 4.31) и рассмотрим их равновесие под
действием момента закрутки торсиона Мт.
Поскольку передача моментов сил от торсиона к осталь-
ным входным валам имеет самостоятельное значение,
изложим расчет передаваемых моментов в общем случае.
Пусть манипулятор имеет п входных
ал о в 1, 2, ..
п
g
и дополнительную замыкающую цепь, содержащую горсион
Т Торсион Т создает момент н^ валу а замыкающей
цепи. Необходимо найти моменты М" на валах 2, 2, ..., п.
По принципу возможных перемещений
Л/т 5фд
(Мн, 8ф) = О,
где 8ф = (8<р 1,..., 8<ри).
Переходя к скоростям и выбрав в качестве независи-
мых координат углы поворота основных звеньев q = [г/ь
«2, • • • > <|т, получим
1
^Фа/^1
<?Ф1Д?1 ••
м
откуда
Mi
М
М"
МГ
п... d^>n/dq
= 0
dyi/dqi.
d^/dq*...
(4417)
В рассмотренном примере
Л/ т,
М“
м\.
-м
5ф27^1 ^Фз7^1
^ф2'/^2 ^Фз'/^а
dq>Jdq2Y
По условиям синтеза
3<Р«/Й«2
0
0
Найдем вид матрицы
^Ф2/^1 dipyldqi
_^ф2'/Й2 ^Фз7^2_
_ ^1/^фу ^1/5Фт
5^2/^Ф2' ^2 /дфз'
= р41/дф2 ^1/дфз’ т =
L д<12 /^ф2' ^2 /^Фз Д
^Ф2'/^1
0фЗ'/^1
ММ»
&Pz/^2
^Фз'/^2_
В итоге имеем
м«
= — М
1/2 и/2
1/2
1/2
о
и/2
-и/2 '
174
1
Рассмотренный пример
показывает, что в кинема-
тически связанных структу-
рах с несколькими степенями
свободы выбор зазоров в
кинематических парах мож-
но осуществить одним упру-
гим элементом.
Этот принцип использу-
ется и в натяжных устрой-
ствах манипуляторов. В этом
случае в состав исполнитель-
ного органа включается до-
полнительная (и + 1)-я пере-
даточная цепь, проходящая
через все звенья манипуля-
тора. На участке между ма-
нипулятором и механизмом
развязки имеется торсион, с
помощью которого и созда-
ется натяжение (рис. 4.32).
Структуру цепи необходимо
выбирать из условия (4.116).
Механизм
развязки
1 г п
Двигатели
Рис. 4.32
При этом реактивные моменты, которые создает момент
закрутки торсиона Мт, в остальных входных валах 1, 2,..., п
можно найти по формуле (4.117).
Раздел
Проектирование
захватных устройств
и передаточных
механизмов
Глава 5
Механизмы захватных устройств
Захватное устройство, служащее для захвата и удержания
объекта, перемещаемого в пространстве манипулятором,
является весьма ответственным элементом конструкции про-
мышленного робота.
Так как перемещаемые объекты имеют самые разные
размеры, форму, массу, прочность, то захватные устройства,
(схваты) выполняются, как правило, сменными. Потребитель
в зависимости от конкретных условий может:
установить схват из комплекта робота;
изготовить сменные элементы (губки, присоски и пр.) для
стандартного схвата;
изготовить специальный схват.
Весьма перспективным направлением является разработ-
ка универсальных захватных устройств, которые могут при-
меняться для удержания различных по размерам, конфигу-
рации и массе объектов.
Существующие захватные устройства можно разделить
на четыре группы в зависимости от характера воздействия
на объект: механические; вакуумные (пневматические); маг-
нитные (электромагнитные); прочие, использующие физико-
химические свойства объекта манипулирования (захватыва-
ние за счет прилипания, прокалывания, притяжения).
Переносимая манипулятором деталь может быть распо-
ложена в схвате различным образом: удерживаться снизу —
односторонний захват, зажата с двух сторон механически-
ми пальцами или иными методами — двусторонний захват,
охвачена со всех сторон («зажата в кулаке») — объемный
захват.
При расчете и конструировании захватных устройств
промышленных роботов приходится учитывать все много-
образие факторов, влияющих на их функционирование:
форму детали, ее свойства, условия протекания технологи-
ческого процесса и т. д.
Основные требования, предъявляемые к захватным уст-
ройствам промышленных роботов: надежное удерживание
детали во время разгона и торможения, сохранность детали
и ее поверхности в процессе захвата.
Массу захвата и его габариты обычно стремятся по
возможности уменьшить, так как увеличение массы ведет
к появлению значительных дополнительных инерционных
сил и увеличению деформаций конструкции робота, а уве-
личение габаритов мешает выполнению рабочих операций
в ограниченном пространстве.
Ряд требований предъявляется к захватному устройству
в связи со спецификой захвата детали, закрепленной на
станке, наличием ошибок позиционирования робота.
Важное требование — возможность захвата деталей в
достаточно широком диапазоне масс и размеров. Жела-
тельно, чтобы этот диапазон был шире, что обеспечивает
схвату определенную гибкость и универсальность. Для
достижения гибкости создаются также быстропереналажи-
ваемые конструкции схватов, позволяющие быстро менять
схват, его губки, обеспечивающие быстроту и простоту
регулировки.
Это требование трудно выполнить с помощью простых
шарнирных схем, так как для них в большинстве случаев,
как будет показано ниже, при захвате деталей различного
диаметра центр схвата смещается. Поэтому губки схвата
делают подвижными.
Следующее требование заключается в возможности само-
установки объекта при его захвате с целью компенсации
неточности программного и действительного положения
объекта. Это требование удовлетворяется введением в кон-
струкцию податливых элементов. При захвате детали про-
извольной формы в общем случае требуется обеспечить
компенсацию линейных и угловых ошибок, положение от-
носительно трех осей, и для этого следует вводить подат-
ливость по шести возможным перемещениям.
При захвате деталей более простой формы число подат-
ливостей может быть уменьшено. Податливости могут быть
177
1
введены как в месте крепления схвата к манипулятору,
так и в механизмах приводов губок и в губках.
Ниже рассмотрим лишь механические захватные устрой-
ства.
захватного устрои-
без специального
5.1. Принципы действия механических
захватных устройств
Механические захватные устройства могут быть с односто-
ронним, двусторонним и объемным захватом, по виду кон-
тактирования как с непосредственным контактированием,
так и с дополнительными фиксирующими устройствами
(гибкие ленты, эластичные камеры и др.), по конструктив-
ному признаку: шарнирные, кулачковые (клиновые), зубча-
тые, винтовые, цепные, комбинированные.
Например, для захвата деталей типа дисков и фланцев
массой до 50 кг применяются пружинные схваты, в кото-
рых усилие зажима создается самой массой детали, распо-
ложенной вертикально, через систему кулачков. Такие само-
зажимные схваты снабжаются специальным механизмом,
удерживающим кулачки в открытом состоянии через цикл,
что позволяет автоматизировать работу
ства на операции разгрузки-выгрузки
тривода и управления.
В качестве привода в механических захватных устрой-
ствах наиболее часто используются пневматический и гид-
равлический приводы, реже — электромеханический. Досто-
инствами пневмопривода являются простота конструкции,
удобство регулирования усилия зажима, возможность рабо-
ты в агрессивных средах и зонах высоких температур,
отсутствие течи (по сравнению с гидроприводом). Основ-
юй недостаток — большие габариты при сравнительно ма-
лых усилиях зажима. Гидравлический привод позволяет
толучить значительно большие усилия при малых габаритах.
Захватные устройства с электромеханическим приводом по
сравнению с рассмотренными выше сложнее и применяются
эедко.
Рассмотрим устройство и принцип действия некоторых
механических захватных устройств. Быстроту срабатывания,
гадежность захвата заготовки, компактность, возможность
самоустановки детали, удобство замены обеспечивает схват
(рис. 5.1) манипулятора токарного обрабатывающего центра.
Схват состоит из корпуса 5, поршня 2 со штоком 3, тарель-
1атых пружин сжатия 4. В пазах корпуса на осях 7 уста-
новлены губки 8 и 9. Малые плечи губок через планки 6
178
шарнирно связаны со штоком. При
зажатии детали планкй устанавлива-
ются в горизонтальном положении
и запирают схват, предотвращая про-
извольное раскрытие его под дей-
ствием сил инерции. При подаче
жидкости в полость 1 поршень пере-
мещается вниз, тарельчатые пружины
сжимаются, губки расходятся. При
снятии давления под действием пру-
жин поршень перемещается вверх,
губки поворачиваются в обратном
направлении, происходит разжим де-
тали.
Использование свойств паралле-
лограммного механизма позволяет
реализовать плоскопараллельный тип
Рис. 5.1
движения (рис. 5.2, а — г). Схемы представляют собой соче-
тание шарнирных и зубчатых механизмов. Схваты подоб-
ного типа используются для захвата деталей с параллель-
ными гранями меняющейся номенклатуры (плиты, короба
и т. д.). В качестве привода используются пневмо- и гидро-
цилиндры.
Схема схвата с параллельными губками нерациональна
при работе с крупногабаритными объектами, конструкция
получается громоздкой. В этом случае применяется схват,
у которого пальцы (губки) перемещаются в направляющей
и каждый палец может иметь независимый привод (рис. 53).
Проста конструкция самоориентирующегося схвата с не-
значительным давлением на захватываемый предмет (рис. 5.4).
179
1
Рис. 5.4
Схват содержит губки /, выполненные в виде упругой гиб-
кой ленты, концы которой закреплены на неподвижном эле-
менте 2 приводного механизма. Подвижный элемент 3 при-
водного механизма поступательного действия присоединен
к среднему перегибу ленты. Два крайних перегиба ленты
служат губками схвата.
Значительный выигрыш в силе зажима деталей дает
система «ломающихся» рычагов (см. рис. 5.1).
Захватные устройства с эластичными камерами («паль-
цами») применяются для захвата изделий, значительно
отличающихся размерами и прежде всего хрупких. Их дей-
ствие основано на деформации эластичной камеры под
действием давления воздуха или жидкости. Поверхности
«пальцев», обращенные к удерживаемой детали, менее элас-
тичны, чем их противоположные стороны, в результате
чего под давлением пальцы деформируются, облегая деталь
и удерживая ее. Причем такие схваты применяются для
удержания деталей как за наружную, так и внутреннюю
поверхность.
С целью сокращения времени на загрузочных операциях
разработаны конструкции двухзахватных устройств последо-
вательного действия. Принцип действия их поясним на при-
мере загрузки станка. Робот, взяв заранее с транспортера
или из тары заготовку, останавливается в непосредственной
близости от рабочей зоны станка. По окончании обработки
предыдущей детали она снимается свободным схватом,
а заготовка — вторым схватом устанавливается на станок.
После этого станок начинает работу, а робот укладывает
обработанную деталь и захватывает следующую заготовку.
Таким образом осуществляется перекрытие машинного вре-
180
1
мени станка и времени, необходимого на манипуляции,
связанные с загрузкой-выгрузкой, что позволяет снизить
время обслуживания станка в 2—3 раза (по сравнению
с работой однозахватного устройства).
Стремление расширить функциональные возможности
захватных устройств, приблизив их к возможностям чело-
веческой руки, реализуется путем создания схватов, у кото-
рых каждый «палец» и составляющие его звенья снабжены
управляемыми приводами. Число степеней подвижности
такой «кисти» может превышать число степеней подвиж-
ности самого робота; и если учесть, что при этом «пальцы»
снабжаются тактильными датчиками, то можно представить,
насколько сложна система управления. Несмотря на это,
в связи с усовершенствованием систем управления рассмат-
риваемые захватные устройства, по всей вероятности, найдут
применение в роботах второго поколения, обладающих ши-
рокой универсальностью и способностью автоматической
коррекции программ в зависимости от условий внешней
среды.
В ряде случаев захватные устройства помимо совмест-
ного перемещения с манипулятором робота должны совер-
шать самостоятельные дополнительные движения. Причем
с целью снижения массы схвата зажим транспортируемых
изделий может производиться от привода, осуществляюще-
го перемещения захватного устройства.
Уменьшение габаритов и требуемой мощности привода
схвата реализовано в конструкции (рис. 5.5). Это достигнуто
введением дополнительных функциональных элементов, обес-
печивающих перемещение за-
жимных губок для подвода их
к объекту захвата и затем ра-
бочее усилие удерживания.
Захватное устройство рабо-
тает следующим образом. При
подаче давления в штоковую
полость цилиндра 1 шток 3
смещается вниз, сдвигая кулису
4 с роликами 5 до упора 2.
Одновременно раздвигаются
шарниры 12 с зажимными губ-
ками. Дальнейшее движение
штока сжимает пружину 6, при
этом клин 7, наезжая на ролики
5, сдвигает их по направляю-
щим кулисы. В результате шар-
Рис. 5.5
181
ниры 12 также будут сдвигаться, сближаясь по прямой
линии, параллельной перемещению роликов.
Установка рычагов 8 — 11 пантографа разной длины
позволяет получить необходимое передаточное отношение
шарнирного механизма, т. е. при небольшом ходе штока
гидроцилиндра большую величину продольного хода губок
схвата.
Для изделий с цилиндрической наружной поверхностью
используются регулируемые самоцентрирующие схваты
(рис. 5.6), обеспечивающие захват цилиндрических деталей
различного диаметра без смещения их центра. Указанная
цепь достигнута введением в конструкцию подвижной приз-
матической опоры. Линейно перемещающийся схват состо-
ит из симметрично расположенных шарнирных многозвен-
ников, включающих в себя ведущее звено 4, ведомые
звенья 8 и 9, губки /0, червяк 2, зубчатые секторы 1 и 3,
жестко соединенные с ведущими звеньями. Ось червяка 2
заканчивается винтом 6, а гайка 5 винтовой пары установ-
лена в направляющих и жестко связана с призматической
опорой 7.
Вращение червяка одновременно передает движение
захватным губкам и призматической опоре. Ее перемещение
должно быть согласовано с перемещением зажимных губок
так, чтобы в момент захвата изделия расстояния от центра
изделия до точек контакта с губками и опорой были равны.
Обслуживание некоторых видов оборудования связано
с необходимостью захватывания изделий при грубом наве-
дении манипулятора на ось объекта захвата. Для этой цели
777777777777.
7777777777777
1
может быть использован схват с дифференциальным меха-
низмом (рис. 5.7) привода губок, позволяющий захватывать
детали, находящиеся между зажимными губками на различ-
ных от них расстояниях.
Устройство работает следующим образом: вращение от
входного вала через конические шестерни 1 и 2 подводится
к корпусу 3; установленные в нем шестерни-сателлиты 7
передают движение на шестерни 4 полуосей 6, опоры кото-
рых расположены в корпусе дифференциала; вращение полу-
осей вызывает перемещение губок 8 схвата, связанных
с полуосями винтовой парой 5, при этом усилие распреде-
ляется равномерно на обе губки.
При неточном подходе манипулятора к объекту 9 обе
губки перемещаются навстречу друг к другу до остановки
одной из них, первой коснувшейся объекта, затем до
касания перемещается вторая. Происходит зажим объекта.
5.2. Кинематические схемы
Наиболее широко в конструкциях захватных устройств при-
меняют механические схваты с двумя жесткими пальцами,
совершающими вращательное, поступательное и, как част-
ный случай поступательного, прямолинейное движения. Ра-
бочая поверхность пальцев, предназначенных для захвата
объекта, представляет собой призму, плоскость, боковую
поверхность цилиндра вращения или комбинацию перечис-
ленных поверхностей. Для схватов удобно использовать
понятия «центр схвата» и «рершина пальца» [17].
Центром схвата будем называть центр окружно-
сти, вписанной в многоугольник (или описанный вокруг
него), образованный рабочими плоскостями пальцев.
Вершиной пальца будем называть точку соприкос-
новения пальца с объектом или центр губки схвата. С точки
зрения выполнения роботом операции снятия-установки
деталей на станок важно, чтобы положение центра схвата
оставалось неизменным при захвате деталей различного
диаметра. Поэтому рассмотрим, как он перемещается для
различных схем схватов.
При вращательном движении пальцев (рис. 5.8, а—г) их
вершины (точки К) перемещаются по дуге окружности,
а положение центра схвата (точка С) зависит от угла накло-
на выходного звена передаточного механизма. При поступа-
тельном движении пальцев (рис. 5.8, д — е) их вершины пере-
мещаются по дуге, а центр схвата смещается вдоль про-
дольной оси, но ориентация самих пальцев в пространстве
183
1
Рис. 5.8
остается неизменной. При прямолинейном движении паль-
цев (рис. 5.8, ж, з) их вершины перемещаются по прямым,
их соединяющим, а положение центра схвата и ориентация
самих пальцев в пространстве остаются неизменными.
Шарнирная установка выходного звена передаточного
механизма в корпусе схвата обеспечивает возможность
поворотного движения пальцев схвата. Простота и надеж-
ность этих конструкций, обусловленная наличием в них
вращательных пар, определила их широкое использование
в промышленных роботах. Существенным недостатком дан-
ных схватов является то, что положение центра схвата,
а также ориентация пальцев зависят от угла поворота вы-
ходного звена, следовательно, такие схваты могут быть
применены лишь для захвата объектов, размеры которых
отличаются незначительно.
Введение параллелограммного механизма позволяет' по-*
лучить поступательное движение пальцев (см. рис. 5.5).
Недостатком схватов, построенных по такой схеме, является
зависимость положения центра схвата от угла поворота
выходного звена.
184
1
Схемы (рис. 5.8, ж, з) поз-
воляют получить прямоли-
нейное движение пальцев, что
делает такие схваты наибо-
лее универсальными, однако
конструкция их более слож-
на, чем в предыдущих слу-
чаях. Захватные устройства
с прямолинейным движени-
ем пальцев работают в ши-
роком диапазоне размеров
захватываемых объектов.
Схемы механизмов схва-
тов на рис. 5.8, а—в, д — ж можно отнести к шарнирным,
на рис. 5.8, в, з — к шарнирно-зубчатым, на рис. 5.8, г —
к кулачковым.
Кинематические схемы схватов на основе плоских шар-
нирных механизмов отличаются большим разнообразием.
Однако у всех захватывание объекта производится с по-
мощью звеньев, несущих губки и совершающих врашатель-
Рис. 5.9
ное или поступательное движение.
На рис. 5.9, а, б показаны кинематические схемы меха-
низмов схватов на основе двух параллельно соединенных
коромыслово-ползунных механизмов со смещенным ползу-
ном [6]. Движение такому механизму сообщается с по-
мощью пневмогидроцилиндра и звена 7, которое является
входным. Оно передается через шатуны 2 и 2' к коромыс-
лам 3 и 3', несущим губки и зажимающим объект 77.
Длина губок может быть регулируемой (рис. 5.9,6).
5.3. Кинематический анализ
Рассмотрим задачу кинематического анализа механизма
схвата (рис. 5.10, а). На рисунке штриховыми линиями
показано начальное положение AB0CQDEQ механизма схвата.
Принимаем, что скорость vB = ds/dr и ускорение ав = d2.s/dt2
входного звена известны. При перемещении звена 1 на рас-
стояние s механизм займет положение ABCDE.
Выведем аналитические зависимости углового перемеще-
ния ос выходного звена DE от перемещения входного звена
1. Очевидно, что угол у0 = 180° — р. — ос©- По теореме синусов
/2/sin у о = /з/sin фо, откуда
sin фо — (^3/^2) sin уо — (^3/^2) sin (180 р осо),
- — — — -- ------- - - — - .
cos Фо = J/1 - (/3Д2)2 sin2 (180° - р - ос0), где /3 = CD.
185
О)
Рис. 5.10
Расстояние B0D определяется суммой
2 и 3 на вертикаль:
проекций звеньев
Во2) = l3 cos у0 + l2 cos фо = /3 cos (180° - ц - а0)
+ h |/1 - (h/h)2 sin2 (180° - ц - а0),
а расстояние
BD = B0D - s = /3 cos (180° — ц — а0)
02 ~ I2 sin2 (180° - ц - а0) - s.
По теореме косинусов
й = 1з + BD — 2l3BD cos у,
откуда
у = arccos [(/j - ll + BD2)/(2/3BD)],
186
1
следовательно,
otf = 180° — р — у.
Угловое перемещение выходного звена
а = а0 — ot,; = а0 — 180° + р + у.
При равенстве длин /2 = /3 =
примут вид:
(5.1)
расчетные зависимости
ф0 ~~~ У0 ~~ 180 — р OCq у
BDq = 21 cos (180° — р — ос0);
BD} = 21 cos (180° — p — ot0) — s;
a = ot0 — 180° + p + arcsin []/4/2 — BD2/(2l)].
Определение скоростей и ускорений механизмов схватов
методом планов. Для определения скоростей и ускорений
заданных точек звеньев механизма используем векторный
метод планов. Построение планов скоростей и ускорений
рассмотрим на примере механизма схвата (рис. 5.10, а).
Положение механизма, размеры звеньев /2, /3, 1А и углы
Ф, а, а0, у принимаем известными.
Масштаб плана скоростей (рис. 5.10, б) рг = v/(pb), где
v — модуль скорости звена I; pb — отрезок, изображающий
вектор v. Единица масштаба плана скоростей [pv] = м/(с • мм).
Выбрав полюс п и значение отрезка nb', изображающе-
го вектор ускорения а, определим масштаб плана ускорений:
ufl = a/(nb'); [pj = м/(с2 • мм).
Скорость и ускорение точки D равны нулю.
Связь между скоростями точек С, В и D представлена
векторными уравнениями:
vc ~ Ув + исв>
Vc — Vd +
В соответствии с этими уравнениями на плане графически
найдены величина и направление вектора скорости гс.
Вектор vE скорости точки Е определяется по теореме
подобия, согласно которой
ed/cd = ED/CD', ed — cd' ED/CD — ed • Z4//3; z. edc— z. EDC = p.
Пользуясь планом скоростей (рис.
угловую скорость звена DE:
da vE (ре)1^ т -. !
©з = -т- = -J---?= --J---, [СОзJ = с .
Ut IDF U
5.10,6), определим
187
1
Связь между ускорениями точек С, В и D может быть
представлена векторными уравнениями:
^С *“
ысв
Як)
aCB>
^CD‘
D
Значения отрезков, изображающих нормальные ускоре-
ния а£в и рассчитываются по формулам:
Ь'Пх — ^св/l^a ~ vCb/(^2^o) ~ (сЬ)2 Рт/ 21k
^СВ^а
ПП2
” СвДОзМв) = (Cd)2 Ц2/(13Ца\
Графическое решение векторных уравнений (рис. 5.10, в)
позволяет определить величину и направление ускорения
а& представленного отрезком nd.
Вектор ускорения аЕ точки Е определяем по теореме
подобия:
ddic’d = ED/CD', dd = dd (ED/CD) = dd (I4//3);
ddd = zl EDC = p.
Пользуясь планом ускорений (рис. 5.10, в), определим
угловое ускорение звена DE:
ез ~ d2ot/dt2 — dCD/lcf) — (n2d) РдДз»
Планы скоростей и ускорений подобных механизмов
целесообразно строить с использованием метода особых
точек Ассура.
Трехповодковая группа 2-3-4-5 имеет три особые точки
Ассура: Я42, Н25, Н45 (рис. 5.11, а). Эти точки принадлежат
базисному звену 3 механизма. Точка Н42 находится на
188
Рис. 5.11
1
пересечении направлений поводков 4 и 2, точки Н25 и Н45
на пересечении направлений поводков 2 и 4 с линией, пер-
пендикулярной направлению движения ползуна 5 и прохо-
дящей через точку F. При определении кинематических
параметров механизма используем точку Ассура Н2 5 (в даль-
нейшем нижний индекс Н относится к точке Н25).
Масштабы планов скоростей и ускорений:
= »/(pb); [nJ = м/(с • мм);
= а/(яЬ'); [ц„] = м/(с2 • мм),
где pb и nb' — отрезки, изображающие на планах скоростей
и ускорений (рис. 5.11, б, в) соответственно векторы скорости
и ускорения входного звена 1.
Векторы скоростей vH, vD и vc графически определяются
с использованием следующих векторных уравнений:
{Vh — е>с
= »f0
( VD='VH
I vD = vE •
М-v
Vfjc — Vg •
VhF0 — ^F
VdHi
VdE>
VCB
vhc‘,
Vc — ^B
vc - VD
Vcb\
VCD)
I
1
г
ГО '
Скорость точки F определяется по теореме подобия, из
которой следует:
fd/dc = ED/DC', fd = de (FD/DC) = de (Ifd/Ьс)-
По плану скоростей (рис. 5.11, б) определяем скорость
(м/с) выходного звена 5 механизма схвата:
»f = (pf) Mv-
Ускорение точки H2s находим, решая совместно два
векторных уравнения:
dpj — $B
<*CD
aCB
4
f
i
г
!
1
1
n
aHF
0
0
aHF>
где отрезки (мм) да плане ускорений, изображающие
нормальные ускорения, соответственно равны:
Ь'И1 = а'св/^a = ^св/^свЦа) ~ (гЬ)2р?/(/2Р«);
= «нс/йа = ^hc/GhcPJ = (h25C)2
= ^HF fa a = ^HFfaHCV-a) = (^25 f)2 Их/УнрРа)-
7CM3
189
1
Ускорение точки D находим из векторных уравнений
; _ Л 1 Ли
aDH\
Rv/( WJ;
лся
^CD
^C£>,
где отрезки на плане ускорений, изображающие нормаль-
ные ускорения Яря и anDE, соответственно равны:
^25n4 = ^bul^a ~ V1)H/^DhP-o) ~ (^25$2
,itM5 = = (de)2 р^/(Цра).
Ускорение точки С находится согласно уравнениям
{ас = &в
== &D
где отрезки на плане ускорений, изображающие нормаль-
ные ускорения а'св и соответственно равны:
Ь'И1 = (c&)2Pv/(/2Pe);
d'n6 = anCD/\ia = vlD/(lCD\ia) = М)2|^/0сдЮ-
Вектор ускорения aF точки F определяется по теореме
подобия, в соответствии с которой
d'f'lc'd1 = DF/CD- d'f = c'd(DF/CD) = c'd’ (lDF /lCD).
Пользуясь планом ускорений (рис. 5.11, в), определим
ускорение (м/с2) выходного звена 5:
= (^Л Ра-
Графоаналитические методы, кинематического анализа
обладают геометрической наглядностью и являются эф-
фективными в анализе механизмов высших классов.
При конструировании механизма схвата важно знать связь
между перемещениями входного звена и выходного звена
(губок схвата). Перемещение выходного звена определяет
максимальный размер захватываемого объекта.
Приведем зависимость между перемещением входного
звена 1 и углом поворота выходного звена 3' для схвата
(см. рис. 5.9, б). Эта зависимость представляет собой функцию
положения смещенного коромыслово-ползунного механизма
и имеет вид [6]:
s = /3 [cos ср + |/1 - (Ai sin ср - л2) At], (5.2)
где 5 — перемещение звена /; = /3//2; А,2 = к/12; 12 и /3 —
длины звеньев 2 и 3; к
тельно точек 02 и 0х.
смещение оси ползуна относи-
190
Эта зависимость позволяет найти значение максималь-
ного раскрытия губок при максимальном перемещении што-
ка 1. Для этого вначале из выражения функции пере-
мещения находим угол <ртах, соответствующий максимально-
му ходу штока smax, затем перемещения губок А и В схвата,
а затем максимальное раскрытие губок по формуле
As = + Sg =
4Oi A sin (фтах/^),
где Sb — перемещения губок А и В.
Для работы с длинными деталями типа валов, труб
необходимо применять схемы механизмов, в которых при
малом перемещении входного звена рычаги, несущие губки,
могли бы захватить деталь большого размера (рис. 5.12).
Этот механизм представляет собой совокупность двух одно-
временно работающих кулисных механизмов, у которых губки
закреплены на качающихся кулисах 3 и 3'.
Перемещения штоков 1 и Г связаны с углом качания
кулис 3 и 3' зависимостью
s = a tg ф,
где s — перемещение звена 1 в направлении оси х; а —
расстояние между осью х и осью штока; ф — угол поворота
рычага от оси у.
Задавая максимальное значение s перемещения штока,
можно определить максимальный угол отклонения рычагов
Фтах ОТ оси у, а задавая ход штока, — минимальный
угол отклонения 9min
Затем можно определить максималь-
ное раскрытие губок As захвата по формуле
As = 20iB [sin (а +
фтах) ~ Sin (« +
Фт1п)1*
Максимальный размер объекта
йтах = Ь - 2L3 sin (а + фт1й).
Минимальный размер объекта
min птах
Недостатком рассмотренных схем схватов на основе
коромыслово-ползунного (см. рис. 5.9) и кулисного
(рис. 5.12) механизмов является необходимость иметь большой
ход штока при большом перемещении губок, что не всегда
возможно реализовать при ограниченных габаритах схвата.
Приведенная на рис. 5.13 схема позволяет получить
большое относительное перемещение губок схвата при малом
перемещении штока. Движение от привода передается через
звено 1 коромыслам 2 и 2', которые приводят в дви-
191
Рис. 5.12 Рис. 5.13
жение кулисы 5 и 5'. Таким образом, в данном случае
имеет место последовательное соединение коромыслово-
ползунного и кулисного механизмов.
Для коромыслово-ползунного механизма перемещение
ползуна связано с поворотом коромысла формулой (5.2).
Зная постоянные параметры этого механизма, для задан-
ных крайних положений штока smin и smax можно найти
экстремальные значения углов поворота коромысла <pmin и
Фтах, решив тригонометрическое уравнение относительно
угла <р.
Этим углам соответствуют два предельных положения
ползунов В и В', зная которые, легко определить
экстремальные значения углов поворота кулис 5 и 5'. Эти
углы можно найти из формулы
tg ф = Х3 sin <р/(1 + Х3 cos ф),
где Х3 = /3Д0; = ^1^2*
Тогда перемещение точки К по оси абсцисс
As = 2L3 [sin (фтах - а) - sin (фт1п - а)].
Максимальное расстояние между губками
= 2L3 sin (фтах - а).
На рис. 5.14 показан механизм схвата, у которого роль
захватывающих рычагов играют коромысла 4 и 5. Этот
механизм можно рассматривать как совокупность централь-
ного кривошипно-ползунного механизма (звенья 1, 2, 4, 6)
и группы Ассура (звенья 3, 5).
Максимальный размер захватываемого объекта
^max = b4 sin (фтах - ₽),
192
1
Рис. 5.14 Рис. 5.15
где Ь4 = О А; р — постоянный угол, характеризующий размеры
рычага схвата; фтах — максимальное значение переменного
угла поворота коромысла, определяется из выражения
s = 2r (1 — coscp) при условии /3 = 15.
Для получения большого хода губок схвата при не-
больших перемещениях входного звена 1 служит также
механизм, показанный на рис. 5.15. Этот механизм можно
рассматривать как совокупность двух плоских четырех-
звенников (звенья 6, 7, 8, 0 и 5, 4, 3, 0) с присоеди-
ненной к одному из них группой Ассура 9-1 и соединенных
между собой звеном 2, или как механизм, образованный из
плоского коромыслово-ползунного механизма (звенья 1, 9, 8),
к которому присоединены группы 2-3, 4-5 и 6-7. Таким
образом, этот механизм является плоским десятизвенным
шарнирным механизмом.
Для плоского четырехзвенника 6-7-8, 0 имеем
/8/6 cos (ф - у) 4- l0l6 cos у + /0/8 COS ф = 0,5 (/? + /о — II - /|),
где lQ — OiO2; Ц — длина звена i.
Подставив значение угла ф в это уравнение, найдем
угол у, а затем значение
ДА = 202A sin Ду,
ГДе Ду Ушах Ymin-
5.4. Кинематический синтез
При синтезе кинематической схемы механизма схвата опре-
деляют основные размеры сю звеньев по заданным кине-
матическим или динамическим условиям.
Синтез механизма схвата по заданным положениям звеньев.
Пусть заданы три положения механизма (см. рис. 5.10), для
которых углы поворота выходного звена 3 соответственно
равны at, а2, аз- Этим углам соответствуют переме-
7 Механика промышл. роботов, кн. 2
193
1
2/3 [/3 cos (180° — р
щения входного звена 1. При известном начальном угле
а0 требуется определить кинематические параметры /2, /3, р.
Пользуясь зависимостью (5.1), составим три уравнения:
cos (ос j - ос0 + 180° - р) =
_ /з - <2 + [/зcos(180° - ц - ot0) + N - S,]2
— а0) + N — Sj ]
COS (а2 - «0 + 180° - р) =
= <3 - *2 + [/3cos(180° - ц - g0) + N - s2]2
2/3 [Z3 cos (180° — ц - а0) + N — s2]
cos (осз — oto "Ь 180° — р) =
_ /з - /2 + [/3 cos (180° - р — ос0) + 7V — s3]2
2/3 [/3 cos (180° — р — ос0) + ТУ — $з] ’
где N = ]//2 — /3 sin2 (180° — р — ос0).
Совместное решение этих уравнений позволяет определить
кинематические параметры /2, /3, р. Ввиду сложности урав-
нений решение рекомендуется выполнять с использованием
ЭВМ.
Приведем более простой пример, не требующий исполь-
зования ЭВМ. Пусть a, s и р заданы. Требуется определить
/ при известных ос и s для одного положения механизма
схвата. Пользуясь зависимостью (5.1), получим уравнение
cos (ос — ос0 + 180° — р) = [21 cos (180° — р — ос0) — s]/(2Q,
откуда
/ = s/{2 [cos (180° - р - ос0) - cos (ос - ос0 + 180° - р)]}.
, ос0 = 60°, а = 50°, то
Например, если s — 0,1 м, р =
решение последнего уравнения позволяет определить, что
I = 0,072 м.
Синтез механизма схвата по заданным углам давления и
размеру захватываемого объекта. Пусть для механизма
схвата (см. рис. 5.10) заданы: s£max
нение точки Е от вертикали
захватываемого объекта; ос0 •
выходного звена DE; у12, у23
в кинематических парах В и С; р — жесткий угол, образо-
ванный звеньями ED и DC; B0D — расстояние, определяю-
щее габариты механизма схвата.
Требуется определить величины: I
максимальное откло-
определяемое размером
максимальный угол размаха
- допускаемые углы давления
2»
194
Длина звена DE
/4 — Sgmax/(2 sin otg).
Угол давления у о = 180° — ot0 — р.
Рассмотрим положение механизма схвата 4B0C0DE0, по-
казанное пунктиром. В этом положении угол ф0 максимален
и при известном допускаемом значении Y23 угла давления
в кинематической паре С может быть определен как
фо = 90° 4- угз- Угол
Фо = 180° “ То ~ Фо = <*о + И - У23 - 90°.
(5.4)
Из ABgCqD по теореме синусов находим:
Z2/sin Yo = B0E>/sin ф0; /3/sin Фо = В0В^пф0,
откуда
sin (180° — «о — М)
»2 — ВоВ------:—ттгтг
sin (90
?2з)
Y23 ~ 90°
sin (90° + Y23)
COSY23
cos(Y23~ao-H)
и-------------
COSY2 3
о
Cos(a0 + И - Y23)
COSY23
(5.6)
В положении ABCDE угол у максимален и не должен
превышать заданного допускаемого значения у i2 угла давле-
ния в кинематической паре В. В предельном случае
можно считать Y == Y12-
Из Д BCD по теореме синусов находим /3/зтф =
= Z2/sin у, откуда
. (12 . \ .Г sin(a0 + p)sinYi2
у — arcsin I — sin ф = arcsin-----z—----------— :
Мз / L c°s(a0 + P — Y23) _
a£ ~ 180° — p — Y-
По известным углу oq и длине /4 определяем мини-
мальное отклонение S£mjn точки Е от вертикали:
«Emin = 2/4 sin af. (5.7)
В Д BCD угол
ф = 180й — ф — у. (5.8)
По теореме синусов В/Э/зтф =/3/8Шф, откуда BD =
= Z3 sin ф/sin ф. Подставив в последнее выражение значение
/3 из формулы (5.6) и углы ф и ф из (5.4), (5.8), получим
BD = -B0Dcos(a0 + И ~ Y23)sin(Yi2 + y)/(c°sY23 sin у 12)-
195
Перемещение входного звена 1
s = BQD — BD —
= B0D [1 + cos (а0 + Ц - Y23)sin(y12 + Y)/(cosY23sin у12)]. (5.9)
Рассмотрим конкретный пример с параметрами:
$£тах = 6,4 М, OCq — 60 ; Ц = 80 \ BqD = 0,7 MJ Y12 ~ 30° J
723 = 30°.
Алгоритм решения: по формуле (5.3) определяем длину
/4; по (5.5)-/2; по (5.6) -/3; по (5.8) - s£min; по (5.9)-
перемещение входного звена 1.
Получаем: /4 = 0,23 м; /2 = 0,52 м; /3 = 0,28 м; s£min =
= 0,23 м; s = 0,16 м.
5.5. Силовой расчет
На рис. 5.16, а показана схема шарнирного механизма
схвата, применяемого в роботах Versatran, УМ-1 и др.
Схват закрывается при подаче давления в правую (на рисунке)
полость гидроцилиндра 1. Угол раскрытия регулируется
винтом 2. Губки 3 обычно выполняются сменными.
В качестве характеристики схвата используют так назы-
ваемое силовое передаточное отношение [12]
К = F/P, (5.10)
где F — сила сжатия детали; Р — усилие привода на входном
звене.
Связь между этими параметрами можно установить на
основе равенства элементарных работ на входе и выходе
1
механизма:
Si Р — б2РТ|,
откуда
К = бзЛ/^i = л/^5>
где 51, 32 — возможные перемещения на выходе и входе
механизма; К8 — 5t/52 — кинематическое передаточное от-
ношение; т| — коэффициент полезного действия (к. п. д.).
Моменты сил трения в шарнирах В и С
(рис. 5.16,б, в,г) можно записать так:
М в = (df/2) + Ki,; Me = (df/2) j/Kiy +
где d — диаметр осей шарниров; f — коэффициент трения;
RBx, &сх, &су — реакции в шарнирах В и С соот-
ветственно.
Так как при малых углах поворота рычагов схвата
значения RCx малы по сравнению с RBy и RCy, то
ими можно пренебречь, тогда
Мв ~ (df/2) RBy\ Мс ~ (df/2) RCy.
Из условий равновесия звена ВС при малых а (рис. 5.16, в)
п Р h Ff^h+dfX
Ву~ 2 df + l3a~ 2\ 12 /’
где /ь /2, 13 — размеры отрезков рычагов схвата. Тогда
силовое передаточное отношение схвата через параметры
механизма выразится так:
При малых углах а кинематическое передаточное отноше-
ние
Xg — (2/i//2)ot,
где а — угол наклона оси звена ВС к линии, перпендику-
лярной оси схвата.
Анализ зависимостей для силового передаточного отно-
шения показывает, что в данном механизме может быть
получено большое значение К при малых углах а, однако
оно падает при уменьшении 13.
При малых углах а в механизме может наблюдаться
явление самоторможения, что можно отнести к достоин-
ствам этой схемы при аварийных ситуациях. Однако
197
*
Рис. 5.17
работа схвата в зоне малых а делает его весьма чув-
ствительным к ошибкам изготовления деталей и сборке.
Кроме того, имеется опасность перехода механизма через
предельное значение а = 0, что недопустимо.
Угол а, при котором происходит самоторможение,
определяется из условия а df/l3. Работа в зоне, близкой
к зоне самоторможения, приводит к низкому к. п. д. этого
механизма, что также является его недостатком.
Значительно большим к. п. д. обладают кулисные механиз-
мы схватов (рис. 5.17, а—г). Наибольшее силовое передаточ-
ное отношение у схвата, построенного по схеме 5.17,в:
K = [G/(/1sin2a)]i1>
где /j — расстояние между осью опорного шарнира и ли-
нией действия силы F; 12 — расстояние между осями
шарнира и пальца на штоке цилиндра.
Все приведенные схемы обладают одним и тем же не-
достатком, связанным с тем, что при захватывании
деталей различного диаметра положение оси детали изме-
няется, при этом могут возникать дополнительно большие
напряжения. Для уменьшения влияния смещения в кон-
струкции между рычагом захвата и губками должны быть
предусмотрены упругие элементы.
Расчет удерживающих усилии в схватах. Из всего
многообразия положения объекта 1 в захватных устрой-
ствах можно выделить три основные схемы удержания их
схватами:
объект непосредственно поддерживается пальцами схвата
2, 3, силы трения практически не участвуют в удержании
(рис. 5.18, а);
198
1
Рис. 5.18
объект удерживается за счет запирающего действия
пальцев при ограниченном участии сил трения (рис. 5.18,6);
объект удерживается только силами трения (рис. 5.18, в).
При удерживании объекта только силами трения не-
обходимая сила зажима детали весом G равна:
при вертикальном линейном перемещении
где f — коэффициент трения; п — коэффициент запаса; аб —
ускорение вертикального движения;
при горизонтальном линейном перемещении
где аг — ускорение горизонтального движения; а — угол скоса
губок;
при вращении захвата в горизонтальной плоскости
где со — угловая скорость вращения схвата; е - угловое
ускорение поворота схвата; R — расстояние от оси вращения
до оси заготовки;
при одновременном торможении всех трех движений
co2R tg а) + sR
На практике обычно встречается сложное нагружение
захватного устройства, при котором имеет место комби-
нация описанный случаев, причем в процессе манипулиро-
вания характер нагрузки и схемы удерживания могут
меняться. Усилие привода определяют с учетом имеющихся
199
1
Рис. 5.19
схем нагружения для критического случая действия нагру-
зок [17].
В случае несимметричного расположения детали (рис. 5.19)
усилия Ri и R2 на крайние сечения пальцев опреде-
ляются по следующим формулам:
если центр тяжести объекта 1 расположен между край-
ними сечениями пальцев 2, 3 (рис. 5.19, а), то
R1= —G; R2 = j-G;
если центр тяжести объекта расположен вне пальцев
(рис. 5.19,6, в), то
К, = Ц-G; R2 = - ~-G,
где G — вес объекта манипулирования.
Для захватных устройств с одной парой, а также
схватов с двумя парами пальцев (рис. 5.19, а) при действии
нагрузки между крайними сечениями можно считать ее при-
ложенной к одному сечению. В случае если нагрузка при-
ложена вне пальцев (рис. 5.19,6, в), усилие привода равно
сумме усилий, найденных для каждого из двух сечений.
Расчет удерживающих усилий проводится в зависимости
от схемы удерживания и формы звеньев. Удерживающие
усилия при непосредственном поддерживании детали пальцем
(рис. 5.20,а) определяют по формулам:
N±- G sin ot2 /sin (»i + a2); N2 — G sin at/sin (aj + a2),
где ocj и a2 — углы контакта детали с пальцем.
Удерживающие усилия для случая, показанного на
рис. 5.20,6:
нормальные усилия
Ni = G/(2 cos aO; N2 = 6/(2 cos a2)*
200
1
о) б) В)
Рис. 5.20
силы трения
FTi = pTVi;
Ft2 = щУ2,
где ocj и а2 — углы контакта пальцев с деталью; ц —
коэффициент трения; для незакаленных пальцев без насечки
(сталь марок 45, 50) ц = 0,12...0,15, для закаленных с острой
насечкой (сталь марок 65Г, У8А, У10А) ц — 0,3...0,35.
При использовании плоской и призматической губок
пальцев (рис. 5.20, в) удерживающие усилия вычисляют по
формулам:
нормальные усилия
Ni — Gtga2; N2 = G/cosa2;
силы трения
FTi —pNi; -FT2 —jx/V2,
где at =90° —угол между векторами сил G и а2—
угол между векторами сил G и N2.
Удерживающие усилия при использовании плоских губок
(рис. 5.20,г): нормальные усилия — N2 — 6/(2ц), силы
трения FT1 = Ft2 = pNi = |x/V2.
Для схемы нагружения (рис. 5.20, д) удерживающие
усилия в i-й точке контакта (i = 1, 2, 3) определяют по
формулам:
201
1
Рис. 5.21
нормальные усилия
Ni = G sin а£/[ц (sino^ + sina2 + sina3)];
силы трения Fi = \iNh
где cq = 180° — a23; a2 *= 180° — a13; a3 = 180° — a12 (a12, a23,
«13 — углы соответственно между векторами сил и N2t
N2 и N3, Ni и N3).
От действия нормальных сил и сил трения FTi воз-
никает удерживающий момент относительно оси вращения
поворотной части пальца (точка А на рис. 5.21, а, 6). Дш
j-го пальца
к
= Е cosaf tga£ ± Cj - p(af ± CftgaO],
i= 1
где ah — расстояния от точки подвеса А до i-й точки
контакта пальца с деталью; к — число точек контакта
Верхнее значение знака при соответствует точке контакта,
лежащей вне оси подвеса пальца.
По значениям удерживающих моментов определяют
усилие привода захватного устройства:
для схвата с клиновым механизмом (рис. 5.22, а)
т
р = Е + р)(ЬпГ\
J= 1
где Mj - момент удерживающих сил на J-м пальце;
Р — угол клина привода; р — приведенный угол трения
202
1
Рис. 5.22
учитывающий сопротивление пар вращения: если оси на
подшипниках качения, р 1°10'; если на подшипниках
скольжения, р ~ 3°; b — длина плеча рычага; т) = 0,95 —
к. п. д. механизма; т — число пальцев схвата, обычно т = 2;
для схвата шарнирного типа (рис. 5.22,6)
*
т
Р == £ Af j cos <р/(М]),
jss 1
где <р — угол рычага при
для схвата с реечным
касании пальцев детали;
механизмом (см. рис. 5.8, з)
т
£ M,/(mczcn),
где тс — модель сектора;
zc — полное число зубьев сектора.
5.6. Примеры расчета схватов
Расчет схвата с клиновым механизмом *. Клиновый механизм
является частным случаем кулачкового, когда профиль
кулачка прямолинейный.
Пример 1. Механизм схвата (рис. 5.23,а) содержит
четыре клиновых механизма с приводом от пневмоцилиндра.
Особенностью схвата является возможность его вращения
вокруг оси х. Это дает возможность быстро забирать
деталь одной парой губок и подводить вторую свободную
пару губок для захвата другой детали.
В основании 6 установлен вал 5 с жестко закреплен-
ным на нем пневмоцилиндром 7. На валу 5 с возмож-
* Пат. 57-97883 Япония, МКИ В 25 J 15/04.
1
ностью поворота вокруг оси
вала размещены барабан 8 с ин-
дивидуальным приводом и че-
тыре схвата 2.
При выдвижении штока 4
пневмоцилиндра перемещается
поршень 3, который обеспечи-
вает зажим пальцев 1 схвата 2.
В зависимости от вида деталей
и в соответствии с программой
работы барабан 8 поворачива-
ет нужный схват под конец
штока 4 пневмоцилиндра.
Для определения силы, с
которой пальцы зажимают де-
таль, необходимо выполнить
силовой расчет механизма схва-
та. Для его выполнения ис-
пользуем принцип возможных
перемещений.
Рис. 5.23
204
л
Силовой расчет. Основной задачей силового расчета
схвата является определение силы, с которой пальцы воз-
действуют на захватываемую деталь при известном усилии
на входном звене. Для его определения удобно исполь-
зовать силовое передаточное отношение К [см. формулу
(5.10)].
На основании принципа возможных перемещений
8Л; = 0, где ЗД- — элементарная работа силы F, на i-м
возможном перемещении точки ее приложения, для данной
схемы нагружения механизма схвата (рис. 5.23) можем
записать
8ЛР
5А
или
Р8Р - F'df - F"d f" = 0,
(5.И)
где 8Р и 88/" — элементарные перемещения соответ-
ственно входного звена и пальцев схвата; F' и F" — силы,
приложенные к пальцам схвата.
В силу симметрии механизма схвата выражение (5.11)
можно записать в виде
Ри8п — Р8 f == 0,
(5.12)
где Рп — проекция силы Р на нормаль п — п к образующей
конуса входного звена; 8 и — элементарное перемещение
точки В в направлении нормали, на котором сила Р
совершает работу.
Несложно показать, что
(5.13)
где а — угол, равный половине угла при вершине конуса 1
(рис. 5.23,6).
Выражение (5.10) с учетом (5.12) и (5.13) приводим к
виду
К = (8и/8/) sin а.
Для определения величин 8и и 8/ рассмотрим
рис. 5.23, в. Звено 2 вращается вокруг точки А, поэтому
точки В и С перемещаются по дуге окружности. Введем
обозначения АВ — Ц; С А — 12. Тогда элементарные пере-
мещения точек В и С составят:
8s2 = h, $ф,
(5.15)
где 8s! и 6s2 — элементарные перемещения точек В и С
соответственно; 8<р — элементарное угловое перемещение зве-
205
I
I
г
на 2. Как следует из рис. 5.23,в, справедливы соотношения:
8и =
ос); 8/ = 6^2 cos ф2-
(5.16)
После подстановки выражений (5.15), (5.16) в (5.14) получим
со8(ф! + ос) .
К — - sin ос. (5.17)
/2 COS ф2 v 7
Выражение (5.17) позволяет рассчитать силовое передаточ-
ное отношение для данного механизма схвата при извест-
ных геометрических параметрах.
Силы, приложенные к пальцам схвата, можно определить
по формуле
г = лг = г -------------sin а.
*2 COS Ф2
П р и м е р 2. Схват (рис. 5.24, а) предназначен для захвата
деталей типа тел вращения и сообщения им вращательного
движения вокруг оси схвата*.
Перемещение толкателя 1 вниз вызывает смещение
кулачка 3, который через шарики 4 воздействует на пальцы 6.
В результате пальцы поворачиваются вокруг осей 5 и
г
I
\
1
♦ Пат. 2008678 ГДР, МКИ В 25 J 15/00.
206
1
рабочие концы пальцев сближаются, что и обеспечивает
захват детали. При обратном движении толкателя 1
пальцы под действием пружины возвращаются в исходное
состояние. Вращение схвата относительно своей оси про-
исходит в подшипниках 2.
Силовой расчет. Используя принцип возможных переме-
щений для данной схемы механизма (рис. 5.24,6), запишем
6т4р 4- 8/4^ 4- = О,
или
2Р„8и - - Г23/2 =0, (5.18)
где Р„ — проекция силы Р на нормаль к образующей
конуса; 8и — элементарное перемещение, на котором сила
совершает работу; Fr и F2 — силы, с которыми деталь
воздействует на пальцы; и 3/2 — элементарные пере-
мещения, на которых совершают работу силы Fi и F2
соответственно.
В силу симметрии механизма выражение (5.18) можно
представить в виде
Рп8п - F6f = 0,
(5.19)
где Fi = F2 = F; 8/ = 8/\ = 8/2.
Проекция силы Р на нормаль к образующей конуса
Рп — Р sin а, (5.20)
где а — угол между геометрической осью и образующей
конуса.
Отношение элементарных перемещений Зи, 8/ выразим
через геометрические параметры механизма схвата. Обозна-
чим (см. рис. 5.31) АС — li', CD = /2; z. АСВ — у.
Элементарное перемещение точки А составит 8s — /,8ф.
Проекция этого перемещения на нормаль к образующей
конуса
Зи = 3s cos (а + ср), или 8и = ^Зф cos (а 4- ф). (5.21)
Элементарное перемещение 8/ составит
5/ = /23ф.
(5.22)
Тогда, подставив выражения (5.20), (5.21) и (5.22) в (5.19),
после преобразований получим
К = F/P — (Ц /12) cos (а 4- ф) sin а.
Силы, приложенные к пальцам схвата,
F = КР = Р /12} cos (а 4- ф) sin а.
207
Рис. 5.25
Расчет
передачи *.
механизма схвата
Схват (рис. 5.25, а)
с приводом от червячной
предназначен для захвата
круглых деталей и состоит из пальцев 6, зубчатых колес
4 и 5, жестко связанных с пальцами и поворачи-
вающихся с помощью червяка 1 и жестко соединенных
между собой колес 2, 3, резиновых дисков 7, попарно
* А. с. 57-156185 Япония, МКИ В 25 J 15/00.
208
установленных на пальцах и поворачивающихся от инди-
видуальных приводов.
При вращении червяка 1 поворачивается червячное
колесо 2. Жестко связанное с ним зубчатое колесо 3
поворачивает колесо 4 и находящееся с последним в за-
цеплении колесо 5. Поворот колес 4, 5 обусловливает
сближение пальцев 6, в результате осуществляется схват
детали. При вращении дисков 7 происходит поворот
детали вокруг своей оси.
Для выбора необходимого усилия привода схвата
необходимо знать силовое передаточное отношение
K = F/P = (F/M1)r1,
(5.23)
где F — сила, приложенная к дискам 7; Р — окружная сила
на червяке 1; Мi — момент на входном звене /; гх—
радиус начальной окружности червяка 1.
Перед тем как определить коэффициент К, выполним
кинематический анализ механизма схвата.
Кинематический анализ. Исходными данными для кине-
матического анализа являются:
закон движения входного звена (червяка 2);
геометрические размеры звеньев.
Для удобства вычислений введем обозначения (рис. 5.25, а):
AiBi = Л2В2 =? Zi; AiDi = A2D2 = l2; AjA2 = /0- Числа зубьев
колес обозначим z2, z3, z4, zs (z4 = z5), а число заходов
червяка — их. За обобщенную координату примем угол
поворота колеса 1 — <рх.
Угловые скорости колес и червяка связаны между собой
следующим образом:
<х>1 = ®4Wi4; w14 = (z2/ni)(z4./z3); со5 = -со4,
где coi — угловая скорость червяка; со4 — угловая скорость
колеса 4 (<о4 = ф4); <о5 — угловая скорость колеса 5 {еа5 =
= — ф4); и14 — передаточное отношение от червяка 1 к
колесу 4.
Тогда положения колеса 5 и червяка 1 будут опре-
деляться углами <р5 и фх соответственно
ф5 = л - Ф4; ф! = ф4(г2/Л1)(г4/г3). (5.24)
Угол поворота червяка в начальный момент времени
принимаем равным нулю (фх — 0).
Выразим координаты точек механизма схвата через гео-
метрические размеры звеньев и обобщенную координату ф4.
В результате получим следующие соотношения (рис. 5.25, а):
209
У Al ~
xBi = sin<p4;
yBi = /icoscp4;
xDi = /2sin(<p4 + P);
yDi = /2cos((p4 + p);
*a2 = 0;
Уа2 ~ ~h'9
xE1 = sin ф4:
У Bi = cos<p4;
xD2 = l2 sin (ф4 + p);
Уб2 = ~h cos (ф4 4- P).
(5.25)
Координаты оси схватываемой детали в момент ее
фиксации определяются из условий:
(xD, - хЕ)2 + (yD, - уЕ)2 = (R + г)2;
(* *£ - xBl)2 + (yBi - у£)2 = (R + г)2; (5.26)
(х0 - хЕ)2 + (yD - у£)2 = (R + г)2;
(*£ - хв)2 + (у£ - ув )2 = (R + г)2,
где R — радиус детали; г - радиус дисков.
Подставим выражения (5.25) в систему уравнений (5.26)
и с учетом симметрии (уЕ — 0) получим:
II - 2/2sin(<р4 + Р)х£ + х2Е = (R + г)2;
/2 — 2/t sinq>4x£ + хЕ = (R + г)2. (5-27)
Вычитая из первого уравнения второе, получим
Подставляя последнее выражение в одно из уравнений (5.27),
получим квадратное уравнение для определения ф4. Система
уравнений (5.27) позволяет определить координату геометри-
ческой оси детали хЕ и значение обобщенной координаты
ф4> при которой произойдет фиксация детали заданного
диаметра.
Скорости точек звеньев определим в проекциях на оси
координат в результате дифференцирования выражений (5.25):
*В1 — Фд/1СО8ф4;
\в2 = -ф4/18Щф4;
*Di - ФЛ cos (ф4 + Р);
^Di ~ ФЛ sin (ф4
<p4/icos <р4;
<p4/i sin <р4;
Ув
(5.28)
₽>;
ф4/2 sin (<р4 + Р),
210
где ф4 — угловаяскорость колеса 4,
ф4 = (04 = COi (n!Z3)/(z2Z4).
Силовой расчет. При захвате детали равновесие звеньев
механизма схвата опишем уравнением вида Q? = 0. где
Ср — обобщенная сила, соответствующая обобщенной
координате ср4:
^ = 0
<?Ч>4
(5.29)
Здесь Fix, Fiy — проекции сил, действующих на звенья
схвата; — момент на червяке.
Вычислив частные производные с использованием выра-
жений (5.28) и подставив их в зависимость (5.29), приведем
ее к виду
/-'01 J2cos(<p4 + ₽) + FBlXliCos<f>4 + FD1Xl2 cos (<p4 + ₽)
₽) - sin <p4
ojz sin (<p4
₽) + FB2ylisin<f>4 + Mi(z2/nl)(zi/z3) = 0, (5.30)
Где * Dij> ** Вгх’ * B2y> *D2x’ * D2y> * B2x> “ B2y
проекции сил, действующих на звенья схвата (рис. 5.25,6).
Рассмотрим равновесием детали в _^юмент захвата. Деталь
под действием сил
FBit FDi, FDi находится в равно-
весии, т. е.
(5.31)
Моментов относительно оси детали действующие силы не
создают.
В силу симметрии имеем (рис. 5.25,6) FBi — FB1\
FDi = Fd2> поэтому обозначим FB = FB = FB; FD = F„ = FD.
Тогда первое уравнение системы (5.31) принимает вид
или
(5.32)
Проекции сил, действующих на звенья механизма схвата:
211
FDl.x = FD(xD1 - xe)/(R + r); FD2X = FD(xD2 - xE)/(R + r);
FBlX = “ Fd (xDi - xe)/(R + r); FB2X = - FD(xD2 - xE)/(R + r);
Fo}y FDyDJ(R + r); FВгУ — FByB2/{R + r)’
(5.33)
Подставляя выражения (5.33) в (5.30) и далее в (5.23), после
преобразований получим выражение для определения сило-
вого передаточного усилия в точке D:
— (Fi)/Ml)r1, (5.34)
или
к =_______________z2z4(# +г)п_______________
D 2w1z3[(x£ — xDi)(/2cosa — GcoscpJ+y^/2sma —
~ Ув. (xDl - x£) (xB - x£) /i sin cp4] ’
где a = cp4 + p.
Действующие на схват силы следующие:
FBl — FD2 ~ KBrxMx', FBi — FB1 — КВГ1М1, (5.35)
где Кв — KD (xn — xE)/(xE — xB).
Таким образом, определив координаты оси детали данного
радиуса, угол ф4 из (5.27) и рассчитав координаты точек
по (5.25), можно по формулам (5.35) с учетом (5.34)
найти усилия захвата детали при известном моменте
Расчет плоского шестизвенного шарнирного механизма
схвата*. Механизм схвата (рис. 5.26,а) состоит из двух
коромысел 3, 3', тяги 4, шатунов 2, 2' и силового
цилиндра. Деталь захватывается тремя съемными пальцами
5, которые установлены на концах коромысел 3, 3' и тяги 4.
Работает механизм схвата следующим образом: шток 1
цилиндра выдвигается и смещает тягу 4 влево, а шатуны 2
и 2' поворачивают коромысла 3 и 3' в шарнирах Съ С2
навстречу перемещающейся тяге 4. В результате пальцы 5
сжимают деталь. При обратном движении штока 1
9
♦ Пат. 8221171 Франция, МКИ В 25 J 15/00.
1
1
цилиндра пальцы 5 разжимаются и деталь освобождается.
Этот схват построен на основе плоского шестизвенного
механизма 2-го класса по классификации И. И. Арто-
болевского.
Одна из основных задач расчета — определить усилия,
необходимые для надежной фиксации детали. Для ее ре-
шения необходимо знать силовое передаточное отношение К,
но сначала нужно выполнить кинематический анализ и
силовой расчет механизма схвата.
Кинематический анализ. Исходные данные:
кинематическая схема (рис. 5.26, а);
геометрические размеры звеньев;
закон движения входного звена механизма xK(t).
Обозначим геометрические размеры звеньев:
— О2С2 ~ = А 2В 2 — ^2>
213
1
Выберем систему координат Оху, за обобщенную коор-
динату примем перемещение хк входного звена 1. Выразим
через обобщенную координату перемещения, скорости и
ускорения точек А, В, D механизма.
Координаты точек А19 А2, Ci9 С2, Bi9 В2, Di, D2,
D3, Ок в системе координат Оху:
Уа^
Уа3 “
— Is > Ус
хв
2
Ув>
2
К
Ув2-
2/i хк).
+ x2-2xK/i)2
хк 2liXK)
(5.36)
Vd
Уя3 — j’ok — о.
Определим положение центра Е цилиндрической детали
(рис. 5.26). Для момента захвата детали
следующие соотношения:
а + R + г = xD1 - хРз; а2 = (R + г)2 - Д,
справедливы
откуда
(5.37)
Выражение (5.37) позволяет определить
входного звена хк = f(R, г, ll9 12, 13, /4, /6)
для фиксации цилиндрической детали радиусом R. Подста-
вим (5.36) в (5.37), после преобразований получим уравнение
I 12 I ~2 I 12 12 ~
перемещение
необходимое
214
1
решив которое, найдем значение хк. Уравнение (5.38) удоб-
нее решать численно на ЭВМ.
Координаты центра Е детали будут следующими:
X- R + г 4- /6 + Хк; уЕ = 0.
Продифференцируем по времени выражения (5.36). Тогда
линейные скорости движения осей пальцев схвата получим
в проекциях по оси координат:
• — ^*«Рз ~.(fi ~ хк)2 ~~ I2] .
2(h-^)2l3
V
• _ Рз G1 *к)
У°' ~ 4/i (G - х„)3 X
_ ... - ® Из - - хк)2 - .
х ]/1 — [/3 + (/i — хк)2 — /2]2/[412(/j — х.)2]
_____________X [(G -хк)2 -Ц- %] _
х |/i - [z2+(Zi - хк)2 - zi]7[4zi(/! - хк)2] ’
Уйз “* 0-
(5.39)
Абсолютные скорости v находим на основании выра-
жений (5.39):
^D2 V*02 + УОг » ~ А-
(5.40)
Таким образом, выражения (5.36) позволяют определить
текущее положение осей пальцев схвата, а выражения (5.39),
(5.10) — скорости их движения в любой момент времени г,
если задан закон движения входного звена хк — хк (t).
Силовой расчет. При фиксации детали силы, действующие
на звенья механизма, уравновешиваются и скорости осей
пальцев схвата равны нулю, поэтому кинетическая энергия 7
также становится равной нулю (Т = 0). Тогда на осно-
вании уравнений Лагранжа для равновесия механизма
необходимо и достаточно, чтобы
1
(5.41)
и
где Pi — силы, приложенные к исходному звену и пальцам
схвата; QK — обобщенная сила, соответствующая обобщенной
координате qK.
Вычислим частные производные в выражении (5.41).
Продифференцировав зависимости (5.36), получим
- х - XJ2]
Х |/1 ~ Рз + ~ Хк)2 ~ ^2]2/[4/з(^1 ~ Хк)2]
дхОк дуОк _ .
А ----- 1 > А ----- В,
дхк дхк
(5.42)
дур _ Ц Рз + (/i — хк)2 — /2] х
dxK 4Zi (/t - хк)3 х
х * х [Qi ~ *к)2 — /2 + /1].
X |/1 — рз + (Z1 — Хк)2 — /2]2/[4/з(^1 ~ Хк)2]
После подстановки выражений (5.42) в (5.41) и некото-
рых преобразований с учетом знаков получим уравнение
равновесия механизма схвата в виде
___________х Рз ~~ ^2 ~ (h. ~~ *к)2]___________р = Q
х ]/1 — рз —12 + (li — хк)2]2/[4/з (li — хк)2]
216
1
i де Fx и Fy — проекции сил, приложенных к пальцам
(рис. 5.26,6); Рх — проекция силы, приложенной к входному
звену, Рх — Р.
Уравнение (5.43) содержит пять неизвестных. Чтобы найти
соотношение между ними, необходимо это уравнение
дополнить еще четырьмя уравнениями. Недостающие урав-
нения получим из условия равновесия детали (рис. 5.26,6).
Под действием сил F
F3 деталь находится в
равновесии, т. е.
£ Fx = 0; £ Fy = 0; £ МЕ (Fx, Fy) — 0.
(5.44)
Силы Fi, F2 и F3 действуют по нормали к поверх-
ностям пальцев и детали, т. е. Flx — F^osyi; F2x = F2cosy2;
F3x = F3. Из уравнений (5.44) получим
F iy = — F2y; F 1х = F2x — ~^зх/2. (5.45)
Из рис. 5.26,6 имеем
Fix = Fiy ctg Yi; F2x = F2y ctg y2, (5.46)
где Yi, y2 — углы между линиями действия сил Fi и F2
и осью х. Выразив углы Yi и у2 через координаты осей
пальцев схвата, несложно показать, что углы Yi и у2
равны, т. е.
Y1 = у2 == Y* (5.47)
На основании выражений (5.45), (5.46) и (5.47) получим
следующие соотношения:
Fj = F2 = F;
Fix — Fcosy; F2x = Fcosy; F3x=-2Fcosy; (5.48)
Flj, = Fsiny; F2y = - F sin у; F3y = 0,
где cosy = (xD1 ~ xe)/(R + r); sin у = yoJ(R + r).
Выражения (5.48) подставим в уравнение (5.47):
I
217
1
2F
2F
4ll(li~xK)3 1
4ll
Введем обозначения:
Уи
0,5
4Zi(/
2
cosy =
Тогда уравнение (5.49) запишется в виде — 2Fca — 2Fb + Р=0,
откуда
F/P = 1/[2 (ас + ВД,
т. е. получено выражение для силового передаточного отно-
шения К, которое для каждой из сил имеет вид:
Kt = К2 = F/P = 1/[2 (ас + Ь)];
Кз — F3/P — 2Fcos у/Р = с/(ас 4- Ь).
Таким образом, по известному значению силового пере-
даточного отношения К и заданной силе Р можно рас-
считать силы Ft, F2, F3, а по заданным значениям сил
Fi, F2, F3 для данного схвата — силу Р, которую необхо-
димо приложить к входному звену.
Расчет механизма ориентирования схвата с двумя
ми свободы*. Рассмотрим пример кинематического
степеня-
анализа
ланетарного ориентирующего механизма
схвата
про-
мышленного робота (рис. 5.27). Особенность схвата: при
повороте головки схвата вокруг одной оси положение
относительно другой корректируется автоматически.
Корпус 20 схвата (рис. 5.27) установлен на манипуляторе
1 с возможностью относительного перемещения по направ-
ляющим 3. В корпусе 20 установлена поворотная головка 14,
* Пат. 57-17674 Япония, МКИ В 25 У 17/02.
218
1
8
6 5
4 3
2
1
15 16 17/ 18 19 20 21 22 23
Рис. 5.27
жестко закрепленная на валу 15. Вал 15 расположен
перпендикулярно оси вращения зажимного устройства 12.
Устройство 12 жестко закреплено на валу 13, который
установлен в поворотной головке 14.
Поворотная головка 14 приводится в движение через
рядовую передачу 4, 7, 8, 19 от приводного вала 2.
При этом головка вращается вокруг вертикальной оси.
Зажимное устройство 12 вращается вокруг горизонталь-
ной оси и движение ей сообщается от приводных валов
2, 23 через коническую передачу 11, 10, зубчатое колесо 9,
дифференциальную планетарную передачу, включающую зуб-
чатые колеса 5, 6, 16, поворотный диск 17, две рядовые
передачи 4, 19 и 22, 21.
При вращении валов 2, 23 зажимное устройство 12
вращается вокруг горизонтальной оси и одновременно
поворачивается вокруг вертикальной оси.
Кинематический анализ. Рассчитаем угловые скорости
головки 14 и зажимного устройства 12.
Так как схват 12 совершает сложное вращательное
движение вокруг осей валов 15 и 13, то для определен-
ности выберем оси х и у в точке О (рис. 5.27). Ось х
направлена по оси вала 15, а ось у — по оси 13 вала
схвата.
Абсолютные угловые скорости головки 14 и схвата 12
следующим образом раскладываются по осям х и у:
d>i4 — о**;
012 — 012 *"Ь
(5.50)
219
1
Так как вокруг оси у схват 12 вращается относительно
головки 14, то
©12 = ©14. (5.51)
Из (5.50) и (5.51) следует, что вначале необходимо
определить движение головки 14, затем — схвата 12.
Поскольку ведущими являются валы 2 и 23, составляю-
щие по осям х и у скоростей ©i2, ©14 будем искать
как функции от ©2, ©2з.
Найдем ©14 = ©14. Из кинематической схемы видно, что
головка 14 не связана с валом 23, а с валом 2 ее
соединяет рядовая передача, состоящая из колес 4, 8, 7,
18 и 19. Следовательно, ©4 = «14.2°)2. Выражая w14>2 через
числа зубьев колес z4, z7, z8, z18, zl9 и определив по
правилу стрелок знак ul4t 2, получим
.. _ Z1 z18 Z4 Z18Z4
Z8Z19*
отсюда
чх ^*18^4
®14 “ (Оз*
^8Z19
Рассмотрим движение схвата 12. Поскольку ©?2
осталось определить только составляющую ©i2 по оси у.
Эта составляющая задает движение схвату 12 относительно
головки 14. Поэтому для ее определения перейдем к об-
ращенному движению, мысленно сообщив дополнительную
скорость (—©14) вокруг оси х всему передаточному ме-
ханизму. В качестве ведущих возьмем звенья 17 и 19. Их
скорости в прямом и обращенном движении будут сле-
дующими :
(5.52)
©23J
©2;
(5.53)
©19
©17 — ©18
©23
(5.54)
©19 — ©19
По формуле для дифференциала
©?2 = ©12 = wil?it(°i9 + ^lljl^l?.
(5.55)
220
Найдем частные передаточные отношения и
в рассмотренном обращенном движении при останов-
ленном вале 17 передаточная цепь от схвата 12 к валу 19
состоит из простых передач 11-10, 9-16, 16-6, 6-5, значит,
„0(17) ..0(17) ..0(17)..0(17).0(17) _
м12, 19 = 10W9, 16 м16,6 м6, 18 —
*10*16
при остановленном вале 19 схват 12 соединяется с валом
17 простыми передачами 11-10, 9-16 и планетарной переда-
чей 16, 17, 5, отсюда
Подставив найденные передаточные отношения в (5.55),
с учетом (5.54) получим выражения для составляющих по
осям хи у скорости со6:
О>12 = <»14;
Выражения (5.52) и (5.56) полностью определяют кине-
матику головки 14 и схвата 12 в зависимости от движе-
ния входных валов 2 и 23.
Расчет дифференциального механизма ориентирования
схвата с тремя степенями свободы. Схема одного из таких
механизмов показана на рис. 5.28. Механизм работает
следующим образом. Корпус 7 схвата крепится на манипу-
ляторе и имеет три поворотные головки 12, 14, 16. Головки
приводятся в движение от валов 1, 2, 30 через систему
зубчатых колес.
Для характеристики вращательного движения головок 12,
14, 16 введем оси: ось х жестко свяжем с головкой 12,
ось у — с головкой 14^ ось z — с головкой 16. Как видно
из рис. 5.27, оси х и z могут совпадать.
Так как головка 12 вращается вокруг оси х, головка
14 — вокруг осей х и у, головка 16 — вокруг осей х, у и z,
221
/7 10 S’8 7 6 5 4 3
Рис. 5.28
то абсолютные угловые скорости со14, со16 расклады-
ваются по осям х, у, z следующим образом:
&12 = «>12; G>n = б>14 + «>Ь; &16 = «>16 + + б>?6. (5.57)
Так как головка 14 вращается вокруг оси у относитель-
но головки 12, а головка 16 вращается вокруг оси z
относительно головки 14, то отсюда следует:
oh = of4 = со?6; со?4 = со?6. (5.58)
Из (5.57) и (5.58) следует, что вначале необходимо найти
Й>12, затем cb14, а затем ю16.
Найдем со12 == со?2. При остановленных валах 2 и 1 дви-
жение от головки 12 к валу 30 передается через вал 24,
содержащий колеса 23 и 22, колесо 26, звено 27 и коле-
со 29. Этот передаточный механизм является планетарным.
Водилом будет сама головка 12, сателлитом — колесо 26, а
неподвижным является колесо 7. Переходя к обращенному
движению, получим
При остановленном вале 30 колесо 27 будет неподвижным
относительно корпуса 5. Сателлит 26, который приводит
в движение головку 12, также будет неподвижен. Следова-
тельно, и{/ °*1) = u(i33°’2) = 0 и угловая скорость головки 12
(5.60)
Определим ©14. Поскольку ©*4 = ©*2, необходимо опре-
делить только угловую скорость ©?4 головки 14 в ее
вращательном движении вокруг оси у относительно голов-
ки 12. Для этого возьмем в качестве ведущих звенья 1, 4,
27 и перейдем к обращенному движению, мысленно
сообщив механизму вращение со скоростью (—©*2) (5.60)
вокруг оси х.
В прямом движении
0)!=©!; ©27 - (“231/z29)®3o; со4 = (-24/23)0)2. (5.61)
В обращенном движении
со? = ©1 - ©J2;
©°27 = ©27 — ©12 — (~z31/z29)©30 ®12»
©4 = - Mil = (-£4Лз)а>2 - G>12-
(5.62)
В обращенном движении угловая скорость головки 14
С0?4 = ©$ = uU2,l,4)to^ + П1^’24?Ю?7 + М?^’427)©2. (5.63)
Найдем частные
„0(27,4) ,,0(1,4) ,,0(1,27).
м14,1 , w14,27> w14,4 •
при остановленных валах
от головки 14 к валу 1 не
что в цепи, соединяющей
передаточные отношения
27, 4 и головке 12 движение
может передаваться, потому
их, находится неподвижное
звено 25 (движение его блокируется звеньями 27 и 4), поэтому
M?i27!’4) = 0
А > X
передаточный механизм, соединяющий головку 14 с ва-
лом 27, состоит из простых передач 20-22, 23-10 и
планетарной 6, 25, 28, отсюда
м14!’г7 “ w2&* 22^2^10^2 ^*б4) ~ (z22/z2o)(”"zlo/Z23)[V(l + г4/гб)]>
передаточная цепь состоит йз тех же ступеней, отли-
чается выходное звено — это вал 4, тогда
м14^427) = (z22/z2o)(“zio/z23)[l/(l +
Подставляем выражения для частных передаточных от-
ношений в формулу (5.62) с учетом (5.61), получим, что
полная скорость головки 3 имеет следующие составляю-
щие по осям хи у:
Юм = а>12;
©14 —
0)2
ю3о-о>12 • (5.64)
Определим ©16. Так как ©f6 = ©f4 = ©f2, ©?6
остается определить только составляющую ©i6. Для этого
вновь в качестве ведущих берем звенья 1, 4, 27 и пере-
ходим к обращенному движению, сообщив всему механиз-
му вращение со скоростью (—©*2) (5.60) вокруг оси х
Найдем в этом движении угловую скорость колеса 18.
Скорости звеньев 1, 4, 27 в прямом и
движениях задаются формулами (5.61), (5.62),
ГЛ0 _ . .0 (27,4)„0 I , .0 (7,4),А0
ю18 — м18, 1 ©I Т ^18, 27 ©27
обращенном
тогда
Найдем частные передаточные отношения
“?£i27), u°i№,
как показано выше при остановленных звеньях 4 и 27
звено 25 неподвижно, следовательно, цепь, передающая дви-
жение от колеса 18 к валу 1, состоит из простой ступени
19-11 и планетарной 8, И, 13
“18,1 = = (~ZU/Z19)
передаточная цепь состоит из простой ступени 19-11 и
двух планетарных - 8, 11, 25 и 25, 27, 28
по аналогии с
В результате
f %. Iм*
0 / 1 | I
©18 = I----— I
<01
210
<»зо
©2 ~ ®12 !•
(5.65)
У
1
Выражение (5.65) задает, с какой угловой скоростью вокруг
оси у относительно головки 12 вращается колесо 18. Для
головки 14 аналогичное выражение получено ранее [см.
(5.64)].
Поскольку в итоге необходимо определить угловую ско-
рость СО16, рассмотрим еще одно обращенное движение. В нем
головке 14 и звеньям, принадлежащим ей, сообщаем допол-
нительное вращение вокруг оси у со скоростью (—оЯ4) =
= ~«?4- втором обращенном движении
со?4 = ш?4 - (014 = 0; (5.66)
«18 = (Dig — «14- (5.67)
При остановленном водиле (головка 14) во втором
обращенном движении получим, что головка 16 приводится
от колеса 18 простой конической передачей 18-15. В ре-
зультате
«16 — (2 18 /21 б) «18*
(5.68)
Выражая со?! через (ох, (о2, (030 из (5.65), (5.67) и (5.68), в
итоге получим, что полная скорость а>1б следующим
образом раскладывается по осям х, у, z:
хТб — «12» «¥б = «14;
(5.69)
Таким образом, кинематика головок 12, 14, 16 описы-
вается зависимостями (5.60), (5.64), (5.69), задающими связь
составляющих их угловых скоростей ng осям х, у, z с угло-
выми скоростями ведущих валов 1, 2, 30.
5.7.* Расчет параметров взаимодействия
схвата с объектом
Виды положений равновесия объекта в схвате. Контакт
объекта с рабочими элементами схвата может осуществлять-
ся по поверхностям, линиям и в дискретных точках. В
* Параграф написан С. Н. Колпашниковым и И. Б. Челпановым.
8 Механика промышл. роботов, кн. 2
225
теории базирования, основные положения которой установ-
лены ГОСТ 21495 — 76, распределенный контакт принято
заменять контактом в дискретных точках так, чтобы при
такой замене объект лишался тех же степеней свободы и
оставалось бы неизменным число налагаемых связей. Так,
контакт по плоскости заменяется контактом в трех точках,
лежащих в этой плоскости, контакт по прямой —
контактом в двух точках, лежащих на этой прямой. При
удерживании объекта схватом непрерывный контакт целе-
сообразно заменять контактом в точках, однако выбор
положения точек контакта не произволен. Когда контакт
осуществляется по линиям, достаточно выделять наиболее
разнесенные точки этих линий (для прямых линий — их
концы). Когда контакт осуществляется по поверхностям,
выделяются точки на их границах.
При несогласованных формах поверхностей контакт
возможен только в дискретных точках, поскольку поверх-
ности контакта объекта и рабочих элементов схвата в
этом случае имеют различную кривизну. Контакт в дискрет-
ных точках имеет место как для гладких поверхностей, так
и для угловых точек (рис. 5.29, а). Случай, когда угловая
точка объекта упирается в линию пересечения плоскостей
рабочего элемента, эквивалентен наличию двух точек контак-
та (рис. 5.29, б). Случай, когда угловая точка объекта
упирается в угловую выемку поверхности рабочего элемента
(рис. 5.29, в), эквивалентен наличию трех точек контакта.
Реакции рабочих элементов схвата, действующие на объект
в точках контакта, представляются в виде суммы
где i — номер точки контакта; N{ — нормальная составляю-
щая реакции, направленная по орту й,- нормали в точке
контакта; Qi — сила сухого трения, действующая в касатель-
Рис. 5.29
226
ной плоскости к поверхностям объекта и рабочих элемен-
тов схвата в точке контакта.
Помимо реакций R, в точках контакта на объект, зажа-
тый в схвате, действуют приложенные силы и моменты. К
ним относятся: сила тяжести, объемные силы инерции,
возникающие- при переносе и ориентировании объекта,
поверхностные силы, возникающие при контакте объекта с
другими предметами и оборудованием. Приложенные силы
и моменты приводятся к условному центру схвата —
точке О, являющейся началом декартовой системы коор-
динат схвата, и представляются проекциями на эти оси
[19].
При правильном захватывании для всех положений
равновесия объекта в схвате осуществляется его жесткое
фиксирование в том смысле, что для выведения объекта из
положения равновесия необходимо приложение сил и момен-
тов, комбинации которых превышают конечные предельные
значения. Положение равновесия при жестком фиксиро-
вании качественно отличается от обычно рассматриваемого
в механике устойчивого равновесия, которое в дальнейшем
называется классически устойчивым. Для классически устой-
чивого равновесия, когда пренебрегают силами трения, при
приложении как угодно малых сил и моментов возникают
смещения того же порядка, а при жестком фиксиро-
вании смещения теоретически точно равны нулю.
Жесткое фиксирование является необходимым условием
надежного удерживания объекта в схвате, поскольку при
работе робота на объект действуют конечные по величине
приложенные силы и моменты. Обычно жесткое фиксиро-
вание по одним координатам осуществляется благодаря
силам трения, по другим — благодаря принудительному
базированию объекта по участкам поверхности рабочих
элементов. *
Исследование положений равновесия проводится в пре-
небрежении силами трения и при учете только нормальных
составляющих реакций. Положение равновесия при учете
только нормальных реакпий называется исходным.
Исходное положение равновесия объекта в схвате может
быть неустойчивым, безразличным, классически устойчивым,
положением жесткого фиксирования.
Примеры положений равновесия и графики зависимостей
потенциальной энергии П системы «схват — объект» вблизи
этих положений приведены на рис. 5.30. В неустойчивом
положении равновесия (рис. 5.30,а) потенциальная энергия
системы имеет максимум, в безразличном (рис. 5.30, б) —
1
постоянна, в классически устойчивом (рис. 5.30, в) имеет
гладкий минимум, в положении жесткого фиксирования
(рис. 5.30, г) — минимум в угловой точке.
На рис. 5.30 приведены также графики зависимостей
предельных значений силы Fx, приложенной к объекту, от
малого смещения по оси х для заданного усилия захваты-
вания Р.
Под действием сил трения жесткое фиксирование
реализуется для положений, которые в пренебрежении сила-
ми трения относятся к положениям классически устой-
чивого, безразличного или неустойчивого равновесия
(рис. 5.30, а—в). Для каждого из этих случаев предельное
значение приложенной силы одинаково: в точках контакта
под действием сил трения, значения которых определяются
коэффициентом трения f и усилием захватывания Р, поло-
жение равновесия сохраняется до тех пор, пока приложен-
ная сила Fx не превысит предельного значения, равного
2/Р.
Для жесткого фиксирования принудительным базиро-
ванием (рис. 5.30, г) минимум потенциальной энергии —
Рис. 5.30
1
неаналитический и достигается в угловой точке, где ее
производная претерпевает разрыв. Предельное значение
приложенной силы определяется согласно принципу виртуаль-
ных перемещений по формуле | Fx | — 2Р tg а.
В рассмотренных примерах поверхности объекта и рабо-
чих элементов схвата призматические или цилиндрические
с параллельными образующими; контакт осуществляется по
образующим. В таких случаях в плоскости, перпенди-
кулярной образующим, рассматривается плоская задача, а об
образующих говорится как о точках. Полагая, что направ-
ление оси z совпадает с направлением образующих контакта,
а ось у совпадает по направлению с вектором h переме-
щения рабочих элементов, положение объекта в схвате при
наличии контакта с обоими рабочими элементами опре-
деляется двумя параметрами: линейным перемещением по
оси х и углом поворота 6 вокруг оси z. В пренебре-
жении силами трения исходное положение равновесия
находится из условия
h — min.
х, 0
Минимум в исходном положении равновесия может быть
аналитическим или неаналитическим, строгим или нестро-
гим. Например, при захватывании выпуклого объекта
плоскопараллельным схватом (рис. 5.31, а), когда контакт
осуществляется в двух точках, положению равновесия
соответствует нестрогий аналитический минимум потенциаль-
ной энергии. По координате х положение равновесия
является безразличным. Если объект имеет эллиптическое
сечение, то для произвольного поворота параметр h
(раскрытие схвата) определяется выражением (рис. 5.31,6)
h — 2|/n2sin20 + b2 cos2 0.
Восстанавливающий момент (рис. 5.?1,в) определяется по
принципу виртуальных перемещений и удовлетворяет ра-
Рис. 5.31
229
венству М —
dh
dO
Р, следовательно, он равен
М — Р(а2 — b2)sin20/]/а2sin20 4- b2cos20.
Устойчивым является положение равновесия, в котором
большая полуось эллипса а направлена по оси х и
h = 2b. Функции h и М непрерывны и дифференцируемы.
В положении равновесия достигается аналитический мини-
мум, и потенциальная энергия может быть представлена
в виде знакоопределенной положительной квадратичной фор-
мы координаты 0. При малых угловых отклонениях от
положения равновесия восстанавливающий момент того же
порядка малости, что й угол поворота 0. При повороте
эллипса вокруг оси z в контакт с поверхностями рабочих
элементов схвата непрерывно вступают все точки контура
эллипса, при этом число точек контакта неизменно и
равно двум.
Если объект имеет угловые точки контакта (рис. 5.32, а),
то, как правило, минимум потенциальной энергии в исход-
ном положении равновесия неаналитический. На рис. 5.32
приведены графики зависимостей потенциальной энергии
(параметра h) от линейного перемещения и поворота
объекта квадратного сечения в уголковом схвате (рис. 5.32, б, в),
а также аналогичные зависимости восстанавливающей силы
F и момента М (рис. 5.32, г, 0). Все зависимости рас-
сматриваются на интервале изменения угла 0 от 0 до
п/2. Из симметрии задачи следует четность h (0) и не-
четность М (0) относительно значения угла, равного к/2.
Рис. 5.32
230
В положении устойчивого равновесия, соответствующем
жесткому фиксированию, контакт объекта с рабочими
элементами осуществляется в четырех точках. При переме-
щении объекта в схвате происходит потеря контакта
хотя бы в одной точке. В положении равновесия
наблюдается разрыв зависимости силы и момента. При
изменении формы рабочих элементов может меняться
число устойчивых положений равновесия, границы области
устойчивости каждого из этих положений. На рис. 5.32, б, г
показаны зависимости потенциальной энергии и восстанав-
ливающего момента системы «схват — объект» для углов
а = 45 и 60°, из которых видно, что число положений
равновесия различно; отличается по значениям и вос-
станавливающий момент.
Значение восстанавливающей силы по оси х, получен-
ное выше с использованием принципа виртуальных пере-
мещений, может быть определено из условий достижения
предельных состояний. Уравнение равновесия верхнего,
подвижного рабочего элемента записывается в виде
р = -j- N2)cosa. Уравнения статического равновесия
объекта под действием силы Fx и реакций в точках
контакта представляют собой уравнения равновесия сил в
проекциях на оси х и у
N4. sin a
— Ni sin a = 0;
+ N2 - (N.
4- N4) cos a — 0
и уравнение равновесия моментов вокруг оси z
(N3-N2)a = (N4-Ni)b.
Исключая из полученных уравнений неизвестные реак-
ции, находим:
*
Р Fx _ Р Fx b
N* ~ 2 cos a + 2 sin a ’ 2 + 2 sin a а
2 2 sin a a
2 cos a
2 sin a
При смешении объекта в положительном направлении
по оси х произойдет отрыв в одной из точек контакта
с верхним
реакция Nt.
рабочим элементом и обратится в нуль
Из условия Ni = 0 находится значение силы
Fx = Р tg а, при котором нарушается равновесие системы.
При перемещении объекта в отрицательном направлении
по оси х вследствие потери контакта в точке 2 обратится
1
в нуль реакция N2. Это произойдет при Fx = — Ptga
(рис. 5.32,3).
Уравнения статики механической системы «схват —
объект». Рассмотрим задачу о жестком фиксировании
объекта, когда схват имеет два рабочих элемента, причем
подвижными могут быть оба рабочих элемента или только
один из них. Перемещение рабочих элементов в процессе
захватывания и создание усилия захватывания в положении
равновесия осуществляются от двигателя с помощью любого
механизма передачи. Предполагается, что механизм схвата
является плоским. В дальнейшем величинам, относящимся
к точкам контакта с верхним рабочим элементом, при-
писывается индекс «1», а с нижним — индекс «2».
Для рассматриваемого типа схватов к системе шести
уравнений статики, определяющих условия равновесия объек-
та, добавляется седьмое — уравнение равновесия системы
«схват — объект», как механизма с одной степенью свободы,
положение которого задается параметром раскрытия h.
В качестве параметра раскрытия могут выступать: рас-
стояние между характерными точками рабочих элемен-
тов, величины угловых перемещений рычагов и др.
Усилие захватывания для схватов с одной степенью
свободы и двумя рабочими элементами определяется как
усилие сжатия шарнирно опертого в точках А} и Л2
стержня рабочими элементами схвата (рис. 5.33, а) при
действии усилия двигателя.
Усилие захватывания зависит от положения точек
и А2 на рабочих элементах. Для симметричных механиз-
мов схвата при симметричном расположении рабочих
элементов относительно оси х (рис. 5.33,6) точки Аг и Л2
целесообразно выбирать симметрично относительно этой оси.
Для несимметричных механизмов схватов расположение
точек Ai и А2 выбирается в каждом конкретном случае
в зависимости от формы и расположения поверхностей
объекта и рабочих элементов.
Рис. 5.33
232
1
Для двигателей с перемещением
усилие захватывания Р выражается
/ выходного
звена
через усилие Q на
выходном звене двигателя в виде:
где $ — расстояние между точками Аг и А2 является
функцией параметра раскрытия h, т. е. s = s (h).
Зависимость передаточного отношения
(5.70)
от параметра h может быть убывающей, возрастающей или
постоянной.
является расстояние s между точками А
ние (5.70) имеет вид
В случае, когда* параметром раскрытия h
и Л2, уравне-
dh ’
Реакции объекта, действующие на рабочие элементы
в точках
контакта, линейно связаны
с усилием захва-
тывания уравнением равновесия механизма схвата:
(5.71)
где i — номер точки контакта; п — число точек контакта;
о, (h) — коэффициенты, зависящие от параметра раскрытия
схвата.
Выделяются следующие частные случаи:
1. Один из рабочих элементов схвата неподвижен (жестко
связан с основанием схвата); уравнение (5.71) записывается в
виде
X = Р,
i-i
где суммирование распространяется только на точки
контакта с подвижным рабочим элементом.
2. Объект и рабочие элементы схвата симметричны
относительно оси х и перемещаются симметрично относитель-
но ее. Уравнение равновесия записывается в виде
1
где суммирование распространяется на точки контакта
только с одним рабочим элементом.
3. Рабочие элементы перемещаются поступательно по
оси у, симметрично относительно оси х, расположение точек
контакта произвольно, возможно несимметрично. Уравнения
равновесия записываются в виде
Y RW cos (- у, R<°) + Y R*2} cos (b Kj2)) = р- (5.72)
i i
В первом слагаемом, относящемся к верхнему рабочему
элементу, множителями являются косинусы углов между
направлением относительно перемещения этого элемента
(противоположного оси у) и соответствующей реакцией
кр. Во втором слагаемом, относящемся к нижнему
рабочему элементу, множителями являются косинусы углов
между направлением оси у и соответствующей реакцией
R$2). При такой записи уравнения все множители являются
положительными.
4. Схват является плоскопараллельным, плоские рабо-
чие элементы перемещаются симметрично по оси у.
Уравнения равновесия записываются в виде
где Ni — нормальные составляющие реакций.
Для случаев 3 и 4 в уравнения равновесия входят
только параметры ориентации реакций, а от координат
точек контакта ничего не зависит. Усилие захватывания
не зависит от положения точек At и Л2, которые
выбираются друг против друга в любом месте рабочих
элементов. Уравнения в форме (5.72) можно использовать
как приближенные при непоступательном перемещении рабо-
чих элементов, когда расстояние между точками считается
значительно меньшим, чем расстояние до осей поворота
последних звеньев схвата.
Для схватов более чем с двумя рабочими элементами
вместо (5.71) записываются уравнения равновесия механизма
схвата в виде
£ ( Z aJt (h) ) = P,
j= 1 \i = 1 /
где к — число рабочих элементов; R^ — реакция в i-й
точке контакта с j-м рабочим элементом.
Рассмотрим сначала случай, когда верхний рабочий
элемент является подвижным, а нижний — неподвижным.
234
1
Так, если с нижним рабочим элементом имеется шесть
точек контакта, а с верхним — одна, то можно считать, что
нижний рабочий элемент осуществляет жесткое фиксиро-
вание (базирование), а верхний обеспечивает увеличение
реакций и тем самым устраняет недостатки, обусловленные
неудерживающим характером связей. Основные уравнения
кинематики малых перемещений точек контакта объекта
с верхним — подвижным и нижним — неподвижным рабочи-
ми элементами записываются различно. Для точек контак-
та с неподвижным рабочим элементом они записываются
в виде
8г-= 8f0 4- ё х rj1) +
(5.73)
Для точек контакта с подвижным рабочим элементом
учитывается его перемещение
/dr<2)\
= 5f0 4- б х r<-2) + 4- ) 5q. (5.74)
\ dg Jq
Три первые составляющие приращения те же, что в пре-
дыдущем выражении, четвертая составляющая характеризует
изменение положения точки контакта при раскрытии схвата.
Если нижний рабочий элемент также является не-
подвижным, то для точек контакта с ним уравнения
кинематики малых перемещений будут иметь вид
= 6г0 4- ё х 4- Sip 4- ( ________ ।
\ /о 7
Условия сохранения контакта во всех точках при пере-
мещении объекта и одновременном раскрытии схвата
записываются в виде системы уравнений
• и,- = 0 (i = 1, 2,..., m).
(5.75)
Полная система уравнений получается после добавления
к ним уравнения (5.71). Общее число неизвестных в этой
системе равно семи; неизвестными являются три составляю-
щие вектора 6г0, три составляющие вектора ё и прираще-
ние dq (составляющие векторов 8/f в полную систему
уравнений не входят).
Как и в случае захватного устройства без подвижных
элементов, возможность относительного перемещения объек-
та без потери контакта во всех точках зависит от
числа точек контакта т. При т = 7 и при независимости
всех уравнений полной системы имеются только нулевые
решения для всех семи неизвестных, т. е. перемещения
1
объекта в схвате возможны только при потере контакта
по крайней мере в одной точке. Так как для потери
контакта необходимо изменение реакций в этой точке от
конечного значения до нуля (приложение конечных дополни-
тельных сил и моментов), то отсюда вытекает, что при
принятых предположениях выполняются условия жесткого
фиксирования.
Реакции в точках контакта конечны за счет прину-
дительного сведения рабочих элементов; усилие захваты-
вания обычно значительно больше сил тяжести, поэтому силы
тяжести могут быть отнесены к числу приложенных. Тогда
исходные положения равновесия определяются без их учета.
При т — 1 в пренебрежении силами трения система
«схват — объект» является статически определимой, неизвест-
ные нормальные реакции находятся из семи уравнений
статики: шести уравнений равновесия объекта и одного
уравнения равновесия механизма схвата. На рис. 5.34 при-
ведены примеры жесткого фиксирования объекта при т = 7.
Распределение числа точек контакта между рабочими
элементами схвата может быть различным. Для схватов с
двумя рабочими элементами возможны следующие сочета-
ния распределения точек контакта: четыре с одним ра-
бочим элементом и три с другим (рис. 5.34, а, б); пять
а)
Рйс. 5.34
236
1
с одним рабочим элементом и две с другим
(рис. 5.34, в, г); шесть с одним рабочим элементом и одна
с другим (рис. 5.34, д,е).
На рис. 5.34,а рабочие поверхности схвата образуют
два двугранных угла со скрещивающимися ребрами,
нижнее основание объекта представляет собой прямоуголь-
ник, верхнее — треугольник. Линии контакта заменяются
угловыми точками. На рис. 5.34,6 имеет место контакт
в виде цилиндра с двумя вилками в четырех точках;
конус, входящий сверху в отверстие цилиндра, обеспечи-
вает условия, эквивалентные трем точкам контакта.
На рис. 5.34, в объектом является шестигранная призма,
опирающаяся на двугранную угловую выемку и поджимае-
мая сверху вилкой. Вилка обеспечивает жесткое фиксиро-
вание по координате линейного перемещения вдоль обра-
зующих призмы. Для жесткого фиксирования цилиндра
с круглым отверстием (рис. 5.34,г) используются: нижний
рабочий элемент в виде конуса, обеспечивающий контакт,
эквивалентный трем точкам, и вилки, а также верхний
рабочий элемент, обеспечивающий контакт в двух точках.
Примеры базирования по всем шести координатам на
нижнем рабочем элементе, реализующем шесть точек
контакта, и использования верхнего рабочего элемента
для увеличения реакции в точках контакта за счет
действия усилия захватывания приведены на рис. 5.34, д,е.
Для этих примеров важно, что реакции в точках
контакта объекта и рабочих элементов схвата пропор-
циональны усилию захватывания и не зависят от ориен-
тации схвата в пространстве. Это свойство определяет
основное преимущество схвата с одной степенью свободы
по сравнению с механическим захватным устройством, не
имеющим подвижных элементов, в виде опоры, форма
которой совпадает с нижней формой рабочего элемента.
Случай т = 7 является нечувствительным в смысле сох-
ранения числа точек контакта к изменениям формы и
размеров, что видно из приведенных примеров. Случай т > 7
соответствует статически неопределимым системам, при этом
малые изменения формы поверхностей приводят к потере
контакта в «лишних» точках.
При т < 7 имеются несущественные координаты, по
которым жесткого фиксирования принудительным базиро-
ванием не осуществляется. Число несущественных коорди-
нат п может быть от 1 до 5, причем п = 5 реализуется,
если число точек контакта равно двум. Необходимым
и достаточным условием существования п несущественных
237
1
координат при удерживании объекта схватом с одной
степенью свободы является реализация контакта в
mQ = 6 — п + 1 точках и равенство ранга определителя
системы уравнений (5.75) для схвата с одной степенью
свободы числу точек контакта щ0. Жесткое фиксирование
объекта в схвате в этом случае осуществляется по
6 — п координатам, п уравнений удовлетворяются тождест-
венно, а неизвестные реакции определяются из т0
остальных уравнений этой системы. Так же, как и в случае,
рассмотренном в п. 2, форму и размеры рабочих
элементов схвата следует выбирать таким образом, чтобы
при выбранном числе и расположении точек контакта
определитель системы уравнений кинематики малых пере-
мещений объекта в схвате (5.75) имел ранг, равный выбран-
ному числу точек контакта. Выбор числа точек контакта
осуществляется исходя из условий обеспечения минимального
числа п несущественных координат для объекта данной
формы.
Примеры жесткого фиксирования объектов, имеющих
несущественные координаты, приведены на рис. 5.35. Шар
(рис. 5.35, я, б) имеет три несущественные координаты —
углы поворота вокруг трех ортогональных осей. Жесткого
фиксирования по этим координатам без сил трения не
обеспечить. Жесткое фиксирование по трем координатам
линейного перемещения обеспечивается реализацией контакта
в четырех точках.
Рис. 5.35
1
При захватывании цилиндра (рис. 5.35, в, г) за цилиндри-
ческую поверхность две координаты — смещение вдоль
продольной оси симметрии цилиндра и поворот вокруг нее —
не фиксируются. Жесткое фиксирование по остальным
координатам осуществляется реализацией контакта в пяти
точках. Если допускается захватывание тел, имеющих
цилиндрическую форму, за торцы, то можно обеспечить
жесткое фиксирование по пяти координатам (не фиксируется
только координата поворота вокруг продольной оси симмет-
рии цилиндра). На рис. 5.35, д приведён пример жесткого
фиксирования трубы двумя конусами по торцам. Пример
жесткого фиксирования шестигранной призмы по пяти
координатам приведен на рис. 5.35, е.
Методика исследования условий равновесия объекта в
схвате и основные качественные выводы полностью сохра-
няются, если механизм схвата по-прежнему имеет одну
степень свободы, но число рабочих элементов больше двух
(например, для схвата с тремя рабочими элементами
типа трехкулачковых патронов, предназначенных для захва-
тывания цилиндрических объектов с торца). При одной
степени свободы записывается одно уравнение равновесия
механизма, аналогичное (5.71), следовательно, для жесткого
фиксирования по всем координатам необходимо также семь
точек контакта. Снижение числа жестко фиксируемых
координат требует снижения числа точек контакта на
столько же единиц.
Если механизм схвата имеет несколько независимых
приводов, то должно быть записано столько уравнений
равновесия механизма, сколько приводов. Поэтому для
жесткого фиксирования объекта по всем координатам
необходимо увеличение числа точек контакта по одной точке
на каждый привод. Так, для случая двух приводов
число точек контакта должно быть равно восьми.
Для плоской задачи жесткое фиксирование объекта
принудительным базированием осуществляется при четырех
точках контакта, если ранг определителя системы урав-
нений (5.75) равен четырем. При наличии несущественных п
координат жесткое фиксирование принудительным базиро-
ванием осуществляется при равенстве числа точек контакта
и ранга определителя системы уравнений (5.75) числу
т0 — 4 — п.
Рассмотрим задачу анализа условий равновесия объекта
в схвате на примере. Квадратный объект со стороной 2а
фиксируется в% схвате (см. рис. 5.32, а). Радиусы-векторы
из начала системы координат схвата в точки контакта
239
1
имеют проекции на оси х и у:
fi = [-п, а]т; г2 = [а, а]т; г3 = [а, ~а]‘;
Г4 = [ —Я, —я]'.
Векторы малых перемещений объекта в точках контакта,
вызванные заданными векторами 6г0 и 0 линейного пере-
мещения полюса объекта и поворота вокруг этого полюса,
определяются выражениями:
8rt = Sr0 4- 60 х fi 4- 6Л; 6r2 — 6r0 + 8$ x r2 + 6/i;
О о **
6r3 = or0 +
бё X f3; 6r4 = 6r0
60 x r4.
Подстановка этих выражений в (5.75) приводит к системе
уравнений относительно составляющих векторов 8г0 и 0:
6rOx sin а — 6гоу cos а + 02a(sin а — cos а) — 6/i cos а = 0;
— 6rOx sin а — 6rOy cos а 4- 0za (cos а — sin а) — 6/i cos а = 0;
6гОу — af)z = 0;
6rOy 4- o02 = 0.
Определитель этой системы
sma
—cos а
a (sin a —cos а)
— cos а
sin а — cos а
a (cos а — sin а)
— cos а
= 2a sin 2а.
0
— d
0
0
a
0
Видно, что A 0, если а 0 и ранг этого определителя
равен четырем, т. е. жесткое фиксирование принудительным
базированием осуществляется по всем трем координатам,
определяющим положение объекта в плоском случае.
Если а = 0, т. е. схват является плоскопараллельным,
определитель системы уравнений имеет вид
Ранг этого определителя равен трем; в этом случае
координата х является несущественной, а жесткое фиксиро-
вание принудительным базированием осуществляется только
по координатам линейного перемещения по оси у и поворота
объекта вокруг оси z.
Характеристики удерживающей способности схватов. Ос-
новной и наиболее важной задачей расчета механической
240
системы «схват — объект» является определение условий
удерживания объекта в схвате в статических и динами-
ческих режимах, когда на объект действуют переменные
нагрузки. Приведенные к условному центру схвата, они
хргут быть представлены в виде главного вектора силы
F = [Fx, Fy, FjT и вектора момента М = [Мх, Му, Мг]‘.
Способность схвата удерживать объект в положении
равновесия приложенных сил и моментов проще всего
задавать предельными значениями этих составляющих по
отдельности (например, предельные значения составляющей
Fx определяются при условии, что только она не равна
нулю).
Однако в общем случае произвольного нагружения все
составляющие силы и моменты не равны нулю. Для
этого общего случая удобно ввести в рассмотрение шести-
мерное пространство. Тогда удерживающая способность
схвата наглядно представляется в виде области жесткого
фиксирования (ОЖФ) в шестимерном пространстве состав-
ляющих силы и вектора момента. Если изображающая
точка значений составляющих приложенных сил и моментов,
определяющая условия нагружения, находится внутри ОЖФ,
то условия равновесия объекта в схвате сохраняются и
перемещений объекта в схвате не происходит. Вход
изображающей точки на границу ОЖФ соответствует
предельному состоянию, при котором становится возможным
перемещение объекта в схвате.
Методика определения границ ОЖФ включает следую-
щие этапы.
1. Определение вида положения равновесия объекта в
схвате. Для механической системы «схват — объект» выяв-
ляются обобщенные координаты объекта, по которым
его жесткое фиксирование в схвате осуществляется без
трения принудительным базированием, и координаты, по
которым жесткое фиксирование обеспечивается только
силами трения (без учета сил трения по каждой
координате реализуется или безразличное, или классически
устойчивое положение равновесия объекта в схвате).
В основе этого этапа лежит составление и анализ
уравнений кинематики малых перемещений объекта в схвате
(5.75). Обобщенные координаты, по которым жесткое
фиксирование обеспечивается только силами трения, опре-
деляются по ненулевым решениям этой системы уравнений.
Существование таких решений говорит о том, что соот-
ветствующие перемещения объекта в схвате происходят
без отрыва в точках контакта. С другой стороны, пе-
ремещения по координатам, по которым реализуется
жесткое фиксирование принудительным базированием, воз-
можны только при потере контакта хотя бы в одной точке.
2. Составление уравнений статического равновесия систе-
мы «схват —объект». Для случаев, когда контакт объекта и
рабочих элементов схвата осуществляется в дискретных
точках, эту систему образуют уравнения
А/ — 0.
(5.76)
3. Определение условий предельных состояний. На этом
этапе определяются такие соотношения между состав-
ляющими векторов дополнительно приложенных сил и
моментов, при которых еще сохраняется положение равно-
весия, но их увеличение приводит к выходу объекта из
положения равновесия. Предельные состояния определяют
границы ОЖФ. Этот этап включает две стадии исследо-
вания. На первой стадии проводится оценка условий
достижения предельных состояний для координат, по кото-
рым жесткое фиксирование осуществляется без сил трения
принудительным базированием. На второй стадии рассчиты-
ваются условия достижения предельных состояний для
координат, жесткое фиксирование по которым обеспечи-
вается силами трения, а также определяются поправки к
результатам, полученным на первой стадии, учитывающие
влияние сил трения. На первой стадии условия предель-
ных состояний получаются для случая контакта в дискрет-
ных точках при разрешимости системы уравнений (5.76)
и (5.71) непосредственно из решений этой системы; для
случаев статически неопределимых задач при дискретном
(в точках) и распределенном (по линиям или поверхностям)
контактах применяется кинематический метод, описанный
ниже.
4. Построение ОЖФ по совокупности условий достиже-
ния предельных состояний, анализ влияния параметров
механической системы «схват — объект» на конфигурации и
размеры ОЖФ.
Основное внимание уделяется этапу построения границ
ОЖФ. На первой стадии этого этапа для статически
определимых задач при дискретном распределении точек
контакта способ определения предельных состояний при
пренебрежении силами трения заключается в следующем.
Предположим, что к объекту приложены сила и момент.
Будем увеличивать составляющие силы и момента до тех
пор, пока не будет достигнуто предельное состояние.
242
Предельные состояния реализуются при отрыве, по крайней
мере, в одной l-й точке контакта, т. е. при обращении
в нуль соответствующей реакции Rt.
Разрешая систему уравнений (5.76) и (5.71) относи-
тельно неизвестных реакций Rt в точках контакта и полагая
Ri — 0, находим соотношение между составляющими силы
и момента (потому что неизвестных Rt становится на
единицу меньше числа уравнений). В результате полу-
чается одно из условий предельного состояния. Полагая
Rt > 0, получаем вместо равенства линейное неравенство
для составляющих векторов F и М; это неравенство
определяет всю совокупность дополнительно приложенных
сил и моментов, при которых сохраняется контакт
объекта и рабочего элемента схвата в l-й точке.
Перебирая точки контакта, т. е. полагая последовательно
/ = 1, 2,..., т0, где т0 < 7 — число точек контакта, получаем
семейство т0 линейных неравенств для дополнительно
приложенных сил и моментов. Совокупность линейных
неравенств выделяет в шестимерном пространстве состав-
ляющих Fx, Fyi Fz, Мх, Му, Mz замкнутую или разомк-
нутую ОЖФ, охватывающую начало координат. На практике
удобно рассматривать двумерные (плоские) сечения ОЖФ
или только предельные значения сил и моментов. Нагляд-
ны и трехмерные сечения ОЖФ.
Для примера на рис. 5.36 изображены трехмерные
сечения этой области для двух видов схватов. Для схвата
с неподвижным нижним рабочим элементом по переменной
Fy ОЖФ является неограниченной (рис. 5.36, а). Для схвата
с симметричным перемещением рабочих элементов сечения
Рис. 5.36
243
1
ОЖФ являются ограниченными и, как правило, симметрич-
ными (рис. 5.36,6). Границы ОЖФ в рассматриваемом
случае представляют собой гиперплоскости, максимальное
число которых имеет место при жестком фиксировании
по всем координатам и равно семи.
В случаях, когда при пренебрежении силами трения
имеются нефиксируемые координаты, объем ОЖФ в шести-
мерном пространстве равен нулю, и имеет смысл рас-
сматривать ОЖФ в пространстве только фиксируемых
координат. Так, для плоскопараллельного схвата строится
трехмерная область в пространстве параметров Fyt Мх, Mz.
Если имеется несколько положений равновесия объекта в
схвате, то ОЖФ различны для каждого из положений
устойчивого равновесия. Для определенного положения
характерные размеры и конфигурация зависят от геометрии
и параметров рабочих элементов. Для захватных устройств,
не имеющих подвижных элементов, размеры ОЖФ про-
порциональны весу объекта. Для схватов эти размеры про-
порциональны усилию захватывания Р. Как было показано,
усилие захватывания, а следовательно, и параметры ОЖФ
зависят от параметра раскрытия схвата, т. е. для объектов
одинаковой формы, но различных размеров поверхностей,
по которым производится захватывание, размеры ОЖФ
могут быть различны.
Целесообразно выделить следующие случаи, представляю-
щие наибольший интерес.
1. Жесткое фиксирование осуществляется по всем коорди-
натам. Несмотря на то что в положении равновесия
объекта в схвате контакт осуществляется по линиям (или
по поверхностям), при любых перемещениях объекта
происходит переход к контакту в дискретных точках. При
любом перемещении объекта контакт по одному ребру или
всем ребрам переходит в контакт в угловой точке или
в угловых точках. Поэтому в подобных задачах контакт
по ребрам можно заменять для предельных состояний
контактом в угловых точках, положение которых известно.
2. Жесткое фиксирование осуществляется по всем коорди-
натам, контакт осуществляется по поверхностям, которые
являются гладкими и не имеют угловых точек. При этом
при любых перемещениях контакт переходит в точечный,
как и в предыдущем случае. Однако положение точек
контакта не может быть определено непосредственно, а
необходимо решение самостоятельных геометрических задач.
3. Жесткое фиксирование осуществляется по некоторым
координатам только за счет сил трения. При этом
244
предельные значения сил и моментов могут быть определе-
ны только для тех обобщенных координат, при изменении
которых происходит изменение условий контакта (контакт в
нескольких точках, по линиям или по поверхностям
переходит в контакт в одной точке). При этом соот-
ветствующие силы и моменты не зависят от упругих
характеристик элементов схвата.
4. Имеется только одна координата, по которой жест-
кое фиксирование осуществляется силами трения. При
этом иногда предельные значения всех сил не зависят от
распределения нормальных составляющих реакций в точках
контакта. Так, при удерживании призматического объекта
схватом с призматическими рабочими элементами предель-
ное значение осевой силы не зависит от распределения
нормальных давлений по образующим. Для объекта в
форме кругового цилиндра предельное значение момента
вокруг оси не зависит от этих давлений.
Глава 6
Передаточные цикловые механизмы
Передаточными механизмами в теории механизмов назы-
вают механизмы, предназначенные для воспроизведения
заданной зависимости между перемещениями звеньев. В
роботах передаточные механизмы могут быть применены
для приведения в движение звеньев основной кинемати-
ческой цепи.
В роботах для решения этой задачи часто применяют
различные виды механизмов с высшими парами, что яв-
ляется не оптимальным с точки зрения возникающих при
этом динамических нагрузок. Однако в этом случае число
звеньев и кинематических пар оказывается наименьшим, что
значительно упрощает систему., Более рационально при-
менение механизмов с низшими парами, так как при этом
можно добиться значительного снижения динамических
нагрузок и повышения быстродействия робота. Однако
широкое их внедрение сдерживается сравнительной слож-
ностью методов их проектирования и большими габари-
тами по сравнению с механизмами с высшими парами.
Первый недостаток может быть устранен изучением и
освоением методов синтеза широким кругом инженеров,
второй — путем применения передаточных механизмов высо-
ких классов.
245
Ниже изложены методы приближенного синтеза переда-
точных механизмов с низшими парами и получивших
значительное распространение в роботах мальтийских
механизмов.
Мальтийские механизмы применяют для поворота про-
мышленного робота, когда необходимо осуществить пре-
рывистое движение рабочего органа, т. е. движение в одном
направлении с периодическими остановками. Мальтийские
механизмы подучили распространение в связи с их кон-
структивной простотой, простотой изготовления и эксплуата-
ции. Эти механизмы нашли применение, например, в ме-
ханизме поворота промышленного робота «Электро-
ника-НЦ».
6.1. Синтез передаточных цикловых
механизмов с низшими парами
Первые работы по алгебраическим методам приближенного
синтеза механизмов принадлежат П. Л. Чебышеву. В даль-
нейшем эти методы были развиты многими советскими и
зарубежными исследователями.
Согласно П. Л. Чебышеву, задача приближенного
синтеза механизмов может быть разделена на три этапа:
выбор основного условия (целевой функции) синтеза и
дополнительных ограничений;
упрощение аналитического выражения основного условия
синтеза;
вычисление постоянных параметров механизма из условий
минимума отклонения от заданной функции.
Рассмотрим задачу синтеза плоского передаточного
механизма шарнирного четырехзвенника методом приближе-
ния функций (рис. 6.1). Входную координату механизма —
угол поворота звена 1 — обозначим через а, выходную
координату — через р. Заметим, что в общем случае эти
углы следует отсчитывать от некоторых прямых, состав-
ляющих с линией AD соответственно углы а0 и р0.
Механизм определяется пятью постоянными парамет-
Рис. 6.1
где 12, 13 — соответственно
длины звеньев 1, 2 и 3, отне-
сенные к длине стойки AD.
Рассмотрим задачу прибли-
женного воспроизведения дан-
ным механизмом заданной
функции
Р = Р (а).
(6.1)
246
При произвольных значениях постоянных параметров
рассматриваемый механизм воспроизводит некоторую дру-
гую функцию
Рм ~ Рм (а, ^1, ^2» а0, Ро)* (6.2)
Задача приближенного синтеза механизма состоит в том,
чтобы так выбрать постоянные параметры механизма /ь
/2, ^з, а0, Ро, чтобы функция рм отличалась от заданной
функции р по возможности мало. Таким образом, мы пере-
ходим к известной задаче приближения функций. Следует
иметь в виду, что теория приближения функций дает явное
решение лишь для сравнительно простых функций, а функция
механизма рм, а следовательно, и отклонение ее от задан-
ной функции имеют весьма сложное выражение. Поэтому
используем метод интерполирования функции. Потребуем,
чтобы в некоторых положениях механизма значения вход-
ной и выходной координат удовлетворяли заданной функции
Р = Р (ос).
Для этого длину звена 2 сделаем переменной, введя еще
одну поступательную пару вдоль оси шатуна ВС. При этом
звенья 1 и 3 можно установить в положения, соответствую-
щие значениям углов и Р,- согласно заданной функции
(6.1), но при этом длина звена 2 будет отлична от 12
и равна /2ф-
Для разности 12 — потребуем, чтобы она обращалась
в нуль в заданных положениях. Если этого удастся достичь
благодаря выбору постоянных параметров, задача будет
решена: входное и выходное звенья механизма будут зани-
мать положения, определяемые заданной функцией. Этот
прием соответствует снятию условия голономной связи
между звеньями 1 и 3 при соединении их шатуном 2
постоянной длины /2.
Составим выражение для квадрата расстояния между
точками В и С. Запишем координаты точек В и С:
)
t
I
хв - /j cos (а + а0); Ув = h sin (а + а0); !
хс = 1 + /3 cos (Р + Ро); Ус = h sin (р + р0)-
Квадрат длины шатуна
^2ф = (ХС “ Хв) + (Ус ~ Ув)2’
Подставляя значения координат точек В и С, получим
/2ф = [1 + ?з cos (Р + Ро) - h cos (а + а0)]2 +
+ [/3 sin (р 4- Ро) - sin (а + а0)]2. (6.3)
247
1
При произвольных значениях углов р и а эта величина
переменная.
Задачей синтеза является такой выбор постоянных пара-
метров, при котором
/1ф - 11 ~ const, ИЛИ 122ф - ll - 0. . (6.4)
Последнее выражение с учетом l2^ после преобразова-
ний может быть представлено в виде
1 4-12 + I2 — I2 4- 2/3 cos (Р 4- р0) — 2/i cos (а 4- а0) —
- 2/1/3 cos (Р + Ро) cos (а 4- а0) 4- 2Ц13 sin (Р 4- р0) sin (а 4- а0),
или
1 4- /3 4" /1 I2 4- 2/3 cos (р 4* Ро) — 2/i cos (ос 4* oto) —
- 2/1/3 cos (Р 4- Ро - а - а0) = 0. (6.5)
Последнее выражение представляет собой при произволь-
ных значениях углов аир функцию отклонения квадрата
расстояния между точками В и С от постоянной величины
/f. В другой терминологии [2] эту величину называют
выражением взвешенной разности.
При синтезе механизма по трем положениям заданными
являются три пары значений углов af, р, (/ = 1, 2, 3), под-
становка которых в (6.5) приводит к системе трех уравне-
ний, позволяющих определить три неизвестные величины.
Если за эти неизвестные принять длины звеньев /ь /2, /3,
а углы а0 и р0 считать выбранными, то система уравнений
получает вид
Pofoi 4- Pifn 4- Р2/21 = Е,-, (6.6)
где Pi (/ = 0, 1, 2) — постоянные коэффициенты, зависящие
только от постоянных параметров механизма; fOi, flb f2i —
функции, зависящие от переменных углов, причем
Ро = - 1Л; foi = cos (af 4- а0);
Pi = 1/^1; fu = cos (Р,- 4- ро);
р2 = (1 + н - II + Ч)/(21,13); (6-7)
Fi = cos (Pf 4- ро - af - а0) (/ = 0, 1, 2).
После определения трех постоянных коэффициентов р0,
Pi, р2 из системы трех линейных уравнений можно найти
и постоянные параметры механизма по формулам
/3 = 1/PoJ ~ 1/Pii /2 = р^/1 4-12 — 2,1^13р2. (6.8)
248
При увеличении числа заданных положений увеличива-
ется число расчетных уравнений системы и изменяется вид
самого выражения условия связи — постоянства длины ша-
туна. Так, при синтезе механизма плоского четырехзвенни-
ка по четырем положениям выражение условия связи не
удается представить в виде обобщенного полинома, напри-
мер, при определении параметров /ь /2, h, Ро-
Условие связи можно представить в виде [2]
I Pifu = Fj (а, р) (j = 0, 1, 2, 3), (6.9)
i = 0
Ро = -tg р0; Pi = - 1/(7з cos ро);
Р2 = Ш Р4 = (1 + И - l22 + /i)/(2G/3 cos Ро).
(6.10)
Особенностью последней системы уравнений является то,
что не все постоянные коэффициенты системы являются
независимыми. Пять коэффициентов р(- (i = 0, 1,..., 4) содер-
жат четыре независимых параметра Р, /2, Поэтому эти
коэффициенты зависимы.
В данном случае имеет место следующая зависимость:
Рз =РоРг;
(6.11).
вначале решается система четырех линейных уравнений от-
носительно четырех постоянных параметров, которые линей-
но выражаются через пятый, например через р0, в виде
Pi = «.Ро
+ ь,-
(i = 1, 2, 3, 4),
(6.12)
где ai9 — известные коэффициенты, не зависящие от
постоянных параметров.
Затем, используя условие связи между параметрами р3,
р0 и р2, получим квадратное уравнение относительно р0 вида
(«зРо + Ь3) = ро (а2ро + Ь2),
или
а2Ро + (Ь2 — а3) Ро — Ь3 — 0,
из которого находим коэффициент р0, затем из (6.12) —
коэффициенты р19 р2, p3i рд., а из (6.10) — постоянные пара-
метры механизма.
249
1
6.2. Синтез мальтийских механизмов
Мальтийский механизм с противоположным направлением
вращения цевки и креста. К числу таких механизмов отно-
сится, например, трехзвенный мальтийский механизм с внеш-
ним зацеплением (рис. 6.2, а) [2]. Такой механизм состоит
из кривошипа а, на конце которого находится цевка Л,
и мальтийского креста Ь, по окружности которого равно-
мерно расположены пазы. Кривошип а совершает равномер-
ное вращение, направление которого указано стрелкой. При
этом цевка входит в паз креста и сообщает ему неравно-
мерное вращение в обратном направлении. Это движение
продолжается до тех пор, пока цевка не выйдет из паза
креста. После этого цилиндрический выступ а, имеющийся
на кривошипе, скользит по цилиндрической поверхности
креста до тех пор, пока цевка кривошипа не войдет в сле-
дующий паз; крест опять повернется и скорость центра
цевки при входе ее в паз будет направлена к центру креста,
и т. д.
Для исключения жесткого удара в момент входа цевки
в паз, а также для облегчения фиксации креста необходимо,
чтобы в момент входа и выхода цевки направление вектора
ее скорости совпадало с направлением оси паза. В эти
моменты скорость креста равна нулю. Условием безудар-
ного зацепления цевки кривошипа с пазами креста является
зависимость
2 (cq + фО = л,
Рис. 6.2
250
где 2oci - угол поворота ведущего кривошипа; 2ср2 — угол
поворота креста.
Угол поворота мальтийского креста называется углом
деления, он зависит от числа z пазов креста: 2<pt = 2k/z.
Крест остается неподвижным при движении кривошипа
на угол 2а0> который определяется из соотношения
2 (oti + ос0) = 2л,
следовательно, с учетом предыдущих соотношений можно
записать
2а0 = 2 (л — осО = л + 2л/г.
Определим время tx поворота креста на угол 2<р2
и время t0 остановки креста. Эти времена должны быть
согласованы с циклограммой движения всех механизмов
машин-автоматов. Время t0 определяется длительностью
выполняемой операции в технологическом процессе. Время
ti поворота креста задается из условия получения наиболь-
шей производительности. Число остановок, которые имеет
крест за один полный оборот, равно числу пазов креста.
Постоянная угловая скорость сок (с-1) вращения криво-
шипа сок = ли/30, где п — частота вращения, мин-1. Тогда
время tj (с) поворота креста с учетом выражения для угла
2«!
2а0 z — 2 30
Г* «ММ
C0K z ли
Время остановки креста
2ос0 z 4- 2 30
to =-----= ----------•
CDK z ли
Зная число пазов z и время остановки креста t0, можно
определить требуемую угловую скорость ведущего звена
кривошипа
z + 2 30 z + 2 л
И == " -9 ИЛИ С0к — .
z to Z t0
Одной из важных характеристик мальтийского креста явля-
ется коэффициент времени работы, который представляет
собой отношение времени поворота креста к времени оста-
новки :
к = ti/to = (z - 2)/(z + 2).
Основными конструктивными параметрами мальтийско-
го механизма являются: расстояние Lмежду осями вращения
251
1
г
кривошипа и креста, длина R ведущего кривошипа, рас-
стояние $ от оси вращения креста до торцов пазов, радиус
г цевки кривошипа, длина h паза креста, диаметр d вала,
на который посажен крест, диаметр dK вала, на который
посажен кривошип (рис. 6.2, б). Параметры R и s определим
из следующих очевидных соотношений:
R — Lsin ф! = Lsin (n/z);
s = Leos q>! = Leos (л/z).
Длину паза креста выбирают из соотношения
h> R + s — L+ г — Lfsin(л/z) + cos(л/z) — 1] + г.
Диаметры вала креста и вала кривошипа:
d > 2 (L — R — г) = 2L [1 — sin (л/z) — r/L];
dK < 2 (L — s) = 2L[1 — cos (л/z)].
Параметры R и L мальтийского механизма находятся
в следующей зависимости:
1 = R/L = sin cpi/sin (о^ + фД
Условимся, что направление отсчета углов otj и ф!
совпадает с направлением угловой скорости; при этом усло-
вии углы будем считать положительными. Выразим угло-
вую скорость со и угловое ускорение £ креста через угловую
скорость кривошипа сок:
со = дф/dz = /сок; с = dco/dt = /сесо2,
где сок = da/dt; i — передаточное отношение;
X (cos а — X)
1 - 2Х cos а + X2 ’ с (1
X (1 — X2) sin а
— 2Х cos а 4- X2)2 ’
Для выполнения условия, чтобы в начале и конце пово-
рота отсутствовали жесткие удары, найдем значение угло-
вой скорости креста
®тах
^тах^к
где /тах — передаточное отношение, зависящее от числа пазов
креста.
Остановимся на силовом расчете мальтийского меха-
низма. Запишем вначале уравнение вращения креста относи-
тельно его оси
Je = М - Мс,
где J — момент инерции креста; е — угловое ускорение;
г
М — движущий момент на валу креста; Мс — постоянный
момент сопротивления.
Преобразовывая это уравнение, получим выражение для
момента на валу креста
М = Мс (1 + Мю2„/Мс).
Обозначим Ло2/Мс = А, тогда последнее уравнение примет
вид
М = Мс (1 + кеА).
Давление ведущей цевки на паз креста Р — M/s. Для
проверки на прочность деталей механизма определяем мак-
симальное значение давления
max ~ Мс [О/^)тах
(&e/s)max
где
(IMnax = 1/(Ь- К) = 1/(L(1 - X));
kjs = X (1 — X2) sin oc/(L(l + X2 — 2X cos a)5/2).
Средняя мощность, необходимая для поворота ведущего
кривошипа, Ncp = Мсрсок, где сок — постоянная угловая ско-
рость ведущего кривошипа; Мср — средний крутящий мо-
мент на валу кривошипа, который может быть найден из
соотношения
Мср = Мс(1 + тА)/г\,
где т| — к. п. д. механизма: ц = 0,75...0,95;
мерные коэффициенты, которые зависят
креста и определяются значениями:
I и тп — безраз-
от числа пазов
z
т
z
т
3 4 5 6 7 8 9
2,000 1,000 0,667 0,500 0,400 0,333 0,286
3,990 3,710 1,079 0,477 0,261 0,163 0,111
10 И 12 13 14 15
0,250 0,222 0,200 0,182 0,167 0,154
0,0795 0,0598 0,0465 0,0373 0,0304 0,0252
Приведенные выше соотношения получены в предполо-
жении, что в передачах механизма отсутствуют зазоры,
звенья его являются абсолютно жесткими, скорость дви-
жения вала ведущего кривошипа постоянна и не зависит
от изменения нагрузки.
Мальтийский механизм с одинаковым направлением вра-
щения креста и кривошипа. К механизмам с таким движе-
нием относится мальтийский механизм с внутренним зацеп-
лением (рис. 6.3), для простоты на рисунке изображен один
из пазов. Особенностью ме-
ханизма является то, что при
входе цевки в паз креста ее
скорость направлена в сто-
рону,
центру
против оположную
креста, при этом
том же направлении, что и
ведущий кривошип.
Угол поворота ведущего
кривошипа, при котором
обеспечивается вращение
креста,
2а* = я + 2 л/z = л (1
+ 2/z),
где z — число пазов креста.
Угол поворота кривошипа, при котором отсутствует
вращение креста,
2а* — 2л — 2а* = я (1 — 2/z).
Время Tj (с) вращения и время г0 (с) остановки креста будут
соответственно равны
z + 2 30 z-2 30
Требуемая угловая скорость (мин-1) ведущего криво-
шипа, при которой обеспечивается заданное время останов-
ки креста,
z-2 30
В мальтийских механизмах рассматриваемого типа время
вращения креста всегда больше времени остановки.
Примем за положительное направление вращение криво-
шипа и креста влево от линии 00 ь а в положении, когда
цевка кривошипа находится вне линии 00ь примем а*=0.
В этом случае, приняв а* = я — а, запишем соотношение,
определяющее угол <р поворота креста:
tg ср = X sin а*/( 1 +
X cos а*).
Угловая скорость со и угловое ускорение £ креста:
со = i*coK; £ = /с*о>к,
где сок — постоянная угловая скорость ведущего кривошипа;
/*, /с* — переменные коэффициенты,
254
1
г
X (cos а* + X)
1 4- 2 A, cos а* 4- X2
г* ________
(1
X (1 — X2)sin а*
4- 2Х cos а* 4- а2)2 ’
Максимальное давление цевки на паз креста определя-
ется соотношением
р = Мс (а* 4- Ь*А)/Ц
где А = Ло2/Мс; Мс — приведенный к кресту момент сопро-
тивления вращающихся деталей; а*, Ь* — безразмерные ко-
эффициенты, зависящие от числа пазов:
z........................ 3 4 5 6 7 8 9 10
о*..................... 2,000 1,414 1,236 1,155 1,110 1,082 1,064 1,051
Ь*..................... 3,458 1,414 0,899 0,666 0,534 0,448 0,387 0,342
Средняя мощность на валу кривошипа, необходимая для
поворота креста, Ncp = Мсрюк, где Мср - средний крутящий
момент на валу ведущего кривошипа.
Глава 7
Передачи промышленных роботов
Передача движения от двигателя к исполнительному звену
манипулятора может быть обеспечена с помощью различ-
ных передаточных механизмов, структура и конструктивные
особенности которых зависят от типа двигателя, вида пере-
мещения исполнительного звена и способа взаимного рас-
положения двигателя и соответствующего ему исполнитель-
ного звена. Передаточные механизмы предназначены для
преобразования одного вида движения в другое, согласова-
ния скоростей и крутящих моментов двигателя и исполни-
тельного звена. Для преобразования движения использу-
ются винтовые, реечные, цепные, тросовые передачи, а также
передача зубчатым ремнем, мальтийские механизмы.
В электроприводах в связи с тем, что электродвигатели
в основном высокоскоростные, а рабочие скорости звеньев
манипулятора невелики, для согласования скоростей исполь-
зуют понижающие передаточные механизмы: зубчатые
цилиндрические и конические, червячные, планетарные, вол-
новые. Тип передаточного механизма выбирают исходя из
сложности его конструкции, коэффициента полезного дей-
ствия, люфта в передаче, габаритных размеров и массы,
свойства самоторможения, жесткости, удобства компоновки,
технологичности, долговечности, стоимости и г. и. Переда-
F
точные механизмы оказывают существенное влияние как на
качество работы привода, так и робота в целом. Поэтому
вопросам проектирования передаточных механизмов следует
уделять особое внимание.
7.1. Винтовые передачи
Передача винт—гайка скольжения. Передача служит для
преобразования вращательного движения в поступательное,
а иногда и для преобразования поступательного движения
во вращательное (рис. 7.1) [45]. Она обладает простотой
конструкции и изготовления, компактностью при высокой
нагрузочной способности, высокой надежностью, плав-
ностью и бесшумностью, возможностью обеспечения мед-
ленных перемещений с большой точностью, дает большой
выигрыш в силе.
К недостаткам передачи следует отнести повышенный
износ резьбы вследствие большого трения, низкий к. п. д.,
наличие люфтов.
Кинематический расчет. Рассмотрим случай преобразо-
вания вращательного движения в поступательное (рис. 7.1).
Перемещение гайки (мм)
$ = фр/с/(2л),
где <р — угол поворота винта, град; р — шаг резьбы, мм;
к — число заходов резьбы.
Скорость гайки
v = сор/с/(2тс),
где со — угловая скорость винта, с
Рис. 7.1
1
Коэффициент полезного действия (к. п. д.) винтовой пары
Пвп = tg Ф/tg (Ф + Р')>
где ф = arctg [рг/(л42)] — угол подъема винтовой линии, град
(Pz — рк — ход резьбы, мм; d2 — средний диаметр резьбы,
мм); р' = arctg [//cos(a/2)] - приведенный угол трения, рад
(/ — коэффициент трения скольжения; а — угол профиля
резьбы, град, для трапецеидальной резьбы а = 30°, для
квадратной а = 0°).
С учетом дополнительных потерь (в резьбе из-за ошибок
изготовления и потерь в опорах) к. п. д. передачи винт —
гайка скольжения
Пвп = (0,90...0,95) tg ф/tg (ф + р').
Обычно к. п. д. передачи имеет значения г|вп = 0,25... 0,70.
Условие самоторможения — условие, при котором пере-
дача движения невозможна, ф р'.
Преобразование поступательного движения во враща-
тельное возможно при ф > 2р'. Угол поворота винта (град)
Ф = 2ns/(pk).
Угловая скорость винта (с ’)
со — 2nv/(pk).
К. п. д. винтовой пары
Г|пв = (O,9O...O,95) tg (ф - p')/tg ф.
Обычно к. п. д. передачи принимает значения г)пв = 0,45...0,70.
Силовые соотношения. Вращающий момент, приложен-
ный к ведущему вращающемуся звену 1 (Нмм),
Т = ~ tg (ф + р'),
£
где Fa — осевая сила, приложенная к поступательно движу-
щемуся ведомому звену 2, Н; d2 — средний диаметр резьбы
ведущего звена, мм.
Мощность на ведущем звене (Вт)
F — Еяг/т|вп,
где v — линейная скорость ведомого звена, м/с.
Если ведомое звено кроме осевой силы Fa нагружено
и радиальной силой Fr, то на ведущем звене возникает
дополнительный момент трения (Н • мм)
9 Механика промышл. роботов, кн. 2
257
где f — коэффициент трения скольжения в резьбе; L2 — рас-
стояние между точкой приложения радиальной нагрузки
и ближайшим рабочим витком резьбы, мм; Lt — расстоя-
ние между крайними рабочими витками резьбы (рабочая
база винтовой пары), мм. Приближенно можно считать
Lt Н, где Н — высота гайки, мм.
Проектный расчет передачи. Основным критерием рабо-
тоспособности передачи винт—гайка скольжения является
износостойкость (невыдавливание смазки между рабочими
поверхностями резьбы винта и гайки)
р„п— —~Г-Р”],
ср nd2hz L J’
где Рср — среднее давление между рабочими поверхностями
резьбы винта и гайки, МПа; h — рабочая высота профиля
резьбы, мм; z — Н/Р — число витков резьбы в гайке; [Р] —
допускаемое давление между рабочими поверхностями резь-
бы винта и гайки, МПа, для стального винта и чугунной
гайки [Р] = 5...6 МПа; для стального винта и бронзовой
гайки [Р]=9...11 МПа.
Высота гайки
Н — yd2,
где у — коэффициент высоты гайки, для цельных гаек у —
= 1,2...2,5, для разъемных и сдвоенных у = 2,5...3,5.
С учетом последних выражений получим
nd2hz
itd2hyd2/p nh/p yd2 p yd2
<[n
откуда находим средний диаметр резьбы винта (мм)
d2 > /Ср |/X/(Y И),
где /ср — коэффициент, зависящий от типа резьбы, для тра-
пецеидальной и квадратной резьб кр = 0,8, для упорной
резьбы кр = 0,65.
По найденному значению среднего диаметра d2 винта
из соответствующих стандартов находят остальные пара-
метры винта. Трапецеидальные, упорные и метрические
резьбы стандартизованы, квадратная — не стандартизована.
Проверочный расчет винта на прочность. При вращении
винт сжимается и скручивается. Условие прочности винта
где оэкв — эквивалентное напряжение в опасной точке вин-
та, МПа;
258
1
ос = 4Га/(л</1)
— сжимающее нормальное напряжение, действующее на
винт, МПа (dt — внутренний диаметр резьбы винта, мм);
т = TJWP
— касательные напряжения, действующие на винт, МПа
(Тк — крутящий момент в поперечном сечении винта, Н • мм;
Wp = TtJt/16 « 0,2d3 — полярный момент сопротивления сече-
ния кручению, мм3);
[а]р - допускаемое напряжение при растяжении, МПа.
Проверка винта на устойчивость. Сжатые винты прове-
ряют на устойчивость. Условие устойчивости
< [су]/ф,
где ос — расчетное напряжение на сжатие, МПа; [оу] =
= окр/[иу] — допускаемое напряжение на устойчивость, М Па
([иу] — допускаемый (требуемый) коэффициент запаса устой-
чивости: для ходовых и грузовых винтов [иу] = 3...5);
<р — коэффициент понижения допускаемого напряжения для
сжатых стержней, выбирается в зависимости от гибкости
стержня X по табл. 7.1.
Тогда условие устойчивости получим в виде
СТс < СТцЛф [«у])-
Критическое напряжение окр определяют по диаграмме
изменения критического напряжения в зависимости от
9* 259
1
гибкости стержня X. На
рис. 7.2 дан качественный
вид этой диаграммы. Для ее
построения сначала опреде-
лим предельную гибкость
Хпр материала винта, при ко-
торой критическое напряже-
ние сгкр в поперечном сече-
нии винта равно пределу
пропорциональности опц ма-
териала винта:
где Е — модуль упругости материала винта, МПа, для сталь-
ных винтов Е = (2,0...2,2)- 105 МПа.
Находим начальную гибкость Хо, при которой критиче-
ское напряжение равно пределу текучести от материала
винта, используя формулу Ясинского
окр = а — ЪЕ.
При окр = от X = Хо, тогда
Хо = (а - сгт)/Ь,
где а и b — эмпирические коэффициенты: для сталей марок
СтЗ, Ст4, 25, 30, 40 а = 321, b = 1,16; для сталей марок
Ст5, Стб, 45, 50 а = 464, b = 3,62.
Для построения кривой 1 диаграммы задаемся гибкостью
X > Хпр и определяем критическое напряжение по формуле
Эйлера окр = л2Е/Х2. На участке 2 гибкость задают в пре-
делах Хо < X < Хпр и критическое напряжение определяют
по формуле Ясинского.
Определяем гибкость винта'
X
где ц = 1/т — коэффициент приведения длины, зависит от
способа закрепления концов винта (т — число полуволн
изгиба винта); I — длина участка винта (рис. 7.1);
— минимальный радиус инерции сечений, мм (Jmin = пJj/64—
минимальный осевой момент инерции сечения, мм4; А =
= л^2/4 — площадь поперечного сечения винта, мм2).
С учетом выражений для ц и imin получим формулу для
определения гибкости винта в виде
X = 4|х//</1.
260
1
В зависимости от того, в какую область диаграммы
(рис. 7.2) попадает значение гибкости X, винты делят на три
группы:
винты большой гибкости X > ХпР; в этом случае крити-
ческое напряжение определяют по формуле Эйлера
<ткр = я2£/Х2 и условие устойчивости винта принимает вид
ос < л2£/(Х2ф [nJ);
винты средней гибкости Хо < X < Хпр; критическое напря-
жение определяют по формуле Ясинского акр = а — ЬХ;
условие устойчивости винта
ЬХ)/(ф [иу]);
винты малой гибкости . X < Хо; для этих винтов скр = ат
и расчет на устойчивость не проводят, так как винты
малой гибкости устойчивости не теряют.
Определение размеров гайки. Высота гайки
Число витков резьбы гайки
z = Н/р,
где р — шаг резьбы.
Витки резьбы гайки проверяют на изгиб
ои = k„Fa/(dH) [о]и,
где кИ = 1,3 — для трапецеидальной резьбы, ка = 1,5 — для
упорной резьбы, ки — 1,9 — для квадратной резьбы; d — на-
ружный диаметр резьбы винта, мм; [ст]и — допускаемые
напряжения при изгибе, для чугунных гаек [и]и = 25 МПа,
для бронзовых гаек [сги] = 40 МПа.
Наружный диаметр D гайки принимают конструктивно:
для бронзовых гаек D = 1,3d; для чугунных гаек D — L,5d.
При этом толщина стенки гайки должна быть более 5 мм,
т. е.
(D - d}/2 5.
Тело гайки проверяют на растяжение
ср = 1,ЗГй/[л (D2 - d2)/4] [о]р,
где [о]р — допускаемое напряжение материала гайки при
растяжении, для чугунных гаек [а]р — 20 МПа, для брон-
зовых гаек [о]р ~ 40 МПа.
Материалы винта и гайки. Материалы винта и гайки
должны представлять антифрикционную пару, т. е. должны
быть износостойкими и иметь невысокий коэффициент тре-
261
ния. Винты выполняют из сталей марок Ст5, 45, 50, 40Х,
40ХГ. Г айки выполняют из оловянных бронз марок
Бр010Ф1, БрОС4-4-4, антифрикционных чугунов марок
АЧВ-1, АЧС-3.
Передача винт—гайка качения. Передача винт —гайка ка-
чения предназначена для преобразования вращательного
движения в поступательное и, наоборот, поступательного
движения во вращательное. По сравнению с передачей
винт —гайка скольжения она характеризуется значительно
большим к. п. д., меньшим износом, большей точностью
хода, повышенной долговечностью [4].
В винтовых шариковых парах между рабочими винто-
выми поверхностями гайки 1 и винта 4 помещены сталь-
ные шарики 3 (рис. 7.3). Скорость перемещения шариков
отличается от скорости ведущего и ведомого звеньев.
Поэтому для обеспечения непрерывной циркуляции шари-
ков концы рабочей части резьбы соединены возвратным
каналом 2.
Замкнутую цепь шариков условно делят на активную
часть (рабочую часть нарезки) и пассивную часть (возврат-
ный канал).
Активная часть шариковой винтовой пары обычно сос-
тавляет z— 1...2,5 витка. При большем числе рабочих вит-
ков к. п. д. шариковой пары снижается из-за увеличения
трения шариков одного о другой.
При вращении винта шарики, зажатые между винтовыми
поверхностями винта и гайки, благодаря трению перекаты-
ваются по ним и передают движение от винта к гайке,
Рис. 7.3
262
перемещающейся поступательно. От проворачивания отно-
сительно своей оси гайка удерживается направляющими
или шпонкой, зафиксированной в корпусе.
Кинематический расчет. Рассмотрим преобразование
вращательного движения в поступательное. Перемещение
гайки (мм)
s = <рр/с/(2л),
где р — шаг резьбы, мм; к — число заходов резьбы; обычно
шариковые винтовые передачи выполняют однозаходными
к = 1.
Скорость гайки (м/с)
v = ырк/(2п).
К. п. д. винтовой пары
Пвп = (0,90... 0,95) tg ф/tg (ф + рк),
где ф — угол подъема винтовой линии по цилиндру диамет-
ром £>ср; рк = arctg [/к/(0,5^ш)] — приведенный угол трения
качения — диаметр шарика, мм; /к — приведенный коэф-
фициент трения качения; при закаленных винтовых поверх-
ностях твердостью >53 HRC и стальных шариках твер-
достью >63 HRC принимают при вращении винта /к =
= 0,004...0,005, при вращении гайки fK = 0,006...0,007).
Так как ркф, то к. п. д. шариковой винтовой пары
даже при малых углах подъема винтовой линии достигает
80—90%. При ф > 2° к. п. д. увеличивается мало, поэтому
выгодно выбирать угол ф малым, так как при этом снижа-
ется необходимый вращающий момент.
Преобразование поступательного движения во враща-
тельное в шариковой винтовой паре практически возможно
всегда, так как ф » 2рк. В этом случае угол поворота винта
(град)
<р = 2ns/(pk).
Угловая скорость винта (с ’)
со = 2nv/(pk),
где v — линейная скорость гайки, м/с.
К. п. д. винтовой пары
Пвп = (0,90.. .0,95) tg (ф - pK)/tg ф.
Силовые соотношения. Вращающий момент на ведущем
звене (Н • мм)
Т — Fa (^ср/2) tg (ф + рк),
1
где Fa — осевая сила, Н; Dcp — диаметр окружности, на ко-
торой располагаются центры шариков, мм.
Мощность на ведущем звене (Вт)
р - Га1'/Т{ы}.
Если ведомое звено, движущееся поступательно, нагру-
жено радиальной силой Fr, то на ведущем звене возникает
дополнительный момент трения (Н • мм)
Tf = FrfK (Dcp/2) (1 + 2L2/L^
где — расстояние между крайними рабочими витками
винтовой поверхности гайки, мм; L2 — расстояние между
точкой приложения радиальной нагрузки и ближайшим
рабочим витком, мм.
Проектный расчет передачи. Внутренний диаметр £>в (мм)
винта находим из условия прочности винта при растяже-
нии (сжатии)
Ов > 1/4Го/(л [а]),
где [ст] — допускаемое напряжение при растяжении (сжатии)
винта, МПа.
Длинные винты, работающие на сжатие, проверяют на
устойчивость (см. выше).
Диаметр шариков (мм) dw = (0,08... 0,15) DB; полученный
результат округляют до ближайшего большего стандарт-
ного значения.
Шаг резьбы (мм) р = /(0,5... 0,6); результат округляют
до ближайшего стандартного значения.
Диаметр окружности (мм), на которой располагаются
центры шариков, £)ср = DB 4- dlu; результат округляют до
ближайшего большего целого значения.
Уточняют значение внутреннего диаметра DB винта.
Наружный диаметр винта (мм) (рис. 7.4) DH = DB +
+ 2dw + А, где A = 0,03...0,12 мм — радиальный зазор.
Угол подъема винтовой линии (град) \|/ = arctg [р/(яРср)].
Число шариков в рабочей части резьбы гш =
= itD^z/d^ — 1, где z = 1...2,5 — число витков в одной замк-
нутой рабочей цепочке. Полученные значения гш округляют
до ближайшего меньшего целого числа. Если при расчете
окажется гш > 65, то следует уменьшить их число, увеличив
при этом диаметр шариков.
Для равномерного распределения нагрузки на шарики
надо подбирать их так, чтобы разность диаметров не пре-
вышала 3 мкм.
264
Рис. 7.4
Профили резьбы передачи. Профили резьбы шариковой
винтовой пары бывают: треугольные (рис. 7.5, а), круглые
(рис. 7.5,б) и круглые с канавкой (рис. 7.5, в).
У резьбы с треугольным и круглым с канавкой профи-
лем имеется пространство под шариком, которое может
служить резервуаром для смазочного материала и продуктов
износа. Для уменьшения трения радиусы гж желоба у винта
и гайки должны быть больше радиуса шариков. При
dw 8 мм радиус желоба гж = 0,51</ш, при > 8 мм радиус
желоба гж = 0,53</ш.
Определение размеров гайки. Число замкнутых рабочих
цепочек в гайке найдем из условия (при этом учтем, что
совф^ 1, так как угол ф мал):
cos ф
« Ист,
где Р — удельная осевая нагрузка, МПа; у = 0,8 — коэффи-
циент неравномерности распределения нагрузки между ша-
риками; и — число замкнутых цепочек; [Р]сг — допускаемая
удельная осевая статическая нагрузка, МПа, определяют
в зависимости от относительного радиального зазора х =
— А/^ш по графику (рис. 7.6).
а) б) 8)
Рис. 7.5
1
Тогда число замкнутых рабо-
чих цепочек в гайке
и > Fa/iz^y [Р]ст);
полученное значение округляют до
ближайшего большего целого чис-
ла.
Рабочая база гайки (мм) Lr —
= pz, где р — шаг резьбы, мм. При
нескольких замкнутых рабочих це-
почках Li — pzu.
Высота гайки (мм)
Н — pzu 4- (1...2) р.
Наружный диаметр гайки при расположении возвратного
канала в гайке (мм):
для чугунной гайки D = 1,5DB + 2ЛШ 4- 10;
для бронзовой гайки D = 1,3£)в 4- 2dlu 4- 10.
Наружный диаметр гайки при расположении возврат-
ного канала вне гайки (мм):
для чугунной гайки D — 1,5£>в;
для бронзовой гайки D = 1,3DB.
Осевой зазор (мм)
с = ]/(2гж - Лш) Д,
где Д — DH — (2<7Ш J- DB) — радиальный зазор, мм. Если техни-
ческие условия на значение Д не установлены, то при
расчете принимают Д = 0,03...0,12 мм.
Определение допускаемых нагрузок. При действии осевой
силы Fa допускаемая осевая статическая нагрузка (Н)
определяется в виде
*
[Рajcr Е^]ст
При действии радиальной силы Fr допускаемая радиаль-
ная статическая нагрузка (Н)
[FjcT = ЩсТ
где Ыст “ допускаемая удельная радиальная статическая
нагрузка, определяемая в зависимости от х по графику
(рис. 7.6).
Проверочный расчет передачи по контактным напряже-
ниям. Условие контактной прочности
max < [п]ншах»
где Од тах
266
максимальные контактные напряжения, МПа.
При действии осевой силы Fa максимальные контактные
напряжения стЯтах определяют по графикам (рис. 7.7, а-в)
в зависимости от Р и х; [<^]нтах ~ допускаемые контакт-
ные напряжения, МПа; для винтовых поверхностей винта
и гайки твердостью >63 HRC допускаемое значение кон-
тактных напряжений принимают [ст]нтах = 5000 МПа.
При действии радиальной силы Fr максимальные кон-
тактные напряжения для винтовой поверхности винта
для винтовой поверхности гайки
где Frl — Fr(Lt 4- L2)/Ll'i e — коэффициент, значение кото-
рого определяют по табл. 7.2 в зависимости от величины v:
для винта
для гайки
7.7
1
а б л и ца 7.2
0,0000
1,000
0,7784
0,8699
1,001
0,7825
0,8774
0,0466
0,1075
1,003
0,7866
0,8811
0,1974
1,008
0,7907
0,2545
1,240
0,7948
0,8885
0,3204
0,3954
1,038
0,8069
0,8958
1,370
1,404
1,416
0,4795
1,060
0,8110
0,5342
0,5819
0,6113
0,6521
0,6716
0,7126
0,7332
0,7579
0,7620
0,7702
0,7743
1,108
1,128
1,140
1,168
1,220
0,8150
0,8190
0,8230
0,8310
0,8350
0,8507
0,8545
0,8661
1,270
1,300
0,9030
0,9065
0.9100
0,9134
0,9428
0,9458
0,9574
0,9705
0,9818
0,9909
0,9973
1,444
1,606
При одновременном действии осевой и радиальной на-
грузок проверку на контактную прочность проводят от-
дельно для каждой нагрузки.
Расчет передачи на статическую грузоподъемность. Рас-
чет шариковых винтовых механизмов на статическую грузо-
подъемность проводят, если частота вращения винта или
гайки не превышает п < 1 об/мин, по условию
Ро Со,
где Ро Fa max — эквивалентная статическая нагрузка, рав-
ная максимальной осевой нагрузке, Н; Со — статическая
грузоподъемность, Н;
Со = (тгРср — Зр) sin р cos ф.
Здесь kz = 0,7...0,8 — коэффициент, учитывающий погреш-
ности изготовления винтовой поверхности передачи; р —
угол контакта шариков с винтом и гайкой, град; для
треугольного профиля р = 45°, для круглого и круглого
с канавкой угол контакта определяют по графику (рис. 7.8).
268
Расчет передачи на долго-
вечность, Расчет шариковых
винтовых механизмов на
долговечность проводят, ес-
ли частота вращения винта
или гайки и > 10 об/мин, по
условию
Рис. 7.8
^й
106
573(0
Шй>
где Lh — долговечность работы механизма, ч; [L]A — до- .
пускаемая долговечность работы механизма, ч;
— эквивалентная динамическая нагрузка, Н (здесь & Fai —
эквивалентная динамическая нагрузка, равная осевой на-
грузке для i-го уровня нагружения, Н; nf — частота враще-
ния винта или гайки при действии Ггй эквивалентной
динамической нагрузки, об/мин; со£ — угловая скорость вин-
та или гайки при действии Ргй эквивалентной динамической
нагрузки, с-1; — продолжительность действия Ff нагрузки,
с);
п
— эквивалентная частота вращения винта или гайки, об/мин;
(О =
— эквивалентная угловая скорость вращения винта или
гайки, с-1; С = (0,2...0,4) Со — динамическая грузоподъем-
ность, Н.
Дифференциальная винтовая передача. Дифференциальная
винтовая передача (рис. 7.9) состоит из винта 3 с двумя
участками резьбы разных шагов (рг и р2), но одного
направления (правого или левого), гайки 1 и стойки 2. При
вращении винта 3 гайка 1 совершает два поступательных
движения: относительно винта 3 и вместе с винтом 3 отно-
сительно стойки 2.
1
Рис. 7.9
I
Полное поступательное перемещение (мм) гайки 1
сительно стойки 2
$2 = Ф! (Pi - р2)/(2л),
OTHO-
i
I
COOT-
И1
где ф! — угол поворота винта, град; pt и р2 — шаги
ветственно первого и второго участков резьбы винта, мм.
Из формулы следует, что дифференциальная винтовая пере-
дача обеспечивает малые линейные перемещения.
Скорость v2 (м/с) перемещения гайки 1 относительно
стойки 2 получим дифференцированием выражения для s2:
v2 = <0i (Pi - p2)/(2n) = ni (pi - р2)/60,
где с»! = ти^/ЗО — угловая скорость винта 3,
частота вращения винта 3, об/мин.
Интегральная винтовая передача. Интегральная винтовая
передача устроена аналогично дифференциальной (рис. 7.9),
но имеет различные направления резьбы (правое и левое)
на резьбовых участках винта.
Осевое перемещение (мм)
гайки 1 относительно стойки 2
= Ф1 (Pi + Рг)/(2тг).
Таким образом, при неболь-
шом угле поворота винта мож-
но получить увеличение осевого
смещения гайки.
Несоосная резьбовая переда-
ча. Несоосная резьбовая пере-
дача (рис. 7.10) состоит из винта
1, гайки 2, свободно вращаю-
щейся в подшипниках 3, наруж-
ные кольца которых установле-
ны в корпусе 4. Корпус 4 пере-
мещается в осевом направлении
i
r
1
\
1
1
вместе с гайкой. При одинаковых шагах резьбы винта
и гайки средний диаметр d2 винта меньше среднего диа-
метра £>2 гайки. Следовательно, угол подъема винтовой
линии винта больше угла подъема винтовой линии
ф2 гайки. При повороте винта на угол cpt точка,
взятая на линии контакта, пройдет путь, равный длине
винтовой линии винта. При этом гайка повернется на угол
(град)
ф2 = [^2 COS ^2/(D2 COS 1I/J] фр
Относительное осевое перемещение (мм) винта и гайки
s2 = 0,5^2 tg Ф1 (1 - sin \|/2/sin ф^ (pt.
Скорость поворота гайки
С02 = [d2 cos ф2/(Р2 cos ФО] С0ь
где со2 — угловая скорость гайки, с-1; coi — угловая скорость
винта, с-1.
Линейная скорость v2 (мм/с) относительного движения
винта и гайки
v2 - 0,5J2 tg Ф1 1 -
«1
бб“’
где = nHi/ЗО — угловая скорость винта, с 1; — частота
вращения винта, об/мин.
7.2. Реечная передача
Реечная передача предназначена для преобразования враща-
тельного движения шестерни в поступательное движение
рейки и, наоборот, поступательного движения рейки во вра-
щательное движение шестерни (рис. 7.11).
1
Основными звеньями реечной передачи являются шес-
терня 1 и зубчатая рейка 2. Рейка образует с неподвиж-
ным звеном поступательную пару.
. Реечную передачу можно рассматривать как частный
случай цилиндрической зубчатой передачи, у которой колесо
обращено в рейку.
Основные соотношения в реечной передаче. Делительный
диаметр (мм) шестерни находят из условия контактной
прочности зубьев
= К, f/1,471 (1/фм + 0,15),
где Тг — крутящий момент на валу шестерни, Н • м; фм =
= 0,2... 1,4 — коэффициент ширины зубчатого венца; Kt =
= 780/Ми/3-
Допускаемое контактное напряжение (МПа) вычисляется
по формуле
И# — (&НИть/8н) &HL>
где Он Пт/» ~ предел контактной выносливости поверхностей
зубьев, соответствующий базовому числу циклов перемены
напряжений, МПа:
для нормализованных и улучшенных сталей с твердостью
<350 НВ
°Hiimb — 2 НВ + 70;
для сталей с твердостью >350 НВ
сгнить = 18 HRC « 1,8 НВ;
SH — требуемый коэффициент безопасности; при нормали-
зации, улучшении и объемной закалке зубьев SH — 1,1, при
повторной закалке, цементации, азотировании, цианировании
&hl —
— коэффициент долговечности, учитывающий влияние срока
службы и режима нагрузки передачи (здесь NH0 — базовое
число циклов изменения напряжений; для сталей NHq —107,
для цветных металлов NHQ = 108; NH — число циклов изме-
нения напряжений); для нормализованных и улучшенных
колес при <350 НВ KHL= 1...2,6, для колес с поверхност-
ной закалкой, азотированием, цементацией при >350 НВ
&hl= 1... 1,8, для длительно работающих передач KHL— 1.
272
Перемещение рейки
s2 = л^о^/ЗбО0,
где eq — угол поворота шестерни, град.
Скорость рейки г2 (м/с)
г2 = <^iC0i./(2 • 1000) = л^^ДбО • 1000),
где (Oi — угловая скорость шестерни, с-1; ть — частота вра-
щения, об/мин.
Для нормальной работы реечной передачи необходимо,
чтобы число зубьев шестерни Z] было больше минималь-
ного числа зубьев zmin: zt > zmin. Из этого условия выби-
рают число зубьев шестерни.
Модуль зубьев т — djz^. Модуль округляют до стан-
дартного значения по ГОСТ 9563-60 (СТ СЭВ 310-76).
Уточняют делительный диаметр шестерни dr — mzi (все
размеры в мм).
Для шестерни, нарезанной без смещения, определяют:
диаметр окружности вершин зубьев dai = dt 4- 2m;
диаметр окружности впадин зубьев dfl =dt —2,5m;
толщина зуба шестерни по дуге делительной окружности
= 0,5лт;
шаг зубьев по делительной окружности шестерни рг — пт.
Шаг зубьев рейки равен шагу зубьев шестерни р2 — р1 —
= пт.
Число зубьев рейки z2 = L2/p2 + 0,5, где L2 — длина
нарезанной части рейки, мм; число зубьев рейки округляют
до целого значения.
Уточняют длину нарезанной части рейки L2 = (z2 — 0,5) р2.
Ширина рейки b2 = ^bddi.
Ширина шестерни = b2 + 0,6 yb^. Полученные значе-
ния округляют до ближайшего стандартного значения по
ГОСТ 6636 - 69.
Высота зуба рейки h = 2,25m.
Высота головки зуба рейки ha — т.
Толщина зуба рейки по средней прямой s2 = 0,5лт.
Осевую силу, действующую на рейку, равную окружной
силе, действующей на шестерню, определяют по зависимости
где F — осевая сила, приложенная к рейке, Н; Ft — окруж-
ная сила, приложенная к шестерне, Н.
Проверка зубьев на контактную и изгибную выносли-
вость проводится так же; как и для цилиндрических
зубчатых передач [45].
273
1
7.3. Тросовая передача
Тросовые передачи предназначены для передачи вращатель-
ного движения и преобразования поступательного движения
во вращательное и наоборот.
Передача вращательного движения от ведущего шкива 1
к ведомому шкиву 2 осуществляется тросом 3 (рис. 7.12, а).
При наличии ведущих гидро- или пневмоцилиндров
происходит преобразование поступательного движения што-
ков 1 во вращательное движение шкива 2 (рис. 7.12,6).
Для преобразования вращательного движения ведущего шки-
ва 1 в поступательное движение звена 4 используют трос 2
и пружину 3 (рис. 7.12, в). Тросы изготовляют плетением
[3 оцинкованной стальной проволоки марок 50, 60, 65.
Кинематические и геометрические параметры. При пере-
даче вращательного движения передаточное отношение
тросовой передачи
<р! CD] Щ R2 О2 D2
(p2~ <o2 n2~ Ki(l-£) “ DiU-e) ~
где (pt и (pa ~ углы поворота ведущего и ведомого
шкивов соответственно, град; («i и со2 — угловые скорости
ведущего и ведомого шкивов соответственно, с"1; пг и п2 —
частоты вращения ведущего и ведомого шкивов соответ-
ственно, об/мин; Ri и R2 — радиусы ведущего и ведомого
шкивов соответственно, мм; Di и D2 — диаметры ведущего
а)
и ведомого шкивов соответ-
ственно, мм; £ — коэффици-
ент упругого скольжения,
е = (Л - Г2)/(ЕЛ).
Здесь Fi — натяжение веду-
щей ветви троса, Н; F2 —
натяжение ведомой ветви
троса, Н; А
— площадь по-
перечного сечения троса,
мм2; Е = vEM — модуль уп-
ругости троса (v = 0,65...0,
85
для тросов с одной свивкой,
v = 0,35 для тросов с двумя
свивками; Ем — модуль упру-
гости материала проволоки
троса, МПа; для стали
Еы = (2Д...2Д) 105 МПа).
274
Окружная скорость на ведомом шкиве (м/с)
v2 = cd2D2/(2 • 1000) = ttD2h2/(60-1000).
Окружная скорость на ведущем шкиве (м/с)
V1 = ^г/(1 ~ е)-
Угол обхвата тросом малого шкива (град)
180° -
l
или
180°
= 180° —
ai
a
а = [2/ - я (D2 - Dt) + |/[2/ - я (О2 + DJ]2 - 8 (D2 - DJ2]/8
— межосевое расстояние, мм;
1 = 2а
+ A(D2 + D1)
(02 - Р1)2
4а
— длина троса, мм.
Силовой расчет. Определим предельные натяжения ветвей
тросовой передачи. Натяжение ведущей ветви троса (Н)
Натяжение ведомой ветви троса (Н)
Предварительное натяжение ветвей троса (Н)
кТ2
/«
— крутящий момент на ведомом шкиве, Нмм; е
где
основание натурального логарифма; /== 0,1 ...0,2 — коэффи-
циент трения скольжения между тросом и шкивом;
к = 1,05... 1,1 — коэффициент запаса предварительного натя-
жения Fo, гарантирующий работу передачи без проскальзы-
вания и мертвого хода
прилегания троса к шкивам.
Мощность на валу ведомого шкива (Вт)
возникающего из-за неплотного
Рвых = Т2п2/9550.
1
Мощность на валу ведущего шкива (Вт)
где т| = 0,90... 0,95 - к. п. д. тросовой передачи.
Расчет на прочность. В процессе работы тросовой
передачи отдельные проволоки троса испытывают напряже-
ния растяжения, изгиба, кручения, смятия. Значения напряже-
ний зависят от многих факторов — конструкции и диаметра
троса, размеров и конструкции шкивов, натяжения троса.
Расчет тросовых передач проводят по максимальному
натяжению ведущей ветви троса
где [F]‘ — допускаемое натяжение троса, Н; Fpa3p — раз-
рывное усилие троса, Н, определяют в зависимости от
диаметра троса d по стандартам; п = 2...5 — коэффи-
циент запаса прочности троса на разрыв.
Для ограничения напряжения изгиба троса должно быть
соблюдено условие £>>(£— 1)где D — наименьший диа-
метр меньшего шкива, измеренный по дну канавки для
троса, мм; d — диаметр троса, мм; 0 = 16...20 — коэф-
фициент, зависящий от режима работы передачи. Диаметр
меньшего шкива следует назначать минимально допусти-
мым.
Наилучшие условия работы троса обеспечиваются полу-
круглой формой канавки шкива. При этом должно
соблюдаться условие RK = (0,53... 0,56) d, где RK — радиус
канавки шкива, мм.
С увеличением отношения RK/d долговечность троса
снижается.
Определение ошибки положения тросовой передачи. Для
определения ошибки положения тросовой передачи запишем
функцию положения
<р2 = (RJR2) (1 — е) Ф1‘
Разложим ее в ряд Тейлора при условии, что ошибка
поворота ведущего шкива равна нулю, т. е. Дерj == 0:
где частные производные равны:
Sifi _ (1 - e)<Pi . g<p2~_ _ Ki(l-e)<Pi
SRt R2 ’ BR2 Ri
Ошибка коэффициента упругого скольжения
Де = (AF/F)e = (ДТ2/Т2)е,
где F — сила натяжения троса, Н; AF — погрешность силы
натяжения троса, Н; Т2 — крутящий момент на ведомом
шкиве, Н мм; ДТ2 — погрешность крутящего момента на
ведомом шкиве, Н-мм.
Выразим угол поворота <Pi ведущего шкива через угол
поворота ф2 ведомого шкива:
(pi — К2ф2/[Кх (1 — е)].
После подстановки и преобразований найдем
Из полученного выражения видно, что ошибка положе-
ния передачи Дф2 зависит от отклонений от номинальных
значений радиусов ведущего и ведомого ДК2 шкивов и
колебаний крутящих моментов (моментов сил сопротивления)
ДТ2.
7.4. Передача зубчатым ремнем
Передача зубчатым ремнем предназначена для передачи
вращательного движения от ведущего шкива 1 к ведомому
шкиву 2 с помощью зубчатого ремня 3 (рис. 7.13, а).
Конструкция зубчатого ремня показана на рис. 7.13,6.
Ремни изготовляют из неопрена, полиуретана и армируют
металлическим тросом, стекловолокном или полиамидным
шнуром. Наличие жесткого и прочного каркаса практически
гарантирует неизменяемость шага ремня. Для повышения
износостойкости зубья ремня покрывают тканым нейло-
ном [44].
Передаточное отношение передачи
i — Ф1/ф2 — C0i/G)2 — ^1/^2 — ^2/^1 — ^2/^1»
г
Геометрические параметры зубчатых ремней. Основным
параметром передачи зубчатым ремнем является модуль
зубьев
где т —
модуль зубьев, мм;
и Р2 — мощность соответ-
ственно на ведущем и ведомом шкивах, Вт; ni и м2 —
1
Рр . о
частота вращения ведущего и ведомого шкивов соот-
ветственно, об/мин (при наличии нескольких режимов и
постоянной мощности — наименьшая частота); 7\ и Т2 —
наибольший крутящий момент на ведущем и ведомом
шкивах соответственно, Н-мм; ц — к. п. д.
Модуль m округляют до стандартного значения: 1; 1,5;
2; 3; 4; 5; 7; 10.
Окружной шаг ремня (мм) рр = пт.
Ширина ремня (мм) b = \|fpm, где фр = 6... 9 — коэф-
фициент ширины ремня. Полученное значение ширины
ремня округляют до стандартного:
1
3;4
5; 8
10
12,5
1,5
3; 4
5; 8
10; 12,5
16; 20
2 3 4 5 7
8 12,5 20 25 50
10 16 25 32 63
12,5 20 32 40 80
16 25 40 50 -
10
50
63
80
Высота зуба ремня (мм) h = 0,6m.
Наименьшая ширина зуба ремня (мм) s = т.
Угол профиля зуба ремня 2ср = 50°.
Толщина ремня (мм) Н = m 4- 1 мм.
Расстояние 8 от впадины зуба до середины несущего
слоя ремня: если т < 4 мм, то 8 = 0,6 мм; если
m > 4 мм, то 8 = 0,8... 1,3 мм.
278
Диаметр троса, мм: если т < 4 мм, то dT = 0,36 мм;
если m > 4 мм, то dr = 0,65 мм.
Шаг между тросами рт = 1,2... 1,4 мм.
Основные параметры передачи (размеры в мм). Число
зубьев меньшего шкива: при m = 2...4 Zj > 14...20;
при т — 5... 10 Zi > 20...26, большего шкива z2 — zri. Значе-
ние z2 округляют до ближайшего целого числа.
Действительное значение передаточного отношения
i = z2/zv
Делительный диаметр меньшего шкива = mzx, боль-
шего шкива d2 = mz2.
Наружный диаметр меньшего шкива
dal — di — 26 + Rzr = mZi — 26 4- Kzls
большего
da2 = d2 —
шкива (мм)
26 + Rz2 = mz2 — 26 + Rz2,
где R = O,213FrA/b — поправка на диаметр шкива, обеспечи-
вающая равномерное распределение нагрузки между зубья-
ми ремня на дуге обхвата, мм [12]. Здесь Ft — окруж-
ная сила, передаваемая ремнем, Н; А — коэффициент
продольной податливости ремня шириной 1 мм на длине
одного шага, мм-мм/Н: при т < 4 мм А = 4,6-10“4т;
при m > 4 мм А = 1,6-10“ 4т.
Диаметр впадин меньшего шкива dfl = dal — 1,8m, боль-
шего шкива df2 = da2 — 1,8m.
Высота зуба шкива Лш = 0,9m.
Ширина шкива В = b + т.
Межосевое расстояние а = (O,5...2,O) m (zj + z2).
Длина ремня L = 2а + Aj + А2/а, где Aj = 0,5n(di +d2);
Д2 = 0,25 (d2 - di)2.
Число зубьев ремня zp = L/(nm). Полученное значение zp
округляют до ближайшего стандартного: 32, 40, 50. 63, 80,
100, 125, 160.
Окончательные значения длины ремня L — nmzp и меж-
осевого расстояния
а = 0,25 [L - Ai + j/(L - AJ2 - 8AJ.
Угол обхвата ремнем меньшего шкива (град)
«! = 180° — 57,3°m(z2 — z^/a.
Число зубьев ремня, находящихся в зацеплении с мень-
шим шкивом, z0 = Zi«1/360°. Рекомендуется принимать
z0 > 6. При z0 < 6 необходимо увеличить межосевое расстоя-
ние.
279
Боковой зазор между зубьями шкива и ремня
f = (0,25... 0,40) т.
Радиальный зазор между зубьями шкива и ремня
е = кш — h = (0,25... 0,35) т.
Силовой расчет передачи. Окружная сила, передаваемая
ремнем (Н),
- 2ZL- 2Г1 - 2Т2 1,91 ♦ Ю4Р1
mzi mz2r| mz^n^
Pi_ = Ik.
V ГГ) ’
l,91-104p2
mz2n2x]
где v — ndint/(6Q-1000) = nd2n2/(60-1000) — линейная ско-
рость ремня, м/с.
Радиальная сила (Н), действующая на валы,
Fr = (1,0... 1,2) Ft.
Предварительное натяжение ремня (Н), необходимое
только для устранения зазоров в зацеплении и правиль-
ного набегания ремня на шкивы:
F о = (1,1 ...1,3) qbv2,
где q — масса 1 м длины ремня шириной 1 мм. кг/(м • мм):
при т < 4 мм q = (15 4- 8,5m) 10“4; при т>4 мм
q = (25 + 8,5т) 10"4.
Расчет зубьев ремня на прочность. Зубья зубчатого
ремня проверяют на смятие
псм = l,98Ft/(zobh) [о]см,
где 1,98 — коэффициент, учитывающий неравномерность рас-
пределения нагрузки по высоте и ширине зубьев, а
также между зубьями; [а]см = О,75пв — допускаемое напря-
жение материала зубьев на смятие, МПа (пв — предел
прочности материала зубьев, зависящий от марки и техно-
логии изготовления ремня, ав = 10... 13 МПа).
Достоинства передач зубчатым ремнем: отсутствие про-
скальзывания ремня; большая нагрузочная способность (до
200 кВт); возможность получения больших передаточных
чисел (до 12); малая вытяжка ремня; небольшие нагрузки
на валы и опоры; бесшумность работы на больших
скоростях; простота в эксплуатации; высокий к. п. д.
(0,92... 0,98).
280
1
7.5. * Волновая передача
Волновые зубчатые передачи (ВЗП) находят широкое при-
менение в электромеханических приводах лучших зарубеж-
ных (ASEA, SKILAM, KUKA и др.) и советских (ТУР-10)
промышленных роботов.
ВЗП выгодно отличаются тем, что имеют малое значе-
ние полного мертвого хода (включающего составляющие
от зазоров и деформаций), постоянство передаточного
отношения, малые габариты и массу при высокой удель-
ной нагрузочной способности.
В обычных зубчатых механизмах деформации самих
зубьев, дисков колес, валов и корпусов нарушают пра-
вильность зацепления зубьев и снижают качество передачи.
Деформации эти незначительны и соразмерны с погреш-
ностями изготовления зубчатых колес. В ВЗП деформация
одного из колес, а именно гибкого колеса, сравнима с
размерами зуба и является необходимым условием зацепле-
ния и передачи движения от одного колеса к другому.
Устройство и принцип действия ВЗП. Простейшая волно-
вая зубчатая передача (рис. 7.14,6) состоит из следующих
основных элементов (рис. 7.14,а): b — генератор волн—
представляет собой два ролика, установленных на водиле,
которое вращается в подшипниках корпуса; 1 — гибкое
колесо — тонкостенная цилиндрическая оболочка, у левого
(по рисунку) торца которой нарезан зубчатый венец с
числом зубьев zj, а правый торец с помощью тонкого
донышка соединен с валом; 2 — жесткое колесо, внутри
которого нарезан зубчатый венец с числом зубьев z2, не
вращается. Передача проектируется таким образом, чтобы
наибольший диаметральный размер по роликам D' был
больше диаметра DB внутренней поверхности гибкого
колеса. Генератор волн, вставленный внутрь гибкого колеса,
деформирует его, и в таком виде гибкое колесо с
генератором волн вставляется внутрь жесткого колеса.
Торцовое сечение показано на рис. 7.14,в, на котором:
Г — контур гибкого колеса до деформации; 1 — контур
гибкого деформированного колеса; 2 — контур жесткого
колеса; w0 — радиальная деформация гибкого колеса. Есл1
мысленно развернуть контуры колес так, чтобы круглый
контур Г превратился в прямую, а кратчайшие рас-
стояния между контурами 1 и Г сохранились в развертке,
* Параграф написан Ю. И. Семиным.
281
1
то получим картину (рис. 7.14, г). Относительно недефор-
мированного контура на гибком колесе появляются две
волны деформации. Зоны вблизи точек Б и Б' называются
вершинами волны деформации, а зоны вблизи точек
В и В' — впадинами. У вершин деформации образуются
две симметричные зоны зацепления зубьев гибкого и
жесткого колес. При повороте генератора волн на угол
фь большая ось Б—Б' деформации также поворачивается
на угол <рь и обе зоны зацепления симметрично пере-
мещаются по периметрам колес.
Если числа зубьев колес равны z2 и zt (угловые
шаги колес 2n/z2 и 2n/Zi), то передаточное отношение
такой передачи можно подсчитать следующим образом. При
остановленном жестком колесе после полного оборота
генератора волн (фь = 2л) вал гибкого колеса повернется в
противоположном генератору направлении на угол, равный
Ф1 = 2л — z2)/zv От углов поворота можно перейти к
282
1
угловым скоростям; тогда передаточное отношение
от генератора волн к гибкому колесу при останов-
ленном жестком
«й> = = = (7 Л)
coj (pi 2Tr(Zi — z2)/Zi z2 — Zi
Если гибкое колесо связать с корпусом, а жесткое с вы-
ходным валом, то после поворота генератора волн на угол
<рь = 2л жесткое колесо повернется в том же направлении,
что и генератор волн, на угол ф2 = 2tc(z2 — zt)/z2. В этом
случае передаточное отношение от генератора волн к
жесткому колесу при остановленном гибком
И) _ _ Фь __ ^71
со2 ф2 2n(z2-Zi)/z2
(7.2)
Выражения (7.1) и (7.2) показывают, что передаточное
отношение волновой зубчатой передачи зависит только от
чисел зубьев колес.
Особенности волнового зубчатого зацепления. Вращающий-
ся генератор волн гонит по периметру гибкого колеса
волну деформации. За один оборот генератора гибкое колесо
испытывает две волны деформации. На рис. 7.15 показан
элемент торцового сечения гибкого колеса. В недефор-
мированном состоянии средняя по толщине обода линия
(нейтральная, или срединная) а—а имеет постоянную кри-
визну. При прохождении вершины волны деформации
срединная линия занимает положение б — б, а при про-
хождении впадины — положение в — в. Очевидно, что напряже-
ния в элементе за один оборот гибкого колеса 4 раза
меняют знак и значение. Для обеспечения долговечности
гибкого колеса (даже ненагруженнои передачи) напряжения
не должны выходить за пределы линейного участка закона
Гука для стали. Поэтому для стальных гибких колес
радиальная деформация w0 и толщина обода hc относи-
тельно невелики: w0 = (0,003...0,015)d}; hc = (0,005...0,03
где di — делительный диаметр недеформированного гибкого
колеса. При таких значениях w0 кривизны характерных
линий (вершин, впадин и т.п.)
деформированного гибкого и
соответствующих окружностей
жесткого колеса отличаются
не более чем на 2%. Малым
значением Wo определяется и
малая разность делительных
диаметров гибкого и жесткого
283
1
колес. Для стальных колес
2w0 « d2 - di = т (z2 - zx). (7.3)
Из этого выражения следует, что разность чисел зубьев
колес z2 — Zi должна быть минимальной, а числа зубьев —
относительно большими. При таких соотношениях w0, z19
z2 зазоры между зубьями в зоне вершины волны малы
и в значительной степени выбираются при нагружении
или даже сборке передачи. Благодаря этому в ВЗП очень
большое число пар зубьев (до 0,3zx) одновременно нахо-
дится в зацеплении (т. е. имеется значительная много-
парность зацепления).
Из вышесказанного можно вывести следующие особен-
ности волновой зубчатой передачи со стальным гибким
колесом:
большое передаточное отношение и в одной ступени;
для передач со стальными гибкими колесами и — 50... 300.
Нижний предел ограничен допускаемыми изгибными напря-
жениями в ободе колеса (чем больше w0/m [см. формулу
(7.3)], тем больше напряжения); верхний предел (при
и — 300 z2 = 600) — технологическими возможностями зубо-
резных станков: нарезать колесо с внутренним числом
зубьев больше шестисот затруднительно;
при одновременном зацеплении большого числа пар
зубьев ВЗП передает большие крутящие моменты при
относительно малых габаритах и массе;
многопарность зацепления и несколько симметричных
зон зацепления дают эффект усреднения ошибок изготов-
ления и монтажа колес и обеспечивают высокую кине-
матическую точность ВЗП и малый люфт ее валов;
малые деформации гибкого колеса (по сравнению с его
диаметром) позволяют выполнить гибкое колесо в виде
глухой оболочки и изготовить герметичные волновые
механизмы, передающие вращение из одной среды в другую
без подвижных уплотнений (см. ниже);
опыт эксплуатации ВЗП выявил их достаточно высокий
к. п. д. Так, для и = 50...300 ц = 0,85...0,6 соответственно.
Виды генераторов волн. Генератор волн в ВЗП служит
для образования, поддержания и движения волн дефор-
мации. По виду энергии, обеспечивающей эти функции,
генераторы подразделяются на механические, гидравли-
ческие, пневматические и электромагнитные.
В механическом генераторе волн на образование волн
деформации энергия затрачивается один раз — при сборке.
В собранной передаче на поддержание волн деформации
284
энергия не затрачивается вообще. При вращении генератора
(если отсутствует внешний момент сопротивления) энергия
расходуется только на преодоление трения в подшипни-
ках и внутреннего трения в материале гибкого колеса.
Гидравлические, пневматические и электромагнитные
генераторы волн требуют непрерывной затраты энергии не
только на вращение, но и на создание и поддержание
самой волны деформации. Это сказывается на их к. п. д.,
который не превышает 8 — 10%.
В приводах робототехнических систем применяются и
наиболее перспективны механические генераторы, в мень-
шей степени могут использоваться гидравлические и пневма-
тические генераторы и совсем трудно использовать
электромагнитные генераторы ввиду их малой жесткости и
относительно большой массы. Гидравлические и пневма-
тические генераторы волн могут применяться как мощные
быстродействующие приводы — усилители. Инерционность
их во много раз меньше, чем у любого другого
механизма такой же мощности. В таких генераторах волн
мощный посторонний источник создает напор жидкости
или газа под плунжерами, деформирующими гибкое колесо.
Давление регулируется достаточно малым (и, следователь-
но, малоинерционным) золотником или быстродействую-
щими клапанами.
Генераторы волн любых типов могут создавать одну,
две, реже три или более волн деформации; генераторы
волн могут деформировать гибкое колесо изнутри (генера-
торы внутреннего расположения) и снаружи (генераторы
внешнего расположения).
Простейший механический роликовый генератор волн
показан на рис. 7.14,6. Гибкое колесо в этом случае
имеет опору в радиальном направлении практически только
в двух точках — точках контакта роликов с внутренней
поверхностью гибкого колеса. Усилия в зацеплении при
передаче крутящего момента вызывают появление радиаль-
ной составляющей, которая заставляет гибкое колесо плот7
нее огибать ролик. Кривизна гибкого колеса в зоне
контакта с роликом увеличивается, следовательно, увели-
чиваются изгибные напряжения в ободе гибкого колеса и
снижаются его прочность и долговечность. Частота враще-
ния роликов оказывается в несколько раз больше частоты
вращения вала генератора волн.
При достаточной быстроходности современных электро-
двигателей работа подшипников роликов генератора с вы-
сокой частотой вращения и с большими радиальными
285
1
агрузками
снижает долговечность ВЗП в целом. Отме-
ченные недостатки практически исключают применение ВЗП
с роликовыми генераторами волн в приводах роботов.
Кулачковый шариковый генератор волн. Необходимость
обеспечить гибкому колесу опору в радиальном направ-
лении по всему периметру колеса приводит к конструкции
кулачкового генератора волн (рис. 7.16). На кулачок 1
эллиптической формы напрессовывается так называемый
гибкий подшипник. Внутреннее кольцо 2 подшипника
деформируется по форме кулачка. Наружное кольцо 3
деформируется телами качения 4 (чаще всего шариками),
которые размещены в сепараторе 5. Толщина и материал
дружного кольца гибкого подшипника выбраны такими, что-
бы обеспечить надлежащую долговечность гибкого кольца.
Гибкий подшипник вставляется
нутрь гибкого зубчатого
колеса 6 и его наружное кольцо испытывает такие же
деформации, как и само гибкое колесо.
Кулачковые генераторы волн обеспечивают хорошие
качественные характеристики ВЗП — большую удельную
нагрузочную способность, высокую крутильную жесткость,
плавность и точность вращения. Гибкие шариковые под-
шипники выпускаются по ГОСТ 23179 — 78. Однако кулачко-
вые генераторы обладают одним недостатком: их при-
веденный момент инерции — наибольший из всех типов
механических генераторов волн.
Например, для волновой зубчатой передачи си — 100,
т = 0,5 мм и внутренним диаметром гибкого колеса 100 мм
можно выбрать гибкий подшипник 815, у которого число
Рис, 7.16
286
шариков zm = 21, диаметр их
— 9,128 мм. Размеры под-
шипника — 0 75 х 0 100 х 15.
Расчеты показывают, что для
кулачкового генератора с ука-
занным гибким подшипником
приведенный момент инерции
7пр = 2,853 • 10" 3 кг • м2. Эту ве-
личину затем сравним с приве-
денным моментом инерции дис-
кового генератора волн. Здесь
любопытно отметить, что 3%
приведенного момента инерции
приходится .на тела качения.
Применение гибкого под-
шипника требует точного изго-
товления кулачка генератора,
лучше всего на станках с
числовым программным управ-
лением или на обрабатываю-
щих центрах.
Рис. 7.17
Дисковый генератор волн. Если увеличить диаметры роли-
ков (см. рис. 7.14, а), получится дисковый генератор волн
(рис. 7.17). Деформирующие диски 1 расположены в парал-
лельных плоскостях и вместе с подшипниками 3 установлены
на эксцентриковом валу 2. Гибкое колесо 4 принимает
форму овала. Двухдисковый генератор волн обеспечивает
опору в радиальном направлении на значительной части
периметра гибкого колеса, правда, не по всей ширине зуб-
чатого венца.
Этот недостаток устраняется в трехдисковом генераторе
волн (рис. 7.18, о). Здесь крайние диски 1 и средний диск 2
придают гибкому колесу 6 форму овала. Каждый диск
на подшипниках 5 установлен на эксцентриках 4, которые
посажены на входной вал 3 передачи. Расположение
деформирующих дисков в торцовой плоскости схематично
показано на рис. 7.18,6. Диски 1 и 2 деформируют
гибкое колесо 6 так, что вблизи вершин волн дефор-'
мации кривизна гибкого колеса постоянна. В зоне, ограни-
ченной углом 2р, наблюдается плотное прилегание гибкого
колеса к деформирующим дискам. Вне этой зоны гибкое
колесо не имеет опоры в радиальном направлении.
С целью увеличения жесткости дискового генератора
волн применяют подкладное кольцо и поддерживающий
диск (рис. 7.19, а). Внутрь гибкого колеса 2 вставляется
287
1
Рис. 7.18
гладкое упругое подкладное кольцо 1. Гибкое и подклад-
ное кольца деформируются одинаково, но не как одно
целое, поскольку в контакте между ними обязательно есть
зазор и, следовательно, относительное проскальзывание.
Деформирующие диски 3 вместе с подшипниками установ-
лены на эксцентриках 4, насаженных на вал б, который
опирается на подшипник 5. Диски имеют буртики, пре-
дотвращающие осевое смещение подкладного кольца. Между
деформирующими дисками на подшипнике 7 установлен
поддерживающий диск 8. Схематично расположение дисков
показано на рис. 7.19,6, из которого видно, что диски 3
придают гибкому колесу 2 форму овала, а поддержи-
вающий диск 8 дает гибкому колесу опору в радиальном
направлении по малой оси деформации (В—В). В зонах,
ограниченных углом 2р, гибкое колесо имеет постоянную
кривизну (подкладное кольцо на рис. 7.19,6 не показано).
288
Рис. 7.19
Если подсчитать приведенный
момент инерции двух-
дискового генератора волн, показанного на рис. 7.17, при-
способленного для ВЗП с внутренним диаметром гибкого
колеса 100 мм, т — 0,5 мм и и ~ 100, то получится
/пр = 4,696* 10“6 кг*м2. Это в 607 раз меньше, чем у кулачко-
вого генератора волн
гибкого колеса эта разность будет увеличиваться.
(см. выше). С увеличением диаметра
Из рис. 7.17 следует, что центры масс левого и правого
по рисунку дисков (в сборе с подшипниками и эксцентри-
ком) находятся в плоскости чертежа на одинаковом рас-
стоянии от оси вращения. Одновременно центры масс распо-
лагаются в двух торцовых плоскостях, расстояния между
которыми чуть больше ширины одного лиска. Узел генера-
тора волн в этом случае является ротором с моментной
неуравновешенностью. Для уст-
ранения этого недостатка не-
обходимо предусматривать на
эксцентриках специальные при-
ливы А, В (рис. 7.19, а).
Составим расчетную схему
для определения корректирую-
щих масс (рис. 7.20). Каждый
деформирующий диск в сборе
имеет массу т (кг), располо-
женную на расстоянии aw от оси
вращения (здесь aw — эксцентри-
Рис. 7.20
289
10 Механика промышл. роботов, ки. 2
ситет деформирующего диска, определяемый из геометри-
ческого расчета волнового зацепления). Центры масс тк
приливов на эксцентриках 4 (см. рис. 7.19) расположены на
расстоянии ек от оси вала. Расстояния между векторами
дисбалансов дисков Ь и корректирующих масс £>к обозна-
чены на рис. 7.20. Векторы дисбалансов равны
D = maw; DK — ткёк к (7.4)
и расположены в плоскости рисунка. Из уравнения суммы
моментов дисбалансов относительно точки А следует:
2MA(D) = DK(h - U - DI. + Dd. +1) - DK(h +1 +12) = 0; (7.5)
- l2 - h - I - l2) - Di-h + h + 0 = 0;
DK = Dl/(l + 2/2). ' (7.6)
Чтобы снизить массу генератора волн, следует увели-
чивать величины ек и /2.
Генераторы волн внешнего деформирования. Гибкое колесо
можно деформировать с наружной стороны, например, двумя
роликами, установленными на водиле. Отмеченные выше
недостатки роликовых генераторов волн в данном случае
проявляются в еще большей степени.
Конструкция кулачкового генератора волн внешнего
расположения показана на рис. 7.21. Во внутренний ку-
лачок / запрессовывается наружное кольцо подшипника 2
нем принимает форму, эквидистант-
ную поверхности кулачка. Тела
качения (шарики) деформируют
внутреннее кольцо и гибкое коле-
со 3, которое принимает требуе- ,
мую форму. Очевидно, «то усло-
вия деформации внутреннего коль-
ца гибкого подшипника такие же,
как и самого гибкого колеса.
У гибких подшипников не пре-
дусмотрена такая возможность
для внутреннего кольца. Поэтому
применение кулачкового генерато-
ра внешнего расположения воз-
можно при индивидуальном изго-
товлении колец подшипника на
прецизионном шлифовальном обо-
рудовании, что, конечно, ограни-
чивает его применение.
Момент инерции этого генера-
и дорожка качения на
290
Рис. 7.22
тора будет в несколько раз больше, чем у кулачкового
генератора внутреннего расположения.
Для внешнего деформирования гибкого колеса можно
применить конструкцию, использующую механизм парал-
лельных кривошипов [36] (рис. 7.22, а). На нескольких
кривошипных валиках 1 на подшипниках установлены
деформирующие шайбы 2, которые через подшипник 3
деформируют снаружи гибкое колесо 4. Кинематика дви-
жения каждой деформирующей шайбы показана на
рис. 7.22,6. Шайба 2 подвешена на четырех кривошипах 1
так, что при одновременном вращении кривошипов любая
точка шайбы (например, М) описывает окружность. Вся
шайба совершает поступательное движение с круговыми
траекториями любых ее точек.
10*
291
1
Расположение деформирующих поверхностей (в данном
случае это будут внутренние поверхности внутренних колец
подшипников 3 на рис. 7.22, а) и гибкого колеса показано
на рис. 7.22, в. Шайбы 2 деформируют гибкое колесо 4
так, что вблизи впадин гибкое колесо имеет постоянную
кривизну — зоны, ограниченные углом 2р.
Таким образом, геометрия деформации гибкого колеса
в описанном внешнем генераторе волн аналогична геометрии
дискового генератора (см. рис. 7.17). Гибкое колесо имеет
внутренние зубья и образует вблизи малой оси деформа-
ции две зоны зацепления с жестким колесом, которое
имеет внешние зубья. Кривошипных валиков должно быть
не меньше трех. Это обстоятельство позволяет применить
мног©двигательный привод (для повышения надежности)
или присоединять к свободным кривошипным валикам
датчики обратной связи. Приведенный момент инерции
внешнего генератора волн с деформирующими шайбами
всего в 3 — 5 раз больше, чем у дискового генератора
волн. И по этому параметру он оказывается предпочти-
тельней кулачкового.
Гидравлический (пневматический) генератор волн. Гибкое
колесо можно деформировать (внутренним и внешним
образом) за счет энергии жидкости или сжатого газа.
На рис. 7.23 показан гидравлический генератор волн.
Гибкое колесо 1 вместе с подкладным кольцом 2 дефор-
л -д
Рис. 7.23
1
а часть плунжеров — с по-
мируется плунжерами 3; плунжеры расположены в два ряда
в шахматном порядке. Под плунжеры нагнетается под
большим давлением жидкость, которая поступает через
отверстие по стрелке Б и сливается через отверстие по
стрелке В. Вращающийся золотник 4 соединяет часть плунже-
ров с полостью нагнетания
лостью слива. Те группы плунжеров, которые находятся под
давлением, деформируют гибкое колесо и образуют вершину
волны деформации; впадина волны приходится на те
группы плунжеров, которые соединены с полостью слива
жидкости. Золотник
он может работать
Работа в шаговом
если давление под
быстродействующих
I
вращается от постороннего привода;
в непрерывном и шаговом режимах,
режиме получается и в том случае,
плунжерами изменяется с помощью
клапанов. Аналогичное устройство
имеет и пневматический генератор волн.
Применение таких генераторов в ВЗП целесообразно
в качестве мощных малоинерционных гидро- или пневмо-
усилителей (здесь волновая передача выступает не только
как передаточный механизм, но и выполняет функцию
двигателя).
Гибкие колеса. Гибкое колесо волновой передачи обычно
представляет собой тонкостенную цилиндрическую оболочку,
на наружной (или внутренней) поверхности которой вблизи
деформируемого торца нарезается зубчатый венец. Генератор
волн, вращающийся внутри гибкого колеса, деформирует его
у одного торца, другой торец остается неизменным. Форма
и величина деформации обязательно должны учитывать
напряженное состояние в материале гибкого колеса, чтобы
напряжения от деформации и от передаваемого крутящего
момента не превышали допускаемых. Допускаемые напря-
жения учитываются при расчете толщины обода гибкого
колеса (см. ниже).
Гибкое колесо соединяется с выходным
корпусом передачи с помощью тонкостенной
диафрагмы, шлицевой муфты или волновой зубчатой муфты.
На рис. 7.24,« гибкое колесо соединяется с жестким
фланцем (который можно присоединить к корпусу) диафраг-
мой, направленной наружу. Внутренняя полость гибкого
колеса может быть при необходимости использована для
размещения ведущего электродвигателя или вспомогатель-
ных устройств. Такая диафрагма довольно жестко фиксирует
продольную ось гибкого колеса (не допускает прецсссиро-
вания ее) и исключает, таким образом, самоустановку
гибкого колеса в передаче.
валом или
плоской
I
I
4
/
i
г
1
I
1
1
L'VMMiЬЧОМ-.М, аЧ(1и>;Ш*(16.Л9№
Рис. 7.24
На рис. 7.24, б соединение тонкостенной оболочки
колеса с валом осуществляется с помощью диафрагмы,
отогнутой от оболочки внутрь. Это соединение допускает
в некоторых пределах прецессию продольной оси колеса
относительно оси вала, т. е. допускает самоустановку
зубчатого венца в передаче. Возможно сварное соединение
встык диафрагмы и тонкостенной оболочки качествен-
ными методами сварки (импульсной, точечно-искровой, ла-
зерной и т. п.).
Гибкие колеса (рис. 7.24, а, б) наиболее предпочтительны,
так как ВЗП с такими колесами обеспечивают высокий
к. п. д., большую крутильную жесткость и не имеют люфта.
Гибкое колесо может быть выполнено в виде тонко-
стенного цилиндра (рис. 7.24, в), на торцах которого
нарезаны зубья. Левый зубчатый венец входит в зацепление
с жестким колесом ВЗП, правый — с жесткой зубчатой
муфтой, соединенной с выходным валом корпусом.
Такое колесо технологично, но из-за наличия боковых
зазоров между зубьями жесткой зубчатой муфты в ВЗП
появляется люфт выходного вала.
Гибкие колеса указанных типов имеют слева по рисунку
упрочняющий поясок шириной а. Благодаря этому пояску зо-
на наибольших изгибных напряжений от деформации гиб-
кого колеса перемещается из зоны зубчатого венца в глад-
кий поясок, в котором нет концентраторов напряжений.
Поэтому опасность возникновения усталостных трещин
в гибком колесе снижается. Уменьшается также и перекос
зубьев гибкого колеса в продольном направлении.
Основные соотношения размеров гибких колес, приведен-
7.24, определены из
ные на рис.
опыта эксплуатации
экспериментальных и промышленных ВЗП. Пример конструк-
294
R = (5... 10)hc; h'shc-(0,05... 0,1) mi h=(o,6...o,9) oc
Рис. 7.25
тивного оформления зубчатого венца гибкого колеса показан
на рис. 7.25.
На рис. 7.26 показаны гибкие колеса двухступенчатых
передач. Длина этих колес определяется из конструктивных
соображений и не превышает 0,5^. Зубчатые венцы I и II
гибкого колеса двухступенчатой передачи (рис. 7.26, а)
имеют разные числа зубьев одного или разных модулей. Они
образуют с двумя жесткими колесами два разных
волновых зацепления. Особенность проектирования этого
гибкого колеса состоит в том, что геометрические
параметры зубьев обоих венцов должны обеспечивать
одинаковую толщину обода по всей длине колеса, иначе
на участке между венцами возникнет «ступенька» и появится
дополнительный концентратор напряжений. Зубья гибкого
колеса (рис. 7.26, б) с одним жестким колесом образуют
волновое зубчатое зацепление, а с другим — волновую
зубчатую муфту. Два волно-
вых зацепления в ВЗП с
кольцеобразными гибкими
колесами несколько снижа-
ют к. п. д. передачи и спо-
собствуют появлению люфта
выходного вала.
Гибкое колесо герметич-
• ной волновой передачи пока-
зано на рис. 7.27.
Жесткое колесо любой
волновой передачи представ-
ляет собой обычное эволь-
вентное колесо с внутренним
Рис. 7.26
295
hs(0,6... 0,9) hc;
^lOhiBrd^lM
Рис. 7.27
или внешним (для передачи внешнего деформирования) зу-
бом и конструкция его не рассматривается.
Для изготовления гибких колес применяются стали с
высокими механическими свойствами. Следует учесть, что
при мелком модуле зубьев (т < 1 мм) операция шлифо-
вания зубьев трудно осуществима, поэтому нарезание
зубьев должно производиться после термообработки заготов-
ки на твердость 34HRC. При большей твердости мелко-
модульный зуборезный инструмент (долбяки или фрезы),
изготавливаемый из инструментальных сталей типа Р18,
не сможет обработать зубчатый венец. Опыт эксплуа-
тации ВЗП показал, что требуемую прочность и долговеч-
ность могут обеспечить стали с сгвр >1150 МПа, ат >
>15 МПа, ст_ 1 >450 МПа при твердости после термо-
обработки 24...34 HRC. Применяются стали повышенной
вязкости, которые менее чувствительны к концентраторам
напряжений, такие, как: 30ХГСА, 38Х2МЮА, 40ХН2МА,
40X13. Для гибких колес герметичных ВЗП применяют
стали типа 12Х18Н10Т. Такие вязкие стали допускают
изготовление гибких колес методами пластического дефор-
мирования (раскатка, глубокая вытяжка).
Для упрочнения поверхности рекомендуется зубчатый
венец гибкого колеса подвергать наклепу, включая впадины
между зубьями. Холодное азотирование зубчатого венца
повышает предел выносливости в 1,3 —1,4 раза и уменьшает
износ зубьев. Благоприятно сочетание электрохимического
полирования с последующим азотированием. Оболочки
гибких колес могут быть и сварными. Чаще всего к
296
цилиндрической оболочке приваривается тонкостенная
диафрагма, тогда материал для сварных гибких колес
должен обладать хорошей свариваемостью.
Напряженное состояние жесткого колеса несравненно
ниже, чем гибкого. Поэтому для изготовления жестких
колес используют простые конструкционные стали (45; 40Х
и т. п.) с несколько меньшей твердостью заготовки, чем
у гибкого колеса. Возможно изготовление жесткого колеса
из высокопрочного чугуна или цветных металлов. В этом
случае жесткое (чугун) и гибкое (сталь) колеса образуют
антифрикционную пару.
Геометрия волнового зубчатого зацепления. Расчет
геометрических параметров волнового зубчатого зацепления
проводится при следующих, подтвержденных теорией и
экспериментом допущениях:
1) профиль зуба гибкого колеса при деформации
остается неизменным;
2) ось симметрии зуба гибкого колеса остается после
деформации нормальной к срединной линии гибкого колеса
(см. рис. 7.15);
3) срединная линия тела гибкого колеса под зубчатым
венцом не изменяет своей длины и обладает свойствами
нейтральной линии криволинейного бруса;
4) зацепление зубьев гибкого и жесткого колес можно
рассматривать в одной торцовой плоскости, нормальной
к продольным осям колес и проходящей примерно
посередине зубчатого венца гибкого колеса.
Генераторы волн внутреннего и внешнего деформиро-
вания (см. рис. 7.18,6; 7.22, в) обеспечивают срединной
линии гибкого колеса постоянную кривизну в пределах
зон, ограниченных центральными углами 2р. В остальных
частях своего периметра гибкое колесо имеет свободную
форму деформации, определяемую упругими свойствами
тонкостенной оболочки колеса. Такая картина деформации
и зацепления показана на рис. 7.28, а.
Постоянная кривизна внутренней поверхности гибкого
колеса в зоне, ограниченной углом 2р, обусловливается
плотным облеганием гибким колесом деформирующего диска
диаметром £>р. При этом не только срединная линия и
внутренняя поверхность, но и все характерные линии гибкого
колеса (впадины, вершины зубьев и т. п.) также имеют
постоянную кривизну. Если предположить, что зубья
гибкого колеса нарезались именно при такой деформации,
то в зоне, ограниченной углом 2р, в каждой полуволне
реализуется чистое внутреннее эвольвентное зацепление.
297
Тогда волновое зацепление жесткого (z2) и гибкого (zj) колес
в указанной зоне можно заменить зацеплением того же
жесткого колеса с числом зубьев z2 и некоторого услов-
ного жесткого колеса с числом зубьев zy
(рис. 7.28, б).
Dp, можно
Обозначив на рис.
7.28, б величины hc и
связать их с радиусом окружности впадин zyy и остальными
параметрами зубчатого венца. Гибкие колеса обычно
нарезаются в недеформированном состоянии, поэтому пред-
лагаемая картина зацепления немного искажается. Однако
эту ошибку можно учесть при определении zy — расчетного
числа зубьев условного колеса. (Подробные выкладки здесь
опускаются.)
1
Геометрия волнового зацепления с использованием
условного колеса принципиально одинакова как для внутрен-
него, так и для внешнего деформирования гибкого
колеса. Здесь и далее индексы «г» и «ж» относятся к
гибкому и жесткому колесам соответственно, а знаки в
формулах относятся: верхний — к внутреннему деформиро-
ванию, нижний — к внешнему. Расчетная схема (рис. 7.29)
волнового зацепления с внутренним деформированием гибко-
го колеса включает следующие обозначения: гс — радиус
срединной линии гибкого недеформированного колеса;
гсу — радиус срединной линии в деформированном гибком
колесе; гЬж и гЬу — радиусы основных окружностей жесткого
условного
колес; гиж и rwy — радиусы начальных
окружностей жесткого и условного колес; aw — угол зацеп-
ления; aw — межосевое расстояние [оно равно эксцентриси-
тету АГО установки деформирующего диска (см.
рис. 7.28, a)]; w0 — радиальная деформация гибкого колеса.
За исходный параметр геометрического расчета прини-
мается максимальная относительная радиальная деформа-
ция гибкого колеса w/rc. Уравнение для определения
расчетного числа зубьев условного колеса выводится из
уравнения срединной линии деформированного гибкого
колеса:
(7.7)
Ряс. 7.29
299
где коэффициент
(7.8)
На основании третьего допущения существует равенство
шагов зубьев по срединной линии недеформированного
и деформированного гибкого колеса:
рс = РУ; 2nrc/zr = 2nrcy/z
у»
откуда
(7.9)
После подстановки выражения (7.9) в (7.7) и преобразования
относительно zy получим расчетное число зубьев условного
колеса
(7.Ю)
При известных параметрах производящего контура w,
Л* и с* далее определяется радиус срединной окружности
деформированного гибкого колеса на участке 2£:
I z
мши*
Су — т
2т
(7.И)
где хг — коэффициент смещения; hc — толщина обода гибкого
колеса под зубом.
На основе опыта проектирования и. эксплуатации ВЗП
для стальных гибких колес предложены следующие эмпири-
ческие формулы:
(7.12)
(7.13)
(7.14)
где при внутреннем деформировании 5 = 1; у = 0,9... 1,1;
при внешнем деформировании 6 = 0,8... 0,9; у = 0,85... 1,1.
Эти зависимости приведены в [23] и получены из
анализа блокирующих контуров двухволновых зубчатых
передач наружного и внутреннего деформирования в диапазо-
не передаточных чисел и — 50... 300.
Далее, из (7.9) определяется радиус срединной окруж-
ности недеформированного гибкого колеса
300
су
(7.15)
Межосевое расстояние в передаче с условным колесом,
равное эксцентриситету установки деформирующих дисков
(или шайб — для внешнего деформирования), получается рав-
ным
или
(7.16)
По межосевому расстоянию можно определить угол
зацепления в передаче с условным колесом (т. е. и в
волновой передаче):
ОС'Ц, — arccos £ ~Ь (^ж
zy) т cos a/(2aw)J.
(7.17)
Передачу внутреннего деформирования чаще всего можно
проектировать при угле зацепления aw = а, тогда в выраже-
ниях (7.13) и (7.14) 6 = 1, у = 1 и w0 = т; в этом случае
значение zy подсчитывается по упрощенной формуле
Zy — z г /(zr + 2k), (7.18)
Для двухволновых ВЗП отмечен возможный диапазон
передаточных отношений и = 50...300. Тогда диапазон
изменения zy, рассчитанных по (7.18), колеблется: zy =
= 3,88... 6,00, а разность гж — zy = 5,88... 8,00. Это указывает
на то, что волновое зацепление есть эвольвентное
внутреннее зацепление с малой разницей зубьев.
Основной особенностью
геометрии такого зацепления
является обеспечение отсут-
ствия заклинивания по вер-
шинам зубьев. При внутрен-
нем зацеплении (рис. 7.30)
кроме точки касания К на
линии зацепления N2K эволь-
венты могут иметь еще и
точку пересечения х, Эта
точка лежит на прямой
линии хх, которая является
геометрическим местом пе-
ресечения эвольвент. Есл и
вершина зуба условного (или
гибкого) колеса выходит из
Рис. 7.30
301
-----ц^1М
Рис. 7.31
впадины между зубьями жесткого колеса, то пересечения
эвольвент не наступает. При этом точка L пересечения
окружностей вершин га2 и лежит
выше
линии
хх.
Если же эти окружности пересекаются в точке L' (при г^),
лежащей ниже линии хх, то происходит пересечение эволь-
вент, т. е. заклинивание при упоре вершин зубьев. Для
проверки на отсутствие заклинивания подсчитывают углы
Ф и ф и сравнивают их, при ф > ф заклинивание отсут-
ствует.
Угловая координата точки L пересечения окружностей
вершин зубьев колес определяется по формуле
COS ф — (г^2 + «i —
(7.19)
Угол ф определяется по номограмме (рис. 7.31), на
которой показаны линии пересечения эвольвент при различ-
ных параметрах колес; эти линии выражают графически
зависимость ф = f (р0; и'; aw), где
и' = z2/zy; ро = га1!тЪ2.
(7.20)
Остальные параметры колес и передачи в целом рас-
считываются так же, как внутреннего эвольвентного зацеп-
ления [36].
Жесткое колесо в передачах внутреннего деформирова-
ния имеет внутренние зубья и нарезается долбяком.
В передачах наружного деформирования жесткое колесо
с внешним зубом нарезается реечным инструментом.
Поэтому расчетные формулы при определении хж — коэф-
фициента смещения производящего контура инструмента —
другие.
При внутреннем деформировании гибкого колеса внача-
ле определяется угол станочного зацепления жесткого
колеса с долбяком
302
1
inv awox = inv a —
(7.21)
где zd = гж — zy; z0 — число зубьев долбяка.
Затем определяется коэффициент
иж — z0 / cos a \
*ж ~ Z------1--------1 ).
2 у cos aw ]
При наружной деформации гибкого колеса угол станоч-
ного зацепления долбяка с гибким колесом '
(7.22)
г
&wOr —
arccos
(7.23)
Затем определяется коэффициент смещения
инструмента
(inv а — inv aw) zd — (inv a — inv awOr) (zy - z0)
шмяа _ _ _j_. _ _ __ -i- _ - -_ — ----- . - _
ЛЖ — ~ .
реечного
(7.24)
Далее определяются остальные параметры:
коэффициент
воспринимаемого смещения
zd ( cos a
2 у cos aw
коэффициент
(7.25)
уравнительного смещения
(7.26)
радиусы окружностей вершин условного г
аж колес
жесткого
(7.27)
(7.28)
где hK = 0,75... 1,00;
высота зубьев колес
h — m(h* + hK 4- с* — Ду);
(7.29)
диаметр окружности вершин зубьев недеформированного
колеса
(7.30)
внутренний DB (наружный d{) диаметр заготовки гибкого
колеса
ау — W1
ЙЖ = W
Z
hK
z
Ж
h
303
1
(7-31)
аж
диаметр окружности вершин зубьев жесткого колеса
аж 9
диаметр деформирующей поверхности дисков Dp (колец
de)
(7.32)
Если в передаче применяется подкладное кольцо (как
на рис. 7.19, а) толщиной hn, то Dp уменьшается, a
увеличивается на 2hn:
(7.33)
Помимо проверки на заклинивание необходимо проводить
проверку по теоретическому коэффициенту перекрытия еа.
Он не является для волновой передачи величиной, строго
лимитирующей ее работоспособность, однако имеются
экспериментальные данные, свидетельствующие о том, что
при снижении е« < 1 ухудшаются некоторые параметры ВЗП
(крутильная жесткость, плавность работы и др.):
(7.34)
ДОЛЖНО быть 8ц > 1,1.
Если зацепление зубьев гибкого и жесткого колес не
удовлетворяет требованиям по отсутствию заклинивания или
коэффициенту перекрытия, то в формулах (7.27) — (7.29)
необходимо взять другой коэффициент hK. В результате
изменяются радиусы гаж и гау, а следовательно, условия
заклинивания и коэффициент перекрытия sa.
Расчет одноступенчатой волновой передачи с внутренним
дисковым генератором волн. Расчет ВЗП, используемых
в приводах робототехнических систем, лучше вести по
крутильной жесткости передачи, которую, в первом прибли-
жении, можно оценить по коэффициенту С статической кру-
тильной жесткости. На рис. 7.32 представлен график
зависимости С —f (Jcr). Проведя на графике для требуемой
жесткости вертикальную прямую, получим в местах ее
пересечения с графиками для дисковых и кулачковых гене-
раторов волн некоторые диапазоны диаметров dcr + AJcr,
которые с некоторой доверительной вероятностью р обес-
304
1
dcr,MM
Рис. 7.32
печат требуемую жесткость ВЗП. Примерные графики из-
менения доверительных вероятностей р —f (Adcr) приведены
на рис. 7.32, справа. В соответствии с этими графиками
большие значения диаметров обеспечат получение требуе-
мой крутильной жесткости ВЗП с вероятностью, близкой
единице. Выбор меньшего диаметра уменьшает вероятность
получения ВЗП с требуемой жесткостью. Задаваясь вероят-
ностью р или степенью риска 1 — р, по графику можно
достаточно точно определить требуемый диаметр гибкого
колеса. По заданным нагрузкам необходимо проверить
полученный диаметр по условию работоспособности при
заданном виде смазки ВЗП. Поскольку dr и dcr различаются
обычно не более чем на 2 %, проверку можно вести по
формуле (см. [13]):
— ]/(ЮЛ/вых)/(^ [^см]),
(7.35)
где Л/вых — расчетный выходной крутящий момент, Н • м;
b — ширина зубчатого венца, м; [осм] — допускаемое напря-
жение смятия, МПа; [осм] == 15...35 МПа для улучшенных
сталей со смазкой — чем лучше условия смазки, тем выше
11 Механика промышл. роботов, кн. 2
305
допускаемое напряжение, [стсм] =* 8 МПа для стальных
зубчатых колес при работе без смазки.
После проверки выбирается больший из двух получен-
ных диаметров.
При заданном передаточном отношении и выбранной
кинематической схеме задают угол зацепления aw = а и опре-
деляют следующие параметры.
1. Числа зубьев гибкого zt и жесткого z2 колес:
при остановленном жестком колесе zx = 2и$;
при остановленном гибком колесе z2 — 2мЙ; zx — z2 — 2.
2. Модуль волновой зубчатой передачи m = d1/z19 где
d} — выбранный диаметр гибкого колеса; модуль округляет-
ся до ближайшего стандартного значения.
3. Толщина обода гибкого кол^а под зубом [форму-
ла (7.12)]
йс = (60 + zx/5)mzx10“4.
4. Исходные параметры инструмента: m; z0; а; Л?; с*.
5. Число зубьев условного колеса (7.18)
zy = zf/(zx + 2/с'),
но сначала выбирается угол р охвата деформирующих
дисков гибким колесом. При этом следует учесть, что
чем больше угол Р, тем больше крутильная жесткость
передачи, но при р > 60° несколько повышаются напря-
жения изгиба в гибком колесе и снижается его надеж-
ность.
По углу р выбирают коэффициент 2k [можно опре-
делить по формуле (7.8)]:
Р, град.............. 40 50 60 70 ’
2к................... 4,38485 4,02946 3,78522 3,62553
6. Коэффициент смещения при нарезании гибкого коле-
са (7.13)
хх = hi + с* + hc/(2m).
7. Угол станочного зацепления при нарезании жесткого
колеса долбяком с числом зубьев z0 (7.21)
inv aw02 = mv a
8. Коэффициент смещения для жесткого колеса (7.22)
cos a
..-..— *
COS Otw02
306
9. Коэффициент воспринимаемого смещения при aw — а
равен у = 0.
10. Коэффициент уравнительного смещения (7.26)
Ду = у - (х2 - Х.1).
11. Межосевое расстояние в передаче (т. е. величина
эксцентриситета установки деформирующих дисков)
т (z2 — zy) cos а
2 cos 'aw
12. Радиус окружности вершин
са (7.27)
зубьев условного коле-
ray = m(zy/2 + hK + - Ду).
13. Радиус окружности вершин
(7.28)
зубьев жесткого колеса
14. Далее проводится проверка на заклинивание зубьев
по формулам (7.19), (7.20) и номограмме (см. рис. 7.31).
15. Проводится проверка по теоретическому коэффи-
циенту перекрытия (7.34)
где
cos = mzy cos а/гду; cos аа2 = mz2 cos а/гв2.
16. В случае заклинивания передачи изменяют значение
/хк. Чем меньше hK, тем лучше выполняется условие от-
сутствия заклинивания, но уменьшается коэффициент пере-
крытия.
17. Исполнительные размеры гибкого и жесткого колес:
высота зубьев колес (7.29)
Ду);
радиус окружности впадин условного колеса (7.11)
м.
2т / ’
к
т
*1
радиус срединной кривой гибкого колеса в зоне зацеп-
ления (послё деформации)
Гсу ~ Гуу Лс/2,
307
радиус окружности гибкого недеформированного колеса
(7.9)
наружный диаметр заготовки гибкого колеса (7.30)
= 2(гс 4- hc/2 4- h);
внутренний диаметр заготовки гибкого колеса (7.31)
= 2 (гс
hc/2);
Внутренний диаметр заготовки жесткого лсолеса
4й2 = 2гв2>
диаметр деформирующего диска (7.33)
су
для увеличения жесткости передачи следует применить
подкладное кольцо, толщина которого h может быть выбрана
в пределах h — (1,6... 2,2)/ic, тогда
18. Проверка правильности расчета:
4- ray — h 4- с*т — га2 4- (h* — hK) т = 0.
(7.36)
Так как расчет ВЗП ведется с точностью, как минимум,
до пятого знака после запятой, то отличие от нуля в
(7.36) не должно быть больше (1...2)10~5.
19. Контрольные размеры колес по измерительным
проволочкам:
для гибкого недеформированного колеса
Afpi =
mz±cos а
cos ар1
(7.37)
где dp — диаметр измерительной проволоки или ролика;
Opi — угол, инволюта которого определяется по формуле
mvocpi =
2tgaxx
mv а н-------
mzi cos a
(7.38)
для жесткого колеса
Mp2 —
mz2
COSOp2
(7.39)
где ap2 — угол, инволюта которого определяется по формуле
308
1
inv ap2 =
inva —
б/р
mz2 cos a
(7.40)
Диаметры измерительных роликов выбирают по мо-
дулю т:
т, мм . . . .0,2 0,3 0,4 0,5 0,6 0,7 0,8 1,0 1,25
dpi мм . . . .0,343 0,572 0,724 0,866 1,008 1,302 1,441 1,732 2,311
После расчета размеров Mpi и Мр2 следует проверить,
не проваливается ли измерительная проволочка во впади-
ну между зубьями больше допустимого. Чтобы этого не
случилось, должно быть
МР1 > dai и Мр2 < da2. (7.41)
Если хотя бы одно из неравенств (7.41) не выполняется,
необходимо взять измерительную проволочку несколько
большего диаметра. Контроль толщины зуба гибкого
колеса по размеру Мр1 (так же, как и измерение всех
остальных наружных размеров гибкого колеса) можно про-
водить только на оправке ввиду податливости гибкого
колеса даже усилиям измерительного инструмента.
Расчет волновой передачи внутреннего деформирования
с волновой зубчатой муфтой. Гибкое колесо (см. рис. 7.26,6)
передачи с волновой зубчатой муфтой представляет собой
тонкостенное кольцо с одним зубчатым венцом с числом
зубьев сдеформированное генератором волн, оно входит
в зацепление с двумя жесткими колесами, число зубьев
одного из них z2 = Zi 4- 2, а другого z3 — zP Такая передача
имеет особенности и ограничения при расчете, так как в
одном волновом зацеплении реализуется передаточное отно-
шение (как в одноступенчатой передаче), а в другом —
осуществляется волновая зубчатая муфта. В обозначениях
параметрам передачи присваивается дополнительный ин-
декс «I» (например, awI; Eqj и т. д.), а параметрам
волновой зубчатой муфты присваивается дополнительный
индекс «м» (например, оси.м; £ам и т. д.).
Расчет передачи аналогичен описанному выше, за исклю-
чением п. 1.
В передаче с волновой муфтой с корпусом можно
соединить как жесткое колесо z2, так и жесткое колесо
z3. В первом случае гибкое колесо вращается и
Zi = 2и(й, а во втором — гибкое колесо стоит, так как
жесткое колесо z3 муфты установлено в корпусе и
Zi = 2wj,2) “ 2. Лучшим вариантом следует считать второй
вариант, так как здесь имеется возможность при селектив-
309
ной сборке несколько уменьшить кинематическую погреш-
ность.
Кроме того, несколько снижается
приведении]
момент инерции передачи, а к. п. д. во втором выше,
чем в первом варианте установки жестких колес.
По окончании расчета передачи (как это указано в
пп. 2 —19) ведется расчет волновой муфты. Зацепление в
муфте — это тоже внутреннее эвольвентное зацепление с ма-
лой разницей зубьев, а разница зубьев z3 — zy на 2 меньше,
чем в передаче. Ряд параметров для зацепления в
муфте уже определен из расчета передачи, это zy; hc;
Xi; h; aw’9 Db; Dp; Ayz и др.
Продолжение расчета:
20. Угол зубчатого зацепления в муфте
cos ocWM = cos awi (z3 - zy)/(z2 - zy).
(7.42)
21. Угол станочного зацепления жесткого колеса муфты
с долбяком с тем же числом зубьев z0
(z3 — zv) (inv a — inv aWM) — 2x t tg a
mv a03 = inv a----------------------------—-
22. Коэффициент смещения при нарезании
колеса муфты
cos a
cos a03
(7.43)
жесткого
(7.44)
23. Коэффициент воспринимаемого смещения в муфте
cos a
COS OtvvM
(7.45)
24. Коэффициент уравнительного смещения в муфте
АУм = Ум ~ (*з - *i)«
(746)
Значение Аум необходимо сравнить с полученным ранее
значением Аух для гибкого колеса и выбрать большее.
При этом допускается в одном из рассчитываемых зацеп-
лений увеличение радиального зазора. Высота зубьев гибко-
го колеса не должна превышать высоты зубьев про-
изводящего контура инструмента. Значение гоум берется рав-
ным гау1.
25. Радиус окружности вершин зубьев жесткого колеса
муфты
(7.47)
К
310
26. Далее проводится проверка на отсутствие заклини-
вания и по коэффициенту перекрытия [формулы (7.19), (7.20),
(7.34) и номограмма (см. рис. 7.31)]. Здесь также возможно
изменение значения hK.
27. Высота зубьев жесткого колеса муфты
h3 = т (hi + hK 4- с* - Дум). (7.48)
28. Внутренний диаметр заготовки жесткого колеса муфты
^вЗ = 2гоз.
29. Контрольный размер по измерительным проволоч-
кам для жесткого колеса муфты рассчитывается по
формулам (7.39), (7.40) подстановкой параметров с индекса-
ми «м».
I
I
1
I
I
1
Раздел
4
Уравновешивание,
развязка движений
и точность
манипуляторов
Глава 8
Статическое уравновешивание,
аккумуляция энергии, динамическая раз-
вязка движений
Под статическим уравновешиванием манипу-
ляторов будем понимать разгрузку приводов от статических
моментов, обусловленных силами тяжести его звеньев и
переносимого груза.
Разгрузка приводов уменьшает мощность двигателей и,
как следствие, уменьшает потребление энергии промышлен-
ным роботом. Но вместе с тем введение в конструк-
цию робота дополнительных механизмов уравновешивания
ведет к ее усложнению, во многих случаях повышает
металлоемкость и инерционность, приводит к дополнитель-
ным нагрузкам отдельных элементов конструкции. Этим мож-
но объяснить, что в большинстве существующих конструк-
ций промышленных роботов используется неполное уравно-
вешивание подвижных частей, хотя с точки зрения теории
осуществимо идеальное уравновешивание.
Уравновешивание статических нагрузок в промышленных
роботах может осуществляться с помощью пружин, противо-
весов или непосредственно приводами робота. Недостатком
второго способа является увеличение общей массы мани-
пулятора, третьего — увеличение необходимой мощности
приводов. Пружинные механизмы широко применяются для
уравновешивания статических нагрузок в роботах, хотя полное
уравновешивание при этом часто не достигается. Роль
пружин могут играть газ и жидкость.
312
Системы уравновешивания можно разделить на активные
и пассивные. В активных системах уравновешивания
используется основной или дополнительные приводы,
а также информация о положении системы. Хотя такие
системы и обеспечивают более точное уравновешивание,
они применяются редко ввиду их сложности. В пас-
сивных системах для уравновешивания используются
неуправляемые источники энергии: гравитационного поля, сил
упругости, сжатого газа.
Статическое уравновешивание манипулятора решает лишь
задачу разгрузки его приводов от сил тяжести звеньев и
переносимого объекта и никак не учитывает характер сил
инерции, возникающих при движении механизма. Между тем
промышленные роботы являются системами, к которым
предъявляются высокие требования по быстродействию.
Быстродействие прямо связано с преодолением сил инерции
системы. Поэтому вопросы распределения масс манипуля-
тора в связи с инерционными свойствами системы имеют
первостепенное значение.
При движении манипулятора с произвольным располо-
жением осей силы инерции звеньев, моменты приводов и
реакции в каждой кинематической паре зависят от движения
в других кинематических парах. Это свойство манипуля-
тора называют динамической связанностью движений или
динамическим взаимовлиянием движений. Для
устранения динамического взаимовлияния производят д и-
намическую развязку движений.
Динамическая развязка движений позволяет упростить
решение задач оптимального управления роботом и аккуму-
ляции энергии [21, 22].
Введение аккумуляторов энергии в манипуляторы значи-
тельно снижает мощность его приводных двигателей,
увеличивает быстродействие [22] и оказывается особенно
эффективным в простых роботах с цикловой системой
управления.
8.1.* Статическое уравновешивание
манипуляторов с помощью пружин
Рассмотрим некоторые конкретные примеры уравновеши-
вающих устройств в конструкциях промышленных робо-
тов.
* Параграф написан М. В. Поповым.
313
1
Универсальный промышленный робот ТУР-10 предназна-
чен для автоматизации основных и вспомогательных
операций в технологическом процессе.
Манипулятор (рис. 8.1) поворачивается вокруг вертикаль-
ной оси; движение схвата осуществляется в вертикальной
плоскости. Для уравновешивания статических моментов от
веса звеньев манипулятора имеется пружинный механизм
(рис. 8.1). Звено 10 уравновешивается с помощью пружины 2,
установленной на поворотной платформе. Усилие пружины
регулируется гайкой /. Пружина 2 через передаточный
механизм 3 цепями 4 и 5 соединена с одним плечом Г-
образного коромысла 6, установленного на валу привода 7
' качания этого звена. Второе плечо коромысла 6 соединено
с шатуном 8 и через звенья параллелограммного механиз-
ма со звеном 10. Звено 9 уравновешивается с помощью
пружины 16. Шток 15 пружины с помощью цепи 14
соединен с кривошипом 13, установленным на валу привода
12 качания звена.
Кривошип 13 шатуном 11 шарнирно соединен со звеном 9.
На штоке 15 имеется резьба, позволяющая с помощью
гайки 17 менять усилие пружины. Усилие пружины регу-
лируется таким образом, чтобы в любом положении мани-
пулятора не наблюдалось самопроизвольного движения.
Механизм подъема электромеханического робота МП-4
(рис. 8.2) состоит из электродвигателя 3, червячной само-
тормозящей пары 2, шестерни 1 и рейки, выполненной
заодно с вертикальным
валом 6. Вал 6 расположен
внутри ротора 5 и связан
с ним в верхней части
шлицевым соединением.
К верхнему фланцу вала
6 крепится манипулятор.
Для разгрузки привода
подъема и опускания
314
1
установлена пружина 4. Очевидно, что с изменением ее
деформации уравновешивающее усилие тоже меняется и
полное уравновешивание во всем диапазоне вертикальных
перемещений невозможно. Это наиболее простое пружинное
уравновешивание привода.
Более сложная схема пружинного уравновешивающего
устройства используется в роботе «Коат-а-Матик» фирмы
«Ретаб» (Швеция) (рис. 8.3). Механизм качания манипулятора
в шарнире В («плече») выполнен в виде параллелограмма,
состоящего из силовой стойки 6 и тяг 11, шарнирно
связанных снизу кронштейном 14, а сверху — щеками 9.
Двигателем является гидроцилиндр 13. Уравновешивание
осуществляется двумя пружинами 4 (вторая на рисунке не
видна), один конец которых с помощью серьги 3 закреплен
на кронштейне 14 эксцентрично относительно оси 2, а второй
конец связан со стойкой 6. При повороте стойки 6
отклоняется серьга 3, уменьшая или увеличивая плечо
пружины 4 относительно оси 1.
Механизм качания
шарнире А («локте») состоит из гидроцилиндра 5, гильза
которого через вилку 12 связана со стойкой 6, а шток 10 —
со звеном 8. Уравновешивающие пружины 7 закреплены
эксцентрично относительно оси качания звена 8. Отсутствие
поступательных степеней подвижности позволило в данном
случае довольно точно уравновесить звенья переносных
степеней подвижности в рабочем диапазоне конфигураций
манипулятора.
Аналогичный уравновешивающий механизм применяется
в промышленном роботе «Универсал-5».
Пневматическое уравновешивание робота «Оливетти»
представляет пример активной системы уравновешивания.
Схема одного из двух манипуляторов робота представле-
на на рис. 8.4. Вертикальное перемещение штанги 4
вместе со схватом 1 внутри каретки 8 осуществляется
через систему шестерен шаговым электродвигателем 7.
На каретке 8 установлен кронштейн 5, удерживающий
корпус пневмоцилиндра 6, поршень 3 которог о другим
концом соединен с фланцем 2, закрепленным на штанге 4. Для
вертикального перемещения применяются два параллельных
двигателя: силовой (пневмоцилиндр), воспринимающий силу
тяжести штанги и схвата, и шаговый электродвигатель,
осуществляющий программное движение, но не выпол-
няющий силовых функций. Такое разделение позволило
унифицировать все шаговые двигатели робота и избежать
применения более мощного и, следовательно, более доро-
гого двигателя вертикального перемещения. Пневматическое
315
Рис. 8.3 Рис. 8.4
уравновешивание применяется и в ряде других роботов.
Рассмотренные примеры, в которых осуществляется лишь
частичное уравновешивание подвижных частей манипуля-
торов промышленных роботов, могут привести к не-
правильному выводу о том, что для создания систем
уравновешивания достаточно лишь интуиции и здравого
смысла. Этот вывод глубоко ошибочен, ибо знание основ-
ных принципов и приемов идеального уравновешивания
помогает добиться простыми средствами большего эффекта
даже при создании систем с неполным уравновешиванием.
Рассмотрим основные принципы построения пассивных
систем уравновешивания манипуляторов.
Уравновешивание кривошипа. У кривошипа, вращающегося
в вертикальной плоскости (рис. 8.5, а), сила тяжести
Р = тд (где т — масса кривошипа) создает относительно
оси вращения О момент Pl sin а (где I = ОС). Поэтому для
точного уравновешивания кривошипа к нему надо приложить
такой же момент, но противоположно направленный. Проще
всего эта задача решается с помощью противовеса D
(рис. 8.5, б), установленного на продолжении кривошипа.
Масса уравновешивающего груза тх — ml/a (где а = OD) при
316
1
кривошипа, и в
результате метал -
ннсвмо-
1> а превышает массу
лоемкость конструкций, а также ее инерционность значи-
тельно возрастают. Поэтому, хотя данному способу прису-
щи и положительные качества — простота, небольшие до-
полнительные нагрузки на элементы конструкции, — уравно-
вешивание с помощью противовесов применяется сравни-
тельно редко.
Заменить постоянную силу тяжести противовеса в ме-
ханизме уравновешивания, в принципе, можез
устройство, обеспечивающее постоянное давление на поршень
цилиндра при его перемещении (рис. 8.5, в). Однако такое
пневмоустройство имеет два недостатка: сложность устрой-
ства и, как правило, необходимость внешнего источника
энергии, так как в процессе эксплуатации происходят
утечки газа. Поэтому, гораздо эффективнее использовать
замкнутый пневмоцилиндр с таким соотношением площади
и хода поршня к объему газовой камеры, которое
обеспечивает почти постоянное давление газа на поршень.
В этом случае усилие, действующее со стороны пневмо-
цилиндра на кривошип, F = pS, где р — избыточное давление
в цилиндре; 5 — площадь поршня (рис. 8.5, в), и значение
неуравновешенного момента определится выражением
Мну = (pSe — QI) sin а,
е — OB = BE — сторона дополнительного параллело
где
грамма.
При переменном давлении р полное уравновешивание
возможно только в одной точке диапазона изменения угла а,
пусть это будет при аА. Предполагая процесс изотерми-
ческим, легко получить для неуравновешенного момента
выражение
Мну = (QI - poSrMcosocj - cos а)/[ Ио/(Se)
cos а],
317
1
где р0 — атмосферное давление; Vo — объем газовой камеры
при а — 0. Используя данное равенство, легко по заданному
предельному значению Мну определить необходимое соот-
ношение V0/(Se), обеспечивающее удовлетворительное
уравновешивание во всем диапазоне изменения угла а.
Как будет видно из дальнейшего, такое пневматическое
уравновешивание близко к уравновешиванию с помощью
пружинных устройств.
Все механизмы уравновешивания, использующие в качест-
ве силового элемента пружину с линейной характеристикой,
могут быть условно разделены на две группы. К первой
относятся те из них, в которых требуемый закон изменения
уравновешивающего момента обеспечивается геометрией
расположения упругого элемента и соответствующим выбо-
ром его жесткости (рис. 8.6, а, б). В механизмах второй
группы необходимый уравновешивающий момент создается
введением промежуточного звена: зубчатой пары, кулисы,
кулачка и т. д. (рис. 8.6, в — е).
Для создания уравновешивающего момента, пропор-
ционального синусу угла отклонения кривошипа О А от
вертикали, в механизмах первой группы необходимо, чтобы
деформация пружины была равна расстоянию BE, а жесткость
пружины определялась выражением
с = Р1/(ОВ • ОЕ).
Действительно, в этом случае момент силы упругости
пружины относительно точки О равен MQ (F) — Fh =
= c BE h — РЬ BE • h/(OB • OE), где h — плечо силы F относи-
318
1
тельно точки О. Но BE • h =
= 25д ове = ОВ • ОЕ sin а. Тогда
M0(F) = Pl• OB• ОЕsinа/(ОВ х
х ОЕ) = Pl sin а.
Наличие в схеме а гибкого
элемента (троса), который мо-
жет вытянуться при эксплуата-
ции, предполагает в этой и
аналогичных ей конструкциях
использование пружин растя-
Рис. 8.7
жения с мягкими характеристиками и регулировку меха-
низма по мере вытягивания троса. Наличие в данной
схеме ролика, с которого сходит трос, теоретически нарушает
уравновешивание, но эти искажения невелики и могут быть
устранены введением дополнительной системы роликов. В
схеме б при наклонном по отношению к кривошипу
расположении упругого элемента применяются пружины
сжатия с малыми деформациями и большими усилиями.
В схемах механизмов в—е вспомогательные элементы
(зубчатая пара с передаточным отношением 2:1, кулиса, у
которой ОЕ = ОВ, или кулачок) предназначены для обеспе-
чения деформации пружины, пропорциональной синусу
половинного угла отклонения кривошипа от вертикали.
Действительно, в соответствии с принципом возможных
перемещений
Pl sin a da — ex dx — О,
где с — жесткость пружины; х — деформация пружины. Пред-
полагая, что при а0 = 0 х0 = О, после интегрирования
получим
г = 2]/Pl/c sin(a/2).
Следует отметить, что и для схем а, б (рис. 8.6) в случае
ОВ = ОЕ деформация пружины также пропорциональна
sin (a/2).
Часто в конкретной конструкции робота диапазон
изменения угла а невелик и тогда появляется возмож-
ность использования наиболее простого пружинного механиз-
ма. Пружина растяжения устанавливается между стойкой и
кривошипом (рис. 8.7), точка Е крепления пружины со
стойкой смещена на угол у относительно вертикали, а
сама пружина выполняется без предварительного поджатия
витков. Жесткость пружины с, ее начальная длина d0,
угол у, расстояния ОЕ — а и ОВ = Ъ выбираются из
условия минимального значения неуравновешенного момента
319
[40] во всем диапазоне изменения угла а:
Мну — cab (1 — dQ/d) sin (у 4- а) — Pl sin а, •
где d — ЕВ = ]/а2 4- b2 — 2ab cos (у 4- а) — текущая длина пру-
жины.
Задача решается численными методами путем перебора
вариантов при условии минимума или максимума Мну или
п
суммы 5 = £ М ну,, где п — число точек разбиения интер-
вала изменения угла а.
Уравновешивание поступательно и вертикально перемещаю-
щегося звена постоянной массы. Для уравновешивания
поступательно и вертикально перемещающегося звена с
успехом могут применяться различные пружинные ме-
ханизмы.
Эффект постоянной силы, необходимой для рассматри-
ваемого объекта уравновешивания, может быть достигнут
за счет пружинного механизма с нулевой жесткостью,
состоящего из параллельно соединенных линейно-упругого
элемента и пружинного механизма с постоянной отрица-
тельной жесткостью (рис. 8.8, а, б).
Элементарные уравнения равновесия статики дают соотно-
шения между усилием Р и упругой силой пружины S:
для схемы а — Pi = 2SX ctg <р;
для схемы б — Р2 = S2 ctg <р.
При жесткости пружин с19 с2 и их деформации /sinср
(/ = АВ = AD — ВО = DO) выражения для Р принимают вид:
Pi — 2сilcos(р = 2с 10А; Р2 = c2lcos(p = с2ОА/2,
т. е. в обоих случаях усилие Р представляет собой ли-
Рмс. 8.8
320
нейную убывающую функцию расстояния ОА и может
трактоваться как усилие пружины с отрицательной
жесткостью с (для первого случая с — 2сдля второго
с ~ сг/^
Соединяя параллельно пружинный механизм с отрица-
тельной жесткостью и линейно-упругий элемент, получим
пружинный механизм нулевой жесткости, у которого сила
упругости постоянна и не зависит от положения уравно-
вешивающего звена. Это постоянное усилие определяется
начальным натяжением линейно-упругого элемента.
Другая группа пружинных механизмов, обеспечивающих
уравновешивание поступательно и вертикально перемещаю-
щихся звеньев, представляет собой пружинные устройства,
дополненные кулисным механизмом.
Вариант с подвижной кулисой А и пружиной сжатия
представлен на рис. 8.9.
Как и при уравновешивании кривошипа, необходимое
постоянное усилие уравновешивания может формироваться
с помощью кулачкового механизма, одна из возможных
схем которого показана на рис. 8.10. Здесь поступательно
движущееся звено 1 с помощью зубчатой рейки сцеплено
с шестерней 2, с которой жестко связан кулачок 3;
на кулачок навита гибкая нить 4, например трос или стальная
лента. Один конец нити прикреплен к кулачку, а другой —
соединен с пружиной 5 в точке А. Второй конец пружины
присоединен в точке В к неподвижному звену. Профиль
кулачка и основные параметры механизма определяются из
условия равенства моментов относительно оси О силы тяжести
поступательно движущегося звена 1 и упругой силы пру-
321
1
живы АВ. Для рассматриваемого случая угол ф опреде-
ляется по формуле
вшф = sin фо/ / 1 “
2 sin фо
PR
где фо — начальное значение угла ф; с — жесткость пру-
жины; L — ОВ; <р — угол поворота кулачка.
Рассмотренные пружинные механизмы обеспечивают пол-
• ное уравновешивание поступательно и вертикально пере-
мещающегося звена постоянной массы. Однако у всех
рассмотренных механизмов, обеспечивающих как полное,
так и неполное уравновешивание, имеется один существен-
ный недостаток: они могут применяться при сравнительно
небольших вертикальных перемещениях уравновешиваю-
щегося звена.
Для устранения этого недостатка можно использовать
различные передаточные механизмы, уменьшающие ход
пружины, но в такой же степени повышающие ее
усилие, т. е. жесткость. В качестве таких механизмов могут
быть использованы редукторы, полиспасты, дифференциаль-
ные блоки, пантографы и т. д. Возможные варианты
механизмов с неполным уравновешиванием (когда механизм
уравновешивания состоит из одной пружины, размещенной
в перемещающемся звене) изображены на рис. 8.11: а —
полиспаст с передаточным числом 1/2", где п — число
подвижных блоков; б — дифференциальная передача, состоя-
щая из приводной шестерни радиуса R и жестко свя-
занного с ней барабана радиуса г — передаточное число
механизма равно (R — r)/R; в — пантографный механизм
Рис. 8.11
322
с передаточным числом а/(а + /), где
I = CD = АЕ = ЕВ.
а = ОС = АС = DE;
Уравновеннвание манипуляторов с взаимно параллельны-
ми и горизонтальными осями шарниров. Рассмотрим шарнир-
ный манипулятор (рис. 8.12, а). Оси шарниров А, В, С гори-
зонтальны и параллельны друг другу, т. е. движения звеньев
манипулятора происходят в подвижной плоскости, прохо-
дящей через вертикальную ось 00 Р
Конструкции пружинных уравновешивающих механизмов
таких манипуляторов зависят от расположения упругих
элементов (они могут располагаться или на подвижных
звеньях манипулятора, или на его основании), а также от
того, что непосредственно «разгружается»: выходной вал
соответствующего привода или сама конструкция манипу-
лятора.
Начнем рассмотрение этих механизмов со случая, когда
упругие элементы установлены на подвижных звеньях
манипулятора и непосредственно не связаны с работой
приводных двигателей. Как было показано выше, для
полного уравновешивания кривошипа необходимо обеспечить
деформацию упругого элемента х ~ sin (а/2). Поэтому в рас-
сматриваемом случае для отсчета углов aj, a2, a3
необходимо создать базовую вертикаль для каждого из
шарниров Л, В, С (рис. 8.12, а). Это может быть выпол-
нено с помощью дополнительных механических передач,
например параллелограммного механизма (рис. 8.12,6) или
независимой системы передач с гибкими звеньями, блок 1
которой неподвижен (рис. 8.12, в). В последнем случае радиу-
сы блоков 1 и 2, 3 и 4 попарно равны, блоки 2, 3
представляют собой одно тело, свободно вращающееся на
1
оси В, а блок 4 свободно посажен на ось С, что при
неподвижном блоке 1 обеспечивает поступательное движение
блоков 2, 3, 4.
Обе схемы имеют как недостатки, так и достоинства.
В процессе эксплуатации параллелограммные механизмы не
должны «складываться», т. е. их внутренние углы всегда
должны быть больше, как минимум, 20°, поэтому у таких
механизмов небольшой диапазон изменения углов аь а2.
Система блоков теоретически допускает любую конфигура-
цию манипулятора, но в процессе эксплуатации гибкие
элементы передач (цепи, тросы, стальные ленты) вытяги-
ваются, вследствие чего необходима периодическая регули-
ровка механизма уравновешивания. Кроме того, возни-
кают технологические трудности при сборке и регулировке.
Полученные таким образом базовые вертикали исполь-
зуются для построения уравновешивающих механизмов,
например, как это показано на рис. 8.13. При этом
жесткости пружин и их установочные размеры (при идеаль-
ном уравновешивании) связаны с размерами и силами
тяжестей звеньев манипулятора следующими зависимостями:
Сз^з^з — Рз®3>
с2а2^2 ~~ ?3^2 + Р2^2 ’
= (Р2 + Рз) Ц + Р Ji>
где Ц = АВ; 1\ — АК; Hi — АН’
с2> сз —
жесткости пружин.
В случае расположения упругих элементов на основании
робота возникает обратная задача получения углов отно-
сительно неподвижной системы координат. Эта проблема
опять-таки решается с помощью системы параллелограмм-
ных механизмов или передач с гибкими звеньями. При*этом
каждое звено, кроме первого, имеет свой собственный
механизм (рис. 8.14,0,6). Поэтому в многозвенном мани-
пуляторе с целью упрощения передаточного механизма
Рис. 8.13
1
Рис. 8.14
предпочтительно упругие элементы располагать на подвиж-
ных звеньях (рис. 8.15).
К основанию 1 манипулятора с возможностью поворота
относительно оси О^О2 прикреплена подвижная опора 3,
к которой с возможностью поворота относительно оси
O3O4 прикреплено плечо 9, с которым в свою Очередь с
возможностью поворота вокруг оси О5О6 связано предплечье
8. Повороты подвижной опоры, плеча и предплечья
осуществляются приводами /6, 11, 10. Подвижная опора 3
Рис. 8.15
325
1
с помощью гибких элементов
13 и 5 связана с пружиной 15
уравновешивания плеча и пру-
жиной 2 уравновешивания пред-
плечья. Гибкий элемент 13 за-
креплен на кривошипе 12, жест-
ко связанном с плечом 9, а
гибкий элемент 5 — на криво-
шипе 6, жестко связанном с
шестерней 20, установленной на
подшипнике оси О3О4. Шестер-
ня 20 находится в зацеплении с шестерней 19, жестко свя-
занной с ведущим блоком 7, установленным на выходном
валу привода 10. Ведущий блок 7 с помощью перекрестной
гибкой передачи 18 связан с ведомым блоком 17, жестко
установленным на предплечье 8. При выполнении опреде-
ленных условий, накладываемых на жесткости пружин и
геометрию уравновешивающих механизмов, статические мо-
менты от сил тяжести плеча 9 и предплечья 8 всегда урав-
новешиваются моментами, вызываемыми силами упругих
деформаций пружин 2 и 15. Пружины воздействуют на под-
шипники 4, 14 горизонтальной оси качания.
В случае, когда исполнительные двигатели реализуют не
абсолютные а2, a2, a3, а относительные <pj, <р2, <рз
(рис. 8.16) углы наклона звеньев, метод построения системы
уравновешивания, расположенной на основании манипуля-
тора, основан на использовании выражения потенциальной
энергии [40].
Потенциальная энергия 17р звеньев для выбранной
системы обобщенных координат представляет собой сум-
му некоторых нелинейных функций, в частности гармони-
ческих от этих координат. Поэтому для построения
уравновешивающего механизма необходимо выбрать так
пружинные устройства, чтобы потенциальная энергия их опи-
сывалась нелинейными функциями обобщенных координат
того же вида.
Потенциальная энергия механизма (рис. 8.16)
Пр = P3Z'3 sin (ср2 + q>2 + Фз) + (P2I2 + ^,Wsm(<₽i + <р2) +
+ [ЛА + (P2+P3)/i]sin<p1.
Она представляет собой сумму трех гармонических
функций, аргументами которых являются линейные формы
обобщенных координат. Упрощенная кинематическая схема
манипулятора, положения звеньев которого относительно
стойки определяются углами <pt, <Pi 4- <р2, <Pi + <р2 + Фз,
326
1
t
16
Рис. 8.17
I
1
г
приведена на рис. 8.17. Оси шарниров, соединяющих
звенья 0 и 1, 1 и 2, 2 и 3, параллельны и сохранят
горизонтальное положение при любых конфигурациях мани-
пулятора. Дифференциалы 13 — 15 кинематической развязки
движений и индивидуальные приводы 10—12 посредством
тросовых передач 16—18 связаны со звеньями 1—3. Тро-
совые передачи пропущены через направляющие ролики и
укреплены на ведомых роликах, жестко связанных со
звеньями манипулятора. С валами приводов 10—12 связаны
дифференциалы 7—9 механизма уравновешивания. Вход
каждого из них связан с выходом предыдущего. Один
вход дифференциала 7 укреплен неподвижно. Выходы этих
дифференциалов кинематически связаны с кривошипами
синусных механизмов 4 — 6,
между ползунами и основанием, помещены пружины. В ре-
зультате кинематической связи между дифференциалами 7—9
углы поворота кривошипов синусных механизмов 4 — 6 равны
соответственно <рь <pt
механизмов возникают моменты, пропорциональные косину-
сам этих углов. За счет кинематической связи между
дифференциалами 7—9 обеспечивается такое суммирование
движений приводов 10—12, что в каждый момент времени
валы двигателей «чувствуют» разгружающие моменты от
на выходах которых, т. е.
4
f
ч
i
г
!
\
1
<р3. А на валах этих
Ф2, Ф1
1
Эти моменты в точности
синусных механизмов 4 — 6.
равны моментам от сил тяжести подвижных звеньев 1—3,
т. е. моменты от сил тяжести звеньев будут скомпенсиро-
ваны усилиями упругих элементов, а приводы будут
разгружены от статических моментов. Нельзя сказать, что
данный метод уравновешивания проще, чем ранее разобран-
ные. Скорее наоборот: наличие дополнительных дифферен-
циалов 7—9 значительно усложняет конструктивную схему,
однако при отсутствии «базовых вертикалей» данный способ
уравновешивания является единственно возможным.
Уравновешивание пантографных манипуляторов. Пан-
тограф представляет собой разновидность параллелограмм-
ного механизма. Размеры механизма (рис. 8.18) выбирают
таким образом, чтобы базовые точки А, К, Н лежали на
одной прямой при любой конфигурации манипулятора: чаще
всего встречается случай, когда АВ = В К = DE; BD = КЕ —
= ЕН. При этом условии вертикальное движение точки А
вызывает строго вертикальное движение схвата — точки Н,
а горизонтальное движение шарнира К — горизонтальное
движение точки Н. При этом вертикальное перемещение
точки Н в AD/AB раз больше, чем перемещение точки
А, а ее горизонтальное перемещение в BD/AB раз превышает
горизонтальное перемещение точки К. Для уравновеши-
вания механизма к нему надо приложить пару сил с
моментом М = Mosina и постоянную силу S:
Мо — Pi 'CiH + Р2' КС2 + Р3 • АС3 — Р
I
I
P4(l - ВС JAB}.
Поэтому комбинация одного из механизмов уравновеши-
вания кривошипа и одного из механизмов уравновешивания
поступательно и вертикально перемещающегося звена по-
стоянной массы полностью решает проблему уравновешива-
ния манипулятора, выполненного по схеме пантографа.
В качестве примера на рис. 8.19 приведена одна из воз-
можных схем уравновешивания. На этой схеме базовые
точки А, К, Н манипулятора лежат на одной прямой,
в этом случае сила тяжести груза не влияет на значе-
ние приведенной пары сил М — Мо sin а, подлежащей уравно-
вешиванию с помощью пружинного механизма.
Уравновешивание манипуляторов с непараллельными ося-
ми шарниров звеньев. Особенность манипуляторов такого
вида заключается в том, что звенья совершают про-
странственное движение. Манипулятор с непараллельными
осями шарниров звеньев изображен на рис. 8.20.
4
/
i
!
1
1
Рис. 8.18 Рис. 8.19
К основанию 1 посредством шарнира с горизонтальной
осью крепятся последовательно соединенные звенья 2, 3 и 4.
Оси шарниров, соединяющих звенья 2 и 3, 3 и 4, парал-
лельны между собой и перпендикулярны оси вращения
звена 2. Угол наклона этих осей к горизонту зависит
от конфигурации манипулятора.
Приводы 5, 7, 9 звеньев установлены на основании 1
и с помощью кинематических зубчатых и тросовых
передач через систему блоков связаны со звеньями 2, 39 4
соответственно. Эти же передачи образуют кинематические
цепи, связывающие подвижные звенья 2, 3, 4 с пружинными
уравновешивающими механизмами 6, 5, 10. Кроме того, на
основании 1 установлены пружинные уравновешивающие
Рис. 8.20
1
механизмы 13, 15 и два дифференциала, которые состоят из
звеньев 16, 17, 18 и 11, 12, 14 соответственно. Вход 17
первого дифференциала кинематически связан с уравнове-
шивающим механизмом 8, вход 14 второго дифферен-
циала — с уравновешивающим механизмом 10, вторые их
входы 11,18 — с уравновешивающим механизмом 6, выходы
12 и 16 дифференциалов связаны с уравновешивающими
механизмами 13 и 15 соответственно. Каждый из уравно-
вешивающих механизмов выполнен в виде синусного механиз-
ма с упругим звеном.
В конструкции уравновешиваются три звена 2, 3, 4.
Моменты, действующие в шарнирах между звеньями 1 и 2,
2 и 3, 3 и 4 от сил тяжести звеньев (Р2, Рз и Р4),
определяются выражениями:
= 0,25P4/4[sin(<pi + ф2 + Фз) + sin(<р2 + ф3 - <pt)];
М2.з = + (Р4 + 0,5Р3)0,5/3 [sin(ср! + ф2) + sin(<р2 - (pj];
Mi.2 = 0,25P4Z4 [sin (ср! + ф2 + ф3) - sin(ср2 + ф3 - Фх)]
+ (Р4 + 0,5Р3)0,5/3 [sin (<pj + <р2) - sin (<р2 - <pi)] +
0,5P2)(2smq>i,
где /2, /3, /4 — длины звеньев 2, 3 и 4 соответственно;
Фь Фг, Фз — углы поворота звеньев 2, 3, 4 относительно
основания 1, звена 2 и звена 3 соответственно.
На входах уравновешивающих механизмов 6, 8, 10, 13,
15 реализуются углы <р19 фх + <р2, Фх + ф2 + Фз, Ф2 — Фь
ф2 + фз — Фх соответственно. Усилия упругих элементов вы-
бираются в соответствии с выражениями:
Те — (Р< Рз
0,5P2)/2/Z;
Ло — Т13 — Р 4^4/(^0>
(Р4 + О,5Р3)/з/(20,
где I — длина кривошипа синусного механизма.
В этом случае при любых конфигурациях манипуля-
тора моменты от сил тяжести Р2, Р3, Р4 звеньев 2, 3, 4
скомпенсированы усилиями упругих элементов и приводные
двигатели разружены от статических моментов.
8.2. Статическое уравновешивание
манипуляторов путем распределения масс
Статическое уравновешивание сил тяжести звеньев и объекта
манипулирования может быть достигнуто с помощью при-
менения противовесов или рационального распределения
масс звеньев. Противовесы увеличивают массу системы
330
и ее инерционность, что не всегда допустимо. Рацио-
нальнее размещать массу звеньев, редукторов и двигателей
так, чтобы выполнялось условие статического уравнове-
шивания.
Для потенциальной системы обобщенные силы, соответ-
ствующие некоторым обобщенным координатам, находятся
по формуле
где П — потенциальная энергия системы; п — число степе-
ней свободы манипулятора. В положении статического
равновесия системы, как известно, обобщенные силы равны
нулю.
Если считать, что на звенья манипулятора действуют
только силы тяжести, то потенциальная энергия манипу-
лятора, как и обобщенные силы, в общем случае яв-
ляется функцией обобщенных координат.
Следовательно, чтобы во всех конфигурациях манипуля-
тора система была уравновешенной, потенциальная энергия
системы не должна зависеть от обобщенных координат,
а обобщенные силы во всех положениях должны быть
тождественно равны нулю [26].
Так как при учете лишь сил тяжести потенциальная
энергия системы зависит только от координат z, центров масс
звеньев и груза, то обобщенные силы находятся по
формулам
где Pt — вес звена; — ордината z центра масс звена;
пъ — масса звена; д — ускорение свободного падения.
В общем случае манипулятор будем называть стати-
чески уравновешенным, если его потенциальная энергия не
зависит от обобщенных координат или его конфигурации.
Для плоского и-звенного манипулятора с поступатель-
ными парами координаты центров масс звеньев могут
быть найдены по формулам:
Ук
qi) cos af + (a* + qk) cos aft -
bkcosaft;
qt) sin a,- + (ak + qk) sin a* + bk cos ak,
331
где oq = Y Уj> Уj *“ постоянный угол между осями j-го и
j=i
j — 1-го звеньев; ак> Ьк — координаты центра масс к-го
звена в системе координат, связанной со звеном; lt —
длина звена. Обобщенная сила, соответствующая силе тя-
жести звена т, имеет вид
п
— 9 Y тк S^n arn я const,
к — т
где п — число звеньев.
Последняя формула показывает, что силы тяжести звеньев
плоского манипулятора с поступательными парами в общем
случае не могут быть уравновешены путем введения
дополнительных масс.
Для плоских манипуляторов с вращательными парами
обобщенная сила, соответствующая силе тяжести звена т,
находится по формуле
где — ордината центра масс звена i.
Используя выражение для уь получим [26]:
к
где sk — sin £
i— 1
т, ]ск + тпапсп
9
mkbksk,
к
Ck COS 9i*
i = 1
Из последней формулы получаем условие статической
уравновешенности:
(Я \
lk Y mi ]lmk’
i—k+1 /
В этом случае Рт = 0 и силы тяжести не совершают
работы при движении манипулятора. Это возможно, если
каждое звено уравновешено относительно своей оси вращения.
Чтобы все звенья манипулятора были статически
уравновешены относительно своих осей вращения, достаточно
их массы распределить таким образом, чтобы центры
масс звеньев лежали на их осях Ь, = 0, а абсциссы
1
удовлетворяли условиям:
йл = b„ = 0; Ьк = 0; актк + 1кМк - 0,
п
где Мк— £
i — k+1
Наряду со статическим уравновешиванием для быстро-
действующих манипуляторов необходимо решать задачу
динамического уравновешивания системы.
8.3. Динамическая развязка движений
Точное решение задач динамического уравновешивания
манипуляторов сложно и не всегда выполнимо, поэтому
вначале рассмотрим частные случаи динамического уравно-
вешивания на примерах.
Динамическое взаимовлияние движений по степеням под-
видности затрудняет управление, построение аккумуляторов
энергии, снижает быстродействие системы при ограничен-
ных усилиях приводов. Поэтому желательно так распреде-
лить массы звеньев манипуляторов и приводов, чтобы это
взаимовлияние устранить или хотя бы уменьшить. Решение
этой задачи рассмотрено в работах [20, 21, 26, 41].
Для развязки движений необходимо, чтобы инерционные
коэффициенты в уравнениях движения манипулятора не
зависели от обобщенных координат, что эквивалентно
условию независимости от обобщенных координат коэф-
фициентов при квадратах и произведениях обобщенных
скоростей в выражении кинетической энергии. Обобщен-
ные координаты, от которых не зависит кинетическая
энергия системы, называются циклическими. Для реше-
ния задачи динамической развязки движений манипулятора
будем использовать выражение кинетической энергии.
Вначале рассмотрим двухзвенные манипуляторы [41].
Считаем, что системы статически уравновешены, т. е. их
потенциальная энергия тождественно равна нулю.
Плоский манипулятор с двумя вращательными парами,
оси которых параллельны (рис. 8.21, а). Его кинетическая
энергия выражается формулой
Т == —(mrf + Ji + ш2/1)<Ф1 + т2/1Г2Ф1 (Ф1 + Ф2)созф2 +
+ у(т2г2 + Л)(Ф1 + ф2)2,
где mi и тп2 — массы звеньев 1 и 0; Ji и J2 — моменты
333
1
a}
Рис. 8.21
центров масс; li9 12 —
расстояния от осей шарниров А и В
инерции звеньев относительно их
длины звеньев; rl9 г2
до центров масс звеньев и С2 соответственно.
Из выражения кинетической энергии следует, что обобщен-
ная координата <Pi является циклической, так как от нее
кинетическая энергия манипулятора не зависит. Для того
чтобы была циклической и координата <р2, необходимо ра-
венство нулю коэффициента при cos<p2 в выражении кине-
тической энергии, т. е. r2lY — 0, что возможно при г2 = О
или = 0.
При /j = 0 система вырождается, а условие г2 = 0
означает условие совпадения центра масс звена 2 с осью
кинематической пары В. Это условие технически выполнимо
и может быть выполнено, например, установкой дополни-
тельной массы на звене 2 из условия
m2r2 = тпг 2и,
где тп — масса противовеса; г2п — расстояние от оси пары В
до центра тяжести противовеса. При этом увеличивается
масса системы, что не всегда приемлемо, поэтому можно
попытаться перераспределить массы звена 2, выполнив
условие г2 = 0.
При г2 = 0 выражение кинетической энергии манипуля-
тора принимает вид
Т = + J1 + т2/1)2ф? + 4-/2(Ф1 + ф2)2.
4W 4Ш
Запишем уравнения
механизма,
используя
метод Лагранжа:
^-= ("itr2 + J1 + ш2/2)Ф1 + -ЫФ1 + Фг);
+ J2
+ m^i + m2/i) Ф1
/2ф2 ® Af i;
334
dt
J2(^l
Ф2) — 0»
где Mi (i — 1, 2) — моменты приводов.
Уравнения движения механизма являются линейными с
постоянными коэффициентами. Эти линейные уравнения
можно разделить относительно фх и <р2 и получить два
независимых линейных дифференциальных уравнения. Поло-
жив ф! = И Ф1 + Ф2 == Фг, получим
где ап = 4- + m2ll', а12 — «/г-
Тогда уравнения движения получают вид
Яцф1=ЛЛ; ai2^f = M2.
Последние уравнения показывают, что движения по
обобщенным координатам манипулятора при условии г2 = 0
не зависят друг от друга.
Плоский манипулятор с двумя вращательными парами.
оси которых перпендикулярны (рис. 8.21,6). Считаем, что
оси Xi и Zi — главные центральные оси звеньев i (i — 1, 2).
Тогда тензор инерции звеньев будет иметь вид
Кинетическую энергию этого манипулятора получим по
формуле
где
2
7П1Г1Ф1
— кинетическая энергия звена 1, совершающего вращатель-
ное движение относительно оси z;
Т2 = 4- v?2 + 4- (Jx2e>i2 + Jy2tay2 +
335
1
— кинетическая энергия звена 2, совершающего пространст-
венное движение.
Здесь vc2 = vB 4- f2 х g>2 — скорость центра масс звена 2
(vB — скорость точки В; &2 — абсолютная угловая скорость
звена 2); сох2, °>у2, <oZ2 — соответственно проекции угловой
скорости звена 2 на оси х2, y2t z2.
Имеем
<ох2 — Ф1 sincp2;
С0у2 — Ф1 cos <р2.
Следовательно, чтобы кинетическая энергия манипулято-
ра не зависела от обобщенных координат <pj и <р2, необ-
ходимо выполнение условий г2 = 0; Jx2 = Jy2 = 0. При этих
условиях движения манипулятора по обобщенным коорди-
натам <Pi и <р2 динамически будут развязаны.
Четырехзвенныи манипулятор (рис. 8.22, в). Ось вращатель-
ной пары А вертикальна, оси вращательных пар В, С и D
горизонтальны и параллельны между собой. Считаем, что
координаты центров масс звеньев заданы в подвижных
системах координат, связанных со звеньями, тогда абсо-
лютные координаты центров масс звеньев равны:
Xi 4-biCi;
yi =
х2 = (a2s2 4- 62с2)з! 4- d2Ci;
у2= - (a2s2 + b2c2) Ci 4- d2Si;
x3 = (Л3$2 4- B3c2) si
d3ci;
Уз — (”“-^3s2 -®3C2)C1
d3Si'9
A3c2 — B3s2 4- /j,
где A3 = a3c3 — b3s3 4- l2; B3 — a3s3 4- b3c3; ah bh di — коор-
динаты центра масс i-ro звена в связанной со звеном
системе координат; sf = sing,; = cos#/ (i = 1, 2, 3).
Найдем обобщенную силу Р3, соответствующую силе
тяжести звена 3:
-qm3
= qm3(a3s3 4- b3c3) 4- qm3(a3c3 -b3s3)s2,
или
qa3m3 sin (q2 + q3) + b3m3 cos (q2 + q3).
Если b3 — 0, a3m3 = 0, to P3 =
находится по формулам:
0, а центр масс звена 3
x3 = d3ci + [(a3c3 + l2)s2 + аз^зСг]^;
y3 = d3si - [(a3c3 4- l2)s2 4-
336
z3 = (азсз + h)c2 ~ a3s2s3 + G-
Обобщенную силу Р2 находим по формуле
= q(m2a2+m3l3c3s2) +
qm3a3c3s2 + q(m3a3s3c2 + m2b2c2).
Если положить Р2 = 0, b2 — 0, т2а2 + 1гтз — 0, то центр
масс звена 2 в этом случае находится по формуле
х2 = a2s2Si + d2Ci; у2 = -n252^i + z2 = а2с2 +
Обобщенная сила Рг равна нулю, так как 5zi/5^1=0.
Найдем проекции абсолютных угловых скоростей звеньев
на связанные с ними оси координат, получим:
0)1
фзт(р2
Ф1 COS(p2
I Ф2 + Фз
о>з = I Ф1 sin (фг + Фз)
Ьф1СО8(ф2 + фз)-
Считаем, что оси систем координат, связанных со
звеньями, совпадают с главными осями инерции звеньев,
тогда кинетическая энергия системы может быть найдена по
формуле
Квадраты скоростей центров масс равны:
= ql (ql + ^i); = d (ql sin2 q2 + 41);
vl = [n3 sin(g2 + <?з) +12 sin<j2]24i + ql (4г + 4з)2
+ ^141 2/г4г(42 + 4з)«
Тогда выражение кинетической энергии манипулятора полу-
чает вид
Т = 1IX (al + Ы) + + J<2> + Л3»] 91
(42> + л2’ - л2>) «2
+ (Л” + Л3) - Л3’) («2 + 9з)2,
где л2) = л2’ + т2а2 + тз12> Л3) = л3> + тзЯ2; тз^з = °-
12 Механика промышл. роботов, кн. 2
337
Условия, при которых манипулятор становится динами*
чески уравновешенным, выглядят тай:
#2^3 = ‘j
W3«2 4“ ^3 2 — Oj J^xy — J^yz ~~ *^ху ~~ dyz — Oj
Л3) = J™ + m3o3; Д2) = J(y2) 4- m2a2 + w3Z2;
- Л? = m3a3d3; J(x2) = m2a2d2 4- m3d3l2.
Уравнения динамики такого манипулятора получают вид:
31 = «iW; ЛЗг + /зЗз = «2(0; ЛЗз + J3q3 = W3(O,
где, Ji = mi (al + bl) 4- m2d2 - m3df 4- J{z1} 4- J£2) 4-
J2 - m2a2 4- m3 (ll 4- aj) 4- Д2) + J<3); J3 = m3aj 4- J<3).
В некоторых случаях удается осуществить независимость
кинетической энергии системы лишь от одной или несколь-
ких обобщенных координат, т. е. получить неполное динами-
ческое уравновешивание манипулятора.
8.4. Аккумуляция энергии
Характерная особенность динамики промышленных робо-
тов — малая доля движений с постоянной скоростью. В об-
щем цикле преобладают режимы разгона и торможения.
В роботах с преобладанием инерционной нагрузки основ-
ная энергия двигателя расходуется на разгон системы и
затем поглощается демпферами. С увеличением быстро-
действия требования к прочностным и энергопоглощаю-
щим характеристикам демпферов ужесточаются.
Свойства и предельные возможности приводов, построенных
традиционно и с аккумулятором энергии. Проанализируем
приводные системы традиционного типа и с аккумулятором
энергии на примере систем с одной степенью подвиж-
нести (рис. 8.22) [21, 22].
При традиционном построении привода (рис. 8.22, а)
мощность двигателя 2 определяют исходя из инерционной
характеристики т подвижных масс 1 и из требуемого
быстродействия. При этом в конечных положениях (позициях)
звена всегда устанавливают регулируемые упоры 2, осна-
щенные демпфирующими устройствами 3. Энергия, которую
получила система от двигателя 2, рассеивается демпфи-
рующими устройствами на малом перемещении. Чем
больше эта энергия (выше быстродействие), тем мощнее
должны быть демпферы и больше усилия торможения.
Движение такой системы с учетом трения описывается
338
Рис. 8.22
уравнением
mR2<? = Мдв — Мд (<р, ф) — Мт,
(8.1)
где R — радиус инерции манипулятора; ф — обобщенная
координата; Мдв, Мд, Мг — соответственно моменты двига-
теля, демпфера и трения в передачах и опорах.
Циклограмма работы системы и ориентировочный гра-
фик изменения моментов Мда, Мд, Мт приведены на
рис. 8.22, в.
Анализ движений системы показывает, что работа двига-
теля (площадь St) равна сумме работ моментов демпфера и
трения (площади S2 и S3 соответственно) в течение полного
цикла движения (от угла — ф1 до угла ф2), т. е.
Si = S2 + S3. Следовательно, при увеличении быстродейст-
12*
339
вия путем повышения Мдв требуемый Мд возрастает
значительно быстрее из-за того, что он действует на
существенно меньшем участке перемещения.
При этом в соответствии с уравнением (8.1) и
рис. 8.22 значительно возрастают ускорения, а следова-
тельно, и нагрузки на участке торможения. Но главное
состоит в том, что повышать быстродействие системы
путем увеличения мощности приводного двигателя принци-
пиально можно лишь до определенного, довольно низкого
предела. Существование предела обусловлено тем, что в каче-
стве ограничений при выборе привода выступают его массо-
габаритные показатели и установленная или потребляемая
мощность. Выбор двигателя по критерию максимума
быстродействия без дополнительных ограничений приводит
к необходимости иметь двигатель с бесконечно большой
мощностью и редуктор с бесконечно большим повы-
шающим передаточным отношением.
Структура привода с аккумулятором энергии (рис. 8.22,6)
включает аккумулятор механической (потенциальной) энер-
гии в виде упругого элемента 5 с жесткостью с; вместо
демпферов-упоров установлены управляемые упоры-фиксато-
ры 6. В положении подвижной массы 1 между упорами-
фиксаторами пружина 5 находится в свободном состоянии
и ее усилие сф = 0. В начальном положении система
поджимается к упору-фиксатору усилием сфй, где фй —
амплитуда перемещения массы 1.
По команде на выполнение движения магнит фикса-
тора убирает упор, и масса 2 под действием усилия сфй
начинает разгоняться, переводя потенциальную энергию упру-
гого элемента в кинетическую. После прохождения сред-
него положения (ф = 0) масса 1 начинает тормозиться в
результате обратного перехода ее кинетической энергии в по-
тенциальную энергию пружины.
Если бы не было трения, то масса 2 обязательно
достигла бы симметрично установленного второго фиксатора
и ее скорость в этом положении была бы равна нулю;
наличие же трения в системе обусловливает необходимость
установки привода 4. Таким образом, в предлагаемой
системе привод используется не для разгона инерционных
масс, на что в традиционных системах затрачивается
основная мощность, а только для компенсации потерь
на трение. Поэтому структуры, построенные по схеме на
рис. 8.22,6, отличаются существенно меньшей мощностью
привода, причем быстродействие от мощности не зави-
сит.
340
При подобном построении системы автоматически
обеспечиваются такие важные выходные характеристики, как
плавность разгона и торможения, а также симметрия
законов разгона и торможения относительно среднего
положения (уменьшаются нагрузки в системе) и выход на
упоры практически с нулевой скоростью (нет необходимости
в демпферах). Эти характеристики иллюстрируются законом
движения массы 1 (рис. 8.22,3). Благодаря согласованию
направлений момента двигателя и скорости движения
звена (т. е. организации автоколебательной системы) работа
двигателя всегда равна работе сил трения (рис. 8.22,г):
Si = S3.
Из уравнения движения системы
(8.2)
следует, что ее быстродействие (время Т выполнения
движения, или полупериод колебаний) при Мдв = Мт опре-
деляется простым соотношением
Т = n]/mR2/c.
(8.3)
Из общих свойств автоколебательных систем следует, что
если условие Мдв = Мт не выполняется, а справедливо лишь
условие Sj = S3, то соотношение (8.3) существенно не
изменяется.
Таким образом, быстродействие системы определяется
собственными динамическими свойствами механического
колебательного контура. Теоретически при известной инер-
ционности mR2 системы всегда можно подобрать жесткость
с так, чтобы обеспечить требуемое быстродействие.
В рамках принятой линейной модели [см. уравнение
(8.2)] предел увеличения быстродействия для таких систем
не существует. На практике же чрезвычайно важно
согласовать характеристики механической колебательной
системы со свойствами привода, т. е. с параметрами
динамической характеристики двигателя и передаточным
отношением редуктора.
Методика выбора параметров привода. Методика расчета
предполагает разделение общего уравнения движения на
два: первое описывает консервативную колебательную
систему без учета потерь энергии и их восполнения и
определяет желаемое движение механической системы, а
второе — процессы, связанные с потерями энергии и ее
восполнением. При этом желаемый закон движения под-
ставляют во второе уравнение и из него определяют
параметры двигателя и передаточное число i редуктора.
341
1
Затем по полученным значениям параметров двигателя
и редуктора выбирают характеристику упругого элемента,
обеспечивающую желаемый закон движения консервативной
системы.
Полное уравнение движения системы (в случае использо-
вания электродвигателя постоянного тока и редуктора)
после приведения всех инерционных составляющих к оси
поворота ведомого звена имеет вид
(mR2 + /да!2) ф + Мт sign ф + сф = Мда/, (8.4)
где
Мдв = Мп sign ф — kityi — Мх sign ф;
/дв — момент инерции ротора двигателя; М„ = Фкмия/Кя —
пусковой момент двигателя; кл = к^Ф2/^ — коэффициент,
определяющий потери в двигателе в зависимости от его
скорости; Мх — момент холостого хода двигателя; Ф —
поток возбуждения; ыя, Кя — напряжение и сопротивление
цепи якоря; kh км — электромагнитная и механическая
постоянные двигателя.
Так как момент сопротивления MTsign(p равен моменту
Мдвь развиваемому двигателем, то
Мт sign ф — iMn sign ф + /с1ф/2 4- iMx sign ф = 0. (8.5)
Учитывая, что количество энергии, поступающей в
систему от двигателя, значительно меньше, чем количество
энергии, циркулирующей в системе с аккумулятором,
для нахождения искомых параметров Мп, кг и i можно
с достаточной степенью точности вместо условия (8.5) исполь-
зовать условие равенства работ в течение заданного времени
движения с амплитудой фв. При этом закон движения
исходной консервативной системы практически не нару-
шается. Принимая этот закон, например, гармоническим
(ф — cos cot); 0 < t < Г, где со — круговая частота; t — теку-
щее время), получим из уравнения (8.4) условие равенства
работ А в виде
О,25/с1фвпо)12
(8.6)
Условие (8.6) графически представлено на рис. 8.23.
Кривая потерь в системе [левая часть уравнения (8.6)]
представляет собой параболу 1, отсекающую на оси ординат
отрезок, равный Мт. Правая часть уравнения (8.6), характе-
ризующая полезную работу двигателя, представлена пря-
мой 2. Если прямая 2 не пересекает параболу 1 [решения
уравнения (8.6) не существует], то потери в системе на
342
1
заданном перемещении при лю-
бом i превышают поступление
энергии и работоспособность
системы обеспечить невозмож-
но.
При пересечении параболы
и прямой вся область значений
i разбивается на три зоны. При
i > Wx (зона /) и i < imin (зона
III) система неработоспособна;
только при imin < i < (зона
II)
поступление энергии превы-
шает потери, и система работо-
способна. При этом целесооб-
разно выбирать значение i,
близкое к imin, что позволяет
Рис. 8.23
получить следующие преиму-
щества:
при меньших значениях i поступление и потери
энергии меньше, чем при i, близком к imax, т. е. к. п. д.
системы возрастает;
так как точка, соответствующая imax, ближе к вершине
параболы, то чувствительность системы к изменению
параметров фЛ и Т при этом меньше, чем при imax;
отсюда следует, что при настройке системы на различ-
ные амплитуды фв при работе с различными грузами,
масса которых влияет на быстродействие Г, избыточное
поступление энергии в систему незначительно; это же
справедливо для параметров двигателя кг, М* и Мп; их
колебания не нарушают работоспособность системы.
При увеличении коэффициентов в уравнении (8.6) парабо-
ла I приближается к оси ординат, а при уменьшении —
к прямой 3 (касательной к параболе в точке с коорди-
натами i — 0; А/фя = AfTp). Условие пересечения прямой 2
и параболы 1 требует, чтобы параметры определялись
для случая, когда парабола предельно сжата, т. е. значение
i следует выбирать при максимальных со и фй; максимум
о соответствует холостому ходу системы (без груза). Эти
соображения определяют следующий порядок выбора дви-
гателя и редуктора:
оценив момент трения в системе и зная минимальное
значение Т и максимальное фв, рассчитываем необходимую
мощность двигателя
343
по каталожным данным выбираем двигатели различных
серий соответствующей мощности;
для каждого двигателя при указанных значениях <рЛ
и Т по уравнению (8.6) или по графику (рис. 8.23)
находим минимальное значение i; если решение отсутствует,
то проверяем двигатель большей мощности;
из всех полученных решений выбираем тот двигатель,
который доставляет в систему минимальное количество
энергии;
при выбранных двигателе и редукторе, зная их пара-
метры Удв и i, необходимые для обеспечения заданного Т,
определяем жесткость с упругого элемента, используя
решение уравнения движения консервативной системы; в рас-
сматриваемом случае это уравнение линейное:
(mR2 4- Удв12)ф 4- с(р — 0 и, следовательно, c = n2(mR2
Отметим, что выбор двигателя осуществлен для макси-
мального значения (ра. При уменьшении фа поступление
энергии в систему превышает потери, что приводит к
«перерегулированию» и ударам об упоры. Поэтому в
системе целесообразно предусмотреть регулирование, с тем
чтобы пусковой момент двигателя можно было изменять
в функции настраиваемого перемещения. В качестве регули-
руемого параметра пускового момента целесообразно
использовать wH, уменьшение которого смещает точку пере-
сечения параболы I (рис. 8.23) и прямой 2 вдоль
вертикальной прямой, соответствующей выбранному значе-
нию i.
Аналитическое выражение зависимости ия = ия (<р) для
рассматриваемого случая легко получить, решив дифферен-
циальное уравнение (8.4) при начальных условиях ср (0) = — фя.
Рассогласование 5 между значениями ФтаХ (максимально
достижимым) и фя описывается выражением
8 = (Е — 1) фа 4-(Е 4- 1) А/со2,
где Е = ехр (—ли/]/со2 — и2); п — kii2/[2 (mR2 4- ^двг2)]» А =
= [i(Mn - Мх) - Мт]/[тК2 4- 7двг2].
При 8 = 0 получаем отсюда искомое уравнение
Пя ^я(^2фо “Ь Мт 4” ?Л/х)/(Ф/см/),
где к2 = со2 (1 - Е) (mR2 4- «Лдв12)/(1 4- Е).
Приведенные закономерности являются основными для
построения привода одной степени подвижности с двумя
1
Рис. 8.24
позициями. Конструктивная схема аккумулятора (см.
рис. 8.22,6) при этом достаточна проста. В случае несколь-
ких позиций по одной степени подвижности аккумулятор
должен обеспечивать выдачу запасенной энергии в произ-
вольном направлении, определяемом программой движения,
только тогда можно по программе изменять направление
движения звена робота, находящегося в любой заранее
настроенной позиции.
Анализ выражений кинетической энергии для различных
структур манипуляторов с двумя степенями подвижности
позволил установить условия динамической развязки, а
также найти конструктивные решения, обеспечивающие вы-
полнение этих условий. Схемы динамически развязанных
исполнительных устройств роботов приведены на рис. 8.24, а, б,
на котором т19 т2 — массы звеньев; т3, т4 — уравновеши-
вающие массы; <pt, <р2 — углы поворота звеньев; фь ф2 —
нормальные координаты [21].
345
1
Г лава 9
Точность механизмов роботов
Точность промышленных роботов характеризуется погреш-
ностью позиционирования и является одной из основных
характеристик промышленного робота. Точность позициони-
рования робота зависит от большого числа факторов, из
которых основными являются: ошибки приводов при отра-
ботке заданных значений обобщенных координат, ошибки
изготовления деталей механизма, ошибки, обусловленные
податливостью звеньев манипулятора. Возможности совре-
менных приводов по отработке заданной программы до-
вольно высоки. Каждая из этих видов погрешностей может
играть основную роль в зависимости от типа робота, его
грузоподъемности, условий функционирования. Поэтому
рассмотрим эти виды погрешностей каждую в отдельности.
9.1. Кинематическая погрешность
манипулятора
Под кинематической погрешностью манипулятора будем
понимать точность, обусловленную ошибками отработки
приводами программных значений обобщенных коорди-
нат.
Под программными значениями координат будем пони-
мать значения обобщенных координат, полученные в ре-
зультате решения обратных задач о положениях манипуля-
тора или измеренные датчиками в процессе обучения ро-
бота и переданные в систему управления. Очевидно, что
в первом случае имеют место ошибки вычисления, а во
втором — ошибки измерений и ошибки, вносимые при пере-
даче значений в память робота. Последний вид ошибок
здесь не рассматриваем. Поэтому считаем, что программные
значения координат обеспечивают теоретически вывод схва-
та робота в заданное положение.
При выполнении технологического процесса схват про-
мышленного робота в каждый момент времени должен
занимать вполне определенное положение в пространстве,
задаваемое программными значениями обобщенных коорди-
нат.
Однако практически программные значения обобщенных
координат воспроизводятся с некоторыми ошибками Дф
(i = 1, ..., и) и поэтому действительное положение схвата
будет отличаться от программного.
1
Под кинематической
погрешностью промыш-
ленного робота будем пони-
мать линейную и угловую
ошибки действительного поло-
жения схвата по отношению
к его программному положе-
нию.
Линейная кинематиче-
ская ошибка манипулятора мо-
жет быть определена следую-
щим образом. Пусть програм-
мное положение схвата в про-
странстве определяется положе-
Рис. 9.1
нием связанной с ним системы координат O„x„ynzn
(рис. 9.1). Действительное положение схвата определяется
положением системы О„х'„Упг'„. Тогда вектор Дг = ОпО„
определяет линейную ошибку манипулятора. Считаем линей-
ную ошибку положения манипулятора малой величиной,
тогда ее можно найти по формуле дифференциала функции
нескольких переменных.
Так как г = г (q^ есть функция обобщенных координат
Qi, то
где Д^ — ошибка обобщенной координаты
В матричной форме координаты точки О„ можно за-
писать так:
[хй] = М1М2М3...МИ_1 (9-2)
где [x„-i] — столбец координат точки Оп в системе
O^iXn-ryn-iZn-i, связанной со звеном и — 1 манипулятора;
[хп] — столбец координат точки Оп в неподвижной системе
Ox0y0zQ; — матрица 4-го порядка перехода от системы
OiX^Zi к системе Oi-1xi_1yi-iZi^1 (i — 1, ...» и).
Взяв дифференциал от (9.2), получим выражение линей-
ной кинематической ошибки в матричной форме
Дхл = ДМ,
П М, [х,_,] + ДМ2 "ff
i = 2 i = 3
Mt [x„_ 1]
+ MtM2 ДЛ/з"п М([х„_1] + ...М1М2М3...ДМ1, "п [%„-!].
i=4 i==s+l
(9-3)
Модуль линейной ошибки
Аг„ = |/(Ах„)2 + (Ауй)2 + (Az„)2, (9.4)
где Дх„, Ауп, Az„ — ошибки позиционирования по осям х,
у, z неподвижной системы координат, зависящие от ошибок
обобщенных координат.
Таким образом, ошибка позиционирования является
функцией декартовых координат точки позиционирования.
Под среднеинтегральной ошибкой робота по некоторому
рабочему объему будем понимать величину
Аг„ = f f f Аг„ (х, у, z) dx dy dz/V. (9.5)
X у z
В том случае, когда интересуются лишь средней ошиб-
кой в конечном числе точек, можно пользоваться средне-
арифметической ошибкой позиционирования
FI я
Arcp = £ (Art/n) = £ (|/(Ах,)2 + (Ay,)2 + (Az,)2/n). (9.6)
I ~ 1 I= 1
Теперь определим угловую кинематическую ошибку
манипулятора. На основании известной теоремы Даламбера—
Эйлера твердое тело, имеющее неподвижную точку, можно
перевести из одного положения в другое одним поворотом
вокруг некоторой оси конечного поворота.
За угловую ошибку манипулятора примем угол, на ко-
торый нужно повернуть схват, чтобы оси системы О^ХпУ^
стали параллельны осям системы O„x„ynzn. Угловую ошиб-
ку манипулятора будем так же, как и линейную, считать
векторной величиной, равной
Аф = Афр, (9.7)
где р — орт оси угловой ошибки схвата.
Если считать угловую ошибку малой величиной, то будет
иметь место следующее векторное равенство:
Аф = £ A^ef, (9.8)
i— 1
*
где ё — орты вращательных пар манипулятора.
Из формулы (9.8) следует матричное равенство
[Дф] = £ М, (9.9)
где [Аф] — столбец координат угловой ошибки в системе
348
1
Рис. 9.2
O0x0y0zo; LOl — матрица 3-го
порядка перехода от системы
О/хда, к системе О0х0уо2о> оп-
ределяемая по формуле
LOi = LiL2L3...Li-iLi; (9.10)
Ц — матрица 3-го порядка пе-
рехода от системы OiX^Zi
к системе
[ej — столбец координат векто-
ра et в системе О^у^.
Элементы матрицы представляют собой соответствую-
щие элементы первых трех строк и столбцов матрицы М£.
Пример расчета кинематической точности манипулятора.
Определим кинематическую линейную и угловую ошибки
манипулятора (рис. 9.2) с тремя вращательными и двумя
поступательными кинематическими парами.
Со схватом 5 свяжем систему координат Exsysz5, напра-
вив ось х5 по оси схвата, а ось z5 по оси вращательной
пары Е. Координаты точки Е в системе Axoyozo равны
хЕ — s3 cos ср!; уЕ = $з sin ; zE = s2,
где s3 = CE; s2 = AC.
По формуле (9.1) находим:
Ах£ = As3 cos (pi
- A(piS3 sinqh;
Ay£ = As3 sin (pi 4- A<PiS3 cos (pt;
Az£ = As2j_____________________________________________________
Ar£ = ]/(Ax£)2 + (Ay£)2 4- (Az£)2 = j/(As2)2 4- (As3)2 4- (A<Pi)2 4-
Угловая ошибка Аф определится формулой
Дф = Аф! 4- Афд 4- Аф5-
(9.П)
Представим выражение (9.11) в матричной форме
[Аф] =
COS ф1
sin ф1
О
— sin фх О
cos ф1 О
О 1
°
О I Аф1
_oj
sin ф1
О
COS фг
О
cos ф1 — sm ф!
Аф4
349
Дф5
COS ф!
siiKpt
0
- Sin (pi
COS (pl
0
0 0 II 0
COS ф4 — sin ф4 | I 0
sin ф4 COS ф4 -I L1—
После преобразований получим формулу для расчета
угловой ошибки манипулятора, изображенного на рис. 9.2:
[Дф4 cos ф1 + Дф5 sin Ф1 sin ф4 |
Дф4 sin ф! — Дф5 cos ф1 sin ф4 I. (9.12)
Дф5 cos ф4 4- Дф1 J
9.2. Кинематическая погрешность
передаточных механизмов
Кинематическая погрешность зубчатой передачи. Из-за нали-
чия погрешностей изготовления и сборки передачи угол
поворота ф2 ведомого звена реальных зубчатых передач
всегда отличается от угла поворота ведомого звена идеаль-
ного механизма (рис. 9.3, а) при одном и том же значении
обобщенной координаты фх:
Фг — Ф1/21 — &Р2 — ФРг! ~
8ф
где бф2 — погрешность положения ведомого звена; 8ф —
погрешность изготовления и сборки передачи.
Алгебраическая разность между погрешностями положе-
ния ведомого звена называется кинематической погреш-
ностью передачи (рис. 9.3, б)
8фх = 6ф2
По методу максимума-минимума минимальное и макси-
мальное значения кинематической погрешности (мкм) пере-
350
дачи определяются по формулам
8ф^„ = Aks (Fi, + F'a);
8<р£„ = к №)2 + (£zi)2 + ]/(Г:-2)2 + (Ezz)2],
где для цилиндрической зубчатой и реечной передач 7-й
и 8-й степеней точности А = 0,71, для остальных степеней
точности А = 0,62, для конической зубчатой передачи 7-й
и 8-й степеней точности А = 0,72, для остальных степеней
точности А — 0,67; F'n и Fj2 — допуск на кинематическую
погрешность первого и второго колеса передачи соответ-
ственно; ks и к — коэффициенты фазовой компенсации, при-
нимаемые в зависимости от передаточного числа и = z2/zt.
и
к
ks
и
к
ks
и
к
ks
1,0... 1,5
0,98
0,30
3,0... 3,5
0,97
0,75
5,0...5,5
0,98
0,85
1,5... 2,0
0,85
0,76
3,5...4,0
0,96
0,80
5,5... 6,0
0,96
0,88
2,0... 2,5
0,83
0,75
4,0... 4,5
0,96
0,90
6,0... 6,5
0,97
0,94
2,5... 3,0
0,93
0,74
4,5...5,0
0,96
0,87
6,5 '
0,98
0,99
— суммарная приведенная погрешность монтажа,
£z = ]/(er tg a/cos 0)2 + (e„ tg p)2,
где a — угол исходного профиля колеса; Р — делительный
угол наклона линии зуба, для конических зубчатых колес —
к образующей начального конуса; ег — монтажное радиаль-
ное биение зубчатого колеса,
е
0,85
et — допуски на погрешности, создающие первичные ради-
альные биения колеса; еа — монтажное осевое биение зуб-
чатого колеса,
ej — допуски на погрешности, создающие первичные осевые
биения колеса.
По вероятностному методу расчета максимальное зна-
чение кинематической погрешности передачи (мкм) [9]
^Фтах
= (5Фтах А) &р,
351
где кр — коэффициент фазовой компенсации, принимаемый
в зависимости от передаточного числа и — z2/Zi и риска р,
его находят по табл. 9.1.
Мертвый ход в зубчатой передаче. В реверсивных меха-
низмах различают прямой и обратный ходы. Вследствие
наличия упругих деформаций звеньев, зазоров в зацеплении
и вращательных парах передачи положения ведомого звена
для одного и того же положения ведущего звена при пря-
мом и обратном ходах всегда различны.
Разность положения ведомого звена для одинаковых
положений ведущего звена при прямом и обратном ходах
передачи называют мертвым ходом. Мертвый ход
проявляет себя в том, что при изменении направления
вращения ведущего колеса ведомое некоторое время оста-
ется неподвижным.
Алгебраическая разность между погрешностями положе-
ний ведомого звена при обратном и прямом ходах назы-
вают погрешностью мертвого хода передачи
SCj; — бфобр бфПр.
По методу максимума-минимума максимальное значение
мертвого хода по дуге делительной окружности ведомого
колеса (мкм)
8С”ах = 0,7 (Еш1 + E„s2) + 1/0,5 (Т2Н1 + Т2н2) + У2 + G2rl + G2r2,
где EHS1 и Eus2 — наименьшее смещение исходного контура
первого и второго колес; THi и Тн2 — допуск на смещение
исходного контура первого и второго колес; +fa — предель-
ное отклонение межосевого расстояния («4-» —верхнее;
«—» — нижнее); Grl и Gr2 — радиальный зазор (люфт) в опоре
вращения первого и второго колес.
По вероятностному методу максимальное значение
мертвого хода (мкм)
В
max
5С
м
max*
Пересчет значений 6фтах и $Gnax, выраженных в мкм, в ми-
нуты получим из пропорции
Зфтах /(1000лd2) = 5фтах/(360 • 60),
откуда
бфтах ~ 6,886фтах/^2>
Аналогично
max
где d2 — диаметр делительной окружности ведомого зуб-
чатого колеса, мм.
Кинематическая погрешность многоступенчатых зубчатых
механизмов. По методу максимума-минимума суммарная
кинематическая погрешность многоступенчатого зубчатого
механизма (рис. 9.4)
Л
max j?
где 5фтах j — кинематическая погрешность j-й передачи;
Ej = ij — передаточный коэффициент погрешности передачи
(ij — передаточное отношение между (/ + 1)-й и последней
ступенями передачи).
По вероятностному методу
где
Дго ~ У ~ У Е^Фшах j 6фт{пу]/2)
1 J=1
Рис. 9.4
353
— координата середины пОля допуска кинематической по-
грешности, мкм (coj = 5фтах j — 8<pmin j — поле рассеяния вели-
чины 6(pj в /-й передаче); — коэффициент, выбираемый
в зависимости от процента риска Р.
10 4,5 1,0 0,27 0,1
0,26 0,35 0,48 0,57 0,61
0,21 0,28 0,39 0,46 0,5
Мертвый ход многоступенчатых зубчатых механизмов.
Найдем зависимость мертвого хода выходного звена много-
ступенчатого зубчатого механизма от мертвого хода ведо-
мого колеса каждой передачи (рис. 9.4).
Рассмотрим соотношение углов поворота одного из
колес передачи при неподвижном другом (рис. 9.5). Мертвый
ход второго колеса при неподвижном первом
5С2 — w2 J п max COS 0tw/^w2*
Мертвый ход первого колеса при неподвижном втором
6С*1 — Ali/rwi «Липах
cos aw/rwl.
Так как начальные окружности перекатываются без
скольжения, то A/t = Д/2 = Тогда
SC2rw2,
откуда
6Ci
“* (rwl!rw 1) SC 2
— ii2 SC2.
Соответственно
SC2 =(1/112)56!
Если механизм сос-
тавлен из нескольких пе-
редач, то можно записать
для каждой передачи:
5С3
i32' 5С2;
(»-1)' SC(B_ 1).
i2i 5СР
354
Для произвольной кинематической цепи мертвый ход
выходного звена при наличии мертвого хода первого ко-
леса 5Ct
~ (»-!)'• • ’йз ^32'^21 оС1
— ini 8С1;
при наличии мертвого хода во всех передачах
5СХ
1пУ §С3
*л2' ^2
^л(п~ 1)' 1) “Ь ^ПП
По методу максимума-минимума суммарный мертвый
ход многоступенчатого зубчатого механизма
п
где SCmaxj- — мертвый ход j-й передачи.
По вероятностному методу
где
— координата середины поля допуска мертвого хода меха-
низма, мкм; t2 — коэффициент, выбираемый в зависимости
от риска Р (см. выше); со} = 6Cmaxj- — bCminj — поле рассея-
ния величины SQ в j-й передаче.
Мертвый ход планетарных механизмов. В планетарных
механизмах зависимость между мертвым ходом и боковыми
зазорами в составляющих передачах более сложная, чем
в механизмах с неподвижными осями.
Мертвый ход в планетарных механизмах зависит от со-
отношения моментов сил трения в опорах сателлитов ТТ2
и приведенного к оси сателлитов суммарного момента
нагрузки и сил трения в опорах центрального колеса zt.
При Тт2 < в передаче движения одновременно участвуют
разноименные профили сателлитов, при Тт2 > Т"? ~ одно-
именные.
Рассмотрим планетарный редуктор, состоящий из двух
цилиндрических передач внешнего зацепления (рис. 9.6) при
1
Тт2 < Тп£. При вращении во-
дила Н против хода часовой
стрелки, а затем в противо-
положном направлении воз-
никает мертвый ход.
По методу максимума-
минимума суммарный мерт-
вый ход (мкм) ведущего во-
дила
8СГ = 8С*Йig>
+ 8С2(->®-
По вероятностному методу
где SCj*2)x и 8С(тах ~ значения мертвых ходов (мкм) обеих
передач механизма;
“Ь ( ~ 1ЯЗ^со2'з)
— координата середины поля рассеяния мертвого хода пла-
нетарного механизма, мкм (^12 и Л^'з — координаты се-
редин полей рассеяния мертвых ходов 6С(^ и обеих
передач соответственно); г2 — коэффициент, зависящий от
заданного процента риска Р (см. выше).
При Тт2 > мертвый ход (мкм) ведущего водила при
расчете методом максимума-минимума 5С™ == ЗСтах®*
Кинематическая погрепность и мертвый ход винтовых
механизмов. Расчет кинематической погрешности и мертвого
хода винтовых механизмов проводится согласно ГОСТ
21095—82 двумя методами.
По методу максимума-минимума минимальная и макси-
мальная кинематическая погрешность
5<Р“ ь. = 0,628Pz; 8<р^ = ]/(8Рх)2 + (EJ2;
мертвый ход
^Стах = Ь' tg ф + ]/[(Ь" - b') tg ф]2 + (Ь tg ф)2 4- G2ai + G22,
где 8Pj — накопленная погрешность шага резьбы — раз-
ность действительных расстояний любых несоседних профи-
лей витков резьбы по образующим среднего диаметра;
Ez = 1/е2 4- (er tg ф)2 — суммарная приведенная погрешность
монтажа (еа — осевое биение винта; ег — рациональное бие-
ние йинта); Ь' и Ь"
предельные отклонения среднего диа-
метра резьбы винта, т. е. минимальное и максимальное
356
отклонения; b — верхнее отклонение среднего диаметра
резьбы гайки; ф — угол профиля резьбы (15° — в трапецеи-
дальной резьбе и 30° — в метрической); Gal и Ga2 — осевые
зазоры в опорах вращения.
При расчете кинематической погрешности и мертвого
хода винтовых механизмов вероятностным методом
в
max
max
k„ l/(8Px)2 + (Ex)2;
м
max
max*
где kp — коэффициент фазовой компенсации, принимаемый
в зависимости от заданного риска Р.
32 10 4,5 1,0 0,27
0,76 0,80 0,86 0,96 0,98
9.3. Статические ошибки манипулятора
Упругие свойства передач манипулятора определяют мат-
рицу жесткости и обратную ей матрицу податливости. Эти
матрицы устанавливают связь между вектором сил и век-
тором упругих перемещений манипулятора [30].
Пусть к подвижным звеньям манипулятора приложены
силы £к и моменты Мк. Эти усилия после их приведения
к обобщенным координатам заменяются приведенными си-
лами Qi (i — 1, ..., и). Всего манипулятор имеет п +1 число
степеней свободы с учетом движения губок схвата. Обозна-
чим ф* — углы поворота исполнительных двигателей (i =
= 1, ...» п + 1).
Матрица податливости устанавливает связь между обоб-
щенными силами Mi (i = 1,..., и + 1) и ошибками обобщен-
ных координат Ag,-, A<pi+1, возникающими от этих сил.
Считая известными приведенные силы Qt (i — 1, ...» п)
и силу зажима F, можно найти моменты двигателей, урав-
новешивающих эту нагрузку, на основе принципа возмож-
ных перемещений
£ Q№h + 1 + f Mfbtyi - FSs = 0. (9.13)
к~ 1 i ~ 1
Связь возможных перемещений валов двигателей 6ф£
с обобщенными координатами запишется так:
6Ф,
(9.14)
357
(9.15)
Последнее равенство говорит о том, что положение губок
схвата в общем случае зависит от всех обобщенных
координат манипулятора.
Подставляя выражения 8ф( и 5s в (9.14) и считая неза-
висимыми возможные перемещения Sqk и 5фп+1, получим
связь между моментами двигателей МД1 и Мд(и+1) (i =
= 1, ..., и):
Объединяя (9.16) и (9.17), получим
(9.16)
(9.17)
17ТМД + 6 = 0; 6 = 6'- MJ+1L7S,
(9.18)
где U — матрица Якоби частных передаточных отношений;
дфи+1
дЯ2
Л
дфй+1
Определим усилия в элементах передач. Присвоим упру-
гим элементам номера j — 1, ..., т.
Если разорвать мысленно элемент у, совершающий вра-
щательное движение, то появится новая обобщенная коор-
дината Ui, тогда
«j, Ф.+i);«=
s(9b ••> Чт «j. Фя+1)
Момент Mj, передающийся на элемент j через передачи,
связывающие его с двигателем, определим на основе прин-
ципа возможных перемещений из условия
Л
Мj Sty = £ или
i=i
(9Д9)
358
1
Тогда относительное угловое перемещение в элементе j
Actj —
(9.20)
где Cj — крутильная жесткость упругого элемента передачи.
При податливом грузе аналогично
где cs — жесткость груза.
Упругие перемещения манипулятора, вызванные дефор-
мацией удерживаемого объекта на величину As и элементов
передач на величины Act; 0 =1, ..., и), приводят к изме-
нению углов поворота ф(- (i = 1, ..., и) и фп+1 валов дви-
гателей, а следовательно, и к изменению обобщенных ко-
ординат манипулятора qt (i = 1, ...» и), причем
Дс/Lj (i — 1,
(9.21)
m
(9.22)
Во второй формуле учтено, что изменение расстояния
между губками схвата за счет податливости объекта при-
водит лишь к повороту вала привода двигателя на угол
Аф*+1 == (^n+1/5s) As. Упругие деформации Дос,- и As выража-
ются через моменты приводов по формуле (9.17) и с учетом
выражений (9.21), (9.22) получают вид
м? (1 = 1,..
ск
Последнюю формулу можно представить в матричной
форме
Аф = — УРЮМД - УРШд+1,
(9.23)
где Аф = [Афх, ..., Аф„]т;
359
пхт;
(i = 1, ..., п; j — 1, ..., m) — матрица размером
да.;
J J
P — диагональная m x m матрица податливости систе-
мы передач; VT =
#n+i
— вектор-столбец
размером т.
Формулу в матричном виде для вычисления ошибок
обобщенных координат получим, подставляя Мд из (9.18)
и Дф из (9.23) в выражение Дф = U \q. Тогда
Д^ = U ^VPV^U-^Q- U~1VPVM^i.
Последняя формула позволяет определить изменения
обобщенных координат манипулятора при действии сил Fk
и Мк, приложенных к его звеньям.
9.4. Динамические ошибки манипулятора
Обозначим деформацию i-ro передаточного механизма, при-
веденную к обобщенной координате qt (i — 1, ..., и), через
Дф. Если qin — программный закон движения привода по
i-й обобщенной координате, то фактический закон движе-
ния выходного звена по i-й координате будет
(9.24)
При заданном законе программного движения qin откло-
нения oq можно рассматривать как новые обобщенные
координаты и для исследования этих отклонений можно
использовать уравнение Лагранжа в виде
а ат
dt daf дщ
причем в этом случае обобщенные силы Qh соответствую-
щие обобщенным координатам af, принимают вид
(9.25)
где — приведенные к координате af жесткости передаточ-
н ых механизмов; — приведенные к координате oq коэф-
фициенты диссипации передаточных механизмов.
360
Составим выражение для кинетической энергии манипу-
лятора с одной вращательной и двумя поступательными
кинематическими парами, имея в виду, что
(9.26)
Тогда
Т— _ {[♦/* + ^з (^Зп Т аз) J (Qm Т а() Т
+ (т2 + /и3) (д2п + а2)2 + т3 (д3„ + а3)2},
(9.27)
где mt (i = 1, 2, 3) — массы звеньев 1, 2, 3; J* = 4- J2 +
4- J3 — сумма моментов инерции звеньев относительно осей,
параллельных оси вращательной пары и проходящих через
центры масс звеньев.
Применяя оператор Лагранжа и учитывая члены не
выше 2-го порядка малости, получим
(J* + m3q3) а 4- (61 4- 2m3q3q3) otj + 4-
4- 2m3q3q1a3 4- 2т3 (q3qr 4- а3 =
== -(J* + m3qj)qt - 2m3q3q3qt;
(9.28)
(т2 4- т3)а2 + 62а2 4- с2а2 = — (т2 4- m3)q2m3a.3 4-
< О
4- Ь3&3 4- (с3 — m3ql) а3 — 2m3q3q^x — —m3q3 4- m3q3qr.
Здесь обозначено qf = qin; 4 — qin; qt — *4П 0— 1» 2, 3), причем
Qi ~ (CiOtj 4“ 6/Otf) (i 1, 2, 3).
Последние уравнения показывают, что динамические
ошибки отклонения звеньев манипулятора от программного
движения зависят от законов программного движения.
Причем ошибка по обобщенной координате q2 — а2 не зави-
сит от законов движения по координатам qr и q2.
Уравнения для at и а3 представляют собой связанную
систему двух дифференциальных уравнений 2-го порядка
с переменными коэффициентами.
При позиционировании в некоторой точке можно поло-
жить qin (t) = const и уравнение (9.28) будет описывать коле-
бание манипулятора вблизи положения равновесия.
361
*
Для манипулятора типа ВПП уравнения (9.28) получат
вид:
(Л + пчзо) «1 + bi&i + = 0;
(т2 + т3) а2 + Ь2а2 + с2а2 s 0;
т3&3 + Ь3а3 + с3а3 — 0.
(9.29)
Система (9.29) линейных уравнений с постоянными коэф-
фициентами позволяет определить собственные частоты
манипулятора в различных конфигурациях, т. е. при различ-
ных значениях обобщенных координат. В этом случае
обычно пренебрегают демпфированием в системе.
Список литературы
1. Артоболевский И. И. Теория механизмов и машин. 1976.
2. Артоболевский И. И., Левитский Н. И., Черкудинов С. А.
Синтез плоских механизмов. М., 1959.
3. Артоболевский И. И., Овакимов А. Г. Об одном свойстве
матрицы, описывающей строение привода манипулятора//Докл.
АН СССР. 1976. Т. 230. № 2.
4. Беляев В. Г. Винтовые механизмы качения в станках с ЧПУ
и роботах. М., 1984.
5. Болотин Л. М., Корендясев А. И., Саламандра Б, Л.,
Тывес Л. И. Цикловые роботы с аккумуляторами механической
энергии. Основы построения привода//Станки и инструмент.
1984. № 4. С. 7-10.
6. Боренштейн Ю. П. Исполнительные механизмы захваты-
вающих устройств. Л., 1982.
7. Бруевич Н. Г. Точность механизмов. М. —Л., 1946.
8. Бурдаков С. Ф., Дьяченко В. А., Тимофеев А. Н. Проектиро-
вание манипуляторов промышленных роботов и роботизирован-
ных комплексов. М., 1986.
9. Вопилкин Е. А. Расчет и конструирование механизмов
приборов и систем. М., 1980.
10. Воробьев Е. И. Синтез пространственных незамкнутых
кинематических цепей по заданному движению объекта//С.: Меха-
ника машин. М., 1977. Вып. 52. С. 11—20.
11. Воробьев Е. И. Синтез механизмов по заданному движе-
нию твердого тела в пространстве//Сб.: Механика машин. М., 1978.
Вып. 52. С. 25—33.
12. Данилевский В. Н., Земмель В. В. Механические захваты
промышленных роботов//Сб. науч. тр. НИАТ. Новые разработки
в области промышленных роботов. 1974. № 386.
13. Иванов М. Н. Волновые зубчатые передачи. М., 1981.
14. Калабин И. В. Дифференциальные механизмы манипулято-
ров//Станки и инструмент. 1978. № 7.
15. Кобринский А. Е., Саламандра Б. Л., Тывес Л. И. Прин-
ципы построения двигательной системы автоматических манипу-
ляторов с программным управлением (промышленных роботов)//
Станки и инструмент. 1976. № 4. С. 3—10.
16. Кобринский А. А., Кобринский А. Е. Манипуляторные
системы роботов. М., 1985.
17. Ковалев Ф. И., Чесных П. П., Кондратьев М. В., Его-
ров О. Д. Проектирование механизмов промышленных роботов.
М., 1984.
18. Козлов В. В., Макарычев В. П., Тимофеев А. В., Юревич Е. И.
Динамика управления роботами. М., 1984.
19. Колпаитиков С. И., Челпанов И. Б. Задачи механики за-
хватных устройств манипуляционных роботов//Изв. АН СССР.
Механика твердого тела. 1984. № 4. С. 32 — 36.
1
20. Корендясев А. И. Автоматические манипуляторы с при-
водами на основании//Станки и инструмент. 1980. № 12.
С. 5—8.
21. Корендясев А. И.. Саламандра Б. Л., Тывес Л. И. Осо-
бенности построения кинематических схем автоматических мани-
пуляторов//Станки и инструмент. 1981. № 2.
22. Корендясев А. И., Саламандра Б. Л., Тывес Л. И. Цикловые
роботы с рекуперацией энергии. Системы с несколькими степенями
подвижности//Станки и инструмент. 1984. № 6.
23. Куклин В. Б., Шувалова Л. С. Волновые зубчатые передачи.
М., 1971.
24. Лебедев П. А. Кинематика пространственных механизмов.
Л., 1966.
25. Левитский Н. И. Теория механизмов и машин. М., 1985.
26. Мелентьев Ю. И., Телегин А. И. Динамика манипулятор-
ных систем роботов. Иркутск, 1985.
27. Овакимов А. Г., Тимофеев И. А. Синтез схемы дифферен-
циального привода для развязки движений в манипуляторах
(Кинематические соотношения)//Изв. вузов. Машиностроение.
1978. № 12. С. 36—41.
28. Овакимов А. Г., Тимофеев И. А. Синтез систем диффе-
ренциального привода для развязки движений в манипуляторах
(передачи привода)//Изв. вузов. Машиностроение. 1979. № 4.
С. 40 -44.
29. Овакимов А. Г., Калабин И. В., Степанов В. П. Развязка
движений и устранение зазоров в дифференциальных передачах
автоматических манипуляторов//Станки и инструмент. 1981. № 12.
С. 13-17.
30. Овакимов А. Г., Калабин И. В., Тимофеев И. А. Расчет
натяжного устройства и усилий в передачах манипуляторов с при-
водом на основании//Станки и инструмент. 1984. № 6. С. 8-10.
31. Петров Б. А. Манипуляторы. Л., 1984.
32. Петров Л. Н. Некоторые вопросы оптимизации мощности
исполнительного органа манипуляционного органа//Вестник ма-
шиностроения. 1981. № 8. С. 17—18.
33. Попов М. В. Выбор параметров звеньев и параметров
уравновешивания ручного манипулятора.//Сб.: Проектирование
механизмов и динамика машин. М., 1980. Вып. 14.
34. Попов С. А. Курсовое проектирование по теории
механизмов и механике машин. М., 1986.
35. Решетов Л. Н. Самоустанавливающиеся механизмы: Спра-
вочник. М., 1979.
36. Скворцова Н. А., Тарабарин В. Б., Тимофеев Г. А. Расчет
геометрии волнового эвольвентного зацепления//Из в. вузов. Маши-
ностроение. 1975. № 7. С. 23—29.
37. Саркисян Ю. Л. Кинематический синтез пространственных
стержневых механизмов // Кинематика,
инамика и точность меха-
низмов. М., 1984.
364
38. Соболь И. М., Статников Р. Б. ЛП-поиск и задачи опти-
мального конструирования//Сб.: Проблемы случайного поиска.
Рига, 1972. Вып. 1.
39. Теория механизмов и машин/Под ред. К. В. Фролова. М.,
1987.
40. Тывес Л. И., ПурцелшУю Г. К. К статическому уравнове-
шиванию звеньев механических рук//Машиностроение. 1981.
№ 5.
41.. Тывес Л. И. К задаче динамической развязки движений
манипуляторов по обобщенным координатам//Машиностроение.
1985. № 2.
42. Фролов В. А. Матсмашческие модели и методы оптималь-
ного конструирования ЭВА и РЭА. Харьков, 1985.
43. Фролов К. В. Методы совершенствования машин и совре-
менные задачи машиноведения. М., 1984.
44. Фомин М. В. Учебное пособие по расчету ременных передач
на ЭВМ. М., 1983.
45. Чернавский С. А., Снсеарев Г. А., Козинцев Б. С. и др. Про-
ектирование механических передач. М., 1984.
46. Чен II., Рос Б. Общая теория кинематического синтеза по
раздельным и бесконечно близким положениям//Конструирование
и технология машиностроения. 1969. № 1. С. 220 — 226.
47. Чен П., Рос Б. Расчетные уравнения для синтеза кинема-
тических цепей ио раздельным и бесконечно близким положе-
ниям// Конструирование и технология машиностроения. 1969. № 1.
С. 227-237.
1
Учебное издание
МЕХАНИКА ПРОМЫШЛЕННЫХ РОБОТОВ
В 3 книгах
Книга 2
Воробьев Евгений Иванович
Егоров Олег Дмитриевич
Попов Сергей Александрович
Расчет и проектирование механизмов
I
i
Заведующий редакцией А. В. Дубровский
Редактор Л. Н. Шатунова
Младший редактор Т. Ф. Артюхина
Художник Е. Н. Урусов
Художественный редактор Л. К. Громова
Технический редактор 3. В. Нуждина
Корректор Р. К. Косинова
i
ИБ № 7118 |
Изд. № ОТ-672. Сдано в набор 13.04.88. Поди, в печать 12.09.88.
Формат 84 х 1081/з2. Бум. тип. № 2. Гарнитура тайме. Печать высокая.
Объем 19,32 усл. печ. л. 19,53 усл. кр.-отт. 18,77 уч.-изд. л. Тираж
44000 экз. Зак. № 1525. Цена 65 коп.
Издательство «Высшая школа», 101430, Москва, ГСП-4, Неглинная ул.,
д. 29/14.
Ордена Октябрьской Революции, ордена Трудового Красного Знамени
Ленинградское производственно-техническое объединение «Печатный
Двор» имени А. М. Горького Союзполиграфпрома при Государственном
комитете СССР по делам издательств, полиграфии и книжной торговли.
197136, Ленинград, П-136, Чкаловский пр., 15.
1