Текст
Б.В.Шабат
ВВЕДЕНИЕ В КОМПЛЕКСНЫЙ АНАЛИЗ
В этой книге дается единое изложение основных понятий теории функций
одного и нескольких комплексных переменных. Первая часть, посвященная
функциям одного переменного, содержит материал обязательного
университетского курса. Вторая часть посвящена функциям нескольких
переменных и содержит материал основного спецкурса.
В последние десятилетия интерес к теории функций нескольких комплексных
переменных значительно возрос — это объясняется тем, что она имеет важные
приложения и богатые связи с другими разделами математики. Первоначальное
изучение этой теории обычно довольно затруднительно. Принятое в книге единое
изложение значительно облегчает знакомство с ней.
ОГЛАВЛЕНИЕ
Предисловие 7
ЧАСТЬ ПЕРВАЯ
ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО
Глава I. Голоморфные функции 13
§ 1. Комплексная плоскость 13
1. Комплексные числа 13
2. Топология комплексной плоскости 17
3. Пути и кривые 20
4. Области 23
§ 2. Функции комплексного переменного 26
5. Понятие функции 26
6. Дифференцируемость 31
7. Геометрическая и гидродинамическая интерпретация 36
§ 3. Элементарные функции 42
8. Дробно-линейные функции 42
9. Геометрические свойства 47
10. Дробно-линейные изоморфизмы и автоморфизмы 50
11. Некоторые рациональные функции 54
12. Показательная функция 58
13. Тригонометрические функции 61
Задачи 65
Глава II. Свойства голоморфных функций 68
§ 4. Интеграл 68
14. Понятие интеграла 68
15. Первообразная 72
16. Гомотопия. Теорема Коши 80
17. Обобщения теоремы Коши 86
18. Интегральная формула Коши 90
§ 5. Ряды Тейлора 93
19. Ряды Тейлора 94
20. Свойства голоморфных функций 100
21. Теорема единственности 103
22. Теорема Вейерштрасса 106
§ 6. Ряды Лорана и особые точки 112
23. Ряды Лорана 112
24. Изолированные особые точки 119
25. Вычеты 127
Задачи 134
Глава III. Аналитическое продолжение 137
§ 7. Понятие аналитического продолжения 137
26. Элементы аналитических функций 137
27. Продолжение вдоль пути 144
§ 8. Понятие аналитической функции 151
28. Аналитические функции 151
29. Элементарные функции 156
30. Особые точки 164
§ 9. Понятие римановой поверхности 170
31. Элементарный подход 170
3 2. Общий подход 174
Задачи 181
Глава IV. Основы геометрической теории 183
§ 10. Геометрические принципы 183
3 3. Принцип аргумента 183
34. Принцип сохранения области 187
35. Принцип максимума модуля и лемма Шварца 192
§11. Теорема Римана 195
36. Конформные изоморфизмы и автоморфизмы 195
37. Принцип компактности 199
38. Теорема Римана 204
§ 12. Соответствие границ и принцип симметрии 206
39. Соответствие границ 206
40. Принцип симметрии 211
41. Эллиптический синус и модулярная функция 216
Задачи 221
Глава V. Дополнительные вопросы 223
§ 13. Разложения целых и мероморфных функций 223
42. Теорема Миттаг-Леффлера 223
43. Теорема Вейерштрасса 230
§ 14. Гармонические и субгармонические функции 238
44. Гармонические функции 238
45. Задача Дирихле 243
46. Субгармонические функции 248
Задачи 254
ЧАСТЬ ВТОРАЯ
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Глава I. Голоморфные функции нескольких переменных 259
§ 1. Комплексное пространство 259
1. Пространство Сп 259
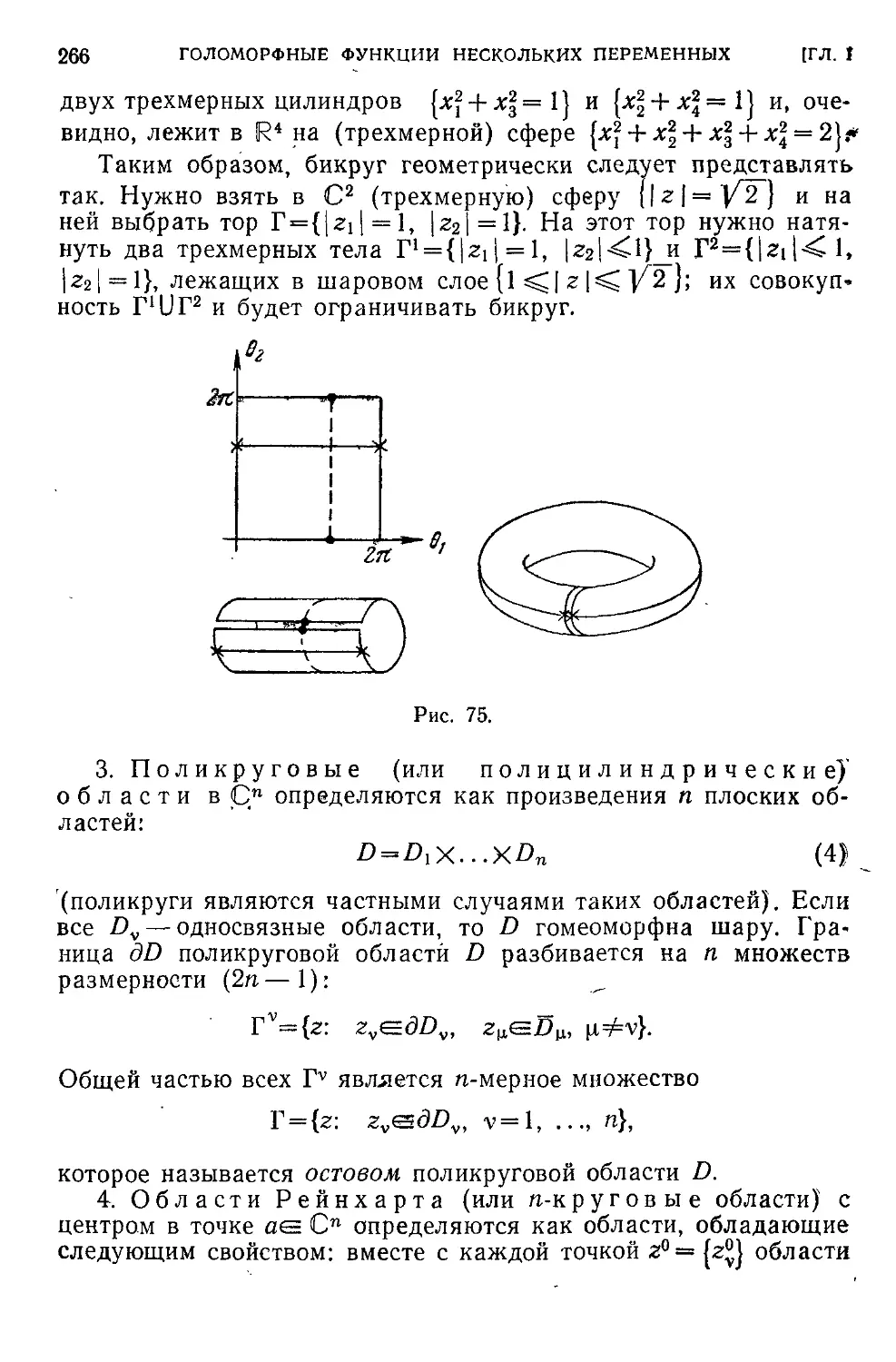
2. Простейшие области 264
§ 2. Понятие голоморфности 270
3. Определение голоморфности 270
4. Плюригармонические функции 277
5. Основная теорема Хартогса 280
§ 3. Голоморфные функции 285
6. Простейшие свойства 285
7. Степенные ряды 293
8. Ряды Хартогса и Лорана 297
Задачи 301
Глава II. Интегрирование 304
§ 4. Многообразия и формы 304
9. Понятие многообразия 304
10. Дифференциальные формы 309
11. Понятие интеграла от формы 314
§ 5. Теорема Коши — Пуанкаре 321
12. Цепи и их границы 322
13. Дифференцирование форм 326
14. Формула Стокса 331
15. Теорема Коши — Пуанкаре 334
§ 6. Интегральные представления 337
16. Формулы Мартинелли — Бохнера и Лере 337
17. Теорема Севери 344
18. Формула Вейля 350
Задачи 355
Глава III. Аналитическое продолжение 357
§ 7. Области голоморфности 357
19. Теорема Хартогса о продолжении 357
20. Понятие области голоморфности 360
21. Голоморфная выпуклость 365
22. Свойства областей голоморфности 372
§ 8. Псевдовыпуклость 377
23. Принцип непрерывности 377
24. Выпуклость в смысле Леви 381
25. Плюрисубгармонические функции 386
26. Псевдовыпуклые области 395
§ 9. Оболочки голоморфности 401
27. Однолистные оболочки голоморфности 402
28. Области разложения 408
29. Многолистные оболочки голоморфности 417
Задачи 422
Глава IV. Мсроморфпыс функции и проблемы Кузена 424
§ 10. Мероморфные функции 424
30. Понятие мероморфной функции 424
31. Первая проблема Кузена 429
32. Решение для поликругов 434
30. Применения. Вторая проблема Кузена 439
§11. Методы теории пучков 445
34. Основные определения 445
3 5. Группы когомологий 451
36. Точные последовательности пучков 455
§ 12. Применения 460
37. Решение первой проблемы Кузена 460
38. Решение второй проблемы Кузена 466
39. Решение д -проблемы и проблемы Леви 469
Задачи 480
Глава V. Особенности и вычеты 484
§ 13. Многомерные вычеты 484
40. Теория Мартинелли 485
41. Теория Лере 492
42. Логарифмический вычет 501
§ 14. Аналитические множества 507
43. Понятие аналитического множества 507
44. Локальное обращение голоморфных функций 515
§ 15. Аналитичность множества особенностей 519
45. Аналитичность множества особых точек 520
46. Существенно особые точки 523
47. Теорема о вложенном ребре 527
Задачи 530
Глава VI. Голоморфные отображения 533
§ 16. Автоморфизмы простейших областей 533
48. Общие теоремы 534
49. Автоморфизмы пространства 540
50. Автоморфизмы некоторых областей 546
§ 17. Инвариантная метрика 551
51. Кернфункция 551
52. Метрика Бергмана 559
53. Поведение кернфункции на границе 564
Задачи 570
Предметный указатель 572
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абеля теоремы 97, 275, 293 Абсолютный октант 267
Автоморфизмы канонических
областей 197
— круга 53
— области 533
— поликруга 550
— пространства 540
нелинейные 541
— шара 546
Автоморфная функция 217
Адамара теорема 235
Аналитическая кривая 377
— плоскость 260
касательная 343, 510, 513
— поверхность 377
компактная 377
— прямая 260
— функция 152, 410
Аналитическое множество 507
компактное 531
локально неприводимое 508
неприводимое 507
— продолжение 137, 143, 410
вдоль пути 145, 410
непосредственное 143, 410
Антиголоморфная функция 277
Антиконформное отображение 38
А-точка 106
База открытых множеств 448
— пучка 446
— и-мерных гомологии 487
Барьер в граничной точке 362, 364
Бенке — Зоммера теорема 378, 520
Бенке — Штейна теоремы 370, 373
Бергмана граница 303
— кернфункция 555
Бесконечная точка 15, 36, 106, 130
Бесконечное произведение 230
Биголоморфное отображение 376,
413,533
Буняковского — Шварца
неравенство 551
Бурмана — Лагранжа ряд 191
Вейерштрасса теорема
подготовительная 289, 514, 516
— теоремы 106, 231, 288
Вейля множество 350
— область 350
— разложение 353
— теорема 351
— формула 350
Векторное поле 40
Верхняя огибающая 250
Ветвь аналитической функции 152
Вложение многообразий 412
Внешнее умножение 311
Выпуклая оболочка 365
— функция 394
Выпуклость 365
в смысле Леви 381
— голоморфная 365, 415
— логарифмическая 294—296
Выпуклость относительно класса 366
— полиномиальная 366, 481
— рациональная 367, 531
Вычет 130
— логарифмический 183, 501
— относительно базисного цикла 488
особого цикла 490
— функции 128, 484
Вычет-класс 498
сложный 500
Вычет-форма 495
Гамма-функция 138
Гармоническая мажоранта 249, 250
наилучшая 252
— функция 238, 242, 390
Геометрия Лобачевского 67, 563
Гиперболическая метрика 563
Гипотеза Бибербаха 136
Глобальное сечение пучка 453
Голоморфизм 195, 307, 376, 413, 533
Голоморфная выпуклость 365, 415
— кривая 355
— нерасширяемость в точке 381
— форма 314
— функция 35, 271
в смысле Вейерштрасса 102,
285
Коши 102
Римана 102. 285
на комплексном многообразий
308
Голоморфное отображение
многообразий 412
— расширение области 361
Голоморфность функции в точке 35,
271
Голоморфный изоморфизм 412
— коцикл 430, 442
Гомологии компактные 497
Гомоморфизм пучков 456
Гомотопические классы 82
Гомотопия 80
Гомотопность кривых 83
Граница 324
— Бергмана 303
— области 24
ориентированная 87
— поликруга 265
— симплекса 322
— цепи 323, 325
— Шилова 237, 303, 570
Граничное расстояние 409
Грина формула 337, 338
Группа автоморфизмов 195, 544
— гомологии 324
— дифференциальных форм 313, 330
— когомологий 331, 434, 451—455
с коэффициентами в пучке 452
покрытия 453
пространства 455
— коциклов 452
— относительных гомологии 500
цепей 500
Даламбера — Эйлера условия 33
Двоякопериоличность 217
де Рама теорема 463,482
Диаграмма Рейнхарта 267
— Хартогса 268
Диаметр множества 88
Дивизор 468
Дигармонические функции 278
Дирихле задача 243, 255, 280
Дискриминант 511
Дискриминантное множество 511,
517
Дифференциал 31
— формы 323
Дифференциальная форма 79, 278,
310—
бистепени (р, q) 314
замкнутая 79, 278, 330, 433
класса Cf(D) 471
СПП
точная 79, 278, 330
эрмитова 384, 561
Дифференциальный коцикл 432
, когомологичный нулю 432
Дифференцирование сложных
функций 272
Дифференцируемость в смысле С
32, 270
R1,270
точке 31
Длина пути 22
Дольбо теорема 461
Дробно-линейные автоморфизмы 52
изоморфизмы 51
функции 42
Дуга аналитическая 208
д -проблема 469
8-функция 341
Евклидова метрика 16, 261
Жордана лемма 134
Жорданов путь 21
Жорданова граница 25
— кривая 23
— область 25
Жуковского функция 55
Задача Дирихле 243, 255, 280
Зацепления коэффициент 486
Идеал кольца 254, 291, 303
Изолированная особая точка 119,
164, 349
Изоморфизм голоморфный 376
— Дольбо 462
— областей 533
— пучков 456
Инверсия 49
Индекс отображения 519
локальный 506, 518
— пресечения симплексов 485
цепей 485
— поверхности относительно точки
501
— пути относительно точки 185
Интеграл 68, 78, 71, 316, 319
— Коши90,274, 321
типа Коши 134
— эллиптический первого рода 209—
211
Интегральное представление Вейля
350
Лере343
Мартинелли — Бохнера 340
Исчерпание множества 320
компактное 108, 363, 368
Каратеодори компактификация 206
Картана теоремы 463, 464, 534
Картана —
Каратеодори теорема 537
Картана — Туллена теоремы 367,
371,415
Келлога теорема 207
Кернфункция 555
Класс-вычет 498
сложный 500
Класс функций 369
й-устойчивый 369
р-устойчивый 370
Кнезера теорема 527
Кограница 452
Кограничный оператор 452
Лере496
Кольцо голоморфных функций 36,
272
— ростков голоморфных функций
445
мероморфных функций 450
Компакт 202
'Компактификация 15, 206, 261
Компактность в себе 202
Копактные гомологии 497
Комплекс 325
Комплексная плоскость 13, 15
— прямая 260
— структура на многообразии 306
Компоненты множества 24
Конформность 37, 207
Конформные автоморфизмы 195
— изоморфизмы 195
Координаты локальные 305
— однородные 262
Коцепь порядка/? 452
Коцикл 331. 430, 433, 452
—, когомологичный нулю 331, 430
Коши интеграл 90
кратный 274
повторный 321
— неравенства 95, 117. 276
— теоремы 84, 128, 484
— формула 90
Коши — Адамара формула 97, 296
Коши — Буняковского неравенство
540
Коши — Гоина формула 92, 340
Коши — Пуанкаре теорема 335
Коши — Римана уравнения 33
касательные 356
неоднородные 434, 470
Коши — Фантапье формула 341
Коэффициент зацепления 486
Кривая 21
— гладкая 23
— жорданова 23
аналитическая 208
— кусочно гладкая 23
— спрямляемая 23
Кпитические точки 510, 513
Круг сходимости 98. 114
Кузена проблема вторая 441. 460, 466
первая 429, 460. 463, 464
Леви выпуклость 381
— определитель 385
— проблема 382, 478
— теоремы 525, 526
— форма 383
Леви — Кшоски теорема 384
Лере кограничный оператор 496
— теория 492—501
— формула 343
Линделёфа теорема 207
Линейная функция 43
Линейное преобразование 544—546
Линии тока 41
Липшица условие 102, 398
Лиувилля теорема 95, 241, 288, 302,
349
Логарифмическая выпуклость 294
— производная 183
Логарифмический вычет 183, 501
— образ 294
— потенциал 255, 521
Локально конечное покрытие 318,
432
Локальное обращение голоформных
функций 188, 515—519
Локальные координаты 305
Локальный индекс отображения 506,
518
— параметр 177, 304
— принцип максимума Росси 423
Лорана ряд 144, 299
^-выпуклость 381
Мартинелли — Бохнера
интегральное представление
340
формула 340
Матрица кососимметрическая 312
— Якоби512
Мероморфная кривая 530
— функция 126, 237, 424, 427
Мероморфное продолжение 523
Метод Коши улучшения сходимости
139,226
Метрика Бергмана 559, 563
— гиперболическая 563
— инвариантная 563
Миттаг — Леффлера теорема 224
Многолистные области 360
Многообразие 304
— гладкое 306
— дифференцируемое 306
— класса Ср 306
С00 306
— комплексно аналитическое 177,
307
— комплексное 307, 355
— наложения над С 409
— ориентируемое 315, 356
— Штейна 417, 478
Множество аналитическое в точке
507
— ветвления 517
— дискриминантное 511,517
— неприводимое 507
— неопределенности функции 124
мероморфной функции 427
— сходимости степенного ряда 303
— тонкое 358
Модель Пуанкаре геометрии
Лобачевского 67
Модулярная функция 217
Монтеля теорема 201
Мореры теорема 101, 335
Наилучшая гармоническая
мажоранта 252
— плюрисубгармоническая
мажоранта 408
— плюрисупергармоническая
мажоранта 407
Непрерывная функция 30
Непрерывность в смысле С 30
С 30, 66
— точке 30
Неприводимая компонента
аналитического множества 509
Неравенство Коши 95, 117, 276
Неравенство Буняковского —
Шварца 551
— Коши — Буняковского 540
— треугольника 551
Носитель комплекса 325
— формы, функции 318, 432
Нуль мероморфной кривой 530
— функции 103
Ньютона — Лейбница формула 77,
333
Область 23
Оболочка выпуклая 365
— голоморфности 362, 402
области Рейнхарта 406
Хартогса 407
трубчатой области 404
— F-выпуклая
Общее положение многообразий 499
точек 322
Объединение областей
голоморфности 373
— путей 70
Ока теоремы 467, 480
Окрестность 17, 174, 410, 446
— проколотая 18
Октант абсолютный 267
Оператор взятия границы 323
— 6/327,330
— а 469
— д 482
— Лапласа 238
— res 495
Определитель Леви 385
Определяющая функция 439
Ориентация многообразия 315, 356
Осгуда лемма 282
— теорема 518
Осгуда — Брауна теорема 349
Особая точка 119, 164
изолированная 119, 164, 349
многозначного характера 166
неизолированная, пример 120
однозначного характера 166
устранимая 119
Остов множества Вейля 350
— поликруга 265
— поликруговой области 265, 335
Остроградского формула 333
Относительная граница 500
— топология 26
Отображение антиконформное 38
— биголоморфное 376, 413, 533
— конформное в точке 37
области 37
второго рода 38
— пучков 455
Парсеваля равенство 553
Первообразная 72
— вдоль пути 76
— локальная 73
Пересечение областей
голоморфности 372
Пикара теорема 219, 220, 554
большая 220
Плоскость аналитическая 260
Плюригармоническая функция 278
Плюрисубгармоническая функция
387
Плюрисупергармоническая функция
407
Поверхность аналитическая 377
— модуля 29, 321
Подготовительная теорема
Вейерштрасса 289, 514, 516
Подпучок 456
Поле мероморфных функций 428
— отношений кольца 450
Поликруг(полицилиндрJ64, 287,
419, 550, 556
максимальный 409
— сходимости степенного ряда 296
Полиномиальная выпуклость 366,
481
Полиэдр 325
— аналитический 350, 367, 373
— полиномиальный 356
Полиэдрическая область 350
Полиэдрическое множество 350
Полунепрерывность 249, 278, 387
Полюс 119,425
— мероморфной кривой 530
Полярная особенность 499
первого порядка 493
Полярное множество мероморфной
функции 425
Порядок Л-точки 106, 519
— ветвления 167
— нулевого множества 468, 509
— нуля 105,530
в бесконечности 106
— общего нуля 506
— полюса 123, 530
— полярного множества 468, 509
— целой функции 234
Последовательность гомоморфизмов
324
точная 324, 331
— комплексных чисел 19
Потенциал комплексный 41
Потенциальная функция поля 40
Предел функции 29, 30
Предельная точка
последовательности 19
Предпучок 448
— мероморфных функций 450
Преобразование линейное 544
положительно определенное
545
унитарное 545
— Рейнхарта 267, 302
Принадлежность компактна» 25
Проблема Кузена вторая
(мультипликативная) 441, 460,
466
первая (аддитивная) 429, 460,
463, 464
— Леви382
Продолжение аналитическое 137,
143,145,410
— мероморфное 523
Производная 34
— аналитической функции 155
— по направлению 33
Пространство комплексное и-мерное
259
проективное 262, 307
— теории функций 262
— топологическое 174
хаусдорфово 175
— С 259
Псевдовыпуклость 377—395
Пуанкаре — Вольтерра теорема 154
Пуассона формула 244
Пути гомотопные 81, 149
— с общими концами 81
— эквивалентные 21
Путь 20
— гладкий 22, 320
—, гомотопный нулю 82
— жор данов 21
— замкнутый 21
— кусочно гладкий 22
— непрерывно дифференцируемый
22
— спрямляемый 22
Пучок 446
— групп 451
— колец 450
— полей 450
— постоянный 451
— ростков голоморфных функций
181,450
дифференциальных форм 450
мероморфных функций 450
функций класса С 451
— тонкий 481
Равенство Парсеваля 553
Радиус мероморфности функции 526
— сходимости 98
— Хартогса298, 395, 397
Радиусы сходимости сопряженные
296
Разбиение единицы 318, 432
Размерность аналитического
множества 512
— комплекса 325
Расстояние 16, 20
— граничное на многообразии
наложения 409
Рациональная выпуклость 366, 531
Ребро множества Вейля 350
Результант 511,516
Рейнхарта область 266, 267, 300, 405
Рельеф функции 29
Римана поверхность 171, 178, 308,
411
— сфера 16
— теорема 204
Римана — Грина формула 85, 333
Римана — Шварца принцип
симметрии 213
Риманово многообразие 176, 411
Росси локальный принцип
максимума модуля 423
— теорема 481
Росток аналитического множества
513
— аналитической функции 151, 410
— дивизора 469
— мероморфной функции 450
Рунге область 355
— теорема 109,193
Руше теорема 186, 506
Ряд Бурмана — Лагранжа 191
— Лорана 114
кратный 299
— степенной 94, 293
— Тейлора 95
— Фурье 117,549
— Хартогса 298
— Хартогса — Лорана 301, 524
р-метрика 261
Связность 24, 26, 308
— линейная 24
Севери теорема 344, 348
Семейство функций компактное 200
равномерно ограниченное
внутри области 199
равностепенно непрерывное
внутри области 200
слабо ограниченное 534
(сильно) ограниченное 535
Серра теорема 466, 482
Сечение пучка 181, 447
Сильное ф-вложение многообразий
412
Симплекс 314
— криволинейный 325
Синус 61
— эллиптический 216. 222
Слабая сходимость 475
Слабое ф-вложение многообразий
412
Сложный класс-вычет 500
Соответствие границ 206—208
Соотношения соседства 177, 305
Сопряженные радиусы сходимости
296
Сохоцкого теорема 123, 544
— формула 135
Сохранение углов 39
Стебель пучка 447
Степенная функция 54
Степенные ряды 94, 293
Степень дифференциальной формы
312
Стереографическая проекция 16, 302
Стерлинга формула 221
Стокса формула 331, 333
Строго плюрисубгармоническая
функция 389
Субгармоническая функция 249, 390
Супергармоническая функция 254
Существенно особая точка 120, 523
Сфера комплексных чисел 16
— Римана 15
Сферическая метрика 16
Сходимость последовательности
множеств 377
— ряда 93
мероморфных функций 224
равномерная 93
Тейлора ряд 95
Тип целой функции 235, 254
Тонкое множество 358
Тор комплексный п -мерпый 355
Точка ветвления 166
бесконечного порядка 167
конечного порядка 167
логарифмическая 167
римановой поверхности 171
— критическая 171, 510, 513
— неопределенности 424
— обыкновенная 171, 509, 512
Точки в общем положении 322
— симметричные 48
Точная последовательность пучков
457
Трансцендентная целая функция 126
Угловое граничное значение 207
Угол в бесконечности 44
Унитарное преобразование 545
Уравнения Коши — Римана 33
касательные 356
неоднородные 434, 470
Условие Липшица 108, 398
Условия Даламбера — Эйлера 33
— локальной однолистности 190, 515
Усредняющее ядро 472
Факторпучок 456
Фату пример 541—544
Форма-вычет 495
Форма дифференциальная 79, 278,
310—314,330,384,433,471,
561
Функционал 202, 417
ф-вложение сильное 412
— слабое 412
ф -расширение функции 413
ф -сужение функции 413
F-выпуклость 366
Характеристическая функция 332,
472
Харнака теорема 242
Хартогса лемма 283
— область 268, 302, 407
полная 268
— ряд 298
— теорема основная 284
— теоремы 252, 357, 520, 523
Хартогса — Лорана ряд 301, 524
Хефера теорема 351,441
Хёрмандера теоремы 478, 567
Цепь 322
Цикл 324
—, гомологичный нулю 324
— особый 489
Циклы гомологичные 324
Шар 264, 287, 546, 557
Шварца лемма 194, 281, 539, 550
— теорема 215
Шилова граница 287, 303, 570
Шпета — Картана теорема 531
Эйлера формула 59
Экстремальная функция 553, 558
Элемент аналитической функции
143,410
канонический 144
Эллиптический интеграл 209
— синус 216, 222
е-окрестность 17, 175
Ядро гомоморфизма 324, 331
Моему учителю —
МИХАИЛУ АЛЕКСЕЕВИЧУ
ЛАВРЕНТЬЕВУ
ПРЕДИСЛОВИЕ
Обстоятельный анализ свойств функций немыслим без вы-
выхода в комплексную область. Вот простой пример: функция
I(х) — -гзг~2~ одинаково хороша (бесконечно дифференцируема)'
во всех точках числовой оси, а ее ряд Тейлора
1 = 1 _ v-2 i Х4 _
перестает сходиться при |х|^>1. Причину этого нельзя понять,
оставаясь в действительной области: ведь точки х=±\, разде-
разделяющие множества сходимости и расходимости ряда, ничем не
примечательны для нашей функции. Но выход в комплексную
область сразу разъясняет явление: на окружности |х| = 1 лежат
точки x=±i, в которых функция / обращается в бесконечность,
из-за них ряд и перестает сходиться.
Переход к рассмотрению функций комплексного перемен-
переменного необходим в целом ряде вопросов. Он столь же естествен,
как переход от поля действительных чисел к алгебраически
замкнутому полю комплексных чисел. И удивительно — для
функций от комплексных чисел, тех самых, которые по знаме-
знаменитой теореме Фробениуса дают единственно возможное рас-
расширение поля действительных чисел с сохранением алгебраиче-
алгебраических свойств, удается построить и анализ, столь же полный и
стройный, как анализ функций действительного аргумента.
Переход к комплексному анализу дает возможность глубже
изучить элементарные функции и установить интересные связи
между ними. Так тригонометрические функции оказываются
простыми комбинациями показательных, например,
8 ПРЕДИСЛОВИЕ
Вскрываются такие неожиданные и замечательные соотноше-
соотношения между действительными и «мнимыми» величинами-, как
скажем
В действительном анализе стройная теория развивается
лишь для однозначных функций, а многозначные часто доста-
доставляют много неприятностей. В комплексном анализе удается
выяснить природу многозначности и построить безупречную
теорию многозначных функций.
Комплексный анализ дает эффективные методы вычисления
интегралов и получения асимптотических оценок, способы ис-
исследования решений дифференциальных уравнений и т.д.—
перечень задач, которые решаются средствами комплексного
анализа, можно продолжать довольно долго. К этому надо до-
добавить, что функции комплексного переменного описывают пло-
плоские векторные поля, причем в комплексном анализе особо вы-
выделяются функции, которым соответствуют поля, наиболее ин-
интересные для приложений — одновременно потенциальные и
соленоидальные. Поэтому комплексный анализ находит много-
многочисленные применения в самых разных областях.
Одной из отличительных и привлекательных черт комплекс-
комплексного анализа является его подлинная комплексность. В нем со-
сочетаются аналитические и геометрические, вполне классические
и самые новые методы. Наряду с очень конкретными и при-
прикладными в нем решаются весьма общие и абстрактные задачи.
В комплексном анализе встречаются и разные разделы ма-
математики, и разные прикладные науки. Его понятия служат
основной моделью, источником и отправным пунктом многих
исследований в функциональном анализе, алгебре, топологии,
алгебраической и дифференциальной геометрии, уравнениях с
частными производными и других разделах математики.
Начальные идеи комплексного анализа возникли во второй
половине 18-го века, и связаны они прежде всего с именем Лео-
Леонарда Эйлера. Основной массив теории был создан в 19-м веке,
главным образом трудами Огюстена Коши, Бернарда Римана
и Карла Вейерштрасса. В наши дни более классическая часть
комплексного анализа — теория функций одного комплекс-
ПРЕДИСЛОВИЕ 9
ного переменного — приобрела уже вполне совершенный вид.
Однако и здесь постоянно возникают нерешенные проблемы как
в связи с новыми постановками математических задач, так и
в связи с приложениями. В более молодой части — теории функ-
функций нескольких комплексных переменных — имеется еще
довольно много белых пятен. Но эта область, особенно богатая
связями со многими разделами современной математики, все
больше и больше привлекает к себе внимание.
По-видимому, наступило время, когда изучающие комплекс-
комплексный анализ должны знакомиться с основами теории функций
не только одного, но и нескольких комплексных переменных.
Эти две части, однако, наряду с общими (сравнительно элемен-
элементарными) свойствами имеют ряд свойств, принципиально отли-
отличающих их друг от друга. Поэтому, по крайней мере на сегод-
сегодняшнем уровне развития науки, их лучше изучать последова-
последовательно, а не параллельно. В Московском университете эта цель
достигается введением наряду с обязательным курсом так на-
называемого основного спецкурса, который должны прослушать
студенты, специализирующиеся в области теории функций.
В литературе имеется много превосходных курсов теории
функций одного комплексного переменного, в последние десяти-
десятилетия появился и ряд руководств по теории функций несколь-
нескольких комплексных переменных. Однако единого изложения двух
частей комплексного анализа еще нет, и эта книга является
первым опытом такого изложения. Она возникла из лекций
читанных автором в Московском университете, причем первая
часть относится к обязательному курсу, а вторая — к основному
спецкурсу. Книга задумана так, что многие ведущие идеи вто-
второй части сначала появляются в первой части, где они иллю-
иллюстрируются на более простом материале функций одного пере-
переменного 1).
Каждая глава сопровождается некоторым количеством за-
задач. Среди них нет упражнений, призванных закрепить навыки
1) Несколько слов по поводу названия книги. Автор отдает себе отчет
в том, что термин «комплексный анализ» у нас не принят. Однако в приня-
принятой терминологии книга должна была бы носить длинное и неблагозвучное
название «Введение в теорию функций одного и нескольких комплексных
переменных».
Ю ПРЕДИСЛОВИЕ
использования методов комплексного анализа, поэтому их на-
набор нисколько не заменяет задачника. Имеются задачи двух
видов — сравнительно нетрудные, иллюстрирующие изложенный
в книге материал, и задачи, в которых формулируются не во-
вошедшие в книгу теоремы; последние иногда снабжаются лите-
литературными указаниями. Резкого разграничения между этими
двумя видами задач умышленно не делается.
Идею написать эту книгу мне подал А. О. Гельфонд, кото-
которому, однако, не довелось увидеть ее готовой. А. А. Гончар про-
просмотрел рукопись и сделал много конкретных замечаний. Ряд
полезных советов дали мне В. С. Владимиров, Б. Я. Левин и
А. И. Маркушевич, В. А. Зорич помог в подборе задач. Этим
моим коллегам я весьма признателен. Особенно многим я обя-
обязан редактору книги Е. М. Чирке, который внимательно прочи-
прочитал рукопись и помог устранить ряд недочетов. Ему принадле-
принадлежит также изложение п. 39 второй части и подбор большинства
задач.
ЧАСТЬ I
ФУНКЦИИ
ОДНОГО ПЕРЕМЕННОГО
ГЛАВА I
ГОЛОМОРФНЫЕ ФУНКЦИИ
Начнем с описания комплексных чисел и действий над ними.
Мы предполагаем, что читатель знает их, и поэтому наше опи-
описание будет кратким, с упором на особенности, нужные для
дальнейшего изложения.
§ 1. Комплексная плоскость
1. Комплексные числа. Рассмотрим множество С упорядо-
упорядоченных пар действительных чисел z= (х, у) или, что то же са-
самое, точек декартовой плоскости хОу или (свободных) пло-
плоских векторов. Два вектора г1=(х1, </i) и z2= (х2, у2) считаются
равными (Zi=z2) в том и только том случае, если Xi = x2 и
yi=y2, векторы z=(x, у) и I = (х, —у), которые изображаются
точками, симметричными относительно оси х, назовем сопря-
сопряженными. Вектор (х, 0) отождествим с действительным чис-
числом х; совокупность всех действительных чисел (ось х) обозна-
обозначим через R. Для действительных чисел и только для нихг = г.
На множестве С введем совокупность алгебраических опе-
операций, превращающих С в поле. Сложение и умножение на
действительное число (скаляр) Я введем так же, как в вектор-
векторном исчислении. После этого мы сможем представить каждый
элемент ге С в так называемой декартовой форме:
г = х ¦ \ + у ¦ i== x + iy, A)
где через 1 = A, 0) и i= @, 1) обозначены единичные векторы
(орты) соответственно осей х и у (обозначение первого орта
опускается).
Умножение в векторном исчислении вводят двумя спосо-
способами: паре векторов zi = xi + iy1 и z2=x2 + iy2 ставят в соответ-
соответствие скалярное произведение по формуле
(zlt z2)=xlx2+yly2, B)
а также векторное произведение по формуле
. C)
') В общем случае векторное произведение двух векторов является вектором,,
перпендикулярным к плоскости перемножаемых векторов. Однако в случае
плоского вектора поля, который только и рассматривается здесь, все вектор-
векторные произведения коллинеарны и поэтому вполне описываются скаляром C).
14 голоморфные функции [гл. г
Но, как хорошо известно, ни одно из этих умножений не удовле-
удовлетворяет аксиомам поля. Поэтому мы введем в С иное умноже-
умножение. Именно, положим по определению i-i=i2 = — 1 и назовем
произведением z^zi вектор, который получается, если перемно-
перемножить Xi + it/i и x2 + iy2 как двучлены по обычным законам ал-
алгебры и положить /2 =—1. Иными словами, по определению по-
положим
D)
(соотношение г'2=—1 получается отсюда как частный случай).
Очевидно, что это произведение выражается через скалярное и
векторное по формуле
(zi, z2)+i[zu z2\ E)
где zi=Xi — iyi — вектор, сопряженный zt.
Мы предполагаем известным, что введение описанных опе-
операций сложения и умножения превращает множество С в поле,
которое называется полем комплексных чисел; его элементы —
векторы z = x+iy— называются комплексными числами. Таким
образом, комплексное число z={x, у) представляет собой упо-
упорядоченную пару, комплекс, составленный из действительных
чисел х и у, которые (в дань исторической традиции) соответ-
соответственно называются действительной и мнимой частью числа z и
обозначаются символами
x = Rez, y — lmz. F)
Числа г= @,у), действительная часть которых равна 0 (в дань
той же традиции), называются мнимыми.
Введенная выше декартова форма A) записи комплексного
числа удобна для выполнения операции сложения (и обратной
к ней операции вычитания). Однако, как видно из D), умноже-
умножение (и деление) выполняется в этой форме довольно громоздко.
Для последних операций (а также для возведения в степень и
извлечения корня) удобнее полярная форма комплексного
числа:
2=r(cos ф+г sin ф), G)
которая получается из B) переходом к полярным координатам
(в такой форме можно представить любое комплексное число
гФО). Полярные координаты комплексного числа z=x + iy —
полярный радиус г = У х2 + у2 и полярный угол ф, т. е. угол ме-
между положительным направлением оси х и вектором z, соот-
соответственно называются его модулем и аргументом и обозна-
обозначаются символами
т=\г\, <p=Argz; - (8)
§ 1] КОМПЛЕКСНАЯ ПЛОСКОСТЬ 15
модуль определяется однозначно, а аргумент — с точностью до
слагаемого, представляющего собой целое кратное 2л. Для про-
простоты письма введем сокращенное обозначение:
cos qp-W sin (f = ei(f (9)
(мы пользуемся здесь тем, что действие возведения числа в
мнимую степень не определено1) и поэтому принятый символ
вакантен), тогда полярная форма G) примет компактный вид:
z = reif. A0)
Пользуясь элементарными формулами тригонометрии и опреде-
определением умножения D), мы получим соотношение
/е'"ф'г2е'ф2 = rir2e' «Pi+<fc>, A1)
которое показывает естественность принятого сокращенного
обозначения (9). Соотношение A1) гласит, что при умножении
комплексных чисел их модули перемножаются, а аргументы
складываются. Так же просто выражается в полярной форме и
операция деления комплексных чисел:
??!!!=-О.еЧФ.-Ф.) A2)
гге142 г2
(если, конечно, ГгфО).
В некоторых вопросах удобно компактифицировать
множество комплексных чисел С. Это делается добавлением
к нему идеального элемента, который называется бесконечной
точкой z — oo. В отличие от конечных точек (гфоо) бесконеч-
бесконечная точка не участвует в алгебраических действиях. Компакти-
Компактифицированную плоскость комплексных чисел (т. е. плоскость С,
пополненную бесконечной точкой) мы будем называть замкну-
замкнутой плоскостью и обозначать символом С. Когда нужно под-
подчеркнуть различие, будем называть С открытой плоскостью.
Описанную компактификацию можно сделать наглядной,
если вместо изображения комплексных чисел точками плоско-
плоскости воспользоваться их сферическим изображением. Для
этого выберем в трехмерном евклидовом пространстве прямо-
прямоугольную декартову систему координат ?, ц, ?, оси 8 и ц кото-
которой соответственно совпадают с осями х и у, и рассмотрим
в этом пространстве сферу
5:
') В п. 12 мы введем это действие и докажем, что формула (9), в кото-
которой справа стоит мнимая степень числа е (основания натуральных логариф-
логарифмов), действительно имеет место.
16
ГОЛОМОРФНЫЕ ФУНКЦИИ
ГГЛ. I
диаметра 1, касающуюся плоскости (х, у) в начале координат
(рис. 1). Каждой точке z(x, y)<^C поставим в соответствие
точку Z(|, ц, ?) пересечения с 5 луча, соединяющего «северный
полюс» N@, 0, 1) сферы с точкой г.
Такое соответствие z—*Z называется стереографической
проекцией. Подставляя уравнение луча Nz (l = tx, ц — ty,
?=1—t) в A3), мы найдем, что в точке пересечения луча со
ф A |2) 1
сферой
и получим урав-
р
нения стереографической проекции
6 =
1 + I г
1 + 1 г I2
(И)
Из последнего уравнения находим, что
узл—\Т ~ 1 ~ ?> и тогда из первых
двух получаем формулы для обрат-
обратного отображения:
г/=А- A5)
X = ¦
1-Г
Рнс.
Из A4) и A5) видно, что стерео-
стереографическая проекция z —* Z уста-
устанавливает взаимно однозначное соответствие между точками
С и S\A/ (очевидно, что точке N не соответствует ни одной
точки z). Условимся считать, что N соответствует бесконеч-
бесконечной точке 2= оо, и тем самым установим взаимно однозначное
соответствие С и S; обычно мы будем отождествлять С со сфе-
сферой S, которая называется сферой комплексных чисел или сфе-
сферой Римана. Открытую плоскость С можно отождествлять
с S\A/ — сферой с выколотой точкой N (северным полюсом).
В соответствии с двумя описанными способами геометриче-
геометрического изображения комплексных чисел мы введем на множе-
множестве С две метрики. Первая из них — обычная евклидова ме-
метрика, в которой под расстоянием между двумя точками z4 =
= Xi + iyi и z2=X2 + iy2 из С понимается
| z2 - zx | = V(x2 - xxf + (y2 - yxf. A6)
Во второй — сферической метрике — под расстоянием между Z\
и z2 понимается евклидово расстояние (в пространстве |, ц, ?)
между их сферическими изображениями. После несложных вы-
выкладок с использованием формул A4) мы найдем сферическое
расстояние между двумя точками zt, г2е С:
§ 1J КОМПЛЕКСНАЯ ПЛОСКОСТЬ 17
Эту формулу можно распространить и на множество С, по-
положив •)
'<*• ~>-FfW- <18>
Очевидно, для любых zit ZjeC имеем p(zltz2)^ 1. Легко прове-
проверить, что введение каждой из этих двух метрик превращает
множество С в метрическое пространство, т. е. что при этом
удовлетворяются обычные аксиомы расстояния2). В частности,
аксиома треугольника для метрики A6) равносильна известному
неравенству
' A9)
В заключение отметим, что на ограниченных множествах
MczC, принадлежащих фиксированному кругу {|z|-^!#}, ?> < оо,
евклидова и сферическая метрики эквивалентны. В самом деле,
если М с {|z|^ R}, то, как видно из A7), для любых точек ги
z2 e M справедливо двойное неравенство
^^,z2)<|z2-z1| B0)
(подробнее об этом см. в следующем пункте). Поэтому сфери-
сферическая метрика обычно применяется при рассмотрении неогра-
неограниченных множеств. Как правило, мы будем рассматривать на
множестве С евклидову метрику, а на С — сферическую.
2. Топология комплексной плоскости. Мы ввели на множе-
множествах С и С метрики, превращающие эти множества в метри-
метрические пространства. Теперь мы введем на рассматриваемых
множествах топологии, соответствующие метрикам. Это де-
делается указанием системы окрестностей.
Пусть е>0—'произвольное число; под г-окрестностыо
UZa = U(zo,e,) точки гоеС (в евклидовой метрике будем пони-
понимать круг радиуса ё с центром в этой точке, т. е. совокупность
точек ге С, удовлетворяющих неравенству
z—zo\<e. A)
Под Ё-окрестностыо точки Zq^ С будем понимать совокупность
точек геС, для которых
рB, zo)<e. B)
') Формула A8) получается из A7), если положить в ней Zi = z, раз-
разделить числитель и знаменатель на г2 и устремить г-2 к со.
2) См Г. Е. Шилов, Математический анализ, Физматгиз, М., 1961,
стр. 25.
2 Б. В. Шабат
18 ГОЛОМОРФНЫЕ ФУНКЦИИ - [ГЛ. I
Формула A8) из п. 1 показывает, что неравенство р(г, со) <е
равносильно неравенству | г | > 1/ —г— 1; следовательно, е-окрест-
ности бесконечной точки на плоскости соответствует внешность
круга с центром в начале координат (пополненная точкой
2= со).
Мы назовем множество Q из С (или С) открытым, если для
любой его точки z0 найдется окрестность Uz принадлежащая
этому множеству.
Легко проверить, что такое введение понятия открытости
превращает С и С в топологические пространства, т. е. что при
этом выполняются обычные аксиомы ').
В некоторых вопросах удобно пользоваться так называе-
называемыми проколотыми окрестностями, под которыми на С и С со-
соответственно понимаются множества точек г, удовлетворяющих
неравенствам
0<|z — 20|<е, 0<p(z, го)<е. C)
В этом пункте мы рассмотрим основные топологические по-
понятия, которыми будем постоянно пользоваться в дальнейшем.
Определение 1. Точка Zo e С (соответственное) назы-
называется предельной точкой множества МаС (соотв. С), если в
любой проколотой окрестности Zq в смысле топологии С (со-
(соотв. С) найдется по крайней мере одна точка из М. Множе-
Множество М называется замкнутым, если оно содержит все свои
предельные точки. Множество, получающееся присоединением
к М всех его предельных точек, называется замыканием М и
обозначается символом М.
Пример. Множество М всех целых чисел {0, ±1, ±2, ...} в С не имеет
предельных точек (и, следовательно, замкнуто). В С оно имеет одну предель-
предельную точку z=oo, не принадлежащую М (М не является замкнутым в С).
В С любое бесконечное множество имеет по крайней мере
одну предельную точку (принцип компактности).
Этот принцип, выражающий полноту сферы комплексных чи-
чисел, можно вывести из аксиомы полноты действительных чисел;
мы опускаем это доказательство. В С принцип компактности
не имеет места (это видно из приведенного выше примера). Он
верен, однако, для бесконечных ограниченных множеств,
т. е. множеств, лежащих в каком-либо круге {|z| <./?}, /?< оо.
Такие множества мы будем называть компактными.
') См. ниже п. 32, а подробнее П. С. Александров, Комбинаторная
топология, Гостехиздат, М., 1947.
§ 1] КОМПЛЕКСНАЯ ПЛОСКОСТЬ 19
Из неравенств B0) п. 1 следует, очевидно, что точка гйф оо
является предельной точкой множества М в топологии С тогда
и только тогда, когда она является предельной точкой М в то-
топологии С. Иными словами, при определении конечных пре-
предельных точек мы можем с равным успехом пользоваться как
евклидовой, так и сферической метрикой. Именно в этом смысле
надо понимать утверждение об эквивалентности этих метрик
в конце п. 1.
Определение 2. Последовательностью {ап} будем назы-
называть отображение в С (или С) множества целых неотрицатель-
неотрицательных чисел (иными словами — функцию целого неотрицательного
аргумента, принимающую комплексные значения). Точку as С
(или С) будем называть предельной точкой последовательности
{ап}, если в любой окрестности а в топологии С (или С) най-
найдется бесконечно много элементов этой последовательности. По-
Последовательность {ап}, имеющую в С единственную предельную
точку а, будем называть сходящейся к а; это будем записывать
так:
lim an = а. D)
П-> оо
Замечание. Между понятиями предельной точки последовательности
{ап} и множества значений {ап} имеется различие. Например, последователь-
последовательность ап = \ (i = 0, 1, 2, ...) имеет предельную точку а—1, а множество {а„},
состоящее из одной точки ап — 1, предельных точек не имеет.
Мы предлагаем читателю доказать следующие утверждения:
1) последовательность {ап} сходится к а тогда и только
тогда, когда для любого е>0 найдется натуральное число N
такое, что для всех п > N выполняется неравенство \ап — а|<8
(если аф оо) или р(ап, а) <е (если а= оо);
2) точка а тогда и только тогда является предельной для
последовательности {ап}, когда существует подпоследователь-
подпоследовательность {cink}> сходящаяся к а.
Комплексное равенство D), вообще говоря, равносильно
двум действительным равенствам. Пусть аф оо, тогда, не огра-
ограничивая общности, можно считать, что и апф оо, и положить
an = otn + tyn, a = a + /p (для бесконечной точки понятия действи-
действительной и мнимой частей не имеют смысла); легко доказать, что
D) равносильно равенствам
liman = a, limpre = p1)- E)
') Для доказательства достаточно воспользоваться соотношением
max (| а„ - а |, | р„ - Р | )< [ ал - а | =
20 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
В случае аФО, Ф оо можно считать, что и апФ0, Ф оо, и по-
положить an = rnel4>n, a = rel<f; тогда D) имеет место, если
limrrt = r, Нтф„ = ф, F)
П-> оо П-> оо
и обратно, если D) имеет место, то имеют место и соотноше-
соотношения F), причем второе — при надлежащем выборе значе-
значений фп1). Если а = 0 или оо, то D) равносильно одному соотно-
соотношению limrn = 0 или Нтг„ = оо (поведение ф„ при этом несу-
П ~> оо п->оо
щественно).
Мы будем пользоваться иногда понятием расстояния между
множествами М и N, понимая под этим нижнюю грань расстоя-
расстояний между любыми парами точек, одна из которых принадле-
принадлежит М, а другая N:
N)= inf p(z', z"); G)
вместо сферической метрики здесь можно, конечно, рассматри-
рассматривать и евклидову.
Теорема 1. Если замкнутые множества М, Ncz С не пере-
пересекаются (Mf]N = 0), то расстояние между ними положительно.
< Пусть, от противного, р(М, N)=0. По определению ниж-
нижней грани существуют последовательности точек г^еУИ и z"n <=
еЛ/ таких, что limp(V, z^) = 0. По принципу компактности по-
П->оо
следовательности z'n и г" имеют предельные точки z' и соот-
соответственно г", причем в силу замкнутости множеств г'еУИ,
z"^N. Переходя в случае надобности к подпоследовательно-
подпоследовательностям, можно считать, что z'n->z', z%->z". По аксиоме треуголь-
треугольника для сферической метрики имеем
p{z , z )^p(z , zn)-t\)[zn, zn)i-p\zn, z у
Но правая часть стремится к 0 при п—> оо; следовательно, пе-
переходя к пределу, получаем, что p(z', z")=0. По аксиоме то-
тождества для той же метрики отсюда следует, что z' = z", а так
как г'еМ, г"еЛ/, то это противоречит условию теоремы, по ко-
которому M{\N = 0y
3. Пути и кривые. Определение 1. Путем у мы будем
называть непрерывное отображение отрезка [а, р] действитель-
действительной оси в С (или С). Иными словами, путь — это комплексно-
значная функция z = z(t) действительного аргумента t, непре-
') Если значения ц>п выбирать произвольно, то {срп} может и не сходиться
при сходимости {On}.
§ 1] КОМПЛЕКСНАЯ ПЛОСКОСТЬ 21
рывная в каждой точке t0^ [а, р] в следующем смысле: для
любого е>0 существует окрестность {fe [a, p]: \t — to\<6],
для всех точек / которой \z(t)—z(t0) | <е (или р[г(/), z(to)]<Ce,
если z(to)= оо). Точки a=z(a) и 6 = z(p) называются концами
пути (если а<Р, то а — началом, a b — концом); путь назы-
называется замкнутым, если z(a)=z(p). Будем говорить, что путь
Y: z — z(t), a ^ t ^ р, лежит на множестве М, если z(t)^M
для всех / е [а, р].
В некоторых вопросах удобно различать понятия пути и кри-
кривой. Чтобы ввести последнее, условимся называть два пути
Yi: z = Zi(/), /e[ai, Pi], и Y2: z = z2(x), x g [a2, P2L
эквивалентными (yi~Y2)> если существует непрерывная воз-
возрастающая функция
такая, что Zi(^) =z2[t@] Для всех t&[ai, Pi]. Нетрудно прове-
проверить, что это отношение удовлетворяет обычным аксиомам экви-
эквивалентности: рефлексивности (y~y)> симметрично-
симметричности (если Yi~Y2> то Y2~Yi) и транзитивности (если
Yi-~Y2 и Y2~Y3, то Yi~Y3)' Мы будем гово- па ^ ,
рить, что путь Y2 получается из yi заменой // > ??
параметра A). ,с
Пример. Рассмотрим пути Yi: z = t, t e [0, 1]; j^j
Y2: г = sin /, / <= 0, i ; Y3: г = cos t, t <
7"
Y4: 2 = sin<, /e[0, я]. '
Рис 2
Множество значений г(^) во всех случаях одинако-
одинаково— это отрезок [0, 1]. Однако лишь Yi — Y2'. пути
уз и Y4 не эквивалентны этим двум и не эквивалентны друг другу — в них от-
отрезок [0, 1] обходится иначе, чем в первых двух (рис. 2). Можно сказать, что
Yi и Y2 эквивалентны пути у$, который получается из уз изменением ориента-
ориентации (об этом см. ниже в п. 14).
Определение 2. Кривой называется класс путей, экви-
эквивалентных в приведенном выше смысле. Иногда, если это не
вызовет недоразумений, мы будем понимать под кривой мно-
множество точек y^ С, которое можно представить как образ от-
отрезка [а, р] при каком-либо непрерывном отображении z=z(t).
В дальнейшем нам придется вводить на рассматриваемые
пути и кривые дополнительные ограничения. Будем называть
путь z=z(t), t e [a, p], жордановым, если отображение z(t):
[а, р]—>С непрерывно и взаимно однозначно. Опре-
Определение замкнутого жорданова пути предоставляется читателю.
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. Г
Путь z(t): [а, р] —>С называется непрерывно дифференци-
дифференцируемым, если в каждой точке / е [а, р] существует непрерывная
производная z'(t) (под производной функции г(^) —x(t) +iy(t)
в точке ^о^(«, р) понимается x'(tQ) +iy'(t0), а в концах от-
отрезка — такая же комбинация соответствующих односторонних
производных). Непрерывно дифференцируемый путь называется
гладким, если г'(/)^=0 при всех ?е[а, р],— это условие вво-
вводится для избежания особых точек. Путь называется кусочно
гладким, если функция z(t) непрерывна на [а, р] и [а, р] можно
разбить на конечное число (замкнутых) отрезков таких, что су-
сужение z (t) на каждый
из этих отрезков опреде-
определяет гладкий путь. Путь
называется спрямляе-
спрямляемым1), если почти всюду
на [ос, р] существует
z'{t), абсолютно интегри-
интегрируемая по Лебегу (т. е.
существует
\\z'{t)\dt =
B)
— длина пути). Всякий
кусочно гладкий путь
спрямляем.
В дальнейшем мы бу-
будем также пользоваться
общепринятыми терминами для описания гладкости функций
(в частности, путей): непрерывную функцию будем называть
функцией класса С0, непрерывно дифференцируемую — функци-
функцией класса С1 и вообще функцию, имеющую в области ее рас-
рассмотрения непрерывные производные до n-го порядка включи-
включительно, будем называть функцией класса Сп.
Пример. Пути у\, Y2 и ^з из предыдущего примера жордановы, Y4 —¦
нет. Окружность г=е", /е [0, 2я], — замкнутый жорданов путь (гладкий);
четырехлепестковая роза z = cos 2teu, te[0, 2я] (рис. 3, а), — замкнутый не-
жорданов (гладкий); полукубическая парабола z=t2(t+i), i^[—1, 1]
(рис. 3,6), — жорданов (непрерывно дифференцируемый кусочно гладкий).
') Всюду в дальнейшем, говоря о спрямляемых путях, мы будем пред-
предполагать, что читатель знаком с соответствующими понятиями теории функ-
функций действительного переменного. Читатели, не знающие этих понятий, вполне
могут обойтись классом кусочно гладких путей.
§ 1] КОМПЛЕКСНАЯ ПЛОСКОСТЬ 23
Путь z = nl+/sin— J, *е , — (рис. 3, в)—жор данов неспр ям ляе-
мый (и, следовательно, не кусочно гладкий).
Такие же ограничения можно ввести и на кривые. Жорда-
нова кривая — это класс путей, эквивалентных некоторому
жорданову пути (так как замены параметров A) взаимно од-
однозначны, то из жордановости пути следует жордановость всех
эквивалентных ему путей).
Определение гладкой кривой требует некоторых уточнений:
мы должны ввести это понятие так, чтобы оно не нарушалось
при замене пути, представляющего эту кривую, любым другим
эквивалентным ему путем. Так как непрерывная и возрастаю-
возрастающая замена параметра A) может перевести гладкий путь в не-
негладкий, то понятие гладкости не инвариантно по отношению-
к таким заменам. Поэтому мы должны наложить на преобра-
преобразование A) дополнительные условия.
Именно, гладкой кривой мы будем называть класс путей,
получающихся из некоторого гладкого пути всевозможными
заменами параметра A), где %{t) ¦—непрерывно дифференци-
дифференцируемая функция с положительной производной. Аналогично мы
будем поступать при определении кусочно гладкой и спрямляе-
спрямляемой кривой. В первом случае мы потребуем, чтобы допустимые
замены параметров были непрерывными и всюду, кроме, быть
может, конечного числа точек, имели непрерывную и положи-
положительную производную (а в исключительных точках имели одно-
односторонние производные). Во втором случае потребуем, чтобы
замены параметров осуществлялись возрастающими абсолютно
непрерывными функциями ').
Иногда мы будем пользоваться и другой, геометрической
трактовкой понятия кривой и тогда понимать под жордановой,
гладкой, кусочно гладкой или спрямляемой кривой множества
точек усС, которые можно представить как образ отрезка
[а, р] при отображениях z=z(t), определяющих соответственно
жорданов, гладкий и т. д. путь.
4. Области. Определение 1. Областью D называется
множество точек С (или С), обладающее следующими двумя
свойствами:
а) для любой точки a^D существует окрестность этой точ-
точки, принадлежащая D (открытость);
') Мы считаем известным, что для спрямляемости пути необходимо и до-
достаточно, чтобы функция z(t) =x(t) +iy(t) имела ограниченное изменение-
(т. е. x(t) и y(t) были с¦ ограниченным изменением), а также что суперпо-
суперпозиция г[?(т)], где z(t)—функция с ограниченным изменением, а *(т)—абсо-
*(т)—абсолютно непрерывная функция, также является функцией с ограниченным из-
изменением. По этому поводу см. Г. Е. Шилов, цит. на стр. 17.
24 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
б) для любых двух точек a, b^D существует лежащий в D
путь с концами а и b (связность).
Точки С, не принадлежащие D, но являющиеся предель-
предельными для ее точек (т. е. такие, что в любой их окрестности
существуют точки, принадлежащие D, и хотя бы одна точка,
не принадлежащая D), называются граничными точками D. Со-
Совокупность всех граничных точек D называется границей этой
области и обозначается символом 3D. Объединение области D
и ее границы 3D совпадает с замыканием D. Точки С, не при-
принадлежащие D и не являющиеся ее граничными точками (т. е,
точки множества С\25— дополнения к В), называются внеш-
внешними точками; для каждой из них существует окрестность, не
содержащая точек D.
Теорема 1. Граница 3D любой области D является зам-
замкнутым множеством.
< Пусть ?0 — любая предельная точка множества 3D; надо
доказать, что ?о е 3D. Возьмем произвольную окрестность U
точки ?о- В U существует точка ? е 3D, и, следовательно, най-
найдется окрестность V точки ?, VczU. В V, а значит и в U, най-
найдутся как точки из D, так и точки, не принадлежащие D. Это
означает, что ?0 — граничная точка D >
В дальнейшем мы будем иногда вводить на границы рас-
рассматриваемых областей некоторые дополнительные условия.
Чтобы их сформулировать, обобщим введенное выше понятие
связности.
Определение 2. Будем говорить, что множество М связ-
связно, если его нельзя разбить на две непустые части Mi и М2 так,
что оба пересечения Л^П-Мг и Л^ПМг пусты. В частности,
замкнутое множество называется связным, если его нельзя раз-
разбить на два непересекающихся замкнутых (и непустых) под-
подмножества. Замкнутое связное множество называют конти-
континуумом.
Свойство множества, выражаемое условие б) из определе-
определения 1 (возможность соединить любые две точки множества
путем, лежащим на этом множестве), называют линейной связ-
связностью. Можно доказать, что любое линейно связное множество
является связным, но обратное, вообще говоря, неверно. Одна-
Однако для случая открытых множеств эти понятия совпадают1).
Пусть множество М несвязно. Максимальные связные под-
подмножества М (т. е. не содержащиеся строго ни в каком другом
связном подмножестве М) называются связными компонен-
компонентами М. Можно доказать, что любое множество является объ-
') Доказательство см. С. С т о и л о в, Теория функций комплексного пе-
переменного, т. 1, М., 1962, стр. 31.
§ 1]
КОМПЛЕКСНАЯ ПЛОСКОСТЬ
25
единением связных компонент (в конечном или бесконечном
числе) '). _
Мы будем называть область DcC односвязной, если ее
граница dD является связным множеством; в противном случае
D называется многосвязной областью. Если число связных ком-
компонент dD конечно, то это число называется порядком связ-
связности области D; если
число таких компонент
бесконечно, D называет-
называется бесконечно связной
областью.
Пример. Множество на
рис. А, а — внутренность лем-
лемнискаты — не является обла-
областью, ибо оно несвязно (но за-
замыкание этого множества связ-
связно). Множество точек, лежа-
лежащих между соприкасающимися
окружностями (рис. 4,6),—
односвязная область (ее гра-
граница— связное множество). На
рис. А, в изображена четырех-
связная область (ее граница
состоит из четырех связных
компонент: окружности, окруж-
окружности с отрезком и двух точек).
Область на рис. А, г— квадрат
{0<х<1, 0<</<1} с выброшенными отрезками
п= 1, 2, ..., — является бесконечно связной.
Иногда мы будем вводить условия иного рода. Мы будем
называть область D жордановой, если ее граница dD состоит
из замкнутых жордановых кривых (в геометрической трактовке
этого понятия). Назовем область D компактной, если суще-
существует круг {\z\<R, /?<oo}, содержащий D. Будем говорить,
что множество М компактно принадлежит области D, если его
замыкание М (в топологии С, т. е. с учетом не только конеч-
конечных, но и бесконечной предельной точки М, если она есть) при-
принадлежит D.
Пример. Прямоугольник йг ~ <] х \ < i, I у\ < у > компактно принад-
принадлежит полосе D = {\ у |<1}, а вдвое более узкая полоса G2=<|(/| < •„-> при-
принадлежит D, но не компактно.
Рис. 4.
31'
') См. Ф. Хаусдорф, Теория множеств, ОНТИ, М.—Л., 1937, стр. 120,
26 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
Компактную принадлежность мы будем записывать симво-
символом Ш (так что М €sD, если MczD). Компактность области D
означает, что D <Ш С.
Далее будет неоднократно использоваться следующая
Теорема 2. Пусть М а С — связное множество и N — его
непустое подмножество. Если N является одновременно и замк-
замкнутым и открытым в относительной топологии1) М, то M = N.
< Пусть, от противного, множество N'=M\N непусто. За-
Замыкание N множества Л/_ в топологии С, очевидно, состоит из
точек его замыкания (N) м в топологии М и некоторого мно-
множества (быть может, пустого), не принадлежащего М. Поэтому
Nf\N'= (Ж)мПА^, а так как JV замкнуто в топологии М, то
(A0m = -'V и, следовательно, N[}N' = N[}N' пусто.
Но так как N и открыто в топологии М, то его дополнение
N' замкнуто в той же топологии (предельные точки N' не могут
принадлежать N в силу открытости последнего, следовательно,
они принадлежат JV'). Поэтому к пересечению N'(\N можно
применить то же рассуждение, что и к Nf]N', следовательно,
N'C\N пусто. Это противоречит определению связности М >
§ 2. Функции комплексного переменного
5. Понятие функции. Определение 1. Говорят, что на
множестве MczC задана функция f, если задан закон, по кото-
которому каждой точке z^M ставится в соответствие комплексное
число w (конечное или бесконечное); обозначения
f: M->C или w=f(z). A)
Согласно этому определению всякая функция однознач-
однозначна (понятие многозначной функции мы введем в гл. III).
Иногда мы будем еще накладывать условие взаимной одно-
однозначности. Функция f: М —* С называется взаимно однознач-
однозначной или однолистной, если она преобразует различные точки
zu z2^M в различные, иными словами, если из равенства
f(zi)=f{z2) следует равенство Zi=z2 (для zi; г2еМ).
Задание / равносильно заданию двух действительных
функций
u = u(z), v = v(z), B)
где и: М —>¦ R и v: M-+ R (мы полагаем z = x + iy и f(z) =
— u + iv). Если еще }фО, Фоо2), то, полагая /(г)=ре**, мы
1) Относительной топологией множества МсС называется топология,
в которой окрестностями точек являются пересечения с М окрестностей
тех же точек в топологии С.
2) Так мы будем писать, если {(г) фО, Ф со для всех г е М,
§ 2] ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 27
можем записать эту функцию в виде двух соотнешений:
p = p(z), ty — ty(z)+2kn (k = 0, ±1, ...) C)
(в точках, где /=0, =оо, функция р = 0 или =оо, а г); не опре-
определена).
Мы постоянно будем пользоваться геометрической иллю-
иллюстрацией понятия функции. Задание B) наводит на мысль ил-
иллюстрировать / в виде двух поверхностей и~и(х,у) nv = v{x, у)
в трехмерном пространстве; однако этот способ неудобен, ибо
он не иллюстрирует пару {и, v) как комплексное число. По-
Поэтому ограничимся представлением о функции f: M.-+C как об
отображении множества М в сферу С .
Чтобы сделать это представление более наглядным, будем
рисовать множества, соответствующие друг другу при рассма-
рассматриваемом отображении. Чаще всего мы будем рисовать коор-
координатные линии (декартовой или полярной системы координат)
и их образы на плоскостях z и ш. Снабдив эти множества чис-
числовыми отметками, мы в простых случаях получим достаточно
хорошее геометрическое представление о функции.
Пример. Функцию
w — z2 D)
в верхней полуплоскости {Im г>0} удобно представить в полярных
(W
координатах. Полагая z=rei<f @<ср<я) и ад = ре'*, мы можем переписать
равенство D) в виде следующих двух:
р=/-2, ф=2Ф E)
(см. правило умножения комплексных чисел в полярных координатах, п. 1).
28
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. I
Из E) видно, что полуокружность {r — rOl 0<ф<я} при рассматриваемом
отображении переходит в окружность с выколотой точкой [р = г0, 0 < ф <
< 2я], а луч {0<г< со, ф = ф0} — в луч {0<р<оо, ф = 2ф0} (рис. 5). Верхняя
полуплоскость Re г>0 переходит в плоскость w с выброшенной положитель-
положительной полуосью. Удобно представить полуплоскость в виде эластичной пленки,
натянутой на две полуоси (положительную и отрицательную, которые шар-
нирно соединены в начале координат) так, что пленка может свободно сколь-
скользить по этим полуосям. Тогда преобразование D)' можно интерпретировать
как деформацию пленки, происходящую оттого, что полуоси складываются
друг с другом.
Отображение D) можно представить и в декартовых координатах в виде
двух равенств:
и=х2 — у2,
F)
(полагаем z = x + iy и w — u + iv и в соотношении w = г2 разделяем дей-
действительные и мнимые части). Положив в F) у=Уо, получим" кривую
Рис. 6.
u = x2—y\, v=2xy0 (je R), соответствующую прямой r/=r/0> —это парабола
¦у\. Лучу
х0
2 2
и = х% - у\
, 0 < у < сю} соответствует дуга параболы
(рис. 6).
Замечание. Мы рассматривали отображение D) в верхней полу-
полуплоскости (хотя оно определено всюду в С) потому, что оно однолистно в
этой области. Во всей плоскости или в любой области D, которая содержит
хотя бы одну пару точек г0 и —г0 (го^0), переходящих в одну точку
иH == Zq, отображение D) неоднолистно и описанные геометрические пред-
представления не столь наглядны.
') Через R+ обозначается совокупность положительных чисел.
§2]
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
29
Иногда пользуются другим способом геометрического пред-
представления функции: в пространстве (х, у, р) рисуют поверхность
p=jf(z)j, которая называется поверхностью модуля или релье-
рельефом функции /. На этой поверхности иногда изображают мно-
множества уровня Argf = const. В простых случаях эти множества
представляют собой линии, и, имея достаточно густую их сетку,
можно составить представление о распределении значений
Рис. 7.
функции / в полярных координатах. На рис. 7 изображена по-
поверхность модуля для функции w — 2.
Перейдем теперь к основному для анализа понятию предела
функции.
Определение 2. Пусть функция f определена в проколо-
проколотой окрестности точки се С; говорят, что число ЛеС является
ее пределом при z, стремящемся к а,
lim f (z) = А, G)
если для любой окрестности UA точки А найдется такая про-
проколотая окрестность U'ay что для всех zef/' значения f(z)
принадлежат UA. Иначе, для любого е>0 найдется б>0 такое,
что из неравенства
0<p(z, а)<б (8)
следует неравенство
p(f(z),A)<E. (9)
Если а, А Ф оо, то (8) и (9) можно заменить неравенствами
0<|г — а\ <б и \f(z) —А\ <е. Если а=оо, Афоо, то их можно
30 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
переписать в виде 6<|z|<oo, \{(z) —А|<е; читатель без тру-
труда распишет эти неравенства и в оставшихся случаях афоо,
Для Афоо мы положим f=u + iv, A=Ai + iA2 и легко убе-
убедимся в том, что равенство G) равносильно двум действитель-
действительным равенствам
lim«(z)'=/41, lim а (г) = Л2. A0)
Если предположить еще, что АфО, и выбрать надлежащим
образом значения argf'), то G) можно переписать в полярных
координатах:
Пт|/(г)| = |Л|, Hmarg/(z)~argA A0')
Так как принятое определение предела функции читается
в точности так, как такое же определение в действительном
анализе, и алгебраические действия над комплексными функ-
функциями проводятся по тем же законам, как над действительными,
то в комплексный анализ автоматически переносятся элемен-
элементарные теоремы о пределах функции в точке (о пределе сум-
суммы и др.) — мы не останавливаемся на их формулировках и
доказательствах.
В некоторых случаях мы будем говорить о пределах функ-
функций по множествам. Пусть дано множество М, имеющее а своей
предельной точкой, и функция /, множество епределения кото-
которой содержит М. Мы будем говорить, что f стремится к А при г,
стремящемся к а по множеству М, и писать
\imf(z) = A, A1)
если для любого е>0 найдется б>0, такое, что для всех
, для которых 0<р(г, а)<б, справедливо неравенство
Л
(),)
Определение 3. Пусть функция / определена в некото-
некоторой окрестности точки ае С; будем называть ее непрерывной
в точке а, если существует
(z) = /(a); A2)
если }(а)фоо, будем говорить о непрерывности в смысле С;
если f(a)=oo — о непрерывности в смысле С (или обобщен-
обобщенной непрерывности).
!) Здееь и далее символом arg w обозначается одно из множества
Arg w значений комплексного числа w; тот же символ применяется и для
обозначения функции arg /(г), геМ.
§ 2] ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 31
По соображениям, о которых мы только что говорили,
в комплексный анализ автоматически переносятся элементар-
элементарные теоремы о функциях, непрерывных в точке (непрерыв-
(непрерывность суммы и др.). — непрерывность здесь надо понимать в
смысле С.
Можно говорить также о непрерывности в точке а по мно-
множеству М, если а является предельной точкой М и предел в ле-
левой части A2) понимается как предел по множеству. Функция,
непрерывная в каждой точке множества М (по М), называется
непрерывной на М. В частности, если f непрерывна в каждой
точке области D, она называется непрерывной в области
(в этом случае она непрерывна в каждой точке D в смысле
определения 3, ибо каждая точка z входит в D вместе с неко-
некоторой окрестностью).
Отметим свойства функций, непрерывных (в смысле С) на
замкнутых (в смысле С) множествах К а С.
1. Любая функция f, непрерывная на множестве К, ограни-
ограничена (т.е. существует постоянная А такая, что \f(z)\ *C А для
всех z e К).
2. Любая функция /, непрерывная на множестве К, дости-
достигает на К своей верхней и нижней грани (т. е. существуют точ-
точки zu z2e=K такие, что |/(г) | < \f(z{) \, \f(z)\>\f(z2)\ для
всех ze/(.
3. Любая функция f, непрерывная на множестве К, равно-
равномерно непрерывна (т. е. для любого е>0 существует б>0 такое,
что |f(zi) — /(z2)|<e, коль скоро zu z2^K и p(zb z2)<6).
Эти свойства доказываются точно так же, как в действи-
действительном анализе, и поэтому на доказательствах мы не остана-
останавливаемся.
6. Дифференцируемость. Пусть функция f = u + iv определе-
определена и конечна в некоторой окрестности точки z0 = x0 + iyo^C
Определение 1. Будем говорить, что f дифференцируе-
дифференцируема в точке z0 в смысле действительного анализа (короче,
в смысле R2), если функции и и о дифференцируемы как функ-
функции (х, у) в точке (х0, у0): дифференциалом f в точке г0 назы-
называется выражение
df = du + idv. A)
Если записать du и dv через частные производные (послед-
(последние существуют в точке z0), то A) можно переписать в виде
df ди , . dv df ди . . ди
где; Ж = Л + 1Ш и а^=^+^-производныеот комплекс-
комплексной функции по действительным переменным. Нам удобно
32 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
переписать формулу для дифференциала еще в одном виде. Рас-
Рассмотрим переменные z — x + iy и z=x — iy; их дифференциалами
будут dz=dx + idy и dz = dx— idy. Отсюда мы находим
dx = -j (dz + dz), dy = -^r (dz — dz)
и, подставляя это в B), после перегруппировки членов полу-
получаем
At д) д]
OZ OZ
где введены обозначения
df 1 / df . df \ \ I ди dv \ i I dv ди
~dz ~ ~2 \~dx l~dy) ~ ~2 \~dx~ + ~~ду) + ~2 \~дх ~ду
иг 2 \дх ^ ду ) 2\дх ду ) "*" 2 \ дх "*" <3i/
Замечание. Представление дифференциала d/ в виде C)
единственно: если df = Adz+B dz, то А=~ и В=-~. В са-
мом деле, подставляя dz=dx+idy и dz = dx — idy, мы полу-
получим, что df= (A + B)dx + i(A — B)dy. Отсюда, как и в действи-
действительном анализе, найдем А + В = -р-, г (Л — В) — -~; решая эту
систему, получим требуемое: Л = j [^ -i-J^j, B=-^{~- +
+'%)¦
Мы вводим основное для всей книги
Определение 2. Функция f называется дифференцируе-
дифференцируемой в точке Zo в смысле комплексного анализа (короче, в смы-
смысле С), если она дифференцируема в г0 в смысле R2 и ее диф-
дифференциал пропорционален dz, т. е. в точке z0
Читателю, незнакомому с комплексным анализом, трудно
оценить сразу важность этого определения — она выяснится по-
постепенно, по мере ознакомления с предметом. Сейчас мы ука-
укажем только, что в отличие от всех предыдущих понятий, кото-
которые представляют собой простой перенос соответствующих по-
понятий действительного анализа, дифференцируемость в смысле
С не сводится к дифференцируемости в смысле R2. Имен-
Именно, дифференцируемость в смысле С требует не только диф-
дифференцируемости в смысле R2, но и выполнения условия E),
которое мы будем называть условием (комплексной) диффе-
дифференцируемости.
§ 2] ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 33
Формулы D) позволяют переписать это условие в виде двух
скалярных равенств:
ди _ ду ди _ _ dv /^.ч
Ж ~ ду ' ~ду~ ~~дх # W
В таком виде условие впервые появилось в работах Ж- Д а-
ламбера и Л. Эйлера и позднее (в более четкой фор-
форме) — у О. Коши иБ. Римана.
Большая ограничительное^ условия комплексной дифферен-
цируемости очевидна: в то время как примеры функций не-
непрерывных, но нигде не дифференцируемых в смысле действи-
действительного анализа, строятся с некоторым трудом (примеры Вей-
ерштрасса или Пеано), нигде не дифференцируемыми в смысле
комплексного анализа оказываются самые «простые» функции.
Например, функция
x + 2iy G)
в смысле С нигде не дифференцируема! В самом деле, для нее
ди
ди , dv п « /^\
-х— — 1, -^— = 2, и первое из условии (о) нигде не выполняется.
Перейдем теперь к рассмотрению производной функции
комплексного переменного. Если f дифференцируема в точке z0
в смысле R2, то ее приращение Af = f(z)—/(^о) в этой точке
можно представить в виде
Af = -g-Az + -J|-Az + o(Az), ' (8)
где Дг = z — z0, Аг = г — г0, а о(Лг) обозначает малую высшего
порядка относительно Дг (т. е. величину, отношение которой
к kz стремится к 0 при Дг—>-0). Полагая Д2=|Дг|е»е, получаем
Дг=|Д2|е"'е и из (8) находим
где ц (Az) = °д стремится к нулю при Аг-^0.
Отсюда видно, что для существования предела отношения
-д^- при Аг -> 0 нужно потребовать, чтобы при стремлении Аг
к нулю величина 0 = argAz стремилась к некоторому пределу ¦&
(рис. 8). Предел -— при таком стремлении Дг к 0 называется
производной по направлению ¦& функции f в точке г0.
Из формулы (9) видно, что эта производная по направлению
dz$ дг дг
3 Б. В. Шабат
34
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. Г
Таким образом, если в точке г0 величина -^
то произ-
производные по направлению в этой точке зависят от направления.
Именно, геометрическим местом (годографом) производных по
направлению -^- в данной точке является окружность с цент-
df
ром -з— и радиусом
df
dz
(см. рис. 8).
Если же / дифференцируема в точке z0 в смысле С, т. е.
df n df
-р- = 0, то эта окружность вырождается в точку -^- и произ-
водные по всем направлениям
/ df \
совпадают они равны -^- .
\ dz I
Определение 3. Произ-
Производной функции f в точке г0
называется
Рис. 8.
если этот предел существует.
Из сказанного выше мож-
можно вывести, что дифференци-
дифференцируемость в смысле С равно-
равносильна существованию производной. Мы, однако, предпочитаем
прямое доказательство.
Теорема. Для того чтобы функция f, определенная
в окрестности точки z0 e С, имела в этой точке производную,
необходима и достаточна дифференцируемость f в точке г0
в смысле комплексного анализа.
•4 Пусть f дифференцируема в точке z0 в смысле С; тогда
она дифференцируема в смысле R2 и ^ = 0 в этой точке. Из
формулы (9) имеем
A/ df
Дг
dz
-~
где г[ —»- 0 при Аг->0; отсюда видно, что существует f'(zo) = -~.
Пусть / имеет в точке z0 производную f'(zQ); тогда для до-
достаточно малых Аг имеем
где т)—»-0 при Az-*0. Таким образом, Af=f'(zo) Az+o(Az), от-
откуда видно, что / дифференцируема в точке z0 в смысле R2 и
§ 2] ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 35
что rff=f (z0) dz, а это и означает дифференцируемость в смы-
смысле С в точке z0 >
Так как производная f'(z), если она существует, не зависит
от направления, то ее можно вычислять, например, в направле-
направлении оси х; мы получим
' ч ' дх дх дх
Определение производной функции комплексного перемен-
переменного совпадает с таким же определением из действительного
анализа, арифметические действия и теоремы о пределах в ком-
комплексном анализе такие же, как и в действительном. Поэтому
в комплексный анализ без всяких изменений переносятся эле-
элементарные правила дифференцирования (дифференцирование
суммы, произведения, частного, сложной и обратной функ-
функции); мы не останавливаемся на их формулировках и доказа-
доказательствах.
В заключение мы должны уточнить сказанное выше о поня-
понятии комплексной дифференцируемости. Строго говоря, диффе-
дифференцируемость в смысле С в одной точке Zo еще не влечет за
собой тех последствий, которые мы имели в виду, говоря о важ-
важности этого понятия, — для этого нужно требовать дифферен-
дифференцируемости в окрестности точки г0. Поэтому мы прини-
принимаем следующее
Определение 4. Функция / называется голоморфной
(или аналитической) в точке zoeC, если она дифференцируема
в смысле С в некоторой окрестности этой точки.
Пример. Функция
/(z)=|z|2=zz, A3)
очевидно, дифференцируема в смысле R2 во всей плоскости С. Однако
-~ — г равна 0 лишь при г—0, поэтому в смысле С она дифференцируема
лишь в точке z=0. Таким образом, функция A3) дифференцируема в смысле
С в точке z=0, но не голоморфна в этой точке.
Мы будем называть функцию f голоморфной на открытом
множестве Qc:C, если она голоморфна в каждой точке этого
множества (для таких множеств, следовательно, понятия голо-
голоморфности и комплексной дифференцируемости совпадают).
Будем говорить, что функция / голоморфна на произвольном
множестве Мс:С, если ее можно продолжить на некоторое от-
открытое множество Q=>M до голоморфной на Q функции.
В частности, голоморфность f в замкнутой области G означает
возможность ее продолжения до функции, голоморфной в более
широкой области D Ш G.
36 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
Наконец, под голоморфностью функции f в бесконечной
точке понимается голоморфность функции <p(z) = n — ] в точ-
точке 2 = 0. Это определение позволяет рассматривать функции, го-
голоморфные на множествах замкнутой плоскости С.
Очевидно, сумма и произведение функций, голоморфных
в области D, также голоморфны в этой области. Поэтому сово-
совокупность всех функций, голоморфных в области D, образует
кольцо, которое мы будем обозначать символом Н (D).
7. Геометрическая и гидродинамическая интерпретация.
Начнем с выяснения геометрического смысла комплексной диф-
ференцируемости. Если функция / дифференцируема в смысле
R2 в точке zeeC, то в окрестности этой точки отображение
w = f(z) можно приблизить с точностью до малых высшего по-
порядка относительно z — z0 аффинным отображением
ди / 1 , ди , ч
" ~ "°= IF ('v ~ Хо) + ~Щ ^ ~ у^>
v ~ v°= 17 (х ~ х°)+ ~д^(У~Уо)>
которое можно записать в комплексной форме '):
w-wo = j^(z-zo) + ^(z-zo) B)
(производные в A) и B) берутся в точке z0). Это отображение
мы будем называть касательным к отображению / в точке z0.
Якобиан отображения f в рассматриваемой точке выра-
выражается через комплексные производные:
/ =
д(и, у)
д(х, у)
дг
1L
дг
C)
(для доказательства проще всего подставить в правую часть
C) выражения -^- и ~ из формул D) предыдущего пункта).
Если /=?0, то касательное отображение B) не вырождено. Эт®
отображение преобразует параллельные прямые в параллель-
параллельные, но, вообще говоря, не сохраняет углы, так что квадраты
переходят в параллелограммы; окружности оно преобразует
в эллипсы.
') Для получения B) достаточно сложить первое уравнение A) со вто-
вторым, умноженным на (, и затем положить х — ха = -^ i(z ~ zo) + (z — z0)],
у— Уо = ~ср- [(г — г0) — (г — г0)]. Заметьте, что это преобразование в точности
повторяет преобразование дифференциала в предыдущем пункте.
§ 2] ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 37
Предположим теперь, что функция / в точке z0 дифферен-
дифференцируема в смысле С. Тогда в этой точке -р- = 0, существует
производная /'(zo) = ~dF и касательное отображение B) прини-
принимает вид
w — wa = f (z0) (z — Zo). D)
Если /'(zo)=?O, то это отображение сводится к растяжению
вектора z — z0 в |/'(z0) | раз и к повороту его на угол argf (z0)
(см. правило умножения комплексных чисел в п. 1). Оно со-
сохраняет ориентацию1) и обладает еще следующими свойства-
свойствами: (а) сохраняет углы, (р) квадраты преобразует в квадраты,
(у) окружности преобразует в окружности. Легко видеть, что
каждое из свойств (а), (Р), (у) влечет за собой остальные два.
Определение. Дифференцируемое в смысле R2 в точке
z0 отображение f называется конформным в этой точке, если
касательное к f в точке z0 отображение сохраняет ориентацию
и обладает одним из свойств (а) — (у). Отображение f: D-*С
конформно в области D, если оно взаимно однозначно и кон-
конформно в каждой точке ге/).
Мы доказали, что если функция / дифференцируема в смы-
смысле С в точке zo и f'(zo)=^=O, то отображение f конформно
в этой точке.
Обратно, пусть отображение f конформно в точке z0. Возь-
Возьмем два вектора: z — zo=l и z — zo=i, касательное отображе-
отображение B) преобразует их соответственно в векторы ~- + -??- и
--¦ лМг- В силу конформности отображения f второй из
них получается из первого поворотом на прямой угол против
часовой стрелки, т. е.
г дг j \ дг дг
Отсюда следует, что в точке z0 мы имеем ¦—- = 0, т. е. суще-
существует f'(zo), а так как касательное к конформному отображе-
отображению не вырождено, то f (z0) фО.
Таким образом, комплексная дифференцируемость функции
f в точке z0 вместе с условием f'(zo)=^0 геометрически означает
конформность отображения f в этой точке.
') Говорят, что аффинное отображение / сохраняет ориентацию, если
оно преобразует любой треугольник г^гз, вершины которого обходятся про-
прой /()/()/()
рру ру ^з, р р д р
тив движения часовой стрелки, в треугольник /(zi)/(z2)/(.Z3) с тем же по-
порядком обхода вершин.
38 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
Замечание. Если отображение g дифференцируемо
в смысле R2 в точке z0, а отображение, касательное к нему
в этой точке, обладает одним из свойств (а) — (у), но меняет
ориентацию на противоположную, то оно называется конформ-
конформным отображением второго рода или антиконформным в этой
точке. Легко видеть, что таким свойством будет обладать ото-
отображение w=f(z), сопряженное к отображению, дифференци-
дифференцируемому в смысле С в точке z0, если 1'(го)ФО.
Функцию w = f(z), сопряженную к голоморфной в некоторой
точке z0 функции f, мы будем называть антиголоморфной в этой
точке. Очевидно, условие антиголоморфности функции g в точ-
точке z0 состоит в том, что g дифференцируема в смысле R2 в не-
некоторой окрестности z0 и что в этой окрестности выполняется
соотношение
?-<>¦ И
Мы видели, что модуль производной f (г0) геометрически
означает коэффициент растяжения, а ее аргумент — угол пово-
поворота отображения, касательного к f в точке z0. Приведем теперь
геометрическую иллюстрацию производной в терминах самого
отображения f (а не касательного к нему). Для этого предпо-
предположим, что производная /' существует и непрерывна ') в ©крест-
ности О точки 20.
Рассмотрим непрерывно дифференцируемый путь у. z = z(t),
t е [а, р], с началом в точке z0 (см. п. 3) такой, что z(tf)e U для
всех t e [а, р]. Отображение f переводит его в путь у*: ш =
— f[z(t)], t e [а, р], также непрерывно дифференцируемый, ибо
по правилу дифференцирования сложных функций
w'(t)=f'[z(t)]-z'(t) F)
существует и непрерывна для всех /е[сс, р]. Обозначим Дг =
— z(t) — z0 и Aw=f[z(t)] — f(zo); так как существует производ-
производная f' (zq) , то существует и
Но так как пути у и у* спрямляемы, то JАз| и \Aw\ при t—*a
представляют собой бесконечно малые, эквивалентные соответ-
соответственно длинам As и As* дуг у и у*, которые отвечают отрезку
[a, t]. Поэтому последнее соотношение можно переписать в виде
|f(zo)| = lim-^-. ¦ G)
') Как мы увидим в дальнейшем, наши требования не независимы: из
существования /' в некоторой окрестности точки г0 следует ее непрерывность
в этой окрестности.
§2]
ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
39
Таким образом, \f (z0) \ геометрически означает коэффи-
коэффициент растяжения длин в точке z0 при отображении f. Как
видно из G), этот коэффициент не зависит от выбора пути с на-
началом в точке г0. Иными словами, все пути с началом zg растя-
растягиваются в этой точке одинаково, т. е. бесконечно малая окруж-
окружность с центром в 20 переходит в кривую, отличающуюся от
окружности с центром в wo=f(zo) на малые высших порядков
(круговое свойство, см. рис. 9).
(z)
(W)
Рис. 9.
Предположим теперь еще, что f'(zo)=J=O, будем считать
и всюду в U, а в качестве у возьмем гладкий путь (т.е.
будем считать z'{t)=hQ для /ё[я, р]); из F) видно, что и соот-
соответствующий путь у* также будет гладким. Тогда углы наклона
к действительным осям хорд Az и Аш при t —* а будут стре-
стремиться соответственно к углам 0 и 8* наклона касательных к у
и у* в точках z0 и до0, т. е. при надлежащем выборе значений
аргументов существуют
lim argAz = 0, lim arg Am» = 8*.
(8)
Положим arg —¦ = arg Am» — arg Az, тогда существует
lim зго!" == эгот г (B i == о G
Таким образом, arg f (z0) геометрически означает угол поворота
пути в точке 20 при отображении f. Из (8) видно, что этот угол
не зависит от выбора пути у с началом в точке г0, все пути
с началом za поворачиваются на одинаковый угол, т. е. угол
между любыми двумя путями у и yi с началом z0 сохраняется
при отображении (свойство сохранения углов, см.
рис. 9).
40
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. I
Выясним теперь гидродинамический смысл комплексной
дифференцируемости и производной. Рассмотрим установив-
установившееся плоскопараллельное течение жидкости. Это означает, что
векторы скорости V этого течения не зависят от времени и оди-
одинаковы во всех точках каждого перпендикуляра к некоторой
плоскости, которую мы примем за плоскость комплексного пе-
переменного z=x+iy (рис. 10). Таким образом, наше поле пол-
полностью описывается плоским векторным полем
V=Vi(x,y)+iV2(x,y). (9)
Предположим, что в окрестности U некоторой точки z0
функции Vi и V2 обладают непрерывными частными производ-
производными. Кроме того, будем счи-
считать, что в этой окрестности поле
(9) потенциально, т. е.
дх
ду
и соленоидально, т. е.
дх
ду
-0 A1)
Рис. 10.
(равенства A0) и A1) справед-
справедливы для всех точек U).
Из условия потенциальности
A0) следует, что в окрестности
U дифференциальная форма Vidx+Vody является точным
дифференциалом некоторой функции ф, которая называется
потенциальной функцией поля. Таким образом, в U имеем
дх
A2)
или, в векторной записи, K=grad ф.
Из условия соленоидальности (И) следует, что и форма
•—V2dx-i-V\dy является точным дифференциалом некоторой
функции \|з, так что в U имеем
* = Ж
ду
A3)
На линии уровня функции \|з имеем d\f = — V2 dx+ Vi dy = 0, т.е.
dy V2
~^="\Г' откуда видно, что эта линия является векторной ли-
') Для плоского векторного поля rot V можно считать скаляром, ср.
сноску на стр. 13.
§ 21 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 41
нией поля V, т.е. линией тока (траекторией частиц жидкости).
Поэтому г|э называется функцией тока.
Построим теперь комплексную функцию
>, A4)
которая называется комплексным потенциалом поля. Сравни-
Сравнивая соотношения A2) и A3), мы видим, что в U выполняются
условия
Они совпадают с условиями комплексной дифференцируемости
F) из п. 6 и, следовательно, показывают, что комплексный по-
потенциал f является функцией, голоморфной в точке z0.
В векторном анализе доказывается, что и обратно, любую го-
голоморфную в точке z0 функцию f = cp + i\|> можно рассматривать
как комплексный потенциал векторного поля V=gradcp, потен-
потенциального и соленоидального в окрестности z0, которое можно
трактовать как поле скоростей некоторого течения жидкости.
Таким образом, голоморфность функции f означает, что эту
функцию можно трактовать как комплексный потенциал пло-
плоскопараллельного установившегося течения жидкости, потен-
потенциального и соленоидального.
Нетрудно выяснить и гидродинамический смысл производ-
производной: имеем
т. е. производная комплексного потенциала представляет собой
вектор, комплексно сопряженный вектору скорости течения.
Пример. Найдем комплексный потенциал бесконечно глубокого тече-
течения над плоским дном, обтекающего препятствие высотой Л, перпендикулярное
к дну. Это плоскопараллельное течение описывается течением в верхней полу-
полуплоскости, обтекающим отрезок длины ft, который без ограничения общности
можно считать лежащим на мнимой оси.
Течение, таким образом, рассматривается в области D, граница dD кото-
которой состоит из действительной оси и отрезка [0, ift] мнимой оси (рис. 11).
Эта граница должна быть линией тока; мы примем ее за линию г|з=О и бу-
будем считать, что всюду в D функция г|з>0. Для отыскания комплексного
потенциала ф-Иф достаточно, следовательно, найти конформное отображе-
отображение D на верхнюю полуплоскость {i|>>0}.
Одну из функций, реализующих такое отображение, можно получить
следующим образом. Отображение г\=г'г переводит D в плоскость с вырезан-
вырезанным лучом Rezi^s—ft2, Imzi = 0 (см. пример в п. 5). Отображение 22=Zi+ft2
сдвигает этот луч в положительную полуось Rez2^0, Im22=0. Если мы
возьмем теперь отображение, обратное к возведению в квадрат:
w ¦
42
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. Г
которое однозначно определено условием 0<arg 22<2я, то в качестве образа
плоскости г2 с вырезанной положительной полуосью мы получим верхнюю
'////////////////777777//
7777777///////////////7/
Рис. 11.
полуплоскость. Остается взять композицию рассмотренных отображений
ш = Vz2 + h2, A7)
и мы получим искомое отображение.
Уравнение линий тока при этом течении мы получим, отделяя действи-
действительные и мнимые части в соотношении (ф + гЧ|зJ= (x+iyJ+h2; для линии
|) = г|)о будем иметь
/ аг
A8)
(соответствие линий тока изображено на рис. 11). Скорость рассматривае-
рассматриваемого течения
1*1
dw
1Г
в бесконечности она равна 1. Можно доказать, что общий вид решений рас-
рассматриваемой задачи
f(z) = VooVz2 + h2, A9)
где t>co>0—скорость течения в бесконечности. Подробнее о применении кон-
конформных отображений в гидродинамике см., например, книгу М. А. Лав-
Лаврентьева и автора •).
§ 3. Элементарные функции
Здесь мы рассмотрим некоторые простейшие классы голо-
голоморфных функций комплексного переменного.
8. Дробно-линейные функции определяются соотношением
w=St> ad-ЬсФО, A)
где а, ..., d — фиксированные комплексные числа, a z — ком-
комплексное переменное; условие ad — ЬсФО накладывается для
') М. А. Лаврентьев и Б. В. Ш а б ат, Методы теории функций ком-
комплексного переменного, «Наука», М., 1965.
§ 31 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 43
того, чтобы исключить случай вырождения в постоянную (при
ad — bc = O числитель A) пропорционален знаменателю). При
с = 0 непременно ёфО и функция A) принимает вид
т. е. обращается в линейную функцию.
Функция A) определена для всех гф , оо (если сфО;
при е = 0 она определена для всех конечных г). Мы определим
d
ее в этих исключительных точках, положив w = oo при z=
С
и ш = — при 2 = oo (в случае с = 0 достаточно положить w = oo
при z=oo). Теперь справедлива
Теорема 1. Дробно-линейная функция A) осуществляет
взаимно однозначное и непрерывное отображение С на С.
* Предполагаем, что сфО, — упрощения в случае с —0 оче-
очевидны. Функция A) определена (однозначно) всюду в С; ре-
решая уравнение A) относительно z:
_ dw-b , .
Z~ a-cw ' KJl>
мы видим, что каждому шф— ,оо соответствует определенное г,
а в силу принятого выше условия точке w =— отвечает
z = oo и w = oo—точка 2 = . Следовательно, A) взаимно
однозначно отображает С на С, остается доказать непрерыв-
непрерывность. Но при гф——, оо непрерывность функции A) оче-
очевидна; непрерывность в этих точках следует из того, что
.. аг + Ь .. аг + b a
hm —-=оо, hm — = —>
d cz + d ^о,, cz + d с
z->
с
Мы хотим теперь доказать, что отображение A) сохраняет
углы во всех точках С. Для гф , оо это следует из того,
что в этих точках существует производная
dw ad — be
dz (cz + df
-Ф0
(см. п. 7). Чтобы установить то же свойство для исключитель-
исключительных точек (из которых обе связаны с бесконечностью: одна
44 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
сама бесконечна, а у другой образ бесконечен), надо ввести
понятие угла в бесконечной точке.
Определение. Под углом в точке z = oo между двумя
путями yi и у2 (проходящими через оо и такими, что их сфери-
сферические изображения имеют касательную в северном полюсе)
понимается угол между образами Ft и Гг этих путей при ото-
отображении
z-+j = Z C)
в точке Z = 0.
Для тех читателей, которые не удовлетворены этим формальным опреде-
определением, мы сообщим геометрические соображения, приводящие к нему. Преж-
Прежде всего докажем, что стереографическая проекция С -> S\JV представляет
собой конформное отображение1).
Рассмотрим в плоскости С гладкий путь у: z = x(t)+iy(t), t e [а, р], и
по формулам A4) п. 1 найдем путь на S, соответствующий ему при стерео-
стереографической проекции:
D)
Путь у*, очевидно, также гладкий, и для квадрата элемента его длины
da из D) получаем
где [ dz\ = Vdx2 + dy2 —соответствующий элемент длины у (ср. с форму-
формулой A7) из п. 1).
Переменные х и у можно принять за координаты на сфере с выколо-
выколотым северным полюсом 5\jV; тогда E) будет служить первой квадратичной
формой на этой поверхности. При этом в стандартных обозначениях (в ко-
которых da2 = E dx2 + 2F dx dy + G dy2) мы будем иметь
откуда и следует конформность стереографической проекции2).
') Под конформностью здесь понимается свойство сохранения углов.
2) В самом деле, угол а между гладкими путями уь Y2eC определяется
по формуле
C0S " =
a угол между их образами на S — по известной из геометрии формуле
cos а* = ——-;— {Е dx\ dx2 + F (dxi dy2 + dyx dx2) + Gdyx dy2);
rfffj da2
из формул G) и F) видно, что в нашем случае cosa*=coscc, т. е. а* = ос.
§ 3] ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 45
Учитывая доказанное, определим угол между путями Yi, Уг<=Св точ-
точке г = оо как угол между сферическими образами Yi> Y2 этих путей в север-
северном полюсе N (предполагается, что Yi и у2 имеют в точке N касательные).
Этому определению можно придать более удобную форму.
Для этого заметим, что преобразованию C) соответствует вращение
сферы. (В самом деле, как видно из формулы A7) п. 1, при этом преобразо-
преобразовании сохраняются сферические расстояния:
а точки S, соответствующие г=±1, — они диаметрально противоположны —
остаются неподвижными.) Поэтому угол в точке N между путями Yi и Уг
равен углу в точке О между путями T'i и Г2, в которые переходят Yi и у2
при этом вращении. Но в силу конформности стереографической проекции
этот угол равен углу в точке 2 = 0 между путями Fi и Гг, в которые пере-
переходят yi и Y2 при отображении C). Таким образом, мы приходим к приня-
принятому выше определению.
Теорема 2. Дробно-линейное отображение A) конформ~
но 1) во всех точках С.
¦« Для неисключительных точек теорема уже доказана.
Пусть yi и Y2 — два пути, проходящие через точку z = и
пересекающиеся в этой точке под углом а (предполагается,
что пути имеют касательные в этой точке). Угол между их
образами yI и у1 пРи отображении A) в точке ш = оо, соот-
соответствующей z = , по определению равен углу между обра-
образами Г* и Г* путей yI и у*2 ПРИ отображении W = — в точке
W = 0. Но
W-
az + b '
и, следовательно, Г* и Г^ можно рассматривать как образы
Yi и Y2 при этом отображении. Так как производная
dW _ be-ad
dz ~ (az+bJ
d
в точке z— существует и отлична от нуля, то угол между
Г* и Г* в точке W=0 равен а. Для точки z = теорема до-
доказана. Чтобы доказать ее для точки г = оо, достаточно приме-
применить то же рассуждение к функции B), обратной к A) >
') Под конформностью в бесконечной точке понимается свойство сохра-
сохранения углов.
46 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
Мы хотим теперь доказать, что совокупность дробно-линей-
дробно-линейных отображений — мы обозначим эту совокупность через Л —
можно рассматривать как группу. Пусть даны два дробно-ли-
дробно-линейных отображения:
их произведением мы назовем композицию отображений L\ и L2,
т. е. отображение
L: z-* LioL2(z).
Отображение L, очевидно, дробно-линейно,
аг + Ь
L: w =
cz + d
(ибо подстановка в выражение Lt вместо z дробно-линейной
функции снова приводит к дробно-линейной функции), и притом
ad— ЬсфО ') (ибо L преобразует С на С, а не вырождается
в постоянную).
Проверим выполнение групповых аксиом.
а) Ассоциативность: для любых трех отображений
Lt, L2, L3eA имеем
Llo(L2oL3) = (LlcL2) oL3. (8)
В самом деле, обе части (8) представляют собой дробно-линей-
дробно-линейное отображение L4 {L2 [L3B)]}. ^>
б) Существование единицы. Единицей, очевидно,
служит тождественное отображение
Е: г-* г. (9)
в) Существование обратного элемента: для
любого LeA существует отображение L~'eA такое, что
L-ioL = LoL-!=?. A0)
В самом деле, обратным элементом для отображения A) слу-
служит обратное к нему отображение B).
Доказана
Теорема 3. Совокупность Л всех дробно-линейных ото-
отображений образует группу, если в качестве групповой опера-
операции рассматривать композицию отображений.
1) В этом можно убедиться и аналитически, если заметить, что
ad — bc= {flidi — b\C\) (a^d^ — 62C2)
§ 3] ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 47
Замечание. Группа Л не коммутативна: пусть, например,
Lt: z-*z+\, L2: z->—; тогда LX°L2: z-* — +\, a l^oL^. z->
1
2+l
9. Геометрические свойства. Приведем два элементарно-
геометрических свойства дробно-линейных отображений. Для
формулировки первого из них условимся называть окружно-
окружностью на С любую окружность или прямую на комплексной
плоскости (при стереографической проекции и тем и другим
соответствуют окружности на сфере Римана); окружности
в собственном смысле будем называть окружностями на С.
Имеет место
Теорема 1. Произвольное дробно-линейное отображение
преобразует любую окружность на С тоже в окружность на С
(круговое свойство дробно-линейных отображений).
< Для случая линейных отображений (с = 0)' утверждение
очевидно, ибо такие отображения сводятся к растяжению с по-
поворотом и сдвигу. Если сфО, то отображение можно переписать
в виде
^йЛ о»
и, следовательно, представить как композицию трех отобра-
отображений:
1
L-, j. Z ^ /\ -\- tjZ) *~/2' ** —^ ' ^*3* ^ —^ ** '
(L — L[O L2 ° L3). Отображения L! (растяжение с поворотом и
сдвиг) и L3 (сдвиг), очевидно, сохраняют окружности на С.
Остается доказать это свойство для отображения
L2: z->±. B)
Для доказательства заметим, что любую окружность на С
можно записать уравнением
Е(х2+у2) +/7iX + /72r/ + G = 0, C)
где, быть может, Е=0, и обратно, любое такое уравнение изо-
изображает окружность на С, быть может, вырождающуюся в
точку или пустое множество1). Переходя к комплексным
') Мы исключаем случай E=Fi=F2=Q = 0.
48 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
переменным z—x+'iy и z=x— iy, т. е. полагая в C) х = -j(z + z),
у = —(z — z), мы переписываем это уравнение в виде
Ezz + Fz + ~F~z + G = 0, D)
где положено F = -j (F{ — iF2), F = -^{Fx + iF2).
Чтобы получить уравнение образа окружности D) при ото-
отображении B), достаточно положить в D) г = —; мы получим
E + Fw + Fw + Gww = Q, E)
т. е. уравнение того же вида, что и D). Случаи вырождения
в точку или пустое множество исключены свойством взаимной
однозначности дробно-линейных отобра-
отображений; следовательно, рассматриваемый
образ является окружностью на С >
Мы видели выше, что произвольная
голоморфная функция /, !'(го)ФО, с точ-
точностью до малых высшего порядка, пре-
преобразует бесконечно малые окружности
с центром в точке z0 в окружности с
центром f(z0). Теорема 1 утверждает,
что дробно-линейные функции точно пре-
Рис. 12. образуют любые окружности на С в
окружности. Легко, однако, видеть на
самых простых примерах, что центр окружности, вообще говоря,
не переходит в центр.
Для формулировки второго геометрического свойства дроб-
дробно-линейных отображений введем
Определение. Точки гиг* будем называть симметрич-
симметричными относительно окружности Г на С, если они лежат на
одном луче с вершиной в центре Г так, что произведение их
расстояний до центра равно квадрату радиуса Г.
Имеем arg(z* — zo)=avg(z— г0) и \z* — zo\\z—го|=/?2
(z0 — центр, R — радиус Г), и, следовательно, симметричные
относительно Г точки связаны соотношением
z*-zo = ==^. F)
z Z
Из рис. 12 ясен способ построения симметричных точек:
если г лежит внутри Г, то достаточно из z провести перпенди-
перпендикуляр к лучу zoz до пересечения с Г в точке ?, а из ? — каса-
касательную к Г до пересечения с лучом в точке z*\ если z лежит
§ 3] ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 49
вне Г, построение производится в обратном порядке (доказа-
(доказательство следует из подобия прямоугольных треугольников zozt,
и zolz*).
Легко устанавливается также следующее свойство, харак-
характеризующее симметричные точки:
(*) Для того чтобы точки z и z* были симметричными от-
относительно окружности Г, необходимо и достаточно, чтобы лю-
любая окружность у на С, через них проходящая, была ортого-
ортогональной Г.
В самом деле, если z и z* симметричны относительно Г,
а у — любая окружность, через них проходящая, то квадрат
длины касательной к у из точки z0
по известной элементарно-геомет-
элементарно-геометрической теореме равен произведе-
произведению секущей |z0 — z*\ на ее внеш-
внешнюю часть |z0 — z\ (рис. 13), т. е.
равен R2; таким образом, касатель-
касательная к у из 20 является радиусом Г, \ \J A,
и эти окружности ортогональны (ее- ^ ^ч. S'
ли у — прямая, то она проходит че-
через 20 и, следовательно, ортогональ-
ортогональна к Г). Обратно, если любая
окружность у на С, проходящая че-
через z и г*, ортогональна к Г (и, в частности, прямая zz*), то,
во-первых, точки z и z* лежат на одном луче с вершиной z0 и,
во-вторых, произведение их расстояний до г0 (по той же эле-
элементарно-геометрической теореме) равно R2; следовательно,
z и z* симметричны относительно Г.
Свойство (*) позволяет переформулировать определение
симметричных точек так, чтобы его можно было применять
к окружностям на С: точки z и z* называются симметричными
относительно окружности Г на С, если любая окружность у, че-
через них проходящая, ортогональна к Г. Очевидно, что в слу-
случае, когда Г представляет собой прямую, это определение совпа-
совпадает с обычным.
Отображение 2—*z*, переводящее каждую точку геС в
точку 2*, симметричную с 2 относительно Г, называется симме-
симметрией относительно этой окружности или инверсией.
Инверсия относительно окружности на С, как видно из F),
осуществляется функцией, сопряженной к дробно-линейной
функции. На основании теоремы 2 предыдущего пункта отсюда
следует, что инверсия является антиконформным отображением
всюду в С.
4 Б. В. Шабат
50 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
(Для случая инверсии относительно прямой это утверждение
очевидно: сдвигом и поворотом переведем эту прямую в действи-
действительную ось, а тогда инверсия сведется к отображению z-*z.)
Теперь желаемое свойство дробно-линейных отображений
получается совсем просто:
Теорема 2. Произвольное дробно-линейное отображение L
преобразует любые точки z и z*, симметричные относительно
какой-либо окружности Г на С, в точки w и w*, симметричные
относительно образа Ь(Г) этой окружности (свойство со-
сохранения симметричных точек).
< Рассмотрим семейство {у} всех окружностей на С, прохо-
проходящих через точки z и z*\ эти окружности ортогональны к Г..
По теореме 1 окружности у преобразуются также в окружЕю-
сти L(y) на С, причем в силу конформности L все окружно-
окружности L(y) ортогональны к L(T). Отсюда следует, что точки до-
и w*, через которые проходят все L(y), симметричны относи-
относительно L(T) J) >
10. Дробно-линейные изоморфизмы и автоморфизмы. В фор-
формулу дробно-линейного отображения
т az + Ь ,п
L: до = —~-т- A)
cz + d v '
входят четыре комплексных коэффициента а, Ь, с и d. Однако
на самом деле отображение зависит от трех комплексных па-
параметров, ибо числитель и знаменатель дроби можно поделить
на один из не равных нулю коэффициентов. Поэтому естественно
ожидать, что при помощи дробно-линейного отображения можно
единственным образом преобразовать три заданные точки в три
заданные. Имеет место
Теорема 1. Каковы бы ни были три различные точки z\,
z2, 23еСи три различные точки wit до2, t»3eC, существует, и
притом только одно, дробно-линейное отображение L, L(zk) =wh,
?=1,2,3.
¦* Существование отображения L доказывается легко: строим
дробно-линейные отображения Li и L2, преобразующие zu z2, z3
и wu Дог. w3 соответственно в точки 0, оо, 1 плоскости ?:
w3 — шг . /q\
гсз-ш, ' W
J • 7"
1- Ь
отображение
Z — Z\
z-z2
Z3
г3
— г2
-zi
L
т
2-
= L<z о
b
и
w
w
— Ш]
— w2
C)
') Заметим, что всякая окружность, проходящая через ш и w*, ортого-
ортогональная L<X), является образом некоторой окружности из семейства {у}.
§ 3] ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 51
которое определяется как функция w = w(z) из соотношения
Z — Zj _ Z3-Z2 _ W-Wj _ W3 — Ш2 , .,
z — z2 Z3 — zx w — w2 w3 — wi' ^ '
и есть искомое. В самом деле, оно, очевидно, дробно-линейное
и преобразует точки zh в wh (k=l, 2, 3).
Докажем единственность этого отображения. Пусть К,
X(zk)=wh (&=1, 2, 3), будет какое-либо дробно-линейное ото-
отображение. Рассмотрим отображение ц = Z.2 ° А, о Li, где L4 и L2
определяются по формулам B); очевидно, ц будет дробно-ли-
дробно-линейным отображением, оставляющим точки 0, оо и 1 неподвиж-
неподвижными. Из условия jj,(oo)=oo следует, что ц — целая линейная
функция: ц(?)=сс?+|3; но из условия j,i @) = 0 получаем, что
C = 0, а из цA) = 1 — что а=1. Таким образом, |i(?) = ?;, т. е.
Li о Я. о L~\ = Е, откуда по групповым законам получаем, что
Я = Li' ° L\ или, согласно C), X = L >
Замечание. Каждая точка zfe и wh входит в соотноше-
соотношение D) дважды, один раз в числителе, другой — в знаменателе.
Читатель может убедиться в том, что это соотношение сохра-
сохраняет силу, когда одна из точек Zk пли wk (или одна zh и
одна wh) является бесконечной: нужно только числитель и зна-
знаменатель дроби, где появляется эта точка, заменить единицей.
Например, в случае Zi=Ws= оо формула принимает вид
1 г3 — z2. w — w\ I
z — z2 1 w — ш2 1
Таким образом, теорема 1 сохраняет силу для точек замкнутой
плоскости.
На основании доказанной теоремы и кругового свойства
(п. 9) можно утверждать, что любую окружность Г на С можно
преобразовать дробно-линейным отображением в любую дру-
другую окружность Г* (достаточно перевести три точки Г в три
точки Г* и воспользоваться круговым свойством). Из тополо-
топологических соображений ясно, что круг В, ограниченный Г, пере-
переходит при этом в один из двух кругов, ограниченных Г* (чтобы
узнать в какой, достаточно выяснить, куда переходит какая-
либо точка гоеВ). Отсюда легко вывести, что любой круг
ВсСможно дробно-линейным преобразованием отобразить на
любой другой круг В*сС.
Дробно-линейное отображение области D на D* мы будем
называть дробно-линейным изоморфизмом, а области D и D*,
для которых такой изоморфизм существует, — дробно-линейно
изоморфными. Только что высказанное утверждение можно
сформулировать так.
4*
52
ГОЛОМОРФНЫЕ ФУНКЦИИ
ГГЛ. Г
Теорема 2. Любые два круга на замкнутой плоскости.
дробно-линейно изоморфны.
Найдем для примера все такие изоморфизмы верхней полу-
полуплоскости {Imz>0} на единичный круг {|ш>|<1}. Использование
теоремы 1 привело бы к некрасивой формуле, поэтому будем
поступать иначе. Фиксируем точку a, Ima>0, которая перехо-
переходит в центр круга w = 0. Точка а, симметричная а относительно
действительной оси, по теореме 2 предыдущего пункта должна
переходить в точку w— оо, симметричную да = 0 относительно
окружности {| до | = 1}. Но точками, которые переходят в нуль и
бесконечность, дробно-линейная функция определяется с точ-
точностью до постоянного множителя; поэтому искомое отобра-
отображение должно иметь такой вид: w — k
z — a\ = \z
поэтому
При действительных z=x имеем \ у
для того, чтобы ось х переходила в единичную окружность, надо
взять |&| = 1, т. е. k — eie. Таким образом, все дробно-линейные
изоморфизмы верхней полуплоскости {Imz>0} на единичный
круг {| w | < 1} определяются формулой
w —
E)
где а — произвольная точка верхней полуплоскости (Ima>0),
а б — произвольное действительное число.
Отображения E) зависят от трех действительных параме-
параметров: 0 и двух координат точки а, переходящей в центр круга.
¦iff
(VJ)
Рис. 14.
Геометрический смысл 6 ясен из замечания, что точка г= оо
при отображении E) переходит в w=eiQ. Изменение этого па-
параметра сводится к повороту круга. На рис. 14 изображены
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
53-
сетка декартовых координат в плоскости z и ее образ при ото-
отображении E).
Дробно-линейный изоморфизм области на себя мы будем
называть дробно-линейным автоморфизмом. Очевидно, что со-
совокупность всех дробно-линейных автоморфизмов какой-либо
области образует группу, которая является подгруппой группы Л
всех дробно-линейных отображений.
Совокупность всех дробно-линейных автомоморфизмов.
С->С, очевидно, совпадает с группой Л. Также очевидно, что
совокупность дробно-линейных автоморфизмов С—>С совпадает
с подгруппой (целых) линейных преобразований г—*az+b. Вы-
Вычислим в заключение группу автоморфизмов единичного круга.
Фиксируем точку а, |а|<1, переходящую в центр круга
ш = 0. Точка а*—1/а симметричная с а относительно окружно-
окружности (|г|=1), должна переходить в точку w= oo; поэтому иско-
искомое отображение должно иметь вид
, z — a , z — a
W = k т- = й, ,
3 -~~ ~тг
а
1 — az
где k и ki — некоторые постоянные. Так как точка z = l перехо-
переходит в точку единичной окружности, то должно быть)й] ' ~а
1-а
(Z)
(ш)
Рис. 15.
= |^i |=1, т. е. ki — e*®, где Э — действительное число. Следо-
Следовательно, искомое отображение должно иметь вид
w ¦¦
l-az '
С другой стороны, очевидно, что любая функция вида F)
где |а|<1 и 6 — действительное число, осуществляет дробно
54 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. Г
линейное отображение единичного круга {|z|<l} на единичный
круг {|до|<1}. На рис. 15 изображен прообраз сетки полярных
координат плоскости w. Он состоит из двух семейств: дуг ок-
окружностей, проходящих через точки аи а* = — (прообраз лу-
лучей), и окружностей, имеющих эти точки симметричными (про-
(прообраз окружностей).
Таким образом, группа дробно-линейных автоморфизмов
единичного круга вычислена. Она зависит от трех действитель-
действительных параметров: двух координат точки а и числа 0.
П. Некоторые рациональные функции.
1. Степенная функция
w=*z", A)
где п — натуральное число, голоморфна во всей плоскости С.
Ее производная -~^ = nzn~x ПРИ «>1 отлична от нуля всюду
при гФО, следовательно, отображение A) при л>1 конформно
в каждой точке ге С\{0}. Записывая функцию A) в полярных
координатах z = reiff, w = pef^:
9 = гп, ф = mp, B)
мы видим, что осуществляемое нашей функцией отображение
увеличивает в п раз углы с вершиной з точке 2 = 0 и поэтому
при я>1 не конформно в этой точке.
Из B) видно также, что любые две точки zt и z2 с одинако-
одинаковыми модулями и с аргументами, отличающимися на целое
кратное 2я/п:
|z,| = |z2|, argz, = arg;z2 + /e-^ C)
(и только такие точки), при отображении A) «склеиваются»,
т. е. переходят в одну точку до. Следовательно, при л>1 это
отображение неоднолистно в С. Для однолистности его в неко-
некоторой области DczC необходимо и достаточно, чтобы D не со-
содержала никаких двух различных точек Zi и г2, связанных соот-
соотношениями C) Ч.
Примером области, в которой отображение A) однолистно,
может служить сектор
Этот сектор гомеоморфно преобразуется в область D* =
!) Область однолистности функции A) при «>1 не может содержать
точку г=0, ибо в любой окрестности 2=0 имеются различные точки, свя-
связанные соотношениями C).
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
55
= {0<arg ш<2я}, т. е. в плоскость до с выброшенной положи-
положительной полуосью. На рис. 16 показано соответствие сеток по-
полярных координат при этом отображении.
\
Рис. 16.
fw=Zs)
Если мы возьмем в плоскости г по-прежнему полярные ко-
координаты 2=rei(P, а в плоскости w — декартовы w = u + iv, то
отображение A) перепишется в виде следующих двух соотно-
соотношений:
u = rn cos mp, v = rn sin mp. D)
На рис. 17 показан прообраз сетки декартовых координат
У/Л
с
У//л\ Y//\ Y//A Y//A
Рис. 17.
плоскости ш при этом отображении. Он составлен из кривых с
полярными уравнениями г =
(пунктирные линии)
56 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
л
г = у ^° (сплошные). При я=2 это обычные гиперболы
х2 — у2=и0 (пунктир) и 2xy = v0 (сплошное линии). В силу кон-
конформности отображения сетка ортогональна, т. е. пунктирные
линии ортогональны сплошным.
2. Функция Жуковского. Так называют рациональ-
рациональную функцию
w-Uz + Ц, E)
2ГТ7
голоморфную в области С\{0}. Ее производная
dw
dz
отлична от нуля всюду в этой области, кроме точек z= ±1, от-
откуда видно, что отображение E) конформно в каждой конеч-
конечной точке гфО, ±1. Точке 2 = 0 соответствует w— oo, и конформ-
конформность в этой точке согласно определению угла в бесконечности,
принятому в п. 6, следует из того, что производная
1A).
dz \ w I
1 _ ~2
отлична от нуля при 2=0. Согласно тому же определению
конформность отображения w — f(z) в точке 2=оо сводится
к конформности w = f\ — \ в точке 2 = 0; но в случае функции
Жуковского f(z)~fi—j, и по только что доказанному ото-
отображение E) конформно в точке 2 = оо. Ниже мы увидим, что
в остальных исключительных точках г=±1 отображение E) не
конформно.
Выясним условия однолистности нашей функции в какой-
либо области D. Пусть г{ и 22 она переводит в одну точку,
тогда
и при 2i=^=22 мы получаем 2iZ2=l. Таким образом, для одно-
однолистности функции Жуковского в какой-либо области D необ-
необходимо и достаточно, чтобы она не содержала никакой пары то-
точек Z\ и 22, для которых ')
l. F)
') Область однолистности функции Жуковского не может содержать то-
точек ±1, ибо в любой окрестности этих точек существуют различные точки,
¦связанные соотношением F).
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
57
Примером области, удовлетворяющей условию однолистно-
однолистности, является внешность единичного круга О={геС: |г|>1}.
Чтобы наглядно представить отображение E), положим z = reilf,
w = u + iv и запишем E) в виде
1 / м
и = -п [г + — cos<p
Z\ Г/
1 / 1 \ .
p, v = -z \r-~ sinf.
G)
Из этих соотношений видно, что окружности {|z| = r0}, го>1,
функция Жуковского преобразует в эллипсы с полуосями
Рис. 18
«л, = тт (г0 Н ) и bra=-z(rQ 1, с фокусами в точках ±1
(ибо av0 — b% = 1 для любого г0). Эти эллипсы изображены на
рис. 18 сплошными линиями; при го->1 имеем 6Го->О и
эллипсы стягиваются к отрезку [—1, l]czR; при больших г0
разность аГо — Ьг„ —— мала и они мало отличаются от окруж-
окружностей. Лучи {ф = ф0, 1<г<оо} преобразуются в части гипер-
М2 V2
бол —5 :-j— = 1 с теми же фокусами ±1 (пунктирные
COS2 ф0 Sin2 фо J V J f
ф0 фо
линии на рис. 18); в силу конформности семейство этих гипер-
гипербол ортогонально описанному выше семейству эллипсов.
Из сказанного видно, что функция Жуковского осуществляет
взаимно однозначное и конформное отображение внешности
единичного круга (включая бесконечную точку) на внешность-
отрезка [—1, 1] действительной оси.
58
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. Т
В точках г = ±1 отображение E) не конформно. В этом
лучше всего убедиться, представив функцию Жуковского в виде
w —:
w + .
(8)
(тождественность этой формулы формуле E) проверяется про-
простой выкладкой). Отображение E), следовательно, представляет
собой композицию отображений
г- 1
z+1 '
со = i
(9)
(последнее отображение обратно к отображению
(w)
Рис. 19.
Первое и третье из отображений (9) дробно-линейны и по до-
доказанному в п. 8 конформны
всюду в С; отображение со = ^2
удваивает углы в точках ?=0
J» и С—°°. которым соответству-
соответствуют точки г=±1. Поэтому ото-
отображение Жуковского удваи-
удваивает углы в этих точках.
Используя разложение (9),
читатель убедится в том, что
функция Жуковского . осуще-
осуществляет однолистное конформное отображение внешности
окружности у. изображенной на рис. 19 (она проходит через
точки ±1 и составляет в них угол а с действительной осью), на
внешность дуги окружности (с концами в точках ±1, составляю-
составляющей в точке w — \ угол 2а с действительной осью) ').
Можно убедиться также в том, что окружности, касающиеся
Y извне в одной из точек ±1, при этом отображении переходят
в замкнутые кривые с характерным острием, напоминающие
профиль крыла самолета (см. рис. 19). Это замечание позво-
позволило Н. Е. Жуковскому создать первый метод аэродина-
аэродинамического расчета крыльев.
12. Показательная функция. Мы определим функцию ег тем
же предельным соотношением, которым она определяется в дей-
действительном анализе:
A)
') Случай а = —- уже разобран выше другим способом.
$ 3) ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ *"~ 59
Докажем существование этого предела для любого гЕС;
для этого положим z=x+iy и заметим, что по правилам воз-
возведения в степень
К'+т
п
О у у2 _]_ y2 \ n
п /г
= п arctg
Отсюда видно, что существуют
Hml+4
П
lim arg 11 +
а значит, существует и предел A), который записывается в три-
тригонометрической форме так:
е*+*у=е*(cos у + i sin у). B)
Таким образом,
1ег|=еНег, argez = Im2. C)
Полагая в B) х = 0, мы получим формулу Эйлера
e"J = cos y + i sin у, D)
которой неоднократно пользовались. Однако до сих пор сим-
символ eiy мы употребляли для сокращенного обозначения правой
части, а теперь можем понимать его как мнимую степень
числа е.
Перечислим основные свойства показательной функции.
1°. Функция ег голоморфна во всей плоскости С. В самом
деле, полагая ez = u + iv, находим из B), что u — excosy,
v = ex sin у; функции и и v дифференцируемы в смысле R2 всюду
в С, и всюду в С выполняются условия комплексной дифферен-
дифференцируемое™
ди dv х Su dv х •
-=— = -3— = е cos и, -х— = н— = — е sin и.
дх ду J ду дх J
Таким образом, функция B) определяет продолжение дей-
действительной показательной функции ех с оси R1 на всю
') Для достаточно большого п точка 1 Н— лежит в правой полупло-
п
(г N
\Л 1 и арктангенса из интервала,
2 ' 2
¦60 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
плоскость С, причем продолженная функция оказывается голо-
голоморфной. Ниже (в п. 21) мы покажем, что такое продолжение
определяется единственным образом.
2°. Для функции ez сохраняется обычная формула диффе-
дифференцирования. В самом деле, производную, когда она суще-
существует, можно вычислять в направлении оси х. Поэтому
(ez)' = ?(excosy + iexsmy) = e*. E)
Показательная функция не обращается в нуль, ибо |ег| =
= ех>0; поэтому {ег)'ф0 и отображение w — ez конформно в ка-
каждой точке С.
3°. Для функции ег сохраняется обычная теорема сложения
ег,+гг = ег1.ег2ш F)
В самом деле, полагая Zh — xh + iyh (k=\, 2) и пользуясь форму-
формулами сложения действительных показательной и тригонометри-
тригонометрических функций, получаем
ех' (cos yi + i sin у,) еХг (cos у2 + i sin y2) =
= ех>+х> {cos (iji + у2) + i sin (г/, + у2)}.
Таким образом, сложению комплексных чисел г4 и г2 соот-
соответствует умножение их образов eZi и егк Иными словами, по-
показательная функция ez преобразует аддитивную группу поля
комплексных чисел в мультипликативную группу этого поля:
при отображении z -* ег
г, + 22 -> ег' • ez\ G)
4°. Функция ег периодическая, с мнимым основным перио-
периодом 2ni. В самом деле, так как по формуле Эйлера e2ni —
= cos 2л + 1 sin 2я = 1, то по теореме сложения для любого геС
имеем
gz+2ni — gZ. g2ni — gz
С другой стороны, пусть ez+T = ez\ умножая обе части на е~г,
получаем ет=\, откуда, полагая T = Ti + iT2, имеем er'(cosr2 +
+ isinr2)= 1. Но тогда eTi = 1, т. е. Г4=0, и cos Г2=1, sin Г2=0,
т. е. Т2=2пп, где п — целое число. Таким образом, T = 2nni и
2я1 действительно является основным периодом.
Из этого рассуждения видно также, что 'для однолистности
отображения w — ez в какой-либо области D необходимо и до-
достаточно, чтобы эта область не содержала ни одной пары точек,
связанных соотношением
(я= ±1, ±2, ...). (8)
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
61
Примером области, удовлетворяющей этому условию, яв-
является полоса {0<1т.г<2я}. Полагая z=x+iy и ш> = рег'*, мы
согласно C) запишем отображение т — ег в виде
р = ех, \р=у. (9)
Отсюда видно, что это отображение преобразует прямые {у=Уо}
в лучи {г|з = г/о}, а отрезки [х=х0, 0<г/<2я}— в окружности с вы-
выколотой точкой {р = е*°, 0<1|з<2п} (рис. 20). Полоса {0<у<2я}
(Z)
преобразуется, следовательно, в плоскость w с выброшенной по-
положительной полуосью. Вдвое более узкая полоса {0<г/<я}
преобразуется при этом в верхнюю полуплоскость 1тда>0.
13. Тригонометрические функции. Из формулы Эйлера для
всех действительных х мы имеем eix = cos x+i sin x, e~ix =
= cos x — i sin x, откуда
cos л: =-
eix+e-ix
eix _ g-ix
Ш
Эти формулы можно использовать для голоморфного продол-
продолжения косинуса и синуса в комплексную плоскость, положив
по определению для любого геС
cos z = •
2г
A)
(голоморфность в С правых частей очевидна).
Все свойства этих функций вытекают из этого определения
и соответствующих свойств показательной функции. Так, обе
они периодические с основным периодом 2я (показательная
функция имеет период 2яг, но в формулах A) есть множитель
при z, равный i), косинус — четная, а синус — нечетная функция.
62
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. I
Для этих функций сохраняются обычные формулы дифферен-
дифференцирования
(cos z)' = i ¦
¦ — — Sin 2,
аналогично (sin г)'=соэ z. Сохраняются также тригонометри-
тригонометрические соотношения, такие, как
sin2 z + cos2 2=1, cos 2 = sin B + j\,
теоремы сложения и т. д.; читатель без труда выведет их из
формул A).
\azszl
Рис. 21.
Тригонометрические функции комплексного переменного
тесно связаны с гиперболическими, которые для любого С
определяются обычными формулами
СП2 =
ег +е
shz —
е-~е
2 ' ¦"**-- 2
Эта связь выражается соотношениями
ch2 = cos/2, sh2 = — i sin iz,
cos2 = ch/2, sin 2 = — ishiz,
B)
C)
которые видны из сравнения формул A) и B).
Пользуясь теоремой сложения и формулами C), находим
откуда
cos (x + iy) = cos x ch у + i sin x sh y,
I cos 2 I = ~j/cos2 x + sh2 у
D)
(мы воспользовались тождествами sin2x=l—cos2* и ch2y —
— sh21/= 1). Эта формула позволяет построить поверхность мо-
модуля (рельеф) косинуса; она изображена на рис. 21.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
63
Для примера рассмотрим еще отображение полуполосы
D = i—^<х<~, у>0>, которое осуществляется функцией
да = sin 2. Мы представим это отображение как композицию уже
известных нам отображений
Z, =
и тогда увидим, что w — sinz однолистно (и конформно) отобра-
отображает полуполосу D на верхнюю полуплоскость. На рис. 22 изо-
изображено соответствие линий при этом отображении: лучам
.л-
2
г
(w=sLnz)
Рис. 22.
{х=хй, 0<г/< °о} соответствуют лежащие в верхней полупло-
полуплоскости части гипербол с фокусами ±1, а отрезкам I—у<лг<
<Y> У = Уо\~ такие же части эллипсов с теми же фокусами.
Из этого рисунка видно, что на вертикальных границах полу-
полуполосы синус принимает действительные значения, по мо-
модулю большие 1.
Тангенс и котангенс для комплексных значений аргумента
определяются формулами
tg z = ¦
Ctg2 =
sin г
E)
и рационально выражаются через показательную функцию:
tg z = — i
eiz-e~iz
eiz+e~iz
ctg z = i
eiz + e~iz
Jz __ „-iz
F)
Эти функции голоморфны всюду в С, за исключением тех точек,
где знаменатели дробей в формулах F) обращаются в нуль
(в этих точках числители отличны от нуля). Найдем такие
точки, например, для ctg z. В них имеем sin z = 0, т. е. eiz = e~iz\
64
ГОЛОМОРФНЫЕ ФУНКЦИИ
[ГЛ. I
отсюда в силу условия (8) п. 12 находим <liz—2inn, z = nn
(л = 0, ±1,...) >)¦
Тангенс и котангенс в комплексной плоскости остаются пе-
периодическими с действительным периодом я, для них сохра-
сохраняются обычные формулы дифференцирования и тригонометри-
тригонометрические соотношения — все эти утверждения легко получить из
формул F).
Рис. 23.
Из формулы D) и аналогичной формулы для синуса находим
cos2 х + sh2 у
На рис. 23 изображен рельеф тангенса. Он имеет резко выра-
выраженные пики над точками z = — + пп (п = 0, ±1, ...), в кото-
которых тангенс теряет голоморфность.
Отображения, осуществляемые функциями w = tgz и w —
= ctg2, представляют собой композицию уже известных отобра-
отображений. Например, w = tgz сводится к таким отображениям:
Zx = 2/2,
w = — г-
') Мы доказали сейчас, что при голоморфном продолжении синуса в
комплексную плоскость не появляется новых точек, где он обращается в нуль.
ЗАДАЧИ
65
Полосу -|—-J < х < -j > эта функция однолистно и конформно
отображает на внутренность единичного круга. Прямые {х = х0}
при этом преобразуются в дуги окружностей, проходящих че-
'Щ
Ш,
V/7A
Ш.
и
ш
щ
1
ш
^,
ш
it
>^
2^.^
<!
^,
-ж
УЛ.
ж
'7//
Ж
{&
[г)
Рис. 24.
(w=tgz)
рез точки ± i, а отрезки -I — ^-<х<^, У = уЛ -в дуги окруж-
окружностей, для которых эти точки симметричны (рис. 24).
ЗАДАЧИ
1. На множестве плоских векторов г=(х,у) введем обычным образом сло-
сложение и умножение на скаляр (действительное число); тогда, отождествляя
действительные числа с векторами вида (х, 0), каждый вектор г—(х,у) мож-
можно записать в виде z=x+iy, где по определению ?=@,1). Однако умноже-
умножение двух векторов Zi = xi+iyi и z2=x2+iy2 определим иначе, чем при опре-
определении комплексных чисел: именно положим
(мы перемножаем двучлены Xi + lyi и x2+iy2 по обычным правилам алгебры
с заменой ?2=1). Такую систему будем называть системой гиперболических
комплексных чисел (Я).
а) Покажите, что (Я) является коммутативной алгеброй с делителями
нуля, и найдите геометрическое место делителей нуля.
б) Пусть z—x—iy; тогда \\г\\=У\г*г\ естественно назвать модулем
числа z. Найдите геометрическое место точек г, для которых ||г|| = 1. Пока-
Покажите, что при умножении гиперболических комплексных чисел их модули
перемножаются. Покажите, что условие ]|z||=0 необходимо и достаточно для
того, чтобы z было делителем нуля.
в) Для z2, \\za\\ Ф 0, и любого z\ определим частное формулой
z2
sgn (z3 « z2),
где sgn x — знак действительного числа х. Покажите, что (z\ J
5 Б. В. Шабат
68 ГОЛОМОРФНЫЕ ФУНКЦИИ [ГЛ. I
г) Для функции w*=f(z) =u+iv введем гиперболическую производную
/' (z) = lim Дщ> i Дг,
Дг->0
если этот предел существует. Покажите, что для существования такой произ-
производной необходимы и достаточны дифференцируемость f в смысле R2 и вы-
выполнение условий
ди _ ду ди dv
дх ду ' ду ~ дх
д) Выясните геометрическую картину отображений w — z*z и w—l %z
(соответствие надлежащим образом выбранных координатных сеток).
е) Положим по определению ё»'= ех (ch у + i sh у) и sin* z = sin x • cos y+
+icosx- sin у. Выясните сходство и отличие этих функций от обычной по-
показательной функции и синуса, а также найдите геометрическую картину
отображений, ими осуществляемых. _
2. Исследуйте на непрерывность в смысле С функции г, z и Rez =
-
3. Пусть и и v — действительные функции двух действительных пере-
, . п, _ ди , . ди dv ,
менных, дифференцируемые в смысле R2, а хи = -=—I-1 -т— , Vv = -^ (-
+ i-= их градиенты. Покажите, что условия дифференцируемое™ в смысле
С функции f=u+iv выражаются равенствами
(V«, Vo)=0, I V«| = | Vt> |,
где (Vu, Vv)—скалярное произведение.
4. Пусть точка z движется по закону z=reu, где г — постоянная, a t —
время. Найдите скорость движения точки w=f(z), где функция f голоморфна
на окружности {|г|=/-}.
(Ответ: izf'(z).)
5. Пусть f голоморфна на окружности Y={!2l==r} и /'(г)=^=0 на у.
Докажите, что условием выпуклости образа f(y) служит неравенство
L /\ I + 1 >0. [Указание: сначала рассмотрите условие выпуклости
/ \z) I
в виде ~ (j + Ф + arg f (rei<f) ) > 0.]
6. Найдите общий вид дробно-линейных отображений, соответствующих
вращению сферы Римана относительно двух ее диаметрально противополож-
противоположных точек.
7. Докажите, что группа дробно-линейных автоморфизмов верхней полу-
полуплоскости состоит из отображений
az + b
^ cz + d '
где а, Ь, с и d действительны и ad — bc>0.
ЗАДАЧИ 67
8. (Модель Пуанкаре геометрии Лобачевского) ')
а) Л-точками называются точки единичного круга U—{\z\<\], Л-пря-
мыми — лежащие в U дуги окружностей, ортогональных к {|г] = 1}. Проверьте
выполнение обычных аксиом связи точек и прямых. Убедитесь, что через
Л-точку, лежащую вне данной Л-прямой, можно провести бесконечно много
Л-прямых, не пересекающихся с данной.
б) Назовем Л-расстоянием между Л-точками zi и z2 величину
1 —- Z1Z2
Проверьте выполнение аксиомы треугольника. Докажите, что если Л-точки
2i, г2 и гз лежат на одной Л-прямой в естественном порядке, то
Рл (zv гз) = Рл (zv г2) + Рл (г2- гзУ
в) Назовем Л-движением дробно-линейный изоморфизм круга U. Пока-
Покажите, что Л-движения сохраняют Л-расстояния.
г) Л-окружностью с центром z0 называется геометрическое место точек,
Л-расстояние которых до z0 постоянно. Покажите, что Л-окружность изобра-
изображается окружностью, имеющей точки г0 и z§ — ljz0 симметричными.
д) Эквидистантой называется геометрическое место точек, Л-расстояние
которых до данной Л-прямой постоянно. Покажите, что эквидистанта изобра-
изображается лежащими в U двумя дугами окружностей, которые пересекают
{|z| = l} в тех же точках, что и рассматриваемая Л-прямая (они не являются
Л-прямыми!).
9. Докажите, что для любого условно сходящегося ряда с комплексными
членами существует такая прямая /с: С, что для любой точки se/найдется
перестановка членов этого ряда, после которой он будет сходиться к s.
(Обобщение теоремы Римана об условно сходящихся рядах с действитель-
действительными членами.)
') По поводу этой задачи см. И. И. Привалов, Введение в теорию
функций комплексного переменного, Физматгиз, М., 1960.
ГЛАВА П
СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ
В этой главе мы рассмотрим важнейшие методы исследова-
исследования голоморфных функций. Они основаны на представлении та-
таких функций в виде специальных интегралов (интегралов Коши)
или в виде сумм некоторых рядов (рядов Тейлора и Лорана).
Начнем с понятия интеграла от функций комплексного пере-
переменного.
§ 4. Интеграл
14. Понятие интеграла. Определение. Пусть дан путь у
класса С1, т. е. непрерывно дифференцируемое отображение
z(t): J -* С, где / = [а, |3] — отрезок действительной оси R1 (см.
п. 3). Пусть на образе этого пути z(J), который мы также бу-
будем обозначать через у, задана комплексная функция f: у-^-С
такая, что функция f °z(t) непрерывна на / (в этом случае мы
просто будем говорить, что / непрерывна на у). Будем называть
интегралом от функции / вдоль пути у число
Р
\fdZ=\f[z(t)\z'{t)dt, A)
у а
где в правой части интеграл от комплексной функции действи-
действительного переменного понимается как соответствующая линей-
линейная комбинация интегралов от действительной и мнимой частей.
Определение без всяких изменений распространяется на ку-
кусочно непрерывно дифференцируемые пути.
Примеры. 1. Пусть у — окружность z — a + reu, t e [0, 2я],
и f(z)i = (z — а)п, где п = 0, ±1, ... — произвольное целое число.
По определению A)
2я
'J (z - af dz = rn+1i J e' (n+I>' dt;
v о
при п ф — 1 имеем
J (z-af dz = rn+4\ J cos(n+ \)tdt + i J s\n(n\
§ 4] ИНТЕГРАЛ 69
а при п — — 1
2Л
Таким образом, целые степени {z— а)" обладают свойством
«ортогональности»
f О при п ф — 1,
Z-fl)nd2= - . ' B)
12m при п = — 1,
которым мы будем неоднократно пользоваться.
2. Пусть у — произвольный путь z = z(t), fe [a, C], класса С1
с концами в точках a=z(a) и 6 = г(Р); тогда
J dz = b-a, § zdz= b2~a2 . C)
V V
В самом деле,
Р Р Р
J d2 = | 2'@ dt = J djc @ + i I dy (t) =
Аналогично
Мы видим, что интегралы C) не зависят от вида пути и
вполне определяются его начальной и конечной точками. По
любому замкнутому пути эти интегралы равны нулю.
Замечание. В принятых нами в определении условиях на
путь и функцию интеграл A) всегда существует (как интеграл
от непрерывной функции) и может пониматься в смысле Ри-
мана. Если путь у лишь спрямляем, то даже для непрерывных
функций ? требуется более общее понятие интеграла, ибо в пра-
правой части A) множитель z'(t) существует лишь почти всюду.
Поэтому в случае спрямляемых путей нужно пользоваться ин-
интегралом Лебега (и тогда естественно считать функцию f такой,
что f °z(t) суммируема на /).
Перечислим основные свойства интеграла от комплексных
функций.
70 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
1°. Линейность. Если fug непрерывны на пути у е С1,
то для любых комплексных постоянных а и b
J (a/ + 6g) dz = a J fdz + b J g dz.
D)
Следует непосредственно из определения.
2°. Аддитивность. Пусть даны два пути уь Y2 е С1, опре-
определенные соответственно функциями Zi{t), t<=[a, pi], и z2(f),
te [a2, р], причем Pi=a2 и 2i(Pi) =z2(cc2). Объединением Y1UY2
этих путей назовем кусочно непрерывно дифференцируемый
путь у. [a, PJ-+C, определяемый функцией
2(t), t<=[a2, p].
Пусть на у задана непрерывная функция /; непосредственно
из определения интеграла следует, что
J fdz=$fdz+ $fdz. E)
Yi U Yj Yi Y2
Замечание. Можно обобщить понятие объединения путей,
отказавшись от условия на расположение отрезков [a, pi] и
[а2, р] и от условия z^Pi) =z2(a2). Тогда yiUy2 уже, вообще го-
говоря, не будет путем; в этом случае мы сохраним свойство E)
по определению (положив интеграл по YiUy2 равным
сумме интегралов по yi и у2).
3°. Инвариантность относительно замены па-
параметра. Теорема 1. Пусть путь у^. z~Zi(x), tefai, Pi]
получается из гладкого пути у: z = z(t), fe [a, p], допустимой
заменой параметра '). Тогда для любой функции f, непрерывной
на у (а следовательно, и на Yi),
[fdz=[fdz. F)
По определению
Yi
Сделаем в правой части замену переменных t=t(%), которая
связывает параметры t и т на наших путях. По теореме из дей-
') Это означает (см. п. 3), что существует возрастающая функция
t = t(x): [ab PJ —•> [a, p] класса С1 такая, что г,(т)=г[<(т)] для всех
те [ai, p,].
§ 4] ИНТЕГРАЛ 71
ствительного анализа (примененной отдельно к действительной
и отдельно к мнимой части интеграла) и правилу дифференци-
дифференцирования сложных функций получим тогда
jfdz=]f[zl(x)]z\{r)dx.
Интеграл справа — это интеграл от / вдоль пути yi >
Из этой теоремы можно сделать важный вывод: интеграл,
введенный нами для пути, имеет смысл и для кривой, под кото-
которой мы понимаем класс эквивалентных путей (см. п. 3). Точнее,
для любого пути, определяющего некоторую гладкую кривую,
интеграл от функции, непрерывной вдоль этого пути, имеет одно
и то же значение.
В соответствии со сказанным в п. 3 мы будем часто в даль-
дальнейшем понимать под кривой множество точек комплексной пло-
плоскости — образ отрезка [ее, р] для любого пути, определяющего
эту кривую. Тогда мы будем говорить и об интеграле по этому
множеству, понимая под ним интеграл вдоль соответствующей
кривой.
Замечание. Теорема 1 сохраняется и для функций, суммируемых на
спрямляемых путях, если допустимой считать монотонную абсолютно непре-
непрерывную замену параметра (в самом деле, тогда можно воспользоваться
теоремой о замене переменных для интеграла Лебега). Поэтому имеет
смысл и понятие интеграла вдоль спрямляемой кривой.
4°. Ориентированность. Обозначим через у~ путь, ко-
который получается из пути у: z=z(t), t e [ос, р], класса С1 за-
заменой переменных t-*a + $ — t (т. е. путь Zi(t)=z(a+$— t),
/е [а, р]), и пусть / — функция, непрерывная на у; тогда
-\fdz.
G)
Это утверждение доказывается так же, как теорема 1.
Мы будем говорить, что путь у~ получается из у переменой
ориентации.
5°. Оценка интеграла. Теорема 2. Для любой функ-
функции f, непрерывной на гладком пути у: z — z{t), t^[a, p], спра-
справедливо неравенство
\\fdz <J
(8)
где \dz\ = Ydx2 +dy2—элемент длины у и справа стоит кри~
волинейный интеграл по дуге.
72 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
¦*Обозначим через / величину интеграла от / по у, и пусть
/= |/|ег'е; имеем
Р
| / | = | e-iQfdz = J е-*6/ [г (/)] г' @ df
V а
(мы внесли постоянный множитель е~г'е под знак интеграла).
Так как интеграл справа — действительное число, то
Р Р
\I\= j Re{e-"f[z(t)]z'(t)}dt^ j \f[z(t)]\\z'(t)\dt= j \f\\dz\ >
a a v
Следствие. Если в условиях предыдущей теоремы
\f{z) |<М всюду на у, где М — некоторая постоянная, то
fdz
(9)
(через |у| мы обозначаем длину пути у).
Неравенство (9) получается из (8), если оценить интеграл
в правой части и заметить, что
15. Первообразная. Определение 1. Первообразной функ-
функции / в области D называется такая голоморфная в этой обла-
области функция F, что в каждой точке геО
A)
Если F— первообразная функции / в области D, то и любая
функция F(z)+C, где С — произвольная постоянная, также яв-
является первообразной f в D. Обратно, пусть Ft и F2 — две ка-
какие-либо первообразные функции f в области D и Ф=Р1 — F2.
Функция Ф голоморфна в D, поэтому ~^г- = 0 в D; но и -^— =
= ф' = р'^ — f2 ^ о в D, поэтому -Q— s= ——^0 в D. Отсюда по
теореме действительного анализа (примененной к функциям
ИеФ и 1тф) мы заключаем, что Ф = С, постоянная в D. Дока-
Доказана
Теорема 1. Если F — какая-либо первообразная функцииf
в области D, то совокупность всех первообразных f дается фор*
мулой
F(z)+C, B)
где С — произвольная постоянная.
5 4]
ИНТЕГРАЛ
73
Таким образом, первообразная функции f в области D, если
она существует, определяется единственным образом с точно-
точностью до постоянного слагаемого.
Перейдем к вопросам существования первообразной.
Сначала мы изучим вопрос о существовании локальной перво-
первообразной, действующей в окрестности некоторой точки. Мы до-
докажем, что локально каждая голоморфная функция имеет пер-
первообразную. Доказательство разобьем на два этапа.
Лемма 1. Пусть функция f непрерывна в круге U =
~{\г — а\ <г) и интеграл от нее по границе 1) любого треуголь-
треугольника А.Ш U равен нулю:
Тогда функция
J f dz = 0.
= J
C)
D)
[a,z]
Рис 25.
где интеграл берется по прямолинейному
отрезку [a, z] a U, является первообразной f
в U (т. е. F голоморфна в U и F'(z)=f(z) .
в каждой точке геУ).
¦« Фиксируем произвольную точку геУ и будем считать \h\
столь малым, что точка z+h^U (рис. 25). Тогда треугольник
Д = {а, z + h, z] Ш U, и по условию C)
[а, г]
[г, z+h]
[а, z+h)
откуда видно, что
h)-F(z)= J
[г, z+h]
E)
(мы воспользовались свойствами интегралов и определением
функции F). Но согласно примеру 2 из п. 14
J f
U, z+h]
J rfg=
[z,z+h]
(мы вынесли постоянный множитель f(z) из-под знака инте-
интеграла); поэтому, используя E), можно написать
^J_ J
F)
[г, z+h]
') Мы считаем, что граница дД ориентирована каким-либо образом (так
что при ее обходе треугольник Д остается все время с одной стороны).
74
СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИИ
[ГЛ. 1Г
Теперь воспользуемся непрерывностью функции f: для лю-
лю0 й 0 \h
р у рр фу
бого е>0 можно найти 6>0 такое, что при \h
[ h] |/() —f(z)
[z, z+h] справедливо неравенство |/()
основании получаем из F), что при \h\ <б
<б для всех
<e. На этом
а это означает, что существует F'(z) =f(z) >
Лемма 2. Если функция fe#(?>) '), то интеграл от f no
границе любого треугольника АшО равен нулю.
4 Пусть лемма неверна и существует треугольник Ad=D та-
такой, что
\fdz
ад
= М>0.
G)
Разобьем Д на четыре треугольника средними линиями и
предположим, что границы А и этих треугольников ориентиро-
ориентированы против часовой стрелки (рис. 26). Очевидно, что интеграл
от / по дА равен сумме интегралов по границам маленьких тре-
треугольников, ибо интегралы по средним линиям (пунктир на
рис. 26) берутся дважды в противопо-
противоположных направлениях и потому сокра-
сокращаются, а остальные части границ со-
составляют дА. Поэтому найдется хотя
бы один маленький треугольник — мы
обозначим его через Д4— такой, что
Рис. 26.
J
<эд,
fdz
4
Треугольник А4 мы снова разобьем средними линиями на
четыре треугольника и по тем же соображениям найдем среди
них хотя бы один — мы обозначим его через Аг — такой, что
I
д
fdz
м
2"
Продолжая наше рассуждение, построим последовательность
вложенных друг в друга треугольников таких, что для инте-
интеграла по границе n-го треугольника справедливо неравенство
fdz
м
4" *
(8)
') Напомним, что через H(D) обозначается совокупность всех функций,
голоморфных в области D.
§4]
ИНТЕГРАЛ
75
Треугольники А„ (мы считаем их замкнутыми) имеют об-
общую точку г0, которая принадлежит Д, а следовательно, и D.
Так как функция / голоморфна в точке г0> то для любого е>0
найдется 6>0 такое, что модуль разности
о) ' (9)
будет меньше е для всех z из проколотой окрестности U' =
= {0<|z — zo|<6}.
В U' найдется хотя бы один треугольник построенной после-
последовательности, пусть это будет А„. На основании (9) и приме-
примеров из предыдущего пункта
J fdz= jf(zo)dz+ J f>(zo)(z-zo)dz-
a (z) (z - z0) dz =
= f a{z){z-zo)dz,
ад„
где |a(z) j <е для всех ге^Д„. Кроме того^для всех ze<3An ве-
величина \г — 20| не превосходит периметра |<?Д„| треуголь-
треугольника An, поэтому по теореме об оценке интеграла
J fdz = J a(z)(z-zo)dz
Но по нашему построению | дАп | =
метр треугольника А, следовательно,
ад |*
где
I
Д
fdz
Учитывая (8), мы получаем неравенство
АКе|о>Д|2,
откуда в силу произвольности числа е заключаем, что М = 0 во-
вопреки предположению G) >
Доказанную лемму 2 мы будем называть основной леммой
интегрального исчисления. Из нее и из леммы 1 непосредственно
вытекает локальная теорема существования первообразной
голоморфной функции.
Теорема 2. Если функция f^H(D), то в любом круге
{| z — z0 \ <г} с D она имеет первообразную
F{z)-
A0)
[г„, г]
76 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
Вопрос о существовании глобальной первообразной, дей-
действующей во всей области D, несколько сложнее. Мы займемся
им в следующем пункте, а сейчас лишь покажем, как из локаль-
локальных первообразных можно склеить первообразную, действую-
действующую вдоль заданного пути.
Определение 2. Пусть в области D задана функция /
и у: z=z(t), t&J, где / = [а, PJcrR1 — произвольный (непрерыв-
(непрерывный) путь, лежащий в D. Функцию Ф@- J~*C мы будем на-
называть первообразной функции f вдоль пути у, если она: 1) не-
непрерывна на / и 2) для любой
точки to^J существует окрест-
окрестность ?/г„сг1) точки zo = z(to),
в которой f имеет первообраз-
первообразную F такую, что
F[z(t)] = O(t) A1)
для всех t из некоторой окре-
t t' стности Ut0 cr /.
**{~JMJ\' Заметим, что если / имеет
Uvj-i-J, 1— Jk-A, ~filt' первообразную F во всей об-
cc't, t, tk tk r " ласти D, то функция F[z(t)]
будет служить первообразной
Рис- 27- вдоль пути у. Однако в опре-
определении не требуется сущест-
существования первообразной во всей D — достаточно, чтобы она су-
существовала лишь локально, в окрестности каждой точки
го^у. Более того, если z(t') =z(t") =z' при ?=fct", то две перво-
первообразные f, из которых одна соответствует окрестности щ>, а
другая — окрестности Uf> , не обязаны совпадать: они могут от-
отличаться постоянным слагаемым (заметьте, что они действуют
в окрестности одной и той же точки z' и по теореме 1 их раз-
разность может быть только постоянной). Поэтому первообразная
вдоль пути, являясь функцией параметра t, может не быть функ-
функцией точки z.
Теорема 3. Для любой функции f^.H(D) и любого (не-
(непрерывного) пути yc^D первообразная f вдоль у существует и
определяется с точностью до постоянного слагаемого.
< Пусть путь у определяется отображением z=z(t): J —¦ D.
Разобьем отрезок /=[а, р] на п отрезков /*= [tk, й] так, чтобы
два соседних пересекались по отрезку {tk<tk+i<t'k, ti = a,t'n =
= Р; рис. 27). Пользуясь равномерной непрерывностью функ-
функции z(t), мы можем выбрать /й столь малыми, чтобы для лю-
любого k=l, ..., п образ z(/ft) содержался в круге UhCiD, в ко-
котором f имеет первообразную (по теореме 2).
§ 4] ИНТЕГРАЛ 77
Среди совокупности первообразных, действующих в t/i (они
отличаются друг от друга постоянным слагаемым), выберем
произвольно одну, которую обозначим через F4. Рассмотрим ка-
какую-либо первообразную, действующую в U2; в пересечении
U1UU2 она может отличаться от F\ лишь постоянным слагае-
слагаемым (ибо это — две первообразные одной функции). Поэтому
среди первообразных, действующих в ?/2, существует одна, мы
обозначим ее через F2, которая совпадает с Л в пересечении
U(]U
Продолжая это рассуждение, мы в каждой ?/& выберем пер-
первообразную Fh так, что Fh==Fh-i в пересечении Uh-if\Uh
(k = l, . . ., п). Функция
O(t)=Fh[z(t)], te=Jk (Л=1, .... п),
будет первообразной функции / вдоль пути у. В самом деле,
она, очевидно, непрерывна на отрезке / и для каждой точки
to^J найдется окрестность, в которой Ф(t) == F [z(t)], где F —
первообразная f, действующая в окрестности z(t0).
Остается доказать вторую часть теоремы. Пусть Q)i{t) и
Фг@ —Две первообразные f вдоль пути у. В окрестности щл
каждой точки г е / мы имеем Ф1 = Я1)[г(г')]'и Фг = /;'B)[2;@]. гДе
рA) и FW — две первообразные функции f, действующие в неко-
некоторой окрестности точки z(t0). Они могут отличаться лишь по-
постоянным слагаемым, поэтому <p(/)=Oi@ —Фг@ постоянна
в ы(о. Но локально постоянная в каждой точке связного мно-
множества функция постоянна на всем множестве1). Поэтому
ФИО — Фг@ = const для всех t е / >
Если известна первообразная функции / вдоль пути у, то ин-
интеграл от f по у вычисляется по обычной формуле Ньютона —
Лейбница:
Теорема 4. Если у: z = z(t), fe [a, |3], — кусочно гладкий
путь и функция f непрерывна на у и имеет первообразную Ф@
вдоль у, то
[ Ф(а). - A2)
•< Пусть сначала путь у гладкий и целиком лежит в обла-
области, где функция f имеет первообразную F. По определению
') В самом деле, пусть % ={t е/ : <р@ =ф(^>)}- Это множество непусто,
ибо содержит t0. Оно открыто, ибо <р локально постоянна и вместе с каждой
точкой t в % входит некоторая окрестность Ut. Но оно и замкнуто, ибо <р
непрерывна (так как она локально постоянна) и поэтому из условий
ф ('л) = ф (*о) и tn -> /" следует, что ф(*")=ф(*о). По теореме 2 из п. 4
]
78 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
интеграла
Э
jfdz=jf[z(t)]z'(f)dt, A3)
V а.
а по определению первообразной вдоль пути для всех /е [а, р]
O(t)=F[z(t)] +const
Так как для всех геу существует F'(z) —f(z), а в силу глад-
гладкости у Для всех ^е [«> Р] существует непрерывная производ-
производная z'(t), то функция Ф для всех t^[a, |3] имеет непрерывную
производную
<b'(t)=f[z(t)]z'(t)
Мы видим, что функция Ф@ является первообразной непре-
непрерывной функции, стоящей под знаком интеграла в правой ча-
части A3).
По формуле Ньютона — Лейбница для функций действитель-
действительного переменного получаем A2).
В общем случае мы можем разбить y на конечное число пу-
путей Yv'- z = z{t), t<=[av, av+\] (ao = a<ai< . .. <an = p), так, что
каждый из них является гладким и лежит в области, где /
имеет первообразную. По только что доказанному
и, складывая все эти равенства, получим A2) >
Замечание 1. Если рассматривать вместо интеграла Ри-
мана интеграл Лебега, то теорему 4 можно точно так же до-
доказать для спрямляемых путей. Однако можно пойти и дальше.
Пусть функция f голоморфна в области D, тогда по теореме 3
существует ее первообразная Ф(?) вдоль произвольного непре-
непрерывного пути yc^D. Учитывая теорему 4, мы определим
интеграл от f no произвольному непрерывному пути yczD как
приращение ее первообразной вдоль этого .пути на отрезке [а, р]
изменения параметра.
Очевидно, что правая часть A2) не меняется при допусти-
допустимых заменах параметра. Поэтому можно рассматривать инте-
интеграл от голоморфных функций и по любым (непрерывным)
кривым.
Замечание 2. Теорема 4 позволяет убедиться в справед-
справедливости сделанного в начале пункта утверждения о том, что в
многосвязной области не каждая голоморфная функция имеет
первообразную, Рассмотрим область ?>={0<|z[<2} и в ней го-
§ 4] ИНТЕГРАЛ . 79
ломорфную функцию f{z) = — \ эта функция не может иметь
в D первообразной. В самом деле, если бы первообразная F
функции f в D существовала, то для любого пути y: z=z{t),
?е [а, р], лежащего в D, первообразной вдоль этого пути слу-
служила бы функция F[z(t)] и, по теореме 4,
где а = 2(а) и Ь=г(р)—концы у. В частности, интеграл от f
вдоль любого замкнутого пути yczD, для которого Ь — а, рав-
равнялся бы нулю. Но мы знаем (см. пример 1 в п. 14), что инте-
интеграл от f вдоль единичной окружности z=eu, t& [0, 2л], т. е.
интеграл
J
В заключение приведем несколько терминологических заме-
замечаний. Вместо интегрирования функций часто говорят об интег-
интегрировании дифференциальных форм. Для функций двух дей-
действительных переменных х и у (линейные) дифференциальные
формы имеют вид
PdQd A4)
где Р и Q — функции от х и у, заданные в плоской области D.
Форма A4) называется замкнутой в D, если Р и Q дифферен-
дифференцируемы и
#=Т A5)
всюду в этой области. Эта форма называется точной, если су-
существует дифференцируемая в D функция ср(л:, у) такая, что
всюду в D
Pd Qd d<$. A6)
Как и в п. 6, будем вместо х и у рассматривать комплексные
переменные z=x + iy и z = x — iy; после перехода к этим пере-
переменным форма A4) примет вид
o = ftdz + f2dz, A7)
где положено fi=-z(P — iQ), f2~'o'{PJr г(?).Однако в комплекс-
комплексном анализе обычно рассматривают частный вид дифферен-
дифференциальных форм, для которых коэффициент при dz равен нулю:
&>=/dz. A8)
80 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИИ [ГЛ. II
Положим f=u + iv и dz = dx + i dy, тогда форма A8) пере-
перепишется в виде линейной комбинации двух действительных
форм
/2 = w dx — v dy + i(vdx+udy).
Условия замкнутости форм coi и со2 в области D состоят в
том, что функции и и v дифференцируемы в D и всюду в D
ди dv ди dv
дх ду ' ду дх
(ср. условие A5) замкнутости формы со). Но это — условие го-
голоморфности функции f в области D. Учитывая сказанное, мы
будем называть форму a=fdz замкнутой в области D, если
функция f голоморфна в этой области.
Форма (o=f dz называется точной в области D, если суще-
существует такая голоморфная в D функция F, что всюду в D
a=dF, A9)
т. е. если / имеет в области D первообразную F.
В п. 20 мы докажем, что производная от голоморфной функ-
функции также голоморфна. Отсюда следует, что всякая точная
форма f dz = dF непременно является замкнутой. Обратное ут-
утверждение неверно, вот пример: форма а — — замкнута в обла-
области Z) = {0< \z\ <2}, но не точна в ней (см. замечание 2). Однако
по теореме 3 каждая замкнутая форма f dz локально т,о ч н а
(в окрестности каждой точки г(еО ее можно представить как
дифференциал функции J /(g)d?).
[го, г]
В следующем пункте мы убедимся в том, что в односвяз-
н о й области у каждой голоморфной функции существует пер-
первообразная. Поэтому в такой области каждая замкнутая форма
точна.
Понятие дифференциальной формы особенно удобно для
функций нескольких комплексных переменных (см. часть II).
16. Гомотопия. Теорема Коши. Эта основная в интегральном
исчислении теорема состоит в том, что интеграл от голоморф-
голоморфной в некоторой области функции по любому замкнутому пути,
который непрерывной деформацией внутри области стягивается
в точку, равен нулю. Она, таким образом, обобщает основную
лемму интегрального исчисления, доказанную в предыдущем
пункте. Мы получим теорему Коши как следствие более общей
теоремы об инвариантности интеграла от голоморфных функций
относительно непрерывных деформаций пути интегрирования
(теорема 1). Перейдем к точным формулировкам и доказатель-
доказательствам.
§4]
ИНТЕГРАЛ
81
Для простоты предположим, что для всех рассматриваемых
путей параметр t меняется на одном и том же отрезке / = [0, 1].
Это предположение не ограничивает общности, ибо ему всегда
можно удовлетворить при помощи допустимой замены пара-
параметра, которая заменит путь ему эквивалентным и сохранит зна-
значение интеграла вдоль пути.
Определение 1. Два пути zu(t): J ~* D и Zi(t): J —> D
с общими концами го(О) = 24@) —а и zo(l) =z1(\) =b назы-
называются гомотопными в области D, если существует непрерывное
Рис. 28.
отображение 2E, t): JxJ—*D (через /X/ мы обозначаем про-
произведение отрезков, т. е. квадрат 0^5<!1, 0<!/<1) такое,
что
2@, t)^zo(t), 2A, t)^zx{t) (*е/),
z(s, 0) = a, z(s, \) = b (se/). { '
Два замкнутых пути zo(t): J —>D и Zi(t): J —*D назы-
называются гомотопными в области D, если существует такое не-
непрерывное отображение z(s,t): JxJ^*D, что
Z(O, t)^Z0{t),
z(s, 0) =
2A, 0 = 2,@
B)
При фиксированном s = so^J функция z (s0, t): J-+D опре-
определяет путь в области D, причем такие пути непрерывно ме-
меняются при изменении s0 и их семейство «связывает» в D пути
Zo{t) и Zi(t) (на рис. 28 эти «промежуточные» пути изображены
пунктиром). Таким образом, гомотопность двух путей в обла-
области D означает возможность непрерывно деформировать их
друг в друга внутри D. На рис. 28 пути уо и yi гомотопны, а у
не гомотопен им.
Гомотопность принято обозначать символом ~, так что если
путь yo гомотопен пути yu to мы будем писать Yo~Yi-
6 Б. В. Шабат
82
СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ
[ГЛ. II
Очевидно, что гомотопность удовлетворяет обычным аксио-
аксиомам эквивалентности (рефлексивности, симметричности и тран-
транзитивности). Поэтому в данной области все пути с общими кон-
концами или все замкнутые пути можно разбить на классы, каждый
из которых объединяет все гомотопные друг другу пути; такие
классы называются гомотопическими классами.
Среди классов замкнутых путей выделяется класс путей,
гомотопных нулю. Говорят, что замкнутый путь у гомотопен
нулю в области D, если существует непрерывное отображение
z(s, t): JXJ-+D, удовлетворяющее условиям B) и такое, что
Zi(^)=const (это означает, что у
непрерывной деформацией внутри
D стягивается в точку). Можно до-
доказать, что два пути yi и Y2 с об-
общими концами гомотопны друг дру-
другу тогда и только тогда, когда их
разность (т. е. объединение путей у^
и у~) гомотопна нулю.
В односвязной области лю-
любой замкнутый путь гомотопен
нулю и, значит, любые два пути с
общими концами гомотопны друг
другу (это свойство можно было
бы принять за определение одно-
односвязности). Поэтому в односвязных областях разбиение на го-
гомотопические классы тривиально.
Так как гомотопность двух путей, очевидно, не нарушается
при допустимых заменах параметра, то это понятие распростра-
распространяется на кривые. Именно, две кривые (с общими концами или
замкнутые) называются гомотопными в области D, если в D гомо-
гомотопны пути yi и Y2, представляющие соответственно эти кривые.
Переходим к доказательству теоремы об инвариантности ин-
интеграла при гомотопных деформациях пути интегрирования.
Теорема 1. Если функция f e H (D), а у\ и у0 — два пути,
гомотопные друг другу в D как пути с общими концами или
как замкнутые пути, то
\fdz-\fdz. C)
Vo Yi
« Будем считать, что отрезком изменения параметра / для
путей Yo и Yi служит / = [0,1]; пусть z(s,t): JXJ-+D — функ-
функция, определяющая их гомотопию (см. определение 1). По-
Построим систему квадратиков /Ст„ (пг, п—\, ..., N), покрываю-
покрывающих квадрат K=JXJ так, что каждый Ктп пересекается с ка-
каждым соседним квадратиком (рис, 29). В силу равномерной
S 4] ИНТЕГРАЛ 83
непрерывности функции z(s, t) квадратики Ктп можно выбрать
столь мелкими, чтобы образ z(Kmn) содержался в круге
Umn<=D, в котором функция / имеет первообразную Fmn (мы
пользуемся тем, что локально каждая голоморфная функция
имеет первообразную). Фиксируем индекс т и будем поступать,
как при доказательстве теоремы 3 из предыдущего пункта. Вы-
Выберем произвольно первообразную Fmi, действующую в Umu
а первообразную Fm2, действующую в Um2, подберем так, чтобы
Fmi=Fm2 в пересечении Umlf]Um2 (мы пользуемся тем, что две
первообразные f в этом пересечении могут отличаться лишь по-
постоянным слагаемым). Точно так же подбираем первообразные
Ртз, ¦ ¦ ¦, FmN (так, что Fm,n+i=Fmn в Um, n+ifl Umn) и строим
функцию
ФтE, t)=Fmn [z (s, t) ] для (s, t)e=Kmn (ra=l,..., N). D)
Функция Фт, очевидно, непрерывна в прямоугольнике
N
Кт = (J Ктп и определена с точностью до постоянного слагае-
л = 1
мого. Мы выбираем произвольно Фь а ф2 подбираем так, чтобы
ф1 = ф2 в пересечении /^ГЖг1)- Точно так же подбираем функ-
функции Фз, . . ., Фя (ТЭК, ЧТО Фт = Фт+1 В KmOKm+l) И СТрвИМ фуНК-
цию
<D(s, t)=<Dm(s, t) для (s, Oe/Cm (m=l,...,N). E)
При фиксированном se/ функция Ф(в, /), очевидно, яв-
является первообразной вдоль пути ys: z = z(s, t), /e/, поэтому по
формуле Ньютона — Лейбница
dz = <D(s, l)-<D(s, 0). F)
Далее разберем отдельно два случая:
а) Пути Yi и Y2 имеют общие концы. В этом случае но
определению гомотопии для любого sg/ имеем z(s,0)=a и
z(s, \)=b. Следовательно, функции ®(s, 0) и Ф{э, 1) локально
постоянны в каждой точке /, и, значит, они постоянны на этом
отрезке. Таким образом, Ф@, 0)=ФA» 0), Ф@, 1)=ФA, 1) и
из формулы F) мы получаем C).
б) Пути yi и Y2 замкнуты. Так как в этом случае z (s, 0) =
= z(s, 1) для любого se/, то O(s, 1) — Ф(в,0) локально по-
постоянна в каждой точке / и, следовательно, постоянна на всем
этом отрезке. Поэтому из F) опять вытекает C) >
') Это можно сделать, так как функция Фг — Ф|, будучи локально по-
постоянной и непрерывной на связном множестве ~ К1Л Кг, постоянна.
84 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
Замечание. Первоначально мы ввели понятие интеграла
для пути и затем убедились в том, что фактически интеграл
определяется не путем, а кривой, т. е. классом эквивалентных
путей. Теорема 1 показывает, что в случае голоморфных функ-
функций можно пойти дальше и утверждать, что в этом случае ин-
интеграл определяется не кривой, а гомотопическим клас-
с о м, которому принадлежит эта кривая.
Из доказанной теоремы просто получается
Теорема 2 (Кош и). Если функция fe#(D), то ее инте-
интеграл по любому замкнутому пути yczD, гомотопному нулю в
этой области, равен нулю:
jfdz = Q, если у~0- (?)
V
¦4 Так как y~0> т0 этот путь можно в D гомотопно дефор-
деформировать в замкнутый путь yi: z = zi(t), re/, лежащий в неко-
некотором круге UczD. По теореме 3 предыдущего пункта функция f
имеет в V первообразную F, и, следовательно, первообразной /
вдоль yi будет функция F[zi(t)]. Так как 2i@) =г1A) =а
(путь yi замкнут), то по формуле Ньютона-—Лейбница
J fdz = F{a)-F{a) = 0.
Но по теореме 1 интегралы от f по y и yi равны, следовательно,
интеграл от / по y равен нулю >
Так как в односвязной области каждый замкнутый путь го-
гомотопен нулю, то для таких областей теорема Коши формули-
формулируется особенно просто:
Теорема 3 (Коши). Если функция f голоморфна в одно-
связной области Da С, то ее интеграл вдоль любого замкну-
замкнутого пути у a D равен нулю. "
Ввиду важности этой теоремы приведем еще ее элементарное доказа-
доказательство в двух дополнительных предположениях: 1) производная f непре-
непрерывна ') в D я 2) у — гладкий жорданов путь.
Из второго предположения следует, что у является границей области G,
принадлежащей области D в силу односвязности последней. Первое предпо-
предположение позволяет применить известную из анализа формулу Римана .—
Грина
JJJ(f)*,. (8)
до а
1) Скоро мы убедимся в том, что это предположение выполняется авто-
автоматически для голоморфных функций.
§ 4]
ИНТЕГРАЛ
85
при выводе которой требуется непрерывность в G частных производных
функций Р и Q (через dG здесь обозначается граница области G, прохо-
проходимая против часовой стрелки). Применяя эту формулу к действительной
и мнимой частям интеграла
f dz = и dx — v dy + i v dx+ и dy,
dG
da
мы получим
Г , , Г Г f dv ди , . / ди dv \ \ , ,
/ dz = \ \ { г н- + ' -^ ^— г Лх dy.
J J J 1 dx <Эг/ \ dx dy ) i y
dG О
Пользуясь символом комплексной производной -^rr (см. п. 6), мы перепишем
последнее соотношение в виде формулы
41 dx dy, (9>
dz "' v '
dO G
которую можно рассматривать как комплексную запись формулы Римана —
Грина.
Так как в силу голоморфности -^т- = 0, то теорема Коши (в сделанных
дополнительных предположениях) непосредственно вытекает из этой фор-
формулы.
Из теоремы Коши (в последней формулировке) просто вы-
выводится глобальная теорема о существовании первообразной
для односвязной обл асти:
Теорема 4. Всякая функ-
функция f, голоморфная в юдносвяз-
ной области D, имеет в этой об-
области первообразную.
< Покажем, что в D интеграл
от f по незамкнутому пути не
зависит от выбора этого пути
и полностью определяется его
началом и концом. В самом деле,
пусть Yi и Y2 — Два пути, соеди-
соединяющие в D точки а и Ъ (рис.30).
Без ограничения общности мож-
можно считать, что для yi параметр
меняется на отрезке [а, р4], а для
Ya — на отрезке [|3i, |3] (a<|3i<p). Обозначим через y объеди-
объединение путей Yi и Уг> это — замкнутый путь, лежащий в обла-
области D. По свойствам интегралов
Рис. 30.
\fdz-\fdz= jfdz,
V,
$6 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. К
но по теореме 3 интеграл от / по любому замкнутому пути у с: D
равен нулю, отсюда и следует наше утверждение1).
Фиксируем теперь точку aeD и будем считать а началом
пути, лежащего в D, конец которого z будем считать произ-
произвольным. Интеграл от f по этому пути (который мы обозначим
через az) является функцией точки z:
f(z)~J/(?)</?. A0)
az
Повторяя в точности рассуждения, проведенные при доказа-
доказательстве теоремы 2 из предыдущего пункта, мы убедимся в том,
что F голоморфна в D и что F'=f в каждой точке z^D, т. е.
что F является первообразной f в области D >
Пример функции f = — в области {0<|.г|<2} (см. замеча-
замечание 2 в предыдущем пункте) показывает, что условие односвяз-
односвязности области в этой теореме существенно: для многосвязных
областей глобальная теорема существования первообразной,
вообще говоря, неверна.
17. Обобщения теоремы Коши. Тот же пример показывает,
что в многосвязной области интеграл от голоморфной функции
по замкнутому пути не обязательно равен нулю, т. е. теорема
Коши в том виде, как она сформулирована в теореме 3 преды-
предыдущего пункта, на многосвязные области не распространяется.
В формулировке теоремы 2 порядок связности несуществен.
Очевидно, что замкнутая кривая гомотопна нулю в области D,
если она является границей некоторой области GcsD (ее можно
деформировать в точку, стягивая в точку область G). Поэтому
теорему Коши можно формулировать еще и так: если функция /
голоморфна в области D, а область G mD и ограничена непре-
непрерывной кривой dG, то интеграл от f no dG равен нулю.
Для применений полезно иметь обобщение этой теоремы на
случай, когда область G не обязательно односвязна. Чтобы
сформулировать это обобщение, введем:
Определение. Пусть-граница компактной2) области G
состоит из конечного числа замкнутых кривых Yv(v==0. • • •>п—!)•
Будем считать, что внешняя граница \о, т. е. кривая, отделяю-
отделяющая точки G от бесконечной точки, ориентирована против часо-
часовой стрелки, а остальные граничные кривые yv (v= 1, .... п— 1) —
') Это утверждение можно получить непосредственно из теоремы 1, если
воспользоваться замечанием, что в односвязной области любые два пути
с общими концами гомотопны друг другу.
_2) Напомним, что компактной называется область G, замыкание которой
s С состоит лишь из конечных точек (G^C),
§4]
ИНТЕГРАЛ
87
по часовой (иными словами, граничные кривые ориентированы
так, что область во время обхода границы всегда остается
слева (рис. 31). Границу области G с такой ориентацией мы
будем называть ориентированной границей и обозначать сим-
символом dG')•
Рис. 31.
Рис. 32.
обобщение
теоремы
Теперь мы можем сформулировать
Коши, о котором говорили выше:
Теорема 1. Пусть функция f^H(D) и G — любая ком-
компактно принадлежащая D область, ограниченная конечным чис-
числом кривых. Тогда интеграл от f no ориентированной границе
области G равен нулю:
jdz = O. A)
< Проведем в G конечное число разрезов Я*, связывающих
компоненты границы этой области (на рис. 32 мы для нагляд-
наглядности изобразим эти разрезы, состоящими из двух берегов).
Очевидно, что замкнутая кривая Г, состоящая из ориентирован-
ориентированной границы dG и совокупностейЛ+= U Av и Л~= U^v, гомотопна
нулю в области D 2). В силу свойств интегралов
\fdz= jfdz+ \fdz+ \fdz= J /dz,
Л+
dQ
а так как Г~0 в Д то по теореме 2 предыдущего пункта мы
получаем A) >
В некоторых вопросах полезно иметь более общий результат о равенстве-
нулю интеграла по границе самой области D, а не только областей, компакт-
компактно ей принадлежащих. Ясно, что без дополнительных условий такой резуль-
результат получить нельзя, ибо функция может не быть' определенной на dD. Мы
') Здесь мы пользуемся геометрическими представлениями об ориенти-
ориентированной границе. Формальное ее определение см. в п. 13 ч. II.
2) Это можно доказать индукцией по числу компонент dD. Заметим од-
однако, что формальное доказательство всего проводимого здесь построения
достаточно громоздко.
свойства голоморфных функции
[ГЛ. ГГ
приведем естественные дополнительные условия, в которых такое обобщение
теоремы Коши имеет место.
Теорема 2. Пусть функция f голоморфна в компактной области D,
ограниченной конечным числом спрямляемых кривых, и непрерывна в D.
Тогда интеграл от f no ориентированной границе этой области равен нулю:
f dz = 0.
B)
dD
¦4 Без ограничения общности можно считать, что D — односвязная об-
область (т. е. dD состоит из одной кривой), ибо приемом, примененным при
доказательстве теоремы 1, общий случай сводится
к этому. Дальнейшее доказательство ') разобьем на
три этапа.
1". Пусть у — спрямляемая кривая и d(y)—ее
У диаметр2); пусть плоскость С покрыта сеткой пря-
прямых, параллельных координатным осям, причем
сторона квадратов сетки
/ ! е<Г7^М- C)
А 1
3J/2
Докажем, что сумма диаметров квадратов_сет-
Рис. 33. KUi пересекающихся с у, не превосходит 9 г2|у1,
где Ivl —длина кривой у.
В самом деле, пусть {Ki}, / е /, — (конечная) совокупность квадратов
сетки, пересекающихся су, и К[ — квадрат со стороной Зе с тем же центром,
что Ки и так же расположенный (рис. 33). В силу условия C) у должна
выходить на границу дК{, следовательно, длина части у, лежащей в Kit
" > е- D)
Кроме того, мы имеем
|
¦ибо
Y П К,-
= 2 IУ П Ki I. а в сумме 2
ie/ is/
I yf]Ki\ не более 9 раз. Из неравенств D) и E) получаем, что
is/
2
is/
2
fe/
E)
мы считаем каждую из длин
F)
2°. Пусть функция f определена на множестве МсС и 6 — положитель-
положительное число. Модулем непрерывности f на М называется величина
М,
w/F)=sup lf(zi)—
для гь
\ г,
Известно, что если М — компактное замкнутое множество, то для непрерыв-
непрерывности f на нем необходимо и достаточно, чтобы Ш/(б) ->0 при 6->0.
') Это доказательство нам сообщил Л. Д. Иванов.
2) Под диаметром d(M) множества М сС понимается верхняя
расстояний \г' — г"\ между точками г', г'ей,
грань
§ 4]
ИНТЕГРАЛ
89
то
Докажем, что если f непрерывна на замкнутой спрямляемой кривой у,
fdz
Iv
G)
где d(y) —диаметр кривой у.
В самом деле, в силу того, что интеграл от dz по у равен нулю, для
любой точки г0 е у имеем
J fdz- J U(z)-f(zo)]dz.
V у
Так как 1/(г) —/(го)К<»/(<2(у)) для всех г
получаем G).
3°. Теперь будем доказывать ут-
утверждение теоремы. Покроем С сет-
сеткой, как в 1°, и представим интеграл
B) в виде
'- у, то отсюда простой оценкой
dD
J
д (ОПКЛ
Рис. 34.
состоит из конечного или счетного
состоит из одной компоненты, а
где первая сумма распространена на
квадраты {Ki}, i e /, пересекающие-
пересекающиеся с dD=y, а вторая — на квадраты,
целиком состоящие из внутренних
точек D (она равна нулю по теореме
Коши).
Для каждого » е / пересечение D П
множества компонент (на рис. 34 Z3 П
D[]Ki2—из трех). К границе каждой компоненты D Л Ki мы применим^ не-
неравенство G), в котором первый множитель заменим величиной со,(е К 2 )—
модулем непрерывности / на D для б = е У 2 (мы учитываем, что диаметр
границы каждой компоненты не превосходит е У 2 и что ш (б) — неубываю-
неубывающая функция от б). Затем мы сложим все такие неравенства (при фиксиро-
фиксированном i) и учтем, что объединение границ всех компонент состоит из у flKt
и некоторого множества точек на dKt, длина которого не превосходит
|dKi| = 4e. Таким образом мы получим
1 idz
d(DUKt)
Подставляя это в (8), будем иметь
IJ
fdz
Ч
Теперь воспользуемся неравенством F), из которого следует, что ^j j
is;
I Y l> получим
90 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
Остается_заметить, что в силу равномерной непрерывности f на D вели-
величина со* (в V2 ) стремится к 0 при е -> 0, а так как е можно взять сколь
угодно малым и оцениваемый интеграл не зависит от е, то он равен
18. Интегральная формула Коши. Здесь мы получим пред-
представление функций, голоморфных в компактной области, при
помощи интеграла по границе этой области. Такое представле-
представление, как мы увидим, находит важные применения как в теоре-
теоретических, так и практических вопросах.
Теорема 1. Пусть f^H(D) и G— компактно принадле-
принадлежащая D область, ограниченная конечным числом (непрерыв-
(непрерывных) кривых. Тогда в любой точке z^G функция f представима
в виде
т
дв
где dG — ориентированная граница G (см. стр. 87).
Величина в правой части этой формулы называется инте-
интегралом Коши.
•4 Возьмем р>0 таким, чтобы круг Up={z': \z' — z\<p}mG,
и обозначим Gp = G\Up. Функция g (g) = y^j голоморфна
в Gp, как частное двух голоморфных функций со знаменателем,
отличным от нуля. По теореме 1 предыдущего пункта (она при-
применима, ибо g голоморфна в некоторой области, компактно со-
содержащей Gp) имеем
2nt J gaQ~ 2m J C-z 2m' J g-z ~U'
ao дв ои
J J
aop дв
где окружность <3?/p={?: |S — zl=p} ориентирована против ча-
часовой стрелки.
Таким образом,
J_ Г f(l)dj _ 1 Г f(Q,
id?
дв ' дЬ„
P
где число р>0 можно считать сколь угодно малым. Так как
функция f непрерывна в точке гу то для любого е>0 можно вы-
выбрать число 6>0 столь малым, что при р<б
1/@ —f(«) 1<в для всех
§ 4) ' ИНТЕГРАЛ 9Г
Поэтому разность')
nz) 2ш" J i-г ~2ni J l
dUP dUP
по абсолютной величине не превосходит — е • 2я = е и, следо-
следовательно, стремится к нулю при р—»0. Но, как видно из B),
левая часть C) не зависит от р, следовательно, она равна нулю
при всех достаточно малых р, т. е.
2m J ? - z '
Отсюда и из B) следует формула A) >
Замечание 1. Если в условиях теоремы 1 точка г лежит
вне 2?, то
2ш J 5-z ~U-
Это утверждение следует непосредственно из теоремы Коши,
ибо здесь функция g(?) = l_ голоморфна в G.
Замечание 2. Если вместо теоремы 1 предыдущего пункта мы исполь-
используем теорему 2, то получим такую теорему:
Теорема V. Если функция f голоморфна в компактной области D,
ограниченной конечным числом спрямляемых кривых, и непрерывна в D, то
1. Г /(?)<*? _ j fW для всех z^D, ^
2m" J ?-2 [ о для всех г
где dD — ориентированная граница D.
Интегральная формула Коши выражает весьма интересный
факт: значения голоморфной в области G функции полностью
определяются ее значениями на границе. (В самом деле, если
значения f на dG известны, то известна и вся правая часть фор-
формулы A), т. е. известно значение / в любой точке 2seG.) Этот
факт принципиально отличает голоморфные функции от функ-
функций, дифференцируемых в смысле действительного анализа.
Из теоремы 1 просто вытекает
Теорема 2 (о ср е днем). Значение функции /ей (D) в
каждой конечной точке z^D равно среднему арифметическому
') Мы воспользовались тем, что ——г * ¦ = 1 (см. пример 1 п. 14)
ZJXt J Q"~ Z
и что постоянный множитель f(z) можно внести под знак интеграла.
92 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
ее значений на любой достаточно малой окружности с цен-
центром в z:
2Я
f(z + pe")dt. F)
о
-< Возьмем круг Up = {z': \z' — г|<р} такой, что UpmD,n
примем его в качестве области G из теоремы 1. По интеграль-
интегральной формуле Коши получим
а так как на dUp имеем ? — z = peu, /е [0, 2л], d'Q = pieudt, то G)
сводится к F) >
Теорема о среднем показывает, что голоморфные функции,
описательно говоря, очень правильно устроены и что их значе-
значения тесно связаны с соседними значениями. Это объясняет на-
наличие у таких функций целого ряда специфических свойств,
которых нет у функций, дифференцируемых в смысле действи-
действительного анализа. Многие такие свойства мы рассмотрим в даль-
дальнейшем.
В заключение приведем формулу интегрального представ-
представления функций, дифференцируемых в смысле действительного
анализа, которая обобщает интегральную формулу Коши.
Теорема 3. Пусть функция f принадлежит классу С1 в за-
замыкании компактной области D, ограниченной конечным числом
спрямляемых кривых. Тогда в каждой точке
Г Wl*L l ( ( df dld
D
J
dD
Эту формулу мы будем называть формулой Коши — Грина;
если f^H(D), то двойной интеграл в ней исчезает, и мы полу-
получаем формулу Коши. _
•4 Исключим из D малый круг Up={t,: \t, — z|^p} и к функ-
функции g(g)= f_j , принадлежащей классу С1 в области Dp==
= D\Up, применим формулу Грина в комплексной записи (см.
формулу (9) п. 16):
dD dU0
.... dg df 1 ж . 1
') Мы имеем -%S- — -jfe-• > ' -¦, ибо функция -~—голоморфно зависит
"Ь "to 6 z ъ ~2
от 5 и ее производная по ? равна нулю.
§ 5] РЯДЫ ТЕЙЛОРА 93
Так как / непрерывна в точке z, то f (?) =f(z) +O(p) для ?ef/p,
где О (р) —>¦ О при р —> 0. Поэтому
и последняя формула при р—*0 дает (8) ') >
§ 5. Ряды Тейлора
В этом параграфе мы, отправляясь от интегральной формулы
Коши, получим представление голоморфных функций в виде
сумм степенных рядов (рядов Тейлора).
Напомним известные из анализа простейшие понятия, свя-
оо
занные с рядами. Ряд (из комплексных чисел) 2 &п называется
п=0
сходящимся, если последовательность его частичных сумм
п
sn = 2 о-к имеет конечный предел s; этот предел называется
суммой ряда.
оо
Функциональный ряд 2 freB). гДе функции fn определены
на некотором множестве МаС, называется равномерно сходя-
сходящимся на М, если он сходится в каждой точке геМ и для лю-
любого е>0 найдется номер N — N(e) такой, что для всех n ^ N
остатки этого ряда
< е для всех
к = п + \
V
Точно так же, как в анализе, доказывается, что ряд 2л fn(z)
га=0
сходится равномерно на множестве М, если сходится ряд с Не-
Неотрицательными членами 2 II fn II. где II/«11= sup | fn(z) | (по-
п = й г^М
следнее условие равносильно тому, что рассматриваемый ряд
') Наше рассуждение доказывает существование
lim
но так как/sC'(D), то двойной интеграл в (8) существует (в этом можно
убедиться, переходя к полярным координатам с центром в точке г) и этот
Чредел совпадает с ним.
94 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
мажорируется на М сходящимся числовым рядом). Без всяких
изменений переносятся и доказательства того, что сумма равно-
равномерно сходящегося ряда из функций, непрерывных на множе-
множестве М, непрерывна на этом множестве и что равномерно схо-
сходящийся на кривой (класса С1 или спрямляемой) ряд из не-
непрерывных функций можно почленно интегрировать по этой
кривой.
19. Ряды Тейлора. Одной из основных в теории функций
комплексного переменного является
Теорема 1. Если функция f^H(D) и z0—произвольная
точка D, то в любом круге U={\z — zo\<R}aD эту функцию
можно представить в виде суммы сходящегося степенного ряда
га=0
< Пусть zef/ — произвольная точка; выберем число г так,
чтобы \z — zo\<r<R, и обозначим через уг окружность
{?: |?— zo\—r}. По интегральной формуле Коши имеем
(С) аг
~ 2ш J с-
Чтобы получить разложение f в степенной ряд, разложим
«ядро» этой формулы в геометрическую прогрессию по степе-
степеням z — г0:
B-г0)" ,„\
t-z
затем умножим обе части на -^-т f(t) и проинтегрируем почленно
по уг. Так как для всех ?еуг имеем
то прогрессия B) сходится равномерно по % на уг. Равномер-
Равномерность сходимости не нарушится при умножении на непрерывную
на уг и, следовательно, ограниченную функцию -$-у/(?). По-
Поэтому наше почленное интегрирование законно, и, выполнив его,
мы получим
V, П=0 ^ 0) п-Ч
§ 5] РЯДЫ ТЕЙЛОРА 95
где
Определение. Степенной ряд A), коэффициенты кото-
которого определены формулами C), называется рядом Тейлора
функции / с центром в точке z0.
Из теоремы об инвариантности интеграла (п. 16) видно, что
коэффициенты сп ряда Тейлора, определяемые по формуле C),
не зависят от радиуса г окружности \r @<r<R).
Отметим простые следствия теоремы 1.
Неравенству Коши. Пусть функция f голоморфна в
замкнутом круге U={\z — zoj<>} и на окружности yr = di/ ее
модуль не превосходит постоянной М. Тогда коэффициенты
ряда Тейлора f с центром в г0 удовлетворяют неравенствам
|с„К-рг (п = 0, 1, ...). D)
« Из формул C), учитывая, что |/(?)|^Л1 для всех ?еуг,
находим
Из неравенств Коши вытекает интересная
Теорема 2 (Лиувилль). Если функция f голоморфна во
всей плоскости С и ограничена, то она постоянна. _
< По теореме 1 в любом замкнутом круге {/={|г|^R),
оо, функция / представляется рядом Тейлора
2
п=0
коэффициенты которого не зависят от R. Так как / ограничена
в С (пусть |/(г) j-^C-M), то по неравенствам Коши для любого
я = 0, 1, ... имеем
1 )-- м
Здесь R можно взять сколь угодно большим, поэтому при
л=1, 2, ... правая часть стремится к нулю при R—* оо. Но ле-
левая часть не зависит от R, поэтому сп=0 для л=1, 2, ... и
/B)=Со >
Таким образом, два свойства функции — быть голоморфной
во всей плоскости С и быть ограниченной — могут сосущество-
сосуществовать лишь на тривиальных функциях (постоянных),
96
свойства голоморфных функций
[ГЛ. II
Теорему Лиувилля можно сформулировать еще и так:
Теорема 2'. Если функция f голоморфна во всей замкну-
замкнутой плоскости С, то она постоянна.
< Функция / голоморфна в бесконечности, значит, lim f(z)
Z -> оо
существует и конечен. Отсюда следует, что / ограничена в неко-
некоторой окрестности {jz|¦<!/?} бесконечной точки. В остальной ча-
части плоскости {|г|^/?} она ограничена,
как непрерывная функция на замкну-
замкнутом ограниченном множестве. Поэтому
/ ограничена в С, а так как она голо-
голоморфна там, то по теореме 2 / =
= const >
Теорема 1 утверждает, что любую
голоморфную в круге функцию в этом
круге можно представить как сумму схо-
сходящегося степенного ряда. Мы хотим те-
теперь доказать, что, и обратно, сумма
любого сходящегося степенного ряда яв-
является голоморфной функцией. Для это-
этого напомним некоторые свойства степенных рядов, известные
читателю из курса анализа.
Лемма. Если члены степенного ряда
Рис. 35.
сп(г-а)п
E)
в некоторой точке гоеС ограничены, т. е.
\cn(z0 — a)"|<M (я = 0, 1, ...), F)
го этот ряд сходится в круге U = {z: \z — a\<\z0 — а\} и на каж-
каждом компактном подмножестве К <Ш11 он сходится равномерно.
< Можно предполагать, что гофа, т. е. \z0 — а|=р>0, иначе
множество U пусто. Пусть множество К <Ш 0, тогда для любой
точки
(рис. 35). Поэтому для любой точки z^K. и для любого
п = 0, 1, ... мы имеем
\cn(z — a)«|<|cn|p«<7".
Но по условию F) |сп|рп-^М, следовательно, для любой z^K
ряд E) мажорируется сходящейся геометрической прогрессией
М
2
п=0
и, значит, сходится равномерно на К.
§ 5] РЯДЫ ТЕЙЛОРА 97
Второе утверждение леммы доказано, а первое следует из
второго, ибо любая точка г'е?/ содержится в некотором круге
{\z— а|<р'}, \г' — а|<р'<р, компактно принадлежащем U >
Теорема 3 (Абель). Если степенной ряд E) сходится
в некоторой точке za<=C, то этот ряд сходится в круге U =
={z: \z — a\<\z0—a\) и на каждом компактном подмноже-
подмножестве U он сходится равномерно.
< Так как ряд E) сходится в точке г0, то общий член
cn(zo — а)" соответствующего числового ряда стремится к нулю.
Но всякая сходящаяся последовательность ограничена, поэтому
выполняется условие леммы, а из леммы следуют оба утвер-
утверждения теоремы >
Формула Коши — Адамара. Пусть дан степенной
ряд E) и
ШУМ=\, G)
где О ^ R ^. оо [мы считаем -~ = оо и — = О]. Тогда в любой
точке z, в которой \z — a\<R, ряд E) сходится, а в любой
точке z, в которой \z — a\>R, расходится ').
¦< Верхним пределом последовательности действительных чи-
чисел ап называется число А такое, что: 1) существует подпосле-
подпоследовательность ап -* А и 2) каково бы ни было е>0, найдется
такой номер N, что а„<А + е для всех n^N. При этом не
исключаются случаи Л = ±оо, только при Л = +оо условие 2)
отпадает, а при А=—оо число Л + е в нем заменяется произ-
произвольным числом (в последнем случае условие 1) выполняется
автоматически и существует liman =—оо). В анализе доказы-
вается, что всякая последовательность алеК имеет единствен-
единственный (конечный или бесконечный) верхний предел.
Пусть 0<R< оо; для любого е>0 можно найти число N та-
та1
кое, что при п !>¦ N имеем Y\ сп I < тг + е> и> следовательно,
(8)
Если \г — a\<R, то можно выбрать е столь малым, что будет
(-Q- + е) | z — а | = q< 1; тогда, как видно из (8), члены ряда E)
при я > N мажорируются членами геометрической прогрес-
прогрессии qn, и, следовательно, ряд E) сходится при \г — a\<R.
') Заметим: это утверждение содержит первое утверждение теоремы Абеля.
7 Б. В. Шабат
98 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
Из условия 1) в определении верхнего предела видно, что
для любого е>0 найдется последовательность nh—*-oo такая,
"ftj
что К|сЯа| >-дг —е, и, следовательно,
{{±)}n\ (9)
Если \г — a\~>R, то можно выбрать е столь малым, что будет
(-?- — ej|z — a\> 1; тогда, как видно из (9), |с„й (z —а)"*|> 1,
и, следовательно, общий член ряда E) не стремится к 0, т. е.
ряд расходится при \г — а|>/?.
Доказательство в случаях R = 0 и R = оо предоставляется чи-
читателям >
Определение. Областью сходимости степенного ряда E)
называется открытое ядро (т. е. совокупность внутренних то-
точек) в множества cf тех точек геС, в которых сходится этот
ряд.
Теорема 4. Областью сходимости степенного ряда E) яв-
является круг {\z— a\<R}, где R — число, определяемое по фор-
формуле Коши — Адамара G)„
< Из предыдущего утверждения следует, что множество <?
точек сходимости ряда E) представляет собой круг {| г—а|</?},
дополненный некоторым множеством точек окружности {|z—а\ —
— R] (быть может, пустым). Поэтому открытым ядром ef яв-
является круг {|z — a\<R) >
Круг (открытый), существование которого только что дока-
доказано, называется кругом сходимости степенного ряда E), а
число R — радиусом сходимости.
Примеры. 1. Ряды
а) S (г)- б) S Л в) S(пг)п-
п=1 п=\ п—1
как видно из формулы Коши — Адамара, имеют соответственно радиусы схо-
сходимости R—°°, 1 и 0. Поэтому круг сходимости первого' из них есть С,
второго — единичный круг {|г|<1}, а третьего — пустое множество.
2. Из той же формулы видно, что кругом сходимости всех трех рядов
оо оо оо
а) 2 Л б) 2 -J-, в) 2 -J
П=\
является единичный круг {|z|<l}. Однако множества точек сходимости всех
трех рядов различны. Ряд а) расходится во всех точках окружности {|г|=1},
ибо его общий член при |zj = l не стремится к нулю. Ряд б) в некоторых
точках окружности {|;г|=1} сходится (например, в г=—1), а в некоторых
§ 5) РЯДЫ ТЕЙЛОРА 99
расходится (например, в z=l). Ряд в) сходится во всех точках этой окруж-
окружности, ибо для любого г, \z\=\, он мажорируется сходящимся числовым
рядом
Переходим к доказательству голоморфности суммы степен-
степенного ряда.
Теорема 5. Сумма степенного ряда
оо
я=0
голоморфна в круге его сходимости.
^ Мы предполагаем, что радиус сходимости ряда R>0, ибо
иначе нечего доказывать. Напишем формально производный
ряд
2 псЛг-аГ'=Ф(г); A3)
со
он сходится или расходится вместе с рядом 2 ncn{z — a)n, а так
как
lim Yn\cn\ = lim
то радиус сходимости ряда A3) тоже равен R. На компакт-
компактных подмножествах круг U={\z — a\<R} ряд A3) сходится
равномерно, следовательно, функция ср(г) непрерывна в этом
круге.
По той же причине ряд A3) можно почленно интегрировать
по границе любого треугольника АШ U:
J ф dz = 2 псп J (z - a)" dz = 0
дА п=\ дА
(по теореме Коши все интегралы в правой части равны нулю,
значит, и интеграл в левой части также). Следовательно, можно
применить лемму 1 из п. 15, по которой функция
оо оо
J Ф (S) dl = J] ncn \ "ft - аГ1 dl = J] с„ (г - аГ
[о, г) n=l La, г] /1=1
7*
100 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
(мы снова воспользовались равномерной сходимостью) в ка-
каждой точке ге?/ имеет производную, равную cp(z). Но тогда и
функция
J
J
[о, г]
в каждой точке г е ?/ имеет производную /'(г)=ф(г) >
20. Свойства голоморфных функций. Отметим несколько
следствий теоремы о голоморфности суммы степенного ряда.
Теорема 1. Производная функции fczH(D) голоморфна
в области D.
< Для любой точки zQ^D мы построим круг U = {\z — Zo| <R},
принадлежащий D. По теореме 1 п. 19 функция / в этом круге
представляется как сумма степенного ряда. По теореме 5 п. 19
производная f = cp представляется рядом, сходящимся в том же
круге. Поэтому к ф можно снова применить теорему 5, и, зна-
значит, ф дифференцируема в U в смысле комплексного анализа >
Из этой теоремы' непосредственно вытекает необходимое
условие существования первообразной, о котором говорилось
в п. 15:
Следствие. Если функция f имеет в области D первооб-
первообразную F, то f голоморфна в D. (В иных терминах: всякая точ-
точная в области D дифференциальная форма f dz — dF является
замкнутой в D.)
Повторным применением теоремы 1 получается .
Теорема ]'. Любая функция f^H(D) имеет в D производ-
производные всех порядков, также принадлежащие Н (D) (бесконечно
дифференцируема).
Следующая теорема утверждает единственность разложения
функции в степенной ряд с данным центром.
Теорема 2. Если функция f в круге {\z — 20|</?} предста-
вима как сумма степенного ряда
я=0
A)
то коэффициенты этого ряда определяются однозначно по фор-
формулам
-«Подставляя в A) г=г0, найдем /(zo)=co. Дифференцируя
ряд A) почленно:
=ci + 2c2(z — z0) +3c3(z — zoJ+ ,..,
§ 5] РЯДЫ ТЕЙЛОРА 101
и затем подставляя z=z0, найдем f'(zo)=Ci. Продифференци-
Продифференцируем A) п раз:
/<«> (г) = п\сп + с\ (г - г0) + c'2(z- zof + ...
(мы не выписываем выражений для коэффициентов), и снова
подставим z = z0; получим n\cn = f(-n^(z0) >
Теорему 2 иногда формулируют так: всякий сходящийся сте-
степенной ряд является рядом Тейлора своей суммы.
Формула B) позволяет писать тейлоровские разложения эле-
элементарных функций. Например, мы имеем
C)
все три разложения справедливы всюду в С (их радиус сходи-
сходимости R— оо).
Сравнивая только что найденные значения сп с первоначаль-
первоначальными их значениями, вычисленными по формуле C) п. 19, по-
получим выражения для производных голоморфных функций:
) = — f f(?)rf? (п=\ 2 ) D)
Если f голоморфна в области О и G<i=D — область, ограни-
ограниченная конечным числом непрерывных кривых и такая, что
z0 e G, то, пользуясь неизменностью интеграла при гомотопной
деформации контура, мы можем заменить в последней фор-
формуле уг ориентированной границей dG. Получим интегральные
формулы для производных голоморфных функций:
^тг^ (-1.».-) (в
dG
(мы пишем г вместо z0 и предполагаем, что геб),
Это формулы получаются из интегральной формулы Коши
--±- Г f{t)d
- 2ni J C-
дв
дифференцированием по параметру z под знаком интеграла.
Наше косвенное рассуждение позволяет избежать доказатель-
доказательства законности такого дифференцирования.
Теорема 3 (Морера). Если функция f непрерывна в
области D и интеграл от нее по границе дА любого треуголь-
треугольника А<Ш D равен нулю, то /еЯ (D).
102 свойства голоморфных функций [гл. и
•^ Для любой точки aeD построим круг U={\z — a|<r}cz?).
По теореме 2 п. 15 функция
[а, г]
голоморфна в U и F''(z) =f{z) в каждой точке z^U. По тео-
теореме 1 отсюда следует, что и / голоморфна в U. Тем самым до-
доказана голоморфность / в каждой точке а е D>
Замечание. Теорема Мореры является обратной к основ-
основной лемме интегрального исчисления (п. 15), по которой инте-
интеграл от голоморфной в области D функции по границе любого
треугольника A<e=Z) равен нулю. Эту теорему можно рассма-
рассматривать также как обратную к теореме Коши (она сильнее по-
последней, в которой требуется, чтобы равнялся нулю интеграл
от / по любому замкнутому пути yczD, а не только по границам
треугольников А ш D). Однако в теореме Мореры вводится до-
дополнительное условие непрерывности функции /. Это условие
существенно: например, для функции, равной 0 всюду в С,
кроме одной точки, где она равна 1, интеграл по границе лю-
любого треугольника равен нулю, однако эта функция не голо-
голоморфна, ибо она даже не непрерывна.
В заключение приведем сводку результатов об эквивалент-
эквивалентности различных определений голоморфности функции в точке:
Теорема 4. Эквивалентны следующие три утверждения:
(R) функция f в некоторой окрестности U точки а имеет
производную f'(z) в смысле комплексного анализа;
(С) функция f непрерывна в некоторой окрестности U
точки а, и интеграл от нее по границе любого треугольника
А<Ш U равен нулю;
(W) функция f разлагается в степенной ряд, сходящийся в
некоторой окрестности U точки а.
Эти три утверждения отражают три концепции в построении
теории голоморфных функций. Обычно функцию, удовлетворяю-
удовлетворяющую условию (R), называют голоморфной в смысле Римана,
условию (С) — голоморфной в смысле Коши и условию (W) —¦
голоморфной в смысле Вейерштрасса.
Импликация (R)=#(C) доказана в теореме Коши (п. 16),
) в теореме Мореры, (R)=^(W) —в теореме Тейлора,
)() — в теореме о голоморфности суммы степенного ряда.
И, наконец, сделаем еще одно
Замечание. Мы убедились в том, что представимость
функции / в круге {\г — a\<R) в виде суммы сходящегося сте-
степенного ряда является необходимым и достаточным условием
ее голоморфности в этом круге. Однако сходимость степенного
§ 5] РЯДЫ ТЕЙЛОРА ЮЗ
ряда в точках границы круга сходимости не связана с голо-
голоморфностью суммы ряда в этих точках. В этом можно убе-
убедиться на простых примерах.
В самом деле, напишем разложение в геометрическую про-
прогрессию
n=0
сходящееся в круге {|2J<1}. Во всех точках окружности
{|г| = 1} ряд F) расходится, ибо его общий член не стремится
к 0. Однако сумма этого ряда голоморфна во всех точках ок-
окружности, кроме 2 = 1. С другой стороны, ряд
оо
V г" '
П = \
сходится во всех точках окружности круга сходимости {|z| = l},
ибо он мажорируется сходящимся числовым рядом V—j. Од-
Однако его сумма f не может быть голоморфной в точке 2=1, так
при стремлении к 1 по действи-
1
тельной оси неограниченно возрастает.
21. Теорема единственности. Определение 1. Нулем
функции / называется любая точка аеС, в которой эта функ-
функция равна нулю, т. е. корень уравнения f(z) =0.
В действительном анализе нули дифференцируемых функций
могут иметь предельные точки, в которых функция остается
дифференцируемой (такова, например, точка х = 0 для функ-
функции f (х) = x2sin —). В комплексном анализе дело обстоит не так:
X }
нули голоморфной функции непременно изолированы, они мо-
могут иметь предельные точки лишь на границе области, в которой
голоморфна эта функция ]). Этот факт выражает
Теорема 1. Если точка а является нулем голоморфной
в этой точке функции f, не равной тождественно нулю ни в
') Заметим, что функция f (z) = г2 sin— перестает быть голоморфной
в точке г—0, ибо при г->0 по некоторым направлениям (например, по на-
направлению мнимой оси) sin — стремится к бесконечности быстрее любой
1
степени —.
г
104 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
какой окрестности а, то существует такое натуральное число п,
что
/B) = (г-а)«ФB), A)
где функция ф голоморфна в точке а и отлична от нуля в неко-
некоторой окрестности этой точки.
< В самом деле, в некоторой окрестности точки а функция f
разлагается в степенной ряд. Свободный член этого ряда равен
нулю, ибо f(a)=O, но все его коэффициенты не могут быть рав-
равными нулю, ибо тогда / = 0 в некоторой окрестности а. Поэтому
найдется отличный от нуля коэффициент с младшим номером,
который мы обозначим через п, и разложение имеет вид
f{z)=cn{z — a)« + cn+1B — а)«+1+:..., спф0. B)
Обозначим через
сумму ряда, сходящегося в некоторой окрестности а, и поэтому
голоморфную в этой окрестности. Так как ф(а) =спф0, то в силу
непрерывности этой функции <рфО в некоторой окрестности а >
Теорема 2 (единственности). Если две функции fit
f2^H(D) совпадают на множестве ?", которое имеет хотя бы
одну предельную точку а, принадлежащую D, то fi = f2 всю-
всюду в D.
< Функция f=fi — /2e#(D); нужно доказать, что /=0 в D,
т. е. что множество & ={z^D: /(z)=0}zDcf совпадает с D.
Предельная точка а является нулем / (в силу непрерывности
последней). По теореме 1 функция / = 0 в некоторой окрестно-
окрестности а, ибо иначе эта точка не могла быть предельной для мно-
множества нулей /.
О ,
Таким образом, открытое ядро &" множества &" (т. е. сово-
совокупность его внутренних точек) непусто — оно содержит точку а.
По построению <& открыто, но оно в то же время и замкнуто
(в относительной 'топологии области D). В самом деле, если
b^D является предельной точкой <& , то по той же теореме 1
функция /sOb некоторой окрестности Ь, т. е. b ej'. Так как D
по определению области связно, то по теореме 3 п. 4 имеем
3~ = D >
Эта теорема также показывает существенное отличие поня-
понятия голоморфности функции от понятия дифференцируемое™
в смысле действительного анализа. В самом деле, две даже
бесконечно дифференцируемые функции действительного пере-
переменного могут совпадать на части области определения, не сов-
совпадая тождественно (рис. 36), Но по доказанной теореме две
§ 5! РЯДЫ ТЕЙЛОРА 105
голоморфные функции, совпадающие на любом множестве, ко-
которое имеет предельную точку в области, где они голоморфны
(например, на маленьком кружке или на
дуге, принадлежащей области), совпадают г
тождественно во всей области.
Заметим еще, что, пользуясь теоремой
единственности, можно несколько упростить ^ , , !
формулировку теоремы 1. Именно, условие, i
что функция f не равна тождественно нулю |
ни в какой окрестности точки а, можно за-
i_
Л i
менить условием, что она вообще не равна о ос р Ь
нулю тождественно (по теореме единствен- рнс зб.
ности эти условия совпадают).
Из теоремы 1 видно, что голоморфные функции обращаются
в нуль, как целая степень (г— а).
Определение 2. Порядком нуля аеС функции /, голо-
голоморфной в этой точке, называется номер младшей отличной от
нуля производной f(ft)(a). Иными словами, точка а называется
нулем / порядка п, если в этой точке
f(a)= ... =/<п-')(а) = 0, }м(а)Ф0 (п>1). C)
Из формул для коэффициентов ряда Тейлора ск— ,, ¦
видно, что порядок нуля совпадает с номером младшего отлич-
отличного от нуля коэффициента тейлоровского разложения функции
в этой точке, т. е. с числом п, которое участвует в формулировке
теоремы 1. Теорема единственности показывает, что голоморф-
голоморфные функции, не равные тождественно нулю, не могут иметь ну-
нулей бесконечного порядка.
Подобно тому, как это делается для многочленов, можно
определить порядок нуля при помощи делимости. Име«но, спра-
справедлива
Теорема 3. Порядок нуля аеС голоморфной функции f
совпадает с порядком наивысшей степени (z— a)k, на которую f
«делится» в том смысле, что частное — . (после продолже-
(z-a)"
ния по непрерывности в точку а) оказывается функцией, голо-
голоморфной в точке а.
< Обозначим через п порядок нуля а и через N наивысший
порядок степени бинома (z -- а), на которую делится /. Из фор-
формулы A) видно, что / делится на любую степень k~^.n:
-(г-аГ»Ф(г),
106 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
поэтому N ^-п. Пусть / делится на (z— a)N, т. е. частное
представляет собой функцию, голоморфную в точке а. Разла-
Разлагая г|5 в ряд по степеням (z— а), мы найдем, что тейлоровское
разложение / с центром в точке а начинается со степени не
ниже N. Поэтому п^- N, и, объединяя это с полученным выше
неравенством, найдем, что N = n >
Пример. Функция f(z)=sinz — г имеет в точке г=0 нуль третьего
порядка. В самом деле, имеем f @) =/'@) =/"@) =0, но Г"@) Ф0. Это видно
также из разложения
z3 г5
/(z) = sinz-z = — gy-+ ...
Замечание. Пусть / голоморфна в бесконечности и равна
там 0; порядком этого нуля естественно назвать порядок нуля
в точке г=0 функции ф (г) = /( — ). Доказанная теорема оста-
нется справедливой и для точки а= оо, если вместо деления на
(г — a)h рассматривать умножение на zh (k=l, 2, ...).
Понятие порядка нуля можно распространить на Л-точки го-
голоморфных функций. Точка йеС называется А-точкой функ-
функции /, если f(a)=A. Порядком Л-точки а функции /, голоморф-
голоморфной в этой точке, называется порядок а как нуля функции
f(z) -A.
22. Теорема Вейерштрасса касается дифференцирования ря-
рядов из голоморфных функций. Как известно, в действительном
анализе почленное дифференцирование рядов требует сходи-
сходимости ряда в какой-либо точке и равномерной сходимости ряда
из производных. В комплексном анализе ситуация упрощается.
Имеет место
Теорема 1 (В е й ер ш т р асе). Если ряд
f(z)=2fB(z) A)
из функций, голоморфных в некоторой области D, сходится рав-
равномерно на любом компактном подмножестве этой области, то
1) сумма этого ряда f голоморфна в D;
2) ряд можно почленно дифференцировать в каждой точке D
любое число раз.
-«Пусть а — произвольная точка D; построим круг U =
={\z — a\<r}mD. Так как ряд A) по условию сходится на U
равномерно, а его члены непрерывны в U, то его сумма / не-
непрерывна в U. Обозначим через у ориентированную границу лю-
§ 5] РЯДЫ ТЕЙЛОРА 107
бого треугольника Adt/. Так как ряд A) сходится на у равно-
равномерно, мы можем проинтегрировать его почленно вдоль у.
= |] \fndz.
п=0 V
Но так как /„ голоморфны в U, то по теореме Коши все
интегралы в правой части равны нулю. Следовательно, равен
нулю и интеграл от / по у. Мы можем применить теорему Мо-
реры, по которой / голоморфна в U. Утверждение 1) доказано.
Для доказательства 2) опять возьмем произвольную точку
«gD, построим круг ?/={|г — a\<r}mD и обозначим через
yr=dU окружность {\z — а\=г). По формуле Коши для произ-
производных имеем
p>(a) = jL Г П*)Ь F = 1,2,...). B)
2яг J (г-а)к
В силу равномерной сходимости на уг ряда
Hz) _ V fn(z) ,„х
{га) (г_а)*+1 W
(он отличается от A) множителем, модуль которого равен —щ-
для всех геуг) мы можем подставить C) в интеграл B). При-
Применяя формулы B) к функциям /„, найдем
оо
^n 2я(- J B-
0
Утверждение 2) доказано >
В анализе особую роль играют ряды, составленные из поли-
полиномов. По теореме Вейерштрасса можно утверждать, что если
ряд из полиномов
f(z)=!iPn(z) D)
п=0
сходится равномерно на каждом компактном подмножестве не-
некоторой области D, то его сумма / голоморфна в D.
Для практики важна обратная задача о приближении про-
произвольной функции, голоморфной в области D, последователь-
последовательностью полиномов, причем обычно требуется, чтобы такое при-
приближение было равномерным на каждом компактном подмно-
подмножестве D. Приведем точную постановку задачи о равномерном
приближении полиномами.
108
СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ
[ГЛ. 1Г
Пусть задана область DcrC и функция /e#(D). Требуется
для любого множества Кшй и любого е>0 построить такой
полином P(z), чтобы
||/-P|k-sup|f(z)-P(z)|<e. E)
Эта задача равносильна задаче построения ряда из полино-
оо
мов 2 Рп (z)> который сходится к / равномерно на каждом
компактном подмножестве области D. В самом деле, если такой
ряд построен, то его частичные суммы с достаточно большими
номерами, очевидно, удовлетворяют
условиям задачи. Для доказатель-
доказательства обратного утверждения восполь-
воспользуемся леммой о компактном исчерпы-
исчерпывании:
Лемма. Для любой области DczC
можно построить компактное исчер-
исчерпывание, т. е. последовательность та-
таких замкнутых {в топологии С) мно-
множеств Кп, что
W i— W г— I— W t— IА\
Л| <— Дг '—• • • • ^— Ая <— ...) \у)
причем все KnczD и каждая точка z<=D принадлежит всем Кп,
начиная с некоторого \D= (J Kn)-
< В качестве Кп можно взять множества
0
Рис. 37.
где р(г, dD)—расстояние от точки z до границы области и
п=\, 2, ... (рис. 37) >
Замечание. Фиксируем точку zo^D и обозначим через Gn
связную компоненту открытого ядра Кп, содержащую г0 (начи-
(начиная с некоторого п=п0 все они непусты). Тогда мы получим
компактное исчерпывание D областями
G1mG2... mGnm..., G)
оо
причем все Gn Ш D и D = (J Gn.
Так как функция p(z, dD) удовлетворяет условию Липшица,
т, е, для всех z', z"^D имеем
Jp(z', dD)-p{z",
§ 5] РЯДЫ ТЕЙЛОРА 109
то границы областей Gn состоят из_конечного числа спрямляе-
спрямляемых кривых. Более того, покрывая Gn конечным числом кругов
достаточно малого радиуса, мы можем построить носледователь-
ность областей G'n с кусочно гладкими границами, также ком-
компактно исчерпывающую D.
Наконец, заметим, что если область D односвязна, то и обла-
области Gn ее компактного исчерпывания можно считать односвяз-
ными.
Вернемся к прерванному рассуждению. Пользуясь леммой,
нетрудно доказать, что если для области D задача о равномер-
равномерном приближении полиномами разрешима, то в ней любую
функцию f^H(D) можно представить рядом из полиномов, рав-
равномерно сходящимся на каждом К Ш D. В самом деле, построим
оо
компактное исчерпывание D = (J Кп, как в лемме, и построим
последовательность полиномов Рп таких, что
М-Рп\\кп<^п (Л = 1, 2, ...)• (8)
Тогда ряд
со
Л (?) + 2 [Рп+1 (г) - Рп (*)] (9)
будет искомым. В самом деле, его п-я частичная сумма равна Рч
и поэтому в силу. (8) он сходится к / равномерно на каждом
К <sD (каждое КшО принадлежит всем Кп, начиная с неко-
некоторого номера, и, следовательно, ||/ — Рп\\к<е Для любого
е>0, если п достаточно велико).
Если область D представляет собой круг U=[\z — a\<R},
то поставленную задачу решают полиномы Тейлора функции f
с центром в точке а:
i^(z-fl)\ A0)
Действительно, мы знаем, что / представляется в U рядом Тей-
Тейлора, причем этот ряд сходится равномерно на компактных
подмножествах U.
Однако степенные ряды сходятся лишь в кругах, поэтому
полиномы Тейлора непригодны для приближения функций в
областях более общего вида. Вопрос о приближении функций
в односвязных областях решает
Теорема 2 (Рунге). Пусть функция f голоморфна в
односвязной области Лс:С и К—'Произвольное компактное.
ПО свойства голоморфных функций [гл. и
подмножество D. Тогда для любого е>0 найдется полином Р
такой, что
Н/-Р|1к<8. (И)
< Построим односвязную область G с кусочно гладкой гра-
границей dG=y такую, что КшвшЭ (см. замечание после
леммы). Для любой точки z<=K по интегральной формуле Коши
имеем
Докажем сначала, это / можно приблизить на К рациональ-
рациональными функциями. Для этого разобьем y на участки точками
gv (v = l, ..., N), взятыми в порядке обхода y. обозначим че-
через Yv участок y между ?v и ?v+1, положим A?v=?v+i— ?v( мы
считаем t,N+i = Zi) и рассмотрим рациональную функцию
Имеем, очевидно,
v=l
Так как функция / двух комплексных переменных z и t не-
прерывна на компактном множестве КХу четырехмерного про-
пространства {г, I) 4), то она равномерно непрерывна на нем. По-
Поэтому для любого е>0 можно выбрать yv столь мелкими, что
/(С) f (Cv)
<е
для всех E;eyv и всех геК. Подставляя эту оценку в A4),
найдем
где IyI —длина y- Возможность приближения / рациональными
функциями вида A3) доказана.
Остается показать, что любую функцию вида A3) можно
приблизить равномерно на К полиномами. Для этого до-
достаточно доказать, что на К равномерно приближается полино-
') Через Ах В обозначается произведение множеств Л и В, т. е. совокуп-
совокупность всех пар (а, Ь), где А 6В
§ 5] РЯДЫ ТЕЙЛОРА " Ш
мами любая функция ? _ , где ?vedG— произвольная точка.
Докажем большее: пусть G' — область такая, что К <Ш G' Ш G
и дополнение Д=С\С связно1); тогда множество
Д: —— приближается равномерно на К полиномами?-
совпадает с Д.
Множество (f непусто, ибо оно содержит внешность круга
{\z\<R}, в котором лежит К- В самом деле, для любого а,
\a\>R, функция —^— голоморфна в {jг|¦<!/?} и, следовательно,
равномерно приближается в этом круге (а значит, и на К)
своими полиномами Тейлора с центром 2=0. Множество If
замкнуто (в топологии Д), ибо если последовательность точек
an^!f сходится к некоторой точке йеД, то и последователь-
последовательность функций —— равномерно на К сходится к —-^— (при
а = оо последнюю надо заменить тождественным нулем), а так
как все —^— равномерно на К приближаются полиномами, то
и —— также. Но в то же время If и открыто: пусть а0 е ^ и:
а — любая точка из круга
\а-ао\< inf \ao-z\\
имеем
(ао-а)"
_J = у
ао-г ' г ао-а Ы (ao-z)n+l '
ao — z n
причем ряд сходится равномерно на К, а так как и, зна-
чит, -, уг приближаются на К полиномами, то частные
(а0 —-Z)
суммы этого ряда — тоже, т. е.
Таким образом, If является непустым и одновременно за-
замкнутым и открытым подмножеством связного множества Д;
по теореме 3 п. 4 ? =Д >
Замечание. По существу тем же методом доказывается,
что любую функцию /, голоморфную на открытом (не обязатель-
обязательно связном) множестве D со связным дополнением,
можно приблизить полиномами равномерно на каждом КшЭ.
') Такую область G' можно построить на основании доказанной леммы
и односвязности области G,
112 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
(Вторая часть доказательства не меняется вовсе; в первой ча-
части нужно построить открытое множество G, Кш G <шЬ, с гра-
границей y=dG, состоящей из конечного числа кусочно гладких
кривых, и заметить, что формула A2) распространяется на этот
случай.)
С другой стороны, для многосвязных областей задача о при-
приближении голоморфных функций полиномами, вообще говоря,
неразрешима. Причину этого мы выясним позже (см. п. 35).
§ 6. Ряды Лорана и особые точки
Ряды Тейлора приспособлены для представления голоморф-
голоморфных функций в кругах. Здесь мы рассмотрим более общие ряды
по положительным и отрицательным степеням (z — a). Такие
ряды представляют голоморфные функции в концентрических
кольцах
V={ze=C: r<\z—a\<R], r>0,R<oo.
Особенно важны разложения в кольцах с нулевым внутрен-
внутренним радиусом, т. е. проколотых окрестностях. Эти разложения
позволяют изучать функции в окрестности точек, где они те-
теряют голоморфность (особых точек).
23. Ряды Лорана. Теорема 1 (Лоран). Любую функ-
функцию f, голоморфную в кольце V = {r<\z — a\<R}, можно в этом
кольце представить как сумму сходящегося ряда
f(z)= 2 cn{z-af, A)
коэффициенты которого определяются по формулам
1 Г /(?)<*?
где r<p<R.
< Фиксируем произвольную точку геУ и построим кольцо
V" = {?: /¦'<!(; — а\ <R'} такое, что z^V'mV. По интегральной
формуле Коши имеем
tM=J- Г ?(?)<*? - ' fii5lEL__L Г ШЛ ™
' yZ) 2ni J ? - г 2ni ) l-z 2я( J ? - z ' ^
dV
где окружности F'={jg — a\=R'} и у' = {\?, — а\ =г'} ориентиро-
ориентированы против часовой стрелки.
§6]
Для всех ? е
екая прогрессия
1
РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ
г — а
113
имеем
Ъ-а
= <7<1» поэтому геометриче-
(г - а)"
сходится равномерно по ? на Г'. Умножая ее на ограниченную
функцию -2^j/(?) (что не нарушает равномерной сходимости)
и интегрируя почленно вдоль Г', получаем
1 Г f (С) dt, =\ , nsn
2я/ J S-z ^ C"lZ Ы; '
п=0
где
~a)
n+x
(п = 0, 1, ...)•
D)
E)
Второй интеграл в формуле C) придется разлагать иначе.
При всех
имеем
поэтому мы получаем
равномерно сходящуюся на у' геометрическую прогрессию так:
I V (С-д)"
п=1
Снова умножая ее на ограниченную функцию -jj—^/(?) и инте-
интегрируя почленно вдоль у', получаем
1 ГШ
2я/ J E-
где
(z-o)" '
(«=1,2, ...).
G)
Заменим теперь в формулах F) и G) индекс п, пробегаю-
пробегающий значения 1, 2 индексом — п, пробегающим значения
Б. В. Шабат
114 свойства голоморфных функций [гл. if
— 1, —2, ... (это ничего не меняет), и обозначим ')
-ар-Ч (я--1, -2, ...); (8)
тогда разложение F) примет вид
-i/W= ft^i'-аГ F')
V' п=--1
Теперь подставим D) и F') в C); получим нужное разло-
разложение A):
/(г)= 2 сп(г-аГ,
п=— °°
где ряд определяется как объединение рядов D) и F').
Остается заметить, что по теореме об инвариантности интеграла
в формулах E) и (8) окружности Г' и у' можно заменить лю-
любой окружностью {|? — а\ = р}, где r<p<R, и тогда эти формулы
примут вид B) >
Определение. Ряд A), коэффициенты которого вычис-
вычисляются по формулам B), называется рядом Лорана функции f
в кольце V. Совокупность членов этого ряда с неотрицатель-
неотрицательными степенями называется его правильной частью, а совокуп-
совокупность членов с отрицательными степенями — главной частью
(естественность названий выяснится в следующем пункте).
Рассмотрим основные свойства рядов по целым степеням
z — а. Как и выше, мы определим такой ряд
S
сп(г-а)п (9)
как объединение рядов
(Si): ЦсАг-аГ и B2): 2 <?B.(z-a)n. A0)
11=0 и--1
Ряд (Si) представляет обычный степенной ряд; его об-
областью сходимости является круг {\z — a\<R), где число R
определяется по формуле Коши — Адамара
оо
') Заметьте, что с с отрицательными индексами до сих пор не
употреблялись.
§6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 115
Ряд Bг) представляет степенной ряд относительно перемен-
переменного Z^j^-z
B2): S c.nZn. A2)
га=1
Поэтому его областью сходимости является внешность кру-
круга {\z— а\>г], где по формуле Коши — Адамара, примененной
к ряду A2),
r= lim V\c-n\- A3)
Число R не обязано быть большим г, поэтому область сходимо-
сходимости ряда (9) может быть пустой. Однако если г</?, то областью
сходимости ряда (9) будет кольцо V={r<\z — a\<R}. Заметим,
что множество точек сходимости ряда (9) может отличаться
от V на некоторую совокупность точек, принадлежащих dV.
По теореме Абеля ряд (9) сходится равномерно на любом
компактном подмножестве кольца V, поэтому по теореме Вейер-
штрасса его сумма голоморфна в V.
Из этих замечаний сразу вытекает теорема единственности
разложения функции в данном кольце в ряд по положительным
и отрицательным степеням:
Теорема 2. Если функция f в кольце V={r<\z — a\<R}
представима рядом вида A), то коэффициенты этого ряда опре-
определяются по формулам B).
< Возьмем окружность у — {\г — а|=р}, г<р</?. Ряд
сходится на ней равномерно, и это свойство сохранится после
умножения обеих частей на произвольную степень (z — а)~п~1
(л=0, ±1, ±2, ...):
оо
Проинтегрируем полученный ряд почленно вдоль у:
f (z) dz
У l*-a>
и воспользуемся тем, что по свойству ортогональности степеней
(п. 14) все интегралы в левой части равны 0, кроме одного, для
116 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
которого k = n и который равен 2го". Мы получим
[™*L (« = 0> ±1> •••)•
а это совпадает с B) >
Теорему 2 можно сформулировать так: всякий сходящийся
ряд по положительным и отрицательным степеням z— а яв-
является рядом Лорана своей суммы.
Формулы B) для коэффициентов ряда Лорана на практике
применяются сравнительно редко, ибо они требуют вычисления
интегралов. На основании доказанной теоремы единственности
для получения лорановских разложений можно использовать
любой законный прием: все такие приемы приведут к одному
нужному результату
Пример. Функция
1 ч
f(z) =
B-1) B-2)
голоморфна в кольцах Vi = {0<|z|<l}, V2={K|z|<2} и У3={2<|г1<оо}. Для
получения лорановских разложений представим эту функцию в виде
f (г) =
2-2 2-1 "
В кольце V] слагаемые представляются такими геометрическими прогрес-
прогрессиями:
1
1 V / 2 \"
~ о" Zj \~o~I (сходится при | г I < 2),
2-2 2 z
2 (И)
оо
j- = -уз~ — ?jz" (сходится при | г | < 1).
Поэтому в Vi функция / представляется рядом
который содержит лишь положительные степени (рядом Тейлора).
В кольце Уг первое разложение A4) продолжает сходиться, а второе
нужно заменить разложением
— оо
г" (сходится при \г\> 1). A5)
г—1 z
§6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ ЦТ
В этом кольце, следовательно, f представляется рядом Лорана
я= — 1 л —
В-кольце Уз разложение A5) продолжает сходиться, а первое разложе-
разложение A4) нужно заменить таким:
— оо
1 11 1 VI (z\n , i i о\
-—5" = Т о" = "о 2и \Т) (сходится при |z I > 2).
Следовательно, в V3
Отметим, что коэффициенты ряда Лорана определяются по
формулам B), которые при п ^ 0 совпадают с интегральными
формулами для коэффициентов ряда Тейлора). Повторяя в
точности выкладки, проведенные в п. 19 при выводе неравенств
Коши для коэффициентов ряда Тейлора, мы получим
Неравенства Коши (для коэффициентов ряда Лорана),
Пусть функция f голоморфна в кольце V=[r<\z — a\<R] и
на окружности yP = {\z — а|=р}, г<р</?, ее модуль не превос-
превосходит постоянной М. Тогда коэффициенты ряда Лорана функ-
функции f в кольце V удовлетворяют неравенствам *
к„К'-~7г (п = 0, ±1, ±2, ...). A6)
В заключение отметим связь между рядами Лорана и ря-
рядами Фурье. Ряд Фурье функции <р, интегрируемой на отрезке
[0, 2я]сК, определяется как ряд
оо
4г + 2j an cos nt + t>n sin nt, A7)
где
2л 2л
t, bn = -^ J у (t)sin ntdt (n = 0, 1, ...) A8)
о
') Однако коэффициенты ряда Лорана нельзя представить по дифферен-
дифференциальной формуле сп=>1 i?i хотя бы потому, что /, вообще говоря, не-
я!
определена при z=a.
П8 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
(мы считаем Ь0 = 0). Такой ряд можно переписать в комп-
комплексной форме. Для этого воспользуемся формулами Эй-
Эйлера
еш,е-ш elnt — e-int
cos nt = g > sin ni — 2I
и, подставив их в A7), найдем
п=1
где положено
2л
=2k J
о
2Я
J (п=-1, -2,...).
J
о
2Я
Ряд
оо
2 спеш A9)
п— — оо
•с коэффициентами
2Я
B0)
и представляет собой ряд Фурье функции ф, записанный в ком-
комплексной форме.
Положим теперь eu=z и q>@ =f(eil) =f{z); тогда ряд A9)
примет вид
оо
2 cnzn, B1)
а его коэффициенты
if 1 Г jz
cn = _L f (etnt) e~lnt dt = —— f{z)-^. B2)
0 Ш I г 1 = 1 Z
Таким образом, ряд Фурье функции cp(t), t^[0,2я], запи-
записанный в комплексной форме, является рядом Лорана функции
f(z)=<p(t), где z=eu, на единичной окружности {|г|=1}.
Очевидно, что и обратно, ряд Лорана функции f(z) на еди-
единичной окружности является рядом Фурье функции f(eu) =<p(/)
на отрезке [0,2я].
§6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ Ц9<
Отметим, что, вообще говоря, даже в случае сходимости
ряда Фурье к функции ф в каждой точке отрезка [0,2я] для
соответствующего ряда Лорана может получиться R = r=\, так
что область сходимости этого ряда Лорана окажется пустой.
Лишь при весьма ограничительных условиях, наложенных на
функцию ф, соответствующий ряд имеет непустую область схо-
сходимости.
Пример. Пусть
asint ,. , ,.
«К*
Положив ei( = 2, найдем соответствующую функцию
'() (
она голоморфна в кольце < I а | < | г | < -j—- >. Как в предыдущем примере,
получим ее лорановское разложение в этом кольце
П=1
Заменяя здесь снова z=e", получим разложение Фурье функции <р:
оо
Ф@= 2 ап sin nt.
24. Изолированные особые точки. Здесь мы начинаем изу-
изучение точек, в которых нарушается голоморфность функций. Рас-
Рассмотрим сначала простейший тип таких точек.
Определение 1. Точка а е С называется изолированной
особой точкой функции f, если существует такая проколотая
окрестность этой точки (т. е. множество @< |г — а\ <г}, если точ-
точка а конечна, или множество {R< | z \ < оо}, если а = оо), в кото-
которой функция f голоморфна.
В зависимости от поведения f при приближении к такой
точке различают три типа особых точек.
Определение 2. Изолированная особая точка а функ-
функции f называется
(I) устранимой точкой, если существует конечный
\imf(z) = A;
(II) полюсом, если существует
120 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. IT
(III)- существенно особой точкой, если / не имеет ни конеч-
конечного, ни бесконечного предела при z-*a.
Примеры.
1. Все три типа изолированных особых точек реализуются. Например,
, sin 2 . „„„„/
функции г и имеют 2=0 устранимой особой точкой для второй из
них это видно из того, что при г Ф 0 справедливо разложение
sin г г2 z4
~~г "зГ "бГ" •'•'
из которого следует, что существует Пт SmZ — 1). Функции —д-, где п —
_1_
целое положительное число, имеют полос в точке 2=0. Функция ez имеет
2 = 0 своей существенно особой точкой, ибо, например, при стремлении
z=x к нулю по действительной оси пределы справа и слева различны (пре-
(предел справа равен бесконечности, а слева — нулю); при стремлении z=iy
к нулю по мнимой оси функция е z = cos i sin — вообще не имеет
предела.
Могут, конечно, существовать и неизолированные особые точки.
Например, функция имеет полюсы в точках z = — (я = ± 1, ± 2, ...),
sin —
2
следовательно, z=0 является для нее неизолированной особой точкой — пре-
предельной точкой полюсов.
2. Более сложный пример особых точек доставляет функция
оо
fB)=2 22"=l+22 + 24 + 28+ .... A)
п = 0
По формуле Коши — Адамара ряд A) сходится в круге {|г|<1}, и, следова-
следовательно, f голоморфна в этом круге. При z -> 1 по направлению действитель-
действительной оси она стремится к бесконечности1), следовательно, точка 2=1 является
для нее особой. Но
/() « 8
¦следовательно, f(z)=z2+f(z2) стремится к бесконечности и когда 2->—1 по
радиусу круга. Аналогично f (г) =z2+24+f (г4), следовательно, f->co и когда
z-> ±i по радиусам круга. Вообще
') Это утверждение не следует из расходимости ряда A) при 2=1
(вспомните замечание в конце п. 14) и требует особого доказательства: при
N
г=х, 0<х<1, имеем f (х) > 2 *2 > гДе N — произвольное натуральное
п=о
число; предел при х->\ суммы в правой части равен N+1, следовательно,
найдется б>0 такое, что f(x)>N при 1 —б<д:<1, следовательно, lim / (л;) —
jc->- 1—0
= оо.
§ 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 121
для любого натурального п, поатому / -»со, когда г стремится по радиусу
к любой «двоичной» точке z = e (?=0, 1, ..., п—1) окружности. Так
как множество «двоичных» точек всюду плотно на окружности {1г|=1}, то
каждая точка этой окружности является особой для f. Таким образом,
f имеет целую линию, составленную из неизолированных особых точек (осо-
(особую линию).
Характер изолированной особой точки z — a тесно связан
с характером лорановского разложения функции в проколотой
окрестности этой точки (мы будем коротко называть его раз-
разложением в окрестности а). Для конечных точек а эта
связь выражается следующими тремя теоремами.
Теорема 1. Изолированная особая точка йеС функ-
функции f является устранимой в том и только том случае, если
лорановское разложение f в окрестности а не содержит главной
части:
f(z)=2 cn(z-df. B)
-* Необходимость. Пусть а — устранимая точка; тогда
существует конечный lim f(z) = А и, следовательно, / ограни-
чена (пусть |/j-^Af) в некоторой проколотой окрестности
{0<|z — a\<R] точки а. Возьмем любое р, 0<р<^, и восполь-
воспользуемся неравенствами Коши
\сп\<$г (п = 0, ±1, ...).
Если п<0, то правая часть стремится к нулю при р—»0,
левая же часть от р не зависит. Следовательно, сп=0 при п<0,
и главная часть ряда Лорана отсутствует.
Достаточность. Пусть в проколотой окрестности точки
а функция f представляется лорановским разложением B) без
главной части. Это разложение является тейлоровским, и, сле-
следовательно, существует и конечен
lim f (z) = с0.
Поэтому а является устранимой точкой >
Замечание. Теми же рассуждениями доказывается и
Теорема V. Изолированная особая точка а функции f
в том и только том случае является устранимой, если f огра-
ограничена в некоторой проколотой окрестности точки а.
Продолжив функцию / в ее устранимую точку а по непре-
непрерывности, т. е. положив / (а) — lim f(z), мы получим функцию,
г->а
122 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. ГГ
голоморфную в точке а (т. е. устраним особенность). Этим и
оправдывается термин «устранимая точка». В дальнейшем мы
будем считать такие точки правильными, а не особыми
точками функции.
Теорема 2. Изолированная особая точка аеС функ-
функции f является полюсом в том и только том случае, если глав-
главная часть лорановского разложения f в окрестности точки а
содержит лишь конечное (и положительное) число отличных
от нуля членов:
№ = 2 cn(z-a)\ N>0. C)
n = -N
¦< Необходимость. Пусть а — полюс; так как
lim/(z) = oo, то существует проколотая окрестность точки а,
в которой / голоморфна и отлична от нуля. В этой окрестности
голоморфна функция ty{z) = jj-г, причем существует lim<p(z) =
1Уг> г->а
= 0. Следовательно, а является устранимой точкой (нулем)
функции ф и в нашей окрестности справедливо разложение
ср (г) = бд, B - af + bN+{ (z - af+l + ... {Ь„Ф0).
Но тогда в той же окрестности мы имеем
'(Z)= фB) ~ (z-a)N ' bN + bN+1(z-a)+ ... ' D)
причем второй множитель является функцией, голоморфной в
точке а, и, значит, допускает тейлоровское разложение
Подставляя это разложение в D), найдем
Это — лорановское разложение f в проколотой окрестности
точки а, и мы видим, что его главная часть содержит конечное
число членов.
Достаточность. Пусть / в проколотой окрестности
точки а представляется лорановским разложением C), глав-
главная часть которого содержит конечное число членов; пусть еще
О. Тогда f голоморфна в этой окрестности, так же как и
§ 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 12$
функция ф(г) = (г — a)Nf(z). Последняя в нашей окрестности
представляется разложением
из которого видно, что а является устранимой точкой и суще-
существует lim ф(г) = с_я ф 0. Но тогда функция f(z)= ф ы-
z->a (z —a)
стремится к бесконечности при z —>а, т. е. а является полю-
полюсом / >
Отметим еще один простой факт о связи полюсов с нулями.
Теорема 2'. Точка а является полюсом функции f в том
и только том случае, если функция ф = -г, ф щк 0, голоморфна
в окрестности а и ф(а)=0.
< Необходимость условия доказана при доказательстве тео-
теоремы 2. Докажем его достаточность. Если ф^О голоморфна
в точке а и ф(а)=0, то по теореме единственности (п. 21) су-
суй
ществует проколотая окрестность этой точки, в которой
В этой окрестности функция / = — голоморфна, следовательно,
а является изолированной особой точкой /. Но lim/(z)=co,
следовательно, а является полюсом f >
Установленная связь позволяет сформулировать
Определение 3. Порядком полюса а функции / назы-
, 1
вается порядок„этои точки как нуля функции ф = у.
Из доказательства теоремы 2 видно, что порядок полюса
совпадает с номером N старшего члена главной части лора-
новского разложения функции в проколотой окрестности по-
полюса.
Теорема 3. Изолированная особая точка а функции f
является существенно особой в том и только том случае, если
главная часть лорановского разложения f в окрестности точки а
содержит бесконечно много отличных от нуля членов.
¦< Теорема, по существу, уже содержится в теоремах 1 и 2
(если главная часть содержит бесконечное число членов, го а
не может быть ни устранимой точкой, ни полюсом; если а — су-
существенно особая точка, то главная часть не может ни отсут-
отсутствовать, ни содержать конечное число членов) >
Поведение функции в окрестности существенно особой точки
характеризует следующая интересная
Теорема 3' (Ю. В. Сохоцкий). Если а является су-
существенно особой точкой функции f, то для любого числа.
124 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. 1Г
j4eC можно найти последовательнбсть точек zn—*a такую,
что
lim f(zn) = А. E)
< Пусть Л = оо. Так как / по теореме V не может быть
ограниченной в проколотой окрестности {0<(г — а\<.г}, то в
этой окрестности найдется точка zu в которой |/Bt) |>1. Точно
так же в < 0<| г — а\< г' „ а > найдется точка z2, в которой
|/(г2) |>2, и т. д., в <0<\z — а\< ~ [ найдется точка гп,
в которой \f(zn) \>n. Очевидно, zn—>a и
lim /(г„)=оо.
П -> оо
Пусть теперь Афоо. Либо Л-точки функции f имеют а своей
предельной точкой, и тогда из них можно выбрать последова-
последовательность Zn—>a, на которой f(zn)—A, либо существует про-
проколотая окрестность {0<\z — a\<r'}, в которой f(z)=hA. В этой
окрестности голоморфна функция
ч^"-' f(z)-A '
для которой а также является существенно особой точкой (ибо
f(z) = A-\ т-у- и если бы ф при z-*a стремилась к конечному
или бесконечному пределу, то / — также). По доказанному
существует последовательность zn-*a, по которой ф(гп) —>¦ оо;
но по этой последовательности
lim f{zn) = A+ lim —,—\ = А >
Совокупность предельных значений функции f по различным
последовательностям точек zn—*a называют множеством не-
неопределенности функции f в точке а. Если а является устрани-
устранимой точкой или полюсом функции /, то ее множество неопреде-
неопределенности в этой точке состоит из одной точки (конечной или
бесконечной). Теорема Сохоцкого утверждает, что для суще-
существенно особой точки реализуется другой крайний случай:
множество неопределенности в такой точке заполняет всю зам-
замкнутую плоскость С.
Несколько слов об изолированных особых точках в беско-
бесконечности. Классификация и теоремы V—3' переносятся на слу-
случай а = оо автоматически. Однако теоремы 1—3, связанные
с характером лорановских разложений, нуждаются в измене-
§ 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 125
ниях. Дело в том, что в конечных точках характер особенности
определяют главные части лорановских разложений, содержа-
содержащие отрицательные степени z— а, которые имеют осо-
особенность в этих точках (отсюда и термин «главная часть»).
В бесконечности же отрицательные степени правильны и особен-
особенность определяется совокупностью положительных степе-
степеней. Поэтому естественно назвать главной частью лорановского
разложения функции в проколотой окрестности бесконечной точ-
точки совокупность членов этого разложения с положительными
степенями. После такого изменения теоремы 1—3 будут спра-
справедливыми и для случая а —сю.
Этот результат сразу получается при помощи замены пере-
переменного г =— : если обозначить
ш
то, очевидно,
lim f(z) = lim q>(w),
0
и поэтому ф имеет в точке ш> = 0 ту же особенность, что / в
точке 2=оо. Например, в случае полюса ф имеет в {0<|да|<г}
разложение
сю
1 ,
заменяя здесь w = —, получим разложение j в кольце
{R<\z\<oo}, R = ±:
f(z) = 2 cnzre + c0 + c,z+ ... +cNzN,
n=-l
где сп = 6_„, СхФО. Его главная часть содержит конечное число
членов. Аналогично рассматриваются случаи устранимой и су-
существенно особой точек.
В заключение приведем классификацию простейших голо-
голоморфных функций по их особым точкам. Согласно теореме Лиу-
вилля функции, совсем не имеющие особенностей (т. е. голо-
голоморфные в С), являются константами. Следующий по простоте
класс составляют целые функции.
Определение 4. Целой называется функция, голоморф-
голоморфная во всей плоскости С, т. е. не имеющая конечных особых
точек.
126 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. If
Точка а = оо является, следовательно, изолированной особой
точкой целой функции f. Если это — устранимая точка, то
f== const. Если это — полюс, то главная часть лорановского
разложения / в окрестности бесконечности представляет собой
полином g(z) =сгг+ ... +cNzN. Вычитая из / эту главную часть,
получим также целую функцию, f — g, но уже с устранимой
точкой в бесконечности. Она является константой, и следова-
следовательно, целая функция с полюсом в бесконечности непременно
является полиномом.
Целые функции с существенной особенностью в бесконеч-
бесконечности называются целыми трансцендентными функциями (та-
(таковы, например, функции ez, sin г, cos z).
Определение 5. Функция, не имеющая в открытой пло-
плоскости С других особенностей, кроме полюсов, называется меро-
морфной.
Целые функции составляют подкласс класса мероморфны'х
функций (они вовсе не имеют особенностей в С). Так как каж-
каждый полюс — изолированная особая точка, то мероморфная
функция не может иметь в С более чем счетное множество
полюсов. В самом деле, в каждом круге {|z|<n}, n= 1, 2, ...,
полюсов может быть лишь конечное число (иначе существовала
бы их конечная предельная точка, которая является неизоли-
неизолированной особой точкой функции, а не полюсом) и все полюсы
можно пересчитать. Примерами мероморфных функций с бес-
бесконечным числом полюсов являются tgz и ctgz.
Теорема 4. Если мероморфная функция f в бесконечно-
бесконечности имеет устранимую точку или полюс (т. е. если она в С не
имеет других особенностей, кроме полюсов), то она является
рациональной функцией.
< Число всех полюсов функции / конечно, ибо в противном
случае в силу компактности С существовала бы предельная
точка полюсов, которая является неизолированной особой точ-
точкой, а не полюсом. Обозначим через av (v = l, ..., п) конечные
полюсы f и через
главную часть лорановского разложения / в окрестности по-
люса av. Обозначим еще
g(z)=dz+]...+cNzN G)
главную часть лорановского разложения f в окрестности а = оо;
если а = оо является устранимой точкой /, положим g = 0,
i 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 127
Рассмотрим функцию
v=l
она имеет все точки геС правильными, и по теореме Лиу-
вилля q>(z)==c0. Таким образом,
п
v=l
т. е. является рациональной функцией >
Замечание. Формула (8) представляет собой разложе-
разложение рациональной функции f на целую часть и простейшие
дроби. Наше рассуждение дает простое доказательство суще-
существования такого разложения.
Иногда мы будем употреблять термин «мероморфная функ-
функция» в более общем смысле. Именно, будем говорить, что функ-
функция / мероморфна в области D, если она не имеет в D других
особенностей, кроме полюсов. И такая функция не может иметь
более чем счетное число полюсов. В самом деле, мы построим
компактное исчерпывание {Gn} области D (см. лемму в п. 22)
и увидим, что в каждой Gn функция / может иметь лишь ко-
конечное число полюсов. Если число полюсов функции f, меро-
морфной области D, бесконечно, то предельные точки множе-
множества полюсов принадлежат границе dD.
25. Вычеты. Это звучит парадоксально, но наиболее инте-
интересными при изучении голоморфных функций являются точки,
в которых функции перестают быть голоморфными — их особые
точки. В дальнейшем мы будем иметь много фактов, убеж-
убеждающих в том, что в особых точках и главных частях лоранов-
ских разложений в их окрестностях содержится основная ин-
информация о голоморфных функциях1).
Мы проиллюстрируем это утверждение задачей о вычисле-
вычислении интегралов от голоморфных функций. Пусть функция /
голоморфна в области D всюду, за исключением изолирован-
изолированного и, следовательно, не более чем счетного множества особых
точек. Пусть область GmD и граница dG состоит из конеч-
конечного числа непрерывных кривых и не содержит особых точек;
особые точки, попавшие в G, мы обозначим аь .. ., ап (их
') Это утверждение допускает физическую интерпретацию. Если тракто-
трактовать голоморфную функцию как комплексный потенциал векторного поля,
скажем поля скоростей течения жидкости (см. п. 7), то особые точки будут
интерпретироваться как источники, стоки, вихри и другие элементы, опреде-
определяющие это поле. Об этом см. М. А. Лаврентьев и Б. В. Ш а б а т, цит.
на стр. 42.
128
СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ
[ГЛ. II
конечное число). Построим окружности yv={\z — av|=r} столь
малого радиуса г, что круги Uv, ими ограниченные, не пе-
пересекаются друг с другом и содержатся в G. Пусть yv ориен-
ориентированы против часовой стрелки (рис. 38). Обозначим
и _
область G \ (J Uv через Gr; функция / голоморфна в (Jr, сле-
V=I
довательно, по интегральной теореме Коши для многосвязных
областей
J fdz =
A)
9G,
Рис. 38.
Но ориентированная граница dGr
состоит из dG и ориентированных от-
отрицательно окружностей \>v(v='> •••
..., л), и по свойствам интегралов мы
получаем
B)
дО
v=l у„
Таким образом, вычисление интеграла от голоморфной функ-
функции по границе области сводится к вычислению ее интегралов
по сколь угодно малым окружностям с центрами в особых точ-
точках функции.
Определение 1. Интеграл от функции / по достаточно
малой окружности yr—{\z— a\=r} с центром в изолированной
особой точке аеС этой функции, деленный на 2ni, называется
вычетом f в точке а и обозначается символом
dz.
C)
По теореме о неизменности интеграла при гомотопной де-
деформации контура вычет не зависит от величины г (при г до-
достаточно малых) и определяется локальным поведением / в ее
особой точке.
Доказанное выше соотношение B) выражает так называе-
называемую теорему Коши о вычетах.
Теорема 1. Пусть функция f голоморфна в области D
всюду, за исключением изолированного множества особых то-
точек, и область G ШИ, а ее граница dG не содержит особых
точек; тогда
jfdz = 2m5]resf> D)
dQ (G) °v
§ 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 12Э
где сумма распространяется на все особые токгм ov функции f,
принадлежащие G.
Эта теорема имеет большое принципиальное значение, ибо
она сводит вычисление глобальной величины, какой яв-
является интеграл от голоморфной функции по границе области,
к вычислению величин локальных — вычетов функции в ее
особых точках.
Как мы сейчас увидим, вычеты функции в ее особых точках
полностью определяются главными частями лорановских раз-
разложений в окрестностях этих точек. Тем самым будет установ-
установлено, что в задаче о вычислении интегралов от голоморфной
функции достаточно иметь информацию лишь об ее особых
точках и главных частях в них.
Теорема 2. Вычет функции f в изолированной особой
точке а е С равен коэффициенту при минус первой степени
z — а в ее лорановском разложении в окрестности а:
resf = c_,. E)
а
¦4 В проколотой окрестности точки а функция / представ-
представляется рядом Лорана
причем на окружности yr={\z — а\=г} при достаточно малых
г этот ряд сходится равномерно. Интегрируя ряд почленно вдоль
ут и пользуясь ортогональностью степеней (п. 14), мы найдем
\ fdz = ?¦_! -2ni.
Вспоминая определение вычета, получим E) >
Следствие. В устранимой точке оеС вычет функции
равен нулю.
Приведем формулы для вычисления вычета функции в по-
полюсе. Пусть сначала а — полюс первого порядка. Лорановское
разложение функции в его окрестности имеет вид
Отсюда сразу получается формула для вычисления вычета
в полюсе первого порядка:
c_,= lim(z-a)/(*). F)
г->а
9 Б. В, Шабат
130 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИИ [ГЛ. 1Г
Особенно удобна для вычислений небольшая модификация
этой формулы. Пусть в окрестности точки а
где ф и \р голоморфны в а, причем ф(а)=^0 и г|?(а) =0,
(отсюда следует, что а — полюс первого порядка функции f).
Тогда по формуле F)
,. (г — а) Ф (г) ~ '-л
С_, = lim -1 , ;,. =
т. е.
Пусть теперь f имеет в точке а полюс «-го порядка; тогда
в проколотой окрестности а
Умножим обе части этого разложения на (z — а)п для устра-
устранения отрицательных степеней в правой части, затем продиф-
продифференцируем п— 1 раз (чтобы выделить справа c_i) и перейдем
к пределу при z-*a. Мы получим формулу для вычисления
вычета в полюсе п-го порядка:
Для вычисления вычетов в существенно особых точках ана-
аналогичных формул не существует, и надо находить главные части
лорановского разложения.
Несколько слов о вычете в бесконечности.
Определение 2. Пусть функция f имеет схэ своей изоли-
изолированной особой точкой; ее вычетом в бесконечности называется
величина
где у% — окружность {\z\ =R)достаточно большого радиуса, про-
проходимая по часовой стрелке.
§ 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 13!
Ориентация yR выбрана так, чтобы во время ее обхода окре-
окрестность бесконечной точки {/?<|г|<оо} оставалась слева. Напи-
Напишем разложение Лорана функции / в этой окрестности:
f(z)= S cnz\
fl= —ОО
Интегрируя его почленно вдоль yR и пользуясь ортогональностью
степеней, мы найдем
res/= -<;_,. (9)
оо
Члены с отрицательными степенями входят в правильную,
а не в главную часть лорановского разложения в бесконечности.
Поэтому, в отличие от конечных точек, вычет в бесконечности
может быть не равным нулю и в том случае, когда z = oo яв-
является правильной точкой функции.
Приведем еще простую теорему о полной сумме вы-
вычетов.
Теорема 3. Пусть функция f голоморфна всюду в плоско-
плоскости С, за исключением конечного числа точек av (v=l, ..., л);
тогда сумма ее вычетов во всех конечных особых точках и вы-
вычета в бесконечности равна нулю:
2j res / + res f = 0. A0)
-* Построим окружность yR = {\z\=R} столь большого ра-
радиуса, что она содержит внутри все конечные особые точки av;
пусть yR ориентирована против часовой стрелки. По теореме
Коши о вычетах
п
1
по теореме о гомотопии (п. 16) величина в левой части равен-
равенства не меняется при дальнейшем увеличении R; следовательно,
эта величина равна вычету / в бесконечности, взятому со зна-
знаком минус (учтите направление обхода). Таким образом, по-
последнее равенство равносильно A0) >
Пример. При вычислении интеграла
dz
(Z8+1J
2
нет нужды вычислять вычеты подинтегральной функции во всех ее восьми
полюсах второго порядка, лежащих внутри окружности {\z\=2). К этой функции
132 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ
применима теорема о полной сумме вычетов, по которой
[ГЛ. 1Г
1
1
(Z8+1J
= 0.
Но функция имеет в бесконечности нуль шестнадцатого порядка, поэтому ее
лорановское разложение в окрестности z= °° содержит лишь отрицательные
степени, начиная с z~16. Поэтому ее вычет в бесконечности равен 0, следова-
следовательно, равна нулю и сумма вычетов в конечных особых точках, т. е. 1=0.
В заключение приведем пример применения теоремы Коши
о вычетах к вычислению несобственных интегралов от функций
действительного переменного. Вычислим
интеграл вдоль действительной оси
ф@ =
ТПс'
dt,
(П)
где t — действительное число (он абсо-
абсолютно сходится, ибо мажорируется
сходящимся интегралом от функции
Рис 39.
Методика применения вычетов такова. Продолжаем подин-
тегральную функцию в комплексную плоскость
затем выбираем замкнутый контур так, чтобы он содержал
отрезок [—R, R] прямой интегрирования и какую-либо дугу,
соединяющую концы отрезка. К этому замкнутому контуру при-
применяется теорема Коши о вычетах, а затем делается предель-
предельный переход при R—*oo. Если при этом удастся вычислить пре-
предел интеграла по дополнительной дуге, то задача будет решена*
Пусть z=x+iy; учитывая, что \eizt\=e~v*, мы будем разли-
различать два случая: f^-О и t<Q. В первом случае мы замкнем от-
отрезок [—R, R] верхней полуокружностью y'Rt проходимой против
часовой стрелки (рис. 39). При R>1 внутри образовавшегося
контура лежит один полюс / первого порядка z = i, вычет в ко-
котором легко находится по формуле F'):
res
1+z2
?1
§ 6] РЯДЫ ЛОРАНА И ОСОБЫЕ ТОЧКИ 133
По теореме Коши о вычетах имеем, следовательно,
R
\f{x)dx+ \f{z)dz = ne-*. A20
-R «'
A3)
Так, как при t^Q на у' имеем \eiiz\ = e~yt^\ и
R2 — 1, то для интеграла по yR справедлива оценка
Jzt
1+Z2
г
dz
из которой видно, что этот интеграл стремится к нулю при
R-*oo. Поэтому, переходя в A2') к пределу при R-+oo, мы
получаем при t^-0
оо
J f{x)dx = ne-K A4')
При ^<0 оценка A3) несправедлива, ибо \еш\=е~у* сильно
возрастает при у-*+оо. Поэтому мы заменим дугу y'R ду-
дугой у? нижней полуокружности (рис. 39). Пусть она прохо-
проходится по часовой стрелке, тогда по теореме Коши о вычетах
лри R>\
R
J
-R
J / (x) dx + J f {z) dz = - 2яг res / = яе'. A2")
4
Так как при ^<0 на yR имеем | eizt | = e~yi^ 1 и |г2+1|^
^R2— 1, то интеграл от f no v^ также стремится к нулю при
Д—> оо, и из A2") в пределе получим
оо
\f{x)dx = neK A4")
— оо
Объединяя формулы A4') и A4"), получаем окончательный
результат:
оо
_? А у — nP-\t\ (\K\
В дальнейшем мы не раз будем пользоваться вычетами для
вычисления различных интегралов. Приведем в заключение
лемму, полезную при таких вычислениях.
134 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИИ [ГЛ. 1Г
Лемма (Жордан). Пусть функция f голоморфна в
{Im z X)} всюду, за исключением изолированного множества
особых точек, и M(R) = max|/(z) | на полуокружности
yR — {\z\ =R, Imz>-0} стремится к нулю при R—*oo (или по по-
последовательности Rn —* со такой, что yR не содержат особых
точек /). Тогда для любого А>0
A6)
стремится к нулю при R—*oo (или по соответствующей после-
последовательности Rn —> оо).
(Смысл леммы состоит в том, что M(R) может стремиться
к нулю сколь угодно медленно, так что интеграл от / по yR не
обязан стремиться к нулю; умножение на экспоненту eiXz с
А>0 убыстряет стремление к нулю.)
< Обозначим через yR = \z = Rei<f: О^^^-^У правую по-
половину уд- В силу выпуклости синуса при ipE 0, у имеем
эшф^: — ф, и, значит, на y^ справедлива оценка \ellz\ =
= e-iR sin <p ^ e "'.Поэтому
т
f(z)ellzdz ^M(R) e n Rdw —
J J
2 2A«q>
V °
и интеграл по y« стремится к нулю при R—>oo. Оценка для
у" = у \ y^ проводится аналогично >
Как видно из доказательства, условие голоморфности / в
этой теореме не существенно.
ЗАДАЧИ
1. Интегралом типа Коши называется интеграл вида
2ш J Z-z
где y — гладкая (или спрямляемая) кривая, a f — непрерывная (или сум-
суммируемая) на у функция. Доказать, что F является функцией, голоморфной
в С\у и равной нулю в бесконечности.
4 задачи 135
2. Пусть у — гладкая замкнутая жорданова кривая, D — область такая,
что y—dD и /еС'(у). Показать, что при переходе через у интеграл типа
Коши испытывает скачок, равный значению f в точке перехода. Точнее: если
?оеу, а г->?о, оставаясь соответственно внутри/? или вне D, то F(z) имеет
предельные значения F*(t,a) и F~(^), причем
(формула Ю. В. Сохоцкого). [Указание: представить F(z) в виде
3. В предположениях предыдущей задачи доказать, что каждое из сле-
следующих условий необходимо и достаточно для того, чтобы интеграл типа
Коши был интегралом Коши:
a)
б)
4. Доказать,
J-
V
j>
У
что
f(Z)dZ
;"/ @ rf? -
интеграл
Ft
Э для всех
¦ 0 для всех
1 Г Г /а
я . J t
геС\й;
я-0, I, 2, ...
— г '
где S=g + iri, О — компактная область, a f — гладкая в D ограниченная
функция, а) является голоморфной в C\D функцией, равной нулю в беско-
бесконечности, б) в любой точке z<=D имеем
dF
[Решение. Утверждение а) проверяется непосредственно. Для доказа-
доказательства б) предположим сначала, что /eC(D) и что f=0 в окрестности SD.
Продолжим f на всю плоскость, считая ее равной нулю вне D, и будем счи-
считать, что в (*) интегрирование распространяется на всю плоскость. Заменой
переменного ?->?+г получим, что
= _± Г f i
В принятых условиях законно дифференцирование под знаком интеграла,
поэтому в любой точке г sD существует
dF_ = __i_ Г Г
dz я -J J
Жdldn
(мы вернулись к прежнему переменному интегрирования). Возьмем теперь
область G шО так, чтобы всюду на dG было f—Q, тогда по формуле Коши—¦
136 СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ [ГЛ. II
Грина из п. 18 получим, что интеграл в правой части равен /(г), — в допол-
дополнительных условиях утверждение доказано. В общем случае нужно восполь-
воспользоваться тем, что любую гладкую в D функцию можно приблизить-
равномерно на любом компакте из D функциями, удовлетворяющими нашим
дополнительным условиям.]
оо
5. Пусть / (г) = ^ anz" голоморфна в замкнутом круге U — {| г \ ^ RY
га=о
и а0 ф 0. Доказать, что тогда / отлична от нуля в круге •! I z | < -.—° .. >,
где М = max [ f (г) |.
гевУ
6. Доказать, что степенной ряд не может сходиться ни в одной гранич-
граничной точке круга сходимости, если там имеется хотя бы один полюс разлагае-
разлагаемой в ряд функции.
7. Доказать, что любая целая функция /, не принимающая значений из-
правой полуплоскости, постоянна.
8. Вывести теорему Сохоцкого для целых функций из теоремы Лиувилля,
9. Пусть а является существенно особой точкой функции /; чем может
служить а для функции -у? (Ответ: предельной точкой полюсов или суще-
существенно особой точкой.)
10. Доказать теорему Сохоцкого для предельной точки полюсов.
11. Пусть / голоморфна в круге |г|<1 и ряд
сходится в точке 2=0. Покажите, что f можно продолжить до целой функ-
функции, причем указанный ряд сходится равномерно на всяком компактном под-
подмножестве плоскости С.
12. Если / голоморфна и равномерно ограничена в правой полуплоскости
и если {(п) =0 для любого целого п > 0, то / = 0.
13 (В. И. Гавр и лов). Если f(z) = z+ 2 anzn голоморфна и одно-
га>2
га
листна в {| z | < 1} и |ол1<« для всех п, то f и все fn (z) = z + ^ akzk
ft=2
однолистны в круге {| г \ < т}, где т — действительный корень уравнения
Оценка т достигается для
[Указание: воспользоваться тем, что
/ (г,) - f Щ
:'/•" " = 2 - , _ з при
П>2
Заметим, что знаменитая гипотеза Бибербаха, по которой для функций
/ (г) = г + 2 апг"' голоморфных в {|г|<1} и однолистных там, |а
п>2
для всех п, до сих пор не доказана и не опровергнута.]
ГЛАВА III
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
В этой главе мы рассмотрим еще одно из самых основных
понятий комплексного анализа — понятие аналитического про-
продолжения. Оно позволит нам, в частности, ввести так называе-
называемые многозначные аналитические функции.
Самые простые задачи приводят к необходимости рассмат-
рассматривать многозначные решения. Например, уравнение z = w2 при
любом фиксированном гфО имеет два решения, отличающиеся
знаком. Совокупность этих решений — мы обозначим ее |Лг—¦
нельзя рассматривать как функцию от z, ибо функция по опре-
определению однозначна. Попытка отказаться от условия однознач-
однозначности в определении функции сразу привела бы к значительным
неудобствам. В самом _деле, какой смысл, например, надо вло-
вложить в сумму Yz+ Уz, если каждое слагаемое принимает два
значения? Самые простые действия анализа с такими «много-
«многозначными функциями» оказались бы весьма затрудненными1).
Понятие аналитического продолжения позволяет снять такого
рода затруднения.
§ 7. Понятие аналитического продолжения
26. Элементы аналитических функций. Мы начнем с изуче-
изучения понятия аналитического продолжения, оставаясь в рамках
теории однозначных (голоморфных) функций. С этой точки
зрения под аналитическим продолжением функции f0, заданной
первоначально на некотором множестве AfcC, мы будем по-
понимать Доопределение ее до функции f, заданной в некоторой
области DzdM, такое, что f голоморфна в D, а ее сужение на
множество М совпадает с fo:
') Если складывать Уг + V~z~ как совокупности, то эта сумма будет уже
трехзначной (ее значения: 2wi, —2aji и 0, где W\ — одно из двух значений
Уг). Складывать лишь значения с «одинаковым» знаком? Но это в ком-
комплексном анализе совсем бессмысленно: пусть Угу — ± A -И), а)/^2=±A —
— i); какие знаки слагаемых в сумме V~z~\ + \z% одинаковы?
138 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
Такую задачу можно решать самыми различными способами. В первой
главе, например, мы аналитически продолжали функции ех, sin x и другие,
заданные на действительной оси R, на всю комплексную плоскость С. Функ-
Функция задана в области С\ {0} (она не определена при г=0); написав
ее разложение в ряд по степеням г:
sin z _ г2 24
мы при его помощи получим продолжение этой функции на всю плоскость С
(такое продолжение равносильно доопределению в точке г — 0 по непрерыв-
непрерывности).
Напротив, сумма ряда
определена (и голоморфна) лишь в круге {|г|<1}, ибо при \г\ > 1 ряд расхо-
расходится. Однако просуммировав эту геометрическую прогрессию, мы найдем,
что /о (г) = -j . и полученная формула дает аналитическое продолжение
функции /о в область С\{1}.
Рассмотрим менее тривиальный пример. Гамма-функция
Эйлера при Ree>0 определяется интегралом по положитель-
положительной полуоси
•-Г'Л, A)
где под tz~l для ^>0 понимается е^~^1п К Функции
оо
Fn(z) = \ e-Hz'ldt (л = 1, 2, ...)
¦ га
— целые, ибо интеграл можно дифференцировать по параметру
в любой точке плоскости. Так как на любом компактном под-
подмножестве правой полуплоскости {Ree>0} последовательность
{/¦*„} равномерно по г сходится к Г (г), то по теореме Вейер-
штрасса гамма-функция голоморфна в правой полуплоскости.
Если х = Re2^0, то интеграл A) перестает сходиться из-за
того, что подинтегральная функция слишком быстро возрастает
пр-и t—>0 (у нас \tz~l \ =<?Re(z-i)in t — fx-i^ а е~1-* I при /-*0).
Мы улучшим сходимость при ^ = 0, если вычтем из е~х началь-
начальные члены ее тейлоровского разложения в нуле и тем самым
получим множитель, стремящийся к нулю при /—>(). При
Ree>0 мы получим на этом пути
1
§ 7| ПОНЯТИЕ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ 139
или, вычисляя элементарные интегралы,
(-0*1
k\ z + k
k=0
dt+\ e~tf~l dL
\
fe=0 1
В этом равенстве второй интеграл справа — целая функция
(см. выше), первый интеграл сходится равномерно по z на лю-
любом компактном подмножестве полуплоскости {Rez> — (п + 1)}
га оо
ибо еч — V ь/ ' = _2j fei стРемится к нулю при ?—>0
со скоростью ^n+1) и, значит, представляет собой функцию, голо-
голоморфную в этой полуплоскости.
Таким образом, равенство B) позволяет аналитически про-
должить разность 1 (z) — 2j—Tj ZT B полуплоскость
k=0
{Rez> — (и+1)}, а сама Г(г) оказывается продолженной до
функции, мероморфной в этой полуплоскости. Так как в каче-
качестве п можно взять любое натуральное число, мы получаем
мероморфное продолжение гамма-функции на всю плоскость.
Мы видим также, что продолженная функция имеет в нуле и
отрицательных целых точках полюсы первого порядка, причем
вычет в полюсе z = —k равен ^-^— (k = 0, 1, 2, .. .). На рис. 40
приведена поверхность модуля гамма-функции, на которой на-
нанесены также линии равного модуля и аргумента.
Метод улучшения сходимости, который здесь продемонстри-
продемонстрирован, называется методом Коши; в гл. V мы еще раз будем
им пользоваться (см. п. 42). Заметим, что мероморфное про-
продолжение гамма-функции в левую полуплоскость можно осуще-
осуществить также, пользуясь функциональным уравнением
которому удовлетворяет эта функция при Re2>0. В самом деле,
при Re 2 > 0 мы можем написать
а потом заметить, что правая часть этого равенства определена
при Re 2 > — 1, 2^=0. Повторяя этот прием достаточное число
140
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. III
раз, мы продолжим гамма-функцию в любую точку
Конечно, задача аналитического продолжения не всегда раз-
разрешима. Вспомним пример из п. 24: функция
«=0
голоморфна в единичном круге ?/={|z|<l}, но окружность
{|z| = l} является ее особой линией, и поэтому аналитическое
продолжение f ни в какую область, строго содержащую U, не-
невозможно,
Рис. 40.
Если функция f (как в этом примере) голоморфна в неко-
некоторой области D и не продолжается аналитически ни в какую
область, строго содержащую D, то мы будем называть D об-
областью голоморфности функции f. В п. 43 мы докажем, что
каждая область DcC является областью голоморфности не-
некоторой функции.
Сейчас мы рассмотрим пример, который заставит нас рас-
расширить принятое понятие аналитического продолжения. Пусть
область D представляет собой плоскость С, разрезанную вдоль
отрицательной полуоси: D = {z = rei<t: —л<ф<я, г>0}, В этой
области определена функция
= to(z)=Vre'
— п < ф < я,
C)
ПОНЯТИЕ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ
141
взаимно однозначно отображающая D на правую полуплоскость
D* = \ w = ре'*: — тг<'Ф<4г> р>0[. Мы имеем хю2 = ге1^—г (так
что /oB) = V^) и в СИЛУ того> чт0 отображение fo:D—>D* вза-
взаимно однозначно, можем воспользоваться правилом дифферен-
дифференцирования обратных функций1),
по которому в каждой точке (z)
гей существует
йг
dw
2w
2fo (г)
Рис. 41.
Таким образом, функция /0 голо-
голоморфна в D.
Рассмотрим теперь сектор
S = {ji ^ ф<я + 6}, где 6>0
(рис. 41). Функция fo непосред-
непосредственно формулой C) продолжается в этот сектор. Так как
при этом 5 взаимно однозначно отображается на сектор
5' = |4 ^Ф^^Ц—г плоскости w, то по тем же соображениям,
что и выше, продолженная функция
- «-2-
f (z) — Yr e 2 > л ^ ф < я + б, D)
голоморфна в 5. Однако f нельзя рассматривать как аналити-
аналитическое продолжение /0 из D в область DU5={—я<ф<л + 6}
по той причине, что f не является функцией в этой
области, ибо она неоднозначна в D\jS. В самом деле, любой
точке zo из пересечения DOS она сопоставляет два значения w:
если считать, что z0 e D, то г0 нужно сопоставить значение
1) В самом деле, в силу однолистности отображения z->w при
имеем hw =^0и, следовательно,
Аш
Дг
1
Дг
Aw
(*)
В силу непрерывности этого отображения Aw ->¦ 0 при &г -> 0, и если суще-
существует iim -г— = -;— ?= 0, то, переходя в (*) к пределу при Дг -> 0, полу-
чим, что существует Iim
Д^
Дг
, равный
dw
~dT
I
dz
dw
142 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
f0(z0) = уТое*~* , где —л<фо<—я + б; если же считать г0 е 5,
то этой точке надо приписать аргумент ф=фо+2л (я<ф<л + б)
и, следовательно, значение функции
. фо+2л
- ЛГг р1 2 ? [у \ (?,)
ш ' п " —' ^^ /0 \ 0/ \ /
(в обоих случаях у нас ro=\z0\).
Между тем если рассматривать f0 только в верхней поло-
половине области D, т. е. верхней полуплоскости ?>+ = {0<ф<зт}, то
функция
f(z) = /;V-T, 0<ф<я + б, (б)
будет аналитическим продолжением f0, ибо она голоморфна в
D+U5 и f\D+=f0. Возникает настоятельная потребность обоб-
обобщить понятие аналитического продолжения так, чтобы оно со-
содержало и рассмотренное выше продолжение f0 из D в DUS,
но не требовало введения многозначных функций.
Заметим, что при аналитическом продолжении однознач-
однозначность нарушается в тот момент, когда расширяющаяся область
определения функции начинает «налезать» на себя, покрывать
еще раз некоторую свою часть (подобно тому, как в нашем
примере сектор S покрывает часть области D, см. рис. 41). Из
этого наблюдения в теории функций возникла идея (восходя-
(восходящая еще к Б. Рим а ну и К. Вейерштрассу) относить
появляющиеся при продолжении новые значения функции не
к старой области, где функция уже определена, а к новой обла-
области, покрывающей старую.
Так, в нашем примере значения f в пересечении Df\S, где
уже определена функция /о, мы будем относить не к области D,
а к сектору 5 (точнее, к S, ибо 5 содержит граничный луч
{ср=я) и не является областью). Таким образом, на пересече-
пересечении Df]S мы будем рассматривать два объекта: 1) часть обла-
области D — сектор ?>о = {—я<ф<—я + 6} — с голоморфной в ней
О
функцией [о и 2) сектор 5 = {я<ф<я + б} с голоморфной в нем
функцией f. Хотя области Do и 5 геометрически совпадают, но
функции / и /о, им отнесенные, различны (они, очевидно, отли-
отличаются знаком), поэтому эти объекты следует считать различ-
различными.
Итак, идея заключается в том, что вместо функции рассмат-
рассматривается новый объект — пара, составленная из области и
заданной в ней функции. Переходим к точным определениям.
ПОНЯТИЕ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ
143
Определение 1. Аналитическим элементом или, короче,
элементом называется совокупность &~={D, f) области DaC
и голоморфной в этой области функции /.
Определение 2. Говорят, что два элемента <&~\ = (DU Д)
и <?F~2= (^2> /г)« области которых имеют непустое пересече-
пересечение Di[)D2, являются непосредственным аналитическим продол-
продолжением друг друга через область А —
связную компоненту Dif\D2— если всю-
всюду в А
fi(z) = /2B) G)
(при этом значения f4 и f2 в других ком-
компонентах пересечения Dif\D2 не обязаны
совпадать, см. рис. 42).
Так, в рассмотренном выше примере
элемент а?, который состоит из области
D = {—я<ф<зх} и голоморфной в ней
функции /^.определенной равенством C), и элемент <&~\, состоя-
состоящий из области Di= 1^"<Ф<~^"( (левой полуплоскости) и го-
Рис 42
ф
ломорфной в ней функции/i (z) = ]/7е 2, у <ср< -^-, составля-
составляют непосредственное аналитическое продолжение друг друга че-
через второй квадрант Л = -J-^- < ср < п>, но не через третий квадрант
А' =]л<ф<-^-[, ибовД' значения/о и fi различны (рис.43).
Рис. 43.
Рис. 44.
Определение 3. Говорят, что элементы &~ — (D, /) и
?? = (G, g) являются аналитическим продолжением1) друг
друга через области Av (v = 0, ..., п—1), если существует та-
такая цепочка элементов e?~v = (Dv, fv), v = 0, ..., п, что: 1)
<^п = &Г, <3"п = &\ 2) области Dv и Dv+i имеют непустое пере-
пересечение и Av является одной из его компонент (v = 0, ..., п— 1);
элемент g^"v+i является непосредственным аналитическим про-
продолжением e7"v (v = 0, ..., п— 1) через Av (рис. 44),
') Уже без слова «непосредственное».
144 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ПГ
Пример. Пусть D — верхняя полуплоскость {1тг>0} и в ней заданы
две функции
з_ (I
ш = / (г) = Уг е 3 , 0 < ф < я,
ш
з {Л
3
{
е 3 , 2л < ф < Зя
(z=re'4>). Они взаимно однозначно и непрерывно отображают D соответ»
ственно на секторы /)* = <0<г1з<^-|- и G* = < -3- < if < л > (мы пола-
полагаем 1|) = агеш). Обе функции обращают функцию ш3=г (так что их можно
з\
считать значениями Vz ) и, по правилу дифференцирования обратных функ-
функций, голоморфны в D. Таким образом, пары е7" = (А /) и & = (Z), g) яв-
являются аналитическими элементами.
Они являются аналитическим продолжением друг друга. В самом деле,
рассмотрим, например, области ?>1 = {0<ф<2л} и 1>2 = {л<ф<3л} и в них со-
з_ t±
ответственно голоморфные функции /i (г) = у г е @ < ф < 2л) и f2 (г) =
3_ г —
= Yr е 3 (л < ф < Зл); элементы еГ', (D,, f,), (?>2> /2). ^ образуют це-
цепочку, которая удовлетворяет всем условиям, принятым в определении 3.
27. Продолжение вдоль пути. Для простоты дальнейших
рассуждений мы несколько конкретизируем понятие элемента.
Определение 1. Каноническим элементом с центром в
точке аеС называется пара <&~а= {Ua, fa), где /„ — сумма схо-
сходящегося степенного ряда с центром в а и Ua — круг сходимо-
сходимости этого ряда. Мы будем называть Ua кругом сходимости эле-
элемента <?Fa и обозначать через Ra радиус этого круга, если афоо,
или радиус его дополнения, если а = оо.
Если аеС, то круг сходимости элемента <>7~а имеет вид
Ua = {z\\z — a\<Ra}, где Ra^C 0°, а функция
Мг)=2сл(г-оГ; A)
га=0
если же а = оо, то Ua = {z :\z\ >Ra}, где /?а> 0, и
га=0
Определения непосредственного аналитического продолже-
продолжения и аналитического продолжения для канонических элементов
несколько упрощаются, ибо их области (круги) пересекаются
по связным множествам и поэтому не надо оговаривать, через
какие компоненты пересечений Av производится продолжение.
§ 7]
ПОНЯТИЕ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ
145
Если канонический элемент 4F\— (Уь, fb) является непосред-
непосредственным аналитическим продолжением элемента <&~а= (Ua, la)
и, кроме того, be. Uа (рис. 45), то такое продолжение сводится
просто к переразложению суммы степенно-
степенного ряда fa в ряд по степеням z— b:
C)
и=0
Заметим еще, что если два канониче-
канонических элемента <?Га и ?ГЬ являются непо-
непосредственным аналитическим продолжением
друг друга, то их круги сходимости Ua и
Ub не могут компактно принадлежать один
другому (если, например, Ub <§ Ua, то fb
голоморфна в большем, чем Ub, круге с
центром b и, следовательно, Ub не может быть кругом сходимо-
сходимости). Поэтому окружности dUa и dUb должны иметь хотя бы
одну общую точку, и из треугольника, изображенного на рис. 45
(только теперь не обязательно beUa), мы заключаем, что
Рис. 45.
\Ra-RbK\b-a\.
D)
Теперь мы займемся понятием аналитического продолже-
продолжения вдоль пути. Без ограничения общности будем предполагать,
что для всех рассматриваемых здесь путей параметр меняется
на отрезке / = [0, 1].
Определение 2. Говорят, что канонический элемент
<&~o=(Uo,fo) продолжаем вдоль пути у: z = z(t), t^J, с нача-
началом в центре a = z@) этого элемен-
1 ^*- та, если существует семейство эле-
элементов
^, = {Ut, ft), te=J, E)
с центрами at = z(t) и ненулевыми
радиусами сходимости, удовлетво-
удовлетворяющее следующему условию. Если
u(to)czJ обозначает такую связную
Рис. 46. окрестность точки to^J, что г(/)е
e(/i, для всех t<=u(t0) (эта окре-
окрестность существует в силу непрерывности пути), то для любого
teu(t0) элемент <?Tt является непосредственным аналитическим
продолжением <&~^ (рис. 46).
Если элементно продолжаем вдоль у, то говорят, что эле-
элемент gT'i семейства E) (с центром в конце b = z(\) пути) полу-
получается из &Го аналитическим продолжением вдоль пути у.
Б. В. Шабат
146 " АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
Прежде всего докажем единственность продолжения
вдоль пути. Для этого условимся считать два канонических
элемента <?7~ = {U, f) и & = {V, g) равными {<?Г = &), если
U=V и в этом круге / = g.
Теорема 1. Если канонический элемент <^~о продолжаем
вдоль пути у, то в результате его аналитического продолжения
вдоль этого пути получается вполне определенный элемент, не
зависящий от выбора семейства, осуществляющего продол-
продолжение.
< Пусть у задается уравнением z = z(t), t^J, а элементы
S"\ и &х получаются продолжением ё?~0 вдоль у: первый при
помощи семейства элементов $~t, а второй — семейства &t
= а?а, t^.J). Рассмотрим множество
оно непусто, ибо содержит точку t = 0.
Это множество открыто (в топологии /). В самом деле,
пусть t0 е с?, т. е. <^0 = 0?ta; в силу непрерывности пути у
найдется окрестность и (/0) с / такая, что для всех t e и (t0)
точка z(t) принадлежит общему кругу сходимости элементов
&Г^ и ??t,,- По определению 2 для всех /ем (tQ) и of t и &t полу-
получаются непосредственным аналитическим продолжением рав-
равных элементов ^"t0 = aft0 и, следовательно, совпадают (см. фор-
формулу C)). Поэтому u(to)c:^'.
Но ? в то же время и замкнуто. В самом деле, пусть
t0 е / — предельная точка <f и и (t0) — такая окрестность, что
для всех t^u(t0) точки z(t) принадлежат меньшему из кругов
сходимости элементов S^u и <&и (обозначим его через W).
В и (to) найдется точка t\ е е и в ней S^t^ = $и- Так как z \t\) e U7,
то (^^0 и (?fy0 являются непосредственными аналитическими про-
продолжениями равных элементов е?"; и ^. Поэтому f; ^^
в пересечении W с кругом сходимости <g~tl и ^,, но тогда по
теореме единственности п. 21 ft = gt всюду в W и, следова-
следовательно, 3~'ta = a?t0, т. е. to e S3.
Итак, непустое подмножество Ж с: / является одновременно
открытым и замкнутым. Отсюда следует (п. 4), что <з =/ и,
в частности, что <&~1 = $х>
Теперь мы хотим доказать, что продолжение вдоль пути
всегда можно осуществить в конечное число приемов, т. е. как
аналитическое продолжение в смысле предыдущего пункта.
Лемма. Радиус R(t) элемента 4F\ из семейства E), осу-
осуществляющего аналитическое продолжение вдоль пути у, яв-
является непрерывной функцией от t на отрезке J, если круги
сходимости всех <&"t компактны.
§7]
ПОНЯТИЕ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ
147
< Для любого to^J найдем окрестность u(t0) такую, что
при teu(t0) элемент 4Ft является непосредственным продол-
продолжением <&~ta (см. определение 2). Из неравенства D) получаем
тогда, что
Это неравенство доказывает непрерывность R в точке t0 >
Теорема 2. Если элемент & получается из $~ аналити-
аналитическим продолжением вдоль пути у, то $ является аналити-
аналитическим продолжением ?f в смы-
смысле п. 26.
< Пусть <*F u /е/, — семейст-
семейство элементов, осуществляющих
продолжение вдоль у. По лемме
радиус R(t) элемента <^"t не-
непрерывен на /, следовательно,
существует е>0 такое, что
R(t)^-e для всех t e /. В си-
силу равномерной непрерывности
функции z(t) на / можно вы-
выбрать конечное число точек tv:
to = O<tl<. . .</„ = 1 так, чтобы
точки zv=z(tv) для v=l, ...
. .., п удовлетворяли неравенству
\zv—2v_i|<e. По определе-
определению 2 отсюда следует, что элемент
Рис. 47.
= eftv является непо-
непосредственным аналитическим продолжением элемента <& =
— a?~tv_l (v=l, ..., п). Но (^) = (^г', а <?Гп) = а?, следова-
следовательно, $ является аналитическим продолжением элемен-
элемента ~~
Пример. Рассмотрим в круге U = {\z—Г|<1} функцию
- Как мы
F)
пункте, в каждой точке
видели в предыдущем
ге[/ существует f (z) — 9f, . , следовательно, f голоморфна
в U и f'(z)—> оо при 2—«-О. Отсюда видно, что пара а? = (U, f)
составляет канонический элемент.
Чтобы получить аналитическое продолжение oF" вдоль пути
\о'- z=eu, O*Ct^,n (верхняя полуокружность {|г| = 1}, рис. 47),
нет необходимости, как сказано в определении, получать тейло-
тейлоровское разложение / в круге U и затем переразлагать его по
степеням z — еи при всевозможных ? е [0, л]. По теоремам 1
10*
148 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
и 2 достаточно рассмотреть круг U'={\z — »|<1} и построить
аналитическое продолжение <^~ по цепочке кругов U, U', V,
где V={|z+l|<l}. Но такое продолжение можно осуществить,
как в п. 26, непосредственно по формуле F), расширяя область
изменения ф в этой формуле: для V—на отрезок [0, л] и для
V—на отрезок Иг > ~5~ • ^ круге V мы получим голоморфную
функцию
и пара a?°=(V, go) составляет элемент, который и является
искомым продолжением <&~ вдоль пути у0. В частности, на отри-
отрицательном диаметре круга V имеем ф = я, следовательно,
(8)
где— х=1г|>0.
Аналогично при помощи цепочки кругов U, U", V, где
f/"={|z+'i|<l}, осуществляется аналитическое продолжение &?~
вдоль пути уь 2==ei', 0^-^>—л (см. рис. 47). Это продол-
продолжение заключается в том, что мы последовательно заменяем
в формуле F) область изменения ф отрезками [—л, 0] и
Г ~, —1-1. В результате мы получаем голоморфную в круге
V функцию
и пара &X = (V, gi) составляет элемент, который является про-
продолжением 47" вдоль пути Yi-
Элемент ^ не равен элементу 0°: хотя круги их сходи-
сходимости одинаковы, но функции отличаются, ибо, например, на
отрицательном диаметре V мы теперь имеем ф=—я и, следо-
следовательно, вместо (8) получаем
gl B) = У- х е~ 2 = - i У- х, A0)
где опять — x=|z|>0. Нетрудно видеть, что gi(z)=—go(z)
для всех z e V.
Заметим, что при построении наших продолжений мы не пользовались
тейлоровским разложением элемента «г. При желании его можно получить,
например, из следующих соображений^ На положительном диаметре круга U
имеем ф=0, следовательно, f(z) = Vx, где z=x>0. В анализе доказывается,
§ 7] ПОНЯТИЕ АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ 14&
что эта действительная функция раскладывается в биномиальный ряд
сходящийся на всем диаметре @,2) (здесь nl\ = n(n — 2)... и последний
множитель равен 2, если я — четное, и 1, если я — нечетное). По теореме
Абеля (п. 19) ряд A1) сходится и для комплексных х=г в круге U и, сле-
следовательно, представляет голоморфную в U функцию (п. 20). На диаметре
@,2) эта функция совпадает с f, а по теореме единственности (п. 21) от-
отсюда следует, что она совпадает с / всюду в U. Таким образом, всюду в U
(-1)" B^" B-1)". A2)
я=1
Можно написать и тейлоровские разложения функций go и gi в круге F;
они имеют вид
go (^ — gi (г) - </ (- г) - Л 1 - ^ в"^ " (г + 1)" I. A3)
В заключение докажем теорему об инвариантности
аналитического продолжения вдоль пути относительно гомо-
гомотопных деформаций этого пути.
Теорема 3. Пусть пути у0: z=zo(t) и уг: z = zi{t) гомо-
гомотопны, как пути с общими концами, и элемент 3" продолжаем,
вдоль любого пути ys'. z = zs(t) (se/), осуществляющего гомо-
топию Yo~Yi- Тогда результаты продолжения ?Г вдоль путей
Yo и Yi совпадают.
< Пусть z — z(s, t): JXJ-+C — функция, осуществляющая
гомотопию Yo~Yi (см- п- 16), так что zs(t)~z(s, t). Обозначим
через a?s (se/) результат аналитического продолжения эле-
элемента <&~ вдоль пути ys и рассмотрим множество
Оно непусто, ибо содержит точку s=0. Пусть So^cf; по лемме
существует е>0 такое, что радиусы R(t) элементов а??0, осу-
осуществляющих продолжение вдоль ys, не меньше е для всех
/е/. В силу равномерной непрерывности функции z(s, t) най-
найдется окрестность u(so)dJ такая, что для всех seu(so) и всех
\z(s, t)-z(s0) 0 К 4. A4>
150
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. Ш
По теореме 2 выберем tv^J так, чтобы точки z°v — z (s0, tv)
для всех v= 1, . •,, п удовлетворяли неравенству
zo _ zo | < _
A5)
и элементы ^v-i и <??" (мы обозначаем afv = a?f°) являлись не-
непосредственными аналитическими продолжениями друг друга.
Обозначим еще zv = z{s, tv), &v = &st и заме-
заметим, что при s^u{s0) в силу A4) и A5)
I zv — zJJ_j I < е для всех v = 1, ..., п (рис. 48).
Элементы &\ и <&\ являются непосред-
непосредственными аналитическими продолжениями
элемента <&~ и, следовательно, друг друга
мы пользуемся тем, что у нас | z\—a j <-j и
\z\ — zx I < —\. Точно так же мы докажем,
что и элементы c7V и ??v являются анали-
аналитическими продолжениями друг друга
Рис. 48. (v= 1, . . ., п). Но элементы &°п и &п имеют
к тому же общий центр (zQn = zn = b) и
О с Г)
поэтому совпадают. Так как soeg, то &п = ??tan~& , сле-
следовательно, и <??„ = a?s = ^°, т. е. sg <э*. Мы доказали, что
u{so)cz(f вместе с s0, т. е. что W — от-
открытое множество.
Но в то же время W является и
замкнутым множеством. В самом деле,
пусть So— предельная точка cf; построим
окрестность u(s0) такую же, как выше. ,
В ней найдется точка se?, так что про- *
должение <3" вдоль ys приводит к эле-
элементу (??°. По тем же соображениям, что
и выше, продолжения вдоль путей ys и
ys приводят к равным элементам, следо-
/ (см. п. 4) и, в
вательно, &н = 0-° и
Таким образом, ef
частности, $1 = $й>
Замечание. Если хотя бы вдоль одного из путей у„, осу-
осуществляющих гомотопию yo~Yl элемент <&~ непродолжаем, то
результаты его продолжения вдоль уо и yi могут оказаться раз-
различными. В самом деле, рассмотрим полуокружности yo и Yi из
разобранного выше примера. Они, очевидно, гомотопны и их
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 151*
гомотопию можно осуществить при помощи дуг окружностей
Ys, (X.s-4.1, проходящих через точки ±1 (рис. 49). Пусть для
определенности уч, обозначает прямолинейный отрезок [1, — 1].
Элемент <&~={U, f) из упомянутого примера можно описан-
описанным выше приемом аналитически продолжить вдоль любой дуги
ys, s=^=Y' Продолжение вдоль уч2 невозможно, ибо, как мы
видели, f'(z) —> оо при 2—>0, а отрезок у'/а содержит точку 2 = 0.
Этого оказывается достаточным для того, чтобы продолжения
вдоль Yo и Yi приводили к различным элементам (см. упомяну-
упомянутый пример).
§ 8. Понятие аналитической функции
Описательно говоря, под аналитической функцией понимает-
понимается то, что получается из аналитических элементов в результате
аналитического продолжения. Здесь мы подробно разберем это
понятие.
28. Аналитические функции. Под (аналитическим) элементом
мы будем сейчас, как в п. 26, понимать пару &?" = (?>, f), со-
составленную из области D и голоморфной в D функции f.
В различных окрестностях фиксированной точки а голоморфная
функция порождает различные элементы. Мы введем понятие
эквивалентности элементов с тем, чтобы отвлечься от несуще-
несущественного различия в выборе окрестностей.
Определение 1. Два элемента а?" = (D, f)_u ?? = (G, g),
области которых содержат одну и ту же точку asC, называются
эквивалентными в точке a (<f? ~ I?), если существует окрест-
окрестность точки а, в которой f=g-
Очевидно, что это отношение эквивалентности удовлетво-
удовлетворяет обычным аксиомам. По теореме единственности (п. 21) для
эквивалентности двух элементов в точке необходимо и доста-
, точно, чтобы функции, принадлежащие этим элементам, совпа-
совпадали во всей содержащей точку а компоненте пересечения их
областей.
Совокупность эквивалентных друг другу в данной точке
аеС элементов называют ростком аналитической функции в
точке а. Смысл этого понятия состоит в локализации по-
понятия элемента: рассматривая вместо фиксированного элемента
класс всех элементов, ему эквивалентных (в том числе и эле-
элементов, области которых сколь угодно малы), мы выделяем
в понятии ростка то общее, что объединяет эквивалентные эле-
элементы. Поэтому росток характеризует локальные свойства функ-
функции в рассматриваемой точке.
Очевидно, росток означает нечто большее, чем просто значе-
значение функции в рассматриваемой точке. В самом деле, пусть.
152 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
а = — л2 и функция / в правой полуплоскости D определена со-
соотношением
г, . У~ (cos -f-+i sin -f-) j
где z = rei(*>. Продолжая элемент (D, /) в левую полуплоскость G
по верхней полуокружности у<ь z = eu, 0-^.t^.n, мы получим
элемент ??°, состоящий из G и функции
/Г (cos-|-+i sin-2-) я Зя ...
g, (z) = e v 2 Ч T<(p<~2~' B)
а продолжение его вдоль полуокружности \>ь z = en, 0^-f^-—л,
приведет к элементу ??1, состоящему из G и функции
Vr (cos -f-+i sin-J- ) Зд
g,(z) = e \ 2 2Л --2-
Элементы ^° и ??' различны/ поэтому различны и их ростки
в точке а=—я2. Однако значения функций go и gi в рассмат-
рассматриваемой точке совпадают: при подсчете go (а) мы полагаем
<p = arga = n и, следовательно, go(a) =eni = — 1, а при подсчете
gi(a) считаем ф = —л и, следовательно, g'i(a) =e~ni — — 1.
К понятию аналитической функции мы придем, если бу-
будем рассматривать совокупности (аналитических) элементов
(•Оа. fa), гДе а пробегает произвольное множество индексов А,
причем предположим, что каждый из этих элементов получается
из любого другого аналитическим продолжением. Голоморфные
функции /а, аеЛ, принадлежащие элементам, будем называть
ветвями рассматриваемой аналитической функции.
Для удобства работы с этим понятием мы несколько кон-
конкретизируем его, заменив произвольные элементы канониче-
каноническими и продолжение — продолжением вдоль путей (п. 27). Так
мы приходим к следующему определению.
Определение 2. Аналитической функцией называется
совокупность канонических элементов, которые получаются из
одного какого-либо элемента <&"={U, f) аналитическими про-
продолжениями вдоль всех путей, начинающихся в центре а эле-
элемента <&~, вдоль которых такое продолжение возможно.
Очевидно, что это понятие не зависит от выбора начального
элемента <&~. В самом деле, пусть i? = (l/, g) — любой элемент,
принадлежащий аналитической функции, которая определяется
начальным элементом <^г. Тогда & получается из &Г продол-
продолжением вдоль пути у- Но и &Г получается из & продолжением
вдоль пути y. а любой другой элемент &6t который получается
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 153
из еТ" продолжением вдоль пути X, можно получить и из &
продолжением вдоль пути у~\}Х (определение объединения
путей см. в п. 14).
Определение 3. Две аналитические функции, опреде-
определяемые каноническими элементами, считаются равными, если
они имеют хотя бы один общий элемент. (По теореме един-
единственности продолжения вдоль пути тогда и все их соответ-
соответствующие элементы равны друг другу.) Две аналитические
функции, определяемые произвольными элементами, считаются
равными1), если какие-либо их элементы эквивалентны друг
другу в смысле определения 1 (тогда и все их соответствующие
элементы эквивалентны).
Теорема 1. Объединение кругов сходимости элементов,
принадлежащих аналитической функции, образует область.
4 Пусть D — это объединение; оно открыто, как объединение
открытых множеств (если г0еО, то z0 принадлежит и кругу схо-
сходимости U некоторого элемента, a U входит в D). Но D и связ-
связно, ибо для любых точек a, b^D можно найти принадлежащие
функции элементы, которые имеют эти точки центрами, а так
как эти элементы получаются друг из друга продолжением
вдоль некоторого пути y> соединяющего а и Ь, то и все точки у
принадлежат D.
Таким образом, D — открытое связное множество, т. е. об-
область >
Заметим, что аналитическая функция не является в этой
области функцией в обычном смысле слова. В самом деле, пусть
f={U, /),где U={\z-1\<\), и
f(z) = V7e'*, --f<cp<^-, D)
— элемент из примера, рассмотренного в предыдущем пункте.
Мы видели, что его можно продолжить в круг 1/={|г+1|<1}
двумя способами, которые приводят к двум различным голо-
голоморфным в V функциям go и gi: gi(z) =—go(z) в V. Таким
образом, аналитическая функция с начальным элементом <&"
каждой точке z^V ставит в соответствие два различных зна-
значения (отличающихся знаком) 2).
Ниже, в § 9, мы введем вместо плоских областей такие
объекты (римановы поверхности), на которых аналитические
') Иными словами, две аналитические функции считаются равными, если
они имеют общий росток (тогда и все их соответствующие ростки равны
друг другу).
2) Этот пример показывает, что аналитическая функция может иметь
в одной точке различные ростки.
54 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ - [ГЛ. III
функции можно будет рассматривать как обычные (однознач-
(однозначные) функции.
Правда, в некоторых случаях аналитические функции можно
рассматривать как обычные функции и в плоских областях.
Например, справедлива такая
Теорема 2 (о монодромии). Если некоторый элемент
o7~=(U, f) аналитически продолжаем вдоль любого пути у,
принадлежащего односвязной области D, то определяемая про-
продолжениями <&" вдоль таких путей аналитическая функция одно-
однозначна в этой области.
< Пусть <&~ имеет центром точку ueDn z — произвольная
точка этой области. В силу односвязности D любые два пути
Yo и Yi. ведущие в D из точки а в г, гомотопны, а по условию
элемент &?~ продолжаем вдоль любого пути, осуществляющего
гомотопию. Следовательно, по теореме об инвариантности ана-
аналитического продолжения (п. 27) элементы аналитической функ-
функции с центром в точке z совпадают. Их значение в точке z мы
и сопоставим этой точке. Таким образом, аналитическая функ-
функция определяет (однозначную) функцию в области D>
Если условие теоремы о монодромии не выполняется (на-
(например, если область D неодносвязна или не все элементы
продолжаются вдоль всех путей yczD), то аналитическая функ-
функция может сопоставлять точкам zgD несколько значений (они
будут значениями различных ветвей аналитической функции
в точке z). Сколько же значений может при этом сопоставляться
фиксированной точке? Ответ на этот вопрос дает
Теорема 3 (Пуанкаре — Вольтерра). Аналитическая
функция может иметь не более чем счетное множество различ*
них элементов с центром в фиксированной точке.
< Пусть аналитическая функция определяется начальным
элементом ^ с центром а и z — произвольная точка области D,
образованной кругами элементов, которые получаются при про-
продолжении <?Г (теорема 1). По теореме 2 п. 27 любой принадле-
принадлежащий функции элемент & с центром в точке z можно получить
при помощи конечной цепочки элементов с центрами a, z,, ...
. . ., zn-\, z, в которой каждый следующий элемент является
непосредственным аналитическим продолжением предыдущего.
Без ограничения общности можно считать, что точки zv
(v=l п—1) рациональны (т. е. Re zv и Im zv — рациональ-
рациональные числа). В самом деле, пусть сначала центры zv элементов
$~'v (v=l, ..., п— 1) произвольны. В сколь угодно малой окре-
окрестности каждой точки z'v возьмем рациональную точку zv и заме-
заменим <^\его непосредственным аналитическим продолжениемо?\
•с центром в zv. Ясно (см. доказательство теоремы 3 из п. 27),что
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 155
при достаточно малых \z'v — zv I результат продолжения по новой
цепочке будет совпадать со старым.
Остается заметить, что множество возможных непосред-
непосредственных аналитических продолжений <&г1 с рациональными
центрами элемента & счетно, так же как и множества эле-
элементов &'2, ..., 3"n-v Так как задание S^n-i и точки z одно-
однозначно определяет элемент & (хотя различные о7~п-\ могут при-
привести к одинаковым &), то множество возможных элементов &
не более чем счетно >
Пример аналитической функции, которая сопоставляет точ-
точкам области D бесконечное (счетное) множество значений, мы
приведем в следующем пункте.
Над аналитическими функциями можно производить обычные
для анализа действия, которые определяются как соответ-
соответствующие действия над их ветвями. Так, производной аналити-
аналитической функции {ofa}, аеЛ, называется аналитическая функ-
функция, элементами которой служат пары<&~'а = {Da, fa), аеД где
(Da> fa)= <&~a- Суммой аналитических функций {^а} и \а?а),
определяемых элементами ?Fa — {Da, fa) и a?a — (Da, ga) с оди-
одинаковыми областями, называется аналитическая функция
с элементами (Da, fa+ga). Аналогично определяются произве-
произведение и частное аналитических функций, однако частное двух
аналитических функций будет аналитической функцией лишь
в том случае, когда делитель отличен от нуля.
Можно определить также композицию двух аналитических
функций {а?~а} и {а?а} как аналитическую функцию с элемен-
элементами (Da, ga°faY, при этом предполагается, что eF'a = (Da, /„),
&a=(Ga,ga) и что f(Da)cz Оадля всех as Л. Например, под е^а)
понимается аналитическая функция с элементами (Da, ef°).
При желании можно определить действия над аналитиче-
аналитическими функциями, не связывая их с рассмотрением областей
элементов. Для этого нужно воспользоваться локализацией по-
понятия элементов, перейдя от них к росткам. Напомним, что ро-
ростком fa аналитической функции в точке а называется класс
эквивалентных элементов при следующем понятии эквивалент-
эквивалентности: элементы (Du /1) и ф2, /г) считаются эквивалентными,
если пересечение /?1ГШ2 содержит точку а и Д=/г в некоторой
окрестности этой точки.
Действия над ростками вводятся естественным образом.
Именно, под производной \'а ростка fa понимается класс элемен-
элементов, эквивалентных (D, /'), где (D, /) — какой-либо представи-
представитель класса fo (очевидно, \'а не зависит от выбора представи-
представителя). Аналогично определяются сумма ia + Sa и произведение.
h'h ростков в данной точке. Совокупность ростков аналитиче-.
156
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. III
ских функций в данной точке а составляет, очевидно, коммута-
коммутативное кольцо.
29. Элементарные функции. Здесь мы рассмотрим важней-
важнейшие примеры многозначных аналитических функций.
1. Корень. Под корнем п-и степени (л — натуральное чис-
число) из z понимается аналитическая функция
w =
определяемая следующим образом. В плоскости С с выброшен-
выброшенной отрицательной полуосью D0 = C\R- рассмотрим функцию
м=
B)
(мы полагаем z — re1®). Она непрерывна в Do и взаимно одно-
однозначно отображает Do на сектор Do = ] <i|)< — >• плоскости
-— (z)
j(w-Vz)
Рис. 50.
комплексного переменного w = pe1^ (рис. 50). Так как wn — z,
то по правилу дифференцирования обратной функции для всех
О существует производная
1
n{h(z)}>
.n-I
C)
(см. сноску на стр. 141).Поэтому пара g?"o= (Do, /0) представ-
представляет собой аналитический элемент. Аналитическую функцию, ко-
которая получается при аналитическом продолжении этого эле-
элемента, и называют корнем п-й степени из г.
Такое продолжение можно описать, например, так. Рассмот-
Рассмотрим область Da={—я + а<ф<я+а} и в ней голоморфную
функцию
п . Ф
-. I— г —
D)
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 157
Очевидно, что элементы <&~а= {Da, fa) при всех aeR будут
представлять собой аналитическое продолжение элемента
(Z)o, /о) (при |а|<я — непосредственное). Совокупность этих
элементов ?Га и описывает нашу функцию.
Объединением областей этих элементов D= [J Da служит,
_ a(sR
очевидно, плоскость С с исключенными точками 2 = 0 и г = оо
(это — единственные точки из С, которые принадлежат грани-
границам всех Da и не принадлежат ни одной Da).
Эту же функцию можно определить и при помощи канониче-
канонических элементов. Примем за начальный, например, элемент а?0
с центром в точке 2=1, который состоит из круга U =
= {\z—1|<1} и голоморфной в нем функции
)-0ft E)
(мы, как и в примере на стр. 149, заметили, что при положи-
п _
тельных z=x функция g0 (х) = Ух, воспользовались биномиаль-
биномиальным разложением этой действительной функции и продолжили
разложение с отрезка @, 2) в круг U).
Элемент ??0 ~ а!Г0, ибо при г=хе@, 2) мы имеем г=х,
Ф = 0 и, следовательно, fQ(x) = g0(x)= Vx, а так как обе функ-
функции /о и ga голоморфны в U, то по теореме единственности
fo(z) =go(z) для всех геС/. По определению 3 предыдущего
пункта аналитические функции, определяемые элементами
<^~0 и &0, совпадают.
п
Каждой точке zo^D аналитическая функция w = Y~z отно-
еит точно п различных значений. В самом деле, значения всех
голоморфных функций, принадлежащих элементам <з7~а (ветвей
нашей аналитической функции), определяются по формуле
w = у rQ e " , F)
где ro=\zo\, фо — одно из возможных значений arg z0, a k — про-
П . фо
извольное целое число. Положив wo=Y~TQe ", мы видим, что
все другие значения w отличаются от w0 множителями е " ,
а эти множители (корни л-й степени из 1) получаются из век-
вектора 1 поворотами на угол, кратный —, т. е. имеют п различ-
158 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ill
ных значений. Таким образом, среди значений F) имеется лишь
п различных значений доо> ^i. •. •, i^n-i, которые получаются,
если положить в F) k = 0, 1, ..., п—1. Эти значения распола-
располагаются в вершинах правильного л-угольника с центром в точке
w = 0, одной из вершин которого служит точка w0 (см. рис. 50).
В заключение несколько слов о ветвях аналитической функ-
п _
ции Yz • В соответствии с определением п. 28 под ветвью этой
функции понимается любой принадлежащий ей элемент (не обя-
обязательно из числа элементов ^а)- Можно также понимать под
ветвью голоморфную функцию, принадлежащую этому эле-,
менту.
г = <
(г)
Рис. 5).
п
По теореме о монодромии (п. 28) ветвь Yz можно выделить
в любой односвязной области G, не содержащей точек г=0 я
2 = сю. Примером такой области служит плоскость с любым раз-
разрезом, соединяющим эти точки (граница области должна быть
связной). На рис. 51 изображена одна из таких областей G и
зл-
злее образ G* при отображении одной из ветвей V z; две другие
27li 4ni
ветви отображают G соответственно на области е 3 G* и е 3 G*,
полученные из G* поворотом на углы -у- и —.
п
Вообще, ветвь у z можно выделить в любой области, кото-
которая не содержит ни одного замкнутого пути, охватывающего
точку 2=0. В самом деле, при обходе таких и только таких
путей величина argz меняется на целое кратное 2я, и, следова-
следовательно, аналитическое продолжение вдоль них какого-либо эле-
элемента может привести к другому элементу. В областях, удовлет-
¦8]
ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
159
ворягещих указанному условию, можно выделить п различных
ветвей нашей аналитической функции. Каждая из таких ветвей
отличается от другой множителями е п и вполне характери-
характеризуется указанием области, в которой она определена, и зна-
значением в одной из точек этой области. (Например, можно го-
говорить о ветви Vz, которая определена в плоскости С с раз-
разрезом вдоль отрицательной полуоси и которая равна 1 при
г=1; другие две ветви Vz в этой области при z=\ принимают
соответственно значения е 3 и е 3 =е 3.)
Л"
(w=Lnz)
1.
Рис. 52.
Над корнями можно производить действия в том смысле,
какой им был придан в конце предыдущего пункта. В частно-
частности, можно рассматривать производную
G)
которая также является аналитической функцией.
2. Логарифм комплексного переменного г
w = Lns;
(8)
можно определить аналитическим продолжением начального
элемента, который состоит из области А) = {—л<ф<я} и задан-
заданной в ней функции
w = In г = In г + ир, — л < ф < я, (9)
которая называется главной ветвью логарифма (как и выше,
Мы полагаем z = re"P). Функция (9) гомеоморфно отображает
А) на полосу Do = {w: — я< Im w < л}, (рис. 52), а так как из
свойств показательной функции (п. 12) следует, что
160 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
ew = elnr• e'f = z, т. е. что функция (9) обратна к показательной,
то по правилу дифференцирования обратных функций в каждой
точке 2oeZ)o существует
-^-Aп2) = 4г = 1. A0)
dz e z
Таким образом, элемент е?~о= (Do, In г) — аналитический.
Аналитическое продолжение элементарно можно, как и выше,
определить при помощи семейства элементов <^"а (а е R), кото-
которые состоят из области Da = {—я + а<ф<л + а} и голоморфной в
ней функции /а(г) =1п r + 1'ф, —л + а<ф<я + а. _Объединением
областей этих элементов по-прежнему служит С с исключен-
исключенными точками z = 0 и z = oo.
Можно определить Ln z также при помощи канонических
элементов. В качестве начального элемента можно принять
круг U—{\z—1|<1} и голоморфную в нем функцию
(которая получается аналитическим продолжением в U с диа-
диаметра @, 2) действительной функции \пх = In {1 + (х — 1)} =
ос. \
= ^(-1)""' (*~1)Д . Элементы (Do, In г) и (U, \nz\v) эк-
вивалентны.
Каждой точке zoe.D—\JDa аналитическая функция Lnz от-
относит счетное множество значений, которые опреде-
определяются по формуле
A2)
где ro=\zo\, ф0—одно из возможных значений Arg z0 и k — про-
произвольное целое число. Все они различны и лежат на вертикаль-
вертикальной прямой Rew = lnr0 на расстоянии, целом кратном 2я, друг
от друга (см. рис. 52). Все эти значения считаются логариф-
логарифмами числа Zo; таким образом, каждое конечное комплексное
число, кроме z = 0, имеет бесконечно много логарифмов.
п
Ветви аналитической функции Ln z, так же как Уг, можно
выделять в любой области G, которая не содержит ни одного
замкнутого пути, охватывающего точку z = 0. В самом деле, про-
продолжение вдоль такого и только такого пути может перевести
канонический элемент в другой элемент с тем же центром,
не равный первому. В каждой области G, удовлетворяющей ука-
указанному условию, можно выделить бесконечно много ветвей
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 16!
Lnz, которые отличаются ..друг от друга постоянными слагае-
п __
мыми — целыми кратными 2го. Поэтому ветви Lnz, как и \/~z,
однозначно определяются указанием области, в котором расч
сматривается ветвь, и ее значения в одной из точек1).
Над логарифмом можно производить действия в смысле,
указанном в п. 28. В частности, производная логарифма
(Lnzy = l A3)
оказывается функцией, голоморфной в области D (все ветви
логарифма имеют одну и ту же производную). Голоморфна и
функция
eLnz = z; A4)
в этом смысле можно описательно говорить, что логарифм яв-
является функцией, обратной к показательной2).
Не так благополучно обстоит дело с алгебраическими дей-
действиями над логарифмами. Например, справедливое равенство
Ln г + Ln г = 2 Ln г
(в самом деле, в обеих его частях стоит аналитическая
функция, определяемая элементом (Do, 2\nz)) нельзя рассмат-
рассматривать как равенство для соответствующих значений логарифма
в фиксированной точке
(в самом деле, действия над совокупностями чисел Lnz0 не
определены, поэтому такое равенство просто не имеет смы-
смысла; если же определить эти действия «естественным» образом
как действия над совокупностями, то получится неправильный
результат: 21nro + 2km = 2(\nro + 2kni), где k — произвольное це-
целое число).
Мы закончим раздел, посвященный логарифму, упоминанием о споре,
который разгорелся в 1712—1713 гг. в переписке между двумя крупнейшими
математиками того времени Иоганном Бернулли и Г. Лейбни-
цем3) о логарифмах отрицательных чисел. Бернулли утверждал, что они
') Это справедливо не для всех аналитических функций. Например,
аналитическая функция е z , которую мы рассматривали в п. 28, в точке
го=—я2 имеет две различные ветви, соответствующие двум значениям
Vza = ± яг; однако значения е±Лг этих ветвей в точке го совпадают.
2) Точнее, в правой части A4) стоит сужение функции иа область D,
ибо левая часть не определена при г=0 и г= °°.
3) Подробнее об этом можно прочитать в книге А, И. М а р к у ш е в и ч а
Очерки по истории теории аналитических функций, Физматгиз, М.—Л., 1951;
мы пользуемся здесь его изложением.
П Б. В. Шабат
162 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
действительны и что 1п(—х)=\пх. Вот один из его доводов в пользу
этого утверждения: из равенства (—хJ=х2 следует, что 21п(—я)=21пл:.
Лейбниц же -утверждал, что логарифмы отрицательных чисел мнимы и что
тождество 1п(—х)=1пл: не имеет места, в частности, 1п(—1)=5^0. Вот один
из доводов Лейбница в пользу последнего утверждения: если подставить
х=—2 в разложение ln(l+jc) = jc й~ + ~5— •••> т0 получится равенство
2, о
1п( — 1) = — 1 — — -z— ..., в котором все члены справа отрицательны,
2i о
и, следовательно, 1п(—1)^0.
В 1749 г. в спор вступил Л. Эйлер. Он опубликовал статью, в которой
утверждал, что ни один из спорщиков не прав. В частности, приведенный
выше аргумент Бернулли он опровергал так. Подобным же_ образом из ра-
равенства {х У — l) = xi можно заключить, что In х + 1п у— 1 = 1п х, т. е. что
In)/"— 1 = 0. Но сам Бернулли открыл, что — — = —, а в последнем равен-
У — 1 2
стве сомневаться нельзя, ибо, писал Эйлер, «это открытие обосновано наиболее
надежными средствами анализа». Приведенный выше довод Лейбница Эйлер
также не считал убедительным. Он привел следующий пример: если поло-
положить в разложении -г-т-— = 1 — х + х2 — х3 + ... один раз х=—3, а другой
1 ~р X
х—1 и сложить результаты, то получится равенство 0=2+2+10+26 + ...,
в котором левая часть равна 0, хотя, как писал Эйлер, «правая часть пред-
представляется отличной от нуля».
В упомянутой статье Эйлер предложил правильное решение спора: лога-
логарифмы отрицательных (как и других комплексных чисел) имеют бесконечное
множество значений. Небезынтересна его аргументация. Значение у=\пх
определяется из уравнения х — еу — [ 1 + 4-1 ' где t — «бесконечно большое
I I \
число» (термин и обозначение Эйлера). Отсюда получается, что y = i\xi — 1 /
а число х ' — «корень с бесконечно большим показателем» — имеет бесконеч-
бесконечно много значений, вообще говоря, комплексных.
Интересно также, что в 1761 г. Ж. Даламбер в этом споре принял
сторону Бернулли против Лейбница и Эйлера.
3. Обратные тригонометрические функции
просто выражаются через корни и логарифмы. Найдем такое
выражение, например, для арккосинуса. Решая уравнение
cos да = z, или y(eiffi) + e~tw) = z, или, наконец,
s>2lw _ 0-yaiw _1_ 1 . П
как квадратное уравнение относительно eiw, найдем
е"» = z + Yz2- 1
(мы не пишем здесь обычный знак ±, ибо по нашему опреде-
определению квадратный корень и так имеет два значения). Остается
заметить, что из последнего равенства
w = Arccos z = i Ln (z + Yz<i ~ 0 A5^
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 163
(мы ставим перед логарифмом i, а не-, как должны были бы,
потому, что в силу соотношения , — z — Vz2 — 1 изме-
z + у г2 — 1
нение знака перед логарифмом сводится к изменению знака пе-
перед корнем, а последний все равно имеет два значения).
Аналогичные выражения справедливы и для других обрат-
обратных тригонометрических функций, например
Arcsin г = - i Ln (iz + V 1 - z2), Arctgz = -~-Ln уз§ . A6)
Формулы A5) и A6) напоминают известные формулы для об-
обратных гиперболических функций, и это неудивительно, ибо в
комплексном анализе тригонометрические функции просто свя-
связаны с гиперболическими (см. п. 13).
Обратные тригонометрические функции представляют собой
аналитические функции, и в формулах A5) и A6) действия
надо понимать так, как принято выше (при помощи ветвей).
4. Общая степенная функция w = za, где а — произ-
произвольное комплексное число, определяется соотношением
w = za = еа Ln z A7)
и представляет собой аналитическую функцию. Для действи-
действительных показателей aeR будем различать три случая:
а) а — целое число. В этом случае функция A7) однознач-
однозначна — многозначность логарифма погашается периодичностью
показательной функции. Поэтому функция голоморфна при а>0
в С (точка z = 0 устранимая), а при а<0 в С\{0} (точка г = оо
устранимая).
б) а = — — рациональное число (мы предполагаем, что дробь
несократима). Здесь многозначность логарифма лишь частично
погашается периодичностью показательной функции, и функция
A7) каждому гФО, фоо ставит в соответствие q различных
q
значений. Она совпадает с аналитической функцией w = Yzp.
в) а — иррациональное число. Здесь различным значениям
aLnz, которые отличаются друг от друга на целое кратное
2ani, соответствуют и различные значения eaLnz. Погашения,
наблюдавшегося в предыдущих случаях, не происходит, и функ-
функция A7) каждому гфО, =?оо ставит в соответствие счетное мно-
множество значений.
Пусть теперь а = а+.ф, р=?0, не является действи-
действительным числом. Простой подсчет
za _ ?(а+/Р) Iln r+i (ф+2?я)] _ ga Jn /¦-$ {(f+2kn)ei Ш In г+а (<р+2?я)]
И*
164 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
(где положено z = rei(f и k — произвольное целое число) пока-
показывает, что в этом случае каждому комплексному числу гФО,
фоо функция относит счетное множество значений, модули
которых г«?-Рф?-2йяр = po6-2ftjtp образуют бесконечную в обе сто-
стороны геометрическую прогресеию со знаменателем q = e~2n^,
а аргументы р \nr + a(f + 2k^a='^o + 2kna— бесконечную в обе
стороны арифметическую прогрессию с разностью d = 2na, если
сс^О, и d = 0, если а = 0.
Например '),
,-' = e'Ln< = e'(IT+2*!tV = e"VT+2*")> fe = o, ±1, ... A8)
5. Общая показательная функция w = az, где
а — произвольное комплексное число аФО, фоо, определяется
соотношением
w = аг = егЬпа. A9)
Этот принятый термин неправомочен. В самом деле, A9)
не является функцией в обычном смысле слова, ибо Lna —
= In|a j +i arga + 2kni (&=0, ±1, . . .) принимает бесконечно
много значений и поэтому az (при нецелых г) многозначна. Но
она не является и аналитической функцией, ибо отдельные ее
элементы, которые получаются, если выбрать для лографма ка-
какое-либо из его значений, не являются аналитическим продол-
продолжением друг друга.
Таким образом, аг следует рассматривать как совокупность
различных (целых) функций
gZ (In I a\+i arg a)e2kniz {h = О Ч- 1 )
30. Особые точки. В п. 24 мы рассмотрели изолированные
особые точки голоморфных функций "(их называют еще особыми
точками однозначного характера). Но, например, точка 2 = 0,
являясь особой для аналитической функции w = Yz, не входит
в классификацию, приведенную в п. 24. Поэтому мы ставим
здесь своей задачей обобщить эту классификацию, введя поня-
понятие особой точки аналитической функции. Как и в п. 24, мы
ограничимся простейшим случаем изолированных особых точек.
Определение 1. Точка йеС называется изолированной
особой точкой некоторой аналитической функции, если сущест-
существует проколотая окрестность V точки а такая, что некоторый
') Неискушенному этот пример должен показаться очень удивительным:
мнимое число /=|/"—1 мы возводим в мнимую степень V— 1 и получаем
бесконечно много значений, да еще все они действительны!
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 165
элемент <^"—{U, /), принадлежащий этой функции, продол-
продолжается аналитически вдоль любого пути ycV.
Таковы, например, точки 2 = 6 и z = oo для аналитических
п _
функций Yz и Ln2 (в качестве V для обеих точек можно взять
кольцо {0< \z\ <оо}). Для функции j= особыми будут как
I +У z
точки 2 = 0 и 2=оо, обусловленные особенностями у z, так и
точка 2=1, обусловленная тем, что в ней одна из ветвей функ-
функции (для которой Yz при 2=1 равен —1) имеет полюс (другая
ветвь, для которой Yz ПРИ ¦г=1 равен 1, правильна в этой
точке).
Классификацию изолированных особых точек аналитических
функций мы будем проводить в зависимости от поведения их
элементов при продолжении вдоль замкнутых путей y^V".
Лемма. Пусть а — изолированная особая точка некоторой
аналитической функции и V — проколотая окрестность такая,
как в определении 1. Если какой-либо
принадлежащий функции элементно при
продолжении вдоль некоторого замкну-
замкнутого пути YodV" не меняется х), то и лю- /
бой элемент <&~, получаемый из <^о про- I
должением в V, не меняется при про- [
должении вдоль любого пути у, гомотоп-
гомотопного Yo в V.
< Пусть К — путь в V, переводящий
с?~0 в <^~, и y' = ^~UyoUA (проходится
в порядке К~, Yo, Я; см. п. 14). Очевидно, ^"" "
Y'~y в V (рис. 53) и имеет с y общие . Рис. 53.
концы, поэтому по теореме 3 п. 27 про-
продолжения вдоль_у и у' совпадают. Но Я" переводит &~ в <&,
Yo не меняет с? 0, а К переводит &Г0 в <&~, т. е. продолжение
вдоль у' не меняет <^"'>
Из этой леммы следует, что продолжение вдоль замкнутых
путей, гомотопных нулю в V, не меняет элементов (ибо такие
пути стягиваются в пути, лежащие в круге какого-либо элемен-
элемента, а продолжение вдоль последних очевидно не меняет элемен-
элементов). Поэтому в нашем исследовании представляет интерес лишь
продолжение вдоль путей, негомотопных нулю в V.
Определение 2. Пусть а — изолированная особая точка
некоторой аналитической функции, V — проколотая окрестность
') Или заменяется элементом, эквивалентным исходному (если рассма-
рассматриваемые элементы не канонические).
166 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
такая, как в определении 1, и Yo^V"— замкнутый жорданов
путь, содержащий точку а внутри. Будем различать два случая:
(I) если обход Yo не меняет исходного элемента функции, то
а называется особой точкой однозначного характера;
(II) если обход yo приводит к элементу, отличному от исход-
исходного, то а называется особой точкой многозначного характера
или точкой ветвления.
В случае (I) продолжение исходного элемента вдоль любого
пути KczV, ведущего в фиксированную точку геУ, приводит
к одному и тому же элементу. В самом деле, если бы существо-
существовали два таких пути Ai и Аг, приводящие к различным элемен-
элементам, то замкнутый путь у = Х^ \]К2с]/' менял бы элемент. Но
путь y либо гомотопен 0 и тогда не может менять элемента по
сделанному выше замечанию, либо гомотопен несколько раз
проходимому (в положительном или отрицательном направле-
направлении) пути Yo и по лемме также не меняет элемента. Это проти-
противоречие доказывает сделанное утверждение.
Из него следует, что в случае (I) продолжение начального
элемента по путям, принадлежащим V, приводит к однозначной,
т. е. голоморфной в V' функции /, которая является ветвью рас-
рассматриваемой аналитической функции1). Точка а является изо,-
лированной особой точкой / в смысле п. 24. В зависимости от
поведения / при приближении к а эта точка может быть устра-
устранимой, полюсом или существенно особой. (Впрочем, если на-
начальный элемент канонический, то случай устранимой точки
исключен, ибо в этом случае круг сходимости элемента содер-
содержал бы точку а.)
В случае (II) аналитическая функция, которая получается
продолжением начального элемента вдоль путей, принадлежа-
принадлежащих V, не допускает выделения в V голоморфной ветви2). Слу-
Случай (II) мы разобьем на два подкласса.
(На) Существует целое число п >• 2 такое, что п-кратный
обход Yo в одном направлении приводит к исходному элементу.
') Продолжение начального элемента по путям, не принадлежащим V,
может привести к другому элементу с тем же центром, так что рассматри-
рассматриваемая аналитическая функция может быть неоднозначной. Так, продолжение
произвольного элемента аналитической функции j= по путям, принадле-
1 +у г
жащим V"={0<|z—1|<1}, приводит к однозначной функции (одной из двух
ветвей ¦—¦ I, но продолжение вдоль замкнутого пути, обходящего точку
1 +У г ]
г=0, переводит элемент, принадлежащий одной ветви, в элемент, принадле-
принадлежащий другой ветви.
2) ХЬтя в V и может существовать голоморфная ветвь рассматриваемой
функции, которая получается из начального элемента продолжением по пу-
путям, выходящим за пределы V (см. ниже пример 5).
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 167
В этом случае а называется точкой ветвления конечного по-
порядка, а наименьшее из чисел п, обладающих описанным свой-
свойством, называется порядком ветвления.
Нетрудно видеть, что порядок ветвления не изменится, если
заменить у0 любым путем у, гомотопным у0 в V. В самом деле,
обозначим через ky путь, который получается ^-кратным обхо-
обходом у в одном направлении (совпадающим с направлением у,
если ?>0, и противоположном ему, если ?<0); если y~Yo. to и
ky~kya и по доказанной выше лемме обходы ky и ky0 либо оба
меняют, либо оба не меняют исходного элемента. Читателю
предоставляется доказать, что если какой-либо замкнутый путь
yczV не меняет исходного элемента, то этот путь гомотопен
целому (положительному, отрицательному или нулевому) крат-
кратному пути пуо, где п — порядок ветвления точки а.
(I-I6) Такого целого числа п, как. в случае (Па), не суще-
существует, т. е. обходы у0 в одном направлении приводят все к но-
новым и новым элементам. В этом случае а называется точкой
ветвления бесконечного порядка или логарифмической точкой
ветвления.
Примеры.
п
1. Функция V~z имеет в точках г=0 и 2= оо точки ветвления порядка п.
Функция Ln г имеет в тех же точках логарифмические точки ветвления.
2. Функция 7=— в точке 2=0 имеет устранимую особую точку, а в
У z
точке 2= оо— существенно особую точку, она является голоморфной целой
функцией (это видно из разложения
Vz 3! 5!
справедливого в кольце У={0<|г1<оо}).
3. Функция У ег + 1 во всех корнях уравнения ег + 1 = 0, т. е. точках
zk — V~Ln (— 1) = ± V~ni + 2kni, имеет точки ветвления второго порядка;
точка г= оо является ее неизолированной особой точкой.
4. Функция -: имеет логарифмические точки ветвления при 2 = 0 и
г=оо;при г=1 одна из ее ветвей в кольце {0<|г—1|<1} (главная ветвь)
имеет полюс первого порядка, остальные ветви голоморфны в этой точке.
5. Разберем подробно пример аналитической функции
w=Vl+ VT.
В точке г=0 внутренний корень имеет точку ветвления второго порядка.
Если в окрестности ?/'={0<|г|<1} мы выберем круг U={\z— V2KV2},
то в U можно выделить четыре различные ветви /v этой функции, характе-
характеризуемые различными знаками обоих корней. Пусть fi ^ одна из этих
168 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
ветвей; элемент 3"\-= (U, /i) после продолжения вдоль окружности уо: г =—е'',
0<?=^2я, перейдет в элемент &~2 = W, /2). где /г — другая ветвь, ибо вну-
внутренний корень при таком обходе изменит знак. Повторный обход Yo
снова приведет к элементу оГъ ибо обходы \а не меняют ветвей внешнего
корня, точкой ветвления которого является г=1. Точно в таком же отно-
отношении находятся две остальные ветви: /3=—fi и /4=—h- Таким образом,
в точке г=0 рассматриваемая функция имеет две различные точки ветвления
второго порядка.
Перейдем к изучению точки 2=1, в которой для одного из значений вну^
треннего корня подкоренное выражение внешнего корня обращается в нуль.
Пусть 1/' = {0<|г— 1|<1}, К = { |г-1/2 |< 1/2} и gv—четыре ветви нашец
функции в круге V. Пусть g\ и g2 (g2=—gi) — ветви, для которых внутрен-
внутренний корень равен — 1 при 2=1. Обход окружности Yb 2 = 1 + — elt,
, не изменит ветви внутреннего корня, но изменит^ знак у внешнего кор-
корня (когда г описывает окружность у\, точка ? = 1 + у z, где рассматривается
выбранная ветвь внутреннего корня, описывает в плоскости ? замкнутый
жорданов путь, содержащий внутри точку ?=0), поэтому при таком обходе
элемент (V, g\) перейдет в (V, gz). Вторичный обход у\ снова изменит знак
внешнего корня и поэтому снова приведет к элементу (V, gi). Оставшиеся
две ветви ^з и gi (gi=—gi), для которых внутренний корень равен 1 при
2=1, при обходе Yi не изменятся (при этом точка ? = 1 + Vz с выбранной
ветвью корня опишет замкнутый жорданов путь, охватывающий точку ? = 2
и не охватывающий ? = 0), следователь-
следовательно такой обход переведет каждый из
элементов (V, g<>) и (V, g4) в себя. Та-
Таким образом, в точке г=1 рассматри-
ваемая функция имеет одну точку вет-
ветвления второго порядка и два правиль-
р _ ел ных, неразветвленных элемента1).
Для изучения функции в точке г =
= оо надо взять проколотую окрестность.
№'={1<|г|<оо) и в ней, например, круг W={\z — 2|<1}. Пусть (W,h\) —
какой-либо из четырех элементов функции в круге W. Обход окружности
уз: z = 2ea, 0^t^2n, приводит к изменению знака как у внутреннего, так и
у внешнего корня (при этом точка ? = 1 + у г при любом выборе ветви кор-
корня опишет замкнутый путь вокруг точки ?=0), поэтому он приведет к дру-
другому элементу. (W, h2). Вторичный обход \з приведет к третьему элементу
(W, hz), трехкратный — к четвертому (W, Л4), и лишь четырехкратный обход
Yo приведет к исходному элементу (W, hi). Таким образом, в точке г=оо,
рассматриваемая функция имеет точку ветвления четвертого порядка.
Остальные точки С являются правильными точками этой аналитической
функции.
На рис. 54 изображен схематически результат нашего исследования.
В заключение приведем один результат, относящийся к точ-.
кам ветвления конечного порядка. Мы покажем, что в окрест-
окрестности такой точки а аналитическую функцию можно разложить.
') Элементы (U, gs) и (U,gt) не являются каноническими, ибо их круг,
сходимости больше U.
§ 8] ПОНЯТИЕ АНАЛИТИЧЕСКОЙ ФУНКЦИИ 169
в ряд по дробным степеням z — а, являющийся обобщением
ряда Лорана.
Теорема. В некоторой проколотой окрестности V' =
= {0<|г — a\<.R) точки ветвления конечного порядка п анали-
аналитическую функцию^) можно представить разложением вида
2 k{ay. A)
k= — оо
¦4 Положим г — a = t,n; когда точка ? описывает в плоскости
Z, достаточно малую окружность A: t,—peix, О -<! т -^ 2л, соответ-
соответствующая точка z = a + t,n описывает п раз окружность у0: z =
~а + рпеи, 0^С(^.2п. Так как начальный элемент рассматри-
рассматриваемой аналитической функции при таком обходе не меняется,
то соответствующий элемент функции w, рассматриваемой в за-
зависимости от переменной ?, не меняется при однократном об-
обходе Я.
Отсюда следует, что ? = 0 является особой точкой однознач-
однозначного характера этой функции и, значит, в некоторой проколотой
окрестности точки ? = 0 она представляется рядом Лорана
о>= 2 с?". B)
п
_ _!_
Подставляя сюда ? = yz — a = (z — а)'1, получаем разложе-
разложение A) >
В зависимости от «главной части» разложения A), т. е. сово-
совокупности членов с отрицательными индексами k, ветви рассма-
рассматриваемой аналитической функции непрерывны в точке (как \^г
или е*г в точке z = 0), стремятся к бесконечности при
/ 1 А
г—>-а(как .— ¦ при г—>0| или не стремятся ни к какому пре-
пределу при z-+a \как е *г при2->0/. Это различие считается
ке так уж существенным, и во всех случаях а называют точкой
ветвления конечного порядка.
Пример. Пользуясь биномиальным рядом, нетрудно написать обоб-
обобщенные лорановские разложения аналитической функции из разобранного вы-,
ше примера 5. В кольце ?/' = {0<|г|<1} имеем
') Точнее, совокупность принадлежащих этой функции элементов, кото-
которые получаются из какого-либо одного продолжением вдоль всевозможных
путей у а У. ¦
170 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
в кольце W' = [l<\z\< оо}
а в кольце V = {0 < | г - 1 | < 1}
Эти разложения хорошо иллюстрируют проведенный выше анализ точек
ветвления рассматриваемой функции.
§ 9. Понятие римановой поверхности
Аналитическая функция может сопоставлять точкам плоской
области несколько (даже счетное множество) значений. В этом
параграфе мы рассмотрим вместо плоских областей многолист-
ные поверхности, которые можно мыслить расположенными над
этими областями и которые имеют над точкой z столько «ли-
«листов», сколько значений приписывает аналитическая функция
этой точке. Поэтому на таких поверхностях аналитические функ-
функции можно рассматривать как функции в обычном смысле слова
(т. е. как однозначные функции).
31. Элементарный подход. Начнем с простейшего примера.
Рассмотрим в области D, которая представляет собой плоскость
С с разрезом вдоль отрицательной полуоси, две ветви ]\ и /г
аналитической функции
w = Vz.' A)
Пусть /i характеризуется условием /';A) = 1, а /2 — условием
/2A)=—1; мы имеем, очевидно, /2B)=—Ы2) для всех геО.
Эти ветви однолистно и конформно отображают D соответ-
соответственно на правую и левую полуплоскости to, которые мы обо*
значим через D\ и /?г.
Возьмем два экземпляра области D и расположим их друг
над другом, как указано на рис. 55, а. На рис. 55 указано также
соответствие берегов разрезов в области D и участков мнимой
оси плоскости w — соответствующие участки отмечены одина^
ковыми рисунками.
Склеим верхний берег разреза на первом экземпляре области
D с нижним берегом разреза на втором экземпляре и в соот-
соответствии с этим склеим Pi и Di вдоль верхней полуоси (все эти
участки отмечены рисунком -|-|-|-)- Затем склеим между собой
ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ
171
оставшиеся свободными берега разрезов на D, отмеченные ри-
рисунком -||-|[- (в трехмерном пространстве при второй склейке
нельзя избежать самопересечений, но мы условимся не отожде-
отождествлять точки луча, по которому происходит самопересечение
поверхности, отмеченные разными рисунками).
Полученная двулистная поверхность (она изображена на
рис. 55, в) называется римановой поверхностью аналитической
функцииУ~г. Этот корень можно рассматривать на ней как функ-
функцию в обычном смысле слова, ибо два значения, которые сопо-
сопоставляет корень каждой точке г0ф0, фоо, мы будем относить
Рис. 55.
двум различным точкам поверхности, лежащим над z0. Точки
отрицательной полуоси R_=(—оо, 0) не составляют исключе-
исключения, ибо над каждой из них также лежит по две точки поверх-
поверхности (мы ведь условились не отождествлять точки различных
листов, принадлежащие линии самопересечения поверхности).
Лишь точкам 2=0 и г = оо корень сопоставляет по одному зна-
значению, поэтому мы будем считать, что над z = 0 и 2= ос лежит
по одной точке поверхности. В этих точках листы нашей поверх-
поверхности соединяются между собой; они называются критическими
точками или точками ветвления поверхности.
Вполне аналогично устроена риманова поверхность-анали-
поверхность-аналитической функции
w = Vz. B)
Она n-листна; над каждой точкой гфО, Фоо лежит по п различ-
различных точек поверхности (они называются обыкновенными ее точ-
точками), над z=0 и z = oo — по одной (критической) точке. На
172
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ III
рис. 56, а, б изображены соответственно части поверхности, ле-
лежащие над окрестностью правильной и особой точки функции
у z. Точки отрицательной полуоси не составляют исключения;
часть поверхности, лежащая над окрестностью такой точки, изо-
изображена на рис. 56, в. Так как самопересечение поверхности мы
не принимаем в расчет, то топологически этот рисунок не отли-
отличается от рис. 56, а — рас-
рассматриваемая часть со-
состоит из трех не связан-
связанных друг с другом кругов.
Риманова поверхность
логарифма
w = Lnz C)
бесконечнолистна. Ее уст-
устройство показано на рис.
57. Мы опять берем об-
область D — плоскость С с
разрезом вдоль отрица-
отрицательной полуоси — ив ней
главную ветвь логарифма
W — /о (Z) ~ 'П I Z I + ' ЙГё Z
Рис. 57. (-Jt<argZ<n).
Эта функция однолистно и конформно отображает D на полосу
Do = {— я < Im w < я};
соответствие берегов разреза и границ полосы указано на рис. 57.
Логарифм имеет в области D бесконечно много ветвей
: = 0, ±1, ...),
§ 9] ПОНЯТИЕ РИМАНОВОП ПОВЕРХНОСТИ 173
отображающих D на полосы Dk, сдвинутые по отношению к Do
на целое кратное 2ni. В соответствии с этим мы берем счетное
множество экземпляров области D и склеиваем верхний берег
разреза на 0-м экземпляре с нижним берегом разреза на 1-м
экземпляре, а нижний берег нулевого разреза — с верхним бере-
берегом разреза на —1-м экземпляре (рис. 57). К оставшимся сво-
свободным берегам мы затем приклеиваем соответственно нижний
берег разреза на 2-м и верхний берег разреза на —2-м экземп-
экземпляре и т. д.
Над окрестностью каждой точки гфО, =^=оо лежит часть по-
поверхности, состоящая из счетного множества отдельных кругов;
каждому кругу мы отнесем ветвь логарифма с соответствующим
номером, действующую в этой окрестности (точки отрицатель-
отрицательной полуоси не составляют исключения). Поэтому логарифм
можно рассматривать на построенной римановой поверхности
как функцию в обычном смысле слова. В точках z = 0 и z=oo
логарифм не определен, поэтсму мы будем считать, что его ри-
манова поверхность не имеет точек над z = 0 и z = oo.
В качестве более сложного примера рассмотрим риманову
поверхность арксинуса
w = Arcsinz. D)
В п. 13 мы видели, что функция z = sin w однолистно и кон-
конформно отображает полуполосу I — — <Reay<-^-, lmw>Q>
на верхнюю полуплоскость г; ясно, что вся полоса-»—— <
< Re w <-g- J- при этом отображается на плоскость z с разре-
разрезами вдоль лучей (—оо, —1] и [1, ос).
Мы обозначим последнюю область через G и через w = go(z) ¦
обозначим ту ветвь арксинуса, которая отображает G на по-
полосу Go = -j—2"<Retu)<-2"> (эту ветвь можно характеризо-
характеризовать также условием go(O)=O). Так как арксинус имеет счетное
множество ветвей, то для построения римановой поверхности
мы должны взять счетное множество экземпляров области G.
К &-му экземпляру (& = 0, ±1, ...) мы отнесем значения k-k
ветви арксинуса w = gii(z), которая отображает G на полосу
Gfe=-|—2~ + k^<Rew <4r + kn> (ее можно характеризовать
также условием gh@) =kn).
Остается склеить между собой отдельные экземпляры обла-
области в соответствии с тем, как склеены их образы G&. Как это
сделать, видно из рис. 58
174
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. III
В результате получится бесконечнолистная риманова поверх-
поверхность, которая имеет над точками г=±1 счетное множество то-
точек ветвления. В точке z = oo она имеет две логарифмические
точки ветвления (одну образуют четные экземпляры области
6/т
k
0'i
I
I
if,
f-
Рис. 58.
G, другую — нечетные). К этому же выводу можно прийти, ис-
исследуя выражение арксинуса через логарифм
Лгсэт z = — I Ln (|Л — z2 + iz).
32. Общий подход. Здесь мы введем общее понятие римано-
вой поверхности как некоторого абстрактного топологического
пространства. Хотя понятием топологического пространства мы
уже не раз пользовались, остановимся на нем подробнее.
Определение 1. Множество X называется топологическим
пространством, если в нем указана система подмножеств, назы-
называемых открытыми множествами, причем:
1) объединение любого числа и пересечение конечного числа
открытых множеств снова являются открытыми множествами;
2) пустое множество и все пространство X являются откры-
открытыми множествами.
Открытое множество, содержащее точку х^Х, называется
окрестностью этой точки.
Когда на множестве X указывается система открытых мно-
множеств (или окрестностей точек), удовлетворяющая требованиям
§ 9] ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ 175
1) и 2), то говорят, что на X вводится структура топологического
пространства. В частности, структуру топологического простран-
пространства всегда можно ввести в метрическом пространстве. Для
этого достаточно объявить окрестностями точки хое1 шары с
центром х0 и произвольным радиусом R в метрике рассматри-
ваемрго пространства, т. е. множества {х^Х: р(х0, x)<R}. От-
Открытыми множествами считаются те, которые вместе с каждой
точкой содержат- и какую-либо окрестность этой точки.
Определение 2. Топологическое пространство X назы-
называется хаусдорфовым пространством, если его окрестности удов-
удовлетворяют следующей аксиоме отделимости: у любых
двух различных точек из X существуют непересекающиеся
окрестности.
Пример нехаусдорфова пространства. Точками X служат точки дей-
действительной оси R; топология вводится так: открытыми множествами объяв-
объявляются ось R, пустое множество и все множества, получаемые из R исклю-
исключением конечного чиСла точек. Читатель легко проверит, что аксиомы то-
топологического пространства (требования в определении 1) выполняются, а
аксиома отделимости — нет.
Перейдем к описанию общего понятия римановой поверхно-
поверхности. Рассмотрим множество 9?, точками которого служат пары
А = {а, fa {г)}, A)
где точка яеСи функция
"n(z — a)n, если аеС,
B)
% , если а = оо,
голоморфна в некотором круге Ua с центром в а; для опреде-
определенности будем считать Ua кругом сходимости соответствующего
ряда B). Введем в 9? топологию следующим образом: под
г-окрестностью U(A) точки ЛеЭ? будем понимать совокупность
точек B = {b, fb(z)} таких, что: 1) b принадлежит е-окрестности
точки а (т. е. {\г — а|<е}, если аеС, и U г |>— J-, если а = оо),
2) элемент (Ub, /ь) является непосредственным аналитическим
продолжением элемента (Ua, fa).
Можно представлять себе точку А как точку римановой по-
поверхности в описанном в п. 31 элементарном смысле, лежащую
над точкой аеС. Дополнительное указание функции /a(z) рав-
равносильно указанию листа, которому эта точка принадлежит.
Окрестность U(А) состоит из точек В того же листа,
176 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
которые проектируются в окрестность точки а (рис. 59); точки
других листов, проектирующиеся в ту же окрестность (как В'
на рис. 59), не считаются принадлежащими U(A).
Нетрудно видеть, что описанная топология вводит на 9t
структуру хаусдорфова пространства. В самом деле, если в этом
пространстве считать открытыми множествами те, которые со-
содержат вместе с каждой точкой и какую-либо окрестность этой
точки, то требования из определения 1
будут выполняться. Проверим выполне-
выполнение аксиомы отделимости: если АфВ,
то либо афЬ, либо а = Ь, но fa4=fb- Для
построения непересекающихся окрестно-
окрестностей О(А) и 0{В) в первом случае до-
достаточно выбрать непересекающиеся ок-
окрестности точекаи&на С, а во втором —
выбрать е столь малым, чтобы е-окрест-
Рис. 59. ность точки а принадлежала кругам схо-
сходимости обоих рядов fa я fb, и в U(A)
включить все точки [с, fc), где (Uc, fc) является непосредствен-
непосредственным продолжением (Ua, fa), а в О(В) —все точки (с, fc), где
(Uc, fc) •—непосредственное продолжение (?/&, /&) (окрестности
Ь{А) и U(В) не пересекаются, ибо иначе элемент (Ub, /ь) сов-
совпадал бы С {Uа, fa))-
Определение 3. Хаусдорфово пространство 91, точками
которого служат пары А={а, fa{z)}, где аеС и fa — голоморф-
голоморфная в точке а функция, а топология введена описанным спосо-
способом, называется римановым многообразием.
Можно определить проекцию риманова многообразия 9? в
С как отображение
»: {a, fa(z)}->a. C)
Глобально это отображение не является взаимно однознач-
однозначным, ибо на 9? существует бесконечно много точек с одной и
той же проекцией. Но локально оно взаимно однозначно. В са-
самом деле, если точка b принадлежит кругу сходимости ряда fa,
то непосредственное аналитическое продолжение (Ub, /ь) эле-
элемента (Ua, fa) вполне определено и, следовательно, в достаточно
малой окрестности U(А) существует лишь одна точка с проек-
проекцией Ь. Очевидно также, что и C), и обратное к нему отображе-
отображение непрерывны, поэтому проекция является локальным гомео-
гомеоморфизмом.
Проекция^ преобразует окрестность U(А) в некоторый круг
плоскости С; совершая дополнительное дробно-линейное ото-
ПОНЯТИЕ РИМАНОВОИ ПОВЕРХНОСТИ 177
бражение этого круга на единичный круг {|?|<1}, можно счи-
считать, что в U(А) определен гомеоморфизм
Ти: ?/(Л)->{Ш<1}- D)
Каждая точка B^U(A) однозначно характеризуется своей
проекцией b и, следовательно, точкой ?,= Ти{В) единичного
круга. Поэтому ? можно рассматривать как локальный пара-
параметр, действующий в окрестности U(A).
Если две" окрестности U, Vczdi пересекаются, то возникает
отображение друг на друга частей параметрических кругов, со-
соответствующих этому пересечению:
a = q>uv@=Tv°T-ul(Q; E)
оно называется соотношением соседства
(рис. 60). Так как соотношение сосед-
соседства является композицией дробно-линей-
дробно-линейных отображений, то оно также дробно-
линейно, т. е. конформно.
Определение 4. Хаусдорфово про-
пространство, которое можно покрыть си-
системой окрестностей, гомеоморфных кру-
кругам, так, что все порождаемые этими гомеоморфизмами соотно-
соотношения соседства оказываются конформными отображениями,
называется комплексно аналитическим многообразием (комп-
(комплексной размерности 1).
Таким образом, доказана
Теорема 1. Риманово многообразие 91 является комплекс-
комплексно аналитическим многообразием комплексной размерности 1.
Комплексно аналитические многообразия высших размерно-
размерностей мы рассмотрим во второй части книги.
Риманово многообразие 9t, очевидно, несвязно. Однако
любое подмножество !ft0 его точек {a, fa(z)}> где fa являются
ветвями одной аналитической функции, связно. В самом деле,
если точки А = {а, fa(z)} и B={b, fb{z)} принадлежат 9t0, то
элементы (Ua, fa) и (Ub, fb) получаются друг из друга про-
продолжением вдоль некоторого пути у: z = z(t), t e [a, р]. Но тогда
и точки At = {at, fat(z)}^di для любого t e [а, р]. Тем самым
определено непрерывное отображение [а, р]—>SR, т. е. путь
t->At, принадлежащий 9lQ и связывающий точки А и В. Таким
образом, Шо даже линейно связно (см. п. 4). Кроме того,
9^о вместе с каждой точкой А содержит и некоторую окрест-
окрестность U(А), т. е. является открытым множеством. Поэтому 5ft0
является областью пространства 9i.
12 Б. В. Шабат
178 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
Мы доказали, что каждой аналитической функции соответ-
соответствует некоторая область риманова многообразия 9?. Очевидно,
что и, обратно, каждой области на Ш соответствует некоторая
аналитическая функция1). Таким образом, доказана
Теорема 2, Между аналитическими функциями и обла-
областями риманова многообразия SR имеется взаимно однозначное
соответствие.
Определение 5. Область 9?0 риманова многообразия С?,
которая характеризуется условием, что голоморфные функции
fa, принадлежащие ее точкам А = {а, fa(z)}, являются ветвями
некоторой аналитической функции, называется римановой по-
поверхностью этой функции.
Мы пришли к общему понятию римановой поверхности.
Смысл этого понятия состоит в том, что каждую аналитическую
функцию мы можем рассматривать на ее римановой поверхно-
поверхности как функцию в обычном смысле слова (т. е. однозначную
функцию). В самом деле, по построению риманова поверхность
имеет столько точек А с данной проекцией а, сколько различных
элементов (Ua, fa) с данным центром а имеет аналитическая
функция, т. е. сколько значений относит аналитическая функция
этой точке а.
Таким образом, аналитическая функция <&~ является функ-
функцией точки на ее римановой поверхности:
&¦'. А = {а, fa{z)}-+fa(a) F)
(а не функцией точки а на плоскости).
На комплексно аналитическом многообразии, каким является
риманова поверхность, можно ввести понятие голоморфной
функции, и тогда окажется, что аналитическая функция голо-
голоморфна на своей римановой поверхности (см. § 9 ч. II).
Римановы поверхности в элементарном смысле, рассмотрен-
рассмотренные в предыдущем пункте, можно рассматривать как модели
общих римановых поверхностей. Заметим, что в теории функций
рассматривают и другие модели. Можно, например, отправ-
отправляться не от многозначных, а от однозначных функций и строить
римановы поверхности так, чтобы эти функции были на них
взаимно бднозначными, — тогда (многозначные) обратные функ-
функции будут (рднозначно) отображать плоские области на по-
построенные поверхности.
Построим, например, поверхность, на которой взаимно одно-
однозначна показательная функция w — ez. Мы знаем, что она перево-
переводит в одну точку такие и только такие точки, разность между
') При этом доказательстве мы пользуемся тем, что на 9? всякая об-
область является линейно связным множеством (докажите это).
§ 9) ПОНЯТИЕ РИМАНОВОИ ПОВЕРХНОСТИ 179
которыми является целым кратным 2ш (п. 12). Поэтому для на-
нашей цели естественно отождествить точки a+2kni, где & = 0,
±1, ... — произвольное целое число.
Иными словами, пусть G — совокупность сдвигов плоскости
С на векторы, целые кратные 2ni:
S: z-*z + 2km (k = О, ± 1, ...). ' G)
Очевидно, что G образует группу (относительно композиции, Tve.
последовательного выполнения преобразований), которая яв-
является подгруппой группы Л всех дробно-линейных преобразо-
преобразований (см. п. 8)., Обозначим через [а]а класс эквивалентности
( У а^р,
V У@ W
Рис. 61.
точки аеС по группе G, т. е. совокупность всех точек S(a), где
SeG (иначе говоря, совокупность всех точек a+2kni, k = 0,
±1, ...). Совокупность таких классов эквивалентности мы обо-
обозначим через C/G; элементы последнего множества можно рас-
рассматривать как отождествленные точки a + 2kni (k = 0, ±1, ...).
Введем теперь на множестве C/G топологию. Для этого под
окрестностью точки [а]0 мы условимся понимать совокупность
точек [z]g, где геС — произвольная точка из окрестности (в то-
топологии С) какого-либо представителя а класса эквивалентно-
эквивалентности [а]а. Таким образом, C/G превращается в топологическое
пространство.
Это пространство можно представить наглядно следующим
образом. Будем выбирать представителей классов эквивалентно-
эквивалентности [z]c, так, чтобы они лежали в полосе {О -*С 1тг<2л}. Доста-
Достаточно малая окрестность точки z0, для которой 0<1пгг0<2л, изо-
изобразится тогда кругом с центром в z0, а окрестность точки zu
для которой Imzi = 0, — совокупностью двух полукругов
(рис. 61). Если мы склеим из нашей полосы цилиндр так, как
это показано на рис. 61, то окрестности всех точек будут есте-
естественными окрестностями на цилиндре.
Таким образом, рассматриваемое пространство C/G с вве-
введенной в нем топологией является цилиндром в трехмерном про-
пространстве. Этот цилиндр можно рассматривать как риманову
поверхность показательной функции (логарифм взаимно одно-
однозначно отображает на нее плоскость С с выколотым началом
координат).
12*
]80 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
Рассмотрим еще один пример. В п. 41 мы введем мероморф-
ную функцию — эллиптический синус w = snz, — которая имеет
два периода: действительный coi и чисто мнимый i'm2; в прямо-
прямоугольнике {0<С Re 2<а>ь 0<^ Im z<a>2} она однолистна. Следо-
Следовательно, для построения ее римановой поверхности достаточно
отождествить точки a + &ia>i + &2J'a>2, где k\ и k2—целые числа.
Иными словами, надо рассмотреть группу Т движений z->-z +
+ ki(x>i + ik2(A2 и рассмотреть пространство С/Т, точками которого
служат классы эквивалентности [а]т точек аеС по группе Т.
Топология в этом пространстве вводится, как в предыдущем при-
примере: под окрестностью точки [а]т понимается совокупность
©
. f777fa
Рис. 62.
классов эквивалентности [z]T, где геС —произвольная точка из
окрестности (в топологии С) какого-либо представителя класса
[а\т. Введение этой топологии превращает С/Г в обычный тор
(рис. 62), который и можно рассматривать как риманову по-
поверхность эллиптического синуса.
В заключение этой главы мы хотим описать другую трак-
трактовку риманова многообразия 9t. Чтобы прийти к этой трак-
трактовке, заметим прежде всего, что в определении точек 31 как пар
{a, fa(z)}, где fo — функция, голоморфная в некоторой окрестно-
окрестности точки asC, выбор такой окрестности несуществен. По-
Поэтому можно считать, что точками Ш служат ростки fa анали-
аналитических функций. Совокупность всех ростков в данной точке а
образует кольцо, которое принято обозначать символом &а.
Множество SH, таким образом, можно рассматривать как поэле-
поэлементное (дизъюнктное) объединение колец 6а по всем аеС:
з?= (J еа.
Далее, на множестве 9? введена топология при помощи
окрестностей, которые можно описать в терминах ростков сле-
следующим образом: окрестность V ростка fa состоит из всех рост^
ков fb, для которых b принадлежит некоторой окрестности Ua,
и существует голоморфная в Ua функция / такая, что элемент
ЗАДАЧИ 181
(Ua, f) является представителем обоих ростков fa и f&. Как мы
видели, эта топология превращает 3? в хаусдорфово простран-
пространство. В этой топологии отображение
р: 91->С,
которое каждому ростку fa ставит в соответствие точку а, яв-
является локальным гомеоморфизмом.
Пространство 9t вместе с отображением р называют пуч-
пучком ростков аналитических функций. Это понятие отражает ло-
локальный подход к понятию аналитической функции. Однако оно
допускает и глобальный подход. В самом деле, рассмотрим про-
произвольную область DcnC и голоморфную в ней функцию /. Эта
функция определяет отображение /: D-*-ffi, которое каждой
точке z^D ставит в соответствие росток fz, порождаемый этой
функцией в точке г. Отображение /, очевидно, непрерывно в то-
топологии 5R, а композиция р °/ является тождественным в обла-
области D отображением.
Такое отображение f называется сечением пучка Ш над об-
областью D. Множество всех сечений SK над областью D образует
кольцо, причем алгебраические операции в нем согласуются с
операциями над ростками в любой точке гей.
Мы ограничиваемся здесь этим описанием. Общее опреде-
определение понятия пучка будет приведено во второй части книги
(см. п. 34).
ЗАДАЧИ
00
1. Докажите, что функция }(z)~ У, пп непрерывна в замкнутом еди-
ничном круге, но непродолжаема аналитически за его пределы.
оо
2. Рассмотрим ряд Л,- ^—, где {ссп}—множество всех рациональ-
n-l z~e' П
оо
ных точек отрезка [0, 2я), а ап — комплексные числа, для которых У, \ ап \ <об.
п = 1
Докажите, что при |z[<l и при |z|>l он .сходится соответственно к го-
голоморфным функциям fi и /г, которые не являются аналитическим продолже-
продолжением друг друга.
3. Докажите: если f голоморфна в единичном круге (/ив каждой точке
окружности 3U, то она голоморфно продолжается в некоторый круг {|г|<р},
где р>1.
4. Постройте пример функции f, голоморфной в круге ?У={|г|<1}, непре-
непрерывной в U и такой, что она голоморфно продолжается до функции, имею-
имеющей существенную особенность в какой-либо точке окружности {|г|=1}. (От-
(От= (z~l)ez~i.)
182 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
5. Пусть D — область с гладкой жордановой границей у; укажите усло-
условия голоморфной продолжаемости в D функции /, заданной на Y- [Указание:
ср. с задачей 3 к гл. II.]
6. Пусть D — произвольная область, у a D— спрямляемая кривая, а / —
¦функция, непрерывная в D и голоморфная в D \ у. Докажите, что f голо-
голоморфна в D.
7. Для произвольного множества ?с:С положительной плоской меры по-
постройте функцию / # const, непрерывную в С и голоморфную в С \ Е. [Ука-
[Указание: ср. с задачей 4 к гл. II.]
8. Покажите, что sin2 является (однозначной) функцией от ?=г(я — г).
9. Докажите, что функция гаA—г)^, где а и р — действительные числа,
допускает выделение голоморфных ветвей в С\ [0, 1], если а+E — целое
число.
1
10. Найдите вычеты ветвей функции е + z в точке 2=1.
11. Является ли функция g(z) =[Ln(z — i)Vf(z), где [ — функция из за-
задачи 1, аналитической в единичном круге?
12. Пусть функция f голоморфна в некоторой области D; обязана ли
V f B) иметь точку ветвления в любом нуле f? (Ответ: нет.)
13. Пусть функция / голоморфна и отлична от нуля в односвязной обла-
области D. Докажите, что для любого целого п>0 найдется голоморфная в D
функция g такая, что gn=f всюду в D; приведите пример, из которого видно,
чго утверждение неверно для многосвязных областей.
14. Опишите особые точки и риманову поверхность функции ffi)=Arctgs,
обратной к w = tgz. [Указание: найдите ее выражение через логарифм.]
15. Постройте конформное отображение тора
х = (R + г cos -ф) cos ф, у = (R + г cos г|)) sin ср, г = г sin "ф
на прямоугольник с отождествленными противоположными сторонами ').
[Указание: дифференциал дуги на торе ds = V(R + r cos i|)J dtp2 + r*d§2;
положив ? = ср, т)= -pr-r , получим ds = (R+r cos i|j) Vd%2 + dr\2. По-
J ri ~r T COS f
0
этому (<р, i|>) -> (\, т)) дает нужное отображение.]
') В следующей главе мы увидим, что такой прямоугольник можно кон-
конформно отобразить на двулистную поверхность над плоскостью (см. зада-
задачу 18 к гл. IV), и тем самым убедимся в том, что тор конформно эквива-
эквивалентен римановой поверхности в элементарном смысле. .
ГЛАВА IV
ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ
Эта глава вводит читателя в геометрическую теорию функций
комплексного переменного. В ней будут рассмотрены основные
вопросы теории конформных отображений, а также так назы-
называемые геометрические принципы, которые касаются лишь са-
самых общих, топологических свойств голоморфных функций.
§ 10. Геометрические принципы
33. Принцип аргумента. Пусть функция / голоморфна в про-
проколотой окрестности {0<|г — #|<г} точки аеС. Мы назовем
логарифмическим вычетом функции / в точке а вычет логариф-
логарифмической производной
~fW = IF Ln ?№ М
этой функции в точке а.
Кроме изолированных особых точек (однозначного харак-
характера) функция / может иметь отличный от нуля логарифмиче-
логарифмический вычет в своих нулях. Пусть аеС — нуль порядка п функ-
функции /, голоморфной в точке а; тогда в некоторой окрестности Ua
имеем f(z) = (z — a)nq>(z)t где ф голоморфна в [/, и не равна
там нулю. Поэтому в Ua
f (г) = п (г - а)" ф (г) + (г - а)п ф' (г) _ 1 гсф (г) + (г - а) ф' (г)
f(z) B-а)"ф(г) г-а ' ср (г)
где второй множитель голоморфен в Ua и, следовательно, раз-
разлагается в Ua в ряд Тейлора, причем свободный член этого раз-
разложения равен п (значению множителя при z—a). Таким обра-
образом, в Ua имеем
fgf = T^r{« + c1(z-a) + C2B-aJ+ ...} =
¦а)+ .... B)
откуда видно, что в нуле порядка п логарифмическая произвол*
ная голоморфной функции имеет полюс первого порядка с выче-
вычетом п; логарифмический вычет в нуле равен порядку этого нуля.
184 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
Если а — полюс функции f порядка р, то у имеет в этой
точке нуль порядка р, а так как
f (г) dz ш f (г) •
то с учетом B) получим, что в полюсе порядка р логарифмиче-
логарифмическая производная функции имеет полюс первого порядка с вы-
вычетом —р: логарифмический вычет в полюсе равен порядку
этого полюса с обратным знаком.
Сделанные замечания позволяют дать метод подсчета числа
нулей и полюсов мероморфных функций. При подсчете мы при-
примем следующее соглашение, которого будем всегда придер-
придерживаться и в дальнейшем: каждый нуль и полюс считается
столько раз, каков его порядок. Справедлива
Теорема 1. Пусть функция f мероморфна1) в области
DczC и G^D — область, граница которой dG является непре-
непрерывной кривой; пусть еще dG не содержит ни нулей, ни полю-
полюсов f. В этих условиях пусть N и Р соответственно обозначают
общее число нулей и полюсов f в области G, тогда
да
где dG — ориентированная граница.
< Так как G €= D, то / имеет в G лишь конечное число нулей
«1, ..., ai и конечное число полюсов Ь\, ..., bm, а так как dG
V
не содержит ни нулей, ни полюсов, то g = у голоморфна в
окрестности dG. Применяя к этой функции теорему Коши о вы-
вычетах, найдем
г 1 т
ш) fdz=Sres ^+Sres -§¦• D)
ас v=i av v=i 6v
Но по сделанному выше замечанию
res g = nv, res g = - pv, E)
где nv и pv — соответственно порядок нуля av и полюса bv; под-
подставляя E) в D) и учитывая принятое соглашение подсчета
нулей и полюсов (по которому N = Zj.uv и P = 2pv)> полу-
получим (З)^
') Напомним, что функция / называется мероморфной в области D, если
она голоморфна всюду в Q, за исключением, быть может, некоторого множе-
множества полюсов.
$ 10] ГЕОМЕТРИЧЕСКИЕ ПРИНЦИПЫ 185
Доказанной теореме можно придать геометрическую форму-
формулировку. Представим dG путем z=z(t), a -^ t <? p\ и обозначим
через Ф@ первообразную функции у вдоль этого пути; по
формуле Ньютона — Лейбница будем иметь
дО
Но, очевидно, Ф(t) =\n f [z(t)], где In обозначает любую ветвь
логарифма, непрерывно меняющуюся вдоль пути dG. Так как
Ln/=ln (/[-И Arg/ и функция ln|/(z)| однозначна, то для вы-
выделения этой ветви достаточно выделить ветвь arg/, непрерывно
меняющуюся вдоль dG. Приращение 1п|/| вдоль замкнутого,
пути dG равно нулю, поэтому
Ф (Р) - Ф («) = i{arg / [г (р)] - arg / [z (а)]}.
Обозначая множитель при i в правой части — приращение
выделенной ветви аргумента — через Дао arg/, мы перепишем,
F) в виде
— dz = i/S.gQ arg/.
dG
Таким образом, теореме 1 можно придать следующий вид:
Теорема 2 (принцип аргумента). В условиях тео-
теоремы 1 разность MeMdy числом нулей N и числом полюсов Р
функции f в области G равна deлeннoмy на 2я приращению
аргумента этой функции при o6xode ориентированной границы
области:
iV-P= 2^Aa0 arg/B). G),
Очевидно, правая часть G) геометрически представляет со-
собой полное число оборотов вокруг точки да = 0, которые сделает
вектор w=f(z), когда z обходит путь dG. Обозначим через dG*
образ пути dG при отображении /, т. е. путь w = f[z(t)\
a-*Ct-*C$; тогда это число будет равно числу оборотов вектора до
при обходе пути dG* (рис. 63). Последнее называют индексом.
пути dG* относительно точки ш = 0 и обозначают символом
ind0 dG*. Теперь принцип аргумента можно прочитать так:
N-P = ~^ga* arg w = indodG\ (8)
Замечание 1. Вместо нулей функции / можно рассмат-
рассматривать ее а-точки, т. е. корни уравнения f(z)=a; для этого
186
основы геометрической теории
[ГЛ. IV
достаточно заменить в наших рассуждениях / функцией f(z)—а.
Если dG не содержит а-точек (и по-прежнему полюсов) функ-
дии /, то
4 \^h ± (9)
дЬ
±
где Na — общее число а-точек / в области G. Переходя к плоскости
(w)
Рис. 63.
w=f(z) и вводя понятие индекса пути dG* относительно точки
а, можно переписать (9) в виде
— P = -z- Дао* arg (w — a) = inda dG*.
(Ю)
Замечание 2. Правая часть формулы G) — приращение аргумента
функции вдоль пути — имеет смысл для произвольных непрерывных функций f,
не равных нулю вдоль этого пути (хотя ее первоначальное определение с ин-
интегралом и связано с производной f, т. е. требует голоморфности функции).
Эта величина, равная индексу образа пути dG*, имеет топологический
характер: она инвариантна относительно топологических преобразований пло-
плоскостей гит. Оказывается, можно ввести и инвариантные относительно то-
топологических преобразований определения порядков нулей и полюсов (не
связанные с производными или разложениями в ряды). Тогда и принцип ар-
аргумента примет топологический характер: он будет справедлив для всех функ-
функций, топологически эквивалентных мероморфным (т. е. получающихся из по-
последних топологическими преобразованиями переменных). Читатели, интере-
интересующиеся этими вопросами, могут найти их подробное изложение в книге
С. СтОилова «Лекции по топологической теории аналитических функций», М.,
1964.
Приведем пример применения принципа аргумента:
Теорема 3 (Руше). Пусть функции fug голоморфны в
замкнутой области G с непрерывной границей dG, и пусть
\f(z)\>\g(z)\ для всех ze=dG. A1)
Тогда функции f и f+g имеют в G одинаковое число нулей.
¦4 Из A1) видно, что / и f+'g не равны нулю на dG1), по-
поэтому, к ним применим принцип аргумента. Так как /?=0 на dG,
') В самом деле, lfl>lgl>0 и |/+g|>lf| — |g|>0 на dG.
§ ТО] ГЕОМЕТРИЧЕСКИЕ ПРИНЦИПЫ 187
то f + g = f\ I + -f-j, следовательно, мы имеем при надлежащем
выборе значений аргументов
Аао arg(/ + §) = Аао arg/ + AaG arg(l + ¦?). A2)
Но так как у < 1 на 0G, то при любом изменении z^dG точ-
точка со = — не выходит из круга {| со | < 1}. Поэтому вектор w = 1 + со
не может повернуться вокруг точки да = 0, и второе слагаемое
в A2) равно нулю. Таким образом.,
откуда по принципу аргумента получаем заключение теоремы >
Теорема Руше полезна при подсчете числа нулей голоморф-
голоморфных функций. В частности, из нее совсем просто получается
основное свойство многочленов:
Т е о р е ма 4. Любой многочлен Р„ степени п имеет в С
ровно я корней.
< Так как Рп имеет полюс в бесконечности, то все его корни
лежат в некотором круге {\z\<R}. Пусть Pn = /-Fg, где f — auzn
(а0ф0) и g=ctizn-l+ .. . +ап; увеличивая в случае надобности
R, можно считать, что на окружности {\z\=R} имеем |/|>|g|,
ибо \f\ = \ao\Rn, a g — многочлен степени не выше я-—1. По
теореме Руше Рп имеет в круге {\z\<R} столько же нулей,
сколько f = aozn, т. е. ровно п >
34. Принцип сохранения области. Так называется следую-
следующая важная
Теорема 1. Если f голоморфна в области D и не равна
тождественно постоянной, то и образ D* = f(D) также является
областью.
< Нужно доказать, что множество D* связно и открыто.
Пусть W\ и w2 — две произвольные точки D*; обозначим через
г4 один из прообразов ш4 в D и соответственно через г2 один из
прообразов w%. Так как множество D (линейно)связно, то суще-
существует путь у: z=z(t), /е[а, р], связывающий в D точки Zi и zz.
В силу непрерывности функции / образ y*: а) = Я2@]> ^[сс, Р],
будет путем, связывающим точки Wi и Шг; он, очевидно, состоит
из точек D*. Таким образом, множество D* связно.
Пусть Wo — произвольная точка D* и zQ — один из ее про-
прообразов в D. Так как D открыто, т,о существует круг
{\г — zQ\< г) mD. Уменьшая в случае надобности г, можно счи-
считать, что {\z — zo|^r} не содержит других two-точек, кроме za
(так как /=?const, то по теореме единственности п. 21 ее ау0-точки
188 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
изолированы в D). Обозначим через y = {\z— го|=л} границу
этого круга; пусть еще
ц = min I f (z) - да01. A)
2 S у
Очевидно, (д,>0, ибо непрерывная функция /(z) —w0 достигает
на y своего минимального по модулю значения, и если бы было
ц = 0, то на у существовала бы и/о-точка функции /, вопреки на-
нашему построению круга.
Теперь мы докажем, что {\w — wo\<[i}ciD*. В самом деле,
пусть Wi — произвольная точка этого круга, т. е. |ш( — шо|<М-
Имеем
f(z) — Wi = f(z) — wo+](wo — wt), B)
причем на у в силу A) \f(z)—шо!^М- Так как у нас
Wq— Wi\ <ц, то по теореме Руше функция f(z) — W\ имеет вну-
внутри у столько же нулей, сколько их имеет там функция f(z)—да0,
т. е. по крайней мере один нуль (точка z0 может быть кратным
нулем функции f(z) —w0). Итак, функция f внутри у принимает
значение wu т. е. ©isD*. Но Wi — произвольная точка круга
{\w — wo\<[i}, следовательно, весь этот круг принадлежит D*,
Открытость D* доказана >
Замечание. Как мы видели, доказательство связности множества D*
требует лишь непрерывности функции f, при доказательстве открытости ис-
использованы теорема единственности и теорема Руше, которые установлены
выше для голоморфных функций. Для произвольных непрерывных функций
утверждение об открытости- образа неверно, в чем убеждает следующий
пример. Пусть f = x2 + iy и ?> = {|г|<1}; тогда D* = f(D) не является открытым
множеством, ибо точки вертикального диаметра D (внутренние точки этого
круга) переходят в граничные точки D*.
Можно, однако, доказать, что принцип сохранения области (так же как
теорема единственности и теорема Руше, на которые он опирается) имеет
топологический характер, т. е. справедлив для всех функций, топологически
эквивалентных голоморфным.
Аналогичное, но несколько более внимательное рассмотрение
приводит к решению задачи о локальном обращении го-
голоморфных функций. Задача эта ставится так.
Дана голоморфная в точке z0 функция w = f(z); требуется
найти аналитическую в точке wo=f(zo) функцию z = g{w) та-
такую, что g{wo)=zo и fog(w)==w в некоторой окрестности w0.
При решении этой задачи следует различать два случая:
I. f'(zo)=fcO. Как при доказательстве принципа сохранения
области, выберем круг {\z — г01-=Сг}, не содержащий других
Шо-точек, кроме центра, и определим (д,>0 по формуле A). Пусть
wi — любая точка круга {\w — ayi|<|i); то же рассуждение (с
применением формулы B) и теоремы Руше) показывает, что
•функция / принимает в круге {\z — 20|<г} значение до4 столько
§ 10] ГЕОМЕТРИЧЕСКИЕ ПРИНЦИПЫ 189
же раз, сколько до0. Но значение ©о принимается в этом круге
лишь в точке z0 и притом, в силу условия f'(zo)?=O, однократно.
Таким образом, функция / принимает в круге {\z— zo|<r}
любое значение из круга {\w — ДОо|<м) и притом только один
раз. Иными словами, функция f локально однолистна в точке z0.
В круге {\w — Wo\<^} тем самым определена функция
z = g(w), для которой g(wo)=zo и f og(w)==w. Из однолистно-
однолистности / следует, что Ддо=?0 при Az=?0, откуда, очевидно, вытекает
существование в любой точке круга {\w — доо|<ц} производной
g>(w) = jj^-, C)
т. е. голоморфность g в этом круге1).
II. f'(z0) =. . . = f(p~1)(z0) = 0, /(p)(z0)^0 (р>2). Еще раз по-
повторим те же рассуждения, выбрав теперь круг {\z — zo|^/"}
так, чтобы в нем, кроме центра, не было ни до0-точек f, ни ну-
нулей производной f (мы снова пользуемся теоремой единствен-
единственности). Как и раньше, выберем (д,>0, возьмем любую точку ш4
из круга {|до — доо|<ц.} и убедимся в том, что / принимает в
круге {\z — zo|<r} значение до4 столько же раз, сколько до0. Из
условий рассматриваемого случая следует, что значение w0 при-
принимается р-кратно в точке z0; так как у нас еще ['(г)Ф0 при
0<|z — zoj<r, то любое значение до4, 0<|до1 — Доо|<ц., прини-
принимается функцией / в круге {\z — Zo\<Cr} в р различных точках.
Таким образом, функция f является р-листной в круге
{\z — zo\<r}.
Выясним аналитический характер решения задачи о локаль-
локальном обращении в этом случае. В некоторой окрестности точки
Zt) имеем
до = f (z) = до0 + (z — zo)p ф (z), D)
где ф голоморфна и отлична от нуля. Отсюда следует, что
р ±
Уф (z) (z — z0) = (до — до0)р > E)
р
где Уф обозначает какую-либо голоморфную в рассматривае-
рассматриваемой окрестности ветвь корня. Эта ветвь разлагается в ряд Тей-
Тейлора с центром za со свободным членом, отличным от нуля, еле-
s
довательно, для функции г|з(г)=Уф(г) (z — z0) имеем i|/(z0)=^0.
Полагая еще (до — ДооI/р = <и, перепишем E) в виде г|)(г)=са и,
') Как видно из C), для существования производной g' нужно еще, что-
чтобы было f фО. В силу непрерывности f и того, что !'{го)ф0, можно счи-
считать это условие выполненным в круге {|г — го|<л}, уменьшая г в случае на-
надобности.
190 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
пользуясь рассмотренным выше случаем I, найдем отсюда z
оо
как голоморфную функцию от о: z = 2 dnan. Заменяя в послед-
о
нем разложении со= (w — Wo)l/p, получим разложение функции,
обращающей /, в обобщенный степенной ряд:
2idn(w-w0)P . F)
«=о
Из него видно, что g является аналитической функцией в круге
{\w — ауо|<|4 и что ©о является для нее точкой ветвления по-
порядка р (см. п. 30).
Из приведенного анализа, в частности, вытекает
Теорема 2. Условие 1'(гй)Ф§ является необходимым и
достаточным условием локальной однолистности голоморфной
функции f в точке г0.
Замечание 1. Достаточность этого условия можно полу-
получить также из общей теоремы действительного анализа о суще-
существовании неявных функций (якобиан р "{. = | f (z) |2 отобра-
о \Х> У)
жения (х, у) —> (и, v) отличен от нуля в рассматриваемой точ-
точке). Однако для произвольных дифференцируемых в смысле
действительного анализа отображений условие Ли' °. ^0 не
а \х' У> z0
является необходимым для однолистности. Это видно из при-
примера отображения f = x3 + iy, якобиан которого равен нулю в
точке z=0 и которое тем не менее однолистно.
Замечание 2. Условие локальной однолистности f'(z) =?0
для всех z&D не является достаточным для глобальной одно-
однолистности функции во всей области D. Это видно, скажем, из
примера функции f(z)=ez, которая локально однолистна в ка-
каждой точке С, но неоднолистна в любой области, содержащей
хотя бы одну пару точек Zi и г2 таких, что z4 — 22 = 2йяг, где
&=?0 — целое число.
Мы изложили выше качественное решение задачи о локаль-
локальном обращении. В заключение заметим, что методы теории
аналитических функций позволяют дать и эффективное количе-
количественное решение этой задачи. Рассмотрим для простоты слу-
случай f{z0) Ф0.
Построим, как и выше, круги {\z — г01^ г} и {\w — Шо|<м)
и при любом фиксированном w из второго круга рассмотрим
функцию
h(c)= СПС) '
§ 10] ГЕОМЕТРИЧЕСКИЕ ПРИНЦИПЫ 191
Она голоморфна в первом круге всюду, за исключением точки
z = g(w), где g— обращение функции /, причем вычет h в этой
точке (полюсе первого порядка) равен г. Следовательно, по
теореме Коши о вычетах
2ni J
G)
где Y = (l? — zo\=r).
Интеграл в правой части зависит от w, и мы получили инте-
интегральное представление обращающей функции g(w). Из него,
действуя так же, как при получении тейлоровского разложения
из интеграла Коши, можно получить и разложение g в степен-
степенной ряд. Имеем
1 = 1 1 = у (w - wo)n
причем это разложение сходится равномерно по ?, на окружно-
окружности y (у нас |/(?) — wo\> \х, на у, a | до — wo\ <ц). Умножая это
разложение на „ . и интегрируя почленно вдоль y> найдем
оо
и=0 °
где
dn = -oZ7 \ ТГ7Г,——Т^ТГ (« = 0,1,...).
Имеем, очевидно, da=z0, а при «> 1 можно преобразовать
полученное выражение интегрированием по частям:
1 --i- Г
п 2nin J
Подинтегральная функция имеет внутри у полюс n-го по-
порядка в точке г0; находя ее вычет по известной формуле (п. 25),
находим окончательное выражение коэффициентов:
«о-о, d^lto^jZ^J. «-1, 2, ... (9)
Ряд (8) с коэффициентами (9) называется рядом Бурмана —
Лагранжа. Его можно использовать для эффективного обраще-
обращения голоморфных функций.
192 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
Пример. Пусть f(z)=ze'az; найдем обращение этой функции в точке
шо=0, соответствующей го = О. По формулам (9) получаем при /г^1
, 1 d"'1 I 2 \" (ап)п~1
"« = — lim - n-i-HTTTl = ', '
п! г -> о Д2 V / B) / п'
и ряд Бурмана — Лагранжа имеет вид
™ .,«-1
- wn. A0)
Можно указать также обобщение ряда Бурмана — Лагранжа
на случай {'(z0) =. . . = p-])(z0) =0, /(p)(zo)=?O, p > 2, но мы на
этом не останавливаемся.
35. Принцип максимума модуля и лемма Шварца. Принцип
максимума модуля выражается следующей теоремой:
Теорема 1. Если функция f голоморфна в области D и
ее модуль \f\ достигает (локального) максимума в некоторой
точке zo^D, то f постоянна.
•4 Воспользуемся принципом сохранения области. Если
f=?const, то она преобразует z0 в точку w0 области D*. Суще-
Существует круг {\w — wq\ <\x]czD*, а в нем найдется точка W\ та-
такая, что |ayi|>|ayo|. Значение W\ принимается функцией f в не-
некоторой окрестности точки z0, а это противоречит тому, что |/|
достигает максимума в этой точке >
Учитывая свойства функций, непрерывных на замкнутых
множествах, принцип максимума модуля можно сформулиро-
сформулировать еще и так:
Теорема 2. Если функция f голоморфна в области D и
непрерывна в D, то 1/1 достигает максимума на границе dD.
< Если f=const (в D, а значит, в силу непрерывности и вВ),
то утверждение тривиально. Если /=?const, то |/| не может до-
достигать максимума в точках D, а так как этот максимум должен
достигаться в Б, то он достигается на dD >
Аналогичное утверждение для минимума модуля, вообще
говоря, несправедливо. Это видно из примера функции f(z)=z
в круге {jz|<l} (минимум |/| достигается в точке z = 0). Од-
Однако справедлива такая
Теорема 3. Если функция f голоморфна в области D и
не обращается в нуль в этой области, что \f\ может достигать
(локального) минимума внутри D лишь в случае / = const.
Для доказательства достаточно применить теорему 1 к функ-
функции g = -f, которая голоморфна в D, ибо /=?0.
Полученные результаты показывают, что поверхность модуля
голоморфной функции, т. е. поверхность в пространстве (х, у, р)
с уравнением р= \f(z) \ (см. п. 5), имеет некоторые структурные
§ Ю]
ГЕОМЕТРИЧЕСКИЕ ПРИНЦИПЫ
193
особенности. Именно, она не может иметь локальных максиму-
максимумов и локальных минимумов, если последние не находятся на
уровне р = 0 (точки а и b на рис. 64). Касательная плоскость
к этой поверхности горизонтальна в тех и только тех точках,
где обращаются в нуль обе производные
Л I f I
что то же самое — обе производные
дх
и
d\f\
дг " дг
ные точки). Простой подсчет показывает, что1)
dz
——
или —
21/1
дг
ду
(стационар-
A)
fi'\f(Z)\
откуда видно, что стационарными точками функции / могут быть
либо ее нули (минимумы 1/1 на уровне р = 0, такие, как точка с
на рис. 64), либо нули ее про-
производной f (точки перевала
поверхности модуля, такие,
как точка d на рис. 64).
Принцип максимума моду-
модуля имеет важные применения
в теории функций. Например,
при помощи этого принципа
легко объяснить, почему теоре-
теорема Рунге (п. 22) несправед-
несправедлива для многосвязных обла-
областей. В самом деле, в неодно-
связной области D существует
замкнутая жорданова кривая
Y, внутри которой есть хотя
бы одна точка г0 ф D. Если не- Рис. 64.
которая функция приближает-
приближается полиномами равномерно на любом компакте К шй, то суще-
существует последовательность полиномов Рп, равномерно сходя-
сходящаяся к / на у- По критерию Коши для любого е>0 найдется
номер N такой, что для всех т, я !> N в любой точке z^y
\Pm(z)—Pn{z)\<e.
По принципу максимума модуля эти неравенства справедливы
и во всех точках области G, ограниченной кривой y, а отсюда
по тому же критерию последовательностью Рп сходится равно-
') Формулы A) получаются формальным дифференцированием по 2 и г
функции | /1 = VJf; законность этого следует из очевидных формул
d\f\ uux + vvx д | /
дх
I/I
UUy + Wy
13 Б. В. Шабат
194 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
мерно в G. По теореме Вейерштрасса (п. 22). lim Pn является
П-»оо
функцией, голоморфной в G. Но в точках Gf]D этот предел^ сов-
совпадает с /, следовательно, / голоморфно продолжается b.G и,
в частности, в точку z0. Так как не любая функция из Н(D)
обладает этим свойством (например, <- им не обладает),
Z Zq
то и не все функции из Н(D) можно равномерно приблизить
полиномами, вопреки тому, что утверждает теорема Рунге.
Простым следствием принципа максимума модуля является
также
Лемма Шварца. Пусть функция f голоморфна в круге
{||l} по модулю не превосходит там 1 (г. е. \f(z)\<^L\
для всех z^U) и f@)=0. То-
Тод д U
!;
гда для
причем
всех z^U
\№\<\г ,
если равенство
B)
дости-
р
гается хотя в одной точке гфО,
то оно справедливо всюду в U,
и в этом случае f(z)=eiaz,
Рис*65 где а — действительная посто-
постоянная.
•* Рассмотрим функцию ф(г) = ; в силу условия f@)=0
она голоморфна в U. Рассмотрим произвольный круг Ur=
= {|z|<r}, г<1| по теореме 2 функция |<р| достигает максимума
на его границе yr = {\z\=r). Но на уг имеем |ф|^—, ибо по ус-
условию |/|<1 1, поэтому всюду в Uг
!ф(г)Ку. C)
Фиксируем z и устремим г к 1; в пределе из неравенства C)
получим, что |ф(г)|<1, т. е. что |/(г)|^|г| для всех z^Ur.
Так как любую точку ге?/ можно погрузить в некоторый круг
Uг, г<1, то неравенство B) доказано.
Если в какой-либо точке Zo^U в B) имеет место знак ра-
равенства, то |ф| достигает в ней максимального значения, рав-
лого 1. Тогда ф является постоянной, модуль которой, очевидно,
равен 1,'т. е. <р(г)н=е*а и f(z)^eiaz. >
Из леммы Шварца следует, что при конформном отображе-
отображении / круга {|2|<1} в круг {|ш|<1}, переводящем центр в центр,
образ любой окружности {|z|=r} лежит внутри круга {|ш|<г}
(рис. 65). При этом образ {|г|=г} может иметь общие точки с
{\w\=r} лишь в том случае, когда / сводится к вращению вокруг
точки г=0, . ,
§ 11] ТЕОРЕМА РИМАНА 195
§ 11. Теорема Римана
Любая голоморфная и однолистная в области D функция f
осуществляет конформное отображение этой области, ибо по
доказанному в п. 34 из однолистности следует, что /'=?0 ни в
одной точке D. Отображения, осуществляемые данными функ-
функциями, мы неоднократно рассматривали выше. Здесь мы рас-
рассмотрим более трудную и более важную для практических це-
целей обратную задачу:
Даны две области Di и D2 и требуется найти (однолистное)
конформное отображение f: Dy-*D2 одной из них на другую.
36. Конформные изоморфизмы и автоморфизмы. Опреде-
Определение. Конформное отображение / области D{ на D2 будем на-
называть еще (конформным) изоморфизмом, а области, допускаю-
допускающие такое отображение, — изоморфными. Изоморфизм области
на себя называется (конформным) автоморфизмом.
Конформные изоморфизмы называют также голоморфными
изоморфизмами или, короче, голоморфизмами.
Легко видеть, что совокупность автоморфизмов <р: D—*D
произвольной области D образует группу, которая называется
группой автоморфизмов этой области и обозначается" символом
A(D). В качестве групповой операции принимается композиция
ф2°ф1 (т. е. автоморфизм ф2 faiB)]), единицей служит тожде-
тождественное отображение е: z-+z, а обратным к ф элементом — об-
обратное к ау = ф(.г) отображение z = q>-l(w).
Богатство группы автоморфизмов области позволяет судить
о богатстве конформных отображений на нее другой области.
Это показывает
Теорема 1. Если f0: Di-*D2 — какой-либо фиксированный
изоморфизм, то совокупность всех изоморфизмов Di на D2 дает-
дается формулой
f = <P°fo. A)
где феЛ(?>2)—произвольный автоморфизм области D2.
¦* Каков бы ни был автоморфизм феЛ(?>2), композиция'
фо^0 будет, очевидно, конформным отображением Dt на D2.
С другой стороны, пусть f: Dx —*D2 — произвольный изоморфизм;
тогда Ф = /°/о' будет конформным отображением D« на себя,
т. е. автоморфизм D2, а из этой формулы следует A) > •
Замечание. Любое конформное отображение f области/)
на D* устанавливает изоморфизм F: A(D) -*A(D*) групп авто-
автоморфизмов этих областей. Этот изоморфизм устанавливается
по формуле
F: ф->/офо/-1. B)
13*
196 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
В самом деле, для любого ф^Л(/)) отображение ф* =
=f°q>°f~l, очевидно, является автоморфизмом D*, т. е. принад-
принадлежит A(D*). С другой стороны, для любого ф*еЛ(/)*) отобра-
отображение f оф* of = феЛ(?>), т.е. F взаимно однозначно преобра-
преобразует A(D) на A(D*). Кроме того,
ф;оф2*=(/оф]оГ1)о(/оф2оГ1)=/о(ф1оф2)оГ1)
т. е. F: ф[ °Ф2—>ф* ° Фг сохраняет групповую операцию и, та-
таким образом, является изоморфизмом рассматриваемых групп.
Это замечание оправдывает принятое выше определение.
В дальнейшем мы ограничимся рассмотрением односвяз-
ных областей D. Выделим три из них, которые будем называть
каноническими: это замкнутая плоскость С, открытая пло-
плоскость С и единичный круг ?/ = {|г|<1}. В п. 10 мы вычислили
группы дробно-линейных автоморфизмов этих областей. Однако
справедлива
Теорема 2. Всякий конформный автоморфизм канониче-
канонической области является ее дробно-линейным автоморфизмом.
< Пусть ф— произвольный автоморфизм С; существует един-
единственная точка гоеС, соответствующая бесконечной точке, по-
поэтому функция ф(г) голоморфна всюду в С, кроме точки z0,
где она имеет полюс. В окрестности полюса порядка п^-2 функ-
функция неоднолистна, следовательно, ф имеет в z0 полюс первого
порядка. По теореме 2 п. 24 и теореме Лиувилля заключаем,
что ф имеет вид ф(г)=—— V В при г0фоо или ф(г) =Az + B
при Zo = oo (А и В — постоянные) и, таким образом, ф является
дробно-линейной функцией. Случай открытой плоскости С рас-
рассматривается аналогично.
Пусть ф — произвольный автоморфизм единичного круга U;
обозначим ф@)=ау0 и построим дробно-линейный автоморфизм
, W — W о
да -> J w
круга U, переводящий точку ш0 в 0. Композиция / = Лоф также
является автоморфизмом V', причем f@)=0. Так как, кроме
того, \f(z) |<1 для всех z^U, то к функции f применима лемма
Шварца из предыдущего пункта, по которой
If(z) l.^-l2! для всех z^u.
Но и обратное отображение z = f~l(w) удовлетворяет усло-
условиям той же леммы, следовательно, \f'l(w) \^C\w\ для всех
откуда, полагая w — f(z), находим, что
(z)\ для всех
§ II] ТЕОРЕМА РИМАНА 197
Таким образом, имеем \f(z) | = |z| для всех ze?/ и по лемме
Шварца заключаем, что f(z)=eiaz. Но тогда ф = Х"'°/ =
— k~l(eiaz) является дробно-линейным отображением >
Учитывая результаты п. 10, мы получаем полное описание
всех (конформных) автоморфизмов канонических областей.
(I) Замкнутая плоскость С:
ad-ЬсФО. (З)
(II) Открытая плоскость С:
w = az + b, афО. D)
(III) Единичный круг U:
Остановимся подробнее на автоморфизмах круга. Как
видно из формулы E), они зависят от трех действительных
параметров: двух координат точки а и числа ее. Покажем, что,
подбирая эти параметры, можно найти один и только один ав-
автоморфизм k^A(U), удовлетворяющий условиям нормировки
k(a) = b, argk'(a) = a, F)
где a, b^U — произвольные заданные точки и aeR—произ-
aeR—произвольное число.
В самом деле, построим автоморфизмы ц: z->eia \Z.^Z и
v: z —> . _6 ; тогда автоморфизм A = v~1o^i определяемый из
уравнения v (до) = ц (z), т. е.
l-6w е 1-az ' V>
будет удовлетворять условиям F). Пусть Xi^A(U)—еще ка-
какой-либо автоморфизм, удовлетворяющий тем же условиям. То-
Тогда автоморфизм f = v°Pi1oji будет, очевидно, удовлетворять
условиям f@)=0, argf'(O)=O, откуда по лемме Шварца (как
и при доказательстве теоремы 2) заключаем, что /(до)=до, т. е.
чт0 f — e — тождественное отображение. Таким образом,
v ° hi ° \i~l = е, откуда fa = v~l. ° ц = к.
По сделанному выше замечанию группа автоморфизмов
A(D) любой области D, изоморфной единичному кругу U, изо-
изоморфна группе A(U), т. е. тоже зависит от трех действительных
параме.тров. Учитывая теорему 1, можно ожидать, что и изо-
изоморфизмы двух областей, изоморфных U, также образуют трех-
параметрическое семейство. И в самом деле, справедлива
198 основы геометрической теории [гл iv
Теорема 3. Если области Dt и D2 изоморфны единичному
кругу, то совокупность конформных отображений Z)t на D2 зави-
зависит от трех действительных параметров. В частности, существует
одно и только одно отображение f: Di—*D2, нормированное
условиями
f(zo) = wo, arg/'(zo) = 6, ¦ (8)
где zo^Di и wQ^D2— произвольно заданные точки и 0eR —
произвольное число.
< Пусть f\: Di-*U и f2: D2-±U—конформные отображе-
отображения, устанавливающие изоморфизм данных областей единич-
единичному кругу. Тогда
l
будет, очевидно, конформным отображением D4 на D2. По тео-
теореме 1 совокупность всех таких отображений задается форму-
формулой /=<p°fo, где ф — произвольный автоморфизм области D2.
Но, как мы видели, A{D2) зависит от трех действительных пара-
параметров. Первое утверждение теоремы доказано.
Пусть /,(zo) = a, arg/;(zo) = 0, и f2(w0)^b, argf2(w0) = %;
построим по формуле G) автоморфизм X единичного круга, нор-
нормированный условиями
Х(а)=Ь, argPi'(a) =« = 6 + 62 — 9!.
Тогда
является изоморфизмом Dl на D2 и удовлетворяет условиям (8).
В самом деле, f(zo) = f~l ° k(a) = f~l(b)= w0 и arg f(z0) =
= -arg/2(^o) + arg^/(a) + arg/iBo)==~~02 + a + ei = e- Суще-
Существование нормированного изоморфизма доказано.
Пусть существует еще изоморфизм g: Di—*D2, нормирован-
нормированный теми же условиями. Тогда (p — f°g~1 будет автоморфизмом
Du нормированным условиями q>(w0)=Wo, агgф/(шo)=O, з
Я = /2офо^~1— автоморфизмом U, нормированным условиями
X(b)=b, argX'(b)=O. По доказанному выше Х = е (тождествен-
(тождественное отображение), следовательно, и ф = /^ °^ °f2 = e- Таким
образом, f°g~Y = e и f=g >
Легко видеть, что различные канонические области не изо-
изоморфны друг другу. В самом деле, замкнутая шгоскость (сфе-
(сфера) С даже не гомеоморфна С и U, а следовательно, ее, нельзя
и конформно отобразить на эти области. Области С и U гомео-
морфны, но конформного отображения, скажем С на U, не су-
5 II] ТЕОРЕМА РИМАНА 199
ществует, ибо такое отображение должно осуществляться целой
функцией f, для которой всюду |/(г)|<1, а тогда по теореме
Лиувилля f=const.
Область, граница которой — пустое множество, совпадает с
С. Области, границы которых состоят из одной точки, представ-
представляют собой плоскость С с выброшенной точкой и, очевидно,
конформно (даже дробно-линейно) изоморфны С. Основной
результат этого параграфа — теорема Римана состоит в том,
что любая односвязная область D, граница которой содержит
более одной точки (и, следовательно, бесконечно много точек,
ибо она связна), изоморфна единичному кругу U.
Для доказательства этой теоремы нам нужно развить неко-
некоторый аппарат, полезный и в других вопросах теории функций.
37. Принцип компактности. Определение 1. Семейство
функций {/}, заданных в некоторой области D, называется рав-
равномерно ограниченным внутри D, если для любого множества
К<Ш D существует постоянная М=М(К) такая, что
\f(z)\<M A)
для всех z^K и всех fe{f}.
Теорема 1. Если семейство функций {/), голоморфных в
области D, равномерно ограничено внутри D, то и семейство
производных {f} также равномерно ограничено внутри D.
¦4 Пусть U={\z — 20|<г} — произвольный круг, ишБ; по-
построим круг V={\z — zQ\<r'}, r'>r, такой, что и VmD. По
формуле Коши для производных в любой точке геУ имеем для
любой f<^{f}
dV
Пусть теперь z^U, тогда для всех %^-dV имеем |? — г|!>/-' — г
и, пользуясь равномерной ограниченностью семейства {f}, полу-
получаем из B)
Доказана равномерная ограниченность {f} в кругах UmD.'
Любое множество К Ш D можно покрыть кругами, компактно
принадлежащими D. По теореме Хейне — Бореля из этого по-
покрытия можно выбрать конечное {t/v)v=r Тогда, если обозначить
Mt(K) =maxMi(?/v), то для всех z<=K и всех /^Ш будем иметь
v
200 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
Определение 2. Семейство функций {/), заданных в не-
некоторой области D, называется равностепенно непрерывным вну-
внутри D, если для любого е>0 и любого множества K^D най-
найдется б = 6(е, К)>0 такое, что
\f(z')-f(z")\<B C)
для всех г'', z"<=K таких, что \г' — z"|<6, и всех f^{f].
Теорема 2. Если семейство функций {/}, голоморфных в
области D, равномерно ограничено внутри D, то оно и равно-
равностепенно непрерывно внутри D.
¦4 Пусть Кшй; обозначим через 2р расстояние между непе-
непересекающимися замкнутыми множествами К и 3D (т. е,
inf|? — z\ по всем zeisT и всем ?edD) и через
= U {|z-zo|<P}
р-раздутие множества К- Так как, очевидно, К(р)шО, то по
теореме 1 найдется постоянная М такая, что
\f'(z)\<M D)
для всех z e К(р) и всех f <= {/}.
Пусть z', z" — две произвольные точки К такие, что
\z' — г"|<р; тогда все точки z прямолинейного отрезка [г', г"}
принадлежат K(v) и, следовательно, для всех zsfz', г"] и всех
fe{f} справедливо неравенство D). Поэтому для всех fe{/} мы
имеем
< М | z' ~ z" \.
Отсюда и следует равностепенная непрерывность семейства {/}
на К, ибо для любого е>0 можно взять 6 = min(p, -^-l^
Определение 3. Семейство функций {/}, заданных в не-
некоторой области D, называется компактным1) в D, если из каж-
каждой последовательности fn функций этого семейства можно из-
извлечь подпоследовательность /nfe, сходящуюся равномерно на
любом
') Будем рассматривать функции, определенные в области D, как точки
некоторого пространства A(D). В этом пространстве введем топологию, на-
назвав сходящейся любук^ последовательность fn, равномерно сходящуюся на
каждом компактном подмножестве K<^D. Тогда компактность семейства
функций {/} сводится к компактности соответствующего множества точек а
пространстве А(?>), Это замечание оправдывает сделанный выбор термина.
§ 11] ТЕОРЕМА РИМАНА . 20!
Теорема 3 (Монтель). Если семейство функций {f}, го-
голоморфных в области D, равномерно ограничено внутри D, то
оно компактно в D.
¦* а) Докажем сначала, что если последовательность fncz{f)
сходится в каждой точке некоторого множества efcrD, всюду
плотного в D, то она сходится равномерно на каждом К <s D.
Фиксируем е>0 и множество КшБ; пользуясь равностепенной
непрерывностью семейства {/}, выберем разбиение D на квад-
квадраты со сторонами, параллельными координатным осям пло-
плоскости z, столь мелкие, что для любых точек z', z"^.K, принад-
принадлежащих одному квадрату, и любой f^{f) справедливо нера-
неравенство
|/B') -f(z") |< -|-. E)
Множество К покрыто конечным числом таких квадратов qv
(р=\, .... Р); так как У всюду плотно в D, то в каждом qp
найдется точка zpe У. Так как последовательность {/„} схо-
сходится на Ш', то найдется число N такое, что
IL(zp)-UzP)l<l F)
для всех пг, n>N и всех zp, р= 1, . . ., Р.
Пусть теперь z — произвольная точка К; найдется точка zp,
лежащая в том же квадрате, что и z, и для всех m, n>N бу-
будем иметь
\U(Z) -fn(z)\<\fm(z) -fm(zp)\ + \fm(zp) -fn(zp)\+]
+ \fn(zP)-fn(z)\<e
в силу неравенств E) и F). По критерию Коши отсюда заклю-
заключаем, что последовательность {fn{z)} сходится для всех ге/С,
причем сходимость равномерна на К.
б) Теперь докажем, что из любой последовательности fncr{f}
можно извлечь подпоследовательность, сходящуюся в каждой
точке некоторого множества &aD, всюду плотного в D. В ка-
качестве У выберем множество точек z — x+'iy^D, обе коорди-
координаты которых х и у рациональны; оно, очевидно, счетно и всюду
плотно в D; пусть ^> = {zv}^,1.
Числовая последовательность fn{z\) ограничена, следова-
следовательно, из нее можно извлечь сходящуюся подпоследователь-
подпоследовательность f/ei=fn (& = !» 2, ...)• Числовая последовательность
fni(z2) также ограничена, следовательно, из нее можно извлечь
сходящуюся подпоследовательность fk2 = fn\ {k = \, 2, ...); по-
последовательность функций fn2 сходится, следовательно, по край-
202 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
ней мере в двух точках: zx и zz. Из последовательности /„2(г3)
извлекаем сходящуюся подпоследовательность fk3 = fn2 {k =
= 1, 2, ...) так, что fn3 сходится по крайней мере в точках zu
z2 и z3. Аналогичное построение можно продолжать неограни-
неограниченно. Остается выбрать так называемую диагональную
последовательность
/ll> /22' • • ¦ > Inn* • ¦ ¦ (')
Эта последовательность сходится в любой точке греё% ибо
по построению все ее члены, начиная с р-ro, выбраны из после-
последовательности fnp, сходящейся в точке zv.
Объединяя доказанное в б) и а), получаем утверждение
теоремы >
Теорему Монтеля часто называют принципом компактности.
Определение 4. Функционалом на семействе функций{/},
определенных в области D, называется отображение /: {f}-*Q
этого семейства в С (это означает, что указан закон, по ко-
которому каждой функции f e {f} ставится в соответствие ком-
комплексное число J(f)). Функционал / на {f} называется непрерыв-
непрерывным, если для любой последовательности /пе{/}, которая равно-
равномерно сходится к /о^{/} на любом КшБ,
lim J(fn) = J(f0). (8)
П ->'оо
Пример. Пусть Н(D)—семейство всех функций f, голо-
голоморфных в области D, и а — произвольная точка D. Рассмотрим
/з-й коэффициент тейлоровского разложения / в точке а:
cP{f)=~
(a)
Это — функционал на семействе H(D); покажем, что он не-
непрерывен. Если fn—+fo равномерно на каждом КшИ, то, взяв
в качестве К окружность y = {\z — a\—r]c=D, мы для любого
е>0 найдем N такое, что \fn(z)—/o(z)|<e для всех n>N и
всех z^y. По неравенствам Коши получим тогда, что для всех
n>N
а это и означает непрерывность функционала cp(f).
Определение 5. Компактное семейство функций {/} на-
называется компактным в себе1), если предел любой последова-
последовательности fne{/}, равномерно сходящейся на каждом
принадлежит семейству {f}.
') Компактные в себе множества называют также компактами.
S И] ТЕОРЕМА РИМАНА 203
Теорема 4. Всякий функционал J, непрерывный на ком-
компактном в себе семействе {/}, достигает своей верхней грани, т. е..
существует функция fo^{fj такая, что для всех f<={f]
\Hh)\>\Hf)\- (9)
¦4 Положим А = sup | J(f) | — это некоторое число, быть мо-
жет, равное оо. По определению верхней грани найдется после-
последовательность fne{/} такая, что \J(fn) | -+А. Так как {/} ком-
компактно в себе, то существует подпоследовательность fn , сходя-
сходящаяся равномерно на каждом КшБ к некоторой функции
/ое{/}. В силу непрерывности функционала имеем
|/(fo)l= Hm \J(fn)\ = A;
отсюда заключаем, во-первых, что Л<оо и, во-вторых, что
U(h)\>U(f)\ Для всех/<={/} >
В дальнейшем мы будем рассматривать семейства функций,
однолистных в некоторой области D. Для доказательства ком-
пактноети в себе таких семейств полезна
Теорема 5 (Г у р виц). Пусть последовательность функ-
функций In, голоморфных в области D, равномерно на любом К <s D
сходится к функции /=?const. Тогда, если f(zo)=O, то в любом
круге {\z—-z0|<r}(=Z) все функции fn, начиная с некоторой,
также обращаются в нуль.
< Пе теореме Вейерштрасса / голоморфна в D; по теореме
единственности существует множество {0<|г — 20|^р}<ш/), на
котором fi=0. Обозначая y={\z — го|=р} и (X=minlf (г) \, имеем
ц>0. Так как /„ сходится на у равномерно, то найдется Л7 та-
такое, что
\fn(z)-f(z)\<ll
для всех геу и всех n>N. Для таких п по теореме Руше функ-
функция fn — f+(fn — f) имеет внутри у столько же нулей, сколько
их имеет там /, т. е. по крайней мере один нуль >
Следствие. Если последовательность функций fn, голо-
голоморфных и однолистных в области D, сходится равномерно на
каждом /С <Ш D, то предельная функция f этой последовательно-
последовательности либо однолистна, либо постоянна.
•* Пусть f(zi)=f(z2), но zx=hz2 (zu 22eO) и f = const. Рас-
Рассмотрим последовательность функций gn(z)=fn(z)—fn{zz) и
круг {\z — zl\<r}, где /-<|Zi — z2|; предельная функция g(z) =
=f(z) —fB2) обращается в нуль в точке zj, следовательно, по
теореме Гурвица и все gn(z), начиная с некоторого номера, об-
обращаются в нуль в этом круге, но это противоречит однолистно-
однолистности функций /„ > ,
204 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
38. Теорема Римана. Любая односвязная область D, гра-
граница которой содержит более одной точки, изоморфна единич-
единичному кругу U.
Идея доказательства такова. Рассмотрим семейство S голоморфных и од-
однолистных в D функций /, по модулю ограниченных 1 (т. е. осуществляю-
осуществляющих конформное отображение D в единичный круг U). Фиксируем точку
a^D и будем искать в семействе функцию, для которой растяжение \f'(a)\
в точке а максимально. Выделив компактную в себе часть S[ семейства S
и пользуясь непрерывностью функционала /(/) = |/'(а)|, мы можем утвер-
утверждать, что существует функция /о с максимальным растяжением в точке а.
Наконец, мы убедимся в том, что /0 реализует отображение D на круг U
(а не только в U, как остальные функции семейства).
Такой вариационный метод, когда ищется функция, обладающая тем или
иным экстремальным свойством, часто применяется в теории функций.
< а) Докажем, что в D существует хотя бы одна голоморф-
голоморфная и однолистная функция, ограниченная 1 по модулю. По
условию граница dD содержит две различные точки а и Р; ко-
корень квадратный 1/ гг_Д продолжается аналитически вдоль
любого пути в области D, и так как D односвязна, то по теореме
о монодромии (п. 28) этот корень допускает выделение в D
двух однозначных ветвей ф1 и фг, отличающихся знаком.
Каждая из этих ветвей однолистна в D, ибо из равенства
<PvBi) =фу(г2) (v=l или 2) следует равенство
Zj-a _ z2-a
г,-0 ~ г2-0 ' U/
а из него, в силу однолистности дробно-линейной функции, —
равенство Zi = z2. Эти ветви отображают D соответственно на
области Д* = ф,(D) и D*2 = q>2(D), которые не имеют общих то-
точек, ибо в противном случае нашлись бы точки zu z2^D такие,
что ф1B1) =ф2(г2), но из последнего равенства снова следует A),
а из него — равенство zi = z2, т. е. ф1(г1)=—фгB2); мы пришли к
противоречию, ибо ФУ=?0 в D.
Область D*2 содержит некоторый круг {\w — а>0|<р}, и, зна-
значит, ф1 не принимает в D значений из этого круга. Поэтому
функция
очевидно, голоморфная^и однолистная в D, ограничена: для
всех z^D имеем |fi(z) |^ 1.
б) Обозначим через S семейство всех голоморфных и одно-
однолистных в D функций, по модулю ограниченных 1. Это семей-
семейство непусто, ибо содержит функцию /i, и по теореме Монтеля
§ II] ТЕОРЕМА РИМАНА 205
компактно. Часть Si семейства S, состоящая из всех функций
/gS, для которых
\Па)\>\П(а)\>0 C)
в некоторой фиксированной точке a^D, компактна в себе. В са-
самом деле, по следствию теоремы 5 из предыдущего пункта пре-
предел последовательности функций fneSi, сходящейся на любом
K^D, может быть лишь однолистной функцией (и тогда при-
принадлежать к Si) либо постоянной, но последний случай исклю-
исключен неравенством C).
Рассмотрим на Si функционал
= \f'(a)\.
По доказанному в предыдущем пункте он непрерывен, и, следо-
следовательно, существует функция fo^Sit реализующая его макси-
максимум, т. е. такая, что
1Г(«Ж|/о(«)| D)
для всех f
в) Так как функция fo^Su то она конформно отображает/)
в единичный круг U. Покажем, что /0(а)=0,—в противном слу-
случае в Si нашлась бы функция
/z\ = /о (г) - /о (а)
1-/о(а)Ы*) '
для которой
вопреки экстремальному свойству D) функции fo-
Покажем, наконец, что f0 отображает D на весь круг U.
В самом деле, пусть /0 не принимает в D некоторого значения
b^U; так как fo(«) =0, то ЬфО. Но и значение Ь* = -т- не прини-
принимается этой функцией в D (ибо |й*|>1), следовательно, по тео-
теореме о монодромии в D можно выделить однозначную ветвь
корня
которая принадлежит S (однолистность проверяется точно так
же, как в п. а), справедливость неравенства |ijj(z)i^l очевид-
очевидна). Но тогда 5 принадлежит и функция
fl (z) — Ф (г) ~ 'Ф (а)
206
для которой
основы геометрической теории
[ГЛ. 17
Но 1+|&|>2У|61, ибо |&|<1, т. е. AeS, и | h'(a) |>|ft(a)|,
вопреки экстремальному свойству функции /0 >
§ 12. Соответствие границ и принцип симметрии
39. Соответствие границ. Приведем без доказательства так
называемый принцип соответствия границ:
Теорема (Каратеодори). Пусть области D и D* огра-
ограничены жордановыми кривыми dD и dD*\ тогда конформное
отображение f: D —* D* можно продолжить на границу D до
гомеоморфизма замкнутых областей D и D*-
Для произвольных гомеоморфизмов теорема, конечно, не-
несправедлива. Например, отображение единичного круга U на
себя, которое в полярных коор-
динатах 2 = rei(f, ш =
ется уравнениями
зада-
зада9 = г, i|5 =
A)
Рис. 66.
очевидно, гомеоморфно, но на
граничную окружность непре-
непрерывно не продолжается.
Точно так же неверна тео-
теорема и для конформных отобра-
отображений на области, границы которых нежордановы. Рассмотрим,
например,конформное отображение/круга f/на область D, изо-
изображенную на рис. 66, в состав границы которой входит часть
кривой u = sin— с предельным сегментом y={w. и = 0, — l^t/^1}.
Можно доказать, что при этом отображении дугам уп, отрезаю-
отрезающими от D области Dn («=1» 2, ...), пересечение замыканий
которых совпадает с у, в плоскости z соответствуют дуги Яп,
отрезающие от U области Un, причем f") Un совпадает с неко-
торой граничной точкой ei<p (рис. 66). В этом смысле при ото-
отображении f точке ei(f соответствует целый отрезок_у, так что /
нельзя непрерывно продолжить в замкнутый круг U.
К. Каратеодори ввел так называемые граничные элементы области, по-
понимая под ними классы в известном смысле эквивалентных сечений этой об-
области. Присоединение к области ее граничных элементов называется ком-
пактификацией по Каратеодори. Он доказал, что конформное отображение
§ 12] СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ 207
областей устанавливает взаимно однозначное и в некотором смысле непре-
непрерывное соответствие граничных элементов этих областей. Поэтому сформу-
сформулированная выше теорема распространяется и на нежордановы области, если
пользоваться при этом компактификацией по Каратеодори вместо обычных
замыканий ').
Приведем, также без доказательства, несколько более точ-
точных результатов о граничном поведении конформных отображе-
отображений областей с жордановыми границами при дополнительных
предположениях об этих кривых. Через dD и 3D* будем обо-
обозначать границы областей и через f: D—*D*— конформное ото-
отображение.
I (Ф. и М. Риссы, И. И. Привалов). Если 3D и 3D* —
спрямляемые жордановы кривые, то f продолжается на dD как
абсолютно непрерывная функция длины дуги. Производная fr
почти в каждой точке t,^dD (в смысле линейной меры) имеет
угловое граничное значение2) f'(t,), конечное и отличное от
нуля, и для любого множества точек eczdD мера образа e* = f(e)
равна
J B)
в частности, множествам eczdD меры 0 соответствуют множе-
множества e*czdD* меры 0.
II (Линделёф). Если 3D и dD* — гладкие жорданов^ьг
кривые, то arg f'(z) продолжается до непрерывной функции в Д.
причем для всего ? е dD
arg/'(?) = e'-e, C)
где б и соответственно б* — углы наклона касательных к кри-
кривым dD и dD* в точках ? и ?* = f(?).
III (Келлог). Если в условиях и обозначениях предыдущей
теоремы, кроме того, углы б и 0*, как функции длины дуги s
и s* соответственно на dD и dD*, удовлетворяют условию Лип-
Липшица
где k и а, 0<а-^1, — постоянные, то производная /' продол-
продолжается до непрерывной и отличной от нуля функции в D (ото-
(отображение «конформно» на границе).
') Подробнее об этом см., например, в книге: А. И. Маркушевнч,
Теория аналитических функций, т. II, «Наука», М., 1968.
2) Угловым граничным значением функции <р в точке ?edD, где д?>
имеет касательную, называется общее предельное значение Ф по всем нека-
некасательным путям yeD с концом в точке ?•
208 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
IV (Шварц). Если 3D и 3D* — аналитические жорда^овы
кривые1), то / продолжается до голоморфной функции в D.
Доказательство утверждений I—III можно найти в книге
Г. М. Голузина «Геометрическая теория функций комплексного
переменного» (М. — Л., 1967); утверждение IV мы докажем в
следующем пункте. Здесь приведем только более простой об-
обратный принцип соответствия границ:
Теорема. Пусть даны области D и ?>*, компактно принад-
принадлежащие С, с жордановыми границами у и у*; если функция f
голоморфна в области D, непрерывна в D и устанавливает
взаимно однозначное отображение у на у*, то и отображение
f: D-+D* взаимно однозначно (т. е. /—конформный изоморфизм).
< Пусть Wq—произвольная точка D*; так как f на у при-
принимает лишь значения из у*, то f=?w0 на у и, в силу непрерыв-
непрерывности, fi=wQ в некоторой граничной полосе G области D. Вели-
Величина
N = ^byarg{f(z)-w0} D)
(где arg обозначает какую-либо непрерывную вдоль пути у
ветвь аргумента и Ду — приращение этой ветви на у), очевидно,
непрерывно меняется при гомотопной деформации пути в полосе
G. Но так как величина D) может принимать лишь целочислен-
целочисленные значения, то она остается постоянной при такой деформации.
По условиям теоремы отображение /: Y"~*Y* гомеоморфно,
следовательно,
•/V = 2^ д\* arg (да - wu) = 1,
ибо при однократном обходе у вектор да — да0 делает один по-
поворот (рис. 67). В силу сказанного выше следует, что и для
любого пути y> гомотопного у в полосе G, имеем
') Дугу у называют аналитической, если ее можно задать путем z—z(t),
< е [а, И, где г(^)—аналитическая функция действительного переменного t на
отрезке [а, р] (т. е. функция, представимая в некоторой окрестности каждой
точки tos. [а, Р] в виде суммы ряда по степеням (t—io), причем г'(t) Ф 0 на
[а, р]. Из теоремы Хейне — Бореля вытекает, что такая функция z(t) про-
продолжается до голоморфной функции комплексного переменного / в неко-
некоторой окрестности отрезка [а, Щ. Поэтому аналитическая дуга — это голо-
голоморфный образ отрезка. Замкнутой аналитической кривой называют голо-
голоморфный образ окружности {И = 1} в плоскости параметра, при котором
z'(t)^=0 на окружности; если отображение z=z(t) еще и взаимно однознач-
однозначно, то у называют аналитической жордановой кривой.
12]
СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ
209
К области ВшБ, ограниченной кривой у, применим принцип
аргумента (п. 33), по которому уравнение f(z)=w0 имеет в D
(а значит, и в D, ибо в полосе G нет да0-точек) точно один
корень. _
Так же доказывается, что для любой точки ио^фИ* число ну-
нулей функции f(z) —wi в области D, равное
Nl = 2я A
равно 0, ибо при обходе у* вектор w — w1 не делает ни одного
полного оборота (рис. 67). Из принципа сохранения области
Рис. 67.
(п. 34) следует, далее, что f не может принимать в D и значений
из у*, ибо в этом случае она должна была бы принимать зна-
значения из дополнения к D*.
Таким образом, f один и только один раз принимает в обла-
области D любое значение w0 из D* и не принимает никаких других
значений, т. е. f взаимно однозначно отображает D на D* >
Замечание. В доказанной теореме D может быть произ-
произвольной областью на С (с жордановой границей), но D* обя-
обязана быть компактной в С, ибо функция f должна быть не-
непрерывной в D в смысле С. Последнее условие существенно: в
самом деле, функция f (z) =z3 голоморфна в верхней полуплоско-
полуплоскости D = {Imz>0} и взаимно однозначно отображает 3D (ось х)
на ось и — границу верхней полуплоскости D* — {lmw>0}, но в
области D отображение f не взаимно однозначно.
Пример. Изучим отображение верхней полуплоскости
D = {Imz>0}, осуществляемое эллиптическим интеграломt пер-
первого рода
= J
dz
V(l-z2)(l-k2z2)
E)
где k, 0<?<l, — параметр и рассматривается голоморфная в D
ветвь корня, которая на отрезке /=[0, 1] оси х принимает поло-
положительные значения.
14 Б. В. Шабат
210
ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ
[ГЛ. IV
Функция F(z; k) непрерывно продолжается в D, и мы вы-
выясним сначала, как она преобразует границу <ЗД т. е. ось х.
Когда z=x описывает слева направо отрезок / = [0, 1], инте-
интеграл E)
F(x, 6) =
dx
V(l~x2)(l-k2x2)
принимает положительные (в силу сделанного выбора ветви
корня) значения, возрастающие от 0 до значения
к =
dx
V{i-x2){i-k2x2)
F)
т. е. F устанавливает гомеоморфизм отрезков [0, 1] оси х и
[0, К] оси и.
При переходе через точку г=1 один из четырех линейных
множителей подкоренного выражения, именно 1—х, меняет
знак. Так как мы рассматри-
рассматриваем ветвь корня, голоморф-
голоморфную в верхней полуплоскости
D, то мы должны считать, что
такой переход происходит в
результате обхода точки 2=1
по малой полуокружности yczD
(пунктир на рис. 68). В резуль-
результате такого обхода arg(l—z)
меняется от 0 до —л, а аргу-
аргументы остальных множителей
не меняются. Поэтому на от-
отрезке /7=1, -г- оси х аргу-
аргумент корня равен — -^ , а аргумент подинтегрального выраже-
выражеж'
-кчн'
/'
ш
в'
-к
1 L
•
У
1
7
V
0
Рис.
л
1 '
и
1
68
В
1
D
Ш
'Л "
Н и
ния а E) равен у; значения
тельно, представить в виде
на отрезке II можно, следова-
следоваdx
V{\-x2)(\-k2x2)
X
dx
X
dx
V(x2-l)(l-k2x2) '
§ !2] СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ 211
где в последнем интеграле корень опять принимает положитель-
положительные значения. Когда х описывает слева направо отрезок // =
= 1, -г\ оси х, точка F(x, k) описывает снизу вверх отрезок
[К, K+iK'] плоскости w, где
i/fe
J
При переходе через точку z — -r еще один множитель подко-
подкоренного выражения, A—kx), меняет знак. Как и выше, мы
убедимся в том, что рассматриваемая ветвь корня на луче
/// = -т-, °°) оси х должна иметь аргумент —л, т. е. принимать
отрицательные значения. Значения F на этом луче представ-
представляются, следовательно, в виде
I Чк х
где в последнем интеграле корень принимает положительные
значения. Замена переменных х~тг показывает, что
тг
CO 1
Г d* — Г
J /(ж2 - lHfe2*2 - П J
rf?
поэтому луч —-г, ooj функция F преобразует (и притом го-
меоморфно) в отрезок [K-?j.Kr, t/C'] плоскости ш (см. рис. 68).
Совершенно аналогично проверяется, что функция F гомео-
морфно преобразует отрицательную полуось х в левую половину
контура прямоугольника, изображенного на рис. 68 (совокуп-
(совокупность отрезков /', //' и ///').
Применяя принцип соответствия границ, можно утверждать,
что эллиптический интеграл первого рода F(z, k) реализует
конформное отображение верхней полуплоскости D на прямо-
прямоугольник с вершинами ±К, ±K+iK', где величины К и К' вы-
выражаются через параметр k no формулам F) и G),
40. Принцип симметрии. Здесь мы рассмотрим один спе-
специальный случай аналитического продолжения, относящийся к
14*
212 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
конформным отображениям. Предварительно докажем так на-
называемую лемму о непрерывном продолжении.
Лемма. Пусть непересекающиеся области Dt и D2 имеют
общий прямолинейный участок границы у1), а функции /4 и f2
соответственно голоморфны в Dt и D2 и непрерывны на множе-
множествах ?>i U у и D2 U у (рис. 69). Тогда, если
/i(z)= /г(г) для всех геу. (О
то функция
|/() для всех DU
|/iB) для всех zeD,UY.
1 h (?) для всех z^D2 { '
голоморфна в области Dy\]y\]D2=D.
< Из условий леммы видно, что / непрерывна в D; для до-
доказательства ее голоморфности по теореме Мореры (п. 20) до-
достаточно проверить, что интеграл от нее по границе любого
треугольника Д шй равен нулю. Если Д
компактно принадлежит Dx или D2, то это
следует из теоремы Коши. Остается рас-
рассмотреть случай, когда Д П у Ф 0.
Пусть у делит Д на две части Ai и Д2;
по свойствам интегралов
dz= J fdz+ J fdz, C)
ад, ад2
Рис. 69. и достаточно показать, что каждый из инте-
интегралов справа равен нулю. Рассмотрим лю-
любую из частей А\ и Дг и для простоты обозначим ее снова через Д.
Обозначим через Th трапецию, которая отсекается от Д пря-
прямой, параллельной y и отстоящей от у на расстоянии h; пусть
Ah = A\Th (рис. 69).
По теореме Коши интеграл от f по <ЗДд равен нулю, следо-
следовательно,
jfdz= \fdz + \fdz= j fdz. D)
ад dfh адй dTh
Пусть y' и у" — основания трапеции Th (предположим, что
они ориентированы одинаково); так как длины боковых еесто-
рон стремятся к нулю при /г—<-0, а функция / ограничена в Д, то
J / dz = J f dz - J fdz + O (h).
dTh Y'
') Отрезок y считается открытым (без концов).
$ 12] СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ 213
Обозначим через l(z)=zo+k(z— zQ) линейное преобразова-
преобразование у' на У"' Делая в интеграле по у" замену переменных
z—*-X(z), получим
jfdz- \fdz= j{f(z)-f[X(z)]k}dz. E)
Y' Y" V
Так как при h~* 0 функция X(z) равномерно на у' стремится
к z, k—> 1 и / равномерно непрерывна в Д, то подинтегральная
функция в E) равномерно стремится к нулю, а значит, инте-
интеграл от / по dTh стремится к нулю при h-*0. Но из D) видно,
что он не зависит от h, следовательно, он, а значит и интеграл
по дА, равен нулю.
Если Д пересекается с y лишь стороной или вершиной, то
доказательство очевидным образом упрощается >
Замечание. Если воспользоваться усиленной формой теоремы Коши,
в которой предполагается, что функция голоморфна в области и лишь не-
непрерывна в ее замыкании, то доказательство леммы существенно упрощается:
по этой теореме каждый интеграл в правой части C) равен нулю.
Функцию /, определенную формулой B) в области D, можно
рассматривать как аналитическое продолжение каждой из функ-
функций fi и /г1). Лемму о непрерывном продолжении поэтому
можно читать так: если две области Dv имеют общий прямоли-
прямолинейный участок границы y и функции /v, голоморфные в Dvt
непрерывно смыкаются на y. то они и аналитически продол-
продолжают друг друга. Для дифференцируемых функций действи-
действительного переменного аналогичное утверждение, конечно, не-
несправедливо (пример: Di и D2 — отрезки (—1, 0) и @, 1) и
f ||)
Перейдем к доказательству принципа симметрии.
Теорема 1 (Ри м а н —Ш в а р ц). Пусть области D{ и D\
имеют жордановы границы dD{ и dD\, причем dDt содержит
отрезок прямой или дугу окружности у, a dD\ — такой же отре-
отрезок или дугу у*. Если функция f4 конформно отображает Dt
на D\, причем U{y)=y*, то ft допускает аналитическое продол-
продолжение в область D2, симметричную с Dt относительно у, и про-
продолженная так функция конформно отображает область-
?»iU y U D2 на D][] y*[] D\, если Dx(\ Da и D]f] D'2 = 0 (рис. 70).
¦4 а) Рассмотрим сначала частный случай, когда y и Y
представляют собой отрезки действительных осей. Определим
*
') Точнее: элемент (Д f) является непосредственным аналитическим про-
продолжением каждого из элементов (Dufi) и (Di,U)-
¦214
ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ
[ГЛ. IV
в области ?>2, симметричной с
функцию
7
Так как при 2eD2 точка
мится к точке х i
то z
Рис 70
относительно отрезка у,
F)
1, а функция fi(z) голо-
голоморфна в Di, то функция f2(z) =fi(z) антиголоморфна в D2
(см. п. 7) и, следовательно, f2 (z) голоморфна в D2. По прин-
принципу соответствия границ /ч непрерывна в Du причем по усло-
условию теоремы /4 на у принимает действительные значения (при-
(принадлежащие отрезку у*). Поэтому, когда точка z^D2 стре-
-*х и f2{z) -*fi{x)=fi(x). Таким
образом, fi(x) =}2(х) для всех
х е у и функции /i и /г удовлетво-
удовлетворяют условиям леммы о непре-
непрерывном продолжении. По этой
лемме функция
f/^BD.UY,
Т(г) \f2(z)BD2
голоморфна в области Di\Jy\JD2-
По построению f конформно
«тображает эту область на D*Uy*U D*r Для частного случая у,
•у* czR теорема доказана.
б) Общий случай приводится к этому частному дробно-ли-
дробно-линейными отображениями. В самом деле, пусть X и Х# — дробно-
линейные отображения, переводящие соответственно y и Y* в
отрезки действительных осей (они существуют по доказанному
в п. 10). Функция gi = h* °fi °irl по доказанному в а) продол-
продолжается аналитически в область X(Dz), симметричную с X(Di)
относительно отрезка My), причем продолженная функция gz
отображает X(D2) на область K(D*2) (мы пользуемся тем, что
дробно-линейные отображения сохраняют симметричные точки,
см. п. 9). Но тогда функция /2 = Х~х ° g2 ° X является аналити-
аналитическим продолжением функции /i в область D2 и отображает D2
на D\ >
Замечание. Отрезок y* b доказанной теореме может со-
содержать бесконечную точку; тогда продолжение / будет меро-
морфным: функция f окажется голоморфной в D всюду, кроме
точки го ^ y> соответствующей бесконечной точке, где она имеет
полюс. Этот полюс непременно первого порядка, ибо f одно-
однолистна в области D (в окрестности кратного полюса функция
многолистна, см. п. 24).
В качестве примера применения принципа симметрии
приведем доказательство теоремы о продолжении, из которой
§ J2] СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ 215.
следует сформулированное в предыдущем пункте утвержде-
утверждение IV.
Теорема 2 (Ш в а р ц). Если граница области D содержит
аналитическую дугу у, то конформное отображение f этой об-
области на единичный круг можно аналитически продолжить че-
через у.
¦4 Пусть у задается при помощи функции z=z(t), аналити-
аналитической на отрезке [a, p]czR и такой, что z'(t)^O (см. опреде-
определение в сноске на стр. 208). Для любой to^[a, fj] найдется
окрестность ?/ = {/еС: \t— to\<r}, в которую z(t) продол-
продолжается, как голоморфная функция комплексного переменного,
причем в силу условия z'(to)=?0 можно считать, что z{t) одно-
однолистна в U. Функция z = z(t) отображает диаметр б cr U, со-
состоящий из точек действительной оси t, на дугу у0 сг у; мы обо-
обозначим через U+ тот из полукругов U\8, который z(t) отобра-
отображает в D. Функция g(z) =f о z(t) в U+ удовлетворяет условиям
принципа симметрии (она преобразует б в дугу единичной
окружности) и, следовательно, аналитически продолжается в U.
Отсюда вытекает, что f(z) аналитически продолжается через
дугу yo >
Принцип симметрии полезен для фактического построения
конформного отображения областей, обладающих свойствами
симметрии.
Пример. Область D представляет собой внешность объединения от-
отрезков [—1, 1] и [—i,i\; обозначим через ?>i ее верхнюю половину (рис. 71).
В D\ однолистна функция W\ = z2 (в D
эта функция неоднолистна), которая отобра-
отображает D\ на плоскость с выброшенным лучом
— l^Rett»i^oo. Поэтому функция ш=уг2+1,
где выбрана нужная ветвь корня, отображает D\
1
(Z)
-i
на верхнюю полуплоскость Dt. Отрезок у. соеди-
няющий через оо точки ±1, переходит при этом
в отрезок у*, соединяющий через оо точки ± у 2 .
Следовательно, к последней функции применим Dt
принцип симметрии, по которому она продол- * I~\nt^ "h" "v?
жается аналитически ') в область /)г, симметрич- ** " *
иую с Di относительно у, и продолженная функ-
функция ш = Уг2+1 (мы обозначаем ее тем же сим- рис 71.
волом) отображает D на внешность D* отрезка
[— V2, К2 ]. Внешность отрезка уже совсем просто отображается на ка-
каноническую область (например, линейной функцией мы отображаем D* на
внешность отрезка [—1, 1], а затем применяем одну из ветвей функции, об-
обратной к фунции Жуковского из п. 11,'—получим отображение на внутрен-
внутренность или внешность единичного круга).
') Точнее, продолжается мероморфно, ибо в бесконечной точке об-
области D функция имеет полюс (первого порядка).
216
ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ
[ГЛ. IV
41. Эллиптический синус и модулярная функция. Рассмотрим
еще два примера более общего характера.
а) Эллиптический синус. В п. 39 мы убедились в
том, что эллиптический интеграл первого рода
z =
dw
(О
где k, 0<?<l, — параметр и рассматривается одна из ветвей
корня в верхней полуплоскости {1тш>0}, конформно отобра-
отображает эту полуплоскость на прямо-
прямоугольник Ro с вершинами ±К,
¦т-+-°гг - ±K+JK'- Обозначим через
}н\ +*! A w = sn(z,k) B)
I
-w-
snz
-i/к
snz
0 I
'/h
Рис. 72.
или, короче, w — snz обращение ин-
интеграла A)—функцию, голоморф-
голоморфную в прямоугольнике Ro и отобра-
отображающую его конформно на верх-
верхнюю полуплоскость {1тда>0}; функ-
функция B) называется эллиптическим
синусом.
Так как функция sn переводит
отрезок [К, K+iK'] в отрезок
1, -т- , то к ней применим прин-
принцип симметрии, по которому она аналитически продолжается
в прямоугольник Ri, симметричный с Соотносительно [К, K+iK'],
причем продолженная функция (мы снова обозначаем ее че-
через sn) отображает Ri на нижнюю полуплоскость {1гпву<0}
(рис. 72). Продолженная функция также удовлетворяет усло-
условию принципа симметрии и по этому принципу аналитически
продолжается в прямоугольник R2, симметричный с R\ относи-
относительно отрезка 2К, 2К + 1К'- Прямоугольник R2 отображается
снова на верхнюю полуплоскость, и притом по построению для
всех гей
sn (z + 4/C) = sn z C)
(см. рис. 72; точка гь симметричная с г относительно отрезка
[К, K+iK'], переходит в точку sn г, а точка 2г = z+]AK, симмет-
симметричная с Zi относительно [2К, 2K+iK'], — снова в точку snz).
Точно так же мы можем продолжить функцию sn в прямо-
прямоугольник У?,, симметричный с Со относительно отрезка [—K+iK',
K+iK'], только, это продолжение будет мероморфным — в точке
iK', отмеченной звездочкой на рис. 72, функция sn имеет полюс
§ 12] СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ 217
первого порядка (см. замечание после принципа симметрии).
Продолженная функция sn отображает #{ на нижнюю полу-
полуплоскость и, по тому же принципу симметрии, аналитически
продолжается в прямоугольник R'2, симметричный с R\ отно-
относительно отрезка [-К+21К.', K + 2iK'\ и этот прямоугольник
она отображает снова на верхнюю полуплоскость. Как и выше,
мы получим, что для всех г е Ro
iK')=snz D)
(см. рис. 72).
Рассуждая точно таким же образом, мы можем продолжить
эллиптический синус sn на всю плоскость С. Продолженная
функция окажется мероморфной: в точках iK'+4Km + 2iK'n,
где т, п — 0, ±1, ... — произвольные целые числа (эти точки
отмечены звездочками на рис. 72), она имеет полюсы первого
порядка, а в остальных точках С голоморфна. Эта функция
обладает также интересным свойством двоякопериодичности —
как видно из соотношений C) и D) и аналогичных им, она
имеет два независимых периода 7\ = 4/С и T2 = 2iK': для любых
целых т, п—±\, ±2, . .. справедливо соотношение
sn (z+AKm + 2iK'n)=snz. E)
Таким образом, функция sn инвариантна относительно не-
некоторой группы движений плоскости С, т. е. линейных преоб-
преобразований вида
z-*z+4Km+_2iK'n (m, я = 0, ±1, ...).
Функции, обладающие свойством инвариантности относительно
некоторой группы дробно-линейных преобразований, назы-
называются автоморфными функциями. Красивой теории автоморф-
ных функций посвящена обширная литература1).
В п. 32 мы говорили о римановой поверхности эллиптиче-
эллиптического синуса.
б) Модулярная функция. Рассмотрим круговой тре-
угольник Т0—АВС, образованный дугами окружностей, ортого-
ортогональных к единичной окружности (рис. 73). По теореме Ри-
мана существует единственное конформное отображение w =
= \i(z) этого треугольника на верхнюю полуплоскость, перево-
переводящее точки А, В и С соответственно в точки ш = 0, 1 и оо. По
принципу симметрии функцию }х можно аналитически продол-
продолжить в треугольники Tf\ k=\, 2, 3, симметричные с То отно-
относительно его сторон. Точки, симметричные вершинам То относи-
') Сщ., например, Л. Р. Форд, Автоморфные функции, ОНТИ, 1936.
¦218
ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ
[ГЛ. IV
В
тельно сторон, противоположных этим вершинам, также лежат
на единичной окружности. (В самом деле, при инверсии, скажем
относительно дуги ВС, дуга окружности {|г| = 1}, содержащая
точку А, перейдет в дополнительную дугу этой окружности и
образ Ai точки А попадет на эту дополнительную дугу.) По
свойствам инверсии (п. 9) стороны треугольников Т\к) снова бу-
будут дугами окружностей, ортогональных единичной окружности.
Продолженная функция ц конформно отображает каждый из
Tf на нижнюю полуплоскость так, что стороны переходят в один
из отрезков @, 1), A, оо),
(оо, 0). Поэтому к ц снова
можно применить принцип
симметрии, и, следовательно,
\х аналитически продолжает-
продолжается в треугольники Tf\ кото-
которые получаются из T\k) от-
отражением относительно их
сторон (заштрихованы на
рис. 73).
Повторяя описанный про-
процесс аналитического про-
продолжения неограниченно, мы
построим голоморфную в
единичном круге I/ функ-
функцию jx, которая и называется
модулярной функцией. Оче-
Очевидно, что модулярная
функция непродолжаема аналитически за пределы U, т. е. U яв-
является ее областью голоморфности. В самом деле, на окружно-
окружности dU = {\z\ = 1} всюду плотны множества точек, получающихся
отражениями каждой из вершин треугольника То; но когда z
стремится по соответствующему треугольнику к точке Ап, полу-
получающейся отражениями вершины А, то ц(г) —»0, а когда z так
же стремится к точкам Вп или С„ (получающихся отражениями
В или С), то n(z) стремится к 1 или оо. Таким образом, ^
нельзя продолжить в U даже непрерывно.
Из построения ясно также, что модулярная функция \к не
принимает в 11 трех значений: 0, 1 и оо. Этим свойством мы вос-
лользуемся в дальнейшем.
Заметим, далее, что четное число отражений относительно
дуг окружностей (инверсий) сводится к дробно-линейному пре-
преобразованию. Дробно-линейные преобразования, которые полу-
получаются четным числом отражений, описанных при определении
модулярной функции, к тому же переводят окружность dU в
§ 12] СООТВЕТСТВИЕ ГРАНИЦ И ПРИНЦИП СИММЕТРИИ 2191
себя, т.е. являются автоморфизмами U. Они, очевидно, состав-
составляют группу Ло, которая является подгруппой группы всех
автоморфизмов U.
Легко видеть, что модулярная функция является инвариант-
инвариантной относительно преобразований группы Ло (т. е. автоморфной
функцией). В самом деле, пусть ХеЛ0 — произвольное отобра-
отображение и ге{/ — произвольная точка; z принадлежит некото-
некоторому треугольнику Т из описанных выше (точнее, его замыка-
замыканию в U), и функция in конформно отображает его на верхнюю
или нижнюю полуплоскость так, что вершины треугольника пе-
переходят в точки 0, 1 и оо.
По построению функция ц, отображает треугольник К(Т) на
ту же полуплоскость, причем соответствующие точки снова пере-
переходят в точки 0, 1 и оо. Поэтому ц, и ц,°Л конформно отобра-
отображают Т на одну полуплоскость с одинаковым соответствием
трех граничных точек, и, следовательно,
ц(г) = цоЬB) F)
(см. п. 36).
Опишем аналитическую функцию, обратную к модулярной.
Для построения этой функции рассмотрим ее ветвь z=n~l(w),
голоморфную в верхней полуплоскости и отображающую эту
полуплоскость на треугольник То. По принципу симметрии эта
ветвь аналитически продолжается в нижнюю полуплоскость че-
через каждый из (открытых) отрезков @, 1), A, оо) и (—оо, 0).
Каждую из продолженных ветвей можно снова продолжить в
верхнюю полуплоскость через любой из этих отрезков. При этом,
если второе продолжение происходит через другой отрезок, чем
первое, то полученная ветвь отличается от начальной (она ото-
отображает верхнюю полуплоскость на один из треугольников
Т^). Этот процесс продолжения можно вести неограниченно;
он и определяет аналитическую функцию, обратную к моду-
модулярной.
Нетрудно видеть, что аналитическая функция, обратная к
модулярной, бесконечнозначна; точки 0, 1 и оо являются ее ло-
логарифмическими точками ветвления. Все значения этой функции
лежат в единичном круге U.
На существовании функции, обратной к модулярной, осно-
основано простое доказательство следующей теоремы, которая пред-
представляет собой далеко идущее обобщение основного свойства
многочленов.
Теорема 1 (Пикар). Любая целая функция, отличная от
постоянной, принимает все (конечные) . комплексные значения,
за исключением, быть может, одного.
220 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
•4 Пусть целая функция / не принимает двух различных зна-
значений а, 6еС. Функция
s ч ' b — a
также целая и не принимает значений 0 и 1. В окрестности
произвольной точки гоеС голоморфна функция y = \x~l°g, где
\х.-х — какая-либо ветвь функции, обратной к модулярной, голо-
голоморфная в окрестности точки wQ=g(z0). Так как функция g
не принимает значений 0, 1 и оо — особых для аналитической
функции ц~1, то функция ф продолжаема вдоль любого пути
Y с С. Так как С односвязна, то по теореме о монодромии
(п. 28) функция ф однозначна и голоморфна в С, т. е. является
целой функцией. Но все значения ц лежат в единичном круге,
следовательно, ф ограничена и, по теореме Лиувилля (п. 20),
постоянна. Но тогда и g, а следовательно и /, постоянна >
Целая функция — это мероморфная (в С) функция, не при-
принимающая значения оо. Теорема Пикара обобщается и на про-
произвольные мероморфные функции:
Теорема 2 (Пик ар). Любая мероморфная в С функция,
отличная от постоянной, принимает все комплексные значения
из С, за исключением, быть может, двух.
< Пусть f — мероморфная функция, не принимающая трех
различных значений а, Ъ, сеС. Эти значения можно считать ко-
конечными, ибо если бы какое-либо из них было бесконечным,
то f была бы целой функцией, не принимающей двух значений,
т. е., по теореме 1, постоянной. Рассмотрим функцию
g ^ = f (г) - с '
она, очевидно, целая (ибо $фс) и не принимает значений
—^— и ¦ . По теореме 1 функция g постоянна, но тогда и f
постоянна >
Замечание. Целая функция егФ0, мероморфная функция
tgzФ±i, следовательно, теоремы Пикара не могут быть усилены
в отношении числа непринимаемых значений (такие значения
называются пикаровскими исключительными значениями).
Можно доказать, что свойство мероморфных функций при-
принимать все значения, за исключением, быть может, двух на са-
самом деле является локальным свойством их поведения в беско^
нечности. Имеет место так называемая большая теорема Пи-
Пикара, по которой любая функция в любой сколь угодно малой
окрестности предельной точки ее полюсов принимает все значе-
значения, за исключением, быть может, двух. Точно так же в любой
ЗАДАЧИ 221
окрестности существенно особой точки любая функция прини-
принимает все конечные значения, за исключением, быть может, од-
одного. В этой формулировке большая теорема Пикара является
существенным усилением теоремы Сохоцкого1).
ЗАДАЧИ
1. Докажите следующее обобщение принципа аргумента: если функция f
мероморфна в замкнутой области D, ограниченной конечным числом непре-
непрерывных кривых, причем на dD нет ни нулей, ни полюсов /, то для любой
функции ф, голоморфной в D,
1
j- J ,
J $
dD k=l k=l
где первая сумма распространяется на все нули, а вторая — на все п о-
люсы функции f в D. При <р=1 получаем принцип аргумента. [Указание:
примените к интегралу в левой части теорему Коши о вычетах.]
2. Пусть f(z) мероморфна в единичном круге U и непрерывна в окрест-
окрестности dU. Доказать, что для любого числа А такого, что |Л|>тах[Д, число
ди
Л-точек в круге V равно числу полюсов._
3. Пусть f(z) непрерывна всюду на С и голоморфна вне некоторого ком-
компакта Кс:С Доказать, что f(K)=f(C\K). [Указание: пусть zo^C\K и
f?=f(z0) на К; тогда нужно рассмотреть функцию g(z)=-^~^— , до-
дог—го
казать, что она имеет конечное число нулей, устранить их и применить прин-
принцип аргумента для непрерывных функций.]
4. а) Найти радиус сходимости ряда A0) из примера в п. 34, который
обращает целую функцию w = ze~az в окрестности точки ш = 0. б) Объяснить,
почему этот ряд имеет конечный радиус сходимости, в) Вывести из б) асим-
асимптотическую формулу Стирлинга для п\ _
5. Пусть fi, ..., fn голоморфны в замкнутой области Д. Доказать, что
функция cp(a:)=|fi(z)|+ ... +|[п(г)| достигает максимума на ее границе dD.
6. Пусть D — полоса <— у < Im г < у> в С. Покажите, что целая функ-
функция ее ограничена на границе области D в С, но не ограничена в D. Од-
Однако всякая равномерно ограниченная в D голоморфная функция / по мо-
модулю не превосходит
sup \f(z)\.
7. Пусть f(z)—голоморфная функция в единичном круге U такая, что
/@) = 1 и |/(г)|<М в U. Покажите, что в круге Iг1^~1ГГ выполняется
неравенство \f{z) — 1|^М • \г\.
8. Докажите, что на поверхности модуля голоморфной функции 1Ф const
внутри всякой замкнутой линии уровня {|/| = с) число минимумов на единицу
больше числа точек перевала.
') Доказательство большой теоремы Пикара (для голоморфных функций)
можно найти в книге А. И. Маркушевича, цит. на стр. 207.
222 ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ [ГЛ. IV
9. Докажите, что всякое голоморфное отображение замкнутого круга О
в себя имеет неподвижную точку. Приведите пример такого отображения, все
неподвижные точки которого находятся на границе круга U.
10. Если f голоморфна в единичном круге U, непрерывна в О и |/(г)| = 1
для всех z^dU, то / — рациональная функция. [Указание. Первый способ:
сначала предположите, что /=^=0 в U, и докажите, что f=const, затем устра-
устраните нули /, не меняя |/| на dU. Второй способ: примените принцип симме-
симметрии.]
11. (Н. Г. Чеботарев). Пусть }(г) голо.юрфна в верхней полупло-
полуплоскости V={\mz>0}, непрерывна в V Л С и f (V) <= V, а / (R) с R. Доказать,
что в этих условиях / — линейная функция. [Указание: по принципу симме-
симметрии / — целая; докажите, что она возрастает на оси х, затем рассмотрите
функцию g(z) = , где х0— единственный нуль f, и докажите, что
z — х0
In g = const.] _
12. Пусть /(г) голоморфна в круге U и постоянна по модулю на его
границе dU. Докажите, что arg f при обходе dU меняется монотонно.
13. Пусть функции /v B круге V голоморфны, отличны от нуля и все
по модулю меньше единицы. Тогда, если /v@)->0, то fv(z) -> 0 равномерно
во всяком внутреннем круге.
14. Докажите, что любой конформный изоморфизм кольца {г]<|г|<Г2} на
кольцо {pi<M<p2} линеен. [Указание: примените принцип симметрии.]
15. Докажите, что любой конформный изоморфизм прямоугольника на
прямоугольник, переводящий все 4 вершины в вершины, линеен.
16. Приведите пример голоморфного (но, конечно, неоднолистного) ото-
отображения кругового кольца на круг и пример такого же отображения круга
на кольцо. _
17. Пусть для функции /: С-> С множество прообразов {г: f(z)=w0)
для любой точки »оеС дискретно, т. е. не имеет предельных точек в С. До-
Докажите, что такая функция не может быть более чем двоякопериодической,
т. е. существуют периоды Wi и а>2 такие, что любой период f имеет вид
o)=n1(Oi+n2CO2, где т и пг — целые числа.
18. Проверьте, что функция KJ=sn (z,k) взаимно однозначно (и конформ-
конформно) отображает прямоугольник {—2K<Rez<2K, —K'<lmz<K'} с отожде-
отождествленными противоположными сторонами на поверхность, которая полу-
получится, если взять два экземпляра плоскости w с разрезами по отрезкам
(—I/ft, —1), A, l/k) и склеить берега разрезов крест-накрест,
ГЛАВА V
ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ
Здесь мы рассмотрим две не связанные между собой темы,
которые, с одной стороны, завершают набор основных сведений
из теории функций одного комплексного переменного и, с другой
стороны, необходимы для теории функций нескольких пере-
переменных.
§ 13. Разложения целых и мероморфных функций
42. Теорема Миттаг-Леффлера. В п. 24 было доказано, что
любая рациональная функция разлагается на сумму некоторого
многочлена (своей главной части в бесконечности) и главных
частей в конечных особых точках. Здесь мы хотим получить ана-
аналогичное разложение для произвольных мероморфных функций.
Через ап {п—\, 2, ...) мы будем обозначать полюсы1) меро-
морфной функции /, а через
п
„(п>
главную часть ее лорановского разложения в полюсе ап.
Если мероморфная функция / имеет лишь конечное число
полюсов, то, вычитая из / сумму ее главных частей в этих полю-
полюсах, мы получим, очевидно, целую функцию h. В этом случае
поставленная задача решается тривиально: функция f разла-
разлагается в сумму целой функции h и своих главных частей. Таким
образом, представляет интерес лишь случай бесконечного числа
полюсов. Здесь вместо конечной суммы мы имеем ряд из глав-
главных частей, и возникает вопрос о его сходимости. Этот ряд, во-
вообще говоря, расходится, и для получения сходящегося ряда
к главным частям приводится вводить поправки, которые, как
мы увидим, можно брать в виде многочленов — отрезков тейло-
тейлоровских разложений главных частей.
') Напомним, что мероморфная функция не может иметь более чем счет-
счетное множество полюсов: в каждом круге {\z\<N}, N.= \, 2, ..., полюсов лишь
конечное число, ибо в противном случае существовала бы их конечная
предельная точка, которая была бы неизолированной особой точкой, а не
полюсом.
224 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
Переходя к точным формулировкам и доказательствам, пре-
прежде всего условимся, что понимать под сходимостью ряда из
мероморфных функций, которые могут обращаться в бесконеч-
ность в некоторых точках.
Определение. Ряд из мероморфных функций назы-
называется сходящимся (соотв. равномерно сходящимся) на мно-
множестве М, если лишь конечное число его членов имеет полюсы
на М и после удаления этих членов ряд сходится (соотв. равно-
равномерно сходится) на М.
Задачу о разложении решает следующая теорема суще-
существования мероморфной функции с заданными полюсами и
главными частями: '
Теорема 1 (Миттаг-Леффлер). Каковы бы ни были
последовательность точек а„еС, lim an = oo и последователь-
П-»оо
ность функций gn вида A), существует мероморфная функция [,
которая имеет полюсы во всех точках ап и только этих точках,
причем главная часть f в каждом полюсе ап совпадает с gn.
< Без ограничения общности можно считать, что ап ф О (ибо
вместо } можно рассматривать функцию f — go, где go — главная
часть f в точке 2 = 0) и что точки ап занумерованы в порядке
неубывающих модулей: |an|<!|an+i| (ft=l, 2, ...). Фиксируем
число q, 0<<7< 1, и обозначим Kn = {z: \г\ <q\an |}. Так как функ-
функция gn голоморфна в круге {|z|<|an|} и Кп компактно при-
принадлежит этому кругу, то gn можно в Кп равномерно прибли-
приблизить полиномом Тейлора
S^T-", B)
степень mn мы выберем так, чтобы для всех z e Кп было
|gl,(z)-Pn(z)!<^r (n=l, 2, ...). C)
При таком выборе Р„ ряд
I>(gnn) f
tt-l
сходится равномерно на любом компакте К из С в смысле опре-
определения 1. В самом деле, для любого К найдется номер JV та-
такой, что К с: Кп Для всех «> VV; члены ряда
/* = S (?»-/>«) D)
lt=N
§ 13] РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИИ 225
голоморфны на /С, и в силу C) этот ряд мажорируется на К
сходящейся геометрической прогрессией. Следовательно, ряд D)
сходится на К равномерно и его сумма fN по теореме Вейер-
штрасса (п. 22) голоморфна в Kn-
Функция / отличается от fN на рациональную функцию
N-1
~2i(gn — Pn) с полюсами ап и главными частями gn (п—\, ...
,..,N—1) и, следовательно, имеет в К заданные полюсы и
главные части. Так как К — произвольный компакт, то / меро-
морфна и имеет в С заданные полюсы и главные части >
Следствие. Любую мероморфную функцию f можно раз-
разложить в ряд
/ = л+2(г„-Л,), E)
я = 1
равномерно сходящийся на любом компакте, где h — целая
функция, gn — главные части f и Рп — некоторые полиномы.
< Занумеруем полюсы / в порядке неубывающих модулей
(точку 2 = 0 можно считать правильной, если вместо f рассмот-
рассмотреть функцию f — g0, где go — главная часть / в этой точке) и
по теореме 1 построим ряд
равномерно сходящийся на любом компакте. Функция f — fo — h,
очевидно, целая >
Примеры. 1. Мероморфная функция ——— имеет полюсы второго по-
порядка в точках ап=пл (я = 0, ±1, ...), причем ее главная часть в полюсе
ап равна gn — ~,—~ w ¦ Ряд из главных частей
со
1
h(z)
(г — ппJ
сходится равномерно на любом компакте (в смысле определения 1), ибо в
любом круге {\z\<R} мажорируется сходящимся рядом 7,-, гтг . По-
¦Ляк (пл — RJ
этому поправочные многочлены Рп в разложении E) не нужны, и остается
найти целую функцию
1 {z) * Ш7 - -и 77^
sin2 г ^J (г — ляJ '
п——о°
Эта функция периодическая с периодом л, поэтому ее достаточно изучить
15 Б. В, Шабат
226 ' ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
в полосе {0<Rez<Tt}. В этой полосе |г —пя|>я(п—1) для п=1, 2, ....
следовательно,
n=m+l
стремится к 0 приг-»-оо в этой полосе. Так как |sin22| = sin2*+sh2y при
этом также стремится к нулю, то и л (г) стремится к нулю при z-> оо,
О<Re 2^Sя. Поэтому Л ограничена в полосе, а в силу периодичности и в С;
по теореме Лиувилля я постоянна и, следовательно, равна нулю. Таким об-
образом, разложение Миттаг-Леффлера имеет вид
оо
т^г^г • F)
2. Мероморфная функция ctg z имеет простые полюсы в тех же точках
пп—пп (я=0, ±1, ...) с главными частями gn——~ • Ряд из главных
частей расходится, но легко видеть, что можно взять поправочные много-
многочлены нулевой степени: ряд
I z-nn +~м
(г — пп) пп
П=—оо П=— оо
(штрих у суммы означает, что при суммировании выпускается индеке/л=0)
сходится равномерно на каждом компакте. Остается найти целую функцию л
в разложении E), что можно сделать так же, как в предыдущем примере;
мы убедимся, что л за 0.
Проще, однако, проинтегрировать . 2 j- по любому пути, соеди-
соединяющему точки 2=0 и 2 и не проходящему через полюсы апФ0. Пользуясь
формулой F), мы получим нужное разложение Миттаг-Леффлера
i- t Ы-Ч-i)
(почленное интегрирование F) законно в силу равномерной сходимости).
Теорема Миттаг-Леффлера и ее следствие являются теоре<
мами существования и не дают информации о том, как факти-
фактически выбирать многочлены Рп и целую функцию к. Для прак-
практических целей полезнее не столь общая, но более конструктив-
конструктивная теорема, при доказательстве которой используется метод
Коши улучшения сходимости.
Теорема 2. Если на некоторой системе окружностей
Yn={|z| =/¦„}, /¦i<r2< • • •, rn—*oo, мероморфная функция f рас-
растет не быстрее, чем zm, т. е. существует постоянная А такая,
что для всех z^yn (n=l, 2, ...)
5 13] РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИЙ 227
то в разложении E) в качестве Рп и h можно принять много-
многочлены степени не выше т.
< Фиксируем любую точку zsC, отличную от полюсов f,
и предположим, что yN содержит z внутри. Функция
Fit)" 1
Fit)" 1_ внутри yN голоморфна всюду, кроме точки ? = 2
и полюсов функции /. Вычет ее в точке z равен f(z), сумму вы-
вычетов в полюсах /, лежащих внутри у^, обозначим через s.
Для подсчета s заметим, что в каждом таком полюсе вычет
функции F совпадает с вычетом функции /^ (?) = -#:—> гДе
Флг (?)= S gn(Z) означает сумму всех главных частей / в полю-
сах, лежащих внутри yN. Функция FN рациональна и кроме
упомянутых полюсов она имеет полюс в точке t, = z с вычетом
фЛ(г), а ее вычет в бесконечности равен нулю, ибо FN имеет
там нуль не ниже второго порядка '). По теореме о полной сум-
сумме вычетов (п. 25) сумма всех вычетов функции FN, т. е.
s + cpN{z)=0, откуда s = — q>N(z) = — 2 gn(z)-
Vn)
Применяя к F теорему Коши о вычетах, найдем
N К NJ
Если бы интеграл в левой части стремился к нулю при
N—+oo, то сходился бы ряд из главных частей / и поправки на
сходимость были бы ненужными. Однако у нас этого, вообще
говоря, нет, и для получения стремящегося к нулю интеграла
нужно под знаком интеграла вычесть из ~г~? начальные члены
ее лорановского разложения в бесконечности, т. е. сумму чле-
членов вида zk+l . Это удобно сделать так: положим 2 = 0 в ра-
равенстве (9) и тех равенствах, которые получаются из него по-
последовательным дифференцированием по z (мы считаем, что
2 = 0 — правильная точка /); получим
1 П(О
2л1 J ?*+1
(*-0.
') Если, конечно, внутри у к есть хотя бы один полюс /.
1*5*
228
ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ
[ГЛ. V
Умножим это равенство на zk и затем вычтем сумму получен-
полученных равенств из (9):
A0)
где
й!
k\
z\
k=0
Наша цель достигнута; в самом деле, оценим левую часть A0),
т. е. величину
* /(?) dj
Х,т US-г)
(мы просуммировали геометрическую прогрессию под знаком
интеграла). Пользуясь неравенствами (8), получаем оценку
lm+l
из которой видно, что RN(z) —»0 при iV—>oo и притом равно-
равномерно на любом компакте >
Пример. Нетрудно видеть, что ctg z ограничен на окружностях
¦I | г | = я(« + -7J-1 >> и = 0 поэтому к функции / (z) = ctg z применима
теорема 2, в которой можно положить т=0. Мы снова получаем разло-
разложение G).
В заключение приведем обобщение теоремы Миттаг-Леф-
флера на случай произвольной области DczC. Без ограничения
общности будем считать, что D содержит бесконечную точку
(этого можно достичь дробно-линейным преобразованием) и
что дйФ0, т. е. что ОфС (в этом случае теорема тривиальна).
Теорема 3. Каковы бы ни были последовательность то-
чек ап е D, не имеющая предельных точек в D, и последова-
последовательность функций gn вида A), существует мероморфная в D
функция f, которая имеет полюсы во всех точках ап, причем
главная часть f в каждом полюсе ап совпадает с gn.
< В случае конечного числа точек ап теорема тривиальна,
поэтому последовательность ап нужно считать бесконечной.
Для каждой ап найдем точку ап s dD, ближайшую к ап (такая
точка существует, ибо непрерывная функция р(?) = |? — а„\ до-
§ 13] РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИЙ 229
стигает минимума на компакте dD)\ очевидно, гп—\ап — <хп\ —*-0
при п—»оо. Для всех ге{|г—ап|>/"„} величину (z— а„)~1
можно разложить в сходящуюся геометрическую прогрессию
z — an z — an — {an — an)
откуда видно, что при \z — an|^2rn функцию (z — ап)~К а
значит, и gn(z) можно с любой степенью точности приблизить
многочленом от переменного (г— an)- Мы подберем много-
многочлены Р„[ ) = Qn(z) так, чтобы при \z — an\^2rn выпол-
\ z — ап /
нялись неравенства
¦-QnB)l<4r. п=\, 2, ... A1)
A2)
(здесь Qn — рациональные функции, голоморфные в D).
При сделанном выборе Qn ряд
сходится равномерно (в смысле определения 1) на каждом
K<^D. В самом деле, для любого такого К найдется число N
такое, что \г — an|^2rn для всех п^- N и всех zeK. Ряд из
голоморфных на К функций
мажорируется на К сходящейся геометрической прогрессией,
и поэтому функция fN голоморфна на /\. Функция / отличается
N- 1
от fN на рациональную функцию 2 (gn ~ Qn), которая в D
п = I
имеет лишь полюсы ап с главными частями gn (n=l, ...
..., N—1) '). Так как К — произвольный компакт из D, то /
удовлетворяет условиям теоремы >
Замечание. Пусть дана произвольная последовательность
точек ап е С и соответствующих функций gn вида A) (если
некоторое an = oo, то соответствующая функция gn является
многочленом относительно г без свободного члена). Пусть
ef—множество всех предельных точек последовательности ап
') Точки а„, в которых эта рациональная функция также имеет полюсы,
не принадлежат D,
230 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
(это множество, как легко видеть, замкнуто). Если в доказа-
доказательстве теоремы 3 выбирать в качестве а„ точку cf', ближай-
ближайшую к ап, то ряд A2) определит функцию /, мероморфную в
дополнении к If (которое является открытым множеством и,
следовательно, состоит из не более чем счетного множества
областей).
43. Теорема Вейерштрасса. Здесь мы рассмотрим разложе-
разложения целых функций на линейные множители, соответствующие
их нулям, аналогичные такому же разложению многочленов:
( J) A)
(через ап мы обозначаем корни многочлена, отличные от нуля;
каждый повторяется столько раз, какова его кратность; через
т оббзначена кратность корня 2=0).
Целые функции в общем случае имеют бесконечное (счет-
(счетное) множество нулей, и мы приходим к необходимости вместо
конечного произведения A) рассматривать бесконечные про-
произведения. Напомним определения и простейшие факты, отно-
относящиеся к таким произведениям. Бесконечное произведение с
комплексными членами
ПA + О B)
называется сходящимся, если все его множители отличны от
п
нуля и частичные произведения П„ = ЦA+сй) имеют предел
17 = lim П„, также отличный от нуля1); число П называется
п ->¦ <*>
величиной произведения B),
Так как 1 + сп = ¦„ " > т0 условие сп-*0 является не-
¦"Л-1
обходимым для сходимости произведения B); оно, конечно,
оо
недостаточно: пример ТТ A + —-]. Для сходимости произведе-
ния B) необходима и достаточна сходимость ряда
iln(l+cn) C)
л-1
') Условие 11=7^0 вводится для сохранения свойства произведений об-
обращаться в нуль, лишь когда один из множителей равен нулю.
§ 13] РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИИ 231
при надлежащем выборе значений логарифмов. В самом деле,
п
пусть ряд C) сходится, т. е. частичные суммы 2„= 2 In (I +ck)
сходятся к конечному пределу 2; тогда частичные произведе-
произведения П„ = es" стремятся к пределу II=es=#0, т. е. B) сходится.
Пусть сходится B), т. е. существует ПтПп=П=?0; выберем зна-
чения логарифмов In Пп так, чтобы In Пп -> In П, а затем по-
положим ln(l + Ci) =1пПь значение 1пA + сг) подберем так, чтобы
ln(l +Ci) + In A + с2) =1пПг и т. д. (считая выбранными значе-
значения ln(l-Hcft) для к=\, ..., п—1, мы подбираем 1пA + с„) так,
я
чтобы 2 In A + ck) = 1пП„). При таком выборе значений лога-
k=i
рифмов Sn=ln Пп->1пП, т. е. ряд C) сходится.
Наконец, бесконечное произведение, множителями которого
служат функции, голоморфные на множестве М, мы будем на-
называть сходящимся на этом множестве, если среди множителей
есть лишь конечное число обращающихся на М в нуль и после
вычеркивания таких множителей произведение оказывается
сходящимся в каждой точке М.
Основной для дальнейшего является следующая теорема
существования целых функций с заданными нулями:
Теорема 1 (К- Вейерштрасс). Какова бы ни была
последовательность точек aneC, liman = oo, существует целая
Л->°о
функция f, которая имеет нули во всех точках ап и только этих
точках, причем порядок нуля f в точке ап таков, сколько чле-
членов, равных ап, имеет данная последовательность.
¦4 Без ограничения общности можно считать, что апф0 (ибо
вместо f можно рассматривать целую функцию -Щ^-, где m —
порядок нуля f в точке г=0) и что точки ап занумерованы в
порядке неубывающих модулей. Подберем натуральные числа
рп так, чтобы ряд
1
r
л=1
равномерно сходился в любом круге {|z|^/?}; для этого до-
достаточно, например, положить рп + 1=п (примените критерий
Коши и воспользуйтесь тем, что а„—>оо).
При таком выборе рп бесконечное произведение
J (S)
232 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ' [ГЛ. V
сходится на любом компакте К из С. Для доказательства
рассмотрим функцию
? p
и заметим, что ее логарифм
при |?|^!<7<1 допускает оценку
i г Р+1
|lng(?, р)К1?Г1A+1?1 + ••¦)<Jfer- 46)
Если теперь обозначить /Си={|г|<<7|ап|}, то для любого
К <?г С найдется номер N такой, что Кcz Кп для всех п^ N.
Для всех таких п в силу F)
и, следовательно, ряд
rt = JV
на /С мажорируется равномерно сходящимся рядом D), т. ё,
представляет голоморфную на К функцию g>(z). Поэтому про-
изведение
оо
I г - \ , , . g., W
f-c I г) 1 — Г I?! —¦ о N
n=JV
сходится и представляет голоморфную и отличную от нуля
функцию на К- Произведение E) отличается от fN множителем
JV=1
ng\ — , Рп\> который обращается в нуль в точках аи ...
..., aN~i и только этих точках.
Так как К — произвольный компакт, то / — целая функция
и имеет заданные нули >
Следствие. Любую целую функцию f можно разложить
в бесконечное произведение, соответствующее ее нулям:
п= 1
( У
~ )еа« рп\ап) t G)
§ 13] РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИЙ 233
где т — порядок нуля f в точке z = 0, g— некоторая целая
функция и числа рп выбраны так, чтобы сходился ряд D).
¦« Будем считать т = 0 (для чего достаточно вместо / рас-
рассмотреть функцию -Ц/г) и расположим нули / в порядке не-
убывающих модулей, повторив каждый нуль столько раз, ка-
какова его кратность. По этим нулям построим по теореме 1 це-
целую функцию
« 1
Отношение -г- является, очевидно, целой функцией без нулей,
/о
поэтому функция g (z) = In / , , неограниченно продолжаема
/о \z)
в С и по теореме о монодромии (п. 28) является целой функ-
функцией. Таким образом, / = e#fo >
Примеры:
, IT , sin г
¦1. Целая функция имеет простые нули в точках а„ = пп («=±1,
V /' z \2
±2,....). Так как ряд Л, \— сходится равномерно на любом компакте, то
можно положить все рп = \, и разложение Вейерштрасса примет вид
где g — некоторая целая функция (штрих у произведения означает, что нуж-
нужно пропустить индекс я = 0). Остается найти g\ а это проще всего сделать,
проинтегрировав разложение ctg г — —, полученное в предыдущем пункте.
Мы' найдем, что g=0, и разложение примет окончательный вид
Л __Це^
ТТ
ЛМ-
(при переходе ко второй форме разложения мы объединили множители с ин-
индексами п и —п, что законно в силу абсолютной сходимости соответствую-
соответствующего ряда). _
2. Целая функция ~=— имеет простые нули в точках а„=игя2 (п —
У г
= 1, 2, ...). Очевидно, можно положить все рп—0, и разложение Вейер-
Вейерштрасса примет вид
л=1
Целая функция g = 0, в чем проще всего убедиться, подставив У г вместо г
во второе разложение (8).
234 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
Приведем без доказательства теорему Адамара, которая
позволяет извлечь некоторую информацию о величинах рп и
функции g, участвующих в разложении G), если известно, как
быстро растет функция /. Чтобы сформулировать эту теорему,
придется ввести понятие порядка целой функции.
Пусть дана целая функция /; обозначим
Af (К) = max |/(z)l. A0)
Если по некоторой последовательности Rn—*oo величина M(R)
растет не быстрее какой-либо степени R, скажем М (Rn) ^ AR™,
где /l=const, то / — полином. Это следует из неравенств Коши
для коэффициентов разложения /(z) = 2 ckzk: имеем
откуда, устремляя п—>оо, находим, что ch=0 при k>m.
Если отбросить этот тривиальный случай, то для оценки
скорости роста M(R) надо взять функции, растущие быстрее
любой степени R- Понятие порядка возникает при сравнении
M(R) с функциями ен*\ Именно, порядком целой функции /
называют нижнюю грань р таких чисел ц, для которых, начи-
начиная с некоторого Ro?=Ro(vi), имеет место неравенство
MiRXeR» A1)
(если таких чисел \i нет, то полагают р = оо и называют / функ-
функцией бесконечного порядка).
Этому определению можно придать более удобную форму.
Число p = inf ^i можно определить еще так: для любого
е>0 M(R)<e*p+\ начиная с некоторого #0(е), М(R)>eRP~?
по некоторой последовательности R = Rn—*°°. Если про-
прологарифмировать дважды эти неравенства, мы получим, что
lnlnAf(fl) . , п , > lnlnM(i?) .
—j v ;<р + е, начиная с некоторого Ro(e), —ln- >p —e
по некоторой последовательности Rn —*°°. Строя такие после-
последовательности R(® для e = -r(k=l, 2, ...), а затем выбирая из
них диагональную последовательность Rn — R^n\ мы увидим,
что по ней —¦. >-р. Поэтому порядок целой функции
тг- ln\n M(R) /)ОЧ
р= hm ¦ j?v ; A2)
формулу A2) можно принять за определение порядка.
$ 13] РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИЙ 235
Пример. Порядки целых функций еаг", sin z, cos Yz и e"Z
соответственно равны ft, 1, т и оо,
Для сравнения скорости роста целых функций одного порядка р вводят
понятие типа. Именно, типом целой функции порядка р называют нижнюю
грань а таких чисел V, для которых, начиная с некоторого Ro=Ro(v), имеет
место неравенство
M(R)<ev*P A3)
(если таких чисел v нет, полагают сг=оо и называют / функцией максималь-
максимального типа; при 0<сг< оо говорят, что f среднего типа, а при сг=О — мини-
минимального типа).
Повторяя рассуждения, проведенные для порядка, можно получить для
типа формулу
_ In M (R)
Rp
Теорема Адамара1). Если f — целая функция конеч-
конечного порядка р, то в ее разложении Вейерштрасса можно при-
принять рп = р — Е(р) и в качестве g взять многочлен степени не
выше ?(р) (через ?(р) обозначается целая часть р).
Пример. Функция порядка 1, следовательно, в ее разложении
Вейерштрасса можно принять g(z)=az + b:
полагая здесь г=0, находим 6 = 0; а так как левая часть и бесконечное про-
произведение— четные функции, то непременно а = 0. Мы доказали, что g^sO.
Приведем теперь обобщение теоремы Вейерштрасса на слу-
случай произвольной области D. Без ограничения общности счи-
считаем, что D содержит бесконечную точку и что граница дйФ0,
Теорема 2. Какова бы ни была последовательность точек
ап е D, не имеющая предельных точек в D, существует голо-
голоморфная в D функция /, которая имеет нули во всех точках ап
и только в этих точках2).
< Последовательность ап считаем бесконечной. Для каждой
точки ап найдем точку а„ е dD, ближайшую к ап; величина
') Доказательство теоремы Адамара можно найти в книге А. И. Марку-
шевича, цит. на стр. 207.
2) Порядок нуля / в точке ап таков, сколько членов, равных а„, имеет
данная последовательность.
236
ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ
[ГЛ. V
Гн = \ап — ап\—>0 при п~*оо. Для всех ге {\z— ап\ >г„] спра-
справедливо разложение
со
!„ z-On_, (. ап-ап\_ V (ап-ап)к
Ш 111A — /х и г
z-an \ г - ап ) -* k(z- anf
k=i
а при \z— а„|>2гг1 оно сходится равномерно по z.
Поэтому при \г — an|>2rn можно выбрать натуральное
число рп так, чтобы было
1П
ь
г - а„ ff, k(z- an)k
При таком выборе рп бесконечное произведение
р" ь
05)
A6)
сходится на каждом Кш D. В самом деле, для любого такого
К найдется число N такое, что \z — ап\>2гп для всех n>iV и
всех z е /С. Ряд из голоморфных на /С функций
n=JV
в силу A5) сходится на К равномерно, следовательно, gN голо-
голоморфна на К, а произведение
голоморфно и не обращается в нуль на К. Поэтому и функция
f, определяемая^произведением A6), голоморфна на К и обра-
обращается на К в нуль лишь в точках а„ е К- Так как /(— произ-
произвольный компакт из D, то / удовлетворяет условиям теоремы >
Замечание. Если предположить, что область D содержит
точку 2=0, которая не является нулем искомой функции f, то
формуле A6) можно придать несколько иной вид. Заменим в
§ 131 РАЗЛОЖЕНИЯ ЦЕЛЫХ И МЕРОМОРФНЫХ ФУНКЦИЙ 237
A6) z на —, ап на ¦— и <х„ на -f-; получим
В частности, если D = C, то надо положить все осп = оо, и тогда
A7) перейдет в формулу Вейерштрасса E).
Мы закончим параграф двумя важными следствиями тео-
теоремы Вейерштрасса. Первое из них выражает связь между ме-
роморфными и голоморфными функциями. Именно, мероморф-
ная в области D функция / в окрестности каждой точки ае D
представляется как отношение двух голоморфных в этой окрест-
окрестности функций: [(г) = ~Щ- (в окрестности правильной точки
Wa \z)
можно принять i|ia(z) = l, а в окрестности полюса i|)a(z) =
= (z— а)Р, где р — порядок полюса). Оказывается, что можно
построить и глобальное представление такого рода, действую-
действующее во всей области D.
Теорема 3. Любую функцию f, мероморфную в области
D, можно представить как отношение двух голоморфных в D
функций (в частности, если D = C, как отношение двух целых
функций).
^'Множество полюсов мероморфной в области D функции
не может иметь предельных точек в этой области (отсюда сле-
следует, что оно не более чем счетно). Пусть ап — последователь-
последовательность полюсов f в D, причем каждый член повторяется в ней
столько раз, какова кратность полюса. По теореме 2 построим
голоморфную в D функцию ф, которая имеет нули во всех точ-
точках ап и только этих точках. Произведение /•т|з = ф, очевидно,
голоморфно в D (каждый полюс погашается нулем i|) соответ-
соответствующего порядка), поэтому / = ~—нужное представле-
представление >
Замечание. Очевидно, что и, обратно, отношение голо-
голоморфных в области D функций является мероморфной в D
функцией. Поэтому эквивалентны следующие два определения:
1) функция называется мероморфной в D, если она не имеет
в D других особых точек, кроме полюсов;
2) функция называется мероморфной в D, если она пред-
ставима как отношение функций, голоморфных в D.
Второе следствие теоремы 2 выражает результат, объявленный
в п. 26. Мы назвали там область D областью голоморфности
238 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
функции f, если f голоморфна в D и не продолжается аналити-
аналитически ни через одну точку границы dD.
Теорема 4. Любая область D сС является областью го-
голоморфности некоторой функции.
¦* Построим последовательность-точек а„ е ?> так, чтобы
она не имела предельных точек в D, но чтобы каждая точка
dD была предельной точкой этой последовательности1). По
теореме 2 строим голоморфную в D функцию /, имеющую точки
ап и только эти точки своими нулями (и, следовательно, не
тождественно равную нулю). Функцию f нельзя аналитически
продолжить ни через одну точку dD, ибо если бы было воз-
возможно такое продолжение в точку а е dD, то а была бы внут-
внутренней точкой области голоморфности функции f, а так как а—
предельная точка нулей /, то по теореме единственности тогда
N0 >
§ 14. Гармонические и субгармонические функции
Мы закончим первую часть описанием двух классов действи-
действительных функций, тесно связанных с голоморфными функциями.
44. Гармонические функции. Определение. Действитель-
Действительная функция и класса С2 называется гармонической в области
D сг С, если всюду в D удовлетворяется уравнение Лапласа
дх2 + ду2 ' {1>
Дифференциальный оператор в левой части A) называется
оператором Лапласа и обозначается символом Д; нетрудно ви-
видеть, что
х 1 ду) \дх +tdy)~ 4 dzdz • (Z)
Связь гармонических и голоморфных функций выражается
следующими двумя теоремами.
Теорема 1. Действительная и мнимая части любой функ-
функции f, голоморфной в области D, являются гармоническими в
этой области.
•* Имеем
') Доказательство существования такой последовательности предостав-
предоставляется читателю.
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 239
откуда видно, что и, оеС2. Далее, -§^ = -j ai"|j:=0 (У нас
-р = 0 в силу голоморфности /, а функция ^4 антиголоморфна)
и аналогично QzQ- = 0 >
Теорема 2. Для любой функции и, гармонической в обла-
области D, локально, в окрестности каждой точки zq e D, можно
построить голоморфную в этой окрестности функцию /, для ко-
которой и является действительной (или мнимой) частью
¦4 Пусть U={\z — zo\ <r} cz D; в силу A) форма
а = — ~- dx + -g^-dy является точной в U (см. п. 15), поэтому
интеграл от со в U не зависит от пути и в U определена функ-
функция
•м-/-?**+?*• (з)
Обычным для действительного анализа способом доказывается,
что v дифференцируема в (/ (в смысле R2) и что ее частные
производные соответственно равны
dv _ _ ди ду _ ди ,.-.
дх ~ ~ду ' ду ~ ~дх ' ^ >
Но это — условия комплексной дифференцируемости функции
f=u+iv, a M = Re/. Функция if = —v+Ju&H(U) имеет и своей
мнимой частью >
Замечание. Если область D односвязна, то это же рас-
рассуждение доказывает существование функции f^H{D), для
которой M = Ref глобально, во всей области D. Для многосвяз-
многосвязных областей теорема неверна.
П р и м ер: в области?>={0< |г| <1} функцияы = 1п| z |= ^ Inzz
гармонична, но условиям D) вместе с и удовлетворяет только
функция v—Argz, определенная в D лишь локально, во всей D
эта функция не определена (она многозначна!).
Установленная связь позволяет распространить на гармони-
гармонические функции некоторые свойства голоморфных функций.
1. Бесконечная дифференцируемость. Любая
гармоническая в области D функция и(х,у) обладает в каждой
точке частными производными всех порядков, которые также
являются гармоническими в D.
•* По теореме 2 строим голоморфную в окрестности U точки
z=x+iy функцию /, для которой u = Re/, и замечаем, чт«»
240 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
^L = ^eff(z), -д—= — lmf'(z). По теореме 1 эти частные произ-
производные гармоничны в U. Применяя к ним уже доказанное, по-
получим существование и гармоничность вторых частных производ-
производных и т. д. >
2. Теорема о среднем. Если функция и гармонична в
круге U' = {?: |? — 2 !</?}, то для любого r<R значение и в центре
круга равно среднему ее значений на окружности {|? — z\—r}:
2л
u(z + re")dt. E)
Доказательство получается отделением действительных ча-
частей в формуле
2л
f(z + reu)dt,
выражающей теорему о среднем для голоморфных функций.
Заметим, что в этой теореме вместо среднего по окружно-
окружности можно брать среднее по кругу U:
¦\\uWo, F)
где da = r dr dt — элемент площади. Для доказательства доста-
достаточно помножить обе части E) на г и проинтегрировать по г
в пределах от 0 до R.
3. Теорема единственности. Если две функции ы4
и U2, гармонические в области D, совпадают на множестве
(? cz D, имеющем хотя бы одну внутреннюю точку, то щ = и«
в D.
< Обозначим и = щ — и2 и рассмотрим множество
(^ = {2eD: u(z)=0}. Открытое ядро $~ по условию непусто;
оно замкнуто в D, ибо если zoeD является предельной точкой
&Г, то существует последовательность г„ е^, lim 2„ = 20, и
функция f=u+'iv, голоморфная в окрестности z0, является мни-
-• О
мой постоянной1), т. е. ы==0 в этой окрестности и zQe.S*. По-
о
этому 4? ^ D >
о
') В рассматриваемой окрестности U найдется точка г„е/, в окрестно-
окрестности VczU которой и se5 0; по уравнениям Коши — Римана в V имеем
-Q-- s= -3— = 0, т. е. V=c=const; тогда f=ic всюду в U,
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 241
Для гармонических функций теорема единственности форму-
формулируется в более слабой форме, чем для голоморфных: тре-
требуется, чтобы множество ef имело не предельную, а внутрен-
внутреннюю точку в D. В такой сильной форме теорема и неверна:
гармоническая в С функция и==х равна нулю на мнимой оси,
не будучи тождественно равной нулю.
4. Принцип экстремума. Если гармоническая в обла-
области D функция и достигает (локального) максимума или ми-
минимума в какой-либо точке Zq e D, то она постоянна в D.
¦Ч Рассмотрим голоморфную в окрестности U точки z0 функ-
функцию f, для которой u = Re/; если и достигает в г0 максимума,
то и модуль голоморфной в U функции ef — также (\ef\=eu);
поэтому /, а следовательно и и, постоянна в U. По теореме
единственности и постоянна и в D. Случай минимума сводится
к случаю максимума, если вместо и рассмотреть функцию
—и >
5. Теорема Л и у в и л л я. Если функция и гармонична
в С и ограничена хотя бы с одной стороны., например: u(z)<M
для всех геС, то u = const. .
•* Так как С односвязна, то существует целая функция /
такая, что u = Ref в С. По условию все значения f лежат в по-
полуплоскости {Re/<M}; пусть Я — дробно-линейное отображение
этой полуплоскости на единичный круг, тогда k°f является це-
целой ограниченной функцией, т. е. константой. Отсюда следует,
что f, а следовательно, и и = const >
6. Инвариантность относительно конформ-
конформных отображений. Если функция и гармонична в обла-
области D и z = z(t) —конформное отображение D* на D, то слож-
сложная функция u°z(?) гармонична в D*.
< Рассмотрим произвольную точку ?0 е D* и ее образ
Zo = z(t,o), в окрестности z0 строим голоморфную функцию / та-
такую, что « = Ref; тогда «°2(t)=Re/° г(?), а так как функция
/°г(?) голоморфна в окрестности ?0, то m°z(?) гармонична в
этой окрестности >
В следующем пункте мы покажем, что теорема о среднем
характеризует гармонические функции, т. е. что справед-
справедлива
Теорема 3. Если конечная в области D функция и, ло-
локально интегрируемая по площади, в каждой точке 2ЕЙ для
всех г-СгоB) совпадает со своим средним по кругу
{ \\}
sk {{ G)
то она гармонична в D.
16 Б. В. Шабат
242 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
Сейчас мы воспользуемся этой теоремой для доказательства
одного утверждения о пределе последовательности гармониче-
гармонических функций, которое понадобится в дальнейшем изложении.
Теорема 4 (Харнак). Предел убывающей последова-
последовательности гармонических в области D функций uh (Л=1, 2, ,,,)
является либо гармонической в D функцией, либо тождественно
равен —оо.
¦4 Пусть сначала и всюду конечна в D; по теореме о среднем
для гармонических функций uh в любой точке z^.D
(8)
для всех r<ro(z), где ro(z) — расстояние от z до dD. В силу
монотонности последовательности uh в (8) можно перейти к
пределу при k -> оо, и мы получим
причем функция и локально интегрируема по площади. По тео-
теореме 3 отсюда следует, что функция и гармонична в D.
Пусть теперь и=—оо в какой-либо точке zo^D. Обозначим
<? = {z^D: u(z)=—оо}; это множество непусто, ибо содержит
г0. Оно открыто: пусть 2ie?° и расстояние от z4 до dD равно
2р; мы имеем
и, следовательно, для любого ге -j | z — zi I < 2 Г
(lSК)
(lS-гКр)
ибо круг {|? — z|'<p} содержит круг \| g — zx |<-| >; таким об-
образом, ] i 2 — 2, К"!"}-^^. Точно так же доказывается и за-
замкнутость У (в топологии ?>), Поэтому <?=D, т.е. ы^—оо
в D >
В заключение этого пункта укажем, что понятие гармонично-
гармоничности распространяется на функции любого числа действительных
переменных. Пусть D — область в л-мерном евклидовом про-
пространстве Rn« Функция ы: D^*R класса С2 называется гармо-
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 243
нической в D, если в каждой точке х = (хи .,,, xn)^D удовлет-
удовлетворяется уравнение Лапласа
±%-0. (9)
Для таких функций остаются справедливыми свойства 1—5 гар-
гармонических функций двух переменных. Эти свойства нуждаются
в специальных доказательствах (ибо приведенные нами доказа-
доказательства основаны на свойствах голоморфных функций), но мы
на них не будем останавливаться.
45. Задача Дирихле. В ряде вопросов анализа используется
задача о гармоническом продолжении функций; мы рассмотрим
эту задачу в простейшей постановке.
Задача Дирихле. Задана односвязная область D с= С
с жордановой границей dD и на dD задана непрерывная функ-
функция и. Требуется гармонически продолжить и в область D, т. е.
построить непрерывную в D и гармоническую в D функцию, ко-
которая на dD совпадает с заданной.
а) Единственность. Покажем, что задача Дирихле не
может иметь двух различных решений. В самом деле, пусть
существуют два решения щ и ыг._Тогда их разность v — ui — и2
гармонична в D, непрерывнее D и равна нулю на dD. Если
максимум или минимум и в D достигается в D, то по_принципу
экстремума v = const в D, а в силу непрерывности и в Л; так как
и==0на dD, то в этом случае уг=О в D. Если же обе эти вели-
величины достигаются на dD, то они равны 0 и опять у=0 в D.
б) Редукция к кругу. Предположим, что задача Ди-
Дирихле разрешима для единичного круга U={\z\<\), и покажем,
что тогда она разрешима и для любой односвязной области D с
жордановой границей dD. В самом деле, по теореме Римана су-
существует конформное отображение /: D—*U, непрерывно про-
продолжаемое в D по принципу соответствия границ (п. 39). Пусть
на dD задана непрерывная функция и; зададим на dU значения
v = u°f-{ и обозначим через v гармоническое продолжение этих
значений в U (оно по предположению существует). Тогда функ-
функция u — v of по свойству 6 предыдущего пункта будет гармониче-
гармонической в D; она непрерывна в Л, а на dD равна u°f-l_°f—u, т. е«
решает задачу Дирихле для D.
в) Решение для круга. Начнем с эвристических сооб-
соображений. Пусть задача Дирихле для единичного круга U и
граничных значений и решена. Построим голоморфную в U
функцию f, имеющую решение этой задачи своей действитель-
действительной частью, Предположим еще, что / непрерывно продолжается
16*
244 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
в U1), тогда в любой точке z&U по формуле Коши
т
Преобразуем правую часть A) так, чтобы ее действительная
часть содержала лишь известные значения Re/ = u на dU. Для
этого возьмем точку 2* = — , симметричную с z относительно dUt
г
воспользуемся теоремой Коши
[Шdt m
2ni J ?-2*
dU
и вычтем B) из A). Так как |?| = 1 и можно положить Z,—eu,
dtt=itsdt и, кроме того,
=
Z-z ?-z* \-l,z
то будем иметь
2Л
Мы достигли поставленной цели: отделяя здесь действитель-
действительные части, получим так называемую формулу Пуассона
2я
где положено еще 2 = ге1ф.
Правая часть формулы Пуассона известна, если заданы зна-
значения и на dU\ покажем, что функция и, определенная в U по
этой формуле, решает задачу Дирихле для круга.
Прежде всего заметим, что ядро интеграла Пуассона
PIT г)- ' \-г2 ,
у<°' ^' 2л 1 - 2r cos (/- <р) + г2
после несложных преобразований (с учетом того, что |?|=1)
можно представить в виде
pit ~\~ 1 '-И2 _ 1 п 1+? (л\
') Это предположение относится к lm/, так как Re/ решает задачу Ди-
Дирихле и, значит, непрерывна в f, ч
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 245"
Поэтому функция и, определяемая интегралом Пуассона, яв-
является в U действительной частью функции
2я
u®J~dt, E)
голоморфной в Ul), и, следовательно, гармонична в U. Остает-
Остается показать, что при z, стремящейся по точкам U к произволь-
произвольной точке go e dU, значение и (г) стремится к «(go).
Для доказательства заметим, что для любой точки 2Е[/
2я
J P(?, z)dt=l. F)
о
Это следует из доказанного выше: функция ы=1 — единствен-
единственное решение задачи Дирихле с граничными данными и=\, и она
удовлетворяет условиям, в которых выведена формула Пуассо-
Пуассона. Далее,
HmP(g, z) = 0 при g?=g0. гЕ[/, G)
причем сходимость равномерна по g на любой дуге у a 6U, не
содержащей какой-либо окрестности точки go, — это видно из
формулы D) (ее средней части).
На основании F) разность между значением и и ее предпо-
предполагаемым пределом при z—>t,0 = eiU равна
2л 2л
А = J и (?) Р (?, z)dt-u (У = | {и (?) - и О Р (?, 2) d/. (8)
о о
Фиксируем е>0 и, пользуясь непрерывностью u(g) в точке go,
выберем б>0 так, чтобы при \t — to\^C2b было
<e; (9)
обозначим Yi = {?e^^^ l^ — ?о|^26} и yz = dU\.y\ и разобьем
интеграл в (8) на интегралы по дугам Yi и Y2- Для первого из
:) Голоморфность функции E) можно доказать дифференцированием под
знаком интеграла: для любой г е(/ имеем
2Я 2Я
Цд__1_ Г g^ Аг Г g« (?) <f/
откуда видно, что при Дг->0 левая часть стргмится к нулю, т. е. суще-
существует f'(z).
246 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ
них в силу (9) при любом ге(/ имеем
J {и(С)-и(Со)}/*(С z)dt
Vi
2л
, z)dt<z[
Yi
[ГЛ. V
, z)dt = e
A0)
(мы воспользовались положительностью ядра Р и равенством
F)).
Теперь положим z=rel<f и будем считать, что [ф — /о|<6;
в силу G) найдется р, 0<р<1, такое, что
1, г)<в
для всех ?^Y2 и всех г, для которых |ф — ^ol<6, 1>г>1—р
(мы воспользовались равномерностью предельного перехода
G)). Поэтому для всех z из области G,
заштрихованной на рис. 74, имеем
l,z)dt
< 2Л1 Г Р (?, z) Л < 2Afe • 2я, (И)
Уг
где М=тах|ыE) |. Объединяя A0) и
Рис. 74.
A1), получим, что для всех геб спра-
справедливо неравенство |А|< A+,4яАГ)е, а
это нам и нужно.
Доказана
Теорема 1. Любую функцию и, непрерывную на границе
dD односвязной жордановой области D, можно единственным
образом гармонически продолжить в D. В частности, для еди-
единичного круга U эта задача решается интегралом Пуассона C),
Заметим, что для круга {|z|<i?} интеграл Пуассона имеет
вид
2л
« в) ^-
dt>
где z = rei(f, %=Reu\ это. получается из доказанного простой
заменой переменных.
В качестве примера применения гармонического продолже-
продолжения приведем доказательство теоремы 3, сформулированной в
предыдущем пункте. Пусть конечная') в области D функция и
') Разумеется, что функция и предполагается локально интегрируемой
ло площади.
5 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 247
в каждой точке гей совпадает со своими усреднениями по кру-
кругам достаточно малых радиусов r<ro(z):
A3)
Отсюда прежде всего вытекает, что и непрерывна в каждой точ-
точке zoeD, ибо при бесконечно малых г— z0 разность u(z)—u(z0)
представляется интегралом по области бесконечно малой пло-
площади (от интегрируемой функции) и, следовательно, эта раз-
разность бесконечно мала.
Фиксируем произвольную точку zo^D и круг U—{\z — zo\<.
R}D no теореме 1 построим функцию h, гармоническую
в U, непрерывную в U и равную и на dU. Нам достаточно пока-
показать, что u=h в U. Так как h по теореме о среднем также удо-
удовлетворяет соотношению A3) при любом ге!7 и {j?—z\<r)aU,
то и функция v = u — h удовлетворяет ему. Из этого следует, что
если v достигает локального максимума или минимума в какой-
либо точке Zi&U, то она постоянна в некоторой окрестности Zi.
Докажем это утверждение для максимума (в случае минимума
доказательство аналогично). Пусть это не так, т. е, v(z)-^i.v(zi)
в круге V—{\z~ Zij <r}, VczU, причем существует точка
г2 е V, в которой v(z2) <v(zi). В силу A3)
B|) = -нк J j°
но в силу непрерывности v существует окрестность точки г2, в
которой v-Cv(Zi)—е для достаточно малого положительного е,
а так как y-^y(zt) всюду в V, то правая часть последнего ра-
равенства строго меньше величины
полученное противоречие доказывает утверждение.
Непрерывная функция v достигает в U своего, максимума М
и минимума т. Если оба экстремума достигаются на dU, где v ==0,
то М = т = 0 и и==0 в U — теорема доказана. Пусть один иа
экстремумов, скажем максимум, достигается в U, тогда множе-
множество ^—{z^U: v{z)—M) непусто. По доказанному она откры-
открыто, а так как v непрерывна в U, то оно в то же время и замк-
замкнуто (в топологии U). Отсюда следует, что W = U_, т. е. v===M
в U; из непрерывности заключаем, что v^=M в U, а так как
и = 0 на dU, то опять и==0 в U, и теорема доказана полностью.
В заключение заметим, что задача Дирихле разрешима
и для пространственных областей при некоторых условиях»
248 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
наложенных на ее границу1). В частности, для «-мерного шара
B={j:eR": \x\<R) эта задача решается при помощи интеграла
Пуассона
дВ
пппП
где <х„ =—-, rR" — площадь «-мерной сферы дВ, a da —
Г(-И
элемент поверхности дВ в точке у (Г обозначает гамма-функцию
Эйлера; ГB) =1, поэтому G2 = 2nR, и при /г = 2 эта формула сов-
совпадает с A2), если еще за-менить da = Rdt). Формула A4) вы-
выводится из формулы Грина2).
46. Субгармонические функции. Логарифм модуля голоморф-
голоморфной функции f является гармонической функцией лишь в окре-
окрестности точек, где f Ф 0, а в нулях lnj/| обращается в —оо, т. е.
теряет гармоничность. Сейчас мы введем более общий класс
субгармонических функций, который, в частности, будет содер-
содержать и логарифмы модулей голоморфных функций.
Одномерным аналогом гармонических функций являются ли-
d2h
нейные функции h(x) =kx + b, для которых-^-у = 0. При помощи
линейных функций можно определить выпуклые функции сле-
следующим образом: функция и(х) называется выпуклой (вниз),
если для любого отрезка [а, р] из области ее определения
и любой линейной функции h(x) из неравенств h(a)^u(a),
п(Р)>«(|3) следует неравенство h(x)^- и(х) для всех х е [а, C].
Субгармонические функции являются двумерным аналогом
выпуклых функций. Они не обязаны быть всюду непрерывны-
непрерывными— можно ограничиться лишь требованием полунепрерывности.
Определение 1. Действительная функция и, —оо ^ и< оо,
определенная в окрестности точки z0, называется полунепрерыв-
полунепрерывной сверху в этой точке, если для любого е > 0 найдется б > 0
такое, что
(и {г) — м(го)<е, если и{гй)=? — оо,
|г-го|<б#-| 1 A)
\u(z)<— —, если u(za)=-oo,
или, что эквивалентно,
lim u(z)^u(z0). B)
') По этому поводу см.: М. В. Келдыш, О разрешимости и устойчи-
устойчивости задачи Дирихле, Успехи матем. наук, вып. 8 A941), 171—292.
2) См. книги: И. И. Привалов, Субгармонические функции, ОНТИ,
М., 1937 и В. С. Владимиров, Методы теории функций многих комплекс-
комплексных переменных, «Наука», М., 1964.
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 249
Если D — область, то функция и: D—*[—оо, оо), полунепре-
полунепрерывная сверху в каждой точке z e D, называется полунепрерыв-
полунепрерывной сверху в этой области. Нетрудно видеть, что для полуне-
полунепрерывности сверху функции и в области D необходимо и до-
достаточно, чтобы для любого ае(—оо, оо) множество меньших
значений {z e D: u(z)<a} было открытым.
Обычным образом определяется полунепрерывность функции
на множестве и доказывается, что функция, полунепрерывная
сверху на компакте К, ограничена сверху и достигает на К
своего наибольшего значения. '
Определение 2. Функция и: D—>[—оо, оо) называется
субгармонической в области D, если 1) она полунепрерывна
сверху в D и 2) для любого достаточно ^алого круга U и лю-
любой гармонической в U и непрерывной в U функции h
h> и на dU=$h> и в U. C)
Такую функцию h будем называть гармонической мажорантой
функции и для круга U.
Отметим несколько простых свойств субгармонических функ-
функций1), которые подчеркивают их аналогию с выпуклыми функ-
циями.
Теорема 1. Если субгармоническая в области D функция
и достигает локального максимума в некоторой точке zo e D,
то она постоянна в некоторой окрестности z0.
•* Пусть и не постоянна ни в__какой окрестности г0- Тогда
найдется достаточно малый круг U cr D такой, что u(z) ^Cu(z0)
для всех ге?/,ав некоторой точке ?i окружности dU=y спра-
справедливо строгое неравенство ы(^) <u(zo). В силу полунепре-
полунепрерывности сверху функции и для достаточно малого е>0 най-
найдется дуга у' cz у, на которой ы(?)<ыB0) — е.
Возьмем дугу у" Шу' и построим непрерывную на у функцию
h(Q, положив ее равной u(z0) —е на у", равной u(z0) на y^y'.
а на дугах y'^y" пусть она линейно зависит от arg(? — zo)—t.
Тогда на у будет н^/г, и по определению субгармоничности
(Z)dt, D)
у
где h(z)—гармоническое продолжение h{t,) в U (см. предыду-
предыдущий пункт). Но правая часть D) строго меньше u(zo)—проти-
u(zo)—противоречие доказывает теорему >
Следующая теорема показывает, что локальное свойство
субгармоничности, выражаемое определением 2, влечет за собой
соответствующее свойство в целом.
') Подробнее см. книгу И. И. Привалова, цит. на стр. 248,
250. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
Теорема 2. Если функция и субгармонична в D и область
G шБ, то для любой функции h, гармонической в G и непре-
непрерывной в U, ¦ -
h>u на dG=$,h>u в G. E)
¦* Положим v = u — А; так как эта функция полунепрерывна
сверху в U, то она достигает в U своего наибольшего значе-
значения М; требуется доказать, что М^.0. Обозначим Ж—
= {геE: v(z)=M); по теореме 1 это множество открыто, а в
силу полунепрерывности v оно также и замкнуто в G. Если оно
пусто, то М достигается на 0G, где v ^ 0, поэтому М -^ 0. Если
У непусто, то ^«=G, и тогда vs=M в G, а в силу полунепре-
полунепрерывности v = М и в G; опять М•<0, ибо о<0 на 6G >
Функцию А, удовлетворяющую условию E), будем называть
гармонической мажорантой функции и для области G.
Теорема 3. Если субгармоническая в области D функция
и в некоторой точке z0 области Gm D совпадает со своей гар-
гармонической мажорантой h для G, то и&= h в G.
< Функция v = u — h субгармонична и неотрицательна в G;
поэтому в каждой точке геб, где v = 0, она достигает локаль-
локального максимума. Множество «? —{z^G: v(z) =0} Непусто (оно
содержит z0), по теореме 1 оно открыто, а в силу полунепре-
полунепрерывности и в то же время и замкнуто в G. Поэтому «? =G >
Следствие.. В условиях теоремы 1 функция и постоянна
во всей области D.
Теорема 4. Пусть иа, где индекс а пробегает некоторое
множество А, — семейство функций, субгармонических в обла-
области D. Если верхняя огибающая семейства, u(z) =sup«a(z)
полунепрерывна сверху1), то она субгармонична в D.
•* Нужно проверить лишь условие 2) в определении субгар-
субгармонической функции. Пусть круг U <ш D, а гармоническая в U
и непрерывная в U функция h <?¦ и на dU. Тогда h ^ иа на dU
для всех as Л, а так как иа субгармоничны, то Л>иа и в U
для всех а е Л. Отсюда следует, что и h i> и в U >:
В предыдущем пункте мы доказали, что гармонические функ-
функции характеризуются тем, что их значение в каждой точке равно
их среднему значению по окружности (или кругу) с центром в
этой точке. Приведем аналогичное свойство и для субгармони-
субгармонических функций, конечно, с заменой равенства соответствую-
соответствующим неравенством.
Теорема 5 (критерий субгармоничности).
Для того чтобы полунепрерывная сверху в области D функция и
') Если множество Л конечно, то это условие выполняется автоматически.
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 251
была субгармонической в D, необходимо и достаточно существо-
существование для каждой точки z&D такого числа го(г)>О, что для
всех г<г0
2п
u(z + re")dt. (в)
б
•* а) Необходимость. Пусть и субгармонична в D, z —
произвольная точка D и г0 — расстояние от z до 3D. Так как и
полунепрерывна сверху, то для любого г<г0 существует сходя-
сходящаяся к и на окружности у — {?: |? — z\=r} убывающая после-
последовательность непрерывных на у функций ukl). Обозначим
через hk гармоническое продолжение uk в круг ?/ = {?: |?—z\<r).
Так как на dU=y имеем ый+1(^)-^ы^(^), то по принципу мак-
максимума такое же неравенство имеет место и для гармонических
функций hk в U, т. е. последовательность hk убывает в U. По-
Поэтому в U определена функция
которая по теореме Харнака (п. 44) либо гармонична в U, либо
тождественно равна —со.
По теореме о среднем для гармонических функций
-re")dt;
переходя к пределу под знаком интеграла (что законно в силу
монотонности), получим, что
Ы*)=-ш] u(z + re")dt.
Если Ъше—оо в U, то там и и =—оо, т. е. F) выполняется
тривиально. В противном случае из субгармоничности и и не-
неравенств u^.hh на dU заключаем, что u(z)*Chk(z) для всех.
/г= 1, 2, ,.., и в пределе при к—>оо получаем, что
2Я
u\z)^n\z)- 2п j и \г + re )at.
Необходимость критерия доказана.
') В качестве таких функций можно, например, взять
«*(?)= max {и (?')-*! ? — ?'!}, А=1, 2, ...,
представляем читателю доказать, что m непрерывны на у и что
252 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
б) Достаточность. Пусть и полунепрерывна сверху в D
и удовлетворяет условию F). Обозначим через h функцию, гар-
гармоническую в круге U <ш D, непрерывную в U и такую^что К>и
на dil. Функция v = u — h полунепрерывна сверху в U, причем
по условию F) и теореме о среднем для гармонических функ-
функций для любой точки z^U и достаточно малых г
2Я
и (г) - A (z) < J- J {«B + reu) -h{z + re")}dt,
о
или
Полунепрерывности и этого свойства достаточно для того,
чтобы для v в круге U было справедливо утверждение теоре-
теоремы 1. Поэтому если М — наибольшее значение v в U, то множе-
множество cf={2e?/: v(z)=M} открыто; в силу полунепрерывности
оно и замкнуто в U. Дальнейшее доказательство идет, как в
теореме 2: если cf пусто, то М достигается на dU и, следова-
следовательно М 4^.0; если «f непусто, то Ж = U и опять М ^. 0 >
Функция h, определяемая в круге U формулой G), назы-
называется наилучшей гармонической мажорантой функции и для
этого круга.
При помощи этого критерия легко доказывается утвержде-
утверждение, сделанное в начале пункта:
Следствие. Если функция f голоморфна в области D,
то функция ы=1п|/| субгармонична в этой области.
¦4 Полунепрерывность функции и очевидна. Если z0 e D не
является нулем f, то Ln f допускает выделение голоморфной
ветви в некоторой окрестности г0; функция « = 1п|/| является
действительной частью этой ветви и, следовательно, гармонична
в этой окрестности. Критерий F) выполняется в точке z0 тогда
(со знаком равенства) по теореме о среднем. Если f(zo)=O, то
u(zo) ——°о и критерий F) выполняется в точке 20 тривиально >
В заключение докажем одну теорему о верхнем пределе по-
последовательности субгармонических функций, которая будет
нам нужна во второй части и которая выражает свойство рав-
равномерности предельного перехода при условии равномерной
ограниченности функций последовательности.
Теорема 6 (Хартогс). Если функции uh субгармоничны
в области D, равномерно ограничены на каждом компактном
подмножестве Due каждой точке D
(> (8)
k ->оо
§ 14] ГАРМОНИЧЕСКИЕ И СУБГАРМОНИЧЕСКИЕ ФУНКЦИИ 253
то для любого множества Кш D и любого е>0 найдется номер
ko, такой, что
uh(z)'<A-fe (9)
для всех ге К и всех k ^ k0.
¦4 Без ограничения общности можно считать, что функции
равномерно ограничены в D, ибо К погружается в область
D' Ш D, на которой uk равномерно ограничены по условию.
Можно также считать, что uk^C0 в D, ибо вместо uk можно рас-
рассматривать функции uk — М, где М — верхняя грань всех ukBD.
Пусть Кш D и расстояние от К до dD равно Зг. Для любой
точки 20е/( из критерия субгармоничности uk мы заключаем,
что
)< J J UbiQdo1). A0)
Воспользуемся теперь леммой Фату2), по которой для лю-
любой ограниченной последовательности измеримых на множе-
множестве Е функций Uh- —оо-^Ый <1 с<оо
lim ukda«^ lim ukda.
к^-оо JEJ JEJ fe->oo
По этой лемме в силу (8)
Tim f f uk @ da < Аяг2;
следовательно, для любого е>0 найдется k0 такое, что при
всех k ^ ka
\\ ( )r2. A1)
Пусть теперь z — любая точка круга {\z — 20|<б}, где б<г.
Так как круг {|? — z\<r+6}m D, то по свойству субгармонич-
субгармоничности
JJ
{IE-zKr+в}
') Для получения неравенства A0) достаточно умножить обе части F)
на г dr и проинтегрировать по г от 0 до г0 (см. п. 44).
2) См., например, В. С. В л а д и м и р о в, цит. на стр. 248. -
254 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
а так как этот круг содержит {|? — 20|<г} и у нас мА-<0, то
в силу A1)
JJ
l
Выбирая б (при фиксированных А, г и е) достаточно малым,
получим, что для всех ге{|г— ?О|<6} и всех k^
Пользуясь леммой Хейне — Бореля, получаем утверждение тео-
теоремы >
Заметим, наконец, что наряду с субгармоническими рассмат-
рассматривают также супергармонические функции — двумерные анало-
аналоги функций, выпуклых вверх. Это — полунепрерывные снизу1)
в области D функции «:?>—> (—оо, оо], для которых для любого
круга U щи и любой функции /г, гармонической в (/ и непре-
непрерывной в U, неравенство и!>/г на 6U влечет за собой такое же
неравенство в U. Изучение таких функций сводится к изучению
субгармонических функций, ибо для супергармоничности функ-
функции и необходимо и достаточно, чтобы функция —и была суб-
субгармонической.
Если всюду заменить гармонические функции двух (действи-
(действительных) переменных такими же функциями п переменных
(см. п. 45), то можно рассматривать субгармонические и супер-
супергармонические функции в областях пространства R™.
ЗАДАЧИ
1. Пусть дана произвольная последовательность точек ояеС, сходя-
сходящаяся к бесконечности. Доказать, что для любой последовательности чисел
4„еС можно найти целую функцию / такую, что f(an) =6„ для всех п= 1,2,...
2. (Теорема Адамара о трех кругах.) Доказать, что если { голоморфна в
{п <;|2| </2) и Af/(/-)=max |/(г)|, то \пМ/(г)—выпуклая функция от р = 1пл,
|г|=г
т. е. для любого re (n, Гг)
(Указание: подобрать а так, чтобы r"^f (ri) = r2^f (гг) и к многозначной
функции га/(г) с однозначным модулем применить принцип максимума.)
3. Доказать, что если f — полином степени п, то
М, (г,) ^ Mf (r2)
Г1 Г2
для любых 0<п<л2. Равенство имеет место лишь для f(z)=c0zn.
') Функция и называется полунепрерывной снизу в точке г0, если функ-
функция —и полунепрерывна сверху в этой точке.
ЗАДАЧИ 255
4. Пусть f —целая функция и as (О, I)—фиксированное число. Дока-
М/(аг)
зать, что Iim „ ... равен 0, если f трансцендентна, и равен а", если
f — полином степени не выше п.
00
5. Пусть f {z) = 2 спгп- целая функция нМ/ (г) < Иг для всех г^го;
доказать, что | сп I =С (—— I m Для всех достаточно больших п. (Указание;
\ п ]
Mf(r)
в неравенствах Коши | сп | < —„— взять такое г, чтобы оценка была
наилучшей; для этого найтн минимум правой части по г.)
оо . "
в. Если f(z)= 5j CnZ"—целая функция и I сп\ ^ I 1 m для всех
iPo \ n J
то М/(г)<е(Л+е)г для любого е > 0 и всех достаточно больших г. (Ука-
заиие: М/ (г)<^] | с„ |гп<2 (^^) " г" + ^п (г), где полином \Р„ доба-
п=0 п=0
влен, чтобы компенсировать конечное число членов, для которых п < п0.
(а+^Аг п
Имеем |/>„(г)|<еч ' , а заменяя— ближайшим целым к, получим
°° JL. °°
Л I—етг \т ^сУ/уг™ , где С —некоторая константа. По фор-
/ й \ * /—— / е \ *
муле Стнрлинга (зад. 4 к гл. IV) У 2nk I— ~ k\, а К2я* < 1 + -дт-
для достаточно больших *, поэтому оценка продолжается так:
{(л+т;)'я]ш
k=0 )
оо
7. Из зад. 5 и 6 следует, что порядок целой функции / (г) = 2 сп?п есть
Пусть
a
— тип
функции
Р =
= Iim -
f; доказать, что
I /
(еар)р =
Iim V
п
п
п.
In
т—
\с
1
р 1
п
—г
¦п\
п
У\ сп 1
П -> оо
Построить целую функцию f данного порядка р и данного типа а, (Ответ;
n-l
256 ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ [ГЛ. V
8. Доказать, что а) не существует голоморфной на R1 функции, отобра-
отображающей R ' на множество с внутренними точками; б) существует целая
функция, отображающая R ' на всюду плотное подмножество С.
9. Пусть D — область в С и последовательность ее точек ап не имеет
предельных точек внутри D. Доказать, что для любых последовательностей
комплексных чисел Ьп и целых чисел kn>0 найдется функция /, голоморф-
голоморфная в D и такая, что для каждого п функция /(г)—Ьп в точке а„ имеет
нуль порядка kn.
10. В кольце SK целых функций задана топология равномерной сходимо-
сходимости па ограниченных подмножествах С. Доказать, что для любого собствен-
собственного замкнутого идеала /с=^"его остов {г: f(z)—O для всех /е/} является
непустым множеством без предельных точек в конечной плоскости.
11. Доказать, что для всякого замкнутого идеала / cz ffC найдется функция
ge/ такая, что I = gSf{ (другими словами, идеал / имеет одну образующую).
12. Привести пример функции ф, гармонической в круге U={x2+y2<.x},
непрерывной в ^\{0}, равной нулю всюду на dU\{0} и не равной нулю то-
тождественно. (Пример показывает, что освобождение одной только точки гра-
границы от условий может привести к неединственности решения задачи Дирих-
Дирихле. Ответ: ш=1 —Re —.1
2 )
13. Если у — гладкая кривая, а функция ц непрерывна на у, то действи-
действительная функция
= J n
называется логарифмическим потенциалом с плотностью ц. Доказать, что
а) ф гармонична вне у; б) если у — окружность {|z| = a} и |х=1, то-ф> по-
постоянна в круге {|г|</-}. '•
14. Пусть ф гармонична в верхней полуплоскости {Imz>0} и равна нулю
всюду на оси х. Доказать, чго <f = ay, где а— неотрицательная константа
(ср. с задачей 11 гл. IV). ••
15. Дано, что /(г) и zf (г) — комплексные гармонические функции (т. е.
комплекснозначные функции, удовлетворяющие уравнению Лапласа). Дока-
Доказать, что f — голоморфная функция.
16. Если гармонические функции <pv положительны в области D и ряд
2фу сходится хотя бы в одной точке «еД то он сходится равномерно на
компактах из D.
17._Пусть ф — действительная функция, гармоническая в замкнутой об-
области D, за исключением конечного числа точек из D, в которых она рав-
равна — оо. Доказать, что зирф = 5ирф.
D до
18. Доказать, что необходимое и достаточное условие субгармоничности
функции феС2 выражается неравенством
. <Э2ф , <Э2ф . .
Дф = -j-ir + -3-5- > 0.
^ дх2 ду2
19. Если функция ф субгармонична, а функция и на R1 выпукла, то их
суперпозиция ы°ф является субгармонической функцией.
20. Доказать, что предел убывающей последовательности субгармониче-
субгармонических функций является субгармонической функцией.
21. Пусть f — комплексная гармоническая в области D функция. Дока-
Доказать, что если |/|=const в fi, то и /=const.
ЧАСТЬ II
ФУНКЦИИ
НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
ГЛА ВА I
ГОЛОМОРФНЫЕ ФУНКЦИИ
НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пожалуй, главную трудность для начинающего при пере-
переходе к изучению функций нескольких комплексных переменных
представляет отсутствие простых, наглядных геометрических
представлений. Поэтому мы с самого начала отметим особенно-
особенности комплексного пространства и подробно опишем ряд простей-
простейших областей в нем.
§ 1. Комплексное пространство
1. Пространство С". Рассмотрим четномерное евкли-
евклидово пространство R2n, точками которого являются упорядочен-
упорядоченные наборы 2« действительных чисел (xit ..., х2п)- Мы введем
в нем комплексную структуру, положив zv=xv+4xn+v (v =
= 1, ..., п). Часто мы будем обозначать xn+v—yv, так что
zv = xv + iyv (v=l, ..., п). Пространство, точками которого яв-
являются упорядоченные наборы п (конечных) комплексных чисел
z=(zb ..., zn)={zv}, A)
мы будем называть «-мерным комплексным пространством и
обозначать его символом О. В частности, при п=\ мы полу-
получаем С1=С— плоскость комплексных чисел. Можно считать,
что при любом п пространство Сп является произведением п
комплексных плоскостей
С" = С X ... X С B)
п. раз
Таким образом, точки «-мерного комплексного пространства
С" — это точки 2«-мерного действительного пространства R2™.
Однако введение комплексной структуры в R2n сразу вводит
в этом пространстве асимметрию — не все координаты в
нем равноправны (например, х4 и хп+1 мы объединяем в ком-
комплекс гь a xi и х2 не объединяем).
Следствием такой асимметрии является, в частности, то,
что не все плоскости при переходе от R2n к Сп оказываются
равноправными. Рассмотрим, например, 2г-мерную плоскость
In
П2г: 2 <Wv = Рц (ц = 1, . •., 2л - 2г), ч C)
17*
260 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
где a^v и Рц — действительные постоянные и уравнения неза-
независимы, т.е. rank(a№v) —2п — 2г. Полагая, как выше, zv =
—xv+ixn+v (v=l, ..., п), будем иметь
^ * • •» *^/»
и поэтому мы сможем переписать уравнение этой плоскости в
виде
2 Kvzv + a;v2v) = Ь» (ц = 1..... л - г,) D)
где а , a^v и Ь^ — комплексные постоянные1).
Среди всех таких плоскостей выделим те, в уравнения ко-
которых не входят переменные zv; такие плоскости будем назы-
называть (комплексно) r-мерными аналитическими плоскостями.
Следовательно, по определению уравнением r-мерной аналити-
аналитической плоскости будет
п
Ar: 2aUv2v=&n (ц= 1, ...,«-г). E)
Только аналитические плоскости будут «настоящими» пло-
плоскостями пространства С™, другие плоскости из R2n ( в частно-
частности, все нечетномерные плоскости) не следует считать плоско-
плоскостями из С™. Например, в С2 множество точек, описываемое
уравнением Zi=Xi + ix3 = 0 (т. е. двумерная плоскость {^ = 0,
х3 = 0) из R4), считается плоскостью, а множество Xi+4x2 = Q
(т. е. двумерная плоскость {xi = 0, x2 = 0} из R4) не считается.
Комплексно (п—1)-мерные аналитические плоскости zv = 0
мы будем называть координатными плоскостями. Комплексно
одномерные аналитические плоскости называются еще аналити-
аналитическими прямыми. Аналитические прямые, проходящие через
заданную точкуz° = (zi, ..., 4)-еС", можно записать уравне-
уравнениями
т .
где «veC — некоторые постоянные (не все равные 0). Обозна-
Обозначая общую величину отношений в F) через ?, мы можем пере-
переписать уравнение аналитической прямой в параметрической
форме:
L: zv = <J + cDv? fteC;v=l л). G)
*) Чтобы перейти от системы C) к D), мы сложили ц-е уравнение C)
с (п — г+|х)-м, умноженным на i, и сгруппировали коэффициенты при
«v и г v.
§ 1] КОМПЛЕКСНОЕ ПРОСТРАНСТВО 261
В С™ естественно вводится структура векторного простран-
пространства: под суммой векторов г'={гН и z"=\z"\ понимается век-
вектор г' + z" = {z'v + z"}, и под произведением вектора z = {zv}
на число ЛеС — вектор kz={Xzv}.
Пользуясь этими операциями, мы можем записать уравнения
аналитической прямой в векторной форме:
L: z = z° + <o?, (8)
где (о=(о)ь ..., (i)n)eCn — направляющий вектор прямой, а
?еС — параметр. Таким образом, аналитическая прямая — это
линейная вектор-функция комплексного переменного ? со значе-
значениями в комплексном пространстве (L: С—>СП).
В С™ можно ввести структуру метрического пространства.
Обычно рассматривают две метрики: евклидову метрику
e(z', z"), или
/~~ /"&
2|<-<|2 = У S«-O2. О)
и еще одну метрику —
p(z', z") = max|z?-z?|, A0)
которую мы будем называть р-метрикой. Очевидно, что р-мет-
рика, как и евклидова, удовлетворяет обычным аксиомам:
а) p(z', z") =p(z", z') —аксиома симметрии;
б) p(z', z")>0 при г*Фг", p(z, z)=0;
в) p(z', z"')-<lp(z', z")+~p(z", z"')—аксиома треугольника.
В соответствии с этими метриками в С™ вводятся и топо-
топологии1). Это делается указанием системы окрестностей: в ев-
евклидовой метрике под е-окрестностью точки г° понимается шар:
В (г°, е) = {геСп: | z - z° |< e}, A1)
а в р-метрике^—поликруг (или полицилиндр):
U(z°, 6)={геС: p(z, г°)<е}. A2)
Очевидное двойное неравенство
р(г', г")<| г' - z" |< Yn P (zf, z") A3)
показывает, что метрики (9) и A0) вводят в О эквивалентные
топологии.
В заключение этого пункта опишем коротко компактифи-
кацию пространства С", т. е. пополнение его бесконечными
') Подробнее об этом см. начало следующей главы (п. 9),
262 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
элементами. Наиболее простой способ компактификации приво-
приводит к так называемому пространству теории функций О. Мы
уже говорили, что С" можно рассматривать как произведение п
комплексных плоскостей С. Но плоскость С присоединением
бесконечной точки пополняется до замкнутой плоскости С, го-
меоморфной сфере (п. 1 ч. I). Естественно поэтому пополнить
С" до произведения п замкнутых плоскостей (сфер)—так мы
и приходим к пространству теории функций
С" - СХ ... X С. A4)
п раз
Таким образом, по определению точками О являются упо-
упорядоченные наборы из пточек, принадлежащих замкнутым пло-
плоскостям С. Бесконечными (несобственными) точками будут те
точки, хотя бы одна координата которых является бесконечной.
Множество всех бесконечных точек О естественным образом
разбивается на п множеств Mv={zeC: zv = oo, г^еС, цфу).
Точки из МУ имеют, следовательно, вид (г1( ..., zv_i, <х>,
zv+i, ..., zn), где z^ (\i4=v)—конечные или бесконечные ком-
комплексные числа. Каждое Mv, а значит и множество всех беско-
бесконечных точек Сп, имеет комплексную размерность п—1. Все
Mv пересекаются в точке (оо, .. ., оо).
Топология в С™ вводится, как в произведении пространств:
под окрестностью точки z = {zl} e Cn понимается произведение
окрестностей точек z^ в замкнутых плоскостях переменных zv.
В этой топологии пространство С" оказывается компактным: из
каждой последовательности точек г^еС" (ц=1. 2, ...) можно
выбрать подпоследовательность, сходящуюся к некоторой точке
г°е=Сп1)-
Другой способ компактификации С™ приводит к так назы-
называемому комплексному проективному пространству Рп. Введем
в пространстве О однородные координаты (щ, ..., ып+\), по-
положив
v=l, .... л, lcoHl/ilcDvP^o). A5)
Однородные координаты точки геСп определяются с точностью
до множителя пропорциональности (т.е.наряду с (coj, ..,, o&n+i)
') Компактность С^ доказывается совсем просто. Можно также вос-
воспользоваться тем, что С" является произведением компактных множеств —?
замкнутых сфер.
§ i] КОМПЛЕКСНОЕ ПРОСТРАНСТВО 263
координатами точки г будут и (Хац taon+i). где Х'ФО— лю-
любое комплексное число). Обратно, любому набору однородных
координат (coi, ..., ©n+i), где ©n+i=?0, по формулам A5) соот-
соответствует точка zeCn (причем координатам с разными отноше-
отношениями A5) соответствуют различные точки). Чтобы устранить
особое положение последней однородной координаты ©п+ь мы
пополним С™ несобственными (бесконечными) точками, и тогда
любым наборам однородных координат ©=(соь ..., ton+i),
|о)|т^0, будут соответствовать точки некоторого пространства
Рп, которое и называется комплексным проективным простран-
пространством. Точкам Рп, для которых сои+1=?0, по формулам A5) соот-
соответствуют точки геС, поэтому Рп действительно пополняет
jCn. Точкам и, для которых соп+1 = О, отвечают бесконечные (не-
(несобственные) точки.
Точнее, точками Р" служат не сами наборы со=(©ь ,,,
• ••, ©n+i), 1 со \фО, а классы эквивалентных наборов, если счи-
считать, два набора со' и со" эквивалентными, когда координаты
ю^.и со" пропорциональны (©" = Я©^, КФОу В самом деле, лю-
любому представителю такого класса эквивалентности (для кото-
которого юп+1=?0) мы ставим в соответствие одну точку z e С™, при-
причем представителям различных классов эквивалентности сопо-
¦ставляются различные точки. Такие классы эквивалентности
можно наглядно представить при помощи аналитических пря-
прямых в пространстве Cn+1. Действительно, эквивалентные наборы
(О=(со1, ..., ©ra+i), |©|=?0, характеризуют аналитическую пря-
прямую в Cn+1:
-?L= ... =I"±L A6)
проходящую через начало координат (замена ш любым Я©,
КФО, не меняет прямой; неэквивалентные со определяют раз-
различные прямые). Поэтому и точки из Ри лучше представлять
как такие прямые. В частности, любая аналитическая прямая
A6), для которой con+i=O, представляет бесконечную точку.
Хорошо известна модель проективной плоскости, которая
получается из сферы в R3 отождествлением диаметрально про-
противоположных точек (пересечения сферы с прямыми из R3,
изображающими точки проективной плоскости). Точно так же
можно представлять при помощи сферы из Rn+1 и действитель-
действительное n-мерное проективное пространство. Мы опишем вкратце
соответствующую модель для Рп.
Так как каждая аналитическая прямая из О+1, проходящая
через начало, вполне характеризуется единичным вектором
©° = -ру, то Р" можно представлять как множество точек сфе-
сферы 5 = {|г| = 1} из Cn+I. При этом, однако, следует отождествить
264 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ I
точки пересечения 5 с аналитической прямой, изображающей
точку Рп. Пусть такая прямая L задается параметрическими
уравнениямиzv = co°? (v=l, ..., п+ 1, |(о°| = 1); так как уравне-
п + \
нием сферы 5 служит 2 2vzv=l, то для точек пересечения L
п + \
и S будем иметь | S I2 *2 | ш° |2 = 1, или | ? | = 1 • Отсюда видно, что
L я S пересекаются по одномерному множеству — окружности
{i?l = l}. лежащей на (двумерной) аналитической прямой и на
Bп+1)-мерной сфере. Таким образом, точки Ри можно еще
представлять как окружности на единичной сфере 5cCn+I (это
находится в соответствии с тем, что Рп имеет действительную
размерность 2п). В частности, окружности, которые получаются
в пересечении S с прямыми L, для которых con+i = O, представ-
представляют бесконечные точки.
В пространстве Ри можно ввести топологию, объявляя
«близкими» те прямые L, которые определяются «близкими»
единичными векторами ©° (или те окружности на S, которые
получаются при ее пересечении с «близкими» прямыми). В этой
топологии Рп оказывается компактным пространством.
2. Простейшие области. Здесь мы опишем некоторые простей-
простейшие примеры областей в пространстве С". Под областью, как
всегда, понимается открытое связное множество, причем откры-
открытость множества означает, что каждая точка принадлежит ему
вместе с некоторой окрестностью, а связность открытого мно-
множества означает возможность связать каждые две его точки z'
и z" путем z(t): /-*Cn, где / = [0, 1] —отрезок действительной
оси, z(t)—непрерывная функция, г@)=г', z(\)—z", причем
для любого t^I точка z(t) принадлежит этому множеству.
1. Ш а р радиуса г с центром в точке йе О определяется как
множество точек
В (a, r)={zzaCn: \z — a\<r). A)
Это — шар с центром а в евклидовой метрике. Границей шара
дВ служит Bп— 1)-мерная сфера
vv
v=l
в пространстве R2n.
2. Поликруг (или полицилиндр) радиуса г с центром
сеС" определяется как множество точек
I/(a, r)={zeCre:|zv — av\<r, v=l,...,«}. B)
§ IJ КОМПЛЕКСНОЕ ПРОСТРАНСТВО 265
Это —шар с центром а в метрике р. Он представляет собой про-
произведение п плоских кругов радиуса г с центрами в точках av.
Можно рассматривать и более общий случай поликруга с цен-
центром а и векторным радиусом г— {г\, . . . , гп):
U(a, г)={геС": \zv — av\<rv, v=l, ...,«}. C)
Границей d(J поликруга является множество всех точек, у ко-
которых хотя бы одна координата zv принадлежит границе v-ro
круга, образующего U, а остальные координаты z^ (|x?=v) про-
произвольно меняются в замкнутых кругах. Эта.граница естествен-
естественным образом разбивается на п множеств
=rv, \zu — а„.\ <г
каждое из которых представляет Bга—1)-мерное образование
(ибо 2га координат точки z связаны одним действительным соот-
соотношением \zv — av\ =rv). Поэтому и вся граница поликруга
п
3U = \JTV является Bп—1)-мерной. Все множества Tv пере-
v = l
секаются по га-мерному множеству
Г={г: \zv — av\=rv, v=l, ..., га},
которое называется остовом поликруга и представляет собой
произведение п окружностей.
Опишем подробнее бикруг радиуса 1 с центром в начале:
Это четырехмерное тело является пересечением двух цилиндров:
х\ + х\<\ и х\ + х\<\.
Граница его — трехмерное тело dU = T[l)T2, где F1={|zi| = l,
j 221 -^. 1} — также трехмерное тело, которое расслаивается в од-
нопараметрическое семейство кругов: Г1 = (J {г, = е('8, | г21^ 1},
е=о
и Г2 — аналогичное тело. Остов бикруга Г = Г'ПГ2 двумерен.
Это — тор r = {|zi| = l, 1221 = 1}; в самом деле, отображение
Zi=eie', Z2 = eie> гомеоморфно преобразует на Г квадрат
{О -^01-^ 2л, 0^92-^2я} с отождествленными, как указано на
рис. 75, противоположными сторонами (ибо e{^v+2lt) = eiev), a
такое отождествление дает тор. Тор Г расслаивается на одно-
параметрические семейства окружностей {2i = ei9', :|г2| = 1} и
{|2i| = l, г2 = е'9'}, О-<0Ь 02<2л (на рис. 75 изображено по одно-
одному представителю каждого семейства). Он служит пересечением
266
ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ. !
двух трехмерных цилиндров {а;2 + л|=П и (лг| + л:| = 1 ] и, оче-
очевидно, лежит в R4 на (трехмерной) сфере [х\ + х\ + х\ + х\ = 2}*>
Таким образом, бикруг геометрически следует представлять
так. Нужно взять в С2 (трехмерную) сферу {|2|=Vz} и на
ней выбрать тор r={|2i| = l, |z2| = l}. На этот тор нужно натя-
натянуть два трехмерных тела Г1 = {|21| = 1, |г21^1}_и r2={|zi|-^l,
|г21 = 1}, лежащих в шаровом слое {l <I| г|^ У2 }; их совокуп»
ность Г1 U Г2 и будет ограничивать бикруг.
Рис. 75.
3. Поликруговые (или полицилиндрические)'
области вС" определяются как произведения п плоских об-
областей:
D)
(поликруги являются частными случаями таких областей). Если
все Dv — односвязные области, то D гомеоморфна шару. Гра-
Граница 3D поликруговой области D разбивается на п множеств
размерности Bп—1):
zv<=dDv,
Общей частью всех Fv является /г-мерное множество
v, v=l, ..., n},
которое называется остовом поликруговой области D.
4. Области Рейнхарта (или п-к р у г о в ы е области) с
центром в точке cg Cn определяются как области, обладающие
следующим свойством: вместе с каждой точкой z°= {г°| области
I]
КОМПЛЕКСНОЕ ПРОСТРАНСТВО
267
принадлежит и любая точка
z = {av + B° ~ flv) eif)v}, 0 Ov < 2я.
Область Рейнхарта с центром в а называется полной, если
вместе с каждой точкой z° ей принадлежат и все точки z = {zv},
для которых \zv — av\ =^)г° ~~ av|. v= 1, ..., /г.
Очевидно, что шары и поликруги являются полными обла-
областями Рейнхарта. При п=\ неполными областями Рейнхарта
будут кольца {r<\z— a\<R}, а полными областями—круги
{\z-a\<R}.
Без ограничения общности можно считать, что центр области
Рейнхарта а = 0 (это достигается сдвигом). Такая область вме-
вместе с каждой точкой {zv} содержит все точки с теми же \zv\,
¦v=l, .... п, и всевозможными аргументами. Учитывая это заме-
замечание, мы можем рассмотреть отображение
z-*a(z) = (\zi\, ..., \zn\) E)
2п-мерного пространства О в n-мерное пространство Rn, точ-
точнее, в так называемый абсолютный октант R" == R+ X ... X R+,
п раз
где R+=[0, оо)—полуось неотрицательных чисел. Это отобра-
отображение а; С" -> R" преобразует область Рейнхарта D во множе-
множество точек fl+cR", которое мы будем называть изображением
(или диаграммой) по Рейнхарту области D. Если D—-полная
область Рейнхарта, то D+ вместе с каждой точкой {|г°|\ содер-
содержит весь прямоугольный параллелепипед {|zv|^|2°|, v= I, ..., п\.
Описанная диаграмма полностью характеризует области
Рейнхарта, а понижение размерности на п единиц для п=2
и я = 3 делает это изображение наглядным. На рис. 76 и
268
ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[Г Л I
77 изображены соответственно диаграммы Рейнхарта шара
{|z|<l} и поликруга {|zv|<l} для я = 2 и 3; на втором из них
показаны множества Fv и остов Г.
Рис. 77.
Кольцо
б. Области Хартогса (или полукруговые области)
с плоскостью симметрии {zn = an} определяются как области, об-
обладающие следующим свойством: вместе с каждой точкой
z°=[z°j области принадлежит и любая точка z = (z°l, ..., z°n_u
ап + {z°n — ап) е' «), 0<9„<2я. Область Хартогса называется
полной, если вместе с каждой точкой z° ей принадлежат и
все точки z, для которых zv = z®
(v=l, ..., п— 1), a \zn — an\<
Очевидно, что области
составляют более широкий
класс, чем области Рейнхарта ').
Области Хартогса с плоскостью
симметрии {г„ = 0} можно изобра-
изображать в пространстве размерности
Bп— 1), если воспользоваться пре-
преобразованием р: Cn->Cn~'X R+,
определяемым формулой
г-»Р(г)={2ь ..., г„_ь |г„|}. F)
Для краткости письма обозначим через 'г= (гь . .. , zn-\) проек-
проекцию точки z в пространство Сп~' и через 'D проекцию D в С™
(т.е. совокупность всех 'г для геО). Изображение палной об-
') Термин «полукруговые области» относится к начальному периоду, ког-
когда теория функций нескольких комплексных переменных была в основном
теорией функций двух переменных. Такие области обладают «круговым свой-
свойством» по одному переменному, т. е. половине всех переменных в С2.
У,
§1]
КОМПЛЕКСНОЕ ПРОСТРАНСТВО
269
ласти Хартогса вместе с каждой точкой ('г°, \zQn |) содержит
весь отрезок {('z°, |гя|): |г„|<|2°)}.
Диаграмма Хартогса понижает размерность на 1 и при п = 2
является вполне наглядной. На рис. 78 изображена неполная
область Хартогса; следует иметь в виду, что точка на этой диа-
диаграмме изображает окружность, а вертикальный отрезок, опи-
опирающийся на 'D, — круг. На рис. 79 изображены шар из С2 и
х.
бикруг; на рисунке хорошо видны трехмерные куски границы
Г1 и Г2 и остов Г бикруга.
6. Трубчатые (или цилиндрические) области
определяются как области, обладающие следующим свойством:
вместе с каждой точкой z° = |z°] области принадлежит и любая
точка 2 = {z° + /yv], — oo<yv<oo, v=l, ..., п. Любую трубча-
трубчатую область можно представить в виде произведения BxRn(y),
где В— так называемое основание области — некоторая область
n-мерного действительного пространства Rn(x), х = (хь ..., хп),
a Rn(y)—действительное пространство точек у={У\ уп)-
Таким образом, трубчатая область полностью характеризуется
ее основанием В — областью «-мерного действительного про-
пространства.
Положив z=x+iy, где х и у — действительные n-мерные век-
векторы, трубчатую область можно символически записать в виде
Т = В + iRn{y) или, подробнее, Т = {х + iy: xeB, у е Rn}.
При п=\ трубчатыми областями будут, очевидно, полосы
{а<х<р, —оо<(/<оо}, а также полуплоскости {х>а} или {х<а}.
Заметим, что отображение ф: zv->eZy (v= I, ..., п) преоб-
преобразует трубчатую область Т в некоторую область Рейнхарта D.
При этом основанию области В соответствует D+ — изображение
D на диаграмме Рейнхарта.
7. Полутрубчатые области составляют более широкий
класс областей, чем трубчатые. Это области, которые вместе с
270 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. t
каждой точкой {'г°, 2°} содержат все точки {'z°, z°n + iyn},
—оо<^п<оо. Иными словами, полутрубчатая область D — это
область вида G+'iRl(yn), где G — область в Bп—1)-мерном
пространстве С" ('г) X R'(*n). Подробнее:
D = {{'z, 4)еС»: ('г, *„)е=О, «/„е= R1}.
§ 2. Понятие голоморфности
3. Определение голоморфности. Пусть в области Z)czCn за-
задана комплексная функция /: D-* С. Пользуясь понятиями
окрестности, введенными в пространстве теории функций Сп и
замкнутой плоскости С, мы обычным образом определяем по-
понятия предела и непрерывности / в точке z°^D и в области D
(см. п. 3 ч. I).
Чтобы ввести дальнейшие ограничения на функцию /, пред-
предположим, что D состоит из конечных точек (DczO) и что f
принимает в D лишь конечные значения (/: D-*-C). Предполо-
Предположим, что / дифференцируема в точке z^D в смысле действи-
действительного анализа (в смысле R2n), т. е. что существует диффе-
дифференциал ')
df-JLdxl + ...+1*LdXbt. . A)
Введя комплексные переменные zv и zv по формулам
_ zv + zv _ zv — zv ,_.
мы можем формально переписать A) в виде
df = ?idzl+...+jLdzn + -ll-dzi + ...+-§-ndzn, C)
где положено для v = l, ..., п
JL=L(JL-i-JL-\ df \ I df , ¦ df \ ,
dzv 2 \ dxv dxn+v}' dzv 2 \ dxv ^ dxn+v )' ^>
Определение 1. Функция /, определенная в некоторой
окрестности точки ге С", называется дифференцируемой в этой
точке в смысле комплексного анализа (в смысле С"), если она
дифференцируема в ней в смысле R2™ и в этой точке
?L (v=l n), E)
dzv
') Как и в случае одного переменного, мы считаем f=u+iv и под df и
df ... ди . dv
•д— понимаем соответственно du+idv и -г \-i-=—.
оху dxv dxv
§ 2] ПОНЯТИЕ ГОЛОМОРФНОСТИ 271
т. е. дифференциал имеет вид
df~§Ldzl+...+-g-dzlg. F)
Заметим, что условия E) комплексной дифференцируемое™
содержат 2п действительных уравнений относительно двух дей-
действительных функций (u = Ref и u = Imf). Таким образом, при
м>1 эта система дифференциальных уравнений переопреде-
переопределена: число уравнений в ней больше числа рассматриваемых
функций. С некоторых точек зрения в качестве пространствен-
пространственного аналога комплексной функции одного комплексного пере-
переменного естественнее рассматривать не одну, а п комплексных
функций от комплексных переменных, т. е. вектор-функцию
/= (/ь ..., /„) вектора z= (zu ..., zn). Однако и это не спасает
положения: записывая условия E) для каждой компоненты fv,
мы получим систему 2п2 действительных уравнений относительно
2п действительных функций, т. е. систему, также переопреде-
переопределенную при п>1.
Переопределенность условий комплексной дифференцируе-
мости функций нескольких переменных влечет за собой ряд
принципиальных отличий пространственной теории от плоской;
с некоторыми из них мы познакомимся в дальнейшем изложе-
изложении. Отметим, что переопределенные системы играют важную
роль в теории уравнений с частными производными и что си-
система E) является одним из основных примеров таких систем.
Определение 2. Функция, дифференцируемая в смысле
О в каждой точке некоторой окрестности точки г°е Сп, назы-
называется голоморфной в точке z°. Функция, голоморфная в каждой
точке некоторого открытого множества QoC" (в частности,
области), называется голоморфной на множестве Q.
Заметим, что при определении понятия голоморфности на
произвольном (не обязательно открытом) множестве М имеется
тонкость, которая видна из следующего примера.
Пример. Пусть множество МаС2 состоит из двух замкну-
замкнутых шаров fi,={|z-@, 1)|<4} и fi2 = ||z + @, 1)|<y}'
соединенных отрезком L = \zl = 0, z2 = x2, \x2\^.-^->. Опреде-
Определим на М функцию
ги гей,,
О, 2<=L, G)
Она, очевидно, непрерывна на М, и для каждой точки
можно построить окрестность ?/2», в которую / продолжается,
272 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
как голоморфная функция. В самом деле, для точек В\, включая
точку @, •„-) пересечения Bt и L, в качестве таких окрестностей
можно ззять шары, не пересекающие?я с В% и продолжить в них
f, положив ее равной z\. Для точек В2 сделаем аналогичное по-
построение, только положим f{z)~—Z\. Наконец, для внутренних
точек L возьмем шары, не содержащие концов этого отрезка, и
положим в них /=0. Однако из теоремы единственности, кото-
которую мы докажем в п. 6, следует, что f нельзя продолжить до го-
голоморфной функции ни в какую связную окрестность Q всего
множества М. В самом деле, из этой теоремы следует, что не
существует голоморфной в Q функции, которая на одном шаре
из Q равна zu а в другом —z4.
Из этого примера видно, что необходимо различать локально
голоморфные на множестве функции, которые в каждой точке
множества можно локально продолжить до голоморфной функ-
функции, и функции глобально голоморфные, которые продолжаются
до функций, голоморфных в окрестности всего множества. В даль-
дальнейшем, говоря о голоморфности функции на множестве, мы,
как правило, будем иметь в виду глобальную голоморфность.
Очевидно, сумма и произведение двух функций, дифферен-
дифференцируемых (в смысле С") в некоторой точке z, также дифферен-
дифференцируемы в этой точке, поэтому дифференцируемые в точке функ-
функции образуют кольцо. В частности, функции, голоморфные
в некоторой области DczCn, образуют кольцо, которое мы бу-
будем обозначать символом H(D).
Справедливо также правило дифференцирования сложных
функций, которое мы сформулируем в следующих двух видах.
Пусть функция f дифференцируема в смысле С™ в точке z° = (г0},
а ш° = /(г°).
(I) Если функция ф дифференцируема в ш° в смысле С, то
Ф ° / дифференцируема в смысле С™ в точке z°.
(II) Если функции фу (v=l, ..., п) дифференцируемы в
смысле Ст в точке ?°, причем фу(?°) = г°, то функция /°ф =
=/(фь . . . , фп) дифференцируема в смысле О в точке ?°.
В частности, пусть / голоморфна в некоторой области DczCn
и z = L(t,)—аналитическая прямая, пересекающаяся с D (т. е.
совокупность линейных функций zv = z° + a>v?, v=l, . . . , п, пе-
переменного ?еС таких, что хотя бы одно значение z^D). Тогда
сужение /на эту прямую (т. е. сложная функция /°L(f;)) го-
голоморфно, как функция одного комплексного переменного на
том открытом множестве плоскости ?, которое попадает в D
при отображении L.
Еще более частный случай мы получим, если рассмотрим
аналитические прямые, «параллельные v-й оси», т. е. прямые
§ 2] ПОНЯТИЕ ГОЛОМОРФНОСТИ 273
zv = ?, z[l = z°tl (ц =И= v). Для этого случая сделанное только что
утверждение означает, что если / голоморфна в области DczCn,
то функция f(z°, .... z°_,, ?, г°+1, ..., z°) будет голоморфной,
как функция одного комплексного переменного, на соответствую-
соответствующем открытом множестве плоскости ?,. Иными словами, функция,
голоморфная в области DczCn, является голоморфной (в смысле
С) функцией по каждой координате zv в отдельности1).
Оказывается, что справедливо и обратное утверждение: если
функция / в некоторой области DczCn голоморфна по каждому
переменному zv в отдельности, то она автоматически будет диф-
дифференцируемой в О в смысле R2n по совокупности переменных
и, следовательно, голоморфной в смысле определения 2. Этот
важный факт составляет содержание так называемой основной
теоремы Хартогса и является далеко не тривиальным. Нетри-
Нетривиальность этой теоремы видна хотя бы из того, что ее дей-
действительный аналог неверен. В самом деле, из существования
частных производных функции действительных переменных не
следует даже непрерывности этой функции. Вот хорошо извест-
известный пример: функция f{x, у) = 2Х]*_ 2 , f@, 0)=0, разрывна в
начале координат, хотя ее частные производные (всех порядков)
всюду существуют. В некотором смысле теорема Хартогса пред-
представляет собой аналог утверждения о том, что функция несколь-
нескольких переменных, которая является многочленом по каждому
переменному, будет многочленом и по совокупности переменных
(см. задачу 16 в конце главы).
Теорему Хартогса мы докажем в п. 5. Здесь же мы приведем
перечень элементарных свойств голоморфных функций несколь-
нескольких переменных, аналогичных свойствам функций одного пере-
переменного. Впрочем, нам удобнее вместо голоморфности рассма-
рассматривать более общее условие:
(А) Функция f непрерывна в области DczCn no совокупности
переменных и в каждой точке z°^D голоморфна по каждой ко-
координате.
(Мы сейчас же убедимся, что из этого условия вытекает и
дифференцируемость по совокупности переменных, т. е. голо-
голоморфность функции. После доказательства теоремы Хартогса
станет ясным, что требование непрерывности излишне, ибо оно
вытекает из голоморфности по каждому переменному.)
Г. Если функция f удовлетворяет условию (А) в замкнутом
поликруге U = {z е О: \zv — av\^.rv}2), то в каждой точке U
') Этот вывод следует также непосредственно из определений 1 и 2.
2) Это означает, что f продолжается до функции, удовлетворяющей усло-
условию (А) в некотором открытом полукруге, содержащем V.
18 Б. В. Шабат
274 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. t
она представляется кратным интегралом Коши
Hz>—®arj -;-J (E,-Zi)...(b,-Ze)' (8)
где Г — остов поликруга, т. е. произведение граничных окруж-
окружностей yv={\lv~av\=r'v).
•^При любом 'ze't/, где 'г и 'U обозначают проекции г и U
в пространство Cn~' (zi, ..., 2n-i), функция f=f('zt'zn) голо-
голоморфна по ?„ в круге {\zn — flnl-^^n}; следовательно, по инте.
гральной формуле Коши из ч. I
При любом ?,„^у„ и любом 'ze'C/ функцию, стоящую под зна-
знаком интеграла, можно представить интегралом Коши по пере-
переменному 2n_i, причем в силу непрерывности f по совокупности
переменных повторный интеграл можно представить как крат-
кратный по произведению Yn-iXYn- Продолжая это рассуждение,
мы и придем к (8) >
В дальнейшем мы будем записывать формулу (8) в сокра-
сокращенном виде:
где будем считать dt,=dt,i ... dt,n и -=—- = 7г—7~\ 7т 7Т-
Так же как в ч. I, из представления функции интегралом
Коши выводится возможность разложения ее в степенной ряд.
Для этого разложим ядро интеграла (9) в кратную геометриче»
скую прогрессию:
1 VI (z-a\k
1А|о
где k=(k\, ..., /г„)—целочисленный вектор, \k\=k{+\. .'±^kn,
kv > 0 и
zn-a \kn
Разложение это можно переписать в виде
2] ПОНЯТИЕ ГОЛОМОРФНОСТИ 275
где A+]l = (fcf+'l, <.., fen+1); при любом z^U он« сходится
абсолютно и равномерно по ? на Г. Умножая его на непрерыв-
непрерывную (и, следовательно, ограниченную) на Г функцию ^.^ и ин-
интегрируя по Г почленно, мы и получаем нужное утверждение:
2°. Если функция f удовлетворяет условию (А) в замкнутом
прликруге U, то в каждой точке z^U она представляется крат-
кратным степенным рядом
f(z)= 2 ck{z-af A0)
I k 1=0
с коэффициентами
* Г f(s)rfs (in
где k= (kit .,, ,kn)—целочисленный вектор (&v^>0) и (г — a)h =
= (z1-a1)fe'...(zra-aj4
3° (Теорема Абеля). Если степенной ряд A0) сходит-
сходится в какой-либо точке ?еО, то на любом множестве
К <^{z: \zv — av\<\%v — av|} этот ряд сходится абсолютно и
равномерно.
¦4 Из сходимости ряда в точке ? следует ограниченность его
членов в этой точке: |сй(? — a)k\K-М для всех &= (kit ..., kn),
kv ^ 0. Обозначим
kv
max l^-flvl =q @<<7v<l, v=l, .... n);
тогда в любой точке z^K будет |сй(г —a)fe|^^ cfe(g — a
где qk = q\l ... qknn. Остается заметить, что кратная про-
прогрессия 2 Mqk сходится >
Так как члены степенного ряда непрерывны по совокупности
переменных, а дифференцирование по любому переменному zv
не нарушает его сходимости, то из 2° и 3° следует
4°. Если_функция f удовлетворяет условию (А) в замкнутом
поликруге U, то в каждой точке z^U она имеет частные произ-
производные всех порядков, непрерывные по совокупности пере-
переменных.
В частности, отсюда следует, что любая функция, удовле-
творяющая условию (А), дифференцируема по совокупности
переменных, т. е. голоморфна, а также что все частные произ-
производные голоморфной функции голоморфны.
Обычным образом доказывается теорема единственности раз-
разложения функции в степенной ряд с данным центром:
18*
276 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
5°. Если голоморфная в точке а функция. { разложена в сте-
степенной ряд вида A0), то коэффициенты этого ряда определяются
по формулам Тейлора:
dz\l ... dzknn
k\ dzk
A2)
еде k\ = kx\ ... kn\.
Пользуясь формулами A1) для тех же коэффициентов и оце-
оценивая входящие в них интегралы, получим
6° (Неравенства К_оши). Если функция f голоморфна
в замкнутом поликруге U = {\zv — av|<>v} и |/| *СМ на его
остове Г, то коэффициенты тейлоровского разложешя f в точке
а удовлетворяют неравенствам
r
где rk = r\' ... а-*".
В заключение остановимся на понятии голоморфности в бес-
бесконечных точках, для чего, как и в теории функций одного пере-
переменного, воспользуемся простыми преобразованиями, перево-
переводящими бесконечные точки в конечные. Эти преобразования, од-
однако, для пространств С" и Р" выбирают гю-разному.
В случае пространства теории функций С" такими преобра'
зованиями служат дробно-линейные преобразования отдельных
переменных: функция / называется голоморфной в бесконечной
точке2° = (оо оо, z°m+1 2°), если функция
/ \~г~ I • • • > ~р > fem+!> ¦ • • > bn) = ф lbl> • • • > Ь/г)
голоморфна в точке (О, ..., 0, zam+i z!)eC°.
В случае комплексного проективного пространства Р" поль*
зуются так называемыми проективными преобразованиями, ко-
которые в однородных координатах имеют вид
л + 1
или в матричной записи
ц=Асо
(здесь ш= (шь ..., o)n+i) и \i= (|j.i,"..., ц.п+1) — векторы, а А =
— (oist)—матрица). Такими преобразованиями бесконечные
точки Р" (для которых con+i = 0) можно, очевидно, перевести
в конечные (цп. ' "ч
§ 2] ПОНЯТИЕ ГОЛОМОРФНОСТИ 277
Функциями точек Р" будут такие функции /(со), которые не
меняются при замене © на А,©, где ХеС\{0}, т. е, однородные
функции (напомним, что точками Р" служат классы эквива-
эквивалентных наборов ©, а не сами эти наборы). Голоморфность
функции f в конечной точке o) = {cov}e Pn понимают как голо-
голоморфность в точке геС", для которой <av служат однородными
координатами, т. е. в точке "' , .... ——). Под голоморф-
\ 0)л+1 мл+1 /
ностью / в бесконечной точке из Р" понимается голоморфность
функции f(Aa) в соответствующей конечной точке (в которую
проективное преобразование и—>-Лш переводит данную беско-
бесконечную).
4. Плюригармонические функции. Здесь мы рассмотрим
вкратце действительные и мнимые части голоморфных функций.
Начнем с простого замечания: • если функция f=u + iv голо-
голоморфна в точке геС", то в окрестности этой точки -~— = 0
(v=l, ..., п), и поэтому функция f = u — iv дифференцируема
в смысле R2™ в этой окрестности, и там для любого v=l, . .. , п
<!к. = ± (Л_ _ .• _^L\ = (JL\ = а (П
dzv 2 [ dxv dyv ) \ dzv ) и> {- }
Такие функции / мы будем называть антиголоморфными в
точке г.
Пусть / голоморфна в точке геС", тогда в силу этого заме-
замечания для ее действительной части и=-п-(/ + /) в окрестности
ди 1 df о
точки z имеем -^~ = -ц- "Н7~• Воспользуемся еще тем, что голо-
морфная функция имеет частные производные всех порядков,
непрерывные по совокупности переменных (это будет доказано
в п. 5). На этом основании можно утверждать, что существует
д2и 1 d2f " , ,
¦ — = — '— и что можно менять порядок дифференци-
OZ^ OZy Z OZ^ OZy
рования, т. e. я~ я—= -~— -д^-] = 0. Таким образом, для лю-
CfZ^ OZV OZV \ OZ^ j
бых ]к, v = 1, ..., п мы имеем
лЙт7 = °- B>
Разделив действительные и мнимые части оператора в левой
части B):
д д J_ / д2 д2 \ , t t д2 д2
dzv
ib
-278 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
мы получим, что условие B) распадается на п2 уравнений с
частными производными второго порядка:
дЧ дЧ = „ дЧ дЧ = „ ,_.
(fi, v=l, . . ., п; уравнения второй группы при fi = v тривиальны).
Определение. Функция и(х, у) класса С2 в области
DczR2n, удовлетворяющая в каждой точке (х, y)^D уравнениям
C), называется плюригармонической в этой области.
При п = 2 плюригармонические функции называют дигармо-
ническими; условия дигармоничности выражаются следующими
четырьмя уравнениями:
дЧ дЧ ~ дЧ дЧ ~
дх, ду, ' дх\ dui
D)
дЧ дЧ „ дЧ дЧ „
Плюригармонические функции связаны с голоморфными
функциями нескольких переменных так же, как гармонические
(в R2) с голоморфными функциями одного переменного. Именно,
справедливы следующие две теоремы:
Теорема 1. Действительная и мнимая части функции f,
голоморфной в области DczCn, являются плюригармоническими
в этой области.
< Для действительной части « = Ref теорема уже доказана.
Так как вместе с / и функция —if^H(D), a Im/ = Re(—if), то
теорема справедлива и для мнимой части >
Обратная теорема справедлива, вообще говоря, лишь ло-
локально.
Теорема 2. Для любой функции и, плюригармонической в
окрестности U точки (х°, г/°)еК2п, существует голоморфная в
точке z°=x° + iy° функция /, действительная (или мнимая) часть
которой равна и.
2л
¦4 Дифференциальная форма со = jpvdxv называется замк-
v=l
нутой в некоторой- области из R2", если в этой области все
и выполняются условия
Рассмотрим в U дифференциальную форму
§2] ПОНЯТИЕ ГОЛОМОРФНОСТИ 279
так как иеС2, то ее коэффициенты принадлежат классу С1;
условия замкнутости этой формы имеют вид
д2и _ д2и д3и _ д2и , _. ,
дх^ dyv ~ dxv дУ), ' ду^ dyv ~ дх^ dxv (Ц, v - 1, . .., п)
и совпадают с условиями плюригармоничности C).
Таким образом, форма F) замкнута в U. Но в действитель~
ном анализе доказывается, что каждая замкнутая форма
© = 2 Pv dxv локально тонна, т. е. существует функция иеС1
v=l
такая, что a = dv, или
Pv = ^T (v-1.....2n); G)
эта функция выражается интегралом
х х 2/г
v(x)= J (о = J 2j Pv ^v.
^° л" v= 1
который не зависит от пути и при фиксированной точке х° яв-
является функцией от х.
В случае формы F) мы имеем
Ti
Til-
°° l
и уравнения G) совпадают с условиями комплексной диффе-
ренцируемости функции f = u + iv. Так как еще /еС в некото-
некоторой окрестности точки z°=x° + iy0, то f голоморфна в этой точке
и и = Re /.
Голоморфная в точке z° функция if==iu — v имеет и своей
мнимой частью >
Первая группа уравнений C) при fi=v дает
дЧ дЧ _„ , , ,
—j- + —у — U. (8)
Складывая эти уравнения для v=l, ..., п, найдем, что опера-
оператор Лапласа от функции и по переменным Х\, у\ хп, уп
а
Аи
Следовательно, плюригармонические функции составляют под-
подкласс класса гармонических функций в пространстве R2n (оче~
видно, правильный при п>1).
•280 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ. ПЕРЕМЕННЫХ [ГЛ. I
Естественно возникает вопрос об определении плюригармо-
нической в некоторой области DcR2n функции по заданным
граничным значениям (задача Дирихле). Этот вопрос решается
не так просто, как в случае гармонических функций. Мы про-
проиллюстрируем возникающие трудности на примере одной из
простейших областей — поликруга ?/ = {zeC": |zv|<l}. Так как
согласно (8) плюригармоническая функция является гармони-
гармонической по каждому переменному zv=xv + iyv в круге {|г„| <1}, то
мы можем последовательно применять интеграл Пуассона из
п. 45 ч. I. Мы получим для любого ге[/
2Л 2Я
и{г)= Jp(g,, z{)dtx ... J u(?)/>(?„, zn)dtn,
о о
где ?v = e'4 ? = {?„} и
— ядра Пуассона. Обозначая через
ЛД?, 2)=ПЯ(?У, zv) (9)
v=l
п-мерное ядро Пуассона, через Qn == [0, 2л] X ... X [0, 2я]
л раз
п-мерный куб и через dt = dt\ . . . dtn элемент объема, перепишем
формулу Пуассона в следующем сокращенном виде:
u{z)= J и (?)/>„(?, z)df. . A0)
В правую часть этой формулы входят лишь значения и на
остове поликрута Г = {?: |?v| = l}, т. е. на /г-мерной части гра-
границы dU (вся граница B/г— 1)-мерна). Отсюда ясно, что нельзя
произвольно задавать значения плюригармонической функции и
на всей границе поликруга. Если подставить „в правую часть
A0) значения какой-либо непрерывной на Г функции ы(?), то
функция «(г), определяемая в U этой формулой, как нетрудно
проверить, будет для всех v=l, ..., п удовлетворять уравне-
уравнениям (8). Однако эта функция, вообще говоря, не будет удов-
удовлетворять другим уравнениям C), т. е. не будет плюригармони-
плюригармонической в U. Для плюригармоничности и (г) на значения ы(?)
нужно наложить дополнительные условия, на которых мы не
останавливаемся.
5. Основная теорема Хартогса. Здесь мы докажем теорему
¦о том, что из голоморфности функции по каждому переменному
§2] ПОНЯТИЕ ГОЛОМОРФНОСТИ 28F
следует ее голоморфность по совокупности переменных, — об
этой теореме уже шла речь в п. 3. Там же было установлено,
что для доказательства этой теоремы достаточно доказать, что
всякая функция, голоморфная по каждому переменному, яв-
является непрерывной по совокупности переменных, т. е. обладает
свойством (А).
Доказательству мы предпошлем ряд лемм. Первая из них
утверждает, что достаточно установить лишь ограниченность
рассматриваемой функции. При этом нам понадобится лемма
Шварца в виде несколько более общем, чем в п. 35 ч. I.
Пусть функция ф голоморфна в круге Ur—-{\z\ <r}czC, при-
причем ф = 0 в некоторой точке zoe(/r и |ср|^М всюду в Ur; тогда
всюду в Ur
(при г = М=\ и 20 = 0 получаем обычную формулировку). Для
доказательства возьмем дробно-линейное отображение Ur на
единичный круг U:
Я: z —> г
Z-Zg
г2 — zaz
обозначим через Я обратное отображение U --*¦ Ur и рассмотрим
функцию ip = ~тт-ф о Я. Она удовлетворяет условиям обычной
леммы Шварца, и по этой лемме |ty(z) |-^|г| всюду в U. Заме-
Заменяя здесь z на k(z), получим неравенство A).
Лемма 1. Если функция f голоморфна по каждому перемен-
переменному zv в поликруге U = U(a, г) ') и ограничена в U, то она
непрерывна в каждой точке U по совокупности переменных.
< Пусть z°, z e U — произвольные точки; распишем прира-
приращение / как сумму приращений по отдельным координатам
п
И~\ f (С,0\ X1 < f /~0 -.0 -;, ^ Л
л/ / Чл / — J-1 \1 \~it • • ¦ > ¦'v-P v' " • " > п)
-f(zb...,^zv+v...,zn)} B)
и рассмотрим v-e слагаемое как функцию фу переменного zv
при фиксированных остальных значениях аргументов. Если
l/l^~2~ B U, то функция ц>ч удовлетворяет условиям леммы
Шварца в только что приведенной форме, и, применяя неравенство
') Это означает, что для любой оеУ и любого v=l, ..., п функция
f(ei, ..., Ov^-i, zv, av+i, ..., an) переменного zv голоморфна в круге
{\zv\ <rv}czC.
¦282 голоморфные функции нескольких переменных [гл. т
A) к каждому слагаемому суммы B), мы найдем, что
v I'v
Отсюда и следует утверждение >
Итак, для доказательства теоремы Хартогса остается дока-
доказать ограниченность в некотором поликруге с центром в а функ-
функции, голоморфной по каждому переменному. Заметим, что огра-
ограниченность в каком-то поликруге, не обязательно с центром в а,
следует из одной лишь непрерывности / по
отдельным переменным. Этот факт состав-
составляет содержание так называемой леммы
О с гуд а:
Лемма 2. Представим поликруг U—
={2еС": \zv\<R] как произведение 'U=
={'2eC'1-1: I zv I </?}') на круг Un =
={г„еС: \zn\<R}. Если функция f('z,_zn)
непрерывна по 'z в 'U для любой zn&jn и
непрерывна по zn в Un для любой 'z^'U, то
существует поликруг W='WxUnaU, в ко-
котором f ограничена (см. диаграмму Хартог-
Хартогса на рис. 80).
< Для фиксированного 'zt='U обозначим
M('z) = max \f{'z, zn)\
и рассмотрим множества efm = {'ze't/: М ('*)< пг). Эти множе-
множества замкнуты, ибо если гг^ е ^т (ц= 1, 2, ...) и 'z^-^-'z, to
и 'ге?т (в самом деле, \f('zw, 2„)|<тдля любого zneC/n, в
силу непрерывности f no 'z тогда и \f{'z, zn) \-^~m для любого
2nef7n, т. е. M('z) Km). Очевидно, Wm образуют возрастаю-
возрастающую последовательность и любая точка 'z^'U принадлежит
всем (fm, начиная с некоторого.
Существует с?м, содержащее некоторую область 'Ga'U.
В самом деле, в противном случае все ?°т были бы нигде не
плотными, но тогда в 'U существовал бы шар Д'сО, свобод-
свободный от точек cf ь в В1 — шар В2, свободный от_точек У2, и т. д.—
мы построили бы последовательность шаров BkaCn~l, которые
имеют общую точку 'z°^'U, и эта точка не принадлежала бы
никакому (?т.
') Напомним, что через 'г—(ги ...
проекцию в С" точки геС".
zn-i) мы условились обозначать
§2]
ПОНЯТИЕ ГОЛОМОРФНОСТИ
283
Таким образом, существует область 'G, в которой \f{rz,zn) \^С
•^ М для любого znet/n. Остается выбрать в 'G поликруг
'W={'z: \zv-zov\<r},n тогда в W='WxUn будет \f\<M >
Чтобы доказать ограниченность / в поликруге с центром в ау
придется использовать голоморфность по отдельным перемен-
переменным. При этом нам потребуется лемма Хартогса, суще-
существенно опирающаяся на свойства субгармонических функций.
Для ее формулировки введем следующие обозначения: rV =
= U('a, R), 'W*=U('a,r) (rnR — скаляры, r<R), Un={\zn\ <R},
V='VxUn, W='WxUn (рис. 81).
Лемма З. Если функция f('z, zn) голо-
голоморфна no 'z в 'V для любого zn^Un и го-
голоморфна по z в W, то она голоморфна во
всем поликруге V.
< Без ограничения общности считаем
'а = 'О. Для любого фиксированного zn^Un
и любого 'ze'V функция f представляется
(в силу голоморфности по 'z) сходящимся
степенным рядом
оо
f (z)— "Si ck (z ){'z)h, C)
где k— (ku .. ., kn-i). Коэффициенты этого
ряда
ck(zn) — ' " Рис. 81.
k\ (d'z)k
голоморфны в круге Un, как производные голоморфной по zn
функции (точка ('0, zn)^W). Поэтому функции т-гт ^n\ck(zn) I
субгармоничны в Un.
Выберем произвольно число р</?; так как для любого'
при |^|-»-оо, то для любого znef/n найдется \k\, начиная с ко»
р ||,
торого будет ттт ^n\ck(zn
0. т- е-
lim 7TT
D)
_Теперь воспользуемся голоморфностью f в W: f ограничена
в W (пусть |/1-<M], и справедливы неравенства Коши
284 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. I
любого zn^Un. Поэтому для любого 2„е(/„ и любого \k\
E)
Таким образом, рассматриваемые субгармонические функции
удовлетворяют условиям теоремы о верхнем пределе (п. 46 ч. I).
По этой теореме для любого а<р можно найти номер ко такой,
что для всех \k\>k0 и всех zn, \zn\^-o, имеем
-r|j-ln|cfcBn)|<ln-i-, т. е.
Отсюда следует, что ряд C) сходится равномерно в любом по-
поликруге U (О, а'), а'<а, но члены этого ряда непрерывны по z,
поэтому и его сумма / непрерывна, а следовательно, ограничена
в U (О, а'). Этот поликруг можно считать сколь угодно близким
к У, а так как V с самого начала можно было немного увели-
увеличить1), то / ограничена и, значит, по лемме 1 и утверждению 4°
из п. 3 голоморфна в V >
Теперь все готово для доказательства основной теоремы.
Теорема Хартогса. Если функция f голоморфна в любой
точке области Z)cC™ по каждому из переменных zv, то она го-
голоморфна в D.
< Достаточно доказать голоморфность / в произвольной
точке z°^D, причем без ограничения общности можно считать,
что 2° = 0. Итак, пусть / голоморфна по каждому переменному
в поликруге U^O, R); требуется доказать, что она голоморфна
в некотором поликруге с центром в 0.
Это утверждение будем доказывать индукцией по числу ком-
комплексных переменных. Для одного переменного оно тривиально;
предположим, что оно верно для функций (п—1)-го перемен-
'0, -g-j. Из предположения следует,
что функция f{fz,zn) непрерывна no'z в '!7_для любого zn^Un =
= {\zn\*CR} и по zn в ип для любого 'z^'U. По лемме Осгуда /
ограничена, а значит, и голоморфна в некотором поликруге
f = 'fX п„, где 'W=U('a, r)<='U (рис. 82). «
/ о
Рассмотрим теперь поликруг V = 'VXUn, где'У = U га, -j-
Очевидно, VczU(О, R), следовательно, f голоморфна по 'z в 'V
') В условия леммы входит голоморфность в замкнутых поликругах.
§ 3]
ГОЛОМОРФНЫЕ ФУНКЦИИ
285
для любого znet/n, а по только что доказанному она голоморф-
голоморфна по z в W. По лемме Хартогса отсюда следует, что она голо-
голоморфна по z и в поликруге V, который уже содержит точку
z = 0. Таким образом, утверждение дока-
доказано и для функций п переменных >
Приведем еще одну формулировку
теоремы Хартогса.
Будем говорить, что функция / голо-
голоморфна в точке аеС" в смысле Р и м а-
н а, если
(R) / голоморфна по каждому пере-
переменному zv в некотором поликруге
U(а, г).
Будем говорить, что / голоморфна в
этой точке в смысле Вейерштрасса,
если
(W) / разлагается в некотором поликруге U(a, r) в степен-
степенной ряд
Рис. 82.
2
|ftl=0
ck{z-a)\
Импликация (W) =ф (R) очевидна, импликация ()^()
составляет содержание основной теоремы Хартогса. Эту теорему
можно, следовательно, сформулировать так:
Понятия голоморфности в смысле Римана и в смысле Вейер-
Вейерштрасса эквивалентны.
§ 3. Голоморфные функции
6. Простейшие свойства. В предыдущем параграфе был от-
отмечен ряд свойств голоморфных функций нескольких перемен-
переменных, которые являются распространением соответствующих
свойств функций одного переменного (интегральная формула
Коши для поликругов, разложимость в степенной ряд, беско-
бесконечная дифференцируемость, неравенства Коши). Здесь мы
продолжим изучение таких свойств.
Начнем с теоремы единственности. В формулировке п. 21
ч. I она на пространственный случай не распространяется: функ-
функция zxZ2, голоморфная в С2 и не равная тождественно нулю,
обращается в нуль на множестве с предельными точками (ана-
(аналитических плоскостях {2i = 0} и {za=0}). Верна такая
Теорема 1 (единственности). Если функция
/e#(Z)) в некоторой точке z° области DaCn обращается в нуль
вместе со всеми частными производными, то f=0 в D.
286 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (ГЛ. I
< Все коэффициенты тейлоровского разложения / в точке га
равны 0, следовательно, /=0 в некоторой окрестности этой точ-
О
ки. Обозначим ^ = {гей: f(z) = O} и е — открытое ядро §*
(совокупность внутренних точек этого множества). Множество
о ' *
в открыто и непусто (оно содержит 2°); как и в ч. I, доказы-
доказывается, что оно замкнуто в D; поэтому «f=?> >
В доказанной теореме, по существу, требуется, чтобы / обра-
обращалась в нуль в 2п-мерной окрестности точки z°. Даже из обра-
обращения в нуль в Bп — 2)-мерной окрестности точки, вообще го-
говоря, не следует тождественного обращения функции в нуль
(пример: f(z)=zn обращается в нуль на B/г — 2)-мерном множе-
множестве {геС": zn=0}). Имеются, однако, случаи, когда обраще-
обращение функции в нуль в /г-мерной окрестности точки влечет за со-
собой тождественное ее равенство нулю:
Если функция /е#(?>) обращается в нуль в действительной
окрестности точки z°^D, т. е. на множестве {z=x+iy^On:
\х — х°\<г, у=у0}, то /=0 в D.
< В некотором поликруге с центром 2° функция / разла-
разлагается в ряд
/B)= 2 Ck{z-Z«)\
1 & 1=0
Полагая здесь у = у°, найдем, что
¦ S Ck(x-x°)k^0
1/М-О
для всех х^{\х — х°\<г}. Дифференцируя это тождество по
xk = **1 • • • xknn, а затем полагая х=х°, найдем, что все ск=0.
По теореме 1 тогда / е= 0 в D >
Теорема 2 (принцип максимума модуля). ?ии
функция f^H(D) и 1/| достигает максимума в некоторой точке
a^D, то /=const в D.
< Рассмотрим любую аналитическую прямую z=/(?) =а + ш?;,
проходящую через точку а. Сужение / на эту прямую — функция
q>a(t,)=fol(t:) — голоморфно в некотором круге {|?|<р}, а
1фи I Достигает максимума при ?=0. По принципу максимума
модуля для функций одного переменного фш (?) =с(со) —посто-
—постоянная, зависящая от <о. Но 9ffl@)=f(a) не зависит от со, по-
поэтому c((o)=const и f=const в, окрестности точки а. По теоре-
теореме 1 f=const в D > _
Если f голоморфна в области Z)c=Cn и непрерывна в D, то
максимум \f\ достигается на границе dD. Однако в С™ при
1 существуют такие области, в которых |f| для любой
ГОЛОМОРФНЫЕ ФУНКЦИИ 287
f(), непрерывной в Д фактически достигается не на всей
dD, а лишь на некотором ее подмножестве. Наименьшее такое
замкнутое подмножество называется границей Шилова обла-
области D. Точнее, границей Шилова области D называется такое
замкнутое множество SczdD, что: 1) для любой /е#(?>), не-
непрерывной в D,
B)| A)
и 2) любое замкнутое множество S, обладающее свойством 1),
Содержит S.
Примеры.
1. Шар B={zeO: |z|<l}. Покажем, что здесь граница
Шилова совпадает с топологической границей. Для этого возь-
возьмем произвольную точку ?е<ЗВ и построим функцию /, голо-
морфную_в В, непрерывную в J3 и такую, что \f(t,) \> \f{z) \ для
всех 2G5\?. Обозначим через
B, 0 =
v=l
скалярное произведение векторов ги^в комплексном простран-
пространстве Сп. По неравенству Буняковского — Шварца
Re(z, ?)<|(z, «|4Slz|,
ибо | ?| = 1, причем равенство Re (г, ?) = |z| = l достигается в В
лишь при z = ?. Поэтому функция /(z) = ete>S) обладает нужным
свойством.
2. Поликруг U = {z^Cn: |zv|<l}. Здесь граница Шилова
составляет лишь n-мерную часть Bя—1)-мерной топологиче-
топологической границы, именно, она совпадает с остовом поликруга. Для
доказательства рассмотрим любую функцию /, голоморфную в
U и непрерывную в (J. Прежде всего заметим, что функция
f('z, ?n) для любого фиксированного ?„, |?„| = 1, является голо-
голоморфной функцией 'z в поликруге 'С/еС". В самом деле, ее
можно представить как предел последовательности функций
фд('г) = /'(/2, z^w), где г^> — какая-либо последовательность то-
точек круга {|2„|<1}, сходящаяся к точке ?„. Так как ('z, zf>) e U
то все фр, голоморфны в 'U, а в силу равномерной непрерывно-
непрерывности f в U последовательность фр, сходится равномерно в 'п. По
теореме Вейерштрасса (см. ниже, теорема 4) отсюда и следует
сделанное утверждение. Точно так же доказывается, что все
функции f(zu ..., zm, ?m+b .... ?„), где m=l, ..., я—1 при
фиксированных ?m+i. •.., ?п, по модулю равных 1, голоморф-
голоморфны по (zi, ,.,, zm) в соответствующих поликругах.
288 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. I
Пусть 7W = max|/B!) | достигается в некоторой точке ?е<3?/,
которая принадлежит одному из множеств rv = {l?v! = l, |?ц|,
H=?v}; перенумеровывая в случае надобности переменные, можно
считать, что оно совпадает с Г". Либо |?n-i| = l, либо по прин-
принципу максимума модуля (он применим по доказанному выше)
/ постоянна по переменному zn-i, и тогда значение М дости-
достигается в некоторой точке, две последние координаты которой по
модулю равны 1. Продолжая это рассуждение, мы получим,
что значение М достигается на остове поликруга r = {|zv| = l,
v=l, ,.., п}. Таким образом, граница Шилова поликруга U
принадлежит Г.
Но для любой точки_?еГ найдется функция /, голоморфная
в Ц_я непрерывная в U, для которой |/(?) J > \f(z) | для всех
\ в качестве такой функции можно взять произведение
п
Ц A + ?vzv)- Таким образом, граница Шилова совпадает с Г.
¦v=l
Теорема 3 (Лиувилль). Если функция f голоморфна
в С" и ограничена, то она постоянна.
¦4 Воспользуемся индукцией по п. При п=\ теорема дока-
доказана в первой части, пусть она верна для функций (п—1)-го
переменного. Возьмем произвольные точки а, ЬеС"; так как
функция f('z, an) по индуктивному предположению постоянна,
то f(a) =f('b, an). Но функция f('b, г„) также постоянна, следо-
следовательно, f(b, an)=f(b). Таким образом, f(a)=f(b), т. е. теоре-
теорема верна для функций п переменных >
В дальнейшем теорема будет усилена (см. п. 18, а также
задачу 9).
Теорема 4 (Вейерштрасс). Пусть последователь-
последовательность функций fn<=H(D) сходится к функции f равномерно на
каждом компактном подмножестве D; тогда f<=H(D) и для лю-
любого k= (&i, ..., kn)
ГЦ 7Т~ \ >
дг" дг"
на любом К ёО.
< По теореме п. 22 ч. I функция голоморфна по каждому
переменному в любой точке z^D и по теореме Хартогса при-
принадлежит H(D). Вторую часть теоремы достаточно доказать
для окрестности произвольной точки 2°eZ) и производной по
одному переменному zv. Возьмем поликруг U=U(z°, r) <ШБ и
воспользуемся формулой Коши
а^ JL 1 Г м
§ 3] ГОЛОМОРФНЫЕ ФУНКЦИИ 289
где Г — остов U. Так как f^-^-f равномерно на Г. то для любого
е>0 найдется цо такое, что Н/ц — fl!r<e для всех ц > ;i0. Если
\U, то из C) будем иметь для всех ге/С и ц ^ (ц0
в Bя)пг,...гя
" Bя)" mm IS-2| |gv — 2V | '
отсюда следует, что -z >~q^~ равномерно на К >
Приведем теперь наиболее содержательное из обобщений на
пространственный случай свойство голоморфных функций — так
называемую подготовительную теорему (Vorbereitung-
satz) Вейерштрасса. Эта теорема обобщает известное свойство
голоморфных функций одного переменного обращаться в нуль
как целые степени г — а: если f(a)=O (но /^0),'то в некоторой
окрестности точки а
где ф голоморфна и не обращается в нуль.
Теорема 5. Пусть функция f голоморфна в некоторой
окрестности U точки аеО и f(a)=O, но f('a, гп)ф0; тогда в
некоторой окрестности V этой точки
f(z) ={(zn — an)h + ci{'z) (zn — an)h~l +'.. . +Cii('z)}(p(z), E)
где k~^> 1—порядок нуля f('a, zn) в точке zn = an, функции cv
голоморфны в 'V, cv('a) =0, а ф голоморфна в V и не обращает-
обращается там в нуль.
< Без ограничения общности считаем, что a — Q. По теореме
единственности для функций одного переменного можно выбрать
г„>0 так, чтобы /('0, гп)ф0 при 0<|znj-Crn, а в ?илу непре~
рывности / найдется поликруг 'V=U('O, r) такой, что }ф0 при
'z^'V, \zn\—rn. Для любого фиксированного 'z°^'V число ну-
нулей функции f{'z°, zn) в круге Vn = {\zn\<rn} равно
J
ибо левая часть F) —целочисленная и непрерывная функция
точки 'z° в 'Vх) и, следовательно, постоянная, а при /2° = /0 она
равна порядку нуля функции f('0, zn) в точке 2п = 0, т. е. k.
') См. лемму в конце пункта.
19 Б. В, Шабат
290 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
Фиксируем 'zg'V, обозначим через z^ = zi?\'z), v= 1, ..., k,
нули функции f('z, zn) в круге Vn и построим многочлен относи-
относительно zn
Р (г) = П (*„ ~ *Г) = 2* + ci ('*) 2Г' + • • • + ck Cz), G)
имеющий эти нули своими корнями. Его коэффициенты голо-
голоморфны в 'V. В самом деле, для любой голоморфной в Vn функ-
функции a(zn) по обобщенному принципу аргумента (см. задачу 1
к гл. IV ч. I)
Г
J
откуда видно, что суммы в левой части — голоморфные функции
переменного 'г в 'V (мы учитываем, что /=?0 при 'ze'V и
2„е<5Уп). Полагая здесь «>(zn) = z?, jn = 1, ..., й, найдем, что
суммы |Li-x степеней корней многочлена G) голоморфны в 'V,
а через эти суммы (как известно из алгебры) рационально вы-
выражаются его коэффициенты, следовательно, с,('г)еЯ('1/). При
'г = 'О все k корней многочлена равны нулю, поэтому и все
cv('0)=0.
Функция
при любом фиксированном 'z^i'V является голоморфной функ-
функцией zn в круге Vn и не обращается в нуль, ибо Р обращается
в нуль того же порядка лишь в точках z™ {'z), в которых и / = 0.
При фиксированном zn^Vn и 'ze'F имеем
2Ш J
а так как РфО на <5Vn (ибо там /?=0), то правая часть, а зна-
значит и ф, голоморфно зависит от 'г1). По теореме Хартогса ф
голоморфна в поликруге V='VxVn >
Подготовительная теорема Вейерштрасса показывает, что го-
голоморфная функция обращается в нуль как многочлен относи-
относительно переменного zn с коэффициентами из кольца Н('а) функ-
функций от 'z, голоморфных в точке 'а. Точнее, все коэффициенты,
') См. лемму в конце пункта.
§ 3] ГОЛОМОРФНЫЕ ФУНКЦИИ 291
кроме старшего, принадлежат идеалу1), который образуют
в Н('а) функции, обращающиеся в нуль в этой точке. Таким
образом, эта теорема позволяет привлечь для исследования мно-
множества нулей голоморфных функций алгебраические методы.
Замечание. Если f#0 и выполняются все условия тео-
теоремы Вейерштрасса, кроме условия f('a, гп)Ф0, то существует
линейная замена переменных г— а—Ахю, DetA^=0, или, в под-
подробной записи,
п
zv - av = 2 «nv^n (v = 1. •.., п), (8)
после которой f переходит в функцию g(w) такую, что
Для доказательства выпишем группу членов
S cft....ftlI(zj-ai)*i ...(zn-an)*«
|ftl = * ' "
тейлоровского разложения / в точке а наименьшего порядка
• \k\ =x, при котором не все коэффициенты группы равны 0. Сде-
Сделаем в ней замену переменных (8), причем матрицу Л подберем
так, чтобы Det/4^0 и чтобы коэффициент при да*
После такой замены f(z) перейдет в функцию g(w), для кото-
которой g(f0, w^ = d,0Kw* + ... Ф 0, что и требуется.
Заметим еще, что при п—2 разложению Вейерштрасса функции /#0
можно придать вид .
f(z,w) = (z — a)k{(w — b)'+Ci(z)(w — 6)'-'+ ... +ch(z)}(f(z,w), (9)
для которого условие f(a, w) Ф0 не требуется (здесь cv — голоморфные в
точке а еС функции, cv(a)=0, k и / — целые числа, ср — голоморфная в точке
(а, 6)еС2 функция, не обращающаяся в нуль). В самом деле, если f(a,w)^s
ФО, то мы имеем разложение (9) с k=0; если же f(a,w) = 0, то из тейлоров-
тейлоровского разложения мы получим, что f(z, w) = (z — a)hg(z, w), где уже
g(a, w)^s 0, и, применяя теорему к функции g, придем к разложению (9).
В заключение этого пункта докажем лемму о голоморфной
зависимости интегралов от параметра, которой мы несколько
раз пользовались при доказательстве подготовительной теоремы
') Напомним, что идеалом кольца R называется множество / его эле-
элементов, которое: 1) является подгруппой аддитивной группы кольца (для
этого разность любых двух элементов из / должна снова принадлежать /)
и 2) для любого элемента/ *= / и любого rei? произведение /ле/. Множе-
Множество всех функций из Н('а), равных нулю в 'а, удовлетворяет обоим этим
условиям, т. е. является идеалом в конце #{'а).
19*
292 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
Вейерштрасса. Мы рассмотрим ее в несколько более общей си-
ситуации.
Лемма. Пусть L^; ?ц = ?ц@—спрямляемая кривая в пло-
плоскости ?д (ц=1, .... m), L = Lxx...XLm и D — область в С";
пусть 1= {lu . .., ?т) и z=(zu ..., г„). Если функция g(t,, z)
непрерывна на LxD, голоморфна по z в D при любом Z, e L и
имеет на LxD непрерывные частные производные -^—,то инте-
интеграл
G(z)=frfe,... Г g(Z, z)dU= f g(?, z)dl A0)
L'i Lm L
голоморфен в D и
^-^-rfS (v=l, .... л).
< Для любого z e D выберем г>0 так, чтобы поликруг
V(z, r)c=D; пусть \hv\<r и ft=@, ..., /iv, ..., 0) 6E С" — вектор,
у которого все координаты, кроме v-й, равны 0. Имеем
~-{G(z + h)-G(Z)} = ^-j{g(Z,z + h)-g(Z, z)}dt,=
и, следовательно,
В силу того, что s dz при фиксированном z равно-
равномерно непрерывна на компактном множестве Lx[0, 1], то для
любого е>0 можно выбрать 6>0 столь малым, что для всех
(?, 9)eLx[0, 1] при |А|<6 будет
+ Qh) dg(?,) . о
о.
Поэтому, оценивая последовательно интегралы в правой ча-
части A2), мы найдем, что левая часть этого равенства при|/г|<б
§ 3] ГОЛОМОРФНЫЕ ФУНКЦИИ 293
не превосходит по модулю е\Ь{\.. ,\Lm\. Таким образом, в каж-
дои точке ге/J все частные производные -=— существуют и вы-
выражаются формулами A1) >
7. Степенные ряды, Здесь мы рассмотрим основные вопросы,
связанные с разложением голоморфных функций в ряды. В п. 5
мы доказали, что любую функцию, голоморфную в поликруге
U(а, г), можно в этом поликруге разложить в кратный степен-
степенной ряд с центром в а. Возникает вопрос о множестве точек
сходимости такого ряда. По аналогии с функциями одного пере-
переменного хочется ожидать, что таким множеством будет поли-
поликруг, дополненный некоторой совокупностью точек его границы.
Однако самые простые примеры показывают, что дело обстоит
иначе.
Примеры. Множество сходимости степенного ряда
оэ
1 ХЧ _„.... A)
-г,г2
(in — скалярный индекс) в С2 представляет собой полную об-
область Рейнхарта {|ziz2| <1}. Для ряда
B)
множеством сходимости в С2 является бикруг {|zi|<l, |Z2|<1},
дополненный аналитической плоскостью {z, = 0}.
Из последнего примера видно, что теорема Абеля в обычной
формулировке (п. 19 ч. I) на функции нескольких переменных не
переносится. Однако можно получить ее аналог, если вместо
множества сходимости рассматривать его открытое ядро,
т. е. совокупность внутренних точек этого множества.
Определение. Областью сходимости степенного ряда
2 ck(z-a)k C)
I ft 1 = 0 "
называется открытое ядро S множества S точек ze<Cn, в кото-
которых этот ряд сходится при каком-либо порядке следования его
членов.
Из леммы 3° п. 3 аналог теоремы Абеля выводится в
следующем виде:
Теорема 1. Если точка z° принадлежит области сходимо-
сходимости S ряда C), то замкнутый поликруг J7={zeQn: \zv — avj^
294 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. I
^ | z°v — av|} также принадлежит S и ряд C) сходится в U абсо-
абсолютно и равномерно').
< Так как 2°eS и S открыто, существует точка ?eS такая,
что | ?v — av | > | z° — av |, v—l,...,n, и ряд (З) сходится в этой
точке. Так как Um{z^Cn: \zv—_av|<|?v— av\}, то по цитиро-
цитированной лемме ряд C) сходится в U абсолютно и равномерно >
Теорему 1 можно сформулировать еще и так: область сходи-
сходимости S ряда C) является полной областью Рейнхарта с цен-
центром в а. Таким образом, полные области Рейнхарта в случае
функций нескольких переменных играют ту же роль, что круги
в случае одного переменного. Эту аналогию подчеркивает и сле-
следующая
Теорема 2. Любая функция f, голоморфная в полной об-
области Рейнхарта ?>с=С" с центром в а, представляется в этой
области тейлоровским разложением
/(*) = S ck{z-af. D)
lftl=0
< Пусть z° — произвольная точка D, тогда поликруг
U = {| zv — av |^|z° — av|} Ш D и по лемме 2° п. 3 функция f пред-
представляется в U тейлоровским разложением с центром в а. Ко-
Коэффициенты последнего вычисляются через производные / в
точке а и, значит, совпадают с ch, т. е. это разложение совпа-
совпадает с D) >
Естественно возникает вопрос: всякая ли полная область
Рейнхарта является областью сходимости какого-либо степен-
степенного ряда? Ответ на него отрицателен, ибо, как мы сейчас до-
докажем, области сходимости обладают некоторым дополнитель-
дополнительным свойством.
Определение. Обозначим через
i|, ..-, ln|zn|) E)
отображение множества {zeCn: Z\ ... г„фО} в пространство R";
логарифмическим образом множества MczCn мы будем назы-
называть множество М* = К(М0), где M0 = {z^M: Z\ ... гпФО). Мно-
Множество М называется логарифмически выпуклым, если его лога-
логарифмический образ М* является выпуклым множеством в Rn.
') Из теоремы 1 следует, что множество S связано: любые две его точ-
точки z' и г" можно соединить с центром (а значит, и друг с другом) кривой,
принадлежащей S. Так как S еще и открыто, то оно в самом деле является
областью.
ГОЛОМОРФНЫЕ ФУНКЦИИ
295
Пример. Множество MczC2, диаграмма Рейнхарта а(М)
которого изображена на рис. 83, а, не является логарифмически
выпуклым; его логарифмический образ Х(М) 1) приведен на
рис. 83, б. Логарифмически выпуклую оболочку М (т. е. пере-
пересечение всех логарифмически выпуклых множеств, содержащих
М) мы получим, если рассмотрим прообраз выпуклой оболочки
множества к{Щ. Диаграмма Рейнхарта такой оболочки ML
отличается от а(М) сегментом, ограниченным отрезком гипер-
гиперболы \Z{\ \z2\=rR (изображена пунктиром на рис. 83).
\z,\\z2\=rR
а)
Рис. 83.
О
Теорема 3. Область сходимости S степенного ряда C) ло-
логарифмически выпукла.
•*Без ограничения общности считаем а = 0. Нам нужно
доказать, что если |' и \" — произвольные точки S* — k(S),
то и l = tl' + (l-t)l"e=S* для любого t, 0<t< 1. В S* суще-
существуют точки \',\" такие, что l'v>tv и |" > g" (v=l, .... п);
J V 1 / Г I °
точки z'=\ev\ и г"=\ех) принадлежат S. Рассмотрим
теперь точк"у | = t%' + (I —1)%" и ее прообраз z={eiv}, где
(z") . Имеем
а так как z', z"eS, то ряд C) в этих точках сходится и выра*
жения в квадратных скобках ограничены; следовательно, и
члены Cft(z)fe ограничены. По лемме 3° п. 3 отсюда вытекает, что
z = {elv) e S, ибо у нас |v < |v и поэтому elv < elv. Но это
означает, что ^=()S*
') Для простоты мы пишем К(М) вместо к(Ма).
296
ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
[ГЛ.1
В дальнейшем мы докажем, что это дополнительное свойство
уже характеризует области сходимости: любая логарифмически
выпуклая полная область Рейнхарта является областью сходи-
сходимости некоторого степенного ряда (см. п. 27).
А сейчас отметим одно важное обстоятельство. Рассмотрим
полную, но не логарифмически выпуклую область Рейнхарта
(скажем, из приведенного выше примера). По теореме 2 любую
функцию f^H(D) можно представить в D степенным рядом.
Но по теореме 3 область сходимости этого ряда логарифмиче-
логарифмически выпукла, следовательно, он сходится по крайней мере в ло-
логарифмически выпуклой оболочке DL области D. Сумма нашего
ряда осуществляет аналитическое продолжение f из D в Dl- Мы
наблюдаем эффект, принципиально
отличающий пространственный слу-
случай от плоского: в то время как
в С1 любая область является обла-
областью голоморфности некоторой фун-
функции (см. п. 43 ч. I), в С" (и>1)
существуют области, из которых
каждая голоморфная функция не-
непременно аналитически продолжает-
продолжается в более широкую область. Этот
эффект обязательного аналитиче-
Рис 84 ского продолжения мы подробно
рассмотрим в гл. III.
Приведем теперь более конструктивный метод описания об-
о
ласти сходимости S данного степенного ряда C). Эта область
исчерпывается поликругами, которые называются поликругами
сходимости. Например, для ряда A), областью сходимости кото-
о
ого служит S = {zeC2: |ziZ2|<1}, такими поликругами будут
2,|<г1, |22|<—>, 0<Г!<оо (рис. 84). Приведем точное
Определение. Поликруг V(а, г) называется поликругом
сходимости ряда C), если UczS, но в любом поликруге [z e С"-
|zv — av| < К}, где r'v^rv (v = 1, ..., п) и по крайней мере
одно неравенство строгое, имеются точки, в которых v ряд C)
расходится. Радиусы rv этого поликруга называются сопряжен-
сопряженными радиусами сходимости.
Теорема 4. Сопряженные радиусы сходимости ряда C)
удовлетворяют соотношению
1*1
lim V\Ck\r*=\ F)
I ft 1-х»
[(пространственный аналог формулы Коши — Адамара).
§ 3] ГОЛОМОРФНЫЕ ФУНКЦИИ 297
•* Положим z = a + t,r (т.е. zv = av+t,rv); при |?|<1 точка г
принадлежит поликругу сходимости U, ряд C) сходится в U
абсолютно, и после перегруппировки членов
сю оо оо
2 \ск\(г-а)* = 2 ЫЛ'*'= 2( 2
|fe|=0 1 fe I —0 H=0 \| k I=H
мы получим ряд по степеням ?, сходящийся при |?|<1. При
:(tl>l этот ряд расходится, ибо в противном случае по лемме 3°
п. 3 ряд сходился бы в некотором поликруге, содержащем U.
Поэтому по формуле Коши'—Адамара для рядов с одним пере-
переменным
/" 2 \ck\rk = i. G)
k | = Ц
В группе членов ряда C) с данным |&|=ц выберем макси-
максимальный член \cm\rm= max | ск\гк. Пользуясь очевидной оценкой
I ft l=n
и тем, что ([л +1)nl]>- -*¦ 1 при ц->оо, мы можем переписать G)
6 виде соотношения
и
Пт Vjcjr» =1,
равносильного F) >
Соотношение F), которое можно записать в виде уравнения
Ф(г,, ..., /-„)=0, (8)
связывающего сопряженные радиусы сходимости ряда C), опре-
определяет границу области cc(S), которая изображает область схо-
о
димости 5 на диаграмме Рейнхарта. Подставив в (8) rv = e=v,
получим уравнение
?(! .... |„)=0 (9)
о о
границы X(S) —логарифмического образа 5, некоторой выпук-
выпуклой области в пространстве R".
8. Ряды Хартогса и Лорана. Кроме степенных рядов в тео-
теории функций нескольких комплексных переменных рассматри-
рассматривают и ряды других типов. Важнейшими из них являются так
называемые ряды Хартогса. Рассмотрим степенной ряд
оо
2 ck(z-a)k A)
|ft|=0
298
ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
{ГЛ. Г
и в произвольной точке z его области сходимости S перегруппи-
руем члены этого ряда, расположив их по степеням одной из
разностей zv — av, скажем я-й (это законно в силу абсолютной
сходимости). Мы получим ряд
2
ц=0
B)
(ц — скалярный индекс), коэффициенты которого gu голоморф-
о о
ны в 'S— проекции области 5 в пространство С"~!.
Заметим, что такая перегруппировка
i|Z/7l членов ряда может привести к расшире-
расширению области сходимости. Например, сте-
степенной ряд
.-z2) 2d
! ft |=o
сходится в бикруге {J|, |}
После перегруппировки членов получаем
ряд
'х
Рис. 85.
ц=0
:-z, '
сходящийся в области {гхф1, |z2|<l}.
Определение. Ряд вида B), коэффициенты ?ц которого —
голоморфные функции 'z= (zu ..., zn-\), называется рядом Хар-
Хартогса с плоскостью центров {zn = an}. Областью сходимости этого
ряда называется открытое ядро Н множества точек ('z, zn) та-
таких, что ряд B) с коэффициентами gu.Cz) сходится в точке г„
и коэффициенты голоморфны в точке 'z. Радиус сходимости
R('z) этого ряда (рассматриваемого как степенной при фикси-
фиксированном 'z) называется радиусом Хартогса.
Так как вместе с каждой точкой z° области сходимости Н
ряда Хартогса принадлежат и все точки z= ('z°, гп), где
\г —a |^|z^"~fln|» т0 Н всегда является полной областью
Хартогса с плоскостью симметрии {zn = an} (см. рис. 85, где
ап = 0). Области этого типа играют для рядов Хартогса такую
же роль, как области Рейнхарта для степенных рядов. В ча-
частности, справедлива
Теорема 1. Любая функция<- f, голоморфная в полной
"власти Хартогса D с плоскостью симметрии {zn = an},
§ 3] ГОЛОМОРФНЫЕ ФУНКЦИИ 299
представляется в D разложением
/(z)=2gu('z)(z»-a«)'1 C)
с коэффициентами, голоморфными в проекции 'D этой области
в С"-1.
< Вместе с каждой точкой z области D принадлежит и поли-
поликруг U='UxUn, где '[/сгО^1 — достаточно малый поликруг с
центром в проекции 'г точки z, a UncC — круг с центром ап,
содержащий точку zn. В U функция f голоморфна по zn при
любом 'ге'У и, следовательно, разлагается в ряд C) с коэф-
коэффициентами
Эти коэффициенты, однако, определены и голоморфны не
только в '[/, но и во всей проекции 'D области D, поэтому и
разложение C) действует во всей области D >
Далее, не каждая полная область Хартогса оказывается об-
областью сходимости некоторого ряда Хартогса: в п. 27 мы пока-
покажем, что области сходимости характеризуются дополнительным
свойством, которым должен обладать радиус R('z).
В заключение опишем вкратце пространственные аналоги
рядов Лорана.
Теорема 2. Всякую функцию f, голоморфную в произведе-
произведении круговых колец П = {геО: rv< \zv — av|<^v}, можно пред-
представить в П в виде кратного ряда Лорана
/(г)= S ck{z-a)k, D)
!ft| = -°°
в котором суммирование распространяется на все целочислен-
целочисленные векторы k=(ku ..., kn), а коэффициенты
с-
BяОя J
где Г — произведение окружностей yv: t,v = av + pveif (v = l, ..., n;
rv<pv<Rv\ 0<t<2n).
< Разложение D) получается обычным образом: мы выби-
выбираем р* так, чтобы (р~, p*)m(rv, RJ, и функцию f в произве-
произведении колец {р~ < | zv — av \ < р+} представляем интегральной
формулой Коши:
е ге
300 ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
Здесь e=(ei, ..., е„)—набор, состоящий из + и —,Ге = у^Х
X ... Xy^"i где Yvv={|Sv~av = PvV) ~ окружность, ориен-
ориентированная положительно, если ev= + , и отрицательно, если
ev =—; суммирование распространяется на все наборы е из
п знаков. Далее мы разлагаем уз~ в соответствующие геоме-
геометрические прогрессии, интегрируем почленно и заменяем инте-
интегралы по Yvv интегралами по yv (с изменением знака, если
ev =—) >
Особенно интересны лорановские разложения в окрестности бесконечных
точек пространства С". Они характеризуются тем, что радиусы Rv с индек-
индексами, соответствующими бесконечным координатам точки, равны бесконечно-
бесконечности. Такими разложениями, в частности, представляются функции, голоморф-
голоморфные в бесконечных точках Си . Запишем для примера разложение функции /,
голоморфной в точке (ai.oo) еС2, где ai=^oo.rio определению п. 3 функция
f I ?,, -у- J = ф (?i, ?2) голоморфна в точке (ах, 0) и, значит, представляется
рядом Тейлора
сходящимся в некотором бикруге {I'd — ail<^i, \Ы<Г?}- Подставляя сюда
t,x — z\, 1,2 — —. получим нужное разложение Лорана функции /:
оо
(г,-о,)*.
оно сходится в окрестности -4 J гг] — asi | < r\, \ z2) > —> точки (аь оо).
Области сходимости рядов Лорана D) являются, очевидно,
областями Рейнхарта. Кроме того, если область сходимости со-
содержит какую-либо точку z° с координатой ^° = av< то в разло-
разложении D) не может быть отрицательных степеней разности
zv-—av, т. е. относительно этой разности D) является тейлоров-
тейлоровским разложением. Поэтому области сходимости рядов Лорана
являются так называемыми относительно полными областями
Рейнхарта. Область Рейнхарта называют относительно полной,
если она при фиксированном v либо не пересекается с пло-
плоскостью {zv = av}, либо вместе с каждой точкой z° содержит и
| j | ° |
z°
а остальные ко-
ковсе точки z, для которых | zv — av j <J | z° — av
ординаты те же, что z° (это условие выполняется для всех v).
ЗАДАЧИ
301
Таким образом, если область Рейнхарта не пересекается ни
с одной из плоскостей {zv=av}, то условие относительной пол-
полноты не накладывает никаких ограничений, пересечение же с
каждой из таких областей влечет за собой дополнительное усло-
условие. Для примера на рис. 86, а и б изображены относительно
полные, а на рис. 86,6 — неполная область Рейнхарта.
•\z,\
б)
Рис. ;
Так же как в случае рядов Тейлора, доказывается, что обла-
области сходимости рядов Лорана являются еще логарифмически
выпуклыми. Всякая функция /, голоморфная в относительно пол-
полной области Рейнхарта D, представляется в D рядом Лорана
D) (и такое представление осуще-
осуществляет аналитическое продолжение
/ в логарифмически выпуклую обо-
оболочку D, если D не логарифмически
выпукла).
Можно рассматривать и другой
аналог рядов Лорана. Именно, вся-
всякую функцию f, голоморфную в об-
области Хартогса вида {геС": 'z^'D,
r('z)<\zn — an\<R('z)}, где 'D —
область из С" (рис. 87), можно
представить в этой области рядом
Хартогса — Лорана
f(z)=
\Х= — оо
G)
Рис. 87.
где gue#(fD). Области сходимости таких рядов характери-
характеризуются дополнительными свойствами радиусов r('z) и R{'z),
которые мы укажем в п. 27.
ЗАДАЧИ
1. Доказать, что в С" всякая действительная гиперплоскость (т. е. ги-
гиперплоскость в R2™) задается уравнением' Re/(г) =а, где l(z)=aizi+...
...+anzn—комплексная линейная функция и aeR, Получить из этого, что
302 " ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ [ГЛ. Г
через любую точку действительной гиперплоскости Sc С" проходит принад-
принадлежащая S аналитическая (комплексная) гиперплоскость.
2. Построить пространственный аналог _стереографической проекции и
ввести с ее помощью сферическую метрику в Сп.
3. Рассмотреть все случаи пересечения сферы {|г| = 1}с:Сп с аналитиче-
аналитическими прямыми г=а+со? (а, соеО, ?еС).
4. Описать сечения шара {|г|<1}с:С2 и бикруга {ki|<l, |2г1<1} трехмер-
трехмерными плоскостями </2=а при различных aeR.
5. Доказать, что преобразование Рейнхарта a(z) = (|zil, ..., |гя|) пере-
переводит любую область DczCn, не пересекающуюся с множеством {zi...zn =
= 0}, в область пространства R".
6. Доказать, что область Хартогса D егС выпукла тогда и только тогда,
когда ее образ C(?>) при преобразовании C(z)'= ('г, |г„|) является выпуклой
областью в R2™.
7. Доказать, что каждая комплексно одномерная аналитическая пло-
плоскость из С" имеет в Рп ровно одну бесконечную точку.
8. Доказать, что любая функция f, голоморфная во всех точках комплекс-
комплексно (и—1)-мерной проективной плоскости Р" из Р", постоянна.
9. Пусть /(г)—целая функция в С" такая, что |/(г)|^сA +|г|)т для
некоторых констант .с, т^О и всех гбС". Доказать, что f (г) — многочлен
степени не выше от.
10. Пусть f(z) голоморфна в окрестности точки а еС" и равна нулю на
некоторой Bп—1)-мерной плоскости, проходящей через эту точку. Дока-
Доказать, что f(z) = 0 в окрестности а. .
11. Доказать, что всякая функция, голоморфная в окрестности точки
ОеС2 и равная нулю на двумерной плоскости z\ = z% равна нулю то-
тождественно в окрестности ОеС2.
12. Пусть f(z) голоморфна в бикруге ?/={|zi|<l, 1г2|<1} и равна нулю на
дуге
-! г2 = Zi, yi = x1sin—>. Доказать, что f(z) = 0 в U.
( xi )
13. Привести пример последовательности точек в единичном поликруге,
сходящейся к началу координат и являющейся множеством единственности
для функций, голоморфных в этом поликруге.
14. Построить пример замкнутого множества на остове бикруга, кото-
которое имеет двумерную меру нуль и является множеством единственности для
функций, голоморфных в бикруге и непрерывных в его замыкании.
15. Доказать, что если функции f и g голоморфны в окрестности замкну-
замкнутого бикруга U и совпадают на подмножестве его остова, имеющем по-
положительную меру размерности 2, то эти fug совпадают тождествен-
тождественно в V.
16. Доказать, что если при каждом фиксированном (г1г . ..,zv_j, z^+[, ...
..., 2°), v= 1 п, функция f(zb ..., zn)
а) является многочленом относительно zv, то она — многочлен;
б) является рациональной функцией от zv, то она — рациональная
функция.
17. Привести пример функции f(zi,z2), голоморфной по Z\ в {|zi|<l} для
"любого z2, |г21<1, непрерывной по zi в {|г2|<1} для любого z\, |2t|<l, и не
являющейся непрерывной по z=(zi,Z2) в бикруге {|2i|<l, Iz2|<lj.
18. Показать, что гармоническая по каждому переменному функция
Х\Хг в С2 не является действительной частью никакой голоморфной функ-
функции. Доказать, что функция является действительной частью голоморфной
функции тогда и только тогда, когда она гармонична на каждой аналити-
аналитической прямой.
ЗАДАЧИ 303
19. Пусть /(г) голоморфна в поликруге C/czC" и f@)=0. Доказать, что
|;(г)|^р(г) sup |/| для всех zef/, где p(z) =max|zvl- Когда имеет место ра-
U «
венство?
20. Доказать, что если f голоморфна в бикруге U={\z\\<l, |г2|<1}, не-
непрерывна в его замыкании, а на остове Г этого бикруга I/] = const, то / —
рациональная функция. __
21. Для функций fe.C2(U) в бикруге U вывести аналог формулы Ко-
ши — Грина для функций на плоскости (п. 17 ч. I).
22. Пусть f(z) голоморфна в окрестности ОеС"и f@, zn)jz™ голо-
голоморфна и не равна нулю в окрестности 0. Доказать, что для всякой функции
g, голоморфной в окрестности 0, найдется голоморфная функция r(z), кото-
которая по гп является многочленом степени <т, такая, что g=r (modf), т. е.
g = qf + r для некоторой функции q, голоморфной в окрестности 0.
23. Пусть / — замкнутый идеал в кольце К всех функций, голоморфных
в окрестности ОеС (каждая — в своей). Доказать, существование конеч-
конечного числа функций /ь ..., ft,e/ таких, что I=f\K+ ... +fhK (т. е. всякая
функция /е/ представима в виде f=f\gi + ¦ ¦ ¦ +fkgh, где все g,^K).
24. Назовем границей Бергмана области D минимальное замкнутое
множество BadD такое, что sup | / (z) | = sup I / B) | для всех функций,
_
голоморфных в D. Очевидно, что В содержится в границе Шилова S области D.
Доказать, что для области ?> = {0 < | Zj | < 1, \г2 I < | гх Г1п |г''} <= С2 эти
границы различны: S = {| гх \ < 1, | г2 1 = 1 zx \~ы |z'Ч, а В = [\ 2,) = 1, | г21= 1}.
25. Построить степенные ряды, для которых областью сходимости яв-
являются
а) шар (геСг-. |zi|2+|z2|2<l},
б) область {ге=С2: |zi| + |z2|<l}.
Построить степенные Ряды, для которых множеством сходимости яв-
являются
а) (геС2: \г}<1}[) {геС2: 1г|<2, г2=0},
+ 0О
б) (J{zeC2:|z|<
71
26. Доказать, что любая выпуклая область Рейнхарта является логариф-
логарифмически выпуклой.
ГЛАВА II
ИНТЕГРИРОВАНИЕ
В предыдущей главе мы уже рассматривали интегральную
формулу Коши для функций нескольких комплексных перемен-
переменных. Однако мы писали ее только для поликругов, и в таком
виде она распространяется лишь на поликруговые области.
Чтобы распространить эту формулу на области более общего
вида, нужно развить соответствующий топологический и анали-
аналитический аппарат.
§ 4. Многообразия и формы
Что и по каким объектам мы будем интегрировать? Здесь
мы дадим ответы на эти вопросы. Интегрировать мы будем по
многообразиям некоторые комбинации произведений диф-
дифференциалов, называемые дифференциальными фор-
м а м и. Выясним подробнее эти понятия.
9. Понятие многообразия. Хотя в этой главе мы будем рас-
рассматривать многообразия только в евклидовом пространстве, но
в дальнейшем нам встретится более общая ситуация многооб-
многообразий в некотором абстрактном пространстве элементов анали-
аналитических функций (пространственный аналог римановых поверх-
поверхностей, ср. п. 32 ч. I). Поэтому мы сразу даем общее
Определение 1. Множество М в хаусдорфовом простран-
пространстве X называется т-мерным многообразием, если выполнены
следующие условия:
1°. Существует семейство окрестностей Uj в относительной
топологии М (/е/, множество индексов / не обязательно счет-
счетное), покрывающих М (M = \j (/,¦) игомеоморфных т-мер-
ному евклидову шару, т. е. для всех /е/ определены гомеомор-
Физмы Ту. U3->Bj A)
на шары Bj = {ti(= Rm: |#|<A)}; переменное t1 = (t{, ....^на-
....^называется локальным параметром, действующим в окрестно-
окрестности Uj.
2°. Если ?/»Л?/3-=?0, то отображение
Tj ° Т1[ B)
открытого подмножества шара Ви которое соответствует пересе-
пересечению L'iOUj, в шар Bj гомеоморфно; отображения B) на-
S 4] МНОГООБРАЗИЯ И ФОРМЫ 305
зываются соотношениями соседства, связывающими окрестности
Ut и U}.
3°. Из покрытия M=\JUjy о котором говорится в 1°, можно
оо
выделить не более чем счетное покрытие М = UUj .
n=i **
(Приведем некоторые пояснения. Хаусдорфово простран-
пространство— это топологическое пространство, для которого справед-
справедлива аксиома отделимости (см. п. 32 ч. I). Относительной то-
топологией на множестве М топологического пространства X на-
называется топология на М, в которой окрестностями объявляются
пересечения с М окрестностей пространства X. То, что в каче-
качестве образов T(U) окрестностей UczM в условии 1° приняты
шары радиуса 1, несущественно; их можно заменить любыми
гомеоморфными им множествами в Rm, например самим Rm.
Гомеоморфность соотношений соседства B) очевидным обра-
образом следует из условия 1°; мы выделили это условие лишь для
удобства дальнейших формулировок.)
Итак, m-мерное многообразие локально устроено так же, как
m-мерный евклидов шар. В каждой окрестности U оно описы-
описывается локальным параметром t=(tu ..., tm), причем пара-
параметры, действующие в пересекающихся окрестностях, связаны
гомеоморфными соотношениями соседства. Локальные пара-
параметры часто называют также локальными координатами.
Функции, заданные на многообразии М, мы можем локально
рассматривать как функции параметра. Однако не всякий на-
набор функций локальных координат определяет функцию на
многообразии: мы должны потребовать независимость этих ло-
локальных функций от выбора параметра, или, иначе, их инва-
инвариантность при изменениях параметра. (Сравните: когда в
физике вводят какие-либо величины как функции координат, то
точно так же требуют их независимости от координат, иначе
они не будут иметь физического смысла. Например, вводя поня-
понятие дивергенции или ротора векторного поля при помощи коор-
координат, дают инвариантные определения этих величин, не завися-
зависящие от выбора координат, и тем самым устанавливают, что эти
величины являются физическими.)
Определение 2. Говорят, что на многообразии М за-
задана функция f, если в каждой окрестности U{czM задана
функция локального параметра Р, действующего в Uf.
!\иГ!ЛП tl<=Bt, C)
причем это задание инвариантно относительно замены па-
параметра: если и^и^ФОЗ, то в части шара В{, соответствующей
20 Б. В. Шабат
306 ИНТЕГРИРОВАНИЕ [ГЛ. II
в силу гомеоморфизма Г< пересечению Utr\Uj, имеем
fi{tl) = f,oT,oT?(ti). D)
Поскольку функция на /n-мерном многообразии в локальных
координатах выражается как функция т действительных пере-
переменных, мы можем говорить о ее дифференцируемости, гладко-
гладкости, наличии у нее вторых частных производных и т. д. Однако
если мы не налагаем на соотношения соседства B) никаких до-
дополнительных ограничений, то лишь свойство непрерывности
функции является инвариантным, а уже свойство дифференци-
дифференцируемости, вообще говоря, неинвариантно. В самом деле, если
какое-либо соотношение соседства B) недифференцируемо, то
функция /, дифференцируемая в зависимости от локальных ко-
координат t\ может оказаться недифференцируемой в зависимо-
зависимости от координат V.
Таким образом, мы приходим к необходимости введения до-
дополнительных ограничений на соотношения соседства.
Определение 3. Многообразие М называется дифферен-
дифференцируемым, гладким или многообразием класса О, если все
соотношения соседства Г/ ° TJ1, его определяющие, соответ-
соответственно дифференцируемы, непрерывно дифференцируемы или
имеют непрерывные частные производные до порядка р вклю-
включительно.
Многообразие в смысле определения 1 можно считать мно-
многообразием класса С0, гладкое многообразие является многооб-
многообразием класса С. Можно ввести также понятие многообразия
класса С°°, имея в виду многообразия, все соотношения сосед-
соседства которых и бесконечно дифференцируемы, т. е. имеют не-
непрерывные частные производные всех порядков.
На гладком многообразии М можно рассматривать диффе-
дифференцируемые и непрерывно дифференцируемые функции, пони-
понимая под ними функции, которые в любой окрестности UczM
дифференцируемо или непрерывно дифференцируемо зависят от
соответствующего локального параметра (это свойство, очевид-
очевидно, является инвариантным относительно замены параметров).
Точно так же на многообразии класса О можно рассматривать
функции классов Сч (q^p), а на многообразии класса С°° —
функции любых классов С*> и бесконечно дифференцируемые
функции.
До сих пор мы говорили о действительных многообразиях и
о дифференцируемости многообразий и функций в смысле дей-
действительных переменных. Однако в четномерном многооб-
многообразии М, пусть размерности 2т, можно ввести комплексную
структуру, если в каждой окрестности UczM вместо действи-
§ 4] МНОГООБРАЗИЯ И ФОРМЫ 307
тельных координат /= (tit ..., /2m) рассматривать комплексные
координаты
?=(&. •••. U); Zv=tv + itm+v (v = l, .... m) E)
и гомеоморфизмы Т; U—у В на шары {|?|<1} в комплексном
пространстве О. I
Соотношение соседства Г/ о 77' Для такого многообразия бу-
будет осуществлять гомеоморфное отображение открытого подмно-
подмножества шара BidCm в шар В3-с:Ст. Это отображение задается
посредством m функций m комплексных переменных
Е? = фЛ?'); v=1, ..., m\ i, /е=/, ' F)
которые можно записать при помощи одной векторной функции
ф<7 = (ф'/, ..., ф<7) в виде
?' = Ф«(?'); i, j(=J G)
(у нас, следовательно, фг/= Г/ ° 77 )• Наиболее интересным для
нас случаем является тот, когда все ф^ являются голоморф-
голоморфными функциями m комплексных переменных, т. е. отображения
ф" = Г/ о 771 — голоморфными гомеоморфизмами, или, как коро-
короче говорят, — голоморфизмами.
Определение 4. Четномерное многообразие М (размер-
(размерности 2т) называют комплексно аналитическим или, короче,
комплексным многообразием (комплексной) размерности пг, ес-
если в нем введена комплексная структура так, что все соотноше-
соотношения соседства фг/ = Г/ ° 77' являются голоморфизмами соответ-
соответствующих открытых подмножеств шаров S,czCm в шары Bj.
Очевидно, что комплексно аналитические многообразия яв-
являются многообразиями класса С°°.
Примеры.
1. Пространство С™ является комплексно аналитическим
многообразием размерности п. Оно покрывается одной окрест-
окрестностью— самим С"; в качестве локальных координат можно
принять комплексные координаты zit .,., zn (они действуют во
всем О).
2. Комплексное проективное пространство Р". Точками его
служат классы пропорциональных наборов комплексных чисел
(соь ..., con+i)- Обозначим через U\ множество всех точек из
Рп, для которых coi^O. Каждой точке из С/4 можно сопоставить
п чисел z\ = -^, ... , z\ = -^-, т. е. точку zl = (z>) е= Ся,
причем это соответствие Uy—*Cn является гомеоморфизмом.
Аналогично определяются множества U^ точек из Рп, для кото-
которых сои=^0, а также координаты z^ = [zty (где z!J— отношения
20*
308 ИНТЕГРИРОВАНИЕ [ГЛ. II
к wu остальных cov) и гомеоморфизмы f/ц,—>С™ (ц = 2, . . . , л).
Таким образом, Ра покрывается конечной системой окрестно-
окрестностей, гомеоморфных пространству С". Легко проверить, что со-
соотношения соседства, возникающие при этом, являются голо-
морфизмами. Следовательно, Р" является комплексно анали-
аналитическим многообразием размерности п.
3. Римановы поверхности аналитических функций одного
переменного являются комплексно аналитическими многообра-
многообразиями размерности 1 (см. п. 32 ч. I). Для функций нескольких
переменных аналогичное понятие будет рассмотрено в п. 28.
На комплексно аналитическом многообразии можно ввести
понятие голоморфной функции:
Определение 5. Функция / называется голоморфной на
/тг-мерном комплексно аналитическом многообразии М, если в
каждой окрестности UczM она представляется как голоморф-
голоморфная функция локального параметра ?= (?ь . .., ?m)eCm, дей-
действующего в этой окрестности.
Это определение инвариантно относительно замены парамет-
параметров при помощи соотношений соседства, ибо голоморфизмы со-
сохраняют свойство голоморфности.
Отметим два простых свойства функций, голоморфных на
связных1) аналитических многообразиях.
Теорема 1 (единственности). Если две функции f
и g, голоморфные на связном комплексно аналитическом много-
многообразии М, совпадают на непустом открытом (в топологии М)
подмножестве М, то они совпадают всюду на М.
¦4 Обозначим через с? открытое ядро совокупности всех то-
точек PeAf, в которых f(P)=g(P)', оно по условию непусто. По-
Покажем, что (f является и замкнутым множеством. В самом
деле, пусть точка Р0^М является предельной точкой cf. В ок-
окрестности UcM этой точки действует локальный параметр
?> = Т(Р), и функции f°T'L(t>), g°T-l(t) голоморфны в точке
^о = Г(Ро) шара ВсСт. В любой окрестности V cz В точки ?°
найдется точка Z,1 такая, что Pi = 7'-1(^1)e cf, и так как f=g
в некоторой окрестности Ри то foT'l^goT~l в некоторой окре-
окрестности t1. По теореме единственности из п. 6 последнее тожде-
тождество справедливо всюду в V, поэтому Po^cf .
Итак, cf непусто и одновременно замкнуто и открыто. Так
как М по условию связно, то отсюда следует, что %"=М, т. е.
f^g всюду на М >
') Определение связности, данное в п. 2 ч. I, годится для множеств лю-
любого топологического пространства. Напомним его: множество М назы-
называется связным, если его нельзя разбить_на две непусты^ части Mi и М2
так, что оба пересечения Mi(]M2 и М\(]М2 пусты (через М, обозначено за-
замыкание множества М().
§ 4] • МНОГООБРАЗИЯ И ФОРМЫ 309
Теорема 2 (принцип максимума). Если функция!
голоморфна на связном комплексно аналитическом многообра-
многообразии Ми |/| достигает максимума во внутренней точке М, то f
постоянна всюду на М.
< Пусть |/| достигает максимума в точке Ро^М; рассмот-
рассмотрим локальный параметр t, = T(P), действующий в окрестности
этой точки. Модуль функции foT~l('Q), голоморфной в точке
^о = Г(Ро), достигает максимума в этой точке; следовательно, по
принципу максимума из п. 6 функция f ° Т~1 постоянна в некото-
некоторой окрестности ?°, и, значит, / постоянна в некоторой окрест-
окрестности точки Ро. По предыдущей теореме / постоянна на всем
М >
Как уже говорилось в начале пункта, наиболее важен для
нас случай многообразий, расположенных в евклидовом про-
пространстве R". В этом случае гомеоморфизмы окрестностей
m-мерного многообразия М и шаров пространства R™ можно
задавать при помощи функций
xv = xv(tu ..., tm), v=l, ..., п. (8)
Впрочем, имеет место теорема Уитни1), по которой произ-
произвольное дифференцируемое многообразие размерности m можно
реализовать как многообразие в пространстве R2m+1.
Определение 6. Гладкое яг-мерное многообразие S cz Rn
называется m-мерной поверхностью, если: 1) 5 связно; 2) для
любой координатной окрестности UczS отображение B—*U,
определяемое по формулам (8), непрерывно дифференцируемо;
3) матрица 1-^гЧ имеет ранг т; 4) все соотношения соседства
\ "'и /
являются непрерывно дифференцируемыми гомеоморфизмами
с не обращающимися в нуль якобианами. ,
10. Дифференциальные формы. Функции на многообразиях
можно рассматривать как формы нулевой степени. Приме-
Примерами форм первой степени являются дифференциалы функ-
функций. Пусть М — гладкое m-мерное многообразие и / — диффе-
дифференцируемая функция на нем. В локальных координатах t = {t]S\
дифференциал этой функции имеет вид
') Точную формулировку и доказательство теоремы Уитни можно найти
в книге: Ж. д е Рам, Дифференцируемые многообразия, ИЛ, 1956,
стр. 32—36.
310 ИНТЕГРИРОВАНИЕ [ГЛ. II
При переходе к новым локальным координатам t—*т диффе-
дифференциал преобразуется к виду со = V-— dx^, где
и
<Эти лА dtv дхи ' ^
Обобщая этот пример, мы будем называть дифференциальной
формой первой степени на гладком многообразии М любое вы-
выражение, которое в локальных координатах t = {t)i}, действую-
действующих в окрестности UczM, имеет вид
»= 2j 0-v.dt C)
и
а при переходе к новым локальным координатам t—*x меняется
так же, как дифференциал, т. е. преобразуется к виду
со = ^j cc^ dXy, где
«, = S«v^-. D)
От форм первой степени можно брать криволинейные инте-
интегралы (т. е. интегралы по одномерным многообразиям). Мы вве-
введем формы второй степени так, чтобы от них можно было
брать интегралы по двумерным многообразиям. Мы будем за-
задавать такие формы в локальных координатах и должны выяс-
выяснить, как меняются их выражения при переходе к другим коор-
координатам.
В простейшем случае плоских областей подынтегральные вы-
выражения двойных интегралов adxdy при замене переменных
(х, у) —>¦ (и, и) умножаются на якобиан: форма adxdy перехо-
переходит в форму а д , *' *\ du dv. Имея в виду более общие случаи,
удобно ввести алгоритм умножения дифференциалов, который
приводит к такому правилу замены на основании формальных
выкладок. Этот алгоритм был найден Э. Картаном и называется
внешним умножением дифференциалов. Мы поясним его сначала
на рассматриваемом простейшем случае.
Условимся считать, что внешнее произведение одинаковых
дифференциалов равно нулю: dxAdx—dyAdy = O (Л — знак
внешнего умножения), а различных дифференциалов — антиком-
мутативно: dx/\dy = —dyAdx. Кроме того, будем предполагать,
что для внешнего умножения соблюдаются обычные правила
.раскрытия скобок. Тогда умножение двух дифференциалов
§4] МНОГООБРАЗИЯ И ФОРМЫ 311
dx = -^- du + ~^~ dv и dy = -jr-_ du + -^-dv формально приведет к
нужному правилу замены:
- f f «« Л *Н-# ?*. Л А. = |fe^» Л *,.
Приведем теперь точное определение в более общем случае.
Определение 1. Внешним умножением дифференциаль-
дифференциальных форм от переменных tu , . ., tm называется умножение, под-
подчиняющееся следующим'законам:
1°. Умножение на скаляр (функцию) коммутативно и ассо-
ассоциативно:
aAdtv = dtvf\a = adtv, dtilAadtv = adtv.Adtv. E)
2°. Умножение дифференциалов антикоммутативно:
), dtvAd(v=O. F)
3°. Умножение линейных комбинаций произведений диффе-
дифференциалов (со скалярными коэффициентами) подчиняется ассо-
ассоциативному и дистрибутивному законам.
Таким образом, внешнее произведение двух форм первой
m ш
степени ю, = 2 avdt%. и ю2=2 bvdtv имеет следующий вид:
V=l V-1
'(aldtl+]... + amdtm)A(bldtl + ... + bmdtm) = (alb2—a2b1)dtlAdt2+ ...
...+ {am-\bm — ambm_x) dtm-\Adtm.
При замене переменных t—*т коэффициенты при произведе-
произведении дифференциалов, как нетрудно проверить прямой выклад-
выкладкой, умножаются на соответствующие якобианы. Например, при
произведении dxiAdx2 будет стоять коэффициент
VV д (tjx, tv)
а\Ь'3 - а'2Ъ\ = 2j Mv - a A) d(Tl,r2) '
где штрих в обозначении суммы показывает, что суммирование
надо вести по всем индексам |i, v при условии I-^ \x<iv ^ т
(упорядоченное суммирование).
Произведение двух форм первой степени является примером
форм второй степени. Вообще же под формой второй степени
на гладком многообразии М мы будем понимать выражение,
которое в локальных координатах t имеет вид
G)
312 ИНТЕГРИРОВАНИЕ [ГЛ. II
где штрих обозначает упорядоченное суммирование (,u<v), a
при замене координат t—*x переходит в аналогичное выражение
с коэффициентами
У' д (и, t,) .„.
2 <8>
Мы можем пользоваться и неупорядоченным суммированием
(без штриха). Для этого условимся считать, что матрица (а^)
к о с о с и м м етр и ч н а , т. е. что а^ = —avii, и тогда перепишем
форму G) в виде
^vdtilAdtv. G0
Закон изменения коэффициентов можно тогда переписать так:
— очевидно, что это равносильно соотношению (8).
Теперь мы можем дать общее определение формы.
Определение 2. Дифференциальной формой степени р
на гладком многообразии М называется выражение, которое в
произвольной системе локальных координат t имеет вид1)
dtV{A ... Л dtVp = -2jav,-v/,dtvi A ... Л dtVp,
(9)
а при замене переменных t—*x переходит в аналогичное выра-
выражение с коэффициентами2)
at. dt,
l>
., t, \
Форма со называется формой класса Сч, если ее коэффициенты
(как функции локальных параметров) имеют непрерывные част-
частные производные g-ro порядка, — это определение инвариант-
') В первой сумме (9) суммирование ведется по упорядоченным систе-
системам индексов 1 ^у\<. ¦ -<Yj> ^ "г> а во второй — по всем системам, но мат-
матрица (а) предполагается кососимметрической по индексам: при четной пере-
перестановке индексов коэффициенты не меняются, а при нечетной меняют знак.
2) Закон изменения коэффициентов дифференциальных форм имеет тен-
тензорный характер. Совокупность этих коэффициентов (а) образует тензор
(кососимметрический, ковариантный).
§ 4] МНОГООБРАЗИЯ II ФОРМЫ 313
но лишь для многообразий класса Сэ (см. определение 3
п. 9).
Дифференциальные формы можно складывать, умножать на
функцию (скаляр), а также умножать друг на друга внешним
образом (при этом произведение формы степени р на форму
степени q является формой степени p + q). Совокупность всех
форм степени р на многообразии М образует группу по сложе-
сложению, которую мы будем обозначать через Qp.
До сих пор мы пользовались записью форм в действитель-
действительных координатах, однако для дальнейшего удобнее комплекс-
комплексная форма записи. Рассмотрим случай гладкого т-мерного
многообразия М, расположенного в комплексном пространстве
С". Если обозначить zv=xv + ixn+v, то эти величины на М будут
функциями локальных координат: zv—-z(t\, ..., /,„), v=l, ..., п.
Дифференциальная форма степени р-^т на многообразии М:
со = 2'аг, ...ipdx^A ... /\dxip='2i' a,dxh A1)
где / = (г,, . . ., ip) — векторный индекс и dxr = dxi{ А ... Л dxip,
в этих локальных координатах принимает вид со = 2'а/^/, где
Чтобы переписать форму A1) в комплексном виде, мы мо-
можем формально перейти от 2п действительных координат xv в
<t> к такому же числу комплексных координат zv, zv. Для упро-
упрощения записей мы положим
v, Zn+v=zv = xv — ixn+v (v=l, . .., п) A3)
и будем рассматривать переход от xv к Zv как обычную замену
переменных.
Подставляя в A1) dxv = у (dZv + dZn+v) и dxn+v =
= -^r(dZv — dZn+v), перепишем эту форму в виде
@ = 2 fidZh A4)
где
д(Х1г %)
6ZV 2 \дху dxn+v)'
1
dZv 2 \dxv dxn+v I' dZn+v 2 \ dxv ^ dxm
(v=l, ..., n).
314 ИНТЕГРИРОВАНИЕ [ГЛ. 1Г
Часто бывает важно различать степени формы A4) по пе-
переменным 2V и zv. Поэтому вводят понятие бистепени формы,
понимая под формой бистепени (р, q) выражение вида
со = 2'/7 jdzi, Л ... Л dz Л dz, Л ... Л dz =
' ' lp 'I 'q
— 2' f/. j dzj Л d2j, A5)
где /=(t'i, ». ., iP) и J=(ju ..., /,)—векторные индексы раз-
размерности соответственно р и q.
Наиболее важен частный случай форм бистепени (р, 0), ко-
коэффициенты которых являются голоморфными функциями п пе-
переменных на множестве MczCn (т. е. голоморфными в 2п-мер-
ной окрестности этого множества). Такие формы записываются
в виде
co = 2'f,- . dz. Л ... Л dz. =^21\,dz,, A6)
г1 ••• гр Н гр
алые» перемен!
голоморфными формами.
Можно рассматривать также формы на комплексно
аналитическом многообразии М комплексной размерно-
размерности m в произвольном хаусдорфовом пространстве. Здесь также
наиболее интересен случай форм бистепени (р, 0), р^.т, кото-
которые имеют вид A6) в локальных координатах (гь ..., zm),
действующих в окрестности Uc:M, причем коэффициенты яв-
являются голоморфными функциями на М и при замене перемен-
переменных г—*'С, меняются по тензорному закону
a it t. \
А'
где / = (/i, ..., ip).
Такие формы называются голоморфными формами на мно-
многообразии М.
11. Понятие интеграла от формы. Дифференциальные формы
степени т введены так, чтобы от них можно было брать инте-
интегралы по /n-мерным многообразиям. Интегралы берутся по ори-
ориентированным многообразиям, поэтому мы должны начать с
этого понятия.
Введем сначала ориентацию в окрестности UczM. Для этого
будем считать, что параметр /, действующий в U, меняется не
в шаре, как раньше, а в /n-мерном симплексе Sm (т. е. что
задается гомеоморфизм Г: U—*Sm). Для определенности пред-
предположим, что одна из вершин симплекса Ро лежит в начале
координат, а другие вершины Pv имеют v-ю координату, рав-
равную 1, и остальные 0 (v = l, ...rm). Введем на Sm ориентацию
§ 4]
МНОГООБРАЗИЯ И ФОРМЫ
315
следующим образом: симплекс (Ро, Pi, . ¦ ¦, Рт) и все, полу-
получающиеся из него четной перестановкой номеров вершин, будем
считать ориентированными положительно; симплексы, номера
вершин которых образуют нечетную перестановку, — ориенти-
ориентированными отрицательно.
Часто неориентированный симплекс мы будем обозначать
через Sm, ориентированные — через S?, где е=+ или е = — в за-
зависимости от ориентации.
На рис. 88 изображены
двумерные симплексы
51 = (P0, Ри Р2) и S- =
= (Ро, Р2, Pi).
При заданном отобра-
отображении Т: U—*Sm мы
введем две ориентации
окрестности U в зависи-
зависимости от той или иной
ориентации симплекса
Sm; ориентированную
окрестность будет иногда
обозначать через Иг.
Пример. Нагляднее все-
всего представляется ориентация
в одномерном случае. Пусть
5' = [0, 1] и U — гомеоморфный образ 51, скажем в С", т. е. жор-
данов путь z=z(t): 5]->1/. Положительной ориентацией U мы будем
считать ту, которая соответствует возрастанию параметра t, т. е. положи-
положительной ориентации отрезка [0, 1]; отрицательной — ту, которая соответствует
убыванию t. Ориентацию гомеоморфного образа в С" двумерного симплекса
52 при заданном отображении z = z(ti, t2): S2 —> U можно представлять как
указание одной из двух сторон V; положительной считается та, с которой
образы Pv — Z(PV) вершин симплекса обходятся в порядке @, 1, 2), и от-
отрицательной— та, с которой они обходятся в порядке @, 2, 1) (см. рис. 88).
Пусть теперь М — связное гладкое многообразие. Назовем
М ориентируемым, если все соотношения соседства, его опреде-
определяющие, имеют положительные якобианы. На каждом ориенти-
ориентируемом многообразии можно ввести две ориентации — положи-
положительную и отрицательную. Для этого достаточно ввести ту или
иную ориентацию в какой-либо окрестности Uc^M; соотношения
соседства позволяют перенести эту ориентацию во все окрестно-
окрестности на М, а условие ориентируемости М обеспечивает, что при
этом мы не придем к противоречию: какой бы цепочкой окрест-
окрестностей, связывающих О с некоторой окрестностью V с: М, ни
пользоваться, всегда получим одну и ту же ориентацию V. То
же условие обеспечивает независимость ориентации от выбора
Рис.
316
ИНТЕГРИРОВАНИЕ
[ГЛ. II
мем, что все соотношения
начальной окрестности U. На доказательстве этих утверждений
мы не останавливаемся1).
Пример. Представим окружность на плоскости (х, у) как одномерное
многообразие, покрываемое четырьмя окрестностями Ui (в Ul и Us дей-
действует локальная координата х, в U2 и (Д — координата у; рис. 89). Ориен-
Ориентируем Ui положительно (т. е. условием возрастания параметра х) и при-
присосе^тт чмеют положительные якобианы. Тогда
на пересечении (А П U2 параметр у должен
возрастать вместе с х (соотношение соседства
Ui и U2 имеет вид у = ——ух — л2), и на
(Л вводится ориентация снизу вверх. Эта ори-
ориентация вводит на Us ориентацию справа на-
налево (в самом деле, условие положительно-
положительности якобиана на пересечении U2 Г) ^з влечет
за собой, что у должен убывать вместе с х).
Далее, G4 окажется ориентированной сверху
вниз и Ui — слева направо. Мы снова пришли
X к исходной ориентации Ui.
Рис. 89.
Перейдем к определению интеграла.
Начнем с интеграла по одной окрест-
окрестности многообразия.
Определение 1. Пусть U — ориентированная окрестность
/n-мерного многообразия М е= С1, t — параметр, действующий в
U и меняющийся в симплексе Sm; интегралом по окрестности U
от формы we=C°(L') степени m назовем
= \f{t)dt{A ... Adtm = s \f(t)dtl ...dtm,
A)
где е означает ориентацию симплекса и окрестности относи-
относительно координат t\, ..., tm, Sm—неориентированный симплекс.
Теорема 1. Определение интеграла инвариантно относи-
относительно допустимой замены параметра.
< Пусть t—ух — допустимая (т. е. гомеоморфная и класса
С1) замена параметр-а, преобразующая Sm на S™, и
/== d(tlt ..., tm)
д (т.,, . . ., тт)
— ее якобиан (непрерывная функция т). По правилам замены
переменных в (неориентированных) кратных интегралах
\f{t)dtx
dtm=
, ... dxm.
B)
') См. П С. Александров, Комбинаторная топология, Гостехиздат,
М. —Л., 1947.
§ 4] МНОГООБРАЗИЯ И ФОРМЫ 317
В силу гомеоморфности отображения t—*x якобиан / в Sm
не меняет знака. Если 7^-0, то отображение сохраняет ориен-
ориентацию, т. е. переводит S? в S™, а так как форма со в новых ко-
координатах имеют вид f °t(x)JdxiA ... Adxm, то по определе-
определению 1 в новых координатах
J со = J fJdxx Л ... Л dx,n = e \ f\J\dxx ... dxm. C)
U cm sm
Если же 7^0, то отображение меняет ориентацию, т. е. пере-
переводит ST в S-s, и по тем же соображениям в новых коорди-
координатах
[ со = f f J dxx Л .. . Л dxm =
U 3„
= — е \ f] dxx ... dxm = s f f\J\dxl ... dxm. (<)
sm sm
В силу B) правые части C) и D) совпадают с правой частью
A) >
Замечание. Мы вводим дифференциальные формы так,
чтобы при замене переменных они менялись, как подинтеграль-
ные выражения соответствующих интегралов. Однако имеется
некоторое отличие: формы при замене переменных умножаются
на якобиан преобразования, а подынтегральные выражения —
на модуль якобиана. Сейчас мы убедились, что именно так и
надо было вводить формы, если желать, чтобы были инвариант-
инвариантными относительно замены переменных интегралы по ориен-
ориентированным окрестностям.
Можно было бы рассматривать так называемые нечетные дифференци-
дифференциальные формы, которые (в отличие от введенных выше четных форм) при
замене переменных умножаются на модуль якобиана. Точнее, нечетной фор-
формой степени р на многообразии М называется выражение, которое в локаль-
локальных координатах t имеет вид ш = 2 av ...v ^v Л ... Л dtvp, а при за-
замене переменных t^-x переходит в такое же выражение с коэффициентами
(ср. с формулами A0) п. 10). Нечетные формы приспособлены для интегри-
интегрирования по неориентированным многообразиям.
Переход от интеграла по окрестности к интегралу по ком-
компактному подмножеству многообразия просто осуществляется
при помощи хак называемого разбиения единицы. Пусть М—•
318 ИНТЕГРИРОВАНИЕ [ГЛ. II
многообразие класса С1 и {Ui}, te/,— его локально конечное1)
покрытие окрестностями; разбиением единицы, соответствующим
этому покрытию, называется система функций е* е С1 (М) та-
таких, что
1) 2 вг(х) = 1, 0-<е*(х)-< 1, для всех х<=М; -
2) "носитель е,, т. е. замыкание множества {х^М: вг(х)Ф0},
является компактным подмножеством ?Д.
Доказательство существования разбиения единицы мы при-
приведем для многообразий М, расположенных в евклидовом про-
пространстве Rn.
Лемма. Для любого открытого множества UcR" и любого
множества Кш1/ существует функция ф: Rn—>[0, l]cR класса
С°° такая, что
1 для всех х ^ К,
О для всех x^Rn\TJ. ^
¦4 Сначала рассмотрим частный случай, когда К={\х\<г} и
U = {\x\ <R} — концентрические шары @<r<.R), Построим
функцию
g[t)J{e~re-lR, t^[r,R],
[О, t^R\[r, R]
и возьмем
R
f ё (т) dx
J gb)dx
r
она принадлежит классу C°°(R), равна 1 на отрезке (—оо, г]
и 0 на отрезке [R, оо). Поэтому функция q>(x) —h(\x\) обладает
нужными свойствами.
В общем случае мы устраиваем конечное (по лемме Хейне —
Бореля) покрытие К шарами Кг такими, что для каждого Кг
найдется концентрический с ним шар (/jcf/ большего радиуса.
¦Для каждой пары (/(,-, Ui) строим, как выше, функцию ф,-, и
тогда
' обладает нужными свойствами >
') Покрытие {Ui} называется локально конечным, если любая точка
имеет окрестность, покрываемую лишь конечным числом U±,
§ 4] МНОГООБРАЗИЯ И ФОРМЫ 319
Теорема 2. Пусть McrR™ — многообразие класса С00.Для
любого его локально конечного покрытия {?Л};е / открытыми
множествами из R™ существует соответствующее этому покры-
покрытию разбиение единицы {ег}.
< Каждая точка х^М имеет окрестность, пересекающуюся
с конечным числом Ut. В каждой U{ мы выберем компактно
принадлежащее ей множество К% так, чтобы объединение Кг по-
покрывало М, и для каждой пары (Ki,_Ui) строим (по лемме)
функцию (pi, равную 1 в Кг и 0 вне Ui. Далее рассматриваем
сумму 2 Фг (х) и замечаем, что она определена в окрестности
каждой точки jteM (ибо там лишь конечное число ф, отлично
от нуля) и положительна в каждой такой точке (ибо эта точка
покрывается хотя бы одним Кг, а там ф,(л:) = 1, остальные же
Ф,-(я)^>0). Функции
eiW-^77. F)
2 М
очевидно, дают разбиение единицы, соответствующее покры-
покрытию {Ui) >
Определение 2. Пусть К — компактное подмножество
«г-мерного ориентируемого многообразия М; интегралом по К
от формы сое С0 (К) степени m называется
= S J е'ю = S J
К ;
где {et} — разбиение единицы, соответствующее некоторому по-
покрытию \JUi=M. (Интеграл по пересечению Kf]Uit где дей-
ствуют локальные координаты tl — (t\, .... t^), определен выше;
в силу локальной конечности покрытия сумма в правой части
содержит лишь конечное число отличных от нуля слагаемых.)
Чтобы убедиться в корректности этого определения, нужно
доказать его независимость от выбора покрытия и разбиения
единицы.
Теорема 3. Пусть {Ut}, [u'j] — два (локально конечных)
покрытия ориентируемого многообразия М и {еД, 1е'\ — соответ-
соответствующие им разбиения единицы. Для любого К<^М и формы
weC°(/C) интегралы от ш по К, вычисленные по этим разбие-
разбиениям, совпадают.
* Интеграл, вычисленный по разбиению {ег),
i кпи,
320 ' ИНТЕГРИРОВАНИЕ [ГЛ. II
в силу тождества 2 ?/ — 1 можно переписать так:
i
кпи.пи
В пересечении К f\ Uif] U\ введем новые локальные координаты,
соответствующие окрестности Uf, в силу инвариантности ин-
интеграла и тождества 2ег=1 будем иметь
i
* ' /СП t/y ' ;' /СП t/^
Мы получили интеграл, вычисленный по разбиению (е'| >
Если М — некомпактное многообразие и Л' — его некомпактное подмно-
подмножество (в частности, N=M), то надо построить исчерпывание Кц компакт-
компактными множествами (/Ci<=/С2с=- • ¦; ИКц^М). Интеграл по N тогда опреде-
ляется как предел при ji->-oo интегралов по компактным множествам ^
если этот предел существует и не зависит от исчерпывания (несобственный
интеграл).
Примеры. 1. Пусть у — гладкий путь z = z(t): [0, 1] —* С",
а / — функция, голоморфная на множестве у (т. е. голоморфная
в каждой точке геу); рассмотрим на у дифференциальную
форму 1-й степени со = ^д~ dzv. Если отображение z = z(t)
v=l
гомеоморфно, то y можно рассматривать как окрестность, а / —
как локальный параметр, действующий в ней. По определению 1
(мы считаем у положительно ориентированным). Так как функ-
функция f голоморфна (т. е. ^- = 0, v=l, ..., п), то подинтеграль-
ная функция справа является производной функции f°z(t), и
по формуле Ньютона—Лейбница (для функций действительно-
действительного переменного) мы получаем
^^ = /И-/(г«), (8)
¦у v=l
§5] ТЕОРЕМА КОШИ - ПУАНКАРЕ 321
где 2° = г@) и zl = z(\)—концы пути. В общем случае отобра-
отображение z = z(t) локально гомеоморфно (в силу условия z'(t)i=O,
принятого нами для гладких путей); разбивая [0, 1] на конечное
число отрезков, мы придем к тому же соотношению (8).
2. Пусть Dv — односвязные плоские области с гладкими гра-
границами dDv: zv=zv(tv) ,^ve[0, 1], и D = D4X.. .XDn — поликруго-
поликруговая область в Сп. Остов этой области T = dDiX- ¦ .XdDn можно
рассматривать как гладкое я-мерное многообразие. Оно являет-
является гладким образом куба Qn = {/eRn: 0^/v^]} при отображе-
отображении z = z(t): Qn—»Cn; ориентацию на Qn и, следовательно, на Г
мы введем условием возрастания всех координат tv. Параметр
t=(tu ..., tn), меняющийся в Qn, можно использовать при
вычислении интегралов по Г, как в определении 1, хотя Г и не
является гомеоморфным образом Qn (это доказывается разбие-
разбиением единицы). Пусть шеС°(Г) —форма бистепени (п, 0), т. е.
имеющая вид co = f dziA . . . Adzn, где / — непрерывная на Г
функция. После введения параметра t форма принимает вид
поэтому, согласно сказанному выше,
Г fdz, Л ... l\dzn= ]f-fL---4r-
j
1
dDn
Таким образом, интеграл от со по Г совпадает с повторным
интегралом. Точно так же повторный интеграл Коши, введенный
в предыдущей главе, можно рассматривать как интеграл по
«-мерному многообразию:
Si-2,--* J t,n-zn B«Г J
au г
Bш)" ,nn
dDl aun г
где мы для краткости обозначили d?> = d?>lA ... Л dtn и
11
§ 5. Теорема Коши — Пуанкаре
В этом параграфе мы рассмотрим многомерный аналог ос-
основной теоремы теории аналитических функций — теоремы
Коши. Центральную роль здесь играет формула Стокса,
21 Б. В. Шабат
322 ИНТЕГРИРОВАНИЕ [ГЛ. II
связывающая две операции: топологическую операцию взятия
границы и аналитическую операцию дифференцирования форм.
Начнем изучение с операции взятия границы.
12. Цепи и их границы. Рассмотрим (замкнутый) ориенти-
ориентированный m-мерный симплекс Sm= {PtoPil ... Ptm}, где Pv —
вершины симплекса, взятые в каком-либо порядке; предпола-
предполагается, что они находятся в общем положении1). Индексы-
to, h, • • •. im образуют перестановку из чисел 0, 1, . . . , т; чет-
четность этой перестановки определяет положительную или отри-
отрицательную ориентацию.
Будем считать, что ориентация Sm индуцирует ориентацию
граней этого симплекса по следующему правилу. Грань Sm-i =
= [Pi ... Pim), получаемую из Sm отбра-
отбрасыванием вершины, которая стоит на пер-
первом месте, будем считать ориентированной
так же, как Sm. Ориентацию других граней
будем вводить так: отбрасываемую верши-
вершину Piy переводим на первое место и при-
приписываем соответствующей грани ту ориен-
ориентацию, которую имеет симплекс \Pi Pi ...
Рнс-90- ...Pt Pt ...Pi ).
'v-l 'v+l ml
На рис. 90 изображен для примера двумерный симплекс
{Р0Р1Р2}, ориентированный положительно. Индуцированная
ориентация его одномерных граней следующая: {Р1Р2},
—{Ро Рг} = {Р2 Ро) н {Ро Pi).
Определение 1. Границей симплекса Sm называется со-
совокупность dSm его (гп—1)-мерных граней, взятых с индуци-
индуцированной ориентацией. Условимся записывать эту совокупность
как сумму:
ds = s%-i+ ... +sS&. (l)
Пример. Для симплекса S2 = {PqPiP2) границей является
dS2 = {Pl P2}+{P2 Po}+{Po Pi)
(см. рис. 90). Граница одномерного симплекса Si = {P0P\)
dS^Pi — Po.
Границу нульмерного симплекса (точки) будем считать рав-
равной нулю.
Определение 2. Будем называть m-мерной цепью ото-
отображение совокупности m-мерных симплексов 5т (л = 1. • • •> Ю
') Это означает, что никакие 3 из Pv не лежат на одной прямой, ника-
никакие 4 не лежат в одной двумерной плоскости и т. д.
§ 5] ТЕОРЕМА КОШИ — ПУАНКАРЕ 323
в какую-либо коммутативную группу (например, группу Z це-
целых чисел). Приписывая каждому S\] его образ nv при этом
отображении как формальный коэффициент, мы можем пред-
представить цепи как формальные линейные комбинации:
Ym=S«vS^. B)
v=l
Границей цепи ут назовем (т— 1)-мерную цепь
дут = 2 «v asS?- (з)
v=l
Цепи одной размерности мы условимся складывать между
собой (покоэффициентно); в частности, будем приводить подоб-
подобные члены (когда это возможно). Совокупность всех т-мерных
цепей (с коэффициентами из данной группы) образует, следова-
следовательно, коммутативную группу, которую мы будем обозначать
через Гт.
Оператор взятия границы можно рассматривать как опера-
оператор, преобразующий Гт в Гпг-ь
д: Тт-*Гт-п D)
причем этот оператор сохраняет групповую операцию
@: Ym + Ут "* ^Y(m + ^Ут)' Т' е- является ГОМОМОрфиЗМОМ.
Теорема. Квадрат оператора д равен нулю, т. е. для лю-
любой цепи Ym^rm
д2 д(д)=0. E)
•* Теорему достаточно доказать для m-мерных симплексов
5т. При т = 0 по определению принято dS0 = 0, значит, и по-
подавно d2S0 = 0. Для m=l имеем S\ = {PoPl}, dSi = P\ — Ро и
d2Si = 0 (опять используется, что граница точки равна нулю).
Пусть т^2; рассмотрим симплекс Sm = {PoPiP2- ¦ ¦} и будем
следить лишь за теми его гранями, которые вносят в d2Sm сим-
симплексы, не содержащие одновременно вершин Ро и Р\. Имеем
причем невыписанные симплексы содержат обе вершины Ро и
Pi, и, далее,
Мы видим, что в выражении d2Sm симплексы, не содержащие
вершин Ре и Р\, сокращаются. Но перестановкой вершин (кото-
(которая может переменить лишь знак) мы любые две вершины Sm
. 21*
324 ИНТЕГРИРОВАНИЕ [ГЛ. II
можем поставить на место Ро и Ри следовательно, в выражении
d2Sm сокращаются все симплексы, и <?2Sm = 0 >
Определение 3. Будем называть циклом любую цепь ут,
граница которой равна 0 (с?ут = 0). Цепь ут, которая является
границей какой-либо цепи ут+\ {ут = дут+\) и которая по дока-
доказанной теореме непременно является циклом, называется цик-
циклом, гомологичным нулю.
Циклы данной размерности т, очевидно, образуют группу
Zm, которая является подгруппой Гт. Точно так же циклы, гомо-
гомологичные нулю, образуют подгруппу Вт группы Zm. Эти под-
подгруппы можно охарактеризовать еще так:
Zm = {Ymerm: aYm = 0} F)
является ядром гомоморфизма д, т. е. совокупностью элементов,
которые д переводит в 0 (обозначение: Zm = kerd), a
Вт = {ут^Гт: ут = дут+1) G)
— образом этого гомоморфизма, т. е. совокупностью элементов
Гт, в которые д переводит элементы Гт+1 (обозначение:
Вт = Шд).
Рассмотрим последовательность двух гомоморфизмов
Г^-^Г^Г^., (8)
(для ясности мы снабжаем оператор д индексом, указывающим
размерность цепей, на которые он действует); доказанная выше
теорема гласит, что
imdm+ic:kerdm. (9)
Последовательности гомоморфизмов, удовлетворяющие этому
условию, называются полуточными; если же вместо включения
имеет место равенство:
im<9,n+1=kerdm, ¦
то последовательность называется точной. Точность последова-
последовательности (8) означает, следовательно, что в Г,„ каждый цикл
гомологичен нулю.
Назовем два цикла уЮ, y{®&Zm гомологичными (Ym~Y®).
если их разность гомологична нулю (yW — у{® е Вт, т. е.
Ут ~ Ym = ^Ym+i)- Классы гомологичных друг другу циклов
образуют факторгруппу
Hm — Zm/Bm, A1)
которая называется группой гомологии. Точность последователь-
последовательности (8) означает, очевидно, тривиальность этой группы
(Ят = 0: все циклы гомологичны нулю).
§ 5] ТЕОРЕМА КОШИ - ПУАНКАРЕ 325
Введенные понятия без труда переносятся на произвольное
гладкое ориентируемое многообразие М. Именно, криволиней-
криволинейным симплексом на М мы будем называть пару ат= (Sm, Ф),
где Sm — ориентированный симплекс и Ф: Sm—*M — непрерывно
дифференцируемое гомеоморфное отображение (сохраняющее
или меняющее ориентацию). Далее, m-мерной цепью на М на-
назовем любую линейную комбинацию ат = 2 nvam\ где nv — эле-
элемент какой-либо группы, а (*?? —(Sm\ ®v)- Границей цепи ат
назовем цепь ]jjnvdom), где да(т = (dSm\ Фу)- Без всяких изме-
изменений переносятся на многообразия определения цикла, гомо-
гомологичных циклов и группы гомологии.
Всюду в дальнейшем (если не оговорено противное) мы бу-
будем рассматривать цепи с целочисленными коэффициентами
nveZ на гладких ориентируемых поверхностях М пространства
Rn или С".
Криволинейный симплекс E, Ф) мы часто будем обозначать
просто символом 5. Мы будем рассматривать конечные наборы
криволинейных симплексов {5} = /(, удовлетворяющие следую-
следующим условиям:
1) каждый симплекс Sp входит в К вместе со всеми своими
гранями Sp-\'<
2) любые два симплекса из К либо не пересекаются, либо
их пересечение является гранью (какой-либо размерности) каж-
каждого из них.
Такие наборы мы будем называть комплексами; размерно-
размерностью комплекса будем называть наибольшую из размерностей
составляющих его симплексов. Объединение точек всех таких
симплексов будем называть носителем комплекса или поли-
полиэдром.
Пусть дан комплекс К на m-мерной поверхности М; тогда
р-мерную цепь @<^р<!т) комплекса К, т. е. линейную комби-
комбинацию ориентированных р-мерных симплексов SpV> e/( с цело-
целочисленными коэффициентами:
V=I
мы будем наглядно представлять как набор этих симплексов,
причем S^ входит в набор nv раз с ориентацией М, если nv>0,
и с противоположной, если nv<0.
На рис. 91 изображено несколько одномерных циклов на
торе Т в R3, который представляет собой носитель двумерного
комплекса. Цикл у0 гомологичен нулю — он ограничивает
326
ИНТЕГРИРОВАНИЕ
[ГЛ. II
одномерный цикл
комбинации циклов
двумерную цепь, носитель которой заштрихован. Циклы Yi и уг
негомологичны нулю и негомологичны друг другу; цикл \2 гомо-
гомологичен циклу— Y2 (это видно из того, 4TOY2 + Y2 ограничивает
двумерную цепь). Можно убедиться в том, что всякий
на торе гомологичен некоторой линейной
i и Y2 с целыми коэффициентами (равными
нулю, если y~0)- Поэтому группа
одномерных гомологии тора с целыми
коэффициентами Н\(Т, Z) изоморфна
прямой сумме двух групп Z.
Любой двумерный цикл на торе
преставляет собой целое кратное са-
самого тора. Поэтому Яг(Г, Z)r*Z.
13. Дифференцирование форм.
Пусть М — многообразие размерности
m класса С2 и со — гладкая форма сте-
степени р<т, заданная на М.
Определение 1. Дифференциал da> формы со определяет-
определяется в локальных координатах t=(tu ..., tm) следующим обра-
образом: если в этих координатах
то в них
= 2' dfVi .Л dUx Л ... Л dtVp,
(О
B)
4
4
где df = 4rdh+ ••• +4r-dtm-дифференциал функции / =
Oti (Jim
iV
Отметим два простых свойства дифференцирования форм:
(I)
(II)
C)
D)
где р — степень формы a>i.
Первое свойство очевидно. Учитывая его, второе свойство до-
достаточно доказать для случая, когда перемножаемые формы яв-
являются одночленами:
со, = / dtv.1 Л ... Л dtnp,
©2 = g dui A ... д dhr
"§ 5] ТЕОРЕМА КОШИ - ПУАНКАРЕ 327
В этом случае мы имеем а){ A (a2 = fgdtfii A ... A dt^ A
A dtVl A ... Л dtVq и
d (©, Л ю2) = {gdf + f dg) А Лц, Л ... Л dt»p A dtVl Л ... Л d
= (dfAdt^A... A dt»p)A(gdtViA... AdtVq)+{fdt^A ... Л dt
А (—1)" (dg Л dtVi Л ... Л dfVff) = de>, Л оJ + (—1)" »i Л
что и требуется.
Теорема 1. Для любой формы со класса С2 квадрат опе-
оператора d равен нулю:
0. E)
< Для форм (j)=fdtlA.. ./\dtm степени m, равной размерно-
размерности многообразия, уже первый дифференциал равен нулю (это
m
следует из того, что df = У, -~ dtv, а внешнее произведение
v=l
одинаковых дифференциалов равно нулю). Для форм степени
m—1 дифференциал da> является формой степени пг, и, следо-
следовательно, й?2со = 0. Для форм степени p^Lm — 2 мы подсчитаем
вклад, который вносит в d2(o дифференцирование по /4 и t2. Оче-
Очевидно, достаточно рассмотреть совокупность тех членов в выра-
выражении со, которые не содержат dt\ и dt2, т. е. форму
<*>1 = 2"/Vi... v dUx Л ... Л dtVp,
где два штриха у суммы означают, что суммирование ведется
по всем индексам vi, ..., vP, для которых 2<vi<.. .^
Мы имеем
Л dtv> Л *"" Л
-^ dh Л dt^ Л • • • Л dUP
(выписаны лишь те слагаемые, которые содержат либо dtu либо
dh, для краткости положено f v =fvj и dzco, =
^ dt\ A dt2 A dtVi A ... Л dtVp + ...; в силу р авенства
смешанных производных выражение в скобках равно нулю,
а так как члены, обозначенные многоточием, не содержат про-
произведения dUAdh, то коэффициент в d2coi при этом произведе-
произведении равен 0.
Перестановкой индексов мы можем любые два дифферен-
дифференциала поставить на место dtiAdh, поэтому можно утверждать,
ЧТО С?2<й = 0 >
328 ИНТЕГРИРОВАНИЕ [ГЛ. II
Пример. В случае га = 3 и р=1, т. е. формы <u=j
имеем
dt2
и теорема 1 сводится к известному из векторного анализа тождеству
divrotf = 0, F)
где f=(fi, h, h) —вектор.
Наше определение дифференциала формы сформулировано
в терминах локальных координат. Однако на самом деле диф-
дифференциал инвариантен относительно координат. Точнее, спра-
справедлива
Теорема 2. Дифференциал гладкой формы на гладком
многообразии меняется по закону изменения дифференциальных
форм.
< Нам нужно показать, что при гладкой (не обязательно го-
меоморфной) замене координат t~*x дифференциал dco перехо-
переходит в то самое выражение, которое получается при вычислении
дифференциала формы со в координатах г.
По свойству (I) можно ограничиться формами вида
со = fdtVi А ... A diVp = fop, G)
где q>p = dtVi A ... Л dtv . Будем рассматривать оз как произве-
произведение формы нулевой степени (функции) / на форму <рр. По
свойству (II) в новых координатах
=df(x)A<fp(x)+f{x)dq>p(x)',
следовательно, все будет доказано, если мы докажем, что
dcpp(x)=0. (8)
Справедливость этого равенства легко доказывается индукцией
по р. При р=1 форма q>i(t) —dtv, и при замене t-^-x по теореме
об инвариантности дифференциала она переходит в дифферен-
дифференциал функции tv(Xi, . . . , Tm); по теореме 1 имеем, следователь-
следовательно, d(f\ = d2tv(x) =0. Пусть (8) верно для всех форм степени не
выше р—1. Тогда ц>р можно рассматривать как произведение
<Pp_iAg^v, и по свойству (II) и индуктивному предположению
получаем, что
=0 >
В качестве примера применения дифференцирования форм
приведем доказательство теоремы существования неявных
функций.
§ 5] ТЕОРЕМА КОШИ - ПУАНКАРЕ 329
Теорема 3. Пусть функции f^z), [i=l, .,., г' (r' = n — r,
\^r4^.n—1), голоморфны в точке аеС" и определитель
/dL \
Detl-,— I, v = r+l, ..., ft, отличен от нуля в точке (аг+\
..., о„). Тогда система уравнений
f^izt, ..., 2„)=0, ц = 1, .... г', (9)
разрешима в некоторой окрестности точки а относительно пере-
переменных zv, v>r, т. е.
24> = gvBb • •• , Zr), \ = Г+],...,П, A0)
причем функции gv голоморфны в точке (п\, ..., аг).
< Мы приведем эту теорему к соответствующей теореме из
действительного анализа. Для этого положим fv. = uil. + ivll,
zv = xv + iyv и будем рассматривать (9) как систему 2г' \равне-
ний относительно 2га неизвестных хч, yv.
д («,, о,, ..., ur,, vГЛ
Для вычисления якобиана -%-,—!—= г отвлечемся
д (хг+1, Уг+i, •••. *Я| Уя)
от системы (9), фиксируем переменные zu . . . , zr и будем рас-
рассматривать fp ..., /, как функции остальных переменных
zr+l, . . ., zn. Учитывая, что эти функции голоморфны, по прави-
правилам внешнего умножения дифференциалов получаем
dfl Л ... Л <'=/(f"""'fr'\^r+1 Л ... Л dzn,
откуда, переходя к комплексно сопряженным величинам, на-
находим
По тем же правилам
dzvAdzv= (dxv+idyv) A (dxv — idyv) =—2idxvAdyv
и аналогично dfllAdfll = —2idullAdvll. Поэтому после перемно:
жения последних соотношений мы получим
du{ Л dv{ Л ... dur, A dvr, =
fr>)
д(гг+
2
dxr+l A dyr+l /\ ... A dxnA dyn
(мы произвели одинаковые перестановки в обеих частях этих
соотношений). Остается заметить, что произведения дифферен-
дифференциалов в левой и правой частях последнего равенства представ-
представляют собой соответствующие 2г'-мерные элементарные объемы
330 ИНТЕГРИРОВАНИЕ [ГЛ. II
(взятые с каким-либо одинаковым для обеих частей знаком) и,
следовательно, их отношение равно искомому якобиану:
<Э(/, fr,)
д (xr+и Уг+и ..., х„, уп)
d(zr
По условию якобиан в правой части A1) отличен от нуля
в точке (аг+ь ..., а„), поэтому в силу теоремы о неявных функ-
функциях из действительного анализа система (9) разрешима в окре-
окрестности точки а относительно переменных хг+и ут+\, ¦ ¦ ¦, хп, уп
(условия непрерывности, требуемые в этой теореме, у нас за-
заведомо выполняются). По той же теореме функции zv=xv+"iyv
(v = r+l, ..., п) дифференцируемы в смысле действительного
анализа (по переменным zu zb ..., zr, zr). Но, дифференцируя
систему (9), находим
dfix dz = = ¦
v=l
(мы воспользовались теоремой об инвариантности дифферен-
дифференциала), откуда в силу условия не равенства нулю определителя
A1) видно, что в окрестности точки (аи ..., ат) дифферен-
дифференциалы dzr+u ..., dzn линейно выражаются через дифферен-
дифференциалы dz{, ..., dzr. Поэтому функции A0) голоморфны в точке
(аи ..., аг) >
Замечание. Соотношение A1) обобщает на пространст-
пространственный случай соотношение между якобианом и производной
голоморфной функции одного переменного:
д (и, V) If// \ 12
д(х,у) ~1< ^Л
(см. п. 7 ч. I).
В заключение этого пункта приведем несколько замечаний
и определений общего характера. Оператор дифференцирова-
дифференцирования d преобразует группу Qp всех дифференциальных форм
степени р на многообразии М (рассматриваются формы и мно-
многообразия из класса С1) в группу Qp+1 форм степени р + 1:
d-Qp—>Qp+l • A2)
Это отображение является гомоморфизмом, ибо он+Ъг —*¦
—*dcoi + rffc>2, однако не на всю группу Qp+1, ибо не каждая
форма степени р + 1 является дифференциалом какой-либо
формы етепени р.
Определение 2. Дифференциальная форма со назы-
называется "замкнутой, если ее дифференциал Ло = 0. Форма ю на-
называется точной, если она является дифференциалом какой-
либо формы: co=c?Q.
i 5] ТЕОРЕМА КОШИ - ПУАНКАРЕ 331
Замкнутые формы степени р на многообразии М образуют
группу (по сложению) Zp, которая является подгруппой Qp.
Мы имеем
ZP = {coeEQP: dco = 0}, A3)
т. е. Zp служит ядром гомоморфизма d (Zp = kercf). Точные
формы образуют группу
ВР = {соеЙР: со = <Ш}, A4)
которая является образом гомоморфизма d (Bp = imd).
По теореме 1 всякая точная форма замкнута (ибо если
<o = d(x>\, то rfco = d2coi = 0), следовательно, Вр является подгруп-
подгруппой группы Zp. По той же причине последовательность гомо-
гомоморфизмов
QP-l JpH+QpA+QW A5)
является полуточной (imdp-jckerdv); точность этой последо-
последовательности (imdp_i = kerdp) означает, очевидно, что каждая
замкнутая форма степени р на М является точной.
Факторгруппа
Hp=Zp/Bp A6)
состоит из классов эквивалентных форм: к одному классу отно-
относятся формы, разность которых принадлежит Вр, т. е. является
точной формой. Точность последовательности A5) сводится к
тривиальности группы Нр (#р = 0).
Очевидна аналогия оператора d дифференцирования форм
с оператором д взятия границы цепей, рассмотренным в пре-
предыдущем пункте; различие между этими операторами состоит
лишь в том, что первый из них повышает размерность (степень)
форм, а второй понижает размерность цепей. Это подчерки-
подчеркивает следующая часто применяемая терминология. Формы, диф-
дифференциалы которых равны нулю, называются коциклами, а
формы, которые являются дифференциалами других форм, —
кого мо логичны ми нулю; факторгруппа Нр называется р-мерной
группой когомологий.
14. Формула Стокса. Аналогия, о которой мы сейчас гово-
говорили, является не только внешней. Глубокую связь между опе-
операторами d и д выражает весьма важная
Теорема. Пусть на ориентируемом пг-мерном многообра-
многообразии М задана р-мерная цепь о, а на ней дифференциальная
форма ю степени р — 1; если М, о, do и а принадлежат классу
О, то
I da= Jo». A)
tr да
Это и есть формула Стокса.
332
ИНТЕГРИРОВАНИЕ
[ГЛ. II
-4 Из принятых нами определений цепи и интеграла следует,
что доказательство теоремы достаточно провести для случая
р-мерного симплекса 5 = {P0-Pi ••¦ Рр}- Введем в S координаты
(tu ..., tp), в которых каждая точка P<sS представляется в
виде суммы векторов:
р
мы положили /0 = 1 —
этих координатах форма за-
шине Р.,
писывается как сумма р членов; мы возьмем один такой член,
например
® = f(tu .... tp)dt2A...AdtP. C)
Пусть Sv будет грань симплекса S, противоположная вер-
уравнением этой грани служит /v = 0 (v = 0, .... р),
Эти грани ориентируем в соответствии
с ориентацией S, в частности, грань So
получит ориентацию {Pi ... Рр), а
грань Si — ориентацию — {Р0Р2 ¦ ¦ ¦ Рр}
(см. рис. 92, где р = 3). Вычислим ин-
интеграл от формы C) по ориентирован-
ориентированной границе dS симплекса:
р
+ J со D)
OS
\>=о sv
Рис. 92.
(мы учли, что на остальных гранях
Sv, v>2, форма (о = 0, ибо там /v = 0,
dtv=O). В обеих гранях So и St мож-
можно пользоваться координатами (t2, ...
,,., tp)=t. На грани So порядок этих координат соответствует
ориентации, a t\ является (линейной) функцией %{t) остальных
р
координат, определяемой из уравнения грани t0— 1 — 2 Л> = 0.
v=l
По определению интеграла от формы (п. 12) получаем, следо-
следовательно,
Ja>= J/[t(O, t]dt, E)
где 5i — неориентированный симплекс (проекция So в простран-
пространство переменных (^, ¦•-, tp)=t, см. рис. 92), a dt-=dh ...
¦ ii dtp — элемент объема. Вводя характеристическую функцию
§ 5] ТЕОРЕМА КОШИ — ПУАНКАРЕ 333
Х@ симплекса Si (т. е. функцию, равную 1 в Si и 0 вне Si),
мы можем переписать правую часть E) в виде интеграла по
всему пространству
J со = J /(т, t)x(t)dt.
So
На грани Si порядок координат (/г, ¦.., tn) противоположен
ориентации, a /i = 0, поэтому мы имеем
J © J/@, t)%(t)dt
s,
и из D) получаем
|й=|{/(т, t)-f(O, t)}%(t)dt, F)
dS
у
С другой стороны, da> = -~ dtx Л dt2 Л ... Л dtp, и, вычисляя
где интеграл берется по всему пространству.
С другой стороны, da> = -~ dtx Л dt2 Л
интеграл по симплексу S, мы получаем
> t)-f(Q, t)}dt
Этот интеграл совпадает с F) >
Примеры.
1. р=\, tn — любое; одномерная цепь а представляет собой линию, ее
граница da состоит из двух точек, причем начало (а) ориентировано отри-
отрицательно, а конец (Ь) —положительно. Форма со нулевой степени — это функ-
функция f. Формула Стокса сводится к формуле Ньютона — Лейбница:
Jrf/= [ / - / (й) - / (а).
50
2. т=р = 2; цепь а пусть представляет собой плоскую область D. Форма
первого порядка имеет вид со = d dtx + /2 dt2, а ее дифференциал rfco =
= \-4т 4т~ I dt\ A dt2. Формула Стокса сводится к формуле Р и м а н а —
\ Oti Ol2 )
Грина:
D dD
334 ИНТЕГРИРОВАНИЕ [ГЛ. II
3. т = 3, р = 2; цепь о пусть представляет поверхность S в R3. Фор-
Формула A) сводится к классической формуле Стокса:
+ Щ; ~ w) dh л dti = Jfl *"•+ f2 rf'2 + h dh-
as
4. m = p = 3; цепь ст— область Z> в R3; формула Стокса сводится к фор-
формуле Остроградского:
= /23 ^2 Л dh + fis rf^i Л dh + /12 rf<i Л dt2.
•J
dD
Приведем два важных следствия из формулы Стокса:
1) Интеграл от замкнутой формы (dco = O) no циклу, гомо-
гомологичному нулю (а = <32), равен нулю:
Jfi>=Jfi>=J"dco = 0. G)
а as 2
2) Интеграл от точной формы (co = dcoi) no циклу (да — О)
равен нулю:
J со = J flfco, = | ю, = 0. (8)
15. Теорема Коши — Пуанкаре. Эта теорема является рас-
распространением на многомерный случай основной теоремы Коши.
Теорема 1. Пусть со — голоморфная форма степени п на
аналитическом многообразии М комплексной размерности п;
тогда для любой (п+l)-мерной цепи oczM с гладкой границей
ш = 0. A)
дсг
< В локальных координатах zv, zv (v=l, ..., п) голоморф-
голоморфная форма со имеет вид
... Adzn, B)
где f^H(M). Она, очевидно, замкнута, ибо в силу голоморф-
голоморфности / дифференциал df выражается лишь через дифферен-
дифференциалы dzv и по свойствам внешних произведений da = Q. Отсюда
следует, что da = Q на всей о, а так как цикл до гомологичен
нулю, то остается воспользоваться следствием 1) из формулы
Стокса >
§ 5] ТЕОРЕМА КОШИ - ПУАНКАРЕ 335
Особенно употребителен следующий частный случай тео-
теоремы 1:
Теорема Коши —Пуанкаре. Если функция f голо-
голоморфна в области DczCn, то для любой (п+1)-мерной поверх-
поверхности G ш D с гладкой границей dG
fdz = O, C)
да
где для краткости положено dz=dz\ Л ... /\dzn.
Отметим принципиальное отличие пространственного случая
от плоского, относящееся к этой теореме: при я=1 области D
и G имеют одинаковую размерность, а
при га>1 размерность G ниже размер-
размерности D (га+1<2га).
Укажем еще более частный случай
теоремы. Пусть /e#(D) и G = GiX-.-
...XGn — поликруговая область (Gv —
плоские односвязные области с гладкими
границами dGv), компактно принадлежа-
принадлежащая D. Остов этой области t=dG\X. ¦.
. . .XdGn является га-мерным циклом, го- рмс 93
мологичным нулю, ибо он является гра-
границей (я+1)-мерных замкнутых областей Sv = dGiX...
. ¦ ¦ X@VX ... XdGn mD. Поэтому для любой такой области G
интеграл по ее остову
{ f dz = 0 D)
г
(ср. с интегральной формулой Коши для поликруговых областей).
Теперь мы приведем пространственный аналог теоремы Мо-
рера, обратной к теореме Коши. В плоском случае для утверж-
утверждения о голоморфности функции f в области D достаточно тре-
требовать равенства нулю интеграла по границам областей спе-
специального вида (треугольников АшО), но на функцию надо
наложить дополнительное условие непрерывности (см. п. 20
ч. I). Аналогично обстоит дело и в пространственном случае.
Роль треугольников здесь играют (м-М)-мерные «призмы» Tv,
которые являются произведением треугольника Av, лежащего
в плоскости С'(гу), на произведение Av прямолинейных отрез-
отрезков [а», гД лежащих в остальных п—1 плоскостях
=n[s, zj) E)
(см. рис. 93, где выделена плоскость zv, а пространство осталь-
остальных переменных гд изображено схематически).
336 ИНТЕГРИРОВАНИЕ [ГЛ. II
Теорема 2. Если функция f непрерывна в области
DczCn и для любой призмы Tv вида E), компактно принадле-
принадлежащей D,
\fdz = 0, F)
arv
mo f<=H(D).
< Достаточно доказать голоморфность f в окрестности про-
произвольной точки a^D. Фиксируем а и рассмотрим функцию
F{z) = J d?, ... J f(g)rf?n; G)
она определена и непрерывна в некоторой окрестности точки а.
Для любого v (v=l, ..., п) ее можно представить в виде
= J
где Fv — интеграл от f no Av (произведению отрезков [а^, z^],
цф\). Функция Fv, очевидно, непрерывна по ^v в окрестности
Uv точки av, и по условию F) для любого треугольника
U
v^v = O. (8)
В самом деле, этот интеграл лишь знаком может отличаться
от интеграла
3AV X Av dTv
где TV — AVXAV и rf^=<if^A ... /\dt,n (мы воспользовались
тем, что на части dTv, отличной от c?AvXAv, т. е. на части
AVX<?AV — совокупности «оснований» призмы Tv, см. рис. 93,—
координата ?v = const, следовательно, d?v=0, и интеграл от f dt,
по этой части границы исчезает).
По теореме Мореры для функций одного переменного отсюда
вытекает, что F голоморфна по переменному zv. Так как рас-
рассуждение применимо для любого zv, то F голоморфна по каж-
каждому переменному в некоторой окрестности U точки а. По тео-
теореме Хартогса F голоморфна в этой окрестности, а значит, там
голоморфна и функция
... dzn
§ 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 337
§ 6. Интегральные представления
Теперь мы можем изучать интегральные представления го-
голоморфных функций. Начнем с наиболее общего, справедливого
для произвольных областей с гладкой границей.
16. Формулы Мартинелли — Бохнера и Лере. Нам понадо-
понадобится формула Грина для областей DcrR™ с гладкой грани-
границей 3D. Она выводится очень просто: обозначим
V = (—\y-4x1A..^..Adxm A)
V
(дифференциал dxv пропускается) и рассмотрим дифферен-
дифференциальную форму степени т— 1:
v=l
где f, g — заданные в D функции класса С2. Дифференциал
этой формы, очевидно, равен
^rf. Л ••• Adxm = (fAg-gAf)dx,
v=1\ "x axv!
д2 д2
где Д = —т + ••• ^ ? ~ оператор Лапласа и dx=d,Xif\ ...
дх\ дхгт
... Л dxm. Применяя формулу Стокса, мы и получим искомую
формулу Грина
3D V = I D
Для областей DcC" эту формулу удобнее писать в ком-
комплексном виде. Для этого введем, как обычно, координаты
7 7 •
Zv = zv, Zn+V = zv (v=l, ..., n),
ПОЛОЖИМ ДЛЯ V = 1, . . . , In
V
v пропускается) и вместо B) рассмотрим форму
л
22 Б. В. Шабат
.338 " ИНТЕГРИРОВАНИЕ [ГЛ. II
где fug — заданные в D функции класса С2 и, как всегда,
д - х { д j д )
dzv 2 \ dxv dyv I' dzv 2 \ dxv dyv
= xn+v). Дифференциал этой формы равен
v=l
d2 , d2 . d2
мы воспользовались тем, что —к--\ ^ = 4 , и поло-
dxv dyv dzv dzv
жили dZ = dZx A ... AdZ2n). Чтобы получить формулу Грина
в комплексной записи:
нужно лишь воспользоваться формулой Стокса.
Формула Мартинелли — Бохнера получается из E) так же,
как интеграл Коши для гладких функций одного переменного
получается из формулы Римана — Грина (см. п. 18 ч. I). Выбе-
Выберем в качестве g фундаментальное решение уравнения Лапласа
с особенностью в точке z — 0 (мы предположим, что D содержит
эту точку). Для п > 1 оно имеет вид
*{Я) I" F)
\v=l
ибо при г ф 0 имеем
dg _ zv d2g __ \z\2-nzvzv Др- = П
dzv \z\2n ' dzvdzv \z\2n+2 ' g
Теперь воспользуемся формулой Грйна E), применив ее к об-
области Dp = D \{| z |<р} (мы исключаем из D окрестность точки
z = 0, чтобы устранить особенность функции g) и к функции
f^H(D). Так как при z^D мы имеем -~ = О, А/ = 0, то эта
формула запишется так:
dD v=l {U|=p} v=l
1 С
2 = 0. G)
§ 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 339
Но на сфере {|z| = p} имеем, очевидно, -^- = -%г и> поль-
зуясь непрерывностью функции / в точке 2 = 0, мы можем
написать, что
[ }
{|2|=p} V=l { 1 2 [ =p} V = 0
где О(р)->0 при р->0. К интегралу в правой части применим
формулу Стокса:
п
J ]? 2V6"+V = n J rfZ, Л ... Л dZ2n,
{lz|=p} v = l {|г|<р}
и заметим, что по свойствам внешнего произведения dZvAdZn+v =
= -2idxvA dxn+v, т. е. dZl А.. .Л rfZ2n = (— 2i)"dx1A ... Adx2n.
Поэтому
xA ... A dZ2n = (- 2t)" J dx, ... dx2n = (- 2i)n^ p2«
{|д:|<Р>
(мы воспользовались формулой для объема шара радиуса р
в пространстве Rm:
„т/1
Р ,
где Г — гамма-функция Эйлера, Т(п + \) = п\), и формула G) пе-
переписывается в виде
1Й(у
dD v=l
Переходя здесь к пределу при р-*0, мы получим
dD v=l
J
v=l
где dz-=dzx A ¦ ¦ ¦ A dzn.
') Очевидно, dz Л Лг^ А../...Л dzn= dzi A--..-</\ dzn A dz, ибо
V V
сделанная перестановка четная (она цикличная при нечетном числе
индексов).
22*
340 ИНТЕГРИРОВАНИЕ [ГЛ. II
Остается переменить обозначения: вместо 2 = 0 мы возьмем
фиксированную точку z еД а точку интегрирования на 3D
обозначим через ?. Тогда мы получим искомую формулу
Мартинелли — Бохнера:
S ffil ^ (8)
dD v=l v
При n = 1 эта формула переходит в интегральную формулу Коши:
ао ао
и поэтому ее можно рассматривать как обобщение последней.
Как и в последней, интеграл в формуле Мартинелли — Бохнера
берется по всей границе области D, которая предполагается
состоящей из одной или нескольких гладких Bя — 1)-мерных
поверхностей. Введя сокращенное обозначение для формы Мар-
Мартинелли — Бохнера
^ (9)
^1^
v=l
мы будем записывать формулу (8) в виде
/(C)o(?, г). A0)
dD
Отметим еще одно свойство формулы Мартинелли — Бохнера,
которое роднит ее с интегральной формулой Коши: вне D пра-
правая часть этой формулы обращается в нуль. Это утверждение
следует непосредственно из формулы Грина E), примененной
к области D (шар из D выбрасывать теперь не нужно, ибо g-
непрерывна в D). Таким образом, для любой функции f^
имеем
f(z) при zs D,
dD I 0 при zeC"\fl.
В частности, для гф-dD
o(?, z) = x(z), A2)
dD
где %{z) — характеристическая функция области D.
§ 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 341
Для тех, кто знаком с понятием обобщенных функций, укажем, что
дифференциал формы Мартинелли — Бохнера (по переменным ?v> ?v) обла-
обладает свойствами б-функции. В самом деле, при ? ф г, очевидно, da> (?, z) = О,
а при ? = г этот дифференциал не существует. При этом для любой области D,
содержащей точку г, имеем
J о (?, г) = J do = 1
(мы формально применили формулу Стокса), и интеграл по D здесь можно
заменить интегралом по всему пространству, ибо das = 0 при t, ф г. Если
формулу Мартинелли — Бохнера A0) переписать в виде
f (z)- J d (/ш) =¦ J f (С) da (С, 2), A3)
D
применив формально к ее правой части формулу Стокса (мы пользуемся
здесь тем, что d (/о) = df Д о) + / das = fda> в силу голоморфности f, и снова
заменяем интеграл по D интегралом по всему пространству), мы увидим,
что A3) сводится к воспроизводящему свойству б-функции.
В заключение приведем общую интегральную формулу,
полученную Ж. Л е р е и названную им формулой К о ш и —
Фантапье. Мы излагаем простой вывод этой формулы,
который нам сообщил Г. М. Хенкин. Обозначим
п
f>{w)= 2 {-l)v~lwvdWl A ..yx..Adwn A4)
v=l
и рассмотрим в пространстве Cn(z)xCn{w) дифференциальную
форму степени 2я— 1
n (п- 1)! б(ш) Л dz
где, как всегда, dz — dzy Л ... Л dzn и
(z, w)=j>j zvwv. A6)
Эта форма имеет особенность на поверхности второго порядка
{z, w) = 0, а в остальных точках пространства она замкнута
в самом деле,
Bш)" [" {г,т)« <*, »>»+1
Непосредственно проверяется, что
)
Adz \= 0
v-i
342 ИНТЕГРИРОВАНИЕ [ГЛ. II
и вообще
а отсюда видно, что форма Q зависит лишь от отношения
переменных wv к одной из них.
В частном случае, когда все wv = zv, т. е. вектор-функция
w -= z, форма A5) совпадает с формой Мартинелли — Бохнера
с особенностью в точке z — О. Поэтому, в силу доказанного
выше, для любой функции /, голоморфной в области DcC",
которая содержит точку z = О, и непрерывной в D, мы имеем
- BяОя J
Вывод формулы Лере основан на том замечании, что вели-
величина интеграла в формуле A7) не изменится, если заменить
в ней функцию w = z любой другой гладкой вектор-функцией
w = %(z) такой, что (z, %{zf)=?=Q для всех zedD.
Для доказательства этого утверждения рассмотрим в про-
пространстве С" (г) X С" {w) два Bя — 1)-мерных цикла у0 — {z e dD,
w — z) и y = {z^dD, w=x(z)}- Покажем, что на эти циклы
можно натянуть 2я-мерную пленку о, не пересекающуюся
с поверхностью особенностей S = {(z, w) = 0} формы A5). Для
этого, пользуясь тем, что Q зависит лишь от отношения пе-
переменных wv, вне S заменим (z, w) переменными (г, ю), где
ш^=-(йу (v=1> ••••п)-
Простой подсчет показывает, что
~J^-6(u>)Adz.
Так как по условию Yo и Y не пересекаются с 5, то на этих
циклах (z, со} = 1. Если соединить теперь точки \z, . 2|2 ) и
(z, {*{x%))) прямолинейным отрезком |(z, (I -1) утрг +
+ t / Х У»-, 0<^< U, то во всех точках этого отрезка
также будем иметь {z, co) = l. Совокупность таких отрезков
для всех z^dD и образует нужную пленку сг.
Так как <9ff = YoUY~ и на сг форма A5) замкнута, то по
формуле Стокса
Yo Y да
§ 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 343
и наше утверждение доказано. Из него следует, что
_ ("-О* \ " - 6 ("*¦ М) Л dz
' ~ Bя/)я J '
(г, X («))"
для любой х. удовлетворяющей поставленным выше условиям.
Нам остается лишь переменить обозначения так же, как
в случае формулы Мартинелли — Бохнера, и мы получим общую
формулу Лере: для области DeCc кусочно гладкой гра-
границей 3D и любой гладкой функции %z(i) такой, что (? — 2,
7г(?))^0 на 0D для всех z^D, любая функция f, голо-
голоморфная в D и непрерывная в D, представляется интегралом
/ (?) " (%z (?)) Л dt, /. пч
ал
(мы пишем %г (g), чтобы подчеркнуть, что выбор функции %
может зависеть от точки z).
Выбирая различным образом функции %, из формулы A8)
можно получать различные интегральные представления. Пусть,
например, дана выпуклая область
где ф — действительная функция класса С1, причем Vqp =
= \-fif- ~а?~) ^ 0 на границе 3D этой области (ф = 0 служит
уравнением dD). В каждой точке ? е сШ можно взять Bм — 1)-
мерную касательную плоскость
}zv-?v)-U- = o, B0)
fc7 U
v=l v=l
а в ней выбрать Bп — 2)-мерную аналитическую касательную
плоскость
п
fev-W-J^O1)- B1)
v=l
') Если выполняется уравнение B1), то, переходя к комплексно сопря-
сопряженным величинам, мы получим, что V (zv — gv) -~- — 0 (для действитель-
ных ф имеем \-5с-\ = -^г~ > т- е- чт0 B1) =^> B0); это и означает, что ан»-
литическая плоскость B1) принадлежит плоскости B0).
344 ИНТЕГРИРОВАНИЕ [ГЛ. II
Выберем в качестве функции % градиент по комплексным пере-
переменным ?, т. е. положим %(?) = Vcp. В принятых условиях
v=l
не обращается в нуль при фиксированном z^D и ?, пробе-
пробегающем dD. Поэтому справедливо представление A8) с такой
функцией %; по сравнению с формулой Мартинелли —Бохнера
оно имеет то преимущество, что в таком представлении ядро
голоморфно зависит от параметра z.
п
Пример. Для единичного шара в С" имеем <р (?) = 2 Sv5v — 1. Vqp = ?,
v=l
п
(I — г, ?) = 1 — 2 Sv2v. поэтому формула Лере для шара ПРИПИ-
ПРИПИ2
ЛИ 1
мает вид
I
v=l
B3)
При n = 1 она переходит в интегральную формулу Коши для единичного
круга:
Замечание. Ядро формулы Лере имеет особенность в тех
точках ?еС\ где (?, — z, %z{t)) = 0. В случае Мартинелли —
Бохнера особенность имеется лишь в точке t, = z, однако
в общем случае могут иметься и другие особые точки вне D.
Поэтому в общем случае интеграл Лере не равен нулю вне
области D, как интеграл Мартинелли —Бохнера.
17. Теорема Севери. Сейчас мы хотим проиллюстрировать
применение формулы Мартинелли — Бохнера. Докажем с ее
помощью одну важную теорему, выражающую условия, при
которых заданная на границе области функция голоморфно
продолжается в эту область.
Теорема 1 (Севери). Пусть дана область D Ш С" (п > 1)
со связным дополнением и с гладкой границей dD = S; на S
пусть задана функция f e С1. Для существования функции
|ей(D)П С1 (D), граничные значения которой совпадают с f,
§ 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 345
необходимо и достаточно, чтобы в каждой точке ? е S
df A dt, |s = О, A)
где d? = dg, A ... A dt,n.
< Необходимость условия A) доказывается просто. В силу
того, что /еH(D)(]C}(D), в каждой точке ?gS выполняются
df п 1 /
условия -^- = 0, v=l, ..., п (мы воспользовались тем, что
~ df
f = f на S, что -~- — О всюду в D и что эти производные не-
непрерывны в D). По теореме об инвариантности дифференциала
(п. 14) при вычислении df \s мы можем пользоваться перемен-
переменными gv, ?v (хотя они и не являются независимыми), но по
,,. vi df ,„
только что доказанному df \s = 2j -gf~dc,v, и, следовательно, по
v=l
свойствам внешнего произведения условие A) выполняется.
Для доказательства достаточности этого условия построим
при помощи формулы Мартинелли — Бохнера по заданным
значениям / функцию
/B)= J/E)(B(S, 2), B)
S
где
п
v=l v
а) Покажем прежде всего, что при выполнении условия A)
функция J голоморфна всюду вне 5. Для этого заметим, что
форма со точна: прямой подсчет1) показывает, что при ^Фг1
') Проделаем этот подсчет (для сокращения письма полагаем z = 0):
(я_1)! V (-I)"
i (S, 0) = ,о„ля' ]j | g |2/i ?v rfSi Л dt2 Л .. /ч- • Л dln Л d? +
v=2 v
?2Л ..
V
, 0).
v=l
346 ИНТЕГРИРОВАНИЕ [ГЛ. II
дифференциал формы
Q,i
по переменным g, Z равен со (g, 2).
Заметим еще, что, в то время как форма Q] имеет особен-
особенность на Bя — 2)-мерной плоскости gI = 21, ее частная произ-
производная
2
v=2
имеет лишь точечную особенность ? = z.
При 2<^5 формулу Мартинелли —Бохнера B) можно про-
продифференцировать по zx под знаком интеграла
?Д. E)
Теперь заметим, что в силу условия A) функция f при диф-
дифференцировании по переменным g, Z ведет себя как постоянная;
ее можно вносить под знак дифференциала. В самом деле,
при geS, ?, -ф Zi имеем
d(fQ1) = rf/AQ1+fco = f(o, F)
ибо Qj содержит множитель d[ и в силу A) первое слагаемое
равно нулю. Беря от обеих частей F) частную производную
по г,, найдем, что при g e S, gj ^ 2,
По сделанному выше замечанию форма -%=*- имеет особенность
лишь в точке t, = z и, следовательно, правильна при JeS и
z efcS, такова же и форма -*=-• Поэтому, переходя в G) к пре-
пределу при g1->z1, мы получим в силу непрерывности, что это
равенство справедливо при всех ?eS и 2^5.
Из этих замечаний видно, что формулу E) при гфв можно
переписать в виде
д!(г
-И
(г) _ Г Лнпа>! (С, гЦ
§ 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 347
где под знаком дифференциала стоит правильная форма.
Так как S —цикл (имеем dS = <92D = 0), то по формуле Стокса
правая часть равна 0. Выделяя вместо переменного zl другие
переменные zv, мы совершенно аналогично построим формы
Ov(?, z), правильные при ?v^=zv и такие, что dQv = co, и точно
так же докажем, что -^- = 0 при всех z<?S. Таким образом,
OZ\
функция / действительно голоморфна всюду вне S.
б) Теперь покажем, что эта функция равна нулю всюду
вне D. В самом деле, в той части Cn\D, где | z, |>max| ?, !>
форма D) неособая, поэтому мы можем воспользоваться со-
соотношением F). Мы получим, что для z, принадлежащих этой
части,
(мы снова воспользовались формулой Стокса и тем, что S — цикл).
Но упомянутая часть дополнения к D содержит внутренние
точка, а так как само дополнение по условию связно, то
в силу теоремы единственности f = 0 во всем дополнении.
в) Докажем, наконец, что граничные значения функции f
совпадают с заданными значениями f. Учитывая свойство ядра
Мартинелли — Бохнера (формула A2) предыдущего пункта), мы
можем написать для любой ^°eS и любой гф.Б
№-%(z)f (?°) = /[/(?)-/(?0)]со(?, г), (8)
s
где % — характеристическая функция области D.
Утверждение будет доказано, если доказать, что правая
часть (8) непрерывна в точке ?°: в самом деле, предельное
значение правой части при z-*t,u извне D, очевидно, равно
нулю; в силу непрерывности будет равно нулю и предельное
значение при z—>• Z,"изнутри D, т. е. /(г) —*-/(g°) при z—>t,°, z^D.
И
р р /) /р
Итак, остается доказать непрерывность функции
Ф(*)= J [/(»-/(E°)]<b(S, z)
s
в точке. ?°. Для этого заметим сначала, что существует интеграл
ф(?°)= jlf (?)- f (S°)l «> (?. ?0)- (9)
s
В самом деле, интеграл берется по Bл — 1)-мерной поверхности
348 ИНТЕГРИРОВАНИЕ [ГЛ. К
и произведения дифференциалов, входящих в форму со:
dly Л . ./v . Л dln Л dg, Л ... Л rig,,,
V
имеют размерность Bя — 1)-мерного элемента объема. Множи-
Множители же при этих произведениях
имеют порядок не выше о 2п_2", ибо f^C1, и, следова-
следовательно, /(?) —Д?°), как и ?v — ?°, имеет порядок не ниже |g —g°|.
Таким образом, порядок бесконечности подинтегральной функ-
функции в (9) по крайней мере на единицу ниже размерности, и,
значит, интеграл (9) сходитсях).
Дальнейшее доказательство проводится обычным для ана-
анализа способом, и мы лишь наметим его ход. Разность
Ф(г) - Ф(g°) = J [f (g) -/(Z0)] [<o(g, *) - <в(g, ?0)]
s
мы разобьем на две части, соответствующие интегрированию
по достаточно малой (относительной) окрестности а точки ?э
и остальной части 5 \ о границы. В силу доказанной сходи-
сходимости интеграла (9) первую часть можно считать малой; в инте-
интеграле по 5 \ а ядро непрерывно, и, следовательно, этот инте-
интеграл сколь угодно мал, если точка z достаточно близка к ?°.
Доказательство того, что f e С1 (D), мы опускаем. >
Замечание. Теорема Севери не верна при я = 1: в самом деле,
функция f = — на границе единичного круга ?/ = {|z| < 1} удовлетворяет
условию A), однако ее нельзя голоморфно продолжить в U. Приведенное
доказательство при п = 1 не проходит, ибо форма Коши у—-— , в отличие
от формы Мартинелли — Бохнера, не является точной на dD, если z^D
(построить Q по формуле D) при я = 1 нельзя). Интеграл
Г
J
dD
конечно, голоморфен при г ф dD, но f не обязательно равна 0 вне D 2).
В качестве примера применения теоремы Севери мы при-
приведем доказательство еще одной теоремы о принудительном
') В этом проще всего убедиться, переходя на S к полярным коорди-
латам с полюсом в точке ?°.
2) См. задачи 1 и 3 к гл. II ч. I.
§ 6]
ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
349
аналитическом продолжении функций нескольких переменных
(ср. пп. 7 и 8) — теоремы о стирании компактных особенностей.
Теорема 2 (О с гуд — Браун). Если функция f голо-
голоморфна всюду в области ОсС" (я>1), за исключением, быть
может, множества К Ш D, то f голоморфно продолжается на
всю область D.
< Выберем в D \ К гладкие Bп— 1)-мерные поверхности St
и S2 так, чтобы они ограничивали соответственно области G{
и G2 со связными дополнениями, чтобы К. Ш G, Ш G2 и чтобы
слой G = G2\ G, <Ш D (рис. 94). Так как / голоморфна в G, то
по формуле Мартинелли — Бохнера для
любой точки zgG
f(z) = Jf (?)<¦> (С, г)- //(?)©(?, г). A0)
s2 s,
По той же причине на S\ и 5'2 выпол-
выполняются условия Севери:
Л
rf/ Л
0.
Рис. 94.
Так как z лежит вне поверхности 5,, то по теореме Севери
второй интеграл в формуле A0) равен нулю, и, следовательно,
для всех zgG
/(z)= j"/(?)*>(?. z). A1)
Но по той же теореме Севери интеграл в правой части A1)
представляет функцию, голоморфную всюду в G2, и, следова-
следовательно, реализует требуемое аналитическое продолжение >
Из этой теоремы видно, что голоморфные функции п^2
переменных не могут иметь изолированных особых точек, — осо-
особенности таких функций обязаны выходить на границу области
или простираться в бесконечность 1). Из этой же теоремы полу-
получается такое усиление теоремы Лиувилля из п. 6: если функ-
функция п^2 переменных голоморфна вне шара {\z\<R} и огра-
ограничена, то она постоянна. (В самом деле, по теореме Осгуда —
Брауна эта функция голоморфно продолжается в шар, т. е.
является целой; но она ограничена: в {\z[>R} по условию,
а в {|z|^^} как непрерывная на компакте функция.)
') Сравните: функция f = — на плоскости г имеет особую точку {0},
а в пространстве (г, да) — особую аналитическую прямую {z = 0}, простираю-
простирающуюся в бесконечность.
350 ИНТЕГРИРОВАНИЕ [ГЛ. II
18. Формула Вейля. Интегральная формула Мартинелли —
Бохнера выписывается для областей достаточно общего вида.
Однако при п>\ она имеет недостаток, существенный для
ряда вопросов: ядро этой формулы со(?, z) неаналитически за-
зависит от z. Мы уже приводили примеры интегральных формул
с аналитическими ядрами —формулу Коши для поликруговых
областей и формулу Лере для выпуклых областей. Здесь
мы приведем еще одну формулу с аналитическим ядром, кото-
которая применима для одного специального класса областей, более
широкого, чем поликруговые области.
Определение 1. Пусть дана область DaCn, а также
конечное число функций Wt<^H(D) и плоских областей
D{ Ш Wi(D), i=\, ..., N. Будем называть полиэдрическим
множеством множество
n = {zeD: Wt{z)s=Du i=\, .... N), A)
если оно компактно в D.
Такое множество не обязательно связно; связное множество
вида A) мы будем называть полиэдрической областью. Часто
рассматривается случай, когда все области Dv являются кру-
кругами; соответствующее множество
П = {гей: \W,(z)\<rt, i=l, .... N] B)
будем называть аналитическим полиэдром. Если все функции Wt
являются полиномами, то B) называется полиномиальным
полиэдром.
В частном случае, когда N = п и все Wt (z) = zt, полиэдри-
полиэдрическая область является поликруговой, а полиэдр — поликругом.
Определение 2. Полиэдрическое множество A) назы-
называется множеством Вейля, если N^n и 1) все его грани
а, = {z е= D: Wt (z) e= dDt, W, (z) s Dh j Ф i) C)
являются Bя— 1)-мерными множествами; 2) пересечение любых k
различных граней B <[ k <! п) — ребро множества Вейля — имеет
размерность не выше 2л — k. Совокупность n-мерных ребер
V..i,,-\n...nafji * D)
множества Вейля называется его остовом. Связные множества
Вейля называются областями- Вейля.
Для получения интегрального представления функций, голо-
голоморфных в областях Вейля, нам понадобится специальное раз-
разложение функций Wh определяющих эти области. Возможность
такого разложения гарантирует
« 6] ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 351
Теорема Хефера. Для любой функции Wtcz H{D), где
D — область в С", существуют п функций Pv(?, z)' (i=l, ..., п)
голоморфных в D X D и таких, что для всех точек ?, ге D
имеет место тождество
Wt (?) - Wt (z) = J) (?? - zv) Plv (?, 2). E)
В общем случае теорема Хефера неэлементарна !), мы при-
приведем ее доказательство в гл. IV. Здесь мы лишь заметим,
что для полиномов тождество E) получается простой перегруп-
перегруппировкой тейлоровского разложения функции Wt в точке z,
причем коэффициенты Хефера P'v также оказываются поли-
полиномами.
Теорема 1 (Вейль). Пусть И — область Вейля A), опре-
определяемая областями Di_c гладкими границами. Тогда любую
функцию /е#(П)ПС(П) в любой точке геП можно пред-
представить формулой
nfi p
где суммирование распространяется на все упорядоченные
наборы индексов A</,< ... <in^N), определяющие ребра
остова области, Р\ — коэффициенты Хефера и dt, = а%\ А ¦ ¦ ¦ A dt,n;
ребра ориентированы условием, что все dDt проходятся в поло-
положительном направлении.
В случае, когда П представляет собой поликруговую область
(N = п, Wi = Zi, i=\, ..., N), остов Г состоит из одного ребра
а, п (и совпадает с остовом в смысле п. 2) и сумма в F)
состоит из одного слагаемого. Коэффициенты Хефера Plv в этом
случае равны 1 при i = v и 0 при i Ф v, т. е. определитель
в формуле Вейля равен 1, и эта формула принимает вид
Таким образом, формула Вейля обобщает интегральную
формулу Коши для поликруговых областей на случай областей
Вейля. Как и формула Коши, она имеет ядро, аналитическое
') Теорема Хефера была доказана в 1942 г.
352
ИНТЕГРИРОВАНИЕ
[ГЛ. II
по переменным ? и г. Для упрощения формальных выкладок
мы приведем доказательство теоремы Вейля в случае п = 2.
А Будем исходить из формулы Мартинелли — Бохнера, кото-
которая в случае областей Вейля из С2 имеет вид
где стг — грань области П. Идея получения формулы Вейля сле-
следующая: мы постараемся применить к (8) формулу Стокса так,
чтобы исчезли неаналитические дифференциалы dZ,v и вместо
граней а{ интегрирование велось по ребрам остова агу, при
этом окажется, что исчезнет и неаналитичность ядра (перемен-
(переменные lv — zv и |g — z\). Весьма существенную роль в этом пре-
преобразовании будет играть разложение Хефера E).
Заметим прежде всего, что форма co(g, z), стоящая под зна-
знаком интеграла (8), точная; она является дифференциалом любой
из N форм
р{
pi
d?.
(9)
Подтвердим это прямой выкладкой, полагая для простоты
письма 2 = 0 и Wt=Wt (?) - Wt @):
(P\l2 -
(P\ dl2 -
S2 - P[ dlx))
= JYJ4- (S
что и требовалось доказать.
Заметим еще, что при геП и ? е о{ лишь разность
^Й)-^(г) отлична от нуля (ибо WiiQ^dDi, a ^(zJeZ),),
а все остальные разности в некоторых точках обращаются
в нуль. Поэтому при геП, Z, е стг лишь форма йг неособая,
а все остальные формы Q/; / ф г, особые, и при интегриро-
интегрировании по грани ог формулу Стокса можно применять лишь так:
/ = l a.
§ 61 ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ 353
(мы воспользовались тем, что голоморфную функцию / можно
вносить под знак дифференциала формы Q,-).
Если складывать эти интегралы, как требует формула (8),
то каждое ребро otj будет встречаться дважды, с противопо-
противоположной ориентацией (со стороны граней ст,- и aj). Поэтому мы
будем иметь
N N
(?, z) = Y /Ш{?2,(?, z)-Q,(?, z)},
где суммирование ведется по всем упорядоченным парам ин-
индексов A <л</<;Л0.
Остается заметить, что при вычитании неаналитические
части ядер (9) сокращаются:
—щщ \У\^2
p\ pi
pi pi
(мы снова воспользовались принятыми выше упрощениями
в обозначениях и разложением Хефера). Мы приходим, таким
образом, к формуле
N
1 V /(»
pi pi
Р Р <*е. do)
р[ Pi
которая совпадает с формулой Вейля при я = 2 >
Замечание. Если множество Вейля A) несвязно, то оно
распадается на некоторое не более чем счетное число связных
компонент (областей Вейля). Теорема 1, очевидно, остается
в силе и в том случае, если П —несвязное множество Вейля.
При этом для z,' принадлежащих какой-либо компоненте,
в формуле Вейля F) отличен от нуля лишь интеграл по остову
этой компоненты, а интегралы по остовам других компонент
обращаются в нуль. Это следует из того, что интеграл Марти-
нелли — Бохнера, из которого выводится интеграл Вейля, равен
нулю вне области.
Аналитичность ядра формулы Вейля используется, напри-
например, в вопросах приближения голоморфных функций функ-
функциями из некоторого класса. Приведем основные факты, отно-
относящиеся к этому.
Теорема 2. Любую функцию /, голоморфную в анали-
аналитическом полиэдре B) и непрерывную в его замыкании, в этом
полиэдре можно разложить в ряд
Ul=o (О
23 Б. В. Шабат
354 ИНТЕГРИРОВАНИЕ [ГЛ. If
где k = {ku ..., kn) и i — (ii in)~ векторные индексы,
[Wt(z)]k = [Wii{z)]ki ... [Win(zj\k", внутреннее суммирование
производится по упорядоченным наборам I =О', <...</„ =g^ tV
и коэффициенты выражаются по формулам
p(' pil
P\n ...Pln
A2)
Ряд A1) сходится равномерно на любом компактном под-
шножестве полиэдра П.
< Разложение A1) получается из формулы Вейля точно
так же, как разложение Тейлора из интегральной формулы
Коши. Для любой точки геПи любой точки ? на остове П
можно написать разложение в сходящуюся геометрическую
прогрессию:
1
П
F», (z)f' ¦ ¦ ¦ [Wjn (z)f" у [Wt (г)]"
При фиксированном z e П это разложение сходится на а ,
«1 ¦" я
равномерно по ?, и, подставляя его в формулу Вейля F), мы
получаем разложение A1) с коэффициентами A2).
Равномерная сходимость ряда A1) на компактных подмно-
подмножествах полиэдра П доказывается обычным образом >
Следствие 1. Любую функцию f, голоморфную в ана-
аналитическом полиэдре П, на любом множестве К ^ П можно
сколь угодно точно приблизить функциями, голоморфными
в области D, которая участвует в определении полиэдра.
Коротко это следствие можно сформулировать так: семей-
семейство функций Н (D) плотно в семействе #(П).
А Частичные суммы ряда A1), очевидно, принадлежат
Я(?>) —они и приближают функции /еЯ(П). Чтобы избежать
словия непрерывности / в П, нужно заменить П полиэдром
= {геП: | U^(z)| <r't}, где все r\<r t и достаточно близки
к последним (г — скалярный индекс) >
В частности, когда П — полиномиальный полиэдр (т. е. все
функции W[ — полиномы), частичные суммы ряда A1) являются
полиномами. Мы получаем
ЗАДАЧИ 355
• • Следствие 2. Любую функцию f, голоморфную в поли-
полиномиальном полиэдре П, на любом множестве ^<еП можно
сколь угодно точно приблизить полиномами.
Области из С", на компактных подмножествах которых
каждая голоморфная функция сколь угодно точно прибли-
приближается полиномами, называются областями Рунге (ср. теорему
Рунге в п. 22 ч. I). Следствие 2 можно сформулировать так:
любой полиномиальный полиэдр является областью Рунге.
ЗАДАЧИ
1. Пусть а1, ..., а2П — (действительно) линейно независимые векторы в С"
2га
и Г —группа преобразований вида z -> г + ~^N^av, где Nv — целые числа.
v=i
Точки z, z' e С назовем эквивалентными, если существует перенос 1еГ
такой, что Я (г) = г'. Доказать, что в множестве С"/Г классов эквивалент-
эквивалентности по этому отношению можно ввести структуру re-мерного комплексного-
многообразия (С/Г называется га-мерным комплексным тором, ср. п. 32 ч. I).
2. Доказать, что любая функция /, голоморфная во всех точках ком-
комплексного тора С"/Г (см. задачу 1), постоянна.
3. Пусть якобиан системы га функций /v, голоморфных в точке а е С",
тождественно равен нулю в окрестности а. Доказать, что в некоторой окрест-
окрестности точки а эти функции связаны голоморфной зависимостью Ф (f fn)~0.
4. Подмножество N многообразия М класса С1 называется подмного-
подмногообразием, если оно является многообразием в индуцируемой топологии и
отображение вложения N-> М всюду имеет ранг, равный размерности N.
Доказать, что всякая функция из С1 (N) является сужением на N функции
класса С1 (М).
5. Пусть М —2т-мерная поверхность класса С1 в С, т, е. образ неко-
некоторой области DdCm при гладком отображении .г ->/ (г), /=(/i fn).
Доказать эквивалентность следующих условий:
а) для любой точки РсМ в касательной плоскости ТрМ нет анали-
аналитических прямых;
б) rank(-j«r, ^ё-1 5= 2т в D (отсюда следует, что п ^2= 2т).
6. Назовем голоморфной кривой систему п голоморфных в области DcrC
функций fv; тогда / = (/i fn) отображает D в С". Доказать, что для
голоморфных кривых имеет место принцип максимума модуля как в евкли-
евклидовой метрике |/ | = У 2 I ^v I2 > так и в метРике max (I fi I • • •> \fn I )•
7. Привести пример голоморфной кривой /: С -> С2, для которой мно-
множество предельных значений по всевозможным последовательностям t, e С,
сходящимся к бесконечности, совпадает с С2. [Указание: воспользоваться
задачей 1 к гл. V ч. I.]
8. Доказать, что множество голоморфных отображений С -> С, обла-
обладающих свойством, указанным в задаче 7, всюду плотно в пространстве
всех голоморфных отображений С->С™ с топологией равномерной сходи-
сходимости на компактах.
9. Дифференциальная форма со в точке Р многообразия М равна нулю,
если в некоторой локальной системе координат все ее коэффициенты
в точке Р равны нулю. Доказать независимость этого определения ог
23*
356 ИНТЕГРИРОВАНИЕ [ГЛ. II
выбора координат. Доказать, что m-мерное многообразие М ориентируемо
тогда и только тогда, когда на нем существует дифференциальная форма со
порядка т, нигде не равная нулю.
10. Пусть f голоморфна в поликруге U а С" и непрерывна на мно-
множестве U U Г, где Г — остов U. Доказать, что f продолжается до функции,
непрерывной в U.
11. Функция f непрерывна на границе dU единичного поликруга UczC
и на каждом одномерном аналитическом круге Av, a = iV ?ц = е |г, р. ф v,
I ?v | < 1} голоморфна по ?v. Доказать, что / продолжается до функции,
голоморфной в U и непрерывной в U.
12. Функция f непрерывна на остове Г единичного поликруга f/crC".
Доказать, что f продолжается до функции, голоморфной в U и непре-
непрерывной в U, тогда и только тогда, когда
(?)$Ad? = O для всех k = (ku ..., kn), йу>0-целые.
13. Пусть D — область в С" со связной гладкой границей 3D и функция
fsC в окрестности 3D. Предположим, что вдоль каждой касательной к 3D
аналитической прямой г = а + ы>Я, а, со е С", Я е С, функция / удовлетворяет
касательным уравнениям Коши — Римана: —=- / (а + соА.) =¦ 0 в точке касания.
Доказать, что f продолжается до функции, голоморфной в D и непрерыв-
непрерывной в D. _
14. Пусть П = BеС: l/>v(z)l^l, v=l п) — полиномиальный по-
полиэдр в С" такой, что Det 1-^-1 Ф 0 на его остове Г. Доказать, что
всякая функция f, голоморфная в П и непрерывная в П U Г, равномерно
приближается полиномами (и потому, в частности, продолжается до функ-
функции, непрерывной в Я).
ГЛАВА HI
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
Любая плоска^ область служит естественной областью
существования голоморфной функции: для любой области DczC
существует функция, голоморфная в D и не продолжаемая
аналитически за пределы этой области (см. п. 43, ч. I). В отличие
от этого, в пространстве С* (п>1) существуют области, из
которых любая голоморфная функция непременно продолжается
в более широкую область. Мы приводили несколько примеров
таких областей, скажем нелогарифмически выпуклые области
Рейнхарта (и. 7) или области с компактными дырками (тео-
(теорема Осгуда — Брауна в п. 17).
Эта глава посвящена в основном описанию пространствен-
пространственных областей, которые служат областями существования голо-
голоморфных функций.
§ 7. Области голоморфности
19. Теорема Хартогса о продолжении. Здесь мы приведем
еще одну простую теорему о принудительном аналитическом
продолжении функций нескольких комплексных переменных.
Теорема 1 (Хартогс). Пусть даны области 'D сг С" ('z)
и Dnc:C{zn); любая функция f, голоморфная в окрестности
(в смысле Сп) множества
.M = ('DXdDn)\J({'z°}xBn), A)
где 'г°е'5, голоморфно продолжается во всю область
D = 'D X Dn (см. рис. 95, где Dn представляет собой круг).
•4 Не уменьшая общности, можно считать, что Dn ограни-
ограничена конечным числом гладких кривых.
Функция
голоморфна в области D = 'DX Dn. В самом деле, при ?„ е dDn
Yi'z^'D точка ('г, ^ей, следовательно, f{'z, ?„), а по лемме
п. 6 и /, голоморфно зависит от 'г в 'D при любом гп ф. dDn;
358
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. ИГ
с другой стороны, при любом 'ze.'D функция /(как интеграл
типа Коши) голоморфно зависит, от zn в Dn. Но при z, при-
принадлежащих некоторой окрестности множества {'z°}XDn, функ-
|Z | у- ция f по условию голоморфна, и для
п""л таких z по интегральной формуле
Коши для функций одного перемен-
переменного zn
1 Г f('z t )
/(z)--9^7 т.-у. ai°n- W)
Рис 95
fi,
\гг\
Таким образом, для z из этой
окрестности ](z)ssf{z) и по теореме
единственности для функций несколь-
нескольких переменных f = f всюду, где /
голоморфна. Но f^H(D), и, следова-
тельно, она дает требуемое аналити-
аналитическое продолжение f >
Пример. Всякая функция /, голоморфная в области из С2, диаграмма
Рейнхарта которой изображена на рис. 96, аналитически продолжается
в бикруг {\z1\<Ru \z2\ <Ri).
Замечание. Как видно из доказательства, условия тео-
теоремы Хартогса можно несколько ослабить, потребовав лишь,
чтобы функция f была: 1) голоморфной
в окрестности множества {'г0} X Dn, 2) не-
прерывной по zn и голоморфной по 'г на
множестве 'D X dDn. Заметим еще, что г
в этой теореме можно поменять роли об-
областей 'D и Dn (и соответственно перемен-
переменных 'z и zn), — для этого достаточно вместо
B) рассмотреть кратный интеграл Коши
по d'D.
В качестве примеров применения тео-
теоремы Хартогса рассмотрим вопрос о сти-
стирании особенностей голоморфных функ-
функций нескольких переменных. Первая из теорем, которые мы
здесь докажем, является пространственным аналогом теоремы
об устранимости изолированной особой точки, в окрестности
которой голоморфная функция ограничена. В случае прост-
пространственной области йсС роль изолированной точки играют
так называемые тонкие множества М cz D. Они определяются
условием, что для каждой точки геД существует окрестность
UZ^D и в ней голоморфная функция ф#0, которая равна Q
R,
Рис. 96.
5 7] ОБЛАСТИ ГОЛОМОРФНОСТИ 359
во всех точках М П Uz. По теореме единственности тонкое мно-
множество не может иметь внутренних точек, оно нигде не плотно
в D. Можно доказать, что дополнение к тонкому множеству
относительно области D связно (задача 3 к гл. V).
Теорема 2. Пусть М — тонкое множество в области D с С"
и функция f голоморфна в D\ M. Если f локально ограничена 1),
то она единственным образом продолжается до функции /,
голоморфной в D.
Л Единственность продолжения очевидна, ибо множество
D \ М связно. Достаточно доказать голоморфную продолжи-
продолжимость f в произвольную точку аеМ, которую без ограниче-
ограничения общности можно принять равной нулю. Выполняя, если
надо, линейную замену переменных, можно считать, что функ-
функция ф, определяющая М в окрестности UQ, удовлетворяет
условию ф('г, 0) Ф 0, где, как всегда, 'г — {ги ..., zn_{). При
достаточно малом р„>0 функция ф('0, zn) ф 0 на окружности
{|zn| = pn}, поэтому числа pv (v=l, .... n—1) можно выбрать
столь малыми, что (p('z, zn)=?0 для всех 'ге'У = {|zv|^pv}
и всех 2„_е dDn = {\zn | = ря}. Отсюда следует, что точки ('г, г„),
где 'zsY, a zn^dDn, не -принадлежат множеству М, т. е.
/ голоморфна в окрестности 'V X dDn.
С другой стороны, при любой фиксированной 'z° e 'V функ-
функция ф^г0, zn) согласно подготовительной теореме Вейерштрасса
имеет конечное число нулей в круге Dn = {12Я | ^ р„}, т. е. f{'z°, zn)
имеет в Dn конечное число особых точек. Так как она по
условию ограничена в Dn, то эти особенности устранимы и,
значит, f{'z°, zn) продолжается до голоморфной в Dn функции.
Продолженная функция J голоморфна в окрестности множества
('V X dDn) U ('О X Dn) и по теореме 1 голоморфна в поликруге
V = 'V X Dn >
В следующей теореме мы усилим ограничение на функцию f,
предположив ее непрерывной в D, но зато ослабим требование
на множество М. Именно, мы предположим, что оно лежит
не на тонком множестве, а лишь на гладкой поверхности раз-
размерности 2п — 1.
Теорема 3. Если функция f непрерывна в области D cz Cn
и голоморфна всюду в D, за исключением множества М, лежа-
лежащего на гладкой поверхности S размерности 2« — 1, то она
голоморфна во всей D.
') Это означает, что для каждой точки геВ найдется окрестность Uz
такая, что f ограничена в (D\M)(]UZ.
360
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. III
¦« Доказательство аналогично предыдущему. Пусть в окрест-
окрестности U точки О е М поверхность S представляется уравне-
уравнением уп = ф {'г, хп), где ф —гладкая действительная функция.
Так как ф('О, 0) = 0, то в силу непрерывности для любого
достаточно малого р>0 найдется такая окрестность 'V точки'О
и такое а>0, что |ф('2, *„)|<р для всех 'ге'1/ и |*„|<а.
Поэтому f голоморфна в 'V Х{\хп\<а, Р<|г/„|<у}> где v>P
достаточно мало. С другой стороны, при фиксированной 'г0 е 'V
функция f('z°, zn) голоморфна по zn в прямоугольнике Dn =
= {1л:га1<а. \Уп\<У) всюду, за исключением гладкой кривой
г/„ = ф('2°, xn), и непрерывна в Dn. Из теории функций одного
переменного известно (см. задачу 5 к гл. III ч. I), что отсюда сле-
следует голоморфность f('z°, zn) в Dn. По теореме 1 (см. замечание
вслед за ней) заключаем, что f голоморфна в 'V X Dn >
20. Понятие области голоморфности. Как мы несколько раз
отмечали, в пространстве не всякая область является областью
существования голоморфной функции —
имеются области, из которых каждая го-
голоморфная функция аналитически продол-
продолжается в более широкую область. Мы хо-
хотим с самого начала подчеркнуть, что в
пространстве, как и на плоскости, в про-
процессе такого продолжения расширяющаяся
область может начать налегать на самое
себя, образуя второй слой, в котором
функция принимает другие значения, чем
в первом слое. Мы приходим, таким обра-
образом, к необходимости рассматривать «мно-
голистные» области, аналогичные римано-
вым поверхностям аналитических функций
одного переменного. Подробнее мы рассмот-
Рис. 97. рим многолистные области в § 9. Сейчас мы
только приведем пример, из которого видно,
что необходимость в таких областях может возникнуть и в
процессе «принудительного» аналитического продолжения.
Пример. Пусть D сг С2 — область, диаграмма Хартогса
которой изображена на рис. 97, это цилиндр {х\ + у\ < 1, | z21 < 2}
с выброшенными квадратами / = {0^лг,<1, у{ = 0, |г2|^1},
// = {0<г/,<1, X] = 0, 1<|г2|<2} и сектором S = {|21|<1,
Xj^sO, Ух^Ь, |z2|=l}. По теореме Хартогса каждая функция
f e H (D) аналитически продолжается через сектор S как сверху
вниз, так и снизу вверх1). В самом деле, рассмотрим, например,
') Мы для простоты говорим о множествах, изображенных на диаг-
диаграмме Хартогса, понимая под ними соответствующие множества из С2.
§ 7] ОБЛАСТИ ГОЛОМОРФНОСТИ 361
первый способ продолжения (сверху вниз): функция f голо-
голоморфна в окрестности полукруга S = {|2, |<Л — е, х^г, | z2\ = 2 — е}
и отрезка {г, = г?, |г2|<2-е}, гд'е | z°| < 1, х°>0, г/° < О, и,
следовательно, продолжается на 2 х {\z2|<2 — е}.
При таком продолжении мы снова попадаем в область D,
но функция не обязана принимать те же значения, которые
она имела. В самом деле, рассмотрим, например, функцию
/0(г,, z2) = Vz\> где рассматривается непрерывная в D ветвь
корня, которая принимает положительные значения на оси хх.
Она, очевидно, голоморфна в D и в точках А и В диаграммы,
которые проектируются в одну точку Р плоскости zu но рас-
расположены по разные стороны S, принимает различные по знаку
значения (переходя из А в В по D, мы должны изменить avgzx
на 2л). С другой стороны, продолжая f0 через S по теореме
Хартогса (как описано выше), мы получим, что значения /0,
скажем, в точке В и ее продолжения в точке А должны быть
одинаковыми.
Таким образом, продолжение /0 привело нас к неодно-
неоднозначной функции; не желая рассматривать такие функции,
мы должны относить продолженные значения ко второму экзем-
экземпляру области D, склеенному с первым по множеству S. Мы
получим пример многолистной области из числа тех, о которых
говорилось выше.
Введем теперь одно из важнейших понятий теории функций
нескольких комплексных переменных.
Определение 1. Область DczCn называется областью
голоморфности функции f, если f голоморфна в D и не про-
продолжаема аналитически за пределы этой области в следующем
смысле1): для любой точки г°еД функция f, голоморфная
в наибольшем поликруге U(z°, r)czD, не продолжается го-
голоморфно ни в какой поликруг U (z°, г'), г' > г (радиусы г и
г' —скаляры). Область называется областью голоморфности,
если она является областью голоморфности какой-либо функ-
функции.
Определение 2. Область G, строго содержащая область D,
называется голоморфным расширением последней, если любая
f e Я (D) продолжается до функции, голоморфной в G.
Второе определение содержательно, когда D не является
областью голоморфности, т. е. лишь в пространственном случае.
Интересную особенность этого случая выражает следующая
простая
') Уточнение существенно, когда f не продолжаема в однолистные об-
области, содержащие D, но продолжается в неоднолистные (как /0 в при-
приведенном выше примере).
362 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
Теорема 1. Если G является голоморфным расширением
области D, то продолжение любой функции f e Н (D) может
принимать в G \D лишь те значения, которые f принимает в D.
4 Пусть, от противного, некоторая функция /€=#(?)) при-
принимает какое-либо значение ш0 в G\D, но не принимает его
в D. Тогда функция g (z) = f, . —, очевидно, голоморфна в D,
но непродолжаем а аналитически в G, ибо в некоторой точке
G\D она обращается в бесконечность. Это противоречит опре-
определению 2 >
Следствие. Голоморфное расширение G ограниченной
области D а С" также является ограниченной областью.
< По теореме 1 функции fv(z) = zv (координаты точки г)
принимают в G\D те же значения, что и в D, т. е.
sup|zv|= sup|zv|, v=l, ..., п. A)
геб г. s D
Но так как D ограничена, то правые части A) конечны, сле-
следовательно, конечны и левые, т. е. G ограничена >
Как для дальнейшего развития теории, так и для прило-
приложений важно уметь находить в известном смысле максималь-
максимальные голоморфные расширения данной области — так называемые
оболочки голоморфности. Этой задачей мы займемся в § 9.
А пока будем учиться характеризовать «нерасширяемые» об-
области пространства С", т. е. области голоморфности (на пло-
плоскости любая область нерасширяема в принятом здесь смысле,
так что поставленная задача интересна лишь при п>\).
Начнем с простых достаточных условий. Будем говорить,
что в граничной точке ? области ДсС" существует барьер,
если для любого множества К Ш D и любого е>0 найдется
функция g<=H{D) такая, что || g \\к = max| g(z)|< 1,но | g(z)|>l
в некоторой точке ге [/(?, е).
Очевидно, что если существует функция f e H (D), неогра-
неограниченная в точке Z, <= 0D (т. е. такая, что f{zv)-+oo по не-
некоторой последовательности zv^D, zv —>?), то в этой точке
существует и барьер. В самом деле, для любых К Ш D и е>0
можно взятъ g(z) — j^~. Обратное утверждение также спра-
ведливо, причем в следующей усиленной форме:
Теорема 2. Для любого множества У cz dD точек, в ко-
которых существует барьер, найдется функция [еЯ(Д), неогра-
неограниченная во всех точках У.
< Прежде всего заметим, что существует не более чем
счетное множество точек dD, всюду плотное на У, и что функ-
§ 7] ОБЛАСТИ ГОЛОМОРФНОСТИ 363
ция, неограниченная на таком множестве, будет неограниченной
и на У. Поэтому У можно считать не более чем счетным мно-
множеством. В этом предположении мы построим последователь-
последовательность ?v e У так, чтобы каждая точка У встречалась в ней
бесконечно часто1). Теперь для доказательства теоремы доста-
достаточно найти функцию fe H (D) и последовательность точек
zv e D так, чтобы |2V — ?v|—>-0 и f{zv)-*-oo.
Сначала мы построим компактное исчерпывание области D,
т. е. возрастающую последовательность замкнутых множеств
сю
RlczR2c ... таких, что (JRk = D, — это делается точно так же,
как при доказательстве леммы из п. 22 ч. I. Теперь мы по-
построим последовательность натуральных чисел pV//oo, точек
2vefl и функций fv^.H{D) так, чтобы для Kv~Rpv и любого
v=l, 2, ... выполнялись условия:
V у
Это можно сделать по индукции: для v=l берем Ki = R\,
в качестве /, —барьер в точке Е,1 Для множества К, и в ка-
качестве zl — точку из1. D\K\, \zl — ?'|<1, в которой \fl(z1)\>l
(она существует по определению барьера), затем выбираем
/С2 = Rpi так, чтобы 21 e Ц2 (можно сделать по условию исчер-
исчерпывания); теперь условия B) выполнены при v=l. Пусть по-
построение сделано для всех натуральных чисел до v—1 вклю-
включительно; мы выбираем в качестве /v барьер в точке t,v для
множества %v (оно уже построено на (v—1)-м шаге), находим
точку z'eD\J(v, Uv-?vl<v> B которой |fvBv)|>l (опре-
(определение барьера), и берем Kv+i = RP так, чтобы г
v
v
v
(условие исчерпывания). Условия B) выполняются, и возмож-
возможность нашего построения доказана.
Наконец, учитывая, что |/VBV)|>1, мы подбираем последо-
последовательность натуральных чисел qv (начиная с ql= 1) так, чтобы
выполнялось неравенство
И-1
^^2^-|/vWv+f* 0*>2), C)
v=l
') Пусть точки множества % как-то занумерованы; для построения по-
последовательности ?v мы возьмем точки в таком порядке: 1; 1, 2; 1, 2, 3;...
364 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
и рассматриваем ряд
Для любого геКд мы имеем | /v B) | ^ 1 при v ^ \л, следо-
следовательно, ряд D) равномерно сходится на Кц- Так как Кп ком-
компактно исчерпывают D, то отсюда следует, что ряд D) схо-
сходится всюду в D и что его сумма f е#(/)) (см. теорему Вейер-
штрасса из п. 6). Наконец, для любого (л=1, 2, ... мы имеем
, —1
v=l v=n+l v=n+l
откуда видно, что /(z^-x» >.
Из доказанной теоремы непосредственно вытекает достаточ-
достаточное условие для областей голоморфности:
Следствие. Если на всюду плотном множестве точек
границы D существует барьер, то D является областью голо-
голоморфности.
Например, в каждой точке ? границы щара В = {| z |< /?}czC"
существует барьер, ибо существует функция
f(z) = -п
V=I
неограниченная в точке g. Следовательно, шар является об-
областью голоморфности. Этот пример обобщает
Теорема 3. Всякая выпуклая область DaCn является
областью голоморфности.
< В силу выпуклости D для любой точки ? е сШ можно
построить Bп — 1)-мерную плоскость
л
2 {av (zv - ?v) + av (zv - tv)} = 0,
v=l
проходящую через ? и такую, что D лежит с одной ее стороны.
В этой плоскости мы возьмем Bга — 2)-мерную !) аналитическую
плоскость
п
v=l
') Указана действительная размерность.
§ 7] ОБЛАСТИ ГОЛОМОРФНОСТИ 365
которая проходит через ? и не содержит точек D. Но тогда
функция f{z) = — голоморфна в D и не ограничена
V=I
в ?, т. е. в ? существует барьер. По следствию D является об-
областью голоморфности >
Однако условие выпуклости не является нзобходимым для
области голоморфности. Это видно, например, из следующей
теоремы:
Теорема 4. Если Dz является областью голоморфности
в пространстве С"(г), a Dw —аналогичной областью в про-
пространстве Cm(w), то произведение Dz X Dw является областью
голоморфности в пространстве Сп+пг (г, w).
< Возьмем функцию f{z)^H{Dz), не продолжаемую голо-
голоморфно в более широкую область, и такую же функцию
g (ш) е Я (Dw). Тогда функция f (z) g О) е Я ('Dz X Dw) и не про-
продолжается голоморфно в более широкую область, чем DZXDW >
Так как в С1 любая область является областью голоморф-
голоморфности, а поликруговые области —это произведения плоских об-
областей, то мы имеем
Следствие. Любая поликруговая область из Сп является
областью голоморфности.
В частности, произведение D двух плоских областей D{ и D2,
из которых по крайней мере одна, скажем Dit не выпукла,
является областью голоморфности, хотя D и не выпукла.
В следующем пункте мы введем обобщенное понятие вы-
выпуклости, которое менее наглядно, чем обычное, но зато дает
необходимое и достаточное условие для областей голоморф-
голоморфности.
21. Голоморфная выпуклость. Выпуклую оболочку множе-
множества М cz Сп можно, очевидно, описать как совокупность М
всех точек 20еС таких, что для любой действительной ли-
линейной функции
Л \Z) = Uq -\- ^j CCVAV \CCV tr: К j
v=l
имеет место неравенство
К sup | Я (г) |
(см. рис. 98, где при га=1 изображены линии уровня линей-
линейных функций).
ggg АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
Предоставляем читателю убедиться в том, что при описа-
описании выпуклой оболочки в С" действительные линейные функ-
функции можно заменить комплексными:
v=l
(av e= С1).
Иными словами, выпуклую оболочку
множества М можно определить как
множество
М = {г°s С": | /(z°) |< sup | /B) |}, A)
ем
где неравенство справедливо для всех
линейных функций / (z).
Рис 98 Мы хотим обобщить понятие вы-
выпуклой оболочки, распространив его
на произвольное семейство F функций (действительных или
комплексных), определенных в области D с С".
Определение 1. F-выпуклой оболочкой множества М czD
называется совокупность точек
МР = {2° s D: I / B°) 1 < sup | f B) |}, B)
где неравенство справедливо для всех функций f^F.
Определение 2. Область D называется F-выпуклой, если
для любого множества К, компактно принадлежащего D, его
/"-выпуклая оболочка также компактно
принадлежит D:
К Ш D => Кр ш D. C)
Форма, в которой принято определе-
определение 2, позволяет устанавливать /^-выпук-
лость области, не выходя за ее пределы.
Это существенно, когда F состоит из
функций, определенных лишь в области D.
Ясно, что в случае, когда F состоит из Рис. 99.
линейных функций, /^-выпуклость совпадает
с обычной (геометрической) выпуклостью (см. рис. 99, где
показано, как невыпуклость области влечет за собой наруше-
нарушение условия C)).
В теории функций особо важную роль играет голоморфная
выпуклость, когда F = H(D), а также полиномиальная выпук-
выпуклость, когда F представляет собой совокупность всех поли-
полиномов Р (z). Полиномиально выпуклую оболочку множества М
§ 7] ОБЛАСТИ ГОЛОМОРФНОСТИ 367
мы будем обозначать через МР, а голоморфно выпуклую — че-
через Мн. Рассматривается и понятие выпуклости, связанное
с другими классами F, например совокупностью всех рацио-
рациональных функций или всех мономов (т. е. кратных степеней
*
zk = zf. . . . z*«).
)
Очевидно, чем шире класс F, тем для большего множества
функций требуется выполнение неравенства B) н поэтому тем
уже /"-выпуклая оболочка множества и, следовательно, тем
шире класс /"-выпуклых областей. В частности, всегда М cz
cz Мн cz МР cz M и все выпуклые области лзляются полино-
полиномиально выпуклыми, все полиномиально выпуклые — голоморфно
выпуклыми.
Примеры.
1. Проиллюстрируем описанное включение в плеском слу-
случае. Любая область DczC1 является голоморфно выпуклой,
а полиномиально выпуклыми будут лишь области со связным
дополнением в С1 (докажите!). Класс геометрически выпуклых
областей уже класса полиномиально выпуклых. Образно говоря,
переход к полиномиальной оболочке плоской области сводится
к заклеиванию в ней «дыр», а к (геометрически) выпуклой обо-
оболочке—еще и к заклеиванию «выемок» вблизи границы.
2. Любой аналитический полиэдр
n = {zeD:|F,(z)|<l, .v=l, .... JV}
(см. п. 18), где функции Wve #(/)), является выпуклым отно-
относительно класса H = H{D). В самом деле, если 1(шП, то для
любого v=l, ..., N имеем || WV\\K =?Сг < 1. По определению
Я-выпуклой оболочки
а отсюда следует, что и Кн ^ П.
Условие выпуклости относительно любого семейства функ-
функций F cz H(D) оказывается достаточным для того, чтобы D
была областью голоморфности.
Теорема 1 (Картан и Туллен). Если область D cz С11
выпукла относительно какого-либо класса FczH(D), то она
является областью голоморфности :).
¦4 Доказывается вполне аналогично теореме о барьере из
предыдущего пункта. Выбираем счетное всюду плитное на 3D
') Выбирая в качестве F совокупность линейных функций /(г), получим
теорему 3 предыдущего пункта.
368 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
множество точек (f и последовательность граничных точек ?ft
так, чтобы каждая точка <? встречалась в ней бесконечно часто.
Далее, исходя из какого-либо компактного исчерпывания 7?, cz
a R2 a ... области D, строим последовательность множеств
Kv = RPv, точек 2veD и функций fv<=H(D) так, чтобы для
любого v=l, 2, ... было: 1) zv^Kv+i\Kv, |zv-?v|<-^-,
2) ||/vll/c ^1, но |fvBv)|>l (для простоты письма мы опускаем
индекс F в обозначении /"-выпуклой оболочки). Построение
делаем по индукции. Для v=l берем K\ = R\ и, пользуясь
/^-выпуклостью, по которой К\ (= D, находим точку гг е D та-
такую, что гхфК\ и Iz1 —?Ч<1; из определения оболочки сле-
следует существование функции g,G F такой, что | gx (zl) \~^t\\gx \\K,
и мы полагаем fi B) = "jijj—• Затем мы выбираем К2 = RP2 так,
чтобы г1 принадлежала /Сг. а значит, и подавно /("г- Далее
предполагаем, что построение сделано для всех натуральных
чисел до V—1 включительно. Тогда берем точку zveZ)\^v
так, чтобы было |zv —?v[< —, находим функцию gv<=F, для
которой 1 g-v(^v) I>lle"vlkv> полагаем fv(z) = ^j~jp^- и выбираем
iCv+i = Rpv+l так, чтобы zv e i*Cv+i \ ^v Построение закончено.
Остается так же, как в теореме о барьере, выбрать нату-
натуральные числа qv так, чтобы при всех ц>1 выполнялись не-
неравенства
и рассмотреть ряд
v=l
Так как ряд сходится равномерно на любом K<^D, то
f^H(D), а так как f(zv)—>oo, то Z) является областью голо-
голоморфности этой функции >
Самое сильное утверждение мы получим, если выберем
в этой теореме F = Я (D):
Следствие. Всякая голоморфно выпуклая область
является областью голоморфности.
Ясно, что для получения необходимых условий для области
голоморфности на класс F надо наложить дополнительные
ОБЛАСТИ ГОЛОМОРФНОСТИ
369
условия (например, если F — совокупность всех линейных функ-
функций, то /-"-выпуклость сводится к обычной выпуклости, а она,
как мы видели, не является необходимой). Мы предположим,
что класс F является устойчивым по отношению к дифферен-
дифференцированию, короче, d-устойчивым, т. е. вместе с любой функ-
функцией f содержит и любую производную —^- .
Для оболочки относительно таких классов справедлива сле-
следующая важная теорема об одновременном продол-
продолжении:
Теорема 2 (Картан и Туллен). Пусть К Ш D и
r = p(K, dD) — расстояние в ^-метрике от К до границы D. Ка-
Какова бы ни была точка 2°, при-
принадлежащая выпуклой оболочке
множества К относительно d-yc-
тойчивого класса F, любая функ-
функция f e F голоморфно продол-
продолжается в поликруг U (z°, r).
Существенно, что U (z°, r)
может выходить за пределы об-
области D (см. схематический
рис. 100,); радиус этого поли-
поликруга не зависит от индивидуальной функции f s F и опре-
определяется лишь расстоянием множества К до dD.
< Так как z°eZ), то любая функция |ef в окрестности 2°
представляется рядом Тейлора
Рис. 100.
где**---
дгп
f(z)= 2 ck(z-z0)k,
I k l=o
D)
Но так как
dzk
dzk
и класс rf-устойчив, то
(б)
т. е. оценка производных в точке 2° сводится к их оценке на Д\
Выберем число г{<г и обозначим через К(п) замыкание
/ураздутия множества К (т. е. объединения всех поликругов
U {г, г,), г
обозначим
/(). Так как K
(ri)
D, то f ограничена на нем, мы
24 Б. В. Шабат
370 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
Если z e К, то U{z, r^czK^, и для оценки производных в пра-
правой части E) мы можем воспользоваться неравенствами Коши
(п. 7):
Н*1
«I
ь ^S: ГТТ
2 „ Г,
ил *
Теперь выберем любое rz.<.r1; для произвольной точки
z е= С/ (z°, r2) имеем
|Cft(z-z°)* КЛ^г,)^I*', G)
откуда видно, что ряд D) сходится в поликруге U (z°, г2). Так
как числа г, и г2 можно выбрать сколь угодно близкими к г,
то D) сходится всюду в U {z°, r). Этот ряд и дает нужное голо-
голоморфное продолжение функции / >
Доказанная теорема сразу приводит к необходимости /•'-вы-
/•'-выпуклости для областей голоморфности в следующей форме:
Теорема 3 (Бенке — Штейн). Если D аСп является
областью голоморфности некоторой функции f из d-устойчи-
вого класса F, то она F-выпукла.
¦4 Возьмем произвольное множество К <Ш D и обозначим
г = р(К, dD). По теореме 2 функция f продолжается в г-разду-
тие множества KF, а так как / по условию не продолжаема
за пределы D, то это раздутие принадлежит D и, значит,
KF^D >
В частности, выбирая F = H (D) (этот класс, очевидно, d-устой-
чив), получим, что любая область голоморфности является
голоморфно выпуклой. Объединив этот факте отмеченным выше
следствием теоремы 1, получим окончательный результат:
Теорема 4. Условие голоморфной выпуклости области
необходимо и достаточно для того, чтобы она была областью
голоморфности.
К сожалению, это условие не является столь наглядным и
эффективно проверяемым, как условие геометрической выпу-
выпуклости. В следующем параграфе мы дадим другую его трак-
трактовку, основанную на теории субгармонических функций. Эта
трактовка, пожалуй, более геометрична и, кроме того, она при-
приведет к некоторым эффективным критериям для областей голо-
голоморфности.
Сейчас мы приведем еще одну формулировку условия F-вы-
пуклости, наложив на рассматриваемые классы дополнительное
ограничение. Именно, мы будем считать, что класс F устойчив
по отношению к возведению в степень, короче, р-устойчив, т. е.
§ 7) ОБЛАСТИ ГОЛОМОРФНОСТИ 371
вместе с каждой функцией / содержит и любую ее натураль-
натуральную степень fm.
Для таких классов теорему об одновременном продолжении
можно несколько усилить:
Теорема 5 (Картан и Туллен). Пусть KmD, r =
= р (К, dD), a F — произвольный класс, одновременно р- и
d-устойчивый. Тогда для любой функции f^F и любой точки
где гх<г — произвольное число и /С(о> — раздутие множества К.
¦4 Пусть гг<гх и точка 2 <= U(z°, r2); тогда ряд Тейлора D)
функции f с центром в точке 2° сходится в точке z и для каж-
каждого его члена справедлива оценка G):
Суммируя эти неравенства, найдем
где через Nn,v обозначено число членов ряда Тейлора функ-
функции п переменных с данной \k\ = v. Но сумма в правой части,
очевидно, равна -, гтг, и, следовательно,
()
О)
Применяя это неравенство к функциям fm (m = l, 2, ...).
принадлежащим классу F в силу его р-устойчивости, получим
Теперь извлечем корень /n-й степени и устремим пг—>°о; будем
иметь | / (z) | ^ Mf (г]). Но здесь z можно считать произвольной
точкой из U (z°, /-!), a Mf{rx) согласно F) совпадает с правой
частью (8) >
Следствие. В условиях и обозначениях предыдущей
теоремы
(Kpf'uDcziK^)^ A0)
24*
372 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
< Любая точка г1, принадлежащая левой части A0), при-
принадлежит и поликругу U (z°, r±) с центром z° e К_Р, поэтому
согласно (8) для любой fsF имеем | f (z1) |<||f ||K(ri); это и озна-
означает, чтог:1 принадлежит /-"-выпуклой оболочке множества К(п) >
Критерий /-"-выпуклости в сделанных предположениях
о классе можно сформулировать так:
Теорема 6. Для того чтобы область D czCn была выпу-
выпуклой относительно некоторого класса F, одновременно р- и
d-устойчивого, необходимо и достаточно, чтобы для любого
множества К Ш D
A1)
¦4 Достаточность условия A1) очевидна. Для доказательства
необходимости обозначим левую часть A1) через t, а правую
через г. Очевидно, t <^.г\ если бы было f<_r, то мы имели бы
р
К Ш D. В силу замкнутости множества К.р оно содержит
точку 2°, для которой p(z°, dD) — f. По-
Поэтому поликруг U(z°, r) касается границы
dD и не может компактно принадлежать D.
Но U (z°, f) согласно теореме 5 содер-
содержится в (/CW)f. Таким образом, оболочка
К(г) некомпактна в D, а это противоречит
/"-выпуклости области >
Мы получили новую характеристику
областей, выпуклых относительно одновре-
одновременно р- и rf-устойчивых классов (в част-
частности, голоморфно выпуклых). Это такие области, в которых
переход от компактных подмножеств к их F-выпуклым оболоч-
оболочкам происходит без уменьшения расстояний до границы. Образно
говоря, такой переход состоит в заклеивании «дырок» и «впа-
«впадин», имеющихся в подмножествах (рис. 101).
22. Свойства областей голоморфности. Области голоморф-
голоморфности в С" —это голоморфно выпуклые области. Мы приведем
несколько их свойств, обобщающих известные свойства выпу-
выпуклых областей.
Теорема 1. Пусть Da, аеД- произвольное семейство
областей голоморфности в Сп и G = f] Da — их пересечение.
о
Каждая связная компонента D открытого ядра G является
областью голоморфности.
¦4 Пусть К <Ш D; так как каждая функция из Я (^^голо-
(^^голоморфна и в D, то H{D) => Я (/)„) и, следовательно,
§ 7]
ОБЛАСТИ ГОЛОМОРФНОСТИ
373
для всех а е А. Поэтому р{Кнф), dDa)~^p{KH(Da), dDa), и, зна-
значит, в силу голоморфной выпуклости Da, для всех а е А имеем
p(Kh{d), dDa)>p(K, dDa)>p(/C, dD). Если бы D не была об-
областью голоморфности, то для некоторого К, было бы
P(Kh(d)> dD)<p(K, dD), и тогда нашлась бы Da, для которой
р(Кнф), dDa)<p{K, dD), вопреки доказанному >
В отличие от пересечения, объединение областей голо-
голоморфности не обязано быть такой же областью (ср. соответ-
соответствующие свойства выпуклых областей). Это видно из простого
примера: {|z1|<l, |22|<2} и {|z1|<2, |z2|<l} являются об-
областями голоморфности в С2, а их
объединение, диаграмма которого
изображена на рис. 102, —нет (это
доказано в п. 7).
Однако, справедлива
Теорема 2 (Бенке — Штейн).
Объединение возрастающей после-
последовательности областей голоморф-
голоморфности Dv'-
'v+l
A)
Рис. 102.
также является областью голоморф-
голоморфности, если D ограничена.
< Доказательство этой теоремы не так просто, и мы разобьем
его на несколько этапов.
I. Прежде всего покажем, что D можно представить как
объединение возрастающей последовательности аналитических
полиэдров (см. п. 18). Для этого выберем последовательность
натуральных чисел pv так, чтобы области Gv = DPv для всех
v=l, 2, ... удовлетворяли условию
sup p(z, dGv+l)<p(Gv-b dGv+i). B)
Возможность такого выбора докажем по индукции. Положим
Gi = Di и выберем р2 столь большим, чтобы для G2 — Dp2 было
sup p{z, dZ))<p(G,, 3D); после этого выбираем рг так, чтобы
граница области G3 = DP3 была столь близкой к dD, что в по-
последнем неравенстве dD можно заменить на dG3' sup p{z, <3G3) <
< p(Gs, dG3). Пусть выбор сделан для всех натуральных чисел,
меньших v; выберем pv так, чтобы для Gv = DPv было
sup р(г, dD)<p{Gv..u dD), C)
;374 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
а затем выберем pv+! так, чтобы Dp = Gv+1 была столь близ-
близкой к 3D, что в последнем неравенстве 3D можно заменить
<9Gv+!, — мы получаем B).
Так как Cv_, <Ш Gv+I и Gv+1 (как область голоморфности)
выпукла относительно класса #(GV+1), то по теореме 6 преды-
предыдущего пункта для оболочки G*-i = (Gv-i)H(G ч имеем
р(Gv-i, aGv+i) = P(Gv-i, aGv+i). D)
Но из B) следует, что для любой точки z°edGv
p(z°, dGv+1)<p(Gv.u dGv+l),
т. e. dGv не пересекается с G*_,. Поэтому для любой точки
z°<==dGv найдется функция ^,еЯ(Сы) такая, что |fz0(z)|<l
в Gv_, и |/го(г)|>1 в некотором поликруге U (z°, г). В силу
компактности множества dGv мы можем из покрытия его такими
поликругами выбрать конечное покрытие Uv — U {z^'v, r<li>v)),
ц = 1, ..., A^v, и построить аналитический полиэдр
, ц=1 iVv}, E)
где f v = fzn,v — найденные выше функции из класса H(Gv+l).
По нашему построению GV_1^IIV^GV для любого нату-
натурального v. Поэтому область D представляется как объедине-
объединение возрастающей последовательности полиэдров Вейля:
D=\Jnv,Uv<c=nvH, F)
V
причем" полиэдр ITV определяется функциями f^ v с: H{Uv+l).
Заметим, что, начиная с некоторого v, все полиэдры IIV можно
считать связными.
II. Покажем теперь, что класс H(D) плотен в каждом
классе Н (Uv), т. е. что любую функцию foe#(IIv) можно на
любом компактном подмножестве Ilv сколь угодно точно при-
приблизить функциями из H(D). В самом деле, пусть заданы
К <шПу и е>0. По следствию 1 теоремы 2 п. 18 существует
функция f,<=#(Ilv+1) такая, что ||f0~ А Наг <у • По тому же
следствию существует f2^H{Uv+2) такая, что ||/2 — /, ||п <-^г,
и вообще для любого ц=1, 2, ... существует функция
^Щ) такая, что
§ 7] ОБЛАСТИ ГОЛОМОРФНОСТИ 375-
Последовательность функций Д,, сходится равномерно на ка-
каждом компактном подмножестве области D, ибо на каждом
таком подмножестве для всех достаточно больших ц и всех
р>0
р р
<
Обозначим f{z)= lim /„(г); по теореме Вейерштрасса
и так как f = fo + (fi-fo) + (f2-fi)+ • ••> то
A-1 Ц=1
III. По построению полиэдры IIV определяются функциями
из классов #(IIV+I), и поэтому они выпуклы относительно этих
классов (см. пример 2 на стр. 367). Мы покажем, что они вы-
выпуклы и относительно класса Н (D). Это на основании II сле-
следует из такого факта: если область G является /"-выпуклой и
класс F' плотен в F, то G является и /"'-выпуклой.
В самом деле, пусть K<^G; в силу /^-выпуклости области G
для любой точки z°^G\Kf существует функция f^-F такая,
чт0 ll/lbr<lf(z°)|. Но тогда найдется б>0 такое, что и
||Л1„ + 6<|/(г°)|. (8)
Так как класс F' плотен в F, то существует функция fi e Fr
такая, что
Iff ~f
Отсюда, пользуясь неравенством (8), мы получим, что
Это означает, что z^^Kf1', таким образом, G\Kf^G\Kf',
т. е. K,f'^G и область G является /"'-выпуклой.
IV. Теперь уже нетрудно доказать, что область D выпукла
относительно класса H{D) = H и, следовательно, является об-
областью голоморфности. Пусть это не так; тогда найдется мно-
множество %<ШО, р(К, dD) = 2rQ>0 и последовательность точек
z^-^D, сходящаяся к точке ?е<3?>, таких, что для всех /eff
376 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
Рассмотрим го-раздутие К(Га) множества К> имеем к}г<>) Ш D
и по уточненной теореме об одновременном продолжении (тео-
(теорема 5 предыдущего пункта) для любой fe# .
ll/IW,ro)<Ufll«w. (9)
Но /С(го) <ш П^ для всех ц., начиная с некоторого а0, и, в силу
выпуклости Пц относительно класса Я, для любой точки
2°едП^\К,(п) найдется функция foe# такая, что \fQ{z°)\>
>\\к\\к(Ы-
Так как lim П =D, то для достаточно больших ц пе-
ресечение dtl^ (] U (?,, г0) непусто и z°e?/(?, r0), а значит,
и U (г*, г0). Поэтому последнее неравенство противоречит (9) >
Для формулировки последней теоремы этого пункта введем
важное
Определение. Отображение qr. D-*¦ D* называется биго-
ломорфным отображением области ?)c:C\ если оно взаимно
однозначно и все компоненты qpv этого отображения (qp =
= (ц>и ..., ф„)) голоморфны в D, а все компоненты ijjv обрат-
обратного отображения ф = (о];1, ..., -ф„) голоморфны1) в D*.
Биголоморфные отображения мы будем называть также
голоморфными изоморфизмами или, короче, голоморфизмами.
Они являются обобщением на пространственный случай кон-
конформных отображений.
Теорема 3. Свойство области быть областью голоморф-
голоморфности инвариантно относительно голоморфизмов. Иными сло-
словами, если D cz С" — область голоморфности и D* — ее образ
при биголоморфном отображении qp, то D* также является
областью голоморфности.
< Пусть К* <Ш D*, тогда в силу гомеоморфности qp и мно-
множество К = у'1 (К*) <Ш D, а так как D — область голоморфности,
то Kikd) <^D.
Легко видеть, что
у(Кнш))=>К*н(о*)- (Ю)
В самом деле, если некоторая точка w° e D* \ qp (Кн (d))> то
2° = qp (ш°) е D \ К и найдется функция f<^H{D) такая, что
') Мы увидим в дальнейшем (см. п. 44), что эти условия не являются
независимыми: из взаимной однозначности и голоморфности <р голоморф-
голоморфность ф-' вытекает.
§ 8] ПСЕВДОВЫПУКЛОСТЬ 377
I f (z°) | >Ц / \\к; обозначим g{w) = f ° cp~l(w); очевидно, g e H (?>*)
и \g(w°)\>\\g\\K*, а это означает, что ш'ей'Х^^.
Из Kh(d)^D заключаем, что <р(/(Я(д))<Ш?)*, и по A0)
K*h{d*)<^D*. Таким образом, D* голоморфно выпукла и, следо-
следовательно, является областью голоморфности >
§ 8. Псевдовыпуклость
Здесь мы познакомимся с другой трактовкой понятия голо-
голоморфной выпуклости, которая имеет два существенных до-
достоинства: во-первых, это понятие можно сформулировать ло-
локально (и в таком виде оно легче проверяется), и, во-вторых,
оно естественно выражается, формулируется в геометрических
терминах.
23. Принцип непрерывности. Начнем еще с одной теоремы
о принудительном аналитическом продолжении. Для ее форму-
формулировки условимся о некоторых терминах.
Определение. Будем называть комплексно г-мерной
аналитической поверхностью в области Ас:С(?) ее образ S
при взаимно однозначном голоморфном отображении qp: A —>
-*• С"(л>г), определяемом функциями
Zv = «Pv(?l. •••> tr), V= 1, ..., П, A)
если ранг матрицы Якоби \-г~] всюду в А равен г.
Комплексно одномерные аналитические поверхности назы-
называют также аналитическими кривыми (если, в частности, все
tpv линейны: <р = а + а>?, то мы получаем аналитическую прямую,
см. гл. I).
Аналитическая поверхность является, очевидно, связным
комплексно аналитическим многообразием. Для функций, голо-
голоморфных на аналитических поверхностях, конечно, справедливы
теорема единственности и принцип максимума, доказанные
в п. 9.
Будем называть (комплексно) m-мерную аналитическую по-'
верхность ScC" компактной, если она является компактным
подмножеством другой m-мерной аналитической поверхности S'.
Для компактных аналитических поверхностей 5 принцип ма-
максимума модуля можно, очевидно, сформулировать так: для
любой функции f, голоморфной на 5 и непрерывной на замы-
замыкании S,
') Напомним, что ||flle= sup | f (г)
2<5
378
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. НГ
Далее, назовем последовательность множеств Mv сходящейся
к множеству М (обозначение: Мч-^-М), если для любого е>0
найдется номер v0 такой, что при всех
Mv С М{> И М <
B)
Ие)
тде через Мт и Mv обозначены е-раздутия соответствующих
множеств (т. е. объединения всех поликругов U(z,_s) с цент-
центрами в точках множеств).
Теорема (Бенке — Зоммер). Пусть Sv — последователь-
последовательность компактных пг-мерных аналитических поверхностей,
принадлежащих вместе с границами dSv области D с: С".
Если Sv сходится к некоторому множе-
ству
F
S, a dSv — K множеству Г и
(рис. 103), то любая функция
/еЯ(D) голоморфно продолжается в
некоторую окрестность множества S.
¦4 Так как ГшО, то существует об-
область GmD такая, что Т<шв; обозна-
обозначим p(G, dD) = r. В силу сходимости
dSy-^T найдется такое v0, что при
Рис. 103.
Для любой' fe H (D) и любой точки
максимума модуля имеем
C)
по принципу
а отсюда в силу C) при v^v0 получаем
\f(z)K\\fh.
Но это означает, что z, а следовательно и вся поверх-
поверхность Sv при v^v0, принадлежит выпуклой оболочке Ghw)-
По теореме об одновременном продолжении (п. 21) отсюда
следует, что любая функция f^H(D) голоморфно продолжается
в r-раздутие Sv всех поверхностей Sv с номерами v^v0.
Наконец, в силу сходимости Sv->S найдется такое v,
что ScSv при всех v^vu и, следовательно, любая f e
голоморфно продолжается в -j-раздутие множества S >
Замечание. Как видно из доказательства, в теореме
Бенке—Зоммера класс H{D) можно заменить классом функ-
§ 8]
ПСЕВДОВЫПУКЛОСТЬ
379*
ций, голоморфных лишь в пересечении D с некоторой окрест-
окрестностью предельного множества S U Г.
Теорему Бенке — Зоммера называют принципом непрерыв-
непрерывности 1). Описательно говоря, она состоит в том, что свойство
функций быть голоморфной в окрестности аналитических по-
поверхностей Sv сохраняется и для предельного множества 5
этих поверхностей.
В качестве примера применения принципа непрерывности
приведем доказательство одной леммы, которая понадобится
нам в следующем параграфе при
изучении продолжения функций, го-
голоморфных в трубчатых областях.
Лемма. Пусть xQ, x1, х2 — три
точки пространства R"(x), не ле-
лежащие на одной прямой, 1{ = [х°, х1]
и /2 = [х°, х2] — замкнутые отрезки,
а Д = х°х1х2 — замкнутый треуголь- х
ник. Если функция f голо-
голоморфна в окрестности множества "
Ui Ш2) X R" {у), то она голоморфно
продолжается в окрестность мно-
множества AxR"(#).
Иными словами, всякая функ-
функция f, голоморфная в окрестности
объединения двух граней трехгранной призмы (рис. 104), непре-
непременно продолжается голоморфно в окрестность всей призмы.
-* Без ограничения общности можно считать, что х°- =
= @, 0,..., 0), ^ = A, 1, 0,..., 0), х2 = (-1, 1, 0,..., 0), ибо
этого можно достичь линейным преобразованием пространства
C"(z) с действительными коэффициентами2). Достаточно дока-
доказать, что f голоморфно продолжается в любую точку а мно-
множества уИ = Л X R" (г/). Можно считать, что а лежит в пересе-
пересечении М с действительным подпространством {у = 0}, т. е.
в треугольнике Л (этого можно достичь сдвигом на вектор
с чисто мнимыми координатами).
Итак, нужно доказать, что / продолжается голоморфно
в любую точку а = {аи а2, 0, ..., 0), где аь а2 — действитель-
действительные числа, удовлетворяющие условию |ail<a2^l (при нашем
Рис. 104.
') Частный случай теоремы Бенке — Зоммера, когда Sv являются замкну-
замкнутыми подмножествами аналитических прямых 'z = 'av и S —таким же под-
подмножеством прямой 'z = 'a= lim 'av, был доказан еще Хартогсом и назы-
V->oo
вается теоремой Хартогса о непрерывности.
2) Такое преобразование переводит R" (х) в себя и не нарушает ни
условий, ни утверждения леммы.
380
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. III
расположении осей это условие того, что a s Д \ (/, (J/2); при
aeliU'2 голоморфность f уже предположена). Для доказа-
доказательства проведем через точки х1, а и х2 параболу
¦р D)
= 1 — а; при а2 = 1 пара-
х2 = ах\
для этого надо взять a =
I-af
бола выродится в прямую х2=\\ и для любого Я,
рассмотрим аналитическую кривую
z3 =
E)
Переменное 2, мы рассматриваем как параметр на S^.
Чтобы доказать компактность 5Х, достаточно показать, что при
zeSji значения г, меняются
в ограниченной области пло-
плоскости г,. Но проекция Sk на
плоскость zx определяется усло-
условием (Re z,, Re г2> 0, ..., 0)еЛ,
которое записывается в виде
X,
и выделяет ограниченную об-
область, заключенную между ги-
гиперболами
(заштрихована на рис. 105). Заметим еще, что аналитические
кривые 5^ при 0<А^5$ пересекают Rn(x) по принадлежа-
принадлежащему А отрезку параболы
х2 =¦ <хх\ + К G)
параллельной параболе D) (изображена пунктиром на рис. 104).
Обозначим
^ = {As@, jj]: f голоморфно продолжается в окрестность SjJ;
это, очевидно, открытое множество. Оно непусто, ибо при до-
достаточно малых Я>0 область F) изменения zlt как видно аз
рис. 185, лежит в сколь угодно малой окрестности точки z, = 0
и, следовательно, SK — в сколь угодно малой окрестности точки
z = 0, где / по условию голоморфна. Но множество ^ в то же
время и замкнуто. В самом деле, если Я0&@, р] — предельная
точка ^, то существует последовательность Si -*Si0, Я„е^;
§ 8] ПСЕВДОВЫПУКЛОСТЬ 381
при этом dSln~+dSlo и / голоморфна в окрестности всех Sk
и dSi0 (заметим, что dSx при любом Ае@, р] принадлежит
множеству {lx U^) X Rn(y), где f голоморфна по условию). Мы
можем, следовательно, применить принцип непрерывности (см.
замечание после его доказательства) и заключить, что Аое<^.
Таким образом, g3 з @, р], и, значит, f голоморфно продол-
продолжается в окрестность 5„, но 5„ содержит точку а >
24. Выпуклость в смысле Леви. Принцип непрерывности
гарантирует возможность голоморфного продолжения функции
из области D в окрестность множества S, которое можно при-
приблизить поверхностями SvczD. Так как 5 можно считать рас-
расположенным в окрестности какой-либо граничной точки D,
то этот принцип имеет локальный характер.
Естественно ввести на область условие локальной непро-
непродолжаемости некоторых голоморфных функций как условие
несуществования последовательности поверхностей, к ко-
которым был бы применим принцип непрерывности. Сформули-
Сформулируем это в следующем виде:
Определение. Область DcC называется выпуклой
в смысле Леви (короче, L-выпуклой) в граничной точке ?, если,
какова бы ни была поверхность S, содержащая ? и такая,
что dSczD, то для любой последовательности компактных
аналитических поверхностей Sv:
SV->S, dSv-+dS, A)
найдется номер v0, начиная с которого все Sv содержат точки,
не принадлежащие D. Область D называется L-выпуклой, если
он^ L-выпукла в каждой своей граничной точке.
Из принципа непрерывности непосредственно вытекает
Теорема 1. Каждая область голоморфности является
L-выпуклой.
¦4 Если D не является L-выпуклой в какой-либо точке
? е 3D, то найдется поверхность S такая, что JeS, dS cz D,
и последовательность компактных аналитических поверхностей
SvczD, 5v->5, dSv->dS; тогда любая f^H(D) голоморфно
продолжается в точку ?, и D не может быть областью голо-
голоморфности >
Этот результат можно сформулировать и локально. Назовем
область D не расширяемой голоморфно в граничной точке ?,
если существует окрестность U$ этой точки и функция f, голо-
голоморфная на открытом множестве U^(]D и не продолжаемая
голоморфно в точку ?.
Теорема 1, очевидно, допускает такой локальный вариант:
Теорема 1'. Если область D не расширяема голоморфно
в точке ? е 3D, то она является L-выпуклой в этой точке.
382 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
Ясно, что любая область голоморфности не расширяема
голоморфно ни в одной точке 3D. Еще в 1911 г. Э. Леви по-
поставил обратную задачу:
Проблема Леви. Является ли область D, не расширяе-
расширяемая голоморфно ни в одной точке границы, областью голо-
голоморфности?
Главная трудность в этой проблеме состоит в переходе
от локального свойства к глобальному. Если D не расширяема
голоморфно в точке ? е dD, то существует локальный барьер —
функция fi{z), голоморфная в U%, П D и не продолжаемая
голоморфно в точку ?. Но как из таких локальных барьеров
построить глобальный барьер, т. е. функцию, голоморфную
во всей области D и не продолжаемую в ?? Эта труд-
трудность была преодолена лишь в 1954 г. К. Ока, который дока-
доказал, что проблема Леви решается положительно для любой
области D с: С".
При помощи теоремы Ока в п. 39 будет доказано, что
условие Z.-выпуклости области D является и достаточным для
голоморфной нерасширяемости, так что эти условия экви-
эквивалентны.
Выпуклость в смысле Леви, в отличие от голоморфной
выпуклости, является локальным свойством границы области,
и поэтому естественно ожидать, что она
легче проверяется. Мы приведем здесь
.. „I несколько критериев. Начнем с простого
' достаточного условия.
Теорема 2. Если области D в не-
некоторой граничной точке ? можно кос-
коснуться извне аналитическим множеством
S={2€=C": f{z) = O}, где f-функция,
рис 105. голоморфная в точке ?, то D является
L-выпуклой в точке ? (рис. 106).
¦4 Условие теоремы означает, что существует функция /,
голоморфная в окрестности f/j точки ?, равная нулю в этой
точке и отличная от нуля в Ut, Л D. Но тогда функция g — -f
голоморфна в U^ftD и не продолжается голоморфно в точку ?.
Таким образом, D не расширяема голоморфно в точке ? и
по теореме Г является L-выпуклой в этой точке >
Отметим, что этот признак обобщает известный признак
обычной (геометрической) выпуклости области. Если вместо
аналитического множества {/ = 0} мы будем рассматривать
опорную гиперплоскость \ 2 av*v ~ Р = 0 (» то получим (необхо-
§ 81 ПСЕВДОВЫПУКЛОСТЬ 383
димый и достаточный) признак выпуклости области в гранич-
граничной точке ?.
Следующий критерий применим к областям с достаточно
гладкой границей. Предположим, что в окрестности Ui неко-
некоторой граничной точки ? область D задается условием
Dnt/c = {z6=?/t: ф(г)<0}, B)
где ф е С2 (f/g) — действительная функция. Предположим еще,
что в точке ?
отличен от нуля.
Тейлоровское разложение ф в точке ? имеет вид
где
±H(z, z) + o(\ z -? |2), D)
v=l M-, v=l
H {z, Z) =
дг„ dzv
, V=l
(все производные берутся в точке ?, свободный член ф(?) = 0,
и о{\ ? — z |2) обозначает малую выше второго порядка при z—>-?).
Для получения D) достаточно написать обычное тейлоровское
разложение по переменным zu zx, ..., zn, zn и заметить, что
так как функция ф действительна, то —— = (——), —т~(—т
dzy \dzv) д% \dzl
поэтому группы членов разложения по переменным zv ком-
комплексно сопряжены соответствующим группам по г, и в сумме
дают удвоенные действительные части (это замечание относится
к первому и второму слагаемым формулы).
Заметим еще, что уравнение
v=l
определяет аналитическую касательную плоскость к поверх-
поверхности {ф = 0} в точке ? (она не вырождена в силу условия
^0). Форма
ц, v=l
384 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
п
„ , d2q> ( d2<f \
является эрмитовой, ибо -%—^=-= -д—з^~ Для всех u. v
oz^ ozv \ azv az^ i
= 1, ..., n в силу того, что <р — действительная функция.
Теорема 3 (Л е в и — К ш о с к а). Пусть область D с: С
в окрестности точки ? е 3D задается условием B), где <реС2
и grad ф |? =9^ 0. Если D является L-выпуклой в точке ?,, то
сужение эрмитовой формы F) на касательную аналитическую
плоскость {L = 0} неотрицательно:
Н(г, 2)lL_o>O. G)
Обратно, если это сужение положительно:
Н(г, z)|L_0>0 (8)
для всех г=?^С. то D является L-выпуклой в точке ?.
¦4 Для упрощения формальных выкладок ограничимся слу-
случаем п = 2 и положим ? = 0. Совершим невырожденное аффин-
аффинное преобразование переменных
azx + bz2->zu 2L(z)->z2,
которое переводит касательную аналитическую плоскость {L = 0}
в плоскость {г2 = 0}. После этого разложение Тейлора D) при-
примет вид
H(z г) + о(|г|2), (9)
где
К (z) = anz\ + 2anzxz2 + a22z\,
J-I [ <y "Л _- fi _^ ~) I f* _-y Zy I /7__ 'У у .. [.. rt _>y >p '
' 11 I 1 1-й I Z 1Z J л ?,?. Z L
(для простоты письма мы полагаем
dzv
dzv
Сужение формы Н на касательную аналитическую плоскость
{z2=0} теперь записывается совсем просто:
а) Достаточное условие. Из (8) следует, что а,у>0.
Возьмем функцию f{z) — z2+ auz2t и рассмотрим аналитическую
поверхность S = {2eC2; /(г) = 0}. На ней z2= — anz], к, ведя
§8]
ПСЕВДОВЫПУКЛОСТЬ
385
подсчет с точностью до малых второго порядка, мы найдем,
что сужение
o(|z|2) =
A2)
Отсюда видно, что qp |s ^ 0 в некоторой окрестности точки
? = О, т. е. что 5 в пределах этой окрестности лежит вне D.
По теореме 2 отсюда сл'едует, что D является /--выпуклой
в точке ? = 0.
б) Необходимое условие. Пусть, от противного,
D является /.-выпуклой в точке ? = 0, а а,у < 0. Из A2) видно, что
поверхность S0=lzeC2: z2— — с
\<r]
аналитическая
при достаточно малых г вся, кроме точки ? = 0, лежит в об-
области D. Из соображений непрерывности ясно, что компакт-
компактные аналитические поверхности
при всех достаточно малых А>0 принадлежат D и что Sx-+SOf
dSi->dS0 при Я —>0. Но это противоречит L-выпуклости D
в точке ? = 0 >
Для случая п — 2 существует еще более эффективный кри-
критерий. Назовем определителем Леей
(Ф) = ~
0
д<р
57
дг,
дг2
A3)
тогда имеет место
Теорема 4. Пусть область ОсС2 в окрестности точки
t,^dD задается условием B), где <р е С2 « gradoplj^O. ?сл«
D является L-выпуклой в точке ?, то в этой точке J?(<p)^O.
Если J?(<p)>0 в точке ?, то область L-выпукла в этой точке.
¦4 Заметим, что в частном случае L(z) = ~k-, к которому
общий приводится невырожденным аффинным преобразованием
25 Б. В. Шабат
386
(как
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
в предыдущей теореме),
-2ЧФ)=-
0
0
1
1
имеем
0
а-п
Ч\
1
2
а-12
1
= Т ап>
[ГЛ. 1ГГ
и теорема сводится к предыдущей. Для доказательства в общем
случае достаточно заметить, что при биголоморфном отображе-
отображении Z-+Z определитель Леви преобразуется по следующему
закону:
(Н)
где ФB) = ф(г) (тождество A4) проверяется прямой выклад-
выкладкой) >
Примеры.
1. Пусть основание В трубчатой области D = B X &г (у) из С2 ограни-
чено кривой <р = х2— Ч1 (xi
сляем определитель Леви:
Заменяя х2 =
¦, вычи-
2
О
О
Отсюда видно, что L-выпуклость таких областей сводится к обычной
выпуклости.
2. Для областей Рейнхарта из С2 с границей ф = 1з2| — ч|>( |2TiJ)=-0
d2 In ф
(ф) - -
16/f (dinЛ!
(мы положили Г] = 1 z\ |). L-выпуклость таких областей сводится, следова-
следовательно, к логарифмической выпуклости, так как ф = | z2 | ^ 0.
3. Для областей Хартогса из С2 с границей ср= | z21 — ф {г{) = 0
?? (ф) - - -J- Д In ф,
где Л —оператор Лапласа. Условие L-выпуклости сводится к субгармонич-
субгармоничности функции — In ф (см. задачу к гл. V ч. I).
25. Плюрисубгармонические функции. Как видно из послед-
последнего примера, L-выпуклость областей Хартогса из С2 сводится
к субгармоничности функций, их определяющих. Оказывается,
$ 8] ПСЕВДОВЫПУКЛОСТЬ * 387
что, вообще, существует глубокая связь L-выпуклости областей
при п = 2 с субгармоническими, а при л>2 с их обобщениями,
так называемыми плюрисубгармоническими функциями. При-
Приведем их определение и простейшие свойства.
Определение 1. Действительная функция ф, — оо^ф<оо,
определенная в окрестности точки 2°еС/}, называется полу-
полунепрерывной сверху в этой точке, если для любого е > 0 най-
найдется б > 0 такое, что
f ф(г) —фB°)<е, если фB0)=^= — оо,
|2-2°|<б=ф! ,ч^1 /оч A)
\ фB)<-—, если фB°) = — оо,
или, иначе, если
firn q>(z)<q>(z°). B)
Функция ф называется полунепрерывной сверху в области,
D с: С", если она полунепрерывна сверху в каждой точке
2°е?) (для этого необходимо и достаточно, чтобы для любого
ае(-оо, оо) множество меньших значений (геО: ф(г)<а}
было рткрытым).
Полунепрерывные функции со стороны больших значений
ведут себя как непрерывные. В частности, на компактах К <s D
такие функции ограничены сверху и достигают своих наиболь-
наибольших значений (ограниченность снизу и достижение наименьших
значений не обязательны).
Совершенно аналогично вводятся полунепрерывные снизу
функции, которые ведут себя как непрерывные, так сказать,
со стороны меньших значений.
Определение 2. Функция ф: D-*-[—оо, оо) называется
плюрисубгармонической в области ОсС", если: 1) она полу-
полунепрерывна сверху в D и 2) для любой точки гоеВ и для
любой аналитической прямой 2 = / (?) = г° + <»?, где шеСп,
geC, сужение ф на эту прямую, т. е. функция ф°/(?), является
субгармонической на открытом множестве {? е С: I (Q е ?)}.
Плюрисубгармонические функции связаны с голоморфными
функциями нескольких переменных так же, как субгармониче-
субгармонические с функциями одного переменного: для любой функции /,
голоморфной в области D с: С", функция
1 = In |f B)| C)
является плюрисубгармонической в этой области. В самом деле,
Ф очевидно полунепрерывна сверху в D, а так как сужение f
на любую аналитическую прямую z = l{?) является голоморфной
функцией от ?, то сужение ф на эту прямую ф ° / (?) = In | / о / (g) | —
25*
388 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
субгармоническая функция. В частности, если /#0 в D, то
функция C) плюригармонична.
Из определения видно, что свойства плюрисубгармонических
функций просто сводятся к свойствам функций субгармониче-
субгармонических. В частности, из теорем, доказанных в п. 46 ч. I, непо-
непосредственно получаются следующие утверждения:
1°. Если плюрисубгармоническая в области D функция <р
достигает локального максимума в некоторой точке 2°еЬ, то
она постоянна в D.
2°. Функция, плюрисубгармоническая в некоторой окрест-
окрестности каждой точки, 2°е?), является плюрисубгармонической
в области D.
3°. Если верхняя огибающая
ф(г)= sup<pa(z)
д
семейства функций <ра, ие/1, плюрисубгармонических в об-
области D, полунепрерывна сверху в D, то она является плюри-
плюрисубгармонической в этой области.
4°. Для того чтобы функция ф, полунепрерывная сверху,
была плюрисубгармонической в области D, необходимо и
достаточно существование для каждой точки геО и каждого
вектора соеС" такого числа ro = ro(z, <o), что
2Я
' Ф (*) <-?г/фB+ «»¦*")<« D)
для всех г<г0 (критерий плюрисубгармоничности).
Для функций класса С2 можно дать более легко проверяемый
критерий. Вспомним, что для субгармоничности функции и(?),
принадлежащей классу С2 в окрестности точки ?0 е С, необхо-
необходимо и достаточно, чтобы в этой окрестности был неотрица-
неотрицателен ее оператор Лапласа:
д л д2и
(см. задачу 12 к гл. V ч. I). Пользуясь правилом дифференци-
дифференцирования сложной функции, мы найдем, что для сужения функ-
функции феС2(В), DcC", на аналитическую прямую z = /(?) =
= z°+ <?>?,, т. е. для сложной функции и (?) = ф ° / (?)
д2и __ Y
ц. v=l
§ 8] ПСЕВДОВЫПУКЛОСТЬ 389
Отсюда получается такой критерий:
Теорема 1. Для плюрисубгармоничности функции ф,
принадлежащей классу С2 в некоторой области D сС", необхо-
необходимо и достаточно, чтобы в каждой точке г° е D для любого
вектора щеС выполнялось неравенство
= 2
(i, V=l
E)
где производные берутся в точке z°.
Заметим, что эрмитова форма Я (ш, ш) — это та самая форма,
которая участвует в теореме Леви —Кшоски из предыдущего
пункта. Назовем еще функцию ф?С2 строго плюрисубгармо-
нической в точке z° e С", если в некоторой окрестности этой
точки gradqp=^=O и Я (со, с5)>0 для всех <о Ф 0. Тогда мы
будем иметь следующий результат, указывающий связь плюри-
субгармонических функций с выпуклостью в смысле Леви:
Теорема 2. Пусть область ОсС в некоторой окрест-
окрестности C/g точки ? е dD задается условием
ф — строго плюрисубгарионическая в f/g функция. Тогда
D выпукла в смысле Леви в точке ?.
•* Утверждение сразу получается из теоремы Леви — Кшоски,
если заметить, что для строго плюрисубгармонической функции
сужение формы Я (со, <в) на касательную аналитическую пло-
плоскость
^-SIH^-W-o F)
v=l
положительно1) для всех z ф t, >
Перейдем к дальнейшему изучению свойств плюрисубгармо-
нических функций. Умножая обе части неравенства D) на эле-
элемент площади сферы {|<о|=1} и интегрируя по этой сфере,
мы найдем
<p(z)a(l)<-L- J dt J <p{z + (i>relt)do= J Ф(z + шг)dor, G)
0 { !} {|| }
') Чтобы получить такое сужение, надо в выражение Я подставить
= zv — ?Vl считая, что эти величины связаны уравнением F).
390 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
где сгA) = ,_ щ—площадь поверхности сферы (внутренний
интеграл не зависит от t). Простой заменой переменного мы
получим отсюда, что для всех достаточно малых г
J
|
(8)
где а (г) = а A) г2" — площадь сферы радиуса г.
Отсюда точно так же, как в плоском случае (см. п. 46 ч. I),
выводится, что любая плюрисубгармоническая функция в об-
области D с: С" является субгармонической функцией 2п дейст-
действительных переменных. Это означает, что для всех точек
геО и всех достаточно малых г, для любой функции h,
гармонической1) в шаре В = {?еС": |g — z| < г} и непрерыв-
непрерывной в В,
Теорема 3. Среднее значение
{|?-z|=r}
плюрисубгармонической в окрестности точки геС" функ-
функции ф является возрастающей функцией от г.
< Согласно G)
2л
5(г)стA)= J <foJL J
{|й>1 = 1} 0
следовательно, достаточно доказать возрастание среднего зна-
значения субгармонической в окрестности точки ? = 0 функции
и (?) •= ф (z + (at,), т. е. величины
2л
Пусть r2>rx и h(?) — наилучшая гармоническая мажоранта
функции и в круге {|?|<г2} (см. п. 46 ч. I). По свойствам.
') Напомним, что гармонической в шаре ?<=С называется функция
А: В->R класса С2, которая в каждой точке ze? удовлетворяет уравне-
2
нию Лапласа ДА = /, —5"= 0-
V-l *V
§ 8] ПСЕВДОВЫПУКЛОСТЬ х 391
субгармонических и гармонических функций имеем тогда
5 (') <
Теперь докажем, что произвольную плюрисубгармоническую
функцию можно аппроксимировать такими же, но бесконечно
дифференцируемыми функциями.
Теорема 4. Для любой функции ф, плюрисубгармони-
ческой в области D cz Cre, можно построить возрастающую по-
последовательность открытых множеств G^ (ц=1, 2, ...),
оо
(jGn = D, w убывающую последовательность функций ср^е
еС^Сбц), плюрисубгармонических в G^, сходящуюся к ф
в каждой точке ге D:
-^ Если ф^ —оо, то в качестве фд можно взять последова-
последовательность фцB)^—(х. В общем случае последовательность фц
строится при помощи усреднений. Возьмем функцию
км-\се Нг12> W<1- do)
I 0, |z|>l,
выбрав постоянную с так, чтобы интеграл от К по всему про-
пространству С" равнялся 1 (фактически интеграл по шару
{|?|<1}, ибо вне шара К = 0). Эту функцию мы используем
в качестве усредняющего ядра, положив
(П)
где dV — элемент 2/г-мерного объема и интеграл берется по
всему С" (фактически по единичному шару). Ясно, что каждая
функция фй определена в —-сжатии области D, т. е. открытом
множестве
): e{z, dD)> —
где е —евклидово расстояние. Ясно также, что G^czG^i для
оо
любого fi и что (J 6^ = 0.
U-1
392 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ПГ
После замены переменных z + ——>•? интеграл A1) примет вид
из которого ясно, что фн е С°° (G^) (в самом деле, подинте-
гральная функция, а следовательно, и интеграл зависят от z
бесконечно дифференцируемым образом). Пользуясь критерием,
который выражается неравенством D), легко установить плюри-
субгармоничность функций фц: для всех z е G^, asC и всех
достаточно малых г
2Л I 2Я ¦)
-L J ФA (z + <brelt)dt = J /С (?) ^- J ф (г + -i- + core") d/} dF >
о I о J
(мы использовали плюрисубгармоничность ф и неотрицатель-
неотрицательность ядра К).
Заменяя dV = dardr, где dar — элемент поверхности сферы
{|?| = г}, а затем делая замену переменных z + — —.>?, мы пре-
преобразуем A1) к виду
Г Г
О {IU=r}
1
= J^(r)dr[i2«-! J
О (it- I-—) ** °
A2)
где sf —j — среднее значение функции ф на сфере j?: |? — г\=— >.
Теперь из теоремы 3 видно, что функции ф^ убывают с ростом ц.
В силу субгармоничности функции ф ее среднее значение
Si— ^ф(г), а так как
1 1
а A) J К (г) г2""'dr = J Kir)a(r)dr= j KdV = \,
то из A2) следует, что Ф^Ог)^ф(z) в любой точке z^D для
всех [л, начиная с некоторого. С другой стороны, в силу полу-
полунепрерывности функции ф для любого е>0 будет ф(?) — q>{z)<&
§ 8] ПСЕВДОВЫПУКЛОСТЬ 393
для всех ?, достаточно близких к г, т. е. 5(— )<ф(;г) + е для
всех (г, начиная с некоторого, и для таких ц из A2) мы по-
получим, что фц(z) < ф(z) + е. Таким образом, для всех zgD
lim ф„ (z) = ф (z) >
Замечание. Предел убывающей последовательности суб-
субгармонических функций является функцией субгармонической
(см. задачу 14 к гл. V ч. I), и это утверждение сразу пере-
переносится на плюрисубгармонические функции. Поэтому теорему
4 можно обратить.
В определении плюрисубгармонической функции требуется,
чтобы ее сужения на аналитические прямые были функциями
субгармоническими. Это свойство допускает следующее усиление:
Теорема 5. Сужение функции ф, плюрисубгармонической
в области D с: С, на любую комплексно пг-мерную аналити-
аналитическую поверхность z = f(?) = {fj (?),..., fn(?)} также является
плюрисубгармонической функцией на открытом множестве
Q {Cm f(?)D}
•«Для простоты формальных выкладок ограничимся случаем
пг — \, т. е. покажем, что сужение ф на аналитическую кривую
z = f(t,) является субгармонической функцией.
Пусть сначала феС2(О). Тогда для и(?) = <р°/(?) по пра-
правилу дифференцирования сложных функций в любой точке
у <Э2Ф 0/ц / dfy \
I
dt,di
И, v=I
Так как ф плюрисубгармонична, то по теореме 1 форма в пра-
правой части неотрицательна, а это и означает, что и (?) — суб-
субгармоническая функция.
Общий случай сводится к рассмотренному при помощи
теоремы 4 и замечания вслед за ней >
Следствие. Для сужения на аналитическую поверх-
поверхность S функции ф, плюрисубгармонической в окрестности S,
справедлив принцип максимума.
В частности, для компактной аналитической поверхности 5
(см. п. 23) этот принцип можно сформулировать так:
IIФ Us = 11 «Piles-
В заключение проведем сравнение понятий плюрисубгармо-
ничности и выпуклости функций нескольких (действительных)
переменных. Мы уже отмечали (в п. 46 ч. I), что субгармони-
394
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. III
ческие функции являются плоским аналогом выпуклых функ-
функций одного переменного. Последние можно определить так:
функция /: [a, &]->R' называется выпуклой (вниз) на отрезке
[a, b] cz R1, если для любых двух точек х', х" е [а, Ь] и
любого t <= @, 1.)
f{txf + (l-t)x"}*?tf(xf) + (l-t)f(x"). A4)
Чтобы подчеркнуть аналогию с субгармоническими функ-
функциями, обозначим через x = txf+{\ — t)x" и через h{x) = tf{xf) +
+ A —t)f{x") — линейную функцию1), принимающую на концах
отрезка [xf, x"] те же значения, что и f (рис. 107). Тогда
условие выпуклости A4) примет вид:
f(x)^.h(x) для всех х е [хг, х"\.
Распространим понятие выпукло-
выпуклости на функции нескольких действи-
действительных переменных. Функция f: D -*• R1
называется выпуклой в области
DczRn, если ее сужение на любую пря-
прямую x = l(t) = x° + e>t, где х°, со е R",
является выпуклой функцией на откры-
открытом множестве Q = {/eR]: /(()eO},
Условием выпуклости дважды
гладкой функции f одного перемен-
переменного t является, очевидно, неравенство fify^O для всех
t^[a, b]. По правилу дифференцирования сложных функций
отсюда получается условие выпуклости функции нескольких
переменных feC2(fl): квадратичная форма
Vov, A5)
(i, V=l
где производные берутся в точке х°, неотрицательна для всех
х° е D и всех со е R".
Таким образом, плюрисубгармоничность является, так ска-
сказать, комплексным аналогом выпуклости. Иными словами, плю-
рисубгармонические функции получаются из выпуклых заменой
действительной структуры комплексной: вместо сужений на
действительные (одномерные) прямые x = t(t) надо рассматривать
сужения на аналитические (двумерные) прямые z = / (?) и вместо
выпуклых функций от t — субгармонические функции от ?. Для
функций класса С2 такой переход состоит в замене квадра-
квадратичной формы A5) эрмитовой формой E).
Рис. 107.
') Функция й является наилучшей линейной мажорантой функции / на
концах отрезка [х', х"] — аналогом наилучшей гармонической мажоранты
б ( 46 I)
р [, ] у
функции на границе области (ср. п. 46 ч. I).
§ 8] ПСЕВДОВЫПУКЛОСТЬ 395
26. Псевдовыпуклые области. Выпуклыми называются такие
области D с: R", которые вместе с любыми точками х' и х"
содержат также и все точки х = tx'-\-{\ — t)x", где t e @, 1).
Существует и эквивалентное1) определение: область D cr R"
называется выпуклой, если функция — \пе(х, dD), где е(х, dD) —
евклидово расстояние точки х до границы области, является
выпуклой в D.
Мы придем к понятию псевдовыпуклой области, если вместо
действительной структуры будем рассматривать комплексную:
Определение. Область D с:С1 называется псевдовы-
псевдовыпуклой, если функция
q>(z)~-lne(z, 3D), A)
где e{z, dD) — евклидово расстояние точки z до границы dD,
плюрисубгармонична в D.
Заметим прежде всего, что на плоскости С любая область
псевдовыпукла. В самом деле, для D = С утверждение три-
тривиально (ибо здесь e(z, 0D) ^ оо). Для D = C\{?} утвержде-
утверждение проверяется простым подсчетом (здесь ^-lne(z, dD) =
= — ln\z — ?,\). Если же граница области состоит более чем из
одной точки, то функция
-lne(z, dD)= sup {_ln|z-S|}
6dO
и, следовательно, субгармонична, как верхняя огибающая суб-
субгармонических функций (см. теорему 4 п. 46 ч. I; в этой тео-
теореме предполагается, что верхняя огибающая полунепрерывна
сверху, но у нас e(z, dD) непрерывна, ибо в силу неравенства
треугольника она даже удовлетворяет условию Липшица, и
не обращается в нуль ни в одной точке z e D).
При п > 1, как мы скоро убедимся, не всякая область
псевдовыпукла: псевдовыпуклость оказывается эквивалентной
выпуклости в смысле Леви. Для доказательства установим
сначала важный вспомогательный результат.
Теорема 1. Для любого ряда Хартогса
/(z)=S ^('z)(z«-aX B)
?№е H{'D), функция qp= — In/?{'z), где R —радиус Хартогса2),
является плюрисубгармонической в области 'D.
1) Эквивалентность этого определения предыдущему следует из резуль-
результатов» которые будут установлены здесь и в п. 27.
2) Напомним, что R ('г) — что радиус сходимости степенного ряда при
фиксированной точке 'г е 'D.
396 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ill
¦«Без ограничения общности положим а„ = 0; кроме того,
для простоты письма будем опускать штрих в обозначении rz,
так что
а) Докажем, что функция R (z) полунепрерывна снизу в об-
области D. Предполагая противное, допустим, что в какой-либо
точке 2° <='D
R (z°) > lim R (г).
z->z-
Пусть сначала R(z°)< oo. Тогда для достаточно малого
е>0 существует последовательность точек zve'?) такая, что
zv-*z° и
R (zv) < R (z°) - е. C)
По определению радиуса Хартогса отсюда следует существо-
существование последовательности точек (zv, z"fy, \z^\ = R(zv), в каждую
из которых функция /, определяемая рядом B), не продол-
продолжается голоморфно. В силу C) последовательность \гЛ огра-
ограничена, и из нее можно выбрать подпоследовательность, схо-
сходящуюся к точке z°n, \z°n\<^R(zu)—e. Точка (z°, 2°) —предельная
для точек (zv, z^), в которые / не продолжается голоморфно,
следовательно, f не продолжается и в эту точку. Но по опре-
определению радиуса Хартогса / продолжается в любую точку
(г°, zn), для которой \zn\<R{z°). Противоречие доказывает
утверждение.
Случай R(z°) = оо приводится к противоречию аналогично.
б) Согласно а) функция ф = — In R {z) полунепрерывна сверху
в 'D. Поэтому остается доказать, что сужение этой функции
на любую аналитическую прямую z = l(t,) = z° + cog, где сое С",
2°е/?), является субгармонической функцией в окрестности
точки ? = 0. Пусть это не так, тогда существует такая анали-
аналитическая прямая z = /(?), что функция
-In*./(?) = «(?) D)
не субгармонична в окрестности ? = 0. Тогда существует круг
U = {\t\<r} и функция h, непрерывная в (/и гармоническая
в U, такая, что н(?)<;/*(?) на 0U, но в некоторой точке goet/
h (Co) - «(У •= inf {h (?) - и (?)} = - е < 0
и
(мы воспользовались тем, что полунепрерывная снизу функция
h — и достигает своей нижней грани на компакте).
§ 8] ПСЕВДОВЫПУКЛОСТЬ 397
Обозначим через #(?)/= — Л(?) — е функцию, гармоническую
в U и непрерывную в U; имеем
g{l)<-uft) на_д?/,
?(?)<-«(?) в С/, E)
По свойству радиуса Хартогса существует точка а„, |а„| =
= /?°/(?0), в которую функция B) при фиксированном z = /(g0)
не продолжается голоморфно. Построим голоморфную в U
функцию G ft) = g (?) + /g ft) так, чтобы G ft0) совпадало с ка-
каким-нибудь значением In а„ (это можно сделать, ибо у нас
gfto) = ln*°/fto) = ln|an|).
Теперь выберем круг U' = {\t,\ < г'} ш U так, чтобы на dV
было g{?)<— ы(?) (это можно сделать в силу E) и полуне-
полунепрерывности сверху функции g + и), и рассмотрим семейство
компактных в смысле п. 23 аналитических кривых
Sx = {(г, г„) еСл:г = 1 ft), zn =
Для любого Яе@, 1) кривая Sx<mD, где ?> = '?> X {|г„| < R(z)},
ибо для всех (z.zJeSj в силу E) имеем | znК Ке~и & —¦
= XRo l(t,) = XR(z). Далее, очевидно, что S^-^-S, и 55^-^-dS!
при К-> 1 и что dSl<^D, ибо на сШ' имеем строгое неравен-
неравенство #(?)<—«(?)> равносильное неравенству | zn\< e-u(^ = R(z).
Таким образом, применим принцип непрерывности п. 23,
по которому функция B) голоморфно продолжается на S{.
Но S] содержит точку (/(?о). ап), в которую, как мы видели,
эта функция непродолжаема.
Противоречие доказывает утверждение >
Связь доказанной теоремы с выпуклостью в смысле Леви
выясняется следующим образом. Для произвольной области
DczC1 назовем радиусом Хартогса в точке 2°eD радиус
R(z°) наибольшего круга с центром 2°, лежащего на пересече-
пересечении D с аналитической прямой /„ = {zeC": 'z = 'z°, zn — Z,}\
R(z°) = e(z°,dD(]tn). G)
Лемма. Для любой L-выпуклой области D cz Cn функция
Ф = — In R (z), где R (z) — радиус Хартогса D в точке z, плюри-
субгармонична в D.
<Для произвольной области D а Сп радиус Хартогса R (z)
полунепрерывен снизу, а функция ср— — lnR(z) полунепрерывна
сверху в D. В самом деле, пусть aeR1 и R (z°) > а; тогда
круг /С={геС": 'z — 'z°, \zn — z° | < а} ш D, и мы обозначим
г = р(дК, dD)~>0. Из рис. 108 ясно, что для любой точки
398
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
[ГЛ. ПГ
z e= U (z°, г) имеем R {z) > а. Таким образом, множество верх-
верхних значений {геД: R (г) > а} открыто для любого а е R1.
Остается доказать, что для L-выпуклых областей сужение
функции <$= — \nR{z) на любую аналитическую прямую
где 2°eD, сое С", является субгармонической функцией в ок-
окрестности точки t = 0. Если
/ш
ф
/0, т. е. 1а параллельна
оси zn, то мы имеем ситуацию плоского
случаяl): R(г)ш = inf \гп-г'\, и, еле-
г' s 3D П 'м
довательно, функция
— \nR{z)\t = sup {—In I z — z'l}
x * '*m _ J^_-l \ tl nil
Рис. 108.
субгармонична, как полунепрерывная свер-
сверху верхняя огибающая субгармонических
функций.
Если же 'со Ф '0, т. е. 1а не парал-
параллельна оси zn, то мы должны повторить
рассуждения, проведенные во второй части доказательства тео-
теоремы 1. Как и там, лредполагая, что функция — \nR{z)\la не
субгармонична, мы найдем точку а е dD, для которой
'а = rz° + '<о?0, | ап — z°n | = R (z° + <o?0), и построим семейство ком-
компактных аналитических кривых
где 'I (Z) = 'z° + 'cog, а остальные обозначения те же, что в F).
При 0<Я<1 кривые S^gfl, а при Я->1 они сходятся
к кривой 5Ь граница которой dS{ Ш D и которая содержит
точку а^дЬ (соответствующую значению параметра ? = ?о)-
Но это противоречит L-выпуклости области D>
Теорема 2. Любая выпуклая в смысле Леей область
D с: С" является псевдовыпуклой.
< Функция е (z, dD) всегда конечна (кроме тривиального
случая D = Cn) и непрерывна, ибо в силу неравенства тре-
треугольника она удовлетворяет условию Липшица. Так как она
положительна в D, то и функция — In e (z, dD) непрерывна
в D.
Рассмотрим всевозможные аналитические повороты
z-+z°+C(z-z°), (9)
') Ср. рассуждение перед теоремой 1 на стр. 395.
$ 8] ПСЕВДОВЫПУКЛОСТЬ 399
где С = (Сцч) — квадратная матрица п-то порядка, второй член
справа понимается как произведение матрицы С на вектор
z — z° и матрица такова, что евклидовы расстояния между
любыми двумя точками С" при отображении (9) сохраняются.
Таким поворотом направление любой аналитической прямой
|в = {геС: z = z° + со?} можно перевести в направление, парал-
параллельное оси zn. Обозначим через Ra{z°) величину радиуса
Хартогса области D, соответствующего направлению со:
Мы имеем, очевидно, для любого
е(г,
где нижняя грань берется по всем векторам сое С1, |ю|=Ь
Если область L-выпукла*), то по лемме для любого фиксиро-
фиксированного со функция —\nka,(z) плюрисубгармонична, и, сле-
следовательно, функция — lne{z, dD), как непрерывная верхняя
огибающая плюрисубгармонических функций, также плюри-
плюрисубгармонична в D>
Теорема 3. Любая псевдовыпуклая область D с С"
является выпуклой в смысле Леей.
< Пусть, от противного, D не является L-выпуклой. Тогда
найдется такая последовательность компактных аналитических
поверхностей Sv, что SV->S, dSv-+dS, причем Sv, dS ш D,
a S содержит точку ?есШ. В силу непрерывности евклидова
расстояния имеем
e(S, dD)= lime(Sv, dD). A0)
V->oo
С другой стороны, так как функция — In e (г, dD) плюри-
плюрисубгармонична, то для нее справедлив принцип максимума
(см. следствие теоремы 5 предыдущего пункта), по которому
для любого v=l, 2, ...
-lne(Sv, a?>)< - In e (<3SV, dD).
Отсюда e(Sv, dD)>e(dSv> dD), а так как <3SV, dS m D и
dS4-*-dS, то e(dS4, dD)^6 и, следовательно, e(Sv, dD)~^b
для всех v и некоторого 6>0. Но тогда из A0) мы получаем,
что e(S, dD)~^6, а это противоречит тому, что 5 содержит
точку ? е 3D >
Таким образом, понятия L-выпуклости и псевдовыпуклости
действительно оказались эквивалентными.
') Легко видеть, что I-выпуклость не нарушается при аналитических
поворотах (9).
400 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ'
В заключение этого параграфа приведем сводку условий,
характеризующих области голоморфности в С".
Теорема 4. Эквивалентны следующие пять условий:
(I) D — область голоморфности (т. е. существует функция
f e Н (?)), не продолжаемая голоморфно в более широкую
область, см. п. 20);
(II) D не расширяема голоморфно в каждой граничной
точке (т. е. для любой точки ? е dD существует окрестность U
и функция /e#(Z) f] U), не продолжаемая голоморфно в точку ?,
см. п. 24);
(III) D голоморфно выпукла (т. е. для любого множества
К <^D голоморфно выпуклая оболочка ^я = {геО: l/(z)| =^||/!!*:
для всех /е #(?>)}<=?>, см. п. 21);
(IV) D псевдовыпукла (т. е. функция — lne(z, dD) является
плюрисубгармонической в D, см. п. 26);
(V) D выпукла в смысле Леей (т. е. не существует после-
последовательности компактных аналитических поверхностей S^->S,
dSv-+dS таких, что Sv, OS ш D, a S содержит точку ? е 3D,
см. п. 24).
¦« Выше были доказаны импликации, изображенные сплош-
сплошными стрелками на схеме
// \
/V \
III IV+--+V
(импликация A)->(П) тривиальна, импликации A)^A11) со-
составляют содержание теоремы 4 п. 21, (II) ->(V) — теоремы 1
п. 24, (IV)*^(V) —теорем 2 и 3 этого пункта).
Изображенная пунктирной стрелкой импликация (II) ->A)
составляет содержание теоремы Ока, решающей проблему
Леви, о которой мы говорили в п. 24; эта теорема будет
доказана в гл. IV. Пользуясь теоремой Ока, мы докажем
сейчас, что (IV) —>(I), и это замкнет цепочку эквивалентностей.
Итак, пусть для некоторой области DcC" функция
qp(z) = — In e(z, 3D)
плюрисубгармонична в D. По теореме 4 п. 25 построим последо-
последовательность функций ФцХф, плюрисубгармонических класса С00
в открытых множествах Gtt, причем G^ образуют возрастающую
последовательность, аппроксимирующую область D изнутри.
Так как функция cp(z)->oo при z->dD, то для любого у.
можно найти номер v = v(jx) такой, что множество
{ze=D: <p(z)<n}<gGv.
§ 91 ОБОЛОЧКИ ГОЛОМОРФНОСТИ 401
Будем считать, что функция \(ц) /*<х>; тогда множества G* = Gvftl)
также образуют возрастающую последовательность, аппрокси-
аппроксимирующую D изнутри. Положим, наконец,
Очевидно, q?eC°°(G^), и простой подсчет показывает, что для
любого шёС"
П .9 • П -О
V д % - V д fv - , 1, ,9
s,t=l s,t=l
В силу плюрисубгармоничности функций cpv сумма в правой
части неотрицательна, откуда следует, что
я;(со, «)>jicoi2,
т. е. что функции ср* строго плюрисубгармоничны. По теореме
Леви — Кшоски п. 24 отсюда вытекает, что открытое множество
не расширяемо голоморфно в каждой своей граничной точке
(см. пункт а) доказательства этой теоремы).
Из этого по теореме Ока следует, что каждая связная ком-
компонента множества D^ является областью голоморфности. Но
при фиксированном г и растущем ц, величина фц(г) уменьшается,
причем lim ф„ (г) = ф(z). Отсюда видно, что существует возра-
Ц->°о
стающая последовательность компонент D*^, аппроксимирую-
аппроксимирующая D изнутри. По теореме 2 п. 22 отсюда можно заключить,
что D является областью голоморфности >
§ 9. Оболочки голоморфности
Если D не является областью голоморфности, то любая
функция f^H(D) голоморфно продолжается в более широкую
область. Возникает вопрос об отыскании так называемой обо-
оболочки голохморфности области D — наименьшей области, в кото-
которую продолжаются все функции из H{D). Этот вопрос важен
как с принципиальной точки зрения, так и с точки зрения
приложений в квантовой физике ')•
') См. Дж. И о с т, Теория квантованных полей, «Мир», М., 1967.
26 Ь. В. Шабат
402 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
27. Однолистные оболочки голоморфности. В п. 20 мы при-
привели пример области D, из которой каждая голоморфная
функция продолжается в более широкую область, причем не-
некоторые функции при продолжении оказываются многозначными.
Желая избежать рассмотрения многозначных функций, мы при-
приходим к необходимости рассматривать многолистные области,
аналогичные римановым поверхностям аналитических функций
одного переменного.
В частности, и оболочки голоморфности могут оказаться
такими многолистными областями (как в упомянутом примере).
Мы рассмотрим понятие многолистных областей в следующих
пунктах, а здесь лишь сформулируем определение оболочки
голоморфности так, чтобы оно охватывало и многолистиый
случай.
Определение. Область D (однолистная или нет) назы-
называется оболочкой голоморфности области D с С", если: 1) D со-
содержит D, 2) любая функция / е Я (D) продолжается до функ-
функции, голоморфной в D, и 3) для любой точки 2° е D существует
функция /ое #(?>), сужение которой на поликруг* U (z°, r), где
г = рB°, 3D), не продолжается голоморфно ни в какой поли-
поликруг U{z°, R), где R>r.
Замечание. Хотя определение сформулировано про запас
и для случая многолистных областей, в многолистном случае оно
нуждается в пояснениях (например, понятий Д=>/)ир {z°, 3D)).
Эти пояснения будут даны в следующих пунктах; здесь же
читатель может понимать под D однолистную область.
В этом пункте мы рассмотрим основные свойства оболочек
голоморфности в предположении их однолистности, а также
вопросы построения оболочек для областей простейших классов.
Прежде всего отметим, что оболочки голоморфности являются
голоморфными расширениями областей в смысле п. 20. Поэтому
по теореме 2 п. 20 любая функция, голоморфная в области D,
принимает в оболочке D этой области лишь те значения, кото-
которые она принимает в D. В частности, оболочка голоморфности
ограниченной области всегда является ограниченной областью
(это утверждение получается из предыдущего, если применить
его к координатам zv, v=l, .... п).
Далее, условие максимальности 3) в определении оболочки
голоморфности можно существенно усилить. Это условие
является условием локальной непродолжаемости некоторой
функции из Н {б), но можно утверждать, что в Я {D) суще-
существует и глобально непродолжаемая функция. Иными сло-
словами, имеет место
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ 403
Теорема 1. Если оболочка голоморфности D области
D cz С" однолистна, то она является областью голоморфности.
< На основании результатов п. 21 достаточно доказать, что Ь
голоморфно выпукла. Пусть К<шб и р(/С» дб) = г; по теореме
об одновременном продолжении (п. 21) любая функция f e H (D)
голоморфно продолжается в поликруг U(z, r) с центром в любой
точке г^-Кдфу Из условия 3) в определении оболочки голо-
голоморфности отсюда следует, что р (г, dD)~^r и, значит,
Р(КНф)< dD)^r. Но так как это расстояние не может быть
больше г, то
^ р(/С, дЗ),
и D голоморфно выпукла >
Следствие. Если область D cz С" имеет однолистную
оболочку голоморфности D, то последняя является наименьшей
областью голоморфности, содержащей D (т. е. пересечением
всех областей голоморфности, содержащих D).
< Если G —область голоморфности, содержащая D, то
G =э D (так как H{G)<=H(D), то любая f e #(G) голоморфно
продолжается в D). Но /5 по теореме 1—область голоморф-
голоморфности, следовательно, D — наименьшая область голоморфности,
содержащая D >.
Замечание. На первый взгляд может показаться, что подобно тео-
теореме 1 из локальной нерасширяемости области выводится ее глобальная
нерасширяемость, т. е. импликация (И)->A) в теореме 4 предыдущего
пункта. Однако в условии (II) рассматриваются функции, голоморфные
не во всей области, а лишь в окрестности граничной точки, и поэтому
доказательство теоремы 1 здесь не проходит. Как мы уже говорили, импли-
импликация (II) -»A) составляет содержание весьма тонкой теоремы Ока, которая
будет доказана в гл. IV.
Для доказательства следующей теоремы нам нужна
Лемма. Если D — область голоморфности, то любая связ-
связная компонента А ее r-сжатия Dr — {z^D: p(z, dD)>r} также
является областью голоморфности.
< Пусть К Ш А и р (/С, <?А) = р; для любых точек z^K
и g e dD на отрезке [z, ?] найдется точка z' e <ЭД такая, что
p(z, O = p(z, z') + pB', ?)>p + r
(рис. 109). Поэтому р (/С, dD) > р + г, атак как D — область
голоморфности, то по теореме 6 п. 21 и
P(W>. dD)>9 + r. A)
26*
404 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
Нам нужно доказать, что р(Кн(Л), <ЭД)>р, т. е. что p{z°, г')>р
для любых точек 2°е/Ся(Д) и 2'<=j3A. Но так как AcD,
то Кн(А) с^Кнш), следовательно z° e^H(D) и согласно A) р + г^.
(°, 3D) < р {z°, z') + р {z't 3D) = р (z°, z7) + г (у нас р (z', dD) = r,
ибо z' e <ЭД). Отсюда и следует, что
p(z°, z')>p >
Теорема 2. ?сли D cz G и эти
области имеют однолистные обо-
оболочки б и соответственно G, то
DczG и
p(dD, dG)>p(d?>, dG). B)
^Так как H{G)czH(D), то
любая функция f^H(G) голо-
голоморфно продолжается в 5, следовательно, б cz G. Пусть
p(dD, dG) = r>0 (для г = 0 теорема тривиальна), тогда D cz Grcz
a(G)r. Очевидно, D принадлежит некоторой связной компо-
компоненте множества (G)r, которая по доказанной лемме является
областью голоморфности. Но тогда и D принадлежит этой
компоненте, а значит, и множеству (G)r; поэтому р (дб, дб) > г >
Следствие. Если D—ограниченная область, имеющая
однолистную оболочку б, то пересечение dD Л дб непусто.
< Применим к областям D и G = б теорему 2:
р (dD, dD) ^ р (дб, дб) = О
(мы воспользовались тем, что оболочка области голоморфности
совпадает с этой областью). Так как dD — компакт (ибо D
ограничена), то из равенства p(dD, дб) — 0 следует, что мно-
множества dD и dD пересекаются >
Перейдем к описанию оболочек голоморфности областей
простейших классов.
1. Трубчатые области. Напомним, что трубчатой
областью с основанием В czRn называется область T = BXRn (у),
т. е. T = {z — х + iy s С": xsfi) (см. п. 2).
Теорема 3. Оболочкой голоморфности трубчатой обла-
сти Т является ее выпуклая оболочка Т.
< Очевидно, Т — В X R" (у), где В — выпуклая оболочка осно-
основания В в пространстве R (х). Покажем, что любая функция
/ е Я (Т) голоморфно продолжается в Т. Область В предста-
представляет собой совокупность точек отрезков [х1, х2], где х1, х2 е В.
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ 40S
Если л:1 и х2 можно соединить в В двузвенной ломаной
[jc1, jc°] U [jc°, jc2], то продолжаемость / в окрестность множества
[jc1, jc2]xR" (у) следует непосредственно из леммы о призме (п. 23).
В общем случае точки х1, х2еВ можно соединить в В
конечнозвенной ломаной (рис. 110). При помощи той же леммы
индукцией по числу звеньев мы снова докажем, что / голо-
голоморфно продолжается в окрестность множества [х1, х2] X R"(#)»
Та же лемма показывает, что функция /
при описанном продолжении остается одно-
однозначной. В самом деле, пусть jc —точка пе-
пересечения двух отрезков [х1, х2] и [Jc1, Jc2]
с концами в Л и в окрестности точки
z = х + iy мы получили два значения / и f.
Рассмотрим призму [х1, х, х1] X R" (у);
функции / и f по цитированной лемме го-
голоморфны в ней, а так как они совпадают
в окрестности точек х1 + iy и Jc1 + iy, то по
теореме единственности они совпадают во Рис- 1!0-
всей призме.
Таким образом, любая функций /еЯ(Г) голоморфно про-
продолжается в Т. Но Г— выпуклая область и поэтому является
областью голоморфности (п. 20). Следовательно, f служит
оболочкой области Т >
2. Области Рейнхарта. В п. 7 мы доказали, что любая
функция /, голоморфная в полной области Рейнхарта]) D с цент-
центром в точке а, голоморфно продолжается в логарифмически
выпуклую оболочку DL этой области. Такое продолжение осу-
осуществляется при помощи разложения / в ряд Тейлора
/(г)= S ck{z-a)\ C)
1 fe | —о
о
область сходимости 5 которого всегда представляет собой
логарифмически выпуклую область (теорема 3 п. 7).
О
Докажем, что S является областью голоморфности. Это
вытекает из следующего более общего результата. Назовем D
областью сходимости последовательности функций ^„ей{D),
если эта последовательность равномерно сходится внутри D
(т. е. на каждом компактном подмножестве D) и сужения /^
на поликруг U(г, г) с центром в произвольной точке zefl
и радиусом r = p(z, dD) нельзя продолжить до функций f^
') Определение полной области Рейнхарта см. в п. 2.
406 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ПГ
голоморфных в поликруге U(z, /?), где R>r, так, чтобы
последовательность /^ равномерно сходилась внутри U (z, R).
Область D называется областью сходимости, если существует
последовательность голоморфных в ней функций, для которой
она является областью сходимости.
Теорема 4. Область D тогда и только тогда является
областью голоморфности, когда она является областью схо-
сходимости.
< Необходимость условия тривиальна: если D — область
голоморфности, то она является областью сходимости после-
последовательности /,! = /, где / — функция, областью голоморфности
которой D является.
Достаточность. Возьмем K^D и обозначим р(/С, dD)=r;
все будет доказано, если мы покажем, что р(Кн(о)> dD)>r,
т. е. что для любой точки z e Ки (о)
p(z, dD)>r. D)
Пусть G — связная компонента пересечения U {z, r) П D, содер-
содержащая г; сужения /№ \в по теореме об одновременном продол-
продолжении (п. 21) можно продолжить до функций fp, голоморфных
в поликруге U(z, г). Покажем, что последовательность /^ равно-
равномерно сходится внутри (/ (z, r). Для этого возьмем любое
число г{<г и заметим, что по теореме 5 п. 21 для любых
натуральных ц и v имеем
II Гц - f V Ну (г, г,) <11 /ц ~
Так как D является областью сходимости и /ураздутие K{ri) <^ D,
то последовательность /^ сходится равномерно на /C(/v- По кри-
критерию Коши отсюда можно заключить, что она равномерно
сходится и на U (z, r{), т. е. внутри U(z, r).
Но по определению области сходимости из этого следует,
что U (z, r) сг D, т. е. что p(z, dD)~^r !>
Теперь совсем просто выяснить вопрос об оболочках обла-
областей Рейнхарта.
Теорема 5. Оболочкой голоморфности полной области
Рейнхарта D является ее логарифмически выпуклая обо-
оболочка DL.
< Мы видели, что каждая функция feff(D) голоморфно
О
продолжается в область сходимости Sf своего ряда Тейлора,
которая по теореме 4 является областью голоморфности. Сле-
Следовательно, все функции класса H(D) продолжаются в пере-
пересечение DL всех областей Sf, f e Я (?>), являющееся логарифми-
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ 407
чески выпуклой оболочкой области D и в то же время (по
теореме 1 п. 22) —областью голоморфности. Таким образом,
DL является оболочкой голоморфности области D >
Следствие. Любая логарифмически выпуклая полная
область Рейнхарта является областью сходимости некоторого
степенного ряда.
< Такая область D по только что доказанному является
областью голоморфности, и, следовательно, существует функ-
функция fe#(Z)), не продолжаемая за пределы D. Тейлоровское
разложение f имеет D своей областью сходимости >
Замечание. Если мы будем рассматривать вместо тейло-
тейлоровских разложений разложения Лорана, то получим более
общий результат: оболочкой голоморфности любой относительно
полной области Рейнхарта (см. п. 8) является ее логарифми-
логарифмически выпуклая оболочка.
3. Области Хартогса1). Для простоты писька ограни-
ограничимся областями с плоскостью симметрии ап = 0 — это не умень-
уменьшает общности.
Теорема 6. Оболочкой голоморфности полной области
Хартогса D = {z = ('z, zn): 'z^'D, |г„ |<r('z)}, проекцией кото-
которой 'D служит область голоморфности в пространстве Са~1,.
является область Хартогса
D = {z = ('г, zn): 'z е='D, | zn |<ev<'*>}, E)
где V {'z) — наилучшая плюрису пер гармоническая мажоранта
функции In г ('z) в области 'D.
¦4 Область Dv вида E), где V строго плюрисупергармони-
ческая в 'D функция, голоморфно не расширяема в каждой
своей граничной точке. В самом деле, пусть g e dDv, % e d'D
и f ('г) —голоморфная функция, для которой 'D является обла-
областью голоморфности. Эта /, как функция в Dv, очевидно, не
продолжается голоморфно в точку ?. Если же ? е dDv и
% ф d'D, то в окрестности ? область Dv задается неравенством
ф(г) = |2„ fe~2V('z) < 1. Так как ф строго плюрисубгармонична
в точке ? (это проверяется непосредственными выкладками),
то по теореме Леви — Кшоски (п. 24) область Dv- голоморфно
не расширяется в точке ?. Отсюда по теореме Ока (которая
будет доказана в гл. IV) мы заключаем, что Dv — область го-
голоморфности.
Из теоремы об аппроксимации плюрисубгармонических
функций (п. 25) мы получаем, что оболочка голоморфности D
') Определение области Хартогса см. в п. 2.
408 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. НС
области D содержится в пересечении всех Dv, где V — произ-
произвольная плюрисупергармоническая мажоранта функции In г ('г)
в 'D. С другой стороны, в п. 8 было доказано, что любая
функция |еЯ(D) представляется в D своим рядом Хар-
тогса
и, следовательно, голоморфно продолжается в область сходи-
сходимости этого ряда Gf = {('z, zn): 'z^'D, \zn|<Rf('г)}. По тео-
теореме 1 п. 26 функция In Rf плюрисупергармонична в 'D, т. е.
Gf является областью вида E), где V — некоторая плюрисупер-
плюрисупергармоническая мажоранта функции In г.
Так как D — пересечение всех Gf, где f<^H(D), а это пере-
пересечение содержит П Dv гэ D, то теорема доказана >
Замечание. Если рассматривать разложения Хартогса —
Лорана, то можно получить более общий результат: оболочкой
голоморфности области D={('z, zn): 'z<=l'D, rl('z)<\ zn\<r2('z)},
проекцией которой 'D служит область голоморфности в про-
пространстве С", является область вида
D = {{'z, zn): 'zts'D, e^™<\zn\<eW*)}, G)
где vx — наилучшая плюрисубгарионическая миноранта функ-
функции — In /¦[, a V2 — наилучшая плюрисупергармоническая мажо-
мажоранта 1пг22).
В теореме 6 (и ее обобщении) существенно, что проекция 'D
области D является областью голоморфности, — иначе области
E) и G) будут не оболочками, а лишь голоморфными расши-
расширениями D. Заметим, что и не всякая область Хартогса имеет
однолистную оболочку. Чтобы в этом убедиться, достаточно
взять в С3 область Хартогса, проекцией которой в С2 является
область из примера в п. 20 с неоднолистной оболочкой.
28. Области наложения. Выше не раз отмечалась необхо-
необходимость рассмотрения многолистных областей, аналогичных
римановым поверхностям над комплексной плоскостью. Здесь
мы изложим основные определения и некоторые результаты,
связанные с этим понятием.
Каждое комплексное многообразие размерности п посред-
посредством локальных координат локально гомеоморфно отобра-
отображается в пространство С". Однако локальные координаты не
') См. В. С. Владимиров, Методы теории функций многих ком-
ллексных переменных, «Наука», М., 1964, стр. 217.
§ §1 ОБОЛОЧКИ ГОЛОМОРФНОСТИ 409
определены глобально на многообразии, т. е. не являются на
нем функциями в смысле п. 9.
Мы выделим специальный класс многообразий условием
существования глобально определенного непрерывного отобра-
отображения в С", всюду локально гомеоморфного. Такие многообра-
многообразия вместе с заданными на них отображениями в С" и будут
предметом нашего изучения в этом пункте.
Определение. Многообразием наложения над простран-
пространством С" (короче: многообразием над С") мы будем называть
пару (М, я), где М — многообразие, а я: М—>С" — локально
гомеоморфное отображение, которое называется проектирова-
проектированием. Если М связно, то (М, я) называется областью наложе-
наложения над С".
Это определение распространяет на пространственный слу-
случай определение римановой поверхности над С (см. п. 32 ч. I).
Как и в плоском случае, проектирование позволяет перенести
на многообразия понятия, введенные в С". Так, мы назовем
поликругом на (М, я) с центром в точке РоеМ и радиусом г
множество U (Ро, г) точек Р^М, содержащее Ро, которое я
гомеоморфно преобразует в точки поликруга U (г°, г), где
2° = я (Ро) — проекция точки Ро:
= {Ре=М: n{P)?=U(z°, г), Ро «= U и я|5 гомеоморфно]. A)
Объединение всех поликругов на (М, л) с данным центром PQ
также является поликругом, который называется максималь-
максимальным; радиус этого поликруга (конечный или бесконечный) на-
называется расстоянием Ро до границы М и обозначается через
р^о, дМ). Под расстоянием до границы некоторого множества
N cr M понимается inf p(P, дМ).
Если М — комплексно аналитическое многообразие
(см. п. 9), то на {М, я) можно ввести понятие голоморфной
функции. Именно, функция /: М->С называется голоморфной
на (М, я), если для любого поликруга U = U{P, r) на (М, я),
функция /°(Jt|jj)~' голоморфна в поликруге U{z, r) = n(U). Оче-
Очевидно, что это определение голоморфности совпадает с приня-
принятым в п. 9. В частности, на (М, я) будут голоморфными все
локальные координаты: 2\,°я(Р), которые коротко обозна-
обозначаются через я,у(.Р) (v=l, ..., п).
Кольцо всех функций, голоморфных в области {М, п) над С",
мы будем обозначать через Н{М).
Важный пример комплексно аналитического многообра-
многообразия над С" доставляет процесс аналитического продолжения
410 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
голоморфных функций. В случае нескольких переменных он про-
проводится в точности так же, как в плоском случае, и мы огра-
ограничимся его кратким описанием. Будем исходить из какого-либо
элемента (?/,/)> т.е. совокупности поликруга U = U(z°, г)с=С"
и голоморфной в этом поликруге функции f(z) = 2 ck{z — z°)k.
t fe I — 0
Точно так, как в случае одного переменного, определяется не-
непосредственное аналитическое продолжение, аналитическое
продолжение и аналитическое продолжение вдоль пути
у: /->С" (здесь / = [0, 1] с= R1, отображение у задается п не-
непрерывными комплексными функциями zv = zv@, ^e/). Дока-
Доказывается, что аналитическое продолжение вдоль пути (если
оно возможно) не зависит от выбора промежуточных точек,
а также не меняется при замене пути у гомотопным ему пу-
путем Yi с теми же концами, если вдоль всех путей ух, 0^т^1,
осуществляющих гомотопию!), продолжение начального эле-
элемента (?/, /) возможно. Приведем теперь основное
Определение. Аналитической функцией п комплексных
переменных называется совокупность элементов (Ua, fa), аеЛ
(А — некоторое множество индексов), каждый из которых полу-
получается из любого другого аналитическим продолжением вдоль
какого-либо пути.
Построим теперь комплексно аналитическое многообразие
над С", связанное с аналитическими функциями. Рассмотрим
множество Ш, точками которого служат пары А = {а, fa}, где
точка аеС и функция
Ш~$сР(г-а)к B)
голоморфна в некотором поликруге Ua с центром в а, кото-
который для определенности будем считать поликругом сходи-
сходимости ряда BJ). Введем в 9t топологию следующим образом:
под окрестностью U (А) точки А е 9t понимается совокупность
точек B = {b, f6}eSR таких, что: 1) р(а, Ь)<г и 2) элемент
(Уь> fb) является непосредственным аналитическим продолже-
') Два пути Yo и \i в D с= С называются гомотопными (как пути с непо-
неподвижными концами), если существует непрерывное отображение \ (t, г):
JXJ-+D такое, что y(t, 0) = Yo @. Y (^, О = Yi @ и у @, г) = у0@),
¦у A, г) = Yo A); через Yt обозначается путь у {t, т): J ->D, где те/ фикси-
фиксировано (ср. п. 16 ч. I).
2) Второй компонентой точки А = {a, fa} можно считать также росток
аналитической функции в точке а е С", т. е. класс эквивалентности голо-
голоморфных в точке а функций по отношению: f ~ g, если /sjb некоторой
окрестности а.
5 9) ОБОЛОЧКИ ГОЛОМОРФНОСТИ 411
нием элемента ((/„, fa). Мы предоставляем читателю доказать,
что эта топология превращает 9? в хаусдорфово пространство.
Определим теперь проекцию 9? в С" отображением
р: {a, fa}->a. C)
Нетрудно видеть, что р — локальный гомеоморфизм и что это
отображение определяет на SR структуру комплексно аналити-
аналитического многообразия комплексной размерности п (ср. п. 32
ч. I); мы будем называть Ш римановым многообразием.
Таким образом, пара (9t, р) является комплексно аналити-
аналитическим многообразием над С" (окрестности U (А) оказываются
на нем поликрутами). Примером голоморфной на (9?, р) функ-
функции является функция
f: A^fa{a), D)
сопоставляющая точке А = {a, fa} свободный член ряда B).
Риманово многообразие SR, очевидно, несвязно. Однако под-
подмножества ffi0 его точек {a, fa} таких, что элементы (Ua, fa)
принадлежат одной аналитической функ-
функции (т. е. являются аналитическим про- А
должением друг друга вдоль какого-либо \ )
пути), связны. Такие множества являются t ^ уц
областями в 9t; мы будем называть их ^ /
римановыми поверхностями. Очевидно, ка- 1«о
ждой области 9?0 сг Ш соответствует анали- '
тическая функция и, обратно, каждой ана- т Сп
литической функции соответствует область z
Sfi,ci рис п]
Пусть 0?о cz ffi — какая-либо риманова
поверхность; через р° и /0 обозначим соот-
соответственно сужения на Шо отображений C) и D). Локально го-
меоморфное отображение р° не обязано быть в целом гомео-
гомеоморфизмом, поэтому оно может переводить в одну т©чку
геС" несколько точек Лс=9?0 (рис. 111). Функция /0, одно-
однозначная на (Шй, р°), будет тогда многозначной, если ее рас-
рассматривать в зависимости от z. Таким образом, и в случае
многих переменных мы можем рассматривать (многозначные)
аналитические функции как (однозначные) голоморфные функ-
функции, если вместо областей в С" перейдем к областям над С",
т. е. римановым поверхностям.
Кроме областей (9t0, p°) рассматриваются и другие модели
римановых поверхностей, эквивалентные этим областям (поня-
(понятие эквивалентности мы сейчас определим). Мы будем далее
заниматься расширением областей наложения и, чтобы можн»
было сравнивать между собой различные модели, введем
412 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
понятия вложения многообразий и сужения функций, связав их
¦с возможностью отображения одного многообразия на другое.
Определение 1. Пусть даны два многообразия (М,, я1)
и (М2, я2) над С"; если существует такое непрерывное отобра-
отображение ф: М,->М2, что на М{
пх = я2 ° ф, E)
то говорят, что первое многообразие {слабо) у-вложено во вто-
второе, и пишут: {Mi, я1) с (М2, я2). Если при этом ф является
ч>
взаимно однозначным отображением М{ в М2, то гово-
говорят, что (Ми я1) сильно (р-вложено в (М2, я2). Если еще
ф —гомеоморфизм Мх на М2, то (М,, я1) и (М2, я2) назы-
называются эквивалентными.
Это определение обобщает обычное понятие включения:
если Mi cz M2 в обычном смысле, то я1 = я2 \м является суже-
сужением функции я2 на Miy и в качестве ф можно принять есте-
естественное отображение вложения ф: Л11->М2, где ф переводит
каждую точку РеМ, в ту же точку Р, рассматриваемую как
точка М21). Очевидно, что эквивалентные многообразия (Ми я1)
и (М2, я2) сильно вложены друг в друга (одно — посредством ф,
другое —ф). В случае слабого вложения (Ми я1) с (М2, я2)
ф
первое многообразие может оказаться «более разветвленным»,
4 _
чем второе. Так, риманова поверхность функции w = yz наД С1
оказывается слабо вложенной в риманову поверхность w — Yz
(в качестве ф надо принять отображение, склеивающие пары
точек первой поверхности, в которых |/? принимает одинако-
одинаковые значения). Всякое многообразие (М, я) над С'1 является
я-вложенным в С".
Обобщая понятие функции, голоморфной на многообразии,
введем понятие голоморфного отображения многообразий.
Пусть даны два комплексно аналитических многообразия {М{, я1)
и (М2, я2) соответственно над пространствами С и С; ото-
отображение ф: М{—>М2 называется голоморфным, если оно не-
непрерывно и все функции
v= I m, F)
голоморфны на (Мь я1). Если еще ф— гомеоморфизм Af, на М2
(тогда непременно пг.= п) и обратное отображение ф: М2-+ М{
также голоморфно, то ф называется голоморфным изоморфиз-
') Так как отображение вложения <р(Я) =Р взаимно однозначно, то
обычное включение является сильным <р-вложением.
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ 413
мом (короче, голоморфизмом) или биголоморфным отображе-
отображением.
Отметим, что если одно комплексно аналитическое многооб-
многообразие ф-вложено в другое такое же, то отображение вложения
ф: М1-*М2 непременно является голоморфным. В самом деле,
по определению вложения функции F)
а последние голоморфны, ибо (М,, я1) — комплексно аналити-
аналитическое многообразие. Эквивалентность -многообразий в этом
случае сводится к голоморфной эквивалентности.
Определение 2. Пусть (Ми л1) с: (М2, я2) и /2: М2->-С —
ф
функция на втором многообразии; функцию f{: М1->С будем
называть ^-сужением функции f2 на первое многообразие (обо-
(обозначение: /1=/21^[), если на М{
/i = /2°<p; G)
функцию /2 тогда будем называть ^-расширением f{.
Если М{ cz М2, а ф — естественное отображение вложения,
то мы имеем обычное сужение /t = f2 |M .
Покажем, что построенное выше риманово многообразие
(Ш, р) является «универсальной моделью» многообразий над С",
т. е. что любое комплексно аналитическое многообразие над С"
можно ф-вложить в риманово многообразие. Точнее, имеет
место
Теорема 1. Пусть D — связное комплексно аналитическое
многообразие, {D, п) — область наложения над С" и f: D->C —
голоморфная на (D, я) функция; существуют связная компо-
компонента Шо а !К и отображение q>: D->9i0 такие, что
(D, я) с: (Я,,, р°), / = /ol*. (8)
где р° = р \я и /0 = f [Яа — сужения на 9t0 отображений C) и D).
< Для любой точки P^D обозначим через q>{P) = A сово-
совокупность точки й = я(Р)еС и голоморфной функции /a(z)
(разложения в ряд Тейлора с центром в а функции fon^iz)).
Пусть ф(?)) — образ области D при построенном отображении;
так как ф непрерывно, а D связно, то ф(О) с= 9t0 — связной
компоненте Ш. По построению я = р°°ф и / = /0°ф, так что (8)
имеет место >
Теперь мы хотим ввести понятие многолистных областей
голоморфности. Определим их как области над С", в которых
существует голоморфная функция, не расширяемая на области,
неэквивалентные данной. Иными словами, примем такое
414 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
Определение. Область наложения (D, я) называется
областью голоморфности, если существует функция [еЯ(D),
обладающая следующим свойством: из того, что некоторая
область (/)[, я')э(Д, я) и функция ДеЯСОО является ф-рас-
ф
ширением функции f, следует, что (Dlt я1) эквивалентна (D, я)
(т. е. что ф взаимно однозначно отображает D на D{).
В этом определении, по существу, используется, что экви-
эквивалентность областей наложения сводится к голоморфной экви-
эквивалентности, и постулируется инвариантность областей голо-
голоморфности при биголоморфных отображениях (для однолистных
областей голоморфности это свойство было доказано в п. 22).
Важные примеры многолистных областей голоморфности
представляют максимальные связные компоненты риманова
многообразия (Ш, р). Для доказательства нам понадобится
Лемма. Если отображение вложения ф области (D, я) над
С" в себя имеет хотя бы одну неподвижную точку, то оно
тождественно.
< Множество всех неподвижных точек отображения ф замк-
замкнуто (ибо ф —непрерывное отображение хаусдорфова простран-
пространства в себя) и по условию непусто. Покажем, что оно открыто.
Пусть Ро — неподвижная точка ф и 0=0 {Ро, г) — поликруг
на (D, я). Обозначим F"= U Пф~!(^); это —открытое множество
на D (в силу непрерывности ф), содержащее Ро, причем проек-
проекция я гомеоморфна на V. По определению ф-вложения на D
имеем я (Р) = я ° ф (Р), а так как на V отображение я гомео-
морфно, то отсюда следует, что q>(P) = P при P^V, т. е. все
точки из V неподвижные. Итак, множество неподвижных точек
отображения ф непусто и одновременно замкнуто и открыто;
так как D связно, то это множество совпадает с D >
Теорема 2. Любая область (9?0, р°) риманова многообра-
многообразия (Ш, р), где Шо — максимальная связная компонента Ж,
является областью голоморфности.
"* Функция fo = f |я голоморфна на (9t0, р°) и (Шо, р°) cz(D, я),
0 ф
причем функция f1 голоморфна на {D, л) и /j ^ = f0; надо по-
показать, что в этой ситуации ф является взаимно однозначным
отображением Шо на D. Так как /,еЯ(Д), то по теореме 1
существует я|з-вложение (D, я) в многообразие (9?, р), для кото-
которого /1* = /j. По построению этого я|з-вложения для А е 9t0
имеем'фоф(Л) = Л и ф°'ф[ф(Л)] = ф['фоф(Л)] = ф(Л), следовательно,
отображение фоф имеет в D неподвижные точки. По лемме
Ф ° я|>СР) =3 р всюду в D, откуда видно, что ф взаимно однозначно
отображает Э^ на ?>>
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ 415
Чтобы сформулировать необходимые и достаточные условия
для областей голоморфности над С", условимся называть об-
область (D, п) голоморфно отделимой, если для любых двух
различных точек Ри P2^D найдется функция f^H{D), разделя-
разделяющая эти точки, т. е. такая, что f(Pi)?=f (Р2)-
Для однолистных областей условие голоморфной отдели-
отделимости выполняется автоматически, ибо в качестве разделя-
разделяющей функции всегда можно взять одну из координат. Для
многолистных областей это не так: вот соответствующий при-
пример. Пусть Г = {|2,|=1, |22|=1} —тор
в С2 и Do = С2 \ Г; возьмем область {D, п)
над С2, диаграмма Рейнхарта которой
изображена на рис. 112. Эта диаграмма
представляет собой лежащую над пер-
первым квадрантом плоскости ? = | zx | + i\z21
часть двулистной римановой поверхности
функции |Л; —A -И) с точками ветвле-
ветвления над ? = 1 +i и ? = <х>. __ |л/(
Рассмотрим произвольную функцию f, '
голоморфную на {D, п). Ее значения на Рис П2.
любом из двух «листов» (D, п) голо-
голоморфны вне шара {|s |^ V^2 }, _ибо многообразие ветвления
(тор Г) лежит на сфере {|г| = \^2}, и- вне шара область не
разветвлена. По теореме Осгуда —Брауна (п. 18) эти значения
продолжаются до целых функций, а так как на Г они должны
совпадать, то они совпадают тождественно (см. задачу 15 к гл. I).
Таким образом, значения f в точках различных листов обла-
области (D, л), лежащих над одной точкой (zu z2), должны совпа-
совпадать: точки (D, л) с одинаковой проекцией не отделимы голо-
голоморфно.
Теорема 3 (К а ртан — Т у л л ен). Область наложения
(D, п) тогда и только тогда является областью голоморфности,
когда она голоморфно выпукла J) и голоморфно отделима.
Мы не будем подробно излагать доказательство, опишем
лишь изменения, которые нужно внести в многолистном
случае.
¦« Необходимость. Доказательство теоремы об одно-
одновременном продолжении (п. 21) без существенных изменений
') Определение голоморфной выпуклости переносится иа многолистные
области без изменений. Например, его можно сформулировать в виде
условия р (К, dD) = p(KH, 3D), где К — произвольное компактное подмно-
подмножество D, а Кн — его оболочка относительно класса функций, голоморфных
на (D, я).
416 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
переносится на многомерный случай1), а из этой теоремы выте-
вытекает голоморфная выпуклость области голоморфности (D, л).
Для доказательства голоморфной отделимости возьмем на
(D, л) функцию f, описанную в определении области голоморф-
голоморфности, и по теореме 1 построим соответствующее ей ср-вложе-
ние (D, л) в риманово многообразие (Ш, р). Из того же опре-
определения следует, что отображение ср взаимно однозначно, т. е.
что ^(Р1)фг^(Р2) для различных точек Рь P2^D. Пусть ср (Pv) =
= ^v(v=l, 2); из (8) и G) имеем f (Pv) = /0 о ф(Pv) = fQ(Av),
а так как А1фА2,то из определения функции /0 следует, что
в точках Р] и Р2 значения функции f или какой-либо ее про-
производной различны (в противном случае Ау = А2). Это и озна-
означает голоморфную отделимость (D, я).
Достаточность. Пусть Kv{v— 1, 2, ...) —компактное
исчерпывание области D (напомним, что D является много-
многообразием, а по нашему определению в п. 9 каждое много-
многообразие счетно исчерпываемо). Пользуясь голоморфной выпук-
выпуклостью D, мы можем считать, что Kv = (Kv)hw)- Покроем дКч
конечным числом поликругов и в пересечении каждого из них
с D \ Kv возьмем по точке Pvi{i = \, ..., kv); через fvi обозна-
обозначим функцию из Я (D) такую, что
Ы (Pvi) = v, ti fvl !kv < 2"^ и fvi (PvJ) = 0, / Ф i.
Функция f =
fvi
l/(Pv«)l>v-l. (9)
Пользуясь голоморфной отделимостью, можно исправить
функцию f так, чтобы она, оставаясь голоморфной в (D, л) и
удовлетворяя неравенству (9), имела в любых двух различных
точках Р, P'^D с одинаковой проекцией л(Р/) — л(Р) различ-
различные элементы (о том, как осуществить такое исправление,
см. книгу Б. А. Фукса2), стр. 193).
Покажем, что (D, л) является областью голоморфности
(исправленной) функции f. Пусть имеется ср-расширение функ-
функции / в область (?),, я1); требуется доказать, что ср взаимно
однозначно отображает D на Dx. Если ср(Р') = ф(-Р). то со-
согласно E) л(Р') = л(Р), а согласно G) f{P') = f(P). Отсюда по
построению f вытекает, что Р' = Р, т. е. ср взаимно однозначно.
Кроме того, ср (D) = D{, ибо в противном случае область ср {D)
') Производные функции / в точке Pe(D, я) можно определить при
помощи дифференцирования степенных рядов для /°я~'(г).
2) Б. А. Фук с, Введение в теорию аналитических функций многих
комплексных переменных, Физматгиз, М., 1962.
§ 9) ОБОЛОЧКИ ГОЛОМОРФНОСТИ 417
имела бы в D, граничную точку, а в этой точке функция
/i=f°cp в силу неравенств (9) не может быть голоморфной >
Замечание. К. Ока доказал в 1953 г., что всякая голо-
голоморфно выпуклая область над Сп голоморфно отделима. По-
Поэтому условия в теореме 3 не являются независимыми.
Области наложения (D, я) над Сп, которые являются об-
областями голоморфности, мы будем называть еще многообра-
многообразиями Штейна. Заметим, что обычно этот термин трактуется
шире: многообразием Штейна называется любое комплексно
аналитическое многообразие X комплексной размерности п,
обладающее следующими тремя свойствами: 1) X голоморфно
выпукло, 2) X голоморфно отделимо, 3) для любой точки Ре!
существует п функций fv, голоморфных на X, которые обра-
образуют локальные координаты в этой точке.
29. Многолистные оболочки голоморфности. В заключение
этой главы мы хотим описать процесс построения оболочек го-
голоморфности для произвольных областей наложения (в част-
частности, областей DaCn). Такая оболочка является областью
голоморфности над Сп, в которую голоморфно продолжается
(в смысле, принятом в предыдущем пункте) любая функция,
голоморфная в данной области. Пример, который был при-
приведен в начале главы, показывает, что задача построения
оболочек голоморфности в классе однолистных областей в об-
общем случае неразрешима. Здесь мы покажем, что эта задача
всегда разрешима в классе областей наложения.
Пользуясь свободой выбора модели в определении областей
наложения, мы будем строить оболочки из несколько необыч-
необычного материала — линейных мультипликативных функционалов
над кольцом голоморфных функций.
Пусть дана область наложения (D, я) над Сп (в частности,
однолистная область DcC, если я — естественное отображение
вложения). Обозначим через D совокупность всех не тождест-
тождественно равных нулю функционалов h:H(D)->C, непрерывных
в топологии равномерной сходимости на компактных подмно-
подмножествах D, а также линейных и мультипликативных, т. е.
таких, что
h(fl + f2)~fi(f1) + h(f!l), М/, •/2) = М/,) • М/2) (l)
для всех /,, fz^HiDj1). Множество D непусто: оно содержит
все функционалы hP(f) = f{P), ставящие каждой функции /<=Н (D)
ее значение в произвольной фиксированной точке Р?)
') Функционалы йеД являются гомоморфизмами кольца Н (D) в кольцо
комплексных чисел С.
27 Б. В, Шабат
418 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. Ш
Мы хотим ввести на D структуру многообразия наложения
над Сп. Для этого прежде всего определим проекцию — ото-
отображение 6 в С". Обозначим через nv(P) = zv °я(Р) координаты
на (D, я); так как они принадлежат H(D), то для любого
/ге=?) определены значения nv = h{nv). Мы положим
ft (А) = (А (я,), '..., А(я„)) B)
и тем самым построим отображение я: D-*Cn.
Докажем, что ft локально взаимно однозначно. Нам пона-
понадобится
Лемм а. Для любого lv^D существует множество К Ш D
такое, что
1МЛКШК О)
для всех f<=H{D).
< Пусть такого множества не существует. Тогда найдется
последовательность компактов KvczD таких, что /Cvcr/Cv+1,
Q KV = D> и функций fv<=H(D) таких, что |/г (/v) I >[|/v kv- На
v=l
основании этих неравенств можно выбрать достаточно высокие
степени ^ = (щ^; так> чтобы ||gvlkv<<p Дл« всех v =
= 1, 2, .... Ряд 2gv сходится равномерно на каждом ком-
v=l
пактном подмножестве D, и по теореме Вейерштрасса его
сумма g^H(D). Yip свойствам гомоморфизма h мы должны
оо
иметь h(g)— 2 h(§v)y н0 так как Mgv)=l для всех v, то по-
v=l
следний ряд расходится. Противоречие доказывает лемму >
Фиксируем h^D и построим степенной ряд
D)
где k = (ku ..., kn) — целочисленный вектор и ^
dz\\ ... dzRnti
Согласно лемме найдем для h множество К.ШЭ и возьмем
произвольное число r<.p(K, dD); по C) и неравенствам Коши
будем тогда иметь
й E)
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ 419
где К(Г) — раздутие множества К,- Отсюда видно, что ряд D)
сходится для всех z из поликруга U(n(h), r)c=Cn.
Если еще фиксировать г, то Lz можно рассматривать как
функционал над кольцом Н (D). Он, очевидно, линеен, а так
как из E) для любой fe^H{D) вытекает оценка
V=I
(см. доказательство теоремы 5 из п. 21), то он и непрерывен.
Пользуясь мультипликативностью h и правилом Лейбница
дифференцирования произведения, легко доказать также, что
он мультипликативен. Таким образом, LZ^D и тем самым
определено отображение
Lz: U(n(h), r)-*D. G)
Применяя формулу D) к функциям / = nv(v = 1, ..., п), мы
найдем Lz(nv) = h(nv) + h(\){zv — h{nv)) = zv, т. е. h{Lz) = z для
всех г e U (n(h), г). Но это означает, что отображение G) ло-
локально обращает B), и локальная взаимная однозначность
отображения я доказана.
Нам нужно доказать, что пара (D, я) является многообра-
многообразием наложения над С". Для этого нам остается ввести на мно-
множестве D топологию, превращающую его в хаусдорфово прост-
пространство, и убедиться в том, что я и его локальное обращение Ьг
являются в этой топологии непрерывными отображениями.
Топологию в D мы перенесем из С" при помощи отображе-
отображения Lz. Именно, поликругом на Ь с центром в точке h и ра-
радиусом г мы назовем образ U (h, г) поликруга U (я (h), rjcC1
при отображении GV, он определен при любом h eD и г <
< р{К,дЬ), где К— множество, соответствующее функционалу h
по лемме. Множество Q cz D мы назовем открытым, если для
любой точки /гей существует такое число г>0, что поликруг
U (h, r)cfl. Остается доказать, что любой поликруг 0 (h, r)cD
является открытым множеством. Пусть я (К) = 0, т. е. соответ-
соответствующий функционал
!ftl.>0
(это предположение не ограничивает общности). Мы должны до-
доказать, что для любого h' e б {h, r)' существует поликруг
б (h', г') а б (А, г). Точка z' = я (А') е U @, г), и, значит, найдется
27*
420 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. III
число г'>0 такое, что U(z', r')c={/@, г). Построим по h'
функционал
L'z{f)= 2 ^h'{Dkf){z-z')k (9)
и сравним его с (8). Так как ряд (9) сходится в U(z', rr), то
по формуле Тейлора
М/)= 21 irDkLz{f)^Az-z')k- ¦ (Ю)
lfc|>o
Но дифференцированием ряда (8) для любого 1 = Aи ..., /„)
получаем
*-'» 21 т
|ftl>l Л
(мы заменили индекс суммирования k индексом j = k — l), от-
откуда видно, что DlLz {f) = Lz (Dlf). Пользуясь этим соотношением,
мы можем переписать A0) в виде
Lz\f)= ^ ~k\^z'^ f)\z"~z) •
lfcl>0
Так как Lz = n~l{z), то Lz,(Dkf) = h' (Dhf) и, следовательно,
последнее разложение совпадает с (9), т. е. L'z{f) = Lz(f) для
любой f^H(D). Отсюда и следует, что U(h', r')czU (h, r).
Таким образом, доказана
Теорема 1. Для любой области наложения (D, я) над С"
можно построить многообразие наложения (D, ft), где D —
пространство всех не тождественно равных нулю линейных
и мультипликативных функционалов над кольцом Н (D),
а проекция п: D->C" определяется по формуле B).
Заметим, что отображение я задает на D локальные ко-
координаты, в которых D можно рассматривать как комплексно
аналитическое многообразие.
Построим теперь вложение (D, я) в (D, ft) в смысле опре-
определения 1 предыдущего пункта. Для этого рассмотрим в D
функционалы специального вида, которые каждой функции
f^H(D) ставят в соответствие ее значение в фиксированной
точке PsD:
(И)
§ 9] ОБОЛОЧКИ ГОЛОМОРФНОСТИ ' 421
Тем самым определено отображение
Ф: P-+hp A2)
области D в D, очевидно, непрерывное. Но по построению
ft о Ф(Р) — n(hP) = я (Я), что и требуется в определении вложения.
Заметим, что отображение Ф локально взаимно однозначно
(ибо из соотношения я ° Ф = я следует, что локально Ф = (ft) ° л)
и голоморфно (как отображение вложения комплексно ана-
аналитических многообразий; см. предыдущий пункт).
Обозначим через D связную компоненту, содержащую Ф(?>),
и через я сужение я на D, тогда (/), я) будет областью над С".
Теорема 2. Область наложения {D, я) является оболоч-
оболочкой голоморфности (D, я).
< Любая функция /е=Я(?)) расширяется (в смысле опре-
определения 2 предыдущего пункта) до функции f<^H{D). В са-
самом деле, при фиксированной / функционалы /ге?) определяют
функцию f: h—>h(f). Эта функция принадлежит Н(Ъ), ибо f
в окрестности h разлагается в степенной'ряд Lz{f). Так как,
в частности, f ° Ф(Р) ~f(hp) — hp{f) = f (Я), то / является Ф-рас-
ширением f.
Остается доказать, что (D, л) является областью голоморф-
голоморфности, а для этого по теореме 3 предыдущего пункта доста-
достаточно убедиться в том, что {?>, й) голоморфно отделима и
голоморфно выпукла. Голоморфная отделимость доказывается
так: если Ь.хфЬ.г, то существует функция /еЯ(О) такая, что
Ь,х{\)фкг{^)\ расширение этой функции f(h) = h{f) и есть функ-
функция из Н ф), разделяющая точки hx и h2.
Чтобы доказать голоморфную выпуклость (D, й), возьмем
произвольное множество 1(<ШО и обозначим р(/С, dD) = r. По
теореме об одновременном продолжении п. 21 (она без изме-
изменений переносится на области наложения) любая feH{D) голо-
голоморфно продолжается в поликруг U {h, r) с центром в любой
точке h, принадлежащей оболочке КНф) множества К, относи-
относительно класса Я (D). Это означает, что степенной ряд, пред-
представляющий функцию f оLz = Lz{f), сходится в поликруге U =
= U (я (h), r). Но по построению области б она содержит
образ 1) при отображении Lz, т. е. U {h, r)cxD и, значит,
р(/г, dD)~^r. Отсюда следует, что р(^я(О)> дЩ^г, а это тл.у
означает голоморфную выпуклость (D, я) >
422 АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ [ГЛ. ИГ
ЗАДАЧИ
1. Пусть[?/ — бикруг {| 2] | < 1, | z21 < 1} и Е — подмножество единичного
круга в С, имеющее 0 своей предельной точкой. Предположим, что функция
/ (zu г2) ограничена в U, голоморфна по г-^ при каждом г2) | г2 | < 1, и голо-
голоморфна по г2 при каждом г1 е Е. Доказать, что / голоморфна в U.
2. Пусть функция / аналитична в области D cz 8\ n по каждой коор-
координате Х\, ..., х2п и в некотором шаре VczD голоморфна по комплексным
координатам zv = xv + ixv+n> v = 1 я. Доказать, что / голоморфна в D
(относительно координат zv).
3. Доказать, что всякая функция, аналитическая по действительным ко-
координатам в области DczC" и плюригармоническая в некотором шаре Кс?)г
плюригармонична во всей D.
4. Доказать, что всякая функция, гармоническая в области ВсС, плю-
рисубгармоническая в некотором шаре FcD, плюригармонична в D. При-
Привести пример функции, аналитической по всем действительным координатам,
плюрисубгармонической в полупространстве х\ > 0 и плюрисупергармони-
ческой при х\ < 0.
5. Описать области DczC", выпуклые относительно класса е?~, состоящег»
из одной функции / (г) = гп.
6. Область Рейнхарта с центром а = 0 тогда и только тогда логарифми-
логарифмически выпукла, когда она выпукла относительно класса мономов га =г
= zfi ... 2*га, где av — целые неотрицательные числа.
7. Если компакт К связен, то его полиномиально выпуклая оболочка К
тоже связна.
8. Если X и Y — непересекающиеся связные полиномиально выпуклые
множества и X\j Y не полиномиально выпукло, то (Х\]У)р связно. ¦
9. Полиномиальный полиэдр Вейля является полиномиально выпуклым
множеством.
10. Всякий компакт К, расположенный в действительном подпростран-
подпространстве С", является полиномиально выпуклым.
11. График комплексной функции ф, гармонической в окрестности
единичного круга, — множество {(г, ф (г)): | г \ =sj 1} — является полино-
полиномиально выпуклым в С2.
12. Пусть К — график функции ф (г) = ] г\ над единичным кругом |z|^l.
Доказать, что для любой области D^K и любого класса еГ голоморфных
в D функций равенство К=К^- невозможно.
- 13. Область сходимости ряда из полиномов (соответственно рациональ-
рациональных функций) является полиномиально (соответственно рационально) вы-
выпуклой.
14. Рационально выпуклая оболочка К% компакта KczCn совпадает со
множеством
{геСя: р (z)ep (К) для всех полиномов р).
15. Доказать, что полиномиально выпуклая оболочка множества MczC2,
состоящего из окружности без малой дуги [Zi = eli, б < t < 2я; z2 = 0} и из
цилиндра <Zi = elt, 0 < t < б; | z2 \ = — j-, содержит круг {| zx К 1, z2 = 0}.
16. Если функция / голоморфна в полиномиально выпуклой оболочке Кр
компакта К, то df {Kp)czf (К).
17. Доказать, что область Д = [геС2:1 2j f+x% > р2} не является областью
-голоморфности.
ЗАДАЧИ 423
18. Доказать, что компакт Л = (|г1|<1, | г2 | ^ | z{ |} нельзя предста-
представить как предел убывающей последовательности областей голоморфности.
19. Пусть О[ и D2 — ограниченные области на плоскости, звездные от-
относительно начала координат, и K,={tz: 0 ^ t ^ I, 2edZ>i X dD2}. Доказать,
что всякая функция, голоморфная в окрестности Д", продолжается до функции,
голоморфной в окрестности DiXD2.
20. Пусть М — дважды гладкое многообразие в С", не имеющее анали-
аналитических касательных плоскостей (отсюда вытекает, что действительная
размерность М не выше я). Доказать, что М является пределом некоторой
убывающей последовательности областей голоморфности.
21. Функция и: D -> R класса С2 тогда и только тогда плюригармо-
нична в области D cz С", когда для всех z <= D и всех aveC
\l, V=l
22. Определение субгармоничности без всяких изменений переносится
на случай пространства Rm, если мажорантой считать гармоническую функ-
функцию 2я действительных переменных. Показать, что плгарисубгармонические
функции в области D с С {— R п) составляют подкласс функций, субгар-
субгармонических в D.
23. Пусть « — полунепрерывная сверху функция в области D, плюрисуб-
гармоническая в D\ E, где Е — относительно замкнутое подмножество D
меры нуль. Доказать, что и плюрисубгармонична в D; если и < <х>.
24. а) Если и плюрисубгармонична в области D с: Сп, то функции ир
(р^\) и е" также плюрисубгармоничны в D. б) Если fefl(D), то функ-
функции 1п+ | f | = max @, In | / ]) и | / \р (р ^ 0) плюрисубгармоничны в D.
25. Пусть D — ограниченная область голоморфности в Сп. Тогда су-
существует плюрисубгармоническая функция и класса С°° в D такая, что
{г е D: и (г) =sj a} €= D для всякого а s R.
26. Пусть К — компакт в С, г° — произвольная точка из его полино-
полиномиальной оболочки Кр, U — окрестность г1 в С" и 5 = (U (] К) U (dU [\ Кр).
Тогда для любого многочлена р выполняется неравенство | р (г°) | ^
^ max |p(z)| (локальный принцип максимума Росси).
27. В обозначениях предыдущей задачи пусть функция и (г) плюри-
плюрисубгармонична в U. Доказать, что
и (г°) < sup и (г).
28. Полиномиально выпуклая оболочка компакта К с. С" совпадает
с множеством
{г е Сп: и (г) =sj sup и для всех функций и, плюрисубгармонических в С"}.
К
29. Обобщенной трубчатой областью называется произведение области
В a R" (х) на область D czR" (у) (при D — R" (у) получаем обычную труб-
трубчатую область). Убедиться, что теорема об оболочке голоморфности труб-
трубчатых областей (теорема 3 п. 27) не распространяется на обобщенные
трубчатые области. Указание: рассмотреть функцию / (г) = —~ ^- в про-
L z,+zi
изведении областей
30. Если р — многочлен или целая функция, то все связные компоненты
множества {х е R": р (х + iy) =?= 0 для V(/ e Rn) выпуклы.
ГЛАВА IV
МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА
В этой главе мы рассмотрим класс функций с особенностями
простейшего типа — мероморфных функций. Главное внимание
будет уделено решению проблем Кузена, которые состоят
в построении мероморфных функций по заданным главным
частям и нулям. Сначала мы рассмотрим элементарное реше-
решение этих проблем в простейших случаях, затем познакомим
читателей с методами алгебраической топологии, которые при-
приводят к общему их решению.
§ 10. Мероморфные функции
30. Понятие мероморфной функции. Определение 1.
Функция / называется мероморфной в области D с: С", если
она; 1) голоморфна всюду в D, за исключением некоторого
множества 3й, 2) не продолжаема аналитически ни в одну
точку & и 3) для любой точки 20е^ существуют окрестность
U и голоморфная в ней функция г|э Ф 0 такие, что голоморф-
голоморфная ъ D[\{U \еР} функция ф = /г|з голоморфно продолжается в U.
Очевидно, что ¦ф(г°) = 0 в каждой точке г0^^3 (иначе вместе
с /tj) и функция / продолжалась бы в некоторую окрестность
точки г0). Если предположить, что для любой 2° е S? функ-
функции ф и ij) не имеют общих множителей, голоморфных в неко-
некоторой окрестности z° и равных нулю в этой точке (на такие
множители всегда можно сократить ф и ф), то ij) будет обра-
обращаться в нуль лишь на множестве еР. Таким образом,
?Р является аналитическим множеством — в окрестности ?/г°
своей произвольной точки оно определяется условием
^ = {геС/г.: -ф(г) = 0}, A)
где o|3S Н (Uz°). Множество S" называется полярным множест-
множеством функции f.
Однако не во всех точках полярного множества $° поведе-
поведение мероморфной функции / одинаково. Точки г0^^3 делятся
на полюсы, в которых функция Ф = /1|з отлична от нуля, и точки
неопределенности, в котарых ср = 0 (мы по-прежнему считаем,
что ф и i|) не имеют общих множителей, голоморфных в точке г°
и равных там нулю). При приближении к полюсу функция
§ Ю] МЕРОМОРФНЫЕ ФУНКЦИИ 425
г Ф
/= ~х~ неограниченно возрастает, а в окрестности точки не-
неопределенности она принимает любое комплексное значение
(именно значение w0 на аналитическом множестве (zg(/x
Ф (г) — woty (z) = 0}, очевидно, содержащем точку неопределен-
неопределенности 2°). Комплексная размерность множества точек неопреде-
неопределенности по меньшей мере на единицу ниже размерности мно-
множества полюсов, ибо точки неопределенности характеризуются
дополнительным условием <р (z) — 0.
Пример. Для функции / =—, мероморфной в С2, полярным мно-
множеством служит аналитическая плоскость {г = 0}. Все точки этой плоскости
являются полюсами, кроме {z = 0, до = 0}, которая есть точка неопределен-
неопределенности.
Как и в случае одного переменного, справедлива следующая
теорема о рациональных функциях (см. ч. I, п. 24):
Теорема 1 (Вейерштрасс, Гурвиц). Любая функ-
функция f, мероморфная в компактифицированном пространстве п
комплексных переменных (Сп или Р"), является рациональной.
< Пусть / мероморфна в Сп; тогда при любом фиксирован-
hom_(z?, ..., Zv-i, Zv+i, ..., zJjeC" она мероморфна по zv
в С (v=l, ..., п). По теореме 4 из п. 24 ч. If является
рациональной функцией от переменного zv. Но функция, ра-
рациональная по каждому переменному при любых фиксирован-
фиксированных остальных, является рациональной (см. задачу 16 к гл. I).
Доказательство в случае пространства Рп предоставляется
читателю >
Теорема 2. Рациональная функция f, существенно зави-
зависящая от п ^ 2 комплексных переменных, имеет хотя бы. одну
точку неопределенности в С'г.
< Если / многочлен, то он имеет хотя бы одну точку не-
неопределенности в бесконечности. В самом деле, мы можем
считать, что -^-@) и -5~\0)^0 и что коэффициент при стар- -
| 2
шей степени zx равен 1 (это можно сделать линейной заменой
координат). Многочлен gb(zx) = f(zu a2, 0, ...,0) — b, где Ъ е С,
при больших а2 имеет большие коэффициенты. Из теоремы
Виета следует, что у него должен быть хотя бы один большой
по модулю корень al{b). По последовательности {af](b), af >
0, ..., 0), сходящейся к точке (оо, оо, 0 0), многочлен f
стремится к пределу Ь; так как b можно выбирать произвольно,
то (оо, оо, 0, ..., 0) — точка неопределенности f. Остается рас-
рассмотреть случай f = —, где р и q — взаимно простые много-
426 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
члены не ниже первой степени. В этом случае точками неопре-
неопределенности будут решения системы уравнений р = 0, <7 = 0,
а в случае «^2 эта система непременно имеет конечные или
бесконечные решения >
В некоторых вопросах удобнее пользоваться другим опре-
определением мероморфной функции, в котором полярное мно-
множество заранее не фиксируется. Более того, в этом новом опре-
определении функция не предполагается заданной в целом во всей
области, а характеризуется лишь ее локальными свойствами.
Описательно говоря, под мероморфной здесь понимается функ-
функция, которая локально представляется как отношение двух
голоморфных функций, причем такие локальные представления
в пересекающихся областях должны быть согласованы между
собой так, чтобы в совокупности они образовывали «единую»
функцию. Особое преимущество это определение имеет при
изучении функций на многообразиях, поэтому мы и рассмотрим
сразу этот случай !).
Пусть дано комплексно аналитическое многообразие М и
область D на нем. Рассмотрим произвольное открытое покры-
покрытие <%f = {Ua} этой области (UaczD — открытые множества,
объединение которых совпадает с D, индекс а пробегает не-
некоторое множество Л) и семейство троек fa — {Ua, ф„, %), <хе=Л,
где фа и г|>а — функции, голоморфные в Ua, причем ни одна
¦фа Ф 0. Кроме того, мы предположим, что выполняется сле-
следующее условие согласованности: если ?/а, Л Ua, Ф 0, то в этом
пересечении
Множество всех семейств {fa}, удовлетворяющих в D опи-
описанным условиям, мы обозначим через 3fl(D).
Наряду с {/а}, аеЛ, рассмотрим еще семейство троек
&3 = С^з» Фз> ^зI Р *= ^> из ^ (^)- Объединением этих семейств
мы будем называть семейство всех троек, принадлежащих
{/а} или {gv}. Два семейства {fa} и {gJ из ffi{D) мы назовем
эквивалентными, если их объединение также принадлежит Tt(D).
Очевидно, что в этом определении существенно лишь требова-
требование, чтобы любые две тройки из объединения {/а} с {g^} удо-
удовлетворяли условию согласованности.
Проверим, что принятое определение эквивалентности удо-
удовлетворяет ' обычным аксиомам. Рефлексивность и симмет-
') Определение, о котором мы сейчас говорим, еще не полностью ло-
локализовано, оно имеет «предпучковый» характер (смысл этого термина
скоро выяснится). В дальнейшем мы приведем еще вполне локализован-
локализованный его «пучковый» вариант.
4 10] МЕРОМОРФНЫЕ ФУНКЦИИ 427
ричность очевидны, а для проверки аксиомы транзитивности
достаточно проверить, что если {fj ~ {gp} и {gp}~{/iY}, то для
объединения {/J и {hy} выполняется условие согласованности.
Возьмем произвольные тройки /„ = (?/„,' cpa, ^а) и hy=(U%, tf, Щ\
для которых Uad и"Ф0, и выберем ?3 = (^з> Фз> %) так> чтобы
A = Ua[}U'?i[}U"=?0 (это возможно, так как (J U'& = D). В силу B)
для объединений {/а| с {gp] и {gp} с {/ц,} на Д имеем сра^ =
= Фр*а И Фр< = <%' a ЗНЭЧИТ> Ф„Ч>ЭД' = ФрФо*, = ^'аФ^Р'
откуда (в силу условия tyg ^ 0) следует, что qy|}'' = i|yp" ').
Определение 2. Мероморфной функцией в области D,
принадлежащей комплексно аналитическому многообразию М,
мы будем называть любой класс эквивалентности f на мно-
множестве Ш(О). Иными словами, мероморфная функция —это
совокупность семейств троек {fa}e=9№(?)) таких, что любые две
тройки из этой совокупности связаны условием согласован-
согласованности B).
Если мероморфная функция / задана в области D cz M, то
в силу условия B) в окрестности каждой точки Ре=?) отноше-
отношение -^~- одинаково для всех троек (Ua, фа, я|за) = /а любого
семейства {fa}, представляющего класс /. В этом смысле и
можно говорить, что мероморфная функция локально пред-
представляется как отношение двух голоморфных функций.
По отношению к мероморфной функции / точки области D
можно разбить на два типа. Будем говорить, что / определена
в точке PeD, если существует тройка fa — Wa, ц>а, tj)a), при-
принадлежащая к какому-либо семейству {/j, которое представ-
представляет /, и такая, что Р е= Ua, а фа и г|за не обращаются
в точке Р одновременно в нуль. Каждой точке Р, в которой
мероморфная функция/ определена, она ставит в соответствие
значение f (¦P) = -f° ,„,— конечное, если if>a(P)^O, и бесконеч-
бесконечна \")
ное, если tya(P) = 0. Это значение, очевидно, не зависит ни от вы-
выбора представителя {fa} класса эквивалентности /, ни от выбора
тройки из семейства {/а}, т. е. определяется рассматриваемой
мероморфной функцией. Множество точек, в которых f опре-
определена, очевидно, открыто. Точки области D, в которых
мероморфная функция /, заданная в D, не определена, обра-
образуют множество неопределенности этой функции.
*) Есл:: i:e избегать деления, то доказательство становится совсем три-
Фа ФЗ Фр Фу Ф« фУ
виальным: из — = —'т и —7- = —— следует, что — =—jr •
% ^ ^ * * 4
428 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
t
Покажем, как можно определить действия над мероморф-
мероморфными функциями. Пусть в области D с M заданы две меро-
морфные функции f и g и семейства троек {/J, {gp}e=9№(?))
соответственно представляют эти функции. Рассмотрим семей-
семейство всех троек hy = {Uy, <fy, i|)Y), у е= Г, (J Uy = D, для кото-
которых существуют fa = (U'a, <р'а, %) е {/„} n\ = (U%, <#, 4#N={gp}
такие, что UyciU'a{\U'^ и в ?/у справедливы соотношения1)
Нетрудно проверить, что {/iY} e= 9И(?>) —условие согласован-
согласованности проверяется простой выкладкой, а остальные условия
очевидны. Класс эквивалентности h на Ш(Б), содержащий
построенное семейство {hy}, и называется суммой мероморф-
ных функций fug (обозначение обычное: h = f + g). Анало-
Аналогично определяется произведение h = fg, только C) нужно
теперь заменить соотношениями
Ф^ФаФр'- %=$$• D)
Пусть / —мероморфная в D функция, не. равная тождест-
тождественно нулю. Из теоремы единственности следует, что тогда
для любой тройки fa = {Ua, фа, г|:а) из семейства {/J, предста-
представляющего класс /, функция ц>аф0 в Ua. Поэтому семейство {ga},
состоящее из троек (Ua, ij)a, фа), которые получаются из fa пере-
перестановкой фа и г|:а, также принадлежит Tt(D). Класс эквива-
эквивалентности на Ш(О), содержащий \ga}, мы назовем мероморф-
ной функцией -у-; очевидно, произведение / • -г- дает мероморф-
ную функцию, тождественно равную 1. Частное двух
мероморфных в D функций / и g Ф 0 мы определим как про-
произведение / • ¦—.
б
Нетрудно убедиться в том, что совокупность функций,
мероморфных в области D, с определенными выше действиями
образует (коммутативное) поле. Очевидно также, что при дей-
действиях над мероморфными функциями их значения подвергаются
тем же действиям: имеем {f + g){P) = f(P)+g(P), fg{P) = f{P)g{P),
') Соотношения C) выражают, что —— = —~ н—§у во всех точках, где
определены обе функции fag.
10] МЕРОМОРФНЫЕ ФУНКЦИИ 429
во всякой точке PgD, где определены функ-
функции fag.
31. Первая проблема Кузена. Естественно возникает проб-
проблема построения глобально определенной во всей области
мероморфной функции f по локально заданным ее «главным
частям», т. е. мероморфным функциям, локально отличаю-
отличающимся от f на голоморфные функции. Приведем общую по-
постановку этой проблемы.
Проблема Кузена I (аддитивная). Дана область/),
принадлежащая аналитическому многообразию М, а также
открытое покрытие ^ = {^а}аеЛ этой области. В каждом Ua
задана мероморфная функция /а так, что выполняется сле-
следую щее условие согласованности:
В любом пересечении Ua^ = UaCiV^ разность /о~/р является
голоморфной функцией.
Требуется построить мероморфную в D функцию f так,
чтобы в каждом Ua разность / — /„ была голоморфной.
Пусть, в частности, D — плоская область; зададимся после-
последовательностью точек ave?), не имеющей предельных точек
Pv c(v)
в D, и последовательностью главных частей gv (z) = V—-—-.
Для любого открытого покрытия {и„} области D обозначим
через fa сумму gv по всем точкам av e= Ual); если же Ua не
содержит точек av, мы положим /„ = 0. Условие согласован-
согласованности при этом, очевидно, выполняется. Проблема Кузена
с этими данными сводится, следовательно, к задаче построения
мероморфной в области D функции с заданными полюсами и
главными частями. Аддитивная проблема Кузена является,
таким образом, естественным распространением этой задачи
на пространственный случай.
Разрешимость задачи для любой плоской области D дока-
доказывает теорема Миттаг-Леффлера (ч. I, п. 42). Однако в про-
пространстве существуют области, для которых не всякая про-
проблема Кузена разрешима.
Пример. Пусть ?> = С2\{0} и cpBj)— функция, голоморф-
голоморфная в С \ {0}, с (неустранимой) особенностью в точке zx = 0.
Рассмотрим покрытие D окрестностями следующих двух типов:
для точек a = (aj, 0), ctj Ф 0, в качестве Ua возьмем шар
В (a, jdjl), а для точек a = (aj, a2), a2 ?= 0, — шар В{а, |сс2|).
') Условимся считать, что в каждом Ua имеется лишь конечное число
точек av.
430
МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА
[ГЛ. IV
В окрестностях первого типа положим /а(z) = 5i?L_j a B окрест-
окрестностях второго типа— /а(г) = 0; эти данные Кузена, очевидно,
согласованы (см. схему на рис. 113).
Допустим, что поставленная проблема Кузена разрешима
и существует мероморфная в D функция f, для которой
f — fa = К голоморфна в Ua (a e D — любое). Тогда (глобально
определенная) функция g = zj, в каждой окрестности Ua пер-
первого типа равная <р{гг) + z2ha(z) и равная ha{z) в каждой Ua
второго типа, голоморфна в D (заметим,
что в Ua первого типа zx Ф 0). По тео-
теореме Осгуда — Брауна g продолжается
в точку 2 = 0 до целой функции. Но тогда
и функция g (zu 0) = (f(z1) (мы пользуемся
тем, что плоскость {г2=0} покрывается
лишь окрестностями первого типа) яв-
является целой, а у нас ср имеет особен-
особенность в точке г, = 0. Противоречие и
доказывает неразрешимость поставлен-
поставленной проблемы Кузена.
Рис ИЗ. Приведем необходимое и достаточное
условие разрешимости проблемы Кузена, »
которое, впрочем, столь близко к самой проблеме, что его
можно рассматривать как изменение формулировки. Имея дан-
данные Кузена {/J для покрытия {Ua} области ДсМ, мы можем
в каждом пересечении С/ар = Ua П U& рассматривать разность
h4 = fa-fp A)
голоморфную в ?/ар в силу условия согласованности. В каждом
Uар очевидно, имеем
/гар + /гра = О, B)
а в каждом пересечении Uafiy = Ua П t/p П Uy —
h 4- h 4- h = 0 (Я\
Любое семейство функций /гаре= H(Ua&)-, удовлетворяющих
условиям B) и C), мы будем называть голоморфным коциклом
для данного покрытия & — {Ua} области D. Если эти функции
связаны с данными Кузена соотношениями A), то коцикл {/гар}
будем называть соответствующим проблеме Кузена {/J. Наконец,
голоморфный коцикл {/гар} мы назовем когомологичным нулю,
если для всех аеЛ существуют функции ha^ H (Ua) такие,
что в каждом пересечении С/ар
"¦& ~ "а ~ "ав* У*/
§ 10] , МЕРОМОРФНЫЕ ФУНКЦИИ 431
Введенные термины и позволяют сформулировать условие
разрешимости, о котором мы говорили:
Теорема 1. Для разрешимости проблемы К,узена {fa} для
данного покрытия <& области D необходимой достаточно, чтобы
соответствующий этой проблеме голоморфный коцикл {ЛаЛ был
когомологичным нулю.
< Если проблема Кузена {/J разрешима, то существует
функция /, мероморфная в D и такая, что все разности
f — fa = ha голоморфны в t/a (ae А). Отсюда для соответствую-
соответствующего голоморфного коцикла /ia» имеем
"ар = /а ~ / р — "з ~ па>
а это и означает, что {/гар} когомологичен нулю.
Пусть, обратно, голоморфный коцикл {hafi}, соответствующий
проблеме Кузена {fa}, когомологичен нулю. Тогда существуют
функции /гае Н (Ua) такгге, что /гр — ha — /гар в каждом пере-
пересечении f/ap, т. е. в каждом Ua& имеем /а — /„ = /L — ha или
/а + К = /р + Лр
для любых а, ре Л. Таким образом, функции fa + ha, меро-
морфные в Ua, не зависят от выбора окрестности Ua и во всей
области D глобально определена мероморфная функция /,
равная fa +ha в каждом Ua. Она и решает рассматриваемую
проблему Кузена >
Перефразируем доказанную теорему. Для данного покры-
покрытия {Uа} области D голоморфные коциклы /гар можно складывать
(поточечно в каждом пересечении f/ag), и относительно этой
операции они образуют группу, которую мы обозначим Z1^)
и будем называть группой голоморфных коциклов для данного
покрытия $Л В этой группе есть подгруппа В1(^) голоморф-
голоморфных коциклов, когомологичных нулю. Факторгруппу
мы будем называть (первой) группой когомологий для покры-
покрытия & области D (с голоморфными коэффициентами).
Элементами Н1№) служат классы когомологичных друг
другу голоморфных коциклов. Тривиальность этой группы
(Я1 (&f) = 0) означает, что для рассматриваемого покрытия все
голоморфные коциклы когомологичны нулю. Поэтому теорему 1
можно сформулировать в таком виде:
Теорема V. Для разрешимости проблемы кузена'с про-
произвольными {/J для данного покрытия <%f области D необходцмо
432 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. PV
и достаточно, чтобы соответствующая группа когомологий была
тривиальной:
Я1 (80 = 0. F)
Введенные выше понятия допускают прямую аналогию
*в классе С°° бесконечно дифференцируемых функций. Пусть
D — область на многообразии М е= С°° и D= [JUa — ее покры-
тие окрестностями на М; пусть еще в каждом пересечении
t/ap=t/an f/p заДана бесконечно дифференцируемая функция /гаE.
Если система таких функций {ha^} удовлетворяет условиям B)
и C), то мы будем называть ее дифференциальным коциклом.
Если при этом выполняется еще аналог условия D), т. е.
в каждом Ua существует функция ha e С°° такая, что Ь$ — па = па„
в f/a|3 для всех a, (J е= А, то коцикл {/гар} называется когомоло-
когомологичным нулю.
Точно так же, как в голоморфном случае, определяется
и первая группа когомологий (с бесконечно дифференцируемыми
коэффициентами). Оказывается, однако, что эта группа всегда
тривиальна:
Теорема 2. Для любого открытого покрытия У/ области D
на многообразии М е= С°° любой дифференциальный коцикл
кого мо логичен нулю.
< Построим для {Ua} разбиение единицы, т. е. семейство
функций eaeC°°(Z)) таких, что: 1) 2еа(/>)=1 для всех точек
асЕЛ
Р е D, 2) носитель каждой еа компактно принадлежит Ua
и 3) каждая точка Р е D имеет окрестность, пересекающуюся
лишь с конечным числом носителей еа. Для этого построим
сначала локально конечное покрытие Vt, i e= /, такое, что для
каждого ie/ задано <х(г)еЛ, при котором V{czUa{l) (суще-
(существование такого покрытия следует из того, что М является
объединением возрастающего семейства компактов; покрытие
^>=={1/7г} называют подчиненным покрытию СМ). Построим раз-
разбиение единицы в/ е= С°°, i е= /, подчиненное покрытию Т (см.
п. 11), и положим еа = 0, если афа{1) ни для какого I, а
eaW = 2e/> сумма по всем j?l, для которых a(/) = a(i). Семей-
Семейство {еа}, очевидно, удовлетворяет указанным условиям.
При помощи этого разбиения единицы мы сгладим функ-
функции Лар, заменив их функциями
ial 0 в Ua\Uia.
§ 10] МЕРОМОРФНЫЕ ФУНКЦИИ 433
При этом мы продолжили hia во всю окрестность Ua, но отлич-
отличной от нуля она оказывается лишь в пересечении Uia. Теперь
в каждой Ua мы можем определить функцию
К *=%%*> G)
здесь суммирование распространяется на все множество индек-
индексов, но в каждой точке Ре(/а отлично от нуля лишь конечное
число слагаемых.
Очевидно, все /jae=C°° и в любой точке каждого пересече-
пересечения ич
h - й« = 2 </4 - h'ta) = 2 et (кф - hta). (8)
I i
Но так как {hap} — коцикл, то в каждой точке пересечения ?/а„г
в силу B) и C) имеем /г,-р — hia~ hai + ht^ = ha&, поэтому со-
согласно (8) в каждом t/ap
Таким образом, семейство {/ij и есть искомое, т. е. {/гаэ} —коцикл,
когомологичный нулю >
Читатель, несомненно, заметил, что введенные здесь термины
аналогичны тем, которые были введены в п. 14 при изучении
дифференциальных форм. Напомним их, ограничиваясь фор-
формами первой степени с коэффициентами класса С°°, которые
в локальных комплексных координатах zv, zv имеют вид
n
ю = Ъ av dzv, (9)
v=l
т. е. формами бистепени @, 1). В отличие от п. 14 мы будем диф-
дифференцировать эти формы лишь по переменным zv (v = 1, . . ., п)
и оператор дифференцирования по этим переменным обозначим
через д. Таким образом,
(напомним, что штрих означает упорядоченное суммирование:
l^[x<v^n). Форма (9) называется замкнутой формой или
коциклом, если дш — 0, т. е.
даи dav
28 Б. В. Шабат
434 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ IV
Коцикл (замкнутая форма) со называется когомологичным нулю
(или точной формой), если существует функция /еГ такая,
что со = df, т. е.
a^ik (v=1> ••••/l)- U1)
Коциклы образуют (по сложению) группу, которую мы обо-
обозначим через Z1, а коциклы, когомологичные нулю, — ее под-
подгруппу В1. Факторгруппу
Я1 = ZVB1
назовем (первой) группой когомологий с коэффициентами
в группе дифференциальных форм (мы ставим значки над
буквами, чтобы отличить эти группы от таких же групп, вве-
введенных в п. 12 на основе обычного дифференцирования d,
по всем координатам zv и zv).
В следующем пункте мы убедимся в том, что связь диф-
дифференциальных форм с проблемой Кузена достаточно глубока
и не исчерпывается сходством терминологии.
32. Решение для поликругов. Здесь будет доказана разре-
разрешимость аддитивной проблемы Кузена в простейшем случае,
когда область D и все области покрытия Ua являются поли-
поликругами. В частности, сюда относится Случай покрытия всего
пространства Сп поликругами. При доказательстве нам пона-
понадобится
Лемма. В любой односвязной области D ci С для любой
функции g е= С°° неоднородная система Коши — Римана
Цг-8Ь) A)
разрешима в классе C°°(D). Если при этом g является голо-
голоморфной (или класса С°°) функцией некоторого параметра,
то и решение f голоморфно (или бесконечно дифференцируемым
образом) зависит от него.
< Пусть сначала функция g финитна, т. е. равна нулю
вне некоторого компакта из D. По формуле Кошн — Грина
(п. 18 ч. 1) имеем тогда
D
где da ~ элемент площади.
Рассмотрим теперь функцию
§ 101 МЕРОМОРФНЫЕ ФУНКЦИИ 435
мы можем продолжить g на всю плоскость, полагая ее равной 0
в C\D, и тогда считать, что интегрирование распространяется
на С. Сделаем еще замену переменного интегрирования ?—>? + г,
тогда будем иметь
Дифференцированием под знаком интеграла (которое, очевидно,
законно) находим
_ 1 Г fii*L
л J J dz ?
dz
или, возвращаясь к старому переменному интегрирования,
_д/_ = _ ± Г Г dg da
dz я J J dl i-z'
Сравнивая это с B), мы убеждаемся, что f удовлетворяет
системе A). Дифференцировать интеграл- D) по z можно любое
число раз, следовательно, feC°°(D). Если g голоморфно зависит
от параметра, то и интеграл так же от него зависит. Для
финитных g лемма доказана.
В общем случае мы возьмем компактное исчерпывание D
односвязными областями Gv (Cv g CvtI, [}GV = D) и построим
функции gveC°°(.D) так, чтобы gv = g в Gv и gv = 0 в D\Gv+l.
По доказанному каждая система
dz ~gv
разрешима в классе С°° (D); мы покажем сейчас, что решения /v
можно выбрать так, чтобы в каждой Gv было
IfvWvK-^r (v=l,2, ...)• E)
В самом деле, выберем решение f, по формуле C), в которой g
заменена функцией glt потом возьмем f2 по той же формуле
с заменой g = g2 и заметим, что разность J2~fi голоморфна
в G, [ибо там -Jj(f2 — fi) = ^2 — ё\ = 0)- По теореме Рунге (п. 22
ч. I) можно подобрать многочлен Pt так, чтобы в Gi было
28*
436 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
теперь видно, что /2 = f2 — Pj удовлетворяет системе -r^ = g2
и условию E) при v=l. Точно такой же прием можно при-
применить и для v = 2, 3, ....
Построенная последовательность fv на каждом компакте
К Ш D равномерно сходится к функции
V=l
В любой G^ функция / представляется как конечная сумма
функций класса С°° и суммы равномерно сходящегося ряда
из голоморфных функций /v+i ~/v> гДе v^ (X (при v ^ jj, на Gy,
имеем fv+i =-1Х- = gj. Следовательно, / е С°° (D) и -г-ь- =
= lim -—¦ =g всюду в D; голоморфная зависимость f от пара-
метра, от которого зависит g, следует из теоремы Вейерштрасса
(п. 22 ч. I) >
Приступаем к доказательству объявленной выше теоремы.
Теорема. Для любого поликруга Z) = {z^C": |zv|<^v},
/?v^oo, и любого его покрытия %f = {Ua} поликругами любая
аддитивная проблема Кузена разрешима.
< С учетом теоремы 1 предыдущего пункта достаточно
доказать, что для рассматриваемого покрытия <%? группа кого-
мологий Я1 (^) тривиальна. Вместо этого мы сначала докажем
тривиальность группы Я1, а затем установим, что Я1 {%f) изо-
изоморфна Я1.
I. Группа Я1 тривиальна. Нам нужно доказать, что каждая
п
замкнутая форма со = 2 avdzv с коэффициентами из С°° (D)
точна, или, другими словами, доказать разрешимость в классе
С°° (D) любой неоднородной системы Коши —Римана
df = <a F)
для "любой формы со eC°°(.D) бистепени @,1), для которой
дсо = О. Перепишем F) в виде системы
df --zv> v=l га, G)
dzv v
и ее разрешимость в классе С°° {D) будем доказывать индук-
индукцией по га.
При га=1 утверждение доказано леммой; предположим,
что оно справедливо, когда число переменных не превосходит
§ 10] МЕРОМОРФНЫЕ ФУНКЦИИ 437
я— 1, и докажем его справедливость для системы G) с п пере-
переменными. Рассмотрим последнее уравнение этой системы
и обозначим через g его решение в круге Dn = {\ zn |< RJ —
функцию от zn, зависящую от 'z — {zx, ..., zn_x) как от пара-
параметра. Решение системы G) мы будем искать в виде f = g + cp,
тогда <р должна быть голоморфной по zn в Dn, а по остальным
переменным в поликруге 'D — {\ zx \<RX, ..., I zn_x |</?„_,} удовле-
удовлетворять системе
(8)
ag ag ^ 5
Так как форма со замкнута и 11-^- = 1__, то — =
для всех jj,, v=l, ..., п—\. Следовательно, форма
«—1
замкнута и, по индуктивному предположению, существует реше-
решение <ре C^i'D) системы (8), зависящее от zn как от параметра.
Остается проверить, что <р зависит от zn голоморфно, а для
этого достаточно убедиться в том, что правые части системы (8)
голоморфно зависят от znl). Но мы имеем
dbv dav d2g dav дап „
dzn dzn dzn dzv dzn dzv ~
для всех v=l, ..., n—\ в силу замкнутости формы со.
II. Группа Нг(^) изоморфна группе Н1. Пусть {/гар} —про-
—произвольный голоморфный коцикл для покрытия {?/а}. Так как
по теореме 2 предыдущего пункта в классе С°° каждый коцикл
когомологичен нулю, то существуют функции ga e C°° (Ua) такие,
что в каждом пересечении [/а|3
К$ = gp ~ ga- (9)
Для любого аеЛ рассмотрим форму
га
azv v
v=l
замкнутую в смысле оператора д. В пересечении Ua& в силу (9)
имеем
cur - coa = а/г„я = О,
1) Это утверждение доказывается индукцией по п при помощи леммы.
438 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
ибо коцикл {йод} голоморфен. Поэтому формы юа, по существу,
определяют единую форму соеС°° (D), лишь по разному зада-
задаваемую в различных окрестностях Ua. Форма со, очевидно,
замкнута в D.
Мы построили соответствие между голоморфными коциклами
{/га|3} и замкнутыми формами со. При этом заданному коциклу
соответствует много форм, но если со и со' соответствуют од-
одному {/zafj], то в каждом [/ар имеем gR - ga = g^ - g'a = AaR, т. е.
разности gp — g& = g'a — ga образуют в D единую функцию
geC°°. В каждом Ua имеем dg'a — dga = dg, ¦ поэтому со'— со =
= dg, т. е. со' отличается от со на точный дифференциал, и,
следовательно, обе эти формы принадлежат одному классу
эквивалентности. Далее, если [A^| и (AaR] эквивалентны, то
в каждом Va!,
где А„ и ha — голоморфные функции; если {AaR} соответствует
форма со, равная dga в каждой Ua, то в силу (9) и A0) имеем
К$ = 8$ + Н ~ (ёа + Ю> и> значит, {Ау соответствует форма со',
которая в каждой [/„ равна Ъ(ga + ha) = dga, т. е. форма, рав-
равная со. Таким образом, фактически мы построили отображение
ZljBl->ZljBl A1)
группы Н1 №) в Я1; это отображение, очевидно, является го-
гомоморфизмом.
Покажем, что построенное отображение взаимно однозначно,
т. е. что его ядро равно нулю. Пусть это не так, т. е. существует
не когомологичный нулю коцикл {/zai5}, которому соответствует
точная форма со = df. В каждом ?/aR имеем AaR = gR — ga и
со = dga в каждой Ua, т.е. там д (ga — f) = 0 и ga~f = Aa — голо-
голоморфная функция. Но тогда AaR = (/ + Ар) — (f + Aa) = AR — Aa,
и коцикл {/zap} когомологичен нулю.
Остается показать, что A1) является отображением на Я1.
Пусть cosC°°(Z)) — произвольная замкнутая форма бистепени
@, 1). Так как по условию все Ua — поликруги, то по доказан-
доказанному в I эта форма локально точна: существует _§„бС°°( Ua)
такая, что со = dga в Ua. В пересечениях ?/ед имеем 5(gR — ga) =
= со — со = 0, т. е. gR — ga = AaR — голоморфные функции. Они,
очевидно, образуют голоморфный коцикл {Aaft}, который со-
соответствует форме со >
§ 10] МЕРОМОРФНЫЕ ФУНКЦИИ 439
Приведенное доказательство без всяких изменений распро-
распространяется на поликруговые области, представляющие собой
произведения односвязных областей. На самом же деле ад-
аддитивная проблема Кузена разрешима для произвольных об-
областей голоморфности — однолистных или многолистных. Однако
в общем случае доказательство разрешимости этой проблемы
требует привлечения новых идей. Мы будем говорить о них
в следующем параграфе.
33. Применения. Вторая проблема Кузена. Здесь мы хотим
привести примеры задач, приводящихся к аддитивной про-
проблеме Кузена. Начнем с одной теоремы о продолжении. Чтобы
ее сформулировать,, условимся называть голоморфную функ-
функцию <р определяющей функцией комплексно (п — 1)-мерного
множества М в некоторой области D, если, во-первых,
М П D = {z<^D: <p(z) = O} и, во-вторых, если какая-либо функ-
функция if>i=#(.D) обращается в 0 на М, то она представляется
в виде -ф = ф/г, где h^H{D). Последнее условие выражает не-
некоторого рода минимальность определяющей функции (так,
для плоскости {zi = 0} функция <p = z1 является определяющей,
а ф = г^ —нет); определяющая функция, конечно, не единственна,
но если ф[ и ф2 — две определяющие функции одного мно-
множества М в D, то их отношение ф]/ф2 —голоморфная в D и
отличная от нуля функция. Чтобы формулировка теоремы
о продолжении имела общий характер, мы воспользуемся
высказанным без доказательства в конце предыдущего пункта
утверждением о том, что аддитивная проблема Кузена раз-
разрешима для любой области голоморфности.
Теорема 1. Пусть DczCn — произвольная область голо-
голоморфности и МсЬ — аналитическое множество, определяю-
определяющая функция которого феЯ(О). Тогда любую функцию g, ло-
локально голоморфную на М, можно продолжить до функции f,
голоморфной во всей, области D.
< Локальная голоморфность функции g на М означает,
что для каждой точки 2°еМ найдется окрестность Со такая,
что g продолжается в ней до функции /оеЯ(Со). Учитывая
это, мы можем рассмотреть такое открытое покрытие {f/J
области D, что в каждой Ua существует голоморфная функция fa,
совпадающая с g в пересечении Ua(]M:
'а Ша!)М ~ & 'иаПМ' w
иа
если Ua(]M пусто, то мы положим fa=0. В любом пересече-
пересечении Uag разность /„ — /р обращается, следовательно, в нуль
на М П &ар> и по свойству определяющей функции в этом пере-
пересечении /а - /6 = фАар, где /гареЯ (?/„„). Мы примем мероморфные
440 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
функции (/о/ф) за данные Кузена для покрытия {Ua} (они,
очевидно, согласованы), и тогда
«ар ф V)
будут образовывать голоморфный коцикл, т. е. удовлетворять
условиям B) и C) предыдущего пункта. Так как D — область
голоморфности, то эта проблема Кузена разрешима, и, значит,
существуют функции ha^H(Ua) такие, что Ар — ha = /гаC в лю-
любом [/ар. Подставляя сюда значение /га|3 из B), найдем, что
fa + Фа = fp + Ф^р в каждом ?/аE. Отсюда видно, что в области D
определяется голоморфная функция /, равная fa + <pha в каж-
каждой окрестности Ua. Но так как ср \м = 0, то, пользуясь еще
соотношением A), мы найдем, что
/I с 1 I
Таким образом, / действительно является искомым продол-
продолжением функции g >
Теорема 1 позволяет получить разложение Хефера, кото-.
рое мы без доказательства применяли в п. 18 при выводе ин-
интегральной формулы Вейля. В основе лежит следующая
Лемма. Пусть DczCn — область голоморфности и {п — k)-
мерная аналитическая плоскость n = {zeC": zl— ... = zk = 0}
имеет с ней непустое пересечение. Тогда любая функция
/(), равная нулю на ПП-О. допускает в D представление
C)
еде все g\,e#(Z)).
< Доказательство будем вести индукцией по k. При k = 1
утверждение очевидно, ибо в качестве gx можно принять
функцию f/z{; пусть оно верно для k — l. Обозначим G = D fifes = 0};
все связные компоненты этого пересечения являются, очевидно,
областями голоморфности в пространстве С" переменных
z,, ..., гй_!, гш zn. Сужение f\{z^0}^H(G) и по условию
обращается в нуль на G П {%\ — • • • — %к-\ — 0}- Отсюда, согласно
индуктивному предположению, вытекает, что в G имеет место
представление
г v _ о / ~ ~ -, \
I гг.=0) — ?а Z\igy\Z\, . , ., Zfc-i, Zk+l, • . ., Zn),
x R ' v=l
где все g°v^H(G). По теореме 1 все g°v продолжаются с G =
= D П {zk = 0} во всю область D до голоморфных функций gv{z].
10] МЕРОМОРФНЫЕ ФУНКЦИИ 441
Рассмотрим теперь разность
k-l
очевидно, ф|, _Ci==0, и, по свойству определяющих функций,
найдется gk^H{D) такая, что <р (г) = zkgk (г) для всех ге/).
Отсюда видно, что представление C) справедливо и для k >
Из этой леммы совсем просто выводится
Теорема 2 (Хефер). Пусть DczCn — область голоморф-
голоморфности и W (г)еЯ (D) — произвольная функция. Существуют
такие функции Pv(g, z)e#(D X D), v= 1, ..., «, чго (9ля всех
?, гей справедливо представление
W4E)-W4z)~ J3(?v-zv)/Mg, г). D)
v=l
•« Разность 1Г(Й-1Г(г)еЯфХ?>), и так как D X ?-об-
?-область голоморфности в С2", а эта разность обращается в нуль на
«-мерной аналитической плоскости П = {г, g: zv = gv, v = 1, ...,«},
то, положив Zv = gv — 2V, Zn+V = 2v (v = 1 /г), мы можем
применить к рассматриваемой разности лемму. Получим нужное
разложение D) >
В качестве следующего примера задачи, приводящейся
к аддитивной проблеме Кузена, мы рассмотрим один простой
случай разрешимости так называемой мультипликативной или
второй проблемы Кузена. Если первая проблема представляет
собой пространственный аналог теоремы Миттаг-Леффлера, то
эта проблема является таким же аналогом теоремы Вейер-
штрасса о существовании голоморфных функций с заданными
нулями. Вот ее постановка:
Проблема Кузена II (мультипликативная). Дано
открытое покрытие ^ = {U^, as Л, области D на аналитичес-
аналитическом многообразии М и в каждой Ua — голоморфная функция fa;
при этом ни одна /а#0 и выполняется следующее условие
согласованности:
В любом пересечении ?/a|3 = Ua (] U$ частное fjf^ является
голоморфной функцией.
Требуется построить голоморфную в D функцию f так,
чтобы в каждой ?/„ частное f/fa было голоморфной функцией,
не обращающейся в нуль.
Замечание. Из условия согласованности следует, что
частное fJf^O в i/ap, ибо там вместе с fjf& голоморфно и
частное у/„.
442 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
Имея данные второй проблемы Кузена {/J для рассматри-
рассматриваемого покрытия <U', мы можем в каждом пересечении рас-
рассмотреть функции
h = — E)
голоморфные и отличные от нуля в силу условия согласован-
согласованности. Эти функции в каждом ?/„» удовлетворяют условию
а в каждом t/apv = Uaf\ [/рП Uy -г- условию
AapApYAva=l. G)
Мы видим, что эти условия представляют собой мультипли-
мультипликативный аналог условий B) и C) п. 31, имеющих аддитивный
характер. Как и в п. 31, просто проверить, что разрешимость
проблемы сводится к построению функций Аа, голоморфных и
отличных от нуля в окрестностях Gа(аеЛ) таких, что
в каждом пересечении С/а|3.
Возникает естественное желание свести вторую проблему
Кузена к первой при помощи логарифмирования. Так как
функции /zap голоморфны и отличны от нуля, то, предполагая,
что пересечения [/а„ односвязны :), мы можем в каждом из них
выбрать некоторую голоморфную ветвь lnAai3 = ga|3, и притом,
в силу условия F), так, что
Из G) мы тогда получим, что в пересечениях t/apv
где feaoY — некоторые целые числа. Если все эти числа равны
нулю, мы приходим к первой проблеме Кузена и, решив ее,
получим решение второй проблемы. Однако, вообще говоря,
это не так, и на область D, кроме условия разрешимости
первой проблемы Кузена, надо наложить еще некоторые топо-
топологические ограничения, которые должны обеспечить возмож-
') Под односвязностью области здесь и далее понимается линейная од-
односвязность: любой замкнутый путь, принадлежащий этой области, гомо-
топен в ней нулю.
§ 10] МЕРОМОРФНЫЕ ФУНКЦИИ 443
ность выбора таких ветвей In/zaf3 = ?а„, чтобы все ka^ оказа-
оказались равными нулю.
Об этих ограничениях мы будем говорить в следующем
параграфе. Здесь же приведем лишь простую теорему, в ко-
которой топологические трудности снимаются условием суще-
существования глобальной (т. е. определенной во всей области D)
функции g, решающей проблему, но не обязательно голо-
голоморфной, а лишь непрерывной.
Теорема 3. Пусть для области D разрешима первая
проблема Кузена и данные fa второй проблемы для покрытия {Ua}
таковы, что существует непрерывная в D функция g, для ко-
которой все частные gjfa непрерывны и отличны от нуля в Ua.
Тогда проблема {fa} разрешима.
•« Предположим сначала, что все Ua односвязны. Тогда
в каждой Ua можно выбрать непрерывную ветвь In(fjg). Мы
выбираем эти ветви произвольно, а затем в каждом пересече-
пересечении Uaa полагаем
1 / , /а . /в
In hm = In In —,
ар g g
где ha& = fjfp и в правой части взяты выбранные ветви. Функ-
Функции g-a|3 = In /za|3 голоморфны в Uafi и удовлетворяют, очевидно,
условиям
0
(т. е. образуют голоморфный коцикл). По условию первая
проблема Кузена {gaj разрешима и существуют голоморфные
в Ua функции ga такие, что
Sap = ?fS ~ 8а (9)
в каждом пересечении 6/а|3. Полагая ha = e8a для каждого
аеЛ, мы получаем голоморфные в Ua и отличные от нуля
функции и из соотношения (9) находим, что ha^ — hjha в лю-
любом Uap. Это равносильно решению второй проблемы Кузена.
Общий случай, когда не все Ua односвязны, приводится
к разобранному при помощи измельчения покрытия. Разобьем
каждую окрестность Ua на односвязные области U'a и поло-
положим f'a =/„ в каждом U'a . По условию все частные g/f'a не-
непрерывны и отличны от нуля. Если теперь положить h'a „ = h^
в каждом пересечении U'a в , то функции [h'a в } будут удовле-
444 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
творять условиям F) и G). Мы находимся в условиях уже разоб-
разобранного случая. По доказанному существует голоморфная в D
функция f такая,, что все частные fjfa голоморфны и отличны
от нуля в С/ц . Но так как f'a =fa в Ua и эти Ua покры-
покрывают Ua, то f решает вторую проблему и для покрытия
Доказанная теорема позволяет усилить теорему 1 о про-
продолжении. В этой теореме предполагается, что множество М
определяется функцией <р, голоморфной в области D. Ока-
Оказывается, можно требовать меньшего: лишь непрерывности qp
в D и ее локальной голоморфности в точках М, и это требо-
требование равносильно предыдущему. В самом деле, справед-
справедливо
Следствие. Пусть DczCn — область голоморфности и
MaD — аналитическое множество комплексной размерности
я—1. Если существует непрерывная в D функция <р, опреде-
определяющая М, то существует и определяющая его функция f,
голоморфная в D.
< Рассмотрим открытое покрытие {Ua} области D, столь
мелкое, что в каждой Ua пересечение Uaf\M имеет голоморф-
голоморфную определяющую функцию fa (это следует из определения
аналитического множества); в тех Ua, которые не пересе-
пересекаются с М, положим fa=sl. Такой выбор /а, если учесть еще
свойство определяющих функций, обеспечивает голоморфность
всех отношений fjf^ в пересечениях С/ар. Поэтому набор {/„}
можно принять за данные второй проблемы Кузена. Наконец,
так как ср и fa обе определяют М в Ua, то все частные ф//а
непрерывны и отличны от нуля в Ua. По теореме 3 рассмат-
рассматриваемая проблема разрешима, и ее решение / обладает
нужными свойствами >
Замечание. В этом следствии условие существования
функции ф не является необходимым: оно вызвано тем, что мы
пользуемся в доказательстве теоремой 3. Очевидно, его можно
опустить, если известно, что в области D разрешима вторая про-
проблема Кузена. В такой области, следовательно, всякое ком-
комплексно (п — 1)-мерное аналитическое множество М имеет
глобальную определяющую голоморфную функцию. Если же
в этой области разрешима и первая проблема Кузена, то по
теореме 1 всякая функция, локально голоморфная на М,
оказывается и глобально голоморфной во всей области. Под-
Подчеркнем, что это свойство может не иметь места, если М не
является аналитическим множеством: пример такого рода
был приведен в п. 3.
§ 11) МЕТОДЫ ТЕОРИИ ПУЧКОВ 445
§ 11. Методы теории пучков
В этом параграфе мы хотим познакомить читателя с новыми
мощными методами, которые возникли при сочетании идей
комплексного анализа с идеями алгебры и топологии. Главная
заслуга в создании этих методов принадлежит французской
математической школе, в первую очередь А. Картану и
Ж. П. С е р р у. Нашей целью являются не сами методы,
а их применения. Поэтому мы подробно прослеживаем связи
этих методов с понятиями комплексного анализа, из которых
они возникли, и примеры применений, но опускаем доказатель-
доказательства некоторых утверждений.
34. Основные определения. Еще в п. 28 ч. I мы ввели по-
понятие ростка аналитической функции, к которому пришли,
желая локализовать понятие аналитичности. Напомним это
понятие для общего случая функций, голоморфных на анали-
аналитическом многообразии произвольной размерности.
Определение 1. Две функции fag, голоморфные
в точке Р аналитического многообразия М, называются экви-
эквивалентными, если существует окрестность (в топологии М) этой
точки, в которой f = g. Любой класс эквивалентности по этому
отношению называется ростком аналитической функции в точке Р.
Росток, содержащий данную функцию /, голоморфную
в точке Р, мы будем обозначать символом гя. Совокупность
всех ростков аналитических функций в точке РеМ будем
обозначать через <дР. Очевидно, <ЭР можно рассматривать как
кольцо, если под суммой и произведением его элементов по-
понимать росток, принадлежащий соответственно сумме и про-
произведению представителей этих элементов (функций, голоморф-
голоморфных в точке Р). Это — коммутативное кольцо с единицей, без
делителей нуля ').
Чтобы прийти к основному в этом параграфе понятию пучка,
напомним определение области наложения над аналитическим
многообразием М, обобщающее определение римановой поверх-
поверхности в ч. I. Прежде всего на множестве ростков
<д= (J (дР A)
вводится топология, в которой окрестностями служат совокуп-
совокупности ростков, принадлежащие одной голоморфной функции,
') В самом деле, если ip и gp — ненулевые ростки, то их представи-
представители f и g — голоморфные функции, не равные тождественно нулю. Но
тогда и fg — такая же функция, т. е. fpgp Ф 0.
446 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
Это делается так. Рассмотрим произвольный росток fPe0
и любую функцию f, его представляющую (т. е. входящую
в класс эквивалентности fp). Пусть U — произвольная окрест-
окрестность точки Р^М, в которой f голоморфна; совокупность
ростков 0 = (J fQ, принадлежащих этой функции, и назы-
вается окрестностью fP.
В определении области наложения участвует еще проекция,
т. е. отображение
я: е-*М, B)
которое каждому ростку fpe(9 ставит в соответствие точку
РетИ. Обратное отображение неоднозначно: оно преобразует
точку Р в совокупность 6Р всех ростков функций, голоморф-
голоморфных в этой точке. Однако топология на в построена так, что
локально, в окрестности U каждого ростка fP, отображение B)
взаимно однозначно, ибо по теореме единственности для любой
Q e U в U существует лишь один росток iQ, соответствующий
этой точке. Очевидно, сужение л \$ является гомеоморфизмом.
Отметим, наконец, что во введенной на в топологии алгеб-
алгебраические действия с ростками (которые определены лишь для
ростков над одной точкой) оказываются непрерывными. Под
этим понимается следующее: пусть f, g, h — ростки из ©р такие,
что h = f + g; тогда для любой окрестности D^c® найдутся
такие окрестности Vv Vgc<8, что для всех f^ej/, и g0 e V
росток f~ + gQ e Uh (мы определили непрерывность суммы, не-
непрерывность произведения определяется аналогично). Для по-
построения окрестностей Vs и Vg достаточно выбрать столь малую
окрестность V точки РеМ, чтобы в ней были голоморфными
функции fug, представляющие соответственно ростки f и g.
Тогда в V будет голоморфной и функция Aeh и, по приня-
принятому выше определению окрестностей, для любых fQ e j/f,
gQeFg сумма fQ + gQ будет принадлежать функции h, ко-
которая, по определению суммы классов эквивалентности, всюду
в V равна f + g. Но это и означает, что fQ + gQ e Uh.
Понятие пучка возникает при алгебраико-топологической
обработке понятия поверхности наложения. При этой обработке
сохраняются все топологические элементы только что описан-
описанной конструкции, а от голоморфных функций остается лишь
их алгебраическая структура— то, что они образуют кольцо.
Определение 2. Пучком некоторых алгебраических
структур (нас будут интересовать лишь кольца или группы)
над топологическим пространством X (базой пучка) называется
§ 11] МЕТОДЫ ТЕОРИИ ПУЧКОВ 447
пара (а?1, сг), составленная из топологического пространства ?Р
и отображения а: ^-*Х (проекции), если выполняются сле-
следующие условия:
1) проекция сг является локальным гомеоморфизмом всюду
на &\
2) для каждой точки Pel в прообразе ?? Р = <5~Х(Р), назы-
называемом стеблем пучка над Р, введена алгебраическая струк-
структура;
3) алгебраические операции в стеблях непрерывны в топо-
топологии if.
Таким образом, описанное выше топологическое простран-
пространство в ростков голоморфных функций с проекцией л, является
пучком колец над комплексно аналитическим многообра-
многообразием М. Этот пример будет для нас основным, ниже мы введем
и другие примеры пучков колец и групп.
Понятие пучка отражает полную локализацию изучаемых
объектов. Однако практическая ценность этого понятия опре-
определяется главным образом тем, что оно позволяет переходить
и к не полиостью локализованным, а иногда и к глобальным
объектам. Такой переход обобщает переход от ростков iP из
пучка (д1) к функциям f, голоморфным в окрестности точки Р,
а затем —если это возможно — к функциям, голоморфным на
всем многообразии М. Поэтому теория пучков дает весьма
мощные методы решения ряда задач, в которых от локальных
свойств нужно переходить к глобальным.
Описанный сейчас переход осуществляется при помощи
важного понятия сечения.
Определение 3. Сечением пучка (^°, а) над открытым
множеством U cz X называется непрерывное отображение
/: [/->(?* такое, что композиция a°f является в U тождествен-
тождественным отображением.
Таким образом, сечения — это обращения сужений проек-
проекции сг на множества Uczif. Условие 1) в определении пучка
показывает, что в достаточно мелких окрестностях каждой
точки Psjf сечения существуют. Совокупность всех сечений
пучка над открытым множеством U cz X мы будем обозначать
символом
?P). C)
Заметим, что в силу локальной гомеоморфности проекции
сечения над связной окрестностью UczX обладают таким
свойством: если два сечения / и g из S^v совпадают в какрй-
') Здесь мы пишем © вместо (©, я); аналогичные сокращения записи
мы будем делать и дальше.
448 МЕЗОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
либо точке Р е U, то / = g всюду в U (доказательство повто-
повторяет доказательство леммы из п. 28). Это свойство вместе
с условием 3) из определения пучка позволяет распространить
на ё?и алгебраические действия, введенные в стеблях &'Р ').
Рассматриваемые в анализе пучки естественным образом
возникают в результате предельного перехода из не вполне
локализованныхобразований, которые называются предпучками.
Определение 4. Говорят, что над топологическим про-
пространством X задан предпучок некоторых алгебраических струк-
структур, если
1) задана база {?/} открытых множеств топологии X, т. е.
такой их набор, что любое открытое множество является объеди-
объединением этих множеств;
2) с каждым множеством U базы ассоциирована алгебраи-
алгебраическая структура ?fv;
3) с каждой парой U, Ке{[/} такой, что V cz U, ассоции-
ассоциирован гомоморфизм
Puv- Sfu-^SPV, D)
причем выполняется следующее условие транзитивности: если
U, V, We{U) и WczVczU, то
Puw = 9vw ° Puv E)
(здесь о обозначает композицию гомоморфизмов).
Важнейшим примером предпучка колец является набор
функций, голоморфных в открытых множествах U, составляю-
составляющих базу аналитического многообразия М, т. е. набор сечений
T(U, &) = Н(U). Гомоморфизмами puv здесь служат естествен-
естественные отображения вложения кольца H(U) в Н (V), которые
каждой функции f e H (U) относят ее сужение f\v на множе-
множество Vcztl (условие транзитивности при этом, очевидно, вы-
выполняется). Описанное выше построение пучка ©, по существу,
можно рассматривать как процесс локализации, приводящий
к © от этого предпучка.
Аналогичный процесс локализации, приводящий от пред-
пучков к пучкам, можно провести и в общем случае. Это
делается при помощи так называемого топологического пре-
предела. Пусть дан некоторый предпучок {SPy} над топологическим
') Пусть даны f, g^dfy, где U — область. Фиксируем точку Р е U и обо-
обозначим f = fp, g = gp; так как f, g^3°p, то определен элемент h = f + g^S^p.
Обращение сг в точке h является сечением в некоторой окрестности Р, и не-
нетрудно видеть, что оно продолжается на U до сечения Ле^у, Мы полагаем
f + g = h; внаших условиях легко доказать, что это определение не зависит
от выбора точки Pet/.
§ II] МЕТОДЫ ТЕОРИИ ПУЧКОВ 449
пространством X. Для каждой точки РеХ мы рассмотрим
базу <U'р окрестностей этой точки; семейство ^fP частично
упорядочено отношением вложения. Назовем два элемента
fu и Sv принадлежащие соответственно ?Ри и ?fy, эквивалент-
эквивалентными в точке Р, если существует окрестность ff'eft'p такая,
что W <=. U П V и
9uw (fu) = 9vw (ev)- F)
Множество классов эквивалентности по этому отношению на-
называется топологическим пределом и обозначается символом
SfP = lim top ?РЦ. G)
В множестве &Р естественным образом вводится структура,
заданная в Sfy.
Покажем теперь, что (J ?РР = ?Р можно рассматривать как
пучок над пространством X. Проекция a: Sf —>X определяется
просто как отображение ёРР->Р. Далее, для каждой окрест-
окрестности U^%?P можно построить отображение рир: с^/-> (?"я,
которое сопоставляет каждому элементу /е^у класс эквива-
эквивалентности \P^.efP, содержащий этот элемент (отображение риР
можно рассматривать как гомоморфизм соответствующих алге-
алгебраических структур). При помощи построенных отображений
мы для каждого элемента fs^p и окрестности U^4/P опре-
определим множество
Набор %>? = {Uf} для всех fE^" и всех U из базы открытых
множеств X можно принять в качестве такой же базы для
топологии в SP. Чтобы убедиться в этом, достаточно доказать,
что если О и Ve^ & и П= 0\ П VB ф 0, то для каждого эле-
элемента ЬРеПв^ найдется WhpczU. По построению PczUf]V
и hP = pup ({) = pVP (g), где fug соответственно принадлежат d5"y
и ff'y. По определению топологического предела существует
открытое множество W с U f\V, содержащее точку Р и такое,
что Puw(f) = Pvw(g)> полагая h = puw(f), мы получаем элемент ?PW,
и тогда искомой окрестностью Whp будет (J PwqW- Наконец,
очевидно, что в построенной топологии проекция а локально
гомеоморфна, а алгебраические операции непрерывны.
29 Б. В. Шабат
450 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
Замечание. Мы обозначаем одним символом ?Ри кольцо
некоторого предпучка, ассоциированное с открытым множе-
множеством Uc:X, и совокупность сечений над U пучка ?Р, кото-
который получается в пределе из этого предпучка. Дело в том,
что при достаточно общих предположениях эти кольца изо-
изоморфны1) и нет опасности их смешать.
Примеры. Символом ^ мы всюду будем обозначать базу
открытых множеств пространства, над которым рассматри-
рассматриваются пучки и предпучки.
1. Пучок 6 ростков голоморфных функций над комплексно
аналитическим многообразием М и соответствующий ему пред-
пучок {<Зи} функций, голоморфных на множествах U^fyf, мы
уже рассматривали. Множество 6У = Г (?/,©) является также
множеством сечений пучка © над U.
2. Предпучок {»#?/} функций, мероморфных на множествах
U^%?, был определен в начале этой главы. Его можно рас-
рассматривать как предпучок полей, причем гомоморфизмами
puv\ аМц-ъ-оМу, как и в предыдущем примере, являются суже-
сужения (они определены, если V с U). Пучок о/Я, который полу-
получается локализацией этого предпучка, называется пучком, рост-
ростков мероморфных функций. Последний можно определить и
независимо от предпучка, если ввести для каждой точки Р^М
стебель <МР как поле отношений в кольце <др. Под этим
понимается следующее: упорядоченные пары (f, g) и (f, g')
ростков из @Р (где g, g' ф 0) считаются эквивалентными, если
fg' = f'g; классы эквивалентности (они называются отношениями)
обозначаются символом m = f/g и объявляются ростками меро-
мероморфных функций. Так как @Р — коммутативное кольцо с еди-
единицей и без делителей нуля, то ростки (отношения) m обра-
образуют коммутативное поле о/КР. Объединение
o4t= U оМр (8)
можно рассматривать как пучок полей.
3. Пучок а?"р''?> ростков дифференциальных форм бистепени
(р, а) над комплексным многообразием М действительной раз-
размерности 2/г можно определить следующим образом. Фикси-
Фиксируем точку Р^М и рассмотрим совокупность дифференциаль-
дифференциальных форм, каждая из которых в некоторой окрестности UpcM
представляется в локальных координатах z — {zx zn),
') Доказательство см. в книге: Р. Ганнинг и X. Росс и, Аналити-
Аналитические функции нескольких комплексных переменных, «Мир», М., 1969,
гл. IV, раздел А, лемма 3.
§ 11] МЕТОДЫ ТЕОРИИ ПУЧКОВ 451
z = (zu ..., zn), действующих в Up, в виде
ffl = 2 fu dzj A dzj, (9)
где / = (/], ..., ip), / = (/i, • • •. jq), 1 =О'ц> iv^n, а коэффициенты
fu~ функции из C°°(Up), кососимметрические по индексам. Две
такие формы, (9) и со' = 2 f'u dz} Л dzp будем считать эквива-
эквивалентными, если существует окрестность точки Р, в которой
f'IJ = fI1 Для всех /, /. Классы эквивалентности по этому отно-
отношению назовем ростками форм бистепени (р, q) в точке Р.
Совокупность таких ростков обозначим через <&~РР' ч) и будем
рассматривать как абелеву группу относительно покозффициент-
ного сложения1). Объединение
& ' = (J в?~р' A0)
мы будем рассматривать как пучок групп. Топология и проек-
проекция в нем вводятся точно так же, как в пучке ©.
В частности, ^°'° = <?F представляет собой пучок ростков
функций из С°°(М).
Можно рассматривать также предпучок, соответствующий
пучку ^(р'ц), который состоит из совокупностей ^%'ч), U^fyf,
форм бистепени (р, q), принадлежащих C°°(U). Гомоморфиз-
Гомоморфизмами puv здесь по-прежнему служат сужения.
4. Постоянные пучки Z, R, С. Пусть каждой точке РеМ
соответствует один и тот же объект, скажем кольцо целых
чисел Z. Тогда мы будем говорить, что над М задан постоян-
постоянный пучок, и будем обозначать его тем же символом, что и
этот объект (в нашем случае — символом Z). Сечением такого
пучка над связной окрестностью U cz M служит набор функций,
каждая из которых постоянна в U (в нашем случае —цело-
—целочисленная постоянная).
35. Группы когомологий. Начнем с определения этих групп
для покрытий. Как мы сейчас увидим, это определение обоб-
обобщает определение, которое было дано в п. 31 при изучении
аддитивной проблемы Кузена. Пусть X — топологическое про-
пространство и над ним задан пучок абелевых групп ?f. Рассмо-
Рассмотрим открытое покрытие W = {Ua}, as Л, пространства X и для
любого целого числа р^О построим мультииндекс a = (a0,..., ap)e
') Разумеется, сумма ростков « + «' определяется как росток, соответ-
соответствующий сумме и + о', где и е ю и и' е ш'.
29*
452 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
еЛр+' = Л X ... X А; символом
?/а=?/а„П ¦•• ПС/а, A)
обозначим пересечение множеств покрытия.
Определение 1. Коцепью порядка/? с коэффициентами
в пучке SP для данного покрытия <2? мы будем называть функ-
функцию h, которая каждому мультииндексу ае/+1 относит неко-
некоторое сечение па^аУи =Г([/а, е?) пучка а?* над Ua, и притом
так, что ha является кососимметрической функцией индексов
а0, ..., ар, составляющих а. Если Ua пусто, то мы будем счи-
считать, что /г„ = 0. Множество всех коцепей порядка р с коэффи-
коэффициентами в & образует "набор групп, который мы обозначим
символом Ср {%Г, &>).
Определим теперь кограничный оператор 6, который каждой
коцепи h порядка р относит коцепь б/г порядка р + 1 по правилу
(справа индекс <xv опускается). Отображение
6: С (&, ?Р) -* Cp+l (<&, ?>\ C)
очевидно, является гомоморфизмом соответствующих групп
коцепей. . ¦
Частными случаями кограничного оператора для пучка
форм <^"(р'ч) являются операторы дифференцирования d (по
всем переменным z, z) и д (по переменным г). Как и для этих
операторов (см. п. 13), в общем случае доказывается, что квад-
квадрат оператора б равен 0:
6-6 = 0. D)
Определение. 2. Коциклом порядка р называется ко-
коцепь h, для которой б/г = 0; совокупность
Z" («Л ^) = {Ае С (W, &): 6Л = 0} E)
называется группой1) коциклов (с коэффициентами в SP). Ко-
Коцикл ЛеС называется когомологичным нулю или кограницей,
если существует коцепь gECH такая, что bg = h; группу
таких коциклов мы будем обозначать символом Вр {%(, 3").
') Конечно, Zp (U, с^°), как и вводимые ниже аналогичные объекты,
является не группой, а набором групп Zp (Ua, 3*), а е Ар+ ; мы называем
их просто группами, чтобы не усложнять и без того громоздкой терминологии.
§ 11] МЕТОДЫ ТЕОРИИ ПУЧКОВ 453
Она является подгруппой группы E), и факторгруппа
№, &) F)
называется р-й группой когомологий (с коэффициентами в Sf)
для покрытия <№.
В частном случае р = 1 коцепи {haoa} определены на пере-
пересечениях ?/аоа, множеств покрытия так, что паощ + ha.,0., = 0 (ко-
(кососимметричность по индексам). Кограничный оператор пере-
переводит их в коцепи порядка 2 такие, что (б/г)аоа,а2 = Аа,а2 — Лаоа2 +
+ haoai в ?/а0а,а2. Поэтому коциклами будут такие коцепи, для
которых еще haia2 + /гаА+ Ла„а, = 0. Кограницей коцепи {ha} по-
порядка 0 является коцепь Fh)a<jai = /гИ| — А , следовательно, кого-
мологичными коциклами первого порядка будут те, для кото-
которых Аа„а, = А«, — Аа„. Мы видим, что введенная здесь термино-
терминология при р = 1 совпадает с той, которую мы рассматривали
в п. 31, а определенная там группа когомологий есть группа
H4W, в).
Рассмотрим еще группу когомологий нулевого порядка.
Коциклами, как показано выше, будут коцепи {ha}, для кото-
которых /га, — /zao = O в каждом пересечении t/aoa,. Следовательно,
каждый коцикл h нулевого порядка определяет сечение пучка ?Р
над всем пространством X, т. е. глобальное сечение — эле-
элемент группы Т{Х, Sf), сужение которого на каждое Ua совпа-
совпадает с ha. Коцепью — 1-го порядка по определению считается
пустое множество, и, значит, кограницей нулевого порядка
является лишь нулевой коцикл. Факторизация по нему три-
тривиальна, следовательно, справедлива
Теорема 1. Нулевая группа когомологий с коэффициен-
коэффициентами в пучке <if над пространством X для любого покрытия <%?
изоморфна группе глобальных сечений этого пучка:
Н°&, ?Г) - Г(Х, <П G)
Теперь мы хотим перейти от групп когомологий для по-
покрытий к группам когомологий самого пространства. Для
этого нужно построить процесс локализации, аналогичный пе-
переходу от предпучков к пучкам в предыдущем пункте. Именно,
мы частично упорядочим множество покрытий по отношению
включения, определим гомоморфизмы, связывающие группы
для двух покрытий, из которых одно мельче другого, и при
помощи таких гомоморфизмов перейдем к топологическому
пределу.
Пусть даны два открытых покрытия W = {Ua}aeA и
У = {l/p}p(SB; будем говорить, что второе покрытие мельче
454 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
первого (обозначение: У¦K'&f), если существует отображение
р: В->А (8)
такое, что V^<^ UP(^ для любого (Jefi. При заданном р ка-
каждой коцепи /ig Cp(fyf) можно сопоставить коцепь р/г е СР(Т"),
полагая для каждого мультииндекса р е Bp+i значение (р/г)я
равным сужению /гр(р) на V^1). Так как у нас б (р/г) = р (б/г)
для любой коцепи h (здесь б —кограничный оператор), то р
индуцирует отображение •
&)^НР(Т, &>), (9)
которое, очевидно, является гомоморфизмом групп.
Лемма. Если Т -< %, то гомоморфизм р* не зависит от
выбора отображения (8).
< Для р = 0 утверждение очевидно в силу теоремы 1, по-
поэтому можно считать, что р^ 1. Пусть наряду с р задано еще
отображение р': В->А такое, что Ур с= С/р>{(}) для всех pefi.
Определим отображение а: Ср+ (%f)—>CpG°), положив для ка-
каждого р е Вр+1 с упорядоченными индексами po<Pi< ••• <$Р
и каждой коцепи h e Cp+I
M)p=Iji(-l)v/zp@o)...pCv)p'(pv)...p'(p/7). A0)
Прямой подсчет2) показывает, что для всех A s Ср+| (^)
p'h-ph. A1)
') В соответствии с принятыми выше обозначениями у нас
Р = (Ро, ..., рр), р (Р) = (р (р0), ..., р (рр)) и Fp = F3o П ••• U %.
2) Проведем этот подсчет для р—1. Пусть р = (р0, р,), p(pv)=av,
p'(Pv) = D; имеем
(р'/г - р/г) = h , , - h .
* Vi aoai
С другой стороны, (<5/OaoC!ia, = й^ - /гао(Х2 + /гао(Х1 и, значит,
[a (вА)]„ = FЙ) , , - (вА)_ _ , = h , ,+h.-(h , + А.
0 0 1 ТП 0 1 0^0 \ 11 0 1
Но по формуле, соответствующей A0) при р = 0, получаем (ah) =h
Ро a
откуда [6(<tA)] =(aA) - {oh) ^h^^-h^^. Таким образом
§ И] МЕТОДЫ ТЕОРИИ ПУЧКОВ 455
В частности, если h — коцикл FЛ = 0), то р'Л — рЛ = б (oh), а зна-
значит, рЛ и р'к принадлежат одному классу эквивалентности при
факторизации по кограницам. Отсюда и видно, что р и р'
соответствует один и тот же гомоморфизм группы Нр (&)
в Н"(Т) >
По этой лемме р* = рит зависит лишь от покрытий (при
заданных X и if). Из нее видно также, что он удовлетворяет
условию транзитивности: если W «< 7° < $Л то
Рига** Ргго" Рит- A2)
Таким образом, мы действительно имеем ту же ситуацию,
что и в предыдущем пункте (с той лишь разницей, что вместо
множеств здесь рассматриваются системы множеств — покры-
покрытия), и можем осуществить желаемую локализацию.
Для этого рассмотрим всевозможные открытые покрытия
пространства X и условимся считать элементы / е Нр (<М) и
g е Нр (Т) эквивалентными, если существует покрытие W та-
такое, что *в<«Л Ж<Т и притом PUw(f) = prW(g).
Определение 3. Множество классов эквивалентности по
этому отношению, т. е.
lim top Hp (&, &>) = Н" (X, &>), A3)
и
называется р-й группой когомологий пространства X (с коэф-
коэффициентами в пучке if).
Замечание. Из этого определения видно, что если для
пространства X существуют сколь угодно мелкие покрытия $Л
для которых Нр{^, ?Р) = 0, то для этого пространства и
НР(Х, ^) = 0.
36. Точные последовательности пучков. Начнем с понятия
отображения пучков, которое вполне аналогично понятию ото-
отображения областей наложения над С* (см. п. 28). Пусть даны
два пучка (if, о) и (J1, х) над одним и тем же пространством X.
Отображением пучков
Ф: if->J A)
мы назовем такое непрерывное отображение топологического
пространства ^ в J*, для которого всюду в if
х о ф ~о. B)
Понятие отображения пучков введено так, что оно сохра-
сохраняет стебли: для любой точки Ре! имеем y(ifp)<^!Tp. Оно
сохраняет также и сечения: если /—произвольное сечение
пучка ifa над открытым множеством U czX, то отображение
456 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
Ф°/ непрерывно в U и т°(ф°/) = а°/ тождественно (по опре-
определению сечения й^и), но это означает, что ф ° / е ^и.
Отображение ф: <?Р ->$ называется гомоморфизмом пучков,
если оно является отображением этих пучков и, кроме того,
сохраняет алгебраические операции во всех стеблях. Гомомор-
Гомоморфизм пучков называется их изоморфизмом, если ф является
взаимно однозначным отображением на J1.
Далее, пусть (^, а) — пучок абелевых групп над X и мно-
множество J1 <= а?"; будем говорить, что (J1, а) является подпучком
пучка {е?', о), если: 1) J1 открыто в ?Р, 2) o(J') = X и 3) для
любой точки PeJf стебель J"P является подгруппой группы й?Р.
Если J1 является подпучком пучка абелевых групп &', то
для каждой точки Р базы X можно образовать факторгруппу
Жр = S^pUp, объединение & таких факторгрупп для всех
Pel, наделенное фактортопологией1), называется фактор-
пучком на X и обозначается символом
<?7J-= U^p/^p- C)
Pel
Примеры.
1. Пусть 0— тривиальный пучок над комплексно аналити-
аналитическим многообразием М (в каждой точке Р е М стебель этого
пучка состоит из одного нуля), С—постоянный пучок, 6 — пу-
пучок ростков голоморфных, а <ЗГ — пучок ростков бесконечно
дифференцируемых функций над тем же М. Здесь каждый
предыдущий пучок является подпучком следующего (проверьте
условие открытости из определения подпучка).
2. Пучок © над комплексно аналитическим многообразием М
является подпучком пучка оМ ростков мероморфных функций
на М. Будем рассматривать в и оМ как пучки аддитивных
групп (относительно сложения); тогда для любой Р е М сте-
стебель 6Р будет подгруппой оМР, и можно образовать фактор-
пучок
\J (А)
Элементами этого факторпучка являются классы ростков ме-
мероморфных в точке Р е М функций, разность между которыми
является ростком голоморфной функции. (Иными словами, эле-
элементами <ж/6 являются классы эквивалентных ростков fpSo^fp,
где ?р и fp считаются эквивалентными, если fp — fpt^@p.\ Как
мы скоро увидим, этот пучок связан с первой проблемой Кузена.
') Под фактортопологией понимается топология в о^Ц", в которой от-
открытыми объявляются множества классов эквивалентности открытых мно-
множеств пространства о?.
§ II) МЕТОДЫ ТЕОРИИ ПУЧКОВ 457
3. Удалим из пучка о/И ростки, соответствующие нулевому
сечению (т. е. функции, тождественно равной нулю на М);
тогда (Ж* = о4С\Щ можно рассматривать как пучок мульти-
мультипликативных групп с умножением как групповой опера-
операцией. Пучок <д* пусть состоит из обратимых элементов колец <дР,
Р^М, т. е. элементов, соответствующих функциям, которые
не обращаются в 0 в точке Р. Очевидно, 6* является подпуч-
подпучком <м , и можно образовать факторпучок
«*•/©•= (J о*;,/©;. E)
Р<=М
Элементами его служат классы ростков мероморфных функ-
функций, не равных тождественно нулю, частное которых является
ростком-голоморфной функции, не обращающейся в нуль (иными
словами, это классы эквивалентных ростков fe #, где V и \"
считаются эквивалентными, если V (Р)"' e ©*). Как мы скоро
увидим, этот пучок связан со второй проблемой Кузена.
Переходим к определению основного в этом пункте понятия
точной последовательности пучков. Пусть даны два гомомор-
гомоморфизма пучков абелевых групп:
е^о — * &\ —?* ^2; F)
будем говорить, что последовательность F) точна в ??х, если
imqp, = ker qp2. G)
Напомним, что символом imqpi = ф[ C?0) обозначается подгруппа
элементов ?РХ, которые являются образами элементов ??0 (об-
(образ гомоморфизма ф^, а символом ker ф2 — подгруппа из ?РХ,
образованная элементами, которые ф2 переводит в нуль
группы ?Р2 (ядро гомоморфизма ф2). Таким образом, точность
последовательности F) означает, что ф2 переводит в 0 те и
только те элементы, которые ф, приносит из Не-
Непоследовательность из любого числа пучков абелевых групп
... -> «5V, -% &t -^i-> SPt+l -+ ... (8)
называется точной, если она точна в каждом а?",:.
Примеры. 1. Точность последовательности
О -U „У, -2* Н2 -U 0, (9)
где крайние элементы— тривиальные пучки (все стебли кото-
которых—группы, состоящие из одного нуля), а г —отображение
вложения, означает, что ф является изоморфизмом <^р1
458 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. TV
на &\. В самом деле, так как ker<p = imi = 0,, то отображе-
отображение ф взаимно однозначно, а так как im ф = ker / = <5*2> то это
отображение на ^2-
2. Последовательность
*), (Ю)
где а?" — подпучок J4, г— отображение вложения, а ф —естест-
—естественный гомоморфизм, который каждому элементу из J" сопо-
сопоставляет класс эквивалентности, его содержащий, точна.
В самом деле, точность A0) в ?Р следует из того, чго i взаимно
однозначно, в члене J* —из того, что ф°г преобразует ??
в нуль, на месте JV^6* —из того, что ф —отображение на.
3. Вообще, точность последовательности пучков абелевых
групп
^",-2!-> ^2-2^^з-^ 0 A1)
означает, что ф2 —гомоморфизм на и
A2)
образ \т.у2 — <&'ъ группы <5 изоморфен ее факторгруппе по
ядру кегф2 = ф1(с?<'1)).
В заключение приведем идею доказательства') одной из
двух теорем, на которых основываются приложения теории
пучков в анализе. О второй из этих теорем мы будем говорить
в следующем параграфе.
Теорема I (о точных последовательностях).
Пусть пространство X хаусдорфово и имеет счетную базу от-
открытых множеств. Тогда всякой точной последовательности
пучков над X
Ъ-+#'-1+&>Л+&»^ъ A3)
соответствует точная последовательность групп когомологий
0-*Я°(Х, <?<")— +Н°(Х, ($')-*-*¦> Я0 (X, &")-?+
—-> Я1 {X, &") -^+ Я1 (X, &) -^-> Я1 (X, &"') -?-+ Я2 (X, &*)-+...
A4)
и так далее, по всем размерностям.
¦4 Прежде всего сопоставим гомоморфизмам пучков гомо-
гомоморфизмы соответствующих групп когомологий. Это делается
так: возьмем произвольное открытое множество U cz X а опре-
определим гомоморфизм сечений ф: Г (С/, ^")->T{U, if), положив
') Подробное доказательство см. в курсах Хёрмандера или Ганяинга и
Росси.
§ 1Ц МЕТОДЫ ТЕОРИИ ПУЧКОВ 459
<p(f) = <Pof B каждой точке Р е ?/ для любой f^T{U, &"). От
сечений естественным образом переходим к коцепям, и тогда
возникает гомоморфизм ф: Cp(%f, &")^-Ср ($?, &). Так как ф
коммутирует с оператором кограницы 6 (имеем фб = бф), то
по ф можно построить гомоморфизм ф*: Нр' (&', <&") -> Нр (%?, ??)
групп когомологий для покрытий1), а от него при помощи
топологического предела перейти к гомоморфизму групп кого-
когомологий самого пространства ф*: НР(Х, <&") -> Нр (X, &). Точно
так же по -ф строится гомоморфизм \J>*: НР{Х, ??)-> Нр {X, &"').
Остается построить гомоморфизм б*, повышающий размер-
размерность группы. Для этого рассмотрим какое-либо покрытие Ж
и последовательность групп коцепей
&"'). A5)
Нетрудно проверить, что она точна в силу точности последо-
последовательности A3). Однако ¦$, вообще говоря, не является ото-
отображением на C(.<2S, &"'), и мы обозначим Ср {%?, tf") = im •$.
Сейчас мы хотим построить отображение Нр\Ж, u?") — Z/Bt
где Z— подгруппа коциклов из Ср(<%?, <&"'), а В — подгруппа
кограниц, в группу Hp+l{^f, <&"). Для этого возьмем коцикл
h e Z; существует коцепь g s Cp (<%?, <з?) такая, что ¦$ (g) = h.
Она не является коциклом, но 6g е Cp+1 (<2S, ?f) и {jj Fg) = б (tyg) =
= 6Л = О. В силу точности A5), где р заменено на р+\, най-
найдется /еСр+1(^, &") такая, что ф(/) = б,§г, причем / — коцикл,
ибо ф Ff) = б (ф/) = б Fg) = 0 и, значит, 6f = 0, так как отобра-
отображение ф взаимно однозначно. Таким образом, мы построили
отображение
6: h-*— ->g—±6g-*— ->/
группы Z в Zp+l (<%f, $"). Нетрудно проверить, что при этом
когомологичные друг другу циклы переходят в когомологич-
ные, так что фактически построен гомоморфизм 6*: Нр {Ш', &"')—>
-*Яр+1(^, &"). Наконец, в условиях, наложенных на про-
пространство X, можно доказать, что топологический предел
групп Нр {<%, &"') будет совпадать с Нр {X, &"'), и мы придем
к нужному гомоморфизму
б*: НР(Х, ?>")->НР+1(Х, ??'). A6)
Точность полученной последовательности A4) ясна из построе-
построений >
') По аналогии с тем, что мы делали в предыдущем пункте для ото-
отображения р при измельчении покрытия.
460 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
§ 12. Применения
Основное содержание этого параграфа составляет исследо-
исследование разрешимости проблем Кузена методами теории пучков.
Приведем их формулировки в пучковых терминах для произ-
произвольного открытого покрытия ^ = {t/J, a e А, комплексно ана-
аналитического многообразия М. При этом мы будем пользоваться
обозначениями предыдущего параграфа.
Первая (аддитивная) проблема. В каждом Ua за-
задана мероморфная функция [аеГ(Уп, сМ) так, что во всех
пересечениях Uafi = Ua f] ?/р выполняется условие согласован-
согласованности fa — /p e Г(?/ар, ©). Требуется найти функцию ^еГ(М,в!)
так, чтобы f — fa<^T(Ua, в) Для всех aGi
Вторая (мультипликативная) проблема. В ка-
каждом Ua задана (не равная тождественно нулю) мероморфная ')
функция fa^T((Ja, oM*) так, что во всех пересечениях ?/а„ вы-
выполняется условие согласованности fjf^ e Г(?/„р, 0*). Требуется
найти функцию /е=Г(уИ, <^) так, чтобы |аеГ({/а, ©*) для
всех аеА
Центральным пунктом решения этих проблем является уста-
установление связи между локально заданными сечениями пучка
в ?/„р и глобальным сечением этого пучка над всем многообра-
многообразием. Методы теории пучков хорошо приспособлены для вы-
выяснения такой связи.
Важной особенностью этих методов является также то, что
они позволяют четко разделить топологическую и аналитиче-
аналитическую части проблемы. В рассматриваемых нами приложениях
топологическая часть проблемы решается теоремой о точных
последовательностях — теоремой I из предыдущего пункта.
Следуя Л. Хёрмандеру, мы используем для преодоления
аналитических трудностей теорему существования решений не-
неоднородных систем Коши — Римана.
37. Решение первой проблемы Кузена. Мы воспользуемся
той же схемой, которая применялась в п. 32 для решения этой
проблемы в случае поликругов. Именно, разрешимость мы
выведем из тривиальности группы когомологий с коэффициен-
коэффициентами в пучке ростков голоморфных функций, а тривиальность
этой группы установим в два этапа: сначала докажем три-
тривиальность такой же группы дифференциальных форм, а за-
затем — изоморфность обеих групп.
Все необходимое для первого этапа доказательства содер-
содержится в следующей теореме Хёрмандера:
') Вторая проблема Кузена формулируется здесь в более общем виде,
чем в § 10: вместо голоморфных рассматриваются мероморфные функции.
§ 12] ПРИМЕНЕНИЯ 461
Теорема II. Пусть D-~произвольная область голоморф-
голоморфности. Тогда для любой дифференциальной формы Q e C°° (D)
бистепени @, a), q>0, для которой д& = О, существует форма
co<=C°°(Z)) бистепени @, q — \) такая, что
да> = Q.
Иными словами, в области голоморфности всякая замкнутая
(относительно д) форма точна.
Под областью голоморфности здесь, как и всюду в этом
параграфе, понимается произвольная область голоморфности
над пространством С" или, если угодно, произвольное много-
многообразие Штейна (см. п. 29). В п. 32 эта теорема была Дока-
Доказана для случая, когда DcC" и является произведением
односвязных плоских областей. В общем случае доказательство
будет изложено в п. 39.
Так как группа когомологий с коэффициентами в пучке
<&~{u'q) для покрытия по определению 2 п. 35 является фактор-
факторгруппой группы форм, замкнутых в пересечениях множеств
покрытия, по подгруппе точных форм, то справедливо
Следствие 1. Пусть %f = {Ua} —покрытие области D на
комплексном многообразии, все множества Ua которого также
являются областями голоморфности. Тогда р-я группа когомо-
когомологий для этого покрытия с коэффициентами в пучке cf'' = gF~ ' q
ростков дифференциальных форм бистепени @, q) тривиальна
для всех р = 1, 2, ... и всех q ^ 0:
НР{Ж, сГ?) = 0 (р = 1, 2, ...). A)
(Мы воспользовались еще тем, что пересечение областей голо-
голоморфности является такой же областью.) Если мы учтем, что
любую область можно покрыть сколь угодно мелкими обла-
областями голоморфности, то по замечанию в конце п. 35 получим
Следствие 2. Для любой области D группы когомологий
с коэффициентами в пучке ростков дифференциальных форм
тривиальны для всех целых р>0:
Hp(D,^") = 0 (p = l, 2, ...)• B)
В основе второго этапа доказательства лежит
Теорема 1 (Дольбо). Для любой области D на ком-
комплексном многообразииг) и любого целого р>0 группа кого-
когомологий порядка р с коэффициентами в пучке ростков голо-
голоморфных функций изоморфна факторгруппе группы Zp всех
') Напомним, что многообразие в нашем определении являетея счетным
объединением компактов.
462 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА (ГЛ. IV
форм бистепени (О, р) из класса C°°(D), замкнутых в D отно-
относительно оператора д, по подгруппе Вр точных форм:
Нр (D, 0) » ZP\BP. C)
¦4 Обозначим через %q подпучок <^q, состоящий из рост-
ростков замкнутых (относительно д) форм. Последовательность
пучков
0-*Z«-U<^~«-ih%q+1^0, D)
где 0 —тривиальный пучок^ а г —вложение, точна. В самом
деле, irru = kerd, так как д переводит замкнутые формы в О,
a imd= %q+i, ибо по следствию 2 ростки замкнутых и точных
форм совпадают.
По теореме о точных последовательностях точна и после-
последовательность соответствующих групп когомологий
O^H°(Z4)^H°{&'4)-+Ho(zq+l)-+-Hl(z4)^>&(&-*)-+... E)
Но нулевые когомологий пучка совпадают с его глобальными
сечениями, поэтому Я°(^ = Г(?, &">) и H°(%q+l) = Zq+l, а по
следствию 2 имеем Я1 {<&"") = 0. Таким образом, мы заключаем
из E), что точна последова-тельность
r(D, «^~')-^>Z'+1-»//I(Z')-*0.
Отсюда следует изоморфизм
+ll Zq+llBq+l F)
(см. пример 3 на стр. 458; мы воспользовались еще тем, что
оператор д переводит @, д)-формы в точные @, д+1)-формы
и, значит, образ T(d, <&~q) совпадает с Bq+l).
Теперь рассмотрим отрезок E) между НР(&ГЧ) и Hp(Srg+1)
и снова воспользуемся тем, что при р>0 эти группы три-
тривиальны:
0-* H^Z"*1)-*^1 (%")-* 0.
Из точности этой последовательности вытекает изоморфизм
Hp+l(z")~Hp(Zq+1) G)
(см. пример 1 на той же стр.). Применяя G) несколько раз,
найдем
§ 12] ПРИМЕНЕНИЯ 463
Остается учесть, что замкнутые относительно д формы бисте-
пени @, 0) совпадают с голоморфными функциями, так что
%° = (д, и воспользоваться изоморфизмом F) >
Замечание 1. Если в покрытии & все элементы Ua
являются областями голоморфности, то из теоремы II выте-
вытекает точность последовательности E), но уже взятой для кого-
мологий покрытия № (подробнее см. Хёрмандер1), стр. 237).
Повторяя дословно доказательство, мы получаем, что
HpW,<d)~ZpIBp, О')
откуда следует, что для таких покрытий НР(ЪС, <3)^HP{D, 0)
(сама D может и не быть областью голоморфности).
Замечание 2. Все рассуждения в доказательстве тео-
теоремы Дольбо проходят совершенно аналогично и в том слу-
случае, когда вместо д рассматривается оператор d дифференци-
дифференцирования по всем переменным zv и zv. Так как в этом случае
пучок %° форм f нулевой степени, для которых df = O, совпа-
совпадает с пучком постоянных С (или R, если рассматриваются
формы с действительными коэффициентами), то справедлива
следующая
Теорема (де Рам). Для любого многообразия М класса
С°° и любого целого р>0 группа когомологий НР(М, С) изо-
изоморфна факторгруппе группы Zp замкнутых на М относи-
относительно оператора d форм степени р по подгруппе Вр точных
форм:
HP(M,C)~ZPIBP. (8)
Из теоремы Дольбо и теоремы II вытекает важное
Следствие. Для любой области голоморфности D
6) = 0 (p=l,2, ...)• (9)
Теперь нетрудно доказать и основную теорему этого пункта:
Теорема 2 (А. К а р т а н). В произвольной области го»
ломорфности D любая первая проблема Кузена разрешима2),
< Последовательность пучков аддитивных групп
Q-+@-+aM-2+oftl@-+Q, (Ю)
где ф — естественный гомоморфизм, который ставит в соответ*
ствие каждому ростку fee# класс эквивалентности, его
')Л. Хёрмандер, Введение в теорию функций нескольких кoм^
плексных переменных, «Мир», М., 1968.
2) Для однолистных областей голоморфности в С" теорема была дока-
доказана К. Ока.
464 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
содержащий, точна (см. пример 2 на стр. 458). По теореме 1
точна и .последовательность
О -* Н° @) -* Я0 (с?) -?* Я0 М7@) -* Я1 @). A1)
Но Я1 {&) = 0 согласно следствию теоремы Дольбо, поэтому
Ф*: T(D, <*#)-> Г (D,
является гомоморфизмом на (мы опять воспользовались тем,
что нулевые когомологии совпадают с глобальными сече-
сечениями).
При заданном покрытии <%? области D данные Кузена {/а}
определяют элемент из F(D, qM\(§\. По только что доказанному
существует элемент /еГ(Д, q/H), для которого qp*(f) совпадает
с элементом, определяемым {fa}, а это означает, что f — fa<=
еГ([/а, 6) в каждой окрестности Ua e <М >
Оказывается, что в С2 класс областей, для которых разре-
разрешима первая проблема Кузена, и исчерпывается областями
голоморфности: справедлива
Теорема 3 (А. К а р т а н). Если в {однолистной) обла-
области DcC2 разрешима любая первая проблема Кузена, то D
является областью голоморфности.
¦4 Если D не является областью голоморфности, то найдется
шар В с центром в граничной точке ? е 3D, в который ана-
аналитически продолжаются все функции f^H(D). Возьмем ка-
какую-либо точку гей П В и на отрезке zt, выберем точку
?°edD, ближайшую к z. Без ограничения общности можно
считать, что ?° = 0 и что плоскость {z2 = 0} содержит отрезок
zt,0 с D П В. Пользуясь тем, что в D разрешима проблема Ку-
Кузена, мы сейчас построим функцию g e Я (D), не продолжаемую
аналитически в шар В, и тем самым придем к противоречию.
Построение функции g делается, как в примере из п. 31.
Выберем какую-либо функцию ф(г2)ЕЯ(С\{0}) с особен-
особенностью в точке Zi = 0 я зададим в указанных там окрестностях
точек о=(а,, OjjeD главные части /„ следующим образом:
5^-, если а,^=0 а2 = 0,
fa B) }
\ 0, если а2 Ф 0.
Эти данные Кузена, очевидно, согласованы. Пусть /~-меро-
морфная в D функция, решающая поставленную проблему
Кузена. Тогда функция g (z) — z2f (z) голоморфна в D, а g(z{, 0) =
= ф(г,). Отсюда видно, что g имеет особенность в точке
0 е= 3D и, значит, не продолжаема аналитически в шар В >
12}
ПРИМЕНЕНИЯ
465
На пространства С", п^З, теорема не распространяется.
Пример. Рассмотрим область D а С3, которая полу-
получается из единичного поликруга U после удаления множества
¦I г: | Zj l^-g-, I z21 ^-9 > I 231^> у i; иными словами, D — поли-
поликруг, у которого грань |z3|=l продавлена внутрь, как на
рис. 114. Покроем D тремя областями голоморфности:
?/
={*: |
|2,|<
A2)
и рассмотрим соответствующий голоморфный коцикл {ha^}.
Разложим /г„„ в ряд Лорана в области ?/123. Так как это раз-
разложение сходится в 1/а„, то мы
получаем, что главные части раз-
разложений /г23 и Л31 совпадают соот-
соответственно с главными частями раз-
разложений этих функций в ряды
Лорана по z2 и по zt. Таким обра-
образом, из равенства
A3)
РИС. 114.
в Um мы получаем, что глав-
главная часть ряда Лорана функции
А12 распадается на две части, одна из которых голоморфна
по 2( и потому продолжается в Uu другая голоморфна по z2
и продолжается в U2. Но из равенства A3) следует тогда, что
главные части разложений Лорана для функций /г23 и /г31 со-
соответственно продолжаются в U2 и Uv Аналогично получаем,
что и правильные части этих функций продолжаются в соот-
соответствующие области. Обозначим через /г, продолжение /г31
в [/], через h2 продолжение /г32 в (/2и положим /г3 = 0 в U3.
Тогда
А, —/г, = ,
ho
/г12 в [/[
и потому {Лар} является кограницей коцепи {Ла}, т. е. первая
проблема Кузена для покрытия A2) всегда разрешима, откуда
следует, что Я1 (?М, &) = 0 для этого покрытия. Согласно заме-
замечанию 1 после теоремы Дольбо, из этого следует, что Hl{D, 0) = О,
т. е. любая первая проблема Кузена в области D разре-
разрешима. Остается заметить, что сама D не является областью
30 Б. В. Шабат
466 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
голоморфности, так как она является не логарифмически вы-
выпуклой областью Рейнхарта.
38. Решение второй проблемы Кузена. Из рассуждений,
проведенных в п. 33, видно, что разрешимость второй проб-
проблемы Кузена зависит также' от некоторых топологических
свойств рассматриваемой области. Мы приведем теорему,
в которой эти свойства выражаются как условие тривиаль-
тривиальности второй группы когомологий с коэффициентами в пучке
целых чисел:
Теорема 1 (Серр). В области голоморфности D любая
вторая проблема Кузена разрешима, если
H2(X,Z) = 0, A)
где Z — (постоянный) пучок аддитивных групп целых чисел.
¦< Рассмотрим точную последовательность пучков мульти-
мультипликативных групп
0-+@Г-1+а4Г-2+а4Г1@'->-0, B)
где 0 —тривиальный пучок, все ростки которого принадлежат
нейтральному элементу (единице) этих групп. Ей отвечает точ-
точная последовательность
Г (D, «Г) -* Г (D, оМ"\&) -> Я1 (D, &). C)
Условие разрешимости рассматриваемой проблемы состоит
в том, что для любого заданного элемента группы V(D,oM*\<d*),
т. е. некоторых согласованных данных второй проблемы Кузена,
найдется элемент |еГ(В,а|), соответствующий заданному
при отображении
Y{D,o4e)->Y(D,oM*\&). D)
Иными словами, условие разрешимости состоит в том, что D)
является отображением на. .Так как последовательность C)
точна, то это условие сводится к тому, что
Я1 (D, О*) = 0. E)
Придадим этому условию другую форму. Для этого рас-
рассмотрим еще одну точную последовательность
о-*z-U ©-*¦>©•-> о, F)
где Z—пучок аддитивных групп целых чисел, г —гомоморфизм
вложения, а е: f-+e2nlt— гомоморфизм пучка в аддитивных
§ 12] ПРИМЕНЕНИЯ 467
групп в пучок ©* мультипликативных групп1). Соответствующая
ей последовательность
H4D, ©)-+Hl{D, ©*)-^//2(D, Z)-+H2(D, 0)
также точна, а так как D — область голоморфности, то здесь
крайние группы тривиальны. Отсюда следует, что средние
группы изоморфны, и в силу условия A) равенство E) дей-
действительно имеет место >
Замечание. Из доказательства видно, что для разреши-
разрешимости конкретной второй проблемы, соответствующей некото-
некоторому сечению из T(D, оМ*\&), необходимо и достаточно, чтобы
образ этого сечения при отображении
a: T{D,c4l'l®*)-*Hl{D,@*) G)
был нулем группы HX(D, в"). Серр доказал также, что для
областей голоморфности а всегда является отображением
на (более того, для любого элемента g e Я1 (D, 6*) найдется
соответствующий ему элемент /еГ(Д, aM*j@*), состоящий
только из ростков голоморфных функций). Таким обра-
образом, если группа Н1Ф,6')Ф®, то найдется сечение из
T(D, eM*l&), для которого проблема неразрешима, т. е. для
областей голоморфности условие A) и необходимо для
разрешимости любой второй проблемы.
Заметим еще, что существуют многообразия, которые не яв-
являются областями голоморфности, хотя вторая проблема Ку-
Кузена на них разрешима. Примером служит область D =
= {0<|z1|<l; |22|<1}U {z! = 0, |22|< 1/2} пространства С2 -
она не является областью голоморфности, но можно доказать,
что в ней любая вторая проблема Кузена разрешима. Из тео-
теоремы 3 предыдущего пункта видно, что D служит также при-
примером области, в которой разрешима вторая, но неразрешима
первая проблема Кузена. В области D а С3 из примера пре-
предыдущего пункта разрешимы и первая и вторая проблемы Ку-
Кузена, хотя сама D не является областью голоморфности. Раз-
Разрешимость второй проблемы следует из того, что Hl{D, <3) = 0,
a H2(D, Z) = 0, так как D гомеоморфна шару.
Простым следствием теоремы Серра является
Теорема 2 (Ока). Если D — D, X ... X Dn — поликруго-
поликруговая область из С™, для которой все области Dv, кроме, быть
') Точность последовательности F) ясна из того, что функции, тожде-
тождественно равные целым числам, при отображении е переходят в 1 и что
каждая функция f Ф 0 локально представляется в виде е 8 (е: <Э -> <Э*
является отображением на). Заметим еще, что" в F) нуль слева — аддитив-
аддитивный, а справа — мультипликативный (единица).
30*
468 ' МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
может, одной, односвязны, то в D разрешима любая вторая
проблема Кузена.
¦< Прежде всего, D, очевидно, является областью голо-
голоморфности. Пусть D2, ¦.., Dn — односвязные области, тогда
#2(D, Z) = H2{Dl, Z), ибо группы когомологий с целыми коэф-
коэффициентами не меняются при (декартовом) умножении на одно-
связную плоскую область (мы не останавливаемся на доказа-
доказательстве этого топологического факта). Но для любой плоской
области группа #2(Z) тривиальна (это следует хотя бы из тео-
теоремы Вейерштрасса из п. 43 ч. I); поэтому H2(D, Z) = 0 >
Замечание. Из теоремы 2 следует, в частности, что вто-
вторая проблема Кузена разрешима в любой односвязной поли-
поликруговой области. Но для произвольных областей голоморф-
голоморфности односвязность еще не гарантирует разрешимости этой
проблемы, вот соответствующий пример (Серр). Область
является областью голоморфности, ибо в каждой точке 1,^-dD
существует барьер: функция /?(z) = {^2+^+^з ~ И + zl + 2з)Г' е
e©%?(D) не ограничена при z->?. Область односвязна, ибо
она гомеоморфна произведению поверхности S = [z\ + z\ +
-f- z2 — 1 = Oj на единичный круг. Тем не менее в D разрешима
не всякая вторая проблема Кузена, например, можно доказать,
что не существует голоморфной в D функции, которая обра-
обращается в нуль на одной из двух компонент пересечения D
с аналитической плоскостью {z2 = /zj и только на этой компо-
компоненте г).
Приведем еще одну формулировку второй проблемы Кузена.
Назовем дивизором А на «-мерном аналитическом многообра-
многообразии М любую целочисленную линейную комбинацию (я—1)-
мерных подмногообразий из М. Если все коэффициенты в этой
комбинации положительны, то дивизор называется положитель-
положительным. Для любой функции f, мероморфной на М и не равной
тождественно нулю, т. е. принадлежащей Г(уИ, аМ*), можно
определить ее дивизор, который обозначается через (f) и пред-
представляет собой комбинацию многообразий нулей f с положи-
положительными коэффициентами (порядками) и ее полярных мно-
множеств с отрицательными коэффициентами (равными порядкам2)
') Неразрешимость хотя бы одной проблемы следует также из того,
что Я2 (D, Z) = Н2 (S, Z) ф 0. Убедиться в последнем можно, заметив, что
S стягивается в множество своих действительных точек, т. е. двумерную
сферу \х\ + х\ + х\= l}, а для нее Я2 (Z) ф 0.
2) Порядки нулевых и полярных множеств мероморфной функции будут
о пределены в следующей главе.
§ 12] ПРИМЕНЕНИЯ 469
со знаком минус). Дивизоры голоморфных функций положи-
положительны.
Если две функции fu /2еГ(?/, &%*), где Uc:M, имеют оди-
одинаковый дивизор, то их частное /,/?' является голоморфной
функцией в U, отличной от нуля; верно и обратное. Поэтому
элементы факторпучка З) = о/Я*1& можно отождествить с рост-
ростками дивизоров. Вторая проблема Кузена теперь формули-
формулируется так: на многообразии М задан произвольный диви-
дивизор Ае®; найти функцию f еГ(М, <Ж), дивизор которой
В этой формулировке особенно отчетливо видно, что вторая
проблема Кузена обобщает задачу о построении мероморфной
функции с заданными нулями и полюсами.
Как и в случае одного переменного, доказывается, что на
любом многообразии М, на котором разрешима вторая про-
проблема Кузена, каждая мероморфная функция представляется
как отношение голоморфных функций. Пользуясь результатом
Серра, который сформулирован в замечании после теоремы 1,
можно доказать, что это верно и для любой области голо-
голоморфности: справедлива
Теорема 3. Каждая функция f, мероморфная в области
голоморфности D, представляется в D как отношение голо-
голоморфных функций.
¦« Представим дивизор (/) функции f в виде разности А' — Д"
двух положительных дивизоров из r(D, 3)\ возьмем элемент
о(А")е Hl{D, <д*) и, пользуясь цитированным результатом Серра,
найдем положительный дивизор А'" такой, что о (А"') — — а (Л").
Так как о — гомоморфизм, то а (Д" + А"') = 0, следовательно-
(по замечанию после теоремы 1), соответствующая проблема
Кузена разрешима и существует функция ty^T(D, ой*), дивизор
которой (ф) = А" + А'". Но этот дивизор положителен, следова-
следовательно, функция i|) голоморфна. Рассмотрим, наконец, дивизор
произведения (fv|>) = (А' - А") + (А" + А"') = А' + А'"; он тоже
положителен, следовательно, и функция qp = fi|) голоморфна на М.
Данная функция_/ = qp/i|> >
39. Решение d-проблемы и проблемы Леви. В начале этого
параграфа мы сформулировали теорему II, которая решает
для областей голоморфности так называемую <Э-проблему,
В общем случае постановка этой проблемы такова:
(Э-проблема. Пусть D — область на комплексном много-
многообразии и / — дифференциальная форма бистепени (р, <?+1)
класса С°°, для которой
470 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
Требуется найти формул бистЪпени (р, q) класса С°° такую, что
dg = f. B)
Так как дд = 0, то условие A) является необходимым для
разрешимости проблемы.
Мы будем решать эту проблему для областей D с=С" в два
шага: сначала решим ее для форм с коэффициентами из про-
пространства L2, затем сгладим полученные решения. Для про-
простоты ограничимся наиболее важным для приложений случаем
р = 0, в общем случае доказательство аналогично 1).
Для первого шага нам понадобятся некоторые обозначения.
Через Lq(ty, D), где D — открытое множество в С и i|)eC2(D),
¦ф^О, мы обозначаем пространство всех дифференциальных
форм /=2' fjdzj бистепени @, q) с коэффициентами из про-
пространства L2 по мере tydV в D, где dV — мера Лебега в С".
Скалярное произведение
(f, h) = Y J ffirtdV'
1 D
превращает L2Q в гильбертово пространство с нормой ||f\\ = (f, /)''*•
1. Сведение к оценкам. Оператор д, заданный на глад-
гладких формах, определяет оператор Т: L2q->L2q+i с плотной обла-
областью определения DT; по определению h принадлежит DT, если
все -тгт^-еLo(яр, D). Аналогичный оператор L2q+\—*¦ L2q+2 обозначим
через 5. Так как дд = 0, то ST = 0. Это значит, что множество
значений Rr оператора Т содержится в пространстве нулей Ns
оператора S, и d-проблема сводится к установлению равенства
Ят = Ms.
Обозначим через Т оператор L2q+\-+L2q, сопряженный Т:
(Tg,h) = (g,T'h), g^DT, h<=Dj*. , C)
Из этого равенства видно, что Rt* ортогонально Nt', его замы-
замыкание Rt* будет ортогональным дополнением к Nt, если Dt*
плотно в L2q+\. В этом случае отыскание формы g из равен-
равенства B) сводится к отысканию формы g e RT* такой, что
(g, ГА) = (/, А), ЛеОг, D)
') Все необходимые сведения из функционального анализа, которые
мы используем при доказательстве, можно найти в книге: К. И о с и д а,
Функциональный анализ, «Мир», М., 1967.
§ 12] ПРИМЕНЕНИЯ ч 471
Так как RT<=NS и f^Ns, то в этом равенстве можно ограни-
ограничиться формами Ае Dp>[)Ns. Если мы докажем оценку
Ns, E)
где с — константа, не зависящая от h, то из неравенства
\if, h)\<c\\f\\'\\rh\\, h<=DT*[)Ns,
будет следовать ограниченность линейного функционала T*h ->
-->(/, h), определенного на Rt*. Из общего вида ограниченного
линейного функционала в гильбертовом пространстве вытекает
существование формы ge Rt*, удовлетворяющей D). Эта форма
будет решением d-проблемы и будет удовлетворять дополни-
дополнительному требованию ||g||^c||/||, если Dt*(]Rt плотно в Rt, ибо
|= sup \(Tg, A)|> sup \{g,®)\ = j
hR j? L
IUII-1 l|<o||-l/e
Итог наших рассуждений подводит
Лемма 1. Если множество Dt* плотно в L^+i, a Dr*f\Rr
плотно в RT и выполняется оценка E), то для любой формы
f^Ns найдется единственная форма g^RT* такая, что dg = f.
Оператор f-*g линеен и непрерывен; имеет место оценка
с той же постоянной с, что и в E).
¦< Ввиду E) пространство Rt* замкнуто; согласно доказан-
доказанному выше существует g^Rr*, удовлетворяющая B) и F).
Единственность g следует из того, что Rt* при выполнении
условия леммы является ортогональным дополнением к NT.
Линейность оператора f—*-g, обратного к Т, следует из линей-
линейности Т; его непрерывность вытекает из F) >
I'. Мы докажем сейчас, что при некоторых ограничениях
на функцию 1|з условие плотности Dt* C\Rt в Rt выполняется.
Сначала найдем явное выражение оператора Т* для форм
/jeC°°(D), равных нулю вне какого-нибудь компакта из D').
Так как
/ V
') Этот класс форм мы обозначаем символом С^° (D).
МРРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА
(ГЛ. IV
ТО
(dg, А) = X 2 / ^Kft dV = - Y ^ J ?/6A
I D
I v D
где
I V D
и ф=— lni|). Таким образом,
Г/г = - 2'
fiv/iv/ dzIt h e Co°° (D),
(8)
и Or* содержит все формы класса Co°(D). Следовательно Dt*
плотно в Lq+i, а для доказательства того, что Dt*[\Rt плотно
в RT, нам достаточно любую форму g<^DT приблизить формами
класса С™ (D) по норме g -> || g || + [| Tg \\. Возможность такого
приближения устанавливается в следующей лемме.
l
Обозначим Dv =
и потребуем, чтобы
убывала на 3D, что
D: | z |< v, p(z,
, v= 1, 2,
была положительной в D и так быстро
lim
a=l, 2, ...,
(9)
где Av = D\DV.
Лемма 2. Если \\> удовлетворяет условию (9), то формы
класса С^ (D) плотны в Lq (ty, D), 0 ^.q^n; если g e L2q имеет
какие-нибудь частные производные, принадлежащие L2q, то
найдется последовательность g\,eCo°(D), которая сходится к g
в L~q вместе с этими производными.
< Обозначим через %v характеристическую функцию мно-
множества Dv. Усредним ее с помощью ядра К(| t, \) — неотрица-
неотрицательной ФО функции из Со" (С™), равной нулю вне единичного
шара; именно положим
-1
A0)
Функция 1veC0°°(D), она равна 1 на Dv и 0 вне DAv; любая
производная от Av порядка а не превосходит по модулю cava,
где постоянная са не зависит от v. Формы
§ I2J ПРИМЕНЕНИЯ 473
принадлежат С™ (D) и сходятся в L~q к g. Так как
= J
то
+
(J/asv! u)
где D^v получилось в результате дифференцирования произве-
произведения gXv по правилу Лейбница; DXV является линейной ком-
комбинацией производных от \ порядка <1а. Так как \D\, ^c'av",
где постоянная с'а не зависит от v, то мы получаем ввиду (9),
что Dagv->Dag в L% >_
Так как операторы д и Г* линейно выражаются через пер-
первые производные, то мы получаем
Следствие. Если г|з удовлетворяет (9), то формы класса
Со"(D) плотны в пространстве Dt*[)Ds no норме h->\\h\\ +
+ || Th 1| +1| Sh || и плотны в DT по норме g -> || g || + || Tg ||. Из
последнего следует, что Вт* ("| /?г плотно в Rt-
Таким образом, оценку E) достаточно получить для форм
из Co°°(D).
II. Оценки в псевдовыпуклых областях. Для
оценки нормы оператора Т* воспользуемся легко проверяемым
коммутационным соотношением
где ф= —Imp, a bv определены в G). Интегрируя по частям
выражение
IIГА ||2 = S S I MvAVl> ^. й е С Ф),
и пользуясь A1), мы получаем
J 6ААЛ> rfy = _ J
Перебрасывая в последнем интеграле -^=- на Av/> мы нахо-
ДИМ, ЧТО
J H,V
474
МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА
[ГЛ. IV
где hj — вектор (hu, ..., hnI). Под знаком второго интеграла
¦стоит выражение, равное
^ ^hji^
2 _
— | dh |2, где | dh | — модуль
/V _
вектора из коэффициентов формы dh и hj — коэффициент h
йри dij1); через #(ф, со), где т = {т1, ..., ©„), мы обозначаем
форму Леви 2j h7 J- щё^. Поэтому
и,
qz gz
dh,,
, A2)
A, V
и мы теперь можем доказать следующую теорему существо-
существования:
Теорема 1 (Хёрмандер). Пусть D — псевдовыпуклая
С C2(D) #( )^| р
р (рр) у
область в С и q>^C2(D) такова, что #(<р,
С
| со
в D,
q) (р | р
где а — положительная константа, © е С. Тогда для любой
/еLJl+i(е~ф, D) такой, что df = O, найдется geЬ2ц{е~ч\ D) такая,
что dg = f и
I \ g \2 e-<f dV ^ a'1 j\f\2e-fdV. A3)
область D ограничена и /eL^+i(l, D), то найдется реше-
решение geijfl, D), удовлетворяющее условию
а)), , A4)
где Д — диаметр области D. (Здесь | h |2 = 2' I ni l2i II h II|j m =
л /
¦< Обозначим через Я, функцию класса C2(D), плйорисуб-
тармоническую в D и стремящуюся к +оо на dD (см. курс
Хёрмандера, стр. 74); если dZ) достаточно гладкая, то в ка-
качестве I можно взять — In р (z, dD); если D = С — функцию | z |2.
Заменяя Я на е\ мы можем считать, что Я>0; добавляя | z |2,
J) Проверим это для q—l. Имеем
•2
Ц < V
dhv
I* ?¦ v
dz»
dzv
§ 12] ПРИМЕНЕНИЯ 475
получаем, что А(.г)—>оо при |г|—>оо. Заменяя теперь Я функ-
функцией и о Я, где и — выпуклая достаточно быстро растущая функ-
функция класса С°° (R1), мы можем считать, что условие (9) выполнено
для любой функции г|зе = ?~еЯ-~ф, 8>0; плюрисубгармоничность X
от этих замен не нарушается. Скалярное произведение в L2(i|3|/V)
мы будем обозначать символом ( )v, норму в этом прост-
пространстве—символом || ||v; в L2(e~<p) соответствующие обозначе-
обозначения ( ) и || ||.
Из равенства A2), где вместо ф надо писать фН—, мы
получаем, что || h ||2 <! a'1 \\ T*h IJ,, h^Ns; по лемме 1 существует
gv e L2 (^1/v) такая, что dgv = f и || gv j|2 < а~г \\ f IP < a1| f ||2. Таким
образом, последовательность gk, k^v, ограничена в L2q(cpi!v),
так как \\gk \\v^l\gk Ik- Из нее можно выделить подпоследова-
подпоследовательность g'k, слабо сходящуюся в этом пространстве (см. Иосида^
стр. 180); это значит, что для любого yeL2(if>I/y) предел
/(о)= lim (g?, о) существует. Линейный функционал v->l{v)
ограничен и потому представим некоторым элементом
т. е. /(»)^TgTo)v. Так как dgk^f и (g, T"h)v= lim (gb r/»)v =
= (f, A)v, то dg = f, а так как L2q(^1/jX)czL2q(^i/v), если n>v, то
ёе П Ll (%v)- Наконец, из того, что ||g||v= sup \(g, f)v|<
V II О || — 1
^— ||f||, мы получаем
а
У а
lim
т. e. geL2,(e"', D), и первая часть теоремы доказана.
Если область D ограничена, то мы можем считать, что OgD,
и в качестве ц> взять а|г|2. Для найденного выше g получаем
\\ffdV.
Функция а~]еаД2 достигает минимума по а при а = Д~2, и мы
получаем оптимальную оценку || g \\L, {D) ^ У~ё Д || / \\L, ф) >
Замечание. Последовательность g'ke~}-lk элементов L2(e"<p}
ортогональна к NT в этом пространстве и тоже слабо сходится
к <?• Поэтому g принадлежит ортогональному дополнению к Nt>
476 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
и этим условием форма g определена однозначно. Как и
в лемме 1, линейный оператор f->g, обратный к д и решающий
<?-проблему, ограничен; его норма не превосходит —^=7 . Наконец,
У а
если е~ф = г|з удовлетворяет условию (9), то ge /?г*, т. е. g — T*h
для некоторой формы h e L2q+i (г|з, D).
III. Гладкость решения. Пусть правая часть B) при-
принадлежит C°°(D); мы хотим найти решение g, тоже принадле-
принадлежащее С°° (D). Сначала мы индукцией по а будем доказывать
существование у специально подобранного решения всех произ-
производных Da порядка а, которые принадлежат L2 на компактных
лодмножествах D; это свойство мы будем записывать так:
Dag^L2q(D, loc), a=l, 2, ... A5)
Лемма 3. Если функция w^L2(C) имеет компактный
носитель 1) и если dw e L2 (С"), то -^-, k = 1, ...,«, тоже при-
azk
надлежат L2(Cn).
< Пусть область D содержит носитель w и wv — последо-
последовательность усреднений A0'). Так как
<Ч
dw\, I dW \ „
и ,- ¦ = (-^- , если носитель w содержится в Dv, то последо-
dwv
ibHUUTb
Деле,
вательность ™v , v=l, 2 сходится в L2(C"). В самом
azk
dw
dzk
так как (^-\ -> |^- в L2(C") при
\ /
Случай ^ = 0. Подберем функцию феС2(О) так, чтобы
//(ф, со)^а|(о|2, шеС", для некоторой константы а >0, и вос-
воспользуемся теоремой 1. Если Я, — произвольная функция из Со° (Z)),
то dXg = Xf + gdX^L2(Cn), поэтому согласно лемме 3 все
Z)!Ag <=L2(C"). Так как в L2(C") порядок дифференцирования
не влияет на результат, то это рассуждение можно применить
к DaXg и получить, что Da+llg e L2(Cn) и т. д. -Значит, для
_ /
') Носителем функции или формы называется наименьшее замкнутое
множество, вне которого она равна нулю.
§ 12] ПРИМЕНЕНИЯ , 477
любого а функция Dag суммируема с квадратом на каждом
компакте, где Я, ф 0. Ввиду произвольности к это и есть свой-
свойство A5).
Случай q>0. Воспользуемся тем, что в равенстве A2)
форма h^Co'(D) и потому г|з можно взять равной 1 на носи-
носителе h. Равенство принимает вид
^'ll^lfHIflcoif + Udcoll2, (OS С (С"), A2')
где норма берется в L2(C) и Фсо = — V V kJ dzj. Заменяя
<в на Daco, мы получаем, что
Это равенство справедливо для любой формы ю, у которой
Da$(a и Dada> e L2(C"); для таких форм существование dDaa,
вытекает из A7).
Подберем (peC°°(Z)) так, чтобы для нее выполнялось усло-
условие теоремы 1, а для г|з = е~ф — условие (9). Решение уравне-
уравнения B) возьмем в пространстве Rt*; это значит, что g = T*h для
некоторой /г е Lo+i (гр). Так как q^l, то можно определить
оператор Я, сопряженный оператору д: Lq-\->Lq; его явный
вид задается формулой (8). Так как Н*Т* — 0 (ввиду равенств
hku= — hikj) и g = T*h, то g ев Dh* и H*g = 0. Поэтому для
>, где Я, е Со° (Д), мы получаем следующее выражение:
* (kg) = Я* (kg) - 2' 2 ^v/ j~; dz, =
Таким образом, если g e L2(D, loc), то й(Ще12(С"). Так
как д (kg) = Эя, A_g + Я,/ и А/ е Со°° (С), то из Dag e L2(?>, loc)
следует, что Dad(kg) e L2(C"), а тогда ввиду A7) dDakg,e
<=L2(Cn) для всех /. Согласно лемме 3 все ^'(l^eL^C11).
Так как kg <=L2(Cn), то мы доказали по индукции, что Z)ag/
для любых / суммируемы с квадратом на каждом компакте,
где кф 0. Ввиду произвольности Я, е Со° (D) это и есть свой-
свойство A5).
478 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
Согласно лемме Соболева о вложении') всякая форма, удо-
удовлетворяющая A5), совпадает в L2 с некоторой формой класса С°°.
Таким образом, доказав A5) для специально подобранных реше-
решений g, мы доказали следующую теорему, которая и решает
д-проблему:
Теорема 2 (Хёрмандер). Если область D псевдо-
выпукла, то уравнение dg = f имеет решение g e C°° (D) бисте-
пени (О, q) для всякой формы f e C°° {D) бистепени (О, <7+1)
такой, что df = O. Для q — О всякое решение обладает этим
свойством.
Эта теорема справедлива и для областей на многообразиях
Штейна, причем для форм любой бистепени (р, q); доказатель-
доказательство можно найти в книге Хёрмандера, цит. на стр. 463.
Замечание 1. Как видно из доказательства, мы брали
g ев Rt*. Согласно лемме 1 этим условием форма g определена
однозначно и она линейно зависит от /. Используя более силь-
сильную лемму Соболева о непрерывности вложения, мы получаем,
что оператор f—*-g, обратный д, непрерывен в следующем
смысле:
Для любого компакта К, a D и любого а^ 0 найдутся C^3= а,
постоянная са{К.) и компакт К' cz D такие, что
max|Z)a?|<ca(/C)max 2 \Dsf\,
К К' s < р
где | (о р = Zi I «/12.
Замечание 2. Так как всякая область голоморфности
является псевдовыпуклой (п. 26), то теорема II, сформулиро-
сформулированная в начале параграфа, является следствием теоремы 2.
В заключение приведем решение проблемы Лев и, кото-
которая связывает локальные и глобальные свойства областей голо-
голоморфности (см. п. 24).
Как мы убедились в п. 26, для решения этой проблемы нуж-
нужно доказать, что любая псевдовыпуклая область является
областью голоморфности; на основании теоремы 2 это вытекает
из следующей теоремы:
Теорема 3 (Хёрмандер). Пусть D — область в С" такая,
что уравнение да = О, имеет решение со е С°° (D) бистепени @, q)
для всякой формы QgC°° (D) бистепени @, q + 1) такой, что
дп = 0. Тогда D является областью голоморфности.
< Мы будем доказывать это индукцией по п. При я = 1
утверждение тривиально, ибо любая плоская область является
См., например, К. И о с и д а, цит. выше, стр. 242.
§ 12] ПРИМЕНЕНИЯ ' 479
областью голоморфности; предположим, что оно справедливо
для областей из С".
Нам нужно доказать, что для любого шара В czD, граница
которого содержит хотя бы одну точку g e 3D, найдется функ-
функция F^H(D), не продолжаемая голоморфно в точку g. Без
ограничения общности можно считать, что ? = 0 и что Ь =
= В (]{zn = 0) непусто. Тогда непусто и открытое множество
d = D fl{zn = 0}, которое мы рассматриваем в пространстве С"~1
точек 'z — {zu ..., zn-x}, a '0 является его граничной точкой.
Мы обозначим через п: z—>'z проекцию С" в С"~ и через
г: 'z—>('z, 0) вложение множества d в D, так что i(d) мы рас-
рассматриваем как подмножество D. Пусть <&'" (D) — совокупность
<0, д)-форм класса C°°{D). Для любой формы а> ^ 3r" (d) от:
переменной 'z мы обозначим через
я*со ту же со, рассматриваемую как
форму от z на множестве d X С.
Символом i*Q будем обозначать
форму от 'z, которая получится из
формы Q e <&~" (D), если положить
в последней гп = 0; таким образом,
Си «= З'4 (d).
Прежде всего докажем, что си-
система
<30 = (о A8)
ет-о-1 / ,ч РИС. 115.
разрешима в классе &ч (d) для
любой замкнутой формы юео^'<7 (d).
Для этого рассмотрим множество G = {zgD: n(z)^d}, за-
заштрихованное на схематическом рис. 115. Так как оно не
пересекается с i{d) и оба этих множества относительно замк-
замкнуты в D, то можно построить функцию феС°°A)), равную 1
на i(d) и 0 на G. С ее помощью мы преобразуем ю в форму
йо = фя*со (которая полагается равной 0 на G, хотя зт'со там и
не определена); очевидно, Qoe<^'?(D) и i*Q0 = a>. Далее пола-
полагаем Q — Qo — г„20, где 20 е <gTq(D) подбирается так, чтобы было
дп = 0. Этот подбор осуществим, ибо последнее равенство пере-
переписывается в виде системы <320 = — дп0, в правой части кото-
которой стоит форма — (Эф Л я*ю е (^""+1 (Д), замкнутая в силу
замкнутости л*(о, а такая система разрешима в классе &Tq (D)
по условию. Очевидно, мы имеем i*Q = i*Q0 = ю. Так как <ЭО = 0,
то по условию существует форма 2e^'''(fl) такая,_что
д2 = п. Полагая а = Г?, мы найдем, что oecf'M и да =
480 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
= С 52 = i*Q = со, т. е. что а является искомым решением си-
системы A8).
Так как d — открытое множество в Сп~ , то по индуктивному
предположению из доказанной разрешимости системы A8) сле-
следует, что d состоит из областей голоморфности. Поэтому суще-
существует функция feff (d), не продолжаемая голоморфно в окрест-
окрестность замкнутого шара Ь. Рассматривая / как замкнутую форму
из e?~0(d), мы, как и в предыдущем абзаце, найдем форму
F ев <&~°(D) такую, что OF = 0 и i*F = f. Построенная F является
голоморфной функцией в D, а так как сужение F \d — f, то F не
продолжаема голоморфно в окрестность замкнутого шара В >
Таким образом, доказана
Теорема (Ока). Любая псевдовыпуклая область D с С
является областью голоморфности.
Как показывает теорема 3, условие псевдовыпуклости об-
области DczC является не только достаточным, но и необходи-
необходимым условием для разрешимости d-проблемы для форм любой
бистепени @, q).
Мы закончим этот параграф доказательством еще одного
критерия для областей голоморфности.
Теорема 4. Область D а С" является областью голоморф-
голоморфности тогда и только тогда, когда HP^D, О) = 0, р — 1, 2, ..., п.
< Согласно теореме 1 п. 37 HP(D, 6) = ZP/BP. Поэтому из
тривиальности всех этих групп когомологий следует разреши-
разрешимость d-проблемы в области D для форм любой бистепени @, р).
По теореме 3 D является областью голоморфности. Обратное
утверждение составляет содержание следствия п. 37 >
ЗАДАЧИ
р
1. (У. Рудин). Если функция / = ~й . гДе Р и Q — взаимно простые
полиномы, голоморфна в области D сг С", то в этой области Q ф 0.
2. Если функция / голоморфна в бикруге {| z \ < 1, | w \ < 1} и не про-
продолжается голоморфно в точку (г0, е'е°), где |го|< 1, то она не продол-
продолжается и во все точки (z, e °), где |г| < 1.
3. Убедиться • в том, что функция -у——j-, голоморфная в шаре В =
= {| г|2 + | ш |2 < 1}, непрерывная в В и равная нулю на плоскости 2 = 0, не
представима в виде 2<р (г, ш), где <р голоморфна в В и непрерывна в В.
{3 5 3 5 )
-г < \z\ <¦ -г-, ~Г < \w \ < ~Т(~ область в С2; множество
M = {(z, w)^D: w = z+ 1} состоит из двух компонент: Л_1={(г, аи)} еМ: 1тг=
= Imi_)>0} и M2 = M\Mu отстоящих на положительном расстоянии друг
от друга. Доказать,-что вторая проблема Кузена: /_. = 1 в D \MU f2 = w—z—l
ЗАДАЧИ 481
в D\ M2 (данные согласованы) — неразрешима. [Указание: в случае разре-
разрешимости мы получили бы функцию f e H (D) такую, что f ф 0 в D\ M{ n
g = fl(z — w — 1)^0 в D \ М2; сравнивая приращения аргументов Дс и &'/
функции f на окружностях {|г| = 1, а> = ± 1} и соответствующие прираще-
приращения аргументов Д^ и Д^' функции g-, мы получим, что Д^ = А" = Д^' и Д^ = Д^,
хотя очевидно, что | Д^ — Д^ | = 2я.]
5. Пусть D — область голоморфности в С и {z e D: zl = 0} = Mi U M2,
где Mi и Mi — открытые непересекающиеся множества на плоскости zt = 0;
тогда существует функция f e Я {D) такая, что f=l на М| и функция f/zi
голоморфна в окрестности М2. [Указание: воспользоваться разреши-
разрешимостью 5-проблемы.]
6. (X. Р о с с и). Пусть К— полиномиально выпуклый компакт в С,
точка z° e К и функция f, голоморфная в окрестности 2/,о этой точки, такова,
что /(г°) = 0 и Re/< 0 на Uzo[}K\z°. Тогда существует функция g, голо-
голоморфная в окрестности К и такая, что g (z°) = 1, а | g (z) \ <1, если ге^\г°.
7. Пучок сУ на многообразии М называется тонким, если для любого
локально конечного покрытия Ua, oe/, на ff" можно определить разбиение
единицы, т. е. семейство гомоморфизмов <ра, ее/, пучка &~ в себя такое,
что: 1) 2 Фа ~ тождественное отображение и 2) для каждого ае/ найдется
а
замкнутое подмножество Va cz Ua такое, что <ра (^х) = 0 для всякого х ф. Fa-
Доказать, что для тонкого пучка ff"
Я?(М, ¦5г) = 0, если <?>1.
Убедиться, что пучок EГ'Р' , ростков дифференциальных форм бистепени (р, q)
с коэффициентами класса С°° на комплексном многообразии М является
тонким.
8. Пусть *Г — пучок на многообразии М, К' —замкнутое подмножество М
и {Ga} — некоторая фундаментальная система окрестностей К. Предположим,
что Нр (Ga, of) —0 для всех a (p фиксировано); доказать, что Я (К, 4F) = 0.
9. Пусть X — компакт, С (X) — кольцо всех непрерывных комплексных
функций на X, G — группа (по умножению) всех функций из С {X), нигде
на X не равных нулю, и Е — подгруппа G, состоящая из функций вида е?г
1бС (X). Доказать, что
G/E~Hl(X,Z).
Это равенство справедливо и в случае, когда X является счетным объеди-
объединением компактов. [Указание: воспользоваться точностью последователь-
последовательности 0 -> Z -> 6 —*" «^ -> 0, где Q м & — пучки ростков элементов С (X) и G
и е —отображение /->еад. ]
10. Пусть К— компакт в С", Р (К) — подкольцо С (К), состоящее из
функций, которые равномерно на К приближаются полиномами от z,
Gp=G{\P(K) и Ep = Ef]P (К), где G и Е определены в задаче 9. Дока-
Доказать, что
GpfEp ~W(K, Z),
если множество К полиномиально выпукло; привести пример компакта
К cz С", для которого этот изоморфизм не имеет места. Доказать, что
в общем случае
pIp(R,
где Ко — рациональная оболочка компакта /С.
31 Б. В. Шабат
482 МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА [ГЛ. IV
11. Пусть К — компакт в С" и функция f голоморфна в окрестности К.
Предположим, что Я1 (К, Z)=0 и 0 & f (К); тогда существует голоморфная
на К функция g такая, что ее = f (голоморфный логарифм /).
12. Пусть X — компакт, функция feC (X) и Nf = {х е X: f (х) = 0}. Пред-
Предположим, что Я1 (X \ Nf, Z) = 0; тогда для всякого целого k > 0 в С (X)
существует функция / .
13. Пусть 6Р — пучок ростков дифференциальных форм бистепени (р, 0)
с голоморфными коэффициентами на комплексном многообразии М, ZPt q —
группа замкнутых и Вр-q — группа точных форм бистепени (р, q) с коэффи-
коэффициентами класса С°° относительно оператора д. Доказать теорему Дольбо:
[Указание^воспользоваться точностью последовательности 0 ->6Р -><5гР' °—>
-э.^Р'1—> ..., которая следует из локальной разрешимости <Э-проблемы,
и задачей 7.]
14. Пусть D — область на комплексном многообразии М (комплексной)
размерности п, Zg и В% — соответственно замкнутые и точные относи-
относительно д формы бистепени @, q) с коэффициентами класса С^° (D) и
В? = В°. 4, где последняя определена в задаче 13. Доказать, что
Н" (D, О) « Z^JB", q > 0,
а если п > 1, то
Hi (D, <д)
Для п= 1 привести пример, когда последнее соотношение неверно.
15. Если D — произвольная область в С", то Hn(D,©) = 0. [Указание:
воспользоваться задачей 14.]
16. Пусть D — область голоморфности в С" и форма f класса С°" (D),
такова, что df голоморфна в D (т. е. df — форма бистепени (р, 0) с голо-
голоморфными коэффициентами); тогда существует форма g степени р— 1
класса С°° (D) такая, что форма f — dg голоморфна.
17. (Сер р). Пусть flcC — область голоморфности, Z и В — группы
замкнутых и точных голоморфных форм бистепени (р, 0) относительно опе-
оператора д = d — д. Доказать, что
Н" (D, С) « ZPlB".
[Указание: воспользоваться теоремой де Рама и задачей 16.]
18. Пусть D — область голоморфности в С" и 9^ (г°) — пучок ростков
голоморфных в D функций, равных 0 вместе с производными порядка ^ k
в фиксированной точке z° e D. Доказать, что
Hq (D, ?Tk (z°) ) = 0, если ,7>1-
[Указание: предварительно установить изоморфизм с подходящей фак-
факторгруппой форм бястепени @, <?) относительно д.]
19. Пусть a(v), v=l,2 — дискретное множество точек в области
голоморфности D czC" и pv — многочлен по z степени kv. Доказать суще-
существование функции fefl {D), у которой начальный отрезок разложения
Тейлора степени ^kv в каждой точке a(v) совпадает с pv. [Указание: сна-
сначала доказать, что Я1 (D, S)=Q, где 9 — пучок ростков голоморфных в D
ЗАДАЧИ 483
функций, равных нулю вместе с производными порядка ^kv в точках a(v>,
затем применить теорему I п. 36 к точной последовательности 0 -> ?? -><3 ->
>6/??>0]
/]
20. Пусть D - область в С", для которой Я1 (D, 6) = 0, и р: С" -> С2 -
проекция на первые две координаты. Предположим, что: 1) в D имеется
аналитическая поверхность, которая на р (D) проектируется взаимно одно-
однозначно, и 2) для каждого a^p(D) множество p~l (a) [\D связно и одно-
связно (т. е. на нем всякий замкнутый путь гомотопен нулю); тогда р (D) —
область голоморфности в С2. [Указание: см. теорему 3 п. 37.]
21. (Гладкая зависимость от параметра решения I проблемы Кузена).
Пусть О —область в С, для которой Hl (D, 6) — 0, и {Ua {t)} — покрытие,
в котором каждый элемент непрерывно зависит от параметра t, изменяю-
изменяющегося на некотором многообразии Д. Пусть /а (z, t) — функция класса Ck,
мероморфная по г в Ua(t) (гладкость — вне объединения полярных мно-
множеств). Предположим, что /а (z, t) — fp (z, ()еЯ (Ua (t) f| U$ (t)) для любых
а, р и t. Тогда найдется функция / (z, t) в DX А, мероморфная по г и
класса Ck вне объединения полярных множеств, такая, что f (z, t) — fa (z, t) e
e# (Ua(t)) для любых а и t. [Указание: воспользоваться существованием
ограниченного линейного оператора, обратного к д; см. замечание 1 после
теоремы 2 п. 39.]
22. (Г. М. Хенкин). Пусть D — строго псевдовыпуклая область в С" с
границей класса С3. Доказать существование гладкой функции f (г, t)
в G X dD, где G — некоторая окрестность D, голоморфной по г и такой, что
ИС: f(z, »-0}ЛО-{0.
[Указание: воспользоваться задачей 21 и доказательством теоремы Леви —
Кшоски из п. 24.]
ГЛАВА V
ОСОБЕННОСТИ И ВЫЧЕТЫ
Основная тема этой главы — особенности голоморфных функ-
функций нескольких переменных. Как мы видели, такие функции
не могут иметь изолированных особых точек: место последних
занимают особые множества. Их изучением мы займемся не-
несколько позже, а сначала рассмотрим теорию вычетов меро-
морфных функций, которая связана с особенностями простей-
простейшего типа — полярными множествами.
§ 13. Многомерные вычеты
Напомним ситуацию, в которой появляются вычеты в пло-
плоском случае. Пусть в области D а С задана функция /, голо-
голоморфная всюду, кроме конечного числа особых точек av
(v=l, ..., N). Обозначим через Yv: z = av + rveu, t e [0, 2n],
окружность достаточно малого радиуса rv. Интегралы от f
по таким окружностям, деленные на 2я/, называются вычетами f
в ее особых точках:
Окружности {yv} составляют базу одномерных гомологии
области D' = D\ U{av}. Это означает, что каждый одномерный
цикл (замкнутый путь) у cr D' гомологичен некоторой линейной
комбинации циклов yv с целыми коэффициентами:
N
У ~ 2 fcvYv-
v=l
Если это разложение известно и известны вычеты Rv, то
по свойствам интегралов
N
| / dz = 2ro 2 kvRv
у v=l
(теорема о вычетах).
Аналогичная ситуация имеет место и в пространстве. Однако
при переходе к пространственному случаю практическое вы-
13]
МНОГОМЕРНЫЕ ВЫЧЕТЫ
485
числение интегралов наталкивается на ряд трудностей, глав-
главным образом топологического характера.
40. Теория Мартинелли. Для изложения этой теории пона-
понадобятся некоторые топологические понятия.
Пусть на ориентируемом многообразии Мг действительной
= (P, Р,
Рр)
р
6)
размерности г заданы два симплекса
Тч = (Р, Q,, . . ., Qq) дополнительной
размерности (это означает, что р + q = r).
Пусть еще эти симплексы трансвер-
сальны, т. е., кроме Р, не имеют других
общих точек (рис. 116). Мы скажем, что
индекс пересечения этих симплексов в
точке Р равен +1, если ориентация г-мер-
ного симплекса (Р, Ри ..., Рq, Q,, ..., Qq)
совпадает с ориентацией Мг, и равен
— 1 в противоположном случае. (На
рис. 116, а индекс пересечения симплек-
симплексов S2 и Г1 в R3 равен +1, а на
рис. 116, б равен —1.)
Пусть теперь в Мг заданы две цепи
ор = 2 avSv и хч = 2 ftvTv дополнительной
размерности (р + q = г), пересекающиеся
друг с другом трансверсально в конеч-
конечном числе точек, которые мы будем счи-
считать общими вершинами симплексов,
составляющих эти цепи. В каждой точке пересечения мы умно-
умножаем индекс пересечения симплексов, принадлежащих этим
цепям, на произведение коэффициентов, с которыми симплексы
входят в цепи. Сумму таких произведений по всем точкам пе-
пересечения цепей ар и х" мы назовем ин-
индексом пересечения этих цепей и обозна-
обозначим символом i(op, х9). (На рис. 117
индекс пересечения цепей ст1 и т2 в R3
ра-
вен1(ст1,т2) = 2- 1 + 1 -(-1)+1 -(-1) = 0.)
Отметим следующие простые свой-
свойства индекса пересечения:
1) ориентируемость:
i К, х«) = - i (- а", х") = - I К, - т9);
Рис
Рис. 117.
2) коммутативность (или антикоммутативность):
1(ор,х") = (-1)рЧ(х",арУ,
3)дистрибутивность
i (aP, Tf + т|) = i (a", rf) + / (а", т|).
486 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
Отметим еще одно, геометрически очевидное свойство: если
обе цепи ор и хч являются циклами (т. е. их границы дар и дхч
равны нулю) и хотя бы одна из них является циклом, гомоло-
гомологичным нулю на Мг (т. е. границей некоторой цепи, принад-
принадлежащей Мг), то
i (о", хч) = 0.
Далее, рассмотрим на ориентируемом многообразии Мг два
гомологичных нулю цикла ор и т?~! (пусть по-прежнему р + q = r);
предположим, что они не пересекаются. Существует цепь TqczMr
такая, что xq~l = dTq, и если Г?с=Мг —еще какая-либо цепь
с границей х^~\ то по отмеченным свойствам индекса пересе-
пересечения
i(ap, Г)-1{а", r?) = iV, Tq-Tq) = 0,
ибо Tq — Т\ — циклл) на Мг, а <тр — цикл, гомологичный нулю.
Таким образом, в наших условиях индекс пересечения цикла ар
с любой цепью Тч с Мг, граница кото-
которой dTq = xq~x, не зависит от выбора этой
цепи и определяется (при заданных Мг
и ор) лишь циклом х4~1. Мы назовем
этот индекс коэффициентом зацепления
циклов аР и т" и обозначим символом
с(ст", xi~l); итак, по определению
c(ap,-t°-l) = i(ap, Г). A)
(На рис. 118 коэффициент зацепления двух одномерных гомо-
гомологичных нулю в R3 циклов т1 и а1 равен 2.)
Отметим следующие простые свойства коэффициента за-
зацепления:
1) ориентируемость:
с (ор, т") = — с(— аР, yi-i) = _ с (от", — х"-1);
2) коммутативность (или антикоммутативность):
с(аР, т"-1) = (-1)р(<7~1)с(т'?-1, 0");
3) дистрибутивность:
с(аР, тч-i + Tf) = с (стр, Tf1) + c(ap, т^1).
Отметим еще одно свойство: если два цикла сгр и аР, гомо-
гомологичные нулю на Мг, гомологичны друг другу на Mr \xq~l
Граница д (Т" - Т{) = хч~1 - т"" = 0.
§ 13] МНОГОМЕРНЫЕ ВЫЧЕТЫ 487
(где т*? — цикл, гомологичный нулю на Мг), то
с (of, т<7-1) = с@Р, т»-1). B)
Пусть, наконец, на многообразии Мг задан какой-либо ком-
комплекс К (см. п. 12). Мы назовем базой р-мерных гомологии К
систему р-мерных циклов о? (v= 1 р) такую, что: 1) циклы о?
гомологически независимы, т. е. из того, что некоторая цепь
р
о = 2 av0v гомологична нулю в К, вытекает равенство нулю
v=l
всех коэффициентов av, и 2) любой р-мерный цикл ор с К.
гомологичен некоторой линейной комбинации 1) циклов ару: ор~
~ 2 Кор.
v=l »
В заключение сформулируем без доказательства
Принцип двойственности (Дж. Александер,
Л. С. ПонтрягинJ). Пусть Sr — сфера действительной раз-
размерности г и К с: Sr — некоторый полиэдр. Тогда для базы
р-мерных гомологии
*У °1 . C)
комплекса Sr\K существует такая база (q— 1)-мерных гомо-
гомологии
полиэдра К (при этом p + q = r), что для всех ц, v = 1, ..., р
где 6jjV —символ Кронекера (равный 1 при n = v и 0 при ^xфv).
Базу D) мы будем называть двойственной к базе C).
Перейдем к задачам вычисления интегралов. Пусть в области
D а С задана мероморфная функция / с полярным множе-
множеством <?Р и требуется вычислить интеграл от формы a> = fdz =
— f{z)dzl А ... Л dzn по некоторому /г-мерному циклу oczD \ <&".
Если а гомологичен нулю в Z)\^°, то по теореме Коши—
Пуанкаре
' f dz = 0.
J
') Здесь, как и всюду в этой книге, мы рассматриваем цепи с цело?
численными коэффициентами.
2) См., например, книгу П. С. Александрова, цит. на стр. 316.
488 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
По той же теореме и по свойствам интегралов, если цикл а'
гомологичен о в Ь\#", то
dz. E)
Отсюда вытекает, что если известна база га-мерных гомо-
гомологии <Т[, ..., (Тр множества D\S" и разложение
р
2 1 (г* \
«vav Щ
v=l
по этой базе, то вычисление интеграла от / по о сводится
к вычислению интегралов по базисным циклам:
р
dz = %kv \fdz. G)
По аналогии с одномерным случаем назовем вычетом функции /
относительно базисного цикла 0V величину
(8)
v
Тогда будет иметь место
Теорема 1 (о вычетах). Если функция f мероморфна
в области D czC" и е7* — полярное множество этой функции,
то для любого п-мерного цикла a<zzD\Sa
р
vRv, (9)
еде kv — коэффициенты разложения о по базе п-мерных гомо-
гомологии D\?P, a Rv — вычеты f относительно циклов этой базы.
"В пространственном случае, в отличие от плоского, оты-
отыскание базы {ov} и разложения F) по этой базе является далеко
не простой задачей. Э. Мартинелли заметил, что в ряде слу-
случаев задача существенно упрощается, если воспользоваться
описанным выше принципом двойственности :). Для возмож-
возможности применения этого принципа предположим, что область D
гомеоморфна 2га-мерному шару. Отождествим все точки гра-
границы D в одну точку и дополним D этой точкой — мы получим
') Вычисления ряда интегралов по этому методу провел А. П. Ю ж а к о в
(см., например, его работу: К теории вычетов функции двух комплексных
переменных, Ученые записки Моск. обл. пед. ин-та, т. СХ, Матем., вып. 7,
A962)).
§ 131 МНОГОМЕРНЫЕ ВЫЧЕТЫ 489
2я-мерную сферу D. Точно так же отождествим все точки пере-
пересечения полярного множества SP функции f с границей 3D
в одну точку и дополненное этой точкой множество <^° обо-
обозначим через <&". Описанный процесс, очевидно, не нарушит
базы га-мерных гомологии {а^ и разложения F) по этой базе.
Иными словами, {о^} останется базой га-мерных гомологии
D \ $° и F) — разложением цикла а по ней.
На основании принципа двойственности мы можем вместо
базы га-мерных гомологии {oj множества D\S" искать базу
(п — 1)-мерных гомологии ть ..., тр самого полярного множе-
множества $", связанную с первой базой соотношениями
C(<V Tv) = <W 0°)
Циклы tv мы будем называть коротко особыми циклами.
Заметим, что коэффициенты kv разложения цикла 0 по базе
{a.J совпадают с коэффициентами зацепления этого цикла
с циклами двойственной базы {tv}. В самом деле, так как о
р _ _
гомологичен 2 ЬцОц в D \ ?Р', то по отмеченному выше свой-
свойству коэффициентов зацепления имеем
/ р
с (а, т\>) = с B ^Л. Ti
\ц=1
а отсюда, пользуясь распределительным законом и соотноше-
соотношениями A0), находим
с (a, tv) = ?v. A1)
Это замечание позволяет находить kv, не зная самой базы {crv}.
Интегралы по базисным циклам av (вычеты функции /) также
можно вычислять, не находя самих этих циклов. В самом деле,
пусть нам удалось найти в D \ 3й какие-либо р гомологически
независимых n-мерных циклов yu> по которым мы можем вы-
вычислить интегралы
'dz = /(yw.), ц = 1, • •., Р-
Пусть еще известны коэффициенты зацепления с (у^, tv) = a^v
этих циклов с циклами двойственной базы {tv}. По сделанному
выше замечанию a^v являются коэффициентами разложения y^
490 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
по базе {0V}, поэтому по теореме о вычетах для любого
ц=1> • ••> Р
v=l
A2)
где Rv — вычет / относительно цикла 0V.
Систему A2) можно рассматривать как линейную относи-
относительно неизвестных вычетов /?v, причем ее определитель про-
пропорционален Det (a^v), который отличен от нуля в силу гомо-
гомологической независимости циклов Уц- Поэтому из этой системы
вычеты легко находятся.
Учитывая отмеченную выше двойственность, условимся на-
называть интеграл / по /г-мерному циклу tfv, деленный на Bга)*,
вычетом относительно особого цикла tv (двойственного (п— 1)-
мерного цикла на S"). Заметим, что это определение подчер-
подчеркивает аналогию пространственного случая с плоским, где
интеграл по одномерному циклу yv> Деленный на 2га, называется
вычетом / относительно особой точки av (нульмерного цикла).
Теорему о вычетах теперь можно сформулировать так:
Теорема 2. Пусть функция f мероморфна в области Z)czC",
гомеоморфной 2п-мерному шару, и &* — полярное множество f,
которое получается добавлением к &* f\D множества S^ f| dD,
отождествленного в точку. Пусть tv, v = 1, ..., р, — база (п— 1)-
мерных гомологии множества &* и Rv —вычет f относительно
особого цикла tv. Тогда для любого п-мерного цикла aczD \ <&"
KRV, A3)
a v»=l
где kv — c (a, xv) — коэффициент зацепления а с особым циклом xv
Примеры:
1. Если /—целая функция п комплексных переменных,
п
п>\, а I (z) =2 av2v + P~ линейная функция, то для любого
v=l
/г-мерного цикла a cz С" \ {I (z) = 0} и для любого целого числа m
J
В самом деле, границей области С" являются бесконечные
точки, которые нужно отождествить в одну. Полярное множе-
множество #"={/ (z) = 0} после пополнения отождествленными беско-
бесконечными точками станет {2п — 2)-мерной сферой #". При п>\
131
МНОГОМЕРНЫЕ ВЫЧЕТЫ
491
любой (п— 1)-мерный цикл на <^° гомологичен нулю (р = 0),
база (tv) тривиальна и, значит, рассматриваемый интеграл
равен нулю.
По тем же причинам равен нулю при п>\ интеграл
I
/ B) dz
Р /
П 2
ц=1\
+
где /—целая функция, а полярное множество^ представляет
собой набор р параллельных плоскостей. (Здесь #" — «букет»
Bп — 2)-мерных сфер, касающихся друг дру-
друга в отождествленных бесконечных точках.)
2. Рассмотрим интеграл
_ Г
~ J
ezw dz Л dw
{z-2w)(w-2z) '
где а — произвольный двумерный цикл из С2,
не пересекающийся с полярным множест-
множеством Sa=S"l[j 3°2, где S"i = {z = 2w] и S°2 =
= {?2>=2Z}.
Пополненное полярное множество §Р
состоит из двух двумерных сфер &*х и #,
пересекающихся в двух точках: {г = О,
до = 0} и отождествленной бесконечности. Нам нужно найти
базу одномерных гомологии ?Р. Очевидно, всякий одномерный
цикл, лежащий полностью на одной из сфер, гомологичен нулю.
Поэтому не гомологичный нулю цикл должен проходить от
точки @, 0) по одной сфере до оо и затем возвращаться
ло другой сфере в ту же точку. Все такие циклы гомологичны
несколько раз проходимому циклу т, который состоит из какого-
либо луча 1Х с:ёР,, идущего из @, 0) в бесконечность, и какого-
либо луча /г с: ^°2> идущего из бесконечности в @, 0) (см. схе-
схематический рис. 119). Пусть, например, /( проходит через точку
{2, 1), а /2 — через точку A, 2), тогда параметрические уравне-
уравнения этих лучей будут иметь вид
'2- „, _ с
U
У нас р=1, следовательно, достаточно вычислить интеграл
от / по какому-либо одному не гомологичному нулю в С2\^
492 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
двумерному циклу у. Выберем в качестве у тор {е{ч, е'*}, где
O^p, г|з ^ 2л, тогда
JfrfzArf»- J J -^«rt—&)•
Y {!ш 1 = 1} {|z| = l}
Так как у нас |до|=1, то при вычислении внутреннего инте-
w
грала нужно учитывать лишь вычет в точке z = —, и, значит,
w2
2я/ -г- 4 о
этот интеграл равен -=—? ¦* , а весь интеграл равен —^-я
(из того, что интеграл отличен от 0, и вытекает, что у не гомо-
гомологичен нулю).
Найдем коэффициент зацепления с (у, т) = а; по определению
он равен индексу пересечения у с двумерной пленкой Г2, на-
натянутой на т. Параметрическими уравнениями Т2 служат
а с тором y эта пленка пересекается лишь в одной точке A, 1),
которая соответствует значениям параметров /, = t2 = -g-, qp =
= if> = 0. В этой точке д , .^ ,у' "' v , > 0 (мы положили 2 = х + г'г/,
w = u + iv), откуда видно, что индекс пересечения i(y, T2) =
= с(у, т) = 1. По формуле A2) находим, что вычет / относи-
относительно особого цикла т равен
Y •
и тогда по теореме 2 получаем значение искомого интеграла:
где с (о, т) — коэффициент зацепления (двумерного) цикла инте-
интегрирования а с особым (одномерным) циклом т.
41. Теория Лере. Здесь мы рассмотрим другой метод вычи-
вычисления интегралов, принадлежащий Ж. Лере, В ряде случаев
этот метод позволяет свести вычисление интеграла от формы со
степени р по р-мерному циклу о к вычислению интеграла
от формы res со степени р — 1, называемой формой-вычетом,
по некоторому (р— 1)-мерному циклу, лежащему на многооб-
многообразии особенностей формы а. Метод Лере также можно рас-
рассматривать как обобщение классического метода вычетов, ко-
§ 13] МНОГОМЕРНЫЕ ВЫЧЕТЫ 493
торый соответствует случаю р = 1 и сводит вычисление инте-
интегралов от форм (й — fdz по замкнутым кривым к вычислению
значений вычетов res / в особых точках / (т. е. нульмерных
интегралов от res/ по этим точкам). Мы изложим этот метод
в его простейшем варианте 2).
Пусть на п-мерном комплексном многообразии М задано
(п — 1)-мерное комплексное подмногообразие^0, которое в окрест-
окрестности Uг" с= М каждой своей точки 2° задается как множество
нулей голоморфной в этой окрестности функции г|зг такой, что
grad арг„ ф 0 в U\\
^0^ = И^: *Mz) = 0}. A)
Пусть на M\S^ задана дифференциальная форма ю степени р,
0< р^.2п, класса С°°, имеющая на ?Т полярную особенность
первого порядка. Последнее условие означает, что в каждой Uz<>,
г°ев^, произведение арг„(о продолжается до С°°-формы на ?/г„.
Лемма. Форма аеС°°(Л}) тогда и только тогда предста-
представила в окрестности U точки z° e S" в виде 2)
а = dip Л Р, B)
где (ЗеС°°(?/), когда в этой окрестности
dip Л а = 0. C)
< Примем if> за одну из локальных координат, определяю-
определяющих SP в окрестности U, скажем за переменную г, (это воз-
возможно в силу условий, наложенных выше натр). Выражение для а
в этих координатах можно разбить на два слагаемых:
а = 2««!... ipdZi1 Л ... Л dZip =dzlA$ + a',
где а' не содержит dz{ (как всегда, мы полагаем Zv = zv,
Zn+V = zv, v=l, ..., п). Таким образом, если а представима
в виде B) при г|з = zx, то а' = 0, а значит, и dzx Л а = 0, т. е. C)
выполняется. Обратно, если dz{ Л а = 0, то и dz{ Л а' = 0, а так
как а' не содержит dzb то это может быть лишь при а'= 0 >
Теорема 1. Если форма и е С°° (М \ S°), имеющая на ?Р
полярную особенность первого порядка, замкнута в M\S", то
') Полное изложение см. в книге: Ж- Л е р е, Дифференциальное и
интегральное исчисление на комплексном аналитическом многообразии,
ИЛ, М, 1961.
2) Для простоты письма мы опускаем индекс z° в обозначениях U,
¦ф и р.
494 особенности и вычеты [гл. v
в окрестности U произвольной точки z0^^ вне <^° она пред-
ставима в виде
<о = ^Лг + со„ <4>
еде формы г, со, е С°° (U). При этом сужение г \#, не зависит
от выбора функции ф и является замкнутой формой.
< Так как у нас фсо е С°° (?/), то d (фю) = йф Л со 4- ф Л dec;
но на М\#" имеем dco = 0 (ибо со замкнута), значит, по непре-
непрерывности d (фю) = йф Л со всюду в U. Таким образом, йф Л со
продолжается на #" до формы ае С°°(?/)> и по лемме найдется
форма C = си, е С°° (U) такая, что
Умножив это равенство на ф, найдем с?ф Л (фсо — фю,) = 0, где
фсо — фсо, е С°° (U); значит, по той же лемме существует форма
r<=C°°{U) такая, что фсо — фсо, = йф Л г. Это равенство вне #"
равносильно D).
Покажем, что сужение г \^ однозначно определяется фор-
формой со. Предположим сначала, что функция ф, определяющая
полярное множество ?Р, задана, и докажем, что из равенства
следует равенство г|^ = 0. Но из E) мы получаем йф Л г +
+¦ фсол = 0, откуда йф Л фю, = 0, а так как ф —функция, от-
отличная от нуля в ?/\#\ то там йф Л со, =0; в силу того, что
йф Л со, е С°° (U), последнее равенство справедливо и всюду в U.
Мы можем применить лемму, по которой найдется форма со2.
такая, что со, = йф А со2. Подставляя это в E), находим
dty А (г + фсо2) = 0; по той же лемме г + фсо2 = йф Л со3, где со3 е
е С°°([/). Отсюда и видно, что сужение г 1^ = 0, ибо на #" у нас
Теперь докажем независимость г ]#, и от выбора функции ф,
определяющей полярное множество. Пусть это множество
(в пределах окрестности U) определяется еще функцией ф;
тогда частное ф7ф = х голоморфно и отлично от нуля в U
(см. п. 33). Пусть мы имеем
где г, в,еС"(С/), Подставляя сюда ф = ф%, найдем
§ 13] МНОГОМЕРНЫЕ ВЫЧЕТЫ 495
здесь со, = —— Л г + и, е С°°(?/), и по доказанному выше г|^ =
Остается доказать замкнутость формы г \^. Но вне #" в силу
замкнутости со мы имеем da = -S- д dr + dco, = 0, причем
в силу непрерывности это равенство справедливо всюду в <&*.
В силу доказанной выше единственности заключаем, что
dr \„ = 0 >
Определение 1. Формой-вычетом замкнутой формы
со е С°° (М \ е^3), имеющей на в^ полярную особенность первого
порядка, называется замкнутая форма, которая в окрестности
каждой точки 2°е#> равна сужению на $* формы г в разло-
разложении D):
res со = г |^. F)
Таким образом, оператор res преобразует группу ZP(M\SP)
замкнутых С°°-форм степени' р в группу Z"'1 (S0) замкнутых
С°°-форм степени р — 1:
res: Zp{M\0>)-*Zp~i(ff>). G)
Замечание. Если форма со голоморфна г) на М \ #", то и
res со голоморфна на &>. Это следует из того, что в случае
голоморфности со формы г и со, при доказательстве теоремы 1
также можно выбрать голоморфными.
Пример. Пусть р равно (комплексной) размерности п
многообразия М, а форма со голоморфна на M\S° и в локаль-
локальных координатах z = (z,, ..., zn), действующих в окрестности U
точки 2°е#>, она представляется в виде
a» = -J-dz = -|d2,A ... Adzn, (8)
где ш, il? ^ Н ([/), a ib \Ф = 0, -—-
0. Тогда можно написать
_Х.
') Определение голоморфной формы см. в п. 14.
496
ОСОБЕННОСТИ И ВЫЧЕТЫ
[ГЛ. V
откуда видно, что
res со = (-1 Г1
dzv
dzx/\ ../ч.. dzn.
(9)
При п = 1 мы получаем обычную формулу для вычета в по-
полюсе первого порядка: res — dz *= *jy, , .
Перейдем к описанию так называемого пограничного опе-
оператора Лере б, который каждой точке 2°^^ сопоставляет
гомеоморф окружности bz°eM\?P (и таким образом увеличи-
увеличивает действительную размерность на 1).
Этот оператор должен обладать следую-
следующими свойствами:
1. В некоторой окрестности Uz« суще-
существуют локальные координаты (zu ..,,
zn) = z с началом 2°, в которых 3й П ?/го
определяется уравнением г„ = 0, а б2°сг[/го
и определяется уравнением 1 zn \ = 1.
2. Совокупность (J 6z образует в
Рис. 120.
M\Sa непрерывную поверхность.
3. При z' ф z" линии bz' и bz" не
имеют общих точек.
Таким образом, совокупность (J bz составляет границу
z ^ &*
трубчатой окрестности многообразия 3й (см. схематический
рис. 120, где <&* изображено линией, а М — трехмерным про-
пространством). В принятых выше условиях построение такого
оператора б всегда возможно, ибо действительные размер-
размерности $° и М отличаются на две единицы.
Пусть теперь а —цикл на <&* действительной размерности
р—1; мы предположим, что носитель этого цикла (т. е. соот-
соответствующий ему полиэдр) компактно1) принадлежит S°.
Обозначим
6а = [J bz;
z e a
мы можем рассматривать 6а как р-мерную цепь на М \$а, если
введем в ней естественную ориентацию, соответствующую
ориентации а. Для этого достаточно ввести ориентацию на ка-
каждой линии 6z, например так: будем считать, что ориентация
в окрестности Uz задается порядком следования локальных
') Это предположение нужно для того, чтобы избежать рассмотрения
несобственных интегралов (см. п. 11).
§ 13] МНОГОМЕРНЫЕ ВЫЧЕТЫ 497
координат z{, ..., zn, а на многообразии иг[\&" — порядком
2], ..., «„_,; тогда положительный обход на hz будет соответ-
соответствовать возрастанию tn в представлении zn = eltn окружности 6z
(см. свойство 1 оператора б).
Легко видеть, что оператор б коммутирует с оператором д
взятия границ Fд = д6), поэтому он переводит циклы снова
в циклы и циклы, гомологичные нулю, в такие же. Таким об-
образом, б устанавливает гомоморфизм групп гомологии
б: H(pU {S») -> Hf (M\f) A0)
(см. п. 12; значок (с) в обозначении групп указывает на то, что
рассматриваются компактные гомологии, т. е. принимаются
во внимание лишь цепи с компактными носителями).
Следующая теорема является обобщением теоремы Коши
о вычетах из ч. I.
Теорема 2. Пусть (р — 1)-мерный цикл вШе? и сое
е С°° {М \ еР) — замкнутая форма степени р, имеющая S° своим
полярным множеством первого порядка; тогда
j со = 2ш J res со, A1)
ба а
где б — пограничный оператор Лере.
¦4 Обозначим через бе, 0<е<1, оператор, который обла-
обладает свойствами 1—3 оператора б, с той лишь разницей, что
в 1 уравнение |г„.|=1 заменено уравнением 1 zn\ = e и при в—>0
трубчатая окрестность а(е), ограниченная поверхностью 6ест =
= (J 6ег> стягивается в а. По формуле Стокса (п. 14) для лю-
г е а
бых 8j и е2, 0<е,<е2<1, имеем
[со— |ш= J da = 0
б б
в силу замкнутости формы, так что интеграл от со по ЬЕа
не зависит от е.
Теперь покроем стA> конечной системой окрестностей {?/у-}уе/,
в каждой из которых действует теорема 1 и, как выше, можно
принять ty{z) — zn. Построим для этого покрытия разбиение
единицы {еу} (см. п. 11) и применим в каждой Uj теорему 1,
в которой положено а|з = .г„; мы получим
32 Б. В. Шабат
498 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
Здесь
{К1} {'Ч
res»
при е~>0, левая часть A2) не зависит от е и равна интегралу
по бо, а вторая сумма в правой части стремится к нулю при
е->0. Поэтому, переходя в A2) к пределу при е->0, мы будем
иметь
Г со = 2га 2j J бу res со = 2га Г res со >
Заметим, что если заменить ст другим циклом а', принад-
принадлежащим тому же классу h e Нрс-\ {??) компактных гомоло-
гомологии на S° (это означает, что о' —<т ограничивает некоторую
р-мерную цепь, компактно принадлежащую 3й), то в силу зам-
замкнутости формы res со интегралы от нее по с и а' по формуле
Стокса совпадают. Учитывая еще, что согласно A0) оператор 6
сохраняет гомологии, мы можем заменить в A1) циклы а и бст
любыми представителями соответствующих классов h e Нр% {<&*)
и 6/г е Нр'(М\еТ). Поэтому формулу A1) можно переписать
в виде
со = 2ш res со. A3)
Ясно, далее, что если к ш добавить точную в М \#" форму
(т. е. являющуюся дифференциалом некоторой формы степени
р —1), то интегралы в A3) не изменятся. Класс форм, отли-
отличающихся от ю на точные формы, является классом когомоло-
гий, содержащим со, а совокупность таких классов для всех
замкнутых форм со степени р + 1 из С°° (М \ 3й) — группой кого-
мологий Нр(М\е7й) (см. п. 13). Мы видим, что класс когомо-
логий из Нр~1 {3й), содержащий res©, зависит только от класса
когомологий из Нр(М\&а), содержащего форму со.-
Определение 2. Пусть со — некоторая замкнутая формаг
представляющая класс со* е Нр (М \ 3°); класс когомологий
из Яр~' (в?3), содержащий форму res со, называется классом-вы-
классом-вычетом и обозначается символом Res ю = Res со*.
Формулу A3) теперь можно переписать в виде
j со* = 2ш j Res а>\ A4)
dh h
<§ 13] - МНОГОМЕРНЫЕ ВЫЧЕТЫ
499
Можно убедиться в том, что оператор Res устанавливает
гомоморфизм соответствующих групп когомологий:
Res: Hp(M\S»)-+Hp-l(Su). A5)
Опишем в общих чертах случай полярных особенностей
выше первого порядка. Пусть опять на n-мерном комплексном
многообразии М задается многообразие 3й, локально описы-
описываемое как множество нулей голоморфной функции ip, для ко-
которой grada|)=^O. Будем говорить, что форма о> е С°° Ш \ в^)
имеет на & полярную особенность порядка q, если произведе-
произведение -ф^со продолжается до С°°-формы на М, a tyi'a, где q'<q,
не продолжается.
Приведем без доказательства теорему, которая сводит вы-
вычисление интегралов от замкнутых форм, имеющих на ?Р по-
полярную особенность выше первого порядка, к уже рассмотрен-
рассмотренному случаю (см. книгу Лере, цит. на стр. 493):
Для любой замкнутой формы со е С°° {М \ ??), имеющей
на 3й полярную особенность, найдется когомологичная ей
форма ш0, которая имеет на $" особенность первого порядка,
Класс когомологий из Нр~1 №), содержащий res ш0, т. е.
класс Res co0, называется классом-вычетом формы ю; он опре-
определяется лишь классом когомологий из Нр(М\?Р), содержа-
содержащим ш.
В плоском случае переход от формы a — fdz к ao = fodz
состоит в замене f(z)= , с~"w + ... + с~' функцией /0 =
\Z ~~ &) Z (X
= —fl— , имеющей в точке а полюс первого порядка и тот же
вычет, что и /. Отметим, что в пространственном случае для
голоморфной ю форма со0 не обязана быть голоморфной и во-
вообще класс-вычет Res со голоморфной формы со может не со-
содержать голоморфных форм 2). Этим и объясняется необходи-
необходимость рассматривать в теории Лере не только голоморфные,
но и формы класса С°°.
Для практики важен также случай, когда форма со имеет
несколько полярных многообразий qTu ..., ?Pm порядков соот-
соответственно qu ..., qm. Предполагается, что ePv находятся
в общем положении, т. е. что во всех точках их пере-
пересечений матрицы, составленные из производных функций, опре-
определяющих эти многообразия, по локальным координатам имеют
наивысший возможный ранг. Мы обозначим #"; = (#",[] ...
') Из замечания вслед за теоремой 1 видно, что это обстоятельство
может возникнуть лишь при рассмотренных форм с полярной особенностью
выше первого порядка.
32*
500 ОСОБЕННОСТИ И ВЫЧЕТЫ {ГЛ. V
... [\S°m, ^° = Af\(#>,U ... U^J и рассмотрим последова-
последовательность гомоморфизмов Ь}, которые ставят в соответствие
циклам а, принадлежащим классам компактных гомологии
из Н{с) (<^°;), циклы Ь'а, принадлежащие классам из Н'с)
6т: Н{с) (S°m) —-> Н(с) {Я*'1) -*...'-* Н{с) (^') --> Н(с) (^°). A6)
Циклы б;<т расслаиваются на гомеоморфы окружностей, обхо-
обходящие SP* и принадлежащие #>;~1. Как и выше, этой последо-
последовательности двойственна последовательность гомоморфизмов
групп когомологий, которая определяет сложный класс-вычет:
l)->H{Spm). A7)
Последовательным применением формулы A4) получается
следующее утверждение:
Для любого (р — пг)-мерного цикла а из класса гомологии
АеЯрУ^1) и любой замкнутой С00-формы со степени р из
класса когомологий со* е Нр (^*°) имеет место формула вычета
J ш* = BшГ| Resma>\ A8)
6mh h
В заключение отметим, что если форма со обращается
в нуль на некотором (п— 1)-мерном комплексном многообра-
многообразии Q cz M, то интегралы от нее и от res со по пересечениям
oflQ и бет Г) Q исчезают. Это дает возможность рассматривать
вместо групп гомологии и когомологий группы относитель-
относительных гомологии и когомологий. Поясним эти понятия на при-
примере группы относительных гомологии. Будем рассматривать
прдмногообразие Q некоторого многообразия М как его под-
подкомплекс :); через СР(М) и CP(Q) обозначим группы р-мерных
цепей на этих комплексах (как всегда, с целыми коэффициен-
коэффициентами). Цепь а^Ср(М) будем называть циклом относительно Q)
если ее граница да cz Q (в частности, равна нулю). Группа CP(Q)
является подгруппой СР(М); факторгруппу
СР(М, Q) = CP(M)/CP(Q)
будем называть группой относительных цепей. Цепь ар е Ср (М)
называется относительной границей, если существует цепь
) Это означает, что каждый симплекс из Q в то же время является
симплексом из М.
§ 13]
МНОГОМЕРНЫЕ ВЫЧЕТЫ
501
ap+i e Cp+i (M) такая, что ар — дар+1 с Ср (Q). Относительные
границы образуют подгруппу ВР(М, Q) группы ZP{M, Q) всех
относительных циклов; факторгруппа
НР(М, Q) = ZP(M, Q)/BP(M, Q)
называется группой относительных гомологии.
При рассмотрении форм со, имеющих полярную особенность
первого порядка на многообразии ?Р и обращающихся в нуль
на многообразии Q (они предполагаются находящимися в общем
положении), можно несколько уточнить описанную выше кон-
конструкцию. Именно, к свойствам 1—3 кограничного оператора
Лере можно добавить еще свойство:
4. Если ze^flQ, то bzcQ.
Тогда этот оператор каждый относительный цикл а е
е= Zp_, (S*, Q)!) преобразует в относительный цикл бст е
^ZP(M\^, Q). Легко убедиться в том, что он устанавливает
гомоморфизм соответствующих групп относительных гомологийг
6:
A9)
Формула вычета A3) для классов относительных гомологии
/ieffrl(^, Q) и 6he=Hp(M\&', Q) сохраняется.
Примеры применения метода Лере для вычисления инте-
интегралов, имеющих важное значение в теоретической физике,
можно найти в книге: Р. Хуа и В. Теплиц, Гомология и
фейнмановские интегралы, «Мир», М., 1969.
42. Логарифмический вычет. Как и в плоском случае, он
оказывается связанным с понятием индекса. Рассмотрим сна-
сначала действительный случай. Пусть в R" задан гладкий (п— 1)-
мерный цикл a: x = x(t), t^In~\ т. е. замкнутая поверхность
класса С1 (здесь х — {хи ..., хп), t = {tu ..., tn_x) и /" — {п — \)-
мерный куб). Предположим, что а не содержит точку х = 0,
и назовем индексом этой поверхности (в смысле А. Пуанкаре)-
относительно х =0 величину
_ 1 Г 1
--17 J TTF
jn-l
Х\ ... Хп
~~дп ' ' ' ~дп~
dxi дх„
dt,... dtn_u
d>
') Под Z(<^, Q) понимается Z(^
нимается и в дальнейших формулах.
); аналогичное соглашение при-
при502 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
где 2„ = —-^ - — площадь n-мерной сферы {|д;|=1}. Индекс
в смысле Пуанкаре является прямым n-мерным аналогом ин-
индекса на плоскости: полагая в A) я = 2и хх = х, х2 = у, получим
Форма под интегралом A)
1Г'^
v
v-1
v=l
имеет особенность в точке х = 0 и замкнута в R"\ {0}, ибо при
хфО
•"• л dXn = div 17Frfjf = °-
\v=l
Отсюда по формуле Стокса мы заключаем, что если два цикла а{
и (т2 гомологичны друг другу в R"\{0} (т. е. разность o-j — сг2
ограничивает некоторую цепь из R", не содержащую точку
х = 0), то интегралы от со по этим циклам равны. Так как базой
(и— 1)-мерных гомологии в R" \{0} служит единичная сфера
{|jc|=1}, то любой рассматриваемый цикл а гомологичен этой
сфере с некоторым целочисленным коэффициентом k. По
только что сделанному замечанию
п
io(o) = j-\e> = ?- J ^(-ir1 xvdXl ../ч .. dxn,
откуда снова по формуле Стокса
*о(*) = -#¦ f ndx^^-Qn,
{\х\<1}
где Qn = — 2„ — объем n-мерного шара {| х | < 1}. Таким образом,
io(a) = k.
Переходя к комплексной структуре, мы рассмотрим четно-
мерное пространство R2" и введем в нем координаты 2v = a;v +
§ 13]
МНОГОМЕРНЫЕ ВЫЧЕТЫ
503
+ ixn+v, zv = xv — ixn+v (v=l,..., n). Индекс Bn—1)-мерного
цикла а, не содержащего точку г = О, записывается формулой
г-о(о)=_4— Г \ х
2" j2n-l
X
Ж
-г
д
zn - zn)
X
которая после простых преобразований определителя перепи-
переписывается так:
• • zn 21 • • • zn
*» <а>-ir (т)" J
1
fin-\
!г|2
а/,
dzn
X
V At rlt (9\
Форму под интегралом B) можно записать в виде
d(Zu .. /\ ..,Zin)
v=l
•' /\ • •
где как всегда Zv = zv, Zn+v — zv (v=l, ..., га). Эта форма
имеет особенность в точке г = 0и замкнута вС\ {0}. По тем же
соображениям, что и выше, о гомологичен целочисленному
кратному границы поликруга U = {\zv\< 1} и
v-1
C)
it at/ v-i
(мы считаем, что dU берется с коэффициентом k, и потому
не ставим множитель перед интегралом).
Оказывается, что подобно тому, как это делалось при вы-
выводе формулы Вейля в п. 18, повторным применением формулы
Стокса можно понизить размерность множества интегрирования
504 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
до га и одновременно исключить неаналитичность подинтеграль-
ной формы. Мы получим тогда формулу для индекса в виде
- 1 Г
- BяОя J
kv
А ¦¦¦ А
тде kT — целочисленное кратное остова поликруга r = {|zv| = 1}.
Эта формула вполне аналогична плоской формуле для индекса
замкнутого пути относительно точки z = 0.
Для формальных упрощений проведем соответствующую
выкладку в случае п = 2. Мы имеем 24 = 2я2, и формула C)
принимает вид
^ dz2 dzx dz2 - z2 dz{ dzx dz2 +
Ч (<*) = - -А- I -г^уг (zi dz2 dzx dz2 - z2 dz{ dzx dz2
kdU
+ 2, dzl dz2 dz2 — z2 dzx dz2 dzs).
Границу бикруга разобьем на две части: Si ={[ zx \ = 1, | z21^ 1} и
•^2 = {l z{ |^ 1, | z2 |= 1}. На S{ имеем z121 = l, z{dz{ +zldzl = 0
и dzldzl = 0, следовательно, соответствующая часть интеграла
io=-— f
8я2 J
kS,
Г
J
fly
An2 J |z|4 UZl
Форма под интегралом точна, она является дифференциалом
формы Q' = —\1-T-2dzxdz2 (в самом деле, du' = — (-г-%- — 22f2 ./'[Х
Z\ \Z \ \ Z\ \\ Z\ \ Z \ j
X dzx dz2 = -v^-dz2dzxdz2, если учесть, что dzxdzx — 0 на SA ,
поэтому по формуле Стокса
1 С ~ 1 Г \ 12 л J
4л;2 J г, ] 2 |2 * ^ BдаJ J | 2
Аналогично интеграл по S2 равен
I3 dzidz2
J
kT
и, складывая полученные выражения, мы получим формулу D)
при ft = 2.
Мы придем к пространственному аналогу логарифмического
вычета, если будем рассматривать следующую задачу. Пусть
в области D cz С" заданы п голоморфных функций
w4 = f4{z), v= I, .... я, E)
131
МНОГОМЕРНЫЕ ВЫЧЕТЫ
505-
независимых в том смысле, что якобиан
d(ft, .... fn)
не равен
тождественно нулю. Предположим еще, что общие нули этой
системы функций, т. е. точки пересечения всех п аналитических
поверхностей fv = {ze D: fv(z) = 0}, образуют изолированное
множество cf. Заметим, что это предположение не следует из
предыдущего (пример: wi = zl, w2 = zlz2 в С2; якобиан равен zu
а общие нули системы заполняют-плоскость \zx = 0}). В области D
пусть дана область G с жордановой гладкой границей S, не
содержащей точек из cf. Требуется определить общее число
нулей системы E) в G с учетом их порядков.
Эта задача решается точно так же, как плоская. Мы выби-
выбираем на 5 параметры т,, ..., т2л_, и рассматриваем индекс
относительно точки w = 0 цикла 5*, который соответствует S
при отображении E). По формуле B) этот индекс равен
¦-t-(t)"J
h
dx2
dfi
fn
dfn
0т,
dfn
dxx
где
n
| f |2= 2 I fv
v=l
Так как под знаком интеграла здесь стоит
_
форма неособая и замкнутая в G\^, то по формуле Стокса
этот интеграл можно представить как сумму интегралов по
замкнутым жордановым поверхностям 5^, каждая из которых
содержит внутри одну и только одну точку а^ е У. В качестве
таких 5Ц можно взять, например, границы компонент множе-
множества Вейля <&'ъ = {ze G: \ fv(z) |< e, v = 1, ..., п] для достаточно
малых е > 0, и мы получим по формуле C)
/\
AdF2n, F)
v=l
где Fv = fv, Fn+V = fv (v=l, ..., n). Если в F) сделать переход
к интегрированию по n-мерному остову Ге = {геб: |/vB)l = 8.
v=l, ..., п} множества &* такой же, как переход от фор-
формулы C) к D), мы получим
N =
1
Bni)n
ге
dhA ... A dfn
fi ...fn
G)
506 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
При достаточно малых е > 0 каждая компонента множества
содержит внутри одну и только одну точку а^ е <jf; интеграл F)
по этой компоненте или равный ему интеграл G) по остову
этой компоненты естественно назвать локальным индексом ото-
отображения E) в точке ац или иначе порядком общего нуля а^
системы E). Мы получаем тогда следующий пространственный
аналог принципа аргумента:
Теорема 1 (о логарифмическом вычете). Пусть
в области DcC" задана система голоморфных функций
f — {fi, ¦ ¦ ¦, fn) c изолированным множеством У общих нулей,
пусть еще G Ш D — область с жордановой границей S, не содер-
содержащей точек У. Тогда общее число нулей f внутри G с учетом
их порядка равно индексу относительно точки f — О образа S*
границы S при отображении /, который можно вычислить по
формуле F) или G) при достаточно малом е > 0.
Пример. Система функций
7,, — ~2 ~2 n7 9
Ш| — *С| — С9, Шо — ^**-1*
с якобианом, равным 4(г^+г|), имеет в шаре В = {\г\ < 1} из С2 один
нуль в точке @, 0). Порядок этого нуля по формуле G) равен
] Г dw1 A dw2 _ 2 Г (A + Z<2)dz\ Л dz2
Bnif «J wxw2 BдаJ J B^-22J,22 '
где Г —остов области Вейля {(г, — г|| < 1, 2|г!22|< lj. Пользуясь мето-
методом Мартинелли, можно доказать, что искомый порядок N — А.
Из принципа аргумента, как и в плоском случае, получается
Теорема 2 (Руше), Пусть в области flcC заданы две
системы функций f = (fu ...,/„) и g = {g[, ..., gn) с изолиро-
изолированными множествами нулей; пусть еще G Ш D — область с жор-
жордановой границей S и всюду на S
! f I > I g I, (8)
где Ifl-VSl/vl2. l?l = V2l?vP. Тогда система f + S =
= {li + gi, ..., fn + gn) имеет в G столько же нулей, сколько
имеет их там система f (с учетом порядка нулей).
< Обозначим через So и Si соответственно Bп— 1)-мерные
циклы, которые получаются из S при отображениях z->f и
z-*-f + g. Через St, O^.t^.1, мы обозначим образ S при ото-
отображении z-*-f + tg. Очевидно, семейство {S*} определяет гомо-
топию циклов So и Si, причем так как по условию на S имеем
\f + tg\^\f\ — ^|gl>0 для всех *е[0,1], то это гомотопия
§ 14] • АНАЛИТИЧЕСКИЕ МНОЖЕСТВА 507
вС"\ {0}, Отсюда следует, что циклы So и S* гомологичны друг
другу в С"\{0} (их разность ограничивает открытое множе-
множество из Сп \{0}, которое заметают циклы S* при изменении t от О
до 1). Но тогда циклы So и S\ имеют одинаковый индекс отно-
относительно точки w — 0, и утверждение следует из теоремы 1 >
Замечание. Если на границе S известен n-мерный цикл Г,
интегрирование по которому по формуле G) приводит к индексу
образа S при отображении г—>,?, то требование теоремы 2
можно ослабить. Именно, достаточно требовать, чтобы нера-
неравенство (8) выполнялось не на всей Bп — 1)-мерной поверх-
поверхности S, а лишь на таком га-мерном цикле Г.
§ 14. Аналитические множества
В этом параграфе мы несколько подробнее рассмотрим по-
понятие аналитического множества, с которым неоднократно
встречались на предыдущих страницах. Такие множества за-
задаются системами уравнений fy(z) = Q, v=l N, где ^ — го-
голоморфные функции, поэтому исследование аналитических мно-
множеств сводится к изучению неявно заданных функций. Частным
случаем этой задачи является задача об обращении голоморф-
голоморфных отображений, и мы рассмотрим ее здесь же.
Основную роль в этих исследованиях играет подготовитель-
подготовительная теорема Вейерштрасса (см. п. 6), которая позволяет заме-
заменять голоморфные функции в левых частях уравнений поли-
полиномами относительно одного из переменных и тем самым
алгебраизировать задачу.
43. Понятие аналитического множества. Определение 1.
Назовем М сг С" аналитическим множеством в точке а е= М,
если в некоторой окрестности U этой точки его можно пред-
представить как множество общих нулей конечного числа голоморф-
голоморфных в U функций fv:
M = {zz=U: Mz) = 0, .... fjv(z) = O}. A)
Мы будем называть М аналитическим множеством, если оно
является аналитическим в каждой своей точке.
Понятие аналитического множества не совпадает с понятием
аналитического многообразия: например, множество {z{z2 = 0}
в С2 в окрестности точки @, 0) не гомеоморфно шару. В этом
примере множество распадается на два отдельных аналитиче-
аналитических множества {гг = 0} и {z2 = 0}, которые уже являются много-
многообразиями. В ряде вопросов важно исключить подобные рас-
распадения. Для этого вводится
Определение 2. Аналитическое в точке а множество М
называется неприводимым в этой точке, если ни в какой окрест-
508 особенности и вычеты [гл. v
ности а его нельзя представить в виде объединения Мх U М2,
где Afj и М2 — непустые и отличные от М аналитические в точке а
множества. Множество М называется локально неприводимым
в точке а, если оно неприводимо в каждой своей точке из
некоторой окрестности а.
Примеры. Аналитическое множество {г^ — z\z\ = 0} приводимо в на-
начале координат С3, ибо оно разбивается на два аналитических множества
{zi — z2z3 = 0} и {2i + г2г3 = 0}. Множество {2^ — 2223 = 0} неприводимо в на-
начале, но не является локально неприводимым'в этой точке, ибо оно приво-
приводимо в точках di = а2 = 0, а3 ф 0 (оно представляется в виде объединения
множеств {г, ± г2 Кг3 = о}, где Vz3 обозначает одну из двух голоморфных
в точке @, 0, а3) ветвей корня). Множество |2j—22гз=0} локально непри-
неприводимо в начале (и в других точках, конечно).
Понятие неприводимости аналитических множеств связано
с понятием неприводимости функций. Голоморфная в точке
аеС" функция f называется неприводимой в точке а, если ее
нельзя представить в виде произведения двух функций, голо-
голоморфных в а, каждая из которых равна нулю в этой точке1).
Отметим простую теорему, относящуюся к разложению
функций на неприводимые множители.
Теорема 1. Любую функцию f, голоморфную в точке а'
и равную там нулю, можно разложить в произведение непри-
неприводимых голоморфных в а функций, причем такое разложение
единственно с точностью до множителей, отличных от нуля
в точке а.
•4 Подготовительная теорема Вейерштрасса (п. 6) сводит
задачу к разложению многочленов (по одному из переменных),
а любой многочлен,' как известно из алгебры, можно един-
единственным способом (с точностью до делителя единицы) пред-
представить в виде произведения неприводимых многочленов. Для
этого достаточно воспользоваться алгоритмом Евклида нахо-
нахождения наибольшего общего делителя >
Следствие. Любое аналитическое в точке а множество М
можно представить как конечное объединение неприводимых
в этой точке аналитических множеств.
Объединяя одинаковые множители в разложении голоморф-
голоморфной в точке а функции / согласно теореме 1, мы получаем
') Напомним, что в алгебре элемент кольца называется приводимым,
если его можно представить в виде произведения двух множителей, не
являющихся делителями единицы. В кольце функций, голоморфных в точке а,
делителями единицы являются, очевидно, функции, отличные от нуля в этой
точке.
§ Н] АНАЛИТИЧЕСКИЕ МНОЖЕСТВА 509
однозначно определяемое (с точностью до множителей, отлич-
отличных от нуля в а) представление
f = fl1-"Cm, B)
где fv голоморфны и неприводимы в точке а, ^ф^ при \i?^v
и пч — положительные целые числа. Каждое множество Му,
которое в окрестности а задается уравнением Д, = 0, неприво-
димо в точке а, и /v является для него определяющей функ-
функцией (см. п. 33).
Мы воспользуемся разложением B), чтобы сформулировать
Определение 3. Пусть / — голоморфная в точке а функ-
функция и /(а) = 0. Число nv (v= 1, ..., т) в разложении B) назы-
называется порядком нулевого множества {fv = 0} функции / в точке а.
Если f мероморфна в точке а, то в окрестности этой точки
f = -у-, где ф и ф голоморфны в а, не имеют общих множите-
множителей, голоморфных и равных нулю в а, и а|)(а) = 0; числа pv, ана-
аналогичным образом определяемые для функции ф, называются
порядками полярных множеств {i))v = 0} функции f в точке а.
Это определение мы и имели в виду в п. 38, когда говорили
о дивизорах мероморфных функций.
Перейдем к описанию простейших аналитических множеств
комплексной размерности п— 1, которые задаются в области
D cz С" при помощи одной голоморфной функции
Af = {zeD: f(z) = O}; C)
предполагается, что [#0 и что градиент
не равен тождественно нулю на каждой неприводимой компо-
компоненте множества М.
Будем различать два типа точек таких множеств.
а) Обыкновенные точки. Точка а аналитического
множества C) называется обыкновенной, если в ней
grad/=^0, E)
т. е. отлична от нуля хотя бы одна из частных производных
df (v-1 п).
dzv
Пусть для определенности
¦¦ 0. По теореме существо-
вания неявных функций (см. п. 13) уравнение М, которое
записывается в виде f('z, zn) = 0, в достаточно малой
510 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
окрестности U точки аеС" можно переписать в виде, раз-
разрешенном относительно zn:
zn = g {'г), F)
где g — голоморфная в 'U функция. Отсюда видно, что в окрест-
окрестности обыкновенной точки а множество М является аналити-
аналитическим многообразием комплексной размерности п—1: за ло-
локальный параметр можно принять переменное t — 'z, а за область
его изменения — окрестность 'U (отображение fU—>M, опреде-
определяемое F), голоморфно, и различным точкам 'U соответствуют
точки {'z, zn) е М, различные просто потому, что их проекции 'z
различны).
Аналитическое множество локально неприводимо в каждой
своей обыкновенной точке — это видно из представимости урав-
уравнением F).
В окрестности обыкновенной точки множество М мало от-
отличается от (п— 1)-мерной аналитической плоскости
<grad /, z ~ а) = 2 *-§- \а (zv - av) = 0, G>
v=l
которая называется касательной аналитической плоскостью1).
б) Критические точки. Так называются точки-анали-
точки-аналитического множества М, в которых
O, (8),
т. е. равны нулю все производные -^— (v=l, ..., п).
Пусть а— критическая точка М; без ограничения общности-
можно считать, что f{'a, zn) #0 (этого можно добиться линей-
линейной заменой переменных). Подготовительная теорема Вейер-
штрасса позволяет записать уравнение М в окрестности а в виде
P(zn) = (zn-an)k + cl('z)(zn-an)k-'+ ... +ck('z) = 0, (9)
где функции cv (v=l, ..., k) голоморфны в окрестности 'U
точки 'а еС" и k~^2, ибо при k = \ точка а была бы,
видно, обыкновенной.
') Здесь и далее для векторов а, >еС* принято обозначение
(а, Ъ) = 2 avbv>
v-i
так что (а, Ь) = (а, Ь).
T41
АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
511
Уравнение (9) имеет k корней
— 1 k
(Ю)
причем функции g^ голоморфны в 'U всюду, кроме точек мно-
множества 'А, в которых это уравнение имеет хотя бы один кратный
корень. Множество 'А называется дискриминантным и, как
известно из алгебры, определяется уравнением
R('z) = 0, A1)
где # —результант многочленов P(zn) и его производной
P'(zn) (по переменному zn). Результант выражается при помощи
определителя, элементами которого являются коэффициенты
многочленов Р и Р' или нулиг), и поэтому представляет собой
функцию, голоморфную в 'U (и не равную тождественно нулю).
Следовательно, дискриминантное множество 'А является анали-
аналитическим множеством (комплексной размерности п — 2) в про-
пространстве С"~ .
Легко видеть, что дискриминантное множество содержит
проекцию в пространство С'1 (V) совокупности критических
точек множества М2). В самом деле, в достаточно малой
окрестности любой точки 'b e= 'U \ 'А множество М задается
') Результантом многочленов
* '
+
+ с. и Q = ,
Q 1
'1 + ... + di называется определитель F + /)-го порядка
, Q) =
где коэффициенты cv занимают / строк, a dv занимают k строк. Если 0o?,
то R (P, Q) = 0 в том и только том случае, если Р и Q имеют хотя бы один
общий корень.
2) Обратное, вообще говоря, неверно: например, для множества
{22 — ;?! = О] в С начало координат является правильной точкой, хотя ее
проекция 2:=0 принадлежит дискриминантному множеству (уравнение
г| = 0 имеет кратный корень).
512 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
уравнениями A0), где g^ — голоморфные в этой окрестности
функции, поэтому каждая из k точек bw = ('&, guCb))e M,
проектирующихся в 'Ъ, является правильной точкой М.
Отсюда следует, что совокупность критических точек обра-
образует на М множество комплексной размерности не выше п ~ 2,
т. е. что действительная размерность этого множества по мень-
меньшей мере на 2 единицы ниже действительной размерности М
(которая равна 2п — 2). В частности, можно показать, что
совокупность критических точек множества М не разбивает
этого множества (так что если М неприводимо, то после уда-
удаления критических точек оно останется связным).
Таким образом, критических точек на аналитическом мно-
множестве сравнительно мало, и основную массу его точек соста-
составляют правильные точки. В окрестности правильных точек
аналитические множества устроены, как комплексно (га — ^-мер-
^-мерные плоскости, а в критических точках ветвится несколько
таких плоскостей.
Переходя к описанию множеств, которые задаются при
помощи нескольких функций, приведем
Определение 4. Пусть дано неприводимое множество
M = {2eD: f, (*)=... =/*(z) = 0}, A2)
где функции fu ..., fm голоморфны в области DcC". Будем
говорить, что это множество имеет комплексную размерность г%
если у матрицы Якоби
A3)
все миноры порядков выше г'= п — г тождественно равны нулю
на М, а хотя бы один минор порядка г' не равен тожде-
тождественно нулю.
В случае одного уравнения (с функцией /^0) мы имеем
г' = 1 и получаем рассмотренные выше множества комплексной
размерности га—1. Как и в этом случае, мы будем различать
два типа точек множества A2):
а) Обыкновенные точки. Так мы будем называть точки
комплексно r-мерного аналитического множества, в которых
ранг матрицы A3) равен г' = п — г (при г'=\ это определение,
очевидно, совпадает с прежним).
Пусть аеМ- обыкновенная точка и для определенности
д(/„..., М
d(zr+1, ..., гп)
§ 11] АНАЛИТИЧЕСКИЕ МНОЖЕСТВА 513
(в случае надобности мы можем переименовать переменные).
По теореме существования неявных функций в некоторой
окрестности точки а мы можем разрешить систему уравнений
/, = 0, .. ., fr, = 0 относительно переменных zr+u ..., zn:
Zr+Ii = gn(zlt ..., гг), ц=1, ..., г', A4)
причем функции g^ голоморфны в некоторой окрестности U
точки (ах, ..., ат) е= С.
Отсюда видно, что в окрестности обыкновенной точки а
множество М является аналитическим многообразием ком-
комплексной размерности г: за локальный параметр можно принять
(Zi zr), а за область его изменения — окрестность U (ото-
(отображение U->M, определяемое A4), голоморфно и, очевидно,
взаимно однозначно).
Из представимости уравнениями A4) видно также, что ана-
аналитическое множество локально неприводимо в каждой своей
обыкновенной точке.
Отметим еще, что в каждой обыкновенной точке множество
имеет комплексно r-мерную аналитическую касательную пло-
плоскость:
(zv-av) = 0, [i=l,..., r'. A5)
dzv
v=l
б) Критические точки. Так называются точки комплек-
комплексно r-мерного неприводимого аналитического множества М, в
которых ранг матрицы A3) даже г' = п — г. Как и в случае
г' = 1, можно доказать, что критические точки образуют аналити-
аналитическое множество комплексной размерности не выше г — 1 и,
следовательно, на множестве М их сравнительно мало (в
частности, они не могут разбивать М).
Используя алгебраические методы, можно доказать сле-
следующее естественное обобщение теоремы 1:
Теорема V. Любое аналитическое в точке аеС" мно-
множество можно единственным образом представить в виде
конечного объедине-ния неприводимых в этой точке множеств.
В некоторых вопросах полезно локализовать понятие ана-
аналитического множества. Для этого вводится
Определение 4. Пусть в окрестностях Ua и Уа точки
аеС заданы два аналитических множества М и N. Будем
говорить, что они эквивалентны, если существует окрестность
WacUar\Va такая, что МП Wa = N[\ Wa- Класс эквивалент-
эквивалентности Ма по этому отношению называется ростком аналити-
аналитического множества в точке а.
33 Б. В. Шабат
5J4 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
Естественным образом определяется понятие объединения
ростков, а также неприводимого ростка как ростка, который
нельзя представить в виде объединения отличных от него
ростков аналитических множеств. Локальной теорией аналити-
аналитических множеств мы здесь заниматься не будем г).
Приведем в заключение теорему, которую можно рас-
рассматривать как обобщение теоремы единственности для функ-
функций одного переменного.
Теорема 2. Если аналитическое в области D аСп мно-
жество
M = {zs=D: Mz)= ... =fn(z) = O} A6)
дискретно, т. е. не имеет связных компонент, отличных от
точки, то оно не может иметь предельных точек внутри D.
< Будем доказывать теорему индукцией по п. Для п=1
она верна, ибо совпадает с теоремой единственности для функ-
функций одного переменного. Предположим, что она верна для
функций (п— 1)-го переменного, но неверна для функций п
переменных. Тогда в ДсС" найдется множество М, удовле-
удовлетворяющее условиям теоремы и имеющее предельную точку
йёВ, Согласно подготовительной теореме Вейерштрасса (для
ее применения, возможно, придется совершить линейное пре-
преобразование переменных z) в некоторой окрестности а мно-
множество М задается уравнениями
Pu(zJ = 0, ц=1, ..., п,
где Рр, — многочлены от zn с коэффициентами, голоморфно
зависящими от 'z. Можно считать, что М содержит последова-
последовательность точек (Vv>, а^), где все 'a(v), v=l, 2 различны.
Рассмотрим результанты многочленов Р^ и Рп:
Рп), |*=1, ••-. п-\,
— голоморфные функции 'г в окрестности проекции 'а точки а.
Так как RiP^, Pn) обращается в нуль в тех и только тех
точках 'г, где Р^ и Рп имеют общий нуль zn, а при 'z, близких
к 'а, все нули Р^ лежат вблизи ап, то в окрестности 'а множество
Ж = {'z e 'D: gl ('z) = ... = gn_t {'z) = 0}
совпадает с проекцией М на эту окрестность. Это множество
удовлетворяет условиям теоремы и имеет 'а своей предельной
точкой. Мы пришли к противоречию с индуктивным пред-
предположением >
') С этой теорией можно ознакомиться по книге: М. Э р в е. Функции
многих комплексных переменных. Локальная теория, «Мир», М., 1965.
515
§ l4] АНАЛИТИЧЕСКИЕ МНОЖЕСТВА
44. Локальное ^вращение голоморфных функций. Задача
ставится так. Пусть в некоторой окрестности точки а е= С" заданы
п голоморфных функций /V) и пусть 6V = /V(a), b = (bu .... bn).
1ребуется найти функции zv = gv(w), для которых gv (b) = av
и которые в какой-либо окрестности точки Ъ удовлетворяют
системе уравнений
М*) = а\ (v=l п). A)
Систему A) мы будем записывать в виде
где / = (Д, . .. t fn) — векторная функция.
Если якобиан системы J(z) = -§Ц- ¦- Ь> отличен От нуля
в точке а (а значит, и в некоторой "окрестности этой точки)
то по теореме существования неявных функций (и. 13) система B)
допускает в окрестности точки b = f{a) голоморфное решение
z-g(w). Это означает, что при /(а)^0 отображение z->f(z)
является гомеоморфным в некоторой окрестности точки а.
Покажем, что для голоморфных отображений верно и обрат-
обратное утверждение1). Пусть векторная функция / осуществляет
голоморфный гомеоморфизм окрестности Ua точки веС"на
окрестность Vb точки b = f{d). Тогда якобиан J(z) этого ото-
отображения не может быть тождественно равным нулю, ибо
в этом случае оказался бы тождественно равным нулю и якобиан
д(х, х1п) ~ I J W I (мы пол ожил и zv = xv + ixn+v, w v = mv + iun+v),
а тогда по теореме из действительного анализа функции щ Щп
были бы зависимыми2) и / не могло бы быть гомеоморфизмом?
ир> ТДКИМО;образом, множество M = {zs=Ua: J(z) = 0} не выше
чем Bп - 2)-мерно, и в силу гомеоморфизма таким же является
его образ М =f(M). Рассмотрим обратное к / отображение
g. vb^-ua. ино непрерывно всюду в Vb и по доказанному выше
голоморфно всюду в Vb\M* (в соответствующих точках z
якобиан 1{г)Ф0). Так как М* - аналитическое множество, то
отображение g голоморфно продолжается в полную окрест-
окрестность Vb (см. п. 19). F
Теперь мы знаем, что всюду в Vb справедливо тождество
fog(w)=w, где / и g-голоморфные функции. По правилам
¦) Напомним, что для отображений класса С°° это обратное утвержде-
утверждение неверно: отображение xv-+x3v (v=l, ..., 2п) пространства С на себя
гомеоморфно а его якобиан обращается в нуль на плоскостях {*v = 0}.
33*
5J6 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
дифференцирования отсюда получается тождество
d(ft,..., fn) д (gu ..., gn) ,
i zn) d(w, wn
C)
справедливое для всех точек z^Ua и соответствующих точек
»е7». Из него и следует, что J{z)=?Q в Ua.
Таким образом, доказана
Теорема 1. Для локальной гомеоморфности голоморфного
отображения f: D-+Cn области D с С необходимо и доста-
достаточно, чтобы якобиан ,, "¦" ! ф 0 в D.
а (гь ..., zn)
Перейдем теперь к изучению задачи локального обращения
в случае, когда якобиан отображения / равен нулю в точке а,
однако а является изолированной точкой1) множества
{z: f(z) = b}. Для простоты мы проведем исследование для п — 2,
причем без ограничения общности примем а = Ь = 0, Итак, мы
рассматриваем систему двух уравнений
h (zu z2) = wlt f2 {zu z2) = w2 D)
и хотим найти в окрестности точки w = 0 ее решения
z1=g1(w1, w2), z2 = g2{wx, w2) такие, что ^@, 0) = g2@, 0)==0.
Из нашего предположения следует, что /г- и f2 не равны
тождественно нулю. Поэтому (сделав, если надо, дополнитель-
дополнительное линейное преобразование пространства 2) мы можем считать,
что fv(zly 0)^0 (v=l, 2). В силу подготовительной теоремы
Вейерштрасса (п. 6) систему D) можно заменить равносильной
ей системой
Pl {z, w) = z\' + С) (z2, w) zkfx + ... + ck{ (z2, w) = 0,
E)
P2(z, w) = z\z + d{(z2, b»J*»-i+ ... +dk2(z2, w)=0,
где cv и ^ — голоморфные функции от z2, wx и w2, обращаю-
обращающиеся в нуль в начале. Исключение zx из E) приводит
к уравнению
R(z2,w) = 0, F)
где R— результант многочленов РЛ и Р2 —голоморфная функция.
Если бы было R{z2, 0)^0, то уравнения E) при w = 0
имели бы общее решение г! = фB2), ф@) = 0, но тогда 2 = 0
была предельной точкой множества {z: f(z) = O}, вопреки пред-
') Это условие заведомо не выполняется, если якобиан / = 0 или если
все функции /v (z) — ^v приводимы и имеют общий множитель, равный нулю
в точке а (как для системы ш1 = г1, ш2 = ztz2 в точке z — 0).
§ 14] АНАЛИТИЧЕСКИЕ МНОЖЕСТВА 517
положению. Поэтому к R можно снова применить подготови-
подготовительную теорему и заменить F) равносильным ему уравнением
Р iy 10)\ = 7^ -+- п (гоЛ 7^-1 4- -4- a (w) = 0. G)
где av —голоморфные функции в некоторой окрестности V
точки w = Q, av@) = 0. Таким образом, отыскание функции
22 = §2(ау) свелось к решению алгебраического уравнения с голо-
голоморфными коэффициентами.
Рассмотрим дискриминантное множество А = {ауеУ: А (да) = 0},
где А — результант многочлена Р (z2, w) и его производной по z2
(см. п. 43). Это множество аналитично, следовательно, оно
самое большее двумерно и не разбивает окрестности V. В точках
V \ А уравнение G) имеет k различных голоморфных корней
zf) = g2^(w), в 'точках же А некоторые из этих корней совпа-
совпадают и теряют голоморфность. Множество А, следовательно,
является множеством ветвления аналитической функции ?2(ШК
Аналогично исследуется зависимость zl = g1(w). Заметим,
что при известной функции z2 — g2(w) функцию gl можно по-
получить, подставляя gf> в каждое из уравнений E) и находя
общий наибольший делитель й^(ги w) многочленов по zu полу-
полученных из левых частей E) после этой подстановки: значение zv
соответствующее значению z?w = g^> (w), будет корнем много-
многочлена dp. На этом пути можно доказать1), что для w е V \ А
каждому значению gf> (w) (возможно, после некоторой линей-
линейной замены переменных) соответствует точно одно значение
2(я) _ ^(м.) (wy Таким образом, 2, = g, (w) оказывается не более чем
й-значной аналитической функцией (уменьшение числа значений
происходит, когда разным zf* соответствуют одинаковые 2^').
В рассматриваемом случае точка w = 0, очевидно, принад-
принадлежит дискриминантному множеству А. Вообще, если ш'еА
и 2°—один из прообразов этой точки при отображении D),
то якобиан отображения / B°) = 0, ибо в противном случае
по теореме 1 это отображение было бы взаимно однозначным
в точке 2° и w° не могла бы принадлежать А. Таким образом,
множество А принадлежит образу множества / = {zs?/: J(z) = 0}
при рассматриваемом отображении.
Пример. Якобиан отображения
') Это —одно из утверждений теоремы Осгуда; см., например, Б. А. фукс,
Теория аналитических функций многих комплексных переменных, Гостех-
нздат М., 1948, стр. 384.
518 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
равный / (г) = 4 (й| + г2), обращается в нуль на аналитических плоскостях
/ = {г1— ± /г2}. Исключая Z], мы придем к биквадратному уравнению
Р (г2, w) = z\ + wxZ2 4~ = 0- Обращение (8) имеет вид
так что функции gv (w) четырехзначны и их ветви голоморфны вне дискри-
минантного множества Д = {ш1=-±ш2}- Это множество является образом
множества / и состоит из двух аналитических плоскостей, на каждой
из которых сливаются по два значения gv; в точке пересечения этих пло-
плоскостей сливаются все четыре значения gv.
Ситуация, аналогичная описанной, справедлива и при
любом п; имеет место
Теорема (ОсгудI) Пусть w = f(z) — система п функций,
голоморфных в некоторой окрестности точки а е С", и а является
изолированной точкой множества {f{z) = b}, где b = f(a). Тогда
{возможно, после некоторой линейной замены переменных)
обращение г = g (w), g (b) = а, этой системы можно получить
следующим образом: zn = gn(w) находится из уравнения
Р (гп, w) = <*„ - anf + a, (w) (zn - aj* + ... + % (w) = 02) (9)
с голоморфными в точке Ь коэффициентами a^, айF) = 0,
а остальные функции zv = gv{w), v=l, .. r, n — \, однозначно
и голоморфно выражаются через gn{w) и ш.
Заметим, что здесь fe=l в том и только том случае, когда
1(а)фО. Если же 7(а) = 0, то gn непременно будет многознач-
многозначной, точнее fe-значной, аналитической функцией, а осталь-
остальные gv — не более чем fe-значными аналитическими функциями
(некоторые из них могут оказаться и однозначными). Множе-
Множеством ветвления Д функции gn будет служить образ множе-
множества / = {/(г) = 0}, а множества ветвления остальных gv при-
принадлежат А.
Таким образом, при отображении f окрестность точки b— f{a)
покрывается образом достаточно малой окрестности точки а
точно k раз. Учитывая геометрический смысл введенного в п. 42
локального индекса, можно утверждать, что в условиях теоремы
Осгуда локальный индекс отображения f в точке а равен
степени k многочлена (9).
!) См. W. F. О s good, Lehrbuch der Funktionentheorie, 2. Aufl., Bd. 2,
Parte 1 (Leipzig, 1929), S. 125. Современное изложение задачи об обраще-
обращении см. в книге М. Эрве, цит. на стр. 514.
2) Это уравнение получается, как и для п = 2 исключением 'г из си-
системы уравнений / (г) = да.
§ 15] АНАЛИТИЧНОСТЬ МНОЖЕСТВА ОСОБЕННОСТЕЙ 519
Заметим, однако, что при п > 1 локальный индекс, вообще говоря, не
выражается через порядки младших членов тейлеровских разложений /\»
в рассматриваемой точке. Так для отображения
wx=^ wz = z\ A0)
локальный индекс в точке 2 = 0 равен б—произведению младших членов
разложений /i и f2. Для отображения же wl = z\, w2 = zl + z2, которое от-
отличается от A0) невырожденным линейным преобразованием и, следова-
следовательно, имеет тот же индекс, произведение таких порядков равно 4.
Подчеркнем, что степень k в (9) совпадает с локальным индексом лишь
при таком выборе переменных, что функции gv (v = Ь ••• > " ~ ') однозначно
выражаются через gn и w.
Следствие. Если f — голоморфное отображение открытого
множества UcC в С" и каждая a^U является изолирован-
изолированной точкой множества прообразов точки b = f(a), то /((/) —
— открытое множество.
Когда условие теоремы Осгуда не выполняется, т. е.
а является предельной точкой множества прообразов b = f(a),
но якобиан отображения не равен тождественно нулю, то суще-
существует содержащее точку а аналитическое множество комплекс-
комплексной размерности г, l^r^n — 1, которое / преобразует в точку Ь.
В этом случае, вообще говоря, b является точкой неопреде-
неопределенности1) для хотя бы одной компоненты gv обращения рас-
матриваемой системы.
Пример. Рассмотрим систему
W2 = Z1Z3, W3 = Z\Z2, A1)
якобиан которой 1 = 2zxz2zz обращается в нуль на трех (комплексно) дву-
двумерных аналитических плоскостях {?,), = 0}, ц = 1, 2, 3. Прообразом то-
точки w = 0 является совокупность трех (комплексно) одномерных аналити-
аналитических плоскостей {z2 = z3 = 0}, {Zi = z3 = 0} и {z2 = Zi = 0}. Обращение A1)
_ -. f
w3
имеет голоморфные ветви вне плоскостей {и>^ = 0}, ц=1, 2, 3; точка w = 0
является точкой неопределенности для всех трех компонент g^,.
§ 15. Аналитичность множества особенностей
Под особыми точками голоморфной функции понимаются
граничные точки ее области голоморфности. Мы видели, что
простейшие такие точки — особые точки мероморфных функ-
функций нескольких комплексных переменных — составляют ана-
аналитические множества. С другой стороны, легко построить
') Термин «точка неопределенности» употребляется здесь в смысле
несколько более общем, чем в п. 30, однако аналогичном (см. приводимый
здесь пример).
520 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
примеры голоморфных функций, особые точки которых образуют
Bя — 1)-мерные множества, заведомо не являющиеся аналитиче-
аналитическими (скажем, функции utej), \i(zxz2) или nBi)[i(z2) в О2, где
ц — модулярная функция из п. 41 ч. I). Однако в предполо-
предположении, что множество особых точек не слишком массивно, мы
докажем здесь его аналитичность и в общем случае. Затем мы
докажем аналитичность множества так называемых существенно
особых точек.
45. Аналитичность множества особых точек. Условие не
слишком большой массивности мы примем здесь в следующей
форме: множество особых точек М пересекается с каждой
аналитической прямой, параллельной некоторому направлению
(скажем, оси zn), не более чем в одной точке. Отсюда следует,
что М не более чем B/г — 2)-мерно.
Теорема 1 (Хартогс). Пусть а — особая точка функ-
функции f и для каждой точки 'z, p{'z, 'a)<e, в поликруге
U={p{z, а)<е} имеется не более одной точки {'z, zn), особой
для этой функции. Тогда найдется поликруг 'V = {p('z, 'а)<6}
такой, что каждой 'ге'1/ соответствует точно одно число zn,
для которого {'z, zn) является особой точкой f в U, причем
функция zn — q>{'z) голоморфна в 'V.
< а) Непрерывность функции ф. Без ограничения общ-
общности считаем а — О. Так как 0 —единственная особая точка /
с проекцией '0, то окружность yo = {'z = 'O, \zn\ = t]}, 0<ii<e,
принадлежит области голоморфности /. Семейство кругов
Ka = {'z = 'a, |zn|<T}} при 'а->'0 стремится к /Со = Г^г = '0,
| 2„ | ^ т]}, причем дКа -*¦ дКо = Yo- Так как Ко содержит особую
точку 0, то по теореме Бенке —Зоммера (п. 23) найдется 6>0
такое, что при р('а, '0)<6 в круге Ка есть хотя бы одна осо-
особая точка /. По условию больше одной такой точки быть не
может, следовательно, функция zn = q>('z) однозначно опреде-
определена в /1/ = {р(/2, '0)<6}. Это же рассуждение доказывает не-
непрерывность ф в точке '0: у нас ф('0) = 0 и для любого е>0
существует такое б>0, что |ф('.г)|<е при p{'z, '0)<б. Так как
за '0 можно принять любую точку из 'V, то ф непрерывна во
всем 'V.
б) Голоморфность функции ф. Число б можно считать
столь малым, что |ф('г:)|<у при 'ге'У, и тогда f будет
{1 2 1
'геТ, -д-е<|г:„ |<-д-е >. Выберем
число р, -g-e<p<-g-e, и точку z°n = peie, тогда f будет голоморф-
голоморфной в поликруге j'ze'V, \zn — г° | <Р — j\- По нашему по-
построению для любой 'ze'I/ точка {'z, ф('г)) — особая для f,
§ 15] АНАЛИТИЧНОСТЬ МНОЖЕСТВА ОСОБЕННОСТЕЙ 521
а все точки ('z, zn), для которых \zn — 2° | <|ф {'z) — z°n\, — пра-
правильные, поэтому
()
является радиусом Хартогса функции / (см. п. 26). По дока-
доказанному выше функция R непрерывна в 'V, а так как у нас
|cp('2)|<!,a|zo| = p>-f-, то /?('z)>|z°|-|<p('z)l>0, и, зна-
значит, \nR('z) непрерывен в 'V.
Голоморфность ф мы выведем из доказанной в п. 26 плюри-
субгармоничности функции — \nR('z). По основной теореме
Хартогса достаточно доказать голоморфность ф по каждому
переменному zv, v= I, ..., п — 1, в некотором круге |zv|<r
при фиксированных z^ = а^, \а^\<.г, ц Ф v. Для простоты обо-
обозначений будем писать R(zv) вместо R(a} zv, ..., а„_,) и
аналогично ф(зу). Так как —In R(zv) субгармонична- в круге
{\zv\<r} и непрерывна в {| zv | ^г}, то
J
In R (re11) dt
о
или, согласно A),
In | ф @) - ре« | > ± J In | Ф (re") - ре«> | dt'). B)
о
Это неравенство справедливо для всех 8е[0, 2л]; интегрируя
его по 6 и меняя в правой части порядок интегрирования (что,
очевидно, законно), будем иметь
2Я 2Я 2Л
J 1п|ф@)-ре'е^9>-^ j dt J 1п|ф(ге")-реш1^8. C)
Известно, что интеграл
который представляет собой логарифмический потенциал с по-
постоянной плотностью распределения на окружности {| ? | = р},
постоянен в круге |?|<р (см. задачу 7 к гл. V ч. I). Так как
у нас |ф('г:)|<р при всех 'геТ, то мы можем, следовательно,
заменить в правой части C) ф(ге'*) значением ф@). Но отсюда
) В этой формуле ф@) = ф(а1, ..., 0, ..., ап) не обязательно равно 0.
522 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
видно, что C), а значит и B), для всех 8 обращается в равен-
равенство, т. е. субгармоническая функция —ln|<pBv) —ре'е| в точке
zv = 0 совпадает со своей гармонической мажорантой. Отсюда
следует (см. п. 46 ч. I), что функция In | ф (zv) — peie | гармо-
гармонична в круге {|zv|<r} при любом 8е[0, 2зт].
Из A) мы имеем
R2 = (Ф - ре'9) (ф - ре"*9) = фф - р (е-Юф + е'9ф) + р2, D)
причем в силу гармоничности In R эта функция принадлежит
классу С°° (по переменным zv и zv) при любом 0. Составляя
разность значений D) при 8 = 80и в = 80 + п, мы увидим, что
e~ie«q> + еге°ф е С°°, а полагая здесь 90 = 0 и -^ , найдем, что
Ф + ф, ф-фе С°°, а значит, Иф? С°°. Остается доказать, что
•?¦-»•
Для этого воспользуемся тем, что вместе с In R и
In 7?2 является гармонической функцией от zn при любом
-5-е, -g-е и любом 0 е [0, 2я]. Уравнение Лапласа для
о о /
In R2 имеет вид
п2 д2т dR1 dR2 q
и функция D) должна удовлетворять ему при любых р и 9 из
указанных отрезков. Подставляя сюда выражение D) и прирав-
приравнивая нулю коэффициент при р3, мы найдем, что
oz oz
ozv dzv
при любом 0, откуда -=—^=- = 0 при \zv\<r. Приравнивая
(с учетом этого) нулю коэффициент при рг, получим, что
при любом 0, следовательно, -^-~- ^ 0 при |zv|<r.
Таким образом, в каждой точке круга {\zv\<r} либо
-д^- = 0, либо -^?- = 0. Чтобы исключить иервую возможность,
OZy OZy
заменим f(zv, zn) функцией f(zv, zn + zv) (зависимость от дру-
других переменных z^, ц Ф v, Ф п, мы не выписываем). Она
удовлетворяет всем условиям теоремы, а уравнением особой
поверхности для нее вместо zn = ф (zv) будет zn = ф (zv) — zv.
§ 15] АНАЛИТИЧНОСТЬ МНОЖЕСТВА ОСОБЕННОСТЕЙ 523
Поэтому, повторяя наши рассуждения, мы найдем, что для ф
в окрестности zv = 0 будет выполняться также одно из условий
_9L = o, -——1=0. Учитывая полученный ранее вывод, най-
найдем, что -~?- = 0 в окрестности zv = 0 >
Справедлива и более общая
Теорема 2 (Хартогс). Пусть аеС"- особая точка фун-
функции f и для каждой 'z, р('г, 'а)<г, в поликруге {p(z, а)<е}
существует конечное число точек (rz,. гЩ, особых для этой функ-
функции. Тогда в некоторой окрестности а особые точки f соста-
составляют аналитическое множество с уравнением
(zn - an)k + с, {'z) {zn - an)k~l + ... + ck i'z) = 0, E)
где функции cv голоморфны в точке 'а.
В п. 47 мы приведем еще один вариант теоремы об анали-
аналитичности множества особых точек.
46. Существенно особые точки. В ряде вопросов особен-
особенности, которые имеют мероморфные функции на своих поляр-
полярных множествах (см. п. 30), можно рассматривать как несуще-
несущественные. Существенно особыми точками в многомерной тео-
теории называют особые точки всех других типов.
Чтобы прийти к независимому определению существенно
особых точек, можно ввести понятие мероморфного продолже-
продолжения. Для этого рассматривают мероморфный элемент как
пару, составленную из поликруга U и мероморфной в нем
в смысле п. 30 функции /. Говорят, что два мероморфных
элемента (Uu Д) и (U2, /2) являются непосредственным меро-
морфным продолжением друг друга, если пересечение иг (] U2
непусто и fi = /2 в0 всех точках голоморфности обеих функций
из этого пересечения. Далее, как обычно, вводится понятие
мероморфного продолжения вдоль пути и под мероморфной
в ш-ироком смысле слова функцией понимается совокупность
элементов, которые получаются из какого-либо одного меро-
морфным продолжением вдоль всех путей, для которых такое
продолжение возможно. Область, вообще говоря, многолистная,
которая при этом определяется, называется областью меро-
мероморфности построенной функции. Граничные точки области
мероморфности некоторой функции и называются ее суще-
существенно особыми точками.
Для доказательства аналитичности множества существенно
особых точек нам понадобится
Л е м м а._Пусть функция f голоморфна в произведении
поликруга 'U = {р ('г, 'а) ^ г} на кольцо Кп = izn- rn ^ I zn-\ ^ Rn}
524 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
и представляется там рядом Хартогса — Лорана
(k — скалярный индекс, gk голоморфны в 'U). Для того чтобы f
мероморфно продолжалась в поликруг U = 'UX{\ zn\^.Rn},
необходимо и достаточно существование конечного числа функ-
функций Яо, .. .,%i, голоморфных e'U и не всех тождественно рав-
равных нулю, таких, что
Хо ('z) gk4 ('z) + ... +%г ('г) gk Цг) = 0 B)
для всех 'z^'U и всех k = — 1, —2
¦4 Достаточность. Рассмотрим функцию
голоморфную в '[/ X С, и для z^'U X Кп образуем произве-
произведение f(z)ty{z) = ф (z). Из A) видно, что условия B) влекут за
собой равенство нулю коэффициентов при всех отрицательных
степенях в разложении <p = fij). Значит, эта функция голо-
голоморфна, а функция / = т~ мероморфно продолжается в поли-
поликруг U.
Необходимость. Если / мероморфно продолжается
в U, то для каждой 'z° e 'U может существовать лишь конеч-
конечное число точек zn, \ zn \ ^ Rn, таких, что ('z°, zn) являются
особыми точками /. В самом деле, в противном случае суще-
существует точка z° = ('2°, г^Е^, предельная для особых, а так
как / мероморфна в г°, то в ее окрестности /=^-, где <р и -ф
голоморфны. По теореме единственности теории функций
одного переменного ty('z°, zn) == 0, а отсюда вытекает, что все
точки пересечения {'z = 'z°) f) U — особые для / (ибо открытое
ядро множества точек этого пересечения, которые являются
особыми для f, одновременно и замкнуто), а это противоречит
голоморфности f в 'V X Кп-
Комплексная размерность множества точек неопределенно-
неопределенности f не превосходит п — 2 (см. п. 30), поэтому множество 'Е
точек 'z^l'U, которые являются проекциями точек неопреде-
неопределенности /, не разбивает 'V. Для fz°ф'Е обозначим через/('2°)
сумму порядков всех полюсов г^ функции f('z°, zn) в круге
(I 2/г 1^*^»}; так как функция I целочисленна и непрерывна на
I 15] АНАЛИТИЧНОСТЬ МНОЖЕСТВА ОСОБЕННОСТЕЙ 525
связном множестве 'U \'Е, то она постоянна. Образуем много-
многочлен
имеющий нулями л-е координаты всех особых точек {'z, zn)
функции / в U с фиксированной проекцией 'г ф. 'Е (все они
будут, очевидно, полюсами, и мы берем -ф так, что порядок ее
нуля совпадает с порядком полюса). Повторяя рассуждения,
проведенные при доказательстве теоремы Веиерштрасса из п. 6,
мы убедимся в том, что функции с^ голоморфны в 'U. Так
как по построению fty является голоморфной функцией zn
в круге {|2„|^7?}, то в ее разложении по степеням zn все
коэффициенты при отрицательных степенях должны быть рав-
равными нулю. Учитывая, что / в 'U X Кп представляется разло-
разложением A), мы заключаем, что условия обращения в нуль
этих коэффициентов имеют вид соотношений B), где Ло=1,.
К = <V (t1 = * > • • • > О >
Теперь мы можем доказать непрерывность расположения
существенно особых точек (аналог части а) доказательства
теоремы Хартогса из предыдущего пункта).
Теорема 1 (Э. Л ев и). Пусть z°— граничная точка обла-
области D мероморфности функции [ и при некотором е>0 окруж-
окружность уо= {'z = 'z°, \zn — z°n\ = е}'с D. Тогда найдется б>0
такое, что при p('a,'z°)<6 в любом круге Ka={'z — 'a>
\zn — z°|^ej есть точки, не принадлежащие D.
•4 Примем 2° = 0 и выберем числа г, г„>0 и конечное
число точек $? — ее' м. так, чтобы поликруги [/ц = {р('2, '0)<г,
\Zti — Zn !</"«} принадлежали D яв совокупности покрывали у0.
В тех и^, где / не голоморфна, мы можем считать, что
/ = ^-, где Ф|1, %е=Н (и„), причем ^('0, $>) = 0, но г^('О, гп)фп
при Q<\zn — t>f)\<rn (для соблюдения этих условий, возможно,
придется уменьшить величины г и гп и сделать линейную за-
замену переменных). Тогда функция /('О, zn) в любом достаточно
узком кольце, окружающем {|zrej = e}, будет голоморфной
всюду, за исключением конечного числа полюсов. Мы мо-
можем, следовательно, выбрать числа 6<г и е', е"(е'<е"<е) так*
что / будет голоморфной в замкнутой области {p('z, '0)^6
s I n I ^ h
Предположим, что теорема неверна и существует точка
'а, р {'а, '0) < б, такая, что / мероморфно продолжается в круг
Л"а = {'2 = 'а, |2„|^е}. Тогда она будет мероморфно продол-
продолжаться и в некоторый поликруг {p('z, 'a)^r|, |2„|^е}, причем.
526 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
можно считать, что 'U = {р {'г, га) ^т}} принадлежит {р {fz, 'a) ^}
На множестве {р('.г, '0)^6, е'<: | 2„ | s^ e"} функция f представ-
представляется рядом Хартогса —Лорана
/B)= 2 gfc('zJ*. C)
где gfe голоморфны в {p{'z, '0)^6}. Так как она мероморфно
продолжается в поликруг 'U X {\ гп |^е}, то по доказанной
выше лемме найдутся функции Яо, ..., Яг<= Я('?/)> не все то-
тождественно равные нулю и такие, что для всех k = —1, —2, ...
и всех 'z e 'U имеем
Яо ('г) §й.г ('z) + ... +h ('z) gk (>г) = 0. D)
Рассмотрим бесконечную линейную систему с / + 1 неизве-
неизвестной !„:
logfc-iCz) + • • ¦ + Sig*('z) = О- Ь = - 1, - 2, .. . E)
ге'С/ она имеет нетривиальное голоморфное решение
ц м('2), поэтому для таких 'г между gv('2:) имеются анали-
аналитические зависимости, выражающие условие существования
такого решения. Но так как gv голоморфны в большем поли-
поликруге {p{'z, '0)^6}, то эти зависимости справедливы и во всем
этом поликруге. Тогда, по той же лемме, функция / меромор-
мероморфно продолжается в поликруг {р fz, '0)^6, |2л|^е}, а это про-
противоречит тому, что ('0, 0) является граничной точкой D >
Дальнейшее доказательство аналитичности множества суще-
существенно особых точек (аналог части б) доказательства теоремы
Хартогса) проходит так же, как в предыдущем пункте. По
аналогии с радиусом голоморфности (радиусом Хартогса) вво-
вводят понятие радиуса мероморфности функции / в точке z°
относительно переменного zn как радиуса RM{'z0) максималь-
максимального круга {'2 = 'z°, \zn — z°n\<R}, в Который / мероморфно
продолжается.
Примерно так же, как в п. 26 (теорема 1), доказывается,
что функция —In RM('z) является плюрисубгармонической
в проекции 'D области мероморфности f (см. книгу Б. А. Фукса,
цит. на стр. 517, стр. 221). После этого можно почти дословно
повторить вторую часть доказательства теоремы Хартогса из
предыдущего пункта. На этом пути получается
Теорема 2 (Э. Л е в и). Пусть а — существенно особая
точка функции f и для каждой точки 'z, p('z, 'a)<e, в поли-
поликруге U = {p(z, а)<е] имеется не более одной точки (% zn),
существенно особой для этой функции. Тогда найдется поли-
§ 15] АНАЛИТИЧНОСТЬ МНОЖЕСТВА ОСОБЕННОСТЕЙ 527
круг 'V ={p{'z, 'a)<6} такой, что каждой 'ге'7 соответствует
точно одно zn, для которого {'z, zn) является существенно осо-
особой точкой f в U, причем функция zn = cp('z) голоморфна в 'V.
Справедлива и более общая теорема, в которой предпола-
предполагается, что f имеет конечное число существенно особых точек
с проекцией 'z, и которая формулируется, как теорема 2
предыдущего пункта.
47. Теорема о вложенном ребре. В заключение мы приве-
приведем вариант теоремы об аналитичности множества особых
точек, который основан на следующей полезной и в других
приложениях теореме о вложенном ребре:
Теорема 1 (Кнезер). Пусть две гиперповерхности
2у = {ф7- (z) = 0}, /=1,2, класса С2 пересекаются по Bп — 2)-
мерному ребру Г так, что во всех точках Г
rankl , , , , 1 = 2 A)
* • ' dzn dzi #' •
Bj и 22 имеют вдоль Г различные касательные плоскости).
Тогда, если существует функция f, голоморфная в тех точках
окрестности Г, где тт(ф,, ф2)<0, но не продолжаемая голо-
голоморфно ни в одну точку Г, то Г — аналитическая поверхность.
¦4 а) Предположим сначала, что в какой-либо точке г°еГ
""И Z Z 1=2' B)
dzt ' ' ' dzn
и примем z° = 0. Рассмотрим аналитическую поверхность
где а, бе С", a Z, е С — параметр. Если для краткости обо-
/ 5ф/ Зф/ А
значить Vф/• = \-z—, ..., ——I то по формуле Тейлора будем
\ о2] azn )
иметь
q>j |So = 2 Re (aZ + bt,2, УФу> + Re 12К,{а) +^-Hj{a, a) + o(\t, f),
C)
где, как и в п. 25,
528 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
(а, Ь) — (а, В) и все производные берутся в точке 2 = 0. По
условию B) векторы Vcpx и Уф2 не коллинеарны, следовательно,
можно выбрать векторы а и Ъ так, чтобы было
(а, УФ,> = 1, (а, Уф2> = - 1, 2 (Ь, УФ;> = -Kj (а) + у Я, (а, а) + 1, D)
/=1, 2.
Тогда формулы C) примут вид
ф1 |So = 21 + %г-ц2 + 12Нг (а, а) + о (| ? |2),
ф2 |So = -21 + I2 - rf + ?2Я2 (а, а) + о (|? |2)
(мы положили ? = | + гг)), откуда следует, что при |?|<р, где р
достаточно мало, вся поверхность SQ, кроме точки ? = 0, лежит
в области min((pi, ф2)<0. В самом деле, при достаточно ма-
малых |?| и 1=7^=0 у нас либо ф^, либо ф2 |s отрицательна,
а при 1 = 0, но цфО отрицательны обе Фу |s.
Теперь, оставив прежние а я b и пользуясь тем, что ни
один из Уфу Ф 0, мы выберем вектор со е С" так, чтобы было
(со, Уфу) =-1, /=1,2, E)
и рассмотрим семейство аналитических поверхностей
St = {z е= С": 2 = at, + bt,2 + at},
где / — положительный параметр. Имеем, очевидно,
ФУ Is, = <Р; ls0 + 2t Re <с0' V(?J \s) + ° W>
откуда в силу условия E) и непрерывности Уфу следует, что
при 0</<т, где т достаточно мало, куски St, для которых
|?|<р (число р мы можем в случае надобности уменьшить),
компактно принадлежат области тт(ф1, ф2)<0.
Семейство St, O^t^.x, удовлетворяет, очевидно, условиям
принципа непрерывности из п. 23. Так как по условию дока-
доказываемой теоремы существует функция /, голоморфная в той
части окрестности точки 2 = 0, где гшп(ф1, ф2)<0, и не про-
продолжаемая в эту точку, то мы пришли к противоречию с этим
принципом. Значит, мы доказали, что во всех точках Г ранг
матрицы B) не превосходит 1.
Но этот ранг ни в одной точке Г не может равняться 0,
ибо тогда в этой точке все производные ^~ = 0. v=l, ..., п,
дц>1
следовательно, и все — = 0, т. е. не выполняется условие A).
§ 15]
АНАЛИТИЧНОСТЬ МНОЖЕСТВА ОСОБЕННОСТЕЙ
529
Таким образом, во всех точках Г
rank
1
F)
б) Теперь мы покажем, что Г — аналитическая поверхность.
Из F) видно, что существует комплексная функция А, такая,
что для всех геГ
G)
Заметим, что 1тЯB)=^0 для всех геГ, ибо если бы X(z°)
было действительным числом, то из G) следовало бы равен-
равенство Vcp2 = АДг^Уф!, где черта —знак комплексного сопряжения,
и тогда ранг матрицы A) в точке z° был бы меньше 2, вопреки
условию.
Рассмотрим произвольный вектор dz — (dzu ..., dzn), ле-
лежащий в касательной плоскости к поверхности Г в точке z.
Он должен принадлежать касательным плоскостям к каждой
из гиперповерхностей 2у, следовательно,
2 Re <Уф2, dz) = 0.
Отсюда в силу соотношения G), где Im X Ф 0, получаем ра-
равенства
0, /=1,2, ¦ (8)
из которых и следует аналитичность Г. В самом деле, из усло-
условия A) видно, что систему ф; = 0, /=1, 2, можно разрешить
относительно одного из переменных,
скажем zn = g('z). Но из (8) видно, что
дифференциал функции g выражается
лишь через dzv и не содержит dzv
(v= I, ..., я — 1), а это и означает ана-
аналитичность g >
'гЛ
Примеры.
1. Пусть ф, = | г, | - 1, ф2 = | г2 | - 1 в С2.
Поверхности 2/={| г/| = 1}, /=1, 2, Пересе-
каются по тору r={|zi|=l, | г21 = 1}. Так
как это не аналитическая поверхность, то из
теоремы Кнезера следует, что всякая функ- Рис- '^1-
ция /, голоморфная в той части окрест-
окрестности Г, где либо | Zi | < 1, либо j z2 \ < 1 (заштрихована на диаграмме Хар-
тогса, рис. 121), непременно голоморфно продолжается на Г.
34 Б. В. Шабат
530 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
2. По той же причине область {) г, |< 1, | z21 < 2} U{| г, | < 2, | г2 | < 1}
не может быть областью голоморфности — этот результат мы получили в п. 7
при помощи логарифмической выпуклости.
Из теоремы о вложенном ребре просто следует теорема об
аналитичности множества особых точек, которая отличается
от доказанной в п. 45 тем, что в ней заранее предполагается
гладкость этого множества, но условие не слишком боль-
большой массивности формулируется лишь в терминах размер-
размерности.
Теорема 2. Если функция f голоморфна в некоторой Хи-
Химерной окрестности Bп — 2)-мерной поверхности Г класса С2
и не продолжается голоморфно на Г, то Г — аналитическая
поверхность.
¦4 Пусть z°e Г — произвольная точка. Так как Г с С2 и
является Bя — 2)-мерной поверхностью, то в окрестности z° она
задается двумя действительными уравнениями q>i = 0, <р2 = 0,
где ф^еС2, и ранг матрицы A) в этой окрестности равен 2.
Так как / заведомо голоморфна в той части окрестности Г,
где т1п(ф1, ф2) < 0, и не продолжается на Г, то Г —аналити-
—аналитическая поверхность >
Небольшой модификацией рассуждений можно доказать
аналог теоремы о вложенном ребре, в котором вместо голо-
голоморфной участвует мероморфная функция. Из этой теоремы
сразу получится вариант теоремы об аналитичности множества
существенно особых точек.
ЗАДАЧИ
1. Мероморфной кривой в области DczC назовем отображение f: D-+C",
компонентами которого являются мероморфные в D функции. Нулем /
называется точка to е А в которой все /v (So) = 0; младший из порядков
нулей /v (v= 1, ..., п) в этой точке называется порядком нуля f. Полюсом
кривой / называется точка ?0 е D, в которой хотя бы одна /\> (So) = °°; по-
порядком полюса / называется старший из порядков полюсов /v B этой точке.
Доказать для мероморфных кривых следующий аналог принципа аргумента:
dD D
(здесь предполагается, что dD — гладкая кривая, f голоморфно продолжа-
продолжается на dD и там f ?= 0; N и Р — число нулей и полюсов / в D с учетом их
порядков; (г, да) = ^zvwv обозначает скалярное произведение). При этом
второе слагаемое справа — неотрицательная величина и обращается в 0 в
том и только том случае, когда кривая f лежит на аналитической прямой,
проходящей через 0 е С".
ЗАДАЧИ 531
2. (А. П. Ю ж а к о в). Доказать, что для любого цикла а, не задевающего
множество особенностей подинтегральной функции,
,2Я + bZl
О
где / — целая функция в С2, к и / — взаимно простые целые положительные
числа, а и 6 ? С.
3. Пусть М — аналитическое множество, относительно замкнутое в об-
области Da С" (это значит, что М— D[\M); тогда множество D \ М связно.
4. Связное аналитическое множество линейно связно.
5. Аналитическое множество неприводимо тогда и только тогда, когда
множество его правильных точек связно.
6. Пусть U — открытое множество в С" я М a U — относительно замк-
замкнутое аналитическое множество. Тогда либо М дискретно, либо содержит
точки, сколь угодно близкие к dU; в частности, всякое компактное аналити-
аналитическое множество дискретно.
7. Пусть М — аналитическое множество в С и L— аналитическая пло-
плоскость (комплексной) размерности к. Если а является изолированной точкой
множества M(]L, то размерность М в точке а не превосходит п — к.
8. Доказать, что неприводимое аналитическое множество М: г% =
в С3 не является аналитическим многообразием; точнее, не существует голо-
голоморфного взаимно однозначного отображения /: B->Mf)U, где В — еди-
единичный шар в С2 и U — окрестность 0 в С3.
9. Одномерное аналитическое множество в С, неприводимое в О,
с точностью до линейной замены координат локально задается системой
уравнений
оо
V^ (v) klm v о п
где т — некоторое целое положительное число.
10. Если одномерное аналитическое множество М с С2 является топо-
топологическим многообразием, то М — аналитическое многообразие в С2.
11. Пусть D — область голбморфности и М — относительно замкнутое
аналитическое множество в D; тогда для любого компакта К а М его обо-
оболочка относительно Н (D) принадлежит М.
12. Пусть К —компакт на замкнутом одномерном аналитическом мно-
множестве МсС". Тогда 1) множество К рационально выпукло, 2) если анали-
аналитическое множество М\ К. неприводимо, то К полиномиально выпукло.
Привести пример полиномиально выпуклого компакта К. а М такого, что
множество М \ К несвязно.
13. Пусть U <= С" — окрестность точки а и функция / е Н (U) такова,
что / (а) — 0 и / ('а, гп) Ф 0. Тогда для каждой jeft (U) существует окрест-
окрестность Уза и функция he.H{V) такая, что g — fh — полином по гп сте-
степени ниже к, где к — порядок нуля f ('а, гп) при гп = ап- (Подготовительная
теорема в форме Шпета — Картана.)
14. Функции fu .... fn голоморфны в точке аеС, и якобиан -gj = 0
в окрестности а.
Доказать, что:
1) существуют голоморфные в а функции gi, ..., gn такие, что
/i?i + ... + fngn = 0, и
2) существует голоморфная в точке / (о) функция F Ф 0 такая, что
34*
532 ОСОБЕННОСТИ И ВЫЧЕТЫ [ГЛ. V
15. Пусть D — область голоморфности в С'! и функции /,еЯ (D), v =
= 1, ..., N, не имеют в D общих нулей; тогда найдутся функции gv<^H (D)
такие, что fxgf + ... + fNgN = 1.
16. Пусть М — аналитическое множество в области D а С", где п ^ 2,
и в каждой точке а е М комплексная размерность М не превосходит п—2.
Тогда любую / е.Н (D\M) можно единственным образом продолжить до
функции из И (D).
17. Если область DczCn является голоморфным расширением области D'
(в частности, D' = D\K, где K<sD), то всякий голоморфизм D' продол-
продолжается до голоморфизма области D.
18. Пусть 2 = {<р (г) = 0}~ гиперповерхность класса С2 в окрестности U
начала координат в С и
S<?2<p
= О
па S для любого вектора а е С". Тогда найдется непрерывная функция
Л (г, 0> голоморфная по г при каждом t, 0 < t < 1, в окрестности нуля
такая, что
ГЛАВА VI
ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ
В этой главе мы рассмотрим основные факты, связанные
с голоморфными гомеоморфизмами пространственных областей.
Заметим сразу, что система Коши —Римана, которая выражает
условия голоморфности системы п функций п комплексных
переменных Bя2 действительных уравнений с 2п действитель-
действительными функциями), при п > 1 переопределена. Это порождает
существенные отличия пространственной теории от плоской.
В частности, в пространстве не имеет места аналог теоремы
Римана о существовании конформного отображения одной
заданной области на другую: даже такие простейшие области,,
как шар и бикруг, в С2 оказываются неотобразимыми друг
на друга!
Мы рассмотрим два подхода к теории отображений —алге-
—алгебраический, связанный с изучением групп автоморфизмов ото-
отображаемых областей, и аналитический, связанный с так назы-
называемой кернфункцией.
§ 16. Автоморфизмы простейших областей
Под изоморфизмом двух областей D, D'czC мы будем
понимать гомеоморфное отображение / = (/i, ..., fn) области D
на D", осуществляемое системой п голоморфных в D функций
fv~fv(z)- Такие отображения называются еще биголоморфными
или голоморфизмами (голоморфными гомеоморфизмами). Изо-
Изоморфизм области D на себя называется автоморфизмом.
Автоморфизмы области D, очевидно, образуют группу, если
под групповой операцией понимать композицию (последова-
(последовательное выполнение) г))°ф автоморфизмов. Как и в п. 36 ч. I,
доказывается, что любой изоморфизм /0: D-+D* устанавливает
изоморфизм групп автоморфизмов отображаемых областей.
Таким образом получается необходимое условие существования
биголоморфного отображения одной области на другую —изо-
морфность их групп автоморфизмов.
На плоскости существует лишь три типа не изоморфных
друг другу односвязных областей: замкнутая плоскость С,.
открытая плоскость С и области, изоморфные единичному
кругу {|z|<l}. В пространстве ситуация значительно сложнее*
534 ГОЛОМОРФНЫЕ ОТОПРАЖЕНИЯ [ГЛ. VI
Мы рассмотрим здесь лишь простейшие факты, связанные
с этими вопросами.
48. Общие теоремы. Начнем с простых теорем об ото-
отображениях пространственных областей. Первые две из них
представляют своего рода теоремы единственности —они утверж-
утверждают, что в некоторых предположениях отображения одно-
однозначно определяются своими линейными частями. Для форму-
формулировки первой теоремы нам понадобится одно определение.
Рассмотрим семейство отображений
f(a) = (C....fr) A)
окрестности точки г — 0, где а пробегает некоторое множество
индексов А, а функции /^а) допускают разложение в кратный
степенной ряд
f:4z)= и 4V- B)
fft|>o KlV
Семейство A) называется слабо ограниченным, если суще-
существуют константы Cfei v ^ 0 такие, что
l'2M<c*.v О)
для всех k = (ki kn) с неотрицательными целыми коорди-
координатами, всех v= 1, ..., п и всех aei
Теорема 1 (А. Картан). Пусть голоморфное отобра-
отображение /=(/i, ..., /„) некоторой окрестности U={\zvl<rv} имеет
линейную часть, совпадающую с тождественным отображе-
отображением, т. е.
fv(z) = zv+ 2 ck,vzk. D)
lft|>2.
Если семейство итераций этого отображения fm (z) = f ° ^|1~I) (г)
(\х = 1, 2, ..., fo)(z) s== z) слабо ограничено, то f{z) = z.
¦* Пусть утверждение неверно. Тогда разложения D) можно
записать в виде
/v (z) = zv + 2 cfe, vzft + ...,
|ft|-=K
где число и^г2 выбрано так, что все ckiV, для которых
К|Л|<к, равны 0, а хотя бы один cft, v, для которого |/г| = и,
отличен от нуля; многоточие обозначает члены разложения
с |&|>и. Итерируя, получим
= zv + 2 S
I * 1-х
§ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ , 535
и, вообще,
Так как по условию семейство [f^} слабо ограничено, то для
всех ц = 1, 2 всех k, \ k\ = H, и всех v = 1 п имеем
где правая часть не зависит от ц. Отсюда следует, что все
такие ckiV — 0, в противоречии с нашим выбором х >
Следствие. Пусть семейство Г голоморфных в U =
= {|zv|<rv} отображений f с компонентами
п
2 с z + 2 c zk
fv (z) = 2 с vzn + 2 ck, vz
слабо ограничено и образует группу (относительно композиции).
Тогда каждое f e Г однозначно определено своей линейной частью-
п
L (!) = 2 Cuv^,, = Сг, г<Эе С = (с^) - матрица, a z = {zl г„) -
ее/crop.
•« Пусть f, gef и имеют одинаковую линейную часть;
тогда ф = f ° g~l е Г и L (ф) = L (/) ° L (g) = z — тождественное
преобразование. Итерации ф<(*> еГи, следовательно, слабо огра-
ограничены. Поэтому по теореме 1 имеем <p(z)^z, и, значит, f=g >
Теорема 2. Пусть ограниченная область D содержит
точку z = 0 и линейная часть голоморфного отображения
f: D -*¦ D в этой точке совпадает с тождественным отображением.
Тогда f{z) = z в D.
¦4 Так как D ограничена, она принадлежит некоторому
поликругу U = {\zv\<M}, а так как f и все его итерации fm
отображают D в D, то и все lfvrt(z)|<M всюду в D. Пусть
поликруг V = {\zv \<rv] ш D, тогда в нем имеют место раз-
разложения
причем в силу неравенств Коши |4ц)м|^~? Т' ОТС!°Да
видно, что семейство итераций f(w слабо ограничено в V, и по
теореме 1 там fv(z) = zv. По теореме единственности эти тож-
тождества справедливы и всюду в D >
Будем еще называть семейство отображений {/(а)}, аеД
компоненты которых в окрестности точки 2 = 0 допускают
разложения B), (сильно) ограниченным в этой точке, если
536 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
существуют постоянная М>0 и вектор г = (ги ..., гп) с по-
положительными координатами такие, что
1М< <5>
для всех k = (ku ..., kn), кц^О, всех v=l, ..., п и всех
аеА Через
д (№ t (аЛ
a (Zi, ..., zn)
мы обозначим величину якобиана отображения f(a) в точке z.
Лемма 1. Пусть семейство голоморфизмов {f(a)}, as A,
окрестности U точки 2 = 0 ограничено в этой точке, fa)@) = 0
ы |/a@)l^ff>0 для всех as Л. Тогда пересечение образов
fa (U), as А, содержит некоторый шар {|да|<р}.
•« Положим 2г = (лг[, ..., х2п), /<a) = («i,..., и2п) и рассмотрим fa>
как действительное отображение
wv= 2 Умху + Фу (х) (v=l, ..., 2rt), F)
где ряды для ф^ содержат лишь члены выше первого порядка
(индекс а мы временно опускаем). Выражение
2га 2п I 2га
v=I v = lV(i=l
является положительно определенной квадратичной формой,
причем в силу условия |/a@)|^cr>0 существует такая не
зависящая от а постоянная /<Ci>0, что ')
2а 2а
С другой стороны, в силу ограниченности {/(а)} в точке г = 0,
в достаточно малом шаре {\x\<R}czU имеем2)
2ге \2
,v=l
>) Напомним, что
J \Xi, . . ., Хчп) v Vя-1» • • •, <-пг
2) Пусть Ф (х) = 2 Vft vxk, тогда | c?v (х) | < | х |21 2 ! Y» v | +
lftl>2 ' llfel-2
+ l-*;l 2 |Vbv|+---l; остается воспользоваться оценками E), которые
I Jfe 1 —з ' J
-справедливы и для j у. I.
§ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ -„у
где /С2 — некоторая положительная константа, также не зави-
зависящая от а. Пользуясь разложением F), находим
2га V/г /2га \>/, /2га
Ъи\) >*, 2*1 -*а 2*;
или, в комплексных обозначениях
ir(z)|>(/t,-/ta|z|)|z|.
Возьмем теперь шар В = {|2|<г}, где r<min(/?, ~-\; на
его границе дВ имеем -~
следовательно, при любом аеУ1 образ fa) (dD) лежит вне шара
{|да!<р}. Так как /№ — голоморфизм и/(а)@) = 0, то отсюда
следует, что fa)(В) => {| w |<р} при любом аеУ1 >
Следующая теорема имеет вспомогательный характер:
Теорема 3. Пусть последовательность голоморфных ото-
отображений f^, ц=1, 2, ..., области D на каждом компакте
К, a D сходится равномерно к отображению f. Тогда, если яко-
якобиан J предельного отображения f в некоторой точке z° e D
отличен от нуля, то найдутся числа ц0 и р такие, что для всех
|ц.^ц0 образ f^(D) содержит шар [\ w — да°|<р}, где w°=f(z°).
< Без ограничения общности принимаем 2° = до° = 0. Семей-
Семейство fm, очевидно, ограничено в точке 2 — 0, и по теореме
Вейерштрасса lim JAz) = J(z). Отсюда следует, что в некоторой
окрестности U точки 2 = 0 отображения f* при м.^(х, гомео-
морфны и |/ц@)|>а>0. Поэтому функции gw = f((i>-fw@),
li^Hi, удовлетворяют условиям леммы, т. е. fw (D) при ц^ц,
содержат шары {| w -fw@)\<2p). Так как fw@)-*0, то най-
найдется (io^Mi такое, что при ju. ^ fx0 образы fw(D) содержат
шар {| w |<р} >
Следующая теорема, принадлежащая А. Картану и
К. Каратеодори, выражает достаточное условие для того,
чтобы голоморфное отображение / некоторой области D в себя,
обладающее неподвижной точкой г°еО (т. е. такой, что
f(z°) = z°), было автоморфизмом этой области. Для ее доказа-
доказательства нам понадобится
Лемма 2. Пусть область D содержит точку г = 0 и голо-
голоморфное отображение f: D-*D таково, что f@) = 0, |/@)j=i?
а итерации fw, |х = 0, ± 1, ..., ограничены в этой точке. Тогда
¦538 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
существует последовательность vs~^ 1 такая, что f^ при s-*-oo
равномерно сходится к тождественному преобразованию в неко-
некоторой окрестности точки z = 0.
А Совокупность итераций fw, где \i = 0, ±1 образует,
очевидно, группу (под f ' понимается тождественное преобра-
преобразование, f(~" обозначает преобразование обратное к f в окрест-
окрестности точки z = 0, которое существует, ибо /@)=^0). По след-
следствию теоремы 1 отображения f1* однозначно определяются
своими линейными частями ?у ), поэтому достаточно найти
такую подпоследовательность vs, для которой b(f^v^)-*-E, где
Е — тождественное отображение.
Заметим, что по определению итераций L (f(lt)) = A^, где
А — матрица L (f), а А^ — ее ц-я степень. Так как последователь-
последовательность b(f ) по условию ограничена, то можно выбрать подпо-
подпоследовательность ц5 @<ц,<ц2< ...), такую, что lim A** = В
существует (т. е. существует предел каждого элемента а^
матрицы A^s, равный соответствующему элементу Ьа^ матрицы В;
а, р=1, ..., п). Так как определители матриц А^ по модулю
равны 1, то матрица В обратима и существует lim A~v's~B~l.
S->°o
Но тогда A^S+1A ^ = A^s+l V'S-^E при s->oo, т. е. последова-
последовательность n.s+1 — Hi = v5 и есть искомая >
Теорема 4. Пусть D — ограниченная область и f: D-> D —
голоморфное преобразование с неподвижной точкой z° e D. Если
(fi. • • -. fn)
I 1 f,,0\ I _
то f — автоморфизм.
•4 Без ограничения общности считаем, что z° = 0. Покажем
сначала, что f — взаимно однозначное отображение. Пусть
f(a) = f (b), где а, Ъ е= D; тогда и f(lx) (a) = fm (b), где fw - итера-
итерации отображения f (\i = 0, 1, ...)• Так как f'w ограничены
в нуле для всех целых ц (в силу ограниченности D), а /@) = 0
и 17@) |=1, то по лемме существует последовательность \is
такая, что /^ сходится к тождественному преобразованию Е
в некоторой окрестности точки 2 = 0. Но f^^ ограничена
в каждой точке ze D, следовательно, из нее по теореме Мон-
теля :) можно извлечь подпоследовательность, равномерно схо-
') См. п. 37 ч. I; доказательство этой теоремы полностью переносится
да пространственный случай.
§ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ
539
дящуюся на любом K<^D. Пусть для простоты {/(IW)} —эта
подпоследовательность; по теореме единственности она сходится
к ? на любом K<^D. Поэтому мы имеем f^s^ (a)-*a и /"V (Ь) —*¦ Ь,
а так как у нас f^ (а) = /^ (Ь), то а = Ь.
Остается показать, что f (D) = D. Последовательность f^s)
удовлетворяет условиям теоремы 3, причем якобиан предель-
предельного отображения всюду в D отличен от нуля. Пусть z^D —
произвольная точка; так как f^) (z)-> z, то по теореме 3 най-
найдутся s0 и р такие, что f^^(D) при s^s0 содержит шар
радиуса р с центром г. Но f^s^(D) czf(D), следовательно,
ге/(й) >
Теорему 4 можно рассматривать как некоторый простран-
пространственный аналог леммы Шварца. В самом деле, ее можно
сформулировать так: если f: D—>D — голоморфное отображение
с неподвижной точкой z°, то |/(z°)|^l, причем равенство
возможно лишь в том случае, когда f — автоморфизм ').
Приведем в заключение другую форму пространственного
аналога леммы Шварца:
Теорема 5. Пусть /, /@) = 0, — голоморфное отображение
единичного шара В ={|z|< 1} с: С", непрерывное в В. Тогда
в любой точке геВ
(8)
•« Рассмотрим сначала комплексную функцию ср: В->С,
ф@) = 0, голоморфную в В и непрерывную в В. Обозначим
М (r) = max|(p(z) |
\г\-г
и положим Ф(*; 2) = ф(<г) = ф(/г„ ..., tzn), где t - комплексное
число, а также
М(г; г) = тах|Ф(*; г)\;
очевидно,
М(г) = maxM (г; О, 0<г<1. (9)
К li
Так как Ф@; z) = 0 для любой геВ, то к функции Ф(*; г)
одного переменного t можно применить обычную лемму Шварца,
') Чтобы убедиться в этом, достаточно заметить, что случай | / (г°) | > 1
невозможен, ибо тогда якобиан итераций f(M в точке г° будет неограниченно
возрастать, а это по теореме Монтеля противоречит ограниченности семей-
семейства итераций.
540 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
по которой для любых ?, |?|^1, игей имеем |Ф(^; г)|^
^111max| Ф(т; г)\, откуда
M(r; z)<rAf(l; г), 0<г<1.
По формуле (9) отсюда получаем сначала М(г; ?)^гМA) для
всех ? ^дВ, а затем
M(r)^rM(l), 0<г<1. A0)
Теперь рассмотрим отображение f = (fi, ..., fn): 5->Сга, удо-
удовлетворяющее условиям теоремы, фиксируем произвольную
точку аеСл и применим неравенство A0) к функции
Po() 2vfv()
v=l
Мы получим, пользуясь еще неравенством Коши—Буняковского:
тах| фа (z) I ^r max
?e=<JB
v=l
flvM*)
<r|a|max|f(C)|. A1)
Пусть z° —одна из точек сферы {\z\-r}, в которой дости-
достигается тах|Д,г)| на этой сфере. Выберем в качестве а вектор
с координатами av = /v(z°). Тогда будет |a| = |f(z°)|, Фо^0) —
= |f(z°)|2; из A1) мы получим
Остается заметить, что в силу нашего выбора z° для любой
точки z, \z\ = r, будет | f(z) |^|/(г°) I >
Следствие. Для любого голоморфного отображения
f:B-+B, /@) = 0, в любой точке гей
lf(z)l<|z|. A2)
< Фиксируем произвольное р, 0<р<1, и рассмотрим ото-
отображение g (z) = f(pz). Оно непрерывно в В, т. е. удовлетво-
удовлетворяет условиям предыдущей теоремы, причем maxj g(t) |^l
Поэтому |g(z)|s^|z| для любого z^B, или, что то же самое,
для любого z^B и любого р, 0<р<1,
|/B)|<.
Устремляя р к 1, получим A2) >
49. Автоморфизмы пространства. В п 36 ч. 1 было доказано,
что любой голоморфный гомеоморфизм комплексной плоскости С
является отображением на С, т. е. автоморфизмом, и непре-
§ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ 541
менно представляет собой линейное преобразование z->az+b.
В пространственном случае оба этих утверждения оказываются
неверными.
В самом деле, пример нелинейного автоморфизма С2
строится совсем просто. Рассмотрим, скажем, отображение
ш1 = г1 + ф(г2), w2 = z2, A)
где ф — произвольная нелинейная целая функция одного ком-
комплексного переменного (например, полином,). Оно голоморфно
в С2, взаимно однозначно (ибо из равенства хю' = хю" немедленно
вытекает, что z'2 = г", а затем, с учетом этого,— что z'{ = z")
и отображает С2 на С2 (ибо произвольное значение (wu ш2)еС2
принимается в точке z1 = w1 — <p(w2), 22 = да2).
Интересный пример (нелинейного) голоморфизма С2 на пра-
правильную часть С2 был построен П. Ф ату в 1922 г. Мы пред-
предлагаем несколько упрощенный вариант этого примера. Возьмем
линейное отображение A: (z1? z2)->( —4г, 4г) и рассмотрим
функциональное уравнение
-3Ф2(Лг), B)
где z = (zv z2) и Л2(г) = ЛоЛ(г) )
Покажем прежде всего, что B) имеет голоморфное реше-
решение вида
2 =z1 + z2 + a|3(z). C)
fe1 2 |
\k\>2
Для этого заметим, что i|) удовлетворяет уравнению
D)
а при исследовании последнего воспользуемся методом мажо-
мажорантных рядов. Мы будем писать 2 ак*к < 2 bkzk, если
I o-k. l^l bk | для всех k (и говорить тогда, что второй ряд мажо-
мажорирует первый), и обозначим || 2 akzk |] = 21 ak I zk. Имеем
so-
lftl-2
542 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ
следовательно,
) E)
Рассмотрим теперь вместо E) уравнение
оно имеет решение 4r = 2(l — / — \fT—2t)= ^j bjt , где
Ц=2
и ряд сходится в окрестности t = 0. Нетрудно видеть, что
¦ф (г) < ^ (^ + г2)'), поэтому ряд для ф, а значит и для ф,
сходится в окрестности точки z = 0. Но из уравнения B) видно,
что если ф голоморфна в бикруге {|2x|<r, \z2\<r}, то она
аналитически продолжается в бикруг {\zl\<.2r, \z2\<2r},
а отсюда следует, что ф —целая функция.
Покажем, что искомое отображение С2 можно взять в виде
/ = (/i> /2). где
fj (z) = ср (z), f2 (z) = ф (Az). F)
Пусть J {z)= ,, {—якобиан этого отображения; сравним
его с якобианом отображения
-С / \ I г9 / \ I /7\
(мы воспользовались уравнением B)). Так как при композиции
отображений их якобианы перемножаются, то из G)
0 1
д (g\,
\, gi) _^
д (ги z2)
1 If
4 2 ':
d(h, h)
д (г„ z2)
а из того, что g (z) = f (Az),' получаем
. 82) _ т(Лт.\ д(Аи At) __ _ 1
, г,) " J {AZ) d{zt,z2) ~ ~ 4
Мы получили, что J(Az) = J(z), откуда находим
где Ап — п-я итерация отображения А. Так как \imAnz = 0 для
любого геС2, то /(г) = / @) = const. Но в окрестности начала,
') Для доказательства можно воспользоваться индукцией по | k \ = ц,
оо
заметив, что E) оценивает коэффициент разложения ||ф(г)||=2 абг*
с фиксированным | k J через коэффициенты с меньшими значениями I ft I.
16]
АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ
543
как видно из B), h (z) = Zj + z2 + .... f2 (z) = - Ix. + ?l + # #.
поэтому /@) = 1 и, следовательно, /(z)e=i.
Отсюда нетрудно заключить, что f — гомеоморфизм. В самом
деле, пусть, от противного, f(a) = f(b), где афЬ— точки С2.
Тогда имеем ф(а) = ф(?), Ф (Аа) = ф (АЬ); но с учетом B) отсюда
следует, что и ф(Л2а) = ф(Л26), а это вместе с последним соот-
соотношением дает f(Aa) = f(Ab). Итак, f(a) = f(b)=$f(Aa) = f(Ab),
и итерированием мы получим
f(Ana) = f(Anb).
Но отображение f локально гомеоморфно, ибо J(z)=?0, а А"а
и АпЬ при достаточно больших п сколь угодно близки к началу,
и мы пришли к противоречию.
Остается показать, что f принимает не все значения из С2.
Прежде всего, ясно, что f не принимает значения A, 1). Дей-
Действительно, если бы в некоторой точке z было <p(z)=l, ф(Лг)=1,
то из B) мы получили бы, что в этой точке и ф(Л2г)=1.
Таким образом, из f(z) = (l, 1) следует, что и /(Лг) = A, 1).
Итерированием найдем, что и f(Akz) = (l, 1) для любого
k = 1, 2, ..., откуда в пределе следует равенство f @, 0) = A, 1).
Но у нас f@, 0) = @, 0), и противоречие доказывает утвер-
утверждение.
Более того, f не принимает ни одного значения из множе-
множества Е — \ (av a2): I aj |^-g-, la^l^lajlj-. В самом деле, пусть
в некоторой точке z имеем ф (z) = au ф (Az) = a2. Из B) тогда
следует, что
Ф (г) 4-Зф (Az) a, 4-3e9
4
и, далее, что итерации f(Az), f\A z), ..., f(A {z) соответственно
равны (a2, a3), (a3, a4), ..., (aft, aft+1), где
= 2, 3, ...).
Из этих соотношений следуют неравенства
3 . 1
•**+!
544
ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ
[ГЛ. VI
из которых для любой точки a = (ait a2) s E сначала при k =
получаем
«2
затем при k = 3
и вообще
_3 _5
4 ' 3
аз
для всех /г = 2, 3, ... Таким образом, ите-
итерации f(Akz) не могут сходиться к точке @, 0) при &->оо, и,
значит, точка а не может приниматься отображением /.
Множество Е, очевидно, имеет полную размерность, и, зна-
значит, пример Фату показывает, что для пары целых функций
(с отличным от нуля якобианом, т. е. функционально незави-
независимых) не имеет места ни аналог теоремы Пикара, ни даже
теоремы Сохоцкого.
В пространстве, как и на плоскости, можно рассматривать
линейные преобразования
(v= 1 п),
которые можно записывать в виде
w = Az + b,
где b = (bl, ..., bn) — вектор, а
(8)
tin)
• ¦ • а'
— квадратная матрица. Линейное преобразование (8) назы-
называется невырожденным, если определитель det А ф 0. Совокуп-
Совокупность невырожденных линейных преобразований в С", очевидно,
составляет группу автоморфизмов этого пространства. Однако
в пространственном случае, в отличие от плоского, она является
лишь подгруппой группы всех голоморфных автоморфизмов
(см. пример в начале пункта).
Добавление вектора b геометрически означает сдвиг, а пре-
преобразование
w = Az, ¦ (9)
которое на плоскости сводится к растяжению с поворотом,
в пространстве имеет несколько более сложный геометрический
§ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ слг
характер. Напомним основные свойства таких преобразова-
преобразований ').
Пространственным аналогом поворота является унитарное
преобразование, т. е. преобразование (9), матрица А которого
удовлетворяет условиям
v=l п). Так как из (9) мы имеем
I w p = 2 Wjw. = 2B a<i\\ {2 dv ^v) = 2 ^^>Vv>
то (9) в том и только том случае является унитарным, когда
оно сохраняет длины векторов (т. е. переводит сферы {\z\~R}
в себя). Доказывается, что в С" существует ортогональный и
нормированный базис, в котором унитарное преобразование
сводится к повороту в каждой координатной плоскости:
Пространственным аналогом растяжения является положи-
положительно определенное преобразование. Так называется линей-
линейное преобразование (9), для которого
(Az, z)=2aS°z zv>0, <> = ^>, A1)
для всех геС и всех ц, v=l, ..., п. Такое преобразование
переводит сферы {\z\ = R} в эллипсоиды, причем в С" суще-
существует ортогональный и нормированный базис, в котором оно
сводится к растяжению в каждой координатной плоскости:
zv -> pv • zv (pv > 0, v = 1, ..., n).
Напомним, наконец, что любое невырожденное линейное
преобразование (9) можно представить в виде композиции не-
невырожденного положительно определенного и унитарного пре-
преобразований (или, что то же самое, любую матрицу Л, deM^=0,—
в виде произведения положительно определенной матрицы Н,
для которой det#=dei^, и унитарной матрицы U: A — HU).
Это представление аналогично разложению плоского преобра-
преобразования z-*az на растяжение и поворот (или, что то же са-
самое, представлению числа а в полярной форме: а = ре'6).
Невырожденные преобразования (9) образуют группу, кото-
которая, очевидно, зависит от п2 комплексных, т. е. от 2п2 дей-
действительных, параметров. Унитарные преобразования состав-
составляют ее подгруппу, которая зависит от п2 действительных
') См. И. М. Г ель фан д, Лекции по линейной алгебре, Гостехиздат,
М.-Л„ 1948.
35 Б. В. Шабат
54G ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
параметров (в самом деле, условия A0) содержат п(п— 1)+
+ п = п2 действительных равенств). Такую же подгруппу со-
составляют и невырожденные положительно определенные пре-
преобразования.
В заключение несколько слов об автоморфизмах компакти-
компактифицированных комплексных пространств. Как известно, пол-
полную группу автоморфизмов замкнутой плоскости С составляют
невырожденные дробно-линейные преобразования z —> аг -,
ad — be фО. Для пространства теории функций Сп их анало-
аналогом служат преобразования
Tzld (Mv-&vCv=*0, v=l, ...,п), A2)
а для комплексного проективного пространства Р^~ невыро-
невырожденные проективные преобразования
(v=l, .... п) A3)
(условия невырождения мы не выписываем; условие пропор-
пропорциональности всех знаменателей формул A3) — мы их берем
даже одинаковыми, включая множитель пропорциональности
в числители, — необходимо для того, чтобы обратное отобра-
отображение не содержало квадратичных членов).
50. Автоморфизмы некоторых областей. Начнем с изучения
групп автоморфизмов простейших областей в С" —шара и
поликруга. Мы убедимся в том, что для них и в простран-
пространственном случае все автоморфизмы являются дробно-линей-
дробно-линейными преобразованиями. Таким образом, пространство С" при
п > 1 существенно отличается от этих областей — его нельзя
рассматривать как шар или поликруг бесконечного радиуса.
а) Шар fi = {zeC": | z |< 1}. Сначала рассмотрим семей-
семейство дробно-линейных (проективных) автоморфизмов. Зададим
точку a = (ah ..., ап), переходящую при таком автоморфизме
в начало, тогда формулы A3) предыдущего пункта (в несколько
иных обозначениях) можно переписать так:
п (v=l, .... «). A)
§ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ 547
Уравнение прообраза сферы {|аи|=1} при этом отображе-
отображении имеет вид
п п I п \
/I {A^v — PjxPv)Z(i^v — 2 Re ^j I yPix + ^j Aflvuv Iz^ =
\L, V=l H = l V V=l /
n
I ., 12 "У Л п = (C)\
n
где Лцу = 2 au)aift)' Мы должны рассмотреть такие отображе-
ния A), для которых B) является уравнением сферы {|г| = 1}.
Условиями этого служат
Лм = Р S (и =5^ VJ Ц, V = 1 . П),
Aw~\^\2 = \y\2-^iAljaia] (ц=1, ...,«), C)
г. /
v=l /
Подсчитаем число независимых параметров, определяющих
рассматриваемые отображения A). Числитель и знаменатель
каждого из уравнений A) можно разделить на одно и то же
число (например, положить в них Y=0- Поэтому отображе-
отображение A) зависит от п2 + 2п комплексных, т. е. от 2п2 + 4/г дей-
действительных, параметров. Условия C) содержат п(п — \) + п +
+ 2п = п2+2п действительных равенств (первое и третье из
этих условий содержат комплексные, а второе — действитель-
действительные равенства). Поэтому группа автоморфизмов шара вида A)
зависит от п2 + 2п действительных параметров.
Особо отметим подгруппу этой группы, которая состоит из
отображений, оставляющих неподвижными центр шара 2 = 0.
Здесь все av = 0, и из уравнений C) при Y—1 мы получим,
что все Рм, = 0, а A^v равны 0 при ц ф v и равны 1 при ц = v.
Мы видим, что эта подгруппа состоит из унитарных пре-
преобразований
a>v=S<>Zll (v=l, .... п), D)
для которых 2aife)a^) = 6 . Уравнения D) содержат 2л2 дей-
k
ствительных параметров, а условия унитарности накладывают
п2 связей, поэтому рассматриваемая подгруппа зависит от п2
действительных параметров.
Пример. Выпишем для автоморфизмов единичного шара
в С2 формулы, в которых участвуют лишь независимые пара-
35*
548 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. УГ
метры. Если по-прежнему обозначить а = (аъ а2) точку, пере-
переходящую в центр шара, и через (z, a) = zxax + z2a2 — скалярное
произведение, то при а Ф О эти формулы будут иметь вид
_ g'9' (г, а) — | а |2 + X У~\ - | а |2 (a2Zi - а1г2)
1- УПТК? |а|[1-(г, а)]
ею> Я [(z, а) - | а 1"] - Kl - 1 а I2 (а»г, - д,г,)
1а|[1-(г, в)]
где X —произвольный комплексный, а 0ц Э2 —действительные
параметры1). Группа автоморфизмов E) зависит от восьми
действительных параметров: четырех координат точки а,
двух —точки X и двух значений 0V (в соответствии со сделан-
сделанным выше подсчетом: я2 + 2га = 8 при п = 2).
Преобразование E) представляется как композиция двух
отображений: дробно-линейного автоморфизма
(г, а) — I а |2 -,/-. ;—т
Ю1 = , i ,, /—Чт . СО, = У 1 — а Г 1—ГТТ / м , F)
1 I а | [1 - (г, а)] г ' ' I а | [1 — (г, а)] к '
переводящего точку z — a в центр шара, и унитарного пре-
преобразования
е<9,
сохраняющего центр. Преобразования G) составляют под-
подгруппу, зависящую от четырех действительных параметров.
Теорема 1. Любой автоморфизм f: В —>В единичного
шара из Сп является дробно-линейным отображением вида A).
•« Пусть f(O) = a; построим дробно-линейный автоморфизм
L: В->В вида A), переводящий точку а в 0; тогда компози-
композиция /r = L°/ будет автоморфизмом шара, сохраняющим его
центр. Если он дробно-линеен, то f = L~l ° F — также; поэтому
достаточно доказать теорему для автоморфизмов, сохраняю-
сохраняющих центр.
Пусть /: В->В, /@) = 0,—такой автоморфизм. К нему и
к его обратному /"' можно применить лемму Шварца из п. 48
(см. следствие на стр. 540), и мы получим, что для всех z e В
одновременно |f(z)|^|z| и I 2 |=^|/(z) |. Поэтому всюду в В
мы имеем I f (z) | з= | z |. Отсюда выведем сейчас, что f является
линейным унитарным преобразованием вида D).
') То, что E) при любом а е В2 \ {0} и любом Я <s С осуществляют ав-
автоморфизм В2, проверяется простой выкладкой.
$ 16] АВТОМОРФИЗМЫ ПРОСТЕЙШИХ ОБЛАСТЕЙ ...
549
Пусть компоненты / в окрестности начала представляются
рядами
fv (*) = ! ^2 a$>z* (v = 1, .... я); (8)
в силу их абсолютной сходимости
1/Р2М)Ш2Ам,
v=l к, I
где
Аы = S 4V)^T. (9)
v=l
a k = (kx, ..., &„), t = (llt ..., /„) — векторы с целыми неотри-
неотрицательными координатами. Полагая гу = rveity> и г = (г; г„),
мы будем иметь
fe, /
Введем новый векторный индекс m = k — l и перегруппируем
последний ряд, записав его в виде
Ф= S Bm(r)e^m'<i+-+m«<«), A0)
I m| = —оо
где
Sm(r)=S^+m,^+- A1)
и суммирование распространяется на все I, для которых /v^0
и /v + mv^0. Мы можем рассматривать A0) как кратный ряд
Фурье, а так как его сумма Ф = |г|2 не зависит от t, то по
теореме единственности разложения в ряд Фурье все Вт = 0
при т ф 0, а
Но рассматривая A1) и A2) как степенные ряды относительно
действительного переменного г = (ги ..., гп), мы получим в силу
единственности разложения в такие ряды, во-первых, что
Akt i = 0 при кф1 и, во-вторых, что Аи {= 0 при / = 0 и | /1 > 1.
Теперь из (9) видно, что a^v) = 0 при fe = 0 и \k\>l, т. е. что
/ — линейное, а значит, унитарное преобразование >
Непосредственным следствием доказанного и сделанных
выше подсчетов является
Теорема 2. Группа всех автоморфизмов шара ВсС
зависит от п2 + 2п действительных параметров, а подгруппа
550 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
автоморфизмов, сохраняющих центр шара, — от п2 действи-
действительных параметров.
б) Поликруг [/ = {геС": |zv|<l}. Подгруппу автомор-
автоморфизмов этого поликруга, зависящую от 3/г действительных
параметров, составляют, очевидно, дробно-линейные преобра-
преобразования
*v~^T*iS- <v-l.....n), A3)
где av, | av |< 1, — комплексные, a 0V — действительные числа.
При п > 1 к этим преобразованиям можно добавить еще те,
которые получаются из них дополнительной перестановкой
переменных wv—> ш^, где ц = ц (v) — взаимно однозначное ото-
отображение множества {1, 2, ..., п) на себя.
Теорема 3. Любой автоморфизм поликруга U сг Сга имеет
вид A3) цл« получается из A3) перестановкой переменных
шч->ш^. Таким образом, полная группа всех автоморфизмов
поликруга расслаивается на п\ классов, зависящих от Зп дей-
действительных параметров1).
< Пусть /—автоморфизм U. Мы можем считать, что
f@) = 0, так как f можно заменить преобразованием L°f, где
/. — дробно-линейный автоморфизм U вида A3), переводящий
/@) в 0. При фиксированном ?edf/ рассмотрим функцию
fv{tt) комплексного переменного t, \t\<l; по лемме П1варца
(п. 35 ч. I) мы получаем, что | fv{tt,) |^| 11, l^v^n. Так как
любую точку z^U можно представить в виде г = тах|2„|-?,
и
где t,^dU, to имеет место неравенство
max | /v (z) | ^ max | zv |,
V V
которое обобщает неравенство Шварца. Так как f~l — тоже
автоморфизм U, то мы получаем, что в U
max|fv(z)| = max|zv|. A4)
zv
Пусть /(v) — плоскость вида 2 Дц^ц = 0, на которой
= тах|г„|. Применяя лемму Шварца на этой плоскости
и
к функциям /ц, мы получаем из равенства A4), что хотя бы
одна из них совпадает на /<v> с функцией eiezv для некоторого
8gR. Так как число индексов ц конечное, а плоскостей
/<v) —континуум, то по теореме единственности мы получаем,
') Среди этих классов лишь один будет группой — тот, который содер-
содержит тождественное отображение, т. е. класс A3).
§ 171 ИНВАРИАНТНАЯ МЕТРИКА 551
с точностью до перестановки переменных, что fv(z) = avzv, где
aveC, |av|=l, v=l, 2, ..., п >
Эта теорема и замечание, сделанное в самом начале пара-
параграфа, приводят к такому заключению:
Следствие. В С" при п>\ поликруг и шар голоморфно
не эквивалентны друг другу.
§ 17. Инвариантная метрика
В этом последнем параграфе мы рассмотрим основные
вопросы, связанные с так называемой кернфункцией, которая
была введена С. Бергманом и оказалась весьма полезной
в ряде задач теории функций.
51. Кернфункция. Рассмотрим произвольную область DczC"
и обозначим через L2h = L2h{D) совокупность всех функций
/ е Я (D), для которых конечна норма
f - (D
где dV — элемент объема в С" и интеграл понимается как не-
несобственный.
Совокупность L2h{D) образует гильбертово пространство со
скалярным произведением
(f,g)=jfgdV. B)
D
Из неравенства Буняковского —Шварца \(f, g) |2<llf II • \\g I! сле-
следует, что это произведение конечно для всех f,g<^ Lh- Из
этого же неравенства обычным образом получается неравен-
неравенство треугольника: для всех f, g^Lh
llf + fiflKilfll+llfifll, C)
причем знак равенства здесь достигается лишь в том случае,
когда либо f = 0, либо g = af. где а^О.
Отметим еще локальную оценку | f \ через^ норму этой функ-
функции в Ь\: если поликруг U (z°, r)mD, то для любой f e Lh(D)
Для доказательства подставим в ||f||y тейлоровское разло-
разложение I с центром 2° и проинтегрируем почленно, вводя
552 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. Vf
в каждой плоскости zv полярные координаты (zv — z°v — pve'°v):
и |/i>o
I/1, Jft|>0 v=l 0
v = l
так как члены полученного ряда неотрицательны, то
0П
Фиксируем точку z°^D и поставим следующую вариа-
ц ио иную зада чу:
Среди всех функций f e Lh (D), нормированных условием
f(z°)=l, найти ту, которая реализует минимум ||/||.
Мы обозначим
Теорема 1. Если класс BZ«(D) непуст, то в нем суще-
существует единственная функция /0, решающая поставленнуш за-
задачу.
¦4 а) Существование. Пусть
Л= inf
(по условию эта величина конечна) и f^ {\x=l, 2, ..^ — мини-
минимизирующая последовательность, т. е. такая последователь-
последовательность f gBz,, что lim ||fwf = А. Так как {||^|1 ограничена,
то в силу оценки D) семейство функций локально равномерно
ограничено в каждой точке z^D. По теореме Монтеля (см.
п. 37 ч. I; доказательство этой теоремы без труда переносится
на функции нескольких переменных) отсюда следует, что это
семейство компактно, т. е. из него можно выделить последова-
последовательность /„ , сходящуюся равномерно в каждой G <Ш D к функ-
ции /0. Очевидно, f0 e Вг„ и
||Ltf = lim || f II2 < lim II/=„ 2<Л,
§ 17] ИНВАРИАНТНАЯ МЕТРИКА 553
а следовательно, и ||/0|?<Л. Так как [оейг„ то отсюда сле-
следует, что || f01|2 = А.
б) Единственность. Пусть есть еще функция gQ <= В „,
для которой ||go||2 = A Тогда так как --tgo ^Bz<>, то
— мы воспользовались неравенством треугольника. Так как
в этом неравенстве имеет место знак равенства и ?йф0,
то ge = а/0, где а ^ 0. Поэтому
2
значит, а=1 и go = fo >
Мы будем называть /0 из теоремы 1 экстремальной функ-
функцией и обозначим
г - / л\ 1 /Г\
Рассмотрим теперь в области D произвольную полную
ортенормальную систему функций (p^eLICZ)), |i= 1, 2, ... Под
ортонормальностью понимается свойство (фц, Фv) = ^цv. гДе
6^=1 при (i = v и 6^ = 0 при (х Ф v, а полнота означает, что
любая функция /eL|(D) представляется рядом
где atl = (f, фр,), сходящимся к / в среднем, т. е. в смысле
нормы A). Заметим, что в нашем случае из оценки D) выте-
вытекает и равномерная сходимость ряда F) в каждой G ш D.
Напомним еще, что условие полноты ортонормальной системы
выражается равенством Парсеваля:
2К12Н1Л!, G)
И = 1
где ац = (/, фц).
Обычным для анализа образом доказывается, что в каж-
каждой ограниченной области D с: С" полные ортонормальные си-
системы из L2h(D) существуют, в неограниченных областях такие
системы могут не существовать (например, их не существует
в С"). Поэтому в дальнейшем области, где существуют такие
системы, мы будем называть областями ограниченного вида.
554 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
Лемма. Для любой ортонормальнои системы у^^ L2h(D)
ряд 21фиB°I2 сходится в любой точке z°^D.
•« Пусть U (z°, г) ш D и т —любое натуральное число;
пользуясь ортонормальностью и неравенством D), находим
откуда
H=l
Теорема 2. В любой полной ортонормальнои системе
е Z,| (?)) экстремальная функция /0 представляется рядом
/О (z) =
(8)
•« Обозначим Ф„ (¦г°) = Фм и 2|фм \2~а (по лемме этот ряд
сходится). Пусть / — произвольная функция из BZ«(D) и
оо
/(z) — 2 Яцфц (г) — ее разложение. Определим числа сец равен-
ствами
и заметим, что условие / (г0) = — ^ (ф° + се^)ф« = 1 влечет за со-
со
бой соотношение 2 ^„ф?. = О- С учетом этого соотношения ра-
венство Парсеваля G) примет вид
И-1
^ l7' ИНВАРИАНТНАЯ МЕТРИКА 555
Отсюда видно, что минимально возможное значение ||f||2
в классе Bz°, равное — , получится в том и только том слу-
случае, когда все % = 0. Таким образом, при / = f0 мы имеем
где — = || /01|2 = -щж ¦> это совпадает с (8) >
Определение. Функция
KD(z,z^ = fQ(z)K(z0) = ^, (9)
где /0 —экстремальная функция, называется кернфункцией об-
области D относительно точки 2°eD.
Следствие. В любой области DcC" ограниченного вида
кернфункция K(z, z°) относительно любой точки г°е/) суще-
существует.
Из теоремы 2 видно, что в любой полной ортонормальнои
системе ф^е!^!)) кернфункция представляется разложением
K(z, ?)=2qv(z)qv(?) (Ю)
1
(мы положили z° = ?). Так как это разложение (при фиксиро-
фиксированной ? е D) сходится равномерно в любой йёОжрц^е
е Н (D), то по теореме Вейерштрасса кернфункция голоморфна
в D относительно своей первой координаты г. Из соотношения
,0 = К(Ъ 2), A1)
которое вытекает из A0), видно также, что она антиголо-
морфна в D относительно второй координаты ?.
Кернфункция обладает интересным воспроизводящим
свойством: для любой fe.Lh{D) и любой точки zeD
(z, l)dV. A2)
Для доказательства достаточно подставить в правую часть
разложения / и К по произвольной полной ортонормальнои
системе Фн ^ L2h(D) и, пользуясь равномерной и абсолютной1)
') Абсолютная сходимость рядов по системам фц следует из неравенства
Коши - Буняковского 2 I VPm. К /^ 1 Ч ^ V^\4>ti\2 • равенства G) и
леммы на стр. 554.
556 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. \'Т
сходимостью разложений в любой G <ш D, проинтегрировать
почленно; учитывая еще ортонормальность системы, мы по-
получим
J f E) К (г,
ц., v-1
Формула A0) позволяет явно вычислять кернфункцию про-
простейших областей. Приведем несколько примеров.
а) Поликруг U = {\zvl<rv}. Полной ортонормальной
системой здесь будет система нормированных мономов
% = h*k = \...uft >••<"• *v>0, A3)
где коэффициенты ЯА>0 выбираются из условия
Вводя в каждой плоскости zv полярные координаты (zv = pe'Sv),
находим из этого условия
v=] 0 v=l
ИЛИ
«-in
kv + l
* r r
х—1 'v'v
Полнота системы A3) следует из того, что рядом по этой си-
системе является ряд Тейлора, а им представляется любая
функция f^H(U); ортонормальность ее очевидна. По фор-
формуле A0) имеем, следовательно,
Положим xv = —^- и r2 = r2 ... г^, тогда
rv
V-1 |ftl>l
* U] ИНВАРИАНТНАЯ МЕТРИКА 557
Так как у нас г, ? е и, тс> UV|<1, и можно переставить по-
порядок суммирования и Дифференцирования; мы получим
1 эЛ ^~ч ,
_^ ...
лпг* дхх ...дхп A- хх) ...A-х„) nnr
v=l
Подставляя значения xv и г2, находим окончательно
б) Шар 5 = {|z|</?}. Полной ортонормальнои системой
здесь опять будет система мономов A3), но условия норми-
нормировки дадут
(|fe)l
*
(для вычисления интеграла по В надо ввести полярные коор-
координаты в R2"). По формуле A0) получим
nnR2n
Схэ
О*-
Теперь заметим, что внутренняя сумма
Zj ~~п— (^l»l) ' • • \Zn~n) П
И ЧТО
оо
^ / I 1\ / , \ и дп 1
(ц+ 1) ... (ц + п)^ =
дхп 1-х (l-x)n+l
п
для всех х, \х\<1. Так как у нас z, ^еб, то -nj Jjzv?v =.
по модулю меньше 1 и, следовательно,
v=l
а5)
558 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
Замечание. Формула A4) показывает, что кернфункция
поликруга U, который является произведением кругов {\zv\<
< rv}, равна произведению кернфункций этих кругов: К (zv, ?v) =
= ——2— rj. Можно доказать, что и вообще кернфункция
произведения областей DiCzCn(z) и D2czCm(w) равна произ-
произведению кернфункций этих областей:
Kd,xdAz> w> S. ®) = Kd№> Z)Kd2(w, <*>)
(см. Б. А. Фукс1), стр. 91).
Особо выделяется кернфункция
K(z) = K(z, z)=Slqv(z)P, A6)
которая, как следует из (9), положительна в каждой точке
области ограниченного вида, ибо она является обратной ве-
величиной минимума ||/||2 в классе всех функций f^L\(D), для
которых f(z) = 1.
Очевидно, можно не накладывать условия f(z) = l, и тогда
будет
! ша
inf
_= inf
К (г) 1Ш2 |/(г)
Поэтому для любой f e L2 мы имеем
A7)
а так как нижняя грань достигается, то существует функция
/ое^, для которой
1Мг)|2 = /ШШ|2; A8)
эта функция также называется экстремальной.
Теорема 3. В любой области ограниченного вида функ-
функция K{z) является плюрисубгармоническоп.
¦4 Так как ф^еЯф), то | ср^ |2 плюрисубгармоничны в D
(см. задачу 24 к гл. III). Но по доказанному выше ряд A6)
сходится равномерно в любой G <Ш D, следовательно, его
сумма также плюрисубгармонична >
В следующем пункте мы убедимся в том, что она и строго
плюрисубгармонична. По теореме 2 п. 25 из этого вытекает,
что если для некоторого ^>0 множество /)( = {гЕ D: K{z)<t)
') Б. А. Фукс, Специальные главы теории аналитических функций
многих комплексных переменных, Физматгиз, М., 1963.
§ 17] ИНВАРИАНТНАЯ МЕТРИКА
компактно принадлежит D, то каждая связная компонента
этого множества является областью голоморфности. Отсюда
как и в п. 25, выводится '
Теорема 4. Если D — область ограниченного вида и для
каждого t>0 множество {z^D: K{z)<t}m D, то D является
областью голоморфности.
Заметим, что в силу субгармоничности функция К не мо-
может достигать максимума во внутренней точке области. Усло-
Условие теоремы 4 состоит в том, что кернфункция К (z) равно-
равномерно стремится к бесконечности при приближении к границе
области D; теорема утверждает, что это условие достаточно
для того, чтобы D была областью голоморфности.
Отметим, наконец, что, как видно из формулы A5), для
шара функция
растет при приближении к любой точке границы с одинако-
одинаковой скоростью п+1 , где d — расстояние до границы. Из фор-
формулы A4) мы видим, что для поликруга, напротив, функция
?Т B0)
V-l V v
растет по-разному при приближении к различным точкам 3U.
Быстрее всего [со скоростью -^А она растет при приближе-
приближении к остову, который является границей Шилова поликруга.
52. Метрика Бергмана. При помощи кернфункции можно
ввести риманову метрику, инвариантную относительно голо-
голоморфных гомеоморфизмов (голоморфизмов). Выясним сначала,
как меняется при таких отображениях сама кернфункция.
Пусть
w = f{z), f = (flt ..., fn) A)
— голоморфизм области flcC" на область D*. По доказан-
доказанному в п. 44 якобиан этого отображения
а(г„...,гп) =Hz)--f7- V)
(мы будем для сокращения письма пользоваться этими обо-
обозначениями) нигде в D не обращается в нуль, а якобиан об-
обратного отображения z = f~1(w)
dz _ d(zb ..., zn)
dw д (o>i wn)
560 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
равен обратной величине —г-- Напомним еще, что при замене
переменных z—>w действительный якобиан (отношение элемен-
элементов объема)
dV"
dV
Теорема 1. При голоморфизме f области D ограничен-
ограниченного вида на D* кернфункции этих областей в соответствующих
точках w — f(z) и со = f (?) связаны соотношением
i)- D)
¦« Пусть ф^ е L\{D) — произвольная полная ортонормаль-
ная система, тогда
будет такой же системой для области D". В самом деле,
D* D* D
следовательно, i]5^eL|(D*); система ортонормальна, ибо
и полна, ибо каждая фе/Д(?>*) представляется в виде
Ф ° ^"' ~dw~' где Ф — Ф ° / "wf~e ^ft (^)> а Умножая разложение ф =
— S Ядфц. на -р-, мы получим ^ = SaM^- Поэтому по фор-
формуле A0) предыдущего пункта мы получаем
'Jt (о) = /. "ф„ I
И у
Из формулы D), в частности, следует, что
z)f, E)
где K(z) = K(z, z)>0 — обратная величина inf ?! ,2 по всем
функциям ф?1/,(О) (см. предыдущий пункт). Отсюда
In К* (ш) = In /<Г B) + In /' (г) + In /' (г),
§ 17] ИНВАРИАНТНАЯ МЕТРИКА ggj
где К* {w) — Kd*{w), и дифференцирование с учетом голоморф-
голоморфности f дает
дЧпК* _ yi б2 In К дга д2$
dw^dwv ~~ 2j dzadzp dw». dwv ' F)
Формула F) показывает, что величины
при голоморфизмах меняются по тензорному закону изменения
дифференциальных форм бистепени A, 1) (см. п. 10).
Определение. Дифференциальная форма
п
2 ga*dza dz&, (8)
a,p=I
где коэффициенты вычисляются через кернфункцшо области D
по формулам G), называется формой Бергмана для этой об-
области1). Эта форма инвариантна относительно голоморфизмов
области -ма 2 в любой области DaCn ограниченного вида
форма Бергмана (8) является эрмитовой и положительно опре-
Гэрмитовость формы выражается равенствами gap = ?pa,
которые вытекают непосредственно из G), если учесть, что
К (z} ^> 0
Положительная определенность означает, что для любого
вектора <в е С, со ф 0, в любой точке гей
S gfapCOa(Op>0. (9)
a, p=I
Для доказательства этого неравенства мы фиксируем
аеС°\{0}, zgD, рассмотрим множество
)
11
a=l
и покажем, что
||ф||2=-— —, A0)
ft S
а, Р
где /С и g-ap вычисляются в точке г.
I) в выражении формы Бергмана мы рассматриваем не внешние, а обыч-
обычные произведения дифференциалов.
36 Б. В. Шабат
562 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
Выберем в D какую-либо полную ортонормальную систему
{ф^}, и пусть ср = 2ацфц- Тогда вариационная задача A0) све-
сведется к отысканию rnin 2 I ац I2 ПРИ условиях
п.
(значения фй и их производных берутся в точке г\ пределы
суммирования по ц мы опускаем). Задача имеет единственное
решение (это доказывается, как теорема 1 из предыдущего
пункта), и для его отыскания мы воспользуемся методом мно-
множителей Лагранжа. Возьмем вспомогательную функцию
VI \Л \
ф (а) = 2л а"й» ~ Ai 2и аЛ ~ Ki2i av.
а
и заметим, что условия ее экстремума имеют вид1)
, = 0 <|*== 1, 2, ...). A2)
Отсюда следует с учетом A1), что для экстремальных значе-
значений аи
d(fn. .
Чтобы найти К2, мы подставим значение ац из A2) в условия A1):
Р Р а, Р " В
Коэффициенты этой системы выражаются через К =
ее производные; решая ее, мы найдем
1 !
' \дгадЦ К дга дЦ
') Для доказательства нужно подставить 0^ = 0^ + г'Р^,, разделить дей-
действительные и мнимые части условий A1) и приравнять производные па
аи и Рн соответствующей вспомогательной функции; A2) выражают ком-
комплексную запись этого.
§ 17] ИНВАРИАНТНАЯ МЕТРИКА ggg
Остается заметить, что
дЧпК _ 1 д*К i дК дК
*> «3 дга 5гр К дга dzp К2 дга ~Щ >
и поэтому Я2 совпадает с правой частью A0) >
Замечание. Положительная определенность формы
Бергмана, выражаемая неравенством (9), означает (строгую)
плюрисубгармоничность функции In /<" (см. п. 25). Этот резуль-
результат сильнее теоремы 3 предыдущего пункта, ибо из плюри-
субгармоничности логарифма функции следует плюрисубгар-
плюрисубгармоничность самой функции, а обратное неверно.
На основании теоремы 2 в каждой области D cz С" огра-
ограниченного вида можно ввести риманову метрику
п
ds2=a^^gaSidzadz&, A3)
по доказанному выше инвариантную относительно голомор-
физмов. Эта метрика называется метрикой Бергмана.
Примеры. Для поликруга U = {|zv |<rv} по формуле A4)
предыдущего пункта метрика Бергмана определяется формулой
(r2 ,1 „Л2 <**«<**„, A4)
„_! [fa \га\ )
где dzadza = dx\ + dy\ = \dza |2. При n = 1 в круге {\z |<г} по-
получаем так называемую гиперболическую метрику
ЫЛ- — (г2 — I г|2J ' ' '
Эта метрика инвариантна относительно конформных отобра-
отображений и, в частности, не меняет своего вида при конформных
автоморфизмах круга, т. е. дробно-линейных преобразованиях
ief(z-a)
w = е'° Г2_пг '• имеем
\dz | _ \dw\
г2 - | г I2' ~ г2 - | w |2
Геометрия, определяемая этой метрикой, является геометрией
Лобачевского; движениями в ней служат Дробно-линейные
автоморфизмы круга (они не меняют расстояний).
Для шара ? = {|z |</?} по формуле A5) предыдущего пункта
36*
564 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
п
где \dzf = 2l dza\2. Из сравнения A4) и A5) можно еще раз
0=1
сделать вывод о невозможности биголоморфного отображения
шара на поликруг.
53. Поведение кернфункции на границе. В этом заключи-
заключительном пункте мы приведем результаты Л. Хёрмандера, от-
относящиеся к поведению кернфункции области голоморфности
на границе области. В их основе лежит утверждение о ло-
локальном характере зависимости от области граничного пове-
поведения ее кернфункции, которое выводится из теоремы суще-
существования Хёрмандера (п. 39).
Теорема 1. Пусть DcC"- ограниченная область голо-
голоморфности с границей 3D класса С2. Пусть еще точка l^dD
обладает окрестностью U такой, что в D' = D(\U существует
голоморфная функция g, которая имеет пик в точке ? в сле-
следующем смысле: 1) |g(z)|^l в D', a sup|g(z)| <1, где
D" = {z<=Z)': p(z, ?) > 6} и б > 0 достаточно мало; 2) lim| g (z)| = 1.
zeD'
Тогда кернфункции Ко и Kd' областей D и D' имеют в_ точке ?
одинаковое граничное поведение, т. е.
A)
D, (г)
z^D'
<* Возьмем функцию х<^С°° (U), равную единице в {р (z, S)}
нулю в окрестности 3U и такую, что 0^%=^1 всюду в U;
будем считать, что х определена всюду в С" и равна нулю
вне U. Для любой функции f^Ll(D') и любого натураль-
натурального р можно найти функцию срeL2(Z)) так, чтобы
p-<P B)
была голоморфной в D (мы считаем, что %fgp определена
всюду в D условием, что она равна нулю там, где % — 0).
В самом деле, условие голоморфности h в D равносильно
условию, что там
d<t = f8pdx, C)
а так как форма в правой части, очевидно, замкнута, a D —
область голоморфности, то по теореме 2 Хёрмандера п. 39
существует решение ф с оценкой
j\
\fgp\2dV, D)
D"
§ 17] ИНВАРИАНТНАЯ МЕТРИКА 5б5
где С — постоянная, зависящая только от выбора функции %
(мы учли, что д% — 0 в D \ D").
При любом заданном е>0 мы можем выбрать р столь
большим, чтобы в D" было
^12Р<2ТсТТ). E)
и тогда будем иметь
D'
J
D" D"
(мы учли D) и то, что 7=1 в D' \ D"). Так как h — fgpe L\ (?)'),
то в силу неравенства A7) из п. 51 отсюда следует, что для
любой z e D'
\h(z)~f (z)gp (z) p < Kw (z) e2 J | f fdV,
D'
и поэтому
\\g()\KD()j\f{v\
I D' J
Выбирая в качестве f экстремальную функцию, для которой
D'
(см. п. 51), получим, в частности, для соответствующей h
I h (z) I2> Kd> (z){\g (z) f - e}2 J | /12 dV. F)'
D'
С другой стороны, по неравенству треугольника, а также B),
4) и E) мы имеем
D' I
J
566 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. Vf
(мы учли, что % = 0 вне D'), откуда, пользуясь оценкой F)
и экстремальным свойством кернфункции, находим для
любой гей'
Так как кернфункция не возрастает при расширении об-
области, то Kd(z)^Kd' B), и утверждение теоремы следует
из того, что \g(z)\->l при z->Z, >
Доказанная теорема позволяет получать локальные оценки
кернфункции при помощи замены области элементарными
областями. Для наших целей в качестве элементарной области
удобно взять эллипсоид
vlJ0), G)
v=l J
где av>0, v = 0, ..., п. Биголоморфное отображение f: zv-+
¦^Тг оТг' преобразует Е в шар B = {\z\<R}; пользуясь
выражением A9-) п. 51 для кернфункции шара и законом ее
изменения при биголоморфных отображениях (см. E) п. 52),
получаем
а° ¦¦• а" т\
j. (8)
- 2 «v I
Придадим этому результату иную форму. Именно, рас-
рассмотрим вместо G) область
G = (zeC": lmzn> 2 аичг„гА, (9)
I м-, v=i J
где билинейная форма эрмитова и положительно определена;
через A = {ailv) мы обозначим матрицу этой формы и через
'Л —эту же матрицу с вычеркнутыми га-й строкой и га-м столб-
столбцом. Унитарным преобразованием переменных 'г (которое не
меняет кернфункции) мы можем привести матрицу 'А к диаго-
§ 17]
ИНВАРИАНТНАЯ МЕТРИКА
567
нальному виду, поэтому с самого начала можно считать, что
= о
где Kv>0, v= 1, ..., «- 1.
Если теперь сделать еще преобразование z„ + -~- zn -v
-^u (м-=1. •••. n—l), zn—>zn, с определителем 1 и поэтому
также не изменяющее кернфункцию, то в новых переменных
матрица А рассматриваемой билинейной формы будет иметь
диагональный вид, причем элемент в последней ее строке
Я„>0 (мы учитываем, что ам,„ = а„м,).
В новых переменных G записывается неравенством 1тг„>
v=l
zvl2> которое в силу просто проверяемого тождества
lmzn-Xn\zn\2 = -r. ln
п-\
можно переписать в виде
'¦+к
v=l
•. Мы
видим, что G представляет собой эллипсоид, и по формуле (8)
можем написать
п-\
\п+1
4Я„ LL
I ZV I2 - Хп
v=l
det
чга+1 -
Im гп -
\
Возвращаясь к старым переменным, получим окончательно
v 1-л п\ det(M)
1тг„-
ц, v=i
Перейдем к доказательству основной теоремы.
Теорема 2 (Хёрмандер). Пусть О = (геС: Ф(г)<0} —
ограниченная область голоморфности и в окрестности точки.
568 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
.?едО функция феС2 « строго плюрисубгармонична. Тогда
\im\z-trlKD(z) = $rK(Q, A1)
D
a (?) — произведение собственных значений сужения формы
Леей
-д-*- — A2)
ц, v=l
со,, = 0 к dD
"и
на аналитическую касательную плоскость V -г-5-
8 точке ?.
< Без ограничения общности считаем ? = 0 и что gradcp
является единичным вектором внешней нормали к 3D в окрестно-
окрестности этой точки. Ось Imzn направим по внутренней нормали,
чтобы было 1т2„ + cp(z) = O(| z |2) при z->0. Тогда по формуле
Тейлора в окрестности 0 область D запишется неравенством
\mza> У
It, v=l
42,
где K(z)= /,-r—^— 2,,2v He меняя ничего в теореме, можно
¦«м С7^м O^v fl
заменить еще zn на zn — г/С (г), т.е. предположить, что в последней
формуле К. (z) = 0. Мы обозначим -^—%:
= a^v, так что
2«nv^zv будет эрмитовой и положительно определенной.
Вблизи точки 0 область D описывается неравенством
я
Im zn > 2j auvznzv + о (| z |2).
Ц, V=l
Теперь мы фиксируем Я и рассмотрим область
GK = \z^Cn: lmzn> JJ а ^г-,+ Я|г [2] .
Если Я > — Яо, где Яо — наименьшее из собственных значений
матрицы А — (allv), \i,v—l, ..., п, то Gx представляет собой
эллипсоид, и по A0) ее кернфункция
где 6^=1 при ц = v и 0 при [x=7^v, 'Ак~{а^ + Яб^,), [i, v='
= I, ..., /г — 1. Фиксируем еще окрестность U точки 0 и обо-
S 1?1 ИНВАРИАНТНАЯ МЕТРИКА 569.
значим G[ = Gk(]U; по теореме 1 кернфункции Ках и KQ'
эквивалентны при z—>0. K
Так как D строго псевдовыпукла в точке 0, то 2 а vz г >
><r|z|2, где о>О-постоянная. Выбирая Я: 0<Я<а и^доста^
точно малую окрестность U, мы добьемся того, что G{ cz D,
и в силу монотонности кернфункции будем иметь KD{z)^K , (z).
Согласно сказанному выше область G'x можно заменить Gk, и
по A3) будем иметь
1шг„
Будем считать, что г->0 по лучу \хпга = \г\; тогда последнее
неравенство примет вид
Шп | г |"+1 KD (z) < ¦$: det ('A,). A4)
Теперь мы рассмотрим эллипсоид С_л, где 0<Л<А0; доста-
достаточно близкие к 0 точки D принадлежат ему, поэтому при
достаточно малой окрестности U точки 0 область D' = Df]Ucz
cz G_v Пользуясь опять монотонностью кернфункции и теоре-
теоремой 1 (в качестве функции g, фигурирующей в ее условиях,
можно взять егг"), мы получим вместо A4)
Um\z\n+'KD(z)>^rdet('A^), A5)
где опять предполагается, что z-»-0 по внутренней нормали
к 3D. Но Я в A4) и A5) можно брать сколь угодно малым;
поэтому, переходя в этих формулах к пределу при А—*0, мы
получим, что существует
det{'A). A6)
rKD(z) = ~n-det{A).
Здесь определитель равен произведению п — 1 собственных
значений формы, которая получается из A2) подстановкой
а>п = 0, ив силу нашего выбора координатных осей совпадает
с сужением A2) на касательную плоскость к dD в точке ? = 0.
Остается заметить, что рассматриваемый нами предел до-
достигается равномерно по ?, поэтому он существует при любом
способе стремления точки геОк граничной точке ? >
570 ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ [ГЛ. VI
ЗАДАЧИ
1. Пусть D — область в С" и K<SD. Тогда любое голоморфное отобра-
отображение f: D -> К имеет одну и только одну неподвижную точку.
2. Пусть б7 —открытое множество в С" и f: U -> Cm — голоморфное ото-
отображение. Если а е U — изолированная точка прообразов b — f (а), то т~^п,
причем т > п в том и только том случае, если существует голоморфная
в точке Ь функция g Ф 0 такая, что g°)'s=0 в окрестности а.
3. Пусть U — открытое множество в С и f: U -> Сш — голоморфное ото-
отображение. Если любая а е U является изолированной точкой множества
прообразов f (а) и множество f (U) открыто в Ст, то т — п. Обратно, если
т — пн любая точка а е U является изолированной среди прообразов / (а),
то множество / (U) открыто.
4. Доказать, что любой голоморфизм f области D на D*, гомеоморфный
в D' преобразует границу Шилова S области D в границу Шилова S* обла-
облает;! D".
5. Если cpi и ф2 — голоморфные отображения области D в себя и
ср = ф, о <р2 — автоморфизм D, то ф! н ф2 — тоже автоморфизмы.
6. Если последовательность голоморфизмов /(v): D -> Dv сходится на
компактных подмножествах области D, то предельное отображение / либо
тоже голоморфизм, либо вырождено в том смысле, что якобиан -—-з^О в D.
7. Если последовательность автоморфизмов (fv ограниченной области D
сходится на компактных подмножествах D к отображению ф и если множе-
множество (f{D)[]D непусто, то ф—автоморфизм D; отсюда следует, что если ф
вырождено, то (f(D)czdD.
8. Пусть D — ограниченная область в С и К— компакт в D. Тогда мно-
множество всех автоморфизмов ф области D таких, что ф (а) е К, где а — не-
некоторая фиксированная точка D, является компактом в топологии равно-
равномерной сходимости на компактных подмножествах D.
9. Пусть || || — произвольная норма в С" такая, что [|Яг|| = | X \ \\z\\ для
любого Я s С, и f— голоморфное отображение единичного (в этой норме)
шара в себя, причем f @) = 0. Доказать, что в этом шаре ||/ (z)||<!||z||.
10. Пусть / — голоморфное отображение единичного шара ВсС"в Ст
такое, что / @) = 0. Тогда для любого числа р > 1 имеет место следующее
обобщение неравенства Шварца:
11. Группа Г автоморфизмов ф области D cz С" называется дискретной,
если множество образов ф (г) фиксированной точки г е D при всевозмож-
всевозможных ф s Г не имеет в D предельных точек. Доказать, что для любой ди-
дискретной группы Г автоморфизмов D ряд 2 I ф'12> ГДе ф'— якобиан отобра-
феГ
жения ф, сходится равномерно на любом компакте из D.
12. Пусть Г —дискретная группа автоморфизмов области D cz С" и
D/T — множество классов эквивалентности по отношению: z'~z", если суще-
существует феГ такой, что Ф (г') = г". Если область D ограничена, а множе-
множество D/V компактно, то D — область голоморфности.
13. Пусть D — область в С2, состоящая из единичного бикруга {|z| < 1,
| w | < 1} и области ¦< (х + iy, w); 0 < х < 2, | у | < у , w — — < — V . До-
Доказать, что всякий автоморфизм D, непрерывный в замыкании бикруга,
является тождественным; это утверждение справедливо и для оболочки
ЗАДАЧИ 571
голоморфности области D. [Указание: воспользоваться задачей 4 и задачей
19 к гл. I.] *
14. Область D cz G называется жесткой, если у нее нет автоморфиз-
автоморфизмов, отличных от тождественного. Примером жесткой области D сг С2 яв-
является бикруг {|г|<1, |да|<1}, из которого вынут меньший бикруг
J г—L <—( w — -a <Т(- [Указание: воспользоваться задачей 17
к гл. V.] ,
15. Доказать, что группа автоморфизмов ооласти U а Ьг, которая полу-
получается из единичного бикруга выбрасыванием бикруга -! U—у < "г >
w _ J- < — |, состоит из двух элементов.
16 Для того чтобы трубчатый конус Т = К X R" (у), где К - конус в R" (х)
с вершиной х = 0, был голоморфно эквивалентен ограниченной области, не-
необходимо и достаточно, чтобы К не содержал прямых.
17 Для того чтобы трубчатая область голоморфности была голоморфно
эквивалентной ограниченной области, необходимо и достаточно, чтобы ее
основание не содержало прямых.
18 Отображение / области ОсСв группу Г преобразовании области
n, r-'m се5я называется голоморфным, если для каждой точки aeD'
голоморфны (по г) отображения (/ (г)) (a): D -> D'. Доказать, что всякое
голоморфное отображение ограниченной области D с С" в группу ортонор-
мальных преобразований С" в себя постоянно. [Указание: воспользоваться
тем, что в неравенстве (} \h\dvJ<V(D) J \h\>dV, где V (D) - объем D,
справедливом для всех AeL^D), равенство достигается только в случае
А==С1°МВезентини). Вычислить кернфункции следующих областей:
а) D, = {zeC4: х, - | г4 |2х2- *§ > 0, х2>0};
б) D2 = {г е С5: хЛ - ^ > °' Л2^з — х§ > 0, *з > °>-
(Ответы: 4
KD(z) = clx2[(xl-\z4\2)x2-x3\ ;
где cv — константы.)