А. А. Боровков
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством высшего
и среднего специального образования СССР
е качестве учебного пособия
для студентов математических
и физических специальностей вузов
1ш
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1 986

ББК 22.17
Б 83
УДК 519.2@75.8)
Боровков А. А. Теория вероятностей: Учеб. пособие для вузов.—
2-е изд., перераб. и доп.— М.: Наука. Гл. ред. физ.-мат. лит. 1986.— 432 с.
В основу положен курс лекций, читавшихся автором в течение ряда
лет на математическом факультете Новосибирского университета (шестой
семестр).
Первое издание вышло в 1976 г. Второе издание значительно перерабо-
переработано и дополнено. Книга охватывает широкий круг вопросов, начиная а
©снований теории вероятностей и кончая элементами теории случайных
процессов.
Для студентов и аспирантов университетов и вузов, а также для спе-
специалистов, желающих изучать теорию вероятностей самостоятельно.
Табл. 2. Ил. 19. Библиогр. 22 назв.
Рецензент:
доктор физико-математических наук профессор В% В. Петров
1702060000-162 ©Издательство .Наука».
0<rU02)-?6 Главная редакция
voovv*y-vu физико-математической
ф
литературы, 197G; с изменениям»
и дополнениями, 1986

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию , , • 7
Предисловие к первому изданию « 9
©ведение » ¦ • 11
Глава 1. Дискретное пространство элементарных событий , • 15
§ 1. Вероятностное пространство * *..,...• 45
§ 2. Классическая схема ....*,..*..« 18
§ 3. Схема Бернулли ..-,..• 21
§ 4. Вероятность объединения событий. Примеры « . . « 24
Глава 2. Произвольное пространство элементарных событии , • % 27
§ 1. Аксиомы теории вероятностей. Вероятностное пространство 27
§ 2. Свойства вероятности ' . . , 34
§ 3. Условная вероятность. Независимость событий и испы-
испытаний 35
§ 4. Формула полной вероятности и формула Байеса . 38
Глава 3. Случайные величины и функции распределения « 43
§ 1. Определения и примеры 43
§ 2. Свойства функций распределения и примеры .... 43
§ 3. Многомерные случайные величины , 55
§ 4. Независимость случайных/ величин и классов событий 59
§ 5. О бесконечных последовательностях случайных величин 67
§ 6. Интегралы , '. 68
Глава 4. Числовые характеристики случайных величин t 75
§ 1. Математическое ожидание 76
§ 2. Условные фупкции распределения и условные математи-
математические ожидания . . ¦ 80
§ 3. Математические ожидания функций независимых случай-
случайных величин • 85
§ 4. Математическое ожидание случайных величин, пе завися-
зависящих от будущего . . , 86
§ 5. Дисперсия 91
§ 6. Коэффициент корреляции и другие числовые характери-
характеристики 93
§ 7. Неравенства 95
§ 8. Обобщение понятия условного математического ожидания 99
§ 9. Условные распределения % 107
1*

4 ОГЛАВЛЕНИЕ
Глава 5. Последовательность независимых испытаний е двум л исхо-
исходами ,114
§ 1. Законы больших чисел 114
§ 2. Локальная предельная теорема , 115
§ 3. Теорема Муавря—Лапласа и ее уточнения . *. . , 4 120
\ 4. Теорема Пуассона и ее уточнения ....... 123
§ 5. Неравенства для вероятностей больших уклонений в схе-
схеме Берпулли 131
Глава в. О сходимости случайных величин и распределений . . . 133
§ 1. Сходимость случайных величин 133
§ 2. Сходимость распределений 140'
§ 3. Условия слабой сходимости ,.»...... 144
Глава 7. Характеристические функции 14.9"
§ 1. Определение и свойства характеристических функции 141)
§ 2. Формула обращения 155
§ 3, Теорема непрерывности (сходимости) 157
§ 4. Другой подход к доказательству теорем сходимости к из-
известному распределению 15ft
§ 5. Применение характеристических функций в теореме Пуас-
Пуассона 1GI
§ 6. Характеристические функции многомерных распределений.
Многомерное нормальное распределение 164
§ 7. Другие применения х. ф. Свойства гамма-распределения 107
§ 8. Производящие функции. Применение к изучению ветвяще-
ветвящегося процесса. Задача о вырождении 17$
Глава 8. Последовательности независимых случайных величии. Пре-
Предельные теоремы - . , 178
§ 1. Закон больших чисел 178'
§ 2. Центральная предельная теорема для одинаково распреде-
распределенных случайных величин .- 179
§ 3. Закон больших чисел для произвольных независимых слу-
случайных величии . 180
§ 4. Центральная предельная теорема для сумм произвольных
независимых случайных величин j 185
§ 5. Другой подход к доказательству предельных теорем. Оцен-
Оценки погрешностей 193
§ 6. Локальная предельная теорема 197
§ 7. Закон больших чисел а центральная предельная теорема
в многомерном случае 201
§ 8. Вероятности больших уклонений 202'
§ 9. Сходимость к другим устойчивым законам 210
V-лава 9. Элементы теории восстановления * 218
§ 1. Процессы восстановления 218
§ 2. Теорема восстановления в решетчатом случае . , . . 219
§ 3. Эксцесс я дефект случайного блуждания. Предельное рас-
распределение в решетчатом случае 223
§ 4. Теорема восстановления и предельное распределение экс-
эксцесса и дефекта в нерешетчатом случае 225
§ 5. Закон больших чисел и центральная предельная теорема
для процесса восстановления • в 230

ОГЛАВЛЕНИЕ 5
Глава 10. Последовательности независимых случайных величин. Свой-
Свойства траектории (О, 8Ъ S2, ...) в целом- 232
§ 1. Законы нуля и единицы. Верхние и нижние функции 232
§ 2. Сходимость рядов независимых случайных величии . , . 238
§ 3. Усиленный закон больших чисел 239
§ 4. Усиленный закон больших чисел для произвольных неза-
независимых слагаемых 244
Глава 11. Факторизациошше тождества 246
§ 1. Факторизациоиные тождества и их первые следствия 240
§ 2. Факторизационные тождества. Свойства траектории
(О, Su S2, ....)• • • 252
§ 3. Распределение S = max @, Q = max S, 256
§ 4. Системы обслуживания " 258
§ 5. Факторизационные тождества для распределений, связан-
связанных с показательной функцией 259
§ 6. Симметричные непрерывно распределенные случайные ве-
величины , 262
§ 7. Тождество Поллачека — Спитцера 263
§ 8. Явные формулы для дискретных блужданий, непрерывных
сверху ....... , ....... 265
Глава 12. Последовательности зависимых испытаний. Дискретные це-
цепи Маркова 270
§ 1. Определения и примеры. Классификация состояний . . . 270
§ 2. Необходимые и достаточные условия возвратности состоя-
состояний. Теорема об однотипности состояний неразложимой
цепи, структура цепи в периодическом случае .... 275
§ 3. Теоремы о случайных блужданиях по решетке .... 279
§ 4. Эргодические теоремы 284
§ 5. Поведение переходных вероятностей для разложимых цепей 292
Глава 13. Информация и энтропия 293
§ 1. Определения, свойства информации и энтропии .... 293
§ 2. Энтропия конечной цепи Маркова. Теорема об асимптоти-
асимптотическом поведении информации длинного сообщения, ее
приложения 298
Глава 14. Мартингалы ¦ 303
§ 1. Определения, простейшие свойства, примеры ...» 303
§ 2. О сохранении свойства быть мартингалом при замене вре-
времени на случайное. Тождество Вальда ...... 307
§ 3. Неравенства ..«,... 314
§ 4. Теоремы сходимости 316
Глава 15. Случайные процессы с непрерывным временем .... 321
§ 1. Общие определения 321
§ 2. Условия регулярности процессов 327

6 ОГЛАВЛЕНИЕ
Глава 10. Процессы с независимыми приращениями 333
§ 1. Общие свойства 33."*
§ 2. Вииеровские процессы, свойства траекторий ..... 335
§ 3. Законы повторного логарифма 337
§ 4. Пуассоновекие процессы 342
§ 5. Описание распределений всего класса процессов с незави-
независимыми приращениями 355
Глава 17. Функциональные , предельные теоремы 350
§ I. Сходимость к вииеровскому процессу (принцип инвариант-
инвариантности) 350
§ 2. Закон повторного логарифма 358
§ 3. Сходимость к пуассоновскому процессу 3 31
Глава 18. Марковские процессы . ч , 36G
§ 1. Определения и общие свойства ЗСГ»
§ 2. Марковские процессы со счетным множеством состояний.
Примеры ...... Ж)
§ 3. Ветвящиеся процессы ........... 37»5
§ 4. Диффузионные процессы . 371)
Глава 19. Процессы с конечными моментами второго порядка. Гаус-
совские процессы , 380
§ 1. Процессы с конечными моментами второго порядка . * . 38'>
§ 2. Гауссово кие процессы 38Я
§ 3. Задача о прогнозе 391
Приложение 1. Теорема о продолжении вероятностной меры 393
При л о ж е и и е 2, Теорема Колмогорова о согласованных распре-
распределениях . 398
Приложение 3. Интегрирование 400
§ 1. Пространство с мерой 400
§ 2. Интеграл но вероятностной мере 402
§ 3. Дальнейшие свойства интегралов . , 405
§ 4. Интеграл по произвольной мере . 410
§ 5. Теорема Лебега о разложении и теорема Радона — Иико-
дима *..... 414
Приложение 4. Доказательство теоремы Хеллн 41!»
Приложение 5. Доказательство теоремы Берри — Эссена. . . 420
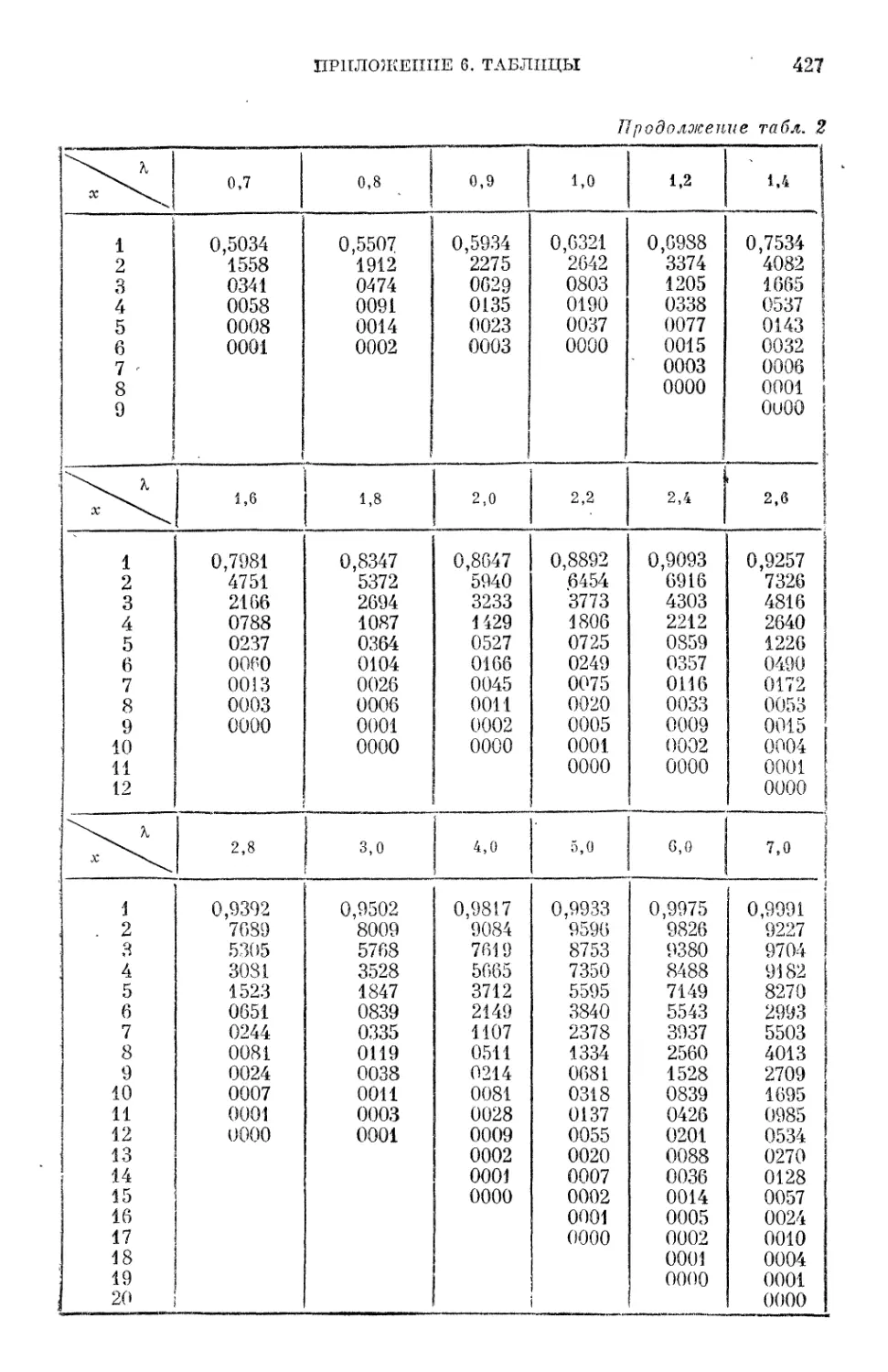
Н р и л о ж е и и е 6. Таблицы 425
Список литературы 429
Предметный указатель , 430

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Первое издание книги вышло в 1976 г., разошлось довольно
быстро, и, судя по отзывам, получило положительную оценку
читателя. Тем не менее, спустя некоторое время у меня как у
автора стали появляться неудовлетворенность некоторыми разде-
разделами книги и соображения, связанные с возможностью улучше-
улучшения ее структуры и пополнения ее в разделах, касающихся слу-
случайных процессов. В результате появился план книги, которая
в первых своих главах (до случайных процессов) мало отличает-
отличается со структурной точки зрения от первого издания (см. преди-
предисловие к первому изданию), но в последующих главах содержит
значительно более полное, чем раньше, изложение основ теории
случайных процессов (сбалансированное, как мне кажется,
с уровнем изложения первых глав). Это делает книгу более пол-
полной и пригодной не только для усвоения основного курса, но it
для изучения предмета в объеме кратких «спецкурсов», скажем,
по теории случайных процессов. Значительные изменения внесе-
внесены и в первую половину книги. Параграф «О сходимости случай-
случайных величии и распределений» из гл. 6 первого издания значи-
значительно расширен и преобразован в отдельную главу. Существен-
Существенной переработке подверглись также главы 3, 4, 6—10. Добавле-
Добавлена глава, посвященная мартингалам.
Но самые серьезные изменения, как уже отмечалось, про-
произошли с разделом, посвященным теории случайных процессов
с непрерывным временем. Здесь излагаются теперь вопросы, свя-
связанные с основаниями теории случайных процессов, изучаются
условия регулярности процессов. Несколько глав посвящены
рассмотрению основных типов случайных процессов, которые до-
допускают конструктивное задание: процессов с независим ылш
приращениями, марковских и гауссовских процессов. Несколько
в стороне от этого пути изложения стоит глава о функциональ-
функциональных предельных теоремах, где излагаются основные результаты
о сходимости процессов, порожденных последовательными сум-
суммами случайных величин, к винеровскому и пуассоновскому про-
процессам; там же устанавливается в качестве следствия закон по-
повторного логарифма.
В связи с тем, что объем книги увеличился, по-видимому, це-
целесообразно привести перечень разделов, которые могут составить
(вариантов тут может быть много) содержание семестрового или

8 ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
лолуторасеместрового курса теории вероятностей. Вот один из
вариантов: гл. 1, 2; § 1 — 4 гл. 3; § 1 — 6 гл. 4 (частично); § 2,
4, гл. 5 (частично); § 1—3 гл. 6 (частично); § 1, 2, 4—6 гл. 7;
§ 1, 2, 4 гл. 8 (§ 4 частично); §1,3 гл. 10; основные результа-
результаты из гл. 12.
Более полное изложение основ теории вероятностей можно
найти в [13], [18], [21]; основ теории случайных процессов —
и [5], [13].
В заключение я хотел бы поблагодарить В. В. Юринского,
А. И. Саханенко, К/ А. Боровкова и других моих коллег, сооб-
сообщивших мпе свои замечания по рукописи. Я глубоко признате-
признателен рецензенту книги В. В. Петрову за его рекомендации по
улучшению изложения. Я благодарен всем, кто так или иначе
помогал мне в работе над книгой.
А. А. Боровков
В н и манию ч и т а т е л я. Значок <4 в тексте означает
окончание доказательства. Нумерация формул, лемм, теорем, па-
параграфов в каждой главе самостоятельная. При ссылках на ма-
материал из других глав используется двойная нумерация. Напри-
Например, ссылка (9.11) означает, что имеется в виду формула A1)
гл. 9; теорема 3.4 означает теорему 4 гл. 3; § 6.2 означает § 2
гл. 6. Текст, напечатанный мелким шрифтом, и параграфы, от-
отмеченные звездочкой, при первом знакомстве с курсом можно
опустить.

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Эта книга написана на основе «Курса теории вероятностей»,
вышедшего в свет в 1972 году. Переработке подверглись почти
ззсе главы «Курса», некоторые из них написаны заново. Автором
руководило при этом стремление к более законченному и связно-
связному изложению, к более простым и наглядным доказательствам.
Появилось несколько новых разделов, предназначенных для бо-
более глубокого изучения предмета.
Предполагается, что читатели в дополнение к традиционно-
традиционному курсу математического анализа знакомы также с элементами
теории меры и, в частности, с понятием интеграла по мере на
абстрактном пространстве и с его простейшими свойствами. Од-
Однако отсутствие этих дополнительных знаний не помешает
успешному освоению книги, если только читатель будет готов
некоторые утверждения принять не в их максимально общей
форме.
Есть и другая возможность. Читатель полностью избежит за-
затруднений, если он при чтении соответствующих разделов озна-
ознакомится с краткими Приложениями, которые помещены в конце
курса и в которых получены все необходимые результаты,
Первые 9 глав книги представляют собой связное целое, и их
лучше читать подряд. Главы 10—13 продолжают изучение тео-
теоретико-вероятностных проблем в трех разных направлениях
(факторизационные тождества — гл. 10, цепи Маркова и теория
информации — гл. 11, 12 и простейшие вероятностные процес-
процессы — гл. 13), с каждым из которых можно знакомиться незави-
независимо от других. В разное время студентам в лекциях предлага-
предлагались все эти три варианта продолжения, и у автора нет основа-
оснований считать, что с методической или познавательной точки зре-
зрения можно отдать предпочтение какому-нибудь одному из этих
вариантов.
Отметим, что доказательства усиленного закона больших чи-
чисел и эргодической теоремы для цепей Маркова базируются в
этой чниге на главе «Элементы теории восстановления», которая
в «Курсе теории вероятностей» отсутствовала. Новыми являются
также разделы о локальной предельной теореме, о больших укло^
нениях и целый ряд других.
По ходу изложения в курсе разобрано значительное количе-
количество задач и примеров. Это не устраняет, однако, необходимости

¦JO ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
в самостоятельных упражнениях. Из имеющихся сейчас сборни-
сборников задач наиболее близким к курсу является, по-видимому*
сборник Л. Д. Мешалкшха, который и рекомендуется читателю*).
Пользуюсь случаем, чтобы поблагодарить здесь 10. В. Прохо-
Прохорова, В. В. Петрова и Б. Л. Рогозина за многие полезные сове-
советы, которые помогли улучшить первый вариант книги. Я глубока
признателен Л. II. Колмогорову, чьи замечания и ценные реко-
рекомендации, особенно методологического характера, способствовали
усовершенствованию второго варианта книги. В связи со вторым
.вариантом я вновь обязан В. В. Петрову, сообщившему мне своя
замечания к повой рукописи, и в большой мере — II. Фрапкенут
с которым я имел много полезных обсуждении при-переводе кни-
книги на немецкий язык. Мне хотелось бы поблагодарить здесь всех,
кто тем пли иным образом содействовал улучшению книги.
1975 г. - ~ А, А. Боровков
*) В дополнение к этому, сборнику можно указать теперь вышедший в
1980 г. «Сборник задач по теории вероятностей» В. А. Севастьянова;
П. П. Чистякова и Л. М. Зубкова (М.: Наука) и книгу «Задачи по теории
л(!роятпострй» Л. В. Прохорова, В. Г. Ушакова, Н. Г. Ушакова, вышедшую
в 1986 г. (М.: Наука).

ВВЕДЕНИЕ
1. Возникновение теории вероятностей относят обычно к
XVII веку и связывают с комбинаторными задачами азартных
игр. Азартные игры трудно считать серьезным занятием. Но
именно они привели к задачам, которые не укладывались в рам-
рамки существовавших тогда математических моделей и стимулиро-
стимулировали тем самым введение новых понятий, подходов и идей. Эти
новые элементы можно встретить уже у Ферма, Паскаля, Гюй-
Гюйгенса и, в более развитой форме чуть позже, у Якоба Берпулли,
Лапласа, Гаусса и др. Имена перечисленных ученых, безусловно,
украшают родословную теории вероятностей, в какой-то мере
связанную, как мы видели, с пороками общества. Впрочем, как
выяснилось, иногда именно это обстоятельство может сообщать
ей в глазах читателей некоторую дополнительную привле-
привлекательность.
Первым руководством по теории вероятностей был трактат
Гюйгенса «О расчетах в азартной игре», вышедший в 1657 году.
Предмет зтого трактата тот же, что и в работах Ферма и Паска-
Паскаля: игральные кости и карточные игры (задачи в рамках § 2
гл. 1). Словно предвидя дальнейшее развитие событий, Гюйгенс
писал: «Я полагаю, что при внимательном изучении предмета
читатель заметит, что имеет дело не только с игрой, но что здесь
закладываются основы очень интересной и глубокой теории».
Трактат Гюйгенса, известный также тем, что в нем впервые вво-
вводится понятие математического ожидания, был включен позднее
Якобом Бернуллп в знаменитую книгу «Искусства предположе-
предположений», опубликованную уже после его Смерти в 1713 году*)»
С этой книгой связано понятие схемы Берпулли (см. § 3 гл. 1)
м доказательство первой предельной теоремы теории вероятно-
вероятностей —- закона больших чисел. Доказательство Бернуллн хотя и
громоздко (ср. с § 1 гл. 5), но математически безупречно,
В конце прошлого и начале этого века стали возникать более
серьезные проблемы, порожденные нуждами естествознания,
и приведите к развитию большого, в значительной мере само-
самостоятельного раздела математики, именуемого сегодня теорией
вероятностей. Эта область знаний вплоть до настоящего времени
*) В переводе на русский книга была впервые издана в 1913 году.
И настоящее время вышло ее новое издание на русском языке (Я. Вернул-
ли. О законе больших чисел.—М.: Паука, 1986).

12 ВВЕДЕНИЕ
находится в состоянии интенсивного развития. Своей строй-
стройностью, современной формой и многими своими достижениями
теория вероятностей во многом обязана трудам наших замеча-
замечательных соотечественников П. Л. Чебышева, А. А. Маркова,
А. И. Колмогорова и др.
То обстоятельство, что увеличение наших знаний о природе
предъявляет все полые требования к теории вероятностей, на
первый взгляд представляется парадоксом. Ведь основной объект
теории вероятностей, как читатель, по-видимому, уже знает,
есть случайность или неопределенность, как правило, связанная
с незнанием. Именно так обстоит дело в классическом примере
с подбрасыванием монеты, где трудно учесть все факторы, влия-
влияющие на положение монеты после падения.
Однако отмеченный парадокс является лишь видимым. На са-
самом дело точных, детерминированных количественных законов
в природе почти по существует. Скажем, классический пример
таких законов — закон о зависимости давления газа от его тем-
температуры — есть на самом деле результат вероятностного харак-
характера о числе соударений частиц о стенки сосуда и их скоростях.
Просто в области обычных температур и давлений случайные
отклонения, которые тут имеют место, с большой вероятностью
очень малы и не регистрируются нашими приборами. Иначе об-
обстоит дело при изучении более редких потоков частиц, скажем,
космического излучения, хотя качественной разницы между эти-
этими двумя примерами нет.
Можно пойти и в несколько ином направлении и указать на
принцип неопределенности, в силу которого для любой пары фи-
физических характеристик, связанных этим принципом, фиксация
одной из них делает невозможным точное определение другой.
Тут уже случайность появляется не как следствие недостаточ-
недостаточности наших знаний, а как принципиальное явление и отраже-
отражение природы вещей. Например, время жизни радиоактивного
ядра случайно по существу, и эта случайность не может быть
устранена увеличением наших познаний.
Таким образом, неопределенность стояла в начале процесса
познания, она будет стоять и на всем пути его. Эти замечания
носят, конечно, общий характер. Но вопрос о том, когда следует
применять методы теории вероятностей и когда пет, по-видимо-
по-видимому, всегда будет определяться соотношением между степенью
ючиости, с которой мы хотим изучать данное явление, и сведе-
сведениями о его природе, которыми мы располагаем.
2. Почти во всех областях человеческой деятельности сущест-
существуют ситуации, когда те или иные эксперименты или наблюде-
наблюдения могут быть повторены большое число раз в одинаковых усло-
условиях. Теорию вероятностей интересуют те эксперименты, резуль-
результат которых, выраженный каким-либо образом, может меняться
от опыта к опыту. События, относящиеся к результату эксиери-

ВВЕДЕНИЕ
мента, которые при этом.могут происходить или не происходить,
называют обычно случайными событиями.
Мы можем, например, подбрасывать монету. Эксперимент
имеет всего два исхода: монета падает либо гербом вверх, либо
.решеткой. При этом до получения результата эксперимента нель-
нельзя сказать, какой именно исход осуществится. Как уже отмеча-
отмечалось, это происходит оттого, что мы практически не в состоянии
учесть все факторы, влияющие на положение монеты в момент
ее падения. Примерно то же самое будет происходить, если вы
при каждой лотерее будете покупать один билет и будете пы-
пытаться предугадать, выиграет он или нет. Или, наблюдая за ра-
работой достаточно сложного механизма, будете пытаться заранее
определить, выйдет он из строя до назначенного срока или после.
В таких ситуациях при рассмотрении результатов отдельных
экспериментов бывает очень трудно обнаружить какие-либо зако-
закономерности. И, стало быть, здесь мало оснований строить какую-
либо теорию.
Однако, если обратить внимание на последовательность боль-
большого числа такого рода одинаковых экспериментов, то обнару-
обнаружится интересное явление. Если индивидуальные результаты
опытов ведут себя очень «неправильно», то средние результаты
обнаруживают устойчивость. Будем, например, повторять наш
"г
л
J/z
о
\
1
V
ч
Z
V
3
Л
i
4
1
5
i
Б
1
7
*^%
8
9
10
1/
—¦—
i
1Z
1 ^
13 п
Рис. 1
эксперимент с подбрасыванием монеты и обозначим через пг
число выпадений герба после первых п испытаний Построим
следующий график: на оси абсцисс отложим число проведенных
экспериментов, а на оси ординат отношение nv/n (рис. 1; график
построен для последовательности исходов ерргрргзгрзгр, где г —
герб, р — решетка).
Мы заметим, что ломаная, соединяющая точки (/г, Пг/п)
с ростом п очень быстро прижимается к прямой пГ/п = 1/2. Что-
Чтобы проверить это обстоятельство, Бюффон *) в XVIII веке
*) Эти данные заимствованы из

14 ВВЕДЕНИЕ
провел 4040 подбрасываний монеты. Из них герб выпал 2048 р,
так что частота выпадения герба пт/п оказалась равной 0,508»
Пирсон провел 24000 бросаний монеты; герб выпал 12012 раз,
пт/п = 0,5005.
Оказывается, это явление имеет общий характер: частота осу-
осуществления какого-либо исхода в последовательности повторя-
повторяемых в одинаковых условиях экспериментов приближается п не-
некоторому числу р е [0, 1] при росте числа экспериментов. Это
объективный закон природы, который лежит в основе теории ве-
вероятностей.
Естественно было бы принять за вероятность некоторого ис-
исхода в эксперименте как раз то число /?, к которому приближает-
приближается частота появления этого исхода. Но такое определение веро-
вероятности (его связывают обычно с именем Мизе'са) оказывается
неудобным. Прежде всего, последовательность частот {nv/n} по-
появления некоторого исхода при проведении одной серии экспе-
экспериментов будет, как правило, отличаться от последовательности
частот появления того же исхода при другой серии эксперимен-
экспериментов. Кроме того, на самом деле мы будем иметь не бесконечную
последовательность частот, а только конечное число ее элемен-
элементов. Получить всю последовательность невозможно.
По-видимому, вероятность надо определять иначе, но так„
чтобы имело место отмеченное желательное свойство частоты:
в каком-то смысле отношение пт1п должно приближаться при
увеличении п к вероятности рассматриваемого события. Отсюда
можно извлечь, в частности, что вероятностями могут быть толь-
только числа р ^ [0, 1], при этом вероятность достоверного событияг
следует считать равной 1.
Мы определим вероятность сначала в несколько упрощенной
ситуации — в так называемом дискретном случае,

Г лав а 1
ДИСКРЕТНОЕ ПРОСТРАНСТВО
ЭЛЕМЕНТАРНЫХ СОБЫТИЙ
§ 1, Вероятностное пространство
Для математического описания экспериментов со случайным
исходами нам потребуется прежде всего понятие пространсп
•элементарных событий (или исходов), соответствующего рассма
риваемому эксперименту. Таким пространством будем иазыва*
любое множество Й взаимоисключающих исходов эксперимен'
такое, что каждый интересующим нас результат эксперимен*
может быть однозначно описан с помощью элементов этого мн
жества.
В самых простых экспериментах мы обычно имеем дело с к
печными пространствами элементарных событий; В рассмотре
пом выше примере с подбрасыванием монеты Q состоит из дв;
элементов — герба и решетки. В опыте с подбрасыванием шест
гранной игральной кости Q также конечно и состоит из 6 эл
ментов. Но даже с подбрасыванием монеты (или игральн
кости) можно связать такие эксперименты, в которых будет i
"возможно обойтись конечными пространствами элементарно
исходов. Рассмотрим, например, такой эксперимент: монета б\
сается до тех пор, пока впервые не выпадает герб, после этс
эксперимент прекращают. Если р будет означать выпадеи
решетки, а г — выпадение герба, то «элементарный исход» этс
эксперимента можно представить в виде последовательное
(рр...рг). Таких последовательностей бесконечно много и i
они различны, так что для однозначного описания всех исход
эксперимента нельзя обойтись никаким конечным пространстве
Рассмотрим конечные или счетные пространства элемент*
пых событий Q. Это так называемые дискретные пространен
Элементы пространства Q мы будем обозначать буквой а> и i
бывать их элементарными событиями (или элементарными i
•ходами).
Само понятие пространства элементарных событий матемаг
чески является неопределяемым — оно исходно, так же как i
яятие точки в геометрии. Конкретная природа Q нас, как п]
иило, интересовать не будет.
Событием мы будем называть любое подмножество А е
элементов из Q (событие А произошло, если произошло как
либо из элементарных событий 0)^4).
Суммой двух событий А и В называется событие АЛ-В(А U i
состоящее из элементарных событий, принадлежащих хотя

16 ГЛ. 1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
одному из событий А или В. Произведением АВ(А П В) называ-
называется событие, состоящее из элементарных событий, принадлежа-
принадлежащих одновременно А и В. Разность событий А и В соответствует
множеству А — В, состоящему из элементов Л, не принадлежа-
принадлежащих В. Q называется достоверным событием. Пустое множест-
множество 0 называется невозмооюным событием. А = Q — А называется
дополнительным событием к А. События А и В несовместны,
если АВ = 0.
Пусть, например, эксперимент состоит в двукратном' подбра-
подбрасывании игральной кости. В качестве пространства элементар-
элементарных событий здесь можно рассмотреть множество, состоящее из
3(> элементов (?, у), где i и j пробегают значения от 1 до 8 и
означают количество выпавших очков соответственно при первом
и втором бросании. События А = U + j < 3} и ? = {/ = 6} несов-
несовместны. Произведением событии А и С = {/ четно) является со-
событие A, 2). Отметим, что если бы нас интересовали события,,
относящиеся лишь к первому бросанию, то мы могли бы рас-
рассматривать и более бедное пространство элементарных событий,
состоящее лишь из 6 элементов i = 1, 2, . . ., 6.
Говорят, что заданы вероятности элементарных событий, если
ла Q задана неотрицательная числовая функция Р такая, что
2 Р (со) = 1 (говорят также, что функция Р задает на Q рас-
нределение вероятностей).
Вероятностью события А называется число
Это определение корректно, так как ряд в правой части абсолют-
абсолютно сходится.
Отметим здесь, что конкретные числовые значения функции Р
нас также интересовать не будут — это есть лишь вопрос прак-
практической ценности той или иноп модели. Ясно, например, что в
случае симметричной игральной кости для исходов 1, 2, .. ., E
надо положить РA) = РB) = . .. = РF) ¦= V»-,; для симмет-
симметричной же монеты надо выбрать значения Р (г) = Р(р) = 1/2г
а не какие-нибудь другие. В эксперименте с подбрасыванием мо-
монеты до первого появления герба следует положить Р(г} = 1/2>
ос
р (рг) = 1/Д р (ррг) = Va3f * • * Поскольку 2 2"""= 1, то фуик-
1
ция Р, заданная таким образом на исходах вида (р...рг), будет
определять распределение вероятностей на Q. Чтобы подсчитать,
например, вероятность того, что эксперимент закончится на чет-
четном шаге (т. е. вероятность события, составленного из исхо-
исходов (рг), (рррг),.'-) надо рассмотреть сумму соответствующих
вероятностей, равную

§ 1. ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО 17
В упоминавшихся во введении экспериментах, где происходп-
ло угадывание, когда выйдет из строя механизм — до назначен-
назначенного срока (событие А) или после,— основанием для количествен-
количественных оценок вероятности Р (А) обычно могут служить только
результаты самих экспериментов. Методы оценок неизвестных
вероятностей но результатам наблюдении исследуются математи-
математической статистикой, содержание которой мы поясним несколько
иозже па примере одной из задач этой главы.
Отметим далее, что далеко не для всех экспериментов можно
построить модели с дискретным пространством элементарных со-
событий. Допустим, например-, что измеряется энергия частиц, воз-
возможные значения которой заполняют отрезок [О, F], V > 0. Ведь
множество точек этого отрезка (т. е. множество элементарных
событий) континуально. Или, если, например, результатом экс-
эксперимента является электрокардиограмма, снятая с больного.
Здесь результатом эксперимента является элемент некоторого
функционального пространства. В этих случаях требуются более
общие схемы.
Из приведенных выше определений, пользуясь абсолютной
сходимостью рядов 2 Р(й), нетрудно получить следующие
свойства вероятности:
1) Р@) = О, P(Q)=1.
2) Р (А + В) = S Р И = 2 Р (<») + 2 Р (со) -
сое л и в we л сое в
- 2 Р(со) = Р(Л) + Р(В) — Р(АВ).
3) Р(Л) = 1~Р(/1).
Отсюда следует, в частности, что для непересекающихся (не-
(несовместных) событий А и В
Р (А 4- В) =* Р (А) + Р (В).
Это свойство аддитивности вероятности сохранится и для со-
совокупности из произвольного числа непересекающихся событий
Аи Л2, ...: если AtAj = 0 при i Ф у\ то
и лл)« 2
Это следует из равенства
и того, что Р I U Ak)->0 при п ~> <».
^ А. А. Боровков

18 ГЛ. 1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
Для произвольных А и В Р(А + ?)< Р (А) + Р (В). Это
неравенство справедливо, очевидно, и для суммы произвольного
числа событий;
Р U
Рассмотрим теперь несколько важных частных случаев.
§ 2. Классическая схема
Пусть Q состоит из п элементов и все исходы равновероятны,
т. е. Р(о>) = 1/л для любого ш е Q. В этом случае вероятность
любого события А определяется формулой
Р (А) = {число элементов А)/пт
Это так называемое классическое определение вероятности (ис-
(используется также термин равномерное дискретное распреде-
распределение).
Пусть задано множество {ah аг, •.., ап}> которое мы будем на-
называть генеральной совокупностью. Выборкой объема к из гене-
генеральной совокупности называется упорядоченная последователь-
последовательность [ctj^aj^ . ..,Я;л).Эту последовательность можно образовы-
образовывать следующим образом: первый элемент щг выберем из всей
генеральной совокупности. Следующий элемент щг выберем из
генеральной совокупности без элемента я^; элемент а$2 выбираем
из генеральной совокупности без элементов щ1 и а)г и т. д. По-
Полученные таким образом выборки называются выборками без воз-
возвращения. Ясно, что в этом случае должно быть k ^ п. Число
таких выборок объема к совпадает с числом размещений
из п по к:
Действительно, в соответствии с процессом выбора на первом
месте может стоять лео6ой из п элементов генеральной совокуп-
совокупности, на втором — любой из (п — 1) элементов и т. д. Более
формальное доказательство можно провести индукцией по
числу к.
Припишем каждой выборке без возвращения вероятность
l/(n)h. Такая выборка будет называться случайной. Это есть,
очевидно, классическая схема.
Подсчитаем вероятность того, что aj{ = #ь uj2 — a2. Так как
остальные к — 2 места могут быть заняты любым из оставшихся
п — 2 элементов генеральной совокупности, то число выборок без
возвращения с элементами at и аг на первых местах равно

§ 2. КЛАССИЧЕСКАЯ СХЕМА 19
(п — 2)ft-2. Стало быть, вероятность указанного события равна
4 {п)к П(п- 1) *
Выборку без возвращения наглядно можно представить как по-
последовательный выбор из совокупности п перенумерованных ша-
шаров, находящихся в урне. Вытянутые шары в урну не воз-
возвращаются.
Но выборку можно образовывать и другим способом. Из урны
вынимается шар и запоминается. Затем он возвращается в урну
и снова производится выбор шара; вынутый шар опять запоми-
запоминается и возвращается в урну и т. д. Полученная таким спосо-
способом выборка называется выборкой с возвращением. При каждом
выборе может быть выбран любой из п шаров. Таких выборов
делается А, поэтому всего выборок с возвращением будет п!\ Если
приписать каждой выборке вероятность 1/пк, то опять будет
иметь место классическая схема.
Подсчитаем, например, вероятность того, что в выборке с воз-
возвращением объема к < п все элементы будут разные. Выборок
с неповторяющимися элементами будет столько же, сколько вы-
выборок без возвращения, т. е. (n)h. Значит, искомая вероятность
равна (ri)Jnk.
Вернемся теперь к выборке без возвращения из генеральной
совокупности {«!, а2, .. ., av). Пас будет интересовать число вы-
выборок объема к ^ /г, отличающихся только составом. Число вы-
выборок без возвращения объема А, имеющих одинаковый состав и
различающихся только порядком элементов, будет А!. Поэтому
число выборок, различающихся составом, будет равно
__ (п
Это число сочетаний из п по к при 0 ^ к ^ п *). Если исход-
Бая выборка случайна, то получим опять классическую вероят-
вероятностную схему, так .как вероятность каждой новой выборки равна
JiL l
Пусть в урне п шаров, из них пх черных и п — пх белых. Про-
Производится выборка без возвращения объема А. Какова вероят-
вероятность того, что в выборке будет ровно АА черных шаров? Всего
(п\
рыборок, различающихся составом, как было показано, I , I. Чер-
*) В дальнейшем для значений к < 0 и к > п положим

20 ГЛ. 1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
(Л
пых hi шаров из всех щ черных шаров можно выбрать , I сяо-
собами. Остальные к — к{ белых шара из всех п — nL белых ша-
in — пЛ
ров можно выбрать I , , I способами. При этом, очевидно, лю-
бой набор черных шаров может сочетаться с любым набором бе-
белых. Поэтому всех выборок объема к, различающихся составом
/пЛ in — пЛ
и содержащих ровно кх черных шаров, будет I , I 7 z . Зна-
чит, искомая вероятность равна
Набор чисел РП][)П @, к), РЯ1,ПA, к), . .., Рпьп(к,к) обра-
образует так называемое гипергеометрическое распределение. Из по-
полученной формулы следует, в частности, что при любом
6<nL<n
у
Пример. В последнее время получила распространение раз-
разновидность лотереи, носящая название «спортлото». Участник
лотереи из 49 наименований видов спорта (обозначенных просто
цифрами) называет шесть. Выигрыш определяется тем, сколько
наименований он угадал из шести других наименовании, кото-
которые в момент розыгрыша лотереи определяются с помощью спе-
специального механического устройства, реализующего на глазах
у публики случайный выбор. Спрашивается, какова вероятность
того, что участник угадает все шесть наименований? Пять наи-
наименований и т. д.?
Нетрудно видеть, что это есть не что иное, как задача о ги-
гипергеометрическом распределении, где в генеральной совокупно-
совокупности, состоящей из 49 предметов, владельцем лотерейного билета
выделено шесть «белых». Поэтому вероятность того, что из слу-
случайно выбранных 0, предметов kL предметов окажутся «белыми»
(совпадут с отмеченными владельцем билета), равна PQy^{k^ k)y
где объем выборки к равен 6. Например, вероятность угадать все
шесть наименований равна
/49\-i
i\49F,6)= «7,2-ЮЛ
ч /
В связи с гипергеометрическим распределением можно сде-
сделать одно замечание о природе задач теории вероятностей и ма-
математической статистики. Зная состав генеральной совокупности,

§ 3. СХЕМА БЕРНУЛЛИ ' 21
мы с помощью гипергеометрического распределения можем вы-
выяснять, каким может быть состав выборки. Это типичная прямая
задача теории вероятностей. Но в естественных науках обычно
приходится решать обратные задачи — по составу выборок опре-
определять природу генеральных совокупностей. Такого рода обрат-
обратные задачи, образно говоря, и составляют содержание математи-
математической статистики.
§ 3. Схема Бсрнулли
Пусть из генеральной совокупности, состоящей из двух эле-
элементов {0, 1}, производится выборка с возвращением объема г.
Всего выборок будет 2Г. Пусть р ~ число из интервала [0, 1]. На
множестве Q всех выборок определим неотрицательную функ-
функцию Р следующим образом: если в выборке содержится ровно к
единиц, то Р (со) = р A — рO~\ ' Чтобы убедиться, что Р есть
вероятность, надо доказать равенство
fr\
Легко понять, что к единиц на г местах можно расположить , )
способами. Значит, выборок, содержащих ровно к единиц, будет
столько же. Теперь уже можно подсчитать вероятность Q:
Р (Q) = 2 (I) / A - рГ" = (р + A - р)Г = 1.
Среднее равенство здесь есть формула бинома Ньютона. Заодно
мы выясняли, какова вероятность того, что в выборке содержит-
содержится ровно к единиц:
Это так называемое биномиальное распределение. Его можно рас-
рассматривать как распределение числа «успехов» в последователь-
последовательности г испытаний с двумя возможными исходами в каждом
испытании: 1 («успех») и 0 («неудача»)." Такую последователь-
последовательность испытаний с вероятностью Р(ю), определенной кар;
ph(l — p)r"hy где к — число успехов в со, называют схемой Бер-
иулли. Оказывается, что испытания в схеме Бернулли обладают
свойством независимости, которое будет обсуждаться в следую-
следующей главе.
Нетрудно проверить, что вероятность появления 1 на фикси-
фиксированном месте в выборке (скажем, на месте с номером s) рав-
равна р. Действительно, удалив из выборки элемент с номером 5,
мы получим выборку из той же совокупности, но объема г — 1.

22 ГЛ. 1. ДИСКРЕТНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
Мы найдем искомую вероятность, если вероятности этих укоро-
чеыиых выборок умножим на р и просуммируем но всем корот-
коротким выборкам. Ясно, что получится р. Поэтому число р в схеме
Бернулли часто называют вероятностью успеха.
Рассуждая таким же образом, обнаружим, что вероятность
появления 1 на к фиксированных местах в выборке равна pk.
Рассмотрим теперь, как ведут себя вероятности различных
всходов Р(к, г), когда меняется к. Обратимся к отношению
г>/7Л л Р (^ г) /? г— А-+1 р
* Х % ' Р {к — 1, г) 1 — р к 1 -—
Очевидно, что оно монотонно убывает с ростом ft, причем при
yzrj^P это отношение больше 1, при —j—j > р— меньше. Это
означает, что вероятности Р(/с, г) сначала возрастают с ростом кг
а затем при ft > p(r + 1) убывают.
Сказанное позволяет оценивать с помощью величин P(ft, г)
вероятности
3=0
ого, что число успехов в схеме Берпулли не превосходит к*
Именно, при к < р(г + 1)
+1-к)р
[етрудно понять, что эта оценка будет весьма точной, если чис-
а ft и г велики, а отношение к/(рг) не очень близко к 1. В этом
чучае сумма
1 1
"*" Л (А, г) + R {к, г) R {к — 1, г) + ' * '
^дет мало отличаться от суммы геометрической прогрессии
' jk " R {к> r) ~~ i
будет справедливо приближенное равенство
Q (к, г)&Р (ft, г) (Г;;1 "nk)Jk * A)
Например, при г = 30, р = 0,7, ft = 16 имеем гр = 21, Р(/с, г) «
05023. Здесь отношение •¦((ГА,1.|11)"р^^ равно 15 • 0,7/5,7 « 1,84.
едовательно, правая часть в A), оценивающая ^(fc, r), равна

§ 3, СХЕМА БЕРНУЛЛИ 23
приближенно 0,023 • 1,84 ~ 0,042. Истинное значение Q(k, r) при
выбранных значениях г, ру к равно 0,040 (с точностью до трех
знаков после запятой).
Формула A) будет использована в примере § 5.2.
Рассмотрим теперь генеральную совокупность, состоящую и:*
п элементов, из них п^ элементов первого вида и и2 = п— п{ вто-
второго вида. Производится выборка без возвращения объема г.
Теорема 1. Пусть п и п{ стремятся к бесконечности тап7
что njn-+p, где р — число из отрезка [0/1]. Тогда для гипер-
гипергеометрического распределения справедливо соотношение
Доказательство. Разделим в формуле для Рпх,п(гУчг)
{см. § 2) числитель и знаменатель па п\ Положив Гъ = г—гь
получим
р ir А
г!
г!
(л- г)!
пг(пг
п \п
м"
п )
\ п
2
п
/ * * * \п
три /г -> оо. ^
При достаточно больших щ в силу доказанного предложения,
>п1,п(?:ъ г) близко к Р(гь г). Поэтому схему Бернулли можно
редставлять себе как выборку без возвращения из очень боль-
roif генеральной совокупности с соответствующим составом (до-
я черных шаров равна р).
Рассмотрим в заключение две задачи.
Представим себе п ячеек, в которые случайно размещаются г
фенумерованных частиц. Каждая частица может попасть в лю-
ю из п ячеек, поэтому всего различных размещений г частиц
п ячейках будет пг. Размещение частиц в ячейках можно нред-
*вить как выборку с возвращением объема г из генеральной со-
'-супности, содержащей п элементов. Мы будем предполагать,
> имеем дело с классической схемой, когда вероятность каж-
X) исхода равна \1пт.
1) Чему равна вероятность того, что в Аню ячейку попало рок-
rt частиц? Остальные r—ri частиц, которые не попали в ячей-
к, распределены по /г -— 1 оставшимся ячейкам. Способов раз-
тить эти г—rt частиц по п—1 ячейкам будет (п—l)r~ri.
г частиц г — п частиц, не попавших в ячейку к, можно

ПРОСТРАНСТВО
выбирать I 1 способами. Поэтому искомая вероятность равна
Эта вероятность совпадает с Р{ги г) в схеме Бернуллп при
р = 1/тг.
2) Подсчитаем теперь вероятность того, что хотя бы одна
ячейка окажется пустой. Обозначим это событие буквой А. Пусть
Ah означает, что ft-я ячейка пуста, тогда
п
4= U Ah.
Чтобы найти вероятность события Л, нам потребуется фор-
формула для вероятности суммы (объединения) событий. При этом
мы не можем воспользоваться аддитивностью вероятности, по-
поскольку в пашем случае события Ак пересекаются.
§ 4. Вероятность объединения событий. Примеры
Вернемся к произвольному дискретному вероятностному про-
пространству.
Теорема 2. Пусть Аи Л2, ».., Аа — события. Тогда
\i=l
Доказательство. Надо воспользоваться индукцией и
свойством вероятности
Р (Л + Я) « Р (/1) + Р (Я) — Р (ЛЯ),
доказанным в § 1. При /2 = 2 утверждение теоремы верно. Пред-
Предположим, что оно верно для произвольных (/г-~1) событий
Аи ..., Лп-1. Тогда, обозначив В = \J Aif получим
р( U АЛ = Р(В + Ап) = Р (В) + Р (Ап) - Р (АпВ).
Подставляя сюда известные значения
получим утверждение теоремы. ^

Обратимся теперь к задаче о ячейках (см. § 3) и найдем ве-
вероятность события А, состоящего в том, что хотя бы одна ячейка
и
окажется пустой. Мы представили А в виде U Ак, где Ak озпа-
чает, что все г частиц пе попадают в /с-ю ячейку. Имеем
Событие Л/{Л/ означает, что все г частик размещаются в и—2
ячейках с номерами, не равными к в /, поэтому '
Аналогично
Р (А1:А,Ат) = ^^ = A - А У, /г, I, т < /г
и т. д. Вероятность события А по теореме 2 равна
Обсуждение этой задачи будет продолжено в примере 4.5.
В качестве примера использования теоремы 2 рассмотрим еще
одну задачу, имеющую много разного рода приложений. Это так
называемая задача о совпадениях.
Имеется п элементов, расположенных в некотором порядке.
Случайным образом они переставляются (все п\ перестановок
равновероятны). Какова вероятность того, что хотя бы один эле-
элемент окажется па своем месте?
Всего перестановок п\. Пусть Ah означает, что /с-й элемент
окажется па своем месте. Это событие содержит (п—1I исхо-
исходов, а его вероятность равна
Событие AkA, означает, что к-й б 1-й элементы попали на свои
места; поэтому
Р (А А) - {п - 2)! Р М Л \ - (п ~~ {r> ~~ 1))f - 1
п
Событие U Ah Ti есть событие, состоящее в том, что хотя бы
один элемент попал на свое место. Таким образом, мы можем

26 ГЛ. 1. ДИСКРЕТНОЕ ВЕРОЯТНОСТПОЕ ПРОСТРАНСТВО
воспользоваться только что доказанной формулой
2! ' 3! * * # п л!
1-4 + 1-1+... + (-*>"
2! 3! т • • • ^ п\
Выражение в скобках есть первые n + \ членов разложения
ряд е~\ Поэтому, если п -*- оо? то
е-\ <

Глава 2
ПРОИЗВОЛЬНОЕ ПРОСТРАНСТВО
ЭЛЕМЕНТАРНЫХ СОБЫТИЙ
§ 1. Аксиомы теории вероятностей.
Вероятностное пространство
До сих пор мы рассматривали такие задачи, в которых мно-
множество исходов состояло не более чем из счетного числа элемен-
элементов. В этом случае вероятность Р(^4) определялась нами с по-
помощью вероятностей Р (со) элементарных исходов со. Ею оказа-
оказалась функция, определенная на всех подмножествах А простран-
пространства элементарных событий Q и обладающая свойствами!
1) РD)>0
2) Р (О) = 1.
3) Для непересекающихся событий Аи AZf •*»-
Однако, как уже отмечалось, легко можно представить себе
задачу, где множество всех исходов несчетно. Например, случай-
ное бросание точки в отрезок [tx, t2] (скажем, эксперимент с из-
измерением температуры) имеет континуум исходов, так как ре-
результатом может быть любая точка отрезка. При этом если в экс-
экспериментах, имеющих конечное или счетное множество неходок,
любая совокупность исходов представляла событие, то в рассмат-
рассматриваемом примере дело обстоит иначе. Мы встретимся с больши-
большими трудностями, если будем считать событием любое подмноже-
подмножество этого отрезка. Здесь в качестве событий нужно выделить
специальный класс подмножеств.
Пусть пространство элементарных событий Q есть произволь-
произвольное множество, а «5$ — некоторая система подмножеств мно-
множества Q.
Определение 1. ?& называется алгеброй, если:
Al. fiei.
А2. Из того, что А е $ф и В е $ф следует, что
A3. Если А е ,«?, то А е s?.
Нетрудно видеть, что в условии А2 достаточно требовать вы-
выполнения лишь одного из приведенных двух соотношений. Вто-
Второе будет выполняться автоматически.
^ Алгебру s4 иногда называют также кольцом, так как в s$>
определены дне операции (сложения и умножения), не выводя-
выводящие из М-. Алгебра $&> является кольцом с единицей, т. к. Q> e «я?
и AQ == QA = А для любого А ^ яФ*

28 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
Определение 2. Класс множеств § называется в-алгеброй
(или о~колъцом, или борелевским полем событий), если свойства
А2 выполняется для любых последовательностей множеств:
А2\ Если {Ап} есть последовательность множеств из- 5, то
П=1 71=1
Здесь, как и в А2, достаточно, чтобы выполнялось лишь одна
из этих двух соотношений. Второе будет следствием равенства
TUJ = и л„.
Таким образом, алгебра есть класс множеств, замкнутый отно-
относительно конечного числа операций дополнения, объединения и
пересечения; а-алгебра есть класс множеств, замкнутый относи-
относительно счетного числа этих операций.
Если задано множество Q и какая-нибудь алгебра или о-ал-
гебра S его подмножеств, то говорят, что задано измеримое про-
пространство <й, т$).
На отрезке [0, 1] все множества-, составленные из конечного
числа отрезков или интервалов, образуют алгебру, по не а-ал-
гебру.
Рассмотрим все о-алгебры, содержащие интервалы (по край-
крайней мере одна такая а-алгебра имеется, поскольку совокупность
всех подмножеств данного множества образует, очевидно, о-ал-
гебру). Легко видеть, что пересечение всех таких о-алгебр (т. е.
совокупность множеств, принадлежащих всем о-алгебрам одно-
одновременно) снова образует а-алгебру. Это есть минимальная о-ал-
гебра, содержащая интервалы; ее называют борелевскоп. Боре-
левскую о-алгебру, грубо говоря, можно представлять себе как
совокупность множеств, полученных из интервалов с помощь»
счетного числа операций объединения, пересечения и взятия до-
дополнений. Это весьма богатый класс множеств, заведомо доста-
достаточный для практических целей. Элементы борелевскон о-алгеб-
о-алгебры называют борелевскими множествами.
Наряду с интервалами (а, 6) борелевскими множествами яв-
являются одноточечные множества {а} и множества вида (a, b]t
|я, 6], [a, b) (а и Ъ могут принимать и бесконечные значения).
Это утверждение следует, например, из представлений вида
(а, 6] - П (а, Ь + ±).
Таким образом, все счетные множества и счетные объедине-
объединения интервалов или отрезков также являются борелевскими.
Если дан какой-нибудь класс 9$ множеств из Q, то мы можем
рассмотреть снова пересечение всех а-алгебр, содержащих $ п
получить таким способом наименьшую о-алгебру, содержащую $}.

§ 1. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Ztf
Определение 3. Наименьшая а-алгебра, содержащая $г
называется о-алгеброй, порожденной классом 9$, и обозначает-
обозначается о{&).
В этих терминах борелевская а-алгебра в га-мерном евклидо-
евклидовом пространстве Дп есть а-алгебра, порожденная прямоугольни-
прямоугольниками или сферами. Если Q счетно, то а-алгебра, порожденная
элементами со ^ &2, очевидно, совпадает с о-алгеброй всех под-
подмножеств Q.
В качестве упражнения предлагаем читателю описать алгеб-
алгебру и а-алгебру множеств на Q = [0, 1], порожденную: а) интер-
интервалами @, 1/3) и A/3, 1); б) полуинтервалами вида (а, 1],
О < а < 1; в) отдельными точками.
Чтобы формализовать какую-либо вероятностную задачу, надо
соответствующему эксперименту приписать измеримое простран-
пространство <Q, g>. Q означает множество элементарных исходов экспе-
эксперимента, а алгебра или о-алгебра 3 выделяет класс событий. Все
остальные подмножества Q, не входящие в S, событиями не явля-
являются. При этом класс событий 8г часто будет удобно определять
как а-алгебру, порожденную той или иной алгеброй эФ.
Выделение той или иной алгебры или а-алгебры событий 3f
обусловлено, с одной стороны, существом рассматриваемой зада-
задачи, с другой стороны — природой множества Q. Как мы увидим,
далеко не всегда можно определить вероятность так, чтобы она
имела смысл для любого подмножества Q.
В гл. 1 уже отмечалось, что в теории вероятностей наряду
с обычной теоретико-множественной терминологией используется
несколько иная терминология, связанная с тем, что множества
из Q (принадлежащие 3?) интерпретируются как события. В свя-
связи с этим само множество Q часто называют достоверным собы-
событием. По аксиомам А1 и A3 пустое множество 0 также принад-
принадлежит 5; его называют невозможным событием. А называется
противополоэюным или дополнительным событием к А. Если
А П В = 0, то события А и В называются несовместными.
Теперь осталось ввести понятие вероятности событий. Рас-
Рассмотрим пространство Q и какую-нибудь выделенную в нем си-
систему множеств s&, образующую алгебру событий.
Определение 4. Вероятность на <й, s&> есть числовая
функция, определенная на множествах из s4> и обладающая сле-
следующими свойствами'.
Р 1. Р (А) > 0 для любого A<=es4.
Р2. P(Q) = 1.
РЗ. Если последовательность {AJ событий такова, что 4Hj =
*= 0 при i Ф /, U A-n ^ ^i то
X
р и лп =2Р(Л). (i)

30 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
Эквивалентным аксиоме РЗ будет требование .аддитивности
A) для конечного набора событий А$ и следующая аксиома не-
непрерывности.
РЗ'. Пусть последовательность {Вп} событий такова, что
сю
Bn+lczBn и П Вп = В€=,&, тогда Р(Вп)-+Р(В) при п-+оо.
Доказательство эквивалентности. Пусть выполнено РЗ
сю
и пусть Вп+1 с~ Л?„, П Вп = Ве яФ. Тогда последовательность
событии В7 Ck = BhBh+u к = 1, 2, ..., состоит из попарно несок-
оо
местных событий и Вп = В + (J С^ для любого м. Воспользо-
h = n
.вавишсь теперь свойством Р3? получим, что ряд P(B±) = Р (В) 4-
сх>
+ 2 Р (Cft) сходится, а это значит, что при п ~> оо
Это и есть свойство РЗ'.
Наоборот, если {Лп} — последовательность несовместных со-
событий, то
^рГи^Л + pf и
и имеют место равенства
2 Р (Л) = Ит 2 Р (Л) = Hm P f 1J
7i=l П-юо ft,—1 ?/~»оо \/i—1
fpf IJ л)-р( U
Последнее рапепство следует из РЗ'. ^
Определен и е 5. Тройка (Q, S&, Р> называется вероят~
постным пространством в широком смысле.
Если некоторая алгебра S образует а-алгебру (S = 0(S)), то
оо
условие (J i,,GS в аксиоме РЗ (для вероятности на <Q, S>)
будет выполняться автоматически.
Определение 6. Тройка <Q, 3, Р>, где S — а-алгебра,
называется просто вероятностным пространством.
Вероятность Р па <Q, S> называют иногда также распреде-
распределением вероятностей на Q или просто распределением на О
(на <Q, S>).
TaKPiM образом, задание вероятностного пространства есть за-
задание счетно-аддитивной неотрицательной меры на измеримом

§ 1. АКСИОМЫ ТЕОРИИ BEPOHTllUUlJMi 01
пространстве, такой что мера Q равна 1. В таком виде аксиома-
аксиоматика теории вероятностей была сформулирована А. Н. Колмого-
Колмогоровым. Введенная система аксиом является неполной и непро-
непротиворечивой.
Построение вероятностного пространства <?2, 5, Р) является
основным этапом в создании математической модели (форхмали-
аации) того или иного эксперимента. •
Дискуссии о том, что следует понимать под вероятностью,
имеют длинную историю и связаны с желанием увязать опреде-
определение вероятности с ее «физической» природой. Однако ввиду
сложности последней такие попытки всегда наталкивались н<?
существенные трудности не только математического, но и фило-
философского характера (см. Введение). Наиболее важные этапы
этой дискуссии связаны с именами Вореля, Мизеса, Бернштойна,
Колмогорова. Появление аксиоматики Колмогорова как бы отде-
отделяет математическую сторону вопроса от всего остального. При
таком подходе «физическая трактовка» понятия вероятности по-
появляется уже в виде теоремы (усиленный закон больших чисел,
см. гл. 5, 7), в силу которой частота появления некоторого собы-
события при неограниченном повторении независимых испытаний
сближается (в строго определенном смысле) с вероятностью это-
этого события.
Рассмотрим теперь примеры наиболее употребимых измери-
измеримых и вероятностных пространств.
1. Дискретное измеримое пространство. Так мы будем назы-
называть пространство <Й, $$>, где Q состоит из конечного или счет-
счетного числа элементов, а а-алгебра S обычно составлена из
всех подмножеств множества Q. Дискретные вероятностные про-
пространства, построенные на дискретных измеримых простран-
пространствах, изучались в гл. 1. Там же рассмотрено много конкретных
примеров.
2. Измеримое пространство (R, Э>, где R — вещественная пря-
прямая (или ее часть), 33 — а-алгебра борелевских .множеств.. Необ-
Необходимость рассматривать такие пространства возникает в тех слу-
случаях, когда результаты интересующих нас наблюдений могут
принимать любые значения из R.
Пример 1. Рассмотрим эксперимент, состоящий в «случай-
«случайном бросании» точки на отрезок [0, 1]. Под этим будем понимать
следующее. Множеством Q элементарных исходов здесь является
отрезок [0, 1]. В качестве -о-алгебры 8? возьмем множество под-
подмножеств В, для которых определено понятие длины (меры Ле-
Лебега) \х(В)у например, а-алгебру 33 измеримых но Борелю мно-
множеств. Слова «произведено испытание» здесь означают, что вы-
выбрана точка «€2 = [0, 1] и вероятность события со ^ В равна
ja(Z?). Ясно, что для вероятностного пространства <[0, 1], ?)? и.)
осе аксиомы выполнены. Мы получили так называемое равно-*
мерное распределение на [0, 1].

32 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
Почему в качестве 8? мы выбрали в этом примере а-алгебру
борелевских множеств §3? Если бы мы на й = [0, 1] рассмотрели
о-алгебру, порожденную «отдельными» точками отрезка, то по-
получили бы множества, лебегова мера которых равна либо 0, ли-
либо 1. Другими словами, мы получили бы множества либо очень
«плотные», либо очень «худые» (счетные), так что интервалы
(а, Ъ) при Ъ — а< 1 не принадлежат этой а-алгебре.
G другой стороны, если рассмотреть на1 Q = [0, 1] о-алгебру
всех подмножеств Q, то задать вероятностную меру на ней так,
чтобы Р ([а, Ь]) « Ъ — а (т. е. равномерное распределение) ока-
оказывается невозможным*).
Если обратиться снова с равномерному распределению Р на
Q = [0, 1], то легко понять, что это распределение невозможно
задать тем же способом, который мы использовали при опреде-
определении вероятности на дискретном пространстве элементарных
событий (т. е. путем задания вероятностей элементарных исхо-
исходов со). Так как в этом примере со есть отдельные точки из [0, 1]
то, очевидно, Р (со) = 0 для любого со.
3. Измеримое пространство </?n, Sn> возникает в тех случаях,
когда наблюдения представляют собой вектор. Здесь Rn -— /г-мер-
иое евклидово пространство (Rn = R{ X . . . X Rn, где Rh .. ., Rn
суть п экземпляров вещественной прямой), Ъп—о-алгебра боре-
борелевских множеств в йп, т. е. о-алгебра, порожденная множества-
множествами В = Bi X ... X Вп, где Вх с: Rx есть борелевские множества на
прямой. Вместо Rn можно рассматривать также какую-нибудь
измеримую часть Q ^ S371 (например, куб, шар), а вместо Ъп —
сужение Ъп на Q. Например, можно аналогично предыдущему
построить вероятностное пространство для случайного бросания
точки в куб Q = [0, 1]п. Здесь полагаем Р (со е В) = \i (В), где
\i(В)—мера Лебега (объем) множества В. Вместо куба [0, i]n
мы могли бы рассматривать и любой другой куб, например,
[а, Ь]п, но только в этом случае надо полагать Р (со е В} =
= \i(B)/\i(Q) = \i(B)/(b — а)п. Это будет равномерное распределе-
распределение па кубе.
В теории вероятностей возникают и более сложные вероят-
вероятностные пространства. Как быть, если результатом эксперимента
является бесконечная числовая последовательность? В этом слу-
случае наиболее подходящим часто оказывается пространство
00
4. Измеримое пространство </?°°, $°°>, где -R°° = И R] есть
1
пространство всех последовательностей (хи х2, ...)? а ^°° есть
N
о-алгебра, порожденная множествами вида П Bjk% Bjk e Sjfe
См. [14], с. 80.

§ 1. АКСИОМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 33
при любых /V, /lt ..., jN, где ЗЭЛ- — а-алгсбра борелевских мно-
множеств из Rj.
5. Если результатом эксперимента является, скажем, непре-
непрерывная функция на отрезке [а, Ь] (траектория движения части-
частицы, электрокардиограмма больного и т. д.), то вероятностные
пространства, рассмотренные выше, окажутся непригодными.
13 этом случае в качестве Q следовало бы взять пространство
С (а, Ь) всех непрерывных функций на [а, Ъ\ или пространство
Пы>ь] всех функций па [а, Ъ\ Вопрос о выборе подходящей а-ал-
гебры здесь несколько усложняется и мы обсудим его поз-
позже в гл.' 15.
Вернемся теперь к определению вероятностного пространства.
'Пусть тройка <Q, «5$, Р> образует вероятностное простран-
пространство в широком смысле (s& есть алгебра). Как мы уже видели,
с каждой алгеброй $$> связана о-алгебра S = a(es$), порожден-
порожденная s&. Существенный интерес представляет следующий вопрос:
определяет ли вероятностная мера Р на $Ф меру на % = o(s^)
и однозначно ли это происходит? Другими словами, достаточно
ли для построения вероятностного пространства <Й, 8, Р> за-
задать вероятность Р лишь на какой-нибудь алгебре s&, порожда-
порождающей % (т. е. построить какое-нибудь вероятностное пространст-
пространство в широком смысле <Q, «s$, Р>, где a(s&)=?5). Ответ на этот
важный вопрос содержится в следующей теореме Каратеодори.
Теорема о продолжении меры. Пусть <Q, «5$, P> —
вероятностное пространство в широком смысле. Тогда существует
и притом единственная вероятностная мера Q, определенная па
5==о(«5#), такая, что
Q (А) = Р (А) для всех isA
Следствие. Каждое вероятностное пространство в широком
смысле <Q, «s$, P) автоматически определяет вероятностное про-
пространство <Я, 5, Р> с S = a (s&).
Этим фактом мы будем широко пользоваться в дальнейшем.
Из него следует, в частности, что для определения вероятности
на измеримом пространстве <й, Э> достаточно задать вероятно-
вероятности интервалов.
Доказательство теоремы Каратеодори отнесено в Прило-
Приложение 1.
В заключение этого параграфа сделаем одно замечание обще-
общего характера. Математика качественно отличается от таких наук,
как физика, химия и др. тем, что она в своих выводах не опи-
опирается постоянно на опытные данные, с помощью которых естест-
естествоиспытатель пытается получить ответы на свои^ вопросы, а раз-
развивается в рамках исходной конструкции или системы аксиом,
которыми человек описал исследуемый объект. Таким образом,
математика и, в частности, теория вероятностей, исследует при-
природу окружающих нас ' явлений методологически иначе — изуча-
Л. А. Боровков

34 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
ются не сами явления непосредственно, а модели этих явлений,,
созданные однажды на основе человеческого опыта. Ценность той
или иной модели определяется соответствием выводов теории и
наших наблюдений и поэтому зависит от выбора аксиом, харак-
характеризующих объект.
В этом смысле аксиомы PI, P2 и аддитивность вероятности
представляются бесспорными и естественными (сравните с заме-
замечаниями во введении о желательных свойствах вероятности).
Счетная аддитивность вероятности и вместе с ней свойство ст-ал-
гебры А2' являются качествами более тонкими и менее контро-
контролируемыми нашей интуицией (так же, впрочем, как и многое дру-
другое, связанное с понятием бесконечности). Введение последних
двух свойств обусловлено главным образом возможностью по-
построения содержательной математической теории. Многочислен-
Многочисленные приложения теории вероятностей, развитой пя сформулиро-
сформулированной в этом параграфе системы аксиом, обнаруживают ее вы-
высокую эффективность и целесообразность.
.§ 2. Свойства вероятности
1) Р @) = 0. Это следует из равенства 0 + Q = Q и свойств
вероятности Р2, РЗ.
2) Р (А) - 1 - Р (А) так как А + А = Q и А Г) А = 0.
3) Если_.4с5, то Р(Л)<1 РE). „Это следует из того, чта
Р(А)+ Р(АВ)=Р{В).
4) Р(Л)<1 (см. свойство 3) у, Р2)'.
5) Р(ЛиВ) = Р(А) + Р(В) — Р(АВ), так как А [) В = А +
+ (В — АВ), Р(В-АВ)^Р (В) - Р (АВ).
6) Р(А U В)^ Р(А) + Р(В) следует из предыдущего.
7) Р ( U Ah) = S Р(Л)- 2 P{AhAt) +
\fe=i / л=1 k<i
2 p D4,4) -...(- lr^P (Л ... Л).
Эта формула была уже доказана и использована для дискрет-
дискретного Q. Здесь читатель может доказать ее точно так же — ис~
пользуя индукцию и свойство 5).
8)Р U 4<2 РD). Так как
\П=1 / П=1
U BnAnf где Bn==O— U Ак%
и события АПВП не пересекаются, то
р и ап Ь= 2 р (?„л
\п=1 / п=1

§ 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. НЕЗАВИСИМОСТЬ СОБЫТИЙ 35
9) Если Ап есть монотонно возрастающая последовательность
оо
множеств Dпс4п+1) и = А (J АП1 то
l
Это другая форма аксиомы непрерывности, эквивалентная Р3\
Действительно, введя в рассмотрение множества Вп = А—4Л,
оо ч
мы получим Bn+i^Bn, П Вп=0< Стало быть, по аксиоме не-
прерывности при п -+¦ оо
Утверждение в обратную сторону получается аналогичным
образом.
§ 3. Условная вероятность/ Независимость событий
и испытаний
Начнем с примеров. Пусть эксперимент состоит в троекрат-
яом подбрасывании симметричной монеты. Вероятность того, что
герб выпадет ровно один раз, т. е. что произойдет одно из эле-
элементарных событий (грр), (ргр), (ррг), в классической схеме
равна 3/8. Обозначим это событие буквой 4. Предположим те-
теперь, что об исходе эксперимента дополнительно известно, что
произошло событие
В = {число выпавших гербов нечетно).
Какова вероятность события А при этой дополнительной ин-
информации? Событие В состоит из 4 элементарных исходов. Со-
Событие же А составляется из 3 исходов события В. В рамках
классической схемы естественно принять новую вероятность со-
события А равной 3/4.
Рассмотрим еще один более общий пример. Пусть задана
классическая схема с п исходами. Событие А состоит из г исхо-
исходов, событие В — из m исходов, а событие АВ содержит к исхо-
исходов. Вероятность события А при условии, что произошло собы-
событие В, по аналогии с предыдущим примером естественно опре-
определить следующим образом:
Р {А/В) =» 1 « У?-%
Полученное отношение равно Р(АВ)/Р(В), так как
Р(АВ)=к/п, Р(В)
Можно перейти теперь к общему определению. Пусть
задано вероятностное пространство <О, S,. Р> и пусть А ж В —
а*

36 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
произвольные события. Если Р(В)^>01 то условная вероят-
вероятность события А при условии, что произошло событие В, по опре-
определению полагается равной
Определение 7. События А и В называются независи-
независимыми, если
Р(АВ) = Р(А)Р(В).
Некоторые свойства независимых событий.
1) Если Р(В) > 0, то независимость А и В эквивалентна ра-
равенству
Доказательство очевидно.
2) Если А и В независимы, то независимы А и В.
Действительно,
- Р (В) - Р (А В) = Р (В) A - Р (А)) - Р (А) Р E).
3) Пусть события /1 и Z?i независимы и независимы также
события А и Z?2, при этом ВкВ2 — 0. Тогда независимы события
А и Si + ?2.
Следующие равенства доказывают это свойство:
Р (А (В, + В2)) = Р (АВ, + АВ2) = Р (ABJ + Р DДа) =
= Р (А) (Р E2) + Р ВД = Р (А) Р (В, + Вг\
Как мы увидим ниже, требование ВХВ2 = 0 здесь существенно.
Пример 2. Пусть событие А означает вьшаденве герба
в первом из двух бросаний симметричной монеты, а событие В —•
выпадение решетки во втором бросании. Вероятность каждого из
этих событий равна 1/2. Вероятность пересечения А В будет равна
Таким образом, события А и В независимы.
Пример 3. Рассмотрим равномерное распределение на квад-
квадрате [О, I]2 (см. § 1). Пусть событие А состоит в том, что случай-
случайно брошенная точка попала в область, расположенную правее
абсциссы а, событие В — в том, что точка попала в область, рас-
расположенную выше ординаты 6.
На рис. 2 обе области заштрихованы. Событие АВ на рисун-
рисунке заштриховано в клеточку. Очевидно, Р {АВ) = Р {А) Р (В)
и, значит, события А и В независимы.

§ 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. НЕЗАВИСИМОСТЬ СОБЫТИЙ
37
Легко проверить также, что если событие В означает попада-
попадание брошенной точки в треугольник FCD (см. рис. 2), то собы-
события А и В будут уже зависимыми.
Определение 8. События Ви В2,..., Вп независимы б сово-
совокупности, если для любых К ix < k < ... < U ^ п, г = 2, 3,.»., п.
Попарной независимости событий недостаточно для независи-
независимости п событии в совокупности. Это показывает следующий
пример.
Пример 4 (пример Бершитейна). Рассмотрим такой экспе-
эксперимент. На пл-оскость бросается тетраэдр, три грани которого по-
покрашены соответственно в крас-
красный, синий и зеленый цвета, а на
четвертую нанесены все три цве-
цвета. Событие К означает, что при
бросании тетраэдра на плоскость
выпала грань, содержащая крас-
красный :цвет, событие С — грань, со-
содержащая синий цвет, и событие
3 — грань, содержащая зеленый
цвет. Так как каждый из трех
цветов содержится на двух гра-
гранях, то Р(Я) = Р(С) = РC) = 1/2.
Вероятность пересечения любой
пары введенных событий равна
111 ^
Т^ ТТ' так как люоая паРа Цветов присутствует только на од-
одной грани. Это означает попарную независимость всех трех со-
событий. Но
Р (КЗС) = 1/4 Ф Р (К) Р C) Р {С) = 1/8. ^
Рис. 2
Теперь легко построить пример, когда при ВьВг Ф 0 свойство
3) независимых событий не будет иметь места.
В качестве примера последовательности событий, независимых
в совокупности, можно привести последовательность исходов в
схеме Берпулли.
Если считать, что каждый исход получен в результате отдель-
отдельного испытания, то мы обнаружим, что любое событие, относя-
относящееся к фиксированному испытанию, будет независимым от лю-
любого события, относящегося к остальным испытаниям. В таких
случаях говорят о последовательности независимых испытаний.
Чтобы дать общее определение, рассмотрим два произвольных
эксперимента Gx и G2 и обозначим <й19 8^, Р3> и <Q2, Qf2, P2>
соответствующие им вероятностные пространства. Рассмотрим

38 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
"также «составной» эксперимент G с вероятностным пространст-
пространством <й, S, Р>, где Q = Qi X Q2 есть прямое произведение про-
пространств fii и Q2, а а-алгебра 5 порождена прямым произведени-
произведением -Si X $2 (т. е. событиями В = В,Х B2l В, е= $,, В2 е= g2).
Определение 9. Мы будем говорить, что испытания Gt
и G% независимы, если для любых В = Bt X JS2, Bi^Si, Bz^i5i
выполняется
P E) = p, (SJ P2 (Я2) = P (Z?! X Q8) P (Q, X 5a).
Независимость п испытаний Giy .. ., Gn определяется анало-
аналогично с помощью равенства
где B = BiX...XBn, Bk^ Sh, <ЙЙ, Sft, P/t> — вероятностное
нространство, соответствующее эксперименту Gfet ft = 1, ..., j^.
В схеме Бернулли вероятность каждой последовательности
X»сходов, состоящей из г пулей и единиц и содержащей к единиц,
равна pk(i — р)''~\ Поэтому схему Бернулли можно рассматри-
рассматривать как результат г независимых испытаний, в каждом из которых
с вероятностью р появляется 1 (успех) и с вероятностью 1 — р
появляется 0 (неуспех), Таким образом, вероятность появления
/г \
к успехов в г независимых испытаниях равна ! , J р A —р)г~1*
Верно и в некотором смысле обратное утверждение: любая
последовательность независимых одинаковых испытаний с двумя
исходами образует схему Бернулли.
В гл. 3 будет приведен ряд замечаний о связи введенных по-
понятий независимости с общепринятым пониманием причинной
зависимости.
§ 4. Формула полной вероятности и формула Байеса
Пусть А ¦— некоторое событие, Ви B2l .. ., Вп — попарно не-
несовместные события, имеющие положительные вероятности и та-
п
кие, что A a \j Bj. Тогда имеет место формула полной веро-
ятности:
Доказательство. Из приведенных условий следует, что
п
А = U BjA. Кроме того, события АВи АВ2, ¦ . ., АВп несов-
3=1
местны, поэтому
р (Л) = 2 Р (ABj) = 2 Р (В}) Р (А/В}). 4

§ 4. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ И ФОРМУЛА БЛЙЕСА 39
Пример 5. В экспериментах на встречных электрон-нози-
тронных пучках вероятность того, что, за единицу времени про-
произойдет / столкновений, сопровождающихся рождением новых
элементарных частиц, равна
/ = 0,1,-..,
где К — положительный параметр (это так называемое распреде-
распределение Пуассона, которое подробно будет рассмотрено в гл. 3,5,
16). Прм каждом столкновении в результате взаимодействия мо-
могут возникнуть различные группы элементарных частиц, при
этом вероятность появления каждой группы фиксирована и не
зависит от результатов взаимодействия при остальных столкно-
столкновениях. В качестве одной из таких групп рассмотрим пару ja-mc-
зонов и обозначим через р вероятность их появления при одном
столновепии. Чему равна тогда вероятность события Ak, при ко-
котором за единкцу времени рождается к пар ц-мезонов?
Допустим, что наступило событие Bh состоящее в том, что за
единицу времени происходит / столкновений. Up и этом условии
будем иметь последовательность/ независимых испытаний, и веро-
ятность появления к пар |и-мезонов будет равна ( h\p (i — pf \
Поэтому по формуле полной вероятности
f- irr^wph A - p)]~h
k\
Таким образом, мы получили снова распределение Пуассона, по
с параметром кр.
Приведенное решение задачи было не формализованным. Фор-
Формальное решение требует прежде всего построения вероятност-
вероятностного пространства. Оно оказывается здесь достаточно сложным.
Обозначим Qj пространство элементарных событий в схеме Бер~
нулли, соответствующей / испытаниям, и пусть со; — элемент Q3.
Тогда в качестве Q можно взять всевозможные нары {(/, со;-)}^0I
гдо цифра указывает число столкновений, (Oj означает последова-
'И'лы-юсть длины / «успехов» и «неуспехов» (<<успех>> — появле-
появление ц-мезонов). Если (Oj содержит к «успехов»,, то следует по-
ЛО'ЛШТЬ
Чтобы получить Р (Ah)i остается просуммировать эти вероятпо-
vni по всем (Oj, содержащим к успехов, и по всем / > & (принцип

40 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
формулы полной вероятности здесь используется веяние при рас-
расслоении Ah на события (/, coj)). Л
Тот факт, что число столкновений частиц описывается рас-
распределением Пуассона, нетрудно понять в силу следующих об-
обстоятельств, .вызванных существом физического процесса. Пусть
событие Bj(t, и) состоит в том, что за интервал времени [t, t + и)
произошло / столкновений. Тогда оказывается, что
а) пары событий B,(v, t) и Bk{v -r t, и), относящиеся к непе-
непересекающимся _ интервалам времени, независимы при всех
v, t, и, /, к;
б) при малых Л вероятность столкновения за время Л про-
пропорциональна Л: '
п, кроме того, P(Bft(f, Д)) = о(Л), &>2.
Иеиользуя снова формулу подпой вероятности при гипотезах
Bj(v, ?), получим для вероятностей Pit(t) ~ P(Bh(v, I)) следу-
следующие соотношения:
Ph (t + Д) = 2 ft@ P (Sfc (и, t + A)/B} (v, t)) =
i—о
к
з-о
+ Ра @ A — Л,Д — о (Д)),, /с > 1;
Преобразуя последнее уравнение, находим
Следовательно, существует производная
po(t) = — Хро@-
Аналогичным образом устанавливаем, что существуют
Ра @ - Ы-1 @ - ^Pft @. к > 1- A)
Заметим теперь, что так как функции Ph(t) непрерывны, то сле-
следует положить /?о @) = 1, /?а@)= 0. Поэтому
Пользуясь индукцией и подставляя в A)" Pk-i(t) = ¦ /^^j—-
устанавливаем (удобно произвести замену рк — е~иик, тогда урав-

§ 4. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ II ФОРМУЛА БАЙЕСА 41
рение A) примет бид uh = - ^ _ ¦¦ ), что
Pk(t) = V^—, A: «0,1, ...
есть распределение Пуассона с параметром \t.
Чтобы понять конструкцию вероятностного пространства в
этой задаче, следует обратиться к множеству Q всех ступенчатых
неубывающих функций x(t)^0, t ^ 0, принимающих значения
0, 1, 2, . .. Каждая такая функция может играть роль элементар-
элементарного события: точки ее скачков будут указывать моменты столк-
столкновений, само значение х{1) будет означать число столкновении
за интервал времени @, ?). Чтобы избежать здесь громоздких
рассуждений, связанных с заданием о-алгебры, можно для наших
.вычислений считать вероятность Р заданной па алгебре зФ
(см. § 1), порожденной множествами {#(?)=&}, i > 0; & = 0,1,...
(ведь все рассматриваемые в этой задаче события являются
именно такими множествами). Приведенные выше рассуждения
показывают, что следует положить
М h
(См. также о пуассоновских процессах в гл. 16.)^
Приведенными примерами мы хотели ие только проиллюстри-
проиллюстрировать применение формулы полной вероятности, но и показать,
что построение вероятностных пространств в реальных задачах
далеко не всегда оказывается простым.
Разумеется, проведение таких построений в каждой задаче
вовсе не обязательно, но рекомендуется все же делать это до по-
появления достаточно твердых навыков.
Пусть события А и Ви ..., Вп удовлетворяют условиям, сфор-
сформулированным в начале § 4. Если Р(Л)>0, то при этих усло-
условиях имеет место формула Байеса:
Ота формула есть просто иная форма записи равенства
Ре в числителе надо воспользоваться определением условной ве~
ятности события А при условии JSj, а в знаменателе — форму-
формулой полной вероятности. ^
Пример 6. Некоторое изделие выпускается двумя завода-
заводами. При этом объем продукции второго зав-ода в к раз превосхо-
превосходит объем продукции первого. Доля брака у 1-го завода Ри

42 ГЛ. 2. ПРОИЗВОЛЬНОЕ ВЕРОЯТНОСТНОЕ ПРОСТРАНСТВО
у 2-го—-TV Предположим теперь, что изделия, выпущенные заво-
заводами за одинаковый промежуток времени, перемешали и в таком
виде пустили в продажу, Какова вероятность того, что вы приоб-
приобрели изделие со второго завода, если оно оказалось испорченным?
Пусть событие 'Bt означает, что выбранное вами изделие с
первого завода, а В% — со второго. Легко видеть, что
Р (lh) = j-T-7,1 Р (#а) = y+Ъ-
Это так называемые априорные вероятности событий Ви /?2.
Пусть событие А означает, что выбрано бракованное изделие.
Нам даны условные вероятности Р (A/Bj) = Р± и Р(А/В2) — Р2.
Теперь, воспользовавшись формулой Байеса, можно ответить на
я о с т а в л е ни ый в о п ро с:
1 -I- к ' 1 "" 1 -|- к 1 2
Р
Аналогично Р (Ь\/А) == р *;> . <4
Вероятности Р (BjA) н.Р (В2/А) называют иногда апосте-
апостериорными вероятностями соответственно событий Ви В2, после
того как произошло событие А.
Пример 7. Студенту предложили решить числовую задачу.
Ответ задачи известен и представляет собой одно из чисел
1,..., к. Решая задачу, студент может либо найти правильный
путь решения задачи, либо ошибиться. Подготовка студента та-
такова, что он находит правильный путь решения задачи с вероят-
вероятностью р. В этом случае ответ, полученный им, совпадает с дан-
данным. С дополнительной вероятностью 1 — р студент ошибается.
В этом случае мы будем предполагать, что в качестве ответа мо-
может получиться любое из чисел 1, . . ., к с вероятностью 1/к.
Известно, что студент получил правильный ответ. Какова при
этом условии вероятность того, что он верно решил задачу?
Пусть Bl (В2) есть событие, означающее, что студент ре-
решил задачу верно (неверно). Тогда но условию априорные веро-
вероятности этих событий равны Р (Вг) = р, Р (В2) =1 — р. Если со-
событие А состоит в том, что студент получил правильный ответ, то
По формуле Байеса искомая апостериорная вероятность Р(В1/А)
равна
p(*)pW) р - *
Очевидно, что Р (/?,//!}> Р Eх) = /> и что_Р(В1/А) близка к 1
при больших к. .

Глава 3
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
§ 1. Определения и примеры
Пусть <Q, 5, Р>-—произвольное вероятностное пространство*
Определение 1. Случайной величиной ? называется из-
измеримая функция ? == §((о), отображающая О в множество дейст-
действительных чисел й, т. е. функция, для которой прообраз ^(i5) =
= {со: ?(со) ^ В} любого борелевского множества Se^ есть дшо-
жество из.о-алгебры &\
В таких случаях говорят также, что % осуществляет измери-
измеримое отображение <?2, g> в <й, 23>.
Например, при бросании монеты О состоит из двух точек: гер-
герба и решетки. Если гербу поставить в соответствие 1, а решетке
О, то, очевидно, получим случайную величину.
Случайной величиной будет также число очков на выпавшей
грани кости.
Расстояние от начала координат до случайно брошенной теч-
течки в квадрат [0 ^ ± ^ 1, 0 ^ у ^ 1] тоже будет случайной вели-
величиной, так как множество {(х, у): х2 + у2 < i\ измеримо. Чита-
Читатель, наверное, заметил, что в этих примерах придумать неизме-
неизмеримую функцию от со, которая отвечала бы какой-нибудь реаль-
реальной задаче, очень трудно. Такое явление имеет место часто, по
но всегда. В гл. 15, посвященной 'Случайным процессам, нас бу-
будут интересовать множества, которые, вообще говоря, событиями
не являются и требуют специальных модификаций для того, что-
чтобы их можно было считать событиями.
Как отмечалось вы иге, из определения случайной величины
следует, что для любого множества В из о-алгебры борелевских
множеств 33 на прямой
Следовательно, иа измеримом пространстве <Л, 33> определена ве-
вероятность Рр {В) = Р (?е ВO которая порождает вероятност-
вероятностное пространство <Д, S3, Р&>.
Определение 2. Вероятность Pg {В) называется распре-
распределением случайной величины %,
Если положить /?=(¦— °о, х)у то получим функцию Fi(x)~
** РA<Сх), определенную на всей вещественной оси, которая
ппаьшается функцией распределения случайной величины g.

44 гл. а. случайные величины и функции распределения
Ниже увидим, что функция распределения случайной вели-
величины полностью определяет ее распределение и часто использу-
используется для описания последнего.
Там, где это не вызовет недоразумений, вместо Fi(x) будем
писать просто F(x).
Так как случайная величина | есть отображение О в Я, то
Р (I ? 1 <Г °°) = ^ • Иногда наряду с такими случайными величи-
величинами бывает удобно рассматривать также случайные величины,
которые могут принимать значения ±°° (они будут осуществлять
измеримое отображение Йвйи {±°о}). Если Р {! 11 = оо) > 0?
то такие случайные величины ?(со) мы будем называть несоб-
несобственными. Каждый случай, когда такие величины будут появ-
появляться, будем особо оговаривать.
Пример 1. Рассмотрим схему Бернулли с вероятностью
успеха р и объемом выборки к (см. § 1.3). Как известно, множе-
множество элементарных исходов Q в этом случае есть множество все-
всевозможных последовательностей из нулей и единиц длины к. За
о-алгебру % возьмем систему, всех подмножеств Q. Определим
на Q случайную величину следующим образом: каждой последо-
последовательности из нулей и единиц поставим в соответствие число
единиц в этой последовательности.
Вероятность г успехов, как мы уже знаем, есть
Поэтому функция распределения F(x) введенной случайной ве-
величины будет определяться следующим образом;
Суммирование здесь ведется по всем целым г, меньшим х. Если
х < 0, то F(x) = 0, если же^> к, то F(x) = 1.
Пример 2. Пусть на отрезок [а, Ь] вещественной прямой
случайным образом бросается точка, т. е. вероятность попадания
точки в некоторое множество из fa, b] полагается пропорциональ-
пропорциональной лебеговой мере этого множества. Q здесь есть отрезок fa, Ь],
a-алгебра % есть класс борелевских подмножеств из [а, 6]. Опре-
Определим случайную величину ? так:
&(со)=<о, <oes[a, Ь],
т. е. случайная величина равна тому числу из [at Ь], в которое
лопала бросаемая точка. Это измеримая функция. Если х < а, то
F(x) = РF<#) = 0. Пусть х&[а, Ъ\ Тогда {| < х} означает,
что точка попала в интервал [а, х) * Вероятность попадания в этот
интервал пропорциональна длине этого интервала, значит,

§ 2. СВОЙСТВА ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ И ПРИМЕРЫ 45
Если же х > 6, то понятно, что F(x)=l. Окончательно находим
О, x<ia,
A)
Эта функция распределения определяет так называемое равно-
равномерное распределение на интервале fa, Ь\
Если fiE)— мера Лебега на </?, S3), то, как мы увидим в сле-
следующем параграфе, нетрудно установить также, что в этом слу-
случае ?i{B)~~
§ 2. Свойства функций распределения и примеры
Пусть F(x) есть функция распределения случайной величи-
величины |. Тогда имеют место следующие свойства F(x):
F1. Свойство монотонности: если Xi^x2, то F{xi)^ F{x?L
F2. lim F (#) = 0 и lim ^ (я) = 1.
F3. Свойство непрерывности слева: lim F (x) = F (x0).
xfx0
Доказательство. Так как {^ < xj s {| < x2}, где xt ^ #2,
то Fl сразу следует из свойства 3) вероятности (см. § 2.2).
Для доказательства F2 рассмотрим две числовые последова-
последовательности {хп} и {уп\ при этом последовательность {хп} убывает
так, что хп ->• —-оо, а последовательность уп возрастает, уп ->- оо.
Введем обозначения Ап = {§ < хп}, 5Л = {? < уя}. Из того, чго
ixj монотонно стремится к —<*>? следует, что последовательность
множеств Ап убывает и П,Лп = 0. В силу аксиомы непрерывно-
непрерывности РЗ' (см. § 1 гл. 2) Р(Ап)~>-0 при п -*¦ оо или, что то же,
lim F(.rn) = 0, Отсюда и из монотонности F(x) следует, что
lim F(x) = 0.
Х-> — сю
Так как последовательность {yj монотонно сходится к оо, то по-
последовательность множества Вп возрастает и U Вп = Й, поэтому
(см. свойство 9) § 2.2) РEп)->-1. Отсюда, как ж прежде, сле-
следует, что
Свойство F3 доказывается аналогичным способом. Пусть А =
{g < xQ}, An = {g < #n}, где последовательность {а:п} возраста-
, х?г f ^o- Последовательность множеств Лп также возрастает
\)Ап~А. Следовательно, Р(Ап)->- Р(А). Это означает, что
liniF(x) =

46 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Нетрудно видеть, что функция F была бы непрерывной спра-
справа, если бы мы положили F (х) = Р (?<!#).
При принятом определении функция F, вообще говоря, не яв-
является непрерывной справа, так как по аксиоме непрерывности
— F(x) = lim (f(x+ -) — F(x))
Сказанное означает, что F(x) непрерывна тогда и только тогда,
когда Р (? = х) = 0 при любом х. Примеры 1, 2 показывают, что
весьма обычны как непрерывные, так и разрывные F(x).
Из приведенных соотношений следует также, что
Р_(*< |< у) = Ps ([ж, й) = F( г, + 0) - F (х).
Теорема 1. Если функция F(x) обладает свойствами F1,-
F2 и F3^ го существует вероятностное пространство. <й, S, Р>
и случайная величина \ на нем .такая, что Fi(x)= F(x).
Доказательство. Построим сначала вероятностное про*
странство <?2, S, Р>.- В качестве Q возьмем вещественную пря*«
мую й, а в качестве 5 возьмем а-алгебру S3 измеримых по Боре*
лю множеств. Как мы уже знаем (см. § 2.1), для построения Bet
роятностного пространства </?, S3, Р) достаточно задать вероят-'
ность Р на алгебре s&, пороя^денной, скажем, полуинтервалами
вида [•, •) (тогда a(*s^)=83). Произвольный элемент А алгебры
<$$ имеет вид конечного объединения непересекающихся полуин-
полуинтервалов:
А= U [аиЬг), аг<Ьг
г=1
(числа а{ и Ъг могут быть бесконечными). Полагаем по опреде-
определению
р <л) =
i
Совершенно очевидно, что в силу Fl, F2 аксиомы PI, P2 вы-
выполнены. Остается проверить счетную аддитивность или непре-
рывность Р на алгебре st>. Пусть Вп е ^, Вп+1 <= Вп, {] Вп==
= B^sfi. Надо показать, что .P(-Z?n)-> РE) или, что то же,
РFп5)->0 (BnBerf). Для этого достаточно убедиться,
что Р (BnBCN) -^ 0 при любом фиксированном N, где CN ==
= [—TV, TV). Действительно, для заданного 8 >_0_ iio свойству F2
выберем TV так, что Р (CN) < 8, Тогда Р (BnBCN) < Р (CN) < &х
lim P (Sn"B) < lim P {BJJCN) + e.

§ 2. СВОЙСТВА ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ И ПРИМЕРЫ 47
Так как 8 произвольно, то сходимость P[BnBCN)-^0 при
п -> оо означает требуемую сходимость Р (ВпВ)-*0. Из сказан-
сказанного вытекает, что можно считать множества Вп ограниченными
(Вп <= [—/V, N) при каком-нибудь N<<x>). Кроме того, не огра-
ограничивая общности, можно считать, что В есть пустое множество.
В силу сделанных выше замечаний Вп допускают представление
Вп- U k,U кп<оо,
где а", Ъ™ конечны. Заметим далее, что для заданного е > 0 и
для любого полуинтервала [а, Ь) всегда можно найти вложенный
в него полуинтервал [а, 6 — 6), б > 0, такой, что- Р([а,Ь—б)) ^
^Р([а, Ь)) — е. Это вытекает непосредственно из свойства F3:
F(b — 6)-+F(b) при б I 0. Следовательно, для заданного 8>0
я множества Вп существуют 6J1 > 0, i =ч 1, ..., кп, такие, что
Присоединим теперь к множеству Бп правые концы полуинтер-
полуинтервалов и рассмотрим замкнутое ограниченное множество
tf»=U [а",Ь?-'б?].
{=1
Очевидно, что
Р (Sn - iCn) = Р (ВХ
Из соотношения К = 0 следует, что Кп == 0 при всех доста-
достаточно больших гс. Действительно, все множества /?п принадлежат
замыканию [CN] == [—N, N], которое является компактом. Мно-
Множества {Лп=[Сдг] — Кп}г7=1 образуют открытое покрытие [CN\
так как U Дп = [Civ](U Кп)= [CN](f) Kn)= [CN]. Таким образом, по
лемме Гейне — Бореля существует конечное подпокрытие
пп П° П0
{Дп}п=1» ^о<°°* такое, что U Ап=[С^]или, что то же, П Кп =»
= 0. Поэтому
по \ п0
U Япо^п <Р U ЯгДп < 2
п=1 / \п=1 / п=1

48 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Итак, для заданного г > 0 нашлось п0 (оно зависит от г) та-
такое, что P(-$rt())<C?- Это значит, что Р(Вп)~>~0 при п -> со.
Выполнение аксиомы 3 доказано.
Итак, вероятностное пространство построено. Остается в ка-
качестве случайной величины % взять тождественное отображение
действительных чисел па себя. Тогда
При изучении функций распределений па основании доказан-
доказанного утверждения часто используют удобную модель выборочного
.вероятностного пространства.
Определение 3. Вероятностное пространство {?2, 5, Р)
называется выборочным для случайной величины %((о), если Q
есть подмножество вещественной прямой R и |(g))= @-
Вероятность Р в соответствии с определением 1 § 1 будет на-
называться распределением §. Этот факт будем обозначать сим-
символом
?^Р. B)
Очевидно, что построение выборочного вероятностного простран-
пространства всегда возможно. Достаточно положить Q = Я, S = Э,
Р (В) « Р (^ G В). Для целочисленных ? пространство <Q, g>
можно выбрать и более «экономным» образом, положив Q =
= {..., -1,0, 1, ...}.
Так как функция распределения F(x) случайной величины ?
но теореме 1 однозначно определяет распределение Р этой слу-
случайной величины, то наряду с B) будем писать также HgSF.
Приведем теперь примеры некоторых наиболее распростра-
распространенных распределении.
1. Вырожденное распределение 1а. Распределение 1а опреде-
определяется соотношением
A, если asB,
al ;~|07 если а^В.
Это распределение, сосредоточенное в точке а: если ?^=§1а» то
P(S = а) = 1» Функция распределения для 1а имеет вид
@ при х^Са9
4 ; 11 при х>а.
Следующие два распределения были описаны в приме-
примерах 1, 2 § 1.
2. Биномиальное распределение В?. По определению ?g==Bp
()
(п -целое, ^ @, 1)), если Р (?=*) «(^)рА A -
. Распределение Вр будем обозначать через В^.

§ 2. СВОЙСТВА ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ И ПРИМЕРЫ Ш
3. Равномерное распределение Uaj&. Если 1>€Ё^а,ъ, то
Р (fe e ii) = -—7tJ~7T\—•> гДе Iх — мера Лебега. Мы видели,.
что это распределение имеет функцию распределения A).
Следующее распределение играет особою роль в теории веро-
вероятностей, мы будем сталкиваться с ним многократно.
А. Нормальное распределение Фа а2 (нормальный закон или
закол Гаусса). Будем писать ?€§Фао2, е^ли
Распределение Фа а2 зависит от двух параметров: а и a > 0.
Если а =з 0, а=1, то нормальное распределение называют стан-
стандартным. Функция распределения Ф0| 4 (будем обозначать ее че-
через Ф(#))»
ОС
Ф (х) = Фод ((- оо, х)) = -^г Г е~/2йм.
— ос
Очевидно, что функция распределения для Фа а2 равна Ф
так что параметры а и о имеют смысл параметров «сдвига» и
«масштаба» распределения.
Тот факт, что формула C) определяет распределение, следует
хотя бы из теоремы 1 и того, что функция Ф(х) (или ф х ~~ а
о
удовлетворяет свойствам F1 — F3, так как Ф(-—оо)=0, Ф(°о)= j?
Ф(х) непрерывна и монотонна. Можно использовать и непосред-
непосредственно тот факт, что интеграл в C) есть счетно-аддитивная
функция множества (см. § 6 и Приложение 3).
5* Показательное распределение Га. Соотношение 5€§Га озна-
означает, что | неотрицательна и
j e~avdu.
)
Функция распределения ?(§§ Га имеет, очевидно, вид
A — е~~ах при ж>0,
Г1ь^ ; [0 при ^<0.
Показательное распределение есть 'частный случай Г-распределе-
ция Га, я, которое мы рассмотрим более подробно в § 7.7.
G, Дискретный аналог показательного распределения называ-
называют иногда геометрическим. Оно имеет вид
Р(Ъ=к) = A-р)рк, ре @,1), fc=O, 1, ...
^ А. А. Боровков

ov j.*i. о. <^i,y члмпъш и^Ш411ЛЫ И ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
7. Распределение Коша Ка>а. Как и нормальное распределе-
распределение, это есть распределение, зависящее от двух параметров а и
о > О, которые также являются параметрами сдвига и масштаба.
Если ??§К<х,G1, то
1 +
Функция распределения К(х) распределения K0,i равна
К(х)
X
i С da
Функция распределения для Ка, о равна/i ( — . Здесь сохра-
сохрапяются все замечания, сделанные по поводу нормального рас-
пределепия.
Пример 3. Предположим, что ъ некоторой точке (а, а),
а > 0, на плоскости находится источник излучения частиц. Следы
излучения фиксируются детектором, который совпадает с осью х
(осью абсцисс). Направление, в котором движутся излучаемые
частицы, случайно и имеет равномерное распределение на ок-
окружности. Другими словами, угол т], составленный этим направ-
направлением с осью ( — г/, 0), имеет равномерное распределение и_я, п
па отрезке [—я, я]. Результатами наблюдений являются коорди-
координаты ~t, §2, • . ¦ точек на оси абсцисс, в которых произошло взаи-
взаимодействие частиц с детектором. Что из себя представляет рас-
распределение случайной величины g = ?л?
Чтобы найти это распределение, рассмотрим частицу, выле-
вылетевшую из точки (а, а) при условии, что эта точка достигла де-
детектора (т. е. при условии, что ц е [—я/2, я/2]). Ясно, что услов-
условное распределение ц при этом условии (P(t]<s [—я/2, я/2] == 1/2))
совпадает с U-rt/2f п/а.' Так как (| — а)/а = tg rj, то
Р E < *•) = Р (а + а tg л < *) «
Р( ц 1 . х — а\ 1.1 . х — а
я ^д ° а / 2 1 л
Поскольку (arctg и)т == 5, то
1 —|- и
X X
, f du С da n
arctg ^r - ——г2 - ——о — т%
J 1 4- м J 1 + w - "
пс—а
" а "
f х — а
*) = - f -^Ц =
к

§ 2. СВОЙСТВА ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ II ПРИМЕРЫ 51
Таким образом, координаты наблюдаемых на оси абсцисс следов
излучения из точки (а, о) имеют распределение Копти Ка, о-
8. Распределение Пуассона 1\к. Мы будем писать ?g§ II?,, если
% принимает только целые неотрицательные значения с веро-
вероятностями
Р(ё = т) = -^-еЛ ц>0, /в = 0, 1,2, ...
Функция распределения, так же как и в примере 1, будет иметь
вид суммы:
2^-г е~11 для #;>0,
Г \Х) = m<JC
О для ж<;0.
Все распределения, рассмотренные в приведенных выше при-
примерах, можно разбить на два типа.
Дискретные распределения.
Определение 4. Распределение случайной ведичпиы ?.
называется дискретным, если ? может принимать лишь конечное
или счетное число значений хи хг> .., так что
Очевидно, что дискретное распределение {р,} всегда можно
задать на дискретном вероятностном пространстве. Характеризо-
Характеризовать такое распределение бывает удобно с помощью таблиц:
Значения
Вероятности
т2.
Pi P-2
?% дискретным распределениям относятся распределения 1«, Вр,,
11л, геометрическое распределение. Производная функции распре-
распределения F(x) для этих распределений всюду равна нулю, за ис-
исключением точек xh х2, .. ., где F(х) терпит разрыв, причем
Абсолютно непрерывные распределения*
Определение 5. Распределение Р случайной величины \
называется абсолютно непрерывным*), если для любого борелев-
*) Имеется в виду абсолютная непрерывность относительно меры Ле-
Лебега. Если на <Л, 23 > задана мера \х (см. Приложение 3), то распределе-
распределение Р называется абсолютно непрерывным относительно tu, если для любо-
любого J5 е ©
в
В этом смысле дискретные распределения также являются абсолютно не-
4*

52 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
«с к о го множества В
D)
в
где f(x)> О, j f(x)dx = 1,
Функция f(x) в равенстве D) называется плотностью рас-
распределения.
Из доказательства теоремы 1 (точнее, из теоремы о единст-
единственности продолжения меры) нетрудно получить, что приведен-
приведенное выше определение абсолютной непрерывности эквивалентно
представлению
для всех хей, Функции распределения, обладающие таким
свойством, также называются абсолютно непрерывными,
• Функция f(x) определяется приведенными выше равенства-
равенствами с точностью до значений на множестве меры 0. Для нее почти
всюду (по мере Лебега) имеет место равенство*) /(#)=—j-—„
dx **
Абсолютно непрерывными являются распределения XJa, &,
Фа>а2»Ка,а, Га. Плотность нормального закона с параметрами
а, а равна
Из приведенных ранее равенств очевидным образом можно полу-
получить и плотности распределений Ua, ь, Ка, о, Га- Плотность для
Ка, а имеет вид, напоминающий вид нормальной плотности, но
имеет более «толстые хвосты» (более медленное убывание при
Ы ~> оо).
Итак, распределения могут быть дискретными и абсолютно
непрерывными. Возможны, конечно, смеси двух типов распреде-
распределений. Но существует еще третий тип, не описываемый преды-
прерывными, по относительно считающей меры т. Действительно, если
положить f{Xk) = Phi m(B) = {числу точек из множества (xlt x2% .«.)? по*
павших в В}у то
р(в) =2 ра=2'К) =
(см. Приложение 3)*
*) Утверждение о единственности «почти всюду» функция / следует
также из теоремы Радона — Никодима (см. Приложение 3)*

§ 2. СВОЙСТВА ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ II ПРИМЕРЫ
53
при
дущимп двумя. Это сингулярный тип. Характеризуется он тем,
что функция распределения F(x) непрерывна, но точки роста
F(x) образуют множество нулевой меры Лебега, (Точка х назы-
называется точкой роста F(x), если для любого 8>0 'F(x+e) —
-~ F(x — е)> 0.)
Таким образом, здесь F(x) непрерывна, d * ¦ = 0 почти
всюду, a F(oo) — F(—<x>)= 1.
Примером такой функции распределения может служить из-
известная кривая Кантора, все изменение которой сосредоточено
на отрезке [0, 1]: F(x)==0
x^Q, F(#)=l при F(x)
L Строится она сле-
следующим образом (процесс
построения кривой Канто-
Кантора показан на рис. 3). От-
Отрезок [0, 1] разбивается на
три равные части [0, 1/3], ,
[1/3, 2/3], [2/3, 1]. На 7и
внутреннем сегменте по-
полагаем F(x)= 1/2. Остав-
Оставшиеся два сегмента снова
разбиваются на три рав-
равные части каждый, й на
внутренних сегментах
F (х) полагается равной
1/9 Z/3 1/5 2/J 7/3 В/9 1
Рис. 3
соответственно 1/4 и 3/4.
Каждый из оставшихся сегментов снова делится на три части и
на внутренних F(х) определяется как постоянная,-равная сред-
среднему арифметическому между соседними, уже определенными
значениями F(x), и т. д. В. точках, не принадлежащих таким
внутренним сегментам, F(x) определяется по непрерывности.
Нетрудно видеть, что суммарная длина «внутренних» сегментов,
ма которых F(х) постоянна, равна
11
9 + 27
гак что функция F(x) растет на множестве меры 0, но без
скачков.
Известна теорема Лебега *) о том, что любаяч функция распре-
распределения F (х) может быть единственным образом представлена
в виде суммы трех компонент: дискретной, абсолютно непрерыв-
непрерывной и сингулярной. Отсюда следует, что произвольная функция
распределения не может иметь более чем счетное число скачков
1
3 -
1
\^
С1'
з
Г
)
1
3
1
1
—
2

*) См. § 5 Приложения 3.

54 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
(это видно и непосредственно: мы перечислим все скачки, если
перенумеруем сначала все скачки, большие 1/2, затем все скач-
скачки, большие 1/3, зате>1 — большие 1/4, и т. д.). Это означает^.
в частности, что Р(х) непрерывна всюду, за исключением, быть
может, счетного или конечного множества точек.
В заключение приведем ряд свойств функций распределения
и плотностей, возникающих 'при переходе к новым случайным
величинам.
Пусть F% (х) = Р (g < х) и g(x) есть борелевская функция
(g(x) называется борелевской, если прообраз g"i(B) = {x\ g(x)^
е В} борелевского множества В есть снова борелевское множест-
множество). Тогда функция распределения случайной величины ц =g(^)
равна
Fg(l) (*) = Р (*(I) < *) = Р U e= g (- 6о, х)).
Если g{x)~ неубывающая функция, для которой определена
обратная g~l{x), то
Fgil) (х) = Р (& < g (*)) ^ ^ (^ И).
Полагая g = F% получим отсюда, в частности, что е'сли ^ непре-
непрерывна, то случайная величина Ц ^ Fi(l) распределена равномер-
равномерно на [0, 1]. Наоборот, пусть ц —- равномерно распределенная
случайная величина и F-— заданная непрерывная функция рас-
распределения. Тогда случайная величина i = F~x (ц) будет иметь
функцию распределения F(x). Мы получили, таким образом,
важный способ построения случайных величин с наперед задан-
заданными распределениями с помощью случайных величин, распре-
распределенных равномерно.
В другом частном случае, когда g(x) = a + bx, b > 0, получаем
^(ь) (х) === ^1 (~~Т—)• Этим соотношением мы'уже в какой-то
мере пользовались при рассмотрении распределений Фа а2 и Ка> „.
Если функция g строго возрастает и дифференцируема (в этом
случае определена gr1), а Ь, имеет плотность j(xI то существу-
существует плотность для g(|), равная
/в«) (у) = / (g-1 (у)) is'1 (у))' = / (*) %
где x^g~l{y), у = g(x) . Аналогичное рассмотрение для убыва-
убывающих g приводит к -общей формуле ¦
При g(x)= а + Ъх, ЬФ О, получаем
Ja+Ы (У) - -Щ- / ^—т—

§ 3. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 55
§ 3. Многомерные случайные величины
Пусть §ь %2, • •., In — случайные величины, заданные на ве-
вероятностном пространстве <й, S, Р>. Каждому со эти случай-
случайные величины ставят в соответствие га-мерыый вектор |(<о) =
= F,@)), |а(о>), ..., gn(©)).
Определение 6. Отображение Q -*¦ йп, задаваемое слу-
случайными величинами ?1? ?2, •.., In, называется случайным век-
вектором или многомерной случайной величиной,
Отображение Q -*- Rn следует рассматривать как измеримое
отображение <Q, 5> на пространство </?п, Эп>, где Эп есть а-ал-
гебра борелевских множеств в Rn. Поэтому для любого борелев-
ского множества В определена функция Pi (В) = Р(^е В).
Определение 7. Функция Р%(Щ называется распреде-
распределением вектора g.
Функция
называется функцией распределения случайного вектора (|i, ¦».
..., |п) или функцией совместного распределения случайных ве-
величин |ь..,, |п.
Приведем некоторые свойства функций распределения слу-
случайного вектора, которые называются свойствами согласо-
согласованности:
FF1. lira /^...^(жц I.., ^n) = F6l..igri-1B:ll ...^n-i)*
FF2. Ню /^...^(tfi, .-.,^n) = 0.
To, что пределы рассматриваются по последнему аргументу, не-
несущественно, так как всегда мойшо перенумеровать случайные
величины.
Доказываются эти свойства так^ же, как свойство F2 функ-
функций распределения одномерной случайной величины. Их можно
дополнить еще двумя свойствами/ подобными F1 и F3, и тогда
каждая функция F(хи ..., хп) с набором таких свойств будет
функцией распределения некоторой случайной величины.
Как и в одномерном случае, рассматривая случайные векто-
векторы ?=(?i, ..., gn), мы можем пользоваться простейшей выбо-
выборочной моделью вероятностного пространству (У, §, Р). Имен-
Именно, пусть Q совпадает с i?n, а а-алгебра 5? = 2)п составлена из бо-
борелевских множеств. Мы закончим построение требуемого ве-
вероятностного пространства, если для любого В ^Ъп положим
Р (В) == Pi (В) = Р (g ge В). Остается в качестве случайной ве-
величины принять само значение элементарного события, т. е. счи-
считать, что |(со) = о), где со есть точка в Rn.

56 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Нетрудно видеть, что функция распределения 1<\г in од-
однозначно определяет распределение Р^ (В). Действительно,
^1,..о?п определяет вероятность на алгебре *5/, порожденной
прямоугольниками {а?<#<<6?; i = 1, ..., п). Например, в дву-
двумерном случае
= [^h.Ea (bi' Ь2> - ^Elf?2 (bi, a2)] - [Flvi2{ax, b2) - F^ (ax, <za)].
Ho §3n = a(«5$), и нам остается воспользоваться теоремой о про-
продолжении меры (см. § 2.1).
Таким образом, по функции распределения ^х ,...,?„ = F
мы всегда можем построить выборочное вероятностное простран-
пространство (Rn, Sn, Pg> a случайную величину ^(со)^оз ад ие.м, ко-
торая будет иметь заданное распределение F^.
Так же, как и в одномерном случае, мы отнесем распределе-
распределение случайного вектора к дискретному типу, если случайный
вектор принимает пе более чем счетное число значений. Распре-
Распределение случайного вектора будет абсолютно непрерывного
типа, если для любого борелевского множества В с: Rn
где, очевидно, /(х) >0, J / (х) dx = 1. -
Это определение можно заменить на эквивалентное, потребо-
потребовав, чтобы
Х1 хп
Действительно, если имеет место E), то мы определим счет-
счетно-аддитивную функцию множеств Q (В) = j / (x) dx (см. свой-
в
ства интеграла в Приложении 3), которая на прямоугольниках
совпадает с Pi(B). Следовательно, Р%(В) = Q (В).
Функция }(х) называется плотностью распределения g или
плотностью совместного распределения \и , *., gn. Для нее почти
всюду имеет место равенство
...дхп
Если вектор | имеет плотность /(^1? ..., дг„), то, очевидно,
любой «подвектор» (?л1? •••j&fts)j ki^n, также имеет плотность,

§ 3. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 57
равную (пусть для простоты кг = i, i = 1, ..., s)
ij * * * xs) — J / («^1? . ». > #n) л^5+1
Пусть в некоторой области А а Rn заданы непрерывно диф-
дифференцируемые функции yi = gi(xi9 ».., хп), которые однозначно
разрешимы относительно хЛ1 ».., хп: x^gj (уъ .,м 1/п),при этом
якобиан / ==
в А Обозначим через В образ А в про-
странстве значений (уи ..., г/п). Пусть далее случайный вектор
^=(gi, ..., ?„) имеет плотность ft(x). Тогда <n*s=s?»(li> • • •» ?*)
будут случайными величинами с плотностью совместного распре-
распределения в точке (уи ..., уп)^В, равной
/n(?/i ••• Уп) — h(xi . . #n)l/l* (8)
¦кроме того
Г
^5 с= ^i; = ] /t ^J>|, » . ., хп) aXjL . . . (IXп —-
А
в
'Это есть, очевидно, обобщение на многомерный случай свойства
плотности, рассмотренного в конце § 2. Формулы G) для инте-
интегралов хорошо известны в классическом анализе как формулы
о замене переменной в интеграле и могут служить доказатель-
доказательством F).
Рассмотрим два важных примера многомерных распределе-
распределений (мы продолжаем список наиболее употребительных распре-
распределений, начатый в § 2).
9. Полиномиальное распределение В". Мы используем здесь
тот же символ В?, что и для биномиального распределения,
с той лишь разницей, что под р будем понимать здесь вектор
г
P—iPi, •••» Рт), Pi^O, S Pi = 1» который можно интерпретиро-
интерпретировать как набор вероятностей г несовместных событий Аь
иЛ,- = й. Для целочисленного случайного вектора v = (Vi, ...., vr)
-будем писать vg=B]J, если для fe=(/ru ,.., ftr), &j^0, 2 kj = n
3=1
справедливо
Справа здесь стоит элемент разложения полинома (р} 4-... 4- рг)п
по степеням ри ,§м рг. Это объясняет название распределения,

58 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Если р — число, то, очевидно, В™ = B™Pil-P)f так что биномиаль-
биномиальное распределение есть полиномиальное при г = 2,
Числа Vj можно интерпретировать как частоты появлений со-
событий Aj после п независимых испытаний (вероятность появле-
появления А) в каждом испытании равна pj). Действительно, вероят-
вероятность любой фиксированной последовательности исходов, содер-
содержащей соответственно ки ..., кт исходов Аи ,.., Аг, равна
Pi ... pr , а число различных таких последовательностей равно
n\/ki\ ... кг\ (из п\ перестановок надо оставить те, которые отли-
отличаются не только перестановками элементов внутри групп ки ...
..., кг). Получим в результате вероятность (8).
Пример 4. Простейшей вероятностной моделью турнира
между двумя шахматистами можно считать следующую. В каждой
партии независимо от исходов предыдущих партий 1-й игрок вы-
выигрывает с вероятностью /?, проигрывает с вероятностью q и делает
ничью с вероятностью 1 — р — q. В этом случае вероятность того,.
что в п партиях 1-й игрок одержит i побед и потерпит j пора-
поражений (i + j ^ я), будет равна
р(«;'. /)- wfr-i-a. рVа-Р-дГ*->.
Допустим, что турнир продолжается до тех пор, пока один из
двух игроков не наберет N выигрышей (ему и присуждается по-
победа). Если обозначить через ц продолжительность турнира
(число партий до его окончания), то
N-l N-1
Р(ц = п)^ 2 p(n — l;N — l, i)p+ 2 P(*-1; *, ЛГ-1)<7.
10. Многомерное нормальное распределение Фа а2. Пусть а
есть вектор а = (а!, ..., аг) и о2=\\оC\\, г, / = 1, ..., г, есть сим-
симметричная положительно определенная матрица, А ='Ня JI —
матрица, обратная к а2 = А~\ Мы будем говорить, что вектор
?=(§i, ..., %г) имеет нормальное распределение ^ё§Фа>а2, если
это распределение имеет плотность
4 ^Х ~" а) А (Х -
Здесь Т означает операцию транспонирования:
Нетрудно проверить, что
(см. так,же § 6.6).

§ 4. НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН 53
§ 4. Независимость случайных величин и классов событий
1. Независимость случайных величин.
Определение 8. Случайные величины %и ..., |rt называ-
называются не зависимыми, если
PfoeEff,, ...)|„еВ„) = Р(?1ев1)...Р(^еЩ (9)
для любых борелевских множеств Ви ..., Вп па прямой.
Можно ввести понятие последовательности независимых слу-
случайных величин. Случайные величины последовательности
{En}^=ij заданные на вероятностном пространстве <О, S,P>,
независимы, если для любого целого числа п выполняется (9)
так, что независимость последовательности случайных величии
сводится к независимости любого конечного набора случайных
величин из этой последовательности. Как увидим позже, для по-
последовательности независимых случайных величин будут незави-
независимыми любые два события, относящиеся к непересекающимся
группам случайных величин из этой последовательности.
Другое возможное определение независимости случайных ве-
величин вытекает из следующего утверждения.
Теорема 2. Случайные величины \и ,.., ??г независимы
тогда и только тогда, когда
Fh...tn(хп • • •» *") = Fit (*i) ... Fln (xn).
Доказательство этой теоремы отнесено нами в п. 3 этого па-
параграфа.
Если распределение ?=(|ь ..., ?п) абсолютно непрерывно,
то важный критерий независимости ^- содержится в теореме 3.
Теорема 3. Пусть случайные величины |t, ..., |п имеют
плотности fi(x), ..., jn(%) соответственно. Тогда для независи-
независимости ?,, ..., \п необходимо и достаточно, чтобы существовала
плотность S{x\i • • •? Хп) вектора | =(^i, ..., |л), равная
Таким образом, если окажется, что плотность § равна про-
произведению плотностей ?j, то это будет означать независимость ?.,.
Мы предоставляем читателю пользуясь этой теоремой убе-
убедиться, что компоненты нормального вектора (§t, .. г, §п) неза-
независимы тогда и только тогда, когда а<ц = 0, <Эц = 0 при i Ф ]'.
Доказательство теоремы 3. Если функция распре-
распределения случайной величины ^ равна
fi(ii)dtH
ж §г независимы, то совместная функция распределения будет

60 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
определяться формулой
- j fAQdh..* j f{tn)dtn= j t., j f1(t1)...fn(tn)dt1...dtn.
— oo —oo —oo —oo
Обратно, предположив, что
Fh-<tn(xn •• •' xn) =* J ««• j fi(h) ^* U(tn)dt1 .,,dtni
получим равенство
— oo — oo
Рассмотрим теперь дискретный случай. Пусть для простоты
компоненты g могут принимать лишь целочисленные значения.
Тогда для независимости gj необходимо и достаточно, чтобы при
всех /Ci, ..,, fcn
Р(I, = klt ..., L = кп) = РA, = к,) tt. P(L = ftB).
Проверка этого утверждения не вызывает затруднений, и мы ос-
оставляем ее читателю.
Понятие независимости является весьма важным в теории
вероятностей и будет использоваться на протяжении всего курса»
Допустим, что мы формализуем какую-нибудь практическую за-
задачу (строим подходящую вероятностную модель, в которой
присутствуют различные случайные величины). Как установить,
будут ли эти случайные величины (или события) независимыми?
В такого рода ситуациях оправдано правило считать независи-
независимыми события и случайные величины, не связанные причинно.
В связи с этим выявление «вероятностной» независимости
в математической модели случайного явления часто связано
с глубоким проникновением в его физическую сущность.
Рассмотрим некоторые простые примеры. Известно, например,.
что вероятность новорожденному оказаться мальчиком имеет
довольно устойчивое значение Р (А) = 22/43. Если В означает
условие, что рождение происходит в день соединения Юпитера
с Марсом, то в предположении, что расположение планет ее
определяет индивидуальных судеб людей, условная вероятность
Р (^4/5) -будет иметь то же самое значение: Р (Л/В) = 22/43^
т. е. фактический подсчет частоты рождения мальчиков при та-
таких специальных астрологических условиях привел бы именно
к частоте 22/43. Хотя такой подсчет в достаточно обширных
размерах, возможно, никем не проводился, нет оснований сомне-
сомневаться в его результатах.

§ 4. НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН 6f
Естественно, что связь между «математической» и причинной
независимостью не следует абсолютизировать. Например, в силу
закона всемирного тяготения несомненно, что полет одного ар-
артиллерийского снаряда оказывает некоторое влияние на происхо-
происходящий одновременно полет другого снаряда. Но очевидно, что
на практике с этим влиянием можно не считаться. Сказанное
поясняет также, что независимость событий и величин в том
конкретном и относительном понимании этого термина, которое
каждый раз имеет место, никак не противоречит принципу все-
всеобщей связи всех явлений.
Любопытно отметить также, что формальное определение не-
независимости событий или случайных величин значительно шире
понятия реальной независимости в смысле принадлежности
к причинно не связанным явлениям. Это следует из того, что
«математическая» независимость может иметь место и в тех
случаях, когда нет никаких оснований предполагать отсутствие
причинной связи. Сказанное можно проиллюстрировать с по-
помощью следующего примера. Пусть г| есть равномерно распреде-
распределенная на [0, 1] случайная -величина. Тогда в разложении ц
в двоичную дробь
случайные величины |ft будут независимыми (см. пример 10.1),
хотя все они связаны по своему происхождению.
Понятно, что это обстоятельство лишь расширяет сферу при-
применения всех утверждений, которые получены нами ниже при
выполнении формального условия независимости*).
С понятием независимости случайных величин тесно связано
понятие независимости о-алгебр.
2. Независимость классов событии. Пусть (Й, 2f, Р) — ве-
вероятностное пространство, а $ФХ и s4-% — классы событий, содер-
содержащиеся в с-алгебре 5.
Определение 9- Классы событий М{ и $Фг называются
независимыми, если для любых событий Ах и А2 таких, что
Ai^sf-i и A2<^s$2, имеет место равенство
Следующее определение вводит понятие независимости после-
последовательности классов событий.
*) Более подробное обсуждение связи причинной и вероятностной неза-
независимости можно найти у А*. Н. Колмогорова в книге [10], из которой заим-
заимствованы приведенные здесь примеры.

ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Определение 1-0. Классы событий {^n}n=i независимы^
если для каждого набора целых чисел пи ..., пк
при любых Ап. е S&n-f
Например, в последовательности независимых испытаний
а-иодалгебры событии, относящихся к различным испытаниям,
будут независимы. Независимость последовательности алгебр со-
событий также сводится к независимости любого конечного набора
алгебр из этой последовательности. Ясно, что подалгебры собы-
событии независимых алгебр событий также независимы.
Теорема 4. а-алгебры %{ и St2, порожденные соответствен-
соответственно независимыми алгебрами событий ?Ф% и *5#2, независимы.
Прежде чем доказывать это утверждение, получим полезную
для дальнейшего теорему об аппроксимации, в силу которой лю-
любое событие А из а-алгебры §1, порожденной некоторой алгеб-
алгеброй s4, можно приближать в известном смысле событиями из з&%
Чтобы быть более точными, введем в рассмотрение «расстояние»
между событиями
d (Л, В)= Р (AB\JAB)=*P (АВ) +Р (АВ) =Р (А-~В)+Р(В-Л)„
Оно обладает свойствами
d(A,B),
d(A,B) + d(B,C)J
D) ' ( '
Первое из этих соотношений очевидно. Неравенство треугольни-
треугольника вытекает из того, что
d(A, С) = Р (АС) + Р (АС) = Р (АСВ) + Р (АСВ) +
+ Р (АСВ) + РBСВ) < Р (СВ) + Р(АВ)+Р (АВ) +
Третье соотношение в A0) получается аналогично путем укруп-
пения событий под знаком вероятности. Наконец, последнее не-
неравенство в A0) есть следствие того, что
Р (А) = Р (АВ) + Р(АВ) = Р (Я) - Р (ВА) + Р {АВ).
Теорема 5 (теорема аппроксимации). Пусть <Q, S, Р> —
вероятностное пространство и §1 есть в-алгебра, порожденная
.некоторой алгеброй М- событий из S. Тогда для любого А ^ %

§ 4. НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН . $3"
существует последовательность An<^s&, обладающая свойством
Jim d{A, An) = 0. A1)
П-*оо
В силу последнего неравенства в A0) утверждение теоремы
означает, что Р (А) = lim P(An) и каждое событие А^% мо-
жет быть с точностью до множества нулевой вероятности пред-
представлено как предел последовательности событий из порождаю-
порождающей алгебры s$ (см. также Приложение 1).
Доказательство*). Событие А^д назовем аппроксими-
аппроксимируемым, если для пего существует последовательность An^s&^
обладающая свойством A1), т. е. d(An, А)->0.
Так как d(A, Л) = 0, то совокупность аппроксимируемых со-
событий Я* содержит М. Поэтому для доказательства теоремы до-
достаточно убедиться, что Я* есть а-алгебра.
Тот^ факт, что §1* образует алгебру, очевиден, поскольку соот-
соотношения 4eS(*, 5eЯ* влекут за" собой A, AUB1 ЛП2?<=Я*.
(Например, если d(A, 4«)->0, d(B, i?A)~>0, то в силу третьего
неравенства в A0) d(AB, AnBn)^d(A, An) + d(B, ?«)->-0,
Пусть теперь
п
Так как Я* — алгебра, то Dn = U Cfe e SI*; при этом
d (?•„, С) = Р (С - Dn) = Р (С) - Р (Dn) -> 0.
Поэтому можно выбрать An^s4 так, что d(Dn, An)<l/n и, сле-
следовательно, в силу A0)
Таким образом, Ce^l* и Я* образует о-алгебру. <4
Доказательство теоремы 4 получить теперь нетруд-
нетрудно. Если Ах^Щц и Л2е^2, то по теореме 5 существуют последо-
последовательности Ain^s^i и А2пЕ=<$&2 такие, что d(Au Ain)-*-Q при
п-*-оо9 i = l9 2. Обозначив Л = AiA2, Bn = AinA2n, получим
d(B, Bn)<d(Au Aln) + d(A2, Ain)-» 0
при п -*- °°,
Р (ЛХА.) = Нт Р EП) = Ню Р (А„) Р (Агп) = Р (Лх) Р D). «
*) Эта теорема является также прямым следствием леммы из Прило-
Приложения 1,

-64 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
3, Связь введенных понятий. Нам понадобится еще следую-
следующее определение. Пусть ? ~ случайная величина (или вектор),
определенная на вероятностном пространстве <й, §, Р>.
Определение 11. Класс 55 множеств из W мы назовем
<5-алгеброй,- порожденной случайной величиной ?, если* о в обра-
образован событиями вида А = |~1E) = (со: |((o)ei?}? где В — боре-
левские множества.
То, что Й| образует G-алгебру, очевидно, поскольку каждой
операции над множествами А соответствует такая же операция
над множествами В = Ь)(А), образующими а-алгебру.
а-алгебру §?, порожденную случайной величиной ?, будем
обозначать также символом о(|).
Рассмотрим, например, вероятностное пространство <Я, Э
Р), где О =/? есть вещественная прямая, а Э — о-алгебра боре-
левских множеств. Если
(О, со<0,
6-6N-{l, о»О,
-то ??<;, очевидно, будет состоять из 4 множеств: й, 0, (со < 0),
{(о-^О). Более «тонких» событии так определенная случайная
величина ^ «выделять» из 53 не может. В то же время очевидно,
что | будет измерима ({|eB}sSi) относительно любой другой
более «богатой» о-подалгебры 931 такой, что о^)^:©!^^.
Если | = 1(о)) = [со] есть целая часть со, то Si будет о-алгеб-
рои множеств, составленных из событий {к ^ со < к + 1},
ft = ..., -1, 0, 1, ....
Если, наконец, |(ш) = ф(о)), где ф непрерывна и монотонна,
ф(оо)=оо? ф(~оо) = — оо? то gs будет совпадать с а-алгеброй бо-
релевских множеств 9.
Лемма 1. Пусть на <Я, S, Р> заданы две случайные ве-
величины ^ м г], величина | является измеримой относительно о(ц).
Тогда Ь, и ц функционально связаны, т. е. существует борелевская
функция g такая, что ?'=g(r|)'
Доказательство. По условию
Обозначим -Bftln = {т|(B))" «G^,«' образы множеств Л^1П па
прямой R при отображении т](со) и положим gn(a:)=fc/2n при
xe=Bktn. Тогда гп(л) = Г2и6]/2п, и поскольку ЛЛ,п^а(т1)", то
5ft,17eS и g"n есть борелевская функция, Так как gn(x)\ при
каждом х, то существует Hmgy, (#)== g (#), который также явля-
ется борелевской функцией. Остается заметить, что по самому
построению I = lim g,, (и) = g{v\). *t
Теперь сформулируем очевидное предложение, связывающее
независимость случайных величии и а-алгебр.

§ 4. НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН 03
Случайные величины ?ь ..., ?п независимы тогда и только
тогда, когда независимы о-алгебры о(^), ..., а(|л).
Это есть прямое следствие определений независимости случай-
случайных величии и о-алгебр.
Мы можем получить теперь доказательство теоремы 2. Заме-
Заметим предварительно, что конечные объединения полуинтервалов
вида [•, •) (возможно, с бесконечно удаленными концами) обра-
образуют алгебру J$, которая порождает борелевскую а-алгебру 3
на прямой: Ъ==а(М).
Доказательство теоремы 2. Так как в одну сторо-
сторону утверждение теоремы очевидно, то достаточно убедиться, что
равенство для совместной функции распределения F(xu ¦.., #п)=*
= f\x (xi) . . . P\n(xv) влечет за собой независимость 0(§4), ..»
..., а(?„). Положим для простоты п = 2 m обозначим Л и Л соот-
соответственно полуинтервалы [xti x2) и [у{, уг). Тогда будут спра-
справедливы равенства
Р(|ге= Д, ?2€=Л) = P^ge^, s2), S2^L?i, l/2))-
Следовательно, если Л?-, г = 1, ..., п, ш А3, / = 1, •.., w,— две
системы не пересекающихся полуинтервалов, то
и Дг,^е и
^ W Д A2)
Но класс событий {(о: |((о) е Л} = |~!(Л), где 4е^, вместе
с «5^ образует алгебру (обозначим ее а(|)) и при этом а (а E))==
= a(g). Мы доказали в A2), что a(gi) и а(|2) независимы.
Следовательно, по теореме 4 будут независимы o(|i)=o(a(|1)I
() (Ы) ^
Сформулируем теперь в виде теоремы следующий факт.
Теорема 6. Пусть <рь ф2 — борелевеше функции и %% и
^ — независимые случайные величины, тогда Г|1 = ф1(^1) и ц2 ==
^фПйз) —также независимые случайные величины*
Доказательство. Нам надо убедиться, что
Р (Ф,3 (Sx) е Вг, Фз (?а) е S2) = Р (Фх FХ) е Вг) Р (ф2 (?а) е В2)> A3)
Но множества {^: Чч {%) е SJ = ф;" E4) == fi^ снова являются
5 А. А. Боровкоз

66 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
борелевскими. Поэтому
и требуемая мультипликативность вероятности A3) следует из
независимости |,-. Л
Пусть {?n}n=i —последовательность независимых случайных
величин. Рассмотрим случайные величины ?й, ?й+1, ..., |m,-где
к <m^oot Пусть a(§ft, ,.., ?>)" (при етг = °о мы будем писать
oEh, 6ft+ij •••)) означает a-алгебру событий, порожденную собы-
событиями П Аи где Аг^ o(rgi).
i—h
Определение 12. о-алгебра o(%k, ..., ?m) называется по-
порожденной случайными величинами gft, ..., ?,„.
Для дальнейшего нам понадобится следующее предложение.
Теорема 7. Для любого А ^ 1 о-алгебра o(tn+h) не зависит
от с(?4, ..., gn).
Доказательство, Чтобы доказать это утверждение, вос-
воспользуемся теоремой 4, Для этого мы должны убедиться, что
алгебра <5#, порожденная множествами вида В = П Ах^ рде ^е
^а(У, не зависит от a(gn+/J). Пусть i4eo(g«+fe), тогда из неза-
независимости a-алгебр a^4), a(?2), f.., а(|п), оAд+л) следует
Р (АВ) = Р(А)Р (А,) „ . Р (Л,г) = Р (Л) . Р (В). ,
Аналогично убеждаемся, что
(надо лишь U ^i представить в виде объединения непересе-
кающихся множеств из s4>). Таким образом, алгебра S& не зави-
зависит от оЦп+к). Следовательно, a(gt, ,.., |п) и a(gn+ft) неза-
независимы. ^
Нетрудно понять, что заключения, аналогичные предыдущим,
можно сделать и относительно векторных случайных величин llv
?г? ..., определив их независимость с помощью соотношений
где Sj—борелевские множества в пространствах соответствую-
соответствующей размерности.
В заключение этого параграфа отметим, что вероятностное
пространство <й, S, P> (<i?n, 33г\ Р^>)? на котором заданы
независимые случайные величины |lt ,.,, ^п с даннышг распре-
распределениями F*. компонент |j, всегда можно построить, если эти
распределения ^ известны. Ото следует непосредственно из.

§ 5. О БЕСКОНЕЧНОМЕРНЫХ СЛУЧАЙНЫХ ВЕЛИЧИНАХ 67
| 3, так как в нашем случае функция совместного распределения ¦
Fi{xu ..., хп) вектора ? = (|i, ..., %п) однозначно определяется
функциями распределения F§. (х) величии ^
§ 5 *. О бесконечных последовательностях случайных величии
Бесконечные последовательности случайных величин ужо
упоминались. Такие последовательности в дальнейшем не ра;$
-будут предметом наших рассмотрений. Однако возникает вопрос,
всегда ли можно на вероятностном пространстве задать беско-
бесконечную последовательность так, чтобы ее координаты обладали
наперед заданными свойствами (например, были одинаково рас-
распределены и независимы).
Как мы видели, конечную последовательность независимых
•случайных величин задать всегда можпо, рассмотрев для «состав-
«составной» случайной величины (§,, ..., rgn) выборочное вероятностное
пространство /?! Х/?2 X ... X Rn = Rn и о-алгебру З^ХЭ^Х...
. .. X Э„ = Э'\ порожденную множествами вида В4 X J52 X ...
. . .X Bncz R'\ где Bi — борелевские множества. На алгебре этих
множеств и достаточно задать вероятность. Однако в бесконечно-
бесконечномерном случае дело обстоит сложнее. Здесь уже недостаточно
теоремы 1 и ее обобщения иа многомерный случай. Надо суметь
сю
задать вероятность на такой алгебре событий из R°° = JJ_ Rhl
замыкание которой относительно счетного числа операций U ш П
образовывало бы а-алгебру §3°°, порожденную произведениями
Пусть N — некоторое подмножество целых чисел. Обозначим
R1 " И ^ь прямое произведение пространств R,, по fee N,
§3Л = ТТ ®и- Мы будем говорить, что распределения Р „г и Р „„ на
х/?1 , S* / и \Я , Э1 J согласованы, если меры па пересе-
пересечении Лд> = Д*' П Я*'"(для /?iV здесь Л/= TV' R7V"), которыо
индуцированы мерами Рл^иРдт//, совпадают. Эти меры на RN
называются проекциями соответственно PN? и РN» на ДхУ.
Ответ па поставленный выше вопрос о существовании бесконеч-
бесконечной последовательности случайных величин содержится в следую-
следующей теореме Колмогорова (доказательство ее приведено в При-
Приложении 2).
Теорема Колмогорова. Задание па конечномерных
пространствах RN согласованных распределений Рл определяет
5*

68 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
на <Д°°, ©°°> такую единственную вероятностную меру Р^, что
каждая вероятность Pjv есть проекция Роо на /?л.
Из этой теоремы следует, is частности, что па соответствую-
соответствующем пространстве всегда можно задать бесконечную последова-
последовательность произвольных независимых случайных величин. Ве:н>
прямые произведения мер, заданных на Ru i?2, ..., для различ-
пых произведении п и и _, очевидно, всегда согласованы.
§ 6. Интегралы
L Интеграл по мере. Как уже отмечалось, задание вероят-
вероятностного пространства означает задание конечной счетпо-аддп-
тивлой меры. Это делает возможным рассмотрение интегралов по
введенной мере
по множеству Q для боролевской функции g и для любой слу-
случайной величины \ на <й, 5?, Р> (напомним, что g{x) назы-
называется борелевской, если lx: g(x)<t) при любом t есть борелев-
скос множество па прямой).
Определение, конструкция и основные свойства интеграла по
мере предполагаются известными читателю. Если читатель1 чув-
чувствует себя недостаточно подготовленным, то мы рекомендуем
ему познакомиться с Приложением 3, где содержатся все необ-
необходимые сведения. Но читатель может и не делать этого, еслм
он готов ограничить себя в дальнейшем только рассмотрело ем
дискретных и абсолютно непрерывных расвределеиий, для кото-
которых интегралы превращаются в суммы или в обычные римаиошл-
интегралы. Для дальнейшего полезно также знание интеграла
Стилтьеса; комментарии по этому поводу см. в п. 2.
Мы уже знаем, что случайная величина ?(о)) индуцирует
меру Р| на прямой, задаваемую равенством
Р| ([х, у)) = Р (х <? < у) = F* (у) - Ft (a-).
С помощью этой меры интеграл A4) можно записать в виде
Это равенство есть результат подстановки ж = |(о)). Доказать
его можно, выписав определения обоих интегралов. Интеграл
в правой части, называемый интегралом Лебега — Стилтьеса от
функции g(x) по мере Р^, может быть записан также в виде
\g(x)dFl(x). A5)
2. Интеграл Стилтьеса* Интеграл A5) часто называется про-
просто интегралом Стилтьеса, как, впрочем, и интеграл Рим а на-—

§ С. Ш1ТЕГРАЛЫ 69
Стилтьеса, который определяется несколько иначе и для более
узкого класса функций g(x).
Если g(x)—непрерывная функция, то интеграл Лебега —
Стилтьеса совпадает с интегралом Римана — Стилтьеса, равным
по определению
N
\ S G) A6)
где предел в правой части не зависит от разбиения х0, хи ..., Хя
полуинтервала \а, Ъ) и выбора точек хл ^ Дй = [#А, xh+i)> Разбие-
Разбиение х0, хи ..., x.v (свое для каждого N) обладает тем свойством,
иле* max (xh+1 — xh) ->• 0 ijpn N->- oo.
h
Действительно, как мы знаем (см. Приложение 3)', интеграл
Лебега — Стилтьеса есть
\g(x)dF(x)= Iim Iim \ gN (x) P^dx), A7)
Ь
а
где gN —- любая последовательность простых функций (принима-
(принимающих конечное число значений), монотонно сходящихся к g(x).
Из приведенных определений видно, что достаточно доказать
ь
совпадение интегралов J в конечных пределах. Так как интс-
а
Ь
грал Лебега — Стилтьеса j gdF от непрерывной функции g
а
всегда существует, то в его определении можно в качестве gN
взять две последовательности простых функций gN и gA-" y по-
постоянных на'полуинтервалах А& и равных на них соответственно
g*(xh) = sup g{x) и g**(xk)= inf g(x).
А
Обе последовательности в A7), построешще по gN ^ g^ t будут,
очевидно, монотонно сходиться с разных сторон к одному и тому
ь
же пределу, равному интегралу Лебега — Стилтьеса J g(x)dF (x).
а
Но для любых xh e As будет выполняться
и, следовательно, интегральная сумма в A) будет заключена
в границах
ь N ь
f gl*d.F (x) < 2 g (xk) [F (xh+l) - F (хк)\ < J g« (x) dF {x).

70 ГЛ. 3. СЛУЧАЙНЫЕ ВЕДШПШЪТ II ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Эти неравенства и доказывают, очевидно, треб}гемое сов-
совпадение.
Нетрудно проверить, что такое же совпадение A7) и A8)
будет и в том случае, если F (х) непрерывна, a g{x) есть функ-
функция ограниченной вариации, при этом
ь ь
J g (x) dF (х) = g (.r) F (х) Ц - j- F (х) dg (x).
а а
Пользуясь здесь этим обстоятельством, мы можем определе-
определение интеграла Римана — Стилтьеса распространить и на случай,
когда g(x) есть функция ограниченной вариации, a F(x) — про-
произвольная функция распределения. Действительно, пусть F(x)=-
~Ра(х) + Рд(х) есть представление F в виде суммы непрерыв-
непрерывной и дискретной компонент, и ?/1? #>, ... есть точки скачков
функции Рл(х):
p!:^Fa(ih + Q)-Fu(Uk)>0.
Тогда следует по определению положить
Jg (x) dF (х) == Ц phg (yh) + J g (x) dFu (x),
где интеграл Римана —- Стилтьеса \gdFu(x) можно понимать
уже, как мы отмечали, в смысле определения A8),
Как общепринято, будем говорить, что \ gdF существует,
^ если J \g\dF конечен/Из определения интеграла Стилтьеса лег-
легко обнаружить, что для ступенчатых F(х) (распределение диск-
дискретно) интеграл превращается в сумму
f g (х) dF (х) = 2 g Ы F (х, + 0)-F (х„)) = 2 g (*ь) Р (I = xh),
к к
х
где xh х2, «..-—точки скачков F(x). Если же F (х) = \ р(х)сх
— ос
абсолютно непрерывна, а р(х) и g(x) интегрируемы ко Римапу,
то интеграл Стилтьеса
превращается в обычный интеграл Римана.
Еще раз отметим, что читателю, плохо знакомому с техникой
интеграла Стилтъеса и интегрированием по мере, можно продол-
жить чтение книги, имея в виду лишь эти две интерпретации
интеграла. Этого вполне достаточно для понимания существа
изложения. К тому же большинство практически важных распре-
распределений относится именно к этим типам — дискретному ппш
абсолютно непрерывному.

§ 8, ИНТЕГРАЛЫ 71
Напомним некоторые другие свойства интеграла Стилтьеса
(непосредственно вытекающие из определений A7) или A6)):
ъ
J dF = F (b) - F (а);
а
Ь
gdF = § gdF + § gdF;
cgdF = с J gJF лри с = const}
если g — функция ограниченной вариации,
3. Интегралы от многомерных случайных величин. Распреде-
Распределение суммы независимых случайных величин. Интегралы во
мере A4) сохраняют свой смысл и для многомерных |(°>)===
= (|1(oi)), ,.., gn(o))) (этого нельзя сказать об интегралах Ри-
Рима на — Стилтьеса A6))-. Имеется в виду интеграл
A8)
где g есть бореловская функция, отображающая Rn в R, так "что
g(|i((o), ..., |„((о)) будет измеримым образом отображать Q в R.
Если </?n, Sn, P|> — выборочное вероятностное пространство
для g, то интеграл A8) можно записать в виде
J g (x) P% (dx), х =^{хг .. v, xn) e Rn»
Обратимся теперь к случаю, когда компоненты ^, ..., |п
вектора 5 независимы и пусть сначала ?г = 2. Для множеств
В = В,ХВ2=г-{ (хь х2): х, е= Д1а х2 е Б2} cz i?2,
где fii и В2 принадлежат R и измеримы, выполняется равенство
Р(|еД) = Ра1еД1, |2efi2) = P(|1efi1)PfeeS*). A9)
В этом случае говорят, что мера P\lt %2(dxu dx2) = Р(|А ^ й^1?
^2 е &2) в Л2, соответствующая (|ь |2), является прямым про-
произведением мер

72 ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАС11РЕДЕЛЫШН
Как мы уже знаем, равенство A9) однозначно определяет
меру в </?2? Э'> по заданным распределениям ?i и ?2 в </?, Э>.
При этом оказывается, что интеграл
^gixuxJP^idx^dXs) B0)
но мере Р|,|.2 можно выразить через интегралы по мерам Р^
и Р^. Именно, справедлива следующая теорема Фубиыи (дока-
(доказательство ее см. в Приложении 3 или см, свойство 5А § 4.8).
Теорема 8 (теорема о повторном интегрировании). Для
борелесской функции g(x, j/)^0 и для независимых ?, и ?2
h (dxl7 dx2) = J [Jg(.rlT *2)
Если g(x, у) разнозначна, то для выполнения равенства B1)
требуется существование интеграла, в левой части B1), Индек*
сы 1 и 2 в правой части B1) можно менять местами,
В Приложении 3 показано, что измеримость g(x, у) влечет
измеримость подынтегральных функций в правой частя B1).
Следствие 1. Пусть g{xu x2) = gi{Xi)gz(xz), Тогда, если
выполнено хотя бы одно из трех условий
¦1)
) ?
2) J
i)g2MPtlt2(dxLi dx^ существует,
3) j gj{zj) Ptjidxj), / = 1, 2, существуют,
TO
J ?i fe) g2 (*3) P^ib №i, ^2) = J gi (^1) Psi (d*i) (g2 B) L (
B2)
Чтобы избежать тривиальных затруднений, предполагаем, что
РE-(У ^0)^1, 7 = 1., 2.
Доказательство. При выполнении первых двух условий
утверждение следствия немедленно вытекает из теоремы Фубпнет.
Для произвольных g{1 g2 положим g! = gf— gj, gj ^ 0, / = 1, 2.
Если jgfdPlj^ °° (будем использовать здесь эту сокращенную
запись интегралов), то
dPh-\ g{ g~ dPh dPtl - J g- g+ dPhdPh +
T 87 dPh dPh = j ff+ dP6l J edPs2 -
J ffi"dP^ -J ^ dP^i I С*Рез +.f ?rJp5i J erdPh -

§ е. интегралы 73
Следствие 2. В частном -случае, когда $ (х^ х2) = IB (#i, х2)
есть индикатор множества В <=? S2, получаем формулу о последо-
последовательном вычислении меры множества В:
= j P (to, |2) <= 5) PEi!
Вероятность события {(#ь |2) е ^ можно записать также
в виде P(l2e^1) = P?2(^x1), где BXl=*{x2: (хх, х2)<= В} мть
«сечение» множества В в точке а?!.
Если В = {(#!, #2): Xj + х2 < х), мы получим
(«х + |2 < л) P6l (dxj = j i'\2 (x - х,) di^x (Ж1). B3)
Мы получили формулу для функции распределения суммы неза-
независимых случайных величин, выражающую F^+i.-, т№регл /'^ и
¦^|л« Интеграл в правой части B3) называется сверткой функ-
функций распределения ^\{{^) п ^1г{х) и обозначается1 Fi^F^ (x).
Таким же образом можно получить равенство
Р (|х -(-
Правую часть здесь молшо рассматривать также как результат
интегрирования ) &^1Х @ ^\2 (х — ^ По частям.
Если хотя бы одна функция распределения имеет плотность,
то а свертка имеет плотность. Это непосредственно следует из
формул для свертки. Пусть, например, . F%2 (х) = j fi2(u) du*
Тогда
— 00 »— 00
X / с»
- J П
<*»OC> \ — ОС
так что плотность }(х) суммы ^ + ^2 равна
оо - сх>

74
ГЛ. 3. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Пример 5. Пусть \и ?2, Л4Ш независимы и равномерно рас-
распределены на [0, 1], т. е. gi, g2, «». имеют одну и ту же функ-
функцию распределения с плотностью
1, «е [0, If,
>; ^[о,и. B4)
Тогда плотность суммы |t +12 равна
0, *9М0, 2],
*, *е[0, 11, B5)
12 — аг, же [1,2].
Присутствующий здесь интеграл равен, очевидно, длине пе-
пересечения отрезков fO, 1| и [х— 1, х]. Плотность суммы |, +12 +
.+1, будет уже склеена из 3 кусков парабол:
0.
(х) = 1
x<=[0,\]t
Вычисление этого интеграла становится наглядным, если
воспользоваться рис, 4, а, где заштрихованные площади соотиет-
\0 х 1
%<*>
ствуют
^1» Si +
1 г
Рис, 4
значениям Нг+Ь%+Ъъ{х) при разных х. Вид плотностей для
|г, ^1 + ^ + |з представлен на рис. 46. Плотность суммы
is + li будет склеена уже из 4 кусков кривых третьего

§ 6. ИНТЕГРАЛЫ 75
порядка и т. д. Если начало координат перенести в точку п/2, то
с точностью до преобразования сжатия внешний вид плотности
суммы ?i + ... + ?д с ростом п все больше будет напоминать
график функции е ' ¦ Мы увидим дальше, что это обстоятель-
обстоятельство .не является случайным.
В связи с рассмотренным примером можно заметить, что если
есть две независимые случайные величины g и rj, где ? имеет
функцию распределения F(x), a ц распределена равномерно на
[О, 1], то плотность суммы § + п в точке х равна
х
}ип (х) = J dF (t) /„ (х - t) = J dF @ = F (я) - F (x - 1).

Глава 4
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
§ 1. Математическое ожидание
Определение 1. Математическим ожиданием, или сред-
средним значением случайной величины |, заданной на вероятност-
вероятностном пространстве <Q, S, Р>, называется число
если интеграл, стоящий в правой части, существует,
В силу сделанных выше замечаний (см, § 3,8) мы можем
М| определить также как
Щ = [ яР^ (ds) = ] xdF (ж), A)
где F(ж) — функция распределения g. Из определения следует,
что М| существует, если iVl | % | < оо. Как нетрудно видеть, М§
не существует,-если, например, 1 —- F(x)>* l/х при всех достаточ-
достаточно больших а\
Мы уже знаем, что если F(x) —ступенчатая функция, то ин-
интеграл Стилтьес-а в A) превратится в сумму
Если F(x) имеет плотность /(.г), то
М^ ~ \ х}(х) ах,
так что М| есть координата «центра тяжести» распределения F
единичной массы на прямой и соответствует естественному по-
пониманию среднего значении этого распределения.
Если g(x) — борелевская функция, то г| —gd) есть снова
случайная величина и
Mg (I) - ) g (I (a))) P (do)) - j g (r) dl< (x) - J x dPga) (x).
Последнее равенство следует из определения A).
Основные свойства математических ожидании совпадают со
свойствами интеграла;
Ml. Если а и Ъ — постоянные, то М {а + Ъс) = а + 6М?.
М2. М (|г + Е2) ^ М|х 4- Мс;2» вела существуют какие-нибудь
два участвующих в равенстве математических ожидания.

" § 1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ 77
МЗ. Если а<1^Ъ,то я<М?<Ь. Всегда Щ^М\Ъ\.
М4. Если % > 0 и MJ- = 0, го | = 0 с вероятностью 1.
М5. Вероятность события А может быть записана в терминах
математических ожиданий с помощью равенства
еде I(А) есть случайная величина, равная индикатору события
A: I(A)~i, если wei, и 1(А)==0 в противном случае.
Дальнейшие свойства математических ожиданий см. в При-
Приложении 3.
Рассмотрим несколько примеров.
П р и м ер 1. Математические о ж и д а н игя7 связан-
\\ ы е со с х смой Бери у л л и. Пусть Н, g= Вр, т. е. % прини-
принимает два значения: 0 с вероятностью q и 1 с вероятностью р, где
р + q == i. Тогда
Mg = 0-Р (? = 0) + I- P(? = 1) = p.
Рассмотрим теперь последовательность исходов в схеме Вер-
пул ли до момента ц появления первого «успеха». Другими сло-
з«ами, рассмотрим последовательность независимых величин |1?
g2, . - •, распределенных к!ак 5? ДО момента времени
Очевидно, что ц является случайной величиной,
р (т, вА) = /"V,
так что т] — 1 имеет геометрическое распределение. Следо-
Следовательно,
77
Если обозначить 5,г =SSa»to, очевидно, М5П == пр. Опреде-
1
лим теперь при некотором целом N > 1 случайную величину ц =
=min{&^l: Sk = N} как «время» достижения последователь-
последовательностью iSn уровня Лг, Имеем

78 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Сумма здесь равна производной /V-ro порядка в точке z = q от
оо
функции ty(z) = 22 =1/A — г),т. е. равна N\/pN+i. Итак, Мг}=
о
= .V//?. Как мы увидим пише, это равенство может быть полу-
получено как очевидное следствие результатов § 4.
Пример 2. Если Е?== Ф о, то
а]/2л
dt
а У 2л
а = а.
Таким образом, ' параметр а нормального закона равен его ма-
математическому ожиданию.
Пример 3. Если §ё=П^, то Мс,--= X. Действительно,
Пример 4. Если ?i§U0>1, то
Ms
с,
о
Из свойства Ml следует, что для fed! ^д,
йл^ - , b — а а -|- (
Если l^K0,i? то М? не существует. Это следует из того, тго
Г xdx
интеграл —¦—-^ расходится.
Рассмотрим теперь пример, близкий по типу примеру t
о подсчете Mr], но более слоя^пый, связанвый с вычислением
среднего значения продолжительности шахматного турнира
в реальной ситуации. В примере 3.4 была описана простейшая
вероятностная модель шахматного турнира. Первый игрок.в каж-
каждой партии независимо от исходов предыдущих партий выигры-
выигрывает с вероятностью /?, проигрывает с вероятностью q, р + q < 1
и делает ничью с вероятностью 1 — p — q. Конечно, это весьма
грубое первое приближение, поскольку независимость па самом
делеэ по-видимому, отсутствует* G другой стороны, трудно пред-

§ I. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ 79
положить, что для уравновешенных игроков высокого класса на-
названные вероятности сильно менялись бы от партии к партии
или в зависимости от предыдущих результатов. Более сложная
модель, учитывающая зависимость р и q от исходов предыдущих
партий будет рассмотрена в примере 12.6.
Допустим, что турнир продолжается до тех пор, пока один
из двух участников не наберет N выигрышей (ему и присужда-
присуждается победа). Именно по такой схеме при iV = 6 был организован
матч на первенство мира по шахматам в 1984 году между
А. Карповым и Г. Каспаровым. Что можно сказать в этом слу-
случае о математическом ожидании Мг\ времени г) _ продолжительно-
продолжительности матча?
В примере 3,4 было показано, что
iY-l N-1
Р(ц = п) = р 2 р(/1-1;Лг-1, i) + gS р(/г-1; *,ЛГ-1),'
где р (п; i, ]) - 7Г/! (я-*-/)! p%ql ^ ~~ р ~~~ qT"^'*¦ Поэтому при
-очевидных соглашениях относительно индексов суммирования
Мч-Т^ГТГ, 2 Щ^2 »(»-!)...
k ¦' г=-0 ' п=о
,.. (/г—г —ЛГ + 1)A —р — д)п-*-\
Сумма по п подсчитана в примере 1 и равна1 у , ,лг+г+Г *
Следовательно,
iV_ ^ (pNq1-]- p'qN) GУ + i)\
q Ad iim ,
* л _L n jto ,•) дг) /„ ( о\г4"Л"
л--1 ,ЛГ +
JV_ у /
y, + q ? \ i
где г ~ р/ (р~^ (]).
В интервью газете «Известия» от 3 марта 1985 г. Карпов со-
сообщил, что в среднем в предматчевых турнирах он проигрывал
1 партию из 20. Такими же показателями, по его словам, харак-
характеризуется и Каспаров. Если в этих условиях применительно
к нашей простейшей модели положить р = q = 1/20 (строго го-
говоря, такое заключение из приведенных данных сделать нель-
нельзя; соотношение р = q == 1/20 скорее можно рассматривать как
одну из возможных гипотез), то при iV = 6 (r = 1/2) путем не-
лосредственного подсчета получим

80 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Таким образом, если верить в адекватность нашей простей-
простейшей модели, то ожидаемая продолжительность турнира оказы-
оказывается очень большой. Некоторым подтверждением правильности
сделанных предположений может служить тот факт, что матч
между Карповым и Каспаровым был прерван по решению пре~
видепта шахматной федерации на 48-й партии ввиду того, что
этот матч чрезмерно затянулся.
Если учитывать результаты проведенного турнира и после-
последующих партий между Карповым и Каспаровым, то оценка (при-
(приближенное значение) чисел р и q может отличаться от 1/20,
Для рассмотренной модели справедливо также следующее
простое неравенство: } \_ ( <Мц<^:~7^~-.
Оно вытекает из соотношения r\N ^ ц < t\2n-u гДе Цк — число
партий до момента, когда суммарное число очков обоих игроков
достигнет N. В силу примера 1 Мцу = N/(p -Ь (/).•
Пример 5. В задаче о ячейках в § 3, 4 гл. 1 рассматрива-
рассматривалась вероятность события А, состоящего в том, что хотя бы' одна
из п ячеек, куда наудачу бросают г частиц, останется пустой.
Найдем математическое ожидание числа Sn%r пустых ячеек
после г бросаний. Если Ak означает событие, состоящее в том,.
что к-я ячейка пуста, a l{Ah) означает индикатор этого собы-
события, то
Заметим теперь, что MSntr близко к 0, если A — 1/?г)г мало
но сравнению с 1/гг, т. е. когда — rln(l — i/n)~~ In n велико. 1\\т
больших п
и требуемое соотношение будет иметь место, если —~~~^— ве-
велико. Ясно, что в нашем случае (ср. со свойством М4) малость
MSn,r будет влечь за собой малость Р (Л) = P(SUtt > 0),
§ 2. Условные функции распределения и условные
математические ожидания
Пусть <Q, S, Р> — вероятпостпое пространство и событхю
Beg обладает свойством Р {В) >> 0. Образуем новое вероятност-
вероятностное пространство <Й, 8?, РвУ, где Рв для любого i^S зада-
зададим с помощью равенства
Легко проверить свойства вероятности Pi, P2, РЗ для меры

§ 2. УСЛОВНЫЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ • 81'
Пусть | — случайная величина па <О, S, Р>. Это есть, очевид-
очевидно, случайная величина и в пространстве <?2, 5, Рв>.
Определение 2. Математическое ожидание | в простран-
пространство <О, 5?, Рц> называется условным относительно В матема-
математическим ожиданием и обозначается М(|/В):
п
По определепию меры Рв
F/5) =J| (со) Р {(Ы/В) = p^L-Jg (со) Р(Ж> П В)= -i^ Ji HP (da>).
Последний интеграл отличается от М2- тем, что интегрирование
в нем ведется лишь по множеству В. Этот интеграл будем
обозначать
М(?; 5)= j ?(
так что
Нетрудно заметить, что функция
Р (xlВ) « Ря (S < а;) = Р (? < ^/1?)
является функт^ией распределения случайной величины г, рас-
рассматриваемой оа (Qi Si P.s).
Определение 3. Функция F(x/B) называется условной
функцией распределения % (в исходном пространстве <^5 S, Р>)
при условии В.
Зпачонио М (%/В) можно записать, очевидно, также и виде
Если а-алгебра стA), порожденная случайной величиной 5Т
не зависит от события В, то P/i (-4) = Р {А) для любого Л е
еа(^). Следовательно,
^ (ж/б) » ^ (;г), М (g/Л) « Mg, М (|; В) = Р (В) М?. B}
Пусть {Вп} — последовательность, быть может, конечная, непере-
непересекающихся событий, такая, что UBH = Q и Р(В„)>0 для лю-
любого п. Тогда
щ =. f t: (со) Р (Жо) « S U Н Р (Ао) «
= 2 М (g; Вй) « 2 Р (В,) М A/Вг). C>
С Af> А. Боровков

¦82 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИИ
Мы получили формулу полной вероятности для математических
ожиданий. Эта формула бывает весьма полезной.
Пример 6. Пусть время службы какого-нибудь механиз-
механизма есть случайная величина | с функцией распределения F(x)9
Известно, что механизм проработал время а» Каково распределе-
распределение оставшегося срока службы? Чему равно его математическое
ожидание?
Очевидно, в этой задаче нам надо найти Р (? — а ^ я/| ^ а)
л М (| — afe^a). Предполагается, конечно, что
В силу выписанных выше формул
Mi
сю
а/?>а) - ^ JariF (я + а).
Интересно отметить следующее. Во многих прикладных за-
задачах, особенно когда речь идет о работе сложных механизмов,
состоящих из большого числа надежных детален, распределение
? можно считать показательным:
Р (х) = Р (I > х) = e~lxxx \i > О,
(Причина этого явления станет я-сной позже, при рассмотрении
теоремы Пуассона и пуассоиовских процессов. Примерами 'таких:
механизмов могут служить электронно-вычислительные устрой-
устройства.) Но для показательного распределения оказывается, что
распределение оставшегося срока службы механизма
совпадает с распределением срока службы нового прибора. Дру-
Другими словами, новый прибор и прибор, проработавший непрерыв-
непрерывно некоторое время а, с точки зрения длительности дальнейшей
безотказной работы эквивалентны.
Нетрудно понять, что показательное распределение (вместо
со своим дискретным аналогом Р (? = к) = q\l—q), к = 0, \,...)
является единственным, которое обладает отмеченным выше за-
замечательным свойством. Это видно из равенства D), в силу ко-
которого с необходимостью
Р(х + а) = Р(х)Р(а).
Пример 7. п агрегатов расположены так, что расстояние
между ?-м и 7-м агрегат-ом равно ац, Ki, ] < п. Каждый агре-
агрегат время от времени нуждается в обслуживании (наладке, ре-

§ 2. УСЛОВНЫЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 83
монте и т. п.)- Предположим, что обслуживание производится
одним рабочим и что каждый очередной вызов на обслуживание
/ п \
с вероятностью р} I JL Pj = 1 ) возникает у /-го агрегата. Если,
\j=i /
например, в данный момент рабочий закончил обслуживание
i-ro агрегата, то с вероятностью р$ (от i ее зависящей) он сле-
следующим будет обслуживать агрегат с номером j; при этом он
пройдет к нему путь длиной пц. Чему равна средняя длина прой-
прой?
денного пути за один переход?
Пусть событие Вг означает, что номер агрегата, обслужива-
обслуживание которого предшествовало данному переходу, равен L Тогда
Р (В{) = Pj и вероятность того, что рабочий от i-то агрегата на-
направится к /-му, / = 1, ..., п, равна pj* Длина перехода при этом
составит aij. Поэтому
№/4J р,{}
3=1
ш по формуле полной вероятности
i=l i,j=l
Полученное выражение позволяет сравнивать различные ва~
рианты расположения агрегатов с точки зрения минимизации
величины М? при заданных ограничениях па ai}. Например, если
atj>l и все агрегаты однотипны (р3 = 1/п), то при ^их располо-
расположении вдоль одной прямой линии получим ai3= \j — i|,
так что Mt, при больших п равно приближенно /г/3. Таким об-
образом, если в день происходит s вызовов, то средняя длина сум-
суммарного перехода составит примерно sn/З. Нетрудно показать,
что расположение агрегатов по окружности будет более выгод-
выгодным, однако и оно не будет оптимальным.
Пример. 8. Как уже отмечалось, не для всех случайных
величин (распределений) существует математическое ожидание.
И соответствующие примеры вовсе не являются патологически-
патологическими — этим свойством обладает, например, распределение Коша
*) Для подсчета этой суммы достаточно заметить, что
У к {к -1)^1. (п - 2) (п ~~ 1) п
(сравните начальные 'значения и приращения этих функций).
6*

8i ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИЯ
Ка. а. Мы рассмотрим теперь одну задачу о случайных блужда-
блужданиях, в которой также появляются случайные величины, не име-
имеющие математических ожиданий. Это задача о так называемой
безобидной игре, В игре участвуют два игрока. Начальный ка-
капитал первого игрока'равен г. Каждую партию этот игрок выиг-
выигрывает или проигрывает с вероятностью 1/2 независимо от исхо-*
"дов предыдущих партий, при этом его капитал соответственно
увеличивается или уменьшается на единицу. Пусть z + Sk— ка-
капитал первого игрока после к-ш партии, a v\(z)—число шагов
до его разорения при игре с бесконечно богатым противником,
когда z есть целое число, т. е.
Если ini*5'|i> — z (т. е. первый игрок никогда не разорится),
h
'МЫ ПОЛОЖИМ T](z) = o°.
Покажем прежде всего, что rj(z) — собственная случайная
величина, т. е. случайная величина, с вероятностью 1 принима-
принимающая конечные значения. Это обстоятельство для первого игро-
игрока будет означать, что он с вероятностью 1 разорится, с каким
бы капиталом z он ни начал играть. В качестве Q здесь можно
взять «выборочное» пространство, состоящее из всевозможных
последовательностей из 1 и — 1. Каждая такая последователь-
последовательность со будет описывать «траекторию» игры. (Например, —1 на
fc-м месте означает, что первый игрок проиграл к-ю партию.)
Мы предоставляем читателю в виде упражнения достроить здесь
вероятностное пространство <0?§,Р>. Очевидно, что надо сде-
сделать так, чтобы вероятность первых п фиксированных исходов
игры (первые п координат со фиксированы) равнялась 2~пв
Положим
i*(z)=P(ri(z)<oo)f u@) = l
n обозначим В{ событие, состоящее в том, что первая координа-
координата со равна 1 (игрок выиграл), и В2 — что эта координата равна
— 1 (проиграл). Замечая, что Р {ц (z) < oo/Bj) = u(z + i) (если
первая партия выиграна, то капитал стал равным z+1), мы но
формуле полной вероятности при 2^1 получим
и (z) « Р (Вх) Р (ll (z) < оо/Вг) + Р (В2) Р (т)(з) < оо/В2) -
- ju(z + l) +±u(z~l).
Полагая 6(z) = u(z+ 1) — u(z), z~>0f мы находим отсюда 6(z)' —
— 6(z-l) = 0, 6(z) = 6==const. Так как u(z + l)=^@)
fe—i
== w @) + 26, то ясно, что б не может быть ничем иным, кроме 0,
u(z)^ 1 при всех z.

§ 3 ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН 85
Итак, в игре с бесконечно богатым противником игрок разоря-
разоряется с вероятностью 1. Это объясняет в какой-то мере тот факт,
что все азартные игроки (не останавливающиеся «вовремя»; вы-
выбор этого «времени» — отдельная задача) рано или поздно кон-
кончают разорением. Даже если игра является безобидной.
Покажем теперь, что хотя ц (z) — конечная случайная вели-
величина, Mr} (z) = ооА Допустим противное, что
17 (З) == Mt)(z)< ОО.
Диалогично предыдущему замечаем, что - М (ц (z)/Bi) = 1 +
+ и (z + 1) (капитал стал равным г+1 и один ход уже сделан).
Поэтому по формуле полной вероятности для математических
ожиданий при z ^ 1 находим
v(z)=±(l + v(z+i)) + ±(i + v (z - 1)), v @) = 08
Из этой формулы видно, что если v(z)<^1 то v(k)<oo п|ш
всех к. Обозначим A(z)== v(z+ I) — v(z). Тогда предыдущее ра-
равенство при z ^ 1 можно записать в виде
или
Из этого равенства находим Д (z) = Д @)— 2z, Поэтому
г-1
Отсюда следует, что Mr\(z)<cO для достаточно больших г. Но
ij(z) —положительная случайная величина, и поэтому Mr] (z)^0.
Полученное противоречие показывает, что предположение о ко-
печпости математического ожидания т]B) неверно.
§ 3. Математические ожидания функций
независимых случайных величин
Теорема 1. 1. Пусть | и ц — независимые случайные ве-
величины, g(x, у) — борелевская функция. Тогда если g^O или
если Mg (|, к]) конечно, то
E)
ла
F)
2. Пусть g(x, y)=igi(x)g2(y). Если gi{l)>0i gz[r\)>0 ила
если Mgx (i>I Mg2(rl) существуют, то

ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Для существования М^(^,г|) необходимо и достаточно суще-
существование Mgi(l) и Mg2(r|). (Случаи P{gi{l) = 0) = 1 или
Р (#2 (Л) = 0) = I во избеоюание тривиальных затруднений здесь
исключаются.)
Доказательство. Первое утверждение теоремы есть пе-
переформулировка теоремы Фубини в терминах математических
ожидании. Первая часть второго утверждения следует непосред-
непосредственно из следствия 3.1 теоремы Фубини. Так как lgi(?)l^03.
I ёг2 (т|)! ^0и эти случайные величины независимы, то
Поскольку М \gx(i)| =^=0, М |g2(ц) \ФОЛ то отсюда следует по-
последнее утверждение теоремы. <4
Замечание 1. Формулу E)' можно рассматривать как
формулу полной вероятности для вычисления Mg(?, т]). Ут-
Утверждение F), не ограничивая общности, можно записать в виде
М?т) = МЩх\4 G)
Чтобы получить отсюда F), надо в качестве % взять gi(|),
а в качестве ц взять ^(л) •—это снова будут независимые слу-
случайные величины.
Примеры использования теоремы 1 были приведены в § 3.6
и будут встречаться в дальнейшем.
Обратное утверждение к F) или G)' неверно. Существуют
зависимые случайные величины g и ц такие, что
Пусть, например, ? и | независимы, !V!^ = Ml, = 0. Положим ц —
= g?. Тогда ^ и т], очевидно, зависимы (за исключением "неко-
"некоторых тривиальных случаев, таких, например, когда ? = const),,
во
Щц - M?2S - М?аМ? - 0 - М?Мп,
§ 4. Математическое ожидание случайных величин,
не зависящих от будущего
Пусть на <?2, Зг, Р> задана последовательность {^л}зТ==г неза-
независимых случайных величин и целочисленная случайная вели-
величина v ^ 0. Пусть ?5k, п = о(|й, ,,., §п) означает о-алгебру, порож-
порожденную га ¦— А + 1 случайными величинами §л, .»., |„.
Определение 4. Случайная величина v называется /^
зависящей от будущего, если событие {v </г} «не зависит от
&,+ !. со.
Случайная величина v называется марковской, или моментом
остановки, если (v ^ w} e g1§ n. Другими словами, в этом случае

§ i. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, НЕ ЗАВИСЯЩИЕ ОТ БУДУЩЕГО 87
звание значений §«, ,.., |п позволяет сказать, произошло событие
{v < п} или нет. ^
На основании предыдущего (см. § 5 гл. 3) ясно, что в нашем
•случае для марковской случайной величины событие (v <с п}
(или (v > п)) и любое событие А из Sn+i, oo независимы. Это
значит, что марковская величина для последовательности неза-
независимых \ь не зависит от будущего.
Пример 9. Пусть v — номер первой случайной величины
в последовательности {^n}rT=^i» которая оказалась больше или
равной N, т. е.
v = inf{&: lh>N).
Если |,.. независимы, то, очевидно, v не зависит от будущего, так
п
как событие {v <! п) = U {>/г ]> iV} е Sltfl.
Любая случайная величина v, не зависящая от последователь-
последовательности gl7 ^о, ... (не зависят o(v) и Йч>00), является, очевадно,
ие зависящей от будущего случайной величиной.
Термин «марковская» станет несколько понятнее после вве-
введения понятия марковости в гл. 12. Термин «момент остановки»
связан с характером большого количества прикладных задач,
в которых такие случайные величины появляются. В качество
довольно типичного примера мы можем рассмотреть следующую
процедуру. Пусть §ft — количество брака в &-й партия продук-
продукции предприятия. Статистический приемочный контроль качества
продукции состоит в следующем. Вся продукция бракуется, если
при последовательной проверке партий обнаружится, что при не-
п
котором п значение суммы $п = Zj !/*• превзошло заданный до-
пустимый уровень а + bn. Помер партии v, при которой это со-'
бытие произошло,
v = mia in: Sn> а + Ьп)
-есть момент остановки всей процедуры проверки. Чтобы избе-
избежать длительной проверки, моментом остановки (в буквальном
смысле) делают также и случайную величину
v* = min in: Sn < —А + bn}1
где А > 0 подбирается настолько большим, чтобы гарантировать
€ высокой вероятностью достаточный уровень качества всей про-
продукции (предположив, например, что ?fe одинаково распределе-
распределены). Ясно, что v и v* удовлетворяют определению марковской
величины ели момента остановки.
Мы предлагаем читателю привести пример случайной вели-
величины v, зависящей от будущего,

88 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пусть & = §, + ,«, + !• v. Это есть сумма случайного числа
случайных величин.
Теорема 2 (Колмогорова — Прохорова). Пусть целочислен-
целочисленная неотрицательная случайная величина v не зависит от буду-
будущего. Тогда, если
2Р(у>*)М|Ь,|<оо, (8)
ТО
2
k=i
Если |ft ^ 0, то условие (8) излишне*
Доказательство. Имеем ¦
(9)
= S M EV; v = п) = 2 М (?„; v = n) =
П=1 « = 1
оо я оо
= 2 2 М (&; v = п) = 2 М (!„; v > /с). A0)
u—\ k=l k=l
Законность перемены порядка суммирования' здесь мы поясним
позже. Так как событие (v > к} = {v > к — 1) Ее зависит от о-ал-
гебры Sa,m, to оно не зависит и от о(|А). Следовательно,
M(c,h; v^ к) = Р (у^к)М1к] и формула (9) доказана. Перемена
порядка суммирования в A0) возможна благодаря абсолютной
суммируемости соответствующих рядов, так как
сю оо
- 2 P(v>A)MUA|<«>
fe=l
но условию теоремы. Если |ft ^ 0, то все 'слагаемые будут неот-
неотрицательны и перемена порядка суммирования станет законной
в любом случае.
Следствие 1 (тождество Вальда). Если случайные вели-
величины ^i, ?2, •. • независимы и одинаково распределены, ЩЬ^ \<Z°o,
а случайная величина v не зависит от будущего, Mv<Coo, шо
MSv^MSiMv.
Доказательство сразу получается, если заметить, что
оо оо оо оо
2 P(v^k)= 2 2 P(v = t)=2 iP(v = ») = Mv, <
Пример 10. Схема цепной реакции. Пусть мы имеем
в качестве исходной одну частицу, которая либо исчезает с ве-
вероятностью q, либо превращается в m таких же частиц с веро-

§ 4. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, НЕ ЗАВИСЯЩИЕ ОТ БУДУЩЕГО
89
ятностыо р = 1 — д. Каждая частица нового поколения ведет себя
таким же образом независимо от судьбы остальных частиц. Чему
равно математическое ожидание числа ?п частиц в п-м по-
поколении?
Рассмотрим «двойную» последовательность 1?/{ ]ii==z-lin==1 неза-
независимых одинаково распределенных случайных величин, прини-
принимающих значения т ш О с вероятностями р и q. Очевидно, что
ff(l)]oo fc.B)]oo ^
последовательности (feft 1й=ь tfe/* U=2» • •• будут независимыми
между собой. С помощью этих последовательностей случайные
величины" ?п (?0 = 1) можно представить в виде
fcB)
tn = li"' + «* • + l:Cn-i%
где в равенстве для t,n число слагаемых ^п-1 еЬть число «частиц-
родителей». Так как последовательность {?)/* 1
?„_! и М|/4" = /?тд? то в силу тождества Вальда
не зависит от
Пример 11. Вернемся к безобидной игре двух игроков,
описанной в примере 8, - но уже ^в случае, когда оба капитала
zt > 0 и zz > 0 первого и второго игроков конечны. Введем слу-
случайные величины gft, изображающие выигрыш первого игрока
в /г-н партии. Очевидно, ^ независимы,
;?
1 с вероятностью 1/2,
— 1 с вероятностью 1/2.
Число 2Х + Sit = zx + 2 Sj будет означать капитал первого
а, a z2 — 5ft — капитал второго игрока после к партий.
Величина
ц = min {к: zi + 5Л == 0 или z2 — 5ft = 0)
есть время до окончания игры, т. е. до разорения одного из иг-
роквв. Спрашивается, чему равна вероятностность Р,- того, что
выи1^рает 1-й игрок (г = 1, 2)?
Ясно, что т] есть марковский момент, при этом 5Л = ~^л с ве-
вероятностью Pz ш 8Щ = zz с вероятностью Pt = 1 — Р2. Поэтому

90 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИИ
Если Mtq<< оо, то в силу тождества Вальда мы имели бы
=0.
Отсюда находим, что Pt = zt/(zt + z2).
Остается проверить -конечность Mr]. Пусть для простоты
Zi~r z2 = lz четко. L вероятностью z ^ Z игра может
закончиться за min(z1, z2)^z партий. Так как в течение игры
суммарный капитал обоих игроков не меняется, то
Это, очевидно, влечет за собой конечность
Мы уже отмечали, что не зависящая от {^} случайная вели-
величина v не зависит от будущего. В то же время v не будет мо-
моментом остановки в смысле определения 4. Приведем теперь
менее простой пример случайной величины v, не зависящей от
будущего, но не являющейся моментом остановки.
Пример 9А. Рассмотрим _ две независимые между собой
последовательности независимых случайных величин ?4, ?2, •.. и
Ль rf2i • • -'¦> 1)€=ёР, Чз€в&- Рассмотрим далее некую систему, со-
состоящую из двух одинаковых приборов. При пуске системы сна-
сначала работает первый прибор случайное время ?t, после чего on
выходит из строя. Его заменяет второй прибор, который рабо-
работает время ?2 (на интервале времени (^, ti + Ег)). Одновремен-
Одновременно в момент выхода из строя, первого прибора он поступает
в ремонт (восстанавливается), время ремонта длится ц2. Ecjiii
г]2 >¦ ?2, то в момент ?, + ^2 отказа второго прибора оба прибора
окажутся неисправными и система дает отказ. Если же ц2 ^ t^>
то в момент ?i + ^2 в строй снова вступает первый прибор и ра-
работает время ?з, а второй прибор поступает в ремонт, который
длится время ц3. Если rj3 > ^3, то система отказывает. Если
}Ь ^ ?з, то второй прибор продолжит работу и т. д. Чему равно
математическое ожидание времени т безотказной , работы
системы?
Пусть v = min{A;>2: Лй^^» Тогда, очевидно, т = ^ + ...
. •. + ?.v, где tj независимы и одинаково распределены {v ^ n) e
eCF(tb •••> S«; т]2, ..-» Лп). Это означает, что v не зависит от бу-
будущего. В то же время, если п., Ф const, то (v<w}^o(Si, . ¦., Sn)
и v не является марковским моментом относительно последова-
последовательности ?ь ?2, .... В силу тождества Вальда Мт = MvM^.
Так как
{v = к} = "и' {П; < U П (^ > W. А > 2д
j

§ 5. ДИСПЕРСИЯ 91
то Р (v = к) = qh~2 (I - q), Л> 2, где
J 0).
Следовательно,
эс оо
Mv - 2AV~S (I - г) = 1 + 2 fV (l — g) = l + —-
1
Тождество Вальда допускает целый ряд обобщений (подроб-
(подробнее об этом будет в § 14,2).
§ 5. Дисперсия
Введем еще одну числовую характеристику случайных
иелпчин.
О о р о я е л е и и е 5. Дисперсией D^ случайной величины |
называется число
D? = М (? - М|J.
Это есть мера «разброса» или «рассеивания» распределения.
Дисперсия равна моменту инерции распределения единичной
массы на прямой. Находим
Dt = щз _ 2М?М? + (ЩJ - Mga ~ (Mg)a. (И)
Дисперсию можно было бы определить так же, как
niinSVl(| — аJ. В самом деле, в силу этого определения
а
in (а2 — 2аЩ) = Mg2 — (MgJT
так как минимум а2 — 2аМ% достигается при а = Mg. Это заме-
замечание показывает, что число а. = М^ является наилучшей оцен-
оценкой (приближением) в среднеквадратичном случайной вели-
величины |.
Величина V D? называется стандартным уклонением.
Пример 12.. &^с^аа2- В примере 2 было выяснено, что
а = М?. Следовательно,
е 2°2
'2л
Последнее равенство получено заменой (х — а)/о = t. Интегрируя

92 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
по частям, получим
2 34 „2
Пример 13. Е€=Пц. В примере 3 было вычислено М?
Поэтому
оо
Щ = ME2 - (MEJ = ^ А2!
(А— 1) JIh _|Х . \} k\lh -ц, 2 ' 2
Пример 14. Для ?€§иод имеем
xadx
В силу A1) D?=i,
Пример 15. Для Е^ВР в силу соотношений |2 = |, М?2 =»
« Mfe = р получаем DJ = р — р2 = рA —• р).
Рассмотрим теперь некоторые свойства дисперсии.
Dl. D|^ О, D5 = 0 гог^ а только тогда, когда Р E = ^) =1«
^^е с — постоянная (не зависит от со).
Первое очевидно, так как Dg == М (| — ЩJ ^ 0,- Пусть
р (? = с) = 1г тогда (М?J = Ml2 = с2 и, значит,
D^ = с2 - с2 = 0.
Если DE = M(g — MgJ-0, то (так как (|—М|)а>0) Р(?—М?=-
«== 0) = 1 или Р(? = М?) = 1 (см. свойство М4).
D2. Если а и Ъ постоянные, то
Это свойство следует непосредственно из определения
D3. Если случайные величины \ и г| независимы, то
Действительно,
D (I + я)> М (? + лJ
= М|2 + 2!V!glV1ii + fVhf - (М|J - (MriJ — 2ЩЩ =
Из этих вычислений видно, что аддитивность дисперсии будет
иметь место не только для независимых | и х\, по и во всех

§ 0. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ 93'
случаях, когда
Пример 16. Пусть v ^ 0 — целочисленная величина, не за-
зависящая от последовательности {|Д независимых одинаково рас-
распределенных величин, Mv<C оо, M?j = а. Тогда, как мы знаем.,
MSV = аЫ\\ Чему равна DSV?
По формуле полной вероятности
DSV = М (Sv — M5VJ =2P(v = к) М EЙ — M5VJ -
« 2 Р (v = к) {М (Sh - akf + (аА - aMvJ] -
- 2 Р (v - /г) Ю^ + а2М (v - Uvf - D^Mv + a2Dv,.
Это равенство эквивалентно соотношению
В такой форме полученное соотношение остается справедли-
справедливым для любого момента остановки v (см. гл. 14), Пользуясь.
им, можно в примере 11 найти математическое ожидание вре-
времени т) до окончания безобидной игры, когда капиталы игроков-
zx и z2 конечны. Действительно, в этом случае а = О,
Отсюда находим
§ 6. Коэффициент корреляции
и другие числовые характеристики
Две случайные величины \ и ц могут быть функционально
(детерминирование) зависимы: ? = g(ii)» могут быть зависимы,
во не функциональным образом; наконец, могут быть независи-
независимыми. Коэффициент корреляции двух величин есть число, с по-
помощью которого пытаются количественно характеризовать сте-
степень зависимости двух случайных величии друг от друга.
У всех случайных величии, которые встретятся в этом разде-
разделе, предполагается существование дисперсии, не равной 0.
Случайная величина | называется нормированной, если
М? = 0 и Dg = 1. Любую случайную величину | можно линей-
линейным преобразованием привести к нормированной, положив ^ =*
= (g — MD/1/D5. Пусть 5 и Ц — некоторые случайные величины,
а ?4 и rji — соответствующие им нормированные случайные ве-
величины.
Определение 6. Коэффициентом корреляции между слу-
случайными величинами g и ц называется число р(%, "Л) == М^чЧ.

<94 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Свойства коэффициента корреляции:
1. 1р(|, п)К1.
Действительно,
О < D (lt ± ni) = М (^ ± ЛгJ = 2 ± 2р (?, ц).
Отсюда и следует, что 1р(|, л)! < 1, А
2. /?а/ш ^ а ц независимы, то р(|, т|) = 0.
Доказательство-следует из того, что §t и r]i Бри этом тоже
независимы.
Обратное утверждение, конечно, не верно. В § 3 приведен
пример зависимых случайных величин g и т] таких, что М? = 07
Myj= 0, М|т]=0. Для них коэффициент корреляции равен 0,
хотя они и зависимы. Однако, как мы увидим в гл. 7, для нор-
нормально распределенных (Е, ц) равенство р(§, г)) = 0 является
необходимым и достаточным для независимости этих величие.
Другой пример, когда некоррелированность случайных вели-
величии влечет их независимость, дает схема Бернулли. Пусть
Р(Б=1) = Р, P(l = 0) = l-p, P(ti = 1) = д, Р (Л = 0) = 1 — у.
Тогда М? = р, Мл = q, Dg==p(l-p), Dn = g(l — g), p(g, Л)«
7—* ... } . '—. Равенство p(^, r])==0 означает, что M?r) =
УРG A — Р) A—9)
или, что тоже, Р(? == 1, л = 1) = Р (I = 1) Р (tj = 1),
O) P(g l)P(S 1 l) P(g l)
( ) )) (
X P (л - 0), и т. д.
Отсюда легко получить, что в общем случае § и л независи-
независимы, если р(/(|), #(л)) = 0 для любых ограниченных измеримых
функций / и g. Достаточно взять / = /(-„эХ), g = 7(_оо, У), получить
отсюда, что Р (& < д:, Л < У) = р D< х) р (Л < У) и воспользовать-
воспользоваться результатами предыдущей главы.
3. 1р(|, л) I ^ 1 тогда и только тогда, когда существуют такие
числа а и Ъ Ф 0, что Р (Л = а + Ь^) = 1.
Доказательство. Пусть Р (л = ^ + ';^) === 1* Обозначим
М^ == а и /Щ = Р; тогда
if- \ ^й< — а а ~\~ bZ — ft — hoc . 7
р(?, Ч) = М?-р • -|6|il = signb.
Предположим теперь, пто 1р(|, л) 1 = 1. Пусть, например,
рA, г])=1. Тогда
Л о свойству дисперсии D1 это может быть только тогда, когда
Р(|1-тI = с)=1.
Если р(|, 1]) = —1, то, рассмотрев 0A,4-1]!), получим

§ 7. НЕРАВЕНСТВА 9S
Если р > G, то случайные величины ? и ц называются поло-
положительно коррелированными; если р < 0, то ? и т] называются
отрицательно коррелированными.
Пример 17. Рассмотрим передающее устройство. Случай-
Случайная величина | означает величину передаваемого сигнала. В ре-
результате помех приемник принимает величину г] = а?+Д (а —
коэффициент усиления, Д — помехи). Предположим, что случай-
случайные величины Д и| независимы. Пусть Мь=я, D^ = 1, а МА0
ОД = а2. Подсчитаем коэффициент корреляции ? и rj;
9 (I, Л) = М (Е ™ а)
+ А — аа
V а2 + а2
Если а — большое число по сравнению с усилением а, то р
близко к 0 и 1] практически не зависит от 5- Если же о мало по
сравнению с а, тогда р близко к 1 и по г\ бывает легко восста-
восстанавливать §.
Рассмотрим некоторые другие числовые характеристики слу-
случайных .величин. В качестве таковых часто используются мо-
моменты более высоких порядков.
Определение 7. Моментом порядка к случайной величи-
величины | называется число М?\ Значение M(s — Щ)/е называется
центральным моментом порядка к, так что дисперсия есть цент-
центральный второй момент |.
Если дан случайный вектор (§i, ..., |п), то величина
M?i . • ф ?ап называется смешанным моментом порядка ki + ...
,.. + kn. Аналогично М (^ — М1г) * , •. (%п — М?7,) п называется
центральным смешанным моментом того же порядка.
Для независимых величин смешанные моменты равны, оче-
очевидно, произведению соответствующих обычных моментов.
§ 7. Неравенства
Теорема 3 (неравенство Коши — Буняковского.) Если ^
и g2 — две произвольные случайные величины, то
Это неравенство иногда называют также неравенством
Шварца.
Доказательство. Требуемое соотношение получается из
неравенства 2iafr| < a2-f Ь2, есля .положить в нем а2 = ll/bA^l,
&2 = й/^^2 и взять математическое ожидание обеих его
частей. ^
Неравенство Коши — Буияковского является частным случаем^
более общих неравенств.

-Ж ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Теорема 4. При г > 1, — + — = 1 справедливо
М | liSs I < [М ! Si П1/Р [МI U |s]1/s (неравекст-eo Гельдера),
[М||-х + la|r]1/r<[M|lir]1/P+ lM||a|Tr (иераввчсгво Л7«и-
ко в ско го).
Доказательство. Так как агг при г>1 есть в области
х>0 выпуклая вниз функция, равная 1 в точке х=1 п имею-
имеющая там производную г, то г(х — 1) ^ хт — 1 при всех # > 0. По-
лагая х = (а/6I/г (« > 0, Ь > 0), получим
пли, что то же, а с? ^ ~ -f-»--. Ьсли положить здесь
а = | ?i |/М | ^| Г» 6 = | ^2 js/M ] ?2 I* и взять математическое ожй,ча-
иие, то мы получим неравенство Гёлъдера.
Чтобы доказать неравенство Минковского, заметим, что в си-
силу неравенства Igi + |о| < i|J + ig2! выполняется
Применяя здесь к слагаемым правой части неравенство Гольде-
ра, получим
i \
Так как (r—l)s==r, 1—у= ~, то отсюда следует неравенство
Мипковского. ^1
Очевидно, что при ?<=,<? = 2 неравенство Гельдера превраща-
превращается в неравенство Коти — Буняковского.
Теорема 5 (неравенство Иенсена). Если М^ существует
и g(x) —выпуклая вниз функция, то g (Щ) ^ М^(^).
Доказательство. Если g (x) выпуклая вниз, то для
каждого у найдется число g* (у) такое, что
Положив здесь х = ^, ?/ = М? и взяв математическое ожидание
•обеих частей этого неравенства, получим
A2)
Часто бывает полезным также
Следствие 2. При любых 0 ,< и < и

§ 7. НЕРАВЕНСТВА 97
Это неравенство показывает, в частности, что если существу-
существует момент порядка и, то существует и момент любого поряд-
порядка v < и.
Неравенство A2) получается из неравенства Гельдера, если
положить в нем gt = IS,!", ?2 = 1, r = u/v, или из неравенства
Иенсена при g(x) = \x\u^v и замене | на g°.
Теорема 6. Пусть ^0 с вероятностью 1. Тогда для лю-
любого s > 0
Р(|>8)<М. A3)
Доказательство. Неравенство доказывают следующие
соотношения:
Щ > М (?; I > г) > еМ A; g > в) - еР (? > е). 4
Если функция g(x)>0 монотонно возрастает, то, очевидно,
{§: g(|)^ ^(е)} == {|: § > е) и, применяя теорему 6 к случайной
величине Л = #(!), получим
Следствие 3. Если g (x) t, g (x) > 0, го
Z? частности, при g(x) = eKx
Следствие 4 (неравенство Чебышева). Д^л произвольной
случайной величины |? имеющей математическое ожидание, спра-
справедливо неравенство
Р(|?_М||>е)<-^-. A4)
Для доказательства A4) достаточно применить теорему 5
к случайной величине Л = E — MgJ ^ 0. «^
Утверждение теоремы 6 также часто называют неравенством
Уебыте ва (или неравенством типа Чебышева), поскольку оно
является по технике доказательства несущественным обобще-
обобщением A4).
С помощью неравенства Чебышева мы имеем возможность
оценивать вероятности различных отклонений g, зная лишь
Щ и D?. В качестве одного из первых применений этого нера-
неравенства можно получить так называемый закон больших чисел
в форме Чебышева (в более общей форме закон больших чисел
будет получен в гл. 8).
Теорема 7. Пусть |,, ?2? ...— независимые одинаково рас-
распределенные случайные величины с математическим ожиданием
7 А. А. Боровков

98 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИИ
M|j = а и конечной дисперсией a2, Sn = 2j?,j. Тогда для любого
е > О
При П -> оо#
Обсуждение этого утверждения будет проведено в гл. 5, 6, 8.
Доказательство теоремы вытекает из неравенства Че-
Чебышева, так как
о о 2 2
М п —п П п ~ по — ° <*
п 7 п п* п
Приведем пример использования неравенства Чебышева в вы-
вычислениях.
Пример 18. Предположим, что мы решили измерить диа-
диаметр лунного диска, используя фотографии луны, полученные
с помощью телескопа. Вследствие атмосферных помех замеры
фотографий, сделанных в разное время, дадут разные результа-
результаты. Пусть ? — а означает отклонение замера от истинного значе-
значения, равного в некотором масштабе а. И пусть М| = а,
о = у Щ= 1. Проведем подряд п независимых друг от друга
замеров и обозначим ?r» =~(?i+ . .. +?а). Тогда, как мы видели,
M'Qn == a, Dt,n = o2/n. Так как дисперсия среднего арифметиче-
арифметического всех наблюдений уменьшается с ростом числа наблюдении,
то величину а естественно оценивать с помощью ?л.
Сколько надо сделать наблюдений, чтобы \t>n — а\ < 0,1 с ве-
вероятностью, большей 0,99? То есть, чтобы выполнялось
Р(|?я-а|<0,1)>0,99 или Р (|U - я| > 0,1)< 0,01. По пера-
2
венству Чебышева Р (| ?п — а* |> 0, 1)^;тйрГоГ Значит, если п
выбрать таким, чтобы ^>() 01 ^0,01, то требуемое неравенство
будет выполнено. Отсюда получаем п ^ 104.
Приведенный пример иллюстрирует возможность использова-
использования неравенства Чебышева для оценок вероятностей тех или
иных уклонений случайных величин. Но этот пример, пожалуй,
еще больше иллюстрирует, насколько грубым с точки зрения
практических подсчетов является неравенство Чебышева. Если
читатель вернется к примеру 18 после знакомства в гл. 8 с цент-
центральной предельной теоремой, то он сможет легко подсчитать,
что на самом деле для получения заданной погрешности доста-
достаточно провести не 10\ а около 670 наблюдений.

§ 8. УСЛОВНОЕ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ 99
§ 8. Обобщение понятия условного
математического ожидании
В заключенно этой главы введем понятие, которое, наряду
с уже введенными, является полезным и важным инструментом
в теории вероятностей. Чтобы дать возможность читателю при
первом чтении книги этот раздел опустить, мы в дальнейшем
избегаем прямого использования проводимых здесь рассмотрений
вплоть до гл. 12, 14.
I, Определение условного математического ожидания (у. м. о).
В § 2 введено понятие у. м.о. относительно произвольного собы-
события В, Р(/>)>0, которое определяется равенством
М(|/Я) = М(&;В)/Р(Я), A5)
где М(ь, В) = ) ЫР = М?/в, /б = /в(«>) есть случайная вели-
в
чипа, равная индикатору множества В. Мы уже видели и будем
убеждаться не раз в дальнейшем, что это очень полезное поня-
понятие. Однако определение A5), с помощью которого это поня-
понятие было введено, обладает тем недостатком, что оно теряет
смысл в случае Р (В) = 0. Как преодолеть этот недостаток?
Тот факт, что условие Р(#)>0 не должно играть суще-
существенной роли, можно проиллюстрировать следующими сообра-
соображения лш. Допустим, что ? и ц независимы, В = {ц=х} и
Р(В)>>0. Тогда для любой, измеримой функции ф(я, у), со-
согласно A5),
м [ф (S, т - ч - "pV-Г1 = ^^Г3 -¦»«•*>•
Последнее равенство справедливо, так как случайные величины
<р(?, х) и /{п=х} как функции соответственно от g и г| независи-
независимы и, следовательно,
Мер (|, ,г) /{^х} = МФ (g, дг) Р (т| = х).
Соотношения A6) показывают, что понятие у. м. о. может
сохранять свой смысл и в случае, когда вероитвюсть условия рав-
равна 0 — ведь само и о себе равенство
для независимых § и ц представляется естественным и с пред-
предположением Р(т) = х)^>0 никак не связано.
Пусть ${ есть а-подалгебра ff. Определим теперь понятие
у. м.о. случайной величины g относительно Я, которое будем обо-
обозначать 1УЩ/§1). Определение дадим сначала для «дискретного»
случая, по так, чтобы оно легко обобщалось»
Напомним, что дискретным называется случай, когда а-алгеб-
ра Ш образована (порождена) не более чем счетном последова-

100 ГЛ. 4, ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
телыюстъю непересекающихся событий Аи А2, ...; U4i = ?2,
Р(-4?)>0- Этот факт мы записываем в виде Я = а(Л1, ^42, ...)»
он означает, что элементами SI являются всевозможные объеди-
объединения множеств Ah А2,
Пусть L2 есть совокупность всех случайных величин (всех
функций ^('со), определенных па <Q, г?, Р>), для которых
М?2<оо.В линейном пространстве L2 можно ввести скалярное
произведение (?, г]) = М?,г] (это делает пространство Ьг гиль-
гильбертовым).
Рассмотрим теперь линейное подпространство Н% всех функ-
функций вида 1((о) = 2 c^Afe (<*>), гДе -^ N — индикаторы мно-
h
жеств Ak. Ясно, что Н% есть пространство всех функций, изме-
измеримых относительно §(, и его можно представлять себе как про-
пространство, натянутое на ортогональный базис [IAk((d)} в L2.
Обратимся к определению у. м. о. Мы знаем, что обычное
математическое ожидание а = Щ для |ei2 можно определить
как единственное значение а, при котором достигается минимум
функции cp(a) = M(?—а}2. Рассмотрим теперь задачу о миними-
минимизации функционала ср (а) = М(| — а (со)J, ? е L2, по всем St-из-
меримым функциям а (со) из Я^.
Определение 8. Пусть | е L2. Я-измеримая случайная ве-
величина а(о)), для которой достигается т!пф(а),—называется
у, м. о. \ относительно §1 и обозначается М
Таким образом, в отличие от обычных математических "ожи-
"ожиданий, у. м. о. ЬЛ (?/3t) есть случайная величина. Рассмотрим ее
подробнее. Ясно, что минимум ср(а) достигается, если в качестве
а (со) взять в L2 проекцию § элемента § на /Лд, т. е. элемент ^е
е//$, для которого ?— %_1_Яьд (см. рис. 5). В этом случае для
любого а е //$
ф(а)==ф(^), если только ег = | п. в.
Итак, в L2 операция у. м. о. есть обычный ортопроектор на
//$ E ~ М(^/Я) есть проекция ^ на Яо|).
Так как для дискретной а-алгебры §t g как элемент Н% име-
имеет вид 1 =2c^Afe9 то условия ортогональности 5 — 1_1_Яд[ (или, -
М(Ъ — ? ) /^ь = ®) однозначно определяют коэффици-

§ 8. УСЛОВНОЕ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
101
еиты ch:
М (IIлк) = скР (А,),
так что
Таким образом, случайная величина М (?/91) постоянна на
Ah и равна на этих множествах усреднению ? по Лк.
Если I и 51 независимы (т. е. Р (?<=/?; А) = Р (? €= Я) Р (Л,,)),
то, очевидно, IV1 (?; Лй) = MIP (Ak) и | = Щ. Если же Я = W,
то § тоже «дискретна», § постоянна па множествах Ак и, зна-
значит, f = ?.
Отметим следующие основные свойства у. м. о., которые по-
позволяют нам освободиться от двух
частных предположений (g e L2
и дискретность 9), которые мы
ввели вначале, чтобы лучше по-
понять смысл у. м. с:
1) ? измерима относительно §(.
2) Для любого события А ^ §1
Первое свойство очевидно.
Второе следует из того, что лю-
любое событие А е §1 представимо в виде
М (|; Л) = 2 М A;
Д^ и, стало быть,
= 2 М (|; A]h) = М (|; Л).
— U
Это свойство довольно ясно: усреднение но множеству А вели-
величины | дает тот же результат, что усреднение уже усреднен-
усредненной по Ajk величины |.
Лемма 1. Свойства 1), 2) однозначно определяют у.м.о.
и эквивалентны определению 8.
Доказательство. В одну сторону утверждение леммы
уже доказано. Пусть теперь выполнены условия 1, 2. Измери-
Измеримость ^ относительно §1 означает, что ? постоянна на множествах
Ah. Обозначим значение g на Ak через ch. Так как Ah e Я, то
из свойства 2 следует, что
и, следовательно, при ш ^ Ah
Ъ === ^ h ^^

|02 ГЛ, 4. ЧИСЛОВОЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
'Теперь можно дать общее определение у. м. о.
Определение 9. Пусть ? есть случайная величина па
вероятностном пространстве <О? Ъ\ Р> и ?l cz g? есть а-подал-
гебра ®. Условным математическим ожиданием g относительно
% называется случайная величина |, обозначаемая M(?/St), ко-
которая обладает следующими двумя свойствами:
1) % измерима относительно Ш.
2) Для всякого ^1е| справедливо Ы A; /I) — М E; Л).
В этом определении случайная величина с, может быть как
скалярной, так и векторной.
Сразу возникают вопросы: существует ли такая величина |,
и единственна ли она? В «дискретном» случае мы видели, что
ответ па эти «опросы положителен. 13 общем случае справедлива
Т е о р е м а 8. Если М J ? | конечно, то функция Е, = Ш (?/§0
в определении 9 всегда существует и единственна с точностью
до значений на множестве вероятности нуль.
Доказательство. Предположим сначала, что Ъ, скаляр-
на, § ^ 0, Тогда функция множества
Q (А) - f idP - М (I: Л), "ils Я,
будет ^epoii па (Q, %), которая абсолютно непрерывна относи-
относительно Р, поскольку Р (Л) = 0 влечет за собой Q (Л) = 0. Сле-
Следовательно, по теореме Радона — Никодима (см. Приложение 3)
существует Я-измеримая функция f=M(?73t), единственная с
точностью до значений па множество меры нуль, такая, что
В общем случае положим | = |+ -~ g~, g+ = max@, |) > 0,
|- = max@, ~g)^0, f^i4" — |", где g* — у. м,о. для g*. Этим
доказано существование у. м. о,, так как g будет удовлетворять
условиям 1), 2) определения 9. Отсюда п;е следует и единствен-
единственность, так как предположение о неединственности g будет озна-
означать неединственность ^+ или |-. Доказательство для векторных
g сводится к одномерному случаю, так как свойствами I), 2)
будут обладать координаты §, существование и единственность
которых памп доказана. Ц
Существо проведенного доказательства достаточно проз-
прозрачно: ведь по условию 2) для всякого А е % "задано М(|; А) =
==j \dP fi т. е. задатгы значения интегралов от | по всем мпо-
л
Жествам 4 ^ 31. Ясно, что это должно определять ЗС-измеримую

§ 8. УСЛОВНОЕ МАТЕМАТИЧЕСКОЕ 0НШДЛШ1Е J03
функцию \ однозначно с точностью до значений па множестве
меры 0.
Смысл М (?/31) остается прежним — грубо говоря, это есть
усреднение \ но «неделимым» элементам 51.
Если 91 = §, то, очевидно, ? = ? удовлетворяет свойствам 1),
2) и, стало быть, М (?/5) = \.
Определение 10. Пусть \ и г) — случайные величины на
^Q, §, Р>, 91 = tf(t|) есть а-алгебра, порожденная случайной
величиной ц. Тогда М(?/Я) называется также условным мате-
математическим ожиданием величины | относительно т].
Иногда для упрощения записи мы будем вместо М(^/о(ц))
писать М (Е/v)). Это не приводит к недоразумениям.
Так как М (|/л) но определению есть а (г))-измеримая слу-
случайная величина, то это означает (см. § 5 гл. 3), что суще-
существует измеримая функция g(x), для которой М (|/г|) = ё(ц).
По аналогии с дискретным случаем можно истолковывать здесь
величину g(x) как результат усреднения ?, по множеству {ц=х}а
(Напомним, что в дискретном случае g(x) = М(|/П = х).)
Определение 11. Если | =/с есть индикатор мио;кества
Ceg, то М Цс1Щ будет называться условной вероятностью
Р (С/%) события С относительно 91. Если 91 = о(т]), то мы бу-
будем говорить об условной вероятности Р (С/ц) события С от-
относительно ц.
2. Свойства у. м. о.
1. У. м. о. обладает свойствами обычных математических ожи-
ожиданий с той лишь раяиицей, что они выполняются почти навер-
наверное (с вероятностью 1):
a) М (а + Ы/Ш) = а + ЬМ (%/Щ.
б) М (I, + ЬуЯ) = М A,/Щ + М E2/Я).
b) Если l^bi п. п., то М{1ь/Ш)^ЫA2/%) п. н.
Чтобы доказать, например, свойство а), надо убедиться, со-
согласно определению 2, что
1) а + ЬМ A/Щ есть ^-измеримая функция,
- 2) М (а + Ъ1; А) = М (а + ЬМ (?/И); А) для любого А^%.
Выполнение 1) очевидно; выполнение 2) вытекает из свойств
линейности обычного математического ожидания (или обычного
интеграла).
Свойство б) доказывается точно так же.
Чтобы доказать свойство вO положим для краткости %\ =
= М (\,\1Щ- Тогда для любого iel
M(fi; Л) = M(?i; Л)<М(Е2; А) = f
Отсюда вытекает, что ^2 — Si ^ 0 п. н.

104 rVf. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
2. Неравенство Чебышева. Если 5 ^ 0, х > 0, то Р (? ^ #/91) ^
< ()
Это свойство вытекает из в), так как Р E ^ я/Я) =
= М(/{^Х}/Я)? где /А—-индикатор события Л, и справедливо
неравенство J
3. Если % и a(g) независимы, то М (g/Sf) = М|. Так как
S — М? является Sl-измеримой функцией, то остается проверить
лишь второе условие определения 9: для любого А ^%
Справедливость этого равенства вытекает из независимости слу-
случайных величин /А и g и соотношений М (|; Л) = Ш (?/а) =
= М?М/А = МA;Л).
Отсюда следует, в частности, что если | и rj независимы, то
М E/т|) = ME. Если о-алгебра Я тривиальна, то, очевидно, так-
также М (|/Я) = MS. •
4. Для |/. ж. о. верпы теоремы сходимости, справедливые для
обычных математических ожиданий, например,
Теорема о монотонной сходимости (см. Прило-
Приложение 3). Если O^gfttg п. п., то М (?„/«) f МA/Щ п.ч.
Действительно, из ?n+1 ^ gn п. н. следует |„+1 ^ ?и п. н., где
In = M En/2t). Поэтому существует Sl-измеркшая ?, такая, что
In t g п. н. В силу обычной теоремы о монотонной сходимости
для любого А^%
• f!«dP-*f fdP,
Так как левые части этих соотношений совпадают, то совпа-
совпадают и правые. Это и означает, что Ъ, = М (В;/Ю.
5. Ег^ц т| скаляриа и измерима относительно 31, Гу1|?|<Соо,
М|!-г]|< оо, то
М(ц1/Щ = ЦМа/Ш). A7)
Другими словами, St-измеримые случайные величины ведут
себя относительно операции у. м. о. как постоянные (ср. со свой-
свойством 1а)). Если ц = 1в (индикатор множества В^Щ, то ут-
утверждение справедливо, так как при любом А е %
М AвЪ/Щ dP = J 1вЫР - J WP - j M
А А АВ
А А АВ АВ
Отсюда и из линейности у. м. о. следует, что утверждение спра-
справедливо и для любых простых функций ц.
Если ? ^ 0, т] ^ 0, то, взяв последовательность простых функ-
функций 0 < цп t т) и пользуясь теоремой о монотонной сходимости

§ 8. УСЛОВНОЕ МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ 105
в равенстве
мы получим A7). Переход к случаю произвольных g и ц осу-
осуществляется обычным образом — путем рассмотрения положи-
положительных и отрицательных частей случайных величин Ъ, и ц.
При этом для того, чтобы полученные разности и суммы имели
смысл, нужно требовать существование М|?|, М|^т]|.-
6. Для у. м. о. остаются справедливыми все основные нера-
неравенства для обычных математических ожиданий, в частности,
неравенство Коша — Буняковского
и неравенство Иепсена: если М 11| < 9° ? TG @ля любой выпуклой
вниз функции ¦
М (я (&)/Я). A8)
Неравенство Копти — Буняковского доказывается точно' так
же, как для обычных математических ожиданий, поскольку до-
доказательство не использует других свойств математических ожи-
ожиданий, кроме линейности.
Неравенство Иеисена вытекает из следующего соотношении.
В силу выпуклости g(x) для каждого // найдется число gx(y)
такое, что g(x)> g(y) + (z — У)g\(y)- Положим здесь х = g,
у = g = М E/21) и. возьмем у. м. о. обеих частей этого неравен-
неравенства. Так как в силу свойства 5
М [(I - I) g, (Ь/Щ = gl (|) М (S - 1/31) = О,
то получим A8).
7. Формула полной вероятности
Ml = ММ (Ъ/Щ
вытекает непосредственно из свойства 2 определения 2 при
A = Q.
8. Последовательное усреднение (обобщение свойства 7):
если §t cz Я4 cz g, то
М(?/Я) = М[М гё/ЯЛ/Я].
Действительно, для любого А е §1 в силу того, что 4 с: Я4, имеем
J М [М (№г)/Щ dP = \u Ц1%х) dP = J gdP = J M (g/a) dP. • •
A A A A
Очевидно, что свойства 1, 3—5, 7, 8 справедливы как для ска-
скалярных, так и для векторных случайных величин §. Следующее
свойство у. м. о. мы выделим особо.

108 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
9. Для ^е?2 при а (со) = М (%/Щ достигается минимум
М (?— а (со)J среди всех %-измеримых функций а (со).
Действительно, М (| — а (со)J = ММ((? — a (co)J/9t), но а (со)
ведет себя как постоянная относительно операции М (>/Щ (см.
свойство 5), так что
М(A~а (<о))а/Я) = М ((? - М (?/Я))а/«) + (М (?/Я) - а (со)J
и минимум этого выражения достигается при а (со) = М )
Это свойство доказывает эквивалентность определений 8 w 9
в случае |eL2 (в обоих определениях у. м. о. определяется одно-
однозначно с точностью до значений па множестве меры 0). В связи
с этим свойством отметим еще раз, что в Ьг операция у. м. о.
есть операция проектирования па Н% (см. пояснения к опре-
определению 8).
Свойство 9 можно перенести на многомерный случай в сле-
следующей форме: при а (со) = М A/Щ достигается min(g —
— а (со)) F(| — а (со) )'г для любой неотрицательно определенной
матрицы V, где min берется по всем Я-измеримым функ-
функциям а (со).
В заключение отметим, что свойство 5 при широких предпо-
предположениях допускает следующее обобщение:
5А. Если ц измерима относительно 91, g(ca, ц) есть измери-
измеримая функция переменных со е Q и ц ^ RJ\ то
М (g (со, т))/Я) = М (g ((о, у)/Щ |„=ч. A9)
Отсюда следует формула (последовательного усреднения или
полной вероятности)
которую можно рассматривать как обобщение теоремы Фубиии
(см. § G и § 3.6). Действительно, если g(co, у) не зависит
от Я, то
М (g (со, У)/Щ - Mg (оз, у), M(g (со, Т1)/Я) = Mg (со, у) |у=ти
По форме это и есть теорема Фубини, но ц здесь — векторная
случайная величина, а со может иметь произвольную природу.
Мы докажем свойство 5А в упрощающем предположении,
что существует последовательность простых функций цп такая,
что g(co, r)n)tg(G>, л), h(®i T)n)tfe(ft), ц) п.н., где fe(<o, г/)—
»=¦ М (g (со, г/)/2(). Действительно, пусть tj^ = J/ft при (u^Akcz Ш.
Тогда
2
С силу свойства 5 отсюда следует выполнение A9) для функ-
функций цп. Остается воспользоваться теоремой о монотонной схо-
сходимости (свойство 4) в равенстве М (#(со, Цп)/Щ = ^(о), Лп).

§ 1). УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ Ю7
§ 9. Условные распределения
Наряду с у. м. о. можно рассматривать условные распределе-
распределения относительно о-подалгебр и относительно случайных величин,
В этом параграфе мы остановимся лишь на последних.
Пусть ? и г] — две случайные величины на^ (О, $, Р) со
значениями, соответственно, в R8 и R\ и W — а-алгебра боре-
левских множеств из Rs.
Олре деление 12. Функция Р {В/у) двух переменных у е
<^ i?/{, В ge Эа называется условным распределением § и/?и усло-
условии ц = (/, если
1) При каждом В Р(В/т}) есть условная, вероятность Р(ь?
<= В/ц) события {^ ^/?} относительно г), т. е. Р(В/у) есть бо-
релевская функция от // такая, что для любого А ^ 53к
М (Р (В/ц); т| е Л) = f Р (В/у) Р (л g*) = P(^g 5, Ч е Л).
2) При каждом у Р(В/у) есть распределение вероятностей
по В.
Функцию Р(В/у) будем иногда записывать в более «расшиф-
«расшифрованной форме» в виде Р(В/у) = Р (? <= B/i] == г/).
Мы знаем, что для каждого iBeSs существует борелевская
функция #в(г/) такая, что geiv) = Р F е ^/Л)« Таким образом,
положив Р(В/у)= gB(y), мы удовлетворим условию 1) опреде-
определения 1. Однако условие 2) при этом из свойств у. м. о. никак
не следует и выполняться совсем не обязано — ведь условная
вероятность Р {? е В/ц) определена при каждом В с точностью
до значений на множестве NB меры нуль (так что существует
много вариантов у. м. о.), и это множество может быть своим
для каждого В. Поэтому если объединение N = (J Nb имеет
Бе §Зв
не нулевую вероятность, то может оказаться, что, например, ра-
равенства
Р (I е= В, U В2Щ) = Р (I <= Дх/ti) + Р(|е Бя/т1)
(аддитивность вероятности) сразу для всех непересекающихся'
St, S2 из Э" не выполняются пи для одного ш из /V, т. е. на
о-множестве ^V иололштельной вероятности функция gB(y) не
будет распределением как функция В,
Однако в случае, когда ? есть случайная величина со зна-
значениями в Rs с о-алгеброй борелевских множеств §3S, gn (ц) ==*
= Р C^g В/ц) всегда можно выбрать таким образом, что gB(y)'
будет условным распределением *)%
*) Подробнее об этом см. [5], [13], [18]*

-108 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Как и следовало ожидать, условные распределения обладают
тем естественным свойством, что у. м. о. выражаются в виде ин-
интегралов не условным распределениям.
Теорема 9. Для любой измеримой функции g(x), отобра-
отображающей Rs в R, такой что' M|g(?)|< оо, справедливо равенство
B0)
Доказательство. Достаточно рассмотреть случай, когда
g(x)^0. Если g(x)= 1А(х) есть индикатор множества А, то
формула B0), очевидно, верна. Стало быть, она верна для лю-
любой простой функции gn (x) (т. е. для функции, принимающей
конечное число значений). Остается взять последовательность
gn t g и воспользоваться монотонностью обеих частей в B0) и
свойством 4) § 8. А
В реальных задачах для подсчета условных распределений
часто можно пользоваться следующим простым правилом, кото-
которое для наглядности мы запишем, в форме
РЛ^*1. B1)
Очевидно, что формально оба условия определения 12 будут
удовлетворены!
Если g 1-г 1] имеют плотность распределения, то этому равен-
равенству будет придан точный смысл.
Определение 13. Пусть условное распределение Р(В/у)
при каждом у абсолютно непрерывно относительно некоторой
меры jx в Rsi
Тогда плотность f(x/y) называется условной плотностью | (от-
(относительно меры [i) при условии ц = у.
Другими словами, измеримая по паре переменных х, у функ-
функция f(x/y) есть условная плотность | при условии ц = у1 если
1) Для любых борелевских множеств 4cff, В d R8
J J / (х/у) \i (dx) P(^g dy) -P^e5,iig4 B2)
2) При каждом у функция f(x/y) есть плотность распреде-
распределения вероятностей.
Из теоремы 9 вытекает, что если существует условная плот-
плотность, то
Если предположить дополнительно, что распределение ц име-
имеет плотность q{y) относительно некоторой меры X в R'\ то B2)

§ 9. УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ 109
можно записать в виде
J J / {xlу) q(y)ii (dx) X (dy) = Р (I €= В, ц е= А). B3)
Рассмотрим теперь прямое произведение пространств Rs и
Rk и на нем прямое произведение мер \хХХ (если C = J3X,4,
B<=zR% AczRk, то цХА,(С)=1а(/?)А,(Л)). В этом пространстве
соотношение B3) означает, очевидно, что совместное распределе-
распределение g и ц в i?s X Л* имеет плотность относительно \х X Я, равную
Справедливо и обратное утверждение.
Теорема 10. Если совместное распределение 7^ и ц в RSSK
XRh .имеет плотность f(x, у) относительно ^Хл, го функция
'!{х/у)^=1Ш1' где
есть условная плотность | при условии ц — у, а функция q(y)
есть плотность ц относительно меры X.
Доказательство. Утверждение теоремы относительно
q(y) очевидно, так как ) q(y) %{dy) = Р (ц е А). Остается за-
л
метить, что f(x/y)=f(x1 y)/q(y) удовлетворяет всем условиям
в определении 13 условной плотности (равенство B3), экви-
эквивалентное B2), выполнено очевидным образом).
Теорема уточняет соотношение B1) в случае наличия плот-
плотностей у распределения % и ц.
Пример 19. Пусть |t, |2-независимы, ^gll^,- E2gl\2.
Чему равно условное распределение g4 при условии, что ?i + !2 =
= ?2? Мы могли бы без труда подсчитать искомую условную ве-
вероятность Р (^х = /f/?i + |2 = п)ч k ^ п, без использования тео-
теоремы 10, поскольку 5i + JUei П>и1+х2 и вероятность события
{§! + g2 = ^} положительна. Оставив этот путь для сопоставле-
сопоставлений, воспользуемся все же формально теоремой 10. Здесь gt
и г) == |i + |г имеют плотности (равные вероятностям) относи-
относительно считающих мер, так что
Поэтому искомая условная плотность (вероятность)" равна
где /? = A,i/(^i + ^2). Таким образом, условное распределение %i

110
ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИИ
при фиксированной сумме ?4 + ?2 = гс есть биномиальное рас-
распределение. В частности, если ?1? . . ., ?г независимы, ?,g§ll>,,
то распределение ?i при фиксированной сумме ^ 4~. , . -Ь ?г = га
будет равно #1/ги от А, зависеть не будет.
Ответ на тот же вопрос, что и в примере 19, для нормально
распределенных случайных величии можно получить, используя
следующий
Пример 20. Пусть Фо д2 есть двумерное нормальное рас-
расM
пределение величин |, и
где а=(а,, а2), щ =
р |, ? ( ) , о2 =
^ \\агз\\% °И ^ М (E>i -~ai)(lj—aj), i, ] = 1, 2. Определитель матрицы
вторых моментов равен
|оа| «anOga—о?2 == о11а22A — р2),
где р есть коэффициент корреляции между ^ и |2. Таким об-
образом, если |р| =^ 1, то матрица вторых моментов не вырождена
и для нее существует обратная матрица
Следовательно, совместная плотность ?, и ^г (относительно ме-
меры Лебега) равна (см. § 3.3)
¦X
2A-V
11
22
Одномерные плотности ?, и ?2 соответственно равны
^/„ч 1 .-(*-alJ/B(Jll) _/,.ч ! "О
11
B4)
B5)
Поэтому условная плотность ^ при условии ?2 = у равна
1
гехр —-
а11 A - р2)
&то есть плотность нормального распределения со средним
ai + 9 ]/ ~~2i (У"~" а2) и дисперсией ОцA — р2).

§ 9. УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ Щ
Отсюда следует, что f(x/y) при р = 0 совпадает с безуслов-*
ной плотностью /(.г) (и, значит, ?t и §2 независимы) и что
у. м. о. gi относительно g2 равно
ЛГ (Si/Sz) = «1 + Р /cin/Oa^Sa—аа)#
Прямую ж = а, + Р к о-п/022 (у —- а2) называют, линией регрессии
§! на §2 Она даст наилучшие средиеквадратические приближения
величины |t при данной %2 = У-
Пример 21. Рассмотрим задачу о вычислении плотности
случайной величины ? = ф(?, rj), где ? и т] независимы. Из фор-
формулы B2) при А = Rk вытекает, что плотность f(x) распреде-
распределения | выражается через условную плотность f(x/y) равенством
Применительно к рассматриваемой задаче под f{x/y) надо по-
понимать плотность случайной величины ф(?, у), поскольку
PgB) P((C)B)
П р и мер 22. Стрельба по цели с коррекцией. Производится
стрельба из орудия по коли с известной геометрической конфи-
конфигурацией. Введем систему
полярных координат, п ] ^Центр цели
начале которых распола-
располагается орудие. Расстоя-
Расстояние г (рпс. 6) от орудия
до некоторой точки, кото- -
рую считают центром це- и ? * Тачка попадания
ли, известно расчету ору- первого Выстрела
дстя точно; азимут нсизве- Рис. 6
стен, но имеется коррек-
корректировщик, который после первого пробного выстрела сообщает
расчету, каково отклонение по азимуту от точки попадания до
центра цели.
Предположим, что рассеивание снарядов при стрельбе (т. е.
отклонение (?, ц) точки попадания от точки прицеливания)
описывается двумерным нормальным распределением с плот-
плотностью j(x, у), определенной в B4) при а = 0. В § А гл. 8 мы
сможем объяснить, почему отклонение (g, r\) нормально. Мы
пренебрегаем здесь тем обстоятельством, что отклонение г) по
азимуту не может превосходить я, а отклонение ? по удаленно-
удаленности не может быть больше г. (Обычно стандартные уклонения
01 и в2 очень малы по сравнению соответственно с г и л, и от-
отмеченное обстоятельство не имеет значения.) Если бы вместе с
удалением г был бы точно известен и азимут [5 центра цели,
то тогда вероятность попадания в цель была бы равна
\ \ f{x,y)dxdyr

112 ГЛ. 4. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
где В(г, [})={(#, у\\(г + х, р+[/)ей/, множество В есть цель,
Но расчету орудия азимут сообщается корректировщиком по ре-
результату пробного выстрела (точку попадания он отождествляет
с точкой прицеливания), т. е. сообщается с погрешностью fi,
распределенной по нормальному закону с плотностью q(y) (см,
B5)), Какова вероятность в этих условиях события А, что вто-
вторым выстрелом орудие поразит цель? Если б = z1 то азимут со-
сообщается с погрешностью z я
р D/6 = 2)= j ) 1(x,y-z)dxdy=B<p{z)%
B(r3)
Следовательно,
]/ 2no
е 2°\{z)dz.
2 -о
Пример 23. Отрезок [0, 1] «наудачу» разламывается (т. о.
с равномерным распределением точки излома) па две части. За-
Затем большая часть снова «наудачу» делится па две части. Ка-
Какова вероятность, что из полученных отрезков можно составить
треугольник?
Эту задачу можно решать, конечно, и прямым «геометри-
«геометрическим» способом. Надо построить вероятностное пространство
<Q, S, Р>, где в качестве Q выбрать квадрат (как множество
значений о)}, со2, равных расстоянию соответственно точек пер-
первого и второго деления от начала координат). Вероятность здесь
определяется соотношением Р (А) = J J f(x, y)dxdy, где
л
О,. если х < 1/2, у < х или х > 1/2, у^ х%
1 i О
;, если х <С 1/2, у ^ г,
1 — X
1
—, если х^1/2. у<С.х.
Остается вычислить интеграл от зтой функции по множеству
В = Si U i52, где
Ва = Ь>1/2; 2(а:-у)<1, 2?/ < 1>,
так как треугольник можно построить' в том и только том слу-
случае, если (©!, оJ)^ В = i?! U В2.
Использование формулы
Р (В) « М [М (/ (В)/©!)J = МР

§ 9. УСЛОВНЫЕ РАСПРЕДЕЛЕНИЯ , Ц$
дает несколько иной путь решения задачи. Здесь для сокраще-
сокращения записи использована буква В также для обозначения собы-
события {(со1? со2)е^}. Так как о)! распределено равномерно на [0, 1],
то надо вычислить лишь Р(В/со1). Если (о4 < 1/2, то со2 распре-
распределено равномерно на [o)i, 1]. Треугольник можно построить, ес-
если 1/2 < оJ < 1/2 + (Oi. Следовательно, " Р (В/(дг) = саА/A — (ох)*
Из соображений симметрии легко находим, что при (Oi > 1/2
Следовательно,
1/2 1/2
Р-{5) = 2 J гЁг^^а: 1 + 2 J ^ = - 1 + 2 In 2. «
О О
Все приведенные выше примеры относились к у. м. о. отно-
относительно случайных величин (а не о-подалгебр).
Потребность в у. м. о. относительно о-алгебр возникает там,
где с помощью у. м. о. относительно случайных величин обойтись
уже трудно. Пусть, например, некоторый процесс описывается
последовательностью случайных величин {?j}?L-oo, которые не
являются независимыми. Тогда описывать распределение g1?
когда фиксирована вся «предыстория» (т. е. значения |0, ?_,,
?_2, ...), удобнее всего с помощью условного распределения gt
относительно о(^0, S-i, •••)• Ограничиться условными распреде-
распределениями относительно случайных величии здесь уже трудно»
Соответствующие примеры содержатся в гл. 12, 14—19,

Глав а 5
ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
С ДВУМЯ ИСХОДАМИ
§ 1, Законы больших чисел
Пусть имеется последовательность испытаний, в каждом из
которых некоторое событие А появляется с вероятностью р не-
независимо от исходов других испытаний. Образуем последова-
последовательность случайных величин следующим образом. Положим
gfe = 1, если событие А в к-м -испытании произошло, и gft = О
в противном случае. Тогда (h<)k^i будет последовательностью
независимых случайных величин, одинаково распределенных по
закону Борнулли: Р (Ik = 1) = р, Р (Ik = 0) = q = 1 — Р, Щи = Р,
D^/t = pq. Сумма Sn = l± + . ¦» + Sn^Bp есть не что иное, как
число появлений события А в п первых испытаниях. Очевидно,
MSn = np,'DSn = прд.
Следующее утверждение носит название закона больших чи-
чисел для схемы Бернулли.
Теорема 1. Для любого е > 0
>(J при п-+оо<
Это утверждение есть частный случай теоремы 4.7. Можно
получить и более сильный результат:
Теорема 2 (усиленный закон больших чисел для схемы
Бернулли). Для любого е > 0 при п -> <*>
P sup -?
>е
-О.
Смысл этого факта состоит в том, что введенное определение
вероятности соответствует интуитивному пониманию вероятности
как предела частоты появления события. Ведь SJn можно рас-
рассматривать как частоту появления события А, для которого
р (Л) = р. И оказалось, что в известном смысле SJn неогра-
неограниченно сближается с р.
Доказательство теоремы 2. Имеем
Р (sup
>е
-P и R-p
A)

§ 2. ЛОКАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
115
Здесь мы опять воспользовались неравенством Чебышева, но с
четвертыми моментами. Раскрывая скобки, находим
М E, - кРу =
i ili-p)) - 2 Mfo-PL + 6 2 M^
- А (де4 + №4) + 3k (k - 1) (pgJ < к + A (fc - 1) = &2, B)
Таким образом, оцениваемая вероятность не превосходит
оо
е~~4 2 ^~2-^0 при гс->оо. ^
Нетрудно видеть, что если бы мы в A) воспользовались
неравенством Чебышева со вторыми моментами, то требуемой
оценки не получили бы.
Можно отметить также, что на самом деле для вероятностей
P(\Sk — kp\>tk) верны я более сильные оценки, чем те, ко-
которыми мы пользовались. Они получены в § 5.
Следствие 1. Если f(x) — непрерывная функция на [0, 1], то при
п-^оо равномерно по р
Mf(Sn/n)-+f(p). C)
Доказательство следует из того, что при любом е > О
М
¦/(р)
+«(|,(?=
'u
¦f(p)
¦-Р
+
/(р)
> 8 < Slip | / (р + X) - f (Р) | + О A).
Следствие 2. Если f(x) непрерывна на [0, 1], то при п -> оо
2
-¦>
"¦*
"«
равномерно по х е= fO, lj.
Это соотношение есть просто другая запись C), так как Р (Sn = Л) =
= I , j pk A — p)n~h (см. гл. J). Из него следует известная теорема Вейер-
штрасса о приближении непрерывных функций полипомами. При этом нуж-
нужные полиномы построены в явном в яде — это полиномы Бернштейна,
§ 2. Локальная предельная теорема
Мы знаем, что Р (Sn = к) =( 7 )pfegn~fe?J g =1 —-р. Однако эта
\л /
формула ори больших п ж к становится весьма неудобной для
вычислений, в связи с чем возникает вопрос об асимптотическом
поведении вероятности РEл = Ал) при тг->оо.
8*

'116 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
В дальнейшем символ ап ~ 6П? где {ап} и {bj — две числовые
последовательности, будет означать, что ajbn ->¦ 1 при п ->- оо.
При этом такие последовательности {ап} и {Ьп} мы будем на-
называть эквивалентными.
Обозначим
H{x) = xlnj + {l-x)ln\^jt P* = i> D)
Теорема 3. /7/ш к ->¦ оо1 п — к ->- оо
Р E. -*) - Р (?-,•) ~ у^,^ ехр {- «Я0»*)}. E)
Доказательство, Воспользуемся формулой Стирлинга,
в силу которой п\ ~ I2nnnve~n при гг ~> °°. Тогда
л ( h n h
" exp J — A In (я — к) In
2лпр* A — р*) \ tl
+ fclnp + (/г —ft)]n(l — р)[ =*
1
ехр (— п \р* Id р* + A — р*) In A — р*) —
- Р* In р - A - р*) In (i-p),]--—^—^ ехр{-геЯ (р.)}.
Если р* = fc/^г близко к р, то для правой части в E) можно
найти другую форму записи, представляющую значительный ин-
интерес. Заметим, что функция II (х) является аналитической в
интервале @, 1). Так как
#' (х) = In - — In j—?, 1Г (*) = !+ -J—f F)
v / p 1 — py x ' x i —- xf- x '
то Н(р)=Н'(р)=0 и при р* — р-+ 0*)
Я (?¦) = i A + 1) (p* - p)« + О (| p* - p \%
Поэтому если p* ~ p m n(p* — pK ->¦ 0, то
P En = *) - ry^L- expf- » (p* - p
УАлпрд { 2pq
*) В соответствии с общепринятыми обозначениями будем писать a(z) =
= o(b(z)) при z->¦ z0, если Ь (z) > 0, lira г-гт = 0, и a (z) = О F (z)) при
| a (z) |
2 ~ь 2Q, если 6 (z) >* 0, lim sup , , , <Z 00.

§ 2. ЛОКАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА Ц7
Если положить Д — —-р==.х (р(х) =-~=е~х % то полним
у npq ' у 2л
Следствие 3. Если z = п(р* — р)= к — пр = о(гг2/3), га
PEn = A)-PEn-np = z)~9(zA)A. G)
Эта формула позволит оценивать вероятности событий вида
{Sv < ft}.
Если р* существенно отличается от р1 то оценка вероятностей
указанных событий может быть произведена с помощью резуль-
результатов §1.3.
Пример 1. В жюри, состоящем из нечетного числа п =
= 2т + 1 членов, каждый человек независимо от других прини-
принимает правильное решение с вероятностью р = 0,7/ Каково мини-
минимальное число членов жюри, при котором решение, принимае-
принимаемое большинством голосов, будет справедливым с вероятностью
не меньшей, чем 0,99?
Положим в этой задаче ^ft == 1, если к-и член жюри принял
правильное решение, и |fe = 0 в противном случае. Нас интере-
интересуют нечетные значения п, при которых Р (Sn^ m) ^0,01. Не-
Несомненно, что высокая точность принятого решения может быть
достигнута лишь при больших значениях п. В этом случае, как
мы установили в § 1.3, вероятность P(Sn^m) равна прибли-
приближенно
Используя теорему 3 и тот факт, что в нашей задаче
II A] = - i In 4/»A - р), II' D) = In i=A получим
,^т^w @-84)П
Справа здесь стоит монотонно убывающая функция а(п). Ре-
Решая уравнение а (л) = 0,01, в качестве ответа получим п = 33.
Такой же результат будет, если мы воспользуемся точными фор-
формулами.
Нетрудно оценить погрешность, возникающую в формуле E). Если в
формуле Стирлинга п\ = ]12лпппе~~п+д{п^ воспользоваться известными Eiepa-
венствами *) ^9п , ^ < 6 (п) < j^, то с помощью прежних рассуждений'
получим следующее уточнение теоремы 3.
*) См., например, [18, т. 1, с, 00],

118 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Теорема 4.
[1 — р*
где
ехр {- пН <**> +е
I е (/с,,,) i = i е {.) -о w - о (гг _ /о | < ^ +
(9)
Соотношение G) можно уточнить следующим образом:
Теорема 5. При всех к таких, что \ р* — р \ ^.-^ min (jo, q), имеет
место равенство Р (Sn = k) = ф(^Д)АA -j- e(/c, w)
1 + & (*, п) - ехр (e(Li!i^ + (| м +1/6) д2)), I е к 1.
Как это нетрудно усмотреть из свойств разложения в ряд функции еху
порядок малости г(к, п) в приведенных формулах совпадает с порядком
малосш показателя экспоненты. Из теоремы 5 следует поэтому, что при
z = к — пр = о(А~4/3) или, что то же, при z = о(я2/3), справедливо G).
Доказательство. Воспользуемся утверждением теоремы 4. В до-
дополнение к формулам (б) можем записать:
iL: (р* — p)R оценим. Учитывая, что
и обозначая для краткости \р* —• р\ =6, получим при б ^ A/2) mm (/>, g)
Отсюда следует, что
A0)
Обратимся теперь к остальным множителям в равенстве (8) и рассмот-
рассмотрим произведение /?*A — /?*). Так как — р ^ 1 — р — />* ^ 1 — /?, то

,§ 2. ЛОКАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 119
1
Отсюда следует, в частности, что при \р* — р \ <. 7>-min (p, q) выполняется
1 1
| р* A __ p*)—pq \<~2 pqf р* A — р*) > у рд.
Поэтому наряду с (9) можно написать, что при значениях к, указанных: в
теореме 4,
1^. - (И)
tinpq
Осталось рассмотреть множитель [/?*(!— Р*)]~'1/2. Так как при \у\ < 1/2
11п A+7) | =
1
то при б =т |р* — р| < (Уг) min (/?, q) будут справедливы соотношения
ря
_2о2_б е ах0,
Р« ! 2 '
- Р*)Г1/2 - [рд]~1/2 ехр °^. A2)
Р?
Используя представления A0), (И), A2) и утвер?кдепие теоремы 3,
закончим доказательство. ^
Из приведенных оценок видно, что границы для числа 0 в формулиров-
формулировке теоремы 5 могут быть сужены, если рассматривать меньшие отклонения
\р* — р|, скажем, до значения a rain (p, q), где а < 1/2.
Найденные соотношения для Р (Sn = к) представляют собой
так называемые локальные предельные георемы для схемы Бер-
Берну лли.
Основная асимптотическая формула, изложенная в теореме 3,
допускает естественное обобщение на полиномиальное распре-
распределение BjJ, p=*(ph . . ., рг), когда в последовательности незави-
независимых испытании при каждом испытании наступает не один из
двух, а один из г^2 возможных исходов Аи .. ., Аг, вероятно-
вероятности которых равны соответственно pL, ..., рг. Пусть Sn есть чис-
число появлений события Aj в п испытаниях,
е __ ( ed> c(r)>) h — Ik h \ n* — к
и положим И (х) = 2 xi ^п {Xi/Pi)' % = (^и • ••» #г). Очевидно, что
*5пёВр. Следующее утверждение является прямым обобщени-
обобщением теоремы 3:

120 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Теорема 6. Если каждое из г переменных kh ..., kr либо
равно 0, либо стремится к <х> при п ~> оо? то
р EП « А) ~ Bя/г) 2 / П ft 1 ехр {^ /гЯ
е^в г0 — число переменных ки . •., &r, we равных 0.
Доказательство. Как и в доказательстве теоремы 3, вос-
воспользуемся формулой Стирлмпга
п\ - И2ппе~ппп .
при д -> оо. Считая, не ограничивая общности, что все /^ -> оог
/ = 1, , •., г, получим
§ 3. Теорема Муавра — Лапласа и ее уточнения
Sn — пр
Пусть а и Ъ — фиксированные числа, ?п =¦ .— -. Тогда
У tlpq
() __2
a Y-npq <z<CbV npq
Если здесь вместо P(Sn—пр =z) подставить ф(гД)Д,'то получим
интегральную сумму 2 ф(^Д)Аг соответствующую интегралу
b
Г
a
Таким образом, соотношения G) делают правдоподобным ра-
равенство
b
lim Р(а<?п<Ь) = |ф (х) dx = Ф (Ъ) - Ф (а), (t3)
где Ф(^) есть функция нормального распределения с парамет-
параметрами @, 1):

§ 3. ТЕОРЕМА МУАВРА — ЛАПЛАСА И ЕЕ УТОЧНЕНИЯ J21
•Это есть теорема Муавра — Лапласа, относящаяся к интеграль-
интегральным, предельным теоремам. В гл. 7 мы получим более общие
интегральные теоремы, из которых A3) будет следовать в ка-
качестве частного случая.
Теорема 5 позволяет получить A3) вместе с оценкой по-
погрешности или, ипаче говоря, с оценкой скорости сходимости.
Пусть А и В — целые числа,
a = (A — np)/l/npq; b = (B — np)tl/npq. A4)
Теорема 7. Пусть b > а, с = max (|a|, |&|)t
p = c "у" Д -f —,
3 G
Тогда если Д = l/\'npq <^. 1/2, p ^ 1/2, ro
a
*de |9<| <1, « = 4,2.
Эта теорема показывает, что левая часть в A5) может быть эквивалент-
эквивалентной Ф(Ь) —Ф(а) и при растущих а и Ъ. В этих условиях ФF) —Ф(а) мо-
может сходиться к 0, и знание относительной погрешности в A3) более удоб-
удобно, так как ее малость всегда позволяет установить малость и абсолютной
погрешности, но не наоборот.
Доказательство. Заметим прежде всего, что при всех к таких,
что \z\ = \к — пр\ <с tfnpq, будут выполнены условия теоремы 5. Дейст-
Действительно, для выполнения неравенства \р* — р} < A/2) min (/?, q) доста-
достаточно, чтобы | к—юр | <; -р—= 1/BД2). Это неравенство будет выполнено,
•если с < 1/BД). Но в силу того, что р ^ 1/2, имеем
с (с2 + 3) А < 1/2> сД<|/2.
Таким образом, при каждом k таком, что a^npq ^ z <C b^/npq, мы 'можем
воспользоваться теоремой 5, в силу которой
«1 п i,q -*Cz<ibYnpq
= 2 ф(гА)Д I1+(ехр (9
¦где |0| < 1. Так как при р ^ 1
то абсолютное значение поправочного члена в A6) но превосходит (подста-
.иим туда гД = с)
охр!

122 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Поэтому
где 10, | < 1.
Преобразуем теперь сумму, стоящую в правой части полученного ра-
равенства. Для этого заметим, что для любой гладкой функции ф(х)
jc-fA
Аф (х) -
(t) dt
1 2/
Но для функции ср (.г) = /—-- е~~х /2 имеем у'(х) = — #ф(я), и наиболыпео
|/2я
значение ф(?) на отрезке [#, # + Д], |ar| ^ с, отличается от наименьшего
( А*\
не более чем на множитель expj с А +—|. Поэтому при \х\ ^с в силу A8)
Аф (о?)
^ J Ф.
Так как
dt
_!_ 1
х+А
ф {t) < _ е 2 I
2
^2, то справедливо представление
A + е^с), • |61|<i.
Подставляя его в A7), мы получим утверждение теоремы.
Таким образом, по теореме 7 разность
1п
| р (х
у) - (Ф (у) - Ф (х)) |
A9)
эффективно, хотя и весьма грубо, оценивается сверху величиной порядка А,
или, что то же, величиной порядка 1/ynpq, если только х = а, у ~ Ъ (под
а и Ъ мы понимаем значения (см. A4)), представимые в виде (к — пр)А,
где к — целое). Если х и у не принадлежат указанной решетке с шагом Д,
то погрешность A9) будет оцениваться величиной того же порядка, так как^
например, при изменении у вероятность Р {а ^ ?п <С у) будет постоянной
на полуинтервалах вида (а + кА, а + (к -\- 1)А), а функция Ф(?/) — Ф(х)
монотонно возрастает с ограниченной производной. Аналогичные доводы
справедливы и относительно левой границы х. Теперь важно отметить, что
порядок оценки Iflnpq не может быть улучшен, так как именно такой по-
порядок имеют по теореме 5 скачки функции распределения ?„.
Теорема 7 позволяет использовать нормальное приближение для
Р (.г ^ ?п <С г/) ив так называемой области больших уклонений, когда х и
у возрастают по абсолютной величине и имеют одинаковые знаки. В этом
случае Ф(у) — Ф(#) и приближаемая вероятность сходятся к 0. Поэтому
приближение естественно считать удовлетворительным, если только
Р (х < tn < у)/(Ф (у) - Ф (х)) -> 1. B0)
Как показывает теорема 7, такая сходимость будет иметь место, когда
с = шах (|я|, \у\) = tf(A~1/3) дли, что то же, с = #(/г1/6).

§ 4. ТЕОРЕМА ПУАССОНА И ЕЕ УТОЧНЕНИЯ 123
При больших значениях с, как это нетрудно проверить с помощью тео-
теоремы 3, соотношение B0), вообще говоря, выполняться не будет.
В заключение отметим, что так как при 6->-оо
то из теоремы 7 немедленно следует, что при каждом фиксированном у
lim Рап<у) = Ф(у).
Позже мы покажем, что это утверждение справедливо и в гораздо более ши-
широких условиях, когда ?п есть нормированная сумма произвольно распреде-
распределенных случайных величин с конечной дисперсией.
§ 4. Теорема Пуассона и ее уточнения
Как было видно из оценок в предыдущем разделе, теорема
Муавра — Лапласа будет обеспечивать хорошее приближение
для оцениваемых вероятностей, если число npq (дисперсия Sn)
велико. Это число будет расти вместе с и, если р и q положи-
положительны и фиксированы. Но как поступать в задаче, где, напри-
например, /? = 0,001, а тг = 1000, так что пр = i? Хотя п здесь велико,
в этой задаче применять теорему Муавра — Лапласа бессмыс-
бессмысленно. Оказывается, что в этом случае распределение Р (Sn = к)
можно хорошо приближать распределением Пуассона П^ при
подходящем значении \х (см. § 4.2). Напомним, что
- 2 е~*?.
Обозначим пр = jjl
Теорема 8. Для всех множеств В
Это утверждение мы могли бы доказывать так же, как ло-
локальную теорему, пользуясь явной формулой для P(Sn = k).
Однако доказательство можно получить более простым и кра-
красивым способом, который можно было бы назвать «методом од-
лого вероятностного пространства». Этот метод нередко исполь-
используется в вероятностных исследованиях и состоит в пашем слу-
случае в том, что на том же пространстве, где заданы Sn, строятся
случайные величины Sn, по возможности близкие к Sn и такие,
что распределение Sn совпадает с распределением Пуассона.
Важно также, что метод одного вероятностного пространства
без каких бы то ни было усложнений допускает обобщение па
случай сумм разнораспределенных случайных величин, когда
вероятность р появления 1 в каждом испытании зависит от но-
номера испытания. Пользуясь этим обстоятельством, докажем здесь
'более общее утверждение, из которого теорема 8 будет следовать
как частный случай,

124
ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Итак, пусть имеется последовательность независимых слу-
случайных величин gi, .. ., gre; ?j^=B^. Обозначим, как и прежде,
п
2 ?;• Формулируемая ниже теорема предназначена для оцеп-
1
3=1
ки РEГП = Л), когда /?j малы, а число \i = 2 Pi «сравнимо с 1».
i=i
Теорема 9. Дял всех множеств В
Прежде чем переходить к доказательству теоремы 9, отме-
отметим одно важное свойство распределения Пуассона, которое нам
понадобится: если щи ц2 независимы, ^el^v тЪ€ЁМ1ц2' mt>
Действительно, по формуле полной вероятности
Р (% + Т|2 = к) = S Р (Г)! = /) Р (Т|а = &-/) =
я
Доказательство теоремы 9. Пусть со,, . .., со„ —не-
—независимые случайные величины, каждая из которых есть тож-
тождественная функция (?(&)ft)=coft) на единичном отрезке с равно-
равномерным распределением. Можно считать, следовательно, что век-
вектор (o=((Oi, . . ., 0)п) задан как тождественная функция на еди-
единичном тг-мерном кубе Q с равномерным распределением.
Построим на Q случайные- величины %} и ?j следующим
образом:
JQ, если o)j< 1 —
если
если
если
1 -— р,у
oj < е
Р\
где яй=
Очевидно, что
независимы, ^j (о))
' Л = 0,1,....
о) независимы, ?j (o))g| В.р.; ^ (со) также-
^. Заметим теперь, что так как 1 — Pj^
*) Этот факт будет очень просто следовать также из свойств характе-
характеристических функций, излагаемых в гл. 7.

§ 4. ТЕОРЕМА ПУАССОНА И ЕЕ УТОЧНЕНИЯ 125
е V то !j(co) =^= ?/(<ю), только если щ^ 11 — pj% e ч или со; е.
[е Pj + Pje v{, lj. Следовательно,,
где 5;« UEj^n^
Теперь можно записать:
еВ,5,^Й)|<РEп#4 B1)
Отсюда очевидным образом следует утверждение теоремы, ^
Замечание. Можно указать и другие конструкции одного вероятно-
вероятностного пространства. С помощью одной из них мы выясним сейчас сущест-
существование более точного пуассоновского приближения для распределения Sn.
Именно, пусть ^ (со) — независимые случайные величины, распределен-
распределенные по закону Пуассона с параметрами г$ = —In A—Рз)^Рз, так что
р (|* = 0) = е~Г> =l-Pj. Тогда Ъ} («) = min (l, l] (со)) ^ В ,
при этом
р (и [ij (^ *е; w}) <2 р(? (<°) >2) = 2
Но при г = —In A —p) справедливо неравенство
- p) In A-p) <p+(t-p
Следовательно, для построенного пуассоиовского приближения
Положив Я = — 2 ^п (* "~ Pj) ^ 2 ^j' пУтем прежних рассуждений по-
лучаем оценку

126 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Эта оценка близости с распределением Пуассона с «чуть сдвинутым»
параметром лучше, чем оценка, полученная в теореме 9. Кроме того, можно
отметить, что в новом построении ^s^g*,Sn^S* и, следовательно,
Р {Sn > &) < P(SI > /с) = nx([fr, оо)).
Вернемся к случаю одинаково распределенных gft. Чтобы из
теоремы 9 получить теперь предельную теорему типа Муавра —
Лапласа (см. A3)), здесь требуется несколько иная, чем преж-
прежде, постановка задачи. Ведь для того, чтобы пр с ростом п оста-
оставалось ограниченным, нам нужно, чтобы р=Р ($л = 1) сходи-
сходилась к нулю, чего нельзя добиться, рассматривая фиксирован ну го
последовательность случайных величин |1? ?2, . * ••
Мы введем в рассмотрение последовательность возрастающих
серий случайных величин:
tB) tB).
fel ? Ь2 у
tC) tC) ?C).
bl у Ь2 ? ЪЗ 1
t(n) p(n) tin) ?(n)
bl » Ь2 ? ЪЗ » . • • » Ьг» •
Это так называемая схема серий. Индекс сверху означает номер
серии. Нижний индекс означает номер случайной величины в
серии.
Пусть в п-ш 'серии случайные величины ?& независимы, t^ ^
Следствие 4 (теорема Пуассона). Если прп -> fi > О
/г ->- оо? го дгра каждом k
Это утверждение является очевидным следствием теоремы 8.
Его легко получить также непосредственно, заметив, что из ра-
(п\
венства Р (Sn = к) = р A — />)'г следует
Р (Sn - к) к + I 1 - /^ М- Г ^
Из теоремы 9 вытекает аналог теоремы Пуассона и в более
общем случае, когда ?/' не обязательно одинаково распределе-
распределены *) и могут принимать значения, отличные от 0 и 1.
*) Обобщение теоремы Муавра-—Ляплагя па случай разпораспределен-
иых величин содержатся в центральной предельной теореме § 8.4.

§ 4. ТЕОРЕМА ПУАССОНА И ЕЕ УТОЧНЕНИЯ 127
Следствие 5. Пусть pjn = P (if = l) зависят от п и j ran,
что
max j9jn--^ G,
з
P (if = 0) = 1- Pjn+ o{Pjn).
Тогда справедливо B2).
Для доказательства следствия надо воспользоваться теоремой'
9 и тем фактом,что Р ( ^ 1^ ^0,^^1))<|о(Pin) = о A),
означающим, что с вероятностью, сходящейся к 1, все l/1 при-
принимают лишь значения 0 или 1. ^
Наряду с этими утверждениями из теорем 9, 8, очевидно,
можно получить и несколько более сильные формулировки; для
любого множества В
lim
Отметим, что в условиях теоремы 8 такая сходимость будет
иметь место и для значений пр -»¦ оо? до таких, что пр2 -»¦ 0. В то-
тоже время уточнение теоремы Муавра — Лапласа в § 3 пока-
показывает, что приближение для распределения Sn с помощью нор-
нормального закона действует, если пр ->¦ °° (мы считаем, что р < q,
1 \
так что npq > -^ пр -> оо I.
Таким образом, существуют последовательности р ^ {р : пр -^
->¦ «эо, ?г/?2 -> 0), для которых применимы оба приближения — и
нормальное, и пуассоновское. Другими словами, области приме-
применений нормального и пуассоновского приближений перекры-
перекрываются.
Далее, из теоремы 8 мы видим, что скорость сходимости в следствии 4
определяется величиной цорядка п~1. Поскольку при п ->- оо
п = 0) — я0 = еп 1п A-^ — ^-^ - f— ^-^
то эта оценка существенно улучшена быть пе может. Однако при больших к
(так сказать, в области больших уклонений) такая оценка для разности
становится грубой. .(Ведь в B1) мы пренебрегаем не только разными зна-
знаками поправочных слагаемых, но и редкими событиями {8п = к} и {?п— &),
которые стоят под знаком вероятностей.) Здесь мы приходим, так же как
в § 4, к необходимости иметь приближения, обладающие малой не только
абсолютной^ по и относительной погрешностью.

128 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Покажем, что соотношения асимптотической эквивале; тности B2) со-
сохраняются и при растущих (вместе с п) к и \i таких, что
к = 0(п2^)\ и. = o(n^)t |fc —ц| = о(У^Г),
Действительно,
П ({fc
k\ \ n J \ n
Надо доказать, таким образом, что при указанных значениях к и \i
1-^-^^1 = 0A). B3)
Мы получим это соотношение вместе с видом поправочного члена. Именно,
покажем, что
B4)
"V7 " 2п
ж, следовательно,
Воспользуемся тем, что при а—>-0
In A — а) =—а — ~ + О (а3)-
Тогда соотношения B3), B4) будут следовать из равенств
<п _ Л) la A - р) + рп = (и - Л) ( - р - ^ + О (р3) j + рп -
В заключение отметим, что приближенная формула Пуассона
P{Sri==k) *!?,-*
широко используется в различных приложениях и обладает, как
показывают опыт и • полученные выше оценки, высокой точ-
точностью даже при умеренных значениях п.
Рассмотрим теперь примеры, где для приближенных вычис-
вычислений используются теоремы Муавра — Лапласа и Пуассона.

§ 4. ТЕОРЕМА ПУАССОНА И ЕЕ УТОЧНЕНИЯ 129
Пример 2. Пусть имеется 104 пакетов с зерном. Известно,
что в этих пакетах имеется 5000 меченых зерен. Какова веро-
вероятность того, что в некотором фиксированном пакете есть хотя бы
одно меченое зерно? Можно себе представить, что меченые зер-
зерна случайным образом распределяются среди пакетов. Тогда
вероятность попадания определенного меченого зерна в выбран-
выбранный пакет будет равна р = 10~4. Так как этих, зерен 5000, то это
число II будет числом испытаний, т. е. п = 5000. Определим слу-
случайную величину gft следующим образом: ^ft == 1, если к-е зерно
попало в выбранный пакет, ?/г = 0 в противном случае. Тогда
5000
$5000 ~ 2 ^k будет числом меченых зерен в нашем пакете. По
теореме 8 Р(?5ооо =0)^^~np = е °'5, так что искомая вероят-
вероятность равна приближенно 1 — е~0>5. Точность этих соотношений
оказывается весьма высокой (в силу теоремы 8 погрешность не
превосходит 2~1-10~4). Если бы мы пользовались теоремой Пу-
Пуассона, а не теоремой 8, то должны были бы представить себе
схему серий случайных величин, распределенных по закону
Бернулли, при этом наши случайные величины составляют пя-
пятитысячную серию. Кроме того, мы считали бы, что для серии
с номером п прп = 0,5. Таким образом, условия теоремы Пуас-
Пуассона были бы выполнены и можно было бы воспользоваться
предельной теоремой для того, чтобы написать уже полученное
приближенное соотношение.
Пример 3. Те же рассуждения можно использовать и в
следующей задаче. Водоем объема F, из которого мы берем про-
пробу объема y<F, содержит п опасных бактерий. Какова веро-
вероятность того, что мы обнаружим эти бактерии в контрольном
сосуде?
Обычно считают, что вероятность р того, что любая заданная
бактерия попадет в пробу, равна отношению объемов v/V. Кро-
Кроме того, обычно также предполагают, что появление одной дан-
данной бактерии в пробе не зависит от того, где находятся осталь-
остальные п — 1 бактерий — в пробе или нет. Иными словами, обычно
постулируют, что механизм переноса бактерий в контрольную
, пробу эквивалентен последовательности п независимых испыта-
испытаний с вероятностью «успеха» в каждом испытании, равной
р = u/V.
Вводя, как п раньше, случайные величины gA, получим опи-
п
сание числа бактерий в пробе с помощью суммы Sn = 21 bt
в схеме Бернулли. Если пи сравнимо по величине с F, то по
теореме Пуассона искомая вероятность
А. А. Боровков

130 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
Модели, аналогичные только что описанной, используются
также для описания числа видимых звезд в некоторой области
неба, расположенной вдали от Млечного пути. Именно, пред-
предполагается, что если в области R имеется п видимых звезд,
то вероятность того, что в подобласти г с= Я будет находиться
к видимых звезд, равна
где р равно отношению площадей S(r)/S(R) областей г и R
соответственно.
Пример 4. Допустим, что вероятность рождения мальчика
постоянна и равна 0,512 (см. и. 1 § 5 гл. 3).
Рассмотрим группу новорожденных в 104 человек и будем
считать, что ей соответствует последовательность I04 независи-
независимых испытаний, результатом каждого из которых является по-
появление мальчика или девочки. Какова вероятность того, что
среди этих новорожденных мальчиков будет но крайней мере
па двести человек больше, чем девочек?
Случайные величины gft определим следующим образом: ?ft =
= 1, если к-й новорожденный оказался мальчиком, и gfe = 0—-
10*
в противном случае. Тогда Sn = ]L ^ есть число мальчиков в
k=i
' зарегистрированной группе. Число npq ~ 0,25 • 104 здесь велико,
поэтому применив интегральную теорему Муавра — Лапласа,
для искомой вероятности получим
Для отыскания численных значений Ф(х) обычно пользу-
пользуются таблицами, имеющимися в большинстве руководств по
теории вероятностей и математической статистике (см. Прило-
Приложение 5).
В приведенном примере А ~ 1/50 и удовлетворительное при-
приближение формулой Муавра — Лапласа будет заведомо обеспе-
обеспечено (см. теорему 7) при с < 2,5.
Если же, допустим, нам потребуется оцепить вероятность то-
того, что доля мальчиков превысит 0,55, то мы будем иметь дело
с вероятностями больших уклонений, где . для оценки
P(«S'M>5500) уже лучше воспользоваться приближенным соот-
соотношением, полученным в § 1.3, , в силу которого (к = 0/i5nf
q = 0,488)

§ 5. ВЕРОЯТНОСТИ БОЛЬШИХ УКЛОНЕНИЙ 131
Пользуясь теоремой 3, находим
Р (Slt > 5500) « J^ Л
То есть если допустить на минуту, что на планете ежегодно
рождается 100 млн. человек и что все родившиеся разбиваются
на партии по 10 тыс. в каждой, то для того, чтобы в какой-
нибудь партии появилось завышение доли мальчиков всего па
3,8%, потребуется ждать в среднем более 107 лет (см. при-
пример 1 § 4.1).
Ясно, что числовые оценки, основанные на нормальном при-
приближении, можно проводить и в задачах примера 3, если числа
"лр, фигурирующие там, окажутся большими.
§ 5. Неравенства для вероятностей
больших уклонений в схеме Бериулли
В заключение этой главы мы получим некоторые полезные
неравенства "для схемы Бернулли. В § 2 мы ввели функцию
которая играет существенную роль в теоремах 3, 4 об асимпто-
асимптотическом поведении вероятности Р (Sn = к), Там же были рас-
рассмотрены простейшие свойства этой функции.
Теорема 10. При z ^ 0
Р (Sn — пр>z)< ехр[— nil[р + -)],
) "Л B5)
Кроме того, при всех р
П( + х)>2х\ B6)
так что каждая из вероятностей B5) при любом р не превосхо-
превосходит ехр {—2z2/n).
Для сравнения с утверждением E) теоремы 3 первое нера-
неравенство теоремы 10 можно записать в виде
Неравенства B5) в какой-то мере близки и к теореме Муавра
Лапласа, поскольку при z = o(tz2/3)
^+ оA).
2npq v '
Последнее утверждение вместе с B6) можно интерпретировать

132 ГЛ. 5. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ ИСПЫТАНИЙ
так: уклонение z от среднего значения пр имеет максимальную
вероятность при р = 1/2.
При z/Hи -*- оо обе вероятности B5) сходятся к нулю при
п -> оо? так как они соответствуют большим отклонениям суммы
Sn от среднего пр. В этом случае их называют вероятностями
больших уклонений.
Доказательство теоремы 10. В следствии 4.3 предыду-
предыдущей главы было установлено неравенство
Применяя его к сумме ?„, получим
Р (Sn > пр + z) < ^(пр+г)м/Ч
Так как е" п = Ц^ ^ и случайные величиные ^независимы, то
1
1
Выражение в квадратных скобках равно Me . Сле-
Следовательно, как сумма двух выпуклых функций, это есть вы-
выпуклая функция от X. Уравнение для точки Х(а) минимума этой
функции имеет вид
-(р + а) A+ р(ех - 1)) + рех = 0.
Отсюда находим
еНа) ^ (р + а) д
р {д — а) '
V Р\е — ))е # ~~ q — a [
exp j — (p + a) In ^-—- —(r^—a)In-
4 )
= exp{—Я(р + а)}.
Первое из неравенств B5) доказано. Второе неравенство сле-
следует из первого, если его рассматривать как неравенство для
числа появлений нулей-.
Далее из D) следует, что Н(р)=П'(р)= 0, IF(x)= -^jzTTy
Поскольку максимум функции x{i — x) на [0, 1] достигается в
точке х = 1/2, то И" (х) > 4,
Об аналогах теоремы 10 для сумм произвольных случайных
величин см. Замечание 1 § 7. 5.

Глава в
О СХОДИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН
И РАСПРЕДЕЛЕНИЙ
§ 1. Сходимость случайных величин1
В предыдущих главах мы уже по раз сталкивались с утвер-
утверждениями, где рассматривалась сходимость в том пли ином
смысле распределений случайных величии или самих случайных
величии. Теперь введем ряд определений, описывающих разные
виды сходимости, и выясним соотношения между ними.
Пусть па вероятностном пространстве <О, 3, Р> заданы
последовательность случайных величин {%п} и случайная вели-
величина ?.
Определение 1. Последовательность {\а} сходится по ве-
вероятности *) к g, если для любого в > О
n-6|>e)->0 при п->оо.
Обозначается это так:
1п~>ь при п~~>-ооа
В этих обозначениях утверждение закона больших чисел для
схемы Бернулли можно было бы записать в виде
Sjll -> /?,
Р
поскольку SJn можно рассматривать как последовательность
случайных величии, заданных па одном вероятностном про-
страпстве.
Определение 2. Мы будем говорить, что последователь-
последовательность |п сходится к % с вероятностью 1 (или почти наверное:
1п~+1 и. н., Ъп-^Ъ), если ?„(©)-> g((o) при п ->¦ оо для всех
о) е Q? за исключением, быть моясет, оз из множества /V cz Q пу-
пулевой вероятности: Р (А^) = 0. Такую сходимость можно назвать
также сходимостью почти всюду (и, в.) относительно меры Р.
Очевидно, что сходимость \н —> 5 влечет за собой сходимость
п. н.
hi —>¦ S- Обратное утверждение, вообще говоря, по верно, в чем
мы убедимся несколько позже. Однако, если |ге монотонно воз-
возрастает пли убывает, то сходимость ^п -*-1 влечет за собой
En—*?• Действительно, предположим, не ограничивая общности,
*) В теоретико-множественпой терминологии сходимость по вероятно-
вероятности означает сходимость по мере.

134 гл. 6. о сходимости случайных величин и распределений
что 1 = 0, %п>0, tnKln-^-l- Отсутствие сходимости ?п—> I оз~
V п.н.
начало бы, что существуют g>0 и множество Л, Р(Л)>б>От
такие, что 8ир^>8при оз е^и при всех п. Ио sap|fe =in, и свд-
занноо означает, что
РAп>е)
при всех га, что противоречит сходимости ?„ -^0.
В этих рассуждениях случайные величины \п могли быть ж
несобственными.
Итак, сходимость по вероятности определяется поведением
числовой последовательности Р (| in — 11 > &). Можно ли ана-
аналогичным образом характеризовать сходимость с вероятностью 1?
Обозначим ?п = sup \\h — \ I (эта случайная величина может
быть и несобственной).
Теорема 1. ^п—*" I тогда и только тогда, когда tn-*-0 или.
П.Н. , 2>
что го же, когда для любого г > 0 тг/??х д -^ оо
|A-S|>8)->0. A)
Доказательство. Ясно, что |„ -*¦ | п. и. тогда и только
тогда, когда tn -> 0 п. н. Но последовательность t,n монотонно
убывает ?nl, ^rt-^0, и нам остается воспользоваться сделанны-
сделанными выше замечаниями, в силу которых ?п -*• 0 п. н. <4
Во введенной терминологии утверждение усиленного закона
больших чисел для схемы Бернулли можно сформулировать в
силу A) как сходимость SJn-*-p с вероятностью 1.
Мы уже отмечали, что сходимость почти наверное влечет
за собой сходимость ио вероятности. Приведем теперь пример,
показывающий, что обратное утверждение неверно. Пусть
<Q, §,Р> есть единичная окружность с о-алгеброй борелов-
екпх множеств и равномерным распределением. Положим §(о))^
= 1, ?п(со)=2 на дуге [г(п), г(п)+ 1/п] и |п(со)=1 на осталь-
п
ном множестве. Здесь г(п) = У, -г. Очевидно, что^п-^|. В то
же время г(?г)-+оо при п ->¦ ^ и множество сходимости \п к ?
пусто (мы не можем указать пи одного со, для которого
g;t(G))Vg(a>)).
Однако если Р(| in— ?| >*0 убывает при п -> °о достаточно
быстро, то сходимость по вероятности будет означать и сходи-
сходимость и. п. Именно, соотношение A) дает следующее достаточ-
достаточное условие для сходимости с вероятностью 1.
сю
Теорема 2. Если ряд 2 Р A ift ~~ ?1 > 8) WPM любом е>0
сходится^ то \п ->- ^ п. л.

§ 1. СХОДИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН 135
Это утверждение очевидно, поскольку
P(U S
Именно этим критерием мы по существу пользовались при
доказательстве усиленного закона больших чисел для схемы
Бернулли.
Обратное заключение о скорости сходимости к пулю вероят-
вероятности Р (| Ьп — ? | > 8) из сходимости п. н. сделать невозможно.
Читатель без труда может построить пример, когда |л -*¦ § п. п.,
а Р A 5д — ? 1 > в) сходится к нулю сколь угодно медленно.
Из теоремы 2 вытекает
Следствие 1. Если t^-v^, то существует подпоследова-
р
телъностъ {nj такая, что |rfe—»-? д. н. при к -*¦ °о9
Это утверждение также очевидно, так как достаточно взять
такие д/г, чтобы Р ( | ^nk — \> \ > е) ^1/&2, и воспользоваться тео-
теоремой 2. ^
Есть еще один важный частный случай, когда из сходимо-
сходимости по вероятности ?п ->¦ ^ следует сходимость gn ->¦ | п. н. Это
случай, когда gn образованы последовательными суммами неза-
независимых случайных величин. Именно, справедливо следующее
п
утверждение. Если ?n = 21lfc> r\k независимы, то сходимость gn
г
/го вероятности влечет за собой сходимость с вероятностью, 1.
Это утверждение будет доказано в § 10.2.
Рассмотрим, наконец, третий вид сходимости случайных ве-
величин.
Определение 3, Будем говорить, что \п сходится к g
в среднем т-го порядка (в средыеквадратическом, если г = 2),
если при п -*¦ °о
Такую сходимость будем обозначать ?л -> |.
Очевидно, что из ^п ->¦ 5 в силу неравенства Чсбышсва сле-
Дус^?п->1- Из п. н. сходимости (и тем более, из сходимости
по вероятности) сходимость ->¦ не следует. Таким образом, схо-
сходимость по вероятности является слабейшей из введенных трех
видов сходимости.
Отметим, что при наличии дополнительных условий из
у
димости ?п->? может, конечно, следовать ?и--^Е. Например,
р (г)
в следствии 4 будет показано, что если ?/г->с;г М|^ЛГ+а <с
при некотором а > 0 и всех /г, то \п -> &•

136 ГЛ. 6. О СХОДИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИИ II РАСПРЕДЕЛЕНИЙ
Опре долепи о 4. Будеда говорить, что последовательность
gn является фундаментальной по вероятности (п. н., 6 среднем)f
если для любого 8 > О
Р fsup 1 S» — Em 1 > «"Л -^ 0,
при п ->• «>, т ->¦ оо.
Теорема 3 (признак сходимости Копти). §п -^ § в каком-
пибудъ смысле (->-, —> , —П тогда и только тогда, когда §п фунда*
ментальна в соответствующем смысле.
Доказательство. Фундаментальность очевидным обра-
образом следует из сходимости в силу неравенств
|Sn-EmK|gn-?| + U,,-H
Slip | gu — gm 1 < Slip I g?1 _ g | + | ^m — g К 2 Slip | ^n _ ^ |,
при некотором Сг*
Для доказательства теоремы в обратную сторону понадобит-
понадобится следующая лемма Бореля — Каителли:
Лемма 1. Пусть {Л „}^=1 — последовательность событий на
<Q, S, Р> и пусть А есть событие, состоящее в том, что про-
произошло бесконечно много событий Ап, т. е.
Л= П U А„ B)
(А составлено из со, принадлежащих бесконечно многим Ап)*
Тогда если 2 Р (Л") < °°- mo P (Л) = °-
Доказательство. Используя свойство вероятности, по-
получим
Верпемся к доказательству теоремы 3. Пусть последователь-
последовательность $п фундаментальна по вероятности. Выберем последова-
тельноеть {ш) так, чтобы
при ?г > /2ft, m > wfe. Обозначим
Тогда Р(ЛА)<2""?г, Р(Л) = 0, где Л определено в B)\
Следовательно, по лемме Бореля — Каптслли с вероятностью 1

§ 1. СХОДИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН 137
произойдет лишь конечное число событий Ah. Это означает, что
для каждого ш ^ Q — Л найдется /н(о) такое, что {Е/Л^) —
'—S/i+i (t0) 1^ 2~~'прн всех k^ko(d)). Отсюда получаем неравен-
неравенство U.Uo)) — gi(a))|<2~/i+1 при всех к>ко(ы), 1>к\{(о),
означающее, что последовательность чисел ^ (со) фундаменталь-
фундаментальна, и что, следовательно, существует значение ?(со), такое, что
||ft(fc>) — s(co) |->-0 при к ->¦ оо. Это означает, в свою очередь, что
П -> оо? к ~> °°.
Пусть теперь ?„ фундаментальна в среднем. Тогда в силу
неравенства Чебышева она будет фундаментальна по вероятно-
вероятности, и, следовательно, существуют случайная величина \ и под-
подпоследовательность {%} такие, что ъпк ~> %• Покажем, что
' П.II.
М | |,t — ^ |г -> 0. Для заданного s > 0 выберем п так, чтобы
М|?/г — ?/Г<8 ПРЫ к~>п, 1^ /г. Тогда в силу леммы Фату (см.
Приложение 3)
Это и означает, что М | ^n — fe f ->¦ 0.
Осталось проверить утверждение теоремы для сходимости
и. и. Мы уже знаем, что если \п фундаментальна ро вероятности
(и тем более п. п.}, то существуют § и подпоследовательность
In такие, что Е,г/, —> ?. Поэтому, если обозначить пНп) =
= min {nh: nh ^ ?г), то
Р (sup | lft - 11 > г\ < Pf sup 1 lh - 1„ I > e/2\ +
\h^n ) \h>n v /
при ?г ->¦ сю. Теорема доказана. ^
Замечание 1. Если в пространстве Lr всех случайных
величии % па <Q, 8, Р>, для которых М|^С <оо, ввести норму
||g|| = (M|gfI/r (неравенство 11^ + |2Н < ligjl + II|2II есть не что
иное, как неравенство Мпиковского, см. теорему 4.4), то утвер-
утверждение теоремы 3 применительно к сходимости -> (это есть
сходимость но норме в Lr) означает, что пространство Lr полно
и, стало быть, является банаховым пространством.

138 гл. 6. о сходимости случайных величин и распределений
Пространство всех случайных величии на <?2, $f, P) можно
метризовать так, чтобы сходимость во введенной метрике была
эквивалентна сходимости по вероятности. Например, можно
положить p(?lf 52)=s= М | -?•'"?? -—? Г* ^ак как всегДа
\*-\-v\ ^ \*\ , UI
то p(|i, 12) удовлетворяет всем аксиомам метрики. Нетрудна
видеть, что соотношения р(|п, Ю~^ 0 и 5п —>¦ 0 эквивалентны.
р
Утверждение теоремы 3 применительно к сходимости ->• будет
означать полноту введенного метрического пространства.
В заключение этого параграфа получим две «теоремы непре-
непрерывности».
Теорема 4. Пусть 1п~^ ^ (?п~>-5) и Н(s) —функция, не-
непрерывная почти всюду относительно распределения случайной
величины ? (т. е. H(s) непрерывна в каждой точке множества В
такого, что P(^gB)= 1). Тогда
Доказательство. Так как вероятности множеств А =
= {<о: 1п(ы)-+ |(о))} и С- {со: ?(<о)е=5} равны 1, то Р(ЛС) =
— Р (Л) + Р (С) — Р (Л + С) = 1. Но на множестве Л С имеет
место сходимость //(gn)-v l/(g). Сходимость п. н. доказана.
Пусть теперь ?n—^ &. Если допустить, что сходимость
•# (Sn) ->- ^ (^) пе имеет места, то найдутся 8 > 0, б > 0 и под-
v
последовательность in) такие, что
Р(\IIAп>)- IIA)\>в)> 8.
По 3L,/-». ? и, значит, найдется подпоследовательность {п"} та-
кая, что \п»—> |, Н Aп»)—>-Я(^). Это
допущению, из которого вытекает, что
кая, что \п»—> |, Н Aп»)—>-Я(^). Это противоречит сделанному
Р(|Я(Ы-#(?I>е)>в. >
Вторая теорема непрерывности касается моментов и связи
со сходимостью в среднем.
Определение 5. Последовательность {|п} называется
номерио интегрируемой, если
(||„|;||„|>^)-*0 при iV-*oo.

§ 1. СХОДИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН 139
Теорема 5. Пусть ?п-»¦!;, {Ц- равномерно интегрируема,
р
Тогда существует Щ и
Если, кроме того, {%гп} равномерно интегрируема, то ?п->?.
Доказательство. Покажем, что М? существует. В силу
свойств интеграла М (?; Ап) —>- О при Р (An) -> О, М | ? | < °°
(см. лемму 3 в Приложении 3). Поэтому при любых N и г
< Km M min (| ?n j + 8, iV)< с + е.
Отсюда следует, что М \ I \ ^ с.
Далее положим для краткости l^n — ^l = Цп. Тогда Цп ->0 и
г\п вместе с §п равномерно интегрируема. Имеем для любых N, с:
< е + 7VP Глп > в) + М (цп; цп > ЛГ). C)
Выберем TV так, чтобы sup M (г]?г; 'n/l>iV)^8. Тогда для такого Л/
Так как е произвольно, то Млп->-0 при 7г~>-оо.
Соотношение М | ^п — ^ |Г —>- 0 доказывается точно так же, как
C), поскольку т]д = 1 \п — ^ |г-^ 0 и г{п равномерпо интегрируемы
вместе с lgjr.
Следствие 2. /?о/ш i?1 ->-1, II (s) удовлетворяет условиям
теоремы 4 и II (^п) равномерно- интегрируема, то
Это утверждение вытекает из теорем 4, 5, так как по тео-
теореме 4 Н&п)-+Н(Ъ).
Условие равномерной интегрируемости {^J будет выполнено,
если выполнено одно из следующих двух достаточных условий:
а) I5J < л, Мг)<оо;
б) М | ^п \1+а < с < °° при некотором а > 0.
Достаточность этих- условий вытекает из соотношений
а) М(|?п|;1Ы>Лг)<М(л;т|>ЛО-*0 при 7V->oo;
б) M(Un|; |gn|>^)<M(|^I1+aAVa; |^|>^)<с/Жа^0
при N -^ оо.
Пользуясь этим замечанием, можно сформулировать еще два
следствия теоремы 5,

140 ГЛ. 6. О СХОДИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН И РАСПРЕДЕЛЕНИЙ
Следствие 3 (теорема о сходимости мажорируемой после-
последовательности). Если ^п->-ъ и l?n|<rl, Мт]<;оог то существу-
ет Ml и М1п-^Щ-
Следствие 4. Если ?rt -»- ?, М 11„ Г6 < г, а > 0, /по ?„ -»- ^„
V ' (г)
Наконец, удобно будет выделить следующее очевидное след-
следствие теоремы 5.
Следствие 5. Если ?п •-> 5 м П (х) — непрерывная ограни-
ограниченная функция, то Mil (In) ->
§ 2, Сходимость распределений
Мы ввели в § 1 три способа характеризовать близость слу-
случайных величин, заданных па одном вероятностном простран-
пространстве. Но как быть, если случайные величины заданы па разных
вероятностных пространствах (или вообще неизвестно где за-
заданы), а их распределения очень похожи? (Вспомним, напри-
например, теоремы Пуассона или Муавра — Лапласа). В этих слу-
случаях надо уметь характеризовать близость самих распределе-
распределений. При удачном определении такой близости мы сможем ко
многих задачах приближать нужные, по труднодоступные рас-
распределения с помощью распределений известных и, как правило,
более простых.
Итак, какие распределения считать близкими? Речь идет,
очевидно, об определении сходимости последовательности функ-
функций распределения Fn{x) к функции распределения F(x). Было
бы естественным, например, считать, что распределения вели-
1
чин Zn =? + тги S сходятся при п -*¦ оо. Поэтому требовать ма-
малость sup\Fn(x) — F(x)\ в определении сходимости было бы
х
неразумно, так как этому условию не удовлетворяют распреде-
распределения ? Н и §,если F (х) = Р (?<#) имеет хотя бы один
разрыв.
Мы определим сходимость Fn к F как такую, которая воз-
возникает при рассмотрении сходимости по вероятности.
Определение 6. Будем говорить, что Fn слабо сходится
к F, и обозначать это Fп =>¦ i7, если для любой непрерывной и
ограниченной функции f(x)
U. D)
Если речь идет о распределениях Рп (В) и Р (В) (В — боре-
левские множества), соответствующих Fn и F, то говорят, что
Рп слабо сходится к Р% и обозначают это Рп =>- Р* Очевидно,

§ 2. СХОДИМОСТЬ РАСПРЕДЕЛЕНИЙ 141
что D) можно записать также в виде
li{x)Pn{dx)-+\f{x)P{dx) или Mf(ln)-+-Mf(t)t E)
(ср. со следствием 5), где \п^вРп, ?€§^-
Другое возможное определение слабой сходимости возникает
из следующего утверждения:
Теорема 6*). Fn=>F тогда и только тогда, когда Fn(x)-+-
.-»- F (х) в каждой точке х, являющейся точкой непрерывности F.
Доказательство. Е^сть выполнено D). Рассмотрим
е>0 и непрерывную функцию /8(?)» равную 1 при t<x, О при
t ^ х + е и меняющуюся линейно на [х, х + е]. Так как
X
Fn (х) = J U (t) dFn (t) < j U (t) dFri (*),
— oo
то в силу D)'
lim sup Fn (x) < j /e (*) dF(t)^F(x + e).
Если х — точка непрерывности Ff то в силу произвольности s
получаем lira sup Fn (x) ^ F (х),
П-*оо
Совершенно аналогично с помощью функции /8 (t) ==»
= /8(^+8) получаем неравенство
Получим теперь обратное утверждение* теоремы. Пусть — М
и N — такие точки непрерывности F, что F(— М)<е/5, 1—
-^(Л)<8/5. Тогда i^(-M)<e/4, l-Fn(iV)<e/4 при всех до-
достаточно больших п. Поэтому, считая для простоты |/| ^ 1, по-
получим, что
и ]jdF F)
будут отличаться соответственно от
N N
j fdFn и - { fdF
м м
-м
*) Во многих учебниках по теории вероятностей высказывание тео-
теоремы принимается за определение слабой сходимости. Однако определение
Рп =-> р в форме
J / (х) Рп (dx) -v J / (Л) р (dx)
для всех ограниченных непрерывных функций /, по-видимому, целесообраз-
целесообразнее, поскольку оно сохраняется и для распределений в произвольных топо-
топологических пространствах (см., например, [12], [1])

142 ГЛ. 6. О СХОДИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН II РАСПРЕДЕЛЕНИЙ
меньше, чем па е/2. Построим на полуотрезке (—Л/, N] ступен-
ступенчатую функцию /а со скачками в точках непрерывности F, ко-
которая отличалась бы от / меньше, чем на е/2. Вне (—Л/, /V]
функцию /в положим равной 0. Можно считать, например, что
k
/eWe 2 f(xj)$){x)% где #0 = —Л/, х1? .,., #Л~ N есть выбран-
пыс нужным образом точки непрерывности F, функция 83(х) —
индикатор полуотрезка {х3-и х3]. Тогда ) fedFn и ] UdF будут
отличаться от интегралов (G) при достаточно больших п мень-
меньше, чем на е. В то же время
J hdFn = 2 / (*;) [рп (xj) - Fn (х^)} -> J UdF.
Отсюда в силу произвольности s > 0 следует сходимость Djj
(надо воспользоваться неравенством
lim sop j fdFn < e + lim sup j jEdFn == e + J fedF < 2e + j jdF
и аналогичным неравенством для lim inf j JdFn). ^
Замечания по поводу другого, в известном смысле, более про-
простого доказательства второго утверждения теоремы 6 см. в кон-
конце § 3 и в § 7.4.
Замечани е 2. Если повторить с очевидными изменениями
приведенное доказательство, то мы получим несколько иной эк-
эквивалент сходимости D): сходимость разностей Fn(y)—Fn(x)-+
-> F(y)— F(x) для любых х и у, являющихся точками непрерыв-
непрерывности F.
Замечание 3. Если F(x) непрерывна, то сходимость Fn =>-
~> F эквивалентна равномерной сходимости sup | Fn (х) —F (х) | -> 0.
х
Доказательство этого утверждения предоставляем читателю.
Оно следует из того, что сходимость Fa(x) ~* F(x) при каждом х
влечет за собой в силу непрерывности F "равномерную сходи-
сходимость па любом конечном отрезке. Равномерная малость Fn(x) —
— F(x) на «краях» обеспечивается малостью F(x) или 1 — F(x).
Замечание 4. Если распределения Fn и F дискретны и
имеют скачки в одних и тех же точках хи х2, ..., то Fn => F
будет эквивалентной, очевидно, сходимости вероятностей значе-
значений хи хг, .о, {F*(xh + 0)—Fn{xh)-*F{xh + Q)-F(xh)).
Введем теперь некоторые удобные для дальнейшего обозна*
чения. Пусть ?„, § — некоторые случайные величины (заданные,,
вообще говоря, на разных вероятностных пространствах) такие,
что ?Р,и ?€§ Р.
Определение 7. Если Рп =ф- Р% то будем говорить, что
|w сходится к \ по распределению и обозначать это ?> => ?.

§ 2. СХОДИМОСТЬ РАСПРЕДЕЛЕНИЙ Ш
Мы используем здесь тот же символ =^7 что и для обозначе-
обозначения слабой сходимости, но это нигде к недоразумениям ие
приведет.
Ясно, что 1п->Е влечет за собой gn =>- g, но не наоборот.
р
, Иногда удобно иметь также простой символ для записи вы-
выражения «распределения gn слабо сходятся к Р». Мы будем за-
записывать это соотношение в виде
Ъп&Р, ' G)
так что символ g?> выражает тот же факт, что и =*% по соеди-
соединяет объекты разной природы так же, как это делает символ
g= в соотношении %g§ P (слева в G) стоят случайные величи-
величины, а справа — распределение).
В этих терминах утверждение теоремы Пуассона можно за-
записать в виде Sn^Il^, а утверждение закона больших чисел
для схемы Бернулли в виде Sn/n ^> 1Р.
Совпадение распределений ? и ц будем обозначать символом
Приведем аналоги теорем 4, 5 в терминах распределений.
Теорема 4А. Если gn =*- g и H(s) удовлетворяет условиям
теоремы 4, то Я(§п)=^-Я(§).
Теорема 5А. Если ?п =^ 1 и i^J равномерно интегрируема,
то существует Ml и М?П->М?.
Есть два пути доказательства этих теорем. Один из них состо-
состоит в сведении их к теоремам 4, 5. Для- этого надо построить слу-
случайные величины In = Fn1^) и ?' = F"(ti), где^ y\^UOiU F~ly
F — обратные функции к Fn, F и доказать, что ?n->s' (известно,
р
что F (т)) ^ F; если F разрывна или не строго монотонна,
то F~l должна быть определена подходящим образом).
Другой путь состоит в проведении доказательств заново па
языке распределений. При наличии незначительных дополнитель-
дополнительных предположений, это оказывается иногда даже проще. Чтобы
проиллюстрировать это, предположим, например, в теореме 4А,
что функция // непрерывна. Надо доказать, что Mg (Н (?п)) —>-
—>- Mg (II (?)) для любой непрерывной и ограниченной функции g.
Но это есть прямое следствие D), E) при f = g°H (f есть су-
суперпозиция функций g ii //).
В теореме 5А предположим, что |n ^ 0 (это не ограничивает
общности). Тогда, интегрируя по частям, получим
оо
) = J Р
(8)

144 ГЛ. 6. О СХОДИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН II РАСПРЕДЕЛЕНИЙ
Так как в силу равномерной интегрируемости
sup Г Р (In >*)<**< sup М (In, In >N)-+0
n N n
при iV-»-o°, то интеграл в (8) сходится равномерно. Так как,
кроме того, P(Sn>^)~>P(S>^) п. в., то
оо оо
lira Mgn = lira J P (ln > ^) cfc = j P (? > x) dx = Щ. <
П->оо ?i->oo q Q
Бывает полезной также следующая
Теорема 7. Пусть §я =>¦ §, ff(s) дифференцируема в точке af
bn -*- 0 ^pw /г ->¦ оо. Тогда
Если //'(а) —О и существует Н" (а), то
H(a + bn^~-II(a^ ^ ^ iin ^
Доказательство. Рассмотрим функцию
( Н(а + х)— II (а)
()
1Я' (а) при я =.0,
которая будет непрерывной в точке х = 0. Так как Ьп|п =*- 0, то
по теореме 4А Ь(Ьп\п)^ /г@) = IV(а). Пользуясь снова этой тео-
теоремой (для двумерных распределений), получим
II (а + ЪЛЛ — II (а)
^—-^ — = h (bnln) ln => IV (п) t
ип
Второе утверждение доказывается точно так же. Щ
Многомерный аналог этой теоремы будет выглядеть несколько
сложнее. При необходимости читатель может получить ее само-
самостоятельно, следуя рассуждениям теоремы 7.
§ 3„ Условия слабой сходимости
Вернемся к понятию слабой сходимости. Мы имеем два кри-
критерия этой сходимости: D) и теорема 6. Однако с точки зрения
применений (проверки их в конкретных задачах) оба эти крите-
критерия неудобны. Значительно проще было бы, например, доказы-
доказывать сходимость М/(?и)—>- М/ (?) не для всех ограниченных не-
непрерывных /, а для функций / из какого-нибудь достаточно уз*

§ 3. УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ 145
кого и просто устроенного класса. Ясно, что совсем узким такой
класс быть не может.
Прежде чем формулировать основные утверждения, введем в
рассмотрение некоторые понятия.
Расширим класс ЗГ всех функций распределения до класса &
функций G, удовлетворяющих условиям Fl, F2 § 3.3 и условиям
G(—oo)^0, G(°°)<1. Функции G из с$ можно называть обобщен-
обобщенными распределениями. Их можно представлять себе как функ-
функции распределения несобственных случайных величин §, прини-
принимающих с положительной вероятностью и бесконечные значения,
так что G(—oo) -Pf^-oo), I —G(oo)-P(? = oo). Мы бу-
будем писать Gn^G, Gne=^, Ge?, если Gn(x)-^ G(x) во всех
точках непрерывности G(x).
Теорема 8 (Хелли). Класс *§ есть компакт относительна
сходимости =>•, т. е. из любой последовательности {Gn), Gn<^&
можно выделить сходящуюся подпоследовательность 6n/j^Ge?»
Доказательство этой теоремы см. в Приложении 4.
Следствие 6. Если любая сходящаяся подпоследователь-
подпоследовательность [Gnh] из {GJ, Gn^&t сходится к G, то Gn =*¦ G.
Доказательство. Если Gnzfi>G, то существует точка х*
непрерывности G такая, что Gn (х0) -^ G(xo)< Так как Gn(«r0)e
е [0, 1], то должна существовать подпоследовательность
Gnk(xQ)-* g^G(x0). Однако по предположению это невозможно*
так как Gn){(x0)-^G (х0). -4
Причина расширения класса ЗГ всех функций распределения
состоит в том, что этот класс не является компактом (в смысле
теоремы 8), а сходимость Fn=> G, Fn&&~, еще не означает, что
С ^ дгЛ Например, последовательность
О, ?<~~?7,
Fn(x)= 1/2, -~п<х^п% (9)
Д, х^>п
всюду сходится к функции G(x) = 1/2 ФЗГ) соответствующей не-
несобственной случайной величине, принимающей значения ±°о
с вероятностями 1/2.
Однако иметь дело с классом *§ тоже не совсем удобно. Дело
в том, что сходимость в точках непрерывности Gn=*- G в классе 9
вовсе не эквивалентна сходимости \ jdGn -> J fdG (см. пример
(9) для /=1), да и сами интегралы J fdG не определяют одно-
однозначно G (они определяют приращения G, но не значения G(—«>)
и G(°°)). Введем теперь два понятия, которые помогут избежать
отмеченных неудобств.
Определение 8. Последовательность распределений {Рп}
(или функций распределения {Fn}) называется плотной, если для
30 А. А. Боровков

146 ГЛ. 6. О СХОДИМОСТИ СЛУЧАЙНЫХ ВЕЛИЧИН И РАСПРЕДЕЛЕНИЙ
любого 8 > 0 существует N такое, что
infPn([-tf,JV])>l-e. A0)
п
Определение 9. Мы будем говорить, что класс 9? непре-
непрерывных и ограниченных функций определяет распределение, если
равенство
= \j{x)dG{x),
для всех /е^ влечет за собой F = G (или М/(?) = М/(т]) для
всех / ^ 3?, где одна из случайных величин \, т] собственная, вле-
влечет i = 1]).
Основной теоремой этого параграфа является
Теорема 9. Пусть класс 3? определяет распределение. То-
Тогда для существования распределения F ^ SF такого, что Fn =>¦ F,
необходимо и достаточно, чтобы*)
1) последовательность {Fn} была плотной;
2) существовал Ига \ jdFn для всех /ej2\
П-*оо
Доказательство теоремы 9. Необходимость оче-
очевидна.
Достаточность. В силу теоремы 8 существует подпосле-
подпоследовательность Fnk => F <~ 2?. Но по условию 1) F^3?~. Действи-
Действительно, если х> N есть точка непрерывности F, то по определе-
определению 8 F(х) = limFnk(x)^ 1 —г . Аналогично устанавливается, что
для x^—N выполняется F(x)<e. Так как 8 произвольно, то
/?(_оо) = 0, F(oo)=l.
Далее, возьмем любую другую сходящуюся подпоследователь-
подпоследовательность F r =>G^. ?F, Тогда для любой /ei?
lim J fdFnk = J /dF, lim j /dF / - J /dG. A1)
Ио по условию 2)
\ \ ' A2)
и, следовательно, F = G. По следствию 6 теорема доказана. Ц
Если доказывать сходимость к «известному» распределению
F е ^", то условие плотности в теореме 9 становится ненужным.
Следствие 7. Пусть класс SB определяет распределение и
F<=$, A3)
*) В таком виде теорема о сходимости распределений сохраняется и
для пространств более общей природы. Роль отрезков [—N, N] в A0) в
этом случае играют компакты. (Ср. с [1], [5], [12], [21].)

§ 3. УСЛОВИЯ СЛАБОЙ СХОДИМОСТИ 147
для любой / s 2\ Пусть, кроме того, выполнено хотя бы одно из
следующих трех условий:
1) последовательность {Fn} является плотной;
2) Fegr;
Тогда F ^ @~ и Fn=> F.
Доказательство следствия почти очевидно. Утверждение
при условии 1) сразу вытекает из теоремы 9. Условие 3) и схо-
сходимость A3) влекут за собой усло-
условие 2). Если выполнено 2), то в соот-
соотношениях (И), A2) F e ST и, значит,
G
Так как, как правило (увидим это
ниже), хотя бы одно из условий 1)—3) _
бывает выполненным, то основной за- О а
дачей становится проверка сходимости Рис. 7
A3) для класса S7.
Отметим также, что в случае, когда доказывается сходимость
к «известному» заранее распределению F<^@~, вся схема рассуж-
рассуждений может быть иной и более простой. Один из таких альтер-
альтернативных подходов изложен в § 7.4.
Приведем теперь несколько примеров классов ??, определяю-
определяющих распределение.
Пример 1. Класс 2?0 функций, имеющих вид
.0, х^а + г.
На отрезке [а, а + е] функции /а>8 определяются как линейные и
непрерывные (график fa,*(x) см. на рис. 7). Это двуиараметрл-
ческое семейство функций.
Покажем, что 2\ определяет распределение. Пусть
для всех / е 5Р0. Тогда
^ («X j fa.edF = j Ja,,dG < G (a + e),.
и наоборот,
G{a)^F(a + z)
для любого е > 0. Если взять в качестве а точку непрерывности
F и G, мы получим
F(a) = G(a], F~G. <
Аналогичным образом легко убедиться, что класс S?o «трапе-
и,иеобразных» функций f(x) = min(/a, e, 1 — /б>е). также определя-
определяет распределение.

148 гл. 6. о сходимости случайных величии и распределений
Пример 2. Класс 2% непрерывных ограниченных функций,
таких, что для каждой / <= 2\ (или / е 20) существует последо-
последовательность fn е= 2?и SUP 1 fn {х) I < Мх для которой lim fn (х) = / (:г)
при каждом х^й,
Пусть J /rf^ = J fdG для всех f^2t. По теореме о сходимо-
сходимости мажорируемой последовательности
HmJ/ndF = J/dF, lim j /ndC = J fdGt fe=2>Q.
Поэтому J fdF = J /dGt f^20; F = G и, следовательно, «2\ опре-
определяет распределения.
Пример 3. Класс Ck всех ограниченных функций f(x) с огра-
ограниченной равномерно непрерывной производной f{k) (x) к-то по-
порядка |U)|
U
Очевидно, Ch определяет распределение, так как обладает
свойствами 2V .
Точно так же убеждаемся, что будет определять распределе-
распределение подкласс Cl cz Ck финитных функций (обращающихся в
нуль вне конечного интервала). Это следует из того, что Cft обла-
обладает свойством класса 3?^ относительно класса 2\ трапециеоб-
разных (и, следовательно, финитных) функций,
Очевидно, что класс Ck удовлетворяет условию 3) следствия 7
и, стало быть, для доказательства сходимости Fn=^- F s ЗГ доста-
достаточно проверять сходимость A3) лишь для /eCft.
Если в качестве 2 взять класс С\ финитных дифференциру-
дифференцируемых функций, то соотношение A3) вместе с условием 2) след-
следствия 1 можно записать в виде
j Fnf'dx -*¦ J Ffdx, Pef, A4)
(Нужно произвести интегрирование по частям в A3), где /' сно-
снова есть финитная дифференцируемая функция.) Критерий сходи-
сходимости A4) иногда бывает полезным. Из него сразу видно, напри-
например, что из сходимости Fn(x)-*- F{x) в точках непрерывности
(т. е. почти всюду) следует A3), так как из названной сходимо-
сходимости и теоремы о мажорируемой сходимости вытекает соотноше-
соотношение A4), эквивалентное A3).
Пример 4. Одним из наиболее важных классов, определяю-
определяющих распределение, является однопараметрическое семейство
комплексиозначных функций {eitx}, t^R.
Изучению свойств J e% xdF (x) будет посвящена следующая
глава.
Все сказанное в этой главе может быть после очевидных из-
изменений перенесено на многомерный случай.

Глава 7
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
§ 1, Определение и свойства характеристических функций
Предварительно отметим, что наряду с вещественными слу-
случайными величинами ?((о) мы с таким же успехом можем рас-
рассматривать и комплекснозиачные случайные величины, понимая
под этим функцию |i((o)+ ?§2((о), где (§i, \г) — случайный век-
тор. Естественно положить М (|г + /?2) = Щх + ?М?2. Комплекс-
позначные случайные величины | = §4 + ig2 и rj == г]! + ir\2 неза-
независимы, если а-алгебры o(§i, §2) и g(t]i, гJ), порожденные соот-
соответственно векторами (§i, |2) и (г\и т]2), независимы. Без труда
проверяется, что для таких величин
Определение 1. Характеристической функцией (х. ф.\
вещественной случайной величины § называется комплексиозпач-
пая функция
тде t — действительное число.
Если функция распределения имеет плотность /(#), то х. ф.
равна ф? (t) = J etXf{x)dx и есть просто преобразование Фурье
функции f(x). В общем случае х. ф. есть преобразование Фурье—•
Стилтьеса над функцией F(x). X. ф. существует для любой слу-
случайной величины ?. Это сразу следует из того, что
|фб(О1 = |
X. ф. представляют собой прекрасный аппарат для исследования
свойств сумм независимых случайных величии.
Свойства характеристических функций.
1. Для любой случайной величины ?
Фь(О)=1 и |ф^(^)|^1 для всех t.
Это свойство очевидно.
Действительно,
Фа?+Ь(*) = Ш1(а1+Ь) = етЫеш1 == етщ (ta).

150 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
3. Если gi, ..., |,х—- независимые случайные величины, то х. ф».
суммы Sn = |i + .., + §п равна
Доказательство следует из свойств математического
ожидания произведения независимых случайных величин. Дей-
Действительно,
*2 ... Meitln = Фб1 @ Ф5з @ ... ФгЛ @. <
Так что свертке F|x*Fs2 соответствует произведение Ф^Ф^.-
4. X. д&. ф*(^) является равномерно непрерывной функцией..
Действительно,
| ф {t + /г) ___ ф до | = | м (e«f+h)l - в1'6) | < М | е»* — 1J—^0
бо теореме о сходимости мажорируемой последовательности
(см. следствие 6.3), так как | eihl— 11 -> Опри fe-^ 0, !ег^-1| ^2.
5. Если существует k-й момент М||| < оо, к ^ 1, го сущест-
существует непрерывная к-я производная функции <pi(t) и ф/г@) =tftM|/4w
Так как | J гже"^/1 (ж) | < | | х | dF (х) = М 111 < оо, то интег-
интеграл J гхег xdF (x) равномерно сходится относительно t. Поэто-
Поэтому возможно дифференцирование под знаком интеграла:
ф' (t) == i j xeilxdF (x), ф' @) - гМ?.
Дальнейшие рассуждения проводятся по индукции. Если для
К к
то
в силу равномерной сходимости интеграла в правой части. Зпа-
пит, фA+1) @) = i'+1M|I+1. < ^
Следовательно, если М|^|г<оо» то в окрестности точки ? = Q
справедливо разложение
Утверждение в обратную сторону верно лишь частично:

§ 1, ОПРЕДЕЛЕНИЕ И СВОЙСТВА X. Ф. 151
Если производная четного порядка q){2k) существует, то
Докажем это свойство для & = 1 (далее можгю использовать
индукцию). Достаточно убедиться в конечности М|Е,|2. Имеем
_ 2ф @) - ф Bh) - Ф (- Щ __ Н*№ 2
Ah" ~ "' V 2ft
1 ак как -—?-^ —> ^ при h ->¦ U, то по лемме срату
/ 2ф @) — ф Bh) — ф (— 2h) \ jyj sin
<p" @) = lim 7-0 == iim ——^
• 2» о
m -i . Sin /г!;
h
6. Если |^0, го ф|(Я) определена в плоскости комплексного
переменного X при ImX^O. При этом \щ(Х) I ^ 1, ф^(^) есть ана-
аналитическая функция в области Ini Я > 0, непрерывная, включая
границу Im % = 0.
Аиалитнчиость следует из возможности тгри Im Я > 0 диффе-
дифференцирования иод знаком интеграла
Непрерывность доказывается так же, как в свойстве А. Сказан-
Сказанное означает, что для неотрицательных g x. ф. ср*(Я) однозначно
определяет функцию ^(s) вещественного переменного s >0,
равную P(s) == ф| (is) = M^~s" и называемую преобразованием
Лапласа (или Лапласа —Стилтъесо) над распределением ?.
Из свойств аналитических функций вытекает и обратное ут-
утверждение: преобразование Лапласа f}(s) шг полуоси 5^0 о<9/ю-
зиачно определяет х. ф. ф|(Я).
7. ф|(?) = ф|(—0 = 9-g@i где.-черта означает комплексную
сопряженность.
Доказательство следует из равенств
Отсюда следует, что если g симметрична (распределена так
же, как — g), то ее х. ф. вещественна. Можно показать и обрат-
обратное, если воспользоваться теоремой единственности, о которой
речь будет идти ниже.
Найдем теперь х. ф. основных законов распределений.
Пример 1. Если g = # с вероятностью 1, т. е, S^^a, то

152 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Пример 2. Если ?ё=Вр, то <p6(J)s=pe" + (l — р)= 1 -h
&р(еи-1).
Пример 3. Если |€=Фо,и то
оо
1 Г
Дифференцируя по ? и интегрируя по частям \хе~~х 2dx
•= — de-x2t2jx получим
Так как ф@)=1, то с = 0,
Пусть теперь г) — нормально распределенная случайная вели-
величина с параметрами (а, о). Тогда ее можно представить в виде
т] = о? + а, рде ? нормально распределена с параметрами @, 1),
X. ф. ц определяется по свойству 2:
Дифференцируя фл@. Для т]§Фм2, получим Мцк = 0 при нечет-
нечетных к и Mrift = Gfe (й-1)(Л-3)...1 при А = 2, 4, ....
Пример 4. Если !^=11,я, то
4 е" " *-Ц 2
Пример 5. Если g имеет показательное распределение Га
с плотностью ае~ах при х ^ 0, то
a—it*
о
Значит, если \ имеет «двустороннее» показательное распределе-
распределение С ПЛОТНОСТЬЮ тг ? , —оо < Х < оо, ТО

§ 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА X. Ф, 153
Если | имеет геометрическое распределение, Р (? = &)=A—p)pks
fc = 0,1, ,..,, то
1-Р
Пример 6. Если | €§ К0I-(имеет плотность —-. $-t то
,пA + х )
^(О™6'1- Читатель может легко доказать это чуть позже, поль-
пользуясь формулой обращения и примером 5.
Пример 7. Если ?€§U0I, то
X. ф. сумм |i + |2» ?i + |г + \*ч .. м рассматривавшихся в при-
примере 3.5, будут равны в силу свойств 3
Как установить, является ли та или иная функция ф характе-
характеристической? Иногда это можно сделать с помощью указанных
свойств. Предлагаем читателю установить, являются ли характе-
характеристическими функции A + ?)""\ 1 + *, sin?, cos* и, если явля-
являются, то каким распределениям соответствуют.
В общем случае поставленный вопрос является сложным.
Сформулируем здесь без доказательства один из известных ре-
результатов.
Теорема Бохнера — Хинчина. Для того чтобы непре-
непрерывная функция <p(/)i обладающая свойством <р@)=1, была ха-
характеристической, необходимо и достаточно, чтобы она была не-
неотрицательно определенной, т. е. чтобы для любых действитель-
действительных ti, ..., tn и любых комплексных чисел ki, .. ., Хп выполнялось
(К — сопряженное к К)
Отметим, что необходимость этого условия почти очевидна,
д
так как если <p(f) = Me ,, то
k=i
Укажем теперь еще два свойства х. ф.
8. Ecjiu распределение \ имеет плотность, то yi(t)-**O при

154 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Это есть прямое следствие теоремы Лебега о преобразованиях:
Фурье. Обратное утверждение неверно. В ^ целом же скорость
стремления к 0 функции ф*@ при UI ->• °° тем выше, чем выше
гладкость F (х). Формулы примера 7 в этом смысле типичны.
Если плотность j(x) имеет интегрируемую /с-ую производную, то
интегрированием по частям получаем
Отсюда следует, что
9. Будем называть распределение ? решетчатым с шагом ре
шетки /г, если существуют а и /г такие, что
2
Случайная величина § имеет решетчатое распределение с ша-
шагом h > 0 тогда и только тогда, когда
Щ -1.
a J
Действительно, если ? решетчата, то
и, следовательно,
Обратно, если верно B), то при t = 2n/h
ф?„а (^) = Mcos t(l — а) + iMsin^E — а) = 1.
Следовательно, М A — cos t (? —- а)) == 0 и по свойству М 4
cos?(? — а)=1, (| — aJn/h = 2д&, &==&(©) с вероятностью 1.
Среди решетчатых распределений важное место занимают рас-
распределения целочисленных случайных величин. Для них а и h —
целые числа, и мы можем положить для простоты а = О, Л = 1.
Тогда Ф*(?) будет функцией переменной z~eu п будет периоди-
периодической по ? с периодом 2я. Значит, в этом случае достаточно -
знать поведение х. ф. па отрезке [—я, я], или, что то же, знать
поведение функции
ife (z) - Mzl = 2 3ftP (g - /с)
па единичной окружности |zl==l. Функция i|:*(z) называется
производящей функцией случайной величины Ь, (или распределен

§ 2. ФОРМУЛА ОБРАЩЕНИЯ J55
ния g). Так как \\i{eu) = q>i{t) есть х. ф., то для производящие
функций остаются справедливыми все свойства х. ф. с теми литш
изменениями, которые вытекают из замены аргумента. Подроб--
нее о применениях аппарата производящих функции см. § 8.
§ 2. Формула обращения
Итак, для каждой случайной величины определена соответ-
соответствующая ей х. ф. Покажем теперь, что класс 5? функций eitx
определяет распределение, т. е. что по х. ф. однозначно восста-
восстанавливается распределение. Этот факт доказывает формула обра-
обращения.
Теорема 1 (формула обращения). Если F(х) — функция
распределения случайной величины ?, а ф(?) — х. ф. ?, то для
.любых точек непрерывности х и у функции F (х)
¦ F (у) -F(x)=±\\m\ e~itx7e-itv ф (t) e-^dt *). C)
Если функция q)(t)/t интегрируема па бесконечности, то ста-
становится законным предельный переход под знаком интеграла,
и можно записать
±)t. D)
Доказательство. Предположим сначала, что существует
плотность /(#), а х. ф. ф(^) интегрируема. Тогда в силу извест-
известной формулы обращения для преобразования Фурье
Утверждение теоремы в этом случае получится, если проин-
проинтегрировать обе части этого равенства в пределах от х до у и по-
поменять в правой части (в силу абсолютной сходимости) порядок
интегрирования **).
*) В литературе формула обращения часто приводится также в виде
Л
Р {у) — F (х) = — lim \ е гХ~~е Ср (t) dt, эквивалентном C).
2я а-^оо J it
~А
**) Формулу D) можно получить из E) и без интегрирования, заметив,
^ito —\И1 _ есть значение в нуле плотности, равной свертке двух
у — х
плотностей: f(x) и плотности равномерного на [—г/, —х] распределения
(замечание но этому поводу см. также в конце § 4.5). X. ф. этой свертки
e—iix e—ity
равна — (р (Q.
{У — х) it

156 " ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Пусть теперь ср(?) — характеристическая функция ? с произ-*
вольным распределением F(x). Рассмотрим на одном вероятност-
вероятностном пространстве с ? случайную величину г), независимую от | я
распределенную нормально с параметрами @, 2о2). Как мы уже
знаем, характеристическая функция ц будет равна е~*"а"\
Это означает, что характеристическая функция g + г], равная
ф @ в , интегрируема. Поэтому будет справедливо равенство
Так как Р (|т]| > б) ->- 0 при любом б > 0 и а -*¦ 0, то в силу гл. б
F%+n =>- i7 (если бы была последовательность ok -** О, и каждому afc
соответствовала бы своя случайная величина r\k, то, очевидно, мы
имели бы I + Tj/t —>¦ S; ^ ^)
V
Значит, если х и у есть точки непрерывности F, то F (у) —
— jF (ж) ===== lim (Fi+^(y) — 1<\+ц(х)). Это вместе с F) доказывает
утверждение теоремы. ^
В доказательстве этой теоремы использован прием, который
можно назвать «сглаживанием» распределений. Он часто приме-
применяется для преодоления технических трудностей, связанных с
формулой обращения.
Следствие 1 (теорема единственности). X. ф, случайной
величины однозначно определяет ее функцию распределения.
Доказательство следует из формулы обращения и из-
того, *что разности F{y) — F{x) однозначно определяют F(x). ^
Для решетчатых распределений формула обращения упроща-
упрощается. Пусть для простоты ? — целочисленная случайная величина
и л|;>! B) = Mz^ есть ее производящая функция. Тогда
J
И
G)
Действительно, переходя к х. ф. щ (t) == 2 е%%2 Р(^ =Л и де-
лая замену в G) z = ^, получим, что интеграл в правой части
G) равен
Здесь все интегралы в правой части, очевидно, равны нулю, кро-
кроме интеграла при / = /с, равного 2я. А
Формула G) есть не что иное, как формула для коэффици-
коэффициентов ряда Фурье и имеет простой геометрический смысл.

§ 3. ТЕОРЕМА НЕПРЕРЫВНОСТИ (СХОДИМОСТИ) ' 157
Функции {eh = eith} образуют ортоиормированиый базис в гиль-
гильбертовом пространстве «S^f—зт, я) комплекснозначпых функций*
интегрируемых с квадратом, со скалярным произведением
я
1
^' g) ^ S"
—л
(f — комплексно-сопряженное к ,g). Если ф^ = 2efeP(S = &)> то
из равенства ф^ = 2^ (ф|» ^) немедленно следует, что
Р(| = /с) = (ф|,ел) = ^г f
§ 3. Теорема непрерывности '(сходимости)'
Пусть {фп@}п=1— последовательность х. ф., a {Fn}n=i—
последовательность соответствующих функций распределения^
Напомним, что знак =>- означает слабую сходимость распределе-
распределений, определенную нами в гл. 6.
Теорема 2 (теорема непрерывности). Для сходимости
Fn=^F необходимо и достаточно, чтобы фп@~>ф@ пРи каоюдом
1, где ф(?) — x.<f>., соответствующая F.
Теорема очевидным образом вытекает из следствия 7 предыду-
предыдущей главы (здесь выполнены сразу два из достаточных условий
следствия 6.7: условия 2) и 3)). Ее доказательство будет получе-
получено также более простым способом в § 4.
В § 1 для неотрицательных случайных величин % было введе-
введено понятие преобразования Лапласа |3 (s) = Me"s^, Пусть Pn(s)*-
р (s) — преобразования Лапласа, соответствующие Fn и F, Спра-
Справедливо аналогичное теореме 2 утверждение:
Для Fn=> F необходимо и достаточно, чтобы $n(s)-+- P(s) при
'каждом s > 0.
Как и теорема 2, это утверждение вытекает из следствия 6.7,.
гак как класс функций {/(#)•= e~sx), s ^ 0, (как и {eitx}) опреде-
определяет распределение (см. свойство 6 § 1) и, кроме того, выполне-
выполнены достаточные условия 2), 3) следствия 6.7.
Теорема 2 обладает одним недостатком — в ней заранее тре-
требуется знать, что функция ф(?), к которой сходятся х. ф., явля-
является характеристической. Между тем таких сведений может не
быть (см., например, § 8.9). В связи с этим возникает естествен-
естественно вопрос, при каких условиях предельная функция ср(?) будет
характеристической.
Ответ на этот вопрос содержится в следующей теореме:

158
ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Теорема 3. Пусть Ф«(?) = J eltxdFn{x) есть последователь-
последовательность характеристических функций и фп@"^ф@ пРи п "*" °° и
при каждом I.
Тогда следующие три условия эквивалентны:
а) ф(?) является х. ф.,
б) ф(?) непрерывна в точке ? = О,
в) последовательность {Fn} является плотной.
Таким образом, если мы установим, что фп@~*"ф@ И выпол-
выполнено одно из трех перечисленных свойств, то можно утверждать,
что существует распределение F такое, что ф является х. ф. F и
Fn ^ F.
Доказательство. Эквивалентность условий а) и в) вы-
вытекает из теоремы" 6.9. То, что из а) следует б), известно. Оста-
Осталось установить, что из б) следует в). Для этого покажем снача-
сначала, что справедлива
Лемма 1. Если ф есть х. ф. ?, то при любом и > 0
Доказательство. Правая часть этого неравенства равна
где F — функция распределения |. Меняя порядок интегрирова-
интегрирования и замечая, что
получим
U
4-J 11-
2 f fi
|x|>2/uV
•! dF{x)-

§ 4. ДОКАЗАТЕЛЬСТВО ТЕОРЕМ СХОДИМОСТИ 159
Пусть теперь выполнено условие б). В силу леммы 1
Hmsup
П— |x|>2
|x|>2/u
Так как ф(?) непрерывна в точке 0 и ф@)=1, то среднее зна-
значение интеграла, стоящего в правой части, может быть сделана
выбором и сколь угодно малым. Это означает, очевидно, выполне-
выполнение условия в). <4
С помощью х. ф. можно не только устанавливать факт сходи-
сходимости распределений, но и оценивать также скорость этой схо-
сходимости в тех случаях, когда удается оценить скорость убывания
фп — ф. С соответствующими примерами мы столкнемся в § 5.
Основные применения аппарата х. ф. встречаются в гл. 8, Иг
16. В этой главе мы также коснемся применений х. ф., однако бо-
более иллюстративного характера. Прежде чем переходить к ним,
рассмотрим еще один подход (возможно, он покажется читателю
более простым) к доказательству теоремы 2 о сходимости распре-
распределений.
§ 4. Другой подход к доказательству теорем
сходимости к известному распределению
При доказательстве с помощью х. ф. сходимости Fn =>¦ F к из-
известному распределению F вместо схемы, изложенной в § 6.3,.
6.2, 7.3, можно предложить другую, которая может оказаться в
этом случае предпочтительнее. Она состоит в следующем.
1. После определения 6.6 слабой сходимости следует доказать
возможность сужения класса функций /, для которых надо прове-
проверять сходимость
$fdFn->$fdF. (8)
Однако сделать это нужно «непосредственно», а не опираясь тта
теорему 6.6, как это было в § 6.3. Таким классом может быть лю-
любой класс, определяющий распределение, например, класс C°k
финитных (отличных от нуля на конечном отрезке) к раз пепре.-
рывно дифференцируемых функций при к ^ 2.
Схема доказательства возможности сужения такова. Пусть С —
класс всех непрерывных ограниченных функций на прямой, С° —
класс непрерывных финитных функций.
Утверждение 1. Если соотношение (8) верно для любой
/еС°, то оно верно для любой /еС,

160 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Доказательство. Выберем ge е С0, 0 < g& ^ 1 так, чтобы
Это всегда возможно, так как для любой функции g^C°, 0 < g <
^ 1, g@)=*l, выполняется l—g(8x)-+0 при 6-^ 0 и по теореме
о мажорируемой сходимости
Пусть /еС, ||/| = sup|/(^)| и (8) справедливо для /е=С°. То-
гда jgB е= С0,
J(l-^/d^|<ll/l(l-Jged^)^||/||(l-JgedF)<e||/^ (9)
Следовательно, в силу равенства / = fg& + /A — ge)
lim sup | J /dFn - J /dF | < lim sup [ | J A - ge) fjFn
+
Так как е здесь произвольно, то для /еС справедливо (8). <4
В (9) использован тот факт, что j dF = 1.
Утверждение 2. .Есл^ соотношение (8) <?е/шо 5дя любой
f е С/?, А ^ 1, го 0/ш ве/?но м для любой /^ С.
Доказательство в силу утверждения 1 очевидно, так как
/еС° можно равномерно приблизить функцией Дб>еС^, Мож-
Можно рассмотреть, например, функции
j
равномерно близкие к /еС и дифференцируемые. Повторив эту
операцию, получим дважды дифференцируемую функцию
и т. д. <4
Для финитной функции / е С\
J /dF = - J Fd/ - - J F/'^, /' e CLi.
Следовательно, критерии (8) можно записать также в форме
A0)
Доказательство теоремы 6.7 после этого можно упро-
упростить (мы уже отмечали это), так как из сходимости Fn\x)-+-
r*F(x\ в точках непрерывности F (следовательно, всюду, за ис-

§ 5. ПРИМЕНЕНИЕ X. Ф. В ТЕОРЕМЕ ПУАССОНА 161
ключением, быть может, счетного множества) вытекает сходи-
сходимость A0) по теореме о мажорируемой сходимости.
Далее вводится понятие х. ф., как это сделано в § 1, и в чис-
числе ее свойств нужно доказать равенство Парсеваля.
Утверждение 3. Если gGCj, fc^2,5gf\ то
dtf
где щ (t) - f eitxdF (x), g (i) = j eiixg (x) dx.
Если F имеет плотность /г, то равенство Парсеваля записыва-
записывается в более привычной в математическом анализе форме
Доказательство. Так как ge^Cl, k>2, то в силу свой-
свойства 8 характеристических функций g абсолютно интегрируема.
Применяя к g(t) .формулу обращения, получим
= ^_ J Me~"?g (t) dt = -^ j" Ф6 (- t) 1 (t) dt.
Доказательство теоремы 2. Пусть ф^ -*- <р (ф„ и ф
суть х. ф. Fn и F соответственно). Тогда для ge C\
t, - (Н)
где функция 1ф„|i ^ \g\ интегрируема. Поэтому по теореме о ма-
мажорируемой сходимости правая часть в A1) сходится к
§ 5» Применение характеристических функций
в теореме Пуассона
Пусть ?;, ,.., ^п — независимые целочисленные случайные ве-
п
личины, 5л = 2?а« P(Ia = 1) =Pa» P(Sfe = O)=- I — /?ft — qk.
i
Формулируемая ниже теорема представляет собой некоторое обоб-
обобщение*) теорем, полученных в § 5.4.
*) Это обобщение не очень существенно, так как результаты, близкие
к теорбме 4, можно получить и пользуясь теоремой 5.4, в которой 1к мо-
может принимать лишь значения 0 и 1. Достаточно заметить, что вероятность
события А= U ^ 2
11 А. А. Боровков
события А= U ^кф0} gft ф \\ оценивается значением 2 qh и, следова-»

162
ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Теорема 4.
!2<
где [х === 2 Ph*
Таким образом, если заданы серии
независимых целочисленных случайных величин
h=l
Qhn%
то для сходимости разности Р (Sn = /с) — Пд ({А:}) к:
О) чтобы
доста-
как 2 Pkn
h=l
' niax /?/ш, го последнее условие всегда вы-
полнено, если max phn ~> 0, fx ^ |i0 = const.
Доказательство. Нам понадобятся два простых вспомо-
вспомогательных предложения. Так как они будут нужны и в дальней-
дальнейшем, то сформулируем их в виде лемм.
Л е м м а 2. Если Re g ^ 0, то
| ер — 1 - Р—Р*/2 К | Р |3/6.
Доказательство. Требуемые неравенства вытекают из
соотношений (в них используется замена t = ру и тот факт, что
U8I ^ 1 при Re 5 ^ 0)
1
J e'df = p j
1
Последнее неравенство доказывается аналогично.
тельно,
где р (^п = Л/л) = Р E*
нами ?^,
образованы случайными величи-

величи§ 5. ПРИМЕНЕНИЕ X. Ф. В ТЕОРЕМЕ ПУАССОНА 163
Лемма 3. Если \ак\ < 1, |&А| < 1; ft = 1, .. м щ то
п п
Таким образом^ если ф&@» tyk{t)—#. Ф^ то при любом t
Доказательство. Обозначим Ап =Па/г, 5Д = Jj6fe. То-
Тогда UJ^l, lSn!<lt
U» - 5J - Un-tOn - Bn^bJ - I (An-i - fi»-i)on + (aft - 6»)fln-il ^
Применяя это неравенство п раз, получим требуемое соотношение.
Доказательство теоремы 4. Имеем *|
ФЙ(<)ЭМЛ- 1 + />,< (е«- 1) + ?ft(Yfc(*)'- 1).
^де 7^ @ есть х- Ф- некоторой целочисленной случайной величи-
величины. В силу независимости случайных величин ?А
Пусть далее ?ё=П„. Тогда
i|)fc(?) = ePft(e "}. Следовательно, разность х. ф.
по лемме 3 можно оценить следующим образом:
П фл - П
где1 по лемме 2 A\е(ви — 1) ^ 0)
2 1<P* -
— cos tf) = pi [ —j- + 2 sm* -j I s A2)
11*

j64 " ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Остается воспользоваться формулой обращения G), в силу
которой
± j «-*"* (Фвп @ _ ф5
2я „
—л
так как
Если в A2) воспользоваться неравенством к" —II < 2, то вы-
выкладки упростятся, необходимость в вычислении двух последних
интегралов отпадет, по оцешш будут несколько хуже:
§ 6. Характеристические функции
многомерных 'распределений.
Многомерное нормальное распределение
Определение 2. Если дай случайный вектор |=(ii, ?2? • • >
..., |п), то его х. ф. (х. ф. распределения ?) называется функция
от вектора t = (tb ..., ?п), равная
= MeihT = Мвм''Е> = М ехр {г .2 tfc?fcj
\ п
здесь |т — вектор-столбец, транспонированный к |, (^, |) — ска-
скалярное произведение.
X. ф. многомерных распределений обладают всеми свойствами
(с очевидными изменениями в формулировках), которые излага-
излагались выше в §§ 1—3.
Ясно, что Ф^@) == 1 и всегда |ф^(/)|<1, q>(~О^ ф|@- Далее,
(?) всюду непрерывна. Если существует смешанный момент
ix1 «• .?»"., то ф^ имеет производную порядка кх +... + кп
Если существуют все моменты некоторого порядка, то в окрест-
окрестности точки ? = 0 справедливо разложение функции <р$(?), ана-
аналогичное A). •

^ § 6. X. Ф. МНОГОМЕРНЫХ РАСПРЕДЕЛЕНИЙ 165
Если известна ф|(?), то х. ф. любой подсовокупности случай-
случайных величин (Е/г1, • ..,|Ц)} очевидно, можно получить, положив
все th, за исключением t^, .. ., ?/*., равными 0.
Следующие теоремы являются простыми обобщениями своих
одномерных аналогов.
Формула обращения. Если А есть «интервал», опреде-
определенный неравенствами ah < xh < bh, к = 1, . . ., я, гг вероятность
Р E е А) непрерывна на гранях этого интервала, то
-и*
и* -i- Г
о-^о Bя)" J
Если существует плотность /(х) случайного вектора |, а х. ф«
ф|(/) интегрируема, то формула обращения может быть записана
в форме
Если функция g{x) такова, что ее преобразование Фурье
интегрируемо (это всегда так для достаточно гладких g(%))<, то
справедливо равенство Парсеваля
Из формулы обращения следует, как и раньше, теорема о вза-
взаимно однозначном соответствии между х. ф. и функциями- рас-
распределения и вместе с ней тот факт, что класс функций {ец*>х)}
в многомерном случае определяет распределение (ср. с определе-
определением 6.9).
Слабая сходимость распределений Рп (В) в га-мерном про-*
странстве к распределению Р (В) определяется так же, как и в
одномерном случае: Рп=^-Р, если ¦ - •
§f(x)dPn(dx)-+$f(x)dP(dx)
для любой непрерывной и ограниченной функции f(x).
Обозначим фп@ и ф(?) х. ф. соответственно распределений
РпИР.
Теорема непрерывности 2А. Для слабой сходимости
Рп=>-Р необходимо и достаточно, чтобы при каждом t и п ->¦ оо
)(
Ф()Ф()
Если удается установить сходимость q>n(t) к некоторой функ-
функции ф(?), то возникает вопрос, будет ли ср(^) х, ф. какого-нибудь

166 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
распределения, или, что то же, будет ли последовательность Ра
слабо сходиться к некоторому распределению Р? Ответы на эти
вопросы содержатся в следующем утверждении. Пусть AN — куб,
определяемый неравенством max | xk \ < N.
к
Теорема непрерывности ЗА, Пусть последователь-
иостъ х. ф. (pn(t) сходится к функции ф(?) при каждом t. Тогда
следующие три условия эквивалентны:
а) ф является х. ф.,
б) ф непрерывна в точке t = О,
в)Нт sup Г dPn(x)~^0 при iV~>oo,
П~юо J
A
Доказательство всех трех теорем проводится так же, как в
одномерном случае.
Пример 8. Многомерное нормальное распределение опреде-
определено как распределение с плотностью (см. § 3.3)
П
где Q(х) = хАхт~ 2 aijXiXj^lA] есть определитель положи-*
тельно определенной матрицы А = \\ац\\.
Это центрированное нормальное распределение, для которого
М | = 0. Распределение вектора ? + а при любом постоянном век-
векторе а также называется нормальным.
Найдем х. ф. ?. Покажем, что
4>l(t) = e 2 % • A3)
где М = А есть матрица, обратная к А, совпадающая с матри-
матрицей 11/Пу11 вторых моментов распределения |:
В самом деле,
Т* 1 Т
dXl...dxn. A4)'
Выберем ортогональную матрицу С так, чтобы САСТ=Е была бы
диагональной матрицей, и обозначим \хи ..., \хп значения диаго-
диагональных элементов. Сделаем замену переменных, положив х~уС
ut~vC. Тогда
хАхт ivyT —-
—тг хАхт^ ivyT

§ 7, СВОЙСТВА ГАММА-РАСПРЕДЕЛЕНИЯ - 167
и в силу свойства 2 х. ф. одномерных нормальных распределений
С другой стороны, так как все моменты | существуют, то в
окрестности точки ^ = О
1 MV + о
Отсюда следует, что .Щ == О, Л~ = М. ^
Из доказанной формулы A3) вытекает следующее свойство
нормальных распределений: компоненты вектора (%и ..., gn) не-
зависимы тогда и только тогда, когда коэффициенты корреляции
р(Ъ>и D^O пРи всех i^h Действительно, если М — диагональ-
диагональная матрица, то А = М~х также диагональна и h(x) равна произ-
произведению плотностей. Обратно, если ?,, ..., %n независимы, то А
диагональна и, стало быть, диагопальна М. <4
§ 7. Другие применения х. ф.
Свойства гамма-раеиределения
1. Свойство устойчивости распределений Фа а2, Ка а. Свой-
Свойство устойчивости, грубо говоря, состоит в сохранении типа рас-
распределения при суммировании случайных величин (это описание
устойчивости не точно, подробнее об этом см. § 8.6).
Сумма независимых случайных величин, распределенных по
нормальному закону, снова имеет нормальное распределение. Дей-
Действительно, пусть ft и |2 независимы и нормально распределены
соответственно с параметрами (аи at), (a2, о|). Тогда х. ф,
h + Ь равна
На ita 1
(t)(t)(t) " *
"
в
Таким образом, сумма §t +12 снова является нормально рас-
распределенной случайной величиной с параметрами (ах + а2, <s\ +
Нормальность распределения сохраняется и при суммирова-
суммировании зависимых величин (компонент произвольного нормально
распределенного вектора). Это немедленно следует из вида х. ф.
многомерного нормального закона, найденного в § 6. Надо лишь
заметить, что для получения х, ф, ii + ,, t + |я достаточно

1G8 ГЛ. 7, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
si выражении для
положить ^ = ... = tn = ?.
Сумма независимых случайных величии, распределенных по
закону Пуассона, снова имеет распределение Пуассона.
Рассмотрим две независимые случайные величины ^1^П^1§
&2€§Пц» X. ф. их суммы равна
<p6l+g2 (t) ^ехр К (**' - 1)] exp j>2 (eu -r l)] -
Следовательно, 5| + |2€§ П^+ц.
Сумма независимых случайных величин, распределенных но
закону Коши, также имеет распрсделецие Коши. Действительно,
__
(t\ _ «
Высказанные утверждения тесно связаны с тем, что нормаль-
нормальный закон и закон Пуассона выступают, как мы видели, в каче-
качестве предельных законов для сумм независимых слагаемых (тем
же свойством обладает и закон Коши, см. § 8.9),
Ведь если 82п/У2п сходится по распределению к нормальному
закону, то ясно, что $П/Уд и (SZn — Sn)/lln также будут сходиться
к нормальному закону, так что сумма двух асимптотически нор-
нормальных величин обязана снова быть асимптотически нормальной.
Равномерное распределение, например, этим свойством сохра-
сохранения вида распределения при суммировании не обладает. Если
It и §2 распределены равномерно на [0,1] и независимы, то F^ и
fitt+\ оказываются существенно разными функциями (см. при-
пример 3.5),
2. Г-распределеняе и его свойства. В этом разделе рассмотрим
еще один весьма распространенный тип 'распределений, тесно свя-
связанных с нормальным распределением и часто используемых в
дриложениях. Речь идет о так называемом гамма-распределении
Пирсона Га, а,. Будем писать, что !€§ Гад», если § имеет плот-
плотность
Х<0г
зависящую от двух параметров а >0 и К > 0, где Г (А.) есть

§ 7. СВОЙСТВА ГАММА-РАСПРЕДЕЛЕНИЯ 169
гамма-функция
Из этого равенства следует, что J / (х; a, %)dx = 1 (нужно сде-
сделать замену ах~у). Если х, ф.
оо
*; «г *-) = ттХГJ **"V'
О
продифференцировать по t и затем произвести интегрирование
по частям, то получим
Так как ф@)== 1, то с*=а\ ф@ A )
Из вида х. ф. следует, что подсемейство распределений Га, >
при фиксированном а также обладает известным свойством устой-
устойчивости: если ^х^Гад1, ^2^ Гад2 незавясимыг от |х + ^2ё
К Г-распределениям относится, в частности, распределение
случайной величины
п
%п ~ 2j bit
тле |i независимы и нормально распределены с параметрами
(О, 1). Это так называемое %г-распредвлеиие с п степенями сво*
воды, играющее важную роль в математической статистике.
Чтобы найти распределение %п достаточно заметить, что в
силу равенства
плотность %i равна
f(X\ 1/2, 1/2),; %f g= Г1/2Д/2»
Это означает, что х. ф. %п равна
фп(«; 1/2, 1/2)«A
и соответствует плотности j(x, 1/2, /г/2).

170 ГЛ. 7, ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
К Г-распределеииям относится также показательное распреде*
ленив Та ^ Та,, t с плотностью
f{x\ а, 1) = шга*, х>0,
и характеристической функцией
Предоставляем читателю с помощью х. ф. убедиться, что если
§= Г<^ и независимы, а,- Ф щ при / Ф I, то
й
В различных приложениях, например, в теории массового об-
обслуживания (ср. с § 11.4), важную роль играет также так назы-
называемое распределение Эрланга. Это распределение с плотностью
/(«г, а, Я) при целом Я. Ясно, что распределение Эрланга есть
Я-кратная свертка показательного распределения.
Найдем математическое ожидание и дисперсию случайной ве-
величины §, имеющей гамма-распределение с параметрами (а, Я);
Щ = _ др' @; а, Я) = ?,
М^ ~ ф'ЧО; а, Я) ^ Mk^?j
Распределения из гамма-семейства и особенно показательное
распределение часто используются с достаточными основаниями
для аппроксимации распределений в, разного рода прикладных
задачах. В связи с этим приведем три примера.
Пример 9. Рассмотрим какой-нибудь сложный механизм.
Выход из строя хотя бы одной из п деталей или узлов, составля-
составляющих этот механизм, означает выход из строя всего механизма.
Распределение срока службы каждого из узлов обычно хорошо
описывается показательным законом. (Причины этого явления
можно понять ,с помощью теоремы Пуассона о редких событиях.
См. также пример 2.5 и гл. 16.)
Таким образом, если сроки службы узлов ?3 независимы и для
узла с номером / выполняется
срок службы всего механизма будет равен T]n = min(!i, ..., %п)%

§ 7. СВОЙСТВА ГАММА-РАСПРЕДЕЛЕНИЯ
и мы получим
Это означает, что х\п снова будет иметь показательное распреде-
распределение, и так как
то среднее время службы всего механизма будет равноf
Пример 10. Обратимся теперь к распределению случайной
величины ?л = шах(?1, . .., ?л), где ?;, независимы и имеют Г-рас-
иределспие с параметрами (а, X). Мы можем рассматривать, на-
например, некоторую систему обслуживания, имеющую п каналов.
(Это может быть, скажем, электронно-вычислительная машина,
решающая некоторую задачу методом перебора и состоящая нз
большого числа малых машин, каждая из которых просматривает
свой вариант.) Канал с номером i занят случайное время |{. Че-
Через какое время освободится вся система? Ото время, очевидно,
будет распределено так же, как случайная величина ?п.
Так как |< независимы, то
Р(^<аО= Р(Д fe<*} j~[P(?i<*)]n. A5)
Если п велико, то для приближенных вычислений представ-
представляет интерес отыскание предельного при п -*¦ °° распределения ?п
(если тг->- °°, то Р (?„ < #)->() при каждом фиксированном х)<
Считая для простоты а = 1 (общий случай сводится к этому
изменением масштаба), по правилу Лоииталя убеждаемся, что
При X -> °о
Полагая при /г -> оо ^ = х (;г) = 1п -—^~—- + ^. и =» const,
получим
р (^ > х).. (ь^)^ г (%) с~и ^ ^ц^
Поэтому при таких х и /г~> оо в силу A5)"

172 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Таким образом, мы получили, что существует
или, что то же,
у •, \п A11 n)
^1п ^
Другими словами, величину ?п при больших п можно предста^
вить в виде
где V^F0>
Пример 11. Пусть |4 и |2 независимы, Ei^ra^lf- ?2^
ё Гад2* Чему равно распределение -«. .^v ? Воспользуемся тео-
ремой 4.10, Так как совместная плотность /(ж, у) для |t и ц =*
^^t'+b равна
а плотность для г) есть
9(У)-/(IT. «. Я-1 + Ха)\
то условная плотность f{z/y) для -gt при условии г| = 1/ равна
В силу формул § 3.2 условная плотность для — =-^~—— (при
У bj + Ц
том же условии %х + |2 = i/) равна
Это распределение не зависит от у (и от а). Поэтому такой
же будет и безусловная плотность v ¦х"Г"« Мы получили так назы-
ваемое бета-распределение В^д2 с параметрами hi, Я2, опреде-
определенное на отрезке [0, 1]. В частности, ггри Кх = К2 ~ 1 Bu« UOf i.

§ 8. ПРОИЗВОДЯЩИЕ ФУНКЦИИ. ЗАДАЧА О ВЫРОЖДЕНИЯ Ш
§ 8. Производящие функции. Применение к изучению
ветвящегося процесса. Задача о вырождении
1. Производящие функции. Мы уже знаем, что если случайная
величина ? целочисдэныа, т. е. Р([) {s = к}\ = I, то х. ф. щ{1)
'будет да самом деле функцией от z = ej\ и наряду с х. ф. распре-
распределение | можно характеризовать производящей функцией
Формула обращения здесь может быть записана в виде
Р (& = *)= Н J в~""ф? О df =2S
-Я izl=l
Читателю полезно отметить, что A6) представляет собой ire
что иное, как формулу для коэффициентов ряда Фурье (ведь
eitk = cos tk + t sin tk).
Если | и ц — независимые целочисленные случайные величи-
величины, то распределение ? + ц будет определяться сверткой после-
последовательностей Р(? = к) и Р (г| = к):
Р(? + Т1 = и)= 2 Р(& = й)Р(г| = л-А)
ft=-oo
(формула полной вероятности). Свертке этих последовательно-
последовательностей отвечает произведение производящих функции
Из примеров, рассмотренных в § 1, ясно, что производящие
функции случайных-величин, распределенных соответственно по
законам Бернулли и Пуассона, равны
iMz)= 1+ p(z-~ 1), i|N(z)=exp{fi(z— 1)}.
Из определения производящей функции видно, что для неот-
неотрицательной случайной величины Ъ,Х) функция .i|)$(z) определе-
определена при Izl ^ 1 и аналитичиа в области \z\ < I.
2. Простейшие ветвящиеся процессы. Обратимся теперь к по-
последовательностям случайных величии, которыми описываются
так называемые ветвящиеся процессы. С простейшим * примером
таких процессов мы уже сталкивались при описании схемы цеп-
цепной реакции в примере 4.10. Рассмотрим более общую схему вет-
ветвящегося процесса. Представим себе частицы, которые могут про-
производить другие частицы того же вида; это могут быть нейтроны
в цепных реакциях, бактерии, размножающиеся по определенным
законам, и др. Пусть в начальный момент времени имеется одна
частица («пулевое поколение»), которая в результате акта «деле-
«деления» с вероятностью /А, к == 0, 1, 2% ..., переходит в к частиц тога

174 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
же типа, 2/л ^ 1« Полученные частицы образуют «первое поко-
ление». Каждая из частиц этого поколения ведет себя точно так
же, как исходная частица, независимо от предыстории и судьбы
других частиц. В результате получаем «второе поколение» и т^ д.
Обозначим ?п число частиц в п-м поколении. Для описания по-
последовательности Сп введем в рассмотрение, как и в примере 4.10,
независимые между собой последовательности независимых оди-
одинаково распределенных случайных величин {^1}}jLb {^J)}jLxi • • -я
где Цп> имеют распределение
p(|f = &) = /„, fc-O, 1, ....
Тогда последовательность ?>п можно представить в виде
?i = li $
Это есть сумма случайного числа случайных величии. Так как
?in\- ^2W)i • • • от ?„»! не зависят, то по формуле полной вероят-
вероятности для производящей функции /<П) (z) == IVfs^^ получим
/(„) (z) = 21 Р (?«-! = *) Mz61 +-+5й =ЦР (?„_! = Л) /ft (z) -
= /(«-!) (/B))» A7)
(П) оо
где /(z) =/(i)(s) = Mz = 2 Д2&. Пусть fn(z) означает п-ю
fe-=o
итерацию функции /(г), т. е. /i(z)=»/(z), /2B) = /(/B)), /3B)-=
= /(/2B)) и т. д. Тогда с помощью индукции из соотношений
A7) заключаем, что производящая функция ?„ равна /г-й итера-
итерации /(z):
Отсюда с помощью дифференцирования в точке 2 = 1 легко полу-
получить рекуррентные соотношения для моментов ?„.
Как найти вероятность вырождения процесса? Под вырожде-
вырождением мы будем понимать событие, состоящее в том, что все ?п,
начиная с некоторого п, равны 0. (Если %п == 0, то, очевидно*
tn+i = Sn+2 =•... « 0, так как (?n+i — 0/?п = 0) == 1.) Обозначим
Ah = {^ft = 0). Тогда вырождение представляет собой событие

§ 8. ПРОИЗВОДЯЩИЕ ФУНКЦИИ. ЗАДАЧА О ВЫРОЖДЕНИИ
175
oo.
U Ah. Так как 4ftcin+i, то вероятность вырождения q равна
Теорема 5. Вероятность вырождения q равна наименьшему
неотрицательному корню уравнения g = /(g).
Доказательство. Имеем Р (Ап) = /п @) ^ 1, и эта после-
последовательность не убывает. Переходя в равенстве
/п+1@) = /(/„@)) A8);
Исследуем по-
по0)
к пределу при п ->¦ <*>, получим q = f(q), q <: 1.
Это уравнение для вероятности вырождения.
ведение его решения. f(z) есть выпуклая (/"(z)>0) неубываю-
неубывающая функция в области z > 0, f(i)=m есть средняя величина
потомства одной частицы. Предположим
сначала, что P(^i1)==l)<l. Тогда ес-
если 7п^1, то f(z)>z при z<l и, сле-
следовательно, д = 1. Если 771 >1, то в си-
силу выпуклости / уравнение q = f(q)
будет иметь на отрезке [0, 1] ровно два
решения: gi < 1 и д2 = 1 (см. рис. 8).
Допустим, что q = gt = 1. Тогда после-
последовательность бте = 1 ~ /п@) монотонно
сходится к 0 и /A — б„)< 1 — бп при
достаточно больших п. Следовательно,
для таких п^ Vm 8
что противоречит монотонности убывания 6„. Это означает, что
q = gi < 1. Наконец, в случае Р (?i1} == l) = f± == 1 имеем f{z)^ z
и, очевидно, g = 0. ^
Рассмотрим теперь более внимательно случай m = 1, который
называют критическим. Мы знаем, что в этом случае вероятность
вырождения g равна 1. Пусть gn=:P(^n) =« /п@) есть вероятность
вырождения к моменту п. Как быстро qn сходится к 1?
В силу A8) gn+i=/(gn). Отсюда следует, что вероятность про-
продолжения (не вырождения) процесса pn = l — qn (к моменту п)
удовлетворяет соотношению
Pn+l =g(Pn) , g (X) == 1 ~ /A - Я).
Ясно также, что 'Yn = /?п — pn+i е^ть вероятность того, что вы-
вырождение процесса совершится на шаге п.
Теорема 6. Если ти = /'(!)= 1, 0 < Ь =*f" A)< oos ro y№ ~
Доказательство. Если второй момент числа потомков
одной частицы конечен (&<°о), то существует ?"@)=***-Ь щ

176 ГЛ. 7. ХАРАКТЕРИСТИЧЕСКОЕ ФУНКЦИИ
следовательно, (g@) = 0, g'@) = /'@) = 1),
g(x) = х — — a* + о(х2).
Полагая здесь х = р1г -* О, для последовательности ап = 1/рп нахо-
находим
Рп~~ рТ}л_1 Ьр2п A + о A)) 5
- 2 tv{F
71 — 1
&11 ^^^ ^i + 2La \^/i+i "~~* ^/-<//>^ 2 ? ~Ри ^^ т—• ^ч
Рассмотрим теперь вопрос о распределении числа частиц ?;„
при условии 'Qn > 0.
Теорема 7. Пусть выполнены условия теоремы 6. Тогда
условное распределение /?п?п (или 2?„/(Ья)) wpw условии ?,п > 0
сходится при п ->¦ ©о к показательному:
Сформулированное утверждение означает, в частности, что при
п -> оо и условии ?п > 0 число частиц t;n имеет величину по-
порядка 72.
Доказательство. Рассмотрим ' преобразование Лапласа
(см. свойство 8 § 1) над условным распределением рп^п (при ус-
условии ?п > 0), равное
М (e"SPnSn /?„ > 0) = f
P
Так как /?n ~^ 0, то при любом фиксированном s > 0
, д р
впРп_ 1 == —-J5.V- Поэтому е SPn ' « A — pN)\ и правая часть в
Ясно, что всегда можно выбрать /V ~ «/5, 5a^ s, 5n I 5 так, чтобы
e~*ni>n _isss__mp^9 Поэтому e~sPnk e A — ру
A9) при 5 == sn может быть записана в виде
<х>
г2р (S» = к) A ~ рл)* = 4- р (?»
Заметим теперь, что
м (Г4"-5 7ьн > о) - м (• ~S)lP"?7Cn > о) -
= rvi [«-"»'" (i - ГE"")РЛ)Д„ > о].

§ 8. ПРОИЗВОДЯЩИЕ ФУНКЦИИ. ЗАДАЧА О ВЫРОЖДЕНИИ 177
Так как е~а < 1, 1 - е~а ^ а при а ^ О, М?п = 1, М (?„/?„ > 0) =
~ 1/р{Щ то оцениваемая положительная разность (sn > 5) не пре-
превосходит
($п — s) pJA (Qn!ln > 0) = % — 5 ->- 0,
Следовательно, цреобразовалие Лапласа A9) сходится при
тг->оо к 1/A + ^). Так как 1/A + 5) есть преобразование Лапла-
Лапласа показательного распределения —
сю
—- то в силу теоремы непрерывности (см. замечание к теореме 2
§ 3) рассматриваемое условное распределение сходится к показа-
показательному*). ^
Утверждения, касающиеся поведения ?п при п -+¦ °° для ветвя-
дщхся процессов в случае \х > 1 (так называемых надкритиче-
надкритических процессов) будут получены в § 14.4 (пример 8) в качестве
следствий теорем о сходимости мартингалов.
*) Приведенные простые доказательства теорем 6, 7 сообщил нам
К, А. Боровков,
а. А. Боровков

Глава 8
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
СЛУЧАЙНЫХ ВЕЛИЧИН, ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
§ 1. Закон больших чисел
Теорема 1 (закон больших чисел в форме Хинчина)\ Пусть
{5п}5Т=1 — последовательность независимых одинаково распреде*
ленных случайных величин, имеющих математическое ожидание,
М^п = &-> и пусть Sn = |i + ... + In. Тогда Зп/п->- а при п~>-°а»
Отметим, что здесь как условие независимости |Л так и само
утверждение теоремы, предполагают, что все случайные величи-
величины gft заданы на одном вероятностном пространстве.
По своему физическому существу сформулированный закон
больших чисел представляет собой простейшую эргодическую тео-
теорему, означающую, грубо говоря, что для случайных величин их
средние значения «по времени» и «по пространству» совпадают.
Еще в большей мере это замечание можно будет отнести к уси-
усиленному закону больших чисел, в силу которого SJn -* p с веро-
вероятностью 1.
При более жестких предположениях (существование диспер-
дисперсии) теорема 1 была получена нами в § 7 гл. 4 в качестве след-
следствия неравенства Чебышева.
Доказательство теоремы 1. Надо доказать, что пря
любом е > О
Р( \ _л п
при п -*- оо. Выписанное соотношение эквивалентно слабом схо-
сходимости распределении Sn/n€==>la. Поэтому в силу теоремы не-
непрерывности и примера 7.1 достаточно- доказать, что для каждого
фиксированного t
X. ф. <р(?) случайной величины ?л в некоторой окрестности 0 об-
обладает свойством |ср(?)--II < 1/2. Поэтому для таких t можно
определить функцию /(?)=1пф(?) (берется главное значение ло-
логарифма). Так как существует математическое ожидание ?п? то
существует
При каждом фиксированном t и достаточно больших п значение

§ 2. ЦЕНТРАЛЬНАЯ ПРОДЕЛЬНАЯ ТЕОРЕМА
определено и
1Шп)п = expU im~Hl@) }->evm - «*"
Так как Ц0)==0, то при п
U imH
§ :2. Центральная предельная теорема
для одинаково распределенных случайных величии
Пусть по-прежнему {\п) — последовательность независимых,
одинаково распределенных случайных величин. Но теперь, кроме
математического ожидания М|л = а, будем предполагать суще-
существование дисперсии D^n ==a2. Как и раньше, Sn = §! + ... + ?я,
а Ф(х)— функция распределения нормального закона с парамет-
параметрами @, 1). Введем еще последовательность случайных величии
Теорема 2. Если 0< о2 < сю, то при п -> оо р(gn<; ^)->ф (#)
равномерно относительно х (•— оо < ж < оо).
В этом случае последовательность {^«} называется асимптоти-
асимптотически нормальной.
Из того, что М?п = 1и из теорем непрерывности (см. теорему
6.5 А и аналог следствия 6.4) вытекает, что наряду со слабой схо-
сходимостью ?>п =*" 5, ?€§ Фод (М/ (Sn) -> M/(S) для любой непре-
непрерывной ограниченной /) имеет место также сходимость M/(Sn)~^
*^M/(S) для любой непрерывной /, такой, что 1/(^I <
< сA + Ы2~е) при каком-нибудь 8 > 0.
Доказательство. Равномерная сходимость здесь является
следствием слабой сходимости и непрерывности Ф(х). Далее, без
ограничения общности можно считать a = 0, так как иначе мож-
можно было бы рассмотреть последовательность {?n = |n-— a}~=i,
ври этом последовательность {?п} не изменилась бы. Стало быть,
для доказательства требуемой сходимости достаточно показать,.
что %n@~>?~"* 2Л когда а = 0. Имеем
ФЬ|(*)вфп0/а/я)* где Ь
Так как существует. М^ то существует ф" (t) ж справедливо'
разложение
Ф (*) = ф @) + W @) + L ф» @) + о (f3) = 1 - if- + о (*=).
12*

'180 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Следовательно, при п -*¦ <*>
4 § 3. Закон больших чисел для произвольных
независимых случайных величин
Перейдем теперь к выяснению условий, при которых справед-
справедливы закон больших чисел и центральная предельная теорема,
в случае, когда gft независимы, но не обязательно одинаково рас-
распределены. Мы не добавим трудностей, если сразу будем рас-
рассматривать более общую задачу, когда даны произвольные серии
li.n, .. ., ?n, n независимых случайных величин, где распределения
|ft, п могут зависеть от п.
п
Обозначим Cn = 2 ?fe,n« С точки зрения последующих резуль-
'татов можно считать, не ограничивая общности, что
Mgftfn = 0. ' A)
Предположим, что выполнено условие: при каком-нибудь $у 2 >
(lM|r (х)
fe=i
При П ~> оо.
Теорема 3 (закон больших чисел). /7/ш выполнении усло-
условий A), (Д.)
Тп g==$In или, что то же, ?**->().
Рассмотрим внимательнее условие (Di). Очевидно, что его
можно записать также в форме
2 M(Uft.n|;|^in|>i)+ 2M(UMf; |6л,п1<1)-^0.
Если
Mi^2M|Eft.n|<e<oo . B)
при п-*- оо, то для выполнения (Di) пеобходимо и достаточно вы-
выполнение условия
Af 1 (х) = 2 М (| &ftift!; 1 **,, | > т) ™> 0 (Л/,)

§ 3. ЗАКОН БОЛЬШИХ ЧИСЕЛ - 181
при любом т > 0 и п -*• °°, которое можно назвать условием типа
Линдеберга (условие Линдеберга (М2) будет введено в § 4), Дей-
Действительно, (т< 1, gi(#)= min(|#|, Uls))f
x (T) + iT1 Jj M ( | lhtn |; I Sft.n К T) < Mx (T) + T'^г @), C)
ftl
Так как Mi@) = Mi < cf а т может быть произвольно малым, то
Z?t ->¦ 0 при п -*• сю.
Обратно (здесь условие B) не требуется), при т<1
2
прк ?г ->• сю и при любом т > 0.
Каждое из условий (Di), (Mi) влечет за собой равномерную
малость М | %,ktn {•
max M|Sfe,n|"-^0 при n-^-oof E)
Действительно, (Mi) означает, что существует достаточно медлен-
медленно убывающая последовательность %п~*0 такая, что Mi(xn)-+-0.
Поэтому
max М 11Кп | < max [тп + М (| %k,n |; I lk,n 1 > тп)] < тп + Mi (тп)->0.
F)
Из E) следует, в частности, свойство пренебрежимой малости
слагаемых |л,п.
Будем говорить, что |&>п пренебрежимо малы, или, что то же,
обладают свойством (?), если при любом е>0
Свойство (S) можно было бы назвать также равномерной схо-
сходимостью |й> п по вероятности к нулю. Свойство (S) сразу следует
из E) и неравенства Чебышева.

182 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Доказательство теоремы 3*). Обозначим
Фл.п (*) - Metlh'\ Дл (t) - <рм (t) - 1.
Надо доказать, что при каждом t и при п -> °о
ф^ (^) =53 |Vf# =S J^J^ ф^ n(f) —>" 1«
В силу леммы 7.3
ft п
1 svi ' —lj 1 == <2j I М(^ — 1 — itzhn)]*
В силу леммы 7.2 (gi(#) = min(|x|, x2)< min(UI, \x3\) при 5 < 2)
|е2'*-— 1 — itxl^minf 2 | ^х|, -^-1^2^ (tx)^. 2h(f)gx(x),
где A(^)=max(UI} UI2)'. Поэтому
Замечание 1. Если {|ft} есть заданная фиксированная (не
зависящая от п) последовательность случайных величин,
п
$п = 2 ^fei М^ = а^г то для нее будем изучать поведение сумм
п
» ^ - 2 ^
te ^ bft ^
где ?ь, n = (I* — ялOдг удовлетворяют A). Если положить, не огра-
ограничивая общности, ал = 0, то условия (Z?i), (Mi) будут в этом
случае иметь вид
Если Zh одинаково распределены, то из теоремы 3 вытекает
в качестве частного случая теорема 1, так как будут выполнены
*) Существует другое, «прямое» доказательство теоремы 3, использую-
использующее не х. ф., а так называемые срезки случайных величин и оценки их
дисперсий. Однако здесь и в связи с дальнейшим нам удобнее использовать
аппарат х. ф.

§ 3. ЗАКОН БОЛЬШИХ ЧИСЕЛ 183
условия B), (Mi) (последнее эквивалентно соотношейию
М (| gft — а 1; \1ъ — а|>та)->0).
Для выполнения (А) достаточно также выполнения следую-
следующего условия: при некотором s, 2 ^ s > 1,
Это утверждение очевидно, так как gi(x)^\x\B при $>1. Усло-
Условие (Ls) можно было бы назвать условием типа Ляпунова (ср. с
условием Ляпунова (Ls) в § 4).
Замечание 2. Условие (Di) (или (Mi)) не является не-
необходимым для сходимости ?п -> 0 даже при выполнении B),
E), на что указывает следующий пример: |ft п принимает зна-
А ' 1 4 2 1
чения —п, 0, п соответственно с вероятностями —, 1 g-, ~.
Здесь Sn^0, так как Р(?п?= 0)< Р (U {Ем ^0»< 2/л-^О,,
M|EftfnH2/ii->-0f М1-2М|Ь,п|==2<оо. В то же время
S М (| Sft.nl; IEft.nl ^ 1)= 2^0,и условия (Dt), (Mf) не выполнены,
' Однако, если потребовать, чтобы
%к п ^ —eft, п, е/t, п >= 0,
п G)
max Eh n ->¦ 0, 2 8^п < с <°°»
то условие (D{) станет необходимым.
Прежде чем доказывать это утверждение, приведем некоторые вспомсь
гательные соотношения, которые будут полезны нам в дальнейшем.
Лемма 1.
При выполнении условия (S) при п ->- со и при каждом t
max | А/г (t) | -* 0. (8)
k-4.ri
Если случайная величина |, М? = 0, ограничена слева: | >> —с, с > 0«
то М|?|< 2с.
Доказательство. В силу леммы 7.2
(*) I < M ( I eitlk'n - 1 I; I gft>n| < e) +
Если воспользоваться здесь условием (S) и произвольностью е, то полу*
чим (8Jt

Положим E+ = max@; &)>0, %~' = — (g — g+) > 0. Тогда ME =r
= Mg+ — ME"" = 0, M | E | = Щ+ + ME~ - 2ME~ < 2c. 4
Из последнего утверждения леммы следует, что условие G) влечет за-
собой выполнение B), E).
Лемма 2. Пусть выполнены условия (S) и B), Тогда для сходимости*
<jp? (?) -> <р (?) необходимо и достаточно, чтобы Л
Доказательство. Заметим, что
! М» I
и, следовательно, по лемме 7.3
? (t) < 1 max j &h W | 2 I Ak @ |-
По лемме 1 в силу условий (S) и B) оцениваемое выражение сходится
к 0 при п -> оо. Поэтому если ф^- (t) -xpjf), то е 1 -*ф@> п наоборот. ^
Следующее утверждение дополняет теорему 3.
Теорема 4. Пусть справедливы соотношения A), G). Тогда условие
(D{) (или условие (М{)) необходимо для выполнения закона больших чисел.
Доказательство. Если выполнен закон больших чисел, то
Ф^ (t) -* 1 и, следовательно, по лемме 2 (напомним, что G) влечет за со-
собой B), E), (S))
h
Кроме того, по лемме 7.2
(I "*
/i=i
кп п
Поэтому, если имеет место закон больших чисел, то в силу G)

§ 4. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 185
е{х — 1
Рассмотрим функцию а (х) — . Нетрудно видеть, что неравенство
| об (д?) | ^ 1, доказанное в лемме 7.2, является при х >¦ е > 0 строгим, и, зна-
значит, существует 6(т) > 0 при т > 0 такое, что ReA — а(х)) ^ б(т) при
х >> т. Это равносильно тому, что Im(l + ix — eix) ^ б(т)# и, следовательно,
1
х < 7^7 *т A + ix ~~ ^гХ) ПРИ
Отсюда находим
мг W = 2 м (I 6М |; | 5М I > т) = 2
fcl л
Im 2
Таким образом, выполнено условие (Л/i), которое вместе с B) влечет за
собой (Di). ^
§ 4. Центральная предельная теорема для сумм
произвольных независимых случайных величии
Как и в § 3, сразу будем рассматривать серии случайных
величия
и их суммы
Е» - S 1Кп- (9)
я = 1
Мы будем предполагать, что ?U, n имеют конечные вторьте момен-
моменты ви}п = D5/t,?i < оо, и считать, не ограничивая общности, что
М?*,„ = 0, 2 о*,п = Du = 1. (Ю)
Введем в рассмотрение условие: при некотором s > 2,
Ц, ^ 2 М min (^,„, | ?ft>n Is) ->0,, (ZJ)
которое будет играть важную роль в дальнейшем. При этом мпо-
гсте рассмотрения, связанные с условием (D2) и с условиями
(Л/2), (L8), вводимыми ниже, будут вполне аналогичны рассмот-
рассмотрениям, связанным с условиями (A), (Ai\), (Ls) в. § 3.
При выполнении A0) необходимым и достаточным для вы-
юлнеиия (D2) является условие Линдебергач
м2(т)г 2 м (I h,n I2; |.-.ih,n | > т) ^о . (Mt)
k

186 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
при любом т>0 и п -> «\ Действительно, положим
= mm(^2, \xV). Тогда (ср. с C), D); т^ 1)
2 М (Й,я; 11и,п | > т) + 2 М
(т) + %S~2M2 @) = М2 (т)
Так как т произвольно, то D2 -*• 0 при и -* <».
Обратно, при т< 1 (условие (8) здесь не требуется)]
при любом тХЗитг-*00. ^
Итак, при выполнении A0) условие (D2) инвариантно по $>2<
Условию (D2) можно придать более общую форму;
2 мй.*л (?*.«)-> о,
fe=l
где h(x)—любая функция, обладающая свойствами h(x)>0 при
х>0, A(x)f, А(ж)-^0 при ж~^0, h(x)-*- с < оо при ^-*•«>. При
этом все основные свойства условия (D2) сохранятся. Условие
Линдеберга выясняет существо условия (D2) с несколько иной
точки зрения. В нем h(x)~ /(т, оо), но т пробегает @,1). Анало-
Аналогичное замечание можно сделать по поводу условий (^Di), {M%)
в § 3.
Аналогично тому, как это было сделано в § 3 относительно
условия (Mi), легко проверить, что условие (М2) влечет за со-
собой сходимость (см. F))
maxD6ft,n->0 A1)
h<4n
и пренебрежимую малость ?fc, „ (свойство (S)). Очевидно также
неравенство
Если {%h} есть заданная фиксированная (не зависящая от п)
последовательность независимых случайных величин, Sn =*
п
•= 2 iki МЕй = йк2 О?л = aj, то для нее будем изучать пове-

§ 4.. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
187
дение нормированных сумм
*п
»2
п
которые, очевидно, также имеют вид (9), где Ь, п ==(^ —^
Условия (Д>)| {Мг) для |* будут иметь вид
n
^ 2 M ((S* - «/.JJ 15* - e* I > тв„) -v о.
A2)
Теорема 5 (центральная предельная теорема). Если по*
следовательности независимых случайных величин {|й,п}?=ь п »
*= 1, 2, ..., удовлетворяют ^условиям A0), (АО, ?ч> ^
-^Ф(х) равномерно по х.
Доказательство. Достаточно убедиться, что
В силу леммы 7.3
Пф*.«(*)-П
Так как по лемме 7.2
< 21 фл.п @ —
/1
(при 5 = 3), то первая сумма в A3) не превосходит
<
. A3)
где A(^)=max(^, UP). Вторая сумма в A3) (снова но лемме

iS8 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
7.2) не превосходит (см. A0), A1))'
7fV"^*° при n~>°°- <
Иногда утверждение теоремы 5 бывает удобным в следующей:
форме:
Следствие 1. Пусть М^,п = 0, D^n~>a2>0 и выполне-
выполнено условие (D2) или (if2), тогда ?п^Ф0)О2- '
Замечание 3. Утверждение теоремы 2 об асимптотиче-
Sn — an
ской нормальности ?п == —77=""' когда §л одинаково распределен
0 уп
ны, можно было бы получить в качестве следствия теоремы 5.
Нужно лишь проверить выполнение условия Липдеберга. Так
как в этом случае #«' = но2, то (см. A2))
M2(x) = ~M((^~-aJ; \lh-a\>xoVn)-+0 при п-^оо
для любого т > 0.
Замечание 4. Достаточным условием для выполнения
(D2), (^/2) является более ограничительное условие .Ляпунова.
Проверять его в ряде случаев легче. Предположим, что выпол-
выполнено A0). Величину
h=l
при некотором s>2 называют отношением Ляпунова порядка s.
Ъ'словие
Ls-+0 (L.)
называют условием Ляпунова. Величина Ls получила название
отношения .потому, что для ?н,п = (Ъ — а}{)/Вп (ak = М^, В\ =*
= О?,пх Ъг от /г не зависят) Ls имеет вид
к
Если |ft одинаково распределены, ah = a, D^ = a2, M | ^ — a
«= fl<C OO, TO
Достаточность условия Ляпунова вытекает из очевидных пе-
раяенств gi(x)<i \x\8 при s > 2, D2^LS.
Замечание 5. Условия (D2) или (М2) не являются не-
необходимыми для сходимости распределения ?п к нормальному.

§ 4. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА Ш
Достаточно рассмотреть следующий пример:?1,п€=Фо,ь ?2,п:==-..
• «•=?п,п=0. Очевидно, что условия A0) выполнены, P(?n<#) —
= Ф(х), а' слагаемые ?ftj n не являются пренебрежимо малыми
и, следовательно, не удовлетворяют условиям (D2), (M2).
Однако, если наряду со сходимостью ?,г€=*Фо,1 потребовать,,.
чтобы %ft> п были пренебрежимо малы,'то условия (D^), (M2)
становятся необходимыми.
Теорема 6. Пусть последовательности независимых .вели-
.величин {bi,n}k=i удовлетворяют условиям A0), (S). Тогда условие
(Д>) (или (Мг)) необходимо и достаточно для сходимости
Доказательство. Достаточность уже доказана. Чтобы
доказать необходимость, воспользуемся леммой 2. Если ф?п@~^
e~t 2& то в силу этой леммы (Ah(t) = Ц)к) n(t)— 1)
При t = 1 выписанное соотношение можно записать в форме-
Обозначим а(х):=(егх — 1 — ix)/x2. Нетрудно видеть, что неравен-
неравенство \и(х)\ < 1/2, доказанное в лемме 7.2, является строгим при
х?=0 и
sup | а (х) | < ~ — б (т),
где б(т)>0 при т > 0. Это означает, что при \х\ ^т>0
6 (т) V
z2
,(т)
i
в силу A4) при п -> ©о дЛЯ любого т >0. ^
Из теорем 4, 6 вытекает следующее утверждение.
Следствие 2. Пусть выполнено A0) гг
Тогда для сходимости ^ё^Фод необходима и достаточна,

190 ГЛ. 8, ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
сходимость
п
Tin ^^ 2mi 5/t,n ?=Г^ *jj
(или сходимость ц\п ->- !)•
Доказательство. Пусть Цп€=$ Ii¦ Случайные величины
?&,п= Slfn—^/i,n в силу A5) удовлетворяют условию G) и удов-
п
летворяют закону больших чисел: 2 Е&,« = % — 1 ->• 0. Следова-
Следовательно, по теореме 4 5^,п удовлетворяют условию (М{):
п
при любом т>0. Но по A5) это условие эквивалентно, очевид-
очевидно, условию (М2) для §ftfn. Отсюда следует ^пё^Фол*
Наоборот, если Ст»ё=» Фод» то выполнено {М%) для g%;n и, зна-
значит, условие A6). Так как, кроме того,
п п
то для ?/t,n выполнено B) и по теореме 3
Пример 1. Пусть |ft, /г=1, 2f ...— независимые случайные
величины с распределениями
{ка с вероятнос1ью 1/2,,
— fca с вероятностью 1/2.
-Здесь (s = 3)
Имеем при 2а + 1 > 0
в\ 2
\

§ 4. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА 191Ч
При а « -1/2
si - 2 *~* ~1п *•
Если а<—1/2, то J3n ограничены при п -> <» и, следователь-
следовательно, не будет выполнено условие пренебрежимои малости сла-
слагаемых.
Аналогичным образом находим при а>-~1/3
с* = is Аза ~
^я \ п у л .* \п) п) J За+1
При а = —1/3 имеем С»~1п?г; если а<—1/3, то Сп ограниче-
ограничены. Так как na+i/3 = o(na+i/2), то при а ^-1/2 Сп = о(Вп) и ус-
условие Ляпунова ^з ^ Сп/Вп-^0 будет выполнено. Следователь-
Следовательно, суммы Srj2a+ 1//га+1/2 при а>—1/2 будут асимптотически;
нормальны с параметрами @, 1), Если же ^ — il/У/с с вероят-
ностями 1/2, то асимптотически нормальной будет величина
Sjyhm. В частности, при больших п величина 15П1 не будег
превосходить 2У1пп с вероятностью, равной примерно 2ФB)~
п
— 1 ~ 0,955. Для сравнения можно заметить, что J^ ггд- растет
п
как Tw/2, а знакочередующиеся суммы 2d ' ч1/-' ограничены по-
стоянпым числом. ^
Очень наглядной и хорошо известной иллюстрацией действия
доказанных теорем является рассеивание артиллерийских сна-
снарядов при стрельбе по цели. Дело в том, что на траекторию
полета снаряда действует большое количество независимых фак-
факторов, влияние каждого из которых само по себе невелико. Это
отклонения в количестве заряда, отклонения в весе и размерах
снаряда, отклонения во влажности и температуре воздуха, на-
направлении и силе ветра на разных высотах и т. д. В результате
отклонение снаряда от точки прицеливания удивительно точно
описывается нормальным законом.
Такого же рода наблюдения можно сделать относительно
ошибок в измерениях, когда на их точность влияет много «мел-
«мелких» факторов. (Существует даже «теория ошибок», главным
пунктом которой является центральная предельная теорема.)
В целом центральная предельная теорема находит чрезвычай-
чрезвычайно много применений в самых разных областях. Это происходит:

192 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
благодаря ее универсальности, ее устойчивости относительно не-
незначительных отклонений от условий теоремы и ее сравнительно
высокой точности даже при умеренных значениях п. Первые дза
отмеченных качества означают, что 1) теорема применима к ве-
величинам §fe, п с любыми распределениями, лишь бы существовали
дисперсии ?fti n и они были «пренебрежимо малы», 2) появление
«умеренной» зависимости*) между b,kt« не меняет нормальности
предельного распределения.
Чтобы проиллюстрировать точность нормального приближения,
приведем такой пример. Пусть Fn(x) = P(Sn/уп<^ х) есть функ-
функция распределения нормированных сумм «Sn, образованных неза-
независимыми величинами gft, равномерно распределенными на
[—УЗ, УЗ], так что D|fe = 1. Тогда оказывается, что уже щш
п = 5 (!) максимальная величина разности \Рп(х)—Ф(х)\ на
всей оси значений х не превосходит 0,006 (максимум достига-
достигается около точек х = ±0,7).
И все же, несмотря на отмеченные обстоятельства, при ис-
использовании центральной предельной теоремы следует проявлять
осторожность. Например, нельзя требовать точности от нормаль-
нормального приближения при оценке вероятностей редких событий, ска-
скажем, при изучении вероятностей больших уклонений (этот во-
вопрос уже обсуждался в § 5.3). Ведь теорема обеспечивает лишь
малость при больших п разности
|Ф(*)-Р(?п<*)|- A7)
Допустим, мы хотим с помощью нормального приближения ука-
указать такое #о, чтобы гарантировать появление события {t,n > хо\
в среднем не чаще, чем 1 раз па 1000 случаев (такая задача мо-
может возникнуть, скажем, у экспериментатора, когда он хочет быть
уверенным, что в отдельном эксперименте событие такого вида
не произойдет). Если даже разность A7) не превосходит 0,02
(что может считаться хорошим приближением), то, используя
нормальное приближение, мы рискуем ошибиться в десятки раз,
поскольку может оказаться, что 1 — Ф(яо)= Ю~3, а Р (?« > х0) ж
?? 0,02 и событие {?„ > xQ} будет появляться значительно ча-
чаще — в среднем 1 раз на 50 случаев.
В связи с этим в § 8 рассматривается задача о вероятностях
больших уклонений, где отыскивается функция Р(п, х) такая,
что Р (Сп > %)/Р {п, х) -*" 1 при п ->• оо, х -*- °°. При этом функция
Р(п, х) оказывается, вообще говоря, отличной от 1 —Ф(#). Надо
отметить, однако, что использование приближения Р(п, х) тре-
*) Существует целый ряд условий, характеризующих допустимую за-
зависимость между ?а# п. Знакомство с пими выходит за рамки настоя-
настоящей книги и требует привлечения специальной литературы. См., напри-
например, [8].

§ 5. ОЦЕНКИ ПОГРЕШНОСТИ 193"
бует выполнения более жестких условий на %kt n. В § 6 приводит-
приводится также локальная предельная теорема, которая устанавливает
сближение плотностей ?,п с плотностью нормального закона и
позволяет оценивать вероятности редких событий другого сорта,
скажем, вида {а < ?n < W, где числа а и Ъ близки.
§ 5. Другой подход к доказательству предельных теорем.
Оценки погрешности
Изложенный в § 1—4 подход к доказательству основных
предельных теорем для распределения сумм случайных величин
основан на х, ф. Однако это далеко не единственный метод дока-
доказательства такого рода утверждений. В настоящее время изве-
известно несколько весьма простых доказательств как законов боль-
больших чисел, так и центральной предельной теоремы, не исполь-
использующих аппарата х. ф. (Это не умаляет значимости последнего,
представляющего собой мощный, хорошо разработанный и весьма
общий аппарат исследований.) Эти доказательства позволяют к
тому же получать в некоторых случаях более общие результаты,
В качестве иллюстрации приведем ниже доказательство цент-
центральной предельной теоремы, обобщающей в известном смысле
теорему 6 и дающей оценку скорости сходимости (правда, не
наилучшую).
Наряду со случайными величинами |ft> „ в схеме серий и при
выполнении A0) рассмотрим независимые между собой и от
последовательности {1ь,«}л=1 случайные величины Л/г,п€§Ф з -•>
OtGFft,n
п
^,n = DSft,m так что г\п = 2 %,Ф0Д*
Обозначим |AftiTl = М | lktn |'\ Vft,n = М | ч&,п |3 = csagn < c3[*ft,n*)»
Ил,* = Jl *\*\d(Fhtn(x) - Ф/|)П (х))| < phtn -h vktn% Ls = 2 jiftin) ЛГ8=
*з) &,-Здесь Fft>n? ф,>п^-
функции распределения ?ftf n и T]ftf и соответственно. Числа L^ и
iV3 суть отношения Ляпунова третьего порядка для последо-
последовательностей i^k, гЛ и {r]ft( „}. Числа [ik^n называются псевдомо-
ментами третьего порядка, а величина Ь% — отношением Ляпу-
Ляпунова для псевдомоментов. Очевидно, что N% ^ dl^ -+• 0, если
*) Если ч?ЕЕФ0 j, to
сю
S = м 1 п |3 = _А^ f *3
О
13 А. А. Боровков

194 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
выполнено условие Ляпунова. Как уже отмечалось для ?ft> n —
а
¦$п, где пи = М?л, $n = 2j Щ/>, gA от /г не зависят,
¦I**I-* И-л = М | g/{ — «л J3. Если к тому же \h одинаково
Вп 1 __
распределены, то L3 = \kj (оЧп).
Нашей первой задачей будет оценка близости М/ (?7г) и
М/(Лп) для достаточно гладких /. Эта задача может представ-
представлять и самостоятельный интерес. Предположим, что / принад-
принадлежит классу С8 всех ограниченных функций с равномерно не-
непрерывной и ограниченной третьей производной: sup | / д) (х) \ ^/3.
ос
Теорема 7. Если /еС3, то
Доказательство. Обозначим
Y — fc 4- -h t +n -I- 4- n
у t 4- 4-t 4-rj 4- 4-.n
Тогда
X/+1 = Z, + ^. „, XL - Zz.+ T|Z, n, A9)
/(U - /(Лп) - 2 [/ (Xl+1) - /№)]. B0)
1
Воспользуемся теперь следующей леммой.
Лемма 3. Пусть /&С3, Z, g и ц суть независимые случай-
случайные величины,
| М/ (Z + I) - М/ (Z + л) |< /з[Ао/6. B1)
Применяя эту лемму к A9), получим
что после суммирования дает A8). <4
Итак, для доказательства теоремы 7 осталось провести
Доказательство леммы 3. Обозначим (g х = М/ (Z + ^).
Очевидно, что gf, будучи усреднением /, обладает всеми свойства-
свойствами гладкости / и, в частности, \g"'{x)\ ^/3. В силу независимо-

§ 5. ОЦЕНКИ ПОГРЕШНОСТИ 195
СТИ Z, | И Г]
м/ (Z +1) - м/ (Z + л) =• .U (*> d (П (*) - ^л («)). B2)
Под интегралом воспользуемся разложением
g(х) = g@) + ^' @) + 4 g' @) + ~ g"' (9«), 0x s L0,, х],
В силу совпадения моментов ? и т| до второго порядка для пра-
правой части B2) получим
Замечание 6. Совершенно аналогично можно получить
представление
IM/ (Q - M/ (л»)! < ^р 2 м U*.« - Л'.») + -^г B3)
при очевидных соглашениях относительно обозначений /4 и Ь^.
Эта оценка может улучшать A8), если разности М (c,fttn—Т\1,п)
малы, Если, напримерДл.тг =—'-•-./- Ли одинаково распределены
и третьи моменты %к п и цк,п совпадают, то справа в B3) будет
стоять величина порядка 1/п.
Теорема 7 обобщает теорему 6 при s = 3. Обобщение состоит
в том, что теперь для сходимости ?п©Фод не требуется пре-
предельной препебрегаемости gft, п. Если, например, 5i, п€=Фо, i/2
(в этом случае fAi,n = °) и ^я->0, то МД?п)-*М/(л), ' т)^Фвд
для любой / из класса С3. Так как С3 определяет распределение
(см. гл. 6), то остается воспользоваться следствием 6.7.
Высказанное утверждение можно усилить.
Теорема 7А.
\Р&п<х)-Ф{х)\<с(ЦУ'\ - B4)
где с — абсолютная постоянная.
Доказательство. Возьмем какую-нибудь функцию Ае
еС3, 0 ^ h ^ 1, такую, что h (х) = 1, ж ^ 0; fe (х) = 0, ж > 1, и
обозначим h>} = sup | hw (х) |. Тогда для функции/ (^) = fe U + -|-
будем иметь /3 == sup | //г/ (х) \ ^ ^3/е3«
Р (?п < 0 < М/ (&,) < М/ (л) + A3 <

196 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Последнее равенство имеет место, так как максимум производ-
производной нормальной функции распределения Ф (t) = Р (ц < t) ра-
равен 1/У2я. Устанавливая точно так же обратное неравенство и
полагая е = (Z/jJI/4, получим B4). ^
Оценка в следствии 2, конечно, не является наилучшей. И все
же неравенство B4) показывает, что мы будем иметь хорошее
нормальное" приближение для Р (?»<#) и в области больших
уклонений (т. е. при \х\ -*¦ °°), по крайней мере для х, при ко-
которых при п -*- °°
()-1/4^oo. B5)
Действительно, в этом случае, например, при х = \х\ >0
1 - Ф
~ Ф
Так как по правилу Лопиталя „
со
1 ( t^ 12, 1 — X^l 2
1/2л J у 2n x
X
то B5) справедливо для | #| < ^il/ ~ 1п/-з при подходящей по-
постоянной с4.
В гл. 17 мы получим обобщение теоремы 7 и следствия 2.
Вопрос об уточнениях и об оценках погрешности в централь-
центральной предельной теореме и в других предельных теоремах явля-
является одним из важных в теории вероятностей, поскольку от от-
ответа на него зависит, насколько точными и эффективными будут
применения этих теорем к задачам практики. Надо, прежде всего,
найти правильный порядок убывания Да = sup | Р (?н <С х) — Ф (х) \
х
по п (или, скажем, по Ls в случае разнораспределенных слагае-
слагаемых). Существует по крайней мере два подхода к отысканию
правильных оценок Дп. Один из них, так называемый метод ха-
характеристических функций, исходит из неулучшаемой оценки
близости характеристических функций
которую читатель может получить самостоятельно, пользуясь
леммой 7.2 и усложнив немного рассуждения в доказательстве
теоремы 5. Основные технические трудности здесь состоят в том,
чтобы с помощью формулы обращения получить такой же по-
порядок малости для Д„.
Второй подход, так называемый метод композиций, был про-
иллюстрировап в этом параграфе в теореме 7 (в какой-то мере
существо его заложено в соотношении B0)). Именно этим мето-

дом в Приложении 5 для случая одинаково распределенных сла-
слагаемых будет доказан следующий общий , результат (Крамер,
Верри, Эссен):
Теорема, Если §А не зависит от п, \к п = (?ft — ак)/Вп, то
где с — абсолютная постоянная.
В случае одинаково распределенных %h правая часть приве-
ценного неравенства превращается в —8 /-¦ * Установлено, что
Здесь надо иметь в виду, что приведенные теоремы и оценка
постоянной с универсальны и выполняются, следовательно, в са-
самых неблагоприятных с точки зрения приближений условиях.
Поэтому скорость сходимости в реальных задачах, как правило,
оказывается лучше.
§ 6. Локальная дредельная теорема
В предыдущих параграфах мы установили, что распределение
п
нормированной суммы Sn = Д, ?j одинаково распределенных и
независимых величин \$ с M?j=O, D?j=a2<oo сходится к
нормальному закону. Допустим теперь, что распределение ?п =
= '—= имеет плотность. Будет ли она равномерно сблия^аться
о у п
с плотностью нормального приближения? Положительный ответ
па этот вопрос позволил бы оценивать вероятности попадания ?п
в произвольные измеримые множества**) и в том числе вероят-
*) См. [22].
**) Слабая сходимость распределений Рп =$» Р означает сходимость ве-
вероятностей Рп (В) ->• р (В) лишь для множеств В, граница которых дВ
(это есть разность между замыканием В и дополнением к замыканию
Н — В) обладает свойством Р (дВ) — 0. Существенность этого условия хо-
хорошо иллюстрируется следующим примером. Пусть ?* целочислеины, а = 1,
а В есть множество всех рациональных чисел. Тогда
Р„ № = Р (In е в) = Р ЫУ» е В) = 1,
если п = к2 (к—-целое), и Рп (В) = 0, в противном случае: так что
lim Pn (В) не существует. В этом примере для предельного нормального
П-»оо
распределения Р, очевидно, выполняется Рп =>¦ Р, Р (дВ) = 1, так как дВ
совпадает здесь со всей вещественной прямой Я.
Одновременно можно заметить, что для любого распределения Р, имею-
имеющего плотность (в том числе для нормального), в силу сч:етности В будем
иметь Р (В) « 0.

198 . ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ности событий вида iSn е Д}?- где' А ~ фиксированный интервал
(из центральной предельной теоремы следует лишь, что Р {8п е
е Д) = Р (In е —^т^ ~~^ ° ПРИ л "*" °°-
V а у л /
Теорема 8. Пусть {%>k}kLi —последовательность независи-
независимых одинаково распределенных случайных величин,
Предположим, что при некотором пг ^ 1 распределение суммы
Sm имеет плотность, и, кроме того, х. ф. срт(?) интегрируемо,.
Тогда плотности распределения fzn (х) случайных величин Cn ^
— _JL_. равномерно по х сходятся к плотности нормального га-
суп
попа ftn(x)-+-y==r-e~x *, .
- Например, плотность равномерного на [—1, 1] распрецеления
удовлетворяет этой теореме, так как для нее 1ф*(?I ^ 1/i2 (см.
пример 7,7) и, следовательно, 1ср2(?I интегрируема. Следователь-
Следовательно, по теореме 6 плотность распределения Sa в точке ио1/п(ог =
А п I
~ 1/3) будет вести себя как ——т=- е (ср. с замечанием к
у ' о у 2кп
примеру 3,4). ' •
Интегрируемость ф2(?) имеет место также во всех случаях,
когда плотность ?л есть функция ограниченной вариации. В этом
. легко убедиться, если проинтегрировать х. ф. по частям.
Доказательство. В силу формулы обращения при п^ m
byr)u Bб)
Здесь, как мы знаем, при каждом I
""'- B7>
Поэтому, чтобы доказать требуемое равенство
f
Mm fln (*) - i f e-V'e-^dt - -^ e-*4 B8)
достаточно убедиться, что фп j —zrpr ] при всех п мажорируемся
V о у п I
интегрируемой функцией.
Так как дисперсия конечна, то ср"@, непрерывна, ф'/@)==
— —а2, Пусть 6 > 0 таково, что при UI < б

§ 6. ЛОКАЛЬНА^ ПРЕДЕЛЬНАЯ ТЕОРЕМА
для заданного г > 0. Тогда при UI < б
109
где ?^[0, ?], I9i!<8. Используя неравенство llnA — р)~- ?| ^ р2?
получаем, что
= -i^l(l + 02), j02|<8, B9)
Отсюда находим, что при
ф»(_1_1|==е-
В дополнительной области
s up
ф
а у п
( * _
t2
—а A-е)
действует оценка
которая справедлива в силу того, что 5т имеет плотность. По-
Поэтому
а К п\
>6
>6
при й->°° в силу интегрируемости \(рт(и)\. Соотношение B8)
доказано. __
Пользуясь тем, что tyn(t/lln) мажорируется интегрируемой
функцией, легко установить, что hn(%) равностепенно по п не-
непрерывны. Это делается с помощью представления B6) точно
так же, как доказывается непрерывность х. ф. Равностепенная
непрерывность дп, непрерывность функции ? и соотношение
B8) влекут за собой равномерную сходимость fin (x) к плотно-
плотности нормального закона. А
Следствие 3. Из доказанной теоремы следует, в частно-
частности, что при 'п -*• °° и при \z\/lfn < с
C0)
где с, а — фиксированные числа. Мы предлагаем читателю

200 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
нить это соотношение с локальной предельной теоремой для схе-
схемы Бернулли (см., в частности, формулу E.7)).
Соотношение C0) можно получить и при более широких ус-
условиях.
Теорема 9. Соотношение C0) останется справедливым,
если в тедреме 8 условие интегрируемости §m(t) заменить на
Фш W
интегрируемость ^ , . t. «
Доказательство. По формуле обращения
При х = —гт=-« у = х Н —j=r в правой части получим
о уп а уп
На
7=r \e ^-- ф
Где i. ^ a^ mn / __.] ->. e * 2# Здесь можно опять исаоль-
lt _ Koynj
о~\/п
зовать теорему о мажорируемой сходимости (по тем же причи-
причинам, что и прежде, и при очевидных изменениях, связанных с
появлением под интегралом множителя 1/?)« Получим в резуль-
результате, что
~itx"dt
о Уп Угк * ^
В дальнейшем нам понадобится несколько более общая постановка за-
задачи. Мы предположим, что распределения случайных величин g/ зависят
от п (схема серий). Следовательно, будут зависеть от п и х. ф. ф (t) = Ф^@ =
Теорема 10. Пусть
1) ф^ (t) при некотором m ^ 1 интегрируемы равномерно по п\
2) sup I фп (t) I < 1 — б < 1 при всех t, \t\ > e > 0, б = б(е);
п
3) фп (t) равностепенно по п непрерывны в точке t = 0. Именно, для за-
заданного е > 0 существует б > 0 такое, что при \t\ «< б
SUP I Ф« @ ~ Ф« (Й) I < et 0 < с1 < I ф^ @) I < с_ < оо.
Тогда справедливо утверждение теоремы 8.

§ 7. ЗАКОН БОЛЬШИХ ЧИСЕЛ 201
'Если в условии 1) Ф™@ заменить на Ф^^)/A +1 t\)t то справедливо
утверждение теоремы 9.
Приведенные условия таковы, что они позволяют получить доказатель-
доказательство теоремы 10, совершенно ничего не меняя в рассуждениях теорем 8, 9.
Соотношение B7), для выполнения которого в условиях схемы серий тре-
требовалось бы условие Линдеберга, следует из B9).
Теорема 10 показывает также,* что переход к схеме серий в локальной
теореме даже в случае одинаково распределенных величин сопровождается
введением целого ряда новых условий.
§ 7. Закон больших чисел и центральная
предельная теорема в многомерном случае
В этом параграфе мы будем предполагать, что ?i, n, ;.., ?п,»
п
есть случайные векторы в схеме серий, М^,п = 0, ?п = 2 ?л,п-
Закон больших чисел ?п~^0 получается немедленно из тео-
<р
ремы 3, если предположить, что условиям теоремы 3 удовлетво-
удовлетворяют координаты |Й1 п.
Чуть сложнее обстоит дело с центральной предельной теоре-
теоремой. Здесь мы будем предполагать, что Mj^>nl2<oo, Где Ы2==з
= (#, х) есть квадрат нормы х. Обозначим
(индекс Т означает транспонирование, так что \и,п есть вектор-
столбец) .
Введем в рассмотрение условие
2 М min (| lhin |M ?*,* Iе) -* 0, 8 > 2, (D2)
h=i
и условие Линдеберга
при п->°° и любом т>0. Как и в одномерном случае, легко
убедиться, что условия (D2) и (М2) при сг^ < с < «> равносильны.
Теорема 11. Если оп-^о2, где о2 — положительно опреде-
определенная матрица, и выполнено условие (D2) (или (М2)), то
Следствие 4. («Обычная» центральная предельная теоре-
теорема.) Если |i, |2, ...— последовательность независимых одинаково
распределенных векторов, М?ь = 0, а2 = М^^ Sn = 25ftf шо

202 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
при п ->• сю
Это утверждение является следствием теоремы 11, так как
случайные величины \ь.,п=^\^1^п удовлетворяют ее условиям.
Доказательство теоремы 11.• Рассмотрим характе-
характеристические функции
<pfc>B W = Me'l'lEft>n), <pn(f) = Mei{tXn) =ПФм(().
Для доказательства надо убедиться, что при любом t и при
Л ->- оо
1
Воспользуемся теоремой 5. Функции q>ftt n(t) и <рп@' можно рас-
рассматривать как характеристические функции
ф^,п (v) = М exp (ivlk,n), Фп (tO == М exp (ivt^)
случайных величин ?л,п = (?ь,п,, 9)» ^ =* (?п»9), где 8 ,
=з UI. Покажем, что скалярные случайные величины 5&,п удов-
удовлетворяют условиям теоремы 5 (или следствия 1) для одномер-
одномерного случая. Очевидно,
S м (ID8 = S м (^,„, еJ = во?,от -> еа^9г > о.
Выполнение условия (Dz) следует из очевидных неравенств
k=l
где gz{x)= min(x2, |xis), s>2. Таким образом, для любых у и 6
(т. е. для любых t) в силу следствия 1 теоремы 5
фп (*)в М exp (zy^} -^ ехр {- 1 у28а29г] = ехр [- 1
§ 8, Вероятности больших уклоненмм
Пусть gi, g2» «*. —последовательность независимых одинаково распре-
распределенных величии, Mgfe = 0, D?ft = 1. Предположим, что надо оценить ве-
вероятность Р (Sn^ х}, когда х зависит от п и х/^п-^оо при д—к сю. Цент-
Центральная предельная теорема в этом случае позволяет лишь заключить, что

§ 8. ВЕРОЯТНОСТИ БОЛЬШИХ УКЛОНЕНИЙ 203
Р (?л ^ я)-* 0. Задача состоит в отыскании функции Р(п, х) такой, что
Отметим еще раз, что в отличие от нормального приближения здесь мы тре-
требуем малость относительной, а не абсолютной погрешности.
Такого рода задачи нередко возникают, например, в математической ста-
статистике при оценке потерь в статистических критериях и в теории падеж-
ности.
В этом параграфе будет изложен метод Крамера исследования вероят-
вероятностей больших уклонений, который в- известном смысле сводит задачу к
центральной предельной теореме.
В дальнейшем будем предполагать, что выполнено следующее основное
условие:
А {условие Крамера). Существует % >> 0 такое, что
f ehjdF (у) = Ме^ < оо. (А)
Смысл этого условия понять нетрудно — оно эквивалентно экспоненци-
экспоненциальному убыванию Р Ц > у) = 1 — F (//). Действительно, интеграл в
(Л) сходится или расходится вместе с интегралом
оо
^ d(i~-F (у)) = I - F @) + % J J* A - F (у)) dy*
Поэтому, если 1 — F(y) ^ ce~w, то (Л) выполнено при X < jx. Наоборот, из
(А) следует по неравенству Чебынтева,. что
Обозначим Я+ = sup {%: Mex*<z оо}. Если, например, 1~ ограничена
сверху, то Х+ = оо. То же самое верно для нормально распределенной g.
Если же Р (I > у) = се~^, fjt > 0, то, очевидно, Х+ = р.
Если выполнено условие (А), то х. ф. tp (t) = Меп% аналитическая в
плоскости комплексного переменного в полосе 0 !> Im t >• —%+. Это следу-
следует из возможности дифференцирования в плоскости комплексного перемен-
переменного функции
<p(t) =
поскольку \ \ye%ty\dF (у) при указанных значениях * равномерно сходит-
сходится. Если условие (А) выполняется и при некоторых отрицательных X, то
(p(t) аналитическая в полосе, содержащей прямую Imt = 0.
Рассмотрим теперь подробнее функцию Ч5 (Я) = Ме^— ср(— гЯ). Очевид-
Очевидно,, что (имеются в виду правые производные)
*' @) - Mg? V @) = Dg, •*- (i) == j |/2^^F (у) > 0.
Нетрудно видеть, что |ф//(Я)/г|)(Я) имеет смысл второго момента случай^
ной величины г] с функцией распределения
G{y)==Tw le%tdF®- [Cf)

204 Г Л, 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Дисперсия этой величины равеа
Так как дисперсия обязана быть положительной, то отсюда следует, что
функции ф и 1ц ф являются выпуклыми на [0, Я+]. Функции
^а (X) « е~а%Ц (X) =Me^s-a), In ypa (X) = — аЯ + In
очевидно, также являются выпуклыми, при этом
Поэтому если a > 0 и ф„ (^+)-> ° (мы полагаем $'а (Х±) = lim
то на полуинтервале [О, Х+) существует единственная точка Я (а), в кото-
которой Фа(Я) =0 и функции фа и In \|)a достигают своего минимума.
/ Y (a)\
Так как *фа (А,) = ^а (Щ — а + яь п\ )» то Условия существования точ-
точк ()
ки к (а) можно записать в виде
Ясно, что при достаточно малых a > 0 эти условия всегда выполнены. Они
выполнены при любом а ^ 0, если '§'(%+) = оо.
Обозначим
Л(а) = —inf (—аЯ, + 1пф(Х)) == аА,(а) — lnij) (X(oc)). C2)
л,
Функцию Л (а) назовем функцией уклонений (смысл такого названия ста-
станет ясным позже). Точка Я (а), где достигается значение Л(а), удовлетво-
удовлетворяет тождеству
)-=a. C3)
Так как 1пгр — выпуклая функция, то производная (i|/(A,)/ij)(X))' =(lni|))" >>
>0 и, значит, функция Х(а), являясь обратной к г|//Ф* будет аналитиче-
аналитической в @, К+). Заметив, что Я,@) = 0, Л@) =0 и что в силу C2), C3)
Л' (а) = X (а) + а^^ (а) - ^^^ X' (а) = Я, (а),]
а
получим Л (а) = I A. (w) du. Так как Я' @) = (Dg) = 1,то отсюда следует,
о
в частности, что Л@) =Л'(@) = 0, Л"@) = 1. Случайную величину ц с
распределением G в C1) нам будет удобно называть преобразованием Кра-
Крамера над случайной величиной |. X. ф. этой случайной величины равна
- j
J Г eiuy
(У) = ""^ГГТгГ- C4)
(Л,) ^ dl {y) - ф (- а) •
Функция распределения для преобразования Крамера над $п в силу C1)
будет иметь вид
у
j udFSn(t), C5)

§ 8. ВЕРОЯТНОСТИ БОЛЬШИХ УКЛОНЕНИЙ 205
а соответствующая х. ф. будет равна в силу C4)
<pSn (и - Щ/Цп (М = ?*(«- a)/t" (W. C6)
Покажем, что C5) есть не что иное, как функция распределения Fz
п
суммы Z = 2 г]Л, где т]й= т) и независимы. Другими словами, преоб-
1 V
разование Крамера над суммой есть сумма преобразований -Крамера над
Л, гг \ ф'(М— Ш 1П
слагаемыми. Это следует из того, что х, ф. Zn равна \-U±—_ iL и совпа-
совпадает с C6). Таким образом,
У У
Fz (У)=Ц-ПA) \ eudFs (t), F (у)=Цпп) \ e~udFz (t). C7)
П J 71 ft <J П
—-СО —OQ
Если Sn имеет плотность fs {у), то Zn также имеет плотность
/ZnW=rn(M^/SnM. ' C8)
Пусть 0 < а < а+. Выберем в формулах C1), C4) К = Ца), Тогда
случайная величина т) с х. ф. g(w) будет обладать свойствами
м/ ч Г (X (а))
М(Ч-«)= ^а-(а)) -« = 0,
Можно сформулировать теперь следующую теорему. Обозначим
1
Теорема 12. Пусть выполнено условие (А) &
(напомним, что -ф(Я) = Л/е*-6, ^+ = sup {К: ^Ск) < оо}). Тогда
F
sn
~ иЛ (a)} J e-**»dFHn (*), D0)
где? а = х/п.
Если, кроме тогоу g имеет плотность^ то
fsn (* + «) = е*Р I- ^А (а) - аХ (ос)} /Hf> (а). D1)
Эта теорема позволяет сводить задачи о больших уклонениях для Sn к
задаче о «нормальных» уклонениях для Нп.
Доказательство следует немедленно из формул C7)-, C8), если
положить в них у = х + а = an + а, X == Х(ос) и заметить, что

206 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Формулы D0), D1) позволяют вычислять F (х + а) и fs (x + a)t
и
поскольку распределение суммы IIп = 2 (^k ~~ а) в области «нормальных
уклонений» известно. Мы знаем, например, что в широких предположениях
в формуле D1) /я (а) ~ •—-~рг —т==-. Для большей точности воспользу-
воспользуемся локальной теоремой 10, где вместо ф«(?) нужно рассмотреть х. ф.
Цх — а, равную
rw" Ф (- tt (a)}
(ясно, что мы находимся в условиях схемы серий, так как распределение
'Hi — а зависит от п через a = xjn).
Введем в рассмотрение условие:
(В). F(ос) имеет плотность, а х. ф. (p[t) такова, что (рт(и — IX) при ка-*
ком-нибудь целом m^i интегрируема по и при всех X е~ [О, Х+.) *).
Нетрудно видеть, что при выполнении этого условия выполняются ус-
условия 1—3 теоремы 10, при этом равномерно по а. Равномерность по а
можно проверять непосредственно. Допустим, например, относительно усло-
условия 2 противное; что существует 8 > 0 и последовательности a*, ik такие,
что \tk\ > е и
• 1 D2)
при к~*оо. Так как а^е [0, о], а < а+, то можно, пользуясь компакт-
компактностью отрезка, не ограничивая общности, считать, что сел ~> ссо е [0, а],
а < og. Далее, производная q)'(t) равномерно ограничена в области
0 ^ Im t ^ —Х(аI поскольку |ф'@ I ^ <Ф/(^(а))» Поэтому вместе с D2)
при к ->' со будет выполняться
I ф (*Л ~~ iX (a ))
I h! > e. ф (- ^ Ы) -> ф (- ^ (%)) > о. | --^гтц^1
Ото противоречит существованию плотности у распределения с х. ф.
Таким образом, условия теоремы 10 выполнены. Это означает, что
равномерно по и, где ?п = —-—;=•-. Сопоставляя это с теоремой 12, получа-
получаем следующее утверждение:
Теорема 13, Пусть выполнены условия теоремы 12 и условие (В),
Тогда
fs W ~ т/о—' ехр ^"~ wA (a^«
а^е по-прежнему а = а?/л, aa определяется формулой C9)«
*) Для етог© достаточно, чтобы интегрируема была фт(?)«

§ 8. ВЕРОЯТНОСТИ БОЛЬШИХ УКЛОНЕНИЙ 207
При любом а > @ гаком, что а = о(}!п),
Р (х < ^ < х + а) —==¦ ехр {- мЛ (а)} т-т-г . D4)
xj^n-*- оо, го
Доказательство. Соотношение D4) получается интегрированием
D1), D3) по а.
Чтобы получить D5), -надо выбрать а = o(ljn) так, чтобы а\(ос) -+¦ оо
(или, что то же, ах/п->¦ оо). Это, очевидно, всегда возможно, и это делает
правую часть в D4) асимптотически эквивалентной D5). ^
В соотношениях D4), D5) следует иметь в виду, что оа->-1, Х(а) ~ а
при а ->- 0.
Замечание 7. Для получения соотношений D4), D5) нет необходи-
необходимости пользоваться локальной предельной теоремой 10, для которой введено
условие (В). Достаточно воспользоваться формулой D0) и теоремой 9, для
которой, как мы знаем, в условии (В) интегрируемость срт(?) можно осла-
Фт (t)
бить до интегрируемости . , ¦ . ¦.
Соотношение D0) при а = оо допускает следующую интерпретацию,
связанную с тем, что интеграл в правой части представляет собой в этом
случае свертку двух распределений. Пусть ^€§ 1\(а) (т. е. Р(у > х) — <М)
х ^ 0) и не зависит от //п. Тогда D0) можно записать в виде
Р (Sn >х) = ехр {- пА (а)} [Р (//„ > 0) - Р (//„ > у)] =
ехр {- ^гЛ (а)} X (a) J e' K^ZP @ < Нп < z) dz
По центральной предельной теореме отсюда следует лишь, что при а > а0
>0
Замечание 8. Соотношение D5) показывает, насколько точным яв-
является неравенство типа Чебыгаева
полученное в § 4.7. Применяя его к случайной величине Sn и выбирая X
= А,(а), мы получим М<?л5л = г|> (Х)п,
)} = ехр {—лЛ(а)},
Замечание 9. Теоремы 12, 13 показывают, что функция Л (а) играет
определяющую роль при описании вероятностей больших уклонений. Соот-
Соотношения D5) позволяют записать для функции Л(а) при каждом а,
в ^ а < а+, равенстве
1 / ?L \
D6)
Л (а) = - lim - In Р [~ > а).

208 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Легко видеть также, что
Л (а) = —lim lim — Р \~ G(a — h, a+h)J. D7)
Э/го последнее соотношение оказывается верным уже без каких бы то ни
было ограничений на распределение ?& и а.
Равенства D6), D7) объясняют в какой-то мере термин «функция укло-
уклонений» для Л (а), которую следует считать определенной при всех а с по-
помощью первого соотношения в C2). Можно отметить также, что если усло-
условие (А) не выполнено, то Л (а) =*= 0 при а >• о!
Замечание 10. Возвращаясь к теореме 9, видим, что если х ^ аои,
а0 > 0, то убывание Р (Sn ^ х) оказывается экспоненциальным. Если
функция \|?(Я) аналитичыа в точке X = 0, то аналитической будет и Л (а)
в точке а = 0, и можно воспользоваться разложением Л (а) = ^ А-^а'*, ГД°
Ak полностью определяются к моментами ?. В этом случае при х/п = а~>-0
получим
f X
ехр {— ?гЛ (а)} ~ ехр I — /г jy^ &ь(
если nas+l = xs+1/ns ->0 при п -> оо. В частности, если х = c(w2/3), то
1/2 ( Х2 Л I X \
«р (- -jr ] ~ 1 - ф [у^ )• (/l8)
Можно отметить, что последний результат согласуется с замечаниями
относительно применимости теоремы Муавра — Лапласа в области больших
уклрпений. Если же окажется, что Л3 ф 0, то пользоваться нормальным
приближением, когда Л3#3//г2 не является малым числом, нельзя.
Функция уклонений Л (а) для некоторых распределений может быть
вычислена в явном виде. Например, для нормального закона с параметра-
параметрами @, 1)
1+ = а+ = оо, X (а) == а, Л (а) = а2/2.
Для центрированного показательного распределения с параметром ji
При Я^г— —, Р (I > х) — 1 При
имеем
Замечание 11. Для схемы Бериулли функция уклонений по-сущест-
ву нами была вычислена и использовалась в § 5.2., В связи с этим можно
отметить, что формулы D5) сохраняются и для решетчатых ?л (|ft имеют
вид М, А > 0, /с—целое), однако при этом х должно быть кратным шагу
решетки.
Из обобщений теоремы 13, которые доступны читателю без преодоления
каких-либо новых трудностей, можно указать следующее. Вспомним, для
чего требовалось условие (В): для возможности использовать формулу об-
обращения (интегрируемость фт) и для оценки h(u)l <1 —б при |и| > 8
(см. условия теоремы 10). Но всего этого можно добиться и несколько иным
путем, введя в Sn «сглаживающее» слагаемое |* с финитной плотностью

§ 8. ВЕРОЯТНОСТИ БОЛЫПЕХ УКЛОНЕНИЙ 200
(гладкой и сосредоточенной на [0, h}) и предположив, что выполнено ус-
условие (С) (это условие иногда также называют условием Крамера):
(С) lim sup | ф (и-Щ | < ф (— i%), X е= [О, X,).
Введение |* будет обеспечивать существование плотности Sn + ?* и
возможность пользоваться формулой обращения, поскольку х. ф. |* ин-
интегрируема (см. доказательство теоремы непрерывности). Из условия (С)
будет следовать, что \ч(и) | <С 1 — б при \и\ >• г (Imu = 0).
Для выполнения условия (С) достаточно*), чтобы F(x) содержала аб-
абсолютно непрерывную компоненту (ведь х. ф., соответствующая этой ком-
компоненте, сходится к 0 при |u|->oo, Imw = 0). Условие (С) заведомо но
будет выполнено, если | дискретна — тогда |ф(?I будет принимать при
\t\ -*- оо значения, сколь угодно близкие (или равные) к 1.
Таким образом, если случайная величина |* не зависит от {%h} и имеет
финитную плотность, сосредоточенную на [0, /г], то ее х. ф. ф*(?) интегри-
интегрируема, аналитична во всей плоскости и плотность Sn + ?* равна
fSn+i* (* + а) = JL j e~itxq,n (t) <р* (I) dt.
Повторяя с очевидными изменениями проведенные выкладки, получим
fsn+t* (^ + й) = ехР 1™ пА (а) — ah (а)) ftin+l** (а) Ф* (— & (а))?
ф* (и — а (а))
где |** также имеет финитную плотность и х. ф., равпую ¦• » / .л . ...
Теперь надо вновь воспользоваться тем, что при а = о(Уп) равномер-*
но по а
Мы получим тогда так же, как в D4), что при а > б, а = о(/гс)
Ф* Н ^ (а)). D9)
Отсюда уже нетрудно получить D4) и D5), пользуясь неравенствами
Р (х + Л < ?н + I* < х + а) < Р (ж < Sn < ж + а) <
и тем, что величина h может быть выбрана произвольно малой. Надо счи-
считать при этом, что а ^ а0 == const > 0. Величина ф*(—iX{a)) в D9) выбо-
выбором h может быть сделана сколь угодно близкой к 1.
Мы доказали таким образом, что верна
Теорема 14. Если выполнены условия (А) и (С), то при дополни-*
тельном условии а ^ а0 > 0 справедливы соотношения D4), D5).
В заключение этого параграфа отметим еще одно свойство функции ук-
уклонений. Будем обозначать Л$(а), А,$(а), ^(А,) функции Л, X и ф, опреде-
определенные выше и соответствующие случайной величине ?. Тогда, если g и г]
*) Условие (С) будет выполнено, если lim sup | ф (и) \ < 1 (lmu =
14 А. А. Боровков

210 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
независимы, то
6(p) + An(a-P). E0)
С другой стороны, так как X,g(P) есть монотонно возрастающая функ-
функция, то можно подобрать $ так, чтобы А,$(р) = 1ц(а — Р). При таком ? в
E0) будет знак равенства и, следовательно,
A|+t| (а) = inf (Л6 (Р) + Лп (а - Р)).
Из соображений симметрии для одинаково распределенных ?& отсюда на-
находим, что
Л
Замечая, что в формуле D5) порядок стремления к бесконечности у
последовательностей пХ2(а) и пА(а) одинаков, мы могли бы эту формулу
записать теперь в виде
р {sn > х) ~ с W (Asn (x))~1/2 ехР (— Asn ^} t
где с (а) заключено в фиксированных положительных пределах. В таком
виде теорема о больших уклонениях становится весьма общей и сохраняю-
сохраняющей свою силу при отклонениях от условий теоремы 14, когда допускается
зависимость между слагаемыми и их разиораспределенность.
§ 9. Сходимость к другим устойчивым законам
Как это видно из предыдущих разделов, нормальный закон занимает
особое место среди других распределений — он выступает в роли предельно-
предельного для нормированных сумм произвольно распределенных слагаемых. Воз-
Возникает естественный вопрос — существуют ли другие предельные законы
для сумм независимых величин?
Из доказательства теоремы 2 для одинаково распределенных случай^
пых величин видно, что характер предельного распределения 8п определяет-
определяется поведением х. ф. в окрестности 0. Если существуют М^ = 0 и М52= о, то
Л это определяет асимптотическое поведение х, ф. Snlfn1 равной срп(?/У«),
которое приводит к нормальному закону. Следовательно, в поисках других
предельных законов для сумм Sn = ^ + ... + In надо отказаться от ко-
конечности дисперсии 1УЩ2, или, что то же, от существования ср"(О). Мы по
будем здесь рассматривать все распределения, обладающие этими свойст-
свойствами, а ограничимся рассмотрением-лишь достаточно «правильных» случаев,
когда при a < 2 выполнено условие (D):
l—F(x) = ax-a"i-o(x~<xI
(О)
F(—x) = bx~*-{-o(x-a<)
при ж->-оо. Здесь предполагается, что по крайней мере одно из чисеп а и
Ъ положительно. Нетрудно вждеть, что для таких распределений \ x%dF (я) =
— оо. Величины Щ, если а > 1, не ограничивая общности, будем считать
равной нулю.

§ 9. СХОДИМОСТЬ К ДРУГИМ УСТОЙЧИВЫМ ЗАКОНАМ 211
' Ответ на поставленный вопрос дает следующая теорема:
Теорема 15. При 0<а<2 существуют последовательности Ап та-
такие , что при п —> оо
закон распределения^ зависящий лишь от параметров а и
Логарифм х. ф. закона Fa, p равен
In <р @ = Г (е»*- 1 - -^_ ] | х у-а-г D {x) dXf E2)
Роль параметров аир поясняется в замечании 13, помещенном в конце
параграфа.
Помимо Fa> р, О <С а <. 2? —1 ^ р ^ 1, предельными, как мы видели, яв-
являются также нормальные законы Ф 2 и вырожденные 1а. Множество
всех этих законов обозначим 2V Далее, нетрудно видеть, что если F — ка-
какой-нибудь предельный закон распределения, то закон отличающийся от F
{ х — а \
изменением масштаба и сдвигом (т. е. закон F\ 1 ), также является
предельным.
Оказывается, что класс законов распределения J?, полученный таким
расширением i?o» исчерпывает все предельные законы для сумм одинаково
раевределеноых независимых величин.
Возможна и другая характеризация класса предельных законов i2\
On ределение-1.
Мы назовем закон распределения F(x) устойчивым, если для любых а\}
tt2, bi .> О, b2 > 0 найдутся а и Ъ >» 0 такие, что
В терминах х. ф. свойство устойчивости можно сформулировать так:
для любых Ьх > 0, ^2 > 0 найдутся а и b > 0 такие, что
q>(f&i)cp(f&2) = eita(p(th).
Класс всех устойчивых законов обозначим i?*. Замечательный факт состоит
в том, что класс всех предельных законов 2? и класс всех устойчивых за-
законов SB* совпадают,
Принадлежность $? с: i?* следует из того, что законы Ф 2? 1а и
Fa, e являются устойчивыми (устойчивость Fat р проще доказывать, пользу-
пользуясь замечаниями 12, 13).
Любопытно отметить, что закон Пуассона (напомним, что его х. ф.
( (и \~х
<p(t) равна exp{ii(eu — 1)}) и гамма-распределение <р (t) = I 1 — — ,см.
V .V а I
§ .7^7) не являются устойчивыми в смысле определения 1. Однако они обла-
обладают другим свойством, называемым безграничной делимостью. Зто свой-
14*

vn. 8. ПРЕДВДЫ1ЫЕ ТЕОРЕМЫ
ство состоит в том, что функция Ф1/П(О при любом п снова должна быть
х. ф. (т. е. величина | с х. ф. ф представима как сумма независимых ?*, п,
к = 1, ..., га, с х. ф. ф1/п). Класс безгранично делимых законов содержит
и себе S7* и играет ту же роль, что и класс 2?: он совпадает с классом всех
предельных законов для сумм независимых одинаково распределенных вели-
величин, но в схеме серий*).
Доказательство,теоремы 15. Общая схема доказательства здесь
примерно та же, что и в центральной предельной теореме. Обозначим
Вп = [aw(a+6)]l^a, Ъп~-г?-~~ Ani гДе Ап выберем позже. X. ф. ?н равна
Так как q>z{t)-+1 при г-vO, то при каждом фиксированном t ш п-+оо
1п
- НАп
— 1
Последнее слагаемое Rn но модулю не превосходит п
дится к 0 при л ->• оо. Действительно, из неравенств
D- — 1
E3)
И CXQ-
вытекает, что при р < 1
|в"-1| <
Так как m= M | g |р < оо при /> < а, то
4m2 ^ const ^
при 2р > а.
Рассмотрим теперь второе слагаемое в правой частя E3). Его можно
записать в виде
где ••)<?
„(„)= Г
*) Подробнее об этом см. [7], [13].
**) Если ос > 1 и, следовательно, существует М| — 0, то удобнее
€то правой части в E4) записать I (ettx — 1 — е^) — dGn (я). В общем

§ 9. СХОДИМОСТЬ К ДРУГИМ УСТОЙЧИВЫМ ЗАКОНАМ 213
Введем в рассмотрение функцию
J 1 + х2
где функция D(t) определена в E2). Интегрируя по частям, находим при
2
v > 0 [ d 1 , = , ^2,2
2
Gn (v) ~Gn @) = п Г _^ dP (хВп) = - п _?!_ A - Р (хВп))
E5)
В силу (D) получаем
lim (в„ (u)-G^ 10)) =
— glim na(vBn)~a + 2 \ lim па (хВь
v2~a n а С г16
= — I • 2 + 2 — dx.
I _|_ у2 а (а + 6) а (а -|- 6) J Ц _|_ ж2J
о
Законность предельного перехода иод знаком интеграла (включая случай
v = оо) здесь нроверяется без труда, и мы предоставляем это читателю*).
Производя «обратное» интегрирование по частям, получим
V
lim (Gn (и) - Gn @)) - -4гт 1* —^-о ^"а^ = G(v)-G @).
0
Совершенно аналогично устанавливаем, что при и < 0
о о
случае мы добавляем и вычитаем \ ——2^(ж^п)» поскольку этот ия~
теграл всегда существует.
*) Если в правой части E5) отбросить I f где vn таково, что Впип -*>
*) Если в правой части E5) отбросить
о
v
v .
, то д j ->¦ 0, а иодынтегральная функция в J мажориру-
О
ется интегрируемой функцией.

214 . ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Таким образом, последовательность Gn(v)/Gn(oo) образует последователь-
последовательность функции распределения
Gn (v) G (v)
Вернемся теперь к E4). Первый интеграл в правой части E4) равен
(x)dG^WY>
J
I 'tx itx \ 1 + ^2
где / (х) ™ i ег — 1 — —-—g ) —~ ^сть при каждом t непрерывная и or-
\ \ -\- х / х
раниченная функция от х. Ограниченность и непрерывность ее при х Ф О
очевидна. В окрестности точки х = 0, пользуясь разложением eitx в ряд,
получаем, что f(x) ведет себя как
На основании E6) и свойств слабой сходимости заключаем, что
Г/ (х) dGn (а) -> j/ (х) dG {x) - j ^ - 1 - ~У 1 « Г04" D (x) dx.
С х
Если теперь положить Ап^= п \ ~~—%dF {xBn)^io получим, что суще-
J 1 -j- ж
ствует
lim lnqv @= f f^-l-TT^lil^r06^^)^^*^- E7)
П-»оо ^П J \ 1 + Л? J
Функция \|), как нетрудно видеть, обладает свойством ty(t) ~>0 при ?~>0 иу
следовательно, непрерывна в точке t =0 (ср. с доказательством непрерыв-
непрерывности х. ф.). По теореме непрерывности (теорема 7.3)' это означает, что <р =
= е^ является х. ф. Сходимость E1) доказана.
Тот факт, что Fa, p зависит только от аир, проверяется непосредствен-
но. Действительно, если обозначить
ВОществешш) ^
то
I / ettx г__ ^ _ _ J | х |-а~1 дх ___ и _|_ iv ^R^ v ___
О
о
С ( itx \
\ [ e*ix — 1 — о 1 1 х I"""" dx = w — гу, и мы получим (см. E2))
J \ 1 + я /
а . Ь __
Числа и и v в этих формулах можно найти в явном виде.
Замечание 12. Формулировку теоремы можно несколько упростить,
рассматривая отдельно случаи а<1, а = 1, а>1 В первом случае не-
нетрудно показать, что пвсиедпий интеграл в E4)
• Г ' * _ • Г 1 ' •Г1Г
П J 1 + х2 ^ п* J 1 й п Х ~* J "ж

§ 9. СХОДИМОСТЬ К ДРУГИМ УСТОЙЧИВЫМ ЗАКОНАМ 215
(надо воспользоваться интегрированием по частям подобно E5)). Одновре-
Одновременно можно заметить, что при а < 1 существует часть интеграла E7),
равная
f I х Г0" D <*) dx^tt\ldG (x).
J x
f
J
ГГ2 I х Г D <*) dxtt\
+ хй J x
Поэтому при а < 1 можно положить Ап = 0, а утверждение теоремы сфор-
аудировать так:
ЗД^^.Ц» E8)
еде Fа о есть устойчивый закон, логарифм х. ф. которого равен
Ы ср* @ - j (eitx - l) U Г* D (яг) dx = U |a J (eiy ™ l) X
Последнее равенство здесь есть результат замены переменных tx = г/.
Если a >¦ 1, то М5=^0 и, как уже отмечалось в сноске па с. 212, лш
можем положить Ап = 0- Логарифм х. ф. распределения Fа о« E8) будет
при этом характеризоваться равенством
In ср* @ = j (ei/x-— I — i^j | x Г0" D (x) dx. , ' F0)
Это выражение интегрированием по частям можно привести к виду,
подобному E9).
В случае а = 1 последовательность Ап устранить ие удается, но можно
найти асимптотическое поведение Ап и показать, что
Ап == р In п + о (In л).
Будем считать для простоты, что а + & = 1. Тогда при a = 1, Вц = ?г
оо
Рассмотрим сначала \ . Ясно, что при достаточно малом е > 0 значение
J
о
в е
/г I —-—dF (хп) будет близко к п\ xdF (хп). Можно считать, кроме того,
J 1 + х2 J
о о
что при некотором с >> О
1— F(x) < min A, еж), х > 0.
Поэтому интегрируя по частям, получаем
8 8
п f xii? (жи) = — m A — F (ел)) + п f (I— F (ял)) ^L
о о
8 с/те (Jrm)/n 8
Здесь пг([ —F(&n))'->•«, re \ = л \ + w j +re j . Находим
О 0 с/п (Ы п)/п
с/п (In n)/n (In n)fn (In п)/п
п \ ^с, п 1 < ге \ с (йл:) dx = f In ^ =
О с/п с/те - с/п
z= с [ЫЫ п — 1п п — Ы с -{• In п] — с [In In n — In с].

216 ГЛ. 8. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
В последнем интеграле аргумент хп > In п ~> оо при п -> оо, так что
8 ? 8
п \ ^ п \ а (хп) dx = a In х\ ¦ = a [In г — In In rc -f- In тг]*
Таким образом,
8
п \ , х— AF (^?г) ^ a In п (~ о (In п) при а = 0).
о
Остальная часть интеграла
оо
п 1 —-— dF (xn) =
&
оо
= _2" A - / (en)) + » f A - F (m)) d (r-j-t) < 7-f-a +
0
Производя такие же вычисления с I % получим, что
— оо
Ап — (а — Ъ) In п + о (In ft). ^
Замечание 13. Устойчивость законов Fa^, описанных в замечании
12, проверяется весьма просто, поскольку в силу E9), F0) lncp*(*&) =
= &а1пф*(?). Так как Fa,& и ^,р отличаются лишь сдвигом аргумента, то
отсюда следует и устойчивость Fa, p.
Чтобы избежать в дальнейшем несущественных оговорок и пояснений,,
мы не будем различать Fa, p и F^ и будем понимать под Fa, p распреде-
распределения с более простыми по форме х. ф. E9), F0).
По поводу роли параметров а и [* отметим следующее. Параметр а ха-
характеризует скорость сходимости к нулю Fat р(—ж) и 1 — Fa, р(ж) при ? ~> оо.
Оказывается, что Fa, p сохраняет свойство (D) с точностью до постоянного
мнояштеля. Параметр р, принимающий значения из отрезка [—1, 1], явля-
является мерой асимметрии распределения Fa> 3. Если, например, р = 1 (а > 0,
Ь =0), то при^ а < 1 распределение Fa, i(s) есть распределение, целиком
сосредоточенное на правой полуоси. Это видно из того, что в этом случае
Fa, 1 (я) можно рассматривать как предельное распределение для нормиро-
нормированных сумм случайных величин lu^O (F(x)= 0 при х < 0). Так как все
допредельные расдределения при этом будут сосредоточены на правой полу-
полуоси, то там же будет сосредоточено и предельное. Аналогично при ^ = —1
(а = 0, Ъ > 0), а<1 распределение Fa,-i(x) целиком сосредоточено на
левой полуоси. При р = 0 х. ф. Fa, о становится вещественной, а самораспре-^
деление Fa, о — симметричным (см. свойства х. ф.).
Как мы отмечали, х. ф. для Fa, p могут быть найдены в явном виде. Что
же касается самих функций распределения Fa, p, то в явной форме извест-
известны лишь немногие законы. Одним из них является закон Кошц F\, о с плот-

§ 9. СХОДИМОСТЬ К ДРУГИМ УСТОЙЧИВЫМ ЗАКОНАМ 217
яюстыо 2/(я2-Ь4я2). Преобразование сжатия в зт/2 раз приводит эту плот-
плотность к виду 1/яA + х2), соответствующему K0,i.
В заключение рассмотрим один пример. В § 11.8 мы увидим, что в без-
безобидной игре, рассмотренной нами в примере 4.8, время разорения r](z) иг-
игрока с начальным капиталом z удовлетворяет соотношению Р (ц (z) ^ n) ~
— z ~]/2/лп при п -*• оо. В частности, при 2 = 1
- Р (Ц A) > п) - У 2/шГ. F1)
Нетрудно видеть (см. об этом также в гл. 11), что r)(z) будет распреде-
распределено так же, как сумма' rji + rj2+ ... -Ь Цг, где r\j независимы и распреде-
распределены как rj(l). Таким образом, при изучении распределения rj(z), когда z
велико, можно в силу F1) воспользоваться теоремой 15 (при а =
Ь = 0, а = 1/2), по которой (см. также замечание 12)
«есть устойчивый закон с показателями а = 1/2, {&==!«

Глав а 9
ЭЛЕМЕНТЫ ТЕОРИИ' ВОССТАНОВЛЕНИЯ
§ 1. Процессы восстановлении
Перейдем теперь к рассмотрению простейших случайных про-
процессов, которые не требуют для своего описания каких-либо спе-
специальных конструкций и целиком определяются последователь-
последовательностями обычных случайных величин.
Пусть {lj}JLi есть такая последовательность, причези ^ не-
независимы и положительны.
Определение 1. Процессом восстановления будем назы-
называть совокупность случайных величин г|(?), зависящих от пара-
параметра t и определенных на <?2,§,Р> равенством
Ti(*)=max{&: Sh<t}, t>0t A)
h
где $k = 2 Ъз« so = О-
3=1
Величины r\(t) определены еще не полностью. Мы не знаем,
чему равны v\(t) на тех исходах ш, на которых уровень t никогда
достигнут не будет. В этом случае естественно положить
т](?)=°°, если все Sk<:tu B)
Обычно случайные величины ?2, ?з, .. ¦ предполагаются оди-
одинаково распределенными и имеющими конечное математическое
ожидание. Распределение случайной величины ^ может быть
произвольным.
Определение A) позволяет рассматривать v\(t) как случайную
функцию, которую можно описать следующим образом. Если на
вещественной оси нанести точки So = О, SU S2, ..., то l»]@)==0i
на полуинтервале [0, «Si), цA)=1 на полуинтервале [Su S2)
и т. д.
Часто процессом восстановления называют и саму последова-
последовательность {?&}/Г=о» Иногда последовательность {Sk} мы будем на-
называть также случайным'блужданием.
Сам термин «процесс восстановления» связан с тем, что функ-
функцию г] (t) и последовательность {SJ часто используют для опи-
описания работы различных физических устройств, содержащих сме-
сменяемые элементы. Если, например, ?j —- время бесперебойной ра-
работы прибора, после которого он выходит из строя и требует
замены или ремонта («восстановления»), то время Sk будет оз-
означать момент к-то «восстановления» прибора, a r\{t) будет рав~

§ 2. ТЕОРЕМА ВОССТАНОВЛЕНИЯ В РЕШЕТЧАТОМ СЛУЧАЕ 219
но числу «восстановлений:», которые произошли до момента вре-
времени t.
Процессы восстановления нередко используются также и в
собственно вероятностных исследованиях, а также при изучения
других процессов, где присутствуют моменты «регенерации»,
после которых развитие процесса начинается как бы сначала,
G примерами такого использования процессов восстановления мы
столкнемся ниже.
В дальнейшем нам иногда понадобится несколько более об-
общая постановка задачи, когда |j могут принимать значения раз-
разных знаков. В этом случае будем предполагать лишь, что
Ml} = а > 0.
Для равнозначных §,• определения A), B) сохраняют свою
силу.
Нетрудно видеть, что
k: Sk>i}
при каждом t является марковской случайной величиной (важно
отметить, что r\(t) таковой-не является). Функция
называется функцией восстановления. Это есть, очевидно, среднее
число шагов случайного блуждания {5Д до первого достижения
.уровня t.
Если ?,->0, то 4\(t) можно представить в виде суммы
где I (A) — индикатор события А. В этом случае для II (t) будет
иметь место равенство
оо
#@ = Мт)(*) = 2 Р№<о. " C)
Так как при каждом t в силу закона больших чисел
Р(Л (*)>*) = P($n<t)~^Q
при п-*- °°, то r|(f) есть собственная случайная величина.
§ 2. Теорема восстановления е решетчатом случае
Одним из основных фактов, на которых строится теория вос-
восстановления,- является так называемая теорема восстановления,
касающаяся поведения функции II (t).
Рассмотрим сначала более простой дискретный случай, когда
случайные величины |j принимают лишь значения, кратные неко-
некоторому положительному числу, которое, не ограничивая общно-
общности, будем считать равным 1. В этом случав Р(^1<С ?), Р (?,, 0

220 ГЛ. 9. ЭЛЕМЕНТЫ ТЕОРИИ ВОССТАНОВЛЕНИЯ
/^2 и H(t) целиком определяются их значениями в целых точ-
точках t — к, к — 1, 2, ...; разность
h{k) = H (к) — II {к — 1) = 2 Р (Sj = к)
(см. C)) есть математическое ожидание числа попаданий после-
последовательности {Sj} в точку к. Положим
qh = р (?х = /с)? рй = Р (^ == /с) при у ^ 2.
Определение 2. Процесс восстановления T](i) будем на-
называть однородным и обозначать т|о(О> если
оо оо
= 1У к = 1 2 У = 1 D>
/г 1
Если обозначить /?(z) производящую функцию
то производящая функция q{z) = Mz" = 2л ^hZ будет равна
* 1
оо оо оо —1 оо
h=i
Как мы увидим позже, термин «однородный» применительно к
процессу r\0(t) вполне оправдан. Одним из свидетельств тому
может служить
Теорема 1.
Доказательство. Рассмотрим производящую функцию*
2) последовательности ho(k) = II0(k) — II0(k — 1);
сю оо сю
*) = 2 Ло (А) = 2 S zfeP (^ = А) =
1 j=i fe^l
Отсюда следует, что ho(k)== I/a. Ц
Процесс т]о@ иногда называют также стационарным. Как
мы увидим позже, его правильнее было бы называть процессом
со стационарными приращениями (см. § 19.1).
Правильное поведение функции Н0(к\ асимптотически при
к -*- оо сохраняется и при произвольном |4.

§ 2. ТЕОРЕМА ВОССТАНОВЛЕНИЯ В РЕШЕТЧАТОМ СЛУЧАЕ 22f
Обозначим через d общий наибольший делитель (о. н. д.) воз-
возможных значений |2:
d = o. н. д. {к: ph>0).
Теорема 2 (теорема восстановления). Если d = 1, ^i — про-
произвольная целочисленная собственная случайная величина, та
h(k)*=H(k)-H(k-l)-+l/a, Н(к)~к/а при /с-^оо.
Для доказательства нам потребуются два вспомогательных
утверждения.
Лемма 1. Если v> I —марковская величина, то о-алгебра,
порожденная случайными величинами v, ?1? ..., |v, и о-алгебра
o(^v+i, ...)» порожденная последовательностью {fv+i, 5v+2, *•.},
независимы. Последовательность {?v+i, %v+2, «..} распределена так
же, как {?2, ^з, ...).
Таким образом, несмотря на случайные номера, элементы по-
последовательности §v+i распределены как \im
Доказательство. Для заданных борелевских множеств
Ви В2, ..., Си ..., Ch обозначим
где Л^ есть заданное множество целых чисел. В силу теоремы 3.4
достаточно доказать, что Р (DVA) = P (Z?2) илиЛ что то же,
P(IVi) = P (flj) Р (Л).
По формуле полной вероятности имеем
Р (DyA) = 2 Р (^ {v = /}) = S P {DiA {v = /}).
jiv " iiV
Но событие Aiv = j} принадлежит o(|i, ..., ^?), в то время как
D;e0(gi+1? ##;? |j+ft). Поэтому события Д и ^{v = y} независимы,
P(Z>^{v = ;}) = P{D-)P{A{v = у»; Р(^) = Р^), /> 1.
Отсюда следует, очевидно, что Р (DVA) == Р (D^P (Л) ^.
Лемма 2. Пусть ?1? ?2J ...— независимые, целочисленные
одинаково и симметрично распределенные случайные величины-
с конечным математическим оэюиданием (M^j = 0) ц о. м. д. воз-
можных значений, равным 1, Положим %п = i ^j* Тогда при
любом целом к
vh = min {^: Zn = &}
есть собственная случайная величина: Р (v^ < оо) = 1.
Доказательство этой леммы содержится в § 12.3 (см. след-
следствие 12.2).
Доказательство теоремы 2. Рассмотрим две незави-
независимые между собой последовательности случайных величин (счи-
(считаем их заданными на одном вероятностном пространстве): после-
последовательности |i, |2, .,., где It имеет произвольное распределение

222 ГЛ. 9. ЭЛЕМЕНТЫ ТЕОРИИ ВОССТАНОВЛЕНИЯ
ж последовательность ?ь ?2« * * • * гДе P,Ui = fc) — gfe, P (^ =» ft') «
== Р {1} = &Н pft при / > 2 (так что ^ — ^ при / ^ 2; процесс
k
-r{{t), построенный по суммам S^ = Zj^j, является однородным).
7=1
Обозначим v = min \n^l: Sn = Sn}> Это есть, очевидно, мар-
марковский момент относительно последовательности (?i?y5i).»,
(g2, ?2)»; *** Покажем^ что P(v < то) == L Положим
^» = 2 (I,- - t'j) при п > 2, Ъг = О, Zo = \х - С
Тогда
v = min Ы > 1: Zn == ~Z0},
По лемме 2 (?j = ^ — ??• имеют при / > 2 симметричное распре-
деление) для каждого целого к величина vk = min{n^ I: Zn=^k}
является собственной. Так как Zn при п ^ 1 и Zo независимы, то
Р(^< оо) = 2P(Z0 = - A) P(Vft < 00) = 1.
Произведем теперь «склеивание» последовательностей {Sr} -и
\Sn]. Так как jSv = Sv и v есть марковский момент, то можно
по лемме 1 заменить |v+i, Sv-нг, ... на |v+i?^v+2j .«.(и тем самым
•iSv+i, Sv+2 на 5V+1, 5v-f2?.. .)» не изменяя при этом распределения
последовательности {^п).
Следовательно, на множестве {Sv<k} выполняется т](/) =
= ц (I) при t ^ к — 1 и, значит,
1 _ м [г)' (й) - т|' (fe - 1); 5V > Л] + М [т] (ft) -TJ (Л
Так как \ц(к)-ц(к~~ 1)\ < 1, то
U(fc)
при к ->¦ оо. Второе утверждение теоремы очевидным образом
следует из первого. ^
Замечание 1. Склеивание {SJ и 1$д| в доказательстве
теоремы 2 можно произвести и раньше, в момент
Y = min {п &* 1: 5П е 5"}
где 5' асть множество точек S' = {SLy S21 . ..}-

§ 3. ЭКСЦЕСС И ДЕФЕКТ СЛУЧАЙНОГО БЛУЖДАНИЯ
§ 3. Эксцесс и дефект случайного блуждания.
Предельное распределение в решетчатом случае
Определение 3. Случайные величины
называются, соответственно, величинами эксцесса и дефекта
уровня t в блуждании {SJ *).
Напомним, что v(t) здесь есть марковский момент, равный
rj(i)+l. Величина %(t) имеет смысл времени, которое еще про-
проработает прибор, работающий в момент t; ^(t) есть время, кото-
которое этот прибор уже работает.
Не следует думать, что сумма %(t)+4(t) распределена так
же, как %j — ведь эта сумма равна значению | со случайным ин-
индексом r\(t). В частности, как мы увидим ниже, может оказать-
оказаться, что М%(?) >> M?j при больших t. С этим обстоятельством
связан кажущийся парадокс в следующем примере. Пассажир,
пришедший на автобусную остановку, через которую проходят*
автобусы с интервалами §i >0, д2 > 0, ..., (Mlj = а), будет
ждать прихода очередного автобуса время %, среднее значение
которого М% может оказаться больше, чем а.
Существенным фактом теории восстановления является ут-
утверждение о том, что в широких предположениях существует
совместное предельное распределение х@ и 4f@ ПРИ * ""*" °°?
так что при больших t распределение %(t) перестает зависеть
от t и становится стационарным. Обозначим это предельное рас-
распределение х@ через Gi
x). E)
Если в качестве распределения ^ взять распределение G, то по
самому его построению -распределение величины %(t) для по-
построенного процесса от t зависеть не будет. В самом деле, в этом
случае {Sj} можно представлять себе как положительные моменты
восстановления лля процесса, который построен по последова-
последовательности {gj} и начало которого отнесено в точку — iV, где N
велико. Так как в силу E) можно считать, что распределения
%(N) и х(^~*~?) совпадают, то распределение величины %(t)
(которую можно отождествить с %(N + t))' от t -не зависит и
совпадает с распределением |i. Формальное доказательство этого
факта мы опускаем, поскольку дальше он использоваться не бу-
будет. Однако читатель может провести его, используя явный вид.
G (х) в E), полученный ниже.
*) В литературе xU) называют часто первым «перескоком» через уро-
уровень t, a 7@ «педоскокомъ. Эти термины весьма наглядны, ио их можно
упрекнуть в недостаточной «литературности»»

224 ГЛ. 9. ЭЛЕМЕНТЫ ТЕОРИИ ВОССТАНОВЛЕНИЯ
Распределение G в решетчатом случае и есть распределение
D), с помощью которого строился однородный процесс восста-
восстановления T\o(t), Этот факт будет доказан чуть позже.
Из того, что распределение %(t) для процесса i]o(O не зави-
зависит от t и совпадает с распределением ?lt будет следовать, что
распределение v\o(t + u)—r\Q(t) совпадает с распределением ц^(и)
и, следовательно, от t также не зависит. Это свойство и опреде-
определяет стационарность приращений процесса восстановления; мы
назвали его однородностью процесса. Оно означает, что распре-
распределение числа восстановлений в интервале времени длины и не
зависит от того, с какого момента мы начали отсчет и, следова-
следовательно, зависит только от и.
Теоремы о предельном распределении %A) и f@ представля-
представляют интерес не только с точки зрения приложений. Они понадо-
понадобятся нам и для целого ряда других задач. Мы рассмотрим опять
сначала случай, когда величины ?j > 0 целочислеины. В этом
случае «время» t можно считать дискретным, и мы будем, как
и прежде, обозначать его буквами п и к.
Теорема 3. Пусть о. п. д. возможных значений g2 равен 1,
существует Щ2 = a, J-t есть произвольная целочисленная слу-
случайная величина. Тогда существует
Km Р (у (к) = i, х (к) = /) - pi+j/a. F)
k-*oo
Из теоремы 3 следует, что
G)
h-юо
H 1
Доказательство теоремы 3. В силу теоремы восста-
восстановления имеем при к > i
оо
Р (Y(fc) = *. X (к) = /) = 2 Р (Si = к - ;, Sm = * + /) -
оо
Ниже мы увидим, что факт существования предельного рас-
распределения для х@ в известном смысле эквивалентен теореме
восстановления (то, что из теоремы восстановления следует (G),
G), уже установлено).
В каких случаях распределение ?i для однородного процесса
восстановления совпадает с распределением §,• при / > 2? Такое

у *. ibUi'iiMA ВОССТАНОВЛЕНИЯ 225-
совпадение эквивалентна тому, что при ? = 1, 2, ,.. справедливо
пли, что то же,
a(P P) P P^
Это означает, что процесс восстановления, порожденный последо-
последовательностью одинаково распределенных случайных величин ?h
?2, ..., является однородным тогда и только тогда, когда |j имеют
¦геометрическое распределение.
Обозначим ^ и х случайные величины с распределением F).
Пользуясь E), нетрудно установить, что 7 и X независимы так-
также лишь в случае, когда gj, / > 2 имеют геометрическое распре-
распределение. Для геометрического распределения ?,-, / ^ 1, независи-
независимы также *((п) и %(гс); х (^)==== Si* Доказательство этих фактов
проводится точно так же, как для показательного распределения
(см. § 4).
Вернемся к общему случаю и вычислим ЬА%. Мелит порядок
суммирования, получим
-1У П.
— a ^ Pj
2a + 2 e
Это означает, в частности, что если распределение g4 таково, что
M|i > 2а2 —я, то среднее значение эксцесса М%(п) при боль-
больших п станет больше, чем М|х = а.
§ 4. Теорема восстановления и предельное распределение
эксцесса и дефекта в перешетчатом случае
Нерешетчатым будем называть здесь случай, когда не суще-
существует такого d > 0, что Р ( U {52 === kd}\ = 1 (<i не обязательно
целое, /с пробегает целочисленные значения). Все основные свой-
свойства процессов восстановления, обсуждавшиеся в § 2, 3, здесь
сохранятся. Аналог основной теоремы восстановления будет иметь
такой вид.
Теорема 4. Если §?, / > 2, нерешетчаты, существует
М12 = а, распределение |, произвольно, то при любом и>0
H(t-u)-+u/a% (8)
H(l)~tta ' (9)
15 д.. А. Боровков

226 ГЛ. 9. ЭЛЕМЕНТЫ ТЕОРИИ ВОССТАНОВЛЕНИЯ
Это утверждение иногда формулируют несколько в иной фор-
форме: для любой функции ограниченной вариации g(u) такой, что
g (и) du
о
выполняется
г ею
Jim - J 8 (и) dll (t - и) =4js («) du. A0)
(Соотношение (8) получается из A0), если взять g{u) = /[0, v].
Чтобы, из (8) получить A0), надо воспользоваться итерирова-
итерированием по частям.)
Доказательство соотношения (8) (или A0)) ока-
оказывается технически значительно более сложным, чем доказа-
зательство теоремы 2. Ограничимся здесь тем, что проведем
Доказательство соотношения (9) (иятегралыкш
теоремы восстановления). С предположением иерешетчатости это
доказательство никак связано не будет. Уже отмечалось, что
случайная величина v(?) = r|(?)+l является марковской,
Sv«) = t + x(t), Mv(*) = #(*) + !. A1)
Предположим сначала, что 5i = S2- В этом случае функции v(t),
%(t), II(t) будем обозначать через v(J), %(t), H(t). Положим
|(8> N) = min {iV, max(e, ?2)} чи снабдим нижним индексом (е, iV)
обозначения v(^), tj(^), a, II(t), %(t), v(t) в том случае, если ^2
заменяется на |(8, лг-,. Очевидно,
«](е, jv) @ t ii(o, N) (t) I ц (i), а(е, я) I aOj N t а при е ->- 0, N -> «>.
A2)
Так как v(8,N) (t)<- t/e, то можно в A1) воспользоваться тожде-
тождеством Вальда, в силу которого
a<efJV)Mv(efjv) (t) =-- t + X(e,iV) @, 0 < X(e,/v) @ < Лг* A3)
В силу A2) по теореме о монотонной сходимости при 8
Используя опять тождество Вальда A3) при 8 = 0 и теорему о
монотонной сходимости при N -^ оо, получим

§ 4. ТЕОРЕМА ВОССТАНОВЛЕНИЯ 227
при любом N>0. Отсюда вытекает, что
I TT-H(t) ..,. H (t)
~ ^ bra -—-
где функция а@, N) может быть выбором N сделана сколь угодно
близкой к а. Отсюда следует (9) для функции H(t). - Если
Ьг?^\>21 то воспользуемся формулой полной вероятности
р
И (t) = ] dP (I, < и) A + Н (t - и)Х
о
в силу которой
1 + Я « — и) -
так как ^г ^1 при каждом фиксированном и,
—^-—— ^1 при всех це@, 0? что Дает равномерную сходи-
п (t)
мость интеграла A4). <4
Проведенное доказательство обнаруживает, что в силу тож-
тождества (Я @ + l)a = ^ + Мх (?)существование предела для H(t)~~
— Hit—и) и сходимость M%(t) — M%(t — а)-»-0 эквивалентны.
Другие утверждения § 2,3 переносятся на перешетчатый слу-
случай без затруднений.
Определение 4. Процесс v)(t) в нерешетчатом случае
называется однородным (и обозначается ^о(^)), если распределе-
распределение первого скачка имеет вид
X
Если обозначить р(Х) х. ф. g2, то х. ф. gi будет равна
сю
g (I) = MeAh = -i J <
dx..
Так как интегрирование здесь ведется по х > 0, то интеграл
существует (как и функция /?(Я)) при всех К, 1тЯ>0 (при
Я, = ?а + ?, -~°° < ? < °°, а > 0 множитель еах равен e~axeltx\ см.
свойство 6 х. ф.). Поэтому при 1Я0
L о
eiKx
15*

223 гл- 9- ЭЛЕМЕНТЫ ТЕОРИИ ВОССТАНОВЛЕНИЯ
Теорема 5. Но (*) = Мг|0 @ == t/a.
Доказательство. Зта теорема доказывается так же, как
теорема 1. Рассмотрим преобразование Фурье — Стилтьеса над
функцией Но (t):
Отметим, "что это преобразование существует при Im X > О и для
него сохраняется теорема единственности, установленная для
х. ф., так как q>(t)=ty(ia + t)/y}p(ia), -~°° < t < °° (мы положили
K = ia + t при фиксированном а > 0) можно рассматривать как
х. ф. некоторого распределения, полученного «преобразованием
Крамера» (см. § 8 гл. 8) над II0(t).
Имеем в силу C)
Ф (Л) = J
- ?лд 1 — р (Л) ^л"
о и
Очевидно, что это преобразование соответствует функции HQ(t) =
= t/a. <
Связи между однородным процессом восстановления rjo(?) и
предельным распределением х@ и ]A) в нерешетчатом случае
те те, что и в решетчатом. Так же, как в § 3, из теоремы вос-
восстановления вытекает
Теорема 6. Если g2 не решетчата, М%2 = а, распределение
|i произвольно, то существует
. р) == A I P E > д:) Jj: A5)
n-f t>
Доказательство. При t > w
о
В силу теоремы восстановления (см. A0)) при g(%)= P(I2>
р> х + и + v) последний интеграл сходится к -^ \ Р {^z^ % + и -\~
о

§ 4. ТЕОРЕМА ВОССТАНОВЛЕНИЯ 2?9
Пусть, как и прежде, Т и X ~~ случайные величины, распре-
распределение которых совпадает с предельным распределением A5).
Из теоремы 6 видно, что каждая из случайных величин ] и )(
имеют плотности, равные ~ Р (?2 ^>х)* Совместное распределение
•у и х может не иметь плотности. Если существует плотность
/'(х) случайной величины ?2, то плотность у и % существует ш
равна — 1 {х + у)* Из теоремы 6 вытекает также, что "f и %
независимы, если только
fp(g.2>«)d« = i-e
X
при каком-нибудь а > 0, т. е. независимость имеет место лишь
для показательного распределения ^^Га-
Кроме того, совпадение P(?i>#) и Р(Е-2>а;) для однород-
однородного процесса восстановления также имеет место лишь для
?2€§Га« Другими словами, процесс восстановления, порожден-,
иый последовательностью одинаково распределенных случайных
величин ^i, ?2, ... будет однородным тогда и только тогда, когда
6;ё§Га. В этом случае процесс v\o(t) называется (см. также
§ 16.4) пуас ооновским. Это связано с тем, что для такого про-
процесса величина п(О=т1о(О при каждом t имеет распределение
Пуассона с параметром t/a.
Пуассоновский процесс обладает и рядом других замечатель-
замечательных свойств (см. также § 16.4). Для негЬ, очевидно, х@ёГа»
но, кроме того, случайные величины y(t) и %(t) независимы.
Действительно, в силу A6) при u<.t
t — u
Р (? (t) > Щ % (t) >v) = e~m+v) + a j e~ait-x+v)dx =
0
(У (t) - t, % (t) > i;) « P (I, > t + v) -
Факт независимости f(?) и х@ заслуживает внимания с точ-
точки зрения его интерпретации. Он означает следующее. Если мы
будем следить за сроком службы некоторого прибора, начиная
с момента времени t, то этот срок будет иметь то же распределе-
распределение, что и срок службы нового прибора (распределение §;€§Г&)
и не будет зависеть от того, сколько этот прибор уже прорабо-
проработал (на первый взгляд явление парадоксальное). Так как рас-
распределение длительности безотказной работы всех механизмов и
приборов, состоящих из большого числа «надежных» элементов!

230 ГЛ. 9. ЭЛЕМЕНТЫ ТЕОРИИ ВОССТАНОВЛЕНИЯ
близко к показательному (см. теорему 17.6), то отмеченное об-
обстоятельство представляет значительный практический интерес.
Если ?j принимает и отрицательные значения, то задачи, свя-
связанные с распределениями ч(п) и х(*0, качественно усложняют-
усложняются. В какой-то мере эти задачи могут быть сведены к случаю
неотрицательных величин, поскольку распределение %(п) совпа-
совпадает с распределением величины %*(п), построенной по последо-
последовательности {?j ^0}? где ?,j распределены так же, как %@).
Распределение %@) может быть найдено методами гл. 11.
§ 5. Закон- больших чисел и центральная предельная
теорема для процесса восстановления
В этом параграфе будем предполагать, что |,- ^ 0.
Теорема 7, Если 0< M?i = а< оо, го w/?w t ~* оо
Доказательство. Основным соотноше^нием, которым мы
здесь будем пользоваться, является равенство
k} = {Sh<th A7)
Так как
то считая для простоты, что -^ = — + Н является целым чис-
числом, получим
где
81 = аA — \ , е j >0. По закону больших чисел ото озна-
означает, что оцениваемая вероятность сходится к 0 при ?
Аналогичным образом оценивается вероятность
Теорема 8. Если M&t — a, D|1 = o2<oo, го

§ 5. ЗАКОН БОЛЬШИХ ЧИСЕЛ 231
Доказательство. На основании A7) имеем
Sh — ак t — ак\
(Sh — ак
По центральной предельной теореме
— ак \
<UO() при
оУ'к ^
Пусть теперь к при t -*¦ °° меняется так, что выполняется
¦=- = v. Считая v фиксированным, можно разрешить это ра-
(/ 1Г~2
va + 2"|/a$l/ 1 + 7Т7"
G у к
венство относительно к:
Подставляя найденное значение к в A8), получим
->Ф(у). A9)
Здесь следует, очевидно, выбрать знак минус, так как только» в
этом случае в обеих частях полученного соотношения будут
стоять возрастающие по v функции.
Так как Ф(и) непрерывна, то наряду с A9)
<* У*
ИЛИ
В следующей главе будет доказан усиленный закон больших
чисел, в силу которого Sk/k -*¦ а п. н. Пользуясь этим фактом,
читатель может наряду с теоремой 7 установить, что x\(t)/t-*- I/a
при t -^ °° с вероятностью 1.

Глава 10
ПОСЛЕДОВАТЕЛЬНОСТИ НЕЗАВИСИМЫХ
СЛУЧАЙНЫХ ВЕЛИЧИИ,
СВОЙСТВА ТРАЕКТОРИИ (О, 8Ъ 5а,...). В ЦЕЛОМ
§ 1, Законы нуля и единицы. Верхние и нижние функции
Первой предельной теоремой, которая была доказана для
распределения сумм одинаково распределенных независимых слу-
случайных величин, был закон больших чисел: Sn/n—>-M%,. Можно
задать вопрос: будет ли вся траектория —, - . |,; ¦ *» начиная
с некоторого п, с вероятностью, мало отличающейся от 1, близка
к М Т. е. будет ли для любого е > О
lira P I sup
<е =1? ' A)
Очевидно, это есть вопрос о почти наверное сходимости гати схо-
сходимости с вероятностью 1.
Утверждение A), называемое усиленным законом больших
чисел, которое будет доказано в этой главе, является частным
случаем так называемых законов нуля и единицы. В качестве
первого такого закона приведем критерий пуля и единицы Бо-
реля — Кантеллн.
Теорема 1. Пусть {-4п}тГ=1— последовательность независи-
независимых событий на <Й, §, Р> и пусть А есть событие, состоящее
в том, что наступит бесконечно много событий Aki т. е* А =
ОС СО
= П U ^k (А составлено из со, принадлежащих бесконечно
n=l h~n
многим Ah) t Тогда Р ( А) = 1 или 0 в зависимости от того, бу-
будет ли
Р (Ак) = оо или 2 Р (А) <
k
Доказательство. В одну сторону (в случае 2 Р (А)
1
это утверждение доказано в гл. 6 (лемма 6.1), причем без ис-
использования независимости Ah.

§ 1. ЗАКОНЫ НУЛЯ И ЕДИНИЦЫ 233
со
Если же ^L P (Ah) = °°> то в'силу независимости Ап
Р (Л) = lim Р ( U Ah) = lim P ( Q - f) л) -
П~.оо \k~n J 7l-*oo у fe=n J
= 1—lim p( П Ah) = 1 —Hm lim P f П^) =
Воспользовавшись неравенством 1аA —а;)< — x, получим, что
[I A — P(^/i))^^ ~"?l * Следовательно,
Предположим, что на <?2, $?, P) задана последовательность
независимых случайных величии {?*i}?T=i- Пусть, как и прежде,
oEi, ..., \п) е-сть о-алгебра, порожденная первыми п случайными
величинами \и ,.., \п, а о(^„, ...)—о-алгебра, порожденная слу-
случайными величинами ?n, In+i, Sn+2,
Определение 1. Событие Л называется остаточным, если
Лео (%п, ...) при любом п > 0.
оо со
Например, событие А = (] {] {bi> Щ, состоящее в том,
n=l h—n
что бесконечно много раз произошло событие {|U>iV}, очевидно,
является остаточным.
Теорема 2 (закон пуля и единицы Колмогорова). Если
А — остаточное событие, то Р (А) = 0 или Р (А) = 1.
Доказательство. Так как Л — остаточное событие, то
А е о (?п+1,...), /г ^ 0. Поэтому событие /I не зависит от о-алгебры
gEu . ••? In) при любом п. Следовательно (см. теорему 3.4), со-
событие А не зависит от о-алгебры o(|i, ...). Так как А е о(^ь ...),
то Л не зависит само от себя:
Но это возможно, если только Р (А) = 0 или 1. ^
71
Обозначим S == sup {0, Su S2, ...}, где *^n == S 5ft• В качестве
примера применения доказанной теоремы сформулируем сле-
следующее

234 гл. to. свойства траектории (о, s,, s2,...) в целом
Следствие 1. Если ?ft, fc = 1, 2, ..., независимы, то либо
р E = оо) = 1, либо Р [S < оо) = 1.
Доказательство следует из того, что событие (S = оо}
остаточно. Действительно, для любого п
{S = сх>} = {sup En_1? 5П, ...)=«,} =
= {sup(O, Sa-Sn-U ...)=°°>eo(gn, ,..).«
Другие примеры остаточных событий получим, если рассмот-
рассмотрим для последовательности независимых величин §1? g2, ... со-
I ]
бытие )ряд 2i%,k сходится?. Теорема 2 означает, что вероятность
I 1 J
этого события может быть только 0 или 1.
оо
Если рассмотреть степенной ряд Zjz'l/t» где 5ft независимы,
то обнаружим, что радиус сходимости этого ряда p=lim sup \l-h \~1/k
ft-^oo
есть случайная величина, измеримая относительно о-алгебры
оAП1 ...) при любом /г({р <ж) е=а(?„, ...), —^^^^о0). Такие
случайные величины также называются остаточными. Так как
в силу сказанного ^р {%) = Р (р < #) = 0 или 1, то отсюда сле-
следует, что р, как и любая другая остаточная случайная величина,
с вероятностью 1 равна постоянной,
В предположении, что элементы последовательности {Ьк}Г=г
не только независимы, но и одинаково распределены, закон пуля
и единицы Колмогорова был распространен Сэвиджем и Хыонт-
том па более широкий класс событий.
Пусть со=(ж1, х2, ...) есть элемент выборочного вероятностно-
вероятностного пространства </?°°, g , Р> для последовательности g=(gt,
g2, ...) (^°° — счетное прямое произведение прямых Rk, /c = l,
N
2, ...; Э°° = o(gi, ...) порождена событиями О Bk a 0"(^lt ..., ?,n)%
где 5fte a(sft) —борелевокие множества на прямой Rk).
Определение 2. Событие А ^ S°° назовем перестановоч-
перестановочным, если
(#1, ^2? • • »j &п-и %v, ^n + lt • • •) S ^
«лечет за собой (хп, х2, ..., ^n-i, ^i, ^n+i ...)^Л. Очевидно, это
условие принадлежности автоматически распространяется на лю-
любые перестановки конечного числа координат. Примером пере-
перестановочных событий могут служить остаточные события.
Теорема 3 (закон нуля и единицы для перестановочных
событий). Если |ft независимы и одинаково распределены и Л
есть перестановочное событие, то либо Р (Л) == 0, либо Р (А) = 1.
Доказательство. В силу теоремы аппроксимации (§ 3. 5)
для любого A eS00 найдется последовательность Ап ^ a(?i, ..., |«)

§ 1. ЗАКОНЫ НУЛЯ II ЕДИНИЦЫ 235
такая, что при п ->- <*>
Введем преобразование
и обозначим J5n = ТпАп. Если Л перестановочно, то ТпА=А,
и для любого ЛеГ Р(ТпВ) - Р (Д). Поэтому Р E„Л) -
= Р (ГЛЛ^Л) = Р(АпА), и, следовательно, Вп будут также аппрок-
аппроксимировать А. Но вместе с Вп-и Лп свойством B) будут обла-
обладать, очевидно, и множества Сп = АпВп. В силу независимости
Ап я Вп это означает, что
Р (А) « lim Р (ЛЙДП) = lim Р2 (Ап) = Р^ (Л). ^
Из этой теоремы вытекает следующий интересный факт.
Определение 3. Последовательность {#nK?=i называется
верхней для последовательности случайных величин {^п}?^, если
события {цп > «п) с вероятностью 1 наступают конечное число
раз. Последовательность {ап} называется нижней, если с вероят-
вероятностью 1 происходит бесконечно много событий {г\п>ап}.
Следствие 2. Если ?ft независимы и одинаково распределе-
распределены, то любая последовательность {aj является либо верхней,
либо нижней для последовательности сумм
п
{Sn}n=l, $П = ^J bk'
7i=l
Другими словами, нельзя подобрать такую «промежуточную»
последовательность {aj, чтобы вероятность события Л == {беско-
{бесконечно много pas Sn > ап) была бы, скажем, равна 1/2.
Для доказательства следствия достаточно заметить, что собы-
событие Л является перестановочным, так как перестановка местами
|i и %n в реализации (?1? g2, *..) отражается на поведении лишь
первых п сумм Su ..., Sn.
Аналогичный факт, конечно, имеет место и для последова-
тельности самих случайных величин \&w/n=i« но его в отлично
от приведенного следствия можно получить проще, так как со-
событие В = {бесконечно много раз \п "> aj является остаточным.
По поводу свойств верхних и нижних последовательностей
для сумм iSn} заметим здесь также следующее. Если РEь —с)^!
и если {ап} является верхней (нижней) последовательностью для
{SJ, то последовательность {Ьп = ап+и — t}n=% также является
верхней (нижней) при любых к > 0 и t. При достаточно больших

238 ГЛ. 10.. СВОЙСТВА ТРАЕКТОРИИ @, Si, S2> . . .) В ЦЕЛОМ
это следует из равенств вида*)
оо
= 2 P(Sk"e=[/\/ + l))P(il/She=[/>/+l))>
2j P ($ь ^ [/» У + 1)) Р (бесконечно много раз Sn + / > ап+а).
При k^k(t) надо, . допустив противное, применить доказан-
доказанную часть утверждения .к нижним функциям. ^|
Из сделанного замечания вытекает, в частности, что Km sup Sn
П-юо
и liminf^ для последовательности сумм одинаково распреде-
71—»оо
ленных независимых величии, не равных 0 с вероятностью 1, не
могут быть конечными. В самом деле, событие В = /Iinisup$n e
е («, &)} является перестановочным и, следовательно, в силу
закона 0 и 1, Р(В) = 0 или Р(Я) = 1. Если'бы Р (В) рав-
равнялась 1, то последовательность F, Ь, ...) была бы верхней для
{5J, а вместе с ней была бы верхней и последовательность
(а, а, *,,), Это означало бы, что
Р Him sup Sn ^ a\ = 1
\ П->оо J
и что предположение Р (-В) = 1 противоречиво. Л
Из теоремы 3 читатель может извлечь также, что для любых
последовательностей {ап} и {Ьп} случайные величины
Jim sup—т и lim in!—
с вероятностью 1 постоянны,
§ 2. Сходимость рядов независимых случайных величии
В этом параграфе остановимся более подробно па сходимости
рядов, составленных из независимых случайных величин. Мы уже
знаем, что такие ряды сходятся с вероятностью 1 или 0. Нас
будут интересовать условия сходимости.
Получим, в частности, ответ на следующий интересный во-
прос. Хорошо известно, что ряд "V -— при а ^ 1 расходится,
сю
а знакочередующийся ряд ^V i~ ^ - сходится при любом а > О
(разность соседних элементов- имеет порядок малости а/п1+а).
*) Пользуясь у. м. о., можно было бы записать точнее: Р(А) =
= Мр l^-lSЛ = \ dP (Sh <; ?) Р (бесконечно много раз Sn-{- t > an+jt)t

§ 2. СХОДИМОСТЬ РЯДОВ 237
00 &
чф Оп
Как будет вести себя ряд ?+—% где бп одинаково распределены,
1 п
независимы, М6П = 0 (например, бп == ±1 с вероятностью 1/2)?
Один из основных путей исследования этих задач состоит в
выяснении связи сходимости п. н. с более простым понятием схо-
сходимости по вероятности. Известно, что, вообще говоря, из сходи-
сходимости по вероятности ?«->•? не следует сходимость п. н. Однако
п
Sn = 2^ %
в рассматриваемом случае, когда Zn = Sn = 2^ % и % незави-
3
симы, это не так. Основным утверждением в этом параграфе
является
п
Теорема 4. Если т],- независимы, Sn=2j ц^ то сходи-
г
мость Sn no вероятности влечет сходимость Sn п. н.
Здесь для определенности под сходимостью будем понимать
фундаментальность, не предполагая заранее, что сумма ряда
известна. Для доказательства.теоремы нам понадобится следую-
следующее неравенство:
Лемма 1 (первое неравенство Колмогорова). Если г], неза-
независимы и при всех j ^ п
ТО
PfmaxISjI^^^PU^I^-a). B)'
Следствие З.
P (шах | Sj | > x)^ < 2P ( | Sn | > x - V2DS~n).
Собственно, Колмогоровым было установлено именно это не-
неравенство (лемма 1 является его незначительным обобщением).
Оно вытекает из B), так как в силу неравенства Чебышева
Р ( 1 Sn - Sj | > У2Жп) < ^y < 1.
Доказательство леммы 1. Пусть т = {min к ^ 1: 1 Sk\ ^
>#}. Обозначим Aj = {t=j}, j = 1, 2, .... Очевидце, что Аг не-
несовместны и, значит,
4
(\\ ^
3=1
>2 P(\Sn-Sj\<a;A}).
i

238 ГЛ. 10. СВОЙСТВА ТРАЕКТОРИИ @, Su Sa, . . .) В ЦЕЛОМ
(Последнее неравенство верно, так как событие {I5n — S3\ < а)Л}
влечет за собой {\Sn\ > х — а)А}.) Но А^ о{х\\,. •., т],), {|5Л —5,-|<
<fl}eo(T|j+1, ..., т]д). Поэтому эти два события независимы,
Лемма доказана. ^
Обратимся к доказательству теоремы. Достаточно доказать
п. н. фундаментальность E?Л, т. е. сходимость для любого 8 > О
при т ~> ©о
j Slip j о д — *3 т ^> ZS \ —>- U. I^Oj
Обозначим
Тогда соотношение C) можно записать в виде
р(д2пг)-^0 D)
При 771 ->¦ оо#
Так как {»Sn} фундаментальна по вероятности, то
/VM = sup P (^!;,iii) ->О
при т?г ->¦ оо, М -> оо, так что рт, м < 1/2 при всех достаточно
больших т и Ж. Для таких /я и М имеем по лемме 1 при а = е,
ж = 2s
/ м \
PJ sup |5n-5m|>2e\ = P^ U 4f,nJ<
< 1™=Г^ Р Um.th) < 2Р ( Ле»7,т).
В силу свойств вероятности
' Р (А%) = lim P С U ^т,Л<2ПшзпрРD!„>т). E)
Обозначим через S предел (по вероятности) -последовательно-
-последовательности 5Я, ^«=={1^ —5|>е}. Тогда P(i?"J->0 при л~> сю,
~4м,т с: S^2 U Вт2% и в силу E)
Соотношение D), а вместе с ним и утверждение теоремы дока-
доказаны. 4

§ 3. УСИЛЕННЫЙ ЗАКОН БОЛЬШИХ ЧИСЕЛ 239
Следствие 4. Если Шцк = 0, 2D%<oq? to Sn п.н. схо-
1
дится.
Утверждение следует из теоремы 4 и фундаментальности Sn
в среднеквадратичном (М (Sn — *SmJ = 2li Dtj^ —>- 0 при m ->¦
ft=m-fl
-*¦ oo? гс-*- °°) и, следовательно, по вероятности.
Оказывается, что если Мци = 0, [r]J <с при всех ft, то усло-
условие 2Dv|fc< °° будет и необходимым для сходимости Sn п. н.*).
В следствии 4 содержится отпет и на вопрос, поставленный
в начале параграфа о сходимости ^—^% где оп одинаково рас-
распределены, независимы, Мбп == 0.
Следствие 5. Ряд 2&пап сходится с вероятностью 1,
если D8k = о2 <С оо, 2а п. < °° •
С учетом сделанного выше замечания можно сказать, следова-
тельно, что ряд 2^— при бд = ±1 с вероятностью 1/2 сходится
тогда и только тогда, когда а > 1/2.
Некоторым обобщением следствия 4 является
Следствие 6 (критерий двух рядов). Для сходимости
ряда 2 чи и. w. достаточно, чтобы сходились ряды ^МцП1 ^Рцп.
Доказательство очевидно, так как последовательности
11 2СП/1 — М%) сходятся п. н. по следствию 4, А
§ 3. Усиленный закон больших чисел
Нетрудно видеть, что если использовать терминологию § 1,
то усиленный закон больших чисел A) означает, что последова-
последовательность {6ra}nLi при любом 8 > 0 является верхней для обе-
обеих последовательностей {Sn} и {—Sn], если только М?х = 0.
Сформулируем предварительно в виде леммы следующее нро-
стое утверждение.
Лемма 2. М | ? I < °° тогда и только тогда, когда
2 Р(Ш>/)<«>.
Доказательство следует очевидным образом иа ра-
равенства
*) Подробнее см. об этом, например, [21].

240 ГЛ. 10. СВОЙСТВА ТРАЕКТОРИИ @, ?,, S2. . . .) В ЦЕЛОМ
и неравенств
Усиленный закон больших чисел получим в качестве след-
следствия одного факта, который представляет и самостоятельный
интерес.
Теорема 5. Если %t одинаково распределены и независи-
независимы, М?1>0,# то случайная величина Z = iniSu является
собственной (с вероятностью 1 конечной).
Доказательство. Пусть i]i = г\A) (см. обозначения
гл. 9) есть номер первой суммы 5А, которая достигла уровня I.
Рассмотрим последовательность {?* = 5^+/*), которая в, силу
леммы 9.1 распределена так же, как {?h}, о не зависит от т]и
?ц *»*л5л1# Для нее построим индекс А = tj2, при котором впер-
вые сумма Sk =2 &? достигла уровня 1. Ясно, что случайные
величины t]i и f|2 одинаково распределены и независимы. Затем
для последовательности I?/*'* = ^т^+па+ь) построим величину
г}3 и т. д. В результате получим последовательность марковских
моментов г\и ц2, .. ., которые определяют моменты «регенера-
«регенерации» исходной последовательности {Sh}, связанные с достиже-
достижением уровня 1.
Обозначим'теперь Zx = inf 5/г, Z2 = 1лf S*ix . ,ss Ясно, что
Zj одинаково распределены и что
Z = inf {Z1? iS^ + Z2, ^2
где по определению iS'r!l > 1, 5Л1+<П2>2 и т. д. Поэтому
2
Это выражение сходится к 0 при N ->¦ «>, если М | Zx| < <х> (см.
лемму 1). Конечность MZ^, в которой нам осталось убедиться,
следует из конечности М% = Мт|A) (см. теоремы гл. 9) и не-
неравенств
Пусть, как и прежде, |J? |2, ... независимы и одинаково рас-
распределены.

§ 3. УСИЛЕННЫЙ ЗАКОН БОЛЬШИХ ЧИСЕЛ 241
Теорема 6 (усиленный закон больших чисел Колмого-
Колмогорова), Для того^ чтобы Sjn—> а, необходимо и достаточно, что-
п. н«
бы существовало М?л = а.
Доказательство. Достаточность. Предположим, не
ограничивая общности, что Щ/г =-0. Тогда из теоремы 4
вытекает, что случайная величина Z8 = infE& + гк) являет-
?t>Q
ся собственной при любом 8 >0 (S&+8& есть суммы случайных
величии Ъя + ^, М {Ik + и) > 0)- Следовательно,
при п -> ©о. Аналогично обнаруживаем, что
(с
h>n к
S
^>2 0 при
/
Так как Р (sup
> 2г \ превосходит суммы двух рассмотрен-
)
S
иых выше вероятностей, то мы получим, что
S
to л S
Необходимость. Заметим, что —— = -~^
Yl Yl
> 1 I < ОС ИЛИ, ЧТО ТО
т. е. событие у >М наступает конечное число раз с ве-
вероятностью 1. По критерию «нуля или единицы» Бореля —- Кап-
оо
телли это означает, что Л г I —
же, 2 Р (Ui I > Л) < °°- Следовательно, по лемме 1 Щх < оо. ^
Таким образом, условие М?д = 0 является необходимым
и достаточным для того, чтобы последовательность {ви}^=1 бы-
была верхней для обеих последовательностей {$п} и {—Sn]. В сле-
следующей главе мы получим в качестве следствий необходимые и
достаточные условия для того, чтобы (ва) была верхней после-
последовательностью для каждой из траекторий {SJ и {—5„} в от-
отдельности. Разумеется, что, например, для последовательности
{SJ ото условие будет шире, чем условие М?/г = 0.
Замечание 1. Мы видели, что в- основе приведенного доказательст-
доказательства усиленного закона больших чисел лежит тождество Вальда. Теперь, поль-
пользуясь доказанным законом, можно несколько усилить утверждение тожде-
тождества. Именно, имеет место следующий факт. Если а = Щ^О, то для мар-
марковского момента v условие IVIv <C оо для выполнения тождества Вальда
MSV = aMv
излишне. Другими словами, это тождество верно и при Mv = оо, или, что
то же, конечность M5V влечет за собой конечность Mv. Если а = 0, то по-
16 а. А. Боровков

242 ГЛ. 10. СВОЙСТВА ТРАЕКТОРИИ @, Su S2, , . .) В ЦЕЛОМ
следнсс утверждение неверно. Читателю нетрудно проиллюстрировать этот
факт на примере безобидной игры, рассмотренной в § 4.2.
Для доказательства приведенного утверждения достаточно убедиться,
что при а >> 0 равенство Mv = сю влечет за собой M$v = оо.
Заметим сначала, что для любого марковского момента, MSV ^ 0. Допу-
Допустив, что MSV <; 0, мы построим так же, как в доказательстве теоремы 4,
последовательность независимых моментов остановок vi, V2, ... таких, что
Sv , Sv^ — $v , ... будут независимы и распределены как Sv. По усилен-
усиленному закону больших чисел это будет означать, что с вероятностью 1 все
Sv , начиная с некоторого N, будут отрицательны. Но это, очевидно, про-
противоречит усиленному закону больших чисел, примененному к Sni n —
= 1, 2, ..., поскольку М|х = а > 0. , ^
Далее, нетрудно видеть, что vN = min (N, v) вместе с v есть марковская
величина. Имеем
MSV = М {Sv; v < N) + М {Sv; v > N} =
- MSVn + M {^v ™ SN; v > N} = MvN-a + MS%,
где $1 = gN+1 + ... + lN+k, ?* =0, v* = max @, v — N) есть марков-
марковская величина относительно последовательности {^n+u ^n+2i .. •}• На ociio- '
вании предыдущего получаем
Так как MvN > M {v; v < N} -+¦ оо при N -+ сю, то утверждение доказано. ^
Для иллюстрации усиленного закона больших чисел рассмот-
рассмотрим следующий пример.
Пример 1. Пусть со—(еь е2, ...) есть последовательность
независимых случайных величии, принимающих значения 1 и 0
соответственно с вероятностями р и G = 1 — /?. Поставим в соот-
соответствие каждой такой последовательности ев число ? = 5 (Г1)) —
сю
= ^V __A так, что со есть двоичное разложение g. Ясно, что воз-
Лт nk
можные значения | заполняют отрезок [0, 1]. Покажем, что ес-
если р = g = 1/2, то распределение g равномерно. Если же /? ^ 1/2,
сю
то распределение g сингулярно. В самом деле, если я =2 8/t2~fe,
где бА принимают значения 0 или 1, то
{% < х} - {8!< б4} П {et - б17 е2 < б2} U {г, = 6i, е, = б2, е3 < бз) U . ..
Так как события в этом объединении не пересекаются, то при
оо
Р(?<*)= 2 P(ei = 6t, .... 8ft =6ft,

§ 3. УСИЛЕННЫЙ ЗАКОН БОЛЬШИХ ЧИСЕЛ 243
Это означает, что распределение § равномерно, т. е. для любого
измеримого по Борелю множества В с: [0, 1] определена вероят-
вероятность Р(? е В) = mes B% равная лебеговой мере В, Обозна-
Обозначь vi ) г °п \
чим оп =* ii Sftir 5n = S 8fe* Тогда множество jx: ^im"===i3| из-
измеримо по Борелю и, стало быть,
mes | x: lim — = -77 > = P f lim ~ = -77 j *
Так как но усиленному закону больших чисел правая часть здесь
равна 1, то
i mes r lim — = —-1 = 1,
Другими словами, для почти всех х ^ [0, 1] доля единиц в двоич-
двоичном разложении х равна 1/2.
(S \
lim —= jd)=1, хотя в силу
предыдущего
mes r lim— = р\ = 0,
так что «носителем» вероятностной меры па [0, 1] является мно-
множество лебеговой меры 0. С другой стороны, распределение слу-
случайной величины \ при р ?=¦ 1/2 также непрерывно. Это следует
из того, что
ft=-l
если х двоичио-иррациопалыю.
Если ^—двоично-рационально, т. е. если при некотором
г<со все bh при к > г равны 0 или 1, то непрерывность следует
из вложения
со оо
{l~x}cz fH8ft = 0}+ П {eft-l}t
h=r k~r
так как вероятности этих событий, очевидно, равны 0. Сингуляр-
Сингулярность F%(x) при р Ф 1/2 доказана. <4
Предлагаем читателю построить график функции распределе-
распределения \.
10*

244 гл. ю. свойства траектории (о, s,, s2 ) в целом
§ 4, Усиленный закон больших чисел
для произвольных независимых слагаемых
Отыскание необходимых и достаточных условий для сходи-
сходимости
когда Ъп t °°, а слагаемые gt, ?2, .. • распределены не одинаково,
представляет собой трудную задачу. Мы ограничимся здесь тем,
что докажем следующую теорему.
Теорема 7 (критерий Колмогорова сходимости почти всю-
всюду). Пусть |ft, й = 1, 2, ..., независимы, М|ь =0, D?& = ол< оо
w, кроме того,
оо 2
П.Н.
Доказательство. Из условий теоремы 7 вытекает, что
(см. следствие 4) ряд ^лА с вероятностью 1 сходится. Поэтому
утверждение теоремы 7 будет следствием следующей известной
леммы анализа.
Лемма 3. Пусть bk t °°, а последовательность хи х2, ... га-
оо
, что рл9 2 ж& сходится. Тогда при п ->• оо
1
Доказательство. Обозначим Хп = 2 ^fe» ^^к что Х„ -*¦ О
п + 1
при п-+о°, X = гаах|Хп|<оо. Используя преобразования Абеля,
получим
п п п—1 п
1 0 1
I
п п—1
lira sup г— 2d ЪьРк ^ lim SUP т-" ^ (^+i — ^) ^* G)
П->оо "п ^ П->оо п -?

§ 4. ПРОИЗВОЛЬНЫЕ НЕЗАВИСИМЫЕ СЛАГАЕМЫЕ 245
Здесь для заданного е >0 можно выбрать N так, что \Хк\ < 8
при к ^ N. Поэтому
1 1 N
« x (bN — ьг) + е (ьп — ад.
Отсюда и из G) следует, что
п
Km sup -т—
Можно было бы доказывать теорему 7 и непосредственно-, ис-
используя неравенство Колмогорова, примерно так же, как это де-
делилось в теореме 4.
Первоначально достаточность в теореме 6 была доказана с
помощью теоремы 5 путем использования срезок
при 11к\ < к,
при
которые имеют дисперсии D^fe,: удовлетворяющие условию
^—1-< оо,и которые с точки зрения закона больших чисел не
1 к
отличаются от gft, так как ^jP {l>k Ф Ьд < °° и, следовательно,
1
происходит-лишь конечное число событий (?& ^ Ski-
Skill p им ер 2. Пусть |ft, /с = 1, 2, ...,— независимые случайные
величины, принимающие значения ^h = ± /са с вероятностями 1/2.
Как мы видели в примере 1 § 7.3 при а > — 1/2 суммы 5П этих
величин асимптотически4 нормальны при соответствующей норми-
нормировке. Будут ли они удовлетворять усиленному закону больших
чисел? Так как D?ft = о2к = /га, то ряд У) -^-- = 2 ^^"^ бУД^т
сходиться при а < 1/2. Таким образом, если а < 1/2, то б^/га—>• 0.
Отметим теперь, что хотя условие а < 1/2 есть всего лишь доста-
достаточное, оно точно определяет границы применимости усиленного
закона больших чисел. Действительно, В2п = DSn ~ п2/2 при
а = 1/2 и, следовательно, величина SJn будет асимптотически
нормальной с параметрами @, 1/У2) (пример 1 § 7.3). Итак,
Sn при а ^ 1/2 не будет удовлетворять усиленному закону боль-
больших чисел, хотя и будет удовлетворять центральной предельной
теореме. Этот факт объясняется, очевидно, существенно различ-
различными нормировками в этих двух предельных теоремах.

Глава 11
ФАКТОРИЗАЦИОННЫЕ ТОЖДЕСТВА
В этой главе мы получим ряд замечательных н весьма полез-
полезных соотношений, устанавливающих связи между разными ха-
характеристиками случайных блужданий, а также связи между
возникающими при этом проблемами и простейшими граничны-
граничными задачами теории функций комплексного переменного.
§ 1. Факторизационные тождества и их первые следствия
Пусть <Й, S, Р) — вероятностное пространство, на кото-
котором задана последовательность {1к}Г=1 независимых одинаково
распределенных случайных величин. Пусть как и прежде
п S&, о
На этом же вероятностном пространстве определим случай-
случайную величину
Это есть время первого достижения нулевого уровня. На тех
элементарных исходах ю, для которых все Sk<0, к>1, поло-
положим гL_ = оо. (Отметим, что определение т|+ отличается от
определения величины ц (х) = min{fc ^ 0; Sh ^ х) при х = 0 (см.
гл. 9), в силу которого т]@) = 0.) Как и т]@), величина ц\
является марковской.
Случайная величина х+ === $ о называется первой неотрща-
¦п+
тельной суммой* Она определена лишь на мпожестве |T]°f<oo].
Совершенно аналогичными свойствами обладают время до-
достижения нулевого уровня
первая неположительная сумма X— === *^,о *
Исследование свойств введенных случайных величии представ-
представляет значительный самостоятельный интерес. Величина т]+, на-
например, есть момент остановки, и знание ее природы весьма
существенно для изучения моментов остановки во многих более
сложных задачах (см. задачи теории восстановления в гл. 9, за-

§ 1. ТОЖДЕСТВА И ПЕРВЫЕ СЛЕДСТВИЯ 247
дачи о статистическом контроле, описанные в § 4.4, и др.). Кро-
Кроме того, величины т|+ и %°+ ' потребуются для описания наведе-
наведения экстремумов
l = suV(Su Sit ...) и Y = inf(Si, Stt ...),
которые играют важную роль в задачах математической стати-
статистики, теории, массового обслуживания (см. § 4) и других.
Обозначим ф (X) = щг (X) = Ме% ^1.
Теорема 1 (факторизационное тождество). Для х. ф. сов-
совместных распределений введенных случайных величин при
Ы < 1, ImA, = 0 справедливо тождество
1 — 2ф (X) =
D (z) [l - М И"/-; т? < оо)],
= 1 - М (/+; х+ = 0, T]of < оо) =1- М (/~; х- =0; т,°_<оо).
D(z)
Доказательство. Обозначим t,n = max {Sii ..., Sn). Ha
множестве {т|+ = к} имеем
С ^* i С С ^ ! С С*
Поэтому
п
ц)п (Я) = Мб* п = 2 М (^ '"» Лн- = ^) + М (в п; ^п <С 0) ==
S. а / I?v(S-jj—S/Л iXSh т / л т\\ -тал- лч
М (/> • р I I пII = А*)) 4- /If /1 ^
где Mt = M (e n; ^n^O). При каждом фиксированном к слу-
случайные величины Sn — Sh и 5fe/ (лч = &) = Х+^ (т)-ь = ^)» где
/(Л) есть индикатор события Л, являются независимыми. Следо-
Следовательно,
ФП (Я.) = 2 4>n~k W M (eiU+; TI+- = й) + Мп.
Умножим теперь обе части равенства на zn, п = 0, 1, ... и про-
просуммируем по п. При этом условимся считать, что при п = 0

248 гл. и. факторизанионные тождества
Для свертки двух последовательностей сп =2%^ n-h справед-
1
ливо равенство
если только ряды, фигурирующие в этом равенстве, абсолютно
сходятся. Так как Ы < 1, |<р(Л) I < 1 при ImA, = 0, то
w=0 fe=l
/0 \
.или, что то же,
где Л2±(Я) означают числитель и знаменатель отношения, полу-
полученного ДЛЯ 1 — 2ф(Х).
Легко понять, что если мы обозначим
то, повторив приведенные рассуждения, придем к равенству
,л,0 0 \
Заметим теперь, что при Ы < 1 функции Аг+(Х) и BZ+(X)
аналитичны в области ImX>0, непрерывны, включая границу
Im/\ = 0, и ограничены при ImX^O. Это следует из того, что
обе эти функции представляют собой равномерно сходящиеся
ряды из функций, обладающих всеми указанными свойствами.
Например,
М\е z , т]+ < ooj = 2j 2 М [е ; Т1-ь =

§ 1. ТОЖДЕСТВА И ПЕРВЫЕ СЛЕДСТВИЯ 249
где М \е% + ;\ti+ = п) есть часть х. ф. неотрицательной случай-
случайной величины (см. свойство 6 х. ф.).
Функции AZ-(X) и Bz~Ck) по тем же причинам обладают
аналогичными свойствами в полуплоскости ImA,<0. Но если
сравнить B) н C), то получим, что при Im?\, —О
Это означает, что функция Az~(к)Вz-(к) (Az+ (X)BZ+Ck)) может
быть через границу ImA, = 0 из нижней (верхней) полуплоско-
полуплоскости аналитически продолжена до целой функции. Так как эта
функция ограничена, то в силу известных теорем она с необхо-
необходимостью равна постоянной. Далее, eiKx-*¦ 0 при ImX *-* — °°, х<
<0 и, следовательно,
Вг_ (- Soo) = 1 - М (/"; х°_ = 0, т,°_ < оо),
4f_(-joo)=l,
Лг_ {%) Вг„ (X) = Az_ (- ioo) Яг_ (- i оо) = Z) (г).=
= I - М (/-; х- = 0, < < оо).
Подставляя в B)' найденное из этого равенства значение
Аг- (%) = -ъ—-ТГ' получим утверждение теоремы. Второе со-
f->z (А)
отношение для D(z) найдем из равенства D(z) = Az+(i°o)X.
ХВ2+Aоо),Щ
При доказательстве теоремы 1 мы в формуле A)" использо-
использовали разложение Мег п на слагаемые,' соответствующие непе-
in \
ресекающимся событиям { U {т)+ = к] \ == {tn ^0} и {t,n < 0). Но
U=i ¦ I
схема доказательства полностью сохранится, если мы рассмот-
рассмотрим разбиение Q на события {?п > 0} и {?„^01. Чтобы сделать
.это, введем случайные величины
г|.|_ == min {к : Sk >> 0} (т|+ = оо, если
т)_ = min {к : 5/. <0} (т|„ = оог если
Величина ц+(ц~) называется временем появления первой поло-
положительной (отрицательной) суммы %+(%-)• Тогда наряду с ра-
равенствами B), C) сможем записать
1 —
2
XI „Я м, { J^U. Y ^ (\\ у zHj^

250 ГЛ. 11. ФАКТОРИЗАЦИОИНЫЕ ТОЖДЕСТВА
Сопоставляя эти соотношения с B), C), мы с помощью преж-
прежних рассуждений сможем доказать следующее утверждение.
Теорема 2.
1 - М (eiU°V+; т,; < оо) ~ D (z) [l - М [eUX V+; Ц+ < оо)], E)
_ м (,"*-,"-; ц_ < о
функция D(z)y определенная в теореме 1, удовлетворяет
также соотношениям
оо оо
я'(*) = 2 2ftp (<sn = а, с.ч<0) = 2 ^"Р E„ = о, 7„ > 0). F)
гг=О п=о
Ясно, что с помощью теоремы 2 можно получить некоторые
другие разновидности факторизационного тождества. Например.,,
такое:
- м (.1АХV+; л+ < оо)] [i - м
Из представлений F) для D(z) вытекает, в частности, что
Р (Sn = 0, Sn < 0) = Р (Sn = 0, Yn > 0)
и что Л (я) ^ 1, если Р EП = 0) = 0 при всех п "> 1.
Доказательство теоремы 2. Получим, например,
первое из соотношений E). Сравнивая C) и D), как и рань-
раньше, находим
_ M (eUxV+; Л+ < оо)] ?г+ (К) = 1, (8)
так как 1 есть значение рассматриваемого произведения в точке
гею. Поэтому в силу C) получаем G)., Остается сравнить G) с
тождеством теоремы 1.
Выражения F) для D(z) получаются, если вспомнить, что в
правой части (8) должно стоять
Так как это произведение также равно 1, то полагая X — — ioo
приходим к одному из требуемых равенств. Второе доказывается
аналогично. ^
Замечание 1. Важно отметить, что теоремы 1 и 2 наряду
с доказательством существования тождеств дают нам также сред-
средство отыскания х. ф. совместных распределений величин % и т].
Речь идет об отождествлении с представлениями в теоремах 1 и 2.

§ 1. ТОЖДЕСТВА И ПЕРВЫЕ СЛЕДСТВИЯ 251
любого представления функции 1 —zqp(A,) при Im^ = Q в виде
7*—7TV или ~г—777» гДе kz±(A) аналитичны соответственно в
ь-г_ \А) Cz^_ (Aj
областях Im к ^ 0, непрерывны включая границу Im к = 0 и
ограничены при 1га Я $0. Если, например,
1 —
ii С2+(гоо) = С'г-(—ioo)= 1, то, как мы видели, \—Щ\ег 4~z +"»Yl+<
<С оо ] можно отождествить с С2+ (Я); С2Т^ (к) с 1 — М [е ' ~~z """»
_ (М
г 4~z +"
П-<°°), a C(z) с D(z).
В общем случае, если некоторую функцию Cz (X), заданную
при 1тЯ = 0, удается представить в виде одного из соотношений
-тт—7Т7 пли ^—ТТГг где С2± обладают указанными выше свои-
ствами, то говорят, что CZ(X) допускает факторизацию. Функция
€Z+Ck) (CZ~(X)) называется положительной (отрицательной) ком-
компонентой факторизации. Задача о факторизации представляет со-
собой разновидность так называемой проблемы Кохии — Римана в
граничных задачах теории функций комплексного переменного.
Получим теперь некоторые следствия теорем 1 и 2.
Следствие 1. Устремляя z ->¦ 1, мы получим
<
1 - ср (X) = [l - М (еШ+; ц+ < оо)] [l _
Аналогичным образом можно, очевидно, написать и другие
тождества такого типа, соответствующие тождествам, которые
можно получить из теорем 1 и 2.
Следствие 2. Если существует M%k = а < 0, mo P (гI <
<оо) = 1, существует Мх- м Р (?<0)=а/Мх« >0.
Доказательство. Первое соотношение следует из зако-
закона больших чисел, так как
при л -*- °°. Следовательно, в рассматриваемом случае
Существование Му- следует из тождества Вальда
и теоремы 9.4, в силу которой Мц. <С оо%

252 ГЛ. 11. ФАКТОРИЗАЦИОННЫЕ ТОЖДЕСТВА
Наконец, поделив обе части тождества в следствии 1 на X и
переходя к пределу при А, -*¦ 0, получим
а =A - Р (Л+ < оо)) МХ- = Р (?< 0) М2_, <
Интересно отметить, что в качестве следствия доказанного
утверждения мы можем получить усиленный закон больших чи-
чисел. Действительно, так как событие {? < °°} является остаточ-
остаточным и Р (?< оо) ^ Р (?^ 0), то из следствия 2 вытекает, что
Р(^<оо) = 1 при а<0. Это означает, что верно утверждение
теоремы 4, из которой и был получен усиленный закон больших
чисел.
Ниже, на основании факторизационыых тождеств, мы полу-
получим некоторое обобщение этого закона.
Во всем дальнейшем в этой главе, чтобвх избежать тривиаль-
тривиальных затруднений, будем предполагать, что %,г с положительной
вероятностью принимает как положительные, так и отрицатель-
отрицательные значения.
Следствие 3. Если а = Mgft = 0, то Р(rj+ = оо ) =
== оо) = 0, так что
1 _ ф (X) = (l _ МеШ+) (l -
Доказательство. Рассмотрим последовательность gft =
= ^ft—8, 8 > 0. Обозначив ?, 5С-, а соответствующие характери-
характеристики для введенной последовательности, получим
где
х- < М (?; f а < 0)< М (|, - е;I, <е)< М(I,; 1г<0)< 0.
Таким образом, вероятность Р(^^0) может быть сделана сколь
угодно малой, так что Р (С <10) = Р (т|+ = оо) = 0. Аналогично ус-
устанавливается, что Р (у ^ 0) = 0, и, следовательно,
§ 2. Факторизациоиные тождества.
Свойства траектории @, 8Ъ 52, ...)
Найдем теперь еще одно представление для компонент фак-
факторизации функции 1— ^ф(Я).
Теорема 3. При Ы < 1, ImA, = 0 функция l — zqCk) допу-
допускает факторизацию
С (X) С (z)
г;/'щ' , C,+ (ioo) = C,_(-ioo) = l, (9)

§ 2. ТОЖДЕСТВА И СВОЙСТВА ТРАЕКТОРИИ (О, S,, S2, . . Л 253'
Сг+ (к) = ехр - 2, т"
?_(*)-* ехр {2
C(Z) =
k=i
Доказательство. Так как Ы < 1, то существует
1юA — 2ф(^)), понимаемый в смысле главного значения. Следу-
Следующие равенства дают нужное разложение
1 - *Ф (X) = ^-^>- в J-2 -^-1- ехр{_2 4 МН =
I /l-l J I k=l )
= ехр!-1 ^ М (е^; Sh > 0I ехр {-1 ^ Р № = 0)] х
4
fe=l j
Требуемые свойства компоненты ?Z+(A,) (Cz_(^)) (аналитичность
яри ImX>0 (IeiX<0), непрерывность включая границу
ImA, = 0 и ограниченность) доказываются точно так же, как для
компоненты Аг+{Аг-) в доказательстве теоремы 1. ^
Так как в формулах (9), A0), очевидно, С2+(г°°) = С2_(—?оо)=:
= 1, то в силу замечания, сделанного к теоремам 1 и 2, мы не-
немедленно получаем
Следствие 4.
1 - М (^V+; Ц+ < оо) - ехр {- 2 4 М (^ Sk > о)];
{ k
-2
;r]_<ooj = exp — 2^ — M [e A;5fe
I fe=i
Следствие 5.
^, p5- =0)
I. Всегда > —Ц < oo,

254 ГЛ. 11. ФАКТОРИЗАЦИОННЫЕ ТОЖДЕСТВА
2. Три следующие условия эквивалентны:
а) Р(Е<оо) = 1,
б) P(S<0)-P(ti+«oo)>01
в) id -Н—- < °° или
Доказательство. Чтобы получить первое утверждение,
надо во втором равенстве следствия 4 устремить z к 1 и вспом-
вспомнить, что D(l) = l-P(x(l = 0, л°+<оо)>Р (|1>0)>0. Эквива-
Эквивалентность б) и в) вытекает из равенства
/t=l
которое получится, если в первом тождестве в следствии 4 поло-
положить А, = 0, z= 1.
Установим эквивалентность а) и б). Если Р(?^0)>0, то
Р (? < оо) > 0 и, стало быть, Р (? < оо) =1, т. к. событие {^ < оо}
остаточное. Наоборот, пусть теперь t — собственная случайная
величина. Выберем N так, чтобы Р(С^АГ)>0, и 6>0 так,
чтобы к = N/b было целое и Р (§4 < —6) > 0. Тогда
SUP (— Ьк + Ъг+1 + • • • + gft+j) < 01.
i>i J
Так как последовательность Ъ>ь+и Zk+2, .. * распределена так же,
как %и §2, ..., то
Следствие 6.
1. Р(?<оо?Т>-оо)-0.,
2. Ясли существует M?i = а < 0,
3. Е^^гг существует Mgx = а = 0,
к
= оо

§ 2. ТОЖДЕСТВА И СВОЙСТВА ТРАЕКТОРИИ (О, Su S2, . . .) 255
Случай а > 0 мы здесь не рассматриваем, поскольку он яв-
является «симметричным» к случаю а < 0.
Доказательство. Первое утверждение следует из того,
что по крайней мере один из двух рядов J^ ^ • или
2^ - расходится, «значит, 'по следствию 5 либо
k=i
р(у _ __ оо) = 1, либо Р(?=оо) = 1.
Второе и третье утверждения очевидным образом вытекают
из следствий 2, 3 и 5. ^
Обобщение усиленного закона больших чисел, о котором мы
упоминали выше, состоит в следующем.
Теорема 4 (односторонний закон больших чисел). Схо~
ili LJ при любом г > 0 является необхо-
необходимым и достаточным условием для того, чтобы
! s \
P(limsup-jp<Oj:=l, A1>
( Sn }
Так как jlimsup-^-<!a| есть остаточное событие и т. к.
S'n = 8п — an снова образуют последовательность сумм незави-
' симых одинаково распределенных величин, то из этой теоремы
немедленно получаем
Следствие 7. С вероятностью 1
S.
limsnp —^ = а,
P(Sh>bk) \
Доказательство теоремы 4. Достаточность. Ес-
Если выполнено условие теоремы, то по следствию 5 Р (swp{Sk —
\ k
—гк) < оо) == 1. Следовательно, {гп) есть верхняя последова-
последовательность для {SJ и
/ S \
Р lim sup — < e = 1.
\ ft-» IX) Л /
А так как г произвольно, то
Р (limsup45-<0) = 1,

258 •> ГЛ. 11. ФАКТОРИЗАЦИЮГШЫЕ ТОЖДЕСТВА
Необходимость. Наоборот, если выполнено равенство
S
A1), то с вероятностью 1 с некоторых пор ~ «<? для любого
€ > 0. Но это значит, что sup(?fe— гк)< <*> с вероятностью 1 и,
к
стало быть, ряд 2* к—— сходится. Щ
Чтобы из этой теоремы получить обычный усиленный закон
больших чисел, достаточно воспользоваться п. 2 следствия 6.
В заключение этого параграфа сделаем одно замечание.
Замечание 2. В доказательстве следствий 2 и 5 фигури-
фигурировало равенство Р (?<10) = Р (т]+ = оо). Более топким фактом
является соотношение
которое мы сейчас в виде упражнения и докажем. Имеем
п=1
Надо убедиться, что вероятность последнего события, которое
обозначим "черев А, равна 0. Но это так в силу того, что Лс^0 =
= (limsiipSn = 01 и Р(Д0) = 0 (см. § ЮЛ). 4
§ 3. Распределение S = max @, g) = max 5*
В разного рода приложениях (одному из низе мы посвятим
следующий параграф) представляет интерес распределение слу-
случайной величины
разумеется, в том случае, когда Р (?<С °°) = 1.
Мы установим здесь, как связано распределение S с рас-
распределением %+> г|+ и с компонентами факторизации функции
ф()
Заметим прежде всего, что случайная: величина т]+ является
марковской. Для таких величин, как легко установить (ср. с лом-
iron 9.1), последовательность ?ц = St^+i,?2 = 5л+-*-2» ••• г[а мно-
множестве {со:г]+<оо} (и ири условии {цл. < со}) распределена так
же, как gj, g2, •¦•» и не зависит от (л+, gt, ...., gn+). Действи-
Действительно,

§. РАСПРЕДЕЛЕНИЕ S 257
Рассматривая новую последовательность {^/J^Li,- мы опять
замечаем, что для псе уровень 0 (уровень %+ для исходной по-
последовательности) будет превзойден лить с вероятностью
Р = Р 01-!- < оо), а распределение ?* = sup (gj + ,. r % + g*) будет
совпадать с распределением ?.
Таким образом, обозначив ?*=тах@, ?*), можно записать,
что
@ на {оз; т]+ = оо},,
S = S (со) - (^+ + 5* _ х+ + 5* ыа {@. % < ^
Так как 5*, как уже отмечалось, по зависят от %+ и ц+1 и рас-'
пределение 5* совпадает с распределением 5, то
М^ = A - р) + М (е144^; ц, < оо) =
- A - р) + Ме'^М
Отсюда вытекает
V Р(?,, >0)
Теорема 5. ?слм ^——~ <С со шш, чго го же, если*
Р = Р(ч+ < оо)< 1, то
Совершенно аналогичным образом можно было бы получить
соотношение
где ро = Р(т]он. <оо)<1.
Факторизационные тождества в этом случае можно записать
в виде
_ р) Л A) 0 -
0) d - М^
Совершенно аналогично можно, найти х. ф. момента времени
0 = min{k:Sh = S), когда впервые достигается максимум S = SQ,
Для этого надо воспользоваться равенством
_ @ на {со: г\+ = оо},
~ lr]f + 9* на {со: т]+ < оо},
где 6* распределена па {т)+ < °°} так же, как 0, и от т)+ не зави-
зависит. Находим
Mze = A - р) + Мг°М (z^; ц+ < оо);
17 А. Л. Боровков

?58 ГЛ. 11. ФАКТОР 113ЛЩЮШ1ЫЕ ТОЖДЕСТВА
и окончательно
Полагая в факториза[дюнном тождестве X = 0, получим так-
также соотношение
1 — z ~ И — М B +; г). < со !! 1 — Fvtz ~ = п - '
L \ ' /JL J [V}7U
§ 4. Системы обслуживания
В этом параграфе покажем, что к изучению распределения
величины S, рассмотренной в § 3, приводит исследование систем
массового обслуживания с очередью.
Представим себе, что в некоторую систему через интервал «я
времени т1т т2, ... поступают «вызовы», которые надо обслужи-
обслуживать. Это могут быть телефонные вызовы; самолеты, прибываю-
прибывающие в аэропорт; клиенты бытовых учреждений; сообщения, со-
содержащие информацию, которую надо обрабатывать,, скажем, па
электронной машине и др. Пусть на обслуживание k-vo вызова
(первый вызов пришел в момент времени 0, второй в момент Ti
л т. д.) тратится время [Зк, k=i, 2, ... . Если в момент прихода
к-то вызова система занята обслуживанием одного из предыду-
предыдущих вызовов, то он становится в «очередь» и ждет своего обслу-
обслуживания, которое начинается немедленно после того, как си-
система обслужит все предыдущие вызовы. Задача состоит в отыс-
отыскании распределения времени ожидания wni которое п-й вызов
ждал начала своего обслуживания.
Предположим, для простоты, что wt = О и найдем, как свя-
связаны между собой значения wn+i и wn. (/г + 1)-ы вызов пришел
позже п-то на время тп, но зато ему придется ждать дополни-
дополнительно (по сравнению с ?г-м вызовом) время рп обслуживания
п-то вызова. Поэтому
если только wn — тп+Р»^О. Если же wn — тп+ Р* < 0, то это-
зшдио wn+i = 0. Таким образом, если обозначить !п-н = $»--ти,
то
Wn+i *= msxx(wn + |n+i, 0), п > i, Wi = 0.
Покажем, что решением этих уравнений является последова-
последовательность
wn = Sn — mini (Si, ..., Sn) = Sn — 'у,,,
где, как и прежде, Sn = 2 bf Так как 54 — ifi ^-0» то достаточ-
достаточно проверить рекуррентное соотношение
Sn+i - Tn-fi = шах @, Su + |w+1 - ifn}%

§ 5. ТОЖДЕСТВА С ПОКАЗАТЕЛЬНЫМИ РАСПРЕДЕЛЕНИЯМИ ыи
Если 5nJ.i>'Yn, то 7n+i = Т'г и и обеих частях A3) будет сто-
стоять Snfl — ч„. Если S^+i^Yn, то iSn+1 = 7n+i и л обеих частях A3)
будет стоять 0. Таким образом, равенство ии = ?п — *{п доказано.
Предположим теперь, что |ft независимы и одинаково распре-
распределены. Тогда разность
Sn — г{п = шах (Sn — 5Ь ..., 5, — S,,) =
= тах@, |„, gn + ?a-i, ..., I/1 + ... + I2)
будет распределена, очевидно, так же, как !$„.-, = max@, ?\, ...
..., Sn- 1) ~ max@t ?w-i). Так что распределение ш„ совпадает
€ распределением лшх@, ?n-i)- Так как ?„ монотонно сходится
к ^ при /г -^ оо, то всегда существует
Km P (wn <x)==F (шах @, Q < х) - Р E < х).
Это распределение называют стационарным распределением вре-
времени ожидания. Как мы уже знаем, оно будет собственным, если
Щ2 = Мрх — Мт, < 0. Если же М^ > MxIt' или М^ - Мтг и
Pi ^ Ti, то стационарное время ожидания будет бесконечным,
§ 5. Факторизацнонпые тождества для распределении,
связанных с показательной функцией
Рассмотрим теперь ряд примеров, когда факторизационные
тождества используются для отыскания явного вида распреде-
распределений х+? Л+1 S и других.
1. Предположим сначала, что Бри х > 0
при некоторых а>0 и 1>^>0. При 2' < 0 распределение gt
может быт]л произвольным. Этот случай замечателен тем, что
для пего распределение yv+ по зависит от г}.ь и является показа-
показательным. Действительно,
о
Р (х+ > л:; Л+ '= п) = j P (т)+ = /?, Sw-i e rfz, х+ > ж) =
= J P (tn-i < 0, S,^ e= dz, ?„ > ж — z) =
— oo
0
( P /? ¦—^ /p ^р//" ^r^ П Q /=- /7^\ —
^ ) i Vb/i -> x — ") • Vbn —1 ^ u: ^ n —1 ^= «z; 1~
— oo
= e~ax \ heaz dP '^-i^ 0? ^л-л <C z) =/? e~axrf
17"

l'Jl. 11. ФЛКТОРИЗАЦИ0Ш1ЫЕ ТОЖДЕСТВА
Отсюда следует, что
Ра = Р (% = П), Р
где р = Pi + p2 + ... Следовательно,
оо со
М (еШ+;у\+ < со) = Гeilxd(p - ре*) = P{aeiXx-axdx-
' г) t)
О О
и если S < оо с вероятностью 1 (т. е. если р < 1), то
Последнее равенство означает, что
р E = 0) = 1 — р, P(S>x) = ре'аа"р)х при х > 0,
ГЗ полученных соотношениях осталось неизвестным лишь чис-
число р (знаем только, что 1 —р = —™, если существует а =М^1<с0;
(см. следствие 2)). Предоставляем читателю с помощью
тождества
1 - ф (I) = (l + 7X^J [l-M (eax-; it < оо)] A4)
убедиться, что аA — р) = \i(l), где [хA)> 0 —единственный по-
положительный корень уравнения \|)(jji)=1, где гр (|л) = ср (—щ) —
= М^ х (я|)' @) <С 0, г|)" (jlx) > 0, ^(jli)-^co при [х-> а. При А, =
= —г|хA) правая часть тождества A4) обязана обратиться в 0).
Отметим также, что в рассматриваемом случае, пользуясь не-
независимостью %+ и г)+, нетрудно найти и распределение п+,
2. Предположим теперь, что при х>0
Р (ЬI <с —х) = Ье~ахх а > 0, 1 > 6 > 0,-
и что 5 с вероятностью 1 конечно. В этом случае заключения,
аналогичные предыдущим, справедливы относительно величин
%_, 1]_. Разница состоит лишь в том, что здесь Р(т]_<;оо) = 1
и, следовательно,

§ 5. ТОЖДЕСТВА С ПОКАЗАТЕЛЬНЫМИ РАСПРЕДЕЛЕНИЯМИ 261
Отсюда находим, в частности, что (см. A2))
1 - Ро = Р (Л°ь = оо) = -щ- -
В заключение следует отметить, что полученные соотношения
позволяют находить стационарное распределение времени ожи-
ожидания для систем обслуживания с ожиданием (см. § 4), когда
хотя бы одна из случайных величин xi или ^ имеет показатель-
показательное распределение (в силу ряда причин такие предположения
можно делать довольно часто. Имеется в виду также, что после-
последовательности {tj} и {[U составлены из независимых и одинако-
одинаково распределенных величин каждая). В самом дело, если, напри-
например, Р (Pjl > х) = е~ах, то для §i == ^ — Ti будем иметь при
х>0
Это означает, что мы находимся в условиях п. 1 этого парагра-
параграфа. Аналогично обстоит дело, если показательным является рас-
распределение Ть
Важные выводы о распределении рассматриваемых случай-
случайных величин E, г]+, %+ и др.) можно сделать, используя каче-
качественные аналитические свойства компонент факторизации
Cz±Ck), определяющих нужные нам распределения. Пусть, на-
например, ф(Х) есть рациональная функция от >v,
П-5Рг1д- A5)
(это будет, в частности, если \г = C — т (см. §4), где Рё§Га1,.
^ ^ Га2 и независимы. Представление A5) возникает и при дру-
других предположениях относительно ?i» связанных с показательным
распределением). Тогда требуемые аналитические свойства CZ;t(K)
(прежде всего аналитичность в соответствующих полуплоскостях)
будут иметь место, если только положить*)
Подробнее об этом см. [3].

202 ГЛ. 11. ФАКТОРИЗЛЦГЮНПЫЕ ТОЖДЕСТВА
гдеЯ^B;), Л^— все нули и полюса функции 1 —zcp(X)\ лежа-
лежащие в нижней полуплоскости.
В связи с изложенным можно отметить также, что если не-
некоторая х. ф. \р{Х) есть рациональная функция, то путем разло-
разложения ее на простые дроби соответствующее ей распределение
можно представить как смесь показательных распределений или
их сверток.
Рассмотрение случаев, когда факторизация позволяет нахо-
находить явные формулы, будет продолжено и § 8.
§ 6. Симметричные непрерывно распределенные
случайные величины
Будем говорить, что распределение gft симметрично, если оно
совпадает с распределением —?,,, и называть распределение ?,,
непрерывным, если функция распределения %к непрерывна. Для
таких величин распределения Sn при всех п также симметричны
и непрерывны и
Р (Sn > 0) = Р (Sn < 0) = 1/2, Р (Sn = 0) = 0.
Стало быть, здесь D(z)^ 1, Р (%+ = 0) = 0 и с вероятностью 1
В силу следствия 5 в рассматриваемом случае t; = °°т 7 = — °°
с вероятностью 1 и ц+ есть собственная случайная величина.
В силу следствия 4
= ехр |_ 2 4| = ехР (^ la A ~ Z)) = ^^^
Отсюда, разлагая в ряд Vl —z, находим, что
При больших п по формуле Стирлиига обнаруживаем, что
1 - -
Аналогичные формулы справедливы и для 1]-, ч„.

§ 7. ТОЖДЕСТВО ПОЛЛЛЧЕКА — СПИТЦЕРА 263
§ 7. Тождество Поллачска — Спнтцера
До сих пор мы получали различные факторизационные тож-
тождества как соотношения между числителями в представлениях
B), C) и D). Обратимся теперь к знаменателям. Получим еще
одно тождество, которое играет важную роль при исследовании
распределений
, ?„) = тах@, ?1? ..., Sn).
Это так называемое тождество Поллачека — Стштцера, связыва-
связывающее х. ф. 5п, 7г = 1, 2, ..., с характеристическими функциями
max@, Sn) тг=1, 2, ... .
Теорема G. При \z\ < 1, 1тК>0
- exp {f 4 Me*max@'efc)L
Если использовать обозначения теоремы 3, то правую часть
Сг+ «>)
этого тождества можно записать в виде — гт^—гтт~
(а — 2) 62+ (А)
Доказательство. Из теорем 1—3 и соотношения B) вы-
вытекает, что
lXSn; ?,, < О) = [ 1 - М (еш- г11"; п- < <*>)Г = ^- (Я.),
где принято М (V* °;^0<0J = 1. Обозначим St = «Sn-ft — 5Л<!
В* == min \k: S'l = 5* — шах @, Si, .. ., 5'"t)) @* есть первый mq^
меит достижения максимума в последовательности 0,5х, ,.., Sn).
'Тогда событие iSn ^ dr, ?„ < 0} можно записать в виде 1*5^^
е—dr, О,"! = п}- Отсюда следует, что
'"; О! = п) = Сг_ (- X). A6)
По последовательность $ь . .., 5П распределена так же, как
суммы %ъ Ei + ^2 7 . • • Д^ + •••-!- 1т гДе 5/i = —?ь. Если поло-
положить 0п = л11п{А:: 5,г=^6гд}, то тождество A0) можно эквивалент-
эквивалентным образом записать в виде
гдп Л\._(Х) есть отрицательная компонента факторизации, функ-
I — z<p* (X) = 1 — 2ф(~Я), соответствующей случайной вели-

264 ГЛ. 11. ФАКТОРИЗАЦИОННЫЕ ТОЖДЕСТВА
чине —?ft. Так как
и функция 1/Сг+(-—д) обладает всеми свойствами отрицатель*
ной компоненты С*-(А,) факторизации функции 1 —zcp*(A,),
а функция 1/Сг.-(—-Я) обладает всеми свойствами положитель-
положительной компоненты, то мы находим, что Сг_ (к) = Cz+ (— X) и
Теперь надо заметить, что
ft-=o
n
/i-0
Так как в правой части стоит свертка двух последовательностей*
то
Полагая % = О, получим
Следовательно,
= expi— ln(l — ,
= exp
Теорема доказана. ^ '

§ 8. ДИСКРЕТНЫЕ БЛУЖДАНИЯ, НЕПРЕРЫВНЫЕ СВЕРХУ 265
§ 8. Явные формулы для дискретных блужданий,
непрерывных сверху
Дискретным блужданием, непрерывным сверху, будем называть блуж-
блуждание частицы, порожденное последовательностью сумм О, Sb S2, ..., когда
%k целочислешш и шах ?/{ (со) = 1.
со
Другими словами, если обозначить fh = Р (^ = /с), то /& — 0 при k ^ 2,
1
2/ft =1. В этом случае, очевидно, х+ = 1 на множестве {rj+ < оо), и в си-
— оо
лу теоремы 5
Это означает, что 5 имеет геометрическое распределение
P(S = k) = A-Р) р\ ^ = 0, 1,
Осталось лишь найти р. Чтобы сделать это, заметим, что по формуле полной
вероятности (по первому скачку) при любом k ^ 2
1 1
Р (•* = *) = .2 ff(S=k-j); 1=2j/^"J-
j—— оо j=_-oo
Таким образом, г = 1/р есть решение уравнения /(г) == 1, где /(z) есть
производящая функция / (z) = Mz*1. Так как /(г) всегда выпукла (см. гл.7),
то это уравнение имеет не более двух корней: один из них z = 1, другой
корень z > 1 возможен лишь в случае MgjL<0. Итак, в случае М^<0
число р < 1 есть единственное решение уравнения 1 = f(p~l).
Оказывается, для блужданий, непрерывных сверху, могут быть пайдеиы
и многие другие явные формулы. Очевидно, что в этом случае последова-
последовательность {Sn} не может «перескочить» ни один целочисленный уровень
х >• 0: если Sn >> х, то обязательно найдется к ^. п такое, что Sh = х.
Задача, которая нас _иптересует, по-прежнему" состоит в отыскании рас-
распределения максимума Sn == max @, ^i, ..., Sn), знание которого, как ужо
отмечалось, бывает важным для многих задач математической статистики,
теории массового обслуживания и др. Отметим, что найти распределение
Sn — это то же самое, что найти распределение
ц(х) = rain {к: Sh ^ х}, г]@) = 0,
так как
{Sn< x) = {Ti (*)>«}. . A7)
Здесь мы считаем ц(х) = оо, если S <С х.
Тояодество § 7 дает двойное преобразование над распределением_$п- Ис-
Исследования этого тождества показывают, что само распределение .$п (пли
т|(ж)), как правило, в явном виде через распределение |а не выражается.
Однако для дискретных блужданий, непрерывных сверху, оказывается,
ммеют место замечательные «двойственные» соотношения, которые мы сей-
сейчас с помощью тождества Поллачека — Спитцера докажем.
Теорема 7. Если ?& целочислеины, то условие Р (b>h ^ 2) = 0 явля*
ется необходимым и достаточным для того, чтобы
пР (ц (х) - и) = хР (Slh - х), х^ 1. A8)

260 ГЛ. ii. ФЛКТОРИЗЛЦПОШ1ЫЕ ТОЖДЕСТВА
С помощью тождества Вальда нетрудно убедиться также, что если су-
существует M2L == а > 0, то блуждание {$п} будет непрерывным сверху тогда
и только тогда, когда Мт) (х) — х/а.
Доказательство. Обозначим
Рх = Р (П (*} = oo) = P(S< *), pXtn - Р (I] (х) = п)г
оо
Qx,n = Р (Л (*) > п) = 2 ^x,/t + /V
Так как для каждого 0 ^ у ^ д?
A] (Ж) = «}С U {!] (у) = k),
то, используя непрерывность сверху, можло написать по формуле полной
вероятности
п
Рх,п ~" 2j Pf/.kPx-y.n-h1
где ^о;о = 1, Ру, о = 0 при г/ >> 0. Следовательно, при \z\ <^: 1 по ираннлу
свертки
оо
рх (z) = М (^*); 1] (х) < оо) = V ЛХ|71^ = Ру (z) Рх„у (z).
/i=0
Полагая ?/==!, pi(z) = /?(з), получим
Px(z) = p(z)px_!(z) = рж(з), а: > 0.
Отсюда можно легко найти производящую функцию последовательно-
последовательности qXj п:
оо П — 1
рх ъ ъ i-zn
Заметим, что здесь число рх A) = Р (т) (х) <С оо) == р (S ^ .г) может
быть и меньшим, чем 1. Используя A7), получим
P(Sn~-=x)^P ()] (х + 1) > и) - Р (Т] (х) > л),
(| __ рХ-\ 1 (z)) __ (j ___ рХ (Z)) рХ (z) A — р B))
= ^ = J__ = J-— §
Наконец, пользуясь абсолютной сходимостью фигурирующих ниже рядов,
находим при |z>| < 1, \z\ < 1
оо оо оо
П—0 ОС—О П—0

§ 8. ДИСКРЕТНЫЕ БЛУЖДАНИЯ, НЕПРЕРЫВНЫЕ СВЕРХУ 2(>7
Обращаясь теперь к формуле Поллачека — Слптцора, можно записать, что
чгч zn ._ 1пах(о,8„) = in 1 — Р (z) _ .,
>^-1-Mi; ^ n) xz — 1аA — yp(z)) =
^ln
Сравнивая здесь коэффициенты при vx, x^\, получим
Учитывая, что /j^(z) = px(s) и сравнивая в A9) коэффициенты при zn,
n ^ 1, получим
Достаточность утверждения теоремы доказана.
Читателю предлагается проверить, что имеет место также равенство
где /х (г) = 2 %пР {$а ~ ^J» JI чт0 /;B) ПРИ lzl ^ 1 является единствен-
п—о
иым в области \р\ ^ 1 корнем уравнения zMp 1 = 1.
Докажем теперь необходимость условия P(gA^2) = 0. Обозначим
4 = Р (^1 = А)« То1'Да в силу A8)
ею
Полагая / (v) = 2 vxfx> получим отсюда
v(uk~{) v(i-f(v))
оо оо
ЭС —1
Мы получили относительно j(v) уравнение
/ (v)
Г (o) =
1 — у •
Сделав замену у = 1 — /, придем к уравнению у' — —¦" ^ 1_ ^ , из которого
находим In j/ = In A — у) + с, f(v) = 1 ~ ?/ = 1 — сA — у).
Но это означает, что /а = 0 при А; ^ 2. ^
Пользуясь полученными формулами, можно, например, найти в приме-
примере 4.8 распределение для времени разорения игрока при игре с бесконечно
богатым противником (суммарный капитал равен оо). Если начальный ка-
иитал первого игрока равен z, то для времени его разорения i](z) получим

268 ГЛ. 11. ФАКТОРИЗАЦИОННЫЕ ТОЖДЕСТВА
где Sn = 2 V» Р Ej = 1) = tf> Р (lj = — 1) =¦= р (р есть вероятность вьтигры-
j—2
ша первого игрока в одной партии). Следовательно, если п и z вместе либо
четны, либо нечетны, то
( п \ —г !*".¦¦
р (т, B) = „) = i-1 n-^ \q2 p 2 B0)
и Р A] (г) == п) == 0 в противном случае.
Представляет интерес вопрос, как быстро убывает P(tj(z) !> и) с рос*
том /2 в случае, когда игрок с вероятностью 1 разорится, т. е. когдаР (т) (z)<c
< оо) = 1. Как мы уже знаем, это будет тогда и только тогда, когда р ^ q.
(Такое утверждение будет следовать так же и из рассмотрений § 12.3).
Применяя формулу Стирлинга так же, как это делалось в локальной
предельной теореме для схемы Берпулли, из B0) уже нетрудно получить,
что при каждом фиксированном z при п-^оо (п и z одной четности) й
p< q
P (ti (z) ^n)~zy — при p=q.
Формулу A8) при P (Sn= x)>0 можно переписать также в виде
Р (ц (х) = n/Sn = х) = х/п, B1)
обозначающем, что среди траекторий {Sk}, к = 0, 1, ..., п, со свойством
Sn = х доля тех, которые имеют абсолютный максимум в последний мо-
момент, составляет х/п независимо от характера распределения |* (при ус-
условии Р (?fe ;> 2) = 0). В таком виде теорема 7 приобретает комбинаторный
характер и может быть доказана комбинаторным путем.
Действительно, пусть | и а означают, соответственно, векторы
l==(Si» •••»?n)» a == (ai» •••»ап)> ^х — совокупность разных векторов а со
г?
свойством 2 % = ^» ^2 —совокупность векторов «из Fx, отличающихся со-
1
ставом координат. Тогда
где схп (а) —соответствующие целочисленные коэффициенты. Далее
•р (т, (з) = И) = ^ Р(| = а)Р(л(*)=|г/6 = в)= 2 Ьхп ИР (Е
2
B2)
где Р (т) (ж) = л/| = «) равны 1 или 0, так что Ь%^Щ1сгп{а) есть доля
таких вероятностей, равных 1. Достаточно показать, что эта доля равна x/nt

§ 8. ДИСКРЕТНЫЕ БЛУЖДАНИЯ, НЕПРЕРЫВНЫЕ СВЕРХУ 269
Мы убедимся в этом пе только для каждого asF}, а более того, для каж-
каждого подкласса Са векторов из Vx, отличающихся от «sFx сдвигом ко-
координат;
где Tla = (al+v ..., ап, ап+1, ..., an+l), an+j = а. (каждому a s V%
в сумме B2) отвечает более широкий класс, распадающийся па подклас-
подклассы вида Са).
Итак, установим, что
Р (т| (х) - пЦ = Tla) = 1 B3)
5ля д; индексов I из п возможных.
Обозначим
Траектория {^}, Л" = 1, ..., и, распадается на х «лестничных моментов»
(точек возрастания сумм S™): ;-й «лестничный момент» равен t\m(j). Оче-
Очевидно, что ц1 (х) = га, если I = m, т + r|m(l), ..., т + Г)т(ж) = т + ^? и что
Ц (х) < Л Для других /. Отсюда следует B3) и вместе с этим равенства
М = п) = ± ^ с*.я (а) Р F = i) = -J Р EП - х).
Если Р (?ft > 2) >0, то из приведенных рассуждений видно, что в этом
случае число «лестничных моментов» траектории [S™] будет ^х, а для
некоторых траекторий, имеющих положительную вероятность, будет строга
меньше х. Это означает, что в сумме B2) выполняется Ъхп («)/^Xjn (о) < ^,
а для некоторых а это неравенство будет строгим. Следовательно в случав
P(>2)>0
Отсюда следует необходимость в утверждении теоремы 7.

Глава 12
ПОСЛЕДОВАТЕЛЬНОСТИ ЗАВИСИМЫХ ИСПЫТАНИЙ.
ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
§ 1. Определения и примеры. Классификация еоетояшш
До сих пор мы изучали последовательности независимых ис-
испытаний. Рассмотрим теперь простойший вариант последователь-
последовательности зависимых испытаний.
Пусть G есть некоторый эксперимент, который имеет конеч-
конечное или счетное множество исходов {Ei4 E2, ...}. Предположим,
что мы неограниченно повторяем эксперимент G. Номер исхода
л-го эксперимента обозначим Хп.
Вообще говоря, вероятности различных значений Ехп могут
зависеть от того, какие события появились на предыдущих п — 1
испытаниях. Если же эта вероятность при фиксированном исхо-
исходе Ехп_1 испытания с номером п — 1 не зависит от исходов ос-
остальных 72 — 2 испытаний, то эта последовательность испытаний
образует цепь Маркова.
Чтобы дать точное определение цепи Маркова, рассмотрим
последовательность целочисленных случайных величии {Х„}^°=п.
Если в п-ы. испытании реализовалось событие Eh то мы будем
считать, что Хп = /.
Определение 1, Последовательность {Хп}™ образует
цепь Маркова, если
Р(Хп — j/XQ = ft0, X1=-kl^ . . ,, ^w-2 == &п-2> ^н-1 = 0 —
= Р(Хп = /7Х„_1 = /)^^). A)
Таким образом, цепь Маркова можно представить себе как
некоторую систему с возможными состояниями {?,, E2i ...}. За-
Задается некоторое «начальное» распределение величины Хо:
затем в целочисленные моменты времени система меняет свое
состояние, при этом вероятность в момент времени и попасть в
состояние Е3, если известна вся предыстория системы, зависит
только от того, в каком состоянии находилась система в момент
л —1. Это свойство кратко можно было бы охарактеризовать так:
при фиксированном настоящем будущее не зависит от прошлого.
Например, ветвящийся процесс {?п}, описанный в § 7.8Т гдо
?п есть количество частиц в w-м поколении, представляет собой
цепь Маркова с возможными состояниями {0, 1, 2, ..,}.

g 1. КЛАССИФИКАЦИИ С0СТОШШИ ^ii
В терминах условных математических ожиданий или услов-
условных вероятностей (см. § 4.8) свойство марковости (так будем на-
называть свойство A)) можно записать также в виде
Р (Хп = j/a (Хо, .,., Х,,^)) - Р (Хп - j/o (Xn-i))r
где о(-) есть о-алгебра, порождегшая случайными величинами,
стоящими в аргументе, пли, проще,
Р (Хп = j/X0, ..., *„_,) = Р (Х„ = №-i).
Такое определение немедленно допускает обобщение на цепи
Маркова, множество состояний которой есть произвольное из-
измеримое подмножество прямой.
Определение 2. Марковская цепь {Хп}™=0 называется
•однородной, если вероятности jiff не зависят от п.
Вопрос существования последовательности {-Xnjn^o» пред-
представляющей собой цепь Маркова с данными вероятностями перс-
хода p^iPij* ^ 0, ^iPij; = 1\ и заданным «начальным» распредс-
3 )
лением \р)[) значения Хо, решается, как и в независимом слу-
случае, с помощью теоремы Колмогорова (см. Приложение 2) и за-
задания согласованных совместных распределений равенствами
(Ло = /i0, Ах = /vj, » t s, Лп = /iu; = Pk^Ph^Ph^k^ *«* Plin-lkn'
которые, как легко видеть, удовлетворяют марковскому свой-
свойству A).
Рассмотрим несколько примеров.
Пример 1. Блуждания с поглощением и с отражением.
Пусть а > I — целое число. Рассмотрим блуждание частицы по
.целым точкам между 0 и а. Если 0 < к < а, то из точки к с ве-
вероятностями 1/2 частица переходит в к—1 или к + 1. Если /г
равно 0 или а, то частица остается в точке к с вероятностью 1.
Это так называемое блуждание с поглощением. Если Хп —
случайная величина, равная координате частицы в мо-
момент /г, то последовательность {XJ образует цепь Маркова, так
как условное распределение случайной величины Хп зависит
только от значения Xn-i. Легко видеть, что эта цепь однородна.
Таким блужданием можно описывать безобидную игру (см.
пример 4.8) в том случае, когда суммарный капитал обоих игро-
игроков равен а. Попадание в точку а будет означать разорение вто-
второго игрока.
Если же частица из точки 0 с вероятностью 1 переходит в
точку 1, а из точки а с вероятностью 1 в точку а—1, то полу-
получим блуждание с отражением. Ясно, что и в этом случае положе-
положения частицы Хп будут связаны в однородную цепь Маркова.
Пример 2. Пусть {^}/Г---)— последовательность независи-
независимых целочисленных случайных величин и d > 0 — целое число»

272 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
п
Случайные величины Хп = 2 Sft(niodd), полученные сложением
Ik по модулю d I Хп = 2 ?л — /d, гДе 7 таково, что 0< Хп < г/),
образуют цепь Маркова. Действительно, Хп = Xn-i + ?n (mod a),
поэтому условное относительно Хь Х2, ..., Хп_! распределение Л/4
зависит только от значения Xn-i-
Если к тому же {|J одинаково распределены, то эта цепь
будет однородной.
Разумеется, все сказанное останется справедливым и при
d = °°, т. е. для обычного сложения. Только в этом случае мно-
множество возможных состояний системы будет бесконечным.
Из определения однородной цепи Маркова следует, что для
нее вероятности р\] перехода из состояния Ег в Е$ на п-м. шаге
не зависят от п. Обозначим эти вероятности рц. Они образуют
матрицу Р = WpijW со свойствами:
Второе свойство есть следствие того, что из состояния Ег систе-
система с вероятностью 1 попадает в одно из состояний Еи Е2, . . ..
Матрицы с указанными двумя свойствами называются стоха-
стохастическими.
Матрица Р полностью описывает изменение состояния систе-
системы за один шаг. Рассмотрим теперь изменение состояния систе-
системы за к шагов. Введем обозначение Р\; (к) = Р (Xk = j/XQ = i)«
При к > 1 по формуле полной вероятности получаем
Pij (к) - 2 Р (Хк-г = s/X0 = i) psj = 2 pie (* - 1) ftj.
Суммирование здесь ведется по всем состояниям. Если обозна-
обозначить Р(к) = \\рц(к)\\ матрицу, образованную вероятностями рц(к)у'
то написанное выше равенство будет означать, что Р(/с)==
= Р(к— i)P или, что то же, P(k) = Ph. Таким образом, матри-
матрица Р однозначно определяет переходные вероятности за любое
число шагов. (Здесь следует добавить, что для однородной цепи
Р (Хп+н - J/Xn = i)~P(Xh= /До = i) = Pij (к).)
Из сказанного видно, что «распределение» цепи будет полностью
определяться заданием матрицы Р и начального распределения
рХ = Р(Хв = й).
Предоставляем читателю в качестве упражнения проверить*
что для любых /с^1и множеств Ви ..., Вп-к
Р {Хп = j/Xn-h « i\ Хд-л-! gB,,, , XQ e 5n~^) = Pij (ft).

§ 1. КЛАССИФИКАЦИЯ СОСТОЯНИЙ 273
Для доказательства этого соотношения можно сначала проверить
его при к = 1, а затем воспользоваться индукцией.
Последовательность независимых целочисленных одинаково
распределенных случайных величин Хп очевидно образует цепь
Маркова, для которой рц =р} = Р (Хп = /). Здесь P(k) = Ph = P,
Классификация состояний*).
Определение 3.
К1. Состояние Ег называется несущественным, если сущест-
существуют такое состояние Е, и целое число ?0>0, что рц{Ъ)>0>
P3i(t)=O для любого целого t.
В противном случае Et называется существенным состоянием.
К2. Существенные состояния Ех и Е, называются сообщаю-
сообщающимися, если существуют такие целые числа ?>0 и s > О, что
р«@>0 и Pa(s)>0.
Пример 3. Пусть система может находиться в одном из
четырех состояний {?\, Z?2, /?3, #J с мат-
матрицей
0
1/2
0
0
'1/2
0
0
0
1/2
0
1/2
1/2
0
1/2
1/2
1/2
(на рис. 9 состояния обозначены точка-
точками, переходы из состояний в состояния —
стрелками, числа па стрелках означают
соответствующие вероятности). В этой цепи состояния Е{ и Е2
несущественны, а Е3 и ?4 являются существенными сообщающи-
сообщающимися состояниями.
В примере 1, описывающем блуждание с поглощением, со-
состояния 1, 2, ...., а~~1 будут несущественными. Состояния 0 и
а существенны, но не сообщающиеся (их естественно называть
поглощающими). В блуждании с отражением все состояния су-
существенны и сообщающиеся.
Пусть {Xri}™^Q — однородная цепь Маркова. Выделим класс
5° всех несущественных состояний. Пусть теперь /^ — какое-ни-
какое-нибудь существенное состояние. Обозначим ?#. класс состояний,
включающий в себя Е{ и все состояния, с ним сообщающиеся.
Если Ej^Sev то Е} существенно, сообщается с Ег я Е\^. Se^
¦ Следовательно, SEi = Ее у Таким образом, все множество суще-
существенных состояний разбивается на непересекающиеся классы
сообщающихся состояний, которые будем обозначать S\ S'\ ... ,
*) Здесь и в § 2 будем следовать в основном работе Л. II. Колмого-
Колмогорова [9] .
IS А. А. Боровков

274
ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
Определение 4. Если класс «S^ состоит из одного со-
состояния Ег1 то это состояние называется поглощающим.
Ясно, что если система попала в существенное, состояние Eh
то она уже никогда не выйдет из класса SEv •
Определение 5. Цепи Маркова, состоящие из одного
класса существенных сообщающихся состояний, называются не-
неразложимыми. Если цепь содержит более одного класса, то она
называется разложимой.
Если состояния перенумеровать так, чтобы сначала шли со-
состояния из 5°, затем из 51 и т. д., то матрица переходных веро-
вероятностей будет иметь вид (см. рис. 10). Здесь подматрицы,
О о и
Sl
V/,
Рис.
зашриховапиьте в клеточку, являются стохастическими. Каждая
из них соответствует некоторой неразложимой цепи. Подматри-
Подматрицы, отмеченные нулями, содержат одни нули.
Одним из основных объектов изучения здесь являются нераз-
неразложимые цепи Маркова. Ими и займемся.
Введем следующие обозначения:
/,• (п) = Р (Хп = у, Хп_х Ф /,..., Хх ф j/X0 = /),
f3(n) есть вероятность того, что система, выйдя из /-го состоя-
состояния, впервые вернется в него через п шагов. Вероятность того,
что система, выйдя из /-го состояния, вновь когда-нибудь вер-
вернется в него, равна F3.
Определение 6.
КЗ. Состояние Е, называется возвратным, если F3—l, и не-
возвратным, если Fj<l.
К4. Состояние Е3 называется нулевым, если Рз3{п)-*-О при
п -> оо? и ненулевым в противном случае.
К5. Состояние Е3- называется периодическим с периодом dh
если возвращение с положительной вероятностью в Е3- возмож-

§ 2. ОДНОТИПНОСТЬ СОСТОЯНИЙ 27S
но только за число шагов, кратное d,>l, и d, есть наибольшее
число, обладающее этим свойством.
Другими словами, dj есть общий наибольший делитель
(о. н. д.) множества чисел {п: /,(/г)>0}. Заметим, что из этого
множества можно всегда выбрать конечное подмножество
Ьг17 ..., nh) такое, что dj есть наибольший общий делитель этих
чисел. Ясно также, что /?#(^) = j3(n) = 0, если пФО (moddj).
Пример 4. Рассмотрим блуждание частицы по целым точ-
точкам па вещественной прямой, задаваемое следующим образом:
частица либо с вероятностью 1/2 сдвигается на единицу вправо,
либо с той же вероятностью остается на месте. Здесь /3A)=1/2Т
а для п> \ fj(n) = Q для любой точки /. Поэтому Fj < 1 и все
состояния невозвратны. Легко видеть, что ри(п)= 1/2п-*¦(), по-
поэтому все состояния нулевые.
Если же точка с вероятностью 1/2 смещается вправо и с той
же вероятностью влево, то мы получим цепь с периодом 2, так
как вернуться в любое фиксированное состояние можно лишь за
четное число шагов.
§ 2. Необходимые и достаточные условия
возвратности состояний. Теорема об однотипности
состояний неразложимой цени,
структура цепи в периодическом случае
Напомним, что производящей функцией последовательности
{ап}™=0 называется функция
где z — комплексное число. Если последовательность {ап} ограни-
ограничена, то этот ряд сходится при Ы < 1.
Теорема 1. Состояние Ej возвратно тогда и только тог-
тогда, когда Pj = 2 Рл G;) ^ °°- Для невозвратного Ej
р.
Fj ^ ttV/ w
Утверждение этой теоремы есть своего рода распространение
леммы Бореля—Каителли па случай зависимых событий Ап =
= {Х,1==/}. События Ап происходят с вероятностью 1 бесконечное
оо
число раз тогда и только тогда, когда 2 Р (^п) = Pj = со.
1
Доказательство. По формуле полной вероятности имеем
18*

278 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
Введем производящие функции последовательностей Ри{п) и
<Ш>
Pi (*) = 2 PU (П) Л F} (z) = 2 U (it) Л
П=1 П=1
Оба ряда сходятся внутри единичного круга и являются там ана-
аналитическими функциями. Выписанная выше формула для рц{п)
после умножения обеих частей на zn и суммирования по п при-
приводят к равенству
Pj(z) = 2/Д1) A + Р}{г) )+ 22/iB) A + Р,B) )+ , . . =
Таким образом,
Пусть Р, = оо. Тогда P}(z)^>- °о при z 11 и, стало быть, F^z)-*- 1.
Из того, что Fj(z)<Fj для вещественных z < 1, получаем, что
^ = 1.
Пусть теперь Fj = l. Тогда F;(z)~>-1 при z t 1, а поэтому
Pj(z)-*-oot Значит, Pj = oo. Если Р^<<», то при z = l получаем
равенство B). ^
оо
Число Pj == 2 Pjj (^) можно интерпретировать как среднее
число попаданий в состояние Е,, если начальным состоянием то-
тоже было Ej. Это следует из того, что число возвращений в Е)
можно представить в виде S I(Xn = j) (здесь, как и прежде,
1 (Л) — индикатор события А). Поэтому математическое ожида-
ожидание числа возвращений равно
оо оо сю
м 2 / (хя = /) = 2 м/ (х„ = л = 2 р« (п) = Л.
п=1 п=1 п=1
Из теоремы 1 вытекает
Следствие 1. Невозвратное состояние всегда является
нулевым.
Это очевидно, поскольку из сходимости ряда 2fti(^)< °°
следует р»(п) -*• 0.
Таким образом, на основании определений КЗ—-К5 мы могли
бы выделить в неразложимой цепи 8 возможных типов состоя-
состояний (каждый ил трех признаков может быть или не быть). Но
на самом деле их оказывается меньше, так как невозвратные со-
состояния автоматически являются нулевыми, а ненулевые— воз-
возвратными. Поэтому возможны лишь 6 типов состояний, которые
порождаются

§ 2. ОДНОТИПНОСТЬ СОСТОЯНИЙ 277
1) Классификацией по асимптотическим свойствам вероятно-
вероятностей Рп{п) (невозвратные состояния, возвратные нулевые, нену-
ненулевые).
2) Классификацией по арифметическим свойствам вероятно-
вероятностей ра(п) или fj(n) (периодичность и непериодичность).
Теорема 2 (теорема солидарности). В неразлооюимой цепи
Маркова все состояния принадлежат одному типу: если хоть од-
одно возвратно, то и все возвратны; если хоть одно нулевое, то и
все нулевые; если хоть одно периодично с периодом d, то и все
периодичны с периодом d.
Доказательство. Пусть Ек и Ej — два различных состоя-
состояния. Существуют числа N и М такие, что
Из формулы полной вероятности
pkh (ЛГ + А/ + и) = 2 Ры (N) pls (n) psh (M)
Us
следует неравенство
Здесь п > 0 — произвольное целое число, а = Pkj(N)> 0? ?> =
= p3h(M)>> 0. Точно так же можно получить неравенство
Следовательно,
ip pkh (л + М + TV) > рф)><*$Рпн (п-М- N). ' C)
Из этих неравенств видно,. что асимптотические свойства у
Pkk{n) и Рп(п) одинаковы. Если Z^ — нулевое, т. е. рЛ?1(/г)-^О', то
и Рзз{п)~*О. Если Ek — возвратное или, что то же^/^^Р/^ОО^
= °°, то
и, значит, Ej — тоже возвратное.
Предположим теперь, что Ек — периодическое состояние с пе-
периодом dh. Если /?^(«)>0, то dk делит п. Обозначать этот факт
будем символом dk/n. Так как
pkk{M + N)>a$>0, то
Покажем, что состояние Ej тоже периодическое и период
его dj равен dk. Действительно, если Рц{п)> 0 для некоторого п%
то в силу C) pkk(n + M + iV)> 0. Следовательно, dk/(n + M + N),
а из того, что dJ(M + N), мы получаем djn и, следовательно,
dk ^ dj. Теперь аналогичным способом можно доказать, что
dj ^ dh. Таким образом, dj = dh, Ц

ГЛ. 12. ДИСКРЕТНЫ!': ЦЕПИ МАРКОВА
Если состояния неразложимой цени Маркова — периодиче-
периодические с периодом d > 1, то цепь называется периодической.
Покажем теперь, что изучение периодических цепей в зна-
значительной мере может быть сведено к изучению непериодиче-
непериодических. Для этого нам понадобится
Теорема 3. Если, цепь Маркова — периодическая с перио-
периодом d, то множество состояний разбивается на d подклассов 4j\,,
х? и ..., xF</_i таких, что с вероятностью 1 за один шаг система
из класса х? k переходит в класс 4Vm, из класса x?d~i система пе-
переходит в х?0.
Доказательство. Выберем какое-нибудь состояние, на-
например, ?\. С помощью этого состояния построим подклассы
Ч'о, ..., l?d-i следующим образом: Е{^х?а, 0 < а < d - 1, если
существует целое число к > 0 такое, что pu(kd + a)> 0.
Покажем, что никакое состояние не может принадлежать сра-
сразу двум подклассахМ. Для этого достаточно доказать следующее
утверждение: если Ег <= ЧГа и для некоторого s pu{s)>0, то
s ^ a(modd).
Действительно, существует число t{ > 0, для которого
Pa(ti)>Q. Тогда в силу определения х?а имеем
К ( + /)>0 С
р
0. Кроме того, /?11E + /1)>0. Следовательно,
и d/(s + ti). Это влечет за собой a«s(modd).
Так как из состояния ?\ можно с положительной вероят-
вероятностью попасть в любое состояние /?,-, то (J гГ« содержит все мно-
множество состояний.
Докажем теперь,
что система из х?а за 1 шаг с ве-
вероятностью 1 переходит в x?a+i (а+1 понимается по moid).
Для этого надо показать, что для
Щ
о
О
0
п
и
о
111
О
0
0
0
О
S
PU
Для этого в свою очередь достаточ-
достаточно показать, что pi3 = 0, если Z?* s
е Wa, E3 & xFa+i. Если допустить
противное, то, учитывая неравен-
Рис. 11 ство ри (kd + а) > 0, получим
Pij(kd + a 4-1)> 0, и, следовательно,
jBJe4/a+i. Полученное противоречие заканчивает доказательство
теоремы. ^
Из доказанной теоремы видно, что матрица периодически
цепи будет иметь вид (рис. 11), где отличны от нуля лишь эле-
элементы заштрихованных клеток.
Из периодической цепи Маркова с периодом d можно обра-
образовать d новых цепей Маркова. Состояниями се-й цепи будут со-

§ 3, ТЕОРЕМЫ О СЛУЧАЙНЫХ БЛУЖДАНИЯХ ПО РЕШЕТКИ 279
стояния из подкласса xFa. Вероятности перехода задаются ра-
равенствами
РЪ = Pi) (d).
В силу только что доказанной теоремы 2 Ри == 1-Новая цепь,
Ej GVa
к кото-рой в известном смысле сводится изучение исходной, уже
во будет иметь подклассов.
§ 3. Теоремы о случайных.блужданиях по решетке
1. Случайное блуждание по целым точкам на прямой. Пред-
Представим себе частицу, которая движется по целым точкам па пря-
прямой. Перемещение из одной точки в другую происходит через
равные промежутки времени. За один таг частица из точки к
с положительной вероятностью р перемещается в точку к+\
и с положительной вероятностью q = 1 — р перемещается в точ-
точку к — 1. Как уже отмечалось, описанной физической системе со-
соответствует цепь Маркова
Л-п = Xn-i Т" t^n = Xq + Оп,
где tn принимает значения 1 и —1 с вероятностями р и q,
?л — 2 ?/<• Состояниями здесь служат целые точки на прямой.
/г =--4 "
Легко видеть, что вернуться в какую-либо точку с положи-
положительной вероятностью можно только за четное число шагов. При
этом /о B) = 2pq > 0. Поэтому это периодическая цепь с перио-
периодом 2.
Исследуем теперь, когда случайное блуждание образует воз-
возвратную цепь. Имеет место следующая
Теорема 4. Описанное случайное блуждание образует воз-
возвратную цепь Маркова тогда и только тогда, когда р — q = 1/2.
Доказательство. Так как 0</?<1, то блуждание
представляет собой неразложимую цепь Маркова. Поэтому в си-
силу теоремы 2 достаточно изучить тип одной точки, например,
пуля.
Воспользуемся теоремой 1. Для этого надо исследовать схо-
ею
димость ряда ^РоЛ'2)- Так как цепь — периодическая с перио-
71-=-1
оо
дом 2, то р0оBк+ 1) = 0. Остается подсчитать 2,РооB^)- Сумма
1
Sn есть координата блуждающей частицы (Хо = 0) после п ша-
шагов. Поэтому РоОBк) = P(S2ii = 0). Чтобы 6^ = 0, необходимо,
чтобы А: суммируемых случайных величин равнялись 1, а остав-
оставшиеся к случайных величин равнялись —1 (к шагов вправо

280 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
и к шагов влево). Поэтому по теореме 2 гл. 5
Р (S2k = 0) ~ * ,-*»<"» _ * (Apq)\
упк упк
Выясним поведение функции ср(/?)= 4/?# = 4/?A—/?) па от-*
резке [0, 1]. В точке р = 1/2 функция ср(/?) достигает единствен-
единственного экстремума, а фA/2)=1. Во всех остальных точках отрез-
отрезка [0, 1] ф(/?)<1. Значит, 4/?д < 1 для рФ 1/2, а это влечет за
оо
собой сходимость ряда 2 Poo BA) и невозвратность цепи. Если
h=l
же р = 1/2, то /?оо B/с) — 1/Уя& и ряд 2 Роо B&) расходится, что
в свою очередь влечет за собой возвратность всех состояний
цепи. ^
Доказанная теорема позволяет сделать также следующее за-
замечание. Если р Ф 1/2, то среднее число возвращений в 0 конеч-
оо
по, ибо оно равно 2 Роо Bк). Это означает, что начиная с ееко-
торого шага частица уже никогда больше не вернется в 0. Час-
Частицу «снесет» вправо или влево от нуля в зависимости от того,
р > 1/2 или р < 1/2. Это легко получить и из усиленного закона
больших чисел.
Если р == 1/2, то среднее число возвращений в 0 бесконечно;
частицу не «сносит». Интересно отметить, что при этом среднее
число возвращений растет не пропорционально числу шагов.
Действительно, среднее число возвращений за первые 2/г шагов
п
есть 2РооB^)-Из доказательства теоремы 4 нам известно, что
й=1 __
рооBк) — 1/Улк. Поэтому " •
Таким образом, в безобидной игре, рассмотренной пами в при-
примере 7 гл. 4, доля «ничьих» результатов с увеличением числа
шагов быстро надает, а отклонения по величине и по длительно-
длительности возрастают.
2. Симметричные случайные блуждания в R}\ &^2, Будем
рассматривать следующую модель случайного блуждания в А-мер-
пом евклидовом пространстве Rh. Если частица находится в точ-
точке (ши ..., mk), то она может переместиться с вероятностью l/2ft
в любую из 2k вершин куба \X} — mj\ = 1, т. е. в точки с коорди-
координатами (wi±l, ..., mk±:l). Такое блуждание естественно на-
вывать симметричным. Если обозначить Хп положение частицы
после тг-го скачка, то мы, как и прежде, получим последователь-*

§ 3. ТЕОРЕМЫ О СЛУЧАЙНЫХ БЛУЖДАНИЯХ ПО РЕШЕТКЕ 281
ттость й-мерных случайных величин, связанных в однородную не-
неразложимую цепь Маркова. Покажем, что все состояния этой
цепи для блуждания на плоскости, как и в одномерном случае,
возвратны. В трехмерном пространстве состояния окажутся уже
невозвратными. Будет доказана, таким образом,
Теорема 5. Симметричное случайное блуждание возвратно
в пространствах одного и двух измерений и невозвратно в про-
пространстве трех и более измерений.
По этому поводу В. Феллер весьма удачно заметил, что по-
пословица «все дороги ведут в Рим» верна только для двумерной
поверхности. Сформулированное нами утверждение примыкает
к известной теореме Пойа о невозвратности при к^2 симмет-
симметричных блужданий в Д\ когда частица за один шаг перемеща-
перемещается на ± 1 по одной из осей координат (%s принимают 2к зна-
значений с вероятностями 1/2к). Обратимся к доказательству теоре-
теоремы. 5.
Пусть к = 2. Нетрудно видеть, что наше блуждание Хп мож-
можно представить в виде суммы двух независимых компонент
• хп = (xl о) + (о, xi), (xl XI) = х01
где Хп, 1 = 1. 2,— уже скалярные (одномерные) последователь-
последовательности, описывающие симметричные независимые случайные
блуждания на прямых. Это ясно, так как двумерная последова-
последовательность допускает представление
X»+i = Хп + gn, D)
где |п принимает 4 значения (±1, 0) +@, ±1) = (±1, ±1) с ве-
вероятностью 1/4 каждое.
С помощью представления D) мы можем исследовать асимп-
асимптотическое поведение переходных вроятностей рц{п). Пусть со-
состояние Хо совпадает с началом координат @, 0), Тогда
pQ0 B/7) = Р (Х2п =@, 0)/Х0 = @, 0)) =
= Р {Х\п = 0Х = 0) Р {Х;п = 0/Х1 = 0) ^ A/ УшьJ - 1/(лге).
оо
Отсюда следует, что ряд 2 Рсо (п) расходится и все состояния
п=0
нашей цепи возвратны.
В случае к = 3 следует поступить аналогичным образом, пред-
представив последовательность Хп в виде суммы трех независимых:
компонент
Хп = (XI 0, 0) + @, XI 0) + (О, О, X»),
где Х]п как и прежде,—симметричные случайные блуждания на

282 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
прямой. Если положить Хо =@, 0, 0), то получим
Ры B«) = (Р (Х\п = OiXl = О)K ~ 1/(лпK/2.,
оо
Здесь ряд 2 Роо (п) будет уже сходящимся, а состояния цепи
71=1
.невозвратными. В отличие от случая прямой и плоскости здесь
частица, выйдя из начала координат, может с положительной
вероятностью никогда туда не вернуться.
Ясно, что эта картина сохранится и для блуждания в любом.
/t-мерном пространстве при к ^ 3, так как 2 (nn)~h/2 < оо цри
п=1
3. Произвольное симметричное случайное блуждание на пря-
прямой. Пусть, как и прежде,
Xn=.X0 + Zl},: E)
но ?j- здесь уже произвольные независимые одинаково распреде-
распределенные целочисленные случайные величины. Теорема 4 может
быть обобщена следующим образом:
Теорема 6. Если ^ симметричны, существует Mi,.(M^.= 0),,
то случайное блуждание Хп образует возвратную цепь Маркова
с нулевыми состояниями.
Доказательство. Достаточно убедиться, что
где Sn = 2 Sj, и что P (Sn = 0) -> 0 при п -> оо. Обозначим
i
p(z) = Mz^1 = 2 2^P (Si = ^)* Тогда производящая функция Sn
— оо
будет равна Mz n = рп (z), и по формуле обращения (см. § 7, 8)
Т
-2д. j
Т 7 F)
__
Последнее равенство справедливо в силу четности вещественной
функции р(г) и получено путем замены z = eu%

§ 3. ТЕОРЕМЫ О СЛУЧАЙНЫХ БЛУЖДАНИЯХ ПО РЕШЕТКЕ 283
Так как Щх = 0, то 1 — р{еи) = оA) при t -+¦ 0, и при до-
зтаточно малом б и 0 ^ / < б
Отсюда следует
я б
Г dt ^ ?dt_ _
Сходимость Р E„ =¦= 0)-»• О следует из F)", так как для всех
z на "окружности Ы = 1, за исключением, быть может, конеч-
конечного числа точек, p(z) < 1, pn(z) -*¦ 0 при п -*¦ <*>. ^
Теорему 6 можно дополнить следующим образом.
Теорема 7. Если о. н. д. возможных значений |j равен \у
то множество значений {Хп} образует один класс существенных
сообщающихся состояний, совпадающий с множеством всех це-
целых чисел.
Утверждение теоремы вытекает из следующей лемглы:
Лемма 1. Если о. п. д. целых чисел at > 0, ..., аг > 0 ра-
равен 1, то существует N такое, что любое натуральное число
h ^ N можно представить в виде
к = х{а{ + ... + хгап
где Xi^O — целые числа.
Доказательство. Рассмотрим функцию L (х) = х^ + ...
... + хгаг, где х==(Х[, ..., хг) есть вектор с целыми координата-
координатами. Пусть d > 0 — минимальное натуральное число, для которо-
которого существует такой вектор х°, что
Покажем, что любое натуральное число, представимое в виде
L(x), делится на d. Пусть это не так, Тогда существуют х, к и
О < а < d, для которых
L(x) = fed + a.
По так как функция Ь(х) линейна, то
Ь(х - кх°) = /cd+ a - kd^a< d,
что противоречит минимальности d в множестве положительных
целых значений L(x).
Все числа аи ..., аг также являются значениями функции
//(^), и поэтому все делятся на d. Так как, по предположению,
наибольший делитель этих чисел равен единице, то d=l.
Пусть к ¦— любое натуральное число. Тогда, обозначив через
О < А остаток от деления к на А == aL + ,,, + ап мы можем

284 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
записать
к = t (ах + ... + аг) + Q = г(аг + ,.. + ar) + 0L{х°) =
== Й! (^ + 0Xi) + #2 (^ + 9^2/ + • » * + ar (t + G^r)*;
где ? + 9#? > О, i = 1, ..., г, при достаточно больших /с. ^
Следствие 2. Если выполнены условия теорем 6, 7Т го
^еяь E) и/? и- любом начальном состоянии Хо с вероятностью 1
побывает бесконечное число раз в любом состоянии к. В частно-
частности, случайная величина v = min {/г: Xft = к} для любых Хо и к
будет собственной.
Если интересоваться периодичностью цепи E), то нужны
более полные сведения о множестве возможных значений ^. Мы
предоставляем читателю убедиться, например, в том, что если
множество возможных значений J-, имеет вид {а + aftd}, к = 1, 2, ...
,.., d>l, о. н. д. (аи а2, ...)=1, о. н. д. (a, d)=l, то цепь бу-
будет периодической с периодом d.
§ 4. Эргодичсскпе теоремы
Рассмотрим следующие два условия:
(A) Цепь неразложима и непериодична.
(B) Существует состояние EQ такое, что время § возвраще-
возвращения в Ео (Р (| == п) = /0 (/г)) имеет конечное математическое
ожидание МН.
Теорема 8 (эргодическая). Условия (А) и (В) необходи-
необходимы и достаточны для того, чтобы при любых i и j существовали
не зависящие от i положительные пределы
lira pi} (/г)-= Рз > О, I, / — 0, 1, 2, ., t
71-^ СЮ
Числа {р(} являются единственным в классе последователь-
последовательностей, образующих абсолютно сходящиеся ряды решением си-
системы уравнений
со
jLJ Pj ~ li
i^o G)
Л= S PftPftif / = 0,1,2, ....
Цепь, обладающая свойством G), называется эргодической.
Числа Pi есть по существу вероятности попадания системы в
состояние Ej через большой интервал времени. При этом оказы-
оказывается, что эти вероятности не зависят от начального состояния
системы. Система «забывает», откуда началось движение. Рас-
Распределение {р) называют стационарным или финальным. Свой-
Свойство G) выражает инвариантность распределения относительно

§ 4. ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ Z5D
переходных вероятностей рц. Другими словами, если Р (Хп = к) =
= pk, то Р (Хп+1 = /с) = 2 Pife также равны /?ft.
Доказательство. Достаточность. Рассмотрим «тра-
«траекторию» цепи Маркова, начинающуюся в состоянии Ео, и рас-
рассмотрим интервалы времени ^ ^ 1, ?2 ^ 1, ..., через которые си-
система возвращается в Ео. Так как каждый раз эволюция системы
начинается из одного и того же фиксированного состояния, то
длительности циклов |fe, образованных попаданиями системы в ЕОу
будут в силу марковости (как и сами циклы) одинаково распре-
распределены и независимы. При этом, очевидно,
Возвратность Еп означает, что |fe есть собственные случайные
величины; непериодичность Ео — что о. и. д. возможных значе-
значений |ft равен 1. Так как
где %(п) есть эксцесс уровня п для процесса восстановления
h
{SJ, S/{ = 2 \i, то по теореме 9.3 (9.2) существует
lim р00 (п) = lim Р (Х (п) = 0) = 1/Мёх > 0. (8)
П->оо П->оо
Докажем теперь существование lim pOj (п) при / ^ 0. Если
7 (/г)— дефект уровня п для блуждания {Sh}, то по формуле пол-
полной вероятности
Poj (п) - S P (Y (") = Л) Р (^« = 7'До = 0, V («) = А)-
fe=i
Отметим, что. в этой формуле вторые множители в силу марко-
марковости от п по зависят:
= Р (Хп = 7'Д0 = 0,
Первые множители сходятся при /г ->- оо к Pji-i/M?ll (Pk =
P(Ii>^))h в силу равенства Р (y(») = A;)= Р (%(п — А;) = 0) ><
Pk-i^Pk-i мажорируются сходящейся последовательностью
-i. Поэтому по теореме о мажорируемой сходимости существует
оо
lim poj (n) = 2 -ШГ Р (А, 7) = ph
при этом
(/г) < S Pk-iP (к, j) < S Pk-iP (Л, /) = ftMgx. (9)
ft=l ' /г=-1

28.6 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
Чтобы установить теперь, что при произвольном i
Ит Pij(n) - Pj>0,
П->оо
покажем сначала, что система из Е{ с вероятностью 1 когда-ни-
когда-нибудь попадет в Ео.
Другими словами, если fiQ(n) есть вероятность того, что си-
система, выйдя из Ei, впервые на п-и шаге попадет в Е^ то
Действительно, состояние Еи как и /?0, возвратно, Рассмотрим
циклы, образованные возвращением системы в состояние Eh и
обозначим Ak событие, состоящее в том, что в течение к-та цик-
цикла система хоть раз попадает в Ео. Тогда в силу марковости со-
события Ak независимы и Р(Л/г) = р>0. Следовательно, по кри-
критерию Бореля с вероятностью 1 произойдет бесконечно много со-
событий Ак, и тем более Р ((J Ah) = 1.
По формуле полной вероятности находим
п
Pij (П) = S /iO (k) Рот(п — /С)'
fe=l
Использование теоремы мажорируемой сходимости дает
ею
lira ptj (n) = S /i0 (/с) /?j == р}ы
П-^оо Jt=l
Так как состояние Eh так же как и /70, является непериоди-
непериодическим и ненулевым, то
Pj = lim р,-;(л)>0.
Докажем теперь необходимость. Необходимость условия
(А) очевидна, так как /?^(д)>0 для каждых i и / при всех до-
достаточно больших п. Необходимость условия (В) следует из спра-
справедливости для Ео равенств F).
Осталось доказать вторую часть теоремы, Так как
то 2pj^1. В силу (9) можно, следовательно, в A0) и в ра-
венстве Poj{n+ 1) = 2 Pok (n) Pit j воспользоваться теоремой о
it=o
мажорируемой сходимости, откуда следует, что
сю
2л = 1. л= 2 PkPkj, (Н)

§ 4. ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ 287
Остается показать, что полученная система имеет единственное
решение. Пусть числа {q) также удовлетворяют G) и 2
сходится. Тогда, меняя порядок суммирования, получим
Ч) = 2 gnPhj = 2 Рю {2 PikQi) = 2 Qi 2 P№№ = 2 ffiPzj B)
/i й \ I J I h I
= 2 Л/i B) BPsi)
для любого /г. Так как 2 Qk = 1» то, переходя к пределу при
/г -*- оо} получим
<7; = 2 (ZftPi = Л- ^
Если цеиь Маркова — периодическая с периодом d, то рц{1)'=:
= 0, если 1ФкA для любой пары состояний Ег и Е31 принадле-
принадлежащих одному подклассу (см. теорему 3). Если же t = kd, то из
только что дока.чаммо" теоремы и из теоремы 3 следует, что су-
|цег,н{ует предел iini /;^ (A:d) = pj >> 0 и не зависит от ?.
Пример 5. В § 11.4 мы видели, что времена ожидания в
системе обслуживания удовлетворяют соотношениям
wn+\ =тах(м>„ + gn+i, 0), u>i=0,
где t,H независимы и одинаково распределены. Ясно, что wn
син:шны в однородную цепь Маркова с множеством состояний
{(), 1 ,..}, если gft целочисленны. Последовательность wn' молено
интерпретировать также как блуждание с задерживающим эк-
экраном б точке 0." Если М?& < 0, то из теорем гл. 8 следует, что
время возвращения в состояние 0 имеет конечное математиче-
математическое ожидание. Поэтому, применяя эргодическую теорему, мы
можем независимо от § 11.4 сделать заключение о существова-
существовании предельного (стационарного) распределения для wn при
и -^ со (пли, принимая во внимание сказанное в § 11.4,— заклю-
h
чепие о конечности supShi Sh= 2 Sj» что составляет содер-
жапие теоремы 10.4). Л
Теорема 9. Пусть цепь Маркова имеет конечное число со-
состояний и удовлетворяет условию (А). Тогда существуют посто-
постоянные с > 0 и q < 1 такие, что для времени возвращения | в лю-
любое фиксированное состояние справедливы неравенства
P(l>n)<cqn. A2)
Эти неравенства означают, очевидно, что условие (В) для
конечных цепей всегда выполнено и, следовательно, эргодическая
теорема для них верна тогда и только тогда, когда выполнено ус-
условие (А),

288 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
Доказательство. Рассмотрим некоторое состояние Ео и
обозначим
г, {п) = Р (Хк фО, к = 1, 2У ..., тгД0 - /).
Тогда, если цепь имеет т состояний, то о(т)<1 при любом /.
Действительно, о (/г) не возрастает с ростом /г. Пусть iV есть на-
наименьшее число, дли которого r}(N)<l. Это означает, что суще-
существует цепочка состояний Е}, Ед1, .. ., E3N такая, что EjN==E0
и вероятность этой цепочки руп . .. PjN_^N положительна. Но легко
видеть, что N ^ т, так как в противном случае указанная це-
1[очка содержала бы по крайней мере два одинаковых состояния,
а следовательно, и цикл, заключенный между этими состояния-
состояниями, который можно было бы из цепочки выбросить, лишь увели-
увеличив ее вероятность. Таким образом, Ту(пг)< 1,
г (m) = max Tj (m) < 1.
з
Кроме того, rJ(nl +n2)^rj(ni)r(n2)<r(ni)r(n2).
Остается заметить, что если ? есть время возвращения в Е{),
то Р (? > ппг) == г0 (nm) ^ г (//г)п. Отсюда следует утверждение тео-
теоремы. ^
Замечание 1. Выполнение условия A2) влечет за собой
экспоненциальную скорость сходимости к пулю разностей
\ра{п)—j)j\. В этом можно убедиться, используя аналитичность
оо
функции Fo (z) = 2/o(^)zn в области \z\ < q~\ q~i > 1 и pa-
веиство
200(«JП=1-^—^-1 A3)
(см. теорему 1; мы считаем, что § в условии A2) относится к со-
состоянию /?<>, так что /о(и) = Р(? = и))« ^ак как ^тоA) = М&=1/Ро»
то Fo (г) = 1 Н j Ь .. ., и из A3) будет следовать ана-
аналитичность в области Ы^1 + 8, в>0 функции Ро (z) — _° =
1= ^ (/H0 (/г)— р0) zn,. которая, о'чевпдио, и будет означать, что
п=1
\роо(п)~ Ро! < сA + г)~п, с = const
Приведем теперь два примера конечных цепей Маркова.
Пример 6. Допустим, что поведение двух шахматистов А
и В и турнирной игре описывается следующим образом. Шахма-
Шахматист А каждую партию независимо от исходов предыдущих пар-
тип выигрывает с вероятностью р, проигрывает с вероятностью q

§ 4. ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ 289
п делает ничью с вероятностью r=l — p —g. Шахматист В менее
уравпошчпеп, он выигрывает партию с вероятностями /Н-е, р и
р — в соответственно, если предыдущая партия была им выиг-
выиграна, сыграна вничью, проиграна. Аналогично ведет себя вероят-
вероятность проигрыша: она равна в этил трех случаях соответственно
ц — е, q, q + s. Кто из> игроков Л м В в длительном турнире набе-
наберет больше очков?
Чтобы ответить па этот вопрос, надо вычислить для каждо-
каждого иг? шахматистов стационарные вероятности рь рг, jh попадания
п состояния Еи Е2, Е3, которые мы отождествим соответственно
с иыпгрышсм, ничьей, проигрышем (ср. с законом больших чисел
и конце параграфа).
Для игрока А цепь Маркова с состояниями Е,, Е2, Ез, описы-
паюшая ход его игры, будет иметь матрицу переходных вероят-
вероятностен
Рл =\ Р г д \
\ р г q )
Очевидно, что здесь р{ = р, рг = г, р3 = q.
Для игрока В матрица переходных вероятностей будет равна
. = I p r g
— 8 г q -|- 8
Уравнения для стационарных вероятностей в этом случае бу-
будут иметь вид
Pi (р + е) + р2р + р3 (р — е) = ри
Pi + Рг + Рз = 1.
Решая эту систему, находим
г['аким образом, доли ничьих при большом числе партий у кгро-
ков Л и В будут совпадать, доля выигрышей у игрока В будет
больше, чем у А, если s > 0, р > g *или 8 < 0, р < q. Если р = q,
то стационарные распределения для исходов партий у игроков у!
н В одинаковы.
И р и м е р 7. Рассмотрим сложение независимых целочислеи-
пых случайных величин \и ?2, ... по некоторому модулю d~> 1
(см. пример 2). Мы полошим ([ж] означает целую часть х)
.V,, ¦ -. О, ^ - |, - [|] d, Х2 = Хх + 12 - р^Ц d и т. д., так
ми» Хп есть остаток от деления на d суммы Xn-i + ?„. Такое
суммирование иногда называют суммированием на окружности
V-' Л. А. Боровков

290 ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
(точки 0 и d склеены в одну). Не ограничивая общности, можем
считать, очевидно, что th принимают лишь значения 0, 1,
..., d — 1. Если Р (In = j) = qj, то
если / ^ &\
если j<u
Допустим, что множество индексов /с, для которых qh > 0, имеет
о. н. д., равный 1. Тогда ясно, что цепь {Хп} будет представлять
собой один класс существенных состояний без подклассов и бу-
будут существовать
lim pi} (n) = ph
удовлетворяющие системе уравнений ^PiPa = Pj, 2 Pj = 1»
г
7*=0, ...,d—1.Заметим теперь, что стохастическая матрица пе-
переходных вероятностей Н/^Н в нашем случае обладает свойствами
у* у» n i
ZjPii = Za Pi) == -1»
i j
Такие матрицы называют дважды стохастическими. Для них ста-
стационарное распределение всегда является равномерным, так как
р3 = 1/d удовлетворяют системе уравнений для финальных веро-
вероятностей.
Таким образом, сложение произвольных случайных величин
на окружности приводит к равномерному предельному распреде-
1 лению. При этом скорость сходимости рц(к) к стационарному рас-
распределению будет показательной.
Нетрудно заметить, что при суммирования но модулю компо-
композиция двух равномерных распределений снова будет равно-
равномерной. В этом смысле ^равномерное распределение является
'устойчивым. Более того, композиция любого распределения с рав-
равномерным также будет равномерной. Действительно, если ц рав-
равномерно распределена и не зависит от §4, то (сложение и вычи-
вычитание здесь происходит по модулю d)
d-l d-1
Pfo + ti = к) = 2 ftP(n = ft-/) == 2 ft7 = i-
Таким образом, если передается некоторый сигнал, принима-
принимающий d возможных значений (например, буквы), и на него
накладывается «случайный» (равномерный) шум, то принимае-
принимаемый сигнал также будет иметь равномерное распределение и,
стало быть, не будет содержать никакой информации о переда-
. ваемом сигнале.
Рассмотренный пример заслуживает внимания и как простей-
простейшая иллюстрация законов, которые возникают при «суммирова-

§ 4. ЭРГОДИЧЕСКИЕ ТЕОРЕМЫ
291
тши» случайных величин со значениями уже не ina числовой оси
а в некоторой группе (множество чисел 0, 1, • • -,, d 1 с опера-
операцией сложения по модулю d образуют конечную %белеву группу).
' Оказывается, что явление, обнаруженное нами в. примере, рав-
равномерность предельного распределения — coxpafi%eTCH и ддя4 зна-
значительно более широкого класса групп,
В заключение этого параграфа мы приведем два утвержде-
утверждения о предельном при п->-°° поведении числа tyi^ri) попаданий
(возвращений) системы в фиксированное состо1ягше /j. 3a вре-
время п. Эти утверждения являются непосредственным следствием
т-еорем 7 и 8 гл. 9, поскольку величины т>(п) Просто совпадают
со значениями в точке п проце-cca восстановлен^ ц(п) порож-
порожденного независимыми одинаково распределеннь,ши величинами
lh ?2, ..., где g4 есть время возвращения систему в СОСТОяпие Eh
Именно справедлива
Теорема 10. Если М |i = а < °°, го при п _>. оо
т/(п)/п-+1/а.
Если цепь эргодична, то отсюда следует, что
пг, (п)/п -> pj.
Если Dgi = о2 < оо? то
еде Ф{х), как и прежде, есть функция нормалычого распределе-
распределения с параметрами @, 1).
Предлагаем читателю в виде упражнения устаповить г1Т0 если
rio соотношение A3) (как и A4)) останется справедЛИВЬШ и в
гкш случае, когда начальное значение Хо = / зай/1еAШП0 па значе-
значение Хо = к.
В доказательстве теоремы б отмечалось, что равенство A6)
дли возвратной неразложимой цепи всегда выпс)Лнепо#
Ро.чюмируя содержание этого параграфа, %>жпо заметить
что изучение последовательности зависимых исг1ЬГтаниц связан-
им\ и цепь Маркова с дискретным множеством состояний во
мчогом может быть осуществлено с помощью результатов ?для
мосцгдоиательпостей независимых случайных ве,пичин Изучение
jiр\'1*нх иидов зависимых испытаний требует, ка^ правило иных
ичдои

292
ГЛ. 12. ДИСКРЕТНЫЕ ЦЕПИ МАРКОВА
§ 5. Поведение переходных вероятностей
для.разложимых цепей
Рассмотрим теперь конечную цепь Маркова общего типа. Как было вы-
выяснено, множество ее состояний состоит из класса S° несущественных сос-
состояний и нескольких классов S1, ..., S1 существенных состояний. Для выяс-
выяснения природы асимптотического поведения pij(n) для таких цепей доста-
достаточно рассмотреть случай, когда существенные состояния образуют один
класс без подклассов. Матрица вероятностей pij{n) в
этом случае имеет вид, изображенный па рис. 12. В си-
силу эргодической теоремы для элементов подматрицы
L существуют положительные пределы pj. Таким об-
образом, осталось выяснить, как ведут себя элементы за-
заштрихованной части матрицы.
Теорема 11. Пусть Ег gee S0. Тогда
Рис. 12
lim
(t) =
0.
Е- е S0.
j > О,
Доказательство. Пусть Ej
Aj (I) =
S{\ Обозначим
Для любого существенного состояния Ег существует такое целое tr, что
Pir(tr) >* 0. Так как переходные вероятности в S] с некоторых пор все поло-
положительны, то существует s% такое, что pn(s) >» 0 для Ег е S0 и для всех:
Ei e S1. Поэтому для достаточно больших t имеют место следующие соот-
соотношения:
где h (i) = 2 />ife (*> = * - 2 /;
то из полученного неравенства следует
1. Если h = max
Таким образом, lim /
к.
lim i4?- (/) = 0.
I ;» oo
t±oo I ; oo
Пусть теперь ?"^ ge 5°, a Ej ge S\ Имеют место равенства
Устремив f и s к ею, мы видим, что первая сумма в последнем выражении
есть оA). Во второй сумме
2
Таким образом,
Pik @ = Н- * A);
з) = Р} 2 Р»л
@ -
При t, S -> oo.
С помощью доказанной теоремы нетрудно убедиться, что существование
lim р..(п) = д ^0 необходимо и достаточно для того; чтобы цель состоя-
ла из двух классов S° я S1 и чтобы S1 не содержал подклассов.

Глава 13
ИНФОРМАЦИИ И ЭНТРОПИЯ*)
§ 1. Определения, свойства информации и энтропии
Предположим, что производится некоторым эксперимент. При
этом событие .4 может произойти с вероятностью 0,99. Тогда ес-
естественно считать, что появление события А не несет в себе боль-
большой информации. Появление же события А несет в себе значи-
значительную информацию, так как оно нами не ожидалось. Пусть,
например, событие А означает, что самолет приземлился благо-
благополучно. Тогда сообщение о том, что произошло событие А (обыч-
(обычно оно маловероятно), будет нести для встречающих (ожидаю-
(ожидающих исхода эксперимента) весьма существенную информацию.
Принята следующая количественная мера информации.
Пусть А и В — события некоторого вероятностного пространства
<Q,«, Р>-
Определение I. Количеством информации I(А/В), кото-
которое заключено в событии (сообщении) В относительно, А, назы-
называется число
Появление события В = А можно интерпретировать как сооб-
сообщение о том, что наступило А.
Определение 2. Число 1(А/А) = 1{А) называется коли-
количеством информации 1(А), заключающейся в сообщении А:
I (A/A) = I (A) = -logP (А).
Из этого определения видно, что чем больше вероятность со-
события А, тем меньше 1 (А). Как правило, в определении инфор-
информации используется логарифм при основании 2, так что единицу
информации несет, например, сообщение о том, что в семье ро-
родился мальчик (или девочка) (предполагается, что эти события
равновероятны, а —-!og2 р = 1 при р = 1/2). В дальнейшем в этом
параграфе везде запись log х следует понимать как log2x.
Если события А ж В независимы, то 1(А/В) = 0. Это означает,
что событие В не несет в себе никакой информации относительно
/I и наоборот. Следует заметить, что всегда 1(А/В) = ЦВ/А),
') Понятия количества информации и энтропии были введены
li !) Шшшошш в 1948 г. Для некоторых частных ситуаций понятие коли-
чм-тил информации рассматривалось и в более ранних работах (например,
Г \;>|>тли, 1928 г.). Изложение § 2 этой главы основывается во многом на
pin им о А. }1. X и и ч и и а [20],

294 . гл. п. информация и зеггропия
Легко видеть, что если события А и В независимы, то
A)
Рассмотрим пример. Пусть случайным образом на одну из
клеток шахматной доски ставится фигура. В этом случае инфор-
информация о том, что фигура находится в клетке с номером к (собы-
(событие А), будет равна /(Л) = log E4 = 6. Пусть Б\ — событие, за-
заключающееся в том, что фигура находится в I строке, а В2 — что
фигура находится в / столбце. Сообщение А можно передать, пе-
передав сначала Ви затем Вг. Имеем
Поэтому
так что при передаче сообщения А «по частям» требуется: сооб-
сообщить то же количество информации, равное 6, что и при одно-
одноразовой передаче. Можно провести и другие примеры, обнару-
обнаруживающие естественность введенных числовых характеристик.
Пусть G есть некоторый эксперимент с исходами Еи .,., EN,
которые осуществляются с вероятностями ри ..., р$.
Информация, полученная нами в результате испытания G,
есть случайная величина /о —Л?(о)), принимающая гшачеиио
— log ph /= 1, ..., УУ, па множестве Е3.
Таким образом, если в вероятностном пространстве <Q, S, Р>
соответствующем эксперименту G, ?2 совпадает с множеством
(ffi, ..., ?^), TO /o(@) = /@)).
Определение 3. Математическое ожидание этой инфор-
информации MJg = — S /;i ^°ь Pj 1газывается энтропией эксперимента.
Мы будем обозначать ее символами
где p = (/?i, ..., Pn). При р^ = 0 про-
Рис. 13 поведение pjlnp^ мы полагаем но
12 е и р е р ьт в н ост и р э в и ым 0.
Энтропия эксперимента есть в некотором смысле мера его
неопределенности. Пусть, например, эксперимент имеет два ис-
исхода А и В с вероятностями р и (/ = 1 — р. Энтропия такого
эксперимента равна
II р =~р log р - A - p)lcg(l -/>) = .
График этой функции представлен па рис. 13. Единственный
максимум /(р), равный log 2 = 1, достигается в точке /? = 1/2.
Это схема с максимальной неопределенностью. Если р уменьша-
уменьшается, то неопределенность вместе с Яр тоже уменьшается, Hp = 0f
если р=--@л1) или A, 0).

§ 1. ОПРЕДЕЛЕНИЯ, СВОЙСТВА ИНФОРМАЦИИ И ЗНТРОДИИ 295
Эти свойства легко усмотреть и в общем случае.
Свойства энтропии.
1. i/(G) = 0, если и только если существует такое /, 1^/^
N, что
2. Н (G) максимально, если /?j =* i/N для всех /.
Доказательство. Так как вторая производная функции
q)(x) = xlogx на [0, 1] положительна, то Ц)(х) выпукла. Следо-
]\
вательно, для любых ох1 ^ 0 таких, что 2* (Ji = Ъ, и любых х{ ^ О
выполняется неравенство
N \ N
Если взять Qi = дг, Xi = pi, то получим
(ж
ж 2 Pij 1оь (ж 2 л) < 2 i Pi
тт I i ! I
Полагая и = [ ^~, „.., -^-/, находим отсюда
Заметим, что если энтропия 11 (G) ровна своему наибольшему
значению II(G) = logN, то с вероятностью 1 /G (о) = log TV, т. с.
информация /о становится постоянной.
3. Пусть G{ и G2 — два независимых эксперимента. Запишем
исходы и соответствующие вероятности исходов в этих экспери-
экспериментах следующим образом:
fEum..,EN\ „ (Аи.ч.,Ам\
I*
Комбинируя исходы этих двух экспериментов, мы получим но-
новый эксперимент;
\PiQi,
Информация /G, полученная в результате этого эксперимента,
ость случайная величина, принимающая значения — log/?^ с ве-
|)оIтиостями ргЯз-> * ^ 1, ..., iV; / = 1, ..., Л/. Но такое же рас-
распределение имеет, очевидно, сумма Jgx + ^g независимых ве-
величин, равных соответственно информапиям от экспериментов
(*[> и С2, Таким образом, информация, полученная от последовав

296 ГЛ. 13. ИНФОРМАЦИЯ И ЭНТРОПИЯ
телъпости независимых экспериментов, равна сумме информации
от этих экспериментов. Так кик при этом, очевидно,
M/G « M/Gl + M/g2,
то мы получаем, что для независимых Gu G2 энтропия Н(G)
равна сумме
энтропии экспериментов Gt и Gz.
4. Если эксперименты Gi и Gz зависимы, то эксперимент G
будет выглядеть следующим образом:
fE.A^E.A,, ...,ENAM\
Will. ^12» • • •» QNM /
где qa = PiPa, a p« есть условная вероятность события Aj при
условии Е{, так что
2 qti = Pi =
2 ft; = » =
i—1
В этом случае равенство Jg = Jgi + ^g2, вообще говоря, уже гге
будет иметь места. Введем случайную величину /2, равную
—log/7,^ на множестве /?,-Л;. Тогда, очевидно; Jg=:Jg1 + /'г* Так
как
то величину /2 при фиксированном i можно рассматривать как
информацию от эксперимента С2 при условии, что произошло
событие Ег. Величину
j=l
мы будем называть условной энтропией H(G2/Ei) эксперимента
G2 при условии Еи а величину
мА = - Ц 9ii log Pii = 2 Р1я (са/?4)
i,i г
условной энтропией H(G2/G{) эксперимента G2 относительно
эксперимента Git Во введенных обозначениях, очевидно,
Мы докажем, что в этом равенстве всегда

§ 1. ОПРЕДЕЛЕНИЯ, СВОЙСТВА ИНФОРМАЦИИ И ЭНТРОПИИ 297
т. е. для двух экспериментов G{ и G2 энтропия II(G) всегда не
превосходит сумльу энтропии II(G\) и II(G2):
H(G)=-H(GiXG2)<H(G1)+H(G2)t
При этом равенство имеет место только в том случае, когда
Чгз=== PSji T> е- когда Gv и G2 независимы.
Для доказательства заметим сначала, что для двух любых
распределений (аь ..,, ып) и (vh ..., vn) справедливо нера-
неравенство
— 2 Щ l°S Щ < — 2 Щ log vu B)
примем "равенство возможно лишь при v{^=-n^ i = 1, ..., п. Это
следует из выпуклости функции log x, в силу которой при лю-
любых пг > О
(равенство возмолшо, если только fli = ^2 = . t. = ««)'• Полагая
у.
«i ~ ^, мы получим B).
Далее имеем
Так как {р^Д, очевидно, образует распределение, то в силу B)
2 Я и
^j > — 2 <Zi; log go = II (&),,
при этом равенство возможно лишь при Цц — РхЪ- ^
5. Как мы видели в п. 3, информация, полученная в резуль-
результате эксперимента G\\ состоящего в n-кратпом повторении неза-
независимых испытаний Gh равна
N
rn = — 2 V;
G
где Vj — число появлений исхода /?j. По закону больших чисел
7 -^Рз ПРИ
В заключение этого параграфа отметим, что рассмотренная
мера количества информации, полученной от эксперимента, мо-
может быть выведена как единственно возможная (с точностью
до постоянного множителя), если отправляться от нескольких
простых требований, которые естественно предъявить к величи-
по, количественно оценивающей информацию*).
*) См., например, [17],

298 ГЛ. 13. ИНФОРМАЦИЯ И ЭНТРОПИЯ
Интересно отметить также связь введенных понятий с веро-
ятностями больших уклонении. Как видно из теорем 5.3, 5.6,
разность между «смещенной» энтропией — 2 pi In pi и эптро-
пией —2j Pi *-n Pj \Рз ~ Vj/n есть относительные частоты появ-
появления ' Е3) является аналогом функции уклонений (см. § 8.8)
в многомерном случае.
§ 2. Энтропия конечной цепи Маркова.
Теорема об асимптотическом нокедешш информации
длшшого сообщения, ее приложения
1. Пусть {-^/<}/Г-1 — стационарная конечная цепь - Маркова,
состоящая из одного класса существенных состояний без под-
подклассов, и пусть Еи ,.,, Z?v — состояния цени. Стационарность
цепи означает, что Р(Х{= /) = pj совпадают с финальными ве-
вероятностями. Тогда, очевидно,
Р (Х2 = /) == У РкРю = Ph Р (Хз = 7) = Pi и т- Д-
/г
Пусть G/t есть эксперимент, состоящий п выяснении значе-
значения Xh (т. е. состояния, и которое попала система на /с-м шаге).
Тогда если ^V-j =*- г, то энтропия /с-го шага равна
II(GhlXk-X = 0 = — 2 Pii bg pij#
i
Энтропия стационарной цепи Маркова есть по определению
число
Я = MH(Gk/Xh^) = H(Gk/Gk^) = ~ 2 Pi2 Pii bg Pii.
г .?
Рассмотрим первые ?г шагов цепи Маркова Хь ..., Хп. Эн-
Энтропия этого сложного эксперимента G{n) = Ct X ... X Gn в силу
марковости равна
Il{G{n)) = H(G±) + IliG./G,) + ,.. + HiGjGn-г) =
= — 2 pj log p? + (^ — i)я ~ ия
при ?г -v oo# Если бы Xfe были независимы, то, как мы видели,
здесь было бы точное равенство.
2, Рассмотрим теперь цепочку (Хи ..., Хп) как некоторое
сообщение (событие) Сп и обозначим, как и прежде, I (Сп) =
== — log P (Сп) количество информации, содержащейся в сооб-
сообщении Сп. Значение 1(Сп) есть функция на пространстве эле-
элементарных событий, равная информации Jа(п)-, содержащейся п
эксперименте G{n\ Покажем сейчас, что, как и для независи-
независимых Хк< эта информация с вероятностью, близкой к 1, ведет себя
асимптотически как пН. Так что // есть приближенное впачеиие

§ 2. ЭНТРОПИЯ КОНЕЧНОЙ ЦЕ1Ш МАРКОВА 299
количества информации, приходящееся в среднем па одно испы-
испытание в последовательности {^ь}/Г-=1.
Теорема 1. При п ->¦ оо
I(Cn) ^-loiP(Cn)_
а а Р
Утверждение теоремы означает, что все цепочки Сп ври лю~
бом б > 0 можно разбить на 2 класса. Для первого класса
(Г)
—~ — И <С б. Сумма вероятностей элементов второго класса
сходится к 0 при а ->¦ °°.
Доказательство. Построим по раиной цепи новую цепь
Маркова {Yh}7=-\ следующим образом. Положим Yft = (Xft, Xh+l).
Состояниями этой цели будут пары состояний (Eh Ej) цепи iXk),
для которых pij>0. Переходные вероятности определяются, очо-.
видно, следующим образом:
(о, ]фк
P i
Заметим, что по индукции легко доказать соотношение
C)
Из определения {Yh\ следует, что для этой цепи верна эргоди-
ческая теорема. Это видно и непосредственно из C), при этом
lim P(U)Ui,l)(n) = PhPhh
Нам потребуется теперь закон больших чисел для числа по-
попаданий m{h>l)(n) цент {Yj}JLi в состояние (А, /) за время п.
В силу этого закона {см. теорему 11.8)
mhl(n)
t
Рассмотрим случайную величину Р(СП)
р (Сп) = Р (Я^^ .. . ЕХп) = Р (?Zl) P (EXJEX1) ..
Произведение здесь берется по всем парам (к, I). Поэтому
P(Cn) = l
logP(Cn)
log P (Cn.) = log p^y + 2 wi(ft>z) (л — 1) log /;/ibj
hj
— Я,

300 ГЛ. 13. ИНФОРМАЦИЯ И ЭНТРОПИЯ
3. Теорема 1 имеет важное следствие. Упорядочим все це-
цепочки Сп длины п в порядке убывания их вероятностей и будем
отбирать наиболее вероятные до тех нор, пока впервые суммар-
суммарная вероятность отобранных цепочек не превзойдет некоторый
заранее заданный уровень а, 0<а<1. Число отобранных цепо-
цепочек обозначим Ма(п).
Теорема 2. Л Для каждого 0 < а < 1 существует один и
тот же
Доказательство. Пусть S > 0 — некоторое число, которое
может быть произвольно малым. Цепочку Сп отнесем к катего-
категории Ки если ее вероятность Р{Сп) >> 2~и(н~6\ Будем говорить,
что Сп принадлежит к категории К2, если
и, наконец, Сп принадлежит к третьей категории К3, если
PF1ft)<2"n(i/+e).
Так как по теореме 1 Р (Сп е Кг [} К^)-^0 при п -*¦ оо? то в ко_
личество Ма(/г) (этим символом мы будем обозначать и само
множество отобранных цепочек) войдут только цепочки из /ч
и Кг. При этом последняя цепочка, вошедшая в Ма(п), обозна-
обозначим ее Са>п, будет из К2. Это значит, что
Ма (п) 2~п{Н+6) < 2 п Р (Q < а + Р (Са,п) < а + 2-n(if-e).
Отсюда следует, что
\оцМ^п)_ < log(a+2-"Gf-6)) + Я + б_
I
В силу произвольности б
log М (п)
lira, suр — 1— ^ //^
С другой стороны, цепочки из К2, принадлежащие Ма(п), име-
имеют суммарную вероятность ^а—Р(К±). Если Ma (w)— число
указанных цепочек, то
Следовательно,

§ 2. ЭНТРОПИЯ КОНЕЧНОЙ ЦЕПИ МАРКОВА 301
Так как Р(Ж)->0 при п -> со, то при достаточно большом п
~~~п >H-b-r^\og^
log Ma (л)
Отсюда следует, что Нтп inf ——'¦ ^ Н. Ц
Можт-ю получить теперь полезную интерпретацию этой тео-
теоремы. Пусть /V — число состояний цепи. Предположим для про-
простоты, что N=-2m. Тогда число всевозможных сообщений дли-
длины п (цепочек Cv) будет равно N11 = 2"т. Предположим далее,
что эти сообщения передаются с помощью двоичного кода, так
что па кодирование каждого состояния нами затрачивается т
двоичных символов. Значит, при таком способе передачи, назо-
назовем его непосредственным кодированием, длина сообщений со-
составит шп (в русском языке, например, для моделирования ко-
которого можно использовать цени Маркова, можно считать N ==--
= 32, ?п = 5). Утверждение теоремы 2 означает, что при боль-
больших п из этих 27ПН цепочек с вероятностью 1 — 8, 8 > 0, будет
передаваться лишь 2нЯ сообщений. Вероятность появления
остальных будет мала, если мы фиксируем малое е. Отсюда
легко установить существование другого — более экономного ко-
кода, с помощью которого па передачу сообщения с большой ве-
вероятностью потребуется меньшее число единиц. Действительно,
отобранные 2nd сообщений можно просто занумеровать с по-
помощью того же двоичного кода и передавать их номер. На это
потребуется, очевидно, nil двоичных единиц. Так как всегда
Н ^ log N = m, то мы получим экономию в длительности сообщо-
• ния в mill > 1 раз.
Это есть частный случай так называемой основной теоремы
кодирования для ценен Маркова: при больших п существует
код, с помощью которого с высокой вероятностью исходное сооб-
сообщение Сп может быть передано последовательностью сигналов
в т/И раз более короткой, чем при непосредственном кодиро-
кодировании.
Приведенный выше способ кодирования, конечно, представ-
представляет собой скорее утрированный пример, чем эффективный ре-
рецепт укорачивания сообщения. По этому поводу следует отме-
отметить, что отыскание действительно эффективных способов коди-
кодирования представляет собой довольно сложную задачу, В азбуке
Морзе, например, разумно более часто встречающимся буквам
ставить в соответствие более короткие последовательности точек
и тире. Но сокращение текста в т/Н раз при этом, конечно, не
достигается. Некоторые приемы сокращения использовались и в
этой книге. Например, часто встречающиеся слова «характери-
«характеристическая функция» были заменены символом «х. ф.». Можно
было бы добиться больших результатов, применяя, скажем, сте-
стенографию. Конструкция кода с высоким коэффициентом, сокра-

ОЧд гл. V6. ИНФОРМАЦИЯ И ЭПТРОШШ
щения, безусловно, будет весьма сложной. Полученные теоремы
указывают верхнюю границу для результата, которого мы при
этом можем достигнуть.
Так как для последовательности независимых равновероят-
равновероятных знаков //=^-^ log iV = щ, то такой текст несократим. По-
Поэтому некоторым критерием при построении различных кодой
может служить близость «новых» сообщений (закодированных
в новом алфавите) • *к последовательности равновероятных сим-
символов.
"Однако при этом следует учитывать, что та «избыточность»
текста, с которой мы «боремся», во многих случаях представляет
собой явление полезное и нужное — ведь иначе было бы невоз-
невозможным выявлять опечатки или восстанавливать пропуски также
легко, как мы восстанавливаем,, например, букву р в слове «ин-
«информация». Читатель, видимо, знает, как трудно читать сильно
сокращенный и формализованный математический текст. Так что
при работе с идеальным кодом (если бы такой удалось найти)
ошибки при передаче информации недопустимы, .поскольку не-
невозможно восстановить пропущенный или искаженный символ в
последователыюстм равновероятных знаков. В связи с этим воз-
возникает одна из основных в теории информации задач о кодиро-
кодировании, которое оставляло бы наименьшую «избыточность», до-
достаточную для ликвидации помех при передаче.

Глава 14
МАРТИНГАЛЫ
§ 1. Определения, простейшие свойства, примеры
В гл. 12 мы рассмотрели последовательности зависимых слу-
случайных величин Хо, Хи ..., связанных в цепь Маркова. Зависи-
Зависимость характеризовалась при этом вероятностями переходов, ко-
которые определяли распределение Xn+i при условии, что Хп из-
известно. Это позволило весьма полно изучать свойства цепей
Маркова.
В этой главе будет рассмотрен другой тип последователь-
последовательностей зависимых случайных неличин,. в котором характериза-
ция зависимости происходит не через условное распределение
Хп+и а лишь через среднее значение Xn+i при условии, что за-
задана «предыстория» Хо, ..., Хпт Оказывается, это также позво-
позволяет получить многие весьма общие результаты об исследуемом
объекте.
Пусть дано вероятностное пространство (Ц, S, Р> и на нем
задана последовательность случайных величии Хо, Хи .... Пусть
далее на <Й, %, Р > выделено семейство (или поток) вложенных
о-алгебр Шп^0: &> s Si s ... ^ Sn ^ S.
Определение 1. Последовательность пар {Хп, 5?я; п>0)
называется мартингалом (говорят- также, что \Хп} есть мартин-
мартингал относительно системы о-алгеб𠧄), если для всех иХК
1) М|Хп|<оо, . (I)
2) Хп измеримы относительно ?5П1
3) М (Хт/Щп) = Хп при любом т>п. B)
Последовательность {Хп, %п; п^О) называется субмартингалом
(супермартингалом), если выполнены условия 1)—3), но знак
«=» в 3) заменен на «^» («^»).
Будем говорить, что последовательность {Хп} образует мар-
мартингал (субмартингал, супермартингал), если для Sn —cj(X0, ...
..., Хп) пары {ХП1 %п} образуют последовательность того же наи-
наименования. Субмартипгалы и супермартингалы часто называют
полу мартингалами.
Ясно, что соотношение B) в силу свойств у. м. о. эквива-
эквивалентно тому, что М (Xri+1ffin) = Хп, поскольку в этом случае
М (ХгпГЯп) = М [М (XwSm-iVSnJ = М (Хп-г/Ъп) = ,.. =Хп.
Аналогично обстоит дело с нолумартингалами.

304 ГЛ. 14. МАРТИНГАЛЫ
Если {Хп} — мартингал, то ЬЛ (Zw+1/a(X0, , .., Хп)) = Хп и по
свойству у. м. о.
М (Хп^/а(Хп))^ М [М (Хл+1/о(Х0, ,. „ Хп))/о(Хя)] ~
Следовательно, для мартингалов, как и для целен Маркова,
М (Хп+1/о (Хо, ,.., Хп)) = М (Хй+1/о (Хп)).
Однако на этом сходство кончается, так как для мартингала
это равенство не сохраняется для распределений, по зато требу-
требуется, чтобы М (Xn+1/a(Xn)) = Х71.
Пример 1. Пусть gn, п ^ 0, независимы. Тогда Хп = §0-Ь ...
. .. + 1п образует мартингал (субмартингал, суиермартиигал), "
если Щп=0 (ML^O», M^n^O). Очевидно, что Х„ связаны
также в цепь Маркова.
V
То же справедливо относительно Хп = Ц^ь при М^п = 1.
Пример 2. Пусть |п, п>0, независимы. Тогда Аг?г-=
= 2|?fc-i?/u; w ^ 1» ^о = So, образует мартингал, если М^, = 0,
так как M(Xn+1/a (Хо, ...; X,,)) = Хп + М ttnln+i/o (Ы) - Хп.
Очевидно, что здесь {Хп} не является цепью Маркова. При-
Пример, последовательности, которая образует цепь Маркова, но не
является мартингалом, можно получить, рассматривая, скажем,
блуждание па отрезке с отражением от границ отрезка (ври-
мер 12.1).
Наряду с множеством @, 1, .. Л индексов для Хп мы будем
использовать и другие, например, { — оо <#<<»} или {/г <-—!},
а также наборы целых чисел, включающие в себя значения ±^,
скажем, @ ^ п ^ °°}. Эти множества будем обозначать одним
символом Jf, а мартингалы (полумартингалы) записывать в
форме 1ХЩ %п; n^Jf). При этом под S-oo будем понимать а-ал-
гебру П §п» а под Soo будем понимать a-алгебру of (J S/t\,
порожденную U Sn, так что $_«> с gn c= g^ c= g при любом
Определение 2. {Хп, $?и; ^e*/f} называется мартингалом
(субмартингалом, супермартингалом) ^ если выполнены условия
определения 1 при любых га е Jf, m e yf, m > д.
Если дай мартингал {ХП1 gn; neyf} и левая граница /?0 мно-
множества ^Г конечна (например, yf == @, 1, ...}), то мартингал
{Zn, Sn) всегда можно продолжить «на всю ось», положив 5П =
г^§По, Хп = ХПо при п<щ. Так же обстоит дело и с правым
концом. Поэтому, если задан мартингал (полумартингал) {Хп>

§ 1. ОПРЕДЕЛЕНИЯ, ПРОСТЕЙШИЕ СВОЙСТВА. ПРИМЕРЫ 305
5?n; n&Jf), то можно всегда, не ограничивая общности, считать,
что задан мартингал (полумартингал) {Хп, %п; —оо<п<<х>}.
Пример 3. Пусть (ffn, —oo<n<oo} — заданная последова-
последовательность вложенных с-алгебр и § есть заданная случайная ве-
величина па <Q, S, Р>, М111 < оо. Тогда {Хп, Sn; ~°° < п < °°}
где Хп = М (?/5Д образует мартингал.
Действительно, по свойству у. м. о. при любом /п ^ °о, ??г > ?г
М (Xm/Sn) = М [М (|/«т)/»п] - М (С/»») = Хп.
Определение 3. Мартингал в примере 3 будем называть
мартингалом, порожденным случайной величиной | (и семей-
семейством {§Т1}).
Определение 4. Множество */Г+ будем называть замыка-
замыканием JT справа, если
1) Jf+=Jf, когда максимальный элемент JT конечен,
2) Jf\ = Ар [} {+оо}? если JT неограничепо справа.
Если Jf = А°+, то будем говорить, что Jf замкнуто справа.
Будем говорить, что мартингал (полумартингал) {Хп, §n, n^Jf}
замкнут справа, если Jf замкнуто справа.
Лемма 1. Мартингал {Хп, ^п; n^Jf) порожден некоторой
случайной величиной тогда и только тогда, когда он замкнут
справа.
Доказательство леммы очевидно. В одну сторону оно
следует из примера 3, В другую — из равенства
М (Xiv/Sn) - ^п, N = sup {k; к е= Jf}%
так что {Хп,^п} порожден XN. ^
Приведем один интересный и более конкретный пример мар-
мартингала, порожденного случайной величиной.
Пример 4. Пусть %ь ?2, ... независимы, одинаково распре-
распределены, М IS] I < °°- Положим
Тогда S-n ^ 8-п+1 и при любом I ^ к < 7г
Последнее равенство справедливо в силу симметрии. Из него
следует, что
Sn - М (Sn!$-n) = 2 М Fл/»-.я) - /гМ (gx/af-rOe
Это означает, что {Хп, ^п; п^—1} образует мартингал, порож-
порожденный !-!.
20 А. А. Боровков

306 - ГЛ. 14. МАРТИНГАЛЫ
Получим ряд вспомогательных утверждений, характеризую-
характеризующих простейшие свойства мартингалов и полумартингалов. При
этом везде будем ограничиваться рассмотрением лишь субмар-
тишгалов, так как соответствующие свойства супермартингалов
сразу получаются переходом к последовательности Yn = —Хч,
если {Хп} — субмартингал. -
Лемма 2. 1) Свойство {Хп, §n; nz=Jf) быть мартингалом
эквивалентно неизменности по ш^п функций множества (ин-
(интеграла)
М(Хт;А)^М(ХпуА) C)
при любом 4е^, В частности, MXm = const.
2) Свойство {Хп, %п; n^-Jf) быть субмартингалом эквива-
эквивалентно монотонному возрастанию по ш ^ п функций множества
М(Хт;Л)^М(Хп;А) D)
при каждом А<^т5п. В частности, MXm | ,
Доказательство является очевидным следствием опреде-
определений. Если выполнено C), то по определению у. м. о. Хп =
= М(ХШ/$П) и наоборот. Пусть теперь выполнено D). Обозна-
Обозначим Yn = M(Xm/Sn). Тогда из D) следует, что ЩУп; A)^M(Xn;
A), M(Yn—Хп\ А)^0 при любом А ^5?п. Отсюда вытекает, что
с вероятностью 1 Yп=М(Хт/^п)'^Хп. Обратное утверждение по-
получается столь же просто. Щ
Лемма 3. Пусть {Хщ т%п; n^Jf)—мартингал и g(x)—вы-
g(x)—выпуклая вниз функция с М j g(Xn) | <С оо. Тогда {g(XnI gn; n <=
g Jf) образует субмартингал.
Если к тому оке g(x) не убывает, то утверждение сохранится
и в том случае, когда {Хп, %п; n^Jf) — субмартингал.
Доказательство. Обозначим ?n+1 =Xnfl — Хп. Тогда
М
Воспользуемся свойствами у. м. о. и, в частности, неравенством
Иенсена, примененным к функции gt (x) — g(Xn + х) (см. § 4.8).
Мы получим
М (gl Aп-н)Ш > gl (M (Sn+i/»n)) - gi @) = g (Хп).
Точно так же проверяется утверждение для субмартингалов.
Л е м м а 4. Пусть {Хп, §n; n ^ Jf) — замкнутый справа суб-
мартингал, Хп(а) = тах(Х„, а). Тогда {Хп(а), Sn; n^Jf) при
любом а — равномерно интегрируемый субмартингал. Если {Хп,
§n; n^Jf) — замкнутый справа мартингал, то он равномерно
интегрируем.
Доказательство. Пусть 7V = sup{fe; k&Jf}. Тогда по
лемме 3 iXn(a), Sn; n^Jf) — субмартингал. Следовательно, при

§ 2. ТОЖДЕСТВО ВАЛЬДА 307
любом с>0 (Х+ = тах@, X))
сР (Хп (а) > с) < М (Хп (а); Хп (а)>с)^
< М (XN (а); Хп (а) > с) < МХ^ (а),
при с -> оо равномерно по п. Поэтому мы имеем требуемую рав-
равномерную интегрируемость
sup М (Хп (а); Хп\а) > с) < sup М (Xjy (а); Хп (а) > с) -+ 0,;
поскольку sup Р (Хп (а) > с)-> 0 при с -> «» (см. лемму 3 в При»
п
ложепии 3; наличие срезки на уровне а позволило избежать
оценки «отрицательных хвостов»).
Если {Xn, gn; n e Jf} — мартингал, то его равномерная инте-
интегрируемость следует из первого утверждения, примененного к
субмартингалу {|XJ, $n;n^JP}. ^
В какой-то мере природу мартингалов поясняет также сле-
следующий пример.
Пример 5, Пусть %,, ?2, ••• — произвольная последователь-
последовательность случайных величин М | ?/> | < °о, gn = 0(g1} # ф >? gn) При
/t^l, So™(^, Й) (тривиальная а-алгебра)
Тогда {Zn, gn; n> i) образует мартингал. Это следует из того,
что
М (Sn+1 - Zn+1/S?n) - М (Хп~+ Ъп+1 - Ы (&Ц-!/»*)/»*) = ^п.
Другими словами, для произвольной последовательности {^J
последовательность Sn можно «подправить» так называемой
«предсказуемой» последовательностью Zn (значение Zn опреде-
определяется по Si, .•., ?n~i) так, что Sn — Zn будет мартингалом.
§ 2. О сохранении евоцства быть мартингалом
замене времени на случайное. Тождество Вальда
В этом параграфе jV = {п > 0}.
Определение 5. Для последовательности {%п; п>д) слу-
случайную величину v будем называть моментом остановки (отно-
(относительно ШЛ), если {v<n}egn при любом пХ).
Очевидно, что постоянная v ~ m является моментом останов-
остановки. Если v — момент остановки, то v = min(v, m) при любом
Фиксированном пг также будет моментом остановки, поскольку

при n*^ гп выполняется v ^ m ^ rc, {v ^ ?г} = Q ^ $n; при n < m
G ^n} = {v <n}^ gn.
Если v — момент остановки, то {v = п} — {v ^ ?г} — {v ^ п —
-l}egn, {v > п} = Q— Ь ^ /г— 1} eg^. Наоборот, если {v =
= п) е gri7 то {v < п) е gn м, следовательно, v — момент оста-
остановки.
Пусть дал мартингал {Х«, Ъп\ п ^ 0}. Типичным примером
момента остановка является момент v попадания Хп в заданное
измеримое множество В:
(v — оо? если все Хп Ф В), Действительно,
{v =, п) - {Хо Ф Д, .. ., Хи-1 ^ Л, Хп е S) е ®я.
Если v — собственны]! момент остановки ({v = oo} = 0)? то
Xv — случайная величина, так как
G-алгвброй Sv будем называть G-алгебру, образованную мно-
множествами А ^ ®, для которых /1 П {v = д} е gn? ?г ~ 0, 1,
Можно представлять себе, что Sv порождена событиями (v ^ п) П
П Вп, /г = 0, 1, ..., где Sn ^ 5?п. Ясно, что v и Xv измеримы отно-
относительно 3?v. Если vt, v2—два момента остановки, то {v2^vi} ^
^$fvf, {va^vJeSv,, так KaK{v2>v1}== U {v2 = ?г} {v! < n}.
1 n
Мы уже знаем, что если {Х„,^ §„} — мартингал, то значение
МХп постоянно при всех п. Сохранится ли это свойство для
MXV, где v — момент остановки? Из тождества Вальда мы зна-
знаем, что для примера 1 это так. В общем случае справедлива
Теорема 1 (Дуб). Пусть {Xn, 8?n; n > 0} мартингал (суб-
(субмартингал) и Vi, v2 — моменты остановки такие, что
M|Xv.|<oo, i-^i/l, (Ъг)
Тогда па множестве {v2 ^ vj
М (XV2/gVl) = XVl (>XVl). F)
Это и есть обобщение мартингальн ого (субмартингалыюго)
свойства для случайного времени.
Следствие 1. Если v2 = v ^0 — произвольный момент оста-
остановки, то полагая Vi^n (это тоже момент остановки), получим,
что па мнооюеетве v ^ п
М (Xv/Bfft) = Xni MXV =

§ 2. ТОЖДЕСТВО ВЛЛЬДА 309
или, что то же, при любом А ^ ?5п П {v > п)
М (Xv; 4) = М (Хп; Л).
Для субмартингалов здесь надо вместо «=» писать «>».
Доказательство теоремы 1. Чтобы доказать (G), доста-
достаточно убедиться, что для любого А^ 8\>х
М (Уv2; 4 П {v2 > vj) = M (XV]; А П {v2 > Vj}). G)
Так как Vi дискретны, то для этого, в 'свою очередь, достаточно
установить G) для множеств An = A(\{vL = n}^$jnj п^-0, 1, ...,
т. е. установить равенство
М (XVa; А, П {v2 > и}) = М (Х„; /1, Л {v2 > и}). (8)
'Тем самым доказательство сведено к случаю Vt = п. Имеем
М (Хп> Ап П {v2 > п}) = М (Х„; /in П {v2 - п}) +
+ М (^Т1; Ап П (v2 > Д + 1}) = М (XV2; Л, П {v2 = п}) + *
Здесь использован тот факт, что (v2^ я+1) S3fn, и свойство C)
мартингала.
Применяя полученное неравенство ш раз, находим
= М (Хп; Ап П {v2 > п}) - М (Хт; ^п П {va > m}). (9)
Последнее выражение в силу E") сходится к нулю для
некоторой последовательности ш -+ о°.
Так как Ап> п = Ап П {/г^л^2 < гл} i Вп = Л/г П {^г ^ v2), то по
свойству интегралов и в силу (9)
М (Xv ; Ля П {л< v2}) - lim M (XVo; АПуГП) - М (Хп; Л f] {v2 > л}).
Мы доказали равенство (8), а вместе с ним и теорему 1 для
мартингалов. Изменения, которые надо внести в доказательство
для субмартингалов, состоят в замене в нескольких местах зна-
знака равенства на неравенство. ^
Условия теоремы 1 бывают выполнены далеко не всегда, да-
даже в довольно простых ситуациях. Рассмотрим, например, без-
безобидную игру (см. примеры 4,8, 4.11), в которой z + Sn есть
капитал первого игрока после п партий в игре с бесконечно бо-
богатым противником и при условии, что игрок еще не разорился.
Пдесь *>G, 5Л= S Ь, Р(?л = ±1) = 1/2, i](z)=*m\n{k: Sh=*
h--=l
-^ ~z) есть, очевидно, марковским момент; последовательность
{Sn; n^Q}, 50 =---0 образует мартингал: 8Ыг) = —z. Следовательно,

310 ГЛ. 14. МАРТИНГАЛЫ
) = — z Ф MSn = 0, и равенство (8) при vA = 0, v2 = г) (z),
2 > 0, тг > 0 не имеет места. В рассматриваемом случае это озна-
означает, что не выполнено условие E") (это связано с тем фак-
фактом, что Мц^) = оо).
Вообще говоря, условия E) теоремы 1 могут быть весьма
трудными для проверки. Поэтому полезными для приложений
являются следующие утверждения.
Положим для краткости
п
с,п = Хп — Xn_lt §0 = Ло, Yn = 2j i bk 15 w == 0, 1, , , . r
о
Лемма 5. Для выполнения E7), E/7) (при Vi = v) доста-
достаточно, чтобы
fV1Fv<oo. A0)
Доказательство почти очевидно, поскольку IXv\ < Уv,
Так как P(v> w)~>G, Myv<o°, то остается воспользовать-
воспользоваться свойством интегралов, в силу которого IV! (ц\ Ап)-*-0, если М | т||<
<оо, Р(Дг)^0. 4
Введем следующие обозначения:
Теорема 2. Пусть {Хп; пХ)} есть мартингал (субмартин-
(субмартингал) и v — момент остановки (относительно {$п = о(Х0, ..., Хп)}).
1) Если
Mv<oo (И)
и при всех п^О на множестве {v ^ «} е gw_t выполняется
пп^ с = const, A2)
то
М | Xv |< оо, !ViXv - MXQ (> МХо). A3)
2) йс^^г, кроме того, Мо2п = М|п < °°7 ^о
A4)
Доказательство. В силу теоремы 1, следствия 1 и лем-
леммы 5 для доказательства A3) достаточно проверить, что условия
A1), A2) влекут за собой A0). Вполне аналогично доказатель-
доказательству теоремы 4.2 имеем
(
=0 \h=Q

§ 2. ТОЖДЕСТВО Б А ЛЬДА ¦ 311
Здесь {v > kl = Q — {v ^ к — 1} е gft_le Поэтому по условию A2)
Это означает, что
сю
MFv<c2P(v>i) = cMv< оо.
Докажем теперь A4). Положим Zn~X\— 2°1- Нетрудно
г
видеть, что Zn — мартингал, так как М (¦X'n+i "~" -^п — Cn-f-i/Sn) ==
= М BХ„?и+1 + ?*+1 - а*/$„) = 0. Ясно также., что М I Zn \ < оо
и что v(/i) = min(v, w) вместе с v есть марковский момент.-Для
пары {Zk}, v(n) условия E'), E") в силу леммы 5, очевидно,
всегда выполнены. Поэтому по первой части теоремы
MZv<n> =0, МА1(I) = М 2 о*. A5)
1
Осталось убедиться, что
lim MX$(n) - MZ^, lira M 2 ^ - М 2 aj. A6)
Я->оо
Второе из этих равенств следует из теоремы о монотонной схо-
сходимости (v (тг) f-v, ol^O). Первое также будет следствием тео-
теоремы О МОНОТОННОЙ СХОДИМОСТИ, ПОСКОЛЬКУ ^v(ri) "^ Zv, -X"v(n)t*
Чтобы убедиться в последнем, заметим, <гто {Х^, 5?1; п ^0}
образует субмартингал и, следовательно, для любого А^%п
М (Х5(п); /1) = М (X?; Л П {v < га}) + М (Xl; A p, {v > п}) <
<М(Х?; ,1 П {v< п}) + М (М (Х^+1/®»)МП {v > n» =
= М (X?; 4 П {v < га + 1}) + М (Xfl+1; 4 П {v > и + 1}) =
Итак, из A5), A6) следует A4), и теорема полностью до-
доказана. А
Из теоремы 2 вытекает уже известное нам тождество Валь-
да, дополненное еще одним полезным утверждением, которое мы
уже использовали (см. пример 4.11).
Теорема 3 (тождество Вальда). Пусть Ъ>и §2, ».. независи-
независимы, одинаково распределены, Sn = |t + ... + ^n, SQ =¦ 0 и суще-
существует М|х = а. Пусть, кроме того, v есгь момент остановки та-
кой) что Mv <C оо. Тогда
MSV = aMv. A7)

312 ГЛ. 14. МАРТИНГАЛЫ
Если к тому же о2 = D^l < оо, то
М [Sv — vaf = aaMv, A8)
Доказательство. Очевидно, что Хп^=- Sn-~ па образует
мартингал и для него выполнены условия A1), A2). Поэтому
MXV = МХ0 = 0f что эквивалентно A7), и МХ^ = Mva2,, что
эквивалентно A8). ^
Пример 6. Иллюстрацией использования теоремы 3 могут
быть примеры 4.11, 4.16, касающиеся безобидной игры, когда
РE/г = ± 1) = 1/2, v = min{A: Sh==Z2 или Sh=—z{} (z{ я z2—-
капиталы соответственно 1-го и 2-го игроков). Рассмотрим те-
теперь случай р == Р (Ъг = 1)ф 1/2. Последовательность Х„ =
^ 0, g == 1 — р, образует мартингал, так как
n
я \^h „ я . л р
М ( ~J = Р~ + q-j- = I* По теореме 3 (вероятности Р1? Р2 оп-
определены в примере 4.11)
Отсюда и из равенства Pi + Р2 = 1 получаем
1
р/ \ Pi
Используя снова тождество Вальда, получим также
Отметим, что эти равенства можно было бы получить и элемен-
элементарными методами*), но это потребовало бы больше места.
В тех случаях, когда ?v имеет достаточно простую природу,
утверждения типа теоремы 2 позволяют получать (или оцени-
оценивать) и само распределение случайной величины v. В этих си-
ситуациях весьма полезным является приводимое ниже следствие
теоремы 2.
Предположим, что мы находимся в условиях теоремы 3, од-
однако вместо условий на моменты §л мы будем предполагать, что
%п удовлетворяют условию Крамера (ср. с § 8,8);
Ир {I) = М^Б < оо
при некотором К Ф 0.
*) См,, например, [18], т.

§ 2. ТОЖДЕСТВО ВАЛЬДА
13
Теорема 4 (фундаментальное тождество Вальда). Пусть v
есть момент остановки такой, что Mv<oo, \Sn\ < с = const на
множестве iv^n). Тогда для значений А,, при которых
справедливо
М
1.
A9)
Замечание 1. Это есть обобщение на случайное время
очевидного равенства Me" n=i|)n(X).
Доказательство. Положим Хп = в пя|Г"п (X). Ясно, что
{Xn, gn; п^О) образует мартингал, МХп = 1. Надо убедиться,
что MXV = МХ0 = 1. Мы докажем это, если проверим, что Х„
удовлетворяет условиям первого утверждения теоремы 2. Для
этого в свою очередь достаточно проверить, что, на множестве
ап = М (|.Хте — Xn_! j/Sn-i
= const.
По
>П-1j —
¦ — 1
Так как |Х„_4| < eu па множестве (v >/г} и при t|)(X)^l, то па
этом множестве ап ^ 2е%с. 4
Пример 7. Вернемся к задаче об игре па разорение, кото-
которая обсуждалась в примере 8. В условиях этой игры теорема 4
дает
е'ЧШ (г|> (^)-v; Sv « z2) + Г^М (гр Wv; S, - - zt) = 1.
В частности, при zt = 22 = z и /? = 1/2 из соображений симмет-
симметрии получаем (в этом случае всегда
-fe
B0)
rl'i\K как i|? (А,) = -7>-(б? + ^~ ), то, сделав замену s = \|)(X), получим
r^==sdhY52 — 1, что после подстановки в B0) (можно взять лю-
любую из ветвей для е%) дает явный вид производящей функции
M.v~v позволяющий путем разложений в ряд элементарных функ-
функции найти в явной форме вероятности P(v = пI п = 1, 2, ,..

314 ГЛ. 14. МАРТИНГАЛЫ
§ 3. Неравенства
В этом параграфе мы получим два полезных для приложений
неравенства для иолумартингалов. Обозначим
Хп = max \Xk\.
О -^ k < п
Теорема 5 (Дуб). Пусть {ХП1 %п; п > 0}—неотрицательный
субмартингал. Тогда при всех х^О, пХ)
Р (Хп > ж)
Доказательство. Пусть
{ft^0: Zfe^x}, v(n) = min(v, n).
Очевидно, что п и v(h) есть моменты остановки, v (/г) =^ 7г, и по-
поэтому по теореме 1 (см. F) при v2 = гс, v1==av(w))
Замечая, что (Хп > ^} = {XV(Vo ^ ж}, по неравенству Чебышева
получим
Из теоремы 5 вытекает
Теорема 6 (второе неравенство Колмогорова). Пусть {Xll7
п\ п ^ 0} мартингал, для которого существует МХ%. Тогда {Xf^
^n'y n^O) — субмартингал, и из теоремы 5 получаем
Первоначально это неравенство было получено Колмогоровым
для сумм -STn = !i +... +?п независимых случайных величин ?п.
Теорема 5 обобщает доказательство Колмогорова на случай суб-
субмартингалов и усиливает неравенство Чебышева.
Докажем теперь одно неравенство, которое понадобится для
теорем сходимости в- следующем параграфе. Оно касается числа
пересечений последовательностью Хп некоторой полосы. Пусть
а < Ъ — два заданные числа. Положим v0 = 0,
Vi ~ min {п > 0: Хп < a}, v2 = mm in > v4: Xn > b}7
n > v2ft-2: Xa ^ a), vZh ==¦ min in > v2ft-i: Xn > 6},

§ 3. НЕРАВЕНСТВА
315
"Пудем считать, что vm =«», если траектория {Хп} при 72
никогда не пересечет соответствующий уровень. В этих обозна-
обозначениях можно определить число пересечений снизу вверх траек-
траекторией Хо? ..., Хп полосы [а, Ь] как случайную величину
(max {к: v2k <; п), если v2
Ю, если v2
п,
Обозначим (а)+= тах@, я)'.
Теорема 7 (Дуб). Пусть {Хп, §ft; д ^ 0} — субмартингал.
Тогда при всех п
M(b)
B1)
Ясно, что само по себе нера-
неравенство B1) предполагает задан-
заданным лишь субмартингал {Xki %k;
)
vt
Рис. 14
Доказательство. v(a, b;
n) совпадает с числом пересече-
пересечений полосы [О, Ъ — а] последовательностью (Хп — а)+. Но
{(Хп — а)+, Щп] п^О} образует неотрицательный субмартингал
(см. пример 4) и, следовательно, можно, не ограничивая общно-
общности, считать а =. О, Хп ^ 0 и доказывать, что
Пусть
A, если v/г < / ^ v/l+1 для какого-нибудь нечетного кг
' ] [0, если v/l</^v/l4-i для какого-нибудь четного к.
На рис. 14 vt = 2, v2 = 5, v3 = 8; т\$ = 0 при / < 2, т|,- = 1 при
3 < У ^ 5 и т. д. Нетрудно видеть (мы используем здесь преоб-
преобразование Абеля), что (Хо ^ 0, т|0 = 1)
о + 2
п—1
+
bv @, Ь; л).
Кроме того (yl^i означает множество нечетных чксел)?
= U

316 • ГЛ. 14. МАРТИНГАЛЫ
Поэтому и в силу того, что М (-Xj/Sfj-i) — Xj__x ^ 0, получим
ЬЦу @, Ь;в)<м| ти (X i - Х^) = 2 М (X, - ХЬ1; ^ = 1) =
1 1
= 2 М [М № - X^/Sj-j); ть = 1] =
1
= 2 М [М (AV^-0 - ^_i; т^ = 1] <
1
< 2 м [ м (ЗД-i) - ^i-i] = 2 м (Xj - х}_г) =
1
§ 4, Теоремы сходимости
Теорема 8 (теорема Дуба о сходимости мартингалов). Пусть
{!„, 5?п; —оо < дг < оо} — субмартиигал. Тогда
1) Z_oo = lira Хп существует п. н., MZioo<oow {Arn, 5n;
П-^ —оо
—oo ^ n <: 00} образует субмартиигал.
2) .Если snpM^J<oo? шо Zoo ™ lira Xn существует п, u.y
fee sup M j Xn | < oo, 7720 M j Хж I <; oo.
3) Последовательность {Xni $n; -<» ^ /? ^ 00} образует суб-
субмартингал тогда и только тогда, когда последовательность [Х^\
равномерно интегрируема.
Доказательство. Так как
{lim Хп > lim Хп) = [) {lim Хп > b > а > lim A^}
а ,Ь
рациоиалыгме
(пределы берутся при /2->—оо), то предположение о расходимо-
расходимости с положительной вероятностью
означает, что найдутся рациональные а < Ъ такие, что
Р (iim Xrt > 6 > а > Иш Хп) > 0. B2)
Пусть \?(я, 5; ттг)—число пересечений снизу вверх полосы
[а, Ь] яоследовательностью ?{ = Х-т, ..., Ут = -X"-i, v (a, b) =
*= lim v(a, fc, m). Тогда B2) означает, что

§ 4. ТЕОРЕМЫ СХОДИМОСТИ 317
По теореме 7 (примененной к последовательности Yh ».., Ym)
B5)
Но последнее неравенство противоречит B3) и доказывает,
что P(limXn = limXn) = 1. Кроме того, по лемме Фату (Xt^ =
MXJ!*, < lim MX+ < MXix< <х>, B6)
Среднее неравенство здесь вытекает ив того, что iXn,3?nl обра-
образует вместе с (Х„, SJ субмаргингал (см. лемму 3) и, стало быть,
NIXt f .
Чтобы доказать, что (Xn, gn; — оо ^п<<*>} — субмартингал,,
нам надо по лемме 2 убедиться, что для любого A eg-oo CS
M(X-ooM)<M(Xn;4). B7)
Положим Xn(a) = inax(Xn, а). По лемме 4 {Хп(а), т$п; п < 0)
есть равномерно интегрируемый субмартингал. Поэтому при лю-
любом —°° < к < п,
M(Xft(a);4)<M(Xn(e);4),
М(Х_00(а);Л)= lim M(Xh(a); A)^M(Xn(a);A). { }
Устремляя а->---оо, по теореме о монотонной сходимости по-
получим B7).
Второе утверждение теоремы доказывается точно так же. На-
Надо лишь в B4), B5) правые части заменить на МХ^ и supM-X",**"
п
соответственно. Вместо B6) получим (здесь пределы берутся при
П -> оо)
и если supM|Xn|<oo, то
М|Х00|<ИгаМ|Хп|<оо,
Последнее утверждение теоремы доказывается точно так жеу
как первое (равномерная интегрируемость позволяет нам наряду
с B8) записать для любого А е g?n
М (Хоо (а); А) == lim M (Xk (а); А) > М (Хп (а); А)).,
Г» обратную сторону третье утверждение теоремы следует из
леммы 4. ^1

318 ГЛ. 14. МАРТИНГАЛЫ
Получим теперь некоторые следствия теоремы 8.
До сих пор (см. § 4.8) мы при изучении сходимости у. м. о.
имели дело с у. м. о. вида М(Хп/$). Теперь из теоремы 8
можно получить полезную теорему сходимости для у. м. о. ино-
иного вида.
Теорема 9 (Леви). Пусть на вероятностном пространстве
(Q, S, Р) задано неубывающее семейство gf, с: gf2 с . . eg
а-алгебр и случайная величина |, М | ?, | < °°- Пусть, как и
преоюде, 8оо = о ([) fin] есть о-алгебра, порожденная событиями
\ п )
из 8?1? 8г2, . •» * Тогда при п -> со
. ¦ B9)
Доказательство. Положим Х„ = М (|/2?п). Мы уже зна-
знаем (см. пример 3), что {Х„, g?n; 1 < /г ^ оо} есть мартингал и, сле-
следовательно, по теореме 8 п. в. существует Нт Хп = Аг(оо). Остает-
П-^оо
ся доказать, что Х^) = M(|/Soo). (т. е. что Х@0) = Хоо). Так как
iXn, Sn; I < w < оо} по лемме 4 является равномерно интегрируе-
интегрируемым мартингалом, то
М (Х(оо); А) = lira М (Хп; А) = М (|; Л) = lira M (М(|/5„); Л)
при А е gfe и при любом к = 1, 2, ... . Это означает, что край-
крайние члены последнего равенства, являющиеся конечными мера-
со
ми, совпадают на алгебре U Srt. По теореме о единственности
продолжения меры (Приложение 1) они будут совпадать при
/ \
всех iea U 5n =^ Sao. Следовательно, по определению у. м. о.
VI/
Х(сю) == М (Шоо) = X«. ^
Можно отметить также, что из равномерной интегрируемо- ..
сти {Хп, Sn; 1</г<оо} следует, что в B9) можно * заменить
па —^*
A)
Из теоремы 8 вытекает усиленный закон больших чисел.
Действительно, обратимся к примеру 4. По теореме 8 суще-
существует предел Х_оо = lim Xr, = \im {SrJn), который измерим от-
П-* — сю п-^-оо
носительно остаточной (тривиальной) о-алгебрьт к, следова-
следовательно, с вероятностью 1 постоянен. Так как М.Х_оо = М^, то
E„//г) ^М|х. ^ - "
п.н.
Можно получить также некоторые обобщения теорем о схо-
сходимости рядов в гл. 10 на случай зависимых слагаемых. Пусть
п . ¦
Хп = Sn = ^ ^ и Х„ образуют субмартингал (М (ln+i/Sn) ^ 0)*

§ 4. ТЕОРЕМЫ СХОДИМОСТИ 319
I Густь, кроме того, М | Хп | << с при всех п и при некотором
с < °°. Тогда существует и. н. предел Soo = ]hnS}l. (Как и
П-»оо
теорема 8, это есть некоторое обобщение теоремы о сходимости
монотонной последовательности. Важнейшую роль при этом иг-
играет условие ограниченности Mj-Xrt|.) В частности, если \h не-
оо
зависимы, M|/i = 0, и ?ft имеют дисперсии °t такие,-что 2
< оо, то
1/2
и, следовательно, *?« ^ *^оо- Л/ьг получали в качестве следствия
теорему Колмогорова о сходимости радов.
Пример 8. Рассмотрим ветвящийся процесс {^J (см. § 7.7)»
Мы знаем, что rQn допускает представление
r;c,e ^ — одинаково распределенные целочисленные случайные ве~
.чичмны, не зависящие между собой и от ?n~i и представляющйе-
«'обом числа потомков t-ik частицы в (п—1)-м поколении. Если
принять So = 1 и обозначить \i = М|.ьо то
Отсюда следует, что Хп ~ —~ образует мартингал, так как
Теорема JO. Последовательность Хп = \х'%п сходится почти
наверное к собственной случайной величине Xf M-X"<°°. Х.ф».
i[)(X) случайной величины X удовлетворяет уравнению
где /(z) = Mz4
Теорема 10 означает, что ц~"п?п имеет при /г ~> сю собственное
предельное распределение.
Доказательство. Так как'Ха^0, МХп = 1, то первое
утверждение немедленно вытекает из теоремы 8.
Так как Mz n равно п~й итерации функции /(z), то для х. ф.
получим (фп(^) == МегЩ)

320 1Л.1*. МЛРТШГГАЛЫ
Поскольку Хп =>¦ X и функция / непрерывна, то отсюда получаем
уравнение для х. ф. предельного распределения ,Х:
В § 7.7 было установлено, что в случае и < 1 процесс ?п вы-
вырождается с вероятностью 1 и, следовательно, Р(Х = 0) = 1.
Убедимся теперь, что в случае и > 1 распределение X не вырож-
вырождено (не сосредоточено в нуле), Для этого достаточно доказать,
что {Х„, 0 ^ п ^ оо} образует мартингал и что, следовательно,
MX = МХП = 0. По теореме 8 для этого достаточно убедиться,
что последовательность Х„ равномерно интегрируема. Чтобы
упростить рассуждения, предположим, что D|>? = а2 < оо и по-
кажем, что в этом случае МХп<с<сю (это, конечно, влечет за
собой требуемую равномерную интегрируемость Х„, см. § 6.1).
Непосредственно проверяется, что справедливо тождество
п
*' v-2 2П VI Г^2 /у \v~\ 2n—2k
Так как
(надо вспомнить равенство Оц = ЬЛ{цг — (М^J)), то
- 2 rvMt. - ,=v 2
Мы доказали таким образом,, что X — невырожденная случайная
.2
величина, MX = 1, ОХ,г~>- - ¦ , ___ л-. Из последнего соотношения
2
нетрудно получить, что DX = — ,__ • . Установить это можно,
доказав, например, фундаментальность Хп второго порядка и тем
самым '(см. теорему 3 § 6.1) сходимость Xrt—>¦ X*

Глава 15
СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
§ 1. Общие определения
Определение 1. Случайным процессом *) натыкается се-
семейство случайных величин !;(/)= ?(?, о), заданных на
одном вероятностном пространстве <Q, $?, Р> и зависящих от
параметра ty принимающего значения из некоторого множе-
множества Т. Обозначать случайный процесс будем символами i%{t),
Последовательности независимых случайных величин ?ь |2т .. •»
рассматривавшиеся в предыдущих параграфах, являются случай-
случайными процессами, для которых 7Т = {1, 2, 3; ...}. То же самое
справедливо и относительно сумм Su S2, ... слагаемых |1? ?г, ... .
Случайными процессами являются также последовательности
{Хп, п = 0, 1, ...} величин, связанных в цепь Маркова, и мар-
мартингалы {Хп; n^Jf}, описанные в предыдущей главе. Такие
процессы, у^ которых множество Т можно отождествить со всей
или с частью последовательности {..'., —1, 0, 1, ...}, обычно на-
называются процессами с дискретным временем или случайными
последовательностями.
Если Т совпадает с некоторым числовым интервалом Т =*
=-[а, Ь] (ото может быть также вся прямая — °° < t < °° или
полупрямая t>0), то совокупность {?(?)> t^T) называют про-
процессом с непрерывным временем.
Простым примером таких процессов могут служить процессы
восстановления (ц{1), к^О), описанные в гл. 9.
В этой главе мы будем рассматривать лишь процессы с не-
непрерывным временем,. Интерпретация параметра t как времени,
конечно, не обязательна. Она возникла исторически, поскольку
в большинстве естественнонаучных задач, которые привели к
появлению понятия случайного процесса, параметр t был вре-
временем, а значение ?(?) было тем, что наблюдалось в момент
времени L
Как случайный процесс можно рассматривать, например, дви-
движение молекулы газа во времени, уровень воды в водохранили-
водохранилище, колебания крыла самолета и т. и.
*) Наряду с термином «случайный процесс» часто используются также
названия «вероятностный» или «стохастический» процесс,
21 Л. А. Боровков

•3ZZ А"'1- 1Э, Li Л У ЧЛ11 LirHlli 11Ги.1Д^ЬЬ.Ы L- li blil'i^l'bL U i lbliVl lil'iilYJLJjJli ii.M
Процессом с непрерывным временем является, например, слу-
случайная функция
/i=-0
где ?л независимы и одинаково распределены.
Рассмотрим некоторый случайный процесс {§@? t^T).
Если фиксировать со <= Q] то мы получим функцию \>{к), t^Tr
которую часто называют выборочной функцией или траекторией
процесса. Таким образом, в роли случайных величин здесь вы-
выступают функции. Как и раньше, можно было бы рассматривать
здесь выборочное вероятностное пространство. Его можно по-
построить, например, так. Рассмотрим пространство SB функций
x(t), t&T, в котором лежат траектории ^(t). Пусть далее Ъ%>-
есть о-алгебра подмножеств из SB, порожденная множествами
вида
для любых /г, любых tu ..., tn из Т и любых борелевских мно-
множеств Bh ..., Вп. Множества такого вида называются цилиндри-
цилиндрическими; всевозможные конечные объединения цилиндрических
множеств образуют алгебру, порождающую ?3^. Если процесс
§(?, со) задан, то он определяет измеримое отображение (Q, ®>
в (<%?,, Э^>, так как, очевидно, ^~1(С) = {со: ?(•, со)^ С) eg? для
любого цилиндрического множества С и, следовательно, |~1(Z?)e
eg для любого В <ее 33^>. Это отображение индуцирует распре-
распределение Р| на <^,33$?>, определяемое равенствами Pg (Z?) =====
===РE (^)). Тройка <<3?,Э^, Р|) и называется выборочным
вероятностным, пространством. В этом пространстве элементар-
элементарный исход «со» отождествляется с траекторией процесса, а мера
Pg называется распределением процесса ?.
Если же, рассматривая процесс {%(?)}, фиксировать значения
времени ?ь t2, .. ., ^rt, то мы получим многомерную случайную
величину ($(tiy со), ..., ^(^,, о))). Распределения таких величии
называют конечномерными распределениями процесса.
В качестве пространства <$ в теории случайных процессов с
континуальным множеством Т значений времени t чаще других
рассматриваются следующие пространства функций.
1. Пространство всех функций на Т
SB = RT = П Rtl
$
где Rt есть экземпляры вещественной прямой (—оо? оо). Это
пространство обычно рассматривают в паре с о-алгеброн

§ 1. ОБЩИЕ ОПРЕДЕЛЕНИЯ 323
подмножеств из i?T, порожденной цилиндрическими множе-*
ствами.
2. С (Г)— пространство всех непрерывных на Т функций (бу-
(будем писать С (а, 6), если Т = [а, 6]). В этом пространстве наряду
с о-алгеброн 23с, порожденной цилиндрическими множествами из
Q(T) (эта а-алгебра уже, чем аналогичная о-алгебра в /?т),
часто рассматривают также о-алгебру $$с(Т) (борелевскую о-ал-
гебру), порожденную множествами, открытыми относительно
равномерной метрики
р (я, у) = sup | у (t) — х (i) |, х,у^.С (T).
Оказывается, что в пространстве С (Г) всегда ^с(Т) = Эс *)•
3. Пространство D(T) функций, у которых в каждой точке t
существуют пределы x(t — 0) й x(t + 0), причем значение x(t)
совпадает либо с x(t — 0), либо с ^(^ + 0). Если Т = [а, Ь], то
предполагается также, что х(а) = х(а + 0), х(Ь) = х{Ъ — 0). Это
пространство называют часто пространством функций без разры-
разрывов второго рода**). Пространство функций, для которых в осталь-
остальных точках x(l) = x(t — 0) (#(?) = x(i'¦ + 0)), будем обозначать
D-(T) (D+(T)). Пространство D+(T) (D-(T)) будем называть
также пространством функций, непрерывных справа (слева).
Например, траектории процессов восстановления, описанных в
гл. 9, принадлежат D+@, °°).
В пространстве D(T) также можно строить борелевскую а-ал-
гебру относительно подходящей метрики, по мы ограничимся ис-
использованием о-алгебры'33d подмножеств из D(T).
После проведенных рассмотрений можно сформулировать сле-
следующее эквивалентное определение случайного процесса. Пусть
$в — заданное пространство функций и © есть а-алгебра его под-
подмножеств, содержащая а-алгебру 39^ цилиндрических множеств.
Определение 2. Случайным процессом ^(fy — ^it, со) на-
называется измеримое (по со) отображение <Й. S, Р> на <«Й?,©, Pt)
(каждому со ставится в соответствие ?(?) = §(?, со) так, что
|g-*(G)={co: g(.)^G}eg для Сев).
Pg называется распределением процесса. Условие Э^ cz ®
нужно для того, чтобы были определены вероятности цилиндри-
цилиндрических множеств и, в частности, вероятности Р E @ ^ Щ, В (= S»
означающие, что §(?) есть случайные величины.
До сих пор как бы предполагалось, что процесс |(?) гадай
й нам известно, что его траектории лежат в $в. Однако это бы-
бывает весьма редко. Чаще процесс пытаются описать теми или
*) См., например, [5].
**) Разрыв второго рода связан либо с учащающимися пезатухающими
колебаниями, либо с уходом на бесконечность.

324 ГЛ. 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
иными сведениями о его распределении. Можно задавать, на-
например, конечномерные распределения. Из теоремы Колмогорова
о согласованных распределениях*) (см. Приложение 2) следует*
что задание согласованных конечномерных распределений опре-
определяет однозначно распределение процесса Pg па пространстве
(RT, S#>. Эту теорему можно рассматривать как теорему су-
существования случайного процесса в (R , ?3к> с заданными ко-
конечномерными распределениями.
Однако пространство (Л , 33я) не очень удобно для изуче-
изучения случайных процессов. Дело в том, что далеко не все часто
употребляемые в анализе соотношения для функций порождают
события — т. е. множества, которые принадлежат о-алгебре йд
и о вероятности которых имеет смысл говорить. Ведь на осно-
основании определения можно с уверенностью сказать, что события-
событиями являются лишь элементы а-алгебры, порожденной событиями
{? (t) е В), t е Т, где В — боролевские множества. Множество
/sup ?(?)< c\i например, может и не быть событием, так как
\t€=T I
мы знаем лишь представление его в виде П {^ (^) <! с}, т. е*
НЕТ
в виде пересечения несчетного числа измеримых множеств, если
Т есть интервал числовой оси.
Имеет место и другое неудобство — распределение Р? на
{R » ЗЭд> не определяет однозначно свойств траекторий ?(?)•
Этот факт связан с тем, что пространство RT очень богато и при-
принадлежность х(') цилиндрическому множеству вида A) не песет
в себе никакой информации о поведении x{t) в точках i, отличных
от tu ..., tn. Это же относится и к произвольным множествам Л
из $&п — грубо говоря, принадлежность х(*)^А может опреде-
определять значения хA) разве лишь в счетном числе точек. (Ниже
мы увидим, что даже такое множество, как {#(?) = 0), не при-
надлежит $$r •) Чтобы задать всю траекторию процесса, недоста-
недостаточно задать распределение па Эд', эту о-алгебру надо рас-
расширять.
Прежде чем приводить соответствующий пример, дадим сле-
следующее
*) Напомним определение согласованных распределений. Пусть Rh t s
е 21,— вещественные прямые, S3/ — а-алгебры борелевских множеств па /?/.
Пусть Тп == {/ь ..., ^} — конечное подмножество чисел из Т. Копечяомер-
ное распределение (ъ(^ь &)<> ¦ • •? ?(**и со)) есть распределение Рт на
(дТп, S5Tn), где ЛГп = Д Л4,»Тп= Д S)t. Пусть даны два конечных
st?,
подмножества Т1 и Т" из /' и (/?', S3'), (/?", S'7) —соответствующие подпро-
подпространства (RT, 53Г). Распределения Рт, и Рт„ па (Л', Э'), (R", S3") согла~
сованы, если их проекции на общую часть пространств /?' и /?х/ (если тако-
таковая существует) совпадают.

§ 1. ОБЩИЕ ОПРЕДЕЛЕНИЯ 225
Определение 3. Процессы ? (t) и r\(t) называются экви-
эквивалентными (или стохастически эквивалентными), если P(S(O==
= т](^)=1 при всех ?^Т. Процесс г] будем называть модифи-
модификацией ?.
Очевидно, что конечномерные распределения для эквивалент-
пых процессов совпадают и, стало быть, совпадают распределе-
распределения Р| и РА в <Д2,Эл>.
Пример 1. Обозначим
(О, 1фа,
и пополним ЗЭя элементами xa{t), a e [0, 1], и элементом ?
^ 0. Пусть y€§ U0,i • Рассмотрим два случайных процесса
и |i(/)j определенных следующим образом: ?0(?)^= #°(?), ^
= #-г@. Тогда, очевидно,
процессы §о и |i эквивалентны и, следовательно, их распреде-
распределения в (R , 23я> совпадают. Однако мы видим, что траектории
этих процессов существенно различны.
Па приведенном примере легко понять, что множество всех
непрерывных функций С(Т), множество/ sup x (t) < х\, элемент
U€=[0,l] /
{x(t)^0} и многие другие не принадлежат Ъц. Действительно,
если допустить противное, например, что С(Г)^33Т, то мы в силу
эквивалентности ?0 и \к должны были бы иметь Р (?0 е
gC@, !))== P(^gC@, 1)), в то время как первая из этих
вероятностей равна 1, а вторая нулю.
Простейший путь преодоления отмеченных выше трудностей
и неудобств состоит в том, чтобы задавать процессы в простран-
пространствах С(Т) или -0G), если это возможно. Если, например,
?(?)еС(Г), r\(i)^ С(Т) и они эквивалентны, то траектории этих
процессов будут с вероятностью 1 полностью совпадать, так как
в этом случае
П {l(t)-4(t)}= n {?(*) = л(*)} = {?(*) =
t рациональны t<~T
= т](?) при всех fG?1},
где вероятность события в левой части равенства определена (это
есть вероятность пересечения счетного числа событий) и равна 1.
Диалогично обстоит дело, например, с событиями isup?(?)<c\ =
Точно такие же рассуждения справедливы для пространств
1ЦТ), поскольку каждый элемент ж(-) из D однозначно опреде-

32G ГЛ. 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
ляется значениями x(t) па счетном всюду плотном множестве
значений t (например, на множестве рациональных чисел).
Итак, допустим, что удалось тем или иным способом устано-
установить, что для исходного процесса %{t) (пусть он задан на
</? , §3/у)) существует его непрерывная модификация, т. е. эк-
эквивалентный ему процесс цA) такой, что траектории r\{t) с ве-
вероятностью 1 непрерывны (или принадлежат D(T)). Сказанное
означает .прежде всего, что мы расширили каким-то образом
G-алгебру §5я присоединением, скажем, множества С{Т) и рас-
рассматриваем теперь распределение ? па о-алгебре 29 =<т(ЭЯ|
С(Т)) (иначе приведенные слета теряют смысл). По распреде-
распределение 1 может быть продолжено с (R , ЗЭл> на </?т, Эг> не
однозначно (это мы видели в примере 1; продолжение можно
задать, положив, например, Р (| е С(Г)) = 0). Сказанное выше
о процессе ц означает, что существует продолжение Рп такое,
что Ръ(С(Т))=Р(г\<=С{Т)) = 1.
Далее, часто бывает лучше совсем не иметь дела с неудоб-
неудобным пространством (R , Э^>. Для этого можно задать распре-
распределение процесса г| на суженном пространстве <С(Г), S3c>-
Ведь ясно, что «с с= §г = а (»д, С (Г)), ъ1 = Эт П С (Т) (пер-
(первая из этих о-алгебр порождена множествами вида A), пересе-
пересеченными с С(Т)). Поэтому, рассматривая распределение г), со-
сосредоточенное на С(Т), можно ограничиться сужением простран-
пространства <2?т, 8Т> до (С(Г),«8с>> определив па последнем вероят-
вероятность как значение Рп {А) = Р (r\ ge A), A e Sc с: Ъ1 - Тем самым
построен процесс ц с непрерывными выборочными траекториями-,
эквивалентный исходному процессу \ (если их распределения
рассматривать в <Л , Эл>).
Чтобы осуществлять, эту конструкцию, надо теперь уметь
выяснять по распределению процесса %, существует для него
непрерывная модификация г) или иет.
Прежде чем переходить к формулировке и доказательству со-
соответствующих теорем, отметим еще раз, что названные выше
трудности носят главным образом математический характер, т. е.
связаны с математической моделью случайного процесса. В ре-
реальных прикладных задачах, как правило, бывает заранее ясно,
является рассматриваемый процесс непрерывным или иет. Если
он «физически» непрерывен и мы хотим построить адекватную
модель, то, конечно, из всех эквивалентных модификаций про-
процесса надо взять непрерывную.
Точно такие же рассуждения остаются справедливыми, если
вместо непрерывных траекторий рассматривать траектории из
D(T). Существо проблемы при этом остается тем же: трудности
устраняются, если есть возможность описать всю траекторию

§ 2. УСЛОВИЯ РЕГУЛЯРНОСТИ ПРОЦЕССОВ 327
процесса !(•) значениями ?(t) лишь на каком-нибудь счетном
множестве значений /. Процессы, обладающие таким свойством,
будем называть регулярными.
§ 2; Условия регулярности процессов
Выясним сначала условия, при которых процесс имеет непре-
непрерывную модификацию. В качестве множества Г, не ограничивая
общности, будем рассматривать отрезок Т = [0, 1].
Очень простой критерий существования непрерывной модифи-
модификации, принадлежащий Колмогорову, основан на знании лишь
двумерных распределений ?(?).
Теорема 1 (Колмогоров). Пусть ^(t)— случайный про\\есс
на [О, 1]. Если при всех I, ? + h из
отрезка [0, 1] ^^-—"Ц>^+/^
Ч+ь B) r^F^^^d»)
при каких-нибудь а > О, Ъ > 0, с <
<°°, то %{-) имеет непрерывную
модификацию. ^ .;
Мы получим это утверждение в 6/7»л n+f>2r- n>r** U
качестве следствия более общей тсо- Рис. 15
ремы, условия которой воспринима-
воспринимаются несколько трудпее, но имеют тот же смысл, что и B).
Теорема 2. Пусть при всех t, t + h из отрезка [0, 1]
где e(fe), q(h)-~ убывающие четные функции от h, обладающие
свойством
2eB-n)<oo, 22n?B-n)<oo.
1 1
Тогда %(•) имеет непрерывную модификацию.
Доказательство. Воспользуемся приближениями процес-
процесса ?(/) с помощью непрерывных процессов. Положим
при t<^[tU}r, tntr+l]. Из рис. 15 видно, что
\ln+l(t)-tn(t)\<
< ! I (tn±lt2*+l) " \ [I (*н+1,2г) + I (*п-И,2г+2)] | <| (« + Р),
«= 1^(^1+1, 2r+i) ~ И^+1, 2r)l, Р==

328 ГЛ. 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Отсюда следует, что
Zn = max | ln.H (t) -5„@|<7 (а + P),
¦ P (Zn > e B~n)) < P (a > e B~n)) + P (p > « B"n)) < 2? B"я)
(здесь неявно введены вероятности на событиях, не иринадле-
жащих 8к» через вероятности событий из %5ц)- Так как здесь
всего 2П отрезков типа [ln, г, ^,r+i], г=0, 1, ..., 2п — 1, то
Р( max |Ui(O-6nU)l>eB-|l))<2'l+1GB-n).
сю
Поскольку 2j2r?^B~n)<: со, то по лемме Бореля — Каптелли для
п. в. со (т. е. для o^/i, Р (А) = I) существует /г (о>) такое, что
при всех п (
Отсюда следует п. и. фундаментальность последовательности ?„,
поскольку
при 72 -> сю и всех /?г > /г, со ^ Л. Следовательно, для о ^ /I суще-
существует lim |n(^) = r\(t), \ln(t)~ ц{1) I ^ en, так что сходимость
является равномерной. Вместе с непрерывностью
5«@ это означает непрерывность r\(t) (здесь мы доказываем,
собственно, полноту пространства С@, 1)).
Осталось убедиться в эквивалентности | и г). Для t = tnr
имеем ^п+л@~Й0 пРи всех ^^О, так что л@ = ?@- Если
t?=tn>r при всех ^г и г, то существует последовательность г,4 та-
такая, что tntrn-^ t, 0< i — ?П)Г?г < 2""'1 и, следовательно,
Р (| I (tn,rn) - 5 @ | > е (* - *n.rrt)) <(?(*- ^.rj,
Р (| Ц*п.гп) - I {0 | > е B"п)) < ?B-*).
В силу леммы Бореля — Кантеллп это означает, что bn.rn->-!@
с вероятностью 1. Одновременно в силу непрерывности r\(t) вы-
выполняется т1(^,гТ1)ч->'П@. Так как g (*л,г„) = ч(^п,г?1), то ^@ =
= r\(t) с вероятностью 1. ^
Из теоремы 1 вытекает
С л е дствие 1. Если
^c\h\l lloglMI14* C),

§ 2. УСЛОВИЯ РЕГУЛЯРНОСТИ ПРОЦЕССОВ 329
при некоторых Ь > а > 0, с < <», го выполнены условия теоремы 1
м, следовательно, для ?(?) существует непрерывная модифи-
модификация.
Условие C), конечно, будет выполнено, если выполнено B),
так что' теорема Колмогорова является следствием теоремы 2.
Доказательство. Положим e(ft)= llog |/*| |~"э, 1 < р < Ь/а.
Тогда
1 1
и по неравенству типа Чебышева
>е(Л))
1о8|Л||11(/Ч
c\h\
где б = & — я ? > 0. Остается заметить, что
Критерий существования модификации ъ@* принадлежащей
пространству D(T), форхмулируется и доказывается сложнее и
с]шзан с более слабыми условиями, накладываемыми на процесс.
Ограничимся лишь формулировкой следующего утверждения:
Теорема 3 (Колмогоров — Ченцов). Если при некоторых
а > 0, р ^ 0, Ь > 0 и при всех t — hi^t^t + hz из отрезка [0,1]
М \l (t) - l(t - Ах) Г | ? (* + Л2) - I (t) f < ck1+\ h = /г, + /г2,
D)
го существует модификация ?(?) ?г-? D@, 1)*).
Условие D) допускает следующее обобщение:
E)
при котором утверждение теоремы также сохранится (здесь 8(/г),
д(Л) имеют тот же смысл, что и в теореме 1).
Следующие два примера иллюстрируют в какой-то мере ха-
характер условий теорем 1—3.
Пример 2. Допустим, что случайный процесс %(t) имеет вид
l{t) = S lhWk(t)i где ф/Д/) удовлетворяют условию Гёльдера
/i=i
1<Рь(*+ ^) — фл@ 1 ^ с|/г|а, a>0, (gi, ..., Sn)—произвольный
случайный вектор, у которого конечны М | ?/г | при некотором
Подробнее об этом см., например, [11].

330. ГЛ. 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ ..
I > 1/а. Тогда процесс ?(?) (он является, очевидно, непрерыв-
непрерывным) удовлетворяет условию B). Действительно,
/t=i
Пример 3. Пусть y€=U0>1, ^ (*) = 0 при t < -у, ?(?)=1 при
люоом
I > 0. Здесь условие B) не выполнено, хотя | S (t + h) — ? (I) | -> 0
при /г-> 0. Условие D), очевидно, выполнено, так как здесь
IV!| \{t) — ^(t — hjI1 ?(? +h2) — %(t)| == 0. (G)
Примерно те же результаты получимг если в качестве %(?)
рассмотрим процесс восстановления для последовательности
Yi, if2, ..., где распределение ^ имеет плотность. В этом случае
вместо F) будет выполняться
М \% @ - I (t - К) 111 (t +h2) ~ l(t) | < c}hh2 < ch\.
В общем случае, когда мы не располагаем данными для по-
построения модификаций процесса !• из пространств С(Т) или
D(T), трудности, отмеченные в .§ 1, позволяет преодолеть введе-
введение понятия сепарабельности.
Определение 4. Процесс |(?) называется сепарабелъным,
если существует всюду плотное в Т счетное множество S такое,
что
Это свойство эквивалентно тому, что для любого интервала /с=Г
Р ( sup I (и) = flip | (и); inf ?(м) = inf g (а)\ == 1.
Дубу принадлежит теорема*), утверждающая, что любой слу-
случайный процесс имеет сепарабелъную модификацию.
Построение сеиарабелъной модификации процесса, так же,
как и построение модификаций из С(Т) или Р(Т), означает рас-
расширение а-алгебры 25д, куда присоединяются несчетные пере-
пересечения вида
Л= П {5(")е[а, b]}=/sup
и распространение на это расширение меры Р с помощью
•) См. [5], [13].

§ 2. УСЛОВИЯ РЕГУЛЯРНОСТИ ПРОЦЕССОВ 331
равенств
т
где под знаком вероятности стоит уже элемент $я.
Можно отметить, что для сепарабельыых процессов такие мно-
множества, как множество всех неубывающих функций, множества
С{Т), D(T) и др. являются событиями. Процессы из С(Т) или
D(T) очевидно, автоматически будут сепарабельными. И наобо-
наоборот, если процесс сеиарабелен и допускает непрерывную моди-
модификацию (модификацию из D(T)), то он сам будет непрерыв-
непрерывным (принадлежать Л (Г)). Действительно, если ц есть непре-
непрерывная модификация ?, то
Р (I (t) = ц (t) для всех te=S) = 1.
Отсюда на основании G) получаем
Р f lim \](u)^l(t)^ lim ц(и) при всех t е Т\ = 1.
Так как lim ц(и) = lim ц(и) = ц(г)у то получаем, что
u-*t
Р(|(^) = т](t) при всех t е= Т) = 1.
В примере 1 процесс ?i@> очевидно, не является сепарабель-
пым. Процесс lo(t) есть его сепарабельная модификация.
Наряду с непрерывностью выборочных траекторий существует
еще один способ характеризовать свойство непрерывности слу-
случайного процесса.
Определение 5. Случайный процесс |(?) называется сто-
стохастически непрерывным, если при всех t^T и h -> О
Здесь мы имеем дело ^ лишь с двумерными распределения-
распределениями l{t).
Ясно, что все процессы с непрерывными траекториями явля-
являются стохастически непрерывными. Но .не только. Разрывные
процессы в примерах 1 и 3 также являются стохастически не-
непрерывными. Разрывный процесс перестанет быть таковым в
точке tOi если точка разрыва т (?(т +0)=^ ?(т —0)) обладает
свойством Р (т = tQ) > 0.
Определение 6. Процесс |(?) называется непрерывным в'
среднем порядка г (в среднеквадратичном при г = 2), если при
всех t е= Т и h -> 0
ли, что то же, М 15 (^ + h) — I (t) \r -> Q,

332 ГЛ. 15. СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Разрывный процесс $(t) в примере 3 будет непрерывным в
среднем любого порядка. Поэтому сама по себе непрерывность в
среднем и стохастическая непрерывность, не очень много гово-
говорят о свойствах траекторий (они говорят лишь, что скачок в
окрестности каждой фиксированной точки t маловероятен). Как
показывает теорема Колмогорова, для того чтобы характеризо-
характеризовать свойства траекторий, нужны количественные оценки для
M\l(t + h) — l{t)\r или для P(\t(t + h)-l(t)\>b).
Из теорем непрерывности для моментов следует, что для сто-
стохастически непрерывного процесса §(?) и любой непрерывной и
ограниченной функции g(x) функция Mg (?(?)) непрерывна.
Это утверждение сохранится, если ограниченность g(x) заменить
условием sup M | g (? (t)) |a < оо при каком-нибудь а > 1.
Последующие гл. 16, 18, 19 будут посвящены изучению тех
типов случайных процессов, которые можно задать явной фор-
формой конечномерных распределений. К ним относятся:
1. Процессы с независимыми приращениями.
2. Марковские процессы.
3. Гауссовские процессы.
В гл. 19, кроме того, будут рассмотрены некоторые вопросы
теории случайных процессов с конечными моментами второго по-
порядка. Гл. 17 содержит предельные теоремы для случайных про-
процессов, порожденных последовательными суммами независимых
случайных величин.

Глава 16
ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
§ 1. Общие свойства
Определение 1. Процесс {?@> ^SK b]}, определенный
на отрезке [а, Ь\ называется процессом с независимыми прира-
приращениями, если для любых U < ti < ... < tnj a^t0, tn ^ Ъ1 случай-
случайные величины g(?0), ?(*i)—?(*o)» ..., l(tn)~l{tn—l) неза-
независимы.
Процесс с независимыми приращениями называется однород-
однородным, если распределение ?(^) — |(^) определяется лишь длиной
интервала tt — t0 и не зависит от t0.
В дальнейшем для простоты везде будем считать, что а = О,
6@) = 0, 6 = 1.
Определение 2. Распределение случайной величины g на-
называется безгранично делимым (ср. с § 8.9), если при любом п
величину § можно представить в виде суммы независимых оди-
одинаково распределенных случайных величин: \ — %it п + ... + §П( п.
Если ф(Х) есть х. ф. §, то отмеченное свойство эквивалентно
тому, что ф1/п при любом п является х. ф.
Из приведенных определений ясно, что распределение §(?)
для однородного процесса с независимыми приращениями ? без-
безгранично делимо, так как ^{t)=- gi, „ + ... + \п, п, где |ь(п =
«= %(Ы/п)— g( (к — i)tln) независимы и распределены как %{tln).
Теорема 1. 1) Пусть {§@» t^O) — стохастически непре-
непрерывный однородный процесс с независимыми приращениями и
пусть ф; (К) = Ме1КШ) есть х.ф. l(t), ф(^) = ф4(^). Тогда
Ф*(М=ФЧМ, A)
ф(Х)^О ?ш дргг каком X. (A) означает, что Ф*(^) обязано быть
х. ф. при любом t.)
2) Пусть ф(Х) <?сгь х.ф. безгранично делимого распределе-
распределения. Тогда существует случайный процесс {?(?)» t ^ 0), удовлет-
удовлетворяющий условиям 1), м такой, что Мег в = ф(^).
Обозначим через S? класс х. ф. всех безгранично делимых
распределений и через S?t класс х.ф. распределений %(t) для
стохастически непрерывных однородных процессов с независимы-
независимыми приращениями. Тогда из теоремы 1 следует, что 3? = 2Y
Класс 9? будет охарактеризован в § 5.
Доказательство. 1) Пусть \it) удовлетворяет условиям
п. 1) теоремы. Тогда 1(?) можно представить в виде суммы

334 ГЛ. 16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
независимых приращений
l(t)=-I,ll(tj)-l(tj-l)}J го = О, *„ = *, tj>tj
i
Отсюда следует, в частности, что
Здесь ? —у 0, <р _?/д1 (Я)->-1 (в силу стохастической петгре-
рывности), фг'п1/п(А)-^ ф'(А) при га-*-°о. Отсюда следует, что
ф/ (А) ->- срг (Л) при /г -> «>. Но ф, (А,) и ф'(А) от /г не зависят, зна-
значит, Ф«(А) = ф'(А.).
Далее, ф*(А) = ф*(А);-> 1 при t-+О и при любом X. Это воз-
возможно, если ф(Л)^О ни при каком А.
2) Заметим предварительно, что если ф ^ «S7, то ф' при лю-
любом J > 0 есть снова х. ф. Действительно,
Ф*(Я.)=»Нтф " (А,),
так что ф' (л) .есть непрерывный в точке А = 0 предел х. ф. По
теореме непрерывности для х. ф. это снова есть х. ф.
Построим теперь случайный процесс l-(t) с независимыми
приращениями, задав его конечномерные распределения. Поло-
Положим 0 = ?o <*!<...<**, А^!(^)—?(^-1), fij^fj —fj-i и заме-
заметим, что
Определим х. ф. совместного распределения ^(^), ..., |(^) ра-
равенством (постулирующим независимость Aj)
М охр \i S Х^ («4 = М exp If 2 A; S Я,] = П Ф B
2 ; S ] П Ф B
Г-J /=-j i 3 = 1 \l=J
Таким образом, мы с помощью ф определили конечномерные
распределения |@ в (R , Эя>> которые, как нетрудно видеть,
согласованы. По теореме Колмогорова существует распределение
случайного процесса §@ в (R г Э«>. Этот процесс по опреде-
определению является однородным процессом с независимыми прира-
приращениями.
Чтобы доказать стохастическую непрерывность 5@» заметим,
что при h -> 0
а(Ш+/)|@) " Фо(я.)г

§ 2. ШШЕРОВСКМЬ in^Mi^^jjx, buunu^uv x*..,_,..,, v,. _„ «35
где
A, если ф (X) ф. О,
0 \0, если ф(?„) = 0.
Таким образом, предельная функция фо(А) может принимать
штъ дна значения: 1 и 0. Но она обязана быть х. ф., так как
непрерывна в точке А, = 0 (ф(А,)=^О в окрестности точки Х = 0)
и является пределом х. ф. Следовательно, фо(А-) непрерывна,
^(t-\-h) — | (/) -> 0 при /г—>-0. ^
Теорема 2. Однородные стохастически непрерывные про-
цессы с независимыми приращениями {^(t); t <= Т) имеют моди-
модификации из пространства D(T)y т. е. процесс §(?) может быть
задан в (D(T), §3d) и, следовательно, не иметь разрывов вто-
второго рода.
Доказательство. Чтобы упростить рассуждения, предпо-
предположим, что существует М?2 A) или, что то же, существует вто-
вторая производная ф" (X). Тогда
' (О)]2 — }щ"@)<с|h|,
так что выполнен критерий теоремы 15.3. Л
В общем случае доказательство усложняется: надо пользо-
пользоваться критерием A5.5) и оценками для
Рассмотрим теперь два наиболее важных представителя про-
процессов с независимыми приращениями — так называемые вине-
ровскис и пуассоновские процессы.
§ 2. Винеровские процессы, свойства траекторий
Определение 3. Винеровским процессом называется одно-
однородный процесс с независимыми приращениями, для которого
распределение <~A) нормально.
Другими словами, это процесс, для которого
е 2 ,, Ф( {%) = ф* A) = е
при некоторых а и а2 ^ 0. Последнее равенство означает, что
приращения ^(t+u)— ?,(u) распределены нормально с парамет-
параметрами (at, o2i). Все совместные распределения §(^i)T «*., ?,(tn)t
очевидно, также будут нормальными.

336 ГЛ. 16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
Числа се и а называются соответственно коэффициентами сно-
сноса и ¦ диффузии. Введя в рассмотрение процесс ?,о(?)~'
~(%(t) — at)/Oi отличающийся от |(?) линейным преобразова-
преобразованием, получим, что для него х. ф. равна
Такой процесс с параметрами @, t) часто называют стандарт-
стандартным виперовским процессом. Расссмотрим его подробнее.
Теорема 3. Существует непрерывная модификация вине-
ровского процесса.
Это означает, как мы знаем, что винеровский процесс {?@»
#е[0, 1]} можно рассматривать, как заданный на измеримом
пространстве <С@, 1), Эс* > непрерывных функций.
Доказательство. Имеем %( + ^)(
I {t + h) - i {t)
1 77= €= фод< Поэтому
yh
h) -
Это означает, что выполнены условия теоремы 15.1. ^
Итак, можно считать, что %(-)^С@, 1). Стандартный вине-
ровский процесс с непрерывными траекториями будем обозначать
iw(t), t&T).
Отметим теперь, что траектории винеровского процесса w{t)y
обладая свойством непрерывности, с вероятностью 1 не диффе-
дифференцируемы пи в какой точке t.
В силу однородности процесса достаточно доказать его не-
недифференцируемость в точке 0. Если бы с положительной вероят-
вероятностью, т. е. па множестве A cz Q, Р(Л)>>0, существовала про-
производная
w' @) - w' @, о)) = lim^-,
то тогда на том же множестве существовал бы
}ira —i > i 1 — lim — ; ]im =
- 2u/ @) - w' @) = u?' @);
Но это невозможно по следующей причине. Независимые раз-
разности w{2~h+i)~- w{2~~h) распределены так же, как wB~k), и с
положительной вероятностью р = 1 — ФA) превосходят У2~/{.
Т. е. независимые события Bh = {^B"A"fl)~- u;B~*)> У2"^} обла-
(Х>
дают тем свойством, что 2 РE^) = оо. По критерию Бореля —
Каптелли это означает, что с вероятностью 1 произойдет беско-

§ 3. ЗАКОНЫ ПОВТОРНОГО ЛОГАРИФМА 337
игчно много событий Bh, так что
Р | lim sup — r , —
Точно так же обнаруживаем, что
Отсюда следует, что
limsup—^ -^
2
liminf -^ ±Гк1 } = - оо = 1?
и, следовательно, процесс w(t) в каждой точке t с вероятностью
1 иедифференцируем.
Имеет место и более сильный факт: с вероятностью 1 не су-
гцествует ни одной точка t% где траектория w(t) имела бы произ-
производную. Другими словами, винеровский процесс с вероятностью i
нигде не дифференцируем. Доказательство этого факта значи-
значительно сложнее и выходит за рамки этой книги.
Читатель может без труда проверить, что w(t) в известном
смысле обладает свойством параболы — именно, процесс w* (t) =
•==—jr-w{ct) пщ любом с>0 снова является стандартным вине-
Ус
ровским процессом.
§ 3. Законы повторного логарифма
С помощью рассуждений, подобных тем, что применялись в
конце предыдущего параграфа, можно установить и значительпо
Вол ее сильный факт: траектория w(t) в окрестности точки ? = 0,
Образно говоря, «полностью зачерчивает» внутренность области,
образованной двумя ветвями кривых У =± у 2 tin In—. Внеш-
Внешность этой области остается нетронутой. Это так называемый ло-
локальный закон повторного логарифма.
Теорема 4.
Р/liminf ">(>> =-lWl,
\ '"*" j/2* In in у J
22. А. А. Боровков

338 ГЛ. 16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
Таким образом, если рассмотреть последовательность случай-
случайП1п~х
Таким образом, если рассмотреть последовательно
ных величин w(tn), tn 4 0, то последовательности у <
ХA±е) при любом е>0 будут для нее соответственно верхнем
и нижней последовательностями.
Для процессов можно было бы естественным образом ввести
понятия верхней и нижней функций. Если, например, процесс
§(?) принадлежит/ С(О, °°) или ^@, °°) (или сепарабелен на
@, °°)), то соответствующее определение для t ->¦ <*> имеет сле-
следующий вид.
Определение 4. Функция a(t) называется верхней (ниж-
(нижней) для процесса 5@? если Для какой-нибудь последователь-
последовательности tn t °° события Лп = /sup (l(t) — а (?)) > 0 с
l
^
ностыо 1 наступают лишь конечное число раз (бесконечное число
раз).
Наряду с теоремой 4 мы получим здесь обычный закон повтор-
повторного логарифма. Доказываются оба эти утверждения практически
одинаково. Докажем второе, а первое получим в качестве его
следствия.
Теорема 5 (закон повторного логарифма)
lUl,
I
y'Ztlnlat
Таким образом, при t ->¦ °° функции У2Пп In ^A ± г) при лю-
любом s > 0 являются соответственно верхней и нижней функциями
для w (t). __
Обозначим w(t) = sup w(u). Для доказательства теоремы по-
и-41
требуется
Лемма I.
Р (w (t) > х) = 2Р (и; (t) > х) = -|=- f е"^7^; * > 0.
х
Здесь справа стоит так называемый удвоенный нормальный
закон.
Доказательство. Введем в рассмотрение случайную ве-
величину %x~mi{u: w(u)>x) (напомним, что и;(-)еС@, °°)):
Это есть момент остановки в том же смысле, что и раньше:
{тх > v) = {ш (у) <i}gS, = o {g (м); м < у},
i
х == у} - Q iw (v - »j < х, w (v)

- § 3. ЗАКОНЫ ПОВТОРНОГО ЛОГАРИФМА 339
Следовательно, при фиксированном тх = v, v ^ t, приращение
w(t)—w(т*)= w(t)—w (v) не зависит от {rx=^v}^^v и распре-
распределено как м;(? — у)^= Фо,*-1> Поэтому на множестве {тх ^ t\
Р (w (t) > х/хх) = Р (w (t) - w (хх) > О/т,) = 1/2,,
Доказательство теоремы 5. Заметим предварительно^
что в силу правила Лопиталя
v
х •>
77 B)
X
При —— -> оо.
Пусть а > 1 и лгА = 12ah\n\nah. Надо убедиться, что при лю-
любом е > 0 .
Р (limsup iy?® < 1 + г) = 1Х C)
г, е. что с вероятностью 1 при всех достаточно больших t
w(t)<(l + e)V2tlnlnt.
Для этого достаточно установить, что с вероятностью 1 происхо-
происходит лишь конечное число событий Bk=i sup w(u)^>
>A +.«) ^/t_il. Рассмотрим события At =/sup m;(m)>A+ e)^ft_11
(см. рис. 16). Тогда, так как хк/Уак-+- оо при А:->• оо^ то
^>(Ак) = 2Р (и;(а") >A + е) хк-г) -
Гг У~а>> \ 2 A + р)У'-* In In а!'-1
1
па In la a1''1
==с(а, е)
"[/in (/с — 1) + In In а (к —
Положим а = 1 + е > 1. Тогда, очевидно, при к -*¦ °°,

340
ГЛ. 10. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
В этих формулах с(а, е) и с(г)—некоторые постоянные, зави-
зависящие от своих аргументов. Полученное соотношение означает,
оо сю
что 2 Р (ДО < оо, 2Р (Bk) < °° {Bk с: Ли) и, значит, по кри-
1 1
терию Бореля — Кантелли события Вк с вероятностью 1 происхо-
происходят лишь конечное число раз.
Рис. 16
Докажем теперь, что при произвольном 8 > 0
sup
w(t)
I XXJLU |JtU/ - i i
\ <-,«, y2t In in
>l-e =1
D)
Очевидно, вместе с C) это и будет означать, что выполнено пер-
первое утверждение теоремы.
Рассмотрим при а > 1 независимые приращения w(ak)— w(ak~l)
и обозначим Вк событие
Bh
= [w (ак) - w (a*-1) > (l - т) Хк}
Так как w(ak)~ w(afi~'i) распределено так же, как w(ak(l — а~1)),
то в силу B), как и прежде, находим
й-1)
1/2я |l - 4rj a:
(l —-|-J2aft lnlna-fe
A _ a
Отсюда следует, что при a>-2/e ряд
расходится, и,
значит, по критерию Бореля с вероятностью 1 наступает беско-
бесконечное число событий Bh.

§ 3. ЗАКОНЫ ПОВТОРНОГО ЛОГАРИФМА 341
Далее, в силу симметрии процесса w(t) из соотношения C)
следует, что при всех достаточно больших к и любом б > О
Имеете с предыдущим это означает, что бесконечное число раз
будет наступать событие
По правая часть этого неравенства может быть сделана выбором
а больше A — г)хк. Действительно,
iA . я\ -1 / Jnlna'1 _ 8
(•ели только A + о) I/ —-—-—r-<Iir, чего в свою очередь легко
добиться, выбрав а достаточно большим. Таким образом, соотно-
соотношение D) доказано.
Второе утверждение теоремы, очевидно, следует из первого в
силу симметрии распределения w(t). ^
В качестве следствия можно получить теперь локальный за-
закон повторного логарифма для t -> 0.
Доказательство теоремы 4. Рассмотрим процесс
{W(u) = uw(i/u); u^Q}, где принято W@) = 0. Захмечательный
факт состоит в том, что процесс {W(u); а^О} также является
стандартным винеровским процессом. Действительно, при t > и
М ехр {IX (W (t) - W (и))} = М exp fa \tw (~\ - uw (Щ =
Независимость приращений проще всего доказать, установив
их некоррелированность. Действительно,
М
[W (и) (W (t) - W (M))J = M [uw (-i) [tw A) - uw A j] =
- M [ив, (!) tw A) - „«u^ A)] = „ - „ = 0.
Для доказательства теоремы остается заметить, что
1
w (t) \ и I W (и)
liin sup—7====-= limsup— - = Ь'гп япр ;
i->oo I/ ?l 111 lll"? u~*0 ~
2m In In — I/ 2m In In ~

342 ГЛ/16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
Доказательство можно было бы провести и повторив рассуж-
рассуждения теоремы 5, где надо выбрать а< 1.
В заключение отметим, что винеровские процессы играют
весьма важную роль во многих теоретико-вероятностных рассмот-
рассмотрениях и служат моделями для описания многих процессов в
природе. Они представляют собой, например, хорошую модель для
описания движения диффундирующей частицы. В связи с от mi
винеровские процессы часто называют также процессами броу-
броуновского движения.
Винеровские процессы оказываются в известном смысле пре-
предельными для случайных ломаных, построенных но точкам
(k/n, SJ^n), где Sh—суммы случайных величин ^, Мс,} = О»
D?j = 1. Об этом подробнее будет сказано в гл. 17, С виперов-
ским процессом тесно связано также понятие стохастического ин-
интеграла и большое количество других конструкций и результатов.
§ 4. Пуассоновскис процессы
Определение 5. Однородный процесс g(?) с независимыми
приращениями называется пуассоновским, если ?@~~"S@) имеет
распределение Пуассона.
Положим для простоты |@) = 0. Если ?A)€ееП^, то ф(Л)=*
= Ме^*A) = expfjLi (егК— l)} и, как мы знаем, '
<р, (X) = МеаШ) - ф' (X) = ехр {|х* {е{К - l)},
так что | (?)€= П^. .
Рассмотрим свойства пуассоповского процесса. Прежде всего,-
\{t) при каждом t принимает лишь целочисленные значения
0, 1, 2, ... Разобьем интервал [0, t) на отрезки [0, ?*), [tutz),..*
..., [tn-i, tn) длиной Ai = ?f — ?{-i, j = l, ..., дг. При малых Д,- рас-
распределение приращений S(^)~"^(^-i) будет обладать свойствами
(о)
Р (I (ti) - ? (*,.!) = 0) = Р (? (А,) - 0) =
Р (Б (^г) ~" I Ui-l) = 1) = liAiC"^* = И-Дг + О (А?),
Рассмотрим «вложенные» рациональные разбиения @?(п)=-
= Ut, ..., tj отрезка [0, t] такие, что 01(п)а 01 [п + 1), 1M2(я) =
= ^2f есть множество всех рациональных чисел отрезка [0, t].
Отметим следующие три обстоятельства.
1) Пусть v(n)—число интервалов разбиения 52(/г), на кото-
которых приращение процесса ? отлично от 0. При каждом (о v(n)
ие убывает при тг->°°. Кроме того, число v(rc) представимо в ви-
виде- суммы независимых случайных величии, равных 1, если ил

§ 4. ПУАССОПОВСКНЕ ПРОЦЕССЫ 343
/ м интервале есть ириращение, и нулю в противном случае. По-
Понтом у в силу E)
!'до 2 Д] ^/max Aj-^Опри п-^оо^ так что при измельчении раз-
1
биения п. в. v (и) f ? (*)€= П^.
2) Так как длина максимального интервала А^ сходится к О
при п -*- °°, то суммарная длина интервалов, содержащих скачки,
сходится к 0.
Следовательно, объединяя оставшиеся (т. е. без приращений
?) и примыкающие друг к другу интервалы Д;-, при каждом о)
получим при п -*¦ °° в пределе v 4-1 интервалов @, а4), (а4, а2),...
¦ •., (av, О» 1Ш которых приращения процесса ? равны нулю.
3) Наконец, в силу E) вероятность того, что хотя бы один
г.качок на интервалах Д;- превосходит единицу, меньше S^(^l) =
-= о A) при п -*• °°, так что с вероятностью 1 приращения в точках
ик равны 1.
Мы получили, таким образом, что на отрезке [0, i] для каж-
каждого со существует конечное число ?(?) точек а4, .. ., aSA) таких,
что ?(w) B рациональных точках интервалов (aft, «ft+i) принимает
одно и то же постоянное значение, равное к. Это означает, что
можно доопределить траектории процесса ?(w)» скажем, по -не-
-непрерывности справа так, что %{и)=~к при всех и, ak<u<ak+l.
Тем самым для исходного процесса §(?) построена модифика-
модификация \(t) с траекториями в D+(T). Эквивалентность ? и g следует
из самого построения, так как в силу 1)
Р A (*) = ? @) = Р (lira v (п) = I (t)) = 1.
Такие непрерывные справа (или слева) модификации пуассо-
иор.ского процесса обычно и рассматривают. С такого рода про-
процессами мы уже имели дело в гл. 9, где определялись более об-
общие процессы — процессы восстановления — сразу с помощью
траекторий. Тот факт, что пуассоповский процесс есть процесс
ипсстановления, вытекает из следующих соображений. Из соотно-
соотношений E) легко установить, что распределения случайных ве-
величин ab a2 — uh а3~а2, ... совпадают и что сами эти величины
пг.члвисимы. Действительно, а^~-ани j^i, #0 = 0, приближается
г\,\шой (fj— Ti-i)A одинаковых интервалов Дг- = Д, где ^ есть
ппмс-р интервала, на котором расположено j-e по счету ^ненулевое

344 ГЛ. 16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
приращение |. Так как
при Д -> 0, то величины а; = а, •— а^и j == 1, 2, 3, •.., распределены
показательно, а значение ?(?)+1 можно рассматривать как время
первого прохождения уровня t суммами я,:
| (t) = шах {к: ah ^ t), 1@+1 = rain {к: ah > t).
Мы получили, таким образом, что пуассоновский процесс ?@
совпадает с процессами восстановления r\(t) (см. гл. 9) для по-
показательно распределенных величин cti, а2, ...; Р(сс/>и) = е~[1ил
Из сказанного и из свойств пуассоновского процесса вытекает
также следующее замечательное свойство показательно распре-
распределенных случайных величин. Количества точек скачкой (т. е.
сумм ak), попавших в непересекающиеся интервалы времени 6Jt
независимы, причем эти количества имеют распределения Пуассо-
Пуассона с параметрами [хб,-.
Пользуясь последним обстоятельством, можно построить и бо-
более общую модель скачкообразного однородного процесса с неза*
висимыми приращениями. Рассмотрим произвольную, не завися-
зависящую от а-алгебры, порожденной процессом ?(?), последователь-
последовательность независимых одинаково распределенных случайных величин
?4, ?2, • • • с х. ф. §Ск). Построим теперь новый процесс fa{t) сле-
следующим образом. Каждому со поставим в соответствие новую
траекторию, полученную из траектории 1-(t) заменой первого еди-
единичного скачка на величину ?,, второго — на величину ?2 и т. д.
Легко видеть, что ?(?) будет также процессом с независимыми
приращениями. При этом значение ?@ будет равно сумме
случайного числа |(?) случайных величии ^, t2, ..., где %(?) по
построению не зависит от {?j.
Поэтому по формуле полной вероятности
М^(« в ^ P(v = к) МеЩ11+'"+1к)
Определение 6. Процесс t>(t), определенный формулой F)
или х. ф. G), называется обобщенным пуассоновским процессом.
Как уже отмечалось, это снова есть однородный процесс с не-
независимыми приращениями. В формуле G) jli определяет интен-
интенсивность скачков процесса ?@» (Н^)—их распределение. Если
к Z,(t) добавить постоянный «снос» at, то процесс ^^) = ^A) + at,

§ 5. ОПИСАНИЕ РАСПРЕДЕЛЕНИЙ 345
очевидно, также будет процессом с независимыми приращениями
сл.ф. Ме^п = eH
Наконец, если на том же вероятностном пространстве задан
ни перовский процесс w(t) с коэффициентами @, а), независи-
независимый от ?(?)» и мы каждому со поставим в соответствие траекто-
траекторию ?@-*~ш@> то вновь получим процесс с независимыми при-
ращениями с х. ф. е
Следует отметить, однако, что этими построениями далеко не
исчерпан весь класс процессов с независимыми приращениями
(и, следовательно, класс безгранично делимых распределений).
Описание всего класса будет дано в следующем параграфе.
Пуассоиовские процессы так же, как и винеровские, часто ис-
используются в качестве математических моделей в разного рода
приложениях.
Пуассоновскнм процессом описывается, например, процесс по-
появления космических частиц определенной энергии в заданном
объеме или процесс возникновения соударений элементарных
частиц в ускорителе. Им же описывается процесс поступления
вызовов на телефонную станцию и многое другое.
Изучение обобщенных пуассоновских процессов в силу пред-
представления F) во многом сводится к исследованию свойств сумм
независимых случайных величии.
§ 5. Описание распределений всего класса процессов
с независимыми приращениями
Мы видели в- теореме 1 § 1, что для описания класса распре-
распределений стохастически непрерывных однородных процессов с не-
независимыми приращениями достаточно описать класс всех без-
безгранично делимых распределений. Пусть, как и прежде, 2 есть
класс х. ф. безгранично делимых распределений.
Лемма 2.-Класс 2 замкнут относительно операций умно-
умножения и предельного перехода (если предел есть снова х.ф.).
Доказательство. 1) Пусть ф^З', ср2 ^ 3?. Тогда ср^ =
= (Ф11/И-Ф->Л|)I> где Ф1/л, <рC1Л0 есть х.ф.
2) Пусть фп е 2, фп ->¦ ср, ф есть х. ф. Тогда для любого m
<Рп/т-^ф1/т» где ф1/т непрерывна в пуле и, следовательно, есть
х. ф. <
Обозначим через 3?л^2 класс х. ф. вида
Ь ф(Х) == iKa + 2cft(*1 ft—l), ^>0, 2c/i<o°-
тот класс будем называть пуассоновским. Мы уже знаем, что он
ответствует пуассоновским процессам со сносом а^и интенсив-

346 ГЛ. 16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
ностью ck скачков величины bkl ^ch(e h — 1 J =-^— Ц(ег'
где t, имеет скачки bk с вероятностью
Лемма 3. X. ф. ф принадлежит 2 тогда и только тогда, когда
Доказательство. Достаточность. Пусть
In фп = я|)п = 2а \1Хпи,п + с^п \е — 1JJ,
h
Ф = lim wn есть х. ф. Очевидно, что q>l/m ^SjxdS, ФпМ->- ф1/т.
Поэтому ф1/м, будучи непрерывным в нуле пределом х. ф., есть
х.ф., ф^ 2\
Необходимость. Пусть, ф^^. Тогда ф(Х)^О, сущест-
существует г|з == In ф, /г(ф1/п — 1) -^ ij),
Интеграл от непрерывной функции, стоящий справа, можпо
рассматривать как интеграл Римана — Стилтьеса. Это означает,
что для Fn существует разбиение вещественной оси на интервалы
Anft такое, что при xnh g= Дпй, гп < сп'2
J (е^ - 1) dFn {х) -
(Рп(А) есть вероятность попадания в Д, соответствующая
Получаем *
ф = lim « (Ф1/п - 1) = lim [в 2 (ettXrt/i - 1) Л, (А„
Теорема 6 (Леви, Хинчин). фе^ тогда и только тогда,
когда функция яр = In ф представима в виде
1|з = Ч> (К; а, ?) = Ла + J (еш - 1 - ^) ^ dV (.r), (8)
где W есть неубывающая функция ограниченной вариации {функ-
{функция распределения с точностью до постоянного множителя),
подынтегральную функцию при х = 0 следует ' считать равной
—Я2/2 (доопределенной по непрерывности).
Доказательство. Пусть if) имеет вид (8). Тогда г|з(X)
есть непрерывная функция, так как она представляет собой (с точ-
точностью до непрерывного слагаемого iXa) равномерно сходящийся
интеграл от непрерывной ограниченной функции. Далее, пусть
Xkn ^ 0, к = 1, ..., /г,— точки измельчающегося разбиения отрезка
[—Уп, У/г). Тогда -ф(Х) можно представить в виде г|з = lim if»,
„ (А) - 2 [i
inakn

§ 5. ОПИСАНИЕ РАСПРЕДЕЛЕНИЙ 347
тде при естественных соглашениях относительно обозначений сле-
следует положить
xkn
Мы получили, что ф есть непрерывный предел последовательности
х. ф. фп е ^д. Остается воспользоваться леммой 3.
Пусть теперь ф ^ 3?> Тогда
= lim п (ф1/п - 1) = lim J (eiU -
^1Г?] (9)
Если положить
^^ ^ A0)
то справа будет стоять lim\|)n, it>n = \|)(^; an, ?„).
Допустим теперь на минуту, что для функций из 3? справед-
справедлива теорема непрерывности:
Лемма 4. Если i|)n = i|)(^; an, Wn)-*"^ и г|) непрерывна в точ-
точке 1 = 0, то/^СК) имеет вид \|з(^; а, Ф), ап-+а, fn=^f (послед-
(последнее, как и для функций распределения, означает сходимость в
точках непрерывности, ^„(ioo)-*- W (±оо)).
Если эта лемма верна, то требуемое утверждение очевидным
образом следует из (9), A0). Осталось лишь провести
Доказательство леммы 4. Отметим сначала, что соот-
соответствие -ф(X; а, 4я) •<->(#, W) взаимно однозначно. Так как в од-
одну сторону это очевидно, то надо убедиться лишь, что \|з однознач-
однозначно определяет а и XF. Каждому г|) поставим в соответствие
функцию
dh =

348 ГЛ. 16. ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
где
IE— = elhX cos hx.
2
l
j e^x (i _ cos Ля) dfe = eiAX ( 1 — -
Поэтому Y (Я) = j eiUdr (а;),
где
ведет себя (с точностью до постоянного множителя) как функция
распределения, для которой ^ (X) играет роль х. ф. Итак, мы по«
лучили цепочку однозиачпых соответствии \p ->• ^ -> Г -> 4х, дока-
доказывающих утверждение.
Вернемся к доказательству леммы 4. Так как в д-> ? , в п есть
х. ф. и еф непрерывна в точке X = 0, то е^ есть х. ф. и, следова-
следовательно, непрерывная функция. Это значит, что сходимость г]?п ->- \|>
равномерна на любом отрезке,
4?n (X + h) + f w (^ - 7а)
и функция y(w) непрерывна. По теореме непрерывности для х. ф.
это означает, что ч(и) есть х. ф. (конечной меры Г), Гп =*- Г (Та
есть прообраз *уи), Ч^ =>¦ V, аЛ ~^ а. Итак, установлено, что
п = lim [гХяп + f f eax - 1 - ~^V) dTn (x)
= На + Г f ^>Л - 1 - -^Ц-) dW (x) = 'ф (Я; а, ?). 4
J \ 1 + х I
Сделаем несколько замечании, относящихся к структуре про-
процесса %(t) и его связи с представлением (8), Функция х? в (8)
соответствует так называемой спектральной мере процесса §(?)•
Ее можно представить в виде jh4/i(x), где ц = ^(оо)— W (—оо),
x?i(x) есть функция распределения. Будем использовать также
запись ?(/!) = J d? (я).

§ 5. ОПИСАНИЕ РАСПРЕДЕЛЕНИЙ 34$
1) Винеровскому процессу соответствует спектральная мера,
сосредоточенная в точке 0. Если гР({0}) = а2, то ЕA)€§ ®а,о2'
2) Пуассоновскому процессу (обобщенному) соответствует
llf Г ^ (х) ^ 1Э
мера т такая, что |™-<оо. Б этом случае
обладает свойствами функции распределения и -ф (Л,; aW) можно
записать в виде
где - ~ • v '
3) Рассмотрим теперь общий случай, во при условии
^F({0}) = 0. Как мы знаем, \?> можно приблизить при малых Д
k = [(к-— 1) Д, /сД)) с помощью выражений вида
ft—— оо Ь
что соответствует сумме пуассоиозских процессов со скачками &Д
оо
и интенсивностью «— ^(Д/г). Если, скажем, \ —^— = ооу
(к A) J ж
то суммарная интенсивность этих процессов со скачками из @, е)
при любом е > 0 будет неограниченно возрастать при Д ->• 0. Это
значит, что с вероятностью 1 на любом временном интервале б
появится хотя бы один скачок меньше любого заданного е > 0,
так что траектории 7z,(t) будут всюду разрывны. Для «компенса-
«компенсации» этих скачков добавляется снос величиной —^~- , который
также может быть «в сумме» неограниченным (если
4) Устойчивым процессам (см. § 8.9) соответствуют гладгае
па полуосях степенные функции х?(х), обладающие свойством
CiW(х)=* х?'(с2х) при подходящих Си с2.

Глава 17
ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
§ 1. Сходимость к винеровскому процессу
(принцип инвариантности)
Уже отмечалось в § 16.2, что винеровские процессы являются
в известном смысле предельными для случайных ломаных, по-
построенных по точкам (к/п, Sh/^n), где 5^ = gi + ... 4- ?-ft — суммы
независимых одинаково распределенных случайных величин
5ь 5г, . •. Придадим теперь этому высказыванию более точный и
общий смысл.
Пусть
Ы, п, ¦ • •> fen, n A),
— независимые случайные величины в схеме серий
и
с конечными третьими моментами М | \ььП |3 = fx/i,n < со.
Будем предполагать, не ограничивая общности (см. § 8.4)\
п h
что D^n === 2 aJ,n == 1- Положим th}Tl = 2 а?,п^ так что ?0 n ^ О,
i=i ' i=i
^л>п = 1, и рассмотрим случайную непрерывную ломаную с узла-
узлами в точках (tk. ^й), где для краткости опущен второй индекс
iv, th = ^t n, ?/?=== Sft, «•
Мы получили случайный процесс на [0, 1] с непрерывными
траекториями, который обозначим
Sr,=sn(t) (рис. 17). Принцип ин-
инвариантности (или функциональ-
функциональная центральная предельная тео-
теорема; смысл, первого названия бу-
будет прокомментирован позже) со-
состоит в том, что для любого фупк-
Рис. 17 цпонала /, заданного на простран-
пространстве С@, 1) и непрерывного в
равномерной метрике, распределение f(sn) слабо сходится:
f(Sn)=>f(w), B)
к распределению /(м>), где w = w(t) — стандартный винеровский
процесс. Обычная центральная предельная теорема является
частным случаем этого факта (надо в качестве f(x) взять хA)).
Высказанное утверждение эквивалентно каждому из следую-
следующих двух фактов:

§ 1. СХОДИМОСТЬ К ВИНЕРОВСКОМУ ПРОЦЕССУ 351
1. Для любого ограниченного и непрерывного функционала /
Mf(sn)-+Mf(w). C)
2. Для любого G из а-алгебры борелевских множеств 53С(о, i> в
пространстве С@, 1) (SC@,i) порождена открытыми миожест-
нами в метрическом пространстве С@, 1) с равномерной метри-
метрикой; уже отмечалось, что8с(о,1) = 93с°'1]) такого, что P(w^dG)=*Ox
где 6G — граница множества G, выполняется
Р^еС)^Р(шЕС). " . D)
Соотношения C), D) суть эквивалентные определения сла-
слабой сходимости распределений Рп процессов sn к распределению
И7 винеровского процесса w в пространстве <С@, 1), ЗЭс(о, d^« ^о-
лее подробные сведения об этом можно найти в [1], [5].
Основное содержание этого параграфа составляют следующие
теоремы.
п
Обозначим, как и прежде, Lz = 2 V>h n-
Теорема 1. Пусть 'L3-+0 при п-^-оо (условие Ляпунова).
Тогда справедливы соотношения сходимости B) —D).
Замечание 1. Условие L3 -* 0 здесь можно ослабить до
условия Лиидеберга. В таком виде высказанная теерема сходи-
сходимости носит наименование принципа инвариантности Донскера —
Прохорова.
Наряду с теоремой 1 получим и более точное утверждение.
Определение 1. Множество G назовем липшийевым, если
AWg(e) ^ W(G{?)) ~ W(G) ^ сг, где G(8) есть е-окрестность С, W —
мера, соответствующая винеровскому процессу.
В дальней]кем буквой с (с индексами или без) будем обоз-
обозначать абсолютные постоянные, не обязательно одни и те же.
Теорема 2. Если G липшицево, то
1Р (sn^G) -Р(шеС)|< cL\{\ E)
В случае |ft, „ = \k/l'n (|7i от п не зависят и одинаково рас-
распределены, M?fc = 0, D|/t = 1) правая часть в E) превращается
и си-|/8.
Аналогичная оценка может быть получена для функционалов.
Функционал / в С@, 1) назовем Липшицевым, если выполнены
два условия:
1) \f(*)-i{y)\<c9(x, у),
2) распределение /(^) имеет ограниченную плотность.
Следствие 1. Если / — Липшицев функционал, то множест-
множество Gv~ {}(х)< и} липшицево (с одной и той же постоянной при
всех z;), так что в силу теоремы 2
sup | Р (/ (w) e v) - Р (/ (sn) < i;)

352 ГЛ. 17. ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Сформулированные выше теоремы будут следствиями форму-
формулируемой далее теоремы 3.
Пусть
Tli.n, ..., TJn, n F)'
— любая другая последовательность независимых случайных ве-
величин в схеме серий с теми же первыми двумя моментами
М%,п = 0> MriSLn =сг^>гИ с конечными третьими моментами. Обоз-
Обозначим Fkt п, Фл, п функции распределения ?ftf n и ix\hi n соответ-
соответственно,
v/lfn = М | Лй.п I3 < oo? iV3 = 2 vh ш
fc=l
Aft,n * J I * I3 \d (Fhtn (x) ~ Фм (ж)
Обозначим через sn (t) случайный процесс, построенный так же,
как процесс sn(t), но по последовательности i^J»
Теорема 3. Для любого А ^ ЭС@| i>
Чтобы доказать теорему 3, получим сначала ее конечномерный
аналог. Обозначим через ^ и i] векторы ?=Ei, ..., ?А), ц =
k h
= A11» •••» 11^). гДе ?й = 2 Sj,«, Лл = 2 'Hi.n» и обозначим 5(е)
е-окрестность множестбк В ^ Rn:
в{е)= и (* + v),
зс--=Я
|bU8
где a? = (#i, ..., я:„), у = (у4, ..., vn), \v\ = max |/;/f|.
/^
Лемма 1. Яг/сгь В —любое борелееское множество из' Rn.
Тогда

"?¦•
Доказательство*). Введем в рассмотрение совокупность
расширяющихся окрестностей
5(8) (к) == U (#ц •. • • ^ft, ^fe+i + УА4-1, ..., ^n + ^n), fc = 0, ..., nt
В = В(е) (га) с В(е) (га - 1) с:... с 7?(е) A) с В(е) @)
*) В основе приводимого ниже доказательства лежит предложенное
А. И. Саханенко обобщение подхода к доказательству, центральной предель-
предельной теоремы, изложенного в § 8.5,

§ i. СХОДИМОСТЬ К ВИ11ЕРОВСКОМУ ПРОЦЕССУ . 353
м обозначим через ек вектор @, ..., О, 1, 0, ..., 0), где 1 стоит на
месте к-ш координаты. Очевидно, что, если х^В{е)(к), то
x + ekvkesB<*>(k-l) при х^В^к, \иК\<е. G)
Далее, наряду с сериями (I), F) рассмотрим совокупность
«переходных» серий
gi,«, ..., |Л.«, T]ft+i,n, ..., Цп,п, Л = 0, ..., П. C)
Обозначим ?(fr)==(Si(^)? •••> 5»(^)) векторы, образованные на-
накопленными суммами А'-й серии, так что
1з(к) = Sa, n + ть+1.»» + • • •*+ Л;, п при / > й.
Лемма 2. Для любой случайной величины б такой, что
Р (| 61 ^ е) = 1, выполняется
Р(^В)<Р(!1еВ(к!) + |АA, (9)
где
А = Р (? (А) + & (fr - 1) е i?(e) (Л - 1)) -
- Р (I (к - 1) + бе (Л - 1) е= й(8) (А - 1)),
) = JU ==((),...,0,1,..., 1).
r-fl
Доказательство, Действительно, в силу G)
- 1))=
Применяя снова те зко выкладки к правой части, получим
Р (С (в - 1) + е (п - 1) б е= 5(s) (и - 1)) <
<Р (?(га - 1) + е(и - 1) в + en_i6 s /?(Е) (и - 2)) =
«= Р (S (и —i) + e (п -2)8е В{е) (л - 24) =
» ^ Р {I (« - 2) + в (в - 2) 6 е i5lE> (п - 2)) + An_lt
= Р (С A) + е @) б е S(e; @)) = Р (t @) + е @) б s S(s> @)) + Д,.
Так как % @) = rj, Р (т) + в @) б е= 5(е)) < Р (т, е 5Bв))г то (9) до-
казапо. ^
д. А. Боровков

354 ГЛ. 17. ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Чтобы получить лемму 1, надо оценить теперь Ah. Нам будет
удобно вместе с (8) рассматривать также серии
и обозначать ?(&, ?/) = (Ci(^ у), . •., 5п(^ ^)) соответствующий
вектор накопленных сумм, так что
Тогда Aft можно записать в виде
Ah = Р (С (&, 0) + F + ?л,п) е (Л - 1) ее #(е) (Л - 1)) -
- Р (Ц/с, 0) + F + л*.п) ^ (Л - 1) G= ?(s) (fe - 1)). (Ю)
Возьмем в качестве б случайную величину, не зависящую от
? и т|. Тогда вероятности, входящие в A0), удобно оценивать»
пользуясь у. м. о., так как, например, в равенстве
Р (? (к, 0) + (б + U,n) е (к - 1) е В(?) (к - 1)) =
= МР ((б + |А,„) е (к - 1) е 5(е) (А - 1) - ? (А, 0)/? (Л, 0)) A1)
множество C = jB<e)(A: — 1) — ?(^, 0) можно считать фиксирован-
фиксированным (см. свойства у.м. о., б и ?ь, п от ?(А:, 0) не зависят). Обоз-
начим через D множество у, для которых уе(к— 1)еС, Тогда
надо оценить разность
Р(б + gfe,neD)-P(б + пл.пе ?>). A2)
Воспользуемся леммой 8.3. Чтобы привести A2) к виду, удоб-
удобному для применения леммы, выберем в качестве б случайную
величину, имеющую трижды непрерывно дифференцируемую
плотность g(t), и положим для краткости Ъ>к,п~%, Ц^п — Ц. Тогда
б + ? будет иметь плотность, равную J dF^ (t) g (у — t) = Mg (у — 5)
так что
D
Если положим теперь / (х) == J g (у — x)dy, то получим, что
Ъ
Р(в + ?е=Я) = М/(?),
где / — трижды непрерывно дифференцируемая функция,

§ I. СХОДИМОСТЬ К UlillJ?lJUliL;KUJVty
Применяя теперь лемму 8.3, получим, что
= J I*31 |<* {Fh,n (x) - Qh,a (x)) |.
Так как правая часть здесь от ?(&, 0) и D никак не зависит, то,
возвращаясь к A0), A1), мы получим ту же оценку
Пусть теперь gi {x) — некоторая гладкая плотность, сосредо-
сосредоточенная на [—1, 1]. Тогда, полагая g(x) = — gA~ , получим
8 \ Ь J
Сопоставляя (9), A3) и A4), мы получим утвержденсе
леммы 1. ^
Доказательство теоремы 3. Эта теорема есть следст-
следствие леммы 1. Действительно, пусть В е /?д таково, что событм'1
-Ьйе^) и {?ei?} эквивалентны (^71 полностью определяется во
ti), тогда, очевидно, {^я eyl(e)} = {^ ей(г)} и утверждение теоре-
теоремы 3 повторяет утверждение леммы 1. ^
Доказательство теоремы 1. Пусть w{i) — стандарт-
стандартный виперовскмй процесс. Положим v\ht п = w D, п) — ^ D-i, n).
Тогда последовательность 'r]1<Ti, ..., r\n, n удовлетворяет всем на-
наложенным выше условиям, так как
Отметим также, что о?1>п= (М |Sft,n|aK;2 <М |§/?з?г|3= шг,?г, так что
Нам понадобится
Л е м м а 3. Р (р (w, sn) > e) <^V3/e3.
Доказательство. Событие j р (ш, ^) >> е} равно U Л^,}
ft
.4А - /sup | w (I) - s' (t) \>г\с /sup j w(t) | >e/2U
Поэтому (^/i ~ ^_! — «га>п, m;@ = aw
(t/G2j)
J

'356 ГЛ. 17. ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Функция (I — ФA)) убывает при t -*- °° значительно быстрее, чем
2~3, Поэтому
'Л
Из доказательства видно, что оценка в лемме 3 является весьма
грубом.
Вернемся к доказательству теоремы 1. Так как
P(^gG)==P (s'n €= G, р (w, s'n) < e) + P (s'n €= G, p (a?, 4) > е)„
TO
r/V
5
и в силу теоремы 3
Р (sn е= G)< Р (и; е G(Se>) + f^S +
в
в
Получим теперь обратное неравенство. Обозначим G{~B) множест-
множество G(-e) = G-EG)<'\ тогда [G(-e)J(e) ^ G°c= G. Меняя местами 5П
и $д в теореме 3 и применяя ее к множеству G(~2e), получим
Р
Меняя местами w и sn в A5) и применяя это соотношение к
(G{e\ находим
rN
Р (s'n с G(-2e)) > P (w e G(~3e>) - -^.
Отсюда и из A0) получаем
P(s»eG)>P (Sn eG°) >P(»e C(-3e)) - -
Если обозначить
Р («»е= G) = W(GF)) - TF (G) = AWG(б)
и учесть, что Ns ^ cL3, ^s^-^s + ^3, то мы получили
— AWG (- Зе) + —± < Р («„ е G) - TF (C)< AWG (Зв) + —±.
A7)

§ !. СХОДИМОСТЬ К ВИНЕРОВСКОМУ ПРОЦЕССУ 357\
Если W(dG) = 0, то очевидно, что
при е-* 0, AWo(db3e)->0. Отсюда и из A7) уже легко получить,
что PMC)h.P(m;gG).
Сходимость f(sn)=> f{w) для непрерывных функционалов сле-
следует из D), так как множество GB = UgC@, 1): f(x)<v} для
точки у, являющейся точкой непрерывности распределения f(w),
обладает свойством
W (dGv) - Р (/ (ш) = v) = 0
и, следовательно,
Р(/ЫО)->Р(/Иеу). <
Доказательство теоремы 2. Если множество G лип-
шицево, то
l
и в силу A7)
Полагая s = Lj 4, получим требуемое утверждение. ^
Название «принцип инвариантности», относящееся к основ-
основным утверждениям этого параграфа, лучше всего иллюстрируется
теоремой 3, в сплу которой для приближенного вычисления
P(sn^A) можно пользоваться значением P\sn^A) для любой
другой последовательности F), обладающей лить теми же пер-
первыми двумя моментами, что и A). В этом смысле главная часть
P(suG/i) инвариантна относительно конкретных распределе-
распределений рассматриваемых последовательностей. Например, вычисле-
вычисление РEпе6') или P(ta(t)^G) можно заменить вычислением
P(^eG) для последовательности в схеме Бернулли, к кото-
которой удобно применять различные численные методы. С другой
стороны, вероятности Р (ш ge G) для целого класса областей G
найдены в явном виде (ель, например, [16]). Мы знаем, например,
что Р (sup w (t) > у) = 2 A — Ф (х)). (Отсюда следует, в частности,
что множество C = UeC@, I): sup#(?)>?/} является Липшице-
вым.) Поэтому для распределения максимума сумм Sn = max Shf^
h
Su = 2sji Щк = 0, D%k = о-2 будем иметь
l
P (Sn > xa Vn) -> 2 A - Ф (x))
и можем использовать это соотношение для приближенного вы-
вычисления распределения Sn, представляющего, как мы видели в
гл. 11, значительный интерес в приложениях.

3^5 l'JI. W. ФУНИЦИиНЛЛЬИЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Точно так же можно приближать совместное распределение
?„, Sn и Sn = minSk (т. е. вероятности вида P{S»<^x 1/7/,,
&п ^>У У Щ Snе В)) с помощью соответствующих формул для
винеровского процесса, приведенных в [16].
Замечание 2. В заключение этого параграфа отметим, что
все утверждения, высказанные выше, сохранятся, если в них
вместо sn(t) рассматривать не непрерывную, а ступенчатую ло-
ломаную sn(t) = ?к,п при t^[tk, tk+i). В этом можно убедиться,
проведя заново все рассмотрения применительно к sn. Другой
путь для получения, скажем, теорем 1, 2 для sn состоит в том,
чтобы воспользоваться уже полученными результатами и оценить
расстояние p(sn» 4). Так как {р (sni si) >e| cz (j {Цк,п\>^}, то
Напомним, что оценку такого же вида мы получили для p(srM w)
и это позволило заменить, где это требовалось, sn на т. Следова-
Следовательно, пользуясь точно такими же рассуждениями, можно ме-
вшть $п на sn. Б этом случае можно рассматривать сходимость
распределений функционалов /(^Х определенных на D@, 1)
(и непрерывных в равномерной метрике р). В ряде случаев ис-
использование sn бывает технически более удобным, чем $п. На-
Например, в случае, когда надо найти предельное распределение
п „
21 ф(?&,п) = п J ф(^п@)^^A»1,п одинаково распределены). Из вы-
k — 1
писанного представления следует, что — ^J ф(?л,п)=>" \(p(w (t))dt.
§ 2. Закон повторного логарифма
Пусть gi, |2, ...— последовательность независимых случайных
Величин,
13 этих обозначениях отношение Ляпунова равно

§ 2. LJAK01I ПОВТОРНОГО ЛОГАРИФМА 359
В этом параграфе мы покажем, что из закона повторного лога-
логарифма для виперовского процесса и из теоремы 2 следует
Теорема 4 (закон повторного логарифма для сумм случай-
случайных величин). Если 5„-»-°°, L3n< с/ln Вп при некотором с < «>f
го
Plira =1=1,
Таким образом, все последовательности, располагающиеся вы-
ше (t-f e)Srty21nljiS,M будут верхними для последовательности
*Sn, а все последовательности ниже A — е)ВпУ2 In In Вп — ниж-
ними.
Условия теоремы, очевидно, будут выполнены для одинаково
и
распределенных gft, так как в этом случае ?3,п = - .» -. 7— т ^н = а{/г.
Доказательство. Обратимся к доказательству закона
повторного логарифма в теореме 16.5 и применим его к последо-
последовательности Sn. При этом не потребуется вносить никаких су-
существенных изменении. Надо лишь вместо w(ak) рассматривать
¦*S\?/>, где nk =min{?i: В;^а{}, п заменить, где потребуется, ah на
&пк- В силу условия Ляпунова шаха): = о(В';1), так что /?72i/t_i~
^ B;lj{ /^' ah при &-> оо.
Ключевым моментом доказательства теоремы 16.5 является до-
доказательство сходимости ряда (при любом 8 > 0)
2 Р / snp w (и) >A + е) а-л,Л A8)
h \и<ак I
и расходимости ряда
где
Xh = ]/2a/f In In a\ ^ (afc) - и; (ак~г) = w (ak (l - a)).
В рассматриваемом случае, если следовать тому же пути, надо
доказать сходимость ряда
A8а)

360
ГЛ. 17. ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
и расходимость ряда
где yh = ]/ 2B*h In In Blk~ xu.\\o асимптотическое поведение ве-
вероятностей событий в A8), A8а) и в A9), A9а) при выполне-
выполнении условия Ь3>п< с/ln Вп будет по существу одинаковым. Чтобы
установить это, воспользуемся, неравенством
B0>
вытекающим из доказательства теоремы 3. В стт^ту этого нера-
неравенства
Л
^ >A + Зк) х j < P (sup w(u)>(l + 2e) *\ +
Поэтому (см. A8а)), полагая n = nb, x^yh-,/Bn, получим
Р (Snh > A + Зе)Ук_Л <Р / sup w(и) >A + 2е) уА_,\ +
Здесль г/h-i - я*-!,
i L3,,,, (in In B;,
In an
Bnh ^ak, In In B2n, ~ In In ak ~ In A:, L3^,,k ^
с
'-jr. Следовательно, при всех достаточно боль-
ших /с (буквой с обозначены различные постоянные)
Р (sn >A + 38)^-J <Р[ sup и>(и)>A + е)^
Так
то полученное неравенство означает, что из сходимости ряда A8)
вытекает сходимость ряда A8а). Первая часть теоремы доказана.

§ 3. СХОДИМОСТЬ К ПУАССОНОВСКОМУ ПРОЦЕССУ 361
Вторая часть доказывается аналогично. Рассмотрим ряд A9а)..
В силу B0) находим
Р E„А - 5„;;_1 >A - Зр.) у,) = Р (sn, A) - S,,h (/'л) >
> A - Зе) А\ ^ р ('«, A) _ ш (,.д) > A _ 2е) А-) -
-^(inln^)-78, B2)
где rk = fi?,,^! В'^-^аГ1 в силу того, что
Первое слагаемое в B2) равно
Как и прежде, в силу B1) рад, составленный из вторых слагае-
слагаемых в B2), сходится. Поэтому установленные, неравенства озна-
означают, что доказанная нами расходимость ряда A9) влечет за
собой расходимость ряда A9а). Теорема доказана. ^
На самом деле условия выполнения закона повторного лога-
логарифма связаны не столько с существованием третьих момснтон,
сколько со скоростью сходимости в центральной предельной тео-
теореме. В какой-то мере этот факт иллюстрируется следующим ут-
утверждением (см. [15]):
. Теорема. Если Вп -* °°, Ba+JBn -*¦ 1 при п ->• о°
suр | Р (SnjBn <х) - Ф (х) | < с (In В,.) ~~б
X
при некоторых 6 > 0, с < °°, то имеет место закон повторного ло-
логарифма.
§ 3. Сходимость к пуасеоновскому процессу
Приведенные в § 1, 2 теоремы показывают, что винеровский
процесс достаточно хорошо описывает эволюцию накопленных
сумм при суммировании «обычных» случайных величин ?hf „,
удовлетворяющих условию Ляпунова. Оказывается, что подобным
же образом пуассоновский процесс описывает эволюцию накоплен-
накопленных сумм, когда случайные величины ?At „ соответствуют появле-
появлению редких событий.

362 ГЛ. 17. ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Рассмотрим независимые случайные величины в схеме серий
li, n, ..., ?п, п, которые для простоты будем считать одинаково рас-
распределенными. Пусть
»P(Sfc,n = 0) = l-pn> Р(?а|П=1)«Рги ЛРп = |А«-^|1>0. B3)
Читателю предлагается проверить, что в этом случае условие
Линдеберга (и, стало быть, Ляпунова) выполнено не будет.
Образуем случайную функцию sn(t) на [0, 1] следующим об-
образом. Положим
к Г
Здесь удобнее использовать ступенчатую, а не непрерывную тра-
траекторию sn(t) (ср. с замечанием 2). Утверждение, которое мы по-
получим в этом разделе, аналогично принципу инвариантности и
состоит в том, что процесс sn(t) сходится в известном смысле к
пуассоновскому процессу 5@ с параметром |л па [0, 1]. Эту схо-
сходимость можно было бы трактовать, конечно, как слабую сходи-
сходимость распределений в D@, 1). Но в рамках настоящей книги
это, по-видимому, нецелесообразно по крайней мере по двум при-
причинам:
1. Нам пришлось бы для этого вводить метрику в 0@, 1) я
изучать ее свойства, что само по себе сложно.
2. Траектории процессов sn(t) и 5@ устроены просто, и ха-
характеризовать их близость можно проще и точнее, ис привлекая
общих концепций. Действительно, как мы видели, траектория
5@ на [0, 1] полностью определяется набором случайных вели-
величии EA); «1, ..., а*A)), где ак есть точка &-го скачка процесса,
-aft+i — осА^Гм. Такую же характеризацию допускают траектории
sn(t): они определяются вектором ($n(l); yjnim. .,ySri{1)/n),r№
7i, y2, • •• суть те значения /, для которых |7-. „ = 1. Будем считать
распределения sn(t) и. 5@ близкими, если близка распределения
двух названных векторов. Это будет отвечать сходимости процес-
процессов в весьма естественном и сильном смысле.
Из сказанного ранее (см. § 16.4) о процессах Пуассона не-
нетрудно понять, что названная сходимость распределений точек
скачков $n(t) эквивалентна сходимости конечномерных распреде-
распределений sn(t) к распределениям 5@ (ступенчатый характер траек-
траекторий sn(t) известен).
Теорема 5. Можно так построить sn(t) и 5@ 1Ш одном
вероятностном пространстве, что
Р (| A) = sn A);
«ft -
IT» * = 1* .... I (!))> 1 - f|. B4)

§ 3. СХОДИМОСТЬ К ПУАССОНОВСКОМУ ПРОЦЕССУ 3G3
Другими словами, траектории ?(?) ш sn(t) с вероятностью
I 21 отличаются лишь малыми (<1/п) отклонениями точек
скачков.
В отличие от теоремы 1 это утверждение уже трудно назы-
называть принципом инвариантности, так как разнообразие распреде-
распределений ikt „, приводящее к такому результату^ не очень велико.
Но сравнению с теоремой оно может быть расширено до всех
распределений такях, что (см. теорему 7.4)
Следствие 2. Пусть В есть множество в JF?\ обладающее
свойством (его также естественно называть липшицевым)
| Р (К,..., ал) е= В(е))~ Р (К?.. м ал) е= Д)|< се.
Тогда us теоремы 5 вытекает, что
*" ^Ь^ E, ... ,Jl)e д)- Р F A) - А, К, ..., а,) <= S)
Доказательство. Из B4) следует, что
2
51> = /г> К ^)еВ) + 7 + т
Точно так же устанавливается обратное неравенство. ^
Доказательство теоремы 5. Пусть %|П = &(—)¦—
— Ц—-^— )> ft = 1, ..., п. Мы докажем утверждение теоремы, если
•осуществим построение |ft( n, rjfe# n на одном пространстве так, что
Р( U {1н.пФЧь,п})<№п B5)
\/ /
(таким построением |(?) будет определен не на всех интервалах
((&—1)М, к/п). Однако дальнейшая «достройка» g(l) нас ипте-
]>рсовать не будет — она может быть любой). Конструкция, при-
приводящая к B5), по существу уже была в теореме 5.9. Мы полу-
получим нужное построение, если рассмотрим независимые о-)п ••., со№>

364 ГЛ. 17. ФУНКЦИОНАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
0)fe§UM И ПОЛОЖИМ
*и
О, если со/. <Se п,
&> 1, если со/г е [я>г_15 .тц),
где яь = П^([0, А;]), & = 0, 1, Тогда ?fe, ft и r)ftf д будут иметь
требуемые совместные распределения,
пкп Ф %,«} = Ц е [l - А) ГР") U [е~Рп + р„ГРп, l]}.
Так как Р (Zkin?=: 4k,n)^pL то теорема доказана. <4
Пуассоновский процесс может выступать в роли-предельного
• и в несколько ином качестве — как предельный процесс для сум-
суммы большого числа однородных «медленных» процессов восста-
восстановления.
Сформулируем постановку задачи более точно. Пусть %(/),
i==l, 2, . .., га,— независимые .между собой произвольные одно-
однородные процессы восстановления в «схеме серий» (т. е. завися-
зависящие от га), для которых
>- А, и при любом фиксированном t
a
при n-^ooi Где rtOl от i не зависит,^0, ?з*\ ••» —случайные ве-
величины, порождающие процесс т]г-(/).
Теорема 6. При выполнении сформулированных условий,
конечномерные распределения процесса
сходятся к распределению пуассоновского процесса ^(t) с пара-
параметром К:
(О сходимости к пуассоновскому процессу см. замечание, пред-
предшествующее теореме 5.)
Доказательство. Докажем сначала сходимость распреде-
распределений приращений ?п(? + и) — rQn{u) к распределению Пуассона с
параметром Xt. Обозначим Ai = r\i(t+и)—r\i(u), Pi = t/au Имеем
(%i(u) —эксцесс для процесса т],-; см. гл. 9)

§ 3. СХОДИМОСТЬ К ПУАССОНОВСКОМУ ПРОЦЕССУ 865
Р (Д, > Z)< P (Xi(w) < t) [P {If < t)}1'1 <
1
^ a. } ^ 2 ' j ^' ^^Г^;'п^ — Pirt,w
Отсюда следует, что
1
P (A{ = 1) = Pi + o(Pi), P(A,- = 0) = 1 - Pi + о(Л). A6)
Мы находимся в условиях следствия 5.5, из которого следует, что
In (t + u)- ln (и) = S Д,"^> Пм. B7)
Осталось доказать асимптотическую независимость прираще-
приращений. Рассмотрим для простоты лишь два приращения на интер-
интервалах @, и) и (п, u + t) и предположим, что tn(u)=k. Более то-
того, предположим, что произошло событие А, состоящее в том, что
восстановления произошли в процессах с номерами iu ,.., ik. Нам
достаточно убедиться, что при этом условии по-прежнему будет
справедливо B7). Пусть В есть событие, состоящее в том, что в
процессах т],- с номерами iu ..., ih на интервале (w, u + ^) вновь
?фоизошли восстановления. Очевидно, что
k
Р (В/А) < S P (gf ° < * + и) <*r,+litn-* 0.
Таким образом, 'вклад процессов Щр 1 = 1, ..., /v, в сумму B7)
при условии .4 пренебрежимо мал. Рассмотрим оставшиеся и — к
процессов. Для них
= Z J (! - *"iB)> d2 И - S7 Jd - *dz))dz = A + o(Pi).
1 и L г *0 J
Так как соотношение BG) для условных (при условии А и
ври i?=ih Z = l, ..., к) распределений Дг- сохраняется, то получим
сю
аналогично предыдущему (роль равенства jEi IP (&i = I) = р%
oo
теперь играет равенство 2 ^P(^i = IIA) = Pi + o(pi)f вытекаю-
вытекающее из B8)):
P (A, = ilA) = Pi + o(Pi), P (A, = 0M) = I - Pi + 0{Pi)%
Остается вновь воспользоваться следствием 5.5. ^

Глава IS
МАРКОВСКИЕ ПРОЦЕССЫ
§ 1, Определения и общие свойства
Марковские процессы с дискретным временем и дискретным
множеством состояний (цепи Маркова) рассматривались в гл. 12.
Напомним, что главным в определении таких процессов было
свойство независимости «будущего» процесса от его «прошлого»,
если фиксировано его «настоящее». Этот же принцип лежит в
основе определения марковского процесса и в общем случае.
1. Определения и общие свойства. Пусть <Q, S, Р> — вероят-
вероятностное пространство, на котором задан случайный процесс
{?(/) = ?(*, (о), IX)}. Обозначим
»,=о(?(и); u<t), Ъи, coy = о(%(и); u>t),
так что величина %(и) измерима-относительно ??/ при u^t и от-
относительно г?[/,оо) при u>t. о-алгебра o(8f(, §п, »)) порождена
значениями %(и) при всех и и для выборочного вероятностного
пространства может совпадать с §.
Определение 1. Случайный процесс ? (?) называется
марковским, если при любых /, А е§/, B^d[t,oo)
Р (АВЦ (t)) = Р (А/1 (*)) Р (ВЦ (t)). A)
Это точно выраженная независимость будущего от прошлого ори
фиксированном настоящем.
Покажем, что приведенное определение 'эквивалентно сле-
следующему:
Определение 2. Процесс |(?) называется марковский,
если для любой ограниченной случайной величины г), измеримой
относительно §[*, «о, .
= М(ЧД@)- " B)
В качестве rj достаточно брать функции ц вида <П===/AE))
при s^ t.
Доказательство эквивалентности. Пусть верно
A). В силу теоремы о монотонной сходимости достаточно дока-
доказать B) для простых функций г]. Для этого в свою очередь до-
достаточно доказать B) дл-я ц = К — индикатора множества Be
^3?[_/too). Пусть А €^§/. Тогда в силу A)
Р (ЛВ) = МР (ЛВ/g (/)) = МР (Ail (t)) P (8,1 (t)) -
= MMUAP№(№(*)) - MIAP(Bjl(t)). C)

§ 1. ОПРЕДЕЛЕНИЯ If ОБЩИЕ СВОЙСТВА 367~
С другой стороны,
Р (ЛИ) = М/д/„ = М/дР (В,%). (А)
Так как (.1), D) верпы для любого /leg,, то это означает, что
РВ% Р{В1())
Наоборот, пусть теперь верно B). Тогда для Ае?,, B<=gf[( a>)
Р (ABil@) = М (М Aл1в/$Ш @1 = М [IJA (IBfti)/t (t)] -
= М [7АМ (Tall (WI (*)] = Р № (*)) Р (Ail (/))•
Осталось убедиться, что в B) достаточно брать г\— /(!(«)),
s5sf. Пусть ^ «? м, < ... < ии. Докажем, что тогда B) верно для
Воспользуемся индукцией и предположим, что B) выполнено
/1—1
для фуикщш Y = И fi(l(ud) (при га = 1 B) выполнено). Тогда,
обозначив g(M'n-i) = Mf/n^O^rt))/^^-])], получим
= М [уМ (/«(S(^))/5 (^,~i))/5fl - М [yg (I (Mn-i
По предположению индукции отсюда следует, что
и, значит, M(ii/S/) измеримо относительно о
М (т)/| @) = М (М (л/®1>/& @) = р^
Мы доказали выполнение B) для функций E), измеримых"
относительно g(?(mi), .. ., |(ип)). Путем предельного перехода
справедливость B) устанавливается для простых, а затем и для
любых %[t, «^-измеримых функций. ^
Приведем еще одно эквивалентное определение марковского
процесса.
Определение 3. Процесс ?(?) является марковским, если
для любой ограниченной функции / и для любых ti < tz < ...
м(/ami(h), .«л(и))-миа(№(и)). F)
Доказательство эквивалентности. Соотпотттеппо
F) очевидным образом следует из B). Пусть теперь выполнено
F). Тогда для любого Лео(^), . Л, §(^))
Обе части в G) являются мерами, совпадающими на алгебре

368 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
цилиндрических множеств. Следовательно, по теореме единствен-
единственности продолжения меры они совпадают и на о-алгебре, порож-
порожденной этими множествами, т. е. на 5^. Другими словами, G)
верно при любом Ле?|п, что эквивалентно равенству
при любом tn<t. Соотношение B) для г) — /(!(/)) доказано. «$
2. Переходная вероятность. Мы выяснили, что для марков-
марковского процесса ?(?) условная вероятность
Р (|@ €= B/ge) = Р (? @ €= Я/? (.9)) 1фИ t > ,9
есть борелевская функция от §(s), которую обозначим
P(l(t)e=B/l(s)) = P{s, l{s); t, It).
Можно считать, что P(s, ж; t, В) как функция от В и # есть ус-
условное распределение (см, § 4.9) §@ up и условии, что g(s)=#.
В силу свойства марковости она удовлетворяет соотношению
()
P(s, x; t, B) = $P(s, x; и, dy)P(u, у; t, В), (8)
которое выте!?ает и.ч равенства
= М [Р (| @ е= Д/5„)/| (••?) = х] = М[Р(и, | (м); *, Д)/| (,?) = xj.
Уравнение (8) носит назвапие у равнения Колмогорова— Чепмэла.
Функцию P(s, x\ t, В) можно использовать для аналитического
задания марковского процесса. Предварительно надо выяснить,
какими свойствами должна обладать функция Px,b(s, i) для того,
чтобы нашелся марковский процесс %(t), для которого
PXtB(s, t) = P(s, x; t, В).
Пусть (SP, Э^>—некоторое измеримое пространство.
Определение 4. Функция Рх< в($, t) называется переход-
переходной функцией па <й?, ©#?>, если она удовлетворяет следующим
условиям:
1) Рх>в($1 t) как функция от В есть распределение вероятно-
степ при каждых s^t, x^85.
2) Рх,в($, t) измерима по х при каждых s < t, B
3) При 0 ^ s <u<t и при всех ж, В
xtdv(s, u)PVtB(u, t)
(уравнение Колмогорова — Чепмэпа).
4) *V*(s, 0 = ^(в)

§ 2, ПРОЦЕССЫ СО СЧЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ 3G9
Здесь свойства 1), 2) обеспечивают функции Рх,в($, t) воз-
возможность быть условным распределением (ср. с § 4.9).
Определим теперь с помощью Px,n(s, t) конечномерные рас-
распределения некоторого процесса ^(t) с начальным условием
5@) = а но формуле
Р (I (tj) e= dyx, „.., I (tn) gee dyn) =
= ^,^@, tJPy^it» *a)- ...-Py^-dyjtn-u tn). (9)
В силу свойств 3), 4) эти распределения согласованы и, значит,
по теореме Колмогорова определяют ?(?) в <-R\, S^>^
По формуле (9) и правилу F)
Р(?(*п)еДп/(&(*1), ..., E(*n-i)) = (jr1, •.., ?п-0)-
= ^Л-1.Лп (^~Ь *») = Р F (««) ^ 5n/6 (^n-i) = Уп-l) «
Можно проверить это равенство и более формально, пользуясь
тем, что интегралы от обеих его частей по множеству {^(^iN5
€=/?<, ..., Ktn-ij^Bn^} совпадают.
Итак, в силу определения 3 мы построили марковский про-
процесс 5@> Для которого
P(Sj Х; t, B)^Px,B(s, I).
Эту функцию мы будем называть также переходной функцией
(или вероятностью) процесса 5@*
Определении е 5. Марковский процесс ?(/) называется од-
однородным, если P(s, x\ t, В) как функция s и t зависит лишь от
разности t — s:
P(s,x; t,B) = P(t-s; x, В).
Это есть вероятность за время t — s попасть из х в В. Если
.Р (и; х, B)=ijp(u; x, y)dy\ функция р(и; ху у) называется
в
переходной плотностью.
Нетрудно видеть, что винеровский и пуассоновский процессы
являются марковскими однородными процессами. Например, для
винеровского процесса
р (и; х, у) =
§ 2. Марковские процессы со счетным множеством состояний.
Примеры
'1. Основные свойства процесса. Не ограничивая общности,
будем считать, что «дискретное» фазовое пространство SB совпа-
совпадает с множеством целых чисел @, 1, 2, ...}. Для простоты бу-
будем рассматривать лишь однородные марковские процессы,
24 а. А. Боровков

370 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
Переходная функция такого процесса определяется набором
функций P(t; г, /) = ?„•(?)> образующих стохастическую матрицу
P(t) = ^Pi}(t)W [pa(t)>0, ^Pij(t) = 1). Уравнение Колмогорова —
Чепмэна здесь принимает вид
Pij(t + s) = %pik(t)p,tj(s),
к
или, что то же, в матричной форме
A0)
Будем рассматривать в дальнейшем лишь стохастически не-
непрерывные процессы, для которых \{t + s) —>\(t) при s -»• 0? что
в рассматриваемых условиях эквивалентно тому, что
P(s)->P{)^E A1)
при s ->¦ 0 (поэлементно). Мы будем предполагать также, что схо-
сходимость в A1) равномерна (для конечного SB это всегда так)*
В соответствии с требованием сепарабельности будем считать,
что \(t) не может менять свое состояние за «нулевое» время бо-
более одного раза (исключаем эффекты, проиллюстрированные в
примере 15, 1, т. е. будем считать, что если ?(?) = /, то с вероят-
вероятностью 1 !(?+$)=/ при se[0,x), т=т(ю)>0). В этом случае
траектории процесса будут кусочно постоянными (для определен-
определенности, непрерывными справа), т. е. ось времени разбивается на
полуинтервалы [0, Ti), [ть Ti + t2), ..., на которых \{1) по-
постоянно.
Обозначим
ft @= Р (I (и) = h 0 < и < III @) = /) = Р (%} > t).
Теорема 1. При выполнении сделанных предположений
(стохастическая непрерывность, сепарабельность)
где <?i<°°; q<>Q, если р«A)*& 1. Существуют
}~Piilt) ^ = gijl гф)х A2)
Доказательство, В силу свойства марковости

§ 2. ПРОЦЕССЫ СО СЧЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ 371
при этом qi{t)\. Поэтому существует единственное решение этого
уравнения qi(t) = е \ где qi<Coo1 т. к. Р(т1>0)==1 и $*>(),
т. к. q{(t)< 1 при pu(t)^ 1.
Пусть далее 0 < tQ < ti < ... < tn < i. Так как события
il(u) = i при u<tn l(tr+t) = j?=i}, г = 0, ..., n— 1; /^i,
несовместны, то
Pu @ = g4 @ + S 2 gt (M P?; (*r+i - tr) ph (t - *r+i). A3)
Здесь по условию A1) pu(t — fr+1)< st при всех /^г', 8^-^-0 при
t -> 0, так что сумма в A3) не превосходит
2 2 Vi(tr)Pii(tr + l- tr)= BtP [
Вместе с очевидным неравенством pu(t)> qt{t) это дает
(т. е. асимптотически 1 — дг(?) и 1 — /?»•(?) при t ~> 0 ведут себя
одинаково). Отсюда следует второе утверждение теоремы.
Пусть теперь tr = HI п. Рассмотрим переходные вероятности
Отсюда следует, что
и что верхний предел, стоящий справа, ограничен. Переходя к
пределу при t -+ 0, получим
Так как 2 Pai^)^^ — Puityi T0
Теорема показывает, что числа
24*

372 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
образуют стохастическую матрицу и имеют смысл вероятностей
перехода из i в / за интервал Л при условии, что процесс ?(?)
иа этом ивтервале покинул состояние i:
Таким образом, эволюцию t>(t) можно представлять себе сле-
следующим образом. Если ,1@) = Хо, то t,(t) находится в состоянии
Хо время тх^Гдт . Затем |(?) переходит в состояние Х{ с веро-
вероятностью Рх хг* Далее, \(t) = Хг на интервале времени [ти %г + т2)*
^2 €§ ^ях ' после чего система меняет свое состояние на X2i и т. д.
Ясно, что последовательность Хо, X",, ... связана в однородную
цепь Маркова с матрицей переходных вероятностей lljojl. Поэтому
дальнейшее изучение ?(?) во многом может быть сведено к изу-
изучению цепи Маркова {Х„; ?г^0), проведенному достаточно под-
подробно в гл. 12.
Мы видим, что эволюция %(?) целиком описывается с помощью
чисел qih q^ образующих матрицу
где принято qu = —q^ так что S Ян = 0. К этому факту можна
3
подойти и аналитически. Чтобы упростить. техническую сторону
рассуждений, будем предполагать, где это потребуется, что эле-
элементы матрицы Q ограничены, а сходимость в A2) происходит-
равномерно но i.
Обозначим через еА матричпозпачпую функцию
еА = Е + 2 Ак/к\.
Теорема 2. Переходные вероятности рц{1) удовлетворяют
системе дифференциальных уравнений
P'(t) = P№, A5)'
P'(t) = QP(t). A6)
Каждая из систем A5), A6) имеет единственное решение
Ясно, что решение получается немедленно, если формально
проинтегрировать A5).
Доказательство. В силу A1), A4)
A7)

§ 2. ПРОЦЕССЫ СО СЧЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ 373
Точно так же из равенства
P(t + s)-P(t) = (P(s)-E)P(t)
получается второе уравнение A6). Законность предельных пере-
переходов обеспечивается сделанными предположениями.
Далее, из A5) следует, что функция P(t) является бесконеч-
бесконечно дифференцируемой, при этом
В связи с методом получения уравнение A5) называется об-
обратным уравнением Колмогорова, а уравнение A8).— прямым
(приращение времени берется после или до основного интервала
времени).
Разница между этими уравнениями становится еще более на-
наглядной в случае неоднородных марковских процессов, когда пе-
переходные вероятности Р (| (^) == //I (s) = i) = p{j (s, t), s ^t за-
зависят от двух временных аргументов: s и L В этом случае A0)
превращается в равенство P(s, t + u) = P(s, ?)Р(?, t+u), обрат-
дР (*? t)
иое уравнение имеет вид ~~~^г— = P(s, ?)(?(s), прямое —
—~—=zQ(t)P(s, t). Читатель может получить эти соотноше-
соотношения самостоятельно.
Каковы общие условия существования стационарного предель-
предельного распределения? Можно воспользоваться здесь подходом, ана-
аналогичным тому, который использовался в гл. 12.
Пусть %(i)(t) есть процесс с начальным значением g<f)@)==&
и с непрерывными справа траекториями. Для заданного i0 обо-
обозначим
v(i) _ min {t ^ д. ?</) (^ = Q _ Vo?
Здесь во второй формуле мы рассматриваем значения t ^ vh-i + 1,
так как при t^vh~i было бы v^ == vfe-b Очевидно, что Р (v^—v/l_1 =
= 1)>0, P(vA — v/;_1e(^, ^ + /г))>0 при любых t>l, /г > 0,
если Pj \ (t) щ^ 1.
Теорема 3. Пусть существует состояние г0 такое, что Mv} <C
< оо, Р (v(l) < со) = 1 при любом i e ^0 с= ^, Тогда существуют
\im pxj(t) =pj
не зависящие от i е й?0.

374 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
Доказательство. Так же, как и для цепей Маркова, мо-
моменты времени vb v2, . ¦. разбивают ось времени на одинаково
устроенные независимые циклы по возвращению (спустя время!)
в состояние i0. Рассмотрим процесс восстановления, порожденный
суммами vft, к — 0, 1, ..., независимых случайных величин v9f
vA — vfc_i, к = 1,2, Пусть
Л (t) = miri {к: vk > t}, y(t) = t — vm)-.u
)
Событие Adv= ^T@e lvi v + dv)] представим в виде произведе-
произведения событий Bdv= Q {vf1^(t—v—di\ ^-i?]}e5m и Cv =
/?>о
= {^(а)^ г0 при ме[Ьу + 1, fj} ^ &~[t-Vt „,,, Имеем
U<0 @ = /. Y@ е [у, р + ^)) = (Р (|(i> («) = yt
1
BdlCv) = J M/B(/BP (^(i> (t) = /
1
О
На множестве Bdv выполняется %(t—v) = i0, и, следовательно, ве-
вероятность под интегралом равна
и не зависит от t и ?'. Так как Р E^) = dli (t — у), то
Pii (*) = j S (v) P (B<lv) = J g (y) dH(t r- v).
0 0
По основной теореме восстановления этот интеграл сходится к
оо
У^~ ] ^ (^) d^- Существование последнего интеграла вытекает из
о
того, что g(v)^ P(v, > v). 4
Теорема 4. Если существует стационарное распределение
еде все строки матрицы Р одинаковы, то оно является единствен-
единственным решением уравнения
Р? = 0. A8)'
Очевидно, что уравнение A8) получается приравниванием
Pf(t) = O в A5). Уравнение A6) дает тривиальное равенство
QPQ

§ 2. ПРОЦЕССЫ СО СЧЕТНЫМ МНОЖЕСТВОМ СОСТОЯНИЙ 375
Доказательство. Уравнение A8) получится, если в A7)
перейти к пределу сначала при ?->оо, а затем при s-> 0. Допу-
Допустим теперь, что Pi есть решение A8), т. е. PiQ = 0. Тогда
PiP(t) = Pl при *<1, поскольку РР Рф
P{kt)-+P при
i
значит, Pi = PJJ = P. ^
2. Примеры.
Пример 1. П у ас ооновский процесс \{t) с параметром X яв-
является марковским процессом, для которого qi = X, qi7 г+1 = Я,
Pi, г+i = 1, i — 0, 1, .... Для него стационарное распределение р
не существует (траектория уходит на бесконечность).
Пример 2. Процессы рождения и гибели. Так называются
процессы, для которых при i ^ 1
А + о (А) при / = i + U
(Д)=
+ о (А) при 7 = i — 1,
о(А) бРи |/~*|>2,
так что
[я^ при ^ - ' + *•
(з[-^.при/-*-1
есть вероятности, соответственно, рождения и( гибели одной ча-
частицы в некоторой популяции, когда эта популяция содержала i
частиц и изменила свое состояние. При i == 0 следует положить
'7о = О. Выяснение условий существования стационарного режима
представляет собой весьма сложную задачу (связанную главным
образом с выяснением условий ухода траектории на бесконеч-
бесконечность). Если таковой существует, то согласно теореме 4 стацио-
стационарные вероятности Pj могут быть найдены единственным обра-
образом из рекуррентных соотношений (см. уравнение A8), здесь
РоК - Pi (Xi + Tfi) + Р2Ч2 = О,
¦
-i ~ Ph (К + b) + Pn+ib+L ^ °»
и условия 2 ft = !•
Пример З. Задача о телефонных линиях в теории массового
обслуживания. Пусть дана система, состоящая из бесконечного
числа каналов связи5 но которым ведутся телефонные разговоры.

376 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
Вероятность окончания разговора в каждой из линий за малый
интервал времени (t, t + Д) равна ЯД + я(Д). Вероятность по-
поступления нового вызова за этот интервал времени равна
4&-ho(A). Таким образом, «входящий» поток вызовов есть не
что иное, как пуассоиовский процесс с параметром X, а число
|(jf) занятых каналов в момент времени. ? есть процесс рождения
и гибели, для которого Xt = X, у г = iy.
В этом случав с помощью теоремы 3 нетрудно убедиться, что
всегда существует стационарное предельное распределение (при
г*о = О), уравнепия A9) для которого примут вид
Хр0 = TPi»
B0)
(X + fk)ph = kpk-A + {к + 1) if/ifc+i,
Отсюда получаем
Pl = Poy^2 = T°(?J,.-M^=GJ ^ B1)
так что ро = е~Кп, а предельное распределение будет, распределе-
распределением Пуассона с параметром Х/у.
Если число каналов связи п конечно, то вызовы, заставшие
все каналы занятыми, получают отказ и надо положить в A9)
Хп = 0, рп+1 = рп+г = ... = 0. В этом случае последнее уравнение
в B0) будет иметь вид ^прп^Хрп^^ Так как формулы B1) при
к < п сохраняются, то получаем для стационарного распределе-
распределения так называемые формулы Эрланга:
Ph = I V I T\
(усеченное распределение Пуассона).
Следующий пример мы выделим в отдельный раздел.
§ 3. Ветвящиеся процессы
Существо математической модели, описывающей ветвящийся
процесс, остается примерно тем же, что в п. 2 § 7. 8. В условиях
непрерывного времени задавать ветвящийся процесс можно сле-
следующим образом. Пусть |(<)@ означает число частиц в момент
времени t при начальном условии g(i) @) = L Каждая частица не-
независимо от других за интервал времени (?, ? + Д) с вероят-
вероятностью |яД + о(Д) переходит в случайное число г| Ф 1 частиц (при
т] = 0 мы говорим, что частица погибла). Таким образом,
i(i)@ = ii1)(')+...+li1)(% B2)

§ 3. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ 377
где Ц"° (t) независимы и распределены как |A)@* Кроме того,
(А); j Ф i; ph = P(i] = fc); pj = 0;
о(Д), B3)
так что здесь д^ —
Формула B3) объясняется тем, что щА есть главная часть
вероятности того, что хотя бы одна частица будет делиться. Оче-
Очевидно, что состояние 0 является поглощающим.
¦• Оно не будет таковым, если рассматривать процессы с имми-
иммиграцией, когда к |<0@ добавляется иуассоновский процесс с па-
параметром X «посторонних» частиц того же типа. Тогда
/?у(Д)=1[гД^-<+1 + о(Д) при у — * ?=0,1,
lh, i+i (А) = А (щр2 + Х) + о(А).
Вернемся к ветвящемуся процессу B2), B3). В силу B2)
имеем
оо
ф«Чм)-м*6@<(>-[м**A)<'>]1 -фЧ*,^- 2«%
где
Из второго уравнения A6) следует, что
Поэтому, дифференцируя B4) по t, получим
оо оо оо
== 2 gii 2 г"Р№ (*) == 2 диЧ>1 (t, z). B5)
По qu == № при I =3^ 1, gu = — jx, и если обозначить
оо / оо
/(«) = 2 qus1 = I* (Ms11 - s) = ц 2р,*' -
то B5) можно записать в виде
Мы получили дифферепциалъное уравнение для ф = ср(^, г) (эк-
(эквивалентное A5)), которое удобнее записать в виде
)
J
Ф@,г)

378 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
Рассмотрим поведение функции fi(y) = MyTi—у па [0, 1]. Оче-
Очевидно, что /i @) = р (г) = 0), /2 A) = 0, /г A) = Мц — 1, /i (у) =
= Мц(г\ — 1)уц~2 >0. Следовательно, fi{y) выпукла вниз и не
имеет нулей на @, 1) ири Мц^1. При Мц > 1 существует точка
де@, 1) такая, что /i(g) = 0, /i(g)<0 (рис. 18), и в окрест-
окрестности этой точки fL(y) = (у — д) Д (д) + О ((г/ — дJ).
д Таким образом, если Mr\^>if z<.qr
Ф t д, то в силу представления т =*
1 \У J
^= . 1_ O(j) получим
(у — «) Л (fi)
-_L>- Ф
==: I Т ^ ===: '
J / \У) llf-. {q)
Рис. 18 г
Отсюда следует, что при t -*• °°,
Ф (t, z) - g + О (e~af), a = - u-Л (g) > 0.
В частности, вероятность вырождения
экспоненциально быстро сходится к g, /?10(oo)=::g. Сравнивая с
§ 7.8, читатель может убедиться, что такой же была вероятность
вырождения для ветвящегося процесса с дискретным временем
(к этому выводу можно прийти и непосредственно). Так как
Pko(t) = [pio(t)]\ то /?/lo(oo) = g7{.
Из B8) следует, что остальная «вероятностная масса» рас-
распределения g(?) быстро уходит при t ->~ °° на бесконечность.
Если Мт]<1, то все приведенные рассуждения сохраняются с
заменой q на 1, так что />ю(°°) = />ло(°°)= 1.
Если Mr) = 1, то
ф
Ф
7,*
^ A)
Таким образом, здесь вероятность вырождения ф(?, O) = piO(t)
также сходится к 1*

§ 4. ДИФФУЗИОННЫЕ ПРОЦЕССЫ 379
§ 4. Диффузионные процессы
Рассмотрим еще один важный класс марковских процессов, иа
этот раз с непрерывными траекториями.
Определение 6. Однородный марковский процесс %(t) в
фазовом пространстве (Я, J?) с переходной функцией P(t, x7 В)
называется диффузионным, если
1) Jim 4- \yP(A,x,dy) = a(x),
2) }im-±-
3) при каких-нибудь б > 0, с <
Обозначим Д?(г) = |(? +А) —?@« '-Тогда приведенные усло-
условия можно записать в виде
Коэффициенты а(х), Ъ{х) называют соответственно коэффи-
коэффициентами сноса и диффузии. Условие 3) есть некоторый аналог
условия Ляпунова. Его можно заменить на условие типа Липде-
берга:
За) М[(Д?(*)J; 1Д|@1>е] = о(Д) при любом е>0.
Из условия 3) и теоремы Колмогорова немедленно вытекает,
что диффузионный процесс ?(?) хможио рассматривать как про-
процесс с непрерывными траекториями.
Стандартный винеровский процесс w(t) является диффузион-
диффузионным процессом, так как для пего
MAw (I) - О, М [Дм; (t)]2 = Д, М [Дм; @14 = ЗА2.
Значит, винеровский процесс имеет нулевой снос и постоянный
коэффициент диффузии. Ясно, что процесс w(t)+at будет иметь
снос а и тот же коэффициент диффузии.
Мы видели в § 2, что «локальная» характеристика Q марков-
марковского процесса |(?) с дискретным SB однозначно определяет эво-
эволюцию процесса. Аналогичная картина наблюдается и здесь: рас-
распределение процесса однозначно определяется коэффициентами
а(х) и Ь(х). Путь для установления этого факта опять лежит
через уравнение Колмогорова — Чепмэпа..

380 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
Теорема 5. Если переходные вероятности P(t, х, В) дваж-
дважды непрерывно дифференцируемы по х, то P(t, x1 В) дифферен-
дифференцируема по X и удовлетворяет уравнению
дР A^л 1J ^
1Г~а ox + Т дх*
и начальному условию Р@7 х, В)= 1в(х). B8)'
Замечание 1. Условия теоремы на гладкость переходной
функции Р на самом деле могут быть доказаны в предположении
непрерывности а и b и условий Ъ > Ьо > 0, |а| < с(|ж| + 1), Ьг <
^сAж|+1).
Доказательство теоремы 5. Обозначим для краткости
¦п' ri nff дР дР
через ги ГХ1 гх соответственно частные производные -^-, -г~-х
д*Р
—2~ и воспользуемся разложением
P(t, у. В) - P(t4 х, В) ^(у-х) Р'х + 1^=^р: +
+ {jL^[P*x(t,yx,B)^P"x(t,x,B)l yxe=(x,y). B9)
Тогда в силу уравнешш Колмогорова — 4епмэна
Р (t + А, х, В)-Р (t, х,В)=*\Р (А, х, dy)[P(t, у, В) -P(t, х, Б)] =
= а(.т)/>;Д + -^-Р;Д + о(Д) + Д, C0)
где
:.({,х,б)]= J
Первый интеграл здесь в силу непрерывности Р"% не превосхо-
превосходит б (в) -- *'¦•• А + о (А) , б(е)~>-0 при е -> 0; второй интеграл
но ycjtoBHio За) есть о(А). Так как 8 произвольно, то Л = о
и из сказанного выше следует, что существует
Из теории дифференциальных уравнений известно, что при
широких предположениях о коэффициентах a, b и при 1? —
= ( — ©о, z) задача Коши B7), B8) для уравнения B7) имеет
единственное решение Р, бесконечное число раз дифференцируе-
дифференцируемое по t, х и z, Отсюда следует, в частности, что P(t1 x, В) имеет

§ 4.. ДИФФУЗИОННЫЕ ПРОЦЕССЫ 38t
плотность p(ty x, z), являющуюся фундаментальным реше-
решением B7).
Из теоремы 5 нетрудно получить также, что вместе с P(t^x^B)
уравнению B7) будут удовлетворять функции и {t1 х) =
= j Ф (z) P (t, х, dz) = М [ф (l{x) (t))] для любой гладкой функ-
функции ф с конечным носителем.
Мы рассматривали в доказательстве теоремы 5 (см. C0)) при-
приращение времени Д, предшествующее основному интервалу.
В связи с этим уравнения B7) называются обратными уравнения-
уравнениями Колмогорова. Аналогичным образом могут быть получены и
прямые уравнения.
Теорема 6 (прямые уравнения Колмогорова). Пусть пере-
переходная плотность p(t, x1 у) такова, что существуют непрерывные
производные
— Г
ду 1
Тогда p(t, x, у) удовлетворяет уравнению
Доказательство. Пусть Ц)(у) — гладкая функция с огра-
ограниченным носителем, и (?, х) =» Мф (g(x) (t)) =* j ф (у) р (х3 t, у) dy*
Тогда
и (t + Д, х) — u(t, x) =»
« J p (xx t, z) [J p (z, Д, у) q(y)dy — J p (z, Д, у) ф (z) dy] dz. C2)
Если воспользоваться разложением в ряд ф(г/) — фB;)| то для вы-
выражения в квадратных скобках мы аналогично тому, как это бы-
было в доказательстве теоремы 5, в силу свойств 1) — 3) получим
Отсюда следует, что существует
Ли
dt
: J p {tb xx z) [a (z) ф' (z) dz + 1
Используя интегрирование по частям, получим
w = J {- ila W p & x> z>] + т i?[b*(z) p {h x*z)])ф (z) dz =

382 ГЛ. 18. МАРКОВСКИЕ ПРОЦЕССЫ
или, что то же,
§Dp(l,x1z)y(z)dz = 0.
Так как ср произвольна, то отсюда следует C1). «4
Как и в случае дискретного <Э?, различие между прямым и об-
обратным уравнениями Колмогорова становится более наглядным
в случае неоднородных процессов диффузии, когда переходные
вероятности P(s, x; t, В) зависят от двух временных аргументов,
а функции а и Ь в условиях 1)—3) будут функциями от s и х.
Тогда обратное уравнение Колмогорова (для плотностей) будет
связывать производные переходных плотностей p(s, x\ t, у) па
первьод двум переменным, а прямое — по вторым.
Вернемся к однородным процессам диффузии. Исследование
условий, при которых существует стационарное распределение
Ъ,{х) (t) при t -*¦ °°, не зависящее от х, может быть проведено с по-
помощью того же подхода, что и в § 2. Теорема 3 при этом пол-
полностью сохранится (надо лишь обозначение ?0 заменить на х0 для
единообразия обозначений в условиях этого параграфа). Доказа-
Доказательство теоремы 3 также сохранится, однако потребует несколь-
несколько более аккуратных рассуждений (в новой ситуации па собы-
событии Bdv выполняется ?(?— u)^dx0 (а не = х0)).
Если стационарное распределение
C3)
существует, то каким образом оно может быть найдено? Так как
зависимость p(t, х, у) при t-+ <*> от t и х становится исчезающей,
то обратные уравнения Колмогорова превращаются при t ~+ °°
в тождество 0 = 0. Если обратиться к прямым уравнениям и
перейти в C2) к пределу сначала но t -*¦ °°, а затем но А -+¦ 0, мы
придем после тех же, что в теореме 3, рассуждений к следующе-
следующему заключению.
Следствие 1. Если выполнено C3) и условия теоремы G>
то стационарная плотность р{у) удовлетворяет уравнению
-1а(у)р(у)У + ^[ЬЦу)р(у)Г = О
(которое получается из C1), если положить —t =0)f
Пример 4. Процесс Орнштейиа — Уленбека .
где w{и\— стандартный винеровский процесс, является однород-

§ 4. ДИс1>ФУЗИ0НИЫЕ ПРОЦЕССЫ 383
пым диффузионным процессом с переходной плотностью
р (t, х, у) = —J-— охр j_ <JLz?p!l C4)
у Ino {Ц { 2а i J
Читателю предоставляется проверить, что этот процесс имеет ко-
коэффициенты а(х) = ах, b (х) = о = const, а функция C4) удовлет-
удовлетворяет прямому и обратному уравнениям. При а < 0 существует
стационарный процесс (определение см. в следующей главе)
плотность распределения которого (она от t не зависит) равна
р {у} = Ига р (х, t, у) =
у^ ер гт
2ла(оо) i 2a"(oo)
В заключение этого параграфа рассмотрим важную для разно-
разного рода приложений задачу об отыскании вероятности того, что
траектория диффузионного процесса не выйдет за пределы задан-
заданной полосы. Для простоты мы ограничимся рассмотрением этой
задачи для шшеровского процесса. Пусть с > 0, d < 0.
Обозначим
U (*, х, В) = Р (ш(х) {и) е= (d, с) при всех м g= [0, f ]; ?г:(зс) @ еВ)=>
= Р (sup ш(х) (и) < с, inf ?^(х) (и) > d, ^(х) @ е=
Опустим проверку того, факта, что функция' U дважды непре-'
рывпо дифференцируема по х, а ограничимся тем, что докажем
следующее предложение:
Теорема 7. Функция U удовлетворяет уравнению B7) с на-
чалъным условием
, В) = 1в(х) C5)
и с граничными условиями
U{t, с, B)=*U(t% d, Я) = 0. C6)
Доказательство. Отметим прежде всего, что функция
U(t, х, В) при x&(d, с) удовлетворяет условиям 1)—3), налага-
налагаемым на переходную функцию P(t, x, В). Действительно, рас-
смртрим, например, свойство 1)*

384 гл. 18, марковские процессы
Надо убедиться, что
с
y-x)U-(b,x,dy)~ba(x) + o(b) C7)
(при а(х)=0 в пашем случае). Но U(i, х1 B) = P(t, ж, В) —
-V(t, я, В), где
V(t, х, В) = Р ((sup ш(х) (м) > с или inf ш(х) (и) < d) fl
.max i
x (с, — d)|P (sup ш(^ (м) >с) + Р f inf ш(х) (и)
Например, первая вероятность в квадратных скобках оценивает-
оценивается, как мы знаем (см. A6.2) и лемму A6.1)), значением
С — X
У А '
При любом х<с ш любом к >*0 это есть о (А*). Поэтому C7) до-
казапо. Точно так же проверяются свойства 2), 3).
Далее, т. к. по формуле полной вероятности при x^(d, c\
с
U(t+A, х, В)= j U (А, х, dy) U (t, у, В\
d
то, пользуясь разложением вида B9) для функции С/, точно так
же, как в C0), получим
U(t + Аг х% В) —U (t, хх В) =
Отсюда следует существование -^- и уравнение B7) для функ-
функции U.
Выполнение граничных и начальных условий очевидно. А

§ 4, ДИФФУЗИОННЫЕ ПРОЦЕССЫ 385
Читатель может убедиться, что функция
и (t, х, у) = —• U(tx х% (—оо, г/)), у е= (<2, c^
играющая роль фундаментального решения для граничной 'зада»
чи C5), C6) (функция и удовлетворяет B7) при граничных ус-
условиях C6) и начальном значении, вырождающемся в б-функ-
цшо), равна
/i=0
Этот ответ можно получить и непосредственно пз вероятностных
соображений (см., например, [16]).
25 А. А, Боровков

Глава 19
ПРОЦЕССЫ С КОНЕЧНЫМИ МОМЕНТАМИ
ВТОРОГО ПОРЯДКА. ГАУССОВСКИЕ ПРОЦЕССЫ
§ 1. Процессы с конечными моментами второго порядка
Пусть {?(?), —<x><t<oo} — случайный процесс, для которого
существуют a (t) = М? (.?), R (?, и) = Ml (t) I (и). Так как от g (t)
всегда можно перейти к изучению процесса %(?)—-а(?), то, не
ограничивая общности, можно считать, что a(t)^O.
Определение 1. Функция R(t, и) называется ковариаци-
ковариационной функцией процесса %{t).
Определение 2. Функция R(t, и) называется неотрица-
неотрицательно (положительно) определенной, если для любых к\ иь ...
..», ик\ аи .. м ah?=0
Очевидно, что ковариационная функция R(t, и) является не-
неотрицательно определенной, так как
2 uiujR (Щ, Щ) == М B &il (иг)У > 0.
Определение 3. Процесс ^(t) называется непредсказуе-
непредсказуемым, если никакая линейная комбинация величин ^(iii),.. ., %(uk)
не равна нулю с вероятностью 1, т. е. если не существует таких
ии ..., мЛ; аь .. ., aft, что Р B а? (mJ = О) = 1.
Если R(t, и) — ковариационная функция непредсказуемого
процесса, то R(ty и) — положительно определенная функция. Ни-
же мы увидим, что в известном смысле верно и обратное утверж-
утверждение.
Непредсказуемость означает, что мы не можем определить
%(th) как линейную комбинацию l(?j), / < Л-
Пример 1. Процесс |@ = 2 SftTfe (Or гДе фл@' линейпо
независимы, |л независимы, не является непредсказуемым, так
как по значениям ^(^), ..., i(tN) можно определить %(t) при
всех остальных t.
Рассмотрим Гильбертово пространство L2 всех случайных ве-
величин 1] на <Q, S, Р> с конечными вторыми моментами, Мт] = 0,
и со скалярным произведением (Лг» Лг) = Mrj1/n2, соответствую-
соответствующим расстоянию |r)i — Л2II = [М (лх — Л2J]1/2* Сходимость в L%
есть, очевидно, сходимость в среднеквадратичном.
Случайный процесс \(t) можно представлять себе как кри-
кривую в Z/2.

§ i. ПРОЦЕССЫ С КОНЕЧНЫМИ МОМЕНТАМИ 2-ГО ПОРЯДКА 387
Определение 4. Случайный процесс ?(?) называется ста-
стационарным (в широком смысле)-, если функция R(t, u) = R(t — u)
зависит лишь от разности t—u. Функция R(s) называется неот-
неотрицательно (положительно) определенной, если таковой оказыва-
оказывается функция R(t, t + s).
Для винеровского процесса R (t, и) = Mw (t) w (и) = min (t, и),
так что процесс w(t) не может быть стационарным. Однако про-
процесс ?(?)= w(t + 1) — w(t) уже будет стационарным.
Очевидно, что для стационарного процесса функция R(s) яв-
является четной, М?2 (t) = R @) = const. Положим для простоты
/?@)=1. Тогда в силу неравенства Коши — Буняковского
IR(s)|<|Ml(t)I(t + s)|<[ME2(t) MS2(f + 6-)]1/2 = Д @) - l.
Теорема 1. 1) Процесс |(?) непрерывен в среднеквадратич-
среднеквадратичE ( Д)| @
) рц |() рр рр
ном E (i + Д)—^> | @ дг/?гг Д ->¦ 0) гог^а и только тогда, когда
функция R(u) непрерывна в нуле.
2) Если функция R(u) непрерывна в нуле, то она непрерыв-
непрерывна всюду.
Доказательство.
1) |l(t + А) - I (t)||2 - М (I (t + А) - I (ОK = 2Л @) - 2Я (Д).
A)
2) R(t + Д)- i? (*)= М (g(^ +A)g(O)—
В соответствии с содержанием гл. 6,15 процесс ?(?)> непрерыв-
непрерывный в среднеквадратичном, будет стохастически непрерывным.
Однако непрерывность в среднеквадратичном не влечет за собой
непрерывность траекторий. Читатель может убедиться в этом,
рассмотрев в качестве примера процесс
где г|@— пуассоновский процесс с параметром 1. Для него
функция
@ при
/? 11\ <
непрерывна, хотя траектории %(t) разрывны.
Если же
B)
при некотором е > 0, то по теореме Колмогорова для ?(?) суще-
существует непрерывная модификация. Отсюда следует, в частности,
что если R(t) дважды дифференцируема в точке ? = 0, то траек-
траектории ?(?) можно считать непрерывными. Действительно, в этом
25*

388 ГЛ. 19. ГАУССОВСКИЕ ПРОЦЕССЫ
случав в силу четности R(t) выполняется i?'@) = 0, /?(Д) —
-Д(О)~Д"F)Д2.
В целом, чем выше гладкость ковариационной функции в ну-
нуле, тем более высокой гладкостью обладают траектории !;(?).
Предположим, что траектории процесса %(?) измеримы (па-
пример, принадлежат пространству D).
Теорема 2 (простейшая эргодическая теорема). Если -
R{s)-+ О при s -> оо? ^ C)
то
о
Доказательство.
т т
о о
В силу четности R(s)
т т т т
ИГ Г
Rit — и) dt du= 2 \ \ R (t — u)dt du.
О V
0 0 0 и -
Сделаем ортогональную замену переменных, положив и
^—(t — u), s = --?=(t + и). Тогда
г/У 5 г/ VI ' т
J R ( у 2v) dv ds^i 2Т \ R (и) dvx
Пример 2. Стационарный процесс белого шума ^(^) опре-
определяется как процесс с независимыми значениями, т. е. как про-
процесс, для которого при любых tu ..., tn значения |(^i), . ¦., S(?n),
. независимы. Для дего
Г1 при з^ = 0%
при
и условие C) выполнено. Однако применять здесь теорему 2
нельзя, так как траектории ?(?) будут с вероятностью 1 неизме-
неизмеримыми (неизмеримым с вероятностью 1 буде^ например, мно-
.жество B^{t: %{t)>0}).

§ 2. ГАУССОВСКИЕ ПРОЦЕССЫ 389
Определение 5. Процесс ?(t) называется стационарным
я узком смысле, если при любых tu , •,, th распределение
(^(U + и), §(?2 + и), ..., \{tk + u)) не зависит от и.
Очевидно, что если ?(?)—процесс- стационарный в узком
смысле, то
Mi(t)l(u) = Ml(t-u)l(O)^R(t-u)
и %{?) будет стационарным в широком смысле. Обратное, конечно,
не верно. Однако существует класс процессов, для которых оба
понятия стационарности совпадают.
§ 2. Гауссовские процессы
Определение 6. Процесс ?,(t) называется гауссовским,
если его конечномерные распределения нормальны.
Будем считать снова, что MS, (t) = О, R (?, и) = М| (t) ^ (и).
Конечномерные распределения полностью определяются х. ф,
где Д=Ш(?г, ^-)И, индекс Г означает транспонирование, так что
Таким образом, для гауссовского процесса конечномерные рас-
распределения полностью определяются ковариационной функ-
функцией R(t, и).
Мы видели, что для непредсказуемого процесса ?(?) функция
JR(t, и) положительно определена. Обратному утверждению мож-
можно придать следующую форму.
Теорема 3. Если функция R(t, и) является положительно
определенной, то. существует непредсказуемый гауссовский про-
процесс с ковариационной функцией R(t, и).
Доказательство. Определим для произвольных tiy .. ., tk
конечномерные распределения |(?i), •••» ё(^) через плотность
где Л есть матрица, обратная к матрице вторых моментов М =
= Ш(^, ^)Н (см. § 7.6). Эти распределения будут, очевидно, со-
согласованы, поскольку согласованными являются матрицы вторых
моментов (матрица для ?(?i), .. ., %{th-i) является подматрицей
матрицы Л). Остается воспользоваться теоремой Колмогорова. -^
II р и м е р 3. Пусть w (t) — стандартный винеровский процесс.
Процесс wQ (t) = w (t) •—twA), t s [0, 1] называется броуновским
мостом (его «концы закреплены»: ш°@) = ш°A) = 0), Корреляцы-

390 ГЛ. 19. ГАУССОВСКИЕ ПРОЦЕССЫ
оиная функция для w° (t) равна
R (t, u)^M{w (t) — tw A)) (w (u) — uw A)) = t A — u)
при u&*t.
Гауссовский процесс i,(t), стационарный в широком смысле^
является стационарным в узком смысле. Это немедленно вытека-
вытекает из того, что для R(t, u) = R(t—u) конечномерные распределе-
распределения ?(?) становятся инвариантными относительно сдвига времени;
поскольку IIД {и + щ U + и) II = WR(U, if) 1L
Если ^(t)—гауссовский процесс, то условия гладкости траек-
траекторий могут быть существенно ослаблены но сравнению с B),
Пусть для простоты гауссовский процесс ?(?) стационарен.
Теорема 4. Если
(±y\ a>3, c<oo,
то траектории |(?) можно считать непрерывными.
Доказательство. Воспользуемся теоремой 15.2 и поло-
}ким ? (h) = log у- при 1 <С Р < а" ¦¦¦ (имеется в виду log na
ос со
основанию 2). Тогда 2 sB""n) = 2 ^~ <°°, и в силу A)
п=1 п—1
: 2 [l - Ф (се (h) (log I)"'2)] = 2 [l - Ф (c (log 1
[• D>
Так как аргумент под знаком Ф неограниченно растет при
Л -> 0, 7 = a - 2fi > 1, то в силу A6.2)
1 — Ф (х) ~ е~х 'ы при х ->- со,
и правая часть в D) не превосходит
д (/г) == с * (log -у-) ехр {— сЛ log у-) f,
так что
сю оо
2 2пд B"п) = сх2 ?г"т/2 ехр {- с2п> + п In 2) < оо,
2
1
так как с2>0, ^>1. Условия теоремы 15.2 выполнены, теорема
4 доказана. ^

§ 3. ЗАДАЧА О ПРОГНОЗЕ 3^
§ 3. Задача о прогнозе
Пусть известно распределение процесса |(?) и известна тра-
траектория %(t) на множестве В<^( — °°, t] (В— либо интервал, либо
конечный набор точек). Что можно сказать о значении ?(? + и)?
Нашей целью будет отыскание случайной величины ?, измеримой
относительно S5 = a(g(i'), v^B) (и называемой прогнозом) та-
такой, что M(E,(t + u) — Q2 принимает наименьшее возможное зна-
значение. Но ответ на этот вопрос известен (см. § 4.8)
Пусть ?(?) — гауссовский процесс, В — {tu ..., 4), 11 < t2 < . ..
...^^o^ + ^t^^-'-ik-A aa = || ME fa) Б (^)lu=i,...,ft,o-
Тогда распределение вектора (?(?4), * •., ?(^o)) имеет плотность
t, ...,Жо)~ У[А1 ехр\-4г
а условное распределение t,(t0) относрттсльно |(?i), ..., ?(?&) име-
имеет плотность, равную отношению
/(*i *о)
>
/(*1? ...,*0)rfx0
Экспоненциальная часть этого отношения имеет вид
( 2 k
{ г ?~i
Это означает, что рассматриваемое условное распределение есть
Ф 2, где а = — у , а-== 1М00. Таким образом, в рассмат-
***** аоо
рииаемом случае наилучший прогноз rQ равен
Средиеквадратнческая ошибка этого прогноза равна У1/а00.
Мы получили линейный прогноз. В общем случае это свойство
линейности обычно нарушается.
Рассмотрим теперь задачу о наилучшем линейном прогнозе
в случае произвольного процесса §(?) с конечными моментами
второго порядка. Для простоты будем считать опять, что В =*
-{?ь ..., tk).
Обозначим //(§) подпространство L2, порожденное случайны-
случайными величинами §(?), — °° < ^ < °°, и через Й"в(|) —- подпростраи-

392
ГЛ. 19. ГАУССОВСКИЕ ПРОЦЕССЫ
ство #(|)', порожденное (натянутое на) ?(?j, ,.., ?(/J. Элементы
к
Нв{Ъ) имеют вид 2 яД(?/)«
Существование и вид наилучшего линейного прогноза в этом
случае устанавливаются следующим утверждением.
Теорема 5. Существует единственная точка ?^#в(|) {про-
екция ^{t+u) на #в(|), /же. 19) такая?
ЧТо
иг + и)-ъ±пвA)< E)
Зго условие эквивалентно тому, что
(G)
Явные формулы для коэффициентов
Рис.19 а$ в представлении ? — 2а,Д (О с°-~
дероюатся в доказательстве.
Доказательство. Соотношение E) эквивалентно урав-
уравнениям
h
Подставляя сюда С = 2
получим
7
G)
или, в векторной форме, Rt+u = aR, где а^{аи ,.., аЛ), Л(+„ =
= (/?U+B, ^), ..., Д(* + а, ^)), R~WR{U, ВН-
ВНЕСЛИ процесс ^@ непредсказуем, то матрица i? иевырождеиа
и уравнение G) однозначно разрешимо:
а = Д|+вД. (8)
Если ^(/) не является непредсказуемым, то либо /?~* все же
существует, и тогда справедливо (8), либо R вырождена. В этом
случае из совокупности ?(/t), ...t l(^) надо выделить лишь l<. k
линейно независимых элементов, для которых все сказанное вы-
выше останется справедливым с заменой к на L
Эквивалентность E) и F) вытекает из следующих соображе-
соображений. Пусть 0 — любой другой элемент Л3(^)9 Тогда i=6-^s
е#*Ш, 4-Ll(*+^)-^ так что
\\l(t + и)- 611 - lig(* + и)-~ ?11 + п^н > Щг + u)— SiL ^
Замечание. Может случиться (если процесс |(I) не явля-
является непредсказуемым), что ?(? +и)^#в(?)# Тогда погрешность
прогноза ? будет равна нулю.

ПРИЛОЖЕНИЕ 1
ТЕОРЕМА О ПРОДОЛЖЕНИИ ВЕРОЯТНОСТНОЙ МЕРЫ
Пусть $Ф есть некоторая алгебра множеств из Q, на которой
задана вероятностная мера Р, т. е. числовая функция, удовлет-
удовлетворяющая условиям Р1 — РЗ гл. 2. Пусть ?Р означает класс всех
подмножеств Q. Для любого A s g> всегда существует последова-
последовательность {Anjn^i непересекающихся множеств из ?& такая, что
ОО
(J Auzd А (достаточно взять Al — Qi An = 0; п>2). Обозначим
Ч {Л) класс всех таких последовательностей и введем на
IP числовую функцию
Р* {А) = inf { S Р (Дг); {Лп} e'Y {A)\.
U=i J
Эта функция (внешняя мера на ^, индуцированная мерой Р па
ч5#) обладает свойствами:
1) Р*(Л)<Р*(Я)<1, если 4сВ,
2) Р* U 4п\ = У^Р(Ап)г если множества Ап^бФ, п = I,
\п=1 / н=1
2, ..., и не пересекаются.
/ 00 \
3) Р* U АЛ< 2 Р*{Ап). для любых Ль А2, „.&&.
\ П=1 / 71 = 1
Свойство 1) очевидно. Свойство 2) вытекает из следующих
рассуждений. Пусть WJ—любая последовательность из ^D), где
А = О Л- Так как U Л^т = 4^^, то Р (Ап)= У] Р(АпВт).
п=1 тп=1 . m=l
Следовательно,
сх) оо оо
2 р {Ап) = 2 2 р (Апвт) = 2 2 р (Ля«).
П=1 ?i W 7П=1 П~1
Но при каждом Л" < <х>
SPDA)<PEm).
71=1
Значит, это неравенство верно и при N = °°, и для люоои
п=1

394 ПРИЛОЖЕНИЕ 1. ПРОДОЛЖЕНИЕ ВЕРОЯТНОСТНОЙ МЕРЫ
сю
Отсюда следует, что Р*(Л)> 2 Р(Л»)- Так как обратное не-
оо
равенство очевидно,'то Р* (Л) = 2 Р(ЛП). А
Для доказательства свойства 3) рассмотрим при некотором
? > 0 последовательности {Лп/^}/Г==1 ее у(Ап) такие, что
Последовательность множеств {Лп/<}^/4==1, очевидно, содержит
ИЛ и, и, значит,
р* (и А.Х 2 2 р (А*) < 2 р* (л„) + е.
it h n=l
В силу произвольности 8 свойство 3) доказано. М
Введем теперь операцию симметрической разности ® над про-
произвольными множествами А, В из Ф с помощью равенства
л е в = А в и лв.
Нетрудно заметить, что
Л Ф 0 = Л, - (Л Ф S) Ф С = 4 Ф (J5 © С).
С помощью этой операции и "функции Р* введем на 9* расстоя-
расстояние р,.положив для любых /1, В^ёР
р(Л, 5) = P*(i0^).
Эта конструкция вполне аналогична топ, которая использова-
использовалась в § 3.4 (мы рассматривали там расстояние d(A4 В) =
=РD® В) между измеримыми А и В). Свойства расстояния р
те же, что и в C.10). Нам понадобятся следующие из них:
1) рD, Я) = Р(Д Л)^0, Р(А, Л) = 0,
2) р(А?) = р(ДВ),
3) р(Л5, С/?)<рМ, С)+р(В, D),
4) p(UA, UB*)<SpD, Bh).
I:
Можно отметить также, что
5) |Р*(Л)-Р*(Я)|<р(Л, В),
и, следовательно, Р*(*) есть функция, равномерно непрерывная
относительно р.
Свойства 1)—3) имеют место в C.10) pi доказываются совер-
совершенно аналогично на основании свойств меры Р** Свойство 4)

ПРИЛОЖЕНИЕ 1. ПРОДОЛЖЕНИЕ ВЕРОЯТНОСТНОЙ МЕРЫ 395
.вытекает из свойства 3) меры Р* и соотношения (Л = 1!ЛП,
В = \}В„)
А®.Вс=.[)(Ап®Вп),
поскольку
А®В = [{\)Ап)П((\Вп)]\)\(ПЖп)Г\(\)Вп)]<=
с [[)АпВп] U [VBnAn] = U {АпВп U АпВп) = U (Лп ® Д„).
Свойство 5) вытекает из того, что
AczB[)(A® В), BaA\J(A®B) A)
ж, значит,
р*(Л) — р*(В)<р*(ле^) = ри, ?),,
р* (Л) _ р* (Л) < Р* (А фВ) = р,(Л, Б).
Аналогично принятому в § 3.4 назовем множество А<^?Р ап-
роксимируемъш, если для него существует последовательность
An<^s&, для которой р(Л, Лп)->0. Совокупность всех апроксими-
руемых множеств обозначим St. Это есть, очевидно, замыкание s4>
относительно р.
Лемма. Я есть а-алгебра.
Доказательство. Проверим, что Я удовлетворяет свой-
свойствам а-алгебры Л1, Л2', ЛЗ гл. 2. Свойство Л^: 1]е| очевидно
выполняется, так как ^с:^. Свойство ЛЗ: А ^91, если Л^§?,
следует из того, что для А^% существуют Ап<^?Ф такие, что
При П -»¦ оо
р(Л, Л„)-*0, р(Л, Лп)-
Рассмотрим, наконец, свойство Л2'. Покажем сначала, что
1
Действительно, не ограничивая общности, можно считать, что
Ап не пересекаются. Тогда в силу свойств меры Р* для любого
8 > 0 имеем
р(л, U4*) = P*( и
при достаточно большом /г.
оо
Пусть теперь Л;г^^. Требуется показать, что Л= |J Лпе21»
71=1
Пусть ШЛ — последовательность множеств из sfi таких, что
р(Ап, Вп)<г/2п. Тогда В= USne§t и в силу свойства 4) расстоя-
расстояния р
Лемма доказана.

396 ПРИЛОЖЕНИЕ 1. ПРОДОЛЖЕНИЕ ВЕРОЯТНОСТНОЙ МЕРЫ
Теперь можно доказать основное утверждение.
Теорема 1*). Вероятность Р может быть продолжена с ал-
алгебры s4> на о-алгебру % до некоторой вероятности Р".
Доказательство, Положим для А е=Я
Р(Л) = Р*(Л).
Очевидно, что_ Р (Л) = Р (А) при Л ё= si>, Р (Q) = 1. Чтобы убе-
убедиться, что Р есть вероятность, надо доказать лишь счетную ад-
аддитивность Р. Докажем сначала конечную аддитивность. Ее до-
достаточно доказать для двух множеств:
Р* (А + В) = Р* (А) + Р* (Я), B)
ще Л, ВеЯ, ЛП5==0. Пусть An<^s4, Bn^s& таковы, что
р(Л, Л„)->0, р(В, Вп)-+0 при ^г-^оо. Тогда
| р* (Л + В) - Р* (Ап + ^)|
Р* (Лп + В„) = Р (Ап + Вп) = Р (Л?1) + Р (Вя) - Р DnSn)., C)
Здесь
Р(ЛЛ)->Р*(Л), Р(Вп)-+Р*(В),
Р (АпВп) < Р* (АпВ) + Р^ (ВпВ) <
5 , Ап) + р (В, Вп) -> 0.
Значит, из C) следует B).
Докажем теперь счетную аддитивность. Пусть Ап^$1 не пере-
оо
секаются. Тогда, полагая Л = (J Лп, из конечной аддитивности
_ п=1
Р получим
U
й=?г+1
Следовательно,
*) Теорема о продолжении меры на минимальную а-алгебрзг, содержа-
содержащую М-, была получена Каратеодори. Метризация нормированных алгебр
Буля М- с помощью расстояния р (Ач В) = Р (А ф В) использовалась мно-
многими авторами (см., например, доклад А. Н. Колмогорова на б съезде поль-
польских математиков в 1948 г.; П. Халмош [191).
Использовать для продолжения меры свойства ее непрерывности отно-
относительно расстояния р (/1, В) = Р* (А ® В) предложил Л. Я. Савельев,

ПРИЛОЖЕНИЕ 1. ПРОДОЛЖЕНИЕ ВЕРОЯТНОСТНОЙ МЕРЫ 397
С другой стороны,
р (А) = Р* (А) < S Р* (А) = 2 Р (Л). <
Теорема 2. Продолжение вероятности Р с алгебры S& па
в-алгебру 51 единственно.
Доказательство. Предположим, что на St существует еще
одна вероятность PL, совпадающая с Р иа rf и такая, что для
некоторого A e?t
Допустим сначала, что е = Pt (Л) — Р (Л) ;> 0. Рассмотрим после-
последовательность {Вп) <=^ч(А) такую, что
2 Р(Вп)-Р(А)<г/2.
п=1
Тогда Рх (А) == Р (А) + 8 > 2 Р (#п) + е/2, что противоречит
г
п==г
оо
принадлежности ^4 cz U /in. Значит,
1
п=1
Так как Р р-пепрерывна в точке 0, то отсюда следует, что и Рг
р-непрерывна в точке 0, а вместе с этим и в любой «точке»
А&У&. Действительно, в силу A)
если только р(Л,5) = Р(Л0 В)-+-0. Поэтому для
Р(Л)= lim Р(В)= lim Рх (В) - РХ(Л).
Пусть St* = a(^) есть о-алгебра, порозкдештая $Ф. Так как
Ts4> c= 9t, то 8t* cz $1 и из полученных утверждений очевидным
образом вытекает
Следствие. Вероятность Р может быть единственным об-
образом продолоюена с алгебры S& на ^минимальную о-алгебру 8(*,
порожденную S4-*
Замечание, a-алгебра St, определенная выше как замыкание
алгебры s4- относительно введенного расстояния р, оказывается во
многих случаях шире о-алгебры $1* = a(*s$), порожденной «5$. Это
обстоятельство тесно связано с понятием пополнения меры. Речь
идет вот о_чем. Пусть s&—% с самого начала есть о-алгебра. Тог-
Тогда меру Р в теореме 1 можно построить весьма просто. Для этого

398 ПРИЛОЖЕНИЕ 2. ТЕОРЕМА КОЛМОГОРОВА
мы продолжим меру Р с <Q, %У на более широкую, чем S а-ал-
гебру, построенную следующим образом. Мы будем говорить, что
множество N из Q принадлежит классу J?, если для N найдется
такое A =A(N)^$, что NczA, P(A) = Q. Нетрудно видеть, что
класс множеств вида В + 7V, где В е $, TV <= «/Г, снова образует
о-алгебру. Обозначим ее Syf. Положив Р (В + JV) = Р(#), мы
получим продолжение меры Р на <Q, S^f >. Такая мера* назы-
называется полной, а проведенная операция — пополнением меры Р,
__ Теперь можно установить, что построенная в теореме 1 мера
Р является полной, а с-алгебра Ш совпадает с %jf.
Если, например, Q = [0, 1], a sf- есть алгебра, порожденная
интервалами, то St*= o(s&) будет, как мы уже знаем, борелевской
о-алгеброй, a SI будет лебеговским расширением $1*, состоящим из
множеств, «измеримых по Лебегу».
ПРИЛОЖЕНИЕ 2
ТЕОРЕМА КОЛМОГОРОВА О СОГЛАСОВАННЫХ РАСПРЕДЕЛЕНИЯХ
Пусть Т — некоторое множество индексов t, Rt при каждом
j есть вещественная,прямая (—°°, °°). Пусть N?= Т—некото-
Т—некоторое конечное подмножество Т. Тогда произведение пространств
JJ есть евклидово пространство размерности, равной
рое конечн
JJ Rt = R
числу п элементов в N, построенное на п осях пространства
RT - П Л*.
Предположим, что для любого конечного подмножества N с: Т
на (RN, 83^), где S3iV — о-алгебра борелевских множеств в RN, за-
задана вероятностная мера Pjv. Тем самым па R1 задано семейство
мер. Это семейство называется согласованным, если для любых
Lcz N и борелевских множеств В из RL
Мера Pl называется проекцией Pjv на 7?L. Множество из RT,
которое можно представить в виде В X RT~N, где В е ^N? a IV —
конечное множество, называется цилиндрическим в /?г. Множе-
Множество В называется основанием цилиндра.
Обозначим W а-алгебру множеств из RT, порожденную цилинд-
цилиндрическими множествами.
Теорема. Если на RT задано согласованное семейство веро-
вероятностных мер, то на- (RT, W) существует единственная вероят-
вероятностная мера Р такая, что при любом N Pn совпадает с проек-
проекцией Р на R k

ПРИЛОЖЕНИЕ 2. ТЕОРЕМА КОЛМОГОРОВА 899
Доказательство. Цилиндрические множества в RT обра-
образуют алгебру. Покажем, что при В ^ $8N соотношения
определяют меру на этой алгебре. Прежде всего, в силу согласо-
согласованности мер Рдт это определение вероятности цилиндрических
множеств корректно (имеются в виду случаи, когда В == 5jX RN~Lf
$.<=ЭЬ. Тогда левая часть будет равна также P(B1xRT~" ))
Далее, введенная вероятность аддитивна. Действительно, пусть
В-, X RT~N и В2 X RT~N2 — два непересекающихся цилиндрических
множества. Тогда, обозначив N = Nt[} N2i будем иметь
= р([в, х /?'v-'Ylu52 х RN~Ni] х RT~N) =
- Р,(Вг X Л*- U B2 X RN-Nt) - РАВг X Д*") +
+ PN (Bt X Л"") = Р (В, X RT~Nl) + P(B2X RT~Ni).
Чтобы проверить счетную аддитивность Р, воспользуемся эквива-
эквивалентностью свойств РЗ и РЗ' (см. гл. 2). В силу этой эквивалент-
эквивалентности достаточно показать, что если 3%п, п = 1, 2, ...— убывающая
последовательность цилиндрических множеств, то соотношения
Р(^п)>?7 /г- = 1, 2, ..., при некотором s>0 означают, что
$ = П «^п непусто. Вложенность множеств «^ означает, что в
п=1
представлениях <%71^=BnxR n выполняется Nn aNn+u Вп^г[\
[\R "czfifl^He ограничивая общности, мы будем считать в даль
нейшем, что число элементов множества Nn = {tu ..., tj равно га,
и через ^i (с различными верхними индексами) будем обозначать
координаты пространства Rt^
Итак, пусть Р (&п) == Pjvn (^n) > е > 0. Докажем, что <В =
= П ^/i непусто. Для каждого борелевского множества Bncz R
существует компакт Кп такой, что
КпаВп, PNjBn-K,l)<e/2n+1.
у jy
Если обозначить Жл = К ,, X R ™, то мы получим
„ - Жп) = P,vn (^. - Л:п) < e/2n+I.
Введем в рассмотрение множества 2)п = П Жъ,» Легко видеть, что
й)„с:?~тоже цилиндры. Так как ^-П^с П {&k—Wh)i
h=l h=l

400 ПРИЛОЖЕНИЕ 3, ИНТЕГРИРОВАНИЕ '
ТО ДЛЯ НИХ
Р (Яп - Фа) < Р I U (ЗВи - Жк)\ < 2 Р № - Ж^) <4'>
Из последнего соотношения следует, что 20п есть убывающая
последовательность непустых цилиндрических множеств. Обо-
Обозначим Хп =(#!, ^з\ *••> #н) некоторую точку основания Дг =
*= П ¦&& X Я n"~Aft цилиндра iZ)n, определяющую цилиндрическое
k—i
множество SSn в i?T. Так как ^),г убывают, то (ж?+р, ^+Р ,
,..., ^г"г>)^ Zn при любом /? > 0. В силу компактности Zn мож-
но выбрать последовательность n[h такую, что х1 —^¦х1 при
к -*• оо. Из этой последовательности можно выбрать последователь-
последовательность /г2ft такую, что х22И ->~х2 и т. д.
Рассмотрим теперь диагональную последовательность точек
(точнее, цилиндрических- множеств) X ldt =
Ясно, что при к-* со X kh-*X = (хг, х2г > %.) (имеется в виду по-^
координатная сходимость). При этом
при любом т. Это означает, что соответствующее точке X множе-
множество 3s={y(t)e=BT:y{ti) = xt, у(и) = хъ ...}е=Кте=д$т при лю-
со
бом т и, значит, <^ ge Г) ^т. Таким образом, ^ не пусто и счет-
пая аддитивность Р на алгебре цилиндрических множеств дока-
доказана. Следовательно, Р есть мера, и остается воспользоваться
теоремой о продолжении меры с алгебры на о-алгебру, порожден-
порожденную этой алгеброй. Щ
ПРИЛОЖЕНИЕ 3
ИНТЕГРИРОВАНИЕ
§ 1. Пространство с мерой
Пусть <Q, g>—измеримое пространство. Мы будем говорить,
что задало пространство с мерой <Q, Ъ, ji>, если па § задана не-
неотрицательная счетно-аддитивная функция ji, т. е. функция, обла-
обладающая следующими свойствами:
1) it ( у Aj\ = ^\i(Aj) для любого счетного набора иепересе-
кающихся множеств А}^Ъ (а-аддитивность).
2) IX(А) > 0 для каждого А <= S.

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 401
3) ji@) = O, где 0 — пустое множество.
Значение \i(A) называется мерой . множества А. Мы будем
рассматривать только конечные и о-конечные меры. В первом
случае предполагается, что ji (?>)<<*>. Во втором —что существует
разбиение Q на счетное число подмножеств А} таких, что
Вероятностное пространство является примером пространства
с конечной (единичной) мерой. Пространство <Д, S3, jx>, где R —
вещественная прямая, S3 — о-алгебра борелевских множеств, a \х —•
мера Лебега, представляет собой пример пространства с а-конеч-
пой мерой.
Можно рассматривать также функции множеств \х(А), удов-
удовлетворяющие лишь условиям 1), 3) и не обязательно неотрица-
неотрицательные. Такие функции называются обобщенными мерами. Лю-
Любая конечная обобщенная мера (т. е. такая, что supjxD)<oo,;
А
int\i(A)>— оо) может быть представлена в виде разности двух
А
конечных неотрицательных мер (теорема Хана о разложении,
см. § 5 этого Приложения). Обобщенные меры нам понадобятся
лишь в § 5. В остальных местах и при отсутствии специальных
оговорок мы везде под мерами будем понимать функции множеств,
удовлетворяющие условиям 1)—3).
Так же, как при изучении простейших свойств вероятности
(§ 2.2), легко устанавливаются следующие свойства меры:
1) ii(A)^ii(B), если AczB.
2) \i ( U А}) < 2 М- (Аз) Для любых А3.
3) Если An^An+l1 иЛ„ = Л, то ii(An)~+ \i(A), или, что то же
самое,
3') если An^>An+i, ПЛ„ = 4, jiD1)<oo? To \i(An)-+- \i(A).
Рассмотрим далее па <Q, §> измеримые функции, т. е. функ-
функции |(со), обладающие свойством {or. ^((о)^В}е§ для любого бо~
релевского множества В на прямой.
Аналогично тому, как это делалось для вероятностной меры,
вводятся понятия сходимости по мере и сходимости почти всюду.
Будем говорить, что последовательность |п сходится к | почти
всюду (п. в.)?п-^-*-?, если ^л (со) -^ g (со) для всех со, за исклю-
исключением множества меры 0.
Будем говорить, что §п сходится к | по мере: ?п->?_»если для
каждого е > 0 при п
Займемся теперь построением и изучением свойств интегралов.
Рассмотрим сначала конечные меры и будем считать их, не огра-
ограничивая общности, вероятностными. В этом случае мы будем вме-
вместо \i(A) писать. Р(А).
К интегралам по произвольным а-конечным мерам вернемся
в § 4 этого раздела.
26 а. А. Боровков

402 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
§ 2. Интеграл по вероятностной мере
i. Интегралы от простых функций. Измеримая функция К о У
называется простой, если множество ее значений конечно. Инди-
Индикатором множества F ^ Ъ называется простая функция
если (ogF,
если оз ф. F.
- Очевидно, что любую простую функцию %(со) можно записать,
в виде
п
где #А, & = 1, 2, ..., /г,— значения, принимаемые |, а /^ =¦
= (со: ^(co) = ^ft}. Множества iy\ попарно не пересекаются л
U Ffc = ?2. Интегралом от простой случайной величины %(со)
называется число
f UP = U (сэ) dP (со) = 2
Интегралом по множеству ieg от простой измеримой функ-
функции ?(со) называется
f ? dP = J ? (со)/А (<о) dP (со).
k
Корректность этих определений (разбиения на множества"/^ мо-
могут быть различны) проверяется очевидным образом.
2. Определение интегралов от произвольных функций.
Лемма 1. Пусть g (со) ^ 0. Существует последовательность
1>((о) измеримых простых функций такая, что gn(co) t ?(со) при*
П ~> сю.
Доказательство. Разобьем отрезок [0, п] на п2п равных
отрезков. Пусть х0 = 0, хи .. м?п2п = Агозпачают точки деления, так
что xi+i — xt = l/2n. Положим F{ == {со: л:< < |(сэ)< ^+1}, г = 1, 2, ..,.
712П-1
г
^ S(o)). §n(co) есть, очевидно, измеримая простая функция, обла-
обладающая тем свойством, что в точке со ^ Й при тг>|(со) выполня-
выполняется неравенство
Лемма 2. Пусть |n 11 ^ 0, т]п t ^^0 — последовательности^
простых случайных величин. Тогда
. lim j ?HdP = lim j v\ndP0

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
Доказательство. Убедимся, что для любого т
Функция \т простая. Следовательно, она с вероятностью 1 огра-
ограничена некоторой постоянной: \т ^ ст. Поэтому при любых пч
8>0
1т — Цп ^ Cm • 1{гт>г\п+ъ) + 8*
Отсюда следует, что
М1т < спР Цт > Цп + е} + е + Мт1я»
Вероятность в правой части при п-+ °® мала:
так как т]п почти наверное (и, следовательно, по вероятностиI
сходится к ?. Поэтому Щте^в + Них К1г)п. Так как 8 произвольно,
ТО
Меняя местами {§п} и {лп}, получим обратное неравенство. <3
Утверждения лемм 1, 2 делают корректными следующие оп-«
ределеиия.
Интегралом неотрицательной функции ^(со) называется число
ndPt A)
где gn — последовательность простых измеримых функций таких,
ЧТО gn t ? При ГС -*- сю.
Интеграл J ЫР будем обозначать также через Щ. Мы будем
J
говорить, что интеграл J ?dP существует, а § интегрируема, если
,IVI^< оо.
Интегралом от произвольной (принимающей значения разных
знаков) функции §(со) называется число
-если хотя бы одно из значений Щ~ конечно. В противном случае
М^ не определено. М^ существует тогда и только тогда, когда
существует М | \ \ < оо (ведь !5l=|+ + g~). Если существует М^,
то существует также М (§; Л) = j idP = Мс,1А для любого А^Ъ\
А
Лемма 3. Если М? существует и Fneg ^сгь последователь*
ность мнооюеств такая, что Р (Fn) ~>0 гсрц и- ->• «^ го

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
Доказательство. Для любой последовательности |?j t
простых функций справедливо (Ат — Щ1 ^ т})
нескольку \lm\lAm\ \l\- Отсюда следует, что
|E|/xm = Ню М (\l |; UK #п)
и, значит, для любого е>0 существует т(г) такое, что
M|||-M(|||;|||<m)<e
при т~^т{ъ). Поэтому для таких т
М(Ш; ^«)-M(|6|; {ISI<w>n) + M(|6l; {|?l>»
(Fn) + e,
3. Свойства интегралов.
II. Если множества А^% не пересекаются и U
j ^
Достаточно доказать это соотношение для |(ш)^0. Для про-*
стых функций равенство B) очевидно, так как
; А
В общем случае, используя определение A), получим
J |dP = lim f |ndP = lira S J |ndP =
3
= 2 Hm j UP= 2j №* C)
Изменение порядка предельного перехода и суммирования здесь
законно, так как в силу леммы 3
v Г ( °° \ ( °°
при N -> °° равномерно по п.
12.

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 403
Для простых функций это свойство очевидно. Поэтому для
\ ^ 0, ц ^ 0 это свойство следует из аддитивности операции пре-
предельного перехода.
В общем случае находим (?* и rj* определяются как и раньше)
J (I + 4)dP = J (S+ + t|+)dP - J (Г + 4~)dP -
¦ - jl+dP - j ГйР + j 4+dP - J rf dP = J УР + J
I 3. ?с./ш а — произвольная постоянная, то
14. Ясли | < rj, то j ?dP < j TjdP.
Доказательство свойств I 3, I 4 очевидно. Так как J ?dP =M?r
то свойства II —14 можно записать с помощью математических
ожиданий следующим образом:
II. Щ = 2М (I; -4?)» ^^^^ Аз не пересекаются^ U ^4j = Q.
14. Щ^Мл, если | ^ т|.
Отметим также следующие свойства интегралов, легко вытека-
вытекающие из свойств 11 —14.
15. | М|| ^ М111.
I 6. Если с] <? < с2, то сЛ <! Щ ^ с2.
1 7. AV^m ^0 и IV1? == 0, то Р (? == 0) = 1.
Это следует из неравенства Чебышева: Ргё^е)^ —==0 при
любом е > 0.
I 8. Если Р (| == т]) = 1 и М? существует, то М? = Мп»
Действительно,
Мц = lim М (т|; | т) | ^ /г) = lim М (|; | ^ | <С ?г) = М^.
§ 3. Дальнейшие свойства интегралов
1. Теоремы сходимости. Ряд теорем сходимости был доказан
в § 6.1 и, в частности, теорема о сходимости мажорируемой по-
последовательности :
Если 1п—>1, \1п\^Ц% Мт]<оо, то существует Щ и М^п~>
Приведем некоторые другие полезные утвер;кдспия о сходимо-*
сти интегралов.
Теорема 1. Если 0 < In t g, то Ml = lim M?,n.

406 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
Доказательство. В дополнение к следствию 6.4 нам надо
здесь доказать лишь, что 1Щп-н>~ оо, если Щ = оо. Положим ?п =
= min(gn, N), lN = min(l,N). Тогда, очевидно, In f lN при га-^оо,
М^п'^М^ч Следовательно, значение М^^М^м выбором/г и iV
может быть сделано сколь угодно большим. ^
Эти теоремы можно обобщить следующим образом. Для того,
чтобы в § 4 было удобно получить распространение теорем сходи-
сходимости на интегралы по произвольной мере, мы Щ будем писать
теперь в форме интеграла ) |dP.
Теорема 2 (Фату — Лебега), Пусть ц и Е; интегрируемы.
Тогда если ^а < t], ^0
lim sup J indP ^ J lim sup ??idP» D)
lim iaf j \ndP > J lim inf \ndPt E)
gu f I, ln > g или ln —> I, ? < ^n < tj, mo
lim JgndP- J^P« F)
Доказательство. Докажем, например, E), положив, на
ограничивая общности, ?= 0. В этом случае
In > Л7г = inf |ft f lim inf %n% цн > 0,;
ii по теореме о монотонной сходимости
lim inf j lndP ^ lim j rindP == j lim inf tndP*
Если E) применить к последовательности rj — |,г, то получим D);
F) следует из предыдущих теорем. ^
2. Связь с интегрированием по мере на прямой. Пусть g(x) —
некоторая борелевская функция, заданная па прямой R (если
S3 — а-алгебра борелевских множеств на прямой и Be Э, то
ix: g(x)eS}G8), Тогда г| = ^(^(со)), очевидно, также будет слу-
случайной величиной. Как мы видели в § 3.2, случайная величина g
индуцирует вероятностное пространство (Д, 33, Р^) с хмерой Р^
на прямой такое, что Р^ (В) = Р (^ е 5)* Следовательно, можно
говорить об интегралах но этой мере. Справедлива
Теорема 3. Если Мц существует, то
Mil = J r]dP = \g{x)Pl{dx)
п К
(в правой части использована несколько иная запись \g(%)dPt(x)L

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 407
Док а з ате л ьство. Пусть сначала g(x) = IB(x) есть инди-
индикатор множества В е 8; Тогда ц = g(?(<o) ) = /а«=в)(<о) и Мц =
= PgeB). Поэтому
б (а) РБ (dx) = Р6 E) = Р (? «= Б) = Мл.
Используя свойства интеграла, легко установить, что утвержде-
утверждение теоремы верно для простых функций g. Применение предель-
предельного перехода распространяет это утверждение на ограниченные
функции. Пусть теперь g > 0. Если функция g(?) 1в (§) =
= 1](со)/{^??) (со) ограничена, то получаем J g (х) dPi(x)= M {ц;
в
^ е 5). Поэтому
J = М (Л; ч < /г).
Переходя к пределу по /г, получим утверждение теоремы. Рас-
Рассмотрение случая, когда g принимает значения обоих знаков, за-
затруднений не вызывает. Щ
Если обозначить
то наряду с интегралом
^g(x)Pl(dx), G)
R
который только что рассматривался, можно рассмотреть также
интеграл Рима па — Стилтьеса
(x)dF(x)t (8)
определение которого дано в § 3.6. Там же было показано, что
для непрерывных функций g(x) эти интегралы совпадают. Кроме
того, в § 3.6 были обсуждены некоторые другие условия совпаде-
совпадения этих интегралов.
х
Напомним также, что если F (х) = J f(t) dt, а функции g(x) и
— оо
f(x) интегрируемы по Римапу, то интегралы G) и (8) совпадают
с интегралом Рпмапа
J g (x) f (x) dx.
3. Произведения мер и повторные интегралы. Рассмотрим дву-
двумерную случайную величину ^^(^ л)? заданную па (fi, S, Р).
Случайные величины % и ц индуцируют выборочное вероятност-
вероятностное пространство (Д2, S32, Р^И1) с мерой Р5|Т1, заданной на эле-
элементах 0-алгебры Э2 борелевских множеств па плоскости (мини-

408 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
мальпая а-алгсбра, порожденная прямоугольниками) п такой, что
Здесь А X В есть множество точек на плоскости («г, у), для ко-
которых х^А,у<^В. Если g(x, у) есть борелевская функция
({(#* y)'S(xi y)^ В} ^W для каждого Ве8), то из предыдущего
легко следует, что
так как оба интеграла равны J 0Pq(cIx) для 0 = g(§, rj).
Пусть теперь | и ц независимы, т. е.
Р {I e A, iigB) = P(^g4)P(iig5)
для любых А, В €= S3.
Теорема Ф у б и и и (теорема о повторных интегралах). Если
g(x, y)> 0 — борелевская функция, g и rj независимы, то
//лл произвольных борелевских функций g(x, у) приведенное ра-
равенство справедливо, если существует Mg(?, i]).
Это же утверждение в гл. 3 мы записывали с помощью инте-
интегралов
, у) Р^ц (dx, dy) == J [ J g (x, у) Рл (dy) ] P5 (^). A0)
Нам будет полезна следующая
Лемма 4. 1. Сечение Вх любого множества В ^ Ъг
Вх^{у: (х, у)^В)
измеримо: Вх е S3.
2. Сечение gx(y)~g(z, у) любой борелевспой функции g (Ъг-из-^
меримой) есть борелевская функция.
3. Интеграл
l ^ (И)
от борелевской функции g есть борелевская функция от х.
Доказательство. 1. Пусть Ж^ — класс всех множеств
из ё2, у которых сечения измеримы. Очевидно, что Ж^ содержит
прямоугольники 5 = 5A>Х5BI где 2?A)^ЗЭ, ВB)е§3. Кроме того,
Жi — а-алгебра. Действительно, рассмотрим, например, множе-
множество B*=\JB{h\ где В{к)^Жи Очевидно, что операция U над мно-
множествами В{к) приводит к тем же операциям над сечениями, так
что Вх = и В(х* е S, Аналогично обстоит дело с другими оде-

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 409
рациями (П и взятие дополнений). Таким образом, Ж{— о-алгеб-
ра, содержащая прямоугольники. Это значит, что S3" с: Ж^
2. Для Б е S3 имеем
g7l(B) = {y: gx(i/)efi} = {y: g(x, у) е Я} ~
= !«/: (*, I/) е ^ (В)} « fe (#)]* е= 9.
3. Интеграл A1) есть результат предельного перехода над
измеримыми функциями и поэтому сам изморим. ^
Доказательство теоремы Ф у б н и и. Докажем сна-
сначала A0) в случае g(x, y)^lB{x, г/), когда теорема Фубшш пре-
превращается в формулу о последовательном вычислении меры мно-
множества fleS2:
Р((?, л) е 5) = J Рп ((х, у) е= 5) РБ (dx) = J Pn EX) P6 (dx). A2)
Введем в рассмотрение функцию множеств
Очевидно, что Q(B)>0, Q@) = Q. Далее, если В = US(A), J5(fe) не
пересекаются, то #х = U В^\ В{хк не пересекаются,
<? (В) = J Рп ( U #*>) Р? (^) = 2 j Рп (^») РБ (rfx) = 2 Q E№>).
Это означает, что ()(#) —мера.
Мера ^(/?) совпадает с Ps(T](fi) = P((E, ii)g^) на прямо-
прямоугольниках В = В{1)ХВ{2). Действительно, для прямоугольников
Х~^ 10 при
Это означает, что меры Q и Р^л совпадают на алгебре, по-
порожденной прямоугольниками. По теореме о продолжении меры
получаем, что Q ==¦¦ P=,ti-
Справедливость A2) доказана. Отсюда следует справедлив
еость теоремы Фубшш для простых функций gx = 2 с$ та1^
Аа%
1
как
J WAj (xt ti)-Ps (fo) = j Mg>. (ж, 11) Рг (dx). A3)

410 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
Если теперь g ^ 0 — произвольная борелевекая функция, то
существует последовательность простых функций gN f g, и нам,
как и в A3), остается воспользоваться операцией предельного
перехода
Mg Aг п) = lira MgN (Ъг я) = lim J MgN (хг ц) Ppo (dx) -
JV-»oo
Для произвольной функции g следует воспользоваться пред-
представлением g =f g+ — g~, g+ ^ Q, g~ ^ 0. A
Замечание. Из доказательства теоремы видно, что ска-
лярность случайных величин § и ц не играет существенной ро-
роли. Утверждение сохранится и в более общей форме (см. свой-
свойство 5А § 4.8) и, в частности, для векторных ? и rj.
§ 4. Интеграл по произвольной мере
Если [х—-конечная мера на <Q, ??>, [х(Й)<«>, то определение
интеграла J Ы\*> но мере \i ничем не отличается от соответству-
соответствующей конструкции интеграла по вероятностной мере (можно .
положить просто J ld[i = ji (Q) | idP, где Р (В) = fi(^)/|i (Q)
А А
есть распределение вероятностей). Если же jli а-конечиа и
|j,(Q) = o°, то дело обстоит несколько сложнее, хотя снова вес
сводится к уже использованным построениям. Сделаем сначала
несколько предварительных замечаний.
Пусть (Q, ЪУ Р> — вероятностное пространство и / = /((о)>
^0 — п. в. конечная неотрицательная измеримая функция (т. о.
случайная величина)» Рассмотрим функцию множества
A4)
Если / интегрируема (м>(Я)<°°)', то jj,D)—конечная о-адци-
тивная функция множества (см. свойство 1.1), удовлетворяющая
условиям 1—3 § 1 этого Приложения. Другими словами, [х ко-
конечная мера на Ш, g>. Если же / неинтегрируема, то м- ^-ко-
^-конечная мера, что сразу следует из возможности представления
fdP
г(интегралы под знаком суммы, равные J fI(k-i<f<k}dPx являют-
А
ся, очевидно? конечными мерами).

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 411
Таким образом, интегралы вида A4) для любых распределе-
распределения Р. и функции / ^ О представляют собой меру. Оказывается,
верно и обратное в известном смысле утверждение.
Лемма 5. Для любой меры \х на <й, Ю найдется распре-
распределение Р на этом пространстве и измеримая функция } ^ 0
такие, что справедливо представление A4).
Таким образом, любая мера представима в виде интеграла от
вероятностной меры (т. е, в виде М (/; А) при соответствующих
функции / и распределении Р).
Доказательство. Пусть \х — а-конечная мера на <Q, т5>
ею
и множества В3^%, 7 = 1, 2, ..., обладают свойствами U Bj = Qf
j = 0 при i Ф ;, \\ (В3) < оо# Положим
Очевидно, что Р (Q) = 1 и Р является мерой. Далее, если A cr Sft,
то |х (А) == 2ftfiX (Bk) P (А). Это означает, что мы должны поло-
положить /@))= 2ft|Ll(b>/j) при Cx)^Bk.
Тогда функция множества
будет совпадать с [i(A):
Здесь, помимо требуемого з^тверждения, мы получили также,
что в представлении A4) множество значений функции /, не
ограничивая общности, можно считать счетным.
Функция /, для которой возможно равенство A4), называет-
называется плотностью меры \х относительно Р (или производной Радо-
Радона — Пикодима меры \х по Р) и обозначается . ^Б« Очевидно,
что изменение функции / = -~s на множестве Р-меры нуль ос-
тавляет справедливым равенство A4),
Пусть теперь \х и Р— две заданные произвольные меры.
Весьма важным в теории вероятностей является вопрос, при ка-
каких условиях эти две меры \х и Р могут быть связаны соотно-
соотношением A4) и единственным ли образом (с точностью до зна-
значений на множестве нулевой Р-меры) определяется при этой

412 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
функция / (подчеркнем, что в предыдущих рассмотрениях мера
Р строилась специальным образом по мере jx или наоборот).
Ответы на эти вопросы содержатся в теореме Радона — Никоди-
ма, которая будет изложена в следующем параграфе.
Теперь же, пользуясь доказанным несложным утверждением
леммы 5, дадим определение интеграла по произвольной мере jx.
Пусть \х — 0-конеч:пая мера на <Й, §> и ? > 0 есть g-измери-
мая функция.
Интегралом \ Ыц- по множеству А е g? от функции | > О по
А
мере fi называется интеграл по распределению Pi
р, A6)
где Р—любая вероятностная мера, удовлетворяющая равенству
A4) (например, мера A5)).
Это определение корректно, поскольку оно не зависит от вы-
выбора Р. Действительно, для простых функций g (g(u>) = #fc при
Г у 7 ^С f rfu г ,п ^ Г d\\, 7Г| X1 / а г> \
1 Ь//и =__ Ў л» I {__ / /7}"' —¦— Т 'У» I //г"* . Ў -у, И М /' 1 I
A A AFfe
Если теперь | > 0 — произвольная функция, то по теореме
о монотонной сходимости ) Ы\ь равен
А
lira fg(n)^P =
П~*оо *J
А
где ?(n) t g есть последовательность простых функций, монотон-
монотонно сходящихся к ? (см. лемму 1). И в том, и в другом случае
полученный результат от выбора Р не зависит, Ц
Интеграл ] ^d\i от произвольной измеримой функции | опре-
А
А
деляется как
А А А
если оба выражения в правой части конечны (в этом случае го-
говорят, что интеграл ) Ы\*> существует). Здесь, как и прежде,
Г = тах@, S)>0, Геттах@, ~Ъ)>0, так что | = g+-g-.
Мы видим, таким образом, что по существу данное опреде-
определение интеграла по произвольной мере эквивалентно той конст-

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 413
рукции, которая использовалась в § 2 этого Приложения. Однако
определение в форме A6) избавляет от необходимости повторять
весь пройденный путь (причем в более сложных условиях) и
дозволяет сразу перенести на общий случай все свойства инте-
интегралов ] % dP. Перечислим основные из них, сохранив их ну-
.мерацию:
11. ]?ф=2 J ?Ф-1 если Аз не пересекаются, U4j = Q.
12. J (g + г|) ^ = j ^4u + J
13. \ ab,d\i=a \ ?ф,.
14. | ?d[i^ j^dy, если ?<;
15. j
16. ЕСЛИ Ci<*?(G))<C2 при СО^Л, ТО
17. Если 1>0 l
I 8. Если [л (g ?= г]) = 0, то j I d\x=* j r\ d\x.
Очевидно, что полностью сохраняются также и теоремы
СХОДИМОСТИ.
Теорема о сходимости мажорируемой после-
последовательности. Пусть |?|^т| и J ?]ф, существует, Тогда?
если In -+¦ I или ?п -* & л. ^., го
j ^n d\\-+- j g ф*
Теорема о монотонной сходимости. ?сд1г 0 < |Л f
j Sn ^И—>- J I d\i«
Теорема Фату—Лебега, Ее формулировка и доказа-
доказательство получаются из теоремы 2 заменой Р на \i.
В заключение отметим, что если Q = Д = (—<», °°), 8? *= S3 есть
<1-алгебра борелевских множеств, \х есть мера Лебега, а функ-
функция g(x) непрерывна, то интеграл j g(%)d\i(x) совпадает
ь
с интегралом Римана j g (x) dx. Это следует из соответствующих
а
замечаний в п. 2 § 3 этого Приложения,

414 . ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
§ 5. Теорема Лебега о разложении
и теорема Радона — Никодмма
Вернемся к вопросу, который был сформулирован в преды-
предыдущем параграфе. При каких условиях на меры \х и А,, заданные
на <О, 3>, мера р, может быть представлена в виде
Здесь мы уже не предполагаем, что мера X обязательно ве-
вероятностная.
Определения. Мера \х называется абсолютно непрерыв-
непрерывной относительно меры X (обозначается jx~<A), если для всяко-
всякого А такого, что Х(А)=0, выполняется \х(А)=0.
Любое множество Nllt называется носителем меры [х, если
(
Говорят, что мера \i сингулярна относительно X, если най-
найдется такой носитель iV* меры Я, для которого ix(Nx) = 0. Или,
что то же, если найдется носитель N» меры ji, для которого
)
Таким образом, последнее определение, в отличие от первого,
симметрично, и можно говорить о взаимной сингулярности мер
\х и X (такое соотношение часто обозначается \х -L X).
Теорема Радона — Никодим а. Для абсолютной непре-
непрерывности pi К% необходимо и достаточно, чтобы существовала
функция /, определенная с точностью до Х-эквивалентности (т. е.
с точностью до значений на множестве Я-меры нуль), такая, что
А
. Как уже отмечалось, функция / называется производной Ра-
Радона— Пикодима -г- меры \к по мере X (или плотностью \х от-
относительно X).
Так как достаточность в утверждении этой теоремы очевид-
очевидна, то получим теорему Радона — Никодима как следствие сле-
следующей теоремы Лебега о разложении меры:
Теорема Лебега. Пусть \х и Х — две о-конечиые меры на
<Q, §>. Существует единственное разложение меры \х на две
компоненты \ха и \хе такие, что
\la<X, JLtc -J- А,.
При этом найдется единственная с точностью до Х-эквивалентно-
*) Это равенство иногда принимается за определение абсолютной не-
непрерывности.

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ 415
era функция /, для которой
xa (A) = J
А
J
А
Очевидно, что если \х •< X, то jxc = О и из теоремы Лебега сле-
следует теорема Радона — Никодима.
Доказательство. Так как jx и X a-копечны, то существу-
существуют возрастающие последовательности вложенных множеств Qfi
и й2п такие, что
р (QS) < оо, Я (Q,1) < оо,; U ЭД = Й- U а*=Й.
п п
Положив Qn = QiJQrt, получим возрастающую до Q последова-
последовательность множеств, на которых
Если мы докажем теорему о разложении для сужепия мер
;|li и X на <Вп, gu>, где Bn = Qn+l — Qn, т5п образована миожества-
-ми ВпА, ieg, то тем самым мы докапаем ее и па всем Q. Доста-
Достаточно будет в качестве \ха и \хс взять суммы соответствующих
компонент по каждому из сужений. Это замечание означает, что
можно рассматривать лишь случай конечных мер.
Итак, пусть \х ш X — конечные меры.
а) Пусть Ф — класс функций / > 0, для которых
J
А
J/dA, < [х (А) при всех 4gS " A7)
А
'{класс Ф не пуст, так как / = 0 принадлежит Ф). Обозначим
а = sup jdX <1 \i (Q) < сю
/SOq
ж выберем последовательность /п такую, что
J fndX-^a.
Положим /п = тах(/1,,*.,/Г1). Тогда, очевидно, fn f /' = sup /rt
и по теореме о монотонной сходимости
m, (is)
Покажем теперь, что f еф, т. е. что для f выполнено A7).
Для этого в силу A8) достаточно заметить, что /пеФ. Пусть
Aki k = 1, .,., п,— непересекающиеся множества, па которых

416 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
/» = Д. Тогда U Ah = Qt
f Adk = 2 f ud% <
A *=1 AAh h=l
Таким образом, для «максимального» элемента /' из Ф также
выполнено A7),
6} Положим
|1в (А) = J /Ш, [lc = Ц — |Хв A9)
А
и докажем, что jnc сингулярна относительно X. Для этого нам
понадобится следующее утверждение о разложении произволь-
произвольной обобщенной меры (определение см. в § 1 этого Приложения).
Теорема Хана о разложении. Для любой обобщен-
обобщенной конечной меры 7 существуют непересекающиеся множества.
D+ e 8? и D~ e g такие, что для любого 4eg
Доказательство. Покажем сначала, что существует мно-
множество Z)^S, на котором t(A) достигает своей верхней границы»
Пусть Вп е g — такая последовательность, что Y (-Вп)->Г =
= sup 7 (^4). Положим B~\JBh и рассмотрим для данного гг раз-
А
биение В на 2П множеств Вп т, т = 1 ».., 2П, вида П Bki где^
/?ft = Bh или В — Bk, к ^п. При п< N каждое Z?rtpm представ-
представляет собой конечную сумму множеств BNi M, 1^A/<22V. Обозна-
Обозначим Dn сумму всех тех Вп т, на которых ^E«, т)^ 0. Тогда
7(O()
С другой стороны, при N > п каждое 2?л, м либо лежит в Z)n?.
либо не пересекается с ним. Поэтому
оо
Отсюда следует, что для множества D = lira U Dh выполня-
h
ется ч(Вп)<ч(О), Г^7(^)« Вспоминая определение Г, полу-
получаем ч(?>) = Г.
Таким образом, существование множества Д на котором т(^)
максимально, доказано. Покажем теперь, что для любого А е 5"
выполняется ^(^^)^0 и т(^4^)^0, где D = Q — Z). Действие
тельно, допустив, например, что 7(^4^)<0? мье придем к проти-
противоречию, так как тогда

ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ • 417
Аналогично, допустив у(АВ)>0, мы получили бы
Нам остается положить D+ = Z), D~~ = D. <4
Вернемся к доказательству того, что мера jic в равенстве
A3) сингулярна. Пусть D~X—множества в разложении Хана
для обобщенной меры
ф/г == [Ас Я*
Обозначим iV== Л ДГ. Тогда АГ = и D+ и при всех nuieg
Отсюда, полагая п -> °°, получаем |i^(Л/V) = 0 и, следовательно,
|АС(^4)= |ис(Л7У). То есть множество N является носителем [хс.
Далее, так как
ра (А) = j.i (Л) - ixc (AN)
то
Это означает, что/' + — / +еФ и, следовательно,
Отсюда вытекает, что ^(ДГ) = 0^ X-(W)= 0 и, значит, jnc сингу-
сингулярна относительно X, поскольку iV есть носитель \хс.
Единственность разложения |i = |ла + [ic может быть установ-
установлена следующим образом. Допустим, что Ц = Н>а + И*—некоторое
другое разложение. Тогдау^^а—\^а = ^с — И-с.. В силу свойства
сингулярности существуют множества N ж N' такие, что |ic(iV)=i
= 0, XGV) = Ot М^(ЛГ') =. 0, Ж/У^-О. Очевидно, ХB))==0, где
D = N + N'. Если допустить, что 7 = Va — №a = Ис — М-с =#= 0tJ то
найдется Ле?, при котором ч(А)?*О. Следовательно, либо
^(АЩ^О, либо 4(AD)=&0. Однако первое невозможно, посколь-
поскольку ^(^^О влечет за собой \*>а (D) === \ха (D) = 0. Второе также
невозможно, поскольку D = NN' и, следовательно, [*с (D) ==*
^()
27 А. А. Боровков

418 ПРИЛОЖЕНИЕ 3. ИНТЕГРИРОВАНИЕ
Единственность функции / (с точностью до ^-эквивалентно-
^-эквивалентности), вытекает из того, что равенства \ха (А) = ] jdX = \ fdXf
А А
j (/~~ f)dX = 0 для всех А влекут за собой равенство / —//==0
А
п. в. Если допустить, например, что Х(А)>0 для 4 = {о: / — /'>
> в), то для такого А мы получили бы J (/ — /') dX >> 0. ^
А
Одним из наиболее существенных приложений теоремы Ра-
Радона — Никодима является доказательство существования и един-
единственности условных математических ожиданий. Пусть 2?0 есть
0-гюдалгебра д и g — случайная величина на <Й,§,Р> такая,
что Щ, существует. Мы определили в § 4.8 условное математиче-
математическое ожидание 1V1 (S/So) величины | относительно §0 как 50-из~
меримую случайную величину *у, для которой
M(y; В)^МA; В) B0)
при любом В е 5?0. Можно считать, не ограничивая общности,
что § ^ 0 (произвольная функция § представима в виде разности
двух положительных). Тоща правая часть в B0) будет мерой
на <Q, So). Так как М E; В) = 0, если Р(В) = 0, то она будет
абсолютно непрерывной относительно Р. Это влечет за собой по
теореме Радона — Никодима существование единственной с точ-
точностью до Р-эквивалентности функции ^ па <Й, 2?о> такой, что
для всякого В eg9
Полученное соотношение, очевидно, эквивалентно B0) и уста-
устанавливает требуемое существование и единственность условного
математического ожидания.
Другое следствие доказанных в этом параграфе утверждений
упоминалось в § 3.6 и касалось теоремы Лебега о том, что лю-
любое распределение Р на прямой /? = (—°°, <») (или соответству-
соответствующая функция распределения) единственным образом предста-
вимо в виде суммы трех компонент Р = Ра + Рс + Ра, где компо-
компонента Ра абсолютно непрерывна относительно меры Лебега
Ра(А)= j f(x)dx; Ре— дискретная компонента, сосредоточенная
А
на не более чем счетном множестве точек хи х2, ..» такр1х, что
Р{х^)^>0; компонента РС имеет носитель лебеговой меры 0 и
непрерывную функцию распределения. Это есть прямое след-
следствие теоремы Лебега о разложении. Надо только из сингуляр-
сингулярной компоненты распределения Р (относительно лебеговой ме-
меры X) выделить дискретную ее часть, удалив сначала все точки
х, для которых Р(я)^1/2, затем все точки х% для которых

ПРИЛОЖЕНИЕ 4. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ХЕЛЛИ 41$
Р(#)^1/3 и т. д. Ясно, что мы получим при этом не более чем
счетное множество х-ъ- и что такое выделение дискретной компо-
компоненты определяет Ро однозначно.
Все сказанное, очевидно, сохранится и для распределений
в /г-мерных евклидовых пространствах Лп,
ПРИЛОЖЕНИЕ 4
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ХЕЛЛИ
Пусть 8Г —- класс всех функций распределения и ^ — класс
функций G, которые обладают свойствами Fl, F2 § 3.2 и свой-
свойствами G(—oo)^0, G(<»)<1. Будем писать Gn^G, Ge?, если
Gn(x)-> G(x) во всех точках х непрерывности функции G.
Теорема Хелли. Всякая последовательность Fn^ЗГ со-
содержит подпоследовательность Fnn =>- F е 2?.
Нам понадобится
Лемма 1. Для сходимости Fn=>F&$? достаточно, чтобы
Fn(x)-+F(x), xcbD,
при п ->¦ °° на каком-нибудь всюду плотном множестве D веще-
вещественных чисел.
Доказательство. Пусть х — произвольная точка непре-
непрерывности F(x). Для произвольных х\ х" ей таких, что х'' ^х^
^#", выполняется
Fn{x')<Fn{x)<Fn(x").
Следовательно,
lim Fn {xf) < lira inf Fn (x) < Km sup Fn (x) < lim Fn {x")»
В силу условий леммы получаем отсюда
F (ж') < lim inf Fn (x) < liai sup Fn (x) ^F(x").
n->oo n-*oo
Полагая х' \ х и х" \х по множеству D и учитывая, что х —
точка непрерывности F(х), получим:
lim Fn(x) = F(x). <
Доказательство теоремы. Пусть D *= [хп] — произ-
рольное счетное всюду плотное множество вещественных чисел,
Последовательность чисел l^n(^i)! ограничена и поэтому со-
содержит сходящуюся последовательность {Fln(x1)}. Обозначим
предел этой подпоследовательности Р(%[). Рассмотрим теперь
последовательность чисел 1^т(#2)Ь Она также содержит сходя-
27*

420 ПРИЛОЖЕНИЕ 5. ТЕОРЕМА БЕРРИ — ЭССЕНА
щуюся подпоследовательность {Р2п(%2)\ с пределом F (х2)*
При этом
Продолжая этот процесс, мы для любого числа к получим к по-
последовательностей
таких, что Пт Ркп(хг) = F(х[).
П-*юо
Рассмотрим диагональную последовательность функций рас-
распределений {Fnn(x)}. Для любого ^gD только к — 1 первых
¦членов последовательности чисел* {Fnn(xpj} могут не принадле-
принадлежать последовательности Fhn (xh). Поэтому lira Fnn (xk) = F (xh).
П-*оо
Ясно, что F(x) есть заданная на D неубывающая ограничен-
ограниченная функция. Ее легко продолжить по непрерывности слева до
неубывающей функции на всей прямой. Теперь видно, что по-
последовательность {FnJ и функция F удовлетворяют условию
леммы 1. -Щ
ПРИЛОЖЕНИЕ 5
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ БЕРРИ — ЭССЕНА
Докажем следующее утверждение (см. § 8.5):
Трорема (Берри — Эссен).- Пусть Ь,к независимы, оди-
одинаково распределены, М^ = 0, Щк = 1, ji = М | ^|3 < оо, Sn =
п
= 2 Efct Sn = Sn/ У п- Тогда при всех п
1
Д„ = sup | Р {1п < х) - Ф (х) | <
X
еде с — абсолютная постоянная.
Доказательство будет проводиться методом композиций.
Основанием для оценки Дп будет, как и в § 8.5, оценка малости
Mg(?n) — Mg (r|), ^1^Фод, для гладких g. Чтобы получить оцен-
оценку для Ап, мы в § 8.5 выбирали g с изменением, сосредоточенным
на малом интервале. Следующая лемма показывает, что такой
выбор g не обязателен. Пусть G — какая-нибудь функция рас-
распределения, y-^G и не зависит от ?п, ц. Положим ()
),. так что Wg (?n)=-MG(^)= Р(Т<ЦЬ)= Р

ПРИЛОЖЕНИЕ 5. ТЕОРЕМА БЕРРИ — ЭССЕНА 421
су < х), Mg {ц) = Р (л + CV < х)- Обозначим
Л„>е - sup
MG (Х~Щ - MG
= sup 1 Р (С» + by< ж) - Р (tj + еу< ж) 1 =
- sup| J Л?(у) [Р &п< х- ъу) - Р(т|< х - еу)]\.
Очевидно, что Лп,е<Ап. Нашей целью будет получение обрат-
обратного неравенства.
Лемма 1. Пусть v>0 таково, что G(v)— C(—v)^ 3/4. Тог-*
да при любом е > О
Доказательство. Предположим, что sup в определений
X
An достигается на положительном значении An(,r) = Fn(a;)— Ф(х)
(отрицательное Ип(х) рассматривается аналогично), и пусть для
заданного 5 > 0 значение х& таково, что
где Fn — функция распределения ?п. При увеличении аргумента
значение &п(хь) меняется мало в следующем смысле. Пусть
\у\ <v9 Тогда v —
An(x6 + е{и- у)) == Fn(x, + е(и~-у))~Ф(х6
Здесь разность в квадратных скобках не превосходит 'г{и —
— у) Ф' @) ^ 2ve/lf2n и,, значив,
Поэтому
J + f
i ii
Так как б произвольно, то отсюда следует утверждение лем-
леммы. <

422 ПРИЛОЖЕНИЕ 5. ТЕОРЕМА БЕРРИ — ЭССЕНА
Следствие 1. 'Для С = ф (^?ЕЕФ0>;1) значение v — 6/S
удовлетворяет условиям леммы 1,
, + е), A)'.
В качестве следующего этапа доказательства оценим An.s*
где, собственно, и используется метод композиций. Обозначим
и (п) = шах Д/г Ук/\1Ь а2 == е2/г.,
Буквой с (с индексами или без) будем обозначать абсолютные
постоянные, не обязательно одни и те же.
Лемма 2. При а "> 1
1 im(n-J)\ .
п
Доказательство. Пусть Нп = 2 Лл» Ла^еФод и незави-
независимы; у, {gj и {т]к} независимы. Основу метода композиций со-
составляет тождество (ср. с теоремой 8.6 и тождеством (8.20)} ,
Р (En + Ч < х) — Р (П + гУ <х) = Р (Sn + ay<x
- Р (Яп + aY < х УТг) = 2 [Р E«-i + (Яп - Ят)
Так как при 7ё(^од выполняется Яп— Нт +
п
то последняя сумма равна 2j Dm, где
m=l
- М 1Ф (Гт - lm)/dm - Ф (Гт -' t\m)/dm]t
dm = п — т + а?% Тт = .
апг
Для оценки слагаемых Dm воспользуемся тем же подходом,
что и в лемме 8.3. Так как первые два момента %т и цт совпа-
совпадают, то, пользуясь разложением в ряд, получим
§q)''B1m+ t)t
dm x
где ф(^=Ф/(дг), ср" =Ф///. Так как функция ф" ограничена, то
. C)

ПРИЛОЖЕНИЕ 5. ТЕОРЕМА БЕРРИ ~- ЭССЕНА
423
Нам понадобится также другая оценка ВШч Чтобы ее получить,
рассмотрим
t) |<
D)
где Ут определяется так же, как Тт, но с заменой ?,»-? па Ят-?.
Интегрированием по частям получаем
< sup i M [<р"(Тт + t) - ф" (Vm + t)] | + sup [ Мф" (Fm + t) |
М
и)] | =
]! = | J ф" (u + t)d [Р (Гт < м)
О [Р (Гт < м) - Р (Vm < и)]
< Ат„! j ф/яг (и) da
поскольку | Р (Гт <^ и)— Р (Fm <С ц) | ^ &m-i (Тт и Fm отличают™
ся от Sm-i/llm — 1 и Ящ-УУ/тг — 1, соответственно, одним и тем
же линейным преобразованием).
Для оценки второго слагаемого в D) заметим, что
Мер"
t) = f сР" (и
L
dut
где
am = ж Vn/dmf rm ==
так что -— Ф
есть плотность Vm =
. Инте-
грируя два раза по частям, находим
Итак,
1 т
Полученные оценки Dm от х не зависят. Поэтому, используя при
т > п/2 только что полученную оценку, а при т ^ п/2 — оцен-
оценку C), в силу которой \Dm\ ^ cjx/тг372, получим
2
m>n/2
2

424 ПРИЛОЖЕНИЕ 5. ТЕОРЕМА БЕРРИ — ЭССЕНА
о п -3/2 1
одесь первая сумма не превосходит -тгп = _—s последняя
z 2уп '
п
не превосходит 1 -^ ^ -4=* Остается оценить среднюю сум-
му (и («) = max
л. У*
1
2 ^!<|Ш(._1)/1 2 и Д.у-
m>n/2 dm m>n/2 V« — я» -|- a j
Последняя сумма не превосходит
1 i ? d^ 1.1^3
3" J (* + 2K/2 3 2а ^ 2а"
< i ?
если а^1. Резюмируя E) и проведенные оценки, получим ут-
утверждение леммы. М
Обратимся теперь непосредственно к доказательству теоремы*
В силу A), B)
2 ,/— . , 2о .„ , 2сии (»— 1) , 2а
г;(га)<|„Д„,в + <2С +
Положим здесь a = max(l, Ac\i). Тогда (jm^ 1)
Отсюда вытекает, что ^(^г)^2с1 при всех /г. Чтобы убедиться
в этом, воспользуемся индукцией. Очевидно, что u(l)=i;(l)^
< 1 ^2с,. Пусть и(/г— 1)^ 2с4. Тогда 1;(л)< 2с4, и (л) = max (у (л),
м(л ~~ 1I^ 2с1# Теорема доказана, ^

ПРИЛОЖЕНИЕ G. ТЛГ.ЛИЦТЛ
425
ПРИЛОЖЕНИЕ б
ТАБЛИЦЫ
Таблица 1. Нормальное распределение
со
1 Г* 2/
Таблица значений функщщ Ф(х) = zrr== \ e~~tl2di. Функция нормаль-
а У 2л J
X
"лого распределения Ф(х) связана с Фо(х) соотношениями Ф(х) = 1 — Фо(аг) =
Ф
X
0,0
од
; о,2
0,3
од .
0,5
0,6
0,7
0,8
0,9
1,0
1,1
\ 1.2
; 1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
; 2,4
2,5
2,6
2,7
2,8
2,9
ж =
Ф0(х) =
0
0,5000
4602
4207
3821
3446 '
3085
2743
2420
2119
1841
1587
1357
1151
09687 ч
0808
0668
0548
0446-
0359
0288
0228
0179
0139
0107
0082
0062
0047
0035
0026
0019
3,0
0,0013
1
0,4960
4562
4168
3783
3409
3050
2709
2389
2090
1814
1562
1335
1131
0951
0793
0655
0537
0436
0351
0281
0222
0174
0136
• 0104
0080
0060
0045
0034
0025
0018
3,1
0,0010
2
0,4920
4522
4129
3745
3372
3015
2676
2358
2061
1788
1539
1314
1112
0934
0778 ч
0643
0526
0427
0344
0274
0217
0170
0132
0102
0078
0059
0044
0033
0024
0018
0,0007
3
0,4880
4483
4090
3707
3336
2981
2643
2327
2033
1762
1515
1292
1093
0918
0764
0630
0516"
0418
0336
0268
0212
0166
0129
0099
0075
0057
0043
0032
0023
0017
3,3
0,0005
4
0,4840
4443
4052
3669
3300
2946
2611
2297
2005
1736
1492
1271
1075
0901
0749
0618
0505
0409
0329
0262
0207
0162
0125
0098
0073
0055
0041
0031
0023
0016
3,4
0,0003

426
ПРИЛОЖЕНИЕ 6. ТАБЛИЦЫ
Продолжение табл. 1
Таблица 2. Распределение Пуассона
оо
Таблица значений функции JjT (х) = > ^_-
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
ОД)
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
х =
Фо(*) =
5
0,4801
4404
4013
3632
3264
2912
2578
2266
1977
1711
1469
1251
1056
0885
0735
0606
0495
0401
0322
0256
0202
0158
0122
0094
0071
0054
0040
0030
0022
00 J 6
3,5
0,0002
6
0,4761
4364
3974
3594
3228
2877
2546
2236
1949
1685
1440
1230
1038
0869
0721
0594
0485
0392
0314
0250
0197
0154
0119
0091
0069
0052
0039
0029
0021
0015
3,6
0,0002
7
0,4721
4325
3931)
3557
3192
2843
2514
2206
1922
1660
1423
1210
1020
0853
0708
0582
0475
0384
0307
0244
0192
0150
0116
0089
0068
0051
0038
0028
0021
0015
3,7
0,0001
8
0,4081
4286
3897
3520
3156
2810
2483
2177
1894
1635
1401
1190
1003
0838
0694
0571
0465
0375
0301
0239
0188
0146
0113
0087
0066
0049
ост
0027
0020
0014
' 3,8
0,0001
9
0,4641 |
4247
3859
3483
3121
2776
2451 j
2148
1867
1011
1379
1170
0985
0823
0681
0559 |
0455
0367
0294
02 НЗ
0183 i
0143
ОНО '
0084 j
0064
0048
0036
0026 |
0019 ' \
0014
3,9
0,0000
ос ^NN4\
1
2
, 3
4
5
6
0,1
0,0952
0047
0002
0000
0,2
0,1813
0175
ООН
0001
0000
0,3
0,2592
0369
0036
0003
0000
0,4
0,3297
0616
0079
0008
0001
0000
0,5
0,3935
0902
0144
0018
0002
0000
0,6
0,4512
1219
0232
0034
0004
0000

ПРИЛОЖЕНИЕ 6, ТАБЛИЦЫ
427
Продолжение табл. 2
X ^Ч>*>^
1
2
3
4
5
6
7 -
8
9
1
2
3
4
5
6
7
8
9
10
11
12
\. К
X N.
1
. 2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 ;
ол
0,5034
1558
0341
0058
0008
0001
1,6
0,7981
4751
2166
0788
0237
ооео
0013
0003
0000
2,8
0,9392
76S9
53E5
3081
1523
0651
0244
0081
0024
0007
0001
0000
0,8
0,5507
1912
0474
0091
0014
0002
1,8
0,8347
5372
2694
1087
0364
0104
0026
0006
0001
0000
3,0
0,9502
8009
5768
3528
1847
0839
0335
0119
0038
ООН
0003
0001
0,9
0,5934
2275
0629
0135
0023
0003
2,0
0,8647
5940
3233
1429
0527
0166
0045
ООН
0002
0000
4,0
0,9817
9084
7619
5665
3712
2149
1107
0511
0214
0081
0028
0009
0002
0001
0000
1,0
0,6321
2642
0803
0190
0037
0000
2,2i
0,8892
6454
3773
1806
0725
0249
0075
0020
0005
0001
0000
5,0
0,9933
9596
8753
7350
5595
3840
2378
1334
0681
0318
0137
0055
0020
0007
0002
0001
0000
1,2
0,6988
3374
1205
0338
0077
0015
' 0003
0000
2,4
0,9093
6916
4303
2212
0859
0357
0116
0033
0009
0002
0000
G,0
0,9975
9826
9380
8488
7149
5543
3937
2560
1528
0839
0426
0201
0088
0036
0014
0005
0002
0001
0000
1,4
0,7534
4082
1665
0537
0143
0032
0006
0001
ОиОО
2,6
i
i
0,9257
7326
4816
2640
1226
0490
0172
0053
0015
0004
0001
оооо 1
7,0
0,9991
9227
9704
9182
8270
2993
5503
4013
2709
1695
0985
0534
0270
0128
0057
0024
0010
0004
0001
0000

428
ПРИЛОЖЕНИЕ 6. ТАБЛИЦЫ
Продолжение табл. 2
1
2
3
4
5
6
7
8
9
40
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
8.0
0,9997
9970
9862
9576
9004
8088
6866
5470
4075
2834
1841
1119
0638
0342
0173
0082
0037
0016
0007
0003
0001
0000
9,0
0,9999
9988
9938
9788
9450
8843
7932
6761
5443
4126
2940
1967
1242
0739
0415
0220
0111
0053
0024
ООН
0004
0002
'0001
0000
10,0
1,0000
0,9995
9972
9897
9707
9329
8699
7798
6672
5421
4170
3032
2084
1355
0835
0487
0270
0143
0072
0035
0016
0007
0003
0001
0000
11,0
1,0000
0,9998
9988
9950
9849
9625
9214
8568
7680
6594
5401
4207
3113
2187
1460
0926
0559
0322
0177
0093
0047
0023
0010
0005
0002
0001
0000
12,0
1,0000
0,9999
9995
9977
9924 -
9797
9542
9105
8450
7576
6528
5384
4240
3185
2280
1556
1013
0630
0374
0213
0116
0061
0030
0Q15
0007
0003
0001
0001
0000
13,0
1
1,0000
1,0000
0,9998
9990
9963
9893
9741
9460
9002
8342
7483
6468
- 5369
4270
3249
2364
1645
1095
0698
- 0427
0250
0141
0076
0040
0020
0010
0005
0002
0001 1
Примечание. При X > 13 вероятность П{х) можно вычислять
приближенно по формуле (ср. с замечаниями в § 4 гл. 5)
Более подробные таблицы можно найти, например, в [2], [6].

СПИСОК ЛИТЕРАТУРЫ
1 Биллингс л и П. Сходимость вероятностных мер.—М.: Наука, 1977,
2. Большев Л. Н., Смирнов Н. В. Таблицы математической статисти-
статистики.— М.: Наука, 1965. ,
3. Б о р о в к о в Л. А. Вероятностные "процессы в теории массового обслу-
обслуживания.— М.: Наука, 1972.
4. Боровков Л. А. Теория вероятностей.—М.: Наука, 1976.
5. Гихман И. И., Скороход А. В. Введение в теорию случайных про-
процессов.™ М.: Наука, 1977.
6. Г н е д е и к о Б. В. Курс теории вероятностей.— М.: Наука, 1969.
7. Г и еде нк о Б. В., Ко л м о го р о в А. II. Предельные распределения
для сумм независимых случайных величии.— М.: Гостехиздат, 1949.
8. Ибрагимов И. A., JI и и и и к 10. В. Независимые и стационарно свя-
связанные величины.-— М.: Наука, 1965.
9. К о л м о г о р о в А. Н. Цепи Маркова со счетным числом состояний//
Бюл. МГУ.— 1937.™ Т. 1, № 3.
10. К о л м о г о р о в А. И. Теория вероятностей. Математика, ее содержа-
содержание, методы и значение. Т. 2.— М.: Изд-во АН СССР, 1956.
11. К р а м е р Г., Л и д б е т т е р М. Стационарные случайные процессы.—
М.: Мир, 1969.
42. Лампер т я Дж. Вероятность.-— М.: Наука, 1973.
13. Лоэв М. Теория вероятностей.—.М.: ИЛ, 1962.
14. Натансон И. П. Теория функций вещественной переменной.— М.: На-
Наука, 1974. ,
15. П е т р о в В. В. Суммы независимых случайных величин.— М.: Наука.
1972.
16. С к о р о х о д А. В. Случайные процессы с независимыми приращения-
приращениями.—М.: Наука, 1986.
17. Фай истей н А. Основы теории информации.— М.: ИЛ, I960.
18. Ф е л л е р В. Введение в теорию вероятностей и ее приложения.
Т. 1, 2.— М.: Мир, 1984.
19. X а л м о ш П. Теория меры.— М.: ИЛ, 1953.
20. Хи н ч и н А. Я. Понятие энтропии в теории вероятностей//УМН.— 1953.—
Т. 8, № 3.
21. Ш и р я е в А. Н. Вероятность.— М.: Наука, 1980.
22. V a n Beak P. An application of Fonder methods to the problem of
charpening the Berry//Esseen inequality. Z. Wahrscheinlichkeitstheorie und
yerw.- 1*972.— B. 23, № 3,- S. 187-196,

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная непрерывность меры 414
Абсолютно непрерывное распределение
51, 5G
Алгебра (множеств) 27
Безобидная игра 84
Бериулли схема 21, 77, 114
Бсрнштейна полиномы 115
Большие уклонения 132, 202
Борелевская функция 54
Борелевское множество 28
— поле 28
Бореля — Каителли лемма (критерий)!
136
Броуновский мост 389
Вероятность 16, 29
—, классическое определение 18
<— переходная 3G9
<— условная 36
Выборка 18
Генеральная совокупность 18
блуждания
223
Дефект случайного
Дисперсия 91
Закон больших чисел 97, 114, 178, 180,
201, 230, 255
усиленный 114, 241, 244, 252,
318
— нуля и единицы 232, 233, 234
— повторного логарифма 337, 338, 359
Измеримое отображение 43
-— пространство 28
Интеграл 68, 402, 412
Информации количество 293
Кольцо (множеств) 27
Корреляции коэффициент 93
Критерий Колмогорова 244
Липшицев© множество 351, 363
Маркова цепь 270
• однородная 271
• периодическая 278
разложимая (неразложимая) 274
Мартингал 303, 304
Математическое ожидание 76
. условное 81, 100, 102
Матрица дважды стохастическая 290
— стохастическая 272
Мера 401
— сингулярная 414
Момент 95
•— остановки 86, 307
Независимые испытания 37
— классы событий 61
— случайные величины 59, 65, 149
— события 36
Неравенство Гёльдера 98
— Иенсепа 96, 105
Неравенство Колмогорова 237, 314
— Коши — Буияковского 95, 105
— Минковского 96
— Чебышева 97, 104
Носитель меры 414
Обслуживания системы 258
Плотная последовательность распределе-
распределений 145
Плотность 411
— переходная 369
•— распределения 52, 56, 73
условная 108
Последовательность верхняя (нижняя)
235
Преобразование Крамера 204
— Лапласа 151
Принцип инвариантности 351, 357
Прогноз 391
Произведение мер прямое 71
Производная Радона — Никодима 411
Производящая функция 154, 173
Пространство вероятностное 30
— выборочное 48, 56, 322
— измеримое 28, 32
— с мерой 400
— элементарных событий (исходов) 15.
27, 29
Процесс белого шума 388
¦— ветвящийся 173, 376
— восстановления 218
однородный 220. 227
стационарный 220
¦— гауссовский 389
— диффузионный 379
— марковский 366
— непредсказуемый 386
— непрерывный в среднем 331
— пуассоповский 229, 342, 361, 375
обобщенный 344
— сепарабельиый 330
— с независимыми приращениями 333.
345
— случайный 321, 323
— стационарный в узком смысле 389
широком смысле 387
— стохастически непрерывный 331
Псевдомомепт 193
Равномерная интегрируемость 138
Распределение абсолютно непрерывное
51
— безгранично делимое 212, 333
— биномиальное 21, 48
— вероятностей 16, 30
— вырожденное 48
— геометрическое 49
— гипергеометрическое 20, 23
— дискретное 51
— конечномерное 322
— Коши 50, 153
— нормальное 49, 152, 425
многомерное 58, 110, 166
— показательное 49, 152, 170
—- полиномиальное 57

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
431
Распределение процесса 322, 323
— Пуассона 39, 51, 426
— равномерное 45, 49, 153
дискретное 18
— симметричное 262
— сингулярное 53, 242
— случайной величины 43, 48, 55
— стационарное 284
— условное 107
— устойчивое 211
— финальное 284
— Эрланга 170
— F (гамма-распределение) 168
— X2 (хи-квадрат) 169
Свертка 73^
Симметрическая разность 394
Случайная величина 43
марковская 86
, многомерная 55
не зависящая от будущего 86
несобственная 44
нормированная 94
— *— остаточная 234
Случайное блуждание 218, 280
, непрерывное сверху 265
Случайные величины, положительно (от-
(отрицательно) коррелированные 95
Случайный вектор 55
Событие 15
— дополнительное (противоположное)
16, 29
— достоверное 16, 29
— невозможное 16, 29
— перестановочное 234
Событий произведение 16
— разность 16
— сумма 15
События независимые 36, 37
— несовместные 16
Состояние возвратное (невозвратное)
274, 275
— нулевое (ненулевое) 274
— поглощающее 274
— существенное (несущественное) 273
Сочетаний число 19
Спектральная мера процесса 349
Среднее значение 76
Стандартное уклонение 91
Стохастическая матрица 272, 370
Стохастически эквивалентные процессы
325
Суб(супер)мартингал 303, 304
Сходимость по вероятности 133
распределению 142
— почти наверное (почти всюду, с ве-
вероятностью 1) 133
— слабая 140, 165
Теорема аппроксимации 62
— Берри — Эссена 197, 420
— Бохнера — Хинчина 153
— Вейерштрасса 115
— восстановления 221, 225
-^ Дуба 308, 314, 315, 316
— единственности 156
— Каратеодори 33
— Колмогорова 67, 398, 319, 327
Прохорова 88
Ченцова 329
Теорема Лебега 414
— Леви 318
Хинчина 346
— локальная предельная 197
— Муавра — Лапласа 120
— непрерывности 138, 157, 165
— о монотонной сходимости 104, 413
— о повторном интегрировании 72, 408
— о продолжении меры 33, 396
— о сходимости мажорируемой последе*
вательности 140
— Пуассона 123, 161
— Радона — Никодима 414
— Фату —Лебега 406, 413
— Фубини 408
— Хана 414
— Хелли 145, 419
— центральная предельная 179, 187, 201,
230
— эргодическая 284, 388
Тождество Вальда 88, 241, 311, 313
— Поллачека — Спитцера 263
— факторизационное 247, 252
Уравнения Колмогорова 381
Чепмеиа 368, 370
Условие Крамера 203
— Линдеберга 185, 201, 379
— Ляпунова 188, 351
Условешя вероятность 36
— функция распределения 81
Условное математическое ожидание 81
Факторизации компоненты 251
Факторизационные тождества 249, 252
Формула Байеса 41
— обращения 155, 165
— полной вероятности 38, 82, 105
— Стирлинга 116, 117
Функция борелевская 54
— верхняя (нижняя) 338
— восстановления 219
— ковариационная 386
— неотрицательно определенная 386
— переходная 368
— производящая 154, 173
— простая 402
— распределения 43, 45, 55
< условная 81
— уклонений 204
— характеристическая 149, 164
Центральная предельная теорема . 179»
187, 101
Цепь Маркова 270
однородная 271
периодическая 278
— разложимая 274
Цилиндрическое множество 322, 398
Эксцесс случайного блуждания 223
Элементарные события (исходы) 15
Энтропия 294
— условная 296
— цепи Маркова 298
о-алгебра 28
— борелевская 28
—, порожденная классом множеств 29
—, — случайной величиной 64, 66