Ю.М. БЕЛОУСОВ, С.Н. БУРМИСТРОВ. А.И. ТЕРНОВ
ЗАДАЧИ
i ПО ТЕОРЕТИЧЕСКОЙ
< ФИЗИКЕ
|
I

Ю.М. Белоусов, С.Н. Бурмистров, А.И. Тернов
Задачи по теоретической физике: Учебное пособие/ Ю.М. Белоусов,
С.Н. Бурмистров, А.И Тернов - Долгопрудный: Издательский Дом
«Интеллект», 2013. — 584 с.
ISBN 978-5-91559-134-8
Книга содержит 460 задач различной степени сложности, которые в раз¬
ное время предлагались студентам МФТИ, и охватывает все основные разде¬
лы теоретической физики: Теория поля, Квантовая механика и Статистичес¬
кая физика. Задачи снабжены подробными решениями и пояснениями. Всем
разделам предшествует краткое теоретическое введение, содержащее необ¬
ходимые сведения для решения и понимания соответствующих задач.
Книга предназначена студентам и аспирантам высших учебных заведений,
изучающим теоретическую физику.
ISBN 978-5-91559-134-8	©	2012,	Ю.М. Белоусов,
С.Н. Бурмистров, А.И. Тернов
© 2013, ООО Издательский Дом «Интеллект»,
оригинал-макет, оформление

ОГЛАВЛЕНИЕ
Предисловие	 6
Часть I. Задачи
Глава 1. Теория	поля	 10
Введение	 10
1.1. Векторы и тензоры в евклидовом пространстве	 40
1.2. Векторы и тензоры в пространстве Минковского	 42
1.3. Релятивистская кинематика	 42
1.4. Уравнения Максвелла	 47
1.5. Движение заряженной частицы во внешнем поле	 49
1.6. Статическое электромагнитное поле	 52
1.7. Свободное электромагнитное поле	 53
1.8. Запаздывающие потенциалы, излучение	 54
1.9. Электромагнитное поле релятивистских частиц	 57
1.10.	Рассеяние электромагнитных волн	 58
Глава 2. Квантовая	механика	 60
Введение	 60
2.1. Операторы и состояния в квантовой механике	 82
2.2. Одномерное движение	 84
2.3. Линейный гармонический осциллятор	 87
2.4. Угловой момент, спин	 88
2.5. Движение в магнитном поле	 90
2.6. Движение в центральном поле	 91
2.7. Квазиклассическое приближение	 93
2.8. Теория возмущений	 93

4 -J\„ Оглавление
2.9.	Релятивистская квантовая механика	 96
2.10. Сложение моментов. Тождественность частиц	 97
2.11. Теория атомов и молекул	 98
2.12. Теория рассеяния	 100
2.13. Теория излучения	 101
Глава 3. Статистическая физика	 103
Введение	 103
3.1. Распределение Гиббса. Термодинамические величины и функции. 142
3.2. Квантовые идеальные газы 	 146
3.2.1. Идеальный ферми-газ	 146
3.2.2. Идеальный бозе-газ	 149
3.2.3. Идеальный газ элементарных бозе-возбуждений	 150
3.3. Неидеальные квантовые системы (жидкости). Основы теории кон¬
денсированных сред	 152
3.3.1. Нормальная (несверхтекучая) ферми-жидкость	 152
3.3.2. Сверхпроводимость. Теория БКШ	 154
3.3.3. Слабонеидеальный бозе-газ. Уравнение Гросса-Питаевского 156
3.3.4. Теория сверхтекучести	 158
3.4. Фазовые переходы и критические явления	 159
3.4.1. Приближение самосогласованного поля	 159
3.4.2. Функционал Гинзбурга-Ландау	 160
3.4.3. Основы теории критических явлений	 163
Часть II. Решения задач
Глава 1. Теория поля	 168
1.1. Векторы и тензоры в евклидовом пространстве	 168
1.2. Векторы и тензоры в пространстве Минковского	 171
1.3. Релятивистская кинематика	 171
1.4. Уравнения Максвелла	 198
1.5. Движение заряженной частицы во внешнем поле	 204
1.6. Статическое электромагнитное поле	 223
1.7. Свободное электромагнитное поле	 233
1.8. Запаздывающие потенциалы, излучение	 235
1.9. Электромагнитное поле релятивистских частиц	 254
1.10.	Рассеяние электромагнитных волн	 266

Оглавление
Глава 2. Квантовая механика	 278
2.1. Операторы и состояния в квантовой механике	 278
2.2. Одномерное движение	 283
2.3. Линейный гармонический осциллятор	 303
2.4. Угловой момент, спин	 306
2.5. Движение в магнитном поле	 311
2.6. Движение в центральном поле	 321
2.7. Квазиклассическое приближение	 332
2.8. Теория возмущений	 337
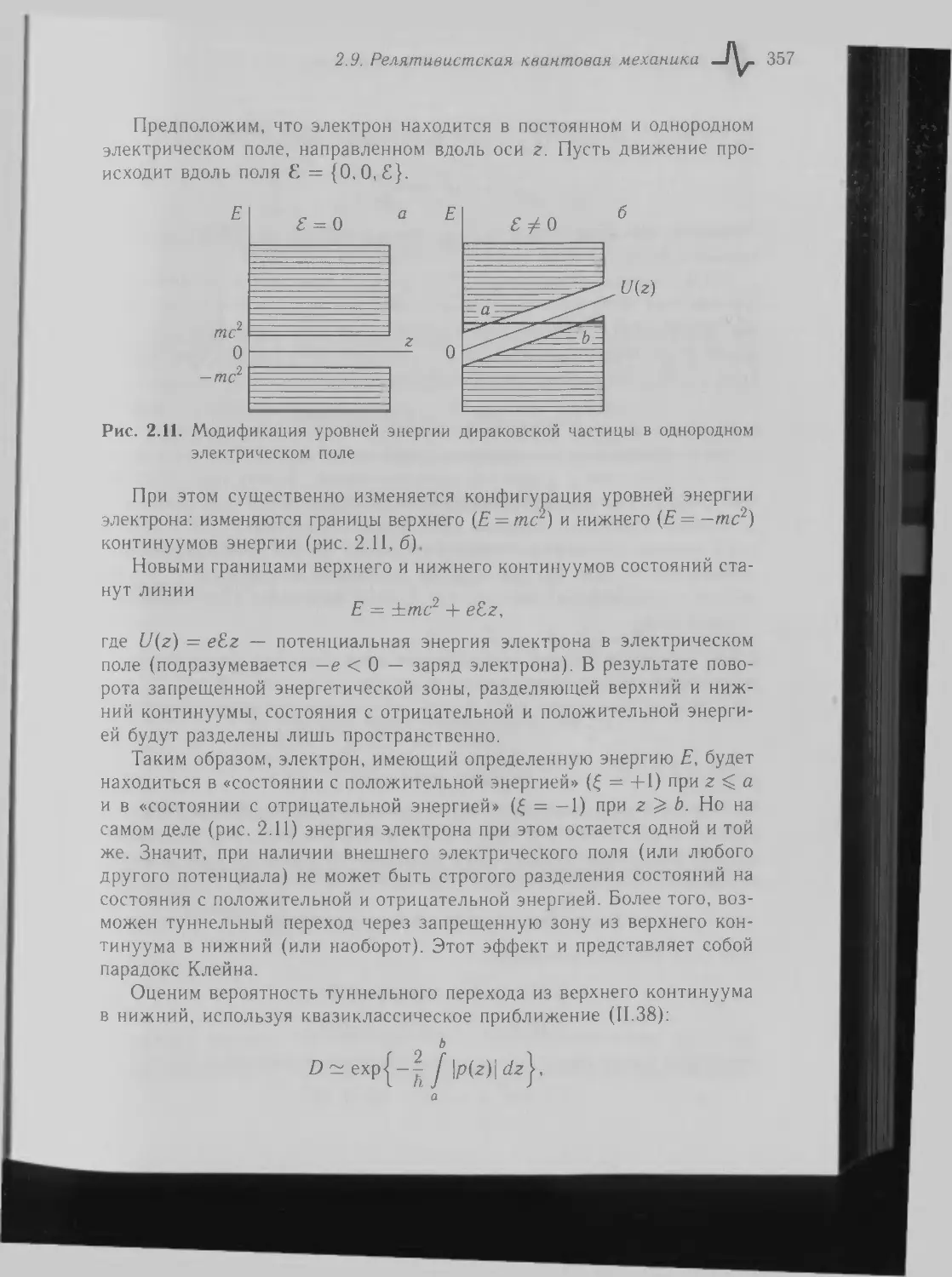
2.9. Релятивистская квантовая механика 	 352
2.10. Сложение моментов. Тождественность частиц	 366
2.11. Теория атомов и молекул	ч ;	 373
2.12. Теория рассеяния	 392
2.13. Теория излучения	 407
Глава 3. Статистическая	физика	 416
3.1. Распределение Гиббса. Термодинамические величины и функции. 416
3.2. Квантовые идеальные газы 	 447
3.2.1. Идеальный ферми-газ	 447
3.2.2. Идеальный бозе-газ	 472
3.2.3. Идеальный газ элементарных бозе-возбуждений	 485
3.3. Неидеальные квантовые системы (жидкости). Основы теории кон¬
денсированных сред	 491
3.3.1. Нормальная (несверхтекучая) ферми-жидкость	 491
3.3.2. Сверхпроводимость. Теория БКШ	 501
3.3.3. Слабонеидеальный бозе-газ. Уравнение Гросса-Питаевского 510
3.3.4. Теория сверхтекучести	 520
3.4. Фазовые переходы и критические явления	 527
3.4.1. Приближение самосогласованного поля	 527
3.4.2. Функционал Гинзбурга-Ландау	 532
3.4.3. Основы теории критических явлений	 555
Дополнения	 573
1. Дельта-функция Дирака и другие обобщенные	функции	 573
2. Цилиндрические функции полуцелого индекса	 575
3. Вырожденная гипергеометрическая функция. Полиномы Лагерра.	577
4. Гамма-функция	 578
Список литературы	 579

ПРЕДИСЛОВИЕ
Изучение теоретической физики невозможно представить себе без
освоения методов решения задач — это не гуманитарная наука. Имен¬
но при решении задач после изучения какого-либо раздела теорети¬
ческой физики приходит как усвоение, так и понимание пройденного
материала. Перед Вами сборник задач по курсу теоретической физики,
снабженных подробными решениями и пояснениями, которые в том или
ином виде предлагались в различные годы студентам Московского фи¬
зико-технического института на так называемом базовом уровне слож¬
ности. Последний термин появился не так давно, но он вполне адекват¬
но отражает требования, которые предъявляются студентам-физикам,
не обязательно специализирующимся как будущие физики-теоретики.
Итак, в данной книге предложены задачи по трем основным кур¬
сам теоретический физики: теории поля, квантовой механике и ста¬
тистической физике в соответствии с теми курсами, которые изучают
студенты Физтеха в бакалавриате (это вовсе не означает, что другие
разделы теоретической физики менее значимы, просто так сложилось со
времен основания МФТИ). Между различными разделами существует
неразрывная связь, которую мы постарались проследить, и поэтому все
задачи объединены в одном сборнике. В соответствии с этим задачник
состоит из трех разделов, каждому из которых предшествует краткое
введение, напоминающее читателю основные понятия, которые будут в
дальнейшем необходимы при решении предлагаемых задач. Это, если
угодно, своего рода теоретический минимум, который должны знать
студенты после изучения курса. Поэтому можно считать данную книгу
также и учебным пособием. Краткое введение не предполагает после¬
довательного вывода формул. Если вывод какой-либо формулы сам по
себе представляет полезную задачу, мы старались сформулировать его
именно в виде задачи. Мы полагаем, что такой подход помогает сту¬
денту лучше понять и усвоить материал. В то же время мы не стре¬
мились составить как можно больше задач, а постарались предложить

Предисловие -1\г ^
и разобрать такое количество задач, которое мы считаем достаточным
для усвоения и понимания основных курсов теоретической физики.
Решение задач дает студенту возможность проверить свои реальные
знания, которые в идеале не должны быть только набором заученных
сведений. Для преподавателя самостоятельно решенная студентом за¬
дача — самый эффективный показатель глубины понимания изучаемо¬
го предмета. Самостоятельное решение задач развивает и воспитыва¬
ет аналитическое и творческое научное мышление. Ответы и методы
решения задач приведены во второй части книги в той же последова¬
тельности, что и условия. В пояснениях к задачам и их решениях мы,
по мере возможности, старались избежать использования сложных ма¬
тематических методов или специального аппарата теоретической физи¬
ки, чтобы изложение было доступно как можно более широкому кругу
студентов-физиков, а не только студентам, которые специализируются
в области теоретической физики. В качестве справочного материала в
конце книги приведены некоторые полезные сведения о специальных
функциях математической физики, часто используемых при решении
различных задач.
Теперь несколько слов о самих задачах. Специфика формулирования
задач часто состоит в том, что трудно найти их истинного автора, поэто¬
му они носят, как правило, «фольклорный» характер. Действительно,
часть задач можно найти в замечательных сборниках задач по теории
поля [3], по квантовой механике [23-25], а также по статистической
физике [31] и, естественно, в соответствующих томах Курса теоретиче¬
ской физики Л. Д. Ландау и Е.М. Лифшица, который составляет осно¬
ву курса теоретической физики МФТИ. Как правило, эти задачи в раз¬
личные годы включались (и включаются в настоящее время) в домаш¬
ние задания студентов. Некоторые из этих задач вошли и в наш сбор¬
ник, поскольку они стали классическими, и без них трудно представить
себе курс теоретической физики. Однако, наряду с такими задачами
читатель найдет в нашем сборнике и много оригинальных задач, учи¬
тывающих особенности курсов, читаемых на разных лекционных пото¬
ках. Поэтому нужно понимать, что данный сборник задач — продукт
коллективного творчества сотрудников кафедры теоретической физики
МФТИ, как работающих в настоящее время, так и и тех, кого уже, к со¬
жалению, нет с нами. Особенно хотелось бы отметить роль В. П. Смил-
ги и В. П. Кузнецова, которые работали на кафедре практически с пер¬
вых лет ее существования и одними из первых начали заниматься со¬
ставлением и подбором задач. Часть из этих задач уже вошла в «Кате¬
хизис» [45] и небольшую книгу «Практическая математика» [46].
Авторы выражают искреннюю благодарность всему коллективу пре¬
подавателей кафедры теоретической физики МФТИ, однако все-таки

8	Предисловие
хотелось бы особо отметить С. П. Аллилуева, С. Т. Беляева, С. С. Гер¬
штейна, Р. О. Зайцева, JI. А. Максимова, внесших большой вклад в ста¬
новление курса теоретической физики и составление заданий, а также
ушедших от нас В. Б. Берестецкого, Б. Т. Гейликмана, В.Н. Горелкина
и И. А. Малкина. Авторы также выражают благодарность доценту ка¬
федры М. Г. Иванову за помощь в подготовке раздела, посвященного
теории поля.

глава ТЕОРИЯ ПОЛЯ
1
ВВЕДЕНИЕ
1.	Понятие тензора
Все физические явления описываются в теоретической фи¬
зике с помощью различных математических моделей, в которых физи¬
ческим объектам ставятся в соответствие математические объекты. Ма¬
тематические объекты описывают физические объекты в пространстве,
задавая их в различных системах координат. При этом любой точке
пространства ставится в соответствие набор координат, число которых
зависит от размерности пространства и которые принято обозначать
как х‘, где индекс i принимает все возможные значения в соответствии
с нумерацией осей системы координат и называется свободным индек¬
сом. Совокупность координат называется радиус-вектором и обычно,
а в трехмерном случае всегда, обозначается как г.
Свойства физических объектов не могут зависеть от выбора систе¬
мы координат, и это определяет свойства соответствующих им мате¬
матических объектов. Например, законы сохранения в физике должны
описываться при помощи математических объектов, имеющих одинако¬
вый вид в разных системах координат. Это — инварианты. Различные
системы координат могут быть связаны между собой с помощью опре¬
деленного преобразования координат, которое с формально-математи¬
ческой точки зрения представляется некоторой заменой, записываемой
обычно в виде х‘ = х‘(г'). Штрихом принято обозначать радиус-вектор в
преобразованной относительно исходной системе координат. Поскольку
при описании физических объектов необходимо использовать преобра¬
зования, имеющие обратные, то для замен координат следует применять
только непрерывные и невырожденные преобразования, т. е. такие пре¬
образования, для которых 1 = det(dxl/дх,к) ф 0, где J — определитель
матрицы Якоби, т. е. якобиан данного преобразования.

Введение
Инвариантам соответствуют математические объекты, не изменяю¬
щиеся при всех заменах (преобразованиях) координат, и эти объекты
называются скалярами. Скаляр не может иметь свободных индексов,
поэтому его можно обозначить как р. Если задан не просто скаляр, а
скалярное поле, т.е. скаляр <р(г) как функция точки пространства с
координатами г, то при замене координат г(г') эта функция изменяет¬
ся так, чтобы прежние значения соответствовали новым координатам
прежних точек:
ф(г')) = ¥>'(г')-
Если преобразования координат линейны, элементы матрицы Якоби
есть просто числа, и выражение для радиус-вектора точки после преоб¬
разования системы координат может быть записано в следующем виде:
дх‘ /к _ дх‘ ,к
и* = 	■
r\ fk	г\	/К
k дх	ох
По дважды повторяющемуся немому индексу принято всегда проводить
суммирование, поэтому знак суммы обычно опускается (правило сум¬
мирования).
Если преобразование координат нелинейно, закон преобразования
справедлив не для радиус-вектора, а для его дифференциала:
dx‘ = —kdx*.
О
дх
Вектором (или контравариантным вектором) называется совокупность
величин А\ которые при преобразовании системы координат изменя¬
ются так же, как и компоненты радиус-вектора:
А‘ = —kA'k.
dx'k
Производная скалярного поля по компонентам радиус-вектора — гра¬
диент — также будет многокомпонентной величиной, при этом ее вид
будет изменяться при преобразованиях системы координат с помощью
обратной матрицы преобразования. Такой объект принято называть
ковариантным вектором (ковектором) и обозначать буквой с индек¬
сом снизу:
др _ dip дх'к _ дх'к ,
дх1 ~ дх^~д7’’ U‘~~d7Uk'
При ортогональных преобразованиях законы преобразования вектора и
ковектора совпадают, и в таком случае отпадает необходимость разли¬
чать эти два объекта и вводить верхние и нижние индексы.

12
Глава 1. Теория поля
Если скалярное поле продифференцировать дважды по компонентам
радиус-вектора, возникнет совокупность величин, характеризующихся
уже двумя свободными индексами, которые преобразуются при замене
координат как произведение компонент двух ковариантных векторов:
Такие математические объекты называются ковариантными тензора¬
ми второго ранга. Соответственно, тензор (контравариантный тензор)
второго ранга — это совокупность величин с двумя верхними индекса¬
ми, которые преобразуются при замене системы координат как произве¬
дения соответствующих компонент двух векторов. Ранг тензора опре¬
деляется числом индексов. В общем случае тензор может быть любого
ранга и содержать как верхние, так и нижние индексы. При этом пози¬
ция индекса имеет значение:
В частности: скаляр — тензор без индексов, вектор —- тензор с одним
верхним индексом, ковариантный вектор — тензор с одним нижним
индексом.
Для тензоров определены следующие операции.
Свертка — суммирование по паре повторяющихся индексов, причем
один из них — верхний, а другой — нижний: Г4"’,/.... При свертке по
одной паре индексов ранг тензора понижается на два. Свертка также
определена для двух тензоров, при этом число пар одинаковых индексов
может быть любым, например: T'i—u...SA? "т/.... Заметим, что, вообще
говоря,
Свертка двух тензоров первого ранга есть не что иное, как их скалярное
произведение: Л'В, = (АВ).
Тензорное или кронекеровское произведение — поэлементное произ¬
ведение компонент тензоров, нумеруемых наборами различных индек¬
сов: Tti - ki...SP4 -mn.... При этом получается тензор, ранг которого равен
сумме рангов тензоров произведения.
Тензорное равенство — два тензора с одинаковым набором верхних
и нижних индексов равны
д2<р _ дх'1 дх!т d2tp _ дх'1 дх'т ^
дх'дхк	дх1дхт	=	~дз?~дР 1т
Pi-ki... = Т'рч"
дх‘ дх' дх'г dx's
rs -dx'p dx'q дхк дх1
если в любой системе координат разность соответствующих компонент
этих тензоров равна нулю. Таким образом, равенство двух тензоров

Введение
означает в М-мерном пространстве наличие системы Ns уравнений, где
s — ранг тензора. Отсюда следует, что векторы и тензоры позволяют
записывать физические соотношения в форме, которая не зависит от
выбора системы координат. Это достигается благодаря тому, что обе
части тензорного равенства при замене координат преобразуются по
одному правилу.
Правильно построенная комбинация тензоров автоматически дает
тензор, но для этого должны выполняться следующие правила баланса
индексов.
• Каждое слагаемое и каждая часть равенства должны иметь одина¬
ковые наборы свободных индексов: индексы с одними и теми же
именами должны стоять в одинаковых (верхних или нижних) по¬
зициях, причем в каждом члене имя каждого свободного индекса
встречается ровно один раз.
• В каждом слагаемом и каждой части равенства могут быть (или от¬
сутствовать) также немые индексы: каждый немой индекс в каждом
члене либо отсутствует, либо встречается ровно два раза (один раз
сверху и один раз снизу).
• Если в одном слагаемом какой-либо индекс встречается три раза
или более, то в формуле присутствует ошибка.
• Если в одном слагаемом какой-либо индекс встречается два раза свер¬
ху, или два раза снизу, то в формуле присутствует ошибка. (Либо мы
работаем с тензорами относительно ортогональных преобразований.)
• Мы можем переименовать какой-либо свободный индекс, если мы
одинаково изменяем его имя во всех слагаемых. При этом надо сле¬
дить, чтобы новое имя индекса не совпало с именем других ин¬
дексов, используемых в каждом слагаемом. Аналогично мы можем
подставить вместо свободного индекса его численное значение.
• Мы можем переименовать любой немой индекс в каком-либо сла¬
гаемом, одновременно заменяя имя обоих его вхождений. При этом
надо следить, чтобы новое имя индекса не совпало с именем других
индексов, используемых в слагаемом.
Можно получить тензор второго ранга, продифференцировав компо¬
ненты радиус-вектора по своим собственным компонентам, и при этом
получится симметричный тензор, компоненты которого инвариантны от¬
носительно любых преобразований координат:
Тензор 6‘k обычно называют символом Кронекера.

&
\
14	Глава 1. Теория поля
Среди различных инвариантов важное место занимает элемент дли¬
ны, квадрат которого есть (dl)2 = dx1 dxi. Поскольку это скаляр, его
величина должна оставаться неизменной при замене координат:
(dl)2 = dx'dxi = ^-r^-^dx,kdx'i.
дх'к дх‘
По определению множитель, стоящий перед dx'kdx' 1, есть смешанный
тензор второго ранга, который можно обозначить как glk. Если оба ин¬
декса будут внизу, получится ковариантный тензор второго ранга
_ дх‘ дх'
ёы~ дх,кдх'‘’
с помощью которого элемент длины можно записать, используя только
компоненты контравариантного вектора:
(dl)2 — gikdx‘dxk.
Тензор gik называется метрическим. Легко видеть, что контравариант-
ный тензор glk оказывается обратным к нему: gikgkl = S-. При замене
переменных метрический тензор преобразуется согласно определению:
_ дх1' дх'1 ,
gik ~ ~д7д7ё'1'
Для тензора второго ранга можно вычислить детерминант. Вычисляя
детерминант обеих частей, получаем g= (J~[)2g', или 77=
Метрический тензор можно использовать для поднимания и опус¬
кания индексов:
Ai = gikAk, Flj = glkFkj, а также
A% = gikA‘Bk = gikAkBi.
Существует еще один важный инвариантный тензор, ранг которого
равен рангу пространства, в котором рассматривается физический объ¬
ект. Это полностью антисимметричный относительно перестановки лю¬
бой пары индексов тензор, ранг которого совпадает с рангом простран¬
ства. Для определенности рассмотрим трехмерный случай, тогда пол¬
ностью антисимметричный тензор является тензором третьего ранга:
ем = —eka = еы‘. Благодаря свойству антисимметрии все 6 компонент
отличаются друг от друга только знаком. Принято определять значение
компоненты для правильного порядка индексов равным +1, т. е. в декар¬
товых координатах ет = ехуг = +1. Запишем связь компонент тензора,
полученных после замены переменных, с исходными:
iki _ <77 7TL P'pyr
дх'р дх'4 дх"

Введение -J\, 15
Выполняя суммирование по дважды повторяющимся индексам с учетом
чередования знаков в сумме, имеем
eikt = Je'ikl,
где J — якобиан преобразования. Если якобиан преобразования равен
единице, что, в частности, имеет место при чистых поворотах, ком¬
поненты тензора остаются неизменными1*. В трехмерном случае тен¬
зор ем называют символом Леви-Чивита.
2.	Векторы	и	тензоры в евклидовом пространстве
В евклидовом пространстве существуют выделенные си¬
стемы координат (декартовы координаты), в которых компоненты мет¬
рического тензора(г,/ — 1,2,3) задаются единичной матрицей. В этом
случае поднимание или опускание индекса не меняет значения компо¬
нент тензора. Матрицы Якоби для перехода между различными декар¬
товыми координатами всегда ортогональные (У-1 = JT), при этом век¬
торы с верхними и нижними индексами преобразуются одинаково.
Кроме специально оговоренных случаев мы будем использовать
для описания евклидова пространства декартовы координаты
г = (x,y,z) = (Х{,Х2,хз), что позволяет не различать верхние и ниж¬
ние индексы. Мы будем обозначать тензорные индексы для евклидова
пространства латинскими буквами и писать их снизу.
В евклидовом пространстве вектор принято обозначать жирной бу¬
квой, или буквой со стрелкой.
Преобразования декартовой системы координат, при которых нача¬
ло координат остается неизменным, сводятся к поворотам вокруг осей,
отражениям в плоскостях и инверсии. При поворотах якобиан / = +1,
при отражении и инверсии J = — 1. Следовательно, тензор eiki ведет себя
как тензор при преобразованиях поворота, но его компоненты изме¬
няют знак при преобразовании отражения. Иными словами, он ведет
себя не совсем так, как положено тензору, поэтому его часто называют
псевдотензором.
Скалярное, векторное и смешанное произведения в тензорных обо¬
значениях принимают вид
(ab) = aibi = dijaibj, (а х b], = etjkajbk, (a[b х с]) = eljkatbjCk.
Как видим, векторное произведение есть свертка псевдотензора и
Двух векторов по двум парам индексов, поэтому получающийся вектор
11 Наличие якобиана указывает, что определенный таким образом тензор
обладает свойствами плотности.

16	Глава	I.	Теория	поля
также не будет истинным и его принято называть псевдовектором или
аксиальным вектором.
Оператор дифференцирования (набла) V в декартовых координатах
есть вектор, компоненты которого имеют вид
В трехмерном евклидовом пространстве часто используемые основ¬
ные функции и операторы, имеющие инвариантный смысл, в тензорных
обозначениях записываются следующим образом:
Vy? = grady?, или grad уф =
OXi
[V х а] = rota, или rota|, = ву*V/a* = е,/*—,
С/Х j
(aV) = Va = а,-V,- — оператор дифференцирования вдоль а,
(VV) = div grad = Д = V, V,- — лапласиан,
div г =	= 3,
rot г|,- = [V X r]j = eijkVjXk = О,
= (aV)r|. = в/, или (aV)r = а,
grad г = - — n.
Интегральная теорема Гаусса в инвариантной форме:
IJI divA dV= JJJ (VA) dV = f(AdS)= f (An )dS.
Элемент поверхности (вектор нормали) направлен наружу.
Теорема Гаусса в тензорной форме:
(Va) = diva = V,ai = p,
OXi
V
v
s
s
V
V
s
s
Интегральная теорема Стокса в инвариантной форме:
JJ (rot A dS) = JJ (dS [V х А]) = f (Adi).
s
s
L

БИБЛИОТЕКА/* \
Московский
физико-технический институт
(государственный университет)
Введение
X
Теорема Стокса в тензорной форме:
дА
//(ro,A*S)s//
S	S
eiik~dXdSi
i = <j) A, dX{.
3.	Векторы	и	тензоры	в	пространстве	Минковского
В четырехмерном пространстве Минковского также суще¬
ствуют выделенные системы координат (лоренцевы координаты), кото¬
рые принято называть системами отсчета. В лоренцевых координатах
компоненты метрического тензора (метрики Минковского) записыва¬
ются в виде = diag(+l, —1, -1,-1) (р, и = 0,1,2,3). В этом случае
поднимание или опускание индекса может изменить знак компоненты
тензора, поэтому верхние и нижние индексы необходимо различать.
С помощью метрики g^v и обратной метрики g^v производится опус¬
кание и поднимание индексов:
/+1
О
О
О
guv = g‘u" = diag(+l, -1, -1, -1) =
\
0 0
-1 0
0 -1
о 0
V"-
o\
о
0
-4
И т.д.
(1.1)
V/i — ^ §fiV’
Тензорные индексы для пространства Минковского будут обозна¬
чаться греческими буквами.
Кроме специально оговоренных случаев мы будем использовать
для описания пространства Минковского лоренцевы координаты
х^ = х = (ct,x,y,z) = (ct, г) = (х°,х\х2,х3), где с — скорость света. Точ¬
ку в пространстве Минковского принято называть событием. Очевид¬
но, что
Хи = (x0,xi,x2,x3) = gM„x" = (х°,-х',-х2,-х3) = (х°, —г).
Часто вектор в пространстве Минковского обозначается буквой, под¬
черкнутой снизу: Ам = А.
Расстояние между двумя событиями s (длина 4-радиус-вектора) на¬
зывается интервалом, квадрат которого равен
s2 = guvix^x1') = хх = (ct)2 - г2.
В общем случае квадрат интервала s2 может быть положительным,
отрицательным, либо равным нулю. Принято называть s2 > 0 времени-
подобным (два события могут произойти в одной точке пространства,
но в разные моменты времени), s2 < 0 — пространственноподобным. На
мировой линии s = 0 (световой интервал).

X
18	Глава	l.	Теория	поля
Относительно преобразований с единичным якобианом (т. е. поворо¬
тов и других преобразований, сохраняющих объем и ориентацию бази¬
са) является тензором полностью антисимметричный тензор ем"а/3. В
четырехмерном случае его принято определять так:
_  gXflXlS _ _gX\l/fJL _	^0123	_	_j_|
В пространстве Минковского с помощью полностью антисимметрич¬
ного тензора е^\^ можно ввести объекты, дуальные скаляру, вектору
и антисимметричным тензорам второго, третьего и четвертого рангов:
1
О!6
Гг 1
Н
^	зельцу'
\cdt’ )'
Оператор дифференцирования в линейных координатах представляет
собой ковариантный вектор и записывается в виде
д Q (\д_
кс dt'
Далее (кроме специально оговоренных случаев) мы будем рассмат¬
ривать линейные преобразования координат, сохраняющие метрику
Минковского. Совокупность таких преобразований включает сдвиги,
пространственные отражения, обращение времени, пространственные
повороты, преобразования Лоренца и их всевозможные комбинации.
4.	Релятивистская	кинематика
Преобразование Лоренца определяет переход из одной инер-
циальной системы отсчета в другую. Для данного преобразования при¬
нят также термин буст. Контравариантные векторы и тензоры в четы¬
рехмерном пространстве принято также называть просто 4-векторами
и 4-тензорами. Стандартное преобразование Лоренца произвольного
4-вектора А^, определенное для случая, когда скорость V системы от¬
счета, движущейся относительно лабораторной, направлена по оси х,
имеет вид2)
(А'°\
( 7
-07
Ап
-Ду
7
А'2
0
0
Ч'3)
10
0
°\
О
О
ч
/А°\
А1
А2
2)	Для описания преобразования Лоренца наряду со скоростью используют
также быстроту в — вещественный параметр, связанный со скоростью соот¬
ношением th<? = V/c.

Введение _/\_ 19
Ковариантные векторы преобразуются с помощью транспонированной
обратной матрицы, которая получается заменой V на -V. Бусты вдоль
осей i/иг получаются соответствующими перестановками строк и столб¬
цов матрицы преобразования.
Контравариантный вектор и его компоненты принято записывать как
Afi = (А0, А) = (А0, А1), а ковариантный вектор соответственно как
Ац = (Ло.Л;) = (Л°,- А) = (А0, -А‘).
Скалярное произведение векторов равно
А*Вр = А= A^Bug^ = АцВиЦ^ = А°В° - АВ = А0В0 - А1 В1.
Элемент интервала между событиями, связанными с движением ча¬
стицы, выражается через ее скорость: ds = с dr = cdt\] 1 - {v/c)2, где
г — собственное время частицы (т.е. время в системе отсчета, где она
покоится) — является инвариантом. При определении четырехмерных
кинематических величин часто используется собственное время т, сов¬
падающее с точностью до множителя с (скорость света) с интервалом
вдоль времениподобной мировой линии.
4-Скорость и 4-ускорение имеют вид
dxм	( v\ „ dwM	d2xм	,,
^ = _ = (1.2)
dx^ ( v\ I,	duм	d2*''
~d?
Из определения 4-скорости и 4-ускорения получаем
и	dxм	dx^	dxn	ds2	,	ц	1	d	u	Л
= — M = — = 1,	и'2®	=	-	—	U^Uu	=	0.
ds ds ds ds rfs	^	2	ds	^
4-Импульс частицы массы m записывается как
= тси^ = (-,р) = {т'ус, myv)\ р =
\ С /	с
где £ — энергия, р — трехмерный импульс.
Энергия покоя £о = тс2 однозначно связана с массой частицы 3> и
представляет собой инвариант.
Общее определение массы может быть получено из инварианта:
Р^Рн = (|) - Р2 = т2с2.
1 Часто в теории относительности и физике элементарных частиц использу¬
ется система единиц, в которой с = 1. При этом для энергии, импульса и массы
используется общая единица измерения, в качестве которой обычно выступают
электрон-вольт (эВ) и производные единицы (1 кэВ = 103 эВ, 1 МэВ = 106 эВ,
1 ГэВ = Ю9 эВ, 1 ТэВ = 1012 эВ). Во многих случаях использование таких еди¬
ниц может специально не оговариваться.

20 ->\r Глава 1. Теория поля
Для безмассовой частицы 4-скорость не определена, но 4-импульс
все равно определен, в этом случае = т2с2 = 0.
Для системы частиц выполняется закон сохранения 4-импульса:
£р£ = £р'£.	(13)
а	b
где суммирование ведется по всем частицам до и после какого-либо вза¬
имодействия между ними (рассеяния, распада, реакции и др.). Суммар¬
ные энергия и пространственный импульс сохраняются, однако теперь
может не сохраняться как число, так и сорт частиц, а также сумма масс
всех частиц. Поэтому в левой и правой частях формулы (1.3) индекс сум¬
мирования обозначен разными буквами. Закон сохранения 4-импульса,
записанный в форме (1.3), очень удобен для решения различных задач с
использованием четырехмерных инвариантов, которые получаются вы¬
делением квадрата 4-импульса любой частицы или нескольких частиц,
входящих в указанное уравнение. Например, для двух частиц с извест¬
ными массами можно записать
Р'2Р2ц = (т2с)2 = (pf + Р% - р'П (pip + Р2Й - р!й).
Реализация метода 4-инвариантов зависит от рассматриваемого процесса.
Упругий процесс — процесс, в результате которого не изменяется ко¬
личество частиц и их сорта (в частности, не изменяются массы частиц).
Неупругий процесс — процесс, в котором изменяется число частиц
или их сорта (в частности, изменяются массы).
Среди кинематических задач, связанных с неупругими процессами,
важное значение имеет задача об определении порогов реакций, в кото¬
рых происходит рождение частиц, отличных от участвовавших в столк¬
новении. Энергетический порог реакции — это минимальное значение
кинетической энергии (Т = £ - тс2) налетающей частицы, необходи¬
мое для рождения новой частицы. Для системы частиц можно опре¬
делить эффективную массу, как энергию в системе центра инерции,
используя инвариантность квадрата 4-импульса:
МэффС2 =/4/W	(1-4)
Как следует из уравнения (1.4), энергия будет минимальной, если в
системе центра инерции частицы покоятся, тогда эффективная масса
просто равна сумме масс всех частиц после реакции:
^4эфф = ^ П1.ь ■
b

Введение _/\, 21
5	Уравнения	Максвелла
1)	Уравнения Максвелла в трехмерной форме. Уравне¬
ния Максвелла принято записывать в виде двух пар: без источников и
с источниками. В трехмерной форме они имеют вид
первая пара,
1 дЕ 4п. ~~ вторая пара,
с дГ + ~с]
Здесь Е — напряженность электрического поля, Н — напряженность
магнитного поля. Из второй пары уравнений Максвелла следует урав¬
нение непрерывности (закон сохранения заряда в дифференциальной
форме):
^ + div j = 0.
Плотности заряда и тока, создаваемые заряженными точечными части¬
цами, равны
p(r,t) = Y^eaS(r-ra(t)), j(r,0 = £>av(0d(r-ra(0),	(1-5)
а	а
где гa(t) — радиус-вектор частицы в момент времени t.
Первая пара уравнений Максвелла позволяет параметризовать элек¬
тромагнитное поле с помощью введения скалярного <р и векторного А
потенциалов:
H = rotA, Е = —grad
2)	Уравнения Максвелла в четырехмерной форме. Скалярный и
векторный потенциал вместе составляют компоненты 4-вектора Afl = (р, А),
при этом электрическое и магнитное поля, будучи производными от
компонент 4-потенциала по компонентам 4-радиус-вектора, представ¬
ляют собой компоненты 4-тензора электромагнитного поля:
/V = д^А„ - д^А^.
Компоненты электрического Е и магнитного Н полей следующим обра¬
зом связаны с компонентами антисимметричного тензора поля:
Ek = Ео*, Нк = -\-ekijF4,

J»-
22 г Глава /. Теория поля
и это можно представить наглядно в виде матрицы:
( 0
Ех
Еу
Ег )
-Ех
0
-Hz
Ну
-Еу
Нг
0
-Нх
\~Ег
-Ну
Нх
0 )
Введение тензора электромагнитного поля позволяет записать уравнения
Максвелла в четырехмерной форме, при этом первая пара определяется
4-дивергенцией дуального тензора F= (1 /2)ey‘'af3Fap:
dvF^y = 0	— первая пара,	(1.6)
duFyL/ = —	— вторая пара.	(1.7)
4-Вектор электрического тока имеет вид /д = (ср, j), а уравнение непре¬
рывности есть 4-дивергенция 4-плотности тока:
= о.
Потенциалы для заданного электромагнитного поля определены неод¬
нозначно: благодаря калибровочной симметрии всегда можно совер¬
шить калибровочное (градиентное) преобразование:
А' = А — grad/, <р' = <Г+^- или А'н =	+	<9М/,
где f(t,x,y,z) — произвольная функция. Данные преобразования остав¬
ляют напряженности электромагнитного поля Е и Н неизменными.
Для того, чтобы частично ограничить произвол, связанный с калибро¬
вочной симметрией, на потенциалы накладывают дополнительные, ка¬
либровочные условия, которые часто называют просто калибровкой.
Обычно используют следующие калибровочные условия:
д^Ау = ^^ + divA = 0 — калибровка Лоренца,
VA = 0	—	калибровка	Кулона,
<р = 0	—	калибровка	Вейля.
При подстановке явного выражения для тензора Fyv через компо¬
ненты 4-потенциала во вторую пару (1.7) имеем уравнение
dvdFAv - dvdvAy = -—'f.
В этом случае удобно выбрать калибровку Лоренца, чтобы получить
волновые уравнения для компонент 4-потенциала:
UAy = -—jy, где -д„ди =	= П	(1.8)
С	с2	dt2
— оператор Даламбера.

Введение _/\_ 23
После выбора калибровки Лоренца остается возможность подверг¬
нуть потенциалы остаточным калибровочным преобразованиям, ко¬
торые, по-прежнему не изменяя полей Е и Н, не нарушают калибровку
Лоренца:
А.'и =	+ Зм/, причем □/ = 0.
Электрическое и магнитное поля, будучи компонентами 4-тензора,
преобразуются при переходе из одной системы отсчета в другую со¬
гласно преобразованиям Лоренца для компонент 4-тензора. В случае
стандартного преобразования Лоренца имеем
и	и'	и _ Чу ~	и	—
П X — Г »	*■* U —	/	~	1	Z	—	/	 »
с	„	с _Е'у + (ЗН’г	с Z-PH'y
ЬУ- ^Zj2'
Заметим, что преобразование компонент электрического поля проще
получить, преобразуя дуальный тензор FM</.
Тензор электромагнитного поля F,#“/ вместе с дуальным тензором F
позволяет определить два инварианта электромагнитного поля:
F^F^ = 2(Н2 - Е2) = /i = inv, F^F^ = 4(ЕН) = /2 = ши. (1.9)
3)	Действие для электромагнитного поля. Уравнения для электро¬
магнитного поля и движения заряженных частиц в общей форме можно
получить, исходя из принципа минимума действия. В самом общем виде
действие представляется как сумма слагаемых, описывающих отдель¬
ные подсистемы и их взаимодействия, поэтому для электрически заря¬
женных частиц и электромагнитного поля, взаимодействующих друг с
другом, оно должно состоять из слагаемых трех типов:
5 = Spart + Sf|e|d + Sjnt,	(I-10)
т. e. действия для частиц, действия для поля и действия, описывающего
взаимодействие частиц и поля. В силу универсальности принципа ми¬
нимума действия, оно обязательно должно быть скаляром, т. е. в нашем
случае 4-инвариантом. При конструировании конкретных выражений
Для действия необходимо учитывать дополнительные условия, в част¬
ности, полученная теория должна быть калибровочно-инвариантна, и,
кроме того, обеспечивать правильный переход в известные выражения
в нерелятивистском пределе (принцип соответствия).
При получении уравнений для поля, взаимодействующего с заря¬
женными частицами, необходимо использовать второе и третье слагае-

24
Глава 1. Теория поля
мые в (1.10). Эти члены удобно выписать в виде действия для электро¬
магнитного поля с источниками:
Здесь интегралы вдоль мировых линий частиц записаны в виде инте¬
грала по пространству-времени и введен 4-вектор плотности тока:
где x%(sa) — 4-радиус-вектор а-й частицы, dxj}/dsa — ее четырехмерная
скорость (1.2), sa = ста — интервал, связанный с собственным временем
частицы, £<4)(х - Xa(s0)) = d(ct - x°(sa))<5(r - ra(sa)) — четырехмерная
(5-функция. Интегрируя в (1.12) по dsa при помощи (Д.7), приходим к
известному выражению (1.5). Заметим, что поскольку элемент четы¬
рехмерного объема d4x — скаляр, плотность лагранжиана £ — также
скалярная функция.
Компоненты четырехмерного потенциала поля являются здесь
независимыми обобщенными координатами, по которым вычисляется
вариация действия. Из условия минимума вариации действия по Лм,
т. е. (55[Лд(х)] = 0, получаем уравнение Эйлера для электромагнитного
поля:
из которого следует вторая пара уравнений Максвелла (1.7) (согласно
определению тензора Fпервая пара (1.6) выполняется тождественно).
4)	Тензор энергии-импульса. Взяв за основу действие для элек¬
тромагнитного поля Sneid (см. (1.10)) или первое слагаемое в (1.11), мож¬
но найти так называемый канонический тензор энергии-импульса:
Определение тензора энергии-импульса (1.13) вообще говоря неодно¬
значно: к нему можно добавить любой тензор 6Т^и с равной нулю
4-дивергенцией:
который обычно выбирают так, чтобы в итоге тензор энергии-импульса
был симметричным: Т^и = TVI1.
= /(-^ - г'"'4»)d<x - М<U1>
(1.12)
(1.13)
pa* _ Тци + 6TvV o^ST^) = о,

Введение -i\r 25
Симметричный тензор энергии-импульса электромагнитного поля
имеет вид
V" = -L	-	Я“^).
При переходе к трехмерным обозначениям тензор распадается на блоки:
JHU
( W
Sx/c
Sy/c
Sx/c\
Sx/c
<7XX
<7xy
о xz
Sy/c
<7ух
(7yy
Gyz
\Sz/c
<7 zx
<7xy
(Jzz /
(•s/c).
VS/c аи )
(1.14)
где плотность энергии w и вектор плотности потока энергии S (вектор
Умова-Пойнтинга) для электромагнитного поля равны
1
^(Е2 + н2),
Ап
[Е х Н].
Плотность импульса g и тензор напряжений cry электромагнитного поля
определяются как
6 = кг|Е * н| = ?■ ч- “	+	'■
Для замкнутой системы, состоящей из электромагнитного поля и
взаимодействующих с ним частиц, выполняется закон сохранения энер¬
гии-импульса:
&7ГоГ = 0,	(1.15)
и это является наглядной иллюстрацией теоремы Нётер, которая гово¬
рит о том, что инвариантности лагранжиана теории относительно ка¬
кого-либо однопараметрического преобразования соответствует локаль¬
ный сохраняющийся ток. В данном случае сохранение энергии-импуль¬
са отвечает инвариантности лагранжиана относительно пространствен¬
но-временных трансляций дУ1 —+	4-	ам.
Если же записать выражение для 4-дивергенции только тензора энер¬
гии-импульса поля, то вместо (1.15) мы получим
ВТ1
(1.16)
где 3^ есть плотность силы, действующей на систему зарядов со сто¬
роны поля. В трехмерном виде данное уравнение запишется как
^ + divS = -(jE),
(1.17)

■3?-
26 JL Глава !. Теория поля
6.	Движение	заряженной	частицы во внешнем поле
Уравнения движения заряженной частицы во внешнем элек¬
тромагнитном поле можно получить из общего принципа минимума дей¬
ствия, причем в данном случае необходимо использовать первое и тре¬
тье слагаемые в (1.10). Действие для одной частицы, взаимодействую¬
щей с полем, удовлетворяющее всем дополнительным условиям, можно
записать в виде
SIxWl = - / (-/fif +	-}l*.	0.18)
а	а
где пределы интегрирования указывают начальное и конечное положе-
ние частицы на мировой линии, L — соответствующая функция Лагранжа
(лагранжиан). Вариация действия (1.18) по координатам частицы xM(s)
при фиксированном поле Ар дает обычное уравнение Лагранжа, из ко¬
торого следуют уравнения движения частицы в ковариантной форме:
mc^f = -F^uv,	(1.19)
ds с
где ds = dxf* dx", и^ = dx^/ds — четырехмерная скорость части¬
цы (1.2). В трехмерной форме эти уравнения записываются как
^ = еЕ + - [v х Н|,	(1.20)
at	с
§ = e(Ev).	(1.21)
Правая часть в уравнении (1.20) представляет собой силу Лоренца, а
уравнение (1.21) (временная компонента (1.19)) есть не что иное, как
закон изменения энергии частицы.
Для системы с	распределенными зарядами	и	токами с	плотностями
соответственно р и	j обычно вводят понятие плотности силы	У (см.	(1.16))
У = р(Е + ^[v х Н] j так, что F = I d3г.
Тогда изменение энергии системы с распределенными зарядами прини¬
мает вид
^ = fd3 r(?v)= J d3r p(vE) = Jd3 r(jE).
Закон сохранения энергии в системе заряженных частиц и электромаг¬
нитного поля можно записать в интегральной форме (см. (1.17)):
dZ dW г,з ,. с dW г,с ...
= Jd"l'vi = -Tr-

Введение _/\, 27
где
d3r(E2 + Н2)
— энергия электромагнитного поля в объеме, через границу которого
вытекает энергия поля, уносимая вектором Пойнтинга, £ — энергия
заряженных частиц, находящихся в рассматриваемом объеме.
Вычисляя по общим правилам на основании (1.18) обобщенный 4-им¬
пульс P,j, = -dL/du^ = тсиц + (е/с)Аполучаем, что обобщенный
импульс заряженной частицы в электромагнитном поле отличается от
кинематического:
Р = р + -А.
с
Функция Гамильтона частицы во внешнем поле равна
[ЩР, г) щ \Jр2с2 + т2с4 + etp = (р - ^A(r) j с2 -I- т2с4 + etp(г).
7.	Статическое электромагнитное поле
Волновые уравнения для компонент 4-потенциала (1.8) пред¬
ставляют собой систему линейных неоднородных уравнений, решение
которых может быть записано в виде
А» =А?+А£,
где АЧ — общее решение однородного уравнения, а А? — частное ре¬
шение неоднородного уравнения, которое определяется распределением
зарядов. Общее решение однородного уравнения представляет собой
свободное электромагнитное поле, а частное решение неоднородного
уравнения может быть получено с помощью функции Грина, которая
удовлетворяет уравнению с точечным источником:
(А	- ^ Д W*; *■'. о = -4^(г	- r')W -	О-	(1-22)
V с dt /
Отсюда следует, что решение для А% имеет вид
А» = -cJ //i(r',f/)G(r,f;r',*V3r'df'.	(1.23)
Физическим условиям удовлетворяет решение	уравнения	(1.22) в форме
запаздывающей функции Грина:
=	(1-24)

X
28	Глава	I.	Теория	поля
Частное решение для компонент 4-потенциала (1.23) после интегриро¬
вания по времени принимает вид запаздывающих потенциалов:
А*( г, 0 = - [ nf''Mf-r1/^V,	(1.25)
к — г|
Самый простой вид частное решение волновых уравнений прини¬
мает в случае статического распределения зарядов и стационарных
токов, когда подынтегральная функция не зависит от времени. В этом
случае решение можно рассмотреть независимо для скалярного и век¬
торного потенциалов, из которых получаются соответственно статиче¬
ское электрическое и статическое магнитное поля.
Скалярный потенциал, создаваемый в точке R, равен
причем здесь приведены выражения для системы распределенных и то¬
чечных зарядов. На больших расстояниях от системы зарядов (|R| » |г|
или |R| » |га|) справедливо разложение по мультипольным моментам:
<p(R) = y?(0)(R) + y>(1>(R) + ¥><2)(R) + ...,
где
/»(R) = |;	^1)(Н) = Ш; yP »(R) = Mgi.	(1.26)
K	2IR
В выражениях (1.26) слагаемые разного порядка по малому параметру
разложения r/R -с 1 имеют смысл полного заряда (нулевого момента),
дипольного (первого) момента и квадрупольного (второго) момента и
для системы точечных зарядов равны
q = J2ea, d = J2 e“r“- Qil	faaiXaj	~ S,,r2a).	(1.27)
a	a	a
Заметим, что след тензора квадрупольного момента (инвариант) равен
нулю: Qu = 0.
Для системы распределенных зарядов сумма заменяется интегриро¬
ванием по плотности распределения зарядов р(г).
Аналогичное разложение по мультиполям имеет место и для энергии
взаимодействия системы зарядов с неоднородным статическим электри¬
ческим полем, если характерный масштаб неоднородности электриче¬
ского поля много больше характерных размеров системы зарядов:
t/ = Х>( R + Г а) = U{0) + t/(1) + и(2) + ...,	(1.28)
а

Введение -J\- 29
где соответственно
i/<°> = $>¥>( R) = W(R).
а
ц(х) = 82$) ^ваГа = _(dE)	t/<2) =	(1.29)
а	1	1
Сила, действующая на систему зарядов, определяется как F = —V(/,
и для системы зарядов, обладающей дипольным электрическим момен¬
том, равна
F = - V(t/(0) + t/(1)) = -qVy + V(Ed) = qE + (dV)E, (1.30)
причем здесь мы учли уравнение Максвелла для статического поля:
rot Е = 0.
Векторный потенциал, создаваемый в точке R, равен
A(R)= f i(r) d3г - У" eaVa
А(К) J c|R — r\ 2^c|R-re|*
где приведены соответственно выражения для системы распределен¬
ных, но ограниченных в пространстве токов, и движущихся точечных
зарядов, а черта означает усреднение по времени, поскольку ограничен¬
ное в пространстве распределение токов не может создаваться заряда¬
ми, движущимися с постоянной скоростью V.
При разложении векторного потенциала по мультипольным момен¬
там обычно ограничиваются первым (дипольным) отличным от нуля
членом, который имеет вид
A(1>(R) = --L f (Rr)j(r) d3r
и выражается через магнитный дипольный момент системы /х:
A(R) =	=	_[М х V]I	(1.31)
где введено обозначение:
M = ^/irxj]d3r = E|[r-xv“1-	<L32>
а
В нерелятивистском случае va = ра/та, поэтому магнитный момент свя¬
зан с моментами импульсов частиц:

30	Глава	1.	Теория	поля
\
где Ма — момент импульса частицы, не зависящий от времени в нашем
случае.
Величина, равная
* - й?	(1-34)
называется гиромагнитным отношением частицы. Если отношение
заряда к массе для всех частиц системы одинаково, можно ввести еди¬
ное гиромагнитное отношение для всей системы (равное 7), тогда маг¬
нитный момент связан с полным моментом импульса:
V =	^	М“	= ^М-	(135)
а
Во внешнем статическом неоднородном магнитном поле силу, действую¬
щую на систему токов, можно разложить по мультипольным моментам.
Обычно учитывается только взаимодействие с магнитным моментом:
F = i j [j(r) х H(R + г)] d3r = rot[Н x ц] = (/xV)H,	(1.36)
где	мы приняли во внимание, что в статическом случае div j	=	0,	а так¬
же	уравнение Максвелла divH = 0. Силу (1.36) можно получить,	введя
эффективную энергию Um магнитного момента в магнитном поле:
Um = -(МН), поэтому F —-VUm.	(1-37)
На систему токов также действует момент силы
К = ^ J [г х [j х Н]] d3г = -[Н х ц].
Под действием момента силы изменяется момент импульса системы в
соответствии с уравнением Лармора:
^ = К = [дхН|.	(1.38)
Если система токов создается зарядами с одинаковыми гиромагнитными
отношениями 7, уравнение (1.38) принимает вид
^=7[МхН] = -[ПхМ],	(1.39)
at
где введена ларморова частота = 7Н, вектор которой направлен
вдоль или против магнитного поля, в зависимости от знака 7 (т. е. заряда).

Введение -И- 31
д.	Свободное	электромагнитное	поле
Общее решение однородного волнового уравнения может
быть представлено в виде плоской волны, т. е. функции, зависящей толь¬
ко от аргумента t - пг/с, где единичный вектор п определяет направ¬
ление распространения поля. Общее решение для потенциалов принято
рассматривать в кулоновской калибровке, тогда
Е = -~ = --А; Н = rot А = --[п х А] = [п х Е].	(1.40)
с dt с	с
Поля Е и Н лежат в плоскости, перпендикулярной единичному вектору
п || г, таким образом, три вектора Е, Н и п взаимно ортогональны и
составляют правую тройку векторов, а поле оказывается поперечным.
Плотность потока энергии в плоской электромагнитной волне равна
S = -^[Е х Н] = -^Е2п - -^Н2п.
47Г	47Г	47Г
Плоская электромагнитная волна может быть разложена в интеграл
Фурье:
A(t, г) = j Ak,>(kr-“()	,	Ак,ш = J A(t, г) е-‘'<кг-“ Vг dt,
(1.41)
Действительная часть фурье-образа представляет собой частный слу¬
чай плоской волны:
A(t,r) = Re{AkuJe'<kr_a'<)}	(1.42)
и называется плоской монохроматической волной. Аргумент такой вол¬
ны (фаза волны) есть ujt — kr = w(t — nr/с), вектор к называется вол¬
новым вектором (|k| = k = из/с = 2п/Х, п = к/|к|). Фазу волны можно
представить в лоренц-инвариантном виде: cat — kr = k^x^, если ввести
четырехмерный волновой вектор:
*' = (?‘)' *"*„ = (f)2-k* = o.
Напряженности электрического и магнитного полей в плоской монохро¬
матической волне принято записывать следующим образом:
E(f,r) = Re{E0e,(kr-u")}, H(t, г) = Re{Hoe,(kr-"‘)}.	(1.43)
Электрическое поле в плоской монохроматической волне может быть
всегда представлено в виде
Е = Re{E0e‘(kr_u'^} = Re{(£0ie(1) + iE0 2e(2))e'<kr-u',)} =
= e(1)|£oi| cos(kr - ut - a) -p e(2)|£o2| sin(kr - ut - a), (1.44)

32
Глава 1. Теория поля
где е*1* и е*2* — единичные (в общем случае комплексные) векторы,
ортогональные друг другу и волновому вектору к. Поэтому с плоской
монохроматической волной можно связать локальный базис или репер,
образованный векторами е(1* и е(2), которые подчиняются условиям
Направление вектора электрического поля в локальной системе коор¬
динат называется поляризацией, которую удобно представлять в виде
единичного вектора е = Ео/|Ео| = eje(l) + еге(2). Плоская монохрома¬
тическая волна всегда поляризована. В локальной системе координат
вектор поля Е описывает эллипс. Если £02 = ±£01 — волна является
циркулярно поляризованной. Если £02 = 0 — волна линейно поляризо¬
вана (см. (1.44)).
Таким образом, линейную или циркулярную (круговую) поляриза¬
цию плоской волны можно задать, выбирая в качестве векторов локаль¬
ного базиса вещественные векторы е(|) и е(2) — для линейной поляри¬
зации или
е<±> = (1/\/2)(е(1> ± ;'е(2*) — для циркулярной поляризации.
9.	Запаздывающие потенциалы, излучение
при этом терять энергию, если поток энергии поля S через бесконечно
удаленную замкнутую поверхность отличен от нуля:
Для этого необходимо, чтобы поле излучения убывало на больших рас¬
стояниях от системы зарядов как
Величина /, определяющая потерю энергии в единицу времени, назы¬
вается интенсивностью излучения.
Такая зависимость полей от расстояния может быть получена из вы¬
ражения для запаздывающих потенциалов (1.25). На больших рассто¬
яниях электрическое и магнитное поле излучения представляют собой
сферическую расходящуюся волну, но связаны между собой так же, как
в плоской волне, т. е. в свободном электромагнитном поле, где теперь
единичный вектор распространения п направлен от излучающей систе¬
мы в точку наблюдения поля.
Для нерелятивистских систем зарядов запаздывающие потенциалы
могут быть разложены по мультиполям. В этом случае наряду с уже
имеющимся малым параметром а//?< 1, где а — характерный линейный
(е(1)*е(2)) = (е(|,2)п) = 0,	е(2)	=	[пх	е(1)].	(1.45)
Система зарядов может излучать электромагнитное поле и
(1.46)
Е,Н l^oo
R'

Введение
размер системы, появляется еще один, связанный с нерелятивистским
характером движения, v/c < 1, где v — характерная скорость движения
зарядов. Поскольку заряды совершают движение в ограниченном объе¬
ме, с ним также связано характерное время Т ~ а/и, что в разложении
запаздывающих потенциалов по плоским монохроматическим волнам
приводит к появлению характерной частоты поля ш ~ с/а » v/a = Т~1.
Таким образом, появляется еще один размерный параметр Л — харак¬
терная длина волны. В зависимости от соотношения между а, А и R
различают три области пространства, в которых рассматриваются поля,
получаемые из запаздывающих потенциалов:
1) квазистатическая зона: а<С/?<С А, в которой можно пренебречь
эффектами запаздывания;
2) индукционная (переходная) область: а < R ~ А, в которой сущест¬
венны эффекты запаздывания, но поле излучения еще не сформировано;
3) волновая зона: а < Л < R, в которой остаются только поля, убы¬
вающие с расстоянием как 1/7?.
Поскольку поля в волновой зоне связаны между собой так же, как
в плоской волне, удобно выбрать кулоновскую калибровку и рассмат¬
ривать только векторный потенциал:
где t' = t - R/c — запаздывающий момент времени, единый для всех
зарядов нерелятивистской системы.
Первый член разложения в формуле (1.47), т. е.
определяется электрическим дипольным моментом системы. Поле в
волновой зоне, создаваемое потенциалом (1.48), называется электри¬
ческим дипольным излучением и равно
причем правые части в (1.49) берутся в запаздывающий момент време¬
ни t' = t - R/c. Угловое распределение интенсивности электрического
Дипольного излучения описывается формулой
cR
(1.48)
[п х [п х d(f')]]
c2R
dl(t) =	1	н
dQ, 47гс2
,2 ИЮ X п]2
47Г С	t'=t—R/c
(1.50)

-Дг Гл
34	Глава	1.	Теория	поля
где dfl — элемент телесного угла, соответствующего направлению п.
Полная интенсивность электрического дипольного излучения равна
,	2d2
= 3?'
(1.51)
Второй член разложения (1.47) дает одновременно выражение век¬
торного потенциала, создаваемого магнитным дипольным и электриче¬
ским квадрупольным моментами: Аг = Am + Aq, где
t'=t—R/c
(1.52)
определяет магнитное дипольное излучение, а электрическое квадру-
польное равно
AQi(R,t) =
6 c?Rdt2 4
или
t'=t-R/c
Aq(r,o = -4-d(0
6 c2R
t'=t—R/c
(1.53)
Для удобства принято вводить вектор Д = ДуП/.
Магнитное поле излучения во втором порядке разложения имеет
следующий вид:
Нт + Hq =	[[№)	х	п]	хп]	+	_L[b(0 х п].
С м\	ОС к
Угловое распределение интенсивности излучения с учетом двух поряд¬
ков разложения содержит интерференционные («перекрестные») чле¬
ны, которые обращаются в ноль при интегрировании по углам, поэтому
полная интенсивность излучения во втором порядке разложения может
быть записана в виде суммы
1т+1°-^2 + Шс
А-
Потери энергии системой заряженных частиц на излучение можно
описать приближенно с помощью работы эффективной силы радиа¬
ционного трения. Например, для одной заряженной частицы можно
записать: / = (Fra(jv). Соответственно, для одной частицы имеем
2е
2е
Frad = t-tV = —т d
Зс
Зс
(1.54)

Введение	35
X
Для системы зарядов, излучающей в электрическом дипольном прибли¬
жении, остается справедливым последнее выражение в формуле (1.54).
Наряду с силой радиационного трения можно также ввести момент
сил, приводящий к потере момента импульса системы частиц:
d№	2	г	j	j-i
— = rd х d .
dt	Зс3 L
10.	Электромагнитное	поле	релятивистских	частиц
Излучение релятивистски движущихся частиц не удается
описать на языке мультипольных моментов, поэтому следует сперва рас¬
смотреть излучение одной релятивистской частицы, а для системы ча¬
стиц результат получается в соответствии с принципом суперпозиции.
Для одной частицы частное решение для компонент 4-потенциала (1.23)
следует записать с помощью запаздывающей функции Грина (1.24), где
плотность заряда и тока (1.5) соответствует одной точечной частице:
га = го(0. при этом v = го(0 — скорость частицы. Для векторного по¬
тенциала имеем
А(г, 0 = £ /	- r'l/c)v(0 <*(!■' - ГоЮ) d3r' dt. (1.55)
CJ k — г|
В результате вычислений4* находим, что векторный потенциал, созда¬
ваемый релятивистски движущимся зарядом, равен
А(г, 0 =
cR( 1 - (nv)/c) t,
Аналогичное выражение имеем для скалярного потенциала:
Ф, О
(1.56)
(1.57)
/?(1 - (nv)/c) /
Потенциалы (1.56) и (1.57) называются потенциалами Лиенара-Ви-
херта. В формулах (1.56) и (1.57) введены следующие обозначения:
R(t') = г - го(/'), R(t') = |R(0|. n(f) = R(t)/R(f) — единичный вектор
в направлении R. Правые части в этих выражениях берутся в запаз¬
дывающий момент времени t, который представляет собой решение
Уравнения
t'-t+ — = 0.	(1.58)
Детали вычислений см. в решении задачи 1.9.1.

V?
36 _J\y. Глава 1. Теория поля
X
Название «запаздывающее время» объясняется тем, что разность вре¬
мен t — t' = R(t')/c в точности равна времени распространения электро¬
магнитного поля из точки формирования го(0 до точки наблюдения по¬
ля. Дифференцирование выражения (1.58) по времени t' дает соотношение
** = 1 _ М,	(1.59)
dt	с
позволяющее установить связь между интервалами времени наблюде¬
ния и запаздывающего времени.
Из потенциалов (1.56) и (1.57) можно получить выражения для на¬
пряженностей электромагнитного поля:
, . _ e{c[w х n] + [п х [[у х w] х п]]}	е(1 - c2/c2)[v х n]
Щ	с3Д(1 - (nv)/c)3	cR2(\	- (nv)/c)3 ’	1	^
4\  е[п х [(п v/c) х w]j , е(1 — v2/c2)(n — v/c)	п
( ’ ’ ~ c2R(l - (nv)/c)3	+	/?2(1	-	(nv)/c)3	’	1>
где w = v(t') — ускорение заряда. Электромагнитное поле, описывае¬
мое формулами (1.60) и (1.61), всегда удовлетворяет условию H(r, t) =
= [п(0 х E(r, f)L т. е. вектор Н всегда перпендикулярен вектору Е и
единичному вектору, направленному от заряда в запаздывающий мо¬
мент времени в точку наблюдения.
На больших расстояниях от частицы в волновой зоне поле равно
Е = е[п ^|(п—wll Н = [п х Е].	(1.62)
c2R( 1 - (nv)/c)
Энергия электромагнитного поля de, испускаемая зарядом в элемент
телесного угла dfl в направлении n = R/Z? в течение интервала времени
t' -i-f + dt1, пройдет через элемент площади dS = R2dQ в течение вре¬
мени от t до t + dt, причем момент излучения f и момент наблюдения t
связаны соотношением (1.58). На больших расстояниях от излучающего
заряда (в волновой зоне, при |го| |г|) эта энергия равна
de = -£-|Е| 2R2dndt,
47Г
где Е определяется формулой (1.62). Поэтому интенсивность излуче¬
ния, т. е. энергия, регистрируемая наблюдателем в единицу времени,
равна
dl _ d2e _ е2 |[n х [(n — v/c) х w)]|2
dfi ~ dfi dt ~ W	(1 - (nv)/c)6
(1.63)

Введение	37
уточним, что формула (1.63) описывает угловое распределение интенсив¬
ности, полная интенсивность излучения / = de/cLt получается из (1.63)
в результате интегрирования по углам.
Чаще представляет интерес мощность излучения, т. е. энергия, излу¬
чаемая частицей в единицу запаздывающего времени Очевидно, мощ¬
ность равна с точностью до знака скорости потери энергии частицей:
Г=^ = -§.	(1.64)
at	at
Мощность отличается от интенсивности излучения. С учетом условия
dt = dt'(\ - (nv)/c) (см. формулу (1.59)) оказывается, что угловые распре¬
деления мощности и интенсивности связаны следующим соотношением:
.2
dW _ сГе _ (,	(nv)^	dl
dtt ~ dt'dn
Подчеркнем, что, как видно из (1.65), отличие мощности от интенсивно¬
сти особенно важно именно в релятивистском случае, если же v/c <С 1,
то различие между этими величинами исчезает.
Таким образом, скорость полных потерь энергии частицы равна
^ = -W=- [ _gLtnx Kn-v/c) х w]]2^n (I 66)
dt	J	47tc	(1	—	(nv)/c)
Непосредственное интегрирование в (1.66) по углам представляет неко¬
торые технические трудности, но для вычисления полной мощности из¬
лучения достаточно заметить, что величина dZ/dt' является реляти¬
вистским инвариантом, поэтому выражение для нее может быть запи¬
сано в релятивистски-ковариантной форме:
^ = |	(1.67)
где wм — вектор 4-ускорения частицы. В собственной системе отсчета
частицы К0, где ее мгновенная скорость равна нулю (vo = 0), выраже¬
ние для мощности излучения (1.67) принимает вид
dZ
dt'
_ dZ о _ 2e2Wo
д0 dt'o Зс3
где w0 — ускорение частицы в собственной (мгновенно сопутствующей)
системе отсчета. Полученная формула называется формулой Лармора.
Поскольку в лабораторной системе отсчета в момент времени t' вектор
4-скорости имеет вид (см. (1.2))
ии _ dx'1 _ dxм _	1	dx1'
ds cdT cVl - v2/c2 dt‘

38 _j\_ Глава I. Теория поля
компоненты 4-вектора ускорения частицы будут равны
Подставляя полученный результат в формулу (1.67), получаем обобще¬
ние формулы Лармора, называемое формулой Лиенара:
магнитной волны начинают ускоренно двигаться, что приводит к излу¬
чению электромагнитных волн. С другой стороны, поле падающей элек¬
тромагнитной волны совершает работу над системой зарядов и ее энер¬
гия поглощается. Таким образом, поле, излучаемое системой зарядов в
результате воздействия поля падающей волны, следует рассматривать
как поле рассеянной волны. Все процессы рассеяния принято описы¬
вать дифференциальным сечением рассеяния:
где dl — интенсивность излучения, уходящего от системы зарядов в
данном направлении в элемент телесного угла dfl в единицу времени,
|S| — плотность потока энергии поля, падающего на единицу площади
системы зарядов в единицу времени.
Обычно рассматривают рассеяние плоской монохроматической вол¬
ны, тогда получают спектральное разложение дифференциального се¬
чения рассеяния. В плоской монохроматической волне
Относительно просто рассмотреть рассеяние системами зарядов в
нерелятивистском приближении. Для одного заряда следует рассмат¬
ривать электрическое дипольное излучение, поэтому
(1.69)
11.
Рассеяние электромагнитных волн
Заряды в некоторой системе под действием поля электро-
ISI = £(Re{E0^-'>})2 = ±(£g, +El2).
dl е2
dn 4-7Г с3
где г определяется из уравнения движения в электрическом поле пада¬
ющей волны, поскольку в нерелятивистском случае действием магнит¬

Введение
ного поля можно пренебречь, а электрическое поле плоской монохро¬
матической волны с той же точностью можно считать однородным:
mr = еЕ + Frad, или г - ^ г = | Re{eE0e-‘“r}.	(1.70)
3 тс т
Частное решение уравнения движения запишем в виде
г =	j Re/ —^Е0е_,'ы<1, где 7 =
тш U + *7 J	3 тс
— естественная ширина линии излучения. Выражение для дифферен¬
циального сечения рассеяния (при условии 7 < 1) имеет вид
da ( е2 \2 [е(|) х п]2 + (£0|/Е02)2[е(2) х п|2	„	?1)
dQ	\тс2 )	1 + (Eo\/E0i)2
Полное сечение рассеяния получается интегрированием дифференци¬
ального сечения (1.71) по всем углам и равно
<тг = у rg,	(1.72)
где го = е2/(тс2) — классический радиус электрона. Сечение рассеяния
(1.72) называется томсоновским.
Рассеяние волны свободной частицей сопровождается действием на
частицу силы со стороны падающей волны. Средняя (по времени) дей¬
ствующая на частицу сила определяется средним значением импульса
поля, который поглощается частицей в единицу времени. Выражение
для силы можно представить в виде
F = arwn,	(1.73)
где а у — томсоновское сечение (1.72), w = E2/(Air) — средняя плот¬
ность энергии поля (импульс поля равен его энергии, деленной на ско¬
рость света), п — единичный вектор в направлении распространения
падающей волны.

ЗАДАЧИ
1.1.	ВЕКТОРЫ	И ТЕНЗОРЫ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
1.1.1. Показать, что скалярное произведение двух действительных
векторов инвариантно относительно преобразований системы
координат.
1.1.2. Показать, что билинейная комбинация, составленная из произве¬
дения компонентов двух векторов AtB, есть тензор второго ранга.
1.1.3. Показать, что тензор 5ц может быть представлен как
х _ дх‘
“ ~ ЭхГ
1.1.4. Убедиться, что тензор 5 ц инвариантен относительно ортогональ¬
ных преобразований системы координат.
1.1.5. Вычислить свертку 6ц.
1.1.6. Вычислить SijSjkSkiSu-
1.1.7. Вычислить eijkemnk-
1.1.8. Вычислить ецквщк.
1.1.9. Вычислить ецквцк.
1.1.10. Вычислить eijkejik-
1.1.11. Преобразовать выражение rot rot а.
1.1.12. Преобразовать выражение div [а х Ь].
1.1.13. Преобразовать выражение rot[a х Ь].
1.1.14. Преобразовать выражение grad(ab).
1.1.15. Считая вектор ц постоянным, вычислить div(/xr).
1.1.16. Вычислить grad(ptr).

/./. Векторы и тензоры в евклидовом пространстве	41
1.1.17. Вычислить rot[/x х г].
1.1.18. Вычислить div(/x/(r)).
1.1.19. Вычислить rot
1.1.20. Вычислить градиент экспоненты elkr.
1.1.21. Считая вектор А постоянным, вычислить div(Ae'kr).
1.1.22. Вычислить rot(Ae'kr).
1.1.23. Показать, используя свойства тензора ецк, что векторное про¬
изведение антисимметрично относительно перестановки сомно¬
жителей.
1.1.24. Используя свойства тензора , получить формулу двойного
векторного произведения:
[а х [Ь х с]] = b(ac) - c(ab).
1.1.25. Вычислить (aV)r.
1.1.26. Преобразовать интеграл fvf(r) div A(r) dV.
Использовать инвариантную и тензорную формы записи.
1.1.27. Используя инвариантную и тензорную формы записи, преобра¬
зовать в интеграл по поверхности объемный интеграл от выра¬
жения (grad /rot А).
1.1.28. В этом и следующих выражениях вычислить поверхностные ин¬
тегралы, связав их с объемными: $s(rdS).
1.1.29. §szdxdy.
1.1.30. Считая вектор с постоянным, вычислить fsr(cdS).
1.1.31. Считая вектор с постоянным, вычислить <fs(cr)dS.
11.32. fs[^Sx А].
11.33. Считая вектор с постоянным, вычислить $s(cdS)A.
1.1.34.	Преобразовать интеграл по контуру от скалярной функции к
поверхностному:
/м.
L
1-1.35. Доказать формулу:
^ [dr х г] = J dS.
L	S

42 _J\_ Глава I. Теория поля. Задачи
1.2.
ВЕКТОРЫ И ТЕНЗОРЫ
В ПРОСТРАНСТВЕ МИНКОВСКОГО
1.2.1. Вычислить е^инХе^н\.
1.2.2. Вычислить е'“'1<хери,>с\.
1.2.3. Вычислить eFv*cXepax\.
1.2.4. Вычислить дуальный к полностью антисимметричному тензору
6^1/х-л скаляр е в 4-мерном пространстве Минковского.
1.2.5. Выразить дважды дуальный тензор Fpv через исходный анти¬
симметричный тензор FpV.
1.2.6. Пусть Gp,v\ = dpFuX + dvFxp + d\Fpv. Записать Gx через FXfi.
1.2.7. Пусть Fpv = дрАи — dvAp. Записать FuX через A'/Xfi.
1.2.8. Выразить F^Fpv через антисимметричный тензор Fpv.
1.3.	РЕЛЯТИВИСТСКАЯ	КИНЕМАТИКА
1.3.1. Записать произведение двух последовательных преобразований
Лоренца для скоростей v\/c = i\\0\ и U2/c = th#2, направлен¬
ных вдоль оси х. Является ли результирующее преобразование
преобразованием Лоренца? Если да, то какой скорости v/c= th в
оно соответствует?
1.3.2. Показать, что матрица буста (преобразования Лоренца) вдоль
оси х может быть представлена в виде матричной экспоненты
Ах(0) = ехр{вах), где в — быстрота (v/c = th#), а ах — неиз¬
вестная пока матрица (генератор буста вдоль оси х). Найти в
явном виде матрицу ах. Записать матрицы бустов и генераторы
бустов вдоль осей у и г.
1.3.3. Показать, что матрица поворота R*(y?) на угол ip вокруг оси х
может быть представлена в виде матричной экспоненты R^(y?) =
= ехр(ipbx), где Ьх — неизвестная матрица (генератор поворо¬
та вокруг оси х). Найти в явном виде матрицу Ьх. Записать
матрицы поворотов и генераторы поворотов вокруг осей у и г.
1.3.4. Показать, что элемент объема d4x — с dt dx dy dz инвариантен
при поворотах, преобразованиях Лоренца и их комбинациях.
1.5. Начало координат системы К' движется со скоростью v отно¬
сительно системы К, а оси координат составляют со скоростью
v = (px,vy) те же самые углы, что и оси системы К. Записать
преобразование Лоренца от системы К к системе К'.

1.3. Релятивистская кинематика _/\- 43
1.3.6. Определить положение осей (х',у') системы К1 (см. задачу 1.3.5)
в системе К в момент времени t = 0 по часам системы К.
1.3.7. Пусть скорости систем отсчета К\, К2, и К' лежат в плоскости
{х,у) лабораторной системы К. Скорость системы К\ относи¬
тельно К равна V| = (У*, 0,0), а скорость системы К' относи¬
тельно К равна\=(Vx,Vy, 0). С какой скоростью v2 = (V2x, V2y, 0)
должна двигаться система К2 относительно системы К\, чтобы
она была неподвижна относительно системы К', т. е. чтобы ее
скорость относительно лабораторной системы К была равна ско¬
рости К' относительно К?
1.3.8. На какой угол будут повернуты оси координат системы отсче¬
та К2 по отношению к осям системы К'? (См. задачи 1.3.5, 1.3.7.)
vo.i
1.3.9. На частицу, движущуюся со скоростью v, действует сила, сооб¬
щающая ей ускорение v. Определить, с какой угловой скоро¬
стью будет поворачиваться спин частицы (прецессия Томаса)
относительно лабораторной системы отсчета, если сила, дей¬
ствующая на частицу, не действует на ее спин.
1.3.10. Два движущихся с одинаковой скоростью v вдоль одной пря¬
мой источника одновременно (в системе источников) испуска¬
ют световые импульсы. Расстояние между источниками (в си¬
стеме источников) составляет I.
С каким временным интервалом световые сигналы будут полу¬
чены приемником, расположенным на прямой, по которой дви¬
жутся источники, впереди по ходу движения?
1.3.11. Плоское зеркало движется со скоростью и в направлении своей
нормали. На зеркало падает монохроматическая волна с ча¬
стотой ис\ под углом в\ к нормали. Определить направление и
частоту отраженной волны, считая, что для покоящегося зер¬
кала справедлив обычный закон отражения. Указание: ввести
4-мерные волновые векторы.
1.3.12. Перейдите в равномерно вращающуюся систему отсчета (систе¬
му отсчета наблюдателя, движущегося равномерно по окруж¬
ности). Как в этой системе отсчета выглядит метрический тен¬
зор? Пусть один из близнецов остается в покое, а другой дви¬
жется по окружности. Кто из близнецов будет младше, когда
они встретятся?
1-3.13. Определить разность фаз при распространении света с часто¬
той ш по и против часовой стрелки по вращающемуся кольце¬
вому волноводу радиуса R с коэффициентом преломления п.

44
Глава 1. Теория поля. Задачи
Данный эффект называется эффектом Саньяка и использу¬
ется для определения угловой скорости вращения в лазерных
гироскопах.
1.3.14.	На плоскости, имеющей щель ширины I, находится наблюдатель
и видит, что со скоростью (Vx, Vy) в сторону щели летит стер¬
жень, который параллелен плоскости и имеет длину L > I (ось х
параллельна плоскости, а ось у перпендикулярна ей). Скорость
стержня такова, что в системе отсчета наблюдателя стержень
имеет длину чуть меньше I. Пролетит ли стержень сквозь щель,
если учесть, что в системе отсчета стержня сокращается как
раз ширина щели? Какой конец стержня пролетит через щель
первым, с точки зрения наблюдателя и с точки зрения стержня?
5.	Частицы с массами т\ и т-2 имеют импульсы pi и рг. Определить:
1) скорость системы центра инерции;
2) энергию в системе центра инерции;
3) энергию второй частицы в системе, в которой первая частица
покоится;
4) относительную скорость частиц.
1.3.16.	В ускорителе производится столкновение потока частиц мас¬
сой т и энергией £ » тс2 с неподвижной мишенью, состоящей
из частиц с той же массой. Определить эффективную массу
пары частиц из пучка и из мишени и скорость системы центра
инерции пары. В качестве примера рассмотреть столкновения
ускоренных протонов (me2 = 1 ГэВ) с неподвижными протона¬
ми (фиксированная мишень) при энергии протонов:
1) £ = 70 ГэВ (Серпуховский ускоритель);
2) £ = 1 ТэВ (Ускоритель лаборатории Ферми, Батавия, США);
3) £ = 7 ТэВ (Большой адронный коллайдер, ЦЕРН, Женева).
1.3.1,7.	В ускорителе на встречных пучках сталкивается поток частиц
с массой т\ и энергией £i mic2 и встречный поток частиц
с массой m2 и энергией £2 тгс2. Определить эффективную
массу пары частиц из первого и второго пучка и скорость си¬
стемы центра инерции пары. Дать численный ответ для встреч¬
ных пучков протонов с энергией £1 = 800 ГэВ и электронов с
энергией £2 = 30 ГэВ (ускоритель «Гера», Германия).
1.3.18.	Какой энергии £' нужно достичь в ускорителе с неподвижной
мишенью, чтобы в системе центра инерции получить такую же
энергию, как и в ускорителе на встречных пучках 7 ТэВ х 7 ТэВ,
т\с2 = /Я2С2 = 1 ГэВ (Большой адронный коллайдер)?

1.3. Релятивистская кинематика	45
1 3.19. Показать, что энергию е и проекцию импульса рх на ось х для
частицы с массой т можно параметризовать, как е = т± cha,
Рх = sh а, где т\ = т2 + р2у + р2г, th а = vx. (В данной зада¬
че мы используем единицы, в которых с = 1.)
1.3.20. 7г°-Мезон пролетает расстояние L и распадается на два 7-кванта,
вылетающих под углами а и /3 к его скорости. Определить вре¬
мя жизни 7г°-мезона в его системе покоя.
1.3.21. Определить массу т частицы, зная, что она распадается на две
частицы с массами т\ и m2, если из опыта известны импульсы
pi и рг этих частиц.
1.3.22. Определить массу т\ некоторой частицы, зная, что она пред¬
ставляет собой одну из двух частиц, образовавшихся при рас¬
паде частицы с массой т и импульсом р. Масса m2 и импульс рг
второй частицы известны из опыта.
1.3.23. 7г°-Мезон, летящий со скоростью v, распадается на два 7-кванта.
Определить минимальный угол разлета 7-квантов 0min.
1.3.24. Ультрарелятивистская частица с массой т и энергией ео упруго
рассеивается на неподвижном ядре с массой М^> т. Опреде¬
лить зависимость конечной энергии частицы е от угла рассеяния в.
1.3.25. Частица с массой mi и скоростью v сталкивается с покоящейся
частицей массы m2 и поглощается ею. Найти массу М и ско¬
рость V образовавшейся частицы.
1.3.26. Ультрарелятивистская частица с массой m и энергией ео рассеи¬
вается на неподвижном ядре с массой М»ти возбуждает его.
Энергия возбуждения ядра Д£ в системе его покоя удовлетво¬
ряет неравенству тс2 -С Д£ -С Мс2. Определить зависимость
конечной энергии частицы е от угла рассеяния в.
1.3.27. Квант света с частотой шо рассеивается на движущемся свобод¬
ном электроне с импульсом ро, составляющем угол во с направ¬
лением распространения кванта (эффект Комптона). Найти
зависимость частоты ш рассеянного фотона от направления его
движения.
1.3.28. Фотон с энергией е = 2 эВ рассеивается на летящем навстречу
в противоположном направлении ультрарелятивистском элек¬
троне с энергией £ = 200 ГэВ е. Найти максимальную энер¬
гию рассеянного фотона. При каком соотношении £, е и массы
электрона m это достигается?

46 -Лг Глава 1. Теория поля. Задачи
Jrz
14
Для нейтрино, образующихся при распаде 7г-мезонов с энер¬
гией 6 ГэВ (масса д-мезона т^с2 « 140 МэВ, масса /х-мезона
тмс2 я» 105 МэВ), определить энергетический спектр, их мак¬
симальную и среднюю энергии и угловое распределение, если
известно, что в системе покоя 7г-мезона распад 7г—*■ р + и про¬
исходит изотропно. Определить характерный интервал углов
вылета нейтрино. Построить графики распределений нейтрино
по углу вылета и энергии.
1.3.30. 7г°-Мезон, летящий со скоростью v, распадается на два 7-кванта.
Найти угловое распределение 7-квантов dw/dQ. в лабораторной
системе отсчета, если в системе покоя 7г°-мезона оно сфериче¬
ски симметрично.
1.3.31. При распаде /Г-мезона К —»- д + е + и определить максимальную
возможную энергию для каждой из трех возникающих частиц.
Считать, что тдс2 = 500 МэВ, тес2 = 0,5 МэВ, тжс2 = 135 МэВ,
ти = 0.
1.3.32. Ускоренный протон сталкивается с покоящимся протоном мише¬
ни. В реакции образуются частица а и античастица а: р -Г р—►
—► р + р + а + а. Найти энергетический порог этой реакции, ес¬
ли частица а — это а) протон р (масса — 1 ГэВ), б) дейтон d
(масса — 2 ГэВ), в) а-частица (ядро гелия 4Не, масса — 4 ГэВ).
1.3.33. В ускорителе со встречными пучками идет реакция е+ + е~ —*-
—> р++р~- Зная энергию электронов и позитронов, найти энер¬
гию и импульсы мюонов. Каков энергетический порог этой ре¬
акции? Сравнить с порогом в случае, когда ускоренные пози¬
троны налетают на неподвижные электроны. Масса электро¬
на — тес2 — 0,5 МэВ. Масса мюона — т^с2 = 100 МэВ.
1.3.34. Протон с энергией £ = 3 ГэВ, рассеиваясь на протоне мишени,
передает ему энергию е = 1 МэВ. Определить угол рассеяния
в системе центра инерции и в лабораторной системе отсчета.
1.3.35. Как связаны в ультрарелятивистском пределе углы рассеяния
двух одинаковых частиц массы т друг на друге в системе непо¬
движной мишени и в системе центра инерции? Энергия нале¬
тающей частицы в системе мишени равна £.
1.3.36. Свободное ядро массой М имеет возбужденное состояние, энергия
которого на величину е превышает энергию основного состояния.
1) Возбужденное ядро испускает 7-квант и переходит в основ¬
ное состояние. Найти энергию 7-кванта.
2) Определить, какую энергию отдачи получит при этом ядро.

г
1.4. Уравнения Максвелла
3)	Определить, с какой минимальной скоростью должно двигать¬
ся возбужденное ядро, чтобы испущенный им 7-квант мог воз¬
будить неподвижное ядро, находящееся в основном состоянии.
1 3.37. Определить максимальную энергию нейтрино, рождающихся при
/3+-распаде ядер
13N—► 13С + е+ + ve и 15O—*■ 15^	+ ие,
предполагая, что протоны с равномерной плотностью распределены
по объему ядер, размер которых До = 1,5 • Ю-13^1/ см (где А —
массовое число), а энергия связи протонов и нейтронов одина¬
ковы. (Разность масс нейтрона и протона тпс2 - трс2 = 1,29 МэВ.)
1.4.	УРАВНЕНИЯ	МАКСВЕЛЛА
1.4.1. Выведите из уравнений Максвелла волновые уравнения для элект¬
ромагнитного поля.
1.4.2. Два уравнения Максвелла позволяют вычислить производные
по времени от полей Е и Н, если эти поля заданы в на некото¬
рой гиперплоскости t = const:
не содержат производных по времени, поэтому их выполнение
может быть проверено на отдельной гиперповерхности t = to-
Пусть уравнения (2) проверены для начальных условий, заданных
в некоторый момент времени t = to- Далее поля Е и Н вычисле¬
ны для произвольных моментов времени с помощью уравнений (1).
При каком условии уравнения (2) будут справедливы при про¬
извольном t, отличном от to?
1-4.3. Модифицировать первую пару уравнений Максвелла, включив
в нее плотность магнитных зарядов (магнитных монополей) рт
и плотность тока магнитных монополей jm таким образом, чтобы
для них выполнялось уравнение непрерывности. Решить зада¬
чу 1.4.2 для модифицированных уравнений.
1-4.4. Переписать уравнения Максвелла в терминах комплексного
векторного поля F = Е + г'Н. Как изменится такая форма урав¬
нений Максвелла в присутствии магнитных монополей (см. за¬
дачу 1.4.3)?
— = -crotE, — = crotH - 47rj.
at	at
(1)
Другие два уравнения Максвелла
divH = 0, div Е = 47Г/9
(2)

Глава /. Теория поля. Задачи
,1.4.5. Подставив в уравнения Максвелла (в трехмерном виде) выра¬
жения для полей Е и Н через потенциалы ip и А, получить
полевые уравнения для потенциалов.
К какому виду при этом сводится первая пара уравнений Макс¬
велла?
1.4.6. Подставив в уравнения Максвелла (в четырехмерном виде) вы¬
ражения для полей Fpv через потенциалы Ам, получить поле¬
вые уравнения для потенциалов.
К какому виду при этом сводится первая пара уравнений Макс¬
велла?
1.4.7. Какой вид принимают полевые уравнения для потенциалов при на¬
ложении калибровочного условия = 0, т. е. ^ ^ + div А — О
(калибровка Лоренца) в трехмерных и четырехмерных обозна¬
чениях?
1.4.8. Какой вид принимают полевые уравнения для потенциалов при
наложении калибровочного условия div А = 0 (калибровка Ку¬
лона) в трехмерных обозначениях?
1.4.9. Какой вид принимают полевые уравнения для потенциалов при
наложении калибровочного условия р — 0 (калибровка Вейля)
в трехмерных обозначениях?
1.4.10. В калибровке р = 0 параметризовать постоянное однородное
электромагнитное поле общего вида (Е и Н — два произволь¬
ных постоянных вектора) с помощью векторного потенциала А.
1.4.11. Для потенциалов = (р, А) общего вида найти калибровоч¬
ные преобразования, после выполнения которых будут выпол¬
нены калибровочные условия:
1)	=	0, т. е.	+ div А = 0 (калибровка Лоренца);
2) div А = 0 (калибровка Кулона)-,
3) р = 0 (калибровка Вейля).
1.4.12. Найти вид остаточных калибровочных преобразований (усло¬
вие на функцию /) для каждой из калибровок:
1) <9МАМ = 0, т. е.	+ div А = 0 (калибровка Лоренца)-,
2) div А = 0 (калибровка Кулона)-,
3) р = 0 (калибровка Вейля).

1.5. Движение заряженной частицы во внешнем поле
\ 4 13. Показать, что из условия инвариантности действия для электро¬
магнитного поля относительно калибровочных преобразований
следует уравнение непрерывности для зарядов и токов.
1 4.14. Действие для электромагнитного поля имеет вид (см. (1.11))
Получить тензор энергии импульса 7’м'/ согласно формуле (1.13).
Является ли данный тензор калибровочно-инвариантным?
1.4.15. Подобрать такую добавку 5Т,1и к тензору энергии-импульса из за¬
дачи 1.4.14, чтобы новый тензор энергии импульса Т^ = T'^+ST^
был симметричен, причем д^6Т^ = 0 при условии выполнения
уравнений Максвелла без источников. Является ли тензор
калибровочно-инвариантным?
Проверить, что dtlT,JV = 0 в отсутствие источников поля.
1.4.16. Вычислить <9М7’М" для тензора из задачи 1.4.15 при наличии за¬
рядов и токов. Получить уравнения баланса энергии-импульса.
1.4.17. Найти след тензора энергии-импульса для электромагнит¬
ного поля.
1.4.18. Найти давление на обкладку плоского тонкого конденсатора
без диэлектрика:
1) исходя из плотности силы рЕ;
2) исходя из перепада давления электрического поля.
1.4.19. Найти давление на стенку соленоида без сердечника:
1) исходя из плотности силы ^ [j х Н];
2) исходя из перепада давления магнитного поля.
1 -5-	ДВИЖЕНИЕ	ЗАРЯЖЕННОЙ	ЧАСТИЦЫ
ВО ВНЕШНЕМ ПОЛЕ
1-5.1. Для релятивистской частицы доказать, что мощность силы (vF)
равна скорости изменения энергии.
1.5.2.	Рассмотреть особенности движения релятивистской частицы с
зарядом е, и массой m в скрещенных однородных полях Е и Н,
угол между которыми равен в.

Глава 1. Теория поля. Задачи
1.5.3. Определить координаты г и время t заряженной частицы в ла¬
бораторной системе отсчета как функции собственного време¬
ни т при ее движении в постоянном однородном электрическом
поле Е. В начальный момент времени частица находилась в
начале координат и имела энергию £о и импульс ро.
1.5.4. Определить координаты г и время t заряженной частицы в ла¬
бораторной системе отсчета как функции собственного време¬
ни т при ее движении в постоянном однородном магнитном
поле Н. В начальный момент времени частица находилась в
начале координат и имела энергию £о и импульс ро-
1.5.5. Определить координаты г и время t заряженной частицы в ла¬
бораторной системе отсчета как функции собственного време¬
ни т при ее движении в постоянных однородных электрическом
и магнитном полях, перпендикулярных друг другу. В началь¬
ный момент времени частица находилась в начале координат и
имела энергию £о и импульс ро.
1.5.6. Определить траекторию движения заряженной частицы во вза¬
имно перпендикулярных и равных друг другу однородных элек¬
трическом и магнитном полях.
1.5.7. Найти кинетическую энергию частицы (Т — £ — тс2) как функ¬
цию собственного времени т при движении ее в постоянных
однородных электрическом и магнитном полях, параллельных
друг другу Е || Н. В начальный момент времени частица поко¬
илась в начале координат.
1.5.8. Определить координаты г и время t заряженной частицы в ла¬
бораторной системе отсчета как функции собственного време¬
ни т при ее движении в постоянных однородных электрическом
и магнитном полях, параллельных друг другу. В начальный мо¬
мент времени частица находилась в начале координат и имела
энергию £о и импульс ро.
1.5.9. Найти кинетическую энергию частицы (Т = £ — тс2) как функ¬
цию собственного времени г при движении ее в постоянных
однородных электрическом и магнитном полях, перпендикуляр¬
ных друг другу Е J. Н. В начальный момент времени частица
покоилась в начале координат.
1.5.10.	Найти время торможения tropM и длину пробега I до остановки
релятивистской заряженной частицы с зарядом е, массой т и
начальной энергией £о в тормозящем однородном электриче¬
ском поле Е, параллельном начальной скорости частицы.

1.5. Движение заряженной частицы во внешнем поле	51
1 5.11- Пучок 7г+-мезонов с начальным импульсом /?о = 200 МэВ/c вво-
Ф дится в линейный ускоритель. Какова должна быть напряжен¬
ность ускоряющего поля Е, чтобы, по крайней мере, половину
пионов удалось ускорить до энергии £ = 200 ГэВ? Какую дли¬
ну должен при этом иметь ускоритель?
Масса 7г+-мезона тс2 — 140 МэВ. Время жизни 7г+-мезона
тж+ = 2,6 ■ 10~8 с, а время полураспада 7г+—►д+ + ь'м равно
Т\/2 = тп+ 2.
1.5.12. Определить частоты колебаний заряженного изотропного про¬
странственного осциллятора, находящегося в постоянном одно¬
родном магнитном поле; собственная частота колебаний (при
отсутствии поля) равна шо (классический эффект Зеемана).
1.5.13. Доказать, что для нерелятивистского электрона (заряд равен -е,
масса равна т), движущегося в поле ядра (заряд — Ze, масса —
М) сохраняется вектор Рунге-Ленца
А = Ze2- --[р х М), ! = 1 + i-, М=[гхр].
г р	р	т	М
1.5.14. По бесконечно длинному прямому цилиндрическому проводу
радиуса г течет ток J. С поверхности провода срывается элек¬
трон, начальная скорость которого vo параллельна оси провода.
Найти наибольшее расстояние R, на которое электрон может
удалиться от оси проводника.
1.5.15. Релятивистская частица с массой т и зарядом е движется в од¬
нородном магнитном поле. Определить изменение энергии ча¬
стицы за один оборот в случае, когда магнитное поле медленно
меняется со временем (так, что изменение поля за период дви¬
жения мало по сравнению с самим значением поля). Доказать,
что величина р2±/Н остается постоянной (является адиабати¬
ческим инвариантом). Вычислить изменение радиуса орбиты и
энергии частицы, если поле изменилось от значения Н\ до #2.
1-5.16. Найти в нерелятивистском случае уравнение движения веду¬
щего центра орбиты заряженной частицы, если магнитное поле
мало меняется на расстояниях порядка радиуса орбиты.
1-5.17. На больших расстояниях магнитное поле Земли представляет
собой поле диполя с магнитным моментом р — 8,1 • 1025 Гс • см3.
Захваченные магнитным полем Земли заряженные частицы сол¬
нечного ветра дрейфуют от полюса к полюсу вдоль силовых
линий в областях, называемых радиационными поясами.

52	Глава	I.	Теория	поля.	Задачи
а) Предполагая, что скорость частицы на экваторе составляет
угол а с плоскостью экватора, определить максимальную ши¬
роту (полярный угол), достигаемую частицей. Найти угол а,
при котором частица достигнет поверхности Земли, если рас¬
стояние от Земли, на котором частица находилась в экватори¬
альной плоскости, значительно больше радиуса Земли.
б) Найти период дрейфа вокруг Земли протона с энергией 10 МэВ,
движущегося в экваториальной плоскости на расстоянии 30000 км
от центра Земли.
1.6.	СТАТИЧЕСКОЕ	ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
1.6.1. Определить квадрупольный момент однородно заряженного эл¬
липсоида относительно его центра.
1.6.2. Найти электрическое поле однородно заряженного по объему
эллипсоида на больших расстояниях с точностью до четвертого
порядка по 1/R.
1.6.3. Определить квадрупольный момент равномерно заряженной ни¬
ти длиной /, если ее заряд равен q. Поместить начало координат
в середину нити.
1.6.4. Вычислить тензор квадрупольного момента нейтральной системы
зарядов, в которой два заряда +q помещены в точках (+а, +а, 0)
и (-а,-а, 0), а два заряда — q помещены в точках (+а,-а, 0)
и (-а,+а,0). Найти систему координат, в которой искомый
тензор имеет диагональный вид.
1.6.5. Определить энергию системы зарядов предыдущей задачи, по¬
мещенной во внешнее однородное электрическое поле Е.
1.6.6. Два разноименных и одинаковых по величине заряда жестко за¬
креплены на расстоянии I друг от друга. Найти силу и момент
силы, действующих на данную систему, помещенную в поле
точечного заряда на расстоянии R I.
1.6.7. Записать энергию £(di,d2,R) взаимодействия диполя db на¬
ходящегося в начале координат, и диполя d2, находящегося в
точке R.
1.6.8. Пусть диполь di направлен вдоль оси г. Получить разложение
энергии £(di,d2,R) при фиксированных di, d2, |R| по сфериче¬
ским гармоникам.

1.7. Свободное электромагнитное поле	53
Я
1 6.9. Потенциал V(r) аксиально-симметричной системы зарядов на
оси z имеет вид
V(0,0,z) = Vo(l- 7^ оУ z>a-
V z\/z2 + а2 )
Найти два главных члена разложения V(r, в) в области г > а.
1.6.10. Тело, ограниченное близкой к сфере поверхностью (сфероид) с
уравнением
/?(0) = /?о[1 + /9/,2(cos 9)\,
заряжено с постоянной плотностью (ЯгМ — полином Лежанд¬
ра). Полный заряд равен q. Найти мультипольные моменты сфе¬
роида в линейном порядке по /3.
1.6.11. Показать, что однородное магнитное поле Н, направленное по
оси z, может быть описано векторным потенциалом А] = (0, Нх, 0).
Градиентным преобразованием перейти к потенциалу Аг = g [Н х г].
1.6.12. Магнитное поле, имеющее составляющую вдоль оси z, убывает
вдоль этой оси с постоянным градиентом дНг/дг = -h = const.
Может ли такое поле быть параллельным оси z во всем про¬
странстве? Найти радиальные компоненты поля вне оси z. Пред¬
ставить картину силовых линий.
1.6.13. Получить формулу F = (//V)H для силы, действующей на маг¬
нитный диполь в неоднородном поле.
1-6.14. Найти в полярных координатах уравнение силовой линии маг¬
нитного диполя. Определить, как меняется поле вдоль силовой
линии.
1.6.15.	Определить энергию взаимодействия магнитного диполя р,
движущегося со скоростью v « с с неподвижным ядром с за¬
рядом Ze.
1 7-	СВОБОДНОЕ	ЭЛЕКТРОМАГНИТНОЕ	ПОЛЕ
1-7.1. Каким условиям должны удовлетворять комплексная амплиту¬
да плоской монохроматической волны Aq = (Ац, Ао) и волновой
4-вектор = (ш/с, к)?
1 ~ 2. Найти тензор энергии-импульса плоской линейно поляризован¬
ной монохроматической бегущей волны.

J?-
54 ->V Глава I. Теория поля. Задачи
1.7.3. Найти тензор энергии-импульса плоской линейно поляризован¬
ной монохроматической стоячей волны.
1.7.4. Показать, что скалярный потенциал произвольного свободного
электромагнитного поля можно обратить в нуль с помощью оста¬
точного калибровочного преобразования, не нарушая калибров¬
ки Лоренца.
1.7.5. Записать уравнения Максвелла для амплитуд Фурье, получа¬
ющихся при разложении произвольной плоской волны по моно¬
хроматическим плоским волнам.
1.7.6. Получить выражение для амплитуд Фурье плоской монохрома¬
тической волны.
1.8.	ЗАПАЗДЫВАЮЩИЕ	ПОТЕНЦИАЛЫ, ИЗЛУЧЕНИЕ
1.8.1. Определить электрическое и магнитное поле гармонически ко¬
леблющегося диполя на расстояниях г, много больших размера
диполя а, но не обязательно больших длины волны Л.
1.8.2. Доказать, что у замкнутой системы заряженных частиц с одина¬
ковым отношением заряда к массе отсутствует дипольное элек¬
трическое и дипольное магнитное излучение.
1.8.3. Два разноименных заряда (е\,т\) и (ег.тг) обращаются один
вокруг другого под действием кулоновского притяжения по кру¬
говой орбите радиуса R (атом Резерфорда). Определить энер¬
гию, теряемую на излучение за один оборот. Найти зависи¬
мость расстояния между зарядами от времени. Определить вре¬
мя, за которое один заряд упадет на другой.
1.8.4. Рассмотрим классическую модель атома гелия, представляю¬
щую собой бесконечно тяжелое ядро с зарядом +2е, вокруг
которого на противоположных концах диаметра вращаются два
электрона с зарядами —е. Чему равны интенсивности диполь-
ного и магнитного дипольного излучения системы? Чему равна
интенсивность квадрупольного излучения? Как будет меняться
со временем радиус орбиты?
1.8.5. Два одноименных заряда (ей т\) и (е2, m2) испытывают лобовое
столкновение. Определить полную излученную энергию, если
задана относительная скорость на бесконечности Voo <С с. Рас¬
смотреть дипольный (е\/т\ т^ег/тг) и квадрупольный (в\/т\ =
= ег/тг) случаи.

1.8. Запаздывающие потенциалы, излучение	55
1 8.6. Тело, ограниченное близкой к сфере поверхностью (сфероид) с
уравнением
Д(0) = ДО[1+/ЗЯ2(СО50)],
заряжено с постоянной плотностью. Полный заряд равен q. Ма¬
лый параметр /3 {/3 < 1) гармонически меняется во времени с
частотой со. Удерживая низшие члены разложения по (3, вычис¬
лить в длинноволновом приближении угловое распределение и
полную мощность излучения.
1.8.7. На невесомой штанге длиной / помещен заряд е с массой т.
1) Найти закон изменения угловой скорости co(t), если в на¬
чальный момент времени ш(0) = и>о-
2) Определить интенсивность излучения dl/dCl и 7.
1.8.8. Электрон вращается .по окружности в однородном магнитном
поле Н. Найти зависимость от времени кинетической энергии
электрона £(0- Определить траекторию электрона в нереляти¬
вистском пределе v < с.
1.8.9.	Определить интенсивность излучения dl/di'l и I для двух оди¬
наковых зарядов е, движущихся равномерно нерелятивистски с
угловой скоростью со по окружности радиуса а и находящихся
на противоположных концах диаметра.
1.8.10.	Два одинаковых заряда е движутся равномерно нерелятивист¬
ски с угловой скоростью со по окружности радиуса а. Насколько
расположение зарядов должно отличаться от диаметрального,
чтобы интенсивности электрического дипольного, квадруполь¬
ного излучений были равны?
1-8.11. Точечный диполь d вращается по окружности радиуса R с угло¬
вой скоростью со, d || R. Найти интенсивность электрического
дипольного, квадрупольного и магнитного дипольного излуче¬
ния при R < Л = 2я-с/со.
1 8.12. Два одинаковых диполя d находятся на расстоянии R от цен¬
тра невесомой штанги и направлены в противоположные сто¬
роны вдоль штанги. Определить зависимость угловой скорости
от времени co(t), если в начальный момент времени оДО) = соо,
масса диполя т, R <С с/со.
1-8.13. Скорость заряженной частицы убывает от vq до 0 за время т.
Найти угловое распределение тормозного излучения, считая уско¬
рение постоянным. Какая длительность импульса излучения At
будет зарегистрирована покоящимся прибором, расположенным
под углом в к направлению движения частицы?

Глава 1. Теория поля. Задачи
1.8.14. Электрон испытывает лобовое столкновение с неподвижным (бес¬
конечно тяжелым) точечным диполем d. Определить потерю энер¬
гии на излучение в результате столкновения. Движение элек¬
трона происходит вдоль прямой.
1.8.15. Равномерно заряженная штанга с линейной плотностью заря¬
да р длиной I в начальный момент времени вращается с угловой
скоростью изо относительно конца штанги. Найти зависимость
от времени u;(t), если масса штанги равна т.
1.8.16. Равномерно заряженная штанга с линейной плотностью заря¬
да р длиной 21 в начальный момент времени вращается с угло¬
вой скоростью изо относительно оси, проходящей через ее се¬
редину. Найти зависимость от времени угловой скорости
если масса штанги равна 2т.
1.8.17. Нейтральная система четырех заряженных частиц жестко за¬
крепленных в вершинах квадрата со стороной 2а (две частицы
с зарядами +q на одной диагонали, и две с зарядами -q на
другой, квадрат лежит в плоскости (х,у), центр квадрата — на
оси г) вращается вокруг оси г с угловой скоростью из. Найти
зависимость от времени угловой скорости вращения, если мас¬
сы частиц равны т, а угловая скорость в начальный момент
времени равна изо-
1.8.18. Магнитный момент ц в начальный момент времени направлен
перпендикулярно внешнему однородному магнитному полю Н =
= (О, О, Я) и прецессирует вокруг него. Найти pz(t), если гиро¬
магнитное отношение равно 7.
1.8.19. Колебательный контур состоит из конденсатора и катушки ин¬
дуктивности. Частота собственных колебаний равна изо-
Пусть катушка идеальная (без потерь), а конденсатор состоит
из двух параллельных пластин площадью s, расстояние меж¬
ду которыми а. Размеры конденсатора малы по сравнению с
Л = 2л-с/из. Определить добротность контура. Добротность кон¬
тура определяется как отношение запасенной энергии к поте¬
рям за период.
1.8.20. Колебательный контур состоит из конденсатора и катушки ин¬
дуктивности. Частота собственных колебаний равна изо.
Конденсатор идеальный (без потерь), а катушка (без сердечни¬
ка) состоит из N витков площадью s каждый, длина катушки а.
Размеры катушки малы по сравнению с А = 2ттс/из. Определить
добротность контура.

1.9. Электромагнитное поле релятивистских частиц
1.8.21. Нерелятивистская заряженная частица с зарядом q и массой т
скользит без трения по поверхности вращения (ось вращения
вертикальна) в горизонтальной плоскости. На частицу действу¬
ет сила тяжести mg и сила нормальной реакции опоры. Частица
теряет энергию за счет электромагнитного излучения, но поте¬
ри за один оборот малы. Определить зависимость z(t).
1) Для поверхности конуса z = kr.
2) Для поверхности параболоида z = г2/а.
1.8.22. Гармонически колеблющийся диполь помещен на высоте h над
идеально проводящей металлической плоскостью. Для случаев
h «С Л и h » Л найти интенсивность излучения диполя в зави¬
симости от угла наблюдения и угла между диполем и нормалью
к плоскости.
1.9.1. Определить напряженности электрического и магнитного поля
произвольно движущегося заряда.
1.9.2. Определить электромагнитное поле, создаваемое электроном,
движущимся равномерно со скоростью V.
1.9.3. Определить силу взаимодействия F двух электронов, движу¬
щихся параллельно друг другу с одинаковыми скоростями V.
1.9.4. Найти мгновенное угловое распределение мощности излучения
заряженной релятивистской частицы dW/dQ в двух случаях:
1) скорость v и ускорение w частицы параллельны в некоторый
момент запаздывающего времени t'\
2) скорость и ускорение взаимно перпендикулярны в момент
запаздывающего времени t'.
Проанализировать нерелятивистский v/c 1 и ультрареляти-
вистский v/c ~ 1 пределы.
1.9.5. Найти энергию излучения релятивистского электрона в одно¬
родном магнитном поле за один оборот. Найти полную мощ¬
ность (в мегаваттах) синхротронного излучения в ускорите¬
ле на встречных пучках электронов и позитронов с энергией
100 ГэВ. Длина окружности ускорителя 30 км, число ускоряе¬
мых частиц в кольце 5 • 1012. Оценить характерную длину вол¬
ны излучения.
1.9.
ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
РЕЛЯТИВИСТСКИХ ЧАСТИЦ

58 ->\r Глава 1. Теория поля. Задачи
1.9.6. Пучок релятивистских электронов пролетает через плоский кон¬
денсатор (электрический ондулятор), к которому приложено
переменное напряжение с частотой ujq. Найти частоту излуче¬
ния электронов (ондуляторного излучения) в зависимости от
угла в между наблюдателем и направлением движения пучка.
1.9.7. Определить зависимость от времени энергии релятивистского
электрона в однородном магнитном поле (скорость электрона
перпендикулярна полю). Проверить, что в пределе t —> оо за¬
висимость согласуется с результатом для нерелятивистского
электрона.
1.9.8. Считая, что в линейном ускорителе частица движется вдоль пря¬
мой под действием постоянной силы, определить потери энер¬
гии на излучение. Определить КПД для ультрарелятивистской
частицы.
1.10.	РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
1.10.1. Определить поляризацию рассеянного электромагнитного поля
для следующих случаев:
1) при рассеянии линейно поляризованной плоской монохрома¬
тической волны свободным электроном;
2) при рассеянии циркулярно поляризованной плоской монохро¬
матической волны свободным электроном.
1.10.2. 1) Найти дифференциальные и полные сечения рассеяния ли¬
нейно поляризованного и естественного света осциллятором с
затуханием (затухание обусловлено вязким трением).
2) Найти полное сечение поглощения.
3) Определить поляризацию рассеянной волны.
1.10.3. Определить дифференциальное сечение рассеяния dcr/d^l плос¬
кой монохроматической циркулярно поляризованной электро¬
магнитной волны электроном, находящимся в сильном одно¬
родном магнитном поле Но, с учетом радиационного трения.
Рассмотреть случаи к || Но и к ± Но, где к — волновой вектор
падающей волны
1.10.4. Определить дифференциальное сечение рассеяния dcr/dil плос¬
кой монохроматической неполяризованной электромагнитной вол¬
ны заряженным гармоническим осциллятором, находящимся в
сильном однородном магнитном поле Но, с учетом радиацион¬
ного трения. Рассмотреть случаи к || Н0 и к _L Hq.

1.10.5.
1.10.6.
1.10.7.
1.10.8.
1.10.9
1.10.10
1.10. Рассеяние электромагнитных волн	59
X
Найти дифференциальное сечение рассеяния циркулярно поля¬
ризованной плоской монохроматической электромагнитной вол¬
ны с частотой ш и волновым вектором к на системе, обладаю¬
щей магнитным моментом /х с гиромагнитным отношением 7е,
в случае если магнитный момент р, совершает под действи¬
ем падающей волны малые колебания около среднего положе¬
ния рь0 ± к. Рассмотреть случай малого гиромагнитного отно¬
шения. Каков критерий малости в этой задаче?
Найти дифференциальное и полное сечение рассеяния линейно
поляризованной плоской монохроматической электромагнитной
волны с частотой ш на конденсаторе. Конденсатор — две па¬
раллельные пластины площадью s каждая, расположенные на
расстоянии а друг от друга, пластины закорочены. Электриче¬
ское поле падающей волны перпендикулярно пластинам. Раз¬
меры конденсатора малы по сравнению с длиной волны.
Найти дифференциальное и полное сечение рассеяния линейно
поляризованной плоской монохроматической электромагнитной
волны с частотой ш на катушке. Катушка состоит из N витков
площадью s, длина катушки — а, катушка закорочена. Маг¬
нитное поле падающей волны направлено параллельно оси ка¬
тушки. Размеры катушки малы по сравнению с длиной волны.
Оценить плотность вещества в солнечной короне, если яркость
короны, наблюдаемой во время затмения, в 106 раз ниже ярко¬
сти фотосферы (видимой поверхности) Солнца.
У сравнительно молодых звезд (так называемых новых), свети¬
мость (полная энергия, излучаемая в единицу времени) резко
меняется в течение нескольких суток: вначале очень быстро
растет, а затем медленно убывает до начального значения. Ме¬
ханизм этого явления — отрыв газовой оболочки звезды в ре¬
зультате нарушения равновесия: световое давление на газовую
(плазменную) оболочку, состоящую на 3/4 из ионизированных
атомов водорода, становится больше, чем гравитационное при¬
тяжение. Оценить критическую светимость звезды массы М
и радиуса R.
Определить дифференциальное и полное сечение рассеяние ли¬
нейно поляризованной монохроматической электромагнитной
волны на сверхпроводящей сфере радиуса г<А. Поля заря¬
дов и токов, наводимые на поверхности сферы внешним элек¬
тромагнитным полем волны, полностью компенсируют внешние
поля внутри сферы.

ГЛАВА
2
КВАНТОВАЯ МЕХАНИКА
ВВЕДЕНИЕ
1.	Операторы	и	состояния в квантовой механике
Состояние физической системы описывается в квантовой
механике при помощи вектора состояния |гр). Совокупность векторов
состояний образует векторное пространство — пространство состояний.
Пространство наделено скалярным произведением векторов \ф) и \tp),
которое обозначается {<р\ф).
Физическим величина^ ставятся в соответствие линейные эрмитовы
операторы: F —> F, причем оператор F+, эрмитово сопряженный опера¬
тору F, определяется согласно соотношению
MF» = (<p\F\i/>)*.	(П1)
Если F+ = F, то оператор называется эрмитовым. Решение уравнения
F|/)=/|/>
дает спектр собственных значений / эрмитового оператора F, которые
являются вещественными и определяют те значения, которые только
и может принимать физическая величина F. Собственный вектор |/}
описывает состояние, в котором значение физической величины F до¬
стоверно равно /. Система векторов |/) обладает свойствами ортонорми-
рованности и полноты, т. е. образует базис в пространстве состояний.
Условия ортонормированности и полноты имеют следующий вид для
дискретного спектра собственных значений:
Ш') = <W>	1/л)(/п|	=	1
и для непрерывного спектра:
</!/') = <*(/-/'), jdf\f){f\ = \.

Введение -l\r 61
Вектор \ф), описывающий произвольное состояние, может быть разло¬
жен по базису:
|# = Е1/"><Ш>+ />1/ХМ.	(П.2)
причем, если (ф\ф) = 1, то квадрат модуля коэффициента разложения
в (II.2) определяет вероятность того, что значение физической величи¬
ны F равно /„, т. е. ш(/„) = |(/„|^)|2 (для дискретного спектра), или со¬
ответствующую плотность вероятности dw(f)/df = |(/|^)|2 (для непре¬
рывного спектра).
Переход к определенному базису означает выбор конкретного пред¬
ставления. При этом совокупность коэффициентов разложения по ба¬
зису (см. (И.2)) однозначно характеризует вектор состояния \ф). Это
дает возможность вместо векторов абстрактного пространства рассмат¬
ривать числовые функции (для непрерывного спектра) или числовые
последовательности (для дискретного спектра).
В координатном представлении состояние характеризуется волно¬
вой функцией в х-представлении ф(х), базис образуют собственные век¬
торы оператора координаты х|х') = х'\х'). То есть
|ф) = J dx \х){х\ф),	\ф) -> ф{х) = (х\ф).	(Н.З)
Скалярное произведение принимает вид: {<р\ф) —► / у>*(х)ф(х) dx. Опе¬
раторам отвечают их конкретные реализации:
х —у х, р-н> —	(П.4)
В импульсном представлении состояние будет характеризоваться вол¬
новой функцией в р-представлении ф(р). При этом
\ф) -4 ф(р) = (р\ф), р -эр, х ► ihщ.	(П-5)
Переход от импульсного представления к координатному
ф(х) = {х\ф)= j др{х\р){р\ф) = J dpфp(x)ф(p)	(II.6)
осуществляется при помощи фр(х) =	,1 -еьрх — собственной функ-
V2nh
Ции оператора импульса в координатном представлении.
Среднее значение оператора в состоянии |ф) можно вычислять по
Формулам
(А) = (ф\А\ф) = J dxф*(x)kф(x) = j dpф*(p)Aф{p).

62 -l\r Глава 2. Квантовая механика
Обобщение описанного формализма на случай систем с нескольки¬
ми степенями свободы не составляет труда. Например, для одной мате¬
риальной точки (три степени свободы) в координатном представлении
будем иметь:
\ф) -* V’(r) = (1#). г-*г, p-+-tW.	(II.7)
При этом среднее значение оператора будет вычисляться по формуле
(А) = (ф\Щ) = J с13гф*(г)Аф(г).
Коммутатор операторов А и В равен [А, В] = АВ - ВА. С учетом (II.7)
находятся значения так называемых фундаментальных коммутаторов
[х/, pa,] = ihSjk, [х/, х*] = [р/, р*] = О,
где /, k = 1,2,3.
Динамика физической системы определяется на основе уравнения
Шредингера:
т||ф(0) = н|Ф(0),	(II-8)
где оператор Н называется гамильтонианом (оператором Гамильтона),
при этом считается, что операторы, как правило, не зависят от време¬
ни (представление Шредингера). В случае д\\/дt = 0 уравнение (II.8)
имеет следующую систему частных решений, называемых стационар¬
ными состояниями:
\'fE(t)) = e-iEt/h№, Н\фЕ) = Е\фЕ),	(И.9)
последнее уравнение есть стационарное уравнение Шредингера. Другой
способ описания временной эволюции системы — представление Гей¬
зенберга, в котором зависимость от времени переложена на операторы:
5s"=(i)„ + i[ax"]'	(ПЛ0)
Оба представления связаны унитарным преобразованием:
|Ф(0) = 0(О|Ф(О)) = 0(0|Фя), Ая = 0+AU,	(11.11)
оператор U(<) называется оператором эволюции. В случае, когда
<9Н/dt — 0, он имеет вид U(0 =
2.	Одномерное	движение
В основе математического аппарата лежит стационарное
уравнение Шредингера (II.9) в координатном представлении:
НфЕ(х) =	+	Щх)}Мх) = ЕЫх),	(Н.12)

Введение _/\, 63
дополненное необходимыми граничными условиями (ограниченность вол¬
новой функции при х —►±оо, непрерывность функции вместе с ее произ¬
водной в точках конечных разрывов потенциала и т.д.). Уравнение (11.12)
определяет энергетический спектр и стационарные волновые функции.
В области энергий, в которой аналогичная классическая частица мо¬
жет совершать только финитное движение, спектр энергий является
дискретным, и невырожденным (связанные состояния). В области энер¬
гий, где аналогичная классическая частица совершает инфинитное дви¬
жение, спектр является непрерывным. В этом случае задачи обычно
ставятся в терминах коэффициентов прохождения и отражения D и R:
|-прош|	;Отр|
_ |/* I п _ Iх
|/Г| ’ R~
,-пад I
1х I
(11.13)
где плотность тока вероятности имеет вид
h = ^(ФМФ'(х)* -ф*(х)-ф'(х)).
3.	Линейный	гармонический	осциллятор
Гамильтониан системы имеет вид
й=Ь+^=Ч2+“+£)’	(П14)
причем во втором способе записи использованы повышающие и пони¬
жающиеоператоры
a+ = -J=(Q-iP), 2=-^(Q + /P),	(11.15)
где Q = х/хо и Р = р/р0 — безразмерные операторы координаты и им¬
пульса. Осцилляторные единицы длины (хо), импульса (ро) и энергии
(£осц) даются выражениями
h
хо = \	—- Ро	= Vfrmco, E0Cn	— hcj.	(11.16)
у fUUJ
Решение стационарного уравнения Шредингера Н|я) = £„|л) позво¬
ляет найти энергетический спектр осциллятора: Еп — hu>(n + 1/2), где
п = 0,1,2, Операторы а+ и	а действуют на	собственные векторы
гамильтониана следующим образом:
[ а+|я) = \/п + 1	\п + 1),	(а+)п
'	г.	'	'	\п) = *74-10),	2|0) = О,	(11.17)
( а\п) = у/п\п - 1),	vn!
причем вектор |0) описывает основное (вакуумное) состояние.
О D	„
и многочастичнои теории эти операторы имеют смысл операторов рож¬
дения и уничтожения.

64 J\j. Глава 2. Квантовая механика
Волновые функции стационарных состояний в координатном пред¬
ставлении имеют вид
MX) = (х\п) = rJ.— Hn(f\e-№ ,	(11.18)
v2 n'.XoVn
где Нп(£) — полиномы Эрмита, которые можно представить в виде
//„(£) — (-1)п^2 ^е~^- Приведем несколько первых полиномов: #о(£) = 1.
//](£) = 2£, #2(0 = (2£)2 - 2. Для волновой функции основного состо¬
яния осциллятора имеем
Ых) = (*|0) = —.
V Хоу/п
Собственные векторы понижающего оператора a\z) = z\z) образуют
систему так называемых когерентных состояний гармонического ос¬
циллятора, причем z — любое комплексное число. Вектор |г) можно
представить в виде разложения по системе собственных векторов га¬
мильтониана (11.14):
00	00	п
|*> = £ и<Ф> = е_5'г|2	(1119)
п=О	п=О
причем состояние (11.19) нормировано на единицу: (z|z) = 1. Очевидно,
что в данном состоянии нет определенного значения энергии. Вероят¬
ность обнаружить в состоянии (11.19) значение энергии Еп
wn = |<«|z)|2 =	(IL2°)
определяется распределением Пуассона.
4.	Угловой	момент,	спин
Угловому моменту сопоставляется оператор J = /ij = {J*. Jz}.
каждая из компонент которого является эрмитовым оператором, и для
них выполняются коммутационные соотношения
[!;,!/] = ieyklk, [j2.J<] = 0.
Общие собственные векторы операторов j2 и Jz
Г j \rm)=j(j+l)\j,m),	(Н21)
\ ]z\j,m) = m\j, m),

Введение _/\, 65
при фиксированном / образуют систему 2/ + 1 ортонормированных век¬
торов (j, m\j, т!) = дтт'. Операторы }± = }х ± i]y действуют на общие соб¬
ственные векторы (II.21) следующим образом:
}±\j,m) = л//(у -+-1) - т(т ± 1)|j,m± 1).	(11.22)
Если система координат поворачивается на угол <р, вокруг направ¬
ления, задаваемого единичным вектором п, то вектор состояния преоб¬
разуется при помощи оператора
R(<p) = exp[/(<pj)] = exp[iV(nj)], т.е. \ф') = RMIV’) (Н.23)
и при ЭТОМ р> = iptl.
Наиболее универсальным представлением, в котором можно рабо¬
тать с векторами |/, т), является матричное представление, где j2 и ]г
диагональны. В этом представлении операторы j2, j,-, j± изображаются
квадратными матрицами размерности 2/ -f 1, а векторы |/, т) — столбца¬
ми той же размерности с одним отличным от нуля (и равным единице)
элементом. Частными случаями углового момента являются орбиталь¬
ный момент и спин.
а)	Орбитальный момент. Для операторов компонент орбитально¬
го момента количества движения М = h\ = [? х р]2) реализуется це¬
лочисленный вариант квантования, т. е. орбитальное квантовое число
/ = 0,1,2, Поэтому возможно рассмотрение в координатном пред¬
ставлении.
В сферических координатах операторы 1, содержат только угловые
переменные. Система уравнений (11.21) сводится к следующей:
(-Aev>Y™ = l(l+l)Ylm\	, [ — 0,1,2,,
j JL yW = mYlm),	I m = 0, ±1,... ± /.
Здесь Д— угловая часть оператора Лапласа, E/m)(0, <р) = {в, р\/, т) —
сферические функции. Приводим их явный вид:
YlM)^ = \/24^1(/ + т)!Р'Д>(С05^)е",1У’	(IL24)
Р\т\х) = (1 - х2)т/2^пРМ,	Р,(х)	=	^^г(*2 - 1)'.
2)
Данное обозначение для орбитального момента соответствует обозначени¬
ям. принятым в [13] и [23]х3аметим, что в ряде учебников (например, [17,20])
применяется обозначение L = М. В нашем издании буквой L мы будем обо¬
значать момент системы частиц.

66 -JU Глава 2. Квантовая механика
где Pt(x) и Р(1т\х) - полиномы Лежандра и присоединенные полиномы
Лежандра. Сферические функции имеют определенную четность, равную
(-1)', они образуют ортонормированную систему:	К/т	]dVL	=	SwSmm'.
Приведем вид некоторых сферических функций:
У<0) = -L,	У,<0)	=	cos	в,	У,(±1)	=	±\Ц-	sin	ве
\f\v	V	4-7Г	V	ОТГ
б) Спин 1/2. Операторы компонент спинового, или собственного,
момента (s = 1/2) S = hs = (П/2)Э действуют в особом спиновом про¬
странстве и изображаются (в представлении, где эг диагонален) в виде
матриц Паули:	%
<7Х =
УоУ -Со) МГ,) <"25>
Собственные функции оператора s* в этом представлении:
хф-Q. *-■/»-(")•	<1126>
они отвечают собственным значениям ±1/2.
В полном пространстве состояний, включающем также и орбиталь¬
ное движение частицы, волновая функция записывается в виде
.(r,o-*(r.oQ+*(r. оСН":))	<"-27>
где |-01.2 (г, t)\2 d3r — вероятности обнаружить частицу в момент t в
объеме г ± г + dr с проекцией спина на ось г, равной ±1/2.
Используя общие формулы для углового момента (11.21), (11.22),
соотношения (11.25)—(11.27) можно легко обобщить на случай спина,
отличного от 1/2.
5.	Движение в магнитном поле
Гамильтониан заряженной частицы со спином s = 1/2 и маг¬
нитным моментом у, в присутствии магнитного поля имеет вид
Н = ^(р-^А)2±а(г)-/х(?1К),	(11.28)
где IK = rot А, р = —tftV, /2 = /0 — оператор спинового магнитного
момента частицы. Гамильтониан (11.28) называется гамильтонианом
Паули.

Введение -J\r 67
Приведем далее три определения оператора магнитного момента, ко¬
торые используются при решении различных задач:
Д = ^ = his = gg о?.	(11.29)
Здесь s — величина спина, go = \e\h/mc — магнетон частицы. Для элект¬
рона т — те — это магнетон Бора, для протона, нейтрона и ядер т = тр —
это ядерный магнетон. Для электрона ge« —2, для протона gp да +5,585
и для нейтрона gn да —3,826.
6.	Движение	в	центральном	поле.	Атом водорода.
Решение стационарного уравнения Шредингера для цен¬
трально-симметричного потенциала
н Mr) = {-£д + Щг)}ыг) = ЕМ г)
с учетом [Н,М2] = [Н,Мг] = 0 можно записать в виде ipEim(r) = Яд(г)х
х	где У';(т) — сферическая функция. При этом уравнение для
/?£/(г) приводится к виду
{£ + -г7г + Ще~ иМ - ^ j }**« = 0	(“•»)
(радиальное уравнение Шредингера). При малых значениях г радиаль¬
ная функция имеет асимптотический вид
КеМ |г—о ~ г1,
что справедливо для любого центрального потенциала, обращающегося
при г —> 0 в бесконечность медленнее, чем 1/г2. При больших значени¬
ях г в случае, если U(r)|г_о -♦ 0. для связанных состояний (при Е < 0)
радиальная функция ведет себя, как
ЕеМ|г^оо ~	где	х2	=
п
Для частицы в кулоновском потенциале притяжения (атом водоро¬
да) U(г) = -Ze21г уровни энергии и радиальные функции для состоя-
Z2 е2
нии дискретного спектра имеют вид Еп = —	— и

68 -l\r Глава 2. Квантовая механика
где а = Н2/(те2) — боровский радиус, Lsk(x) = е*х s—j(e
dx"
-*xs+k)
при¬
соединенный полином Лагерра, п = пг + 1+ 1 = 1,2,3,... — главное
квантовое число. Квантовое число пг = 0,1,2,..., определяющее сте¬
пень полинома в (11.31) и, соответственно, число узлов радиальной функ¬
ции, называется радиальным квантовым числом.
Приведем явный вид радиальных функций водородоподобного ато¬
ма для нескольких нижних состояний:
'Z\3/2C
*•-(!
-Zr/a
zу/2
*•-(£
2 -—
a J
-Zr/2a
(11.32)
Для решения уравнения (11.30) бывает полезно использовать под¬
становку XEi{r) = rREt(r), тогда уравнение переходит в
j2	h2l(l	+1)
2 т
dr1
2 тг
- U(г)
|х£/(г) =
о
(11.33)
с обязательным граничным условием xei(0) = 0. Функция XEi(r) долж¬
на удовлетворять условию нормировки на положительной полуоси
/0°° \XEi(r)\2dr = 1. По форме уравнение (11.33) совпадает с одномерным
уравнением Шредингера.
7.	Квазиклассическое	приближение
Две линейно независимые волновые функции — решения
одномерного уравнения Шредингера (11.12) в квазиклассическом при¬
ближении имеют вид
ip£ = у== expji^ Jр(х) dx^, р(х) — \J2т(Е - U(x)).	(11.34)
Условия применимости данного приближения, или условия квазиклас¬
сичности, записываются следующим образом:
h
д_(\
дх \р
« 1,
hm
ди
Р3
дх
(11.35)
где F = —dll/дх — сила, действующая на частицу.Таким образом, тре¬
буются большие значения классических импульсов р(х) и плавный ход
потенциальной кривой. Условия (11.35) нарушаются вблизи классиче¬
ских точек поворота, и это потребовало разработки методов сшивания
или согласования решений по обе стороны от точки поворота.
Например, при переходе из классически запрещенной области
(U(x) > Е при х > хо) в классически разрешенную область (U(x) < Е

Введение -JU 69
при х < хо), где х0 — точка поворота, условие согласования выглядит
так:	г	\ х
'‘Wl— -57га“рЬМ)|Л};
•«о
х0
V'WUoo = ^^ysin{^/p(A:)djc + ?}•	(II36)
Важнейшими приложениями квазиклассической теории3* являются
правило квантования Бора-Зоммерфельда:
ь
J xj2m{E - (Дх)) dx = тгп(п + I)	(11.37)
a
(классически разрешенная зона а < х < b находится между двумя клас¬
сически запрещенными) и формула Гамова для коэффициента прохож¬
дения через потенциальный барьер:
ь
D = expj—^ J |р(х)| dxj	(11.38)
а
(классически запрещенная зона а < х <Ь находится между двумя клас¬
сически разрешенными).
8.	Теория	возмущений
Методы теории возмущений основаны на возможности пред¬
ставления гамильтониана системы в виде Н = Н*0) + V, где Н(0) — га¬
мильтониан невозмущенной задачи (соответствующее уравнение Шре¬
дингера имеет точное решение), а V — оператор возмущения, его вклад
в решение мал.
а)	Стационарная теория. Решается стационарное уравнение Шре¬
дингера (11.9) Н|фп) — Еп\фп), векторы состояния \фп) и уровни энер¬
гии Еп находятся приближенно в виде степенных рядов по малому па¬
раметру, входящему в оператор возмущения.
Если в нулевом приближении мы имеем невырожденный уровень
энергии Е(п \ которому отвечает вектор 10пО)), то поправки первого и
второго приближения к уровню энергии имеют вид
£(•) = <n|V|n>,	=	(и-39)
кфп
3) Теория Вентцеля-Крамерса-Бриллюэна (ВКБ).

70 _/\, Глава 2. Квантовая механика
и поправка первого приближения к вектору состояния:
,||40)
кфп	Lk
Здесь при вычислении матричных элементов используются собственные
векторы невозмущенного гамильтониана |^40)).
Если в нулевом приближении уровень энергии £^0) s-кратно вырож¬
ден, т. е. £^0) —> {iV'na)}. a = l,s, то правильные векторы нулевого при¬
ближения | фп)= Л а са\'Фп>1) и соответствующие поправки к энергии
вычисляются, исходя из системы уравнений
J2[(na\V\n/3)-E^Sap\cp = 0.	(11.41)
Р
Условие совместности системы (11.41) дает так называемое секулярное
Е-0)
уравнение для определения поправок Е„
\(na\V\n/3) — Е^6ар\ — 0.	(11.42)
б)	Нестационарная теория. В этом случае оператор возмущения за¬
висит от времени: V = V(t). При этом задача становится нестационар¬
ной и необходимо рассматривать временную эволюцию состояния. Удоб¬
но перейти к представлению взаимодействия:
|Ф(0> = 0о(01*/(0>,
где Uo(0 = е-<н(0,/й — оператор эволюции невозмущенной системы. Век¬
тор состояния в представлении взаимодействия |Ф/(0) подчиняется урав¬
нению Шредингера в представлении взаимодействия:
т||Ф/(0> = 0+У(оОоФ/(0 = У/(0|ф/(0). (II43)
Решение уравнения (11.43) можно записать в общем виде с помощью
Г-экспоненты или хронологически упорядоченного ряда
t
|Ф/(0> = т ехр(-| I V/(0 df) |Ф/(*о)>.	(11.44)
to
Здесь введено обозначение
t
Texp (-Ljv,(f)df) =
to
оо . п 1	1	1
= Е h. (4) / dt> / di" • • • / ^}V/(0V,(O ■ • • Vi(t(n)), (11.45)
n—0	/0	to	tо

Введение _/\„ 71
где все операторы, стоящие справа, берутся в более ранние моменты вре¬
мени, т. е. t(n) ^ t(n~X) < ...t"^ t'. Обычно выбирают to = 0 или t0 = -оо.
Если до включения возмущения (при t < to) система находилась в
собственном состоянии невозмущенного гамильтониана IV'n0*). то при
t > to вектор состояния |ФП(0) можно записать в виде
|Ф„«)> - 00(0£ал*«)№Г> =
k	k
Точное выражение для коэффициентов ank(t) получается из (11.44):
ank{t) = (^0)|Тexp(-i } Vtndf) |^0)>,
to
откуда с точностью до поправок первого приближения с учетом малости
возмущения (см. (11.45)) получаем
<
ank(t) ~ а%>«) + aj»(t) = Snk-{f dt1 Vkne‘^‘',	(11.46)
to
где Vkn =	ukn	=	(£<0)	-	£<0))//i.
Вероятность квантового перехода из состояния п в состояние k в
общем случае определяется с помощью формулы (11.44):
t
Wnk =
<^0)|fexp (~fw,(f)df)\^)
to
В первом порядке теории возмущений следует оставить только линей¬
ный по V член в ряде (11.45):
= -
* А2
J №\ytf)\№)d<\ =±\f e^'VUOdt1 . (11.47)
to	to
Вероятность переходов в единицу времени из начального состоя¬
ния i в близкие конечные состояния /, относящиеся к непрерывному
спектру, под действием постоянного возмущения V имеет вид
dwi, = Ц-\Vfi\26(E, - Ei) dv,,	(11.48)
где dv, обозначает число этих состояний. Интегрирование в (11.48) по
энергии конечных состояний дает золотое правило Ферми:
Щ = %Ш*Р,т.	(11.49)
причем р, = dv,/dE, — энергетическая плотность конечных состояний.

72 -JU Глава 2. Квантовая механика
Если возмущение периодически зависит от времени V(0 = V е ш1+
+	то обобщением формулы (11.48) будет
dw± = ~\V£\26(E, - Ei ± М duf,	(11.50)
где верхний знак отвечает поглощению, а нижний — излучению энергии
системой.
в)	Адиабатическое приближение. В рамках данного приближения
гамильтониан системы Н(0 считается зависящим от времени, но не
разделяется на гамильтониан невозмущенной задачи и оператор воз¬
мущения, дающий малый вклад в решение. Малым параметром здесь
является скорость изменения Н(?): предполагается, что гамильтониан
изменяется медленно по сравнению со всеми временными масштабами
системы, т. е. рассматриваются адиабатические изменения. При этом
необходимо иметь в виду, что медленное изменение вектора состояния,
рассматриваемое в течение достаточно большого промежутка времени,
может привести к весьма существенному итоговому изменению исход¬
ного вектора.
Предполагается, что гамильтониан системы зависит от некоторого
параметра £(t), который является заданной плавной функцией време¬
ни: Н(£) = Н(£(£)). Данный параметр может описывать расстояние меж¬
ду взаимодействующими подсистемами, напряженность внешнего поля
и т.п. (в общем случае таких параметров может быть несколько).
В каждый момент времени можно определить мгновенные собствен¬
ные векторы гамильтониана ^(^(О)). отвечающие значениям энергии
£л(£(0)- Они находятся из уравнения
щтшт) = Ептшт).
Данную систему состояний можно использовать в каждый момент вре¬
мени t в качестве базиса.
При адиабатическом изменении параметров вероятности квантовых
переходов системы между мгновенными собственными состояниями га¬
мильтониана Н(£(0) оказываются экспоненциально малыми [17,19,22].
Поэтому система, находившаяся первоначально в состоянии |^л(£(0))),
относящемся к невырожденному мгновенному значению энергии £л(£(0)),
будет и в последующие моменты времени оставаться в подобном мгно¬
венном собственном состоянии (т. е. в состоянии |V>n(£(0))> отвечающем
уровню энергии £„(£(£)))• Таким образом, вектор состояния успевает
«подстраиваться» под изменения гамильтониана, медленно меняясь со
временем, и тем точнее, чем меньше величина £ = d£/dt.

Введение JX,. 73
Однако вектор |?/у,(£(£))) с течением времени приобретает некоторую
фазу. В общем случае эта фаза состоит из двух частей: динамической
фазы, возникающей вследствие обычной временной эволюции стацио¬
нарного состояния (с унитарным оператором эволюции U(£), см. (11.11)),
и геометрической (или топологической) фазы, которая отражает то¬
пологию пространства параметров. Данную фазу принято называть фа¬
зой Берри.
9.	Релятивистская	квантовая	механика
Релятивистское волновое уравнение для свободной части¬
цы со спином s = 1/2 (уравнение Дирака) имеет вид
ih— Ф(г, 0 = Н0Ф(г, t) = {с(йр) + Д/лс2}Ф, Ф =
/
■ф2
Фз
W
(II 51)
где волновая функция Ф(г, t) представляет собой четырехкомпонентный
спинор, или биспинор, а матрицы Дирака обладают следующими алгеб¬
раическими свойствами:
{SiSj + а/а, = {3,-, а,} = 2бу,	( а,- = piE, = -75Е,,
а.Д+ДЗ,- = 0, Р2 = 1,	\	Ё„Ёт = \6пт + ienm,E,.
В так называемом стандартном, или дираковском, представлении мат¬
рицы ai, Р, Е,- можно записать в блочном виде, выразив их через мат¬
рицы Паули:
о> 3 = (о °> Но °)	<||52>
Обобщение уравнения (11.51) на случай наличия внешнего электро¬
магнитного поля, описываемого четырехмерным потенциалом Ам = {ф, А},
дает
г7).^Ф(г, 0 = |са(р+ +/3тс2 - еф|ф(г, £),	(11.53)
гДе — е < 0 — заряд электрона.
Уравнение (11.53) можно записать в явно релятивистски ковариант-
ной форме:
{^{д^ + -А- тс}ф(г, t) = 0,	(11.54)

74 -l\r Глава 2. Квантовая механика
где введены 7-матрицы: 70 = 70 = Р, 7‘ = —7< = P&i> имеющие следую¬
щий вид в представлении (11.52):
нх :> +-Н °>
10.	Сложение моментов. Тождественность частиц
а)	Сложение моментов. Задача сложения моментов подра¬
зумевает следующее. Предполагаем, что для двух систем (или частиц),
которые характеризуются операторами угловых моментов ji и j2, извест¬
ны решения одночастичных задач (см. (11.21))
J j 1,21/1.2> т\з) = У 1,2(/1.2 + 1)1/1,2. ^1,2).
1 jl,2z|/l,2< "11,2) = ^1,21/1,2> ^1,2)-
На основании этого нужно найти решение задачи
j ]2\J,M) =J(J+W,M),
где j = ji + }2 — оператор суммарного углового момента. То есть нужно
найти общие собственные векторы и спектр операторов j2 и j2. Об¬
щее решение данной задачи дает следующую связь между квантовыми
числами:
М — т\ + m2, J = j\ +/2, /1 +/'2 - 1,	•••-	l/'i	—	/21 -	(II.55)
Соотношение (11.55) называется правилом треугольника.
Векторы нового базиса |JM) = \j1j2JM) (общие собственные векторы
операторов j2, j\, j2, j2) связаны с векторами старого базиса \j\m\j2m2) =
= \jiml)\j2m2) (общими собственными векторами операторов jf, ji2, j^, j2Z)
линейным преобразованием
IЩ = J2 1/1 »»i/2»»2>(/1 mi/2m2|/M) = £
ГП\,ГП2	ТП\,ТП2
Коэффициенты разложения C™1/2m2 (которые можно выбрать веществен¬
ными) называются коэффициентами Клебша-Гордана. Практическую
важность представляют соотношения ортогональности
52 Cli^hm2Cimhm2 = Ь/'ймМ',	(II.56)
mi,m2
Е Ci^m2Cfm[hm, =	(11.57)
J.M

Введение -J\, 75
б)	Тождественность частиц. Частицы, обладающие всеми одинако¬
выми физическими характеристиками, в квантовой механике неразли¬
чимы и называются тождественными. Состояние частицы характери¬
зуется как ее координатой в конфигурационном пространстве г, так и
значением внутренней переменной ms — проекцией спина, т. е. опреде¬
ляется парой переменных:
{r,/ns}EE£-	(11.58)
Волновая функция системы двух тождественных частиц, зависящая
от двух аргументов (11.58), при перестановке частиц местами будет опи¬
сывать физически то же самое состояние, поэтому она должна быть
собственной функцией оператора перестановки двух частиц Р12:
Р12Ф(£ь&;0 = ф(£2.£ь0-
Симметрия волновой функции относительно перестановки частиц одно¬
значно связана с их спином:
1 3
Ф(6.6;0 = -Ф(6.£1;0 при s	- ферми-частицы;
Ф(£ь&; 0 = +Ф(^2.6:0 ПРИ s = 0,1,2,... — бозе-частицы.
Если система состоит более, чем из двух частиц, то
Ф(б • ■ •& • • -6 • • • .£лб О = ±ф(6 •••&•••& • • • >£лб *).	(11.59)
где верхний знак относится к бозе-частицам (бозонам), а нижний — к
ферми-частицам (фермионам).
Для описания состояний системы тождественных частиц, взаимо¬
действием которых друг с другом можно пренебречь, выбирается базис
невзаимодействующих частиц — одночастичный базис. При этом ка¬
ждое возможное состояние N частиц должно удовлетворять переста¬
новочной симметрии в соответствии с формулой (11.59). Для ферми-
частиц такие базисные состояния могут быть записаны в виде детер¬
минанта Слэтера:
^ Фп\(£\)
тМй) •
Фп„(£ i)N
Фп,,л2	.яд,(£ь&. •••.&)= ^7det
•фщ (6)
чМ6) •
\Фп, (£v)
Фп2(Ы ■
■ ■
Легко видеть, что если среди индексов, нумерующих одночастичные сос¬
тояния n\,ri2, ■ ■. riN есть два одинаковых, то два столбца определителя
окажутся одинаковыми, и функция тождественно обратится в ноль. От-

76 _/\, Глава 2. Квантовая механика
сюда следует принцип Паули: в системе тождественных фермионов в каж¬
дом однофермионном состоянии может находиться не более одной частицы.
Для системы бозе-частиц базисные состояния определяются полно¬
стью симметризованной по всем перестановкам суммой, которая иногда
называется перманентом:
К.П2 пЛьб. ••■•&) =	£	ЩпАШпЛЬ)•. .<МЫ.
У ' ОТ
где суммирование ведется по всем перестановкам У различных индек¬
сов п\, «2, • • • пы, а числа Л7,- указывают, сколько частиц находится в
состоянии г, т. е. сколько из этих индексов имеют одинаковое значение г
(очевидно, что £Л7,- — ^0-
В системе двух невзаимодействующих нерелятивистских частиц спи¬
новые и координатные переменные частично разделяются, при этом фор¬
мальное выражение имеет одинаковый вид для ферми- и бозе-частиц:
= £ Cs,Al5y<f)„2(r1,r2)x(S,Ms).	(11.60)
S,Ms
Здесь п\ 2 — полный набор квантовых чисел одночастичных состоя¬
ний (без учета спина), х(5, М$) — спиновая функция, описывающая
состояние с определенным значением суммарного спина двух частиц S.
Координатная часть волновой функции (11.60) равна
Ф^П2(гьГ2) = -^= (V’n, (г 1) 'Фт (г2) + (-l)srpnf(r2)^n2(ri)).
11.	Теория	атомов	и молекул
а)	Атомная система единиц. Часто в решениях задач ис¬
пользуется атомная система единиц (а. е.) е = h = те = 1. Приведем
значения некоторых характерных величин для атомов.
h2
А. е.	длины (боровский	радиус):	а	=	—* = 0,529 • 10-8 см.
тее
А. е.	энергии:	Еа	=	— =	= 27,21 эВ.
а h
е2	«
А. е.	скорости:	va	=	— = 2,2 ■ 10 см/с.
h
А. е. времени:	та	=	=	-^-т	=	2,42 ■ 10 17 с.
е тее
А.е. частоты:	иа	=	=	4,13	•	1016 с-1.
П3
6	Q
А.е. напряженности электрического £0 = — = 5,14 • 10 В/см.
поля:	а

Введение _J\„ 77
Решения уравнения Шредингера для связанных состояний водоро¬
доподобного атома приведены ранее в (11.31) и (11.32).
б)	Сложный атом. Большинство атомов периодической системы эле¬
ментов Менделеева обычно рассматриваются в рамках нерелятивист¬
ской теории. При этом описание и классификация состояний и уров¬
ней энергии проводится в соответствии со стационарной теорией воз¬
мущений. В нулевом приближении учитываются только кулоновские
взаимодействия, а качестве невозмущенного гамильтониана атома Но
выбирается сумма одночастичных гамильтонианов, в которых взаи¬
модействие электронов с бесконечно тяжелым ядром и парное взаи¬
модействие между собой заменяется центрально-симметричной частью
самосогласованного потенциала, вид которого, естественно, неизвестен.
Однако это позволяет задать общие свойства одночастичных состоя¬
ний частиц в центральном поле, которые определяются стандартным
полным набором одночастичных квантовых чисел п, I, т и проекцией
спина ms, поскольку в нерелятивистском описании спиновые и коорди¬
натные переменные каждого электрона разделяются.
Из одночастичных состояний частицы в центральном поле строит¬
ся многочастичный базис невозмущенных состояний атома, содержа¬
щего N электронов, в виде слэтеровских детерминантов. Выбор тако¬
го представления позволяет с хорошей точностью считать каждый де¬
терминант Слэтера соответствующим невозмущенным состоянием. По¬
скольку все магнитные взаимодействия рассматриваются в виде возму¬
щения, в нулевом приближении наряду с энергией всегда существуют
интегралы движения, определяющие состояние атома как целого: пол¬
ный спин атома S и полный орбитальный момент L. Таким образом,
состояние атома в нулевом приближении будет полностью определено
указанием числа электронов с одинаковой энергией (на одной элек¬
тронной оболочке), зависящей только от двух одночастичных кванто¬
вых чисел п и / (конфигурацией), определенным значением полного
орбитального и полного спинового моментов:
|Ф(0)> = Е Е^;ш|конфиг.,Т,5)|Т,М)|5,М5).
5,/Vfs L.M
Кратность вырождения уровня энергии в нулевом приближении равна
^0 = E(25 + 1)(2L + 1)’
S.L
где суммирование проводится по всем возможным (разрешенным прин¬
ципом Паули) значениям полного спина и орбитального момента атома.

78 -l\r Глава 2. Квантовая механика
Поправка первого порядка определяется нецентральной частью само¬
согласованного поля и обусловлена по-прежнему только кулоновскими
взаимодействиями. В первом приближении состояния с различными L и S
при заданной конфигурации имеют различные поправки и вырожден¬
ный уровень энергии расщепляется. Правильные состояния нулевого
приближения |Ф*0') теперь имеют заданное значение полного орбиталь¬
ного и спинового моментов:
|Ф<°)) = |конфиг., Z., S)|Z-, Af)|S, Afs),
а расщепленные уровни энергии имеют кратность вырождения
N1 = (2S + 1)(2L + 1).
В следующих порядках теории возмущений учитываются более сла¬
бые взаимодействия, в частности, для свободного атома всегда следует
учесть спин-орбитальное взаимодействие, а также другие магнитные
взаимодействия или релятивистские поправки. В этом случае интегра¬
лом движения атома как целого должен быть полный угловой момент
J = L + S,
а правильные состояния будут иметь вид
|Ф) = |конфиг.,£,5)|А,5,У,Му),
где
\L,S,J,Mj) =	£	Cj/mSMs\L,M)\S,Ms).
M+Ms=Mj
Кратность вырождения уровней понижается до N2 = (27-f 1).
Уровни энергии атома принято называть термами. Для них вво¬
дятся спектроскопические символы, указывающие значения основных
квантовых чисел, определяющих кратность вырождения:
2S+'Lj.
При определения основного терма невозбужденного атома (уровня с ми¬
нимальной энергией) применяются эмпирические правила Хунда. Для
первого порядка теории возмущений первое правило Хунда гласит: энер¬
гия атома имеет минимальное значения в состояниях с максимально воз¬
можным значением полного спина S. Если при этом возможны несколь¬
ко различных значений полного орбитального момента, минимальную
энергию имеют состояния с максимальным значением L.
Для второго порядка теории возмущений формулируется второе
правило Хунда: минимальную энергию имеет терм с J = \L - S|, если

Введение -J\- 79
электронная оболочка заполнена меньше, чем наполовину, и с J — L + S
в противном случае.
Во внешнем магнитном поле гамильтониан атома принято представ¬
лять в виде
Н = Но + Vz + Vd,
где Но — гамильтониан свободного атома,
Vz = MoW + 2S)	(11.61)
— оператор так называемого зеемановского взаимодействия, где ро —
магнетон Бора электрона,
VD = А £ A2(ra) =	sin2	ва	(11.62)
2 тс ^	8	тс	^
— оператор диамагнитного взаимодействия, который всегда можно учи¬
тывать как малое возмущение к гамильтониану свободного атома.
Учет оператора Vz в качестве малого возмущения возможен толь¬
ко в относительно слабых полях, когда poDi много меньше величины
спин-орбитального взаимодействия.
12.	Теория рассеяния
Постановка задачи на рассеяние частиц с импульсом р = hk
на потенциале V(r) предполагает исследование решения уравнения
Шредингера
НтЫг) = {-^Д + V(r) jv'k(r) - ЕМ г),
отвечающего асимптотическому граничному условию на больших рас¬
стояниях
^(r)Uoo ~ e‘kr + №^±eikr,	(11.63)
где k = yj2mE/h, углы 9 и <р характеризуют направление импульса р' = hk'
рассеянной частицы. Амплитуда рассеяния f(6, ф) определяет дифферен¬
циальное сечение рассеяния do — \f(9, <p)\2d£l. Полное сечение рассеяния
получается в результате интегрирования do по углам: о = J \f(9, tp)\2d$l.
Борновское приближение предполагает вычисление амплитуды рас¬
сеяния по формуле
Щ = ——2 Г V(r)e-‘vd3x,	(11.64)
2,7th J

80 _/\^ Глава 2. Квантовая механика
где q = к' - к характеризует изменение импульса при рассеянии, причем
q = 2ksm(0/2), где в — угол рассеяния. Условием применимости борнов-
ского приближения является выполнение хотя бы одного из соотношений
^!«1,	^£«1.	(Н.65)
г	hv
В формулах (11.65) Ко и а — характерная величина потенциала и его
радиус действия, v = hk/m — скорость частицы.
При рассеянии центральным потенциалом формула (11.64) упрощается:
ОО
2т
/(0) = -=£ [ V(r) sin qrrdr.
п q J
Метод парциальных волн применяется в случае центрального по¬
тенциала и предполагает разложение функции (11.63), которое имеет
вид
^ь(г) = Е ~Pi(cose),
kr
i=о
где «/(г) — парциальная волна, представляющая собой решение радиаль¬
ного уравнение Шредингера (11.33) с Е = h2k2/(2m) и граничным условием
Ul(r) |г_оо ~ С sin (kr - у +	.	(11.66)
Слагаемое ф в формуле (11.66) называется фазой рассеяния.
Знание фаз рассеяния позволяет найти амплитуду рассеяния
ОО
т = Е - D^tcose) (п.67)
1=0
(формула Факсена-Холыпсмарка), а также полное сечение рассеяния
°°	А
<r = '£(2l + l)^sin26l.	(11.68)
i=o	k
Важное значение в теории рассеяния имеет соотношение, называе¬
мое оптической теоремой:
а = ~j~ Im/(0),	(И.69)
связывающее полное сечение рассеяния (11.68) и амплитуду рассеяния
вперед.

Введение _J\, 81
13.	Теория излучения
Последовательная теория, рассматривающая процессы из¬
лучения и поглощения фотонов, предполагает, что поле излучения, или
свободное электромагнитное поле, является квантованным, и поэтому
должно описываться при помощи оператора векторного потенциала
Aradir, 0 = £ y^{ek,A?Me-iM-kr) +	(II.70)
к,А
где ск+А и ск,А — операторы рождения и уничтожения фотона с вол¬
новым вектором к и состоянием поляризации А = 1,2, екд — единич¬
ный вектор поляризации фотона, удовлетворяющий условию попереч-
ности (kek-A) = 0. Операторы с^Л и ск,л удовлетворяют коммутацион¬
ным соотношениям: [с^а.с^д,] = <5kk'<5аа'- Предполагается, что поле
заключено в куб объемом V = L3, и при L —* оо величина L не входит
в наблюдаемые величины.
Взаимодействие нерелятивистской частицы со спином s = 1/2 с по¬
лем излучения (11.70) при выборе кулоновской калибровки имеет вид
V =	—	(Ararfp)	+	A2rad	-	p(a$Crad),	(11.71)
тс	2 тс
где Scrad = rot Arad, е, т и р — электрический заряд, масса и магнитный
момент частицы.
Поскольку квантовая система, взаимодействующая с полем излуче¬
ния, считается нерелятивистской, то взаимодействие (11.71) будет харак¬
теризоваться малым параметром a = e2/hc~ 1/137 -С 1 (постоянная
тонкой структуры). Поэтому расчеты можно вести по теории возму¬
щений. В этих условиях наиболее существенную роль играют кван¬
товые переходы с излучением или поглощением минимального числа
фотонов. Если речь идет об излучении или поглощении одного фотона
системой типа атома, то в (11.71), как правило, можно пренебречь квад¬
ратичным по А слагаемым, описывающим двухфотонные переходы, и
слагаемым с магнитным моментом, которое содержит лишнюю степень
параметра а по сравнению с первым слагаемым.
Приведем выражение для полной вероятности излучения фотона в
дипольном приближении, которое сопровождается переходом квантовой
системы из состояния |/) в состояние |/) (см. также задачу 2.13.3):
где d/i = (f\d\i) — матричный элемент оператора дипольного момента кван¬
товой системы (системы нерелятивистских частиц), шц = (£,- - E[)/h —
частота перехода.

ЗАДАЧИ
2.1.	ОПЕРАТОРЫ	И СОСТОЯНИЯ
В КВАНТОВОЙ МЕХАНИКЕ
2.1.1. Для операторов инверсии 1 и трансляции Та найти обратные и
эрмитово сопряженные.
2.1.2. Найти собственные значения и собственные функции операто¬
ра инверсии I.
2.1.3. Найти собственные значения и собственные функции операто¬
ра трансляции Та.
2.1.4. Найти явный вид операторов ехр(г'у>1) и expQpxaj, где ip и а —
вещественные числа.
2.1.5. Проверить эрмитовость основных операторов (координаты, им¬
пульса, момента импульса, оператора Гамильтона). Доказать
соотношения (условия полноты)
= i /1а)<л| d\ = i.
п
2.1.6. Доказать справедливость равенств
(А§)+ = В+А+, (АВ ...F)+ = F+...B+A+.
2.1.7. Показать, что А+А — эрмитов оператор (при любом А) и что
(А+А) ^ 0.
2.1.8. Доказать, что \ф) есть собственный вектор эрмитового опера¬
тора А тогда и только тогда, если (^|А2|^) = (V’lAIV')2-
2.1.9. Коммутатор двух эрмитовых операторов А и В равен [А, В] = ihC
где С — эрмитов. Доказать соотношение неопределенностей:
((А-(А))2Х(В-(В))2)^^!.

2.1. Операторы и состояния в квантовой механике ->V 83
2.1.10. Пусть А, В и F — эрмитовы операторы, и для них выполняют¬
ся следующие соотношения: [A, F] = [В, F] = 0, но [А, В] ф 0.
Доказать, что спектр оператора F вырожден.
2.1.11. Доказать справедливость соотношений
[АВ, С] = А [В, С] + [А, С] В,
[А, ВС] = В[А, С] + [А, В]С.
2.1.12. Проверить справедливость коммутационных соотношений
[%F( %)] =	[р„ G(x)] =
2.1.13. Раскрыть коммутаторы [Та,х], [Та, рх].
2.1.14. Раскрыть коммутаторы
[р*./(г)]> [Рж.Дг)], x.expQap*)], где г= у/х2 + у2 + г2.
2.1.15. Получить выражение для оператора скорости частицы массы т.
2.1.16. Показать, что (r|G(?)|r') = U(r)6{r - г').
2.1.17. Доказать справедливость соотношения ([А, В] ф 0)
е€А§е-«А = § + в] + ^2[А, [А, §]] + ....
2.1.18. Чему равен оператор
ехр(^ар) U(г) ехр(-^ар),
где а — постоянный вектор?
2.1.19. Оператор трансляции Та действует на векторы состояний с опре¬
деленной координатой |г) следующим образом: Та|г) = |г — а).
Как действует этот оператор на произвольный вектор состоя¬
ния | гр)?
2.1.20. Используя переход от х- к ^-представлению и наоборот, полу¬
чить вид оператора координаты в импульсном представлении и
оператора импульса в координатном представлении.
2.1.21. Записать стационарное уравнение Шредингера в импульсном
представлении.

84 _J\- Глава 2. Квантовая механика. Задачи
2.1.22. Эрмитов оператор с дискретным спектром /(А) зависит от веще¬
ственного параметра А. Собственные значения, /„(А), и собст¬
венные векторы, |л(А)), этого оператора также зависят от А. До¬
кажите следующее соотношение (теорема Фейнмана-Гельмана):
эх {Щ д\ '
2.1.23. Используя оператор координаты свободной частицы в представ¬
лении Гейзенберга, найти закон движения и «расплывания» вол¬
нового пакета.
2.2.	ОДНОМЕРНОЕ	ДВИЖЕНИЕ
2.2.1.	Найти уровни энергии и собственные функции частицы в по¬
тенциальном ящике (с бесконечно высокими стенками):
Щх) =
О,	0 < х < а,
оо, х < 0, х > а.
Найти (х) и ((х — (х))2) для п-го стационарного состояния. По¬
казать, что при п —» оо найденные величины принимают клас¬
сические значения. Найти фазовый объём, приходящийся на
одно квантовое состояние.
2.2.2. Найти уровни энергии и собственные функции частицы в по¬
тенциальной яме вида
щх) = 1~и°’ М<а’
[О,	\х\	>	а,
используя симметрию потенциала (U(x) — U(-x)).
2.2.3. Используя формулу (см. задачу 2.1.22)
дЕ« _ /„\дН\„\
дХ ^дХ^’
вычислить силу, с которой частица действует на стенку потен¬
циального ящика.
2.2.4. Найти уровни энергии и собственные функции частицы в по¬
тенциальной яме вида
оо,	х < О,
U(x) =	—Uo,	0 < х <	а,
О,	х > а.

2.2. Одномерное движение	85
Указать условие существования по крайней мере одного дис¬
кретного уровня энергии в такой яме.
2.2.5. Пусть в потенциальной яме задачи 2.2.2 существует единствен¬
ный уровень энергии с очень маленькой энергией связи: |е| -с
•С h?/(2ma2) (т. е. на < 1, где х = у/2т\е\/К). Найти вероят¬
ность обнаружения частицы вне потенциальной ямы. Можно
ли истолковать полученный результат на основе классической
механики?
2.2.6. Найти уровень энергии и собственную функцию связанного со¬
стояния частицы в поле (5-ямы:
U(x) = ~-х06(х).
т
2.2.7. Для связанного состояния частицы в поле (5-ямы найти (х), (х2),
(р), (р2). Рассмотреть разные способы вычисления (р2). Прове¬
рить, выполняется ли соотношение неопределенностей.
2.2.8. Решить задачу 2.2.6 в импульсном представлении.
2.2.9. Найти уровни энергии и собственные функции связанных со¬
стояний частицы в поле двух (5-ям:
fc2
U(x) = xq(S(x - а) + S(x + а)).
т '
Отдельно рассмотреть случай удаленных 5-ям (xoа » 1).
2.2.10. Найти разрешенные зоны энергии для частицы, движущейся в
одномерном периодическом поле вида
°°	h20
а) U(x) — У —-б(х-па) (модель Кронига-Пенни);
' т
п=—оо
оо 2
б) и(х) = - У —^ 6(х - па).
' т
п=—ос
Рассмотреть предельные случаи /Зой 3> 1 (или хф > 1, сильная
связь) и /Зо« <С 1 (или хф -С 1, слабая связь).
2.2.11. Определить волновые функции частицы в однородном поле
V(x) = -Fx.
2.2.12. В условиях действия потенциала задачи 2.2.9 (при хф » 1) ча¬
стица в начальный момент времени t = 0 находится в левой
яме. Найти вероятность обнаружения частицы в правой яме в
момент времени t.

86
Глава 2. Квантовая механика. Задачи
2.2.13. Найти коэффициенты прохождения и отражения:
а) для прямоугольной ямы;
б) для прямоугольного потенциального барьера (рассмотреть слу¬
чаи, когда энергия падающей частицы больше и меньше высоты
потенциального барьера).
2.2.14. Для частицы, находящейся в связанном состоянии в поле <$-ямы
(см. задачу 2.2.6) найти вероятность «ионизации» при внезап¬
ном изменении параметра ямы от хо до х\.
2.2.15. Частица массы т свободно движется вдоль оси х с энергией Е
и попадает в область действия (5-потенциала (см. задачу 2.2.6).
Найти коэффициенты прохождения и отражения, нарисовать
графики.
2.2.16. В условиях задачи 2.2.5 найти фазу отраженной от потенциала
задачи 2.2.4 волны e‘kx+tv> относительно падающей из беско¬
нечности —e~lkx . Выразить ее через энергию слабосвязанного
уровня (ka -С 1).
2.2.17. На плоскость г = 0, разделяющую области пространства с
потенциалами
падает снизу волна де-Бройля, направление которой составляет
угол в\ с осью г. Найти закон преломления и показатели пре¬
ломления для обеих сред. Найти коэффициенты отражения и
прохождения. При каких условиях будет наблюдаться полное
внутреннее отражение? Каково при этом поведение волны во
второй среде?
2.2.18.	Частица массы т движется в одномерном потенциальном поле
вида:
Найти зависимость числа связанных состояний от параметров
а и А.
2.2.19.	Найти функцию Грина G(x,x') уравнения Шредингера для сво¬
бодной частицы при £< 0 в одномерном случае. Используя эту
функцию, найти энергию связанного состояния частицы в поле
U\, z < О,
U2, z > О,
U(x) =
+оо,	х	<	О,
—А6(х - а), х > 0.
U(x) = ~—х0 6(х).
т

2.3. Линейный гармонический осциллятор	87
2.3.	ЛИНЕЙНЫЙ	ГАРМОНИЧЕСКИЙ	ОСЦИЛЛЯТОР
2.3.1. Найти распределение по импульсам для основного состояния
гармонического осциллятора.
2.3.2. Для одномерного гармонического осциллятора вычислить (п\х2\п),
{п\р2\п) и сравнить с классическим результатом для х2 и р2.
2.3.3. Воспользовавшись понижающим и повышающим операторами,
а и 2+, найдите средние значения операторов х4 и х2*+1 в га-м
стационарном состоянии линейного гармонического осциллятора.
2.3.4. Вычислить произведение дисперсий ДрДх для n-го состояния
осциллятора.
2.3.5. Найти для гармонического осциллятора а и 2+ в представлении
Гейзенберга.
2.3.6. Вычислить [2, /(2+)], если [2,2+] = 1.
2.3.7. а) Частица движется в потенциальном поле
2 2
1 т / \ tflUJ X
V(x) = —.
Определить вероятность нахождения частицы вне классических
границ для основного состояния.
б)	Найти энергетические уровни частицы, движущейся в по¬
тенциальном поле вида
V(x) =
оо, х < О,
2 2
тио х	„
„	,	х	>	0.
2.3.8. Написать уравнение Шредингера для осциллятора в р-представ-
лении и определить распределение вероятностей различных зна¬
чений импульса.
2.3.9. Для когерентного состояния осциллятора \г) показать, что
^ = ММ'+ 1/2).
где Н — гамильтониан гармонического осциллятора с частотой ш.
2-3.10. Для когерентного состояния осциллятора |z(0) вычислить сред¬
нее значение операторов х и р и сравнить результат с класси¬
ческой траекторией в фазовом пространстве осциллятора.

Глава 2. Квантовая механика. Задачи
2.3.11. Найти волновую функцию для когерентного состояния осцил¬
лятора |z) в координатном и импульсном представлении.
2.3.12. Заряженный гармонический осциллятор находится в основном
состоянии в однородном электрическом поле £ || х, которое вне¬
запно выключается в момент времени t — 0. Определить веро¬
ятность обнаружить осциллятор на n-м возбужденном уровне
энергии при t > 0.
2.3.13. В когерентном состоянии гармонического осциллятора найти
(Дх2)(Др2).
2.4.	УГЛОВОЙ	МОМЕНТ,	СПИН
2.4.1. Раскрыть коммутаторы
а)	[1„г2];	б)	[!«,р2];	в)[1„(?р)];	г)	[1г, (рг)р*];
д) [ti, Р*Р/];	е)	[U±];	ж) [I+.L];	з)	[Т«,р*];
и)	[1«, х*];	к) (1„/(г)].
2.4.2. Найти Тг1,-, используя коммутационные соотношения и свойс¬
тво следа Тг(АВ) = Тг(ВА) или Тг[А, В] = 0.
2.4.3. Доказать, что собственные значения оператора I2 равны /(/ + 1),
исходя из того, что все координатные оси равноправны и воз¬
можные значения проекции т на данную ось равновероятны.
2.4.4. Используя соотношение неопределенности для М* и М^, опре¬
делить минимальное значение выражения
(/,/|М2 + М2|/,/>.
2.4.5. Преобразовать оператор е‘Ыг\±е~‘а1г.
2.4.6. Показать, что в состоянии 11, т) (определена проекция на ось z)
выполняются соотношения:
а) (I) - (\у) = 0;
б) <ш = -<Ш = у;
в) (1?) = (12,) = (Д12) = 1[/(/+1)-т2].
2.4.7. Для системы с I = 1 найти матрицы операторов I2, \г, 1+, 1_ и
общие собственные векторы операторов I2 и \г.

2.4. Угловой момент, спин
2.4.8. Найти собственные значения и собственные векторы операто¬
ра ]п — (jn) для квантовой системы с угловым моментом / = 1,
где п — единичный вектор с составляющими n = {sin0cosy>,
sin в sin ip, cos в).
2.4.9. Исходя из свойств оператора момента j и векторного операто¬
ра А при преобразованиях поворота, получить коммутационные
соотношения
[j,, А*] = ielklAi.
2.4.10. Доказать тождества
[j2. А] = i([A х j] - [j x A]);
[j2, [j2, A]] = 2(j2A + A]2) — 4j(jA),
где j — оператор момента, a A — произвольный векторный опе¬
ратор, т. e. [ji, А*] = ieikiAi.
2.4.11. Найти собственные функции и собственные значения матриц
Паули.
2.4.12. Вектор поляризации спина Р определяется как вектор с компо¬
нентами Р, = (<?,•) = (х|5;|х> = Х+5,х где х - спиновая функ¬
ция данного состояния. В состояниях
найти Р, и |Р|.
2.4.13. Получить соотношение сг,<7* = 1Й,-* + г'е,и<т/.
2.4.14. Доказать, что (<тА)(«гВ) = (АВ) + i(B[А х В]), где А и В —
обычные (не спиновые) векторные операторы.
2.4.15. Вычислить и антикоммутаторы {Э±,ах}, {Э±,ау}, {Э±,а2}.
2.4.16. Вычислить Tr<7,-<7ft, Ivaidkdi.
2.4.17. Вычислить (ста)*, где а — обычный вектор.
2.4.18. Найти явный вид оператора ехр[г'а(стп)].
2.4 19. Найти собственные значения и собственные функции спиново¬
го оператора дп = (стп0), где п0 — единичный вектор с состав¬
ляющими По = {Sin во COS Ifio, Sin во Sin (fio< cos #o}-

Глава 2. Квантовая механика. Задачи
2.4.20. Записать оператор, преобразующий спинор (спиновую волновую
функцию х) при повороте системы координат на угол а вокруг
оси с направлением, заданным единичным вектором п. Найти
явный вид оператора преобразования спинора при повороте си¬
стемы координат, при котором ось z совмещается с направле¬
нием no = {sin0ocos<po,sin$osinipo.cos0o}-
2.4.21. Используя результат предыдущей задачи, найти волновые функ¬
ции частицы со спином 1/2 в случае, когда проекция ее спи¬
на на направление no = {sin во cos ро, sin во sin ро, cos #о} равна
соответственно ±1/2. Сравнить с результатом задачи 2.4.19.
2.4.22. Электрон находится в состоянии с проекцией спина на ось г,
равной 1/2. Какова вероятность различных значений, которые
может принимать проекция спина на направление, задаваемое
вектором по? (См. задачи 2.4.19 и 2.4.21).
2.4.23. Используя результат задачи 2.4.20, решить следующую геомет¬
рическую задачу: система координат поворачивается на угол р\
вокруг оси П( и затем на угол р2 вокруг оси пг. Найти угол и
направление оси вращения для результирующего поворота.
2.4.24. Записать спиновые матрицы Sx,Sy,Sz для частицы со спином 1
(взяв в качестве базиса состояния с определенной проекцией
спина на ось г).
2.4.25. Используя представление матриц предыдущей задачи, найти для
частицы со спином 1 спиновую функцию состояния, отвечающего
проекции спина +1 на направление п0 = {sin во cos ро, • • • }• Най¬
ти вероятности различных проекций на ось Oz в этом состоя¬
нии. Исследовать специально случай во, близких к нулю и к ■к,
а также к -к/2. Чем отличаются при во = 7г/2 состояния со спи¬
ном вдоль оси х (ро = 0) и со спином по оси у (ро = тг/2)?
2.5.	ДВИЖЕНИЕ	В МАГНИТНОМ ПОЛЕ
2.5.1.	Найти волновые функции и спектр энергии для заряженной ча¬
стицы во внешнем однородном и постоянном магнитном поле,
направленном по оси z. (Указание: использовать в качестве
векторного потенциала А вектор с компонентами Ах = Аг = 0,
А у = ЗОс.) Определить число состояний, приходящихся на ин¬
тервал (рг ч- рг + Арг) и один дискретный уровень, предпола¬
гая, что система заключена в ящик объема V (линейные раз¬
меры которого значительно больше ларморовского радиуса).

2.6. Движение в центральном поле	91
2.5.2. Найти уровни энергии и волновые функции заряженной бес-
спиновой частицы в однородном магнитном поле, направленном
вдоль оси г, используя цилиндрическую систему координат.
2.5.3. Показать, что в однородном магнитном поле, переменном во
времени, волновая функция частицы со спином распадается на
произведение координатной и спиновой функций.
2.5.4. Найти зависимость от времени спиновой функции покоящегося
мюона, если в начальный момент
и включается магнитное поле ЗГ, направленное вдоль оси х.
Найти (Эх), (Эу), (Эг) и убедиться, что магнитный момент мю¬
она совершает прецессию вокруг магнитного поля. Получить
вид спиновых операторов в представлении Гейзенберга.
2.5.5. Найти оператор спина электрона в однородном магнитном по¬
ле ЗС в представлении Гейзенберга. Считать, что других взаи¬
модействий, изменяющих спиновое состояние электрона, нет.
2.5.6. Частица со спином 1/2 находится в однородном магнитном поле
ЗС(0 вида
где ЗСь ЗСо, ш — постоянные величины. При £ = 0 частица нахо¬
дится в состоянии с проекцией спина на ось г, равной sz = 1/2.
Найти вероятность перехода частицы к моменту времени t в со¬
стояние, в котором проекция спина на ось г будет равной sz = —1/2.
2.5.7. Можно ли определить магнитный момент р свободного элект¬
рона на основании измерения напряженности создаваемого им
поля? (Использовать соотношение неопределенностей).
2.5.8. В сверхпроводнике проделано цилиндрическое отверстие, в ко¬
тором существует магнитное поле, параллельное оси цилиндра.
(В толщу сверхпроводника магнитное поле не проникает). По¬
казать, что поток магнитного поля внутри отверстия должен при¬
нимать дискретные значения. Найти квант магнитного потока.
2.6.1.	Записать уравнение Шредингера для двух частиц с массами т\
и m2, взаимодействующих по закону U(r\ - гг) в системе цен¬
тра масс. Какой вид имеет волновая функция Ф(г1,гг)?
ЗС = {3Ci cosujt, ЗС) sin ш?, ЗСо},
2.6.
ДВИЖЕНИЕ В ЦЕНТРАЛЬНОМ ПОЛЕ

92
Глава 2. Квантовая механика. Задачи
2.6.2. Определить интегралы движения для частицы, движущейся в
произвольном центральном поле.
2.6.3. Найти волновую функцию основного состояния атома водорода
в импульсном представлении.
2.6.4. Найти среднее значение операторов г2, 1 /г, р2 для основного
состояния атома водорода. Убедиться в том, что выполняется
теорема вириала.
2.6.5. С помощью теоремы Фейнмана-Гельмана (см. задачу 2.1.22)
получить (1 /г) и (1 /г2) в произвольном состоянии атома водо¬
рода. Используя теорему Эренфеста для радиального движения
d(pr)/dt = (Fr), получить (1 /г3) для состояний атома водорода
2.6.6. Записать стационарное уравнение Шредингера для атома водо¬
рода в импульсном представлении.
2.6.7. Найти уровни энергии трехмерного изотропного осциллятора и
кратности их вырождения, разделяя переменные:
а) в декартовых координатах;
б) в сферических координатах.
Определить четность состояний. Обсудить связь задачи с мо¬
делью ядерных оболочек и получить первые три магических
числа: 2, 8, 20.
2.6.8. Найти уровни энергии и волновые функции частицы в трехмер¬
ном потенциальном ящике:
Сравнить порядок следования уровней энергии в этой задаче и
в предыдущей, имея в виду, что задача о потенциальном ящике
также обсуждалась в связи с моделью ядерных оболочек.
2.6.9.	Найти уровни энергии состояния частицы в трехмерной потен¬
циальной яме вида
2.6.10. Найти энергию связанного состояния частицы в мелкой дву¬
мерной потенциальной яме. Сравнить с результатом для трех¬
мерной потенциальной ямы.
с / > 0.
г < а,
г > а.
г < а,
г ^ а.

2.8. Теория возмущений
2.7.
КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
2.7.1.	Найти в квазиклассическом приближении уровни энергии и соб¬
ственные функции:
а) линейного гармонического осциллятора;
б) частицы, движущейся в поле
2.7.2.	Найти в квазиклассическом приближении уровни энергии и соб¬
ственные функции частицы в поле
2.7.3.	Найти в квазиклассическом приближении коэффициент про¬
хождения через потенциальный барьер
Получить приближенное выражение для коэффициента прохож¬
дения, считая, что г0 < 2Ze2/E. Обсудить связь этой задачи с
элементарной теорией альфа-распада и получить закон Гейгера-
Неттола.
2.7.4. Найти в квазиклассическом приближении коэффициент про¬
хождения через потенциальный барьер
при условии 0 < Е < Uq-
2.7.5.	Исходя из правила квантования Бора-Зоммерфельда, получить
выражение для смещения энергетических уровней частицы при
изменении потенциальной энергии на малую величину 6U(x).
оо, х < О,
х ^ О,
х > 0.
х
2.8.	ТЕОРИЯ	ВОЗМУЩЕНИЙ
2.8.1.	Найти с помощью теории возмущений поправки к уровням энер¬
гии линейного гармонического осциллятора, возмущенного по¬
лем вида: а) V = ах\ б) V = Ах3 + Вх4.

Глава 2. Квантовая механика. Задачи
2.8.2. Найти поправки к уровням энергии и векторам состояния од¬
номерного гармонического осциллятора, помещенного в одно¬
родное поле.
2.8.3. Определить расщепление первого возбужденного уровня энер¬
гии трехмерного изотропного гармонического осциллятора и най¬
ти правильные векторы нулевого приближения при воздействии
на него возмущения вида V = аху.
2.8.4. Предположим, что в случае вырожденного энергетического спект¬
ра все матричные элементы оператора возмущения для состоя¬
ло)
нии, относящихся к данному уровню энергии Ь„ равны нулю.
Показать, что при этом поправки к уровню энергии и правиль¬
ные векторы нулевого приближения можно найти из уравне¬
ния (11.41) для эффективного оператора возмущения
ОеК - V V
с(0> _ Fi0) v ’
k.u
которым можно пользоваться только при действии на состоя¬
ния, относящиеся к уровню энергии Е(„°\
2.8.5. Определить поправки ко второму возбужденному уровню энер¬
гии трехмерного изотропного гармонического осциллятора и пра¬
вильные векторы нулевого приближения при воздействии на него
возмущения вида V = /Зхуг.
2.8.6. Уровни энергии невозмущенной системы зависят от парамет¬
ра Л, и при некотором значении Ао два уровня энергии совпа¬
дают: ^[^(Ао) = £f(A0). В начальный момент времени система
находится на первом уровне в состоянии Найти вероят¬
ность того, что система будет находиться в момент времени t
в состоянии V,2°)> если на нее накладывается малое постоянное
возмущение V. Считать, что матричные элементы V\\ = V22 = 0,
но V12 = VJ ф 0.
2.8.7. Найти вероятность того, что при /3-распаде трития ион 3Не+
окажется: а) в ls-состоянии; б) в 2б-состоянии; в) в 2р-состоя-
нии, если атом трития находился в ls-состоянии.
2.8.8. Определить вероятность процесса, при котором ядро, связанное
гармоническим потенциалом, останется в основном состоянии
после испускания 7-кванта (эффект Мессбауэра).

2.8. Теория возмущений	95
2.8.9. Найти вероятность перехода частицы, находящейся в связанном
состоянии в поле <$-ямы, в непрерывный спектр под влиянием
2.8.10. Найти вероятность перехода между состояниями дискретного
спектра под действием возмущения
2.8.11.	Для заряженного линейного гармонического осциллятора, на¬
ходящегося первоначально в основном состоянии, определить
вероятности переходов в различные возбужденные состояния
под влиянием однородного электрического поля вида
Рассмотреть пределы мгновенного и адиабатически медленного
включения поля.
2.8.12. На мюон, покоящийся в сильном однородном магнитном по¬
ле 9Со || г, падает слабое циркулярно поляризованное радиоча¬
стотное поле h(0 ± ДСо. Найти зависимость от времени спи¬
новой функции х(0 и поляризации мюона Р(0 = (х(0|^|х(0).
если в начальный момент х(0) = Xi/2-
2.8.13. Квантовая система описывается гамильтонианом Н(£(0), зави¬
сящим от некоторого параметра £(/), медленно (адиабатически) ме¬
няющегося во времени, так что в каждый момент времени имеет
решение задача на собственные значения Н(£(0)|^га(£(0)) —
= £п(£(0)|^/г(£(0))- Показать, что для невырожденного уровня
энергии En(£(t)) эволюция состояния во времени может быть
представлена в виде
Получить уравнения для определения фазы 7 и найти эту фазу
(фаза Берри).
2.8.14.	Рассмотреть задачу о покоящемся положительном мюоне, нахо¬
дящемся в однородном магнитном поле. Напряженность поля 9С
составляет постоянный угол в с осью z и медленно вращается
вокруг нее. Предполагая, что вектор 96 совершает полный обо¬
рот вокруг оси z, определить фазу Берри.
внешнего поля вида V(t)=Fx cos ujt в случае, когда huj>h2x^/(2т).
'О, t< 0,
£=<£0-, O^t^r,
Т
£о> t > т.

Глава 2. Квантовая механика. Задачи
РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА
.9.1. Выяснить, какие из указанных ниже операторов коммутируют с
гамильтонианом свободной релятивистской частицы со спином
s= 1/2 (и являются интегралами движения):
.9.2. Показать, что уравнение Дирака инвариантно относительно ка¬
либровочного преобразования. Как при этом преобразуется вол¬
новая функция?
9.3. Найти решения уравнения Дирака, описывающие свободную
частицу, имеющую определенный импульс и энергию. Для кон¬
кретизации спинового состояния частицы использовать опера¬
тор (Ер)/р (продольной поляризации).
9.4. а) Найти оператор скорости \х в теории Дирака в случае сво¬
бодного движения.
б) Показать, что четная часть этого оператора [v*] допускает
простую классическую интерпретацию.
в) Показать, что его нечетная часть {у*} осциллирует с часто¬
той и = 2Е/Н (Zitterbewegung).
Указание: оператор, описывающий физическую величину F, мож¬
но записать в виде F = [F] + {F}, где
.9.5. Оценить вероятность рождения пары е+е~-пары в однородном
постоянном электрическом поле в квазиклассическом прибли¬
жении (парадокс Клейна).
9.6.	Показать, что в нерелятивистском пределе уравнение Дирака
переходит в уравнение Паули.
.9.7. Найти релятивистские поправки порядка (v/с)2 к нерелятивист¬
скому гамильтониану атома водорода с помощью разложения
гамильтониана Дирака, описывающего состояния в кулоновском
б) 1 = 1 [г х р] =
в) i2;
а) р = -fAV;
ж) j2;
з) (Sp)/р\
[F] = i(F + AFA), {F} = I(F - AFA); A = |.

2.10. Сложение моментов. Тождественность частиц	97
поле ядра, по степеням v/c. Провести классификацию получен¬
ных поправок.
2.9.8. Найти энергетический спектр заряженной дираковской части¬
цы в однородном магнитном поле.
2.9.9. Найти в нерелятивистском пределе выражение для плотности
заряда и тока заряженной дираковской частицы, находящейся
во внешнем электромагнитном поле.
2.9.10. Показать, что преобразование зарядового сопряжения позволя¬
ет интерпретировать решения уравнения Дирака с отрицатель¬
ными значениями энергии как волновые функции античастиц.
2.9.11. Предполагая, что состояния электронного и мюонного нейтрино
представляют собой суперпозиции состояний нейтрино l^i) и \vi)
с определенными массами т\ и m2'.
{We) — W\) COS 0 + Wl) sin0,
WW) = Ни) sin0 + W2) COS 0,
найти вероятность перехода нейтрино в состояние \vд) к момен¬
ту времени t, если при t = 0 оно было электронным (осцилля¬
ции нейтрино).
2.10.	СЛОЖЕНИЕ МОМЕНТОВ.
ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ
2.10.1. Найти собственные значения и собственные функции операто¬
ров S2 и S* системы двух электронов (S = ?i -f £2). Установить
связь перестановочной симметрии спиновой функции с суммар¬
ным спином 5.
2.10.2. Найти собственные значения и собственные функции операто¬
ров L2 и Lz системы двух частиц с орбитальными моментами
/, = /2 = 1 (L = 1] + 1г)- Воспользоваться соотношениями орто¬
гональности для коэффициентов Клебша-Гордана. Определить
связь между квантовым числом суммарного момента L и пере¬
становочной симметрией координатной волновой функции.
2.10.3. Найти собственные значения и собственные функции операто¬
ров j2 и )г частицы со спином 1/2 в случае, когда орбитальное
квантовое число равно / (j = 1 + s).

98 -Л. Глава 2. Квантовая механика. Задачи
2.10.4. Вычислить средние значения операторов (Is), (lj) и (js) в со¬
стоянии |/, s,j, mj).
2.10.5. Показать, что оператор Р12 = ^(1 + <xi<T2) является оператором
обмена спинами, т.е. Pi2?iP12 = <?2-
2.10.6.	Найти уровни энергии и волновые функции стационарных со¬
стояний двух невзаимодействующих тождественных частиц в
потенциальном ящике
если этими частицами являются:
а) ферми-частицы со спинами s — 1/2;
б) бозе-частицы со спинами s — 0;
в) бозе-частицы со спинами s = 1.
Чему равна в каждом из этих случаев энергия основного со¬
стояния N частиц?
2.10.7.	Может ли распасться на две альфа-частицы нестабильное ядро
8Ве*, находящееся в состоянии с J = 1?
2.11.1. Найти смещение уровня энергии основного состояния атома во¬
дорода под влиянием конечных размеров ядра. Ядро считать
равномерно заряженным по объему шаром радиуса го.
2.11.2. Вычислить электрическую поляризуемость атома водорода, на¬
ходящегося в основном состоянии. Показать, что для нахож¬
дения поляризуемости атома, находящегося в основном состо¬
янии, достаточно знать лишь
2.11.3. Найти расщепление в однородном электрическом поле уровня
энергии атома водорода с п = 2 (эффект Штарка). Найти пра¬
вильные волновые функции нулевого приближения.
2.11.4. Найти величину сверхтонкого расщепления основного состоя¬
ния атома водорода.
2.11.5. Найти уровни энергии атома водорода в основном (Is) состоя¬
нии в однородном магнитном поле.
2.11.6. Для свободного атома водорода написать правильные функции
возбужденных состояний с п — 2 с учетом спин-орбитального
взаимодействия (спин ядра считать равным нулю).
0,	0	<	х	< а,
оо, х < 0, х > а,
2.11.
ТЕОРИЯ АТОМОВ И МОЛЕКУЛ

2.11. Теория атомов и молекул	99
2.11.7.
2.11.8.
2.11.9.
2.11.10.
2.11.11.
2.11.12.
2.11.13.
2.11.14.
2.11.15.
Найти величину тонкого расщепления состояния атома водоро¬
да с главным квантовым числом п и орбитальным квантовым
числом /. Выразить величину этого расщепления в атомных
единицах энергии. Нарисовать схему расщепленных уровней с
п = 3.
Пользуясь правилами Хунда, определить значения квантовых
чисел L, S и / в основных состояниях следующих атомов: а) крем¬
ния, б) фосфора, в) серы, г) ванадия, д) кобальта, е) церия. Для
случаев а), б) и в) найти все термы. Записать спектроскопиче¬
ские символы полученных состояний.
С помощью второго приближения теории возмущений опреде¬
лить зависимость от расстояния R энергии взаимодействия:
а) атом 4- ион; б) атом + атом. Оба атома находятся в S-состоянии.
Желтый дублет атома натрия соответствует оптическим перехо¬
дам 2Рз/2 —> 2S\/2', 2Р\/2	2S\/2-	Определить	расщепление	это¬
го дублета в слабом и сильном магнитном полях. Сравнить по¬
лученные картины расщепления линий натрия с расщеплением
синглетной линии кадмия, отвечающей переходу lD —> 1Р.
Вычислить энергию основного состояния атома водорода из ва¬
риационного принципа. В качестве пробных функций взять:
а) ф(г) = (7га3)-1/2 ехр(-г/а);
б) ф\г) = (7г62)-3/4 ехр(-г2/2Ь2).
Определить параметры а и Ь.
Найти диамагнитную восприимчивость атома гелия в основном
состоянии, исходя из волновой функции вида
ф ~ exp[-Z'(r 1 + г2)1,
где Z' находится из условия минимума энергии.
Показать, что газ атомов, обладающих в основном состоянии пол¬
ным моментом / = 0, но при этом L = S ф 0, парамагнитен (па¬
рамагнетизм Ван Флека).
Определить зависимость вращательного квантового числа мо¬
лекулы водорода Яг от суммарного спина S протонов.
Найти энергетический спектр двухатомной молекулы, считая,
что энергия взаимодействия ядер описывается модельным по¬
тенциалом Кратцера:

too -Л, Глава 2. Квантовая механика. Задачи
2.11.16.	Отрицательный мюон захватывается протоном, образуя рр-атом,
«боровский радиус» которого в 207 раз меньше соответствую¬
щего радиуса атома водорода. На таких расстояниях уже ока¬
зываются существенными ядерные силы, и мюон может захва-
титься протоном. Однако скорость захвата существенно зави¬
сит от величины суммарного спина р-атома S =	+ sp. Таким
образом, время жизни отрицательного мюона в среде сильно
зависит от величины суммарного спина 5. Образовавшийся мед¬
ленный рр-атом, как и нейтрон, взаимодействует с ядрами сре¬
ды контактным образом, однако при этом взаимодействии сле¬
дует учитывать также магнитное сверхтонкое взаимодействие,
которое, как и для атома водорода в s-состоянии имеет изо¬
тропный контактный характер. Построить контактный оператор
сверхтонкого взаимодействия рр-атома с ядром, обладающим
спином /, при котором изменяется суммарный спин S рр-атома.
2.12.1.	Найти в борновском приближении эффективные сечения рас¬
сеяния частицы в полях:
Записать критерии применимости борновского приближения для
рассматриваемых случаев.
2.12.2. С помощью «золотого правила» Ферми получить формулу для диф¬
ференциального сечения рассеяния в борновском приближении.
2.12.3. Определить фазы рассеяния ф в борновском приближении.
2.12.4. Для модельного потенциала отталкивания
найти фазы рассеяния ф. В предельном случае 2m/3/ft2<l найти
приближенное выражение для фаз ф -С 1, и, выполнив сумми¬
рование ряда разложения амплитуды рассеяния по парциаль¬
ным волнам, получить замкнутое выражение для амплитуды /(#).
Сравнить полученное выражение с борновским приближением.
2.12.5.	Показать, что при рассеянии медленных частиц на потенциале
с малым радиусом действия а наиболее существенную роль иг¬
рает рассеяние s-волн (/ = 0).
2.12.
ТЕОРИЯ РАССЕЯНИЯ
a)V=je~xr; б) V = р в) V-
— Vo, г < а,
0, г>а.
V(r) = l /3 > 0

2.13. Теория излучения
2.12.6.	Показать, что при рассеянии медленной частицы массы т, рас¬
сеивающий потенциал может быть заменен контактным псевдо¬
потенциалом
где а — длина рассеяния (см. задачу 2.12.5). Данное выражение
часто используется для описания рассеяния медленных нейтро¬
нов ядрами.
2.12.7. Записать выражение для эффективного псевдопотенциала, опи¬
сывающего рассеяние медленного нейтрона на молекуле водо¬
рода Н2.
2.12.8. Найти сечение рассеяния медленных частиц на сферически-сим-
метричной прямоугольной потенциальной яме. Определить, при
каких соотношениях между глубиной Vo и радиусом ямы а пол¬
ное сечение намного превышает геометрическое значение 7га2
(резонансное рассеяние) и, наоборот, обращается в ноль (эф¬
фект Рамзауэра).
2.12.9. Найти сечение рассеяния медленных частиц на сферически-сим-
метричном прямоугольном потенциальном барьере.
2.12.10. Найти сечение рассеяния частиц на непроницаемой сфере ра¬
диуса а. Отдельно рассмотреть предельные случаи:
а) медленных частиц (ka -С 1);
б) быстрых частиц (ka » 1).
Обсудить характер зависимости от угла в дифференциальных
сечений упругого рассеяния.
2.12.11. Найти полное сечение рассеяния быстрых частиц (ka ;» 1) на
черном шаре радиуса а.
2.12.12. Найти дифференциальное сечение рассеяния:
а) а-частиц на а-частицах;
б) протонов на протонах.
2.12.13. Вычислить сечение упругого рассеяния быстрых электронов ато¬
мом водорода в основном состоянии.
2.13.1. Вычислить матричные элементы (2p|x|ls), (2p|y|ls) и (2p|z|ls)
для атома водорода. Какие правила отбора они определяют?
2.13.2. То же, что и в задаче 2.13.1, но для матричных элементов (2p|p*|ls),
2.13.
ТЕОРИЯ ИЗЛУЧЕНИЯ
(2p|Py|ls) и (2р|рг|1з).

102	Глава	2.	Квантовая	механика.	Задачи
2.13.3. Найти угловое распределение фотонов, излучающихся в пере¬
ходе |2р) -» |Is) атома водорода, и время жизни \2р) состояния.
Выразить это время в атомных единицах времени.
2.13.4. Нейтрон находится в однородном магнитном поле 9£о || z. Опре¬
делить время жизни состояния с проекцией спина на направ¬
ление поля ms = +1/2. Получить численное значение времени
жизни для IKo = 1 кГс.
2.13.5. Найти сечение фотоэффекта на атоме водорода под действи¬
ем плоской монохроматической волны с частотой щ для случая
hu> » /, где / — потенциал ионизации атома. Сравнить резуль¬
таты вычислений при классическом и квантовом описаниях па¬
дающей электромагнитной волны.

глава СТАТИСТИЧЕСКАЯ ФИЗИКА
3
ВВЕДЕНИЕ
1.	Основные	принципы	статистической	физики
1.1.	Распределение Гиббса. Термодинамические величи¬
ны и функции. Из квантовой механики известно, что физическая си¬
стема, характеризуемая гамильтонианом Н, имеет набор собственных
состояний, обозначаемых вектором |п). Вектор |я) является собствен¬
ной функцией гамильтониана:
Н|л) = еп\п),
где еп — соответствующее собственное значение энергии или, другими
словами, соответствующий уровень энергии системы.
Статистическое описание физической системы означает ее вероятност¬
ное описание с введением некоторой функции распределения wn — w(\n}),
которая задает вероятность найти систему в состоянии |п). Вообще го¬
воря, функций распределения может быть много. Статистическая физи¬
ка изучает физические системы, которые подчиняются каноническому
распределению Гиббса, и такие системы называются термодинамиче¬
ски равновесными. При термодинамическом равновесии вероятность wn
найти систему в состоянии |я) зависит, прежде всего, от энергии этого
состояния е„ и дается распределением Гиббса
Wn~\ ехр(_тО'
Нормировочный множитель Z называется статистической суммой, опре¬
деляется из условия Ylnwn = 1. и равен сумме по всем возможным со¬
стояниям системы, взвешенным с гиббсовской экспонентой:
z = £«P (-Ь).
п

104 •Ar Глава 3. Статистическая физика
Внешний неотрицательный параметр 7^0 — называется температу¬
рой. Условие Т ^ 0 просто означает, что состояния системы с ростом их
энергии становятся менее вероятными. Также видно, что вырожденные
состояния с одинаковой энергией, хотя и с разными квантовыми чис¬
лами, имеют одинаковую вероятность, при нулевой температуре 7 = 0
система может находиться только в состоянии с минимальной энергией.
Если же физическая система состоит из двух независимых и невза¬
имодействующих друг с другом подсистем, так что полный гамильто¬
ниан Н = Hj + Нг есть сумма двух гамильтонианов подсистем Hi и Нг,
соответственно,
|п) = |ni) <g> |п2),
£п = £\п + £2 п<
то распределение Гиббса есть простейшее распределение, удовлетворя¬
ющее условию произведения вероятностей для статистически независи¬
мых случайных величин: w(e\п + £2п) = w(£in)w(s2n)-
Статистическую сумму можно записать и в операторном виде, кото¬
рый не зависит от выбранного нами энергетического представления:
Z = Y.e~£jT = E(nle~Wrl«> =	= Тге-й/7\
п	п	п
Соответственно, статистический оператор или матрица плотности дает¬
ся соотношением
w = -e-^T.
Z
Числом состояний Г(е) называется число состояний с энергией, не
превышающей заданную:
Г(е) = Е®(£ ~ £п)-
П
Плотность состояний g(e) определяется как производная
g(e) = ^jf- = 'ES(e-en).
П
Знание плотности состояний бывает удобным, так как статистическая
сумма может быть записана в виде однократного интеграла по энергии:
Z = J g(e)e-£/Td£.
Чтобы увидеть связь статистической физики с традиционной термо¬
динамикой, определяем энергию системы как обычное среднее значе-

Введение _/\, 105
ние статистической величины, подчиняющейся распределению вероят¬
ности wn:	„
Е = (е) = J2£nwn = Тг(Нш).
л
Нетрудно увидеть следующие соотношения для энергии:
„ cMnZ
E=-S0-
и для среднего квадрата флуктуаций энергии или дисперсии:
((АЕ)2) = ((е-(е))2) = ^,
где /3 = 1/Т — обратная температура.
Свободной энергией F называют следующую величину:
F = — TlnZ,
и тем самым распределение Гиббса принимает следующий вид:
wn = exp
Чтобы получить традиционные термодинамические соотношения,
установленные в термодинамике между энергией Е, свободной энерги¬
ей F и энтропией S,
F = Е - TS,
с _ дР
ВТ'
нужно определить энтропию как среднее значение логарифма функции
распределения с обратным знаком:
S = — (In ш) = — wn In w„ = — Tr w\n w.
Действительно,
F—E I	a-En/T	I	J__n
7 I r 7
\	л
tl
С другой стороны, используя условие J2nWn = 1, получим
-	w„\n	^	+	^2wn	In	е_е"/г	j	=
„	е-е«/Т
= 2^ In —о»„ In о/л.

106
Глава 3. Статистическая физика
Сравнивая два равенства, видим, что термодинамическое и статистиче¬
ское больцмановское определения энтропии полностью эквивалентны.
Если система обладает N состояниями с одинаковыми энергиями
е, = ... = eN и, следовательно, равными вероятностями заполнения со¬
стояний w\ = ... = wn = 1 /N, то ее энтропия будет S = In TV. С помо¬
щью плотности состояний g(e) энтропия представима в виде следую¬
щего интеграла по энергии:
В зависимости от экспериментальных условий и типов изучаемых
процессов удобно вводить разные термодинамические потенциалы и пе¬
ременные. Свободная энергия F = F(T,V) — термодинамический потен¬
циал, зависящий от температуры Т и объема V, и ее дифференциал,
равный
служит для определения энтропии S и давления Р.
Энергия £ = E(S, V) — термодинамический потенциал, выраженный
в переменных: энтропия, объем:
Переменным давление Р и температура Т соответствует термодинами¬
ческий потенциал Ф = Ф(Т,Р) (потенциал Гиббса):
Пары (Т, S) и (V, Р) называются сопряженными переменными. Переход
от одной сопряженной переменной к другой сопряженной переменной
осуществляется с помощью преобразования Лежандра, основанном на
дополнении дифференциала до полного дифференциала, например, для
dF(T, V) = -SdT - PdV,
£(S, V) = F + TS,
dE(S, V) = TdS-PdV.
Ф(Т,Р) = F + PV = E — TS + PV,
d4>(T,P) = -SdT+ VdP.
И наконец, энтальпия (тепловая функция) W = W(S,P):
W(S,P) = Ф + TS = E + PV,
dW(S,P) = TdS+VdP.
T-+S:
dF=-SdT = (-SdT-TdS) + TdS, или d(F + TS) = T dS.

Введение	107
1.2.	Идеальный больцмановский газ. Идеальным газом называет¬
ся газ, в котором пренебрегается взаимодействием между частицами.
В отсутствие взаимодействия между частицами задача о нахождении
статистической суммы существенно упрощается и в силу идентично¬
сти частиц сводится в целом к задаче об определении статистической
суммы одной частицы. Действительно, если гамильтониан системы Н =
— Hi+.. .+Hiv есть сумма N одинаковых невзаимодействующих гамиль¬
тонианов, то энергия состояния, характеризуемого набором {п\, ..., пдг}
квантовых чисел каждого отдельного гамильтониана Н(, равна сумме
энергий отдельных частиц:
Отсюда полная статистическая сумма разбивается на произведение N
одинаковых статистических сумм, взятых по состояниям каждой от¬
дельной частицы, т. е.
Таким образом, полная статистическая сумма Z сводится к произведе¬
нию всех одночастичных статистических сумм 2q:
которую также можно выразить через g(e) =	5(е	- еп) — одноча¬
стичную плотность состояний.
При использовании в вычислении статистической суммы классиче¬
ских формул для энергии системы необходимо учесть следующие обсто¬
ятельства. Во-первых, состояния системы N частиц классифицируются
набором импульсов и координат
представляющих точку в фазовом пространстве, а энергия системы являет¬
ся одновременно функцией координат и импульса е(р, q) = e(pi,qi; • • •
• ■ •; ры, Чм)- Здесь подразумевается, что вектора р, = {ра,} и q, = {qai}
включают в себя и пространственные компоненты а= 1,2,	где
d — размерность геометрического пространства, в котором находятся
частицы газа. Поэтому сумма по состояниям, т. е. сумма по всем воз¬
можным р и q, превращается в интеграл по всей области доступных
У* g-{eni+...+enN)/T _
{щ пц)
У е Е*|^Х'"Хе е^/т =
{Л|„...,Ллг}
Z = 4- zo = Ee-£"/T= j g(e)e-‘'Tde,
(p>q) = (рьяг. • • •; Рлг. ялг).

108
Глава 3. Статистическая физика
импульсов р и координат q. Число возможных состояний dr в элементе
фазового пространства dpdq равно
Во-вторых, следует обратить внимание на тождественность одинако¬
вых частиц. Если поменять местами две одинаковые частицы i и /, то
состояние системы будет характеризоваться другой точкой в фазовом
пространстве, которая получается заменой координаты и импульса г'-й
частицы координатой и импульсом /'-й частицы или (р,, q,... р;, qj) —►
—> (р;, qj... р;, q,). При такой перестановке не изменяется не только
энергия, но и состояние системы, т. е. обе такие точки фазового про¬
странства, хотя и разные, на самом деле представляют для одинаковых
частиц одно и то же состояние системы. Другими словами, полное чи¬
сло различных состояний меньше, чем f dr в число раз, равное числу
всевозможных перестановок одинаковых частиц. Если система состоит
из N одинаковых частиц, то полное число всевозможных таких пере¬
становок будет N\, а число состояний будет равно
Таким образом, при использовании классических выражений для
энергии идеального газа из N одинаковых частиц полная статистиче¬
ская сумма дается соотношением
Соответственно, одночастичная плотность состояний g(e) будет равна
dr =
где одночастичная статистическая сумма zq равна
г°=!Ше~Л’Л,Т=1е{£)е~',Т'‘‘-
Достаточное приближение, которое используется для N\ в макроско¬
пическом пределе jV —> оо, дается формулой Стирлинга: ЛП « (N/e)N.

Введение	109
В вычислении го можно продвинуться дальше, если из полной энер¬
гии частицы или молекулы газа выделить кинетическую энергию, свя¬
занную с поступательным движением центра массы частицы, и внутрен¬
нюю энергию, связанную с внутренними степенями свободы, которые
в зависимости от типа частиц или молекул могут представлять враща¬
тельные, колебательные, электронные типы движений и возбуждений:
£л(р) = £+е"ВН)‘
В простейшем приближении для описания внутренних типов дви¬
жения предполагается их независимость друг от друга, что позволя¬
ет представить внутреннюю энергию как сумму вращательной, колеба¬
тельной энергий и учесть по отдельности вклады электронных и ядер¬
ных степеней свободы. В целом, имеем
о°	,
кин„(вн) _ (вн) 1а3, Г	V/2«r_	v(mLY\m
Z о = Zq Z{
— ZqBh) [ d3r [ J-l- e-”2!2"'7 = v(-^\
0 J J (2trfi)	\2жН2)
где V — объем, занимаемый газом, и статистическая сумма по внут¬
ренним состояниям
2(вн) _	е-^’И)/т	= e-f(T)/T
П
есть некоторая функция, зависящая только от температуры. Отсюда
свободная энергия идеального газа дается соотношением
F(T, V) = -NT\n eJ	3/2	+	Nf(T).
Давление идеального газа не зависит от внутренних степеней свободы
частиц и равно
р _ _dF_ = NT
dV V '
а термодинамический потенциал Ф = F + PV пропорционален числу ча¬
стиц и равен
р /2тгй2\3/2
Ф(Р, Т) = NT\n f	+Nf(T) = Nn(P,T).
Здесь ц(Р, Т) — химический потенциал частицы или термодинамиче¬
ский потенциал, приходящийся на одну частицу. Энтропия S = —dF/dT
и энергия Е = F + TS даются соотношениями
s = N\ne^(K~Sj'2 + \N-Nf (ТУ, Е — ^NT - NTf'(T).

110 -Ar Глава 3. Статистическая физика
Из формул, приведенных выше, можно вывести распределение Больц¬
мана для среднего числа частиц /(е), которые имеют энергию е. Вероят¬
ность того, что частица находится в состоянии с энергией е, пропорцио¬
нальна ехр(—е/Т), а поэтому и среднее число частиц в этом состоянии
пропорционально той же экспоненте, т.е. /(е) ос ехр(-е/Г). С учетом
гого, что f(e) нормируется на полное число частиц:
J dr /(е) = N,
имеем
Пе) =
Zo
С другой стороны, ezo/N = e~F/NT или
£о _ e-(F+NT)/NT _ e-(F+PV)/NT _ g-i>/NT _ g-м/Г
где /г — химический потенциал, введенный выше. Окончательно для
распределения Больцмана будет
f(e) = <>-£>/г.
Энтропия газа, выраженная через больцмановскую функцию распреде¬
ления числа частиц, дается выражением
S = J drf\nj.
2.	Квантовые идеальные газы
2.1.	Термодинамический потенциал О. Распределение
Гиббса для систем с переменным числом частиц. При рассмотрении
термодинамической системы с макроскопически большим числом ча¬
стиц N —► оо, взаимодействующих между собой, часто удобно полагать,
что число частиц N в системе не фиксировано и, соответственно, рас¬
сматривать термодинамические потенциалы в зависимости от химиче¬
ского потенциала ц — переменной, сопряженной к числу частиц. Пере¬
ход к термодинамическим потенциалам, зависящим от химического по¬
тенциала как от независимой переменной, выполняется с помощью пре¬
образования Лежандра. Для дифференциала свободной энергии имеем
dF(T, V,N) = -SdT-PdV + fidN.
Используя соотношение /.idN = d(/iN) - jV dn, найдем
d(F - fiN) = -SdT-PdV-Ndn.

Введение _/\, 111
Далее, введем термодинамический потенциал = fi(7\ V,fi) = F - /iN,
и тогда число частиц определится производной:
Если учесть соотношение для потенциала Гиббса Ф = Л//х, то потенци¬
ал Q можно записать в следующем формально простом виде: О = —PV.
Аналогичное преобразование можно выполнить и для другого тер¬
модинамического потенциала — энергии. Обозначая Е = Е — /хУУ и с
учетом Е = E(S, У,/х), имеем для дифференциала:
При обобщении распределения Гиббса на систему с переменным чи¬
слом частиц мы должны учесть, что состояние системы уже характери¬
зуется кроме набора квантовых состояний |п) с соответствующими им
энергиями Еп еще и дополнительным параметром Nn — числом частиц
в этом состоянии. Таким образом, состояние системы характеризуется
вектором |К) = \ri,Nn), и в роли внешнего параметра выступает хими¬
ческий потенциал /х, а не полное число частиц. В этой ситуации вместо
свободной энергии F и энергии Е, когда фиксируется число частиц в си¬
стеме, мы должны использовать в распределении Гиббса термодинами¬
ческие величины F и Е, т. е. вероятность найти систему в состоянии |АГ)
дается выражением	_	_
Окончательная формула распределения Гиббса с переменным числом
частиц записывается следующим образом:
Обычно это выражение для вероятности называют также большим ка¬
ноническим распределением.
Условие нормировки wk — 1 Дает выражение для определения
термодинамического потенциала Г2(ц):
n,N„
Отсюда легко проверяется соответствие между термодинамическим и
статистическим определениями среднего числа частиц в системе:
dE=TdS-PdV -Nd/л.
Щц) = -T\nJ2 еОУ.-А.лО/7'
N*WnNn-
n,N„

112	Глава	3.	Статистическая	физика
2.2.	Идеальный ферми-газ. Перейдем к рассмотрению свойств
ферми-систем. В этом случае возможные числа заполнения квантового
состояния |п) равны либо Nn = 0, либо Nn = 1, а возможные энергии
состояний Nnen — либо 0, либо еп. Распределением Ферми называют
среднее число частиц в квантовом состоянии |п) с энергией еп:
1
/(£«) = Л NnWnN„
О • 1 + 1 ■
1 I Ju~en)/T	(е„-Ю/Т	,	1	'
Nn=0	1	+	в	в	+	1
Полное число частиц в системе N можно найти суммированием по всем
возможным состояниям системы |п):
»)/Т
+ 1
Это равенство определяет связь между химическим потенциалом р и
числом частиц N в ферми-системе.
Потенциал П найдем из соотношения
g—Cl/T = ^ e(uNn-enNn)/T _	J2(e(fi~£n)/T)K	=
n,N„	N„=	0	n
= П £ (e0j-£")/r)yV" = ПО + e^-e")/T).
n Nn=0	n
Отсюда полный потенциал П равен следующей сумме по состояниям
системы |я):
П = -7]ГЧп(1 + е^~£п^т).
П
Рассмотрим низкотемпературные свойства ферми-газа. Высокотем¬
пературные свойства могут быть приближенно описаны распределением
Больцмана и совпадают со свойствами классического газа. Ниже мы
имеем ввиду ферми-газ частиц или газ электронов со спином 1/2 и
энергетическим спектром частицы ер = р2/(2т).
При нулевой температуре распределение Ферми принимает вид сту¬
пеньки /(ер) = 9(р- ер). Физически это означает, что ферми-частицы
последовательно по энергии занимают все состояния до химического
потенциала, тем самым реализуя минимальное значение полной энер¬
гии — основное состояние ферми-газа. Граничную энергию, представля¬
ющую химический потенциал р при 7 = 0, называют энергией Ферми
£f — р(Т = 0), а соответствующий ей пограничный импульс pF — им¬
пульсом Ферми. Соответственно, в импульсном пространстве частицы

Введение -l\r из
полностью заполняют все состояния внутри сферы радиусом р = рр,
которая называется ферми-сферой или ферми-поверхностью. Импульс
Ферми зависит только от плотности ферми-газа п = N/V:
Pf = Л(3тг 2я)1/3,
и вычисляется из равенства
..	0 V 47г з
N = 2 о
(2тгft)3 3
Соответственно, энергия Ферми равна
„2	ь2„2/3
Полная энергия газа дается выражением
*r = 0) = 2/|$e,№,> = §*,*.
а соответствующее давление или уравнение состояния при Т — 0 выра¬
жением
иг = 0) =	~	V--V3,
5 m V Г/ 3V
Отсюда можно найти скорость звука с в идеальном ферми-газе при
нулевой температуре согласно
_ /дЯ _ vf
° ~ V дР Уз’
Здесь р — mN/V — плотность газа, а скорость Ферми определена как
скорость частиц на поверхности Ферми vp — pp/m.
Ферми-газ при Т Сер называют вырожденным, а при Т » sf —
невырожденным. О температуре Тр ~ ер говорят как о температуре
вырождения.
Термодинамические функции ферми-газа удобно вычислять, исполь¬
зуя понятие одночастичной плотности состояний g{e). Тогда, например,
энергия и число частиц ферми-газа даются выражениями
Е = j deeg(e)f(e) = J de~
eg(e)
-Щ/г + !
о	о
oo	oo
g(g)
N = J deg(e)f(e) = J de
+ 1

114
Глава 3. Статистическая физика
Важной характеристикой ферми-газа, как газа частиц, имеющих спин
и несущих магнитный момент, являются его парамагнитные свойства и,
в частности, спиновая парамагнитная восприимчивость. В невырожден¬
ном ферми-газе, когда Т » ер, парамагнитная восприимчивость, соглас¬
но свойствам классического парамагнитного газа, подчиняется закону
Кюри хр ~ 1/^- В вырожденном ферми-газе закон Кюри нарушается и
парамагнитная восприимчивость газа остается конечной при нулевой
температуре.
2.3.	Идеальный бозе-газ. Для бозевской статистики заполнение
квантового состояния |п) частицами ничем не ограничено. Число ча¬
стиц в одном и том же состоянии может быть равно любому целому
неотрицательному числу Nn = 0,1,2,..., а возможные энергии для раз¬
ных заполнений равны Nnen = 0, е„, 2e„, 3£„ Распределением Бозе
называют среднее число частиц в квантовом состоянии |п) с энерги¬
ей еп:
Полное число частиц в системе N можно найти суммированием по всем
возможным состояниям системы |п):
Это равенство определяет связь между химическим потенциалом и чи¬
слом частиц в бозе-системе. Для сходимости и положительной опреде¬
ленности функции распределения необходимо, чтобы химический по¬
тенциал в бозе-системе не превышал бы минимально возможного зна¬
чения энергии для состояний системы /i ^ emin.
Потенциал П найдем из соотношения
Отсюда полный потенциал П равен следующей сумме по состояниям
системы |я):
/(£«)= J2 NnwnNn =
ОО
N„=О
\ е(и-еп)/Т	е2(ц-еп)/Т	е(еп-ц)/Т	_	j
00	м
= ПЕ (е(м~£л)/г) = П(1 - е^~е"^т)~ .
п Na=О
п
П
Равенство N = —дП/дц выполняется.

Введение -l\r 115
Для реализации при Т = О основного состояния газа со спектром
частиц ер = р2/(2т) все бозе-частицы следует поместить в одно и то же
состояние с минимально возможной энергии, т.е. в состояние с р = 0.
В одном квантовом состоянии будет находиться макроскопически боль¬
шое число частиц. Волновая функция основного состояния будет про¬
изведением одночастичных волновых функций всех частиц. Явление
макроскопически большого заселения квантового состояния получило
название конденсации Бозе-Эйнштейна. О накоплении частиц в одном
и том же квантовом состоянии говорят, как о конденсации частиц в
это состояние. Частицы, находящиеся в макроскопически заселенном
состоянии, называют конденсатными частицами или конденсатом. Ча¬
стицы, которые находятся вне конденсата и заполняют возбужденные
состояния, называют надконденсатными частицами или надконденса-
том. С повышением температуры число частиц в возбужденных р > 0
состояний растет, а число конденсатных частиц уменьшается. Темпера¬
туру перехода Тс, при которой исчезает макроскопически большая засе¬
ленность квантового состояния или плотность конденсата обращается в
нуль, называют температурой бозе-эйнштейновской конденсации. Пере¬
ход в бозе-газе из конденсированного состояния в неконденсированное
состояние и, наоборот, представляет собой пример фазового перехо¬
да конденсированной среды из одного термодинамического состояния
в другое.
Максимально возможное число частиц, которое может находиться
во всех возбужденных состояниях, достигается при максимально воз¬
можном значении химического потенциала. В идеальном газе бозонов —
это р = 0, и для газа объемом V имеем
Значение дзета-функции Римана равно С(3/2) « 2,612.
При достаточно низких температурах, по крайней мере, не меньше,
чем N — max[Nex(Г)] частиц с необходимостью должно находиться в
основном состоянии с р = 0, т. е. в конденсате. Температура бозе-кон-
денсации Тс определяется из условия N = max[Nex{T)] и зависит от
плотности бозе-газа п = N/V:
max
о

116 -J\r Глава 3. Статистическая физика
Само существование перехода бозе-эйнштейновской конденсации, а так¬
же вид особенности в поведении теплоемкости в точке перехода зависит
от размерности пространства и вида ограничивающего внешнего потен¬
циала ловушки, в которую заключен бозе-газ.
2.4.	Идеальный газ элементарных бозе-возбуждений. Бозевскую
статистику можно применять к изучению теплового равновесия элек¬
тромагнитного излучения и к элементарным бозевским возбуждениям
в конденсированных средах. Излучение или электромагнитные волны
можно описывать как набор квантов электромагнитного поля — фото¬
нов, энергия которых определяется импульсом и поляризацией фотона.
Возбуждениям упругой конденсированной среды, представляющим
колебания атомов около положений равновесия, соответствуют звуко¬
вые волны, которые описывают как набор квантов поля упругой дефор¬
мации — фононов, энергия которых также определяется импульсом и
типом или ветвью волны. Звуковые волны просто выглядят в жидкости,
где имеется одна продольная акустическая ветвь. В кристаллической
среде ветвей звуковых волн больше: всегда имеется одна продольная и
две поперечные акустические ветви. В средах со сложными кристал¬
лическими решетками, содержащих v > 1 атомов в элементарной ячей¬
ке, существует еще 3(и - 1) ветвей, которые называют оптическими. В
акустических ветвях частота звуковой волны обращается в нуль при
нулевом волновом векторе, а в оптических ветвях частота при нулевом
волновом векторе остается конечной.
Примером конденсированных сред, в которых существуют элемен¬
тарные возбуждения бозевского типа, являются магнитоупорядоченные
среды. Волны, сопровождающиеся переворотом спина и распространя¬
ющиеся по магнитной системе, получили название спиновых волн, а
соответствующие им кванты названы магнонами.
Механизм, обеспечивающий тепловое равновесие возбуждений, за¬
ключается в рождении и поглощении элементарных возбуждений кон¬
денсированной средой. Это обстоятельство ведет к следующей особен¬
ности элементарных возбуждений. Полное число элементарных возбуж¬
дений N не фиксировано, а целиком определяется условием теплового
равновесия, т. е. температурой, N = N(T). Отсюда, полное число эле¬
ментарных возбуждений не может служить независимой переменной,
которую можно задавать по своему усмотрению, а должно определяться
из условий термодинамического равновесия — минимальности термоди¬
намических потенциалов: свободной энергии F или потенциала Гибб¬
са Ф. Поскольку производная потенциалов по числу частиц есть хими¬
ческий потенциал:
/dF\ /5Ф\

Введение _J\, 117
то условие минимальности совпадает с условием ц = 0. Равенство нулю
химического потенциала есть общее свойство для элементарных воз¬
буждений, когда их полное число не сохраняется. На это условие мож¬
но посмотреть и с точки зрения условия химического равновесия для
реакции рождения и поглощения элементарного возбуждения:
среда + возбуждение среда.
Отсюда для термодинамического равновесия дср + /хВозб = Мер. поэтому
/Чвозб = 0.
В первом приближении, если пренебречь взаимодействием между
элементарными возбуждениями, возбуждения можно рассмотреть как
идеальный газ частиц с р = 0. Энергия такой частицы es = hujs{k), где
ms(k) — частота s-й ветви или типа возбуждений, к — волновой вектор
и р = hk — импульс возбуждения. Распределение возбуждений или их
среднее число в различных квантовых состояниях с волновым вектором
к и частотой ujs дается формулой
/(ws(lк)) = ^Лк)/Т _ ^ •
Это распределение называется распределением Планка.
Применим распределение Планка для описания так называемого чер¬
ного излучения, т. е. термодинамически равновесного электромагнитно¬
го излучения или газа фотонов. Учитывая две возможные поляризации
фотона и дисперсию uj{k) = ck, где с скорость света, для плотности
фотонного газа найдем
СЮ
* [ d3k 1	_	713	[	x2dx	2«3){Т\3
К ) V J (2п)3еш/т-1 ttW e*-l ~ \hc) '
o
Свободную энергию F можно вычислить с помощью П-потенциала. Так
как ц = 0,
СЮ
F — fi = 2TV J у^1п(1 -е~ш,т) = Ц- J*21п(1 -e~h£klT)dk.
о
Вводя переменную х = hck/T и интегрируя по частям, получим
СЮ
р- у 7,4 Г x2<ix к2 VT*
Зтт2Н3с3 J ех — I ~~	45	(Дс)3
о
Нетрудно получить выражение для энтропии:
dF 4тг2/7’\3

118	Глава	3.	Статистическая	физика
и теплоемкости
Энергия равновесного газа фотонов будет равна
Представления о газе фононов используются и для описания тепло¬
вых свойств твердых тел, обусловленных тепловыми колебаниями ато¬
мов около некоторых положений равновесия — узлов решетки атомов.
Если имеется 3и типов нормальных колебаний кристаллической решет¬
ки с дисперсией ш = ш5(к), то фононная часть свободной энергии твер¬
дого тела дается выражением
Здесь g(u) — спектральная плотность фононных колебаний, т. е. плот¬
ность фононных состояний, отнесенная к единице объема тела:
Общее число различных звуковых волн в твердом теле или полное
число состояний фононов определяется числом колебательных степе¬
ней свободы твердого тела, которое за вычетом трех степеней свободы
поступательного и трех степеней вращательного движений тела как
целого равно 3N - 6. В пренебрежении числом 6 по сравнению с числом
атомов N » 1 это дает условие
Спектр фононов ограничен по частоте. Из-за дискретности решетки ато¬
мов длина волны звука не может быть меньше минимального расстоя¬
ния а между атомами. В низкочастотном пределе ш -+ 0 звуковые воз¬
буждения представляют собой длинноволновые акустические фононы с
частотами ш ~ k, и спектральная плотность g(uj —» 0) ~ оА
Пользуясь соотношением E = F— T(dF/dT), найдем фононный вклад
в энергию твердого тела:
Fph = VTT f ln(l - е-^'Т) = VT f di0g(uj) in(! _ „-Ли/Т)
J (2тг)	J
s= 1

Введение _/\, 119
а затем и в теплоемкость согласно, С = (дЕ/дТ)у'-
В пределе высоких температур Т » hu>mах, пользуясь для малых значе¬
ний х < 1 приближением е* - 1 = х и x/shx — 1, обнаруживаем клас¬
сическое поведение энергии и теплоемкости:
Eph — V J dujg(u) Т = 3NT, Cph=vJ dug(u>) = ЗУУ.
Для интерполяции между областями низких и высоких температур час¬
то используется модель Дебая, в которой низкочастотная спектральная
плотность g(u>) = аи>2 распространяется на область всех частот вплоть
до максимальной частоты шр, которая называется дебаевской часто¬
той. Ей соответствует температура Дебая 0д = hu>o, порядок величины
которой hu/a. Коэффициент а и дебаевская частота шд должны быть
согласованы между собой условием нормировки. Отсюда найдем выра¬
жение для интерполяционной спектральной плотности в модели Дебая:
g(w) = 9^fl(u
v U)D
В результате для энергии и теплоемкости в модели Дебая получим:
е0/г
„ 9N f ,	2	huj	П.,Г	(	,
“ 4 У * ё| У Лх
х3
Г
о
,	в0/г
(/ка/27") _ 9NT3	f , х4
:рн = ™	=	[	dx
P uD J sh huj/2T 4 Ql J
sh2 x/2
При низких температурах 7"<C©d верхний предел интегрирования мож¬
но заменить на бесконечность. Поэтому
с Зтг4 А, Г4 „	12тг4.,
Eph — ^ q3 и ph ~	5
ш3
При высоких температурах 7"» ©о воспроизводится классический
результат.
Оптические ветви часто бывают малодисперсионными шопт(к) «
= const = и>о■ В рамках приближения Эйнштейна, полностью пренебре¬
гающим зависимостью от волнового вектора, оптическая ветвь в спек¬
тральной плотности g(uj) аппроксимируется ^-образным пиком вблизи

120 -J\r Глава 3. Статистическая физика
wo, т.е. g(w) 6(и — wo). При комбинировании дебаевских и эйнштей¬
новских членов температура Дебая будет понижена, так чтобы сумми¬
рование по всем фононным состояниям давало бы тоже число колеба¬
тельных степеней свободы.
3.	Неидеальные	квантовые	системы (жидкости).
Основы теории конденсированных сред
В отличие от идеальных газов, где энергия газа складыва¬
ется из энергий отдельных частиц, в системе взаимодействующих ча¬
стиц определение уровней энергии в общем случае представляет собой
сложную и часто невыполнимую задачу. Поэтому, хотя и основные идеи
и методы описания конденсированных сред могут быть одними и теми
же, тем не менее конкретная реализация этих идей и методов различна
в различных случаях и типах конденсированных сред.
3.1.	Нормальная (несверхтекучая) ферми-жидкость. Систему вза¬
имодействующих ферми-частиц принято называть ферми-жидкостью. В
ферми-жидкости спектр элементарных возбуждений или квазичастиц,
обладающих импульсом р и энергией е(р), имеет структуру, которая
полностью подобна спектру частиц идеального ферми-газа. При нуле¬
вой температуре, отвечающей основному состоянию ферми-жидкости,
все квазичастицы в импульсном пространстве полностью заполняют об¬
ласть |р| < рр, которая ограничена импульсом Ферми рр. Величина им¬
пульса Ферми не зависит от взаимодействия и определяется только плот¬
ностью частиц ферми-жидкости п. Величина импульса Ферми совпада¬
ет с его значением для идеального ферми-газа той же плотности п.
Число квазичастиц равно числу частиц жидкости. Следует отличать
импульсное распределение N(р) истинных частиц жидкости от импульс¬
ного распределения квазичастиц п(р) = в(рр — р). Функция N(р) при
р = 0 несколько меньше единицы и убывает при увеличении р от нуля
к р = рр- При р = Pf функция jV(p) испытывает скачок конечной ве¬
личины, после чего в области р > Pf продолжает убывать до нуля с
увеличением импульса р. Величина скачка при р = pF зависит от вза¬
имодействия частиц в жидкости.
Энергия основного состояния жидкости при Т = 0 не сводится к сум¬
ме энергий квазичастиц е(р). Имеется только общее утверждение, что
энергия жидкости £ представляет собой некоторый функционал плот¬
ности, зависящий только от функции распределения п(г, р):
£ = £[л(г,р)] = [ E[n(r,p)](2s + \)-~^d3r.
J	(Z7rh)

Введение
Для спина s = 1/2 множитель 2s + 1 = 2. Когда нужно учитывать спи¬
новые эффекты и магнитное поле, предполагается, что функция рас¬
пределения na{r, р) = пар{г, р) зависит от спина и представляет собой
матрицу 2x2.
Равновесное состояние при 7/0 и, вообще, любое возбужденное
состояние ферми-жидкости может быть получено путем последователь¬
ного перемещения одной или нескольких квазичастиц из области внут¬
ри ферми-сферы наружу. О каждом таком перемещении говорят, что
рождается квазичастица вне ферми-сферы и дырка внутри ферми-сфе-
ры. Таким образом, под дыркой подразумевается незаполненное состо¬
яние. Энергию отдельной квазичастицы е[«(г, р)] определяют как ва¬
риационную производную полной энергии по функции распределения
согласно
Соответственно, при возникновении одной квазичастицы в точке г = R
с импульсом р = q и изменении функции распределения на 2<Sn(r, р) =
= (27г/г.)3<5(р — q) <5(r — R), энергия ферми-жидкости увеличивается на е.
В однородной ферми-жидкости при 7 = 0 равновесная функция рас¬
пределения квазичастиц просто равна ступеньке «о(р) = 9(Рд - р)< а
энергия квазичастицы е зависит только от ее импульса е(«о(р)) = £о(р/
Вблизи ферми-поверхности функцию £о(р) можно разложить по степе¬
ням разности р — рр, и тогда
£(р) = ео(р) ~ so(Pf) ~ vF{p - Pf), IР ~ Pf\ « Pf-
Коэффициент vp называется скоростью Ферми и часто его выражают
через другой коэффициент, называемый эффективной массой т* согласно
Величина т* зависит от взаимодействия частиц в ферми-жидкости и
отличается от массы истинных частиц жидкостей.
Энергия квазичастиц меняется при изменении функции распределе¬
ния. Разложим полную энергию ферми-жидкости по малым отклонени¬
ям функции распределения от равновесной 6п = п — по'-
£ = £[п0(р)] + J e0(p)6n(p)VdTp+^J f(p,p')6n(p)6n(p')VdTpdTP'+...,
5£ = Цп + <?«]-£[п] = [ SE[n(r,p)]-^-3d3r =
J	(27ТП)

122	Глава	3.	Статистическая	физика
где V = f d3r — объем жидкости, и drp = 2Ф3р/(2тгН)3. Отсюда энергия
квазичастицы равна
£(Р) = £о(р) + j /(P. Р') <Ир') drP' + ... = £г0(р) + <*Ф(р)].
где функция Ландау /(р, р') = /(р', р) — симметрична и определена вто¬
рой производной
/(р,р') = <52£/^(р)<5я(р')|л=п,=По(р).
Функция Ландау /(р, р') обусловлена взаимодействием между квазича¬
стицами и определяет физические характеристики жидкости, в частно¬
сти, эффективную массу т*.
3.2.	Сверхпроводимость. Теория БКШ. Согласно теории БКШ (Бар-
дина-Купера-Шриффера) в сверхпроводнике с синглетным s-спарива¬
нием электроны с противоположными спинами связаны в куперовские
пары. Количественной мерой связи является сверхпроводящий параметр
порядка Др, зависящий от температуры и определяющий спектр одно¬
частичных возбуждений, энергия которых равна
= S +14
яг.
где £р = р2/(2т) - ер — энергия электрона с импульсом р, отсчитанная
от поверхности Ферми. Поскольку энергия элементарных возбуждений
(квазичастиц) не может быть меньше |ДР|, то возбужденное состояние
сверхпроводника отделено от основного энергетической щелью. Элемен¬
тарные возбуждения обладают спином 1/2 и появляются парами.
Величина параметра порядка определяется из самосогласованного
уравнения для величины сверхпроводящего параметра порядка:
Д = — V -1	^£р'	^	д	.
рр 2ер/ р
где Урр/ — потенциал взаимодействия между электронами с импульса¬
ми р и р', и f(sp) — равновесная фермиевская функция распределения
квазичастиц, равная
В простейшем приближении VPP' изотропно и постоянно в узком энер¬
гетическом слое вблизи поверхности Ферми Ьизо £д:
VPP' —
[g. ICpI	и	|£Р'|</гшо-
[0, |£р|, или \iP'\>hjjD.

Введение _J\, 123
Л
В случае притяжения g < 0 уравнение имеет нетривиальное решение
со щелью при Т = 0, равной
До = 2hwD ехр(—1/Л); А = |g|N(0),
где Ы(0) = трр/(2тг2Н3) — плотность состояний с фиксированной проек¬
цией спина на поверхности Ферми, А — безразмерная константа связи.
Критическая температура Тс определяется как температура, при ко¬
торой впервые появляется нетривиальное Д / О решение уравнения для
щели:
Тс = — /ги>0ехр(-1/А).
7Г
Здесь 27/7Г и 1,14, где In 7 = С « 0,577 — постоянная Эйлера. Величи¬
ны До и Тс в модели БКШ связаны универсальным соотношением
= — и 3,52.
Тс 7
Предельное температурное поведение щели вблизи нуля температуры и
Тс даются формулами
'Д0(1 - у/2пТ/А0е-л°'т), Т -О,
А(Т) =
т-*тс.
7С(3)V Ъ
Приведем предельные формулы электронного вклада в теплоемкость
сверхпроводника. В пределе низких температур Т —* 0 электронная теп¬
лоемкость в сверхпроводящем состоянии экспоненциально вымерзает
по отношению к теплоемкости в нормальном состоянии:
С.(Т) = 3/2 / Ар \ 5/2 Ао/т
Сп(Т) тг3/2 \ Т )
В окрестности сверхпроводящего перехода при Т <ТС теплоемкость CS(T)
превышает теплоемкость Сп(Т) и нарастает прямо пропорционально бли¬
зости \Т — Тс\ к точке перехода. В самой точке перехода Тс теплоем¬
кость испытывает скачок по отношению к значению в нормальном со¬
стоянии С„{Тс). В модели БКШ относительная величина скачка теп¬
лоемкости в точке сверхпроводящего перехода является универсальной
величиной
Cs(Tc) - Сп(Тс) _	12	_1/|0
Сп(Тс) 7С(3) ~ ’ ’
Знание разности плотностей термодинамических потенциалов для
нормального Fn(T) и сверхпроводящего FS(T) состояний дает возмож-

124
Глава 3. Статистическая физика
ность определить величину термодинамического критического магнит¬
ного поля Нс согласно
Приведем формулы для температурного поведения термодинамического
критического магнитного поля в двух предельных случаях:
Здесь Нс(0) = \J4TTiV(0) До — термодинамическое критическое магнит¬
ное поле при нулевой температуре.
3.3.	Слабонеидеальный бозе-газ. Уравнение Гросса-Питаевского.
Конденсированный слабонеидеальный газ частиц с нулевым спином —
газ. в котором характерная энергия межчастичного взаимодействия ма¬
ла по сравнению с температурой бозе-эйнштейновской конденсации. В
основе теории лежит утверждение о том, что почти все частицы га¬
за находятся в конденсированном состоянии: Np±о = N - Np-о -С N. В
этих условиях основную роль в столкновениях между частицами иг¬
рают парные столкновения частиц с малыми импульсами. В силу малых
скоростей рассеиваемых частиц учитывают лишь вклад от s-рассеяния.
Матричный элемент двухчастичного взаимодействия gpp> заменяется
на его значение при нулевых импульсах: gp,p< =g = const. В коорди¬
натном представлении это соответствует контактному взаимодействию
между частицами U(г, г') = gS(r - г').
Эффективный гамильтониан для N бозонов:
где р,- — импульс г-й частицы и К(г) — внешний потенциал. Константа
взаимодействия g связана с длиной s-рассеяния а соотношением g —
= 4тгh2a/m, где m — масса частицы. Взаимодействие между частицами
предполагается отталкивательным, т. е. g > 0. При притяжении меж¬
ду частицами а < 0 однородное состояние бозе-газа термодинамически
неустойчиво.
В первом приближении волновая функция системы бозонов Ф(гь гг,.. •
...,глО есть симметризованное произведение одночастичных волновых
функций. В конденсированном состоянии все бозоны находятся в одном
и том же состоянии с одночастичной функцией гр(г) и, следовательно,
^ = Fn(T) - FS(T).
N
Ф(Г1,Г2,...Гл,) S3 nV’O-i)-
1=1

Введение	125
Одночастичную функцию V>(r;) нормируют на полное число частиц:
f d3n |ф(г,)|2 = N.
Плотность частиц п(г) дается выражением п(г) = |^(г)|2. а энергия
системы
Е[ф(г),г1>*(г)] = j d3r(|^|VV>(r)|2+ V(r)|V>(r)|2 + ^|ф)|4)
представляет собой функционал от одночастичной комплексной функ¬
ции ф(г), называемой волновой функцией конденсата.
Оптимальное значение энергии достигается минимизацией функци¬
онала энергии Е[г1),ф*] при условии сохранения полного числа частиц
N- J d3r\-ip(r)\2 = const.
С введением множителя Лагранжа р в качестве химического потенци¬
ала газа необходимо минимизировать выражение Е - pN. Уравнение,
которому подчиняется волновая функция конденсата
-Ц-У2ф(г) + V(r)4>(r) + g|V>(r)|V(r) = /#(«0.
Am
называется уравнением Гросса-Питаевского и имеет вид нелинейного
уравнения Шредингера.
В отсутствие внешнего поля V(r) = 0 для однородного состояния
конденсированного бозе-газа уравнение Гросса-Питаевского дает зна¬
чение химического потенциала:
Р = ё\Ф(г)\2 =gn,
что согласуется с соотношением р = dE/dN, где
N(N-\)g	N*_
2 V *2V
и V — объем газа. Давление конденсированного газа равно
р --ЁЁ. - g"2 - sp2
dV 2	2т2’
где р = тп — массовая плотность газа. Скорость звука, определяемая
как и = (дР/др)1/2, при 7 = 0 равна

126 •Аг Глава 3. Статистическая физика
Корреляционная длина £ характеризует пространственный масштаб,
на котором меняется волновая функция конденсата:
с _	^	^
2yjmgn 2у/ггщ'
Приближение, в котором можно пренебречь кинетическим членом
в уравнении Гросса-Питаевского, называется приближением Томаса-
Ферми. В нем распределение плотности имеет вид
п( г) = \ф(г)\2 =	,
а пространственные границы конденсата определяются из условия V{r) = p.
Условие малости характерной энергии взаимодействия gn по сравне¬
нию с температурой бозе-эйнштейновской конденсации Тс ~ h2n2/3/m
интерпретируют в терминах разреженности или малой плотности газа,
вводя газовый параметр п1//3а. Разреженность n'/3a <С 1 означает, что
длина рассеяния частиц друг на друге а много меньше среднего рас¬
стояния между частицами я-1/3. Корреляционная длина £ охватывает
большое число частиц газа: £ » я-1'3.
Нестационарное обобщение уравнения Гросса-Питаевского для опи¬
сания эволюции волновой функции конденсата ф(т, t) во времени имеет
следующий вид:
ihJF =	+
Энергия элементарного возбуждения с импульсом р в слабонеиде¬
альном конденсированном газе дается боголюбовским соотношением:
:(р) = пй+еп) -(гп)2 =
y/gnm,
\/gnm.
Равновесное распределение возбуждений по импульсам имеет вид обыч¬
ного бозевского соотношения:
1
№ =
,Ф)/Т _
Следствие неидеальности бозе-газа — это появление надконденсат-
ных частиц при абсолютном нуле температуры. Плотность конденсата
яо(0) при 7 = 0 меньше полной плотности газа я, при этом отношение
яо(0)/я зависит от величины газового параметра:
яо(0) _ .	(mg)3/2nl/2 _ ,	8	/па3	.	1	1
1 - Т 2 3 = 1 - ? V — = 1 - -4-4 < 1-
Зтг h,	з	V	7Г	247Г я£3

Введение
127
Об этом свойстве говорят как о явлении обеднения конденсата. Послед¬
нее равенство означает, что из конденсата объемом порядка куба кор¬
реляционной длины £3 взаимодействие выталкивает примерно одну ча¬
стицу в надконденсатное состояние.
Повышение температуры ведет к тепловому обеднению конденсата:
где и — скорость звука в газе.
3.4.	Теория сверхтекучести. В жидком 4Не при температуре 2,17 К,
которая называется Л-точкой, происходит фазовый переход второго рода
из нормального состояния Не I в сверхтекучее состояние Не II. Сверх¬
текучее состояние характеризуется способностью жидкого 4Не проте¬
кать через капилляры без трения, не обнаруживая вязкости.
При абсолютном нуле температур жидкость находится в энергетиче¬
ски наинизшем или в основном состоянии. При отличной от нуля темпе¬
ратуре жидкость переходит в возбужденное состояние. При достаточно
низких температурах это будет слабовозбужденное состояние, которое
можно описать как совокупность элементарных возбуждений или ква¬
зичастиц, обладающих определенным импульсом р и соответствующей
энергией е(р).
В жидком 4Не закон дисперсии элементарных возбуждений е(р)
имеет немонотонную зависимость. После начального линейного возрас¬
тания при достаточно малых импульсах энергия е(р) достигает мак¬
симума и далее убывает, проходя через минимум А = е(ро) при опре¬
деленном значении импульса ро, после которого энергия возбуждений
опять растет с увеличением импульса. Начальный линейный участок
е(р) = ср называется фононным, а элементарные возбуждения пред¬
ставляют фононы или звуковые колебания, распространяющиеся со ско¬
ростью с = 240 м/с. Элементарные возбуждения с энергией вблизи ми¬
нимума и законом дисперсии, который аппроксимируется параболиче¬
ской функцией
называются ротонами. Ротонная щель А, импульс ро и эффективная
масса ротонов т зависят от давления и при нулевом давлении равны
по(Т) - п0(0) — ——-^2 ~ —Т2, T^p = gn,

128 -i\r Глава 3. Статистическая физика
Термодинамически равновесное распределение элементарных возбуж¬
дений в 4Не имеет вид распределения Бозе с равным нулю химическим
потенциалом:
С хорошей точностью термодинамические величины сверхтекучего ге¬
лия представляют собой сумму фононного и ротонного вкладов.
В рамках двухжидкостной модели сверхтекучести при малых до-
критических скоростях v < vc течение жидкого гелия II представляется
в виде суммы двух независимых друг от друга течений: нормального
течения с нормальной скоростью v„ и сверхтекучего течения со сверх¬
текучей скоростью vs. Каждому из течений соответствует своя компо¬
нента, нормальная или сверхтекучая, и каждая со своей эффективной
плотностью: рп и ps, в сумме составляющие полную плотность жидко¬
сти р. Импульс единицы объема или поток массы жидкости слагается
из потоков нормальной и сверхтекучей компонент:
j ~ РпУп "I" psvs.
При Т ф 0 из всей жидкости только ее часть, которой отвечает плот¬
ность, равная ps = р — рп, может обладать сверхтекучими свойствами и
протекает без трения сквозь самые узкие капилляры. Отношение рп/р,
равное нулю при Т = 0, с повышением температуры увеличивается и
достигает в Л-точке значения, равного единице.
Кроме отсутствия вязкости, течение сверхтекучей компоненты об¬
ладает еще двумя важными свойствами: оно всегда потенциально, т. е.
rot vs = О,
и не сопровождается переносом тепла или энтропии. Энтропия, кото¬
рая в Не II определяется статистическим распределением элементарных
возбуждений, переносится только течением нормальной компоненты с
нормальной скоростью \п.
4.	Фазовые	переходы и критические явления
4.1.	Фазовое равновесие и фазовые переходы. Разные
состояния вещества, которые могут быть одновременно в термодинами¬
ческом равновесии друг с другом, представляют собой различные фазы
одного и того же вещества. Условия термодинамического равновесия
двух фаз друг с другом — следующие.
Равенство температур фаз 1 и 2 отвечает их тепловому равновесию:
Т\ = Т2.

Введение -l\r 129
Равенство давлений выражает условие механического равновесия меж-
фазной границы:
Р\ = Рг.
Равенство химических потенциалов обеих фаз означает равновесие по
отношению к переносу частиц из одной фазы в другую:
Р\(Р\, Т\) = р2{Рг, Т’г)-
Уравнение
/XI (Р(Т),Т) = р2(Р(Т),Т)
неявно определяет кривую фазового равновесия или бинодаль Р = Р(Т).
Дифференцирование по температуре дает формулу Клапейрона-Клаузиуса:
dP(T) = L
dT	T(v2-v O'
Величина L= T(s2 — si) называется скрытой теплотой фазового пере¬
хода, a si,2 и У] 2 — удельные энтропии и удельные объемы, т. е. прихо¬
дящиеся на одну частицу.
Если уравнение р\ = р2 имеет решения не при всех температурах,
то кривая равновесия фаз Р = Р(Т) имеет точку окончания, которая на¬
зывается критической точкой. За критической точкой не существует
двух различных фаз. Критическая точка — это особая точка хотя бы од¬
ной из функций /л или /Х2. Температура и давление в критической точке
называются критической температурой Тс и критическим давлением
Рс = Р(ТС).
Точка, в которой в термодинамическом равновесии могут одновре¬
менно находиться три фазы, называется тройной точкой. Равновесие
более, чем трех фаз одного и того же вещества невозможно.
Если в точке фазового перехода производная первого порядка
(др/дТ)р = —s или (др/дР)т — v при фазовом переходе испытывает ска¬
чок, т.е. si ф s2 или У) ф Уг, то о переходе говорят как о фазовом пе¬
реходе первого рода. Когда первые производные совпадают, то переход
обычно относят к фазовым переходам второго рода.
Вне кривой фазового равновесия (бинодали) Р = Р(Т) выбор той или
иной фазы вещества определяется энергетическими соображениями. Пол¬
ностью устойчивой (стабильной) фазой является фаза с наименьшим
значением /х. Фаза с большим /х становится неустойчивой (нестабиль¬
ной). Для характеристики неустойчивости фазы и рода фазового пере¬
хода важную роль играет область возможного существования фазы за
кривой фазового равновесия Р = Р(Т) и положение границы ее термо¬
динамической устойчивости (спинодали) P = PS(T), которая определяет¬
ся нарушением одного из термодинамических неравенств (дР/до)т < О,

130	Глава	3.	Статистическая	физика
СР = T(ds/dT)p > 0. В области обратных значений этих неравенств фа¬
за становится абсолютно неустойчивой.
Есть две возможности. Первая — когда граница спинодали отстоит
от бинодали — характерна для фазовых переходов / рода. Тогда в обла¬
сти между бинодалью и спинодалью фаза с большим р может существо¬
вать в метастабильном состоянии. Метастабильная фаза представля¬
ет собой неполное термодинамическое равновесие и, обладая конечным
временем жизни, в конце концов перейдет в стабильную фазу. Хотя и
метастабильная фаза в целом неустойчива, тем не менее она устойчива
по отношению к достаточно малым гетерогенным флуктуациям. С
наличием области метастабильности связаны явления перегрева или
переохлаждения фазы, когда фаза с большим р может существовать
в гомогенном (однородном) состоянии достаточно длительное время.
Предельно возможные границы перегрева или переохлаждения ограни¬
чены спинодалью.
Вторая возможность реализуется, когда граница спинодали совпа¬
дает с бинодалью, и нет области существования фазы по другую сторо¬
ну фазового перехода. Это характерно для фазовых переходов II рода.
Явления перегрева или переохлаждения при фазовом переходе II рода
отсутствуют.
Если кривая фазового перехода первого рода Р = Р(Т) заканчива¬
ется критической точкой, то в этой же точке заканчивается также и
спинодаль.
4.2.	Приближение самосогласованного поля. В настоящее время
фазовый переход второго рода рассматривается как спонтанное нару¬
шение симметрии. Количественная характеристика степени нарушения
симметрии называется параметром порядка ip, который может быть мно¬
гокомпонентной величиной. Параметр порядка всегда равен нулю по
одну сторону фазового перехода и плавно нарастает при удалении от
точки перехода по другую сторону перехода. Смысл и число компонент
параметра порядка ц> определяется физикой конкретного фазового пе¬
рехода. Например, при ферромагнитном переходе параметр порядка —
намагниченность или магнитный момент единицы объема; для антифер-
ромагнитного упорядочения — это вектор антиферромагнетизма, пред¬
ставляющий собой разность намагниченностей двух магнитных подре-
шеток; для критической точки перехода пар-жидкость — это отклоне¬
ние плотности жидкости от ее критического значения. При переходе
в сверхпроводящее или сверхтекучее состояние параметр порядка уже
комплексная волновая функция. Для сверхтекучей ферми-жидкости ти¬
па 3Не с р-спариванием параметр порядка становится еще сложнее и
представляет собой комплексную 3x3 матрицу.

Введение -lw 131
Для более детального описания фазового перехода второго рода вво¬
дится понятие локального значения параметра порядка <^(х) в точке х,
определяемое как среднее по объему, содержащему большое число частиц,
но малому по сравнению с полным объемом всей системы V. В этом слу¬
чае говорят о р(х), как о поле параметра порядка, и поле ip(x) представ¬
ляет собой макроскопическую или классическую переменную. Харак¬
терный пространственный масштаб, на котором параметр порядка ip(x)
меняется существенно, должен быть велик по сравнению с расстояни¬
ем между частицами или постоянной решетки. Параметр порядка ip(x)
может изменяться или флуктуировать от одной точки к другой точке.
Одной из основных характеристик параметра порядка, наряду с его
средним значением (у>(х)), является корреляционная функция или кор¬
релятор
К(х,х) = (<p(x)ip(x )).
Символ (Л) означает термодинамическое среднее величины А. При Т> Тс
в неупорядоченной фазе (р) = 0, а коррелятор экспоненциально зату¬
хает при |х - х'| —► оо:
Х(х,х')~ехр(-|х-х'|/£)-
Корреляционная длина £ = £(Г) неограниченно возрастает при прибли¬
жении к точке перехода. В упорядоченной фазе ниже температуры пе¬
рехода коррелятор не спадает на больших расстояниях и стремится к
квадрату среднего значения параметра порядка (ip)2.
Если задать <^(х) в каждой точке системы, то можно представить
свободную энергию F (при заданном объеме) или термодинамический
потенциал Ф (при заданном давлении) как функционал от ip(x). Обыч¬
но в общей теории фазовых переходов не конкретизируют вид внеш¬
них условий и тип термодинамического потенциала и, также, для всех
термодинамических потенциалов используют одно и тоже обобщенное
название — эффективный гамильтониан.
Эффективный гамильтониан может разложен в бесконечный интегро-
дифференциальный ряд по степеням параметра порядка р(х) и его про¬
изводным. Учет в разложении наинизших степеней ip(x) и Vyp(x) назы¬
вается разложением Ландау и приводит к гамильтониану Ландау:
Kl = J^(Vp)2 + |v22 +	-/z(x)v>]dx.
Чтобы упорядочение ip ф 0 возникало ниже Тс и отсутствовало (т. е.
р = 0) выше Тс, достаточно предположить, что а меняет знак, обраща¬
ясь в нуль в точке перехода:
Т — Т
а = ат, т——се > 0.

132 -J\r Глава 3. Статистическая физика
Величина г называется близостью к точке перехода или безразмерной
температурой. Коэффициенты cub, соответственно, жесткость и кон¬
станта взаимодействия, меняются не столь сильно и считаются посто¬
янными. О члене с <р* говорят как о взаимодействии флуктуаций. Па¬
раметр h(x) представляет собой обобщенное внешнее поле. Наличие
кубического члена с р3 в гамильтониане приводит к фазовому пере¬
ходу первого рода, когда в точке перехода нарушается непрерывность
и возникает скачок параметра порядка при переходе из одной фазы в
другую.
Вероятность W[p(x)\ заданной конфигурации поля упорядочения р(х)
равна
Г[уэ(х)] = Z-1 ехр(-1К/. [ф(х)\/Т), Z = ^ ехр(—Э-С/. [<р(х)]/Г),
Ч> (х)
где Z — статистическая сумма. Наибольшей вероятностью обладает кон¬
фигурация, для которой ;Нф[</?(х)] минимальна. Необходимое условие
следующее:
<ЯКДу?(х)] _ q
Мх)
В приближении самосогласованного (среднего) поля флуктуации пара¬
метра порядка р считаются пренебрежимо малыми, а равновесные свой¬
ства системы определяются условием экстремальности 1Кф[</>(х)] по у>(х).
Приближение самосогласованного поля дает следующие характеристи¬
ки фазового перехода второго рода.
Для среднего равновесного значения параметра порядка (р) = ро
имеем
{О	при т > О,
(а\т\/Ьу/2 ~ |г|*/2 при т < 0.
Теплоемкость в точке перехода испытывает конечный скачок:
АС = С(т = +0) - С(т = -0) - -^г.
Обобщенная восприимчивость, определяемая как х = 9{p)/dh, ведет
себя в слабом внешнем поле h hc по закону Кюри:

Введение	133
а в сильном магнитном поле h^> hc согласно соотношению
X = i/з 'ТТз ~ Л_2/3. h > hc =	•
3b h	b'/2
По мере приближения к Тс корреляционный радиус £, т. е. размер обла¬
сти, в которой значения <р скоррелированы, неограниченно возрастает,
предшествуя появлению дальнего порядка в точке перехода:
£ = (с/ат)~1//2 ~ т-1/2, т > 0.
В самой точке перехода Т — Тс отсутствует характерный и естествен¬
ный масштаб длины в силу £ = оо, и коррелятор К(х, х') ведет себя сте¬
пенным образом:
К(х,х') ~ |x-x'r(d“2),
где d — размерность пространства.
Теория самосогласованного (среднего) поля справедлива, пока флук¬
туации параметра порядка в объеме ~ £d с линейным размером ~ £
малы по сравнению с равновесным значением tpo- В противном случае
необходимо учитывать флуктуации параметра порядка. Для обычного
пространства d = 3 из условия
((Д^)2) = ((у? - <р0)2) = ^ ~ -Д- « <Ро ~
•ч £ а|т|	о
получаем критерий применимости разложения Ландау или теории са¬
мосогласованного поля:
Ь2Т2
Gi < |т| « 1,	(I)'
Первое неравенство выражает близость к точке перехода, необходимую
для возможности разложения Ландау. Второе неравенство обеспечива¬
ет малость флуктуаций. Непосредственная окрестность точки перехода
|т| < Gi, в которой развиваются сильные флуктуации параметра поряд¬
ка, называется флуктуационной или критической областью фазового
перехода. При Gi > 1 области применимости теории самосогласованного
поля (разложения Ландау) нет.
Безразмерный параметр Gi, независящий от температуры, называет¬
ся числом Гинзбурга-Леванюка. Поясним его смысл из вида последней
формулы. Здесь £о = (с/с*)1/2 совпадает по порядку величины с корре¬
ляционным радиусом (длиной когерентности) вдали от точки перехода,
грубо говоря, при Т = 0, когда |т| ~ 1. Величина ес = а2/Ь по порядку

134
Глава 3. Статистическая физика
величины представляет собой плотность энергии конденсации упорядо¬
ченной фазы также вдали от точки перехода. С учетом того, что пара¬
метр а играет роль межчастичного расстояния или периода решетки,
еса3 есть характерная энергия конденсации или выигрыш в энергии
при полном упорядочении низкотемпературной фазы на одну частицу.
Основное условие для малости числа Gi — это £о > я- К веществам с
Gi < 1, прежде всего, относятся сверхпроводники и сверхтекучий 3Не,
в которых Gi ~ (а/£о)4 или ~ (Тс/ер)4- К веществам с относительно
небольшими числами Gi ~ 0,1 относятся некоторые ферромагнетики и
сегнетоэлектрики с температурами Кюри порядка сотен кельвин. При¬
мером, где совсем нет области применимости разложения Ландау в силу
Gi ~ 1 и флуктуационная область занимает всю область фазового пере¬
хода, служит сверхтекучий 4Не. Здесь длина когерентности £о состав¬
ляет несколько межатомных расстояний, а энергия конденсации поряд¬
ка нескольких кельвин сравнима с температурой перехода около 2 К.
4.3.	Функционал Гинзбурга-Ландау. Использование микроскопи¬
ческой теории БКШ для описания поведения сверхпроводника в маг¬
нитном поле представляет собой математически сложную задачу. Вбли¬
зи точки сверхпроводящего перехода из уравнений микроскопической
теории может быть получено упрощенное описание поведения сверх¬
проводника в магнитном поле, получившее название теории функцио¬
нала Гинзбурга-Ландау.
Функционал Гинзбурга-Ландау есть разность свободных энергий
сверхпроводящего и нормального состояний вблизи критической тем¬
пературы Тс:
^-У„ = ДУ№(Г),^(г),А(г)]= J Л3гД/^(г)Ж(г),А(г)),
Первые три слагаемые обусловлены проявлением сверхпроводящего со¬
стояния. Последнее слагаемое — энергия магнитного поля величиной
h = rotA. Функционал Гинзбурга-Ландау представляет собой первые
члены разложения свободной энергии в ряд по малости и медленно¬
сти пространственного изменения сверхпроводящего параметра поряд¬
ка. Коэффициент а(Т) = ао(Т - Тс) обращается в ноль при Т = Тс и
положителен при Т > Тс в силу ао > 0. Два остальных коэффициен¬
та — /3 и 7 — положительны и не зависят от температуры.
где плотность разности свободных энергий A.F равна

Введение
Функционал Гинзбурга-Ландау обладает свойством калибровочной
инвариантности. При калибровочном преобразовании вектор-потен¬
циала А(г):
так что значение свободной энергии не меняется.
В теории функционала Гинзбурга-Ландау сверхпроводящий пара¬
метр порядка, который является комплексной величиной, также приня¬
то называть волновой функцией конденсата куперовских пар. Норми¬
ровка или единицы измерения волновой функции ф(г) в рамках теории
Гинзбурга-Ландау содержат элемент произвола и могут быть выбраны
из соображений удобства. Величину коэффициента пропорционально¬
сти в соотношении -0(г) ~ Д(г) можно изменить переопределением или
выбором единиц измерения для коэффициентов а, /3, 7 в разложении
свободной энергии.
Кроме естественного для теории БКШ выбора = Д(г), где Д(г) —
сверхпроводящий параметр порядка (сверхпроводящая щель), часто ис¬
пользуется представление в котором
где т — масса электрона. Такой выбор 7 позволяет использовать ана¬
логию с квантовомеханическим движением частицы массой 2т и элек¬
трическим зарядом 2е. В этом случае
где п — плотность электронов.
Уравнения, которые отвечают требованию минимальности функци¬
онала Гинзбурга-Ландау, называются уравнениями Гинзбурга-Ландау
и находятся из приравнивания к нулю вариационных производных. Из
условия 6(AJ)/6il>*(r) = 0 находим
А(г) - А(г) + Vx(r)
волновая функция приобретает дополнительную фазу
7 = 1/2 т,
| (-iftV - Ц А(г)) ф(т) + аф(г) + /3\ф(г)\2ф(г) = 0.
Варьирование по ф(г) дает комплексно сопряженное уравнение.

136	Глава	3.	Статистическая	физика
Варьирование по вектор-потенциалу и условие J(AJ)/(5A(r) = 0 при¬
водят к уравнению Максвелла
представляет собой плотность сверхпроводящего тока.
Для границы сверхпроводник-изолятор или сверхпроводник-вакуум
используется естественное граничное условие, которое зануляет поверх¬
ностный интеграл, возникающий при варьировании функционала по ф*
или ф:
Здесь п — внешняя нормаль к поверхности сверхпроводника S. Это
граничное условие означает отсутствие сверхпроводящего тока через
границу сверхпроводника:
Граничное условие для магнитного поля h(r) — это непрерывность поля
на границе. Уравнения Гинзбурга-Ландау вместе с уравнением Макс¬
велла и граничными условиями представляет собой замкнутую систему
уравнений, описывающую поведение сверхпроводника в магнитном по¬
ле вблизи критической температуры.
В однородном состоянии \7ф = 0, и в отсутствие магнитного поля
возможны два состояния: нормальное с ф = 0 при всех температурах и
сверхпроводящее с ф = фо — (—а//?)'/2 только при Т ^ Тс. Плотность
энергии сверхпроводящего состояния меньше энергии нормального со¬
стояния при всех Т < Тс на величину
где НС(Т) ~ (Тс — Т) — термодинамическое критическое поле.
Если волновая функция ф(г) — действительная величина (ф — ф*),
то плотность сверхпроводящего тока прямо пропорциональна вектор-
потенциалу и описывается соотношением Лондонов:
rotrotA(r) = roth(r) = —js(r),
с
где выражение
(js)n = (jsn)|s = 0.
с А
4тг S2'

Введение _J\, 137
Здесь величина ns = Ат^Щ2 — называется плотностью сверхпроводя¬
щих электронов, а
г—2 л 4б I I (О 47Гб
5	= 4^—2_|V,I =  frts
с	тс
представляет собой квадрат обратной глубины проникновения магнит¬
ного поля в сверхпроводник <5. Это видно из уравнения Лондонов, к кото¬
рому сводится уравнение Максвелла в кулоновской калибровке divA = 0:
V2A = А/62.
Уравнение описывает эффект Мейсснера — выталкивание магнитного
поля из объема сверхпроводника. Сверхпроводящие незатухающие то¬
ки, которые экранируют внешнее магнитное поле, текут в приповерх¬
ностном слое сверхпроводника толщиной порядка <5. Магнитная индук¬
ция, определяемая как среднее поле по объему сверхпроводника V, рав¬
на нулю:
В = р/ МО d3r = (h) у = 0.
v
В магнитном поле при Н < НС{Т) энергетически выгодно сверхпро¬
водящее состояние и ф = фо- Для Н > Не(Т) уже выгоднее нормаль¬
ное состояние с ф = 0. Такой переход с разрушением сверхпроводимо¬
сти магнитным полем — фазовый переход первого рода, так как волно¬
вая функция (сверхпроводящий параметр порядка) меняется скачком с
ф = ■фо на ф = 0.
Внешнее магнитное поле, при котором в нормальном состоянии ста¬
новится выгодным спонтанное образование зародышей сверхпроводя¬
щей фазы, называется верхним или вторым критическим магнитным
полем Нс2{Т). Это критическое поле находится из линеаризованного
уравнения Гинзбурга-Ландау
о	2	1
|(-tW - уА(г)) ф(т) + а(Т)ф(г) = 0, А(г) = -[Нхг],
как магнитное поле Я, при котором впервые появляется нетривиальное
решение с ф(г) ф 0, и равно
Hfii(T) = \а(Т)\-^ ~ (Тс — Т).
Отношение верхнего критического поля Нс2 к термодинамическому
полю Нс не зависит от температуры:
ML2= с^-У2 = яУ2.
ИЛТ) ФЗттЬе'у

138	Глава	3.	Статистическая	физика
Безразмерный параметр я называется параметром Гинзбурга-Ландау и
является важнейшей характеристикой сверхпроводника. Этот параметр
можно представить и как отношение двух длин:
я-т.
«л-
Первая представляет собой глубину проникновения магнитного поля 6(Т),
а вторая — сверхпроводящая корреляционная длина £(Г) — характери¬
зует пространственный масштаб, на котором меняется сверхпроводящий
параметр порядка или волновая функция:
£(Т) = I ^ -	1
2|а(Л|	(Гс-Г)|/2‘
Последнее очевидно из линеаризованного уравнения в нулевом магнит¬
ном поле:
^ (-ihV)1 ф{г) + аф(г) = 0, или £2V2 ф(г) + ф(г) = 0.
С введением элементарного кванта потока магнитного поля фо = псН/е —
= 2 • 10~7 Гс • см2 выражение для верхнего критического поля приобре¬
тает наглядный вид:
Нс2(Т) = —.
2тг ?(Т)
В зависимости от величины параметра Гинзбурга-Ландау я возни¬
кает два разных типа поведения сверхпроводника в магнитном поле, и,
соответственно, различают два рода сверхпроводников. К сверхпровод¬
никам первого рода относят сверхпроводники с я < \/\/2 или Нс > Нс2.
Ко второму роду относятся сверхпроводники с я > 1/\/2 или Нс < Нс2.
При уменьшении внешнего магнитного поля в сверхпроводнике / ро¬
да сверхпроводящее состояние выгодно уже при достижении полем зна¬
чения Я = Нс > Нс2 и, следовательно, будет выгоднее образовать скач¬
ком мейсснеровское состояние с конечным значением сверхпроводяще¬
го параметра порядка. Это приводит к фазовому переходу I рода. На¬
оборот, в сверхпроводнике II рода уже в поле Я = Нс2 > Нс начнется
образование зародышей сверхпроводящей фазы со сколь угодно малым
значением параметра порядка. Переход к сверхпроводящему состоянию
будет фазовым переходом II рода в силу плавного нарастания величины
сверхпроводящего параметра порядка при переходе через критическую
точку.

Введение -И, 139
4.3.	Основы теории критических явлений. При подходе к точке пе¬
рехода корреляционный радиус £, неограниченно возрастая, становится
единственной самой большой длиной в системе, которая превышает все
остальные возможные длины, например, межчастичное расстояние (по¬
стоянную решетки), радиус межчастичного взаимодействия. В каждой
области (ячейки) размером £ и объемом V^ суммарный параметр
фс = 22
xev(
растет с увеличением £. Систему в целом вблизи перехода можно пред¬
ставить как совокупность макроскопических областей (ячеек) взаимо¬
действующих друг с другом. Если все линейные размеры измерять в
единицах £, а суммарный параметр порядка в единицах Фс, то изме¬
нение близости к переходу т не приводит к изменению термодинами¬
ческих величин и корреляционных функций. В рамках такой гипотезы
подобия, или масштабной инвариантности, поведение всех термодина¬
мических величин в зависимости от т и корреляторов, как функций
расстояний, выражаются степенными законами.
В теории критических явлений особое поведение физических вели¬
чин в окрестности точки фазового перехода характеризуют критически¬
ми индексами, описывающими степенную зависимость физических ве¬
личин от их близости т к точке перехода. Критические индексы а, (3, у
и S вводятся, соответственно, для теплоемкости С, параметра порядка р
при т < 0, восприимчивости х в слабом и сильном внешнем поле Л:
C~|r|-Q, (р ~ (-т)0 (т < 0),	Х~М_7> X ~ Л1/<5_1.
Для характеристики корреляций поля параметра порядка tp в неупо¬
рядоченной фазе при т > 0 и в самой точке перехода т = 0 вводят два
индекса: индекс корреляционный длины и согласно
(¥>(x)v?(x/))|x-x'Hoo~exp(-|x-x'|/0.	£~т_1/	(т	>	0);
и индекс аномальной размерности (индекс Фишера) £ согласно
<¥>(хМх'))|х-х'|-оо ~ |х - x'|-(d-2+c) (т = 0);
где d — размерность пространства. Критические индексы универсаль¬
ны, т. е. зависят только от числа компонент параметра порядка. Сте¬
пень точности описания не позволяет различать логарифмическое по¬
ведение In |т| на фоне степенного. Нулевому значению индекса соответ¬
ствует как стремление к постоянному пределу, так и логарифмическое
поведение.

140 ->\r Глава 3. Статистическая физика
Масштабная инвариантность или скейлинг становится возможным в
силу того, что в критической точке корреляционный радиус обращается
в бесконечность и тем самым исчезает естественная единица длины
или масштаб. Подобное изменение расстояний (скейлинг) в отсутствие
характерного размера или масштаба:
х —► х' = Ах
не может изменить состояния системы, так как это преобразование сво¬
дится к изменению единицы длины. При масштабном преобразовании
(скейлинге) физический параметр Л(х), характеризующий систему, на¬
пример, параметр порядка р, плотность энергии е, температура т, внеш¬
нее поле h, умножаются на некоторую степень Л согласно закону
Л(х) —> Л'(х') = А~ЛМ(х).
Показатель степени Д^ называется масштабной (скейлинговой) размер¬
ностью величины А.
Исходя из требования масштабной инвариантности можно связать
скейлинговые размерности с критическими индексами и получить ряд
скейлинговых соотношений между индексами. Очевидно, что Ах = — 1
и Д{ = — 1. Из условия £ ~ т-" следует Дт = 1/м, а с учетом ip ~
имеем А1р = /3/и. Размерности термодинамически сопряженных вели¬
чин в сумме равны d, например, Д^ + Дh = d. Скейлинговые соотношения
а + 2/3 + 7 = 2, /36 = /3 + 7,
с d + 2 — £	,	~
s = J^rrc =
позволяют выразить через два индекса, например, ги(, все остальные
индексы.
Эксперимент и численный расчет в трехмерном случае демонстриру¬
ют для индексов теплоемкости и Фишера относительно малые значения:
а < 0,1 и С < 0,05. Если положить а = 0 и С = 0, то оценка остальных
индексов дает /3 = 1/3 ~ 0,3, 7 = 4/3 ~ 1,3, м = 2/3 ~ 0,7 и <5 = 5 вме¬
сто значений в теории самосогласованного поля (3 = 1/2, 7 — 1, м = 1/2
и 8 = 3.
Критические индексы зависят от размерности пространства d. В про¬
странстве d ^ 4 критические индексы самосогласованного поля удовле¬
творяют всем скейлинговым соотношением, что неверно при d < 4. Раз¬
мерность пространства d = 4 называется верхней критической размер¬
ностью и может быть взята в качестве исходного нулевого прибли¬
жения для развития теории возмущения (е-разложение) с математи¬

Введение	141
чески непрерывным переходом к пространству меньшей размерности
^ — 4-t-. Физический смысл в подобных разложениях имеют лишь це¬
лые значения е — 1,2,3.
Приведем первые члены е-разложения критических индексов для п-
компонентного параметра порядка:
4 ~п I	я — 1	3
а ~ 2(л+~8)е	’	2	2(п	+	8)
7=1 + 2&т1)6 + ---’ ^3 + е + -’--
\ п 2	*	 п 2
2	4(n	+	8)f	_	2(п	+	8)2

ЗАДАЧИ
3.1.	РАСПРЕДЕЛЕНИЕ	ГИББСА.
ТЕРМОДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ И ФУНКЦИИ
3.1.1. а) Проверить, что уравнение состояния идеального газа PV = NT
не зависит от энергетического спектра его частиц е = ер и раз¬
мерности пространства d. Найти энергию и теплоемкость газа
частиц со спектром ер = cpk (k > 0).
б) Рассмотреть температурное поведение теплоемкости С(Т) для
газа частиц со спектром ер = ср + р2/(2т) в d = 3.
3.1.2. Идеальный газ объемом V находится во внешнем поле U(г).
Найти поправку к теплоемкости газа от внешнего поля в пре¬
деле высоких температур Т —* оо.
3.1.3. Найти, как изменится свободная энергия и теплоемкость идеаль¬
ного газа, заключенного в цилиндрический сосуд высотой Я, если
поместить сосуд с газом в однородное поле тяжести U(z) = mgz.
3.1.4. Цилиндрический сосуд радиуса R с идеальным газом внутри по¬
местили во внешнее поле с потенциалом U(r) = Uo(r/R)2 (Яо > 0).
где г — расстояние от оси цилиндра. Найти, как при этом из¬
менится свободная энергия и теплоемкость газа.
3.1.5. Идеальный одномерный газ из N » 1 частиц массой m нахо¬
дится в двухъямной ловушке с потенциалом
U(x) = ти> ^х ~
Найти свободную энергию газа и оценить его теплоемкость в
низко и высокотемпературном пределах.
3.1.6. Идеальный газ N частиц находится в ловушке с гармоническим
потенциалом
/ 2 2	2 2 2 2\
Щх,у,г) = тЬх	±“?г)..

3.1. Распределение Гиббса. Термодинамические величины и функции	143
Найти одночастичную плотность состояний, химический потен¬
циал и теплоемкость газа.
3.1.7.	Идеальный двумерный газ помещен в осесимметричную ловуш¬
ку с потенциалом
О,	r<R,
Uo In r/R, г > R (Uo > 0).
U(r) =
Показать, что одночастичная плотность состояний растет экспо¬
ненциально с энергией. Найти теплоемкость газа и обосновать,
что система обладает предельной температурой Гпр = Uo/2, вы¬
ше которой газ невозможно нагреть.
3.1.8.	Идеальный трехмерный газ помещен в центрально-симметрич¬
ную ловушку с непроницаемой сердцевиной радиуса R и внеш¬
ним потенциалом
U(r) =
оо,	г = R,
Uo\nr/R, r>R(Uo> 0).
Найти теплоемкость газа и предельную температуру, выше ко¬
торой газ невозможно нагреть.
3.1.9.	Идеальный двумерный газ находится в ловушке с непроницае¬
мой стенкой радиуса R в центральном поле с притяжением к
центру ловушки:
U(r) =
оо,	г	=	R,
-U0\nR/r, г < R (Uo > 0).
Вычислить энергию газа, теплоемкость и показать, что суще¬
ствует предельная температура Гпр, ниже которой газ не может
быть охлажден.
3.1.10.	Термодинамическая система представляет собой ансамбль из
N > 1 невзаимодействующих двухуровневых систем с одинако¬
вой энергией возбуждения, равной е. Кратность основного уров¬
ня энергии равна g\, а возбужденного уровня — g2. Найти эн¬
тропию системы: а) с помощью статистического определения
энтропии; б) через распределение Гиббса. Определить теплоем¬
кость системы и показать, что область отрицательных темпера¬
тур отвечает термодинамически неустойчивым состояниям си¬
стемы с инверсной заселенностью.

144 -J\r Глава 3. Статистическая физика. Задачи
Состояние аморфных веществ (стекол) при низких температу¬
рах описывают, как состояние с макроскопически большим на¬
бором различных двухуровневых систем, у которых энергия воз¬
буждения е представляет случайную величину с плотностью
распределения р(е), нормированной на число двухуровневых си¬
стем в единице объема /0°° р(е) de — N. Предполагая, что плот¬
ность распределения двухуровневых систем р(е) остается ко¬
нечной и непрерывной при е = 0, найти поведение теплоемко¬
сти аморфных веществ в пределе низких температур.
3.1.11. Найти намагниченность, магнитную восприимчивость, энтро¬
пию и магнитную теплоемкость N классических магнитных мо¬
ментов величиной р во внешнем магнитном поле Н.
3.1.12. Найти намагниченность, магнитную восприимчивость, энтро¬
пию и магнитную теплоемкость N частиц, обладающих спи¬
ном 5 и эффективным магнетоном Бора рЭф, во внешнем маг¬
нитном поле Н. Рассмотреть переход к классическому пределу
большого спина S —> оо.
3.1.13. Квадрупольный момент молекул с аксиально-симметричным рас¬
пределением электрического заряда можно представить в ви¬
де: Qik = Q(3n,n*. - Sik), где n — единичный вектор, направлен¬
ный вдоль оси молекулы. Энергия Е квадрупольного момента
во внешнем электрическом поле, потенциал которого равен <р,
выражается через вторые производные по координатам:
Г-П	1 tfifi
E-Qikaik, где <гЛ - 6^^-
Найти средний квадрупольный момент газа в пределе высоких
температур или слабого поля.
3.1.14. Изменение температуры магнетика при его адиабатическом на¬
магничивании или размагничивании во внешнем магнитном по¬
ле называется магнитокалорическим эффектом. Найти величи¬
ну эффекта, т. е. отношение изменения температуры к измене¬
нию величины магнитного поля, предполагая известными на¬
магниченность и теплоемкость магнетика.
3.1.15. В ферромагнетике при быстром адиабатическом изменении на¬
правления вектора намагниченности относительно кристалло¬
графических осей, которое может быть достигнуто поворотом
ферромагнитного монокристалла в сильном постоянном магнит¬
ном поле, также возникает магнитокалорический эффект, при¬
водящий к изменению температуры магнетика (J1.B. Киренский,

3.1. Распределение Гиббса. Термодинамические величины и функции	145
1939). Найти изменение температуры при адиабатическом по¬
вороте одноосного ферромагнетика в сильном магнитном поле
на 90°. Константа магнитной кристаллографической анизотро¬
пии К(Т) зависит от температуры, а свободная энергия, связан¬
ная с магнитной анизотропией, равна Faн = К(Т) sin2 в, где в —
угол между направлением вектора намагниченности и кристал¬
лографической осью кристалла.
3.1.16. На примере орто- и параводорода рассмотреть влияние ядер-
ного спина на вращательный вклад в теплоемкость газа моле¬
кул, образованных двумя одинаковыми атомами. Найти тепло¬
емкость смеси орто- и параводорода: а) при заданной концен¬
трации и б) термодинамически равновесной.
3.1.17. Определить степень однократной тепловой ионизации а(Т) од¬
ноатомного идеального газа плотностью п, если энергия одно¬
кратной ионизации равна /,, а масса электрона m много меньше
массы атома Ма.
3.1.18. Найти степень диссоциации а, энтропию S и теплоемкость Ср
диссоциирующего идеального газа двухатомных молекул АВ,
образованных разными атомами А и В. Энергия диссоциации
молекулы равна /. Теплоемкости каждого из газов АВ, А и В
считать постоянными.
3.1.19. Найти средние квадраты термодинамических флуктуаций ос¬
новных термодинамических величин: давления, объема, темпе¬
ратуры, энтропии и корреляции между ними.
3.1.20. Найти средний квадрат термодинамических флуктуаций числа
частиц и корреляцию между флуктуациями химического по¬
тенциала и числа частиц.
3.1.21. Линейный отклик системы на внешнее малое воздействие V = —qf,
где q — обобщенная координата, а / — возмущающая сила,
можно описать с помощью восприимчивости х. которая опре¬
деляется как производная среднего значения координаты (q) по
возмущающей силе согласно
В термодинамически равновесных системах средний квадрат
флуктуации координаты ((Aq)2) и восприимчивость х взаимо¬
связаны друг с другом. При достаточно высоких температурах
Т » hue, где ш — характерные частоты возбуждений в системе,

Глава 3. Статистическая физика. Задачи
термодинамические флуктуации можно считать классически¬
ми, и соотношение между ((Aq)2) и х существенно упрощается.
Найти соотношение между ((Aq)2) и х< предполагая термоди¬
намические флуктуации в системе классическими.
КВАНТОВЫЕ ИДЕАЛЬНЫЕ ГАЗЫ
.1. Идеальный ферми-газ
.2.1. Найти поведение теплоемкости и химического потенциала вы¬
рожденного ферми-газа в области низких температур Т, много
меньших энергии Ферми ер.
.2.2. Вычислить химический потенциал двумерного идеального фер¬
ми-газа с поверхностной плотностью ris при произвольной тем¬
пературе. Масса фермиона m и спин равен 1/2.
2.3. Найти поведение парамагнитной восприимчивости вырожден¬
ного ферми-газа в слабом магнитном поле Н в области низких
температур Т, много меньших энергии Ферми ер. Масса фер¬
миона т, спин равен 1/2 и магнетон Бора (3 = eh/(2mc).
2.4. Найти изменение импульса Ферми и энергии Ферми при пол¬
ной поляризации магнитным полем идеального газа атомов 3Не.
Определить зависимость скорости звука от магнитного поля
при нулевой температуре.
2.5. Свойства примесных атомов 3Не, растворенных в сверхтекучем
гелии 4Не, в первом приближении можно описать как идеаль¬
ный газ фермиевских возбуждений (примесонов) с импульсом р
и энергией ер = —Д + р2/(2714), где Д/6д ~ 2,8 К — энергия
растворения атома 3Не в 4Не и М ~ 2,ЗМНез — его эффектив¬
ная масса. Эти параметры, хотя и незначительно, зависят от
давления Р и концентрации 3Не. «Сверхтечь» из тонких ка¬
пилляров пропускает только сверхтекучую компоненту 4Не и
не пропускает нормальную компоненту. Определить возникаю¬
щее осмотическое давление П между чистым 4Не и раствором
3Не-4Не при нулевой температуре и малых концентрациях 3Не,
считая Д и М постоянными. Осмотическое давление определя¬
ется равенством химических потенциалов 4Не:
/х4(Р, п3) = д4(Я- П, 0),
где пз — плотность атомов 3Не. Как изменится осмотическое
давление при полной поляризации ядерных спинов 3Не в маг¬
нитном поле?

3.2. Квантовые идеальные газы	147
3.2.6. При сжатии металла размер и форма ферми-поверхности изме¬
няются. Пусть при давлении Р = Рс происходит так называе¬
мый топологический электронный переход, в результате кото¬
рого электроны могут заполнять новый участок электронного
спектра с законом дисперсии ер = Д + р2/(2т) (Д > 0). Найти
изменение термодинамического потенциала П, теплоемкости и
сжимаемости металла при таком переходе.
3.2.7. Идеальный газ N » 1 фермионов массой т и спином 1/2 нахо¬
дится в гармонической ловушке с потенциалом
+	t
Найти в квазиклассическом приближении энергию Ферми, низ¬
котемпературные поправки к термодинамическим величинам,
распределение плотности частиц и распределение частиц по
импульсу.
3.2.8. Идеальный газ нейтронов находится в однородном поле тяже¬
сти U = mgz над идеально отражающей горизонтальной поверх¬
ностью. Число нейтронов, приходящихся на 1 см2 поверхности,
N » 1. Найти распределение плотности нейтронов по высоте
при нулевой температуре. Какой высоты имеет смысл делать
ящик, чтобы нейтроны не рассеивались в пространстве?
3.2.9. Для накопления электронов в центр ловушки поместили боль¬
шой положительный заряд +Q. Пренебрегая взаимодействием
электронов друг с другом, найти энергию Ферми при числе ча¬
стиц N » 1. Показать, что система из одних связанных уровней
термодинамически неустойчива при конечных температурах.
3.2.10. Для малых металлических частиц, имеющих небольшое число
электронов N, дискретность спектра энергетических уровней
начинает играть существенную роль при низких температурах
Т < S, где J — характерное расстояние между уровнями. Вели¬
чина энергетического интервала 6 приблизительно равна £f/N,
где ер — энергия Ферми. Предполагая для простоты эквиди¬
стантность энергетического спектра, оценить теплоемкость и
спиновую восприимчивость металлической частицы в зависи¬
мости от четности числа электронов N в металлической части¬
це при Т < 6.
3.2.11. В графене (монослой графита) зависимость энергии от импуль¬
са р = (рх,ру) описывается безмассовым дираковским спектром
Ер = vcг р, где v — скорость электрона и ег = {сгх,ау) — мат-

148
X
Глава 3. Статистическая физика. Задачи
рицы Паули, и соответственно ер = ±и|р|. Найти одночастич¬
ную плотность состояний g(e), а также теплоемкость С(Т), в
условиях когда химический потенциал у фиксирован внешними
условиями. (В плотности состояний учесть двукратное вырож¬
дение по спину электрона и наличие двух одинаковых кониче¬
ских зон.)
3.2.12. В условиях предыдущей задачи оценить парамагнитную вос¬
приимчивость графена.
3.2.13. Идеальный газ из N ;» 1 электронов находится в тонком коль¬
це радиуса R. В направлении, перпендикулярном к плоскости
кольца, приложено магнитное поле величиной Я. Найти ток
намагничения, который протекает по кольцу в зависимости от
потока через кольцо Ф = я7?2Я и химического потенциала.
3.2.14. Найти осцилляционное поведение намагниченности двумерно¬
го слоя электронного газа в перпендикулярном к слою магнит¬
ном поле (эффект де Гааза-ван Альфена).
3.2.15. Идеальный газ N » 1 электронов массы m находится в осе¬
симметричной ловушке, ограниченной по вертикали размером L
и в горизонтальном направлении гармоническим потенциалом
U(x,y) = ти>2(х2 + у2)/2. Вдоль вертикальной оси г приложе¬
но магнитное поле напряженностью Я. Оценить диамагнитную
восприимчивость электронного газа, предполагая малость ча¬
стоты ловушки ш и циклотронной частоты шс = еН/(тс) по
сравнению с температурой Т.
3.2.16. Идеальный газ N ^> 1 двумерных электронов массы т находится
в гармонической ловушке с потенциалом U(x, у) = ти2(х2+у2)/2.
Перпендикулярно плоскости ловушки приложено магнитное по¬
ле напряженностью Я. Оценить диамагнитную восприимчивость
электронного газа, предполагая электронный газ вырожденным,
а циклотронную частоту и)с = еН/(тс) и частоту ловушки ш
малыми по сравнению с температурой Т.
3.2.17. В графене (монослой графита) зависимость энергии от импуль¬
са р = (рх,Ру) описывается безмассовым дираковским спектром
ер = vcr • р, где v — скорость электрона и <т = (сгх,ау) — мат¬
рицы Паули. В перпендикулярном к слою магнитном поле Я
спектр становится дискретным:
£п = eo\/Hsign(n)> £0 = Й» . (я = 0,±1,±2,...).

3.2. Квантовые идеальные газы	149
Вырождение каждого магнитного уровня по центру орбиты элект¬
рона точно такое же, как и для обычного спектра ер = р2/(2т),
и равно eH/(2nhc). Плотность состояний в магнитном поле да¬
ется обычным соотношением:
ш £
п=—ос
(Множитель v = 2 х 2 = 4 включает в себя двукратное вырож¬
дение по спину и наличие в графене двух одинаковых подзон.)
Оценить намагниченность и диамагнитную восприимчивость в
графене при нулевой температуре.
3.2.18. Определить корреляционную функцию для флуктуаций плот¬
ности в идеальном ферми-газе. В низкотемпературном преде¬
ле вырожденного газа найти корреляционный радиус и период
фриделевских осцилляций.
3.2.2.	Идеальный бозе-газ
3.2.19. В идеальном бозе-газе бесспиновых частиц массой т и плот¬
ностью п найти плотность конденсата по(Т).
3.2.20. Найти энергию, давление и теплоемкость идеального конден¬
сированного бозе-газа бесспиновых частиц массой т. Темпера¬
тура газа равна Т.
3.2.21. Для идеального бозе-газа частиц со спектром ер = р2/(2т) опре¬
делить размерности пространства d, в которых невозможно яв¬
ление бозе-эйнштейновской конденсации.
3.2.22. Найти адиабатическую сжимаемость и адиабатическую скорость
звука в идеальном конденсированном бозе-газе.
3.2.23. Определить поведение теплоемкости СР(Т) идеального бозе-газе
при постоянном давлении вблизи точки бозе-эйнштейновской
конденсации.
3.2.24. Рассмотреть бозе-эйнштейновскую конденсацию идеального га¬
за бозонов со спином единица в магнитном поле. Определить
температуру перехода в конденсированное состояние в зависи¬
мости от величины магнитного поля. Рассмотреть температур¬
ное поведение парамагнитной восприимчивости.
3.2.25. Идеальный газ N » 1 бозонов массой m находится в симмет¬
ричной гармонической ловушке с удерживающим потенциалом
U(r) = mu2r3/2. Найти температуру бозе-эйнштейновской кон¬

150	Глава	3.	Статистическая	физика.	Задачи
денсации, поведение химического потенциала и теплоемкости
вблизи перехода. Определить плотность конденсата и теплоем¬
кость газа во всей области бозе-конденсации.
3.2.26. Для газа бозонов в симметричной гармонической ловушке най¬
ти термодинамические флуктуации температуры, а также вли¬
яние термодинамических флуктуаций частоты ловушки ш на
размытие температуры бозе-эйнштейновской конденсации.
3.2.27. Рассмотреть идеальный газ N » 1 бозонов с обычной диспер¬
сией ер = р2/(2т) в шестимерном пространстве.
а) Показать, что в макроскопическом пределе бозе-газ в гар¬
монической ловушке с частотой ш изоморфен газу в однород¬
ном шестимерном пространстве, заключенном в ящике объемом
Уб = ^6. где / = \j2nh/mu — осцилляторная длина.
б) Найти коррелляционный радиус пространственных корреля¬
ций вблизи точки бозе-эйнштейновской конденсации.
3.2.28. Какой следует выбрать удерживающий потенциал ловушки,
чтобы наблюдать бозе-эйнштейновскую конденсацию в одно¬
мерном пространстве?
3.2.29. Идеальный газ N 1 бозонов массой т заключен в ящик, кото¬
рый находится в однородном поле тяжести. Оценить как зави¬
сит температура бозе-эйнштейновской конденсации от высоты
ящика Н. Найти распределение числа частиц по высоте при
температурах ниже температуры конденсации.
3.2.3.	Идеальный газ элементарных бозе-возбуждений
3.2.30. Показать, что теплоемкость Сь(Т) одномерных фононов с дис¬
персией £р = ср и теплоемкость С/(Т) одномерных фермионов
с фиксированной проекцией спина и дисперсией £р = р2/(2т)
совпадают в низкотемпературной области при условии равен¬
ства скорости звука с скорости Ферми Vf.
3.2.31. Размерное квантование фононного спектра в малых частицах
влияет на их удельную теплоемкость. Оценить величину эф¬
фекта на примере изотропного упругого тела в форме куба раз¬
мером L х L х L с закрепленными гранями. Возможным изме¬
нением упругих констант в малых частицах пренебречь.
3.2.32. В сверхтекучем гелии при больших импульсах энергетический
спектр элементарных возбуждений существенно отклоняется от
линейного звукового поведения и имеет минимум величиной
Д/&в = 8,7 К вблизи волнового вектора po/h — 1,9 • 108 см-1.

3.2. Квантовые идеальные газы
Поведение вблизи минимума спектра аппроксимируется пара¬
болой с эффективной массой т = 0,16Л1Не4:
Возбуждения с таким спектром называют ротонами. Найти вклад
ротонного участка энергетического спектра возбуждений в сво¬
бодную энергию, энтропию, теплоемкость сверхтекучего гелия,
воспользовавшись неравенствами Д> Г и р\ » 2тТ.
3.2.33.	Не очень близко к температуре Кюри плотность магнонных воз¬
буждений в ферромагнетике невелика и газ магнонов можно
рассматривать как идеальный. Длинноволновый спектр магно¬
нов в изотропном ферромагнетике во внешнем магнитном по¬
ле Н дается соотношением
где /3 — эффективный магнетон Бора, т. е. отношение магнит¬
ного момента иона к его спину, М — намагниченность ферро¬
магнетика и а — его магнитная жесткость. Найти влияние маг¬
нонных возбуждений на намагниченность и теплоемкость фер¬
ромагнетика при температурах, малых по сравнению с темпе¬
ратурой Кюри.
3.2.34. Полное описание вещества при ультравысоких температурах
Т > тс2 должно учитывать рождение пар: частица — антича¬
стица. Рассмотреть влияние рождения пар: бозон — антибозон
на температуру бозе-эйнштейновской конденсации в ультраре-
лятивистском пределе, считая, что разница числа бозонов и чи¬
сла антибозонов N = Nb — N-^ остается постоянной и задается
начальными условиями.
3.2.35. При учете квантовых эффектов черная дыра может не только
поглощать, но и рождать частицы. Состав излучения зависит от
массы черной дыры: для тяжелых черных дыр это в основном
безмассовые частицы (фотоны, нейтрино, гравитоны), а в спек¬
тре легких черных дыр начинают присутствовать и частицы с
ненулевой массой (электроны, позитроны и другие). Термоди¬
намическое равновесие черной дыры может быть описано как
состояние абсолютно черного тела, нагретого до температуры
hoj(k) — PH + /3Mak2,
hx
2-7Г с
GM

Глава 3. Статистическая физика. Задачи
Здесь х — ускорение свободного падения на поверхности чер¬
ной дыры, G — постоянная тяготения Ньютона, М — масса
черной дыры и Rg = 2GM/c2 — ее размер или гравитационный
радиус. Предполагая, что излучение черной дыры в основном
связано с испусканием фононов, оценить время жизни черной
дыры массой М.
НЕИДЕАЛЬНЫЕ КВАНТОВЫЕ СИСТЕМЫ (ЖИДКОСТИ).
ОСНОВЫ ТЕОРИИ КОНДЕНСИРОВАННЫХ СРЕД
.1. Нормальная (несверхтекучая) ферми-жидкость
.3.1. Определить эффективную массу квазичастиц т* в ферми-жид¬
кости, зная функцию Ландау /(р, р') и массу т истинных ча¬
стиц, образующих ферми-жидкость.
.3.2. В пределе низких температур, малых по сравнению с энергией
Ферми, теплоемкость ферми-жидкости пропорциональна тем¬
пературе: С{Т) = 7Т. Постоянная 7 называется постоянной Зо-
ммерфельда. Выразить постоянную Зоммерфельда через эффек¬
тивную массу квазичастиц т* и импульс Ферми pp.
3.3. Ферми-жидкость обладает магнитными свойствами, поскольку
наличие спина у частиц означает наличие у них магнитного мо¬
мента. Определить спиновую восприимчивость ферми-жидко¬
сти при нулевой температуре, предполагая, что спиновая часть
взаимодействия между квазичастицами в функции Ландау
/то-'(Р. Р') = /(р. р') + С(Р. PV • о-'
имеет чисто обменное взаимодействие.
3.4. Неравновесные состояния ферми-жидкости описываются функ¬
цией распределения квазичастиц, зависящей от координат, им¬
пульсов и времени п = n(r,p,t). При нулевой температуре или
при достаточно низких температурах столкновения между ква¬
зичастицами становятся настолько редкими, что ими можно
полностью пренебречь. В отсутствие столкновений между ча¬
стицами справедлива теорема Лиувилля о тождественном об¬
ращении в нуль полной производной по времени от функции
распределения:
dn дп

3.3. Неидеальные квантовые системы (жидкости)	153
где {//, п} — скобки Пуассона для гамильтониана Н и функции
распределения п. Используя следующее кинетическое уравнение:
дп	(Мдп _ дН_дп = Q
dt	др дг	дг др
рассмотреть малые колебания функции распределения при
Т = 0. Найти условия, когда возможно распространение неза¬
тухающих волн, получивших название нуль-звук. Считать, что
функция взаимодействия квазичастиц не зависит от импульсов
/(р.р') = /о.
3.3.5. Энергия основного состояния взаимодействующего неоднород¬
ного электронного газа во внешнем электрическом поле У (г)
может быть записана в виде функционала плотности £ = £[п(г)]:
£[«(«•)] = -J eV(r)n(r)dr+l- j ^^Idrdr1 +
+ £одн [«(г)] + ^неодн [^(г)Ь
где п(г) — плотность электронов. Однородная часть
„	, ,	3	[	(Зтг2)2/3П2пь/3 ,	З/ЗЧ1/3	[	2	4/3	w
£—l«(r)l - s у —*-}У	+ -
представляет собой сумму кинетической энергии Томаса-Ферми,
обменной энергии и корреляционной энергии, которой мы здесь
пренебрегаем. Неоднородная часть представляет собой разло¬
жение по градиентам плотности:
£неодн [«(г)] = ^2-J	dr + • • •
В простейшей модели металла (модели «желе») положительные
ионы заменяются однородным положительным фоном с плот¬
ностью п+, равной электронной плотности, чтобы обеспечить
условие электронейтральности. Оценить поверхностное натя¬
жение металла в модели «желе», используя простейшую вариа¬
ционную функцию
/1 - (\/2)е*'ь, х < 0,
”{(1/2)е-х/*, х > 0
с вариационным параметром Ь для аппроксимации профиля элект¬
ронной плотности вблизи плоской границы х = 0.
3.3.6. В условиях предыдущей задачи определить работу выхода элек¬
трона из металла в модели «желе».

Глава 3. Статистическая физика. Задачи
.2. Сверхпроводимость. Теория БКШ
3.7. Определить плотность состояний элементарных возбуждений
vs(e) в сверхпроводнике с синглетным s-спариванием вблизи
поверхности Ферми.
3.8. В сверхтекучей A-фазе 3Не спектр элементарных возбуждений
имеет вид
где £р = р2/(2т) — ер — энергия, отсчитанная от уровня Ферми,
и в — полярный угол вектора р. Соответственно, энергетиче¬
ская щель в спектре возбуждений обращается в нуль на се¬
верном в = 0 и южном в — 7г полюсах ферми-сферы. Оценить
поведение плотности состояний элементарных возбуждений z/s(e)
в области энергий е < А.
3.9.	Взаимодействие между электронами можно представить как сум¬
му двух вкладов. Первый вклад описывает притяжение, обу¬
словленное фононами, и существенен в узкой области энергий
~ Hlod £f вблизи ферми-поверхности. Второй вклад — это
прямое кулоновское отталкивание, действующее в широкой об¬
ласти энергий hujc ~ Ер вокруг ферми-поверхности. Аппрокси¬
мируя электрон-электронное взаимодействие кусочно-гладкой
функцией
где g > 0 — величина притяжения, а V > 0 — отталкивания,
найти критическую температуру сверхпроводящего перехода Тс.
Оценить величину изотопического эффекта a = —d In Tc/d\nM,
предполагая, что дебаевская частота шд м-1'2, где М — мас¬
са иона.
.10. Для описания сверхпроводимости в ряде металлов, например,
MgB2 с Тс = 39 К используется представление о наличии двух
перекрывающихся незаполненных электронных зон. Найти тем¬
пературу сверхпроводящего перехода в модели БКШ для двух¬
зонного сверхпроводника, предполагая, что спаривание между
электронами возможно только внутри одной и той же зоны, а
матричные элементы, отвечающие внутризонному и межзонному
электрон-электронному взаимодействию, равны gij (i,j = 1,2).
~g+V,	|£р|	и	|£р-1 <
V,	fkJo	<	|£р|	и	|£р<|	^	hue,
.0,	|£р|,	или	|£р/1 >	fkJc,

3.3. Неидеальные квантовые системы (жидкости)	155
3.3.11. Электрон-электронное взаимодействие в кристаллах может за¬
висеть от ориентации импульсов электронов относительно кри¬
сталлографических осей. Для примера рассмотрим слоистый ме¬
талл, в котором каждый слой представляет собой квадратную
решетку, в узлах которой находятся ионы. Пусть ось z перпен¬
дикулярна слоям, оси х и у направлены вдоль сторон квадрат¬
ной решетки ионов, а потенциал притяжения между электрона¬
ми с импульсами р = (х,рг) и р' = (х',р'г) анизотропен и равен
^	Гgcos20*.cos26v, |£р|	и |£р/1 < hujD « eF,
РР	\0,	|£р|,	или |£р/1 > Тюсо-
Здесь	— угол между проекцией	х импульса р на плоскость
слоя и направлением кристаллографической оси х, а £(р) —
энергия электрона, отсчитанная от энергии Ферми ер. Такое
взаимодействие означает, что электроны с импульсами, парал¬
лельными осям х и у притягиваются сильнее, чем для направ¬
лений, повернутых на угол 45° относительно осей х и у. Найти
зависимость сверхпроводящей щели Др от импульса и ее вели¬
чину при нулевой температуре.
3.3.12. В сверхтекучей A-фазе 3Не спектр элементарных возбуждений
имеет вид
£р = ^2 +Д2 sin2 в,
где £р = р2/(2т) — ер — энергия, отсчитанная от уровня Фер¬
ми, и в — полярный угол вектора р. Оценить низкотемператур¬
ное при Д поведение теплоемкости С$(Т) в A-фазе гелия.
3.3.13. Спиновая парамагнитная восприимчивость — важнейшая харак¬
теристика сверхпроводящего (сверхтекучего) состояния. Опреде¬
лить температурное поведение спиновой восприимчивости хЛП
для ферми-системы с синглетным s-спариванием куперовских
пар в модели БКШ. Спектр возбуждений в магнитном поле ра¬
вен eptr = V^2 + Д2 - усгН, где у — эффективный магнетон Бо¬
ра фермиона и £р = р2/(2т) — ер — энергия, отсчитанная от
уровня Ферми.
3.3.14. В нормальном состоянии ферми-система обладает большей спино¬
вой восприимчивостью Хп п0 сравнению с восприимчивостью Xs
в сверхпроводящем (сверхтекучем) состоянии. В достаточно силь¬
ном магнитном поле может оказаться, что спин-поляризован-
ное состояние в нормальной фазе обладает меньшим значением

156
Глава 3. Статистическая физика. Задачи
свободной энергии, чем в сверхпроводящей (сверхтекучей) фа¬
зе. Оценить предельное магнитное поле Нр, называемое пара¬
магнитным пределом Клогстона-Чандрасекара, выше которого
сверхпроводящее (сверхтекучее) состояние не может существо¬
вать. Для нулевой температуры выразить поле Нр через вели¬
чину энергетической щели До. Эффективный магнетон ферми-
она равен /х.
3.3.15. Согласно теории БКШ возбужденные неспаренные состояния
в сверхпроводнике отделены от основного состояния энергети¬
ческой щелью А(Т). При изменении числа электронов на еди¬
ницу: N —> N ± 1 энергия сверхпроводника должна изменить¬
ся на ±Д. Знак плюс или минус зависит от того, четное или
нечетное было исходное число электронов N. Найти разность
SCl(T) = П„еч — Пчет термодинамических потенциалов П для сверх¬
проводящих состояний с нечетным и четным числом электро¬
нов. Оценить температуру Т*, выше которой такой эффект чет¬
ности числа электронов становится существенно подавленным.
3.3.3.	Слабонеидеальный бозе-газ.
Уравнение Гросса-Питаевского
3.3.16. Пользуясь уравнением Гросса-Питаевского, найти пространст¬
венное поведение плотности бозе-конденсата вблизи бесконеч¬
ной непроницаемой стенки.
3.3.17. В симметричной гармонической ловушке с частотой ш, создаю¬
щей удерживающий потенциал V(r) — ти2г2/2, находится сла¬
бонеидеальный конденсированный газ N » 1 бозонов. В при¬
ближении Томаса-Ферми для уравнения Гросса-Питаевского
оценить размер конденсатного облака, химический потенциал
и энергию газа.
3.3.18. Бозе-конденсат с притяжением между частицами может быть в
метастабильном, относительно долгоживущем состоянии, если
он ограничен в пространстве и число частиц меньше критиче¬
ского значения Nc. Оценить критическое число частиц Nc, вы¬
ше которого метастабильное состояние конденсата становится
абсолютно неустойчивым и происходит коллапс газа в случае
симметричной гармонической ловушки с частотой uj. Исполь¬
зовать гауссову функцию:

3.3. Неидеальные квантовые системы (жидкости)	157
с вариационным параметром Л, который задает характерный раз¬
мер газового облака. Длина рассеяния частиц друг на друге
равна а < 0 и осцилляторная длина ловушки / = (Н/тш)1^2.
3.3.19. Пользуясь нестационарным уравнением Гросса-Питаевского для
волновой функции конденсата:
ihlH = _inV2^+	+ ё^2^’
вывести уравнение непрерывности для плотности газа р — т\г^\2
^ -j- div j = О
и определить плотность потока массы j.
3.3.20. Вывести боголюбовский спектр элементарных возбуждений
однородного слабонеидеального конденсированного бозе-газа,
пользуясь нестационарным уравнением Гросса-Питаевского
и рассматривая в линейном приближении малые отклонения
волновой функции конденсата от его однородного равновесного
состояния.
3.3.21. Найти линейное натяжение прямолинейного квантованного вих¬
ря или энергию, отнесенную к единице его длины, в слабоне¬
идеальном конденсированном бозе-газе, используя для аппрок¬
симации плотности конденсата на расстоянии г от оси вихря
функцию
, ч nor
П(П = -j j
г + а
с вариационным параметром а.
3.3.22. Солитоном называют уединенную волну, представляющую со¬
бой локальный колоколообразный волновой импульс, который
сохраняет свою форму в процессе его распространения с неко¬
торой постоянной скоростью в одном направлении в простран¬
стве. Показать, что одномерное нестационарное уравнение Грос¬
са-Питаевского допускает существование солитонных решений
для плотности бозе-конденсата п(х, t) со следующими свойства¬
ми: п(х, t) = п(х - ct) и п(х, t) —» по при х —* ±оо, где по — рав¬
новесная плотность и с — скорость, с которой движется солитон.
3.3.23. Бинарная смесь двух бозе-конденсатов образована бозе-части-
цами с массами т\, тг и плотностями щ, П2, соответствен¬
но. Определить две ветви боголюбовского спектра возбужде¬
ний, и из требования положительности квадрата скоростей зву¬

158	Глава	3.	Статистическая	физика.	Задачи
ка найти условие для устойчивости однородного состояния сме¬
си двух бозе-конденсатов. Константы взаимодействия между
бозонами равны (г,/ = 1,2), причем gn, £22 > 0.
3.3.4.	Теория сверхтекучести
3.3.24. Пользуясь представлениями об элементарных возбуждениях в
сверхтекучей жидкости и преобразованием Галилея, найти усло¬
вие на максимально допустимую или критическую скорость vc
бездиссипативного течения жидкости (критерий Ландау). Энер¬
гия элементарного возбуждения с импульсом р равна е(р).
3.3.25. Поток элементарных возбуждений, обладающих импульсом, в
сверхтекучей жидкости сопровождается переносом части массы
жидкости и вкладом в полный импульс жидкости. При малых
скоростях импульс единицы объема Р, вносимый элементарны¬
ми возбуждениями, пропорционален скорости течения жидко¬
сти v, т. е. Р = pnv. Определить коэффициент пропорциональ¬
ности или плотность нормальной компоненты рп.
3.3.26. Показать, что критическая скорость течения жидкости, необ¬
ходимая для одновременного рождения двух элементарных воз¬
буждений, не превышает критическую скорость, которая необ¬
ходима для рождения одного элементарного возбуждения.
3.3.27. В цилиндрическом сосуде радиуса R находится сверхтекучий
Не II. Определить критическую угловую скорость вращения со¬
суда Пс, при которой становится энергетически выгодным рож¬
дение первого квантованного вихря. Радиус кора вихря равен
£ -С R, плотность сверхтекучей компоненты равна ps.
3.3.28. Определить фононный вклад в плотность нормальной компо¬
ненты Pn,ph* предполагая разность нормальной и сверхтекучей
скоростей w = v„ — vs не малой по сравнению со скоростью
звука с.
3.3.29. Найти плотность нормальной компоненты в идеальном конден¬
сированном бозе-газе.
3.3.30. Атомы 3Не, растворенные в малой концентрации в сверхтеку¬
чем 4Не, представляют в первом приближении идеальный газ
фермиевских возбуждений (примесонов) с импульсом р и энер¬
гией ер = — ео + р2/(2Л4), где £о — энергия растворения атома
3Не и М — его эффективная масса. При малых скоростях при¬
месные частицы не взаимодействуют со сверхтекучей компо¬
нентой раствора и полностью увлекаются нормальным движе-

3.4. Фазовые переходы и критические явления
нием. Найти примесный вклад в плотность нормальной ком¬
поненты слабого раствора 3Не-4Не с массовой концентрацией с.
31. Найти температуру, при которой становится выгодным спонтан¬
ное рождение квантованных вихрей в тонкой (квазидвумерной)
сверхтекучей пленке толщиной d. Плотность сверхтекучей ком¬
поненты равна ps, радиус кора вихря равен £.
г.1. Замкнутая (изолированная) система состоит из двух термоди¬
намических подсистем, представляющих собой две разные фа¬
зы вещества. Из требования максимальности энтропии для рав¬
новесия замкнутой системы вывести условия равновесия фаз.
.2. Термодинамическая система, например, жидкость-пар, описы¬
вается термодинамическим потенциалом Ф, в котором разло¬
жение по действительному параметру порядку <р, содержит ку¬
бический член:
Определить температуру перехода тс в упорядоченную фазу <рф О
и род фазового перехода. Найти зависимость параметра поряд¬
ка Iр от температуры т, определить границы устойчивости (точ¬
ки спинодали) упорядоченной и неупорядоченной фаз. Прове¬
рить, что точка й = 0ит = 0 представляет собой критическую
точку системы.
.3. Для описания фазовых переходов в сегнетоэлектриках часто
используют разложение термодинамического потенциала вплоть
до членов шестого порядка:
где р — вектор спонтанной поляризации, а т — приведенная
температура. Определить значения параметров т и а, при кото¬
рых возникает трикритическая точка с изменением в ней рода
фазового перехода из неупорядоченной фазы в упорядоченную.
Найти линию фазовых переходов, значение параметра порядка,
и теплоемкость вблизи трикритической точки. Показать, что в
трикритической области а2 <С \т\ верхняя критическая размер¬
ность пространства d вместо четырех становится равной трем.
(Принять во внимание энергию неоднородности ~ (Vp)2).
ФАЗОВЫЕ ПЕРЕХОДЫ И КРИТИЧЕСКИЕ ЯВЛЕНИЯ
1. Приближение самосогласованного поля
Ф =	(Ь	>	0).

Глава 3. Статистическая физика. Задачи
4.4.	Переходы с нарушением трансляционной симметрии и возник¬
новением длиннопериодических структур, например, волн за¬
рядовой плотности в сегнетоэлектриках, волн спиновой плот¬
ности или геликоидальных структур в антиферромагнетиках,
пространственно-неоднородной фазы FFLO в сверхпроводниках,
можно описать добавлением в разложение термодинамического
потенциала членов с пространственными производными более
высокими, чем второго порядка:
Найти условие на коэффициент жесткости S (точку Лифши¬
ца) для возникновения пространственно неоднородной струк¬
туры, ее период, а также линии и род фазовых переходов в
зависимости от приведенной температуры т и коэффициента
жесткости 6. Найти индекс корреляционной длины и в точке
Лифшица.
.2. Функционал Гинзбурга-Ландау
4.5.	Комплексность сверхпроводящего параметра порядка ф = \ф\ х
хехр(г'0) приводит к эффекту квантования магнитного потока в
сверхпроводнике. Наряду с вектор-потенциалом А(г) градиент
фазы V0 также дает вклад в плотность сверхпроводящего тока:
Доказать, что поток магнитного поля Ф через замкнутый кон¬
тур С, на котором сверхпроводящий ток тождественно равен
нулю js = 0 и параметр порядка отличен от нуля ф ф 0, всегда
кратен целому числу п квантов магнитного потока фо = -кНс/е.
Найти пример простейшего вихревого состояния, несущего не¬
сколько квантов магнитного потока.
4.6. Для предельного сверхпроводника второго рода с параметром
Гинзбурга-Ландау к 1 найти: а) энергию на единицу длины
прямолинейного квантового вихря; б) нижнее или первое кри¬
тическое магнитное поле Нс\.
4.7. Коэффициент 7 перед градиентным членом в разложении Гинз¬
бурга-Ландау для свободной энергии сверхпроводящего кри¬
сталла должен отражать анизотропию направлений в кристал¬
ле и представляет собой тензор второго ранга 7у (i,j = 1,2,3).
Ф - Jdx^y- + У' + |(VV)2 + j(VV)2]. (a.d > 0).

3.4. Фазовые переходы и критические явления -IV 161
В одноосном кристалле с тетрагональной или с гексагональной
симметрией:
Щ = (6ц - ni/ij)7х + л,-п/7ц,
где п — единичный вектор в направлении оси симметрии кри¬
сталла. (В кристаллах с кубической симметрией 7j_ = 7ц.) Рас¬
смотреть анизотропию верхнего критического поля, т. е. зави¬
симость поля Нс2 от угла в между осью симметрии кристалла п
и направлением внешнего магнитного поля.
3.4.8. Параллельно плоской поверхности сверхпроводника приложено
внешнее магнитное поле. Показать, что образование сверхпро¬
водящей фазы начинается в приповерхностном слое сверхпро¬
водника, и оценить соответствующее поверхностное критиче¬
ское поле Нс3. Найти диапазон магнитных полей, в котором
возможно явление поверхностной сверхпроводимости, заключа¬
ющееся в наличии сверхпроводящей фазы в приповерхностном
слое и ее отсутствии в объеме сверхпроводника.
3.4.9. Имеется тонкая пластина сверхпроводника первого рода с па¬
раметром Гинзбурга-Ландау я «С 1 и толщиной D. Пластина
находится во внешнем магнитном поле Но, параллельном плос¬
костям пластины. Найти распределение сверхпроводящего тока
и магнитного поля в пластине и определить критическое значе¬
ние толщины пластины, при которой изменяется род фазового
перехода в магнитном поле.
3.4.10. Определить критическую плотность сверхпроводящего тока js,
который может протекать по тонкой пленке сверхпроводника
толщиной d, много меньшей корреляционной длины £ и глуби¬
ны проникновения магнитного поля S. Считать плотность сверх¬
проводящего тока однородной по сечению пленки.
3.4.11. Определить период осцилляций температуры сверхпроводяще¬
го перехода тонкого полого цилиндра радиуса R и толщиной
d -С £,<5, Л в зависимости от величины потока магнитного поля
Ф = 7г/?2Я, направленного вдоль оси цилиндра (эффект Литт¬
ла-Паркса).
3.4.12. Определить коэффициент поверхностного натяжения для гра¬
ницы между сверхпроводящей и нормальной фазами в сверх¬
проводнике первого рода с предельно малым параметром Гин¬
збурга-Ландау х <С 1, когда можно пренебречь глубиной про¬
никновения магнитного поля и считать, что магнитное поле не
проникает в сверхпроводящую область.

162 ->\r Глава 3. Статистическая физика. Задачи
3.4.13. Найти в сверхпроводнике второго рода сх»1 энергию и си¬
лу взаимодействия двух параллельных вихревых линий, рас¬
положенных на расстоянии г » £ друг от друга. Показать, что
квантованные вихри с одинаковым направлением циркуляции
сверхпроводящего тока отталкиваются, а с противоположно на¬
правленными — притягиваются.
3.4.14. Показать, что вихревая линия, параллельная поверхности сверх¬
проводника, притягивается к его поверхности. Определить силу
притяжения.
3.4.15. Металл с магнитными атомами, в котором могут сосущество¬
вать и конкурировать два явления: сверхпроводимость и ферро¬
магнетизм, можно назвать ферромагнитным сверхпроводником.
Например, халькогениды HoMogSg, HoMogSee и борид ЕГШ14В4.
Считая температуры сверхпроводящего перехода Тс и Кюри в
близкими, ферромагнитный сверхпроводник можно описать в
рамках теории функционала Гинзбурга-Ландау с двумя взаи¬
модействующими параметрами порядка: сверхпроводящим ф(г)
и намагниченностью М(г), используя следующее разложение
для плотности свободной энергии, отсчитанной от нормального
состояния:
AF = а(Т)\ф\2 + ^\ф\4 + ^>М2 + ^М4 + CM2|V>|2.
Константа взаимодействия G > О, что соответствует подавле¬
нию сверхпроводимости при появлении ферромагнитного упо¬
рядочения. Коэффициенты разложения а(Т) = с*о(Т - Тс) и
А(Т) = Aq(T — в), а остальные не зависят от температуры. Для
случая Тс> 0 определить возможные фазы, найти род фазовых
переходов и построить фазовую диаграмму состояний в зави¬
симости от константы взаимодействия. Считать, что ферромаг¬
нитное состояние энергетически гораздо выгоднее, чем сверх¬
проводящее.
3.4.16. Пусть в изотропном ферромагнитном сверхпроводнике одновре¬
менно реализуются ферромагнитное и сверхпроводящее состо¬
яния. С учетом энергии магнитного поля величиной h = rot А и
энергий неоднородности функционал Гинзбурга-Ландау имеет вид
Д 3= j d3r ДД(М(г), V’(r), ^*(r), А(г)),
AF = %(VM)2 + ^M2 + f M4 + (h ~ 47rM)2 +
2	2	4	о7Г
+ \ I (-<W - |a)^|2 + а(Т)\ф\2 + ||У>|4 + GM2H2.

3.4. Фазовые переходы и критические явления	163
При температурах заметно ниже точки Кюри в и сверхпроводя¬
щего перехода Тс абсолютные величины вектора намагничено-
сти М и сверхпроводящего параметра ф можно считать фикси¬
рованными. Найти условие на коэффициент магнитной жестко¬
сти Ст, при котором однородное ферромагнитное упорядочение
становится неустойчивым и возникает спин-спиральная фаза,
в которой вектор намагниченности М равномерно поворачива¬
ется в плоскости, перпендикулярной выделенной оси при дви¬
жении вдоль этой оси. Такая магнитная структура называется
антиферромагнитным геликоидом. Определить период гелико¬
ида (шаг спирали) в зависимости от глубины проникновения
магнитного поля S. Возможность состояний с квантованными
вихрями не рассматривать.
3.4.17. В нормальной фазе при температуре выше температуры сверх¬
проводящего перехода возможны флуктуации сверхпроводяще¬
го параметра порядка ф(г). Определить пространственную кор¬
реляционную функцию (ф(г)ф*(г')), пренебрегая членом чет¬
вертого порядка в функционале Гинзбурга-Ландау.
3.4.18. Возможность флуктуационного рождения сверхпроводящих ку-
перовских пар в нормальной фазе при температуре выше темпе¬
ратуры сверхпроводящего перехода Тс создает дополнительный
вклад в диамагнитную восприимчивость металла. Вычислить
флуктуационную поправку к диамагнитной восприимчивости
во внешнем магнитном поле Н при Т > Тс для нульмерного
сверхпроводника — сферической гранулы малого радиуса та¬
кой, что R £ и R <С S.
3.4.19. В нульмерном сверхпроводнике — малой грануле с характер¬
ным размером R -С £(Т) — найти поведение квадрата модуля
сверхпроводящего параметра порядка |^о(Г)|2 в области тем¬
ператур, близких к критической точке перехода Тс в объем¬
ном сверхпроводнике. Найти условие малости размытия фазо¬
вого перехода, если объем гранулы V, а среднее расстояние
между уровнями энергии вследствие размерного квантования
равно 5е.
3.4.3.	Основы теории критических явлений
3.4.20. Одномерная модель Изинга представляет собой одномерную це¬
почку из N полуцелых спинов s = 1/2, для которых возможно
всего два состояния: вверх и вниз. Каждый спин в цепочке
взаимодействует только с ближайшим соседним спином. Свойс¬

164	Глава	3.	Статистическая	физика.	Задачи
тва такой системы, находящейся в однородном магнитном поле,
могут быть описаны гамильтонианом
N
ж = -j^2 <w+1 -
;=i	i
где J — обменная константа, сг, на узле / принимает значения ±1,
а р — эффективный магнетон Бора и Н — магнитное поле. Най¬
ти теплоемкость С(Т) в нулевом поле, намагниченность М(Т,Н)
и магнитную восприимчивость \(Т,Н) цепочки. Для простоты
использовать циклическое граничное условие а^+1 = о\.
3.4.21. Для одномерной цепочки спинов в модели Изинга с гамиль¬
тонианом
% = -] J2 °icri+1
<r,=il
найти корреляционную функцию или термодинамическое сред¬
нее 7т). Здесь k, т нумерует номер узла цепочки. Рассмот¬
реть случаи ферромагнитной / > 0 и антиферромагнитной J < О
цепочек и определить корреляционный радиус £ — характерное
расстояние, на котором исчезает корреляция между ориентаци¬
ями двух выделенных спинов.
3.4.22. В одномерной цепочке Изинга обменная константа взаимодей¬
ствия J принимает случайные значения Д и /г с вероятностью р\
и рч — 1 —pi, соответственно. Найти теплоемкость цепочки С(Т).
3.4.23. В ферромагнитной системе изинговских спинов ст,- = ±1 обмен¬
ная константа имеет дальнодействующий характер и одинакова
для всех пар спинов независимо от расстояния между ними. Га¬
мильтониан такой системы из N частиц во внешнем магнитном
поле Н можно представить в виде
^ £Т‘<7/ °‘Н > °)-
/,/= 1	i=l
Найти статистическую сумму Z. В термодинамическом пределе
N —> оо определить свободную энергию, отнесенную к одному
спину, и найти уравнение для среднего значения спина или на¬
магниченности. Сравнить полученное уравнение с приближен¬
ным описанием намагниченности в теории самосогласованного
(среднего) поля.

3.4. Фазовые переходы и критические явления
3.4.24. В пренебрежении пространственными флуктуациями парамет¬
ра порядка теплоемкость в точке сверхпроводящего перехода
испытывает скачок. В приближении разложения Гинзбурга-Лан-
дау рассмотреть влияние флуктуаций параметра порядка на по¬
ведение теплоемкости в нормальной фазе вблизи точки перехо¬
да Тс. Оценить величину близости к точке фазового перехода
т = \Т- Тс\/Тс или число Гинзбурга-Леванюка Gi, когда флук-
туационная поправка к теплоемкости становится сопоставимой
с величиной скачка. Проанализировать случай произвольной
размерности пространства d.
3.4.25. Классическая ЛТ-модель представляет собой двумерную квад¬
ратную решетку, в узлах которой находятся двухкомпонентные
спины Sr единичной длины |Sr| = 1. Период решетки равен а.
Гамильтониан такой системы, в которой каждый спин взаимо¬
действует обменным образом только с ближайшими соседями
с ферромагнитной константой взаимодействия / > О, определя¬
ется выражением
Найти корреляционную функцию спинов KrT> — (SrSr/), распо¬
ложенных в узлах г и г', и оценить корреляционный радиус
£ = £(7) при высоких 7 » / и низких 7	/ температурах. При
низких температурах воспользоваться континуальным прибли¬
жением, когда направление спинов меняется незначительно от
узла к узлу, и система может быть описана эквивалентным га¬
мильтонианом типа
с киральным полем п(г) = п(;е, у), в котором п — двухкомпо¬
нентный вектор с наложенным ограничением n2 = 1.
3.4.26.	Сверхтекучесть в 4Не вблизи A-точки описывается с помощью
параметра порядка ф(г) — комплексной волновой функции бозе-
конденсата. Плотность сверхтекучей компоненты: ps = т\\ф|2.
Плотность потока сверхтекучей компоненты:
Свободная энергия единицы объема 4Не при наличии сверхте¬
кучего движения дается соотношением
K = -jj:s*rs*r+> + sys"r+a.
г,а
J (Vn)2dxdy
j* = -f	-	W)	=	P,V,.
F{i>, Vs) = FoWO + Psv2/2.

166
Глава 3. Статистическая физика. Задачи
Предполагая справедливость гипотезы масштабной инвариант¬
ности (скейлинга) для сверхтекучего перехода в A-точке, опре¬
делить критический индекс для плотности сверхтекучей ком¬
поненты ps, зная индекс теплоемкости а.
3.4.27.	Вычислить критический индекс корреляционной длины и для
однокомпонентного параметра порядка <р и эффективного (Я =
— Ki/T) гамильтониана
с точностью до первого порядка в е-разложении, предполагая
справедливость гипотезы масштабной инвариантности (скейлин¬
га). Зная индекс v, найти индексы теплоемкости а, параметра
порядка /3 и восприимчивости 7.

ЧАСТЬ
РЕШЕНИЯ ЗАДАЧ

глава ТЕОРИЯ ПОЛЯ
1
1.1.
ВЕКТОРЫ И ТЕНЗОРЫ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
1.1.1.	По определению скалярного произведения в старой системе координат
(ab) = dibjgij.
В новой системе координат (7 — матрица Якоби)
Здесь Е — единичная матрица, 7 — матрица Якоби. — инвариант
относительно преобразований системы координат, для которых JTJ = Е,
т. е. для ортогональных преобразований.
1.1.5. 3.
1.1.6. 3.
1.1.7. 5im8jn — 8inSjm.
akbm (Jikhn) UjmJjl)gnl — 0-kbm8kn8ml — Q-kbmgkm-
1.1.2.	AtB, = JikA'kJjnB'n = JikJjn(A'kB'n).
1.1.8. 2Si„.
1.1.9. 6.
1.1.10. -6

1.1. Векторы и тензоры в евклидовом пространстве	169
1.1.11. Запишем выражение с помощью оператора V и воспользуемся
формулой двойного векторного произведения, помня о том, что вектор¬
ная функция а должна стоять справа от V:
[V х [V х а]] = V(Va) - (VV)a = grad div a - Да.
1.1.12. В этом примере мы воспользуемся как правилом дифференциро¬
вания произведения двух функций, так и свойством смешанного произ¬
ведения относительно перестановки сомножителей. Индекс с у вектор¬
ной функции означает, что в данном выражении она не дифференциру¬
ется (это не тензорный индекс):
(V|a х Ь]) = (V[a х Ьс]) + (V[ae х Ь]) = (Ь, [V х а]) - (а, [V х Ь]).
1.1.13. Воспользовавшись правилами дифференцирования произведения
функций и свойствами двойного векторного произведения относительно
перестановки векторных сомножителей, получим
|V х [а х b]] = [V х [ас х b]] + [V х [а х Ьс]] =
= a(Vb)-(Vac)b-b(Va) + (Vbc)a = adivb-(aV)b-bdiva+(bV)a.
1.1.14. Переставлять местами векторы в формуле V(ab) можно, исходя
из формулы двойного векторного произведения: а(Ьс) = [Ь х [а х с]] +
+ (Ьа)с. Поскольку скалярное произведение симметрично относительно
перестановки сомножителей, получаем
grad(ab) = |ах rot b] + [b х rot а]	+	(aV)b + (bV)a.
1.1.15. V(pr) = (pVr) = (p grad r) = (pin).
1.1.16. Воспользуемся формулой для градиента скалярного произведе¬
ния и формулами действия оператора V на радиус-вектор: V(pr) = р..
1.1.17. [V х [р х г]] = 2р.
1.1.18. V(/x/(r)) = (р grad /(г)) = f'{pn).
1.1.19. [V х pf(r)] = -[р х V/(r)| = -f'[p	х	n]	= /'[n x	p\.
1.1.20. Воспользуемся формулой градиента скалярного произведения и
правилом дифференцирования сложной функции:
Ve'kr = e‘kr(V(ikr)) = ikeikr.
1.1.21. (VAe‘kr) = (AVe‘kr) = i(Ak)e,kr.
1.1.22. [V x Ae'kr] = [Velkr x A] = i[k x A]eikr.
1.1.23. [a x b], = eijkUjbk = elkjakbl = -eljkbjak = -|bx a],-.

170 ->\r Глава I. Теория поля. Решения задач
1.1.24.	i-я компонента двойного векторного произведения равна
eijkCLjekmnbmCn = eijk&mnkCLjbmCn — (5im5jn Slrl djm ) CLj Ьт Cn — ajbjCj — QjbjCi.
1.1.25.	В тензорных обозначениях:
dxt
UXi	r-
1.1.26. Запишем подынтегральное выражение с помощью оператора на-
бла и применим формулу интегрирования по частям:
Jf(VA)dV = f f(AdS)- J (AV)fdV = ff(AdS)- J (A grad f) dV.
V	S	V	S	V
Тот же самый результат легко получить, используя тензорные обозначения:
/ lWtdv = jiAtdSt~SdVAtlk1'
V	S	V
1.1.27. Представим выражение в форме дивергенции с помощью опера¬
тора набла:
(V/)[V х А] = V(/[V х А]) - /(V[V х А]) = div(/[V х А]),
поскольку для любого вектора (V[V хА]) = div rot А = 0.
Таким образом, имеем
J (grad/rotA)dV= J div(/[V х A]) dV = ff[VxA]dS.
V	V	s
В тензорных обозначениях этот же результат можно получить, ис¬
пользуя интегрирование по частям:
/(grad/rotA)dKs	j	§Lelua£dV = j,eJ£
V	V	S	V
В силу того, что
д2 п
ешд^жк=0'
получаем искомый результат.
1.1.28. 3V.
1.1.29. V.
1.1.30. $v(cV)rdV = cV
1.1.31. fvV(cr)dV = cV.

1.3. Релятивистская кинематика	171
1.1.32. /„[V х A] dV = fvrotAdV.
1.1.33. fv(cV)AdV.
1.1.34. /s[dS x V]/ = /s[grad/ x dS].
1.1.35. Умножим подынтегральное выражение на произвольный посто¬
янный вектор с:
(с[г х dr]) = ([с х г] dr).
Поскольку rot [с х г] = 2с, получаем
J rot [с х г] dS = 2с J dS = с j> \dr х г].
1.2.	ВЕКТОРЫ И ТЕНЗОРЫ
В ПРОСТРАНСТВЕ МИНКОВСКОГО
1.2.1. е^хер1/хх = -4!.
1.2.2. ^жАер1/хА =-3!^-
1.2.3. е^*херахх = -2! ОД - 6*6$.
1.2.4. е=^е'"'жАем1,ХА = -1.
1.2.5. Fpv = -Fpu.
1.2.6. Gx = -др?х».
1.2.7. FuX = -d~AvX*.
1.2.8. F^Fpv = -F^Fpv.
1.3.	РЕЛЯТИВИСТСКАЯ КИНЕМАТИКА
1.3.1. Является, v/c = th(0j + 62).
1.3.2. Предположим, в соответствии с условиями задачи, что матрицу
буста для преобразования х = Ахх' действительно можно записать в
виде матричной экспоненты
^7	/?7	0	0	^
Лх(/?(0)) = 01 7 ° О
п 0	0	10
^0 001/
= ехр(0а*), 7 =
1
/3 = the,

172
X
Глава I. Теория поля. Решения задач
где /3 = v/c. Продифференцируем это выражение по в и положим 9 = 0:
d\x(9)
d9
0=0
0=0 dP
= а.
/3=0
где мы учли, что d(3/d9\e=o — 1. Поскольку dj/d^p-o = 0, мы находим
генератор буста вдоль оси х:
d\x(9)
< 0
1
0
0^
= ах =
1
0
0
0
0=0
0
0
0
0
0
0
Ч
d9
Для проверки необходимо вычислить экспоненту в явном виде:
«21 а»
ехр(9ах) = ^ ]/\ах-
k=0
Учитывая, что все нечетные степени ах совпадают между собой, а также
совпадают между собой все четные степени, кроме нулевой, т. е. а°х = Е,
ахк ~ ах’ ахк~1 = ах Для всех к = 1,2,..., получаем, что
/ch9	she	0	0\
//1ч п , „	2/ , л ,1 shfl	сЬЙ	О	О
ехр(вах) = Е + ах sh в + a^(ch в - 1) =
* 0	0	10
^ О	О	О	1 у
где Е — единичная матрица. Ясно, что 7 = ch в, /З7 = sh в, а поэтому
условие /3 = v/c = th9 действительно позволяет параметризовать все
относительные скорости систем отсчета, допустимые в специальной тео¬
рии относительности, вещественными числами.
Переставляя столбцы и строки в матрицах, находим генераторы бу-
стов для осей у и г:
У0 0 1 о\
0 0 0 0
10 0 0
\0 О О О/
а, =
/О 0 0 l\
0 0 0 0
0 0 0 0
\ 1 О о о/
1.3.3.	Предположим, что матрицу поворота на угол ip вокруг оси х, т. е.
матрицу преобразования х = Rx(ip)x\ действительно можно записать в

1.3. Релятивистская кинематика
виде матричной экспоненты
Л	0	0	0	\
0	10	О
О 0 cos tp -siny>
^0	0 sin у?	cos ip	;
= exp (ipbx).
(1)
Мы используем матрицы 4x4, поскольку рассматриваем повороты, как
преобразования четырехмерного пространства Минковского. Дифферен¬
цируя по углу <р, находим
\0 0 1 О/
Для проверки вычислим экспоненту в явном виде, учитывая, что bx = Е,
b2xk = (-1 )k+lb2x, bxk~[ = (-1)*+16л: для всех k = 1,2,— В результате
ехр(y>bx) = Е + bx sin <р + b2x{\ - cos ф),
что и приводит к матрице (1). Циклически переставляя пространствен¬
ные столбцы и строки в матрице Ьх, можно найти генераторы поворотов
вокруг осей у и z.
1.3.4. При замене координат элемент объема умножается на модуль яко¬
биана: d*x = d*x'-\Dx/Dx'\. Для поворотов и бустов \Dx/Dx'\ = 1 (см. яв¬
ный вид соответствующих матриц в решениях задач 1.3.2 и 1.3.3).
1.3.5. Введем единичный вектор n = \/v и будем работать в системе
единиц, в которой с = 1. Разложим радиус-вектор г на продольную и
поперечную компоненты по отношению к скорости:
Г|р = riitljfj, r±i = г,- - Г||; = {6ц - ГЦПj)rj
и, аналогично,
dRx^) = bx exp(v?6x)|¥,=0 = bx =
d(f v=o
/000 o\
0 0 0 0
0 0 0 -1
имеем
/ц = щп/j, r>u = r'i- rj,,- = (6ц - nlnj)ft\
в системах отсчета К и К' соответственно.
В этих обозначениях преобразование Лоренца имеет вид
f = 7(* - v/Г/),

174
\
Глава I. Теория поля. Решения задач
В четырехмерных обозначениях — (/, гг) получаем:	где
матрица преобразования Лоренца (т. е. буста) имеет вид
AJJ(-v) = (Л° ЛП = ( 7	\
\Ло A'jJ	Sij	+	(7 - 1)я(л//
В нашей задаче я, = (яья2,0) = (cos у?» sin у?, 0), где у> — угол меж¬
ду скоростью v и осями координат к и х'.
1.3.6.	Уравнения, определяющие положение осей х' и у' в системе от¬
счета К в момент времени t — 0, имеют вид
у' = 0 = у + (7 - 1)л2(я1ДС + п2у) (ось х'),
х1 = 0 = X + (-у — \)П\(П\Х + п2у) (ОСЬ!/'),
откуда находим
_	(7-1)тя2	(7~ 1) tg у?
1 + (7-1)п2	1 + 7 tg2 у;
_	1 + (7- 1 )n2i	_	1 +7Ctg2y>
(7 — l)n,n2	(7 — 1) ctg у?
(ось л:'),
(ось у').
Возможен геометрический способ решения этой задачи, использую¬
щий эффект лоренцева сокращения длины (рис. 1.1).
Проведем две прямые, перпендику¬
лярные скорости у, на расстояниях /02
и /04 = /о2\/1 — V2 от общего в момент
времени t = t' = 0 начала координат О
и О' систем отсчета К и К'. Первая из
этих прямых будет пересекать оси х и у
в точках 1 и 3. Затем через эти точки мы
проведем прямые, параллельные скоро¬
сти v, до пересечения со второй прямой
в точках 5 и 6. Тогда проходящие через
точки 0 и 5 и точки 0 и 6 прямые и бу¬
дут искомыми положениями осей х' и у'
с точки зрения системы отсчета К в
момент времени t = 0 по часам систе¬
мы К. Обозначая Z102 = <р, Z205 = гр\,
Z206 = ip2, Z105 = у>\ = гр\ — ip, Z603 =
= Г>2 — V>2 — (тг/2 — <р), получим
Рис. 1.1. Геометрический
соб решения задачи 1.3.6
спо-
tg^ = it = 7tgy>’ ^2=^= 7Ctg</?,

1.3. Релятивистская кинематика
tg¥>2 = tg(<^2 - ТТ/2 + ф) =
tgpi = tg(^l -ч>) =
tg^i - tgy> _ (7 - 0 tg уз
l + tgi/>itg¥J 1 + 7 tg2 <p
.4	(7	— l)ctgy>
' Vt	T7 rr~ •
1 +7ctg2v5
Последние две формулы и определяют положение осей системы от¬
счета К'.
1.3.7.	Из релятивистского закона сложения скоростей:
где в нашем случае &ц = Vx, v± = Vy, V = Vx, v|| = V^x, Wj. = V2y< сле¬
дует, что
Таким образом, система Я2 будет двигаться относительно системы К\
со скоростью Vy( 1 - V%/c2)~1'2 — 7*Vy, направленной вдоль оси у.
1.3.8.	Хотя системы X' и Яг движутся относительно лабораторной си¬
стемы координат Я с одинаковыми скоростями, но их оси оказываются
по разному ориентированными по отношению к направлению скорости
V = (Vx, Vy, 0). Это связано с тем, что два последовательных преобразо¬
вания Лоренца К —> К\ —> Яг с относительными скоростями, не парал¬
лельными друг другу, т.е. vi = (У*,0,0,) и V2 = (0,^xVy,0) не экви¬
валентны одному преобразованию Лоренца, а требуют еще и поворота
осей системы отсчета Яг.
При переходе от системы Я' к системе отсчета Я имеем соотношение
где A(V) — матрица преобразования Лоренца (см. задачу 1.3.5). Далее,
при переходе от системы Яг к системе К\ будет
х, = A(v2)x2, где v2 = (0,ухУу,0).
И наконец для перехода от системы К\ к Я получим
x = A(vi)x1, где V] = (К*, 0,0).
х = А(У)х', где V = (K,,^,0)f

176	Глава	/.	Теория	поля.	Решения	задач
Таким образом,
х = A(vi)x, = A(v!)A(v2)jc2 = A(V)jc'.
Отсюда мы имеем следующее условие связи:
x' = A(-V)A(v,)A(v2)x2.
Используя результаты задач 1.3.5 и 1.3.7, получаем, приравнивая
результат матрице поворота в плоскости (х,у):
х' = A(-V)A(vi)A(v2)*2 = R(6>) jc2,
где в — угол поворота вокруг оси г. В явном виде будем иметь
(
-7&
„2 , „2
~10у
°\
~10х	irijc+ri*	(7 - \)пхПу О
-10У (7 - 1 )ПхПу п2х+уп2у О
О	О	О 1/
Ч/ъ
0
10у
о\
/1
0
1
0
0
0
7 0у
0
7/7*
0
0
\ о
0
0
ч
\0
I Ъ	Ъ0х	о о\
Ъ0х	7х	О О
О	0	10
\ 0 001/
о
„2
0\
--(7
7
— (ч-1)пхПу О
7
—(Лх+7«у) О
7
О	1/
Л	о	о о\
О	cos#	sin в О
О -sin# cosd О
\0	0	01/
где n = \/V — единичный вектор в направлении скорости V с компо¬
нентами п = (пх, пу, 0) = (cos 1р, sin ip, 0), а также
Ъ =
(l-/32)l/2 coscpd +72 tg2^)'/2’
7 =
(1-(/£ + #))1/2'
Угол поворота осей системы отсчета А2 по отношению к осям систе¬
мы К' определяется формулами

X
1.3. Релятивистская кинематика	177
1.3.9.	Пусть частица движется со скоростью v вдоль положительного
направления оси х лабораторной системы отсчета А (см. задачу 1.3.8).
Пусть за малый промежуток времени St скорость частицы изменилась
на величину S\ = i/St. Если считать, что частица покоится в систе¬
ме Я2, а сила, действующая на нее (например, на ее заряд, если это
электрическое поле), вызывает только изменение скорости, не затраги¬
вая ее спин1*, то изменение направления спина при этом носит кинема¬
тический характер, связанный с релятивистским эффектом, описанным
в задаче 1.3.8.
Направление спина остается неизменным в системе Яг (инерциаль-
ная мгновенно сопутствующая система отсчета), но оси системы Яг
поворачиваются относительно системы К' (при <5v = 0 или St = 0 на¬
правления осей в системах Яг, Я' ив лабораторной системе Я совпада¬
ют). Таким образом, имеет место прецессия мгновенно сопутствующей
системы отсчета и, соответственно, прецессия спина (прецессия Тома¬
са). Для вычисления скорости томасовской прецессии воспользуемся
результатами задачи 1.3.8.
В рамках нашей задачи будем считать, что
V = v + <5v = (о 4- 6vx, Svy, 0), vi = v + <5уц = (v + Svx, 0, 0),
/ \
v2 =
0, , ,0
(v + Svx)2
\ V 1	C2	)
Формула, связывающая угол поворота координатных осей в с уг¬
лом ip, определяющим направление скорости V (tg</> = Vy/Vx)
tg6>=fr— .?■)-?££
1 +7tg y>
при малых углах 9 и <р (нас интересуют малые промежутки времени St)
дает
0 ~ (7 — \)р.
Учитывая, что в = uSt (и — угловая скорость прецессии Томаса), а также
Svv	Svu	wSt
in ~	y	 Z.	—
V + Svx	V	V
где w = |v| — абсолютная величина ускорения частицы, получим
, ,.WV	~/2VW
w = (7-l)-	-
v2 (1 + 7 )c2
11 Спин частицы мы моделируем некоторым вектором, связанным с частицей.

178	Глава	/.	Теория	поля.	Решения	задач
В векторной форме данное выражение имеет вид
.2
и> —
7
г [v X V].
(1+7Г
Мы учли, что в — угол поворота системы К2 относительно К' по ча¬
совой стрелке, т.е. ш = -ueZ} v = vex, v = wty, где tx,ey,tz — орты
системы отсчета К.
1.3.10.	По существу исследуемый в задаче эффект — это эффект До¬
пплера. В системе отсчета наблюдателя К испускание световых сигна¬
лов происходит не одновременно (относительность одновременности), а
в моменты
ct\ = 7 (ct[ + (Зх\), и ct2 = 7(^2 + 0х2),
где 0 = v/c и х'2 = х\ — I. В системе движущихся источников К' испус¬
кание сигналов осуществляется одновременно: t[ = t2, т.е.
ct2 - ct\ = 'y0(x2 - х\) — -7(31.
Здесь, как и обычно, 7 = (1 — /?2)-1/2. Прием наблюдателем световых
сигналов произойдет при пересече¬
нии мировых линий сигналов
Ct-Ct\=X — X\ и ct — ct2
-х2
и мировой линии наблюдателя х = О
(рис. 1.2) Сигналы будут приняты в
моменты времени
ct2o = ct2 — х2, ctio = ct\ — X\.
Интервал времени между приемом
сигналов равен
Рис. 1.2. Прием световых сигналов,
испущенных движущимися источ¬
никами. Пунктирной линией обо¬
значены мировые линии сигналов,
штриховой линией обозначены ги¬
перболы, задающие масштаб длины
на плоскости Минковского
ct2o - Ctю = ct2 - ct\ + X\ - x2,
где
X\ —x2 = (ct\-ct2)0+l y/l- (32 = /7,
поскольку в системе К расстояние
 между источниками вследствие ло-
ренцева сокращения есть I у/1 — /З2, но Х\ и х2 взяты в разные моменты
времени, и источники успевают сместиться на (t\ - t2)v:
ct20 - ctio = 7/3/(—1 +0) +I \/\-02 =
='(тВ|+^)='
1-/?
= /
1-0

1.3. Релятивистская кинематика	179
Задачу можно решить проще, если ввести 4-мерный волновой век¬
тор к- Представим себе, что два световых импульса распространяют¬
ся вместе с двумя последовательными максимумами радиоволны. Для
этой волны в системе источников длина волны и период задаются рас¬
стоянием между источниками У = сТ = /, о/ = 2тсс/1, поэтому
U = (2тг//,27г//,0,0).
В системе отсчета наблюдателя получаем
k =
< 7
7/3
0
0^
7/3
7
0
0
0
0
1
0
1°
0
0
ч
( 2тг/1\
2тг/I
О
\ 0
/ 27Г
т
27Г
7
7(1 + /3)
7(1 + /3)
О
О
/
В этой системе будет выполняться
ш = ^7(1 + /3) = ^£0+£
и мы приходим к тому же самому результату:
2тг
Т '
сТ = I
1-/3
1+0'
Данная формула описывает так называемый продольный эффект Допп¬
лера: частота волны и = l/Т, принимаемая приемником в системе К,
больше частоты, испускаемой движущимся источником (и > и1). В слу¬
чае же, если источник не приближается, а удаляется от приемника,
в окончательном результате необходимо заменить /3 на —/3, поэтому
получится, что v < v’.
1.3.11.	В этой задаче используется основной принцип специальной тео¬
рии относительности — ковариантность (форминвариантность) законов
физики. В задачах на столкновения используется частный случай ин¬
вариантности — инварианты столкновений. В нашем случае — это ко¬
вариантность 4-векторных законов отражения.
Пусть направление вектора нормали к зеркалу совпадает с направле¬
нием скорости (n' = \/V) движения зеркала (рис. 1.3). Существование
компоненты скорости, параллельной зеркалу, не влияет на характер от¬
ражения плоской волны, поэтому наше условие не является ограниче¬
нием общности решения.

180	Глава	I.	Теория	поля.	Решения	задач
В системе покоя зеркала К' угол падения равен углу отражения,
частота волны при отражении не меняется:
и>[ = и>2,
(kin) = -(kin),
ki - (k',n)n = kj - (k2n)n.
Исключая из последней формулы (Цп), получаем
Г"
~ ^1’
W2 = к', - 2(k|n)n.
Для записи этих формул в 4-векторной форме введем в системе от¬
счета К' 4-вектор нормали к зеркалу л' = (0,п), где п = (1,0,0). В ла¬
бораторной системе К будем иметь
п = 7 (п + /?) = 7/?-
п1 = 7(1 + /Зп'°) = 7,
п2 = п'2 = 0,
п3 = л'3 = 0.
То есть л = (7/3,7п), где /3 = V/c. Так как n2 = 1, то, как и должно
быть,
л'2 = -п2 = -1 = л2 = 72(/32 - 1).
В системе К1, принимая во внимание, что
k — (w/c, k) = ш/с(1, к/k)
является 4-вектором, имеем
k!2 = k[ + 2(k[n')n\
к2Ч
вЛ
L.,
к|
Рис. 1.3. Отражение
света от движущегося
зеркала
и, в силу ковариантности последнего соотноше¬
ния, оно должно иметь эту же форму (быть фор-
минвариантным) и в лабораторной системе от¬
счета К, т. е.
k2 = k\ + 2(й[Л)л.
В компонентах эта формула имеет вид
ш2(1,п2) =wi(l,n1) + 2wi72(/3- (ппОН/З.п),
где П] = cki/u>i, п2 = ск2/щ2.

1.3. Релятивистская кинематика	181
Для частот мы получаем следующее условие связи:
= (1 +Р2 ~ 2/3 cos #i)72u>i.
умножая пространственные компоненты на вектор п, учитывая, что
(ПП2) = — cos 021 находим
а _ cos в\ - 2/3 _ (1 + /З2) cos в\ -2/3
C0S 2	ч;2	1	- /З2	1+	/З2	- 2/3 cos 0i
Более прозрачная формула для углов может быть получена с помощью
преобразований
зеркало «убегает» от волны, и отражения не происходит: 02 = я- — 0\.
1.3.12.	В «системе карусели» (системе наблюдателя, движущегося по
окружности) р' = р + Ш. Чтобы не загромождать запись, переобозна-
чим х° = ct, как t (т. е. положим с = 1). Тогда
ds2 = dt2 - dx2 - dy2 - dz2 = dt2 - dr2 - r2 dp2 - dz2 —
= dt2 - dr2 - r2 {dp1 — ft dt)2 — dz2 =
= (1 - r2Cl2)dt2 + 2r2ft dp' dt - dr2 - r2 dp'2 - dz2 =
= [1 _ (** + y'2)ft2] dt2 + ft(/ dy' - I/ dx') dt - dx'2 - dy'2 - dz'2.
02	\	/3	,	0\
=	и	П0ЭТ0МУ	>0i-
Интересно, что при
имеем 02 > 7г/2, а при cos$i < /3, т. е. при
Соответствующий метрический тензор задается матрицей
/1 - (х* + y'2)ft2 -ftjj' ft/ 0 \
-Qy'	-10	0
ftx'	0-10
О	0	0	—1у

182 -Ar Глава 1. Теория поля. Решения задач
Старше будет неподвижный близнец (интервал между двумя точ¬
ками, разделенными времениподобным интервалом, максимален вдоль
прямой).
1.3.13.	Будем решать задачу в инерциальной (не вращающейся) систе¬
ме, связанной с центром кольцевого волновода.
Волновой 4-вектор для света с частотой со, распространяющегося
вдоль оси х в неподвижной среде с коэффициентом преломления п,
имеет вид
*'±
-(ш, ±псо, 0,0).
с
Это соответствует волновому вектору в сопутствующей системе отсчета
для света, распространяющегося по направлению вращения (+) и про¬
тив направления вращения (-):
ck±
( 7
7/3
0
0^
7/3
7
0
0
0
0
1
0
^0
0
0
ч
( w \
±псо
О
V о У
^ W7(l ± п/З) ^
±u>i(n ± /3)
О
О
У
Таким образом, волновое число для света, распространяющегося по и
против вращения, составляет по абсолютной величине
ck± = ату(п ± /3).
Будем считать, что датчик расположен в диаметрально противополож¬
ной точке по отношению к источнику. Чтоб достичь датчика, свет дол¬
жен пройти половину окружности 7гR в ту или другую сторону. Набег
фазы составляет
ip± = k±nR=^.
С
Разность фаз будет равна
= ч>+ - ч>- =
ui^2f3'KR
Если волновод вращается с угловой скоростью Q = v/R, то
Sip ■
В низшем порядке по (3 =
Sip ■■
= ‘QooVL-kR'2 = ЦиоПБ.
с	с
v/c будет 7 » 1, и мы получаем
2a>f2S

1.3. Релятивистская кинематика	183
X
учет отличия 7 от 1 был бы в данном случае превышением точности:
в специальной теории относительности вращающееся тело не может
иметь ту же геометрию, что и поступательно движущееся. Учет 7 ф 1
потребовал бы расчета релятивистских упругих деформаций во враща¬
ющемся интерферометре. Такой расчет существенно более сложен, и
кроме того он зависит от конструкции интерферометра.
1.3.14. Пролетит ли стержень через щель, или столкнется с плоскостью
не зависит от того, из какой системы отсчета наблюдается этот процесс.
С точки зрения неподвижного наблюдателя очевидно, что стержень,
длина которого меньше, чем ширина щели, свободно пролетит через
нее. Поскольку по условию задачи стержень параллелен плоскости, то
оба конца пролетят через щель одновременно.
С точки зрения наблюдателя, связанного со стержнем, длина стерж¬
ня L больше, чем ширина щели /, но в системе стержня иначе опре¬
деляется одновременность: события, одновременные для системы непо¬
движного наблюдателя, в системе стержня происходят тем раньше, чем
Оольше они смещены вперед:
,/	t-Vr\\/c2
V1 - v2 /с2
Таким образом, прохождение стержнем щели в системе самого стержня
совершается не одномоментно, как в системе неподвижного наблюдате¬
ля, а в разные моменты времени: для переднего конца раньше. То есть
стержень в своей системе отсчета наклонен по отношению плоскости,
за счет чего плоскость пролетает мимо него, не задевая стержень края¬
ми щели.
1.3.15. Положим с = 1. В ответах скорость света будет вновь восстанов¬
лена из соображений размерности. Энергия частиц имеет вид
£1 = yj т\сА + pf с2 = yjm\ + р^,	£2 = у/ т^с4 + р\сг = \]т\ + р\.
Скорость системы центра инерции (СЦИ) V определим с помощью пре¬
образования Лоренца для суммарного вектора 4-импульса, описываю¬
щего переход от лабораторной системы к СЦИ, учитывая, что в этой
системе
pj + р2 = 0 = 7(pi + р2 - V(£j + £2)),
т. е.
V _ r2 р! + р2
£, + £2'

184 -l\r Глава I. Теория поля. Решения задач
Энергию в СЦИ (т. е. М — эффективную массу) найдем из условия
инвариантности четырехмерного скалярного произведения:
(р, +Р2)2 = т\ + т\ + 2(рхр2) = (£; + £^)2-(р;+Р;)2 = (£{ + £2)2 = М2,
так как в СЦИ р( + р'2 = 0. В итоге
М = [m2 + т2 + 2(£i£2 - р\ + р2)] '/2,
£ = Afc2 — [т2с4 + т2с4 + 2(£[£2 - р[с + р^с)]1/2.
В системе отсчета, в которой покоится первая частица (pj = 0, £J = mi),
имеем
(PiEj = £l£2 “ (Р1Р2) =
т. е. в этой системе отсчета энергия второй частицы равна
£9 =
£i£2 - (Р1Р2) _ £l£2 — (pip2)c2
т\	mic2
По определению относительной скоростью двух частиц называется ско¬
рость второй (или первой) частицы в системе отсчета, где первая (или
вторая) покоится. Тогда из условия
£9 =
тг
получаем
1 {РА) г
 = —1— = (UiHs),
уД - V&H т'т2
где и = 7(1, v) — четырехмерная скорость частицы. Как и должно быть,
относительная скорость не зависит от масс частиц, а зависит только от
их скоростей. Таким образом,
(и.\Ц.г)
-1—2
и является релятивистским инвариантом.
1.3.16.	Мы будем считать с = 1 и измерять энергию, импульс и массу
в одинаковых единицах ГэВ = 109 эВ. В ответе скорость света будет
восстановлена из соображений размерности.
Хотя набор статистических событий при неподвижной мишени (в
силу ее плотности) происходит быстрее, чем при работе ускорителя
на встречных пучках, но достижение большой энергии (эффективной

1.3. Релятивистская кинематика	185
\
массы) в ускорителе на встречных пучках выгоднее, так как в этом
случае энергия не тратится на бесполезное движение центра инерции
сталкивающихся частиц, что и показывает сравнение результатов ре¬
шения задач 1.3.16, 1.3.17 и 1.3.18.
Пусть неподвижная мишень состоит из частиц массы т, как и уско¬
ряемые частицы. Тогда эффективная масса будет равна
М = [2т(т + £)]1/2 » (2т£)1/2 (при £ » т),
а скорость системы центра инерции:
V=-P-
т + £
Если восстановить в последней формуле скорость света, то получим
.2'
V
с
/ Е — тс‘
~ (l - -g-'j ПРИ £ > тс2-
] Е + тс
• т =	1 ГэВ,	£	=	70 ГэВ, Мс2 = 12 ГэВ, V/c = 1 -	0,014;
• т =	1 ГэВ,	£	=	1000 ГэВ, Мс2 = 45 ГэВ, К/с =	1 - 0,001;
• т =	1 ГэВ,	£	=	7000 ГэВ, Мс2 = 118 ГэВ, V/c =	1 - 0,000143.
1.3.17. Положим	с-	1. В случае встречных пучков
М= [m? + ml + 2(£1£2+piP2)]1/2«2(£i£2)1/2 при £, »т,,£2>т2,
V	=	~	р/	« р1 ^ при	£[£2 > mim2,
Cl	+ С2 С) + С2
и конкретно:	М	=	2/800	• 30 ~ 310 ГэВ, — = §qq + gQ =	0,92.
1.3.18.	Положим с =	1. Из условия (р(р2)	= £2 + р2 = /п£'	получаем
£' = (g2+p2) « — = 98 • 103 ТэВ.
m
m
1.3.19.	Проверим выполнение обязательной связи энергии, импульса и
массы £2 - р2 = т2, т. е.
е2 - р2 - р2у - р2 - т]_ ch2 а - mx sh2 а - р2у - р\ =
= т2х-р2-р2 = т2+р2+р2-р2-р2 = т2.
е cha

186 -l\r Глава 1. Теория поля. Решения задач
1.3.20. Закон сохранения четырехмерного импульса дает соотношение:
р = kx + k2, где р, kx, k2 — 4-импульсы л-мезона и двух 7-квантов. Так
как ((^i -k2)p) = k2 -k2 = 0, то (kxp) = (k2p). Кроме того, из закона
сохранения проекции импульса на ось у, перпендикулярную импульсу
7г-мезона, следует, что \k\y\ = |/s2i/|.
Таким образом, получаем систему уравнений
{£i(l - о/с cos а) = £2(1 — о/с cos/3),
£1 sin а = £2 sin (3,
откуда следует, что
sin а — sin /3
о = с	—
sin(a — /3)
Время жизни 7г-мезона есть время жизни в его системе покоя, т. е.
_ ^ /1 у2 _ ^ л/sin о: sin /3
T~^V - «COS&+!"
1.3.21. Имеем соотношение Р = Р{+р2. Возводя в квадрат и полагая
с = 1, получим
пг = т] + т\ + 2^yJ(р^ + т^)(р% + т\) - (р,р2)).
В обычных единицах трехмерные импульсы pi и pi надо разделить на с,
чтобы получить размерность массы.
1.3.22. Имеем соотношение Р = Р{ + р2- Отсюда р{ = р - р2 и, возводя
в квадрат (с = 1), получим
т\ = т2 + т\ - 2	(р2	+	т2)(р* + пф - (рр2)).
В обычных единицах трехмерные импульсы pi и pi надо разделить на с,
чтобы получить размерность массы.
1.3.23. Закон сохранения 4-импульса дает р = р1 + р2. Возведем это ра¬
венство в квадрат (с = 1) и получим уравнение
т2 = 2£i£2(1 — cos#),
которое необходимо решить совместно с законом сохранения энергии
£\ + £2 = £, что приводит к следующему результату:
. 2 в	т2	т2
Sin — = 	 =
2	4е,(£ — е,)	4£2х(1	—	х)'

1.3. Релятивистская кинематика	187
гдел: = е\/Е. Максимум функции х(1 - х) будет достигаться при х = 1/2,
х. е. при е\ = ег = £/2. Отсюда
sin2 % = ^ = 1 - У2, т.е. cos^ = -.
2	£2	2 с
1.3.24. Положим с = 1. Поскольку ео > т и М » т, то ео « |ро|, и
задача фактически сводится к задаче о комптон-эффекте на непо¬
движной частице массы М.
Вводя обозначения для 4-импульсов частиц: k^, k — импульсы рас¬
сеиваемой частицы до и после рассеяния, р и р' — импульсы ядра до и
после столкновения, получаем закон сохранения 4-импульса системы:
ко + р = к + /Ф.
Перенося k в левую часть равенства и возводя в квадрат, получим
(ко + Р - к)2 = р'2>
откуда следует, что
М2 + 2(k0p) - 2(kp) - 2(k0k) - М2,
поэтому (kp) + (кко) = (коР)’ т-е- + еео(1 — cos в) — £qM. В итоге
получаем
Ео м	ео
£ -
М + £о(1 - COS б)	jro	(1_cos0)-
Мс2
1.3.25.	Закон сохранения 4-импульса дает равенство Р{+ Р.2= Р- Возво¬
дя данное соотношение в квадрат, найдем массу образовавшейся частицы:
1/2
М =
2 ,	2	,	2m\m<i
т.\ 4-	+
V1 - и2/с2.
Скорость этой частицы есть скорость центра инерции сталкивающихся
частиц:
у _	Pi	  miv
£i/c2 + m2	щ -р m2\/1 _ у2/с2
1.3.26.	Введем обозначения для 4-импульсов частиц: ко, k — импульсы
рассеиваемой частицы до и после рассеяния, р нр* — импульсы ядра до
и после возбуждения. Получаем закон сохранения 4-импульса системы:
к>о + р = к + Р*, откуда (предполагая, что с = 1) имеем
(ко+р- k)2 к М2 + 2 М£ - 2 МФ - 2ее'(1 - cos в) = р*2 = (М + Д£)2.

188 -Ar Глава 1. Теория поля. Решения задач
Так как частица ультрарелятивистская, то для нее можно считать, что
^ = k2 « 0, т.е. ео ~ |ро|, £ ^ |р|. Таким образом, находим
, = 2Ме + М-(М + А£.у _ е - AS.
2(М + е(1 — cos 0))	1 + _^(,_cos0)
Afc
1.3.27.	Обозначим 4-импульсы частиц следующим образом:	—	им¬
пульсы фотона до и после рассеяния, р^ и р — импульсы электрона до и
после столкновения и получим закон сохранения 4-импульса системы:
+ р0 = k + р. Перенося k в левую часть и возводя в квадрат, находим
(Ьо+Рц-Ю2 =Р2’
откуда
(кРц) + (££о) = (£0Ро), или
е(£о - cpocos^i) + е(ео - eocosd) = е(£о - cpocosOo).
Здесь в — угол между импульсами падающего и рассеянного фотона,
а в\ — угол между импульсом рассеянного фотона и импульсом перво¬
начального электрона. Тогда имеем
_	е0(£0	-	сро cosflp)
So — cosfficpo + ео(1 - cos#) ’
При ро — 0, £о = тс2 получаем формулу для энергии рассеянного фо¬
тона на покоящемся электроне (см. также задачу 1.3.24).
1.3.28.	Обозначим 4-импульсы частиц: k, k' — импульсы фотона до и
после рассеяния, р и р' — импульсы электрона до и после столкнове¬
ния. Запишем закон сохранения 4-импульса: p + k=p' + и, возводя
в квадрат, найдем, что
(p + k-k!)2=p2, или (pk') + (kk') = (pk).
Обозначив через в угол рассеяния фотона, получим (полагая с — 1)
. _ e(S+p)		2Sp	S
S + e + (p — e) cos в
„ ,	(„	m	\	.	.	m	S	.	2
\	2£_	У	C°S	l	+	We	+	VeA
Мы использовали здесь условие £»ти малость угла А = п - в (усло¬
вие Д «С 1 означает, что рассеянные фотоны летят в основном вдоль
начального импульса электрона).

1.3. Релятивистская кинематика
Энергия рассеянного кванта будет максимальна при А — 0, т. е. при
лобовом столкновении и рассеянии кванта «назад» (строго по пучку
электронов). Энергия фотона при этом равна
е' =	»	172	ГэВ	>	е.
1+тс
4 е£
Отсюда видно, что в случае ультрарелятивистских электронов проис¬
ходит существенное «ужесточение» квантов света.
1.3.29.	Положим с= 1. Энергия нейтрино ео в системе центра инер¬
ции определяется из уравнения pQ^	+ £<,„• из которого следует
условие
т. е. ml - 2тпе = т2^. Окончательно находим
£о = т\~ т\ - 31 МэВ.
2 tYl-n
Таким образом, в системе центра инерции энергия нейтрино фиксиро¬
вана и связана с массами остальных частиц (для любых углов вылета
нейтрино).
В лабораторной системе отсчета энергию нейтрино можно найти при
помощи преобразования Лоренца:
е = уеоО + ocos в0), где 7 = (1 - v2)
Здесь v = Ртг/стг — начальная скорость 7г-мезона. Мы видим, что в ла¬
бораторной системе энергия нейтрино зависит от во — угла между им¬
пульсами нейтрино и начального 7г-мезона. Энергия может изменяться
в пределах
Emin = Ео (1 - и) 7 < £ < £о(1 + 1*Ь = Етах,
причем в условиях нашей задачи
Emin = 0,40 МэВ, етах = 2666 МэВ (7*. = 43).
В системе покоя 7г-мезона угловое распределение нейтрино изотроп-
то, т. е.
aN dflo 11 . л I dtpo
где No — полное число нейтрино, dN — dN(6o,4>o) — число нейтрино,
импульсы которых лежат в телесном угле dflo-

190	Глава	1.	Теория	поля.	Решения	задач
Из соотношения е = 7во(1 + ncos#o) следует, что de = vjeo dcosdo-
Учитывая, что dpo = dip, так как при лоренц-преобразовании компо¬
нента импульса нейтрино, поперечная по отношению к направлению
скорости 7г-мезона, не изменяется, и, интегрируя по dp, получаем рас¬
пределение нейтрино по энергиям в лабораторной системе отсчета:
dNe =	1	d	_ de
N0	207е0	£max	£min
Поскольку правая часть данного выражения не зависит от энергии
нейтрино, то равновероятны любые значения е из интервала [£тах, етт]-
Рис. 1.4. Энергетическое (а) и угловое (б) распределения нейтрино, вылетаю¬
щих при распаде 7г-мезона. Сплошная линия отвечает 7* = 3, штри¬
ховая линия соответствует 7^ = 5
Поэтому распределение по энергиям в лабораторной системе имеет сту¬
пенчатый характер (рис. 1.4, а). Ступенчатость энергетического спек¬
тра продуктов двухчастичного распада движущейся нестабильной ча¬
стицы — это характерное свойство двухчастичного распада. Среднее
значение энергии легко находится:
- = етт + £„■„ _ 1333 МэВ
Нетрудно убедиться в том, что полное число нейтрино действительно
равно Nq\
£max	eoO+i'b
j мГ = ъ^Го / de = L
£min	^о(1	—	v)~f
Направляя ось х лабораторной системы отсчета вдоль скорости 7г-ме-
зона и совершая обратное преобразование Лоренца, получаем
J £о = е(1 - v cos 0)7,
I Pox = £о cos 9 = e(cos в - v)j,

1.3. Релятивистская кинематика -»1г 191
откуда следует связь между углами:
РОх	л	cos	в — v , п	d	cos	в
— = cos во = ;	л-	d cos0o = -5	т.
£0	1	— U COS 6>	72(1 - OCOS0)
Учитывая эту связь и исходя из (изотропного) распределения по углам
в системе пиона, получаем распределение нейтрино по углам уже в
лабораторной системе:
dN _	1 - у2/с2	dQ
No (1 — v/ссоъв)2 47г ’
причем здесь мы восстановили скорость света с. Нетрудно проверить
очевидное условие
1
f dN= Г 1 ~ у dCl = l-и2 Г
J Nо J (1 - ocos^)2 47г	2	J
-1
dx _ .
1 )
(1 — vx)
2
где х = cos в.
Заметим, что угловое распределение нейтрино в лабораторной си¬
стеме имеет резко анизотропный характер: наблюдается так называ¬
емый прожекторный эффект (рис. 1.4, б). Вследствие закона сохра¬
нения импульса основная часть вылетающих нейтрино сосредоточена
в узком конусе, ось которого направлена вдоль начального импульса
пиона. Данный конус имеет раствор Ав ~ \/1 — о2 ~ m^/e*. Получен¬
ное нами анизотропное угловое распределение, сильно вытянутое вдоль
скорости распадающейся частицы, характерно именно для безмассовых
вторичных частиц, к которым относится и нейтрино.
1.3.30. Поскольку 7-квант, как и нейтрино, является безмассовой ча¬
стицей, угловое распределение 7-квантов находится способом, полно¬
стью аналогичным рассмотренному в задаче 1.3.29.
1.3.31. Из закона сохранения 4-импульса рк — р +р +р следует (при
с=1):
Q1к ~ О2 =	-	28-еГПК	= (pv + pj2.
Заметим, что 4-вектор (р + р ) времениподобен. Действительно, в
системе центра инерции пиона и нейтрино:
(Р +р)2 = (р'+р’)2 = & +О2 > 0.
. )2 = (р' +р')2
—и	—7Г —У
Таким образом,
V	_	тк + ml — (р’ + p^)min
£— =  ~

192 -l\r Глава 1. Теория поля. Решения задач
но, поскольку ти = 0, то (р^ + pj2min = (£* + fi'Jmin = ml, т. е.
2 2 2 2 2 2
q   тКс ”1" мес — тпс
emax ~	2тк	'
Аналогично получаем
с _ т2кс2 + т\с2 - т2ес2 с __ т2кс2 - (Ме + т„)2с2
t-ж max-	2тк	,	t-umax	^
причем в окончательных формулах мы везде восстановили множитель с2.
1.3.32. В системе единиц, в которой с = 1, эффективная масса систе¬
мы — это энергия в системе центра инерции. Минимальная энергия
в системе центра инерции — суммарная энергия покоя всех частиц.
Таким образом мы считаем, что конечные частицы покоятся в системе
центра инерции.
Поэтому, если обозначить массу протона как тр, а массу частицы а
как та, то минимальная энергия в системе центра инерции, при которой
может родиться пара аа, — это 2(та + тр). С другой стороны энер¬
гия в системе центра инерции выражается через квадрат суммарного
4-импульса рt + р2, где р, и р2 — четырехмерные импульсы начальных
частиц. Таким образом,
Цта + тр)2 < (р{ +р2)2 = р* + р? + 2(р,р2) = 2т2р + 2(£,£2 - Р1Р2),
2(та + тр)2 - Шр < £i£2 - pip2.
Поскольку перед столкновением вторая частица покоилась, то £2 = тр,
р2 = 0. В этом случае получаем минимальное значение энергии нале¬
тающей частицы, а также соответствующий порог реакции:
2(та + тр)2 - ml	2	2тас2(та + 2т„)
Cl ^	,	У	—	C.J трс —	,
тр	н	тр
причем в последнем равенстве мы восстановили множитель с.
а) тр = та = 1 ГэВ, 7 = 6 ГэВ.
б) тр = 1 ГэВ, та = 2 ГэВ, 7 = 16 ГэВ.
в) тр = 1 ГэВ, та — 4 ГэВ, 7 = 48 ГэВ.
1.3.33. Положим с — 1. Пренебрегая потенциальной энергией взаимо¬
действующих частиц находим, что минимальная энергия мюона и ан¬
тимюона в системе центра инерции на большом расстоянии друг от
друга равна 2тр. Энергия в системе центра инерции выражается через
квадрат суммарного 4-импульса рх + р0 начальных частиц:
4ml < (рх + р2)2 = Р* + Р* + 2(7,Р2) = 2т2е + 2(£i£2 - р,р2),
2-т2е^ £i£2 -р,р2.

1.3. Релятивистская кинематика ->\г 193
В случае встречных пучков £ 1 — £2 — £ встреч! Pi — P2i Pf £встреч *4 '
минимальная энергия начальной частицы и порог реакции равны
2ml -т2е< £ встреч + Р? = 2£встреч ~
,2
£ встреч ^ тН'	^встреч — (тц ™е)с ■
В случае неподвижной мишени вторая частица вначале покоится,
поэтому £2 = те, рг = 0, следовательно
2ml-ml it,т.. £, > 2 £ - т„ - г<"е - ~ 40 ГэВ.
1.3.34.	Пусть с = 1. Записываем закон сохранения 4-импульса:
Ei + Р-2 = & + —2’
где в системе покоя мишени (2-й частицы) начальные и конечные 4-им¬
пульсы первой и второй частиц имеют вид
= (£ - е, pj),
(т + Е, рг).
Из условия (р, -р')г= (Р2-^2 слеДУет. что (£,^) =	или
£(£ - г) - ppl cos 0 = т(т + е).
Поскольку р = л/£2 — m2, р( = \/(£ — £)2 ~ т2> 70 получаем
/(£ + т)(£ — е — т) _ м£ + тсг)(£ - е - юс2)
C0S у (£-m)(£-e + m) у (£ - mc2)(£ - е + тс2) ’
причем в последней формуле мы восстановили скорость света с. Оценки
дают, что в ~ 1°.
В системе центра инерции первой и второй частицы имеем
~ ^20—10^’
и это означает, что m(£ — е) = £q + Ро cos#o> следовательно,
= (£,р)-	|pj =
= (т, 0),	\Р2	=
т(£-е)-£ о
cos 0о 	2	•
Ро
Определим £о из условия рю + Рго = 0 в системе центра инерции,
а также учитывая (рх + р.,)2 = (р,0 + Р20)2. т. е. 2т2 + 2т£ = (2£о)2, от¬
куда имеем (
„2	m(£ + m) 2   с2 г _ т(£ - т)
£0 =	2	’	Ро — ^0 ~ т -	2	'

194	Глава	1.	Теория	поля.	Решения	задач
И в итоге получаем
cos во = 1 - 2-	=	1-2
.2 '
£ - т	Z-mc
В последней формуле восстановлена скорость света с. Согласно оценкам
во ~ 2°.
1.3.35.	Скорость ультрарелятивистской частицы v в лабораторной си¬
стеме выражается через скорость системы центра инерции (СЦИ) V
и скорость частицы в СЦИ vo по формулам сложения скоростей (мы
полагаем, что с = I, во — угол рассеяния частицы в СЦИ):
Vcose = _p>^fo + v osinff = ^e0fZZt
1 + t>0 V COS во	1 + Vo V cos во
откуда следует, что
faff— fosinflp-y/l - V2
Vo COS во + V
Заметим, что в частном случае, когда vo — 1 (или оо = с — в обычной
системе единиц), данная формула описывает явление аберрации, т. е.
изменения угла наклона световых лучей при переходе между инерци-
альными системами отсчета.
Скорость СЦИ будет равна (с учетом £ » т)
Z + m V Z + m	Z' V	V	£	’
Считая далее, что vo ~ 1, V ~ 1 (нас интересуют ультрарелятивистские
частицы), находим
sinft> =	J	во
й _ V £ 1 -Ь cos во	V	£ ё 2 ’
где мы восстановили скорость света с. Последняя формула будет неспра¬
ведлива в узком интервале углов
тг - S < в0 < 7г, где	6 ^
т. е. угол во не должен быть близок к п.
1.3.36.	Положим с= 1. Обозначим массу возбужденного ядра М* =М+е,
где М — масса невозбужденного ядра. Закон сохранения 4-импульса
дает соотношение р* = р + k, где р*, р, k, — 4-импульсы возбужденного
ядра, невозбужденного ядра и 7-кванта.

1.3. Релятивистская кинематика	195
■К
1)	Энергия испущенного 7-кванта. Перенося k в левую часть
равенства и возводя в квадрат, получаем
М*2 - 2ЛГе7 = М2,
где е7 — энергия испущенного 7-кванта. Поэтому получаем
М*2 - М2 _ (ЛГ - М)(М* + М) _ е(2М + е)
е-у =
2ЛГ	2М*	2	(М	+	е)	V	2Л1с:
е 1 -
Таким образом, энергия излученного 7-кванта е7 меньше величины энер¬
гии возбуждения, так как часть энергии тратится на отдачу ядра массы М.
2)	Энергия отдачи ядра. В выражении для закона сохранения
4-импульса перенесем р в левую часть равенства и возведем в квадрат:
(р* - р)2 = М*2 +М2- 2£АГ = £ = О,
т. е. кинетическая энергия, сообщенная ядру, равна
Е_М= (ЛГ~М)2 - е2 -
2ЛГ	2М-?	2Мс2'
3)	Скорость возбужденного ядра. Вначале рассмотрим про¬
цесс возбуждения налетающим 7-квантом покоящегося ядра, находя¬
щегося в основном состоянии. Чтобы возбудить такое ядро, необходима
энергия 7-кванта, большая, чем энергия возбуждения е, так как часть
ее будет потрачена на энергию движения образовавшегося возбужден¬
ного ядра. Таким образом, закон сохранения 4-импульса теперь будет
иметь вид k' +р = р*, где k! — 4-импульс налетающего 7-кванта. От¬
сюда следует, что (&' + р)2 = р*2, т. е.
2е\М + М2 = М*2, откуда = М	=е(1	+ -£?).
Далее мы будем считать, что исходное возбужденное ядро движет¬
ся, и его 4-импульс: р*' = (£*', р*')- Начальная скорость возбужден¬
ного ядра должна быть такой, чтобы 7-квант, испущенный им, имел
энергию бу. Из закона сохранения 4-импульса р*' — р + k' следует, что
(р*' - k')2 = р2, т. е.
ДГ2 - 2е;(£*' - (p*'n')) = М2, где п' = k'/|k'|.
Очевидно, ^то наиболее выгодным является излучение 7-кванта в на¬
правлении движения возбужденного ядра, т. е.
М*2 — 2е'(£*' - |р*'|) = М2.

196	Глава	/.	Теория	поля.	Решения	задач
Отсюда получаем
ул _ V*) =	=	м'2-м2 V* = М'2-М2 ~ _L
71	’	1	+	Г	2	е;уи*	’	М,2	+ М2~Мс'
Легко видеть, что минимальная скорость возбужденного ядра должна
быть в точности такой, чтобы после испускания 7-кванта в направлении
вперед ядро остановилось.
Выше во всех окончательных формулах восстановлена скорость света с.
1.3.37.	Положим с — 1. При /3+-распаде ядра происходит реакция
nAz —> n+\Az 1 + е+ + ve,
где N — число нейтронов в ядре, Z — число протонов, е+ — позитрон,
ve — электронное нейтрино, А — число нуклонов в ядре. Закон сохра¬
нения 4-импульса для этой реакции записывается в виде
Рг=Рг-х+Р + Ь где
— 4-импульсы ядер, позитрона и нейтрино соответственно. Отсюда име¬
ем (р^ - k)2 = (рг_] + р)2, т. е.
М% - 2Mze = (рг_1 + р)2-
Таким образом, максимальная энергия нейтрино оказывается равной
_ Mz - (pz_j + p)min	-	(Mz-1 + m)2
emax	2^	2Мг
(см. задачу 1.3.31), где Mz-1, m — массы первоначального и дочер¬
него ядер, а также позитрона.
Масса ядер определяется числом протонов и нейтронов и их энер¬
гией связи по формуле Вайцзеккера:
AMZ = mpZ + тя(Л -Z) - аА + (ЗА2/Ъ + 7Jfl + e{A,2^Z)1.
Энергия связи в нулевом приближении пропорциональна числу нук¬
лонов в ядре Л и не зависит от их заряда (член ~ -аА). Энергия связи
уменьшается на величину энергии поверхностного натяжения (/?Л2/3) и
энергии кулоновского расталкивания протонов (каждый из Z протонов
взаимодействует с остальными Z — 1, т. е. кулоновские силы не насыща¬
ются, в отличие от ядерных (см. первое слагаемое), и пропорциональны
Z(Z - 1) ~ Z2 и обратно пропорциональны радиусу ядра R ~ Л1/3. Име¬
ется также тенденция к симметрии: ядра с Z = Л/2 наиболее устойчивы
(большая энергия связи). Этот эффект учитывается наличием в форму-

1.3. Релятивистская кинематика	197
пе Вайцзеккера члена е(А/2 - Z)2/А. Из-за принципа Паули взаимо¬
действие нейтронов с протонами больше, чем нейтронов с нейтронами
и протонов с протонами, т. е. при данном А образование системы из
I = А - Z — N выгоднее, чем при Z ф N.
Используя формулу Вайцзеккера, получаем
_ (Mz - Mz-1 - m)(Mz + Mz-1 + m)	M - m-
emax -	2Mz
.	, 2Z — 1	2Z — 1 — Л
= -(mn - mp) -me +	e д '
В данной задаче первоначальное и дочернее ядра являются зеркаль¬
ными, т. е. у них число |А - 2Z\ одинаково. Например, у ядра i3N7 —
7 протонов, 6 нейтронов, поэтому А - 2Z = -1; у дочернего ядра 13С —
6 протонов, 7 нейтронов, и, следовательно, A — 2Z = 1. Аналогично, для
ядра 15O8 величина А - 2Z = -1, а для 15N7: A -2Z — 1.
Поэтому для ядер 13N7 и )508 значение величины 2Z - А - 1 = 0, и
симметричный член не вносит вклада в общий результат. Чтобы найти
коэффициент 7 в кулоновском члене, будем считать заряд ядра Ze рав¬
номерно распределенным по шару радиуса R = r0Al‘3 (г0 = 1,5 ■ 10~13 см).
Плотность заряда в ядре:
(Ze	п
 г, r<R,
4/Зтг Я3
О,	г	>	R.
Электростатический потенциал ядра имеет вид
■ Ze_r
ф) = { 2R
-©]•
Ze/r,	г	>	R.
Z2
Кулоновская энергия взаимодействия протонов в ядре:
1	г ...	3 (Ze)2	Зе2 Z2
U - 2	у P4>dV -	5 R	ЪгоаХ/3	7л,/3.
Зе2
т. е. 7 = — = 0,577 МэВ. Таким образом,
Ъго
Стах = 7А2/3 - (тп - тр) - те = 7Л2/3 - 1,8 МэВ,
т. е. = 1,4 МэВ; = 1,7 МэВ. Сравнение с экспериментом дает
следующие относительные ошибки:
A(N> = 1>7~1-4 =0,18; д(О) = 1,9 ~ 1,7 = 0,11.
1,7	1	*9

198 -Ar Глава I. Теория поля. Решения задач
1.4.	УРАВНЕНИЯ	МАКСВЕЛЛА
1.4.1. Выпишем уравнения Максвелла, содержащие временные произ¬
водные:
ЭН	,	ЭЕ	,	т»	Л	■
— = -crotE, — = crotH -47TJ.
Продифференцируем их по времени:
Э2Н	,	ЭЕ Э2Е . ЭН . д\
—r = -crot—, —f = c rot —-4тг-±
dt	dt dt	dt	dt
Подставим выраженные через исходные уравнения Максвелла произ¬
водные dH/dt и ЭЕ/dt в правые части уравнений, воспользуемся тож¬
деством rot rot а = grad diva — Да и выразим дивергенции полей через
два оставшихся уравнения Максвелла:
~ - с2 A ) Н — 47гс rot j, ( JL - с2 Д j Е = -4тг (grad р + Ц).
1.4.2. Уравнение divH = 0 будет выполняться при всех t всегда. Урав¬
нение div Е = 4тгр будет выполняться тогда и только тогда, когда всюду
выполнено уравнение непрерывности dp/dt + div j = 0.
Уравнения, включающие дивергенции полей Е и Н, можно рассмат¬
ривать не как динамические уравнения, а как уравнения, определяющие
начальные условия.
1.4.3. Первая пара в присутствии магнитных монополей:
rot Е = —— —jm, div Н = 47rpm.
с dt с
В задаче 1.4.2 условием выполнения уравнения divH = 47rpm станет урав¬
нение непрерывности для монополей: dpm/dt + divjm = 0.
1.4.4. Комплексная запись уравнений Максвелла:
j• с л	гг idF , 4тг/.
divF = 47rp, rotF = - — Н 1.
с dt с
В присутствии магнитных монополей величины рт и ]т входят в урав¬
нения как мнимые части р и j, т. е. р = ре + ipm, j = je + i)m. Здесь pe и
je — плотности электрических зарядов и токов.
Заметим, что комплексные уравнения Максвелла симметричны (в силу
их линейности) относительно одновременного умножения F, р и j на
произвольный ненулевой комплексный множитель. В частности умноже¬
ние на —г соответствует переходу от тензора к дуальному тензору Fyiv.

1.4. Уравнения Максвелла	199
1.4.5. Первая пара уравнений Максвелла дает тождество. Из второй
пары получаем
А<р + - div А = -4л-р,
С С/1
(^т2 -c2A + c2graddiv^A + cgrad^ = 47rcj.
с.
1.4.6. Первая пара уравнений Максвелла дает тождество. Из второй
пары получаем
dvdvA» + d»dvAv =	Л или ПА» + d»dvAv =	/м.
с	с
1.4.7. В трехмерной записи:
□у? = -4я-р, ПА = -^j, где □ = Д —
с	с	at
47Г
В четырехмерной записи: [14м = — —/м. где □ = —о„сг.
1.4.8. Ду? = -4тгр, (I|j - д) А + \ grad % =	■
14‘9' ^divA = -47rp’	~ A + graddiv)A = т*-
1.4.10. А = —ctE + ^[Нхг].
1.4.11. ус/ = <р + А' = А - grad/ или А'» — А» + d»f.
1)	□/ - QVAV\ 2) Д/ = div А; 3)	= -cip.
1.4.12. 1) □/ = 0; 2) Д/ = 0; 3) Ц = 0.
1.4.13. Тензор электромагнитного поля FMl/ инвариантен относительно
калибровочных преобразований, поэтому единственный член, инвари¬
антность которого надо проверить, — действие взаимодействия:
5in i = -lJA^d4x,
и
где U — четырехмерная область интегрирования в пространстве-времени.

200 -l\r Глава 1. Теория поля. Решения задач
При калибровочных преобразованиях изменяется четырехмерный по¬
тенциал: 5Ад = <9М/, вследствие этого происходит изменение действия:
ssM = -l-f (d^rd'x = i J (-ад") + fd^r)d4x.
и	и
Первый член в полученном равенстве является пблной 4-дивергенцией,
его можно переписать как интеграл по границе области U — трехмер¬
ной поверхности 8U, поэтому
SSM = -±f fr dV^+'-jНд^П d4x.
au
Выберем функцию / так, чтобы она обращалась в нуль на границе U.
Теперь условие инвариантности действия при калибровочном преобра¬
зовании сводится к равенству
1
6SM='-Jf(d^)d4x = 0.
Это условие должно выполняться для произвольной функции /, обра¬
щающейся в нуль на границе области интегрирования. Таким образом,
всюду в области интегрирования должно выполняться уравнение непре¬
рывности для зарядов и токов:
диГ = §7 + div j = О,
и это является еще одной иллюстрацией теоремы Нётер: инвариантно¬
сти теории относительно калибровочных преобразований отвечает за¬
кон сохранения электрического тока.
1.4.14.	В соответствии с формулой (1.13) имеем
^ = F^jd^/
dL
0(V1a) ~ 17’
откуда получаем выражение для канонического тензора энергии-импульса:
Тензор Т^и не является калибровочно-инвариантным, поскольку выра¬
жение д„А\ не является калибровочно-инвариантным.
SL =	5F^F^	=	F^5F^	_	F“l/(dfMu	-	ди6Ам)	_	F^d^SA..
167т	87т	8л	4л	’

1.4. Уравнения Максвелла ->V 201
1.4.15. Естественно попробовать модифицировать тензор T^v из преды¬
дущей задачи так, чтобы он полностью выражался через тензор элек¬
тромагнитного поля Для этого надо дополнить выражение dvA\ до
риХ = диАх — д\Аи. То есть мы предполагаем, что новый тензор имеет
вид	.	,	.
ррХр	F*XF ч	FM
^‘-Чг+ъЧг' ^ =
Поднимая второй индекс, получим
£?мЛ ри,	FylXF	ч	FmA
7= _F r_x + puf Г» А 6Три = Г — QXAV.
47Г	107Г	47Г
Используя четырехмерную запись уравнений Максвелла и полагая /д = 0,
проверяем, что дрбТ^ = dpT*11'. (См. также решение задачи 1.4.16).
Тензор калибровочно-инвариантен в силу того, что выражается че¬
рез калибровочно-инвариантный тензор электромагнитного поля F^v.
1.4.16. Дифференцируя тензор энергии-импульса, имеем
рн^р	рн^р
Я ТН — r vX л. Я L Liii =
^	^	4тг + " 16тг
_ (dpF^ ) с ^ pp\dpFvx^ . рр\ dyFfix _
4тг иХ	4тг	8тг
= -~jXFvА - F^a-L(2^F„a - d„FpX) =
С	о7Г
- --jXFvл - F^^dpF.x + dxF„„ + d„FA#1) = -;/Л^А,
С	07Г	С
и это полностью соответствует (1.16). Здесь были использованы уравне¬
ния Максвелла. При v = 0 отсюда можно получить уравнение баланса
энергйи, а при v = п = 1,2,3 — уравнение баланса импульса (см. (1.17)).
1.4.17. Т% = 0.
1.4.18. Вне тонкого плоского конденсатора электрическое поле Е = 0.
Внутри Е = 47г<7, где о — поверхностная плотность заряда на пластине.
Таким образом, если пластины лежат в плоскостях z — 0 (положитель¬
но заряженная) и z = а (отрицательно заряженная), то электрическое
поле и плотность заряда имеют вид
Е = 4-7гстег 0(г)9(а — г), р = cr(S(z) — 6(z — а)).
Здесь 0(г) — 0-функция Хевисайда (Д. 13).
1)	На поверхности пластины электрическое поле испытывает ска¬
чок, поэтому мы не можем непосредственно воспользоваться формулой
для плотности силы рЕ, поскольку произведение данных обобщенных

202	Глава	1.	Теория	поля.	Решения	задач
функций не определено (разрывы 0-функций приходится как раз на
поверхности, на которых локализован заряд). Чтобы доопределить про¬
изведение рЕ, можно рассуждать двумя способами.
а)	Поле Е представляет собой суперпозицию полей, создаваемых от¬
дельными пластинами, причем силу взаимодействия пластины с соб¬
ственным полем следует считать равной нулю. Таким образом,
p = Pi + P2,	p\=a8(z), p2 = -a6(z-a),
Е = Е] + Ег, Ei = 2naez sgn(z), Ег = 2ттаег sgn(a — z).
Произведения Е1Р2 и Е2Р1 хорошо определены. Давление, действующее
на первую пластину, равно
б)	Мы можем рассмотреть бесконечно тонкую пластину, как пре¬
дельный случай пластины конечной толщины d, равномерно заряжен¬
ной по объему. В этом случае внутри пластин поле будет изменяться
линейно от нуля до максимального значения. Регуляризованные таким
образом величины имеют вид
2)	Компонента агг тензора напряжений Максвелла соответствует дав¬
лению (отрицательное давление — это натяжение) вдоль оси z и имеет
вид	2
стгг =	= -27ГСГ20(z)0(a - z).
07Г
Перепад давления на поверхности равен давлению, действующему на
данную поверхность:
0,	z < -d,
(z + d)/d, -d^z^O,
Е = 47гсгег < 1,	0 < z < а,
(z-a)/d,	a^z^a + d,
О,	z > a + d,
р =	+	d)Q(-z)	-	0(z	-	а)в(а	+	d	-	z)).
Давление, действующее на первую пластину, равно
о
-d
Р\ = <Угг{о - е) - <тгг(0 + е) = 2-ка2.

1.4. Уравнения Максвелла	203
1.4.19.	Ход решения практически полностью совпадает с ходом реше¬
ния задачи 1.4.18.
Вне длинного соленоида магнитное поле Н = 0. Внутри Н = (4n/c)J,
где J — поверхностная плотность тока в обмотке соленоида. Таким обра¬
зом, если обмотка лежит на поверхности цилиндра г = а (г2 = х2 + у2)
и образует правый винт с осью г, то
4тг	" -
Н = — JezQ(a - г),	)=Jl5(a-r),	1 = (—у/г, х/г, 0).
1)	На поверхности обмотки магнитное поле испытывает скачок, по¬
этому мы не можем прямо воспользоваться формулой для плотности
силы “[j х Н], так как произведение данных обобщенных функций не
определено (разрывы 0-функций приходится как раз на поверхности, на
которых локализован ток). Чтобы доопределить произведение - [j х Н],
можно рассуждать двумя способами.
а)	Поле Н представляет собой суперпозицию полей, создаваемых
отдельными участками обмотки, причем силу взаимодействия участка
обмотки с собственным полем следует считать равной нулю. В отли¬
чие от задачи 1.4.18 обмотка связана и не может быть естественным
образом разбита на два участка. Выделим маленький участок обмотки
с размерами много меньше а.
Поле, создаваемое всеми остальными участками на поверхности рас¬
сматриваемого участка, будет непрерывным. Сам участок в малой окрест¬
ности (много меньше его размеров) создает поле, аналогичное полю
бесконечной плоскости, по которой течет однородный поверхностный
ток У. Так, если мы выделили участок обмотки вокруг точки (а, 0,0),
то ток на этом участке (в малой окрестности) равен
j, = JtyS(x - а),
а создаваемое этим участком поле (в малой окрестности) равно
Hi = 2nJez sgn(a — х).
Вычитая Нг = Н - Hi, получаем, что магнитное поле, создаваемое осталь¬
ными участками намотки, есть среднее арифметическое между полями
внутри и снаружи соленоида.
Произведение ^ [ji х Нг] хорошо определено. Давление, действую¬
щее на обмотку, направлено наружу и равно
а+е
Я, = [ hyH2zdx = ^J2.
J	С
а—е

204	Глава	1.	Теория	поля.	Решения	задач
б)	Мы можем рассмотреть бесконечно тонкую обмотку, как предель¬
ный случай обмотки конечной толщины d с постоянной плотностью то¬
ка. Аналогично задаче 1.4.18, в этом случае внутри обмотки поле меня¬
ется линейно от нуля до максимального значения, и мы легко получаем
тот же ответ.
2) Компоненты ахх = ауу тензора напряжений Максвелла соответ¬
ствуют давлению вдоль осей х и у:
^0(а-г) = ^У20(а-г).
Поскольку аху — 0, а ахх = оуу, в плоскости (х,у) давление изотропно.
Перепад давления на поверхности задает давление, действующее на
данную поверхность:
2п
Р = ауу(а - е) - <Туу (а + е) = -jJ2.
с
1.5.	ДВИЖЕНИЕ	ЗАРЯЖЕННОЙ	ЧАСТИЦЫ
ВО ВНЕШНЕМ ПОЛЕ
1.5.1.	Сила, действующая на частицу, есть производная ее импульса по
времени:
р _ dp _ тх , mv(vv)
" Tt " V\ - о2/с2	о\ 1-,2А2)3/2’
а ее мощность соответственно равна
т(хх)
(vF) —
(1 - «70
что совпадает с производной энергии по времени dZ/dt. См также фор¬
мулы (1.19), (1.21).
1.5.2.	Направим ось z по магнитному полю, а ось у так, чтобы вектор
электрического поля лежал в плоскости {у, г), как показано на рис. 1.5.
Тензор электромагнитного поля в нашем случае может быть записан в
виде матрицы
Fр1/ =
/б 0	—	£sin0	—EcosO\
0	0	-Н	О
Es'md	Н	О	О
У Е cos 0	0	0	0	у
(1)

1.5. Движение заряженной частицы во внешнем поле -Л- 205
Систему уравнений движения частицы представим в матричной форме:
d_
dr
( и0\
их
иу
W
0	О
о	о
Л sin# —ui
Л cos в 0
Л sin#
ш
0
О
Acos#\
О
О
0 /
( и0\
их
Uy
W
(2)
где
еН
Л _ еЕ _
тс'	тс'
Поскольку коэффициенты полученной системы обыкновенных диффе¬
ренциальных уравнений постоянны, решение ищется в виде экспонент,
показатели которых находятся из характеристического уравнения
А4 + А2(ш2 - Л2) - Л2ш2 cos2 в = 0
и равны
(3)
Рис. 1.5. Ориентация маг¬
нитного Н и электрического
Е полей в декартовой си¬
стеме координат. Скорость
дрейфа V направлена вдоль
оси X
где 1\ и /г — соответствующие инварианты
электромагнитного поля. В общем случае
существуют два действительных и два мни¬
мых решения:
А j _2 = ±>г, Аз 4 — ±г'П,	(4)
явный вид которых легко получается из (3).
Таким образом, мировая линия частицы за¬
висит только от 4-инвариантов: ее собствен¬
ного времени и двух инвариантов электро¬
магнитного поля.
Имеется два простейших случая, когда /г = 0, но 1\ ф 0. В этом
случае поля ортогональны, но не равны друг другу. Следовательно, мо¬
жет быть выбрана система отсчета, в которой либо Е ф 0, но Н = 0,
либо Е — 0, но НфО. Пусть Е > Н, тогда 11 = 0 и имеются только
действительные корни Ai,2 = ±е\/Е2 - Я2/(тс). Видно, что координа¬
ты и время частицы экспоненциально растут с ростом собственного
времени частицы. Пусть Н > Е, тогда отличны от нуля только мнимые
решения А34 = ±iCl. При этом происходит ограниченное движение в
плоскости, параллельной плоскости (у, г), смещающейся в направле¬
нии оси х с постоянной скоростью V = с[Е х Н]/Н2, которая описы¬
вает дрейф ведущего центра орбиты частицы, представляющей со¬
бой окружность с центром на оси х. Угловая скорость частицы равна
П = eVH2 -Е2/(тс).

206	Глава	1.	Теория	поля.	Решения	задач
1.5.3.	В этом случае /г = 0 и 1\ < 0, поэтому мнимые корни (4) общего
решения задачи 1.5.2 Азд = 0, а действительные =±Л. Из системы
уравнений (1) задачи 1.5.2 следует, что йх = йу = 0, и, согласно началь¬
ным условиям,
х(т) = £т. у(т) = &т.	(1)
m	m
Решение для системы, определяющей две другие компоненты, предста¬
вим в виде
сям: )—(-,)-•
Из начальных условий определяем
fl=£o_f^£>	где	Z0=Jc2p2+m2c4'
2mc	2	me	'
и получаем для компонент 4-скорости равенство
ио(т) = —^ ch Лг + — shA-r, иг(т) = sh Лт -I- — сЬЛт. (2)
тс	тс	тс	тс
Выполняя еще раз интегрирование в (2) с учетом начальных условий,
находим уравнения траектории в параметрическом виде:
*(т) = ^зЬАт+^сЬАт-1),	(3)
z(r) = %(chAr-l) + ^shAr.	(4)
eh	eh
Из уравнения (3) выражаем т через t:
тс ,	{ eEt + рог + J(eEt + ро*)2 + т2с2 + р20х + р\
Т = — In < 	- —
еЕ I	со/с	+ рог
Подставляя это соотношение в (4) и (1), находим законы движения в
трехмерной форме:
г(0 = ^ | у/(eEt + р0г)2 + т2с2 + ^	^	^	J,
(5)
,А сро*. Г	+ р0г + у/(eEt + р0г)2 + т2с2 + р\х + р*
х(0 = -^1п^   5-7—	f,	(6)
еЕ {	£о/с + р0г	1
закон движения по оси у, т. е. y(t) получается аналогично закону x(t)
заменой рох —► роу в множителе перед логарифмом.

1.5. Движение заряженной частицы во внешнем поле ->v 207
При малых значениях ро и t, т. е. при ро -С тс и eEt тс оказы¬
вается, что t = т, и выражения (5) и (6) переходят в законы нереляти¬
вистского движения в однородном электрическом поле:
*<!> = ач+Й<!.
m 2m
Если с момента начала движения прошло достаточно большое время,
т. е. t > mc/{eE), то скорость частицы ста¬
новится близкой к скорости света с, даже
если начальная скорость была мала. Законы
движениячв этом пределе:
z(t) — ct —
x(t)
срох
еЕ ’
. 2 eEt
v ln •
еЕ me
Движение вдоль оси z под действием однород¬
ного электрического поля при рох = роу = 0
(см. формулу (5) и рис. 1.6) называется ги¬
перболическим движением.
1.5.4. В отличие от предыдущей задачи здесь /[ > 0, поэтому х = 0, а
мнимые корни (4) общего решения задачи 1.5.2 определяются частотой
О = ш. Теперь сохраняются компоненты 4-скорости мо и иг, и при этом
зависимости t(r) и г(т) имеют вид
Рис. 1.6. Гиперболическое
движение
t(r) = -^т, г(т)
тс
РОг РОгС л
-^T=~e^L
(1)
Как видим, собственное время частицы и время в лабораторной систе¬
ме отсчета имеют разный масштаб, но связаны между собой линейно:
время в лабораторной системе отсчета течет быстрее.
Для компонент 4-скорости, лежащих в плоскости, перпендикуляр¬
ной магнитному полю (поперечные компоненты), имеем
(иЛг)) = 0+
\Uy(r)J
О'"'+iC>
С учетом начальных условий находим
их(т) = — cos сот + — sin шт,
me	me
РОу
Uu(t) = — COS CUT -
P Ox
me	me
Траектория движения в параметрической форме имеет вид
sin шт.
cos шт),
у(т) — ~^тг sin wr + ^^-(соsujt — 1).
сР0х .
еН
еН

208 -i\r Глава I. Теория поля. Решения задач
Решение можно представить в лабораторной системе отсчета, осуще¬
ствив замену
еНс,
£о
t.
Траектория частицы представляет собой винтовую линию, ось которой
параллельна оси г и проходит через точку плоскости (х,у) с коорди¬
натами хо = сроу/(еН), уо = -срох/(еН). Шаг винтовой линии в лабо¬
раторной системе отсчета равен h = 2npozc/(eH), и радиус вращения:
ро = cVpqx + Р()у/(еН). Частота вращения частицы в лабораторной си¬
стеме отсчета равна ljq = (еЯс)/£о-
1.5.5.	В этой задаче снова /2 = 0, поэтому, в зависимости от соотноше¬
ния между величинами полей, можно перейти в систему отсчета, где
останется либо электрическое, либо магнитное поле, и свести задачу
к одной из двух предыдущих. Однако такой подход требует проведе¬
ния двукратного преобразования Лоренца, поэтому кажущаяся просто¬
та превращается в весьма трудоемкий процесс. Гораздо эффективнее
решить задачу сразу в лабораторной системе отсчета.
Положим для определенности Н > Е, тогда я = 0, а частота равна
П= — \/Н2 - Е2 =
еН'
тс ’
где Я' — магнитное поле в системе отсчета, движущейся вдоль оси х
со скоростью
V = с
[Е х Н]
Н2
(1)
Из системы уравнений (2) задачи 1.5.2 следует, что йг = 0, и соглас¬
но начальным условиям имеем
иг{т)
_ £0г
тс ’
г(т)
РОг
Т.
Для системы уравнений, определяющих оставшиеся три компоненты,
остается одно действительное собственное значение (я = 0) и два мни¬
мых (±гП). Определив соответствующие собственные векторы, запи¬
шем решение для компонент 4-скорости в виде
(ио(т)^
их(т)
\uy(T)J
= а0
+ а+
( 1
ш/ А
\iQ/Ay
(
I eiQr + а_
\
ш/ А
in/А у
<Пт

1.5. Движение заряженной частицы во внешнем поле	209
учитывая начальные условия, получим
_о;2(£о - рохУ) _ ЫЕоУ -fp*) CQSПт _ ЛДо^ sjn
ао
(г)
me2 U2
mc3fi2
тсП
(г)	-	ср0х]	sin fir + — cos fir.
me fi ' c	'	mc
(2)
«Л7-) =
Aw(£o -РаДО
[ (^° "c ~~ Cj0°x) cos + sin fir
mc2fi2
mc2fi2
Проводя дальнейшее интегрирование, получаем выражения, определя¬
ющие траекторию частицы в параметрическом виде:
2 ,
t(r)-
' = (1) Р
*м-(£) {
-ро,П V
 о	Г
£oV-c
ес2Н1
VZ0-poxV
т —
тс
Z0V -с ро.
ес Н'
sin fir + ^(cosfir - l)j j,
fir-i-g(cosfir - !)]},
г * H
у ~ w
Z0V-
ec H'
с P°JC (1 _ cosQr) _|_ sin fir
en
(3)
Для проекции 4-скорости на ось х мы получили слагаемое, не завися¬
щее от времени, которое определяет скорость дрейфа ведущего центра
орбиты частицы. Заметим также, что отношение Н/Н' есть лоренцев-
ский фактор, определяющий преобразование координат при переходе из
лабораторной системы в систему отсчета, движущуюся относительно
нее со скоростью (1), в которой отлично от нуля только магнитное поле,
равное по величине Н'.
Переход к случаю Е > Н осуществляется простой заменой fi —> ix,
cos fir -^chxr и sin fir —► i sh xt.
1.5.6.	В этом случае оба инварианта электромагнитного поля равны
нулю и соответствующая система уравнений движения оказывается вы¬
рожденной. Поэтому решение удобно получить предельным переходом
Е —> Н, исходя из результатов, полученных в задаче 1.5.5.
Положим Н = EV 1 + S2, Н2 - Е2 — Е282, Г2 = Л<5. Выполняя предель¬
ный переход <5 —► 0 в выражениях (3) задачи 1.5.5, получаем
ct
£о
тс
Ро.
т
г +
еЕрру
2 т2с
т+£^т2 +
У=тТ +
m
2m с
еЕ
(еЕ)2
6 (тсУ
(еЕ)2
6 (тс)
(Zo~PoxC)t3,
(£о - Р0хС)т3,
ДГД2^° ~	2 = ДГТ-
2 (тс)2	т

ziu _l \ _ /лава 1. Теория поля. Решения задач
1.5.7.	Поскольку оба инварианта электромагнитного поля отличны от
нуля, получаем два действительных и два чисто мнимых собственных
значения, при этом структура системы уравнений такова, что она рас¬
падается на две независимых подсистемы:
Первая подсистема в точности совпадает с подсистемой системы урав¬
нений, определяющий движение частицы в электрическом поле. Таким
образом, для кинетической энергии частицы получаем
1.5.8. Как видно из системы уравнений (1) предыдущей задачи, наша
задача сводится к задаче о движении частицы в однородном постоянном
электрическом поле для определения t(r) и z(r) и к задаче о движении
частицы в однородном постоянном магнитном поле для определения
х(т) и у(т). Однако, в отличие от задачи 1.5.4 теперь простого соот¬
ношения между собственным временем частицы и временем в лабора¬
торной системе отсчета нет, и оно определяется из первой подсистемы,
как в задаче 1.5.3.
1.5.9. Согласно соотношениям (2) задачи 1.5.5 с учетом начальных усло¬
вий нашей задачи имеем
1.5.10.	Запишем уравнение, определяющее изменение энергии частицы
в трехмерной форме:
(1)
Т(т) = шс2(ио(т) - 1) = тс2(сЬЛт - 1).
при Е > Н.
при Е < Я,
d£
dt
или, что то же самое:
£d£
е\сЕ dt.
V£2 - (me2)2

1.5. Движение заряженной частицы во внешнем поле	211
Поскольку тс2 < £ ^ £ о, то для полного времени торможения получаем
где 7'0 = £0 — тс2 — начальная кинетическая энергия частицы. В од¬
нородном поле сила, действующая на частицу, постоянна, поэтому ее
работа по торможению частицы до полной остановки, равная кинетиче¬
ской энергии частицы, есть
Этот очевидный результат также полезно получить из уравнений дви¬
жения. Поскольку Е || г, а импульс имеет отличную от нуля только
г-компоненту, имеем
Проинтегрировав данное уравнение в пределах 0 < t < 1торм> находим
необходимое выражение для I = z(lTOpM) - z(0).
1.5.11.	Время жизни частицы определяется в системе отсчета, в кото¬
рой она покоится. Число пионов, не успевших распасться к моменту
собственного времени т, определяется экспоненциальным законом ра¬
диоактивного распада:
где то — время жизни пиона, а т\/2 = то In 2 — период полураспада.
Промежутки собственного времени и времени в лабораторной систе¬
ме отсчета связаны соотношением dr = dt\J\ — {v/c)2 (см. (1.2)), по¬
этому необходимо найти временную зависимость скорости частицы в
лабораторной системе. Движение пиона в линейном ускорителе опреде¬
ляется уравнением движения в постоянном однородном электрическом
поле, поэтому, аналогично предыдущей задаче имеем
е\Е1 — То, откуда 1=ут=,-
\е\Е
\е\Е, p(t) = р0- \e\Et,
откуда получаем уравнение
V(тс)2 + (р0 - |е|£/)2
Ро - \e\Et
N(t) = N(0)e~T/TO,	N(t1/2)	=	iyV(O),
o'	о	о
\J(po + \е\Et)2 + (тс)2
тс dt
cp(t) + E(t)
сро 4- £о

212 •Ar Глава L Теория поля. Решения задач
где ро и £о — соответственно импульс и энергия пиона в начальный
момент времени, p(t) = ро + \e\Et.
Из результатов предыдущей задачи видно, что длина пробега части¬
цы определяется изменением ее энергии:
1
/ = x{t) - х(0)
\е\Е
(Ш-е о),
поэтому время полураспада и длина ускорителя L (длина пробега пио¬
на) связаны соотношением:
_	__ !„<->_ тс i„ ср(Т) + Е(Т)
4/2 — Го 1П2 — 1П ——	,
'	\е\Е	сро	+	£о
где £(7) = L\e\E + £0.
Согласно начальным условиям, пион, влетающий в ускоритель, вначале
является нерелятивистским: сро ~ £о ~ тс2, соответственно, £(7) » £о,
поэтому в формулах можно считать ср(Т) яз £(7) яз \e\LE. Получаем
го In 2
тс , £(7)
Ч*	О	У
И Е	тс~
откуда находится необходимая величина ускоряющего электрического
поля Е\
ЦТ)
тс
In
0,6 - 104 CGSE = 1,8 • 10 В/см.
|е|то1п2 тс-
Длина ускорителя при этом должна быть равна
ЦТ) ^ 1 1 1л5
\е\Е
1,1 • 10 см = 1,1 км.
1.5.12. Колебания происходят с тремя частотами:
'	/V	,	еН
01,2
I о0 +
\2mcJ	2тс'
Оз — Оо-
Частота шз = ujq соответствует колебаниям вдоль поля. Частоты и>\,2 со¬
ответствуют вращениям по окружности в плоскости, перпендикулярной
полю в одну и в другую сторону. Большая из частот соответствует на¬
правлению вращения, соответствующему правилу Ленца (направление
тока связано с направлением поля левым винтом).
1.5.13.	Продифференцируем вектор А по времени и примем во внима¬
ние, что в центральном поле момент импульса сохраняется (М = 0):

1.5. Движение заряженной частицы во внешнем поле	213
Учитывая, что р = -Ze^r/r3 и подставляя определение момента импуль¬
са, получаем, что правая часть равенства обращается в ноль.
1.5.14.	Введем цилиндрическую систему координат, ось z которой сов¬
падает с осью провода, причем направление оси z задается направле¬
нием тока. Запишем второй закон Ньютона для частицы в магнитном
поле:
ес г тж1 и	2J	|	|	.
— [vxH], Н = —Пц>,	nJ = 1.
с	ср
Здесь энергия частицы £ = const, поскольку магнитное поле не совер¬
шает работы.
Проектируя это уравнение на направление пг, получаем
есН .	2	е]	р
г=-р = 1Г-р
Интегрируя данное равенство, получаем закон сохранения:
.	2е].
Z ——In р = const.
В начальный момент времени скорость частиц параллельна проводу (знак
скорости в начальный момент может быть определен из условия, что
частица удаляется от провода под действием магнитного поля), т.е.
частица со скоростью, параллельной пг, находится на расстоянии г от
оси провода. В момент наибольшего удаления от провода скорость ча¬
стицы остается прежней по абсолютно величине, она снова параллельна
проводу, но направлена в обратную сторону:
2е].	2е].	п
-Щ - -g-lnr = v0 -
Знаки, с которыми входит скорость Vo в данное тождество, можно про¬
верить, исходя из того, что г < R. Отсюда
?-ехр(^)=«р(й£!).
1-5.15. Будем полагать, что магнитное поле мало изменяется за время
оборота частицы т, движущейся по окружности в плоскости, перпен¬
дикулярной направлению однородного магнитного поля Н, т. е. выпол¬
няется условие r\dH/dt\ Н. Это означает, что т Т, где Т — время,
за которое поле Н изменяется существенно (на величину порядка Н).
В основу наших расчетов положим уравнения движения частицы и
электромагнитного поля (без учета излучения частицы). В уравнениях

214 -Аг Глава 1. Теория поля. Решения задач
поля мы положим р = 0 и j = 0, считая, что в области движения части¬
цы внешние заряды и токи отсутствуют:
Данные уравнения мы будем решать методом последовательных при¬
ближений с учетом малости изменения поля Н.
В нулевом приближении мы пренебрегаем индукционным элек¬
трическим полем, считая, что магнитное поле однородное и постоянное,
т. е.
Решая данное уравнение с начальными условиями г(0) = го и v(0) = vo,
находим
что мы поместили начало координат в центр круговой траектории. Из
соотношения (3) легко получаем
— радиус круговой траектории частицы.
В первом приближении мы учитываем индуцированное внеш¬
нее электрическое поле, но не учитываем производимое им индукцион¬
ное магнитное поле. Тогда в системе (2) произойдут изменения:
Уравнение для rotE решаем по аналогии с уравнением rotA = Н при
Н = const:
(1)
' divH = О,
rot Н = О,
dH/dt = 0.
(2)
Из формул (2) с учетом р = £v/c2 получаем
d\ ее,
Л= 7Г|ухН|-
[v х Н].
V = ^[(г-г0) xH]+v0 = j[r х Н].
(3)
В последнем равенстве мы положили vq = -^-[го х Н], и это означает,
г = ——j[Н х v], откуда R =
есН	есН	еН
(4)
(5)
(6)

1.5. Движение заряженной частицы во внешнем поле
где h = Н/Я. Из уравнения divE = 0 следует, что Д/= 0. Поэтому
скалярная функция / — решение уравнения Лапласа — может быть
только функцией времени: / = f(t), и это значит, что V/ = 0.
Оценки порядков величин. Убедимся в том, что напряжен¬
ность электрического поля Е, полученная нами в (6), — действительно
величина первого порядка малости по параметру т/Т:
Тс с Т
где мы учли, что г ~ от. Индукционное магнитное поле Н\ имеет поря¬
док величины
Я, ~ Ifг~ -^£«£«Я,
с Т с Т
что и оправдывает наше приближение.
Адиабатический инвариант. Итак, из уравнения (5) имеем
dE еН, г , ,,	Я Е 2	/7\
_ = _(v[rxh])	= Sa?l’!,	(7)
где мы	учли	соотношение (3). В итоге,	поскольку р = £v/c2, из выра¬
жения	(7)	получаем дифференциальное	уравнение
2 dp _ 1 dH
pit ~ hJF’
откуда следует, что
— = — — J = const.
Н Н
Мы получили адиабащцческий инвариант — величину, сохраняющу¬
юся приблизительно при медленном изменении магнитного поля.
Применения полученных формул. 1) Изменение энергии ча¬
стицы за период вращения находится по формуле:
. п dE 7гс , dH
~ ltT ~ 7н ~dt'
2)	Приращение энергии и радиуса вращения частицы при изменении
магнитного поля от Н\ до Яг:
£г - £i = \/с2/Яг + т2с4 - у/c2JH\ + т2с4 ~	- Я]),
с ГТ
если v/c<1. И, наконец, для радиуса вращения (4) с учетом R = - у jj
находим
cVl (	1	1	\	_____	/?2	/яГ

216 -l\r Глава 1. Теория поля. Решения задач
1.5.16.	Для заряженной нерелятивистской частицы в магнитном поле
уравнение движения имеет вид
тг= -[г х Н(г)],	(1)
с
где г — радиус-вектор частицы, v = г — ее скорость. Будем считать,
как и в задаче 1.5.15, что в области движения частицы отсутствуют
внешние источники (заряды и токи), отсутствует электрическое поле
(Е = 0), и для напряженности магнитного поля выполняются соотно¬
шения (следующие из уравнений Максвелла)
divH = 0, rot Н = 0,	2? = 0.
at
Таким образом, поле предполагается постоянным, но неоднородным: на¬
пряженность поля зависит от пространственных координат. Движение
заряженной частицы в таком поле складывается из трех видов движе¬
ния: быстрого вращения вокруг магнитной силовой линии (ларморова
прецессия), движения вдоль силовой линии и медленного дрейфа в на¬
правлении, перпендикулярном к силовым линиям. Переход к прибли¬
жению ведущего центра (дрейфовому приближению) означает выде¬
ление среди всех видов движе¬
ния ларморова вращения и усред¬
нение уравнений движения по пе¬
риоду вращения частицы. В ре¬
зультате такого усреднения полу¬
чается простое уравнение, описы¬
вающее движение некоторой эф¬
фективной частицы (фактически,
ларморова кругового тока), коор¬
дината которой в каждый момент
времени совпадает с положени¬
ем центра ларморовской круговой
траектории («ведущий центр»).
Такая частица осуществляет быстрое движение вдоль силовых линий
и медленный дрейф — в перпендикулярном направлении (рис. 1.7).
Введем очевидные обозначения:
r = R + p, причем (ph) = 0, h = —.
П
Здесь вектор R называется радиус-вектором ведущего центра орбиты,
V = R — скорость ведущего центра, р — радиус ларморовской окруж¬
ности, который, вообще говоря, может меняться в неоднородном по¬
ле (рис. 1.7, а). Для выполнения усреднения уравнения (1) необходима
Рис. 1.7. Приближение ведущего цен¬
тра для движения заряженной части¬
цы в неоднородном магнитном поле

1.5. Движение заряженной частицы во внешнем поле	217
слабая неоднородность поля: поле должно мало изменяться на рассто¬
яниях, сравнимых с радиусом круговой орбиты, и скорость движения
частицы по круговой орбите o_l также должна мало изменяться за вре¬
мя ~ т, где т = 2п/са — период вращения. (Для движения по окруж¬
ности ш = еН/{тс), р = vj_/ш.) Таким образом, должны выполняться
условия
^	< 1 И у « 1,
где L — характерное расстояние, на котором существенно (на величи¬
ну ~ И) меняется поле, а Т - характерное время, за которое ведущий
центр смещается на L.
Производим разложение Н(г) по степеням р с линейной точностью
по е:
H(r) ~ H(R) + (pV)H(R),	(2)
далее везде будем опускать аргумент R и считать, что H(R) = Н. Под¬
ставляя (2) в уравнение (1), получаем
R + P=^{[pxH(r)] + [RxH(r)]}~
~ — {[р х Н] + [R х Н] + [р х (pV)H] + [R х (pV)H]}.	(3)
тс 1	’
Второе слагаемое в правой части (3) содержит (R)x = Vx — скорость
дрейфа частицы, которая перпендикулярна полю Н. Предварительно бу¬
дем считать, что V^/v ~ е, т. е. полагаем, что данное отношение мало.
Это подтвердится в дальнейшем. Оценка порядков величин слагаемых
в уравнении (3) дает #
р , L шр , ujL , cjLp , шр
—  —I—	£ -4—  		 —I—
г2 Т2 t T TL tL
Элементарный анализ показывает, что нулевое приближение по е обес¬
печивают первые слагаемые в левой и в правой частях уравнения, а
остальные представляют собой поправки, линейные по е.
Главный член дает просто движение частицы в однородном магнит¬
ном поле по круговой траектории: р = са[р х И]. Интегрируя это урав¬
нение, находим
р — ш[р х И].
При усреднении по периоду ларморовой прецессии члены, линейные
по р, уходят: р ~ р ~ р ~ О, а также R = R, R = R. В итоге имеем
R~—{[RxH] + [px(pV)H]}.
tn Г	J

218 -l\r Глава 1. Теория поля. Решения задач
Последнее слагаемое в точности соответствует средней силе, действу¬
ющей на магнитный диполь в слабонеоднородном магнитном поле, ко¬
торая была получена в задаче 1.6.13. Используя результат этой задачи,
находим
R« — [R х Н] + i(/xV)H,	(4)
тс	т
р = х ^ = fc ^х ^х = ~Tcp2h-
Средний магнитный момент ларморова тока частицы вне зависимости
от знака заряда (напомним, что щ ~ е) направлен против поля: лар-
моров ток — элементарный диамагнетик. Вводя обозначение Р = тR,
приводим (4) к виду
P=J[V х Н] + (/zV)H.
Данное уравнение по смыслу существенно отличается от уравнения (1),
ибо оно описывает движение ведущего центра, т. е. эффективной ча¬
стицы (с радиус-вектором R), причем второе слагаемое в правой части
уравнения представляет собой силу, действующую на магнитный мо¬
мент в неоднородном магнитном поле (рис. 1.7, б).
Далее, с требуемой нам точностью мы должны считать2*, что V =
= V|| + V_l ~ V|| ~ V||, так как |VX|/|VX|~| V±/T\-\T/v\~ Ух/о~е<1.
Поэтому, преобразуя левую часть уравнения (4), получаем
V*V|| -	=	0||h	+ D||h«0||h + Ujj(hV)h,	*
Подставив в правую часть уравнения (4) Н = ИЯ, будем иметь
d||h + ojj(hV)h ~ w[Vx х h] - ^(hV)h - g£h(hV)tf. (5)
Векторно умножая левую и правую части уравнения (5) на h и учиты¬
вая, что и± = сор, находим
Vx = ^i/2[h х (hV)h|.
и
Дифференциальный оператор (hV) = d/ds представляет собой про¬
изводную по естественному параметру (длине) вдоль силовой линии
2)	Необходимо заметить, что Vx = dV±/dt ф (V)x = Rx и Vy ~Уц Ф (V)ц = Йц,
т. е. Vx и V|| не являются продольной и поперечной составляющими вектора
ускорения.

1.5. Движение заряженной частицы во внешнем поле -Аг 219
магнитного поля, вектор h — единичная касательная к этой линии. Из
аналитической геометрии известно, что
(hv)i, > £ - г.
OS Г]
(6)
где п — единичный вектор главной нормали к силовой линии, а 77 —
радиус кривизны силовой линии. Введем единичный вектор бинормали
к силовой линии b = [h х п] (рис. 1.8) и запишем окончательную фор¬
мулу для скорости поперечного дрейфа в виде
LJT)
Ь.
(7)
Скорость поперечного дрейфа, как и предполагалось ранее, мала, по¬
скольку (как следует из (7)) V± т j L. r^‘ vp/L ~ ve. Поперечный (или
градиентный) дрейф возникает вследствие неоднородности магнитного
поля, направлен перпендикулярно полю и ме¬
няет зрак в зависимости от знака заряда.
Скалярно умножая уравнение (5) на h с
учетом (h(hV)h) = О, получаем
»ц = -
2Н dl
dH
2Hv\\ dt
В силу того, что и2 + Oj_ = v2 = const (энергия
частицы строго сохраняется ввиду отсутствия
электрического поля), имеем
*4
dt
dv i
dt
v\ dH
= ~1Tit' откуда
= const.
П
(8)
Рис. 1.8. Естественный
базис: h — единичный
вектор, касательный к
силовой линии, п —
главная нормаль, Ь —
бинормаль; точка О —
центр кривизны
Последнее равенство в (8) получается в резуль¬
тате решения дифференциального уравнения.
Таким образом, показано, что в магнитном по¬
ле, медленно меняющемся вдоль траектории частицы, приближенно (по
крайней мере с точностью до е2) сохраняется величина v\/H. Мы по¬
лучили тот же самый адиабатический инвариант, что и в магнитном
поле, медленно меняющемся во времени (задача 1.5.15).
1-5.17. В первом приближении магнитное поле Земли является полем
точечного магнитного диполя Ш1, расположенного в ее центре и на¬
правленного примерно вдоль оси вращения. Выберем декартову систе¬
му координат таким образом, чтобы направление магнитного момента

220	Глава	I.	Теория	поля.	Решения	задач
Земли совпадало с направлением оси г, т. е. ОЯ = (0,0, £Ш) (рис. 1.9)3).
Величину 9Я оценим из экспериментально известного значения напря¬
женности магнитного поля Земли на ее поверхности в экваториальной
области г-0,34 Гс.
Поле магнитного диполя, как известно, описывается формулой
„ Зп(9Яп) - т
н = 7
и имеет в сферической системе координат компоненты (см. решение
задачи 1.6.14)
Hr = mlSSll} = 9(1)
г3	г3
На экваторе Земли (г = R^ ~ 6400 км при в = 7г/2, где Rg — радиус
Земли) напряженность поля будет равна Н = Hg(R^, тт/2) = 9Я/Д|. От¬
сюда величина магнитного момента Ш = ///?| ~ 8 • 1025 Гс • см3.
Элементарная оценка показывает, что влиянием гравитационного по¬
ля на движение заряженной частицы в магнитном поле Земли можно
пренебречь при кинетической энергии частицы Т = mv2 /2, большей,
чем ~ 1 эВ для протонов и ~ 10~3 эВ для электронов (Т ^ GmM^/R^).
Здесь G = 6,67 • 10“8 см3/(г • с2) — гравитационная постоянная, М^ =
= 6 • 1027 г — масса Земли, Rg = 6400 км — ее радиус, m — масса
частицы, и — ее скорость.
Дальнейшее рассмотрение задачи будет существенно опираться на
дрейфовое приближение, разработанное в задаче 1.5.16. Заметим, что
малая абсолютная величина напряженности магнитного поля в около¬
земном пространстве с существенным запасом компенсируется боль¬
шой протяженностью поля, поэтому критерии применимости дрейфово¬
го приближения оказываются выполненными (в этом можно убедиться
далее).
1)	Дрейф частицы в экваториальной плоскости. На рис. 1.9
схематически изображена одна из силовых линий магнитного поля Зем¬
ли (см. решение задачи 1.6.14).
Пусть заряженная частица движется в экваториальной плоскости,
т. е. с нулевой проекцией скорости на силовую линию магнитного по¬
ля (в = 7г/2, цц =0, v_i = и). Тогда ее движение будет складываться
из быстрого вращения вокруг «местной» силовой линии со скоростью
!| В действительности полярность магнитного поля Земли противоположна
географической, поэтому на рис. 1.9 верхняя точка земного шара отвечает
южному географическому полюсу, а нижняя точка — северному.

1.5. Движение заряженной частицы во внешнем поле
X
и± = v = •у/27'/т (Т — кинетическая энергия частицы в нерелятивист¬
ском случае при v/c < 1), радиусом орбиты p = v/u> и периодом т = 2п/и>
(сj = еН/(тс)) и медленного дрейфа в экваториальной плоскости, пер¬
пендикулярно силовым линиям, со скоростью
Vx = п—I*1 х п] - -—[h х п].
2uit]	muirj
(2)
-1
При е > 0 частица (например, протон) дрейфует с востока на запад.
Приведем в качестве примера численные оценки для протона (трс2 =
= 940 МэВ, е — 4,8 • 10~ю CGSE) с энергией 7=10 МэВ, дрейфующего
в экваториальной плоскости на расстоянии го = 3 ■ Ю4 км от центра Зем¬
ли. В этом случае напряженность поля Земли Н = ЭЛ/гц = 3,0-10~3 Гс,
скорость частицы и = v± = с у]2Т/(трс^) — 0,15 с = 4,4 • Ю4 км/с, лармо¬
рова частота ш — еН/(трс) = 30 с
радиус ларморовской круговой
траектории р = V\_/uj — 1500 км.
Для расчета скорости дрей¬
фа (2) необходимо найти радиус
кривизны г] магнитной силовой
линии на экваторе. Воспользу¬
емся для этого формулой (6) за¬
дачи 1.5.16 и запишем:
, период вращения т = 2п/ш = 0,21 с,
Z
dh
dh
/ ds
ds
del
de
Рис. 1.9. К вопросу о движении заря¬
женных частиц в магнитном поле Земли
i = |(hV)h| =
где изменение угла в происхо¬
дит при смещении вдоль сило¬
вой линии вблизи экватора, т. е.
в — к/2 + £ при е —* 0. Элемент длины силовой линии (уравнение си¬
ловой линии: г(в) = го sin2 в) равен
ds = |<71| = у/(dr)2 + r2(d6)2 ~ го d6.
Отсюда, очевидно, следует, что ds/dO\в=^/2 = го- Используем далее фор¬
мулу (2) задачи 1.6.14 и получим, что единичный вектор вдоль силовой
линии h = Н/Н при в = 7г/2 + е с линейной точностью по е равен
h ~ —2enr -I- rig при е —* 0.
(3)
Из простых геометрических соображений следует, что dno/dO = -пг.
Тот же результат можно получить и прямым расчетом, используя явный
вид для компонент вектора пв (см. задачу 1.6.14). Поэтому в целом

222	Глава	1.	Теория	поля.	Решения	задач
из (3) следует, что dh/dO\e=1T/2 = —3nr. В итоге получаем, что радиус
кривизны равен rj = r0/3 = Ю4 км и, следовательно, скорость попереч¬
ного дрейфа
V± = — = 0,009 с = 3,3 • 103 км/с,
пиар
т. е. эта скорость действительно намного меньше скорости ларморовско-
го вращения. При такой скорости частица, дрейфуя, совершит полный
оборот вокруг Земли за время tj_ = 27rro/Vj_ — 57 с, двигаясь с угловой
скоростью fi = V±/ro = 0,11 с-1. Для сравнения, угловая скорость су¬
точного вращения Земли равна fig = 27r/rg ~ 7,3 • Ю5 с-1 (rg = 24 ч =
= 86400 с), т. е. отношение угловых скоростей fi/fig = 1500.
2)	Отражение от зеркальных точек. Из рассмотрения общей
задачи о движении заряженной частицы в слабонеоднородном магнит¬
ном поле (задача 1.5.16) следует, что в рамках нашей задачи существует
два интеграла движения. Во-первых, сохраняется энергия частицы £
(вследствие отсутствия электрического поля), и это — точный интеграл
движения. В нерелятивистском приближении сохранение энергии сво¬
дится к сохранению величины v2, т. е. модуля полной скорости части¬
цы. Во-вторых, имеется адиабатический инвариант J = о2/Н, наличие
которого характерно именно для движения в слабонеоднородном поле,
которое рассматривается в дрейфовом приближении. Таким образом,
это — приближенный интеграл движения.
На основании этого можно записать для продольной (по отношению
к полю) скорости движения частицы следующее соотношение:
у Н = ±y/v2-JH.
Это значит, что частица, двигаясь по винтовой траектории вдоль сило¬
вой линии возрастающего по модулю магнитного поля, отражается от
области, где Н > у2//. При уц = 0 скорость частицы имеет только по¬
перечную компоненту у_|_ = у, и частица, вращаясь, изменяет знак про¬
дольной скорости Уц. Это происходит независимо от знака заряда и
является следствием сгущения силовых линий и, тем самым, появле¬
ния перпендикулярной к скорости составляющей магнитного поля Hj_
и соответствующей составляющей силы Лоренца
F„ = х Hj_] = у [[р х h] х Hj_] •
В этом и проявляется так называемый эффект «магнитного зеркала»,
заключающийся в отражении частиц от областей с увеличивающимся
значением напряженности магнитного поля. Принцип магнитного зер¬
кала используется для создания магнитных ловушек для плазмы, фоку¬

1.6. Статическое электромагнитное поле -*\г 223
сировки частиц в ускорителях, электронной оптике и т. д. Для космиче¬
ских частиц магнитной ловушкой является само магнитное поле Земли.
Дело здесь в том, что магнитное поле Земли — неоднородное, причем
напряженность поля повышается (силовые линии сгущаются) по мере
приближения к магнитным полюсам (см. рис. 1.11). Частицы, захвачен¬
ные в такую магнитную ловушку, могут удерживаться в ней доволь¬
но долго — они оказываются «запертыми», потому что они совершают
финитное движение в некоторой бграниченной области вокруг Земного
шара. Так образуются радиационные пояса вокруг Земли, представля¬
ющие собой слои заряженных частиц высокой энергии.
Пусть скорость заряженной частицы в экваториальной плоскости
Земли составляет угол а с этой плоскостью. Тогда из сохранения вели¬
чин v\/H, v и формулы (1) получим величину минимального полярного
угла в, достигаемого частицей:
о2 cos2 a v2	2	sin60
ЯОг/2 )-Н(0У °™УДа C0Sa=VW^r
При этом частица столкнется с земной поверхностью, если 6(a) < в£,
где в^ — полярный угол, при котором силовая линия г = го sin2 в пе¬
ресекает поверхность Земли, т. е. Д5Д0 = sin2 вj, где Rj = 6400 км —
радиус Земли. Это происходит, если а > а^, где
2	sin6	(Д^Ло)3
cos aj =	2	—	-
Vz COS2 -h 1
V4 - 3R6/r0
При го = 3 • Ю4 км, получаем в^ = 27° при = 86°, соответствующая
географическая широта равна 90° — 0^ = 63°.
Таким образом, движение заряженной частицы в магнитном по¬
ле Земли (магнитного диполя) можно представить как результат трех
движений:
1) ларморова вращения вокруг силовой линии;
2) осцилляций между северной и южной зеркальными точками;
3) дрейфа поперек силовой линии магнитного поля.
1.6.	СТАТИЧЕСКОЕ	ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
1.6.1.	Исходим из известного выражения для тензора квадрупольного
момента (1.27)
Qij = J p(R)(SXiXj-SiiR2)d3R.

224 •Ar Глава I. Теория поля. Решения задач
Введем вспомогательный тензор
Qii = J p(R)3XiXj d3R, т. e. Q4 = Q,, - IfyQu-
v
Заметим, что Q,y ведет себя, как тензор относительно более широкого
класса преобразований координат, чем Q,y: помимо поворотов он допус¬
кает произвольные линейные преобразования координат, в частности,
растяжения.
Расположим оси х, у, z вдоль полуосей эллипсоида а, Ь, с. Перейдем
к координатам
, х , у , z
Х=а' У=Ь'
и получим р' = pabc, причем в новой системе координат эллипсоид вы¬
глядит, как шар единичного радиуса. В штрихованных координатах ком¬
поненты тензора Q,; равны
Q'a = lsijQ'kk =	/	p'(R')R'Vr'	=
Л'<1
= 6ijPabc J R'2 AttR'2 dR' = SljPabc j R'2 d4R'.
R'< 1	R'<	1
После вычисления интеграла мы получим
Q'ij = SypobcЦ- = IqSi,.
В исходных (не штрихованных) координатах для компонент тензора Q,y
находим
/3 а2 0	0	\
О 3 Ь2 О
п 1
Q‘i = 5
у 0	0 Зс2у
Окончательный результат для тензора Q,y имеет вид
Qxx = |(2а2-62-с2), Qyy = | (2ft2-а2-с2),	=	|(2c2-a2-&2),
где <7 = (47г/3)abcp.
i.6.2.	Определение поля E с точностью до четвертого порядка по 1/R
соответствует определению потенциала с точностью до третьего поряд¬
ка по 1 /R, т. е. с точностью до квадрупольных членов. Поскольку ди-

1.6. Статическое электромагнитное поле
польный момент эллипсоида относительно центра равен нулю (в силу
центральной симметрии распределения зарядов), получаем
Д	2 Д
„ Ч п п * к Q'jXiXj ^ n QijhkXj QijXidjk
е„ = - VW » р v(fi + 5-^г-v»« -	 -
—	i ^ QijXjXj^ _ QkjXj
Д3 2R7	k R5
Если считать вектор R столбцом, то на матрично-векторном языке на¬
пряженность поля Е будет иметь вид
E = SB + 5n^R-«?.
Д 2/?7 Д5
Мы можем переписать выражение без помощи матриц, если введем
единичные собственные векторы е, тензора Q и собственные числа А;
(из задачи 1.6.1 следует, что Ai = q/5(2a2 - b2 - с2) и т.д.):
Е= <?R + 5 EA(e.R)2R Е, Ai(e,R)e,
~ Д3	2Д7	Д5
С учетом выбора осей координат вдоль осей эллипсоида (см. задачу 1.6.1)
собственные векторы е, — это базисные векторы используемой системы
координат. Окончательно получаем
£ _ <?R + ^ Е; XX? д _ Еi XX,е,
Д3 2Д7	Д5
1.6.3.	Выберем ось х вдоль нити. Тогда, учитывая, что dq = -jdx, получаем
1/2	з
Qyy = Qzz = J(3yy - *2)y dx=-
l'2	__q_?
12 ’
1/2
Qxx = —Qyy — Qzz — “g“
-1/2
Недиагональные элементы тензора Q(/ равны нулю.
1.6.4.	Единственные ненулевые компоненты квадрупольного момента —
Qxy = Qyx = \2qa2. Чтобы диагонализовать матрицу, необходимо повер¬
нуть систему координат в плоскости (х,у) на угол 7г/4. Пусть ось х'
проходит через положительные заряды, а ось у' — через отрицательные.
Тогда QX>X' = -Qy'y' = \2qa2, Qz>z- = Qzz = 0.

226	Глава	l.	Теория	поля.	Решения	задач
1.6.5. Для однородного поля Е могут отличаться от нуля только потен¬
циал <р и его первые производные = —£*. В мультипольном разло¬
жении для энергии (1.29) они взаимодействуют с суммарным зарядом
и дипольным моментом, которые для рассматриваемой системы равны
нулю. Ответ: 0.
1.6.6. Потенциальная энергия диполя в поле заряда q имеет вид
U= -(dE) = 2^.
R3
Дифференцируя данное выражение, находим силу:
Ft = -V,- U =	=	3qdkX.kX'	-	2*
R3	R5	R3
3(dR)R - dR2
F = q———г	.
R5
Здесь d = el, где вектор 1 направлен от заряда —е к заряду е.
167 е (<М,)Я2 - 3(d,R)(d2R)
R5
1.6.8. Энергия взаимодействия диполей имеет вид
Р _ dizd2Z — 3di2 cos в {dix sin в cos y> + d2y sin 9 sin p + d^z cos 9)
R3	'
Учитывая явный вид сферических функций:
Y20) = \/5-( 1 -3cos20),	Y<">	=	A/^cos0sin0-e±,v
V	V	^
и вводя обозначение d,2± = d^x ± id2y, получим
^  /б7г Г /8 d\zd2z у(0) d\zd2— y(+i)  d\zd2+ у(~ 1) 1
~ V 5 \V з Я3 2	я3 2	я3 2 /■
1.6.9. Представим потенциал взаимодействия в виде
[-ИЖ)
У(0,0,г) = У0( 1-	 )	=	У0
гу z2 + а2
2ч -1/2
Учитывая условие г » а, находим приближенное выражение:
то.г) и У0
Зо^ _ 7а^
2 г2 8г<
(1)
Общее выражение для энергии взаимодействия системы зарядов с по¬
тенциалом внешнего поля (О^ — октупольный момент)
а\ ~ Я I (dr) , QijXiXj , OijkXiXjXk
Я	г3 +	2г5	+	6г7

1.6. Статическое электромагнитное поле -‘V 227
при 9 = 0, т. е. на оси г, принимает вид
Г\\	У	, dz ,	Qzz	, Ozzz
( . )	*	?	2?	в?"'
Сравнивая данное выражение с (1), находим
4 = 0, dz = \v0a\ Qzz = О, OZZ2 = -jV0a4.
Исходя из аксиальной симметрии и свойства Qkk = 0, получаем
dx = dy = 0, Qij = 0.
Из аксиальной симметрии, полной симметрии октупольного момента
относительно перестановок индексов (0,у* = Оу1* = СЦ- = Okji) и свой¬
ства Okki — 0 следует, что у октупольного момента отличны от нуля
компонента Ozzz и компоненты
П	—Г)	—Г)	—О —О	—О	—	®ггг
^xxz — KJxzx — ^zxx	—	wyyz ~	^yzy	— ^zyy	—	2	*
Подставляя г = г cos 9, х — rsm9, у = 0 (по причине аксиальной сим¬
метрии мы можем положить угол у> = 0) получаем
V(r, 9) « ^ cos6 -)- cos9(cos2 9 sin2 6*).
г	6	г	V	2	/
1.6.10.	При /3 = 0 (для равномерно заряженного шара) все мультиполь-
ные моменты кроме суммарного заряда обращаются в нуль (это соот¬
ветствует нулевому порядку по /3). Остальные мультипольные моменты
создаются распределением зарядов, которое является разностью плот¬
ности зарядов сфероида и шара, такое распределение отлично от нуля
в тонком слое у поверхности сферы. Объем этой области линеен по /3,
отсюда следует, что при вычислении интегралов по этой области доста¬
точно определить подынтегральное выражение в нулевом порядке по /3,
т. е. можно пренебречь отличием координат точки в слое от координат
точки на поверхности сферы. Таким образом, мы можем заменить инте¬
грирование по объему интегрированием по поверхности сферы, считая,
что на ней имеется поверхностный заряд с плотностью
а = PR0f3P2(cos9) = рЯ0/3^(3cos2 0 - 1), где р =	%	.
*	47г/?о/3
+1
Qzz = J cr(3z2 - R$) ds =
-l
Qzz = g^3?o/3, Qxx = Qyy = — 2 Qzz-
J рЯ5У-(3x2 - 1)22tt dx = |тгрЛ&3,

228 •Аг Глава 1. Теория поля. Решения задач
Заметим, что поверхностная плотность заряда <т{в) пропорциональна
сферической гармонике У2(0>. Все остальные мультипольные моменты
равны нулю (в линейном порядке по /3) в силу ортогональности сфе¬
рических гармоник.
1.6.11. Нетрудно убедиться непосредственной проверкой в том, что
rot Ai = rot Аг = Н, где
Ai = (0, Нх, 0), A2 = i[Hxr] = (-Х-Ну,Х-Нх,0), Н = (0,0,Я).
Градиентное преобразование не должно изменять наблюдаемых вели¬
чин — напряженностей электромагнитного поля, поэтому полагаем
Ai = А2 + grad / и имеем систему уравнений
< Нх = У-Нх + ^/, откуда / = f(x, у) = Х-Нху + с.
о = о + |-/,
OZ
1.6.12. Нам надо найти свободное (без источников) магнитное поле,
удовлетворяющее условиям
^ = -А, rot Н = 0, divH = 0.
дг
Такое поле определяется неоднозначно. Для уменьшения этой неодно¬
значности введем дополнительное условие — аксиальную симметрию
(симметрию относительно поворотов вокруг оси z на произвольный угол).
Аксиально-симметричное поле удобно описывать в цилиндрической
системе координат. При этом компоненты поля не зависят от угла ip:
Нр = и(р, г),	=	v(p, z), Нг = w(p, z).
Интеграл по окружностиconst, z = const пропорционален ЯДр, г),
однако, поскольку rotH = 0, этот интеграл должен равняться нулю,
таким образом, Яv = 0.
Поскольку rot Н = 0, мы можем искать поле Н, как градиент неко¬
торого скаляра:
Н = grad ф{р,г).
Уравнение div Н = 0 требует, чтобы скаляр ф удовлетворял уравнению
Лапласа:
div Н = div grad ф = Дф(р, z) = 0.

1.6. Статическое электромагнитное поле
В цилиндрических координатах получаем
I , г,	г,
А ф(р,г)
1 д
рдрР
д д2 \ . п днг
д2-ф
dz2
-h.
Таким образом,
1 д д ,	,
-—p—iP = -h
р др др
д'ф
др
Поскольку поле должно быть конечно во всех точках, получаем /(г) = О,
т. е.
иР = Up,
Отсюда находим
^ = \р2 +
дНг
дг
д2гр
дг2
= ^'(г) = -h.
Н.
-?V--hz + c
г ~ дг ~ Пг + С
-h(z - z0),
где мы положили с = hzp. На силовой линии должно выполняться усло¬
вие dr || Н, т. е. касательная к силовой линии должна быть направлена
вдоль магнитного поля. Поэтому
dp _ dz
Но
—, или
Нг
2dp
+
dz
г - го
О,
откуда находим уравнение силовои линии:
p2(z - г0) = с.
Схема силовых линий приведена на
рис. 1.10. Поскольку Нр = (1/2)hp, то
при р ф 0 радиальная компонента поля
Нр не может обратиться в нуль, т. е. по¬
ле не может во всем пространстве оста¬
ваться параллельным оси z. Заметим
также, что при z = Zo составляющая по¬
ля Hz обращается в нуль, и поле целиком определяется радиальной
составляющей.
1.6.13. Пусть система заряженных частиц совершает финитное движе¬
ние в магнитном поле в ограниченной области пространства. Опреде¬
лим усредненную по времени силу, действующую на одну из частиц
(для нескольких частиц нужно будет лишь просуммировать выражение
по номеру частицы):
Рис. 1.10. Схема силовых линий
Р = |[гхН(г(0)].

230 ■Аг Глава I. Теория поля. Решения задач
Введем обозначение г = R + г', где R — радиус-вектор фиксированной
внутренней точки рассматриваемой области пространства. Считаем по¬
ле слабонеоднородным, т.	е.	расстояние, на котором	такое	поле	суще¬
ственно	(на	величину ~	Я) меняется по модулю и	направлению,	го¬
раздо больше размеров области, занятой частицами. Для напряженно¬
сти поля используем разложение по г до первой производной: Н(г) =
= H(R + г') = H(R) + (r'V)H(R), где оператор V действует на коорди¬
наты фиксированной точки с радиус-вектором R. Тогда будем иметь
F = ^[г' х Н] + [Я х (r'V)H],
где H(R) = Н. При усреднении по бесконечному (на практике — боль¬
шому) временному интервалу полной производной по времени от любой
финитной функции /(0 получаем ноль:
g=l,m	1	/ 4= lim U,0+T =	0.
dt Г—к»	Т	J dt T—*oc Т t0
to
Таким образом, для средней силы имеем выражение
F = -[г' х (r'V)H],
С
или, в записи по компонентам:
Fi = ~^ijkX'iX,m'^mHk = “@ijk	mHk■
Поскольку выполняется равенство ^ftx'jx'm ~ 0, мы можем представить
интересующее нас среднее в виде
xjxm = 2 ^XjX'm ~ xjx'm) = 2xlxn(^tj^nm ~ filmfinj) = 2X'lXnelnPeimP'
Подставляя это соотношение в выражение для средней силы, получим
—	Q	t	Q
Fi	2^&jik£jmpxixn&lnp^m^k —	^(.^im^kp	~	^ip ^km )X/Xn& I np^mj^k	=
= -^einkWnViHk + ~сх'1х'пе,шЧ kHk-
В данном выражении второе слагаемое обращается в нуль, посколь¬
ку VpFlk = divH = 0, а первое описывает вклад магнитного момента
/х =	[г'	х	г']	в	среднюю	силу.	Таким образом, имеем
F = V(7ZH),
где мы считаем Ji — const.

1.6. Статическое электромагнитное поле
Полученное нами выражение V(/^H) отличается от выражения (/xV)H,
которое фигурирует в условии задачи. В силу очевидного соотноше¬
ния V(/xH) - (mV)H = [fix [V хН]] два выражения будут совпадать,
когда rot Н = 0, т. е. когда внешние токи (создающие магнитное поле)
отсутствуют в области движения частиц.
1.6.14.	Поле магнитного диполя имеет вид
Пусть диполь направлен вдоль оси г декартовой системы координат:
р. = (0,0, р). Будем вести рассмотрение в сферической системе коорди¬
нат, считая, что длина определяется выражением
dl2 = dl2 + dig + dip, где dlr = dr, dig = rd6, dlv = rsin0dip. (1)
В таком случае метрический тензор является единичной матрицей, и мы
можем не различать верхние и нижние индексы в таких сферических
координатах. Получим в явном виде компоненты ортонормированных
базисных векторов сферической системы координат:
Напряженность магнитного поля диполя имеет в такой системе коор¬
динат следующие компоненты:
На силовой линии магнитного поля должно выполняться условие
dl || dVL, т. е. касательная к силовой линии должна быть направлена
вдоль магнитного поля. Таким образом, уравнение касательной имеет
вид
н _ 3(/хп)п - /х
г
п = -
г
НГ = { пгН) = м^^, Нв = (пвН) = -р^, Н<р = (п^Н) = 0.
г	г
Абсолютная величина напряженности поля равна
dl = АН.

232 -l\r Глава 1. Теория поля. Решения задач
dr Нг r> 4 л
ЙГ ил" 7Ж“№=2с1вЛ
Отсюда с учетом (1) получаем дифференциальное уравнение
dr rd9
Hr
Интегрируя данное уравнение при условии г(7г/2) = го, находим урав¬
нение силовой линии магнитного диполя:
г(в) = го sin2 в.
На этой силовой линии (рис. 1.11) компоненты магнитного поля и
его модуль ведут себя следующим
образом:
и р2соъв	и
Пг — -з . fi „ 1 Пд
r0 sin
3 ■ 5 ,
/"о sin I
Рис. 1.11. Схема силовых линий маг¬
нитного диполя
Н =
р \/3 cos2 в + 1
sin6 в
(2)
1.6.15. В системе отсчета, связанной с ядром, имеем
E = -V— = Цг, Н = 0.
г г3
В движущейся системе отсчета, в которой в данный момент времени
диполь покоится, определяем компоненты магнитного поля при помощи
преобразования Лоренца с линейной точностью по v/c (т. е. пренебрегая
членами ~ (v/c)2):
Н' = --[v х Е] =	=	1^1
с	с	г3	тсг
.з •
Поэтому энергия взаимодействия магнитного диполя с внешним полем,
вычисленная в движущейся системе, есть
£' = -(/Ш') = i(/x[v х Е]).
Нетрудно показать, что в том же приближении можно получить £ — £'.
Следовательно, окончательно находим
£ = i(/x[v х Е]) = i([/x х v|E)
Ze
тсг
Ы).
Видим, что движущийся магнитный момент по отношению к внешнему
полю Е эквивалентен электрическому дипольному моменту:
d = -[v х /х].
с

1.7. Свободное электромагнитное поле	233
1.7.	СВОБОДНОЕ	ЭЛЕКТРОМАГНИТНОЕ	ПОЛЕ
1.7.1. Амплитуда волны и волновой 4-вектор должны удовлетворять
условиям:	=	0 и	=	0, или в трехмерных обозначениях:
А°со - (А0к) = 0 и (1/с2)щ2 - к2 = 0.
1.7.2. Для плоской волны, бегущей вдоль оси г, отличны от нуля сле¬
дующие компоненты тензора энергии-импульса:
• Т00 = w — (Е2 + Н2)/(8тт) — Е2/(47г) — плотность энергии;
• Т03 = Г30 = Sz/c = w — плотность потока энергии (Sz) и объем¬
ная плотность импульса (Sz/c2) вдоль оси z\
• Г33 = azz = w — давление вдоль оси г.
1.7.3. Зададим стоячую волну потенциалом
А = Ао cos(uit) cos(kr).
Если uj = ck и (A0k) = 0, то потенциал удовлетворяет волновому урав¬
нению и калибровке Лоренца (или Кулона, поскольку при <р = 0 они не
различаются). В этом случае напряженности полей равны
Е = Ео sin(utf) cos(kr),	Ео	=
Н = Но cos(wO sin(kr),	Но	= [к х Ао],
выполняется	условие |Ео| = |Но|, и векторы	Ео, -Н0 и к	образуют	пра¬
вую тройку.	Выберем направление осей	х, у	и z вдоль этих векторов. В
результате будем иметь (см. (1.14))
г2
w = crzz = -^{sin2(a;0cos2(kr)+ cos2(wOsin2(kr)} =
ОТГ
=	{1 - cos(2wl) cos(2kr)},
F2
Sz — sin(2o;0 sin(2kr),
107Г
r2
aXJC = —а у у = g^{-sin2(w/)cos2(kr) + cos2(u>l) sin2(kr)} =
= -j^-{cos(2u;0 - cos(2kr)}.
Остальные компоненты тензора энергии-импульса равны нулю.
1.7.4. Искомая калибровочная функция находится стандартным образом:
А = А' + grad/,	=	°,	f(r,t) = c j <p'(r, tf) dt'.

234	Глава 1. Теория поля. Решения задач
1.7.5. Для случая, когда заряды и токи равны нулю, проделаем преоб¬
разование Фурье уравнения Максвелла div Е = 0:
Jf div Е(г, 0e-i(kr~ut)d3T dt =
= f dtj e-‘(kr-“"(EdS) - JJ (EV)e-,(kr-“()d3r dt = t'(kEk,J = 0.
Здесь мы считаем, что интеграл по бесконечно удаленной замкнутой
поверхности равен нулю.
Рассмотрим преобразование Фурье второго уравнения этой же пары.
Для левой части соответствующего уравнения Максвелла получаем
JJ rot Н(г, t)e~i(kt~u>i)dirdt = f dt j [V x H]e~i(fa-ut)d3r =
= - J dt J e-,(kr-wl)[HxdS]+ JJ [H x V] e-i(kr-u'')d3r dt= -t[Нк ы x к].
Правая часть этого же уравнения дает
lfd3rj ^e~Kkr~ul)dt = -i-c JJ E(r,t)e~i{'a-“,)d3rdt= -/^Ek,w.
Таким образом, имеем
[kxHU = -^Ek,„.
Совершенно аналогично проводится преобразование Фурье для дру¬
гих двух уравнений Максвелла:
(kHk,u) = 0, [кхЕк,ш] = ^Ны.
1.7.6. Запишем для определенности электрическое поле плоской моно¬
хроматической волны:
Е = Re{Eoe‘(kr_w°()} = ei|£i| cos(kr - wt - a) =f е2|£г| sin(kr -ut - a).
(1)
Необходимо проделать преобразование Фурье для косинуса и синуса:
JJ cos(k'r - dt - a)e'(kr_u',_“)d3r dt =
_ ^ JJ ei\(k+k')r-(4,+u')t-a]d3t dt + ]_ JJ ei|(k-k')r-(u>-w')<+ai^3r ^ _
= 1(2тг)4 [<5(k + k') 6(u + d) e~ia + <5(k - k') 6(u - d) eia]. (2)

1.8. Запаздывающие потенциалы, излучение —1\<- 235
Выражение для фурье-образа синуса очевидно. Подставляя полученные
выражения (2) в формулу преобразования Фурье поля (1), получаем
Ек,ш = ^(2тг)4 [(ei|£i! =f ге2|£2|)е~‘а<5(к + к')<5(ш + и>') +
+ (е,|£,| ± ге2|£2|)е'а<5(к - к')5(и - о/)]. (3)
Выражение (3) можно переписать в виде
Ек,и; = ^(2тг)4 [Е5£(к + k')*(w + J) + Ео<5(к - k')<*(w - и/)].
1.8.	ЗАПАЗДЫВАЮЩИЕ	ПОТЕНЦИАЛЫ,	ИЗЛУЧЕНИЕ
1.8.1.	В соответствии с условием задачи полагаем, что дипольный мо¬
мент d зависит от времени гармонически, т. е.
d(l) = Аше~ш\ поэтому d(l') = d^ — 0 = Аше~1(ш*~кг\ (1)
где t' — t — г/с — запаздывающее время, г — расстояние от диполя до
точки наблюдения поля, k = и/с. Будем считать, что расстояние до точ¬
ки наблюдения много больше линейных размеров диполя (г » а). Кро¬
ме того предполагается, что а<Л, где А — характерная длина вол¬
ны излучаемых электромагнитных волн. Эти два условия обеспечива¬
ют возможность применения дипольного приближения. В формуле (1)
величина вообще говоря, комплексная, т.е. на окончательном этапе
от выражения необходимо брать действительную часть.
Векторный потенциал диполя на больших расстояниях имеет вид
A(r, t) = —d(0 =	d(l')-
сг	г
Подставляя в условие калибровки Лоренца данный вектор-потенциал,
получим
Это значит, что <p(r,t) = — div(d(t')/r) с точностью до константы инте¬
грирования, не зависящей от времени, которая здесь нас не интересует.
В итоге имеем для скалярного потенциала
ф, t) = - div(^P) = *5^(1 - i(kr)).

236 -i\r Глава 1. Теория поля. Решения задач
где п = г/г. Переходим к вычислению напряженностей полей:
Е = —- V</p = i{(3n(nd) - d)(l - i{kr)) + {kr)2[n x [d x n]]},
H = rot A = — ik
с dt	f
V x -
r J
= з (n x d] (i'(kr) + (kr)2),	d = A{t').
Как видно, в окончательном результате существенную роль играет
параметр kr ~ г/А. В зависимости от значения данного параметра элек¬
тромагнитное поле может иметь различный вид на разных расстояниях
при г>а (рис. 1.12).
а)	Квазистатическая зона: а -С г <С Л {kr <С 1). В этой обла¬
сти можно пренебречь эффектами запаздывания, тогда напряженности
полей
E=3nM-d н = 0
г3
отвечают полю квазистатического электрического диполя, в пределе
kr —> 0 мы получаем просто статический диполь.
а < г < А	Переходная	зона	а<Л</’
Н 1 1
О а '	■	' А а<г~А	г
Квазистатическая	Волновая зона
зона
Рис. 1.12. Условное обозначение трех характерных зон для поля, создаваемого
системой движущихся зарядов
б) Волновая зона: a -С А -С г (kr^> 1). В этой области напря¬
женности полей имеют вид
E = y[nx[dxn|] =[Hxn], Н = — [п х d].
Напряженности полей убывают с расстоянием, как 1/г, а кроме того они
они связаны между собой так же, как они связаны в поле плоской элек¬
тромагнитной волны, распространяющейся вдоль единичного вектора п.
в) Промежуточная (индукционная) зона: а -С г ~ A (kr ~ 1).
В этой области важны все члены в исходных выражениях для по¬
лей: эффекты запаздывания существенны, но поле излучения еще не
сформировано.
1.8.2.	Пусть в системе для всех частиц выполняется: е;/т, — а = const.
Тогда для полного дипольного электрического момента получим
d = ]Г e,r, =а^2 m,r, = aR ^ /я„ где R = £±01*1
; ; 2-- т‘

1.8. Запаздывающие потенциалы, излучение	237
— координата центра инерции. В замкнутой системе, где отсутствуют
внешние силы, полный импульс сохраняется: R = const, R = 0, поэтому
d = О, следовательно, 1ц = 0.
Полный магнитный момент можно записать в виде
т = ^ Ее‘1г‘ х V,] = ~ х m,v,] = |-М,
i	i
где М = £.[г, х р(] — полный момент количества движения системы.
Если суммарный момент внешних сил равен нулю, то в изолированной
системе М = О, М = 0, следовательно, = 0.
1.8.3.	Вначале мы имеем задачу двух тел. Переходя в систему центра
инерции и вводя обозначения
„	т\Т\+т2Г2	т,т2
R =	  ,	г	= г, - г2, ц =
т\+ т2 ’	'	т\	+	т2’
где R — радиус-вектор центра инерции системы, г — радиус-вектор
относительного движения зарядов, /х — приведенная масса, получаем
П = (/х/от))г, гг = (/х/т2)г, и, следовательно, дипольный электрический
момент системы равен
е\ £г\
eiri + e2r2 = /i, т I
\т 1 т2 j
Уравнение движения эффективной частицы с приведенной массой в по¬
ле неподвижного кулоновского центра имеет вид
„г = -!аа!£.
Вычислим интенсивность дипольного излучения (энергию, теряемую
системой в единицу времени), предполагая, что потери энергии за один
оборот малы по сравнению с полной энергией4*:
/= -
<9£ _ 2d2 _ 2|eie2|2 / е, __ е2 \2 \_
dt Зс3 Зс3 V^i «2)
г4'
4)	При решении данной задачи (и некоторых задач, следующих ниже) предпо¬
лагается, что потеря энергии системой дЕ /dt за период движения мала по
сравнению с полной энергией £. Или: движение частицы, например, в ато¬
ме идет по очень пологой спирали, так что заряд в любой момент времени
излучает, как заряд на круговой орбите. Математически это означает, что
при расчете интенсивности излучения мы считаем, что £ = const, а затем
вычисляем потери энергии дЕ/dt по невозмущенному движению. Как правило,
для этого необходимо выполнение условия v/c 1.

238 -Лг Глава I. Теория поля. Решения задач
Энергия, излучаемая системой за один оборот, будет равна
хр - / ?££ - / . 27ГР/2 гЗ/2 _ 47r^'/2|eie2|3/2 (£i_ _ е2 \2 1
v ' |е,е2|1/2	Зс2 \т\	т2) г5/2’
поскольку из условия pv2/г = |eie2|A2 (ускорение — центростремитель¬
ное, движение плоское) следует, что скорость частицы на орбите равна
leie2|l/2	(j)
U 1/2 1/2 * v ;
/X Г
Анализ двух последних формул показывает, что энергия, излучаемая
системой за оборот, действительно мала, как и предполагалось:
2 |eie2| р ппы а
<5£
Найдем далее изменение расстояния между частицами и время па¬
дения одной частицы на другую (фактически, время жизни атома в
классической электродинамике). Поскольку кинетическая энергия си¬
стемы теряется на излучение, то
dt _	,	_	dt	dr	„	_	pv2	_	|eie2|	_	_	\e\e2\
dt	dr	dt'	ГДС	r	r	2r '
В результате мы получаем следующее уравнение:
(iL _ £2_V_L
\mi т2) г4’
j£l£2| dr _ _ 2(£i£2>^ Х ~	-’	Ч2
2г2 Л	Зс:
Интегрируя это уравнение (с начальным условием г(0) = го), находим
закон изменения радиуса орбиты:
,2 / .	ч	2	\	1/3
/ \ 2 \ */■>
) t) .
\т 1 т2) )
4|eie2|
В момент падения частиц друг на друга r(tnад) = 0, т. е. время падения
равно
3 3/	ч	-2
4	_	г0с	(е, е2 )
*пад —	I	1	_	I
^2/
Наиболее наглядный вид полученные результаты приобретают, если их
выразить через приведенные величины: р = r/ro, т — t/tnад, и = v/vo,
] = ///о (рис. 1.13), т. е.
Р = (1_г)1/3, и =	1	/	=
(1-т)|/6’	(1	—	т)4/3	*

1.8. Запаздывающие потенциалы, излучение -IV 239
В заключение приведем некоторые численные оценки для атома во¬
дорода, полагая, что е\ = е2 — е — заряд электрона, т\ = т — масса
электрона (mi < т2) и го = 0,529 • 10~8 см — размер атома. В этом слу¬
чае время жизни такого атома будет равно
U *	- 3,2 • КГ13 с.
4е
Предположения, в рамках которых рассматривалась задача (малость
энергетических потерь за период вращения), нарушаются при условии,
что электрон в атоме перестает быть нерелятивистским, т. е. v —> с. Это
может произойти в случае (см. (1)), если
го < гкл =	= 2,8 ■ 10~13 см,
тс
т. е. на очень малых расстояниях (гкл — классический радиус электро¬
на). На расстояниях ~ 10-13 см, строго говоря, уже становится непри¬
менимой сама классическая электродинамика, ибо она становится внут¬
ренне противоречивой. В частности, на рисунках 1.13, б и в видно, что
вблизи момента падения (при t —> tnад или т —> 1) скорость частицы, как
и излучаемая ею энергия, бесконечно растут.
г/го	а	v/vo	б ///о	в
Рис. 1.13. Падение одной частицы на другую при дипольном излучении: а —
зависимость расстояния между частицами от времени; б — зави¬
симость скорости частицы от времени; в — зависимость интенсив¬
ности излучения от времени (т — отношение времени к времени
падения)
В этой связи заметим, что результат, полученный нами в данной за¬
даче (очень маленькое время жизни атома), указывает на неправиль¬
ность классических представлений (в данном случае, о движении элек¬
трона в атоме). Эта и другие трудности, возникшие в классической тео¬
рии, как раз и стимулировали создание и развитие квантовой механики.

240 -Ar Глава 1. Теория поля. Решения задач
1.8.4.	Как и в предыдущей задаче, вычислим интенсивность для невоз¬
мущенного движения (без учета потерь на излучение). Если электроны
вращаются вокруг ядра гелия, все время находясь на противоположных
концах диаметра, то электрический дипольный момент тождественно
равен нулю и электрическое дипольное излучение отсутствует. Маг¬
нитный дипольный момент для невозмущенного движения постоянен,
поэтому магнитное дипольное излучение также отсутствует. Найдем
вклад квадрупольного излучения.
Пусть п — единичный вектор, направленный от ядра к первому элек¬
трону, а N — единичный вектор, направленный вдоль оси вращения.
В силу симметрии собственные направления квадрупольного момен¬
та задаются единичными векторами n, N, 1 = [N хп]. Соответствую¬
щие собственные числа равны —2Qo, Qo. Qo. где Qo = 2eR2. Тензор
квадрупольного момента можно выразить через компоненты собствен¬
ных единичных векторов:
Qij — Qo(-2nitij + N,Nj + /|7у).
Для вычисления интенсивности квадрупольного излучения нам нужно
вычислить Qjj для невозмущенной траектории (считая, что R постоян¬
но). При этом N — 0, а векторы п и 1 вращаются вокруг N с постоянной
угловой скоростью ш. Это означает, что
~ = n = cc[N хп]= оЛ, ^ = i = w[N х 1) = —щп;
dt	dt
Qij = Q0w(-2«,7y - 2l,nj - riilj - litij) — -3Qoaj(nilj + /,яу),
Qij = 6Qow2(n(7iy - /,•//),	=	12Q0w3(/,«y + riilj).
Полная интенсивность квадрупольного излучения:
, _ QijQij _ (12)2 • 2Qgux6 _ 32e2/?V _ 32e2R(Rj)3
Q ~ .	—	c2	c	„5	—	r	5	—	j-	5
180c	6 • 5c	5c	5c
Ускорение электрона при круговом движении Rlo2 вычислим из закона
Кулона и второго закона Ньютона:
п. Л _ >	е2	\	_ 7е2
m\R2	(2 R)2)	4	mR2'
Полная интенсивность излучения дает нам скорость потери энергии:
dtl 73е8
1Ч = ~77 =
dt lOcVfi5'
Полная энергия системы будет равна
„	0mv2 „2е2 е2	,2	7е2	Те2	7е2	Те2
£ = 2—г	2— + — = m(Ru>) - — = mR 5 - — = — —,
2 R 2R v ’	2 R	4mR	2	R	4	R

\
1.8. Запаздывающие потенциалы, излучение	241
где мы учли соотношение (1). Получаем дифференциальное уравнение
относительно R = R{t):
73е8	7е2	■	ч	■	8	•	72е6
—5—3-5 =	2R'	0ТКУДа	4Й3/?	=	——5—Г-
Юс m R	4R1	5с	т
Интегрируя данное уравнение (при условии /?(0) = /?о)> окончательно
5 cDm3
находим
R\t)=Rb-^-3t.
1.8.5.	Предположим, что суммарные потери энергии малы по сравне¬
нию с начальной кинетической энергией системы. Поэтому определим
интенсивность электромагнитного излучения исходя из того, что дви¬
жение частиц происходит под действием электростатических сил (без
учета потерь энергии на излучение)5*.
Движение двух взаимодействующих частиц сводится к равномерно¬
му движению их центра масс и движению частицы с приведенной мас¬
сой ц в поле силы взаимодействия двух частиц. Пусть частицы движут¬
ся по оси х, причем начало координат совпадает с положением центра
масс системы. Если R — расстояние между частицами, то в системе
центра масс:
т]Х[+т2х2=0. Xx = _R_m_^ X2 = +R- т'
т 1 4- m2	т\	+	т2	т\	+	т2
Компоненты дипольного момента имеют вид
dx = Х\в\ + *2е2 = Rm'e2 ~ W2<?l = Rq, dy = dz = 0.
mi + m2
Интенсивность дипольного излучения равна
h = biif =
Полные потери энергии за счет электрического дипольного излуче¬
ния удобно вычисляются, если перейти от интегрирования по времени
к интегрированию по скорости v — R. В этом случае (с учетом того, что
dt = dv/R) имеем
+00	+Иоо	+»«.	-и„
Iddt= f	f %Rdv=2-^ [
J	J	3c3	R	J	Зс3	3yc	J
dv
R2'
5)	См. также сноску на с. 237.

242 ■Аг Глава 1. Теория поля. Решения задач
Здесь R находится из уравнения движения в системе центра масс (ниже
р — приведенная масса):
я = Щ, р =	(1)
pR2	т\+т2
Из закона сохранения энергии (опять не учитывая потери на излучение)
получаем
pdL pv2 , е\е2	1	р	,	2	2\
-t = -2+-T' 0ТКУДЗ R = 2^^~V)-
Для полной излученной энергии находим
6£d =	/	(vl	-	v2)2dv	=	/(1	-	u2)2du	=
6с е\е2 J	6с	е\е2 J
Я РУ°с 16
6c3ei62 15
где и = v/Voo — нормированная скорость.
Взяв определенный интеграл, получаем полную энергию, излучен¬
ную в дипольной моде:
sz - 16 q2 ^°°")3 - ^v°° (v°°)3 « ^2°
d 45 е\е2 2 \ с /	2	V с /
Дипольный момент обращается в ноль, если удельные заряды рав¬
ны, т. е. если е\/т\— еч/т^- В этом случае нам нужно рассмотреть
следующий член мультипольного разложения, который учитывает элек¬
трическую квадрупольную и магнитную дипольную моды.
Для равных удельных зарядов магнитный момент пропорционален
моменту импульса и сохраняется вместе с ним (см. решение задачи 1.8.2).
Квадрупольный момент, из соображений симметрии, диагоналей:
п -п _ Q** _ „„2	„2	 D2m]e2 + m\e\ _ о2„/
чггг — Wyy — ~Д~ — &\х1	£2Х2	— —К —	-у	—	—К Ц .
z	(mi	+	т2)
Вычисляем интенсивность квадрупольного излучения:
I = Ml -	_	я
/2
d R*
180с5 ~~ 180с5 ~~ 30с5 V dt3
Находим третью производную по времени, учитывая (1):
~ = 2 RR + 6 RR = 2^-RR + 6 RR = 2^-( Щ )r + 6 RR =
dt3	dt	dt	\pR2	J
= 2(-2)^|RR + 6RR = (6 - 4)RR = 2RR.

1.8. Запаздывающие потенциалы, излучение
Далее вычисления проводим аналогично дипольному случаю:
Q J Q J 30 с5 R \Ъус J R2
— OO	—Woo	—Voo
t2	+/*°°	/2	7	"У
= 4 - T f v2(v200 -v2)2dv=^—^^	u2(l-u2)2du.
30eie2c5 J	°°	30e,e2c5	J
Полная энергия квадрупольного излучения равна
(т)5 ~ 4 (т)"«	« 4-
и вновь оказывается много меньше исходной энергии частицы.
1.8.6.	Электрический дипольный момент сфероида равен нулю. Маг¬
нитный дипольный момент также равен нулю в силу центральной сим¬
метрии зарядов и токов. Электрический квадрупольный момент имеет
следующие ненулевые компоненты (см. задачу 1.6.10):
Qzz =	= !?ЯоА> cos(ojt), Qxx = Qyy	=	~^Qzz-
Магнитное поле квадрупольной волны имеет вид (г — радиус-вектор
точки наблюдения)
,, IQ х п]	г	„	~
Hq — -—г , п — , Q —	Qft.jH .1 ■
6 с г	г
_ Q2 - (Qn)2 dn _ niQi-Q^nk - (n-Q^n,)2	dU
Q	~	36c5 4тг ~~	36c5	4тг'
В рассматриваемом здесь аксиально-симметричном случае:
QL (cos2 в+^ sin2 - Q2zz (cos2 в - Х- sin2 в} dfl
dlQ = 36? 47г ’
и угловое распределение интенсивности имеет вид
^	cos2 9 sin2 в.
dil 64тгс5
Полная интенсивность равна
/<? =	=	120?’	где	^гг	=	lqR2°^ = l^o/W sinM-

244	Глава	1.	Теория	поля.	Решения	задач
1.8.7.	Запишем баланс энергии с учетом потерь на излучение в диполь-
ном приближении:
dt / с т12 2 г ^ л2	2е2Г 4
£ = —*, U--pi
Получаем дифференциальное уравнение
2е2/2 4	„w	rf	1	4е2
,2	I 4	n a;	a i
ml uju =	3-а;, откуда — 2— = ——
3 ~	- з	,	2	о	з	•
Зс	ш dt и Зс т
Интегрируя данное уравнение с начальным условием ш(0) = шо, находим
= 1/2
\и»0 Зс т,
Полная интенсивность излучения изменяется только за счет умень¬
шения частоты u(t). Распределение интенсивности по углам меняется
с частотой ш, поскольку вектор d вращается. Поэтому
где п — единичный вектор, задающий направление излученной волны.
Пусть штанга вращается вокруг оси z. Поскольку после усреднения
по времени должно получиться аксиально симметричное распределе¬
ние, вектор п можно взять в плоскости (x,z), т. е. n = (sin 0, O,cos0),
тогда, очевидно, d = —c^2e/(cos(a^?), sin(u;?), 0). Следовательно, для уг¬
лового распределения имеем
~ = 6 1	(1	- cos2M) sin2 в).
dn 4тгс3 v	’
При усреднении по периоду cos2(uit) — 1/2, и поэтому
1й ЛУЬ. ,	2	т
d£i = ~4пР~2 "*"cos
1.8.8.	Запишем баланс энергии с учетом потерь на излучение в диполь-
ном приближении (w — ускорение электрона):
dt .	2	>	2e2w2	е	г
-гг — Id — rd = W = —[v x H ,
dt	Зс3	3c3	me
поскольку электрон вращается по окружности со скоростью v ± Н. Да¬
лее имеем
9 е2Н2 2 _ 2е2Н2

1.8. Запаздывающие потенциалы, излучение
Получаем дифференциальное уравнение для кинетической энергии:
dE 4е4Я%	„/л	9 с J 4е4Я2,
откуда £(') = £"еЧ“^у'
1.8.9.	Электрический дипольный момент равен нулю, магнитный ди-
польный момент постоянен, лидирующий член — квадрупольный. Мгно¬
венное распределение зарядов аксиально симметрично (ось симметрии
соединяет заряды). В базисе, образованном собственными осями, квад¬
рупольный момент имеет вид
Qii = Qn diag(l, -1/2, -1/2), Qn = 4ea2.
В лабораторной системе выразим квадрупольный момент через собствен¬
ные векторы eQ:
Qy = 4ea2(t\it\j - ^e2ie2/ - ^e3l-e3/^.
Собственные векторы вращаются с угловой скоростью uj. Ось вращения
перпендикулярна еь будем считать, что она параллельная е3. В этом
случае ё] = сое2, ё2 = -соеь ё3 = 0. Находим производные:
Qy = 6еа2ио (eue2j + e2ie\j), Qy = 12ea2uo2 (-eue\, + e2le2l),
Qy = -24ea2u3 (eue2j + e2ie\/).
Полная интенсивность не зависит от времени:
j _ QijQy = 2(24)2e2q4u>6 = 32е2аУ = 2QW
Q ~ 180с5 ~	180с5	_	5с5	5с5
Для углового распределения интенсивности имеем
\2
,, niQi/Q^nk - (то,,щ) dQ
d'Q = ~	36?	4?’
QyQjk = (24ea2uj3)2 (euelk + e2ie2k),
n = (sin в cos <p, sin в sin p, cos 9) — единичный вектор в направлении точ¬
ки наблюдения.
Удобно проводить вычисления, предполагая, что в данный момент
времени векторы ei,e2 направлены вдоль осей х,у. При этом вместо
усреднения по времени можно усреднить по углу р:

246	Глава	I.	Теория	поля.	Решения	задач
1.8.10.	Пусть 2а — угол между направлениями на заряды. Чтобы вы¬
числить дипольный и квадрупольный моменты, выберем начало коор¬
динат в центре окружности, ось г направим по оси вращения, ось х —
по биссектрисе угла между зарядами. Тогда имеем
Остальные компоненты d и Q,y обращаются в нуль.
Для решения задачи необходимо вычислить интенсивность диполь-
ного la и квадрупольного Iq излучения. С этой целью в лабораторной
(не вращающейся) системе выразим мультипольные моменты через соб¬
ственные векторы е, тензора Qij. Поскольку (см. задачу 1.8.9) ё] = ше2,
ёг = —шеь ёз = 0, получим для дипольного излучения:
do	,	2	jo	2е2	a2	lj*	о
= 2еа cos aej, откуда Id — --d =  	5— cos a,
Зс	3c3
и для квадрупольного излучения:
и получим квадратное уравнение и2 - (К - \)и + 1/4 - 0 для определе¬
ния cos2 а. В интервал [0,1] попадает один корень:
dx = 2еа cos a, Qxx = 4еа2 cos2 a,
Qzz = -2ea2, Qyy = -Qxx - Qzz = 2ea2(l - 2 cos2 a).
Qij - 2ea2 [2 cos2 а ецец - e2ie2j + (1 - 2 cos2 о)е3,е3у],
Q,j = -8ea2uj3(\ + 2 cos2 a)[eue2j + e2ie\j]\
Приравняем интенсивности:
Введем обозначение
u = \[K-\-s/K2-2K] = Х-[К{\-у/Г^2/К)-\].
и = ~
С учетом малости величины l/К разложим корень в ряд:
Окончательно находим

1.8. Запаздывающие потенциалы, излучение	247
1.8.11.	При вращении выполняется соотношение d = —o;2d, поэтому
/d = ^d2 = ^d2.
3 с3	Зс3
Пусть начало координат совпадает с центром окружности, а враще¬
ние происходит вокруг оси z. В момент времени, когда d || х, выпишем
квадрупольный и магнитный дипольный моменты. Для этого предста-,
вим диполь как пару зарядов величины ±d/e, находящихся на рассто¬
янии е друг от друга и перейдем к пределу е —> 0. Для магнитного
момента будем иметь
ц =	[(Я	+ е)2 - R2] е2 -> ^ег.
Магнитный дипольный момент ц от времени не зависит, поэтому маг¬
нитное дипольное излучение отсутствует: /м = 0. Далее
Qxx = 2- [(R + в)2 - R2] - 4dR,	Qyy =	=	-2dR.
2
Окончательно получим (по аналогии с задачей 1.8.9)
,	32 d2R2u6
1.8.12.	Суммарный дипольный момент системы d = 0. Квадрупольный
момент в два раза больше, чем в задаче 1.8.11, соответственно интен¬
сивность квадрупольного излучения больше в четыре раза. Запишем
уравнение баланса энергии:
dZ , с	П2 2	,	128d2R2uj6
Iq, £ = mRzu\ Iq =
dt ‘v’	~	   5c5
Получаем дифференциальное уравнение для u(t):
п п2 ■	128d2R2J‘ , ш d 1	256d2
2 mR'ww = г ,	-4-г-	=	——г	=	г, откуда
5с5	си	dt	J	5тс
it\-( 1	256rf2	.Г'74
Lj + 5	)	'
1.8.13. dk = (£g)%]„*»£b Д< = r(l - g cos»).
1.8.14. Решение задачи во многом похоже на решение задачи 1.8.5. Ин¬
тенсивность излучения и полная излученная энергия даются формулами
ОО	Voo	Uoo

248	Глава	/.	Теория	поля.	Решения	задач
Электрон будет лететь по прямой только, если он летит вдоль вектора d.
Электрон отразится только в том случае, если он подлетит к диполю со
стороны «минуса» и оттолкнется от него. Учитываем уравнение движе¬
ния электрона и закон сохранения энергии:
ъ	Е\е\	2d\e\	-	Л „	4|e|3d	7	1	,
R = —— =	—^	>	0,	откуда	Д£ = - ■1	dv,
т	R т	Зтс	J	R3
-Ооо
I W __	nTKVn„	J_ _ m(t4 - a2)
2 + R2 2 ’ УД д2 2|e|rf ’
и для полной потери энергии на излучение получаем окончательно
д£ = !	У /я2	2Лз/2 Л,_
-0<х>	-1
Зтг
1.8.15.	Дипольный момент относительно неподвижного конца штанги
равен d = pi2/2. Кинетическая энергия — £ = тш212/6. Решение полно¬
стью аналогично решению задачи 1.8.7 (с заменой т —» m/З, е —» р1/2).
Поэтому приводим результат:
/1 „2/2\ _1/2
+ 1 — )
\w0 с т.)
1.8.16.	Квадрупольный момент вдоль оси штанги относительно ее непо¬
движного центра равен Qn = 4pl3/3. Кинетическая энергия равна £ =
= тш212/3. Решение полностью аналогично решению задачи 1.8.12 (с за¬
меной d —> д/2/6, /и —» рт/3). В результате:
ГА | > х64^Г1/4
Й
1.8.17.	Собственные оси квадруполя направлены по диагоналям квадрата
и по оси г. Соответствующие собственные числа равны Qn = —Q22 — 12<7а2,
<2зз = 0 (см. задачу 1.6.5). Обозначим единичные собственные векто¬
ры е, (г = 1,2,3). Тогда для них выполняется: ё) = ше2, ё2 = — шеь ёз = 0.
Далее:
Qij = Ща2(еиеч - е2(е2/),	Q;/	=	96qa2uj3(-eue2j	-	e2ie4).

1.8. Запаздывающие потенциалы, излучение
Интенсивность излучения и уравнение баланса энергии:
l0 = Ml = m£^L = _*£,	£	= 4 maW.
180с5	15	с5	dt
Окончательно имеем
...	(	1 ,512«W.)-,/4
ш(0-	— + Тс—ъЧ
\ш0	тс	/
1.8.18.	Уравнение движения (без учета радиационного трения) описы¬
вает прецессию магнитного момента вокруг поля Н (ниже М обозначает
механический момент):
dT =	= ^_7Н х я] = к х /*!•
Находим интенсивность излучения дипольного магнитного момента:
,	2	„г	2са4, 2 2ч	27V, 2	2dt
3с3^ ~ Зс3	_	Зс3	Мг dt'
£ = -(дН) = -Яцг.
Получаем дифференциальное уравнение относительно уг\
= 2^я3(д2 _	2	ч
dt	Зс3
Интегрируя данное уравнение с начальным условием /хг(0) = 0, окон¬
чательно находим
4 ггЗ
бус
1.8.19.	Электрический дипольный момент конденсатора равен d = qa.
Вычисляем интенсивность дипольного излучения (при гармонических
колебаниях) и усредняем ее по периоду колебаний:
2 ".о	2а2ш4 9	т~	а2и>4 о
Id = —-d = —j-q2, поэтому Id = ——q0,
Зс	Зс	ос
где qo — амплитуда колебаний заряда на конденсаторе. Энергия кон¬
денсатора равна £с = 2irq2a/s. Полная энергия колебательного контура
есть £ = 2nqQa/s. Уравнение, описывающее баланс энергии, имеет вид

250	Глава	I.	Теория	поля.	Решения	задач
Находим решение уравнения:
,0 = ,0(0)ехр(-^/).	£ = £„е*р(-^<
Добротность будет равна
Q 3 ~~3 = "~2 ~ » !•
asui 4-л- as
Добротность велика, поскольку размеры конденсатора много меньше дли¬
ны волны. Это позволяет считать, что заряд на конденсаторе колеблется
почти гармонически (затухая за Q/(2it) периодов) с частотой ш «шо-
1.8.20.	Ход решения аналогичен ходу решения задачи 1.8.19. Магнитный
момент катушки равен р = INs/c. Получаем интенсивность магнитного
дипольного излучения (при гармонических колебаниях) и усредняем ее
по периоду:
,	2	..2	г2	т	Nsu	,2
= ТдМ = ~'ТГ 1 - П0ЭТ0МУ =	7Т~^0'
где /о — амплитуда колебаний тока в катушке. Энергия катушки рав¬
на £д = 2ttN2sI2/(ас2). Полная энергия колебательного контура равна
£ = 2irN2sIq/(ас2). Записываем дифференциальное уравнение баланса
энергии и решаем его:
dZ _т
dt ~
4	/	4	\
V	Q.SUJ	т'	т	I	/а\	I	CIS	Li)	.	\
откуда /0 = ——3/0, /0 = /о(0)ехр	—jM.
127ГС	V	127ГС	/
Находим закон изменения энергии и добротность:
asu>4 Л	б7гс3	3	Л3
£ = £0ехр -==V ,	Q=^3=-^-»l.
V 67ГС )	asu)	4ж	as
Заметим, что формула для добротности оказывается такой же, как и в
задаче 1.8.19.
1.8.21.	Частица будет скользить в горизонтальной плоскости при усло¬
вии взаимной компенсации силы тяжести mg и вертикальной состав¬
ляющей N_l силы реакции опоры N. Центростремительное ускорение
создается горизонтальной составляющей Nц.
1)	Коническая поверхность, k = N\\/N± = mw/(mg) = w/g, где
w — ускорение частицы. Находим далее ускорение и кинетическую
энергию:
,	V2	2	^	-г-	1	2	1
w = kg=-=v2-, T=-mvz = -mgz.

1.8. Запаздывающие потенциалы, излучение
\
Интенсивность излучения и полная энергия равны
Зс2 Зс3	Зс3
d£
' dt'
£ = Т + U = -mgz.
Записываем дифференциальное уравнение и решаем его:
4 k2q2g	,А	4 k2q2gt
z = if-, откуда z(t) = zq - ^ ft.
9 me	9mc
2) Параболоид вращения. Общий ход решения аналогичен, по¬
этому приведем только основные формулы. Находим ускорение, полную
механическую энергию и интенсивность излучения:
dz	_ 2 г	_	jV|| _	mw	_	w
dr	a	N±	mg	g’
n	r	n	z	v2	т	1	2
® = 2g-= у,	T =	2mv — mgz,
- 2A
3c3 3cJa
Записываем дифференциальное уравнение и решаем его:
2 — -
4 q2g
3 тс'
—z, откуда z(t) = z0exp(—
а	\	3	тс	а	)
1.8.22.	Пусть в соответствии с условием задачи диполь di расположен
в плоскости (х, г) на расстоянии h от идеально проводящей плоскости
(т.е. плоскости (х,у), рис. 1.14).
d,
Vd..-"
h'
ез
~д
>?=-AV
ei
d2
Рис. 1.14. Излучение диполя вблизи проводящей плоскости

252	Глава	1.	Теория	поля.	Решения	задач
При решении задачи используется так называемый метод изобра¬
жений, в соответствии с которым исходная задача с граничными усло¬
виями (в нашем случае граничные условия нужно ставить на плоскости
(х,у)) заменяется на эквивалентную задачу определения поля в расши¬
ренной области без граничных условий, но с учетом зарядов-изобра¬
жений — фиктивных зарядов, расположенных таким образом, чтобы
обеспечить выполнение необходимых граничных условий.
В данной задаче система зарядов вблизи проводящей плоскости об¬
ладает зеркальной симметрией, поэтому можно заменить проводящую
плоскость «отражением» в ней исходного диполя, т. е. диполем 62, рас¬
положенным, как и диполь di, в плоскости (х, z), но в полупространстве
z < 0 (рис. 1 14). При этом мы учитывали, что зеркальным изображе¬
нием положительного заряда является отрицательный и наоборот.
В итоге мы имеем конфигурацию двух гармонически колеблющих¬
ся диполей, изображенную на рис. 1.14. Пусть расстояние от средней
точки между диполями (она находится в начале координат) до точки
наблюдения в волновой зоне равно г. Расстояния от диполей до точки
наблюдения можно записать в виде
П.2 = г ± Л(пе3),	(1)
где п — единичный вектор, направленный от центра системы в точку
наблюдения. При этом считается, что h <С г.
Далее мы рассмотрим общий случай, когда длина волны поля излу¬
чения может быть сравнима по величине с расстоянием между диполя¬
ми: А ~ h (при условии, что А <С г). С учетом введенных обозначений
(рис. 1.14) выражения для диполей di и d2 можно записать в виде
d| = dcos0de3 + dsin 6dt\, d2 = dcos#de3 - dsin9dt\, (2)
где d — величина диполя, 64 — угол между диполем и нормалью к
проводящей плоскости, т. е. ез.
Временную зависимость диполей при гармонических колебаниях за¬
даем следующим образом:
d,(f) = doi cos= d0i cos[w^ ~	~ ujh('nt3'1
d2(0 = d02 cos [w(t -	= d02 cos [w(t - 0 +
Полная напряженность магнитного поля в волновой зоне равна сумме
вкладов от каждого диполя в отдельности:
Н = -{J- {[d„, х „] cos [а, (<-{)-
С
а»/г(пе3)
+
-I- [d02 X n] cos |w (г - 0 + fa,A^ie3)j |.

1.8. Запаздывающие потенциалы, излучение	253
Здесь мы пренебрегли слагаемыми ±h (пез) (см. (1)) в знаменателе, но
не можем отбросить их в запаздывающем времени, потому что именно
благодаря этим слагаемым проявляется интерференция между полями
излучения истинного и фиктивного диполей. Учитывая (2), приводим
выражение для магнитного поля к виду
•2j '	г	/	,\л	\шИ(пс3)'
Н —	х	ез]	cos0dcos[w(/	-	cos
+
+ [п х е; ] sin в a sin |w
sin
uh( ne3)
]}•
где do — амплитуда колебаний диполя. Для углового распределения
интенсивности излучения, усредненного за период колебаний, имеем
{[п х e3]2cos20dcos2(a(ne3))+[n х ei]2sin20dsin2(a(ne3))}.
ail	^
Здесь мы ввели обозначение а = uh/c — h/X, где Л = Х/(2тт). Вводя да¬
лее сферические углы вектора п (рис. 1.14) и интегрируя по углу у>,
получаем для полной интенсивности
- J cos2 9d( 1 - x2) cos2(qjc) + sin2 Sd (1 + x2) sin2(ax)j dx,
причем интегрирование по углу в производится только по верхнему по¬
лупространству. Отсюда находим общий результат:
/ :
COS в а
sin 2а 11
~2а 3J
¥{(
+ (cos2+ ^) [l - (i- - -L) sin 2a - jL cos2a]}.
(3)
Теперь рассмотрим некоторые предельные случаи выражения (3).
Во-первых, исследуем случай h X, что соответствует а —> 0. В этом
пределе находим
т	4 из dn 2 л
/ = —cos ва-
Зс3
(4)
В данном случае истинный и фиктивный диполи представляют собой
единую систему, размеры которой малы по сравнению с длиной вол¬
ны. Поэтому запаздывание поля излучения между диполями не играет
никакой роли. Это означает, что вместо того, чтобы складывать магнит¬
ные поля, можно просто вычислить вначале полный дипольный момент

254	Глава	I.	Теория	поля.	Решения	задач
системы, а затем найти интенсивность излучения. Эту программу дей¬
ствительно несложно реализовать. Учитывая (2), легко находим, что
суммарный дипольный момент равен
d = 2dcos#d ез.
Вычисление полной интенсивности с таким значением d действительно
приводит к результату (4). Из выражения (4) также видно, что эта ин¬
тенсивность обращается в ноль, если диполь расположен параллельно
плоскости: costf^ = 0. Это значит, что в данном случае необходимо най¬
ти вклад квадрупольного излучения. Здесь мы этого делать не будем,
ибо ограничиваемся исследованием только дипольного излучения.
Второй предельный случай: /г»А, и это соответствует условию а-* оо.
В таком пределе из (3) получается следующий результат:
. _ 2о/4
Зс3
То есть, система диполей в таком приближении излучает в точности
так же, как один диполь, причем излучение не зависит от ориентации
диполя (нет зависимости от угла во). Это происходит потому, что усло¬
вие А фактически означает, что зеркальная поверхность удалена от
излучающего диполя на столь большое расстояние, что уже не оказы¬
вает на его излучение никакого влияния.
1.9.	ЭЛЕКТРОМАГНИТНОЕ	ПОЛЕ
РЕЛЯТИВИСТСКИХ ЧАСТИЦ
1.9.1.	Основываясь на выражении для запаздывающих потенциалов
г±*=4)
вычислим поле, создаваемое точечной заряженной частицей, движение
которой задано функцией г = го(0, при этом v = го(0 — скорость ча¬
стицы. Вначале перепишем (1) в следующем эквивалентном виде:
Л"(х) = 1 [d'x'P^rSft-S - 1^1).
с1 J |г г | V	с	)
(2)
Учитывая далее, что 4-плотность тока заряженной частицы имеет вид

1.9. Электромагнитное поле релятивистских частиц	255
вычисляя интеграл по d3x' в (2), получим
А £ Ldt'^
_ е f dx'1
~ cj
dx»8(t-t') dt'
|r-ro(f')|	cj	dt'	\ftf)\	R(t')'
Здесь мы применили формулу (Д.7) для 5-функции от сложного аргу¬
мента, и под величиной t' мы понимаем решение уравнения
Rtf)
f(t') = 0, или f +
t- О,
(3)
где R(/') = г - го(0- Rtf) = |R(OI- И, наконец, учитывая, что
dftf) _	_	(nv)	j	|
т =
dt'
где n = R/R, получаем
Л°(г, t) = <p(r, t) =
R( 1 - (nv)/c)
A(r, t) =
e\
cR( 1 - (n\)/c)
(4)
Потенциалы (4) называются потенциалами Лиенара-Вихерта. Время t'
есть запаздывающее время, поскольку разность времен t — t' — R(t')/c
в точности равна времени распространения электромагнитного поля из
точки формирования (местоположение частицы ro(t')) до точки наблю¬
дения поля. Заметим, что все величины в правых частях (4) берутся в
запаздывающий момент t'.
Напряженности полей в точке наблюдения можно вычислить по из¬
вестным формулам:
Н = rot А,
и	А	1	дА
Е = - grad —
В целом данное вычисление не составляет проблемы, но является не¬
сколько громоздким. Поэтому ограничимся некоторыми указаниями.
Прежде всего необходимо представить напряженности полей в виде
н _ e[Vt' х w] +
cR
h-M\
С )
G)»
e[V(nv) x v]
Щ
2/?^l
E =
¥)
’(я)
cR
eV(nv)
(-
¥)
и
с dt
ev d /1 \	ew
^ _ W'jdt' \Rj	(nv)	j
d(nv)
dt'

256	Глава	I.	Теория	поля.	Решения	задач
где w = v — ускорение частицы. Затем можно воспользоваться некото¬
рыми вспомогательными формулами:
(1\ - М
7\r) r2 ’
dt' _	1	—./ _	п	д
dt (1 — (nv)/c) ’	(I-(nv)/c)’	dt'
v(-] =	5	 =	(nw)	+v[n x [tl x-v|!
\RJ R2(\ — (nv)/c) ’ dt'	R
R\ 1 - (nv)/c)
X7( v _ n((nw) - \2/R)/c + n(n\)/R V
1	’	(1	— (nv)/c)	+	R'
Здесь две первые формулы получаются путем почленного дифферен¬
цирования соотношения (3). Остальные результаты следуют из первых
двух формул.
После проведения вычислений получаем следующие выражения:
,.2>
е
(' ~ ?)(П~ , g[nx [(""PHI
Е(г, t) = 4 / V	^(5)
«•(l-М)	с*(	1-
<*>)
иЛ.	с2)[УХП1 , e(c[w х п] + [п х |[v х w] х п]]) /сч
'	/	/ W3	/	/ ч\ 3	*	' '
Заметим, что в этих формулах все величины в правых частях берутся
в запаздывающий момент времени t'. Нетрудно проверить, что всегда
выполняется Н = [п х Е].
Каждое из выражений (5) и (6) для напряженностей полей содержит
два слагаемых: первые слагаемые зависят только от скорости частицы и
не зависят от ускорения, а вторые слагаемые пропорциональны ускоре¬
нию w частицы. Первые слагаемые имеют квазистатический характер,
убывая с расстоянием, как R~2, в то время, как члены, зависящие от
ускорения, описывают поперечное поле излучения, для которого поля
Е и Н ортогональны друг другу и радиус-вектору R, и изменяются, как
R~l с ростом R.
1.9.2.	Если ускорение частицы равно нулю, то в формулах (5) и (6)
задачи 1.9.1 остаются только первые слагаемые. Именно они и описы¬
вают статические поля, создаваемые равномерно движущимся зарядом.
Запишем эти поля в виде
<-?)(-г»)
(Rv)\3
Е(г, 0 =
(*-
V
н(г,*) = ££И.	(1)

1.9. Электромагнитное поле релятивистских частиц	257
Заметим, что в формулах (1) поля выражены в терминах запаздываю¬
щего времени t'. Установим, как они будут выглядеть в момент времени
наблюдения t. Воспользуемся сле¬
дующими геометрическими сооб¬
ражениями.
На рис. 1.15: О — точка наблю¬
дения, S — точка, в которой за¬
ряд находится в момент времени t,
S' — точка, в которой он находил¬
ся в соответствующий запаздыва¬
ющий момент t1, в' — угол меж¬
ду направлением движения и ра¬
диус-вектором R(0 положения ча¬
стицы в момент t'. Начало отсчета
времени выбрано так, что в момент
t = 0 заряд находится на кратчай¬
шем расстоянии (равном р) от точ¬
ки наблюдения.
Рис. 1.15. К вопросу о выводе связи
между напряженностями полей в за¬
паздывающий момент времени t' ив
момент времени наблюдения t
Расстояние S'M равно (vR{t')/с) cos в' = (R(^)v)/c, поэтому отрезок
ОМ равен R{t') - (R(t')\)/c. Эта величина входит в знаменатель фор¬
мулы (1). Из треугольников OMS и S'SM следует, что
Л?(*') _ (R(*')v))2 = ОМ2 = R2(t) - MS2 = R2(t) -	sin2	в'.
Из рисунка видно, что R(t') sin в' = р = R(t) sin в, а также
R(f') - -R(t') = R(0-
С
Объединяя все эти результаты и подставляя их в (1), окончательно на¬
ходим выражения для напряженностей полей в следующем виде:
Е =
eR
ч
R3 (.	.	2Л3/2’
V ~ 7 в)
н
-|vxE|,
С
где все величины в правой части взяты в момент времени t. Данный
результат можно получить также и из статического кулоновского поля
заряда, используя преобразование Лоренца.
1.9.3. Указание: использовать результат предыдущей задачи. Приводим
ответ:	/	,,2\	/	i/2>
Fx =
е\е2
О-Я
COS в
Fy =
е\е2
г>2	/	,,2	\	3/2	>	У	г>2	/ и2	ч	3/2	’
R (l-^sin2*)	R	(l-fsin^j

258 ->\r Глава 1. Теория поля. Решения задач
где R — радиус-вектор от еч к е\, в — угол между векторами R и V,
заряды движутся вдоль оси х.
1.9.4.	Как следует из формул (5), (6) задачи 1.9.1 (см. также (1.62)), на
больших расстояниях от частицы выражения для напряженностей по¬
лей выглядят следующим образом:
т. е. содержат только волновые поля (поля, спадающие, как 1/R и со¬
здающие конечный поток энергии на бесконечности).
Общее выражение для углового распределения мощности излуче¬
ния имеет вид (в соответствии с (1.66))
где все величины в правой части взяты в запаздывающий момент вре¬
мени t'. Здесь v и w — скорость и ускорение частицы, n = R/R —
единичный вектор в направлении наблюдения.
Далее мы будем считать, что заряд ускоряется в течение короткого
интервала времени, при этом скорость и ускорение не успевают суще¬
ственно измениться, тем самым мы будем рассматривать мгновенное
угловое распределение мощности.
1)	Скорость v параллельна ускорению w (в момент време¬
ни t1). При этом угловое распределение мощности излучения имеет вид
причем угол в отсчитывается от направления w или v.
2)	Скорость v перпендикулярна ускорению w (в момент
времени t'). Выберем систему координат так, чтобы ось z была направ¬
лена вдоль скорости, угол в будет отсчитываться от направления ско¬
рости, азимутальный угол отсчитывается от направления ускорения.
Угловое распределение мощности будет иметь вид
(1)
dW _ е2 |[nx[(n-v/c)xw]]f
dCl	4тг с3	(1 — (nv)/c)5
dW _ е2 |[п х [п х w]]|2 _ e2w2
dn 4тгс3 (1 — (nv)/c)5	47гс3	Л
V
 COS
с
5 ’

1.9. Электромагнитное поле релятивистских частиц	259
3)	Выводы (рис. 1.16). При о/с <С 1 оба распределения переходят
в нерелятивистскую формулу для интенсивности дипольного излуче¬
ния. На рис. 1.16 соответствующие диаграммы изображены штриховой
линией.
Рис. 1.16. Угловое распределение мощности излучения релятивистской заря¬
женной частицы: о — скорость параллельна ускорению (7 = 2), б —
скорость перпендикулярна ускорению (7 = 1,2); штриховая линия
отвечает случаю v/c -С 1
При v/c —> 1 (ультрарелятивистский предел) диаграмма излучения
«вытягивается» в направлении движения частицы. Наблюдается «про¬
жекторный эффект», сопровождающий излучение релятивистских ча¬
стиц: основная часть излучения происходит в конус очень узкого рас¬
твора 6в < I/7 = у/1 — v2/с1 = /пс2/£, ось которого направлена вдоль
скорости. В этом можно убедиться, анализируя знаменатели в угловых
распределениях. В самом деле, раствор конуса по порядку величины
можно определить из следующего приближенного соотношения:
. (nv)	1 v /)	1	V , в2 1 / -2	, л2\
1 — -—- = 1— cos#~l 1- — ~ -(7	+в ),
с	с	с	2	2
откуда и следует приведенная выше оценка б). Вне этого конуса мощ¬
ность излучения очень быстро спадает.
1.9.5.	Как следует из формулы (1.66) (см. также (1.63) и (1.65)), ско¬
рость полных потерь энергии заряженной релятивистской частицей за
счет излучения получается в результате интегрирования по углам со¬
ответствующего углового распределения мощности:
_d* = w= fdWd^ = J_ / Kn,x.[(n-v/c)xwl]|2da (1)
dt	J dfl 4тгс J (1 — (nv)/c)
где v — скорость, w — ускорение частицы, п — единичный вектор в
направлении наблюдения.
6)	Здесь использовано приближение 1 — {v/c)2 = (1 — v/c)(\ +v/c) « 2(1 — v/c).

260 •Ar Глава 1. Теория поля. Решения задач
Далее прежде всего заметим, что мощность излучения или потеря
энергии частицей в единицу запаздывающего времени (1) является ре¬
лятивистским инвариантом. Для того, чтобы убедиться в этом, вна¬
чале перейдем в собственную (мгновенно сопутствующую) инерциаль-
ную систему отсчета Ко, где мгновенная скорость частицы равна нулю
(v0 = 0). Выполняя интегрирование по углам в выражении (1) в этой
системе, получим
где wo — ускорение частицы в мгновенно сопутствующей системе от¬
счета, dt'0 = dr — интервал собственного времени частицы, в — угол
между ускорением wo и направлением наблюдения излучения п в мо¬
мент времени t'0. Отсюда видно, что излучение в мгновенно сопутствую¬
щей системе отсчета фактически имеет дипольный характер, ибо подын¬
тегральное выражение в (2) переходит в известное угловое распределе¬
ние интенсивности излучения дипольного момента при замене d = ewo.
Полная скорость потерь энергии в системе Ко описывается нереляти¬
вистской формулой для полной интенсивности дипольного излучения.
Далее вспомним, что наряду с энергией излучение уносит также и
импульс, причем в волновой зоне импульс поля, излучаемый в проме¬
жуток времени dt' в телесный угол dCl, направлен по вектору п (по
радиус-вектору точки наблюдения). В этой связи рассмотрим четырех¬
мерный вектор потерь энергии-импульса частицы за время dt':
В силу симметрии углового распределения дипольного излучения отно¬
сительно замены в —► 7г — в полная потеря импульса частицей в систе¬
ме Ко равна нулю: dp — 0. Поэтому в мгновенно сопутствующей систе¬
ме отсчета
Перейдем далее в лабораторную систему отсчета (в которой скорость
частицы равна v), используя преобразование Лоренца. Учитывая, что
—dZ = —dZо7, и, соответственно, dt'0 = dr = dt'/7, где 7 = 1/y/l — о2/с2,
получим, что скорость потерь энергии является лоренц-инвариантом:
7Г
dZ _ dZo
dt' к0 dt'0
I
о
dP^ = (-dZ/с, -dp).
dP£ = (-dEo/c,0).
dZ _ dZo _ dZo _ 2e2wo
dt' dr dt'0 3c3
(3)

1.9. Электромагнитное поле релятивистских частиц	261
(формула Лармора). Формулу (3) можно записать в релятивистски-
инвариантном виде, заменяя Wq релятивистским инвариантом, перехо¬
дящим в Wg в системе отсчета Ко- Таким инвариантом является четы¬
рехмерный квадрат 4-ускорения частицы w^ = du^/ds (см. (1.68)), где
= dx^/ds — 4-скорость частицы. В мгновенно сопутствующей систе¬
ме отсчета w11 = (0,wo/с2), поэтому	=	—wо/с4. Таким образом,
в лабораторной системе скорость потерь энергии имеет вид
=_2£с
'dt1 ~	3
w^w^.	(4)
Заметим, что тот же самый результат можно было бы получить, непо¬
средственно проводя интегрирование в (1), однако это потребовало бы
существенно больших технических усилий.
В рамках нашей задачи ускорение частицы создается внешним элек¬
тромагнитным полем — на частицу действует сила Лоренца:
wu =	= ^fi(Ev), Е + ![v х H]Y
me	me Vc	с	J
В случае синхротронного излучения, т.е., когда частица движется в
однородном магнитном поле по круговой траектории, выполняется Е = 0,
vlH, и поэтому (4) приводится к виду
-^l = W=^,v2H2.	(5)
dt'	Зт	с
Для электрона, движущегося в ускорителе в однородном магнитном поле
с постоянной по модулю скоростью, имеют место следующие соотношения:
еН п v mc2vy	..	mcvy	, п „
и> =	, R = - = ——, т.е. еН =——s L = 2ttR,
тсу	ш сеН	R
где ш — частота вращения, R — радиус круговой траектории, L — дли¬
на окружности ускорителя. Движение электрона мы считаем реляти¬
вистским, т.е. v ~ с или 7 = £./(тс2) » 1. При выполнении всех этих
условий формула (5) принимает вид
8/Л1 = 8/Лт4
3 L2	3 L2	UcV '
Форма частотного спектра существенно зависит от соотношения меж¬
ду характерным углом раствора конуса 6в, в котором находится основ¬
ная часть излучения релятивистской частицы (см. задачу 1.9.4), и пол¬
ным углом Ав, на который отклоняется вектор скорости за все время
движения частицы (или за период движения, например, в ускорителе).

262	Глава	I.	Теория	поля.	Решения	задач
Для синхротронного излучения, испускаемого электроном, движу¬
щимся по круговой траектории в магнитном поле, выполняется условие
Д0 3>7~*. При этом излучение в заданном направлении п (в конус с
раствором 69 ~ 7-1 и осью вдоль направления наблюдения п) опреде¬
ляется участком траектории, на котором вектор скорости поворачивает¬
ся на угол 69 ~7-1 Длина этого участка, очевидно, равна rsj / = Л/7и
называется длиной формирования излучения или длиной когерентности.
Итак, при наблюдении синхротронного излучения в заданном на¬
правлении п будет регистрироваться последовательность коротких им¬
пульсов. Оценим их длительность. В конус с углом раствора 7-1 части¬
ца излучает в течение промежутка времени
так как v ~ с. Наблюдатель регистрирует это излучение в течение ин¬
тервала времени (см. (1.59))
At = (1 - (nv)/c)At' ~ 7~2At'.
Или, окончательно, с учетом того, что частота обращения по окружно¬
сти равна wo = еНс/8. = v/R ~ c/R, имеем
Это и есть длительность импульса излучения, фиксируемая наблюдателем.
Между длительностью импульса и шириной его спектра имеется
известное из теории интеграла Фурье соотношение Дш Д^ ~ 1 (анало¬
гичное по происхождению соотношению неопределенности в квантовой
механике АЕ At ~ К). Это значит, что импульс длительностью Д^ мож¬
но разложить в спектр частот шириной вплоть до частот порядка
При малых частотах мощность излучения растет с ростом частоты ш,
поэтому (6) есть оценка положения максимума в спектре излучения.
Наблюдатель регистрирует не только излучение на основной частоте
обращения электрона, но также и высшие ее гармоники, которые в за¬
висимости от энергии частицы могут попадать в область видимого света
(«светящийся электрон») или лежать выше — вплоть до рентгеновской
области.
Итак, характерная длина волны синхротронного излучения (соот¬
ветствующая частоте wc)
R
R
С	U1Q
(6)

1.9. Электромагнитное поле релятивистских частиц	263
Среднее расстояние между частицами по окружности ускорителя L/N ~
~ 60 А. При случайном, но равномерном распределении частиц по тра¬
ектории излучение некогерентно (L/N А), поэтому полная мощность
излучения
Гп°лн _ NW = £с / £ \^ 15 МВт
3 L \тс J
1.9.6.	Ондулятор представляет собой устройство, обеспечивающее перио-.
дическое движение заряда по траектории, близкой к прямой (рис. 1.17).
Будем считать, что движение электрона по оси ондулятора (вдоль оси х)
происходит с большой (вообще говоря, релятивистской) скоростью.
Однородное периодически изме¬
няющееся во времени электриче¬
ское поле, приложенное в перпен¬
дикулярном к движению электро¬
на направлении (вдоль оси у), вы¬
зывает малые колебания части¬
цы в поперечном направлении.
Используемое приближение пред¬
полагает, что эти колебания прак¬
тически не влияют на движение
электрона со скоростью v ~ с вдоль оси ондулятора (скорость движения
частицы вдоль оси у много меньше скорости вдоль оси х).
Рассмотрим данную задачу в системе отсчета К', которая движется
относительно лабораторной системы вдоль оси х со скоростью vx, где
vx — продольная скорость частицы, усредненная по периоду поперечных
колебаний (условно можно назвать эту систему «системой пучка»). В
системе К' электрическое поле на разных участках конденсатора ко¬
леблется уже не синхронно. Чтобы определить частоту поля в системе
пучка, введем четырехмерный волновой вектор стоячей волны в кон¬
денсаторе, который в лабораторной системе имеет компоненты
k£T = (u0/c, 0,0,0).
С помощью преобразования Лоренца получаем тот же вектор в движу¬
щейся системе К':
Кт = ~(7шо. -/frywo, о, 0),
где /3 = v/c. Для достаточно слабого поля (если в движущейся систе¬
ме К' электроны остаются нерелятивистскими) частота ондуляторного
излучения в системе пучка не зависит от направления и совпадает с
частотой вынуждающей силы k= ушо/с.
Рис. 1.17. Излучение электрона в пе¬
риодическом электрическом поле

264	Глава	1.	Теория	поля.	Решения	задач
Далее рассмотрим волновой 4-вектор ондуляторного излучения в си¬
стеме К'. В предположении о том, что излучение испускается в плос¬
кости (х,у), он имеет следующие компоненты:
k,fl = - (7^0,7шо cos 0',7Wo sin #',()),
с
где в' — угол между волновым вектором к' и осью х. При помощи
обратного преобразования Лоренца переходим в лабораторную систему:
( 72oi0(1 + /3cos0')\
72w0(/3 + cos в')
\
7wo sin (
О
/
UJ
\
ш cos в
ш sin в
\ о
Отсюда получаем связь между углами в лабораторной и в движущейся
системах отсчета:
k' р + cos в'
COS в
1 + Р cos в'
COS в =
— Р + cos в
1 — PcosQ
а также искомую частоту ондуляторного излучения:
U
ck =7 шо(1+/3cos0') =
(1)
■ Р COS в
Как следует из формулы (1), для ондуляторного излучения характер¬
на пространственная дисперсия: под фиксированным углом к оси онду¬
лятора испускается определенная частота. Кроме того, как видно из (1),
с точки зрения спектрального состава ондуляторное излучение суще¬
ственно отличается от синхротронного. В самом деле, в случае реляти¬
вистского движения фактор (1 — (nv)/c) ~ (1 — (3cos6) ~ 7~2 (см. за¬
дачу 1.9.5), следовательно максимум мощности излучения должен при¬
ходиться на частоты порядка
2
ис ~ wo7 — ио
(2)
(ср. с формулой (6) задачи 1.9.5). Указанное отличие двух видов излуче¬
ния связано с разными условиями формирования синхротронного и он¬
дуляторного излучения. Для ондуляторного излучения полный угол Ав,
на который отклоняется вектор скорости за все время движения части¬
цы, невелик и удовлетворяет условию Ав < j~l -с 1. Это означает, что
длина формирования ондуляторного излучения, вообще говоря, боль¬
ше, чем для синхротронного: излучение собирается не с малого участка
траектории, а фактически со всей траектории движения. Общий харак¬
тер излучения остается синхротронным: все излучение направлено в

1.9. Электромагнитное поле релятивистских частиц
А
265
узкий конус вперед по движению, однако максимум мощности падает
на несколько другую величину7'.
1.9.7.	Мощность синхротронного излучения (или полное количество по¬
терь энергии на излучение заряженной частицей в единицу запаздыва¬
ющего времени) имеет вид (см. формулу (5) задачи 1.9.5)
dt _ V _	2^ = &V, ! _ „
М^снихр	3c	3m с	Зт	с
Полагая, что потери энергии за период движения в магнитном поле
малы, приходим к дифференциальному уравнению
HP О	7	2е4#2
£ = тс 7,	^	=	тс27	=	-^синхР,	или	^	-	7^5	•
Решая данное уравнение, находим зависимость энергии от времени.
£	<Л	т- Зт3с5
7=—9=cth 	)•	Т ТГТТл-
'	тс2	\	г	/	2е’Я
В пределе больших 1 - fo находим для кинетической энергии
Т = £ — me2 = mc2|cth^ ) - lj « £оехр(-2-).
Это соответствует формуле для энергии нерелятивистского электрона
в магнитном поле, полученной в задаче 1.8.8.
1.9.8.	Полагая, что векторы скорости и ускорения сонаправлены, т. е.
w || v, имеем	^
w = -Ц.
m'y
Мощность электромагнитного излучения, определяющая энергетические
потери для частицы в единицу времени, постоянна и может быть пред¬
ставлена в виде
„2Г.„	..	.o'!	2е2	6	2	=	2eV
1	з «W
Wra„p = ||{7*w2+76i(v»)2} = |5
Мощность силы, действующей на ультрарелятивистскую частицу в элект¬
рическом поле, т.е. работа, совершаемая электрическим полем в еди¬
ницу времени, равна
2И3£
(eEv) ~ |е|£с, КПД ^ 1 --LL
7)	Оценку для характерной частоты излучения (2) можно получить методом,
использованным в задаче 1.9.5, см. формулу (6).

266	Глава	I.	Теория	поля.	Решения	задач
1.10.	РАССЕЯНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
1.10.1.	Поле падающей волны имеет вид
Еп = Re{E0exp(-iM- кг))}, Нп = (к0 хЕ„],
где к0 = к/|к|, к — волновой вектор падающей волны. Уравнение дви¬
жения нерелятивистского электрона в поле падающей волны:
т'т = еЕП + ^[ухНп|й еЕп да еRe{E0 exp(-iu;l)}.
В данном случае силой -[vxHn], действующей со стороны магнитного
поля можно пренебречь, так как |ЕП| = |НП|, а v/c « 1. Электрическое
поле можно считать однородным (пренебрегая слагаемым гкг в пока¬
зателе экспоненты), поскольку kr ~ v/c -С 1. Заряд движется с ускоре¬
нием, поэтому
а2
A — er = — Re{Eo exp(-ic<;f)}-
m
Поле дипольного излучения:
с /d a d±(t-R/c)	[[d(/ — R/c) х n] х n]
Erf(R, t) = j-r	j-r	.
где n = R//? = (sin0cosy?,sin0sin93,cos#) — единичный вектор в на¬
правлении наблюдения. Символ «±» обозначает проекцию на плоскость,
перпендикулярную направлению рассеяния.
Вектор амплитуды колебаний поля Еа с точностью до нормировоч¬
ного множителя задает вектор поляризации:
_ Еох _ Е0 - п(пЕ0)
~ |Еох| _ |Еох| ’
1) Для падающей волны, линейно поляризованной по оси х, оче¬
видно, Ео ~ (1,0,0) = е*, и мы получаем вещественный вектор поля¬
ризации, т. е. поляризация линейная: а ~ е* — пхп. Для п = ±e* вектор
поляризации рассеянной волны не определен, поскольку в этих направ¬
лениях волна не рассеивается.
2) Для циркулярно поляризованной в плоскости (х,у) волны Ео ~
~ е± = -^=(1,±г, 0), и мы получаем
а ~ е+ \= sin в е±ир п.
\/2

1.10. Рассеяние электромагнитных волн
267
В этом случае для рассеяния строго вперед или строго назад вектор
поляризации рассеянной волны совпадает с вектором поляризации па¬
дающей. Однако, поскольку для рассеяния назад направление распро¬
странения волны меняется на противоположное, рассеянная назад вол¬
на имеет направление вращения электрического поля относительно вол¬
нового вектора противоположное направлению вращения в падающей
волне. Для рассеяния на угол 7г/2 рассеянная волна поляризована ли¬
нейно. При рассеянии на промежуточные углы мы получаем проме¬
жуточные (эллиптические) поляризации, причем в случае рассеяния в
переднюю полусферу направление вращения поля совпадает с направле¬
нием вращения в падающей волне, а для рассеяния в заднюю полусферу
направление вращения меняется.
Если в малой окрестности положения электрона изобразить ориенти¬
рованную кривую, которую описывает конец вектора Еп в данной точке
пространства (отрезок для линейной поляризации, или окружность для
круговой), то поляризация излучения, рассеянного в направлении п,
соответствует тому, как проецируется эта кривая на плоскость зрения
наблюдателя, который смотрит на электрон со стороны вектора п.
1.10.2.	Пусть электромагнитное поле падающей волны имеет вид
тогда вектор Умова-Пойнтинга, описывающий плотность падающего по¬
тока излучения, т. е. Sn = (с/47г)Еак°, где к0 = к/|к| — единичный век¬
тор вдоль волнового вектора падающей волны, после усреднения по
периоду будет равен
Как и в предыдущей задаче, вначале необходимо записать уравнение
движения осциллятора в поле падающей волны:
где первое слагаемое в правой части обусловлено квазиупругой силой,
следующие два слагаемых — силой Лоренца, и последнее слагаемое
есть сила радиационного трения (см. (1.70)):
Еп = Re{Eo exp(-i(u;t - кг))},
|S„| - ^(Е0Е$).
тг = -ти>1т + еЕп + ^[vx Н„] + Frad,
(1)
(2)
Основное условие применимости выражения (2) состоит в том, что си¬
ла |Frad| должно быть мала по сравнению с другими членами уравнения.
Поэтому, поскольку в нулевом приближении (в пренебрежении всеми

268	Глава	l.	Теория	поля.	Решения	задач
малыми добавками) уравнение (1) имеет вид т'г = —тш^г, то отсюда
находим г = — и это учитывается во втором приближенном равен¬
стве формулы (2). Далее мы обозначим
2e2wo
"fr — о 3 ’
3 тс
это есть постоянная затухания, связанная с радиационным трением.
Если существенную роль играют также и другие факторы, вызывающие
диссипацию энергии (например, столкновения атомов, их тепловое дви¬
жение), то в левую часть уравнения (1) необходимо ввести слагаемые
вида -т^'г, где 7' — постоянная затухания, характеризующая величи¬
ну диссипативных эффектов неэлектромагнитного происхождения. То¬
гда величина 7 = 7Г + 7' есть полная постоянная затухания (полная
ширина линии). В итоге мы получаем следующее уравнение:
г -I- 7Г + JqT = — Е0	(3)
и т
В (3) нами сделаны следующее стандартные приближения: мы прене¬
брегли в правой части гкг в показателе экспоненты (поскольку kr ~
~ v/c -С 1), а также опустили магнитную часть силы Лоренца (рассмат¬
ривая предельно нерелятивистский случай v/c —> 0). Амплитуда волны
Ео — величина комплексная, но операцию выделения действительной
части можно отнести на один из последних этапов в вычислениях, по¬
скольку мы используем пока только линейные операции. Решая урав¬
нение, находим
Г(0 =
т и>0 — ш — I'yuj
— устоявшийся режим для вынужденных колебаний (собственные ко¬
лебания осциллятора затухают за время ~ 7-1 и здесь нас не инте¬
ресуют). Учитываем далее, что электрический дипольный момент ко¬
леблющейся частицы равен d = ег, поэтому d = —ш2ег, выделяем ве¬
щественную часть и, усредняя по периоду движения, получаем сред¬
нее значение интенсивности вторичного излучения в телесный угол dft
(см. (1.50)):
y^lfd х ПН2 =	Л*—тг;-2 21 tEo х ПИ2йП,
о7гс	07Гс т \<jj — а;о) + 7 ш
где n = R/R — единичный вектор в направлении точки наблюдения.
Множитель | [Ео х п]|2 зависит от поляризации падающей волны. За¬
метим, что
I [Е0 х п]|2 = [Е0 х п][Е5 х п] = |Е0|2 - (Е0п)(Е» = (6у - л.-Я/^До/,

1.10. Рассеяние электромагнитных волн	269
следовательно, дифференциальное сечение рассеяния можно записать
в виде
= -L£. = ( е" V	(6	-	-	п	п	)^
dQ	UcV	(w2-4)	+	72w2	|Eo|2
(4)
Здесь e2/{mc2) = гкл — классический радиус заряженной частицы. На¬
помним далее, что вектор Е0 — комплексный, но он поперечен: (Е0к) = 0.
В плоскости, перпендикулярной вектору к, можно разложить ампли¬
туду Ео по взаимно перпендикулярным (вообще говоря, комплексным)
ортам е(|* и е(2), которые вместе с волновым вектором к (в дальнейшем
будем использовать также к0 = к/|к|) образуют правую тройку век¬
торов: (е(1)е(2)) = (е(12)к) = 0, е(2) = [к0 х е(|)] (см. также (1.45)). При
помощи этого локального базиса описывается поляризация исходной
волны. Как видно из (4), непосредственно с поляризацией падающей
волны связана функция
ВД,
РЦ |Е0|2 ’
называемая тензором поляризации.
Если поляризация падающей волны линейная, то для ее описания
достаточно одного вещественного вектора поляризации, например, е(|),
и поэтому pij = е(Ре^\ а дифференциальное сечение рассеяния равно
(	) и„= (J - wg) + 7V ^ ~ (ne(U)2') •	(5)
Данную формулу можно записать в несколько ином, эквивалентном,
виде, если заметить, что (1 - (ne(1))2) = sin2#, где в — угол между век¬
торами п и е(|).
Если поляризация падающей волны правая или левая циркулярная,
то вместо вещественных векторов е*1* и е*2* рассматривают орты е(,) =
= -^=(е(1)+(7е<2)), где I = ±1, причем I = +1 отвечает правой, а I = -1 —
v2
левой циркулярной поляризации. При этом тензор поляризации прини¬
мает вид
„.. _ ifx k°k°) — — е k°
Рч — £ \ ч	< I)	2	Чп п'
где мы учли, что
£ efef* = 6ц - Щ.
п=1,2
Дифференциальное сечение рассеяния в этом случае:
(g)„^T(^-i+7v<i+(nk0);)-	<б)

270 -l\r Глава I. Теория поля. Решения задач
Данную формулу можно записать по-иному, если заметить, что
(1 -I- (nk°)2)/2 = (1 + cos2$)/2, где д — угол между направлением рас¬
пространения падающей волны к и направлением рассеяния п.
Для естественного света усредним вектор е(|) в формуле (5) по всем
направлениям, перпендикулярным вектору к, используя соотношение
В результате мы получим дифференциальное сечения рассеяния есте¬
ственного света, которое в точности совпадает с (6).
Полное сечения рассеяния получается в результате интегрирования
по углам любого из выражений (4), (5) или (6), не зависит от поляри¬
зации падающей волны и имеет вид
_ 8я- ji	w4
аР о~ГклТ~2 27F7	2	2	*
Л (w0 — ui ) -I- 7 w
Полученное нами полное сечение рассеяния характеризуется следую¬
щими отличительными чертами.
Для частот, много меньших частоты связи (и <С wo) сечение рассея¬
ния сгр ~ (w/wo)4, т. е. интенсивность рассеяния длинноволнового излу¬
чения обратно пропорциональна четвертой степени длины волны (закон
рассеяния Рэлея). В области частот, близких к wo, сечение рассеяния
демонстрирует резонансное поведение, т. е. сильно возрастает. Ширина
максимума характеризуется постоянной затухания 7. На высоких ча¬
стотах (и) » wo) сечение приближается к томсоновскому сечению для
свободной частицы (1.71). Следует однако иметь в виду, что примени¬
мость данной формулы в области высоких частот ограничена: кванто¬
вые эффекты начинают играть существенную роль, когда энергия кван¬
та излучения Нш ~ тс2. Резко выраженное резонансное рассеяние при
w ~ wo называется резонансной флуоресценцией.
Поляризация рассеянной волны исследуется теми же методами, что
были применены в задаче 1.10.1, общие выводы — такие же.
Сечение поглощения можно определить, как отношение энергии,
поглощенной в единицу времени в единичном интервале частот к вели¬
чине падающего потока энергии в этом же частотном интервале. Энер¬
гия, поглощаемая в единицу времени, есть не что иное, как мощность
силы трения:
1^ПОГЛ = (РтрГ) = Я17|г|' ,
откуда после выделения вещественной части и усреднения по времени
следует
W - е2 7^2|Eq12
w погл о / 2	2\2	2	2	*
2m (Шо — ш ) + 7 w

1.10. Рассеяние электромагнитных волн	271
При этом сечение поглощения оказывается равным
Wno?n е2 47TC7W2
(Тпогл — ттг г —	2,2	2\2	,	22'
|S„| тс (и>о — и>) +7«
Видно, что вблизи резонансной частоты	сечение	поглощения так¬
же имеет резонансный характер. Сечение поглощения можно назвать
полным сечением, так как оно учитывает влияние всех диссипативных
процессов как электромагнитного, так и неэлектромагнитного проис¬
хождения, ибо при расчете мы не интересовались будет ли поглощенная
энергия в дальнейшем излучена в виде рассеянной электромагнитной
волны или рассеется другим способом.
1.10.3. См. задачу 1.10.4 в случае шо = 0.
1.10.4. Запишем уравнения движения осциллятора в поле Но и поле
волны:
тг = -ти)1г+ ^г'г + еЕ„ + -[г х (Нв + Н0)1,
Зс3	с
Ев = Еп Re(eei(kr“a")), (ее*) = 1, (ек) = О,
где е — вектор поляризации падающей волны (по условию задачи поля¬
ризация должна быть циркулярной). Далее мы делаем стандартные при¬
ближения (см. задачу 1.10.2): пренебрегаем магнитной составляющей
силы Лоренца, а также опускаем kr <С 1 в показателе экспоненты. Для
режима установившихся колебаний г ~ е~ш‘, поэтому г = —ш2г. Счи¬
таем, что внешнее поле Но направлено по оси z. В итоге уравнение
приводится к виду
г + Ц)г + 7Г + ин [ez х г ] = ^ Re (ее-1"'),
2е2 ш2	еНо
7 ~~ 3 тс3 ' UH ~ тс'
где ez — вещественный единичный вектор вдоль оси г. Будем искать
решение для установившихся колебаний в виде r(t) = р0е~,ш‘. Усред¬
ненная по периоду плотность потока энергии в падающей волне и усред¬
ненная интенсивность рассеянной дипольной волны в направлении п =
= (sin 0 cos у?, sin 0 sin (/?, cos0) имеют вид
did = ^(|Ро|2-(р0п)(р$п)уа
07Г	87Г	С
поэтому дифференциальное сечение рассеяния:
da = ^	-	nmtpoufydSl.
|Sn | с t,n

272 ->\r Глава 1. Теория поля. Решения задач
Уравнение движения для комплексной амплитуды р0 приводится к
виду
-из2р0 + ш1р0 - iuj'YPo - iuu>H[ez х р0] = —е.	(1)
т
Для компоненты poz вклад векторного произведения обнуляется, и мы
получаем
1	еЕП
РОг
2 2
и>о — ш — гсы'у т
где е2 есть проекция вектора е на ось г. Проекция уравнения (1) на
плоскость (х,у) дает
из\ — ш2 — iuj') —шшн	\{ рох\	еЕ„
iuiu>H	ujq — J1 — iuj'y J\poyJ	m
где ex, ey — проекции вектора поляризации e. Обращая матрицу, полу¬
чаем решение для амплитуды:
Г ujq — uj2 — iuj'y	iuiuiH
ч	п\	2	2,,
рох\	V	—1шшн	и>о	—	из	—	iuj'y	J	/ех
РОу J ш ( [uj0 — uj — iuj'y] —	\e,
а)	Случай k|| H0. При этом вектор поляризации ортогонален на¬
правлению поля: (еНо) = 0. Выберем для циркулярной поляризации
е = ej*' = (1, ±{, 0)/\/2. Получаем
р _ еЕп(ш1 - из2 - iuj'y т	_	eEne\^
т([ш1 — о? — iuj'y]2 — из2ujji)	т(и>1 — из2 — iu>7 ± изизн)
Тогда дифференциальное сечение рассеяния для правой (левой) цирку¬
лярной поляризации будет иметь вид
fda\^ ( е2 \2	ш4	1,,
УШ) ~ {^) U-Jl±u>UH)i + J1^°S
Заметим, что полученные дифференциальные сечения содержат знаме¬
натели, обладающие характерным резонансным поведением. Так в слу¬
чае слабого поля (изн < изо) для падающей волны правой (левой) цир¬
кулярной поляризации резонансное условие выполняется для частот
из ~ шо ±и;#/2, и это полностью соответствует расщеплению частот во
внешнем магнитном поле, имеющему место в эффекте Зеемана.
В пределе сильного поля нужно считать, что изн 3> из, изн > изо, изн 3> 7.
В этом приближении находим следующее выражение:
/Лт\(±> pda\ecT	9 и2	1

1.10. Рассеяние электромагнитных волн	273
которое является справедливым как для циркулярно поляризованного,
так и для естественного света.
б) Случай k_L Но. Тогда для циркулярной поляризации выберем
вектор поляризации в виде е —	= (0,1, ±г)/\/2. Считая, что и>ц мно¬
го больше чем из, изо, 7, находим
(
Ро =
еЕп
V2 т
\
\ll1q — UJ — iuf'y] — UJLUH
2	2
CJq — CJ — lUJ 7
~2	2	• i2	2	2
Jq — UJ — lUJ^l — UJ UJfi
±i
2	2
cjq — a; — *017
V2m(Jl — uj2 — iuj)
fo\
0
V1/
По существу мы получили, что сильное магнитное поле «заморажива¬
ет» движение осциллятора в перпендикулярном к полю направлении и
при этом не влияет на его продольное движение. Для обеих цирку¬
лярных поляризаций получается одинаковое сечение рассеяния, кото¬
рое также совпадает с сечением для естественного (неполяризованного)
света:
do
1 2
-г
(wg - и/)* + w 7'
1.10.5.	Для магнитного дипольного рассеяния
(1 - cos 0).
|=»п| - 4п -
dl„
dil
47Г с3
(р2-(рп)2),
do _ dlц
Ш
с4/У2
Здесь ц — магнитный дипольный момент, п — единичный вектор в
направлении наблюдения. Уравнение эволюции во времени магнитного
дипольного момента имеет вид
А = 7еМ = 7e[/Lt X Н].
Магнитное поле циркулярно поляризованной волны вращается вокруг
волнового вектора: dH/dt = [из х Н], где из = ±uk/k = ±шк°, к0 =
= (0,0,1). (Волновой вектор направлен по оси г) Поэтому
А = 7е((А х Н] + \ц х Н]) = 7е2[[д х Н] х Н| +7е[ц х [из х Н]].
Критерий малости гиромагнитного отношения в данной задаче:
7еН -с из. Он означает, что угловая скорость прецессии магнитного мо¬
мента в поле Н мала по сравнению с частотой падающей волны. Для
малого гиромагнитного отношения имеем
А ~ 7е[р х[ихН]] = 7е[и>(мН) - H(/iw)] = 7ew(/iH) и 7eu>(/j0H).

274	Глава	1.	Теория	поля.	Решения	задач
Таким образом, магнитный дипольный момент совершает малые коле¬
бания в плоскости, натянутой на векторы ш || к0 и д0. Поскольку маг¬
нитный момент совершает малые колебания около среднего положения,
при усреднении по времени /I заменяем на д0:
(МоН)2 = pomojHiHj.
Усредним теперь произведение Я/Я/ по времени:
В силу того, что вектор /7 совершает гармонические колебания, остава¬
ясь параллельным оси г, диаграмма направленности рассеянной волны
отвечает магнитному дипольному излучению с осью симметрии г.
1.10.6.	Поле падающей волны внутри конденсатора компенсируется по¬
лем зарядов, наведенных на обкладках конденсатора. Плотность наве¬
денных зарядов и их дипольный момент имеют вид
Находим далее угловое распределение интенсивности дипольного излу¬
чения (ниже в — угол между радиус-вектором точки наблюдения R и
вектором Ео падающей волны) и сечение рассеяния:
= Я2 slnwtcosujt sin20	=	Я2^	diag(l,	1,0).
^	0	0	Оу
Учитывая что fiz — О, получаем
(МоН)2 = /zoz/V^IdiagO, 1,0)]// = \н^1 = 1-Н2р\
da = (i _ (nk0)2) dQ = sin2 в dn.
2c	>	’	2	с4
s
E ^ _ asE
47Г ’	47Г
(^)cosM)

1.10. Рассеяние электромагнитных волн —'у- 275
1.10.7.	Поле падающей волны внутри катушки компенсируется полем
токов, наведенных в обмотке. Наведенный ток и соответствующий маг¬
нитный дипольный момент:
, саН	asH	(asHo \	,
м =	47	= “ \~4jT ) costwi)'
Угловое распределение интенсивности магнитного дипольного излуче¬
ния (ниже 0 — угол между радиус-вектором точки наблюдения R и
вектором Но падающей волны) и сечение рассеяния:
din	и2	. 2 /1	1	/	asu;2	ы \2	. 2 п
—^	sin"	в	=	—т	-r-Но sin" в,
d-Pl	4тгс3	8тгс3	V	4тг	у
2 „2 4	.	„1.1	,4
da	!	din	aVta’	.	2	а	Г	,	aVuT
— = = —£ = T-rSin 0,	(7=	da	=	т-
|Sn I dQ 167Г C	J	67Гс
1.10.8.	Для грубой оценки можно считать угловое распределение рас¬
сеянного света по направлениям близким к изотропному. Это долж¬
но быть справедливо для близких к Солнцу участков короны, которые
освещаются фотосферой практически изотропно из нижней (со стороны
Солнца) полусферы. Толщину ближайших к Солнцу слоев короны D
оценим как диаметр Солнца. Корону считаем практически прозрачной.
Яркость соответствует энергии, излучаемой в единицу времени с
единицы наблюдаемой площади. Полная интенсивность света, рассеян¬
ного участком короны вдоль луча зрения, равна интенсивности на один
электрон /е, умноженной на число электронов:
Аюлн расе = A- nsD.
Здесь п — плотность электронов в короне, s — площадь малого участка
короны, перпендикулярного лучу зрения. Отношение яркостей равно
Ю_6 = £ =	=	...	/-п£>..- = aTnD,
/0/(4тг4)	/0/(4тгД|)
где cry — томсоновское сечение рассеяния для свободной частицы (1.72),
7?0 — радиус Солнца, /© — полная интенсивность излучения (свети¬
мость) Солнца. В итоге
£	£	3	(тС2\2 гг 1 /\6	-3
n=^D = DSi{T] = 5'10 “ '
1.10.9.	Для оценки критической светимости звезды приравняем силу,
действующую на систему электронов и протонов, связанных кулонов-
скими силами, со стороны излучения фотосферы (видимой поверхно¬

276 ->\r Глава I. Теория поля. Решения задач
сти) звезды, т. е. световое давление — силе гравитационного притяже¬
ния звездой.
Сила светового давления на систему зарядов есть средняя по времени
сила радиационного трения, и ее можно представить в виде (см. (1.73))
F = arwn,
где п — единичный вектор в направлении распространения волны, па¬
дающей на систему зарядов, W = Е2/(47г) — средняя плотность энергии
в этой волне, ар = 8ят§/3 — сечение томсоновского рассеяния волны
на заряде, Гр = е2/тс2 — классический радиус электрона.
Так как «тг ~ 1/т2, и масса протона много больше массы электрона
(тр ~Э> те), а сила гравитационного притяжения GmM/R2 ~ т, где G —
гравитационная постоянная, М — масса звезды, R — радиус ее фотосфе¬
ры, то выражая среднюю плотность энергии поля w через светимость
звезды согласно / = AtxR2wc, получаем
 («О ^кр _ ОтрМ
tW~°t
где a— сечение томсоновского рассеяния на электронах оболочки
(атмосферы) звезды. Поэтому критическая светимость будет равна
= 4тгcGmLM	0 g Ю5М
р 4е)
Отметим, что в формулу не входит R — радиус фотосферы звезды. Это
связано с тем, что световое давление, как и гравитационное притяжение
пропорциональны R~2.
Для Солнца получаем отношение светимости /0 к критической /©кр:
1@_ =	4 ■ 10м	_ 4 • 10*	^ 0	ю_4
7©кР	O,6 1O5Af0	1,3 Ю38
т. е. человечество в этом плане может не беспокоиться.
1.10.10.	В силу условия г<^А внешнее поле вблизи сферы считаем прак¬
тически однородным, и предполагаем, что рассеянная волна создается
дипольными электрическим и магнитным моментами, которые индуци¬
руются падающей волной.
Полное электрическое поле в центре сферы должно быть равно ну¬
лю, из этого условия получаем дипольный электрический момент:
Ео cos(wO
+ i —~ Ir ~ r3^‘° cos^^'

1.10. Рассеяние электромагнитных волн
Магнитное поле в центре сферы должно быть равно нулю, поэтому
Но cosM) + /[VX (J3f^ d~ = 0, д = J |r|—v- dp = - j H0 cos(ujt).
Электрический и магнитный дипольные моменты оказались одного по¬
рядка, поэтому необходимо учесть как электрическое, так и магнитное
дипольные излучения. При этом угловое распределение интенсивности
и дифференциальное сечение рассеяния будут содержать интерферен¬
ционный член.
Запишем магнитное поле в волновой зоне:
u _n(nx/i) , |dx n]
"волн —	2 т !,
c'R	сгР
и найдем интенсивность излучения магнитного и электрического мо¬
ментов в телесный угол dtt:
dl = (SBMH(nR2) dn) = C-^R2Н20л„ = A [n(n x Д) + [d x n]]2,
47Г	47ГС
dl = — [fi2 - (Дп)2 + d2 - (dn)2 + 2(/i|d x n])].	(1)
47Г С
Последнее слагаемое в (1) — интерференционный член. Пусть ампли¬
туда поля Ео направлена вдоль оси х, а амплитуда Но — вдоль оси у,
тогда, поскольку у = d/2 (см. формулы выше), имеем
dI = Аы? ^	_	^(пег/)2	+	(пег)	-
dl =	Еа	[| - sin2 0 cos2 у? - sin2 в sin2 tp + cos в
8тг с3	L5
dn.
,6 4
, Г UJ
dcг = —Г
с
- - sin 0 cos ю — sin в sin ц> + cos в
5
При интегрировании по телесному углу оказывается, что вклад интер¬
ференционного члена равен нулю, поэтому

глава КВАНТОВАЯ МЕХАНИКА
2
2.1.	ОПЕРАТОРЫ	И	СОСТОЯНИЯ
В КВАНТОВОЙ МЕХАНИКЕ
2.1.1. H = i+ = i, т-‘ = т_а = т+
2.1.2. Собственные значения: Л = ±1, собственные функции: 'ф(-х) =
= ±гр(х) — четные и нечетные.
2.1.3. Пусть Та'ф(х) = A(a)xp(x). Собственные значения можно опреде¬
лить из следующих предположений:
• |A(a)| — 1 — условие отсутствия неограниченного роста функции при
х —у ±оо.
• А(а)А(Ь) = А (а + Ь) — следствие группового свойства операторов
трансляции 1а1ь = Та+&.
Исходя из этого, имеем А (а) = е‘Ка, где Im К = 0. Собственные функ¬
ции — функции Блоха 1рк(х) = е‘Кхик(х), ик(х + а) = ик(х).
2.1.4. Для решения задачи необходимо использовать разложение экс¬
поненты в ряд Тейлора.
• Для оператора ехр(г</?1) после разложения сгруппируем слагаемые,
содержащие четные и нечетные степени оператора I (четные сте¬
пени I дают единичный оператор, а нечетные — снова оператор I).
В итоге
exp(iVI) = 1 cos ip + il sin <p.
• Для оператора expQp^aj переходим в координатное представление
и раскладываем экспоненту
expQp^a^M = exp(a^)^M ^ Ф(х) + аф'(х) + ~гр"(х) + ...=
= ip(x + а).
Таким образом, мы имеем дело с оператором трансляции.

2.1. Операторы и состояния в квантовой механике
2.1.7. Для доказательства эрмитовости А+А необходимо использовать
свойство (А+)+ = А и результат задачи 2.1.6. Далее
(А+А) = (ip\A+A\ip) = тА+)(Щ)) = ||А|</>}||2 ^ О
ввиду неотрицательности квадрата нормы вектора.
2.1.8. Если |ф) — собственный вектор оператора А, то сразу получаем
утверждение задачи. Обратно: если верно утверждение, указанное в усло¬
вии, а именно (А2) = (А)2, то ясно, что (ДА2) = (V'KA - (А))2|^) =
откуда следует, что А|^) = (А)|^>).
2.1.9. Пусть
f(A) = (i»\m,	( ДА = А — (A)i,
< Л Л и тогда < Л Л Л „
\ (В) = (#*№>	[ ДВ = В — (В) 1,
при этом, очевидно [ДА, ДВ] = ihC. Введем в рассмотрение вектор \ip)
такой, что
\р) = (ДА - »7ДВ)|^), тогда (tp\ = (^>|(ДА + г'7ДВ).
Здесь мы учли эрмитовость операторов, действительность средних значе¬
ний, а также 7* = 7 по определению. Построим следующую конструкцию:
Ш = НИН2 - ШДА + «7ДВ)(ДА - /7ДВ)|^> =
= (ДА2) + 72(ДВ2) + 7А(С) >0,
ибо квадрат нормы вектора положительно определен. Мы получили квад¬
ратный трехчлен относительно 7. Для того, чтобы это выражение было
положительным, нужно, чтобы его дискриминант D < 0, т. е.
А2(С)2-4(ДА2)(ДВ2) <0.
Отсюда и следует утверждение, которое следовало доказать.
2.1.10. Предположим, что спектр оператора F невырожден. Оператор F
должен обладать полной системой собственных векторов F |F,) = F; |F,-).
Поскольку [A, F] = 0, то
AF|F,> = FA|F,) = F,A|F,),
т. е. вектор A|F,) — также собственный вектор оператора F и отвечает
тому же собственному значению F,. Мы считаем, что спектр F невы¬
рожден, поэтому каждому F,- должен отвечать в точности один соб¬
ственный вектор, т. е. A|F,) = A,|F«). Аналогичное рассмотрение для one-

280	Глава	2.	Квантовая	механика.	Решения	задач
ратора В приводит к соотношению B|F,) = В,IF,). Отсюда следует, что
для любого собственного вектора |F()
(АВ - BA)|F() = (А,В, - B,Ai)|F/> = 0.
Система векторов |F,) полна, поэтому получаем противоречие.
2.1.12. Указание: вычислить коммутаторы
(х,й1 =	1р*-*'] =
и воспользоваться определением функции от оператора.
2.1.13. [Та, х] = аТа, [Та,рж] =0.
2.1.14. Приводим ответы, штрихом обозначается производная функции
по ее аргументу, т. е. по г.
[Рх./М] = -ihf'(r)-r<
[Рх./(О] =	+	^rw}.
x,expQapx)] - -aexpQapx).
2.1.15. Оператор скорости по определению есть производная по времени
от оператора координаты. Поскольку последний явно от времени не
зависит, имеем
где Т — оператор кинетической энергии. Далее
[U(г), г] - О, [Г,г] =
Таким образом, v = р/т.
2.1.16. Указание-, воспользоваться свойством функции от оператора
^(?)1/п) = F(fn)\fn), если /|/л) = fn\fn)-
2.1.17. Обозначим ^АВе~^А = Q(0- Легко получить, что
Р_ г
L2 т’
= —г/г—.
dQ(0
= [A,Q(0], ^P = [A,[A,Q(0]], и т.д.,
Ъ L	dt
откуда имеем разложение в ряд Тейлора:
0(0 = е«АВ<Г«А = В + i [А, В] + | [А, [А, §]]+..

2.1. Операторы и состояния в квантовой механике _/W81
2.1.18. U{г-а). Использовать результат задачи 2.1.17.
2.1.19. Пусть Та|•ф) = |0). Найдем связь двух векторов состояний \ф) и
|0) в координатном представлении, т. е. связь волновых функций. Спро¬
ектируем полученные состояния на состояние |г):
(г|Та|0) = <Г 10) = 0(г).
Выражение слева «расщепим» при помощи единичного оператора 1г =
= J|r')(r'| d3r':
(г|ТаТг|0> = f d3r'(r|fa|r')<r'|0) = J d3r'{r\r' -a)0(r') =
= J d3r'6{r-r'+ a.)tp(r') = V>(r + a).
Окончательно в координатном представлении Та0(г) = ф(г + а).
2.1.20. Оператор координаты в координатном представлении есть опе¬
ратор умножения на (действительное) число х (см. (II.4), для простоты
ограничиваемся одномерным случаем). Пусть оператор координаты дей¬
ствует по схеме <р(х) = хф(х). Перейдем к импульсному представлению.
С этой целью вначале запишем
оо	ОО
«	Г	;«'v	-
(1)
V2n h
L= [ e,£^(p{p')dp' =	f	хе*гГф(р')	dp',
!ttk J	V2tXh	J
где ip(p) и ip{p) — функции в импульсном представлении. Воспользуемся
1 ipx
условиями ортонормированности и полноты и умножим (1) на -j==e ь ,
а затем проинтегрируем по х. В результате в левой части получим
оо	оо
// 2hie<ie~**L	dxdp'= / S(j> ~ dp' = &&)•
-оо	-ОО
В правой части (1) будет
оо	ОО	;
.// ^e^W)dxdp' = II ^(Р')(-^)е^ахйР' =
-ОО	-оо
ОО
= I 5(p-p')[ih-^j^(p')dp' = т^ф{р).

282	Глава	2.	Квантовая	механика.	Решения	задач
Здесь мы проинтегрировали по частям по р', имея в виду убывание
функций на ±оо. Таким образом, мы получили, что в импульсном пред¬
ставлении
Ф(Р) =
Аналогично можно получить и выражение для оператора импульса
в координатном представлении (см. (II.5))
2.1.21.	Действуя по той же схеме, что и в предыдущей задаче, получим
ОО	ОО
Uof —о)х'
= Е(р(р).
2^(Р) + J dp'vlp') 2^ J dxU(x)eJeLn£L
—оо	—ОО
2.1.22. Будем считать, что собственные векторы оператора /(А) норми¬
рованы на единицу: (п\п) = 1. Продифференцируем по А левую и пра¬
вую части уравнения
?(А)МА))=/я(А)|я(А)>	(1)
и получим
^И)+/0)|И = ^|»> + /.(Л)|;|Л>.	(2)
Умножим все слагаемые в (2) слева на бра-вектор (я|, учтем соотноше¬
ние (1) и эрмитовость оператора /(А). В результате получаем утвержде¬
ние теоремы.
2.1.23. Вначале, используя результат задачи 2.1.17, найдем явный вид
операторов координаты и импульса в представлении Гейзенберга для
свободной одномерной частицы (см. (11.11)), т. е. для Н = р2/(2т):
хн =	=	х	+1—,
т
рн = <?£й(ре_*й( = р,
где х и р — операторы в представлении Шредингера. Среднее значение
координаты (xH)t = (‘Фн^нЩ'фн) имеет вид
(хя), = <х)о ± ^(р)о = х0 + v0t,
т. е. эволюционирует во времени, как координата свободной классиче¬
ской частицы массы т.

2.2. Одномерное движение	283
Для того, чтобы определить закон расплывания волнового пакета, най¬
дем зависимость от времени дисперсии координаты (Дх2)( = (х^) — (хя)2,
которая характеризует эффективную ширину пакета. Учитывая, что
{x2H), = (х2)0 + - (х р + рх)0 + —2 (р2)о,
т'	т2
получаем
(Хи)? = (х)о + 2^-(х)о(р)о + ~~2 (Р)о•
(Дх2)( = (Дх2)0 -I- ^(ДхДр + ДрДх)о + А;(Др2)о-
2.2.	ОДНОМЕРНОЕ	ДВИЖЕНИЕ
2.2.1.	В данной потенциальной яме возможен только невырожденный
спектр энергии частицы. Волновая функция частицы удовлетворяет
уравнению
^ + Ц(Е - и(х)Шх) = О,
h
должна быть непрерывна в точках 0 и а и нормирована на единицу.
При х ^ 0 и х ^ а должно выполняться -ф(х) = 0, а при 0 < х < а
справедливо уравнение
■ф" + к24>( х) = 0, k2 =
п
т. е.
-ф(х) = C\tkx + c2e~lkx.
Из условий непрерывности ip(x) получаем ip(Q) — C\-\-c2 = Q, т. е. ip(x) =
= с sin/гх, а также ip(a) = csin/гх = 0, поэтому
fc2(,2	2fc2
,	п	П	К	7Г	П	2
ka — n-x, Ьп = —— 	хП ,
2 т	2 та2
1~2 . жп п .
, ,/ - sin —х, 0 < х < а,
Фп(х) = ( V а а
О,	х	<	0,	х	>	а,
где n = 1,2,3... . Таким образом, состояние определяется одним кванто¬
вым числом. (Подумайте о том, может ли п быть равным 0, —1, —2,....
Нет ли вырождения по энергии?)

284	Глава	2.	Квантовая	механика.	Решения	задач
Дальнейший расчёт удобно вести в естественной (для данной зада¬
чи) системе единиц: h = 1, т = 1, а = 1, тогда
р 7г2"2	/ / ч fv^si
Еп = —, V’nW = < 0
sin 7гпх, 0 < х < а,
х ^ 0, х ^ а.
Таким образом,
1 1
(п|х|л) = Jхх1>2п(х) dx = - - — J sin ах dx\a=inn = ^
о	о
т. е. в обычных единицах (я|х|я) = а/2, а также
1
(л|(Дх)2|я) = (я|х2|л) - (л|х|я)2 = J х2грп(х) dx - ^ =
1 д Г	Л	I	11	1
и в обычных единицах {я|(Дх)2|л) = Н —
2(7ГП)2.
Классическая плотность вероятности найти частицу в интервале
(x,x + dx) есть р(х) = 1/а (скорость частицы в ящике постоянна). То
есть в классическом пределе
x=Jxp(x) = |,	(Дх)2	=	^,
о
что совпадает с квантовым результатом при п » 1.
Волновая функция частицы в импульсном представлении:
1 1
грп(р) = (р\п) = J(р\х)(х\п) dx - J ~^=e~ipx\/2 sin nnxdx =
о	о
. (р-пп\
, п sin --- ■■■
_.{£-пж)	I 2	)
= —12 >/¥е	2	 2	V 2 •
Р ~(П1г)
В квазиклассическом приближении (п з> 1) распределение по импуль¬
сам вблизи р = ±П7г имеет вид
оо	оо
7Г£Г	J	ТГЕ	J X	*
— ОО

2.2. Одномерное движение	285
где е = р ± пл, что соответствует классической плотности вероятности
распределения по импульсам:
р(р) = U(p-p„)+ ^(р+рп), Рп = \ДГп = ЯП.
Фазовая плоскость, как и траектория частицы на ней, — понятие
классическое, поэтому рассмотрим эту часть задачи в квазиклассиче-
ском приближении: h —> 0, п —* оо при конечном hn. Фазовые объёмы
для состояний с энергией Е < Еп и Е ^ Еп+\ имеют вид
Г„ = 2рпа = 2лКп (рп = \/2тЁп -	,
Г„+1 = 2pn+ia = 2л П(п + 1).
Следовательно, объём, приходящийся на одно квантовое состояние,
ДГЛ = Гл+, — Г„ = 2лН.
2.2.2.	Используем оператор инверсии I. Поскольку в координатном пред¬
ставлении
Н =	+ U(x), а также U{x) = U(-x),
2 m dx2
получаем [I, H] — 0.
Таким образом, волновые функции невырожденного дискретного спек¬
тра данной задачи (£ < 0) обладают определенной четностью
Г Н'Фе(х) = ЕфЕ{х),
\ IфЕ(х) = ±Фе(х),
и данная система уравнений будет заведомо совместна. Обозначая
=	=	kl	=	2-^,
h	п
получим уравнения для определения Фе(х) при \х\ < а:
Ф"е(х) + к2фЕ(х) = 0
и при |jc| > а:
Ф"е(х) - х2ф(х) = 0.
Таким образом, для четных состояний получаем Фе(+\х) = A coskx
при |х| < а и Фе^^ — Ве~н\*\ при |х| > а. Вследствие явного учета
четности функции граничное условие достаточно поставить в одной из

286	Глава	2.	Квантовая	механика.	Решения	задач
точек х = ±а. Из условия непрерывности логарифмической производ¬
ной для функции 'ФеМ при х = а получим
У>е(д + 0) _ У>е(Д ~ 0)
грЕ(а + а) #(д - 0) ’
Т'е‘ 2
ktgka = x, k2 = kl~x2, или	=	l	+	tg2&a.	(1)
На основании этого имеем
ka
| cos£a|
koa
при обязательном дополнительном условии tgka > 0, которое следует
из (1). Уровни энергии определяются формулой Еп — -h2x%/(2m), где
я = 0,1,2,... (рис. 2.1).
I tg ka > Oi
I tg ka > О I
Рис. 2.1. Определение уровней энер¬
гии для четных состояний
Рис. 2.2. Определение уровней энер¬
гии для нечетных состояний
Четное состояние существует при малой глубине Uo ямы (koa > 0).
N четных состояний существует при koa ^ (N — 1)7г. Из условия непре¬
рывности функции
г/>(а - 0) = ф(а + 0)
В = Ае*а cos ka.
получаем
Условие нормировки дает
а	оо
1 = 2\А |2 {^J cos2 kxdx+ J cos2 kae~2*(x~a) dx^j,
откуда в результате несложных вычислении имеем
1
2 \ —1/2
sin2£a , cos ka
+
В = Ae*a cos ka.

2.2. Одномерное движение ->V 287
Для нечетных состояний волновая функция должна иметь вид
Фе ’М =
где
{A sin kx,	\х\ < а,
В sign(jc) е—,	\х\>а,
sign(x) =
1,	х > О,
-1, х < 0.
Уровни энергии для нечетных состояний определяются из уравнения
kctgka = -x,	62 =	-	х2, т. е.	= l + ctg2^a
или
kd
| sin Дга| = —— при igka < 0.
RoCL
Как видно из рис. 2.2, нечетные дискретные состояния существуют
при условии koa ^ -к/2, (ka/(koa) = 1, когда koа = тт/2), т. е.
2 fc2
Uo > \—2.
о та
Это и есть условие существования хотя бы одного нечетного состояния
в такой яме. N нечетных состояний существует при koa ^ nN/2.
Из непрерывности функции тр(а + 0) = ф(а — 0) следует
В = Ае*а sin ka.
Учитываем условие нормировки нашей функции
а	оо
= 2|Л|2^ sin2 kx dx + sin2 ka j	dx'j
1
о
и получаем итоговый результат:
. sin26а , sin ka\ ^	„	л	*a	■	и
1	  1	,	В	=	Ae	sin	ka.
2ka	xa	1
2.2.3.	Сила, действующая на частицу со стороны потенциальной ямы,
представляет собой оператор F = -dU/dx = -dW/dx. Рассмотрим вна¬
чале яму конечной глубины Uo, имея в виду дальнейший предельный
переход Uo —> оо. При этом
U(x) = U0(9(x — а) + 1 - 0(х)),

288	Глава	2.	Квантовая	механика.	Решения	задач
где 0(х) — ступенчатая функция Хевисайда (Д.13):
е(*) =
Отсюда следует, что
F = -^ = U0{6(x)-6(x-a)).
Второе слагаемое данного выражения представляет собой оператор
силы, действующей на частицу со стороны правой стенки потенциаль¬
ного ящика. Нетрудно получить, что Fnp = -UoS(x-a) = dU/da = dW/da.
Используя теорему Фейнмана-Гельмана (задача 2.1.22), для среднего
значения этой силы находим
аЙ Л дЕ„ _ тг2/г2л2	2Еп
/ 1C I \	\
<n|Fnp|n> = {п — п) = — =
_ з
та
Заметим, что мы нашли среднее значение силы, действующей на
частицу со стороны правой стенки потенциального ящика. Сила, кото¬
рая действует на стенку ящика со стороны частицы, имеет, очевидно,
противоположный знак.
2.2.4. Получим решение задачи о состояниях дискретного спектра в
данной потенциальной яме на основании анализа нечетных решений
задачи 2.2.2.
Граничные условия, накладываемые на волновую функцию в точке
х = 0ина^и^'в точке х = а, совпадают с соответствующими гра¬
ничными условиями для ■)/>£ *(х). Однако область, где волновая функция
отлична от нуля, уменьшается вдвое. Поэтому	*(х) нужно умножить
на V2. В итоге получим волновые функции в виде
Ых) = м. *>°.
\о, х ^ 0.
2.2.5. При исследовании данной задачи используем следующие пред¬
положения.
• Считаем, что яма мелкая, и тогда, как это следует из анализа за¬
дачи 2.2.2, в ней присутствует единственный дискретный уровень
энергии, отвечающий четной волновой функции. Таким образом,
koa <S 1, или 2mt/° д2 ^ j
h

2.2. Одномерное движение	289
Мы используем здесь обозначения задачи 2.2.2, т. е.
rr	Ы	h2X2	<2   у2 J2
=	|е1	= ^Г’ k~ko-^-
• Полагаем, что энергия связи мала по сравнению с глубиной ямы:
|е| <С С/о, или я < ко-
Оказывается, что при этих предположениях также и ka <С 1, и мы
решаем приближенно (с учетом малости ка) трансцендентное уравне¬
ние для определения значений энергии:
(koa)2 cos2 ка = (ка)2.
В результате имеем
я2 « коа2 = яо-
Получается, что значение энергии связи |е| = |ео| гораздо меньше глу¬
бины ямы (как и ожидалось):
|е0| = tA = Uo(k0a)2 « С/о.
Волновая функция в этом приближении имеет вид
'Вое~К°\х\, \х\ > а,
-фо(х)
I Aq coskx, \х\ < а,
причем Ло ^ В0 = Л|*а_о = %/**)•
Вероятность нахождения частицы в пределах ямы при этом
W:
и
яо J cos2 kxdx ~ 2xofl <SC 1,
и, как мы убеждаемся, с подавляющей вероятностью (~ 1) частица бу¬
дет находиться вне пределов ямы, т. е. в классически недоступной обла¬
сти. Очевидно, что это существенно квантовое явление, и классическая
интерпретация для него невозможна.
Необходимо заметить, что при а —> 0, С/о —> оо, но при условии
Uoa = const, пределом данного потенциала является <5-яма (см. детали в
задаче 2.2.6), в которой (как и в мелкой яме конечной глубины) имеется
всего одно (четное) состояние дискретного спектра :
2
U(x) = --яоб(х) = lim
171	а-+	О
*2
п Яр
2 та
в(а - |х|)
= lim [—С/ов(а
а—+ О

290 _J\,. Глава 2. Квантовая механика. Решения задач
2.2.6.	Полагая Е < 0 и вводя обозначение
2 _ 2т\Е\
.9	1
h2
получаем уравнение, которому удовлетворяет волновая функция дис¬
кретного невырожденного спектра частицы в виде
ф"(х) — (х2 — 2xoS(x))ip(x) = 0.	(1)
В точке разрыва потенциала х = 0 потребуем непрерывности ф(х):
ф(+0) = ф(-0).
При этом производная ip'(x) терпит разрыв, величину которого находим
из уравнения	(1),	интегрируя его в пределах от —е до	е	при	г	—*	0:
V/(+0) - г/’Ч-О) = -2хоф(0).	(2)
При этом, как	и	должно быть, выполняется условие непрерывности	плот¬
ности потока вероятности: /(+0) = /(—0), где
j(x) = ^(ф(х)ф'(х)* -ф*(х)ф'(х)).
Нормированное решение ищем в виде
'Схе~хх, х > 0,
Ф(х) =
Счехх, х < 0.
Из непрерывности ф при х = 0, получаем С{ = С% — С. Тогда условие (2)
дает х = хо, т. е. при Е < 0 имеем всего один дискретный уровень с
энергией	2
С   Й Хо
Ео~-^Г
и волновой функцией
Фо(х) = у/хое_х°|х| ^
нормированной на единицу.
2.2.7.	В импульсном представлении волновая функция дискретного уров¬
ня задачи 2.2.6 будет иметь вид
Фо(р) = (Р\0) = f dx{p\x){x|0) =

2.2. Одномерное движение	291
Легко найти (0|х|0) = 0, (0|р|0) = 0, а также
ОО	ОО
(0|х2|0) = J xe~2*°^x2dx = a J e~axx2dx =
—оо	О
d2 °[
~ adaI J
e~axdx = 4
da J	a2
2 ’
a=2xo *0
и, кроме ТОГО,
оо
да!|0> - I	Р-
— оо
= {х0Н)2.
a—xh
Соотношение неопределенности для данного состояния имеет вид
<(Дх)2)((Др)2> = -^х2h2 = у > у
— абсолютный минимум для когерентного состояния гармонического
осциллятора.
2.2.8.	Фурье-образ потенциала равен константе, и уравнение Шредин-
гера в импульсном предсталении (см. решение задачи 2.1.21) принимает
простой вид:
2 00
р / \ I h*o
2т
Полагаем Е = —Н2х2/(2т) < 0, и, считая, что интеграл в (1) сходится,
обозначим его С:
С = J dp'<p(p').
Таким образом, уравнение (1) свелось к алгебраическому. Его решение
дает выражение для функции
= (2)
п р + п х
Согласно определению константы С получаем уравнение, из которого
находится уровень энергии:

292	Глава	2.	Квантовая	механика.	Решения	задач
откуда имеем (ср. с задачей 2.2.6)
2т
Неизвестная константа С в (2) определяется из условия нормировки:
Интеграл легко вычисляется с помощью методов теории функций ком¬
плексного переменного: следует взять вычет в полюсе второго поряд¬
ка, например в верхней полуплоскости в точке z = Шяо, после чего
получаем С=у/2тШяо. В итоге нормированная волновая функция в р-
представлении имеет вид
в полном соответствии с формулой (1) решения задачи 2.2.7.
2.2.9.	Очевидно, что данный потенциал представляет собой четную функ¬
цию U{-x) = U(x), поэтому гамильтониан коммутирует с оператором
инверсии:
и можно искать решение уравнения Шредингера, как общие собствен¬
ные функции операторов Н и I, т. е. в виде четных и нечетных функций.
Запишем общий вид четного и нечетного решения на всей числовой
прямой, исключая сами ^-функции (Е < 0, я2 — 2m\E\/h2):
Учитываем условия «сшивания» решений: непрерывность функции
при х = а
— ОО
откуда
[Н, I] О,
Ве*х, х < -а,
-фм{х) = A ch ях, -а < х < а,
Be *х,	х > а,
Be**,	х < -а.
) U) = A sh ях, -а < х < а,
-Ве~*х, х > а.
гр(а + 0) = гр(а - 0)
(1)

2.2. Одномерное движение
X
293
(2)
и конечный разрыв производной (см. решение задачи 2.2.6)
1ф'(а + 0) — яр'(а - 0) = -2хо'Ф(а)-
Условие совместности уравнений (1) и (2) с учетом явного вида ?/>(+)(х)
и гр(~\х) дает трансцендентное уравнение для нахождения уровней
энергии:
— = \±е~2*а,
мо а
(3)
где верхний знак отвечает четному, а нижний — нечетному уровню
энергии.
Анализ уравнения (3) показывает (рис. 2.3), что в данном потен¬
циале в общем случае существуют два дискретных уровня энергии —
четный и нечетный. Четный уровень лежит ниже и присутствует всегда,
нечетный лежит выше и существует только при хоа > 1/2. Таким об¬
разом, при малых расстояниях меж¬
ду ямами остается только четный
уровень.
Если ха «С 1, то х ~ 2хо и энер¬
гия четного состояния
£(+) = -4
2
П Х0
2т ’
Рис. 2.3. Графический анализ урав¬
нения (3)
т. е. при малом расстоянии две (5-ямы
действуют, как одна, но с удвоен¬
ным значением хо. Если же ямы да¬
леки друг от друга (при хоа 3> 1),
то уровни энергии экспоненциально
мало отличаются друг от друга и в конце концов сливаются. В резуль¬
тате мы получаем задачу о двух (5-ямах, независимых друг от друга.
Находим нормировочные коэффициенты для четной и нечетной вол¬
новых функций:
^ sh 2ха
ch2 ха
2 ха
sh2xa
2 ха
+
sh2 ха
ха
-1/2
-1/2
В<+) = А^еха ch ха,
В<_) = А(~^е*а sh ха.
2.2.10.	Рассмотрим пункт а) данной задачи. Прежде необходимо заме¬
тить, что вследствие инвариантности потенциала относительно транс¬
ляций на величину а (период одномерной кристаллической решетки),

294	Глава	2.	Квантовая	механика.	Решения	задач
т. е. U(x + а) = U(x), гамильтониан нашей задачи будет коммутировать
с оператором трансляции Та (см. задачу 2.1.1):
[Н,тв] = 0.
Поэтому мы можем искать решение в виде общих собственных функций
операторов Н и Т„:
Г Щ{х) = Егр(х),
\ Таф(х) = А(а)ф(х),
где Л(а) (собственное значение оператора трансляции) имеет вид Л(а) =
= e±lKa, a \тК — 0 (квазиимпульс). Собственные функции оператора
трансляции согласно теореме Блоха должны удовлетворять условию,
которое следует из (1):
ф(х + а) = e‘Kaip(x).	(2)
Запишем общий вид решения уравнения Шредингера (1) в двух смеж¬
ных областях:
О <	х	<	а	(область 1):	ф(х)	= c\eikx + d\e~,kx,
а <	х	<	2а	(область 2):	гр(х)	= C2e‘k<-X~a) + d2e~lk(x~a\
h2k2
причем Е —	>	0. Условия сшивания в точке х = а
%/j(a + 0) = ф(а - 0),
ф'{а + 0) - ip'{а -	0) = 2/Зо^(0)
после элементарных вычислений дают связь между коэффициентами с\,
d\, С2, d2, которую можно записать в матричном виде:
о=ч:>
где матрица А имеет вид
А
(„ika (1 I	„—ika	@0
V ik)	ik
 Jka 00	p—ika
\	ik
(-S)I
Нетрудно заметить, что бе!Л = 1.
Далее мы применим формулу (2) и получим
ф(х + а) = c2eik{x+a-a) + d2e-ik(x+a-a) = c2eikx + d2e~ikx = е‘Каф(х).

2.2. Одномерное движение ->\г 295
Таким образом, имеем
U)-*“G>	<4)
и, сравнивая (3) и (4), видим, что задача свелась к проблеме диагона-
лизации матрицы А (матрица сдвига), а е‘Ка = А(а) — играет роль соб¬
ственного значения этой матрицы. В результате получаем уравнение на
собственные значения
А2(а) - 2РХ(а) + 1 = 0,
где 2р = SpA — след матрицы А. Решение уравнения дает
Ai,2(a) = e±lKa = р± i\/l - р2,
откуда следует, что cos Ка = р или, конкретнее:
cos Ка = cos/га + ^ sin ka.	(5)
k
Это и есть так называемое дисперсионное соотношение.
Анализ соотношения (5) показывает, что энергетический спектр ча¬
стицы в таком поле	имеет зонную структуру. В самом деле,	задавшись
некоторым значением энергии Е, мы находим k	= \J2mE/h	и	затем из
уравнения (5) можем найти значение Ка (рис. 2.4).
Случай 1. Энергия Е такова, что \р\ — |cos/fa| < 1. При этом К
является вещественным числом, что и требуется для функции Блоха,
а сама функция — распространяющаяся модулированная волна. Эти
области значений Е называются разрешенными зонами энергии.
Случай 2. Энергия Е такова, что \р\ = |cos/fa| > 1. При этом ве¬
личина К — комплексная, и частицы с такими К не могут распростра¬
няться внутри большого кристалла. Эти области значений энергии —
запрещенные зоны.

296 J\r Глава 2. Квантовая механика. Решения задач
Разрешенные зоны чередуются с запрещенными, не перекрываясь
между собой. Ширина разрешенных зон увеличивается с ростом \ka\.
Условие Роа С 1 (слабая связь) описывает случай, близкий к свободно¬
му. Это значит, что К ~ k + 2тгп/а, и поэтому зависимость Е(К) пара¬
болическая. В противоположном предельном случае fioа 3> 1 (сильная
связь) интервалы разрешенных значений энергии фактически превра¬
щаются в отдельные дискретные уровни ka яз -кп.
2.2.11.	Наиболее просто эта задача решается в импульсном представ¬
лении, когда уравнение Шредингера сводится к дифференциальному
уравнению первого порядка:
р2 - ihF-d
?)Фе(р) = О-
^2 m	dp
В результате решения этого уравнения получаются функции
Мр) = ШГгещ
нормированные условием
оо
/ Фе(р) Фе> (р) dp — 6(Е - Е').
— ОО
Переходя к координатному представлению, получаем
ОО
=ш1 фмА'1'’=(I+4
— оо
оо
где Ф(х) = —р J cos^ + tx^dt — функция Эйри,
о
2.2.12.	При исследовании данной задачи используем следующие пред¬
положения.
а)	<5-Ямы находятся достаточно далеко друг от друга, т. е. в системе
ям имеется два дискретных уровня энергии, отвечающих связанным со¬
стояниям. Однако ямы не бесконечно далеки, следовательно, ^Е^
(см. решение задачи 2.2.9).
б) Система, рассматриваемая нами, — приближенно двухуровневая,
т. е. отброшен весь непрерывный спектр — считается, что частица не
выходит из ям.

2.2. Одномерное движение ->\г 297
Как это следует из рис. 2.5, в любом из стационарных состояний
•ф(+\х) или ф(_)(*) выполняется
\ip{±) (~х)\2 = \ip{±)(x)\2,
поэтому вероятность обнаружения частицы вблизи левой и правой ямы
одинакова — частица не локализована
вблизи ни одной из ям.
С целью построить состояние, в котором
частица (хотя бы в начальный момент вре¬
мени) была бы локализована в окрестности
одной из ям, воспользуемся линейной ком¬
бинацией функций
Ф(х, t) — C\e л М + Сге ft V’ '(*)•
(1)
Очевидно, что в начальный момент
времени
Ф(х,0) = С{ф(+\х) + С2гр(-)(х).
Если положить С\ = Сг, то мы полу¬
чим состояние (рис. 2.5), в котором ча¬
стица локализована вблизи правой 5-ямы. Обозначим это состояние
Ф(х, 0) = 1ра(х)- По аналогии можно построить состояние гр-а(х) с ло¬
кализацией частицы вблизи левой 5-ямы. Окончательно
'Фа(х) = -~(ll>i+){x) + 1р{-](х)),
ф-а(х) = -~{г!)(+){х) - ф{~](х)),
и обратно
ф(+)(х) = ~^=(фа(х) + Ф-А*)).
f
ф( \х) = -^=(фа(х) - ф-аМ).
Итак, волновая функция состояния (1), в котором частица в началь¬
ный момент времени локализована вблизи правой 5-ямы, имеет вид
i£(+)<	,	,	,	i£<-)<
Рис. 2.5. Стационарные со¬
стояния для системы двух
5-ям

298 -JL- Глава 2. Квантовая механика. Решения задач
В соответствии со статистической интерпретацией, вероятность об¬
наружить частицу локализованной вблизи левой ямы, если в начальный
момент она была локализована в правой, равна
W-a = 7
i£(+)( <£<—><
2_ 1
/
e ft — e ft
1 - cos
4
2
V
2.2.13.	При рассмотрении задачи о нахождении коэффициентов отра¬
жения и прохождения (11.13) мы будем исходить из потенциала
Учет условий непрерывности волновой функции гр и ее производ¬
ной гр' в точках х = ±а/2 дает систему из четырех уравнений. В ре¬
зультате решения этой системы имеем
Волновая функция частицы будет иметь вид
etkx + Ae tkx,	х <—а/2,
гр(х) — <	Ce‘k'x + De~‘k>x,	\х\ < а/2,
Beikx,	х > а/2,
где
^ п	?,2 _ 2т(Е + U0)
^ о,	«1 —	2
П
ie lka{k\ — k2) sin k\a
2kk\ cos k\a - i(k2 + k2) sin k\a ’
2kk\e~ik'a
2kk\ cos k\a — i(k\ + k2) sin k\a
Таким образом, для коэффициента отражения получаем
о_ 1/Л _|„|2_	(*?-*“)sin2
1,'пад1 I I	л	(.2(.2	2	.	/,2	,	.2ч:
1/Л	1	1	4k2k2	cos2 k\a + (k2 4- k2)2 sin2 k\a ~
(k2 — k2) sin2 k\a
Ak]k2 + (k2 — k2)2 sin2 k\a'
Величина R обращается в ноль при k\а = ^у/2т(Е+ U0) = пп, п = 1,2,...,
а также, естественно, при k — k\, (Uq = 0).

2.2. Одномерное движение	299
Коэффициент прохождения имеет вид
D
1/Гш1 _
I /г
= \в\2 =
4fe?fe2 cos2 k\а + (k2 + k2)2 sin2 k\a
Ak\k2
Ak\k2 + (k2 - k2)2 sin2 k\a '
Очевидно, что выполняется равенство D + R = 1.
Полученные результаты для коэффициентов прохождения и отраже¬
ния будут справедливы и в случае потенциального барьера (рис. 2.6)
О,	|*| > а/2,
Uq, \х\ < а/2,
Щх) =
если в формуле k\ = Щ-(Е + (Jo) осуществить замену (Jo
h
При 0 < Е < Uo нужно допол¬
нительно положить k\ =Лщ, где В
Щ-(ио-Е). В результате
■Uq.
классический
Г
получаем
R =
(х2 + ft2)sh2xia
Ax\k2 + (х\ + k2)2 sh2 х\ а ’
D =
Ax2k2
Рис. 2.6. Коэффициент прохождения
для потенциального барьера
Ax2k2 + (х\ + k2)2 sh2 х\ а'
Из рис. 2.6 видно, что коэф¬
фициент прохождения D в кван¬
товом случае достигает максимального значения D = 1 (классический
предел) лишь при k\a = 7г«, п = 1,2, Между этими максимумами
находятся минимумы, причем значение D в этих точках растет с ростом
величины E/(Jo- Данные отличия в поведении квантового коэффици¬
ента прохождения от классического связаны с проявлением волновых
свойств частиц.
2.2.14. Wi = I —	~'2
4xqX|
2.2.15. R =
2
ХО
2 I (.2
Хо + k
(х0 + Х\)
D —
/ хр - х\ У
\ х0 + Х\ )
xl + k2’
где Е■■
h2k2
2т
> 0.
2.2.16. В соответствии с условием (см. также задачу 2.2.4) выбираем
решение в виде
\Asmk\x,	0	<	х	<	а,
Ф(х) =
-е lkx + elkx+lv = elv^2i sin (kx + (p/2), x^a.

зоо_Л, Глава 2. Квантовая механика. Решения задач
Здесь введены стандартные обозначения:
Е=^’	=	+	Ы	=	Ы	(D
Решение в области 0 < х < а следует из граничного условия ip(0) = 0;
<р — дополнительная фаза, приобретенная отраженной волной.
Условие непрерывности логарифмической производной при х — а дает,
что
kacig(ka + ip/2) = k\acigk\a.	(2)
По условию задачи в яме должен быть один слабосвязанный уровень.
При глубине ямы
i/о г
~2ь2
7Г П
8та2
в ней появляется первый дискретный уровень энергии (см. задачу 2.2.4),
но его энергия |г| = 0. Поэтому предположим, что глубина ямы Uo =
= i/ominO + А)- где Д -С 1. Раскладывая (2) в предположении Д «С 1
и ka <С 1 («медленные» частицы), получаем условие для определения
фазы:
<23	7Г2Д
С‘П = -ж-
Величину Д можно связать с энергией е слабосвязанного уровня.
Для этого в уравнении, определяющем связанные уровни энергии,
ctgКа = -^, где \е\ = К2 = k\ - хг
проведем разложение, считая, что ха -С 1, Д -С 1 (ko связано с Uq обыч¬
ным соотношением (1)). В результате найдем
7Г2Д
к~
8 а
поэтому окончательно
.	<х>	X
g2~~T = “V Е
2.2.17.	Вначале введем обозначения
t2 .2	.2J
Е ~ U\ —	>	0,	Е-и2	=	^-> 0.
2т	2т
Таким образом, мы считаем величины k и q действительными.

2.2. Одномерное движение	301
В полупространстве z < 0 (область 1) волновая функция — решение
уравнения Шредингера будет иметь вид
</>i(r ) = eikT+Aeik'r,
где А — амплитуда отраженной волны, к и к' — волновые векторы
падающей и отраженной волны. В полупространстве z > 0 (область 2)
волновая функция описывает только прошедшую волну
V>2 (г) = Beiqr.
Здесь q — волновой вектор прошедшей волны.
На плоскости 2 = 0 должны выполняться условия
Г Мх,у) = Мх,у),
\ip[(x,y) = ф'2 (х,у),
откуда следует равенство фаз и амплитуд этих функций. Если напра¬
вить ось у перпендикулярно плоскости падения, то условие равенства
фаз запишется совсем просто (рис. 2.7):
kxx = k'xx = qxx, или /гsin ^ = Дгsin= ^7sin 6>",
(1)
откуда немедленно следует 9 = 9' (закон отраже¬
ния) и закон преломления:
sin в
sin в
По аналогии с оптикой определим показатель
преломления:
4 V0"
Z
©
X
/
\ ®
г
\
к/
\ к
Рис. 2.7.
Наклонное
падение
волны де
" = 1 =
Е- U2
Е — U\'
Бройля на потенци¬
альную ступеньку
Это показатель преломления второй «среды» относительно первой. Ес¬
ли же принять п = 1 для U = 0, то получим показатели преломления
обеих «сред» относительно вакуума:
т = д/i -
(А
Е ’
Теперь используем условия равенства амплитуд

302 _J\ - Глава 2. Квантовая механика. Решения задач
Решаем эту систему и находим коэффициенты прохождения и отражения:
Г) 1/У I	Di	2	_	4 qzk2
I; чад I	/	\Щ
1/Л кг' '	(kz+q2)2’
n_ l/Tl _ м,2_ (кг-Чг?
1/Л 1 1	(*2 + 9г)2'
Полное отражение возникает, когда Е < U2, и тогда q =	ix —	чисто
мнимая величина. При этом из равенства (1) следует
q2z — q2-q2x = -х2 - k2 sin2 в < 0,
поэтому и qz = ixz — чисто мнимое. При таких условиях R = 1, а плот¬
ность потока прошедшей волны равна нулю. Волновая функция в обла¬
сти 2 пропорциональна e~HzZ, т. е. экспоненциально убывает.
2.2.18. Единственное связанное состояние в яме существует при —р- >
2.2.19. Функция Грина свободного уравнения Шредингера должна удо¬
влетворять уравнению с ^-функцией в правой части:
(Н - Е) G(x, х1) = { - £ £ - £} G(x, х’) = 6(х	- х').	(1)
Используем разложение в интеграл Фурье:
6(х -х') = J ^.е‘Цх-х'\ G(x,x') = J ~G(k)eik(x-x'l
Подставляя эти разложения в (1), находим (р = hk, Е = -|£| < 0)
G(k) =	1	2т
h2k*.p. h2k2 + \E\'
2т
При переходе к функции G(x, х') необходимо вычислить интеграл (х2 =
= 2m\E\/h2)
Jk(x-x')
G(*,*') = А [
7Г П J
k2 + х2 h2x
Интеграл вычисляется методом теории вычетов, но нужно иметь в виду,
что при х — х' > 0 контур интегрирования следует замыкать в верхней,
а при х — х' < 0 — в нижней полуплоскости.
Общее решение уравнения Шредингера при U{x) ф 0, Е < 0 с уче¬
том граничных условий при х —» ±оо будет выглядеть так:
ОО
1!>(х) = -Л- [ e-^x-x'\U(x')^{x')dx\
h х J
— ОО
выбор U(x) = — К2xq5(x)/т приводит к результату задачи 2.2.6.

2.3. Линейный гармонический осциллятор	303
2.3.	ЛИНЕЙНЫЙ	ГАРМОНИЧЕСКИЙ	ОСЦИЛЛЯТОР
2.3.1. \(f>0(p)\2dp = -Д-- ехр(-^Л dp, р0 = \fhmuj.
V жРо	V Ро/
2.3.2. Для расчетов используем выражение операторов х и р для гар¬
монического осциллятора через операторы а+ и а (см. (11.15)):
х=^=(а++а), р = i^={a+ - а), х0 = \ —, Ро = Vhmu.
у/2	уД	V	»
Тогда получим, что
(х2) - (п|х2|«) = ^(п|2+а + аа+|«) = х\(п +	= -^2_,
2	\	2/ ти}
(р2) = (м|р2|«) = Ц(п\а+а + аа+|я) = р20(п +	= тЕп,
где Еп — Нсс(п + 1/2) — энергия квантового осциллятора.
Для классического осциллятора общее решение уравнений движе¬
ния имеет вид
хкл = A sin(w? + tp), ркл = тшА cos (cat + ф),
где А — амплитуда колебаний, а <р — начальная фаза. Нетрудно найти
т	2
*кл = j [ A2 sin2М + <p)dt=-r =
I J	2	ти}
0
Ркл = ('М2Х2Л = т£кл-
Известно, что согласно принципу соответствия в пределе п —► оо
выражения для квантовых средних должны переходить в соответствую¬
щие выражения для классических средних для одного и того же значе¬
ния энергии (Еп = Екл). Заметим, что для гармонического осциллятора
данное равенство выполняется не только при п —► оо, но и для любых п.
2.3.3. (х4) = (л|х4|«) = ^(6п2 + 6п + 3),
(х2*+‘) = (л|х2*+1|п) = 0, k = 0,1,....
2.3.4. Др Дх =у/(Ар2)ф(Ах2) = Еп/ш = h(n + 1/2), см. задачу 2.3.2.
2.3.5. ан = аехр(—iujt), аф = а+ехр(ги2)- Использовать результат за¬
дачи 2.1.17.

304	Глава	2.	Квантовая	механика.	Решения	задач
2.3.6. Полагая, что функция /(а+) допускает разложение в ряд Тейлора:
m-±qp<rt.
k=0
получаем [а,/(а+)] = /'(а+).
[°° e-^dy
2.3.7. a) w — —	j—	~ 0,16.
/о°° е~ dy
б) Е'п — Е%п+\ = huj{2n + 1 + 1/2) = 2Ью(п + 3/4).
2-3-8-
|ЛИ|2ф = 5v7^expK«)1"“(«)‘i'’-
2.3.9.	Когерентное состояние |z) является собственным вектором опе¬
ратора а, отвечающим собственному значению z (комплексному). На
основании этого имеем
(z|H|z) _ МФ+а + ^\z) _ bw{z\z*z + ^\z)
(ф) “	(ф)	~	{z\z)
2.3.10.	Эволюция во времени когерентного состояния определяется га¬
мильтонианом гармонического осциллятора Н = hu[a+a + g), т-е.
|z(0) = expf-^Ш^ |z(0)). Это означает, что
(x)t = (z(t)\x\z(t)) = <z(0)|enH'xe-nH*|z(0)) = <z(0)|xff|z(0)),
(p)t = <Ф)|р|Ф)) = <2(0)|рЯ|2(0)).
где хя, ря — операторы координаты и импульса в гейзенберговском
представлении (см. задачи 2.1.17 и 2.1.23). Несложный расчет приводит
к результату
(x)t — (xjocoswt + ^^sinu>l,	Г (х)о = (z(0)|x|z(0)),
muJ	где \г\
(р)( = (р)0coswt - muj(x)osmujt,	^ 'Р'° ~
(z(0)|p|z(0)).
Таким образом, эволюция во времени средних значений координаты
и импульса в когерентном состоянии квантового осциллятора в точно¬
сти соответствует закону изменения координаты и импульса классиче¬
ского осциллятора при движении по классической траектории.

2.3. Линейный гармонический осциллятор •Аг 305
2.3.11.	Основное состояние гармонического осциллятора |0) представ¬
ляет собой когерентное состояние с z = 0. Вектор состояния |0) опре¬
деляется из уравнения а|0) = 0 (см. (11.17)). После перехода к коорди¬
натному представлению это уравнение принимает вид
(f+^)lM£) = 0 с решением ф0(О = Се V.
(Использованы обозначения: £ = х/хо, фо(0 = (£|0) — волновая функ¬
ция основного состояния в координатном представлении.)
Уравнение для (£|z) — волновой функции когерентного состояния
1	.	d.
>/2 ' <*£
является модификацией предыдущего уравнения с заменой £ —»£ — у/2z
Поэтому искомая функция имеет вид
(£|z) - СехрГ-^(£- V2z)2
2'
В импульсном представлении по аналогии получаем
1/„	_	ч2!
{p\z) = Сех р
2 \ро	7 J
Фактически обе функции являются собственными функциями ос¬
новного состояния, «сдвинутыми» в комплексной плоскости на число г.
2.3.12.	Гамильтониан заряженного осциллятора в однородном электри¬
ческом поле (в системе единиц т = 1, h = 1) имеет вид
H = f + ~~e£x.	(1)
Волновая функция основного состояния осциллятора с гамильтониа¬
ном (1) при К 0 в осцилляторных единицах имеет вид
4>(Q, 0|«о = e~iEt	^(с?_е£)2.
7Г 1
Сравнивая с когерентным состоянием (см. задачу 2.3.11), видим что в
нашем случае параметр z = е£/\/2. Таким образом, вероятность обна¬
ружить осциллятор в момент времени t > 0 на п-м возбужденном уровне
энергии равна
(<?£)2п _(е£)2
we — -—т-e 1'
п\
в соответствии с (11.20).

306 _l\- Глава 2. Квантовая механика. Решения задач
2.3.13.	(Дх2)(Др2) = /г2/4, причем это соотношение остается постоян¬
ным во времени. Таким образом, когерентное состояние минимизирует
соотношение неопределенностей для координаты и импульса. Поэтому
когерентные состояния в наибольшей степени соответствуют классиче¬
скому представлению о движении частицы по траектории.
2.4.	УГЛОВОЙ	МОМЕНТ,	СПИН
2.4.1. а) 0; б) 0; в) 0; г) г(рг)<?;*,р,; д) г(е^/р/р,+е,;ур^ру); е) ±1±; ж) 21г;
з)	ieikjPj\ и) ieikjXf, к) 0.
Равенство нулю результатов в п.п. а), б), в), и к) связано с тем,
что они отвечают коммутаторам 1 ,• со скалярными операторами. Такие
операторы не преобразуются при поворотах системы координат, а опера¬
тор 1; описывает преобразование векторов состояний именно при таких
поворотах.
Одинаковая структура результатов в п.п. з) и и) есть следствие то¬
го, что % и р* являются компонентами векторных операторов, т. е.
преобразуются при поворотах, как компоненты векторов (см. также за¬
дачу 2.4.9).
2.4.2. Trl; = 0.
2.4.3. Поскольку все оси координат равноправны, то
<i2> = (?) + (?) + (Е> = з(5).
Исходя из равновероятности различных значений 1г имеем
/Т2\	1	Л 2	2^2	/(/ + 1)
(1,) = ——- > т	=	■■ ■	>	т	=	—-.
\г/	21+1	^,	21+1 z-'	3
т=—1	т=0
Окончательно получаем, что I2 = (I2) = 1(1 + 1).
2.4.4. Исходя из коммутационного соотношения [M^MJ = ihNlz по¬
лучаем (в соответствии с решением задачи 2.1.9)
<дй2>т,„<дйг>- = 7<Й->2 =
ибо усреднение проводится по состоянию 11,1). В силу симметрии за¬
дачи относительно осей х и у можно считать (ДМ2)тщ = (ДМ2)тщ.

2.4. Угловой момент, спин	307
Учитывая также, что (М*) = (Му) = 0 (см. решение задачи 2.4.6), окон¬
чательно получаем
<Мм?+м;|и>т1п = л’(1 + ^)=)й.
2.4.5. е±ю\±. Использовать результаты задач 2.1.17 и 2.4.1.
2.4.6. Поскольку (см. (11.22)),
1±|/, т) = у/1(1 + 1) - т(т ± 1)|/, т ± 1),	(1)
то (1±) ~ (/, m\l, т ± 1) = 0. Отсюда получаем (1*) ± i(\y) = 0, поэтому
(I) = (I) - 0.
Далее, из соотношения (1) имеем (1^_) = 0, откуда
<12 - I2} ± i{\x\y + у*> = 0,
и поэтому (I2) = (I2), (\х\у + \у\х) — 0. Исходя из этого и учитывая так¬
же, что (Уу - \у\х) = 1'(1г), получаем (\х\у) = -(\у\х) = im/2.
Наконец, имея в виду, что (1^ +1^) = (I2 —1|), нетрудно получить
утверждение в) данной задачи.
2.4.7. Из формулы (1) задачи 2.4.6 следует, что
(/, т'|1±|/, т) = У/(/+ 1) - т(т ± \)8т^т±х.
Очевидно также, что (/, т'\\г\1, т) = т6т',т, (1,т1 |12|/, т) = /(/ + l)6m',m.
Полагая / = 1, получаем в представлении, где I2 и \г диагональны,
(о
1
0^
У
0
0^
i+ = V2
0
0
1
, \- = Т2
1
0
0
,
V0
0
V
1
V
<0
1
о)
У
-1
0 ^
1 =
1
72
1
0
1
1 - —
’ у~ л/2
1
0
-1
V0
1
V
1
°У
Л
0
0 N
/1
0
0^
1г =
0
0
0
»
I2 = 2
0
1
0
1°
0
-V
1°
0
V

308
Глава 2. Квантовая механика. Решения задач
2.4.8.	Используя результат задачи 2.4.7 и решая уравнение на собствен¬
ные векторы и собственные значения }nip\ = \ip\, получаем, что соб¬
ственные значения равны Л — 0, ±1, а собственные векторы в представ¬
лении, где j2 и j* диагональны, имеют вид
2.4.9.	При повороте системы координат новые координаты г' физиче¬
ского объекта выражаются через старые следующим образом: г' = Rvr,
где R<p = R^n) ~~ матрица поворота (оператор преобразования коор¬
динат). Поворот осуществляется на угол вокруг оси, направление
которой задано единичным вектором п.
Компоненты векторного оператора при этом должны преобразовы¬
ваться по обычному векторному закону (так же, как и компоненты век¬
тора г), т. е.
Отсюда для поворота на бесконечно малый угол 6<р имеем (с линейной
точностью по 5<р)
А' — (i-/<fy(nj))A(l + i(fyj(nj)) ~ A-/<5</?[(nj), А] = А-(5</з[п х А], (2)
последнее равенство в (2) следует из формулы Эйлера для поворота
вектора на малый угол. Переписывая (2) в тензорных обозначениях,
получим	^	^	^
л, ft, A*] = -iekuriiki = ieikiitiAi,
откуда и следует утверждение задачи.
2.4.10.	Докажем первое соотношение. Перейдем к тензорным обозна¬
чениям и получим
А' = e-‘V(nj)Ae'V(nj) = R(¥?n)A.
О)
[j2. А,] = [Ы*,А,-] = J* [j*, А«] + []*, A;]J/
I*, AilJA =
= iekiilkki + iekiiAi\k = ieukAi]k — ге^/^А/,
Закон преобразования оператора в (1) выбирается обратным по отношению
к закону преобразования вектора состояния (П.23) с тем> чтобы согласовать
изменения средних значений: (ip'\A\xl>') = (tplA'lip).

2.4. Угловой момент, спин	309
что и доказывает утверждение задачи. Данный результат необходимо
использовать при доказательстве второго соотношения.
2.4.11.	Собственные функции и собственные значения матриц Паули на¬
ходятся из решения уравнений ст,ХА; = Фхл,> где i = x,y,z. Поскольку
для любой матрицы Паули of = 1, то собственные значения А,- = ±1. Нор¬
мированные на единицу собственные функции матриц dx,dy,dz имеют
вид
Xa,=±i = ^(±i). Хау=±. = ^(±.)
1\ /0
(0)
^sintfcos 6^
0
, б) р, =
sin в sin 5
, Р| = 1 в обоих случаях.
V)
\ COS в j
ХАг=1 = Xl/2 =	Хлг=-1 = X—1/2 — у J
Последние две функции описывают состояния х±1/2 (П.26), в которых
проекция спина на ось г равна ±1/2.
2.4.12. а) Р,
2.4.13. При получении соотношения необходимо учесть основные свой¬
ства матриц Паули: of = 1, {о;,?/} = Зуоу + d/di = 0 (t ф j), [5;, о/] =
= d{Oj — djdi = Zieijkdk (последнее есть следствие основного коммута¬
ционного соотношения для компонент спинового момента).
2.4.14. При доказательстве использовать результат задачи 2.4.13.
2.4.15. d\ = 0, {d±,dx} = 2 • i, {d±,dy} = ±2i • 1, {ст±,стг} = 0.
2.4.16. Тгст,ст* — 2фу, Tr didkdi = 2ie,-*/.
|a|* -1, k — четное,
|a|*—1 (ст-a), k — нечетное.
2.4.18. ехр[1а(стп)] = cos a ± i(dn) sin a.
2.4.19. С учетом явного вида матриц Паули имеем
2.4.17. (ста)* =
cos tin е ™ sm <
sin tin — cos f
Решая далее уравнение на собственные функции и собственные зна¬
чения апЧ!я — сФ4, получим, что с2 = 1, откуда с = ±1, а собственные

310 -JL. Глава 2. Квантовая механика. Решения задач
функции (нормированные на единицу) имеют вид
0о \	/	. 0о
cos —	\	/ — sin —
Ф,= |	\ ’	Ф“1=	в
ет sin у J	\e,v,° cos у
Заметим, что эти функции, как и обычно, определены с точностью до
общего фазового множителя еп.
2.4.20.	Искомый оператор преобразования спинора имеет вид R(cm) =
exp
(см. (11.23)).
Для того, чтобы ось z оказалась совмещенной с направлением век¬
тора по, необходимо осуществить поворот системы координат на угол во
вокруг оси с направлением, заданным единичным вектором п, лежа¬
щим в плоскости хОу, а также перпендикулярным оси z и вектору по.
Несложный расчет показывает, что п = {-sin <ро, cosy?o> 0}. Поэтому
матрица оператора преобразования спинора будет иметь вид
R(#on) = exp г'у(стп) = cos у - i sin у (sin у>одх - cos ч>оду) =
cos — sin — e "fi0
2 2
. - sin ye,¥>0 cos у
Действуя оператором R на функции Ф±1 предыдущей задачи, получим
с точностью до общего фазового множителя х±!/2 (см. (11.26)).
2.4.21. Действуя оператором R-1 на собственные функции оператора аг,
т. е. на x±i/2 (см. (11.26) и задачу 2.4.20), очевидно получим Ф±1 (см. за¬
дачу 2.4.19). Это и есть состояния, в которых проекция спина на ось по
равна ±1/2. Для того, чтобы получить явный вид матрицы R-1, доста¬
точно в выражении для R произвести замену во —> -во.
2.4.22. По условию задачи электрон находится в состоянии с проек¬
цией спина на ось г, равной 1/2, т. е. xi/2 (см. (11.26)). Представим
это состояние в виде суперпозиции состояний Ф4=±1 с определенным
значением проекции спина на ось по (см. задачу 2.4.19), образующих
ортонормированный базис в спиновом пространстве электрона:
xi/2= 22 1ф«Хфт1х1/2) = (Ф/‘Х1/2)Ф1 + (Ф1,Х1/2)Ф—1 =
«=±1
= cos уф, - sin уФ-1-

2.5. Движение в магнитном поле ■Аг 311
Поэтому wis = 1) = cos2(0o/2), w(s = -1) = sin2(0o/2) — вероятности
найти частицу в состояниях с проекцией спина на ось по, равной ±1/2.
2.4.23.	Угол поворота и направление оси вращения:
^2	1„	„Л	Ч>\	^2
П =
1
sin
cos | = cos ^ cos ^ - (nin2) sin у sin y,
■ |^ni sin у cos y- ± n2 cos у sin у - [ti! x п2] sin ^ sin ^ |.
2.4.24. См. решение задачи 2.4.7.
2.4.25. Спиновая функция состояния, отвечающая проекции спина +1
на ось по, совпадает с функцией ф\, найденной в решении задачи 2.4.8
для орбитального момента I = 1. Вероятности различных проекций спи¬
на на ось z в этом состоянии:
ш(±1) = ^(1 ± cos0o)2, да(0) = ^ sin2 0О.
При Оо —> 0 и во —иг функция переходит в
( о\
\7
— функции,
описывающие состояния с проекцией спина на ось г, равной ±1. При
Оо —► тг/2, <ро 0 и уо -* тг/2 решение переходит в ^
функции, описывающие состояния, в которых проекция спина на оси х
и у равна +1.
(Л ,
(-Л
v/2 и
V2
W
\1 /
2.5.	ДВИЖЕНИЕ В МАГНИТНОМ ПОЛЕ
2.5.1.	Гамильтониан системы
Й=2^[р'+(^-^)2 + р'.
коммутирует с операторами ру и р2. Поэтому собственные функции Н
можно искать в виде
Фе
РуРг
Сехр
fayy + PzZ)]f(x),

312
Глава 2. Квантовая механика. Решения задач
где f(x) удовлетворяет уравнению
ГМ + Y [(я -	-	J<4(х - хо)2]/(х) = 0.	(1)
Здесь шн = ^ (е > 0) и хо = Решение уравнения (1) выражается
через решение уравнения Шредингера для гармонического осциллятора
с частотой шя (см. (11.18)). В итоге
Первое слагаемое в (2) описывает энергетические уровни попереч¬
ного движения (уровни Ландау). Они являются дискретными и ну¬
меруются квантовым числом п. Движение вдоль поля не квантуется,
квантовое число рг может принимать значения —оо < рг < оо. Уровни
энергии (2) вырождены, ибо они не зависят от квантового числа ру,
которое также может изменяться от —оо до оо.
Если ограничить область движения частицы ящиком в виде куба с
ребром L, то рг и ру становятся дискретными:
потому что предполагается граничное условие ip(xi + L) = ip(xi). Исхо¬
дя из того, что в классическом пределе на одно квантовое состояние
(в одном измерении) приходится фазовый объем 2nh (см. задачу 2.2.1)
получим, что число квантовых состояний в объеме V в расчете на ин¬
тервал Арг и на один дискретный уровень равно
Из условия 0 < хо < L (центр классической орбиты внутри объема V, и
радиус орбиты пренебрежимо мал по сравнению с L) имеем Apy = e%L/c.
Поэтому окончательно
(2)
Pi = —m, щ = о, ±1,...,
2.5.2.	С педагогической точки зрения полезно найти уровни энергии в
данной задаче путем выделения асимптотик без привлечения специаль¬
ных функций.

2.5. Движение в магнитном поле	313
Векторный потенциал однородного поля записывается в виде
А=1рСхг].
Направим, как обычно, ось г вдоль магнитного поля, тогда компонен¬
ты векторного потенциала в цилиндрической системе координат будут
равны
Аг = 0, А р = 0, А^ = ]pip.
Гамильтониан частицы массы Af с зарядом е (е > 0) имеет вид
Н — — {$ — -А^2 — — у2 — е^\ + е ^ п2	(1)
Н~2Л1Г с) ~ 2МУ 2Мс 8Мс2	Ш
Введем ларморову частоту и>н = е'КЦМс) и учтем, что оператор про¬
екции момента импульса на ось z равен 1г = —id/dip, тогда гамильто¬
ниан (1) в цилиндрических координатах примет вид
G h2 ( д2 , 1 д д ,	1	д2	\	, г' д , 1	2	2
н	ттт	+	+	in	+	+	ъМи>нР	■	(2)
2м\дг2	рдр др р2 д</J 2 д<р
Гамильтониан (1)-(2) коммутирует с операторами \г и рг, поэтому
решение стационарного уравнения Шредингера в цилиндрических коор¬
динатах
Нф(г,р, р) = Еф(г,р, <р)
следует искать в виде общей собственной функции трех операторов: Н,
\г и р2, т.е. ф(г, р, <р) = фг(г)Ф(<р)Я(р), где
фЛг) = фРг (г) = -~= е^г, Ф(у>) = Фт(<р) = -±= е‘т*.
Таким образом, имеем
ДтЧ> Лргг
гр{г'р'‘р) = 7^7Ш*{Р)'	(3)
Для радиальной функции R(p) получаем обыкновенное дифферен¬
циальное уравнение
h2
h'
"ж
(Мы представили полную энергию в виде суммы Е — Ег + Ер, где Ег =
= рЦ(2М) — энергия продольного движения частицы.) Потенциальная
энергия в (4) зависит квадратично от переменной р, как и для гармо¬
нического осциллятора, поэтому ее удобно измерять в осцилляторных

314	Глава	2.	Квантовая	механика.	Решения	задач
единицах: Ен = Ишне. Поделим уравнение (4) на /кщ/ и введем безраз¬
мерную переменную
f	V2 р	12 Мшн
где рн = у/Ть/(Ми>н) — осцилляторная единица длины (11.16). В безраз¬
мерных переменных уравнение принимает вид
R" + i«'+(e_| + |_|!)S = 0.	(5)
Выделим асимптотики уравнения (5). При £ —» 0 имеем
До +	-	^До = 0.
Ищем решение, как обычно, в виде степенной функции R0 ~ £s и по¬
лучаем для s уравнение и его решение в виде
s(s - 1) + s - т2 = 0, —► s = ±т.
Таким образом, асимптотика радиальной функции при £ —*► 0 есть
Д|5_о~£|т|.
Для определения асимптотического решения при £ —> оо на основа¬
нии (5) получаем уравнение
Д~ - ]^2Доо = 0.
Ищем решение в виде /?<*, ~ e_Q^ и с асимптотической точностью по¬
лучаем а = 1/8, т. е.
/г|€_оо ~ е_«,/в.
Таким образом, полную радиальную функцию можно представить в виде
Д(£) - е-€2/8£|т|а;(£)>	(6)
учитывающем особенности поведения в нуле и на бесконечности.
Подставляя функцию Д(£) в виде (6) в радиальное уравнение (5) и
вводя новую переменную z согласно z = £2/4, получим уравнение для
функции w(z):
d2w , ,, , , . \dw ,
z—F + (|m| + 1-2)— +
\m\ — m + \
£ —
■  	 dz	'Г 2 (7)
причем функцию w(z) мы будем далее искать в виде суммы степенного
ряда (вообще говоря, бесконечного)
ОО
w(z) = akzk.	(8)
k=0

2.5. Движение в магнитном поле
\
Подставляя в (7) решение в виде суммы (8) и производя преобразование
индекса суммирования таким образом, чтобы сгруппировать члены с
одинаковыми степенями г, находим
\т\ — т + V
0.
Y^zk[(k+ \)(k + 1 + \m\)ak+1 + (e-k -		)ak
k=0
Для того, чтобы левая часть данного уравнения обратилась в ноль, необ¬
ходимо и достаточно потребовать, чтобы коэффициенты при всех степе¬
нях z были бы равны нулю. На основании этого получаем рекуррентные
соотношения для коэффициентов а*:
2k + \т\ — т + 1 - 2е	,Q..
ам ~	2(к + 1)(Л + 1 + М) '	(
Заметим, что в ряде (8) отношение двух последующих коэффициен¬
тов согласно (9) при k » 1 стремится к пределу
gft+i
Clk
и будет таким же, как и у функции ег, разложенной в ряд
00
'-'Li-
k=0
Поэтому при z —> оо мы получим w(z)~e2 или w(£)~e^ /4, т. е. радиаль¬
ная функция (6) при £ —► сю будет экспоненциально расти: /?(£) |^_оо ~ ^ /8.
Единственная возможность избежать данного неограниченного роста —
«оборвать» ряд (8) при некотором k = пр и превратить его в полином.
При этом должно выполняться условие
,\т\ — т + \	1	о	<\п\
Епр — пр 4“	2	’	^р —	’	’	’	*	*	■	'	(	)
Число пр, как и обычно, называется радиальным квантовым числом
и определяет количество нулей многочлена w„p(z).
Окончательно получаем энергетический спектр заряженной частицы
в однородном магнитном поле2’:
Епрг = Гшн(п+'-) + £ n = np+W^ = 0,l,2,...,	(И)
где мы ввели главное квантовое число п. Данный результат находится
в полном согласии с формулой (2) решения задачи 2.5.1. Уровни энер¬
гии (11) вырождены по значению проекции момента на направление
2) В учебнике [13] рассматривается задача для электрона с зарядом е = — \е\,
поэтому проекция т входит в выражение для энергии с другим знаком.

316	Глава	2.	Квантовая	механика.	Решения	задач
магнитного поля: каждому фиксированному значению числа п отвечают
состояния с т — — п, —п + 1, ..., 0,1,... оо.
Для функции w(z) мы получаем ряд (8), определяемый рекуррент¬
ными соотношениями (9) и сводящийся к вырожденной гипергеомет-
рической функции F(-np, \т\ -I-1 , z), которая является регулярным при
z —> 0 решением уравнения (7). При условии (10) гипергеометрическая
функция превращается в присоединенный полином Лагерра (см. (Д.24)),
т. е.
_2
wnpm(z) = а0
1 _ пр z л. __иАцрпИ—— +
(Н + 1) 1 (Н + 1НН + 2) 2
- a0F(-np, \т\ + 1,2) -
Восстанавливая исходные обозначения, запишем общий вид радиаль¬
ной функции /?(р), нормированной условием /0°° \R{p)\2pdp = 1:
	И
Fnpm(p) =	,	:
Рну/пр\(\т\ +
2.5.3.	Утверждается, что координатные и спиновые переменные в урав¬
нении Паули разделяются только в случае наличия однородного маг¬
нитного поля, возможно, зависящего от времени. Предполагая возмож¬
ность такого разделения, ищем решение уравнения Паули
ihj( Ф(г, t) = (Нш - р0(<тЮ)*(г, /).	0)
где
йш = 2^(р-|а)2+о<г).	*>°.
в следующем виде:
Ф(г, о =/(r, t)x(t)-	(2)
Здесь х(0 — спиновая функция, зависящая только от времени. Подста¬
вим (2) в (1) и потребуем, чтобы функция /(г, t) подчинялась уравнению
Шредингера для бесспиновой частицы
t) = Нш/(г, t).	(3)
Тогда для спиновой функции мы получим
ihjtx(t) = -po(ZK)x(t)-	(4)
Уравнения (3) и (4) будут независимыми, если магнитное поле ДС —
однородное, т. е. не зависит от координат.

2.5. Движение в магнитном поле	317
2 5 4 По условию задачи магнитное поле постоянное и однородное
поэтому переменные в уравнении Паули разделяются, и уравнение (4)
задачи 2.5.3 принимает вид
ih~x( 0 = -АП^Х(0.	(1)
с учетом явного вида матрицы 5, уравнение (1) переходит в
ю=ч:;:>
- начальное условие. Решаем далее систему дифференциальных урав¬
нений для si и S2 и получаем
x«) = ("smY	<2>
ХУ ' \i sin Ш/
Используя (2), находим средние значения
= х+&хХ z (CTi/) = s'n	(£Tz)	~	cos	2Ш.
Поскольку (Д)х = аю(^)х. то ясно- что в плоскости У°г• перпендику¬
лярной к направлению магнитного поля, происходят периодические во
времени изменения средних значений магнитного момента мюона. Это
интерпретируется, как прецессия магнитного момента вокруг направле¬
ния магнитного поля.
Перейдем к представлению Гейзенберга. Из формулы (1) следует,
что гамильтониан Н = -hfldx и поэтому
—. v	—iiittTxsT	  рг
(<Тх)н = е ахв ~ °х'
(5	_	е-‘шЭхЭуе‘ШЭх	=	ду	cos 2Ш + дг sin 2Ш,
(рг)н = е-‘ш9хЭге‘п‘Эх = dz cos 2fit - Эу sin 2Ш.
При вычислении необходимо использовать соотношение е,ш°х =
= cos Ш + id sinfif а также свойства матриц Паули. Таким образом,
в представлении Гейзенберга матрицы Паули (и спиновые операторы
? = (1/2)5;) изменяются во времени, как компоненты трехмерного
вектора.
2 5 5 Данную задачу можно решить двумя способами: 1) используя
унитарное преобразование, связывающее представления Шредингера и
Гейзенберга (11.11) и 2) непосредственно решая уравнения Гейзенберга
(11.10). Первый способ был применен при решении задачи 2.5.4, здесь
мы воспользуемся вторым способом.

318 -]\г Глава 2. Квантовая механика. Решения задач
Направим магнитное поле по оси г, тогда спиновый гамильтониан
электрона в однородном магнитном поле примет вид
Н = 2/io^sz.
Здесь до = eh/(2mc) — магнетон Бора, —е < 0 — заряд электрона. Для
решения задачи воспользуемся уравнением Гейзенберга (11.10). Полу¬
чаем (с учетом [s„s±] = ±s±)
ff=o, ^ = fe.
Полученные уравнения легко решаются:
%(t) =%,	s±(t)	=	e±ia"s±,
где ш = 2до ОС/К.
Окончательно будем иметь (ср. с задачей 2.5.4)
s'x(t) = s* cos cat - sу sin ait,
sy(t) = sy cos uit + s* sin cat.
2.5.6.	Уравнение эволюции спина в лабораторной системе координат
имеет вид (см. задачу 2.5.3)
«л|х(0 = Нх(0 = -до (#К)х(0 = -7(&К)х(0.
где 7 = е/(тс) — гиромагнитное отношение для спинового момента,
S = (К/2)а — оператор спина. Здесь наряду с постоянным полем !Но,
направленным	по	оси	г, имеется также поле ОСь	вращающееся	в	плос¬
кости хОу	с	угловой	скоростью ш = uik. Поэтому	гамильтониан	явно
зависит от времени.
Перейдем в систему координат К', вращающуюся относительно ла¬
бораторной системы К с угловой скоростью ш. При этом спиновая функ¬
ция подвергнется преобразованию, отвечающему повороту на угол ait:
х' = еЪ(шЭ)1х = еЪ(*ш)‘х-
Функция х' будет удовлетворять преобразованному уравнению
ih^x'V) = Knx'(t), где Н;„ = е^Не-*^1 - (Ьш).
С учетом явного вида гамильтониана
Н = —7 [Э-Ci (S* cos ait + Sy sin ait) + 1KoS2]

2.5. Движение в магнитном поле
получим
= -7(s^ff), Кп = {и,, о, Wo + ^} •
Таким образом, мы перешли к некоторому эффективному полю [K'ff, но
зато теперь наш гамильтониан H'[f не зависит от времени.
В новой системе координат магнитное поле однородно и постоянно
во времени. Магнитный момент частицы должен прецессировать вокруг
направления магнитного поля (см. задачу 2.5.4). Перейдем теперь в
представление Гейзенберга, учитывая, что dH'eU/dt = 0:
Хн = х" = еь^еП*х' =	=	еь^^х! ■
Как видно, переход к представлению Гейзенберга эквивалентен еще од¬
ному повороту — вокруг направления вектора Г2 — —7^eff на Угол ^t.
Спиновая функция х" не зависит от времени (как и должно быть), ибо
новый вид уравнения эволюции:
= 0. потому что Н"„ = 0.
В итоге решение исходного уравнения х(0 записывается при помощи
оператора эволюции, представляющего собой два последовательных по¬
ворота. Поскольку х"(0 = х"(0) = х'(0) = х(0)- решение принимает вид
хМ-е-^е-^ЫО).
Введем обозначения
Ul\
ujq = 'уСКо, wi = 7^1.
Г2 = \J{uj -f- шо)2 + cof,
COS e=Ko+uh +
где 9 — угол между векторами IKo и “К'еff. Тогда
(Sco) = wSz, (§П) = —Г2 (S^ sin 9 + Szcos 9).
Вероятность переворота спина к моменту t равна
(«* = -5) = |Х^,/2Х(0|2 - sin26>sin2(y)
,2
. 2
sin
(и + ^о) +
(и -Г ш0)2 -Г u)\t
Вероятность переворота спина имеет резонансный характер. При усло¬
вии Tfj <с ЭГо (ш) < шо) она мала при всех значениях частоты ш кроме

320	Глава	2.	Квантовая	механика.	Решения	задач
узкой области вблизи точки резонанса ш —► —шо = —Ipo'Ko/h. В резо¬
нансной области вероятность может быть близкой к единице в некото¬
рые моменты времени t.
2.5.7.	Магнитное поле движущегося электрона обусловлено как его соб¬
ственным магнитным моментом, так и его движением. Поле спинового
магнитного момента — поле магнитного диполя !КСП ~ р/г". Магнитное
поле движущегося заряда (о <С с)
3"Сорб
i[vx£]
v е ре
rsj	  /-ЧУ	  .
,2 mr JL
с г тс г
Для реализации эксперимента необходимо выполнение условия
2£а*«1, т. е. -£-£«1.
Щеп	тс	р
Но импульс движущегося электрона точно не известен. Если считать,
что область локализации электрона ~ Аг, то в соответствии с соотно¬
шением неопределенностей ртщ > Н/Аг, и тогда получим
д
тс р
Если р — спиновый магнитный момент свободного электрона, то
р — ро = eh/(2mc), следовательно Аг » г, что противоречит разумной
постановке опыта, ибо для проведения эксперимента требуется Дг<Сг —
локализация частицы.
2.5.8.	Решение задачи основано на возможности описать сверхпрово¬
дящее состояние при помощи волновой функции вида
ф = y/ale14’,	(1)
где ns(г) — плотность сверхпроводящих электронов, <р(г) — фаза, общая
для всех частиц, находящихся в сверхпроводящем состоянии. Исполь¬
зуем выражение для плотности тока вероятности при наличии магнит¬
ного поля М = rot А:
ih I /т /	,41	еА
) = ^[ФГ)Ф-ГФф)]-^гГФ= rV(P-f:A
Zm	тс
h — е
L т	тс
(2)
где мы учли вид функции (1). Проинтегрируем (2) по замкнутому конту¬
ру /, проходящему глубоко внутри сверхпроводника, полагая, что плот¬
ность ns постоянна на контуре интегрирования:
Л f (j d\) = Ц f (Vip d\) - f (A d\).	(3)

2.6. Движение в центральном поле —1\ - 321
Левая часть (3) обращается в нуль, так как в толще сверхпроводника
47Г .
магнитного поля нет, т. е. 1К = 0, следовательно rot 1К = — j = 0, по¬
этому и j = 0. Далее
f(Adl)= JJ rot A dS = jj‘Md$ = Ф,
i
где Ф — поток вектора магнитного поля сквозь площадь, окруженную
контуром. И наконец
j (Vpd\) = j) = j) dp = 2жn, n = 0, ±1, ...,
/
где использовано условие однозначности волновой функции, вследствие
чего изменение фазы должно быть равно 2-кп. Окончательно получаем,
чт0	о
т , 2ппс
Ф = пФ0, Фо = 	.
е
где Фо — квант магнитного потока.
2.6.	ДВИЖЕНИЕ	В ЦЕНТРАЛЬНОМ ПОЛЕ
2.6.1.	Система двух частиц описывается волновой функцией Ф(гь г2, t),
которая подчиняется уравнению Шредингера
т^Ф(гьГ2,0 = НФ(г,, г2, t),
ot
причем гамильтониан в координатном представлении имеет вид
Н = -^Д,-^Д2 + У(г,-г2).
2 т\	2 т2
Введем координату центра масс R и относительную координату г:
„ miri+m2r2
R = 	;	.	Г	= Г]-Г2.
т\ + m2
Проделав далее замену переменных rj, г2, Д|, Д2 —» R, г, Ди, Дг
(используя правило дифференцирования сложной функции), приведем
гамильтониан к виду
где М = т\ + m2, р = wim2/M — соответственно полная и приведенная
массы. Ввиду того, что система стационарна, полагаем, что волновая
функция будет иметь вид
Ф(гь г2,0 = е_Я£'Ф(Н)^(г). Е - Епм + Еот.

Глава 2. Квантовая механика. Решения задач
Полная энергия складывается из энергии движения центра масс £цм и
энергии относительного движения £отн- Функции Ф(К) и гр(г) должны
подчиняться уравнениям
-|1двФ(11) = £цМФ(К),	(1)
h2
~АГ + Щг)
■ф(г) = £отн^(г).	(2)
Из уравнения (1) следует, что функция Ф(И) описывает свободное дви¬
жение центра масс: Ф(Н) = Ce«PR, характеризуемое полным импуль¬
сом Р и энергией £цм = Р2/(2М).
2.6.2. Операторы I2, l*, 1У, 1г, I коммутируют с гамильтонианом и явля¬
ются интегралами движения в произвольном центральном поле.
2.6.3. Используя явный вид волновой функции основного состояния
водородоподобного атома в координатном представлении31
г3/2	7
ipm(r) = —?=е Zr,
у7Г
перейдем в импульсное представление:
ф(р)=(гж2! а3хе~1(гр]фт{г)=Щ
1
(Z2+p2)2'
2.6.4. Приводим ответы: (r2) = 3/Z, (1 /r)=Z, (p2)=Z2. Учитывая, что
средняя кинетическая энергия (Т) = (р2/2), а средняя потенциальная
энергия (U) = —(Z/r), убеждаемся в справедливости теоремы вириала
для кулоновских сил:
2(f) + (0) = 0.
2.6.5. Запишем выражения для радиального гамильтониана и энерге¬
тического спектра водородоподобного атома:
G Рг ,1(1+1) Z
Н 2
72
£" ~	,2 •
г_
2п<
11 В данном разделе при решении задач об атоме водорода мы используем
атомную систему единиц h = m = е = 1.

2.6. Движение в центральном поле	323
Учитывая теорему Фейнмана-Гельмана (задача 2.1.22), а также оче¬
видные соотношения
ЗН 1 деп Z	/1 \ Z
3z=~? az = получаем \-r) = S'
где угловыми скобками обозначено среднее по произвольному состоя¬
нию атома водорода \nlrn).
Имея в виду далее, что
аЙ	/ +1/2 деп Z2	/ 1 \	Z2
ИГ =	а^ = 7’	получаем Ы	= Л7Т77^
Здесь мы использовали связь квантовых чисел п = nr + I + 1 для ато¬
ма водорода. При дифференцировании выражений, например, по /, мы
считали зависимость от I непрерывной, т. е. вместо реальной дискрет¬
ной переменной / мы рассматривали некоторую фиктивную непрерыв¬
ную переменную, равную I в точках, отвечающих целым значениям
/ = 0,1,....
Из теоремы Эренфеста для радиального движения
легко получить, что
(Нрг - РгН) = 0, откуда	=
На основании этого окончательно находим
Z3
(/+1/2)/(/+1)
/>0.
2.6.6.	Уравнение Шредингера в импульсном представлении, как извест¬
но, является интегральным, причем роль ядра играет фурье-образ по¬
тенциала (см. задачу 2.1.21). В атомной системе единиц уравнение имеет
вид	2
(£- - е)ф(Р) = - / W(р - Р')<А(р')>
где
Щр) = J dhe-^Uir)
— фурье-образ потенциала взаимодействия. Для кулоновского потенци-
Z	Z
ала U(г) = — нетрудно получить W(p) = j~2’ и уравнение примет
г	27г	р
вид
(р'2 - 2Е)ф(р) = 4 [<Рр'-Щ-2.	(1)
7Г1 J	|Р — Р |

324	Глава	2.	Квантовая	механика.	Решения	задач
Уравнение (1) можно свести к одномерному интегральному уравнению,
точное решение которого впервые было найдено В. А. Фоком (1935 г.).
2.6.7.	Уравнение Шредингера для трехмерного изотропного осциллято¬
ра имеет вид
|-^А + —у—|^(г) = £У>(г).	(1)
а)	Декартова система координат. Поскольку гамильтониан
уравнения (1) можно записать в виде суммы
о vf h2 92 I
Н-2-Д	2 тдх* +	2	/’
где Xj = x,y,z, то очевидно, что решение может быть представлено в
виде
*,«(r) = CWO)W Я1.Я2.ПЗ = 0,1,2	 (2)
Еп =	п = п\ + П2 + пз, я = 0,1,2,...,	(3)
где u°cn(Xi) — собственные функции гамильтониана одномерного осцил¬
лятора (11.18):
у 2я'я,-! льо\/п	V	о/
Здесь Hni(Xj) — полиномы Эрмита, хо = у/Н/(тш) — осцилляторная
единица длины (11.16). Поскольку четность полиномов Эрмита #„,(*,-)
равна /„, = (-1)"', то состояния (2) и уровни энергии (3) также харак¬
теризуются определенной четностью
/„ = (-1)л'+«2+«з = (_!)«
При вычислении кратности вырождения уровней энергии (3) заметим, что,
если задать п\, то число «2 будет принимать значения «2 = 0,1, ...,п — п\,
т. е. всего п — п\ + 1 различных значений. Число пз всегда фиксировано
соотношением пз — п — п\ — пч- Поэтому полная кратность вырождения
уровня энергии будет равна
£(„_„1 + 1) = 1(п + 1)(я + 2).
Л|=0
б)	Сферическая система координат. Решение уравнения (1)
будет иметь вид
il>Elm(r)=REi(r)Ytm)(6,ip),

2.6. Движение в центральном поле
X
325
где У/т)(0, </>) — сферическая функция, а функция /?н(г) должна удо¬
влетворять уравнению
Г 2тЕ
R"(r) + ±R'(r)+ ,
I *
г2 /(/+!))
''о г2 J
/?(г) = О,
(4)
Где го = y/h/(mco) — осцилляторная единица длины (11.16). Переходя в
уравнении (4) к безразмерным переменным, получим
/(/+1)
R"{q) + 2-R\q) + Ье - q2 -	}/?(<?) = О,
4	1	q	)
(5)
где q = г/г0, е = E/(fkj).
Исследуем асимптотики функции R(q). При q —> 0 имеем следую¬
щий асимптотический вид уравнения (5):
-/?0
-До = 0.
Ищем решение этого уравнения, как обычно, в виде Ro ~ qs и получаем
для s уравнение и его решения в виде
s(s - 1) + 2s - 1(1 + 1) = О, —V S\ = I, S2 = —(/+1).
Следовательно, асимптотика радиальной функции при q —> 0 имеет вид
Д|9—о ~ ql, поэтому сделаем подстановку R(q) = qlu(q). Для функции
u(q) получим уравнение
и" +	+ (2е - q2)u = 0.
q
Асимптотику функции u(q) при q —► оо определим из уравнения
- 42“оо = 0.
2
Подставляя в данное уравнение иао ~ e~aq > находим а = 1/2. Таким
образом, радиальную функцию с выделенными асимптотиками можно
записать в виде
R(q) = e~q2/2qlw(q),	(6)
учитывающем особенности поведения в нуле и на бесконечности.
Введем новую переменную согласно £ = q2, и получим уравнение
для функции w(£):
d2w
' de
Функцию ге>(£) мы будем далее искать в виде суммы степенного ряда
ОО
®(£) = Y1 а^к-	(8)
k=0

326 J\r Глава 2. Квантовая механика. Решения задач
Подставляя в (7) решение в виде суммы (8) и, группируя члены с оди¬
наковыми степенями £, находим
ОО
^£*[(*4- 1)(* + /+ §)«*+! - (К/_£+ I) “*)“*] = °-
k=0
Отсюда, приравнивая нулю коэффициенты при £*, найдем рекуррентные
соотношения для коэффициентов а*:
 	(/	+	3/2	— е) 4- 2k
ak+i - аь у + щ2(к +1) + 3)'
Поскольку в ряде (8) отношение двух последующих коэффициентов
в соответствии с (9) при k » 1 стремится к пределу
Д*+1
а*
k>\ k'
то при больших значениях аргумента, т. е. при £ —> оо мы получим
ш(£)~е^ или w(q)~eq (см. решение задачи 2.5.2). Поэтому радиальная
функция (6) при q—> оо будет экспоненциально расти: /?(<7)|?_+0О ~ еч /2.
Чтобы избежать данного неограниченного роста, необходимо «оборвать»
ряд (8) при некотором k = пг, т. е. свести его к полиному. При этом
должно выполняться условие
^ (/ + § - е) = -яг, пг = 0,1,2	 (10)
откуда получаем уровни энергии:
Еп = huo(l + 2пг +	+	|),	п — 2пг + / = 0,1,2,... .
Здесь пг — радиальное, I — орбитальное и п — главное квантовое
число.
Для функции о>(£) мы имеем ряд (8), который определяется рекур¬
рентными соотношениями (9) и сводится к вырожденной гипергеомет-
рической функции F(—nr,l + 3/2, £), которая является регулярным при
£ —» 0 решением4) уравнения (7). При условии (10) гипергеометриче-
4)	Второе линейно независимое решение уравнения (7) при г —> 0 ведет себя
~ г“(2/+|\ что несовместимо при Ос условием нормировки /0°° \R(r)\2 г2 dr = 1,
а в случае / = 0 это решение приводит к расходимости при г = 0 среднего
значения кинетической энергии —h2/(2т) f Ф*(г)ДФ(г)d3x.

2.6. Движение в центральном поле	327
ская функция превращается в присоединенный полином Лагерра (см.
(Д.24)), т.е.
И f	и_/я.	  11	Д
Wnrl(0 = do
,	Пг£	Пг(Пг	-	1)	Г	.
(I + 3/2) 1	(/ + 3/2)(/ + 3/2 + 1) 2
= a„F(-nr,l+ 3/2,0 =
Здесь константа ао определяется из условия нормировки. Восстанав¬
ливая исходные обозначения, запишем общий вид радиальной функ¬
ции R(r), нормированной условием /0°° \R(r)\2r2 dr = 1:
R-M-fs,(11)
Таким образом, полная волновая функция в сферической системе
координат
■Фпш{т) = Rni{r)Ylm)(e,v)
зависит от трех квантовых чисел: п, I и m (функцию (11) можно запи¬
сать с учетом пг = (п — 0/2), в то время, как уровни энергии опреде¬
ляются только главным квантовым числом п. Поэтому имеется вырож¬
дение: уровню энергии с определенным значением числа п отвечают
функции с / = п, п — 2 О, если п — четное (п/2 + 1 значений /), или
с 1 = п,п- 2,..., 1, если п — нечетное ((« + 1)/2 значений /). Кроме
того, для каждого / существует 21 + 1 различных значений магнитного
квантового числа m (уровни энергии не зависят от т).
На основании этого заключаем, что уровни энергии имеют опреде¬
ленную четность5) /„ = (-1)'1 = (-1)г и полную кратность вырождения
(для четного и нечетного п), равную
£ (2/+l)= J2 (2/+1) = ±(л + 1)(л + 2),	(12)
/=0,2,...	/=1,3
что полностью соответствует результату п. а).
Потенциал изотропного гармонического осциллятора можно исполь¬
зовать в качестве модели самосогласованного поля, которое действует
на каждый нуклон в ядре (модель ядерных оболочек). При этом най-
5)	В сферических координатах четность волновой функции определяется пол¬
ностью угловой частью, т.е. сферической функцией Y„(0,<p). Поскольку при
преобразовании инверсии 0 —► тг —	</?—>7г + у>, имеем У1т(ж — в, -к + ф) =
= (-\)‘У‘т(в^).

328
X
Глава 2. Квантовая механика. Решения задач
денные нами уровни энергии (3) представляют собой спектр одноча¬
стичных уровней для рассматриваемой модели. Если главное квантовое
число принимает значения п = 0,1,3, то максимальное число нуклонов,
которые могут находиться на соответствующих уровнях равно 2, 6, 12
(удвоение кратности вырождения (12) связано с тем, что нуклоны име¬
ют спин 1/2). Максимальное число нуклонов, которые можно разме¬
стить на всех уровнях, начиная с нулевого и заканчивая рассматрива¬
емым, будет равно 2, 8, 20. Это и есть значения магических чисел для
данной модели оболочек.
2.6.8.	Уравнение Шредингера для данного потенциала допускает раз¬
деление переменных в сферической системе координат, и его решение
можно представить в виде (см. (11.33))
гР( г) = й;(г)К/т)(0,^) = l-xi(r)Ylm\6,<p).
В результате такой подстановки мы получаем для функции xi(r) так
называемое «укороченное» радиальное уравнение
х'/(г)+ (k2 - 1Х±й^Х1(г) = 0, где Е =
(1)
Функция xi удовлетворяет данному уравнению при 0 < г < а, и должна
быть равна нулю при г = 0 и при г ^ а.
Случай 1 = 0. В этом случае уравнение (1) и граничные условия
Х/(0) = Х/(а) — 0 имеют точно такой же вид, как и в одномерной задаче
(см. задачу 2.2.1). На основании этого сразу получаем решение:
ЕПго
J1*1
■к п о I
W"'’
1	.	ППг	г,
sin—-г, 0 < г < а,
\/2паг а
0,
а,
где nr = 1,2,3,... — радиальное квантовое число.
Случай I > 0. При помощи замены xi(r) — \frlP(r) уравнение (1)
приводится к виду
Ч>" + V +
k2 _ (/+1/2)2
if = 0.
Решениями данного уравнения являются функции Бесселя полуцелого
порядка /±ц+i/2)(kr). Поэтому общее решение уравнения (1) можно за¬
писать в виде
ХМ = C\ji(kr) + C2rii(kr),

2.6. Движение в центральном поле	329
где мы используем сферическую функцию Бесселя
h(x) =	,/2(*)
и сферическую функцию Неймана
пМ = \[Цм1+х/2(х) = (-1 ),+1У^/_(Ж/2)(*).
При малых значениях аргумента имеют место следующие асимптотиче¬
ские представления:
i-,+1	Г2/—ПИ
о - (2/+ !)!!’ "/WU-o  	(2)
Учитывая граничное условие х/(0) = 0, а также асимптотику (2),
приходим к выводу о том, что решение уравнения (1) необходимо вы¬
брать в виде6* xi(r) = cji(kr). Граничное условие xi(a) — 0 определяет
значения k и, следовательно, — уровни энергии и собственные функ¬
ции. Должно выполняться условие
ji(ka) = 0, или Jl+\/2(ka) = О,
поэтому окончательно находим
где А„,1 — корни функции Бесселя 1/2(х), пг = 1,2,... — радиальное
квантовое число, определяющее номер корня в порядке возрастания его
величины. Вырождение по орбитальному квантовому числу отсутствует —
значение энергии однозначно определяет число I. Вырождение по маг¬
нитному квантовому числу т существует, ибо оно обусловлено сфери¬
ческой симметрией задачи.
Используя значения корней Л„д, можно определить порядок распо¬
ложения уровней энергии, начиная от основного состояния:
Is, 1 р, Id, 2s, If, 2р, lg, 2d, 1 h, 3s, 2/,...,
где состояния с /= 1,2,3,4,5,... обозначаются буквами s,p, d,f,g,h,...,
число перед буквой нумерует уровни с одинаковым I в порядке воз¬
растания их значений (очевидно, в данном случае это число просто
6)	См. также сноску на с. 326.

330	Глава	2.	Квантовая	механика.	Решения	задач
равно пг). Для сравнения приведем порядок расположения уровней для
изотропного пространственного осциллятора (см. задачу 2.6.7, число
перед буквой теперь равно п + 1)
Is, Ip, [1 d, 2s], [1/, 2p], [lg, 2d, 3s],... .
Для уровней энергии осциллятора характерно вырождение по квантово¬
му числу I, поэтому состояния, отвечающие одному и тому же уровню,
заключены в скобки. Заметим, что отличия в порядке расположения на¬
чинают проявляться лишь для сравнительно высоко лежащих уровней
энергии.
2.6.9.	Как и в предыдущей задаче, представим решение уравнения Шре-
дингера в виде
1.
Введем очевидные обозначения
п	п
(см. задачу 2.2.2) и тогда радиальное уравнение Шредингера для опре¬
деления функции хАг) в случае связанных состояний примет следую¬
щий вид:
х'/И	+ ^k2 - 1(1	= 0 для 0 < г < а,	(1а)
х"{г) + (-х2 ~	*^Х;(Г)	=	0	для г^а,	(16)
Решение уравнения (1а), удовлетворяющее граничному условию х/(0) = 0.
представляет собой сферическую функцию Бесселя xi{r) =Aji(kr) при
0 <	г	<	а. Решением уравнения (16), экспоненциально убывающим	при
г —»	оо,	является	сферическая функция Ханкеля мнимого аргумента
(см. (Д.17)):
X/(r) = Bhjl)(ixr) при г ^ а;
^\х) = jt(x) + irii(x).
Из условия непрерывности логарифмической производной на границе
ямы г = а получим
М ы^р.О)	(2)
li(ka) h\\ixa)
Очевидно, что это и есть трансцендентное уравнение, определяющее
уровни энергии связанных состояний в яме.

2.6. Движение в центральном поле -*\г 331
Для s-состояний (/ = 0) уравнение (2) приобретает совсем простой
вид:
kcigka = —х.
Данное уравнение фактически совпадает с уравнением, определяющим
уровни энергии для нечетных состояний задачи 2.2.2 (см. также зада¬
чу 2.2.4). Обсуждение вопросов о существовании связанных состояний
и о количестве уровней энергии можно повторить здесь без особых
изменений.
2.6.10.	Уравнение Шредингера в импульсном представлении для дву¬
мерной потенциальной ямы имеет вид (см. задачу 2.6.6)
(|l-£^(p) = -|d2p'W(р-р')ф(р') = - /d2q W(q)<t>(p-q)} (1)
где q = р — р' — переданный импульс,
Г(ч) =	/	^xe~l^U(r)
(27Г п) J
— фурье-образ потенциала взаимодействия. Полагаем, что потенциал
обладает аксиальной симметрией U(г) = (Д|г|) = U(r), поэтому для фу-
рье-образа будет также UT(q) = W(q).
Не конкретизируя вид потенциала, предположим, что он имеет ми¬
нимум, равный -t/o и радиус действия а (т. е. при г < а потенциал от¬
личен от нуля). Тогда из очевидных свойств преобразования Фурье сле¬
дует, что область локализации фурье-образа W(q) в импульсном про¬
странстве ограничена значением q < К/а.
Далее мы полагаем, что яма мелкая, и координатная волновая функ¬
ция связанного состояния при больших значениях г имеет вид убываю¬
щей экспоненты ф(г) ~ е~*Г, причем выполняется условие ха <С 1 (см.
также задачу 2.2.5). Поэтому область локализации функции в импульс¬
ном представлении, т. е. ф(q), должна быть ~ Нх К/а. Таким обра¬
зом, при q —> оо функция ф(q) убывает значительно быстрее, чем W(q).
При этом доминирующую роль в интеграле (1) играет область |<7| < h/a,
поэтому мы можем вынести W(q) из-под знака интеграла в точке q « 0.
В результате получим
(I-- Е)ф(р) =-W( 0) I d2pф(p).
Пусть С = J d2p ф(р) и тогда

332 _/\ - Глава 2. Квантовая механика. Решения задач
Из условия согласования находим
ОО
1 = - r(0) 2* 1 7Т% “ - г,0> 2”-(ё +1£|) Г
о
Учтем также, что
Г(0) ~
(2rrh)
и получим
, / ft2 \ 2ft2 „ ft2 ( 2ft2 \	,оч
£““wexph^> (2)
Таким образом, в мелкой двумерной яме, как и в симметричной од¬
номерной, всегда существует одно связанное состояние. Причем, как
это видно из (2), глубина залегания соответствующего уровня энергии
экспоненциально мала по сравнению с глубиной ямы. В трехмерной яме
связанное состояние есть не всегда (см. задачу 2.6.9).
2.7.	КВАЗИКЛАССИЧЕСКОЕ ПРИБЛИЖЕНИЕ
2.7.1.	Случай а) Исходя из правила квантования Бора-Зоммерфельда,
имеем
ь	х0
Jp(x)dx= j \j2mE - т2са2х2 dx = nh^n + ij,	(1)
-Xo
где xo = \/2E/(muj2) — классическая точка поворота. Вычисляя инте¬
грал (1), получим Етг/ш, откуда найдем уровни энергии:
En = fka(n + ^y п = 0,1,2
Построим волновую функцию, исходя из правила согласования ква-
зиклассических решений при переходе из классически запрещенной об¬
ласти в классически разрешенную (11.36):
(-I)"
;exp{-zi}, х <-а,
ipn(x) = С <
sin{z2 + 7г/4}, -а<х < а,	(2)
exp{-z3}, х> а,
uvw)\
где мы обозначили
—а	а	х
21 = ъ J ью| da, Z2 ={-j Р(о da, z3=l-J ip(oi

2.7. Квазиклассическое приближение	333
При расчете нормировочного множителя, как и обычно, пренебрегаем
вкладом экспонент и считаем, что sin2 а =1/2 (функция быстро ос¬
циллирует), поэтому С ~ у/2muj/iг. Вычисляя интегралы, окончательно
получаем
Еп
Z2 =
huj
— V 1 “ (—) +arcsin(-) +
Хо V ЧХо /	ЧХо/
Z1.3	-
Еп_
hu>
Полный вид решения легко восстанавливается, если учесть, что
С
1
2%/|р(х)|
2тг^/х2 -х%	\
nyfcl
Случай б) Прежде всего заметим, что условия применимости ме¬
тода ВКБ (плавный ход потенциала взаимодействия) выполняются вплоть
до х = 0, а в точке х = 0 необходимо поставить граничное условие
ф(0) = 0 (рис. 2.8).
Поэтому должно выполняться условие (для
классически разрешенной области)
*°
sin{- Jр(х) dx +	= О,
о
что приводит к модификации правила кванто¬
вания Бора-Зоммерфельда:
3
J р(х) dx = irh(n +	.
(3)
Рис. 2.8. Потенциал за¬
дачи 2.7.1 (случай б)
Из соотношения (3) получаем уровни энергии:
Еп = hu>(2n + !), и = 0,1,2,...,
которые совпадают с нечетными уровнями для случая а). Волновые
функции ipn{x) связаны с функциями (2) очевидным соотношением (ср.
с задачей 2.2.4):
~	fV2ll>2n+iM. *>°-
■фп(х) = \	.	п
О,	х	<	0.

334	Глава	2.	Квантовая	механика.	Решения	задач
2.7.2. В данной задаче, как и в задаче 2.7.1 п. б) необходимо поставить
специальное граничное условие при х = 0, т. е. гр(0) = 0. Это приводит
к следующему виду правила квантования:
Е!р   ч
jР(0 di = J >/2т(Е - F£) d£ = тгh[n + ^ J.
о	о
В итоге получаем энергетические уровни:
„ _ /ЗтгhF\2/3(	ЗЛ2/3
П \2\/2т/	("+4)
и согласованные квазиклассические функции. В классически разрешен¬
ной области функция имеет вид
и в классически запрещенной:
2.7.3. Согласно формуле Гамова (11.38) коэффициент прохождения че¬
рез потенциальный барьер равен
ь
D ~ ехр|—^ J \p(x)\dx},
а
где
Ь	Ь	2Ze*/E
J \p(x)\dx = J ^2m(U(x)-E)dx = V2m J \J^--Edx.
a	a	ro
Вычисляя интеграл, получаем
D ~ exp|-^-^^(arccos у/а - у/а(\ - q)) j,	(1)
r F
где a = —-—о. В случае, если q < 1, выражение (1) упрощается:
2Ze
D
Г 27гZe2 /2т 1	,оч
~е1ф|	(2)

2.7. Квазиклассическое приближение
X
335
Следует заметить, что выражения (1) и (2) определяют коэффициент
прохождения лишь по порядку величины, т. е. показывают его экспо¬
ненциальную малость. Поскольку условия применимости метода ВКБ
нарушаются в точке х = го (резкий скачок потенциала), то условия сши¬
вания решений в данной точке требуют
уточнения. В точном выражении в отли¬
чие от (2) появляется предэкспоненциаль-
ный множитель ~ 1.
Данная задача рассматривалась впер¬
вые в связи с теорией а-распада. С точ¬
ки зрения квантовой механики а-распад
представляет собой типичное явление про¬
хождения частицы через потенциальный
барьер.
Итак, а-частица вначале «заперта» в
области х ^ го (зона действия потенциа¬
ла притяжения ядра, рис. 2.9). Для того,
чтобы выйти из ядра, т. е. излучиться, а-частица должна преодолеть
потенциальный барьер (при х > го на частицу будут действовать куло-
новские силы отталкивания).
Вероятность а-распада (или прохождения через барьер) в единицу
времени А пропорциональна коэффициенту прохождения D: А = nD, где
п — число столкновений со стенкой барьера в единицу времени.
Величину п можно оценить следующим образом: п ~ v/ro, где v —
характерная скорость частицы в потенциальной яме. Далее
Рис. 2.9. Потенциал, исполь¬
зуемый в теории а-распада
_Р_
та
h
таг0
поэтому п ~
™ У1'
таг о
Период полураспада Г)/2 связан с вероятностью распада в единицу
времени А известным соотношением:
' 1/2
In 2 _ таг0\п2
~ hD
= С\ ехр
£l
L V~e
(3)
где последнее равенство является следствием (2). Логарифмируем (3) и
получаем соотношение
In Г,/2 = Л + -|,
которое и представляет собой закон Гейгера-Неттола. Величины А и В,
разумеется, несложно выразить через исходные данные задачи.

336 JXr Глава 2. Квантовая механика. Решения задач
2.7.5.	Пусть возмущенный потенциал имеет вид U(x) = Uo(x) + 6U(x),
где Uo{x) — начальный потенциал, a U(x) — малое изменение потен¬
циальной энергии. Будем считать, что дискретные уровни энергии при
наложении возмущения изменяются по схеме: £„0) —> Еп = Е^ + 6Еп.
Для поиска поправки 6Еп представим формулу квантования Бора-Зо-
ммерфельда в виде
Ь+бЬ
■rch(n + 1 ) = J ^2m(£i0) 4- SEn - U0(x) - 6U(x))dx,	(1)
a+6a
где 6a и 6b характеризуют возможные сдвиги точек поворота. Очевидно,
что должно выполняться
U0(a + 6а) + 6 U (а) = £<0) + 6Еп,
откуда легко получить, что
5Еп - 6U(а)
\6а\
U'(а)
т. е. |5а| -С 1 и \8b\ «С 1, если выполнены условия квазиклассичности.
Нетрудно показать, что изменение интеграла за счет сдвига точек по¬
ворота ~ (<5а)3/2 (или ~ (6Ь)3/2), и в линейном приближении соответ¬
ствующие поправки должны быть отброшены. Поэтому оставляем в ин¬
теграле (1) в пределах интегрирования только а и Ь, и, проводя разло¬
жение подынтегрального выражения с линейной точностью по 6U(x),
6Еп, получаем
, ^ f 6U(x)dx	If	dx	_	2	Г
I ^2m(Uo(x) - £f) / / yj2m(U0(x) - £<0)) T /
Vo(x)
где T — полный период классического движения частицы в потенциале
Uo(x), v0(x) — классическая скорость частицы.
Данный результат может быть получен и в первом приближении тео¬
рии возмущений, если в качестве невозмущенной функции взять квази-
классическую функцию. В этом случае при расчете интегралов нужно
пренебречь вкладом экспонент и заменить квадрат синуса на 1/2 под
знаком интеграла, считая, что функция быстро осциллирует.

2.8. Теория возмущений JV 337
2.8.
ТЕОРИЯ ВОЗМУЩЕНИЙ
2.8.1.	Для расчетов используем выражение оператора координаты х для
гармонического осциллятора через операторы а и а+ (хо — осциллятор-
ная единица длины (11.16)):
х= ^~(а+ +а),
V2
хо
П_
тси
Случай а) Поправка первого приближения -
поправка второго приближения:
*f = £-
2 2
а х0
г(0)
кфп
с-(О)
(_п п + 1N
\hu> hui J
О (см. задачу 2.3.3),
(1)
2ти
где Vnk = (n|V|*>, 40) = М« + 1/2).
Случай б) Для слагаемого Дх4 в операторе возмущения поправка
первого приближения найдена в задаче 2.3.3, для Ах3 необходимо вы¬
числять поправку второго приближения. Суммарная поправка равна
АЕп
Ь/м*
\rnuj)
2 1
пг + П + -
4 hu> V muj )
',2 + n+55
2.8.2.	Оператор энергии взаимодействия с однородным полем имеет вид
V = ax= ^(а+ + а),	(1)
V2
где а — некоторая константа взаимодействия.
Поправка к уровням энергии (с учетом второго приближения теории
возмущений) найдена в задаче 2.8.1, формула (1). Как видим, поправка
■* оказалась не зависящей от постоянной Планка, поэтому она имеет клас¬
сическую интерпретацию. Действительно, если бы мы записали полный
гамильтониан с учетом возмущения (1) и выделили бы полный квадрат,
мы бы получили, что все уровни энергии сдвинулись на одинаковую
величину, совпадающую с полученной по теории возмущений, но при
этом и изменилось бы равновесное значение координаты осциллятора.
Для нахождения смещения положения равновесия осциллятора по тео¬
рии возмущений необходимо знать «поправленные» векторы состояния.
Поправки к векторам состояний находим по формуле (11.40):
\фя) = |л) + |^1)) = |Л> + AjjL(v^|п - 1) - v^T+T)|n + 1)).

338 -М- Глава 2. Квантовая механика. Решения задач
Вычислим теперь среднее значение координаты для состояния \грп) с уче¬
том поправок первого приближения:
(•ф„\х\фп) = ^{(п\(а + а+)\гр^) + (-ф^Ца + а+)\п)) =
= ^—(s/n{n\a+\n - 1) - \J{n + l)(n\a\n -)-1)) = —^-j.
Пш '	тш
Полученный результат в точности совпадает с тем, который получается
в результате выделения в гамильтониане полного квадрата.
2.8.3. Состояния трехмерного изотропного гармонического осциллятора
определяются тремя квантовыми числами, принимающими целые неот¬
рицательные значения |пь«2.«з)- Первый возбужденный уровень энер¬
гии трехкратно вырожден. Обозначим состояния следующим образом:
|1) = |1,0,0),	|2)	=	|0,1,0),	|3)	=	|0,0,1).
Оператор возмущения выразим через повышающие и понижающие опе¬
раторы (см. задачи 2.8.1 и 2.8.2)
V = ^ах0(а+ + ах)(а+ + ау),
где ш — частота осциллятора, xq = yjh/(mu) — осцилляторная единица
длины (11.16).
Легко видеть, что все диагональные матричные элементы оператора
возмущения равны нулю, а отличны от нуля только два недиагональных:
Vn = V22 = I/33 = У\Ъ = 1^23 = 0,	1/)2	=	К21 = ^ах0-
Таким образом, получаем, что состояние |3) = |0,0,1) — правильное и
имеет энергию, совпадающую с энергией первого возбужденного уров¬
ня невозмущенного осциллятора. Два других правильных состояния
определяются линейными комбинациями
|±Д) = -^(|1,0,0) ±10,1,0»
и отвечают поправкам к невозмущенному уровню энергии, равным соот¬
ветственно ±Д, где Д = ах\/2.
2.8.4. Поскольку в рассматриваемом случае все матричные элементы
оператора возмущения для состояний, относящихся к вырожденному
уровню энергии Е„°\ равны нулю, то общий вид вектора состояния с

2.8. Теория возмущений	339
учетом первого приближения теории возмущений определяется стан¬
дартным образом в соответствии с (11.40):
I ал * ю +	<■>
где штрих означает отсутствие в сумме слагаемых с п = k, р = v. Со¬
ставим теперь из состояний (1), относящихся к одному и тому же уров¬
ню энергии £„°\ линейные комбинации
I =	(2)
и подставим их в уравнение Шредингера:
(Н<°) + У)|Фла} = £па|Ф„а>.
Теперь мы можем получить систему алгебраических уравнений, ана¬
логичную системе (11.41), из которой определяются поправки второго
порядка к уровню энергии и, соответственно, коэффициенты линейных
комбинаций (2), дающих правильные векторы первого приближения:
Уравнение формально сводится к стандартному (см. (11.41)), если ввести
оператор возмущения Veff.
2.8.5.	Второй возбужденный уровень трехмерного изотропного гармо¬
нического осциллятора шестикратно вырожден. Обозначим состояния
так же, как и в задаче 2.8.3:
|1) = |2,0,0), |2) = 10,2.0), |3> = |0,0,2),
|4) = 11,1,0), |5) = 11.0,1), |6) = |0,1,1).
Для состояний |4)-|6) отличны от нуля только диагональные матрич¬
ные элементы эффективного оператора возмущения Veff задачи 2.8.4.
Таким образом, получаем трехкратно вырожденный уровень, смещен¬
ный на величину —Д, где
„2 3’
4 т ujq
которому соответствуют три произвольные линейно независимые ком¬
бинации состояний |4)-|6).

340	Глава	2.	Квантовая	механика.	Решения	задач
При действии оператора возмущения Veff состояния |1)-|3) «смеши¬
ваются», поскольку отличны от нуля как диагональные, так и недиаго¬
нальные матричные элементы:
Vn = V22 = У33 = — ^Д. V12 = У23 = У\з = -Д.
Таким образом, получаем секулярное уравнение третьей степени, корни
которого, однако, легко находятся и равны
5 .
£1,2 = Д, £3 = -g Д.
Правильный вектор состояния для поправки £3 равен
|£3) = А(|2,0,0) + |0,2,0) + |0,0,2)).
Для двукратно вырожденного уровня £1,2 правильными будут линейные
комбинации, ортогональные вектору состояния |ез) и имеющие вид
|1) = Л(^|2’0’0) + |0’2’0))"|0’°’2>)’
!H) = У§(|(|2’0’0) +10’°’2)) -1°.2.0>)-
Как видим, шестикратно вырожденный уровень энергии расщепился
на три: невырожденный, один двукратно и один трехкратно вырожден¬
ный уровни энергии. Учет более высоких порядков теории возмущений
уже не сможет качественно изменить картину.
2.8.6.	В невозмущенной задаче уровни энергии очень близки или сов¬
падают, поэтому применим теорию возмущений для близких уровней
энергии. Сформируем линейные комбинации волновых функций нуле¬
вого приближения ф = С\ф^] + Сг^0* и подставим их в уравнение
(Н<°) + у)ф = Еф. В результате для нахождения коэффициентов Сь Сг
мы получим систему
(Н"-Е уСЛ = 0	(!)
V Яи Hn-E)\cJ
где введены обозначения
Я™-«»|Н|Й»)) = |^ + й°’’	т.».	1.2.
^ Vтт	171	ф	П.

2.8. Теория возмущений -*\г 341
Вообще говоря, здесь не предполагается, что уровни энергии в невоз¬
мущенной задаче совпадают, т. е. £,(0) Ф Е^]. Из условия разрешимости
системы (1) находим значения уровней энергии для линейных комби¬
наций ф\х
£i,2 = ^{(^11 + Нм) ± ^}.	=	\J(Н11 - #22)2 + 4|//i2|2.
Из системы (1) находим коэффициенты С\, Сг, позволяющие построить
функции -01.2 = с;-20<о) + С^ф^, нормированные на единицу, т. е.
[ с\'2= [/3,2(1 ±а)]1/2.	_Нп+Н22 а _	,ч,
\ Cj2 = ±[/32i(l Т «)]1/2.	’	21*«1‘
Далее выразим через ф\х ф\°2 =	—	^2л^г)- Здесь мы учли,
что det С = — 1. Функции ф\$ описывают состояния с определенной энер¬
гией, поэтому, восстанавливая зависимость от времени, получим
ф|0)(л:, t) = С\ф2е~лЕг* - С\ф\е~тЕд'	(3)
Полученная нами волновая функция описывает состояние, в котором
ф‘О)(х,0) = ^[0), как и требуется по условию задачи. Подставим в соот¬
ношение (3) функции ф\ и ip2, выраженные через ф^. В результате
получим функцию ф{0)(х, t) в виде разложения по состояниям ф^, при¬
чем коэффициенты разложения теперь будут зависеть от времени. В
соответствии с вероятностной интерпретацией квадрат модуля коэффи¬
циента перед ф2°* должен быть равен вероятности обнаружить систему
в момент t в состоянии ф^-
W =
с\с\
(К.Л2 1	1	(hw)2	\	2	)
(М	(М
Здесь мы использовали соотношения (2).
2.8.7.	/3-Распад трития 3Н —> ^Не + е~ + ме представляет собой быстрый
процесс, в течение которого изменяется потенциальная энергия элек¬
трона в атоме:
UH(r) = -el - UHe(r) =	(1)
поскольку ядро трития превращается в ядро изотопа 3Не. Время распада
можно оценить, как время пролета /3-электрона через область, зани¬
маемую атомом tp ~ а/ир, где а — радиус воровской орбиты, vp —

342 _/\, Глава 2. Квантовая механика. Решения задач
скорость ,9-электрона. Поскольку энергия /3-электрона имеет порядок
нескольких кэВ, то цд/с ~ 10-1 » vaT/с ~ а ~ 1/137, где оат ~ e2/h —
скорость атомных электронов. В итоге получаем, что tp гораздо меньше
характерных атомных времен:
Это означает, что волновая функция электрона не успевает изме¬
ниться за время tp, в течение которого меняется гамильтониан (1). Вме¬
сте с гамильтонианом меняется и система его собственных функций,
поэтому мы можем разложить исходную волновую функцию электро¬
на i/;H в поле 1/н(г) по собственным функциям в поле t/неМ:
где коэффициенты разложения Сп — (^е|^Н) = /^e*ipHd3x опреде¬
ляют вероятности перехода электрона wn — \Сп\2 в одно из связанных
состояний иона Не.
Имея в виду явный вид радиальных функций электрона в тритии и
в гелии:
2.8.8.	При резонансном испускания 7-кванта ядром, переходящим из
возбужденного состояния в основное, энергия испущенного 7-кванта е7
должна быть в точности равна энергии возбуждения ядра: е7 = е. Из¬
вестно, что для свободно движущегося ядра такой процесс не идет,
потому что этому мешает отдача ядра, возникающая вследствие дей¬
ствия закона сохранения импульса (см. задачу 1.3.36). Оказалось, что в
твердом теле связанные ядра-излучатели могут излучать 7-кванты «без
отдачи». Причем процесс возможен именно потому, что ядро связано, а
не свободно.
В дальнейшем рассмотрим простую одномерную модель, предпола¬
гающую, что ядро-излучатель связано гармоническим потенциалом:
= Ц Сп'Фпе + J Ск'Фк*dk,
получим окончательно
(1)

2.8. Теория возмущений
J^. 343
где М — масса ядра. Вектор |п) теперь характеризует состояние ядра в
пространстве в целом.
В отличие от этого, если бы ядро было свободным, то его простран¬
ственное состояние следовало бы характеризовать собственным векто¬
ром оператора импульса \k'), где p|fe') = hk'\k'). При испускании 7-кванта
свободным ядром это состояние переходит в \k' — k), где Hk — импульс
испущенного 7-кванта.
При движении в гармоническом потенциале импульс уже не будет
интегралом движения, и начальное состояние ядра |п) не является соб¬
ственным вектором оператора импульса. Поэтому теперь невозможно
применить закон сохранения импульса по схеме \k') —» \k' - k), как для
свободного случая. Однако состояние ядра |п) можно разложить по
собственным векторам оператора импульса:
Дальнейшие рассуждения будут существенным образом использо¬
вать тот факт, что рассматриваемый нами процесс является быстрым по
сравнению с характерным временем движения в гармоническом потен¬
циале. Приведем оценку времени взаимодействия. Длина волны 7-кванта
намного больше размеров ядра, ибо Ни)*, ~ he/А7 -С Hc/R„m ~ 40 МэВ.
Поэтому время взаимодействия можно оценить, как т7 ~Л7/с~ш“1.
Поскольку энергия 7-кванта гораздо больше характерной энергии коле¬
баний ядра Ни) (см. (1)), то время взаимодействия т7 оказывается много
меньше тялра ~ ш-1 — характерного времени эволюции состояния ядра
в гармоническом потенциале.
На основании этого делаем вывод о том, что процесс испускания
7-к ванта действительно является быстрым. Одновременно и так же быст¬
ро срабатывает и закон сохранения импульса. Поэтому можно считать,
что в выражении (2) каждое состояние с определенным значением им¬
пульса |к') получает сдвиг: \k') —► \k' — k). Коэффициенты в разложении
не изменяются. Следовательно, вектор конечного состояния ядра можно
записать в виде
Очевидно, что состояние |/) не является собственным вектором гамиль¬
тониана (1), но его можно разложить по полной системе собственных
векторов {|л)}:
(2)
|/) = J \k' - k){k'\n) dk' = J e-ik*\k')(k'\n) dk' = е~ш\п).
n'

344 Глава 2. Квантовая механика. Решения задач
Отсюда видно, что вероятность того, что ядро при испускании перейдет
в одно из состояний гармонического осциллятора, равна
Wn^n, = \{п'\е-т\п)\2.
Энергия испущенного 7-кванта при этом е7 = е — Ни(п' — п), где по¬
следнее слагаемое — это энергия, забираемая ядром. Случай п' — п
отвечает условию е7 = е, следовательно, это и есть условие резонанс¬
ного испускания. Вычислим вероятность резонансного испускания из
основного состояния осциллятора:
+оо
Wo—.о = |(0|е-,'**|0)|2 =	J e-ikxe~(*) dx
— ОО
Мы получили так называемый фактор Дебая-Уоллера.
2.8.9.	Гамильтониан задачи имеет вид
= е
й = 1г^ад + у<е'"‘ +
Для невозмущенной задачи
=	40)	=	£о = -^
— волновая функция и энергия связанного состояния в (5-яме (см. зада¬
чу 2.2.6). В основу вычислений положим общую формулу для вероят¬
ности переходов в единицу времени в состояния непрерывного спектра
под действием периодического возмущения (11.50):
w = ^г- J \Fvq\25(Eu - Е0 - Ни) du,	(1)
где v — квантовое число, нумерующие состояния непрерывного спектра.
Прежде всего рассмотрим случай Ни 3> |£Ь|. т. е. приближение, ког¬
да ^-потенциал не действует на частицу в конечном состоянии. Тогда в
качестве волновой функции конечного состояния можно просто выбрать
функцию свободной частицы:
1 ь	h2k2
ipk(x) = —=eikx, тогда v = k, -00 < k < 00, Ek = ——.
V27T	2	m
Вначале необходимо вычислить матричный элемент
рьп — ^ [ хе-*о\х\+ikxdx —	Ь

2.8. Теория возмущений
X
345
а затем использовать формулу (1), имея в виду правило (Д.7) для
<5-функции:
w
= ^[Ы2 + Ы2]
ft
dk
dEk
k\2 = ±-^\j2m(hw + До)-
Окончательно получим
w =
\E0\3/W^-\Eo\-
(2)
Заметим, что данная формула применима и при более слабом огра¬
ничении Ни > |£о|. В этом случае в качестве функций нулевого прибли¬
жения необходимо выбрать точные собственные функции невозмущен¬
ного гамильтониана (для непрерывного спектра). Поскольку невозму¬
щенный гамильтониан коммутирует с оператором инверсии, то можно
рассматривать отдельно четные и нечетные функции. Очевидно, что
четные функции дадут нулевой вклад в матричный элемент. Нечетные
решения имеют вид ipk(x) = (l/\/7r)sin£x. Вычисление вероятности с
этими функциями приводит нас опять к формуле (2).
2.8.10. Вероятность квантовых переходов из начального состояния |г) в
конечное состояние |/) в первом порядке временной теории возмущений
имеет вид (см. (11.47))
ща) = х\ j Vftoe^'dt'
_ \Vo„\2
4ft
|/(0I2
(1)
причем верхний предел интеграла t необходимо в дальнейшем устре¬
мить к бесконечности. Чтобы не получить при t —* оо расходящийся
интеграл, воспользуемся следующим приемом: в выражении (1) возьмем
интеграл I(t) по частям. При этом получим
т
е'У
iujfi
2	г
1 + - arctg -
7Г	Т
2т f е
inuy J t‘
e^'dt'
'2 + т2'
Здесь первое слагаемое описывает поправку первого приближения к
начальной волновой функции при t > 0 и не дает вклада в переходы.
Квантовые переходы описываются вторым слагаемым, и после устрем¬
ления t —> оо интеграл легко берется. Окончательно находим
W,	I	V	g-2ШЦТ
W[t	2 2 е
и OJfi

346 -i\r Гпава 2. Квантовая механика. Решения задач
2.8.11.	Гамильтониан рассматриваемой системы имеет вид
^2 2 2
Tj Р . TYlUJ X	р
н = 2^ + — -«£*.
причем последнее слагаемое должно учитываться по теории возмуще¬
ний. Вероятность квантовых переходов из основного состояния п = 0 в
различные возбужденные состояния п в первом порядке теории возму¬
щений определяется квадратом модуля коэффициента (с. (11.46)):
< = i'f	VM^'dt = i j d-^e~d,'.	(1)
—оо	—оо
Мы воспользовались здесь приемом, описанном в предыдущей задаче,
т. е. проинтегрировали один раз по частям и отбросили внеинтегральное
слагаемое, считая, что оно не вносит вклада в квантовые переходы.
Очевидно, что в условиях данной задачи единственным возможным
переходом будет переход в состояние п — 1, потому что только матрич¬
ный элемент У,о отличен от нуля для осциллятора:
У,о = -е£<1|х|0> =	хо	=	\/Х
V2	V	тш
Вследствие конкретной зависимости электрического поля от времени
(см. условие) интегрировать в выражении (1) нужно от нуля до т (пред¬
полагается, что t —* оо, поэтому t^> т). В результате для вероятности
перехода получим
• 2/шт\
1П (т)
Sln 1 ~ 1	е2Е2
Го_*, = Г0- ■ 4 V , Го
(т)
2hmu>'
В случае мгновенного включения поля (ит < 1) имеем ГЬ-ц ~ Го. При
адиабатически медленном включении поля (щт> 1) получим Го_*1 ~ О,
т. е. переходы в возбужденные состояния практически не происходят.
2.8.12.	В основу решения задачи положим уравнение эволюции для спи¬
новой функции мюона:
ih§-tx( 0 = Нх(0 =-мо^экЫО.	(1)
где гамильтониан в представлении Шредингера имеет вид
Н = -цо(ЭЛо) - /хо(^Ь) =
= -цо(Э^Ко) — poh(ax cos u>t + оу sin oat) = H0 + V(t),	(2)

2.8. Теория возмущений
347
причем Но = -роЛоВг = -(hujо/2)стг, где введено обозначение шо = 7IK0,
7 = е/{тс) — гиромагнитное отношение для спинового момента.
а)	Теория возмущений. Вначале применим для решения урав¬
нения (1) нестационарную теорию возмущений, считая малым воздей¬
ствие радиочастотного поля h. Тогда в нулевом приближении мы имеем
двухуровневую систему:
приближения, описывающая вклад состояния х-1/2. равна (см. (11.46))
где мы ввели обозначение ид = 7Л. Таким образом, спиновая функция
с учетом поправки первого приближения должна иметь вид
Это можно реализовать либо при ид С |ш + и>о|, т. е. система должна
быть далека от резонанса: ш	— wo> либо при малом времени действия
возмущения. Оба варианта не позволяют детально рассмотреть резо¬
нансные явления, и поэтому мы обратимся к точному решению.
б)	Точное решение. Мы уже рассматривали эту задачу ранее
(см. задачу 2.5.6), ниже предлагается другой способ ее решения. Урав¬
нение Шредингера (1) сводится к системе уравнений
Данную систему можно свести к системе уравнений с независящими
от времени коэффициентами при помощи подстановки
Если в начальный момент х(0) = Х1/2 (а10> — 0. то поправка первого
о	о
(3)
Условия применимости теории возмущений предполагают, что lajg | -С 1.
Сх = е-Ъш‘а, С2 = е12ш,Ь.

348	Глава	2.	Квантовая	механика.	Решения	задач
Систему уравнений для функций a(t) и b(t) запишем в матричном виде:
i0-< :)(;> Q-(i>
где мы обозначили е — ш + шо- Решение системы (4), удовлетворяющее
необходимому граничному условию, можно записать в виде матричной
экспоненты:
CHt>
(5)
Здесь Л — матрица, имеющая следующий вид:
л = (£ w') = °(
\wi -е/ V
= n { е/П wi/fi\
wi/П —e/Sl)’
и мы ввели обозначение7) П = yj'е2 + ш2. Поскольку Л2 = П2 ■ I, то все
четные степени матрицы Л будут пропорциональны единичной матрице,
и мы приходим к соотношению
е‘м — cos
Подставим (6) в решение (5) и определим a(t) и b{t):
. sin Ш ( £ \
t_n~ W'
°) = cosm(‘| + ,
Наконец, восстанавливая зависимость от времени в экспонентах, полу¬
чаем искомую функцию xtt) в виде
х(0
Icos(?0+/Ssin(?0]e"'¥,>
.uj] . (\
» — sin —t)e 2
П 42/
Вероятность переворота спина, вычисленная при помощи данной функ¬
ции, в точности совпадает с найденной в задаче 2.5.6. Реализация усло¬
вия <§; |е| позволяет получить результат теории возмущений (3). Точ¬
ный и приближенный результаты согласуются также и при малом вре¬
мени действия возмущения Ш С 1.
7)	Введенные нами обозначения П, wo, и ш\ совпадают с аналогичными обо¬
значениями задачи 2.5.6

2.8. Теория возмущений	349
Приведем также значения проекций вектора поляризации мюона:
Р*	= sin 0[cos#(l _ cos fii) cos wt - sin fit sinwl],
Py	= sin 0[cos0(l - cos fit) sinwf + sin fitcosw/],
Pz = cos2 в + sin2 в cos fit,
где sin0 = u>i/n, cos 9 = e/fl, что совпадает с обозначениями задачи 2.5.6.
Заметим, что фактически мы нашли оператор эволюции для дан¬
ной	задачи, который, как нетрудно сообразить, будет иметь	вид	U(0 =
= е~5ш°г‘е‘А‘,	где первая экспонента отвечает начальной замене	пере¬
менных (переходу СьСг -> а, Ь). Подумайте, совпадает ли этот опера¬
тор с оператором эволюции, полученным другим методом в задаче 2.5.6.
2.8.13.	Вначале рассмотрим динамическую часть фазы, приобретаемой
вектором \фа(Ш) (см- условие задачи). Заметим, что временная эво¬
люция состояния неконсервативной системы может быть представлена
в виде
где оператор эволюции определяется как хронологически упоряченная
экспонента:
Пусть начальное состояние является одним из собственных векто¬
ров мгновенного гамильтониана в момент времени /(л), совпадающим
с моментом времени оператора Н(?(л)) в соответствующем я-м члене
разложения правой части соотношения (1) (см. также (11.45)). Тогда
оператор Н(£(л)) может быть заменен соответствующим собственным
значением энергии, а в силу невырожденности уровня энергии мгно¬
венное состояние останется тем же самым. Поскольку параметр £ из¬
меняется во времени медленно, на интервале времени At = t — to т,
где т — характерное время изменения параметра, можно считать, что
состояние будет близко к собственному состоянию для всех сомножите¬
лей членов ряда Т ехр. В этом случае действие оператора эволюции сво¬
дится к умножению исходного вектора состояния на фазовый множи¬
тель exp fgE„(^(t'))dt/Sj. При этом в силу невырожденности уров¬
ня энергии состояние по-прежнему будет мгновенным собственным век¬
тором гамильтониана в текущий момент времени.
!*(*)) = U(l, fo)|*o),
(1)

350 -J\, Глава 2. Квантовая механика. Решения задач
Для интервала времени At ^ т представим решение в виде, записан¬
ном в условии задачи, которое теперь должно удовлетворять уравнению
Шредингера
ш||Ф(и(0)> = н(ШИи(0)>.
В силу того, что гамильтониан зависит от времени только через пара¬
метр £(0, уравнение Шредингера принимает вид
ift|i*(u(0)> = [-w)+Eam)mt,m) +
+ *^(0(^Ш£(0)))е‘'7(()е fi° М .
Производную от состояния |i/>n(£(t))) по параметру £ можно представить
в виде	^
д-шт) = £ш£(0))<^0)||^п(£(0)>«
ее1
тт мт)\шт-
Здесь мы воспользовались адиабатическим приближением и опустили
в сумме все слагаемые с k ф п, имея в виду, что вероятности перехо¬
дов в эти состояния экспоненциально малы. Таким образом, с учетом
мгновенного стационарного уравнения Шредингера получаем
in§-t№,sm =
Поскольку уровень энергии £„(£(0) невырожден, состояние |Ф(/, £(0))
также должно соответствовать этому же уровню энергии. Поэтому в
правой части полученного уравнения можно заменить значение £„(£)
действием гамильтониана Н(£). Таким образом, видим, что в правой
части уравнения Шредингера появляются дополнительные члены, кото¬
рые обязаны обратиться в нуль, что возможно при выполнении условия
7(о = ттт д
<Ы£(0))-
Нетрудно показать, что функция 7(0 является действительной. В самом
деле, продифференцируем условие нормировки 1 = (^л(£)|^л(£)) и най¬
дем соотношение
о = то щ Фляг + то =2не{^}.
которое, по существу, и доказывает данное утверждение.

2.8. Теория возмущений	351
Если параметр £ изменяется периодически с периодом Т, описывая
замкнутую траекторию в параметрическом пространстве, изменение фа¬
зы за период можно выразить через интеграл по замкнутому контуру Г
в параметрическом пространстве:
г
7 = J dt'y(t) = i j d£{ipn(Z(t)) ~ фп(£(Щ.
(2)
2.8.14.	Состояния с определенными значениями проекции спина sm =
= ±1/2 на направление магнитного поля определяются векторами (см.
задачу 2.4.19)
(1)
|+)и =cos-|+) -t- sin
|-)и = - sin -|+) + cos 2е<¥,|-)>
где векторы |+) и |—) описывают состояния с положительной и отри¬
цательной проекциями спина на ось z (см. (11.26)).
Два состояния |±)jc (1) отвечают значениям энергии ^ро'К/2. Та¬
ким образом, энергетический спектр невырожден. Пусть теперь маг¬
нитное поле адиабатически медленно вращается вокруг оси z при по¬
стоянном угле в (рис. 2.10). В этом случае применимо адиабатическое
приближение, из которого следует, что частица, находившаяся перво¬
начально в основном состоянии, в нем и оста¬
нется, а вектор состояния будет отличаться
от исходного вектора (1) фазовым множителем
(найденным в формуле (2) задачи 2.8.13).
Периоду Т изменения параметров соответ¬
ствует изменение азимутального угла <р от 0
до 27г, поэтому для фазы Берри имеем
27Г
= i J с1<рм{х 1^1х)эс
= —
= —2 /d<p( 1-COS0) =
о
2тг в
J dip J sin в1 d6' = — дщП,
Рис. 2.10. Среднее зна¬
чение спина мюона в
медленно вращающем¬
ся магнитном поле
где П — телесный угол, под которым из нача¬
ла координат видна траектория, описываемая
средним значением спина (рис. 2.10), дщ; = 1/2 — проекция спина на
направление магнитного поля.

352 -Up Глава 2. Квантовая механика. Решения задач
2.9.
РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ МЕХАНИКА
2.9.1.	Приводим результаты расчета коммутаторов:
а)	[рь Н0]	= О,
б)	[I;, Но] = iceijkajPk	ф-	О,
в)	[I2, Но]	=	+	Ьр*)	Ф	О,
г)	Но]	= iceijkakpj	ф	О,
д) [s2, Но] = О,
е) [J;, Н0] = О,
ж) [j2, Но] = О,
з) [(Sp),Ho]=0,
и) [75, Но] = 2imc2i
Р2 ф 0.
Таким образом, для свободной дираковской частицы интегралами
движения являются: три компоненты импульса р,-, три компоненты и
квадрат полного углового момента j, а также оператор продольной по¬
ляризации (Ёр)/р. В отличие от нерелятивистской теории компонен¬
ты орбитального и спинового моментов не являются интегралами дви¬
жения, что является особенностью релятивистского движения. Опера-
для безмассовой частицы (например, для безмассового нейтрино).
2.9.2.	Калибровочное преобразование — это одновременное преобразо¬
вание потенциала электромагнитного поля и волновой функции:
Таким образом, градиентное преобразование потенциала, дополненное
умножением волновой функции на фазовый калибровочный множитель,
оставляет инвариантным уравнение для электрона во внешнем поле (его
удобно записать в ковариантном виде (11.54)).
2.9.3.	Уравнение Дирака для свободной частицы в гамильтоновой фор¬
ме имеет вид
чем ip(r) удовлетворяет стационарному уравнению — уравнению на соб¬
ственные значения гамильтониана Дирака. Кроме того, -ф(г) должна
тор 75 (оператор киральности) является интегралом движения только
или Л" -> А'» = А»
Ф(х) -» Ф'(;с) = e*cfM Ф(х).
»Й^Ф = Н0Ф = {с(Йр) + /?тс2}Ф.	(1)
Для стационарных состояний можно записать Ф(г, t) = e~ft£V(r)> при-

2.9. Релятивистская квантовая механика -Д,. 353
быть собственной функцией оператора импульса, потому что операторы
трех компонент импульса р коммутируют с гамильтонианом:
| Нд^(г) = Еф(г),
\ рф(г) = рф(г).
Условия (2) указывают на то, что решения уравнения (1) следует искать
в виде плоских волн
ф(г) = ц(р,£)Чрг>,	(3)
где и(р,Е) — не зависящий от координат и времени биспинор. Учиты¬
вая (3), перейдем к так называемой «расщепленной» форме записи ста¬
ционарного уравнения Дирака:
| с(ар)х = (Е- mc2)ip,
\ с($р)<р = (Е + тс2)х■
Здесь мы использовали формулы, выражающие дираковские матрицы в
блочном виде через ст-матрицы Паули (11.52):
ч: s> ч -°,> -
ст, О
О
(5)
а также ввели обозначения
— двухкомпонентные функции. Условие совместности системы уравне¬
ний (4) имеет вид
с2(Эр)(&р) = Е2 - т2с4.
С учетом тождества дпдт = 5пт 1 + ienmkdk (задача 2.4.13) из этого со¬
отношения получаем
Е = £ЕР = £у/с2 р2 + /и2с4,	(6)
где £ = ±1 — знак энергии. Двум знакам энергии отвечают два типа ре¬
шений уравнения Дирака, соответствующие различным знакам энергии
в экспоненте, т. е. различным типам зависимости функций от времени.
Рассмотрим далее так называемый знаковый оператор

354 _/\, Глава 2. Квантовая механика. Решения задач
записанный в общем виде и в импульсном представлении. Очевидно он
коммутирует с гамильтонианом Но, и поэтому его собственные значе¬
ния могут быть использованы для классификации состояний, собствен¬
ных для Ид. Собственные значения оператора Л есть £ = ±1, причем
£ — +1 соответствует положительному (£ > 0), а £ = — 1 — отрицатель¬
ному знаку энергии (£ < 0). Для свободного движения энергия Ер, им¬
пульс р и £ (знак энергии) являются интегралами движения и могут
одновременно принимать определенные значения. Далее, из (4) следует,
что биспинор ы(р,£) можно представить в виде
( *
ц(р,£) = N1 С(Э р)
\££р + тс2<у3
где N — нормировочный коэффициент, a <р — остающийся пока неопре¬
деленным двухкомпонентный спинор, нормируемый условием ip+ip = 1.
Нормировочный коэффициент в (8) легко находится:
Осталось найти функцию <р. Неоднозначность в выборе р связана с
наличием спиновой степени свободы у дираковской частицы. Рассмот¬
рим оператор (Ер)/р, где р = |р|. Собственные значения этого операто¬
ра характеризуют проекцию спина на направление движения, т. е. это —
оператор продольной поляризации. Оператор продольной поляризации
коммутирует с гамильтонианом, следовательно, физическая величина,
соответствующая ему, является интегралом движения. Поэтому к урав¬
нениям (2) можно добавить уравнение
^V(r) = sV’(r),
где собственное значение s = ±1 называется спиральностью частицы.
Используя (8), а также явный вид матриц Е, (5), сводим это уравнение
к двухкомпонентному:
(£р) ip = spp>,	(9)
т. е. к уравнению для паулиевских спиноров с определенным значени¬
ем проекции спина на направление импульса. Ясно, что уравнение (9)
определяет двухкомпонентный спинор, собственный для оператора (<тп),
где п = р/р. Такие функции были найдены нами в задаче 2.4.19. На
этом можно было бы и завершить решение данной задачи, но представ¬

2.9. Релятивистская квантовая механика _/\, 355
ляется полезным получить также другой вид решения уравнения (9)
с явной зависимостью от спиральности s. Такое решение может быть
представлено в виде
_	0	+	«Рг/р)‘/2	N
^	V2\s(\-	spz/p)U2ei6/
(10)
где tg<5 = ру/рх■ Если ввести сферические координаты вектора п = р/р,
то эти функции перейдут в функции Ф±1 задачи 2.4.19. Объединяя на¬
ши результаты (10) и (8), мы получаем нормированные собственные
функции операторов Но, р, Л и (£р)/р:
(
Фр.Ыг, t)
Г
\
<(-«£)>•?)
'ЫП'-Ъ
1/2
1/2
1/2
(11)
/
2.9.4.	Перейдем в гейзенберговское представление и вычислим опера¬
тор dx/dt, представляющий собой, очевидно, х-компоненту оператора
скорости:
^ = V* = ^[Но,х] = ljca ][рх,х] = са\.
Данный результат не поддается интерпретации в духе принципа соот¬
ветствия. Во-первых, поскольку собственные значения оператора а\ рав¬
ны ±1, то оказывается, что собственные значения операторов компонент
скорости равны ±с, хотя в действительности скорость может принимать
любые значения в промежутке от -с до +с. Во-вторых, матрицы а;
не коммутируют между собой, что должно приводить к принципиаль¬
ной невозможности одновременно измерить хотя бы две компоненты
скорости.
И, наконец, в теории Дирака происходит так называемое «расщеп¬
ление» понятий скорости и импульса, т. е. отсутствуют обычные, анало¬
гичные существующим в релятивистской классической механике связи
между операторами скорости и импульса. Эти сложности в физической
интерпретации оператора скорости, связаны с интерференцией состоя¬
ний с различными знаками энергии.

Глава 2. Квантовая механика. Решения задач
В последовательной одночастичной теории физические величины дол¬
жны описываться операторами, не смешивающими между собой состоя¬
ния с различными знаками энергии. Такие операторы называются чет¬
ными (или «одночастичными»). Четный оператор переводит волновую
функцию с определенным знаком энергии в функцию с тем же знаком
энергии, а нечетный оператор — в функцию с другим знаком энергии:
[?]Ф(±) = Ф(±),	Д}Ф(±)	= Ф(т).
Найдем четную часть оператора скорости:
[V*] = с[а,] = ±<Ух + ЛуД) = 2^{Йь Н0}Л = ^Л.
Отсюда следует, что четная часть оператора скорости для решений с
положительной энергией (£ = +1) связана с оператором импульса со¬
отношением, соответствующим связи между скоростью и импульсом в
классической релятивистской теории — четная часть оператора скоро¬
сти допускает простую классическую интерпретацию.
Нечетная часть оператора скорости {v*} = ^(vx — AvxA) антиком-
мутирует с гамильтонианом, потому что
чг{у*} = пДу* - уД) = -{уЛт2-
Up	Z	Lip
Отсюда следует, что
Jpv,}.i[H0,{v,}] = -!{v,}H „
Интегрирование этого уравнения с учетом dHp/dt = 0 дает
2iHnt
{v*} = c{Si} = c{ai(0)}e ft .
Таким образом, нечетная часть оператора скорости не имеет класси¬
ческого аналога и характеризуется быстрыми осцилляциями с частотой
~ 2\E\/h, вызывая явление Zitterbewegung («дрожащее движение»), ко¬
торое, по существу, и затрудняет физическую интерпретацию операто¬
ров в теории Дирака.
2.9.5.	Система уровней энергии свободного электрона Дирака
Е — £ \J с1 р2 + т2с4, £ = ±1
представляет собой два континуума состояний для положительных и
отрицательных значений энергии, которые разделены энергетической
щелью АЕ = 2тс2 (рис. 2.11, а).

2.9. Релятивистская квантовая механика	357
Предположим, что электрон находится в постоянном и однородном
электрическом поле, направленном вдоль оси z. Пусть движение про¬
исходит вдоль поля £ = {0,0,£}.
б
Щг)
Рис. 2.11. Модификация уровней энергии дираковской частицы в однородном
электрическом поле
При этом существенно изменяется конфигурация уровней энергии
электрона: изменяются границы верхнего (Е = тс ) и нижнего (Е = -тс1)
континуумов энергии (рис. 2.11, б).
Новыми границами верхнего и нижнего континуумов состояний ста¬
нут линии
Е = ±тс2 + e£z,
где U(z) = e£z — потенциальная энергия электрона в электрическом
поле (подразумевается — е < 0 — заряд электрона). В результате пово¬
рота запрещенной энергетической зоны, разделяющей верхний и ниж¬
ний континуумы, состояния с отрицательной и положительной энерги¬
ей будут разделены лишь пространственно.
Таким образом, электрон, имеющий определенную энергию Е, будет
находиться в «состоянии с положительной энергией» (£ = +1) при z < а
и в «состоянии с отрицательной энергией» (£ = -1) при z ^ Ь. Но на
самом деле (рис. 2.11) энергия электрона при этом остается одной и той
же. Значит, при наличии внешнего электрического поля (или любого
другого потенциала) не может быть строгого разделения состояний на
состояния с положительной и отрицательной энергией. Более того, воз¬
можен туннельный переход через запрещенную зону из верхнего кон¬
тинуума в нижний (или наоборот). Этот эффект и представляет собой
парадокс Клейна.
Оценим вероятность туннельного перехода из верхнего континуума
в нижний, используя квазиклассическое приближение (11.38):
ь
D~ ехр{-| J |/?(z)|dzj,
а

358 -Л, Глава 2. Квантовая механика. Решения задач
где \p(z)\ — -у/т2с4 — (Е — e£z)2. Вычисляем интеграл и получаем, что
„2„3 •
П	/	т	С	\
Очевидно, что такой же вид должна иметь и вероятность обратного тун¬
нельного перехода — из нижнего континуума в верхний.
Итак, наложение электрического поля не приводит к локализации
дираковской частицы — она может оказаться в состоянии с противо¬
положным знаком энергии в результате туннельного перехода, причем
вероятность такого перехода растет с ростом поля и стремится к еди¬
нице в том случае, если напряженность поля равна
£ = гКр = ^ = 1,3-1016 В/см
г еп
— так называемому швингеровскому значению.
В соответствии с дырочной интерпретацией Дирака при переходе
электрона из нижнего континуума состояний в верхний появляется па¬
ра частиц: электрон в верхнем континууме с энергией Е > 0 и «дыр¬
ка» в нижнем континууме (среди состояний с Е < 0). Эта «дырка» ин¬
терпретируется, как античастица по отношению к электрону, т. е. по¬
зитрон. Следовательно, мы описали процесс рождения электрон-пози-
тронной пары.
2.9.6.	Уравнение Дирака, описывающее движение заряженной частицы
во внешнем электромагнитном поле, имеет вид
т£ф(г,0 = (с(аУ)+ ртс2 - еф)Ф(гД),	(1)
^	^	в
где У =? р + -А, — е < 0 — заряд электрона.
^		i_ р.
Считаем состояние Ф(г, t) стационарным: Ф(г, t) = e к ф(т). В даль¬
нейшем будем полагать Е > 0, т. е. мы фиксируем знак энергии (счита¬
ем энергию	положительной, ибо в нерелятивистской	квантовой	механи¬
ке имеются	только	состояния с положительной энергией).	Представим
далее, как и обычно, волновую функцию в виде ф(г) =	и
\х(г)/
шем (1) в «расщепленном» виде:
Г (Е - тс2 + еф)р = с(аУ)х,
\ (Е + тс2 -)- еф)х = с(аУ)р.
Исследуем эту систему в нерелятивистском пределе и в слабых полях, т. е.
Е~тс2 + е, \е + еф\<^тс2.	(3)
запи-

2.9. Релятивистская квантовая механика	359
В этом случае (2) перейдет в
Г (е + еф) ф) - с{Э7) х(г),
\ (е + еф + 2тс2) х(г) = с(ЭУ) ф).
Из второго уравнения с учетом (3) находим
*(Г) "	(4)
откуда видно, что в нерелятивистском приближении двухкомпонентный
спинор х(г) имеет по отношению к ф) порядок малости (о/с) « 1. Это
и позволяет (в случае положительной энергии Е > 0) говорить о двух
нижних компонентах дираковского спинора как о малых.
Подставим (4) в первое уравнение системы и получим с линейной
точностью по (о/с) уравнение для двухкомпонентного спинора ф)\
(е + еф)ф) = -^(ЭУ)(ЭУ)ф).
Преобразуя правую часть данного уравнения, находим
(<тТ)(аТ) =	+ ieijkdk) = У + i-dkeijk(^ikj + А ,-ру) =
= у>2 + ie-dkeiik[ Pi, Ay] = У + ^(ЯК),
с	с
где IK = rot А. В результате получаем нерелятивистское уравнение, опи¬
сывающее движение частицы со спином 1/2 в электромагнитном поле:
Это и есть уравнение Паули, а <р(г) — паулиевский двухкомпонентный
спинор.
2.9.7.	В уравнении Дирака для электрона во внешнем электромагнит¬
ном поле
ih~ Ф(г, 0 = (c{aV) + Ртс2 - еф) Ф(г, 1)
положим
U (г) = -еф(г) = -Ц~, А = О,
т. е. будем считать, что внешнее поле — чисто кулоновское, при этом,
очевидно, У = р + ^А —+ р, и, как и ранее, -е < 0 — заряд электрона.

360 -l\r Глава 2. Квантовая механика. Решения задач
“ Ft
Полагаем, что задача — стационарная: Ф(г,t) — е~ ь 1р(г), фикси¬
руем знак энергии Е > 0. Переходим к «расщепленной» форме записи
уравнения Дирака:
(Е - тс2 + еф)<р = с(Эр)х,
(Е + тс2 + еф)х = с(Э р)<р.
Из второго уравнения системы (1) выражаем х(г):
Х(г) =   ~2 -с(стр)<р(г)и_0 - ^Щф)<	(2)
Е + тс + еф	*	2тс
т. е. в нерелятивистском приближении функция х(г) имеет по отноше¬
нию к ip(г) порядок малости (и/с) <С 1. Подставляем результат (2) в
первое уравнение (1) и получим (пока еще точное) уравнение для <р(г):
(.Е - тс + еф)ф) = с* (ар)-	-2 -(Эр)ф).	(3)
Е + тс + еф
Переходим к нерелятивистскому приближению:
Е~тс2 + е, |е + еф\ -С тс2,
и в дальнейшем при разложениях будем ограничиваться членами по¬
рядка (v/с)2. Поэтому
—A i-i±4).
2тс V 2тс )
(Е + тс2 + еф) 1 = (2 тс2 + е + еф) 1 ~ —,
2 тс'
При этом уравнение (3) принимает вид
(£ +еф - ы)Ф) = -(^^(frpMr).	(4)
В правой части уравнения (4) преобразуем слагаемое
- (Эр)еф(Эр) = (Эр) U(r)(ap) = U(r) р2 + '[(?р),£/(г)](ар) =
= U (г) р2 + (5ц + ieijkdk)(-ihV iU(r))vi =
= U(r)p2 - ih((vu(r))p) + h2^-\oi). (5)
Здесь { = i[r x p] — орбитальный момент. Уравнение (4) при этом пе¬
рейдет в
(с+еф-ыУм=

2.9. Релятивистская квантовая механика	361
Далее, в правой части (6) преобразуем первое слагаемое:
(е + еф)р2 = р2(е + еф) + [(е + еф),р2\ ~ ^-p[U(r),p] - [U(r), pip =
= £ - h2(V2U(r)) - 2ih((VU(r))p). (7)
Здесь мы учли, что на решениях уравнения в рассматриваемом при-
о2
ближении (е + еф)<р(г) ~ |~^(г)> а также использовали правило диф¬
ференцирования произведения функций.
Теперь вспомним общий вид нашей (четырехкомпонентной) волно¬
вой функции (1) с учетом (2). Запишем условие нормировки функции
ф(г) с точностью до (v/c)2:
1= Jip+(r)ip(r)d3x~ J d3x j<^+(r)</>(r) + -^2^((CTVV(r))+((CTVV(r)) j.
(8)
Здесь мы использовали вид оператора импульса: р = —t'ftV. Заметим,
что мы хотим получить приближенное уравнение для двухкомпонент¬
ной паулиевской (нерелятивистской) функции, которую в дальнейшем
будем обозначать ^П(г)- Две компоненты такой функции должны, как
всегда, описывать две возможные ориентации спина, и условие норми¬
ровки для фп(г) должно иметь традиционный вид:
1= J фи+(г)фи(г)с13х.	(9)
Наше приближенное уравнение (6) пока записано для двухкомпонент¬
ной функции ip(г) (верхние компоненты биспинора ф(г)), но функция <р(г)
имеет существенно иное условие нормировки, следующее из (8).
В связи с этим в условии нормировки (8) проинтегрируем по частям
второе слагаемое:
f d3x((aV)^)+((£VV) = - j d3x<p+(Ap) = - J d3x(A<p+)v>.
Симметризуя эти два варианта, из условия (8) мы получим
1 = j d3x\^p+p- £-^[(Д</?+)^ + <£+(Ду?)] j.	(10)
Для согласования нормировочных условий (9) и (10) с точностью до (v/c)2
положим
^(r,= (1 + ii)v<r)' или *(г)" (‘ - IS?K(r)'

362 -Л, Глава 2. Квантовая механика. Решения задач
где мы учли, что р2 = —h2A. Это есть не что иное, как каноническое
преобразование волновой функции, ибо оно сохраняет значение норми¬
ровочного интеграла, т. е. вероятность.
Теперь подставим в уравнение (6) соотношение (7), а также функ¬
цию <р(г), выраженную через ipu(r). В итоге получим окончательный
вид приближенного уравнения:
(е + еф-^уп(г) = 9фп(гУ,	(11)
V =	+ ±(—V(v2t/).
8т с 2т2с2 dr г 8 \rncJ
В правой части полученного уравнения сгруппированы поправки к дви¬
жению электрона в кулоновском поле. В порядке следования это: реля¬
тивистская поправка, спин-орбитальное взаимодействие и контактное
взаимодействие.
2.9.8.	Пусть магнитное поле направлено по оси z: 9С = {0,0, Э-С). Вы¬
берем вектор-потенциал так же, как в нерелятивистском случае в за¬
даче 2.5.1, т. е. А = {0,!Kjc, 0}. Тогда стационарное уравнение Дирака
будет иметь вид Но^(г) = Еф(г), причем
HD = с(,аУ) + рте2, 1Р = р+^А, -е < О
— заряд электрона. Перейдем к «расщепленной» форме записи уравне¬
ния Дирака:
=("!'!>	«о
\х(г)/	\с(д'5,)р	= (Е-\-тс)х-
Выразим из второго уравнения системы (1) х(г) через р(г) и подставим
результат в первое уравнение:
(Е2 - m2c4)tp(г) = c2(<rIP)(<rIP)yj(r).	(2)
л~	~2 eh ^
Используем тождество (задача 2.9.6) (ЭТ)(а7) = IP + — (егДС), и тогда
уравнение (2) примет вид
{Й + (Ру + ^Х) + Pf + у^г}у>(г) ~Е Ф)-	(3)
Полученное уравнение формально имеет вид уравнения Шредингера
Heff<£(r) = £effy?(r), причем легко заметить, что Heff коммутирует с one-

2.9. Релятивистская квантовая механика -Л,- 363
раторами ру и р2. Это значит, что можно искать решение уравнения (3)
в виде
ф) = Ce^y+P‘z)f( х).	(4)
Далее положим f(x) =	и	приведем	уравнение	(3)	к	следующему
\hU)J
виду:
1
2 me2
[£2 - m2c4 д e/LcJC - c2p2]/i,2(x). (5)
Уравнение (5) есть не что иное, как нерелятивистское уравнение для
осциллятора H'f[/i,2(x) = Д'^/угС*), причем
й' _ Р« j. mcfiy'^ у' — у 4_ сРу о —	^	^
ПрГГ — _ Т п л , X — X ~у” ..|	'	Ь	1	я	«	/2	*
еП 2т 2	еЛ	me	dx
Ясно, что должно выполняться Е'еП = Ш(л' + 1/2) и на основании этого
получаем
Е2 - т2с4 - с2р2 = ehc‘K(2n' + 1 ± 1).
Очевидно, что 2л' + 1 ± 1 — всегда четное число. Обозначим его 2л и
получим окончательный результат:
ЕпРг = yJm^+^^+2ehc^<n.	(6)
Поскольку в соотношении 2л' + 1 ± 1 = 2л знак ± относится к ком¬
понентам /l,2(x) функции /(х), то ясно, что общий вид функции ф)
(формула (4)) должен быть таким:
(PW.W - ехр [Н(Р»» +	( &иГ(/) J,
где w°cu(x) есть обычное решение уравнения Шредингера для гармо¬
нического осциллятора (11.18). Коэффициенты С\$ можно определить,
если конкретизировать спиновое состояние частицы, для этого нужен
еще один оператор — спиновый интеграл движения.
Найденные нами уровни энергии (6) не являются эквидистантными
в отличие от уровней Ландау (задача 2.5.1). Уровни энергии вырождены
по спину с кратностью 2 (кроме основного состояния л = 0) и по ру —
с бесконечной кратностью.

364 _/\, Глава 2. Квантовая механика. Решения задач
2.9.9. Плотность заряда и плотность тока для дираковской частицы
имеют вид
р - еФ+Ф, j = есФ+аФ,
причем эти выражения справедливы как для частицы во внешнем элек¬
тромагнитном поле, так и для свободной частицы.
Действуя стандартным образом, перейдем в уравнении Дирака к «рас¬
щепленной» форме записи (см., например, задачу 2.9.6), выразим две
нижние компоненты х(г) через две верхние <р(г) и перейдем далее к
нерелятивистскому пределу Е ~ тс2. В итоге получим с линейной точ¬
ностью по v/c (формула (4) задачи 2.9.6)
*(г) “	” "Кme‘^v{r). *(г) = О'
Далее необходимо учесть, что р = — ihV, а также связь матриц а, с
S-матрицами Паули (формула (5) задачи 2.9.3). В итоге находим, огра¬
ничиваясь линейными по v/c членами,
р ~
j - ^ ((V<p+)y> ~ ^)) -	^ rot{у+Эф).
Полученные выражения совпадают результатами нерелятивистской тео¬
рии для плотности заряда и тока частицы со спином 1/2, обладающей
зарядом е и собственным магнитным моментом р = eh/(2mc).
2.9.10. Решения уравнения Дирака для свободного электрона, отвеча¬
ющие определенным значениям импульса р и энергии Е = £Ер, могут
характеризоваться различными значениями знака энергии £ = ±1 (см.
задачу 2.9.3). При этом решения с положительным знаком энергии £ = +1
описывают состояния частиц, а решения с £ = — 1 должны описывать
античастицы. Волновая функция античастицы (с положительной энер¬
гией) получается из решения уравнения Дирака с £ = -1 в результате
применения операции зарядового сопряжения.
Операция зарядового сопряжения при использовании стандартного
представления для матриц Дирака (11.52) вводится по следующей схеме:
Фс(гД) = 5сфТ(г,0,	(1)
где Фт = 7°Ф* («Т» — операция транспонирования биспинора), Sc =
2 0^
= 77 = —OL2-
Исследуем далее, как преобразование (1) будет действовать на кон¬
кретные решения уравнения Дирака в виде плоских волн (формула (11)

2.9. Релятивистская квантовая механика	365
задачи 2.9.3). Исходя из функции с отрицательным значением энергии,
получаем функцию античастицы:
То есть с точностью до несущественного фазового множителя мы по¬
лучаем ту же самую функцию — свободные электроны и позитроны
описываются одними и теми же волновыми функциями.
Мы видим, что при преобразовании (1) изменяется знак энергии и
направление импульса, но не меняется спиральность s. Волновая функ¬
ция античастицы должна описывать состояние с противоположным (по
отношению к частице) знаком заряда. Изменение знака заряда не за¬
метно в (2), так как это соотношение записано для свободных частиц.
Но если предположить, что волновая функция электрона с отрицатель¬
ной энергией удовлетворяет уравнению Дирака с зарядом — е < 0 (мы
записываем уравнение в ковариантной форме (11.54)):
то зарядово сопряженная функция будет удовлетворять уравнению
которое отличается от (3) именно знаком заряда.
2.9.11. Мы полагаем, что нейтрино — нейтральные массивные дираков-
ские частицы. Кроме того, мы считаем, что нейтрино определенного
типа (например, электронное или мюонное), или, как принято говорить,
определенного аромата, не являются состояниями с определенной мас¬
сой, а представляют собой суперпозицию таких состояний:
Состояния \v\$) в (1) удовлетворяют уравнениям Дирака соответствен¬
но с массами т\ и m2, а 9 — угол смешивания нейтрино.
Эволюция во времени состояний |i/[) и |г^г) дается выражением
ис(-£.-р.«) =
 —i£u(£, р, s) = г£Ф€,PiS(r, t). (2)
(3)
{
We) = И) COS# + Wi) s'n0>
Wu) — ~W\) sin# + \i>2) COS#.
(1)
h(0> = e-K£l‘h(0)>; MO) = e-^'MO)),

366 Глава 2. Квантовая механика. Решения задач
где £,,2 = у/р2с2 -(- т22сА. Если в момент t = 0 рождается электронное
нейтрино, то его состояние эволюционирует во времени следующим
образом:
| ue(t)) = cos0e-ft£|'|t/i(O)) + sin 0e~ft£2<|i/2(O)) =
= (e~ кЕ>‘ cos2 в + е~ьЕ2‘ sin2 IMO)) +
+ cos0sin#(e-ft£2' -	|г/Д0)).
Вероятность того, что нейтрино, родившись в момент t = 0, как элек¬
тронное, перейдет в момент t в состояние |i/M), имеет вид
Р(ие -+ vj - |(1/д|г/в(0>|2 = 2 sin226*
.	(ml	- т])с3
1 - cos '	'	t
2ph
Здесь мы предположили, что р ;» т\^с. Вероятность появления ней¬
трино нового сорта периодически зависит от времени, поэтому "данное
явление и носит название осцилляций,
2.10.	СЛОЖЕНИЕ МОМЕНТОВ.
ТОЖДЕСТВЕННОСТЬ ЧАСТИЦ
2.10.1.	Система состоит из двух частиц со спином 1/2. Одночастичные
спиновые функции обозначаем, как и обычно: Х1/г(1.2) и х—1/2(1.2), где
индексы 1,2 нумеруют частицы. Должно выполняться условие
si,2zX±i/20.2) = ±^х±1/г(1.2),
где s/2г — одночастичные спиновые операторы, действующие только
на спиновые функции первой или второй частицы. Обозначим искомые
функции ipsM, причем
f S2iI>sm = S(S + 1)V\sm.
I SzV’SAf = Мхрзм,
где S = S1+S2 — оператор суммарного спина.
Сразу находим общие собственные функции операторов S2 и S2,
отвечающие собственным значениям S = 1, М = ±1:
^1,1 = Xi/2(1)xi/2(2), ^1,-1 = X—1/2(1) х—1/г(2).
Применим к функции V'i.i понижающий оператор S_ = ?i_ + ?2_. С уче¬
том правил действия этих операторов получаем
‘Фю =	(xi/2(l)X—1/г(2) + X—1/г(1)Х1/2(2)).

2.10. Сложение моментов. Тождественность частиц	367
Спиновая функция t/’o.o должна иметь вид
0о,о = ^Х1/2(0Х-1/г(2) + Вх-1/2(1)Х1/г(2),
где коэффициенты А и В находятся из условий ортогональности и нор¬
мировки. Окончательно находим
'Фо.о = ^|(xi/2(1)X-i/2(2) - X—1/2(1)Х1/г(2)).
Спиновые функции ipsM обладают определенной симметрией по от¬
ношению к перестановкам спиновых переменных 1 <->■ 2: они симметрич¬
ны при S = 1 и антисимметричны при S = 0.
Заметим в этой связи, что для нахождения функций rpsM можно
было бы воспользоваться оператором спинового обмена Р12 (см. зада¬
чу 2.10.5). Он действует на спиновые функции следующим образом:
Pi20sm(1>2) = 0sm(2, 1). т. е. как раз переставляет спиновые перемен¬
ные. Оператор Р12 коммутирует с S2 и Sz, а поэтому искомые функции
должны быть и его собственными функциями: Pi20sm(1,2) = A0sm(1,2).
Легко видеть, что А = ±1, а собственные функции должны быть сим¬
метричными (А = 1) или антисимметричными (А = —1). Поэтому можно
сразу составить из одночастичных функций симметричные и антисим¬
метричные комбинации, и тогда останется только определить значения
квантовых чисел S и М.
2.10.2.	Рассматриваем задачу в представлении, где lf 2 и 11,22 диаго-
нальны, индексы 1,2 нумеруют частицы. Пусть 0/,,2m,,2(l, 2) — решения
одночастичной задачи. Они удовлетворяют уравнениям
f i?,2^i,2mi.2(l>2) = h,2(l\,2 + 1)^1.2т,/2(1.2),
\ li,2*0/i,2^11,2(1» 2) — Д11,2*0/1,2>ni,2(1* 2),
где l\ — I2 — 1, а т\ и m2 пробегают значения 0, ±1. Необходимо найти
функции Ф/.ль удовлетворяющие условиям
Г £2ФШ = L(L + 1)Фш,
\ ЦФьм = МФш<
где L = li +12 — оператор суммарного орбитального момента. Всего
мы должны получить девять состояний: пять состояний с L = 2; три
состояния с L = 1 и одно — с L = 0.	л
Сразу находим общие собственные функции операторов L2 и Lz,
отвечающие собственным значениям L = 2, М = ±2:
Ф2,2 = 01.1(1)01,1(2),	Ф2.-2	=	01,—1 (1) 01,-1 (2).

368 -l\r Глава 2. Квантовая механика. Решения задач
Применяем к функции Фгд понижающий оператор L_ =	12_, а к
Фг,-2 — повышающий оператор L+ = lj+ -И2+. Учитывая правила дей¬
ствия операторов L±, lj± и 12±, получаем
Фг,1 = ^=(V>i,o(l) ^1,1(2) + ^м(1)^1,о(2)),
Ф2-1 =	(^1,0 (1) ^1,-1 (2) + ^1,-1(1)^1.о(2)).
Далее, действуя понижающим оператором L_ на Ф23, находим
Фг.о = ^(^1,-1(1)^1,1(2) + ^1,1(1)^1,-1(2) + 2^1,о(1)^1,о(2)).
Для построения состояний с моментом L = 1 воспользуемся соотно¬
шениями ортогональности для коэффициентов Клебша-Гордана (11.56)
и (11.57). Вначале выпишем явный вид уже известных коэффициентов:
/-*2,±2	  |	/">2,4:1	  />2,±1	  1
1,=Ы,1,±1 ~	°1,±1,1,0 ~ °1,0,1,±1 ~
r2,0 _ 1 г2,0 _ /2
''±1Л'т1 ~ л/6’ 1Д1'° ~ V 3'
Далее используем соотношение ортогональности для коэффициентов с
М' = М = 1, L' = 2, L = 1. Оно сводится к выражению
^ ($+1.1.0+ ci£Li) = o.
Соотношение ортогональности, записанное для коэффициентов со зна¬
чениями М' = М = 1 и L' = L = 1, дает просто условие нормировки, по¬
этому получаем
Фщ = ^=(^1.о(1)^и(2) -^i,i(l)^i,o(2)).
Функция Фц-i определяется отсюда тривиально и равна
Ф,,_, = -^(^1,о(1)^1,-1(2)-^,-1(1)^1,о(2)).
Действуя на функцию Ф^ понижающим оператором L_, получим
Ф.,0 = ^(V’i,-i(l)V;i,i(2) — "01,1 (1) V7!,—1 (2)).

2.10. Сложение моментов. Тождественность частиц -*V 369
Осталось построить последнюю функцию Фо.о с L — 0. Вновь вос¬
пользуемся соотношениями ортогональности для коэффициентов с
М' = М = 0:
и = 2, L = 0: ^(С°+м_1 + С°'°11+1) +	=	0;
L' = 1, L = 0: ^- C°;°lili+i) = 0.	(1)
Решая систему уравнений (1) и используя условия нормировки, получаем
Фоо = -4=(*.-i<1)*.i(2) + V,i,i(1)V’i.-i(2) - V’i,o(l)V;i,o(2)).
v3
Полученные нами функции ФLM обладают симметрией по отноше¬
нию к перестановкам частиц 1 <-> 2: они симметричны при L = 0,2 и
антисимметричны при L — 1.
2.10.3.	Искомые волновые функции должны быть собственными для
следующего набора взаимно-коммутирующих операторов: j“, jz, l“, s2,
где 1 и s — орбитальный и спиновый моменты электрона, a j = 1 + s —
полный момент.
Волновая функция должна быть собственной для оператора проек¬
ции полного момента |г, т. е.
}2Ф = туФ.	(1)
Поскольку ]г = 12 + ?г = -г'^ + ^Эг, то, учитывая явный вид матри¬
цы дг, получаем, что уравнение (1) эквивалентно системе
£*=/(»•/-г)*.
Ф
=0-
= +
Интегрируя эти уравнения, легко получаем
V>i=/i(0)e‘'(m'_*h	(2)
Далее, искомая функция должна быть собственной для оператора I2,
12Ф =/(/+ 1)Ф,	(3)

370 Глава 2. Квантовая механика. Решения задач
и это позволяет конкретизировать функции f\(6) и f2(6) в (2). Учиты¬
вая (3), приходим к выводу о том, что
01 - С\ г/"'-*) (в, <р), 02 = с2 у(т,+*\е, ч>),
(т\
где Yt (в, <р) — сферические функции.
Наконец, искомая функция должна быть собственной для оператора j2:
|2Ф =/(/+1)Ф,
(4)
причем оператор j2 имеет вид
Р =
1 + !* + т
4
I2 - 1г +
В результате из соотношения (4) получаем систему уравнений для опре¬
деления констант Ci и С2:
1(1 + 1) - /(/ + 1) + т, + Ij Ci + ^ 1(1 + 1) - т) - 1с2 = О,
_	0 - ту “ ^С| + \l(l + 1) - /(/ + 1) - ту + ^ С] - 0.
Условие совместности для данной системы дает два решения: j = 1+1/2
и / = I ~ 1/2- Окончательно, определяя из системы Ci и С2, получаем
нормированные функции (сферические спиноры) в виде
04)
(.ПЕу(т^){в,г))
/
/у - my + 1
V 2/ + 2
7-т/ (Уг)
VV 2/ '
/
(<?. v>)
("•/-j)
(«.¥>)
7+4 + 1 vM)(e ,
\ V 2/ +2
2.10.4.	(/s/ту|(is)|/s/ту) = I (/(/ + 1) - 1(1 + 1) -
(/s/ту|(ij)|/s/ту) = - {j(j 4-1) +1(1 + 1) —	;
(Isjtrij|(ps)|Isjmj) = X- (j(j + 1) - 1(1 + i) + !).

2.10. Сложение моментов. Тождественность частиц	371
2.10.5.	Прежде всего заметим, что оператор Р]2 = (1/2)(1 + д\Э2) свя¬
зан с оператором квадрата суммарного спина системы двух частиц со
спином 1/2. В самом деле
Таким образом, при действии оператором Pi2 на симметричную функ¬
цию (5 = 1) функция умножается на +1, а при действии этим опера¬
тором на антисимметричную функцию (S = 0) последняя умножается
на —1. С учетом симметрий^функций такое действие оператора оказы¬
вается полностью эквивалентным перестановке частиц 1 <-> 2 (см. также
задачу 2.10.1). Как известно, любая функция двух переменных может
быть записана в виде суммы симметричной и антисимметричной функ¬
ций, поэтому действие оператора Pi2 на произвольную спиновую функ¬
цию двух частиц также будет сводиться к перестановке частиц.
Для того, чтобы доказать формулу Р\2Э\1?^ = Э2, заметим, что
выполняются соотношения
Правые части этих равенств совпадают, что, по существу, и доказывает
утверждение задачи.
2.10.6.	Одночастичные координатные функции и уровни энергии (за-
а)	Ферми-частицы со спином 1/2. Полная волновая функция Ф
(произведение координатной и спиновой функций) должна быть анти¬
симметричной, поэтому в случае щ ф п2 возможны два варианта:
S2 = (si + s2)2 = ^(<г, -I- а\ + 2<ti<72),
откуда легко получить, что
если S = 1,
если S = 0.
дача 2.2.1) имеют вид
О < х < а,
^nin2=Mxi,x2)xs(S,M) и Ф„|Л2 = iPs(x\,x2)xa(S,M),

372 -А. Глава 2. Квантовая механика. Решения задач
где грА и ips ~ антисимметричная и симметричная комбинации одноча¬
стичных функций (1), ха и Xs — функции системы двух спинов, найден¬
ные в задаче 2.10.1. Таким образом, ха отвечает значению суммарного
спина 5 = 0 (одна функция), a xs отвечает состояниям с 5 = 1 (три
ж2Н2
функции). Энергия состояния двух частиц £„,„2 = j(n^ + п\).
2 та
В случае щ = П2 = п может реализоваться только симметричная ко¬
ординатная функция ips, поэтому спиновая функция должна быть ан¬
тисимметричной: ха. т. е. такому состоянию отвечает значение 5 = 0.
n2h2
Энергия состояния двух частиц равна Епп — —^п2.
та
Энергия основного состояния N частиц:
тг2/)2
+\)(N + 2), если N = 2п,
п 24 та
£ =
ТГ2/)2
^Ц(М+1)(М2 + 2М + 3), если N = 2п +
24 та
б) Бозе-частицы со спином 0. Полная волновая функция (она
же — координатная) может быть только симметричной:
Ф«,Л2 =^s(x 1,X2) = -^[rpni(Xl)lpn2(X2) + ФтШ’фпгМ]-
ж2Н2
Энергия двух частиц: ЕП]П2 = - i—г(«1 +пЬ-
2 та
в) Бозе-частицы со спином 1. Полная волновая функция Ф
(произведение координатной и спиновой функций) должна быть сим¬
метричной, поэтому возможны два варианта (ri\ ф п2):
ФЛ|Л2 = ^s{x\.x2)xs(S,M) и ФЛ1„2 = i/ja(xi,x2)xa(S,M),
где спиновые функции имеют точно такой же вид, как и общие соб¬
ственные функции операторов L2 и Lz из решения задачи 2.10.2. Следо¬
вательно, ха отвечает значению суммарного спина 5 = 1 (три функции),
a xs отвечает состояниям с 5 = 0,2 (шесть функций). Энергия двух
частиц: £Л|„2 =	+	п\).
2 та
В случае щ = п2 = п может реализоваться только симметричная ко¬
ординатная функция ips, поэтому спиновая функция должна быть так¬
же симметричной: xs> т. е. такому состоянию отвечают значения 5 = 0,2.

2.11. Теория атомов и молекул —373
Энергия основного состояния N частиц для случаев б) и в) одина¬
кова и равна
2.10.7.	Спин а-частиц равен нулю, и их общая волновая функция дол¬
жна быть симметрична по отношению к перестановкам пространствен¬
ных переменных. В системе центра масс такая перестановка приводит к
преобразованию г —> -г, где г — относительная координата. При дан¬
ной замене угловая часть волновой функции а-частиц должна умно¬
жаться на (-1)L — четность состояния (L — полный орбитальный мо¬
мент). Число L должно быть четным, потому что волновая функция
симметрична. Поэтому и полный момент ядра Be также должен быть
четным. Следовательно, при J = 1 распад невозможен.
2.11.	ТЕОРИЯ	АТОМОВ И МОЛЕКУЛ
2.11.1.	Гамильтониан системы имеет вид
Н = Н(0) + V,
р(0)	Г	ez
Н ~ 2т	Т'
причем решение невозмущенной задачи известно (основное состояние
атома водорода):
/7(0) _
со ~
е
'2а’
V>(0)(r) =
'ira°
,-г/а
а -
те
— боровский радиус. Ядро представляет собой равномерно заряженный
по объему шар радиуса гр, поэтому электростатический потенциал та¬
кого ядра равен
U(r) =
- — ,	Г	tiro,
е2 г2	Зе2
0<r<ro'
Возмущение определяется отличием потенциала U(r) от кулоновского
в области ядра (г < г0), т. е. V = U(r) + е2/г. При расчете поправки
первого приближения по теории возмущений = (V>(0)|V|t/>(0)) можно
считать, что rp ~ 10-13 см<а~ 10~8 см. Окончательно получаем

374	Глава	2.	Квантовая	механика.	Решения	задач
2.11.2.	Пусть атом водорода помещен в однородное электрическое поле
£ = {0,0, £}. Взаимодействие с внешним полем приводит к модифика¬
ции гамильтониана:
H = ^-i + £rcos6> = H(0) + V,	(1)
где мы используем атомную систему единиц h = т = е = 1. В форму¬
ле (1) £ есть отношение напряженности внешнего электрического по¬
ля к внутриатомному £а = е/а2 ~ 5,14 • 109 В/см, поэтому практически
всегда £ -с 1, т. е. можно использовать теорию возмущений.
Если атом находится в основном состоянии, описываемом волновой
функцией ^(0)(г) — ■фюо = (1/\[к)е~г, то поправка первого приближе¬
ния к энергии £(01> — (ф(°)|У|ф(°)} = 0 в силу сферической симметрии
основного состояния и, как следствие, равенства нулю среднего значе¬
ния дипольного электрического момента.
Для вычисления следующей поправки к энергии (квадратичной по
полю) необходимо использовать второй порядок теории возмущений.
На классическом языке такая поправка соответствует индуцированному
дипольному моменту, возникающему под действием того же поля. В
этом случае поправка к энергии будет иметь вид
42) = -1а£2, где <* =	(2)
— поляризуемость атома.
Поправку к энергии во втором приближении теории возмущений
можно выразить через поправку первого приближения к волновой функ¬
ции ip^ при помощи известного соотношения
£<2) = (^(,,|У|ф<°>) = J ф(|) (г) £r cos в^(0> (г) d3x.	(3)
Функция должна удовлетворять уравнению первого приближения
теории возмущений:
(Н<°> - £<°))^(|)(г) = -VV>(0)(r).
Конкретизируя данное уравнение, получим
(	1	.	1 , 1\ ,/п/ \ £rcos0 _г 2
:Д
-r + ^(1)(r) =	=	—j=£re-rY{0)(6,<p),
\[ъ	у/Ъ
где У,(0) (#,</>) = yJZ/A-K cos в. Предполагая, что искомая функция имеет
вид ^(l)(r) = /(r)e~'T1(O,(0, ip), где f(r) = а + br + сг2, подставляем ее в
уравнение и, определяя коэффициенты, находим окончательно

2.11. Теория атомов и молекул	375
Вычисляя интеграл (3), получаем
ОО
42) = -|£2/r4(l + 0e-2^r = -?£2.
о
Следовательно, с учетом (2) поляризуемость атома равна а = 9/2 или,
в обычной системе единиц, а = (9/2)а3.
2.11.3.	Гамильтониан имеет в точности такой же вид, как и в зада¬
че 2.11.2 (формула (1)). Взаимодействие с электрическим полем по-преж¬
нему описывается по теории возмущений, и используется атомная си¬
стема единиц h — т = е — 1.
Атом водорода находится в возбужденном состоянии с п = 2. В этом
случае энергетические поправки оказываются пропорциональны первой
степени £ — имеет место линейный эффект Штарка. Причиной этого
является «случайное» вырождение уровней энергии, благодаря которо¬
му возбужденные состояния не обладают определенной четностью, и у
атома появляется отличный от нуля средний дипольный электрический
момент.
Для невозмущенной задачи п = 2, поэтому = -Z2/8, причем
данный уровень энергии вырожден с кратностью п2 = 4, поэтому необ¬
ходимо применять теорию возмущений для вырожденных уровней энер¬
гии. Итак, в невозмущенной задаче уровню Е4 отвечают четыре соб¬
ственные функции гамильтониана Н(0):
г/>200 = д20(r)Y^(0, ¥>),	^210	= Л2,(Г)У,(О)(0, <р),
ik\±\=R2Ar)Y[±l\o,v),
где в явном виде
«2.М= (§)3/Vf2(l-f), *,«-(§ )3/Vf|,
=	COS9,	lf).±v/^sta^.
Вычисления показывают, что отличны от нуля лишь следующие мат¬
ричные элементы оператора возмущения:
(V^oolVIV^io) = (‘^io|V|‘02Oo) =
Решая секулярное уравнение, получаем поправки к уровню энергии Е^:
44 = тз|, £<;> = о.

376 -А. Глава 2. Квантовая механика. Решения задач
Таким образом, исходный уровень энергии Епод действием элек¬
трического поля расщепляется на три уровня с энергиями:
Ех.з =	±	£,(‘]	=	т	3|,	£2 = £f •
Уровню энергии Е\ отвечает состояние (правильная функция нулево¬
го приближения) ф\ = (l/\/2)(t/>2oo + ^210)- уровню Ез соответствует со¬
стояние = (1/л/2)(^200 — ^210). а уровень Е% двукратно вырожден —
ему отвечают две линейно независимые функции: ф^и и V^i-i-
2.11.4.	Ядро атома водорода (протон) обладает собственным магнитным
моментом /Гр. Взаимодействие магнитного момента электрона с магнит¬
ным полем ядра приводит к расщеплению атомных уровней по зна¬
чению полного углового момента атома. Поскольку значение ядерного
магнитного момента примерно в 103 раз меньше, чем значение орбиталь¬
ного магнитного момента электрона, то и соответствующее расщепле¬
ние примерно в 103 раз меньше, чем расщепление тонкой структуры
(см. задачу 2.11.7). Поэтому та^ое расщепление называют сверхтонким
расщеплением.
Гамильтониан сверхтонкого взаимодействия имеет вид
VCBT = -(/Жя),
где введены обозначения:
Д =	= rot A; A = -[/ipXV]^,
Др = /Гр<Хр — оператор магнитного момента протона, /хо — магнетон
Бора. Таким образом,
vcbt = —/i0/ip<7[vх[Эр х v]]i = -iioppa[apA-(apv)v]-r. (D
Расчет ведем далее по теории возмущений, оператором Гамильтона
невозмущенной задачи является гамильтониан атома водорода Н<0) =
= р2/(2т) - е2/г, в волновых функциях нулевого приближения прост¬
ранственные переменные отделены от спиновых ^0)(r,s,sp) = фхоо(г) х
х x(s,Sp), V’ioo(r) = - г—е~'!а — координатная волновая функция ос-
V па3
новного состояния атома водорода, а = Я2/(/ие2) — боровский радиус.
Поправка к энергии, связанная со взаимодействием (1), равна
£св.т = J ^Х+^Гоо(г)Усв т ^юо(г)х-

2.11. Теория атомов и молекул
Для основного состояния вследствие сферической симметрии коорди¬
натной части волновой функции взятие интеграла по угловым пере¬
менным в (2) дает усредненный по направлениям гамильтониан (1), в
котором нужно заменить оператор V,Vy —> (1/3)<5;/Д. В результате (1)
сводится к
£св.т =	yAto/vlV’ioo(0)|2x+(££p)X-	(3)
Здесь мы учли, что Д(1/г) = -47гб(г), см. также (Д. 12).
Поскольку (ЭЭР) — 2S2 — 3 1, то правильными функциями нулево¬
го приближения будут собственные функции оператора квадрата сум¬
марного спина S = (1/2)(<т + Эр) (т. е. tpsM* см. задачу 2.10.1). С учетом
того, что IV’ioo(O)!2 = (7га3)-1, из выражения (3) получим
{8 роРр	^	_	|
3 ioPp	Н)
5 = 0
а
Таким образом, исходный уровень энергии расщепляется на два в соот¬
ветствии со значением суммарного спина электрона и протона, причем
один	из	этих	уровней трехкратно вырожден по проекции	суммарного
спина (S =	1,	М = 0, ±1),	а второй уровень — невырожденный	(S	=	0).
Подставляя численные значения величин, находим частоту перехода:
Аитеор = Es=' ~	=	1417	МГц.
Данное теоретическое значение отличается от экспериментально изме¬
ренного Дг^ксп = 1420 МГц. Причина расхождения результатов состоит
в том, что в действительности магнитный момент электрона не равен
в точности магнетону Бора ро> а отличается от него на величину Д/зд,
называемую аномальным магнитным моментом.
2.11.5.	В задаче рассматривается эффект Зеемана для основного состо¬
яния атома водорода с учетом его сверхтонкой структуры.
Атом водорода, находящийся в основном состоянии, помещен в од¬
нородное магнитное поле ДС = {0,0, Д-С}. После проведения стандарт¬
ных преобразований гамильтониан принимает вид
Н = |^-- + Усвт+Ш(1г + 2?г),	(1)
2т г
где VCBT- — гамильтониан сверхтонкого взаимодействия (формула (1)
задачи 2.11.4), П = е<К/(2тс) — ларморова частота, 1г и ?г — операто¬
ры проекции орбитального момента и спина электрона на ось г. Мы

378 -JL- Гпава 2. Квантовая механика. Решения задач
пренебрегли в (1) квадратичным по полю ТС членом, считая его вклад
в поправку к энергии малым по сравнению с линейным. Это можно
сделать при ТС -с Ю9 Гс.
В качестве оператора возмущения выберем Vщ = Ш(1г + 2зг). Га¬
мильтониан невозмущенной задачи Н(0) включает сверхтонкое взаимо¬
действие VCBT-, поэтому в нулевом приближении мы имеем два уров¬
ня с энергиями Ео + Д£о,ь Здесь Ео = —е2/(2а) — энергия основного
состояния атома водорода, Д£о,1 — поправки сверхтонкой структуры
(см. задачу 2.11.4) — соответственно для состояний с суммарным спи¬
ном S = 0 и 5 = 1. Волновые функции невозмущенной задачи имеют
вид =^юо(r)ipsM, где V’ioo(r) — координатная волновая функция
основного состояния атома водорода, грзм ~ спиновые функции элек¬
трона и протона (задачи 2.10.1 и 2.11.4).
Поскольку (■^iooPzIV’ioo) = 0, то вся содержательная часть будет ка¬
саться вычислений со спиновыми функциями. Обозначим состояния сле¬
дующим образом: |1) = |-0оо), |2) = |V>io), |3) = |-0п>, |4) = |V>i-i) и за¬
метим, что последние три состояния относятся к трехкратно вырож¬
денному уровню с S = 1, а состояние 11) — к невырожденному уровню
с S = 0. Отличные от нуля матричные элементы оператора возмущения
равны
(1|Ущ|2) = (2|Vjc|1> = <3|Vjc|3) = -(4|V«|4) = Ш. (2)
Учитывая малость сверхтонкого расщепления, мы можем считать невоз¬
мущенные уровни энергии близкими. Поэтому, записывая секулярное
уравнение, включим в него наряду с матричными элементами (2) также
и сверхтонкие поправки Д£о,ь
АЕ0 - £(1)	Ш	О
Ш Д£, - £(1)	О
О	0	Д£,	+	Ш	-	£(1)
0	0	О
Из секулярного уравнения получаем
£$ = ^{(Д£0 + Д£.) Т V(A£i - Д£0)2 + 4(Ш)2|,
£^4 = Д£( ± т.	(3)
Проведем анализ результатов. Во-первых, состояния |3) = |^ц) и
|4) = IV’i-i). относящиеся к уровню сверхтонкой структуры с S = 1, по¬
лучают линейные по полю поправки ±Ш. Тем самым снимается вы¬
0
О
О
AEi - Ш - £(1)
= 0.

2.11. Теория атомов и молекул
рождение по проекции суммарного спина М, уровень энергии с S = 1
расщепляется на три уровня.
В слабом поле, когда вклад магнитного поля много меньше вкла¬
да сверхтонкого взаимодействия (Ш -С АЕСВ.Т = АЕу — Д£о, это спра¬
ведливо для < 103 Гс), поправки получают также состояния |1) = |-0оо)
и |2) = {'Фю)■ Эти состояния относятся к разным уровням сверхтонкой
структуры: S = 0 и S = 1, но они отвечают одному и тому же значению
проекции суммарного спина М = 0 (рис. 2.12). Данные поправки квад¬
ратичны по полю:
Д£..,т т'
7(1)
'1,2
АЕ 1 — АЕо'
но ввиду наличия малого знаменателя АЕ\ — АЕо (малости сверхтонко¬
го расщепления) вклад этих поправок может быть существенно больше,
чем вклад отброшенного квадратичного по "К члена в гамильтониане.
Рис. 2.12. Эффект Зеемана с учетом сверхтонкой структуры для основного
состояния атома водорода (po2i = hCl, АЕСЛТ = АЕ\ — Д£о)
В сильном поле, когда Ш ДВ) — Д£о> поправки, относящи¬
еся к состояниям |1) и |2), равны
£<’> ~ тШ,	(4)
а правильные функции
•01,2 =	^	0ю)
описывают состояния, которые характеризуются значениями проекций
электронного и протонного спина на направление магнитного поля по
отдельности.

380 —J\- Глава 2. Квантовая механика. Решения задач
Заметим, что в данном приближении состояния |3) и |4) получают
поправки
£<‘> ~ ±Ш,	(5)
и при этом в состояниях |3) = \iptt) и |4) = IV’i-i) проекции электрон¬
ного и протонного спина на ось z также имеют определенные значения
(как и в состояниях ^1,2)-
Это и понятно, ибо в случае сильного поля можно вначале учесть
взаимодействие с полем, а затем, повторно применяя теорию возмуще¬
ний, — сверхтонкое взаимодействие. Взаимодействие с магнитным по¬
лем в (1) влияет только на проекцию спина электрона и не затрагивает
спин протона. Поэтому, сопоставляя (4) и (5), мы видим, что в сильном
поле (до учета сверхтонкого взаимодействия) мы имеем два двукратно
вырожденных (по значениям проекции спина протона) уровня энергии,
отвечающие поправкам Е\l)2 = E['l ~
2.11.6.	Гамильтониан атома водорода с учетом релятивистских и спи¬
новых поправок приведен в решении задачи 2.9.7, см. формулу (11).
Поправки содержат оператор спин-орбитального взаимодействия, ко¬
торый с учетом U(г) = -Ze2/г может быть записан в виде
Veo = ^^ = 4(r)(si),
2 тс г
где 1 и s — операторы орбитального и спинового моментов электрона.
Правильные функции нулевого приближения должны быть собствен¬
ными функциями операторов, являющихся точными интегралами дви¬
жения (т. е. коммутирующих не только с Н(0) = р2/(2т) — е2/г, но и
с Vе0, играющим роль оператора возмущения). Стандартные решения
уравнения Шредингера, пропорциональные сферическим функциям
4pnim(r) = Rni(r)Y\m\6,<p), не подходят для наших целей, ибо эти функ¬
ции являются собственными для оператора 1г, а данный оператор, как
легко проверить, не коммутирует с Vе0: [(sl),lz] ф 0.
Однако оказывается, что [(sl),j2] = 0, т. е. точным интегралом дви¬
жения является проекция на ось z полного углового момента ]z = 12-Г?г.
Это значит, что искомые функции должны быть общими собственными
функциями для полного набора наблюдаемых Н(0), I2, s2, j2, )2, к кото¬
рому можно перейти от стандартного набора Н(0), I2, s2, sz, 12. Эти два
набора эквивалентны, ибо по сути данный переход есть не что иное,
как задача сложения моментов: j = 1 + s.

2.11. Теория атомов и молекул	381
Итак, правильный вектор состояния атома водорода должен опре¬
деляться следующими квантовыми числами: |nljm/), где мы опустили
квантовое число s, потому что оно всегда имеет значение s = 1/2. В
координатном представлении этим векторам отвечают функции, най¬
денные в решении задачи 2.10.3. Воспользуемся результатами данной
задачи и конкретизируем их для п — 2.
Для п = 2 имеется восемь состояний, из которых в двух состояни¬
ях орбитальный момент равен нулю. Поэтому волновые функции этих
состояний можно записать в виде
где |±) — собственные векторы оператора ?2, а в представлении, где s2
диагоналей, им соответствуют функции x±i/2 (П.26).
Для значения орбитального квантового числа I = 1 возможны два
состояния с полным моментом /=1/2 и четыре состояния с / = 3/2.
Используя общие результаты задачи 2.10.3, получаем
Соответственно для полного момента / = 3/2 мы должны записать че¬
тыре состояния. Выпишем только два состояния с положительными про¬
екциями полного момента (остальные два легко написать самостоятельно):
Соответствующие векторы состояний имеют вид
|2,0,1/2, ±1/2) = |2,0,0)|±),
или в виде векторов состояний:
|2,1,1/2, +1/2) = -L(V2|2,1, +1)|-) - |2,1,0)|+)),
|2,1,1/2, -1/2) = -J=(|2,1,0)|-) - у/212,1, -1)|+».

382 _J\, Глава 2. Квантовая механика. Решения задач
2.11.7. Указание: Провести расчет по теории возмущений, положив в ос¬
нову гамильтониан Дирака для кулоновского поля в нерелятивистском
приближении (задача 2.9.7). В качестве гамильтониана невозмущенной
задачи Н<0) использовать нерелятивистский гамильтониан атома водо¬
рода, возмущение V должно включать релятивистскую поправку, спин-
орбитальное взаимодействие и контактное взаимодействие. В качестве
правильных функций невозмущенной задачи выбрать функции, собствен¬
ные для следующего набора коммутирующих операторов: I2, ?2, j2, jz,
где j = 1 + s — полный угловой момент электрона, см. задачу 2.10.3.
Уровни энергии атома водорода с учетом релятивистских поправок:
с _	(е2\ f, , ZV Г п ЗЦ
ni 2n2Wl п2 1/+1/2	4J/’
где п — 1,2,... — главное квантовое число, / = 1± 1/2 — внутреннее
квантовое число (формула Зоммерфельда).
2.11.8. Приводим ответы, в электронных конфигурациях указаны толь¬
ко электроны на незаполненных оболочках.
Атом
Конфигурация
Возможные термы
Нормальный
терм
nSi
15Р
leS
23V
27С0
58 Се
3s23p2
3s23p3
3s2 Зр4
3d3As2
3d1 As2
4/5rf6s2
'So, lD2,3Po,3 P\,3P2
45з/2, 2P|/2> 2 7*3/2, 2-Оз/2. 2jC>5/2
'S0,'D2,3Po,3Pi,3P2
3P0
45з/2
3 Pi
2
4^9/2
'G4(3//4)
Элемент Се представляет собой одно из немногих исключений из
правила Хунда. В скобках записан терм, определенный согласно прави¬
лам Хунда (отличающийся от истинного).
2.11.9.	При исследовании взаимодействия составных частиц таких,
как атомы, с другими атомами или ионами можно использовать тео¬
рию возмущений, рассматривая изолированные атом и ион (или дру¬
гой атом), как невозмущенную систему, а потенциальную энергию их
электростатического взаимодействия — как оператор возмущения. По¬
скольку скорости относительного движения атомов невелики, мы мо¬
жем считать, что ядра атомов (ионов) покоятся (приближение Борна-
Оппенгеймера).
Считая, что составные частицы находятся на большом расстоянии
друг от друга по сравнению с их размерами (ra < R), найдем энергию

2.11. Теория атомов и молекул	383
их электрического взаимодействия в виде разложения по степеням 1 //?.
Первый неисчезающий член такого разложения (в силу электронейтраль¬
ности атома) дает оператор возмущения нашей задачи (см. также (1.29)):
V = —d£,	(1)
где d — дипольный момент атома, £ — внешнее электрическое поле
(при га «С R его можно считать приблизительно однородным на расстоя¬
ниях ~ га).
Искомый потенциал взаимодействия получается в результате расче¬
та по теории возмущений с оператором возмущения (1) и волновыми
функциями, описывающими состояние изолированного атома (иона).
а)Атом + ион. В этом случае £ = ZeR/R3 (поле иона на больших
расстояниях, Ze — заряд иона), оператор возмущения имеет вид
V = -p(dR) = -|dz (d [, = £*„*«),
если считать, что R ffОг. Поправка первого приближения теории воз¬
мущений £(|) = (?//0)|у|^;(0)) = 0 в силу сферической симметрии S-со¬
стояний. Во втором порядке теории возмущений имеем
/7(2) _ у' |(00[У|пт)|2
е(0) _ £7(0) ’	W
п.тф О С00
где индексы 00 относятся к S-состояниям атома и иона (наинизшим
по энергии), индексы п,т нумеруют их возбужденные состояния. Из
формулы (2) ясно, что £*2) < 0, а также £(2) ~ I//?4, и в итоге получаем
общее выражение для потенциала взаимодействия в виде
U(R) = £(2) =	где С = const.
R
Взаимодействие такого типа называется поляризационным.
б) Атом + атом. В этом случае, учитывая, что напряженность
электрического поля для атома с дипольным моментом di имеет вид £ =
= [3(din)n-di]/£3, где n = R/£, из (1) получаем оператор возмущения
v - (З.аа> - 3(a,n>(d,n> = j_(j^ +
(см. задачу 1.6.7). Аналогично п. а) имеем £(1> = 0, а вычисление по¬
правок второго приближения дает
£/(£) =--^т, где С = const.
R
Именно такой зависимостью энергии от расстояния характеризуются
силы притяжения Ван-дер-Ваальса.

384 Л Глава 2. Квантовая механика. Решения задач
2.11.10.	Гамильтониан атома, находящегося в однородном магнитном
поле IK, имеет вид
й = нЕ(*+;*<'■>)’+1/+£н*
а
где — е < 0 — заряд электрона, суммирование производится по всем
электронам атома, U — энергия взаимодействия электронов с ядром
и друг с другом, S =J2a*“ ~ оператор суммарного спина электронов.
Проводя стандартные преобразования (в частности, выбирая вектор-
потенциал в виде \а — (1/2)[ДС х г„]), получим
H = Ho + ^-JC(L + 2S) + -^^[;Kxr«l2-
2тс	8тс ^
а
где L — полный орбитальный момент атома, Но — гамильтониан атома
в отсутствие поля (см. (11.61), (11.62)).
Имея в виду дальнейшее рассмотрение задачи по теории возмуще¬
ний, сделаем ряд приближений. Во-первых, отбросим в (1) член, квад¬
ратичный по напряженности поля Jf, считая, что в достаточно сла¬
бом поле он вносит малый вклад в решение по сравнению с линейным
по !К слагаемым. Далее, полагая, что поле направлено по оси г, полу¬
чим Н = Н0 + Vjc, где Vjc = Ш(£г + 2SZ) — оператор взаимодействия
с магнитным полем, П = е‘К/{2тс) — ларморовская частота.
а)	Слабое поле. В этом приближении считается, что поправка,
связанная с магнитным полем, т. е. Д£щ, гораздо меньше тонкого рас¬
щепления уровней Д£ТОНк8), и поэтому можно применить теорию воз¬
мущений к каждому уровню тонкой структуры. При этом оператором
возмущения является Vjc, а невозмущенные уровни — это уровни энер¬
гии атома с учетом расщепления тонкой структуры, характеризующие¬
ся определенными значениями квантовых чисел L, S, J (т. е. собствен¬
ными значениями операторов L2, S2, J2, где J = L + S). Правильными
векторами нулевого приближения в этом случае являются |L,S,J,Mj)
(собственные векторы для операторов L2, S2, J2, Jz). Расчет в первом
порядке теории возмущений дает
л гО)	a/i	1	+	1)	— L(L -(-1) + S(S + 1)
Д£'к = httgMj, где g = 1 +	27(7ТТ)
есть так называемый фактор Ланде. Отсюда следует, что магнитное поле
полностью снимает вырождение по магнитному квантовому числу Mj,
каждый уровень тонкой структуры расщепляется на 27+ 1 подуровней.
8> Это будет справедливо при +С -С 105 Гс.

2.11. Теория атомов и молекул	385
Конкретно для атома натрия находим, что уровень 2Рз/г расщепля¬
ется на четыре компоненты:
Д£2(р = ihSlM,, М] = ±^, ±^,
з/2 з.	1	2	2
а каждый из уровней 2Л/г и 2Si/2 расщепляется на две компоненты:
Д£<}>/2 = \hSlMj, Mj = ±1;
AEjJ = 2 ШМ/, Afy = ±1.
Спектр наблюдаемых частот, в соответствии с правилом Бора, имеет
вид
0) _ -(О)
ш = 2 й ' + n(g2MJ2 - £,мл) ее + Дш,	(2)
причем здесь необходимо учитывать правила отбора для дипольного
электрического излучения
AJ = 0,±1, ДМу = 0,±1, AL = ±1, AS = 0.
Применяя эти правила, видим, что вместо линии 2Рз/г 2Si/2 в маг¬
нитном поле возникают шесть переходов с частотами (см. (2)) Аш = ±П,
±(1/3)П, ±(5/3)П, а вместо линии 2Р\/2 —* 2S1/2 — четыре перехода с
частотами До; = ±(2/3)П, ±(4/3)Г2. Таким образом, в слабом магнит¬
ном поле вместо резонансного дублета наблюдается спектр, состоящий
из 10 близких спектральных линий (аномальный или сложный эффект
Зеемана).
б)	Сильное поле. В данном случае считается, что Д£;н » Д£тонк,
т. е. расщепление в магнитном поле велико по сравнению с интервалами
тонкой структуры, но по-прежнему настолько мало, что можно прене¬
бречь квадратичным членом в (1). При этом также можно применить
теорию возмущений, но необходимо сначала учесть влияние магнит¬
ного поля, а затем (если нужно) — спин-орбитальное взаимодействие,
ответственное за тонкую структуру.
Правильными векторами нулевого приближения в данном случае яв¬
ляются |£,S, Ml,Ms), т. е. общие собственные векторы для операторов
L2, S2, L2, Sz. В первом приближении теории возмущений получаем
поправку к энергии:
Д£$ = hn(ML + 2 Ms)
и наблюдаемые частоты (с учетом правила отбора AMs = 0):
uj = ш о + ПА.Mi, A.Mi = 0, ±1.

386 -A, Глава 2. Квантовая механика. Решения задач
Таким образом, в сильном поле наблюдается триплет спектральных ли¬
ний шо, wo ± П (простой или нормальный эффект Зеемана).
В случае кадмия термы '£) и 1Р являются синглетными, т. е. для них
S = 0, / = L и, следовательно, g = 1. Поэтому независимо от величи¬
ны напряженности магнитного поля будет наблюдаться простой эффект
Зеемана.
2.11.11. Параметры функции ф(г), выбранной для применения вариаци¬
онного метода, определяются, исходя из того, чтобы вычисленное при
помощи этой функции среднее значение гамильтониана
(Н> = f Г(г)Нф(г)й3х, где H = -^A-ej,
имело бы минимум при условии, что функция ф(г) является нормиро¬
ванной. Вычисляя интегралы и находя минимумы для средних значений
гамильтониана (Н), получаем:
случай а) а = —х, (Н) = — -х—г (точное решение);
те	2	fi
„	,	Зч/я-	h2 .г;.	4 me4	1	те4
случаи б)	b	=	——2,(
2.11.12. Гамильтониан атома гелия, записанный в атомной системе еди¬
ниц, имеет вид
н = --а1--а2-	(1)
I	I	Г,	Г2	Г12
где г12 — |Г] — гг |. В выражении (1) первые два слагаемых описывают
кинетическую энергию электронов, третье и четвертое слагаемые —
притяжение электронов к ядру (для гелия Z = 2) и последнее слагаемое
описывает кулоновское отталкивание электронов.
Первая часть задачи предполагает минимизацию среднего значения
гамильтониана (1), найденного при помощи пробной функции ф ~
~ ехр[—Z'(r\ + гг)], и нахождение значения вариационного парамет¬
ра Z'. Нормируем пробную функцию и получаем
ф = —e~Z'(n+r2)
7Г
При вычислении среднего значения гамильтониана (Н) нам встретятся
интегралы	.	.
(Ь)-{$-*■	<2)
по поводу их вычисления — см. задачу 2.6.4, а также интеграл
(_L\ = (£)* [	(3)
2/	\*	J	J	^г\ + г\-2гхг2соъв

2.11. Теория атомов и молекул -*\г 387
В интеграле (3) зафиксируем вначале значение п и проинтегрируем по
угловым переменным, относящимся к гг, совместив ось z с направле¬
нием вектора п. В результате получим
7
2^ j	sin	вйв
' Атх
—> Г> > Г2-
Г\
4-7Г
—, г2 > Г\.
Г2
J ^г\ + г\-2г\п COS в
С учетом данного результата приводим интеграл (3) к виду
ОО	Г\
(1)	= (4Z'3)2{ f ne-^dn f rle-^dn +
12	0 0
oo	Г2	lie
+	J r2e-2Z'r*dr2 J fa-^dn}	= Z'(2 - И)	=	|z'. (4)
Собирая далее результаты (2) и (4), получаем для среднего значения (Н)
следующее выражение:
(Н) = -2 ZZ' + ^Z'+Z'2,
где мы учли, что — (Ai) = — (Д2) =Z'2, как это следует из решения
задачи 2.6.4. Заметим, что наша пробная функция фактически есть про¬
изведение двух функций основного состояния атома водорода с един¬
ственным отличием Z —> Z', поэтому использование результатов зада¬
чи 2.6.4 является корректным.
Минимизируем (Н) и находим
Z' = Z - —
16’
т. е. для гелия Z' = 27/16. Полученное значение Z' имеет прозрачный
физический смысл — это значение эффективного заряда ядра, кото¬
рое «чувствует» электрон при движении в общем кулоновском поле
ядра и второго электрона — часть заряда ядра Z экранируется вторым
электроном.
Найдем далее диамагнитную восприимчивость основного состояния
гелия. Запишем общий вид гамильтониана для атома гелия в однород¬
ном внешнем магнитном поле (в обычной системе единиц):

388 _/\ . Глава 2. Квантовая механика. Решения задач
обозначения совпадают с обозначениями задачи 2.11.10. Заметим, что в
основном состоянии гелия L = S = 0, поэтому линейное по слагаемое
не дает вклада в поправку к энергии. Следовательно,
£<1) = Г-2<£Р<Х Га]2) = /-2 g** £ ^>-
8тс а=1.2	8тС	0=1,2
где угловые скобки (...) означают усреднение по состоянию с пробной
функцией с зарядом Z'. Диамагнитная восприимчивость равна
е2			La3a2
дХ2 ~	66mc2 Z'2 Z ’
где а = е2/(he) ~ 1/137 — постоянная тонкой структуры. Численное зна¬
чение восприимчивости: \ — -2,77 • Ю~30 см3.
2.11.13. В этом случае поправка первого порядка для зеемановского
взаимодействия Vz (см. (11.61)) равна нулю. Оценим поправку второ¬
го порядка для возмущения Vz к уровню энергии атома с L = S ф О
и J = 0. Поправка второго порядка содержит энергетический знамена¬
тель, равный разности энергии основного терма и соответствующего
возбужденного состояния. Среди всех возможных энергетических зна¬
менателей следует учесть только те, которые относятся к одной конфи¬
гурации основного терма, поскольку расстояние между уровнями энер¬
гии с одной и той же конфигурацией имеет величину порядка а2Ео ~ А,
где А — эффективная величина спин-орбитального взаимодействия. Та¬
ким образом, оценка поправки второго порядка есть
дг(2) „ V 1(Д^.7,^|Уг1Д5,0,0)|2 ^ р№
eLS0-eLSj	А	■
J,Mj
Легко видеть, что IA^VI^d*! > где ~ поправка первого при¬
ближения для диамагнитного взаимодействия (11.62). Вспомним также,
что поправка второго приближения к основному состоянию всегда от¬
рицательна, поэтому газ таких атомов, находящихся в основном состо¬
янии c/ = 0hL = S/0, будет парамагнитным.
2.11.14. Для определенности будем считать, что молекула водорода на¬
ходится в основном состоянии (терм £+). В приближении Борна-Оп-
пенгеймера полная волновая функция молекулы представляет собой про¬
изведение электронной и ядерной волновых функций. Ядерную подси¬
стему молекулы водорода образуют два протона, поэтому соответствую¬
щая ядерная волновая функция есть функция двух тождественных ча¬

2.11. Теория атомов и молекул -Аг 389
стиц. В системе центра инерции ядер волновая функция ядер представ¬
ляет собой произведение координатной функции /?(R), где R = R2-R| —
взаимное расстояние ядер, на спиновую функцию Vvm. характеризую¬
щуюся значением суммарного спина ядер / (задача 2.10.1).
При перестановке ядер местами, т. е. при преобразовании R —► -R
координатная функция умножается на (—1)*, где К — вращательное
квантовое число. Спиновая функция ядер меняет знак при перестановке
спинов, если суммарный спин / = 0, и не меняет знак, если / = 1. По¬
скольку полная ядерная функция должна быть антисимметричной (си¬
стема двух фермионов), то при суммарном ядерном спине 1 = 0 возможны
только четные значения вращательного квантового числа К = 0,2,4,...
(параводород), а при / = 1 — только нечетные К (ортоводород).
Заметим, что волновая функция электронной подсистемы не меня¬
ется при преобразовании R —> -R, если, как предполагалось выше, мо¬
лекула находится в состоянии с электронным термом Е+.
2.11.15.	Потенциал Кратцера был предложен для описания колебательно¬
вращательного спектра двухатомной молекулы (рис. 2.13). Константа D
характеризует минимальное значение потенциала, которое достигается
при г = Ь.
Отделяем движение центра масс, и Щг)
для волновой функции относительного
движения ядер получаем уравнение
г/Ъ
n	U	1	1	1	1	г-
где р — приведенная масса ядер. Ре-	1	2	3	4	5
шаем далее задачу методом разделе¬
ния переменных в сферической систе¬
ме координат и, полагая, что
1	2	3	4	5
гр(г) = R(r) У(кМ)(в,	Рис-	2	13-	Потенциал
Рис. 2.13. Потенциал Кратцера
находим уравнение для радиальной функции R(r):
Сделаем замену переменной согласно соотношению р = 2г\/-2.рЁ/Н,
поскольку нас интересует дискретный спектр. Введем обозначения:

390 _/\, Глава 2. Квантовая механика. Решения задач
В результате наше радиальное уравнение принимает вид
R"{p) +	+	{	-^±J2	+	"	-	i }r(p) = 0.
Р	I	р	Р	4 J
Данное уравнение формально совпадает с радиальным уравнением,
описывающим движение в кулоновском поле.
В состояниях дискретного спектра функция R(p) должна стремиться
к нулю при р —► оо. Отсюда получаем условие обрыва соответствующе¬
го степенного ряда, которое одновременно фиксирует уровни энергии.
Условие обрыва ряда имеет вид п — А — 1 = v = 0,1,2,..., причем
под Л здесь следует понимать положительный корень уравнения (1), т. е.
В итоге получаем дискретные уровни энергии:
,{(» + i) + \/(/r+i)! + 'r!} .
Безразмерный	параметр 72 пропорционален приведенной массе	ядер р,
и поэтому можно	считать,	что 72 » 1. Если при этом	и -С 7,	К	7,
то выражение для Evk можно разложить по малому параметру I/7. В
результате получим	*
Я»х = -^ш2 + /Цо+1) + ^(я+±) -
ъп2 (	, п2 зп2 ( , п /„ ,	i\2	...
2/~ \ 2/ +2) +"” (2)
где мы ввели частоту колебаний ш и момент инерции J:
I /2D ,	,2
Ш=Т\ —, / = рЬ .
о \ р
Второе слагаемое в выражении (2) описывает колебательные уров¬
ни, характеризующиеся колебательным квантовым числом v. Третье сла¬
гаемое дает энергию вращательных уровней с постоянным моментом
инерции. Четвертое слагаемое учитывает ангармоничность колебаний и
ведет к некоторому понижению колебательных уровней. Наконец, пятое
слагаемое дает поправку к энергии, обусловленную взаимодействием
между вращением и колебанием ядер.

2.11. Теория атомов и молекул —1\г 391
2.11.16.	Оператор контактного сверхтонкого взаимодействия двух ча¬
стиц со спинами si и s2 имеет вид
Vcont = ^S]S2-
Данный оператор линейно связан с оператором квадрата суммарного
спина системы S2, где S = si+s2 (см., например, задачу 2.11.4), по¬
этому его действие на общие собственные векторы операторов S2 и Sz
(обозначаемые, как |S,Af)) не приводит к изменению квантовых чи¬
сел S и М. Таким образом, оператор Vco„t сохраняет суммарный спин
системы.
Суммарный спин рр-атома может принимать два значения S — 0,1.
Покажем, что оператор s^a — spa изменяет значение суммарного спи¬
на S. Действительно,
(s^-spz)|l,±l) = 0, но
(sM2 — SpZ)11,0) = |0,0), (Sp2 -spz)|0,0> = |1,0).
Несложно проверить также, что
(sp+ - Sp+)|1,+1> = 0,	(sM± — sp±)|l,0) = 0,
(sM_ -sp_)|l,+l) = —-ч/2|0,0), (Sp± - sp±)|0,0) = TV2|1,±1).
При рассеянии pp-атома ядром должен сохраняться полный спин
системы «ядро + рр-атом», т. е. F = sM + sp + I = S + I, который может
принимать значения \S -1\ ^ F ^ S +1 (здесь I обозначает спин ядра).
Поскольку S принимает значения 0 или 1, полный спин F имеет возмож¬
ность сохраниться при изменении суммарного спина рр-атома только в
случае, когда F = I. Таким образом, искомый эффективный оператор
контактного магнитного сверхтонкого взаимодействия Q должен обла¬
дать свойством
(S = l,F,Mf|Q|S = 0 ,F',M'f) =
Будем искать оператор Q в виде
Q = Л(5р -Sp)I.
Запишем два возможных состояния системы «ядро + рр-атом» с пол¬
ным спином F = /, обладающих максимальными значениями проекций
полного спина на ось z:
|S = 1 ,F = I,1) = уХ|1,0)|/./> - -J=|l,+l>|/./- 1>,
\S = 0,F = 1,Г) = |0,0)|/, /).

392 -l\r Глава 2. Квантовая механика. Решения задач
Подействуем далее оператором Q на состояние с 5 = 1 и в результате
найдем
^{(Sp2 - Sp2)I2 + - [(SM+ - Sp+)I_ + (Sp_ - sp_)i+]}|5 = 1,1,1) =
= MI + l)y 7^-jlO. 0)|/,/) = A ^/(/+1)1 s = 0, F = /,/).
Таким образом, мы можем записать итоговое выражение для операто¬
ра Q в виде
Q = -7-1 ,,(sM-Sp)I.
2.12.
>/7(7+7)
ТЕОРИЯ РАССЕЯНИЯ
2.12.1.	Для нахождения амплитуды рассеяния в борновском приближе¬
нии необходимо вычислить интеграл
2пН
[ V(r)e lvd3x =	[	V(r)	sin	qrrdr,
J	hqJ
а для получения полного сечения — проинтегрировать \f(9)\2 по углам:
7Г
а = J \№\2dn = 2тг у |/(0)|2sin ede.
о
Выше положено, что q = к' — к, q = 2ks'm(0/2). Условие применимости
получается из анализа интеграла
m
2л7?
/яJif
— V(r)eikzd3x
Результаты расчетов имеют вид
/ та У
« 1.
а) /= --
2 та
47Г
ftV + ?2)
4/г + х2
_ 2тЕ
ь2 '
kZ =
Условие применимости: ат/х	h2	(для любых энергий) или а -с Ни,
где v - hk/m — скорость частицы (для быстрых частиц)
б) / = lim
*■—>0
2 та
h2(x2 + q2).
2 та
п q

2.12. Теория рассеяния	393
Условие применимости: a <SC hv.
2ir ( т Voa2 \ 2 .	1	sin4fc
~k?\ h ) [ ~ (2ka)2	(2kaj
sin Aka
,3
sin2 2ka
"(2 ka)4
Условия применимости: 2m Voa2 <C h2 (при любых энергиях) или 2т х
х Voa2 <С h2(ka) (для быстрых частиц).
2.12.2.	В данном подходе исследуются индивидуальные отклонения
одной частицы в поле рассеивающего потенциала. Предполагается, что
до взаимодействия с потенциалом движение частицы свободное, и ее
состояние можно описать функцией, собственной для оператора им¬
пульса с собственным значением р и энергией Е = р2/(2т). В резуль¬
тате взаимодействия с рассеивающим центром у частицы появляется
определенная вероятность совершить квантовый переход в состояние с
импульсом р' и энергией Е' = р'2/(2т) (т. е. рассеяться).
В соответствии с «золотым» правилом Ферми вероятность кванто¬
вых переходов в единицу времени между состояниями непрерывного
спектра дается формулой
где роль возмущения играет сам рассеивающий потенциал У(г). В ка¬
честве интервала конечных состояний du/ выберем d3p', при этом вол¬
новая функция конечного состояния нормирована на (5-функцию: Vy =
= (27г^)_3/2е‘р r/h. Начальную волновую функцию нормируем на еди¬
ничную плотность потока (|jHa41 = 1): ‘Фр = (m/p)^2eipr^h. Подставим в (1)
также разность энергий Е' — Е = (р'2 — р2)/(2т) и получим
Данное выражение имеет размерность площади и представляет собой
дифференциальное сечение рассеяния. Исключаем (5-функцию, перехо¬
дя к сферическим координатам (т. е. заменяя d?p' по формуле d3p' =
dwp = ~\Vfi\2S(Ef - Ei) duf,
(1)
= p,2dp'dQ = -p'd(p'2)dVT), и интегрируя no d(p'2). В итоге имеем
где q = (р' - р)/h. Это и есть искомое дифференциальное сечение.

394 -И,. Глава 2. Квантовая механика. Решения задач
2.12.3.	Радиальное уравнение Шредингера для парциальной волны
щ(г) = rRi(r) имеет вид
{л'^-?7(г) + ф(г) = 0’	(1)
У dr	г	h	J
где k2 = 2mE/h2. Обозначим далее решение свободного уравнения У/(г),
{d^~l^7^ + k2}Mr) = 0-	(2)
Умножим почленно уравнение (1) на о/(г) и уравнение (2) на щ{г) и
вычтем друг из друга. Полученный результат проинтегрируем по от
нуля до г. В итоге будем иметь (с учетом vi(0) = U/(0) = 0)
Г
Vi(r)jrm(r) - Ui(r)jVi(r) = |г / V(r')vi{r')ui(r')dr'.	(3)
0
Перейдем далее к пределу г —> оо. Предполагаем, что при г —> оо по¬
тенциал V(r) стремится к нулю быстрее, чем 1/г, поэтому интеграл в
правой части сходится. Вспоминая, что функция цДг) есть на самом
деле сферическая функция Бесселя ji{kr) (см. задачу 2.6.8), используем
асимптотики для ыДг) и ji(kr):
//Ml*-оо ^ Sin (х - у ) ,	~	Sin	(х. - у + S/J ,
где St — фаза рассеяния. Тогда из уравнения (3) находим
ОО
sin<5, =	[ V(r)ji(kr)ui(r)dr.	(4)
п k J
о
Заметим, что полученная формула — точная. Таким образом, чтобы
найти фазу <5/, необходимо знать точное решение уравнения (1). Но,
если считать влияние потенциала V(r) малым, то ц/(г) должна мало
отличаться от свободной сферической волны (т. е. фактически от /) (kr)),
и, следовательно, фазовый сдвиг ф —» 0. Имея в виду этот факт, из (4)
получим
ОО
sin6i~6i~-^- f V(r)[ji(kr)]2dr.
hkJQ
Найдем теперь амплитуду рассеяния. С этой целью подставим выра¬
жения для фаз с учетом малости ф в формулу разложения амплитуды

2.12. Теория рассеяния Л 395
по парциальным амплитудам (11.67). Будем также иметь в виду, что
//(jc) = y/icxj2Ji+\/2(x). В итоге находим, что
Д0)~ i£(2/+l)<5;/Mcos0)~
1=0
°г	°°
—	/	r2dry(r)[^(2/+l)^(/;+1/2(x))2P;(cos0)].
п О	'=°
Из теории	бесселевых функций	известно, что сумма в квадратных скобках
вычисляется	точно	и равна	sm qr/(qr),	где	q = 2k sin(0/2).	Таким	об¬
разом, мы пришли к амплитуде рассеяния в борновском приближении.
2.12.4.	Разделяя переменные в сферической системе координат, нахо¬
дим уравнение для парциальной волны ы/(г) = rRi(r):
{ —2 + Ь2 ~ -Т
I dr2	г2
/0 + 1) + ^
п
| щ(г) = 0.
(1)
При помощи замены u/(r) = y/rip(r) уравнение (1) приводится к виду
^"+У + {*2-^[(/+1) +2^]j^ = 0.
Решениями данного уравнения являются функции Бесселя J±„(kr), где
1\2 , 2т0
2/
v=\ 1 +
В связи с этим решение уравнения (1), удовлетворяющее граничному
условию ц/(0) = 0, выбираем в виде (ср. с задачей 2.6.8)
и,(г) = c^JAkr).
Асимптотику этого решения при больших значениях аргумента мы при¬
равняем граничному условию для парциальной волны (при г —> оо):
Ui(r)|r_oo ~ с sin (kr - Y + J) = с sin (kr - у + £,).
Отсюда мы и находим фазы рассеяния:
6i=-\ {\/(/+D +?PM/+D}-

396 -1\г Глава 2. Квантовая механика. Решения задач
= (2)
Рассмотрим предельный случай 2m(3/h2	1.	В	этом	пределе	получим
6,	кт.Я~	..
Й2(2/ + 1)	’
очевидно, что при этом должно выполняться условие |<5/|	1.	Суммиру¬
ем далее ряд разложения по парциальным амплитудам (11.67) с учетом
|<5/| «С 1 и находим
| ОО	п	ОО
т - г£(2/+ l)6tP,(cas0) a -^£P;(COS0).
* (=0 hk 1=0
Для вычисления суммы используем производящую функцию полиномов
Лежандра:
1	°°
= £VP,(z),
V1 - 2хг + X2	1=0
в которой необходимо положить х = 1, г = cos#. В итоге получаем вы¬
ражение для амплитуды рассеяния в виде
пт(3
2kh2 sin((9/2)
Нетрудно проверить, что в результате расчета в борновском прибли¬
жении получается выражение для амплитуды, в точности совпадающее
с (2).
2.12.5.	Условие «медленности» частиц ka -С 1 означает, что энергия ча¬
стицы настолько мала, что соответствующая длина волны де Бройля
велика по сравнению с радиусом действия потенциала V(r) (Л » а).
В таких случаях в рассеянии частиц низкой энергии будут участво¬
вать только парциальные волны с малыми значениями /. В этом можно
убедиться, исходя из простых качественных соображений. При г > а
на частицу с / ф 0 будут действовать лишь центробежные силы оттал¬
кивания, поэтому частица не сможет приблизиться к рассеивающему
центру ближе, чем на расстояние р = y/l(l + \)/k. Если р> а, то она не
попадет в область действия потенциала и не будет принимать участия
в рассеянии.
Рассмотрим и более строгие соображения. Общий вид радиального
уравнения для парциальной волны:
{ ^ " ¥у{г) + *2}“'(г) = °- (1)
Полагаем, что на больших расстояниях потенциал стремится к нулю быст¬
рее, чем 1/г2. Тогда при г^> а в уравнении (1) можно пренебречь вкла¬

2.12. Теория рассеяния —i	оэ<
дом члена с У(г) по сравнению с центробежным потенциалом 1(1 + 1 )/г2.
При этом уравнение (1) превратится в свободное радиальное уравнение
с решением
щ(г) = a\ji(kr) + a2ni(kr),	(2)
где ji(x) и «Дя) — сферические функции Бесселя и Неймана (см. (Д. 15),
(Д.16)). В области сравнительно малых расстояний а -С г \/k в урав¬
нении (1) можно пренебречь как потенциалом V(r), так и членом k2
по сравнению с /(/+ 1 )/г2. Решение уравнения в данной области будет
иметь вид
щ(г) = ctr'+1 + с2г~‘.	(3)
В области а < г « l/k решение (2) должно переходить в (3). Вос¬
пользуемся асимптотическим видом функций ji(x) и «/(х) при малых х
(Д.20) и получим
(2/+1)!!	k‘
fll_Cl k>+1 ’ 02 °2 (21 — 1)!!'
А теперь рассмотрим асимптотику решения (2) в дальней области (/гг» 1),
учитывая асимптотический вид функций ji(x) и д/(х) при х —> оо:
, ..	(2/+1)!! . Л /тг\ , k‘	Л	/тг\
^;(г)|*л->оо ~ С1 ^(+1 sin^r	2 J (2/— 1)!! C°Sч 2/’
Исходя из граничного условия для парциальной волны должно быть:
ц;(г)|Аг_оо ~ sin(£r - hr/2 + Si), откуда
h21+l
tg5' = (21 + 1)!! (21 — 1)!! ^
Отношение c2/c\ не зависит от k, ибо мы пренебрегли в уравнении
членом k2 в области а < г -с \/k. Отсюда делаем вывод о том, что при
низкоэнергетическом рассеянии (ka 1) существенный вклад вносит
лишь рассеяние s-волн, потому что с ростом / фазы рассеяния tg<5/ ~ ф
стремятся к нулю.
Из выражения (4) следует, что максимальное значение фазы Si до¬
стигается в случае, когда I = 0, при этом <5о — (c2/c\)k. Соответствую¬
щая парциальная амплитуда равна
I“ =	» 7 * I "	(5)
т. е. она не зависит от k. Величина а называется длиной рассеяния. Рас¬
сеяние при этом будет изотропным, а его сечение равно а = 47га2.

398 _М, Глава 2. Квантовая механика. Решения задач
2.12.6. Указание: Воспользоваться выражением для амплитуды рассея¬
ния в борновском приближении.
2.12.7. Нейтрон практически не взаимодействует с электронами, поэто¬
му можно учитывать только рассеяние на ядрах молекулы, т. е. на про¬
тонах. В таком случае рассеяние на каждом ядре может быть описа¬
но псевдопотенциалом, приведенным в задаче 2.12.6, в котором теперь
т — приведенная масса. Принимая Мп « Мр = М и помещая начало
координат в центр масс молекулы, расстояние между ядрами которой
определяется радиусом-вектором R, имеем
V* =	г	-	R/2) + 6(г + R/2)).
2.12.8. Предположим, что потенциал рассеяния задан формулой
V(r)
{О, г > а,
-Vq, г^а.
В соответствии с выводами, сделанными в задаче 2.12.5, в случае
рассеяния медленных частиц (ka -С 1) вклад в сечение всех парциаль¬
ных волн с I ф 0 является малым по сравнению с вкладом от рассеяния
s-волн. Поэтому запишем радиальное уравнение для s-волны:
и'о(г) + k2u0(r) = 0, г>а,
и'о(г) + М?и0(г) = 0, г < а,
где мы ввели обозначения Е = h2k2/(2m), V0 = h2x\/{2m), к2 = k2 + х20.
Решение, удовлетворяющее условию ыо(0) = 0, имеет вид
ио(г)
\А sin(&r + J0), г > а,
I В sin хг,	г	<	а.
Условие непрерывности для логарифмической производной при г = а дает
х cos ха _ kcos(ka + 5o)
sin ха sin(fea + 5о) ’
откуда для фазы рассеяния мы получим
ka
ka
L ха
tg ха — tg ka
Jo = arctg —tgxa - ka, или tgJQ = ■ -^a 	.	(1)
ka ,
1 -I—- tgxa tg ka
Рассмотрим различные частные случаи данного решения.

2.12. Теория рассеяния	399
Если хоа < 1 (яма малой глубины), то, очевидно, также и ха «С 1, и
можно разложить тригонометрические функции в (1). В итоге найдем
2 (х0а)4
So = ^ка¬
ст ~ 47га
(2)
3	  9
Тот же результат дает и борновское приближение (задача 2.12.1). Отме¬
тим, что сечение в данном приближении не зависит от знака потенци¬
ала — оба знака ±Vo приведут к выражению (2).
Далее, в случае ka < 1, и k <С хо, т. е. при малых энергиях относи¬
тельного движения и сравнительно глубоких потенциальных ямах мож¬
но пренебречь вторым слагаемым в знаменателе (1), ибо он является
величиной второго порядка малости по ka. В результате получим
(3)
Если выполняется условие tg ха = ха, то из (3) следует, что Jo — 0.
о = сто — 0, т. е. при некоторых значениях энергии и глубины ямы она
не приводит к рассеянию s-волн (эф¬
фект Рамзауэра).
Если же выполняется соотношение
сг/(47га2)
3
ха =
(2 П + 1)7Г
(4)
то сечение достигает максимального
резонансного значения
сг ~
4-7Г
и в этом случае
*2 = ?[(2п+1Д
- хо-
Данные значения k2 определяют так
называемые виртуальные уровни энер¬
гии. При k —► 0 условие (4) совпа¬
дает с условием появления связан¬
ного s-состояния в сферической яме
(ctgxoa = 0). То есть при таком зна-
0	2	4	6	8	хоа
Рис. 2.14. Сечение рассеяния мед¬
ленных частиц: на сферической яме
глубины Vo и радиуса а (сплошная
линия) и на сферическом барьере
высоты Vo и радиуса а (штриховая
линия), Vo = ft2xj)/(2m), ka = 0,5
чении хо в яме появляется новый
уровень с нулевой энергией, и падающая волна вступает с ним в ре¬
зонанс. При этом сечение рассеяния характеризуется резкой энергети¬
ческой зависимостью, что видно на рис. 2.14 (резонансное рассеяние).

4UU ^ I ja I JlUOll . /wufl/ниоил ЛИ-AUIIUIVU. я |/И*Ь1»м/> uui/u>
2.12.9.	Потенциал рассеяния задается соотношениями
Радиальное уравнение для парциальной s-волны имеет вид
(u%(r) + k2u0(r) = 0, г > а,
|uo(r) + /efwo(r) = 0, г ^ а,
где £ = h2k2/(2m), Уо = h2xl/(2m), k2 = k2 - х\. Решение уравнения в
области г > а имеет вид
uo(r) = Asm(kr + 6о), г > а.
В области действия потенциала (г < а) существуют два варианта реше¬
ний, удовлетворяющих условию ио(0) = 0, а именно
где х\ = x/xg - k2. В случае низкоэнергетического рассеяния, очевид¬
но, k2 Xq, поэтому х\ ~ хо. Из условия равенства логарифмических
производных при г = а получим
С ростом хоа (с увеличением высоты барьера Уо) сечение рассеяния
медленных частиц, как это видно из рис. 2.14, монотонно стремится к
Данная задача допускает точное определение фаз рассеяния. Запишем
радиальное уравнение для парциальной волны ы/(г) (при г > а)
uo{r) = В\ sin&ir,	если	k2 ^ Хд,
ио(г) = Вг sh x\r,	если	k2 < xg,
Lxia
Если ka —» 0, то xi = xq, и сечение принимает вид
<5о = arctg — thxifl — ka.
пределу а = 4я-а2, который отвечает низкоэнергетическому рассеянию
на непроницаемой сфере (см. задачу 2.12.10).
2.12.10.	Потенциал рассеяния задается соотношениями
г > а,
г ^ а.

где Е = h2k2/(2m). Граничные условия для функции щ(г) имеют вид
Г и,(а) = О,
\ ui^lr^oc ~ sin(kr - ln/2 + St).
Общее решение уравнения записывается через сферические функции
Бесселя и Неймана:
Реализация граничных условий дает возможность определить фазы рас¬
сеяния
и получить точное выражение для сечения
Рассмотрим некоторые частные случаи результата (2).
а)	Медленные частицы (ka < 1). В соответствии с результатом
задачи 2.12.5 можно утверждать, что в этом случае фазы рассеяния (1)
настолько быстро убывают с ростом I, что при вычислении сечения
фактически можно ограничиться только учетом вклада s-волн. В самом
деле, учитывая асимптотики сферических функций Бесселя и Неймана
(задача 2.6.8), нетрудно получить из (1), что tg5; (ka)2l+l\ka^0 -*■ 0.
Окончательно в этом пределе имеем
т. е. получается учетверенное геометрическое сечение. Такой результат
объясняется преобладанием волнового аспекта в процессе рассеяния.
Пространство за сферой заполняется частицами, идет дифракция, и это
приводит к росту эффективного сечения. Заметим также, что в этом
пределе сечение изотропно.
б)	Быстрые частицы (ka » 1). С ростом энергии частиц вклад
в рассеяние парциальных волн высокого порядка (/ > 0) становится все
более значительным. Предполагая, что ka » 1, разобьем сумму (2) на
два слагаемых: а = а\ 4- стг-
В слагаемом <у\ сгруппируем члены, для которых 0 ^ I ^ ka. Пар¬
циальные волны с такими значениями / будут давать вклад в сечение
рассеяния, потому что для них k2 > 1(1 + 1)/а2 (ср. с задачей 2.12.5). С
учетом ka » 1 функции jt(ka) и rii(ka) можно заменить их асимптоти¬
ками при /га —» оо (Д.18).
щ(г) = Aji(kr) + Brit(kr).
ОО
(2)
а = ^(/га)2 = 47га2,
k
(3)

402 -1\г Глава 2. Квантовая механика. Решения задач
В слагаемом o<i присутствуют члены с / > ka. В классической кар¬
тине таким волнам отвечают частицы с большими прицельными пара¬
метрами yjl{l + \)/k > а. Такие частицы вносят малый вклад в рассея¬
ние. Для оценки можно положить ka » 1, / » 1, но ka /. В этом пре¬
деле работают асимптотические представления (2) из задачи 2.6.8. В ре¬
зультате получаем, что tg<^ —♦ 0, т. е. слагаемым стг можно пренебречь.
Очевидно, что существует область значений I ~ ka, где ни одна аппрок¬
симация не верна. Однако, чем больше ka, тем точнее результат будет
описываться при помощи слагаемого о\. Итак, в нашем приближении
\ka\
сг СГ,|*а»1 ~ ]Г]^(2/+l)sin2|fca- j ,	(4)
1=0
где [ka] есть целая часть ka. Для оценки выражения (4) можно заме¬
нить сумму интегралом. Тогда в ведущем приближении по ka получим
ka
47Г f
¥ J
dx( 2х + 1) sin^
, хп
ka
2 J
~ 27га2,
(5)
da I dQ.
500
т е. удвоенное геометрическое сечение.
Такой, на первый взгляд, странный результат объясняется проявле¬
нием волновых свойств частиц, и, в частности, наличием дифракции.
Численный расчет по точной форму¬
ле (рис. 2.15) показывает, что угловое
распределение рассеявшихся частиц
обладает резко выраженной анизо¬
тропией: в пределах узкого конуса с
угловым раствором Д0~7г/(&а), на¬
правленного вдоль падающего пуч¬
ка, рассеивается примерно половина
всех частиц.
Иначе говоря, половина рассеян¬
ной волны (в пределах конуса Д#)
интерферирует с падающей и фор¬
мирует «тень», находящуюся за сфе¬
рой. Другая же половина отража¬
ется более или менее изотропно во
всех остальных направлениях, фор¬
мируя обычное геометрическое сече¬
ние 7га2 (дифференциальное сечение
100
10
1
о
7г/2
в
Рис. 2.15. Дифференциальное се¬
чение рассеяния на непроницаемой
сфере радиуса а при ka = 20, нор¬
мированное на классическое сече¬
ние а2/4
при этом ~ а2/4). Анализ и детальные аналитические оценки этих яв¬
лений приведены, например, в [26].

2.12. Теория рассеяния	403
2.12.11.	Наличие неупругих процессов легко учитывается в рамках фа¬
зовой теории рассеяния при помощи модификации формулы разложения
амплитуды f(6) по парциальным волнам (11.67): фактор е2'5' заменяется
на комплексное число тц, по модулю меньшее единицы, т. е. \rji\ < 1.
Таким образом можно описать изменение полного числа частиц в пучке,
происходящее при неупругом рассеянии.
Для модели черного шара, применяемой в теории рассеяния ней¬
тронов ядрами, коэффициенты гц выбираются следующим образом:
VI
= (■• '
(о, (
> ka,
< ka,
т. е., если прицельный параметр р < а, то частицы полностью погло¬
щаются сферой, а если р > а, то «не замечают» ее. Полное сечение
рассеяния делится на упругое и неупругое:
® = Оупр "4" °неупр>
причем амплитуда упругого рассеяния вычисляется по обычной формуле
2 ik
1=0
m = 'E^1(vl-DPi(cose),
откуда получаем
<7„п п =	,
k
_ \ка\
ступр = 72 Х](2/ + !) -7га ■	(*)
1=0
Полное сечение рассеяния находим из оптической теоремы (11.69),
которая верна и в случае наличия неупругих процессов:
[ka]
'-Т'"*» i-tEtb2*8"*-	(2)
1=0
Сравнивая (1) и (2), заключаем, что <тнеупр — ка2.
2.12.12.	Волновая функция, описывающая движение двух тождествен¬
ных частиц в системе центра масс, имеет вид (см. задачу 2.6.1)
Ф(ГьГ2,51,52) = <£(R)i/>(r)x(si,s2)-	(1)
Здесь R = (1/2)(п + г2) — координата центра масс, функция <I>(R) опи¬
сывает движение центра масс системы; г = rj — г2 — относительная
координата, функция гр(г) описывает движение частицы с приведенной

404	Глава	2.	Квантовая	механика.	Решения	задач
массой р = т/2; x(si>52) — спиновая функция двух частиц. Мы предпо¬
ложили, что потенциал взаимодействия не зависит от спинов, поэтому
спиновые и координатные переменные разделяются.
Согласно постулату тождественности полная волновая функция Ф
должна быть симметричной или антисимметричной относительно пере¬
становки частиц 1 <-> 2. Сразу же заметим, что координата R не меняет¬
ся при указанной перестановке, поэтому симметризации или антисим¬
метризации подлежит только произведение t/>(r)x(si, S2).
а)	а-частицы. Спин а-частиц равен нулю, поэтому полная волно¬
вая функция (совпадающая с функцией ф(г)) должна быть симметрич¬
ной относительно перестановки 1	2. При такой перестановке отно¬
сительная координата меняет знак: г —► -г, и в сферической системе
координат это эквивалентно замене в —* -к — в, ip -* р + ж, г —> г. В со¬
ответствии со сказанным вид функции ф(г) при больших значениях г
должен быть следующим:
Jkf
iMr)Uoo ~ e'kr + е~‘кг + {№ + /(тг -в))е—.	(2)
Рассмотрим смысл отдельных слагаемых в формуле (2). Два первых
слагаемых описывают начальное движение частиц в системе центра
масс. Если считать, что частицы движутся по оси z, то первое сла¬
гаемое в (2) описывает начальное состояние частицы с приведенной
массой р, налетающей на покоящийся рассеивающий центр из —оо (со¬
стояние А на рис. 2.16), а второе слагаемое в (2) описывает состояние
такой же частицы, летящей из +оо (состоя¬
ние В на рис. 2.16).
Третье и четвертое слагаемые в (2) учи¬
тывают две возможности по рассеянию ча¬
стицы с массой р в поле рассеивающего цен¬
тра. Частица, летящая	из —оо, может испы¬
тать рассеяние на угол	в и будет зарегистри¬
рована детектором, находящимся в точке С
дественных частиц	(рис.	2.16), но тот же детектор зарегистри¬
рует и частицу, летящую из +оо, которая
рассеялась на угол ■к — в. В силу тождественности частиц обе эти воз¬
можности учитываются одновременно в волновой функции (2).
Дифференциальное сечение рассеяния вычисляется, как отношение
числа	частиц,	рассеявшихся в единицу времени	в элемент телесного
угла	dn	в	направлении	детектора, к плотности	потока в каждой из
падающих волн:
1 г/лч ,

2.12. Теория рассеяния	405
б)	Протоны. Полная волновая функция должна быть антисиммет¬
ричной относительно перестановки частиц. Важную роль здесь играет
спиновая функция в (1). В силу того, что протоны имеют спин 1/2, в
качестве спиновых функций будут выступать функции х(5,Л4), соб¬
ственные для операторов квадрата суммарного спина S2 и проекции
суммарного спина S* (задача 2.10.1). Известно, что в состоянии с сум¬
марным спином S = 0 спиновая функции антисимметрична, значит ко¬
ординатная функция должна быть симметричной, т. е. она должна сов¬
падать с (2). В состояниях с 5 = 1 спиновые функции симметричные,
поэтому функция ip(r) должна быть антисимметризована. Подводя итог,
можно сказать, что в состояниях с полным спином протонов, равным S,
дифференциальное сечение рассеяния равно (см. также (11.60))
das = \№ + (-i)snn-e)\2dn.
Если же пучки исходных частиц неполяризованы, то будет наблю¬
даться среднее значение эффективного сечения. Считая, что все спино¬
вые состояния равновероятны, получим
da = ^das=o + ^das=i-
2.12.13.	Для описания упругого рассеяния быстрых электронов на ато¬
ме (не обязательно на атоме водорода) можно использовать борнов-
ское приближение, если скорость налетающего электрона велика по
сравнению со скоростями атомных электронов. Поскольку масса атома
гораздо больше, чем масса электрона, можно считать, что атом является
неподвижным в течение всего процесса рассеяния. Тогда в формуле
борновского приближения
m = -г?з1 e~iv Vir) d3x, q = k' - k,	(1)
27ХП J
как и обычно, ftk и hk' — импульсы электрона до и после рассеяния,
m — масса электрона.
С точки зрения воздействия на электрон, атом представляет собой
систему зарядов. Это распределение зарядов создает электрический по¬
тенциал, на котором и рассеивается заряженная частица. Потенциал
атома создается зарядом ядра и зарядом электронов, распределенным
по объему атома, т. е.

406 -И, Глава 2. Квантовая механика. Решения задач
где -ер(г) — плотность заряда электронов в атоме. Подставляя V(r) в
выражение (1) и учитывая значения интегралов
J r	q2	J	|г-г|	q2
получаем
f(0) = *£[Z-F(q)], где F(q) = [ р(г)е~*Ч3х.	(2)
па	J
Выражение (2) определяет так называемый атомный формфактор.
Он зависит от распределения плотности электронов в атоме и от ве¬
личины q — передаваемого при рассеянии импульса. Если плотность
электронов обладает центральной симметрией, то формулу (2) можно
упростить:
ОО
F(q) = — J sin qrp(r)rdr.	(3)
о
Для атома водорода (Z — 1), находящегося в основном состоянии,
электронная плотность р(г) определяется очевидным образом:
p(r) = IV’iooWI2 = -^е~2г/а,
па
где а — боровский радиус. При помощи выражения (3) находим форм¬
фактор
F(q) =
1 +
(qa)
2
-2
4
Определяем далее дифференциальное сечение рассеяния
do = 4a2^ +8>.
((qa)2 + 4)
Для вычисления полного сечения заметим, что dn — 2л sin вйв =
= (2n/k2)qdq, поскольку q = 2k sin в/2. В итоге имеем
_ nai 7(ka) + 72(ka)2 + 192
3	((ka)2	+	4)3
7тг
r^l
ka^> 1	3fe
Критерий применимости борновского приближения (если положить
Vo ~ е2 /а) дает условие ka » 1, поэтому данное приближение приме¬
нимо лишь для достаточно больших энергий налетающих электронов.

2.13. Теория излучения	407
2.13.	ТЕОРИЯ	ИЗЛУЧЕНИЯ
2.13.1. (210|х|100) = 0, (210|у1100) = 0, (210|z|100) =
(21 ± 1|х|100) - ±^|, <21 ± 1 |уIЮО) =	|,	(21	±	l|z|100)	- 0.
(Ответы приведены в атомной системе единиц.)
2.13.2. (210|р,|100) = 0, (2101^1100) = 0, (210|рг|100) = г~,
(21 ± 1|р*|100) = ±i^f (21 ± 1|Р(/|Ю0) =	(21	±	1	|рг1100) = 0.
(Ответы приведены в атомной системе единиц.)
2.13.3. Уравнение Шредингера, описывающее атом водорода, взаимо¬
действующий с вторично-квантованным полем фотонов, имеет вид
{гй|-Н(0>-У}|Ф) = 0, V = 2L(Ap), -е < 0.	(1)
Здесь Н(0) = р2/(2т) — е2/г — гамильтониан атома водорода, V — опе¬
ратор возмущения. Возмущение периодически зависит от времени, по¬
тому что вектор-потенциал фотонного поля (11.70) записывается так:
Х(г’ ') = £	+	е;,Ас+А^)},	(2)
к,А
где с^А и Ск,А — операторы рождения и уничтожения фотона с волновым
вектором к и состоянием поляризации Л = 1,2, а вк,л — единичный век¬
тор поляризации. Вектор-потенциал A(r, t) нормирован на объем V = L3,
потому что поле фотонов рассматривается в кубе с длиной ребра L при
циклических граничных условиях.
Рассмотрим квантовый переход, совершаемый атомом водорода из
состояния 2р в состояние Is, который сопровождается излучением одно¬
го фотона с волновым вектором к и поляризацией Л. Фотон излучается
из вакуума, поэтому мы имеем дело с процессом спонтанного излуче¬
ния. Начальное и конечное состояния полной квантовой системы, вклю¬
чающей атом и электромагнитное поле, имеют вид |i) = |2р\ 0,0, ..., 0)
и |/) = |ls;lk,A.0. • ..,0), причем 1к,л — число заполнения, отвечающее
наличию одного фотона.
Поскольку (1к,А,0, ... ,0|с£Л|0,0, ... ,0) = 1, то в матричный эле¬
мент оператора возмущения (/|V|i), отвечающий нашему процессу, вно¬
сит вклад только одно слагаемое из суммы (2), которое включает опе¬
ратор рождения с^А и зависит от времени, как е‘ш>. Поэтому дифферен¬

408
А
Глава 2. Квантовая механика. Решения задач
циальная вероятность нашего квантового перехода в единицу времени
запишется следующим образом (см. (11.50)):
dw?f = Ц | (ДV+Ji> 126(Е, - Е, + Ли) dvh	(3)
^“5
где £, и £/ — начальная и конечная энергия атома водорода (для состо¬
яний 2р и Is). В этой формуле предполагается далее провести интегри¬
рование по энергии конечных фотонов.
Учитываем, что
,	dC'k	,3	k2 dkdSl. з	ш1 d(hw)	. з
ai// = -rL =	5—L = —5	5L a\l,
1	(2n)	(2tt)3	he	(2n)
так как энергия фотона Е^ — hw = hkc, и dk = dca/c. Интегрируя в (3)
по энергии конечных фотонов при помощи J-функции, получаем
(Ck.AP/i)
тс
dfl, где pfi = (2p\e ,krp|ls) (4)
и мы ввели обозначение иц = (£) — Ef)/h.
Поскольку характерное значение величины (kr) ~ ka ~ huja/(hc) ~
~ е2/а ■ a/(hc) ~ а ~ 1/137 <С 1, т. е. является малым для атомных
процессов, то можно разложить экспоненту в (4) и пренебречь величи¬
ной (кг) по сравнению с единицей9'. Учитывая, кроме того, что
1
тР fi —
видим, что матричный элемент оператора возмущения сводится к матрич¬
ному элементу оператора дипольного электрического момента d = —ёг.
В итоге мы получаем дифференциальную вероятность перехода в ди-
польном приближении
dW^^K^fdn.	(5)
В формуле (5) необходимо провести суммирование по поляризациям
конечных фотонов при помощи формулы
Е(емМеЫ/ = ^/-^-	(6)
А=1,2	Й
9) По той же причине мы пренебрегли слагаемым с магнитным моментом во
взаимодействии (11.71).

'/.Id. 1 еирин UvJ;jytcrn*A —
В результате получим угловое распределение вероятности излучения:
где к0 = к/|к|. Интегрируя в (7) по угловым переменным10*, получа¬
ем полную вероятность излучения фотонов, сопровождающего переход
атома 2р —► Is:
Воспользуемся далее результатами задачи 2.13.1 и увидим, что
независимо от значения квантового числа т — 0,±1 начального состоя¬
ния (а = h2/(те2) — боровский радиус). Имея также в виду, что
fuvi/ = £2 - Е\ = Зе2/(8а), находим из формулы (8)
— постоянная тонкой структуры. Подставляя численные значения физи¬
ческих величин, получаем, что вероятность Wy ~ 6,35 • 10® с-1, время
жизни 2р-состояния т ~ 1,57 • 10—9 с или г = (3/2)®а_3тат, где тат =
= ha/e2 = 2,4 • 10~17 с — атомная единица времени.
Наконец, проведем анализ углового распределения излученных фо¬
тонов. Оно будет различным для начальных состояний атома водорода с
квантовыми числами т = 0 и т = ±1 (рисунки 2.17, а и б). Обозначим
через и в сферические углы волнового вектора к. Учитывая значения
матричных элементов оператора d для начальных состояний т = 0 и
т = ± 1 (задача 2.13.1), получаем на основе формулы (7)
^ = т4з|[к°хйл1|2^’
(7)
(8)
|d/,|2 = е2 |(2p|r|ls)|2 =
[|(2p|x|ls>|2 + |(2p|y|ls)|2 + |(2p|z|ls)|2] -	еа))\
dWi,|m=0 = U7sin20dO, dWifU=±i = W- l-(\ + cos20)dn, (9)
где при помощи W мы обозначили величину
|0) При интегрировании можно воспользоваться соотношением (к?к°) = 8ц/3,
где угловыми скобками обозначен интеграл — <f(...) dC2.

410	Глава	2.	Квантовая	механика.	Решения	задач
Заметим, что для вывода соотношений (9) можно использовать фор¬
мулу |[к° х d/,]|2 = (d£dр) - (k°d£)(k°d/,). Интегрирование по углам в
выражениях (9) в обоих случаях дает один и тот же результат (8).
Рис. 2.17. Угловое распределение излучения 2р-состояния атома водорода
2.13.4.	Нейтрон — электрически нейтральная частица со спином 1/2,
обладающая собственным магнитным моментом /г = — цп = — 1,913/^„,
где ця = eh/(2mpc) — ядерный магнетон.
Взаимодействие нейтрона с электромагнитным полем (с классиче¬
ским внешним и вторично-квантованным полем излучения) имеет вид
V = -Д(9С0 + yCrad), где Д = 1пЭ,
‘Яга[1 = Tot A rad —
где мы воспользовались формулой (11.70).
Гамильтониан невозмущенной задачи записывается в виде: Н(0) =
= —Д9<о = о = цпЭ2Ло, так как ось г направлена вдоль поля 9Со-
Волновые функции, собственные для невозмущенного гамильтониана:
Ai = Xi/2 —	*2 = X-1/2 ~ (i)'
Эти функции отвечают уровням энергии невозмущенного гамильтониана
£}°2 = ±цп^Ко- Как видно, энергия нейтрона в магнитном поле зависит
от ориентации магнитного момента по отношению к направлению по¬
ля. Причем два разных состояния ориентации магнитного момента об¬
ладают различной устойчивостью в отношении взаимодействия с по¬
лем фотонов. Поэтому оказываются возможными спонтанные переходы
нейтрона между состояниями, отличающимися ориентацией магнитно¬

2.13. Теория излучения	411
го момента. Такие переходы сопровождаются изменением ориентации
спина и одновременным испусканием фотона. Это и есть излучение
магнитного момента нейтрона во внешнем магнитном поле.
В нашем случае возможен переход нейтрона из состояния xi в состо¬
яние Х2, которое обладает большей устойчивостью. Проводя начальные
преобразования по аналогии с задачей 2.13.3, мы можем записать диф¬
ференциальную вероятность излучения фотона с волновым вектором к
и поляризацией Л в виде
dW>,\ = Ц\Уп\2du, = ^L|[k х е;,Л]м21|2<т,	(1)
где мы ввели обозначения ш\2 = 2р.п'Къ, ц2\ = Mn(X2|^|xi)- Выражение (1)
можно переписать в виде
dW^ = ^^1ек,лт21|2dtt, где m2i = [к х /х21).
Далее суммируем по поляризациям излученных фотонов, как в зада¬
че 2.13.3. В итоге получаем
^12 = -4з|[к°хМ21]|2^,
2тгпс
где k° = k/k, и мы учли, что к[к х д21] = 0. Интегрируем по углам
вылета фотона так же, как и в задаче 2.13.3, и находим полную ве¬
роятность излучения в единицу времени:
(2)
Очевидно, что излучение имеет магнитно-дипольный характер (ср. (2)
и формулу (8) задачи 2.13.3).
Вычисляем матричные элементы:
(/* 21 )х = /*т	(/*21 )у — t'/*m	(/*21)2	= 0
и получаем окончательное выражение для полной вероятности излуче¬
ния, сопровождаемого переворотом спина в магнитном поле (так назы¬
ваемый спиновый свет нейтрона):
1 v/ — 64 о
“ 3 п*с3 '
Проведем численные оценки. Для напряженности поля Э-Со = 1 кГс
получаем время жизни т се 1,9 • 1028 с ~ 5,9 • Ю20 лет. Таким образом,
в лабораторных условиях вероятность данного процесса чрезвычайно
мала. Однако в сверхсильных полях ~ 1013 Гс, существующих вблизи

412 _/\„ Глава 2. Квантовая механика. Решения задач
астрофизических объектов таких, как нейтронные звезды, вероятность
может сильно возрасти, при этом время время жизни т может составить
~ 10 с. Это указывает на большое значение данного процесса именно в
астрофизических приложениях.
2.13.5.	Фотоэффектом называется реакция «выбивания» электрона из
атома падающим фотоном (в задаче речь идет о фотоэффекте на атоме
водорода).
В соответствии с условием задачи полагаем, что в начальном со¬
стоянии в системе находятся один фотон и атом водорода в основном
состоянии, т. е. | i) = | Is; lk,а. 0,0, ...,0), а конкретно
— энергия и волновая функция основного состояния атома водорода,
а = h2/(те2) — радиус воровской орбиты. Атом взаимодействует с вто¬
рично-квантованным полем фотонов, описываемым вектор-потенциалом
A(r, t) (см. (11.70)). Оператор, описывающий взаимодействие, имеет обыч¬
ный вид:
V = -^(Ap)
тс
и играет роль оператора возмущения в рассматриваемой задаче (—е < 0 —
заряд электрона). В результате акта взаимодействия происходит иони¬
зация атома, т. е. атомный электрон переходит в непрерывный спектр.
Энергия ионизации в данном случае равна / = -Е\ = е2/(2а).
Далее мы предположим, что энергия вылетающего из атома электрона
велика по сравнению с /, а это значит, что электрон является быстрым,
следовательно, можно пренебречь влиянием атома на состояние элек¬
трона и выбрать конечное состояние системы в виде |/) = |р; 0,0, ..., 0),
а конкретно
Vy = ^p(r) = ^U>	(1)
— энергия и волновая функция свободного электрона.
Вероятность процесса в единицу времени, во время которого систе¬
ма поглощает энергию радиационного поля, рассчитывается согласно
формуле (см. (11.50))
dwit =	Ц- | Vfi\26(Ei -Ef + hw) dvh	(2)
где Ei	и	Ef	—	начальная	и конечная энергии электрона,	а	в	матрич¬
ный	элемент	V/,	= (/|V|i)	вносит вклад только одно	слагаемое	из	сум¬

2.13. Теория излучения	413
мы (11.70), включающее оператор уничтожения ск,А, так что (0,0, ...
• ■ -, 0|см|1к>А, 0, ... ,0) = 1. Поэтому Vfi = (/|VkiA|i), где
^е‘кг(екдр).	(3)
Поскольку для волновой функции (1) мы использовали нормировку
на объем куба периодичности L3, то связь дифференциальной вероятно¬
сти перехода с дифференциальным сечением определяется соотношением
da = ^-	= L3— = L3—,	(4)
JVC
где j = v/L3 — плотность потока вероятности при нашем выборе нор¬
мировки (для падающих фотонов, очевидно, v = с).
Запишем матричный элемент:
[e->+ikrpe~r/ad3x.	(5)
ша J
В этом выражении можно пренебречь импульсом фотона по сравнению
с импульсом электрона, имея в виду, что из закона сохранения энергии
(см. (2)) следует
т. е. мы считаем электрон нерелятивистским, а поэтому
fojj
hk (
Р ~ V2 тс2
1/2
I «1.
При вычислении интеграла в (5) удобно вначале проинтегрировать по
частям, имея в виду, что р = — tftV и перенести действие производной
на плоскую волну. Кроме того необходимо учесть, что fuj » /, откуда
следует, что pa/h » 1. Расчет интеграла при этом условии дает
87ГЙ4
—г Р
ар
Для дальнейших вычислений заметим, что
= L3Pd^™	(6)
'	(2тг ft)3	(2nh)	2(2nh)
Подставляем теперь значение матричного элемента (5) в (2) и, учитывая
(4) и (6), интегрируем по энергии конечных электронов при помощи

414	Глава	2.	Квантовая	механика.	Решения	задач
^-функции (берем интеграл по d(p2)). В итоге дифференциальное сече¬
ние нашего процесса приобретает вид
<to = 64(£)(s?) (й),/2|е1ЛП|2‘,!!'	(7)
где п = р/р — единичный вектор в направлении вылета электрона.
Проводим усреднение по поляризациям начального фотона в выра¬
жении (7), используя формулу (6) задачи 2.13.3, разделив результат на
два. В результате получаем дифференциальное сечение фотоэффекта
для неполяризованных фотонов:
j 7/2
da = 32аа2j |[k° х n] f dfl,
где а = e2/(hc), k° = k/k — направление волнового вектора падающего
фотона. Интегрируя по угловым переменным, получаем окончательный
результат — полное сечение фотоэффекта:
256	2( 1 \7/2	/оч
" = хоа (к) '	(8)
В заключение сделаем несколько замечаний относительно полуклас-
сического описания фотоэффекта. При таком подходе электромагнит¬
ное поле описывается классически, т. е.
А(г, t) = A0<riM~kr) + \*Qei(ut~kl),	(9)
а частицы описываются методами квантовой механики. Все, сказанное
о выборе начальных и конечных состояний для электрона и о прибли¬
жениях остается	в силе, да и (по большей части) методы	решения	со¬
храняются.	В	основе также лежит формула для вероятности	переходов
в единицу времени (2). Оператор электромагнитного взаимодействия,
очевидно, имеет вид
V = —— (AV).
тс
Для определенности будем считать, что плоская волна распростра¬
няется вдоль оси г, а вектор электрического поля (т. е. поляризация)
направлен вдоль оси х, тогда ось z совпадает с направлением векто¬
ра к, а А0 = {Ло.0,0} (Ло считаем вещественной величиной). Тогда
дифференциальная вероятность переходов в единицу времени, проин¬
тегрированная по энергиям конечных электронов, имеет вид
dWif = ^\Vfi\2dn,
47Г п
Vfi
iehAo
f — <Г
-jрг d
1 (,-r/a
тс
L3/2
дх
.sf^P .
d х.	(10)

2.13. Теория излучения ->\г 415
Для вычисления интеграла в (10) тоже нужно вначале проинтегриро¬
вать по частям. Сечение процесса равно дифференциальной вероятно¬
сти, деленной на плотность потока падающих фотонов. Усредненный по
времени вектор Пойнтинга направлен вдоль оси z и равен
а плотность потока фотонов, т. е. число фотонов, падающих в 1 секунду
на единичную площадку есть / = S/(hw). В итоге
da = 32 6	(-)	, где рх = pcos</?sin0.
импса Vp/ \ ft /
Интегрирование по углам дает результат, полностью совпадающий с
формулой (8).

глава СТАТИСТИЧЕСКАЯ ФИЗИКА
3
3.1.	РАСПРЕДЕЛЕНИЕ	ГИББСА.
ТЕРМОДИНАМИЧЕСКИЕ ВЕЛИЧИНЫ И ФУНКЦИИ
3.1.1. а) Статистическая сумма равна Z — zff/N1, где N — число частиц
газа, а одночастичная статистическая сумма го имеет вид
2о= [d*x [ ЛРе-"/т.
J J (2пП)“
Для спектра ер — срк мы имеем го = AVTd^k, где А — постоянная ве¬
личина, V — d-мерный объем, занимаемый газом, и Т — температура.
Соответственно, свободная энергия равна
F = -Т\п « -NT In = -NT In ^--NTlnV- NT( In T.
N\	N	N	\kj
Определяем давление согласно P = -(dF/dV)т и получаем P = NT/V.
Энтропия газа равна
5=-(1), = лг(г+|птг)+л'|"1,+л,(г)1"7'-
Соответственно, энергия газа Е = F + TS = (d/k)NT прямо пропорцио¬
нальна температуре, а теплоемкость не зависит от температуры:
Щй)*
При этом можно сказать, что на каждую степень свободы в энергии
частицы приходится по равной доле \/k в ее энергии и теплоемкости,
б) Запишем свободную энергию газа:
ОО
F(T, V) = -NT In j e-'Tg(e)de,
о

3.1. Распределение Гиббса. Термодинамические величины и функции	417
выраженную в терминах одночастичной плотности состояний g[e) на
единицу объема
, ч 4-7Г у, ^dp(e)	2m3	1	е2
ст(е)  	=	-зт	 -	   .
(27гЛ)	de	7г	h	[тс	+	\/т2с2 + 2те) \/т2с2 + 2те
В области низких температур Т -С тс2 термодинамические функции
определяются поведением g(e) при малых энергиях е < Т <С тс2:
Производя интегрирование, получим
-Л/Лп
еУ Г
N 2тг2ftV
: -ЛГЛп
еУ Г
+
6ЛТ
N 2тг2ft3c3	тс2	'
■o-s:
Отсюда для теплоемкости имеем низкотемпературное разложение:
Ci, = 3w(l —
\ тс /
В области высоких температур Т ;§> тс2 в силу расходящегося ха¬
рактера плотности состояний с ростом энергии
g[s » тс2) =
т
V2me
т2с _ mV2me
2^~'Th3	2Л3
1 -
2тсг
+
-)
вклад в интеграл вносит область е ~ Т —*с». Используя высокоэнерге¬
тическое разложение для g(e), найдем
F= -ЛГ7Чп
еУ
ЛГ
-NT In
еУ / тГ
еУ /
/V V
27ГЙ"
3/2
27V
тс2Т
Соответственно высокотемпературное поведение теплоемкости примет
вид
Cv = \N[ 1 +
1 / 2тс2 \
3 У~яТ J'
Таким образом, теплоемкость газа зависит от температуры и изменяет¬
ся в пределах между 3N и ЗЛ7/2.

418 -l\r Глава 3. Статистическая физика. Решения задач
3.1.2.	Свободная энергия газа определяется выражением
F(T, V) = -NTIn	[d3г [ JlPe-(c(p)+u(r))/T _
N J J (2тгhf
= F0(T, V) - NT In p J d3re~U(t)/T.
Рассматривая потенциал внешнего поля, как возмущение, разложим
экспоненту:
AF = F-F0 = -NT\ ni J d3r(\-"f- + ^ + ...).
Далее, раскладывая логарифм, найдем поправку к свободной энергии
газа:
A F = N(U) + nW\/2) +...,
где (А) = И-1 / Л(г)й3г обозначает среднее от величины Д(г) по объе¬
му V. После двукратного дифференцирования по температуре получим
высокотемпературную поправку к теплоемкости:
A c = nA-^)\
Т
3.1.3.	Изменение свободной энергии во внешнем поле U(z) = mgz опре¬
деляется выражением
н
AF = -NT\n —!r— [ d2r [ dze~mgzlT.
nR2H J J
Простое интегрирование дает:
AF = —NT In -I— (1 - e-msH,T) = NЦУ- - NT In sh т8иНЦТ.
mgH'	'	2	mgH/2T
Отсюда получим для изменения теплоемкости во внешнем поле:
АСу — n( 1 - у/27П
V sh mgH/2Т )
Предельное поведение АСу в области высоких и низких температур
дается выражениями
\г кг /	,	T^>mgH,
ACV = N х I \2Т	®
[l,	Т	<	mgH.

3.1. Распределение Гиббса. Термодинамические величины и функции	419
3.1.4.	Изменение свободной энергии во внешнем поле определяется
формулой
. 21
Af=-«n„JL j Лехр[-^(1)
r<R
Несложное интегрирование дает:
AF= -NT\n^-(\ -e-Uo/T) = nQ-NT In
t/o	L	Uo/Zl
Отсюда получим для изменения теплоемкости во внешнем поле:
АСу = iv/l - (^2П2).
V sh2 Uo/2Tj
3.1.5.	Свободная энергия газа определяется выражением
F(T,N) = -AT In jj J dx J ^e-(e(/,)+c/(x))/r =
= -NT\n
Ti (	1/2	%xo	[	dxe~m“2
N\2nh2J J
Далее удобно ввести безразмерную переменную s = \/ти2х\/{2Т), рав¬
ную квадратному корню из отношения высоты потенциального барьера
между ямами к температуре. Тогда для свободной энергии получим
F - -A^7’ln|^j[e_s2erfi(s)-l-es2(l -erf(s))]
где erf(s) обозначает интеграл вероятности (функцию ошибок):
erf(s) = — [ e~*2dx,
\ 7Г J
О
a erfi(s) — интеграл вероятности (функцию ошибок) от мнимого аргумента:
erfi(s) == 2 [e*dx.
I	у	7Г	J
О
Теплоемкость определяется второй производной по температуре
С(Т) = —Т(д2Р/дТ2). Сначала рассмотрим низкотемпературное поведе-

420	Глава	3.	Статистическая	физика.	Решения	задач
ние, когда температура существенно ниже высоты барьера, разделяю¬
щего две ямы Т -С тш2х\/2. Пользуясь разложениями при s 1
и ^	2	,	2	s3,	2	s5,
y/nS	у/И Ъ	V?r 10
ft/ \	2	2	s3,	2	s5,
(s)	v^3+^10	’
найдем теплоемкость и соответствующую ей энергию газа при низких
температурах:
C(7’) = |^+18yv(-^)2,
4	\тш	Хо/
E=^NT + 6N- Г23 2 2 .
2	(mu>24)2
При высоких температурах мы воспользуемся асимптотическими
разложениями при большом аргументе s > 1:
11	3	1
erf(s) = 1 + е (~А=-
\ у/1TS
erfi(s) = е$2 (~
V V7T
+
1 1
2у/п s3
+
2у/и s3 Ьура
4 >/7Г S5
!_1..Л
/^s5	;■
В результате найдем высокотемпературное поведение теплоемкости и
энергии газа, когда температура существенно превышает высоту барье¬
ра между ямами Т » ти2х 1/2:
C(T)/N
С(Т)
у/ж\2Т )
.2
Е = NT- Nr^^- +
+
mu'
2 Т )	'
В целом система демонстри¬
рует интересное немонотонное по¬
ведение теплоемкости (рис. 3.1).
С понижением температуры теп¬
лоемкость уменьшается от значе¬
ния N, характерного для гармо¬
нической ловушки, и проходит через минимальное значение при темпе¬
ратуре, несколько превышающей высоту барьера; после чего начинает
расти, достигая своего максимума, а затем опять уменьшается, прибли¬
жаясь к своему предельному значению 3N/2 при нулевой температуре.
Т/То
Рис. 3.1. График теплоемкости газа,
отнесенной к одной частице, как функ¬
ция безразмерной температуры Т/То

3.1. Распределение Гиббса. Термодинамические величины и функции	421
3.1.6.	Одночастичная плотность состояний определяется выражением
sie) = S d'r S Ш6(е'с(г-,)1
где е(р, г) = р2/(2т) + U(г) — энергия одной частицы. Проводя инте¬
грирование по импульсу, получим
Щ Г)<£
Последний интеграл легко вычисляется с помощью замены переменных
х —► X\j2/(mu2x) и т.д. Окончательно,
е2
g(e) =	  [	dxdydz	\Д	-	(х2	+	у2	+	z2)	=	,	.
87Г h LOxUJyUJz J	2n UJxLUyLdz
x2+y +z <e
Свободная энергия для газа из N частиц с одночастичной плотно¬
стью состояний g(e) дается выражением
„-е/т _
F=-NT ln^ J deg(e)e
OO
fdee2 e-£/r
J
= -iVf In
.2h WxUiyUJzN
eT
= -NT In
h uixUiyUJzN
Химический потенциал и теплоемкость находим, соответственно, диф¬
ференцированием свободной энергии по числу частиц и температуре:
/х=|£ = -ЗЛп   C(T) = -T^L = 3N.
dN	h(u>xU>yuJzN)'/3	дТ2
3.1.7.	Одночастичная плотность состояний определяется выражением
8(£) = /Л/<Й5'5(£-£(р'г))’
где е(р, г) = р2/(2m) + U(г) — энергия одной частицы. Проводя инте¬
грирование по импульсу, получим
Rec/Uо
f d^r.T^L [ 2x,dr.
<2"в	(2’"1)	о

422 •Ar Глава 3. Статистическая физика. Решения задач
Окончательно плотность состояний дается выражением
g(<r) = —7г/?2 ехр(2е/Uo)
/пп
и нарастает экспоненциальным образом с увеличением энергии, что свя¬
зано с медленным ростом потенциала ловушки.
Вычислим свободную энергию газа из N частиц согласно
F=-NT\r\1 [ dee(e)e-£/T =
J deg(e)
ОО
= -«rin[if^/«eexp(|-i)
= -NT In
e mR2 TU0
N 2h U0 - 2 T
Написанная формула верна при Т < Uo/2. При Т > Uo/2 интеграл рас¬
ходится и термодинамическое равновесие невозможно. Таким образом,
существует предельная температура Гпр = Uo/2, выше которой систе¬
му нагреть нельзя. Физическая причина заключается в том, что из-за
медленного роста потенциала ловушки частицы с возрастанием энергии
расходятся очень далеко, и их кинетическая энергия оказывается малой
по сравнению с потенциальной.
Теплоемкость находится двукратным дифференцированием свобод¬
ной энергии по температуре:
.&F	Uo 4 2
c(t) = -t—2=n(-^
дТ2 \Uo~
2 Т
и обращается в бесконечность при стремлении температуры к предель¬
ному значению Uo/2. Такой теплоемкости соответствует следующая энер¬
гия газа в ловушке:
Uo
Е = NT
Uo — 2Т'
3.1.8.	Свободная энергия газа определяется выражением
_ . . . / „2
F =
л
r>R
е (2тгтТ)3/2
-jvrinl [d>rf-£P-3 ехР(-/1- m =
N J J (2nh) FV 2mT	T J
(2тгН)
= -NT In
N (2тгЛ)3
R
oo
4tr J drr*exp(--ylnj^)
Последний интеграл сходится только при Т < С/о/3, тем самым опре¬
деляя предельную температуру Тпр = С/о/3, при которой еще возможно

3.1. Распределение Гиббса. Термодинамические величины и функции	423
термодинамически равновесное состояние газа. Физически это связано
с экспоненциальным ростом плотности состояний с увеличением энер¬
гии. Вычисляя интеграл, находим свободную энергию:
е (2тгтТ)3/2
F = -NT In
N (2тгЙ)3
■ 4nR
U0-3T
а затем и теплоемкость газа
о2 г*
С(Т) = -T^=N
дТ2
которой соответствует энергия газа
3 + f_%_y
2 ^ \ Uo - ЗТ)
E=NT{bv~ir)-
3.1.9.	Прежде всего рассмотрим одночастичную плотность состояний
g(e) для частицы газа с энергией e(p,r) = р2/(2m) + U(г):
R
2пт
&) = ! *гI= Ш /
r<R	U(r)<e
2т:г dr.
U(r)<e
При е > 0 нижний предел интегрирования равен г = 0, а при е < О
равен г = Rexp(e/Uo) < R. Окончательно найдем
■(Е) £>0'
2h2 |exp(2£/t/o), е<0.
Свободная энергия дается выражением
ОО
F=-NT 1п^ J deg(e)e~e/T =
— ОО
0	оо
= -NT'“[*w(Iехр® - т)*■+ /ЯК-Т)*).'
—оо	0
Первый интеграл сходится только при условии Т > С/о/2. Тем самым газ
в рассматриваемой ловушке не может быть охлажден ниже предельной
температуры Тпр = Uq/2. Физически это связано с экспоненциально ма¬
лой плотностью состояний при отрицательных энергиях частиц газа.
Вычисляя интегралы, получим свободную энергию:

424 ->v Глава 3. Статистическая физика. Решения задач
Отсюда находим теплоемкость:
. 21
С(7) = N
1 +
\2T-Uo)
и соответствующую ей полную энергию газа в ловушке:
e = nt( 1 - —U\, V
V 27 — Uo )
При Т —> 7пр теплоемкость газа стремится к бесконечности, а его энер¬
гия неограниченно уменьшается.
3.1.10.	а) Если уровни энергии не вырождены, то число состояний с
энергией Е = пе есть число сочетаний из N по п:
Г (£ = пе) = С%	т
(N — л)! л!'
Если нижний уровень gi-кратно вырожденный, а верхний — £2-кратно
вырожденный, то число состояний с энергией Е = пе будет равно
r(£ = ne)=^-^Q.
Соответственно, энтропия системы дается выражением
S(E) = In Г(£ = пе) = {N - п) lng, + n\ng2 + In —
(N — п)\п\
В макроскопическом пределе N —► оо и п —> оо достаточно ограничить¬
ся приближением
S(£) « (N - n)\ngi + n\ng2 + N\nN - (N - n)\n(N - n) - n\nn.
Обозначая максимально возможную энергию ансамбля двухуровневых
систем как Emax = Ne, найдем для энтропии:
S(E) = n(lng, + In	V
\	^max	E	Emax	\	E	g\	J	J
Температуру системы определяем из равенства 1/7 = dS{E)/dE\
Т =
Отсюда можно найти долю возбужденных двухуровневых систем или
заселенность возбужденного уровня п(Т)/N как функцию температуры:
п(Т) _ Е	g2

3.1. Распределение Гиббса. Термодинамические величины и функции	425
и выразить энтропию также как функцию температуры:
5(7) = n(lng, + In	=
\	£max	~	E I £max /
= wfln(g, +g2e~e/T) + £-	./—A
V	1 g\ + g2 e ' )
Так как энтропия	связана	со	свободной энергией соотношением S(T) =
= -dF/dT,	то	несложно	найти и свободную энергию системы, которая
оказывается равной
F(T) = -M71n(g, +g2e~'/T)= -T\nz%.
б) При использовании распределения Гиббса для определения сво¬
бодной энергии необходимо только вычислить статистическую сумму
системы. В данном случае, когда система представляет ансамбль неза¬
висимых подсистем, это нетрудно выполнить, так как полная статисти¬
ческая сумма Z сводится к произведению статистических сумм всех
независимых подсистем, т. е. Z = zff, где Zq — статистическая сумма
отдельной двухуровневой системы:
zo =g\ +g2e~£/T.
Очевидно, что оба подхода дают одинаковый результат.
Зная энтропию S(T), нетрудно найти теплоемкость системы:
С(Т) = N4 glg2g е/Т,т i = Л4
T2(gi+g2e-'/T)2 Т
— е~е/т, Т^е,
g\
glg2
(g\ + gif ’
T > £.
Максимум теплоемкости лежит в области температур Т ~ е.
Предельные выражения для энтропии очевидны. При Т = 0 все двух¬
уровневые системы находятся в основном состоянии, и 5(7 = 0) = N\r\g\.
В пределе высоких температур Т —* оо все состояния — основное и воз¬
бужденное — становятся равновероятными, так что заселенность воз¬
бужденных состояний становится равной n/N = gi/{g\ + £2). а энтро¬
пия достигает своего максимального значения 5(7 —> 00) = AHn(gi +£2)-
Характерной особенностью рассматриваемой системы является то,
что ее энергетический спектр ограничен сверху. В этом случае можно
осуществить аномальные состояния с инверсной заселенностью, когда
заселенность возбужденных состояний (верхних энергетических уров¬
ней) превышает заселенность основных состояний (нижних уровней). В
нашем случае — это n/N > g2/(g\ + gi)- Предельный случай инверсной
заселенности реализуется, когда все двухуровневые системы находятся

426 ->\r Глава 3. Статистическая физика. Решения задач
только в возбужденном состоянии, так что n/N = 1, и энергия систе¬
мы достигает своего максимального значения £max = Ne. Очевидно, что
инверсные состояния термодинамически неустойчивы и должны распа¬
даться. Рассматривая функцию Т = Т(Е) при всех допустимых значе¬
ниях энергии 0 ^ Е ^ £тах, мы можем формально охарактеризовать ин¬
версные состояния как состояния с отрицательной температурой. При¬
чем, чем менее отрицательна температура, тем большей энергией об¬
ладает система. Энергия системы достигает максимума при Т = —О,
а соответствующая ей энтропия S(T = -0) = \ng2 меньше максималь¬
но возможного значения. Если термодинамические величины (заселен¬
ность, энтропия, теплоемкость) при переходе от области нормальных
состояний с Г^О к области инверсных состояний с Т < 0 при увели¬
чении энергии меняются плавным образом, то температура испытывает
скачок от Т = +оо к Т — —оо.
Теплоемкость отдельной двухуровневой системы с энергией возбуж¬
дения е определяется выражением
с(£) = g2 g.g2g~e/r
T2(gl+g2e-''y
Усредненное значение теплоемкости С(Т) для ансамбля двухуровневых
систем со случайными значениями энергии возбуждения £ и их числом,
задаваемым распределением р(е), будет равно
ОО
С(Т) = J c(e)p(e)de =
О
оо	оо
= /4/ glg2g е/Т,т 2 p(e)de=T [ * 2p(xT)dx.
J T2(&+g2в-£/г)2	J	te>+g2e-*)
Если функция р(е) непрерывна и остается конечной в нуле, то в пределе
низких температур Т —> 0 теплоемкость аморфного вещества (стекла)
будет линейна по температуре:
ОО
J1-X
С(Т) = Тр(0) [ g‘g2xV* dx „ Тр(0).
{ (&+ё2е-х)
При gi = g2 интеграл легко вычисляется и равен тг2/6.
3.1.11.	Энергия магнитного дипольного момента во внешнем поле Н рав¬
на ~(МН), где р. = цп, р — величина момента, ап — единичный вектор,
указывающий направление момента в пространстве.

3. /. Распределение Гиббса. Термодинамические величины и функции ->V 427
Поскольку магнитные моменты независимы, и, соответственно, в пол¬
ной энергии их энергии складываются, то статистическая сумма сво¬
дится к произведению N одинаковых статистических сумм каждого из
моментов, деленного на N\ для учета неразличимости магнитных мо¬
ментов, т. е. Z = z%/N\, где
г0 = Jехр(-(-дН)/Г)) dn = j ехр(МН/Л)^.
Интеграл вычисляется по всему пространству изменения единичного
вектора п и нормирован на одно состояние в полном телесном угле
П = 47г.
Выбирая ось г вдоль направления магнитного поля Н, мы находим:
20 = Ь /S[n6deld<pexр(^Т^) = \/exp(^)dx =
0 0 -1
где через а = pH/Т обозначено отношение характерной магнитной энер¬
гии к температуре. Соответственно, свободная энергия равна
F = NT\nN\ - NT\n(sh а/а).
Полная намагниченность или полный магнитный момент определя¬
ется выражением
*~(5S),~S
где функция
£(а) = cth а - 1/а
называется функцией Ланжевена. Предельное поведение намагничен¬
ности в слабых и сильных полях имеет вид
„	(Hp2N/3T, рН^Т,
[у\ — I
\pN(l-T/pH), рН^>Т.
В пределе бесконечно большого поля наступает насыщение М = pN,
когда все магнитные моменты ориентируются вдоль направления маг¬
нитного поля.
Магнитная восприимчивость определяется соотношением \ = дМ/дН
и равна
где £,-(«)-

428 -J\r Глава 3. Статистическая физика. Решения задач
Положительность восприимчивости означает парамагнитный отклик на
магнитное поле. В слабом поле или при высоких температурах
х = \ ^ (pH « Т).
Изменение магнитной восприимчивости, обратно пропорциональное тем¬
пературе, называется законом Кюри. В сильном поле или в пределе низ¬
ких температур магнитная восприимчивость падает степенным образом
с ростом величины поля:
Х = Н~ (рН*Т),
п
что характерно для систем с бесщелевым спектром возбуждений.
Вычисление энтропии S = —dF/dT дает
S(H) = InN\ + W(ln	-	~гЦрН/Т)).
В рамках классической статистической физики имеет смысл говорить
только об изменении энтропии при физическом процессе, а не об аб¬
солютном значении энтропии. Поэтому найдем изменение энтропии в
магнитном поле или магнитную часть энтропии:
AS(tf) = S(H) - S(0) = In -5-^Г -	.
Предельные выражения для слабого и сильного поля:
, 2
AS(H) =
-№)■ ""«г,
-JV 1п^, рН^>Т.
Упорядочение магнитных моментов в поле ведет к уменьшению энтро¬
пии системы, и в пределе бесконечно большого поля, когда система на¬
ходится в полностью упорядоченном состоянии, полное изменение эн¬
тропии стремится к минус бесконечности. Таким образом, можно счи¬
тать, что в нулевом поле система имела бесконечную энтропию и была
бесконечно вырождена. Магнитная часть теплоемкости находится из
соотношения
А Ст(Т,Н) = Тд^ТгН) = N (pH / Т)2 L'(pH / Т) =
_д,л _ M<WL) = ij(ff' “н<<т'
V sbVW (лг, ,,//»т

3.1. Распределение Гиббса. Термодинамические величины и функции ■Аг 429
Интересно отметить, что теплоемкость магнитных моментов совпадает
с изменением теплоемкости идеального газа в однородном поле тяже¬
сти, если в соответствующем выражении заменить энергию магнитного
момента pH на среднюю энергию частицы в поле тяжести mgH/2.
3.1.12.	В отсутствие магнитного поля энергия частицы не зависит от
ее спина, и кратность вырождения по энергии равна 2S + 1 — числу
возможных проекций спина на некоторую ось. Магнитное поле полно¬
стью снимает вырождение с образованием 2S + 1 равноотстоящих друг
от друга магнитных уровней. При этом энергия n-го уровня равна Еп =
= рЭфпН, где ръф — эффективный магнетон Бора, а целое число п про¬
бегает подряд 2S + 1 значений от -S до S. В силу независимости ча¬
стиц и аддитивности их энергией полная статистическая сумма дается
произведением одночастичных сумм Z = Zq, где Zo вычисляется сумми¬
рованием геометрической прогрессии:
zo= £ е~Е»П = £ (е^Г = Sh(‘h+J^5)a.
n=-S	n=-S	1
Здесь через а — p^SH/T обозначено отношение характерной магнит¬
ной энергии к температуре. Свободная энергия равна
F = -NT\n sh(* + 1 /2S)a
sha/25 '
Полная намагниченность или полный магнитный момент определя¬
ется выражением
где функция
®sw=(' + 23)c,h(1 + s)',-5cH,e
называется функцией Бриллюэна. Для спина S= 1/2 функция Брил-
люэна принимает простой вид ®1/г(а) = tha. В пределе большого зна¬
чения S —» оо функция Бриллюэна переходит в свой классический ана¬
лог — функцию Ланжевена £(а). Предельное поведение намагниченно¬
сти в слабых и сильных полях имеет вид
М =
Hp%S(S+\)N
3 Т
рЭфН < Т,
P^SN(l - S~xe~^H/T), МэфЯ > Т.

430	Глава	3.	Статистическая	физика.	Решения	задач
В пределе бесконечно большого поля наступает насыщение, и М — /хЭфSN,
когда все спины ориентируется вдоль направления магнитного поля.
Магнитную восприимчивость найдем из определения \ — дМ/дН:
где
х = NlZ>sjS?Vs(tb*SH/T),
s(a)	(2s)	sh2 a/2S	(1 + 2s)
1
sh a/2S V 257 sh2(l + l/25)a
Положительность восприимчивости означает парамагнитный отклик на
магнитное поле. В слабом поле или при высоких температурах
ЛГ/4ф5(5 +1) , и ^
X = Н ф ЗТ  (МэфЯ < Т)
и температурное поведение магнитной восприимчивости демонстрирует
закон Кюри. Множитель S(S + 1) отражает тот факт, что в квантовой
механике собственное значение S2 равно S(S + 1). В сильном поле или
в пределе низких температур, в отличие от классического случая, маг¬
нитная восприимчивость вымерзает экспоненциальным образом:
X = мф e-'W7 (МэфЯ>7)-
Такое низкотемпературное поведение напрямую связано с наличием энер¬
гетической щели рЭфЯ в спектре возбуждений.
Вычисление энтропии S = —dF/dT дает:
s(7-.tf)=w(insh(!t;/f“-aW).
где а = рЭф5Н/Т.
В отличие от классической системы магнитных моментов здесь име¬
ет смысл уже говорить об абсолютном значении энтропии. Предельные
выражения для слабого и сильного поля:
5(7, Я) =
Упорядочение спинов в магнитном поле ведет к уменьшению энтропии
системы, и в пределе бесконечно большого поля, когда система нахо¬
дится в полностью упорядоченном и единственном состоянии, энтропия

3.1. Распределение Гиббса. Термодинамические величины и функции -IV 431
обращается в нуль. Магнитная часть теплоемкости находится из соот¬
ношения
Отметим, что следующее отношение не зависит от температуры и маг¬
нитного поля, оставаясь постоянной величиной:
Переход к классическому пределу должен происходить, когда посто¬
янная Планка h —* 0. Так как эффективный магнетон Бора пропорци¬
онален h, то он также должен исчезать в классическом пределе. Это
можно компенсировать устремлением величины спина S к бесконечно¬
сти, так что величина /хЭфS остается постоянной и переходит в класси¬
ческий магнитный момент, т. е.
Функция Бриллюэна при этом переходит в функцию Ланжевена.
3.1.13.	В отсутствие внешнего поля ось квадруполя ориентирована в
пространстве случайным образом, поэтому средний квадрупольный мо¬
мент молекул газа Qik равен нулю. Действительно:
Запишем статистическую сумму N квадруполей во внешнем поле
Z = zq/N\, где го — статистическая сумма отдельного квадруполя:
и интеграл вычисляется по всему пространству изменения единичного
вектора п и нормирован на одно состояние в полном телесном угле
Ст(Т,Н) =	=	N(^SH/T)2V's(^SH/T)	=
[^)2е-^н/т, Д*фЯ » Т.
ТСт{Т,Н) = j
Н\(Т,Н)
Г Дэф с
\S-
Дэф ^ ^ * В»
с условием дэф5 = дкл = const.
00
Qik = Q{3{nink) - 6ik) = О
в силу того, что среднее по пространственному углу Г2 равно
z0 = j exp(—Qik(Tik/T) йП/4тг,

432	Глава	3.	Статистическая	физика.	Решения	задач
Q = 4я\ В пределе высоких температур разложим экспоненту до вто¬
рого порядка и усредним по углу:
1 (Qik)crik - (QikQim)® ik® lm .
20 = 1	=—	“I	s	h . .. .
T	2T
Второе слагаемое обращается в ноль, а при вычислении последнего сла¬
гаемого мы воспользуемся также соотношением
/►. и \ ^ik^lm ”Ь Silfikm “I- 3im3kl
(ninkntnm) =	—	.
После алгебраических вычислений найдем
г0 = 1 + Дг0 = 1 + Q2(3SuSkm ~
5 Г
Свободная энергия N квадруполей во внешнем поле равна
F=-NT In 20 = -NT 1п(1+Дг0) ~ -NTAz0 = -	-J‘kSim)aikaim	_
5 T
Средний квадрупольный момент находим из соотношения
Qik =^~ = ~1тЩЗ6‘,6ы -	=	~l^rN(3alk - 6ikau).
Зависимость от температуры отвечает закону Кюри. Соотношение для
следа отдельного квадруполя Qu = 0 сохраняется, естественно, и для
следа средней величины Qu = 0.
3.1.14.	В условиях адиабатичности магнетик находится в теплоизоли¬
рованных условиях, не поглощая и не отдавая тепло. Поэтому энтропия
магнетика не меняется, оставаясь постоянной. Рассматривая энтропию
5(7, Н) как функцию температуры и внешнего магнитного поля, в усло¬
виях адиабатичности для изменения энтропии мы запишем:
-HEWS),"-*
Отсюда для величины магнитокалорического эффекта имеем:
dT _ (dS/dHh
dH (dS/dT)H ‘
Производная (dS/dT)n = Сн/Т, где Сн — теплоемкость магнетика в по¬
стоянном магнитном поле. Вторую производную преобразуем, пользуясь
цепочкой равенств
(<dS/dT)H = -d2F/dHdT = -d2F/8TdH = (дМ/дТ)н,

3.1. Распределение Гиббса. Термодинамические величины и функции	433
где М — намагниченность магнетика. Окончательно, найдем:
dT _ Т(дМ/дТ)н
dH ~	Сн
Поскольку Сн/Т > 0, охлаждение магнетика (dT < 0) или его нагрев
(dT > 0) целиком зависит от знака производной и знака изменения
магнитного поля dH. Более обычная ситуация реализуется, когда
(дМ/дТ)ц < 0, поэтому при выключении магнитного поля (dH < 0)
будет происходить охлаждение магнетика. При использовании парамаг¬
нетиков метод адиабатического размагничивания особенно эффективен,
если исходная температура достаточно низкая, поскольку теплоемкость
парамагнетика при низких температурах становится малой благодаря
тому, что Оц r>j Г3.
3.1.15. Свободная энергия, которая обусловлена вкладом магнитной ани¬
зотропии, дает для соответствующей энтропии выражение
с _ (9F,„\ _ (дК(Т)\	2Й
~\~дТг)н	_ \ ~дТ /н	°-
С другой стороны, изменение энтропии определяется равенством
AS = % Д7\
Т
Отсюда, поскольку полная энтропия в процессе поворота ферромагне¬
тика не меняется, находим изменение температуры:
При повороте на 90° полное приращение равно A(sin2#) = 1.
3.1.16. Вклад в энергию двухатомной молекулы, связанный с вращени¬
ем молекулы относительно ее центра инерции, может быть приближен¬
но описан с помощью гамильтониана Н = h2k2/(2J), где hk — оператор
вращательного момента молекулы и / — ее момент инерции (см. также
задачу 2.11.14). Энергетические уровни даются выражением
Ekjc. = ^K(K+ 1),
где К = 0,1,2,... — вращательное квантовое число, и каждый уровень
энергии вырожден 2К 4-1 раз по проекции Кг оператора момента к.
Соответствующая одночастичная статистическая сумма равна

434 -JV Глава 3. Статистическая физика. Решения задач
где мы обозначили через То = h2/(2J) — характерную вращательную
энергию молекулы. Отсюда вращательная часть свободной энергии, от¬
несенная к одной молекуле, определится как FBp = -Ппго-
Если молекула образована двумя одинаковыми атомами, то возни¬
кает специфика, связанная с перестановкой тождественных частиц и
соответствующей ей симметрии волновых функций ядер. Наиболее яр¬
ко эффект проявляется в молекуле водорода, где Го « 85 К — одно из
наибольших значений. Обратим внимание на спин ядра атома водорода,
который является протоном, т. е. фермионом со спином i— 1/2. Тогда
полная волновая функция двух ядер, включающая в себя произведе¬
ние спиновой и пространственной (орбитальной) частей, должна быть
антисимметричной. При перестановке ядер или изменении направле¬
ния радиус-вектора, равного разности радиус-векторов положений ядер,
пространственная (орбитальная) часть волновой функции умножается
на (—1)*. В свою очередь, изменение знака спиновой части волновой
функции будет зависеть от суммарного ядерного спина /, который в на¬
шем случае может быть либо равен нулю, когда ядерные спины антипа-
раллельны, либо единице, когда спины параллельны. Число состояний
с полным спином 1 = 0 всего одно, и оно антисимметрично по переста¬
новке ядер. Число состояний со спином / = 1 будет равно трем, и они
все симметричны по перестановке ядер. Таким образом, в целом полная
волновая функция ядер при их перестановке умножается на (-1)/_1+л
и требование антисимметричности волновой функции двух фермионов
приводит к тому, что I + К обязано быть четным числом.
Водород с / = 1 называется ортоводородом, а с / = 0 — параводо¬
родом. Соответственно, в ортоводороде — три ядерных состояния, и
вращательные числа К принимают только нечетные целые значения. В
параводороде — всего лишь одно ядерное состояние, и вращательные
числа К принимают только четные целые значения. Отметим, что при
столкновениях молекул полный спин ядер / может изменяться, и об
этом говорят как об орто-пара конверсии. В газе малой плотности веро¬
ятность столкновений невелика, и процесс орто-пара конверсии доста¬
точно медленный. Смесь, в которой все возможные спиновые состояния
ядер представлены в равной вероятности, называется статистической
смесью и, соответственно, в ней молекул ортоводорода в три раза боль¬
ше молекул параводорода.
В чистом параводороде одночастичная статистическая сумма запи¬
сывается следующим образом:
zp =	(2Я	+	1)ехр[~^*(К+1)|.
/(=0,2,...

3.1. Распределение Гиббса. Термодинамические величины и функции	435
а в чистом ортоводороде как
z0—	^2	3(2/С	-Ь	1)	ехр
К=1,3,...
-ЦК(К + 1)
Отсюда в пределе низких температурах Т -С Го найдем
zp = 1 + 5е-6Т°'т + ...,
z0 = 9e~2T°'T + 2le-l2T°'T + ... .
Чтобы найти степенную асимптотику при высоких температурах 7» То,
удобно воспользоваться формулой типа Эйлера-Маклорена для медлен¬
но изменяющихся функций:
N	N+1/2	,
£»- / тЛп-^ + ^лГ-^лГ + ....
п=О
-1/2
где Л/(А) = f^(N + 1/2) — /w(—1/2) — разность производных &-го по¬
рядка на границах в точках N + 1/2 и —1/2.
Асимптотические разложения статистических сумм zp и zo по об¬
ратной температуре имеют одинаковую структуру в обоих случаях:
17,1
1 Т0
2 То
Zp	2 То + 6 + 30 7 + 315 т2 + ‘ " ’
0	Д2Гц 6	30	7	315	72	’/
Далее находим предельные поведения теплоемкости пара и ортоводоро¬
да на одну молекулу:
2
СР(Т) =
Со(Т) =
1 + _L^2 + Ji/M3
+ 45 V Г / ^ 945 V Т ) ’
7	7о,
Т » Го;
ZOO^ye-lor./r г<<Го>
Данная высокотемпературная асимптотика удовлетворительно работает
только в области 7 > 107Ь. Обе функции Ср(7) и Са(Т) с понижением
температуры проходят через максимумы и далее экспоненциально вы-

436	Глава	3.	Статистическая	физика.	Решения	задач
мерзают (рис. 3.2). Для ортоводорода максимум теплоемкости численно
весьма невелик. Существенная количественная разница в теплоемкости
пара и ортоводорода в области невысоких температур начинается уже
при Т < 57о. Величины 67о и 107о в показателях экспонент представ¬
ляют собой разницу между первым возбужденным и нижним уровнями,
соответственно.
1	2	3	4	Т/То	6	7	8	9	10	11	Т/То
Рис. 3.2. График температурной зависимости теплоемкости параводорода (р-Нг)
и ортоводорода (о-Нг) в области низких температур (а) и промежу¬
точных температур (б)
При полном тепловом равновесии между пара и ортомолекулами каж¬
дое ядерное спиновое состояние, пара или орто, должно быть учтено толь¬
ко один раз в статистической сумме с весом (2/Г+1) ехр[-7оЯ'(/С+1)/7'],
т. е. одночастичная статистическая сумма будет суммой статистических
сумм пара и ортосостояний:
Zeq = ZP + 2о =	(2 - (-1)*)(2/( + 1)ехр
к=о
-Цк(к + 1)
Вероятность в тепловом равновесии найти молекулу в состоянии с вра¬
щательным числом К равна
ш* = -!-(2-(-1)*)(2Я+1)ехр
Zeq
То
К(К+ 1)
Вероятность найти молекулу в парасостоянии с четными К будет рав¬
на сумме ш/с по всем четным вращательным числам, а вероятность в
ортосостоянии — по всем нечетным. Соответственно, для вероятностей
получим
Zp
— и
Zeq	<>eq
Таким образом, при тепловом равновесии отношение чисел молекул ор¬
то и параводорода х(Т) зависит от температуры согласно
Zo
Ze,
No
Zo

3.1. Распределение Гиббса. Термодинамические величины и функции	437
и изменяется от 0 до 3 с ростом температуры от 0 до оо. Термодинами¬
ческое равновесие при орто-пара конверсии можно рассмотреть и с
точки зрения условия равновесия для химической реакции типа о р,
когда равновесие относительно взаимного превращения достигается при
условии равенства химических потенциалов пара и ортомолекул:
Отсюда следует предыдущее соотношение. Используя равенства Мр =
= Nzp/(Zp -I- zp), N0 = Nz0/(z0 + z0), где N — полное число всех мо¬
лекул, можно проверить, что свободная энергия равновесного газа Feq
есть сумма свободных энергий пара и ортоводорода Fp и F0, т. е.
Если ядро атома водорода было бы бесспиновой частицей, то в сум¬
му по вращательным числам входили бы только четные числа.
3.1.17.	Посмотрим на процесс ионизации атома А как на химическую
реакцию
При тепловом равновесии должно выполняться равенство суммы хи¬
мических потенциалов веществ в левой и правой частях уравнения.
Действительно, пусть
Термодинамический потенциал зависит от числа частиц каждого из ве¬
ществ Ф = Ф(Р, Г;М,М>,Л7з), но в тепловом равновесии при фиксиро¬
ванных давлении Р и температуре Т числа частиц N2 и N3 есть функции
числа частиц N\. Требование минимума потенциала дает
А А+ + е~.
А\ А2 + Аз,
N1 N2, N3.
<9Ф]	9Фг	<9Фз
ад	ад	ад
дФ2 + дФз _ q
Так как ДМ> = -ДМ и ДМ = -ДМ, то имеем р\ - Р2 - Рз — О-

438	Глава	3.	Статистическая	физика.	Решения	задач
Химический потенциал одноатомного газа с энергией частиц ер =
= р2/(2т) + ео дается выражением
МЛ Т) = -ТIn
Т ( mT \3/2
1 \2тг h2)
ge
-го/Г
где g — кратность вырождения или статистический вес нижнего уровня
частицы. Таким образом, в равновесии имеем следующее равенство:
£а + Т\ П
(2%Н V
аТ\МаТ)
2 \ З/2-l
—£i+T\n
Pi ( 2nh2 \3/2
&т\м,т)
+ Т In
Ре (2пН‘
geT V mT
2 \ 3/2'
и энергия электронов отсчитывается от нуля £е = 0, а Ра, Pi и Ре — пар¬
циальные давления атомов, ионов и электронов, соответственно. Далее
найдем, что
Г In
j Ра gegi
( mM,
j. \ 3/2"
[ PiPe ga
{ М
2тг И2)
= £i ~£а= /,,
где мы ввели потенциал ионизации атома согласно /, = £,• — еа.
Вводя степень ионизации газа а = Ni/N как отношение числа иони¬
зованных атомов к полному числу атомов, будем иметь с учетом N-, =
= Ne = aN и числа неионизованных атомов, равного Na = (1 — a)N,
для парциальных давлений, выраженных через полное давление Р =
= Ра + Л + Ре-
Pa~Na~( 1 — a)/V,
Л ~	~	MV,
Ре ~ Ne ~ MV
Р ~ (1 + a)N
Pi
Ре
1 — а
1 + a
a
1 + a
a
1 + a
P,
P,
P.
Учитывая, что /И, ~ Ma в силу m С Ма и что кратность вырождения
состояний электрона с одной и той же энергией равна ge = 2, получим
-М _ ga / 2nh \
а2Р 2gi \ m )
2 \ 3/2 ^/,/7-
7-5/2
= вд.
Здесь К(Т) — константа равновесия реакции, а выражение
1
МЛ Г) =
VT+mj)
полностью определяет зависимость степени ионизации от полного дав¬
ления и температуры.

3.1. Распределение Гиббса. Термодинамические величины и функции
В пределе низких температур степень ионизации газа становится экс¬
поненциально малой величиной. Посмотрим, при какой температуре сте¬
пень ионизации достигает 50%. Выразим сначала полученный ответ
для а через плотность неионизованного газа п = N/V, используя соот¬
ношение Р = (1 + а)пТ
Величину пТК(Т) удобно записать в явном безразмерном виде:
которая имеет смысл температуры вырождения электронного газа той
же плотности п, что и плотность неионизованного газа атомов. Напо¬
ловину ионизованным газ становится при пТК(Т) = 2, т. е. при темпе¬
ратуре, удовлетворяющей уравнению
Наиболее интересный случай возникает в пределе достаточно разре¬
женного газа, когда Те -С /;. Решая уравнение с помощью последова¬
тельных приближений и используя в качестве первого приближения
Т « /,, во втором приближении найдем
Таким образом, заметная ионизация газа достигается уже при темпера¬
туре, заметно меньшей потенциала ионизации атома. В случае, когда Те
сравнима с /, или превышает для достижения той же половинной
степени ионизации уже необходима большая температура порядка /,.
3.1.18.	Для химической реакции
АВ^± А + В,
N{ N2,N3
тепловое равновесие достигается при следующем условии на химиче¬
ские потенциалы щ, ц2, мз> соответственно, газов АВ, А, и В:
^1+4 пТК(Т)- 1
2 пТК(Т)
вводя температуру Те согласно
или Т =
U
Т «	^
(3/2)1п(22/3/,/7е)
если In » 1.
/ е
е
Ml = М2 + М3-

440	Глава	3.	Статистическая	физика.	Решения	задач
Химический потенциал ц и энтропия S идеального газа с постоянной
теплоемкостью Ср даются выражениями
ц(Р, Т) = £0 + Т\пР-СрТ\пТ-<;Т= Т\пР + Х{Т),
= ы(ср+(-^1Ау
Здесь постоянная £ называется химической постоянной газа, а посто¬
янная ео — химический потенциал при нулевой температуре или мини¬
мальная энергия частицы газа, от которой отсчитывается ее кинетиче¬
ская энергия.
Введем степень ионизации газа а = (N — N\)/N как отношение чи¬
сла диссоциированных молекул к полному числу исходных молекул N.
Далее с учетом стехиометрии реакции для числа атомов Л и В, т. е.
N2 = N3 = N — N\, найдем парциальные давления газа молекул Р\ и
атомов Р2, Рз, выраженные через полное давление Р = Р\ + Р2 + Рз в
системе:
N1 =	(1 - a)N, N2	— N3	=	aN\
Р\   N\   1 — Q Р2   Рз   N2	  Q
Р	N\	+	N2 + N3	1 + q ' P	P	N1	+ N2 + N3 1 + a
Из условия на	химические потенциалы	имеем
т'п	+	Х1	= Пп гп;+ *2 + T’ln + хз.
1 + а	1	+	ol	1	+	а
Отсюда получаем, что степень диссоциации определяется выражением
а(Р, Т) =	1
V\ + PK(T)’
а константа равновесия реакции К(Т) равна
„Ci-Сг-Сз
= jWsr*" •
Энергия диссоциации дается соотношением I = е02 + еоз — £оь
Энтропию находим как сумму энтропий каждой из компонент смеси
газов:	3
(=1
Продолжая далее, найдем
з
s = x>(c* + s-ite)
Д|=Д2+МЗ
S = J2K (cpi + у) - (jV'+A/2)r(M2+— = N^Cpi + а(Ср2 + Срз - СрХ) -
1=1
- (1 - a)j - In Р2 + Ср2 In Т + С2 - In Р3 + Ср3 In Т +	.

3.1. Распределение Гиббса. Термодинамические величины и функции -*\г 441
Отсюда получаем окончательный результат для энтропии:
S - n(cp\ + а(СР2 + Срз - Ср\) - (1 - а)у -
— 2 In -р—j—^ + (Ср2 + Срз) In Т +	+	Сз	~	2 In P^j.
Теперь мы можем найти теплоемкость, как T(dS/dT) при постоян¬
ном давлении Р. При дифференцировании по температуре нужно учесть,
что степень диссоциации зависит от температуры. Итак,
^ = СР2 + Срз + (1 - a)j + la' -	+ (СР2 + Ср3 - СрХ)Та'.
Это выражение можно упростить, выразив производную а' = да/дТ
через а. Действительно,
, схРК' а(1 — а2)(1п/(У
° _ 2 2
-Т(\пК)' = Ср2 + Срз-Ср1 +у,
j^i _ а(1 - а2)(СР2 + Срз - Ср\ + 1/Т)
Окончательно для теплоемкости, отнесенной к одной частице, получим
— (1 - а)Ср\ + а(СР2 + Срз) +	2~--~ (Ср2 + Срз - Ср\ + - j .
Предельные значения теплоемкости при а = 0иа = 1 очевидны.
3.1.19.	Для вычисления средних значений прежде всего необходимо най¬
ти функцию вероятности для флуктуаций термодинамических величин.
С этой целью рассмотрим среду, ограниченную объемом Vo, в котором
находится Nq частиц при температуре То и давлении Pq. Среда может
обмениваться энергией с термостатом, так что ее энергия не сохраняет¬
ся. Пусть в объеме V' «С Vo, который занимают N' частиц, изменились
давление, температура, энтропия и другие возможные величины, но
полное число частиц в среде No и полный объем среды Vo не изме¬
нились. Изменение энергии в среде, связанное с флуктуацией, равно
U = Е\ - До = e(v',s')N' + e(v,s)N - e(vo, sq)N0,
где e', £ представляют энергию в области флуктуации объемом V' и вне
ее — объемом Vo - V'. Соответственно, o', v, vo — удельные объемы
частиц в области флуктуации, вне ее и в исходной среде. То же самое

442 ->\r Глава 3. Статистическая физика. Решения задач
относится и к удельным энтропиям s', s, so, отнесенным к одной части¬
це. Используя сохранение полного числа частиц и полного объема:
Л/q = N' + N, V0 =V'+ V,
будем иметь
U = (е' - e0)N' + [е(и, s) - фо. So)]A(.
В силу N' <с No и V' <С Vo мы можем разложить разность энергий во
втором слагаемом. Воспользовавшись тем, что ds(v, s) = Т ds - Рdv,
найдем
U = АЕ + 7o(s - s0)N - P0(v - v0)N,
где АЕ — изменение энергии N' частиц, которые занимают объем V'.
Из сохранения объема NqVq = Nv + N'v' имеем
N(v - uo) = -N'(v' - uo) = — Д V,
где Д V — изменение объема, связанного с N' частицами. Что касается
энтропии, то в силу второго закона термодинамики, ее полная величина
не обязана сохраняться и может увеличиваться, т. е.
sN + s'N^soNq, или (s - s0)jV ^ -(s' - s0)N' = -Д5,
где AS — изменение энтропии, связанное с флуктуацией N1 частиц. Та¬
ким образом, энергия флуктуации удовлетворяет следующему неравенству:
и > (/min = АЕ- ToAS + PoAV.
Флуктуации, которые происходят с сохранением энтропии, т. е. до¬
статочно медленно, адиабатически, без диссипации энергии, мы будем
называть термодинамическими флуктуациями. Им соответствует энер¬
гия (минимальная работа) U = Umin, которая выражается только через
термодинамические функции среды. В реальности всегда есть диссипа¬
ция энергии, которая зависит от скорости изменения параметров флук¬
туации, например, объема флуктуации V' = V'(t), и тогда U - Umin ос
ос (dV'/dt)2 > 0. Как минимум здесь должна возникнуть вторая сте¬
пень производной, чтобы увеличивалась энтропия и была положитель¬
ной диссипация энергии независимо от направления процесса. Вероят¬
ности нетермодинамических флуктуаций зависят от конкретного типа
процесса, а также и от кинетических диссипативных коэффициентов
среды, например, вязкости, теплопроводности. Для термодинамических
флуктуаций результаты носят универсальный характер.
Ниже мы уберем индекс ноль у всех величин, стоящих перед флук¬
туациями, и представим минимальную энергию Umm в удобном для вы¬
числений симметричном виде по флуктуирующим переменным, которые

3.1. Распределение Гиббса. Термодинамические величины и функции	443
все равноправны. Считая флуктуации малыми по сравнению со сред¬
ним значением самой флуктуирующей величины, мы будем пренебре¬
гать всеми членами выше второго порядка по отклонениям от средних
величин. Рассматривая АЕ, как функцию энтропии и объема, разложим
АЕ в f/min по отклонениям AS и Д V:
(/„,„-£§ AS+ffдг+
+mi^+^s*v+'S(Ay)1-TAS+PAV=
4(1 А5+|^Д1')а5-1(^Д5+^Ду)дГ>1(Д7-Д5-ДРДЮ.
Для термодинамической устойчивости среды относительно флуктуаций
необходимо выполнение условия
Umm = \(ATAS-APAV)>0.
Вероятность найти среду с энергией термодинамической флуктуации,
равной Umin, будет определяться распределением Гиббса:
1V7	(	Umi„\	(	AT	AS	—	APAV\
W cx exp^——J oc exp(^	—	J.
Предэкспоненциальный множитель проще находить из условия норми¬
ровки полной вероятности на единицу.
а)	Флуктуации энтропии и давления. Выберем в качестве
независимых переменных S и Р. Тогда
Здесь Ср — теплоемкость при постоянном давлении, и мы учли с помо¬
щью определения и перестановки смешанных производных от энталь¬
пии W, что (dV/dS)P = d2W/dS8P = (dT/dP)s. Члены с ASAP со¬
кращаются, и в результате для распределения вероятности имеем
ЩДД, АР) = А ехр
{dV^(APf - ^(AS)2
Постоянная А может быть определена из условия нормировки плотно¬
сти вероятности W(AS, АР):
J j W(AS, АР) d(AS) d(AP) = 1.

444	Глава	3.	Статистическая	физика.	Решения	задач
Для средних флуктуаций энтропии и давления, согласно
(х2) — J x2W(x,y)dxdy и (ху) = J xyW(x,y)dxdy,
находим
((AS)2) = Ся, ((ДЯ)2) = _г(|^)5, (ASAP) = 0.
Из последнего соотношения видно, что термодинамические флуктуации
давления и энтропии происходят независимо друг от друга, а из поло¬
жительности первых двух следуют необходимые условия термодинами¬
ческой устойчивости среды на теплоемкость Ср > 0 и адиабатическую
сжимаемость (dP/dV)s < 0. С учетом того, что плотность р ~ 1/V, по¬
следнее неравенство эквивалентно положительности квадрата скорости
звука (dP/dp)s > 0.
б)	Флуктуации температуры и объема. Выбирая в качестве
независимых переменных Т и У, имеем
Здесь Су — теплоемкость при постоянном объеме, и мы учли с помо¬
щью определения и перестановки смешанных производных от свобод¬
ной энергии F, что (dS/dV)T-d2F/dTdV-(дР/дТ)у. Члены с ATAV
сокращаются и в результате для распределения вероятности имеем
Отсюда, аналогично, найдем для средних флуктуаций температуры и
объема:
Последнее равенство означает, что температура и объем являются тер¬
модинамически независимыми переменными, подобно паре — давление
и энтропия, и флуктуируют независимо друг от друга. Необходимые
условия термодинамической устойчивости среды подразумевают поло¬
жительность Су, т. е. Су > 0, и отрицательность изотермической сжи¬
маемости (dV/дР)т < 0.
W(AT,AV) ос ехр
<(Д Т)2)) = ^-, {(AV)2) =-т(^) т, (AT AV) = 0.

3.1. Распределение Гиббса. Термодинамические величины и функции	445
В нашем рассмотрении мы не учитывали члены третьего и более вы¬
соких порядков по отклонениям. Для этого, по крайней мере, необходи¬
мо, чтобы средние квадраты флуктуаций были много меньше квадрата
самой величины, например, ((ДГ)2) «С Т2, т. е.
„ i «i
Т2	Cv N
Таким образом, относительная флуктуация термодинамических вели¬
чин обратно пропорциональна корню из числа частиц N.
в)	Корреляции термодинамических переменных. Для при¬
мера рассмотрим корреляционные средние (ДУДР) и (ASАТ). Итак,
имеем
*PAV={w)t{AV)1 + (ff)virAl'-
Усредняя по флуктуациям и учитывая, что (ATAV) = 0, получим
<ДРДК} = (!£)г«ДГ>гН-Г.
Аналогично находим
(AS АТ) = Т.
3.1.20.	Обобщение минимальной энергии (минимальной работы) £/min,
рассмотренной в предыдущей задаче, на случай флуктуации числа ча¬
стиц N дается выражением
Umin = АЕ- TAS + PAV- pAN = ^(ATAS - APAV + Ар AN).
где р — химический потенциал. Переменные температура, объем, чис¬
ло частиц — термодинамически независимы и флуктуируют независи¬
мо друг от друга. Поэтому средний квадрат флуктуации числа частиц
можно вычислить, считая температуру и объем постоянными. Тогда ми¬
нимальная энергия будет равна
Umin = AF-pAN,
где F = Е - TS — свободная энергия. После разложения флуктуации
свободной энергии ДF при постоянных Т и V до второго порядка, най¬
дем, что вероятность флуктуации W(AN) пропорциональна следующей
гиббсовской экспоненте:
W(AN) ос ехр

X
446	Глава	3.	Статистическая физика. Решения задач
Отсюда сразу находим, что
((AN)2) =
(dn/dN)T,v'
Пользуясь тем, что A/i — (dfi/dN)r,v AN при постоянных Т и V, полу¬
чаем, что переменные ц и N — термодинамически зависимые перемен¬
ные, и
(А^ AN) = Т.
3.1.21.	Статистическая сумма определяется гамильтонианом Н(р, q) =
= Но(р, q) - qf и имеет вид
2кл</)~ fdpdqe-Wo-4f>/T.
Дифференцируя свободную энергию F(f) по /, находим
дF	Td\nZ„ ^dZw/df , х
d(q) _
d2F т
’ 1 d2ZK„
N
I
Ю
1
(q2) - (q)2 . ((Aq)2)
df
df2
\zw df
\zu df J
T2 T
Отсюда получаем искомое соотношение:
((Aq)2) = ТХ,
которое представляет собой одно из утверждений флуктуационно-дис-
сипационной теоремы для термодинамически равновесных классических
систем.
Этот результат может получен и с использованием понятия о ми¬
нимальной энергии флуктуации t/min из предыдущих задач. Обозна¬
чим для удобства Q = (q). Тогда для дифференциала потенциала F(f)
имеем cLF(f) = —Qdf. Сопряженный потенциал F(Q) вводится согласно
F(Q) — F + Qf, и его дифференциал равен dF(Q) = fdQ. Минимальная
энергия или минимальная работа при флуктуации термодинамической
переменной Q будет равна
=дгюь/до - ||лс-;дс+!0<д«>г - Ш(ЛС)2 “ 11Г'
Последнее соотношение после усреднения с гауссовой экспонентой
—(AQ)2/2Т\ даст то же равенство ((AQ)2) = Т\, где x~l = d2F/dQ2.

3.2. Квантовые идеальные газы -JVr 447
3.2.	КВАНТОВЫЕ ИДЕАЛЬНЫЕ	ГАЗЫ
3.2.1.	Идеальный	ферми-газ
3.2.1. Запишем энергию и число частиц ферми-газа, используя понятие
одночастичной плотности состояний g(e):
оо	оо
Е-/*«*(<)/(£) =
О	О
оо	оо	^
N = Jdeg(e)f(e) = J	■
о	о
Химический потенциал неявно определяется из второго уравнения. При
вычислениях в области низких температур полезно следующее разло¬
жение по температуре:
ОО
/ т (_ 2)и f(m)+f"(/x)-
о
Интегрируя оба выражения по частям и применяя последнее равенство,
найдем низкотемпературные Т eF разложения для энергии и хими¬
ческого потенциала:
Е(Т) = Е(Т = 0) + ^ T2g(eF), /х(Г) = е, -
Отсюда следуют линейные законы для низкотемпературного поведения
теплоемкости и энтропии:
C(T) = jTg(eF) и Sm = ^7gM.
Линейный закон роста теплоемкости и энтропии ферми-газа с темпе¬
ратурой не зависит от размерности пространства d. Для химического
потенциала это свойство не выполняется. Учитывая, что для d-мерного
газа плотность состояний g(e) ~ e^d~2^2, знак производной химическо¬
го потенциала по температуре d^i/dT2 ~ — (d — 2) меняет знак с поло¬
жительного при d— 1 на отрицательный при d = 3 и больше.
3.2.2. Вводя поверхностную плотность ферми-частиц ris, имеем
ns = 2 [ d2P ,	1	=	*![/“+1п(1 + в-'*/г)1.
J (2nh) е(Р /2т-е)/г _ j тг Lr	J

л
448 -V Глава 3. Статистическая физика. Решения задач
Отсюда химический потенциал /х = /х(Г) равен
\ef - Te~eflT, Т -с ef,
h(T)=ef+Tln(l -	=
-T\n(T/EF), Т^>Ер,
где ef = 'KtPris/m — энергия Ферми.
3.2.3.	Энергия частицы в магнитном поле будет равна ер ± /ЗН в зави¬
симости от ориентации спина вдоль или против магнитного поля. Число
частиц со спином вдоль или против поля будет равно
N.
ОО	ОО
+ = У def(E - (ЗН) g(E), N-=l-f dEf(E + (ЗН) g(E).
о	о
Множитель 1/2 отражает тот факт, что в определение плотности состо¬
яний включено две проекции спина. Полный магнитный момент М —
= (3{N+ — N-) будет равен
М
= £fdeme-0H)-f(e + l3H)]g(e)-
ОО
В слабом магнитном поле можно разложить под интегралом разность
функций распределения и найти парамагнитную восприимчивость со¬
гласно М = хрН\
ХР = (3> jdE(-?M)g(E).
О
Спиновая (парамагнитная) восприимчивость вырожденного ферми-газа
называется также восприимчивостью Паули и при низких Т -С ef тем¬
пературах для нее имеется разложение
ХР = P2g(£F)	ln	•
Оставаясь конечной при нулевой температуре, парамагнитная восприим¬
чивость Паули с ростом температуры ведет себя по-разному в зависи¬
мости от размерности системы, подобно случаю с химическим потен¬
циалом. Нетрудно видеть, что д2 \пg(e)/ds* = -{d/2 - 1 )/е2, где d —
размерность пространства.
3.2.4.	При полной поляризации газа в состояние с одним и тем же им¬
пульсом можно поместить только один фермион, а не два, как в случае
нулевого магнитного поля. Поэтому размер ферми-сферы увеличится и

3.2. Квантовые идеальные газы	449
будет равен рр = 2*/3ро, где ро — импульс Ферми без учета магнитного
поля. Соответственно, энергия Ферми равна ер = 22/3ео. где во — энер¬
гия Ферми в нулевом поле.
Пусть N+ (JV_) — число частиц с магнитными моментами, ориен¬
тированными вдоль (против) магнитного поля. Тогда соответствующие
импульсы Ферми и числа частиц удовлетворяют соотношениям
р3+ — 6tt2N+,	р3_ = 6ir3N-, pi — 3n2N, и N+ + AL = N.
Отсюда	»
,з
(-) +(—) =2’
V ро )	\	ро	/
, Ро ) V Ро
Для энергий Ферми фермионов с магнитными моментами, ориентиро¬
ванными вдоль и против поля, имеем
£-£ = 2 0Н, или (?±)2-^)2 = 2Ж,
2т 2т	\ ро / V ро / £о
где 0 — магнитный момент фермиона. Два уравнения на р+ и р_ полно¬
стью определяют зависимости р+ и р_ от магнитного поля Н. В полях
Н > Нс = £о/(2^30) ферми-газ становится полностью поляризованным.
Отношение квадратов скорости звука дается соотношением
с2(Н) _	2р0	с2(Н	^	Нс) _ 2i/3.	_	Ро
с2(0)	Р++Р-’	с2(0)	’	V3m'
Химический потенциал газа в магнитном поле будет
р(Н) = £0- (ЗНр-±^-.
Р++р-	Р++Р-
3.2.5.	В пренебрежении взаимодействием между атомами примеси 3Не
свободная энергия единицы объема раствора при Т = 0 дается выражением
Д(я4, Лз) = ^40>(«4) - П3А + |^лз,
где ро = Й(37г2/гз)‘/3 — импульс Ферми. Дифференцируя по Яз, найдем
химический потенциал 3Не:
М.—А+А-
Химический потенциал 4Не в растворе равен
(0) дА 3 д In М ро
М4_^4 “ д^Пз~ Ъ~д^2МПз-

450 -J\r Глава 3. Статистическая физика. Решения задач
Зависимость Д и М от плотности п4 несущественна, и в первом приближе¬
нии ею можно пренебречь, положив — /Д0). Изменение химических
потенциалов частиц в растворе приведет к изменению давления, кото¬
рое можно выразить из приращения термодинамического потенциала П:
dP = П3 d/сз + п\ d/Z4.
С учетом dfx4 яз d/j.[0> = 0 найдем осмотическое давление:
П 3	«3
n = J"3w/"3 = Jliid’l3 = lmn>'
О	О
которое приблизительно равно давлению идеального ферми-газа.
В полностью поляризованном растворе осмотическое давление уве¬
личится в
22/з
раз.
3.2.6.	Новый участок электронного спектра дает вклад в изменение
плотности одночастичных состояний g(e) = go(e) + Sg(e), где
Sg(e) =
О,	е	<	Д,
[7(5 —Д)1/2, е^Д = VmV2m/n2h3).
Изменение потенциала Н определяется выражением
SCI = ~tJ de Sg(s) ln(l + е(м-е)/г),
которое после интегрирования по частям принимает вид
оо
-?7 [ SLZ
з J е(Е-"
д
Предельные случаи в зависимости от соотношения между температу¬
рой Т и отклонением химического потенциала от порога зоны (ц — Д)
даются формулами
' -^(4 - V2hT5'2 [с(5/2) + |(3 - ^2)С(3/2)^Д^
SCI = <	7>д-Д,
-17(М - А)5/2 - у77'2(м - Д)1/2, Т « g - Д.

3.2. Квантовые идеальные газы
Отсюда при стремлении Т —> 0 имеем корневую аномалию в электрон¬
ной теплоемкости:
При изменении давления Р меняется химический потенциал /х — /а(Р),
и в случае малых изменений имеем
Та же аномальная часть, связанная с 6£1, имеется и у термодинамиче¬
ского потенциала Ф(Р, Т). При нулевой температуре будем иметь
Отсюда следует, что модуль объемного сжатия
тоже имеет корневую особенность. Конечные температуры Т > |/х - Д|
размывают и сглаживают особенности в электронных свойствах.
3.2.7.	Простейший способ ввести квазиклассическое описание — это
использовать приближение локальной плотности для функции распре¬
деления Ферми
где е(г, р) = р2/(2т) + U(r) — классическая энергия частицы и ц —
химический потенциал, определяемый из нормировочного условия на
полное число частиц:
ц-А = ц(Р)-ц(Рс)*%(Р~Рс).
Р<Рс,
Р>Рс.
/(г,р) = (е(£(г’р)-^)/г-)-1) \
оо
О
Здесь мы ввели одночастичную плотность состояний:

452	Глава	3.	Статистическая	физика.	Решения	задач
С введением плотности состояний легко вычисляются термодинамиче¬
ские функции, например, энергия газа:
ОО
cyt\ _ Г £v(e)de
Е(Т) - J
О
При Т= 0 химический потенциал определяет энергию Ферми eF=р(Т=0).
Из нормировочного условия имеем
eF = h{3Nu;xu)yLJz)[/3.
Соответственно, энергия газа Ео при 7 = 0 равна
'/	г4	ч
Eq = j eu(s) de = —3—F-	= -Nef.
/	4П ШхШуШг	4
Низкотемпературные поправки к энергии, химическому потенциалу, эн¬
тропии и теплоемкости очевидны:
E(T) = Eo + ^1*v(eF), n(T) = eF-\~-
О	3	£f
S(T) = ^Tv(ef), C(T) = ^Tv(eP).
Здесь v(eF) = Ер/(h3uxujyujz) = 3N/ef — плотность состояний на поверх¬
ности Ферми.
Распределение плотности частиц п(г) в ловушке можно найти ин¬
тегрированием функции распределения /(г, р) в импульсном простран¬
стве. При 7 = 0 выполнено /(г, р) = 0(ef - е(г, р)) и тогда
“(г)=2/ше(ср-г(г-р))ш(Ш<е'-Щг)>3,2‘
8 N (	х2	у2	г2 \3/2
п2 RxRyRz V	Я2	Л2	Я2 У '
Найденное выше распределение плотности фермионов называется рас¬
пределением Томаса-Ферми и в данной ловушке имеет форму эллип¬
соида с полуосями Rx, Ry и Rz согласно

3.2. Квантовые идеальные газы	453
Интегрируя функцию распределения /(г, р) по координатам, найдем
импульсное распределение для частиц. При 7 = 0 получаем
"(р) = (2S5 / Л0(№ “£<г р,) = 7 3 (‘" з) ''
для р < Pf и п(р) = 0 в обратном случае. Это уравнение является ана¬
логом импульсного распределения в виде^тупеньки 0(1 — р2/Рр) в одно¬
родном ферми-газе. Заметим, что значения граничного импульса рр =
= h[3n2n(r — О)]1/3 в обоих случаях совпали.
3.2.8.	Рассмотрение аналогично предыдущей задаче. Одночастичная плот¬
ность состояний, отнесенная к 1 см2 поверхности, дается выражением
ОО
м(е) = 2 [ dz [ d ^ б(е - | mgz) =
J J (2nh) V 2т	)	Ъж К
(2 те)3'2
3mg
Химический потенциал р находится из условия нормировки:
'(e) de
»=Ч'-
(2тгНУ	J	e‘£“w/,+l
о
Отсюда при 7 = 0 находим энергию Ферми ер = р(Т = 0) и погранич¬
ный импульс рр\
Pf	ъ(	157r2Nm2g^ '^5
Распределение плотности нейтронов по высоте дается при 7 = 0 соот¬
ношением
п[г) ‘2 /	ш^сг' й - т*2) = 3^? (‘ ■
Таким образом, использование ящика высотой большей, чем zmax =
= ep/(mg), не имеет смысла, так как плотность нейтронов при z > zmax
пренебрежимо мала. Это остается справедливым, пока температура до¬
статочно низкая 7 <С£д. Распределение в импульсном пространстве так¬
же легко находится:
"(р)=/ ^ke(£F ~ h ~=0 ~	1е(р'_ р2)-

454 -IV Глава 3. Статистическая физика. Решения задач
3.2.9.	В потенциале U(r) = -eQ/r энергия k-ro уровня равна £* = —£о/&2,
где £о = m{eQ)2/{2К1). При 7 = 0 электроны будут последовательно запол¬
нять уровни в соответствии с принципом Паули. На каждый уровень мо¬
жет быть помещено 2k2 электронов. Таким образом, для заполнения пол¬
ностью последнего л-го уровня необходимо следующее число электронов:
Отсюда номер последнего заполненного уровня п и (ЗТ^/2)1/3, а его энер¬
гия и, соответственно, энергия Ферми будет приблизительно
Полная энергия всех электронов: Е w —3jNef-
При конечной температуре условие нормировки примет вид
и это условие невозможно удовлетворить при конечной температуре.
Причину такого поведения можно увидеть и из сильной расходимости
плотности состояний при е —у —0:
3.2.10.	При температуре 7 = 0 вырождение последнего по энергии уров¬
ня, занятого электронами, — разное в случае четного числа и нечетного
числа электронов. Так как один и тот же уровень энергии может быть
занят максимум двумя электронами с противоположными спинами, то
в случае с четным числом электронов, уровень Ферми полностью занят.
При нечетном числе электронов на уровне Ферми находится только
один электрон, и состояние двукратно вырождено по проекции спина.
Из условия 7 <с S следует, что только уровни, наиболее близкие к уров¬
ню Ферми, могут существенно влиять на низкотемпературные свойства
частицы. Для оценки теплоемкости в пределе 7 —> 0 достаточно учесть
только уровни, отстоящие от уровня Ферми не более, чем на S. Соот¬
ветственно, статистическая сумма Z и свободная энергия F для четного
числа и нечетного числа электронов приблизительно равны
П
п(п + l)(2n + 1)	2^з
N =	2k2	=	2
6	п»1	3
Z4eT = 1 + Ае~6/Т +	F4er	«	-ATe~s'T-
ZHe4 = 2e~s/T + 4e~2S/r + ..., FHe4 » S - 7 In 2 - 2Te~s/T.

3.2. Квантовые идеальные газы	455
Дважды дифференцируя по температуре, для теплоемкостей прибли¬
женно найдем
с„„»	и С„„ = 2(1)!е-‘/Т
Таким образом, в пределе Т —► О поведение теплоемкостей качественно
совпадает, хотя и отличается по величине.
В поведении спиновой восприимчивости разница оказывается более
существенной. Действительно, в магнитном поле Н каждый уровень
расщепляется на два магнитных подуровня, симметрично отстоящих
относительно уровня в нулевом поле н£ ±0Н, где 0 — магнитный мо¬
мент электрона. В слабом поле 20Н < 6 при четном заполнении ме¬
таллической частицы для возбуждения магнитного состояния необхо¬
димо затратить энергию S — 20Н > 0. Наоборот, в случае нечетного
заполнения в силу вырожденное™ уровня Ферми по спину, энергия
возбуждения отсутствует и электрон на этом уровне будет вести себя
подобно свободному спину, т. е. обладать заметной восприимчивостью.
В слабом	поле	получим
S-20H	6	6	S+20H
Z4tт = 1	+	£	т	т	+ е	т + е	т	+...=
= l + 2(l + ch^y-s/T + ... ;
S—0H	S-0H	2S-0H	2 S-0H
Z„e4 = е~ Т +е Т + 2е т + 2е т + ...-
= 2ch^<r4/7'(l + 2e-‘5/7') + ... .
Отсюда находим спиновую восприимчивость, используя соотношение
x = -T(d2(\nZ)/dH2y.
Хчет «	8(у)е-4/Г И	Хнеч«у-
Таким образом, мы приходим к качественно разному поведению для
восприимчивости при Т —» 0.
Более подробное рассмотрение дает следующий результат для раз¬
ности в энергиях нечетного и четного заполнения электронами метал¬
лической частицы:
6F(T) = FНеч{Т) - F4eT(T) = -Tin
где
/m = nth?f = exp(Elnthif)
k,a	k,a
и k обозначает номер уровня, а а — проекцию спина.

456	Глава	3.	Статистическая	физика.	Решения	задач
3.2.11.	Для плотности состояний имеем
g(e) = v [ ~Г2 [<*(е - VP) + <5(е + vp)] = г'—7^2-
J (2пп)	2nh	v
гдег/ = 2х2 = 4 — кратность вырождения по спину и числу кониче¬
ских зон.
Дифференцируя по температуре выражение для энергии, отнесен¬
ной к единице площади,
[ deeg(e)
J е^)/Т)
+ 1
Е(Т)
—оо
и, считая химический потенциал фиксированным, найдем
С(Т) =
ОО
ч!
de |е|е е — р
2тгh2v2 J ATch2(e — р)/2Т Т
Наиболее интересен случай, когда химический потенциал проходит че¬
рез коническую точку спектра, т. е. р = 0. В этом случае ферми-поверх-
ность вырождается в точку и единственный параметр, имеющий размер¬
ность энергии, — это температура. Параметром длины будет £(Т) = hv/T.
Окончательно
ОО
С(Т) = JL[L2 [ ..dxf = и-а3) 72
2-кh2v2 J 4ch2x/2	27Г д2у2
0
Такая зависимость является простым следствием конической формы изо-
энергетической поверхности и плотности состояний g(e) ~ |е|. Действи¬
тельно, только электроны вблизи конической точки с энергией |е| < Т
вносят вклад в тепловое возбуждение системы. Число таких электро¬
нов порядка N(T) ~ Tg(e ~ Т), и, соответственно, энергия теплового
возбуждения Е(Т) ~ TN(T) ~ Т\ В результате это дает С ~ Т2.
Зависимость С(Т) ~ Т2 справедлива пока |/х| < Г. В обратном пре¬
деле |/z| Т возбуждения находятся вдали от конической точки, ферми-
поверхность представляет окружность вместо точки, и температурная
зависимость теплоемкости становится привычной, т. е. линейной и про¬
порциональной плотности состояний на уровне химического потенциала:
C(T) = ^Tg(\p\) = ^MT, (И» Г).
•J	■З п и
В условиях, когда фиксируется число частиц, температурные зависимо¬
сти сохраняются, но численные коэффициенты могут измениться. От¬

3.2. Квантовые идеальные газы	457
метим отдельно случай g(T = 0) = 0. Эта точка является фиксированной
точкой в том смысле, что при изменении температуры остается д(7) = 0.
Если ц(Т = 0) = цо ф 0, то можно выделить две области температур
T<g.\fi\ и 7»|^|. При низких температурах, пока 7« |//|, зависи¬
мость /х(Г) имеет обычное фермиевское поведение /Д7) — /хо T2/g,o-
В области 7 > |д0| поведение ц(Т) становится нетрадиционным со сте-
пеннным спаданием:	7) ~ цо\цо\/Т.
3.2.12.	Энергия электрона в магнитном »поле равна ер±(ЗН, где 0 —
эффективный магнитный момент частицы. Полный магнитный момент,
выраженный через функцию распределения /(е), дается соотношением
М
ОО
= f | deg(e)[He-pH)-f(e + 0H)\,
где g(e) = v\e\/(2txh2v2) — плотность состояний с учетом двух проекций
спина. Дифференцированием по магнитному полю найдем восприимчи¬
вость хр — —дМ/дН:
ОО
п2
—оо
оо
= у I de[g{£-m+g(e + m}(-^) =
— ОО
оо
"	^	Iе	+	^	~	+	|е	+	/л	+	Щ
~ 2тгftV Т J 47	ch2(e/27)
Далее мы используем соотношение
— ОО
ОО
J \х +а
— ОО
—=— dx = 2 ln(2 ch а),
ch х
и в итоге получаем следующую зависимость:
w(r'H)-dv/s!7'",[2H+ch f)l-
Отметим, что g и 0Н входят в ответ симметричным образом. Предель¬
ные соотношения даются простыми выражениями. При 7 = 0
{P2g(g) ~ const, 0Н < \ц\ (слабое поле),
02g(0H) ~ Н, (ЗН > |/х| (сильное поле).

458 ->\r Глава 3. Статистическая физика. Решения задач
При конечных температурах в пределе слабого поля 0Н <с Т имеем
ХР(Т) = —2/32Т 1п(2chр/2Т) *
Z'Kfx v
{02g(p) ~ const,	Т	|/х|	(низкие температуры),
2 In 202g{Т) ~ Г, Т » |/i| (высокие температуры).
3.2.13.	Уровни энергии жесткого ротатора в зависимости от величины
магнитного потока через кольцо Ф = nR2H даются соотношением
/	ф	\	2
-л(Ф) =eoyi — ^ J , ео =
h2
2m/?2 ’
где фо = ■кНс/е — квант магнитного потока, и орбитальное число п =
= 0, ±1,±2,— Термодинамический потенциал Q с учетом двух про¬
екций спина определяется выражением
П = -2Г£1п(1 + e0‘-«.(*))/rj>
П
а ток, который течет по кольцу, будет равен
/ =	=	-Ог	V	де„(ф)/Эф
^ дФ	Z_,	еыФ)-ц)/т + , •
Для вычисления тока воспользуемся формулой суммирования по
Пуассону:
ОО	ОО	ГГ
£ Д(л) = £	f	dnF(n)e2nikn.
п=—оо	k——ОО —оо
Отсюда, сдвигая переменную л —> п - Ф/(2фо), находим ток:
ОО
Jlirikn
]=Щ У еп‘кф/ф° f dn ■
*R2 „Ч. J ,
пе
„	р^о"2-и)/т , .
к=-оо	 „	е
= —^ ^sin(7r6<J>/0o) Im / dn
оо
пе2шкп
k=1
где 0 = eh/(2mc) — электронный магнетон Бора.
е(Е0**-Ь)/Г _|_ | ’

3.2. Квантовые идеальные газы	459
При больших температурах в случае невырожденного газа электро¬
нов, когда распределение Ферми переходит в больцмановское распре¬
деление, интеграл легко оценивается:
оо	оо
/_	2nikn	Г	0
dn—¥	«е^г1т / dnne2*ikn-ean !Т =
е(с0п2-и)/т + ,	J
—оо	—оо
_ си/Т(^Т\312с-ЫкТ/е0)2
* .	V	£о	)
Химический потенциал ц можно выразить через полное число частиц
согласно
ОО	I	—
N = 2^2 е<#л_£л(ф))/г w 2ем/г J йпе~€ЛФ)1Т) = №/т	.
П	—ОО
Тогда находим, что
/* = N^e-^kT^\
2ео
и ток в кольце равен
] =	I—	у'	е-(7гА7'/£о)2	$\п(тт1гФ/фо).
nR so ^
Поскольку условие невырожденности газа подразумевает 7» ер »
и e0(Af/4)2 ео, то фактически в сумму дает вклад только лишь пер¬
вый член с k = 1, и амплитуда тока экспоненциально подавлена темпе¬
ратурой.
Перейдем к противоположному пределу вырожденного газа и рас¬
смотрим случай нулевой температуры. В этом случае
!k = J dn nsin(2nkn)Q(fj, — едя2) =
27rfeyV/eo cos(2nky/n/£0) - sin(27rfey/^/go)
и ток в кольце при 7 = 0 равен сумме
2Л2
2nky/n/£0cos(2nk^n/eo) - sin(27rfe yV/e0)
7Г/?2 f-f	TT2fe2
«=1
Осцилляции тока будут не только по напряженности магнитного по¬
ля, но и в зависимости от химического потенциала, т. е. от постепенного

460	Глава	3.	Статистическая	физика.	Решения	задач
заполнения электронами энергетических уровней. Период осцилляций
соответствует изменению значения корня V/x/eо на единицу. Амплиту¬
да тока при этом будет нарастать пропорционально VJi/eо или числу
электронов.
Ненулевой ток в кольце означает, что кольцо будет обладать намаг¬
ниченностью величиной Л4(Ф) = 7г#2/(Ф)/с.
3.2.14.	При движении электрона в магнитном поле его уровни энергии
дискретны:
£п = Пин(п + 1/2) (сон = — И л = 0,1,2,...)
V	тс	/
и вырождены по положению центра орбиты электрона. Число вырож¬
денных состояний на каждом уровне Ландау одинаково и с учетом двух
проекций спина равно eHS/(nhc), где S — площадь, занимаемая элек¬
тронным газом. Введем обозначения: п = N/S — плотность электронов
и ер = -кГРп/т — энергия ферми-газа электронов без магнитного поля.
Вычислим термодинамический потенциал:
ПнМ = ~Т~ £ 1п(1 + е^-^/т).
п—0
Рассмотрим сначала предел слабых полей. При /кщ/< min{Т,£р} от
суммирования можно приближенно перейти к интегрированию с помо¬
щью формулы суммирования Эйлера-Маклорена:
ОО
п„(ц) = - тf dn In (1 + в0*-«.)/Г) _
л=—1/2
J_ e_HS hu>H |n=°°
24 7Гhe е(*п-н)/т + j |n=_,/2
oo
~S~ [ С
2nh J
o
d= £ I 1 с m (huH) ,
a£e*'T+ i + 2* \h2e-*'T+l+“
Первое слагаемое, полученное интегрированием по частям, не зависит
от поля и соответствует потенциалу электронов при Н = 0, а второе
описывает уже влияние магнитного поля. Разложение в ряд происхо¬
дит по параметру {Ьшн/ min{7\£/r})2 -с 1. Магнитный момент единицы
площади равен

3.2. Квантовые идеальные газы	461
где п — электронная плотность. Следовательно, диамагнитная воспри¬
имчивость равна
xm__
р/ту
Выше мы учли, что химический потенциал в двумерном ферми-газе
равен
/i = nn(e£f^ - 1)
и Ниц — 2/гдЯ, где /г,в = eh/(2mc) — электронный магнетон Бора.
Рассмотрим теперь температуру 7 =? О, которая является особой в
том смысле, что для нее не существует приближения слабого поля.
Введем целое число N:
Кин 2
имеющее смысл последнего полностью заполненного уровня Ландау, и
запишем энергию системы:
4=0
eHS к N(N+1) , с.	,	1\
м =
Намагниченность на единицу площади равна
\_дЕ_ =
' SdH ~
= -п/хв(2ЛЖ)+^мвЛГ(Л7Н).
Изучим поведение намагни¬
ченности в ситуации, когда чис¬
ло полностью заполненных уров¬
ней меняется на единицу. Если -
уровень с номером N +1 бли¬
зок к заполнению, то намагни- Рис. 3.3. График осцилляций намагни¬
ченность стремится к	ченности в зависимости от обратной ве¬
личины магнитного поля
Л4_ = —пцв-
Здесь мы учли, что eH(N + \)/{тхКс) —> п. Если уровень N + 1 уже за¬
полнился, и только начал заполняться следующий, то
М+ = пцв-
В итоге поведение зависимости М = М(Н) выглядит следующим обра¬
зом (рис. 3.3).

462 -*\r Глава 3. Статистическая физика. Решения задач
Всякий раз, когда происходит полное заполнение уровня Ландау,
намагниченность испытывает скачок величиной 2пцв, а в промежутках
меняется по линейному закону. В точках
. 7Гh2n N+ 1/2
намагниченность всякий раз обращается в ноль. В целом, можно го¬
ворить об осцилляциях намагниченности в зависимости от обратного
поля 1/Я. Период осцилляций Д равен
Здесь фо = ixhc/e — квант потока ил - плотность электронов. Осцил¬
ляции магнитного момента или намагниченности, периодические по об¬
ратному магнитному полю, и составляют эффект де Гааза-ван Альфена
в магнитном поле.
Рассмотрение ненулевой температуры можно провести с помощью
формулы суммирования по Пуассону:
где По(м) — термодинамический потенциал в отсутствие поля:
-1/2 *=‘-1/2
Полагая
/(„) = _T—2hwH In(1 + е,
представим термодинамический потенциал f2//(/x) в виде
о оо
Пн(р) = ПоМ + ДПяМ = ПоМ + ^2 £(-1)* Re /*,
По(/х) = -Г— I de 1п(1 + е^-£)/г).
7Г h J
о
Интеграл /* определяется выражением
оо
I„ = -T J dee2iriks/hoJH In(1 + е^~е)/т).
о

3.2. Квантовые идеальные газы	463
Интегрируя 4 два раза по частям, получим
ОО
Лп(1 +e“IT)~ J de
Re/' = Re2„i*
g2ink£/huiH
= Re
e(.-M)/r + 1
0
OO
Г f e2*ike/h“H de
(2тгДг)2 [/ 4 ch2(e - ц)/2Т T \ +
o
Дальнейшее упрощение возникает в предположении достаточно низ¬
ких температур и вырождения газа электронов Т ц. Вклад в инте¬
грал набирается вблизи е — ц ъ узкой области порядка Т. Обозначая
х = (е — ц)/Т и распространяя нижний предел интегрирования до -оо,
приближенно получим
ОО
/ fc \ 2 Г	Г	JZnikTx/huju
Re 4 « (^|) Re e2*ikli/hw" I -—dx - 1
4 ch2 x/2
Учитывая значение интеграла
ОО
/
ах =
4 ch2 х/2 sh 7га ’
найдем для части потенциала ДП/Д/х), зависящей от магнитного поля,
окончательное выражение:
дS!„W = Щ V'(-l)*-'(§2£)г С1 -	cos	МЛ
жН	\2nkJ	\	sh	2ж kT/hwn	)
При Т = 0 сумму можно оценить с помощью соотношения
ОО
/(*) = Е(-в*—=*2 ПРИ М^1/2-
(7rfe)
Функция /(х) периодична, и ее период равен единице. Термодинамиче¬
ский потенциал, а вместе с тем и намагниченность, содержат осцилли¬
рующий член, период осцилляций Д(1/Я) которого определяется усло¬
вием ц/(Иин) — 1. При конечной температуре амплитуда осцилляций
уже первой гармоники экспоненциально быстро падает с ростом тем¬
пературы как ехр[-2тг2Т/(Нсан)], и уже при Т > 2тт2Нсон осцилляции
де Гааза-ван Альфена становятся несущественными. Физически это
связано с температурным уширением уровней энергии и замазыванием
дискретной картины магнитных уровней.

464	Глава	3.	Статистическая	физика.	Решения	задач
3.2.15.	Энергетический спектр электронов в магнитном поле дается со¬
отношением
£п,.п2(Рг) =	-I-1/2) + haj2(n2 + 1/2) +
где «ь яг = 0,1,2,... и частоты ид, ш2 равны
/ 9 ш2с . и)с	еН
ы,Л«^ + т±т. *е = -.
Термодинамический потенциал Q с учетом двукратного вырождения по
спину равен
00	°Г г л
Я = -2Т J2 / ^1п(1 + е(м~е""л*Ы)/г).
п,.п2=0 _ос
Оценить двойную сумму можно с помощью приближенной формулы
ОО
р(п{ + -,п2 +	«
ЛьЛ2=0
ОО ОО	оо	оо
00,0)
J J F(x,y)dxdy + ~ J F'x(0,y)dy+^ J F'y(x,0)dx
576
00	о
Условие применимости формулы предполагает малое изменение функ¬
ции F при изменении ее аргументов «1,2 —»«1,2 + 1, т. е. идд 7. Тогда
ОО ОО	ОО
^ = f JF(ni,n2)dnidn2 - ^ J dn2 ~
00	о
ОО
[ dF(nuO) . h2uiMjj2 <Э27(0,0)
24 J дц П'+ 576	a^2	’
0
где мы обозначили для краткости
ОО
7(м,л,,л2) = -27 J ^1п(1 + в('*-*("|Л*))/г).
— ОО
Далее введем новые переменные согласно £1,2 = ЙшцгЛцг и найдем по¬
тенциал П с учетом идшг = ш2 и ш2 + ш2 = 2ш2 + и>2:
ОО ОО	оо
1 t f с ^ л, л, 2u2+Jc fdF(0,0 л, , ftVc>27(0,0)
n = J FKub) dt‘db - ~^T J -W~di +176 •-5?-
0 0 0

3.2. Квантовые идеальные газы	465
Здесь функция F(£i.6) = Дм-С 1.6) равна
ОО
^1.Ы = -27’ J ^jflnO + е(д-€'-6~р*/2т)/г)-
—оо
Выделяя слагаемое, зависящее от магнитного поля, найдем
АП{Н)
dF( O.Q
дц
di,
где цв = eh/(2mc) — магнетон Бора.
Можно показать, что последний интеграл выражается через произ¬
водную полного числа частиц по химическому потенциалу с обратным
знаком как -h2uj2{dN/др). Действительно, выражение для полного чи¬
сла частиц имеет вид
N(ji) = J
g(e) de
е^-ц)/Т j ’
где g(e) — плотность состояний, равная
°°
*<•)-*/й./Л/^(‘-ft-
— ОО
ОО
-2/
pj+pt	mu; V + у1)
2 т	2
L dpz (е - р1/2т)в(е -р\/2т)
к2 2
п и
Подставляя g(e) в выражение для N(p) и переходя к переменной £ =
= е - р2/(2т), получим
ОО	ОО
вд = ет.Ш/
еа+Рг/2т-в)/Т _|_ j
—оо	О
С другой стороны после интегрирования по частям находим
оо	ОО	ОО
J F(0,S)dS = -27 J ^ J d£ ln(l + e(^-p'/2m)/7') =
О	“оо	О
оо	оо
[ Ldp, [ Zdt = _
J 2жН J е-(й-е-Рг/2т)/7'
K2uj2N{p).
+ 1

466	Глава	3.	Статистическая	физика.	Решения	задач
Окончательно имеем
An/m_^2ajV
ДО(Я)_——,
что дает следующее выражение для диамагнитной восприимчивости
_ а2 А П(Н) = _&dN_
Х~	дН2 ~ з дц'
При низких температурах Т <С ц производная dN/дц равна bN/2ц, а
при высоких равна N /Т.
3.2.16. Решение задачи аналогично предыдущей. Диамагнитная восп¬
риимчивость дается тем же выражением
х з дц'
Вычисляя производную при низких Т -с ц температурах, найдем
v =	_	2	ц2в	д.1/2
*	3	п2ш2	‘ЗПш
с корневой зависимостью от полного числа частиц N.
При huc > Т в диамагнитной восприимчивости необходимо учиты¬
вать также и вклады от осцилляций намагниченности, обусловленные
дискретностью магнитных уровней.
3.2.17. Запишем термодинамический потенциал О в магнитном поле:
=	£	1п(!	+е,‘‘-'->/г)-
п=—ос
Так как формально уровни энергии ничем снизу не ограничены, то удоб¬
но рассмотреть разность термодинамического потенциалов для разных
значений химических потенциалов:
п= — ос
В реальной ситуации имеется минимальная энергия До < 0, ниже кото¬
рой не существует электронных состояний. Естественно предполагает¬
ся, что абсолютное значение |£о| гораздо больше всех остальных энер¬
гетических параметров задачи. В дальнейшем, мы устремим Ц2 к До. что
соответствовало бы полностью незаполненным верхней е > 0 и нижней
е < 0 подзонам, и будем от этих значений отсчитывать термодинамиче¬
ский потенциал.

3.2. Квантовые идеальные газы -l\s 467
Для суммирования по уровням используем формулу Пуассона:
оо	оо
£ F(n) = /o + Re£/*;
п=—оо	k=\
оо
/0 = J F(n) dn, /*>о = 2 f F(n)e2irikn dn.
о	о
Начнем с простейшего вклада, отвечающего гармонике k = О
ОО
.	еН	Т [	,	,	1 + в04,_е*)/г
/о = — v-—r- Т / ая In 7 гтт =
и	2тгhe J	1 e(M2-en)/r
— оо
оо	ОО
9	/■	|	I	-,(ei-*)/r	г	I	j.
-47” / <fe|e|ln±±*—_ = -Г / deg(e)ln —
■е\	J	11 1+е(м_г)/г	7	s 1 +
= —i/
где g(e) = ^|e|/(27r/i2o2) — плотность состояний в отсутствие магнитно¬
го поля. Итак, /о равно значению в нулевом поле и вклада в намагни¬
ченность не дает, так как не зависит от магнитного поля.
Перейдем к ненулевым гармоникам
ОО
/*>о = -2и^-Т [ dn e2nikn In 1 + е<"‘~ЕП)'Т
2nhc J	1+е(м-*»)/г’
-ОО
-2 11 fin   91<т1/7(Г /с-2
Делая замену переменных п = е\е\/е20 и dn = 2|e|de/£o» имеем
оо	.
Д>0 = ~2i/—/ ^|ф2^И/41п1±4
27г/1 у У	1	+	в
, Jl*2-e)/T'
— оо
Далее интегрируем по частям:
О оо
2l/ £о
— ОО
где /(х) = 1/(е* + 1) — фермиевская функция распределения. Для даль¬
нейшего, поскольку нас интересует только действительная часть /*, удоб¬
но ввести интеграл Френеля S(x):
X
S(x) = j
j 7Г 9
as sin -s .

468 ■Лг Глава 3. Статистическая физика. Решения задач
Интегрируя еще раз по частям, получим
оо
Re/*>0 =
2тгh2v2 4тгДе3/2
ОО
J deS{2\fk\e\/eo)
dfje-щ) df(e - ц2)
де	де
При низких температурах производная фермиевской функции распреде¬
ления /(е — ц) сосредоточена в узкой ~ Т области вблизи химического
потенциала, а при 7 = 0 просто равна — <5(е — ц). Интегралы по энергии
быстро сходятся, и второе слагаемое, полагая ~ £о, можно опустить.
Тогда для зависящей от магнитного поля поправки в термодинами¬
ческий потенциал П(/л) получим
ДПя(м) =
ОО
v2 == J £3/2	\	de	)I t=0
8к2П2,
«	1	—OO
8ttW f- k3/2
A=1
В пределе слабого магнитного поля ео |/х| для анализа поведения
суммы удобно воспользоваться следующим асимптотическим разложе¬
нием интеграла Френеля:
Six) = ^ - fix) cos ще - gix) sin
цх) = -L + 1Г(-1ГИ' у"?-11-X- 4-, + —
■кх кх ^	(кх )	КХ	к	X
ТП—1
g(x) = -L V(-l)w1'3'	=	4з	+	•	•	•	•
S кх ^	(кх	)	к	х
ГП— О
С помощью этого разложения можно легко выделить монотонную и ос¬
циллирующую части термодинамического потенциала ДП// = ДП^оп) +
+ ДП^С):
Ло|г> = f- ■ .
И	8к	h	o	f-f	2/fe	7	16тг2 V fic /
*=i
ДП^С) = -v-4n х
я	8к	h	о
СЮ
X
Л=1
^r/(2^l^l/eo) _j2Kkfi2\ g(2Vk\ix\/e0)	/2тг^2\'
f-?.	^	°	^2	V	4	А

3.2. Квантовые идеальные газы	469
Монотонная часть дает расходящийся при Н —► О вклад в диамагнит¬
ную восприимчивость:
Последний результат мы представили в форме, традиционно принятой
для электронного газа с обычным квадратичным спектром. Для этого
мы ввели эффективную массу, зависящую от энергии тэф(г) = |е|/и2,
так чтобы плотности состояний формально совпадали для дираковского
и квадратичного спектров:
g(£) = "Tljm = Яэф(е) =
2nh v	2nh
Соответствующий эффективный магнетон Бора
а < \ _ еh _ ehv2 1
Рз*(£) ~ 2тэф(е)с ~ ~2ГЩ
также зависит от энергии и обращается в бесконечность в конической
точке е = 0. В целом, точка нулевого магнитного поля Н — 0 являет¬
ся особой точкой термодинамического потенциала, а расходимость вос¬
приимчивости указывает на неустойчивость однородного состояния в
слабом магнитном поле.
Частота осцилляций термодинамического потенциала (эффект де Га-
аза-ван Альфена) равна /г2/£о ~ $/Н- Такие же осцилляции в зави¬
симости от отношения /х2/// возникают и в намагниченности и маг¬
нитной восприимчивости. В этом, в частности, наблюдается отличие
от обычных систем с квадратичным законом дисперсии, где период ос¬
цилляций зависит от отношения /i/Я. Пользуясь понятием эффектив¬
ной массы тзф(е), здесь также можно провести аналогию с квадратич¬
ным спектром, для которого период осцилляций зависит от отношения
ц/(Ни>с). Действительно, определяя эффективную циклотронную часто¬
ту шс,эф(е) = еН/{стЭф(е)), легко убеждаемся, что
М = /д
2шс.эф(ц) 4‘
Выпишем далее первый член разложения Af^sc) в слабом поле по
малому отношению ео/\ц\:
4 2 2 Е cos(27r^22/£°) +•■• =
Н	16тг|м1	H	v	(7rfe)
4
1б7г|ц| k2U2
В2(ц2/е20) + ...	(е0<|м|).

470
Глава 3. Статистическая физика. Решения задач
Здесь ВгС*) — периодическая функция с периодом равным единице и
совпадающая на отрезке [0,1] с полиномом Бернулли второй степени
Следующие члены разложения могут быть также выражены через поли¬
номы Бернулли более высоких степеней. Хотя и осциллирующие члены
в термодинамическом потенциале малы по сравнению с монотонным
членом, но после дифференцирования по магнитному полю намагни¬
ченность M(osc) = -дАП^/дН и восприимчивость ^<osc) = dAf(osc)/cW
приобретают большие по абсолютной величине значения.
Теперь проанализируем противоположный предел сильного поля, ко¬
гда so » \р\. Для оценки суммы
проведем следующее рассуждение. При малых аргументах интеграл Фре¬
неля S(x) ведет себя приближенно как
Соответственно, основной вклад в сумму вносят члены с большими номе¬
рами до тех пор, пока номер k не превысит k ~ ko ~ е\/р2	1.	В	этих
условиях, когда функция медленно меняется при изменении ее аргумен¬
та, для оценки суммы можно воспользоваться следующей приближен¬
ной формулой:
о
Далее учитывая, что
S(2Vk\n\/eо) _ л- /2|/х|\3 _ тг3 Г2\ц\\7^ +
k3/2	6	V е0 /	336	V ео )
получим
о

3.2. Квантовые идеальные газы -»\у 471
Отсюда дифференцированием по напряженности магнитного поля с уче¬
том того, что Sq — 2ehv2H/с, находим намагниченность в пределе силь¬
ного поля, когда до > И:
м =	=	-А>фМ&эф(м)Н-
По существу это вклад наинизшего уровня Ландау, который единствен¬
ный выживает в пределе сильного поля. Интерпретируя ответ, можно
считать, что на этом наинизшем уровне находятся все электроны, число
которых £Эф(м)|м|, и каждый несет магнитный момент /3Эф(м)- Магнит¬
ных осцилляций, пока выполняется до > Н> нет-
3.2.18.	Корреляционная функция i/(г) флуктуаций плотности частиц
Дп(г) — п(г) — п в ферми-газе определяется соотношением:
(Дл(г[) Дл(г2)) = п5(г 1 - г2) + nv(r), r=\t\- г2|,
где п — средняя плотность газа и г — радиус-вектор. Корреляционная
функция связана с функцией распределения следующим соотношением:
пи(г) — — 2 |У
e‘pi/h d3p
1\
е(Е,-Ю/т + j (27гЙ)3
ОО
. _ f dp р %\г\(рг / К)
J е1'Р-н)/т + i '
О
Мы рассмотрим наиболее интересную область температур, отвечающую
вырожденному ферми-газу 7 ер. Вычисляя последний интеграл по
частям, получим
ОО
/=5* [( sin PL-.Pi: cos PL) (дд/dp)dp
г2 J ' ft ft ft / 47ch2(ep — p)/2T
o
При 7 -C sf можно положить p = p(T = 0) = др. Далее, вклад в ин¬
теграл набирается в области импульсов, близких к поверхности Ферми
\ер — р\ « vp\p - pF|	^ < ер, и удобно перейти к переменной интегри¬
рования £ = Ер - ер « vp(р - рр). Распространяя нижний предел инте¬
грирования, т. е. — р, до —оо, приближенно получим
ОО
/ » _|1 f [(^y + i}eipFrlhe*rlhVF + с.с.
dH
47ch £/27

472	Глава	3.	Статистическая	физика.	Решения	задач
Используя соотношение
оо	оо
Г e±i(r/^r ^ ^ г e±*Tr/hvFdx ^ ъТг/hVF
J 47'ch2£/27’ ~~ J 4Гch2х/2 ~ shnTr/hvF'
—оо	— ОО
найдем
, _ tyF (	_ A oin	nTr/hvf!
г V ft pFc ft / shnTr/hvF’
Наиболее интересны корреляции между частицами на расстояниях,
превышающих средние расстояния между частицами, т.е. при r^>h/pF ~
~ п-1/3. Тогда с учетом п = р3Р/(Зп2Н3) для корреляционной функции и(г)
найдем
2
, .	_ 9п 1	+ cos(2pFr/h) ( пТг/Hvf \	ft
V Г 4	{pFr/h)4 VshTrTr/ftyfJ Г	pF'
Отсюда видно,	что при	Т — 0 корреляционная функция медленно спада¬
ет степенным	образом	с расстоянием, т. е. флуктуации	плотности	кор-
релированы. Кроме того, корреляционная функция также осциллиру¬
ет с периодом, определяемым диаметром ферми-поверхности 2pF. Ос¬
цилляции с таким периодом в физических характеристиках называют
фриделевскими осцилляциями. Конечная температура разрушает про¬
странственные корреляции в ферми-газе. Как следствие, корреляцион¬
ная функция экспоненциально быстро затухает на расстояниях, боль¬
ших корреляционной длины г > £(Г), которая равна
m = tr
3.2.2.	Идеальный бозе-газ
3.2.19.	Если при заданной плотности бозе-газа понижать его темпера¬
туру, то при Т — Тс химический потенциал газа обращается в нуль и
остается нулем вплоть до абсолютного нуля температур р(Т < Тс) = 0.
Плотность надконденсатных частиц при Т ^ Тс дается соотношением
3/2	/	Т	\
Соответственно, плотность конденсатных частиц конечна и равна
п0(Т) = п- пех(Т) = п
■АГ

3.2. Квантовые идеальные газы	473
3.2.20.	Энергия конденсированного газа определяется интегралом
ОО
Е= [ —тг- = VT(J^')V2^= f
J (2nh) e p! - 1 \27rft / vW * - 1
= ^гМйГ “Hi7'""'7'»17 ~ vtW1-
Теплоемкость Су при постоянном объеме имеет вид
Давление конденсированного газа Р можно вычислить с помощью по¬
тенциала ft = -PV:
/ жТ \ 3/2	9
-УТШ «W—f*-
Отсюда давление идеального бозе-конденсированного газа равно
/ т \3/2
Р{Т) = Т[~^)	С(5/2)	~	Тъ'\
и не зависит от объема газа. Это приводит к расходящимся значениям
для изотермических коэффициентов расширения и сжимаемости газа,
а также для теплоемкости при постоянном давлении.
Поскольку ц = 0, то свободная энергия газа F легко находится из
соотношения F = fiN + П:
Д=П = -|£~-К7'5/2.
J
Далее находим энтропию S, согласно 5 = —dF/dT:
S =	=	\CV	~	VT3'2.
Так как энтропия газа зависит от его объема, то значения адиабати¬
ческих коэффициентов расширения и сжимаемости остаются конечны¬
ми в отличие от их изотермических аналогов. При изменении Т и V
вдоль адиабаты отношение Т/Тс остается неизменным и, следователь¬
но, соотношение между надконденсированной и конденсированной фа¬
зами в адиабатическом процессе остается неизменным.

474 •Ar Глава 3. Статистическая физика. Решения задач
3.2.21. Выразим максимально возможное число частиц во всех возбуж¬
денных состояниях е > 0 в виде интеграла от одночастичной плотности
состояний g(e):
ОО	ОО
maxlAUD] = / ^ = Т J 1*2*.
О	о
Результат зависит от поведения g(e) при малых значениях энергии е.
Если интеграл сходится и неограниченно убывает с понижением темпе¬
ратуры, то при некоторой температуре необходимо ввести конденсацию
частиц на наинизший уровень энергии, так как все частицы уже не
смогут быть размещены в возбужденных состояниях. В противополож¬
ном случае расходящегося интеграла, когда значение max[Nex(T ф 0)]
превышало бы полное число частиц N, нормировка на полное число
частиц в газе всегда будет удовлетворяться при значении химического
потенциала, меньшем его максимально возможного, т. е. при р < 0. За¬
селенность основного уровня е = 0 тогда пропорциональна ограничен¬
ному по величине фактору [ехр(—/х/7’)—1]—1 и, тем самым, не возникает
макроскопической заселенности основного уровня.
В пространстве размерности d и при обычном законе дисперсии ер =
= р2/(2т) одночастичная плотность состояний g(s) пропорциональна
£(d-2)/2 g результате, бозе-эйнштейновская конденсация в идеальном
газе бозонов отсутствует при Т ф 0 в пространстве размерностью d ^ 2.
3.2.22. При адиабатическом процессе (S = const) в идеальном конден¬
сированном бозе-газе выполняется соотношение РУ5/3 = const. Отсю¬
да, адиабатическая сжимаемость равна
_1(^ = 3J Т-Ь/2
V\dP)s 5Р(Т)
и остается конечной при Тф 0 в отличие от бесконечной изотермической
сжимаемости. Пользуясь тем, что р(дР/др) = -V(dP/dV) (р 1/V-
плотность газа), найдем квадрат адиабатической скорости звука из опре¬
деления:
С2=» =5Р(Г)^5/2_
5 \dpJs 3 р
Значение адиабатической скорости звука при 7/0 также конечно в
отличие от нулевого значения изотермической скорости звука.
3.2.23. Воспользуемся соотношением для теплоемкостей Ср и Cv:
r _r (dP/dV)s
р v(dP/dV)T'

3.2. Квантовые идеальные газы	475
Величины С„ и (dP/dV)s непрерывны в точке перехода Тс, и расходи¬
мость Ср связана с обращением в нуль знаменателя. Итак,
„ (дР\ 25 Р2{ТС) _	{5«Ь/2)\2(N\2t
Lv\dv)s~ 4 Тс V2C(3/2)) \v) с'
Давление Р найдем, пользуясь условием (дР/дц)т,v = N/V. Тогда
Р = Р0(Т) + ^,
где Р0(Т) — давление при ц — 0. Тогда
Вблизи Тс химический потенциал приблизительно равен
9С2(3/2)(Т-Те)2а(т т,
^ ~ 16тг Те
С учетом dTc/dV = -(2/3)Tc/V найдем основной вклад в обратную
сжимаемость при Т —> Тс:
{w)T = Jj^V‘iT-T‘)e{T'TA
и окончательно при Т —► Тс
с = 25тгС2(5/2)л, Т
3<4(3/2) Т-Тс Т-Тс
3.2.24.	Обозначим магнитный момент бозона через /3. Трем проекциям
спина в магнитном поле Я отвечает три уровня энергии
£ра = 2т + а^И' =
Связь между плотностью газа п = N/V и химическим потенциалом р,
дается соотношением
d3p	1
П ст5±1 ^ 12т+а13Н~1х)/Т - 1
ОО
( *	2	[	\fedE
<r=U,±I

476 Глава 3. Статистическая физика. Решения задач
Обозначим через Го температуру конденсации при Я = 0:
2nh2n2'3
То =
[ЗС(3/2)]2/3т
При Я —* оо все бозоны будут находиться в одном спиновом состоянии
и в конденсированном состоянии с ц = —pH. Температура конденса¬
ции Гоо вырастет за счет уменьшения вырождения основного уровня
энергии и будет равна Г^ = 32/3Го. Таким образом, предел сильного
поля означает /ЗЯ;» Г^ или Го. В этом пределе
Перейдем к пределу слабого поля /ЗЯ <с Го. В области конденсации
ц, ~ —/ЗЯ, поэтому и |^| <с Го. Пользуясь разложением
ОО
tJ
Tn,dX, = С(3/2) - 2у/тгу/а - С(1/2)а + ... при а -> +0,
- 1
найдем связь между химическим потенциалом, температурой и магнит-
ным полем:
/Го\3Я 	2\/тг у/—pH — ц 4- уГр 3" 'У/ЗЯ — р,
vr; “	ЗС(3/2)	•
Отсюда, полагая р = -/ЗЯ, найдем температуру бозе-конденсации в сла¬
бом поле:
Тн , 4^(^2 + 1) [pH olJ „г
7^~1+	9С(3/2)	V	V	/?Я<<Г°-
Запишем намагниченность газа на единицу объема (Г > Тн):
м = /з [	(	!	1	^	_
Р J (2nh)3	_	,	е(£+дя-м)/г _ J -
y/xdx
а( mT \3/2 2	,	PH	[
ch(x — р/Т) — ch(PH/T) ’
где мы перешли в интегрировании к переменной х = р2/2тТ. В пределе
слабого поля, устремляя Я к нулю, найдем намагниченность М = ^Я>
где восприимчивость х(Г) равна
х(г) = £('”Д'13/!Д- /
” ’ rbrtV vW
y/xdx
ch(jc — /i/Г) — 1 ‘
0

3.2. Квантовые идеальные газы -»1г 477
Оценивая интеграл вблизи точки бозе-конденсации, когда |/х| « Г, и
полагая Т — То всюду, кроме расходящихся членов, найдем
3/2 / жТо	8тг	02п
ИЛ I 9£2(3/2) Т — То
При высоких температурах Т » Го для восприимчивости мы должны
иметь обычный закон Кюри х(Л = 202п/(ЗТ).
При низких температурах Т То, когда бозе-газ находится в конден¬
сированном состоянии, намагниченность становится нелинейной функ¬
цией магнитного поля даже в слабых полях. Более того, точка Я = 0 —
особая точка, так как в ней снимается вырождение конденсата по раз¬
ным проекциям спинов. При любом Я > 0 конденсат имеет только толь¬
ко одну проекцию спина. Представим намагниченность газа М(Т,Н),
т. е. магнитный момент единицы объема, как сумму намагниченности
конденсата и надконденсата:
М(Т, Я) = 0пс + 0п(еа% - 0п(:х2_{.
С другой стороны, для полной плотности частиц п имеем соотношение
П = п< + п™+п™+п%_,.
Отсюда находим намагниченность с учетом ц = — 0Н\
М(Т,Н) = 0{п -	-	2п{?}_х)=
•з/о	00
of ™т у'2 2 [ ( Vidx	2Vidx \
~ РП P\2nh2) sfr J \ех+0Н/т - 1 е*+20Н/т - 1/'
о
В пределе слабого поля Г » /ЗЯ > О, пользуясь разложением для ин¬
тегралов, получаем
М(Т,Н) = (Зпс{Т) + 2л/^^2)+---	РпеЛТ),
где, соответственно, пс(Т) и пех(Т) — плотности конденсата и надкон¬
денсата в нулевом магнитном поле Я = 0. Отсюда поведение парамаг¬
нитной восприимчивости конденсированного газа в слабом поле описы¬
вается выражением
..IT и\	у/п(2\/2 + I) 0	Пех(Т) It	1	(J, ДМ1
*(7’W)-	ЗС(3/2)	—\Iw 7h (Т>>РН)'
которое расходится в пределе Я —» 0.

478	Глава	3.	Статистическая	физика.	Решения	задач
В пределе сильного поля /?# » Т намагниченность экспоненциаль¬
но мало отличается от намагниченности насыщения
М(Т, Н) = fin -	(e-WT + *±^е-2,
где «е?°,(7’) = пе]С(Т)/3 — плотность надконденсатных частиц в пределе
бесконечного магнитного поля. Соответственно, магнитная восприим¬
чивость оказывается экспоненциально малой:
Х(Т.Н) = («-W + i+S^-«w/r),
что связано с малым тепловым возбуждением на магнитные уровни,
отстоящие от основного на /ЗН и 2/ЗН.
3.2.25.	Прежде всего определим одночастичную плотность состояний
газа в гармонической ловушке:
, Л [ d3pd3r х( р2 mui2r2\ [ d3pd3r Г(.	2	2ч
g(e) = У ^ Ч£ - 2^ - — j= У '(£ -р -г
Последний интеграл можно рассмотреть, как интеграл в шестимерном
пространстве R = (р, г):
где мы учли, что площадь поверхности шестимерной сферы равна я-3.
Вычисляя последний интеграл с подстановкой /?2 = р, находим плот¬
ность состояний в ловушке:
g(e) =
2(М3’
Температуру бозе-эйнштейновской конденсации Тс находим из условия
ОО
о
Откуда Тс = huj(N/((З))1/3. Число надконденсатных частиц равно
ОО
N„(T) = [ d££\	*— = -^С(З) =N(T/Tcf.
J 2(МV/r-l	(Aw)	'	’

3.2. Квантовые идеальные газы	479
Энергия конденсированного газа определяется соотношением
ОО
Е(Т) = / 2 (М3 ес/т - 1 = 2(^15 =
о
Дифференцированием по температуре находим теплоемкость конденси¬
рованного газа:
С(Т) =	=	щ^КЛТ)	~	Г3.
Рассмотрим поведение химического потенциала /х(7') вблизи темпе¬
ратуры перехода Тс. Для его определения запишем
N
Г dee2	1	_	Т3	f	dxx2
~ J 2(M3	-1 2(Кш)3 J e~
V -1
.3
2(M3
(ад3) + тт) = <Й?<<3)'
При оценке интеграла мы учли, что вблизи Тс химический потенциал
1^1 « т Тс. Отсюда находим
ц(Т) =-Щ*±(Т - Тс)в(Т - Те), при \Т-ТС\ « Тс.
7Г
В отличие от привычного случая трехмерной ловушки, представляющий
собой кубический ящик, здесь производная дц/дТ испытывает конеч¬
ный скачок.
Переходя к переменной х = е/Т и дифференцируя энергию газа по
температуре, представим выражение для теплоемкости в следующем виде:
С(Т)
ОО
д
f dxx
J 2(М
дТ J 2(Пи,)3 ех-»/т - 1
О
оо	оо
4Г3 [ dxx3	Г4	Г dxxУ~"/г д(ц/Т)
~ 2(М3 J ex~'llT - 1	2(М3 J (ех-*/т - I)2 дТ
о	о
Учитывая непрерывность ц и скачок производной дц/дТ, найдем вблизи Тс

480 -l\r Глава 3. Статистическая физика. Решения задач
И с учетом значения интеграла, равного 6£(3), получаем для скачка
теплоемкости в точке бозе-эйнштейновской конденсации следующее
выражение:
АС(Тс) = С{Тс - 0) - С(Тс + 0) =
7Г
Таким образом, бозе-эйнштейновская конденсация в гармонической ло¬
вушке представляет собой пример фазового перехода второго рода.
3.2.26.	Термодинамические флуктуации температуры описываются
формулой
КАТ)2) = -1- = 15С(3) 7?	15	(М3
U ’ 1 С(Т)	2тг4 NT	2тг4 Т ■
Флуктуации температуры малы ((ДГ)2} < Г2, пока	Чтобы най¬
ти термодинамические флуктуации частоты, разделим обе части равен¬
ства на (hu>)2\
Л Гш) / 2тг4 т
Эта величина не зависит от того, рассматриваем ли мы флуктуации при
постоянной частоте или при постоянной температуре. Считая теперь
температуру заданной величиной и имея для приращений
Т	1	Т
А~ = ТА-А- = ЦД(М.
Тш (М
найдем
((Дш)2> = ^^.
' 2тг4 Т
Относительная флуктуация частоты мала, пока Нш Т.
Для оценки влияния флуктуаций частоты ловушки на температуру
перехода Тс учтем, что АТС = (Я/<(3))'/3Д(Лщ). Отсюда
<(дгс)!> = (ЛГ/С(3))!/3((ДМ!) =
г-л q (6) ic
Таким образом, относительная величина термодинамических флуктуа¬
ций температуры перехода приблизительно равна
sj {(АТС)2)
Это приводит к размытию перехода в системе с конечным числом частиц.
Другая причина размытия температуры перехода связана с дискретно¬
стью уровней в ловушке. Действительно, поведение химического потен¬

л
3.2. Квантовые идеальные газы -Jb 481
циала |д(7)| ~ (Т — Тс) вблизи Тс было найдено в непрерывном пределе
и —> 0, который справедлив, пока \ц(Т)\ » Нш. Обратное неравенство
приводит к области, где существенна дискретность уровней в системе:
или ‘ .
hw hw ~ ’	тс	~	тс	jv'/s
Следовательно, относительная величина размытости температуры пере¬
хода из-за дискретности энергетического спектра имеет порядок М-1/3,
и влияние термодинамических флуктуаций на фоне дискретности спек¬
тра не сказывается, пока отношение ЛМ^/М-1/3 = JV-1/6 <с 1. Таким
образом, в качестве параметра макроскопичности гармонической ло¬
вушки выступает величина М1/6 » 1.
3.2.27.	а) Плотность одночастичных состояний в шестимер¬
ном пространстве описывается выражением
-3_5	,	.2,	„	\	3
£2.
8(£)= [	¥l**Es(£-PL)	= v6 [ n3P5dP б( е--?-) =	У*(Л!-\
J	(2тгЛ)6 V	2m)	J (2nhf V 2т)	2	\2пП2)
Подставляя объем Кб	= /6 = [2-кК/ (тиз))3, найдем
g(£) = Щ*'
Поскольку плотность состояний оказалась идентичной плотности со¬
стояний газа в гармонической ловушке, то все термодинамические функ¬
ции и тепловые свойства двух разных систем будут также идентичны. В
частности, бозе-эйнштейновская конденсация в шестимерном простран¬
стве будет фазовым переходом второго рода.
б) Корреляционная функция и(г) флуктуаций плотности
Ап(г) = п(г) - п определяется соотношением
(An(fi) Дл(г2)) = л<5(г! - г2) + пи(г), г= |п - г2|,
где n — N/V6 — средняя плотность газа и г —- радиус-вектор в про¬
странстве d = 6. Корреляционная функция связана с функцией распре¬
деления выражением
пи(г)
[ eipr/
= I / в(«Р-м)/г _
■рг/П	d6p	2
1 (2nh)6
Мы рассмотрим наиболее интересную область температур выше темпе¬
ратуры бозе-эйнштейновской конденсации, но близкую к ней. Вблизи
Т =ТС химический потенциал ц мал, и интеграл определяется областью

482 -Ar Глава 3. Статистическая физика. Решения задач
малых импульсов е ~ р2/(2т) ~ р <С Т. Поэтому, разлагая экспоненту,
находим
Jpr/h
еу' ар
П1у(г)
2 тТ
/
р + 2m\p\ (2nh)
Поскольку мы ограничились малыми импульсами р < (2тТ)1/2, то мы
подразумеваем расстояния г > h/\/mTc.
Интеграл можно оценить, используя уравнение Пуассона в простран¬
стве размерностью d = 6:
V2u - х2^ =-<5(г), или	-	х2!*	=-<5(г)
и формулы для фурье-образа и(г). Решение этого уравнения выражает¬
ся через функцию Бесселя мнимого аргумента K^ipc)'.
и(г) ~ уК2(хг)
С другой стороны, Uq — фурье-образ функции ы(г) — удовлетворяет
уравнению (q2 + х2)^ = 1, т. е.
и(г)
[ eiv
/	„2	1	2
J q + х
А
qx + х2 (27г)6
Таким образом, приходим к выражению
,4
nv{r) ~	К2(хг),
где
2т\р\ _ 6^2С1/З(3) /Л/у/6 1Т-Тс
h2 ^ \vj \ Тс '
Пользуясь тем, что Лг(* » 1) ~ е~к/>/х, находим асимптотическое по¬
ведение корреляционной функции на больших расстояниях г> х-1:
7/2
Отсюда видно, что на расстояниях г > 1/2х корреляции между части¬
цами экспоненциально быстро затухают. Величина £(Г) = 1/2х назы¬
вается корреляционным радиусом и равна
?т = ^(£),/6\/= i/a.

3.2. Квантовые идеальные газы
где показатель степени v называется критическим индексом. В про¬
странстве d = 6 среднее расстояние между частицами приблизительно
равно (Vb/N)x/6. При приближении к точке перехода Тс корреляцион¬
ный радиус £(7") корневым образом расходится и обращается в беско¬
нечность в самой точке перехода. Отметим, что критический индекс
г/ = 1/2 совпадает с соответствующим критическом индексом в самосо¬
гласованной теории Ландау фазовых переходов второго рода.
3.2.28.	Для существования бозе-эйнштейновской конденсации при ко¬
нечной температуре необходимо, чтобы плотность состояний g(e) обра¬
щалась в нуль при е = 0. В квазиклассическом приближении плотность
состояний дается выражением
Пусть при малых х удерживающий потенциал ловушки имеет вид U(х) =
= А\х\п (п > 0). Тогда из оценки интеграла можно увидеть, что g(e) ~
~ £(2—л)/2л Поэтому вблизи центра ловушки при х —> 0 потенциал U(x)
должен нарастать быстрее, чем гармонический, т. е. п < 2.
3.2.29.	Квазиклассические уровни энергии частицы в поле тяжести
U(x,y,z) = mgz с наложенным ограничением z > 0 для движения в на¬
правлении оси z описываются выражением
где £о = (Этт2 mg2 ft2/8)'/3. Ниже мы будем предполагать, что темпера¬
тура Т ;» £о, чтобы в процесс бозе-эйнштейновской конденсации было
вовлечено много уровней. В противном случае задача сводится к бозе-
конденсации в системе из нескольких уровней.
В этих предположениях одночастичную плотность состояний g(s)
проще всего оценить, согласно
U(x)^e
н
о
где S — площадь дна ящика. В результате найдем

484 ■Ar Глава 3. Статистическая физика. Решения задач
Температуру Тс бозе-эйнштейновской конденсации находим из уравнения
ОО
JV = [ de f}£) .
J ее/т' - 1
о
Вводя поверхностную плотность частиц п = N/S, имеем
mgH	оо
Зп h, g V J е - 1 J е 1 с - 1
О	mgH
ИЛИ
7ыт*с'2
п — 	5~Т—
Зтг h g
{]«&- J
О	mgH/Tc
Для открытого или неограниченного по высоте ящика Н = оо находим,
что
п=у/ЫТ5с/2 3^,с/оч	т	_	(2тг)3/5	kfhg2n2\l/5
-г (2тг)3/5
<(5/2)' или	т“-Н»
Зтг п g 4	С	7 (5/2)
В другом предельном случае, когда mg# < Тс или Н —> 0, для оцен¬
ки Гс достаточно провести разложение числителя подынтегрального вы¬
ражения во втором интеграле. В результате получим
\РЫТЬС'2 3mgH Г sfxdx _ (mTc)3/2H ^С (3/2)
Зтг2h3g 2 Тс J ех - 1	л/27г2Л3	2
о
Отсюда имеем
2тг й2 / я \ 2/3
7V =
С 7 (3/2) m
(йГ-
что совпадает с обычным однородным случаем для объемной плотности,
равной п/Н. Таким образом, температура перехода с увеличением
высоты ящика # падает и при
m\mgJ
выходит на насыщение.

3.2. Квантовые идеальные газы -IW 485
Ниже температуры конденсации Тс конденсатные частицы находят¬
ся в состоянии с нулевым импульсом и в области минимального значе¬
ния потенциала, т. е. на дне ящика. Распределение числа надконденсат¬
ных частиц Nex(z) по высоте можно найти интегрированием функции
распределения /(е(р, г)) в импульсном пространстве:
2/3
Nex(z) sj (2^)3 e|p2/(2m)+mgz,/7. _ j S{2nh2) \[ъ J
dx \fx
gx+mgz/T _ | '
Оценивая последний интеграл, найдем в предельных случаях:
2/3
NeAz)
= s(^- V
V2tt ft2/
mfT)’ ’<*■
e-mgz/T	z	>	—.
mg
3.2.3.	Идеальный газ элементарных бозе-возбуждений
3.2.30.	Термодинамический потенциал фононов, отнесенный к единице
длины, описывается выражением
ОО
ПЬ(Т) = Т j 4L\n([-e-cWT).
— ОО
Интегрируя по частям, найдем
ОО
«*<”=- / йЫЬ -
—оо
Г2
= к/"vb = ш
о
Дифференцируя энергию Еь(Т) по температуре, находим теплоемкость
одномерных фононов Сь(Т) = тгТ/(ЗНс) — линейную по температуре.
Для фермионов с фиксированным значением проекции спина термо¬
динамический потенциал П/ записывается следующим образом:
ОО
ЩТ) = -Т j ^1п(1 +е(^-Р2/2т)/Г)_

486	Глава	3.	Статистическая	физика.	Решения	задач
Интегрируя по частям, найдем
ОО
Пг(Т) = —2 [ ^—-р2,2т	=	-2Е,(Т),
'	J	2пП e(r?/2m-n)/T + J	Р	"
—ос
ОО
с ,т\ о f de m £	~ \/2m (2 з/2 п2 Т2 \
E^ = 2J 2^V&eW+l 2^1зе^ +T^J-
о
Здесь мы ограничиваемся низкотемпературным приближением Г <с £д.
Вводя импульс и скорость Ферми, согласно ед = p2/(2m) = mv2/2,
получим
£/W = fie'+®£’ Г<<£-
Отсюда для теплоемкости одномерных фермионов с фиксированной про¬
екцией спина находим С/(Т) = 7г7У(3?Шд). Таким образом, при с = од
теплоемкости совпадают, и по термодинамическим свойствам при низ¬
ких температурах обе системы эквивалентны. Преобразование ферми-
онной системы в эквивалентную ей по свойствам бозевскую упругую
среду называется бозонизацией. Аналогия, в первую очередь, связана
с возможностью линеаризации закона дисперсии фермионных возбуж¬
дений Ер — £д « ±уд(]р| - pF) вблизи ферми-поверхности, которая пред¬
ставляет в одномерном случае две точки при р = ±pF.
3.2.31.	Для твердого тела конечного размера из N частиц и объемом
V = L3 фононный вклад в теплоемкость равен
где {п} = (п],П2, пз) означает сумму по всем разрешенным 3N нормаль¬
ным модам упругих колебаний, а плотность состояний определяется
как g(u>) = 5Z{n}	- шл)- Конечный размер тела L ведет к ограниче¬
нию максимального значения длины волны упругих колебаний и, следо¬
вательно, к существованию минимального ненулевого значения часто¬
ты колебаний wmin ~ u/L, где и — скорость звука. Поэтому, в пределе
Т —> 0 теплоемкость вымерзает экспоненциально:
С(Т) ~ N(Hwmin/T)2e~^T (ftiCmin < Т).
Это меньше, чем было бы объемное значение С* ~ АДГ/вд)3. Здесь
©д — температура Дебая. Наибольший интерес представляет область

3.2. Квантовые идеальные газы
humin < Г < ©о, так как в пределе Т > 0д теплоемкость выходит
на классическое значение Дюлонга-Пти С(Т) = 3N, не зависящее от
размера тела.
Частоты нормальных колебаний твердого куба размером L х L х L
с закрепленными гранями равны
где «/ и И; - скорости продольного и поперечного звуков в изотропном
упругом теле. Для оценки плотности состояний воспользуемся следу¬
ющим рассмотрением. Используя формулу
три раза для трех суммирований с условием, что каждый раз производ¬
ная dF/dri\n=o = 0, можно получить
Полагая F(q2) = 6(ш - nuq/L), найдем вклад в плотность состояний от
одной звуковой ветви, скорость которой равна и,
Л
wn1.n2.n3 — ‘
52!
(пь«2,«з = 0,1,2,...),
п=0	о
£ F(n) = JF(n) dn + \F{0) - if'(0) + ... .
Л|,Л2
оо
F(/^ -f AZ2 + Л3) = /	^2	dri3	F(tl	1	4-^2	+	^3)	+
оо
оо
+ | J dn\ dn2 F(n2i + n\) + I j dn\ F(n2) +...
0
0
^ J 4irr2drF(r2) + I • ^ J 2itrdrF(r2) + | J drF^r2) + ... .
00	00	00
0
0
0
Суммируя плотности состояний от одной продольной и двух поперечных
ветвей звукового спектра и вводя усредненные скорости распростране¬
ния звука согласно

488	Глава	3.	Статистическая	физика.	Решения	задач
найдем полную плотность состоянии:
, V 3 L3	2 , 9 L2	9 L
ё(ш> ~ К 1^31ш + 7	+	Т	-=-	+	••	•	•
4 7Г «3	4	ТГИ2	4	7ГW1
Второе и третье слагаемые обусловлены дискретностью спектра коле¬
баний в частице конечных размеров. Подставляя g(u>) в выражение для
теплоемкости и вычисляя три интеграла с подстановкой x = hu>/T и
бесконечным верхним пределом, найдем
cm ~ 2п*( 7 Yl3 + 27С(3) ( Т Yl2 +37Г т l
С[Т) ~-ь-\т) 1 +-ьг{гш2)1 ТШ[
Отсюда при промежуточных температурах tbjmm -с Т < 0д для поправ¬
ки к объемному значению теплоемкости, отнесенной к единице объема
с = С/L3, получим
с(7) _ с.(т\ — 27С(3) (JL-Y- + — ——
1 ' Ь( ’ 2тг \Кй2) L 4 hUiL2'
Положительность поправки означает, что существует температура, вы¬
ше которой с > сь, и ниже которой с < Сь.
3.2.32.	Свободная энергия ротонов (как бозе-газа с /г = 0) равна
F = Q = Т/ ^ 1п(1 - е~^т) « -тг(Г).
Здесь мы разложили логарифм, имея в виду малость экспоненты в силу
неравенства Т -с Д, и ввели плотность ротонов яДТ’) согласно
ОО
пг= [	=	e-YYL	f	dpp2e-(P-Po)2/2mT
J (2nh) 2n h J
0
Далее, пользуясь тем, что в силу неравенства p20/{2m) » Т вклад в
интеграл набирается в окрестности |р -ро| ^ (2тТ)1^2, найдем
= 2рЦтТ)''2 Л/т
Г{>	(2п	К2?'2	'
Дифференцированием выражения для Fr находим энтропию Sr и теп¬
лоемкость Сг ротонного газа на единицу объема:
с _ (А , 3\	„	(А2	,	Д	,	3\
sr-n\j + 2J и Cr-«r^ + - + iJ.
В области Г > 0,8 К ротонный вклад играет основную роль в термоди¬
намических функциях сверхтекучего гелия.

3.2. Квантовые идеальные газы -Л. 489
3.2.33.	Тепловое возбуждение магнонов приводит к изменению значе¬
ния термодинамического потенциала магнетика при Т = О, так что
П(Г) = П(0) + flm(T). В результате изменяется намагниченность и теп¬
лоемкость магнетика. Равновесное значение намагниченности и тепло¬
емкости связаны с потенциалом П соотношениями
Л
1 ^	^	Тд2П
м = и c = ~vW2'
где V — объем тела. Термодинамический потенциал Пт газа магнонов
описывается соотношением
Пт(Т) = - j ^ln(l + e-W0.
Это дает поправки к намагниченности и теплоемкости, обусловленные
тепловым возбуждением спиновых волн:
АМ(Т) = М(Т) - М0 = — [	[	—
v ' v '	J	(2тг)3	e	-1 J (2тг
Cm(T) = lTj
3k 1
(2тг)3 еПшк/т - 1 ’
d3k Кил,	_ 9Em(T)
(27r)3 eftw*/r -	1	_	9T
где Mо — намагниченность при Т = 0, а Ет(Т) — энергия газа магно¬
нов. Из первого соотношения видно, что спиновые возбуждения умень¬
шают намагниченность ферромагнетика пропорционально числу магно¬
нов в единице объема. Вводя переменную х = (3Moctk2/T, представим
интегралы в виде
ОО
АМЖ_ Р( т \3/2 2 [ x'/2dx .
АЛ*(Г)	8 \п/ЗМоа)	J ex+0H/T - 1 ’
о
ОО
Г	<Т\-дЕ™	F	-	Т( Т V/2	2	f xV2<iX
Lm(D-	дт,	£rn -	g ^7Г/ЗЛ|оа j	^	J e*+L
+0H/T
1
Оценивая интегралы в слабых /ЗН <С Т и сильных /?Я ;» Г полях, най¬
дем для вклада магнонов в намагниченность
™~fU=r*
3/2 /С(2/3) -	/?Я	«	Г,
wr,	/?Я	»	г,

490	Глава	3.	Статистическая	физика.	Решения	задач
и в теплоемкость
Ст(Г) 16 \тг/ЗМоа) ' 0jte-0H/T
з/2 Г §С(5/2) - |с(3/2)^, PH « Т,
Т
рн » т.
Температурная зависимость Г3/2 для магнонного вклада при Н — О
называется законом Блоха. Эта зависимость справедлива при темпера¬
турах достаточно удаленных от температуры Кюри, при приближении к
которой необходимо учитывать как ограниченность возможных волно¬
вых векторов по величине, так и взаимодействие магнонов друг с дру¬
гом. В сильных магнитных полях отклонение намагниченности от Мо
и магнонная часть теплоемкости экспоненциально малы, что связано с
наличием энергии активации PH спиновых волн в магнитном поле.
3.2.34.	Рассматривая рождение пар, как химическую реакцию Ь + Ь^ 7,
и учитывая, что химический потенциал гамма-квантов равен нулю, для
соотношения химических потенциалов бозонов и антибозонов мы най¬
дем /ль + рр = 0. Разность плотностей бозонов и антибозонов, которая
сохраняется, имеет вид
Здесь ер дается релятивистским выражением ер = C\Jp2 + m2c2. Упро¬
щая выражение, найдем
Поскольку числа заполнения бозонов и антибозонов должны быть неот¬
рицательны, то \ръ\ ^ тс2. При температуре бозе-эйнштейновской кон¬
денсации должно быть \рь(Тс)\ = тс2, и тогда
В ультрарелятивистском пределе Тс » тс2 можно положить ер = ср, и
тогда
(2тгй)3 Vв<*я-«>/г _ 1 e^P+едП _ 1)'
)
ОО
п _ [ Р2 dP	sh	(тс2/Тс)
J 27г2Й3 ch(v/p2c^+m2c^/7'c) - ch(тс2/Тс)
ОО
ОО
р1 dp тс2/Тс _
2тг2Й3 ch(рс/Тс) - 1 _
О
о

3.3. Неидеальные квантовые системы (жидкости)	491
Отсюда Тс = h(3hcn/m)'/2. Без учета рождения пар Тс ~ hen}/3. Для
выполнения условия Тс > тс2 необходима высокая плотность /г-1/3 <
•С hi (тс), т. е. среднее расстояние между частицами должно быть мень¬
ше их комптоновской длины.
3.2.35.	Полная интенсивность излучения фононов абсолютно черным
телом площадью 4ttR2 равна 47гД3<тГ4, где <7 = 7г2/(60ft3с2) — посто¬
янная Стефана-Больцмана. Потери массы черной дыры в процессе ее
испарения даются уравнением баланса энергии:
-4-Шс2) = 4nRlaT4 =
he6
dC ’	8	210 15тг g2m2'
Время жизни черной дыры оказывается конечным и равным
т = 15 ■ 210тг4 /м2	=	5 •	=	-^2= (£) V
О
Последнее равенство записано в планковских единицах массы Мр =
= (Лс/87гС)*/2 и времени tp = (ftG/c5)1/2.
3.3.	НЕИДЕАЛЬНЫЕ КВАНТОВЫЕ СИСТЕМЫ (ЖИДКОСТИ).
ОСНОВЫ ТЕОРИИ КОНДЕНСИРОВАННЫХ СРЕД
3.3.1.	Нормальная (несверхтекучая) ферми-жидкость
3.3.1. Воспользуемся тем, что импульс единицы объема жидкости ра¬
вен плотности потока массы, и тем, что число истинных частиц массой
т в ферми-жидкости равно числу квазичастиц. С учетом того, что ско¬
рость квазичастицы равна де/др, плотность потока квазичастиц дается
выражением
и, соответственно, плотность потока массы жидкости будет j = mi. С
другой стороны, импульс единицы объема жидкости равен интегралу
У = J рпс1тр.
Таким образом, приходим к равенству
jpndTp = m J	n(p)drp.

492 -Ar Глава 3. Статистическая физика. Решения задач
Варьируя это равенство по функции распределения, найдем
J рбп d.Tp = т J щдпйтр + т J п{р)^^-drp-
= т J щ6пйтр + гп [ dTPn(P(j f(p,p')6n(p')dTpl
= m I щSn dTp + m I dTp6n(p) ^ dTpm(p')-^f(p', p).
Ввиду произвольности Sn и с учетом симметричности /(р, р') имеем
равенство
Р _ де , [ 5/(PV)„/ /ч
™~dp + J	)dTp'-
которое после интегрирования по частям и с учетом зануления подын¬
тегрального выражения на бесконечно удаленной поверхности р' — оо
примет вид
Для равновесной функции распределения при Т = О
дп дп де	р	ч	р	г/	.
щ, “ *щ = Цг~w> = ргtip~^>•
При определении эффективной массы т* нас будут интересовать зна¬
чения импульса на поверхности Ферми |р| = pp. Выберем направление
вектора р за полярную ось и введем угол х> равный углу между векто¬
рами р — ррп и р' = ррп':
р _ де
т др
+ [ f(pFn, ppW) S(p' - pF) f 2py f* =
i=Pf J	Pf	(2tt h)
(2тг hf
= --£ + //»+	*TT-
где dFlx = 27rsinx^x ~ элемент телесного угла. Используя vp = pp/m*
и вводя определение параметра Ландау F\, представляющего собой усред¬
ненное с косинусом угла по поверхности Ферми взаимодействие между
квазичастицами
2
*=Зтк1
найдем связь между эффективной массой т* и параметром F\:
1==^(1 + т)’ или т* = л(1 + т)-

3.3. Неидеальные квантовые системы (жидкости)
В жидком !Не значение F\ = 6,25 и, соответственно, т* = 3,08т, где
т — масса атома 3Не. В металлах или полупроводниках т* может быть
как больше, так и меньше электронной массы. В так называемых тя-
желофермионных металлах на основе церия или урана эффективная
масса т* может превышать массу электрона в 100 и более раз.
«
3.3.2.	Эффективная масса определяет энтропию S и теплоемкость С
жидкости в пределе низких температур Т <с Теплоемкость нахо¬
дим с помощью дифференцирования энергии по температуре при за¬
данном числе частиц N. Изменение энергии жидкости в единице объе¬
ма при температурном изменении равновесной функции распределения
6п = п(Т) — по можно записать в виде
<5£ = J е6пйтр= J £o6ndTp+ j дебпдтр^ J ео 6пйтр.
Пренебрежение вторым слагаемым в данном случае оправдано только
тем обстоятельством, что в пределе низких температур вклад от остав¬
ленного слагаемого линеен по температуре Т, а вклад от отброшенного
слагаемого, который обусловлен взаимодействием квазичастиц, — бо¬
лее низкого порядка, чем первая степень температуры. Действительно,
д(5е) _ [ t д(5п)
дТ ~ J ‘ ~дТ~ р’'
а также учтем, что при Г —> 0 имеет место разложение
% = pie-») + ....
Производная дц/дТ равна энтропии, которая как и теплоемкость, будет
линейна по температуре. Следовательно, величина 8е — второго поряд¬
ка по Т, и наше приближение будет оправдано. Тогда при фиксирован¬
ном числе частиц жидкости N = const имеем
С(Л» /ео(р)%drp и 0 = J^dTp,
причем в низшем порядке по температуре Т в производной функции п
по Т можно заменить точные значения е на ео- После этого вычисления
становятся тождественными вычислению для случая идеального газа
с заменой в плотности состояний массы частицы m на эффективную
массу т*. Таким образом, теплоемкость ферми-жидкости равна

494 •Ar Глава 3. Статистическая физика. Решения задач
где 7 — постоянная Зоммерфельда и g(£p) — плотность состояний на
поверхности Ферми. В силу линейной температурной зависимости эн¬
тропия и теплоемкость совпадают. Положительность теплоемкости дает
необходимое условие устойчивости ферми-жидкости т* > О или F\ > —3.
3.3.3.	Когда ферми-жидкость находится в магнитном поле Я, то квази¬
частицы приобретают дополнительную энергию от приложенного поля
и изменения функции распределения Sn^iр) = па(р) — по(р):
6еа(р) = -/За-Н + Тг„/ [	(рр')	Sna>	(р') Фтр>, drp =
j	(27ГП)
где (3 — эффективный магнетон Бора, ег — матрицы Паули. Спиновая
восприимчивость вычисляется согласно
* = М = Ji Тг<т //?<7^(p)rf7> = /3MTr°- f <rtin*(p)dTp.
В линейном приближении по магнитному полю можно пренебречь изме¬
нением химического потенциала, так как он меняется лишь во втором
порядке по магнитному полю Я. Поэтому приблизительно
X%/3J/Tr<T / <Tn£rS£a(p)dTP'
Sea(p)^-P<rH + Tr<T. j W(pp')^i^(p,)rfv.
Так как n'0(e) — -6(e — £/?) = — S(p - Pf)/vf, to интегрирование в обоих
интегралах происходит по поверхности Ферми, и существенны значе¬
ния только при |р| = |р'| = рр. Предполагая решение в виде (5е<т(р) =
= -ар)рстн, найдем уравнения для определения (их:
£(р) = 1+2 J «р,Р')дп;{; \(p')dTP,,
х = —2/32 J ap)^-drp = /?2^СЫ = 02g(eF)Z(PF),
где g(£/0 — плотность состояний на поверхности Ферми. Мы воспользо¬
вались тем, что Tr^o-cr^cr = 2ег и Тг„(аН)а = 2Н. Независящая от
спинов часть взаимодействия /„^(р, р') естественно выпадает из ре¬
зультата. Выберем направление вектора р за полярную ось г и введем
угол в, равный углу между векторами р = ррп ир' = рдп'. Тогда
z(pf) = 1 - J	m	=	ciPF^ppn1),

3.3. Неидеальные квантовые системы (жидкости)	495
где d£le = 27г sin в de — элемент телесного угла. Отсюда
где Zo — обменный параметр Ландау, равный с точностью до множителя
усредненному значению обменного взаимодействия по поверхности Фер¬
ми. Окончательно, спиновая восприимчивость в ферми-жидкости равна
... . Р2вШ
Х l+Zo'
Условие устойчивости (критерий Стонера) парамагнитного состояния
ферми-жидкости определяется соотношениями \ > О или > —Е Ес¬
ли Zo становится равным —1, то \ обращается в бесконечность, что
означает наличие ферромагнитной неустойчивости. В жидком 3Не Zo «
~ -0,67. Металл Pd, где Zo « -0,9, еще ближе к магнитной неустой¬
чивости.
3.3.4.	Рассмотрим малые отклонения функции распределения 6п = п-по
от равновесной функции «о- При этом также изменяется и энергия ква¬
зичастиц Н:
n = n0(p) + 6n(r,p,t) и Я = ео(р) + Й£[л(г,р,0]-
В линейном приближении по 6п и 6е из уравнения Лиувилля найдем
dSn	dSn део	дпо дбео	_ q
dt	dr dp	dp dr
Скорость квазичастиц равна у — део/др, и производная имеет вид
дпо/др = удпо/де. Решение ищем в виде бегущей волны
6n(r, р, t) = Sn(p) elkr~lut,
где к — волновой вектор и ш — частота колебаний. Изменение энер¬
гии квазичастиц, выраженное через функцию взаимодействия /(р, р'),
можно записать в виде
5е = |/(p,pOMpVkr-‘^V, dT„. = 2-0-3.
Поэтому
(w-kv)6n(p) = -(ky)^ f f(p,p')6n(p')dTp>=-(kv)^fo J 6n(p')dTp-,
где для упрощения анализа мы положили /(р, р') = /о = const, а также
Т = 0. Решение уравнения имеет вид <5л(р) = n'0(e)is(e), где в — угол

496 •Ar Глава 3. Статистическая физика. Решения задач
между векторами v и к. Поскольку п'0(е) = -6(р — pF)/vF, поправка
<5я(р) отлична от нуля только на поверхности Ферми, т. е. |р| = pF и
|v| = vF. Подставляя <5я(р), найдем
(и - kv) и(в) = kvFo [	До	= -Л-h = Otefo.
J	™	7Г	П Vf	7Г n
Здесь Fo — безразмерный параметр Ландау, m*pF/(n2h3) — плотность
состояний и dFl = 2'къ\пвдв — элемент телесного угла.
Далее
и(в)	COS	в	[	/л/,	dCla’	ш
= ъ ! v^>-r~ и s=z—t-
F0 s — cos 9 J	47Г	vfk
Из условия самосогласования
1 f msdQe [ cosO dCle ( [ ,ai\dCl
ft у TT = ]	17	[J 1,(9 >
47Г
находим
7Г
1
Fo
f cosd 27rsinOdd _ 1 f xdx
J s — cos в 4n 2 J s — x'
-1
Дисперсионное уравнение
1	s	in	s +1	i
■5- =	о	In 7	~	1.
Fo	2	s -1
имеет действительные решения только при Fo > 0, так как правая часть
изменяется в пределах (+оо, 0) при изменении s от 1 до +оо. Таким об¬
разом, если Fo > 0, что отвечает отталкиванию квазичастиц на ферми-
поверхности, то имеется действительное решение s = s(Fo), которое да¬
ет незатухающую волну со звуковым спектром:
u>(k) = s(F0)vFk.
Такие звуковые волны в ферми-жидкости называются бесстолкнови-
тельным звуком или нуль-звуком. Если Fo —> +0, то s —> 1. Для Fo > 1.
s « -у/До/3. Следовательно, незатухающие волновые процессы возмож¬
ны только при условии, что скорость квазичастиц vF не превышает фа¬
зовую скорость волны и/к. В жидком 3Не значение До = 10,8, и ско¬
рость нуль-звука примерно 197 м/с. В процессе распространения нуль-
звука поверхность Ферми вытягивается в направлении распространения
волны и сплющивается в противоположном направлении.
При До < 0 действительных решений дисперсионного уравнения нет,
и моды колебаний ферми-поверхности — затухающие.

3.3. Неидеальные квантовые системы (жидкости)	497
3.3.5.	Поверхностное натяжение о определяется минимизацией по па¬
раметру b разности энергий металла при наличии поверхности раздела
между двумя частями металла и при ее отсутствии:
2а = 2Е\п(х)\ - Е[п].
Здесь энергии отнесены к единице площади поверхности, ап — объем¬
ная электронная плотность и п(х) — плотность электронов при наличии
поверхности.
Поскольку при образовании поверхности изменением в распреде¬
лении положительного фона пренебрегают, то вклад в поверхностное
натяжение от кулоновского взаимодействия между зарядами проще вы¬
числить, используя скалярный потенциал Энергия взаимодействия
зарядов на единицу площади равна
£эл = | / {п+(х) - п(х))ф) dx.
Без поверхности п(х) = п+ = п и £эл — 0. Изменение электростатиче¬
ской энергии взаимодействия, вносимое образованием поверхности и
перераспределением электронной плотности в поверхностное натяже¬
ние, будет равно
е- J (n+(x)-n(x))<p(x)dx,
о*/Ь\	0~*/Ь
п+(х) = пв(-х) и п(х) - п
Г/ РЧ»\	о-’Ч"
уравнения Пу<
j- = —4пе[п+(х) - л(х)].
Потенциал <р(х) найдем с помощью уравнения Пуассона
aVw
дх
Отсюда <р(х) — 47гeb2n(x). Вычисляя далее интеграл, получим
же п b .,з
оЪЛ = —-— = АЬ .
Вклад от кинетической и обменной энергий дается соотношением
—оо
j /о	ОО
- !	е2	I	[п^ъ(х)	-	n^3e(-x)]dx =
b = -ъвь.

498	Глава	3.	Статистическая	физика.	Решения	задач
Здесь мы ввели обозначения:
О	оо	1/2
-/* = j (l-ex/2)kdx + j(ex/2)kdx = j	~	1	dx	+
-оо	0	0
Выполняя вычисления, найдем значения /5/3 и /4/3:
/5/з = ^(1-2“2/3)+^-^arctg	lnd-2-1/3)-! In 6 «0,572,
/4/3 = ^(l-2-'/3)-^+V3arctg	ln(l-2-'/3)-| In 6 «0,339.
Вклад от энергии неоднородности вычисляется проще:
ОО
_ П2 [
<Тнеод “ 2т J
72п
h2n Iff e2xdx f
72mb 4 IJ 1 - ex/2 J
OO
■2xj- r2e~2xdx\ h2n In2 С
mb 72
Окончательно для поверхностного натяжения получим
а(Ь) =АЬ3-ЗВЬ+
О
Отсюда видно, что не выгодны как малые значения Ь, так и большие.
Оптимальное значение & находится из условия минимума да/db = 0 и
положительности значений Ь. В результате будем иметь
, „<М = 2 Ьо{^Щ-2в).
Для анализа формул удобно ввести безразмерный радиус Вигнера-
Зейца, как радиус сферы в атомных единицах, объем которой прихо¬
дится на один электрон:
4-7Гг3 _ 1	h2
~5 —	Г’	аВ	~	2	*
о	пав	те
Коэффициент В меняет знак при rs — 2*/3(37г2)2/3/s/3/5/4/3 « 4 и, сле¬
довательно, при больших плотностях преобладает кинетический член,
а при низких плотностях — обменный вклад. При малых плотностях

3.3. Неидеальные квантовые системы (жидкости)	499
или больших rs > 4 можно приближенно полагать АС <С В2 и считать
вклад в В только обменным (В < 0):
В итоге, при малых плотностях или больших rs > 4 поверхностное на¬
тяжение положительно и уменьшается с ростом rs.
При больших электронных плотностях или малых rs < 1 можно пре¬
небречь обменным вкладом по сравнению с вкладом от кинетического
члена, а также воспользоваться тем, что опять AC <tc В2. После чего мы
приходим к следующим оценкам:
io * Vm » «»4/2 (|)1/3 (^)'1/3 * 0ЛЬ„,гГ,
/и ,	2В3/2	е2 1 9 /33/2 е2 0,0754
а1/2 » аЗЛ9/2 40	а3	,9/2	•
Видно, что при малых rs < 1, поверхностное натяжение становится от¬
рицательным и растет по абсолютной величине с уменьшением rs. Фи¬
зическая причина лежит в том, что электроны, вытекая в приповерх¬
ностную область, уменьшают свою плотность и кинетическую энергию.
Этот вклад в поверхностное натяжение имеет отрицательный знак и
становится определяющим при малых rs < 1. Таким образом, металли¬
ческое состояние с высокой плот¬
ностью электронов обладает по¬
верхностной неустойчивостью, свя¬
занной с отрицательным значени¬
ем поверхностного натяжения.
Как функция rs, поверхност¬
ное натяжение (рис. 3.4) в про¬
стейшей модели «желе» растет с
отрицательных значений, прохо¬
дит через нулевое значение около
rs ~ 2,8, достигает положитель¬
ного максимума rs, и начинает
спадать с ростом rs, оставаясь по¬
ложительным. Для лучшего количественного согласия с эксперимен¬
тальными значениями поверхностного натяжения металлов необходи¬
Рис. 3.4. График зависимости поверх¬
ностного натяжения как функции ради¬
уса Вигнера-Зейца в модели «желе»

500
X
Глава 3. Статистическая физика. Решения задач
мо учитывать корреляционную энергию электронной жидкости и дис¬
кретность положительных ионов. Для большинства обычных металлов
rs = 2ч-6.
3.3.6.	Условие равновесия электронов в металле при сохранении числа
электронов / n(r) dr задается условием постоянства множителя Лагран¬
жа, который в данном случае часто называется электрохимическим по¬
тенциалом и равен
С =	= -Mr) + ц[п( г)].
Электрический потенциал у>(г) определяется обычным образом:
, .	[ п+(г')-п(г') , ,
Ф) = е j |r _f/| dr -
а химический потенциал д[п(г)] равен
А*[«(г)] =	+	г£т!"(г)]	=	МоднИг)]	+	М„еод[«(г)].
6п( г)
6п( г)
Однородная часть — сумма кинетической и обменной энергий, отнесен¬
ных к одной частице:
А*ОДн(л) —
Ц2(3п2п)2/3	f ^ \
2т
&
Работа выхода W есть работа по удалению электрона из металла и
определяется как разность электрохимических потенциалов электрона
вне и внутри металла:
W = С(оо) - С(-оо) =
= -е[ф(оо) - ¥>(-оо)] - ^одн(л),
где мы учли, что для одного элек¬
трона р{оо) = 0, а внутри метал¬
ла электронная плотность ста¬
новится однородной п(-оо) = п.
Разность электростатических по¬
тенциалов ф(оо) — <р(—оо) возни¬
кает вследствие нарушения ло¬
кальной электронейтральности
вблизи границы металла с вакуумом и образования двойного электри¬
ческого слоя. Скачок электрического потенциала чувствителен к виду
Рис. 3.5. График зависимости работы
выхода электрона как функции радиу¬
са Вигнера-Зейца в модели «желе»

3.3. Неидеальные квантовые системы (жидкости)	501
распределения электронной плотности и может быть выражен как ди-
польный момент двойного слоя:
ОО
у>(оо) - <р(-оо) = 47ге J х(п+(х) - п{х)) dx.
— ОО
Это соотношение можно получить из уравнения Пуассона. Подчерк¬
нем, что работа выхода электрона складывается из двух вкладов. Пер¬
вый — энергия связи электрона в металле, как нейтральной частицы.
Второй вклад связан с притяжением удаленного электрона к поверхно¬
сти металла и равен работе по преодолению потенциального барьера,
образованного двойным слоем на поверхности металла.
Для вариационного распределения электронной плотности п(х) из
предыдущей задачи найдем
w=WV - *2<34^2-3- +	=
2т	\7г/
- ?L\!L(]L\2 - iY^2/3i + f-!4!273!
2 V 4 / r2 \2ttJ rs '
В качестве b можно использовать значение b = Ьо, которое минимизи¬
рует поверхностную энергию.
В области малых плотностей или больших rs> 2 работа выхода
(рис. 3.5) всегда положительна и убывает. С уменьшением rs < 2 работа
выхода проходит через максимум и затем неограниченно уменьшается,
приобретая отрицательное значение при rs < 0,5. Это также указывает
на неустойчивость однородного металлического состояния для высоких
значений электронной плотности (rs < 1).
3.3.2.	Сверхпроводимость. Теория БКШ
3.3.7.	В сверхпроводнике с синглетным s-спариванием спектр элемен¬
тарных возбуждений вблизи ферми-поверхности дается выражением
£р = \Ар + д2; £р = vf(p-Pf) (I P~Pf\<^Pf)-
По определению плотность состояний, отнесенная к единице объема,
равна
Поскольку нас интересует область значений |р - р?| < Pf, то прибли¬
женно можно заменить р1 dp —> (p2F/vF)d£. Тогда
^	=	Аг, /'d(l~	>- 1'(0) -£,)-

502	Глава	3.	Статистическая	физика.	Решения	задач
Окончательно имеем
{0,	при	е	<	Д,
1	 =	.	при	е	>	Д,
•фе2 - Д2
где i/(0) — плотность состояний на поверхности Ферми в нормальном
состоянии. Плотность состояний квазичастичных возбуждений в щели
при £ < Д тождественно обращается в ноль.
3.3.8.	Плотность состояний, отнесенная к единице объема, равна
=21ш6{‘-с')=1 £ /й*(е - ve+*-"*») =
= 1/(0)
I J ^ J d^S^£ - V £2 + A2 sin2 o'j.
Здесь мы учли две проекции спина элементарных возбуждений и то,
что нас интересует область энергий е -С ер. Последнее позволяет вы¬
полнить замену р2 dp —► (p2F/vp)d^. Далее
^s(£) =	°	 ==sinfl^6>,
Ц \/е2 — Д2 sin 0
sin 0<e/A
где г/(0) — плотность состояний на поверхности Ферми в нормальном
состоянии. Вычисление интеграла дает
, ,	1/(0)	е	,
^(е) = — д1п
£ +Д
1/(0)
(е/Д)2, е < Д,
1, е»Д.
Таким образом, при е < Д мы имеем ненулевую плотность состояний
элементарных возбуждений.
3.3.9.	Линеаризованное самосогласованное уравнение для щели
2 Р
(2тгй)3
служит для определения температуры сверхпроводящего перехода Тс,
как температуры, при которой впервые возникает нетривиальное реше¬
ние Др ф 0. Так как вклад в интеграл дает область импульсов вбли¬
зи ферми-поверхности |р — pF\	pF, то можно заменить дифференциал
d3p’ на 4n(pF/vF)d£'. Тогда
Д(0 = -ад J d? th^2{?Te)W

3.3. Неидеальные квантовые системы (жидкости)	503
где N(0) = р2р/(2-к2Н3ир) — плотность состояний на поверхности Ферми
с фиксированной проекцией спина. Решение ищем в виде кусочно-глад¬
кой функции
'Дь |£| < hwD,
Д(0 = < Д2, hojD < |£| < hoJc,
0, hjJc < I£|.
В результате получим систему двух линейных уравнений:
hug
A, = (A-/i)LiA,-/iL2Д2, U = j
о
hue
дг = -„L, д. - „/.гдг,	*(w)	- '"О-
Ншо
Здесь Л = gN(0) — безразмерная константа электрон-фононного притя¬
жения, g = VN(0) — константа кулоновского отталкивания электронов,
и In 7 = С « 0,577 — постоянная Эйлера. В оценке интегралов исполь¬
зовали обычное приближение слабой связи fiwc. ^ Т’с- Условие су¬
ществования нетривиального решения однородной системы линейных
уравнений (обращение в ноль детерминанта) дает уравнение
(1 - (Л - g)Li)(l + gL2) - g?L\L2 = 0
или
Отсюда температура сверхпроводящего перехода описывается обычной
формулой БКШ с некоторой эффективной константой А — ц*\
27
Тс = —hjJo exp
7Г
ш-
где /г — кулоновскии псевдопотенциал:
1 + ^ In (wc/wc) ’
В силу hjjc ~ £f > Tmd происходит логарифмическое ослабление куло¬
новского отталкивания за счет большого значения кулоновского лога¬
рифма \n[£F/(hjjD)\ » 1. Даже при А < ц еще возможно существование
сверхпроводимости.

504 ->\r Глава 3. Статистическая физика. Решения задач
Величина изотопического эффекта дается формулой
d(In Тс) _ 1
d(\nM) 2
1 -
* \ *
-Р )
Кулоновское отталкивание всегда ведет к уменьшению изотопического
эффекта.
3.3.10.	Обобщение самосогласованного уравнения на щель для сверх¬
проводника с двумя перекрывающимися зонами, каждая из которых
имеет свою щель, описывается соотношениями
—
Здесь £Pi = (£2. + (Д,!2)1/2. Для простоты предполагаем £р, = p2/(2m,)-
—ер — энергетический спектр электронов, отсчитанный от энергии Фер¬
ми, и с эффективной массой т, в каждой из зон. Вблизи ферми-поверх-
ности приближенно можно положить £Pi = од,(р, — pFt) и дифференци¬
ал d3pi/(2nh)3 заменить на	где JV; = p2F,/(2n2h3VFi) — плотность
состояний в г'-й зоне на уровне Ферми. Из эрмитовости матрицы
следует gik = g*ki. Взаимодействие обрезается на частоте порядка деба-
евской частоты шд.
Для определения температуры сверхпроводящего перехода Тс перей¬
дем к линеаризованным уравнениям
huJo	hoJ[)
A^-guN^ j dt-x th(\£Tc) -g12A/2A2 j dt2ih{b£Tc),
0	0
hu>D	hu>D
Д, = -Й.МД, /	J
26
Отсюда приходим к системе двух линейных уравнений
Ai = Л\\L А\ -(- А12Д Дг- Kk = -gik^k (». k = 1,2),
Д2 = Л211Д1 + Л221Д2, L = ln^^).
Условие существования нетривиального решения дает уравнение
(1 - XnL)(l - A22L) - A12A21L2 = 0.

3.3. Неидеальные квантовые системы
(жидкости)	505
Отсюда, выбирая наибольший корень, найдем
1 ч Ац + Л22 + V (Ац — А22)2 + 4Ai2 А21
I - Лэф -	2
и затем критическую температуру для двухвонного сверхпроводника:
Таким образом, в каждой из зон имеется свой конденсат куперов-
ских пар, который возникает благодаря притяжению электронов внутри
зоны и за счет межзонных переходов пар частиц. Наличие двух пе¬
рекрывающихся зон благоприятствует сверхпроводимости и увеличи¬
вает критическую температуру за счет межзонных переходов в силу
А12А21 == |gi2|2M^2 > 0. При ненулевом перекрытии g\% ф 0 сверхпрово¬
дящие щели Д] и Д2 возникают при Т = Тс во всех зонах одновременно.
3.3.11.	Запишем уравнение для щели при Т = 0:
т. е. величина щели зависит от направления в кристалле, и щель из¬
меняет знак с прохождением через нулевое значение всякий раз при
повороте на 90°. Такой сверхпроводник называют сверхпроводником с
d-спариванием, поскольку симметрия щели относительно осей кристал¬
ла аналогична электронной dxг_уг орбитали в атоме.
Максимальная величина щели находится из уравнения
Тс = — Нссо ехр(-1/Аэф).
7Г
Сразу видно, что
Др = Д cos 2в„ ~ (р2х - р2у),

506	Глава	3.	Статистическая	физика.	Решения	задач
где N(0) = p2F/(2-K2h3VF) — плотность состояний на поверхности Ферми
с фиксированной проекцией спина. Решение существует для притяже¬
ния g < 0, и максимальная величина щели равна
|Д| = -^2/гщ0е“2/|А|, Л = gN( 0).
Ve
Как обычно, предполагалась слабая связь |А| -С 1 и |Д| <с hujo-
3.3.12.	Для вычисления низкотемпературного поведения теплоемкости
воспользуемся тем, что изменение полной энергии ферми-системы при
варьировании функции распределения /р элементарных возбуждений
равно
й
(2-кП)Л
где мы учли наличие двух проекций спина. Отсюда получаем теплоем¬
кость:
ОО
о г	г	2	«	г	_2
г =9	_	[i*P	[
S J(2nh)3PdT J nh3 J
0
cLQ. £p	1
4tt 4 Г ch (ep/27)
Вклад в интеграл по р набирается в окрестности импульса Ферми \р—рр\ <с
<С pf, в которой можно воспользоваться приближением £,p~vf(p — Pf) = £•
Тогда
оо тг/2
Cs = 2u(0) [d£ [ sin6с10?-Щ-—;—l-	,
J J	47	ch	(e(f)/27)
о о
где i^(0) = p2F/(ir2h3vF) — плотность состояний на уровне Ферми. При
9 = 0 щель в спектре £■(£) обращается в нуль. В пределе Т —> 0 главный
вклад в интеграл дает область углов в < £/Д, и приближенно
°о ?/Д
Cs = 2i/(0) [d£ [ 9d9	=
J	J	47 ch (£/27)
0	0
oo
/m87"3 f a x4	t3
0
Теплоемкость сверхтекучего (сверхпроводящего) состояния со щелью,
которая обращается в нуль в изолированных точках на ферми-поверх-
ности, при Т —> 0 пропорциональна Г3 вместо традиционного поведения
~ ехр(—А/Т).

3.3. Неидеальные квантовые системы (жидкости)	507
3.3.13.	В сверхпроводнике с синглетным спариванием куперовские па¬
ры не обладают суммарным спином и не дают вклада в спиновый маг¬
нитный момент. Спиновый момент определяется только вкладом от спи¬
нов нормальных возбуждений:
где /(ер(Т) — фермиевская функция распределения. Раскладывая / пре¬
деле слабого магнитного поля, получим
Вклад в интеграл дает область импульсов вблизи ферми-поверхно-
сти \р — рр| <g:pF, и можно заменить дифференциал р2 dp на (p2F/vF) di
с интегрированием по £ в бесконечных пределах. Тогда
Здесь Хп — спиновая восприимчивость в нормальном состоянии, a Y(T) —
функция Иосиды, равная
Функция Иосиды Y(T) описывает долю нормальных электронов в сверх¬
проводнике.
3.3.14.	Парамагнитная восприимчивость \s в сверхпроводящем состоя¬
нии меньше нормальной восприимчивости \п- Следовательно, нормаль¬
ное состояние поляризуется сильнее, чем сверхпроводящее, и в доста¬
точно большом магнитном поле окажется, что поляризованное нормаль-
М = ^^/(ер<т), £ро- = А2 - рсгН.
Парамагнитная восприимчивость \s = дМ./дН тогда равна
ОО
Xs = -
d*p df _	2	f	P2	dP	1
(2-Kh?dev	J	Tr2fi3	47’ch2(£p/27')
/
0
oo
— oo

508	Глава	3.	Статистическая	физика.	Решения	задач
ное состояние будет иметь более низкую свободную энергию, чем по¬
ляризованное сверхпроводящее состояние. В этом случае, когда сво¬
бодные энергии Fn(H) и FS(H) сравняются, произойдет фазовый пере¬
ход с разрушением сверхпроводимости. При этом должно выполняться
условие	2	2
Fn(0)-*£- = Fs(0)-*j-, или
{Хп -Xs)H2 = Fn(0) _ Fs{0) = Hfr)
Отсюда находим предельное магнитное поле, выше которого сверхпро¬
водимость не может существовать:
и !Т\   Нс(Т)
р{ ’ Га t ™
у4тг(хп - Х>)
При Т = 0 парамагнитный предел равен
и /п\	Ис(0)	\/27п/(0)	До	До
ПрУд) = - .	=		 =- =  = .
Л/47ГХгг V Ажц v(0)
В поле Нр(0) происходит разрушение синглетного состояния куперов-
ской пары, так как обоим спинам электронов в паре становится выгод¬
нее ориентироваться вдоль магнитного поля.
3.3.15.	Термодинамический потенциал сверхпроводника складывается
из энергии конденсата куперовских пар и термодинамического потен¬
циала газа нормальных возбуждений. Так как конденсат куперовских
пар содержит четное число электронов, то разность термодинамических
потенциалов сверхпроводника с нечетным числом электронов Пнеч и
с четным числом электронов Пчет равна разности термодинамических
потенциалов газа нормальных возбуждений с нечетным числом возбуж¬
дений Пвдч и с четным числом возбуждений n[nJT:
5П = Пнеч - Пчет = fiW - п{й.
Для вычисления потенциала П^ = —T\nZ газа нормальных возбужде¬
ний, состояние которых характеризуется импульсом р и спиновой пе¬
ременной сг, определим статистическую сумму, которая равна произве¬
дению статистических сумм для каждого отдельного состояния с энер¬
гией £Pi(T:
2 = Пг‘ = П(1 +е ^е‘)’ для краткости I = (р,ст).
i	i
Здесь /3=1/7’ — обратная температура, и мы учли, что состояние с энер¬
гией £( может быть свободно или занято лишь только одним возбуждением.

3.3. Неидеальные квантовые системы (жидкости)	509
Далее представим Z в виде суммы двух слагаемых Z = Z4eT + ДеЧ:
[П ('++П (‘ -
i i
z
~ 2
, + IIthT
i
[П(1+«-л)-no
/ i *
z
" 2
1 - Пth t
i
Очевидно, что Z4eT состоит из суммы всевозможных произведений толь¬
ко четного числа экспонент, a ZHe4, наоборот, из суммы всевозмож¬
ных произведений только нечетного числа экспонент. Соответственно,
Z4eT и ZHe4 представляют статистические суммы для сверхпроводников
с четным и нечетным числом нормальных возбуждений. Окончательно,
7	1	р—
<m =	-	пй	=	-Г1п	fs	=	-Пп	;
^чет	1	+ в
„(О = - п .ь £=Е'# - *Е / А|л c,h
i	i	о	v	7
В сверхпроводнике ер(Т = (£2 + Д2)1/2 и
 	°°	.-./г
am=2V^Ide"'clh^=M0)VI^b
Здесь 1/(0) — плотность состояний и V — объем сверхпроводника. При
Т < Д основной вклад в «(Г) дает малая окрестность х = е — Д ;$ Д
вблизи е = Д:
ОО
а(Г) « 4i/(0)Ve-A/r [ -^Le~x'T = 2v(0)Vs/2^TAe-^T « 1.
У V2Ax
о
В результате находим
6П = Д - ТIn Л/Эф, М,ф = i/(0) Vs/2nTA.
При 7 = 0 очевидно, что = Д. Число можно трактовать как
эффективное число состояний, которые занимают нормальные возбуж¬
дения при Т < Д.
В нормальном состоянии Д = 0 и
оо	2
а(Т) = 4i/(0)VT J dx lncthx = yi/(0)VT.

510 ->\r Глава 3. Статистическая физика. Решения задач
Эффект четности в нормальном состоянии мал:
6П ™2Texp(-n2v(0)VT/2),
если температура Т велика по сравнению со средним расстоянием меж¬
ду энергетическими уровнями 5е г\_/
3.3.3.	Слабонеидеальный бозе-газ.
Уравнение Гросса-Питаевского
3.3.16.	Пусть стенка совпадает с плоскостью х = 0, а газ занимает по¬
лупространство х > 0. Волновая функция конденсата ф(х) может вы¬
брана действительной и удовлетворяет уравнению
2m'
с граничными условиями ф(х = 0) = 0 и ф(х = оо) = фо = (p/g)1^2- До-
множая обе части уравнения на ф'(х) и интегрируя, получим с учетом
граничных условий первый интеграл:
- рФ2(х) = -%Фо-
Решение уравнения дает волновую функцию
П
ф(х) = фоЩх/20, £
2т/т/1 ’
которая восстанавливает свое объемное значение на расстоянии поряд¬
ка корреляционной длины £.
3.3.17.	Волновая функция конденсата ф(г) может выбрана действитель¬
ной и удовлетворяет уравнению
h2 _2 , , mui2r2 , ,	,3	,
~2m	—2~xl)+g'l} =
В приближении Томаса-Ферми, пренебрегая градиентным членом, най¬
дем распределение плотности газа п(г) = ф2(г):
U — 1:ти>2Г2	,2	2	г\2
n(r) = —^-g	=	^(/?2-г2),	р=^-,
где радиус R — размер конденсатного облака. Число частиц N в ловуш¬
ке удовлетворяет соотношению
N
= Jn(r)4*r2dr=^4nf(R2-r2)r2dr=^^R5.

3.3. Неидеальные квантовые системы (жидкости)	511
Отсюда можно найти радиус облака и химический потенциал:
i1/S ,/15аЛГ\*/5	4тг	h2a
\47rmo; /	\	I	/
т
_ тш2
2	\47гта/
15gA/ А 2/5 _ hw / 15аУ\2/5	1={Л_)>/2
\irmu)2)	2	V	/	/*	Vmw/
Здесь а — длина рассеяния частиц газа и / — осцилляторная длина
ловушки. Пользуясь тем, что fi — dE/dN и // ~ АТ2/5, найдем полную
энергию газа:
Е =	~	Л/7/5.
Справедливость приближения Томаса-Ферми предполагает выпол¬
нение неравенства
-^—о'ф < Н'Ф-
2mR2
Это дает следующее условие на полное число частиц в ловушке: N^>1/а,
что подразумевает необходимое требование N » 1.
3.3.18.	Вариационная волновая функция, удовлетворяющая условию нор¬
мировки N = f i/j2(r)d3r, имеет вид
ч	V72 А372	/	AV4
^=—3747372- ехР(
<-¥)■
Подстановка вариационной функции в выражение для энергии
ОО
Е( А) = j	+	^ти2г2гр2+
дает следующее выражение для полной энергии газа
Е(А) - ^
3(л« + ^)+та>], ,= У|2Л-.
Безразмерный параметр 7 характеризует силу межчастичного вза¬
имодействия. При отталкивании частиц друг от друга 7 > 0 минимум
£(А) всегда абсолютно устойчив при любых значениях А, т. е. всегда
Е(А) ^ £min.
При притяжении между частицами 7 < 0 это становится не так
(рис. 3.6) потому, что при А —► оо отрицательный член с А3 доминирует,
и £(А) —> —оо, тем самым указывая на неустойчивость или коллапс
газа в ловушке. Условие Е (А) = 0 дает положение локального мини¬

512	Глава	3.	Статистическая	физика.	Решения	задач
мума. При достаточно малых значениях |'у| минимум в £(А) существу¬
ет, указывая на то, что возможно метастабильное состояние газа —
устойчивое при достаточно малых изменениях А. При |7| < 1 имеем
£т|п = (3/2)Йщ^(1 + 7/3).
С ростом |7| локальный мини¬
мум в £(А) исчезает, метастабиль¬
ное состояние не существует и про¬
исходит коллапс газа. Исчезнове¬
ние локального минимума происхо¬
дит при Ас и 7с, удовлетворяющим
условиям £'(А) = 0 и £"(А) = 0:
Рис. 3.6. Зависимость энергии газа
от вариационного параметра А при
разных значениях параметра межча-
стичного взаимодействия 7
3(А - А"3) + З7А2 = 0
3[(1 + ЗА-4) + 27А] =0.
Отсюда Ас = 51/4 и 7е = —4/55/4.
Окончательно находим критическое
число частиц в ловушке, при котором исчезает потенциальный барьер,
препятствующий коллапсу газового облака:
Nc
2\/27г /
0,67т
55/4 |в|
Численный расчет дает 0,57 вместо 0,67.
3.3.19.	Нестационарные уравнения Гросса-Питаевского
ih7n = _2^у2^+	2Ф<
-ih
дф
аГ
дф*
dt
домножим на ф* и ф и вычтем одно из другого:
Пользуясь тождеством
di\(фУф*) = фУ2ф* + (Уф) ■ (Уф*),
и таким же тождеством для сопряженных величин, получим уравнение
непрерывности для плотности газа р = т\ф\2:
др
dt
+ divj = О,

3.3. Неидеальные квантовые системы (жидкости)	513
где плотность потока массы дается соотношением
j = -j(rW-W) = pv-
Если мы запишем волновую функцию в терминах амплитуды и фазы
ф = \ip\exp(i6), то скорость конденсата v дается простым выражением
v = —V0.	*
т
При условии, что поведение V# — несингулярно, течение бозе-конден-
сата потенциально и удовлетворяет условию rot v = 0. Сингулярные ли¬
нии, на которых rotv ф 0, называются вихревыми линиями или нитями.
Циркуляция скорости вокруг нити
/vd = £[*l,
где [0] — приращение фазы при обходе вокруг нити. Для однозначности
волновой функции ф необходимо, чтобы Щ — 27т, ил - целое число.
Это дает условие квантования циркуляции.
3.3.20.	Однородное и равновесное состояние бозе-конденсата с плотно¬
стью п и химическим потенциалом ц описывается следующей волновой
функцией:
Фо (t) = ^ne~iftt/ri и $5(0 = Vne,,lt/h (п = \фо\2),
которая является решением нестационарного уравнения Гросса-Пита-
евского. Химический потенциал ц связан с плотностью конденсата со¬
отношением g = gn, где g — константа взаимодействия между бозе-
частицами. Представим волновую функцию в виде ф = фо + 6ф и, соот¬
ветственно, ф* — Фо + 6ф*. Далее линеаризуем уравнение Гросса-Пи-
таевского для ф и сопряженной функции ф* по малым отклонениям 6ф
и дф*. В итоге получим
= ~^?Чф + 2gn6ф + gФo6ф*,
= ~^Чф* + 2\ёп8ф*+ёф$6ф.
Решение системы линейных уравнений ищем в виде суммы незави¬
симых фурье-гармоник, характеризуемых волновым вектором к и ам¬
плитудами «к и Ок^
6ф(г, 0 =	]Г [ukeikr~‘^‘ + и*ке~‘кг+ш],
к
6ф*(г, 0 = eitit/h £ \vkeikT~iUkt + uje-ikr+fa'<] •
к

514 •Ar Глава 3. Статистическая физика. Решения задач
В результате получим пару связанных уравнений для определения ам¬
плитуд «к и Ок, которые в нашем простейшем случае являются действи¬
тельными величинами:
k =	+	2gn	- gj uk + gnvk,
+ 2gn- g)vk+gnuk.
Условие существования нетривиальных решений, когда детерминант,
составленный из коэффициентов при неизвестных зануляется, дает спектр
возбуждений:
^ = Ой-+2‘п - ")! - ■*v = (ъг+еп)' -
Отсюда приходим к боголюбовскому спектру возбуждений
Отношение амплитуд ик и Ок равно
, vk 1	h2k2 \
Нормировка самих амплитуд ик и Ok — произвольна. Для квантовоме¬
ханических приложений удобен выбор и\ - v\ = 1 или
1	U
цк= / г2	и vk =	-==.
VI -Li	V\-Ll
3.3.21. Чтобы найти энергию вихря, мы должны из полной энергии газа
с вихрем вычесть энергию однородного газа с тем же числом частиц
газа N. В этом случае плотность газа вдали от вихря будет несколько
отличаться от плотности однородного газа по, что порождает неудоб¬
ства при сравнении энергий газа EV(N) и Eo(N).
В этом случае удобнее анализировать энергию газа в зависимости
от химического потенциала g:
E(g) = E(N) - gN = j *(£ |VV>|2 + \g\MA - m2)
и сравнивать энергии газа с вихрем и без вихря при фиксированном хи¬
мическом потенциале. Это автоматически обеспечивает в газе с вихрем
-hut k Ok
= (~
\ 2
V
2 m

3.3. Неидеальные квантовые системы (жидкости)	515
те же самые характеристики газа вдали от вихря как и в однородном
безвихревом случае и, в частности, ту же плотность «о в силу простой
связи р = gno■
Энергия вихря на единицу длины равна
АЕ = Ёи-Е0 = J rf2r^|V^|2 + ^H4-H^I2-(5£lV>o|4-Ml^l2)].
ИЛИ
ДЕ = J d2r^\X7rp\2+ £{ф20-\ф\2)2 .
Записывая конденсатную волновую функцию с вихрем в цилиндриче¬
ских координатах г и tp, как гр(г,<р) = n'/2(r) ехр(гу>), придем к
d£=J2"dr[i;{?w) +^? + 1(л“-“)2/
Подставляя вариационную функция п = nor2/(г2 + а2), получим
л cv \ ро*2 ( 1 , 1 R , °2 \	е	Ь	27ГЙ.
АЕ(а) — ^— ( - + In —I	j > £ = о /	 и	х	=	>
27Г V4	а 8$ )	2^/mgno	т
где р0 = тпо — плотность конденсата, £ — корреляционная длина и
х — квант циркуляции. При вычислении вклада от второго слагаемого
интеграл, логарифмически расходящийся при г —► оо, обрезан на радиу¬
се R, представляющем собой радиус цилиндрического сосуда, в котором
находится бозе-газ. Естественно, R 3> а. Минимизируя АЕ(а) по вари¬
ационному параметру а, находим а = 2£ и линейную энергию вихря:
Д£=1г(|"|+?) = ^1л(1-058!)-
Численное расчет линейный энергии дает тот же ответ с коэффициен¬
том 1,035 вместо 1,058.
3.3.22.	Однородное стационарное состояние бозе-конденсата описыва¬
ется волновой функцией
где химический потенциал р связан с амплитудой /о и плотностью кон¬
денсата по соотношением р = gno = gfl- Представляя волновую функ¬
цию ф в виде
ф(х, 0 =

516	Глава	3.	Статистическая	физика.	Решения	задач
и разделяя уравнение Гросса-Питаевского на действительную и мни¬
мую части, получим систему из двух уравнений:
Ищем солитонное решение с амплитудой /(х, t) = /(х - ct) и фазой
у>(х, 0 = <^(х - ct). Это дает упрощение: / = -с/' и ф = -су/. Тогда
ncf<p' = ~(f"-f<p'2)+gf3-tif,
W' = £(2/V + /^").
Введем сверхтекучую скорость согласно о = hip'/т и перепишем
уравнения в виде
«Ф =	+	^mu2/u2	+	g/3	-	g/,
2с/' = 2f'v + fv'.
Домножая второе уравнение на /, получим первый интеграл:
с/2 - fv = const = с/о,
где использованы граничные условия / = /оио = Онах = ±оо. Отсюда
найдем v = и(/):
»ф-р).
Далее подставляем v = v(f) в первое уравнение:
ti- + i»cy(i-S)-g/J+rf = o.
Первый интеграл получим умножением уравнения на /'. Постоян¬
ную интегрирования определим из граничных условий /' = 0, / = /о при
х = ±оо и связи р — gf. В результате
Далее удобно перейти к переменной п = /2 (плотность):

3.3. Неидеальные квантовые системы (жидкости)	517
Результат интегрирования дает следующий профиль плотности
/ ,ч	,	,	ч. ,2 х — ct	тс2
П\Х, I) — Пшin + (По Пmin) th — , nmjn —	,
g
где ширина солитона зависит от его скорости:
Скорость солитона также выражается через значение минимальной плот¬
ности:
„,	/ ^min
С — U\	,
V Ло
где и = (gno/тУ/2 — скорость звука в бозе-газа.
Изменение фазы вдоль солитона можно найти интегрированием со¬
отношения ip' = mv/h:
оо
у?(+оо)-<р(-оо) = -^ f  (n0-nmin)dx   = -2arccos(\ 5е!2.\
ft J по ch (х/2£с) — (по — Лш1п)	VV По)
— ОО
По аналогии с нелинейной оптикой солитоны с обеднением плотности
частиц газа лт|П < «о называют темными солитонами. Для статическо¬
го солитона с = 0 изменение фазы максимально и равно -п. Волновая
функция представляет собой кинк и имеет вид 1р(х) = /oth(x/2£).
3.3.23.	Обобщение выражения для энергии смеси двух конденсирован¬
ных бозе-газов имеет вид
5/Н-
Константы взаимодействия между разными бозе-частицами gn и g%\
одинаковы gn =g2i> ая, = |^;|2 — плотность г-компоненты смеси. Неста¬
ционарные уравнения Гросса-Питаевского можно записать в виде
ihlH =	+ £n|V>l|Vl +^12|^2|2^1 = Ц.
ihln =	+Я21|^1|2^2 +g22|V’2|2V’2 =
Стационарное равновесное решение для волновых функций бозе-кон-
денсатов
V>i(0 =	и	ф2(0	=

518 -IV Глава 3. Статистическая физика. Решения задач
приводит к следующим значениям химических потенциалов:
№ = ё\\п\ +&12Я2 И g2 — g21«l + £22«2-
Чтобы найти спектр возбуждений смеси, рассмотрим малые возму¬
щения волновых функций согласно ■ф; —> rpi + 5i/>i и гр* —> ф* + 6ф*, и
найдем линеаризованные уравнения, которым подчиняются возмущения
первой компоненты:
_ _^_V2^ + (2gun, -(- ^12^2)5ipi + Un ф\ 5ф*+
+gi2 V’lV’ii ЭД»2 + gi2 Ф1Ф2 Щ,
_ ,^Г = __|_у2<5фГ + (2gnn, +г,2л2)^Г +guV»f2^i+
+£l2 V’l* Ф2 <5^2 + §12 V’l* ^2 <^2,
и возмущения второй компоненты:
= ~^v2^2 + (2^22«2 + g2l/Il)^2 + g22 Ф2 Щ +
+£21 Ф2Ф1 H\ + £21 Ф2Ф1 Щ,
- ih-= ~2^V2^2* + (2^22«2 +g21«l)#2 + g22 ^2 2 ^2+
+£21 Ф2Ф1 Щ + £21 Ф2Ф\ 5Ф\-
Решение системы линейных уравнений ищем в виде суммы по волно¬
вым векторам к независимых фурье-гармоник с амплитудами ц(к и uik:
6ф\(г, 0 = e-iw</n£[uIke‘'kr-‘^ + u|,ke-ikr+iWk<],
k
6ф2(г, 0 =	Е [u2ke‘kr“‘“k< + u2V_ikr+‘W].
k
Аналогичные соотношения можно выписать и для сопряженных вели¬
чин. В результате получим четыре уравнения на определение амплитуд
Ui и Vi, которые оказываются действительными величинами:
= (v 1 + £u«i + £12^2 - Pi)ui + AnWi + A12U2 + Ai2n2.
-fkckv 1 = (771 + gurii + g\2n2 - g\)vx + AnUi + Al2v2 + Д12Ы2,
bu]yU2 = (ry2 + g22«2 + £21«1 ~ g2)^2 + A22V2 + Al2Ul + AtfVl,
-tkcbV2 = (772 + g22n2 + g2ini — g2)v2 + A22U2 + Д12Щ + Al2“l-

3.3. Неидеальные квантовые системы (жидкости)
X
519
Здесь для краткости мы ввели обозначения
h2k2 .	h2k2	Л
= 2тГ	=	2тг"	22	’
All=gllrtl. А22=^22«2-	А]2	=	fl2\/«l«2	=	g2lVnln2-
Нетривиальное решение системы уравнений существует при обра¬
щении в ноль детерминанта, составленного из коэффициентов при неиз¬
вестных амплитудах, т. е.
Vi - ft^k
Дп
Д12
Д12
Дп
г)\ +
Д12
Д12
Д12
Д12
772 - Йч;к
Д22
Д12
Д12
Д22
Г)2 + Ншъ
Частота элементарных возбуждений в смеси двух бозе-конденсатов опре¬
деляется из биквадратного уравнения. Это означает существование в
смеси двух ветвей возбуждений: шц и w2k. Квадрат частоты каждой из
них определяется из соотношения
1-2 2 *
ft “>1,2 = 2
у/(е% - е$2 + ШД^тд - Д„)(772 - Д22)
где е,- = (r)f — Д2)1/2 — боголюбовский спектр возбуждений каждой из
компонент смеси в отдельности. Длинноволновая область спектра (k —> 0)
представляет собой две звуковые ветви ац>2 = u.\$k со скоростями звука
цц2, определенными соотношениями
2 1
“1,2 = О
и\ + и\ ±
[и\ - ц2)2 +
4А?2
m\m<i
где ы? = Д,,/т, = guni/trii — квадрат скорости звука в отдельной г-ком¬
поненте. Требование положительности квадрата скорости звука приво¬
дит к условию gug22 > gi2- Это эквивалентно требованию положитель¬
ной определенности матрицы из констант взаимодействия
(£ll £пЛ
\£21 £22/
При нарушении этого требования однородная смесь двух бозе-конден¬
сатов неустойчива, и происходит ее расслоение на отдельные компоненты.

520	Глава	3.	Статистическая	физика.	Решения	задач
3.3.4.	Теория сверхтекучести
3.3.24.	Возможность сверхтекучего движения Не II в капилляре огра¬
ничена по скорости некоторой критической скоростью vc. Рассмотрим
жидкий 4Не при нуле температуры в основном состоянии, протекающий
по капилляру с однородной постоянной скоростью v. Если жидкость
испытывает трение о стенки капилляра, то часть ее кинетической энер¬
гии переходит в тепловую энергию. Это приводит к нагреву жидко¬
сти и ее переходу в возбужденное состояние. Возбужденное состояние
жидкости характеризуется наличием элементарных возбуждений и, тем
самым, трение или наличие вязкости у жидкости будет проявляться
в рождении элементарных возбуждений. Конечное время жизни или
затухание рожденных элементарных возбуждений будет приводит к ре¬
лаксации жидкости в основное состояние и замедлению потока жидко¬
сти с соответствующей диссипацией энергии. Необходимым условием
для существования бездиссипативного течения жидкости является за¬
прет на спонтанное рождение элементарных возбуждений.
В системе отсчета, в которой жидкость покоится, энергия элемен¬
тарного возбуждения с импульсом р равна е(р). Согласно принципу
относительности Галилея для инерциальных систем в лабораторной си¬
стеме отсчета, в которой жидкость движется с однородной и постоянной
скоростью v, энергия элементарного возбуждения подвергнется доппле¬
ровскому сдвигу и будет равна е(р) + pv. Спонтанное рождение элемен¬
тарного возбуждения становится энергетически выгодным при условии
£(р) + pv < 0. Рождение возбуждений с импульсами, направленными
против скорости течения v — наиболее выгодно. Необходимое условие
для бездиссипативного течения
• £(р)
v <vc = min
Р
определяет максимально допустимую или критическую скорость тече¬
ния жидкости и называется критерием сверхтекучести Ландау.
Минимум отношения е/р определяется из условия экстремума
de/dp = 0, которое дает
de _ е
dp ~ р'
Геометрически это отвечает точке, где прямая, проведенная из начала
координат, касается кривой е(р). Для спектра возбуждений в Не II эта
точка лежит несколько правее точки ротонного минимума и критиче¬
ская скорость
\/Ро + 2тА-ро д

3.3. Неидеальные квантовые системы
(жидкости)	521
составляет 58 м/с. В слабонеидеальном конденсированном бозе-газе с
боголюбовским спектром возбуждений критическая скорость равна ско¬
рости звука. Идеальный конденсированный бозе-газ с частицеподобным
спектром возбуждений е = р2/(2ЛТ) не обладает свойством сверхтеку¬
чести в силу нулевого значения критической скорости.
При ненулевых температурах Т ф 0 в жидкости уже существуют
тепловые элементарные возбуждения в термодинамически равновесной
концентрации. Тем не менее, при малых скоростях течения v < vc воз¬
можность изменения числа элементарных возбуждений за счет дополни¬
тельного рождения элементарных возбуждений отсутствует. Жидкость
может оставаться тогда в том же состоянии и поддерживать бездисси-
пативное течение.
3.3.25.	Элементарные возбуждения, обладающие импульсом, вносят
вклад в полный импульс жидкости. Плотность импульса или импульс
единицы объема, вносимый возбуждениями с функцией распределения
л(р), равен
Течение жидкости с постоянной и однородной скоростью v приводит к
изменению энергии возбуждений вследствие допплеровского сдвига:
где е(р) — энергия возбуждений и р — импульс в системе координат, в
которой жидкость покоится и описывается равновесной функцией рас¬
пределения п(е). Далее имеем
Коэффициент пропорциональности между плотностью импульса и ско¬
ростью называют плотностью нормальной компоненты р„. При малых
скоростях интеграл легко оценивается, и с учетом усреднения по на¬
правлениям импульса р
е -» е(р) - pv,
для плотности нормальной компоненты найдем

522 -l\r Глава 3. Статистическая физика. Решения задач
Поток элементарных возбуждений обязательно сопровождается и пере¬
носом части жидкости. Доля переносимой массы жидкости равна рп/р,
где р — полная плотность жидкости.
Вычисление р„ для фононных возбуждений с ер — ср дает
2тг2 Т4
Pn'ph ~ 45 йзс5 ~ Т •
а для ротонных возбуждений
_	2w'/2Pq	„-А/Т	_ ро „ ^ -А/Т
Рп,г	2\3/2	гт*\/2 *-3	QT г	’
3(2тг ) ' Т ' h	3	Т
где пг — плотность ротонов. В Не II плотность нормальной компоненты
есть сумма фононного и ротонного вкладов рп = рпр^ + рп г.
3.3.26.	Для одновременного рождения двух элементарных возбужде¬
ний необходимо выполнение условия
e(pi) + е(р2) + (pi + p2)v < О,
где v — скорость течения жидкости. Это выражение удобно переписать
в виде
e(q)+£(p-q) + pv<0.
Условие минимума по q дает соотношение между скоростями возбуж¬
дений:
v(q) = ^ = <Me^Uv,p_q,
которое отвечает двум возбуждениям, распространяющимся в направ¬
лении р с одинаковыми скоростями. Критическая скорость о2 опреде¬
ляется как минимум отношения
,я,е(ч) , !_ _!^(Р — q)
e(q) + е(р — q)	q	Ip	—	q|
o2 = mm	H——	= min ^^
IPI	|p|
e(q) , . _i g(p - q)
|c|| min I. 4" |p cj| min .	,	.	,
^	|q|	lp-q|	^	Tf	|q|	+	|p-q|	^ rr
^	|p|	>Vc~w\	*0e-
Здесь мы учли, что vc — критическая скорость для рождения отдель¬
ного возбуждения, определяемая минимумом отношения e(q)/q, и учли в
последней дроби неравенство для сторон треугольника. Равенство о2 = ос
заведомо достигается при рождении двух одинаковых возбуждении с
P\ = Р2 = Рс. где рс — импульс, отвечающий критической скорости vc.

3.3. Неидеальные квантовые системы
(жидкости) I I 523
3.3.27.	При вращении сосуда с гелием в предположении о безвихревом
движении сверхтекучей компоненты rot vs = 0 только нормальная ком¬
понента жидкости будет вращаться вместе со сосудом, а сверхтекучая
компонента будет оставаться неподвижной. Нормальные возбуждения,
сталкиваясь и взаимодействуя со стенками сосуда, увлекаются враще¬
нием подобно обычной вязкой жидкости. Сверхтекучая компонента, не
взаимодействуя со стенками, остается в покое. Такая ситуация сохра¬
няется, пока скорость стенок достаточна мала и они не могут рождать
элементарные возбуждения. Если допустить рождение элементарных
возбуждений в виде квантованных вихрей, циркуляция сверхтекучей
скорости вокруг которых отлична от нуля, т. е. я ф 0, то наличие вих¬
рей будет имитировать вращение сверхтекучей компоненты как целого.
Число вихрей при этом будет пропорционально удвоенной частоте вра¬
щения 2Г2, деленной на квант циркуляции я.
Чтобы найти критическую скорость вращения Пс, необходимо опре¬
делить две величины: энергию вихря £ и его момент импульса L, ко¬
торые представляют собой изменение кинетической энергии и момента
импульса всей жидкости. Изменение обусловлено возникновением цир¬
куляции сверхтекучей скорости vs вокруг оси вихря. Спонтанное рож¬
дение вихря становится выгодным при достижении неравенства £вр =
= Е — ЬП < 0. Действительно, в системе отсчета, в которой жид¬
кость движется со скоростью v, энергия возбуждения подвержена до¬
пплеровскому сдвигу е + pv, и условие е + pv < 0 позволяет спонтанно
рождать возбуждение. В нашем случае для возбуждения на расстоя¬
нии г от оси сосуда сверхтекучая компонента движется со скоростью
v = vs = — [Г2 х г] и
где 1(г) = [г х р] — момент импульса. Интегрируя последнее соотно¬
шение по всему объему, придем к £вр = £ — Lfl, где £ = / edV и
Наименьшей энергии вихря £вр соответствует расположение вихря
в центре сосуда вдоль оси цилиндра. Условие квантования циркуляции
сверхтекучей скорости по замкнутому контуру, охватывающему вихре¬
вую нить, имеет вид
£ + pv* = £ — р[П X Г] = £ - 1(г) • П,
L = fldV.
где Ш4 — масса атома 4Не. Если контур не охватывает нить, то цирку¬
ляция равна нулю. Скорость vs — я/(2жг) имеет только азимутальную

524 ->V Глава 3. Статистическая физика. Решения задач
компоненту. Момент импульса вихря параллелен оси вращения, и его
величина в расчете на единицу длины нити равна
L= J d2r [г х psvs]2 = Ps f d2rrvs = ixpsR2,
где ps — плотность сверхтекучей компоненты. Мы учли также, что в
данной геометрии вектор сверхтекучей скорости не имеет г-компоненты.
Энергия вихревой нити на единицу длины нити дается интегралом
£=/¥л=!/Ш22^=ir'nf-
€
Из условия £вр = Е — LJ7 = 0 находим критическую скорость вращения:
л1с — о 1П —
2nR £
Ей соответствует линейная критическая скорость
Vc = ncR=-L In*
m^R £
По порядку величины это оценка справедлива и для критической ско¬
рости рождения вихрей в капиллярах и отверстиях с характерным диа¬
метром 2 R.
3.3.28.	Воспользуемся соотношением, которое определяет нормальную
плотность:	з
ft<w,w=/(li?p',(e''-p'v)'
Для фононов п(е) — функция распределения Бозе и ер = ср. Выбирая
ось г вдоль направления относительной скорости w = \п — vs, имеем
ОО	7Г
р COS в
g(cp—pw cos в)/Т _ j
О
1	ОО
3 Л-	Т4 О	.../„	_4
Pn,ph(w)w =	Jр2 dp J sin в dO
о о
1
Г4 Г xdx Г e3de _ Г4 8 а>/с тг'
47г2Й3с4 7(1- xw/c)* J — 1	47г2Й3с4	3(1-	ш2/с2)3	15
-1	О
Отсюда фононный вклад в нормальную плотность равен
„	,_л _	р«.ра(0)	. /лч _ г^г4
A.^(w) - (1 _ да2/с2)3 -	А»п^(0) -	.
Нормальная плотность увеличивается с ростом относительной скоро¬
сти w и расходится при w = с.

3.3. Неидеальные квантовые системы (жидкости) -IV 525
3.3.29. В идеальном газе спектр возбуждений имеет вид ер = р2/(2т).
Согласно результатам предыдущей задачи
p(w)w= [ d3p	9	[	d3p	р + OTW
J (2nh)3 g(p2/2m-pw)/r _ J J (2nh)3 g(P2/2m-mw2/2)/T _ j '
Из двух слагаемых в числителе слагаемое^: р зануляется в силу сим¬
метрии. Тогда
/ \ _ Г d3p	1
~т J (2тгh)3 е^Пт-т^/2)/Т _ j •
При w = 0 плотность нормальной компоненты совпадает с плотностью
надконденсатных возбуждений:
/ тТ \3/2	/ т \3/2
рп(0) = mnex(T), nex(T)=i^L J C(3/2) = n(^J .
При w > 0 последний интеграл имеет особенность в точке р = mw и
расходится. В этом смысле p„(w > 0) обращается в бесконечность ана¬
логично фононному вкладу в нормальную плотность при w > с. Это
коррелирует с утверждением о том, что критическая скорость в иде¬
альном конденсированном газе равна нулю.
3.3.30. Воспользуемся соотношением, которое определяет плотность
нормальной компоненты при малых скоростях:
1 [ 2( дщ\г, d3p
PnJ= 3 J ^\~дё)
Здесь п,(е) — фермиевская функция распределения для примесей, и
множитель 2 учитывает две проекции спина возбуждений. Для вычис¬
ления pnj удобно энергию растворения eq включить в химический по¬
тенциал. Тогда
2М [ дщ 2d3p
Рп'1 3 J £ де (2тгП)3 ’
После однократного интегрирования по частям получаем
где N3 — концентрация атомов 3Не, р — плотность раствора, с —
= M3N3KM3N3 +	— массовая концентрация, и М34 —- массы
атомов 3Не и 4Не. Сверхтекучий раствор 3Не-4Не — пример сверхте¬
кучей системы, в которой плотность нормальной компоненты остается
конечной при нулевой температуре.

526
Глава 3. Статистическая физика. Решения задач
3.3.31.	Чтобы найти искомую температуру, необходимо оценить сво¬
бодную энергию отдельного вихря
где Е — энергия и 5 — энтропия вихря в пленке радиуса R. Спонтанное
рождение вихрей происходит при условии F < 0. Поле сверхтекучей
скорости для вихря с осью, перпендикулярной плоскости пленки,
определяется выражением
в соответствии с условием квантования циркуляции сверхтекучей ско¬
рости по любому замкнутому контуру, охватывающему вихревую нить:
Здесь Ш4 — масса атома гелия. Энергия вихря представляет собой ки¬
нетическую энергию сверхтекучего движения:
Интеграл ограничен сверху размером пленки, а снизу размером кора £,
представляющего собой нормальную область, где сверхтекучее движе¬
ние отсутствует.
Кор вихря размером £ занимает площадь 7г£2, и его центр может
быть помещен в любую точку пленки площадью kR2. Соответственно,
энтропия равна логарифму числа возможных размещений вихря площа¬
дью 7г£2 на пленке площадью 7rR2:
Итак, свободная энергия отдельного вихря имеет вид
F = Е — TS,
я = <£ vsdl = vs(r) 2-кг =
/
€
Температура Гбкт. равная
называется температурой Березинского-Костерлица-Таулеса. При Т> Гбкт
в сверхтекучей пленке становится энергетически выгодным рождение
вихрей в силу F < 0, что приводит к разрушению сверхтекучего состояния.

X
3.4. Фазовые переходы и критические явления	527
3.4.	ФАЗОВЫЕ ПЕРЕХОДЫ И КРИТИЧЕСКИЕ ЯВЛЕНИЯ
3.4.1.	Приближение самосогласованного поля
3.4.1. Если Si и S2 — энтропии первой и второй фаз, то энтропия всей
системы:
S = S1(£bV'1,M) + S2(£2?V2,JV2),
где £ji2 — энергия, V\i2 — объем и ЛД2 — число частиц в первой и
второй фазах. Из максимальности энтропии следует, что dS = 0:
dS = I ^ + $dV, - %-dNi) + (Ф- + ^-dV2 - £dN2) = 0.
rf£,
Л ' тГ'1 Tr‘'lJ ' V £2 ' т2~'“ t2
Учитывая, что в замкнутой (изолированной) системе
£ = Е\ + Е2 = const	и	dE\	=	-dE2,
V — V\ + V2 = const	и	dV1	=	-dV2,
N — N1 + N2 = const	и	dN\	=	-dN2,
получим
J__J_	F\ _ £2	IA	_ P2
T\ ~ T2’	Ti~ T2	T{	T2'
Отсюда для условия равновесия фаз: Т\ = Т2, Р\ = Р2, р\ = р2.
3.4.2.	Для определенности считаем а > 0 (а < 0 сводится к замене (р —>
—► —<р). Энергия неупорядоченной фазы Ф(р = 0) = 0. Выгодности упо¬
рядоченной фазы отвечает условие Ф ^ 0. Точку фазового перехода или
точку бинодали тс можно найти из условия Ф = 0 и дФ/др = 0. Это
дает температуру фазового перехода тс и значение параметра порядка
в точке перехода <рс:
2 а2	2 а
Tc~9j	И {Р°~~ЪЬ'
Конечный	скачок	параметра	порядка в точке перехода	означает,	что
это переход первого	рода. При	т	<тс значение параметра	порядка	на¬
ходим из условия минимальности энергии:
^ = <р(т + ар + btp2) = 0.
Абсолютному минимуму энергии отвечает корень с максимальным от¬
рицательным значением параметра порядка. Итак,
Г о	при	т > тс,
фо(т) = \ (а 4- \Jа2 — 46т)
2 Ь
при Т < То

528	Глава	3.	Статистическая	физика.	Решения	задач
Точки спинодали (точки абсолютной неустойчивости фаз) можно най¬
ти из условия нарушения минимальности энергии, когда вторая про¬
изводная д2Ф/дф2 меняет знак с положительного значения на отрица¬
тельное, т. е.
<Э2Ф
= о.
tp=ip0
Отсюда получаем точку спинодали (точку максимального переохлажде¬
ния) для неупорядоченной фазы rs_ = 0 и точку спинодали (точку мак¬
симального перегрева) для упорядо¬
ченной фазы rs+ = а2/(4Ь). Очевид¬
но, что rs_ <тс < ts+, и области тем¬
ператур ts_ <т <тс и тс < т < т3+
отвечают областям метастабильно-
Рис. 3.7. Диаграмма фазовых со
стояний. Сплошной линией пока
зана бинодаль. Пунктирными ли
ниями обозначены спинодали
Значение параметра а = 0 выде¬
ленное. При а = 0 в точке фазово¬
го перехода тс = 0 параметр порядка
<рс = 0 и фазовый переход в упорядо¬
ченную фазу становится переходом
второго рода. Таким образом, точка
а = 0 и т = 0 является точкой, где
меняется род фазового перехода, т. е. является критической точкой.
Видно также, что в критической точке точки бинодали и спинодалей
совпадают, так как при переходе второго рода нет области метастабиль¬
ности фаз.
3.4.3.	Если а > 0, то переход при т = 0 в сегнетоэлектрическую упоря¬
доченную фазу является фазовым переходом второго рода. Роль члена
~ р6 не существенна, так как при этом род перехода и качественное по¬
ведение системы в непосредственной окрестности точки перехода т — 0
не меняется. При \т\<^а2/Ь этим членом можно пренебречь в силу
Ьро « арщ где р§ ~ |т|/а.
При а < 0 поведение системы качественно меняется и возникает
переход первого рода в точке, определяемой условиями
Ф(р) = 0 и ^ = (т + ар2 + 6р4)р = 0.
Отсюда находим точку фазового перехода первого рода:
3 а2
Тс 16 Ь

3.4. Фазовые переходы и критические явления	529
и значение параметра порядка, который скачком возникает сразу ниже
точки перехода:
Таким образом, линия фазовых переходов в зависимости от коэффици¬
ента а дается соотношением	*
О	при	а ^ О,
3 а2
Теъ при а<0’
и точка а = т = 0, в которой происходит смена рода фазового перехода,
называется трикритической (рис. 3.8). Во всей области существования
сегнетоэлектрической фазы параметр порядка определяется уравнением
— а + \/а2 — 4 Ьт
2Ъ
(знак минус перед корнем отвечает либо отсутствию действительных
решений, либо большему значению потенциала Ф). Потенциал Фо сег¬
нетоэлектрической фазы дается соот¬
ношением
Ф0(т) = Ф(р0) =
= а3 - 6аЬт - (а2 - 4Ьт)3/2
24 Ь2
Теплоемкость, определяемая как
С(т) = —д2Ф/дт2, обращается в ноль
в неупорядоченной фазе и равна
см =
в сегнетоэлектрической фазе. Тепло¬
емкость характеризуется различным
поведением в двух областях: в окрест¬
ности, близкой к трикритической точке, т. е. а2 < |т| и в далекой окрест¬
ности а2 > |т|. При фазовом переходе вдали от трикритической точки
скачок теплоемкости конечен и АС ~ 1/|а|. Вблизи окрестности три¬
критической точки имеем усиление особенности в поведении теплоем¬
кости вида |т|-1/2.
Для определения верхней критической размерности трикритической
точки, т. е. точки, в которой коэффициент а = 0, используем критерий
Рис. 3.8. Диаграмма фазовых со¬
стояний сегнетоэлектрика. Сплош¬
ной линией показан фазовый пере¬
ход второго рода. Пунктирной ли¬
нией — фазовый переход первого
рода

530	Глава	3.	Статистическая	физика.	Решения	задач
слабости флуктуаций параметра порядка в объеме ~ £d с линейным
размером порядка корреляционной длины £
Здесь х ~ 1/М — восприимчивость, и d — размерность пространства.
Корреляционую длину можно оценить, используя энергию неодно¬
родности порядка c(Vp)2 и сравнивая ее с энергией ~ |т|р2. Тогда £ ~
~ (с/\т\)[/2. При а = 0 равновесное значение ро можно оценить из соот¬
ношения тро ~ bpg, согласно которому рд ~ \т\/Ь. Окончательно имеем
В пределе т —> 0 неравенство всегда удовлетворяется при d > 3 и не
удовлетворяется при d < 3. Соответственно, для трикритической точки
или для взаимодействия в шестой степени ~ рб верхняя критическая
размерность равна трем. Линия кроссовера т ~ av отделяет трикрити-
ческое поведение от обычного критического. В теории самосогласован¬
ного поля для трикритической точки индекс кроссовера <р = 2.
3.4.4.	Для анализа фазовых состояний удобно представить параметр
порядка у>(х) в виде разложения в ряд Фурье
Неустойчивость неупорядоченной фазы с у? = 0 будет связана с по¬
явлением отрицательного значения r(q). При <5 > 0 минимум r(q) в за¬
висимости от волнового вектора q достигается при q = 0 и впервые r(q)
меняет знак при т = 0. Следовательно, в области <5 > 0 при г = 0 про¬
исходит обычный фазовый переход второго рода в упорядоченную од¬
нородную фазу с ро = (М/а)1/2 и q = 0. Потенциал этой однородной
фазы равен
= I^qe,q\
ч
и записать термодинамический потенциал в виде
ч
где коэффициент r(q) будет равен
r(q) = т + Sq2 + ~-

3.4. Фазовые переходы и критические явления -г 531
В области значений 6 < 0 минимум r(q) достигается при ненулевом
значении волнового вектора
а знак r(q) изменяется с положительного на отрицательный при темпе¬
ратуре перехода
При т < тт+ становится выгодной модулированная упорядоченная фаза,
в которой параметр порядка изменяется в пространстве согласно соот¬
ношению
Период пространственной структуры L определяется из условия
Термодинамический потенциал модулированной упорядоченной фазы най¬
дем из соотношения
где (...) означает усреднение по периоду пространственной структуры.
С учетом того, что (cos2qx) = 1/2 и (cos4qx) = 3/8, имеем
где ipm — амплитуда модуляций параметра порядка. Минимизируя Фт,
находим амплитуду модуляций и термодинамический потенциал фазы из
Переход в модулированную упорядоченную фазу из неупорядочен¬
ной фазы является фазовым переходом второго рода, поскольку при
этом параметр порядка ipm, или амплитуда модуляций пространствен¬
ной структуры, меняется плавно.
Сравнивая Фт и Фо, мы видим, что при достаточно больших отри¬
цательных г потенциал Фо становится меньше, чем Фт. Переход из
модулированной упорядоченной фазы в упорядоченную однородную фа¬
_ <52
Тт+ “ 2d'
фМ = Фт cosqx.
фш = \{ф2(*)) + ^г(у>2(х)> + ^~{ф2(х)) + f (</(х)),

532 ->\r Глава 3. Статистическая физика. Решения задач
зу происходит при равенство Фт(тт_) = Фо(тт_). Это дает температуру
перехода, равную
V2
Тт~~ V3^V2Tm+-
Переход при тт_ является переходом первого рода со скачком модуля
параметра порядка и периода пространственной структуры.
Точка параметров 6 — 0 и т = 0, которая называется точкой Лифши-
ца, является точкой, в которой сходятся две линии фазовых переходов
второго рода и одна линия фазового перехода первого рода. При <5 < О
в области температур т„_ < т < тт+ существует модулированная упо¬
рядоченная фаза. Область существования однородной упорядоченной
фазы: т < тт_ при 6 < 0 и т < 0 при 8 > 0. В точке Лифшица сосу¬
ществуют три фазы (рис. 3.9).
Корреляционную длину £ при 8 = 0 вблизи перехода можно оце¬
нить, сравнивая энергии тр2 /2 и энергию неоднородности d(V2tp)2 /4
в пренебрежении членом ip4 в си¬
лу его малости. Считая, что в
этом случае тр2/2 ~ d(V2p)2/4,
и оценивая d(V2p)2 ~ dtp2/Г,4, по¬
лучим, что £ ~ (d/т)1/4. Поэтому
критический индекс 1/4 вме¬
сто 1/2 вдали от точки Лифшица.
Особенностью точки Лифши¬
ца <5 = О также является стремле¬
ние к бесконечности периода мо¬
дуляции пространственной струк¬
туры, что связано с уменьшением <5.
Это аналогично уменьшению кор¬
реляционной длины £ ~ 81/2 с пе¬
реходом к закону £ ~ т~1/4 вместо
£ ~ т~|//2. Это способствует росту
флуктуаций параметра порядка. В результате вблизи точки Лифшица
расширяется флуктуационная область, а верхняя критическая размер¬
ность увеличивается, становясь больше четырех.
3.4.2.	Функционал Гинзбурга-Ландау
3.4.5.	Для циркуляции вдоль контура С с необходимостью имеем
°=/(1ув-А)"|-|дв-ф-
с
упорядоченная
неоднородная
фаза /'
/
неупорядоченная
однородная фаза
упорядоченная
однородная фаза
О	8
Рис. 3.9. Диаграмма фазовых состоя¬
ний. Сплошными линиями показаны
фазовые переходы второго рода. Пунк¬
тирной линией — фазовый переход
первого рода

3.4. Фазовые переходы и критические явления	533
В силу однозначности параметра порядка, как функции координаты г,
приращение фазы Ав при полном обходе контура и возврате в ту же
точку должно быть кратно 2тгп, что и приводит к квантованию магнит¬
ного потока Ф = пфо.
Простейший пример вихревого состояния в сверхпроводнике можно
описать следующим поведением параметра порядка:
ф(г) - \ф\е1в^\ в(т) = narctg(y/x) и п — целое.
Здесь arctg(у/х) = — азимутальный угол в цилиндрической системе
координат (р, <р, г). Градиент фазы равен
Ось г, которая соответствует р = 0, представляет собой особую линию,
называемой вихревой линией. Изменение фазы при обходе по любому
контуру, охватывающему вихревую линию, равно 2-яп. Так как сверх¬
проводящий ток js на бесконечно удаленном от вихревой линии контуре
обращается в ноль, то полный поток магнитного поля, переносимый
одной вихревой линией, квантуется:
Для выполнения условия однозначности параметр порядка обращается
в ноль в центре вихря на вихревой линии ф(р = 0) = 0. Квантованный
вихрь представляет собой пример топологического дефекта.
3.4.6.	а) Количественное описание структуры вихря заметно упроща¬
ется в предельном сверхпроводнике II рода с я » 1. В этом случае цен¬
тральная область вихря, называемая кором вихря, представляет собой
приближенно нормальную область, внутри которой параметр порядка
изменяется от нулевого значения в центре вихря до равновесного зна¬
чения фо вне кора вихря. Радиус кора приблизительно равен корреля¬
ционной длине £(Т).
Магнитное поле вихря h(p) в области вне кора р > £ описывается
уравнением
h -I- 62 rot rot h = h — $2V2h = пфо^г^(р) (p ?Z £)>
где ег — единичный вектор, задающий направление вихревой линии и
пфо — полный поток магнитного поля, созданного вихрем. Точное ре¬

X
534	Глава	3.	Статистическая	физика.	Решения	задач
шение уравнения выражается через функцию Бесселя нулевого порядка
от мнимого аргумента (функцию Макдональда) Ко(х):
,	.	fin	(S/p),	S<P<6,
2п6	2п6	|	у	2^	ехр(—р/«5), Р>5.
Поле в центре вихря остается конечным, достигая максимального зна¬
чения порядка
.A, Inf.
2тг<52	£
Образование вихря связано с дополнительной энергией. При вычис¬
лении энергии вихря при я 1 можно пренебречь изменением энер¬
гии конденсации сверхпроводящей фазы в коре вихря, и тогда энергия
вихря будет складываться из энергий магнитного поля и сверхпроводя¬
щих токов в области вне кора. Энергия вихревой линии, отнесенная к
единице ее длины, т. е. линейное натяжение, приближенно выражается
формулой
Г j2 Г h" <52 / 47г . X21	2 Фо 1 <5	г
е"=У ‘Чвт + втЫ )“‘jS?lnr 4»<-
Вклад от области кора в энергию вихря порядка (Н2/87г)7г£2, т. е. при¬
мерно в In к » 1 раз меньше, и поэтому не существен. Так как еп ~ п2
и п2 ^ |я|, то состояние из \п\ вихрей с одиночным квантом потока
фо энергетически более выгодно, чем состояние с одним вихрем, но
несущем сразу \п\ квантов потока.
б) В присутствии внешнего магнитного поля h необходимо также
учитывать энергию намагниченности вихря во внешнем магнитном поле
-Mh, где М — полный магнитный момент вихря. Из связи js = с rot М,
где М — плотность магнитного момента, создаваемым циркулирующим
сверхтекучим током, и уравнения Максвелла rot(h - 47гМ) = 0 нахо¬
дим для полного магнитного момента вихря на единицу его длины
соотношение
4-л-Л4„ = 47г JJ т d2р = JJ h d2p = пфо-
Поле, при котором становится энергетически выгодным появление вихря,
находится из условия еп — МпН = 0. Наименьшему возможному полю,
которое называется нижним (первым) критическим магнитным полем

3.4. Фазовые переходы и критические явления
535
Нс 1, соответствует вихрь с одним квантом потока фо, или Нс\ = 4тге\/фо.
Для сверхпроводника II рода сх»1 это дает
Таким образом, вблизи Тс также имеем НС\(Т) ~ (Тс - Т).
По мере превышения внешним полем критического значения Нс\ рас¬
тет число вихрей и увеличивается проникновение магнитного поля в
сверхпроводник. Эффект Мейсснера становится неполным. Состояние
сверхпроводника в промежуточных полях Нс\ < Н < Нс2 называется сме¬
шанным или вихревым. Плотность числа вихрей N связана с магнитной
индукцией соотношением В = №фо- Среднее расстояние между вихре¬
выми линиями зависит от магнитного поля примерно, как (фо/В)'/2.
Исчезновение сверхпроводящего состояния при поле Н = Нс2 представ¬
ляет собой фазовый переход второго рода. При этом расстояние между
вихрями становится порядка размера их кора £(Т), так что коры, со¬
стоящие из нормальных областей, фактически сливаются. В смешанном
состоянии вихри образуют регулярную периодическую пространствен¬
ную структуру называемую вихревой решеткой Абрикосова. Обычно —
это треугольная решетка.
3.4.7.	Верхнее критическое поле Нс2, при котором в сверхпроводнике
второго рода происходит переход, соответствует максимальной темпера¬
туре, при которой впервые появляется нетривиальное решение линеари¬
зованного уравнения Гинзбурга-Ландау. Выберем ось z вдоль оси сим¬
метрии п, а оси х и у расположим в базисной плоскости. В этой системе
координат запишем линеаризованное уравнение Гинзбурга-Ландау:
Введем параметр анизотропии е согласно 7ц = c27j. и сделаем замену
координаты и вектор-потенциала:
Тогда в новых переменных уравнение будет выглядеть так же, как и в
изотропном случае:
In я = Нс
\п X	In	X
■у (pi + ^у)'Ф + ’2’^г‘Ф =	Da	=	T-ihVа - Ца
z = ez\ Az=A’z/e,
у = у\ Ау = Ay,
х = хАх = А'х.

536	Глава	3.	Статистическая	физика.	Решения	задач
Соответственно нашему преобразованию и соотношению h = rot А мы
выразим компоненты магнитного поля в штрихованных величинах че¬
рез исходные величины:
W = {еНх,еНу,Нг}.
При этом величина магнитного поля Н' будет равна
И' = |h'| - Ve2(Hl + Ну) + Н2 = HVe4in26 + cos20,
где в — угол между осью симметрии и направлением магнитного поля.
Воспользовавшись результатом для изотропного случая, сразу получим
= Ид = Нс2 V е2 sin2 в + cos2 О
ьно
Нс2(0)
he 7х
или окончательно
с\а(Т)\	Нс2(	0)
heVr)f_i(7± cos2 0 + 7ц sin2 в)	Vcos2 в + е2 sin2 в
В кристаллах с кубической симметрией выполняется 7j_ =7ц, и вели¬
чина Нс2 не зависит от ориентации поля по отношению к осям кристал¬
лической решетки.
3.4.8.	Поверхностное критическое магнитное поле Нсз соответствует
максимальной температуре, при которой впервые возникает нетриви¬
альное решение линеаризованного уравнения Гинзбурга-Ландау с уче¬
том граничных условий для параметра порядка на границе сверхпро¬
водник-вакуум:
2(-iftV-^A)V(r)+a(7Mr) = 0, А= 1 [Н х г];
= 0.
s
Направим ось х вглубь сверхпроводника, занимающего полупростран¬
ство х > 0, а ось z — вдоль магнитного поля Н, приложенного парал¬
лельно поверхности сверхпроводника. В калибровке для вектор-потен¬
циала А = (0, Нх, 0) имеем
7h2 cPxl> 7 (2еН\2( ihc д\2	7Й2 д2ф
+	[х+2ТнёТу) *-Te7 = -e(7W
(х = 0) = 0.
'dyJ 2 дг
дф
дх
Решение, которое можно представить в виде
ф - eip»y/heip'z/hf(x)

3.4. Фазовые переходы и критические явления	537
ведет к уравнению, аналогичному уравнению Шредингера для осцил¬
лятора с массой I/7, у которого положение центра орбиты смещено в
точку х = хо:
-^/'Ч^(*-*о)2/+^/ = £/, Г(х = 0);
Xo = S’ = ^ и ^ = 1«(Л = |а(Г)|.
Благодаря граничному условию собственные значения Е кроме номера
уровня п = 0,1,2,... и импульса рг зависят также от расстояния цен¬
тра орбиты хо до границы сверхпроводника, т. е. Е = Еп(хо) + чр2г/2.
Минимальное положительное значение Е достигается при pz = 0, п = 0
и некотором значении хо-
Последнее уравнение, которое в безразмерных переменных
X	х0	.2	7^	Йс	,	,	Еп(х о)
г = _, 2о = _, Л= —= —, £f,(2o) = —,
сводится к уравнению
-f"{z) +	=	(v	+	£n(Zo)	=
имеет ограниченные на бесконечности решения — функции параболи¬
ческого цилиндра Dv с индексом и\
Еп(хр) 1 _ „	1
fuvH
Дисперсия Еп(хо) или en(zo) определяется условием на границе
fix = 0) = 0v{-x о/А) = 0, или /'(z = 0) = D'^-zo) = 0.
Численный расчет дает для минимального собственного значения emin »
«0,295 или £min « 0,59£оо, где £оо = 1/2 — собственное значение
энергии нижнего уровня осциллятора — очевидное решение при хо = 0
и хо = оо. Оптимальное положение центра орбиты zjj, отвечающее £min,
можно определить, дифференцируя граничное условие D^^-zq) = 0
по Zq и используя условие минимума u’(Zq) = 0. Тогда найдем, что
Д"(г.)(-4) = 0, и из уравнения на f(z) при z = 0 получим Zq =
= 2(£mjn)*^ « 1,1. Пространственно решение локализовано вблизи
поверхности в области z < 1.
Магнитное поле Нс3, при котором впервые возникает нетривиальное
решение гр(х) Ф 0 с поверхностным зародышем сверхпроводящей фазы,
определяется из соотношения
£min _ |о:(7')|
/ = ОЛг - го) = ‘ - *„(«,) - ^
hwH hujH
= £гт

538 -J\r Глава 3. Статистическая физика. Решения задач
Отсюда поверхностное критическое магнитное поле Нсз равно
и _	1 МЛ|с Нс2(Т)	,
н« - 2 --ZZT “ 1'69Нй<г)'
а оптимальное значение *о — порядка корреляционной длины £(Т):
Хо = 2emin£(7’) » О.бЭ^Г).
Наличие поверхности может способствовать возникновению сверх¬
проводящей фазы в параллельном к поверхности магнитном поле. Тол¬
щина возникающего при Нсз сверхпроводящего слоя — порядка кор¬
реляционной длины. По мере уменьшения напряженности магнитного
поля сверхпроводящий слой уширяется и при Нс2 заполняет весь объем.
В диапазоне полей Нс2 < Н < Нсз может наблюдаться явление поверх¬
ностной сверхпроводимости.
Значение £min можно оценить, используя вариационный метод для
уравнения Шредингера. Вариационная функция f(x) = exp(-bx2) с ми¬
нимизацией энергии Е по отношению к Ь и хо дает 2£вар = (1 - 2/7т)1/2
ИЛИ £вар « 0,60£<30.
3.4.9.	Направим ось х перпендикулярно плоскости пластины и поло¬
жим х = 0 в середине пластины. Границы пластины находятся в точ¬
ках х = ±D/2. Ось z направим вдоль магнитного поля. Соответственно,
сверхпроводящий ток течет вдоль оси у.
Решение задачи удобно провести, используя безразмерные единицы:
f=±.	ф1= Н.
‘ Фо'	13’
г г_2	.	/2е
h =
V 5 2 = 47Г7(т) ^
h и _ 2л/тг|«|.
hcV2’	с (3^ '
А
А =
HCV2S‘
Здесь фо — равновесное значение параметра порядка, 6 — глубина про¬
никновения магнитного поля и Нс — термодинамическое магнитное по¬
ле. В безразмерных единицах функционал Гинзбурга-Ландау равен
(^r-A)/f-|/|2 + !T + h:
а уравнения Гинзбурга-Ландау принимают вид
— а)2/ - / + I/I2/= о,
rot h = -(f/2x) (Г V/ - /V/*) - А|/|2, h = rot А.

3.4. Фазовые переходы и критические явления	539
Учитывая, что величины f(x) и А(х) = (0, а, 0) изменяются только вдоль
оси х, получим
^( = х2/(а2-1 + |/|2).
ах
Правая часть уравнения стремится к нулю*при к —» 0, и в первом' при¬
ближении ею можно пренебречь. К тому же, если df/dx ф 0, то в силу
к <с 1 вклад градиентного члена в функционал Гинзбурга-Ландау ве¬
лик и энергетически невыгоден. В результате имеем \{х) = const, что
также удовлетворяет граничному условию df/dx = 0 на краях пласти¬
ны при х = ±d/2. Уравнение Максвелла принимает форму уравнения
Лондонов:
d2a ,9
-ТТ = -/■а-
dx
С учетом h = da/dx и граничного условия непрерывности тангенциаль¬
ной компоненты магнитного поля на поверхности пластины, т. е.
h(x = ±d/2) = ho, находим распределение магнитного поля h = (0,0, h)
и вектор-потенциала в пластине:
A(x) = Ao_gg/>	а(х) = — sh(x/)
ch(/rf/2) ’ w / ch(/d/2) ’
Конкретное значение параметра порядка /, которое реализуется, от¬
вечает минимуму свободной энергии А7 = AJ(T, В), где В — магнит¬
ная индукция, определяемая как среднее магнитное поле по объему
пластины V:
B=I/h dV.
При фиксированном внешнем магнитном поле следует перейти к термо¬
динамическому потенциалу
Д?(Г,Ь) = ДУ(Г,В)- Г dV^,
J 4п
зависящему от внешнего магнитного поля Н. В безразмерных единицах
потенциал У, приходящийся на единицу площади пластины, и который
мы ниже будем минимизировать, равен
2 d/2
Д?(/)-£ / dx{fp-l‘ + :2
2 + 4- + h2 — 2hoh
-d/2

540 -J\r Глава 3. Статистическая физика. Решения задач
Вычисление вклада от трех магнитных членов дает
7 г*.		(Ш-\\
J/2	Л	2ch (/d/2)	V Id
d/2
Г K2dx-dh\	^	(~СГ + 0’
_J/2	2ch	(fd/2)	\ fd )
d/2
hdx = d^y ^d) .
J	fd	2 ch (Ш2)
-d/2	'	'
В итоге для термодинамического потенциала получим
дт Н2С( 2 , /4	,2 Ufd/2)\
d — 87г \	+2~h°~fd/2~)'
Из условия d(AT)/df — 0 находим связь между / и /го:
Ag-/2o-/2)[i+ch(	mUhi-
В нормальном состоянии пластины / = 0. Следовательно, критическое
поле hcr для данного значения / определяется из условия равенства
потенциалов
АПП _ А?(/ = 0)	,2	Н2С
d	d	°8тг'
Отсюда
(/) = 1 /!(2-./2)
сгЧ> 2 1 - th(/d/2)/(/d/2)'
Уравнения для ho(f) и hcr(f) при ho = hcr позволяют определить крити¬
ческое магнитное поле пластины.
Рассмотрим предельные случаи. В толстой пластине (d ;» 1) в точке
перехода значение / близко к единице и
hcr « -L(l + 1/d), d»l,
или в обычных единицах
Hcr*Hc(l+6/D), D^>6.
Разрушение сверхпроводящего перехода в толстой пластине является
фазовым переходом первого рода, так как параметр порядка в точке
перехода испытывает конечный скачок.

3.4. Фазовые переходы и критические явления	541
В тонкой пластине (d <С 1) вблизи точки перехода значение / -С 1 и
в точке перехода при
и
к«а1Г
обращается в ноль. Соответственно, фазовый переход становится фа¬
зовым переходом второго рода. В обычных единицах критическое поле
пластины будет равно
л/24<5,
D
Нсг = -Чг-Яс, £)< 6.
Определим толщину пластины Do, при которой меняется род фазо¬
вого перехода. Рассмотрим поведение разности
AJ(/) _ A3~(/ = 0) _ Н[
d	d	8ж
(■-¥!)
при малых значениях /. Видно, что толщина do = у/Ъ выделена тем,
что коэффициенты при /2 и /4 обращаются в ноль одновременно при
h\ = 12/d2. Действительно, при do < л/5, когда ho < y/\2/d, энергети¬
чески выгодно состояние с малым значением /:
2	1	- hid2/12
1 - (/iod2/12)(d2/5)
В обратном случае, если d > у/Ъ, то вблизи / = 0 не существует мини¬
мума разности потенциалов при h20d2/\2 —» 1. Но сверхпроводящая фаза
может быть энергетически выгодна уже при h20d2/\2 > 1. Для этого
требуется конечное значение /, удовлетворяющее условию
2	hid2/12 - 1
(hid2/\2)(d2/Ъ) - 1 ’
и переход становится фазовым переходом первого рода. В обычных еди¬
ницах Do — л/5<5.
3.4.10.	Выберем ось z в направлении сверхпроводящего тока, ось х на¬
правим в перпендикулярном к плоскости пластины направлении. Усло¬
вие d «С £ обеспечивает в первом приближении постоянство параметра
порядка ф по сечению пленки, которое также согласуется с граничным
условием di/>/dx = 0 на обеих сторонах пленки. В противном случае
S/ф ~ ф/d, и вклад в функционал Гинзбурга-Ландау от градиентного
члена становится слишком большим и энергетически невыгодным.

542	Глава	3.	Статистическая	физика.	Решения	задач
Второе условие d. -С 6 позволяет в первом приближении пренебречь
возможным изменением вектор-потенциала А, магнитного поля и из¬
менением плотности тока по сечению пленки. Относительная величина
поправок имеет порядок {d/5)2 <С 1. В этом приближении
О*
47е2|'0|2
и магнитное поле пренебрежимо мало: h = rot А « 0. Соответственно,
для плотности свободной энергии Гинзбурга^Ландау получим
Условие минимума AF относительно ф дает
 — -Ь- - а + /3\ф\2 = 0.
87е2 \ф\4
Полагая \ф\ = ф0/, где ф\ = \а\//3 — равновесное значение параметра
порядка, находим
и =	~(Г' - Т)Щ
Величину jc называют критической плотностью сверхпроводящего тока.
Если рассмотреть js как функцию /2, то видно, что она обращается в
нуль при / = 0 и / = 1, а при /2 = 2/3 имеет максимум. Таким образом,
jc является максимальным значением плотности тока, которое может
быть совместимо со сверхпроводящим состоянием. В точке перехода к
нормальному состоянию при js = jc параметр порядка ф скачком ме¬
няется от у/2/3 до нуля. Физический смысл найденного значения jc
можно увидеть из соотношений
1 сНс(Т)	,т	.	.
i‘~m^ri=enAT)v‘{T)-
С учетом того, что ns{T) — плотность сверхпроводящих электронов,
величине
ml hvp
= зУЗРеШ)’
где Vf и рр — скорость и импульс Ферми, можно придать смысл кри¬
тической скорости элементарных возбуждений (квазичастиц), при до¬
стижении которой происходит разрыв куперовских пар. В этом смысле
критическая скорость пропорциональна ширине сверхпроводящей щели
Д(7’), т. е. vc ос A(T)/pF.

3.4. Фазовые переходы и критические явления -г 543
3.4.11.	Условие d -С £ позволяет в первом приближении пренебречь из¬
менением модуля параметра порядка по толщине цилиндра: \ф\ и const.
Условия 6 R и d R также позволяют приближенно считать, что
вектор-потенциал А практически не изменяется в пределах толщины
цилиндра, и не делать различия между магнитными полями внутри и
вне цилиндра.
Выберем вектор-потенциал А таким образом, чтобы он имел только
компоненту Av в цилиндрических координатах (р, <р, г). Подставляя
■ф = \ф\е‘т
в плотность свободной энергии
7 (_lW _ |А^|2 + а{Т)щ2 + ||^|4 + ^
A F--k
получим
(ve - ^a)2|V>|2 + а(ТМ2 + ||^|4 +
Пользуясь тем, что V# и А приближенно постоянны по сечению ци¬
линдра, представим V# — [2е/(Йс)]А в виде среднего от интеграла по
контуру, перпендикулярному оси цилиндра и представляющему собой
окружность внутри цилиндра:
™ - !а - / (™ -!	('"1	-	!ф)	-	К-- 0
Здесь [Д0] = 27гл, где [Д0] — приращение фазы при полном обходе
вокруг оси цилиндра и п — произвольное целое число, которое обеспе¬
чивает однозначность параметра порядка. Магнитный поток через ци¬
линдр равен Ф = ttR2H, и фо — квант потока. В результате
AF = Й 6’ -	+	«<	+	"2
Целое число п выбирается из условия минимума свободной энергии,
т. е. п соответствует неравенству
1 Ф ,1
П~2 фо	2'
Критическая температура сверхпроводящего перехода Тс = ТС(Н) опре¬
деляется условием
а(Тс) + 2R* (" ~ £)2 = °’ а(Тс) = а°(Гс ~ Тс0)'

544	Глава	3.	Статистическая	физика.	Решения	задач
Относительное изменение критической температуры равно
^	~	-	х-У-
Тсо 2R аоТсо V Фо] V R J \	фо)
Зависимость АТС/ТСо от Ф состоит из периодически повторяющихся
параболических дуг с периодом фо с максимальным отношением
А Тс =	7^2	„	^(7- = 0)\2
До	8R2а0Тс0	V 2Л / '
3.4.12.	Пусть при х —► +оо имеется сверхпроводящая фаза с ф = V’o. а
в левом полупространстве при х —> — оо — нормальная фаза с ф = 0.
Выберем ось z вдоль магнитного поля Н и вектор-потенциал Л вдоль
оси г/, так что /г = dA/dx. Все величины ф, Я, А зависят только от х.
Ось х перпендикулярна плоскости границы.
В пределе я -с 1 или <5 —► 0 магнитное поле проникает только на глу¬
бину 6 •С £, и в первом приближении мы можем считать, что магнитное
поле совсем не проникает в те области, где ф ф 0. Поэтому в уравнении
Гинзбурга-Ландау мы можем полностью пренебречь магнитным полем
и вектор-потенциалом, полагая Я = А = 0 при х > 0, т. е.
Ф" + аф + РФ3 — О,
и приближенно считать, что ф(х) — 0 при х < 0. В нашем приближении
будет Я — Нс при х < 0. Домножая уравнение на ф', получим первый
интеграл:
-2f-V’/2 + аф2 + |ф4 = const = аф20 +
Здесь мы учли, что ф'(оо) = 0, и ф(оо) = фо = (М/Р)1^2 представляет
собой равновесное значение параметра порядка. Далее имеем
Фо V2t\ ф\У ?	2|а|	’
где £ — корреляционная длина. Решение уравнения есть
ф(х) = V>oth-^.
Свободная энергия сверхпроводящей фазы, отнесенная к единице пло¬
щади границы, равна
ОО
Fs = J dx^-ф'2 + аф2 + |V>4).
о

3.4. Фазовые переходы и критические явления Лг 545
Поверхностное натяжение ons представляет собой разность между Fs
и свободной энергией сверхпроводящей фазы Fsо, отвечающей случаю,
если бы все полупространство х ^ 0 была заполнено однородной сверх¬
проводящей фазой с ф(х) = фо. Итак,
Л
ОО	ОО
VNS = FS-Fs0 = j дх(^ф'2 + аф2 + |ф4) - J dx(-^j =
ОО
= frdx\2e4+(i- 4)2]
2 pj	_	ф1 V	ф1)
О
оо	оо
= £L [ dx(\ - £) =
0 J	V	ф\)	47г	J	ch4x 8тг 3 ^
о	о
В конце мы учли, как а2//3 выражается через термодинамическое кри¬
тическое поле Нс.
3.4.13.	Пусть две вихревые нити параллельны оси z и проходят в плос¬
кости z = 0 через точки г, = (х\,у\) и г2 = (*2, г/г)- Магнитное поле h
описывается уравнением с двумя источниками магнитного потока:
h + S2 rot rot h = 0oi^2(r - n) + ф0262(г - r2),
где ф01 = фо^г и ф02 = ±фовг- Знак плюс (минус) отвечает одинаковым
(противоположным) направлениям циркуляции, ег — единичный вектор
вдоль оси г, фо — квант потока. Магнитное поле является суммой двух
полей, создаваемых каждой из нитей:
h(r) = h,(r) + h2(r), h,(г) = h0(r- г,) = К0ЛГ ~ r'h
27гд	\ о /
где ho(r) — магнитное поле отдельного вихря, выраженное через функ¬
цию Макдональда Ко-
Вклад вихрей в энергию системы на единицу длины вдоль оси г
описывается выражением
Е = /h2 + ^r0t h)2 d2r — Е\ + Е2 + UB3,
где Ej — энергия отдельной вихревой нити:
= J * + й2Г' . = J 2>

546 •Ar Глава 3. Статистическая физика. Решения задач
а энергия взаимодействия нитеи дается соотношением
Ц _ Г h|h2 + J2(rot hi) • (rot h2) rf2r
J	4тг
Пользуясь тождеством
В rot A = div[A x В] + A rot B,
преобразуем последний интеграл к следующему виду:
^вз = J (hi + S2 rot rothi)~d2r + ^div[h2 х rothi]d2r =
Ф01 -h2(ri)
4n	4л
<J> [h2 x rot hi] d\.
Интеграл по бесконечно удаленной поверхности равен нулю, поскольку
магнитное поле вихрей экспоненциально спадает при условии г —+ оо.
В результате
у„(г, - гг) = isL^l = =
™	07Г	д
(Фо\Фо2)
8тг2(52
1п|^|-	€	<	|Г1	-г2|	< 5,
х \ 1/2
^ е-Ь-М, |ri - г2| > 6.
,2|г, - г2|
Таким образом, когда направления магнитного потока в обоих вихрях
совпадают {фтфт) > 0, вихри отталкиваются, а вихри с противопо¬
ложными направлениями магнитного потока (вихрь-антивихрь), т. е.
(Ф01Ф02) <	_	притягиваются.
Сила, действующая на первый вихрь со стороны второго вихря, рав¬
на по определению
р _ dUB3 _	1	Э(4>ШЬ2(Г|))	_
вз дг\ 4тг дг\
= -^[00. х rot Н2] - ^;(0oi • V)h2 = i[js2(n) х ф01].
Здесь мы учли равенство V(AB) — А х rot В + (AV)B при А = const,
а также то, что h2 = h2(х,г/) не зависит от z, и воспользовались урав¬
нением Максвелла roth = (47r/c)js. Структура полученного выражения
совпадает со структурой силы Лоренца. Обобщение выражения для си¬
лы, действующей на вихрь, на случай произвольного числа вихрей,
очевидно:
F - ~ [js х ф0],

3.4. Фазовые переходы и критические явления
где js — суммарная плотность тока в коре вихря, наведенная всеми
остальными вихрями. Вихревая линия может находиться в равновесии,
если сумма токов от всех остальных вихрей на данной вихревой линии
обращается в ноль. Это условие можно выполнить, если каждый из вих¬
рей поместить в узлы симметричной периодической решетки, например,
квадратной или треугольной.
3.4.14.	Пусть вихревая линия находится на расстоянии х от поверхно¬
сти сверхпроводника. Магнитное поле описывается уравнением
где г0 = (х, 0) и вектор ф0 параллелен поверхности и оси г. Гранич¬
ные условия на поверхности х = 0 — непрерывность магнитного поля
и отсутствие сверхпроводящего тока через границу сверхпроводника —
имеют вид
Чтобы найти магнитное поле, воспользуемся методом изображений,
рассматривая бесконечный сверхпроводник, в котором имеются два вих¬
ря с противоположными направлениями магнитного потока (вихрь-ан¬
тивихрь), расположенные на равном расстоянии от поверхности сим¬
метрично относительно х — 0. В силу симметрии граничные условия
удовлетворяются автоматически. В силу однозначности решения поле,
созданное парой вихрь-антивихрь в области х > 0, совпадает с полем
одного вихря у поверхности сверхпроводника. Пользуясь результатами
предыдущей задачи, найдем энергию взаимодействия вихря с поверхностью:
где ho — поле, создаваемое вихрем изображения. Сила притяжения вих¬
ря к поверхности сверхпроводника равна
h + 62 rot rot h = ф0б2(г - r„),
h = 0 и (js)x = 0 при х — 0.
dUB3(x) _ ф0к'0(2х)
dx	2п
87г2<52 1 (тг/хб)1/2 ехр(—2х/6), х > 6.
Внешнее магнитное поле Я, параллельное вихревой нити, наоборот, от¬
талкивает ее от поверхности вглубь сверхпроводника с силой, опреде¬
ляемой экранирующим мейсснеровским током

548 ->V Глава 3. Статистическая физика. Решения задач
текущим вдоль поверхности в направлении оси у и перпендикулярно
нити. В результате
F°tt = Рзфо =
Полная сила, действующая на вихрь у поверхности, равна сумме F =
= Sприт 4“ Тотт ■
3.4.15.	Физическое состояние системы определяется минимумом сво¬
бодной энергии. Приравнивая производные от AF по М и ^*, найдем
(Л(Г)+ВМ2 + 2G|V>|2)M = 0,
(а(Г) + Р\ф\2 + GM2)V> = 0.
Система имеет четыре возможных решения и, соответственно, четыре
возможные фазы. Нормальная немагнитная ./V-фаза:
ip = 0 и М = 0, AFN = 0.
Сверхпроводящая немагнитная S-фаза, если Т ^ Тс:
ф2 = фЪ = --р и м = 0- Ар* = ~^-
Нормальная ферромагнитная S-фаза, если Т ^ в < Тс:
ф = 0 и М 2=М20 = -1, A Ъ =
И, наконец, SS-фаза ферромагнитного сверхпроводника, если Т ниже
Тс и в\
,2 аВ — AG ЛЛ2 А/3 — 2aG
V =	о	и	М	=			5-,
РВ - 2G	рв	- 2G
AFsf = AFp —— (аД ~ Л°)2 = AFS - i-{AP ~ 2aG)2
SF F 2В PB-2G1	S	4p рв-202 '
Из последнего соотношения видно, что энергия SS-фазы всегда больше,
чем энергия S-фазы или энергия S-фазы, если константа взаимодей¬
ствия G велика: G2 > рВ/2 или велико безразмерное отношение
у/2 G ^ .
g y/PB '
Следовательно, при g > 1 SS-фаза не реализуется и осуществляется
одна из /V, S, S-фаз, которая имеет наименьшую энергию. В результате
при Т > Тс будет /V-фаза. Ниже Тс будет переход второго рода к S-фазе.

3.4. Фазовые переходы и критические явления •Аг 549
При Т < в становится возможным существование f-фазы. Однако, пе¬
реход к Е-фазе, как более выгодной, произойдет при температуре То,
когда энергии конденсации S-фазы и Е-фазы сравняются:
а (То) = А\Тр)
2(3	4В*	'
Переход при температуре То с разрушением сверхпроводящего состоя¬
ния и возникновением ферромагнитного упорядочения будет фазовым
переходом первого рода, так как при этом скачком меняется сверхпро¬
водящий параметр порядка от фо к нулю, а намагниченность скачком
увеличивается от нуля к Mq.
При относительно малой константе взаимодействия g < 1 энергия
SE-фазы в области ее существования всегда будет меньше, чем энер¬
гия S-фазы или Е-фазы. Переход из S-фазы в SE-фазу происходит на
линии А(Т)(3 = 2a(T)G. Поскольку на этой линии намагниченность М
обращается в ноль, то переход является
фазовым переходом второго рода. На ли¬
нии а(Т)В = A(T)G будет иметь место пе¬
реход из SE-фазы в F, который также яв¬
ляется фазовым переходом второго рода,
так как на линии перехода сверхпрово¬
дящий параметр порядка ф обращается в
ноль.
Итак (рис. 3.10), при g < 1 с пониже¬
нием температуры будем последовательно
иметь фазовые переходы второго рода: из
нормальной немагнитной фазы в сверхпро¬
водящую немагнитную фазы, потом в фазу
ферромагнитного сверхпроводника и далее
в нормальную ферромагнитную фазу. Ес¬
ли уравнение а(Т)В = А(Т) G не имеет ре¬
шения при любой Т < То, то фаза ферро¬
магнитного сверхпроводника существует и
при нуле температуры. Точка на фазовой
диаграмме g = 1 и Т = То представляет собой трикритическую точку, в
которой сходятся две линии фазовых переходов второго рода и линия
фазового перехода первого рода, а также соприкасаются S, SF и Е-фазы.
3.4.16.	Если вектор намагниченности M(r) = const, то магнитное поле
в объеме сверхпроводника экранируется: h = 0 и А = 0, и появляется
дополнительная энергия 2лМ2. Если быстро менять направление век¬
тора М на длине, гораздо меньшей глубины проникновения магнитного
Рис. 3.10. Диаграмма фазо¬
вых состояний ферромагнит¬
ного сверхпроводника. Сплош¬
ными линиями показаны фа¬
зовые переходы второго рода.
Пунктирной линией — фазо¬
вый переход первого рода

550	Гпава 3. Статистическая физика. Решения задач
поля 5, то магнитное поле не экранируется, h « 47гМ, и энергия 2лМ2
пропадает. С другой стороны, это приводит к отличным от нуля век¬
тор-потенциалу А и VM, что увеличивает вклады градиентных членов
в энергию системы. Период структуры будет определяться балансом
между уменьшением магнитной энергии и ростом градиентной энергии.
Пусть ось магнитной спирали направлена вдоль оси х и вектор на¬
магниченности вращается в плоскости у — z, перпендикулярной оси х,
с волновым вектором q:
Мх = 0, Му = М sin qx, Mz = М cos qx
так, что М2(х) = const. Из уравнения движения для намагниченности
-Ст^ + (А + 2в\ф\2 + ЬМ2)М = h - 4лМ
dx
видно, что \ф\2 = const и вектор h(x) также описывает спираль с тем же
волновым вектором. Это согласуется также и с уравнением Гинзбурга-
Ландау для ф. Чтобы найти связь между h и М, запишем уравнение
Максвелла или уравнение Лондонов:
rot(h - 4тгМ) = — js =
с	О
Для решения удобно ввести вектор индукции В = h — 47гМ. Тогда
, . „	В	4тгМ	d2	В	В 4тгМ
rot rot В = --5	S-,	ИЛИ 		7 = 	5-.
6	5	dx2	8	82
В результате получаем следующие соотношения:
п 47гМ	,	q282	.	..
В -= s-s- и h — - ■ . 947гМ.
1 + q2S2	1	+	q262
Величину волнового вектора найдем из условия минимума функ¬
ционала Гинзбурга-Ландау. Выпишем часть функционала, зависящую
только от волнового вектора:
AFq = %VM)2 + (h. 4тгМ)2 +
I	07Г	87ГЙ
Из условия h = rot А или h = (0, -dAz/dx,dAy/dx) находим
Ах = 0, Ау = ^ cos qx, Az = ^sinqx; и А2 = ^.
В результате получим
л I- '-т -2\ц2 _l 27гМ"

3.4. Фазовые переходы и критические явления	551
Дифференцирование по q приводит к уравнению
= 0.
47гб2
(1 +q2S2)2
Если магнитная жесткость большая, т. е. Ст > (47nS2)1/2, то решением
уравнения является q — 0, и намагниченность однородная: М = const.
При Ст < (47г<52)1/2 энергетически выгоднее неоднородное решение с
геликоидальным упорядочением. При этом волновой вектор будет равен
Период геликоида L = 2n/q. При Ст < (47г<52)1/2 он приблизительно равен
L = 2тг(Ст52/4тг)1/4 ~ 61/2.
3.4.17.	Выше температуры перехода Тс и вне непосредственной окрест¬
ности Тс флуктуации сверхпроводящего параметра порядка достаточ¬
но малы \ip\2 -с а//3, и можно пренебречь членом четвертого поряд¬
ка. В этом же приближении также можно не рассматривать и флук¬
туации магнитного поля, вызванные флуктуациями сверхпроводящего
тока, которые пропорциональны \ф\2. По определению корреляционной
функции
£	r')e~J/T
К( г, г') = <ф( г)Г(г')) =	_J/r ,
Lj Z-, е
V>*(r) ф(т)
где сумма берется по всем реализациям полей ф(г) и гр*(г), а Д —
функционал Гинзбурга-Ландау, ограниченный квадратичными членами
Д№(г)Ж(г)] = J d3r(^^L+am\2)-
Вычисления удобно провести в фурье-представлении:
Ф(г) = £<V'4r и Ф*(г) = ХЖе_,чг’
ч	ч
в котором Д принимает простой диагональный вид:
ь2 2
1/2
я
а корреляционная функция равна
(Ф(г)Г(г')) = £<«УЧГ-‘Ч'Г = £<|'0ч12)е'ч(г_г,)
чч'	ч

552 Глава 3. Статистическая физика. Решения задач
yh q /2 + а
Последнее равенство возникает, если гармоники с разными q флукту¬
ируют независимо друг от друга, т. е. (фчф*,) ~ £qq'.
Для вычисления среднего используем метод производящего функ¬
ционала Z:
\^ - X/fV’q '^q+fjq V’q + V’q ^q)
EEe 4
o-r *1 _	*4	L'	T
Z[r?q, ??„]-	-	K4 ~ _.fc2„2
EEe 4
ф; фч
Искомый коррелятор равен второй производной:
4	<4	Sr]q
Для вычисления Z воспользуемся преобразованием однородного сдвига
полей ф^ и ф*, по которым ведется суммирование:
^q-^q+^q И ф* -У ф* + £*.
При такой замене переменных значение сумм, входящих в определе¬
ние Z, не меняется, поскольку суммирование по фч и ф* ведется в
бесконечных пределах от — оо до +оо. Далее
^—г - Е [(^+Cq)^'(V’q+?q)+J)*(V’q+?<l) + (V'q +£q)»Jql
Е Е е 4
«/>,*+£,* Vq+C,
Е ч,*кчлч v-'	_	Е Ф'цк~'-Фч
= еч ЕЕе 4
ФЦ Фч
где мы выбрали величину сдвига £q = -Kqr)q и £* = -r]*Kq, чтобы изба¬
виться от линейных членов по фq и ф*. Отсюда находим производящий
функционал:
Z[Vq<Vq] = ^P{J2VqKqVq) = ехр( £ Г]* (Kq6q q- )щ>) .
Ч	q.q'
Это дает следующий результат:
(ФЧФЦ') — Sq<5qq' — 2 2/9	<W>
7 п q /1 + 01
который приводит нас к корреляционой функции
Д(г-г') = J ^ Е е?
d\	Т	ciq(r-r')	=	2Г
(2тг)3 7йУ/2 + a	yh2	47г|г	-	г'|	’

3.4. Фазовые переходы и критические явления	553
Здесь £ = Д(7/2а)'/2 ~ (Т — Тс)~'/2 — корреляционная длина или ха¬
рактерный размер области, в которой формируется новая фаза, возни¬
кающая в бесконечном объеме при Т — Тс.
3.4.18.	Благодаря малости размера гранулы по сравнению с длиной ко¬
герентности R <с £ можно приближенно считать параметр порядка гр
постоянным. Малость размера гранулы по <5равнению с глубиной про¬
никновения S позволяет пренебречь эффектами экранирования магнит¬
ного поля и приближенно считать магнитное поле внутри частицы рав¬
ным внешнему магнитному полю Я. Тогда зависящими от флуктуаций ip
в функционале Гинзбурга-Ландау остаются только градиентный и квад¬
ратичный члены. Членом с \ip\A пренебрежем в силу приближения ма¬
лости гр. Итак, рассмотрим только существенные члены:
А7= j d3r^^)2\iP\4a(T)\ip\^ = V^L(A2)+a(T)
\iP\z=Va\iP\',
где V — объем, а (А2) — среднее по объему гранулы. Выбирая вектор-
потенциал в калибровке А=[Нх г]/2, вычислим
R	7Г
■2/а Г . Г	.	H2R2
(А2) = 1 [d3r[H х г]- = 2nHJ4 [г4dr [sin26>sin вd6
V ' V J 4	(4тгй3/3)	J	J
(4тгй3/3) J	J	10
о	о
Влияние магнитного поля сводится здесь к изменению коэффициента
а —у а, т. е. к уменьшению температуры сверхпроводящего перехода.
Полная намагниченность равна производной от свободной энергии
F = -T\nZ:
dF	_dZ/dH
M = -m = Tz-
где Z — статистическая сумма. Далее
J dip* dip[V(2e2'y/c2)\ipfd(A2)/dH] ехр(-ДТ/Г)
J dip* dipexp(—A3/T)
М =
ОО
J d\ip\2\ip\2 exp(-Va\ip\2/T)
2 цт/еУ2 о	 2	Te2^R2	Н
5 с2 °г	5	с2	а(Т)+e2^H2R2 / 5с2
у d\ip\2 exp(-Va\ip\2/T)

554	Глава	3.	Статистическая	физика.	Решения	задач
Флуктуационная намагниченность отрицательна и соответствует диа¬
магнетизму, т. е. выталкиванию магнитного поля из области гранулы.
При приближении к точке сверхпроводящего перехода, когда а{Тс) — О,
намагниченность неограниченно нарастает. В слабом поле флуктуаци-
онный вклад в диамагнитную восприимчивость равен
дМ
дН
2 Te2yR2
5 с2а(Т)
1
Т - Тс
3.4.19.	В нульмерном сверхпроводнике, благодаря неравенству #<£(7"),
основной вклад в статистическую сумму Z вносит пространственно¬
независящая часть параметра порядка ф(г) = ф. Термодинамическое сред¬
нее для величины \ф\2 определяется выражением
Фо =
J d-ф* \ф\2 ехр(— У(а\ф\2 + /3\ф\*/2)/Т)
J dtp* dTPexp(-V(a\Tp\2 + 0\ф\*/2)/Т)
в котором интегрирование ведется по всем возможным значениям ф и ф*.
Величины а = ао(Т — Тс) и /3 — суть параметры разложения Гинзбур¬
га-Ландау. Далее имеем
Фо
/2/3 Т\
с
1/2 1
ю
^ dxxexp(—(sx + x2))
_ 1
(2 0Т\
\ V )
°? 0
J dxexp(-(sx + X2))
F(s) =
s, где
( v V/2
S а\2(3т)
y/ir 1 - erf(s)
и erf(s) — интеграл вероятности или функция ошибок:
erf(s)
/
е ,2 dt.
Предельные выражения для F(s) даются соотношениями
s » 1,
F(s)
Г_1_
2s'
1
у/п
-S,
7Г — 2
2тг
s, |s| < 1,
s < -1.

3.4. Фазовые переходы и критические явления -IV 555
Прежде всего отметим, что параметр порядка фо = Фо(Т) — регу¬
лярная функция температуры, плавно нарастающая с понижением тем¬
пературы. Точка Т —Тс ничем не вы¬
делена. Тем самым, строго говоря,
сверхпроводящий фазовый переход в
нульмерной системе отсутствует. Бла¬
годаря флуктуациям параметр поряд¬
ка отличен от нуля в заметной об¬
ласти температур при Т > Тс. При
s < -1 величина ф% принимает значе¬
ние ф1 « -а/Р, которое равно значе¬
нию в случае объемного сверхпровод¬
ника при Т < Тс, а при s > 1 вели¬
чина щ стремится к нулю. В области
|s| < 1 различие, благодаря конечно¬
сти объема гранулы, существенно.
Такое поведение (рис. 3.11) пара¬
метра порядка характеризуют как
размытие области фазового перехода. Область размытия определяется
неравенством
Рис. 3.11. Зависимость сверхпро¬
водящего параметра порядка от
температуры для гранулы (сплош¬
ная линия). Пунктирной линией
показан случай массивного сверх¬
проводника
1 >
a2(T)V _ H2(T)V VN(0)T2 (Т - Тс)2
2/37'	8тг Т	Т	Т2
где N(0) — плотность состояний на поверхности Ферми с данной про¬
екцией спина. Вводя характерное расстояние между энергетическими
уровнями 6е ~ (jV(O)l/)-1 и учитывая Т ~ Тс, приходим к следующей
ширине размытия области сверхпроводящего перехода:
Тп =
I Т-Тг
Если тс -С 1, то ширина размытия области перехода относительно неве¬
лика, и в области температур тс <^\Т - Тс\/Тс <С 1 приближенно можно
пользоваться формулами теории функционала Гинзбурга-Ландау.
3.4.3.	Основы теории критических явлений
3.4.20.	Статистическая сумма Z определяется выражением
2= Е
а \,...уоц
Введем матрицу
gJ<7\<T2 +
иН J
т^ет
1 (У\(ТЧ
ет
сг 1<72 +
ей*
(Г2<ТЗ+ г <?2
е1/Т+^Н/Т
/Т
1	,	иН
juNat + ‘y-(TN
■ет
е~"т \
J/Т-цН/Т ■

556	Глава	3.	Статистическая	физика.	Решения	задач
Тогда статистическая сумма Z запишется как
Z = E£"-£Ww..7™«Tr7*-=Ai
0\	(72	<7«
где Лт — максимальное собственное число матрицы Т:
Xm = eJ/T ch^- + е у/7у 1 + е4у/гsh2 ^L.
Выбирая только максимальное значение, мы подразумеваем макроско¬
пический предел N » 1. Свободная энергия равна
F(T,H) = —NT\nXm(T,H).
В нулевом магнитном поле теплоемкость равна
С(Т) = N (J/T)2
ch (J/T)
и непрерывна как функция температуры. Последнее указывает на от¬
сутствие фазового перехода при конечной температуре.
Далее находим магнитный момент М = —dF/dH и восприимчивость
X = дМ/дН:
М = цЫ- ^(цН/Т)
Ve~4J/T + sh2(^H/T)'
_ h2N	e~u/Tch (цН/Т)
X T [<r4'/r + sh2(мЯ/Г)]3/2'
Высокотемпературный предел Т» |/| дает результат для свободных спи¬
нов М —	/	Т). Низкотемпературное поведение зависит от зна¬
ка J. Для ферромагнитной цепочки (/ > 0) при Т —> 0 имеем насыще¬
ние: М = fiN. Для антиферромагнитной цепочки (/ < 0) поведение при
Т —► 0 зависит от величины магнитного поля. Пока /гЯ < 2|/|, полный
магнитный момент М = 0. При цЯ > 2|/| все спины выстраиваются в
одном направлении: М = fiN. Восприимчивость в нулевом поле, равная
Х(т)=^еи/Т,
при Т —> 0 расходится, если / > 0, и зануляется, если / < 0.
3.4.21.	В обозначениях предыдущей задачи коррелятор спинов в узлах
тип можно представить в виде
(о’т'Тл) = Z ^2 ^2 . . . ^2	'	■	'	Tom_{omVrnTomom+i	'	'	'
0\	<Т2	(JN
■ • • Ton_w°nTonon+i • • • ToNo, = Z-1 Tr(Tm-lSTn-mSTN-n+l).

3.4. Фазовые переходы и критические явления ->v 557
Матрицы Т и S имеют вид (для краткости положим a — J/Т)
В представлении, где матрица Т диагоналвна, т. е.
А+ = 2ch а,
Т
матрица S принимает вид
-ft
А_ = 2sha,
"С о>
Перемножая матрицы и вычисляя след, найдем
('РтРл) =
Z-1 Тг
/А”-1 0 \ /О 1\/а;-’ 0 \/0 l\/A^-m+1	о
\ о АГ7М оД о \пГт/ \ 1 оД
+
дМ—т+1
В результате получим
yj-(m-n)уп-п ^N-{m-n)уп-п	/д \т—п
<<Tffi(Tn> = “	~	V W ’
где в последнем равенстве мы учли предел N —» оо. Окончательно с
учетом симметрии т <=* п имеем
М = (th i)1”'"1 - (sp.fll—1/«п.
Корреляционная длина £(Г) равна
Г jn/т
При высоких температурах корреляционная длина не превышает рас¬
стояния между ближайшими спинами. С понижением температуры £(Г)
неограниченно возрастает, обращаясь в бесконечность при нулевой темпе¬
ратуре. Тем самым, дальний порядок, ферромагнитный, когда (атстп) = 1,
или антиферромагнитный, когда {сттап) = (— l)lm_nl, возникает только
при 7 = 0.

558 Глава 3. Статистическая физика. Решения задач
3.4.22. Пусть в данной случайной реализации цепочки Изинга из пол¬
ного числа N =	+	N% обменных констант, N\ констант имеют зна¬
чение J\, a N2 констант — значение /2. Используя рассмотрение двух
предыдущих задач, найдем статистическую сумму Z, отвечающую дан¬
ной реализации констант:
Z = Tr(7fTf) = Tr(Af|A^{ + A^Afi),
где матрица Т и ее собственные значения А+ и А_ равны
„	(	еа	е~а\	А+	=	2ch	а,	у,,
т=\ -с q и \ о и « = «1,2 = -=г-
\е е / А_ = 2sha,	Т
В макроскопическом пределе N\, N2—>ос следует ограничиться толь¬
ко максимальными значениями А]+ и А2+. Тогда свободная энергия равна
F(NUN2) = -T(Ni In А,+ + N21п А2+) = ~Nt($ In A1+ + ^ In A2+).
Усредняя по всем случайным реализациям, найдем среднюю свободную
энергию F — {F(Ni,Ni)) и среднюю теплоемкость С(Т) = -T(d2F/dT2):
F = —NT(pi In Ai+ + p2 In A2+),
2 2	2	2	Г/	2	2	i
C(T) _ piot\ +P2CX2 + P\P2[{ot\ -I- a2)chai cha2 — 2aia2 she*: sha2j
N	(pi	ch	a\ + p2 ch a2)2
3.4.23. Для вычисления статистической суммы Z представим гамиль¬
тониан системы в виде
Is 9 N
^ = -ОЛ/Ё0-') -мЁ
2N
1= 1	f=l
и воспользуемся формулой
еЬ*/4а = (£)'/2 J dm e~am2+bm (fl > Q)
— ОО
для линеаризации квадратичного члена с суммой по спинам. Обозначая
через вектор сг все возможные состояния системы, имеем
rr	J	~

3.4. Фазовые переходы и критические явления	559
где функция f(m) равна
г/ \ т2 ТI Го ufJm + pH\
f(m) = у - 7 ln 2ch^ ^-)
В термодинамическом пределе N —* оо основной вклад в Z дает окрест¬
ность точки т = то(Т,Н), где /(т) минимальна. Условие df{m)/dm — О
дает самосогласованное уравнение:
iUJm0 + pH
пг о = tn -	.
В нулевом магнитном поле Н — 0 при Т > J уравнение имеет только
тривиальное решение то — 0, а при Т < J возникает нетривиальное ре¬
шение с то ф 0, которое вблизи Т = J принимает вид то = [3(7’—У)//]1/2
и стремится к mo = 1 при Т = 0. В слабом магнитном поле Н —► 0 при
Т > J значение то подчиняется закону Кюри:
m -
то =
Т -
Свободная энергия, отнесенная к одному спину, приближенно равна
ЗШ»^_Г1П[2сЬ(^)].
Чтобы проиллюстрировать физический смысл параметра т, проин¬
терпретируем представление Z, как статистическую сумму системы с
гамильтонианом
m	N
H[m, а] = — m2 - (Jm +
1	i=	1
1/2 °°
Соответствующая эффективная свободная энергия в зависимости от m
равна
F[m] = -71п^е-я1т‘т1/7'.
а
Вычисляя минимум .F[m] по отношению к параметру т, из условия
dF[m]/dm — 0 получаем соотношение
1=1	<Т	1=1

560	Глава	3.	Статистическая	физика.	Решения	задач
Поскольку (а) есть термодинамическое среднее значение спина на уз¬
ле г, то параметр т имеет смысл средней намагниченности в системе.
Кроме того, уравнение, определяющее то(Т,Н), совпадает с уравнени¬
ем для намагниченности в теории самосогласованного (среднего) по¬
ля. Следовательно, для рассмотренной модели с бесконечным радиу¬
сом взаимодействия приближение самосогласованного (среднего) поля
является точным.
3.4.24.	Выше точки сверхпроводящего перехода Тс в нормальной фазе
можно пренебречь в первом приближении членом четвертого порядка в
функционале Гинзбурга-Ландау:
Здесь а(Т) = ат, где т = (Т - Тс)/Тс — близость к точке перехода. Вы¬
числение удобно проводить в фурье-представлении:
Термодинамический потенциал AF^-TlnZ, где статистическая
сумма Z является суммой по бесконечному числу реализаций поля па¬
раметра порядка ф(х). Перебор всех возможных фурье-компонент фу
эквивалентен перебору всех возможных реализаций поля ф(х):
Вычисляя в данном произведении значение суммы с фиксированным к,
найдем
A5'[V>(x),V>*(x)] = Jdx[j|-ihS7ip\2 + а(Т)\ф\2 .
ф(х) = £>ke““,
к
в котором функционал приобретает вид
Re i/'k.Im ifa
k ReV'k
Re г/

3.4. Фазовые переходы и критические явления	561
Окончательно, получаем выражение для статистической суммы:
7Г Т
г = П
k ат + ~/h k /2
и тогда термодинамический потенциал равен
жТ	^	I	жТс
AF=-TY In ln
™-4-л,Й2Ь2/ 9	^
ат + ~fh2k2/2	ат + -yh2k2/2
Поскольку из дальнейшего будет видно, что наиболее сингулярное
поведение связано с областью малых волновых векторов к и малостью
ат, то в остальных местах выражения для AF можно пренебречь раз¬
личием между Т и Тс. Тогда сингулярная поправка в теплоемкость
С — -Td(AF)/dT2, обусловленная флуктуациями параметра порядка,
будет равна
:п t ч ^~\^{AF) _	а2	_ fVdddk (2a/jh2)2
ОСiing(r)- lc dr2 -2^{aT + jh2k2/2)2 J (2n)d (k2+2arhh2)2'
где Vd = Ld — объем в пространстве размерности d. Вычисление ин¬
теграла дает следующую сингулярную поправку в теплоемкость при
d< 4:
АГ м _ КА ~ d) (2а\ 5 / П ¥	1_
OCsinglr; - (27r)MsjnM/4)	{т)	т(4-<о/2-
где	Sd — поверхность d-мерной сферы. При d =	4	особенность	поправ¬
ки	— логарифмическая SCsmg ~ 1п(1/т).	В	размерности d>4	особен¬
ности вообще не возникает, и роль флуктуаций параметра порядка не
существенна.
В обычной размерности d = 3
SCsing(r) - g7r ^д2 J	(tJ	.
Сравнивая эту величину со скачком теплоемкости, возникающим при
полном пренебрежении пространственными флуктуациями параметра
порядка
Va
АС =
0ТС'
где 0 — коэффициент при |V>|4, оценим число Гинзбурга-Леванюка

562 -l\r Глава 3. Статистическая физика. Решения задач
3.4.25.	Для решения задачи удобно ввести угловые переменные
S* = cos и Syt = sin ipt,
в которых гамильтониан примет вид
Д; = -y]Tcos(yjr - <^г+а).
г,а
Представим коррелятор спинов в виде
2т	2т	у	„
(SrSr'} =	=z~l	J ... J (Пd4>xy^-^eJ	^ ^ ,
О 0 х
где Z — статистическая сумма:
2i	2f	j
/Г	ч	r	2^cos(^x-^x + «)
■■■ j{\[dipx)eT"
О	0 х
Рассмотрим сначала область высоких Т » / температур и корреля¬
тор между ближайшими соседними спинами в узлах г и r + а. При
Т » / экспоненту в формулах, приведенных выше, можно разложить
в ряд, и мы ограничимся членами ряда по J/Т -С 1 не выше линейного.
Принимая во внимание, что
2*
j dp>x eiipt = О,
убеждаемся в том, что в коррелятор между ближайшими соседними
спинами в узлах г и г + а из всей суммы по узлам ненулевой вклад
внесет только слагаемое сх = г. Поэтому
2т
(е'<'*-<*+*>) * j j d<pr	cos(pr	- *>r+a) =
о
В пределе высоких температур мы ожидаем быстрое спадание кор¬
реляции в направлении спинов с ростом расстояния между ними, и в
первом приближении мы можем пренебречь какой-либо корреляцией
между исходным спином и спином, следующим за ближайшим сосед¬
ним спином. Тогда приближенно можно записать:
^e‘('fir-Vr+n.)^ яз (e‘(4>'-Vr+,)'j ^e‘(<Pr+,-‘Pr+2.)'j . . . ^g‘(v»г+(л-|).-¥’г+/|.)^>

3.4. Фазовые переходы и критические явления	563
где следует взять кратчайший путь от узла г к узлу r+яа. Окончательно
(SrSr+na) ~ (J/2T)n = e-nmT/J) (Т » /),
т. е. коррелятор спадает экспоненциально с расстоянием между спина¬
ми, и корреляционный радиус £ ~ 1/ ln(27’//)	1.
В пределе низких температур Т / энергетически выгодно макси¬
мальное значение cos(<^r — <^г+а), или чтобы фг медленно менялось на
расстоянии между двумя соседними узлами. Другими словами, корре¬
ляционный радиус должен быть гораздо больше периода решетки. В
этих условиях можно использовать приближение
/	\	1	(фг — Уг+а)
cos(y>r - ffir+л) « 1	j	’
Далее опуская единицу, которая приводит к сдвигу уровня отсчета энер¬
гии, и используя приближение
а
где а __ постоянная решетки, приходим к эквивалентному гамильтониану
Н=Ц (Vrfdxdy
с учетом правила перехода от суммы по узлам к интегралу по площади
a2Y,~* J dxdy ■
Г
В параметризации пх = cos у> и пу = sin у? имеем n2 = 1 и
Н = ^ j (Vn)2dxdy.
Распределение Гиббса с гамильтонианом Н[ф)] является гауссо¬
вым, и можно воспользоваться соотношением
^giMr)-¥>(r')]^ _ е—<[<^(г)—<р(г')|2>/2
для средних величин, распределенных по Гауссу. Среднее значение
i((v?(r) - ф'))2) = (<р2(г)) - (ф)ф'))
можно вычислить, используя фурье-представление
ф)=y. wlv (*>;=^-ч)>
q

564	Глава	3.	Статистическая	физика.	Решения	задач
в котором коррелятор имеет вид
ШФ')) = 5>Ч¥у>*‘чг+‘ч'г'.
чч'
и гамильтониан диагоналей по
H = lj:jq2\<pq\2.
ч
В нашем случае распределение Гиббса ~ехр(-Я/7’) представляет со¬
бой гауссовское распределение для флуктуирующей величины ipq. В
результате это дает
(</V/y> = <Ы2)<*-ч.ч' и (1^ч12) = Т2-
Jq
В итоге мы получим, что
\{\Ф) - Ф')\2) = £ 72 0 - е'ч(г_г,)) -
q ^
оо	2-к	оо
_ Г [ qdq Г d.0   t<7|r-r'|cos6>л _ Т Г 1 - J0(q\r - г'|)
0	0	о
Интегрирование по углу 0 выдало нам функцию Бесселя нулевого ин¬
декса Jq(x). Интеграл по q расходится на больших волновых векторах
логарифмически. Расходимость связана с неприменимостью контину¬
ального приближения на больших q ~ 1/а, с которыми связаны быстрые
изменения поля у? на масштабах порядка периода решетки а. Поэтому
мы должны устранить расходимость интеграла на волновом векторе
q ~ 1/а. Это дает следующую оценку для среднего значения:
и, соответственно, степенное поведение корреляционной функции с бес¬
конечным радиусом корреляции в низкотемпературной области Т <с /:
/	„	\	Т/2ж/
<srsr,> =	=	.
Из вида коррелятора спинов можно заключить, что в АТ-модели,
строго говоря, нет спонтанного спинового упорядочения. В противном
случае из того, что при |г — г'| —у оо коррелятор спинов расщепляет¬
ся (SrSr<) —► (Sr)(Sr») и обращается в нуль, следует (Sr) = 0. С другой

3.4. Фазовые переходы и критические явления	565
стороны, по мере уменьшения температуры в области Т ~ / должно
происходить изменение поведения коррелятора от экспоненциального к
степенному. Согласно гипотезе подобия или теории скейлинга в точке
фазового перехода корреляционная функция имеет степенную зависи¬
мость от расстояния, причем для размерности пространства d — 2 дол¬
жно быть
(SrSr/> ~ |г - г'Гч*
Это соответствует критическому индексу Фишера, зависящему от тем¬
пературы, т. е. г] = T/2ttJ. Наивысшая температура 7вкт ~ /. при кото¬
рой экспоненциальное спадание коррелятора сменяется на степенное,
соответствует специфическому фазовому переходу, который называется
переходом Березинского-Костерлица-Таулеса.
3.4.26. Масштабная размерность плотности термодинамического потен¬
циала равна размерности пространства d, т. е. трем. Поэтому из раз¬
мерности psv2 имеем соотношение APs + 2ДУ, = 3. Так как согласно
ih ip* Vip — ipVtp*
масштабные размерности гр сокращаются, то масштабная размерность
vs равна AVs = 1 и, следовательно, APs = 1. Последнее означает, что
ps ~ £-1, где £ ~ \т\~и — корреляционный радиус, имеющий ту же мас¬
штабную размерность = 1. Отсюда ps ~ тv и, используя скейлинго-
вое соотношение vd — 2 — а, окончательно получим критическое пове¬
дение ps ~ (-t)(2_q)/3 (т ^ 0) с индексом (2 - а)/3.
3.4.27. При подходе к точке фазового перехода характерный масштаб
флуктуаций параметра порядка р неограниченно возрастает. Длинно¬
волновые флуктуации ip описываются гамильтонианом Ландау
Я = Я[<А,;<7о] = J dx	+ go<P* -
в котором поле <р(х) сглажено. Сглаженность означает, что в фурье-раз-
ложении
<р(х) = J2 Фче'чх
Ч<Чо
отсутствуют гармоники с большими волновыми векторами q > qo- Ре¬
шение проблемы сводится к анализу статистической суммы
Z = Tre~w = [ П d<pqe-Hte"4o],
ЖЧо

566 ->V Глава 3. Статистическая физика. Решения задач
представляющей собой многомерный интеграл по всем значениям ipq,
изменяющимися в интервале от —оо до +оо. Прямое вычисление инте¬
грала представляет собой затруднительную задачу.
Интегрирование по части импульсов в интервале волновых векторов
А<7о < qo (А < 1) или сглаживание SA приводит к новому эффективному
гамильтониану ЯА = S\H, который следует определить согласно
e~SxH = / П dvqe-"^\
Xq0<q<qo
и, соответственно, разделить поле v?(x) на медленную </?о(х) и быструю
<£>i(x) части:
у?(х) = у?о(х) + ф\(х),
<Ро(х) = J2 ФчеЩ% и <МХ) = J2 Фче‘"х-
Ч<Мо	Xq0<q<qo
Согласно гипотезе подобия гамильтониан ЯА — S\H должен иметь ту
же структуру, что и исходный гамильтониан Я, а в самой точке фазо¬
вого перехода не изменяться.
Для сравнения ЯА = S\H и исходного гамильтониана Я необходимо
произвести обратное изменение пространственного масштаба до преж¬
него размера:
q -»q' = а~‘<7,
и одновременное преобразование масштаба или растяжение D\ поля
параметра порядка у?(х):
Фч Фц' = ^х 1Фхq' = %х Vq-
Растяжение D\ преобразует гамильтониан Я, в котором изменяет вол¬
новой вектор в Л-1 раз, длину в А раз, и поля в ZA раз:
DxH[ipq\qо] = H[Zx<Px-'q''’ А_1<7о] =Я'[^;А_,<7о]-
Последовательное применение сглаживания SA и растяжения D\ на¬
зывается ренормировкой гамильтониана: Rx = D\S\. Ренормированный
гамильтониан
#АЯ[у>ч;д0] = Я[ДАу?А-1ч; А_|<7о] = #' [<Pq'; И
описывает флуктуации нового поля в неизменной области волновых век¬
торов q < qo. Если система находится в точке фазового перехода, то
ренормированный гамильтониан не должен изменяться и зависеть от

3.4. Фазовые переходы и критические явления	567
выбора волнового вектора qo• В противном случае после многократного
ренормирования мы придем к достаточно большим масштабам (малые
Xqo), которые превышают корреляционную длину и отвечают некорре¬
лированным гауссовым флуктуациям поля ip.
Рассмотрим ренормирование гамильтониана свободного поля Но в
пространстве размерностью d:
А
Н0[фч-,Яо] = ^ J ^2 + Го)1^ч12^уг
Я<Чо
Так как <рч с разными q не взаимодействуют друг с другом, то сгла¬
живание сводится к появлению постоянного слагаемого, возникающего
при интегрировании по <рч в интервале векторов от Xqo до qo и приво¬
дящего к сдвигу отсчета энергии:
= i J (Я2+то)\Ф*Е lnf4^
?<л,„
Постоянное слагаемое, как несущественное и не зависящее от tp, мы
опускаем. Ренормированный гамильтониан будет равен
RxH[pq\qo] = J (АУ+ то)|<А,|2^.
Ч<Чо
Для гамильтониана свободного поля точка то = 0 — точка фазового
перехода. В этой точке ренормированный гамильтониан не изменяется,
если мы выберем
zA = л-^2»/2.
При этом то преобразуется по закону
го -* то = А~2то,
соответствуя масштабной размерности = 2.
Рассмотрим теперь гамильтониан Ландау Н = Но + Hi, где Hi — га¬
мильтониан взаимодействия:
f 4/ u	[f[	ddqi	ddq2	d%_
Hi — So I Ф (x) dx — go JJJ	(2т)й	(27r)rf	(2^)^'
<?l.?2.?3<?0
Его прямое интегрирование затруднительно из-за члена с взаимодей¬
ствием у?4, поэтому интегрирование мы проводим по теории возмуще-

568	Глава	3.	Статистическая	физика.	Решения	задач
ний, выбрав в качестве нулевого приближения гамильтониан свободно¬
го поля Но- Воспользуемся тождеством
I П dv*e н'е
e-S>H _	«■<£«	 Г	П	е-Н,	=	{е-Н,)ое
J П dpqе ° Xqo<q<qo
-Hi „-Но
-SxHo
Xq0<q<q0
и представим сглаженный гамильтониан как
SxH = SXH0 - \n(e~H‘)o.
Вычисление последнего слагаемого проводим в виде разложения в ряд
по константе взаимодействия go, предполагая ее малой:
п=О
(е % = £<-1>"§( f dx(vo(x) + <Pi(x))4
Сглаживание не затрагивает медленную компоненту (у>о(х), которая иг¬
рает при вычислениях роль внешнего параметра. Мы ограничимся здесь
только первым и вторым порядком по константе взаимодействия go:
(е Н‘)о = 1 - go((<Po + <Pi)4)o + ^(Vo + Ф\)*(ф'о + ф'\)*)о + • • •
Для краткости мы опустили знаки интеграла. Рассмотрим первый порядок:
((фо + <Pi)4)o = Фо + 4ф\(ф\)о + Ьфо(ф2\)о + *Фо(ф\)о + (ф\)о =
= ^ +	6^СЛ + С(Л2),	Gx = (rf) о и	Gf = (v\)o.
Члены	с	нечетным числом	ipi обнуляются.	Итак, в первом	порядке по go
имеем
SXH = SXH0 -go j dx [yjJ(x) + 6y>§(x)GA + G^2)].
Последний член, независящий от у?о. представляет собой непринципи¬
альный сдвиг уровня энергии и может не рассматриваться. Второй член
означает сдвиг то, т. е. температуры фазового перехода:
т0 -+ Sxt0 =	т0 + 6т0 = т0 +	12g0GA + O(go).
В точке	фазового перехода должно быть	т* = то + бто —	0. Константа
взаимодействия в первом порядке остается той же самой:
go -> Sxg0 = go + 0(g§),

3.4. Фазовые переходы и критические явления	569
и для определения ее сдвига необходимо рассмотреть второй порядок
теории возмущения. Рассматривая в разложении логарифма 1п(е-я,)о
члены, пропорциональные g\<pQ, найдем
go -+ Sxgo = go- 36g*0Kx,
где неприводимый коррелятор Кх дается соотношением
= ^[(<rf(x)<rf(x'))o - (<rf(x))(rf(x')o].
Растяжение Dx дает следующие преобразования для то:
Dxro = Z\\d = Л-2т0
и для go:
Dxgo = Z{\3d = Ad-4g0 = X~ego (d = 4 - e).
Последнее соотношение легко увидеть из представления члена с вза¬
имодействием в виде трехкратного интеграла по волновым векторам.
Размерность d = 4 в некотором смысле выделена, и в дальнейшем мы
считаем е< 1.
Ниже мы будем интересоваться волновыми векторами медленной
компоненты, гораздо меньшими быстрой компоненты (А -С 1), и для упро¬
щения можно положить волновые векторы медленного поля равными
нулю, т. е. рассматривать компоненту у?о(х), как приближенно постоян¬
ную величину. Для вычисления Кх можно воспользоваться следующим
соотношением для средних от гауссовых интегралов:
J dxdx' (rf(x)d(x'))о =
= J dxdx1 (yj2(x))o(<gi(x'))o + 2 J dx dx' (tpi(x)</?i(x'))o (ум(x') ipi(x))o-
Это соотношение можно получить из среднего для фурье-гармоник
(Фч<Р-чФч'Ф-Ч')о = (<Pq<P-q)o(<Pq'V>-q')o + (<Pq<P-q)o <5ч'.-Ч + (^Ч<Р-ч)о
пользуясь независимостью фурье-гармоник
(Vq^q^O = (IV’q^O^q'.-q	(Ф-q = V’q)
и соотношением (|<А)|4)о = 3(|<^ч|2)о- Итак,
?0
Кх = J dxdx1 (¥>i(x)<^i(x'))o(vi(x/)^iW)o = У (|<^ч|2)о<|¥’-ч|2)о-

570 ->\r Глава 3. Статистическая физика. Решения задач
Выберем то таким образом, чтобы ренормированное то обратилось в
нуль, и тем самым, чтобы система находилась в точке фазового пере¬
хода, т. е. (|v?q|2)o = 1 /q2- Тогда
где Sd — площадь сферы единичного радиуса в d-мерном пространстве.
В первом наинизшем приближении нам достаточно положить е = 0. Учи¬
тывая, что S4 = 27г2, получим
Малый параметр, по которому ведется разложение, будет go In А <С 1.
Ренормированное значение константы взаимодействия g(A) = R\go
с учетом растяжения равно
В нашем приближении go 1. С точностью до первого порядка по g
мы можем заменить go на g и получить уравнение ренорм-группы
Функция /(g) называется функцией Гелл-Манна-Лоу. Она была опре¬
делена нами в низшем первом порядке разложения по константе взаи¬
модействия g и, вообще говоря, подлежит дальнейшему вычислению и
уточнению.
Неподвижную или фиксированную точку ренорм-преобразования g*,
в которой константа взаимодействия не меняется, находим из условия
Малость б <с 1 оправдывает наше приближение малой величины кон¬
станты взаимодействия.
Масштабная размерность АТ величины т подразумевает, что т при
ее ренормировании R\ подчиняется скейлинговому закону:
Чо
ddq 1 _
А-£ — 1
(2ж)“ qA (2n)d
е
Ка = -А1пА и SAg0 =g0 +-^golnA-f O(gg).
Дифференцируя no In А, получим
/(Г) = 0:
т —» т(А) = R\t = А Атт, или	■	-Дт-
a In А

3.4. Фазовые переходы и критические явления	571
Найдем размерность величины т вблизи неподвижной (фиксированной)
точки g*. Для этого нужно вычислить ренормированную величину т с
точностью до первого порядка по е. Начнем с вычисления значения G\\
0Л-|л^(х)= I 0<Ыя)|2) = ^ /
Xqo<q<4o	bqo
Чо
qd-'dq
q2 + то
При вычислениях с точностью до первого порядка по е достаточно
положить d — 4. Тогда приближенно новая температура фазового пере¬
хода г* определяется из уравнения
Яо	Я	о
3
0=т*+ i?>е° I 7Т7 = г‘+ 2?ё0 J4 (‘ - 77т)'м'
Xqo	Xqo
Ренормирование то нам дало уравнение
Чо
Rxt0 = А~
то + 5?го/,(1-?Т^)
Xqo
dq.
Однако, при анализе этого уравнения мы должны иметь в виду, что в
результате учета взаимодействия флуктуаций произошел сдвиг точки
фазового перехода из то = 0 в новую точку то = т*, и, следовательно,
нам уже нужно отсчитывать температуру от новой точки фазового пе¬
рехода т*. То есть, мы должны рассмотреть ренормирование величины
г' = то — т*. В результате в первом порядке по go получим
Чо
3go
т(А) = Rxt^ =	-	^t'q	j
1 + 3S® 1пАК,
2тг2
1пт = In то - 2 In А + ln^l + In А^ « In то - ^2 - In А.
Заменяя go на g, получим уравнение ренорм-группы на величину т:
Arte). Arte)-2-^,+ ....
Наконец, полагая g = g* = 2тт2е/9, найдем масштабную размерность вели¬
чины т в неподвижной (фиксированной) точке — точке фазового перехода

X
572	Глава	3.	Статистическая	физика.	Решения	задач
Критический индекс v для корреляционной длины £ ~ \t\~v равен
i = l2 + T2 +
что в интересующем нас случае е = 1 дает приближенное значение
v = 7/12 «0,6.
Пользуясь скейлинговым соотношением du = 2 — а при d — 4-е,
находим в первом по е приближении критический индекс для теплоемкости:
е
6'
Критический индекс /3 параметра порядка <р(х) найдем, пользуясь
соотношением (3 = vA^. Выше мы нашли, что при масштабном пре¬
образовании фурье-компонента параметра порядка ipq умножается на
множитель 1 = A<d+2)/2. Соответственно, сам параметр порядка у>(х)
переходит в Z^l\~dip(x) = \~(d~2^2ip(x) в силу </>(х) = f <pq ddq/(2n)d и
q —*• A_lg. Таким образом, в нашем приближении масштабная размер¬
ность параметра порядка равна
д —	—	j	_	£
*ч>	2	2‘
Далее легко находим
Индекс восприимчивости 7 можно определить из скейлингового со¬
отношения а + 2/3 + 7 = 2, и он равен
7=1 + | + 0(е2).
Индекс Фишера С в линейном приближении по е оказывается рав¬
ным нулю, т. е. £ = 0(е2). Дело в том, что в линейном приближении по g
или по с коэффициент при q2\tpq\2 после сглаживания S\, как мы виде¬
ли, не меняется. Вместе с этим и масштабный коэффициент Z\ остается
тем же, что и для гамильтониана свободного поля, т. е. Z\ — A-<d+2)/2.
Соответственно, поведение коррелятора К(х,х') — (<p(x)ip(x')) в точке
фазового перехода не изменяется по сравнению со случаем гамильто¬
ниана свободного поля, для которого К(х, х') ~ |х — x'|~(d~2).
Итак,
1 а 1	7	7	/-	л
«=-,	/3=-,	7=0.	v	—	|2	’	<	= °
в линейном е-разложении при е = 1. Эти значения неплохо согласуются
с экспериментом.

ДОПОЛНЕНИЯ
1.	ДЕЛЬТА-ФУНКЦИЯ	ДИРАКА
И ДРУГИЕ ОБОБЩЕННЫЕ ФУНКЦИИ
^-Функция Дирака является обобщенной функцией (распределени¬
ем) и определяется как линейный функционал на множестве так назы¬
ваемых основных(или «хороших») функций Ф. Если функция f(x) € Ф,
то (5-функция определяется как функционал, ставящий в соответствие
функции f(x) ее значение в точке х = 0:
№)]=/( 0).	(Д.1)
При практических расчетах, как правило, достаточно ограничиться
подходом, при котором (5-функция (не являющаяся функцией в обычном
смысле) понимается, как ядро линейного интегрального оператора. В
этом случае функциональное равенство (Д.1) переписывается в виде
ОО
f f(x)S(x) dx — /(0).	(Д.2)
— ОО
Таким образом, все вычисления с (5-функцией должны рассматриваться
в интегральном смысле, как в формуле (Д.2). В остальном, соблюдая
известную осторожность, с (5-функцией можно обращаться, как с обыч¬
ной функцией.
Функции из пространства Ф должны обладать гораздо лучшими свойства¬
ми, нежели функции i/>(х) € i2(K), которые обычно используются в квантовой
механике. (Пространство L2 квадратично интегрируемых функций представ¬
ляет собой реализацию гильбертова пространства.) Примером конкретной
реализации пространства Ф является пространство Шварца S: пространство
бесконечно дифференцируемых комплекснозначных функций, которые убыва¬
ют вместе со своими производными на бесконечности быстрее любой степе¬
ни 1/х. Такие функции принято называть «хорошими» функциями.

574	Дополнения
Используя (Д.2), можно получить различные соотношения с участи¬
ем (5-функции:
6(-х) = 6(х),	(Д.З)
х6(х) = О,	(Д.4)
6(ах) = ±*(д), а ф О,	(Д.5)
f(x)6(x - а) = f(a)S(x - а),	(Д.6)
WW) = ±	<Д V
где f(xj) = 0, Xi	—	простые (некратные) корни, п — число таких	корней
на всей оси х.	На	основе (Д.2) можно получить выражение	для	произ¬
водной от (5-функции:
ОО
f f(x)6'(x)dx = -f'(0),	(Д.8)
— ОО
а также обобщение (Д.8)
f(x)6M(x)dx = (-l)nfM(0).
I
Важными для приложений являются различные представления (5-функ-
ции в виде пределов последовательностей функций из пространства L2,
например,
Г/ ч	sin	Я* .. К	•	1	К	,п„,
S(x) = lim 	=	lim	—=е	=	lim	--5-5	,	(Д.9)
К—*оо ЛХ К-юо у/л	Л—оо Л К X +1
причем эти пределы понимаются также в интегральном смысле, т. е.
переход к пределу осуществляется после вычисления интеграла соглас¬
но (Д.2).
Функции, находящиеся под знаками пределов в (Д.9) при достаточ¬
но больших, но конечных значениях К, характеризуются наличием рез¬
ких положительных максимумов в точке х = 0, в то же время инте¬
гралы от этих функций по всей числовой прямой остаются равными
единице. Это — примеры так называемых сглаженных (физических
или «размазанных») (5-функций, которые дают возможность получить
наглядное представление о математической (5-функции.

2. Цилиндрические функции полуцелого индекса	575
Используя первое из равенств в (Д.9), нетрудно показать, что
ОО
8(х) = g- / eikxdk.	(Д. 10)
— ОО
Это — интегральное представление (фурье-]зазложение) 5-функции.
Обобщение 5-функции на трехмерный случай производится очевид¬
ным образом и дает соотношение
5(г) = 8(х)8(у)8(г) =-^ [ eikr dk,	(Д-11)
(2тг) J
где интегрирование ведется по всему k-пространству. Важное значение
имеет равенство
Д(1) = -47г5(г),	(Д-12)
которое говорит о том, что 1 /г является решением уравнения Пуассона
с точечным источником (фундаментальным решением).
Еще одним примером обобщенной функции является ступенчатая
функция или Q-функция Хевисайда:
0(дс) = |°’ Х<	(Д-13)
\\, х^О.
По аналогии с (Д.9) функцию 0(x) можно представить в виде предела
= llm[i a.c'gi + i].
Важным для приложений является соотношение, понимаемое также в
смысле (Д.2),
в'(х) = 8(х),	(Д-14)
т. е. 5-функция является производной 0-функции.
2.	ЦИЛИНДРИЧЕСКИЕ	ФУНКЦИИ
ПОЛУЦЕЛОГО ИНДЕКСА
Функции Бесселя с индексом и = 1 + 1/2, где / = 0,1,2,..., появ¬
ляются при решении уравнения Шредингера методом разделения пе¬
ременных в сферической системе координат. Обычно рассматриваются

576 Дополнения
функции следующих типов:
п(х)	=	W<X)	(Д. 15)
— сферическая функция Бесселя;
пМ =	=	(-1)'+' У™/_(<+1/2)(*)	(Д.16)
— сферическая функция Неймана;
h(i'2\x) = j,(x) ± in,(x)	(Д.17)
— сферические функции Ханкеля 1-го и 2-го рода.
Эти функции являются решениями дифференциального уравнения
„"(*)+(l_ W+i)jU/(je) = 0
и обладают следующим асимптотическим поведением при х —*• оо:
/7(*)|*-оо~ sin(x- 1уУ	«/(х)|х^0о~ -cos(x-у),	(Д.18)
А,(1)М|х-.оо ~ Г(,+1)<?“ A{2)(jc)U-oo ~ il+xe~ix.	(Д.19)
Заметим, что в случае чисто мнимого аргумента (х — ip) только функ¬
ция hf\x) стремится к нулю при р -► оо. При малых значениях аргу¬
мента справедливы приближенные формулы
/+1	*
/7WU-°*pT+Wv	(Д.20)
где (2/ + 1)!! = 1 - 3 - 5... (2/ + 1).
Сферические функции Бесселя, Неймана и Ханкеля можно выра¬
зить через элементарные функции, например,

3. Вырожденная гипергеометрическая функция. Полиномы Лагерра	577
3.	ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ.
ПОЛИНОМЫ ЛАГЕРРА
Вырожденная гипергеометрическая функция F(a, с, х) определяется
при помощи ряда
rv	ч	,,	ах , а(а + 1) *2 , а(а + 1)(а + 2)	х3	,	,ПОп
F(a. с. х)	=	1 +	- д +	2! + ф + 1)(с + 2)	31	+	■ ■	■'	(Д 21)
где а и с	—	некоторые константы, причем с ф —k,	где	k	= 0,1,2,—
Эта функция является частным решением уравнения Куммера
x^ + (c-x)^-aF = 0.	(Д-22)
dx	dx
При а ф -п, где п = 0,1,2,..., функция (Д.21) имеет следующую асимп¬
тотику при х —► оо:
F(a,c,x)\x-. оо-Щ^-V,	(Д-23)
где Г(х) есть гамма-функция. Если с ф —k (k = 0,1,2,...), то второе
линейно независимое решение уравнения Куммера (Д.22) может быть
представлено в виде
Ф(х) = xl~cF(a - с + 1,2 - с, х).
Возвращаясь к функции F(a,c,x) (Д.21), заметим, что при выполне¬
нии условия а — -п (л = 0,1,2,...) она превращается в полином сте¬
пени п (происходит «обрыв» гипергеометрического ряда):
г-/	ч	, пх , п(п- 1)х2 ,	,	(-1)"	„п
F(—П, С, X) = 1 гг Н 7 гг ггг + . . . Ч ;——гг	7—;	гг-^ •
v	7	cl!	с(с+1)	2!	с(с	+	1)... (с + п - 1)
Данный полином с точностью до общего множителя представляет собой
присоединенный полином Лагерра, т. е.
=	<Д-24>
причем
Lsn(x) = exx-s£*(e-xxs+n).	(Д.25)
Для присоединенных полиномов Лагерра выполняется	следующее усло¬
вие ортонормированности:
ОО
J Lsn(x)Lsk(x)e-xxsdx = n\r(n + s+l)6nk.	(Д.26)

578	Дополнения
4.	ГАММА-ФУНКЦИЯ
Гамма-функция Г(лг) определяется при помощи интеграла
ОО
Г(*) = Je~‘tx~ldt, Rex >	О	(Д.27)
о
и удовлетворяет следующим функциональным соотношениям:
Г(х + 1) = хГ(х),	(Д.28)
Г(х)Г(1 - х) = —22д:_|Г(х)Г(х + 1/2) = Г(2х)Г(1/2).
Если аргумент принимает целые значения, то из формулы (Д.28) сле¬
дует, что
Г(л + 1) = л!,	(Д.29)
и это означает, что гамма-функция является обобщением понятия фак¬
ториала на случай произвольного комплексного аргумента.
Гамма-функция, определенная формулой (Д.27), является аналитиче¬
ской при всех значениях аргумента, кроме точек х = -п (п = 0,1,2,...),
в которых она имеет полюсы первого порядка с вычетами, равными
(-1 )"М
Приведем некоторые конкретные значения гамма-функции:
Г(1) = 0! = 1,	Г(п) = (л — 1)!,
Г(1/2) = д/SF,	Г(3/2) = у/тг/2.
При больших значениях аргумента |z| > 1 и при условии, что | argx| ^
^ 7г - е, е > 0, (тем самым исключаются точки, в которых расположены
полюсы Г-функции) асимптотическое поведение гамма-функции описы¬
вается формулой Стирлинга
rW = yfe-VHM, вд»| + ^_ + _1? + ...,
или
п\ = Г(я 4-1) = пГ(п) =	Н(п).	(Д.ЗО)

СПИСОК ЛИТЕРАТУРЫ
Литература по теории поля
1. Ландау Л.Д., Лифшиц Е.М. Теория поля. — М.: Наука, 2001.
2. Джексон Дж. Классическая электродинамика. — М.: Мир, 1965.
3. Батыгин В.В., Топтыгин И.Н. Сборник задач по электродинамике. — М.:
РХД, 2002.
4. Алексеев А.И. Сборник задач по классической электродинамике. — М.:
Наука, 1977.
5. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродина¬
мика. — М.: Наука, 1985.
6. Белоусов Ю.М. Методы теоретической физики. Ч. 1: Уч. пос. — М.:
МФТИ, 2010.
7. Новожилов Ю.В., Яппа Ю.А. Электродинамика. — М.: Наука, 1978.
8. Пановский В., Филипс М. Классическая электродинамика. — М.: Физ-
матгиз, 1963.
9. Соколов А.А., Тернов И.М., Жуковский В.Ч., Борисов А.В. Квантовая
электродинамика. — М.: Изд-во Моск. ун-та, 1983.
10. Кузнецов В.П., Смилга В.П. Движение заряженной частицы во внешнем
слабонеоднородном магнитном поле. Дрейфовая теория: Уч.-метод, пос. —
М.: МФТИ, 2001.
11. Фомичев С.В., Толоконников С.В. Излучение заряженных частиц в ваку¬
уме: Уч.-метод, пос. — М.: МФТИ, 2003.
12. Киселев В.В. Классическая электродинамика. Семинары по курсу «Теория
поля»: конспекты и упражнения: Учеб. пос. — Протвино: ИФВЭ, 2005.
Литература по квантовой механике
13. Ландау Л.Д., Лифшиц Е.М. Квантовая механика. — М.: Наука, 2010.
14. Берестецкий В.Б., Лифшиц Е.М., Питаевский Л.П. Квантовая электро¬
динамика. — М.: Наука, 1989.
15. Мессиа А. Квантовая механика. — М.: Наука; Т. 1, 1978; Т. 2, 1979.
16. Блохинцев Д.И. Основы квантовой механики. — М.: Наука, 1976.

580	Список	литературы
17. Давыдов А.С. Квантовая механика. — М.: Наука, 1973.
18. Дирак П.А.М. Принципы квантовой механики. — М.: Наука, 1979.
19. Белоусов Ю.М. Курс квантовой механики. Нерелятивистская теория. Уч.
пос. - М.: МФТИ, 2005.
20. Балашов В.В., Долинов В.К. Курс квантовой механики. — М.: Изд-во
Моск. ун-та, 1982.
21. Елютин П.В., Кривченков В.Д. Квантовая механика. — М.: Наука, 1976.
22. Зелевинский В.Г. Лекции по квантовой механике. — Новосибирск: Сиб.
унив. изд-во, 2002.
23. Галицкий В.М., Карнаков Б.М., Коган В.И. Задачи по квантовой меха¬
нике. — М.: Наука, 1992.
24. Флюгге 3. Задачи по квантовой механике. Т. 1, 2. — М.: Мир, 1974.
25. Гольдман И.И., Кривченков В.Д. Сборник задач по квантовой механике. —
М.: Гостехиздат, 1957.
26. Аллилуев С.П., Зяблюк К.Н. Избранные вопросы квантовой теории рас¬
сеяния: Уч. пос. — М.: МФТИ, 2005.
27. Тернов А.И. Основы релятивистской квантовой механики: Уч. пос. — М.:
МФТИ, 2002.
Литература по статистической физике
28. Ландау Л.Д., Лифщиц Е.М. Статистическая физика. Ч. 1. — М.: Наука,
1976.
29. Хуанг К. Статистическая механика. — М.: Мир, 1966.
30. Румер Ю.Б., Рывкин M.LU. Термодинамика, статистическая физика и ки¬
нетика. — М.: Наука, 1972.
31. Кубо Р. Статистическая механика. — М.: Мир, 1967.
32. Максимов Л.А., Михеенков А.В, Полищук И.Я. Лекции по статистиче¬
ской физике: Уч. пос. — М.: МФТИ, 2011.
33. Зайцев P.O. Введение в современную статистическую физику: курс лек¬
ций. — М.: Едиториал УРСС, 2005.
34. Квасников И.А. Термодинамика и статистическая физика. Т. 2. Теория
равновесных систем: Статистическая физика. — М.: УРСС, 2002.
35. Абрикосов А.А. Основы теории металлов. — М.: Наука, 1987.
36. Халатников ИМ. Теория сверхтекучести. — М.: Наука, 1971.
37. Де Жен П. Сверхпроводимость металлов и сплавов. — М.: Мир, 1968.
38. Ландау Л.Д., Лифщиц Е.М. Статистическая физика. Ч. 2. — М.: Наука,
1976.
39. Тинкхам М. Введение в сверхпроводимость. — М.: Атомиздат, 1980.
40. Варламов А.А., Ларкин А.И. Теория флуктуаций в сверхпроводниках. —
М.: Добросвет, 2007.
41. Шмидт В.В. Введение в физику сверхпроводников. — М.: МЦНМО,
2000.

Список литературы	581
42. Сан-Жам Д., Сарма Г., Томас Е. Сверхпроводимость второго рода. — М.:
Мир, 1970.
43. Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых
переходов. — М.: Наука, 1982.
44. Квасников И.А. Термодинамика и статистическая физика. Т. 1. Теория
равновесных систем: Термодинамика. — М.: УРСС, 2002.
Литература по общим вопросам *
45. Белоусов Ю.М., Кузнецов В.П., Смилга В.П. Катехизис. Руководство по
математике для начинающих изучать теоретическую физику: Уч. пос. —
М.: МФТИ, 2005.
46. Белоусов Ю.М., Кузнецов В.П., Смилга В.П. Практическая математика.
Руководство для начинающих изучать теоретическую физику. — Долго¬
прудный: ИД «Интеллект», 2009.
47. Никифоров А.Ф., Уваров В.Б. Специальные функции математической фи¬
зики. — Долгопрудный: ИД «Интеллект», 2007.
48. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и про¬
изведений. — М.: Физматгиз, 1963.
49. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 2. — М.:
Наука, 1974.
50. Новиков И.Д., Фролов В.П. Физика черных дыр. — М.: Наука, 1986.

Учебное издание
Заявки на книги присылайте по адресам:
zakaz@id-intellect.ru
solo@id-intellect.ru
id-intellect@mail.ru
тел. (495) 579-96-45
факс (495) 617-41-88
В заявке обязательно указывайте
свои реквизиты (для организаций) и почтовый адрес!
Подробная информация о книгах на сайте
http://www.id-intellect.ru
Юрий Михайлович Белоусов
Сергей Николаевич Бурмистров
Алексей Игоревич Тернов
ЗАДАЧИ
ПО ТЕОРЕТИЧЕСКОЙ
ФИЗИКЕ
Компьютерная верстка — А.А. Пярнпуу
Корректура авторов
Художник - С.Ю. Биричев
Ответственный за выпуск — Л.Ф. Соловейчик
Формат 60x90/16. Печать офсетная.
Гарнитура Ньютон.
Печ. л. 36,5. Тираж 2000 экз. Зак. М-1441.
Бумага офсетная № 1, плотность 80 г/м2
Издательский Дом «Интеллект»
141700, Московская обл., г. Долгопрудный,
Промышленный пр-д, д. 14,
тел. (495) 617-41-85
Отпечатано в типографии филиала ОАО «ТАТМЕДИА» «ПИК «Идел-Пресс»
420066, г. Казань, ул. Декабристов, д. 2