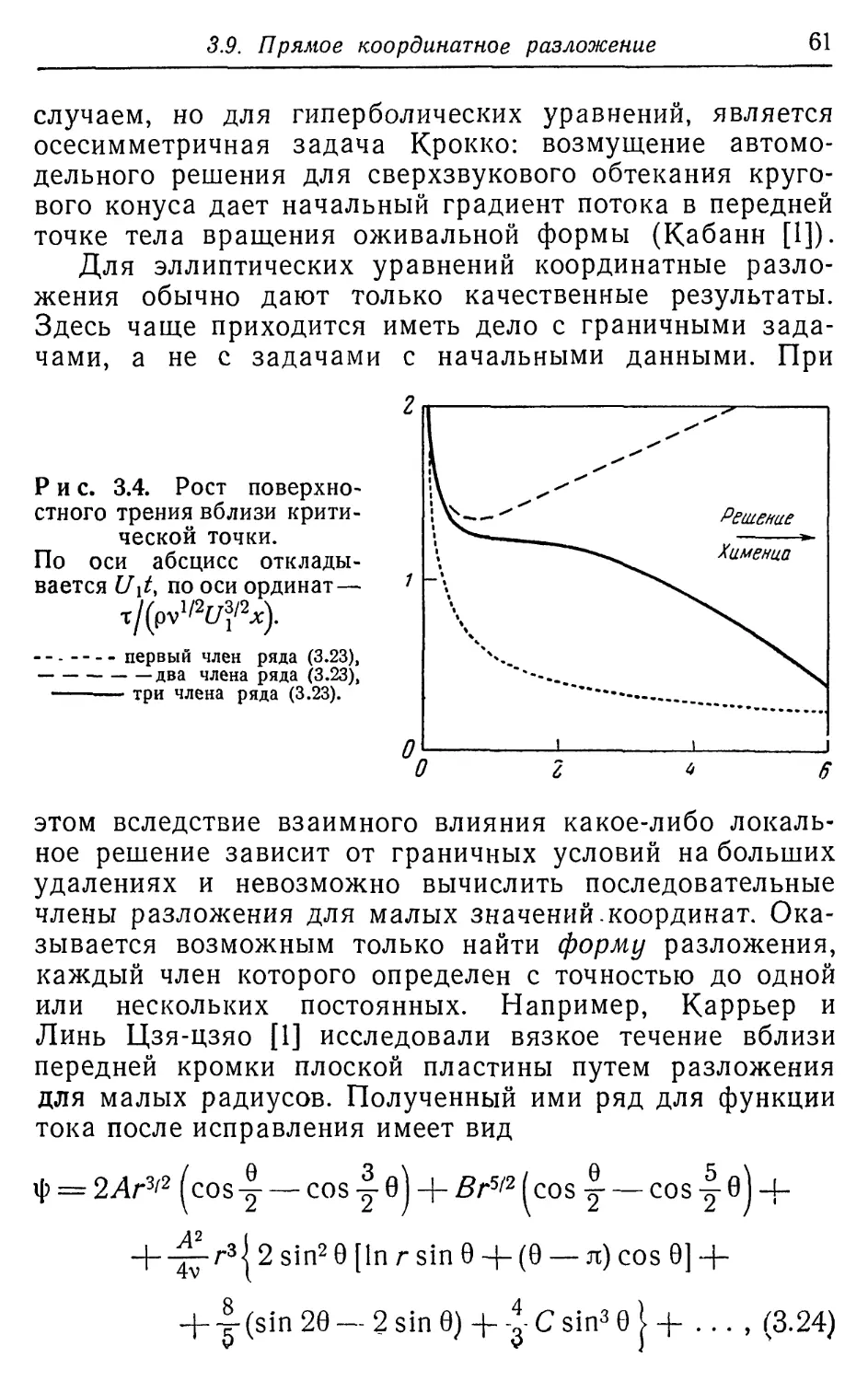
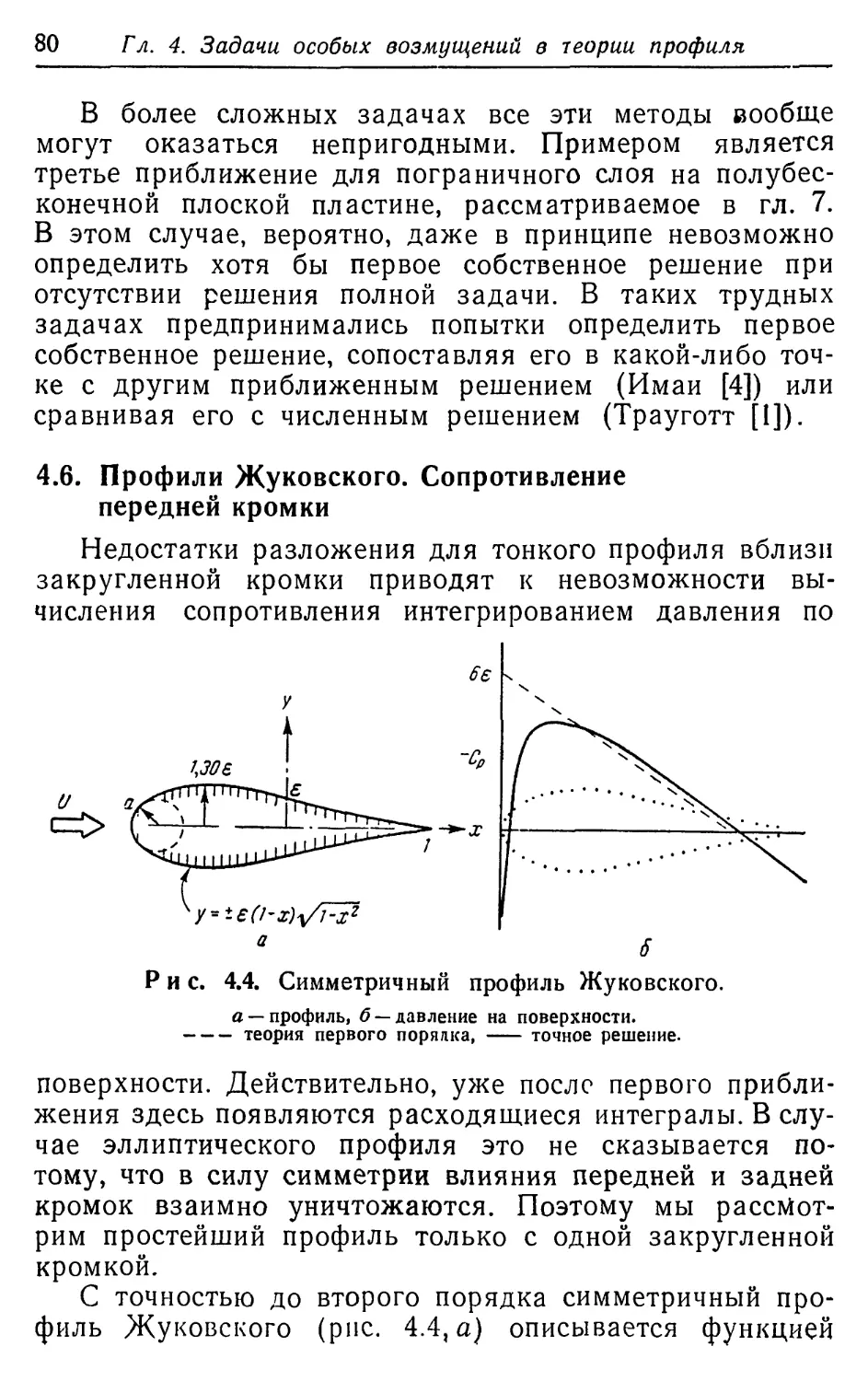
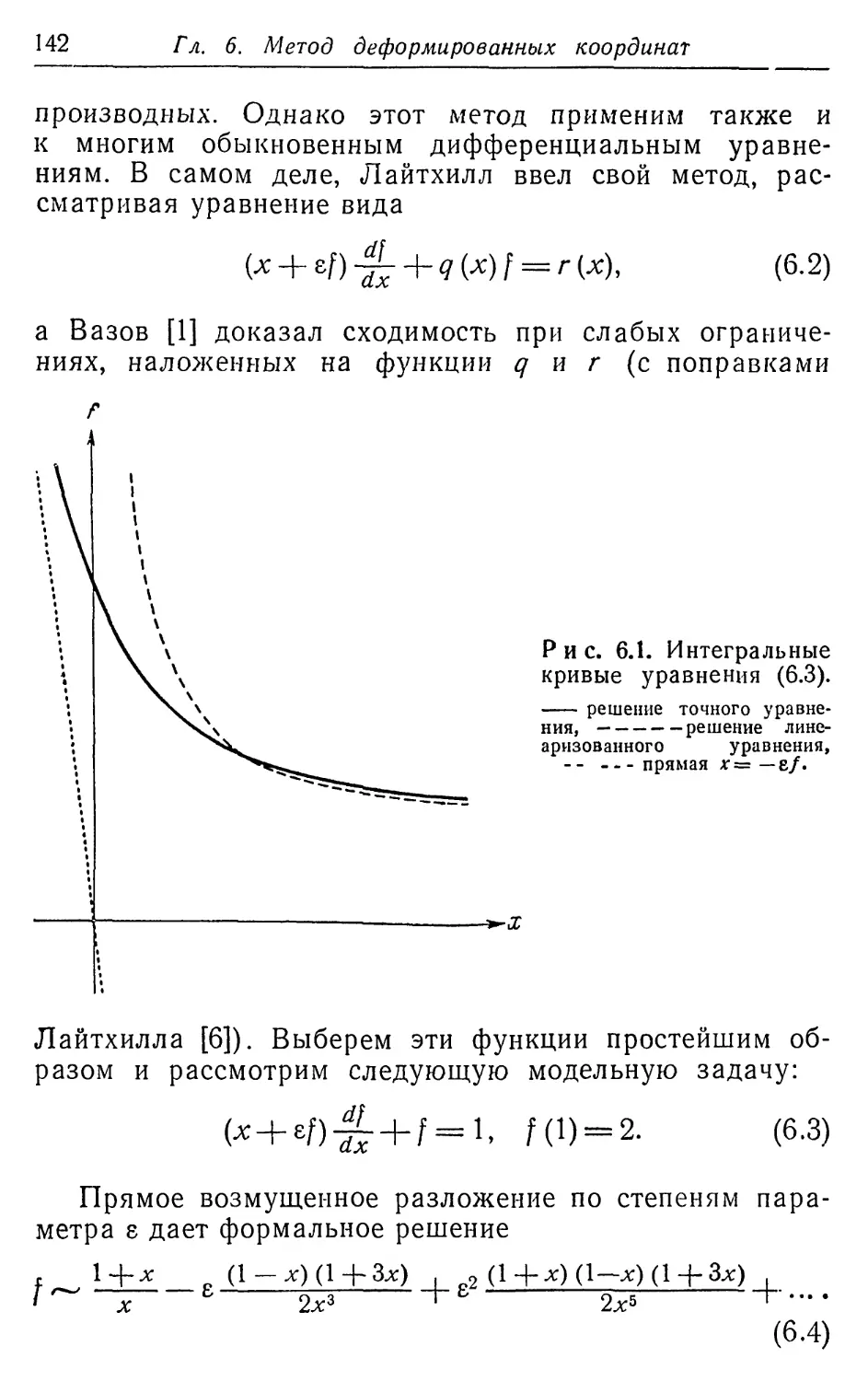
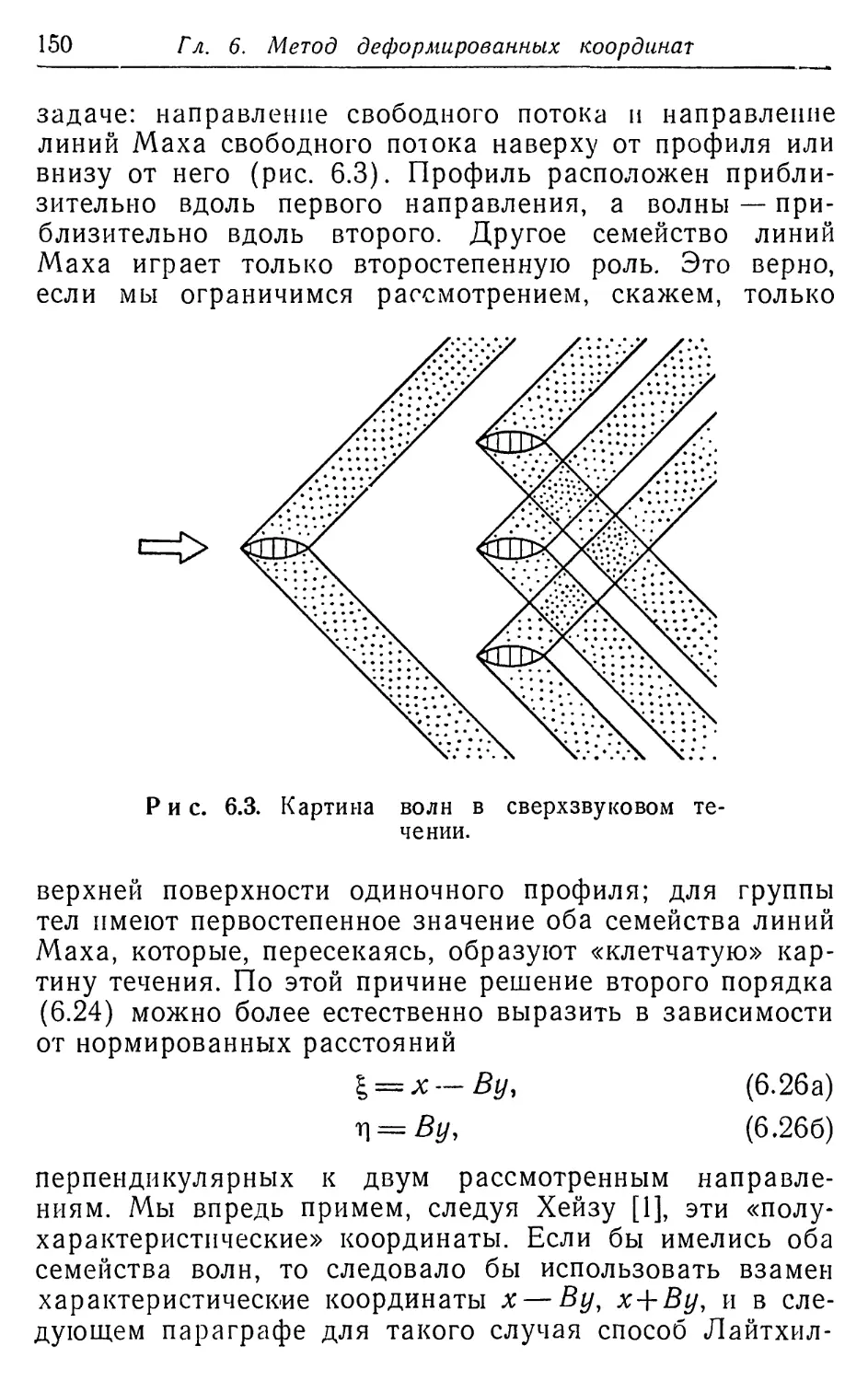
Текст
МЕТОДЫ
ЗОММ У Iff EHHH
В МЕХАНИКЕ
ЖИДКОСТИ
PERTURBATION
METHODS IN
FLUID MECHANICS
by
Milton Van Dyke
Department of Aeronautics and Astronautics
Stanford University
Stanford, California
1964
ACADEMIC PR ESS
New York • London
М. Ван-Дайк
МЕТОДЫ
ВОЗМУЩЕНИЙ
В МЕХАНИКЕ
ЖИДКОСТИ
Перевод с английского
В. А. СМИРНОВА
Под редакцией
А. А. НИКОЛЬСКОГО
ИЗДАТЕЛЬСТВО «МИР»
Москва 1967
УДК 532/533 + 517 944
Книга известного американского ученого, посвящен-
посвященная систематическому изложению теории и приложений
методов возмущений; таким методом автор считает лю-
любой метод приближенного решения задач, в котором
так или иначе содержатся малые величины. Основное
содержание книги составляет исследование задач «осо-
«особых возмущений», в которых сколь угодно малое изме-
изменение параметра возмущения приводит к конечным из-
изменениям решения.
Примеры, рассматриваемые автором, относятся к
механике жидкости в широком смысле слова — от тече-
течений несжимаемой идеальной жидкости до гиперзвуко-
гиперзвуковых течений вязкого газа, — однако изложенные авто-
автором общие методы несомненно найдут обширные при-
применения в других разделах механики и физики. Книга
представит интерес и для математиков, так как она со-
содержит обширный «экспериментальный» материал в ви-
виде примеров по сложной и мало разработанной совре-
современной проблематике.
Редакция литературы по математическим наукам
Инд 2-4-3
ПРЕДИСЛОВИЕ РЕДАКТОРА
ПЕРЕВОДА
Если первой тенденцией в исследованиях по механике
является максимальное упрощение задачи для того,
чтобы иметь возможность получить эффективное реше-
решение, то вторая состоит в учете возможно большего числа
влияний, что способствует расширению, круга практиче-
практически важных решаемых задач. Математическому вопло-
воплощению последней тенденции и посвящена книга амери-
американского ученого Милтона Ван-Дайка, перевод которой
предлагается вниманию читателя.
Учет влияния, вообще говоря, обусловливает не ко-
коренное, а лишь некоторое изменение задачи, которое
может быть учтено как в первом, так и — при необходи-
необходимости — в последующих приближениях. Таким образом,
речь идет о представлении решения в виде ряда по не-
некоторой в общем случае малой величине возмущения и
об отыскании одного или нескольких членов ряда.
Книга охватывает различные аспекты и примеры
приближенного решения многих конкретных задач раз-
различными авторами в различное время. По существу, к
методу возмущений автор книги относит любой метод
приближенного решения задач, в которых так или иначе
содержатся величины, малые по сравнению с некото-
некоторыми исходными, и использование этой малости лежит
в основе метода. Величиной возмущения может быть
Предисловие редактора перевода
один из безразмерных параметров (числа Маха или Рей-
нольдса набегающего потока, относительная толщина
профиля, удлинение крыла конечного размаха и т. д.),
одна или несколько координат пространства — времени;
возмущению могут подвергаться как краевые условия,
так и сами дифференциальные уравнения, описывающие
процесс. Автор книги ставит перед собой задачу иссле-
исследования только «рациональных приближений», опреде-
определяя их как приближения, допускающие возможность бес-
бесконечного продолжения процесса уточнения решения за-
задачи (в основном путем построения асимптотических
разложений). При этом он вводит термин «иррациональ-
«иррациональные приближения», определяя последние как такие, ко-
которые не становятся точными ни при каком известном
предельном переходе (к числу их он относит, например,
известный метод Кармана — Цяня расчета дозвукового
обтекания профиля). В книге рассматриваются некото-
некоторые примеры «регулярных возмущений» (терминология
автора книги), которые становятся малыми вместе с па-
параметром возмущения (например, задача обтекания
идеальной несжимаемой жидкостью тела, близкого к за-
заданному). Однако основное содержание книги состав-
составляет исследование задач «особых возмущений», таких,
в которых сколь угодно малое изменение параметра воз-
возмущения приводит к конечным изменениям решения. Ти-
Типичным примером такой задачи является задача о влия-
влиянии вязкости на обтекание тел.
Задачи особых возмущений часто встречаются в ме-
механике жидкости и являются в этой области, по словам
автора, «скорее правилом, чем исключением». В книге
содержится ряд примеров, когда даже в классических
проблемах удалось получить новые результаты за счет
того, что была установлена особая природа задачи.
Предисловие редактора перевода
В книге для исследования задач особых возмущений
даны два общих метода (гл. 5 и гл. 6). Эти методы были
развиты в последние десятилетия трудами многих вы-
выдающихся ученых, причем существенный вклад был вне-
внесен самим Ван-Дайком. Первый метод — метод сращива-
сращиваемых асимптотических разложений— представляет со-
собой обобщение теории пограничного слоя. Он включает
в себя нахождение так называемых внутреннего и внеш-
внешнего разложений и сращивание их определенным обра-
образом. Второй метод — метод деформированных коорди-
координат— восходит к идеям Пуанкаре, предложен Лайтхил-
лом и развит рядом работ последующих ученых (так на-
называемый метод Пуанкаре — Лайтхилла — Го).
В обоих методах приходится оперировать с асимпто-
асимптотическими расходящимися разложениями, сращивать
два таких разложения и производить ряд рискованных
с точки зрения математики действий. Строгое математи-
математическое обоснование рассматриваемых методов практиче-
практически отсутствует. Тем более интересным представляется
проникновение автора в суть этих вопросов путем иссле-
исследования множества примеров. В некоторых случаях в
качестве простых моделей, демонстрирующих существен-
существенные черты методов, используются обыкновенные диффе-
дифференциальные уравнения, однако основная часть приме-
примеров дается из механики жидкости, т. е. из области урав-
уравнений в частных производных.
Несмотря на то что рассматриваемый в книге мате-
материал касается механики жидкости в классической ее по-
постановке— от несжимаемого течения до гиперзвуковых
обтеканий как идеальной, так и вязкой жидкостью, —
изложенные в книге общие методы, несомненно, найдут
обширные приложения и в новейших разделах гидро-
гидроаэродинамики: в динамике разреженного газа, магнито-
магнитогидродинамике и др.
8 Предисловие редактора перевода
Книга М. Ван-Дайка представляет большой теоре-
теоретический и практический интерес для ученых-гидромеха-
ученых-гидромехаников, и для них ее появление будет важным событием.
Представляется целесообразным рекомендовать эту кни-
книгу и представителям других областей механики, а также
представителям других точных наук, ибо методы, проде-
продемонстрированные здесь на задачах гидромеханики, без-
безусловно имеют гораздо более общее значение. Настоя-
Настоящая книга может заинтересовать и математиков, так как
она содержит обширный «экспериментальный» материал
в виде примеров по сложной и мало разработанной со-
современной проблематике.
Л. А. Никольский
ПРЕДИСЛОВИЕ К РУССКОМУ
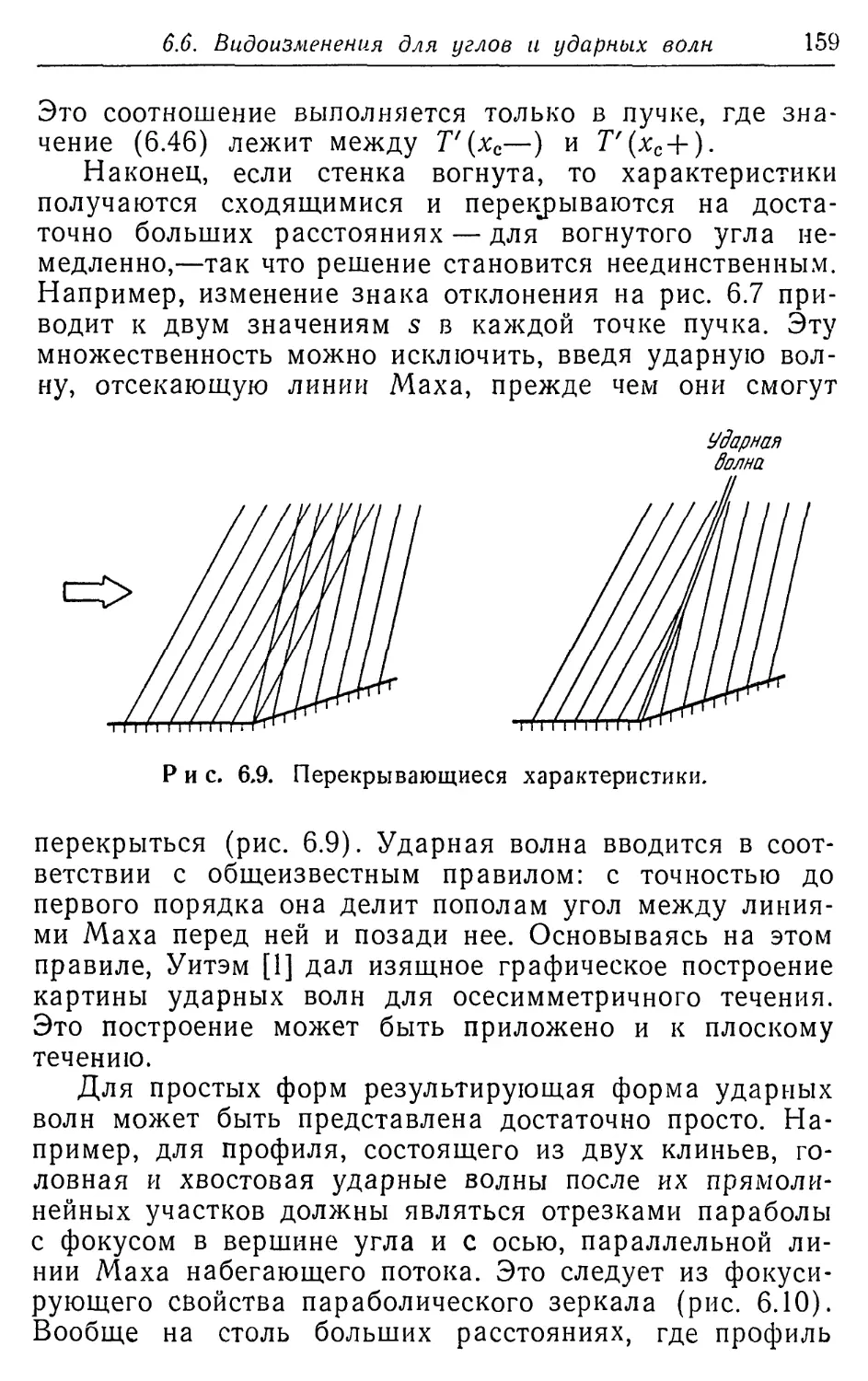
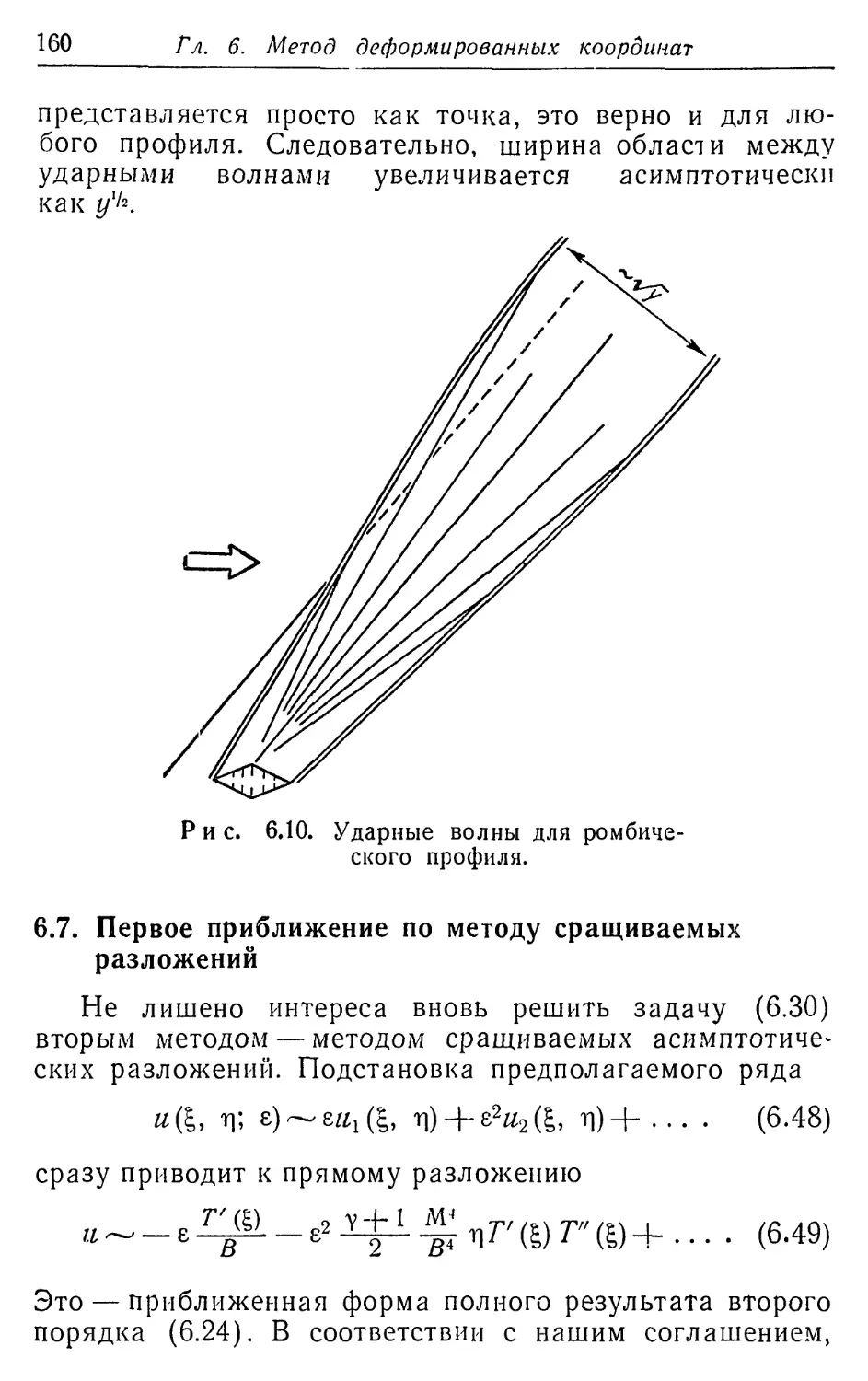
ИЗДАНИЮ
Мне было очень приятно во время своего пребыва-
пребывания в Советском Союзе увидеть, что моя книга перево-
переводится на русский язык, и убедиться в заботе моих кол-
коллег о точном ее воспроизведении. Приятно также, что в
русское издание удалось внести некоторые мелкие ис-
исправления исходного текста.
Методы возмущений в настоящее время находятся
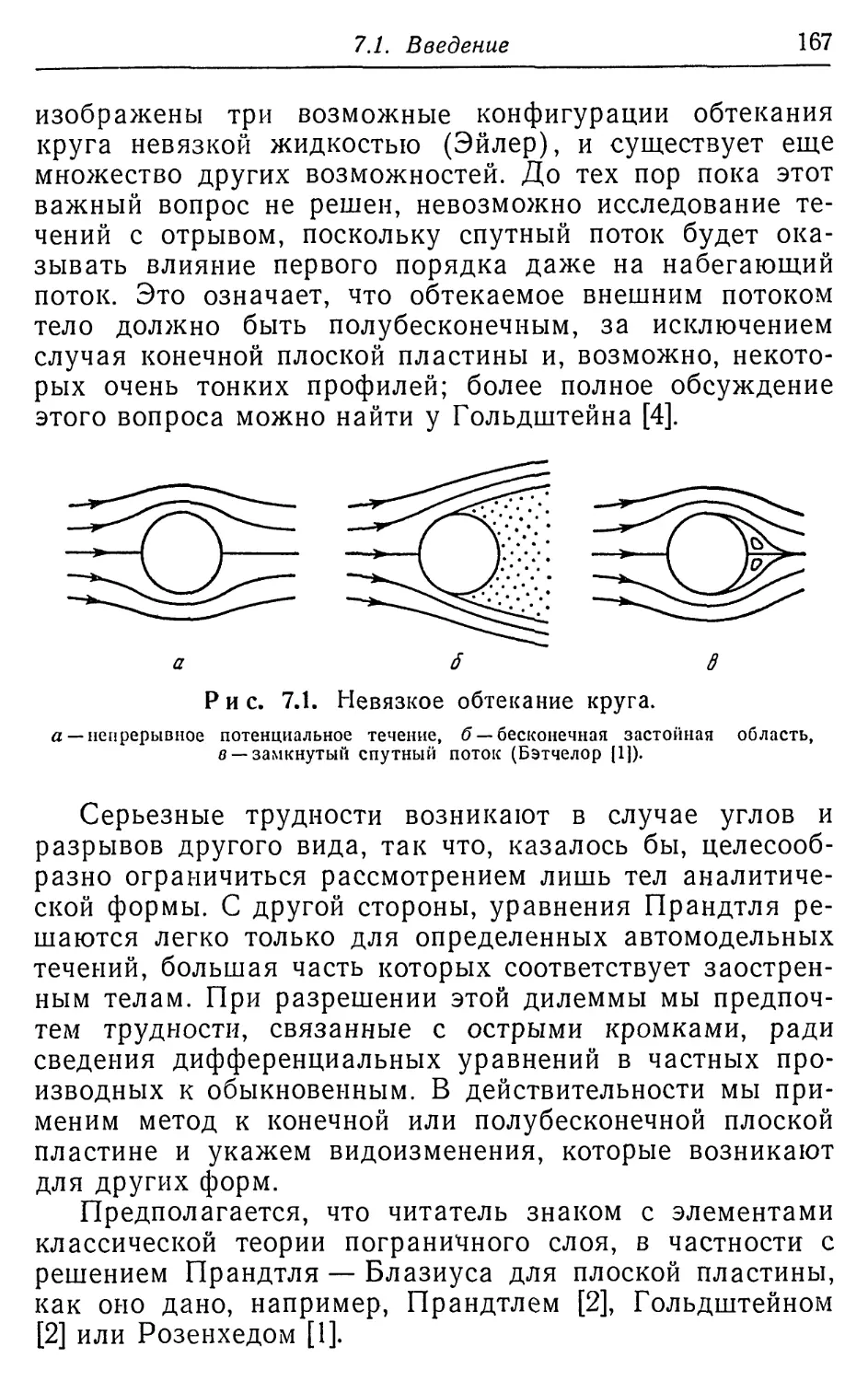
в стадии быстрого и плодотворного развития. Во многих
отраслях механики этими методами получены замеча-
замечательные результаты как в Советском Союзе, так и в
странах английского языка. Этим методам, несомненно,
предстоят еще более замечательные приложения, и я
надеюсь, что моя книга окажет некоторую помощь моим
молодым коллегам, которые возьмут на себя эту работу.
Я неизбежно проявлял тенденцию к ссылкам на
статьи, написанные по-английски, и поэтому не смог от-
отразить в должной мере существенный вклад советских
исследователей в развитие предмета. К счастью, мой
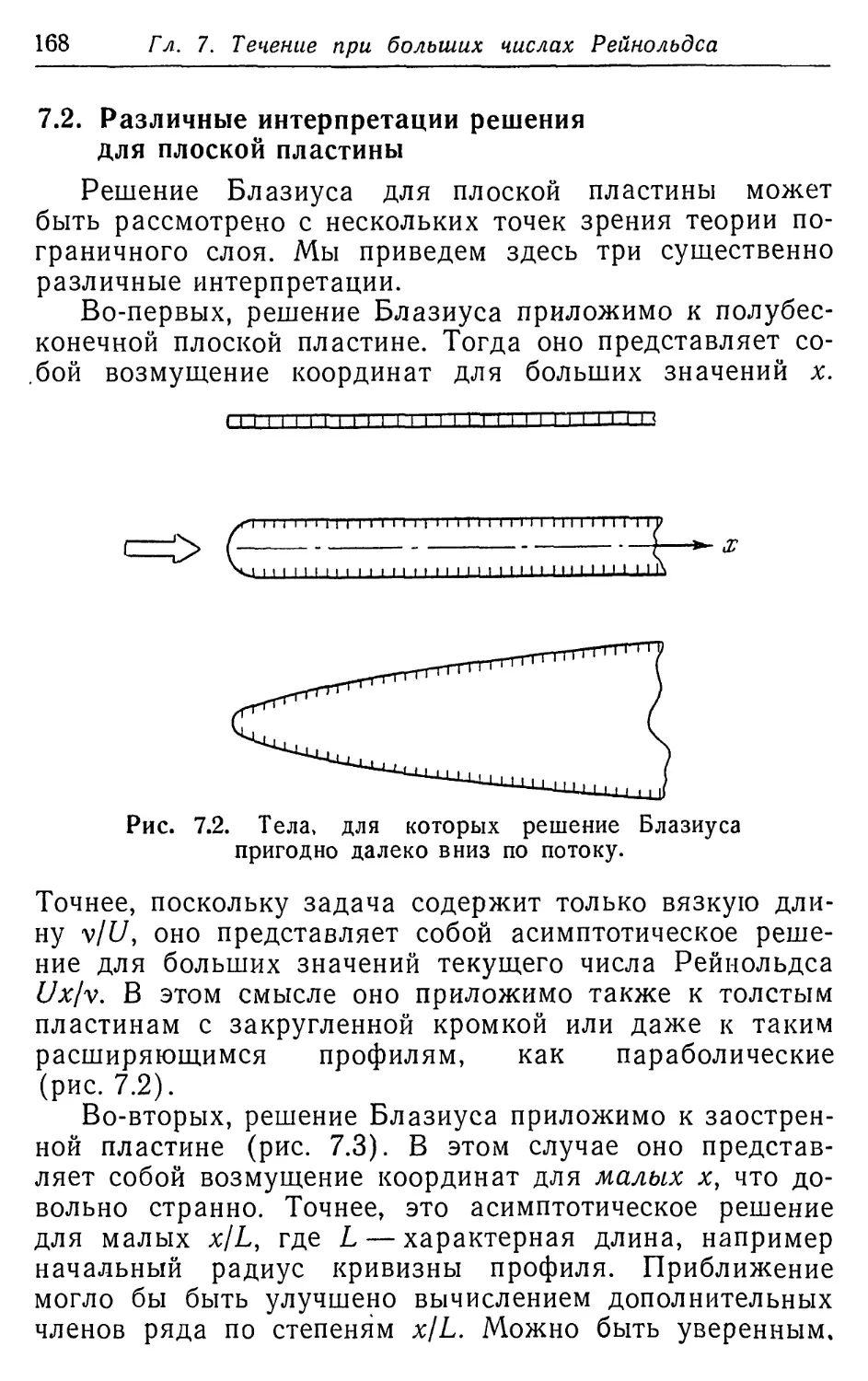
давний друг, профессор А. А. Никольский, напишет пре-
предисловие к переводу, и я надеюсь, что он сообщит так-
также дополнительные сведения о работах советских уче-
ученых.
Милтон Ван-Дайк
Москва, декабрь 1965 г.
ПРЕДИСЛОВИЕ
Эта книга посвящена главным образохм исследова-
исследованию задач особых возмущений, возникающих в меха-
механике жидкости. В частности, в ней дается единое пред-
представление двух сравнительно общих методов, которые
были развиты за последние пятнадцать лет в работах
Лагерстрома, Каплуна, Коула, Лайтхилла и Уитема.
Основное внимание мы уделяем тем задачам, которые
непосвященному могут показаться патологическим ас-
аспектом теории возмущений, но это оправдывается не
столько новизной этих приемов, сколько тем фактом, что
особые возмущения представляются в механике жидко-
жидкости скорее правилом, чем исключением, и во все боль-
большем количестве встречаются в современных исследова-
исследованиях. Тем не менее книга начинается с изложения общих
методов, приложимых в равной мере как к регулярным,
так и к особым возмущениям, поскольку возможен по-
последующий независимый учет характера возмущений.
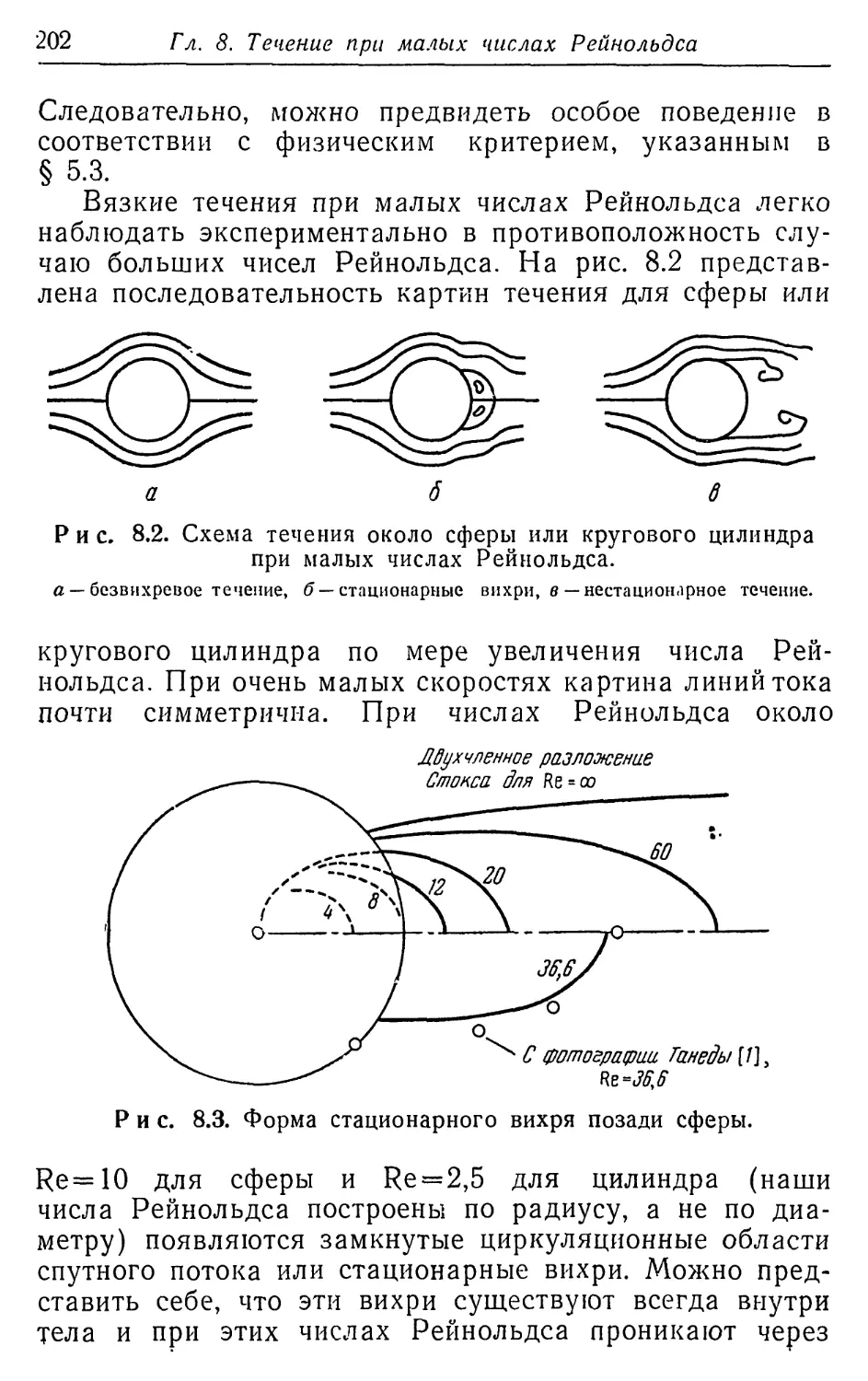
Общие методы вводятся в основном с помощью при-
примеров, причем последние, за исключением нескольких
математических моделей, взяты из механики жидкости.
Несомненно, что эти методы могут быть непосредственно
использованы и в других разделах прикладной механики,
и я надеюсь, что книга окажется полезной для исследо-
исследователей и в этих областях. Тем не менее оба общих ме-
метода, упомянутых выше, были изобретены в связи с за-
задачами течения жидкости, были развиты и получили
приложения преимущественно в этой области. Приводи-
Приводимые примеры в основном ограничиваются теми, которые
в середине века считались относящимися к классической
аэродинамике. Очевидно, однако, что задачи особых воз-
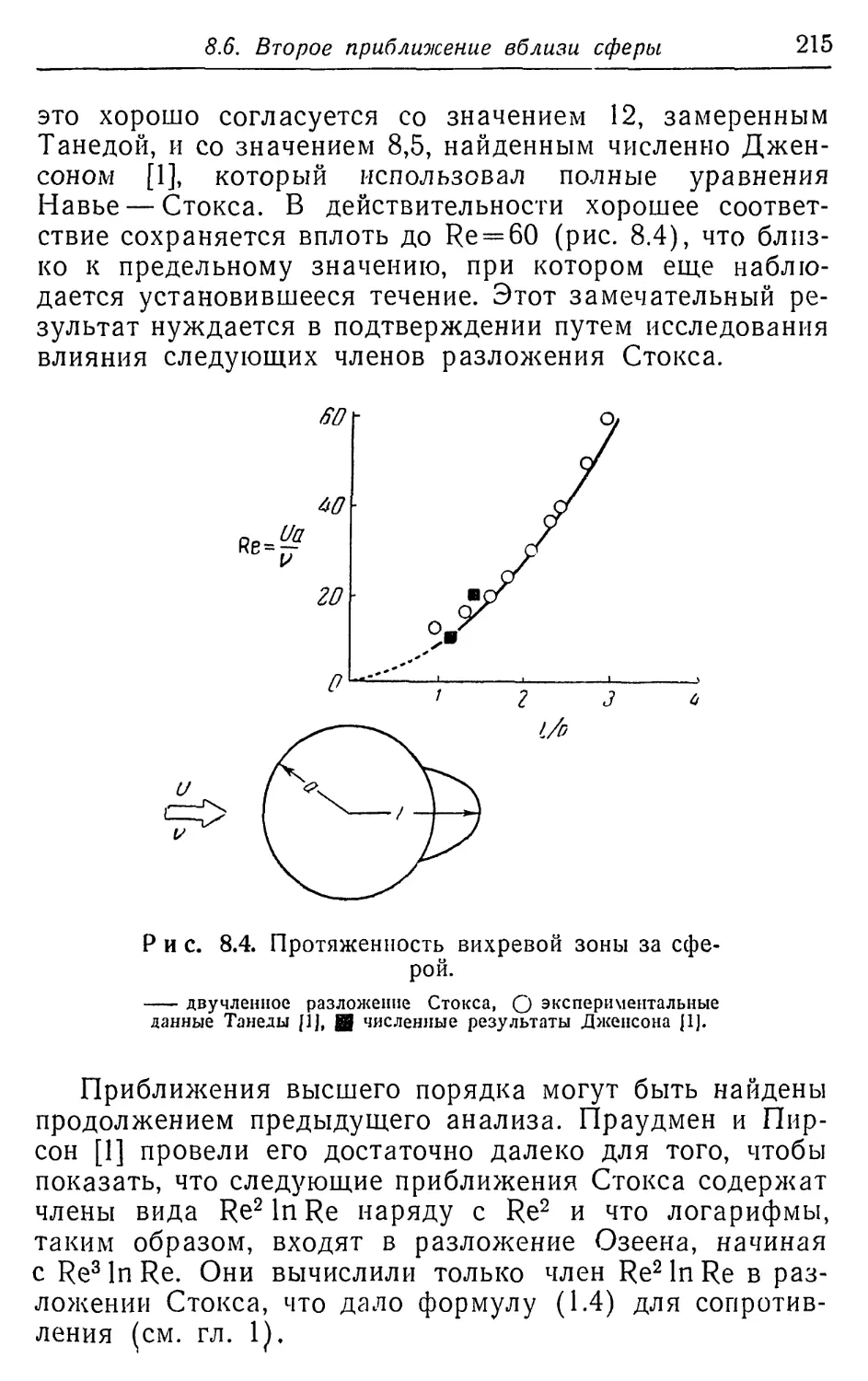
возмущений в изобилии содержатся в таких новых разде-
разделах, как теория неравновесных течений, теория течений
излучающего газа, магнитогидродинамика, динамика
плазмы, динамика разреженного газа. Рассматриваемые
методы определенно получат там плодотворные примене-
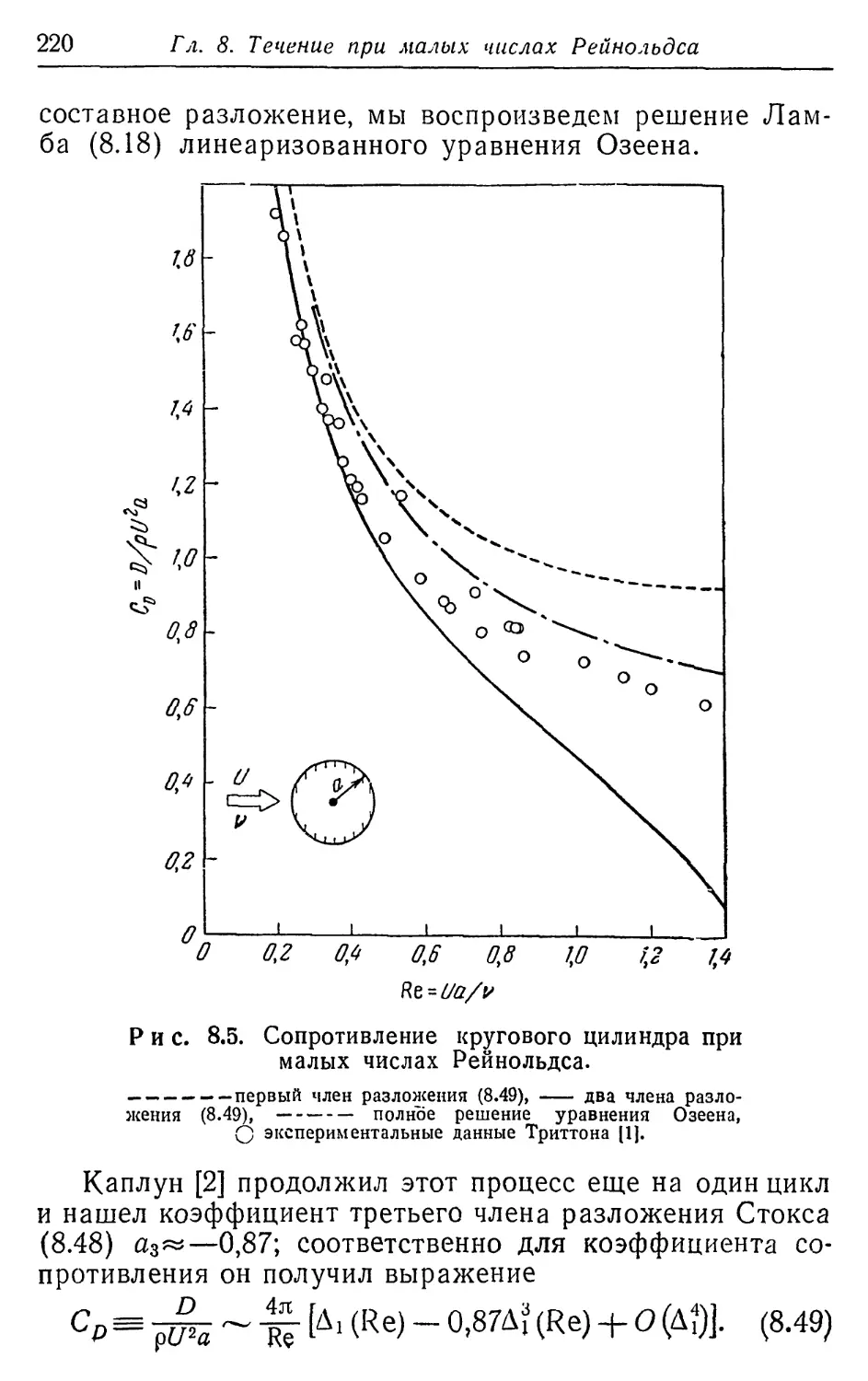
12 Предисловие
ния, так же как и в океанографии, метеорологии и дру-
других областях великого мира движения жидкости.
Начало этой книге было положено заметками, под-
подготовленными для курса, который я читал в 1959 г. на
Отделении аэронавтики и астронавтики Станфордского
университета. Естественно, многое в книге взято из моих
собственных исследований и работ моих учеников. Боль-
Большая часть этих работ была выполнена по заказу Научно-
исследовательского управления военно-воздушных сил.
Центральным пунктом книги является исследование
(в гл.4) потенциального обтекания симметричного тонко-
тонкого профиля потоком несжимаемой жидкости. Хотя эта
задача сравнительно проста и для ее решения достаточно,
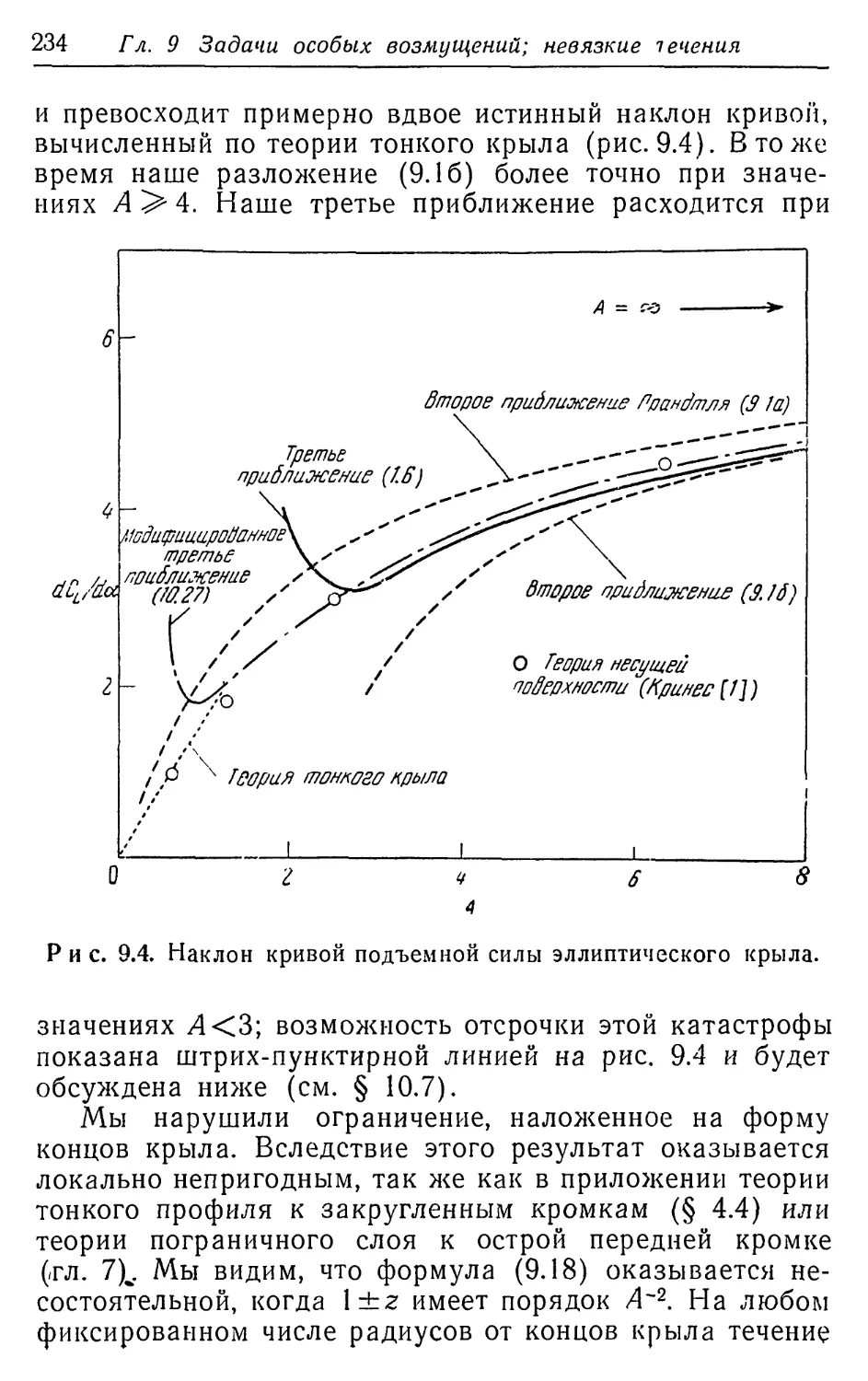
использовать двумерное уравнение Лапласа, она обла-
обладает основными чертами задач как регулярных, так и
особых возмущений. В частности, она служит для вве-
введения двух общих методов исследования задач особых
возмущений. Ссылки на эту основную задачу повто-
повторяются во всех последующих главах.
Я рекомендовал бы читателю не пренебрегать упраж-
упражнениями. Они предусматривают в краткой форме многие
дополнительные детали, дальнейшие ссылки на литера-
литературу, обобщения и развитие материала, изложенного в
основном тексте.
Я обязан прежде всего П. А. Лагерстрому, который
не только является моим учителем, коллегой и другом,
но и сыграл выдающуюся роль в развитии одного из
двух главных методов исследования задач особых воз-
возмущений. Многие из изложенных в книге идей носят
отпечаток моего сотрудничества с Р. Т. Джонсом,
М. А. Хислетом и их коллегами по Эймской лаборато-
лаборатории. За полезные замечания и критику я в долгу перед
многими другими коллегами, в частности перед О. Бург-
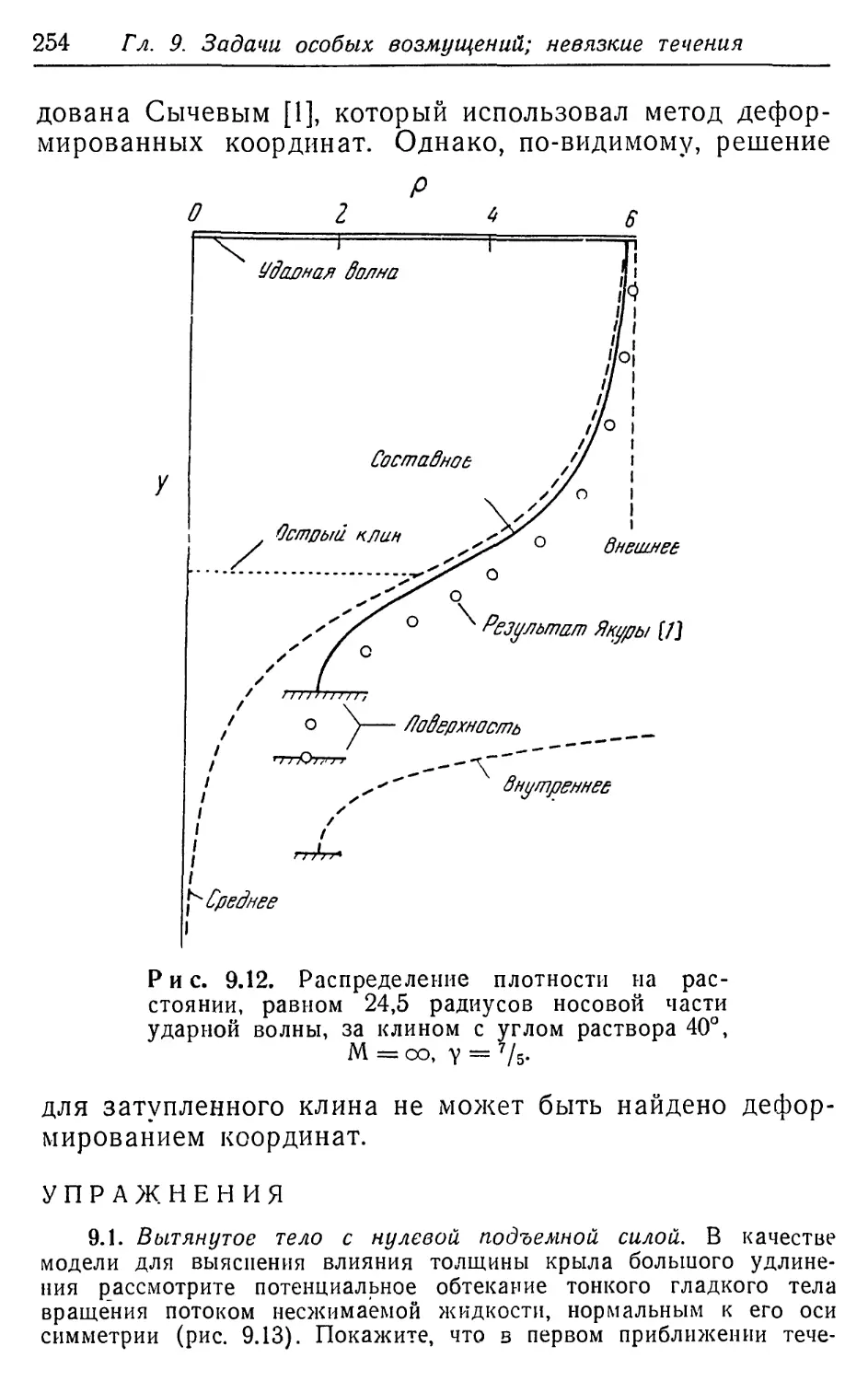
графом, Чжан Ай-ди, Г. Эмануэлем, С. Каплуном,
С. Надиром, Б. Перри, А. Ф. Пилау. Эта книга не была
бы написана без помощи и ободрения со стороны моей
жены Сильвии, и ей я посвящаю этот труд как дар
любви.
Милтон ВаН'Цайк
Станфорд, Калифорния
Май, 1964 г.
Глава 1
СУЩНОСТЬ
ТЕОРИИ ВОЗМУЩЕНИЙ
1.1. Приближения в механике жидкости
Механика жидкости явилась одним из основных ис-
источников теории нелинейных дифференциальных урав-
уравнений в частных производных. В отличие от основных
уравнений многих других разделов математической фи-
физики уравнения, описывающие движение жидкости, су-
существенно нелинейны (точнее квазилинейны) независимо
от того, учитываются или не учитываются вязкость и
сжимаемость жидкости. Единственным важным исклю-
исключением является хорошо исследованный случай безвих-
безвихревого движения несжимаемой невязкой жидкости, сво-
сводящийся к уравнению Лапласа. Тогда при отсутствии
свободных границ нелинейность проявляется лишь алге-
алгебраически в уравнении Бернулли.
В силу этой существенной нелинейности точные ре-
решения в любом разделе механики жидкости получаются
редко. Обычно это автомодельные решения, для которых
вследствие высокой степени симметрии, присущей за-
задаче, дифференциальные уравнения в частных производ-
производных сводятся к обыкновенным дифференциальным урав-
уравнениям. Нужда в точных решениях столь велика, что
решение — несколько нестрого — называется «точным»
даже в том случае, когда интегрирование полученных
обыкновенных дифференциальных уравнений может
быть осуществлено лишь численно. Лайтхилл [1] дал бо-
более или менее полный список таких решений для невяз-
невязкой сжимаемой жидкости:
а) установившееся сверхзвуковое обтекание выпукло-
выпуклого угла;
б) установившееся сверхзвуковое обтекание вогну-
вогнутого угла;
в) установившееся сверхзвуковое обтекание кругово-
кругового конуса без угла атаки;
14 Гл. 1. Сущность теории возмущений
г) течение от импульсивного вдвигания бесконечной
плоскости в покоящийся газ;
д) течение от импульсивного выдвигания бесконечной
плоскости из покоящегося газа;
е) течение от равномерного расширения кругового
цилиндра в покоящемся газе;
ж) течение от равномерного расширения сферы в по-
покоящемся газе.
Далее, по Шлихтингу [1], может быть дан аналогич-
аналогичный список для течений несжимаемой вязкой жидкости:
а) установившееся течение между бесконечными па-
параллельными плоскостями, в цилиндрической тру-
трубе с круговым сечением или между круговыми
концентрическими цилиндрами;
б) установившееся течение между неподвижной и
скользящей плоскостями или концентрическими
круговыми цилиндрами;
в) установившееся течение между концентрическими
вращающимися цилиндрами;
г) плоское или осесимметричное течение навстречу
бесконечной плоскости;
д) течение, образованное установившимся вращени-
вращением бесконечного плоского диска;
е) установившееся плоское течение между расходя-
расходящимися плоскостями;
ж) течение от импульсивного или синусоидального
движения бесконечной плоской пластины в ее соб-
собственной плоскости.
Для этих автомодельных течений типично то, что они
связаны с идеализированными геометрическими обра-
образами, далекими от большинства практически интересны к
форм.
Для того чтобы продвинуться дальше, необходимо
использовать приближенные методы. (Иной, недавно
возникший путь — составление программ для вычисли-
вычислительных машин.) Приближения представляют собой ис-
искусство, и обычно с успешными аппроксимациями связа-
связаны имена знаменитых ученых:
12. Рациональные и иррациональные приближения 15
теория крыла Прандтля;
метод Кармана — Цяня для профиля в дозвуковом
потоке 1);
приближение Прандтля — Глауэрта для дозвуковых
течений;
разложение Рэлея — Янсена для дозвуковых течений;
приближения Стокса и Озеена для вязкого течения;
теория пограничного слоя Прандтля;
метод Кармана — Польгаузена для пограничного
слоя;
теория Ньютона — Буземана гиперзвукового обтека-
обтекания.
Во многих важных областях успешные аппроксима-
аппроксимации еще должны быть найдены. Примерами являются
отрывные вязкие течения, гиперзвуковое обтекание за-
затупленных тел.
1.2. Рациональные и иррациональные приближения
Наиболее полезные аппроксимации имеют место, ко-
когда один или несколько из параметров или переменных
задачи малы (или велики). Этой величиной возмущения
часто является один из безразмерных параметров:
разложение Рзлея — Янсена число Маха <g^ 1,
теория тонкого профиля относительная толщина <^ 1,
теория несущей линии удлинение ^> 1,
течение Стокса, Озеена число Рейнольдса <<^ 1,
теория пограничного слоя число Рейнольдса ^$> 1,
теория Ньютона — Буземана число Маха ^> 1, (у—1)<^ 1,
метод квазистационарности приведенная частота <^ 1,
теория свободно-молекуляр- число Кнудсена ^> 1.
ного течения
Необычным примером является исследование Гара-
бедяна [1] осесимметричного течения со свободными ли-
линиями тока, которое представляет собой приближение,
1) В СССР независимо от указанного метода приближенная тео-
теория профиля в дозвуковом потоке была дана в работе С. А. Хри-
стиановича «Обтекание тел газом при больших дозвуковых скоро-
скоростях», Труды ЦАГИ, вып. 481, 1940. — Прим. ред.
16 Гл. 1. Сущность теории возмущений
основанное на предположении, что число измерений
пространства лишь слегка отличается от двух.
Во всех этих случаях говорится о возмущении пара-
параметров. Величиной возмущения может также быть одно
из независимых переменных (в безразмерной форме):
ряд Блазиуса для пограничного слоя расстояние <^ 1,
импульсивное движение в вязкой
или сжимаемой жидкости время<^ 1.
В таких случаях говорят о возмущении координат.
Приближения такого типа становятся все более точ-
точными по мере стремления величины возмущения к нулю
(или бесконечности). Они являются таким образом
асимптотическими решениями. В принципе можно улуч-
улучшить результат, рассматривая его как первый шаг в
схеме последовательных приближений. Получающиеся
ряды, хотя и необязательно сходящиеся, по построению
представляют собой асимптотические разлооюения. Прак-
Практически обычно вычисляется только первое приближение,
иногда — второе. Основной смысл второго приближения
часто состоит в том, что оно помогает понять первое.
Лишь в редких случаях вычисления проводятся до пя-
пятого или шестого приближений. Но возможность беско-
бесконечного продолжения этого процесса имеет фундамен-
фундаментальное значение. Мы будем называть приближение та-
такого типа рациональным приближением.
С другой стороны, некоторые очень полезные при-
приближения не становятся точными ни при каком изве-
известном предельном переходе. Примерами являются сле-
следующие приближения:
Метод Кармана — Цяня для профиля в дозвуковом
потоке (Липман и Паккет [1]);
теория скачка и волны разрежения и ее распростра-
распространение на осесимметричные и трехмерные течения
(Хейз и Пробстин [1]);
локальная линеаризация Спрейтера для околозвуко-
околозвуковых течений (Спрейтер [2]);
теория Честера — Чизнелла в динамике ударных волн
(Честер [3]);
теория Мотт-Смита структуры ударных волн (Мотт-
Смитт[1]).
1.2. Рациональные и иррациональные приближения 17
Будем называть такое приближение иррациональным
приближением. Если дальнейшее исследование не вы-
выявит асимптотического характера приближения, то ир-
иррациональное приближение представляет собой тупик.
Приходится принимать любую ошибку, которую оно вно-
вносит, и нет возможности увеличить точность последова-
последовательными приближениями.
В этой книге рассматриваются только рациональные
приближения. Таким образом, мы будем иметь дело с
асимптотическими разложениями решений уравнений
движения жидкости для малых или больших зна-
значений некоторого параметра или независимого пере-
переменного.
Часто удобно обозначить величину возмущения через
е и определить ее так, чтобы она была мала. Например,
в теории пограничного слоя за е можно взять величину,
обратную числу Рейнольдса или корню из него.
Следует предположить, что при стремлении е к нулю
течение стремится к некоторому пределу, который может
быть назван основным решением. Например, при боль-
больших числах Рейнольдса вязкое обтекание большей части
полубесконечных тел стремится к соответствующему об-
обтеканию невязкой жидкостью. Это стремление не являет-
является равномерным, что ясно из идей теории пограничного
слоя. Однако для тел, на которых пограничный слой от-
отрывается, мы еще не знаем соответствующего предела
или — более того — не уверены в самом существовании
предела (см. § 7.1).
Если.мы имеем возмущение параметра, основное ре-
решение часто оказывается равномерным параллельным
потоком или иным тривиальным течением. Тогда оно
обычно рассматривается как «нулевое приближение», а
первое его возмущение называется первым приблиэюе-
нием или решением первого порядка. С другой стороны,
в большей части случаев с возмущением координат ос-
основное решение не является тривиальным решением пол-
полных уравнений (например, одно из упомянутых выше
автомодельных течений) и обычно само рассматривает-
рассматривается как первое приближение.
18 Гл. 1. Сущность теории возмущений
f.3. Примеры разложений по малому возмущению
Эти общие замечания могут быть иллюстрированы
некоторыми типичными разложениями по малому воз-
возмущению, для которых трудолюбивые исследователи вы-
вычислили несколько членов. В методе Рэлея — Янсена,
или М2-разложении, влияние сжимаемости при дозву-
дозвуковых скоростях исследуется путем возмущения основ-
основного решения для несжимаемой жидкости. Поправка
первого порядка пропорциональна квадрату числа Ма-
Маха М набегающего потока, и высшие приближения выра-
выражаются последовательными степенями М2. Симасаки [1]
вычислил шесть членов ряда для дозвукового обтекания
кругового цилиндра без циркуляции. Для максимальной
скорости gmax (которая достигается на поверхности ци-
цилиндра в концах диаметра, перпендикулярного потоку),
отнесенной к скорости U на бесконечности, и при зна-
значении показателя адиабаты у =1,405 он нашел разложе-
разложение
^ = 2,00000 +-
+ 7,53386M6-f- 25>69342М8 + 96,79287М10+ .... A.1)
Предполагается, что этот метод дает сходящиеся ря-
ряды, если течение чисто дозвуковое. (Доказательство схо-
сходимости для достаточно малых М2 было доложено
Вендтом в 1948 г., но не опубликовано1).) Из поведе-
поведения коэффициентов разложения видно, что сходимость
становится сомнительной, когда М приближается к кри-
критическому значению, примерно 0,40, при котором gmax
становится звуковой (см. упражнение 10.6).
В теории тонкого профиля решение для удлиненного
объекта находится как возмущение равномерного пото-
потока. Ханцше [1] вычислил разложение для тонкого эллип-
эллиптического профиля с относительной толщиной е без угла
атаки в дозвуковом потоке сжимаемой жидкости. Он на-
1) Сходимость разложения еще ранее доказана в работе
М В. Келдыша и Ф. И. Франкля «Внешняя задача Неймана для
нелинейных эллиптических уравнений с приложением к теории крыла
в сжимаемом газе», Изв. АН СССР, 1934. -—Прим. ред.
1.3. Примеры разложений по малому возмущению 19
шел разложение
Wi T ] , A.2а)
где
A.26)
В разложении A.2а), как и во многих задачах теории
возмущений, неожиданно появляется логарифм вели-
величины возмущения. По причинам, которые будут изло-
изложены в § 10.5, неизвестный следующий член, который,
как оказывается, будет иметь порядок е4, должен быть
включен вместе с членом е4 In e в приближение четвер-
четвертого порядка.
При малых числах Рейнольдса вязкое обтекание трех-
трехмерных тел описывается приближением Стокса. Для тел,
симметричных относительно среднего поперечного сече-
сечения, лучшая оценка дается приближением Озеена. Гольд-
штейн [2] вычислил шесть членов ряда Озеена для со-
сопротивления сферы. Его результат для коэффициента
сопротивления в зависимости от числа Рейнольдса
Re=?/a/v, где а — радиус сферы, имеет вид
^D:==W2'a^~" Re Г "^ 8 Ke"~ 320 Ke "+" 2560 Ke ~
30179 122 519 \
2150400 Ke ¦ 17 203 200 Ke ' '")' (i'6>
Здесь последний коэффициент исправлен Шенксом
[1]. Решение полных уравнений Навье — Стокса отлича-
отличается от приближения Озеена, начиная со второго члена
разложения. Согласно работе Праудмена и Пирсона [1],
это решение имеет вид
^ ] A.4)
При больших числах Рейнольдса вязкое течение
вблизи поверхности тела описывается уравнениями
20 Гл. 1. Сущность Теории возмущений
Прандтля пограничного слоя. Поскольку они нелиней-
нелинейны, обычно требуются дополнительные приближения.
Разложения по возмущениям^ координаты для малых
расстояний от критической точки некоторых гладких сим-
симметричных плоских форм, начатые Блазиусом, были до-
доведены Тиффордом [1] до шестого члена. Для коэффи-
коэффициента местного поверхностного трения на параболе это
дает (Ван-Дайк [11])
——1,93186 (—
V а
т
Л1051 (-^-J — 5,02892 L^-Y + 8,14109 (^J —
+ ...]. A.5)
Здесь х — расстояние от критической точки вдоль по-
поверхности тела, Re — число Рейнольдса, построенное по
радиусу а кривизны в вершине параболы.
Обтекание тонкого крыла большого удлинения А по-
потоком несжимаемой жидкости описывается приближе-
приближением Прандтля несущей линии. Вычисление приближе-
приближений высших порядков будет проведено в гл. 9. Для
эллиптического крыла наклон кривой коэффициента
подъемной силы няйаен (Ван-Дайк [12]) в виде
2 16 In Л 4/7 о
+ (Ч241
A.6)
Для известной своей трудностью задачи гиперзвуко-
гиперзвукового обтекания затупленного тела были предприняты
попытки решения в приближении Ньютона — Буземана
разложением в ряды по 1/М2 и (у — \I{у+\). Честер
[2] дальше всех продвинулся в этих разложениях для
тел вращения, порождающих параболоидальную удар-
ударную волну При М = оо он нашел для отношения наи-
наименьшего расстояния Д ударной волны к радиусу b
1.4. Задачи регулярных и особых возмущений 21
кривизны в ее вершине следующее разложение:
А _ Y-l -,/T/Y-lf2 , 13fY-ll2
\ag . 13 f у-If
В следующих главах каждый из этих примеров бу-
будет рассмотрен подробно.
1.4. Задачи регулярных и особых возмущений
При наиболее благоприятных условиях решения, по-
полученные методом возмущений, приводят к результатам,
удовлетворительным в целом. Часто ряды не могут пред-
предполагаться сходящимися, особенно при возмущении
параметра. Тем не менее асимптотический характер этих
рядов означает, что несколько членов разложения могут
давать вполне достаточную точность всюду в поле тече-
течения при разумно малых е. Такая равномерная точность
результатов представляется имеющей место, например,
в разложениях Рэлея — Янсена при числах Маха, мень-
меньших критического. В таком случае говорят о задаче ре-
регулярных возмущений.
С другой стороны, может случиться, что решение,
найденное непосредственно методом возмущений, не яв-
является равномерно точным во всем поле течения. Наи-
Наиболее известным примером является безотрывное вязкое
обтекание при больших числах Рейнольдса. В нем воз-
возмущения основного невязкого течения неприемлемы
вблизи поверхности тела и должны дополняться при-
приближением пограничного слоя. В этом случае не только
первое приближение локально несостоятельно, но и
в приближениях высшего порядка — если они вообще
могут быть вычислены —трудности лишь нарастают, так
что в области неоднородности решение при этом скорее
ухудшается, чем улучшается. В этом случае говорят о
задаче особых возмущений.
Задачи особых возмущений возникают в механике
жидкости часто. Они изучались с нарастающей интен-
интенсивностью в последние годы одновременно с развитием
22 Гл. 1. Сущность теории возмущений
необходимого математического аппарата. Даже некото-
некоторые классические задачи получили новое освещение за
счет того, что был осознан их особый (в рассматривае-
рассматриваемом смысле) характер. По этим причинам настоящая
книга посвящена в основном задачам особых возмуще-
возмущений.
Для исследования задач особых возмущений недавно
были развиты два более или менее общих метода. Один
представляет собой обобщение понятий теории погра-
пограничного слоя и называется нами методом сращиваемых
асимптотических разложений. Другой метод представ-
представляет собой развитие идеи, восходящей к Пуанкаре; его
мы называем методом деформированных координат. Ма-
Математическое обоснование обоих этих способов находит-
находится в зачаточном состоянии. Так, пока не может быть точно
установлено, когда и какой из методов приложим, какой
из них предпочтительнее в данной проблеме, как свя-
связаны между собой два этих метода. Тем не менее мы
попытаемся вникнуть в суть дела путем изучения раз-
различных примеров. В некоторых случаях в качестве про-
простых моделей, демонстрирующих существенные черты
методов, используются обыкновенные дифференциальные
уравнения. Однако мы по возможности старались брать
наши примеры из современных работ по механике жид-
жидкости, т. е. обычно имели дело с уравнениями в частных
производных.
Поскольку мы касаемся способов, имеющих довольно
обширные применения, то наши примеры будут — так же
как и уже приведенные результаты — относиться как
к невязким, так и к вязким течениям и к диапазону ско-
скоростей от гиперзвуковых до скоростей, обеспечивающих
несжимаемое течение. Мы предполагаем, что читатель
знаком с физическими основами этих задач; это часто
полезно и для понимания математической стороны во-
вопроса. Предполагается также достаточное знакомство с
элементарными операциями анализа, основами теории
дифференциальных уравнений в частных производных и
общими понятиями теории функций комплексного пере-
переменного, включая, в частности, представление об анали-
аналитической функции как результате аналитического про-
продолжения.
Глава 2
НЕКОТОРЫЕ ЗАДАЧИ
РЕГУЛЯРНЫХ ВОЗМУЩЕНИЙ
2.1. Введение. Исходное течение — обтекание круга
Для иллюстрации некоторых методов теории возму-
возмущений мы рассмотрим сначала несколько связанных ме-
между собой задач регулярных возмущений. Эти методы
будут систематизированы в следующей главе. В следую-
следующих главах будут рассмотрены усложнения, связанные
с особыми возмущениями.
Поскольку точные решения чрезвычайно редки, есте-
естественно стремление использовать их возможно более
полно. Так, часто рассматриваются различные возмуще-
возмущения какого-либо одного точного решения для исследо-
исследования тех или иных эффектов. В обычной аэродинами-
аэродинамической задаче об обтекании тела безграничным потоком
жидкости могут быть произведены возмущения:
i) дальних граничных условий (в набегающем по-
потоке) ;
ii) ближних граничных условий (на поверхности
тела);
Hi) уравнений движения.
В свою очередь каждая из этих возможностей может
быть осуществлена различными путями. Например, точ-
точное решение об обтекании кругового конуса сверхзвуко-
сверхзвуковым потоком невязкого газа было подвергнуто возмуще-
возмущениям типа (i) для исследования влияний:
а) угла атаки (Стоун [1]);
б) углового колебательного движения (Кавамура и
Цянь[1]);
возмущениям типа (ii) для выяснения эффектов:
¦в) кривизны носовой части для тел оживальной фор-
формы (Кабанн [1]);
24
Гл. 2. Некоторые задачи регулярных возмущений
г) отклонений от круговой формы поперечных сече-
сечений (Ферри и др. [1]);
д) малого затупления (Якура[1]);
и возмущениям типа (ш) для учета влияния
е) малой вязкости (Ханцше и Вендт [1]).
Для того чтобы продемонстрировать эти возможно-
возможности и избежать излишних вычислений, возьмем в каче-
качестве основного точного решения бесциркуляционное
обтекание круга безграничным потоком невязкой несжи-
несжимаемой жидкости (рис. 2.1). Наряду с потенциалом ско-
скорости удобно ввести в рассмотрение и функцию тока,
Рис. 2.1. Исходное течение — бесциркуля-
бесциркуляционное обтекание круга невязкой несжимае-
несжимаемой жидкостью.
поскольку далее мы будем рассматривать и вихревое те-
течение, для которого потенциал не существует.
Для плоского несжимаемого течения функция тока
определяется в декартовых координатах соотношением
d\\> = udy — v dx. B.1)
В невязкой жидкости она удовлетворяет уравнению
V2i|) = -co(i|)), B.2)
которое выражает тот физический факт, что при отсут-
отсутствии вязкости завихренность неизменна вдоль линии
тока. Это уравнение нелинейно, если завихренность
со(я|)) не является линейной функцией от я|). Если набе-
набегающий поток равномерный, то завихренность обра-
обращается в нуль и я|) удовлетворяет уравнению Лапласа
Ф„-Ь^ + ^ = О. B.3а)
2.2. Круг в потоке с малой завихренностью 25
Здесь и далее в книге нижние индексы употребляют-
употребляются для обозначения частных производных. Граничные
условия будут следующие:
в набегающем потоке ф(г, 0) -.> Ur sin 9 при /*—>оо, B.36)
на поверхности тела ф {а, 0) = 0. B.3в)
К этому нужно прибавить условие, исключающее цир-
циркуляцию. Таким условием является требование симмет-
симметрии течения относительно линии 0 = 0:
ф(г, в) = -ф(г, -6). B.3г)
Решение получается наложением на равномерный
поток течения от диполя, помещенного в центре круга,
¦ — -?-) sine. B.4а)
Соответствующий потенциал скорости равен
B.46)
Обе последние зависимости могут быть выражены
одной комплексной:
) eiQ B.4в)
у
2.2. Круг в потоке с малой постоянной
завихренностью
Рассмотрим сначала малые возмущения условий в
набегающем потоке. Пусть набегающий поток представ-
представляет собой параллельное течение с малой постоянной
Рис. 2.2. Обтекание круга
потоком с малой постоян-
постоянной завихренностью.
завихренностью (рис. 2.2), скорость в котором опреде-
определяется формулой
(j)(^) B.5а)
26 Гл. 2 Некоторые задачи регулярных возмущений
Функция тока равна (с точностью до аддитивной по-
постоянной)
B.56)
а завихренность —
= -6-^. B.5в)
Уравнение и граничные условия полной задачи та-
таковы:
Фгг + ^ + ^ = е^. B.6а)
ф->?/ [г sin 0 + Ie-?A — cos 20)] при г->оо, B.66)
ф(а, в) = 0. B.6в)
Для единственности решения мы должны добавить,
например, требование, чтобы тело не вызывало допол-
дополнительной циркуляции.
Если безразмерный «параметр завихренности» емал,
то представляется вероятным, что течение будет лишь
слегка отличаться от предыдущего решения для безвих-
безвихревого движения. В этом предположении будем искать
решение в виде
ф(г, 0; е) = фо(г, 0) + eiMr, 6)+ .. . , B.7)
где -фо — основное решение B.4а). Подставляя ряд B.7)
в уравнение B.6а) и граничные условия B.66), B.6в)
полной задачи и приравнивая члены с одинаковыми сте-
степенями е, получаем для возмущения первого порядка
я|н следующую задачу:
.. | ^1г 1 "Фюе и /о йа\
x\hrr + -у -т- -рг- — -?•' (z.«a)
ф1->1^г2A --cos 20) при г->схэ, B.86)
фа(я, 0) = О. B.8в)
В этой задаче частным решением, соответствующим
неоднородному члену в правой части уравнения B.8а),
2.2. Круг в потоке с малой завихренностью 27
является вихревая часть набегающего потока B.56).
Таким образом, удобно представить решение в виде
^=i^2(l-cos2e) + Xl(r,e). B.9)
Наличие частного решения позволяет привести диф-
дифференциальное уравнение к однородному — к уравне-
уравнению Лапласа вместо уравнения Пуассона, — так что для
дополнительного решения %i получается задача
Х1гг + ~ + ^ = 0> BЛ0а)
Х\—> const при г—>оо, B.106)
Xl(#, 6) = — \Ua(\ —cos26). B.10в)
Эта задача также легко решается разделением пере-
переменных, как решалась основная задача B.3); здесь
опять будет единственное решение, свободное от цирку-
циркуляции. Объединяя полученные результаты, получаем
полное решение первого порядка
^-cos26- -a\. B.11)
Это основное решение состоит из равномерного по-
потока — диполя на бесконечности — и его отображения
относительно круга — диполя в начале координат. По-
Подобным же образом возмущение первого порядка состоит
из вихревой части набегающего потока, ее отображения
относительно круга и константы, приводящей функцию
тока к нулевому значению на поверхности.
Обычно в конце такого выражения пишут « + •••»
или « + О(е2)», чтобы подчеркнуть, что найденный ре-
результат верен до величины первого порядка по малому
параметру е. Однако в этом нетипичном случае разло-
разложение по возмущению конечно, и полученное решение
является точным (см. Ламб [2]). Для любого иного про-
профиля скорости в набегающем потоке задача была бы
нелинейной и возмущенное решение выражалось бы бес-
бесконечным рядом по степеням е (см. упражнение 2.4).
28
Гл. 2. Некоторые задачи регулярных возмущений
Это решение было использовано Холлом [1] как мо-
модель для учета влияния завихренности на показания
трубки Пито в спутной струе или в пограничном слое.
Легко показать, что нулевая линия тока -ф = 0 начинает-
начинается выше по течению при у^еа/4. Следовательно, изме-
измеренное давление торможения больше, чем та же вели-
величина непосредственно выше по течению; этот эффект
наблюдался в экспериментах. Холл исследовал ту же
задачу для сферы, что связано со значительными услож-
усложнениями.
2.3. Малая деформация круга
Рассмотрим следующий тип возмущений — возмуще-
возмущение граничных условий на поверхности тела. При этом
Рис. 2.3. Обтекание одно-
однородным потоком деформи-
деформированного круга.
обнаружатся некоторые черты теории возмущений, ко-
которые не проявлялись в предыдущем примере. Пусть
форма тела (рис. 2.3) определяется уравнением
= аA- 8Sin20).
B.12)
Это уравнение можно рассматривать или как первое
приближение для эллипса, или как точное описание бо-
более сложной кривой.
Как и прежде, попытаемся представить возмущенное
решение разложением по степеням е
ф (г, 6; 8) = ф0 (г, 6) + e\\h (г, 0) + ...
B.13)
и подставим его в уравнение и граничные условия пол-
полной задачи. В уравнении движения B.3а) и в условиях
в набегающем потоке B.36) мы вновь приравняем чле-
2.3. Малая деформация круга 29
ны с одинаковыми степенями е и получим для первых
двух членов разложения
У2ф0 = 0, i|>0-»?/rsin9 при г—>со, B.14а)
у2ф! = 0, ф! —> 0 при г->со. B.146)
Однако в условии обтекания появляются усложнения.
В точной записи это условие будет иметь вид
%[a(l— esin26), в]Ч-еф1[аA ~esin28), 0]+ ... =0.
B.15а)
Здесь параметр возмущения е входит как явно, так
и неявно (в первом аргументе функций). Следовательно,
непосредственно приравнять нулю члены с различными
степенями е здесь невозможно. Для этого необходимо
предварительно разложить функции в ряды с тем, что-
чтобы получить их явную зависимость от 8. Если предпо-
предположить, что функции -фо и хр± являются аналитическими
по г, то можно разложить их в ряды Тейлора вблизи
г = а. Сохраняя только линейные члены, получаем
фо(а, 6) — га sin2 Щг {а, в) + еф,(а, в) f . . . —0. B.156)
Сравнение коэффициентов при одинаковых степе-
степенях 8 теперь возможно и дает соотношения
фо(а, в) = 0, B.16а)
^(а, 9) = asin2e\|Hr(a, 6) = -^ UaC sin 6 — sin 30). B.166)
Последнее выражение получено с использованием
основного решения B.4а) для а|H.
Задача для возмущения B.146), B.166) имеет теперь
ту же форму, что и основная задача, и ее решение мо-
может быть написано непосредственно. Таким образом,
полное приближение первого порядка находится в виде
^-sine--^ sin Зб)+О (s2).
B.17)
- Значения на поверхности тела, которые обычно пред-
представляют наибольший интерес, могли бы быть получены
30 Гл. 2 Некоторые задачи регулярных возмущений
простой подстановкой значения B.12) для г на поверх-
поверхности тела. Однако в связи с уже введенным приближе-
приближением уместно упростить результат, отбросив члены выс-
высшего порядка как несущественные. Это достигается
опять-таки разложением в ряд Тейлора вблизи основ-
основного значения г = а. Так, например, для скорости на по-
поверхности тела можно найти выражение
..)• B.18)
2.4. Круг в жидкости с малой сжимаемостью
Рассмотрим теперь возмущение уравнений движе-
движения. Пусть жидкость почти несжимаема, т. е. число Маха
набегающего потока мало. Удобнее работать с потен-
потенциалом скорости, поскольку связь между функцией тока
и скоростью усложнена теперь переменностью плотно-
плотности. Пусть вектор скорости будет q=Ggradcp. Тогда
полное уравнение для потенциала плоского течения со-
совершенного газа будет
(Осватич [1]). Здесь М — число Маха набегающего по-
потока. Преобразование к полярным координатам дает
уравнение
i Vr , Фее ] .до [У д , Фе д
Удобно так выбрать масштаб длин, чтобы радиус
круга был равен единице. Тогда граничные условия при-
принимают вид
в набегающем потоке ф—>/*COS0 при Г—>оо, B.20а)
на поверхности тела Фг A, 0) = 0. B.20б)
К этому нужно добавить требование симметрии, ис-
исключающее циркуляцию.
2А. Круг в жидкости с малой сжимаемостью 31
Вместо того чтобы применить, как прежде, разло-
разложение по возмущениям, мы воспользуемся случаем и
продемонстрируем способ итераций как другой путь по-
построения последовательных приближений. С этой целью
все члены, представляющие влияние сжимаемости, на-
написаны выше в правых частях дифференциальных урав-
уравнений. Пренебрежение ими приводит к основному реше-
решению B.46) для несжимаемой жидкости при U = a=\.
Чтобы вычислить в первом приближении влияние сжи-
сжимаемости, мы подставим основное решение в нелиней-
нелинейную правую ча'сть и вновь решим уравнение. Дифферен-
Дифференциальное уравнение первого приближения будет таково:
B.21)
В способе итераций удобнее вычислять полное реше-
решение на каждой стадии, а не только малую поправку к
предшествующему результату. Тогда полные граничные
условия B.20) будут иметь место во всех приближениях.
Чтобы подчеркнуть отличие от предыдущего случая, мы
используем римские цифры в индексах последователь-
последовательных приближений.
Как легко заметить, член с (у—1) в дифферен-
дифференциальном уравнении не влияет на первое приближе-
приближение ф1. Влияние сжимаемости в первом приближении
не зависит от термодинамических свойств газа.
Следуя Рэлею [1], мы найдем разделением перемен-
переменных частное решение итерационного уравнения B.21),
обращающееся в нуль на бесконечности,
77^-T7t)C0s 0- TTcos39]-
К этому должно быть добавлено решение однород-
однородного уравнения — уравнения Лапласа, — чем восстанав-
восстанавливаются граничные условия. Окончательный результат
32 Гл. 2 Некоторые задачи регулярных, возмущений
Вычисление на основе этого выражения максималь-
максимальной скорости на поверхности воспроизводит первые два
члена ряда A.1) Симасаки, приведенного в гл. 1.
Приближения высшего порядка могут быть найдены
повторением итерационного процесса, причем единствен-
единственным усложнением является стремительное увеличение
объема вычислений. Его можно уменьшить путем при-
применения теории функций комплексного переменного и
систематизации выкладок.
2.5. Влияние малой вязкости
Можно попытаться исследовать влияние вязкости та-
таким же путем, как исследовалось влияние сжимаемости.
Удобно иметь дело с функцией тока, которая в плоском
несжимаемом течении удовлетворяет уравнению
B-24)
Здесь v — кинематическая вязкость. Если мы опять
введем такие безразмерные переменные, что ?/ = а=1,
то v можно заменить на Re, где Re = Ua/v — число Рей-
Рейнольдса, взятое по радиусу. Это уравнение выражает то
обстоятельство, что завихренность переносится с местной
скоростью (левая часть уравнения) и одновременно рас-
рассеивается вязкостью (правая часть уравнения).
При бесконечном значении числа Рейнольдса правая
часть уравнения B.24) обращается в нуль, что приво-
приводит к уравнению B.2) для г|). Следовательно, основное
невязкое решение B.4а) становится точным в этом пре-
предельном случае. Положим, что мы пытаемся действовать
способом итераций для получения возмущенного реше-
решения при больших числах Рейнольдса. Уравнение следует
преобразовать к полярным координатам, и к граничным
условиям нужно добавить требование отсутствия сколь-
скольжения на поверхности тела. Однако и без детальных вы-
вычислений ясно, что попытка применения итераций ока-
окажется неудачной. Правая часть уравнения обратится
в нуль, если в нее подставить основное решение, так
что число Рейнольдса не фигурирует в задаче.
Разрешение этих трудностей дается теорией Прандтля
пограничного слоя. Несмотря на их внешнее сходство,
2.6. Пограничный слой; разлоо/сение по координате 33
задачи о течениях жидкости с малой сжимаемостью и
с малой вязкостью существенно различны. Для первой
основное решение является подходящей- аппроксимацией
всюду в поле течения, в то время как для второй оно
непригодно вблизи поверхности тела даже при сколь
угодно больших числах Рейнольдса. Поэтому влияние
малой сжимаемости составляет задачу регулярных воз-
возмущений, а влияние малой вязкости — задачу особых
возмущений.
2.6. Пограничный слой; разложение по координате
Задачи особых возмущений и основные идеи теории
пограничного слоя будут обсуждаться в следующих гла-
главах. Здесь же целесообразно просто привести известные
результаты Прандтля. При больших числах Рейнольдса
Рис. 2.4. Координаты теории
пограничного слоя для круга.
вязкость существенна только внутри тонкого слоя, при-
примыкающего к поверхности тела, где уравнение B.24)
для яр может быть приближенно заменено уравнением
ФЖ* — ФА* = v$yyy + 4^&- B.25а)
Здесь х и у — криволинейные координаты вдоль поверх-
поверхности тела и по нормали к ней (рис. 2.4). При выводе
было произведено одно интегрирование исходного урав-
уравнения по у и порядок уравнения снижен до третьего.
Последний член есть функция интегрирования, q — ско-
скорость на поверхности тела в невязком обтекании.
Из требования равенства нулю скорости на поверх-
поверхности тела следуют два граничных условия:
0)-фДх, 0) = 0. B.256)
34 Гл. 2. Некоторые задачи регулярных возмущений
Третье условие, а именно условие, что скорость на
внешней границе пограничного слоя стремится к значе-
значению скорости на поверхности тела в невязком обтека-
обтекании, может быть записано в виде
HmiMx, y) = q. B.25в)
г/->оо
Здесь необходимо иметь в виду, что у —> оо означает
большие значения у только в масштабе малой толщины
пограничного слоя.
Во всех предыдущих примерах имелись только воз-,
мущения параметра. Теперь для пограничного слоя на
круге мы рассмотрим возмущения координат. В рамках
теории Прандтля это вновь будут регулярные возму*
щения.
Положим, что расстояние х от критической точки
мало по сравнению с радиусом а круга. Тогда функцию
тока можно разложить в ряд по х/а, и из симметрии
следует, что в разложение войдут только нечетные сте-
степени. Разложение удобно написать в виде
B.26)
который является обычной формой ряда Блазиуса (см.
Шлихтинг [1]).
Скорость невязкого обтекания на поверхности круга
мы возьмем из основного решения
и подставим в уравнение и условия задачи пограничного
слоя B.25). После приравнивания одинаковых степеней
х/а мы получим последовательность задач для обыкно-
обыкновенных дифференциальных уравнений
B.28а)
Упражнения 35
Первая из этих задач представляет собой классиче-
классическую задачу Хименца о вязком течении у критической
точки на плоскости, остальные — ее возмущения.
Численное интегрирование (Тиффорд [1]) дает зна-
значения f" @) = 1,2325877 и /? @) = 0,7244473. Исходя из
этого, получим следующее разложение для коэффициен-
коэффициента поверхностного трения:
= ^=-[,973- — 2,732 (-? + ...]. B.29)
Эта величина обращается в нуль при я/а =1,6, что
указывает на отрыв пограничного слоя на круге на уг-
угловом расстоянии от критической точки около 92°. Эта
оценка была уточнена вычислением еще четырех членов
ряда (см. Шлихтинг [1]), и было получено значение
109°, но сам факт отрыва пограничного слоя делает не-
непригодным предшествующий анализ. Получающийся
мощный спутный поток решительно изменяет обтекание
тела. Таким образом, хотя уравнение Прандтля B.25а)
имеет место всюду, но скорость невязкого обтекания q
не определяется формулой B.27), а остается неизвест-
неизвестной (см. рис. 7.1). Эксперименты показывают, что от-
отрыв потока в действительности происходит примерно
при 81°.
Ряды Блазиуса оказываются совместимыми лишь для
тех тел, для которых из решения следует отсутствие от-
отрыва. Примером является парабола в равномерном те-
течении, для которой разложение вида B.29), содержа-
содержащее шесть членов, дано уравнением A.5) гл. 1.
УПРАЖНЕНИЯ
2.1. Пульсирующий круг. Равномерный плоский поток несжи-
несжимаемой невязкой жидкости обтекает круговой цилиндр, радиус кото-
которого слегка меняется во времени по закону a[\ + sf )]. Вычислите
потенциал скорости с точностью до первого порядка по 8. Найдите
функцию тока и покажите, что она не обращается в нуль на по-
поверхности.
2.2. Круг с малой пористостью. Равномерный поток несжимае-
несжимаемой невязкой жидкости обтекает полый круговой цилиндр, в поверх-
поверхности которого нормально к поверхности высверлено много малых
цилиндрических пор. Предполагается, что нормальная составляющая
36
Гл. 2. Некоторые задачи регулярных возмущений
скорости на поверхности равна произведению некоторого малого sи
перепада давления на внешней и внутренней поверхностях цилиндра
(давление внутри цилиндра считается постоянным) и что полный
поток через поверхность равен нулю. Вычислите функцию тока внеш-
внешнего обтекания приближенно до порядка 8 и внутреннее давление.
Знаки величин выбирайте из физических соображений. Каков соот-
соответствующий результат для жидкости с малой сжимаемостью, если
сохранить только линейные по s и М2 члены?
2.3. Гофрированный квазицилиндр. Рассмотрим бесконечно длин-
длинное тело вращения (рис. 2.5) радиуса а[1 + 8 sin (z/b)]. Вычислите
приближенно трехмерный потенциал скорости для равномерного
Рис. 2.5. Бесконечный го-
гофрированный квазицилиндр.
a[?~esin(z/bji
несжимаемого набегающего потока (без циркуляции), перпендику-
перпендикулярного оси вращения тела, сохраняя лишь линейные по 8 члены.
Используя разложения для функций Бесселя, упростите решение для
случая, когда длина волны столь велика, что молено оставить лишь
линейные по afb члены. Интерпретируйте результат как квазидву-
квазидвумерный. Покажите, что в другом предельном случае, когда ajb
очень велико, возмущение представляет собой плоскую гармониче-
гармоническую функцию вблизи поверхности, причем Э входит только как па-
параметр. Подтвердите этот результат физическими соображениями.
2.4. Круг в потоке с параболическим профилем скорости. Кру-
Круговой цилиндр радиуса а расположен симметрично в параллельном
несжимаемом невязком потоке жидкости, имеющем параболический
профиль скорости u=U(\ + ll2&y2/a2). Найдите точное выражение для
завихренности ©(ф) и разложение, определяющее со в виде ряда
до членов порядка 82 включительно. Получите возмущенное решение
для течения и покажите, что в членах порядка 8 возникают труд-
трудности, связанные с тем, что возмущения, вызванные телом, возра-
возрастают, а не убывают далеко вверх по потоку.
Глава 3
АППАРАТ ТЕОРИИ ВОЗМУЩЕНИЙ
3.1. Введение; предельные переходы
Примеры, приведенные в предыдущих главах, слу-
служили для демонстрации различных приемов решения
задач о возмущениях. Теперь мы попытаемся классифи-
классифицировать и обобщить те из них, которые имеют общее
значение. Мы начнем с обсуждения некоторых обозна-
обозначений, определений и уместных в том или другом слу-
случае процессов исследования.
Мы имеем дело с нахождением приближенных реше-
решений уравнений движения жидкости, которые близки
к точным решениям в некотором нужном нам смысле.
Этим вызывается необходимость введения различных
видов равенств, которые (в порядке уменьшающейся
степени точности) будут выражаться следующими сим-
символами:
s тождественно равно,
= равно,
~> асимптотически равно (при некотором
данном предельном переходе), C.1)
« приближенно равно (в каком-либо нуж-
нужном нам смысле),
ос пропорционально.
Как указывалось в гл. 1, мы рассматриваем прибли-
приближения, которые зависят от предельного перехода и кото-
которые становятся точными при стремлении величины воз-
возмущения к нулю или к некоторому иному критическому
значению. Часто встречаются двойные или множествен-
множественные предельные переходы, в которых две или более ве-
величин возмущений одновременно стремятся к своим пре-
предельным значениям. Поскольку порядок выполнения не-
нескольких предельных переходов не может быть, вообще
говоря, изменен, часто приходится уточнятьотноситель-
38 Гл. 3. Аппарат теории возмущений
ную скорость стремления к пределам. Это уточнение вво-
вводит параметр подобия задачи. Ниже приведены некото-
некоторые известные примеры.
а) Теория малых возмущений для плоского транс-
трансзвукового обтекания крыла с относительной тол-
толщиной е (Карман [1]):
б) Гиперзвуковая теория малых возмущений для
тела с относительной толщиной е (Хейз и Проб-
стин [1]):
8->0,
М—>со
в) Приближение Ньютона — Буземана для гипер-
гиперзвукового обтекания затупленного тела (Коул [1]):
М->оо, 1 j
г) Гиперзвуковая форма, приближения Ньютона —
Буземана для тонких тел с относительной толщи-
толщиной 8 (Коул [1]):
0,
1
М—>оо,
(у — 1)М2е2
В последнем примере можно было бы ожидать по-
появления двух параметров подобия, однако лишь один из
них оказывается существенным.
Величина возмущения никогда не определена един-
единственным образом. Например, параметр толщины для
удлиненных тел может быть взят в виде относительной
толщины, максимального наклона, среднего наклона
и т. д. Конечно, его можно также изменить введением
постоянного множителя; например, упоминавшееся выше
число Рейнольдса по радиусу обычно для сферы берется
по диаметру. Следует цак можно шире использовать
3.1. Введение; предельные переходы 39
возможности этой свободы выбора, заменяя очевидный
параметр таким, который более выгоден в каком-либо
отношении. Эти возможности настолько разнообразны,
что не укладываются ни в какие правила. Мы можем
лишь подсказать их, перечислив несколько примеров, в
которых остроумный выбор величины возмущения, обыч-
обычно основанный на посторонних рассуждениях, приводит
к упрощению или улучшению результатов.
а) (М2—1) вместо (М — 1) в трансзвуковой теории
малых возмущений; при этом результат оказы-
оказывается справедливым также и в смежных режи-
режимах дозвукового и сверхзвукового течений (Спрей-
тер[1]).
(б) l/i^M2—1 вместо 1/М в гиперзвуковой теории
малых возмущений; тогда результат имеет место
также и в смежных режимах сверхзвукового тече-
•ния (Ван-Дайк [1]).
в) (y~ 1)/(V+1) вместо (у—1) в приближении
Ньютона — Буземана для гиперзвукового течения,
этот параметр может быть отождествлен с отно-
отношением плотностей при переходе через сильную
ударную волну (Хейз и Пробстин [1])
г) ({lnRe/4+v—1/2) вместо In Re для вязкого обте-
обтекания круга при малых числах Рейнольдса (здесь
Y — постоянная Эйлера) При этом два первых
члена в разложении Стокса объединяются (Кап-
(Каплун [2], § 8.7).
д) е/A—е) вместо е для расстояния отошедшей
ударной волны при обтекании затупленного тела
сверхзвуковым потоком в приближении Ньюто-
Ньютона — Буземана. Здесь е — отношение плотностей
при переходе через прямой скачок, и указанный
вначале параметр обращается в бесконечность
при М-»1 одновременно с величиной расстоя-
расстояния ударной волны от тела (Сербии [1])
ё) (i4 + ?Re-V»+\..J вместо (А2 + 2АВ Re-V*+...)
для сопротивления затупленного тела в ламинар-
ламинарном потоке при.больших числах Рейнольдса..Этот
40 Гл. 3. Аппарат теории возмущений
параметр подсказывается теорией и лучше согла-
согласуется с известными результатами (Имаи [5]).
ж) 2яA+2/Л+\..) вместо 2лA—2/Л + ...) для на-
наклона кривой подъемной силы эллиптического
крыла большого удлинения А. При этом наклон
кривой стремится к нулю при А -»0, как и должно
быть (см. гл. 9).
з) l/Y^-r~l2* где ? — параболическая координата,
вместо х в рядах Блазиуса для пограничного слоя
на параболе. При этом радиус сходимости стано-
становится бесконечным (см. гл. 10).
и) s/B + e) вместо s в теории струй (Гарабедян [1]),
где 2 + е — число измерений пространства. При
этом увеличивается радиус сходимости.
3.2. Функции сравнения и символы порядка
Решения задач механики жидкости зависят от коор-
координат, например х, у, г, /, а также от различных па-
параметров. Одна или несколько из этих величин при
надлежащем их определении могут считаться исчезающе
малыми в возмущенном решении. Рассмотрим поведе-
поведение решения в зависимости от одной такой величины
возмущения, фиксируя остальные координаты и пара-
параметры. Таким образом, мы попытаемся описать поведе-
поведение функции f(e), когда s приближается к нулю. Такая
ситуация уже возникала при рассмотрении граничных
условий в набегающем потоке B.36), B.66) и т. д., где
требовалось описать поведение решения далеко от тела.
Существует несколько возможных описаний, обла-
обладающих различной степенью точности. Мы рассмотрим
шесть из них в порядке увеличения точности. Во-первых,
можно просто установить, существует ли предел. Напри-
Например, sin2e имеет предел при е->О, в то время как
sin 2/в предела не имеет. Однако мы будем касаться
лишь тех проблем, в которых предполагается существо-
существование предела.
Во-вторых, можно описать предельное значение ка-
качественно. Имеются три возможности: функция в пре-
3.2. Функции сравнения и символы порядка 41
деле может
а) обращаться в нуль, / (е) -> О,
б) быть ограниченной. /(е) < оо,
в) бесконечно возрастать, f (e) -> со
при е -> 0.
Особенность этого способа описания состоит в том,
что случай а) заключается в случае б)—обращаю-
б)—обращающаяся в нуль функция также и ограничена. Однако есте-
естественно, где это возможно, использовать описание а),
поскольку оно более точно.
В-третьих, можно описать предельное значение коли-
количественно. Опять имеется три возможности, из которых
только вторая является уточнением качественного опи-
описания:
при е -> 0.
а)
б) lim / (б) = с = const,
в) lim / (е) = оо
В четвертых, можно качественно описать скорость
приближения к пределу. Только случаи а) ив), указан-
указанные выше, могут быть уточнены таким образом. Это
может быть сделано путем сопоставления с некоторым
набором функций сравнения. Последние являются функ-
функциями столь простыми, что их предельное поведение
можно считать интуитивно известным. Сравнение осу-
осуществляется использованием символов порядка О
(«О большое») и о («о малое»). Они являются необхо-
необходимым средством учета степени приближения в возму-
возмущенных решениях.
Символ О применяется в тех случаях, когда сравне-
сравнение f(e) с некоторой функцией сравнения 6(е) показы-
показывает, что отношение /(s)/6(e) остается ограниченным при
е-»0. Мы пишем
f(e) = O[6(e)] при е-* О, если lim-^ < оо. C.2)
Если это отношение стремится к нулю, то применя-
применяется символ о взамен О. Мы пишем
= o[6(s)\ при ?->0, если lim!?v = 0. C.3)
е»0 °W
42 Гл. 3. Аппарат теории возмущений
Ниже приведены примеры:
sin 2е = О (е), 1 — cos е = О (е2) = о (е),
/1-е2 = 0A), arcsec(l+e)-=OF1/2) = o(l), C.4)
ctge = Of—j, exp(—l/e) = o(em) для любого m.
Так же как и сам параметр возмущения, функции
сравнения могут быть определены не единственным об-
образом, и иногда отличный от очевидного выбор функции
сравнения может оказаться более выгодным. Например,
в первом из примеров C.4) при определенных условиях
может оказаться полезной замена оценки на следующие
эквивалентные ей:
sin 2г = О Bе), O(tgs), О (j^j) и т' д*
Естественно в качестве функций сравнения брать
действительные степени е, поскольку эти функции обла-
обладают наиболее простыми свойствами. Однако этот набор
неполон. Он непригоден, например, для описания In 1/е,
который при стремлении е к нулю стремится к бесконеч-
бесконечности, но медленнее, чем любая степень г. Степени е
должны, следовательно, быть дополнены при необходи-
необходимости логарифмом, экспонентой, функцией In In и т. д.
или эквивалентными им функциями, например
}), Ar ch К0(е) = О (in ln{
, exp(—ch~) =
Часто, как в формуле A.4), lne пишется там, где In 1/s
был бы более уместен.
Символы порядка не обязательно описывают действи-
действительную скорость приближения к пределу, они дают
лишь верхнюю границу. Так, формально было бы пра-
правильно заменить первый из примеров C.4) следующими
оценками:
Sin 2е = 0A-), оA), 0(е1/2), 0(8^ и т. д., C.6)
3.3. Асимптотические представлении и ряды 43
однако мы предполагаем, что всегда дается наиболее
тонкая оценка. Это предписывает, например, выбор в ка-
качестве функций сравнения наибольшей возможной сте-
степени е и применение символа о только при отсутствии
сведений, достаточных для применения символа О. Ко-
Конечно, результат может быть только верхней границей
из-за недостатка соответствующей информации.
Математический порядок величины, выраженный сим*
волами О и о, теоретически не совпадает с физическим
порядком величины, поскольку не принимаются во вни-
внимание множители пропорциональности; следовательно,
Кг считается величиной О(е) даже в том случае, когда К
равно десяти тысячам. В физических задачах имеется,
однако, по меньшей мере некоторая надежда, почти не-
неизменно оправдывающаяся, что эти две оценки доста-
достаточно близки. Так, если ошибка в физической теории со-
составляет О (г) и 8 выбрано разумно, то можно ожидать,
что численная ошибка не будет превосходить некоторого
умеренного кратного -е: возможно, она будет 2е или
даже 2пе, но почти определенно не достигнет 10е.
Правила для простых операций с символами порядка
очевидны на основе этой физической связи. Например,
порядок произведения (или частного) равен произведе-
произведению (или частному) порядков; порядок суммы или раз-
разности равен порядку преобладающего слагаемого, т. е.
члена порядка sm с наименьшим значением m и т. д.
Символы порядка можно интегрировать как по е, так
и по другим переменным; дифференцировать соотноше-
соотношения порядка в общем случае нельзя. Тем не менее в фи-
физических проблемах обычно предполагается, что диффе-
дифференцирование по другим переменным законно, так что
производные имеют тот же порядок, что и сами функ-
функции. О других свойствах символов порядка можно про-
прочитать в 1 гл. книги Эрдейи [1].
3.3. Асимптотические представления; асимптотические
ряды
Пятая схема описывает количественно скорость, с
которой функция приближается к своему пределу. Она
представляет собой уточнение четвертой схемы (приме-
44 Гл. В. Аппарат теории возмущений
нение символов порядка), так же как третья схема яв-
является уточнением второй. Мы просто восстановим мно-
множитель пропорциональности и запишем
/(е)~?б(е) при 8—>0, C.7а)
если
= с, C.76)
т. е. если
f(e) = c6(e)+o[fi(e)]. C.7в)
Это асимптотическая форма или асимптотическое пред-
представление функции, которое составляет первый член в
асимптотическом разложении, рассматриваемом далее.
Вот некоторые примеры
sin2e~2e, Arseche~ln~, ]Л — е2~1,
fe1
В шестой схеме предыдущее описание, обеспечиваю-
обеспечивающее наибольшую точность, которая может быть достиг-
достигнута при применении одной функции сравнения, уточ-
уточняется добавлением дальнейших членов. Будем считать
разность между данной функцией и ее асимптотической
формой некоторой новой функцией и определим ее
асимптотический вид. Результат может быть записан
следующим образом:
при ?->0, C.9а)
где вторая функция сравнения 62 (е) должна быть вели-
величиной более высокого порядка малости, чем первая,
или
C.96)
а ошибка — величиной еще более высокого порядка ма-
малости:
f (г) = с А (е) + с2Ь2 (е) + о [62 (8)]. C.9в)
Следующие члены могут быть добавлены повторением
этого процесса. Таким образом, получается асимптотике-
3.3. Асимптотические представления и ряды 45
ское разложение или асимптотический ряд из /V членов,
который можно записать в виде
N
= 2^А(8) при е—>0 C.10а)
и определить так:
N
/00= 2^А(?) + ^К(еI при 8->о. (З.Юб)
Если бы функция /(е) была известна вместе с функ-
функциями сравнения 6^(8), то коэффициенты сп асимптоти-
асимптотического разложения могли бы быть вычислены последо-
последовательно в виде
/(*)- 2 слбя(е)
cm=lim f^ . C.11)
Если все функции сравнения представляют собой це-
целые положительные степени 8, то говорят об асимптоти-
асимптотических степенных рядах. Когда число N членов увели-
увеличивается беспредельно, получаются бесконечные асимп-
асимптотические ряды, которые могут быть сходящимися или
расходящимися.
Некоторые примеры асимптотических разложений
даны ниже:
Arseche~ln~ — i-
-|е+1^е»+...). C.12)
/2=0
Первые два из них сходятся, три последних расходятся.
Граничные условия на бесконечности надлежит рас-
рассматривать как асимптотические соотношения. Например,
46 Гл. 3. Аппарат теории возмущений
условие B.66) будет впредь записываться в виде
при г->оо. B.660
Необходимо учесть, что эта запись допускает возмож-
возможность ошибки порядка о (г). В действительности для рас-
рассматриваемой задачи следующий член асимптотического
разложения представляет собой 0A); функция тока в
набегающем потоке должна быть определена лишь с
точностью до константы, которая физически соответ-
соответствует смещению критической линии тока.
3.4. Асимптотические последовательности
Только что описанный процесс построения разложе-
разложения член за членом эффективнее, чем метод, применен-
примененный для получения возмущенных решений в гл. 2. Его
особенностью является то, что для построения возму-
возмущенного решения каждой задачи требуется специальная
система функций сравнения
6i(e), 62(e), 63(е), ..., C.13)
которые расположены по убыванию порядка: 6n+i(e) =
=о(8п). Это — асимптотическая последовательность,
связанная с задачей. Ее нельзя задать произвольно, по-
поскольку она должна быть достаточно полной, чтобы
описывать, например, логарифм, если он появится в за-
задаче. С другой стороны, существует неограниченная воз-
возможность выбора различных частных асимптотических
последовательностей:
sin 2г — 2г — -|- г3 -f- -Д-е5 -h ...
— 2 tg e — 2tg3e — 2tg5e-f ...
— 2 ln(l -Ьг)+-]пAЧ-г2) — 21n(l+e3
Две последние формы иллюстрируют то обстоятельство,
что выбранные последовательности не обязательно эк-
эквивалентны: порядок соответствующих членов неодина-
неодинаков. Однако и асимптотическая последовательность и
3.4. Асимптотические последовательности 47
само асимптотическое разложение определяются един-
единственным образом, если выбрана величина возмущения
(например, е) и функции сравнения (например, ет,
In 1/e, In In 1/е и т. д.).
Мы видели, что оди-н из способов исследовать задачу
возмущений состоит в том, чтобы заранее предположить,
какую форму будет иметь решение в виде ряда. Для
этого требуется угадать подходящую асимптотическую
последовательность. Простейшей возможной является
последовательность целых степеней еп, использованная
в примерах гл. 2. Могут встречаться также и дробные
степени, особенно в задачах особых возмущений. Приве-
Приведем несколько примеров:
1, е1/2, е, е3/2, ...Безотрывное ламинарное обтекание
гладких тел при больших числах
Рейнольдса Re, s=l/Re (Ван-Дайк
[9])
1, е3/4, ... Отрывное течение Озеена при боль-
больших числах Рейнольдса Re, e=l/Re
(Тамада и Мияги [1])
В некоторые члены последовательностей могут входить
логарифмы; см. следующие примеры:
1, е, 821пе, е2, 831пе, е3, ... Осесимметричное те-
течение при малых чис-
числах Рейнольдса Re,
s = Re (Праудмен и
Пирсон [1])
1, 821п8, е2, 841п28, еЧпе, е4, ...Сверхзвуковое обте-
обтекание осесимметрич-
ных тонких тел, е—
параметр толщины
(Бродерик [1])
sine, e, e2lne, е2, ... Приближение Нью-
Ньютона—Буземана для
плоского гиперзву-
гиперзвукового обтекания за-
затупленных тел, е^
= (Y-1)/(Y + 1) (Че-
(Честер [1])
48 Гл. 3. Аппарат теории возмущений
(lne)-1, (In г), Aпе)~3, ... Плоское вязкое те-
течение при малых чис-
числах Рейнольдса Re,
e=Re (Каплун [2];
Праудмен и Пирсон
[1])
1, 8, е2, е3, еЧпе, е4, ... Дозвуковая теория
тонкого профиля с
закругленным носи-
носиком, е — параметр
толщины (Ханцше
[1])
1, е1/2, 8, 83/21п8, 83/2, ... Ламинарное обтека-
обтекание плоской пласти-
пластины при больших чис-
числах Рейнольдса Re,
е=1 /Re (Гольдштейн
[3]; Имаи [4])
В последних двух примерах ранние исследователи
получали ошибочные решения, поскольку они не подо-
подозревали о наличии логарифмических членов. Другие
примеры, возникающие в теории пограничного слоя,
были рассмотрены Стюартсоном [2], который показал,
что в асимптотическом решении задачи об обтекании
кругового цилиндра далеко вниз по потоку фигурирует
даже функция In In.
Экспоненциально малые члены встречаются редко и
обращение с ними затруднительно. Следующий пример
показывает, что оценка О (е~{^) имеет весьма малое
практическое значение:
C.15)
Естественно возникает вопрос, как удостовериться в
правильности сделанного выбора асимптотической по-
последовательности. По-видимому, общего правила не су-
существует, но некоторую помощь могут оказать следую-
следующие принципы:
3.5. Сходимость и точность асимптотических рядов 49
а) Сомнительные случаи проверяются: излишний
член выпадет при построении для его коэффи-
коэффициента однородной задачи, решением которой
(если оно единственно!) является нуль.
б) При первом намеке на затруднения нужно иметь
в виду возможность наличия логарифмических
членов.
в) Итерации иногда (но не всегда!) автоматически
приводят к надлежащей последовательности.
Обычно чувствуется, когда решение развивается пра-
правильно: все члены согласуются, запутанные выражения
часто упрощаются. С приобретением опыта можно на-
научиться распознавать, когда отсутствие таких успокаи-
успокаивающих признаков внушает мысль о перепроверке пред-
предположенной формы ряда. Однако единственным совер-
совершенно надежным процессом является такой, в котором
асимптотическая последовательность не устанавливается
заранее, а определяется — член за членом — в ходе ре-
решения. Этот метод будет продемонстрирован в гл. 7 и 8.
3.5. Сходимость и точность асимптотических рядов
Мы видели, что бесконечные асимптотические ряды
могут или сходиться для некоторого диапазона значе-
значений е или расходиться при всех е. В задачах возмущений
исследователь часто не знает, сходятся ли полученные
им ряды, и не заботится об этом. Эта точка зрения была
убедительно изложена Джеффрисом [1]. Было бы ошиб-
ошибкой считать, что сходимость необходима практически.
Математическая сходимость зависит от поведения чле-
членов бесконечно высокого порядка, в то время как в фи-
физических задачах исследователь может вычислить только
несколько первых членов и надеяться, что они быстро
приближаются к истинному решению. Для расходящих-
расходящихся рядов это требование 'может иногда даже лучше вы-
выполняться, чем для сходящихся. Так, разложение
Л(е) 1 е2 + 84 г6+ C16)
для функции Бесселя имеет бесконечный радиус сходи-
сходимости, но для получения точного результата требуется
50
Гл. 3. Аппарат теории возмущений
много членов, если е не слишком мало. Для е>4, нацри-
мер, первые три члена увеличиваются по величине (так
что ряд имеет вид как бы расходящегося), и нужно по
крайней мере восемь членов для достижения точности
в третьем знаке. С другой стороны, асимптотическое раз-
разложение
C.17)
расходится для любых е, даже сколь угодно малых, но
несколько членов дают хорошую точность при умеренно
Нужно
идти до
Пд-
Нужно остановиться
здесь
ПпппПП!
1 4 6 8 Ю 12
4 6 8
Рис. 3.1. Поведение членов ряда.
а — медленно сходящийся ряд, б —расходящийся ряд.
По оси абсцисс откладывается номер члена п, по оси ординат —
абсолютная величина я-го члена.
малых 8. Один первый член дает верный до третьего
знака результат для A/е) =4.
Полезность асимптотических разложений основана на
том, что ошибка по определению имеет порядок первого
отброшенного члена и, следовательно, быстро стремится
к нулю при уменьшении е. Для фиксированного значе-
значения е ошибка может быть уменьшена вначале увеличе-
увеличением числа членов, но если ряд расходится, то в конце
концов достигается точка, за которой добавление членов
увеличивает ошибку (см. рис. 3.1). Эти свойства часто
являются идеальными для практических целей, в част-
частности при возмущениях параметров того вида, которьщ
3.5. Сходимость и точность асимптотических рядов Й1
используется в теории тонкого профиля. Там практиче-
практический интерес представляют только малые значения 8
и вычисляется только несколько членов, так что точка
увеличения ошибки не достигается.
Имеются, однако, другие проблемы, в которых 8
должно быть настолько велико, насколько возможно.
Это имеет место для таких возмущений параметра, как
в разложении для больших или малых чисел Рей-
нольдса. Это почти всегда справедливо для возмущений
координат, поскольку естественно стремление распро-
распространить результат как можно дальше от начала от-
отсчета. При этих условиях вопрос сходимости приобре-
приобретает практический интерес. Как будет показано в гл. 10,
иногда можно увеличить скорость и радиус сходимости
или даже превратить расходящиеся ряды в сходящиеся.
/%<? сходимости
Возможная
особенность
Рис. 3.2. Комплексная плоскость величины
возмущения е.
С физической точки зрения ясно, что величина возму-
возмущения s — положительная действительная величина. Од-
Однако часто оказывается полезным математическое иссле-
исследование, основанное на рассмотрении аналитического
продолжения в комплексной плоскости (рис. 3.2). Это,
в частности, полезно, когда решение представляет собой
степенной ряд по величине возмущения. Так, в методе
Рэлея —Янсена рассматривается комплексная М2-пло-
скость, в теории тонкого профиля — комплексная пло-
плоскость относительной толщины и т. д. В этом случае
можно использовать все преимущества мощных методов
теории функций комплексного переменного.
52 Гл. 3. Аппарат теории возмущений
При этом существенно знать принцип аналитического
продолжения и хорошо представлять себе его значение.
Аналитическую функцию можно разложить в степенной
ряд в каждой регулярной точке, но этот ряд сходится
лишь в круге, простирающемся до ближайшей особой
точки. Функция, определенная в некоторой области или
даже на прямолинейном отрезке, обычно может быть
единственным образом распространена на значительно
большую область плоскости комплексного переменного
(возможно, на многолистную риманову поверхность) при
помощи аналитического продолжения.
Иногда на основании нескольких первых членов воз-
возмущенного решения представляется, что ряд сходится,
но имеет ограниченный радиус сходимости, причем по-
последнее обстоятельство не вытекает из физической сущ-
сущности задачи. В соответствии с только что изложенными
соображениями это должно быть результатом существо-
существования особенности в комплексной плоскости переменно-
переменного е где-либо не на положительной действительной оси.
Некоторые примеры, которые будут приведены в гл. 10,
наводят на мысль о том, что обычно в этих условиях
особенность лежит на отрицательной действительной оси,
а именно при е = — 1, если сделан наиболее естественный
выбор переменного (рис. 3.2). Это искусственное огра-
ограничение может быть исключено перенесением особенно-
особенности в бесконечность путем применения простого конформ-
конформного отображения, а именно преобразования Эйлера
± C.18)
При этом радиус сходимости простирается до другой
ближайшей особенности в плоскости комплексного пере-
переменного е и возможность использования ряда часто зна-
значительно расширяется.
3.6. Свойства асимптотических разложений
При подстановке предполагаемого решения в виде
ряда в уравнения задачи возмущений должны осуще-
осуществляться такие операции, как сложение, умножение и
дифференцирование. Сложение и вычитание вообще за-
3.6. Свойства асимптотических разложений 53
конны; умножение допустимо, если результат является
асимптотическим разложением; дифференцировать асимп-
асимптотические разложения ни по переменной разложения,
ни по другим переменным в общем случае нельзя. Эти
и другие свойства асимптотических разложений рассмот-
рассмотрены в книге Эрдейи [1]. Результаты формальных преоб-
преобразований оказываются непригодными в достаточно об-
общем случае, охватывающем и такие часто встречаю-
встречающиеся ряды, как ряды с логарифмическими членами.
Поэтому на практике такие операции, как дифференци-
дифференцирование по тем или иным переменным, выполняются
формально, без попытки обосновать их законность. Если
они окажутся незаконными, то в решении возникнут не-
неравномерности.
В физических задачах коэффициенты асимптотиче-
асимптотического разложения будут зависеть от пространственных и
временных переменных, иных, чем е. Ряды называются
равномерно пригодными или равномерно точными (в про-
пространстве или времени), если ошибка мала равномерно
по этим переменным.
Примеры неравномерности (неоднородности) по х:
,— = О (е), но неравномерно вблизи X = О,
Vх C.19)
elnx=O(e), но неравномерно вблизи Х = 0, со.
Задачу особых возмущений лучше всего определить
как задачу, в которой ни одно асимптотическое разло-
разложение не является равномерно пригодным во всей рас-
рассматриваемой области. Неоднородности, иллюстриро-
иллюстрированные примерами C.19), возникают в практических
задачах особых возмущений. Например, первая встре-
встречается в теории дозвукового тонкого профиля с закруг-
закругленной передней кромкой, вторая — при острой перед-
передней кромке или в плоском вязком течении при малых
числах Рейнольдса.
Мы видели, что каждая функция имеет единственное
асимптотическое разложение, если выбраны функции
сравнения или асимптотическая последовательность.
С другой стороны, часто делается утверждение, что раз-
различные функции могут иметь одинаковые асимптотиче*
54 Гл. 3. Аппарат теории возмущений
<ские разложения. Степень этой неединственности может
быть осознана на следующем примере:
п = 0
По отношению к функциям сравнения еп эти две
функции имеют одинаковые асимптотические разложе-
разложения вплоть до любого конечного члена. Их разность так
мала, что она становится очевидной только в том слу-
случае, когда рассматривается вся бесконечная последова-
последовательность степеней е, например при их суммировании.
В данном примере это легко показать применением пре-
преобразования Эйлера C.18): асимптотические разложе-
разложения рассматриваемых двух функций по степеням нового
переменного е оказываются различными (и конечными):
1 1-е,
1+8
1+е
-Не _ . _ C-2°б)
1 — е + е • е~1/г — еее'11г.
1+е
Величину ?~1/8 называют трансцендентально малой
по сравнению с последовательностью степеней е, по-
поскольку она представляет собой о(ет) для любого сколь
угодно большого т. Подобным же образом на другом
уровне величин само s трансцендентально мало по срав:
нению с последовательностью (lne)~m. Эта последова-
последовательность появляется, например, в исследовании пло-
плоского вязкого течения при малых числах Рейнольдса.
Возможности действий с трансцендентально малыми чле-
членами будут рассмотрены в гл. 8 в связи с этой задачей.
3.7. Последовательные приближения
Задачи возмущений в механике жидкости обычно
сводятся к системам дифференциальных уравнений —
обыкновенных или в частных производных — с соответ-
соответствующими начальными и граничными условиями; мо-
"гут также встретиться интегро-дифференциальные урав-
3Jj Последовательные приблюисения 55
нения, как в задаче с учетом излучения,. Существуют
два систематизиюов/аншых способа нахождения решения
последовательными приближениями; оба они описаны
в предыдущей главе:
i) подстановка • ряда предполагаемого вида;
И) последовательные приближения к основному при-
приближенному решению (итерации).
В первом ^етоде, который обладает несколько боль-
большей общйостыю, ведущая идея состоит в том, что, по-
поскольку разложение должно иметь место хотя бы в
асимптотическом смысле для произвольных значений
величины возму1щения е, члены одного порядка по е
должны по отдельности удовлетворять каждому равен-
равенству. Таким образом, следует приравнивать одинаковые
степени е, члены' вида em lnn e с одинаковыми тип
и т. д.
Каждый из этих, методов имеет свои преимущества
и недостатки, что м>,ожно иногда использовать для соз-
создания некоторой их комбинации. Наиболее важные их
особенности состоят в1 следующем.
а) Итерации могугг начинаться только в том случае,
когда известно соответствующее начальное при-
приближенное решение. Решения в виде ряда обла-
обладают большим автоматизмом, поскольку они мо-
могут давать оанов<ное пршближение при подста-
подстановке в уравнения задачи ряда с неопределенной
заранее асимптотической последовательностью
Соответствующий пример будет приведен в гл. Т..
б) При применении итераций не нужно угадывать,
вида асимптотической последовательности. Сле-
Следовательно, оно будет надежнее, чем подстановка-
ряда, если не оставлять асимптотическую после-
последовательность неопределенной. Например, приме-
применение итераций часто (хотя в задачах особых
возмущений не-всегда) дает логарифмы в членах
высшего порядка, которые пропускаются, если
предполагаемый ряд выбирается степенным.
в) Разложение в ряд обеспечивает более система-
систематичные сведения о третьем и следующих членах,
56 Гл. 3. Аппарат теории возмущений
поскольку оно дает только существенные резуль-
результаты, в то время как итерации в нелинейных про-
проблемах дают некоторые члены высшего порядка,
учет которых не имеет смысла, так как не учтены
другие члены того же порядка. Например, в ре-
решении Рэлея — Янсена для круга (§ 2.4) следую-
следующий итерационный шаг дал бы, очевидно, не
только члены порядка М4, которые верны и со-
совпадают с вытекающими из разложения в ряд,
но и некоторые члены порядка М6 и М8, кото-
которыми следует пренебречь, поскольку они не-
неполны.
г) Итерации дают на каждом шаге группу членов
приблизительно одного порядка, на что требуется
несколько шагов при применении ряда. Напри-
Например, в теории обтекания осесимметричных тонких
тел каждый шаг итераций добавляет следующие
группы членов:
[1], [821пе, е2], [841п2е, еЧпе, е4]
Какой бы метод ни применялся, существуют общие
для всех возмущенных решений черты. Основное реше-
решение может быть линейным или нелинейным, но все при-
приближения высшего порядка определяются линейными
уравнениями с линейными граничными условиями. Ис-
Исключением являются трансзвуковая и гиперзвуковая
теории малых возмущений, где применяется специфиче-
специфический двойной предельный переход с тем, чтобы сохра-
сохранить в возмущениях существенные нелинейности задачи.
В этих частных случаях только третий член и члены
высшего порядка удовлетворяют линейной задаче. В ос-
остальных случаях возможна суперпозиция возмущений
первого порядка, так как они линейно независимы. На-
Например, можно сложить три возмущения, изученные по
отдельности в § 2.2, 2.3, 2.4, и получить решение первого
порядка для обтекания слегка деформированного круга
слегка завихренным потоком слегка сжимаемой жидко-
жидкости. Однако приближения высшего порядка будут свя-
связаны с произведениями различных величин возму-
возмущений.
3.7. Последовательные приближения
Уравнения, определяющие приближения высшего
порядка, линейны, но обычно содержат переменные ко-
коэффициенты, зависящие от предыдущих приближений.
Часто удается упростить вычисления, учитывая уже из-
известные соотношения для этих предшествующих резуль-
результатов. Простой пример будет приведен в теории тон-
тонкого профиля (гл. 4), где как дифференциальные урав-
уравнения, так и граничные условия будут использованы
для упрощения их аналогов в последующих прибли-
приближениях.
Как и в решении Рэлея — Янсена (§ 2.4), задачи
для приближений высших порядков, как правило, от-
отличаются одна от другой лишь появлением в дифферен-
дифференциальных уравнениях последовательно усложняющихся
неоднородных членов (зависящих от предшествующих
приближений). Этим членам соответствует некоторое
частное решение. Обычно лучший способ найти некото-
некоторое частное решение — это просто угадать его. Только
после того, как эта попытка окажется неудачной, сле-
следует применять более изощренные приемы.
Нужно также иметь в виду и те немногочисленные
задачи, в которых общий вид частного решения может
быть выражен через предыдущие приближения. Мы ил-
иллюстрируем эту возможность двумя примерами из тео-
теории малых возмущений для осесимметричных течений
сжимаемой жидкости. Во-первых, в приближенной ли-
линеаризованной теории винта в сверхзвуковом потоке
найдено, что потенциал скорости во втором приближе-
приближении должен удовлетворять неоднородному, волновому
уравнению
^ ^е, C.21 а)
а первое приближение является решением однородного
уравнения П2ф1 = 0. Берне [1] заметил, что частное ре-
решение ф2 всегда выражается через решение первого
порядка в виде
- М
Ф2= 1_M2^Pl8' C.216)
Во-вторых, если попытаться улучшить линеаризован-
линеаризованную теорию дозвукового или сверхзвукового обтекания
Гл. 3. Аппарат теории возмущений
'тел вращения, рассматривая нелинейные члены, то
потенциал второго приближения должен удовлетворять
уравнению
C.22а)
где снова П2ф4 = 0. Ван-Дайк [2] нашел, что с точностью
.до членов третьего порядка частное решение равно
Ф2 = М» [Ф„ (ф, - Ц± j^w гф1г) -1 яр?,] • C.226)
Частные решения такого вида обычно находятся пу-
путем проб, а не путем систематического анализа. Анало-
Аналогичные решения некоторых однородных уравнения для
вязких течений были найдены Линь Дун-цзи и Ша-
фом [1].
3.8. Перенос граничных условий
Часто граничные условия заданы на поверхности,
положение которой слегка меняется с изменением пара-
параметра возмущения е. Поверхность может быть границей
твердого тела (как для слегка деформированного кру-
^га в § 2.3), свободной линией тока, ударной волной
Рис. 3.3. Примеры переноса граничных условий.
и т. п. (рис. 3.3). Для того чтобы осуществить система-
систематическую схему разложения, нужно в каждом случае
выразить граничные условия через величины, опреде-
определенные в основном положении поверхности, соответ-
соответствующем 8 = 0. Иначе е войдет в возмущенные выраже-
выражения как явно, так и неявно, результат будет неоправ-
3.9. Прямое координатное разложение 59
данно усложнен, ряды не будут асимптотическими раз-
разложениями и отпадет возможность приравнивания чле-
членов одинакового порядка.
При переносе граничных условий используются све-
сведения о том, как меняется решение в окрестности основ*
ной поверхности. Часто бывает известно, что решение
является аналитическим по координатам; в этих слу-
случаях перенос осуществляется разложением в ряды Тей-
Тейлора около значений на основной поверхности. В пер-
первом приближении это обычно сводится к простому пере-
переносу граничных условий с деформированной на основ-
основную поверхность. С другой стороны, в теории осесим-
метричных тонких тел решение имеет особенность на
оси, но перенос можно осуществить, используя то обстоя-
обстоятельство, что вблизи оси потенциал скорости меняется
как In г, или радиальная компонента скорости меняется
как 1/л
После того как решение найдено, часто требуется
найти параметры течения на поверхности тела или на
других поверхностях. Эти величины могут быть най-
найдены в простейшей форме повторением процесса пере-
переноса, выражением их через значения на основной по-
поверхности. Оба эти процесса переноса будут описаны
в гл. 4 (см. также упражнения 2.1, 2.3 и 3.2).
3.9. Прямое координатное разложение
Задачи возмущений, в которых малая величина
представляет собой безразмерную комбинацию, вклю-
включающую в себя координаты (пространство — время), а
не только параметры, имеют определенные специфиче-
специфические черты. Ценное исследование различий между пара-
параметрическими и координатными разложениями было
дано Чжаном [1]. Существенным моментом является от-
отсутствие производных по параметру и, следовательно,
возможность вычисления решения для одного значения
параметра без рассмотрения других его значений. При-
Приближение обычно ищется или.для малых, или для боль-
больших значений одной из координат Эти случаи полезно
различать как прямое и обратное координатные разлФ
щ$ния соответственно,
60 Гл. 3. Аппарат теории возмущений
Прямое координатное разложение является есте-
естественным для задач с дифференциальными уравнениями
параболического или гиперболического типа. Решение
раскладывается для малых значений переменной, по-
подобной времени, которая, конечно, может быть про-
пространственной координатой, а не реальным временем.
Величина возмущения должна возрастать вместе с этим
переменным, обратного влияния нет, так что каждый
член возмущенного ряда не зависит от следующих чле-
членов и может быть вычислен, когда до него дойдет оче-
очередь. Результатом является возмущенное разложение,
описывающее начальные стадии развития решения от
известного основного начального состояния.
Ниже дан типичный пример прямого координатного
разложения. Гольдштейн и Розенхед [1] вычислили на-
нарастание пограничного слоя на цилиндре, импульсивно
приводимом в движение. Применялось разложение по
степеням времени, уравнения задачи были параболиче-
параболическими. Вблизи критической точки на круге, например,
для поверхностного трения было получено
C.23)
где U\ — градиент скорости в критической точке при
иевязком обтекании, а х— расстояние вдоль поверхности
тела. Этот ряд, очевидно, расходится для больших зна-
значений времени (см. рис» 3.4), где он должен был бы
приближаться к решениям Хименца для установивше-
установившегося обтекания. Такая неоднородность обычно возни-
возникает в прямых координатных разложениях (см., одна-
однако^ 10.6—10.8).
Случаем, в котором роль переменной, подобной вре-
времени, играет пространственная координата, является раз-
разложение Блазиуса по степеням расстояния х от крити-
критической точки для установившегося пограничного слоя на
цилиндре. Уравнения пограничного слоя B.25а) явля-
являются параболическими как для установившегося, так
и для неустановившегося движения. Результат A.5)
для параболы является сходящимся, по-видимому,
только для х/а<я/4 (Ван-Дайк [11]). Другим таким же
3.9. Прямое координатное разложение
61
случаем, но для гиперболических уравнений, является
осесимметричная задача Крокко: возмущение автомо-
автомодельного решения для сверхзвукового обтекания круго-
кругового конуса дает начальный градиент потока в передней
точке тела вращения оживальной формы (Кабанн [1]).
Для эллиптических уравнений координатные разло-
разложения обычно дают только качественные результаты.
Здесь чаще приходится иметь дело с граничными зада-
задачами, а не с задачами с начальными данными. При
Рис. 3.4. Рост поверхно-
поверхностного трения вблизи крити-
критической точки.
По оси абсцисс отклады-
откладывается Uit, по оси ординат—
первый член ряда C.23),
два члена ряда C.23),
- три члена ряда C.23).
Решение
Химениа
этом вследствие взаимного влияния какое-либо локаль-
локальное решение зависит от граничных условий на больших
удалениях и невозможно вычислить последовательные
члены разложения для малых значений.координат. Ока-
Оказывается возможным только найти форму разложения,
каждый член которого определен с точностью до одной
или нескольких постоянных. Например, Каррьер и
Линь Цзя-цзяо [1] исследовали вязкое течение вблизи
передней кромки плоской пластины путем разложения
для малых радиусов. Полученный ими ряд для функции
тока после исправления имеет вид
= 2Ar3'2 (cos-^
|- — cos |-e)-f
-^-r3j 2 sin2 6 [In r sin 0 + @ — я) cos 0] +
~(sin20 — 2sin0)-f ^
.. , C.24)
62
Гл. 3. Аппарат теории возмущений
где 9=0 на пластине. Постоянные Л, 5, С, ... зависят
от граничных условий далеко от области пригодности
разложения и, следовательно, неопределимы в рамках
проводимого исследования.
Исключение составляет необычный случай задачи с
начальными данными для эллиптических уравнений.
В обратной задаче сверхзвукового обтекания затуплен-
затупленного тела (рис. 3.5) задается отошедшая ударная >волна
Рис. 3.5. Сверхзвуковое обте-
обтекание затупленного тела.
и ищется порождающее ее тело. Хотя течение вблизи
оси является дозвуковым, можно разложить функцию
тока по степеням расстояния вниз по потоку от ударной
волны и последовательно найти коэффициенты разло-
разложения. Кабанн [3] вычислил семь членов ряда при
М = 2. Для параболической ударной волны функция то-
тока вблизи оси определяется выражением
3 а
85 / х \2 215 / х \з
18 { а ) 27 { а )
7051 /^\5_ 1817 909 ( х
11945
324
243
2916
¦ C.26)
Помимо таких редких исключений, прямые координат-
координатные разложения могут эффективно прилагаться к эллип-
эллиптическим уравнениям только при условии, что с этими
уравнениями обращаются как с параболическим-и и об-
обрывают ряды на конечном числе членов.
Исследование обтекания затупленного тела настолько
трудно, что некоторые ученые пытались ввести еще одно
независимое переменное g тем, чтобы перевести урав-
3.10. Обратное координатное разложение 63
нения в параболические или гиперболические. Так, Ка-
банн [2] рассмотрел импульсивное начало движения, раз-
разлагая функции неустановившегося течения по степеням
времени. Он полагал, что точность будет увеличиваться
с увеличением числа Маха. При М = оо и y = 7/5 он на-
нашел для отношения расстояния Д ударной волны от но-
носовой точки тела к радиусу кривизны а носовой части
гладкого тела следующее выражение:
Л 1 (ш\ (п п 7
Здесь п — число пространственных измерений: д = 2 для
плоского течения ип = 3 для осесимметричного. Можно
ожидать, что результат будет более точным для пло-
плоского течения, поскольку он является точным для одно-
одномерной задачи о поршне, п—\. Ряд, очевидно, расхо-
расходится для больших значений времени, но Кабанн пытал-
пытался оценить его предел как максимум, доставляемый дву-
двумя известными членами. Это дает Д/а = 0,107 для пло-
плоского случая, что можно сравнить со значением 0,377,
полученным точными численными расчетами для круго-
кругового цилиндра. Мы обсудим это расхождение в § 10.7.
3.10. Обратное координатное разложение
В противоположность прямым разложениям, которые
обычно имеют конечный радиус сходимости, обратные
разложения для больших значений координаты обычно
являются расходящимися асимптотическими рядами. Им
также свойственна неопределенность независимо от типа
уравнений. Для эллиптических уравнений ситуация та-
такова же, как и при прямом разложении, однако неопре-
неопределенные постоянные могут иногда быть связаны с про-
простыми интегральными свойствами решений. Так, первые
несколько постоянных в разложении для дозвукового
течения далеко от конечного тела могут быть отожде-
отождествлены с его подъемной силой, сопротивлением, момен-
моментом и т. д. (Имаи [3]; Чжан [1]). Для параболических
и гиперболических уравнений неопределенность возни-
возникает вследствие того, что разложение происходит в на-
направлении, противоположном направлению изменения
64 Гл. 3. Аппарат теории возмущений
переменной, подобной времени. Таким образом, на ран-
ранних стадиях появляются собственные решения, постоян-
постоянные множители которых зависят от определенных дета-
деталей предшествующей истории. Иногда некоторые из них
можно найти без детального знания предыдущего дви-
движения, используя некоторые общие законы сохранения
(см. § 4.5), но чаще эти постоянные остаются неопреде-
неопределенными.
Форма обратного координатного разложения широко
меняется в зависимости от типа уравнений, числа изме-
измерений задачи и протяженности тела. В некоторых зада-
задачах главный член разложения очевиден. Например, это
будет невозмущенный поток для установившегося те-
течения далеко от конечного тела, коническое течение
далеко вниз по потоку от вершины затупленного конуса
и соответствующее установившееся течение для больших
значений времени после импульсивного начала движе-
движения. В дальнейшем это основное решение подвергается
возмущению с тем, чтобы найти степень даваемого им
приближения. Иногда приближение бывает алгебраиче-
алгебраическим и выражается через отрицательные степени боль-
больших координат, как это имеет место для бесциркуля-
бесциркуляционного потенциального течения далеко от конечного
тела (Имаи [3]). Очень часто наряду с алгебраическими
появляются логарифмические члены, как это имеет ме-
место для потенциального циркуляционного движения или
вязкого течения далеко от тела (Чжан [1]). В задачах,
зависящих от времени, часто встречаются экспонен-
экспоненциальные члены, как, например, в неустановившихся
вязких течениях или течениях со свободными линиями
тока (Келли [1]; Керл [1]).
Сошлемся на один пример. Ряды Блазиуса для по-
пограничного слоя (§ 2.6) представляют собой прямое ко-
координатное разложение для малых расстояний от кри-
критической точки. Для параболического цилиндра мы мо-
можем дополнить это приближение обратным разложением
для больших расстояний. Очевидно, что главный член
представляет собой решение для плоской пластины, по-
поскольку далеко вниз по потоку радиус носовой части
пренебрежимо мал по сравнению с рассматриваемыми
расстояниями. Возмущение этого основного решения
З.П Изменение типа уравнений и характеристик 65
дает в дополнение к A.5) следующее выражение для
коэффициента поверхностного трения:
/^Г[1 + 0,3006
C.27)
Здесь х — абсцисса, a Ci — неопределенный постоянный
множитель в первом из бесконечной последовательности
собственных решений для задачи об обтекании плоской
пластины (§ 7.6).
Иногда первый член отнюдь не очевиден. Возможные
усложнения можно показать на примере течений со
свободными линиями тока. В плоском течении ширина
застойной зоны далеко вниз по потоку увеличивается
как л:]/2, а в осесимметричном течении она растет по не-
неожиданно сложному закону xl'*(lnx)-lf* (Левинсон[1]) *).
3.11. Изменение типа уравнений и характеристик
Любопытной чертой методов возмущений является то,
что они могут менять тип рассматриваемых дифферен-
дифференциальных уравнений в частных производных. Ярким
примером этого является приближение Прандтля погра-
пограничного слоя. Эллиптические уравнения Навье — Стокса
внутри пограничного слоя заменяются параболическими
уравнениями, а вне его — эллиптическими или гипербо-
гиперболическими в зависимости от того, является ли внешнее
течение дозвуковым или сверхзвуковым. В теории по-
поверхностных волн эллиптическое уравнение Лапласа
также заменяется нелинейным гиперболическим уравне-
уравнением в приближении мелкой воды (Сгокер [1]). Наобо-
Наоборот, гиперболические уравнения невязкого сверхзвукового
течения становятся эллиптическими з линеаризованной
теории конических течений2) и в приближении тонкого
тела (Уорд [1]).
Эти изменений типа уравнений влекут за собой зна-
значительные изменения в области влияния и зависимости
1) Этот результат был независимо получен М. И. Гуревичем.—
Прим. ред.
2) Тип уравнений меняется и при точной нелинейной постановке
задач о конических течениях. — Прим. ред.
66 Гл. 3. Аппарат теории возмущений
и в соответствующих граничных условиях. Так, уравне-
уравнения Прандтля пограничного слоя, поскольку они являют-
являются параболическими, можно интегрировать шаг за
шагом вниз по потоку. Обратное влияние, связанное с
их бывшей эллиптичностью, как бы отбрасывается; од-
однако оно проявится в приближениях высшего порядка
(см. гл. 7). Подобным же образом в теории тонкого
крыла должно быть наложено условие Жуковского —
Кутта на дозвуковой задней кромке, так как ее влияние
вверх по потоку в приближении этой теории потеряно1).
В основе возможности таких изменений типа лежат
некоторые предположения о гладкости. Всюду, где эти
предположения не выполняются, должен приниматься
во внимание истинный тип уравнений, иначе возмущен-
возмущенное решение окажется неприемлемым по крайней мере
локально. Так, теория пограничного слоя непригодна
вблизи угловых точек, так же как теория мелкой воды
и приближение тонкого тела. Таким образом, задачи
особых возмущений возникают здесь как результат раз-
разрывности граничных условий.
Часто тенденция к изменению типа уравнений ока-
оказывается неполной: возмущенные уравнения становятся
лишь «менее гиперболичными» или «более эллиптичны-
эллиптичными». Для гиперболических уравнений это означает, что
характеристические поверхности меняются. Примером
этого является сверхзвуковая теория малых возмуще-
возмущений, где на каждой стадии истинные характеристики
приближенно заменяются в возмущенных уравнениях
конусами Маха невозмущенного потока. Как и прежде,
этот недостаток является несущественным для достаточ-
достаточно гладких тел, однако другие случаи приводят к неод-
нородностям (см. гл. 6 и упражнение 3.4).
УПРАЖНЕНИЯ
3.1. Видоизмененное гиперзвуковое правило подобия. В соответ-
соответствии с гиперзвуковой теорией малых возмущений коэффициент дав-
давления на тонком клине или конусе с углом раствора 2е имеет вид
Найдите другую форму зависимости, которая должна быть пред-
1) Условие Жуковского — Кутта накладывается и при точной
постановке задачи. — Прим. ред.
Упражнения 67
почтительнее для толстых тел, исходя при этом из ньютоновской
теории неупругого удара, согласно которой коэффициент давления
в некоторой точке поверхности тела, обтекаемого гиперзвуковым
потоком, равен удвоенному квадрату синуса угла, образованного на-
направлением потока с поверхностью тела. Покажите степень получае-
получаемого улучшения путем численного сравнения с полным решением
при М = оо. Выясните, можно ли распространить этот результат на
толстые тела при меньших скоростях, если руководствоваться сверх-
сверхзвуковым правилом подобия
Cn ~
3 2 Перенос условия обтекания. Малая сфера пульсирует в по-
покоящемся газе Ее радиус меняется во времени по закону е/(/) и
вызывает слабые расходящиеся волны, потенциал которых удовле-
удовлетворяет акустическому уравнению (p^ = c2V2(p. Покажите, что если
функция / достаточно гладкая, то условие обтекания приближенно
может быть перенесено в центр сферы и записано в виде
Вычислите ф', используя это условие Какой гладкостью должна
обладать функция р Что произойдет с решением, если это требова-
требование будет нарушено?
3.3. Оценка максимального значения по координатному разло-
разложению. Испытайте идею Кабанна оценки значения C.26) при беско-
бесконечном значении времени, применив ее к выражениям C.23) и A.5),
где ответ известен. Следует ли при отсутствии экстремума выбирать
значение, в точке перегиба? Попытайтесь придумать лучшую или
более рациональную схему такого типа.
3.4. Эффект изменения характеристик. Математической моделью
установившегося сверхзвукового обтекания верхней поверхности тон-
тонкого профиля является следующая задача
уу ^ ^ в ф* (°' У) = ° ПРИ У > °-
ср^ (х, 0) = е/' (jc), где f (х) = 0 при х < 0
Решите ее, пренебрегая сначала правой частью дифференциаль-
дифференциального уравнения, и последовательными приближениями найдите ре-
решение второго порядка. Сравните с точным решением для того,
чтобы установить, при каком наложенном на функцию f ограниче-
ограничении п е приближение будет пригодно вблизи поверхности Иссле
дуйте, что произойдет на больших расстояниях
Глава 4
НЕКОТОРЫЕ ЗАДАЧИ
ОСОБЫХ ВОЗМУЩЕНИЙ
В ТЕОРИИ ПРОФИЛЯ
4.1. Введение
Мы займемся теперь задачами, в которых прямая
схема возмущений, применявшаяся до сих пор, теряет
смысл в некоторых областях поля течения. В этих слу-
случаях отношение последовательных членов не мало, как
предполагалось, так что приближения в этих областях
перестают быть асимптотическими разложениями. Вслед-
Вследствие таких неоднородностей можно ошибиться в расче-
расчете или даже потерять существенные результаты, такие,
например, как поверхностное трение и теплопередача в
вязком течении при больших числах Рейнольдса или
как сопротивление тонкого профиля. Более того, обычно
на некоторой ранней стадии становится невозможным
перейти к высшим приближениям даже формально. Это
задачи особых возмущений. Для других разделов мате-
математической физики (иных, чем механика жидкости) они
рассмотрены в превосходном обзоре Фридрихса [5].
Прототипом задачи особых возмущений является тео-
теория Прандтля пограничного слоя. Мы, однако, подойдем
к вопросу путем изучения более простой задачи об об-
обтекании тонкого профиля потоком несжимаемой жидко-
жидкости. Поскольку движение описывается двумерным урав-
уравнением Лапласа, которое линейно, оказывается возмож-
возможным представить результат в аналитической форме и
выразить главную идею более ясно. Эта задача также
прекрасно подходит для введения двух основных мето-
методов, которые были предложены для исследования задач
особых возмущений. Благодаря этому настоящая глава
является краеугольным камнем всей книги. Следующие
главы посвящены лишь приложению и распространению
на другие задачи идей, изложенных здесь в связи с
принятой нами за эталон задачей об обтекании тонкого
профиля.
План решения этой задачи следующий. Сначала мы
вычислим формально разложения для общего симмет-
4.2. Формальное разложение для тонкого профиля 69
ричного профиля. Затем для некоторых специальных
форм мы покажем неоднородности и неединственности,
которые возникают в окрестности критической точки из-
за нарушения предположения о малости возмущений.
Наконец, мы исправим эти недостатки, во-первых, пу-
путем использования интуитивных физических соображе-
соображений, во-вторых, сращиванием с локальным решением
в духе теории пограничного слоя и, в-третьих, путем де-
деформирования координат в случае закругленной кромки.
4.2. Формальное разложение для тонкого профиля
Рассмотрим обтекание тонкого профиля равномер-
равномерным плоским потоком несжимаемой невязкой жидкости.
Для простоты ограничимся исследованием симметрич-
симметричного течения, так как оно содержит все существенные
интересующие нас черты явления, однако подобным же
Рис. 4.1. Симметричное обтекание тон-
тонкого профиля.
образом могут быть исследованы и эффекты асимметрии,
обусловленные изгибом крыла и углом атаки. Более де-
детальные сведения по этому вопросу читатель может найти
в современных обзорах теории тонкого профиля, данных
Лайтхиллом [4], Джонсом и Коэном [1] и Туэйтсом [1].
Мы используем декартовы координаты и будем счи-
считать, что хорда профиля совпадает с отрезком оси х,
длина которого может быть принята за единицу. Далее
предположим, что форма профиля задана уравнением
у=±гТ(х)у где е — некоторый параметр толщины, а
Т(х) —функция порядка единицы, которая дает рас-
распределение толщины (рис. 4.1). Изменение е дает семей-
семейство аффинно подобных профилей.
Течение безвихревое, и в целях возможного распро-
распространения результатов на трехмерные течения удобно
70 Гл. 4 Задачи особых возмущений в теории профиля
рассматривать потенциал скорости ср. Пусть он норми-
нормирован так, что вектор скорости определяется в виде
q = ?/gradcp, где U — скорость набегающего потока. То-
Тогда полная задача запишется в виде
дифференциальное ф -4- ср = 0, D.1а)
уравнение: хх ' уу
условие в набегаю- Ср—х-\- О A) при X1-\-у1—> оо, D.16)
щем потоке:
условие обтекания: —— = ± еТ'(х) при у = ± гТ (х). D.1 в)
Второй член в асимптотическом условии D.16) на-
накладывает требование, чтобы потенциал возмущений на
бесконечности стремился к нулю, хотя в действительно-
действительности он имеет порядок 0A /г) для конечного тела. Это
требование обеспечивает единственность решения, так
как оно исключает возможность наличия циркуляции.
Эту, казалось бы, безобидную задачу, включающую
только простейшее линейное дифференциальное уравне-
уравнение эллиптического типа, трудно решить с нужной точ-
точностью. Обычный численный метод конформных отобра-
отображений, развитый Теодорсеном (Аббот и Дёнхоф [1]),
трудоемок и неточен, поэтому приближение тонкого про-
профиля не только интересно теоретически, но и полезно
практически. Оно еще более полезно в случае дозвуко-
дозвукового сжимаемого течения, для которого уравнение дви-
движения нелинейно, и в случае трех измерений, когда кон-
конформное отображение неприменимо.
Мы будем искать асимптотическое разложение ре-
решения при стремлении параметра толщины е к нулю.
В пределе профиль вырождается в линию, которая не
вызывает возмущений в набегающем потоке, так что
основное решение представляет собой равномерный па-
параллельный поток. Предположим, что асимптотический
ряд при данной функции Т(х) имеет вид
Ф (х, У\ е) — х -+ ecpj (х, у) + 82ср2 (х, у) + е3ф3 (х, у)-+....
D.2)
Подразумевается, что разложение продолжается беско-
бесконечно по целым степеням е- Это представляется прд-
4.2. Формальное разложение для тонкого профиля 71
внльным для несжимаемой жидкости, если профиль не
слишком затуплен (см. упражнение 4.3). Однако для
дозвукового обтекания сжимаемой жидкостью профиля
с закругленной передней кромкой наш пример A.2)
показывает, что, начиная с члена еЧпе, появляются ло-
логарифмы 8.
Для того чтобы подставить это разложение в полную
задачу и приравнять члены с одинаковыми степенями е,
мы должны перенести условие обтекания D.1 в) на ось
у — О. Предположив, что cpn(#, у) аналитичны по у при
у = 0, мы можем разложением в ряды Тейлора получить
равенство
[cp2i/(x, 0 ±) ±
± Т%уу{х, О ±)+j Т>%ууу(х9 О ±)]+. • • D.3)
и аналогично для фх. Здесь у = 0± относится к верхней
и нижней сторонам разреза, в который вырождается
профиль в пределе при е—*0 и на котором фу разрывно
(фя- непрерывно). Это разложение, хотя и существенное
для получения ряда желаемого вида (см. § 3.8), являет-
является источником неоднородностей, с которыми мы столк-
столкнемся позже. Можно предвидеть трудности из-за появ-
появления производных все более высоких порядков.
Таким образом, мы получаем последовательность
задач, которые линейны как по условиям обтекания, так
и по дифференциальным уравнениям, причем первая
из них представляет собой обычную задачу линейной
теории тонкого профиля. Эта последовательность задач
такова:
Фи,+ Фц,„ = 0« D-4а)
ср, —оA) при x2-\-if->cx), D.46)
%у(х, 0±)=±Г(х); D.4в)
<P2«+(P2W=°- D-5a)
Ф2 = оA) при х24 у2-^со, D56)
Ъу(х, 0 ±)= ± Т'(х)<р1х(х, 0) + Г(х)%уу(х, 0) =
(*. 0)]'; D 5в.)
72 Га 4 Задачи особых возмущений в теории профиля
Ъ=о(\) при %2 + if ->co, D.66)
cp3i/ (*, 0 ±) = ± Г (х) ф2^ (х, 0) + Г (*) Г (х) ср^ (х, 0) +
D.6в)
Сокращенные формы условий обтекания второго и тре-
третьего порядка D.5в) и D.6в) получены путем использо-
использования как дифференциальных уравнений, так и усло-
условий обтекания, взятых из предыдущих приближений.
В результате этого видоизменения каждая задача фор-
формально оказывается такой же, как первая. Любое при-
приближение высшего порядка может рассматриваться как
первое приближение для некоторого фиктивного профи-
профиля, функция толщины Тп(х) которого равна выраже-
выражению, заключенному в последние квадратные скобки в
условии обтекания.
Параметры течения на поверхности профиля можно
выразить через степенные ряды по е, если связать их,
снова через ряды Тейлора, с компонентами скорости на
оси. Поскольку на оси уПу дается условием обтекания,
требуется только найти Ц)Пх(х, 0). Так, например, ско-
скорость q на поверхности определяется выражением
± = 1 + еФи (х, 0) + е* [ц>2х (х, 0) +
+ Т(х) Т"{х)+\Т'2 (Х)]+ .... D.7)
Конечно, этот процесс является другим возможным ис-
источником неоднородностей.
4.3. Решение задачи обтекания тонкого профиля
Каждую из задач высшего порядка для тонкого про-
профиля мы свели по форме к задаче первого порядка. Эта
основная задача может быть решена различными пу-
путями. Обычно простейший способ — использовать тео-
теорию функций комплексного переменного; лучший метод
4 3. Решение задачи обтекания тонкого профиля 73
состоит в том, что фх — 1Ц)У рассматривается как функ-
функция комплексного переменного z=x + iy, удовлетворяю-
удовлетворяющая граничным условиям. Полезная таблица таких ре-
решений дана Джонсом и Коэном [1]. Методы, основанные
на применении комплексного переменного, имеют, одна-
однако, тот недостаток, что они не могут быть обобщены на
трехмерные течения.
Другой метод, который допускает такое обобщение,
состоит в замене тела распределением особенностей.
Источники, диполи и другие особенности могут быть
расположены или на поверхности, или внутри тела.
В теории тонкого профиля они, естественно, распола-
располагаются на отрезке оси между передней и задней кром-
кромками. В нашей симметричной задаче используются толь-
только источники и стоки, причем для конечного тела сум-
суммарные интенсивности источников и стоков должны быть
равны.
Точечному источнику единичной интенсивности, по-
помещенному в начале координат, соответствуют формулы
<p = -Lin Yx2 + y2 =-^rRealln^, D.8a)
^ = ^r^TW D*8б)
%=~Ш^- D.8в)
Для достаточно гладкого профиля соображения непре-
непрерывности показывают, что местная интенсивность источ-
источников должна равняться удвоенному наклону поверхно-
поверхности профиля. Это соотношение в такой же степени при-
приближенно, как и примененный выше перенос условия
обтекания на ось. Таким образом, решение какой-либо
из задач тонкого профиля D.4), D.5) и т. д. опреде-
определяется выражениями
1 3'гК'(х — 1)<Р& °+) ^ ,Л п ч
b D*9a)
ц. к.
74 Гл. 4. Задачи особых возмущений в теории профиля
что может быть проверено прямой подстановкой, или
(в комплексной форме)
з. к.
п. к.
Для вычисления значений на поверхности, как и в D.7),
требуется только величина
3. К.
3. К. /
= iv. P. f -*Ц-й\. D.10)
ЗХ J X — 5
п. к.
Здесь берется главное значение в смысле Коши инте-
интеграла, расходящегося для значений х между передней
и задней кромками профиля. Таблица профильных инте-
интегралов D.10) для некоторых функций Т(х) дана Ван-
Дайком [4].
4.4. Неоднородности для эллиптического профиля
Большая часть дозвуковых профилей имеет закруг-
закругленную переднюю кромку. Простейшим конечным про-
профилем такого рода является эллиптический профиль,
который мы теперь детально исследуем. Пусть функция
толщины будет Г(л:) = |/—х2, что соответствует эл-
эллипсу с отношением полуосей 8, занимающему отрезок
¦—1 -<х-< 1 (рис. 4.2). Радиус кривизны передней и зад-
задней кромок равен в2.
Подстановка в формулу D.10) этого значения Т(х)
дает решение задачи первого порядка D.4) для ф1зс на
оси в виде
,cpv(;c, 0) = —— V.P. __ __
для X2 < 1,
~Ж~ D.Н)
4.4. Неоднородности для эллиптического профиля 75
В более общем виде комплексная возмущенная ско-
скорость во всем поле течения (из таблицы Джонса и Коэ-
на) определяется как
•Pu-*Pi, = i-7rf=r- DЛ2)
При надлежащем выборе ветви функции это воспроиз-
воспроизводит результат D.11) на оси. Тогда соотношение D.7)
Рис. 4.2. Эллиптический профиль.
дает известный результат линейной теории тонкого про-
профиля, а именно из него следует, что скорость на поверх-
поверхности постоянна для эллипса, <?/?/= 1+е. Это значение
является точным на миделе эллипса, где достигается
максимум (рис. 4.3).
То обстоятельство, что скорость на поверхности в ре-
решении первого порядка оказалась конечной даже на
концах профиля, вводит в заблуждение. В соответствии
с D.12) возмущенная скорость имеет особенность на
передней и задней кромках. Предположение о малости
возмущений нарушается вблизи критических точек, и
вследствие этого в этих областях решение теряет смысл.
Решение типа тонкого профиля не является равномерно
пригодным вблизи кромок.
Возмущенная скорость имеет особенность вида е//*1/2.
где г — расстояние от критической точки. Следователь-
Следовательно, область неоднородности представляет собой круго-
круговую окрестность кромки радиусом порядка е2. Как и
можно было предвидеть на основании физических сооб-
соображений, эта величина имеет порядок радиуса кривизны
передней кромки.
76
Гл. 4. Задачи особых возмущений в теории профиля
Недостатки возмущенного решения усиливаются в
приближениях высшего порядка. Задача D.5) для ф2
идентична с таковой' для фА. Следовательно, второе при-
приближение для скорости на поверхности, согласно D.7),
будет
а , , 1 „ х2
D.13)
и имеет особенность порядка квадрата е/г1^. Первое и
второе приближения для е = 0,5 в сравнении с точным
Рис. 4.3. Скорость на поверхности эллиптического про-
профиля, е = 0,5.
первое приближение, второе приближение D.13),
точное решение D.14а), О результат применения правила Лайт-
хилла D.316).
решением даны на рис. 4.3, где отчетливо видна расхо-
расходимость ряда вблизи критической точки. Последующие
члены могут быть вычислены аналогично, и можно по-
показать, что 2/г-е приближение будет иметь особенность
вида (е/г^2J71. Знак при этом последовательно меняется
в тщетной попытке привести к нулю скорость в критиче-
4.5. Неединственность. Собственные решения 77
ских точках наложением последовательно усиливающих-
усиливающихся особенностей. (Как и в первом приближении, компо-
компоненты скорости нечетного порядка также имеют особен-
особенности, но добавляют лишь регулярные члены к величине
скорости на поверхности.) Таким образом, решение
улучшается на каждом шаге всюду, за исключением ок-
окрестностей кромок радиусом порядка е2, где оно стано-
становится все хуже и хуже.
Формальное разложение для тонкого профиля может
быть проверено сравнением с полным решением, которое
легко получить применением конформного отображения
или разделением переменных в эллиптических коорди-
координатах. Точный результат для скорости на поверхности
имеет вид
± = * + ?
U Y\ + е2 [х2/0 — х2)} '
разложение этог
^ | _i_ р . р* рЗ
U — 1 "Г ь 2Ь 1—л:2 2 1—
Формальное разложение этого выражения для ма-
малых е дает
что подтверждает и расширяет наш результат D.13).
Более того, это разложение делает очевидным источник
неоднородности. Особые члены появляются при бино-
биномиальном разложении знаменателя, которое оправдано
только в том случае, когда
1-*2>TTF- DЛ5)
Это условие нарушается вблизи критических точек
х=±1.
4.5. Неединственность. Собственные решения
Проверка, проведенная выше, важна потому, что для
тонкого профиля с закругленной передней кромкой ре-
решение не будет единственным. Условия обтекания D.4в),
D.5в) и т. д. имеют особенности на закругленной кром-
кромке. Следовательно, к решению можно добавить какую-
78 Гл. 4 Задачи особых возмущений в теории профиля
либо гармоническую функцию, которая в этих точках
имеет особенности, а в других точках не влияет на гра-
граничные условия. В рассматриваемой задаче одна из та-
таких функций соответствует точечному источнику, поме-
помещенному на одной кромке, и стоку той же интенсивно-
интенсивности, помещенному на другой:
Ф = ^ [in /U+lJ + J/2 ~ In /(*-1J + </2Ь D.16а)
х 4-1 х—1
DЛ6В)
Очевидно, что добавление этой функции не влияет на
задачи D.4), D.5) и т. д., за исключением передней
и задней кромок, где решение для эллипса так или
иначе имеет особенность.
Это наш первый пример собственного решения.
Смысл собственных решений в обратных координатных
разложениях был пояснен в § ЗЛО. Настоящий пример
относится к параметрическому разложению, но оно мо-
может рассматриваться также — поскольку мы имеем дело
с задачей особых возмущений — как обратное коорди-
координатное разложение. А именно, решение для тонкого про-
профиля становится достаточно точным на расстояниях от
кромок,, больших по сравнению с их радиусом е2. Соб-
Собственное решение D.16) представляет собой результат
незнания деталей течения вблизи кромок.
Производная по а: в D.16) также является собствен-
собственным решением для эллиптического профиля. Оно соот-
соответствует диполям на передней и задней кромках (ин-
(интенсивности которых теперь не обязательно должны
быть равны, чтобы удовлетворить условиям в набегаю-
набегающем потоке). Подобным же образом последовательным
дифференцированием по х можно построить бесконеч-
бесконечную последовательность собственных решений с про-
прогрессивно усиливающимися особенностями: квадруполя-
ми, октополями и т. д.
Для того чтобы решение стало единственным, нужно
определить постоянные множители перед каждым воз-
возможным собственным решением. Это можно попытаться
4.5. Неединственность. Собственные решения 79
сделать следующими способами, которые приведены в
порядке увеличения их совершенства.
(i) Принцип минимальной особенности. Согласно
этому весьма надежному, но несколько загадочному ут-
утверждению, в некоторых случаях неединственности истин-
истинное решение соответствует наименьшей возможной осо-
особенности. Для эллиптического профиля этот принцип по-
позволяет исключить все собственные решения в решении
первого порядка, все, кроме источников во втором и треть-
третьем приближениях, все, кроме источников и диполей в чет-
четвертом и пятом и т. д. Обоснование этого принципа будет
дано позже в § 5.6, где будет обсуждаться процесс сра-
сращивания с локальным решением типа пограничного слоя.
(п) Общий закон сохранения. Иногда возможно най-
найти закон сохранения, который будет служить для опре-
определения собственного решения. Для эллиптического про-
профиля закон сохранения масс позволяет исключить соб-
собственное решение D.16) типа источника. Это удобнее
осуществить, работая не с потенциалом скорости, а с
функцией тока, которая гарантирует сохранение общей
массы. Тогда допустимым собственным решением с наи-
наименьшей особенностью является не источник, а диполь
(см. упражнение 4.1). Отсюда (и из принципа мини-
минимальной особенности) следует, что для эллиптического
профиля неопределимость отодвигается до четвертого
приближения.
(ш) Сращивание с дополнительным разложением.
Далее в этой главе мы обобщим идею Прандтля о де-
детальном исследовании области неоднородности. Суще-
Существенной чертой этого способа является возможность
сращивания с дополнительным асимптотическим разло-
разложением, имеющим место в области неоднородности. Этот
процесс служит для исключения всех собственных реше-
решений в разложении для тонкого профиля в случае эллипса.
В предыдущем параграфе мы не использовали ни одного
из подобных методов, а просто сравнивали разложение
с известным точным решением.
80
Гл. 4. Задачи особых возмущений в теории профиля
В более сложных задачах все эти методы вообще
могут оказаться непригодными. Примером является
третье приближение для пограничного слоя на полубес-
полубесконечной плоской пластине, рассматриваемое в гл. 7.
В этом случае, вероятно, даже в принципе невозможно
определить хотя бы первое собственное решение при
отсутствии решения полной задачи. В таких трудных
задачах предпринимались попытки определить первое
собственное решение, сопоставляя его в какой-либо точ-
точке с другим приближенным решением (Имаи [4]) или
сравнивая его с численным решением (Трауготт [1]).
4.6. Профили Жуковского. Сопротивление
передней кромки
Недостатки разложения для тонкого профиля вблизи
закругленной кромки приводят к невозможности вы-
вычисления сопротивления интегрированием давления по
Рис. 4.4. Симметричный профиль Жуковского.
а —профиль, б — давление на поверхности.
теория первого порядка, точное решение.
поверхности. Действительно, уже после первого прибли-
приближения здесь появляются расходящиеся интегралы. В слу-
случае эллиптического профиля это не сказывается по-
потому, что в силу симметрии влияния передней и задней
кромок взаимно уничтожаются. Поэтому мы рассмот-
рассмотрим простейший профиль только с одной закругленной
кромкой.
С точностью до второго порядка симметричный про-
профиль Жуковского (рис. 4.4, а) описывается функцией
4.6. Профили Жуковского 81
толщины Т(х) = (\—x)Y^—х1- Относительная толщи-
толщина равна е на середине хорды и C У 3/4) е « 1 ,ЗОг в
точке наибольшей толщины. Для возмущения первого
порядка ^-компоненты скорости на оси формула D.10)
дает выражение
1
(flx(x* 0) = —— V.P. Г l+6-2g—dl=\—2x* D.17)
ПХ V * J /1 — ?2 (* - I)
Х2< 1.
Во втором приближении для скорости на поверхно-
поверхности мы получаем
?=1+8 A-2*)- |82|^A+2хJ+... . D.18)
Из уравнения Бернулли для коэффициента давления
на поверхности находим
x(\+2f + .. . . (А.Щ
Коэффициент сопротивления можно вычислить ин-
интегрированием давления по поверхности профиля:
Cd =
d
1
= E \Cp(x) Г(х)dx. D.20)
Однако подстановка разложения D.19) для тонкого про-
профиля показывает, что член второго порядка дает инте-
интеграл, расходящийся вблизи передней кромки. Сохраняя
только члены первого порядка, получаем для сопротив-
сопротивления отрицательную величину:
1
Cd * 2е2 J A - 4х2)
-1
Этот результат, очевидно, неверен, так как, согласно
принципу Даламбера, сопротивление должно быть рав-
равно нулю. Поскольку из-за неточности теории первого по-
порядка не выявляется возрастание давления вблизи кри-
критической точки (рис. 4.4,6), эта теория не учитывает
82
Гл. 4 Задачи особых возмущений в теории профиля
положительную добавку к сопротивлению, которая дол-
должна в точности компенсировать только что вычислен-
вычисленное давление на остальной части профиля.
Джонс [1] показал, что это сопротивление передней
кромки можно все же найти, вычисляя сопротивление
не путем суммирования давлений, а по теореме количе-
количества движения для контура, который не проходит через
область непригодности решения вблизи передней кром-
кромки. Его можно также получить, уточняя значения дав-
давления на поверхности вблизи передней кромки методом,
который будет рассмотрен ниже, причем только этот
метод является удачным для второго и высших прибли-
приближений.
Сопротивление передней кромки, которое должно
быть прибавлено к интегралу давлений по поверхности,
в линейном приближении оказывается одной и той же
величиной для любого профиля с закругленной перед-
передней кромкой, в том числе и для профиля Жуковского.
Эта величина определяется выражением
Dn.K. = уяр?/2а, D.22)
где а — радиус передней кромки, равный 4s2 для про-
профиля Жуковского, изображенного на рис. 4.4. Она как
раз равна сопротивлению бесконечной параболы с той
Рис. 4.5. Схема,
определяющая сопро-
сопротивление параболы.
же кривизной при вершине, определенному — следуя
Прандтлю и Титьенсу [1] —как сопротивление носовой
части, отделенной разрезом (в котором давление равно
давлению во внешнем потоке), в пределе при движении
разреза в бесконечность вниз по течению (рис. 4.5).
Справедливость этого утверждения следует из того фак-
4.7. Двояковыпуклый и прямоугольный профили 83
та, что любой профиль с закругленной кромкой при
уменьшении его толщины аппроксимируется параболой
на все большем расстоянии вниз по течению от перед-
передней кромки (это расстояние измеряется в радиусах пе-
передней кромки). Такую соприкасающуюся параболу мы
используем ниже (см. § 4.8).
Подобное же нарушение принципа Даламбера про-
происходит для несущего профиля нулевой толщины. В этом
случае, однако, интегрирование определенных по линей-
линейной теории давлений на поверхности дает ложное сопро-
сопротивление, а не тягу. Так, для наклонной плоской пла-
пластины, очевидно, получается результирующая нормаль-
нормальная к пластине сила, имеющая составляющую вниз по
потоку. Разгадка этого парадокса снова связана с осо-
особенностью на передней кромке. Дополнительная тяга
передней кромки, требующаяся для сведения сопротив-
сопротивления к нулю, может быть определена методами, раз-
развитыми для симметричных профилей (Карман и Бюр-
Бюргере [1], стр. 51—52).
4.7. Двояковыпуклый и прямоугольный профили
Рассмотрим два других профиля; один из них имеет
острую переднюю кромку, а другой — затупленную
/
I
s-
Рис. 4.6. Двояковыпуклый профиль.
переднюю кромку, но с иным, чем у эллипса, затупле-
затуплением. В первом случае функция толщины Т(х) = 1—х2
определяет двояковыпуклый профиль, составленный из
двух дуг парабол (рис. 4.6).
Действуя, как и прежде, для первого приближения
получаем
D.23)
84 Гл. 4. Задачи особых возмущений в теории профиля
В критической точке на острой кромке возмущенная
скорость логарифмически бесконечна и ведет себя как
s in г даже на поверхности. Опять эта особенность
усложняется в приближениях высшего порядка. Так, во
втором приближении скорость на поверхности опреде-
определяется выражением
-¦^•'"'тй—с—^)]- <4-24)
Здесь особенность в критических точках имеет вид
(elnrJ, и можно показать, что п-й член имеет особен-
особенность вида (elnr)n. Следовательно, разложение непри-
непригодно у кромок внутри круга радиусом порядка е~^е.
Поскольку эта величина меньше, чем любая степень е,
на практике ею обычно пренебрегают; кроме того, на
задней кромке неоднородность смазывается влиянием
вязкости. Тем не менее очень важно понять и исправить
этот небольшой дефект решения (так же как и более
серьезные для случая закругленной кромки).
Особенности в этом примере так слабы, что практи-
практических трудностей не возникает. Все собственные ре-
решения можно исключить с помощью принципа мини-
минимальной особенности, поскольку даже решение с осо-
особенностью наименьшего порядка — собственное реше-
решение D.16) типа источника — имеет в критической точке
особенность более высокого порядка, чем в любом члене
разложения для тонкого профиля. Более того, интеграл
D.20)для коэффициента сопротивления сходится. Таким
образом, формальное решение теории тонкого профиля
может быть вычислено до членов сколь угодно высо-
высокого порядка для профиля с острыми кромками.
Далее рассмотрим предельный (в известном смысле)
случай тонкого прямоугольного профиля (рис. 4.7), ко-
который может быть представлен функцией толщины
T(x)=H(l—x*)=H{x+l)—H(x—l). Здесь Я —еди-
—единичная функция Хевисайда, равная нулю для отрица-
отрицательных значений аргумента и единице для положи-
положительных значений. С учетом разрывности этой функции
4.7. Двояковыпуклый и прямоугольный профили 85
формула D.10) дает
ja(i+i)-6(s-i)^ D.25a)
-1
Здесь 6 — дельта-функция Дирака (производная от #),
равная нулю для всех значений аргумента, за исключе-
исключением нуля, где она обращается в бесконечность так, что
интеграл от нее равен единице. Ее появление здесь имеет
очевидную физическую интерпретацию: приближение
тонкого профиля для распределения источников дает в
этом случае просто концентрированный источник на пе-
передней кромке и сток равной интенсивности на задней.
Рис. 4.7. Прямоугольный профиль.
Интегрирование в D.9), очевидно, должно включать в
себя все источники на оси; следовательно, в этом при-
примере оно должно быть продолжено хотя бы немного за
каждую из кромок. Мы можем продолжить интегриро-
интегрирование до бесконечности и получить выражение
= i J
-4-Ij?. D.256)
В соответствии с физическим смыслом это, очевидно,
собственное решение D.16) типа источника при С = 2.
Скорость в первом приближении имеет теперь вбли-
вблизи кромок особенность вида е/г. Это наводит на мысль
о том, что область неоднородности имеет размер поряд-
порядка толщины 8 кромки (это же следует и из физических
соображений). Если попытаться вычислить второе при-
приближение, то окажется, что интеграл D.10) на передней
и задней кромках расходится. Особенность может быть
86 Гл. 4 Задачи особых возмущений в теории профиля
ослаблена интегрированием D.10) по частям, и это пои
казывает, что для гладкого профиля такого, что Т = 0
на каждой кромке, возможно другое представление:
D.106)
%Ax,0) = V.P. | dl.
П. К.
Это выражение еще расходится для рассматриваемой
негладкой формы, но лишь логарифмически. Если про-
произвольно отбросить бесконечные члены, то результат
будет
. D.26)
Третий член представляет собой собственное реше-
решение D.16) типа источника, второй — собственное реше-
решение типа диполя. Ни одно из них не может быть исклю-
исключено по принципу минимальной особенности, так как
первый член имеет более сильную особенность, однако
из соображений непрерывности следует, что собственно-
собственного решения типа источника не должно быть. Эта ошибка
обусловлена нашим весьма произвольным толкованием
расходящегося интеграла. По этой же причине можно
ожидать, что правильным будет только главный член
разложения. Таким образом, интенсивность диполя во
втором члене заменяется неопределенной постоянной.
Тогда для скорости на поверхности во втором прибли-
приближении формула D.7) дает
D.27)
Интенсивность С диполя в собственном решении мо-
может быть определена только при сращивании с дополни-
дополнительным разложением, имеющим место в окрестности
кромок. Как будет следовать из упражнения 4.3, это
приводит к появлению в асимптотической последова-
последовательности логарифмических членов, начиная с е2 In 8.
4.8. Поправочный множитель для закругленных кромок 87
Такое усложнение связано с тем фактом, что более за-
затупленный, чем эллипс, профиль в действительности
нельзя представить распределением источников на оси.
4.8. Поправочный множитель
для закругленных кромок
На предыдущих примерах были показаны некоторые
трудности, которые возникают от неоднородностеи в
задачах особых возмущений. Теперь мы перейдем к
исследованию этих трудностей у их истоков путем исклю-
исключения соответствующих неоднородностеи.
В следующем параграфе нами будет введен довольно
общий метод, приложимый к широкому классу задач
особых возмущений. Он имеет то преимущество, что в
случае необходимости его можно применять формально,
почти не пользуясь физическими соображениями. Но
сначала мы обоснуем этот способ, применив близкую
процедуру, которая построена в основном на физической
интуиции. Для простоты мы рассмотрим только закруг-
закругленные кромки, примером которых является эллиптиче-
эллиптический профиль, и ограничимся только вычислением ско-
скорости на поверхности тела.
Рис. 4.8. Соприкасаю-
Соприкасающаяся парабола для про-
профиля с закругленной пе-
передней кромкой.
Рассмотрим симметричное обтекание какого-либо
профиля с закругленной передней кромкой и с относи-
относительной толщиной е (рис. 4.8). Так же как и для эллип-
эллипса, разложение для тонкого профиля становится непри-
непригодным на расстояниях от передней кромки, меньших,
чем величина порядка радиуса а носовой части, которая
пропорциональна е2. В этой окрестности профиль может
быть аппроксимирован параболой, имеющей тот же ра-
радиус кривизны при вершине. Бшее того, приближение
88 Гл. 4. Задачи особых возмущений в теории профиля
становится лучше с уменьшением относительной толщи-
толщины, т. е. обеспечивает заданную точность на увеличиваю-
увеличивающемся числе радиусов носовой части.
Точные значения скорости на поверхности параболы
легко вычислить или получить предельным переходом
из результата D.14а) для эллипса в виде
Здесь s — расстояние, отсчитываемое от кромки, а ?/г- —
максимальная скорость на параболе. Последняя вели-
величина, очевидно, почти равна скорости U набегающего
потока, но ее значение в дальнейшем не потребуется.
Разлагая это выражение формально для малых значе-
значений радиуса а носовой части (точнее для малых значе-
значений отношения a/s), получим ряд
-^-+...). D.29)
Величина q взята в кавычки, чтобы отметить, что это
только формальный результат. Это тот результат, ко-
который получался бы из теории тонкого профиля. Он
может быть в действительности получен из решения
второго порядка D.13) для эллипса. Два члена, данные
здесь, образуют второе приближение, поскольку радиус
носовой части имеет порядок е2. В разложении нет чле-
членов порядка 8, так как возмущения первого порядка на
поверхности параболы обращаются в нуль.
Мы теперь утверждаем, что отношение этих двух вы-
выражений является поправочным множителем, который
обращает формальный результат теории тонкого про-
профиля для скорости „#" на каком-либо профиле с радиу-
радиусом а носовой части в равномерно пригодное прибли-
приближение q,
Это утверждение основывается на том, что вблизи
передней кромки, где возмущения велики, точные зна-
значения скорости на профиле близки к соответствующим
значениям на параболе. С другой стороны, далеко от
кромки поправочный множитель приближается к едц-
4.8. Поправочный множитель для закругленных кромок 89
нице, и поэтому решение типа тонкого профиля вновь
получается там, где оно пригодно.
Это правило можно упростить. Знаменатель уже был
разложен формально, так что от дальнейшего разложе-
разложения не будет вреда; то же верно для „д" в решении
типа тонкого профиля. Следовательно, если мы вспо-
вспомним, что „q"/U имеет вид 1+О(е), и сохраним только
члены порядка е2, то получим более простое правило:
Здесь черта сверху означает, что формальное решение
второго порядка „92" превращается в равномерно при-
пригодное до второго порядка решение. Это следует пони-
понимать в том смысле, что как главный, так и второй (по-
(порядка по е) члены являются правильными всюду на
профиле для возмущения скорости или коэффициента
давления.
Это правило впервые было получено Лайтхиллом [4]
путем совершенно иных рассуждений (эти рассуждения
будут приведены ниже в § 4.12). Он показал, что это
правило приложимо также для профиля под углом ата-
атаки и для несимметричных профилей. В последнем слу-
случае, однако, вблизи носовой части возмущения верны
только до первого порядка. Впредь мы будем ссылать-
ссылаться на соотношение D.306) как на правило Лайтхилла.
В качестве примера мы приложим это правило к пе-
передней кромке эллиптического профиля, для которого
величина „qJ'W определяется формулой D.13). При
s = x+\ и а = г2 получим
Особенность на передней кромке устранена и заме-
заменена точным нулем. Конечно, особенность на задней
кромке осталась, так что решение несимметрично по х,
но и она может быть исключена повторным применением
правила Лайтхилла при 5=1—х. После дальнейших
упрощений это дает вполне однородный результат
90 Гл. 4. Задачи особых возмущений в теории профиля
На рис. 4.3 этот результат сравнивался с точным ре-
решением и с решением типа тонкого профиля, что под-
подтвердило его равномерную пригодность.
Весьма поучительна интерпретация данного выше вы-
вывода правила Лайтхилла с точки зрения теории кон-
конформных отображений. Если мы будем искать отобра-
отображение равномерного потока на поток, обтекающий тон-
тонкий профиль, то приближение типа тонкого профиля не
может воспроизвести резкие изменения величин вблизи
круглой носовой части. Однако мы можем использовать
композицию двух отображений: равномерного потока на
параболу, а этой параболы — на тонкий профиль. Тео-
Теория тонкого профиля отвечает требованиям последнего
отображения, в то время как первое должно быть про-
произведено точно. Два члена в формуле D.306) соответ-
соответствуют этим двум отображениям.
4.9. Локальное решение вблизи
закругленной кромки
Теперь мы рассмотрим обтекание профиля с закруг-
закругленной передней кромкой с точки зрения теории Пранд-
тля пограничного слоя. А именно мы исследуем детали
течения в области неоднородности, введя растягиваю-
растягивающие эту область переменные. Так мы получим локаль-
локальное решение, которое дополнит ряд для тонкого про-
профиля и будет сращиваться с ним (см. следующий
параграф). Связь между этим формальным способом и
предыдущими интуитивными рассуждениями станет яс-
ясной в процессе исследования.
Для определенности мы рассмотрим эллипс; прило-
приложение полученных результатов к другим профилям с
закругленной носовой частью окажется очевидным. Рас-
Рассмотрим неоднородности только вблизи передней кром-
кромки; окрестность задней кромки исследуется точно таким
же образом. Для простоты мы опять изучим скорость
только на поверхности, однако этот метод, очевидно,
может быть приложен ко всему полю течения. Мы ис-
исследуем второе приближение, и с тем, чтобы показать
эффективность метода, положим, что в каждом члене
оно содержит собственные решения D.16) типа источ-
4.9. Локальное решение вблизи закругленной кромки 91
ника с неизвестными множителями. Тогда формальный
ряд теории тонкого профиля для скорости на поверхно-
поверхности в соответствии с формулами D.13) и D.16) примет
вид
D.32а)
Конечно, можно использовать закон сохранения мас-
массы (как указывалось в § 4.5) и получить Ci = C2 = 0.
Однако мы хотим показать, что тот же результат полу-
получится и в процессе сращивания с локальным решением;
это окажется необходимым в более трудных задачах.
Поскольку рассматриваемые неоднородности имеют
место вблизи передней кромки, удобно перенести туда
начало координат (рис. 4.2), полагая s = x-bl. Тогда
эллипс определится уравнением
y=±eV2s-s2 D.33а)
и ряд D.32а) теории тонкого профиля для скорости на
поверхности запишется в виде
Я
U
_s) J 28 LsB-s) s B - s) J
при 8->0 для i- = O(D. D.326)
о
Это асимптотическое разложение непригодно в области,
где s = O(&2), поскольку там третий член имеет порядок
единицы, что противоречит предположению о его ма-
малости.
' ' Мы намерены ввести новые независимые и зависи-
зависимые переменные (обозначив их прописными буквами),
которые в области неоднородности имели бы порядок
единицы. Очевидно, что для s такое увеличение осуще-
осуществляется множителем 1/е2 и что другая декартова коор-
координата у преобразуется так же, поскольку было пока-
показано, что область неоднородности представляет собой
круг. Таким образом, мы вводим новые координаты
D.34.)
92 Га. 4. Задачи особых возмущений в теории профиля
В этих переменных эллипс описывается уравнением
У=± /25 —е252. D.336)
Зависимое переменное ф должно быть соответственно
преобразовано введением функции Ф=ф/е2. Однако по-
последнее преобразование несущественно для рассматри-
рассматриваемой задачи, поскольку как дифференциальное урав-
уравнение, так и граничные условия линейны относительно ф.
*~s
Рис. 4.9. Локальное течение — обтекание со-
соприкасающейся параболы.
Теперь мы рассмотрим результат, получающийся при
стремлении е к нулю и при фиксированных значениях
новых переменных. При этом, поскольку относительная
толщина стремится к нулю, мы непрерывно увеличиваем
окрестность передней кромки таким образом, что радиус
носовой части остается конечным. В пределе профиль
принимает вид
Г~±/25~ для е-^0 при 5 = 0A), D.33в)
т. е. становится бесконечным параболическим цилинд-
цилиндром с единичным радиусом кривизны носовой части.
Уравнение Лапласа не меняется от произведенного пре-
преобразования координат. Следовательно, локальная за-
задача опять представляет собой задачу потенциального
обтекания параболы (рис. 4.9).
Для единственности решения требуются дополнитель-
дополнительные граничные условия. Очевидно, что течение должно
быть симметрично относительно оси S. С другой сто-
4.10. Сращивание вблизи закругленной кромки 93
роны, не является очевидным, что поток далеко впереди
должен быть равномерным. Однако иные предположе-
предположения привели бы к более сильным особенностям на бес-
бесконечности и поэтому могут быть исключены по прин-
принципу минимальной особенности (§ 4.5). Нельзя, однако,
утверждать, что скорость набегающего потока равна
его исходной скорости U; мы обозначим ее, как прежде,
через Ui и определим эту величину сращиванием с реше-
решением для тонкого профиля. Заметим, что значения Ui
не требовалось при выводе правила Лайтхилла в пре-
предыдущем параграфе, поскольку там оно сокращалось.
Граничная задача для фE, У) легко может быть ре-
решена для скорости на поверхности. Однако результат
можно получить и из соотношения D.28) в виде
для е->0 при 5 = 0A). D.35)
Таким образом, мы имеем два различных асимптотиче-
асимптотических приближения к решению для малых е. Разложение
D.326) теории тонкого профиля пригодно всюду, за ис-
исключением окрестности передней кромки, где имеет
место локальное решение D.35).
Теперь полезно ввести некоторые термины, которые
будут применяться и в следующей главе. Следуя Кап-
Каплуну [1], Лагерстрому и Коулу [1], мы назовем ряд тео-
теории тонкого профиля внешним разложением. Это
результат, получающийся при стремлении е к нулю при
фиксированных значениях внешних переменных s и у
(или х и у). Подобным же образом локальное решение
является первым членом внутреннего разложения, кото-
которое получается при стремлении е к нулю с фиксирован-
фиксированными значениями внутренних переменных 5 и У. (Ин-
(Индекс в Ui теперь расшифровывается как обозначение по-
понятия «внутренний» (по английски inner— Ред.).)
4.10. Сращивание с решением вблизи
закругленной кромки
В общем случае, как и в приведенном примере, внут-
внутреннее и внешнее разложения дополняют друг друга:
одно имеет место в той области, где другое непригодно.
При этом весьма важна возможность сращивания двух
94 Гл. 4. Задачи особых возмущений в теории профиля
разложений. Сращивание. существенно для успеха ме-
метода, и мы подробно обсудим его в следующей главе,
здесь же мы примем без доказательства, что в рассмат-
рассматриваемом примере так же, как и во многих других за-
задачах, приложим следующий принцип асимптотического
сращивания:
/тг-членное внутреннее разложение /г-член-
ного внешнего разложения равно я-член- С4 3б^
ному внешнему разложению /тг-членного * * '
внутреннего разложения.
Здесь m и п — произвольные целые числа, равные
или неравные. По определению m-членное внутреннее
разложение д-членного внешнего разложения находится
переписыванием последнего во внутренних переменных,
асимптотическим разложением для малых е и обрыва-
обрыванием результата на m-м члене. Обратный процесс дает
правую часть равенства D.36).
Мы теперь используем этот принцип для того, чтобы
найти неизвестные постоянные С\ и С2 во внешнем раз-
разложении D.326) и величину Ui во внутреннем решении
D.35). Для начала мы знаем только первый член внеш-
внешнего разложения, соответствующий невозмущенному по-
потоку, и не знаем ни одного члена внутреннего разло-
разложения. Выберем т = /г=1, чтобы найти первое прибли-
приближение для эффективной скорости набегающего потока
иг во внутренней задаче. Удобно представить последо-
последовательность действий в следующем виде.
Одночленное внешнее разложение: q~^Ut D.37а)
переписанное во внутренних переменных: = Ut D.376)
разложенное для малых е. = U, D.37в)
одночленное внутреннее разложение: = U. D.37г)
Одночленное внутреннее
разложение:
переписанное во внешних
переменных:
разложенное для малых е:
/ 1 ?2 \
— Ut 1 — -j- \- . , D.38в)
\ 4 5 /
одночленное внешнее
разложение: ^= U^. D.3Вг)
4.10. Сращивание вблизи закругленной кромки
95
Приравнивая D.37г) и D.38г) в соответствии с прин-
принципом сращивания D.36), получаем
Ut = U. D.39)
Таким образом, эффективная скорость на бесконеч-
бесконечности для внутреннего решения в первом приближении
совпадает с реальной скоростью набегающего потока,
что физически правдоподобно. Можно показать (см. уп-
упражнение 4.2), что это сращивание нельзя было бы вы-
выполнить, если бы внутреннее решение имело особенность
на бесконечности. Это оправдывает использование
нами принципа минимальной особенности.
Теперь проведем обратный процесс, чтобы найти вто-
второй член внешнего разложения. Полагая т—\ и /г = 2,
мы получим следующие результаты.
Одночленное внутреннее
разложение:
переписанное во внешних
переменных:
разложенное для малых е:
двучленное внешнее
разложение:
Двучленное внешнее q^
разложение: 1
переписанное во
sB
ci
i 11
— s) \ )
D.40а)
D.406)
, D.40в)
D.40г)
D.41а)
одночленное
внутреннее
разложение:
U
С,
, если Сх Ф 0,
со
1. если С, = 0.
D.41г)
Сравнивая выражения D.40г) и D.41г), мы нахо-
находим, что они сращиваются только при d = 0. Следова-
Следовательно, в решении первого порядка для тонкого про-
профиля не может быть собственного решения тида источ-
источника.
96 Гл. 4. Задачи особых возмущений в теории профиля
Теперь еще раз проведем процесс в обратном на-
направлении с тем, чтобы найти второй член во внутрен-
внутреннем разложении. Положим т = п = 2.
Двучленное внешнее
разложение: q~ U (\ -f-?), D.42а)
переписанное во внутренних
переменных: = U A + е), D.426)
разложенное для малых е: = <[/ A -{- е), D.42в)
двучленное внутреннее
разложение: = U A + е)- D.42г)
Последний результат показывает, что второй член во
внутреннем разложении должен быть порядка е. Теперь
из D.336) следует, что ошибка при приближенной за-
замене носовой части эллипса соприкасающейся парабо-
параболой имеет порядок лишь е2. Следовательно, внутреннее
решение есть решение для параболы с точностью не
только до первого, но и до второго порядка при условии,
что Ui уточнено. Мы найдем далее
г- ¦¦
Двучленное внутреннее п л/ iaatk \
разложение: q—> иt \/ 1 , ос > D.4<за)
переписанное во внешних
переменных:
разложенное для малых е: = U-ь [ 1 —~- — + • • • Ь D.43в)
\ 4 s )
двучленное внешнее
разложение: = U\. D.43г)
Сравнение показывает, что с точностью до второго по-
порядка
Ul = U(l+e). D.44)
Физически это означает, что, хотя характер течения
вблизи передней кромки зависит только от местной фор-
формы профиля и до второго порядка таков же, как для
соприкасающейся параболы, эффективная скорость на
бесконечности для этой параболы слегка отличается от
истинной скорости набегающего потока. Она увеличена
влиянием относительно удаленных частей профиля, дей-
действие которых можно считать обусловленным дополни-
дополнительными к параболе стоками. Таким образом, парабо-
параболическая носовая часть обтекается потоком, как бы
4 10 Сращивание вблизи закругленной кромки 97
ускоренным с тем, чтобы обеспечить обтекание и ос-
остальной части профиля.
Мы могли бы теперь вернуться к внешнему разложе-
разложению, выбрать т = 2, п = 3 и показать, что сращивание
решений приведет к условию Со = 0: в решении второго
порядка для тонкого профиля нет собственных решений
типа источника. Собственные решения типа диполя и
собственные решения высших порядков могли бы быть
исключены подобным же образом.
Этот процесс в принципе можно продолжать до бес-
бесконечности. Однако, начиная со следующего шага, сле-
следует принять во внимание, что внутренняя задача долж-
должна рассматриваться уже не для параболы, а для более
сложной формы
4 о" 32
для е->0 при s = O(l). D.45)
Эта форма получается разложением соотношения D.336)
и учетом требуемого числа членов (рис. 4.10). Решение
Рис. 4.10. Последовательные внутренние
разложения для формы эллипса.
Верхняя кривая Y == YS, средняя кривая
Y = yr2S(l--:lU&2S), нижняя кривая
Y V
можно найти, взяв за основное решение обтекание со-
соприкасающейся параболы и применив к нему воз-
возмущение координат. Конечно, внутреннее разложение
D.45) для формы профиля расходится для больших S,
а именно для 5>2/е2. Следовательно, внутреннее раз-
разложение непригодно при S=oo. Этот результат мож-
можно получить и из известного точного решения, введя
98 Гл 4 Задачи особых возмущений в теории профиля
внутренние переменные и произведя разложение, что
дает
Я = 1 + в _
-I/ 1 4- ( ~ >
2S Г1 , 3 2 S , 3 з S
1+2S [М"8Н" 4 8 1 + 2S "+" Т 8 1+2S
Отсюда видно, что особенность при S = oo появляется,
начиная с пятого члена внутреннего разложения. Эта
расходимость не имеет значения, поскольку внутреннее
разложение не применяется па столь больших расстоя-
расстояниях.
4.11. Сращивание с решением вблизи острой кромки
Теперь мы приложим тот же метод к случаю острой
кромки. Пример двояковыпуклого профиля (§ 4.7) по-
показывает, что исследование острых кромок приводит к
появлению логарифмических особенностей в разложе-
разложении теории тонкого профиля. Эти особенности так сла-
слабы, что, не обращая на них особого внимания, можно
вычислить неограниченное число членов. Тем не менее
представляет интерес выяснить источник появления ло-
логарифмических членов, исследуя течение в непосред-
непосредственной окрестности кромки.
Для простоты мы рассмотрим только переднюю
кромку двояковыпуклого профиля — распространение
результатов на любую острую кромку очевидно. При
смещении начала координат в переднюю кромку (см.
рис. 4.6) профиль описывается уравнением
у= ±е Bs — 52). D.47а)
В § 4.7 было показано, что разложение D.24) теории
тонкого профиля непригодно на расстояниях, меньших
чем s = O(e~]/&), от передней кромки. Поэтому удобно
пользоваться следующими внутренними переменными:
D.48)
4.11. Сращивание вблизи острой кромки
99
В этих переменных уравнение профиля запишется так:
У =-. ± г B5 — e-1/eS2). D.476)
При стремлении 8 к нулю второй член этого выраже-
выражения стремится к нулю быстрее, чем любая степень е.
Рис. 4.11. Внутреннее решение для профиля
с острыми кромками.
Следовательно, если закругленная кромка представ-
представляется параболой только с точностью до второго по-
порядка, то острая кромка аппроксимируется клином
с точностью до любого порядка (рис. 4.11). Поскольку
Рис. 4.12. Конформное отображение
обтекания клина.
• = \2-i arc tg 2е]( g 2e)
угол клина исчезающе мал, наш профиль аппроксими-
аппроксимируется уравнением
Г~±2е5 для г->0 при 5 = 0A). D.47в)
Соответствующим внутренним решением является
симметричное потенциальное обтекание этого клина при
наименьшей возможной особенности на бесконечности.
Его можно найти (см. рис. 4.12) элементарным кон-
конформным отображением равномерного параллельного
потока, а также разделением переменных в полярных
100 Гл. 4. Задачи особых возмущений в теории профиля
координатах, причем этот метод может быть распро-
распространен и на трехмерные задачи. Таким образом, внут-
внутреннее решение для скорости на поверхности находится
в виде
г г oarc tg 2е/(л-агс tg 2е) л г. Г) П\ (A AQ\
q ~ U io для 8—>U при o = U(l). D.4У)
Здесь в противоположность случаю закругленной кром-
кромки даже первый член внутреннего разложения расхо-
расходится на бесконечности. Он дает неограниченные значе-
значения скорости при 5 —* оо, так что множитель ?/2- теперь
нельзя интерпретировать как некую эквивалентную ско-
скорость набегающего потока, а можно лишь рассматри-
рассматривать как скорость на поверхности при 5=1. Как и для
закругленной кромки, [/,- можно найти сращиванием
с внешним разложением для тонкого профиля.
Для осуществления сращивания нам нужно внеш-
внешнее разложение внутреннего решения D.49). Это тре-
требует введения малых дробных степеней в формальный
ряд по степеням экспонент и осуществляется примене-
применением следующего правила:
s° = exp (In s8) = exp (e In s) = 1 -f e In s + -9- e2 In2 s + .. .,
D.50)
которое не будет пригодным для малых 5. Оно не-
неверно при е In 5 = 0A), или при s = O(?~1/?). Этот ре-
результат объясняет таинственнее появление логарифми-
логарифмических членов в разложении теории тонкого профиля
для острой кромки.
При сращивании двух разложений мы не обязаны,
как в случае закругленной кромки, переходить от одного
приближения к следующему, а можем сразу исследо-
исследовать нужное приближение. Рассмотрим, например, вто-
второе приближение. Тогда приложение принципа сращи-
сращивания D.36) при пг = п = 2 будет иметь следующий вид:
Двучленное внешнее разложение:
^]} D.51а)
переписанное во внутренних переменных:
« ul 1 + | г [2 + (t -e-4'S) '"^'-ilJ }' D-51б>
4 11. Сращивание вблизи острой кромки 101
разложенное для малых е:
двучленное внутреннее разложение:
5-ln2)]i D.51г)
переписанное во внешних переменных:
. D.51д)
Двучленное внутреннее разложение:
q - ?/;Sarc ** 2е/(л"агс *g 2e), D.52а)
переписанное во внешних переменных:
= f//(,1'es)arCtg2e/(It-arCtg2e), D 526)
разложенное для малых е:
двучленное внешнее разложение:
[l + \ г (in s + \)], D.52г)
переписанное во внутренних переменных:
)] D-52д)
При получении формулы D.52в) было использовано
правило D.50). Дополнительный последний шаг D.51д)
или D.52д) потребовался потому, что сравнение двух
результатов должно быть произведено или только во
внешних, или только во внутренних переменных. Так,
приравнивая D.52г) и D.51д) (см. также упражнение
4.5), получаем
— In 2 — -|) + ...]. D.53)
Это дополняет до второго порядка внутреннее разложе-
разложение D.49). Читатель может, используя соотношение
D.24), найти следующий член в разложении D.53) пу-
путем сращивания при т = п==$.
102 Гл. 4. Задачи особых возмущений в теории профиля
4.12. Сдвиговая поправка для закругленных кромок
Вернемся к особенности на закругленной кромке и
дадим иной способ ее исправления. Это послужит для
введения второго общего метода трактовки задач осо-
особых возмущений, который будет подробно описан в гл.6.
Рассмотрим простейший профиль с закругленной
кромкой — параболический. Мы должны исследовать
полное поле скоростей, поскольку скорость на поверх-
поверхности искажается из-за переноса граничных условий.
Для параболы у= ±е]/2я' с радиусом е2 при вершине
комплексная скорость с точностью до первого порядка
может быть получена из соответствующего выражения
D.12) для эллипса в виде
h f-O(e2), z = x±iy. D.54)
Сравним это выражение с точным результатом, ко-
который находится конформным отображением или разде-
разделением переменных в параболических координатах,
**-1*>=х-ущ=чт- D-55)
Легко видеть, что первое приближение D.54) ста-
становится точным, если начало координат просто сдвинуть
на величину 72?2. Это убирает из вершины особенность
вида корня квадратного и переносит ее внутрь пара-
параболы, в ее фокус, который является особой точкой кон-
конформного отображения. Таким образом, теория тонкого
профиля дает для параболы распределение источников
точное, но смещенное на половину радиуса кривизны
при ее вершине.
Это замечательное свойство должно приближенно
сохраняться для любого профиля с закругленной кром-
кромкой. По этой причине Мунк [1] поддерживал идею изме-
изменения абсциссы путем сдвига передней кромки профиля
на половину ее радиуса. Очевидно, что простое переме-
перемещение всего конечного профиля было бы неправильно,
поскольку при этом задняя кромка оказалась бы не на
месте. Для эллипса (рис. 4.2) равномерное сжатие вдоль
оси х, очевидно, обеспечивает требуемый сдвиг обеих
4 12. Сдвиговая поправка для закругленных кромок 103
кромок, но в то же время производит неограниченное ко-
количество более сложных деформаций. Чтобы сохранить
выгоды, даваемые применением теории функций комп-
комплексного переменного, мы вместо этого деформируем
единственное переменное z = x + iy.
Лайтхилл [2] предложил следующий принцип нахож-
нахождения деформированных координат, с помощью которых
восстанавливается равномерная пригодность в широком
классе задач особых возмущений:
Приближения высших порядков имеют не большую /456}
особенность, чем первое приближение. ^ * '
Мы продемонстрируем этот принцип, приложив его
к разложению теории тонкого профиля для эллипса.
Необходимо исследовать третье приближение, поскольку
второе уже имеет особенность не большую, чем первое.
По этой причине деформирование имеет порядок г2,
а не е.
Распространение формулы первого приближения
D.12) на приближения высших порядков дает разло-
разложение теории тонкого профиля
-iVy =1+
Теперь предположим, что, как и в случае параболы,
этот результат становится равномерно пригодным, ес-
если z заменить слегка деформированной координатой ?.
Положим
.., D.58)
где деформирующая функция 22, которая равнялась — 1/2
для параболы, подлежит определению. Подстановка
этого значения в формулу D.57) и повторное разложе-
разложение по степеням г дают соотношение
^--2t)+--- D'59)
104 Гл. 4 Зас/ачи особых возмущений в теории профиля
Очевидно, что третий член не будет иметь особен-
особенность более сильную, чем второй, при ?=±1 (а также
при ? = 0), если мы положим
г2(С) = -¦§-, или —\С3, или .... D.60)
Рассмотрим для простоты первую из этих возможно-
возможностей, что обеспечивает равномерное сжатие вдоль абс-
абсциссы, уже предложенное выше. Тогда решение первого
порядка примет вид
Ф* - Щу = 1 + е (l - ]/ -^т ), D.61а)
где
^ .. . D.616)
В данном случае можно исключить ? и получить
решение в явном виде, что невозможно при каком-ни-
каком-нибудь ином выборе z2. В общем случае приходится до-
довольствоваться неявным представлением решения че-
через ? как через параметр. Это приближение равномерно
пригодно с точностью до первого порядка, что может
быть проверено сравнением с точным решением
Поскольку мы оперировали с решением вместо того,
чтобы ввести деформирование координат в основную за-
задачу, примененный выше прием в действительности пред-
представляет собой некоторое видоизменение метода Лайт-
хилла, предложенное JVL Ф. Притуло [1] (см. упражне-
упражнение 6.4).
Приложение подобных рассуждений к общему про-
профилю привело Лайтхилла [4] к правилу D.306) исправ-
исправления теории топкого профиля вблизи закругленных
кромок. Однако в противоположность данному выше на-
нашему выводу этого правила способ Лайтхилла приме-
применим лишь к закругленным кромкам и оказывается не-
непригодным для острых, прямоугольных и т. п. кромок.
Упражнения 105
УПРАЖНЕНИЯ
4.1. Теория тонкого профиля с использованием функции тока.
Воспроизведите исследования § 4.2 и 4.3, применяя функцию тока
взамен потенциала скорости. Выведите решение для эллиптического
профиля и убедитесь в том, что неопределимые собственные реше-
решения типа источника исключаются автоматически
4.2. Сращивание решений и принцип минимальной особенности.
Локальная задача симметричного обтекания соприкасающейся пара-
параболы (рис. 4.9) имеет собственные решения, которые содержат осо-
особенности на бесконечности. Покажите, что наименее особое из них
добавляет к выражению скорости на поверхности член [53/(l + 25)]V2
с некоторым постоянным коэффициентом. Это можно сделать, на-
например, введя параболические координаты g и г] и найдя решения
задачи потенциала в виде полинома по {^Л-щ). Покажите далее,
что для любого профиля с закругленной передней кромкой сращи-
сращивание с решением теории тонкого профиля приводит к исключению
этого собственного решения, что находится в соответствии с прин-
принципом минимальной особенности.
4.3. Сращивание с локальным решением для прямоугольной
кромки. Введите внутренние переменные, подходящие для передней
кромки прямоугольного профиля, изображенного на рис. 4.7 Пока-
Покажите, что с точностью до первого порядка внутренним решением
является решение для обтекания полубесконечной прямоугольной
плиты толщиной 2, на гранях которой скорость на поверхности
выражается через параметр t (Милн-Томпсон [1], § 10.6):
где rtS=/*2=Tf—Arch*
Осуществив сращивание с внешним решением D.27), покажите,
что коэффициент собственного решения равен С=7г— 1пDя/е), так
что асимптотическая последовательность для разложения D.2) тео-
теории тонкого профиля содержит логарифмические члены, начиная
с 821п 8.
4.4. Правило исправления решения в случае острых кромок.
Придумайте правило с поправочным множителем для случая острых
кромок, аналогичное правилу D 306) Лайтхилла Обсудите пер-
перспективы аналогичного исследования прямоугольных кромок, а так-
также острых вершин осесимметричных удлиненных тел.
4.5. Точное решение для двояковыпуклого профиля. Милн-Томп-
Милн-Томпсон ([1], § 6.51) дает точное решение для симметричного потенциаль-
потенциального обтекания двояковыпуклого профиля, образованного дугами
окружности С точностью до какого порядка в теории тонкого про-
профиля их можно заменить параболическими дугами? В координа-
координатах, показанных на рис. 4.6, точная скорость па поверхности опре
деляется выражением
q _ 4 ch r\ — cos /гя/2
V~"~nr 1 + ch 2т) п '
106 Гл. 4. Задачи особых возмущений в теории профиля
где
х = — ! к, п = — arc ctg ?.
ch т) — cos ля/2 я &
Получите из этих соотношений внешнее и внутреннее разложения
и сравните с результатами § 4.7 и 4.11. Покажите, что прирав-
приравнивание выражений D.51г) и D.52д) взамен D.51д) и D.52г) не
приводит к равенству D.53). Объясните причины этого различия
и сделайте выводы.
4.6. Одновременное сращивание для эллиптического профиля.
Покажите, что взамен сращивания шаг за шагом, как это делалось
в § 4.10, можно сразу срастить трехчленное внешнее разложение
D.32) с двучленным внутренним разложением D 35).
4.7. Правила исправления течений вблизи носовых частей тел
вращения. Предложите правило, аналогичное D.306), для осесим-
метричных тел с закругленной носовой частью при осесимметричном
обтекании несжимаемой жидкостью. Используйте тот факт, что
распределение скорости на поверхности параболоида вращения та-
таково же, как на параболическом цилиндре. Примените полученное
правило к эллипсоиду вращения, образованному вращением кривой
эллипса, изображенного на рис. 4.2, вокруг оси х, для которого тео-
теория тонкого тела дает следующее выражение (Ван-Дайк [8]) ско-
скорости на поверхности:
Сравните с точным выражением
1 + е2 (Аг seen s — У"Г^ё?I(УТ=ё? — г2 Ar seen s)
Подобным же образом получите правило для исследования об-
обтекания заостренных тел вращения и приложите его к веретено-
веретенообразному телу, образованному вращением кривой, изображенной на
рис. 4.6, для которого теория тонкого тела дает формулу
JL = 1 Д- е2 Г 2 A — Зх2) In — 2 —3+1 1л:2] 4- О (е4 In2 e).
4.8. Теория малых возмущений для параболоида вращения. Рас-
Рассмотрите осесимметричное обтекание несжимаемой жидкостью пара-
параболоида вращения г=у2г2х. Выведите аналог уравнений D.4) для
первого возмущения, но не переносите условие обтекания на ось.
Проведите решение разделением переменных в параболических ко-
координатах, покажите, что возмущения имеют порядок е2, а не s
и что потенциал течения имеет вид
1 \Г г2 -I- г2 у
цх+ ' г* la UL3rJL±[ О(еЧпе)
Упражнения 107
Покажите, что этот результат станет точным, если начало координат
сместить вниз по потоку на половину радиуса носовой части.
Разложите приведенное выше приближение формально для ма-
малых значений г порядка е и, получив тем самым решение теории
тонкого тела, проверьте, что оно удовлетворяет приближенному
уравнению сргг + Фг//"=0 теории тонкого тела. Улучшите этот резуль-
результат, применив метод итераций к полному уравнению Лапласа для
нахождения решения второго порядка теории тонкого тела в виде
Найдите вид функции f из соображений размерности, использо-
использовав тот факт, что е2 — единственная характерная длина в задаче,
и таким образом завершите решение, за исключением остающегося
неизвестным множителя собственного решения. Интерпретируйте это
как форму частного решения уравнения Лапласа применительно
к теории тонкого тела. Найдите неизвестную постоянную сравнением
с точным решением. (Роль, которую играет здесь искусственный па-
параметр е, и приложение метода сращиваемых асимптотических раз-
разложений описаны в статье Чжана [1]. Обтекание параболоида до-
дозвуковым потоком сжимаемой жидкости исследовано Ван-Дай-
ком [7].)
4.9. Дозвуковая теория топкого профиля. Для симметричного
дозвукового течения сжимаемой жидкости, когда уравнение Лапла-
Лапласа D. Га) заменяется уравнением B.19а), сформулируйте задачи пер-
первого и второго порядка, соответствующие задачам D.4) и D.5).
Покажите, что изменение вертикального масштаба (преобразование
Прандтля — Глауэрта) сводит первую из них к эквивалентной за-
задаче для несжимаемой жидкости. Проверьте, что общий вид част-
частного решения (§ 3.7) для уравнения второго порядка определяется
(Ван-Дайк [2]) выражением
. Y+1 М2 \ y+1 M2
А+ 4 1-мОф|~ 4 Т=Ж
Найдите решение второго порядка для волнистой стенки
y=Esmx. Вычислите коэффициент давления на поверхности исходя
из формулы
СР = - 2Ф1Х - [A - М2) vl + <р?„ + 2Ф2 J + ...
и проверьте, что он удовлетворяет правилу подобия во втором при-
приближении для профиля (Хейз [2]):
если при М=0
то для
р J/1-M2 W^ 4 A-М'J р(
Глава 5
МЕТОД СРАЩИВАЕМЫХ
АСИМПТОТИЧЕСКИХ РАЗЛОЖЕНИЙ
5.1. Историческое введение
В предыдущей главе мы ввели метод исследования
задач особых возмущений, который представляет собой
обобщение теории пограничного слоя, предложенной
Прандтлем [1]. Этот метод в прошлом назывался мето-
методом «внутреннего и внешнего разложений» или «двух
асимптотических разложений». Мы предпочитаем, сле-
следуя Бретертону [1], называть его методом сращиваемых
асимптотических разложений.
Идеи, лежащие в основе метода, развивались в тече-
течение многих лет. В пятидесятых годах этим методом поль-
пользовались Фридрихе [3, 4] и его ученики. Он был систе-
систематически развит и приложен к течениям вязких жид-
жидкостей в работах сотрудников Калифорнийского
технологического института. Каплун [1] ввел формаль-
формальные внутренний и внешний предельные переходы для
теории пограничного слоя и соответствующие внутрен-
внутреннее и внешнее разложения. Впоследствии, изучая тече-
течения при малых числах Рейнольдса, Каплун и Лагер-
стром [1] провели глубокий анализ процессов сращива-
сращивания (см. также Лагерстром [1]). Каплун [2] использовал
эти идеи для исследования парадокса Стокса для плос-
плоского течения при малых числах Рейнольдса. Лагерстром
и Коул [1] осуществили оценку метода путем сравнения
с новыми точными решениями уравнений Навье — Сток-
Стокса для обтекания со скольжением расширяющегося кру-.
гового цилиндра. Коулс [1] приложил метод к некото-
некоторым специальным решениям для сжимаемого погранич-
пограничного слоя.
Независимо Праудмен и Пирсон [1] использовали ме-
метод для изучения обтеканий сферы и кругового ци-
цилиндра при малых числах Рейнольдса. Гольдштейн [3,4]
5 1. Историческое введение 109
и Имаи [4] дали первое правильное развитие решения
Блазиуса для пограничного слоя на полубесконечной
плоской пластине. Тинг [1] решил загадку о вязком
сдвиговом слое между двумя потоками, движущимися
с разной скоростью.
После этого периода развития метод сращиваемых
асимптотических разложений был приложен ко множе-
множеству проблем механики жидкости. Большая часть ран-
ранних приложений относилась к вязким течениям. Напри-
Например, Жермеи и Гиро [1, 2], а также Чоу и Тинг [1] вы-
вычислили влияние кривизны на структуру ударной волны.
Меррей [1] и Тинг [2] определили влияние внешней за-
завихренности на пограничный слой вблизи передней
кромки плоской пластины и на большом удалении от
нее. Чжан [1] выяснил поведение вязкого течения далеко
от конечного тела. Течения при малых числах Рей-
нольдса были исследованы для эллипсоида Бричем [1],
для вращающейся сферы — Рубиновым и Келлером [1],
для кругового цилиндра в сдвиговом потоке — Бретер-
тоном [1] и т. д.
Этот метод может с успехом применяться также и
к невязким течениям. Предыдущая глава дает примеры
течений несжимаемой жидкости; Коул и Миссайтер [1]
рассмотрели трансзвуковое обтекание тонких тел. Ме-
Метод, как нам представляется, менее популярен в Совет-
Советском Союзе, но Б. М. Булах [1] использовал его для ис-
исправления линеаризованных сверхзвуковых конических
течений и их приближений высшего порядка в окрест-
окрестности головной ударной волны1). Подобным же обра-
образом Френкель и Уотсон [1] попытались решить задачу
о «псевдотрансзвуковом» обтекании треугольного кры-
крыла, которая зозникает в том случае, когда головная вол-
волна близко прилегает к передней кромке. Якура [1] ис-
исследовал энтропийный слой, образованный малым затуп-
затуплением тела в гиперзвуковом потоке.
') В последнее время этот метод был успешно применен и в
других работах; см., например, Сычев В. В, К теории сильного
взрыва в теплопроводном газе, ПММ, 29, вып. 6; Н е й л а п д В. Я.,
Сычев В. В., Асимптотические решения уравнения Навье — Стокса
в областях с большими, локальными возмущениями, М. Ж. Г., 1
A966), № 4. — Прим. ред.
110 Гл. 5. Метод сращиваемых асимптотических разложений
После 1960 г. в изобилии появились работы, посвя-
посвященные приложениям метода как в различных разде-
разделах механики жидкости, так и в других отраслях при-
прикладной математики. Некоторые недавно исследованные
примеры будут рассмотрены в следующих главах этой
книги.
5.2. Неоднородности прямого разложения
Прежде чем обсуждать детали метода сращиваемых
асимптотических разложений, полезно составить пред-
представление о том, как возникают задачи особых возму-
возмущений. Что является источником возмущений? Можем
ли мы предсказать, к задаче каких возмущений — ре-
регулярных или особых — приведет данная физическая
проблема?
Классический признак особого поведения знаком нам
по теории Прандтля пограничного слоя: малый пара-
параметр является множителем при одной из старших про-
производных в дифференциальных уравнениях. Тогда в пря-
прямой схеме метода возмущений эта производная теряется
в первом приближении, так что порядок дифферен-
дифференциальных уравнений снижается. В связи с этим должны
быть отброшены одно или несколько граничных усло-
условий, и вблизи границ, на которых они были наложены,
приближение нарушается. Так бывает, за исключением
того маловероятного случая, когда исходные граничные
условия согласуются с упрощенными дифференциаль-
дифференциальными уравнениями.
Часто оказывается полезным исследовать обыкно-
обыкновенные линейные дифференциальные уравнения как ма-
математическую моцель, показывающую существенные
черты более сложных задач. Простая модель, которая
показывает потерю старшей производной в теории по-
пограничного слоя, дана Фридрихсом [1] в виде уравнения
& ^ l E-1)
с точным решением
1 p-xfe
f (x; e) = A - a) \_e-VB 4- ax. E.2)
5.2. Неоднородности прямого розлолсения
111
Однако если положить е = 0, то дифференциальное
уравнение станет уравнением первого порядка, так что
оба граничных условия не могут быть удовлетворены,
если только не окажется случайно, что а=\. Точное ре-
решение показывает, что условие при х = 0 должно быть
Рис. 5.1. Решение
задачи-модели.
внутреннее решение,
внешнее решение,
точное решение.
отброшено. Тогда приближенное решение для малых в
будет
f,(x\ е) — A —-а)-\-ах. E.3)
Как следует из рис. 5.1, это является хорошим при-
приближением всюду, за исключением «пограничного слоя»,
где х = О(г). Если ввести увеличенную внутреннюю ко-
координату X, соответствующую этой области, и положить
/ (х; &)^F (Х\ е), X = —, E.4)
то исходная задача E.1) преобразуется в следующую:
U Г , и Г Р-, /Гчч ^ г-« / 1 \ 1 /г-г*\
= I. E.5)
dX2
dX
Если теперь положить 8 = 0, то решением дифферен-
дифференциального уравнения, удовлетворяющим внутреннему
граничному условию, будет функция A — е~х) с произ-
произвольным множителем. Наложение внешнего граничного
112 Г л 5. Метод сращиваемых асимптотических разложений
условия привело бы к обращению этого множителя в
единицу. Однако точное решение показывает, что этот
результат неверен. Внешнее граничное условие должно
быть отброшено при отыскании внутреннего решения,
так же как было отброшено внутреннее граничное усло-
условие для внешнего решения. Взамен этого внутреннее ре-
решение нужно срастить с внешним при помощи принципа
сращивания D.36). Таким образом, мы найдем равно-
равномерно пригодное первое приближение для малых е
1—а-\-ах при е—>0 для фиксиро- E.6а)
ванного х > О, ^ '
ванного
(I—a)A-е x) при e—>0 для фиксиро-
eJ* E.66)
В задаче особых возмущений признак, характеризуе-
характеризуемый потерей старшей производной, чаще всего отсут-
отсутствует. Так, в теории тонкого профиля (гл. 4) неодно-
неоднородность обусловлена не дифференциальными уравне-
уравнениями, а граничными условиями. Подобным же образом
для вязкого течения при малых числах Рейнольдса все
производные высшего порядка в приближенных уравне-
уравнениях Стокса сохраняются; неоднородность здесь свя-
связана скорее с бесконечной протяженностью жидкости.
Очевидно, что было бы полезно иметь более надежный
признак для обнаружения неоднородности.
5.3. Физический критерий однородности
В физических проблемах можно установить более
общий признак особого поведения, основанный на сооб-
соображениях размерности. Мы видели, что присущая про-
проблеме неоднородность может подавляться исключи-
исключительными граничными условиями, так что можно дать
только необходимый, но не достаточный признак неодно-
неоднородности. Поэтому вместо признака неоднородности мы
установим следующее правило как положительный кри-
критерий однородности:
Возмущенное решение равномерно при-
пригодно в координатах пространства и вре- /57ч
менп, если параметр возмущения е не пред- ^ ' '
ставляет собой отношения двух длин,
5 3 Физический критерий однородности 113
Для понимания этого критерия рассмотрим сначала
возмущения параметра. Геометрия задачи будет опре-
определяться типичным главным размером, который мы мо-
можем назвать первичной характерной длиной. Примерами
являются радиус кругового цилиндра в гл. 2 и длина
хорды тонкого профиля в гл. 4. Эта длина является
естественной основой для образования безразмерных
координат (в неустановившихся течениях требуется так-
также характеристическая скорость) — из этих величин
составляются непосредственно внешние переменные. Не-
Неоднородность может проявиться только тогда, когда
среди параметров задачи есть вторичная характерная
длина, отношение которой к первой стремится к нулю
или бесконечности при стремлении е к нулю. Эта вто-
вторичная длина при надлежащем ее выборе является ос-
основой для внутренних переменных.
Нам уже знакома задача, включающая две незави-
независимые длины, — задача потенциального обтекания тон-
тонкого профиля с закругленной носовой частью. Ее гео-
геометрия характеризуется длиной хорды, за исключением
окрестности передней кромки, где главную роль играет
радиус носовой части. Поскольку отношение этих двух
длин стремится к нулю как квадрат относительной тол-
толщины профиля, то наш критерий E.7) наводит на мысль,
что решение типа тонкого профиля может быть особым.
В гл. 4 было показано, что эта возможность реализует-
реализуется; при этом внешние переменные были основаны на
хорде профиля, а внутренние —на радиусе носовой
части.
Наш критерий указывает, что при возмущении ко-
координаты никогда нельзя гарантировать однородность
решения по остальным координатам. Последние могут
быть сделаны безразмерными с использованием или
первичной характерной длины или возмущенной коор-
координаты. И поскольку отношение этих двух длин стре-
стремится к нулю или бесконечности, они обеспечивают мас-
масштабы для внутреннего и внешнего разложений.
Укажем примеры возмущений параметра, которые
дают лишь один масштаб характерной длины и, следо-
следовательно, необходимо являются регулярными согласно
нашему критерию. Обтекание круга жидкостью с малой
114 Г л 5. Метод сращиваемых асимптотических разложений
сжимаемостью (§ 2.4) содержит радиус круга в каче-
качестве единственной характерной длины, и параметр воз-
возмущения образуется отношением скоростей или энергий,
а не длин. Задача о слегка деформированном круге
в потенциальном потоке (§ 2.3) содержит две длины,
но одного порядка, и при е —> 0 их отношение прибли-
приближается к единице, а не к нулю или бесконечности.
Приведем теперь случаи возмущения параметра, ко-
когда существует две независимые длины и вследствие
этого возникает неоднородность (рис. 5.2). Несущее
Рис. 5.2. Задачи особых возмущений, включаю-
включающие две независимые длины.
крыло характеризуется хордой и размахом; их отноше-
отношение обращается в нуль в теории несущей линии Пранд-
тля (см. § 9.2) и становится бесконечным в приближе-
приближении крыла малого удлинения. Тело в вязком потоке
характеризуется не только геометрической длиной, но
также и масштабом длины v/U, связанным с вязкостью.
Их отношение есть число Рейнольдса, которое стремится
к нулю в течениях Стокса (гл. 8) и становится беско-
бесконечным в теории пограничного слоя (гл. 7). Этот при-
пример показывает, что вторичная характерная длина не
всегда является геометрическим размером.
Далее рассмотрим некоторые возмущения координат,
которые являются особыми (рис. 5.2). Вязкое сверхзву-
сверхзвуковое обтекание конуса или клина (включая плоскую
пластину) может быть найдено приближенно для рас-
расстояний от вершины, больших по сравнению с длиной
5 3. Физический критерий однородности 115
v/i/. Аналогично при исследовании течения газа с диссо-
диссоциацией или химическими реакциями можно ввести
длину релаксации; так же может быть исследовано
влияние малого затупления. В случае импульсного
приведения в движение тела в вязкой жидкости можно
получить разложения по степеням времени, отнесенного
к характерной длине и скорости. Вязкое течение далеко
от тела может быть представлено разложением по отри-
отрицательным степеням расстояния, отнесенного к харак-
характерному размеру тела.
Укажем теперь задачи, в которых имеются две неза-
независимые длины, но которые тем не менее являются
задачами регулярных возмущений. Потенциальное обте-
обтекание волнистой стенки, остроносого профиля или тон-
тонкого тела любой формы, на котором не образуется кри-
критических точек, представляют собой задачи регулярного
возмущения по параметру толщины. Задача об обтека-
обтекании круга равномерно завихренным потоком (§ 2.2) об-
обнаруживает внешние симптомы неоднородности па бес-
бесконечности, где отношение возмущения к основному ре-
решению в разложении B.11) растет как ег; однако здесь
решение является точным и, следовательно, равномерно
пригодным. В то же время какое-либо другое распреде-
распределение завихренности привело бы к задаче особых воз-
возмущений (упражнения 2.4 и 5.7). В невязкой жидкости
разложение для течения вдали от тела регулярно так-
также и для случая импульсивного приведения в движе-
движение. Даже неоднородность в теории пограничного слоя
Прандтля, являющаяся прототипом неоднородности во-
вообще, исчезнет, если заменить фиксированную твердую
поверхность тела эластичной подвижной пленкой, точки
которой имеют ту же скорость, что и жидкость в потен-
потенциальном течении.
Задача может содержать и более двух независимых
длин, что приведет к множественному предельному пе-
переходу; тогда возможно и несколько неоднородностей.
В случае трех слоев можно говорить о внешнем, сред-
среднем и внутреннем разложениях. Примером является
вязкое течение при больших числах Рейнольдса и боль-
больших или малых числах Прандтля, когда толщина тепло-
теплового пограничного слоя будет значительно больше или
116 Г л 5 Метод сращиваемых асимптотических разложений
меньше толщины вязкого слоя. Пример для невязкого
течения будет рассмотрен в § 9.9.
Возмущение координат иногда можно заменить воз-
возмущением параметра. Например, вместо разложения
для больших расстояний от вершины затупленного кли-
клина (§ 9.9) можно рассматривать решение задачи об об-
гекании клина конечной длины, у которого величина
затупления стремится к нулю. В геометрии кониче-
конических течений угол играет роль длины. Следовательно,
в конических течениях возможна неоднородность, если
параметром возмущения является отношение двух уг-
углов. Примерами являются эллиптический сильно сжа-
сжатый конус, для которого прямое возмущенное решение,
очевидно, становится непригодным вблизи передних кро-
кромок, так же как это было в теории тонкого профиля, и
круговой конус под бесконечно малым углом атаки,
вблизи поверхности которого обнаруживается существо-
существование вихревого слоя Ферри [1].
5.4. Роль составного и внутреннего разложений
Мы видели, что задача особых возмущений, как
правило, включает две независимые длины. В ре-
результате прямое возмущенное решение в координатах,
отнесенных к первичной характерной длине, оказывает-
оказывается неверным в области, где существенной является вто-
вторичная характерная длина. Вторичная характерная дли-
длина не всегда очевидна. Ясно, что это хорда для крыла
большого удлинения, толщина для профиля с плоско
затупленной передней кромкой, вязкая длина v/U для
течения при малых числах Рейнольдса. Однако при боль-
больших числах Рейнольдса это будет корень квадратный из
произведения вязкой и геометрической длин. Для про-
профиля с закругленной передней кромкой это будет не
толщина, а радиус кромки, который пропорционален
квадрату толщины, деленному на длину хорды. Обте-
Обтекание заостренного профиля дозвуковым потоком (§6.4)
является весьма тонкой задачей, граничной между одно-
однородными и неоднородными задачами; в ней размер об-
области неоднородности экспоненциально мал и не может
быть непосредственно сопоставлен с каким-либо фпзиче-
5.4. Роль составного и внутреннего разложений 117
ским размером. Подобное замечание относится и к вих-
вихревому слою на слегка наклоненном конусе в сверх-
сверхзвуковом потоке.
Непосредственное возмущенное решение дает асимп-
асимптотическое разложение вида
/ (х, у, z; 8) ~ 2 bn (e) fa (х, у, г) E.8)
для ?->0 при фиксированных х, у, z.
Здесь 6п(е) образуют соответствующую асимптоти-
асимптотическую последовательность, х, у, z — координаты, при-
приведенные к безразмерному виду отнесением их к пер-
первичной характерной длине. Это разложение применимо
там, где функции fn регулярны. Эти функции приобре-
приобретают особенность в какой-либо точке, если течение в
ее окрестности определяется вторичной, а не первичной
характерной длиной. Такая точка лежит в бесконеч-
бесконечности, если вторичная длина является большей. Для
того чтобы видоизмененное разложение было равномер-
равномерно пригодно, оно должно зависеть также от координат,
приведенных к безразмерному виду отнесением их к
вторичной характерной длине. Поскольку отношение
первичной и вторичной длин является функцией от е,
это равносильно зависимости также и от е. Таким обра-
образом, равномерно пригодное разложение должно иметь
более сложный вид
/ (х, у, z\ 8) « 2 6Я (е) gn (X, у, Z\ 8) равномерно при е -> 0.
E.9)
Поскольку параметр возмущения е входит теперь
как неявно в функции gn, так и явно в асимптотическую
последовательность бп, написанное выражение не яв-
является асимптотическим разложением в обычном смыс-
смысле. Мы назовем его составным разложением. Такие раз-
разложения обсуждались в связи с задачами особых воз-
возмущений Эрдейи [2], который назвал их «обобщенными
асимптотическими разложениями». Имеются два возра-
возражения по поводу работы с составными разложениями.
Во-первых, с ними трудно производить действия; оче-
очевидно, такая обычная операция, как приравнивание
одинаковых степеней е, должна быть пересмотрена и,
118 Гл. 5. Метод сращиваемых асимптотических разложений
как будет видно из дальнейшего, составные ряды не
определяются однозначно. Во-вторых, они излишне со-
сочетают в себе сложности как прямых разложений, так и
области неоднородности (см., однако, § 10.3 и 10.4).
Проще изолировать трудности, связанные с неодно-
неоднородностью, построением дополнительного внутреннего
разложения, пригодного в окрестности этой неоднород-
неоднородности. Это достигается введением новых внутренних ко-
координат, которые имеют порядок единицы в области не-
неоднородности. Тогда внутреннее разложение имеет вид
f{x, у, z; s) = 2lAn(&)Fn(X> V, Z) E.10)
для е->0 при фиксированных X, Y, Z.
Мы обозначаем внутренние переменные пропис-
прописными буквами. Асимптотическая последовательность
Ап (г) может отличаться от асимптотической последова-
последовательности 6д(е) для внешнего разложения. Часто они
совпадают, но в § 6.3 будет приведен пример, в котором
они оказываются различными. Если область неоднород-
неоднородности представляет собой окрестность точки, лежащей
на конечном расстоянии, то внутренние координаты
X, Y, Z обычно приведены к безразмерному виду при
помощи вторичной характерной длины. Если неодно-
неоднородность имеет место вдоль линии, как в теории погра-
пограничного слоя, то изменяется только координата, нор-
нормальная к этой линии. Для случая неоднородности на
бесконечности координаты иногда должны быть рас-
растянуты введением различных функций от е для разных
направлений. Подобно внешнему разложению, внутрен-
внутреннее разложение является асимптотическим рядом в обыч-
обычном понимании, так что к нему применимы обычные
операции.
Часто бывает полезно предварительно ввести и зави-
зависимое переменное, которое так же, как и независимое,
имело бы порядок единицы во внутренней и внешней
областях. Тогда главные члены в асимптотических по-
последовательностях Дп(е) и 6п(е) будут равны единице.
Степень растяжения в общем случае будет различной
для зависимого и независимого переменных. Следуя
Каплуну [1], а также Лагерстрому и Коулу [1], мы мо-
5.4. Роль составного и внутреннего разложений 119
жем формализовать этот процесс следующими опреде-
определениями.
Внешние переменные: безразмерные независимые и
зависимые переменные, основанные на первичных
характерных величинах задачи.
Внешний предел: предел при стремлении параметра
возмущения е к нулю при фиксированных значе-
значениях внешних переменных.
Внешнее разложение: асимптотическое разложение
для е-* 0 при фиксированных внешних перемен-
переменных. В принципе получается из точного решения
последовательным применением внешнего пре-
предельного перехода в соответствии с выбранной
внешней асимптотической последовательностью.
Внутренние переменные: безразмерные независимые
и зависимые переменные, растянутые при помощи
соответствующих функций е так, что они имеют
порядок единицы в области неоднородности внеш-
внешнего разложения.
Внутренний предел: предел для е —> О при фиксиро-
фиксированных значениях внутренних переменных.
Внутреннее разлооюение: асимптотическое разложе-
разложение для е —> О при фиксированных внутренних пе-
переменных. В принципе получается из точного
решения последовательным применением внутрен-
внутреннего передельного перехода в соответствии с вы-
выбранной внутренней асимптотической последова-
последовательностью.
Составное разлооюение: какой-либо ряд, который сво-
сводится к внешнему разложению, когда он разла-
разлагается асимптотически для е —> 0 во внешних пе-
переменных, и к внутреннему разложению — во
внутренних переменных.
Метод сращивания двух дополнительных асимптоти-
асимптотических разложений сводит задачу особых возмущений
к ее простейшим возможным элементам. Если тем не
менее внутренняя задача первого приближения ока-
окажется «невозможной», то можно предположить, что сама
120 Га 5. Метод сращиваемых асимптотических разложений
по себе задача является нерешаемой. Например, оче-
очевидно, что распространение теории тонкого профиля
гл. 4 на дозвуковой сжимаемый поток в случае закруг-
закругленной передней кромки приводит к внутренней задаче
дозвукового обтекания параболического цилиндра, для
которой общее решение неизвестно. Вязкое обтекание
заостренного профиля при больших числах Рейнольдса
приводит к внутренней задаче вязкого обтекания полу-
полубесконечной плоской пластины, для которой существуют
только частные решения. Одно из преимуществ рассмат-
рассматриваемого способа состоит в том, что даже в этих «не-
«невозможных» ситуациях можно использовать численные
результаты или даже экспериментальные данные для
того, чтобы получить внутреннее решение. Так, в своей
теории несущей линии Прандтль отстаивал возмож-
возможность использования экспериментальных данных по про-
профилям для получения того, что, как будет показано в
§ 9.2, является внутренним решением.
5.5. Выбор внутренних переменных
Решающим шагом в методе сращиваемых асимпто-
асимптотических разложений является выбор внутренних пере-
переменных. Возникают следующие вопросы:
а) Какие независимые переменные должны быть рас-
растянуты?
б) Как они должны быть растянуты?
в) Как должно быть растянуто зависимое перемен-
переменное?
Ответ на первый вопрос зависит от выяснения осо-
особой природы задачи, включая сюда положение неодно-
родностей и их «форму», а именно появляются ли они
в окрестности точки, линии или поверхности.
Нужная степень растяжения обычно очевидна, если
можно вычислить несколько членов внешнего разложе-
разложения. Например, формальное решение типа топкого про-
профиля для эллипса, как было показано в § 4.4, оказалось
непригодным в окрестности порядка е2 передней
кромки; соответственно были увеличены внутренние ко-
координаты. Физические соображения могут подсказать
5 5. Выбор внутренних переменных 121
или подтвердить выбор надлежащего растяжения как
масштаба вторичной характерной длины задачи.
С другой стороны, можно искать растяжение путем
проб. Руководящей идеей здесь является то, что внут-
внутренняя задача должна обладать наименьшей возмож-
возможной вырожденностью, что она должна включать в пер-
первом приближении какие-либо существенные элементы,
упущенные в первом внешнем решении, и что внутрен-
внутреннее и внешнее решения должны сращиваться. В каче-
качестве примера рассмотрим задачу E.1). Пытаясь задать
произвольное растяжение только независимого перемен-
переменного, положим
!(х;е) = Р(Х;в), Х = -^> E.11)
тогда задача примет вид
d*F . а (?) dF _ а2 (е)
dX2 "" е dX ~ е а'
Поскольку старшая производная была потеряна во
внешнем пределе, d2F/dX2 должна теперь быть сохра-
сохранена во внутреннем пределе. Это означает, что множи-
множитель сх(е)/е, стоящий перед dFjdX, не должен обращать-
обращаться в бесконечность при е —> 0. Если он обращается в
нуль, то решение, удовлетворяющее внутреннему гранич-
граничному условию (которое также должно быть сохранено),
есть просто X с постоянным множителем, но это ре-
решение нельзя срастить с внешним решением E.3).
Остается лишь одна возможность, а именно, что о/е при-
приближается к константе, причем это дает также наимень-
наименьшую вырожденность дифференциального уравнения. По-
Положив эту константу равной единице, мы без потери
общности получим предыдущий результат E.4) и E.5).
В этом примере было бы излишне растягивать зависи-
зависимое переменное, поскольку внутренняя задача первого
приближения однородна, но в общем случае необходимо
допустить возможность независимого растяжения каж-
каждого переменного, как зависимого, так и независимого.
Внутренняя переменная почти всегда, как и в пре-
предыдущем примере, образуется линейным растяжением.
Исключение составляет задача о вихревом слое на
122 Гл. 5 Метод сращиваемых асимптотических разложений
наклонном конусе (Мупсои [1]). Это иллюстрируется сле-
следующей моделью:
д^-g—ef = O, f(l) = l. E.13)
Решая последовательными приближениями или под-
подставляя ряд по степеням 8, получим прямое (внешнее)
возмущенное решение
f(x\ e)~l+-r^(*1-'*--l) + O(s2), тпФ\, E.14а)
f(x\ е)~1 4-е Inх + О(е2), /71=1. E.146)
Здесь имеется особенность при х = 0 для т>1 и при
х = оо для т<Л. Представляется вероятным, что для
тф\ подходящей внутренней координатой будет
х = хг-тт-^ E.15)
и это подтверждается исследованием или результирую-
результирующего внутреннего уравнения
Л""^-/ = 0, E.16)
или точного решения
хе, т=\. E.176)
В специальном случае пг=\ из E.146) следует, что
область неоднородности вблизи начала координат экс-
экспоненциально мала, х = О(е~Х1г). Можно предположить,
что, так же как для заостренного профиля в § 4.7, под-
подходящим внутренним переменным будет переменное,
получающееся линейным растяжением,
Х = хе]*, E.18)
однако при этом дифференциальное уравнение остается
непреобразованным
так что простое растяжение неэффективно. Вместо этого
можно, основываясь на точном решении E.176), счи-
5.6. Роль сращивания 123
тать, что подходящая внутренняя координата опреде-
определяется нелинейным искажением
Х=:х\ E.20)
которое преобразует дифференциальное уравнение к
виду
Xf = 0
Таким образом, складывается представление, что пре-
преобразование с дробной степенью нужно использовать
в том случае, когда неоднородность в экспоненциально
малой области обязана своим происхождением не гра-
граничным условиям, а однородному оператору вида хд/дх
в дифференциальном уравнении.
5.6. Роль сращивания
Методу сращиваемых асимптотических разложений
свойственна потеря граничных условий. Нельзя ожи-
ожидать, что внешнее разложение будет удовлетворять ус-
условиям, которые наложены во внутренней области, и
обратно, внутреннее разложение в общем случае не бу-
будет удовлетворять условиям в удаленной области. Та-
Таким образом, лишь благодаря исключительному стече-
стечению обстоятельств внутреннее решение для эллиптиче-
эллиптического профиля (§ 4.10) оказалось удовлетворяющим
граничному условию в набегающем потоке. Внутреннее
решение для острой кромки не обладает этим свойством
(§ 4.11). Таким образом, неудовлетворенные граничные
условия вообще присущи как внутреннему, так и внеш-
внешнему разложениям. Потеря условий восполняется сра-
сращиванием двух разложений.
Для дифференциальных уравнений в частных произ-
производных сращиванию обычно целесообразно предпослать
приложение принципа минимальной особенности (§ 4.5).
Опыт показывает, что только одно из возможных реше-
решений, а именно то, которое имеет наименьшую особен-
особенность в своей области неоднородности, может быть сро-
щено с дополнительным разложением. Например, внут-
внутреннее решение для тонкого профиля с закругленной
носовой кромкой, как было показано в § 4.9, представ-
124 Гл. 5. Метод сращиваемых асимптотических разложений
ляет тобой симметричное обтекание соприкасающейся
параболы. На рис. 5.3 представлены первые две из бес-
бесконечного числа возможностей. Все они, кроме первой,
дают неограниченную скорость на бесконечности и в
Рис. 5.3. Возможные схемы симметричного обтека-
обтекания параболы.
связи с этим не могут быть срощены с разложением
теории тонкого профиля (упражнение 4.2).
Хотя принцип минимальной'особенности часто умень-
уменьшает число возможностей, он не всегда позволяет вы-
выбрать единственную картину течения. Например, он
исключает собственное решение типа источника для про-
профиля с закругленной носовой частью в линеаризован-
линеаризованном решении, но не во втором приближении. Так и
должно быть, поскольку собственное решение типа ис-
источника должно действительно фигурировать во внеш-
внешнем решении второго порядка для гладкого профиля,
Рис. 5.4. Профиль, для которого
линеаризованное решение совпа-
совпадает с решением для эллипса.
который отличается от эллипса только в окрестности
передней и задней кромок (рис. 5.4).
Сращивание представляет собой основную черту ме-
метода. Возможность сращивания основана на существо-
существовании области перекрытия, в которой пригодны как
внутреннее, так и внешнее разложения. Используя это
перекрытие, можно получить точное соотношение между
5.7. Принципы сращивания 125
конечными частными суммами. Реализация этой
замечательной возможности осуществима только для
возмущения параметра, которое неоднородно в коорди-
координатах, или для возмущения координаты, которое неод-
неоднородно по другим координатам. Нельзя срастить два
различных параметрических разложения, таких, как
разложение для больших и малых значений числа Рей-
нольдса или числа Маха; невозможно срастить два раз-
различных координатных разложения, таких, как разложе-
разложение для малых и больших значений времени или рас-
расстояния. Такие ряды могут перекрываться в том смысле,
что они имеют общую область сходимости, но процесс
аналитического продолжения дает только приближен-
приближенное соотношение для некоторого конечного числа чле-
членов (см. § 10.9).
Сращиванию может быть противопоставлен некий
другой процесс, который мы назовем численным склеи-
склеиванием. Этот процесс состоит в связывании двух рядов
условием равенства их численных значений и, возмож-
возможно, численных значений некоторых производных на ка-
какой-то произвольной промежуточной границе. Хотя ре-
результат может быть практически полезным — или даже
численно неотличимым от результата сращивания — по-
подобное склеивание неприятно с эстетической точки
зрения и обычно не является более простым. Кроме того,
сращивание дает лучшие, чем склеивание, результаты
для приближений высшего порядка. Мы считаем, что
склеивание должно отбрасываться, как только оказы-
оказывается возможным заменить его сращиванием, которое
обеспечивает незаметное гладкое соединение двух ре-
решений.
5.7. Принципы сращивания
Существование области перекрытия означает, что
внутреннее разложение внешнего разложения должно
с точностью до соответствующего порядка согласовы-
согласовываться с внешним разложением внутреннего разложе-
разложения (Лагерстром [1]). Этот общий принцип сращивания
может быть дан в различных специальных формулиров-
формулировках. Изучение существующей по этому вопросу лите-
126 Г л 5. Метод сращиваемых асимптотических разложений
ратуры приводит к выводу, что выбор формулировки
принципа сращивания является до некоторой степени
делом вкуса исследователя.
Прандтль при сращивании своего приближения по-
пограничного слоя с внешним невязким течением приме-
применил (не вводя специальной формулировки) то, что мы
назовем принципом предельного сращивания:
Внутренний предел внешнего предела равен ,^ 22}
внешнему пределу внутреннего предела. ^ ' '
Является ли это примитивное правило верным, зависит
не только от задачи, но также и от выбора независимых
переменных, которые сращиваются. Оно, очевидно, при-
пригодно для касательной скорости в пограничном слое, ко-
которая должна для больших значений аргумента прибли-
приближаться к скорости невязкого течения. Однако оно не-
непригодно для нормальной скорости или функции тока,
где первый повторный предел в E.22) равен нулю, а
второй — бесконечности. Такие же трудности возникают
в плоском течении при малых числах Рейнольдса (гл.8).
Мы можем улучшить это простое правило, описав
более точно предельное поведение сращиваемых вели-
величин (ср. § 3.2 и 3.3). Взамен простых пределов мы ис-
используем асимптотические представления. Это дает сле-
следующий принцип сращивания:
Внутреннее представление внешнего пред-
представления равно внешнему представлению E.23)
внутреннего представления.
Здесь внешнее (или внутреннее) представление озна-
означает первый ненулевой член в асимптотическом разло-
разложении во внешних (или внутренних) переменных. Это
правило обеспечивает сращивание в тех случаях, когда
предельный принцип E.22) дает только тривиальный
результат. Например в § 8.7 мы увидим, что оно доста-
достаточно для плоских течений при малых числах Рей-
Рейнольдса.
Этот принцип распространяется на приближения выс-
высшего порядка при сохранении дальнейших членов в
асимптотических разложениях. Мы должны допустить,
что число членов может быть различно во внутреннем
и внешнем разложениях, поскольку нормальный поря-
5 7. Принципы сращивания 127
док сращивания (§ 5.9) требует разницы па единицу
при четных шагах. Таким образом, мы получаем прин-
принцип асимптотического сращивания, введенный в гл. 4:
/я-членное внутреннее разложение /z-член-
ного внешнего разложения равно /z-член- ,г сул \
ному внешнему разложению /тг-членного * ' '
внутреннего разложения.
Здесь m и п — два целых числа; практически m обычно
выбирается равным п или п-\-\.
Иногда порядок необходимой для применения этого
правила нумерации членов разложения может пока-
показаться неясным; тогда полезен иной вариант правила.
Может показаться неясным, как нумеровать члены, на-
например, в следующих случаях: когда асимптотическая
последовательность имеет пропуски (например, когда
в степенном ряде по е коэффициент при е3 тождествен-
тождественно равен нулю), когда асимптотические последователь-
последовательности для внутреннего и внешнего разложений суще-
существенно различны (например, одна из них содержит
целые степени е, а другая — половинные), когда появ-
появляются логарифмические члены (например, г71 In е имеет-
имеется наряду с sn). Во всех этих случаях неопределенность
исключается применением следующего варианта правила:
Внутреннее разложение порядка А
внешнего разложения порядка 6 равно
внешнему разложению порядка 6 внутрен-
внутреннего разложения Порядка Д.
E.246)
Здесь 6(е) и Д(е)—две любые функции сравнения
(не обязательно одинаковые), которые могут входить
(а могут и не входить) в асимптотические последова-
последовательности для внутреннего и внешнего разложений. Ко-
Конечно, эта измененная форма сводится к исходному пра-
правилу сращивания E.24а), когда нумерация членов не
вызывает сомнений. Во всем последующем изложении
мы будем для простоты полагать, что нумерация оче-
очевидна, так что пригодна исходная форма правила.
Принцип сращивания представляется достаточным
для любых проблем, к которым приложим метод сра-
сращиваемых асимптотических разложений. Он будет при-
применяться во всей этой книге. В следующем параграфе,
128 Г л 5 Метод сращиваемых асимптотических раз южении
однако, мы дадим другой принцип, который позволяет
получить более глубокое представление об основных
свойствах области перекрытия.
5.8. Промежуточное сращивание
При внешнем предельном переходе теории тонкого
профиля (гл. 4) рассматриваемая точка оставалась на
фиксированном расстоянии от передней кромки, в то
время как относительная толщина s стремилась к нулю.
При внутреннем предельном переходе для эллиптиче-
эллиптического профиля это расстояние уменьшалось как в2. Со-
Совершенно очевидно, что два предельных перехода могут
С
Рис. 5.5. Промежуточный пре-
предельный переход для эллипти-
эллиптического профиля.
быть переставлены местами, поскольку имеется просвет
между внутренней и внешней областями. То, что этот
просвет существует, может быть разъяснено рассмотре-
рассмотрением точки, расстояние которой от передней кромки
уменьшается только как е (рис. 5.5). При внутреннем
переходе эта точка в конце концов выходит из любой
окрестности передней кромки и в то же время остается
вне области пригодности внешнего решения.
Чтобы перекрыть этот просвет, Каплун [2] ввел по-
понятие континуума промежуточных пределов, лежащих
между внутренним и внешним пределами. Хотя он рас-
рассмотрел очень общий класс пределов, для иллюстратив-
иллюстративных целей достаточно рассмотреть только предел, свя-
связанный со степенями малого параметра. Если s — внеш-
5.8. Промежуточное сращивание 129
няя переменная, связанная с неоднородностью при 5 = 0,
то вводится промеоюуточное переменное
s^~, 0<a<<v E.25)
здесь сс = О дает внешний предел, а а = щ — внутренний,
например ссг = 2 для эллиптического профиля. Предел
при е, стремящемся к нулю при фиксированном значе-
значении 5, называется промежуточным пределом, а его по-
повторное применение в связи с соответствующей асимп-
асимптотической последовательностью приводит к промежу-
промежуточному разложению.
Введение промежуточного предела в дифференциаль-
дифференциальное уравнение и граничные условия приводит к проме-
лсуточной задаче. Хотя мы ввели очень много предель-
предельных переходов, они ведут только к нескольким различ-
различным задачам. Все промежуточные пределы, в сущности,
сводятся к единственной промежуточной задаче, кото-
которая часто совпадает с внутренней задачей. Например,
полагая в уравнении D.33а) для эллиптического про-
профиля s = s/ea и у~у/&а и устремляя е к нулю, получаем
E.26)
Таким образом, промежуточная задача представляет
собой задачу о симметричном обтекании параболы с ра-
радиусом носовой части &2~а.
Промеоюуточное решение — это решение промежуточ-
промежуточной задачи. Его отличие от полного решения должно
равномерно стремиться к нулю в промежуточном пре-
пределе. Так, для эллиптического профиля промежуточное
решение для скоростей на поверхности тела в соответ-
соответствии с решением D.28) будет
Знаменатель разложить нельзя, поскольку результат
не является однородным вблизи критической точки.
Этот пример показывает, что промежуточное решение
не обязательно является промежуточным пределом пол-
полного решения, который здесь просто равен Uu по может
иметь более сложную структуру.
130 Г л 5 Метод сращиваемых асимптотических разложений
Хотя просвет между внутренним и внешним преде-
пределами был перекрыт промежуточным решением, еще не
очевидно, что там существует область перекрытия. Пос-
Последняя обеспечивается теоремой распространения Кап-
Каплуна, которая утверждает, что диапазон пригодности
внутреннего или внешнего пределов распространяется
хотя бы немного в промежуточный интервал. Мы опус-
опустим доказательство этой теоремы, правильность которой
будет очевидна из частных примеров. Таким образом,
мы можем срастить промежуточное разложение с внеш-
внешним разложением на одном конце интервала и с внут-
внутренним разложением на другом его конце. Часто про-
промежуточное разложение идентично с внутренним раз-
разложением — как в нашем примере эллиптического
профиля — или содержится в нем как частный случай.
Тогда мы можем просто срастить внутреннее и внешнее
разложения во внешней области перекрытия.
Для сращивания требуется, чтобы в области пере-
перекрытия разница между внешним (или внутренним) и
промежуточным решениями обращалась в нуль в про-
промежуточном пределе. Так, для эллиптического профиля
мы сращиваем промежуточное решение E.27) с внеш-
внешним равномерным течением, рассматривая следующий
предел:
[и- и,/'-
lim
s фиксировано
= lim [?/ — ?/,+ O(e2-«)]. E.28)
Эта величина обращается в нуль, если Ui = U и а<2.
Следовательно, внешняя область перекрытия есть
0<а<2.
Обобщение этого правила на приближения высших
порядков можно назвать принципом промежуточного
сращивания:
В некоторой области перекрытия
промежуточное разложение разности
между внешним (или внутренним)
разложением и промежуточным раз- E.29)
ложением должно обращаться в нуль
с точностью до соответствующего
порядка.
5.9. Порядок сращивания 131
Рассмотрим, например, по два члена как промежу-
промежуточного, так и внешнего разложений для скорости на
эллиптическом профиле и допустим наличие собствен-
собственного решения типа источника D.32а). Разность между
двумя разложениями в промежуточных переменных
будет
разложение этого выражения дает
E.31)
Эта величина обращается в нуль с точностью до по-
порядка е, т. е. до второго порядка по степеням е, если
Ui = U(l+&), Ci = 0 и 0<а<1. Первые два из этих ре-
результатов были найдены асимптотическим сращиванием
в гл. 4, а третий означает, что внешняя область пере-
перекрытия сжата до половины ее первоначальной ширины.
5.9. Порядок сращивания
Все наши предшествующие рассуждения основыва-
основывались на предположении о полной симметрии между
внутренним и внешним пределами, так что эти два члена
можно было бы поменять местами. Однако мы до
сих пор употребляли слово «внешний» для обозначения
прямого или основного приближения, и здесь мы настаи-
настаиваем на необходимости сохранения этого соглашения.
Точнее, мы определяем это название исходя из того,
что внешнее решение с точностью до первого порядка
независимо от внутреннего. Проверка состоит в том, что
в каждое из этих решений вводится изменение первого
порядка и выясняется, будет ли это влиять на другое
решение. Например, в теории тонкого профиля набе-
набегающий поток лишь слегка возмущается удвоением ра-
радиуса носовой части тела, в то время как течение вблизи
носовой части резко меняется при удвоении скорости
набегающего потока. ......
132 Гл 5 Метод сращиваемых асимптотических разложений
В общем случае сращивание должно производиться
шаг за шагом, как показано сплошными стрелками на
рис. 5.6. Основное решение определяет внутреннее реше-
решение, которое в свою очередь оказывает вторичное влия-
влияние на внешнее разложение и т. д. Этот порядок яв-
является нерушимым, например, в прямой задаче теории
пограничного слоя. Иногда этот обычный порядок сра-
сращивания можно сократить. Очевидным случаем является
Внутреннее
разложение
Рис. 5.6. Порядок сращивания
внутреннего и внешнего разло-
разложений.
задача с начальными условиями, в которой все гранич-
граничные условия наложены во внешней области. Тогда мож-
можно вычислить неограниченное число членов внешнего
разложения, как показано пунктирными стрелками на
рис. 5.6, а затем срастить его с внутренним разложе-
разложением для дополнения решения. Такая ситуация может
возникнуть в механике жидкости при формулировке
обратной задачи; пример будет дан в § 9.9.
Подобное же сокращение процедуры для внутрен-
внутреннего разложения возможно в более тонком случае, ко-
когда неоднородность так слаба, что не влияет на внеш-
внешнее течение. Примером является двояковыпуклый про-
профиль, рассмотренный в § 4.7 и 4.11. С другой стороны,
для профиля с закругленной передней кромкой пример,
представленный на рис. 5.4, показывает, что могут быть
вычислены только два члена разложения, а затем по-
появится необходимость обратиться к сращиванию с внут-
внутренним разложением.
5.10. Построение составного разложения 133
Когда применяется стандартный порядок, сращива-
сращивание будет само выявлять каждый новый член в асимп-
асимптотической последовательности и, следовательно, вид
этого члена не должен предполагаться заранее извест-
известным. Например, переписывая во внутренних переменных
любое количество членов разложения D.146) теории
тонкого профиля для эллипса и проводя разложение для
малых е, найдем на каждой стадии, что следующий член
во внутреннем разложении будет порядка следующей
высшей степени 8. Пример, в котором асимптотические
последовательности различны для внутреннего и внеш-
внешнего разложений, будет рассмотрен в § 6.3.
5.10. Построение составного разложения
Представление решения задачи особого возмущения
в виде внутреннего и внешнего разложений может вы-
вызвать затруднительный практический вопрос о том, где
нужно переходить от одного разложения к другому.
Грубый рецепт состоял бы в том, чтобы такой переход
совершался бы в точке пересечения кривых, однако в
этом случае результат содержал бы несвойственные яв-
явлению угловые точки. Более того, для эллиптического
профиля, например, внутреннее и внешнее решения пер-
первого приближения для скорости на поверхности тела
вообще не пересекаются (рис. 5.7).
К счастью, поскольку эти разложения имеют общую
область пригодности, оказывается легко построить из
них одно равномерно пригодное разложение. Результат
по необходимости является более сложным, чем любое
из составляющих, и в действительности представляет
собой составное разложение в смысле § 5.4. Построение
в принципе может быть осуществлено разными путями.
Результаты могут быть различны, поскольку составное
разложение не единственно, однако все они будут экви-
эквивалентны с точностью до принятого порядка.
На практике применяются два существенно различ-
различных метода. Первый может быть назван аддитивным
составлением. Сумма внутреннего и внешнего разложе-
разложений поправляется вычитанием их общей части, так что
последняя не считается дважды. Общая часть иногда
134 Г л 5 Метод сращиваемых асимптотических разложений
может быть найдена проверкой. Иначе она может быть
вычислена как внутреннее разложение внешнего разло-
разложения или наоборот. Таким образом, в очевидных обо-
обозначениях, где /И означает m-членное внутреннее раз-
разложение и т. д.1), правило аддитивного составления бу-
будет выглядеть так:
dm, n) __
' с
I
E.32)
()
\0
Можно проверить это правило, взяв m-членное внутрен-
внутреннее и /2-членное внешнее разложения от обеих частей
внешнее разложение
Составное разложение E 36)
Рис. 5.7. Внутрен-
Внутреннее и внешнее ре-
решения первого по-
порядка для скорости
на поверхности
гонкого эллипти-
эллиптического профиля.
равенства. Использование асимптотического принципа
сращивания E.24) показывает, что внутреннее и внешнее
разложения воспроизводятся в соответствующих обла-
областях.
l) fy означает /г-членное внешнее (outer) разложение; ин-
индекс с означает составное (composite) раздо^ение. — Прим. перед.
5.10. Построение составного разложения 135
Действия с разностями, хотя в принципе и несколь-
несколько отличные от предыдущего, приводят к тому же пра-
правилу. Внешнее разложение делается равномерно при-
пригодным прибавлением к нему решения внутренней за-
задачи для разности между точным решением и его внеш-
внешним разложением; внутреннее разложение поправляется
аналогично. Символически это можно записать в виде
Принцип асимптотического сращивания показывает,
что это правило эквивалентно правилу аддитивного со-
составления E.32).
Второй метод может быть назван мультипликатив-
мультипликативным составлением. Внешнее разложение умножается на
поправочный множитель, состоящий из отношения внут-
внутреннего разложения к внешнему разложению этого внут-
внутреннего разложения (или проводится аналогичная опе-
операция для внутреннего разложения). Это дает
Am) An) f(n)f(m)
dm, n) __ с{п) И е(т) 'о 'о Ч /г 04л
'С lo If(m)fn) ' ' ' Ып)]М Г Кт)](«) _ ЫппШ ' [° V
Vi \о Vo U VI \0 ~Vo \i
В первой форме нетрудно узнать ту, которая дает соот-
соответствующий поправочный множитель, примененный
для профилей с закругленной кромкой в § 4.8. Послед-
Последняя форма показывает симметричность внутреннего и
внешнего предельных переходов.
Аддитивное и мультипликативное правила составле-
составления связаны тем, что отношение двух величин, близких
к единице, может быть разложено в ряд по формуле
бинома. Аддитивное правило обычно проще в приложе-
приложении, мультипликативное иногда дает более простые ре-
результаты. Каждое из них можно применять даже в тех
случаях, когда внутренняя проблема не может быть ре-
решена аналитически, а решение известно только в чис-
численном виде или из эксперимента.
Мы продемонстрируем эти два метода, рассматривая
скорость на поверхности тонкого эллиптического про-
136 Г л 5. Метод сращиваемых асимптотических разложений
филя. Исходя из двух членов внешнего разложения
D.13) и одного члена внутреннего разложения D.46),
мы получим в качестве равномерно пригодного возму-
возмущенного решения первого порядка при помощи аддитив-
аддитивного составления E.32) следующий результат:
а при помощи мультипликативного составления E.34)
^ / ОТ
E.36)
Здесь s=l+x или 5=1—х в зависимости от того, ка-
какую неоднородность мы исправляем: па передней или
на задней кромке; действительно однородное решение
получается поочередным рассмотрением каждой кромки
(упражнение 5.3). Другие виды множественной неодно-
неоднородности (см. § 9.13) могут быть исследованы повтор-
повторным приложением правил составления.
Составное разложение имеет точность по крайней
мере не меньшую, чем точность каждого из его состав-
составляющих. Так, соотношения E.35) и E.36) дают ошибку
не более чем О (г2) вдали от кромки и О(е) вблизи нее.
В действительности аддитивный результат E.35), оче-
очевидно, дает ошибку, в точности равную е в критической
точке. Мультипликативный результат E.36) имеет то
преимущество, что в этой точке он является точным.
Расширение составного результата применением двух
членов как внутреннего, так и внешнего разложений
приводит снова к формуле E.36), но и для аддитивного
и для мультипликативного составлений. Это означает,
что вследствие совпадения ошибка E.36) в действитель-
действительности нигде не превосходит О(е2). Улучшение, обуслов-
обусловленное применением составного разложения, показано
на рис. 5.7.
УПРАЖНЕНИЯ
5.1. Однородное приближение для модели Фридрихса. Обра-
Образуйте двумя различными путями составное разложение решения
E.6). Обсудите различие получившихся результатов и сравните их
с точным решением. Исследуйте приближения высшего порядка.
Упражнения 137
5.2. Однородное приближение для двояковыпуклого профиля.
Постройте приближение для скорости на поверхности тонкого
двояковыпуклого профиля в несжимаемой жидкости, которое было
бы равномерно пригодно до порядка б всюду, за исключением зад-
задней кромки.
5.3. Правила составления для двух неоднородностей. Предло-
Предложите правила, аналогичные E.32) и E.34), для построения состав-
составных разложений в случае двух изолированных неоднородностей, ко-
которые имеют место, например, для тонкого профиля с критическими
точками на передней и задней кромках. Примените полученные ре-
результаты к исследованию скорости на поверхности эллиптического
профиля и сравните с точным решением.
5.4. Внешнее, среднее и внутреннее разложения. Покажите, что
возмущенное решение задачи
для 0-<!^-С1 требует сращивания трех разложений. Вычислите
последовательно два члена прямого (внешнего) разложения, два
члена' среднего разложения и один член внутреннего разложения.
Выберите новые увеличенные переменные, подсказанные предыду-
предыдущим разложением, и проведите сращивание на каждом шаге.
5.5. Модель с неисчезающими старшими производными. Вы-
Вычислите три члена приближенного решения по степеням 8 для урав-
уравнения
Определите положение неоднородностей для 0<?.*<Л и размер их
областей. Вычислите главный член во внутреннем разложении,
найдя константу сращиванием. Вычислите второй член и образуйте
равномерно пригодное второе приближение.
5.6. Импульсивное движение малой массы на пружине. Малая
масса подвешена на невесомой пружине и испытывает сопротивле-
сопротивление, пропорциональное скорости. К массе прикладывается вертикаль-
вертикальный импульс / (ударом молотка). Показать, что при надлежащем
выборе переменных задача сводится к следующей:
?</+</ + </ = 0, у@) = 0, еу@) = 1.
Покажите, как нарушается прямое (внешнее) приближение для
малых е. Вычислите внутреннее разложение и составное приближе-
приближение. Исследуйте возможность применения метода к случаю, когда
сопротивление отсутствует и основное уравнение принимает вид
L38 Гл. 5. Метод сращиваемых асимптотических разложений
5.7. Круг в потоке с распределением скорости по закону гипер-
гиперболического косинуса. Покажите, что при замене в упражнении 2.4
параболического профиля скорости в набегающем потоке на
u = U ch(l^e у/а) получается линейное уравнение и что прямое
возмущенное решение остается при этом неизменным до порядка в.
Дополните решение до порядка s введением дополнительного
разложения, пригодного на большом расстоянии от круга. По-
Постройте равномерно пригодное составное приближение.
Глава 6
МЕТОД
ДЕФОРМИРОВАННЫХ КООРДИНАТ
6.1. Историческое введение
В конце сороковых годов Уитэм и Лайтхилл в Ман-
Манчестерском университете занимались задачами, связан-
связанными с положением головной ударной волны в сверх-
сверхзвуковом потоке. В результате Лайтхилл [2] разработал
общий метод устранения неоднородностей из возмущен-
возмущенных решений нелинейных задач. Впоследствии этот ме-
метод был приложен к широкому классу задач механики
жидкостей и, таким образом, успешно конкурирует с ме-
методом сращиваемых асимптотических разложений.
Основная идея этого метода состоит в том, что ли-
линеаризованное решение может быть правильно по фор-
форме, но не совсем правильно расположено. Исправление
заключается в том, чтобы слегка деформировать коор-
координаты путем разложения некоторых из них, так же
как и зависимых переменных в асимптотические ряды.
Первое приближение — которое становится той же функ-
функцией деформированных переменных, какой она была от
исходных координат, — вследствие этого становится рав-
равномерно пригодным. Подобным же образом можно дей-
действовать и с приближениями высшего порядка. Дефор-
Деформирование координат заранее неизвестно и должно оп-
определяться почленно в процессе решения задачи.
Это деформирование определяется принципом, уже
введенным в § 4.12:
Приближения высших порядков имеют
не большую особенность, чем первое F.1)
приближение.
Это останавливает катастрофическое усложнение осо-
особенностей, которое сделало бы прямое возмущенное
разложение непригодным в области неоднородности.
Лайтхилл заметил, что иногда можно допустить слабое
140 Гл. 6. Метод деформированных координат
увеличение особенностей (упражнение 6.1), однако про-
проще придерживаться приведенного выше принципа.
Этот принцип, без сомнения, не определяет деформи-
деформирование единственным образом, однако неединствен-
неединственность часто может оказаться не недостатком, а преиму-
преимуществом. Поскольку как независимые, так и зависимые
переменные разложены, решение находится в неявной
форме, причем деформированная координата входит как
параметр. Эта неявность (отнюдь не нежелательная)
существенна во многих задачах. Часто требуется найти
только равномерно пригодное первое приближение. То-
Тогда нет нужды решать уравнения второго порядка, до-
достаточно просто исследовать их для того, чтобы опре-
определить деформирование.
Аналогичное деформирование независимого пере-
переменного было применено Пуанкаре [1] для получения
периодических решений нелинейных обыкновенных диф-
дифференциальных уравнений. По этой причине Цянь Сюэ-
сэнь [1] в обзорной статье ввел для него название «ме-
«метод ПЛГ», где Г стоит для обозначения приложений
к вязким течениям, данных Го Юн-гуаем [1, 2]. Мы пред-
предпочитаем говорить о методе Лайтхилла или о методе
деформированных координат, поскольку последнее на-
название отражает существенные черты метода.
Было показано, что этот метод всегда может быть
с успехом применен для исследования гиперболических
дифференциальных уравнений, в частности в задачах
с волнами, первоначально распространяющимися в од-
одном направлении; именно для задач такого типа и был
изобретен метод. Сам Лайтхилл приложил его непо-
непосредственно [3] к коническим ударным волнам в устано-
установившемся сверхзвуковом потоке. Уитэм применил его
к исследованию ударных волн на осесимметричных те-
телах в установившемся сверхзвуковом полете [1] и к рас-
распространению сферических ударных волн в звездах [2].
Легра [1, 2] исследовал сверхзвуковые профили, а Рао
[1] — звуковые шумы.
Важное обобщение метода было дано Линь Цзя-цзяо
[1] для гиперболических уравнений в случае двух пере-
переменных, когда деформированная координата Лайтхилла
может интерпретироваться как одна из характеристик.
6.2. Обыкновенное дифференциальное уравнение 141
Линь выбрал характеристические параметры в качестве
основы для теории возмущений, что равносильно дефор-
деформированию обоих семейств характеристик. Это позво-
позволяет исследовать волны, распространяющиеся в обоих
направлениях.
Вследствие гибкости метода Лайтхилла он представ-
представляет собой не определенный набор правил, а общую
идею приближения. По этой причине трудно когда-либо
утверждать, что этот метод непригоден. Тем не менее
метод, по-видимому, не подходит для эллиптических
уравнений, несмотря на исследование Лайтхиллом [4] об-
обтеканий сжимаемой жидкостью профилей с закруглен-
закругленной кромкой, общие черты которого изложены в § 4.12.
Подобным же образом, несмотря на попытку Го, метод
представляется неподходящим для параболических
уравнений, где он даже приводит к ошибочным резуль-
результатам (У Яо-цзу [1]; Леви [1]). В соответствии с этим
в позднейшем обзоре, носящем то же название, что и
основная статья, Лайтхилл [6] рекомендует применять
его метод только для дифференциальных уравнений ги-
гиперболического типа.
Полезно сопоставить метод деформированных коор-
координат с методом сращиваемых асимптотических разло-
разложений. Сила и в то же время слабость первого из них
состоит в том, что для зависимых переменных исполь-
используется только одно асимптотическое разложение. Иссле-
Исследование упрощается так же, как и результат, и устра-
устраняется вероятность появления «невозможной» нелинейной
задачи для первого члена внутреннего разложения.
С другой стороны, принцип, используемый для опреде-
определения деформированных координат, так груб по сравне-
сравнению с детальным описанием области неоднородности,
даваемым внутренним разложением, что едва ли сле-
следует удивляться тому, что приложения метода Лайт-
Лайтхилла не универсальны.
6.2. Модель: обыкновенное дифференциальное уравнение
Наша преданность механике жидкости заставляет
нас в первую очередь подчеркивать приложения метода
деформированных координат к уравнениям в частных
142
Гл. 6. Метод деформированных координат
производных. Однако этот метод применим также и
к многим обыкновенным дифференциальным уравне-
уравнениям. В самом леле, Лайтхилл ввел свой метод, рас-
рассматривая уравнение вида
а Вазов [1] доказал сходимость при слабых ограниче-
ограничениях, наложенных на функции q и г (с поправками
Рис. 6.1. Интегральные
кривые уравнения F.3).
решение точного уравне-
уравнения, решение лине-
линеаризованного уравнения,
-- ---- прямая # = — е/.
Лайтхилла [6]). Выберем эти функции простейшим об-
образом и рассмотрим следующую модельную задачу:
Прямое возмущенное разложение по степеням пара-
параметра s дает формальное решение
2х~3
!-*) A+3*)
2J
F.4)
6.2. Обыкновенное дифференциальное уравнение 143
Это — знакомая ситуация, возникающая в задаче осо-
особых возмущений. Ряды сходятся, но радиус сходимости
стремится к нулю при приближении х к нулю. Разложе-
Разложение не будет равномерно пригодным вблизи * = 0. Точ-
Точное решение
/(J 1 F-5)
конечно при х = 0. Полное уравнение имеет особенность
вдоль линии x = —ef (рис. 6.1), однако линеаризация пе-
переносит особенность в точку х = 0, и в приближениях
высшего порядка эти особенности лишь увеличиваются
вместо того, чтобы исправляться.
Метод деформированных координат позволяет сдви-
сдвинуть особенности в линеаризованном решении в направ-
направлении их истинного положения путем деформирования
координаты х. Мы разложим как х, так и f по степе-
степеням е с коэффициентами, зависящими от новой вспомо-
вспомогательной координаты, например s. Поскольку деформи-
деформирование слабое, то главным членом разложения для х
является само s. Таким образом, мы положим
f (*; в) ~ fx (s) + г\2 (s) + e2fз (s) -Ь • • •. F.6а)
где
X ~ S + &Х2 (S) + 82Х3 (S) -4- F.66)
Подставляя эти выражения в уравнение F.3) и при-
приравнивая одинаковые степени е, получаем
Ш'=\, F.7а)
(sf2y = r](sx^2-x2~f1) = [x2(l -fx)-i П] . F.76)
и т. д. Решение для /\
fds)^1^ F.8)
удовлетворяет граничному условию. Тогда уравнение
для f2 принимает вид
и его решением будет
h (*) = у - "F
144 Гл. 6 Метод деформированных координат
Однако если мы ищем только первое равномерно при-
пригодное приближение, то это решение нам не потре-
потребуется; деформирование х2 может быть найдено просто
исследованием уравнения для f2 без его решения.
Деформирование выбирается в соответствии с прин-
принципом F.1), который в данном случае означает, что /2
должно иметь не большую особенность, чем /V Очевид-
Очевидно, простейшим путем осуществления этого является
устранение неоднородности в правой части уравнения
F.9) для /2. Положим
+ ^1 = const, F.11)
хотя константа могла бы быть заменена любой регуляр-
регулярной функцией 5.
Для метода характерно, что дальнейший выбор де-
деформирования остается открытым. Наиболее очевидный
выбор х2 = — {l+2s)/2s дает однородно пригодное пер-
первое приближение
/(*; e)~l±?+...f F.12а)
В этой простой задаче оказывается возможным исклю-
исключить параметр s, что дает в явном виде первое прибли-
приближение
/(J^-+l-f F.12b)
С другой стороны, может быть удобно сделать дефор-
деформирование равным нулю при #=1, где наложено гра-
граничное условие. Тогда мы возьмем х2= {3s2—1— 2s)/2s,
и равномерно пригодное первое приближение будет та-
таково:
/(х;е)~1±?, (б.13а)
3$2-2\-28 . F.136)
В этом случае исключение 5 показывает, что первое
приближение является точным решением F.5), так что
ряды F.13) не продолжаются,
6.3. Сравнение с методом сращиваемых разложений 145
При я' = 0, где формальное разложение F.4) расхо-
расходится, точное решение F.5) или F.13) дает f@; e) =
= B/е + 4)У*. Результат F.12), вытекающий из первого
выбора деформирования, дает вместо этого /@; е) ~
~ B/е+1I/г, что согласуется с точным решением до пер-
первого порядка по е.
6.3. Сравнение с методом сращиваемых разложений
Естественно исследовать относительные достоинства
и возможности применения метода деформированных
координат и метода сращиваемых асимптотических раз-
разложений. Для этого в рассматриваемом примере нужно
найти внутреннее разложение, чтобы дополнить прямое
внешнее разложение F.4) в области его неоднородности.
Внешнее разложение оказывается непригодным, ко-
когда х2 становится малой величиной порядка е, поскольку
тогда последовательные его члены не уменьшаются по
величине, как предполагалось. Это показывает, что об-
область неоднородности находится там, где х = О(е1/2). То-
Тогда внешнее разложение наводит на мысль, что /имеет
порядок е/2. Поэтому мы вводим внутренние перемен-
переменные X и F, которые будут порядка единицы в области
неоднородности, полагая
Х = фг> F = f*m- F-14)
Уравнение F.3) во внутренних переменных принимает
вид
• (x+n4r+f=el/2- FЛ5)
Наличие члена е1/2 наводит на мысль, что в этом случае
асимптотические последовательности существенно раз-
различны для внутреннего и внешнего разложений. В то
время как внешнее разложение F.4) производится по
целым степеням е, внутреннее разложение содержит
половинные степени и имеет вид
f (х; е) ~ е-' ^ \F, (X) 4 s^-F2(X) + eF3(*)+...]. F.16)
146 Гл. 6. Метод деформированных координат
Подставляя это разложение в дифференциальное
уравнение F.15), получаем
= 0, F.17а)
i/==l F.176)
и т. д. Общее решение для Ft будет
рг {X) = УХ* + 2СХ — X. F.18)
Очевидно, что граничное условие является внешним
и должно быть поэтому отброшено и заменено сращива-
сращиванием с внешним разложением. Мы приложим асимпто-
асимптотический принцип сращивания E.24) для т=п = \. Сле-
Следуя схеме, введенной в гл. 4, мы получим такие ре-
результаты.
1 1 ¦ X
Одночленное внешнее разложение: \ ^———, F.19а)
переписанное во внутренних _ ^ _i___L_ /g jgd)
переменных: ' ^}l2x '
разложенное для малых е: = —По hi» (б.19в)
Vй X
одночленное внутреннее = 1 = _L /g19гч
разложение &У2х х '
Одночленное внутреннее с 1 \лГ у2_\ог у] /a on*\
разложение ?V2l ' J v
переписанное во внешних
переменных:
F.206)
разложенное для малых е: =—~ +..., F.20в)
одночленное внешнее = _^L F 20г)
разложение: х
Приравнивая F.19г) и F.20г), мы получаем С4=1. Сле-
Следовательно, решение первого порядка, полученное мето-
методом сращиваемых асимптотических разложений, будет
иметь вид
fix; e)~
1 I у*
——— для ?—>0при фиксированном X, F.21а)
-t[V1+2C^-1\
V (т
~"Т для8~>ОпРи фиксированном х/е1/2. F.216)
6.4. Неоднородности в теории сверхзвукового профиля 147
Равномерно пригодное составное приближение мо-
может быть построено одним из методов, изложенных в
§ 5.10, что дает
fix, e)~
1/ D-J Ч —+Ь аддитивный; F.21в)
A ¦+ х) ~|/ (— ] -| , мультипликативный. F.21 г)
Дальнейшие члены внутреннего разложения могут быть
найдены продолжением этого процесса.
Представляется, что в этом примере метод дефор-
деформированных координат является более простым. Мы от-
отложим более детальное сравнение до § 6.8.
6.4. Неоднородности в теории сверхзвукового
профиля
Простым течением, в котором метод деформирован-
деформированных координат оказывается эффективным, является
сверхзвуковое обтекание тонкого профиля. Классиче-
Классическое линеаризованное решение Аккерета основано на
приближенном уравнении
Здесь ср — потенциал возмущенной скорости. Мы счи-
считаем его нормированным так, что скорость равна
q=U grad(x + y). Хотя решение Аккерета является под-
подходящим первым приближением на поверхности про-
профиля и вблизи него, оно дает неверный результат на
больших расстояниях от профиля. Согласно этому ре-
решению, возмущения распространяются без изменения
вдоль линий Маха свободного потока до бесконечности
(рис. 6.2), в то время как в действительности линии
Маха не являются ни прямыми, ни параллельными и
в поле течения образуются и разрушаются ударные
волны.
Эта неоднородность на больших расстояниях в неко-
некоторых отношениях является более тонкой, чем неодно-
неоднородность, имеющая место, например, в приближении
148 Г л 6 Метод деформированных координат
Стокса для вязкого течения при малых числах Рей-
нольдса (см. гл. 8). Там можно использовать первое
приближение для оценки величины членов, отброшен-
отброшенных в уравнении движения, и показать, что они в конце
концов превосходят величины оставленных членов. Од-
Однако в настоящей задаче нелинейные члены действи-
действительно всюду малы по сравнению с линейными, хотя их
вклад становится преобладающим. Здесь имеет место
а 5
Рис. 6.2. Картина течения у сверхзвукового профиля.
а — линеаризованная теория, ? —нелинейная теория.
то, что Хейз [1] назвал кумулятивным эффектом, имея
в виду, что на больших протяженностях влияние этих
членов возрастает до первого порядка. Чтобы увидеть
это, необходимо действительно вычислить второе при-
приближение. Это означает, что нужно решить нелинейное
уравнение для потенциала B.19) последовательными
приближениями, начиная с линейного решения Акке-
рета. Положив в уравнении B.19) <р=х + ф и сгруппи-
сгруппировав линейные члены в левой части, представим урав-
уравнение в удобной форме
фуу — В2фхх = М2 \~Y~ {^Фх +Фх+ Ф1) (Фхх + Фу у) +
Ч- Bфх + фх) фхх + 2 A + фх) фуфху + ф2уфуу] • F.23)
Пусть верхняя поверхность профиля описывается,
как и прежде (рис. 4.1), уравнением у = гТ(х). Тогда
6.4. Неоднородности в теории сверхзвукового профиля 149
формальное второе приближение для компоненты скоро-
скорости вдоль потока над профилем находится приложением
итераций к уравнению F.23) в виде
« _ 1 о т' (Е)
и ~ 1 ° в
Г (I) Г (I) - Т (I) Г (I)] + О (ез), F.24)
где 1~х — Ву (Ван-Дайк [2]). На поверхности это вос-
воспроизводит общеизвестное решение второго порядка
Буземана. Однако вдали от профиля второй член немал
по сравнению с первым, как предполагалось в процессе
последовательных приближений, поскольку он растет
линейно с у вдоль любой линии Маха свободного потока
х — By = const. Очевидно, разложение непригодно в уда-
удаленной от профиля области, где у = О(г~1).
Член с у, доставляющий затруднение, пропорциона-
пропорционален (y+1). Это следует из того обстоятельства, что
неоднородность обусловлена лишь «псевдотрансзвуко-
«псевдотрансзвуковым» членом (у-\-1)М4фхфХХ1 который содержится в не-
нелинейной правой части дифференциального уравнения
F.23) и может быть получен в явном виде преобразова-
преобразованием к косоугольным координатам, введенным позднее
(см. также Хейз [1]). Вклад всех нелинейных членов яв-
является однородным и имеет второй порядок, кроме псев-
псевдотрансзвукового члена, для которого, несмотря на его
малость, имеет место кумулятивный эффект первого по-
порядка. Следовательно, этот член должен быть сохранен
в дополнение к линейным членам при разыскании рав-
равномерно пригодного первого приближения. До этого по-
порядка условия обтекания могут быть наложены на оси,
что обсуждалось в § 3.8 и 4.2. Таким образом, задача
для первого приближения примет вид
,y ,' F.25а)
Фу(х> 0) = еГ(*), F.256)
Ф(х, у) = 0 в набегающем потоке. F.25в)
Удобно предварительно произвести преобразование
координат. Имеются два различных направления в
150
Гл. 6. Метод деформированных координат
задаче: направление свободного потока и направление
линий Маха свободного потока наверху от профиля или
внизу от него (рис. 6.3). Профиль расположен прибли-
приблизительно вдоль первого направления, а волны — при-
приблизительно вдоль второго. Другое семейство линий
Маха играет только второстепенную роль. Это верно,
если мы ограничимся рассмотрением, скажем, только
Рис. 6.3. Картина волн в сверхзвуковом те-
течении.
верхней поверхности одиночного профиля; для группы
тел имеют первостепенное значение оба семейства линий
Маха, которые, пересекаясь, образуют «клетчатую» кар-
картину течения. По этой причине решение второго порядка
F.24) можно более естественно выразить в зависимости
от нормированных расстояний
\ = х — Ву, F.26а)
ч] = Ву, F.266)
перпендикулярных к двум рассмотренным направле-
направлениям. Мы впредь примем, следуя Хейзу [1], эти «полу-
«полухарактеристические» координаты. Если бы имелись оба
семейства волн, то следовало бы использовать взамен
характеристические координаты х — Вг/, х+Ву, и в сле-
следующем параграфе для такого случая способ Лайтхил-
6.4. Неоднородности в теории сверхзвукового профиля 151
ла будет заменен обобщением Линь Цзя-цзяо [11, упо-
упоминавшимся выше.
Переписанная в этих косоугольных координатах за-
задача F.25) принимает вид
при
= 0, F.276)
Ф = 0 в набегающем потоке. F.27в)
Линеаризованное решение есть ф=—еГ(?)/Б, так что
?п —0тт = О- Хотя это и неверно в нелинейном решении,
поскольку волны слегка отличаются от линий Маха на-
набегающего потока, Хейз указал, что члены фц и </>w
появляющиеся здесь, представляют в действительности
эффекты второго порядка, подобные тем, которые уже
были отброшены. Следовательно, их также можно от-
отбросить, и задача для равномерно пригодного первого
приближения упрощается:
fcfl+^r"l?fcfc6-=0, F.28а)
Н&0) = -г?М, F.28б)
^ = 0 в набегающем потоке. F.28в)
Теперь мы оказываемся в благоприятном положении,
имея хорошо поставленную задачу для безразмерного
возмущения компоненты скорости, параллельной по-
потоку, определяемой в виде
з'=4г = #* = #*• F-29)
Мы предпочитаем работать с этой величиной, поскольку
она имеет большее физическое значение, чем потенциал
скорости ф. Таким образом, задача, которая подлежит
решению, окончательно принимает вид (штрих в и'
впредь отбрасывается)
ии°' F*30а)
-е-^1, F.306)
0 в набегающем потоке. (б.ЗОв)
152 Гл. 6 Метод деформированных координат
6.5. Первое приближение по методу деформированных
координат
Приложим к этой задаче метод деформированных
координат. Как с физической (см. рис. 6.2), так и с ма-
математической точки зрения ясно, что должна быть де-
деформирована координата g, описывающая линию Маха.
Введем слегка деформированное переменное 5 вместо g
и положим
, t)-\- ..., F.31а)
••> Л = *. F.316)
Преобразование производных определяется форму-
формулами
; д д F.326)
Подставляя разложения F.31) для и в задачу F.30)
и приравнивая одинаковые степени е, находим
Т' (s)
lht == 0, ^i E, 0) ¦= g— , Й! = 0 в набегающем потоке,
F.33а)
Й j й^' F.336)
Очевидно, uL та же функция от деформированного
переменного 5, какой она была в линеаризованной тео-
теории по отношению к переменному g:
Ulis,()^-I^L. F.34)
Деформирующая функция g2 теперь должна быть вы-
выбрана в соответствии с принципом F.1), заключающим-
заключающимся в том, что и2 должна иметь не большую особенность,
чем Mi при By = r\ = t, стремящемся к бесконечности.
6.5. Первое приближение; деформированные координаты 153
Простейший способ обеспечения этого состоит опять в
том, чтобы обратить в нуль правую часть уравнения
F.336) для ш, положив
так что
la(s, t) = f (s) -1^ |г ^' (s). F.36)
Для наших целей достаточно сделать деформацию
равной нулю на оси у = 0, положив произвольную функ-
функцию /(s) равной нулю. Из соображений неразрывности
следует, что до первого порядка вертикальная скорость
также является той же функцией от s, какой она была
от g в линеаризованной теории. Следовательно, если
вернуться к декартовым координатам, то равномерно
пригодное первое приближение для компонент скорости
будет
F.37а)
где параметрическое переменное 5 определяется неяв-
неявным выражением
X-By~s- ^f1 tf4/7v(s)+ .... F.376)
Это решение имеет простую физическую интерпрета-
интерпретацию. Линии 5 = const в действительности представляют
собой исправленные линии Маха, вычисленные с ис-
использованием скоростей первого приближения. Можно
показать (Ван-Дайк [2]), что наклон отходящего семей-
семейства характеристик равен
dx~ ву~ 2 Б2 и^"
и интегрирование приводит к зависимости
F.39)
что согласуется с результатом F.376), если постоянная
интегрирования равна s.
154 Гл. 6 Метод деформированных, координат
Таким образом, решение, полученное деформирова-
деформированием координат, дает компоненты скорости, которые
постоянны вдоль исправленных линий Маха и имеют
значения, определяемые линеаризованной теорией на
профиле. Это противоречит линеаризованной теории, со-
согласно которой скорость в какой-либо точке равна ско-
скорости у основания линии Маха набегающего потока,
проходящей через эту точку (рис. 6.4). Формальная тео-
теория второго порядка F.24) пытается улучшить эту
Испрадленная ч //
характеристика^/'
' \ Характеристика
/ сдободного потока
Рис. 6.4. Исправление линий Маха.
оценку, связывая значение у основания исправленной
линии Маха со значениями у основания линии Маха на-
набегающего потока путем разложения в ряды Тейлора.
Конечно, последние неприменимы при у —> оо. Равно-
Равномерно пригодное первое приближение, полученное де-
деформированием координат, оказывается, таким образом,
состоящим из простых волн (волны разрежения Прандт-
ля — Майера) и может быть сравнено с решением, по-
полученным на этой основе Фридрихсом [2].
Уитэм [1] принял данную выше физическую интер-
интерпретацию за основу более эвристического вывода рав-
равномерно пригодного первого приближения. Он ввел
«основную гипотезу, состоящую в том, что линеаризо-
линеаризованная теория всюду дает пригодное первое приближе-
приближение для течения при условии замены в нем приближен-
приближенных характеристик точными или по меньшей мере до-
достаточно хорошим приближением к точным». Проверка
F.39) дает действительно достаточно хорошее прибли-
приближение к характеристикам, и тогда гипотеза Уитэма при-
приводит сразу к решению F.37), которое мы вывели бо-
6.5. Первое приближение; деформированные координаты 155
лее формально методом деформированных координат.
Уитэм занимался главным образом приложением своего
метода к телам вращения- его результаты являются ос-
основой для вычисления звуковых ударов.
Неявный характер деформирования, очевидно, су-
существен для равномерной пригодности решения. В до-
достаточно простых случаях, однако, зависимость может
быть разрешена и решение получено в явной форме.
Рис. 6.5. Гладкая вы-
пуклая стенка.
111111 м 11111 I
Рассмотрим, например, гладкую выпуклую стенку, изо-
браженную на рис. 6.5, где Т(х) = — -V для х>0. Урав-
Уравнение F.376) принимает вид
Ц1^у F.40а)
Это соотношение может быть разрешено в виде
Тогда формула F.37а) определяет компоненты скорости
в любой точке
г> АИ V X By tn лл\
В-ц-^-^^гв^г У . F.41)
В этом примере ясно виден источник неоднородности в
формальном разложении теории тонкого профиля. Для
данного у решение может быть разложено по степе-
степеням е, но результат не является равномерно пригодным
вблизи i/ = oor
156 Гл. 6. Метод деформированных координат
6.6. Видоизменения для углов и ударных волн
Может случиться, что устранение грубых неоднород-
ностей из задачи возмущений вызовет появление до-
дополнительных трудностей, которые должны в свою оче-
очередь быть исследованы для получения истинно однород-
однородного решения. Для рассматриваемой задачи это имеет
место в том случае, когда профиль содержит углы или
возникают ударные волны. Хотя эти детали и несуще-
несущественны для главной линии нашего изложения, мы в
целях полноты представления укажем те дополнитель-
дополнительные видоизменения, которые здесь потребуются.
Предыдущий результат равномерно пригоден для
выпуклой стенки, наклон которой изменяется непрерыв-
непрерывно и постепенно (V имеет порядок единицы). Однако
Рис. 6.6. Область не-
непригодности решения по-
позади угла.
с физической точки зрения очевидно (рис. 6.6), что ре-
результат становится непригодным даже на поверхности
для расстояний порядка е вниз по потоку от угла, если
только угол не лежит на оси у = 0. То же самое имеет
место для некоторой области, где кривизна так велика
(Г" имеет порядок е), что изменение наклона на рас-
расстоянии порядка толщины профиля составляет ощути-
ощутимую долю полной величины его изменения.
Данная трудность возникает из-за наложения усло-
условий обтекания на оси, а не на поверхности, что было бы
точнее, и соответственно из-за того, что деформирова-
деформирование обращается в нуль на оси. Ее можно избежать, вы-
выбрав функцию интегрирования f(s) в формуле F.36)
так, что деформирование обращается в нуль точно на
поверхности и s = x на профиле. Это дает
f (s) = Ц±- §- гТ (s) Г (s)~BT (s). F.42)
6.6. Видоизменения для углов и ударных волн
157
Таким образом, решение, которое равномерно пригодно
на поверхности даже при быстром изменении кривиз-
кривизны или для случая угла, определяется формулой F.37а)
и заменой зависимости F.376) соотношением
F.43)
Это эквивалентно результату уравнений (92) и (93)
Уитэма [1], хотя и несколько проще.
Теперь решение равномерно пригодно для любого
гладкого выпуклого профиля, хотя еще нужно ввести
ударные волны для вогнутой стенки. Это верно неза-
независимо от того, насколько быстро изменяется кривизна,
однако в пределе, когда кривизна становится разрывной
¦=>
Рис. 6.7. Угол как предел гладкой стенки.
(рис. 6.7), картина характеристик показывает, что ре-
решение не определено в пучке Прандтля — Майера, исхо-
исходящем из угла. Например, положив Т(х)=—хН(х), где
Н— единичная функция Хевисайда, мы получим выпук-
выпуклый угол, изображенный на рис. 6.7. Подстановка этого
выражения в F.376) или F.43) и решение для 5 дают
с точностью до первого порядка по 8
x-By
М4
для X—By<0,
для X — Зу ^
F.44)
158
Гл. 6. Метод деформированных координат
Однако 5 не определено для
что как раз и представляет собой область пучка
Прандтля — Майера.
Эта трудность легко преодолевается временным не-
небольшим сглаживанием угла, так что получающиеся
характеристики, проведенные через любую точку, под-
подходят к поверхности в точке с определенным наклоном,
Рис. 6.8. Сглаживание
выпуклого угла.
как показано на рис. 6.8. Очевидно, 5 приближенно рав-
равно хс всюду в пучке, если угол лежит в точке (хс, ус).
Следовательно, в пучке T(s) остается постоянной, имею-
имеющей значение Т(хс), в то время как V меняется от
Т'(хс—) до Т'(хс + ). Значение Г', связанное с какой-
либо точкой (х, у) в пучке, находится из соотношения
F.43):
±±фг{у — уе)Г, F.45)
так что
— Ву)-(хс-Вус)
F.46)
Подстановка этого выражения в формулу F.37а) дает
компоненты скорости в пучке
R — — _ — —
F.47)
6.6. Видоизменения для углов и ударных волн
159
Это соотношение выполняется только в лучке, где зна-
значение F.46) лежит между V(хс—) и Г/(л:с+).
Наконец, если стенка вогнута, то характеристики
получаются сходящимися и перекрываются на доста-
достаточно больших расстояниях — для вогнутого угла не-
немедленно,—так что решение становится неединственным.
Например, изменение знака отклонения на рис. 6.7 при-
приводит к двум значениям s в каждой точке пучка. Эту
множественность можно исключить, введя ударную вол-
волну, отсекающую линии Маха, прежде чем они смогут
Ударная
Волна
<=>
Рис. 6,9. Перекрывающиеся характеристики.
перекрыться (рис. 6.9). Ударная волна вводится в соот-
соответствии с общеизвестным правилом: с точностью до
первого порядка она делит пополам угол между линия-
линиями Маха перед ней и позади нее. Основываясь на этом
правиле, Уитэм [1] дал изящное графическое построение
картины ударных волн для осесимметричного течения.
Это построение может быть приложено и к плоскому
течению.
Для простых форм результирующая форма ударных
волн может быть представлена достаточно просто. На-
Например, для профиля, состоящего из двух клиньев, го-
головная и хвостовая ударные волны после их прямоли-
прямолинейных участков должны являться отрезками параболы
с фокусом в вершине угла и с осью, параллельной ли-
линии Маха набегающего потока. Это следует из фокуси-
фокусирующего свойства параболического зеркала (рис. 6.10).
Вообще на столь больших расстояниях, где профиль
160
Гл. 6. Метод деформированных координат
представляется просто как точка, это верно и для лю-
любого профиля. Следовательно, ширина области между
ударными волнами увеличивается асимптотически
как г/1/з.
Рис. 6.10. Ударные волны для ромбиче-
ромбического профиля.
6.7. Первое приближение по методу сращиваемых
разложений
Не лишено интереса вновь решить задачу F.30)
вторым методом — методом сращиваемых асимптотиче-
асимптотических разложений. Подстановка предполагаемого ряда
я F, л; е)~8/^F, л) + ?2%а, Л)+... • F.48)
сразу приводит к прямому разложению
... • F.49)
Это — приближенная форма полного результата второго
порядка F.24). В соответствии с нашим соглашением,
6.7. Первое приближение; сращиваемые разложения 161
приведенным в § 5.9, мы назовем это внешним разложе-
разложением, несмотря на то что областью его неоднородности
является окрестность бесконечно удаленной точки.
Внешнее разложение непригодно, когда т] = О(8), и
в этой области и имеет порядок е. Это наводит на
мысль ввести внутренние переменные, такие, что внут-
внутреннее разложение примет вид
F.50)
Подстановка этого разложения в дифференциальное
уравнение F.30а) дает для первого приближения
Это — нелинейное дифференциальное уравнение в част-
частных производных. Однако оказывается, что его можно
линеаризовать, поменяв местами зависимые и незави-
независимые переменные и находя решение для ?(?Л, Н). Урав-
Уравнение принимает вид
и его общим решением будет
Ц1^г ^i^- F.53а)
Функция интегрирования g находится сращиванием с
внешним решением F.49), что, очевидно, дает
g(Ui)*=(TTl(-BUi). F-536)
где (Г7) — функция, обратная Т. Например, в случае,
представленном на рис. 6.5, мы имеем Г7(х)=—х, так
что (T')-l(—BUi)=BUun тогда решение F.53а) для
Ui дает результат F.41), полученный прежде методом
деформированных координат.
Это внутреннее решение равномерно пригодно, по-
поскольку внутреннее уравнение F.51) в действительности
представляет собой полное уравнение F.30а). В этом
простом примере не было введено упрощений с по-
помощью внутреннего разложения, которое состоит из од-
одного члена.
162 Гл. 6. Метод деформированных координат
6.8. Полезность метода деформированных
координат
Объективная оценка метода деформированных ко-
координат получается при сопоставлении его с методом
сращиваемых асимптотических разложений. Представ-
Представляется, что, как и в двух предыдущих примерах, послед-
последний метод приложим всегда, когда приложим первый.
Обратное, к сожалению, неверно. Следовательно, метод
сращиваемых разложений является более действенным
и, возможно, более обоснованным.
Однако в случае, когда метод деформированных ко-
координат приложим, он дает значительные упрощения.
Это хорошо показывают предыдущие примеры, которые
демонстрируют два следующих преимущества метода
Лайтхилла:
i) требуется решить только прямые (внешние) воз-
возмущенные уравнения, которые линейны;
ii) этот метод непосредственно дает единственное
равномерно пригодное разложение.
Второе преимущество менее важно, поскольку мы
видели в гл. 5, что внутреннее и внешнее разложения
можно скомбинировать несколькими путями в одно рав-
равномерно пригодное составное разложение. С другой сто-
стороны, первое преимущество часто оказывается весьма
существенным, потому что в нелинейных задачах урав-
уравнение для главного члена внутреннего разложения
может быть трудно или даже невозможно решить. Так,
в обоих наших примерах первая внутренняя задача не-
нелинейна, в то время как метод деформированных коор-
координат приводит только к линейным уравнениям. Триум-
Триумфом метода Лайтхилла является то, что он достигает
цели, избегая кропотливого анализа области неодно-
неоднородности.
Однако по этой же причине метод не всегда может
быть успешно применен. Хуже того, может показаться,
что он успешно применяется, в то время как на самом
деле результат получается неверным. Поэтому основным
является вопрос: когда безопасно применять метод де-
деформированных координат? В настоящее время нельзя
6.8. Полезность метода деформированных координат 163
дать общего ^правила, можно предложить лишь некото-
некоторые признаки.
Один определенный признак состоит в том, что бес-
бесполезно деформировать координаты в задаче возмуще-
возмущений, которая является особой из-за того, что старшая
производная в уравнении множится на малый параметр.
Так, метод Лайтхилла нельзя применять в теории по-
пограничного слоя Прандтля. Здесь попытка применения
метода обычно приводит к нулевому результату, как
можно видеть из -задачи-модели § 5.2. Однако при опре-
определенных условиях метод приводит к конечному, но не-
неверному результату. Это положение было исследовано
Леви [1], который предложил математическую модель,
показывающую соответствующие существенные труд-
трудности.
Метод деформированных координат оказывается ус-
успешным в тех случаях, когда особенность, предсказы-
предсказываемая прямым первым приближением, действительно
существует, но слегка смещена. Он дает неверные ре-
результаты в тех случаях, когда истинная особенность
оказывается особенностью другого типа или несуще-
несущественной. Первый случай, по-видимому, имеет место
для гиперболических уравнений, второй — обычно для
эллиптических. В эллиптических уравнениях появляется,
например, логарифмическая особенность на острой
кромке в теории тонкого профиля, обтекаемого несжи-
несжимаемой жидкостью. В § 4.11 было показано, что это.
соответствует в действительности малой дробной сте-
степени е. Следовательно, в этом случае метод деформи-
деформирования координат является несостоятельным, в то вре-
время как метод сращиваемых асимптотических разложе-
разложений оказывается успешным.
Профиль с закругленной кромкой в несжимаемой
жидкости представляет собой исключение, поскольку
особенность вида корня квадратного существует в тео-
теории тонкого профиля и просто сдвинута от передней
кромки приблизительно в фокус соприкасающейся па-
параболы (см. § 4.12). По этой причине Лайтхилл [4] был
в состоянии использовать свой метод для нахождения
однородного второго приближения для профилей с
закругленной кромкой. То, что этот случай является
164 Гл. 6. Метод деформированных координат
исключительным, показывает то обстоятельство, что все
попытки распространить решение Лайтхилла на при-
приближения высшего порядка, на дозвуковые течения сжи-
сжимаемой жидкости или на другие формы кромок оказа-
оказались безуспешными. Все эти проблемы успешно иссле-
исследованы методом сращиваемых асимптотических разло-
разложений (Ван-Дайк [3]).
Указанные обстоятельства побудили Лайтхилла [6]
рекомендовать ограничить применение его способа лишь
гиперболическими уравнениями. Это — нежелательное
ограничение для мощного метода. Будем надеяться, что
дальнейшие исследования не только выяснят, при каких
условиях можно применять метод деформированных
координат в его современном виде, но и внесут усовер-
усовершенствования, которые с надежностью позволят при-
приложить метод к другим задачам, в частности к задачам,
включающим эллиптические и параболические урав-
уравнения.
УПРАЖНЕНИЯ
6.1. Более слабый принцип деформиро'вания. Покажите, что
равномерно пригодное решение задачи F.3) получается методом
деформированных координат, если принцип деформирования F.1)
ослабить и свести только к требованию, чтобы второе приближение
имело бы не большую особенность, чем квадрат первого.
6.2. Задача Каррьера [1]. Приложите метод деформированных
координат к задаче
показав, что равномерно пригодное первое приближение имеет вид
с надлежащими значениями констант а, Ъ, с, d, g. Вычислите зна-
значение f@).
6 3. Запаздывающее деформирование. Покажите, что в прило-
жении"метода деформированных координат к задаче
первое деформирование определено только задачей третьего по-
порядка. Сравните это решение с решением, полученным методом сра-
шиваемых асимптотических разложений.
Упражнения 165
6.4. Метод Притуло. Притуло [1] указал, что если вычисленное
прямое возмущенное решение окажется неоднородным, то деформи-
деформирование координат, требующееся для превращения его в равномерно
пригодное, может быть найдено непосредственно решением только
алгебраических, а не дифференциальных уравнений. Покажите это,
подставив разложение F.66) в решение F.4) и определив деформи-
деформирование до порядка е2.
6.5. Распространение цилиндрических волн Рассмотрите нели-
нелинейную модельную задачу
Найдите область неоднородности прямого разложения для малых
8 и */^>1. Покажите, что мегод деформированных координат дает
точное решение.
Глава 7
ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
ПРИ БОЛЬШИХ ЧИСЛАХ
РЕЙНОЛЬДСА
7.1. Введение
Обратимся теперь к прототипу задач особых возму-
возмущений — к задаче вязкого обтекания тел при больших
числах Рейнольдса. Для исследования этой задачи была
разработана теория пограничного слоя Прандтля. Не-
Несколько позже выяснилось, что теория пограничного
слоя дает главный член в асимптотическом разложении
для больших чисел Рейиольдса. Однако попытки вычис-
вычислить следующие члены разложения приводили сначала
к существенным заблуждениям, противоречиям и ошиб-
ошибкам. Ситуация прояснилась после систематического при-
приложения метода сращиваемых асимптотических разло-
разложений. Здесь, используя этот метод, мы покажем, как
теория Прандтля может быть представлена в качестве
первого шага в схеме последовательных приближений.
Практическая полезность такого усовершенствования
подсказывается оценкой Лагерстрома и Коула [1], по
которой второе приближение может позволить достаточ-
достаточно точно определить коэффициент поверхностного трения
до чисел Рейнольдса, равных 10 или даже 5.
Простоты ради мы рассмотрим только плоское уста-
установившееся ламинарное течение несжимаемой жидкости
около изолированного тела в однородном параллельном
потоке. Для начала исследования нам нужно основное
решение для бесконечного числа Рейнольдса. Конечно,
реальное течение становится неустановившимся и тур-
турбулентным, когда число Рейнольдса превосходит некото-
некоторое определенное значение, но это не относится к делу,
поскольку нашей конечной целью является получение
приближения для умеренных значений числа Рей-
Рейнольдса. К сожалению, в случае, когда вероятен отрыв
потока от тела, соответствующее предельное решение
для конечных тел неизвестно. Например, на рис. 7.1
7.1. Введение
167
изображены три возможные конфигурации обтекания
круга невязкой жидкостью (Эйлер), и существует еще
множество других возможностей. До тех пор пока этот
важный вопрос не решен, невозможно исследование те-
течений с отрывом, поскольку спутный поток будет ока-
оказывать влияние первого порядка даже на набегающий
поток. Это означает, что обтекаемое внешним потоком
тело должно быть полубесконечным, за исключением
случая конечной плоской пластины и, возможно, некото-
некоторых очень тонких профилей; более полное обсуждение
этого вопроса можно найти у Гольдштейна [4].
а 6
Рис. 7.1. Невязкое обтекание круга.
а —непрерывное потенциальное течение, б — бесконечная застойная область,
б —замкнутый спутный поток (Бэтчелор A]).
Серьезные трудности возникают в случае углов и
разрывов другого вида, так что, казалось бы, целесооб-
целесообразно ограничиться рассмотрением лишь тел аналитиче-
аналитической формы. С другой стороны, уравнения Прандтля ре-
решаются легко только для определенных автомодельных
течений, большая часть которых соответствует заострен-
заостренным телам. При разрешении этой дилеммы мы предпоч-
предпочтем трудности, связанные с острыми кромками, ради
сведения дифференциальных уравнений в частных про-
производных к обыкновенным. В действительности мы при-
применим метод к конечной или полубесконечной плоской
пластине и укажем видоизменения, которые возникают
для других форм.
Предполагается, что читатель знаком с элементами
классической теории пограничного слоя, в частности с
решением Прандтля — Блазиуса для плоской пластины,
как оно дано, например, Прандтлем [2], Гольдштейном
[2] или Розенхедом [1].
168 Гл. 7. Течение при больших числах Рейнольдса
7.2. Различные интерпретации решения
для плоской пластины
Решение Блазиуса для плоской пластины может
быть рассмотрено с нескольких точек зрения теории по-
пограничного слоя. Мы приведем здесь три существенно
различные интерпретации.
Во-первых, решение Блазиуса приложимо к полубес-
полубесконечной плоской пластине. Тогда оно представляет со-
.бой возмущение координат для больших значений х.
'И I I I I I I I I I I I I I I I I I I I ГП
,.
Рис. 7.2. Тела, для которых решение Блазиуса
пригодно далеко вниз по потоку.
Точнее, поскольку задача содержит только вязкую дли-
длину v/f/, оно представляет собой асимптотическое реше-
решение для больших значений текущего числа Рейнольдса
Uxfv. В этом смысле оно приложимо также к толстым
пластинам с закругленной кромкой или даже к таким
расширяющимся профилям, как параболические
(рис. 7.2).
Во-вторых, решение Блазиуса приложимо к заострен-
заостренной пластине (рис. 7.3). В этом случае оно представ-
представляет собой возмущение координат для малых х, что до-
довольно странно. Точнее, это асимптотическое решение
для малых x/L, где L — характерная длина, например
начальный радиус кривизны профиля. Приближение
могло бы быть улучшено вычислением дополнительных
членов ряда по степеням x/L. Можно быть уверенным.
7.2. Интерпретации решения для плоской пластины 169
что результат непригоден в непосредственной близости
от передней кромки, где x = O(v/U). Таким образом, мы
встречаемся с ситуацией, которая иногда возникает в
других разделах механики жидкости, например для
тел степенной формы в гиперзвуковой теории малых
возмущений (Хейз и Пробстин [1], § 2.6), когда возму-
возмущение координат пригодно для малых (или больших),
но не слишком малых (или больших) расстояний. Мож-
Можно предположить, что неоднородности на передней
Рис. 7.3. Тело, для которого решение Блазиуса
пригодно вблизи передней кромки.
кромке могли бы быть устранены построением третьего
разложения для этой области. Однако эта предельная
задача будет, очевидно, такой же, как и для самой по-
полубесконечной пластины. Конечно, течение очень близко
от кромки дается приближением Каррьера и Линя, опи-
описанным в § 3.9. Однако это приближение не является
внутренним решением в смысле гл. 5: оно не перекры-
перекрывается с решением Блазиуса и из-за этого не может
быть срощено с ним (§ 10.9).
В-третьих, решение Блазиуса приложимо к конечной
плоской пластине (рис. 7.4). Тогда оно представляет
собой возмущение параметра и является асимптотиче-
асимптотическим решением для больших чисел Рейнольдса UL/v,
построенных по длине пластины. Такое положение воз-
возникает только потому, что основное невязкое решение
одно и то же для конечной и полубесконечной пластины
и потому что уравнения параболические, так что спут-
нцй поток за задней кромкой не влияет на пограничньщ
170 Гл. 7. Течение при больших числах Рейнольдса
слой. Конечно, этот результат не является равномерно
пригодным и оказывается несостоятельным у обеих кро-
кромок. Вопрос о неоднородности на передней кромке уже
был обсужден; вопрос о неоднородности на задней кром-
кромке, вероятно, даже более сложен.
Различие между этими тремя интерпретациями ре-
решения Блазиуса проявляется в приближениях высшего
\j = —
v Re
Рис. 7.4. Обозначе-
ния для конечной
плоской пластины.
" i i i i i i i i i i i i i I I I I
порядка. Мы рассмотрим параллельно первую и третью
точки зрения для конечной и полубесконечной плоской
пластины; относительно второй см. Ван-Дайк [10].
7,3. Внешнее разложение для плоской пластины.
Основное невязкое течение
Пусть L — длина конечной пластины или произволь-
произвольная характерная длина для полубесконечной пластины
(скажем, расстояние от передней кромки до красной чер-
черты, нанесенной на пластину!). Решение в действитель-
действительности не должно зависеть от L в последнем случае; для
первого то же будет иметь место в первом приближении.
Удобно ввести безразмерные переменные, отнеся все
длины к L и скорости к U. Это эквивалентно выбору та-
таких единиц, что L = f/=1 (рис. 7.4). Тогда в декартовых
координатах уравнения Навье — Стокса эквивалентны
уравнению B.24) для безразмерной функции тока i|) при
замене v на величину, обратную числу Рейнольдса Re,
построенному по длине L,
Re = ^. G.1)
7.3. Внешнее разлоокение для плоской АлаСтиньь 171
Добавляя граничные условия обращения в нуль скоро-
скорости на пластине и условие в равномерном набегающем
потоке, получаем полную задачу:
ф(х, 0) = 0, G.26)
( 1, конечная пластина,
Ч> (х, 0) = 0 дИ 0<к G.2в)
у { оо, полубесконечная,
ф(х, у)~у в набегающем потоке. G-2г)
Мы ищем асимптотическое решение этой задачи при
стремлении числа Рейнольдса к бесконечности. Посколь-
Поскольку параметр возмущения входит в задачу только как
I/Re, можно попытаться предположить, что соответ-
соответствующая асимптотическая последовательность состоит
из степеней I/Re. Однако теория Прандтля показывает,
что это неверно. Поэтому мы выберем более безопасный
путь, оставив последовательность неопределенной и
предположив, что прямое (внешнее) разложение имеет
вид
для Re-» со при фиксированных X, у > 0. G.3)
Подставив это выражение в полную задачу и перейдя к
пределу при Re-»oo, мы получим для условий в набе-
набегающем потоке G.2г)
Ф^*^ У)'— ^m s /р-ч У в набегающем потоке. G.4)
Имеющийся здесь предел может быть нулем, бесконеч-
бесконечностью или конечным. Если он равен нулю, то задача
однородна и решение (если оно единственно) есть ipi = 0.
Если предел бесконечен, то задача теряет смысл. Следо-
Следовательно, существенный результат получается только в
том случае, когда предел конечен. Не ограничивая
общности, мы положим
61(Re)=l. G.5)
172 Гл. 7. Течение при больших числах Рейнольдса
Тогда уравнение для первого приближения совпа-
совпадает с уравнением для невязкого течения
Ч = 0, G.6а)
согласно которому завихренность просто переносится
конвективно, а ее вязкая диффузия в этом приближении
отбрасывается. Первый интеграл этого уравнения был
дан в § 2.1 в виде
Щ h). G.66)
Это означает, что завихренность —V2% является неко-
некоторой функцией coi только от функции тока и, следова-
следовательно, постоянна вдоль линии тока. Форма этой функ-
функции определяется течением далеко перед телом. Она-об-
Она-обращается в нуль в рассматриваемой задаче, как и дол-
должно быть в том случае, когда набегающий поток яв-
является безвихревым. Следовательно, задача для первого
члена внешнего разложения принимает вид
у2ф, = 0, G.7а)
Мх, 0) = 0, G.76)
^iC*> У) — У в набегающем потоке. G-7в)
Здесь условие прилипания ipiy(jt, 0)=0 отброшено, по-
поскольку оно не может быть выполнено. Порядок диффе-
дифференциального уравнения понижен на единицу за счет
того, что членом, соответствующим вязкости, мы прене-
пренебрегли, и соответственно должно быть отброшено одно
граничное условие. Вопрос о том, какое из граничных
условий должно быть отброшено, для простых задач
можно решить математически; в нашей задаче следует
руководствоваться данными эксперимента и физической
интуицией.
Решение этой задачи
Ы*> У) = У G.8)
представляет собой просто равномерный параллельный
поток — при бесконечном числе Рейнольдса плоская пла-
пластина не вызывает возмущений. Решением для какого-
либо другого цилиндрического тела в случае, когда нет
отрыва потока, является соответствующее потенциальное
течение идеальной жидкости.
7.4. Внутреннее разложение. Сращивание 173
7.4. Внутреннее разложение. Уравнения
пограничного слоя. Сращивание
Потеря высшей производной является классическим
характерным признаком задачи особых возмущений
(§ 5.2), и мы знаем, что основное невязкое решение не-
непригодно вблизи поверхности, где оно не удовлетворяет
условию прилипания. Таким образом, область неодно-
неоднородности представляет собой окрестность линии, а не
точки, как было в задачах об обтекании тонкого про-
профиля (гл. 4). Координаты порядка единицы в области
неоднородности будут получены увеличением нормаль-
нормальной координаты у при оставлении координаты х неиз-
неизменной.
Прандтль пришел к подходящему увеличению коор-
координаты с помощью физической интуиции и сравнения с
простыми точными решениями. До некоторой степени,
однако, можно поступать и формально. Пусть ширина
области неоднородности (пограничного слоя) имеет по-
порядок Ai(Re), где Ai — функция, обращающаяся в нуль
при бесконечных значениях аргумента. Тогда надлежа-
надлежащим образом увеличенная (внутренняя) нормальная
координата определяется в виде y = r//Ai(Re), где растя-
растягивающий множитель l/Ai(Re) еще должен быть опреде-
определен. Что касается зависимого переменного, ясно, по
крайней мере физически, что и — \\>у должно быть вели-
величиной порядка единицы как внутри пограничного слоя,
так и вне его, так что
Таким образом, ф должно быть увеличено во столько
же раз, что и у.
Обобщая на приближения высшего порядка, предпо-
предположим, что внутреннее разложение, пригодное внутри
пограничного слоя, имеет вид
ф(х, у;
тля Re—>оо при фиксированных X, Y, G.9а)
где
174 Гл. 7. Течение при больших числах Рейнольдса
Функции Ап образуют асимптотическую последователь-
последовательность, такую, что все 4я п имеют порядок единицы в по-
пограничном слое, где У=ОA). Определим Дь подставив
это разложение в уравнение Навье —Стокса G.2а), ум-
умножив результат на Д4 и устремив Re к бесконечности.
Это дает
4)[^} <7Л0>
Как и прежде, появляющийся здесь предел может быть
нулем, бесконечностью или конечной величиной. Пер-
Первые две возможности ведут к вырожденным решениям,
которые не могут удовлетворить внутренним граничным
условиям и быть срощены с внешним течением. Следо-
Следовательно, мы выберем третью возможность. Это озна-
означает, что мы вновь, как и в предыдущем разделе, при-
применяем принцип минимальной особенности (см. § 5.5).
Без потери общности положим этот постоянный предел
равным единице, что дает
Д! (Re) = Re~1/2, Y = Re1/2r/. G.11)
Таким образом, мы получаем известный результат: тол-
толщина пограничного слоя пропорциональна Re~1/2.
Уравнение G.10) для первого члена внутреннего раз-
разложения теперь принимает форму
^ ^^^ 0 GЛ2а)
Выражение в левой части представляет собой полную
производную, и уравнение может быть записано в виде
W~ O^iууу ~t~ ^lx^iyy ^iy^uy) = 0' G.126)
так что интегрирование дает уравнение третьего по-
порядка
™~ М**1УТ ^ 1КМлгГ==: f (ХУ G.12в)
Функция интегрирования f(x) пропорциональна гра-
градиенту давления на поверхности в невязком течении.
Это показывается при сращивании с основным невязким
течением, что определяет f(x) и также обеспечивает вы-
выполнение внешнего граничного условия.
7 А. Внутреннее разложение. Сращивание 175
Применим принцип асимптотического сращивания
E.24) при пг=п=1. Достаточно (и на данной стадии бо-
более удобно) вместо самой функции г|) срастить величину
фу, которая с физической точки зрения интерпретирует-
интерпретируется как касательная скорость. Используя предыдущие
результаты G.3), G.5), G.8), G.9) и G.11), мы полу-
получаем для любого плоского тела следующие результаты.
Одночленное внешнее
разложение: $у"^"Ф\у(х> У)* G.13а)
переписанное во внут- __ ^ lx Y \ ,j jo^)
ренних переменных: ^}у у ' ]ЛЩ" / ' °
разложенное для _ ^
больших Re:
одночленное внут-
внутреннее разложение: = i^
Одночленное внутреннее
разложение: \ру ^ х?
переписанное во внеш-
внешних переменных: =zW1Y(x, у КЙё"), G.146)
разложенное для
больших Re: =Ч\у(х, оо)-{-..., GЛ4в)
одночленное внешнее
разломсение: =у?1У(х, оо). G.14г)
0^-4-
и; -f-
0).
У).
Y
i/"i?p" '
^(^0)+....
G.13в)
G.13г)
G.14а)
Здесь мы использовали определенные свойства функций
i|)i и ЧХ1: в формуле G.13а) учли то обстоятельство, что
\pi(x, у) аналитична по у при у = 0, а в G.14в) предпо-
предположили, что Wiy имеет предел при У, стремящемся к
бесконечности. Приравняв два конечных результата, мы
получим требуемое условие сращивания
Ч„(х,оо) = Ъ1в(х,0). G.15а)
Это знакомое требование, состоящее в том, что каса-
касательная скорость на внешней границе пограничного слоя
(У=оо) должна приближаться к скорости невязкого те-
течения tyiy(x, 0). Если бы мы сращивали саму функцию
if>, то результат был бы
(Г) при К->оо. G.156)
176 Гл. 7. Течение при больших числах Рейнольдса
Это же можно получить из G.15а) интегрированием, и
это показывает, что условие сращивания для первого
члена асимптотического разложения при больших У по-
понято правильно.
Условие сращивания можно использовать для на-
нахождения функции интегрирования f(x) путем оценки
уравнения G.12в) пограничного слоя при У—»оо. Ре-
Результатом является обычное уравнение Прандтля для
пограничного слоя
^ууу+^г^\уу-^1у^у=-%у^ 0)ф1ху(*, 0).
G.16а)
Выражение в правой части представляет собой безраз-
безразмерный градиент давления на поверхности в невязком
течении, получаемый из интеграла Бернулли. Это урав-
уравнение действительно справедливо для любого плоского
тела, причем х— расстояние вдоль поверхности, а у —
расстояние по нормали к ней, поскольку кривизна по-
поверхности влияет только на второе приближение теории
пограничного слоя. Подходящими граничными условия-
условиями являются условие сращивания G.15) и условие ра-
равенства нулю скорости на поверхности, которое, если г|э
нормировано так, что оно обращается в нуль на поверх-
поверхности тела, имеет вид
^(х, 0) = ^1К(;с, 0) = 0. G.166)
Условие сращивания G.15) оставлено, несмотря на то
что оно уже было использовано для исследования функ-
функции интегрирования. Такое двойное использование усло-
условия объясняется тем, что точка У=оо особая.
Уравнение пограничного слоя G.16а) является пара-
параболическим— в нем х есть подобное времени перемен-
переменное, тогда как исходное уравнение Навье — Стокса было
эллиптическим. Это изменение типа уравнения (см.
§ 3.11) означает, что влияние вверх по потоку подав-
подавлено. По этой причине в первом приближении совсем не
учитывается влияние задней кромки и последующего
спутного потока на пограничный слой на плоской пла-
пластине.
7.5. Решение для плоской пластины 177
7.5. Решение задачи о пограничном слое
для плоской пластины
Решение G.8) для невязкого обтекания плоской пла-
пластины показывает, что градиент давления отсутствует, и
задача пограничного слоя принимает вид
^.kkk+VVk-Vuk^O- G.17а)
?,(*, 0) = 0, G.176)
°<*<' G.17в)
полубесконечная, 0 < X < со, v '
Wiy(Xi оо)=1. G.17г)
Для конечной пластины пограничные слои на верхней и
нижней поверхности у задней кромки сливаются и от-
отходят от пластины без отрыва в виде спутного потока
(рис. 7.5). Очевидно, что приближение пограничного
слоя продолжает оставаться пригодным в спутном по-
потоке, и градиент давления там по-прежнему равен нулю.
Рис. 7.5. Пограничный слой и спутный поток
для конечной пластины.
Единственное необходимое изменение состоит в том,
чтобы заменить условие прилипания G.17в) требова-
требованием симметрии
4iyy(x> 0) = 0 для 1<х. G.17вО
Мы будем, однако, рассматривать пограничный слой в
деталях только до задней кромки, поскольку за ней те-
течение не автомодельно.
Автомодельное решение существует на пластине
вследствие того, что задача обладает некоторым группо-
групповым свойством, что позволяет свести ее к обыкновенному
178 Гл. 7. Течение при больших числах Рейнольдса
дифференциальному уравнению. Это свойство выражает-
выражается тем фактом, что задача G.17) инвариантна1) отно-
относительно преобразования
Чг^сЧг» х->с2х, Y->cY. G.18)
Как и в теории размерностей, где инвариантность по от-
отношению к изменению масштаба скорее является физи-
физической необходимостью, чем, как здесь, математическим
условием, это означает, что решение (если оно един-
единственно) содержит переменные XYU x и Y не по отдель-
отдельности, а только в комбинациях, которые инвариантны
по отношению к этому преобразованию. Здесь возмож-
возможны следующие варианты:
= функция от
G.19)
Мы выберем последнюю форму, введя множитель 2 для
соответствия с обычным обозначением Фолкнера — Скен
(Шлихтинг [1]; Розенхед [1], стр. 222):
Т1 (х, Y) =
Возвращаясь в этой формуле к исходным размерным пе-
переменным, мы видим, что длина L в выражении для
ft и г\ исчезает в соответствии с тем фактом, что она
произвольна для полубесконечной пластины и не харак-
характерна для пограничного слоя на конечной пластине. Это
другой способ обоснования группового преобразования.
Подстановка формул G.20) в задачу G.17) погра-
пограничного слоя дает
/Г + /1/Г = 0, G.21а)
f1(O) = f1/(o) = O, G.216)
К(оо)=1. G.21в)
*) В случае конечной плоской пластины при этом преобразова-
преобразовании длина изменяется от 1 до с2. Следовательно, для того чтобы
установить существование инвариантности, существенно сознавать,
что пограничный слой на пластине не подвергается действию спут-
ного потока.
7.5. Решение для плоской пластины 179
Это — задача Прандтля — Блазиуса без множителя 2,
который имеется в ранних исследованиях. Она должна
решаться численно. Сам Блазиус склеивал решение в
рядах для малых ц с асимптотическим разложением для
больших т). Однако Вейль [1] указал на то, что это опас-
опасное занятие, поскольку первый ряд имеет только умерен*
ный радиус сходимости (а второй, вероятно, расходит-
расходится). Безопаснее —а в настоящее время в связи с появ-
появлением электронных машин и проще — интегрировать
численно от т) = 0 до некоторого разумно большого зна-
значения, скажем до г) = 5 или г]=10.
Это — двухточечная краевая задача, в которой тре-
требуется выполнение предположения, что f[ удовлетворяет
условию G.21в) для больших т|. Однако в рассматривае-
рассматриваемой задаче этого усложнения можно избежать, исполь-
используя другое групповое свойство решения. Дифферен-
Дифференциальное уравнение G.21а) и начальное условие G.216)
инвариантны относительно преобразования
fl-+cfl9 т|->14. G.22)
Следовательно, можно интегрировать задачу G.21), за-
заменив условие G.21в) требованием fi @) = 1 с последую-
последующим выбором константы с, удовлетворяющей условию
на бесконечности (Гольдштейн [2]; Розенхед [1], стр.223).
Существенные для наших целей результаты числен-
численного решения содержатся в разложениях для малых и
больших т|:
fI Ol) = \ ЗД2 + О (if), аг = 0,469600, G.23а)
Мл)~т1 —Pi + exp, pj =1,21678. G.236)
Здесь «ехр» обозначает члены, которые экспоненциаль-
экспоненциально малы для больших т). Отсюда видно, что завихрен-1
ность, вызванная наличием стенки, убывает в погранич-
пограничном слое сильнее, чем любая степень г\. То, что это
правильно для пограничного слоя, подсказывается анало-
аналогией с диффузией тепла (Розенхед [1], стр. 216) и опре-
определенными математическими доводами (Стюартсон [2],
Чжан [1]). Мы увидим впоследствии, что условие экспо
180 Гл. 7. Течение при больших числах Рейнольдса
ненциального убывания завихренности должно быть на-
наложено в тех случаях, когда оно не выполняется авто-
автоматически.
7.6. Единственность решения Блазиуса
Рассмотренное выше решение задачи G.17) не един-
единственно с математической точки зрения. К нему может
быть прибавлено любое из бесконечного дискретного
ряда собственных решений, каждое из которых удовлет-
удовлетворяет уравнению G.21а) и условиям G.216) и экспо-
экспоненциально убывает на бесконечности (Стюартсон [2];
Либби и Фокс [1]). Эти решения имеют вид
Г (*, Y) = Стх1/2~хгпет (п), G.24а)
где Ст — произвольные постоянные и
А,ш=1, 1,887, 2,818, 3,800, 4,740,.... G.246;
Первое из этих собственных решений равно произ-
производной по х от решения Блазиуса G.20):
М1} = С1Х-1/2[Л(т|)-т,К(т,)]. G.25)
Оно физически соответствует небольшой неопределенно-
неопределенности в положении начала отсчета по оси абсцисс. Подоб-
Подобным же образом собственные решения высшего порядка
представляют дальнейшую неопределенность в деталях
течения вблизи передней кромки, однако их не так про-
просто интерпретировать, как первое. Стюартсон [2] рас-
рассматривал вопрос о том, как возникает неопределенность
в любом разложении вниз по потоку для пограничного
слоя вследствие того, что не наложены начальные усло-
условия (см. § 3.10).
Мы можем соответствующим образом избавиться от
всех собственных решений на этой стадии, используя
принцип минимальной особенности (§ 4.5). Однако бо-
более поучительно понять, почему может прилагаться
этот принцип. Характерная длина L и связанный с ней
7.7. Течение, обусловленное толщиной вытеснения 181
параметр Re — искусственны; следовательно, безразмер-
безразмерные переменные должны входить только как Rei|), Rex
и Re у с тем, чтобы L исчезала из результата. Решение
Блазиуса обладает этим свойством. Первое собственное
решение G.25) обладает им только в том случае, когда
константа Ci имеет порядок Re. Но это означало бы,
что оно принадлежит третьему приближению (§ 7.11),
а не первому. Таким же образом собственные решения
более высокого порядка сдвигаются к приближениям
высших порядков. Это типичное рассуждение, вклю-
включающее в себя понятие искусственного параметра; даль-
дальнейшее обсуждение этого вопроса можно найти у
Лагерстрома и Коула [1], Чжана [1], а также в упраж-
упражнении 4.8.
Эти рассуждения неприложимы к затупленной плос-
плоской пластине (рис. 7.2), которая имеет реальный гео-
геометрический размер L. Действительно, в этом случае
все собственные решения должны быть сохранены в
асимптотическом разложении решения первого порядка
пограничного слоя. Они не исключаются принципом ми-
минимальной особенности, поскольку появляются члены
с большей особенностью. Например, для параболы раз-
разложение содержит член х~х12\пх между решением Бла-
Блазиуса и первым собственным решением. Результирую-
Результирующее выражение для поверхностного трения было дано
уравнением C.27) в гл. 3, а в § 10.9 мы покажем, как
константа С\ может быть приближенно найдена связы-
связыванием с другим разложением вблизи передней кромки
или склеиванием с численным решением.
7.7. Течение, обусловленное толщиной вытеснения
В § 5.9 было показано, что в прямой задаче погра-
пограничного слоя надлежит следовать нормальному порядку
сращивания (см. рис. 5.6). Мы, следовательно, перейдем
ко второму члену во внешнем разложении G.3).
Форма множителя 62(Re) вместе с условиями сра-
сращивания находится сращиванием с решением для по-
пограничного слоя. На этой стадии сращивания tyy недо-
недостаточно; необходимо срастить саму функцию я|) или
одновременно обе производные tyx и ^у. Используя все
182 Гл. 7. Течение при больших числах Рейнольдса
предыдущие результаты, мы найдем соответствующие
разложения.
Одночленное внутрен- ^ _! j/^ (tj)
нее разложение: Y УТзёГ /1VI"
переписанное во вне*
р ^ _ у2х f (KJl/) G<26б)
шних переменных: j/^e '! ^ Y2x / '
разложенное для = _* y^(V^± ___ р + ехр\
больших Re: ^е у ]/2лг /
G.26в)
двучленное внешнее _ „ L_ r, /2лГ, G.26г)
разложение: ]/"Re"
переписанное во внут- = У^ 1 р |/^-. G.26д)
ренних переменных: ^е j/^Re ri v A'
Двучленное внешнее
разложение: ^^ у -|- 62 (Re) я|?2 (^, #), G.27а)
переписанное во внут-
ренних переменных
- = _У + 6 (Re) ^ / .„^
: ]fRe \ у Re
G.276)
разложенное для ^ _J1_ « б2 (Re) [i|j2 (xt0)+... ].
больших Re: УТ&
G.27в)
Здесь мы использовали в равенстве G.2бв) асимптоти-
асимптотическое разложение G.236) для функции Блазиуса fu a
"в G.27в)—тот факт, что ty2, подобно %, — аналитиче-
аналитическая функция по у при у = 0>
Теперь мы приложим принцип асимптотического
сращивания E.24) при т=1 и п = 2. Сравнение G.26д)
и G.27в) показывает, что 62 (Re) должно быть равно
Re~I/a с некоторым множителем; мы выберем
^. G.28)
Из этого следует, что
ф2(дг, 0) = — faY2x. G.29а)
Физическая интерпретация этого соотношения в терми-
терминах толщины вытеснения пограничного слоя известна.
7.7. Течение, обусловленное толщиной вытеснения 183
Подстановка в G.27) показывает, что внешнее разло-
разложение для функции тока обращается в нуль при
y = $iRe-l/2BxL2. Таким образом, пограничный слой вы-
вытесняет' внешний невязкий поток так же, как твердая
парабола с радиусом носовой части Pj/Re. Условие сра-
сращивания G.29а) представляет собой условие обтекания
этой вытесняющей параболы, линеаризованное по тео-
теории тонкого профиля и снесенное на ось (§ 4.2).
Другая форма с несколько отличной физической ин-
интерпретацией вытекает из дифференцирования по # фор-
формулы G.29а):
~*Ы*. 0) = р1/1/2^. G.296)
Это — составляющая второго порядка нормальной ско-
скорости во внешнем течении, рассмотренная на поверх-
поверхности, где она должна быть равна наклону вытесняю-
вытесняющей параболы. С этой точки зрения эффект вытеснения
пограничного слоя действует подобно поверхностному
распределению источников. Это—условие обтекания
тонкого профиля, данное в § 4.3. Подробное описание
различных интерпретаций эффекта вытеснения дано
Лайтхиллом [5].
Подстановка внешнего разложения G.3) в полное
уравнение G.2а) дает линейное уравнение для я|J
&)*Ф, = 0. G.30а)
Нелинейные конвективные члены разбиваются на
два, как обычно в схеме возмущений. Два члена пред-
представляют соответственно конвективный перенос завих-
завихренности второго порядка вдоль линии тока первого
приближения и перенос завихренности первого порядка
вдоль линий тока, исправленных во втором приближе-
приближении. Последний член в нашей задаче обращается в нуль,
как это всегда бывает в тех случаях, когда набегающий
поток является безвихревым. Вязкость не оказывает
влияния на этой стадии, поток вне пограничного слоя
считается невязким по меньшей мере до второго порядка
и до любого порядка, когда завихренность в нем равна
нулю. Тогда уравнение G.30а) имеет первый интеграл
¦ G.306)
184 Гл. 7. Течение при больших числах Рейнольдса
Однако внешняя завихренность второго порядка со2
также обращается в нуль в том случае, когда набегаю-
набегающий поток является безвихревым, так что if>2 удовлетво-
удовлетворяет тогда уравнению Лапласа.
7.8. Второе приближение для пограничного слоя
на полубесконечной пластине
Для полубесконечной плоской пластины задача обте-
обтекания с учетом толщины вытеснения имеет вид
V2i|>2 = 0, G.31а)
О для х<0, G.316)
— ра /2х для х > 0, G.31b)
ф2(х, у) —о {у) в набегающем потоке. G.31г)
Условие G.316) симметрии течения служит для исклю-
исключения циркуляционного движения. Это — линеаризован-
линеаризованная задача теории тонкого профиля для безвихревого
обтекания вытесняющей параболы # = PiB.x;/ReI/2. Мы
рассмотрим только скорость на поверхности, которая
была найдена в § 4.8. Однако полное решение очевидно
из теории функций комплексного переменного:
G.32)
где Real обозначает действительную часть.
Вид зависимости A2(Re) в G.9а) и условие сращи-
сращивания для tp2 находятся, как прежде, приложением
принципа сращивания для т = п = 2. Продолжая процесс
G.13), получаем в качестве двучленного внутреннего
разложения двучленного внешнего разложения вели-
величины г|)у:
Двучленное внутреннее двучленного внешнего ф = 1 -\- -.
у К Re
G.33а)
Мы выписываем здесь второй член в правой части, по-
поскольку его коэффициент будет отличен от нуля в дру-
других задачах, включая и задачу о конечной пластине.
7.8. Второе приближение; полубесконечная пластина 185
В обратном процессе мы имеем
Двучленное внешнее двучленного внутреннего ф =
= 1 + ReI/2Д2 (Re) W2y (*, оо). G.336)
Здесь мы предположили, что предел xF2y(Jt, оо) су-
существует; в отношении случаев, когда это не так, см.
упражнение 7.2.
Сращивание приводит к мысли, что мы можем во-
вообще выбрать
A2(Re) = -^-, G.34)
так что как внутреннее, так и внешнее разложения про-
производятся по обратным половинным степеням числа
Рейнольдса. Это верно для тел аналитической формы
(Ван-Дайк [9]). Для тел с угловой точкой, как мы уви-
увидим в § 7.11, это верно только до второго порядка. Сра-
Сращивание обеспечивает для тела произвольной формы
условие для функции Чг2г(^, оо), в физической интер-
интерпретации — условие возрастания касательной скорости
на границе пограничного слоя. Для пластины мы имеем
^2Г(х, оо) = 0, G.35)
поскольку скорость, обусловленная вытеснением, обра-
обращается в нуль при у = 0. Бесконечный параболический
цилиндр имеет единственное в своем роде свойство: в
приближении тонкого профиля скорость на его поверх-
поверхности совпадает со скоростью в свободном потоке.
Подставляя внутреннее разложение G.9) в полное
уравнение G.2а), мы вновь получим в качестве уравне-
уравнения для 4*2 полную производную:
G.36)
Это выражение обращается в нуль только для плоской
пластины. Для любой другой формы правая часть бу-
будет содержать члены, пропорциональные местной кри-
кривизне поверхности (Ваи-Дайк [9]).
Граничные условия на поверхности будут 4*2 (*, 0) =
= "Ф*2у(л;, 0)=0 для любого тела. Следовательно, для
186 Гл. 7. Течение при больших числах Рейнольдса
полубесконечной плоской пластины Ч^ удовлетворяет
полностью однородной задаче; решение должно обра-
обращаться в нуль, если оно единственно. Оно могло бы
быть* неединственным при наличии любого из собствен-
собственных решений G.24), однако доводы § 7.6 показывают,
что ни одно из них не может появиться до следующего
приближения. Таким образом, W2(x, Y)=0 и полное
второе приближение имеет вид
Ф(л:, у; Re)~
у— ¦-—=0! Real У (*+«/) , внешнее, G.37а)
/1 I уъГ )~~*~ rT ' внутреннее. ((.
I/Re
7.9. Второе приближение для пограничного слоя
на конечной пластине
Обсуждая возможности улучшения решения Блазиу-
са последовательными приближениями, Прандтль [2,
стр. 108—109] писал:
«Вместо простого параллельного потока следует рас-
рассмотреть поток вокруг параболического цилиндра...,
слегка изменяющего распределение давлений... Вычис-
Вычисления должны были бы быть повторены для этого но-
нового распределения давлений, и в случае необходимости
процесс должен быть повторен на основе новых изме-
измерений толщины вытеснения».
Однако мы видели, что из-за неожиданного совпа-
совпадения с параболой эта процедура во втором приближе-
приближении ничего не добавляет к результату для полубеско-
полубесконечной пластины.
С другой стороны, для конечной пластины предло-
предложенный Прандтлем процесс дает существенный резуль-
результат. В деталях это было проделано Го [1], рассуждения
которого, однако, могут быть подвергнуты критике с не-
нескольких точек зрения. Поскольку уравнения погранич-
пограничного слоя являются параболическими, решение Бла-
зиуса применимо выше по течению от задней кромки. За
задней кромкой очень трудно вычислить толщину вы-
7.9. Второе приближение; конечная пластина 187
теснения (Розенхед [1]). Го делает, возможно, резонное
предположение, что ее можно считать постоянной вели-
величиной, равной толщине вытеснения у задней кромки
(рис. 7.6). Тогда в течении, обусловленном толщиной вы-
вытеснения, скорость на поверхности увеличивается не-
незначительно.
Рис. 7.6. Предполагаемое распределение тол-
толщины вытеснения для конечной пластины.
Соответствующая задача теории тонкого профиля
может быть решена методами, изложенными в гл. 4.
Так, условие сращивания G.35) второго порядка долж-
должно быть заменено следующим:
хр (х со)- Р' 1 1
Эта функция логарифмически бесконечна на задней
кромке, и разложение в ряд там расходится. Тем не
менее Го решает уравнение G.36) пограничного слоя
второго приближения путем соответствующего разложе-
разложения ^2 в виде
Ч'2 (х, У) = ^- [xlph (т|) + -i x3% (л) +...]. G.39)
Задачи для первых девяти fn были проинтегрированы
численно, и остаток вычислен приближенно. Таким об-
образом, Го оценивает сумму медленно сходящихся рядов
для суммарного поверхностного трения. Для одной сто-
стороны пластины результат имеет вид
Re
188 Гл. 7. Течение при больших числах Рейнольдса
где г — напряжение трения. Этот результат находится
в превосходном соответствии с экспериментами вплоть
до Re=10. К сожалению, однако, перепроверка ряда
показывает, что второй коэффициент едва ли пре-
превосходит 3 и не равен 4,12. Это расхождение обуслов-
обусловлено дополнительным эффектом, не учтенным Го и об-
обсуждаемым в следующем параграфе.
7.10. Местное и суммарное поверхностное трение
Рассмотрим вновь полубесконечную пластину. Исходя
из двучленного внутреннего разложения G.376), вычис-
вычислим коэффициент местного поверхностного трения:
т 0,664 , 0 , п л\\
Здесь Rex=Ux/v — местное число Рейнольдса, построен-
построенное по расстоянию от передней кромки. Первый член мо-
может быть проинтегрирован, в результате чего получится
классическое значение коэффициента суммарного по-
поверхностного трения на одной стороне пластины:
х
f cfdx
п 1 328
F x /Re*
Второй член в формуле G.41) не может быть про-
проинтегрирован, за исключением случая, когда его коэф-
коэффициент равен нулю, поскольку асимптотическое разло-
разложение непригодно вблизи передней кромки. Тем не менее
второй член в суммарном поверхностном трении был
остроумно вычислен Имаи [4]. Он обошел трудности на
передней кромке, рассматривая баланс количества дви-
движения на удаленном контуре (рис. 7.7). Это соответ-
соответствует исследованиям Джонса по сопротивлению перед-
передней кромки в теории тонкого профиля (§ 4.6). Исполь-
Использовав решение Блазиуса в пограничном слое и течение,
обусловленное толщиной вытеснения во внешнем по-
потоке, Имаи нашел
УЬ ' Re, *"••• <7'43>
7.10. Местное и суммарное поверхностное трение 189
Примечательно, что потребовалось 50 лет для того, что-
чтобы раскрыть то обстоятельство, что один член решения
пограничного слоя порождает два члена в сопротивле-
сопротивлении трения.
Хотя детали довольно сложны, этот результат почти
очевиден в свете сказанного в § 4.6. Первый член в раз-
разложении G.43) появляется в результате интегрирования
поперек пограничного слоя и дает классический резуль-
результат G.42). Второй член появляется от интегрирования
nX Течение, одуслодленное
\\ / Зь/темением
\ ) Течение длаэиусп
Рис. 7.7. Контур, на котором рассматривается ба-
баланс количества движения для полу бесконечной
пластины.
вдоль оставшейся части контура, где течение невязкое.
Это есть, следовательно, как раз сопротивление перед-
передней кромки D.22) для вытесняющей параболы с ради-
радиусом носовой части a = p?/Re при значении константы
72:гф1> равном 2,326.
Второй член формулы G.43), таким образом, пред-
представляет силу на передней кромке. Конечно, силу можно
считать приложенной в этой точке только с точки зре-
зрения теории пограничного слоя. Действительно, эта
дополнительная сила должна быть результатом увеличе-
увеличения местного поверхностного трения по сравнению с зна-
значениями, даваемыми решением Блазиуса вблизи передней
кромки, где местное число Рейнольдса имеет порядок
единицы. О течении в этой области неизвестно ничего,
кроме того, что оно, вероятно, имеет форму C.24).
Сосредоточенная сила появится также и на передней
кромке конечной плоской пластины, поскольку это явле-
190
Гл. 7. Течение при больших числах Рейнольдса
ние представляет собой местный эффект. Это обстоя-
обстоятельство было, однако, упущено Го. С этими дополни-
дополнительными соображениями, пересматривая сделанное
прежде, следует заменить коэффициент 4,12 в формуле
G.40) на что-нибудь около 2,3. Результат опять-таки
находится в разумном соответствии с экспериментом,
если учесть еще некоторое возможное влияние третьего
приближения.
Может возникнуть вопрос, не появляется ли также
сосредоточенная сила на задней кромке. Естественно
считать, что это так, но в то время как передняя кромка
обращена к свободному потоку, задняя кромка укрыта
сравнительно толстым пограничным слоем. Вследствие
этого сила, возникающая на задней кромке, будет добав-
добавлять лишь член третьего порядка, пропорциональный
Re/2. Такое различие между передней и задней кром-
кромками отчетливо показано в численном решении для ко-
конечной плоской пластины, проведенном Янссеном [1].
7,11. Третье приближение для полубесконечной
пластины
Теория пограничного слоя в третьем приближении
рассматривалась только для полубесконечной пластины.
На этой стадии трудности, возникающие из-за неанали-
неаналитичности передней кромки, становятся еще более серьез-
серьезными. По этой, а также по другим причинам первые по-
попытки Олдена[1] и других исследователей были ошибоч-
ошибочными. Правильное решение было дано Гольдштейном [3]
и Имаи [4] и подробно изложено в книге Гольдштей-
на [4].
Во всех этих исследованиях использовались парабо-
параболические координаты ]), но мы можем получить резуль-
результат и в декартовых координатах. Третий член во внеш-
внешнем разложении, как легко видеть, исчезает, поскольку
1) Методом асимптотических разложений в параболических ко-
координатах задача о полубесконечной пластине решалась Н. Е. Ко-
чиным в работе «Задача об обтекании вязкой жидкостью полубеско-
полубесконечной пластины» (К о чин Н. Е., Собрание сочинений, т. II,
стр. 493—507, Изд-во АН СССР, 1949). Изложение этой работы
Н. Е. Кочина содержится также в известной книге: К о ч и и Н. Е.,
К и б е л ь И. А., Розе Н. В , Теоретическая гидромеханика,
часть II, стр 485—497, Физматгиз, F963. — Прим. ред.
7.11. Третье приближение; полубесконечная пластина 191
он представляет вытесняющий эффект второго члена в
пограничном слое, который обращается в нуль. Уравне-
Уравнение для третьего приближения в пограничном слое будет
иметь вид (поскольку 4^ = 0)
д /ш i ш w -i-W W W w —W W \
dY \ ZYYY* r ix^'dYY^ х1ГГ^Зх \Y^ 2>xY ^ UY Г SYJ—
Чтобы уравновесить неоднородные члены правой части,
во внутреннем разложении G.9) должен быть член, со-
содержащий А3 (Re) =1/Re3/2. Это приводит к задаче, ре-
решенной Олденом. Однако результирующая завихренность
оказывается убывающей только алгебраически для боль-
больших значений rj, что неприемлемо (см. § 7.5). Эта труд-
трудность обусловлена острой передней кромкой. На теле
аналитической формы корректно определенный погра-
пограничный слой существует, начиная с критической точки,
и экспоненциальное убывание завихренности получается
автоматически. Вблизи острой кромки пластины прибли-
приближение пограничного слоя непригодно. Оно становится
пригодным далеко вниз по потоку, однако экспоненци-
экспоненциальное убывание завихренности не обеспечивается и дол-
должно быть навязано как дополнительное условие.
Это достигается добавлением к W3 члена, содержа-
содержащего 1п#. Тогда, для того чтобы решение было незави-
независимо от L, должен существовать соответствующий член
вида
Таким образом, получится внутреннее разложение, име-
имеющее форму
G-45)
f32 Ol) , fsi '
Re1
3/2
Хотя задача лля f32 однородна, решением будет не нуль,
а первое собственное решение G.25). Экспоненциальное
убывание завихренности в f3\ может быть достигнуто
надлежащим выбором константы CL.
192 Гл. 7. Течение при больших числах Рейнольдса
Однако остается еще одна трудность. Решение для /3j
не единственно из-за первого собственного решения, и
не известно, как определить его константы. Таким обра-
образом, местный коэффициент поверхностного трения опре-
определяется как
Е51^+^г+- р-46)
а суммарное поверхностное трение (Имаи [4])—как
1,328 . 2,326 , 1ПО InRe^ 0,204 + 2С,
G.47)
где константа С\ неизвестна. Как показал Гольдштейн
[4], подобные же неопределимые константы появляются
ив приближениях высшего порядка. Они зависят от не-
некоторых деталей течения вблизи передней кромки. Мо-
Можно ли хотя бы в принципе определить их без точного
решения задачи, в настоящее время неизвестно. Имаи [4]
оценил величину Си склеивая G.47) при Rex==l с ре-
результатом приближения C.24) для передней кромки.
7.12. Влияние изменения координат пограничного слоя
Решение пограничного слоя можно скомбинировать
с внешним разложением для получения составного ре-
результата методами, описанными в § 5.10. Взамен этого
мы рассмотрим существенно иной путь построения един-
единственного равномерно пригодного разложения. Это пред-
предложенный Каплуном [1] метод оптимальных координат,
в котором независимые переменные изменяются так, что-
чтобы сделать решение пограничного слоя равномерно при-
пригодным.
Прежде всего мы должны выяснить, как влияет на
решение пограничного слоя изменение координат. Этот
вопрос оставался неясным в предыдущих параграфах,
когда мы рассматривали последние исследования полу-
полубесконечной плоской пластины, проведенные в параболи-
параболических, а не в традиционных декартовых координатах.
Положим, что все исследование Прандтля погранич-
пограничного слоя повторено в другой системе координат. Это
7.12 Влияние изменения координат пограничного слоя 193
значит, что уравнения Навье — Стокса записаны в новой
системе, функция тока и координата, нормальная к по-
поверхности, увеличены множителем Re1/2, осуществлен
предельный процесс Re->oo, результирующее уравнение
пограничного слоя решено при условии нулевой скорости
на поверхности и решение срощено с основным невязким
течением. Тогда окажется, что, хотя внешнее разложение
инвариантно, решение пограничного слоя не обладает
этим свойством, так что оно дает измененное поле те-
течения. Различные системы координат дают решения по-
пограничного слоя, которые идентичны на поверхности и
отличаются лишь незначительно внутри пограничного
слоя — так что поверхностное трение одинаково, — но мо-
могут сильно отличаться вне пограничного слоя.
По этой причине решение пограничного слоя обычно
пересматривается вне пограничного слоя, где оно заме-
заменяется невязким обтеканием, получаемым при сращива-
сращивании. Однако точка зрения Каплуна совершенно иная. Он
использует преимущества изменения координат, выбирая
специальную систему координат, в которой решение по-
пограничного слоя приближается к внешнему обтеканию
настолько близко, насколько это вообще возможно.
Нет необходимости повторять вывод решения погра-
пограничного слоя при изменении координат. Если решение
было вычислено в какой-либо удобной системе коорди-
координат, то соответствующий результат в какой-либо другой
системе определяется по простому правилу. Положим,
что решение пограничного слоя для установившегося
плоского обтекания какого-либо тела было вычислено в
координатах (х, у), которые не обязательно ортогональ-
ортогональны, но для удобства выбраны так, что форма тела опре-
определяется уравнением у = 0. Тогда так же, как для пло-
плоской пластины в § 7.8, три классических первых шага
метода пограничного слоя дают решение, верное до по-
порядка Re~1/2, в виде
для Re -> оо при фиксированных лг, у > О, G.48а)
(х, ууЩ+...
для Re->oo при фиксированных х, у У Re. G.486)
194 Г л 7 Течение при больших числах Рейнольдса
Теперь положим, что другая система координат (с-, rj)
введена так, что снова для удобства тело описывается
уравнением т] = 0. [Введенную здесь координату г\ сле-
следует отличать от переменной Блазиуса в формуле G.20)!]
Если преобразование регулярно на поверхности, то мы
получим разложение в ряды Тейлора
х = х&, л) = *F, 0) + 0(Л), G.49а)
У = УA,г\) = Wn ft, 0) + О (л2). G.496)
Поскольку внешнее разложение инвариантно при изме-
изменении координат, то его выражение в новых координа-
координатах находится просто применением преобразования
G.49) к формуле G.48а). Однако это неприменимо к ре-
решению пограничного слоя. Его новая форма находится
введением G.49) в G.486), разложением в ряд Тейлора
и отбрасыванием члена порядка Re во внутренних пе-
переменных. Таким образом, решение в новой системе ко-
координат должно иметь вид
Ч"
6, Л), У& Ч)]+у=Ых(Ъ Л).
G.50а)
Ь цг, [х (I, 0), ц /Те у- (|, 0)] + .... G.506)
/Re
Последнее решение представляет собой корреляционную
теорему Каплуна.
7.13. Различные системы координат
для плоской пластины
В декартовых координатах (х, у) решение погра-
пограничного слоя для полубесконечной пластины дается фор-
формулами G 37). Пусть введены параболические коорди-
координаты (?, ц) соотношениями
_ 2 h G.51)
Параболические координаты более естественны для этой
задачи (см. § 10.6), поскольку в отличие от декартовых
координат все тело и только тело описывается уравне-
7.13. Различные системы координат; плоская пластина 195
нием г] = 0. Они, следовательно, предпочтительнее для
этой задачи, так же как и для других задач математи-
математической физики, включающих в себя полуплоскость. При-
Приложение корреляционной теоремы G.50) дает решение
в параболических координатах в виде
З^-j- . . ., внешнее, G.52а)
) -+-..., внутреннее. G.526)
Упрощение результата очевидно. Более того, в то время
как в декартовых координатах завихренность погранич-
пограничного слоя бесконечна вдоль всей вертикальной линии
у
Рис. 7,8. Системы коорди-
координат для полубесконечной
пластины.
Вверху —параболические коорди-
координаты, внизу —сжатые прямоуголь-
прямоугольные координаты.
х=0, в параболических координатах она имеет особен-
особенность только в начале координат. Таким образом, видно,
что параболические координаты в этой задаче удобнее,
чем декартовы.
Поучительно рассмотреть третью систему, которая
окажется худшей, чем декартовы координаты. Она мо-
может быть определена как система «сжатых прямоуголь-
прямоугольных» координат (|, г]), изображенных в нижней части
рис. 7.8 и определяемых формулами
G.53)
196 Гл. 7. Течение при больших числах Рейнольдса
Применение корреляционной теоремы дает для решения
пограничного слоя в этой системе
-J^ Rea 11/ 21 + i (V 1 + 4л—l) + .... G.54а)
У Ке
Теперь мы исследуем поведение решения погранич-
пограничного слоя во внешней области в каждой из этих систем
координат. Образуем двучленное внешнее разложение
одночленного внутреннего разложения. Использование
асимптотической формы G.236) для функции Блазиуса
дает _
декартовы координаты: у _ У~х-\- .... G.55а)
У Re
о
параболические: grj — ¦ g-|- ¦••» G.556)
У Re
сжатые прямоугольные: т} —=• у 2f -|- • • • • G.55в)
К Re
Сравнение с соответствующими внешними разложениями
G.37а), G.52а) и G.54а) показывает, что параболиче-
параболические координаты воспроизводят два члена, декартовы
координаты — только один, а сжатые прямоугольные ко-
координаты— вообще ни одного. Соответственно мы ска-
скажем, что решение пограничного слоя в параболических
координатах содержит не только основное невязкое те-
течение, но и течение, обусловленное толщиной вытесне-
вытеснения. Решение пограничного слоя равномерно пригодно
до порядка Re~1/a, так что внешнее разложение излишне.
Координатные системы, обладающие таким свойством,
называются оптимальными.
В соответствии с этим определением декартовы коор-
координаты не являются оптимальными. Однако они ведут
к решению пограничного слоя, которое содержит основ-
основное невязкое течение и, следовательно, равномерно при-
пригодно до первого порядка. Мы можем, следовательно,
7 14. Определение оптимальных координат 197
сказать, что декартовы координаты полу оптимальны в
этой задаче. В противоположность этому решение по-
пограничного слоя в сжатых прямоугольных координатах
совершенно бесполезно во внешнем потоке.
7.14. Определение оптимальных координат
На идею об отыскании оптимальных координат Кап-
Каплуна натолкнул тот факт, что если уравнения Навье —
Стокса приближенно представить линеаризованными
уравнениями Озеена (гл. 8), то решение пограничного
слоя будет точным решением в параболических коорди-
координатах (упражнение 8.1). Это вместе с другими уже упо-
упомянутыми рассуждениями наводит на мысль, что парабо-
параболические координаты могут быть предпочтительными для
плоской пластины и в том случае, когда рассматривают-
рассматриваются полные уравнения Навье — Стокса; выше будет по-
показано, что это оказывается верным.
Возникает вопрос, как найти оптимальные коорди-
координаты для других форм. Очень простой ответ был дан
Каплуном. Найдем решение до порядка Re~1/2 в какой-
либо удобной системе координат (х, у)\ оно будет иметь
вид G.48). Тогда оптимальная координатная система
определится формулами
^опЛ-*' У) = Ф2С*:» У)> ЛоптС^» y) = ]\>i(x, у)- G.56а)
Оптимальные координаты не единственны, однако наи-
наиболее общий их вид следующий:
1опт(*> У) = Л[Ф2(*> У)Ь ,- с_ч
, , ч1 G.ODO)
Ф2(*> у)Ь
где F\ и F2 — произвольные функции.
В качестве примера рассмотрим снова полубесконеч-
полубесконечную пластину и решение пограничного слоя G.37) в де-
декартовых координатах. Используя обобщение G.566)
только для того, чтобы отбросить ненужный постоянный
множитель, мы получим из формулы G.56а)
y)=l, G57)
1^
198 Гл. 7. Течение при больших числах Рейнольдса
Эти координаты не ортогональны; ортогональная система
получится из G.566), если положить F2(^i) = 1/г|?2, что
дает параболические координаты G.51).
Каплун [1] приводит и другие примеры. Интересным
является случай течения, нормального к бесконечной
плоской стенке. Декартовы координаты здесь являются
оптимальными, и решение пограничного слоя удовлетво-
удовлетворяет полным уравнениям Навье — Стокса.
7.15. Развитие идеи оптимальных координат
Оптимальные координаты, возможно, существуют
также для теории пограничного слоя второго приближе-
приближения и приближений высшего порядка, хотя правила для
их нахождения еще неизвестны. Они, возможно, могут
быть найдены также для трехмерного и сжимаемого по-
пограничных слоев.
Более существенным было бы обобщение на другие
виды задач особых возмущений. Мы можем спросить,
например, могут ли быть найдены оптимальные коорди-
координаты для задач об обтекании тонкого профиля (см. гл.4).
Для простой проверки рассмотрим скорость на поверх-
поверхности эллипса с относительной толщиной 8 (рис. 4.2).
В соответствии с формулами G.48) двучленное внешнее
и одночленное внутреннее разложения D.13) и D.46)
принимают вид
для е->0 при фиксированном s > О, G.58а)
U
s
s
для ?->0 ПРИ фиксированном S==-y
G.586)
Замена абсциссы s, измеряемой от передней кромки, но-
новой координатой а, обращающейся в нуль вместе с я,
преобразует внутреннее решение G.586) к виду
ъ-V
'(%г- G-59)
Это аналог корреляционной теоремы Каплуна G.506).
Двучленное внешнее разложение этого выражения дает
просто единицу. Следовательно, в этом примере все
Упражнения 199
координаты являются полуонтнмальными и оптимальных
координат нет.
Подобное обстоятельство заслуживает дальнейшего
изучения, так же как и вопрос о связи между оптималь-
оптимальными координатами Каплуна и деформированными ко-
координатами Лайтхилла (гл. 6). Они объединяются идеей
достижения однородности путем изменения независимых
переменных. Их отличие на первый взгляд заключается
в том, что Каплун меняет внутренние координаты, в то
время как Лайтхилл деформирует внешние. Однако это
не очень существенно, поскольку имеется двойственность
в определении внутреннего и внешнего разложений
(§ 5.9). Более существенное различие обусловлено спо-
способом, которым определяются измененные координаты.
В то время как Каплун требует, чтобы внутреннее реше-
решение было возможно более пригодно во внешней области,
Лайтхилл налагает более грубое условие невозрастания
особенности. Вполне можно себе представить, что после
соответствующего обобщения и уточнения обоих методов
они окажутся двумя сторонами одной медали; см. также
§ Ю.4.
УПРАЖНЕНИЯ
7.1. Пограничный слой на клине. Рассмотрите симметричное
вязкое обтекание полубесконечного клина с углом раствора |3я. Най-
Найдите потенциальное течение и укажите, как должно быть изме-
изменено условие в набегающем потоке G.2г) для уравнений Навье —
Стокса. Обсудите возможность применения решений пограничного
слоя как возмущения координат и как возмущения параметра.
Используя групповое свойство, покажите, что уравнение погранич-
пограничного слоя Прандтля G.16а) может быть сведено к уравнению
Фолкнера — Скен
Считая заданными необходимые численные свойства функции /, най-
найдите течение, обусловленное толщиной вытеснения. Найдите орто-
ортогональные оптимальные координаты. Определите решение погранич-
пограничного слоя второго порядка. Имеется ли сосредоточенная сила на
передней кромке?
7.2. Пограничный слой на плоской пластине в течении со сдви-
сдвигом. В качестве модели влияния внешней завихренности на погра-
пограничный слой рассмотрите полубесконечную плоскую пластину под
нулевым углом атаки в параллельном потоке с постоянной завихрен-
завихренностью; скорость потока U — cot/. Сформулируйте задачу для вто-
200 Гл. 7. Течение при больших числах Рейнольдса
рого приближения в пограничном слое, показав, что условие сра-
сращивания имеет вид
Ч'2 (*, У) ~аУ2 + ЬУ+ОA) при У -> со.
Покажите, что из-за взаимодействия между эффектом вытеснения
и внешней завихренностью возникает градиент давления второго по-
порядка для пограничного слоя. Сведите задачу к обыкновенному
дифференциальному уравнению третьего порядка с соответствую-
соответствующими граничными условиями. (Четкое исследование этой спорной
задачи вместе с ссылками на более ранние работы дано Мер-
реем [1].)
7.3. Обратная задача пограничного слоя. Положим, что мы ре-
решаем обратную, а не прямую задачу теории пограничного слоя
в следующем смысле: мы ищем тело, которое обусловливает данное
невязкое течение вне пограничного слоя. Объясните, почему асимпто-
асимптотические последовательности для внутреннего и внешнего разложе-
разложений не являются последовательными степенями Re~'/2, как в прямой
задаче. Проведите решение так далеко, как только возможно прак-
практически для верхней поверхности тела, чтобы вне пограничного слоя
получилось равномерное параллельное течение
7.4. Корреляционная теорема второго порядка. Покажите, что
аналогом правила GJ506) для задачи второго порядка является
ф--^^^, о),
+ УЖ цхц F, 0) Wu [ ] -f 1 Re r)^ (g, 0) Viy[ ] J ,
где все квадратные скобки содержат те же аргументы, что и первая.
7.5. Скользящий подслой. Если на поверхности допускается
малое скольжение, то второе из граничных условий G.166) заме-
заменяется следующим:
ЧГ1Г(х. 0) = е?1КК(х, 0), e<;i.
Найдите решение пограничного слоя для полубесконечной плоской
пластины до порядка 8, возмущая решение для 8 = 0. Обратите вни-
внимание на то, что возмущение представляет собой производную по У
от основного решения (Линь Дун-цзи и Шаф fl]). Покажите, что
это приближение непригодно в тонком подслое вблизи поверхности.
Постройте первый член дополнительного разложения, пригодного
в этой области.
Глава 8
ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
ПРИ МАЛЫХ ЧИСЛАХ
РЕЙНОЛЬДСА
8.1. Введение
Рассмотрим теперь обтекание тел поiоком несжима-
несжимаемой жидкости при малых числах Рейнольдса на приме-
примерах сферы и кругового цилиндра (рис. 8.1).
Рис. 8Л, Обозначения с/=1
для сферы и кругового i ^>
цилиндра. _ /
Любой студент знаком с вычислениями Милликена
сопротивления капли масла при помощи приближения,
развитого Стоксом в 1851 г.:
р D ^ 6я р L/a ~ (R ] \
Второе приближение было найдено Озееном в 1910 г.:
+ |-Re). (8.16)
Однако только в 1957 г. было показано, как можно
вычислить последующие члены, используя метод сращи-
сращиваемых асимптотических разложений [см. формулу (\А)].
Классический признак особого поведения здесь отсут-
отсутствует: производные высшего порядка сохраняются в
уравнениях Навье — Стокса в пределе при Re->0. Од-
Однако задача содержит две характерные длины: радиус a
и вязкую длину v/U. Их отношение представляет собой
число Рейнольдса, так что в пределе при Re->0 вязкая
длина становится значительно большей, чем радиус тела.
202
Гл. 8. Течение при малых числах Рейнольдса
Следовательно, можно предвидеть особое поведение в
соответствии с физическим критерием, указанным в
§ 5.3.
Вязкие течения при малых числах Рейнольдса легко
наблюдать экспериментально в противоположность слу-
случаю больших чисел Рейнольдса. На рис. 8.2 представ-
представлена последовательность картин течения ^ля сферы или
Рис. 8.2. Схема течения около сферы или кругового цилиндра
при малых числах Рейнольдса.
а —безвихревое течение, б —стационарные вихри, в— нестационарное течение.
кругового цилиндра по мере увеличения числа Рей-
Рейнольдса. При очень малых скоростях картина линий тока
почти симметрична. При числах Рейнольдса около
Двухчленное разложение
С токса для Re = оо
С фотографии Танеды [1],
Рис. 8.3. Форма стационарного вихря позади сферы.
Re=10 для сферы и Re = 2,5 для цилиндра (наши
числа Рейнольдса построены по радиусу, а не по диа-
диаметру) появляются замкнутые циркуляционные области
спутного потока или стационарные вихри. Можно пред-
представить себе, что эти вихри существуют всегда внутри
тела и при этих числах Рейнольдса проникают через
8 2. Решение Стокса для сферы и кругового цилиндра 203
поверхность тела (рис. 8.3). При числах Рейнольдса
около Re = 65 для сферы и Re=15 для цилиндра течение
становится нестационарным и сопровождается колеба-
колебаниями спутного потока. Течение становится нерегуляр-
нерегулярным, и начинается отрыв вихрей при числах Рейнольдса
около Re=100 для сферы и Re = 20 для цилиндра.
8.2. Решение Стокса для сферы и кругового цилиндра
Стоке указал, что при малых скоростях силы инер-
инерции, представленные конвективными членами в уравне-
уравнениях Навье — Стокса, мало существенны, поскольку они
имеют порядок квадрата скорости. Следовательно, при
малых числах Рейнольдса силы давления должны при-
приблизительно уравновешиваться одними вязкими силами.
В первом приближении Стоке отбросил конвективные
члены. В результате этого для плоского течения полу-
получается бигармоническое уравнение для функции тока
Этот результат формально следует из уравнения G.2а)
при Re->0. Соответствующий результат для осесимме-
тричного течения таков:
2 , sin 0 д ( 1 д
Пусть длины сделаны безразмерными путем отнесения
их к радиусу а и скорости — отнесением к скорости набе-
набегающего потока U (рис. 8.1). Тогда граничное условие
обращения в нуль скорости на поверхности примет вид
в) = фгA, 6) = 0, (8.3а)
а условие равномерности набегающего потока — вид
( г sin 0 для плоского
течения,
{ . при г->оо. (8.36)
— г2 sin2 G для осесимме-
2 тричного течения
В случае цилиндра нужно еще добавить условие симмет-
симметрии для исключения циркуляции.
204 Гл. 8. Течение при малых числах Рейнольдса
Рассмотрим сначала обтекание сферы. Условие (8.36)
в набегающем потоке подсказывает, что нужно разде-
разделить переменные и искать решение в виде \|) = sin29f (г).
Это приводит к следующему:
', г2, г, -Ц. (8.4)
Условие в набегающем потоке показывает, что здесь
не должно быть члена с г4 и что коэффициент члена с г2
равен 1/2. Тогда из условия на поверхности (8.3а) опре-
определяются коэффициенты при г и \\г и получается при-
приближение Стокса
j( }) (8.5)
Первый член соответствует равномерному потоку, а тре-
третий— диполю в центре сферы, причем оба дают безвих-
безвихревое течение. Второй член, который представляет всю
завихренность, Ханкок [1] назвал «стокслетом»; Ханкок
использовал линейное распределение этих трех элемен-
элементов для того, чтобы построить модель движения плыву-
плывущего червя. Для невязкого течения стокслет отсутствует
и коэффициент при диполе равен —1/2 вместо 1/4. Вы-
Вычисление поверхностного трения дает 2/3 от сопротив-
сопротивления (8.1а); остающаяся треть представляет собой
сопротивление давления (Томотика и Аои [1]). Картина
течения симметрична впереди и сзади тела, и вихри от-
отсутствуют, как на рис. 8.2, а.
Рассмотрим теперь круговой цилиндр. Условие в на-
набегающем потоке (8.36) наводит на мысль искать реше-
решение в виде \|) = sin8f (г), что приводит к выражению
ф = sin в|г3, rlnr, г,М. (8.6)
Наложение условия (8.3а) на поверхности сводит это к
следующему:
± — -| г*] sin в. (8.7)
Мы можем привлечь принцип минимальной особенности
(§ 4.5), выбирая /г = 0, так что функция тока и скорость
8.3. Парадоксы Стокса и Уайтхеда 205
возрастают с ростом г как можно медленнее; тогда
ф~C(r In r-^ + y7Jsin9' (8-8)
Второй член соответствует равномерному параллельному
потоку, третий — диполю в центре круга, а первый пред-
представляет собой двумерный стокслет, содержащий всю
завихренность. Однако решение не может быть завер-
завершено, поскольку ни при каком выборе константы С не
удовлетворяется условие (8.36) в набегающем потоке.
Трудность состоит в том, что в противоположность реше-
решению для сферы стокслет здесь обладает большей особен-
особенностью на бесконечности, чем равномерный поток, и обу-
обусловливает таким образом существование неограничен-
неограниченных скоростей вдали от тела.
8.3. Парадоксы Стокса и Уайтхеда
Отсутствие решения уравнения Стокса для плоского
обтекания любого цилиндрического тела неограничен-
неограниченным потоком известно как парадокс Стокса, Сам Стоке
[1] считал его указанием на отсутствие установившегося
течения; тело, движущееся из состояния покоя, вовлек-
вовлекло бы в движение непрерывно увеличивающееся коли-
количество жидкости. Однако это объяснение теперь при-
признано неверным (см. следующий параграф).
В действительности аналогичные трудности возни-
возникают и для трехмерных тел, хотя они и отодвигаются ко
второму приближению для конечных тел, поскольку, как
обычно, возмущения для трехмерных течений являются
более слабыми, чем для двумерных. (Относительно об-
обтекания полубесконечных тел см. упражнение 8.2.) Так,
Уайтхед[1] потерпел неудачу при попытке улучшить при-
приближение Стокса для сферы путем итераций. Полные
уравнения Навье — Стокса дают (Гольдштейн [2]):
'о w - 4v ж +2 ct§е *' ~2 ?)№»'
(8.9а)
где
гJ , sin 0 d I 1 д \ /а „...
Ь() <8-96)
206 Гл. 8. Течение при малых числах Рейнольдса
Подстановка первого приближения (8.5) в конвективные
члены правой части уравнения (8.9а), которые были от-
отброшены Стоксом, дает итерационное уравнение
Г д2 , sin9 _д_ ( 1 jM]2 __
[дг2 ~^ г2 00 UinO дд)\ ф"~
A^)os6. (8.10)
Легко найти частное решение, которое удовлетворяет
условиям на поверхности (8.3а),
^). (8.11)
Однако скорость не ведет себя надлежащим образом на
бесконечности и не существует дополнительной функции,
которая могла бы быть добавлена для ее исправления.
В следующем приближении скорость обратилась бы в
бесконечность на бесконечности, как в первом прибли-
приближении (8.8) для кругового цилиндра.
Отсутствие второго приближения к решению Стокса
для обтекания трехмерных тел неограниченным потоком
известно как парадокс Уайтхеда. Сам Уайтхед рассма-
рассматривал его как указание на возникновение разрывов
в поле течения, связанных с образованием застойной
зоны. Однако это объяснение также признано теперь
несостоятельным.
8.4. Приближение Озеена
Подобно тому как парадокс Даламбера был разре-
разрешен указанием Прандтля на то, что при больших числах
Рейнольдса течение становится задачей особых возму-
возмущений, парадоксы Стокса и Уайтхеда, как показал Озе-
ен, обусловлены особой природой течения при малых
числах Рейнольдса. В то время как область неоднород-
неоднородности при больших числах Рейнольдса представляет со-
собой тонкий слой вблизи поверхности тела, при малых
числах Рейнольдса она является окрестностью бесконеч-
8.4. Приближение Озеена 207
но удаленной точки. Источник трудностей может быть
обнаружен исследованием относительной величины чле-
членов, отброшенных в приближении Стокса.
Как следует из правой части уравнения (8.10), нели-
нелинейные конвективные члены вдали от тела имеют поря-
порядок Re/r2. Типичный вязкий член — произведение опера-
операторов в левой части уравнения (8.10)—в приближении
(8.5) выглядит так:
д2 Г sin G д ( 1 д У] . / 3
Таким образом, отношение отброшенных членов к сохра-
сохраненным таково:
Конвективные члены ^ /п ч /о 1 о\
Вязкие члены = O(Rer) при г->оо. (8.13)
Хотя это отношение мало вблизи тела при малых Re,
оно становится сколь угодно большим на достаточно
больших расстояниях несмотря на малость Re. Таким
образом, приближение Стокса становится непригодным,
когда произведение Re r имеет порядок единицы. Это
происходит на расстояниях порядка v/t/, причем нужно
иметь в виду, что вязкая длина является тогда сущест-
существенным характерным размером. Аналогичная трудность
еще в большей степени возникает для плоских течений,
где незавершенное приближение Стокса (8.8) для ци-
цилиндра дает оценку
Конвективные члены = Q Q
Вязкие члены v ' F v '
Эти неоднородности являются источником особого
поведения приближения Стокса. В трехмерных течениях
трудности замаскированы, поскольку первое приближе-
приближение ведет себя достаточно хорошо. В области неоднород-
неоднородности, где Re/*= 0A), скорость достигает своего значе-
значения в набегающем потоке, так что оказывается возмож-
возможным наложить граничные условия в набегающем потоке.
Это — исключительный случай, который встречался уже
прежде во внутреннем решении для профиля с закруг-
закругленной носовой частью (см. § 5.6).
208 Гл 8 Течение при малых числах Рейнольдса
Это объяснение парадоксов Стокса и Уайтхеда было
предложено Озееном [1], одновременно указавшим и вы-
выход из положения: вместо того чтобы отбросить все кон-
конвективные члены, он заменил их линеаризованной фор-
формой, пригодной вдали от тела, где появляются трудности.
Например, в уравнении движения вдоль оси х в декарто-
декартовых координатах
иих -\-vay+- wuz + -у = v (ихх + иуу + u2Z) (8Л5)
Стоке вообще отбрасывает первые три члена, а Озеен
заменяет их приближенно величиной Uux. Тогда в пло-
плоском течении безразмерное уравнение G.2а) для функ-
функции тока принимает вид
— Re -^-) V2ip = 0. (8.16)
Это дает специально подобранное для этой задачи одно-
однородное приближение вида, который будет обсужден
ниже (см. § 10.2). Основная идея состоит в том, чтобы
обнаружить те члены, пренебрежение которыми в пря-
прямом возмущенном решении приводит к неоднородности,
и по мере возможности сохранить их после упрощения
в области неоднородности. Если получающиеся уравне-
уравнения могут быть решены, то результатом будет равномер-
равномерно пригодное составное приближение, такое, как рассма-
рассматривалось в § 5.4.
Таким образом, уравнения Озеена дают равномерно
пригодные первые приближения как для плоского, так и
для трехмерного течений при малых числах Рейнольдса.
В принципе можно было бы улучшить решение последо-
последовательными приближениями, и результат, вероятно, со-
сохранял бы пригодность на каждой стадии. Однако
практически, несмотря на линейность уравнений Озеена,
их решение достаточно сложно, так что второе прибли-
приближение до сих пор неизвестно. Проще разбить составное
разложение на составляющие его внутреннее и внешнее
разложения, которые впоследствии могут быть вновь
объединены. Этот процесс будет осуществлен в следую-
следующих параграфах.
Уравнения Озеена допускают иную, существенно от-
отличную интерпретацию. При произвольных числах Рей-
8.4. Приближение Озеена 209
нольдса они описывают вязкое течение на столь больших
расстояниях от конечного тела, что скорость прибли-
приближается к ее значению в свободном потоке. С этой точки
зрения теории малых возмущений приближение Озеена
было использовано для изучения спутного потока вдали
от тела (упражнения 8.1 и 8.3). В таком приложении ур
в уравнении (8.16) обычно представляет не полную
функцию тока, а ее возмущение, причем это изменение
влияет только на вид граничных условий. Эта вторая
интерпретация приближения Озеена, естественно, остает-
остается пригодной и при малых числах Рейнольдса и будет
использована нами в дальнейшем.
Решение уравнений Озеена для сферы было дано са-
самим Озееном [1] в виде
|^)/2]e (8Л7)
Решение для кругового цилиндра было дано Ламбом [1]
для компонент скорости в декартовых координатах. На-
Например, компонента, нормальная к невозмущенному по-
потоку, имеет вид
1 j sin 20
У* ~ In D/Re) — у + 1/2 \ 2r2 ~^
()]} (8.18)
Здесь y = 0,5772... — постоянная Эйлера, а Ко — функция
Бесселя.
В обоих этих решениях условия на поверхности были
удовлетворены только приближенно в рамках основного
предположения, что числа Рейнольдса малы. Мы позже
реконструируем эти результаты. Решения для произволь-
произвольных чисел Рейнольдса были получены Гольдштейном [1],
а также Томотика и Аои [1]. Эти более сложные резуль-
результаты имеют ограниченное значение, поскольку вопреки
мнению самого Озеена они столь же хороши качествен-
качественно, сколь непригодны количественно при больших чис-
числах Рейнольдса. Например, приближение Озеена дает
пограничный слой, толщина которого имеет порядок Re~r,
210 Га 8 Течение при малых числах Рейнольдса
а не Re~1/2, как в правильной теории Прандтля. С физи-
физической точки зрения это расхождение можно объяснить
тем обстоятельством, что в приближении Озеена завих-
завихренность, образованная на поверхности тела, переносит-
переносится в большей степени поперек потока, чем вдоль поверх-
поверхности. Детали картины течения, вычисленные Томотика и
Аои, представляли бы некоторый интерес, если бы Яма-
да [1] не указал, что численные неточности искажают их
качественный характер даже при малых числах Рей-
Рейнольдса. Например, Томотика и Аои предсказали суще-
существование стационарных вихрей (рис. 8.2,6) при произ-
произвольно малых числах Рейнольдса, в то время как Ямада
показал, что в приближении Озеена эти вихри появляют-
появляются позади кругового цилиндра, начиная лишь с Re= 1,51.
8.5. Второе приближение вдали от сферы
Теперь мы улучшим решение Стокса для сферы при-
приложением метода сращиваемых асимптотических разло-
разложений. Наше изложение по идее следует Каплуну и Ла-
герстрому [1], однако по обозначениям ближе к исследо-
исследованию Праудмена и Пирсона [1].
Будем считать приближение Стокса (8.5) главным
членом асимптотического разложения для малых чисел
Рейнольдса, которое мы назовем разложением Стокса.
Мы видели, что этот ряд непригоден вдали от тела, где г
имеет порядок Re. Поэтому введем надлежащим обра-
образом сжатую радиальную координату р, положив
p = Rer, (8.19)
и рассмотрим второе асимптотическое разложение, при-
пригодное в отдаленной области. Мы назовем его разложе-
разложением Озеена, поскольку течение далеко от тела пред-
представляет собой малое возмущение равномерного потока,
В соответствии с соглашением, принятым в § 5.9, разло-
разложение Озеена является внешним разложением, а разло-
разложение Стокса — внутренним. Соответственно выберем
обозначения, за исключением радиального переменного:
поскольку обозначение R для него неуместно1), мы бу-
х) В английском издании R означает число Рейнольдса. — Прим.
ред.
8.5. Второе приближение вдали oi сферы 211
дем использовать р для внешнего и г для внутреннего
переменного.
Мы могли бы, как в предыдущей главе, записать два
разложения, оставив неопределенными их асимптотиче-
асимптотические последовательности. Однако мы предпочитаем по-
показать, как сращивание автоматически определяет фор-
форму каждого члена в том случае, когда, как в этой про-
проблеме, оно производится в соответствии с обычным
порядком (§ 5.9).
Записывая решение Стокса (8.5) в переменных Озе-
ена (8.19) и производя разложение для малых Re, полу-
получаем в качестве двучленного разложения Озеена
2-Озеен A-Стоке) ф = у "^гР2 sin2 9 — -| -^-р sin2 0, (8.20)
где первый член соответствует однородному потоку. Ис-
Исходя из возможности сращивания, разложение Озеена
следует представить в виде
*р281п20 +
для Re—>0 при фиксированном р. (8.21)
Подстановка в полное уравнение (8.9) дает для ф2 клас-
классическое линеаризованное уравнение Озеена (8.16)
в виде
(«02_coee?+«j?^)i0»fc = O, (8.22а)
где
Полагая
= е'/2 Re xih =
сводим уравнение (8.22) к следующему:
2 = 0. (8.24)
Разыскивая, как и прежде, решение вида ср2= sin2Of (p),
получаем
212 Гл. 8. Течение при малых числах Рейнольдса
Решение, обращающееся в нуль на бесконечности,
будет
-р/2. (8.26)
Любое другое решение уравнения (8.24), обладающее со-
соответствующей симметрией, имеет большую особенность
в начале и, следовательно, может быть исключено как
несращиваемое по принципу минимальной особенности
(§ 5.6).
Таким образом, исходное уравнение (8.22) для \|J
сводится к следующему:
Ib-p(l-cos0)/2sin2 0g (8.27)
Его частным решением является функция
ф2 = — 2с2 A + cos 9) [1 — e-P(i-cos0)/2jj (8.28)
где первый член представляет потенциальный источник
в начале, который прибавлен для того, чтобы компенси-
компенсировать сток, соответствующий второму члену, и свести,
таким образом, к нулю поток через любую поверхность,
охватывающую тело. Любая другая дополнительная
функция, обладающая этим свойством, не дающая ско-
скорости на бесконечности и имеющая нужную симметрию,
будет иметь в начале особенность более высокого по-
порядка и, следовательно, окажется несращиваемой.
Полученное выражение является фундаментальным
решением уравнения Озеена, описывающим поле возму-
возмущений, образованное на больших расстояниях любым
конечным трехмерным телом с нулевой подъемной силой.
Постоянная с2 зависит от некоторых деталей течения
вблизи тела; мы найдем ее, используя принцип асимп-
асимптотического сращивания E.24), Записывая разложение
Озеена (8.21) в переменных Стокса и разлагая в ряд
для малых Re, получаем
1-Стокс B-Озеен) i|> =* у г2 sin2 9 — c2r sin2 Э (8.29)
Это решение сращивается с решением (8.20), если по-
постоянная с2 равна 3/4.
8.6. Второе приближение вблизи сферы 213
Таким образом, мы нашли два члена в разложении
Озеена (8.21). Переписанное в переменных Счокса, оно
принимает вид
l|>~-i Г* Sin2 0 -1 JL A + COS 0) [1 _^-Re M1-COS0V2]
для Re->0 при фиксированном Re г. (8.30)
Мы можем построить равномерно пригодное составное
разложение, комбинируя полученный результат с при-
приближением Стокса (8.5) по правилу E.32) для аддитив-
аддитивного составления. Результат дает равномерное прибли-
приближение для поля возмущений. Он является решением
(8.17) уравнения Озеена, найденным самим Озееном.
Это подтверждает установленный в § 8.4 факт, что ли-
линеаризованные уравнения Озеена дают равномерное пер-
первое приближение. Вблизи тела последний член в реше-
решении (8.17) обращается в стокслет приближения Стокса;
по аналогии его можно назвать «озееплетом».
8.6. Второе приближение вблизи сферы
Перейдем ко второму члену в разложении Стокса.
Двучленное разложение Стокса разложения Озеена
(8.21) таково:
2-Стокс B-Озеен) ф = j (Bг2 — 3r) sin2 9 -f
4™Rer2(l — cos 0) sin2 9. (8.31)
Для возможности сращивания разложение Стокса долж-
должно иметь вид
I) eW2(r, 9)+... . (8.32)
Уравнение для W2, очевидно, представляет собой уравне-
уравнение Уайтхеда (8.10) без множителя Re. Его частное ре-
решение (8.11) остается пригодным, и исходное приближе-
приближение Стокса (8.5) определяет единственную дополнитель-
дополнительную функцию с нужной симметрией, которая имеет на
214 Гл 8. Течение при малых числах Рейнольдса
бесконечности не большую особенность. Таким образом,
мы положим
?2= С2Bг2 - Зг + 1) sin2 в —
— —- Bг2 — Ъг + 1 — у + 4f) sin2 6 cos 9. (8.33)
Постоянная С2 находится сращиванием. Осуществляя
разложение Озеена для (8.32), находим
2-Озеен B-Стокс) ф =
(8.34)
Это выражение сращивается с (8.31), если С2 = 3/32.
Таким образом, мы нашли два члена разложения
Стокса для функции тока в окрестности сферы:
_| ReB + 1+-^) cos в]. (8.35)
Это выражение обращается в нуль не только на сфере
и вдоль оси симметрии, но также и вдоль кривой
2г2-\-г
Это уравнение приближенно описывает границу стацио-
стационарного вихря. Она построена на рис. 8.3. Вихрь появ-
появляется только при числах Рейнольдса настолько боль-
больших, что нельзя ожидать пригодности разложения Сток-
Стокса. Тем не менее оно поразительно точно согласуется с
экспериментальными данными Танеды [1] при Re = 36,6
(см. нижнюю часть рис. 8.3). Нижний по потоку конец
вихря расположен при
r,=4(/l+3Re-l). (8.37)
Следовательно, вихрь впервые появляется в поле тече-
течения при Re = 8. Если не говорить о его интенсивности, то
8.6. Второе приблио/сение вблизи сферы
215
это хорошо согласуется со значением 12, замеренным
Танедой, и со значением 8,5, найденным численно Джен-
соном [1], который использовал полные уравнения
Навье — Стокса. В действительности хорошее соответ-
соответствие сохраняется вплоть до Re = 60 (рис. 8.4), что близ-
близко к предельному значению, при котором еще наблю-
наблюдается установившееся течение. Этот замечательный ре-
результат нуждается в подтверждении путем исследования
влияния следующих членов разложения Стокса.
60 х
20
2 3
i/o
Рис. 8.4. Протяженность вихревой зоны за сфе-
сферой.
двучленное разложение Стокса, О экспериментальные
данные Танеды /1], Ц численные результаты Джексона |1].
Приближения высшего порядка могут быть найдены
продолжением предыдущего анализа. Праудмен и Пир-
Пирсон [1] провели его достаточно далеко для того, чтобы
показать, что следующие приближения Стокса содержат
члены вида Re2 In Re наряду с Re2 и что логарифмы,
таким образом, входят в разложение Озеена, начиная
с Re3 In Re. Они вычислили только член Re2 In Re в раз-
разложении Стокса, что дало формулу A.4) для сопротив-
сопротивления (см. гл. 1).
216 Гл. 8. Течение при малых числах Рейнольдса
В соответствии с этими результатами число Рей-
Рейнольдса, при котором появляется вихрь, является ре-
решением трансцендентного уравнения
l--^Re + ^Re2lnRe + O(Re2) = 0. (8.38)
К сожалению, это уравнение не имеет действительного
корня, если не отбросить в нем ни одного из трех чле-
членов. Логарифмический член ограничивает разложение
Стокса значениями Re, малыми по сравнению с едини-
единицей. До тех пор пока не найдены методы увеличения
диапазона приложимости таких рядов (см. § 10.7), мы
не можем сказать, является ли поразительная точность
второго приближения Стокса чем-то большим, чем про-
простое совпадение.
Вследствие симметрии второй член в квадратных
скобках в уравнении (8.35) ничего не добавляет к сопро-
сопротивлению, которое в соответствии с первым членом пре-
превосходит значение, указанное Стоксом, в A+3/8 Re) раз.
Но второй член является частным решением Уайтхеда
для нелинейных членов; по этой причине приближение
Озеена, в котором отброшены нелинейные члены вблизи
тела, тем не менее дает сопротивление, верное до вто-
второго порядка, по крайней мере для симметричных тел
(Честер [4]).
8.7. Приближения высшего порядка
для кругового цилиндра
Парадокс Стокса для плоского течения более порази-
поразителен, чем парадокс Уайтхеда для случая трех измере-
измерений. Поэтому его разрешение методом сращиваемых
асимпотических разложений более существенно, несмот-
несмотря на практический недостаток, заключающийся в том,
что решение не может быть проведено с большой точ-
точностью. Мы исследуем типичный пример кругового ци-
цилиндра, объединяя метод работы Каплуна [2] и Прауд-
мена и Пирсона [1].
Исследование в основном аналогично исследованию
обтекания сферы, однако в нем появляются интересные
руличия. В частности, сращивание проходит на пределе
8.7. Приближения высшего порядка; круговой цилиндр 217
возможного и соответственно асимптотическая последо-
последовательность меняется медленно. Именно для этой задачи
Каплун и Лагерстром [1] изобрели свой изощренный ап-
аппарат промежуточных пределов и разложений и принцип
промежуточного сращивания (§ 5.8). Однако мы увидим,
что принцип асимптотического сращивания E.24) вполне
достаточен, хотя простой принцип предельного сращива-
сращивания E.22) ока. -мвается непригодным.
В качестве первого члена разложения Стокса рассмо-
рассмотрим решение (8.8) бигармонического уравнения
при Re—>0 для фиксированного г. (8.39)
Следует допустить, что множитель А\ зависит от числа
Рейнольдса, поскольку наша асимптотическая последо-
последовательность не определена. Хотя это приближение не
может удовлетворить условию (8.36) равномерного по-
потока на бесконечности, его можно срастить с равномер-
равномерным потоком, рассматриваемым как первый член разло-
разложения Озеена (Лагерстром и Коул [1], § 6.3). Перемен-
Переменное Озеена вновь взято в виде p = Rer, так что длины
отнесены к вязкой длине v/U, а не к радиусу а. То-
Тогда разложение Озеена начинается с члена, соответст-
соответствующего невозмущенному потоку,
ф — "JUT P Sin G —|— ... при Re -> О для фиксированного р > 0.
(8.40)
Записывая приближение Стокса (8.39) в переменных
Озеена и производя разложение, получаем
1-Озеен A-Стокс) \\> = ^^ 1п Ж Р Si° °* (8*41)
Это разложение сращивается с разложением (8.40), ко-
когда Ai(Re) = (ln I/Re), или в более общем случае, ко-
когда Ai(Re) = (In l/Re + й), где k — любая постоянная;
позже мы используем эту свободу выбора.
Перекрытие в этом случае настолько мало, что для
того, чтобы осуществить сращивание, мы должны допу-
допустить относительную ошибку порядка Аь что ненормаль-
ненормально по сравнению с ошибкой порядка Re в приближении
218 Гл. 8. Течение при малых числах Рейнольдса
Стокса для сферы. Таким образом, мы имеем дело с
медленным разложением по степеням Дь в котором бес-
бесконечное число членов соответствует только одному пер-
первому члену для сферы.
Дальнейшее разложение приближения Стокса (8.39)
в переменных Озеена дает
2-Озеен (ЬСтокс) Ф = -^ [l +^i (Re) (in p — k — "§•)] P sin 9*
(8.42)
Из этого следует, что для осуществимости сращивания
разложение Озеена (8.40) должно продолжаться так:
*~-^-[psine + A1(Re)*2(p, 9)+ ...]. (8.43)
Подстановка этого разложения в полное уравнение
G.2а) показывает, конечно, что фг удовлетворяет лине-
линеаризованному уравнению Озеена (8.16). Подходящее ре-
решение может быть найдено так же, как и в случае сферы
(Праудмен и Пирсон [1]). Однако вводить функцию тока
здесь бесполезно, поскольку ее можно записать только
в виде бесконечного ряда, в то время как компоненты
скорости определяются замкнутыми выражениями.
Мы, очевидно, нашли для плоского течения аналог
решения (8.28), причем озеенлет в нем представлен воз-
возмущениями, вызванными бесконечно малым сопротив-
сопротивлением в начале координат. Это фундаментальное ре-
решение, данное Озееном (Розенхед [1]), определяет
декартовы компоненты скорости в виде
д (р sin 9)
yp)}, (8.44a)
(8.446)
Член с In p представляет опять потенциальный источник
в начале, который уравновешивает сток, соответствую-
8.7. Приближения высшего порядка; круговой цилиндр 219
щий слагаемому, содержащему функцию Бесселя KQ.
Для малых р имеет место приближенное представление
д (р sin 0) ^2 У'1 У г ' ^wo " ) г ^ vr iXI г;' ("-45а)
d ^2s Q. — с2 sin G cos 6 + О (р In p), (8.456)
где 7 = 0,5772... — постоянная Эйлера. Интегрирование
этих уравнений дает
(8.46)
Используя этот результат, находим, что разложение
Озеена (8.43) ведет себя вблизи тела следующим обра-
образом:
1-Стокс B-Озеен) ф =
(8.47)
Тогда сращивание с разложением (8.42) в соответствии
с принципом асимптотического сращивания дает с2= 1.
Второй член в разложении Стокса (и вообще любой
член конечного порядка), очевидно, снова является ре-
решением бигармонического уравнения, поскольку нели-
нелинейные члены порядка Re трансцендентально малы в
масштабе степеней Ai(Re). Сращивание или приложение
принципа минимальной особенности показывает, что
каждый из этих членов представляет собой кратное пер-
первого приближения (8.8). Удобнее, следуя Каплуну [2],
устранить второй член путем такого выбора постоян-
постоянной k, что разложения (8.42) и (8.47) сращиваются со-
совершенно: & = 1п4—y+1/2- Тогда разложение Стокса
предполагается в виде
rlnr — -хГ +-9- — JsinG,
где
Образовав при помощи аддитивного составления разло-
разложений (8.43) и (8.48) равномерно пригодное двучленное
220
Гл. 8. Течение при малых числах Рейнольдса
составное разложение, мы воспроизведем решение Лам-
ба (8.18) линеаризованного уравнения Озеена.
О 0,2 0,4 0,6 0,8 1,0 f,2 1,4
Рис. 8.5. Сопротивление кругового цилиндра при
малых числах Рейнольдса.
первый член разложения (8.49), два члена разло-
разложения (8.49), полное решение уравнения Озеена,
О экспериментальные данные Триттона A].
Каплун [2] продолжил этот процесс еще на один цикл
и нашел коэффициент третьего члена разложения Стокса
(8.48) а3~—0,87; соответственно для коэффициента со-
сопротивления он получил выражение
D ~-g-[Ai(Re)-O,87Aj(Re) + 0(AOl. (8.49)
Упражнения 221
Первый член дает классический результат Ламба [1, 2].
Сравнение с измерениями Триттона [1] показывает пре-
предел полезности этого результата (рис. 8.5). На том же
рисунке для сравнения показаны результаты Томотика и
Аои [1] полного численного решения линеаризованного
уравнения Озеена (8.16).
С формально математической точки зрения мы дол-
должны были бы исчерпать все степени А| в решении (8.48),
прежде чем рассматривать нелинейные поправки урав-
уравнения Стокса, которые имеют трансцендентально малый
порядок по Re. На практике, однако, такие члены суще-
существенны. Первый из них (см. упражнение 8.5) имеет
порядок ReAi; при Re>0,06 он оказывается больше,
чем Д?. Праудмен и Пирсон [1] кратко обсудили вопрос
о том, как можно вычислить эти члены, необходимые для
того, чтобы показать некоторую асимметрию в картине
течения, такую, как при появлении стационарных
вихрей.
УПРАЖНЕНИЯ
8.1. Решение Озеена для плоской пластины и плоского спутного
потока. В параболических координатах G.51) уравнения Навье —
Стокса для функции тока в плоском течении дают уравнение
д д
Выведите соответствующее линеаризованное уравнение (8.16) Озе-
Озеена. Разделением переменных найдите решение Озеена для полубес-
полубесконечной плоской пластины в равномерном потоке и для течения
далеко от конечного тела с нулевой подъемной силой. Покажите,
что в первом случае приближение пограничного слоя в параболи-
параболических координатах является полным решением Озеена. Сравните
поверхностное трение с известным значением, получающимся из
уравнений Навье — Стокса далеко вниз по потоку. Во втором слу-
случае выразите постоянные множители для обоих членов, представ-
представляющих спутный поток, и для потенциального течения в зависимости
от сопротивления тела. Свяжите решение с выражением (8.44).
(Первый случай впервые был исследован более сложным путем
Льюисом и Каррьером [1], в отношении второго см. Имаи [1] и
Чжан [1].)
8.2. Вязкое обтекание тонкого параболоида. В параболоидаль-
ных координатах (ср. упражнение 8.1) уравнения Навье —Стокса
222 Гл. 8. Течение при малых числах Рейнольдса
дают для осесимметричного потока
L 1ц \ * дт\ ^ dl) * 12ц2 n ^ ^ J
где
D2__ Ь\ Г д ( 1 д \ , д ( 1 д
Найдите решение Стокса для параболоида вращения. Покажите,
что его можно срастить с равномерным потоком таким же предель-
предельным образом, как и в случае кругового цилиндра. Вычислите вто-
второй член в разложении Озеена. Опишите, как мог бы быть продол-
продолжен этот процесс. Что это дает для оценки точности известного
приближения Озеена для эллиптического параболоида (Вилкин-
сон [1])? Каково отношение поверхностного трения к сопротивлению
давления в приближении Озеена по сравнению с 1 : 1 для круга
и 2 : 1 для сферы (Томотика и Аои [1])?
8.3. Спутный поток осесимметричного тела. Вычислите главный
член в разложении функции тока вдали от конечного тела вра-
вращения в вязком течении, определив постоянные через сопротивление
тела, как в упражнении 8.1.
8.4. Вязкое обтекание тонкой параболы. Покажите, что при-
приближение Стокса для параболического цилиндра никак не может
быть срощено с равномерным потоком. Покажите, что оно, по-види-
по-видимому, сращивается с приближением Озеена для плоской пластины
до первого'порядка и с приближением Озеена для параболы до
второго порядка; при продолжении решений методом сращиваемых
асимптотических разложений оказывается, однако, что ни в одном
из этих случаев не получается правильный главный член. Что пред-
представляет собой истинный предел приближения Озеена? (См. Лагер-
стром и Коул [1], стр. 877.)
8.5. Трансцендентально малые члены для кругового цилиндра.
Полагая, что разложение (8.48а) известно до любого нужного порядка,
найдите форму «следующего» члена с точностью до неопределимых
постоянных. Покажите, что он имеет порядок ReAj. С каким чле-
членом разложения Озеена нужно было бы его сращивать?
8.6. Об одной возможности применения метода деформирован-
деформированных координат. Покажите, что двучленное разложение Стокса (8.35)
могло бы быть найдено применением метода деформированных ко-
координат с деформированием только радиуса, если было бы известно,
что деформирование должно обращаться в нуль вдоль оси сим-
симметрии вниз по потоку.
Глава
НЕКОТОРЫЕ ЗАДАЧИ
ОСОБЫХ ВОЗМУЩЕНИЙ
ДЛЯ НЕВЯЗКИХ ТЕЧЕНИЙ
9.1. Введение
Как уже было указано в гл. 5 и 6, метод сращивае-
сращиваемых асимптотических разложений был изобретен для
исследования задач особых возмущений в теории вязкой
жидкости, в то время как метод Лайтхилла деформиро-
деформированных координат был развит применительно к задачам
распространения волн. До сих пор не ясно, может ли
метод Лайтхилла, дающий хорошие результаты для ги-
гиперболических уравнений, быть обобщен на случай эл-
эллиптических и параболических уравнений. С другой
стороны, метод сращиваемых асимптотических разло-
разложений был с успехом применен к ряду задач невязкого
течения. Действительно, мы применили его в гл. 4 для
теории тонкого профиля в идеальной жидкости, а в §6.7
дали его приложение к гиперболическим уравнениям
сверхзвукового обтекания.
Настоящая глава посвящена рассмотрению еще трех
примеров невязких течений, содержащих неоднородности.
Эти примеры охватывают диапазон скоростей от дозву-
дозвуковых через трансзвуковые до гиперзвуковых. Первым
примером является классическая теория Прандтля несу-
несущей линии, которая представляется в новом свете после
обнаружения ее особой природы. Второй пример —
обтекание тонкого конуса сверхзвуковым потоком с чис-
числом Маха, близким к единице, в котором линеаризован-
линеаризованное решение должно быть исправлено с тем, чтобы опре-
определить положение ударной волны. Третьим примером
является энтропийный слой, вызванный малым затупле-
затуплением клина в гиперзвуковом потоке. Первый и третий
примеры мы исследуем методом сращиваемых асимпто-
асимптотических разложений, а второй — методом деформиро-
деформированных координат, однако полезно было бы выяснить,
можно ли было выбрать иной метод в каждом из этих
случаев.
224 Гл 9 Задачи особых возмущений; невязкие течения
9.2. Несущее крыло большого удлинения
Описание поля течения, вызванного конечным несу-
несущим крылом при дозвуковых скоростях, представляет
собой одну из наиболее трудных задач теоретической
аэродинамики. Вязкостью можно пренебречь, за исклю-
исключением ее роли в условии Жуковского — Кутта на задней
кромке; в существенных своих чертах эта задача линей-
линейна, так что влияния толщины, кривизны и угла атаки
могут исследоваться отдельно. Кроме того, дозвуковая
задача эквивалентна задаче для несжимаемой жидкости
в соответствии с правилом Гётерта (Джонс и Коэн [1],
стр. 49). Однако даже полученная после всех этих упро-
упрощений задача невязкого несжимаемого обтекания крыла
нулевой толщины и бесконечно малого наклона к потоку
достаточно сложна. Ее прямое исследование по теории
несущей поверхности требует решения сингулярного
интегрального уравнения, содержащего двойные инте-
интегралы.
Для крыла большого удлинения теория несущей ли-
линии Прандтля сводит задачу к решению сингулярного
интегрального уравнения, содержащего лишь однократ-
однократные интегралы. Остается, однако, неясным, как улучшить
исследование Прандтля для получения более точных
приближений. Например, известное выражение для на-
наклона кривой подъемной силы плоского эллиптического
крыла с удлинением А
dCL 2я
~da~ = 1+2/Л (9Ла)
можно с точностью этого приближения записать в виде
^L^2n(\ -+.-••). (9.16)
da \ А ' / v '
однако никакое обобщение метода Прандтля не может
дать следующего члена разложения, который, как мы
увидим, имеет порядок, отличный от Л.
Фридрихе [3] указал, что эта задача представляет со-
собой задачу особых возмущений. В ней существуют два
характерных размера: размах крыла является первичной
характерной длиной, а хорда — вторичной. Их отношение
9.2. Несущее крыло большого удлинения
225
стремится к бесконечности при увеличении удлинения.
Следовательно, согласно нашему физическому критерию
(§ 5.3), эта задача возмущения параметра может ока-
оказаться особой. Эта возможность реализуется для несу-
несущего крыла (а также и для крыла с нулевой подъемной
силой, см. упражнение 9.1). Неоднородность может быть
исследована применением метода сращиваемых асимпто-
асимптотических разложений. Второе приближение окажется
эквивалентным теории Прандтля несущей линии. Однако
применение принципа сращивания, как будет показано,
исключит интегральные уравнения, которые сведутся к
квадратурам, что коренным образом упростит исследо-
исследование. Более того, продолжение процесса сделает воз-
возможным вычисление приближений высшего порядка.
Рассмотрим для простоты плоское крыло нулевой
толщины, форма которого в плане симметрична как от-
относительно направления потока, так и относительно на-
направления размаха (рис. 9.1, а). В качестве единиц ско-
скорости и длины возьмем скорость набегающего потока и
— t
L
i
/
Рис. 9.1. Внутренний и внешний пределы для плоского не-
несущего крыла.
а —полная задача, б— внутренний предел, б —внешний предел.
половину размаха крыла. Перенос условий обтекания
исключается тем, что мы рассмотрим крыло, лежащее
в плоскости у = 0, к которой набегающий поток наклонен
под углом а. Тогда форма крыла в плане может быть
выражена уравнением х= ±A~lh{z), где А — удлинение,
а полухорда h (z) — аналитическая функция порядка
единицы. Сначала мы предположим, что при г=±1
функция h обращается в нуль столь гладко, сколь это
226 Гл. 9. Задачи особых возмущений; невязкие течения
необходимо для того, чтобы избежать дополнительных
неоднородностей на концах крыла. Влияние смягчения
этого ограничения будет рассмотрено позже.
Полная задача для безразмерного потенциала ско-
скорости ф имеет вид:
уравнение: V2cp == ф^ -{- цуу + ф22 = 0, (9.2а)
условие обтекания: уу = 0 при у = 0, | х\ < A~lh (z),
(9.26)
условие в набегающем потоке: <р ^ х cos a -f- у sin а, (9.2в)
условие Жуковского: фх < оо при у ~ 0, х = Л/г (г).
(9.2г)
Принятый здесь вариант условия Жуковского представ-
представляет простейшее выражение того, что физическое тре-
требование конечности скорости на задней кромке выпол-
выполняется.
Физически очевидно, что, когда удлинение А стремит-
стремится к бесконечности, течение на любом расстоянии вдоль
размаха приближается к плоскому обтеканию плоской
пластины с шириной, равной местной длине хорды
(рис. 9.1,6). Это можно показать формально, введя уве-
увеличенные внутренние переменные, которые имеют поря-
порядок единицы вблизи крыла,
<р=.А~1Ф{Х, У, г), (9.3а)
где
Х = Ах, (9.36)
Y = Ay. (9.3в)
Эти координаты отнесены не к полуразмаху, а к харак-
характерной хорде, которая является уместным масштабом
длины в сечении, нормальном к размаху.
В новых переменных полная задача (9.2) преобра-
преобразуется к виду
Фхх + Фгу + А~2ф*, = 0, (9.4а)
Фк = 0 при У = 0, \X\<h(z), (9.46)
Ф — X cos а -\- У sin а в набегающем потоке, (9.4в)
ФА<оо при Г = 0, X = fi{z). (9.4г)
9 2. Несущее крыло большого удлинения 227
Решением этой задачи при Л = оо будет выражение
а\ = X cos a + Im W{X -4- iYf — A2 (г) —
— h (z) In [X + IY + ]/"(^+-/ГJ-Л2(г)]} sin a, (9.5)
которое может быть представлено в действительном виде
при использовании эллиптических координат. Как легко
видеть, это решение для плоского обтекания плоской
пластины с хордой 2h(z) при угле атаки ос (рис. 9.1,6).
Таким образом, в первом приближении координата по
размаху z играет роль только параметра. В этом месте
исследования мы требуем от этого решения только того,
чтобы оно давало циркуляцию Г, которая равна произ-
произведению 2ш на коэффициент при In (x2+y2I''2 в выра-
выражении ф
Исходя из уравнения (9.4а), относительную ошибку
в этом первом приближении вблизи крыла следовало
бы, казалось, считать величиной порядка А~2. Однако
для того, чтобы найти второе приближение, нельзя вос-
воспользоваться простой итерацией. Вычисление ФХ7 по фор-
формуле (9.5) дает выражение, которое ведет себя как
arc tg УД вдали от рассматриваемого сечения крыла в
соответствии с циркуляционным характером потока. Ча-
Частное решение итерационного уравнения будет, следова-
следовательно, вести себя как X2-\-Y2 и будет доминировать над
равномерным потоком на расстоянии порядка А в мас-
масштабе внутренних переменных. Это расхождение, анало-
аналогичное тому, которое обнаружил Уайтхед при попытке
улучшить решение Стокса для обтекания сферы (§ 8.3),
показывает особый характер задачи. Мы исследуем ее
в следующем параграфе, построив дополнительное внеш-
внешнее разложение. Как будет показано, сращивание прину-
принудит ввести во внутреннее разложение член относитель-
относительного порядка Л*; возникающая ситуация аналогична
той, которая имела место в теории пограничного слоя
(§ 7.3).
228 Гл. 9. Задачи особых возмущений; невязкие течения
9.3. Метод сращиваемых асимптотических
разложений в теории несущей линии
Во внешнем пределе (рис. 9.1, в) крыло сжимается
в линию особенностей, которые должны давать решения
уравнения (9.2а). Первую возможность представляют
собой вихри, поскольку они обладают нужной симмет-
симметрией по отношению к у. Мультиполи высшего порядка
на этой стадии могут не рассматриваться, поскольку,
как будет доказано, они несращиваемы в соответствии
с принципом минимальной особенности. Интенсивность
вихря Г будет, очевидно, обращаться в нуль при Л->оо
и, следовательно, может быть предположительно разло-
разложена в ряд вида
Г (г; A)~A-1y2(z) + A-\(z)+ .... (9.7)
Вихри, сбегающие с крыла, должны быть продолжены
как свободные вихри, располагающиеся вдоль линий
тока вниз по потоку до бесконечности. Следовательно,
предположение о том, что угол атаки мал, является за-
заметным упрощением, так как в этом предположении мо-
можно сохранить только члены, линейные по а. Тогда вих-
вихри, сбегающие с задней кромки, можно считать парал-
параллельными оси х (рис. 9.1, в). Потенциал такой системы
вихрей легко вычисляется при помощи закона Био — Са-
вара. Таким образом, внешнее разложение находится
в виде
при А -> оо для фиксированных х, у, z. (9-8)
Начиная с этого места, мы существенно отклоняемся
от классической теории несущей линии Прандтля и до-
достигаем тем самым существенного упрощения. Прандтль
нашел распределение циркуляции Y2C2), решая инте-
интегральное уравнение. Однако в пределах точности его
теории циркуляция может быть найдена непосредствен-
непосредственно сращиванием с внутренним решением. Это можно
сделать формально, однако результат очевиден из того
факта, что все кривые, охватывающие одни и те же вих-
9.3. Сращиваемые разложения в теории несущей линии 229
ревые линии, дают одну и ту же циркуляцию (рис. 9.1).
Во внутреннем пределе циркуляция определяется фор-
формулой (9.6). Поскольку это выражение не зависит от
размера контура, сращивание с разложением (9.7) дает
у2 И = 2яаА (z). (9.9)
Таким образом, с точностью до первого порядка сбегаю-
сбегающая с крыла завихренность представляет собой цирку-
циркуляцию около плоской пластины с длиной, равной мест-
местной длине хорды, в плоском потоке при истинном зна-
значении угла атаки. В теории Прандтля циркуляция
соответствует приведенному («эффективному») углу
атаки, однако разница представляет собой величину
высшего порядка. Таким образом, двучленное внешнее
разложение (9.8) принимает вид
1
_\ ^ + (^_Q2 [
Теперь вернемся к внутренней задаче и будем искать
второе приближение. При получении внутреннего разло-
разложения из (9.10а) лишенные смысла расходящиеся инте-
интегралы устраняются предварительным интегрированием
по частям, что дает
1
I (9.106)
Введем далее внутренние переменные (9.3) и разложим
результат в ряд для больших значений А; получится дву-
двучленное внутреннее разложение двучленного внешнего
разложения для ф:
Двучленное внутреннее двучленного внешнего Ф==
Acb4KV.P
230 Гл. 9 Задачи особых возмущений; невязкие течения
интеграл здесь нужно понимать в смысле главного зна-
значения Коши. Весьма примечательно, что этот интеграл
уже фигурировал в гл. 4 в формуле D.10) при исследо-
исследовании тонкого симметричного профиля и что он встре-
встречается также в иных вопросах механики жидкости, на-
например в сверхзвуковой теории обтекания тонких тел.
Первый член в формуле (9.11) уже был срощен с
внутренним решением (9.5). Второй член нуждается в
поправке относительного порядка Л, так что внутрен-
внутреннее решение (9.3а) должно иметь разложение
Ф-Л^ФД*, Г, z) + A-4\{X, Y, z) + ...
при Л->оо для фиксированных X, К, z. (9.12)
Подстановка в полное уравнение (9.2а) показывает,
что как Ф2, так и Ф4 удовлетворяют двумерному урав-
уравнению Лапласа по X и У. Поэтому из соотношения (9.11)
следует, что Ф2 представляет просто результат умень-
уменьшения угла атаки в местном решении для плоской пла-
пластины от его геометрического значения а до эффектив-
эффективного значения
р.
(9.13)
f
-1
Это известный результат теории несущей линии. Система
сбегающих с крыла вихрей индуцирует направленные
вниз скорости в окрестности крыла, которые постоянны
вдоль хорды в каждом сечении, перпендикулярном раз-
размаху. Таким образом, система сходящих вихрей как бы
уменьшает угол атаки в каждом сечении. Однако здесь
мы сводим вычисления к квадратурам, учитывая, что для
больших значений А это уменьшение угла мало по срав-
сравнению с геометрическим углом а, в то время как теория
несущей линии приводит к интегральному уравнению,
поскольку указанный факт в ней не используется. Наш
результат может быть получен как второй шаг в ре-
решении методом итераций интегрального уравнения
Прандтля.
Из внутреннего решения мы использовали только со-
соотношение (9.6) между циркуляцией и углом атаки, ко-
которое эквивалентно наклону кривой подъемной силы.
9 4. Результаты третьего приближений 231
Прандтль предлагал заменить такую теоретическую
кривую экспериментальной, что должно было учесть вли-
влияние толщины и вязкости. Это практический пример ут-
утверждения (§ 5.4), что метод сращиваемых асимптоти-
асимптотических разложений может быть приложен даже в тех
случаях, когда внутренняя задача «невозможна» и мо-
может быть решена только численно или экспериментально.
9.4. Результаты третьего приближения
Предшествующий анализ был продолжен еще на
один цикл для получения третьего приближения (Ван-
Дайк [12]). Здесь мы остановимся лишь на некоторых
наиболее интересных его чертах.
Получение трехчленного внешнего разложения дву-
двучленного внутреннего разложения дает, согласно приве-
приведенным выше физическим соображениям, поправку уз
к интенсивности вихрей (9.7). Кроме того, оно показы-
показывает появление на этой стадии следующих особенностей
высшего порядка в точках несущей линии. Эти особен-
особенности представляют собой диполи с вертикальной осью,
но мы назовем их дивихрями, чтобы подчеркнуть их фи-
физическую интерпретацию как производных по х от вих-
вихрей, представляющих первый момент распределения за-
завихренности на крыле. Таким образом, трехчленное
внешнее разложение оказывается равным сумме разло-
разложения (9.10) и выражения
1аУГ2 У ± [НЧЪ-7=М=Ш=, (9.14)
4 х* + у* дг Jx VWJ/V + </24-^-SJ '
причем величина h в (9.10) изменена множителем (9.13).
Трехчленное внутреннее разложение этого результата
может быть вычислено после дальнейшего интегрирова-
интегрирования по частям. Удивительно то обстоятельство, что ожи-
ожидаемому следующему члену порядка А~3 во внутреннем
разложении (9.12) предшествует член порядка А~г\пА.
Как обычно (см. § 10.5), этот логарифмический член вы-
вычислить легче, чем степенной. Он обусловливает даль-
дальнейшее изменение эффективного угла атаки (9.13), а
также изменение кривизны линий тока, вызванное вбли-
вблизи крыла системой сходящих вихрей (рис. 9.2).
232 Гл. 9. Задачи особых возмущений; невязкие течения
Нелогарифмический член включает эти и другие
более сложные местные течения, причем все они могут
быть найдены методами теории функций комплексного
переменного. Далее коэффициенты всех членов вида
Рис. 9.2. Искривление линий то-
тока вблизи крыла, обусловленное
системой вихрей, сходящих с зад-
ней кромки.
In (x2 + y2L* дают распределение циркуляции или подъ-
подъемной силы по размаху, которая определяется в виде
. J ^
-г Л ~21п А BЛ/2 + ЗМ") 4-
A
(9.15)
Здесь Гоо — значение (9.6) для плоского течения, а ае
определяется формулой (9.13). Тогда в соответствии
с правилом Жуковского — Кутта наклон кривой подъем-
подъемной силы равен
dC Г ()
9.5 Прилооюение к эллиптическому крылу
233
9.5. Приложение к эллиптическому крылу
Пусть эллиптическое крыло с удлинением А
(рис. 9.3) имеет полухорду
4
h (г) = —1/1 —z2.
Циркуляция определяется по формуле (9.15)
Г __ 2 . 4 1пЛ 3-2г2 ,
(9.17)
In 2
\-z2
3 — 2z2
\—z2
In
—1
\-Z2\
.. . (9.18)
Интегрируя это выражение вдоль размаха, получаем в
соответствии с формулой (9.16) наклон кривой подъем-
подъемной силы, уже указанный формулой A.6) в гл. 1. Первые
Рис. 9.3. Плоское
эллиптическое
крыло.
два члена образуют полученное нами ранее видоизмене-
видоизменение (9.16) результата Прандтля (9.1а).
К счастью, это один из тех редких случаев, когда
удается найти решение для несущей поверхности.
Решение Прандтля имеет то преимущество, что оно
обращается в нуль при Л = 0, хотя вблизи этого значения
234 Гл. 9 Задачи особых возмущений; невязкие течения
и превосходит примерно вдвое истинный наклон кривой,
вычисленный по теории тонкого крыла (рис. 9.4). В то же
время наше разложение (9.16) более точно при значе-
значениях А > 4. Наше третье приближение расходится при
dCL/da
I-
Третье
приближение AВ)
А = *э
Второе приближение Рраи dm л л (S /а)
.о-
Модифицированное
третье
приближение
G0.27)
второе придлижение C. /б)
О Геория несущей
поЗерхности (принес [1])
/Р ч Геория тонкого крыла
/
Рис. 9.4. Наклон кривой подъемной силы эллиптического крыла.
значениях Л<3; возможность отсрочки этой катастрофы
показана штрих-пунктирной линией на рис. 9.4 и будет
обсуждена ниже (см. § Ю.7).
Мы нарушили ограничение, наложенное на форму
концов крыла. Вследствие этого результат оказывается
локально непригодным, так же как в приложении теории
тонкого профиля к закругленным кромкам (§ 4.4) или
теории пограничного слоя к острой передней кромке
(гл. 7)^. Мы видим, что формула (9.18) оказывается не-
несостоятельной, когда 1±г имеет порядок А-2. На любом
фиксированном числе радиусов от концов крыла течение
9.5. Приложение к эллиптическому крылу
235
не может стать плоским независимо от того, сколь велико
удлинение. Очевидно, для этой области необходимо еще
другое асимптотическое разложение. Первый член такого
разложения соответствует обтеканию плоской полубеско-
полубесконечной пластины параболической форАмы в плане
(рис. 9.5); это относится к концу любого плоского
ос
Рис. 9.5. Предельная задача для окрестности закруг-
закругленного конца крыла.
крыла, форма которого определяется аналитической кри-
кривой. В этом решении вблизи конца крыла все исходные
координаты должны быть увеличены умножением на А2.
В этой усложненной проблеме существуют еще иные
неоднородности. Известно, что вихревая пелена стремится
свертываться, так что наше внешнее решение непригодно
далеко вниз по потоку, где х имеет порядок А/а. Далее
профили иного сечения, чем плоская пластина, обычно
должны были бы исследоваться с помощью теории тон-
тонкого профиля для внутренней задачи, что привело бы
к неоднородностям на передней и задней кромках, рас-
рассмотренным в гл. 4, и к их более сложным аналогам
вблизи концов крыла. Неоднородности могут возникать
также в углах стреловидного крыла или при других раз-
разрывах формы в плане, на отклоняемых элеронах и т. д.
Крыло с малой стреловидностью серповидной формы в
плане было исследовано Турбером [1], применившим
236 Гл. 9. Задачи особых возмущений; невязкие течения
метод сращиваемых асимптотических разложений. Он
нашел, что в этом случае логарифмический член появ-
появляется во втором приближении.
9.6. Сверхзвуковое обтекание тонкого
кругового конуса при числах Маха,
близких к единице
Для тонких веретенообразных тел в сверхзвуковом
потоке обычная линеаризованная теория (см., например,
Уорд [1]) не дает сведений об интенсивности головной
ударной волны. Ее можно найти только при сохранении
некоторых нелинейных членов и при учете особой при-
природы возмущенного решения. Эта задача была исследо-
исследована как методом деформированных координат (Лайт-
хилл [3]), так и методом сращиваемых асимптотических
разложений (Булах [1]). Мы применим первый способ
к задаче настолько простой, что сможем провести реше-
решение еще на один шаг сверх полученных ранее резуль-
результатов.
Рассмотрим тонкий круговой конус с углом раствора
2е при нулевом угле атаки в потоке, скорость которого
М>7
Рис. 9.6. Сверхзвуковое обтекание тонкого ко-
конуса при числах Маха, близких к единице.
настолько превышает скорость звука, что течение являет-
является коническим (рис. 9.6). Если скорость течения лишь
немного превышает скорость звука, то существенные
9.6. Сверхзвуковое обтекание тонкого конуса 237
черты явления описываются трансзвуковым уравнением
малых возмущений (Осватич и Берндт [1])
Фгг + -т1 - (М2 - 1) <Рхх = (V + 1) <РХ<РХХ. (9-19а)
Здесь ф — возмущенный потенциал скорости, такой, что
Бектор скорости равен U grad (# + ср). В этом приближе-
приближении условие обтекания можно линеаризовать и, посколь-
поскольку тело гладкое, перенести на ось (§ 3.8) в виде
limrq>r = e2;t. (9.196)
г-»0
Соотношения косого скачка уплотнения налагают два
условия на головной волне, положение которой неиз-
неизвестно:
Ф = 0, ) (9.19в)
2 M»sln»a-1 при j; = tga. Q
На поверхности конуса коэффициент давления опреде-
определяется выражением
Ср=-2<рх — е*. (9.20)
Эта задача была решена численно Осватичем и Съё-
дином [1]. Вместо этого мы будем искать ее решение
аналитически путем асимптотического разложения для
малых 8. Предполагая, что число Маха фиксировано, мы
пересмотрим трансзвуковую природу задачи; соответ-
соответственно наше решение будет пригодно только в верхней
части трансзвукового режима.
Прямое возмущенное разложение приводит к труд-
трудностям на конусе Маха набегающего потока. Возмущен-
Возмущенный потенциал в первом приближении обращается там
в нуль как корень квадратный, что вызывает появление
особенностей в приближениях высшего порядка за счет
дифференцирования. В соответствии с этим мы вводим
деформированное коническое переменное 5, полагая
^ Ф (х, г; е) ~ ^ (s) + е4Д> (S) +- ?% (s) -f- ?8/4 (s) + . . .,
(9.21а)
^\^~s + z%(s) + z6r^s)+ .... (9.216)
238 Гл. 9. Задачи особых возмущений; невязкие течения
В разложении (9.216) нет членов порядка е2, поскольку
мы установим, что деформирование обращается в нуль
с точностью до этого порядка. По этой же причине урав-
уравнение, описывающее ударную волну, берется в виде
—1 tg а — 1 -f- kg* + k^ + (9.22)
9.7. Второе приближение и положение
ударной волны
Когда разложения (9.21) подставляются в дифферен-
дифференциальное уравнение (9.19а), члены с е2 дают известное
линеаризованное уравнение для f\
(l_s*)f» + A = o. (9.23)
Условию обтекания (9.196) и первому условию на удар-
ударной волне (9.19в) удовлетворяет решение
f 1 (S) = — (Аг sech 5 - /Г^2"). (9.24)
Второе условие на ударной волне (9.19г) удовлетворяется
автоматически, и поэтому в разложение (9.22) не входит
член порядка г2.
Члены порядка е4 в дифференциальном уравнении те-
теперь дают для второго приближения уравнение
(9.25а)
где
0=-
М2 — 1 '
Интегрируя и налагая условия обтекания и первое усло-
условие на ударной волне, получаем
f2 (S) =~Q (Ar sech 5 — /l — s2Ar sech 5 — ]Л — s2).
(9.26)
Это трансзвуковая форма теории малых возмущений для
решения второго порядка (Ван-Дайк [2]), выраженная в
деформированном переменном, которое должно быть
определено.
9.7. Второе приближение и положение ударной волны 239
Члены порядка е6 в дифференциальном уравнении
дают теперь для третьего приближения следующее урав-
уравнение:
1 s2 (Ar sech sJ
2 (l-s2K/2 J ' s 3~ ^'^s'^Tct'3'
(9.27)
На этой стадии возникают непреодолимые трудности при
отсутствии деформирования. Первый член правой части
имеет особенность вида G2(l—52)~1/2 при 5=1, что вызы-
вызывает аналогичную особенность в величине скорости. Этот
дефект устраняется подходящим выбором деформирую-
деформирующей функции r3(s).
Простейший выбор, постоянное растяжение
r3(s) = j02, (9.28а)
был с успехом применен Лайтхиллом [3] для нахожде-
нахождения положения ударной волны в том приближении, кото-
которое он осуществил. Однако это исключает неоднород-
неоднородности вблизи ударной волны ценой введения допол-
дополнительных неоднородностей на оси, что сделает невоз-
невозможным наложение условия обтекания в следующем
приближении. Этой трудности можно избежать, выбрав
вместо этого линейное деформирование
rz(s) = ±G2s. (9.286)
Теперь можно использовать второе условие на удар-
ударной волне для того, чтобы найти отклонение ударной
волны от конуса Маха набегающего потока. На ударной
волне, согласно формулам (9.216), (9.22) и (9.286),
(
(9.29)
Подстановка в условие (9.19г) дает
О = -J К (9.30)
240 Гл. 9 Задачи особых возмущений; невязкие течения
и решением будет
h = ~G\ (9.31)
Это трансзвуковая форма результата теории малых
возмущений, найденного Лайтхиллом [3] и Булахом [1].
Этот результат, до которого они довели свое решение,
приложим к тонкому конусу любого поперечного сече-
сечения. Следующий параграф дает для этого новое обосно-
обоснование.
9.8. Третье приближение для давления на конусе
После проведенного выше деформирования уравнение
(9.27) для третьего приближения упрощается и прини-
принимает вид
Аг sech 5 Аг sech 5
1 __ 52 /1 _ 52
1 1 _1_ s2(ArsechsJ
2" /1 — 52 " 2A—52K/2
K }
После интегрирования и наложения условия обтекания
и первого условия на ударной волне находим
f3 (s) = 4" °2 [D ~ 1п 2) '/:Г:=:Г^2 + (In 2 — 1) Аг sech s +
(9.33)
Интеграл, входящий в это выражение, имеет следующее
свойство:
~ (i + T1 2 - In 2) — -^s2 In s + О (s2) — (9.34a)
s2K'2 In A - s2) + O[(l — sf2]. (9.346)
9.8. Третье приблиоюение для давления на конусе 241
Члены порядка е8 дают уравнение для четвертого при-
приближения, которое при приближенном представлении
правой части вблизи 5=1 принимает вид
(9-35)
Особенности в правой части и, следовательно, также в
четвертом приближении для скорости устраняются вы-
выбором специальной формы следующего члена деформи-
деформирования:
г4 (s) - - 1 Gh [3 + УТ^~$ In A — 52)]. (9.36)
Множитель 5 вновь служит для предотвращения появле-
появления неоднородностей на оси. На ударной волне отсюда
следует разложение
Тогда подстановка во второе условие на ударной волне
(9.19г) дает
kA = -±G*. (9.38)
Выражая эти результаты через исходные параметры,
находим для ударной волны
Г
12 L М2 -J
(9.39)
Коэффициент давления на поверхности (9.20) может
быть записан в соответствии с трансзвуковым правилом
подобия Осватича и Берндта [1] в виде
Как можно было предвидеть, эти результаты представ-
представляют собой асимптотические разложения для больших
242 Гл 9 Задачи особых возмущений; невязкие течения
значений известного параметра трансзвукового подобия
(Y+l)e2/(M2—1). Первые три приближения для давле-
10т
Рис. 9.7. Давление на тонком конусе в трансзву-
трансзвуковом течении.
первое приближение, второе приближе-
приближение, третье приближение, О численные результаты Осва
тича и Съёдина |1].
ния на поверхности на рис. 9.7 сравниваются с числен-
численным решением Осватича и Съёдина.
9.9. Гиперзвуковое обтекание тонкого
затупленного клина
В § 5.3 было указано, что при невязком сверхзвуко-
сверхзвуковом обтекании малое затупление носовой части тела
приводит к неоднородностям ниже по потоку. При уда-
9.9. Гиперзвуковое обтекание затупленного клина 243
лении от носовой части течение почти всюду прибли-
приближается к течению для заостренного тела. Однако на по-
поверхности энтропия — поскольку она постоянна вдоль
линии тока — имеет то значение, которое она получает
за прямым, а не за косым скачком, и некоторые другие
параметры течения также отличны от соответствующих
значений для заостренного тела. Эти изменения имеют
Рис. 9.8. Энтропии- г^
ный слой на затуплен- I ^
место поперек энтропийного слоя (рис. 9.8), толщина
которого для плоского течения является величиной по-
порядка радиуса затупления.
Влияние малого затупления как задача особых воз-
возмущений впервые было исследовано Гиро [1]. Он рассма-
рассматривал прямую задачу, когда задано тело. Более простой
анализ возможен для обратной задачи, когда задана
ударная волна и ищется форма тела. Это исследование
было осуществлено Якурой [1] для течения совершенного
газа при бесконечном числе Маха с применением метода
сращиваемых асимптотических разложений. Мы рассмо-
рассмотрим лишь частный случай его решения для затуплен-
затупленного клина, предполагая, что клин тонок. Несмотря на
упрощение исследования, в нем сохраняется примеча-
примечательный эффект расщепления энтропийного слоя на два
подслоя, так что в исследовании потребуется введение
внешнего, среднего и внутреннего разложений.
Рассмотрим течение за гиперболической ударной вол-
волной (рис. 9.9). Предположим, что наклон s ее асимптот
244 Гл. 9. Задачи особых возмущений; невязкие течения
будет мал, и будем считать радиус кривизны ее носовой
части равным е3 с тем, чтобы первое приближение соот-
соответствовало заостренному клину. Таким образом, мы
вводим возмущение параметра для малого радиуса но-
носовой части, в то время как Якура вводил возмущение
Рис. 9.9. Обозначения для гиперболической ударной волны.
координат для больших х. Ударная волна определена
уравнением
Г/2 = е2х2_е4. (9.41)
В обратной задаче форму тела удобнее всего находить
исходя из того условия, что на границе тела функция
тока обращается в нуль. Функцию тока мы введем, по-
положив, как это обычно делается для сжимаемой жид-
жидкости,
d\p = ри dij — pv dx. (9.42)
Уравнения сохранения имеют следующий вид:
неразрывности: (ри)х + (Pv)y = 0> (9.43а)
количества движения вдоль оси х: р (иих -\- vuy) -\- рх = 0, (9.436)
количества движения вдоль оси у: р (u,vx -\- w \-\-p — 0, (9.43в)
энтропии: и (р/ду)х + v (р/ру)у = 0. (9.43г)
Последнее из этих уравнений выражает тот факт, что
энтропия постоянна вдоль линии тока между ударными
9.9. Гиперзвуковое обтекание затупленного клина
245
волнами, и эквивалентно уравнению сохранения энергии.
Можно использовать это свойство, выбрав в качестве
нового независимого переменного функцию тока и поме-
поменяв ролями у и я|) применением преобразования Мизеса
теории пограничного слоя. Тогда дифференциальные
уравнения (9.43) примут следующий вид:
V
наклон линии тока:
неразрывности:
количества движения по
нормали к линии тока:
интеграл Бернулли: а2-
интеграл энтропии:
дх и '
д"ф ри '
"cU ""¦"" chj) ~~ '
I vt> I ^Y P i
г ^ y —1 Р
4-= /(¦)•
(9.44а)
(9.446)
(9.44в)
(9.44г)
(9Г.44д)
Пусть переменные течения сделаны безразмерными
отнесением скоростей и плотностей к их значениям U и
Роо в набегающем потоке, а давлений — к p<x>U2. При этом
предыдущие уравнения не изменятся 1). Тогда, поскольку
наклон ударной волны равен
dy - гх (9.45)
dx
соотношения Ренкина — Гюгопио дадут начальные усло-
условия
2 о х2
V = 7-г ?
9 =
Y+1
V+1
Y-1 '
11=1 —
2
хУх2 —г2
Y+1
— е2
//=?}/" X2 — ?2
при
= С
— 82.
(9.46)
1) Уравнение (9.44г) уже записано в безразмерных перемен-
переменных. — Прим. ред.
246 Гл. 9. Задачи особых возмущений; невязкие течения
Вследствие этого интеграл энтропии (9.44д) на ударной
волне оценивается следующим образом:
9.10. Решение теории малых возмущений
для затупленного клина
При стремлении к нулю параметра возмущения 8 рас-
рассмотренная выше задача сводится к гиперзвуковой зада-
задаче малых возмущений для острого клина (Хейз и Проб-
стин [1], гл. II). Начальные условия (9.46) наводят на
мысль о возможности улучшения этого основного реше-
решения разложением по степеням е2. Таким образом, мы
произведем обычное для гиперзвуковой теории малых
возмущений разложение (Хейз и Пробстин [1], гл. II),
положив
а ~ 1 4- e2tf j (*, *i) + е%2 (х, ФО Н- .. ., (9.47а)
v ~ гъг (*, ф2) + е%2 (х, ф2) + • • - (9-476)
Р ~ ?2А {х, Ф0 + е*р2 (х, фО + ..., (9.47в)
р ~ pj (л:, ф2) -f- е2р2 (^, ФО + • • •, (9.47г)
У— ъуЛх, ^i) + ?3y2(^5 Ф0+ • • • • (9.47д)
Здесь
Ф1 = | (9.48)
является функцией тока, отнесенной к характерной тол-
толщине ударного слоя для х=О(\).
Подставляя эти разложения в полную задачу (9.44)
и (9.46) и приравнивая члены с одинаковыми степенями
8, получаем для первого приближения нелинейную си-
систему, решение которой просто совпадает с решением
для плоского клина
Л = —и, ==*; ^рр
(9'49)
Y-1" У1~ Y+1
9.11. Среднее разложение для энтропийного слоя 247
Линейные уравнения для второго приближения также
могут быть решены в замкнутом виде. Однако, имея в
виду нашу цель, заметим, что интеграл энтропии (9.44д/)
дает для второго приближения
Л.-7-^ = 4-1- (9.50)
Pi Pi *i
Таким образом, существует особенность при г|I = 0. Легко
видеть, что давление регулярно, в то время как плотность
на поверхности тела имеет особенность вида 1/\|^. Подоб-
Подобным же образом скорость v регулярна, а у имеет особен-
особенность вида l/i|)i и и — особенность вида 1/ф2. Эти неодно-
неоднородности усложняются в третьем приближении и в при-
приближениях высшего порядка.
9.11. Среднее разложение
для энтропийного слоя
Прямое разложение по малому возмущению нару-
нарушается вблизи поверхности, поскольку решение для
острого клина непригодно в качестве первого приближе-
приближения в энтропийном слое. Мы исследуем эту неоднород-
неоднородность методом сращиваемых асимптотических разложе-
разложений.
Поскольку неоднородность имеет место вдоль линии,
как в теории пограничного слоя, то нужно увеличить
только нормальную координату я]^. В соответствии с фор-
формулами (9.47г), (9.49) и (9.50) внешнее разложение
плотности для малых г|н ведет себя следующим образом:
(9.51)
Это наводит на мысль ввести новое независимое пере-
переменное
Мы будем называть его средним переменным, поскольку
для того, чтобы достичь поверхности тела, потребуется
еще одно увеличение.
248 Гл. 9 Задачи особых возмущений; невязкие течения
Сравнение с
дующую форму
гг —^ 1 -|- г2и]
/?~ е2/
Р~ Pi
У ~ ^Уо (*» i
внешним
средних
(х, ф) +
i(^ Ф) +
h (х, ф) +
(л:, ф) 4-
разложением
разложений:
е4и2{х, фL- •
?3^2(х,ф)+ .
&*Р2(х, ФL- •
е2р(^ Ф)+ •
:, ijj) 4-е3^ (л:,
подсказывает сле-
(9.53а)
(9.536)
(9.53в)
(9.53г)
Ф)+ . .. . (9.53д)
Подстановка в полные уравнения (9.44) и сращивание
с главными членами внешних разложений (9.47) в соот-
соответствии с принципом асимптотического сращивания
E.24) дает для первого приближения
| ^х, (9.54а)
^=^-, ^(^.00) = ^-. (9.546)
, (9.54в)
?L = _J^(^i)V^4f , p,(x, oo) = 1+L f (9.54r)
p7 y + i \y + 1/ Ф2 y—i
2Й, + ^ + _?!_ |l = о, Й, (x, oo) = - -H_, (9.54д)
•^ = -i-. ^(x, ф) = Х=1ф при Ф->сх:, (9.54е)
Л|» Pi Y +1
Эти уравнения можно решить последовательно, что дает
- 2 - 2
2Y /1+Ф2\1Л? (9.55)
(Y+1J
9.12. Внутреннее разложение для энтропийного слоя 249
Это разложение тоже непригодно на поверхности те-
тела, где в первом приближении компонента скорости и
становится бесконечной, а плотность — нулевой. Для
второго приближения интеграл энтропии (9.44д') дает
р, г р, (9'56)
Можно показать, что р2 регулярно; следовательно, в
силу формулы (9.55), р2 имеет особенность вида \р~{2~2/у).
9.12. Внутреннее разложение
для энтропийного слоя
Такая неоднородность среднего разложения пока-
показывает, что для полного решения требуется третье асимп-
асимптотическое разложение. В соответствии с формулами
(9.53г), (9.55) и (9.56) наше среднее разложение для
плотности при малых я|) ведет себя как
у^ ^ '' •
Это наводит на мысль ввести следующее новое внутрен-
внутреннее переменное:
?^1 = |, (9.58)
которое представляет собой функцию тока, нормирован-
нормированную по отношению к радиусу носовой части ударной
волны.
Тогда сравнение со средним разложением подсказы-
подсказывает следующую форму внутренних разложений:
14- tf-WUb (х, V) + . . ., (9.59а)
-., (9.596)
.., (9.59в)
-., (9.59г)
у ~ еГ0 (х, W) + c3-2/vy! (л:, ХУ) + . . . . (9.59д)
250 Гл. 9. Задачи особых возмущений; невязкие течения
Подстановка в полное уравнение и сращивание со
средним разложением дают
Г0(х,оо) = т%-Тх, (9.60а)
(9.606)
, (9.60в)
\ (9.60г)
. (9.60д)
Последовательное интегрирование этих уравнений при-
приводит к формулам
р 2 ,, 2у
К v-1 Г dt
Y + l J
w
Это последнее разложение пригодно на поверхности
тела. В частности, оно дает асимптотическую форму тела,
которое порождает гиперболическую ударную волну,
\ t г dt
8 ~ Y ТГТ^Г
о
Х-
Ly+1
Здесь Г — гамма-функция. Первый член представляет
собой результат для острого клина, изображенного пунк-
пунктирной линией на рис. 9.9. Второй член дает асимптоти-
асимптотическое значение толщины вытеснения энтропийного слоя.
Как и в вязком пограничном слое, поток массы умень-
9.12. Внутреннее разложение для энтропийного слоя 251
шен, поскольку энтропия, а следовательно, и темпера-
температура увеличены действием затупления, а плотность
соответственно уменьшена. Следовательно, в прямой за-
задаче (рис. 9.10, а) ударная волна отодвигается от тела
Рис. 9.10. Вытесняющий эффект затупления.
а —прямая задача, б —обратная задача.
в областях вниз по потоку, хотя вблизи носовой части
она проходит ближе к телу. В обратной задаче (рис.
9,10,6) соответственно должно быть сдвинуто тело. Даль-
Дальнейшая аналогия между энтропийным и вязким погра-
пограничным слоями очевидна из формул (9.54в) и (9.606):
в первом приближении давление поперек слоя не ме-
меняется.
¦ L **"
6
Рис. 9.11. Независимые характерные длины для
затупленного клина.
а —толстый клин, б —тонкий клин.
Исследуя толстый клин, Якура [1] нашел следую-
следующее приближение, которое добавляет к (9.62) член ви-
вида лг1. Это достаточно для хорошего описания тела, за
252 Гл. 9. Задачи особых возмущений; нсвязкие течения
исключением окрестности малого радиуса вблизи его
носовой части. Исследование Якуры содержит только
внутреннее и внешнее разложения. Наше среднее
разложение вводится с помощью двойного предельного
перехода (см. § 5.3), в котором наклон и носовой радиус
одновременно обращаются в нуль. На рис. 9.11 показано,
как при этом появляются три независимые длины, харак-
характеризующие три разложения, в которых мы предположи-
предположительно приняли, что L имеет порядок единицы.
9.13. Составное разложение
для затупленного клина
Для гого чтобы показать изменение параметров тече-
течения в возмущенной области между ударной волной и
телом, мы хотим соединить отдельные разложения в одно
составное разложение. Это даст полезную иллюстрацию
метода образования составного разложения из более
чем двух составляющих (см. упражнение 5.4).
Рассмотрим сначала плотность. Применяя мульти-
мультипликативное правило E.34) к среднему и внутреннему
решениям, получаем
что пригодно в обоих подслоях энтропийного слоя. Ясно,
что это выражение принимает различные формы в сред-
среднем и внутреннем пределах. Повторение процесса
с целью комбинирования этого выражения с внешним
решением оставляет результат неизменным. Следова-
Следовательно, мы получили нужное равномерное приближение,
пригодное во всех трех областях.
Если вместо сделанного выше мы используем адди-
аддитивное правило E.32), то равномерно пригодное прибли-
приближение получится в виде
Хотя эти две формы и эквивалентны, первая из них
является предпочтительной вследствие ее простоты.
9.13. Составное разложение для затупленного клина 253
Она также соответствует результату Якуры для толсто-
толстого клина.
Для ординаты у наши три приближения могут быть
записаны так:
2 y 1
внешнее: у ~*> . -. &х + r ^ я|?, (9.65а)
2
среднее: у ^ —-т-у ех +
(9.656)
\1/Y
внутреннее:
V_1 Г I ?4 \1/Y
Результат как аддитивного, так и мультипликативного
составлений излишне сложен. Более простая форма
находится в виде
[ оо _ ]
Л. (9.66)
Это соответствует результату, который Якура нашел с
помощью аддитивного составления из двух своих разло-
разложений.
На рис. 9.12 показано распределение плотности между
ударной волной и телом, определенное по формулам
(9.63) и (9.66), на расстоянии 24,5 радиусов от вершины
гиперболической ударной волны при 8 = 0,437, что соот-
соответствует клину с углом раствора 40°. Там же показаны
внешнее, среднее и внутреннее приближения и резуль-
результат Якуры, в котором клин не предполагается тонким.
Расхождения положений поверхности указывают на не-
неточности, обусловленные столь большим значением s.
Якура [1] приложил метод сращиваемых асимптоти-
асимптотических разложений также к осесимметричным задачам:
к обтеканию затупленного конуса, который порождает
гиперболоидальную ударную волну, и тела, которому
соответствует параболоидальная ударная волна при
М = оо. Последняя задача с равным успехом была нссле-
254 Гл. 9. Задачи особых возмущений; невязкие течения
дована Сычевым [1], который использовал метод дефор-
деформированных координат. Однако, по-видимому, решение
Ударная долна
Состадное
Остоыи клин
ъзультат Я куры [1]
¦ Яодерхность
внутреннее
i
"Среднее
Рис. 9.12. Распределение плотности на рас-
расстоянии, равном 24,5 радиусов носовой части
ударной волны, за клином с углом раствора 40°,
М = со, у = 7/s-
для затупленного клина не может быть найдено дефор-
деформированием координат.
УПРАЖНЕНИЯ
9.1. Вытянутое тело с нулевой подъемной силой. В качестве
модели для выяснения влияния толщины крыла большого удлине-
удлинения рассмотрите потенциальное обтекание тонкого гладкого тела
вращения потоком несжимаемой жидкости, нормальным к его оси
симметрии (рис. 9.13). Покажите, что в первом приближении тече-
Упражнения 255
ние является плоским в каждом сечении, но что прямые итерации
приводят к трудностям, аналогичным парадоксу Уайтхеда (гл. 8).
Применяя метод сращиваемых асимптотических разложений, най-
найдите следующее приближение Приложите Bdiue решение к эллип-
эллипсоиду вращения и сравните полученный результат с правилом Мун-
ка [2], согласно которому скорость на поверхности эллипсоида равна
проекции максимальной скорости на касательную плоскость в рас-
рассматриваемой точке. Приложите ваше решение также к веретено-
веретенообразному телу с параболической образующей. Объясните, почему
не требуется поправки в вершинах эллипсоида. Придумайте и при-
примените поправку для концов веретенообразного тела.
Рис. 9.13. Поток, нор-
нормальный к тонкому телу
вращения.
9.2. Несущее крыло с острыми концами. Вычислите по фор-
формулам (9.15) и (9.16) во втором приближении наклон кривых на-
нагрузки по размаху и подъемной силы для крыла, форма которого
в плане образована двумя дугами параболы. Придумайте поправку,
которая делает решение равномерно пригодным вблизи концов кры-
крыла. Обсудите соответствующую поправку для среднего сечения ром-
ромбовидного в плане крыла.
9.3. Течение над волнистой стенкой, близкое к равновесному.
Рассмотрите установившееся плоское течение невязкого газа с виб-
вибрационной или химической неравновесностыо. При равновесном
числе Маха, равном VY, линеаризованное уравнение для потен-
потенциала скорости будет иметь вид (Винченти [1])
ду* дх2 + 8 дх \ ду2 дх2 ) ~ '
где 0<А<1 и 8 пропорционально времени релаксации. Исходя из
известного результата для равновесного потока (е = 0) над волни-
волнистой стенкой y=xs\nx, найдите путем итераций поправку по-
порядка et. Полезно использовать косоугольные координаты %=х — у
и т\ = у (см. § 6 4). Исправьте результат в области его неоднород-
неоднородности далеко над стенкой. Образуйте равномерно пригодное первое
приближение Сравните с решением Винченти.
Г л а ва 10
ПРОЧИЕ АСПЕКТЫ
ТЕОРИИ ВОЗМУЩЕНИЙ
10.1. Введение
Эта последняя глава посвящена различным специаль-
специальным вопросам теории возмущений. Прежде всего мы
рассмотрим несколько методов, разработанных для за-
задач особых возмущений и отличных от тех двух стан-
стандартных методов, которые были введены в предыдущих
главах. Далее мы обсудим весьма своеобразную роль
логарифмических членов в возмущенных разложениях.
Затем мы исследуем в некоторых деталях захватывающие
возможности получения достаточно точных результатов
при помощи расходящихся или медленно сходящихся
рядов. И наконец, мы опишем способы связывания двух
различных разложений в тех случаях, когда их нельзя
срастить в смысле метода асимптотических разложений.
10.2. Метод составных уравнений
Мы уже видели (гл. 8), как Озеен устранил неодно-
неоднородности в приближении Стокса для течения при малых
числах Рейиольдса, частично включив в уравнения от-
отброшенные ранее конвективные члены. Та же идея мо-
может быть приложена к любой задаче особых возмуще-
возмущений, в которой неоднородности обусловлены дифферен-
дифференциальным уравнением. Можно поступить следующим
образом:
а) определить члены дифференциальных уравнений,
пренебрежение которыми в прямом приближении по-
порождает неоднородности;
б) возможно проще аппроксимировать эти члены,
сохранив их существенные черты в области неоднород-
неоднородности;
в) попытаться решить получившиеся составные урав-
уравнения.
10 2. Метод составных уравнений 257
Эту специальную процедуру с успехом использовали
Лайтхилл [1] для определения положения ударных волн
и Чжен [1] — для расчета вихревого слоя на наклонен-
наклоненном конусе.
Однако метод составных уравнений, по-видимому,
всегда оказывается хуже двух более систематиче-
систематических методов, введенных ранее. Его недостатки можно
было заметить при исследовании течений при малых чис-
числах Рейнольдса (гл. 8), когда внутреннее и внешнее
разложения сравнительно просто сопоставить с состав-
составным решением уравнений Озеена. Так, он вытесняется
методом деформированных координат в задаче ударных
волн (§9.6; Лайтхилл [3]) и методом парных асимптоти-
асимптотических разложений в задаче вихревого слоя (Мунсон[1]).
Можно продемонстрировать недостатки метода со-
составных уравнений, вернувшись к исследованию погра-
пограничного слоя на полубесконечной плоской пластине
(гл. 7). Используем приобретенный выше (§ 7.14) опыт
и перейдем к параболическим координатам. Уравнения
Навье — Стокса дают для функции тока уравнение, при-
приведенное в упражнении 8.1. Непосредственное прибли-
приближение состоит в устремлении величины v к нулю и при-
приводит к уравнению
Это уравнение непригодно в пограничном слое, где оно
заменяется уравнением
J*AtJ = 0, (Ю.2)
полученным применением метода Прандтля к полному
уравнению.
Теперь мы будем искать составное уравнение, которое
включает в себя оба эти приближения. В уравнении
A0.1) отсутствует только первый член уравнения A0.2).
Прибавив его к A0.1), получим составное уравнение
258 Гл. 10. Прочие аспекты теории возмущений
Поскольку наши координаты являю!ся оптимальными
для этой задачи (§ 7.13), можно предположить, что под-
подходящим решением этого уравнения является решение
Блазиуса, выраженное в параболических координатах,
(Ю.4)
Однако проверка показывает, что это выражение не яв-
является решением. В действительности простого решения
не существует. Объединяя трудности, имеющиеся во вну-
внутренней и внешней областях, мы приходим к неразреши-
неразрешимой задаче.
Конечно, это составное уравнение не является един-
единственным. К нашей форме A0.3) может быть добавлен
любой из отброшенных в полном уравнении членов и
любое кратное уравнения для потенциала. Таким обра-
зом, зная решение A0.4), мы можем построить неогра-
неограниченное число других составных уравнений, которым
оно удовлетворяет. Одно из таких простейших уравнений
будет
) = 0, (Ю.5)
однако нет никаких доводов для такого выбора уравне-
уравнения.
10.3. Метод составных разложений
Более обещающим методом прямого получения равно-
равномерно пригодного решения является подстановка пред-
предполагаемого составного разложения (см. § 5.4). Латта[1]
показал, что часто можно вывести требуемую форму раз-
разложения, исследуя внутреннее («пограничного слоя»)
решение. Это указывает на конечное число определенных
функций, которые должны быть взяты за основу разло-
разложения.
Мы иллюстрируем этот метод модельной задачей E.1)
Фридрихса. Внутреннее решение E.66) включает функ-
функцию е~х1е. Поскольку эта функция сохраняется при диф-
10.3. Метод составных разложений 259
ференцировании, других функций не требуется. В соот-
соответствии с этим Латта предположил, что составное
разложение имеет вид
f(x; B)~[fl(x) + efi(x)+ ...] +
+ e-**\k1W + th2(x)-\- ...]• A0.6)
Подстановка в уравнение E.1) и объединение членов с
одинаковыми степенями е и множителями е~х'е дают
fj = af A[ = 0f f1(O) + A1(O) = O. fiO)=l. A0.7a)
fm= fm-l~®> Ki~ Ьт-1 — ®> (Л(\7^\
Отсюда мы получаем /i=(l—а)+ах, h\=—A—а) и
fm = /zm = O. Следовательно, решение будет таково:
f(x; е)~A—я)A — е-*ъ) + ах. A0.8)
Предполагается, что этот результат равномерно пригоден
в интересующем нас интервале (Xlx-^l с ошибкой,,
меньшей чем любая стейень 8. Из сравнения с точным
решением E.2) следует, что это предположение верно.
В более сложных задачах внутреннее решение вместе
с его производными может указывать не на одну, а на
несколько быстро меняющихся функций. Например, если
мы рассмотрим линеаризованное уравнение Озеена (8.16)
в декартовых координатах для полубесконечной плоской
пластины, то решение пограничного слоя содержит до-
дополнительную функцию ошибок erfc(,///2Re-1%1/2) и мы
должны включить также ее производную ехр (—y2/4Re~lx)
(производные высшего порядка не добавляют новых
функций). Может также оказаться необходимым обоб-
обобщить аргумент функций, допуская, что он может быть
гладкой функцией всех координат, которые опреде-
определяются в ходе исследования. В результате этих двух
модификаций составное разложение для функции тока в
течении Озеена около плоской пластины должно быть
взято в виде
Ф(*, у;
+ erf с Их, iO/Re-^IM*. У) 4-Re-1/2A2(x, y)+ .. .] +
l- (Ю.9)
260 Гл. 10. Прочие аспекты теории возмущений
Изменение аргумента, разрешенное функцией g, суще-
существенно в этом случае, в то время как в предыдущем
примере оно было излишним. В действительности ока-
оказывается, что функция g(x,y) должна быть равна
1/2[{х2+У2L2 — х\ половине квадрата параболической
координаты г], что естественно приводит к оптимальным
координатам Каплуна (§ 7.13). Читатель может закон-
закончить решение или обратиться к работе Латта [1] для
уточнения деталей.
Могут также возникнуть дальнейшие усложнения,
особенно в нелинейных задачах. В модельной задаче §6.2
быстро меняющиеся функции были подсказаны внутрен-
внутренним решением F.18), но число их производных беско-
бесконечно. Необходимо также указать, что рассмотрение вну-
внутреннего решения не всегда подсказывает правильную
форму функций для разложения.
10.4. Метод многих масштабов
Только что упомянутые трудности могут быть устра-
устранены, если предположит^ более общую форму для со-
составного разложения. Как было указано в § 5.3, возму-
возмущенное решение является особым, если оно включает в
себя два различных масштаба длин для одной из коор-
координат. В соответствии с этим Кокрен [1] и Махони [1]
предположили, что решение зависит от этой координаты
отдельно в каждом из этих двух масштабов. Это озна-
означает, что такая «чувствительная» координата заменяется
двумя координатами, и, таким образом, число независи-
независимых переменных увеличивается. Тогда можно применить
обычное асимптотическое разложение. Подобная идея
была выдвинута также Коулом и Кеворкяиом [1].
Для иллюстрации мы вновь используем модельную
задачу E.1) Фридрихса. Вид внутреннего решения (или
другие рассуждения) показывает, что решение зависит
как от Jt/e, так и от самого х. В соответствии с этим мы
предположим, что асимптотическое разложение имеет вид
f(x; е)~Мх, X) + ef2{x, Х) + г%(х, *)+ ..., A0.10а)
где
Х = х!г. A0.106)
10.4. Метод многих масштабов 261
Это разложение должно быть однородным не только для
0<л:<1, но и для (ХХ^оо. Для того чтобы обеспе-
обеспечить однородность при Х->оо, что соответствует е->0
при х>0, следует наложить определенные ограничения;
это обстоятельство в действительности составляет основ-
основную трудность в рассматриваемом методе.
Конечно, мы должны заменить обыкновенное диффе-
дифференциальное уравнение уравнениями в частных произ-
производных, однако, как будет видно, при этом не возникнет
существенных усложнений. Подставив в задачу E.1)
предполагаемое разложение и приравняв одинаковые
степени 8, получим систему уравнений
hxx + fix = 0> 00.11а)
f2xx-hfix = a-2flxX-flx1 A0.116)
fmXX + fmX — %f(m-l) xX~~~f(m-l) x f(m-2) xx> m ^ 3.
A0.11b)
Номинально эти уравнения являются уравнениями в
частных производных, однако первое из них формально
тождественно с первым внутренним уравнением [уравне-
[уравнение E.5) при 8=1], и это всегда так. Его решением будет
fx(x, X) = c1(x) + dl(x)e~x, A0.12)
где функции интегрирования С\(х) и di(x) пока произ-
произвольны.
Применяемые в дальнейшем соображения имеют по-
поразительное сходство с теми, которые были использо-
использованы в методе Лайтхилла деформированных координат
(гл. 6). Если наше составное разложение A0.10) яв-
является равномерно пригодным, то отношения /2//i, /3//2
и т. д. должны оставаться величинами порядка единицы
при 8->0. Мы, следовательно, должны потребовать, чтобы
выполнялось следующее условие:
Каждое приближение должно иметь не
большую особенность, чем предшествую-
предшествующее, или стремиться к нулю не медленнее
его при е->0 для произвольных значений A0.13)
независимых переменных. То же условие
должно выполняться для всех производ-
производных.
Аналогия с принципом F.1) Лайтхилла очевидна.
262 Гл. 10. Прочие аспекты теории возмущений
Так же, как в методе деформированных координат,
можно получить равномерно пригодное первое прибли-
приближение, исследуя уравнение второго порядка, но не решая
его. В нашем примере уравнение второго порядка
A0.116) принимает вид
[(x)e-^. A0.14)
Любое частное его решение будет содержать член
(а — С[)Х. Но тогда второе приближение имело бы боль-
большую особенность, чем первое при Х->оо; следовательно,
этот член должен быть отброшен с помощью выбора
с[(х) = а. Подобным же образом остающееся частное
решение будет содержать член —d[Xe~x, благодаря ко-
которому производная f при Х->оо во втором приближе-
приближении будет стремиться к нулю медленнее, чем в первом.
Мы, следовательно, должны уничтожить всю правую
часть уравнения, полагая d[(x)—-0. Значения постоян-
постоянных Ci и di могут быть теперь найдены заменой /Y на
х/г в формуле A0.12) и наложением граничных условий
задачи E.1). Результат в точности совпадает с форму-
формулой A0.8), полученной методом Латта.
В более сложных задачах необходимо по меньшей
мере одно обобщение. Как и в предыдущем методе, мо-
может оказаться необходимым обобщить увеличенную ко-
координату A0.106), полагая
х=-?&-,
где g— гладкая функция, положительная при положи-
положительных значениях аргумента и определяемая в ходе
исследования. Читатель может проверить, что в рассма-
рассматриваемом примере, исходя из принципа A0.13), g'(x)
следует положить равной единице. В общем случае, ко-
конечно, функция g должна обращаться в нуль в точках
неоднородности, е может быть заменено некоторой дру-
другой степенью или функцией от параметра возмущения и
асимптотическая последовательность может содержать
другие функции е, а не целые его степени. В результате
того что вводится новое переменное X, число независи-
независимых переменных в дифференциальных уравнениях в част-
10.5. О логарифмических членах 263
ных производных возрастает только на единицу, однако
функция g должна зависеть от всех исходных независи-
независимых переменных. Некоторые примеры этого даны Кок-
реном [1].
Мы показали, что этот метод, а также метод, рассма-
рассматриваемый в предыдущем параграфе, превращают вну-
внутреннее решение метода сращиваемых асимптотических
разложений в равномерно пригодное приближение. Та-
Таким образом, они, по-видимому, дают ответ на вопрос
о том, как обобщить понятие оптимальных координат
(§ 7.15). Роль функции g состоит -в том, чтобы обеспе-
обеспечить свободу, необходимую для превращения координат
в оптимальные. Возможно, что при дальнейшем разви-
развитии один из этих методов заменит методы, применявшие-
применявшиеся прежде, как наболее гибкий и надежный способ иссле-
исследования задач особых возмущений.
10.5. О логарифмических членах
Энтузиасты методов теории возмущений постоянно
удивляются появлению логарифмических членов там, где
для этого нет никаких разумных оснований. Современ-
Современная история механики жидкости насчитывает не одного
известного исследователя, павшего жертвой той вполне
правдоподобной гипотезы, что применяемое им разло-
разложение содержит лишь степени малого параметра. Как
указывалось в гл. 3, при первом же намеке на затруд-
затруднения следует подозревать появление логарифмических
членов. Наличие этих членов как в параметрических,
так и в координатных разложениях было достаточно
полно иллюстрировано предыдущими примерами; см.,
например, формулы A.2), A.4), A.6), C.24), C.27),
G.47), (8.38), (8.48), (9.18) и (9.40). В различных зада-
задачах вязких течений Стюартсон [2, 3] обнаружил члены
вида In In, но, к счастью, такие случаи редки.
Источники появления логарифмических членов раз-
различны. В некоторых задачах они появляются как есте-
естественный результат цилиндрической симметрии. Так об-
обстоит дело, например, в теории тонкого тела (§ 9.8), где
логарифмы описывают существенно особую природу по-
поведения вблизи оси таких функций, как функция Бесселя
264 Гл. 10. Прочие аспекты теории возмущений
Ко и обратная гиперболическая функция Аг sech, кото-
которые фигурируют в более полных теориях.
Другим общим источником логарифмов является ма-
малая экспоненциальность. Этот случай иллюстрируется
примером D.50), в котором видна степень неоднородности
разложения. Такая ситуация всегда возникает при обте-
обтекании малого угла, которое описывается уравнениями
эллиптического типа, как для двояковыпуклого профиля
(§ 4.7). Если исследователь уверен в том, что дело об-
обстоит именно так, то можно превратить решение в равно-
равномерно пригодное простой заменой логарифмов степенями,
близкими к целым (упражнение 9.1; Мунсон [1]).
В обратных координатных разложениях для вязких
течений логарифмы часто требуются для выражения
экспоненциального убывания завихренности (§ 7.11).
В других задачах их источник еще более неясен. Многие
из этих задач представляют собой задачи особых возму-
возмущений. Исследователю остается лишь размышлять о том,
что описание с помощью дробных степеней не может
исчерпать бесчисленные процессы, происходящие вовсе-
ленной, и о том, что логарифмы представляют собой
следующие по простоте функции.
В этой последней группе разложения, как правило,
начинаются с простых степеней параметра возмущения,
а его логарифмы входят линейно только во второй, тре-
третий или даже пятый член. Таким образом, логарифмы
появляются обычно при целых степенях, которые после-
последовательно увеличиваются, хотя часто только в переме-
перемежающихся членах. В задаче особых возмущений наличие
логарифмов, скажем, во внутреннем разложении влечет
за собой их появление во внешнем разложении на сле-
следующем этапе из-за сдвига в порядке членов, который
имеет место при переходе от внутренних к внешним пе-
переменным.
Когда логарифм впервые появляется в членах выс-
высшего порядка, он сопровождается алгебраическим членом,
содержащим туже степень величины возмущения. Лога-
Логарифмический член гораздо легче вычислить, чем этот
алгебраический член, поскольку первый удовлетворяет
однородному дифференциальному уравнению. Тем не ме-
менее эти два члена должны рассматриваться как состав-
10.6. Улучшение рядов. Естественные координаты 265
ляющие одного шага в процессе последовательных при-
приближений. Такая тесная взаимосвязь этих двух членов,
очевидно, отражается тем обстоятельством, что видоизме-
видоизменение величины возмущения (§ 3.1) переносит константу
логарифмического члена в соответствующий алгебраи-
алгебраический.
Для тех значений, которые величина возмущений
принимает практически, ее логарифм незначительно отли-
отличается от единицы; поэтому алгебраический член в дей-
действительности может иметь большую величину, хотя он
имеет более высокий порядок малости. Более того, опыт
подсказывает, что эти два члена всегда имеют противо-
противоположные знаки и что их сумма часто оказывается зна-
значительно меньшей, чем каждый из них; таким образом,
сохранение только логарифмического члена может ухуд-
ухудшить точность. Примером этого является разложение
A.6) для подъемной силы эллиптического крыла. Для
значения Л = 6,37 оно дает
dCr
_^ = 2яA —0,314 — 0,074 + 0,088 ...), A0.16)
в то время как Кринес [1] вычислил точное значение,
равное 4,55. Два члена дают ошибку 6%, логарифмиче-
логарифмический член увеличивает ее до 15%, а его алгебраический
компаньон снова уменьшает ее до 3%. Таким образом,
представляется вероятным, что последние члены в таких
рядах, как A.2) и A.4), хотя и имеют теоретический
интерес, но не представляют практической важности до
тех пор, пока не вычислен следующий член. То же заме-
замечание относится и к /z-й степени логарифма, которая
должна быть объединена с членами, содержащими низ-
низшие степени логарифма.
В § 8.6 мы видели, что появление логарифмических
членов может резко ограничить диапазон приложимости
рядов для возмущений. Мы вернемся к этому вопросу
позже в § 10.7.
10.6. Улучшение рядов. Естественные координаты
Можно вычислить только несколько членов возму-
возмущенного разложения, обычно не больше, чем два или три.
и почти никогда не больше, чем семь. Получающиеся
266
Гл. 10. Прочие аспекты теории возмущений
ряды часто медленно сходятся или даже расходятся. Тем
не менее эти несколько членов содержат значительную
информацию, из которой исследователь должен извлечь
все что возможно.
Эта точка зрения была убедительно изложена в пре-
превосходной статье Шенкса [1], который привел несколько
замечательных примеров, включая несколько примеров
из механики жидкости. Простейшим примером является
числовой ряд
который сходится, но исключительно медленно. Седьмая
частная сумма, показанная ниже во втором столбце,
верна только в первой цифре, и потребовалось бы
400 000 членов для получения точности в шестом знаке.
Тем не менее первые семь членов действительно дают
величину я с точностью, большей чем шесть значащих
цифр, как показано путем образования следующей схемы:
1 4,0000000
2 2,6666667 3,1666667
3 3,4666667 3,1333333 3,1421053
4 2,8952381 3,1452381 3,1414502 3,1415993 A0.18)
5 3,3396825 3,1396825 3,1416433
6 2,9760462 3,1427129
7 3,2837385
Здесь третий столбец образован из второго нелинейным
преобразованием
q q __ s2
Чг&-. A0.19)
Повторение этого процесса дает следующий столбец,
причем последний столбец дает результат, верный с точ-
точностью до шести значащих цифр. Применение преобра-
преобразования еще один раз вдоль нижней диагонали дает
дальнейшее улучшение точности. Это и другие связанные
с ним преобразования подробно обсуждаются в статье
Шенкса.
10.6. Улучшение рядов. Естественные координаты
267
Важным предварительным этапом в задаче возмуще-
возмущений является подходящий выбор величины, по которой
ведется разложение (см. § 3.1). Для координатных раз-
разложений это означает использование системы естествен-
естественных координат, что, без сомнения, совпадает с понятием
Рис. 10.1а. Разложения для функции тока на оси за
параболоидальной ударной волной при М = 2, у = 7Д-
Декартовы координаты.
оптимальных координат. Однако для некоторых задач
можно выбрать специальные системы координат, кото-
которые приводят к наиболее удовлетворительным результа-
результатам. Хорошим примером может служить преимущество
параболических координат по сравнению с декартовыми
или любыми другими координатами в задачах, содержа-
содержащих параболические границы. Роль параболических ко-
координат в теории пограничного слоя для предельного
268
Гл. 10. Прочие аспекты теории возмущений
случая полубесконечной плоской пластины была обсу-
обсуждена в гл. 7.
Вторым примером является обратная задача об об-
обтекании затупленного тела (рис. 3.5) с параболоидаль-
-0,50
Рис. 10.16. Разложения для функции тока на оси яа
параболоидальной ударной волной при М = 2, у = 7/5.
Параболические координаты.
ной ударной волной. Введем параболические координа-
координаты g, г] в соответствии с равенством
х+ iy == у 6 [(? + 'ЛJ-Ь1]. A0.20)
так что ударная волна с радиусом носовой части Ъ опи-
описывается уравнением г] = 1. Тогда ряды Кабанна C.25)
для функции тока вблизи оси с их беспорядочным изме-
10.7. Приближения рациональными дробями 269
нением знака переходят (Ван-Дайк [6]) в знакоперемен-
знакопеременные (после первых двух членов) ряды
¦ф 1 8 /Л ч 1 ,л ч9 i 155 /л ч~
^ = -2~3-A-^)--Т8-A-^J+-^ГA-Т]K-
15235,- ч4 . 35416,.. чс 5 656 651 71 4fi ,
A —г]L +-о7о-A — *]M Еоо9— A — Л) 6+ ....
648 ^А -и "Г 243 V1 " 5832
A0.21)
При использовании этих координат — и в этом состоит
одно из их преимуществ — отчетливо видно, что разло-
разложение расходится в передней точке тела, хотя и не так
сильно, как разложение в декартовых координатах (см.
рис. 10.1а и 10.16). Возможность дальнейшего улучше-
улучшения этого ряда мы обсудим в следующем параграфе.
Третьим примером является ряд Блазиуса A.5) для
поверхностного трения на параболе. Преобразование его
к параболическим координатам (при этом Ъ в формуле
A0.20) заменяется на а) дает (Ван-Дайк [11])
— 2,99343?п н- ... . A0.22)
Численная проверка (упражнение 10.3) подтверждает ос-
основанную на теоретических соображениях догадку об
увеличении при этом радиуса сходимости почти на 50%.
10.7. Приближения рациональными дробями
Применение нелинейного преобразования Шенкса
A0.19) к первым трем членам степенного ряда 1+ае+
62 дает простую рациональную дробь
которая часто является более точным приближением в
сумме ряда, чем сумма исходных трех членов. Напри-
Например, она дает точную сумму, если ряд является геомет-
геометрической прогрессией (как сходящейся, так и расходя-
расходящейся). Это до некоторой степени объясняет успешное
применение преобразования Шенкса к такому ряду, как
A0.17), который, очевидно, является «почти геометриче-
геометрическим»,
270 Гл. 10. Прочие аспекты теории возмущений
Когда известно более чем три члена степенного ряда,
Шенкс [1] предлагает строить рациональные дроби выс-
высшего порядка. Так, из первых пяти членов ряда A.3)
Гольдштейна для сопротивления сферы в приближении
Озеена он получает
Re r _ 73920 + 66600 Re + 10880Re2
6я Д~~ 73920 + 38880 Re + 689 Re2 '
где Re — число Рейнольдса, отнесенное к радиусу. Это
хорошо согласуется с более точными вычислениями,
вплоть до Re= 10, в то время как исходный ряд стано-
становится непригодным для вычислений при Re>-1. Знамена-
Знаменатель рациональной дроби A0.24) обращается в нуль при
Re = —1,97 и Re = —54,5. Второе из этих значений слиш-
слишком велико, но первое наводит на мысль, что сходимость
исходного ряда A.3) ограничена особенностью при Re =
= —2. Это правдоподобно, поскольку, как следует из
формул (8.17) и (8.18), естественным параметром для
течения Озеена является х/2 Re, для которого особен-
особенность может лежать в точке —1 комплексной плоскости
(см. § 3.5).
Подобным же образом Ваи-Туйл [2] построил рацио-
рациональные дроби при помощи ряда Кабанна C.25) для
течения за параболоидальной ударной волной при М = 2
и соответствующего ему разложения A0.21) в параболи-
параболических координатах. Последнее имеет вид
2ф _ 1 — 0,73878 A - тр — 37,827 A — тр2 + 72,098 A—трз /109^
^2 1 -{- 4,5946 A — тр — 13,212 A — тр2 — 3,5958 A — rp3' ^R uZ0>
В то время как исходные ряды на поверхности тела рас-
расходятся (рис. 10.1а и 10.16), это выражение хорошо со-
согласуется с численными решениями и дает величину от-
отхода ударной волны Д, верную до четвертой значащей
цифры. Преимущество параболических координат пора-
поразительно подтверждается тем обстоятельством, что в де-
декартовых координатах соответствующая рациональная
дробь становится бесконечной в поле течения между
ударной волной и телом.
Мы можем сделать смелую попытку применить тот
же метод к другому результату Кабанна, относящемуся
10.7. Приближения рациональными дробями Ti\
к задаче обтекания затупленного тела. Из его двучлен-
двучленного разложения C.26) по степеням времени для рас-
расстояния отхода ударной волны от тела, импульсивно
приведенного в движение, мы можем образовать рацио-
рациональную дробь, которая остается ограниченной при бес-
бесконечном значении времени, в надежде оценить стацио-
стационарное значение этой величины. Для М = оо и у = 7/ъ это
дает
Для плоского течения (п=1) получается значение 0,429,
которое значительно ближе, чем исходный результат,
подходит к точному численно найденному значению 0,377
для кругового цилиндра. Этот успех показывает, по-ви-
по-видимому, что стоит потратить время на вычисление даль-
дальнейших членов разложения. Как уже было указано в
§ 3.9, соответствие будет худшим для осесимметричного
течения, где рациональная дробь A0.26) для сферы дает
значение 0,214, в то время как численное значение равно
0,128. Другие проверки этого способа экстраполяции
прямого координатного разложения на бесконечность
предлагаются в упражнениях 10.7 и 10.8.
Очень нужным был бы способ, аналогичный способу
рациональных дробей, для улучшения рядов, содержа-
содержащих логарифмические члены, подобно ряду A.4). В этом
направлении еще не получены достойные внимания ре-
результаты, однако мы приведем один пример, где удалось
добиться хотя бы частичного успеха. Ряд A.6) для
подъемной силы эллиптического крыла по аналогии с ре-
результатом (9.1а) Прандтля можно переписать в виде
dC, 2зх
— L-~ — A0.27)
da , , 2 , 16 Л . . , 7\ 1
В самом деле, результат в такой форме естественным об-
образом был получен (с другими, неверными константами)
в исследовании Кринеса [1]. Точность существенно улуч-
улучшена, например при Л = 2,55 ошибка уменьшена с И до
1%. Однако эта модификация имеет тот недостаток, что
272 Гл. 10. Прочие аспекты теории возмущений
она еще обращается в бесконечность (рис. 9.4), хотя
при меньшем значении Л, чем исходный ряд. Очевидно,
здесь еще остается место для дальнейшего улучшения.
10.8. Преобразование Эйлера
Преобразования, использованные в предыдущем па-
параграфе, несмотря на их очевидную полезность, имеют
тот недостаток, что их обычно приходится применять
произвольно и вслепую, без понимания соответствую-
соответствующего механизма. Это неизбежно, когда неизвестны ни
характер, ни положение особенности, которая ограничи-
ограничивает сходимость. Кроме того, ясно и без слов, что да-
далеко не всегда удается получить такое замечательное
улучшение, как в предыдущих примерах.
При дальнейшем выяснении вопроса об источнике
расходимости появляется возможность действовать бо-
более рационально и, следовательно, с большим успехом.
Так, могут быть случаи, когда известно положение осо-
особенности, но неизвестен ее характер. Как было указано
в § 3.5, в прикладной механике часто случается, что сте-
степенные разложения, физически осмысленные только для
положительных действительных значений величины воз-
возмущения, имеют радиус сходимости, ограниченный осо-
особенностью где-либо в комплексной плоскости, обычно на
отрицательной оси в точке —1, если переменные выбра-
выбраны наиболее естественным образом. То, что дело об-
обстоит именно так, можно или установить из общих рассу-
рассуждений, или обнаружить по виду соответствующей
рациональной дроби, как в A0.24), или просто заподо-
заподозрить.
В § 3.5 было выдвинуто предположение, что при этих
условиях обычно можно улучшить ряды, преобразуя их
к степеням нового параметра
Этот результат представляет собой частный случай
дробно-линейного преобразования. Целью такого преоб-
преобразования Эйлера является перенос особенности из точ-
точки е = — 1 в бесконечно удаленную точку. Если в комп-
комплексной плоскости других особенностей не существует,
10.8. преобразование Эйлера 273
то радиус сходимости становится бесконечным. Беллман
[1] исследовал результаты применения этого преобразо-
преобразования в различных задачах прикладной механики. Мы
приведем три примера, взятые из гл. 1.
Во-первых, рассмотрим еще раз ряд Блазиуса A.5)
для поверхностного трения на параболе, который был не-
несколько улучшен преобразованием к более естественным
параболическим координатам A0.22). Разложение в па-
параболических координатах, очевидно, имеет радиус схо-
сходимости, равный единице, что следует из существования
особенности при g=i в конформном преобразовании для
параболы. Следовательно, подходящим преобразованием
Эйлера будет разложение по степеням ?2/A+?2) после
устранения множителя g (поверхностное трение пред-
представляет собой нечетную по \ функцию). Это дает (Ван-
Дайк [11])
\ I VTte cf ~ 1,23259 (-y-JL-) - 0,49384
- 0,10650 (-^j3 - 0,04733
A0.29)
Коэффициенты теперь уменьшаются быстрее, чем 1/д2,
и это наводит на мысль, что даже далеко вниз по по-
потоку ряд сходится быстрее, чем ^1/п2 — тс2/6. Если это
так, то при ? = оо ряд должен воспроизводить значение
Блазиуса 0,664 для плоской пластины (§ 7.10). После-
Последовательные частные суммы имеют следующие значения:
1,743, 1,045, 0,894, 0,827, 0,789, 0,765, ..., A0.30)
и более детальное исследование оставляет мало сомне-
сомнений в том, что эта последовательность действительно
сходится к значению Блазиуса. Таким образом, радиус
сходимости ряда Блазиуса может быть расширен до бес-
бесконечности.
В качестве второго примера мы займемся улучше-
улучшением ряда Честера A.7) для расстояния ударной волны
от затупленного тела, перед которым возникает парабо-
274 Гл. 10. Прочие аспекты теории возмущений
лоидальная ударная волна при М = оо. Есть основания
полагать (Ван-Дайк [6]), что этот многообещающий ме-
метод приводит к разложению, сходящемуся при у<п/б,—
значение, которое практически не достигается, однако
скорость сходимости остается удручающе малой. При
у = 7Д, когда параметр возмущения (у—1I(у+1) соста-
составляет всего 7б, разложение принимает вид
A = ^.(i_0,667+0,433 — 0,306+ ...); (io.3i)
это выражение непригодно для конкретных вычислений.
Следуя рекомендации пользоваться естественными
координатами (§ 10.6), сначала перепишем этот резуль-
результат в параболических координатах A0.20). Тогда значе-
значение т] в носовой точке тела определится так:
93 „ 631 « , \
w^:w+-4 A0.32)
Имеется ряд признаков, указывающих на то, что такой
выбор е является наиболее естественным. Одним из них
является то обстоятельство, что ряд теперь колеблется
почти как геометрическая прогрессия с особенностью при
е = — 1. Далее соответствующее преобразование Эйлера
A0.28) дает
1 - 3 Г ? i 13 ( г \з } 177 ( е \'4 , "I
1"~T]o-i:?8LT4:7"h'8O" qr7J ~^22Ш\Т+7) ••••]•
A0.33)
Этот результат представляет собой безусловный успех.
Коэффициенты последних двух членов убывают сильнее,
чем обратный квадрат их показателей, что предсказы-
предсказывает быструю сходимость даже при е = оо. В то же время
даже y = °o соответствовало бы только значению 8=1,633,
а для реальных газов у не может превосходить 5/3, так
что е не превышает 0,817, а е/A+е) не превышает0,450.
При у = 7/б последовательные частные суммы ряда
A0.33) дают для расстояния ударной волны следующие
значения:
— = 0,0950, 0,0973, 0,0978, ... A0.34)
10.9. Связывание координатных разложений 275
Если к этим суммам приложить преобразования Шенкса
A0.19), то получится значение 0,0979. Различные числен-
численные расчеты дали значения, заключенные между 0,0980
и 0,0990. Интересно отметить, что, хотя это приближение
и основано на предположении, что у близко к единице,
его теперь можно применять вплоть до у^00, где оно
предсказывает расстояние ударной волны примерно в
три раза большее, чем при y = 7/s- Предшествовавшие
менее успешные попытки улучшить ряд Честера путем
применения рациональных приближений были предпри-
предприняты Ван-Дайком [6] и Ван-Туйлом [1].
В качестве третьего примера мы еще раз рассмотрим
ряд A.3) Гольдштейна для сопротивления сферы по
Озеену. Как было указано в § 10.7, и теоретические и
численные исследования наводят на мысль, что в нем
имеется особенность при Re = —2. Тогда применение со-
соответствующего преобразования Эйлера дает
J L U Re j~ 8642 + Re j ~
1 / Re \з 2459 / Re \4 9469 / Re \5
~4"I 2 + Re J ~~ 134400 \2+Rej "" 537600 \ 2 + Re J ""
A0.35)
Этот ряд имеет признаки сходимости при всех Re, хотя
и менее ярко выраженные, чем в предыдущих двух при-
примерах. Для Re = 20 результат получается менее точным,
чем A0.24) при дробно-линейном преобразовании, но
имеет то преимущество, что сохраняет смысл npnRe = oo,
где A0.24) дает CD = 0, а следующая рациональная дробь
с кубическим полиномом в числителе предсказывает от-
отрицательное сопротивление. При Re = oo последователь-
последовательные частные суммы ряда A0.35) будут
CD^9,42, 7,07, 4,83, 4,68, 4,51, 4,34, ... A0.36)
Они убывают довольно нерегулярно, но не представляет-
представляется невероятным, что они стремятся приблизительно к
значению 3,33, вычисленному Стюартсоном [1].
10.9. Связывание координатных разложений
Сращивание, как оно применялось в методе сращи-
сращиваемых асимптотических разложений, связывает два па-
параметрических разложения, имеющих место в соседних
Гл. 10. Прочие аспекты теории возмущений
пространственно-временных областях, для одного и того
же предельного перехода. Иногда оказывается возмож-
возможным связать подобным же образом другие виды раз-
разложений. В этом и в последнем параграфах мы рас-
рассмотрим два вида задач, в которых это возможно сде-
сделать.
Иногда в одной и той же задаче могут быть связаны
между собой различные координатные разложения. Если
оба они представляют собой сходящиеся ряды, то этот
процесс сводится к аналитическому продолжению, кото-
которое в принципе просто. Практические осложнения иллю-
иллюстрированы разложением Кабанна для функции тока за
параболоидальной ударной волной, записанной в пара-
параболических координатах в виде A0.21). Этот ряд схо-
сходится только примерно на трех четвертях расстояния от
волны до тела (рис. 10.1), что обусловлено существова-
существованием предельной линии в физически нереальном продол-
продолжении поля течения вверх по потоку от волны (Ван-
Дайк [6]). Этот ряд можно использовать для вычисления,
например, до половины расстояния от волны к телу, и
новый ряд, начатый оттуда, будет достигать тела. Од-
Однако такой новый ряд нельзя получить прямо из исход-
исходного оборванного ряда, поскольку он был бы эквивален-
эквивалентен ему и имел бы ту же область сходимости. Выход из
создавшегося положения (Льюис [1]) состоит в том, что-
чтобы использовать исходный ряд только для получения
новых начальных данных в промежуточной точке, а даль-
дальнейшие коэффициенты находить с помощью дифферен-
дифференциальных уравнений.
Более часто встречаются случаи, когда существуют
прямое и обратное разложения для малых и больших
значений координат соответственно. Последнее обычно
не сходится и является только асимптотическим разложе-
разложением, содержащим логарифмические члены и неопреде-
неопределенные константы (§ ЗЛО). Тем не менее такие два ряда
могут быть связаны — и тем самым константы опреде-
определены— если прямой ряд имеет бесконечный радиус схо-
сходимости. Мы продемонстрируем это для пограничного
слоя на параболе.
Преобразуя обратное разложение C.27) к параболи-
параболическим координатам A0.20) и перенося логарифмические
10.9. Связывание координатных разложений 277
члены в левую часть, получаем
A0.37)
Приравняем теперь это выражение той же величине, по-
полученной из прямого разложения A0.29), используя то
обстоятельство, что, ряд
1 / V \3
6 V 1Ч-Б2 У ""
сходится при ?2<1оо. Отсюда, учитывая также, что на
параболе 12 = 2х, получаем
-0,499 (-^-0,084 [j^-f- 0,034
- 0,018 (тт|гM- 0,01 lf-^-N-... A0.39)
для всех ?2-<оо. Далее, проводя формально разложение
для малых 1/A+ ?2) и сравнивая с разложением A0.37),
получаем (Ван-Дайк) [11]) для прежде неопределенной
константы С\ следующее значение:
d= 1 4- (— 1,34+1,00 + 0,25 + 0,12 +
+ 0,09 + 0,07+ . . .)'0,664« 1,89. A0.40)
Конечно, этот результат получен только приближенно
как частная сумма бесконечного ряда, однако он полу-
получен асимптотическим связыванием, а не численным скле-
склеиванием при некотором большом конечном значении |.
Склеивание с результатом численного интегрирования от
носовой точки при ?=6,8 дает Ci= 1,83.
Такого рода связывание невозможно в том случае,
когда прямой ряд имеет лишь конечный радиус сходи-
сходимости или является асимптотическим разложением.
К последней категории относится, например, приближе-
приближение C.24) Каррьера и Линя [1] для вязкого течения
вблизи передней кромки полубесконечной плоской
пластины, которое логически не может быть связано
с разложением высшего порядка для пограничного
278 Гл. 10. Прочие аспекты теории возмущений
слоя (§ 7.11). Имаи [4] произвел склеивание для поверх-
поверхностного трения при Ux/v=\, однако пригодность полу-
полученного таким образом результата сомнительна.
10.10. Связывание различных параметрических
разложений
Разложения для различных предельных значений од-
одного и того же параметра (например, для малых и боль-
больших чисел Рейнольдса) могут быть связаны, как и в пре-
предыдущем параграфе, при условии, что одно из них яв-
является сходящимся всюду. Такие примеры неизвестны,
хотя разложение A0.35) близко подходит к этим тре-
требованиям.
Разложения для двух различных параметров могут
быть связаны в конечном виде только в том случае, ко-
когда одно из них удовлетворяет соответствующему прави-
правилу подобия. Так, разложения теории тонкого профиля
или тонкого тела для дозвукового сжимаемого потока
могут быть получены из разложения Рэлея — Янсена па
степеням М2, однако обратное невозможно.
В качестве простейшего примера рассмотрим плоское
обтекание параболы у= ±гBхI/\ имеющей радиус но-
носовой части е2. Разложение потенциала скорости по сте-
степеням М2 было осуществлено Имаи [2] вплоть до члена
(Y+1)M4. Разлагая этот результат формально при ма-
малых е, получаем
+ О[М4, (ч>-М)М6, е3], A0.41а)
где [ср. A0.20)]
?2 = Vx2^-t/ + х + О (е2),
A0.416)
Чтобы превратить это двойное разложение для ма-
малых е и М2 в единое разложение для малых е, мы дол-
должны просуммировать ряд по М2. Эта, на первый взгляд,.
Упражнения 279
невыполнимая задача разрешается применением прави-
правила подобия во втором приближении дозвуковой теории
малых возмущений (Ван-Дайк [5]), согласно которому
у\ М, у, е)<~
A0.42)
где Р=A—М2I/г и каждая функция имеет тот же аргу-
аргумент, что и первая. Предыдущее двойное разложение
A0.41) совместимо с этим правилом только в том слу-
случае, когда его можно заменить следующим разложе-
разложением:
. е - 1 М2 9 Л rj2 . 1 Р + лМ
р 4 Р2 \ I2 + ti2 4Р2?2 /
_ vj-i ли 2г _?_ +1п12 + ^1 + О(?з)? A0в43а)
16 Р4 L (^2 + 'П2J 4Р2?2 J^ V h К }
где _
I , A0.436)
T|2 = "/x2H-pv — ^;
это представляет собой решение второго порядка теории
тонкого профиля. Соответствующее связывание для па-
параболоида вращения проведено Ван-Дайком [7].
УПРАЖНЕНИЯ
10.1. Уравнение Лайтхилла с применением многих масштабов.
Решите задачу F.3), используя метод многих масштабов, и пока-
покажите, что результат не совпадает с формулой F.12в), а является
некоторым иным, в равной мере приемлемым решением. Попытай-
Попытайтесь также решить эту задачу методом Латта составных разло-
разложений.
10.2. Задача, не допускающая сращивания. Покажите, что ме-
метод многих масштабов может быть с успехом применен в задаче
ef"+/=l, f @) =/'@) = 1, в то время как метод сращиваемых асимп-
асимптотических разложений оказывается непригодным.
10.3. Оценка радиуса сходимости. Оцените радиусы сходимости
рядов A.5) и A0.22), используя критерий Коши, и сравните со зна-
значениями s/a=Jt/4 и ?2=1, получающимися путем конформных отобра-
отображений для потенциального течения. Сделайте то же для рядов A.7>
280 Гл. 10. Прочие аспекты теории возмущений
и A0.21) и сопоставьте с особенностями в способе последователь-
последовательных приближений рациональными дробями.
10.4. Подъемная сила эллиптического крыла. Вычислите первые
три приближения для выражений A.6) и A0.27) при Л = 8/я (отно-
(отношение осей 2:1). Оцените полную сумму и сравните с значе-
значением 2,99, полученным Кринесом.
10.5. Приближения рациональными дробями для трения на па-
параболе. Постройте приближения рациональными дробями для раз-
разложений (Г1.5) и A0.22) и попытайтесь таким путем найти пре-
предельное значение далеко вниз по течению.
10.6. Критическое число Маха для круга. Критическое число
Маха (при котором впервые достигается местная звуковая ско-
скорость) приближенно представляется последовательными частными
суммами ряда A.1) Симасаки:
0,4659, 0,4206, 0,4090, 0,4043, 0,4020, 0,4008, ...
Оцените истинное значение и сравните с собственной оценкой
Симасаки 0,40. Оцените радиус сходимости ряда A.1), сравните
с данным Симасаки значением 0,50 и сопоставьте с критическим
числом Маха Рассмотрите возможность применения преобразования
Эйлера к ряду A.1).
10.7. Трение в носовой точке цилиндра, импульсивно приведен-
приведенного в движение. Попытайтесь экстраполировать ряд C.23) на бес-
бесконечные значения времени и сравните результат со значением
Хименца для установившегося обтекания (Шлихтинг [1]).
10.8. Отрыв потока на импульсивно приведенном в движение
круговом цилиндре. На круговом цилиндре радиуса а, импульсивно
приведенном в движение со скоростью V в вязкой жидкости, по-
поверхностное трение изменяется вначале со временем, пропорцио-
пропорционально величине (Гольдштейн и Розенхед [1])
• 1 + 2,8488 cos 0 U?\ — [0,8795 cos2 9 — 0,2330 sin2 9] U^X ,
где 0 — угол, отсчитываемый от передней критической точки. Най-
Найдите положение точки отрыва потока как функцию времени. Экстра-
Экстраполируйте результат на бесконечное значение времени и сравните
с известным значением 9=109° (Шлихтинг [1]).
ЛИТЕРАТУРА
Аббот, Дёнхоф (Abbott I. H.f Doenhoff A. E.)
[1] Theory of wing sections, Dover, New York, 1959.
Беллман (Bellman R.)
[1] Perturbation methods applied to nonlinear dynamics, /. Appl.
Mech., 22 A955), 500—502. Русский перевод: Беллман Р.,
Метод возмущений в приложении к нелинейной динамике, сб.
Механика, № 2 D2) A957).
Берне (Burns J. С.)
[1] Airscrews at supersonic forward speeds, Aeronaut. Quart, 3
A951), 23—50.
Бретертон (BrethertonF, P.)
[1] Slow viscous motion round a cylinder in a simple shear, /.
Fluid Mech., 12 A962), 591—613.
Б р ич (Breach D. R.)
[1] Slow flow past ellipsoids of revolution, /. Fluid Mech., 10
A961), 306—314.
Бродерик (BroderickJ. В.)
[1] Supersonic flow round pointed bodies of revolution, Quart. J.
Mech. Appl. Math., 2 A949), 98—120.
Б у л a x Б. М.
[1] О некоторых свойствах сверхзвуковых конических течений
газа, ПММ, 25 A961), вып. 2, 229—241.
Б э т ч е л о р (В a t с h е I о г G. К.)
[1] A proposal concerning laminar wakes behind bluff bodies at
large Reynolds number, /. Fluid Mech., 1 A956), 388—398.
В азов (WasowW.)
[1] On the convergence of an approximation method of M. J. Light-
hill, /. Rat. Mech. Anal, 4 A955), 751—767.
В а н - Д а й к (Van DykeM. D.)
[1] The combined supersonic-hypersonic similarity rule, /. Aero-
Aeronaut ScL, 18 A951), 499—500. Русский перевод: Ван
Д а и к М. Д., Объединенный закон подобия для сверхзвуко-
сверхзвуковых и очень больших сверхзвуковых скоростей, сб. Меха-
Механика, № 2 A2) A952), 64—65.
[2] A study of second-order supersonic flow theory, Rep. NACA
№ 1081, 1952.
282 Литература
[3] Subsonic edges in thin-wing and slender-body theory, Tech.
Note NACA № 3343, 1954.
[4] Second-order subsonic airfoil theory including edge effects, Rep.
NACA № 1274, 1956.
[5] The similarity rules for second-order subsonic and supersonic
flow, Rep. NACA № 1374, 1958.
[6] A model of supersonic flow past blunt axisymmetric bodies
with application to Chester's solution, /. Fluid Mech., 3 A958),
515—522.
[7] The paraboloid of revolution in subsonic flow, /. Math and
Phys., 37 A958), 38—51.
[8] Second-order slender-body theory — axisymmetric flow, Tech.
Rep. NASA № R-47, 1959.
[9] Higher approximations in boundary-layer theory. Part 1. Gene-
General analysis, /. Fluid Mech., 14 A962), 161 — 177.
[10] Higher approximations in boundary-layer theory. Part 2. Appli-
Application to leading edges, /. Fluid Mech., 14 A962), 481—495.
[11] Higher approximations in boundary-layer theory. Part 3. Para-
Parabola in uniform stream, /. Fluid Mech., 19 A964), 145—159.
[12] Lifting-line theory as a singular perturbation problem, Arch.
Mech. Stos., 16 A964), № 3.
В а н - T у й л (VanTuylA.)
[1] The use of rational approximations in the calculation of flows
with detached shocks, Rep. U. S Naval Ord Lab. № 6679, 1959.
[2] The use of rational approximations in the calculation of flows
with detached shocks, /. Aerospace Sci., 27 A960), 559—560
В ей ль (WeylH.)
[1] On the differential equations of the simplest boundary-layer
problems, Ann. of Math., 43 A942), 381—407.
Вендт (Wendt H.)
[1] Die J3nsen — Rayleighsche Naherung zur Berechnung von Un-
terschallstromungen, Siizsber. Heidelberg. Akad. Wiss., Math.'
Naturwiss. Kl.,7 A948), 147—170.
В и л к и н с о н (W i I k i n s о n J.)
[1] A note on the Oseen approximation for a paraboloid in a uni-
uniform stream parallel to its axis, Quart. J. Mech. Appl. Math., 8
A955), 415—421.
В и н ч е и т и (V i n с e n t i W. G.)
[1] Non-equilibrium flow over a wavy wali, /. Fluid Mech., 6
A959), 481—496
Гарабедян (Garabedian P. R.)
[1] Calculation of axially symmetric cavities and jets, Pacific J.
Math., 6 A956), 611—684.
Г и po (Guiraud J. P.)
[1] Ecoulement hypersonique d'un fluide parfait sur une plaque
plane comportant un bord d'attaque cTepaisseur finie,
С R. Acad. Sci. Paris, 246 A958), 2842—2845.
Литература 283
ГоЮн-гуай (Kuo Y. Н.)
[1] On the How of an incompressible viscous fluid past a flat plate
at moderate Reynolds numbers, /. Math, and Phys, 32 A953),
83—101.
[2] Viscous flow along a flat plate moving at high supersonic
speeds, /. Aeronaut ScL, 23 A956), 125—136. Русский перевод:
К у о, Обтекание вязким газом плоской пластины, движущейся
с большими сверхзвуковыми скоростями, сб. Механика, № 6
D0) A956), 3—26.
Гольдштейн (Goldsteins.)
[1] The steady flow of viscous fluid past a fixed spherical obstacle
at small Reynolds numbers, Proc. Roy. Soc, Ser. A, 123 A929),
225—235.
[2] Modern developments in fluid dynamics, Oxford Univ. Press,
London — New York, 1938. Русский перевод второго издания
A943): Гольдштейн С. (ред.), Современное состояние
гпдроаэродинамики вязкой жидкости, ИЛ, 1948.
[3] Flow of an incompressible viscous fluid along a semi-infinite
flat plate, Tech. Rep. Eng. Res. Inst. Univ. Calif. № HE-150-144,
1956.
[4] Lectures on fluid mechanics, Wiley, New York, 1960.
Гольдштейн, Розенхед (Goldstein S., Rosenhead L.)
[1] Boundary layer growth, Proc. Cambridge Philos. Soc, 32
A936), 392—401.
Джексон (JensonV. G)
[1] Viscous flow round a sphere at low Reynolds numbers (<40),
Proc. Roy. Soc, Ser. A, 249 A959), 346—366
Д ж e ф ф p и с (J e f f г е у s H.)
[1] On the relation to physics of the notion of convergence of se-
series, Philos. Mag [7J, 2 A926), 241—244.
Джонс (JonesR. T.)
[1] Leading-edge singularities in thin-airfoil theory, /. Aeronaut.
ScL, 17 A950), 307—310.
Д ж о н с, К о э н (J о n e s R. Т., С о h e n D.)
[1] High speed wing theory, Princeton Univ. Press, Princeton, 1960.
Ж е р м е н, Г и р о (Germain P., Guiraud J. P.)
[1] Conditions de choc dans un fluide done de coefficients de vis-
cosite et de conductibilite thermique faibles mais non mils,
C. R. Acad. Sci. Paris, 250 A960), 1965—1967.
[2] Conditions dc choc et structure des ondes de choc dans un
ecoulement stationnaire de fluide dissipatif, ONERA Publ.
№ 105, 1962.
И м а и (I m a i I.)
[1] On the asymptotic behaviour of viscous fluid flow at a great
distance from a cylindrical body, with special reference to Fi-
lon's paradox, Proc. Roy. Soc, Ser. A, 208 A951), 487—516.
284 Литература
[2] Application of the M2-expansion method to the subsonic flow
of a compressible fluid past a parabolic cylinder, Proc. 1st.
Japan Nat. Cong. Appl. Mech., 1952, 349—353.
[3] On the asymptotic behaviour of compressible fluid flow at a
great distance from a cylinder in the absence of circulation, /.
Phys. Soc. Japan, 8 A953), 537—544.
[4] Second approximation to the laminar boundary-layer flow over
a flat plate, /. Aeronaut ScL, 24 A957), 155—156.
[5] Theory of bluff bodies, Tech. Note Inst. Fluid Dynamics and
Appl. Math. Univ. Maryland № BN-104, 1957.
Кабанн (Cabannes H.)
[1] Etude de Fonde de choc attached dans les ecoulements de re-
revolution, Rech. Aero., № 24 A951), 17—23.
[2] Etudes du depart d'un obstacle dans un fluide au repos, Rech.
Aero., N2 36 A953), 7-12.
[3] Tables pour la determination des ondes de choc detachees,
Rech. Aero., № 49 A956), 11—15.
Кавамура, Цянь (Kawamura R., TsienF. H.)
[1] Aerodynamic stability derivatives of axisymmetric body moving
at hypersonic speeds, Proc. 3rd Intern. Cong. Aero. Sci., Spar-
Spartan Books, Baltimore, 1964.
Каплун (К a p 1 u n S.)
[1] The role of coordinate systems in boundary-layer theory, Z. an-
gew. Math. Phys., 5 A954), 111 — 135.
[2] Low Reynolds number flow post a circular cylinder, J. Math.
Mech., 6 A957), 595—603.
Каплун, Лагерстром (Kaplun S., Lagerstrom P. A.)
[1] Asymptotic expansions of Navier — Stokes solutions for small
Reynolds numbers, /. Math. Mech., 6 A957), 585—593.
Карман (Karman vonT.)
[1] The similarity law of transonic flow, /. Math, and Phys., 26
A947), 182—190. Русский перевод: Карман Т., Закон подо-
подобия для трансзвукового потока, сб. Газовая динамика, ИЛ,
1950, 173—182.
Карман, Бюргере (Karman von Т., Burgers J. M.)
[1] General aerodynamic theory — perfect fluids. Division E. Aero-
Aerodynamic Theory (D u r a n d W. F., ed. ), vol. 2, Springer, Ber-
Berlin, 1935. Русский перевод: Карман Т., Бюргере И,
Теоретическая аэродинамика идеальных жидкостей, Д ю-
рэнд В. Ф. (ред.), Аэродинамика, т. II, раздел Е, Оборон-
гиз, 1939.
К а р р ь е р (С а г г i е г G. F.)
[1] Boundary layer problems in applied mathematics, Cotntn Pure
Appl. Math, 7 A954), 11—17.
Каррьер, Линь Цзя-цзяо (Carrier G. F., Lin С. С.)
[1] On the nature of the boundary layer, near the leading edge of
a flat plate, Quart. Appl. Math., 6 A948), 63—68.
Литература 285
Келли (Kelly R. E.)
[1] The final approach to steady, viscous flow near a stagnation
point following a change in free stream velocity, J. Fluid Mech
13 A962), 449—464.
Керл (Cur le N.)
[1] Unsteady two-dimensional flows with free boundaries. I. Gene-
General theory. II. The incompressible inviscid jet, Proc. Roy. Soc,
Ser. A, 235 A956), 375—395.
Кокрен (CochranJ.)
[1] A new approach to singular perturbation problems, Ph. D. Dis-
Dissertation, Stanford Univ., 1962.
Ко у л (Cole J. D.)
[1] Newtonian flow theory for slender bodies, /. Aeronaut. ScL, 24
A957), 448—455.
Коул, Кеворкян (ColeJ. D., Kevorkian J.)
[1] Uniformly valid asymptotic approximations for certain non-li-
non-linear differential equations. Nonlinear Differential Equations and
Nonlinear Mechanics (L a S a 11 e J. P., Lefschetz S.,
eds.), Academic Press, New York, 1963, 113—120.
Коул, М и с с а й т е р (Cole J. D., M e s s i t e r A. F.)
[1] Expansion procedures and similarity laws for transonic flow.
I. Slender bodies at zero incidence, Z. angew. Math. Phys., 8
A957), 1—25.
Ко у л с (Coles D.)
[1] The laminar boundary layer near a sonic throat, Preprints Heat
Transfer Fluid Mech. Inst., Stanford Univ. Press, Stanford,
1957, 119—137.
Кринес (Krienes K-)
[1] Die elliptische Tragflache auf potentialtheoretischer Grundlage,
Z. angew. Math. Mech., 20 A940), 65—68.
Лагерстром (LagerstromP. A.)
[1] Note on the preceding two papers, /. Math. Mech., 6 A957),
605—606.
Лагерстром, Коул (Lagerstrom P. A., Cole J. D.)
[1] Examples illustrating expansion procedures for the Navier —
Stokes equations, /. Rat. Mech. Anal., 4 A955), 817—882.
Лайтхилл (Light hill M. J.)
[1] The position of the shock-wave in certain aerodynamic prob-
problems, Quart. J. Mech Appl. Math., 1 A948), 309—318.
[2] A technique for rendering approximate solutions to physical
problems uniformly valid, Philos Mag. [7], 40 A949), 1179—
1201.
[3] The shock strength in supersonic „conical fields", Philos. Mag.
[7], 40 A949), 1202—1223.
[4] A new approach to thin aerofoil theory, Aero. Quart., 3 A951),
193—210.
286 Литература
On displacement thickness, J. Fluid Mech., 4 A958), 383—392.
A. technique for rendering approximate solutions to physical
problems uniformly valid, Z. Flugwiss., 9 A961), 267—275.
Л а м б (LambH.)
[1] On the uniform motion of a sphere through a viscous fluid,
Philos. Mag. [6], 21 A911), 112—121.
[2] Hydrodynamics, 6th ed., Cambridge Univ. Press, London — New
York, 1932. Русский перевод: Л а м б Г., Гидродинамика, Гос-
техиздат, 1947.
Латта (Latta G. Е.)
[1] Singular perturbation problems, Ph. D. Dissertation, Calif. Inst.
Tech., 1951.
Л е в и (Le v e у H. C.)
[1] The thickness of cylindrical shocks and the PLK. method, Quart.
Appl. Math., 17 A959), 77—93.
Левинсон (L e v i n s о n N.)
[1] On the asymptotic shape of the cavity behind an axially symmet-
symmetric nose moving through an ideal fluid. I, Ann. of Math. B),
47 A946), 704—730.
Легра (Legras J.)
[1] Application de la methode de Lighthill a un ecoulement plan su-
personique, С R. Acad. Scl. Paris, 233 A951), 1005—1008.
[2] Nouvelles applications de la methode de Lighthill a l'etude des
ondes de choc, ONERA Publ. № 66, 1953.
Л и б б и, Ф о к с (L i b b у P. A., F о х Н.)
[1] Some perturbation solutions in laminar boudnary-layer theory.
Part I The momentum equation, J. Fluid Mech., 17 A963),
433—449.
ЛиньДун-цзи, Ш а ф (LinT. C, Schaaf S. A.I
[1] Effect of slip on flow near a stagnation point and in a boun-
boundary layer, Tech. Note NACA № 2568, 1951.
Линь Ц з я - ц з я о (Lin С. С.)
[1] On a perturbation theory based on the method of characteristics,
/. Math, and Phys., 33 A954), 117—134.
Липман, Паккет (L i e p m a n n H. W., Puckett A. E.)
[1] Introduction to aerodynamics of compressible fluid, Wiley, New
York, 1947. Русский перевод: Липман Г. В., Паккет А. Е.,
Введение в аэродинамику сжимаемой жидкости, ИЛ, 1949
Льюис (Lewis G. Е.)
[1] Two methods using power series for solving analytic initial va-
value problems, Ph. D. Thesis, New York Univ., 1959.
Лыоис, Каррьер (L e w i s J. A., Carrier G. F.)
[1] Some lemarks on the flat plate boundary layer, Quart. Appl
Math, 7 A949), 228—234.
Литература 287
М а х о н и (М a h о п у J. J.)
[1] An expansion method for singular perturbation problems, /.
Austral Math. Soc, 2 A962), 440—463.
Мер р ей (Murray J.D.)
[1] the boundary layer on a flat plate in a stream with uniform
shear, /. Fluid Mech., 11 A961), 309—316
Милн-1омпсон (Milne-Thompson L. M.)
[1] Theoretical hydrodynamics, 4th ed., Macmillan, New York, 1960.
Русский перевод: Милн-Томпсон Л. М., Теоретическая
гидродинамика, «Мир», 1964.
М о т т - С м и т (М о 11 - S m i t h H. M.)
[1] The solution of the Boltzmann equation for a shock wave, Phys.
Rev., 82 A951), 885—892. Русский перевод: Мотт-Смит Г.,
Решение уравнения Больцмана для ударной волны, сб. Меха-
Механика, № 1 A7) A953), 72—85.
М у н к (М u n k М. М.)
[11 General theory of thin wing section, Rep. NACA № 142, 1922.
[2] Fluid dynamics for aircraft designers, Ronald Press, New York,
1929.
M у н с о н (М u n s о n A. G.)
[1] The vortical layer on an inclined cone, /. Fluid Mech., 20 A964),
625—643.
О з е е н (OseenCW.)
[1] Ober die Stokes'sche Formel, und iiber eine verwandte Aufgabe
in der Hydrodynamik, Ark. Math. Astronom. Fys., 6 A910),
№ 29.
О л д е н (А 1 d e n H. L.)
[1] Second approximation to the laminar boundary layer flow over
a flat plate, /. Math, and Phys., 27 A948), 91 — 104.
Осватич (OswatitschK.)
[1] Gas dynamics, Academic Press, New York, 1956.
Осватич, Берндт (Oswatitsch K-, Berndt S. B.)
[1] Aerodynamics similarity at axisimmetric transonic flow around
slender bodies, KTH Aero. TN 15, Roy. Inst. Tech. Stockholm,
1950.
Осватич, Съёдин (Oswatitsch К., S j 6 d i n L.)
[1] Kegelige Oberschallstromung in Schallnahe, Qsterreih. Ing.-Arch-.,
8 A954), 284—292
Прандтль (Р r a n d 11 L.)
[1] Ober Flussigkeiten bei sehr kleiner Reibung, Verh. Ill Internat.
Math. Kongr., Heidelberg, Teubner, Leipzig, 1905, 484—491; Vier
Anhadlungen zur Hydrodynamik und Aerodynamik (P r a n d 11
L., В et z A., eds.), Gottingen, 1927.
[2] The mechanics of viscous fluids. Division G. Aerodynamic theory
(Durand W. F., ed.), vol. 3, Springer, Berlin, 1935, 34—208.
288 Литература
Русский перевод: Прандтль Л, Механика вязких жидко-
жидкостей, Дюрэнд В. Ф. (ред), Аэродинамика, т. III, раздел Ж,
Оборингиз, 1939, 47—237.
Прандтль, Титьенс (Prandtl L., Tietjens О. G.)
[1] Applied Hydro- and Aeromechanics, McGraw-Hill, New York,
1934. Русский перевод немецкого издания: Титьенс О, Гид-
ро- и аэродинамика. По лекциям Л. Прандтля, ОНТИ, 1935.
Праудмен, Пирсон (Proudman I., Pearson J. R. A.)
[1] Expansions at small Reynolds numbers for the flow past a
sphere and a circular cylinder, /. Fluid Mech., 2 A957), 237—
262. Руский перевод: Праудман И., Пирсон Дж., Разло-
Разложения по малым числам Рейнольдса в задачах обтекания сфе-
сферы и кругового цилиндра, сб. Механика, № 2 D8) A958).
ритуло М. Ф.
[1] Об определении равномерно точных решений дифференциаль-
дифференциальных уравнений методом возмущений координат, ПММ, 26
MQfi9.\ яып Я 444—452.
Пуанкаре (Р о i n с а г ё Н.)
[1] Les methodes nouvelles de la mecanique celeste, vol. I, ch. 3,
Dover, New York, 1892.
Pao (Rao P. S.)
[1] Supersonic bangs, Aero. Quart., 7 A956), 21—44.
Розенхед (Rosenhead L, ed.)
[1] Laminar boundary layers, Oxford Univ. Press, London — New
York, 1963.
Рубинов Келлер (Rubinow S. I., Keller J. B.)
[1] The transverse force on a spinning sphere moving in a viscous
fluid, J. Fluid Mech., 11 A961), 447—459.
Рэлей (Rayleigh)
[1] On the flow of a compressible fluid past an obstacle, Philos.
Mag. [6], 32 A916), 1—6.
Сербии (Serb in H.)
[1] The high speed flow of gas around blunt bodies, Aero. Quart.,
9 A958), 313—330.
Симасаки (Simasaki 1)
[1] On the flow of a compressible fluid past a circular cylinder, II,
Bull. Univ. Osaka Prefecture, Ser. A, 4 A956), 27—35.
CnpeftTep(SpreiterJ. R.)
[1] On the application of transonic similarity rules to wings of
finite span, Rep. NACA № 1153, 1953.
[2} Aerodynamics of wings and bodies at transonic speeds, /. Aero-
Aerospace Set., 26 A959), 465—487. Русский перевод: Спрей-
тер Дж. Р., Аэродинамика крыльев и тел при околозвуковых
скоростях, сб. Механика, № 2 F1) A960).
Литература 289
Стокер ( S toker J. J.)
[1] Water waves, Wiley, New York, 1957. Русский перевод: Сто-
Стокер Дж. Дж , Волны на воде, ИЛ, 1959.
Стоке (Stokes G. G.)
[1] On the effect of the internal friction of fluids on the motion of
pendulums, Trans. Camb. Phil. Soc, 9 A851), Part II, 8—106;
Math, and Phys. Papers, vol. 3, Cambridge Univ. Press, Lon-
London—New York, 1901, 1—141.
Сто у н (S to ne A. H.)
[1] On supersonic flow past a slightly yawing cone, /. Math, and
Phys., 27 A948), 67—81
Стюартсон (Stewartson К.)
[1] On the steady flow past a sphere at high Reynolds number
using Oseen' approximation, Philos. Mag. [8], 1 A956), 345—
354.
[2] On asymptotic expansions in the theory of boundary layers, /.
Math and Phys., 36 A957), 173—191.
[3] Viscous flow past a quarter-infinite plate, J. Aerospace ScL, 28
A961), 1 — 10.
С ы ч е в В. В.
[1] О методе малых возмущений в задачах обтекания тонких за-
затупленных тел гиперзвуковым потоком газа, Журн. прикл. мех.
и техн. физ. A962), вып. 6, 50—59.
Тамада, М и я г и (Т a m a d a K-, М i у a g i T.J
[1] Laminar viscous flow past a flat plate set normal to the stream,
with special reference to high Reynolds numbers, /. Phys. Soc.
Japan, 17 A962), 373—390.
Танеда (TanedaS.)
[1] Studies on wake vortices (III). Experimental investigation of
the wake behind a sphere at low Reynolds numbers, Rep. Res.
Inst. Appl. Mech. Kyushu Univ., 4 A956), 99—105.
T и н г (Т i n g L.)
[1] On the mixing of two parallel streams, /. Math, and Phys., 38
A959), 153—165.
[2] Boundary layer over a flat plate in presence of shear flow,
Phys. Fluids, 3 A960), 78-81.
Тиффорд (Tifford A. N )
[1] Heat transfer and frictional effects in laminar boundary layers.
Part 4. Universal series solutions, Tech. Rep. Wright Air Dev.
Center № 53-288, 1954.
T о м о т и к а, А о и (Tomotika S., А о i T.)
[1] The steady flow of viscous fluid past a sphere and circular cy-
cylinder at small Reynolds numbers, Quart. J. Mech. Appl. Math.,
3 A950), 140—161. Русский перевод: Томотика С, Аой Т.,
Установившееся движение сферы и цилиндра в вязкой жид-
жидкости при малых числах Re, сб. Механика, № 2 A2) A952).
290 Литература
Трауготт (TraugottS. С.)
[1] Evaluation of indeterminate second-order effects for the Rayleigh
problem, Phys. Fluids, 5 A962), 1125—1126.
T p и т т о н (Т г i 11 о n D. J.)
[1] Experiments on the flow past a circular cylinder at low Reynolds
numbers, /. Fluid Mech., 6 A959), 547—567.
T у р б e p (T h u r b e r J. K.)
[1] An asymptotic method for determining the lift distribution of a
swept-back wing of finite span, Ph. D. Dissertation, New York
Univ., 1961; Comm. Pure Appl. Math., 28 A965), 733—756.
Туэйтс (Thwaites В., ed.)
[1] Incompressible aerodynamics, Oxford Univ. Press, London —
New York, 1960.
У Яо-цзу (Wu Y. Т.)
[1] Two dimensional sink flow of a viscous, heat-conducting, com-
compressible fluid; cylindrical shock waves, Quart. Appl. Math., 13
A956), 393—418.
Уайтхед (W h i t e h e a d A. N.)
[1] Second approximations to viscous fluid motion, Quart. J. Math.,
23 A889), 143—152.
У и гэм (Whitham G. В.)
[1] The flow pattern of a supersonic projectile, Comm. Pure Appl.
Math., 5 A952), 301—348.
[2] The propagation of weak spherical shocks in stars, Comm. Pure
Appl. Math., 6 A953), 397—414.
У орд (Ward G. N.)
[1] Linearized theory of steady high-speed flow, Cambridge Univ.
Press, London — New York, 1955.
Ф е р р и (Fe r r i A.)
[1] Supersonic flow around circular cones at angles of attack, Tech.
Note NACA № 2236, 1950.
Ф е р р и, Н е с с, К а п л и т a (F e r r i A., Ness N., К а р 1 i-
ta Т. Т.)
[1] Supersonic flow over conical bodies without axial symmetry,
/. Aeronaut. Set., 20 A953), 563—571. Русский перевод:
Ф е р р и А., Н е с с Н., Каплита Т , Сверхзвуковое обтека-
обтекание конических тел, не обладающих осевой симметрией, сб.
Механика, № 3 B5) A954), 3—19.
Френкель, У о т с о н (F г а е n k е 1 L. E., Watson R.)
[1] The formulation of a uniform approximation for thin conical
wings with sonic leading edges, Pros. Symp. Transsonicum
(Oswatitsch K., ed.), Springer, Berlin, 1964, 249—263.
Фридрихе (FriedrichsK. О.)
[1] Theory ot viscous fluids. Fluid Dynamics, Ch. 4, Brown Univ.,
1942.
Литература 291
[2] Formation and decay of shock waves, Comm. Pure Appl. Math
1 A948), 211—245.
[3] Special topics in fluid dynamics, New York Univ., 1953, 120—130.
[4] Special topics in analysis, New York Univ., 1954.
[5] Asymptotic phenomena in mathematical physics, Bull. Amer
Math. Soc, 61 A955), 485—504.
Ханкок (Hancock G.J.)
[1] The self-propulsion of microscopic organisms through liquids,
Proc Roy. Soc, Ser. A, 217 A953), 96—121.
Ханцше (Hantzsche W.)
[1] Die Prandtl — Glauertsche Naherung als Grundlage fur ein Ite-
rationsverfahren zur Berechnung kompressibler Unterschallstro-
mungen, Z. angew. Math. Mech., 23 A943), 185—199.
Ханцше, Вендт (Hantzsche W, Wendt H.)
[1] Die laminare Grenzschicht an einem mit Oberschallgeschwindig-
keit angestromten nicht angestellen Kreiskegel, Jahrbuch der
deutschen Luftfahrtforschung, 1 A941), 76—77.
Хейз (Hayes W. D.)
[11 Pseudotransonic similitude and first-order wave structure, /.
Aeronaut. ScL, 21 A954), 721—730. Русский перевод: Хейз,
Псевдотрансзвуковое подобие и структура волн в первом
приближении, сб. Механика, № 1 C5) A956), 57—74.
[2] Second-order pressure law for two-dimensional compressible
flow, /. Aeronaut. ScL, 22 A955), 284—286.
Хейз, Пробстин (Hayes W. D., Probstein R. F.)
[1] Hypersonic flow theory, Academic Press, New York, 1959. Рус-
Русский перевод: X e й з У. Д., Пробстин Р Ф., Теория гипер-
гиперзвуковых течений, ИЛ, 1962
Холл (Hall I. M.)
[1] The displacement effect of a sphere in a two-dimensional shear
flow, /. Fluid Mech., 1 A956), 142—162
Ц я н ь Сюэ-сэнь (T s i e n H. S.)
[1] The Poincare — Lighthill — Kuo method, Advances in Appl.
Mech., vol. 4, 1956, 281—349. Русский перевод: Цянь Сюэ-
сэнь, Метод Пуанкаре — Лайтхилла — Го, сб. Проблемы ме-
механики, вып. II, ИЛ, 1959, 7—62.
Честер (Chester W.)
[1] Supersonic flow past a bluff body with a detached shock. Part
I. Two-dimensional body, /. Fluid Mech., 1 A956), 353—365.
Русский перевод: Честер У., Сверхзвуковое обтекание тупо-
тупоносого тела с отсоединенной ударной волной, часть I, двумер-
двумерное тело, сб. Механика, № 5 D5) A957), 19—31.
[2] Supersonic flow past a bluff body with a detached shock. Part
II. Axisymmetrical body, /. Fluid Mech., 1 A956), 490—496. Рус-
Русский перевод: Честер У., Сверхзвуковое обтекание тупоно-
тупоносого тела с отсоединенной ударной волной, часть И, осесим-
метричное тело, сб. Механика, № 6D6) A957), 19-24.
292 Литература
[3] The propagation of shock waves along ducts of varying cross
section, Advances in Appl. Mech., vol. 6, 1960, 119—152. Русский
перевод: Честер У., Распространение ударных волн в кана-
каналах переменного поперечного сечения, сб. Проблемы механики,
вып. IV, ИЛ, 1963, 100—127.
[4] On Oseen's approximation, J. Fluid Mech., 13 A962), 557—569.
ЧжанАй-ди (Chang I. D.)
[1] Navier — Stokes solutions at large distances from a finite body,
J. Math. Mech., 10 A961), 811—876.
Чжен (Cheng H. К.)
[1] Hypersonic flows past a yawed circular cone and other pointed
bodies, /. Fluid Mech., 12 A962), 169—191.
Ч о у, Т и н г (ChowR. R., TingL)
[1] Higher order theory of curved shock, /. Aerospace ScL, 28
A961), 428—430.
Ш е н к с (S h a n k s D.)
[1] Non-linear transformations of divergent and slowly convergent
sequences, /. Math, and Phys., 34 A955), 1—42.
Ш л и х т и н г (S chlichting H.)
[1] Boundary layer theory, 2nd English ed., McGraw-Hill, New York,
1960. Русский перевод первого немецкого издания: Ш л и х-
ти н г Г., Теория пограничного слоя, ИЛ, 1956
Эрдейи (Erdelyi А.)
[1] Asymptotic expansions, Dover, New York, 1956. Русский пере-
перевод: Эрдейи А., Асимптотические разложения, Физматгиз,
1962
[2] An expansion procedure for singular perturbations, Atti Accad.
Sci. Torino, Cl. ScL Fis. Mat. Nat, 95 A961), 651—672.
Я к у p a (Y a k ц r a J. K.)
[1] Theory of entropy layers and nose bluntness in hypersonic flow,
Hypersonic flow research (Riddel 1 F. R., ed.), Academic
Press, New York, 1962, 421—470. Русский перевод: Я к у р а Дж ,
Теория энтропийных слоев и затупление носка в гиперзвуко-
гиперзвуковом течении, Ридделл Ф. Р. (ред.), Исследования гиперзву-
гиперзвуковых течений, «Мир», 1964, 206—325.
Ямала (YamadaH.)
[1] On the slow motion of viscous liquid past a circular cylinder,
Rep. Res. Inst. Appl. Mech. Kyushu Univ., 3 A954), 11—23.
Я н с с е н (JanssenE.)
[1] Flow past a flat plate at low Reynolds numbers, J. Fluid Mech.,
3 A958), 329—343 Русский перевод: Ян сен Е., Обтекание
плоской пластины при малых числах Рейнольдса, сб. Меха-
Механика, № 1 E3) A959).
ИМЕННОЙ УКАЗАТЕЛЬ
Аббот (Abbott I. H. 70, 281
Аои (Aoi Т.) 204, 209, 210, 222,
289
Беллман (Bellman R.) 273, 281
Берндт (Berndt S. В.) 241, 287
Берне (Burns J. С.) 57, 281
Бетц (Betz A.) 287
Бретертон (Bretherton F. Р.)
108, 109, 281
Брич (Breach D. R.) 109, 281
Бродерик (Broderick J. В.) 47,
281
Булах Б. М. 109, 236, 240, 281
Бургграф (Burggraf О.) 12
Бэтчелор (Batchelor G. К.) 167,
281
Бюргере (Burgers J. M.) 83,
284
Вазов (Wasow W.) 142, 281
Ван-Дайк (Van Dyke M. D.)
5_7, 20, 39, 47, 58, 60, 74,
107, 149, 153, 164, 170, 185,
231, 269, 273—277, 279, 281
Ван-Туйл (Van Tuyl A.) 270,
275, 282
Вейль (Weyl H.) 179, 282
Вендт (Wendt H.) 24, 282, 291
Вилкинсон (Wilkinson J.) 222,
282
Винченти (Vincenti W. G.) 255,
282
Гарабедян (Garabedian P. R.)
15, 40, 282
Гиро (Guiraud J. P.) 109, 243,
282, 283
Го (Kuo Y. H.) 140, 141, 186—
188, 190, 283
Гольдштейн (Goldstein S.) 19,
48, 60, 108, 167, 179, 190, 192,
205, 209, 280, 283
Гуревич М. И. 65
Дёнхоф (Doenhoff A. E.) 70,
281
Дженсон (Jenson V. G.) 215,
283
Джеффрис (Jeffreys H.) 49,
283
Джонс (Jones R. T.) 12, 69,73,
82, 188, 224, 283
Дюрэнд (Durand W. F.) 284,
287, 288
Жермеи (Germain P.) 109, 283
Имаи (Imai I.) 40, 48, 63, 64,
80, 109, 188, 190, 192, 221,
278, 283
Кабанн (Cabannes H.) 23, 61—
63, 284
Кавамура (Kawamura R.) 23,
284
Каплита (Kaplita Т. Т.) 290
Каплун (Kaplun S.) 11, 12, 39,
48, 93, 108, 118, 128, 192 193,
197—199, 210, 216, 217, 219,
220, 284
Карман (Karman ven T.) 38,
83, 284
Каррьер (Carrier G. F.) 61, 164,
221, 277, 284, 286
294
Именной указатель
Кеворкян (Kevorkian J.) 260,
285
Келдыш М. В. 18
Келлер (Keller J. В.) 109, 288
Келли (Kelly R. Е.) 64, 285
Керл (Curie N.) 64, 205
Кибель И. А. 190
Кокрен (Cochran J.) 260, 285
Коул (Cole J. D.) 11, 38, 93,
108, 109, 118, 166, 181, 217,
222, 260, 285
Коулс (Coles D) 108, 285
Кочин Н. Е. 190
Коэн (Kohen D.) 69, 73, 224,
283
Крииес (Krienes К.) 234, 265,
271, 280, 285
Лагерстром (Lagerstrom P. A.)
11, 12, 93, 108, 118, 125, 166,
181, 210, 216, 222, 284, 285
Лайтхилл (Lighthill M. J.) 6,
11, 13, 69, 89, 103, 104, 139—
142, 163, 164, 183, 199, 236,
239, 240, 257, 285
Ламб (Lamb H.) 27, 209, 221,
286
Ла-Салль (La Salle J. P) 285
Латта (Latta G. E.) 258—260,
285
Леви (Levey H. C.) 141, 163,
286
Левинсон (Levinson N.) 65,
286
Легра (Legras J.) 140, 286
Лефшец (Lefschetz S.) 285
Либби (Libby P. A.) 180, 286
Линь (Lin С. С.) 61, 140, 141,
151, 277, 284, 286
Линь (Lin Т. С) 58, 200, 286
Липман (Liepman H.) 16, 286
Лыоис (Lewis G. Е.) 276, 286
Лыоис (Lewis J. A.) 221, 286
Махони (Mahony J. J.) 260,
287
Меррей (Murray J. D.) 109,
200, 287
Милликен (Millikan) 201
Милн-Томпсон (Milne-Thomp-
(Milne-Thompson L. M.) 105, 287
Миссайтер (Messiter A. F.)
109, 285
Мияги (Miyagi T.) 47, 289
Мотт-Смит (Mott-Smith H. M.)
16, 287
Мунк (Munk M. M.) 102, 255,
287
Мунсон (Munson A. G.) 122,
257, 264, 287
Надир (Nadir S.) 12
Нейланд В. Я. 109
Hecc (Ness N.) 290
Озееи (Oseen С. W.) 208, 209,
213, 287
Олден (Alden H. L.) 190, 191,
287
Осватич (Oswatitsch К.) 30,
237, 241, 242, 287, 290
Паккет (Puckett A. E.) 16, 286
Перри (Perry В.) 12
Пиллоу (Pillow A. F.) 12
Пирсон (Pearson J. R. A.) 19,
47, 48, 108, 210, 215, 216, 218,
221, 288
Прандтль (Prandil L.) 82, 108,
120, 126, 167, 186, 231, 287,
288
Праудмен (Praudman I.) 19,
47, 48. 108, 210, 215, 216, 218,
221, 288
Притуло М. Ф. 104, 165, 288
Пробстин (Probsiein R. F.) 16,
38, 39, 169, 246
Пуанкаре (Poincare H.) 6, 22,
140, 288
Pao (Rao P. S.) 140, 288
Ридделл (Riddell F. R.) 292
Розе Н. В 190
Розенхед (Rosenhead L.) 60,
167, 178, 179, 187, 218, 280,
283, 288
Именной указатель
295
Рубинов (Rubinow S. I.) 109,
288
Рэлей (Rayleigh) 31, 288
Сербии (Serbin H.) 39, 288
Симасаки (Simasaki Т.) 18,288
Спрейтер (Spreiter J. R) 16,
39, 288
Стокер (Stocker J. J.) 65, 289
Стоке (Stokes G. G.) 201, 205,
216, 289
Стоун (Stone A. H.) 23, 289
Стюартсон (Stewartson К.) 48,
179, 180, 263, 275, 289
Сычев В. В. 109, 25-1, 289
Съёдин (Sjodin L.) 237, 242,
287
Тамада (Tamada К.) 47, 289
Танеда (Taneda S) 202, 214,
215, 289
Теодорсен (Theodorsen) 70
Тинг (Ting L.) 109, 289, 292
Титьенс (Tietjens О. G.) 82,288
Тиффорд (Tifford A. N.) 20, 35,
289
Томотика (Tomotika S.) 204,
209, 210, 221, 222, 289
Трауготт (Traugott S. С.) 80,
290
Триттон (Tritton D. J.) 220,
221, 290
Турбер (Thurber J. К.) 235, 290
Туэйтс (Thwaites В.) 69, 290
У Яо-цзу (Wu Y. Т.) 141, 290
Уайтхед (Whitehead A. N.)
205, 227, 290
Уитэм (Whitham G. В.) 11,139,
140, 154, 155, 157, 159, 290
Уорд (Ward G. N.) 65, 236,
290
Уотсон (Watson R.) 109, 290
Ферри (Ferri A.) 24, 116, 290
Фокс (Fox Ш 180, 286
Франкль Ф. И. 18
Френкель (Fracnkel L Е.) 109,
290
Фридрихе (Friedrichs К. О.) 68,
108, ПО, 224, 290
Ханкок (Hancock G. J.) 201,
291
Ханцше (Hantzsche W.) 18, 24,
48, 291
Хейз (Hayes W. D.) 16, 38, 39,
107, 148—151, 169, 246, 291
Хислет (Heaslet M. A.) 12
Холл (Hall I. M.) 28, 291
Христианович С. А. 15
Цянь (Tsien F. H.) 23, 284
Цянь (Tsien T. S.) 140, 291
Честер (Chester W.) 16, 20, 47,
216, 291, 292
Чжан (Chang I. D.) 12, 59, 63,
64, 107, 109, 180, 181, 221,
292
Чжен (Cheng H. K.) 257, 292
Чоу (Chow R. R.) 109, 292
Шаф (Schaaf S. A.) 58, 200,
286
Шенкс (Shanks D.) 19, 266,
270, 292
Шлихтинг (Schlichting H.) 14,
34, 35, 178, 280, 292
Эйлер (Euler L.) 167
Эмануэль (Emanuel G.) 12
Эрдейи (Erdelyi A.) 43, 53,117,
292
Якура (Jakura J. K.) 24, 109,
243, 244, 251—254, 292
Ямада (Jamada H.) 210, 292
Янссен (Janssen E.) 190, 292
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомодельное решение 13—14,
17, 177
Аддитивное составление 133,
252—253
Асимптотическая последова-
последовательность 46
в теории тонкого профи-
профиля 70
выбор 47
различие между внешней
и внутренней 119, 145
члены логарифмические
15, 47—48, 53, 56, 71, 84, 86,
98, 263—265, 271
экспоненциальные 48
Асимптотическая форма см.
Асимптотическое представле-
представление
Асимптотические разложения
16, 45; см. также Асимптоти-
Асимптотические ряды
единственность 53—54
свойства 52—54
точность 49—52
влияние логарифмиче-
логарифмических членов 265
улучшение 265—275
— решения 16
— ряды 45
бесконечные 45
: ошибки 51
степенные 45
— — сходимость 49, 52
Асимптотического сращивания
принцип 94, 127, 135, 175, 182,
217, 248
Асимптотическое представление
функции 44, 126
Атаки угол эффективный 230,
231
Блазиуса разложение обратное
63, 277
— решение для плоской пла-
пластины 177—180
— единственность
180-181
— ряд 16
для пограничного слоя
на круговом цилиндре 34—35
— — — — параболе 20,
60, 269, 273
Величина трансцендентально
малая 54, 219, 222
Веретенообразное тело враще-
вращения 106
Вихрь за круговым цилиндром
и сферой 202—203, 210, 214—
215
Внешнее разложение 93, 115,
119
в теории несущей линии
228, 230
для пограничного слоя
на плоской пластине 170—173
энтропийного слоя 247
определение 119
Внешние переменные 93, 119
Внешний предел 119
Внутреннее разложение 93, 115,
119
в теории несущей линии
229
— — для пограничного слоя на
плоской пластине 173
Предметный указатель
297
Внутреннее разложение для по-
пограничного слоя на плоской
пластине полубесконечной 191
энтропийного слоя
249—252
определение 119
Внутренние переменные 93, 119
выбор 120—123
для несущего крыла боль-
большого удлинения 226
энтропийного слоя 249
— — определение 119
Внутренний предел 119
Возмущение координаты 16
— — для пограничного слоя
на плоской пластине 168—169
— — замена возмущением па-
параметра 116
особое 21, 113—115
регулярное 21, 115
— параметра 16
особое 21, 113—115
регулярное 21, 115
Возмущения величина 15,38—40
выбор 38—40
Вторичная характерная длина
113, 224
Вязкое течение см. Течение вяз-
вязкое
Гиперболическая ударная вол-
волна 243
Гиперболические уравнения, из-
изменение характеристик 66
координатное разложение
обратное 63
прямое 60
Гиперзвуковая теория малых
возмущений 38, 39, 56, 246
Гиперзвуковое обтекание затуп-
затупленного клина 242—254
тела 20—21, 63, 273—
275
— правило подобия 38
видоизмененное 66
Гофрированный квазицилиндр
36
Граничных условий возмуще-
возмущения 23, 25, 28
отбрасывание ПО, 112,
123, 172
Граничных условий перенос
58—59, 67, 71
разрывность 66
Групповое свойство 177—178,
199
Даламбера парадокс 206
Двойной предельный переход
37, 252
Двояковыпуклый профиль 83—
87, 98, 105, 137
Деформирование запаздываю-
запаздывающее 164
Деформированный круговой ци-
цилиндр 28—30
Деформированных координат
метод см. Метод деформиро-
деформированных координат
Дивихрь 231
Длина характерная вторичная
ИЗ, 224
первичная 113, 224
Длины характерные различные
ПЗ—116, 224, 252, 260
Дозвуковое течение см. Тече-
Течение дозвуковое
Дополнительное решение 27
Единственность разложения
асимптотического 53—54
— решения Блазиуса для пло-
плоской пластины 180—181
для тонкого профиля
77—79
Жуковского — Кутта условие
66, 226
— профиль 80—83
Завихренности внешней влия-
влияние 200
— экспоненциальное затухание
в пограничном слое 179—180,
191, 264
Задачи особых возмущений 21,
53, 68
— в теории профиля
68—107
218
Предметный указатель
Задачи особых возмущений для
возмущения координат 113—
115 '
. параметра 113—
115
малого затупления
243
— невязкого течения
223-255
— при больших и малых
Re 206
признаки ПО, 112—
113
— регулярных возмущений 21 —
22, 23—36, 113—115
Закругленная кромка, локаль-
локальное решение 90—98
— — неоднородность в теории
тонкого профиля 77—83
— — поправочный множитель
87—90, 106
— — сдвиговая поправка 102—
105
Запаздывающее деформироса-
ние 164
Затупленное тело 20—21, 62,
63, 268, 270, 271, 273—275
Затупленный клин в гиперзву-
гиперзвуковом потоке 242—254
Изменение типа уравнений
65-66, 176
— характеристик 65—67
Импульсивное начало движе-
движения затупленного тела с ги-
гиперзвуковой скоростью 63,
270, 271
— кругового цилиндра в
вязкой жидкости 280
Интегралы профильные 74
Иррациональное приближение
15—18
Искусственный параметр 107,
181
Источник плоский 73
Источников распределения для
профиля 73, 87, 102
Итерации 31, 55
Квазицилиндр гофрированный
35
Клин затупленный в гиперзву-
гиперзвуковом потоке 242—254
— пограничный слой 199
— потенциальное обтекание
99—100
Координатное разложение см.
Разложение по координате
обратное 63—65
— — прямое 59—63
Координат преобразование
в пограничном слое 192—-
199
Координаты возмущение см.
Возмущение координаты
— естественные 267
— оптимальные 196, 197—199,
267
— параболические 105, 194,
267—270, 273, 274
— полуоптимальные 197, 199
— полухарактеристические 150
— сжатые прямоугольные 195,
197
Корреляционная теорема 194
второго порядка 200
Коэффициент давления в до-
дозвуковой теории тонкого про-
профиля 107
— поверхностного трения на
круговом цилиндре 34, 35
параболе 20, 269,
273
плоской пластине
конечной 187, 189—190
— полубесконеч-
— полубесконечной 188—192
Критерий однородности физи-
физический 112—115, 225
Критическое число Маха 18,
280
Кромка закругленная см. За-
Закругленная кромка
— острая см. Острая кромка
Круговой конус, возмущение
решения для сверхзвукового
потока 22
сверхзвуковое обтекание
при М~1 236—242
— цилиндр 23—36
— — в потоке с параболиче-
параболическим профилем скорости 36
Предметный указатель
299
Круговой конус в потоке с по-
постоянной завихренностью
25—28
сжимаемом 18, 30—
32, 280
деформированный 28—30
— — 'обтекание вязкое 32—35
невязкое безвихревое
23-25
отрыв потока 35, 167,202,
280
— — пограничный слой 33—35
пористый 35
при малых Re 216—221
коэффициент со-
сопротивления 220
приближение Рэлея—Ян-
сена 18, 31
Стокса 203—205
пульсирующий 35
Крыло эллиптическое 20, 224,
233—236
— — большого удлинения 20,
224-231
Кумулятивный эффект 148, 149
Лайтхилла мегод см Метод
деформированных координат
— правило 89, 90
Линии Маха исправленные
153—154
Логарифмические члены 19,
263—265
— — в асимптотическом разло-
разложении 19, 47, 49, 53, 55—56,
71, 84. 86. 98, 100, 106, 191,
215—219, 263-265, 275
обратном координат-
координатном разложении 64, 65
— — — решении для вязкого
течения 191, 215—219
теории несущей линии
231, 236
— — — — тонкого профиля
34, 86, 98, 100, 106
— — источник появления 98,
100, 263—264
— — как функции сравнения 42
— — связь с соседними алге-
алгебраическими членами' 264—
265
Маха линии исправленные
153—154
— число критическое 18, 280
Метод деформированных коор-
координат 22, 139—165
для гиперзвукового
обтекания затупленного тела
253—254
— — — — сверхзвукового об-
обтекания конуса 236—242
— — — — эллиптических и
параболических уравнений
141, 163—164, 223
неприменимость 163,
254
— полезность 162—164
связь с оптимальными
координатами 199
— — — сравнение с методом
сращиваемых асимптотиче-
асимптотических разложений 141, 145—
147, 162—164
— сходство с методом
многих масштабов 261
— Лайтхилла см. Метод де-
деформированных координат
— многих масштабов 260—263,
279
— ПЛГ 140; см. также Метод
деформированных координат
— составных разложений 258—
260
— сращиваемых асимптотиче-
асимптотических разложений 22, 108—
138
— — дЛЯ затупленного
клина в гиперзвуковом пото-
потоке 242—254
— — круга при ма-
малых Re 216—221
несущего кры-
крыла большого удлинения 224—
236
— сферы при ма-
малых Re 210—216
— — неприменимость,
пример 279
— — сравнение с мето-
методом деформированных коор-
координат 141, 145—147, 162—
164
300
Предметный указатель
Минимальной особенности
принцип 79, 93, 95, 105, 123,
181, 212, 219
Многих масштабов метод 260—
263, 279
Множественный предельный пе-
переход 37, 115
Множитель покравочный для
кромки закругленной 87—90,
105
острой 105
Мультипликативное составле-
составление 135, 252, 253
Мунка правило 255
Навье—Стокса уравнения 170,
205, 221
Неединственность решения Бла-
зиуса для плоской пластины
180—181
для тонкого профиля
77—80,
Неоднородности область см.
Область неоднородности
Неоднородность 53; см. также
Задачи особых возмущений
— в коническом течении 116
— — модельной задаче ПО—
112
прямом координатном
разложении 60
¦— — теории крыла большого
удлинения 227, 234, 235
— сверхзвукового про-
профиля 147—152
— возмущения координат 114—
115
— для затупленного клина в
гиперзвуковом потоке 247,
249
эллиптического профиля
74—77
— множественная 115
— предсказания ПО
— у острой кромки 84
плоской кромки 85
— физический критерий 112—
116, 225
Несущей линии теория 15 -20,
223—236, 255
Нулевое приближение 17
Ньютона—Буземана теория 15,
20, 38, 39, 47
Область неоднородности 75, 145
в теории тонкого профи-
профиля 75, 84, 85
для пограничного слоя
173
при малых Re 206—207
экспоненциально малая
' 84, 122—123
— перекрытия 124, 125, 130
Обратное координатное разло-
разложение 63—65
Одновременное сращивание 106
Однородности физический кри-
критерий 112—115, 225
Озеена приближение 15, 19,
206—210
для параболоида 221 —
222
— плоского спутного по-
потока 221
плоской пластины 221,
250
— — — пограничного слоя
209—210
сферы 19, 209, 270,
275
— разложение 209—213, 221—
222
— течение отрывное 47
Озеенлет 213, 218
Оптимальные координаты 196,
197—199, 267
Основное решение 17, 132
Особое возмущение 21, 113—
115
Особых возмущений задачи см.
Задачи особых возмущений
Острая кромка 83—84, 98—
102, 105
Отрыв течения 47, 166—167,
202, 214—215, 278
Парабола, комплексная ско-
скорость на 102
— коэффициент поверхностного
трения 20, 269, 273
Предметный указатель
301
Парабола, пограничный слой на
20, 269, 273, 276—277
— приближение тонкого про-
профиля 88, 102
— разложение Рэлея—Янсена
278
— симметричное обтекание 124
— скорость на поверхности
88
— соприкасающаяся 83, 87,
90—92, 96, 97, 105
— сопротивление 82
Параболические координаты
105, 194, 267—270, 273, 274
— уравнения, метод дефор-
деформированных координат 141,
163—164, 223
координатное разложе-
разложение обратное 63
прямое 60
Параболоидальная ударная
волна 20, 62, 267—268, 270,
273—274
Параболоид вращения 106, 107
Парадокс Даламбера 206
— Стокса 205
— Уайтхеда 205—206
Параметр искусственный 107,
181
— подобия 38
для гиперзвуковых тече-
течений 38
— трансзвуковых тече-
течений 38, 242
Параметра возмущение см.
Возмущение параметра
Параметрическое разложение
см. Разложение по парамет-
РУ
Первичная характерная длина
113, 224
Первого порядка решение 18
Первое приближение 17
Передняя кромка закругленная
77—83, 87—98, 102—105
острая 83—84,98—102. 105
плоская 84—86, 105.
плоской пластины, вяз-
вязкое обтекание 61, 188-189
сопротивление 81—83,
188- 189
Передняя кромка, сопротивле-
сопротивление отрицательное 81
Перекрытия область 124, 125,
130
Переменное промежуточное 129
— среднее 247
Переменные внешние см. Внеш-
Внешние переменные
— внутренние см. Внутренние
переменные
Перенос граничных условий
58—59, 67, 71
Переход предельной двойной
37, 252
множественный 37, 115
ПЛГ метод 140; см. также Ме-
Метод деформированных коор-
координат
Плоская пластина, второе при-
приближение теории пограничнэ-
го слоя 184—188
интерпретации решения
Блазиуса 168—170
конечная 169—170, 177,
178, 186—188
метод составных уравне-
уравнении 257—258
— — оптимальные координаты
196, 197
— — передняя кромка 61,
188—189
поверхностное трение
187—192
¦ приближение Озеена 221,
259
— — решение теории погра-
пограничного слоя 177—192, 194—
198, 257- 258
— — течение, обусловленное
толщиной вытеснения 181 —
184
— — третье приближение тео-
теории пограничного слоя 190—
192
Поверхностное трение см. Ко-
Коэффициент поверхностного
трения
Пограничный слой в потоке с
постоянной завихренностью
199
координаты 33
302
Предметный указатель
Пограничный слой на клине 199
круговом цилиндре
22 35
параболе 20, 269, 273,
276—277
— плоской пластине
177—J92, 194—198, 257—258
нарастание 60
обратная задача 200
преобразование коорди-
координат 192—198
приближение Озеена
206—210
— — приближения высшего по-
порядка 166
теория 17—19, 166—200
уравнение первого поряд-
порядка 176
Подобия параметр см. Пара-
Параметр подобия
— правило см. Правило подо-
подобия
Подслой скользящий 200
Полуоптимальные координаты
197, 199
Полухарактеристические коор-
координаты 150
Поправочный множитель см.
Множитель поправочный
Пористый круговой цилиндр 35
Порядка символы см. Символы
порядка
Порядок сращивания 131 —132
Последовательность асимптоти-
асимптотическая см. Асимптотическая
последовательность
Последовательные приближе-
приближения 54—58
Потенциал скоростей для круга
в дозвуковом течении 30—32
несжимаемой
жидкости 25
плоской пластины 73
Правило «исправления тече-
течения» у двух кромок 136, 137
кромки закруглен-
закругленной 89—98, 102—105
острой 98 -102,
105
__ носка тела враще-
вращения 106
Правило Лайтхилла 89, 90
— Мунка 255
— подобия гиперзвуковое 38,
66
видоизмененное 66
дозвуковое во втором
приближении 107, 279
трансзвуковое 38, 242
Прандтля—Блазиуса решение
167
различные интерпрета-
интерпретации 168—170
Предел внешний 119
— внутренний 119
— промежуточный 129, 217
Предельного сращивания прин-
принцип 126, 217
Предельный переход см. Пере-
Переход предельный
Представление асимптотическое
44, 126
Преобразование Эйлера 52, 54,
272—275
Приближение нулевое 17
— Озеена см. Озеена прибли-
приближение
— первое 17
— рациональными дробями
269—272
— Стокса см. Стокса прибли-
приближение
Приближения иррациональные
15-18
— последовательные 54—58
— рациональные 15 — 18
— роль в механике жидкости
13—22
Принцип минимальной особен-
особенности 79, 93, 95, 105, 123, 181,
212, 219
— нахождения деформирован-
деформированных координат 103, 139
— сращивания асимптотиче-
асимптотического 94, 127, 135, 175, 182,
217, 248
— — предельного 126, 217
промежуточного 130, 217
Промежуточная задача 129
Промежуточное переменное 129
— разложение 129
— решение 129
Предметный указатель
303
Промежуточное сращивание 128
принцип 130, 217
Промежуточный предел 129, 217
Профиль двояковыпуклый 83—
87, 98, 105, 137
— Жуковского 80—83
— прямоугольный 84—87, 105
— эллиптический, внешнее и
внутреннее решения 133
комплексная скорость на
104
одновременное сращива-
сращивание 106
решение вблизи кромки 90
составное 135—136
сдвиговая поправка 102—
104
скорость на поверхности
тонкий, дозвуковое обте-
обтекание 18
в несжимаемой жид-
жидкости 74—77, 103—104
Профильные интегралы 74
Профиля теория, задачи осо-
особых возмущений 68—107
сверхзвукового 147—162
тонкого 15. 18, 48, 51, 53,
57, 68—107, 278
Псевдотрансзвуковое обтекание
109
Псевдотраисзвуковой член 149
Пульсирующая сфера 67
Пульсирующий круговой ци-
цилиндр 35
Разложение асимптотическое
см. Асимптотическое разло-
разложение
— Блазиуса обратное 63, 277
— внешнее см. Внешнее раз-
разложение
— внутреннее см. Внутреннее
разложение
— координатное см Разложе-
Разложение по координате
обратное 63—65
прямое 59—63
— — связывание 275—278
Разложение Озеена 209—213,
221—222
— параметрическое см. Разло-
Разложение по параметру
связывание 278—279
— по координате 16
— — — для эллиптических
уравнений 62—63
неоднородность ИЗ
обратное 63—65
особое 21, 113—115
прямое 59—63
регулярное 21, 115
— — — связывание 275—278
— — — сходимость 49
параметру 18—21
особое 21, 113—115
— — — регулярное 21, 113
связывание 278—279
сходимость 49—51
— промежуточное 129
— Рэлея—Янсена см. Рэлея—
Янсена разложение
— составное см. Составное раз-
разложение
— среднее см. Среднее разло-
разложение
— Стокса 210, 213—221
Распространения теорема 130
Расстояние ударной волны от
затупленного тела 20—21,
62—63, 273—275
Рациональные приближения
15-18
Регулярное возмущение 21, 115
Регулярных возмущений за-
задачи 21—22, 23—36, 113—
115
Решение автомодельное 13—14,
17, 177
— асимптотическое 16
— Блазиуса см. Блазиуса ре-
решение
— дополнительное 27
— основное 17, 132
— первого порядка 18
— промежуточное 128
Решения единственность см.
Единственность решения
— собственные см. Собствен-
Собственные решения
304
Предметный указатель
Рэлея—Янсена разложение 15,
18, 21, 51
для круга 18, 31, 56,
57
— параболы 278
Ряды асимптотические см.
Асимптотические ряды
— Блазиуса см. Блазиуса ря-
ряды
— равномерно пригодные 53
— — точные 53
Свойство групповое 177—178,
199
Связывание разложений коор-
координатных 275—278
— — параметрических 278—
279
Сжатые прямоугольные коорди-
координаты 195, 197
Символы порядка О и о 41
операции с 43
связь с физическим по-
порядком величины 43
Склеивание 80, 125, 192, 277,
278
Скользящий подслой 200
Слой пограничный см. Погра-
Пограничный слой
— энтропийный см. Энтропий-
Энтропийный слой
Собственные решения в обрат-
обратном координатном разложе-
разложении 23—26
пограничном слое на
плоской пластине 180—181
теории тонкого про-
профиля 78—80, 86, 90—98, 105,
124
Соприкасающаяся парабола 83,
87, 90—92, 96, 97, 105
Сопротивление круга при ма-
малых Re 220
— передней кромки 81—83, 189
— сферы при малых Re 19,
201, 270, 275
Составление аддитивное 133,
252—253
— мультипликативное 135, 252—
253
Составное разложение 116—
120, 133—136, 219, 258—260
для затупленного клина
252—254
построение 133—136
Составные уравнения 256
Сращиваемых асимптотических
разложений метод см. Метод
сращиваемых асимптотиче-
асимптотических разложений
Сращивание 123—125, 275—276
— в теории тонкого профиля
93—101
— для определения собствен-
собственных решений 79
— и принцип минимальной осо-
особенности 105, 123—124
— одновременное 106
— промежуточное 128
Сращивания порядок 131—132
— принцип см. Принцип сра-
сращивания
— условие для пограничного
слоя 175—176
Среднее переменное 247
— разложение 115, 137, 243,
247—249, 252-254
Стокса парадокс 205
— приближение 19
для кругового цилиндра
203—205
параболоида 221
— параболы 222
сферы 203—205, 210—
213
— разложение 210, 213—221
Стокслет 204, 213
Сфера, отрыв потока 202—203,
214—215
— пульсирующая 67
— решение Озеена 19, 211 —
212, 270, 275
Стокса 203—205, 210—
213
— сопротивление 19, 201, 270,
275
Сходимость асимптотических
рядов 45, 49—52
— разложения Рзлея—Янсена
18
— улучшение 265—275
Предметный указатель
305
Тело вращения веретенообраз-
веретенообразное 106
«исправление течения» у
носка 106
параболоид 106, 221
тонкое 106
эллипсоид 106, 255
— затупленное см. Затуплен-
Затупленное тело
Теорема корреляционная 194
второго порядка 200
— распространения 130
Теория малых возмущений ги-
гиперзвуковая 38, 39, 56, 246
— несущей линии 15—20, 223—
236, 255
— Ньютона—Буземана 15, 20,
38, 39, 47
— профиля, задачи особых
возмущений 68—107
сверхзвукового 147—162
тонкого 15, 18, 48, 51, 53,
57, 68—107, 278
— свободно-молекулярного те-
течения 15
— тонкого тела 47, 59, 106, см.
также Теория профиля тон-
тонкого
Течение вязкое около круга и
сферы 201—205
параболоида 221
передней кромки плос-
плоской пластины 61, 188—189
при больших Re 166—
200
малых Re 201—222
— гиперзвуковое см. Гиперзву-
Гиперзвуковое обтекание
— дозвуковое около круга 30—
32
параболы 278—279
тела вращения, част-
частное решение 58
тонкого профиля 107
правило подобия 107, 279
уравнение для потенциа-
потенциала 30
— над волнистой стенкой 255
— обусловленное толщиной
вытеснения пограничного слоя
181—185, 188—190
Течение с постоянной завихрен-
завихренностью' около круга 25—28,
35—36
— — — плоской пласти-
пластины 199—200
— — свободными линиями то-
тока 65
— сверхзвуковое около затуп-
затупленного тела 20, 62—63, 206,
270—271, 273—274
тонкого конуса 236—
242
— профиля 147—161
— тела вращения,
частное решение 57—58
— трансзвуковое 56
около тонкого конуса 238
— — правило подобия 38, 242
— — теория малых возмуще-
возмущений 238
Течения отрыв см. Отрыв те-
течения
Тип уравнений, изменение 65,
66, 176
Тока функция см. Функция
тока
Толщина вытеснения погранич-
пограничного слоя 182, 183
— — течение обуслов-
обусловленное 181—185, 188—190
— — энтропийного слоя 250
Точность асимптотических раз-
разложений 49—52
влияние логарифмиче-
логарифмических членов 265
улучшение 265—275
Трансзвуковое течение см. Те-
Течение трансзвуковое
Трансцендентально малая ве-
величина 54, 219, 222
Уайтхеда парадокс 205—206
Угловая точка сверхзвукового
профиля 156—159
Угол атаки эффективный 230,
231
Ударная волна гиперболиче-
гиперболическая 243
параболоидальная 20, 62.
267—268, 270, 273—274
306
Предметный указатель
Уравнения гиперболические см.
Гиперболические уравнения
— изменение типа 65, 66, 176
— Навье—Стокса 170, 205,
221
— параболические см. Парабо-
Параболические уравнения
— составные 256
— эллиптические см. Эллипти-
Эллиптические уравнения
Условие Жуковского—Кутта 66,
226
— сращивания для погранич-
пограничного слоя 175—176
Условия граничные см. Гранич-
Граничные условия
Физический критерий однород-
однородности 112—115, 225
Функции сравнения 41—46
выбор 42—43
Функция тока для вязкого те-
течения у передней кромки
плоской пластины 61
затупленного тела в
сверхзвуковом потоке 62,
266—268, 270
круга в плоском по-
потенциальном течении 24
потоке с посто-
постоянной завихренностью 26
деформированно-
деформированного 28-29
плоского течения не-
несжимаемой жидкости 24
сжимаемой
жидкости 244
— пограничного слоя на
тонкой пластине 170—178,
180—187, 193—196, 200, 257
тонкого профиля 105
Характеристик изменение 65—
67
Характерная длина: вторичная
ИЗ, 224
первичная 113, 224
Характерные длины различные
113—116, 224, 252, 260
Цилиндр круговой см. Круго-
Круговой цилиндр
Число Маха критическое 18,
280
— Рейнольде а 32
большое 166—200
малое 201—222
Члены логарифмические см.
Логарифмические члены
— экспоненциальные см. Экспо-
Экспоненциальные члены
Эйлера преобразование 52, 54,
272—275
Экспоненциальное затухание
завихренности 179—180, 191,
264
Экспоненциальные члены асим-
асимптотической последователь-
последовательности 48
Эллипсоид вращения 106, 255
Эллиптические уравнения, ме-
метод деформированных коор
динат 141, 163—164, 223
разложение координа1
ное обратное 63
прямое 61—62
Эллиптический профиль см,
Профиль эллиптический
Эллиптическое крыло см. Кры-
Крыло эллиптическое
Энтропийный слой 243, 247—
252
толщина вытеснения 250
Эффект кумулятивный 148, 149
Эффективный угол атаки 230,
231
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие к русскому изданию 9
Предисловие 11
ГЛАВА I. СУЩНОСТЬ ТЕОРИИ ВОЗМУЩЕНИЙ 13
1.1. Приближения в механике жидкости . . . . 13
1.2. Рациональные и иррациональные приближения ... 15
1.3. Примеры разложений по малому возмущению ... 18
1.4. Задачи регулярных и особых возмущений .... 21
ГЛАВА 2. НЕКОТОРЫЕ ЗАДАЧИ РЕГУЛЯРНЫХ ВОЗМУЩЕНИЙ . . 23
2.1. Введение. Исходное течение — обтекание круга . . 23
2.2. Круг в потоке с малой постоянной завихренностью 25
2.3. Малая деформация круга 28
2.4. Круг в жидкости с малой сжимаемостью 30
2.5. Влияние малой вязкости 32
2.6. Пограничный слой; разложение по координате ... 33
Упражнения ..... 35
ГЛАВА 3. АППАРАТ ТЕОРИИ ВОЗМУЩЕНИЙ 37
3.1. Введение; предельные переходы 37
3.2. Функции сравнения и символы порядка ... .40
3.3. Асимптотические представления; асимптотические
ряды . . 43
3.4. Асимптотические последовательности 46
3.5. Сходимость и точность асимптотических рядов . . 49
3.6. Свойства асимптотических разложений 52
3.7. Последовательные приближения . 54
3.8. Перенос граничных условий 58
3.9. Прямое координатное разложение 59
ЗЛО. Обратное координатное разложение 63
3.11. Изменение типа уравнений и характеристик ... 65
Упражнения 66
Оглавление
Г Л Л В Л 4. НЕКОТОРЫЕ ЗАДАЧИ ОСОБЫХ ВОЗМУЩЕНИЙ В ТЕО-
ТЕОРИИ профиля 68
4.1. Введение 68
4.2. Формальное разложение для тонкого профиля ... 69
4.3. Решение задачи обтекания тонкого профиля ... 72
4.4. Неоднородности для эллиптического профиля ... 74
4.5. Неединственность. Собственные решения .... 77
4.6. Профили Жуковского Сопротивление передней кромки 80
4.7. Двояковыпуклый и прямоугольный профили ... 83
4.8. Поправочный множитель для закругленных кромок 87
4.9. Локальное решение вблизи закругленной кромки . . 90
4.10. Сращивание с решением вблизи закругленной кромки 93
4.11. Сращивание с решением вблизи острой кромки . . 98
4.12. Сдвиговая поправка для закругленных кромок . . 102
Упражнения . 105
ГЛАВА 5. МЕТОД СРАЩИВАЕМЫХ АСИМПТОТИЧЕСКИХ РАЗЛО-
РАЗЛОЖЕНИИ 108
5.1. Историческое введение 108
5.2. Неоднородности прямого разложения ПО
5.3. Физический критерий однородности 112
5.4. Роль составного и внутреннего разложений . . . .116
5.5. Выбор внутренних переменных 120
5.6. Роль сращивания 123
5.7. Принципы сращивания 125
5.8. Промежуточное сращивание . 128
5.9. Порядок сращивания 131
5.10. Построение составного разложения 133
Упражнения . 136
ГЛАВА 6. МЕТОД ДЕФОРМИРОВАННЫХ КООРДИНАТ 139
6.1. Историческое введение 139
6.2. Модель: обыкновенное дифференциальное уравнение 141
6.3. Сравнение с методом сращиваемых разложений . . 145
6.4. Неоднородности в теории сверхзвукового профиля 147
6.5. Первое приближение по методу деформированных
координат 152
6.6. Видоизменения для углов и ударных волн .... 156
6.7. Первое приближение по методу сращиваемых разло-
разложений 160
6.8. Полезность метода деформированных координат . . 162
Упражнения 164
Оглавление
ГЛАВА 7. ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ ПРИ БОЛЬШИХ ЧИС-
ЧИСЛАХ РЕЙНОЛЬДСА 166
7.1. Введение 166
7.2. Различные интерпретации решения для плоской
пластины . 168
7.3. Внешнее разложение для плоской пластины. Основ-
Основное невязкое течение 170
7.4. Внутреннее разложение. Уравнения пограничного слоя.
Сращивание 173
7.5. Решение задачи о пограничном слое для плоской .
пластины . 177
7.6. Единственность решения Блазиуса . 180
7.7. Течение, обусловленное толщиной вытеснения ... 181
7.8. Второе приближение для пограничного слоя на по-
полубесконечной пластине 184
7.9. Второе приближение для пограничного слоя на ко-
конечной пластине 186
7.10. Местное и суммарное поверхностное трение . . . 188
7.11. Третье приближение для полубесконечной пластины 190
7.12. Влияние изменения координат пограничного слоя . . 192
7.13. Различные системы координат для плоской пластины 194
7.14. Определение оптимальных координат 197
7.15. Развитие идеи оптимальных координат 198
Упражнения 199
ГЛАВА 8. ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ ПРИ МАЛЫХ ЧИСЛАХ
РЕЙНОЛЬДСА 201
8.1. Введение 201
8.2. Решение Стокса для сферы и кругового цилиндра 203
8.3. Парадоксы Стокса и Уайтхеда 205
8.4. Приближение Озеена 206
8.5. Второе приближение вдали от сферы 210
8.6. Второе приближение вблизи сферы . 213
8.7. Приближения высшего порядка для кругового ци-
цилиндра 216
Упражнения . 221
ГЛАВА 9. НЕКОТОРЫЕ ЗАДАЧИ ОСОБЫХ ВОЗМУЩЕНИЙ ДЛЯ
НЕВЯЗКИХ ТЕЧЕНИИ 223
9.1. Введение 223
9.2. Несущее крыло большого удлинения 224
9.3. Метод сращиваемых асимптотических разложений в
теории несущей линии 228
9.4. Результаты третьего приближения 231
9.5. Приложение к эллиптическому крылу 233
9.6. Сверхзвуковое обтекание тонкого кругового конуса
при числах Маха, близких к единице 236
9 7. Второе приближение и положение ударной волны 238
9.8. Третье приближение для давления на конусе . . . 240
9.9. Гиперзвуковое обтекание тонкого затупленного клипа 242
9.10. Решение теории малых возмущений для затупленно-
затупленного клина 246
9.11. Среднее разложение для энтропийного слоя . . . 247
9.12. Внутреннее разложение для энтропийного слоя . . 249
9.13. Составное разложение для затупленного клина . . 252
Упражнения . 254
ГЛАВА 10. ПРОЧИЕ АСПЕКТЫ ТЕОРИИ ВОЗМУЩЕНИЙ 256
10.1. Введение 256
10.2. Метод составных уравнений 256
10.3. Метод составных разложений 258
10.4. Меюд многих масштабов 260
10.5. О логарифмических членах 263
10.6. Улучшение рядов. Естественные координаты . . . 265
10.7. Приближения рациональными дробями .... 269
10 8. Преобразование Эйлера 272
10.9. Связывание координатных разложений 275
10.10. Связывание различных параметрических разложе-
разложений 278
Упражнения 279
Литература 281
Именной указатель 293
Предметный указатель 296
М. Ван-Дайк
МЕТОДЫ ВОЗМУЩЕНИЙ
В МЕХАНИКЕ ЖИДКОСТЕЙ
Редактор Г. М. Ильичева
Художник И. А. Литвшико
Художественный редактор В. И. Шаповалов
Технический редактор Л. М. Харьковская
Сдано в производство 8/П 1967 г.
Подписано к печати 7/VII1 1967 г.
Бумага тип. № 1 84хЮ8732=4,88 бум. л.,
16,38 печ. л. Уч.-изд. л. 15,09. Изд. № 1/3747
Цена 1 р. 29 к. Зак. 564
ИЗДАТЕЛЬСТВО
«МИР»
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2
имени Евгении Соколовой
Главполиграфпрома
Комитета по печати
при Совете Министров СССР.
Измайловский проспект, 29.