Краткий курс физики - Черноуцан А.И.

Автор: Черноуцан А.И.

Теги: физика

ISBN: 5-9221-0292-3

Год: 2002

Похожие

Последняя тайна бога. Электрический эфир

Решение задач по физике

Физика. Том 1

Минимальная физика

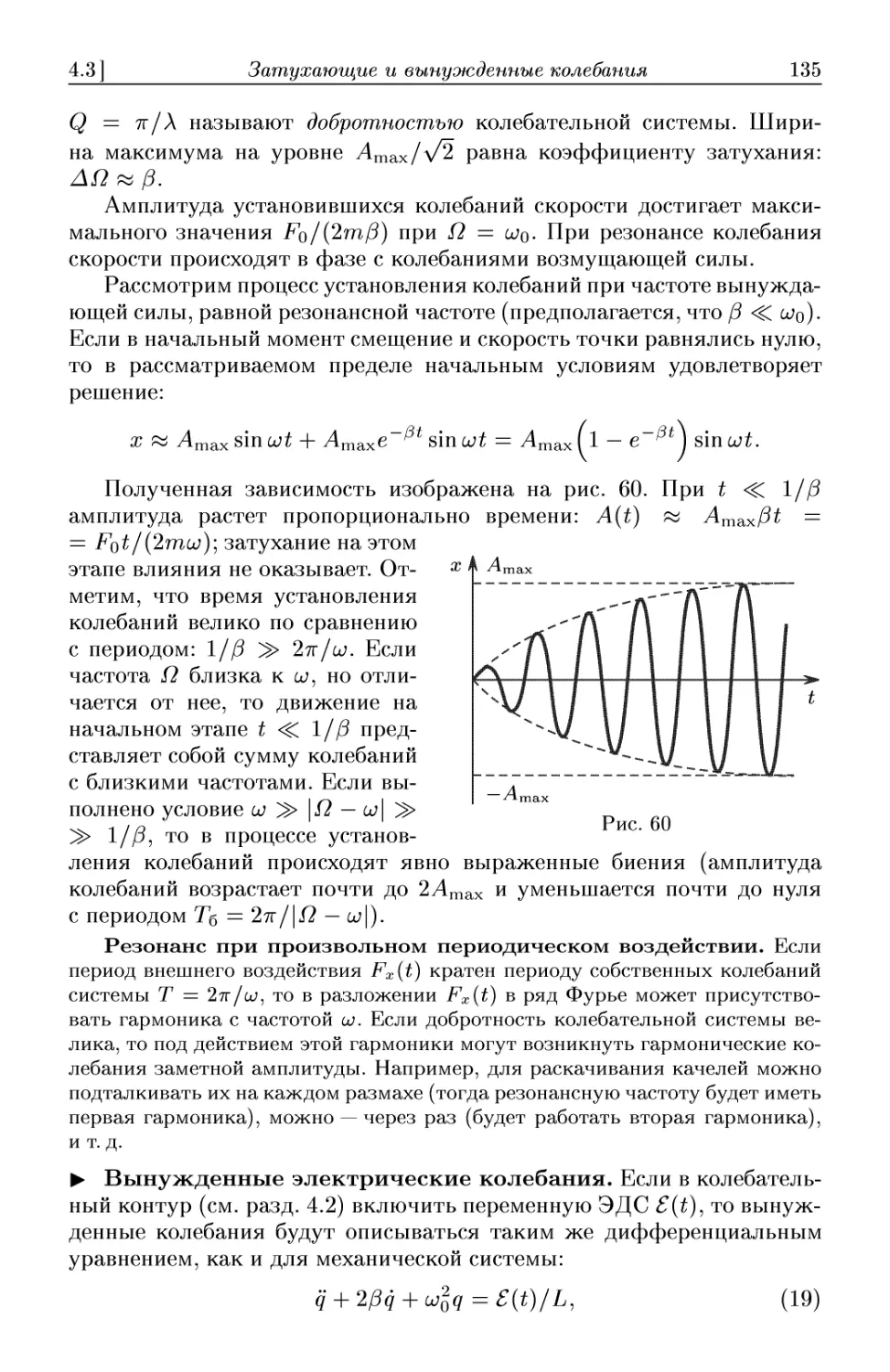
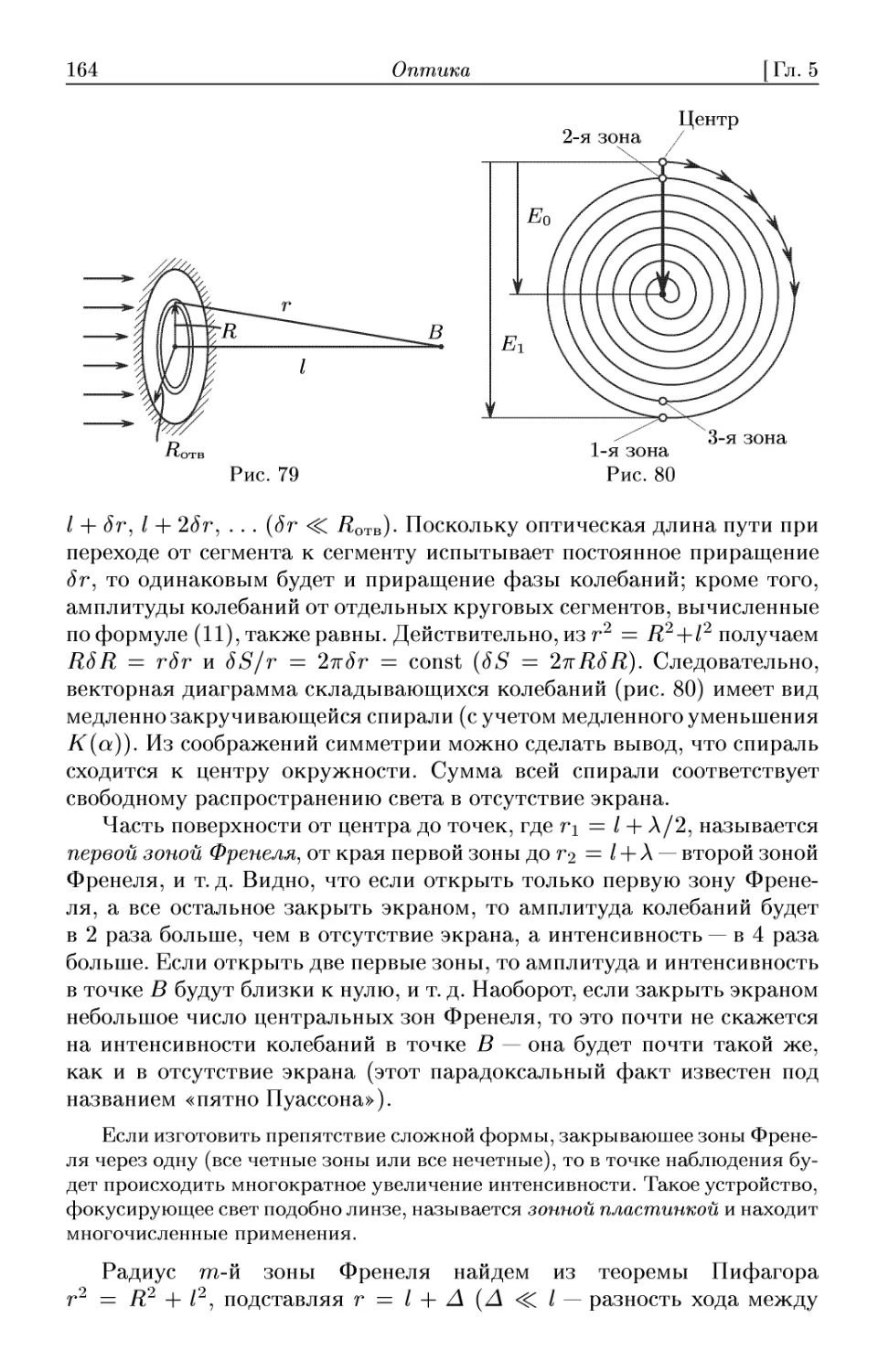
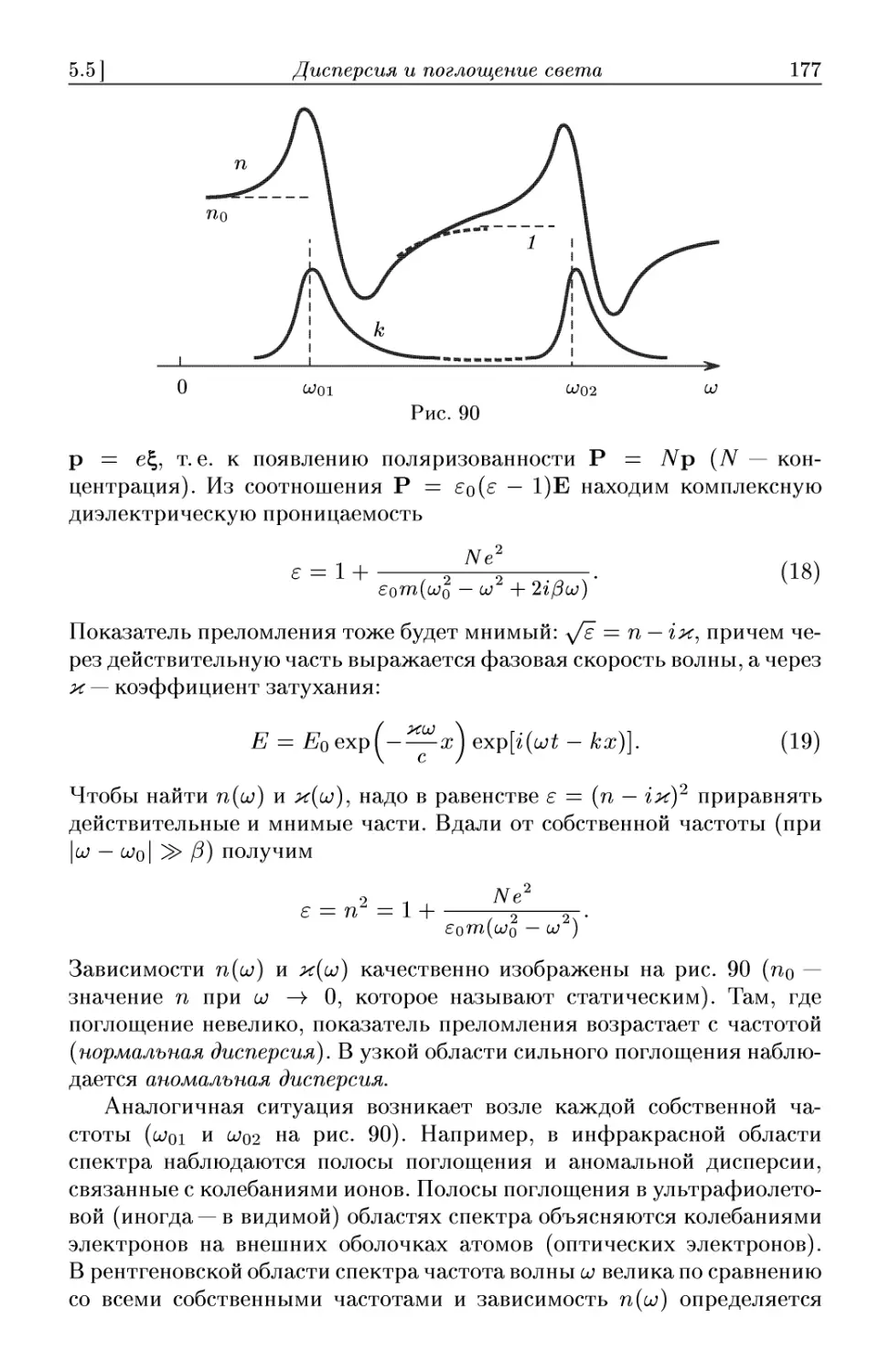
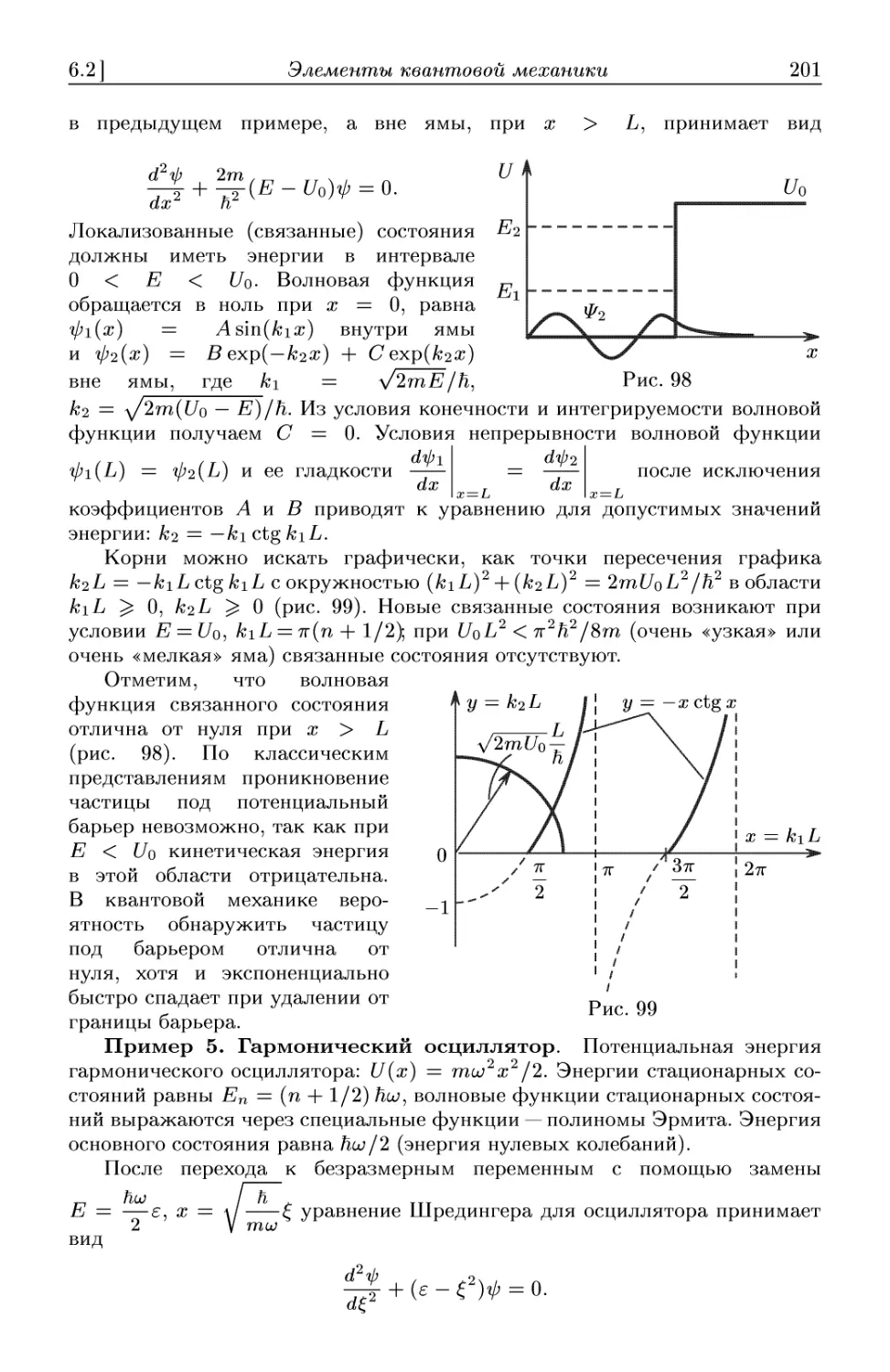
Текст

УДК 530.1
449
ББК 22.3
Черноуцан А. И. Краткий курс физики. — М.: ФИЗМАТЛИТ,
2002. - 320 с. - ISBN 5-9221-0292-3.
Книга содержит сжатое изложение всех основных вопросов курса физики,
включенных в программы подготовки бакалавров и специалистов по инже-
инженерным и физическим специальностям технических вузов. Она не претендует
на роль основного учебника, но является полезным дополнением к известным
курсам физики, приведенным в списке литературы. Ее удобно использовать
для повторения пройденного материала непосредственно перед зачетом, кол-
коллоквиумом или экзаменом, а также для быстрого восстановления в памяти
забытого материала.
Книга будет полезна не только студентам, но и преподавателям, а так-
также тем инженерам и научным сотрудникам, кому понадобится вспомнить
отдельные разделы подзабытого курса физики.
ISBN 5-9221-0292-3 © ФИЗМАТЛИТ, 2002

ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Физические основы механики 7
1.1. Кинематика точки 7
1.2. Кинематика твердого тела 10
1.3. Динамика 12
1.4. Закон сохранения импульса 16
1.5. Закон сохранения энергии 19
1.6. Закон сохранения момента импульса 24
1.7. Задача двух тел. Приведенная масса 29
1.8. Поле тяготения 30
1.9. Неинерциальные системы отсчета 33
1.10. Динамика твердого тела 35
1.11. Специальная теория относительности 40
Глава 2. Молекулярная физика и термодинамика 47
2.1. Основные положения и определения 47
2.2. Первое начало термодинамики 49
2.3. Второе начало термодинамики 53
2.4. Энтропия. Свободная энергия 56
2.5. Кинетическая теория идеального газа 60
2.6. Реальные газы. Уравнение Ван-дер-Ваальса 66
2.7. Равновесие фаз. Фазовые переходы 68
2.8. Поверхностное натяжение 70
2.9. Явления переноса в газах 72
Глава 3. Электродинамика 76
3.1. Электрический заряд. Закон Кулона 76
3.2. Электрическое поле. Напряженность поля 77
3.3. Электростатическое поле. Принцип суперпозиции для на-
напряженности и потенциала 78
3.4. Теорема Гаусса 82
3.5. Электростатика проводников 85
3.6. Электростатика диэлектриков 88
3.7. Конденсаторы 93
3.8. Энергия электростатического поля 95
3.9. Постоянный ток 98
3.10. Магнитное поле. Сила Лоренца и закон Ампера 103
3.11. Вычисление магнитной индукции 105
3.12. Циркуляция и поток вектора магнитной индукции 107

Оглавление
3.13. Магнитное поле в веществе 110
3.14. Электромагнитная индукция 115
3.15. Уравнения Максвелла 120
Глава 4. Колебания и волны 125
4.1. Гармонические колебания. Сложение колебаний 125
4.2. Свободные незатухающие колебания 128
4.3. Затухающие и вынужденные колебания 132
4.4. Упругие волны 137
4.5. Электромагнитные волны 145
Глава 5. Оптика 152
5.1. Геометрическая оптика. Фотометрия 152
5.2. Интерференция света 156
5.3. Дифракция 163
5.4. Поляризация света. Формулы Френеля 170
5.5. Дисперсия и поглощение света 176
5.6. Тепловое излучение 179
5.7. Световые кванты 185
5.8. Принцип работы лазеров 189
Глава 6. Квантовая механика. Атомная физика 193
6.1. Строение атома. Модель Бора 193
6.2. Элементы квантовой механики 197
6.3. Структура и спектры сложных атомов 214
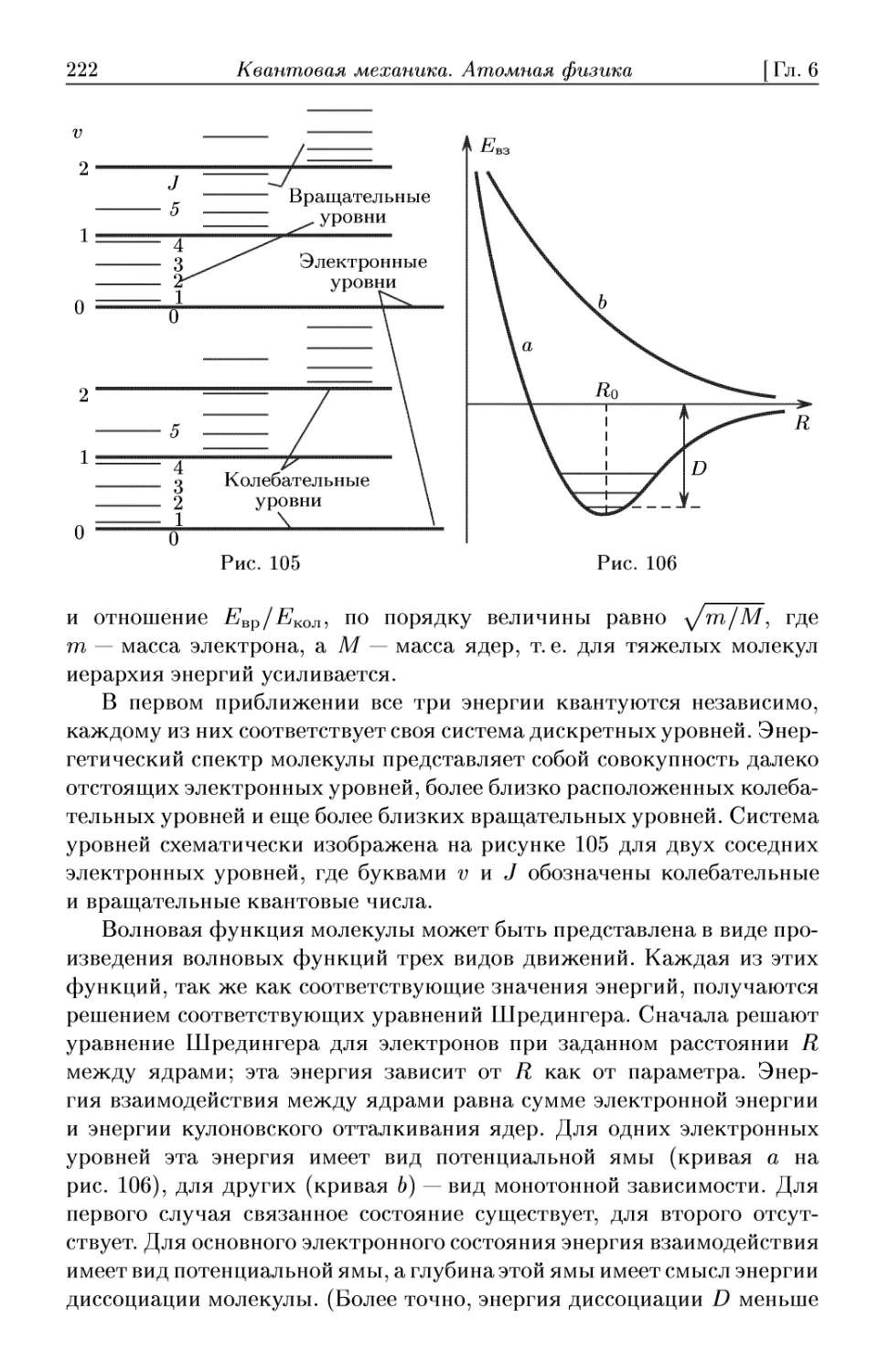
6.4. Элементы физики молекул 221
Глава 7. Квантовая теория кристаллов 228
7.1. Элементы квантовой статистики 228
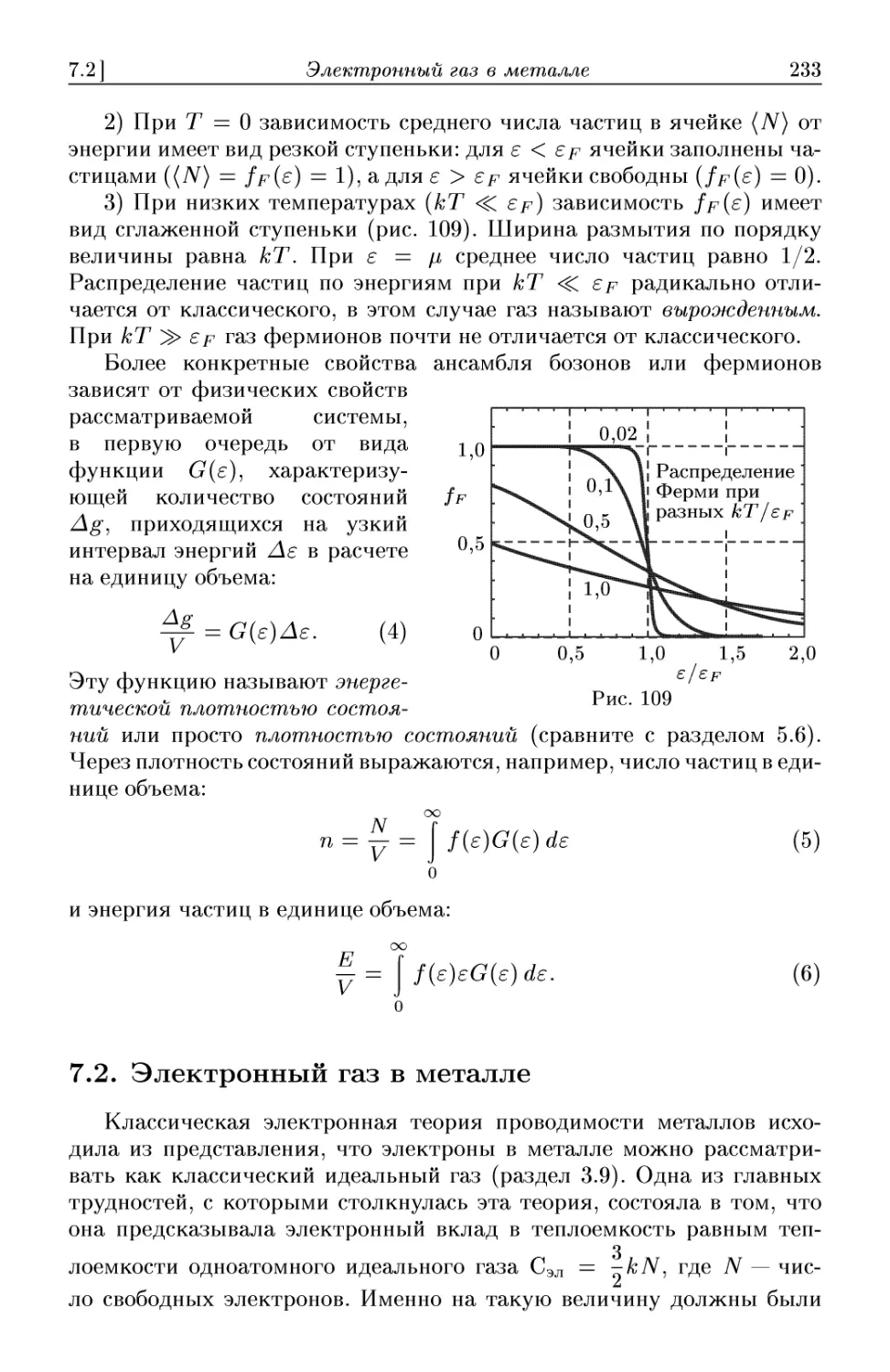
7.2. Электронный газ в металле 233
7.3. Теплоемкость кристаллической решетки. Фононы 237
7.4. Электроны в периодическом поле. Энергетические зоны . . . 242
Глава 8. Элементы ядерной физики 252
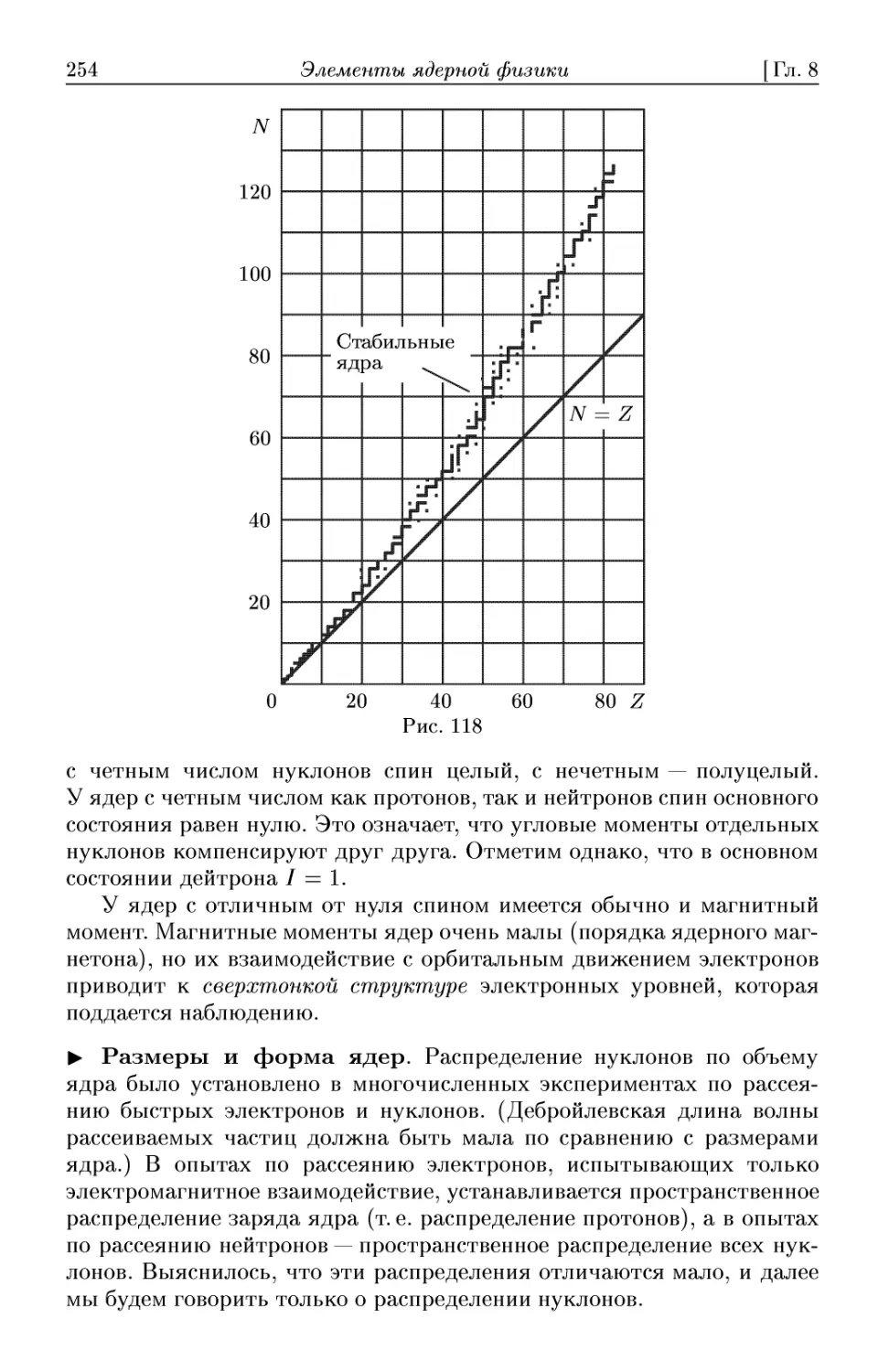
8.1. Основные свойства ядер 252
8.2. Ядерные силы. Модели ядер 258
8.3. Радиоактивность 263
8.4. Ядерные реакции 272
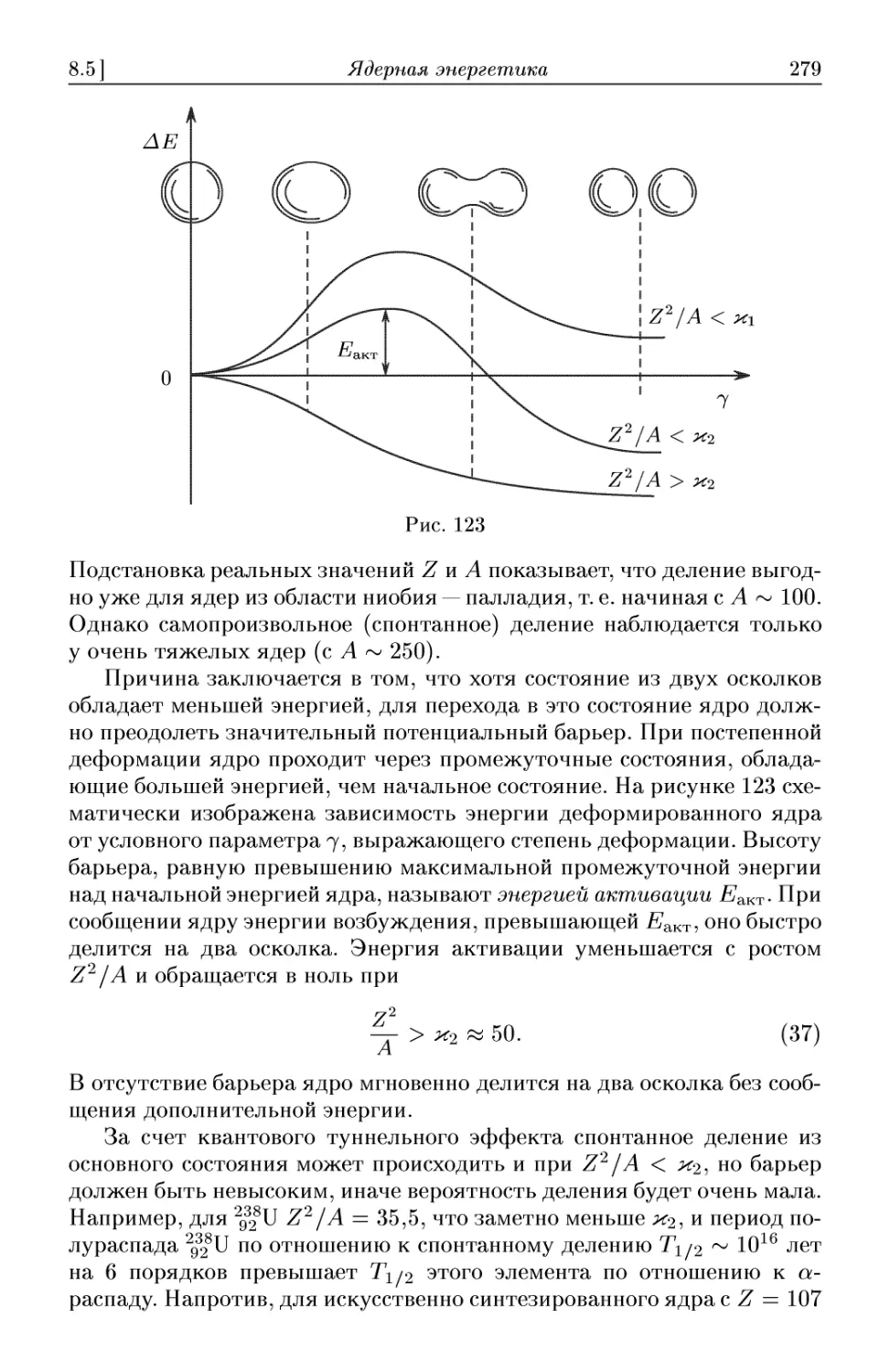
8.5. Ядерная энергетика 278
8.6. Элементарные частицы 286
Список литературы 299
Приложения 301
Предметный указатель 308

Предисловие
Книга содержит сжатое изложение всех основных вопросов курса
физики, включенных в программы подготовки бакалавров и специ-
специалистов по инженерным и физическим специальностям технических
вузов. Она не претендует на роль основного учебника, но является
полезным дополнением к известным курсам физики, приведенным в
списке литературы. Ее удобно использовать для повторения пройден-
пройденного материала непосредственно перед зачетом, коллоквиумом или
экзаменом, а также для быстрого восстановления в памяти забытого
материала.
Несмотря на краткость, изложение материала является цельным и
логически связанным, сопровождается выводом многих утверждений
и формул и разбором многочисленных примеров, поясняющих поло-
положения теории и иллюстрирующих их практическое использование при
решении задач. Фактически студент при подготовке к экзамену найдет
в книге ответ на любой вопрос, причем в объеме, который можно
считать достаточным для получения хорошей или отличной оценки.
В полезности такого краткого курса с примерами убеждает опыт
использования аналогичного пособия, написанного автором для школь-
школьников (Культура и традиции, 1993-1999, Эксмо Пресс 1999, 2001). Это
пособие оказалось эффективным как при подготовке в обычные техни-
технические вузы, так и в элитные университеты физического профиля. Дан-
Данное пособие для студентов выходило ранее (в сокращенном варианте и
без последних глав) в составе многопредметного справочника (Меж-
(Международная программа образования, 1995; АСТ-Астрель, 2000, 2002) и
было опробовано в нескольких вузах. Автор успешно использовал его
при обучении студентов как физических, так и обычных технических
специальностей в Российском государственном университете нефти и
газа им. И. М. Губкина.
Книга будет полезна не только студентам, но и преподавателям,
а также тем инженерам и научным сотрудникам, кому понадобится
вспомнить отдельные разделы подзабытого курса физики.
Несколько слов о структуре книги. Материал разбит на 8 глав, а
каждая глава — на несколько разделов. Нумерация рисунков в книге
сплошная, формулы нумеруются отдельно в каждой главе, а приме-
примеры—отдельно в каждом разделе. Примеры набраны мелким шрифтом,
кроме того мелким шрифтом набран материал, выходящий за рам-
рамки программы для инженерно-технических специальностей. В конце
книги помещены несколько приложений и предметный указатель, что

6 Предисловие
позволит использовать книгу в качестве справочника. Изложение всего
материала ведется в единицах СИ.
Автор выражает глубокую благодарность Андрею Полянину, в свое
время вдохновившего автора на написание данной книги и сыгравшего
роль первого сурового редактора. На идеологию книги и отбор мате-
материла большое влияние оказали соратники автора по журналу «Квант»
А. Л. Стасенко, А. А. Леонович и др., а также сотрудники кафедры
физики РГУ нефти и газа им. И. М. Губкина и других вузов, сделавшие
много полезных замечаний. Автор благодарен редактору данного изда-
издания И.Н. Жетвиной, много сделавшей для устранения многочисленных
недочетов, сотрудникам издательства О.А. Пениной и В.В. Худякову
за их самоотверженную помощь в придании книге окончательного
вида. Все оставшиеся недочеты лежат на совести автора, и он просит
сообщать о них в издательство или ему лично по электронной почте
alexei_chernoutsan@mtu-net.ru.

Глава 1
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Механическим движением называется изменение положения тела
по отношению к другим телам. Как видно из определения, механи-
механическое движение относительно. Для описания движения необходимо
определить систему отсчета, которая включает в себя тело отсчета,
жестко связанную с ним систему координат и набор синхронизирован-
синхронизированных между собой часов. Механика изучает движение модельных объек-
объектов — материальной точки и твердого тела. Положение этих объектов
определяется конечным числом независимых параметров (т. е. они об-
обладают конечным числом степеней свободы). Кинематика занимается
описанием движения без выяснения его причин.
1.1. Кинематика точки
> Основные определения. Скорость и ускорение. Материаль-
Материальной точкой называется тело, размерами которого при описании его
движения можно пренебречь (в сравнении с пройденным расстояни-
расстоянием). Положение точки в момент времени t задается радиусом-векто-
радиусом-вектором г, проведенным к этой точке из нача-
начала координат (рис. 1). В процессе движения
конец радиуса-вектора описывает простран-
пространственную кривую — траекторию. В прямо-
прямоугольной декартовой системе координат по-
положение радиуса-вектора задается тремя его
проекциями на оси — координатами ж, у, z.
Движение точки полностью определяется за-
заданием закона движения — одной векторной
функции г(?) или трех скалярных функций
x(t), y(t), z(t). Для компактной записи ради-
радиуса-вектора (или любого вектора) через его
проекции используют единичные орты i, j,
k: r = xi + yj + z\l. Путь — длина участка
траектории, пройденного точкой за рассматриваемый интервал време-
времени. Путь — величина скалярная, неотрицательная и не убывающая со
временем. Перемещением точки называется вектор Ay = г — го, соеди-
соединяющий начальное положение точки с конечным и равный разности
радиусов-векторов в конечный и начальный моменты времени.
У
Рис. 1

8 Физические основы механики [ Гл. 1
Скорость точки равна производной от радиуса-вектора по време-
времени: v = dr/dt. Скорость направлена по касательной к траектории.
Средняя (по времени) скорость за конечное время At определяется как
отношение перемещения к интервалу времени: vcp = Ay /At. (Средняя
скорость пути равна отношению пройденного пути к интервалу време-
времени.) Движение называют равномерным, если v = const. Равномерное
движение происходит по прямой. Равномерным движением по задан-
заданной криволинейной траектории называют движение с постоянным
модулем скорости. (Пример — равномерное движение по окружности.)
Ускорение точки равно первой производной от скорости по времени:
а = dv/dt. Ускорение лежит в той же плоскости, что и участок тра-
траектории, и направлено «внутрь» траектории (в частном случае, когда
траектория является прямой линией, ускорение направлено вдоль этой
прямой). Проекцию ускорения на направление скорости называют тан-
тангенциальным ускорением и обозначают аТ, она опре-
определяет быстроту изменения модуля скорости и равна
производной от модуля скорости: ат = dv/dt. Другую
компоненту ускорения, перпендикулярную скорости,
называют нормальным ускорением (рис. 2) и обозна-
обозначают ап; она характеризует быстроту изменения на-
направления скорости и равна ап = v2/R, где R — ра-
радиус кривизны траектории (т.е. радиус окружности,
~ наиболее близко примыкающей к траектории в данной
рис< 2 точке). Среднее ускорение за время At определяется
как аср = Av /At. Движение называют равноускорен-
равноускоренным, если а = const. Равноускоренным движением вдоль заданной
траектории называют движение с аТ = const.
> Прямая и обратная задачи кинематики. Задачу определения
характеристик движения по известному закону движения называют
прямой задачей кинематики.
Пример 1. Пусть закон движения имеет вид: х = RcosLot, у = Rs'mout.
Найдите уравнение траектории, скорость и ускорение.
Решение. Исключая время (с помощью тождества sin2 Lot-\-cos2 tot = 1),
находим уравнение траектории: х2 + у2 = R2 (окружность радиуса R).
Дифференцируя исходные выражения по времени, получим
(компоненты скорости),
(компоненты ускорения).
.,- = — со R sin cot
dt2
dx
~ ~dt
_ dy_
dt
d x
= — coRsincot,
= LO R COS LOt
= — LO2 RcOSLOt
= — lo2 RsinLot

1.1] Кинематика точки 9
Модуль скорости v = y/v% + v2, = cuR и модуль ускорения а = о;2Я не
зависят от времени и связаны соотношением а = г? //2. Ускорение направлено
перпендикулярно скорости к центру окружности: а = — uj2t.
Задачу определения закона движения по известному ускорению а(?)
называют обратной задачей кинематики. Для однозначного решения
этой задачи нужно знать начальные условия — положение и скорость
точки в начальный момент времени.
Пример 2. Равноускоренное движение. Пусть известны ускорение
точки а = const и ее начальные скорость vo и положение го. Найдите
траекторию и закон движения точки.
Решение. Последовательно интегрируя, находим сначала скорость точ-
точки v = JQ a dt = vo + а?, а затем ее положение г = Jo v dt = го + vot H—at .
Точка движется в плоскости векторов vo, а по параболе, что видно
в системе координат, где ось у направлена по а, а ось х — перпендикулярно а
(х = хо + voxt, у = уо + voyt + -at2).
Во многих случаях задача кинематики не сводится ни к прямой,
ни к обратной. В этом случае для определения закона движения при-
приходится решать дифференциальное уравнение. Иногда это уравнение
можно решить разделением переменных.
Пример 3. При решении задач динамики часто возникает уравнение
dv/dt = — av2 (торможение тела происходит с ускорением, пропорциональ-
пропорциональным квадрату его скорости). Найдите зависимость скорости движения тела
от времени, если начальная скорость равна vq. Найдите также зависимость
скорости тела от его перемещения s.
Решение. Разделяя переменные, получим: dv/v2 = —adt. Интегри-
Интегрируя левую часть уравнения от vo до и, а правую — от 0 до t, находим
(v~1 — Vq1) = at, т. е. v = vo/(l-\-voat). Интегрируя далее, можно определить
закон движения s(t) и, исключив ?, найти v(s). Однако можно поступить
проще: поскольку vdt = ds, уравнение с разделенными переменными можно
записать в виде dv/v = —ads. Интегрируя, получим ln(v/vo) = —as, откуда
v = vo exp(—as).
> Движение по окружности. Движение по окружности можно
описывать с помощью угловых переменных: угла поворота ср, угловой
скорости uj = dip/dt и углового ускорения е = duj/dt. Если угол
измерять в радианах, то длина дуги равна s = ipR. Отсюда следует,
что
о dv о v2 2 о
v = ojR, аТ = — = еп, ап = — = uj п.
dt it
В случае равномерного движения по окружности нормальное ускоре-
ускорение ап иногда называют центростремительным.
Формулы для нормального и тангенциального ускорений можно вывести,
если записать скорость в виде v = vz, где т — единичный вектор, направ-
направленный вдоль скорости. Получим а = (dv/dt)z + v(dz/dt) и учтем, что
dz/dt = n(d(p/dt) = n(v/R), где п —единичный вектор, перпендикулярный

10 Физические основы механики [ Гл. 1
к скорости и направленный вдоль радиуса. Этот вывод справедлив и для
произвольной траектории, если принять соотношение с/т = n(ds/R) за опре-
определение как направления нормали п, так и радиуса кривизны R.
> Относительность движения. Сложение скоростей. Если дви-
движение точки рассматривается из двух систем отсчета К и К\ оси
которых остаются все время параллельными друг другу, то между
скоростями точки v и v' относительно эти
момент времени выполняется соотношение
скоростями точки v и v' относительно этих систем отсчета в каждый
v = v' + vK, A)
где yk — скорость системы К' относительно системы К. Такое же
соотношение выполняется и для ускорений: а = а' + з.^.
1.2. Кинематика твердого тела
> Основные определения. В механике твердым телом называют
идеализированное тело, расстояние между любыми двумя точками
которого не меняется (т.е. отсутствуют деформации). Выделяют два
простых движения твердого тела — поступательное и вращательное.
При поступательном движении отрезок, соединяющий любые две
точки тела, перемещается параллельно самому себе. Поскольку все
точки тела движутся одинаково, достаточно описать движение одной
точки. При вращательном движении все точки твердого тела движут-
движутся по окружностям, центры которых лежат на прямой, называемой
осью вращения (при этом скорости всех точек перпендикулярны оси
вращения). Угловые скорости всех точек в каждый момент времени
одинаковы, поэтому вводят вектор угловой скорости ю, направляя его
вдоль оси вращения по движению буравчика. Распределение линейных
скоростей точек тела можно представить с помощью векторного про-
произведения х)
v = ю х г, B)
где радиусы-векторы проводятся из любой точки на оси. В случае
неподвижной оси вращения вектор углового ускорения е = day/dt также
направлен вдоль оси.
> Плоское движение твердого тела определяют как движение,
при котором скорости всех точек тела параллельны некоторой плос-
плоскости. Если с любой точкой тела (или его мысленного продолжения)
) Это уравнение является частным случаем важной математической фор-
формулы dA/dt = со х А, выражающей производную по времени от любого
вектора А, который вращается с угловой скоростью со.

1.2]
Кинематика твердого тела
11
А
связать поступательно движущуюся систему координат, то относи-
относительное движение будет чистым вращением вокруг неподвижной оси,
перпендикулярной плоскости движения.
Пример 1. Качение колеса без проскальзывания со скоростью v удобно
представить как сумму поступательного движения со скоростью v и враща-
вращательного движения с угловой скоростью ш (рис. 3). Скорость любой точки от-
относительно земли можно найти по закону
сложения скоростей A). Скорость нижней
точки колеса О' должна быть равна нулю,
откуда следует связь между v и о;: v = ujR.
Ускорения всех точек направлены к цен-
центру колеса.
> Мгновенная ось вращения. Ес-
Если какая-то точка тела (или его мыс-
мысленного продолжения) в данный мо-
момент неподвижна, то существует про-
проходящая через нее прямая неподвиж-
неподвижных точек, которую называют мгно-
мгновенной осью вращения. Распределение
скоростей в этот момент описывается формулой B). Мгновенная ось и со
могут менять свое положение как в пространстве, так и относительно
тела. В частности, в примере 1 можно получить скорости всех точек
колеса как результат чистого вращения относительно мгновенной оси,
проходящей через точку касания О'. Угловое ускорение е может быть
непараллельно мгновенной оси.
> Сложение угловых скоростей. Движение относительно
вращающейся системы отсчета. Движение твердого тела с непо-
неподвижной точкой представляет собой в каждый момент времени чистое
вращение вокруг мгновенной оси. Если это движение можно пред-
представить как вращение с угловой скоростью a>i относительно системы
отсчета, вращающейся с угловой скоростью Ю2, то результирующая
угловая скорость равна ю = coi +Ю2. Для доказательства надо обобщить
закон сложения скоростей A) на непоступательное движение системы
отсчета:
V = VOTH+Vnep, C)
где vnep — переносная скорость данной точки системы отсчета. В слу-
случае вращающейся системы отсчета
V = VOTH + СО X Г.
D)
Если относительное движение представляет собой чистое вращение, то
получим v = coiXr + GJXr = (a>i + ©2) х г, т.е. результирующее
движение представляет собой вращение с угловой скоростью (a>i +©2)-

12 Физические основы механики [ Гл. 1
Пример 2. Круговой конус с углом полу раствора а положили на бок
и покатили без проскальзывания так, что его ось вращается с угловой ско-
скоростью coi (рис. 4). Найдите угловую
скорость и угловое ускорение конуса.
Решение. Во вращающейся сис-
системе отсчета, в которой ось кону-
конуса неподвижна, происходит враще-
вращение вокруг этой оси с угловой скоро-
скоростью 0J. Связь между ш\ и ио2 найдем
из условия неподвижности точки А:
ио\1 = (лJГ, или ш\ = о;2 sin а. Из это-
этого соотношения следует, что вектор
со = coi + 0J направлен горизонталь-
но, по линии соприкосновения конуса
с плоскостью, которая, конечно же,
является мгновенной осью вращения. Вклад в угловое ускорение дает толь-
только вращение вектора 0J с угловой скоростью coi: е = dco/dt = coi x 0J,
? = UJ\UJ2 COS OL.
Формула D) является частным случаем формулы для производной
по времени от любого вектора А:
dA fdA\
\ / отн
где первый член — скорость изменения А относительно вращающейся
системы координат (см. также сноску к формуле B)).
При изучении неинерциальных систем отсчета (см. разд. 1.9) нам по-
понадобится связь между ускорениями точки в неподвижной и вращающейся
системах отсчета. Ее можно получить, применив E) к каждому из двух
членов в D):
dw gJvoth dr
— = h со х — =
dt dt dt \ ai / о™
—Г— + 0) X Voth + 0) X (Voth + 0) X Г) =
V at / Отн
= аОТн + 20) X Vqth + 0) X (o) X r)
Последний член представляет собой переносное ускорение данной точки
системы отсчета (нормальное, или центростремительное, ускорение). Видно,
что кроме относительного и переносного ускорений, возникает дополнитель-
дополнительное слагаемое, которое называют кориолисовым ускорением.
1.3. Динамика
> Первый закон Ньютона утверждает, что существуют такие си-
системы отсчета, в которых любое тело, не взаимодействующее с други-
другими телами, движется равномерно и прямолинейно. Системы отсчета,
существование которых постулирует этот закон, называются инерци-
альными.
Из закона сложения скоростей видно, что любая система отсчета,
движущаяся с постоянной скоростью относительно инерциальной, так-
также является инерциальной. Практически точно инерциальной можно

1.3] Динамика 13
считать гелиоцентрическую систему, связанную с Солнцем и удаленны-
удаленными звездами. Земля является инерциальной системой только прибли-
приближенно, вследствие суточного вращения ускорение точек ее поверхности
достигает 0,034 м/с . Кроме того, Земля движется вокруг Солнца, но
соответствующее ускорение на три порядка меньше (проверьте это).
> Масса. Импульс. Из первого закона Ньютона следует, что в инер-
циальных системах отсчета ускорение тела возникает только в резуль-
результате его взаимодействия с другими телами. Это ускорение зависит
от инертности тела, т. е. его способности сопротивляться изменению
скорости, а также от интенсивности и направления действия на него
других тел.
Масса тела т — это скалярная положительная величина, характе-
характеризующая инертность тела. Эксперименты показывают, что при вза-
взаимодействии двух тел их ускорения ai и а2 в инерциальной системе
отсчета направлены в противоположные стороны, а отношение модулей
ускорений а±/п2 не зависит от характера и интенсивности взаимодей-
взаимодействия. Это позволяет определить отношение масс двух произвольных
тел как величину, обратную отношению ускорений, возникающих при
их взаимодействии друг с другом: m\/m<i — ач/а\. Чтобы определить
абсолютную величину массы т, необходимо определить эталон массы.
В системе СИ за эталон массы принимают 1 килограмм A кг). Мас-
Масса обладает свойством аддитивности: сумма масс частей, на которые
можно разделить тело, равна массе всего тела. Как показывает теория
относительности, это свойство является приближенным и нарушается
при сильном взаимодействии между частями тела. Например, масса
ядра оказывается меньше суммы масс образующих его нуклонов.
Импульсом частицы называют векторную величину, равную произ-
произведению массы частицы на ее скорость:
р = 771V. F)
Определение F) действует только при и С с, где с — скорость света;
более общее определение, верное при любых v < с, вводится в теории
относительности.
> Сила. Силой, действующей на тело массой т при его взаимодей-
взаимодействии с другим телом, назовем величину F = та, где а — ускорение,
сообщенное этой силой телу т в инерциальной системе отсчета. Более
общее определение имеет вид: F = dp/dt. В ньютоновской динамике
оба определения эквивалентны, но в динамике теории относительно-
относительности определение импульса изменяется, и оказывается верным толь-
только второе определение. В системе СИ сила измеряется в ньютонах
(Н = кг-м/с2).
Изменение импульса точки за время t под действием силы F равно
интегралу от силы: Ар = p(t) — р@) = Jo Fdt. Эту величину называют
импульсом силы. Средняя (по времени) сила равна Fcp = Ар/At.

14 Физические основы механики [ Гл. 1
> Второй закон Ньютона. Если на материальную точку одновре-
одновременно действуют N тел с силами II, ..., Fyy, то ускорение тела а
определяется векторной суммой этих сил:
F 1 " dp "
а = — = — V Е или -тг = У Е.
т т ^ J dt ^ J
3=1 3=1
Силу F называют равнодействующей (или результирующей) сил II,
..., Fyy. Второй закон Ньютона называют уравнением движения тела,
так как он позволяет (в принципе) рассчитать движение тела или
системы тел, но только в том случае, если известна зависимость сил
взаимодействия между телами от их взаимного расположения и скоро-
скоростей. Ниже мы кратко напомним свойства сил, которые возникают при
решении механических задач.
> Третий закон Ньютона утверждает, что силы Fab и Бвд, с ко-
которыми действуют друг на друга два взаимодействующих тела Л и В,
направлены вдоль одной прямой в противоположные стороны и равны
между собой по модулю:
> Дальнодействие и причинность. Поле. В ньютоновской меха-
механике считалось, что третий закон Ньютона выполняется для любых
взаимодействующих тел независимо от природы взаимодействия и от
того, находятся ли тела в непосредственном контакте или взаимодей-
взаимодействуют на расстоянии с помощью гравитационных или электромагнит-
электромагнитных сил. Однако выполнение этого закона для дальнодействующих сил
означает мгновенную передачу информации об изменении положения
тел. Само понятие дальнодействия противоречит постулатам теории
относительности, запрещающим передачу информации со скоростью,
превышающей скорость света. Современная физика отказалась от
дальнодействия, введя нового участника взаимодействия — материаль-
материальное силовое поле (электрическое, гравитационное и др.), заполняющее
все пространство. На тело в данной точке пространства действуют
не удаленные тела, а поле в окрестности этой же точки; это поле
создается удаленными телами (источниками поля). Изменение поля
передается от точки к точке и распространяется с конечной скоростью
(скоростью света). Ньютоновская механика оказывается верной только
при малых скоростях i; <с, в этом нерелятивистском пределе можно
пользоваться как дальнодействующими силами, так и полем. Удобно
изучать движение точки (или системы точек) во внешнем стацио-
стационарном поле, создаваемом неподвижными источниками (пример: поле
тяжести Земли). Силовое поле называется центральным, если сила,
действующая со стороны поля на помещенную в него материальную
точку, направлена в сторону центра поля (силового центра), а модуль

1.3] Динамика 15
силы зависит только от расстояния г до этого центра:
F(r) = Fr(r)r-.
Здесь Fr(r) — проекция силы на радиальное направление; Fr > О
соответствует отталкиванию, Fr < 0 — притяжению. Поле называет-
называется однородным в области пространства, если сила одинакова во всех
точках этой области: F = const.
> Силы природы. Все разнообразие действующих в природе сил
можно свести к нескольким фундаментальным взаимодействиям (гра-
(гравитационному, слабому, электромагнитному и сильному). Однако для
практических целей такой подход непригоден, и кроме фундаменталь-
фундаментальных дальнодействующих сил (в механике это сила тяготения), надо
знать свойства различных сил, возникающих при контакте макроско-
макроскопических тел. Перечислим кратко силы, возникающие при решении
механических задач.
1. Сила тяжести mg (сила тяготения у поверхности Земли).
2. Сила упругости при продольной деформации тела пропорци-
пропорциональна деформации: Fynp = — kx, где к — жесткость тела (закон
Гука). В пределе бесконечной жесткости возникают сила (нормальной)
реакции N или сила натяжения нити Т, которые определяются из
самих уравнений движения. (Силы такого типа называют реакциями
связей.)
3. Сила сухого трения. Сила трения скольжения: FTp = /iiiV, где
/ii — коэффициент трения скольжения. Сила трения покоя FTp ^ /i2^5
где /i2 — коэффициент трения покоя (при решении задач считают, что
Hi — Ц2)- Сила трения покоя также относится к реакциям связей.
4. Сила сопротивления движению в жидкости или газе зависит от
скорости и поперечных размеров тела. При малых скоростях и малых
размерах тела сила пропорциональна скорости (сила вязкого трения),
при больших скоростях сила пропорциональна площади поперечного
сечения и квадрату скорости (сила лобового сопротивления).
> Принцип относительности Галилея. Принцип относительности
Галилея утверждает, что все законы механики имеют одинаковый вид
во всех инерциальных системах
отсчета. Пусть система К' дви- k v ^ z'
жется относительно системы К
с постоянной скоростью V. Вы- К К'
берем системы координат с па-
параллельными осями, причем оси
х и х' направим вдоль V (рис. 5);
время будем отсчитывать от мо-
момента полного совмещения осей.
Тогда координаты и время собы- ис'
У
У

16 Физические основы механики [ Гл. 1
тия в системе К' будут выражаться через координаты и время в К
с помощью преобразований Галилея:
x' = x-Vt, y' = y, z' = z, t' = t. G)
При преобразованиях Галилея остаются неизменными разность скоро-
скоростей двух точек и расстояние между ними; значит, не меняются силы
взаимодействия между материальными точками. Кроме того, преоб-
преобразования Галилея не меняют ускорения точки. Следовательно, не
меняются обе части равенства, выражающего второй закон Ньютона,
т. е. уравнение движения имеет одинаковый вид в разных системах
отсчета (инвариантно относительно преобразований Галилея).
Преобразования Галилея основаны на утверждениях о независи-
независимости хода времени и длины отрезков от системы отсчета, которые
считались неотъемлемыми свойствами пространства и времени. Тео-
Теория относительности пересматривает представления о пространстве
и времени и показывает, что преобразования Галилея верны только
при V <С с; их заменяют преобразования Лоренца, верные при любых
скоростях V < с.
1.4. Закон сохранения импульса
> Система материальных точек. Центр масс. Пусть система со-
состоит из N материальных точек. Силы, действующие на j-ю точку, под-
подразделяются на внутренние Ц\, действующие со стороны остальных то-
точек системы, и внешние, равнодействющую которых обозначим 1) Fe.
В соответствии с третьим законом Ньютона сумма внутренних сил
равна нулю, т. е. сумма всех сил, действующих на точки системы, равна
сумме внешних сил. Если тела системы не взаимодействуют с внешни-
внешними телами, то систему называют замкнутой (или изолированной).
Центром масс (центром инерции) системы материальных точек
?7ii, ..., тn называют точку, положение которой определяется радиу-
радиусом-вектором
_ -\ h mNrN
ц
_
ц
+ • • • + tun
Связанную с центром масс поступательно движущуюся систему отсче-
отсчета будем называть системой центра масс.
Если масса распределена непрерывно (в пространстве, по плос-
плоскости, вдоль линии), то составляющие систему материальные точки
получаются при мысленном разделении объема тела на маленькие
) Верхние индексы «i» и «е» у сил происходят от латинских слов internus —
внутренний и externus — внешний.

1.4] Закон сохранения импульса 17
области. Распределение массы по объему задают с помощью плот-
плотности: dm = p(r) dV. Например, определение (8) для непрерывно
распределенной массы принимает вид
э(г) dV
р(г) dV
Тело с постоянной плотностью называют однородным.
> Импульс. Импульс системы определяется как сумма импульсов
составляющих его частиц:
Продифференцировав уравнение (8) по времени, найдем, что импульс
системы выражается через скорость центра масс:
р = Шуц, (9)
где т — масса системы. Значит, в системе центра масс импульс системы
точек равен нулю.
Просуммируем уравнение второго закона Ньютона dp/dt = F по
всем точкам системы и учтем, что все внутренние силы уничтожаются:
(скорость изменения импульса системы равна результирующей внеш-
внешней силе).
> Закон сохранения импульса. Из уравнения A0) следует, что им-
импульс замкнутой системы сохраняется. Закон сохранения импульса
является следствием однородности пространства (равноправия всех его
точек) и поэтому носит универсальный характер. Область действия
этого закона выходит за пределы ньютоновской механики, в рамках
которой мы его вывели. Даже при учете конечной скорости распростра-
распространения сигнала (явление запаздывания), которое приводит к нарушению
третьего закона Ньютона, закон сохранения импульса выполняется
точно, если учесть импульс передатчика сигнала — силового поля.
Импульс незамкнутой системы сохраняется в следующих случаях:
1. Если сумма внешних сил равна нулю.
2. Если результирующая внешняя сила перпендикулярна некоторо-
некоторому направлению, то сохраняется не вектор импульса системы, а проек-
проекция импульса системы на это направление.

18 Физические основы механики [ Гл. 1
3. Если взаимодействие продолжается очень короткое время At,
а внешние силы Fe ограничены г), то изменением импульса системы
FeAt можно пренебречь (считать, что At —> 0).
> Движение центра масс. Продифференцировав по времени урав-
уравнение (9), с учетом A0) получим уравнение движения центра масс:
т. е. центр масс движется так, как двигалась бы воображаемая матери-
материальная точка с массой, равной массе системы, если к ней приложить
результирующую внешнюю силу.
Пример 1. Тонкий стержень длиной / и массой т вращается в горизон-
горизонтальной плоскости вокруг одного из своих концов с угловой скоростью ш.
Найдите силу натяжения в середине стержня.
Решение. Центр масс внешней половины стержня движется по окруж-
3
ности радиусом -/ под действием только одной внешней силы — искомой
4
1 3 3
силы натяжения. Из уравнения A1) получим: Fu = (-m)u;2(-/) = -тш21.
Отметим, что центр масс замкнутой системы движется равномер-
равномерно, следовательно, система центра масс является инерциальной.
> Реактивное движение. Изменение скорости корабля в глубо-
глубоком космосе (вдали от гравитирующих тел) возможно только за счет
выбрасывания наружу части массы — ракетного топлива. Уравнение
движения космолета при наличии внешней силы F и реактивной струи
легко получить, записав закон изменения импульса A0) в инерциальной
системе отсчета, связанной в данный момент с кораблем:
mZ\v + Z\Mu = FAt,
где и — скорость струи относительно корабля, а ЛМ- масса выбро-
выброшенного за время At топлива. Разделив на At, получим уравнение
Мещерского:
ma = F — /т,
где /i = AM/At = —Am/At — расход топлива в струе. Второй член
в правой части называют реактивной силой.
Запишем уравнение Мещерского для движения по прямой в отсут-
отсутствие внешней силы: m(dv/dt) = —{dm/di)u. Считая и постоянной
и обозначив начальную массу корабля то, найдем зависимость скоро-
скорости корабля от его массы: v/u = — ln(m/mo) (уравнение Циолковско-
Циолковского).
х) При этом импульсы частиц системы могут заметно измениться под дей-
действием очень больших внутренних сил (взрыв, удар).

1.5] Закон сохранения энергии 19
1.5. Закон сохранения энергии
> Работа — скалярная величина, являющаяся мерой изменения энер-
энергии. Работа внешних сил равна изменению энергии
А = Е2-Е1. A2)
Опираясь на это соотношение как на исходное, мы будем определять
различные виды энергии. (Уточнение этого принципа с учетом тепло-
теплообмена будет дано в гл. 2.) Работа силы на малом участке пути опреде-
определяется как скалярное произведение силы и перемещения: 5 А = (F • cfr),
а работа на всем пути равна:
2 2 2
А = [(F-dr) = [Fr|dr| = \F\dr\cosa,
ill
где FT — проекция силы на направление движения точки ее приложе-
приложения, а а — угол между силой и этим направлением. Работа и энергия
измеряются в джоулях (Дж = Н • м).
Пример 1. Работа постоянной силы F
2 2
А = J(F ¦ dr) = (F ¦ Jdr) = F • (r2 -
1 1
равна скалярному произведению силы на полное перемещение и не зависит
от траектории точки приложения.
Пример 2. Работа центральной силы (силы со стороны центрального
поля, см. разд. 1.3) равна
2 г2
А = [(F-dr) = [ Fr(r)dr
1 п
(проекция dr на радиальное направление равна изменению расстояния г до
центра). Работа зависит только от начального п и конечного Г2 расстояний
до силового центра и не зависит от траектории.
> Мощность. Средняя мощность — отношение работы к интервалу
времени. Мгновенная механическая мощность равна
D dA (F-dr) f ч
Мощность измеряется в ваттах (Вт = Дж/с).
> Кинетической энергией называется энергия, связанная с движе-
движением точки и зависящая от ее скорости. Скорость тела изменяется под

20 Физические основы механики [ Гл. 1
действием результирующей силы F, работа которой равна
2 2 2 . v2
Г j 1
Л = Fr|rfr| = т \aTv dt = т\ —v dt = т \v dv = -j
2
— -mv1
2""^i•
1 ! .
A3)
Видно, что в соответствии с общим принципом A2) кинетическую
энергию можно определить как Ек = mv2/2. Полученное тождество,
утверждающее, что изменение кинетической энергии равно работе ре-
результирующей силы, называют теоремой о кинетической энергии.
Кинетическая энергия системы точек определяется как сумма
кинетических энергий всех точек системы. Изменение кинетической
энергии системы равно работе всех сил, действующих на ее точки.
Кинетическая энергия системы равна:
где т — масса системы, уц — скорость ее центра масс, ЕОТН ~~ кинети-
кинетическая энергия в системе центра масс (теорема Кёнига).
> Консервативные силы. Потенциальное поле. Сила взаимо-
взаимодействия между точками называется консервативной, если работа этой
силы зависит только от начального и конечного положения точек, но
не зависит от траектории их перемещения. Силы, не удовлетворяющие
этому условию, называют неконсервативными. Внешнее стационарное
поле называется потенциальным, если работа поля при перемещении
точки зависит только от ее начального и конечного положения, но
не зависит от ее траектории. (Эквивалентное утверждение — работа
поля при перемещении точки по замкнутой траектории равна нулю.)
Потенциальное поле — это поле консервативных сил взаимодействия,
создаваемое неподвижными внешними источниками. Из примера 1 сле-
следует, что однородное поле потенциально (пример — поле тяжести). Из
примера 2 следует, что любое центральное поле потенциально. Потен-
Потенциальным будет также поле, являющееся суперпозицией нескольких
центральных полей (создаваемое несколькими источниками). Следо-
Следовательно, электростатическое поле и стационарное поле тяготения
являются потенциальными. Из примера 2 также следует, что сила
упругости, создаваемая легкой пружиной, является консервативной.
Система точек, между которыми действуют только консервативные
силы, называется консервативной системой.
> Потенциальная энергия. Потенциальная энергия характеризует
взаимодействие между материальными точками и зависит от их взаим-
взаимного расположения. Потенциальная энергия материальной точки во
внешнем потенциальном поле определяется следующим образом. Раз-
Разность потенциальных энергий для двух положений точки определим

1.5] Закон сохранения энергии 21
как работу поля по ее переносу из одного положения в другое:
- Еп(т2) = А12 A5)
(эта работа не зависит от траектории). Следовательно, изменение по-
потенциальной энергии Е^ — Е\ равно работе сил поля, взятой с об-
обратным знаком. Если перемещение частицы в поле осуществляется
очень медленно с помощью внешней силы, то работа внешней силы
будет равна по величине и противоположна по знаку работе поля, т. е.
А\2 = Е<х — Е\ в соответствии с общим принципом A2).
Равенство A5) дает определение разности потенциальных энергий,
т. е. определяет потенциальную энергию с точностью до константы.
Чтобы сделать определение однозначным, надо задать значение по-
потенциальной энергии в какой-то точке пространства (обычно задают
точку, в которой потенциальная энергия равна нулю).
Пример 3. Работа силы тяжести mg при перемещении точки массой т
с высоты hi на высоту hi равна mgh\ — mghi- Отсюда следует, что по-
потенциальная энергия точки в поле тяжести равна ЕП = mgh, где высота
отсчитывается от оговоренного нулевого уровня. Потенциальная энергия
системы точек в поле тяжести равна
Еп = ^mjghj = mg — = mgh4,
k\
где т — масса системы, /гц — высота ее центра масс.
Пример 4. Работа силы упругости равна $**(—kx)dx = -kx\ kx\,
где Ж1, Х2 — начальная и конечная деформации пружины. Следовательно,
потенциальная энергия упругой пружины равна Еп = —кх , где за нуль
принята энергия недеформированной пружины.
Пример 5. Работа сил трения, сопротивления отрицательна как на
каждом участке пути, так и вдоль замкнутой траектории. Следовательно,
эти силы не удовлетворяют условию консервативности, т. е. являются некон-
неконсервативными.
Потенциальную энергию консервативного взаимодействия двух
частиц можно определить как потенциальную энергию одной частицы
в поле другой частицы. Ответ не зависит от того, какую из частиц
выбрать в качестве источника поля.
> Связь силы с потенциальной энергией. Записав равенство A5)
для двух близких точек, лежащих на некоторой оси х, получим
Еп(х) — Еп(х + dx) = Fx dx. Следовательно, проекция силы на произ-
произвольное направление выражается через производную от потенциальной
энергии:
F. = -°? A6)
(частная производная означает, что Еп рассматривается как функция
одной переменной х). Получаем, что вектор силы равен градиенту

22 Физические основы механики [ Гл. 1
потенциальной энергии:
Для центрального поля формула A6) принимает вид
_ dEu(r)
A8)
> Механическая энергия системы определяется как сумма ее
кинетической энергии, потенциальной энергии взаимодействия между
ее частицами и потенциальной энергии во внешнем поле:
j 3<n j
Первые две суммы образуют собственную механическую энергию си-
системы.
Кроме того, в соответствии с теоремой Кёнига A4) кинетическая энергия
системы равна сумме двух членов — энергии ее движения как целого mv^/2
и кинетической энергии в системе центра масс Еота. Сумму Еота и по-
потенциальной энергии взаимодействия частиц иногда называют внутренней
энергией системы.
> Изменение механической энергии. Изменение кинетической
энергии равно работе всех сил, приложенных к точкам системы (урав-
(уравнение A3)). Изменение потенциальной энергии равно работе всех кон-
консервативных сил (внутренних и внешних, включая работу потенциаль-
потенциальных полей), взятой с обратным знаком. Значит, изменение механиче-
механической энергии равно работе всех неконсервативных сил, как внешних,
так и внутренних:
ДЕмех — ^неконс- B0)
> Закон сохранения механической энергии: механическая энер-
энергия замкнутой консервативной системы остается постоянной. Это
утверждение является частным проявлением общего фундаментально-
фундаментального принципа сохранения энергии: полная энергия замкнутой системы
сохраняется. Полная энергия, кроме механической, включает в себя
также различные виды внутренней энергии: тепловую, химическую,
ядерную. Общий принцип сохранения энергии выходит далеко за пре-
пределы ньютоновской механики, в рамках которой мы получили закон
сохранения механической энергии. Этот принцип тесно связан с фун-
фундаментальным условием однородности времени (равноправием всех
моментов времени), он является основанием всего здания современной
физики.

1.5] Закон сохранения энергии 23
Условие консервативности эквивалентно требованию независимого
сохранения двух слагаемых полной энергии: механической и внутрен-
внутренней. Если, например, внутри системы действуют силы трения, работа
которых отрицательна, то механическая энергия уменьшается (уравне-
(уравнение B0)), переходя во внутреннюю (в этом случае говорят, что в системе
выделяется тепло). Механическая энергия может также изменяться
в том случае, если в системе присутствует какой-нибудь механизм,
способный производить работу за счет внутренней энергии (топлива):
двигатель внутреннего сгорания, человек.
Пример 6. Упругий удар. При центральном ударе упругих шаров
сохраняется и импульс системы, и ее механическая энергия:
+ rri2V2x = miuix +
2 2 2 2
Вместо второго уравнения удобно использовать условие, что относитель-
относительная скорость шаров не меняется по величине, но изменяет свой знак:
vix — ^2ж = и^х — и\х. Это уравнение можно вывести из первых двух, но оно
становится очевидным при переходе в инерциальную систему центра масс
(относительная скорость при таком переходе не меняется). В этой системе
отсчета полный импульс системы равен нулю, и после удара скорости шаров
просто меняются на противоположные (оба закона сохранения при этом
выполняются). Решая два линейных уравнения, находим конечные скорости
шаров:
(mi —
Ul =
Ulx , U2x •
mi + ТП2 m\ + ТП2
При упругом ударе о движущуюся стенку (rri2 ^> mi) получим
U2x ~ ^2ж, Ulx ~ —Vlx + 2г?2ж-
Пример 7. Неупругий удар. После абсолютно неупругого удара шары
движутся поступательно с одинаковой скоростью, т. е. как одно составное
тело (вращения не возникнет, если в системе центра масс удар центральный).
Скорости сравниваются в результате действия неконсервативных сил, т. е.
при неупругом ударе обязательно выделяется тепло. Чтобы убедиться в этом,
найдем с помощью закона сохранения импульса конечную скорость шаров:
mivi + m2V2 = (mi + 7712I1, после чего вычислим уменьшение механической
энергии:
V Ш2^2 (Ш1 + f^2)u2 mim2 (vi — V2J
2 2 2 ~~ mi + m2 2
Еще проще получить этот ответ в системе координат, связанной с центром
масс, где шары после удара покоятся.
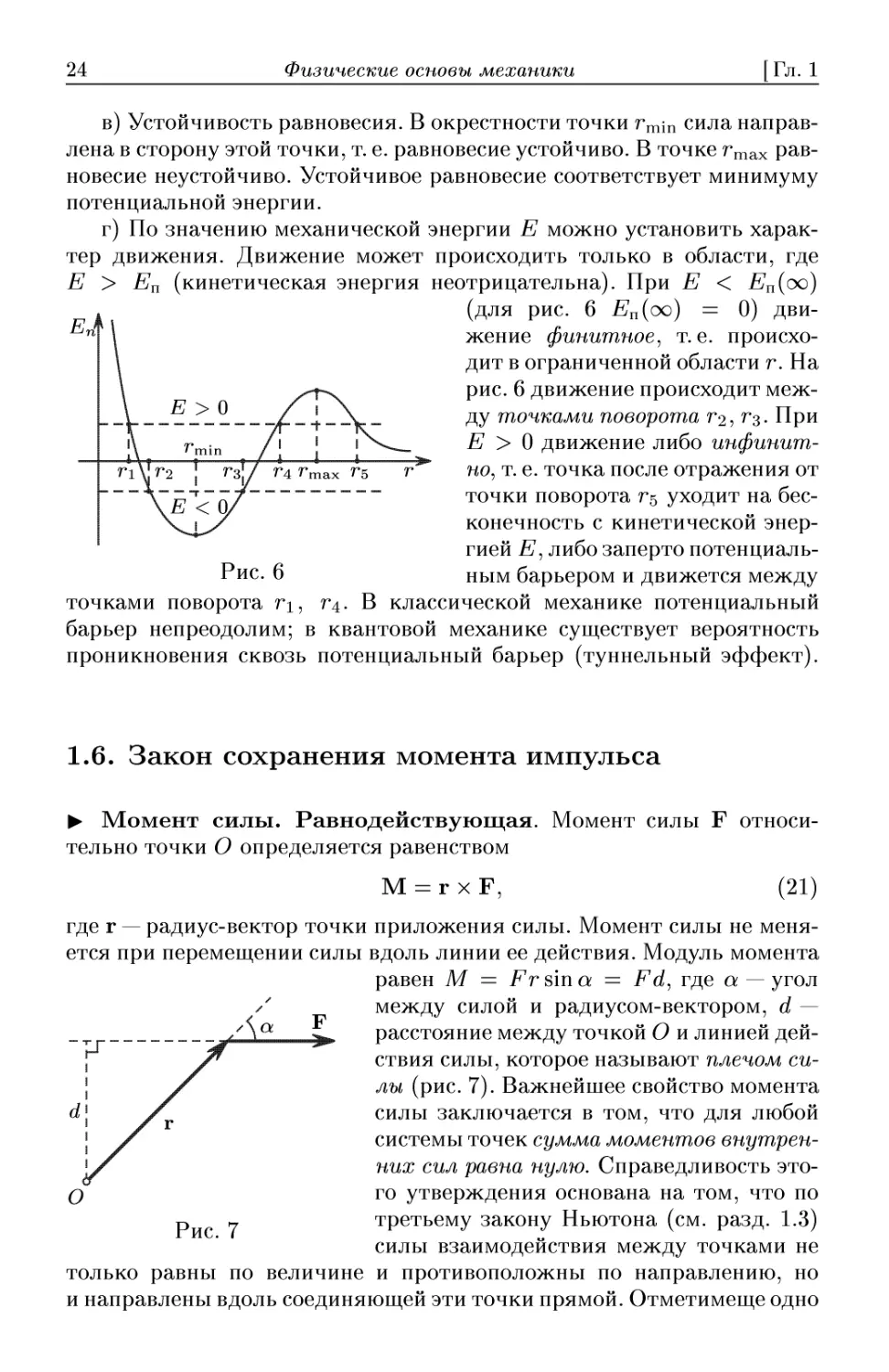
> Потенциальные кривые. Устойчивость. Если известна потен-
потенциальная энергия одномерного движения в потенциальном поле Еи(г)
(рис. 6), то, опираясь на соотношение A6) между силой и энергией,
можно выяснить:
а) Направление силы (F > 0 при 0 < г < гт-ш и при г > rmax).
б) Точки равновесия (F = 0 при г = гт-ш и г = rmax).

24
Физические основы механики
[Гл. 1
в) Устойчивость равновесия. В окрестности точки гт-ш сила направ-
направлена в сторону этой точки, т. е. равновесие устойчиво. В точке гтах рав-
равновесие неустойчиво. Устойчивое равновесие соответствует минимуму
потенциальной энергии.
г) По значению механической энергии Е можно установить харак-
характер движения. Движение может происходить только в области, где
Е > Еп (кинетическая энергия неотрицательна). При Е < Еп(оо)
(для рис. 6 Еп(оо) = 0) дви-
движение финитное, т.е. происхо-
происходит в ограниченной области г. На
рис. 6 движение происходит меж-
между точками поворота Г2, гз- При
Е > 0 движение либо инфинит-
но, т. е. точка после отражения от
точки поворота г§ уходит на бес-
бесконечность с кинетической энер-
энергией Е, либо заперто потенциаль-
Рис. 6 ным барьером и движется между
точками поворота ri, r4- В классической механике потенциальный
барьер непреодолим; в квантовой механике существует вероятность
проникновения сквозь потенциальный барьер (туннельный эффект).
1.6. Закон сохранения момента импульса
> Момент силы. Равнодействующая. Момент силы F относи-
относительно точки О определяется равенством
M = rxF, B1)
где г — радиус-вектор точки приложения силы. Момент силы не меня-
меняется при перемещении силы вдоль линии ее действия. Модуль момента
равен М = Fr sin a = Fd, где а — угол
между силой и радиусом-вектором, d —
расстояние между точкой О и линией дей-
действия силы, которое называют плечом си-
силы (рис. 7). Важнейшее свойство момента
силы заключается в том, что для любой
системы точек сумма моментов внутрен-
внутренних сил равна нулю. Справедливость это-
этого утверждения основана на том, что по
р rj третьему закону Ньютона (см. разд. 1.3)
силы взаимодействия между точками не
только равны по величине и противоположны по направлению, но
и направлены вдоль соединяющей эти точки прямой. Отметимеще одно

1.6] Закон сохранения момента импульса 25
свойство момента сил: если сумма сил равна нулю, то они создают оди-
одинаковый суммарный момент относительно любой точки пространства.
Равнодействующей системы сил называют силу, равную их вектор-
векторной сумме и приложенную таким образом, что ее момент относительно
любой точки пространства равен суммарному моменту этой системы
сил.
Пример 1. Вычислим суммарный момент сил тяжести, действующих на
точки системы:
М = J2TJ х
где т — масса системы, гц — радиус-вектор центра масс. Видно, что равнодей-
равнодействующая сил тяжести проходит через центр масс, т. е. центр масс является
такэюе центром тяэюести.
Моментом силы относительно оси z называют проекцию Mz на
эту ось момента сил относительно любой точки на этой оси. Если
разложить как г, так и F в B1) на две составляющих, параллельную
оси и перпендикулярную к ней, г = гц + r_L, F = Е[| + Fj_, то составля-
составляющие, параллельные оси, не дадут вклада в проекцию момента на ось.
Следовательно, Mz = (rj_ x Fj_)^. В плоскости, перпендикулярной оси,
получим такую же картинку, как на рис. 7, только вместо г и F надо
написать r_L и Fj_. Соответственно модуль момента относительно оси
также равен произведению силы на плечо, а выбор положительного
направления вдоль оси можно заменить более наглядным выбором
положительного направления вращения вокруг этой оси.
> Моментом импульса материальной точки относительно точки О
называют величину
L = г х р, B2)
где г — радиус-вектор материальной точки, проведенный из точки О,
р — ее импульс. При движении с постоянной скоростью момент им-
импульса не меняется. Модуль момента импульса равен произведению
импульса на плечо. Моментом импульса относительно оси z называ-
называется проекция Lz на эту ось момента импульса L относительно любой
точки на этой оси. Момент импульса относительно оси определяется
проекцией импульса точки на плоскость, перпендикулярную к оси:
Lz — (rj_ х p_l)^. Все эти свойства абсолютно аналогичны соответ-
соответствующим свойствам момента силы.
Производная по времени от момента импульса материальной точки
относительно точки О
dL dr dp „ , _.
равна моменту результирующей силы относительно точки О (член
v х р = 0 в силу параллельности векторов v и р.)

26
Физические основы механики
[Гл. 1
vdt
Рис. 8
> Движение в центральном поле. Так как на частицу в цен-
центральном поле действует сила, направленная в сто-
сторону центра поля, то момент этой силы относи-
относительно центра тождественно равен нулю. Следо-
Следовательно, вектор L момента импульса относитель-
относительно центра сохраняется. Из определения B2) сле-
следует, что движение происходит в одной плоскости,
перпендикулярной L, и что сохраняется величина
L = mvr sin а. Эта величина пропорциональна ско-
скорости «заметания» площади радиусом-вектором г:
ds/dt = -г{vdt) sin a/dt = L/2m (рис. 8), так что
утверждение о сохранении момента импульса при
движении в центральном поле оказывается эквивалентным знамени-
знаменитому второму закону Кеплера.
Пример 3. Прицельный параметр. Сохранение момента импульса
в центральном поле позволяет связать прицельный параметр b частицы, при-
приближающейся издалека к силовому
центру, (рис. 9) с минимальным рас-
расстоянием п, на которое она прибли-
приблизится к центру в процессе движе-
движения. {Прицельным параметром на-
называют расстояние от центра поля
до линии движения частицы в от-
отсутствие взаимодействия.) В тот мо-
момент, когда расстояние до центра
р q минимально, скорость частицы на-
направлена перпендикулярно радиусу-
вектору, и закон сохранения момента импульса имеет вид
mvob =
где vo — начальная скорость частицы, vi — ее скорость в момент максималь-
максимального приближения к центру. Отсюда можно выразить v\ и подставить в закон
сохранения энергии -mv2 = -mv2 + En{ri).
А А
Пример 3. Угол рассеяния. Большое значение для астрофизики
и атомной физики имеет задача о рассеянии частицы на кулоновском (или
гравитационном) центре. Рассмотрим частицу массой т, налетающую на
силовой (отталкивательный) центр Fr = Л /г2 с начальной кинетической
энергией Ек = mv2/2 и прицельным параметром 6, и найдем угол рассея-
рассеяния в.
Решение. Из соображений симметрии ясно, что изменение импульса за
все время пролета направлено вдоль оси z (см. рис. 10 ) и равно
|Лр| = Apz = 2mv0 sin@/2).
За время dt изменение импульса (в проекции на ось z) равно
dpz = Fzdt = Fcos (pdt = —~ — cos ш = cos tpdtp,
r Vip/r L
где v^p = r{d(p/dt) — азимутальная (перпендикулярная к радиусу-вектору)

1.6]
Закон сохранения момента импульса
27
Рис. 10
компонента скорости (см. рис. 11), через которую выражается момент им-
импульса частицы: L = mv^r. Интегрируя по ср от — (тг — 9)/2 до (тг — 9)/2,
получим
Приравнивая два выражения для Apz и учитывая, что L = mvob, получаем
Эта формула будет нами использована при обсуждении опытов Резерфорда.
> Эффективная потенциальная энергия. Применение законов
сохранения энергии и момента импульса позволяет установить, как за-
зависит от времени расстояние до цен-
центра г, точнее, свести эту задачу к од- г^/^\
номерному движению. Для этого на-
надо разложить скорость частицы на
две компоненты (рис. 11): радиальную
vr = dr/dt и перпендикулярную к ней
азимутальную v^. Момент импульса
выражается через азимутальную ско-
скорость: L = mrVp. Следовательно, ме-
механическую энергию точки можно пред-
представить в виде:
/ 2 . 2 \
Рис. 11
Видно, что зависимость r(t) такая же, как при одномерном движении
с эффективной потенциальной энергией, определяемой равенством
B4)

28
Физические основы механики
[Гл. 1
Вид эффективной потенциальной
кривой определяется значением L,
которое можно вычислить из на-
начальных условий.
На рис. 12 качественно изоб-
изображена зависимость эффективной
потенциальной энергии Е^ от рас-
расстояния г для разных значений L
(Lo = 0, Li < L2 < L3) в слу-
случае Еп = —b/r. Видно, что при
любом L условие финитности дви-
движения остается одним и тем же:
Е < 0.
Рис. 12
> Момент импульса системы
материальных точек. Моментом импульса системы относительно
точки О называется сумма моментов импульса материальных точек,
составляющих эту систему. Момент импульса системы равен
L = Гц х р + LOTH, B5)
где LOTH — момент импульса в системе центра масс. Одно из следствий
этого равенства: если импульс системы равен нулю, то L не зависит
от выбора точки О. Суммируя уравнение B3) по всем точкам системы
и учитывая, что суммарный момент внутренних сил равен нулю, полу-
получим
^ = Ме, B6)
т. е. производная по времени от момента импульса системы равна
суммарному моменту внешних сил.
> Закон сохранения момента импульса. Из уравнения B6) сле-
следует, что момент импульса замкнутой системы сохраняется. Закон
сохранения момента импульса является фундаментальным законом,
отражающим изотропность пространства, т. е. равноправие всех его
направлений. Как и в случае законов сохранения импульса и энергии,
действие закона сохранения момента импульса выходит за пределы
ньютоновской механики, в рамках которой он был выведен.
Момент импульса незамкнутой системы сохраняется в следующих
случаях:
1. Если суммарный момент внешних сил Ме равен нулю. (Пример:
система взаимодействующих частиц в центральном внешнем поле.)
2. Если момент импульса внешних сил относительно некоторой оси
равен нулю, то момент импульса относительно этой оси сохраняется.
Пример 4. Если грузик на конце невесомой нити движется по горизон-
горизонтальной окружности, то момент импульса относительно любой точки на оси
вращения (кроме центра окружности) не сохраняется, а момент импульса

1.7] Задача двух тел. Приведенная масса 29
относительно оси вращения сохраняется, так как моменты сил тяжести и на-
натяжения нити относительно этой оси равны нулю.
3. Если внешние силы ограничены, то изменением момента импуль-
импульса Z\L = MeZ\? за время удара At можно пренебречь.
1.7. Задача двух тел. Приведенная масса
> Приведенная масса. Рассмотрим замкнутую систему двух взаи-
взаимодействующих между собой частиц. Решить задачу об их движении
(задачу двух тел) — значит определить положение точек во все мо-
моменты времени исходя из заданных начальных условий. Положение
точек выражается через положение центра масс гц(?) (см. (8)) и их
относительное расположение Г12 = i*i — Г2:
77121*12 ГП1Г12
Г=г + г2=гц-
Uli + 7712 mi + 7712
Движение центра масс является равномерным, а его начальные поло-
положение и скорость определяются из начальных условий (см. уравнения
(8), (9)). Получаем, что решение задачи двух тел сводится к определе-
определению 1*12.
Из условия однородности и изотропности пространства и одно-
однородности времени следует, что частицы должны взаимодействовать
центральными силами, т.е. Fi2 = — F21 = F, где F параллельна i*i2,
а ее модуль F зависит только от |r*i21 - Запишем уравнения движения
каждой точки:
F = TTli о~, — F = 7712 о~¦•
dt dt
Разделим первое уравнение на mi, второе на Ш2, а затем вычтем второе
уравнение из первого. В результате получим:
, F = ту— или F = а ту—,
mi m2) dt dt
где приведенная масса \i определяется равенством
- = — + —. B7)
fi mi UI2
Видно, что поведение вектора Г]_2 определяется решением задачи о дви-
движении частицы массой /i в центральном поле.
Отметим еще некоторые полезные свойства приведенной массы. Импуль-
Импульсы частиц pi, р2 в системе центра масс (СЦМ) равны по модулю (полный
импульс равен нулю, р2 = — pi, |pi| = |рг| = р) и выражаются через их
относительную скорость (не зависящую от системы отсчета):
'_FM_ _ Р2_М _ |Р
.mi m2 t

30 Физические основы механики [ Гл. 1
Кинетическая энергия системы в СЦМ также выражается через их относи-
относительную скорость
~2 ~2 ~2 2
Е = — + = = ^отн
к 2
2т2 2а 2
Эта формула уже возникала раньше — при разборе неупругого удара (раздел
1.5, пример 5).
1.8. Поле тяготения
> Закон всемирного тяготения. Две точечные массы mi, Ш2,
находящиеся на расстоянии г друг от друга, притягиваются с силой
тяготения (гравитационной силой), равной
B8)
7
Г
где 7 ~ 6,67 • 10~n H • м2/кг2 — гравитационная постоянная. Сила
тяготения — центральная сила, т.е. она действует вдоль линии, соеди-
соединяющей частицы.
Силу, действующую на материальную точку массой т в централь-
центральном поле тяготения (гравитационном поле), создаваемым неподвижной
точечной массой М, можно записать в виде (см. разд. 1.3):
F =-7—о-- или FJr) = -7—о". B9)
г г г
Тем самым роль «заряда» для поля тяготения играет инертная мас-
масса т. Иногда это свойство формулируют как равенство гравитацион-
гравитационной и инертной масс. Потенциальную энергию точки в центральном
поле тяготения можно найти, используя соотношение между силой
и потенциальной энергией (формула A8)): —jmM/r2 = —dEn/dr, т.е.
Еи = —jmM/r + const. Константу обычно полагают равной нулю, т. е.
принимают за нуль потенциальную энергию на бесконечности:
Еп = -7^. C0)
> Принцип суперпозиции. Если поле тяготения создается несколь-
несколькими точечными массами Mi, ..., Мдг, то сила, действующая на мате-
материальную точку массой т, и ее потенциальная энергия вычисляются
по формулам:
F-TF - Ут
где г — радиус-вектор точки массой т, г3¦, — радиус-вектор точки мас-
массой Mj. Если источник поля представляет собой непрерывно распреде-
распределенную массу, то суммирование в C1) надо заменить интегрированием.

1.8]
Поле тяготения
31
> Напряженность и потенциал поля тяготения. Из уравне-
уравнений C1) видно, что как сила, действующая на материальную точку
массой т в поле тяготения, так и ее потенциальная энергия пропорцио-
пропорциональны т. Таким образом, удельные значения силы и энергии (отноше-
(отношения F/т и Еп/т) не зависят от величины т, т. е. представляют собой
характеристики поля. Их называют, соответственно, напряженностью
и потенциалом поля тяготения:
= — = *
т' т
Напряженность поля имеет простой физический смысл: она представ-
представляет собой ускорение свободного падения любой точечной массы, по-
помещенной в данную точку поля. Напряженность и потенциал поля
тяготения, создаваемого точечной массой М, имеют вид:
Mr
Ч> = -7"
М
C2)
Напряженность и потенциал поля, создаваемого несколькими массами,
вычисляются с помощью принципа суперпозиции. Запись уравнения
аналогична C1), для разнообразия запишем ответ для случая распре-
распределенной массы:
= - 7
Р(г')
(г-г'J |г-г
-dV,
C3)
Пример 1. Покажите, что напряженность поля тяготения внутри тон-
тонкого сферического слоя равна нулю.
Решение. Для доказательства рассмот-
рассмотрим вклад в напряженность поля в точке А
небольших участков В и С сферы, отсекае-
отсекаемых от нее тонким конусом с вершиной в точ-
точке А (рис. 13). Отношение площадей этих
участков, а значит, и отношение их масс,
равно отношению квадратов расстояний от
этих участков до точки А. Следовательно, на-
напряженности, создаваемые этими участками
в точке А, равны по величине.
Напряженность поля, создаваемого тон-
тонкой сферой массой М вне ее, оказывается
равной напряженности, создаваемой точечной
массой М, помещенной в центр сферы. Доказательство этого результата
требует громоздкого интегрирования (первым его проделал Ньютон). В гл. 3
Рис. 13

32 Физические основы механики [ Гл. 1
это утверждение будет доказано с помощью теоремы Гаусса. Такой же ответ
годится для любой сферически распределенной массы, в частности, для
любой сферической планеты.
Пример 2. Пусть масса М распределена по отрезку длиной /. Вычислить
напряженность и потенциал на продолжении отрезка, на расстоянии х от его
центра.
Решение. Масса dm, заключенная на отрезке длиной dy, равна М dy/l.
Интегрируя, получим
Г Mdy М
g(x) = -7
x+l/2
Mdy M . x + l/2
= ^ln
x-l/2
Видно, что симметричное, но несферическое тело нельзя заменить точечной
массой, помещенной в ее центр. Этот пример является также иллюстрацией
того, что напряженность и потенциал связаны соотношением gx = —дср/дх,
аналогичным соотношению A6).
> Движение в центральном поле тяготения. Законы Кепле-
Кеплера. Движение в центральном поле тяготения подчиняется общим зако-
законам движения в центральном поле. Однако оно обладает некоторыми
особенностями, отраженными в первом и третьем законах Кеплера,
сформулированных им для планет Солнечной системы.
Первый закон Кеплера утверждает, что финитное движение (Е < 0)
материальной точки в центральном поле тяготения происходит по за-
замкнутой траектории —эллипсу, в одном из фокусов которого находится
центр силы притяжения (Солнце).
Второй закон Кеплера фиксирует постоянство секторной скорости,
т.е. скорости «заметания» площади радиусом-вектором движущейся
точки. Он относится к любому центральному полю и является прямым
следствием закона сохранения момента импульса (см. пример 2 из
разд. 1.6).
Третий закон Кеплера утверждает, что квадраты периодов дви-
движения относятся как кубы больших полуосей эллиптических орбит:
ТЦТ1 = а\1а\.
Дополним первый закон Кеплера утверждением, что инфинитное
движение в центральном поле тяготения происходит либо по параболе
[Е = 0), либо по гиперболе (Е > 0). В качестве дополнения к третьему
закону Кеплера приведем связь между удельной энергией движения
и большой полуосью: \E\/m = jM/Ba). Видно, что период движения
однозначно определяется удельной энергией движущегося тела.

1.9] Неинерциальные системы отсчета 33
> Космические скорости. Первой космической скоростью называ-
называют скорость движения по круговой орбите вблизи поверхности плане-
планеты. Она определяется из уравнения движения спутника mg = mvf /R
и равна v\ = л/gR = -\/^М/ R, где М — масса планеты. (Для Земли
v\ « 7,9 км/с.) Вторая космическая скорость — минимальная ско-
скорость, которую надо сообщить телу на поверхности планеты, чтобы
оно преодолело силу тяготения и ушло на бесконечность. Как видно
из разд. 1.7, условием инфинитности движения является неравенство
Е ^ 0, т. е. вторая космическая скорость находится из уравнения
mv^/2 - jmM/R = 0 и равна v\\ = ^2jM/R = ^2gR. (Для Земли
v\\ ~ 11,2 км/с.)
1.9. Неинерциальные системы отсчета
> Определение сил инерции. Во многих случаях удобно решать
задачу динамики непосредственно в неинерциальной системе отсчета
(НСО), а не пересчитывать ответ, полученный сначала в инерциальной
системе отсчета. Для этого вводят силы инерции, определенные следу-
следующим образом. Во втором законе Ньютона выделяют из ускорения точ-
точки а в виде отдельного слагаемого ее ускорение относительно НСО аотн,
а все остальное переносят в другую часть равенства и называют силой
инерции:
= ша =^ ^2 ^ = ш(а°тн + а*) =>
=> ^2 Fi + (~ша*) = ^аотн => ^2,Щ +?ИН= таотн.
Приходим к следующему определению сил инерции:
FHH = -ша*, C4)
где а* определяется кинематическим соотношением
а ^ З-отн i ^
и зависит от параметров НСО и положения и скорости частицы в НСО.
Разберем конкретные случаи.
> Поступательно движущиеся НСО. В этом случае а* равняется
ускорению системы отсчета (см. формулу A)), т.е. для силы инерции
получим выражение
Fhh = -ma.K.
Видно, что сила инерции полностью эквивалентна силе тяжести.
При решении задач их удобно объединять вместе, т. е. введение
силы инерции оказывается эквивалентным замене напряженности
поля тяготения (т.е. ускорения свободного падения, см. разд. 1.8):
g => g* =g + a* =g-aK.
2 А. И. Черноуцан

34 Физические основы механики [ Гл. 1
Пример 1. Сосуд с жидкостью движется с постоянным горизонтальным
ускорением а. Найдите угол /3 между поверхностью жидкости и горизонта-
горизонталью.
Решение. Перейдем в систему отсчета, связанную с сосудом, где непо-
неподвижная поверхность жидкости должна быть «горизонтальна», т. е. перпен-
перпендикулярна вектору g* = g + а* = g — а. Отсюда следует, что tgj3 = a/ g.
Принцип эквивалентности сил инерции и сил тяготения был поло-
положен Эйнштейном в основу общей теории относительности, которая
является релятивистской теорией гравитации и объясняет возникно-
возникновение гравитационных сил искривлением пространственно-временного
континуума в присутствии внешних масс.
> Равномерно вращающаяся система отсчета. В этом случае
кинематическое соотношение для ускорения C5) имеет вид: а = аотн +
+ю х [ю х г] + 2ю х vOTH (см. разд. 1.2). Второй член связан с поворотом
вектора переносной скорости ю х г вместе с системой отсчета, направ-
направлен в сторону оси вращения и равен и2R (R — расстояние до оси),
т. е. представляет собой нормальное (центростремительное) ускорение
данной точки системы отсчета. Третий член (ускорение Кориолиса)
связан, во-первых, с поворотом vOTH вместе с системой отсчета и, во-
вторых, с изменением переносной скорости ю х г за счет перемещения
частицы из одной точки вращающейся НСО в другую. Соответственно
сила инерции C4) представляет собой сумму двух членов, первый из
которых называют центробежной силой, а второй — силой Кориолиса:
Fhh = F46 + FKOp = ma;2R + 2mvOTH x ю. C6)
Центробежная сила инерции направлена от оси вращения (R, направ-
направлен от оси вращения перпендикулярно к ней). Так как она не зависит
от скорости частицы, то ее действие неотличимо от (неоднородного)
поля тяготения. Например, на поверхности Земли измеряемая сила тя-
тяжести представляет собой сумму силы тяготения и центробежной силы
инерции. Сила Кориолиса направлена перпендикулярно скорости. В се-
северном полушарии для движения вдоль поверхности горизонтальная
составляющая силы Кориолиса направлена вправо, что проявляется
в образовании циклонов, размывании правого берега рек и др.
Пример 2. Найдите отклоняющее действие силы Кориолиса на тело,
свободно падающее с высоты h на экваторе Земли.
Решение. Так как отклонение маленькое, то в первом приближении
можно подставлять в силу Кориолиса C6) скорость «невозмущенного» па-
падения v = g?. Так как вектор со перпендикулярен v, то сила Кориоли-
Кориолиса направлена в сторону востока, равна 2mvuj и сообщает горизонтальное
ускорение аВОст = 2oogt. Интегрируя, находим горизонтальную скорость
^вост = gut2 и горизонтальное перемещение sBOct = -goot3. Подставив сюда
о
время падения t = y/2h/g, найдем конечное отклонение. Например, для
h = 300 м отклонение составляет и 10 см.

1.10] Динамика твердого тела 35
1.10. Динамика твердого тела
> Вращение вокруг неподвижной оси. Момент импульса твер-
твердого тела относительно неподвижной оси вращения z (см. разд. 1.6)
равен
\LZ\ = ^RjrrijVj =oj^2<mjR2j = Izoj, C7)
где Rj — расстояние от точки rrij до оси вращения, и мы использовали
соотношение Vj = ujRj. Направление проекции совпадает с направле-
направлением ю, т. е. определяется по правилу буравчика. Величина
R)
) = [ R2 dm C8)
называется моментом инерции твердого тела относительно оси z. Про-
Продифференцировав C7) по времени и учтя, что dLz/dt = Mz, где Mz —
момент внешних сил относительно оси вращения (уравнение B6)),
получим
Mz = Ize, C9)
где е = dcxj/dt — угловое ускорение. Это уравнение называют основным
уравнением динамики вращательного движения твердого тела вокруг
неподвижной оси. Вычислим еще кинетическую энергию вращающего-
вращающегося твердого тела:
^f = l^T.mjR] = \h^ D0)
и работу внешней силы при повороте тела:
A=\dr-F= Umdt х г) • F = Umdt) • (г х F) = f(M-dq>),
где dq> = codt.
Пример 1. К концу нити, намотанной на блок с моментом инерции /
и радиусом Я, привязали тело массой т и отпустили. Найдите ускорение
тела.
Решение. Запишем второй закон Ньютона для тела: mg — Т = та
и уравнение C9) для блока: ТR = 1е. Учтем также кинематическое соот-
соотношение а = eR (нить по блоку не проскальзывает). Решая эти уравнения,
получим а = g/(l + I/mR2).
> Свойства момента инерции. Момент инерции C8) — скалярная
аддитивная величина, характеризующая распределение массы тела по
отношению к оси. Из уравнений C9), D0) видно, что момент инерции

36 Физические основы механики [ Гл. 1
является мерой инертности твердого тела по отношению к вращатель-
вращательному движению, т. е. играет ту же роль, что масса для поступательного
движения.
Пример 2. Вычислите момент инерции однородного диска массой т
и радиусом R относительно оси симметрии.
Решение. Разбив диск на тонкие круговые полоски и интегрируя, полу-
получим
= г2 dm = г2 ( 2 )
2
о
Такой же ответ верен и для сплошного однородного цилиндра.
Теорема Штейнера связывает момент инерции / относительно про-
произвольной оси с моментом инерции /о относительно параллельной ей
оси, проходящей через центр масс твердого тела:
/ = /0 + та2, D1)
где т — масса тела, а — расстояние между осями. Например, момент
инерции диска относительно оси, перпендикулярной плоскости диска
о
и проходящей через его край, равен -mR2. Минимальный момент инер-
инерции среди всех параллельных осей получается для оси, проходящей
через центр масс.
Теорема о взаимно перпендикулярных осях: момент инерции плос-
плоского тела относительно произвольной оси z, перпендикулярной его
плоскости, равен сумме моментов инерции относительно двух взаимно
перпендикулярных осей х и у, лежащих в плоскости тела и пересекаю-
пересекающихся с осью z:
h = 4 + Iy
Например, момент инерции тонкого диска относительно оси симмет-
симметрии, лежащей в его плоскости, равен Ix = Iy = -Iz = -mR2.
Приведем моменты инерции некоторых тел различной формы.
1) Тонкий обруч (относительно оси симметрии): / = mR2. Такой
же момент инерции имеет тонкостенный цилиндр (без торцов).
2) Тонкий стержень длиной / (относительно перпендикулярной
к стержню оси, проходящей через его середину): / = —ml2. Такой
же момент инерции имеет плоский прямоугольник относительно оси,
проходящей через середины противоположных сторон длиной /. Отно-
Относительно края стержня момент инерции равен / = -ml2.
о
3) Плоский прямоугольник относительно оси, перпендикулярной
его плоскости и проходящей через его центр: / = —т(а2 + Ь2). Такой
же момент инерции имеет прямоугольный параллелепипед относитель-
относительно оси, проходящей через середины противоположных граней.

1.10]
Динамика твердого тела
37
4) Тонкая сфера относительно оси симметрии: / = -mR2.
о
5) Однородный шар относительно оси симметрии: / = -mR2.
о
6) Цилиндрический слой с внутренним радиусом R\ и внешним R2'.
> Плоское движение твердого тела. Плоское движение есть су-
суперпозиция поступательного движения центра масс и вращательного
движения в системе центра масс (см. разд. 1.2). Движение центра
масс описывается вторым законом Ньютона и определяется резуль-
результирующей внешней силой (уравнение A1)). Вращательное движение
в системе центра масс подчиняется уравнению C9), в котором надо
учитывать только реальные внешние силы, так как момент сил инерции
относительно центра масс равен нулю (аналогично моменту сил тяже-
тяжести, пример 1 из разд. 1.6). Кинетическая энергия плоского движения
равна Ек = -mv2. + -/о^2 (см. уравнение A4)). Момент импульса от-
относительно неподвижной оси, перпендикулярной плоскости движения,
вычисляется по формуле (см. уравнение B5)): Lz = ±mvnd ± Iquj, где
d — плечо скорости центра масс относительно оси, а знаки определя-
определяются выбором положительного направления вращения.
Пример 3. Найдите ускорение круглого тела, которое скатывается без
проскальзывания по наклонной
плоскости (рис. 14).
Решение. Уравнения движения
имеют вид: mg sin a — FTp = та,
FTpR = Is. Условие отсутствия
проскальзывания (г; = ujR) приводит
к уравнению а = eR (см. пример 1 из
разд. 1.2). Решая уравнения, находим
ускорение: а = gs'ma/(l + I/mR2).
Так как сила трения покоя работы не
совершает, то механическая энергия
сохраняется.
Пример 4. При упругом ударе
шарика массой т о край неподвижного стержня длиной / и массой М,
расположенного перпендикулярно его скорости, конечные скорости
шарика и, центра стержня V и угловую скорость его вращения ш определяют
из трех уравнений:
1) закона сохранения импульса: mv = ти + MV,
2) закона сохранения энергии: mv2/2 = ти2/2 + MV2/2 + (М/2/12)о;2/2,
3) закона сохранения момента импульса (например, относительно точки
удара): 0 = MV(l/2) - (M12/12)uj.
> Движение с неподвижной точкой. Угловая скорость вращения,
направленная вдоль оси вращения, меняет свое направление как в про-
пространстве, так и по отношению к самому твердому телу. Уравнение
Рис. 14

38
Физические основы механики
[Гл. 1
движения
которое называют основным уравнением движения твердого тела
с неподвижной точкой, позволяет узнать, как изменяется момент
импульса L. Так как вектор L в общем случае не параллелен вектору ю,
то для замыкания уравнений движения надо научиться связывать эти
величины друг с другом.
Пример 5. При вращении наклонной гантельки вокруг вертикальной оси
(рис. 15) момент импульса L = ri x pi +Г2 х р2 направлен перпендикулярно
гантельке, он направлен под углом к оси вращения и сам вращается с угловой
скоростью со.
Проблему связи между L и ю решает теорема о главных осях
инерции, утверждающая, что для любой точки тела существуют три
взаимно перпендикулярные оси, при вращении относительно кото-
которых вектор L параллелен оси вращения:
~Li = Iidii (i = 1,2,3). Моменты инерции
относительно этих осей называют главными
моментами инерции. Если вращение проис-
происходит вокруг произвольной оси вращения,
то, разложив угловую скорость по главным
осям ю = Ю1+Ю2+Ю35 мы сможем вычислить
момент импульса: х
ГП2
-F
L =
/2Ю2
D2)
(Аналогично, разложив вектор L, мы най-
рис 15 Дем вектор ю.) Если главные оси проведены
через центр масс (центр инерции) тела, то
их называют свободными осями. При вращении вокруг любой из сво-
свободных осей сохраняются как импульс, так и момент импульса тела, т. е.
для поддержания вращения к телу не надо прикладывать ни внешнюю
силу, ни внешний момент сил. (В примере 5 результирующая сила
равна нулю, но в точках крепления оси возникает пара сил, момент
которых обеспечивает изменение L со временем.) При свободном вра-
вращении устойчивым оказывается только вращение относительно двух
свободных осей — с минимальным и максимальным главными момен-
моментами инерции.
Пример 6. В каком случае выбор свободных осей является однознач-
однозначным?
Решение. В том случае, когда все три главные моменты инерции раз-
различны. Если же два главных момента из трех равны (/i = /2), то любая ось,
лежащая в плоскости, проходящей через эти оси, также будет свободной:
L = /coi + 1@2 = /со. Если же равны все три главные моменты инерции (как,
например, у однородного куба), то свободной будет любая ось, проходящая
через центр масс.

1.10] Динамика твердого тела 39
Пример 7. Известны три главные моменты инерции. Выразите момент
инерции относительно оси, составляющей углы 715 72 и 7з с главными осями.
Решение. Выразим двумя способами кинетическую энергию вращения
с угловой скоростью из относительно указанной оси. С одной стороны, она
равна
/о,2
Е= 2
а с другой стороны —
_ Ьшш _ (Leo) _ 1\ш\
~~ 2 ~" 2 ~" 2
2 2 2 2 2 '
где Ьш = Ioj — проекция L на со. Поскольку ил/ш = cos7;, получаем
/ = /l COS2 71 + ^2 COS2 72 + /3 COS2 73.
Пример 8. Свободный симметричный волчок. Нутация земной
оси. Выясним, как меняется положение оси вращения относительно твердого
тела (в системе отсчета, связанной с этим телом). Ограничимся случаем
свободного симметричного волчка, т. е. свободно вращающегося твердого
тела, у которого 1\ = /2 = /j_, /3 = /ц ф /_ь (Таким волчком является,
в частности, Земля.) Для симметричного волчка вектор L = /цсоц + /_i_a>_i_
лежит в одной плоскости с осью симметрии 3 и с вектором со = соц + со±.
В инерциальной системе отсчета вектор L сохраняется, из чего следует, что
в системе отсчета, связанной с самим вращающимся телом, вектор L совер-
совершает в данный момент вращение с угловой скоростью со, т. е. подчиняется
уравнению:
dL
—- = со х L.
dt
Это уравнение называется уравнением Эйлера (обычно записывают систему
трех уравнений, получающихся при проектировании этого уравнения на оси
1,2,3 с учетом соотношения D2)). Сложность этого уравнения заключается
в том, что сам вектор со не постоянен, но связан с вектором L линейным соот-
соотношением D2). Для симметричного волчка сох L перпендикулярно плоскости
со, L, следовательно, dL\\/dt = I\\d(O\\/dt = 0 (oj\\ = const). Для со± получаем
уравнение:
t-L—JT = (ШН +ю^) х (^||®|| + J-L®-l) = (/_l - ^|)го|| х a>-L
или
- = П х ш,
где \l = соц. С7то уравнение показывает, что в системе отсчета,
связанной с волчком, ось вращения совершает круговое движение вокруг оси
симметрии 3 с угловой скоростью ft. В случае земного шара относительное
отличие между моментами инерции мало, и наблюдается медленное (с пери-
периодом в десятки суток) движение оси вращения Земли (нутация земной оси).
> Гироскопы. Гироскопом называют твердое тело, быстро враща-
вращающееся относительно своей оси симметрии. Задачу о движении оси
гироскопа можно решать в гироскопическом приближении: L = /со, оба

40 Физические основы механики [ Гл. 1
вектора направлены вдоль оси симметрии. Уравновешенный гироскоп
(закрепленный в центре масс) обладает свойством безынерционности:
его ось перестает двигаться, как
только исчезает внешнее воздей-
воздействие (М обращается в нуль). Это
позволяет использовать гироскоп
для сохранения ориентации в про-
пространстве. На тяжелый гироскоп
(рис. 16), у которого центр масс сме-
смещен на расстояние d от точки за-
закрепления, действует момент силы
тяжести, направленный перпендику-
перпендикулярно L. Так как dJj/dt _L L, то L
О Ўmg и ось гироскопа совершают регуляр-
Рис. 16 ное вращение вокруг вертикальной
оси (прецессия гироскопа). Конец вектора L вращается по горизонталь-
горизонтальной окружности радиусом L sin а с угловой скоростью
Р \dL/dt\ mgds'ma mgd
L sin a Iuj sin a Iuj
Угловая скорость прецессии не зависит от угла наклона оси а.
1.11. Специальная теория относительности
Специальная теория относительности Эйнштейна (СТО) расши-
расширяет границы классической ньютоновской физики, действующей в об-
области нерелятивистских скоростей, малых по сравнению со скоростью
света с, на любые, в том числе релятивистские, т. е. сравнимые с с,
скорости. Все результаты релятивистской теории при v/c —У 0 пере-
переходят в результаты классической нерелятивистской физики (принцип
соответствия).
> Постулаты СТО. Специальная теория относительности опирает-
опирается на два постулата:
Первый постулат (принцип относительности Эйнштейна): все
физические законы — как механические, так и электромагнитные —
имеют одинаковый вид во всех инерциальных системах отсчета (ИСО).
Иными словами, никакими опытами нельзя выделить какую-то одну
систему отсчета и назвать именно ее покоящейся. Этот постулат явля-
является расширением принципа относительности Галилея (см. разд. 1.3)
на электромагнитные процессы.
Второй постулат Эйнштейна: скорость света в вакууме одинакова
для всех ИСО и равна с « 3-Ю8 м/с. Этот постулат содержит сразу два
утверждения:
а) скорость света не зависит от скорости источника,

1.11] Специальная теория относительности 41
б) скорость света не зависит от того, в какой ИСО находится на-
наблюдатель с приборами, т. е. не зависит от скорости приемника.
Постоянство скорости света и независимость ее от движения источника
следуют из уравнений электромагнитного поля Максвелла. Казалось оче-
очевидным, что такое утверждение может быть верным только в одной систе-
системе отсчета. С точки зрения классических представлений о пространстве —
времени, любой другой наблюдатель, двигаясь со скоростью v, должен для
встречного луча получить скорость с + v, а для испущенного вперед луча —
скорость с — v. Такой результат означал бы, что уравнения Максвелла
выполняются только в одной ИСО, заполненной неподвижным «эфиром»,
относительно которого и распространяются световые волны. Однако попыт-
попытка обнаружить изменение скорости света, связанное с движением Земли
относительно эфира, дала отрицательный результат (опыт Майкельсона —
Морли). Эйнштейн предположил, что уравнения Максвелла, как и все законы
физики, имеют один и тот же вид во всех ИСО, т. е. что скорость света в любой
ИСО равна с (второй постулат). Это предположение привело к пересмотру
основных представлений о пространстве — времени.
> Преобразования Лоренца. Преобразования Лоренца связывают
между собой координаты и время события, измеренные в двух ИСО,
одна из которых (К') движется относительно другой (К) с постоянной
скоростью V. При таком же выборе осей координат и отсчета времени,
как в преобразованиях Галилея (формула G)), преобразования Лорен-
Лоренца имеют вид:
/ x-Vt , , ., t-(V/c2)x (ЛО,
х = =, у = у, z = z, t = . =. D3)
ГлТТо/ 9 ГлТТо/ 9 ^ '
yl — V2/ с2 V1 — V2/ с2
Часто удобно пользоваться преобразованиями для разности координат
и времен двух событий:
Ах' = j(Ax - VAt), At' = j[At- (V/c2)Ax].
D4)
Ay' = Ay, Az' = Az,
где для краткости введено обозначение
7= л L, ,. 7^1- D5)
Преобразования Лоренца переходят в преобразования Галилея при
|/ < с. Они выводятся из второго постулата СТО и из требования
линейности преобразований, выражающего условие однородности про-
пространства. Обратные преобразования из К' в К можно получить из
D3), D4) заменой V на -V:
Ах = j(Ax' + VAt'), At = j [At' + (V/c2)Ax'].
D6)

42 Физические основы механики [ Гл. 1
> Сокращение длины. Длина движущегося отрезка определяется
как расстояние между точками, где концы отрезка находились одно-
одновременно (т.е. At = 0). Рассмотрим твердое тело, которое движется
поступательно со скоростью v, и свяжем с ним систему отсчета К'. Из
уравнения D4) (в котором надо положить V = v, At = 0) получим, что
продольные размеры движущегося тела сокращаются:
/ = /о/7 = Wl-«2/c2, D7)
где /о — собственный продольный размер, т. е. измеренный в системе
отсчета К', в которой тело неподвижно. Поперечные размеры движу-
движущегося тела не изменяются.
Пример 1. Квадрат, движущийся со скоростью v = 0,8с вдоль одной из
своих сторон, превращается в прямоугольник с углом между диагоналями,
равным arcctg y/l — v2/c2 = arcctg 0,6 и 59°.
> Относительность хода времени. Из преобразований Лоренца
видно, что время протекает по-разному в разных ИСО. В частно-
частности, события, происходящие в системе К одновременно (At = 0), но
в разных точках пространства, в К' могут быть не одновременными:
At' = — jVAx/c2 может быть как положительным, так и отрицатель-
отрицательным (относительность одновременности). Часы, движущиеся вместе
с системой отсчета (т.е. неподвижные относительно К1', или Ах' = 0),
показывают собственное время этой ИСО. С точки зрения наблюда-
наблюдателя в системе К, эти часы отстают от его собственных (замедление
хода времени). Рассматривая два отсчета движущихся часов как два
события, из D6) получим:
At = jAr = . Лт D8)
у/1 - V2/c2 V У
где Ат = At' — собственное время движущихся часов (точнее, свя-
связанной с ними ИСО). Равноправие всех ИСО проявляется в том, что
с точки зрения наблюдателя К' часы, неподвижные относительно К,
будут отставать от его собственных. (Заметим, что для контроля за
движущимися часами неподвижный наблюдатель в разные моменты
времени использует разные часы.) Парадокс близнецов заключается
в том, что СТО предсказывает различие в возрасте двух близнецов,
один из которых оставался на Земле, а другой путешествовал в глу-
глубоком космосе (космонавт будет моложе); казалось бы, это нарушает
равноправие их систем отсчета. На самом деле, только земной близнец
все время находился в одной ИСО, космонавт же поменял ИСО для
возвращения на Землю (его же собственная система отсчета неинерци-
альна).
Пример 2. Среднее собственное время жизни нестабильного мюона
г = 2,2 • 10~6 с, т.е. ст ~ 660 м (с — скорость света). Благодаря эффек-
эффекту замедления времени, с точки зрения земного наблюдателя космический

1.11] Специальная теория относительности 43
мюон, летящий со скоростью v, близкой к скорости света G У?> 1), живет
в среднем jt, пролетает от места рождения в верхних слоях атмосферы
расстояние порядка с^т, что позволяет регистрировать его на поверхности
Земли.
> Сложение скоростей в СТО. Если частица движется со скоро-
скоростью v' относительно ИСО К1', то ее скорость относительно К можно
найти, выразив dx, dy, dz, dt из D6) и подставив в vx = dx/dt,
vy = dy/dt, vz = dz I dt:
_ vx + v _v_^/y^vw _»;yrvw D9)
x~ l + v'xV/c2J v~ l + v'xV/c2 ' z~ l + v'xV/c2 • ( '
При vx, V <C с происходит переход к нерелятивистскому закону сложе-
сложения скоростей (формула A)). Важное свойство формулы D9) состоит
в том, что если V и v' меньше с, то и v будет меньше с. Например,
если мы разгоним частицу до V = 0,9с, а затем, перейдя в ее систему
отсчета, снова разгоним ее до v' = 0,9с, то результирующая скорость
окажется не 1,8с, а A,8с)/1,81 < с. Видно, что превзойти скорость
света не удается. Скорость света является максимально возможной
скоростью передачи взаимодействий в природе.
> Интервал. Причинность. Преобразования Лоренца не сохра-
сохраняют ни величину интервала времени, ни длину пространственного
отрезка. Однако можно показать, что при преобразованиях Лоренца
сохраняется величина
s22 = (cAtJ - (АхJ - (AyJ - (AzJ = (cAtJ - (AvJ, E0)
где ^12 называется интервалом между событиями 1 и 2 (At = t<i — t±,
Ay = Г2 — i*i). Если s\2 > 0? то интервал между событиями называют
времениподобным, так как в этом случае существует ИСО, в которой
Ay = 0, т. е. события происходят в одном месте, но в разное время. Та-
Такие события могут быть причинно связанными. Если, наоборот, s\2 < 0,
то интервал между событиями называют пространственноподобным,
так как в этом случае существует ИСО, в которой At = 0, т.е. собы-
события происходят одновременно в разных точках пространства. Между
такими событиями не может существовать причинной связи. Условие
c\At\ < \Ay\ означает, что луч света, испущенный в момент более
раннего события (например, t\) из точки ri, не успевает достигнуть
точки Г2 к моменту времени t^- События, отделенные от события 1
времениподобным интервалом, представляют по отношению к нему
или абсолютное прошлое (^2 — t\ < 0), или абсолютное будущее
(^2 — t\ > 0); порядок следования этих событий одинаковый во всех
ИСО. Порядок следования событий, отделенных пространственнопо-
добным интервалом, может быть разным в разных ИСО.

44 Физические основы механики [ Гл. 1
> Лоренцевы 4-векторы. Четверка величин (Ах, Ау, AZJ AT) =
= (А, Ат), которые при переходе из системы К в систему К' преоб-
преобразуются так же, как (ж, у, z, ct), т.е. (см. D3)):
, ,_АХ- (У/с)Ат л,_л А,_А л ,_АТ- (У/с)Ах
/1 ^2/с2 Л ^7с2
л/ / лЛ 7
E1)
называется лоренцевым четырехмерным вектором (или, коротко, ло-
ренцевым 4-вектором). Величины Ах, Ау, Az называются простран-
пространственными компонентами 4-вектора, АТ — его временной компонен-
компонентой. Сумма двух 4-векторов и произведение 4-вектора на число —
тоже 4-векторы. При изменении ИСО сохраняется величина, анало-
аналогичная интервалу: А = А^. — (А) , а также скалярное произведение
(АТВТ — А • В). Физическое равенство, записанное в виде равенства
двух 4-векторов, остается верным во всех ИСО.
> Импульс и энергия в СТО. Компоненты скорости преобразуют-
преобразуются не так, как компоненты 4-вектора (сравните уравнения D9) и E1)),
потому что в выражении v = dr/dt преобразуются как числитель, так
и знаменатель. Следовательно, величина X^777/ivj5 соответствующая
классическому определению импульса, не может сохраняться во всех
ИСО. Релятивистский 4-вектор импульса определяют как
dr m dr diet) me
- P = m -
dr
где dr = dt yjl — v2/с2 — бесконечно малое изменение собственного
времени частицы (см. D8)), т.е. измеренное в ИСО, скорость которой
равна скорости частицы в данный момент (dr не зависит от того, из
какой ИСО мы наблюдаем за частицей.) Пространственные компонен-
компоненты 4-вектора образуют релятивистский импульс
р = -^= , E2)
Гл 9/ 9 v '
у/1 — v2/c2
а временная компонента рТ оказывается равной Е/с, где Е — реляти-
релятивистская энергия частицы:
E3)
поэтому 4-вектор (р, Е/с) называют ^-вектором энергии — импульса.
Отметим, что релятивистские энергия и импульс связаны простым
соотношением:
Р = ^- E4)

1.11] Специальная теория относительности 45
В соответствии с E1), энергия и импульс при переходе в другую ИСО
преобразуются по закону
E'= f~Vpx . E5)
/1 V2/2 V J
Рх \ PyPy, Pz Pz, E f
y/l - у2/с2 У У у/1 - V2/c2
Релятивистская энергия частицы не равна нулю при v = 0, т. е. она
состоит из энергии покоя тс2 и кинетической энергии:
Е= .тС\, =тс2 + Ек, E6)
причем релятивистская кинетическая энергия при v/c ^ 1 переходит
в классическую кинетическую энергию Ек = mv2/2. Так как величина
(Е/сJ — р2 сохраняется, ее можно вычислить в системе отсчета, где
частица в данный момент покоится:
^-р2 = т2с2 или Е2-р2с2=т2с4. E7)
С
Для частиц с массой, равной нулю (фотоны), связь между энергией
и импульсом принимает вид:
Е = рс E8)
(см. также E4)). Подставляя в E7) Е = тс2 + Ек, получим удобное
соотношение между импульсом и кинетической энергией:
р2с2 = ЕК(ЕК + 2тс2).
> Неупругий удар. Взаимосвязь энергии и массы. Запишем
закон сохранения релятивистской энергии для неупругого удара двух
тел массой т каждое, летевших навстречу друг другу с одинаковой
скоростью v:
2 2
тс тс , , о
+ = Мс2.
Видно, что масса М составной частицы больше суммы масс начальных
частиц. Увеличение внутренней энергии при неупругом ударе на ЛЕ
привело к увеличению массы на ЛЕ /с2. Этот пример иллюстрирует
общее соотношение Эйнштейна между релятивистской энергией поко-
покоящегося тела и его массой:
Е = тс2. E9)
Релятивистская энергия включает в себя все виды внутренней энергии.
Пример 3. Пусть энергия покоящегося тела равна Е. Найдите импульс
этого тела в системе отсчета, движущейся со скоростью —v.

46 Физические основы механики [ Гл. 1
Решение. В соответствии с формулами релятивистского преобразова-
преобразования E5) импульс равен р' = (Ef/c2)v = ^. Видно, что получилась
22
формула для релятивистского импульса с массой т = Е/с2.
Пример 4. Ускорители на встречных пучках. Предположим, что
для достижения порога какой-нибудь реакции частицы во встречных пучках
надо разогнать в ускорителе до кинетической энергии атс . До какой кине-
кинетической энергии потребовалось бы разогнать одну частицу, если бы другая
частица находилась на неподвижной мишени?
Решение. В нерелятивистском случае энергия в СО центра масс равна
половине энергии налетающей частицы. Именно эта энергия может пойти
на реакцию, а другая половина недоступна — она остается в виде кинети-
кинетической энергии системы. В релятивистском (а особенно ультрарелятивист-
ультрарелятивистском) пределе ситуация кардинально меняется. Вычислим энергию одной
из частиц в СО, где другая частица покоится. Запишем условие инвари-
инвариантности Е2 — р2с2 для энерги и импульса системы. В СО центра масс
Е = 2атс2 -\-2mc2, р = 0; в СО, где одна из частиц покоится, Е = Е\ -\-тс2,
р = pi, где Ei, pi —энергия и импульс движущейся частицы. После преоб-
преобразований, с учетом тождества Е2 — р\с2 = т2с4, для кинетической энергии
налетающей частицы получим: Е\ — тс2 = 2тс2а(а + 1). Например, при
а = 100 получим, что одну частицу надо 2
идет примерно 1/100 энергии частицы.
> Основной закон релятивистской динамики. Приложенная
к частице сила равна, как и в классической механике, производной от
импульса:
F = ?, F0)
а = 100 получим, что одну частицу надо разогнать до 20200тс2. На реакцию
но релятивистский импульс E2) отличается от классического. Под дей-
действием приложенной силы импульс может неограниченно возрастать,
но из определения E2) видно, что скорость будет меньше с. Работа
силы F0)
fF-dr = \^-vdt= fv-dp =
равна изменению релятивистской энергии. Здесь были использованы
формулы E2) и E3), а также формула р • dp = E dE/с2 (см. E7)).

Глава 2
МОЛЕКУЛЯРНАЯ ФИЗИКА
И ТЕРМОДИНАМИКА
2.1. Основные положения и определения
> Два подхода к изучению вещества. Термодинамический подход
заключается в установлении связей и соотношений между эксперимен-
экспериментально определяемыми (феноменологическими) параметрами (их на-
называют термодинамическими параметрами), опираясь на несколько
постулатов (начал термодинамики).
Статистический подход опирается на молекулярно-кинетические
представления о строении вещества (основные положения молекуллр-
но-кинетической теории):
1. Все тела состоят из огромного числа мельчайших частичек веще-
вещества— атомов и молекул.
2. Молекулы вещества находятся в непрерывном хаотическом дви-
движении.
3. Молекулы взаимодействуют между собой: на больших расстоя-
расстояниях притягиваются, на малых отталкиваются.
Термодинамические параметры вычисляются в рамках конкретной
модели внутреннего строения вещества (т. е. модели движения и взаи-
взаимодействия атомов и молекул), посредством усреднения по огромному
числу состояний системы. Статистическая физика использует методы
теории вероятностей и математической статистики. Классическая тео-
теория опирается на классические законы движения молекул, квантовая
статистика— на законы квантовой механики.
> Количество вещества. Моль. Количество вещества в системе,
т. е. число содержащихся в ней структурных единиц — атомов или
молекул, измеряется в молях. Моль любого вещества содержит опре-
определенное число молекул, называемое числом Авогадро, равное числу
атомов в 12 г углерода: TVa ~ 6,02 • 1023моль~1. Для числа молей
получим:
N т ( v
A)
где N — число молекул в системе, т = moN — масса системы (то —
масса одной молекулы), \i — uioNa — молярная масса вещества.

48 Молекулярная физика и термодинамика [ Гл. 2
> Равновесные и неравновесные состояния. Уравнение со-
состояния. Термодинамическая система, находящаяся при неизменных
внешних условиях, приходит в равновесное состояние, в котором от-
отсутствуют потоки любого типа (например, потоки массы и энергии).
Термодинамические параметры равновесного состояния (давление р,
температура Т, объем V или плотность р, молярная масса ц и др.)
связаны уравнением состояния. Уравнение состояния идеального газа
(уравнение Клапейрона— Менделеева)
pV = vRT, B)
где R ~ 8, 31 Дж/(моль • К) —универсальная газовая постоянная, было
получено эмпирически и хорошо выполняется для разреженных газов
(см. разд. 2.5). Уравнение Ван-дер-Ваальса
C)
является одним из приближенных уравнений состояния реальных плот-
плотных газов (см. разд. 2.8). Процесс изменения состояния называют
равновесным (квазиравновесным), если он происходит столь медленно,
что каждое промежуточное состояние можно считать равновесным.
Равновесные процессы являются обратимыми.
Равновесная термодинамика рассматривает равновесные состоя-
состояния и процессы. Она позволяет сделать ряд выводов о характере и на-
направлении протекания неравновесных процессов, происходящих между
начальным и конечным равновесными состояниями, но не дает количе-
количественного описания этих процессов. Неравновесные системы — предмет
физической кинетики и неравновесной термодинамики. Отметим, что
время прихода в равновесие (время релаксации) уменьшается вместе
с размерами системы, поэтому можно говорить о локальном равновесии
в маленькой части неравновесной системы (например, вводить темпе-
температуру, меняющуюся от точки к точке).
> Простые термодинамические системы. Однородная и изо-
изотропная термодинамическая система, химический состав которой не
меняется, называется (термодинамически) простой. К простым систе-
системам относятся, в частности, однокомпонентные (чистые) газы и жидко-
жидкости. Простая система обладает двумя степенями свободы, т.е. только
два ее термодинамических параметра можно считать независимыми.
Равновесные состояния простой системы можно изображать точками
на плоскости (например, в координатах (р, V)), равновесные процес-

2.2] Первое начало термодинамики 49
сы — линиями на этой плоскости. Работа, совершаемая простой систе-
системой против внешних сил, равна
v2
8A = pdV, A= \ p(V)dV, D)
Vi
где p(V) называется уравнением процесса. Так как работа не является
функцией состояния, то бесконечно малая работа обозначена 5 А, чтобы
отличить ее от бесконечно малого изменения функции (дифференциа-
(дифференциала).
Наличие связи между любыми тремя параметрами простой системы,
налагаемой уравнением состояния, приводит также к связи между
их производными. Выразив изменение Т через изменения р и V:
dT = ( —— I dV + ( —— I dp и применив это выражение к изотермическому
\dV / p \ dp ) v
процессу (dT = 0), получим
() () () i.
\dTJp\dpJv \dV)т
Это соотношение связывает между собой три коэффициента:
1 (dV\ ( ,
а = — I ) (температурный коэффициент объемного расширения),
Vb V дТ J p
/3 = — ( —— ) (температурный коэффициент давления),
ро \оТ J v
К = —V\ —— ) (изотермический модуль всестороннего сэюатия).
V оу / т
2.2. Первое начало термодинамики
> Внутренняя энергия. Теплообмен. Температура. В отличие
от механической энергии, которая может изменяться только за счет
работы, внутренняя энергия может изменяться как за счет работы, так
и при контакте с телами, имеющими другую температуру, т.е. в про-
процессе теплообмена. Энергия, переданная при теплообмене (подведении
тепла), называется количеством теплоты или теплотой и обозна-
обозначается Q. Теплота считается положительной, если система получает
энергию, и отрицательной, если отдает.
При теплообмене энергия переходит от тела с большей темпера-
температурой к телу с меньшей температурой. Любая температурная шкала
должна удовлетворять этому свойству. Эмпирические температурные
шкалы основаны на косвенных измерениях, т. е. на измерениях пара-
параметров, монотонно зависящих от температуры. Газовая шкала темпе-
температур опирается на уравнение состояния идеального газа B). Термоди-
Термодинамическая, или абсолютная шкала температур определяется на основе
второго начала термодинамики.

50 Молекулярная физика и термодинамика [ Гл. 2
С точки зрения классической молекулярно-кинетической теории,
внутренняя энергия термодинамической системы равна сумме кине-
кинетической энергии движения ее молекул и потенциальной энергии их
взаимодействия. Внутренняя энергия U = U(V, Т, . . .) — функция
состояния термодинамической системы г), она является важнейшей
характеристикой термодинамической системы.
Термодинамика должна определять любую величину феноменологиче-
феноменологически, вне зависимости от представлений о внутреннем устройстве веще-
вещества. Принципиальную возможность такого определения дает представление
о гибкой адиабатической оболочке, которая позволяет изменять форму си-
системы и совершать над ней работу, но исключает ее теплообмен с внешними
телами. В этом случае работа внешних сил Ае при переходе системы из
состояния 1 в состояние 2 не зависит от процесса перехода, а зависит только
от начального и конечного состояний системы, что позволяет определить
разность внутренних энергий следующим образом: U2 — U\ = АеA —»¦ 2).
> Первое начало термодинамики. Общий закон сохранения энер-
энергии с учетом процесса теплообмена и внутренней энергии имеет вид:
т. е. изменение полной (механической+внутренней) энергии системы
равно работе внешних сил и теплоте, полученной при теплообмене
с внешними телами. Иногда закон сохранения энергии формулируют
как невозможность создания вечного двигателя первого рода (который
производил бы работу из ничего). Первым началом термодинамики
называют обычно применение этого закона к термодинамической си-
системе, механическая энергия которой не меняется. Кроме того, в тер-
термодинамике удобнее использовать работу системы против внешних сил:
А = -Ае. Получаем
A E),
т. е. подведенная к термодинамической системе теплота идет на изме-
изменение ее внутренней энергии и на совершение системой работы против
внешних сил.
> Первое начало для простой системы. Теплоемкость. Исполь-
Используя уравнение D), запишем первое начало термодинамики для простой
системы, получившей бесконечно малое количества теплоты:
SQ = dU + p dV. F)
Отношение 5Q к изменению температуры dT называют теплоемко-
теплоемкостью системы С в данном равновесном процессе (измеряется в Дж/К):
С dT = dU + p dV. G)
г) Зависимость U = U(V, Т, . . .) называют калорическим уравнением со-
состояния, в отличие от термического уравнения состояния р = p{V, T).

2.2] Первое начало термодинамики 51
Считая U в G) функцией двух переменных (К, Т), запишем
где Су = I "яг7) ~~ теплоемкость при постоянном объеме (см. урав-
уравнение G)). Получаем:
[(|^)]K (9)
Отсюда видно, что теплоемкость для процесса V(T) зависит от зна-
значения производной dV/dT. Так как параметры (К, Т) можно менять
независимо, то эта производная, а значит, и теплоемкость в данной
точке может иметь любое значение.
> Энтальпия. Процесс Джоуля — Томсона. Если равновесный
процесс изменения состояния происходит при постоянном давлении, то
подведенная теплота
Q = AU + pAV = A{U + pV) = AI (р = const) A0)
равна разности энтальпий I = U + pV в конечном и начальном
состояниях. Энтальпия используется также для описания процесса
Джоуля — Томсона — стационарного просачивания вещества сквозь
пористую перегородку (дросселирования). Этот процесс применяется
для получения сверхнизких температур. В процессе Джоуля — Томсо-
Томсона сохраняется энтальпия вещества, прошедшего сквозь перегородку:
Ul +P1V1 = U2 +P2V2-
> Внутренняя энергия идеального газа. Внутренняя энергия
идеального газа зависит только от его температуры. Существуют экс-
экспериментальные подтверждения этому факту:
1. При расширении газа в пустоту внутри жесткой адиабатической
оболочки равны нулю как работа газа Л, так и полученная теплота Q,
а следовательно, и AU; было обнаружено, что в этом неравновес-
неравновесном процессе температура идеального газа не меняется (опыты Гей-
Люссака и Джоуля).
2. Температура идеального газа не меняется в процессе Джоуля —
Томсона.
Второе начало термодинамики позволяет доказать уравнение
(ди\ п /о\
7Т77 = 0, исходя из термического уравнения состояния B).
\oV Jт
> Процессы в идеальном газе. Из уравнений G), (8) получим
изменение внутренней энергии и первое начало термодинамики для
идеального газа:
dU = CvdT, 5Q = CvdT + pdV. A1)

52 Молекулярная физика и термодинамика [ Гл. 2
Эксперименты показывают, что в широких пределах изменения
температуры Су не зависит от Т, и можно записать U = СуТ + const.
Рассмотрим конкретные процессы.
1) Изотермический процесс (dT = 0). В этом случае dU = 0, т. е.
5Q = pdV, Q = А = J p(V) dV = vRT In №\ . A2)
Vi
Теплоемкость данного процесса можно считать равной бесконечности.
2) Изобарный процесс (dp = 0). Вводя теплоемкость при постоян-
постоянном давлении, с учетом уравнения состояния B) получим
Ср dT = CvdT + pdV = Су dT + vR dT.
Сокращая на dT, получим соотношения между теплоемкостями (урав-
(уравнение Майера):
Cp = Cv + iyR, Ср = су + -, С^р = С^у + Я, A3)
где с = С /т — удельная теплоемкость, а С ^ = С j \i — молярная,
теплоемкость газа (измеряются в Дж/(кг • К) и Дж/(моль • К) соот-
соответственно).
3) Адиабатический процесс. Если равновесный процесс происходит
без подвода тепла (SQ = 0), то
CydT = -pdV => iyCliydT =
dT R dV
Интегрируя, получим уравнение адиабатического процесса (уравнение
Пуассона):
TV1'1 = const или pV1 = const, A4)
где безразмерный параметр 7 = Ср/Су = 1 + (R/C^y) называется
показателем адиабаты. Через 7> с учетом уравнения Майера A3),
можно выразить теплоемкости газа:
г R ~ jR
4) Политропный процесс. Политропным называется процесс, теп-
теплоемкость которого постоянна (С = const):
CdT = CvdT + pdV =Ф (Су -C)dT = -p dV.

2.3]
Второе начало термодинамики
53
Проведя такие же вычисления, как для адиабатического процесса,
получим уравнение политропного процесса:
где п = 1 +
R
рУп — const,
_ ср-с
— показатель политропы.
— C/_i Cv — С
5) Цикл Карно. Циклом Карно называется замкнутый цикл, состо-
состоящий из двух изотерм (при температурах 7\ и Т2, 7\ > Т2) и двух
адиабат. Коэффициентом полезного действия замкнутого цикла на-
называют величину
А _ Q.-Q, _ Q2
V — 7Г "" —п ~ i ~ 7Г' v10^
где Л — работа за цикл, Q\— теплота, полученная от нагревателя, Q^ —
теплота, отданная холодильнику. В замкнутом цикле AU = 0, поэтому
Q1 -Q2 = A.
Для цикла Карно (рис. 17) из уравнения A2) имеем:
Из уравнения Пуассона A4) нахо-
находим:
Отсюда следует, что V2/Vi = V3/V4.
Поэтому для КПД получим:
v = i-^, A6)
V
Рис. 17
т. е. КПД цикла Карно зависит только
от отношения температур холодильника и нагревателя.
2.3. Второе начало термодинамики
> Формулировки второго начала. Приведем две наиболее извест-
известные формулировки:
1. Невозможен процесс, единственным результатом которого было
бы совершение работы за счет теплоты, взятой у теплового резервуара
при постоянной температуре (формулировка Томсона). Эта же форму-
формулировка, но выраженная другими словами, утверждает невозможность
создания вечного двигателя второго рода (т. е. производящего работу
за счет внутренней энергии теплового резервуара).

54 Молекулярная физика и термодинамика [ Гл. 2
2. Невозможен процесс, единственным результатом которого была
бы передача энергии от более холодного тела к более горячему (фор-
(формулировка Клаузиуса).
Формулировки Томсона и Клаузиуса эквивалентны.
> Теорема Карно. Циклом Карно называют цикл, в котором рабочее
тело получает теплоту только от резервуара при постоянной темпера-
температуре 7\ (нагревателя), а отдает — только резервуару при постоянной
температуре Т<± (холодильнику). Теорема Карно утверждает, что КПД
произвольного цикла Карно не может превышать КПД обратимого
цикла Карно, работающего при тех же 7\ и Т^. Из этого немедленно
следует, что КПД обратимого цикла Карно зависит только от 7\ и T<z
и не зависит от природы рабочего тела.
Покажем в общих чертах, как можно доказать теорему Карно. Предпо-
Предположим, что КПД обратимой машины меньше, чем необратимой. Подберем
объем рабочего тела обратимой машины так, чтобы она совершала за цикл
такую же работу, как необратимая. С учетом A5) неравенство для КПД
приобретает вид A/Q°6 < A/Qieo6, откуда следует Qf> > Qie°6- Пустим
обратимую машину в обратную сторону так, чтобы работа необратимой
машины потреблялась обратимой. За цикл объединенной машины ее работа
будет равна нулю, а нагреватель получит энергию Q°6 — Qie°6 > 0, целиком
взятую у холодильника. Мы пришли к противоречию с формулировкой
Клаузиуса.
Так как нам известен КПД одной из машин Карно — газовой A6),
то теорему Карно можно записать так:
—п ^ —г или tjt ~ tjt ^ °>
Qi 11 11 i2
причем равенство соответствует обратимому циклу Карно.
Термодинамическая шкала температур. Теорема Карно позволяет
определить шкалу температур, не зависящую от свойств конкретных тел.
Отношение температур двух тел определяют, присоединив к ним обратимую
машину Карно; так как отношение Q1/Q2 зависит только от их температур,
то его можно принять равным отношению термодинамических температур:
9i/02 = Q1/Q2. Как видно из A7), отношение термодинамических темпера-
температур равно отношению газовых температур (в той области, где газовая шкала
определена).
> Второе начало: вычисление внутренней энергии. Второе
начало термодинамики позволяет вывести важное соотношение для
внутренней энергии простой системы, которое не может быть получено
в рамках первого начала:

2.3]
Второе начало термодинамики
55
Покажем, как можно получить A8) из теоремы Карно. Рассмотрим
(бесконечно) малый обратимый цикл Карно и изобразим его в координатах
(р, V). Работа системы за цикл, равная
площади маленького параллелограмма pi
(рис. 18), не изменится при замене адиабат
вертикальными отрезками, длина которых
AT. Умножив на высоту АУ,
dTJy
получим 6 А = (—) ATAV. Теплота,
полученная на верхней изотерме, равна
SQi = AU+pdV = (|^) AV + pAV,
где для приращения AU при постоянной
температуре использовано (8). Из теоремы
Карно и уравнения A7) имеем
V
Рис. 18
ЛТ
~тг
дТ L
ATAV
AT
p\AV
'dU\
,dv)T'
откуда получим A8).
Приведем несколько примеров применения формулы A8).
1) Внутренняя энергия идеального газа. Подставим в A8) уравне-
уравнение состояния р = —uRT. В результате получим \-^rj) = 0, т.е.
V \oV)т
внутренняя энергия идеального газа не зависит от объема.
2) Внутренняя энергия газа Ван-дер-Ваальса. Выразив давление
из уравнения состояния C) и подставив в A8), приходим к формуле
(dU\ _ ai/_
\дУ)т ~ V2
. Следовательно,
dU = Cv dT + ^ dV.
Кроме того, имеем
(Ш\ =^\(дЖ\]=?=\(д-?-\]=?=(аЛ\ =
(
дт [\dv
(
дТ\ V
>Т dVl\dTJv\ - LV-/TJ
т. е. Су не зависит от объема. В области температур, где Су слабо
зависит от Т, можно записать
2
и = Су 1 —. A9)
3) Общая формула для Ср — Су. Подставляя A8) в уравнение (9)
и фиксируя давление (р = const), получим:
г г т(дЛ (ду\ т(дЛ fdv
cp-cv = t ^_) ^_) = -т ^_j [w

56 Молекулярная физика и термодинамика [ Гл. 2
(здесь использовано соотношение между производными, рассмотрен-
рассмотренное в конце разд. 2.1). Неотрицательность полученного выражения
( др\ . п
следует из условия механической устойчивости: ( 77— I ^ U.
> Неравенство Клаузиуса. Неравенство A7) является частным
случаем неравенства Клаузиуса, относящегося к любому замкнутому
циклу. Если в замкнутом цикле система получает теплоты Qi, ...
..., Qn от внешних резервуаров, имеющих температуры 7\е, . . ., Тдг,
то удовлетворяется неравенство
N
Ё|Н° или Ш<0. B0)
г=1 г **
Для обратимого процесса неравенство превращается в равенство,
а температура резервуара, с которым система в данной точке цикла
обменивается теплом, равна температуре системы: Те = Т. В этом
случае получим
^=0. B1)
обр
Равенство B1) служит основой для определения еще одной функции
состояния — энтропии (см. разд. 2.4).
2.4. Энтропия. Свободная энергия
> Определение энтропии. Уравнение Клаузиуса для обратимого
цикла B1) можно переформулировать как условие независимости ин-
интеграла
А
от пути равновесного перехода из состояния А в состояние В. Это поз-
позволяет определить функцию состояния — энтропию, точнее, разность
энтропии в двух состояниях:
При равновесном процессе без подвода тепла энтропия не меняется
(адиабатический процесс можно называть изоэнтропным). Первое на-
начало термодинамики F) для равновесного процесса в простой системе
приобретает вид:
TdS = dU + pdV. B3)

2.4] Энтропия. Свободная энергия 57
> Примеры вычисления энтропии.
1. Процесс с постоянной теплоемкостью. Изменение энтропии при
изменении температуры от 7\ до Т<± равно
т2
^ (^) B4)
2. Энтропия идеального газа. Подставляя в B3) выражение для
внутренней энергии идеального газа (И), с учетом уравнения состояния
рУ = l/RT получим
Иногда условно записывают S = v(CMv \пТ + R\nV), имея в виду, что
в приложениях всегда возникает разность энтропии.
3. Энтропия газа Ван-дер-Ваальса. Подставляя в B3) зависи-
зависимость A9), с учетом уравнения состояния C) имеем
,с ~ dT , аи2 dV , р „. ^ dT , uRdV
dS = vC»v— + — ^ + -dV = vC»v— + ^-^,
S = u [C^v In T + R \n(V - vb)}.
> Направление неравновесных процессов в теплоизолиро-
теплоизолированной системе. Рассмотрим неравновесный процесс, переводящий
систему из равновесного состояния 1 в равновесное состояние 2. Орга-
Организуем циклический процесс, вернувшись из 2 в 1 при помощи любого
равновесного процесса. Запишем для этого цикла неравенство Клаузи-
уса B0) и для равновесного процесса учтем определение энтропии B2).
Получим:
2
pk^-Si- B6)
Если неравновесный процесс происходит в адиабатической оболочке,
то левая часть равенства обращается в нуль, что дает
52^5Ь B7)
т. е. в любом процессе без подвода тепла энтропия не убывает. Равновес-
Равновесное состояние теплоизолированной системы соответствует максимуму
энтропии.

58 Молекулярная физика и термодинамика [ Гл. 2
> Примеры неравновесных процессов.
1. Теплообмен. Рассмотрим простейший пример: теплообмен меж-
между двумя телами с одинаковой теплоемкостью С и начальными тем-
температурами 7\ и 7~2. Из уравнения теплового баланса следует, что
в результате теплообмена оба тела достигнут одинаковой температуры
Тк = -G\ + Тг). При этом согласно B4) изменение энтропии системы
будет положительным:
(аргумент логарифма больше единицы, так как среднее арифметиче-
арифметическое больше среднего геометрического).
2. Расширение идеального газа в пустоту. Внутренняя энергия
и, следовательно, температура идеального газа при расширении его
в пустоту остаются постоянными. Изменение энтропии находим из
формулы B5):
Q|y B8)
Возрастание энтропии при адиабатическом расширении в пустоту (уве-
(увеличении V при постоянной U) можно доказать для любой простой си-
системы. Если рассматривать S в B3) как функцию переменных (U, V),
то получим (||)^ = ? > 0.
3. Смешение газов. Рассмотрим теплоизолированный сосуд, раз-
разделенный перегородкой на две равные части, в каждой из которых
содержится по одному молю идеального газа при одинаковых темпера-
температурах и давлениях. При убирании перегородки газы смешиваются; из
формулы B8) следует, что энтропия системы увеличивается на 2/2 In 2
(энтропия смешения). В случае различных газов начальное состояние
отличается от конечного; газы можно снова разделить, совершая ра-
работу над специальными поршнями, пропускающими молекулы только
одного сорта. Однако для одинаковых газов начальное и конечное
состояния системы тождественны, и энтропия не должна меняться.
Отсутствие непрерывного перехода от почти одинаковых к полностью
тождественным молекулам называют парадоксом Гиббса.
> Статистический смысл энтропии. Формула Больцмана
Б = к\пП B9)
(А; — постоянная Больцмана) связывает энтропию макроскопического
состояния со статистическим весом этого состояния, т.е. числом
различных микроскопических состояний, которые его реализуют. Чем
больше J2, тем больше вероятность состояния; при неравновесных
процессах система переходит от менее вероятных к более вероятным

2.4] Энтропия. Свободная энергия 59
состояниям. Логарифм обеспечивает аддитивность энтропии: статисти-
статистический вес системы, состоящей из двух независимых подсистем, равен
произведению их статистических весов. (Подробнее статистический
смысл энтропии обсуждается в разделе 7.1.)
Чтобы проиллюстрировать формулу B9), вычислим пространственную
часть энтропии газа. Разобьем объем на маленькие ячейки объемом v. Каж-
Каждая молекула может быть помещена в любую из V/v ячеек, т. е. число незави-
независимых состояний равно ft = (V/v)N, где N — число молекул газа. Для энтро-
энтропии получим S = к In ft = kN\n(V/v) = vR\n(V/v). Квантовая статистика
утверждает, что одинаковые частицы принципиально неразличимы, т. е. ft
надо разделить на число перестановок между ними N\. В результате для
пространственной части энтропии получим выражение S = kN\n(V/Nv).
Нетрудно убедиться, что таким образом удается разрешить парадокс Гиббса.
> Третье начало термодинамики. Третье начало термодинамики
(теорема Нернста) утверждает, что при приближении температуры
к абсолютному нулю энтропия любой системы стремится к опреде-
определенному конечному значению, не зависящему от значения остальных
термодинамических параметров. Энтропию системы при Т = О при-
принимают равной нулю. Статистическое объяснение: при Т = О система
находится в наинизшем энергетическом состоянии, кратность которого
(равная статистическому весу системы ft при Т = 0) невелика, и в со-
соответствии с формулой Больцмана B9) энтропия пренебрежимо мала.
Следствия третьего начала: при Т —У 0 теплоемкости Су и Ср системы,
а также ее температурные коэффициенты объемного расширения а
и давления /3 стремятся к нулю.
> Система в термостате. Свободная энергия. Рассмотрим из-
изменение состояния системы, находящейся в тепловом контакте с тер-
термостатом, имеющим постоянную температуру Т. Такую же темпера-
температуру будет иметь сама система в начальном и конечном равновесных
состояниях. Неравенство B6) после «цепочки» преобразований Q/Т ^
^ S2-S! => (J/2-?/i)+A ^ TS2-TS! => U1-TS1-(U2-TS2) ^ А
принимает вид:
#1-«Ъ ^Л, C0)
где ^ = U — TS — новая функция состояния, называемая свободной
энергией. Если объем системы не меняется, то в рассматриваемом
неравновесном процессе
т.е. свободная энергия не возрастает. Другими словами, равновесное
состояние системы постоянного объема, находящейся в тепловом кон-
контакте с термостатом, соответствует минимуму свободной энергии. Для
равновесного процесса неравенство в этих уравнениях превращается

60 Молекулярная физика и термодинамика [ Гл. 2
в равенство. Из формулы B3) следует, что
-pdV. C1)
Поэтому естественными переменными для свободной энергии являются
объем и температура: Ф = &(V, Т).
Если система в термостате находится в механическом контакте
(легкий поршень, гибкая оболочка) с внешней средой, имеющей фикси-
фиксированное давление р (такое же давление будет у самой системы в равно-
равновесном состоянии), то работа против внешних сил равна А = p(V2 — V\)-
Из C0) получим
#1 + РУ\ ^&2+ PV2 ИЛИ ФХ ^ Ф2, C2)
где Ф = Ф + pV = U — TS + pV — термодинамический потен-
потенциал Гиббса (при обратимом процессе Ф = const). Равновесному со-
состоянию для системы в термостате и гибкой оболочке соответствует
минимум Ф(р,Т). Так как йФ — —SdT + V dp, то естественными
переменными для термодинамического потенциала являются давление
и температура: Ф = Ф(р, Т). При постоянных давлении и температуре
термодинамический потенциал пропорционален количеству вещества:
Ф(р, Т, гп) = гпф (ф — удельный термодинамический потенциал) или
Ф(р, Т, N) = N/л (/л — термодинамический потенциал в расчете на одну
частицу, или химический потенциал).
Канонические уравнения состояния. Естественные перемен-
переменные. Хотя функции U, /, S, Ф, Ф могут рассматриваться в любых независи-
независимых переменных, для каждой из них существуют естественные переменные.
Для энтропии это переменные (?/, V), для энтальпии — (?/, р), для свободной
энергии — (V, Т), для потенциала Гиббса— (р, Т). Функция в естественных
переменных называется каноническим уравнением состояния. Зная любое
каноническое уравнение, можно получить как термическое, так и калориче-
ское уравнения состояния. Например, — ( ) дает выражение для p(V, T),
\oV /т
а выразив S(V, Т) = -(?—) , найдем U(V,T) = V + TS.
\дТ /у
2.5. Кинетическая теория идеального газа
> Основное уравнение кинетической теории идеального газа.
С точки зрения молекулярно-кинетической теории, газ считается иде-
идеальным, если можно пренебречь потенциальной энергией взаимодей-
взаимодействия его молекул (по сравнению с кинетической энергией) и размерами
молекул (по сравнению со средним расстоянием между ними). Давле-
Давление газа на стенку возникает в результате многочисленных упругих
соударений молекул между собой и со стенками сосуда. (Удары можно
считать в среднем упругими, так как газ находится со стенкой в тепло-
тепловом равновесии.) Основное уравнение кинетической теории идеального

2.5]
Кинетическая теория идеального газа
61
газа выражает давление через средний квадрат скорости молекул:
11 9
р = зп(ру) = зпш°^2) = зп^пост^'
где п = N /V — концентрация молекул, то — масса одной молекулы,
р = ttiov — ее импульс, {eUOCT) = (-mov2) — средняя кинетическая
энергия поступательного движения молекулы.
Если связь энергии и импульса отличается от классической, то
последнее равенство в C3) приобретает иной вид. Для газа фотонов
имеем р = еIс (см. разд. 1.11). В результате получим
Р= з
C4)
> Число ударов о стенку. Число молекул AN, попадающих за
время At на плоский участок поверхности площадью AS, равно
AN _ n(v)
ASAt
C5)
Формулы для вычислений. Формулы для переноса через площадку
числа частиц, импульса, энергии и т. д. получают разбиением молекул на
удобные группы и расчетом их вклада в вычисляемую величину. Наиболее
общий подход — разбиение на
группы, имеющие почти одинаковую
скорость v. Выделим группу молекул,
имеющих величину скорости от v
до v + dv и направление в телесном
угле сШ.Число молекул данной груп-
группы в единице объема равно dn(v, v-\-
+dv; dfi) = dn(v, v + dv)dn/4ir.
Чтобы найти, сколько молекул данной
группы попадает на плоский участок
площадью AS за время At, надо
построить на этом участке косой
цилиндр (рис. 19), направляющая ко-
которого имеет длину vAt и составляет
Рис. 19
угол в с осью х. Все молекулы выделенной группы, находящиеся в этом
цилиндре (и только они!), попадут на площадку AS за время At. Производя
последовательные интегрирования, можно вывести C5) и многие другие
формулы, например, для энергии, проносимой через площадку:
АЕ mon{v3)
ASAt
C6)
> Определение температуры в кинетической теории газов.
В кинетической теории газов доказывается, что если две подсистемы
(из одинаковых или разных молекул) могут обмениваться энергией, то
в состоянии равновесия оказываются равными средние кинетические

62 Молекулярная физика и термодинамика [ Гл. 2
энергии поступательного движения их молекул. Исходя из этого, кине-
кинетическая теория газов определяет температуру как величину, пропор-
пропорциональную средней кинетической энергии поступательного движения
молекулы:
(еПост) = \кТ, C7)
где к — постоянная Больцмана, которая выражается через уни-
универсальную газовую постоянную и число Авогадро (см. разд. 2.1):
к = R/Na ~ 1,38 • 10~23 Дж/К. Коэффициент пропорциональности
выбран так, чтобы уравнение состояния идеального газа
р = пкТ = укТ C8)
(оно получается из основного уравнения C3) и определения темпера-
температуры C7)) совпадало с уравнением B), в котором используется газовая
шкала температур.
Средняя квадратичная скорость поступательного движения моле-
молекул с учетом C3) и C7) вычисляется по формулам
поГ [Зр /ЗкТ [ШГ , .
Vkb = у/Щ = ^_?= ^_ = ^__, C9)
где р = топ — плотность газа.
> Внутренняя энергия идеального газа. Важной характеристи-
характеристикой идеального газа является число степеней свободы его молеку-
молекулы ъ. У одноатомной молекулы есть только три степени свободы, со-
соответствующие поступательному движению: ъ = in = 3. У жесткой
двухатомной молекулы, кроме поступательных, есть еще две враща-
вращательные степени свободы (полярные углы, задающие ее направление
в пространстве): i = in + гвр = 3 + 2 = 5. У жесткой многоатомной
(нелинейной) молекулы —три вращательные степени свободы, поэтому
i = 6. В классической статистической физике доказывается теорема
о равнораспределении энергии по степеням свободы: на любую степень
свободы, которой в выражении для энергии молекулы соответствует
член ах2 или /Зх2, приходится средняя энергия ^кТ в расчете на одну
молекулу. Формула C7) находится в полном соответствии с утвержде-
утверждением этой теоремы. Средняя энергия одной молекулы и внутренняя
энергия всего газа принимают вид:
(е) = \%фкТ, U = N(e) = \i^vRT. D0)
Физическое число степеней свободы гф в случае жестких молекул
совпадает с математическим. Однако, когда оказываются возбужден-
возбужденными колебательные степени свободы (при Т ~ 103 К), то на каж-
каждую колебательную степень свободы будет приходиться (с учетом по-
потенциальной энергии колебаний) средняя энергия кТ. В результате

2.5] Кинетическая теория идеального газа 63
получим гф = гп + гвр + 2гкол, где гкол обозначает математическое
число колебательных степеней свободы. Для TV-атомной молекулы
гкол = 37V — (гп + iBp) (например, для мягкой двухатомной молекулы
гф = 3 + 2 + 2F-5) = 7).
Из D0) получим выражения для теплоемкостей идеального газа
и его показателя адиабаты (см. разд. 2.2):
При комнатных температурах измеряемая теплоемкость соответствует
модели жестких молекул — колебательные степени свободы оказываются
невозбужденными или, как говорят, «замороженными». Однако при повы-
повышении температуры до ~ 103 К теплоемкость начинает возрастать, т. е.
колебательные степени свободы «размораживаются». Наоборот, при пони-
понижении температуры до нескольких десятков Кельвинов происходит «вымора-
«вымораживание» вращательных степеней свободы, сопровождающееся соответству-
соответствующим уменьшением теплоемкостей. Объяснение явлению вымораживания
степеней свободы дает квантовая механика: если средняя энергия теплового
движения кТ мала по сравнению с расстоянием до ближайшего дискретного
уровня, то данный вид движения не возбу ж дается.
> Смесь идеальных газов. Закон Дальтона: давление смеси (двух)
идеальных газов равно сумме их парциальных давлений:
р = Pl + р2 = (щ + п2)кТ = (vx + v2)RT.
Внутренняя энергия смеси равна сумме внутренних энергий
U — -^HViRT + -12V2RT. Эта формула позволяет ввести:
эффективное число степеней свободы: i(v\ + и2) = i\Vi + ^2^2,
эффективные молярные теплоемкости: (^i + ^2)CM = ^i
эффективную молярную массу: (v\ + ^2)/^ — ^iA*i + ^2/^2•
> Распределение Максвелла. Распределение молекул по скоро-
скоростям описывается следующими функциями:
, ч j dn(vx, vx + dvx) ?( Ч7 dn(v,v + dv)
(p(vx) dvx = , f(v)dv = ,
П т П D2)
Ф(у) dvx dvy dvz = —-— ——— — -.
in
Определение любой функции распределения основано на утвержде-
утверждении, что доля молекул, попадающих (в среднем) в очень маленький
интервал данной переменной (скорости, проекции скорости, энергии),
пропорциональна ширине этого интервала (dv обозначает физически,
а не математически, бесконечно малый интервал — он должен содер-
содержать большое число молекул.) Среднюю долю молекул, обладающих
некоторым признаком (например, попадающих в заданный интервал

64
Молекулярная физика и термодинамика
[Гл.2
скоростей), можно трактовать как вероятность того, что произволь-
произвольная молекула обладает данным признаком. Поэтому функцию распре-
распределения иногда называют плотностью вероятности.
Перечислим свойства функции распределения (на примере f(v)):
1) Доля частиц (вероятность) в конечном интервале (vi, V2)'.
= J f(v)dv.
2) Нормированность:
[ f(v)dv = 1.
D3)
3) Вычисление среднего от любой функции скорости x(v):
ОО
(X(v))= \x(v)f(v)dv. D4)
о
Между тремя функциями распределения, определенными в D2),
существуют следующие связи:
f(v) = Ф(у)Атгу2, <P(vXjvyjvz) = <p(vx)ip(vy)(p(vz).
Функция (р является четной функцией, т. е. можно написать: ip = ip(v%.).
Функция ^(v) зависит только от v2 = v\ + Vy + v\. Связь между Ф и ip
удовлетворяется только функцией ip(vx) = Лехр(—(v2). Коэффици-
Коэффициенты Л и ( определяются из двух условий: а) нормировки функции ip,
б) требования, чтобы (v2) = ~(v2} = kT/mo, см. C9). Ответ выглядит
так:
k!/2
/(«) =
\
3/2
ехр
D5)
ЛтгкТ; *Ч 2kT
Обычно именно последнюю формулу называют распределением
Максвелла (рис. 20). Функция f(v) достигает максимума при
скорости vB = B/гТ/тоI/2, ко-
которую называют наиболее вероят-
вероятной скоростью. Значение функ-
функции f(v) в этой точке равно
f(vB) = 4е-1BтткТ/т0)-1/2. На-
Например, при увеличении Т в 4 ра-
раза максимальная скорость станет
в 2 раза больше, а соответству-
соответствующее значение функции f(vB) —

2.5] Кинетическая теория идеального газа 65
в 2 раза меньше; напомним, что площадь под кривой f(v) равна еди-
единице.
Средняя (или среднеарифметическая) скорость молекул вычисля-
вычисляется в соответствии с правилом D4):
сю
(v) = \ vf(v)dv =
J
о
Приведем также распределение молекул по энергиям поступательного
движения:
Интегралы для вычислений. Для вычисления средних величин
с распределением Максвелла нужно уметь вычислять интегралы
типа In = J^° xn exp(—/Зж2) dx. Приведем два первых результата:
1о = ~л/п/3~1 '2, /i = ~/3~1. Дальнейшие интегралы получим диффе-
дифференцированием по /3. Например, /2 = = -у/тг /3~3'2.
dp 4
> Распределение Больцмана. Если газ находится во внешнем си-
силовом поле, то концентрация молекул зависит от координат. Из условия
механического равновесия газа можно получить:
/ \ / \ Г sn(r) - еп(гоI
п(г) = п(г0) ехр \ ,
L kl \
D6)
где sn(r) — потенциальная энергия молекулы во внешнем поле (рас-
(распределение Больцмана). Частным случаем распределения Больцмана
является барометрическая формула:
n(h) = n0 ехр у- kT j, p(h) = n(h)kT =
кт у
Поясним на примере барометрической формулы, как выводится рас-
распределение Больцмана. Условие равновесия в поле тяжести вертикального
цилиндра с площадью основания s и высотой dh имеет вид: s dp = —p(s dh)g.
r\ / гт7 dn mog
Отсюда с учетом уравнении р = пк! и р = топ получим — = п.
dh kT
Интегрируя, приходим к барометрической формуле.
> Распределение Максвелла — Больцмана. Оба распреде-
распределения — Максвелла D5) и Больцмана D6) — содержат выражение
ехр(—е/кТ). Распределение Максвелла — Больцмана выражает веро-
вероятность того, что произвольная молекула из сосуда, содержащего N мо-
молекул, находится в области пространства (ж, x + dx] у, y + dy; z, z + dz)
и имеет скорость в интервале (vx, vx + dvx; vy, vy + dvy; vz, vz + dvz):
dN dn(r) d3r п(г)Ф(лг) ,q ,o л ( e \ ,q ,o , ai_.
— = ^— = -L±±id8rd8v = Лехр(-—)d3rd3v. D7)
3 А. И. Черноуцан

66
Молекулярная физика и термодинамика
[Гл.2
Здесь d3r = dx dy dz, d3v = dvx dvy dvZj e = -m$v2 + ?n(r) — меха-
механическая энергия молекулы, А — коэффициент, который можно найти
из условия нормировки. Общее распределение Максвелла — Больцма-
на применимо к любым видам энергии молекулы: энергии вращения,
энергии колебаний, потенциальной энергии, зависящей от ориентации
молекул, и т. д.
2.6. Реальные газы.
Уравнение Ван-дер-Ваальса
> Изотермы реального газа. Если температура газа меньше кри-
критической (см. ниже), то при равновесном изотермическом уменьшении
его объема наблюдаются следующие процессы (рис. 21):
1. До точки А давление возрастает. Если температура далека от
критической, то вплоть до точки А хорошо выполняется уравнение
состояния идеального газа.
2. На участке АВ давление
в системе не меняется. В сосу-
сосуде появляется жидкость, отде-
отделенная от газа четкой границей
(поверхностью раздела). Газ, на-
находящийся в равновесии с жид-
жидкостью, называют насыщенным
паром. Отношение масс жидко-
жидкости и пара в произвольной точ-
точке равно отношению горизон-
горизонтальных отрезков, на которые
эта точка делит отрезок АВ:
тж/тп = АС/СВ. Участки
V
Рис. 21
изотерм AL\ и L^B соответствуют метастабильным состояниям, т. е.
состояниям, в которых система может существовать некоторое время,
но потом быстро переходит в устойчивое состояние на линии АВ. (Имея
в виду процессы при постоянном давлении или объеме, их называют пе-
переохлажденным паром или перегретой жидкостью.) Существование
метастабильных состояний объясняется тем, что образование малень-
маленьких зародышей новой фазы (жидкости в паре или пара в жидкости)
невыгодно из-за поверхностной энергии (см. разд. 2.8).
3. После точки В давление резко возрастает. В сосуде находится
только жидкость.
Чем выше температура, тем короче горизонтальный участок изо-
изотермы. Наконец, при критической температуре Тк от горизонтального
участка остается только точка перегиба К (рис.21). Давление в этой
критической точке называют критическим давлением рк, а объем
одного моля газа в этом состоянии — критическим объемом VK. При
Т > Тк изотерма представляет собой плавную монотонную функцию.

2.6] Реальные газы. Уравнение Ван-дер-Ваальса 67
Область выше критической изотермы называют (истинным) газом (его
нельзя изотермически перевести в состояние «жидкость + пар»), а об-
область под критической изотермой делится на три: жидкость, ненасы-
ненасыщенный пар и жидкость + насыщенный пар. Из области «П» в область
«Ж» можно перейти плавно, обойдя область «П + Ж», т. е. газ и жид-
жидкость отличаются только количественными показателями.
> Уравнение Ван-дер-Ваальса для одного моля идеального газа
имеет вид
/ \
D8)
(Уравнение C) из разд. 1.1 для v молей получается подстановкой
Уд = V/v.) Постоянная b учитывает уменьшение свободного объ-
объема для движения молекул за счет их собственного объема; счита-
считается, что эта константа равна учетверенному объему всех молекул:
b = 47Va • ^7Г^3- Член a/V^ учитывает уменьшение давления за счет
взаимного притяжения молекул; это особенно ясно видно из выражения
для внутренней энергии газа Ван-дер-Ваальса: U = С^уТ — a/V^.
Среднее взаимодействие между молекулами описывают модельным вы-
выражением для потенциальной энергии, содержащим два члена: первый со-
соответствует сильному отталкиванию на малых расстояниях (~ 10~ м),
второй — ван-дер-ваальсовским силам притяжения на больших расстояниях
(рис. 22):
Минимум Еп соответствует среднему расстоянию между молекулами в от-
отсутствие теплового движения. При кТ <С Em\n движение молекул сводится
к колебаниям возле дна ямы (твердое тело), случай кТ ~ Em\n соответствует
жидкому состоянию, а случай кТ ^> Em\n — газообразному. Ввиду крутого
наклона левой ветви кривой, соответствующей отталкиванию молекул, по-
положение точки поворота при сближении молекул газа слабо зависит от их
средней энергии (см. также разд. 1.5).
> Изотермы газа Ван-дер-Ваальса. Вычисление критиче-
критических параметров. На рис. 23 изображены изотермы газа, описы-
описываемого уравнением D8). На участке K\K<i не выполняется условие
механической устойчивости (-^гт ) ^ 0> переход между правой и ле-
\oV Jт
вой ветвями происходит по горизонтальному участку А В. Правило
Максвелла: положение отрезка АВ определяется условием равенства
заштрихованных площадей. (В противном случае изотермический цикл
AK\K<iBА производил бы работу, что противоречит второму началу
термодинамики.) Участки АК\ и К^В соответствуют метастабильным
состояниям.

68
Молекулярная физика и термодинамика
[Гл.2
\?пост/
р А
Рис. 22
Рис. 23
В критической точке выполняются сразу два условия: (-^гт ) =
\oV Jт
= 0. Выразив р из D8) и подставив в эти уравнения, найдем:
д2Р
dv2
Ук = 36,
1 а
27F'
27 Ш'
Критические параметры удовлетворяют соотношению: pKVK = -RTK.
8
Если ввести относительные переменные v = V/VK, тг = р/рк и в = Т/Тк,
то D8) принимает вид:
(и_1)GГ +зО = ^,
единый для всех газов. Следовательно, уравнение Ван-дер-Ваальса удовле-
удовлетворяет экспериментально установленному принципу соответственных со-
состояний, который утверждает, что если две относительные переменные двух
газов совпадают, то совпадает и третья. Этот закон хорошо выполняется для
большинства газов.
2.7. Равновесие фаз. Фазовые переходы
> Условия равновесия фаз. Фазой называется часть системы,
однородная по физическим и химическим свойствам. Одно и то же
по химическому составу вещество может находиться в разных фазах.
Примерами двухфазной системы являются: (жидкость+насыщенный
пар), (твердое тело+жидкость) и (твердое тело+пар).
Условия равновесия фаз: 1) равенство давлений — механическое
равновесие; 2) равенство температур — тепловое равновесие; 3) равен-
равенство химических потенциалов (или удельных потенциалов Гиббса) —
равновесие по отношению к переходу вещества из одной фазы в дру-
другую. Последнее условие соответствует минимуму термодинамического
потенциала Гиббса Ф = /jliNi + ^{N — N\) (см. разд. 2.4) по отноше-
отношению к числу частиц в одной из фаз N\. Условие /xi(p,T) = ^(р^Т)
дает (для простой системы) уравнение для кривой сосуществования
р(Т); двухфазная простая система имеет только одну степень

Лед
Пар
2.7] Равновесие фаз. Фазовые переходы 69
свободы. Так, давление насыщенного пара (положение горизонталь-
горизонтального участка изотермы, см. разд. 2.6) является однозначной функ-
функцией температуры (кривая парообразования); то же самое относится
к зависимости температуры плавле-
плавления от внешнего давления (кривая А Р
плавления) и к зависимости от тем-
температуры давления пара над твердой
поверхностью (кривая возгонки).
На рис. 24 приведены все три кри-
кривые — парообразования (I), плавле-
плавления (II) и возгонки (III) — для во-
воды. Точка пересечения этих кривых
называется тройной точкой (для во-
воды U = 0,01°С, р3 = 610,5 Па). Рис. 24
Для существования трехфазной си-
системы должны выполняться сразу два условия: /in(p,T) = /лж(р, Т)
и /лж(р, Т) = /iTB(p,T), которые однозначно определяют ее давление
и температуру.
> Фазовый переход первого рода. Теплота и энтропия пере-
перехода. Чтобы в двухфазной системе перевести часть вещества массой т
из одной фазы в другую, не меняя при этом давления и темпера-
температуры, надо сообщить системе теплоту Q = mq, которую называют
(скрытой) теплотой фазового перехода (q — удельная теплота пере-
перехода). При переходе вещества в новую фазу ее энтропия изменяется
на AS = Q/T = mq/T, а внутренняя энергия на AU = mq — mpAv
(v = V/т — удельный объем). Величину As = q/T называют удельной
энтропией перехода, а Аи = q — pAv — изменением удельной внут-
внутренней энергии при переходе. Переход вещества между фазами двух-
двухфазной системы, связанный с поглощением (выделением) теплоты пе-
перехода и сопровождающийся скачкообразным изменением внутренней
энергии, энтропии, плотности (объема) и др., называется фазовым пере-
переходом первого рода. (Название связано с тем, что скачок испытывают
величины, являющиеся первыми производными термодинамического
/ дФ \ ( дФ \
потенциала Гиббса: S = — (-^=; I и V = ( -7— } .)
V оТ J р \ор J т
> Уравнение Клапейрона — Клаузиуса. Если изменить темпе-
температуру двухфазной системы, то ее давление изменится таким образом,
что химические потенциалы (или удельные потенциалы Гиббса) фаз
останутся равными: 6,ф\ — d</>2, или —s\ dT + v\ dp = — S2 dT + V2 dp
(см. разд. 2.4). Получаем, что наклон кривой фазового равновесия
равен
dp As q
dT Av TAv
D9)

70 Молекулярная физика и термодинамика [ Гл. 2
(уравнение Клапейрона — Клаузиуса). Например, для перехода
лед — вода при атмосферном давлении температура плавления
равна 273 К, q = 3,34 • 105 Дж/кг, vB - ул = -0,91 • 10 м3/кг,
и мы получим —— = —1,1 • 107 Па/К. Знак минус объясняется
аномальным свойством воды: при плавлении (таянии) ее плотность
увеличивается.
Пример 1. Если непрерывно подводить к жидкости теплоту, то в тот
момент, когда ее температура достигает значения, при котором давление
насыщенного пара равно внешнему давлению, наступает интенсивное паро-
парообразование во всем объеме жидкости, которое называют кипением. Уравне-
Уравнение D9) определяет зависимость температуры кипения от внешнего давле-
давления. Пренебрегая удельным объемом жидкости и выражая удельный объем
RT
пара из уравнения состояния идеального газа: v = , получим прибли-
приближенное уравнение — = ^. Например, для воды (/л = 18 г/моль) при
dT RT
атмосферном давлении р = 105 Па температура кипения равна Т = 373 К,
удельная теплота q = 2,26 • 106 Дж/кг, и мы получим — = 3,5 • 103 Па/К.
> Фазовый переход второго рода. При фазовом переходе второго
рода (точка Кюри перехода из ферромагнитного состояния в парамаг-
парамагнитное, точка перехода жидкого гелия в сверхтекучее состояние и др.)
плотность, внутренняя энергия, энтропия (первые производные тер-
термодинамического потенциала Гиббса) изменяются непрерывно, а раз-
различного вида производные этих термодинамических функций (воспри-
(восприимчивости) — теплоемкость, сжимаемость, диэлектрическая или маг-
магнитная проницаемость и т. д. — изменяются скачком или проявляют
критическое поведение (стремятся к бесконечности при приближении
к точке перехода). (Название «фазовый переход второго рода» связано
с тем, что скачок испытывают вторые производные термодинамиче-
термодинамического потенциала Гиббса.) Фазовый переход второго рода происходит
сразу во всем объеме. В результате перехода происходит качественное
изменение внутреннего строения — появляется (или исчезает) дополни-
дополнительная симметрия.
2.8. Поверхностное натяжение
> Коэффициент поверхностного натяжения. Молекулы в по-
поверхностном слое жидкости обладают большей потенциальной энер-
энергией по сравнению с молекулами в объеме (меньше «соседей», энергия
взаимодействия с которыми отрицательна, —см. рис. 22). При постоян-
постоянной температуре дополнительная энергия пропорциональна площади
поверхности U:
E0)

2.8] Поверхностное натяжение 71
где удельную свободную энергию поверхности а называют коэффи-
коэффициентом поверхностного натяжения. При равновесном изотермиче-
изотермическом изменении площади прямоугольного участка поверхности рабо-
работа внешней силы равна изменению свободной энергии C0). Поэтому
Л = АФПОВ = aAU = o~Lx, где L — длина прямолинейного отрезка
границы, х — его перемещение. Отсюда следует, что на отрезок границы
действует сила поверхностного натяжения, перпендикулярная к это-
этому отрезку и направленная по касательной к поверхности жидкости:
^пов = oh. E1)
Равновесие соответствует минимуму свободной энергии, следователь-
следовательно, жидкость или жидкая пленка стремятся уменьшить свою поверх-
поверхность: в невесомости жидкая капля принимает форму шара.
> Термодинамика поверхностного слоя. Так как ^пов является
функцией (Т, X7), то d№ = a dE + ^~l^ dT. Отсюда с учетом C1) по-
получим выражения для энтропии поверхностного слоя, его внутренней
энергии и теплоты, поглощаемой поверхностным слоем при изотерми-
изотермическом увеличении площади:
S S u * + ts
При увеличении температуры Т коэффициент поверхностного натяже-
натяжения а уменьшается и при критической температуре обращается в нуль.
> Добавочное давление под искривленной поверхностью. Из
условия механического равновесия поверхностного слоя следует, что
давление внутри выпуклой поверхности должно быть больше, чем
снаружи. Добавочное давление Ар в случае сферической поверхности
найдем, увеличив (мысленно) радиус шара на dR и приравняв работу
внешних сил над поверхностным слоем к изменению его свободной
энергии: ApdV = a dU =^ Apd(-7rR3) = а ^Dтг/22). В результате
получим
AV=\. E2)
Обобщением этой формулы является формула Лапласа'.
где Ri, R2 — главные радиусы кривизны (радиусы кривизны в сечении
поверхности взаимно перпендикулярными плоскостями, проходящими
через нормаль к поверхности в данной точке).

72 Молекулярная физика и термодинамика [ Гл. 2
> Краевой угол. Смачивание. Поверхность жидкости образует
с твердой поверхностью угол, который называют краевым. Величи-
Величина краевого угла зависит от соотно-
п у шения между коэффициентами по-
Возлух ж~в-^!
^ Уг\ w верхностного натяжения на грани-
. Жидкость ^ , ч ^
i Чах жидкость — воздух (сгж_в), жид-
,< гг !>„ >,1 кость — твердое тело (а^-т) и твер-
СГт~в Тв. тело СГж"т дое тел0~ ВОЗДУХ (^т-в). Из усло-
условия механического равновесия эле-
Рис 2^
мента жидкости на линии пересече-
пересечения трех сред (рис. 25) имеем ат_в = аук-т + сгж_в cos ^ (на единицу
длины). Отсюда получим
cosfl= а-*-а*-\
Если cos 0 > 0, то говорят, что жидкость смачивает поверхность.
Если правая часть последнего равенства больше или равна +1, то на
поверхности твердого тела образуется молекулярная пленка жидкости
(полное смачивание жидкостью твердого тела); в сосуде жидкость
образует со стенкой нулевой угол. Если правая часть равенства меньше
или равна —1, то имеет место полное несмачивание.
> Капиллярные явления. Если жидкость смачивает поверхность
тонкого капилляра, то она поднимется по нему на высоту /г, определя-
определяемую условием механического равновесия.
В случае капилляра круглого сечения радиуса г радиус кривизны
мениска равен R = г/ cos 0, и давление под мениском (см. E2)) должно
быть меньше атмосферного на величину 2а / R = 2а cos в jr. Прирав-
, , 2<т cos в
нивая к pgli, находим высоту подъема жидкости: а = .
2.9. Явления переноса в газах
> Средняя длина свободного пробега. Среднее число столкнове-
столкновений в единицу времени выделенной молекулы с другими молекулами
газа равно
z = по» л/2, E3)
где п — концентрация молекул, (v) — средняя скорость движения мо-
молекул, а а — эффективное сечение для упругих соударений молекул.
В модели твердых шариков а = 7rd , где d — диаметр шарика. Мно-
Множитель л/2 учитывает движение встречных молекул; в качественной
теории явлений переноса его обычно опускают.
Для определения числа столкновений траекторию молекулы, имеющую
вид ломаной линии, окружают цилиндрической поверхностью радиуса d.

2.9] Явления переноса в газах 73
Движущаяся молекула столкнется с любой неподвижной молекулой, центр
которой окажется внутри этого цилиндра. За единицу времени молекула
проходит расстояние (v), объем цилиндра равен nd (v), число попавших
в него молекул равно z = тгс/ (v)n.
Средняя длина свободного пробега молекулы равна
Л = М= 1 . E4)
z палД
Полное число соударений между молекулами в единице объема в еди-
единицу времени равно:
_ zn _ n(v) _ n2a(v)V2
Эффективное сечение некоторого процесса взаимодействия между стал-
сталкивающимися частицами (по отношению к выделенному результату этого
взаимодействия, например, рассеянию в заданный телесный угол, погло-
поглощению и т. д.) определяют следующим образом. Рассмотрим неподвижную
молекулу (мишень) и налетающий на нее пучок молекул интенсивности
I = nv (интенсивность пучка — число частиц, проходящих в единицу
времени через единичную площадку, перпендикулярную скорости молекул).
Эффективным сечением процесса называют отношение числа столкновений
в единицу времени, приведших к выделенному результату, к интенсивности
пучка:
а = AN/I. E6)
Ослабление пучка молекул, распространяющихся в газе, на пути dx равно
dl = — Ian dx = —(//Л) dx,
где а — сечение упругого рассеяния молекул, п dx — число рассеивающих
центров на пути dx (на единицу площади), Л = 1/'(па). Интегрируя, получим
зависимость интенсивности пучка от пройденного им расстояния:
/ = /оехр(—пах) = /о ехр(—ж/Л), E7)
т. е. вероятность того, что молекула испытает соударение на интервале
(ж, х + dx), равна \dl\/lo = ехр(—ж/Л) d(x/X). Среднее расстояние, прой-
пройденное молекулой до столкновения, равно
оо
(х) = Жехр(--)— = Л.
о
> Качественная модель явлений переноса в газах. Явления
вязкости, теплопроводности и диффузии объясняются переносом им-
импульса, энергии и концентрации за счет хаотического теплового дви-
движения. Вязкостью называют возникновение силы трения между па-
параллельно движущимися слоями, если скорости слоев различны. Если
скорость направленного движения и параллельна оси х и меняется
только в направлении оси у (рис. 26), то между слоями жидкости

74
Молекулярная физика и термодинамика
[Гл.2
dy
возникает сила, пропорциональная площади
и градиенту скорости и:
<V
E8)
Рис. 26
где г\ — коэффициент вязкости (или просто вяз-
вязкость). Возникновение силы объясняется пере-
переносом вдоль оси у импульса рх молекулами, пе-
пересекающими площадку за счет теплового дви-
движения.
Если в направлении у меняется не скорость
направленного движения молекул, а температура газа, то поток тепло-
теплоты в направлении оси у равен
dT
dy
E9)
где к — коэффициент теплопроводности (или просто теплопровод-
теплопроводность).
Если вдоль оси у меняется концентрация меченых молекул газа п\
(полная концентрация п должна быть постоянной), то поток меченых
молекул в направлении оси у (самодиффузия) определяется законом
Фика:
j = _Ddn1^ щ
где D — коэффициент диффузии.
Обозначим за g(y) величину, поток которой вдоль оси у нас интере-
интересует. В случае вязкости это — импульс направленного движения моле-
молекул: g{y) = mou(y), в случае теплопроводности — средняя энергия теп-
теплового движения: g(y) = (г) = сут^Т (су —удельная теплоемкость),
в случае диффузии: g{y) = ni(y)/n. Будем считать, что каждая
молекула газа переносит через площадку то значение параметра g,
которое имеют (в среднем) молекулы газа в том месте, где произошло
ее последнее соударение. Тогда для потока величины g в направлении
оси у можно получить выражение
1 и, Q"
/~ч -*- / \ \ о (С\Л \
Для грубой оценки можно считать, что поток частиц через единичную
площадку равен n(v), и что частицы, пересекающие площадку в точке
у, испытали последнее соударение в среднем на расстоянии Л. Получа-
Получаем G ~ n(v)[g(y - Л) - g(y + Л)], т. е. G ~ n(v)X(dg/dy).
Покажем, как можно учесть, что последние соударения частиц перед
пересечением площадки происходят на разных от нее расстояниях. Будем
считать, что после соударения молекула летит в одном из шести направлений,

2.9] Явления переноса в газах 75
задаваемых осями координат. С расстояния у прилетят молекулы, испытав-
испытавшие соударение в цилиндре объемом S dy, полетевшие в направлении —у
и не испытавшие более соударений на пути у (рис. 26). С учетом E5) и E7)
получим g(y)dN = [g-(O) + У-^-\ -^-exp\-jj(Sdy). ИнтегРиРУя п0 У>
получим вклад молекул, летящих со стороны положительных у. Вычитая
вклад противоположно летящих молекул, приходим к формуле F1).
> Формулы для коэффициентов переноса.
1. Подставляя g = movx в формулу F1), получим поток импульса,
который равен силе трения E8) для единичной площади. Для вязкости
имеем:
г] = -nmo(v}\ = -p(v)\. F2)
2. Подставляя g = cyuioT в формулу F1) и сравнивая с E9),
находим коэффициент теплопроводности:
к = -nmo(v)cvX = -p(v)cv\. F3)
3. Подставляя g = rti/пв формулу F1) и сравнивая с F0), получим
выражение для коэффициента диффузии:
D = l(v)X. F4)
Из формул F2) — F4) следуют два важных факта:
1) Длина свободного пробега обратно пропорциональна р, что вид-
видно из уравнения E4); поэтому вязкость и теплопроводность газов не
зависят от давления (закон Максвелла). Этот вывод остается верным до
тех пор, пока длина свободного пробега мала по сравнению с размерами
сосуда.
2) Отношение вязкости и теплопроводности не зависит от темпера-
температуры.
Если длина пробега становится сравнимой с размерами сосуда (раз-
(разреженный газ), то вязкость и теплопроводность начинают зависеть от
плотности. Например, при вычислении потока теплоты между стен-
стенками, расположенными на расстоянии d <^i Л (ультраразреженный
газ), можно считать, что после удара о стенку, имеющую темпера-
температуру 7\, каждая молекула приобретает (в среднем) энергию сут^Тх,
летит без соударений к противоположной стенке и отдает ей энергию
сугпо(Т2 — Т\). Из формулы C5) следует, что число попадающих на
стенку молекул равно -n(v)SAt. Отсюда получим: q = -p(v)cyAT',
т. е. к — -p(v)cyd.

Глава 3
ЭЛЕКТРОДИНАМИКА
3.1. Электрический заряд. Закон Кулона
> Электрический заряд — физическая величина, определяющая
интенсивность электромагнитного взаимодействия.
Свойства заряда:
1. Носителями электрического заряда являются заряженные эле-
элементарные частицы — протон и электрон (а также их античасти-
античастицы — антипротон и позитрон — и некоторые нестабильные частицы:
тг-мезоны, /i-мезоны и т.д.). Заряженные частицы взаимодействуют
между собой с силами, убывающими с расстоянием так же медленно,
как гравитационные, но во много раз превышающими их по величине.
2. Все заряженные элементарные частицы обладают одним и тем
же по величине зарядом, который называют элементарным зарядом
и обозначают буквой е. Опыт показывает, что заряд элементарных
частиц не зависит от их скорости.
3. Заряд элементарных частиц может быть положительным или от-
отрицательным. Одноименные частицы отталкиваются, разноименные —
притягиваются. За положительный заряд принят заряд протона +е.
Заряд электрона —отрицательный (—е).
Если в состав макроскопического тела входит различное количество
электронов Ne и протонов Npj то оно оказывается заряженным. Заряд
тела всегда представляется числом, кратным величине элементарного
заряда: q = e(Np — Ne).
Закон сохранения электрического заряда: полный заряд замкнутой
системы, т.е. алгебраическая сумма зарядов всех тел, постоянен. Это
утверждение очевидно, если в системе не происходит превращений
элементарных частиц. Но закон сохранения заряда имеет более фунда-
фундаментальный характер — он выполняется в любых процессах рождения
и уничтожения элементарных частиц.
> Закон Кулона описывает взаимодействие покоящихся точечных
зарядов, т.е. элементарных частиц или заряженных тел, размеры ко-
которых малы по сравнению с расстоянием между ними. Сила взаимо-
взаимодействия двух точечных зарядов в вакууме (кулоновская сила) прямо
пропорциональна произведению зарядов и обратно пропорциональна
квадрату расстояния между ними:
F = k^-, A)
Г

3.2] Электрическое поле. Напряженность поля 77
где к — коэффициент пропорциональности, зависящий от системы еди-
единиц. Сила взаимодействия направлена вдоль прямой, соединяющей
заряды; одноименные заряды отталкиваются, разноименные — притя-
притягиваются.
В СИ единица заряда кулон (Кл) определяется через еди-
единицу силы тока ампер, а коэффициент в формуле A) равен
к = 9,0 х 109 Н • м2/Кл2, или к = 1/Dтгео), где е0 = 8,85 х 1(Г12 Ф/м -
электрическая постоянная. В гауссовой системе (СГС) к принимается
равным единице, и единица заряда определяется законом Кулона.
Сила, действующая на заряд q со стороны нескольких зарядов
Qi, Q2, • • • равна суперпозиции сил:
B)
Распределение заряда по пространству задается пространственной
плотностью заряда р(г), по поверхности — поверхностной плотно-
плотностью заряда сг(г), по линии — линейной плотностью заряда А (г):
dq = pdV, dq = adS, dq = Xdl. C)
Система зарядов называется электронейтральной, если ее полный
заряд равен нулю. Простейший пример электронейтральной системы —
электрический диполь, состоящий из двух точечных зарядов q и — q.
Дипольным моментом электрического диполя называется вектор
Р = <?1, D)
где 1 = г+ — г_ — вектор, проведенный от заряда — q к заряду q.
Обобщением на произвольную электронейтральную систему является
определение
где q = ^2 qi — сумма всех положительных зарядов, г+ = ^2 qi^i/q —
Qi>0 qi>0
центр положительных зарядов, r_ = ^ qi^i/q — центр отрицательных
Qi<0
зарядов.
> О системах единиц в электростатике. Все формулы будут при-
приводиться в СИ. Для перехода к гауссовой системе (СГС) в большинстве
случаев достаточно положить к = 1. Если формула записана через Eq,
то надо сначала заменить ео на 1/Dтг&).
3.2. Электрическое поле. Напряженность поля
> Электромагнитное поле. Взаимодействие заряженных частиц
друг с другом осуществляется посредством электромагнитного поля.
Это означает, что: а) заряженные частицы создают в окружающем про-
пространстве электромагнитное поле, б) на заряженную частицу действу-

78 Электродинамика [ Гл. 3
ет электромагнитное поле, существующее в данной точке пространства
в данный момент времени. Поле, создаваемое точечным источником,
пропорционально его заряду; воздействие поля на заряженную частицу
пропорционально заряду этой частицы.
> Электрическое поле. Электромагнитное поле представляет со-
собой совокупность двух взаимосвязанных полей — электрического и
магнитного. Действие электрического поля на заряженную частицу не
зависит от ее скорости, а действие магнитного поля пропорционально
скорости частицы. Источниками электрического поля служат любые
заряженные частицы, магнитное поле создается движущимися заряда-
зарядами. Соотношение между электрическим и магнитным полями меняется
при переходе в другую инерциальную систему отсчета. Свойства полей
полностью описываются системой четырех уравнений Максвелла (см.
разд. 3.15). Уравнения Максвелла релятивистски инвариантны.
> Пробный заряд. Напряженность электрического поля. Для
определения характеристик электромагнитного поля используют поня-
понятие точечного пробного заряда, внесение которого в исследуемое поле
его не искажает (т.е. не приводит к смещению источников поля). Для
этого величина пробного заряда должна быть достаточно малой. Сила,
действующая на неподвижный пробный заряд </, пропорциональна его
величине и определяется только электрическим полем:
F, = </Е. E)
Эта формула определяет напряженность электрического поля. Она
же дает ответ на вопрос, какая сила действует на любой заряд </,
движущийся или неподвижный, со стороны электрического поля. В СИ
напряженность измеряется в Н/Кл или в В/м.
3.3. Электростатическое поле. Принцип
суперпозиции для напряженности и потенциала
> Электростатическое поле. Стационарное электрическое поле,
создаваемое системой неподвижных зарядов, называется электроста-
электростатическим полем. Напряженность электростатического поля может
быть определена с помощью закона Кулона B).
1. Поле точечного заряда. Если внести пробный заряд q в поле
точечного заряда Q, то из B) и E) получим:
где Ег — проекция Е на радиальное направление.
F)

3.3]
Электростатическое поле, Принцип суперпозиции
79
У
El
dE
'jtdE
/
dq
'//|2аочч
/ ^
Рис. 27
Л dEx
dq
Рис. 28
2. Поле системы зарядов. Используя принцип суперпозиции полей,
имеем:
E = Ei + Е2 + --- = Vfc-
В случае непрерывного распределения заряда суммирование надо
заменить интегрированием, см. C). (Сравните с формулами для поля
тяготения в разд. 1.8.)
Пример 1. Заряд равномерно распределен по дуге окружности радиусом
R с линейной плотностью Л (рис. 27). Угловой размер дуги равен 2схо.
Вычислите напряженность в центре окружности.
Решение. Напряженность направлена по оси у, проходящей через сере-
середину дуги и центр окружности. Напряженность поля, создаваемого в точ-
точке О элементом дуги с угловым размером da, равна dE = kdq/R2, где
dq = XRda. Проектируя на у и интегрируя, находим:
а0
. XRda . 2Asin ao
к ц— cos a = к-
RA
R
Пример 2. Поле отрезка. Заряд равномерно распределен по отрезку
прямой с линейной плотностью Л. Вычислите напряженность поля в точке А,
положение которой по отношению к отрезку задано расстоянием у до прямой
и двумя углами а,\ и схч (рис. 28).
Решение. Вклад в напряженность от элемента dx равен dE = kXdx/r2,
его проекции на оси х и у равны dE cos а и dE sin ex. Интегрировать удобно
по углу а после подстановки г = у/ sin а и замены переменной: х = —у ctg a,
dx = уdexj sin ex. Для проекций Ех и Еу получим:
Ех = к — (sin «2 — sin ai),
Еу = к — (cos ai — cos аг).
Если ai = тг — «2 = ск (точка А лежит на перпендикуляре, проведенном
через середину отрезка), то Ех = О, Еу = 2&А cos а/у. Если в этом равенстве
а —>- 0 (прямая), то Е^ = 2кХ/у. Если aa = 0, «2 = тг/2 (полупрямая), то
Ех = Еу = кХ/у.
> Потенциал электростатического поля. Как и любое стацио-
стационарное центральное поле, электростатическое поле является потенци-

80 Электродинамика [ Гл. 3
альным (см. разд. 1.5). Это означает, что работа поля при перемещении
пробного заряда из одной точки пространства в другую не зависит от
траектории. Сказанное позволяет определить потенциал электроста-
электростатического поля ip(r):
Ая{1 -> 2) = W,(ri) - Wq(r2) = ф(п) - р(г2)], (8)
где Aq(l —У 2) — работа поля при переносе пробного заряда q из точки ri
в точку Г2, VK^(r) = q(f(v) — потенциальная энергия точечного заря-
заряда q во внешнем электростатическом поле (в этой главе энергия будет
обозначаться буквой W). Величина </?(ri) —</?(г2) называется разностью
потенциалов между точками ri и Г2. Для однозначного определения
Wq(r) и ер (г) надо выбрать точку, где они обращаются в нуль. В СИ
потенциал измеряется в вольтах (В).
Зная напряженность Е(г), можно вычислить разность потенциалов
и потенциал:
- <р{т2) = JEdr, ip(r) = ^Edr, (9)
где го — точка, в которой потенциал принят равным нулю. Зная потен-
потенциал </?(г), можно найти проекцию напряженности на любое направле-
направление / (исходя из (9) для двух близких точек):
El = ~ln A0)
и вектор напряженности:
> Потенциал поля точечного заряда и системы зарядов.
Потенциал поля точечного заряда Q можно найти с помощью фор-
формулы A0):
п dtp dcp , Q / \ i Q
Er = --f- => -f- = -k-ъ ==> (p(r) = k— + const.
dr dr r ^v ' r
Обычно потенциал принимают равным нулю на бесконечности. В этом
случае:
Потенциал поля системы зарядов равен сумме потенциалов полей
отдельных зарядов (принцип суперпозиции для потенциала):
Если заряд распределен непрерывно, суммирование надо заменить
интегрированием.

3.3]
Электростатическое поле, Принцип суперпозиции
81
Пример 3. Поле диска. Источником поля является тонкий диск
радиусом R, равномерно заряженный с поверхностной плотностью а.
Вычислите потенциал в точке Л, расположенной на оси диска на
расстоянии х от его центра (рис. 29).
Решение. Вклад в потенциал тонкого
кольца, заключенного между окружностями
радиусов г и г + dr, равен
= k-
dq
= k
а 2тгг dr
Vs2 + r2 V^ + r2
(все точки кольца расположены почти на оди-
одинаковом расстоянии от точки А). Интегрируя,
находим потенциал кольца:
я
<т 2тгг dr
Г
= k
Рис. 29
Затем с помощью A0) определим напряженность (она направлена вдоль х):
dip
Ех = —^ = 2irka(l-
dx V
В пределе R —»¦ оо получим поле бесконечной плоскости: Ех = 2тгка = .
Пример 4. Поле диполя. Найдите потенциал и напряженность элек-
электростатического поля вдали от диполя, изображенного на рис. 30.
Решение. Потенциал в точке, задаваемой радиусом-вектором г, на боль-
большом расстоянии от диполя (г = |г| ^> /)
равен:
, N kq kq kq kq (p • r)
(p(r) = и и /с—о—,
Г\ Г2 Г — S Г + S Г
1 г
где s = (-•-), Р = ql (см. разд. 3.1).
Чтобы найти напряженность, исполь-
используем тождества: grad(l/r3) = —3r/r5
и grad (p • г) = р. В результате имеем:
Отсюда для модуля напряженности полу-
получим Е = kpr~3y/3 cos2 (9 + 1. Такие же
выражения верны для поля любой элек- Рис. 30
тронейтральной системы с отличным от
нуля дипольным моментом (см. разд. 3.1) на большом от нее расстоянии.
> Диполь во внешнем поле. Маленький диполь с дипольным
моментом р = ql во внешнем поле обладает потенциальной энергией
Wu = 4<р(т+) -
_) = q^-l = -pE, = -(p • E).

82 Электродинамика [ Гл. 3
Эта энергия изменяется как при повороте диполя — на диполь со сто-
стороны поля действует вращательный момент:
М = 1 х (qE) = р х Е,
так и при перемещении диполя в неоднородном поле — на диполь
действует сила:
F = *Е(г+) - *Е(г_) = q — l = р— = рх— + ру— + pz — .
Равновесная ориентация с минимальной энергией соответствует поло-
положению р || Е, ориентированный таким образом диполь втягивается
в область более сильного электрического поля.
3.4. Теорема Гаусса
> Поток вектора напряженности. Потоком вектора напряженно-
напряженности через плоский участок площадью ds называется
AФ = (E-ds) = Ends = E cos в ds, A4)
где ds = n ds, n — вектор нормали к плоскости, в — угол между Е и п,
Еп = Е cos в — проекция Е на направление нормали. Знак d<E> зависит
от выбора направления нормали. Поток вектора напряженности через
поверхность S конечных размеров определяется как
Ф
= \Ends. A5)
В случае замкнутой поверхности направление нормали выбирается
в сторону внешнего пространства.
Аддитивность потока: если электростатическое поле является су-
суперпозицией нескольких полей Е(г) = ^ Е^, то для любой поверхности
Поток вектора напряженности поля точечного заряда Q через пло-
площадку ds равен
d<?> = Er cos в ds = ±fc-4 ds± = ±kQ d?2,
r
где ds± = \ds cos 0\ — проекция ds на плоскость, перпендикулярную г;
df] = ds±/r2 — телесный угол, под которым площадка видна от заря-
заряда Q; знак « + » соответствует острому углу между п и г, а знак « —» —
тупому углу. Поток через замкнутую поверхность равен AirkQ, если
заряд Q находится внутри этой поверхности, и нулю — если снаружи.
> Теорема Гаусса. Поток вектора напряженности электростатиче-
электростатического поля через замкнутую поверхность выражается через полный

3.4] Теорема Гаусса 83
заряд внутри этой поверхности </охв (охватываемый поверхностью):
в = ^. A6)
Теорема Гаусса и силовые линии. Для графического изображения
полей используют силовые линии (линии напряженности) поля, которые
проводятся по следующим правилам: а) касательная к силовой линии направ-
направлена вдоль вектора Е в каждой точке пространства; б) густота силовых линий
пропорциональна величине напряженности в данной области пространства.
Поток вектора напряженности пропорционален числу силовых линий, прони-
пронизывающих поверхность. (По такому же правилу можно ввести линии любого
векторного поля.) Теорема Гаусса означает, что силовые линии начинаются
и заканчиваются на зарядах, а в пустом пространстве непрерывны. Отметим,
что теорема Гаусса и непрерывность силовых линий являются следствием
того, что кулоновская сила убывает с расстоянием как 1/г2.
Кроме силовых линий, используются также эквипотенциальные поверх-
поверхности, которые перпендикулярны силовым линиям (работа поля при пере-
переносе пробного заряда вдоль этой поверхности должна быть равна нулю).
> Вычисление напряженности с помощью теоремы Гаусса.
Если соображения симметрии позволяют построить замкнутую поверх-
поверхность (ее называют гауссовой), на части которой вектор Е перпенди-
перпендикулярен поверхности и имеет постоянную величину Е, а на остальной
части Е направлен вдоль поверхности (Е _1_ п), то можно найти Е,
применив к этой гауссовой поверхности теорему Гаусса.
Пример 1. Поле заряженной нити. Найдите напряженность поля,
создаваемого бесконечной равномерно заряженной нитью (рис. 31).
Решение. Напряженность в любой точке пространства направлена
вдоль перпендикуляра к нити, а значение Ег
зависит только от расстояния г до нити. В ка- А А А
честве гауссовой поверхности можно выбрать 1 1 1
цилиндр радиусом г и образующей длиной /,
ось которого находится на нити. Записав тео- / \ i
рему Гаусса A5), найдем напряженность:
„ о . XI _ Л 2/сА
Ег 2nrl = — ==* Ег = = 1 1
?0 27Г60Г Г 14
(сравните с примером 3 из разд. 3.3). Разность If
потенциалов двух точек равна рис 31
А г2
^^1П
Пример 2. Поле заряженной плоскости. Найдите напряженность
поля, создаваемого бесконечной равномерно заряженной плоскостью
(рис. 32).
Решение. Напряженность всюду перпендикулярна плоскости, а Ех за-
зависит только от расстояния до плоскости. В качестве гауссовой поверхности
можно выбрать цилиндр, основания которого площадью S расположены
симметрично относительно плоскости. Поток через эту поверхность равен

84
Электродинамика
[Гл. 3
Ex{x)S - Ex{-x)S = 2EXS. Записав
теорему Гаусса, найдем напряженность:
?0
- = -Ех{-х) =
(см. пример 3 из разд. 3.3). Приняв (р = О
при х = О, получим ip(x) = |ж|.
Пример 3. Поле заряженного
шара. Найдите поле равномерно заря-
заряженного шара радиусом R.
Решение. Поле равномерно заря-
с* ^ женного шара является центральным.
В качестве гауссовой поверхности можно выбрать сферу радиусом г. Если
г > Я, то внутрь поверхности попадает весь шар (дОхв = q), и мы имеем:
Ег • 4тгг2 = q/eo. Если г < R, то </Охв = qr3/R3, и теорема Гаусса принимает
вид: ?V • 4тгг2 = qr3/{eqR3). Окончательно получим:
pR3 -
Е =
3?0
;- При Г > Я,
при г < R
(/? — плотность заряда). Исходя из формулы для радиальной составляющей
напряженности Er = —dcp/dr (см. разд. 3.3), находим
/г- при г > R,
2
qr
2
qr
— ^—о- + const = — &—о- Н—&— при г < R
< 2Я3 2Я3 2 Я
(константа определяется из условия непрерывности потенциала на поверх-
поверхности шара).
> Теорема Ирншоу. С помощью теоремы Гаусса можно убедиться
в справедливости теоремы Ирншоу, которая утверждает, что точечный
заряд в пустой области пространства не может находиться в состоянии
устойчивого равновесия под действием электрических сил. Действи-
Действительно, в этом случае напряженность поля остальных зарядов на ма-
маленькой сфере, окружающей заряд, должна быть всюду направлена
внутрь сферы (если рассматриваемый заряд положительный), но это
противоречит теореме Гаусса (все остальные заряды находятся вне
сферы).
Уравнения Максвелла в электростатике. Условие потенциальности
электростатического поля
Е • dr = О
rot Е = О
представляет собой одно из уравнений Максвелла (в интегральной и диф-
дифференциальной форме) для случая электростатики. Второе уравнение —

3.5] Электростатика проводников 85
теорема Гаусса (для объемного распределения заряда):
г 1 г р
Подставив сюда Е = —grad (p, получим уравнение Пуассона для потенциала:
1. 1 Р Л Р
divgrad<^ = , или Аш = .
?0 ?0
3.5. Электростатика проводников
> Поле в проводнике. Потенциал проводника. Проводником
называется вещество, способное проводить электрический ток. Для
этого вещество должно содержать свободные заряды, способные пере-
перемещаться по объему проводника. В электростатике рассматривается
состояние, в котором заряды пришли в равновесие (т. е. отсутствует
направленное движение зарядов — электрический ток). Это значит, что
всюду в объеме проводника напряженность поля должна быть равна
нулю. Отсюда следует, что:
1. Потенциал всех точек проводника имеет одинаковое значение,
которое называют потенциалом проводника.
2. Поверхность проводника является эквипотенциальной. Линии
напряженности перпендикулярны к поверхности проводника.
3. Объемная плотность заряда в проводнике равна нулю (из теоре-
теоремы Гаусса следует, что заряд в любом объеме внутри проводника равен
нулю). Некомпенсированные заряды распределены по поверхности
проводника.
4. Напряженность поля вблизи поверхности проводника связана
с поверхностной плотностью заряда на этом участке поверхности:
Эту формулу можно получить из теоремы Гаусса A6), если в качестве
гауссовой поверхности взять маленький цилиндр, одно основание которого
проходит вне проводника вблизи его поверхности, а другое — внутри провод-
проводника: ES =
> Уединенный проводник. Потенциал уединенного проводника
пропорционален его заряду:
где С — электроемкость проводника, зависящая от его формы и раз-
размеров и от диэлектрической проницаемости среды вокруг проводника.
Электроемкость измеряется в СИ в фарадах (Ф), а в СГС — в см.
Например, потенциал и электроемкость уединенного шара радиусом R
равны

86
Электродинамика
[Гл. 3
> Соединение проводников. При соединении проводников с раз-
различными потенциалами проводящей проволокой их потенциалы вы-
выравниваются. Если проводники расположены далеко друг от друга,
то потенциал каждого из них можно рассчитывать как потенциал
уединенного проводника, и закон сохранения заряда позволяет найти
потенциал ipf проводника после соединения:
(электроемкость проволоки можно считать пренебрежимо малой и ее
заряд не учитывать). Если электроемкость одного из проводников
очень велика, то его потенциал почти не меняется. Например, при со-
соединении проводника с землей (заземлении) его потенциал становится
равным постоянному потенциалу Земли, который принимают равным
нулю.
> Проводники во внешнем электрическом поле. При внесении
любого проводника во внешнее поле свободные заряды перераспреде-
перераспределяются таким образом, чтобы напряженность результирующего поля
(суперпозиции внешнего поля и поля зарядов проводника) равнялась
нулю внутри проводника. Например, если к незаряженному проводни-
проводнику поднести положительный точечный заряд, то на ближней поверхно-
поверхности проводника соберутся отрицательные заряды, а на дальней — поло-
положительные, и заряд с проводником будут притягиваться. (Это явление
называется электростатической индукцией.) Так как распределение
зарядов на проводнике обычно не
известно, то расчет по принци-
принципу суперпозиции применить невоз-
невозможно. В некоторых случаях за-
задачу удается решить косвенным
путем.
Пример 1. Поднесем точечный
заряд q > 0 к поверхности зазем-
заземленного проводника на расстояние а,
малое по сравнению с его размера-
размерами. В этом случае конечный про-
проводник можно заменить бесконеч-
бесконечным полупространством из провод-
проводника (рис. 33). На плоской поверх-
поверхности проводника находятся отрица-
отрицательные наведенные заряды. Требу-
Требуется найти Епл, создаваемую этими
Рис. 33 зарядами в любой точке свободного
пространства (при этом распределение этих зарядов неизвестно!) Начнем
с того, что найдем Епл внутри проводника, в точке, симметричной по от-
отношению к рассматриваемой точке пустого пространства. В этой точке Епл
q су
= О

3.5] Электростатика проводников 87
компенсирует напряженность, создаваемую в этой же точке зарядом q. Сле-
Следовательно, Епл внутри проводника точно совпадает с полем воображаемого
заряда (—д), помещенного в ту же точку, что и заряд q. Последний шаг: поле
зарядов проводника Епл симметрично относительно плоскости (все заряды
расположены на поверхности!). Значит, вне проводника Епл точно совпадает
с полем воображаемого заряда (—q), но расположенного симметрично заря-
заряду q. Этот воображаемый заряд называют «изображением» заряда д, а сам
метод — методом электростатических изображений. Теперь можно найти:
а) силу притяжения заряда и проводника F = kq2/BaJ; б) напряженность
поля во всем пространстве вне проводника (она равна напряженности двух
зарядов -\-q и — q)\ в) распределение зарядов на поверхности проводника —
зная напряженность поля возле поверхности, по формуле A7) можно опре-
определить а.
> Принцип единственности. При решении задач с неизвестным
распределением заряда помогает принцип единственности, который
можно сформулировать следующим образом: существует единственное
распределение зарядов по поверхности проводников и единственное
поле Е(г) в пространстве между ними, при котором напряженность
поля внутри проводников равна нулю, а потенциалы или заряды про-
проводников имеют заданные значения. Если удастся угадать такое рас-
распределение зарядов или такую конфигурацию поля, при котором эти
условия выполняются, то это решение и будет правильным. Например,
заметив, что эквипотенциальная поверхность ср = О для поля двух
зарядов q и — q совпадает с их плоскостью симметрии (см. рис. 33),
можно сделать вывод, что их поле с той стороны от этой плоскости, где
находится заряд q, совпадает с полем заряда q и проводящей плоскости
(см. предыдущий пример).
Пример 2. Проводящий шар в однородном поле. Рассмотрим про-
проводящий незаряженный шар в одно-
однородном поле Ео. Заряды на шаре рас-
распределятся так, чтобы создать внут-
ри шара поле (—Ео). Чтобы подобрать
такое распределение зарядов, рассмот-
рим два воображаемых шара такого °
же радиуса, но равномерно заряжен-
заряженных по объему, один — зарядом плот- >
ностью /9, другой — плотностью —р.
(Поле такого шара было рассмотрено
в примере 3 из разд. 3.4.) Если центр Рис. 34
положительного шара смещен на малое расстояние 1 по отношению к центру
отрицательного (рис. 34), то в области их пересечения поле равно
т. е. является однородным. Плотность заряда внутри пересечения шаров
равна нулю. Устремим теперь 1 к нулю, а р к бесконечности, так чтобы
pl/Ceo) = Ео. В итоге получим правильное распределение зарядов:
а = <7ocos#, где ао = pi = ЗеоЕо, а также найдем поле, создаваемое

Электродинамика
[Гл. 3
зарядами проводящего шара вне шара: оно совпадает с полем точечного
диполя с дипольным моментом р = (pV)l = AneoR Ео (см. пример 4 из
разд. 3.3).
3.6. Электростатика диэлектриков
> Поляризация диэлектрика. Поляризованность. Диэлектри-
Диэлектриком называют вещество, которое не проводит электрический ток, сле-
следовательно, в этом веществе отсутствуют свободные заряды (или их
ничтожно мало). Тем не менее, в присутствии диэлектрика происходит
ослабление электрического поля. Это свидетельствует о том, что при
помещении диэлектрика в электрическое поле в объеме и на поверх-
поверхности появляются макроскопические заряды. Указанные заряды воз-
возникают в результате поляризации диэлектрика — смещении связанных
зарядов отдельных молекул или кристаллической решетки друг отно-
относительно друга. При поляризации средний дипольный момент молекул
становится отличным от нуля, и возникает дипольный момент объе-
объема диэлектрика. Степень поляризации в данной точке диэлектрика
характеризуют поляризованностъю Р, определяемой как суммарный
дипольный момент молекул в расчете на единицу объема:
р =
AV
где п — концентрация молекул. Для построения макроскопических
уравнений поля в диэлектрике можно упрощенно считать, что все
молекулы в объеме AV имеют одинаковый дипольный момент
> Поляризованность и связанные заряды. Механизм образова-
образования макроскопических связанных зарядов проще всего представить
в случае однородной поляризации (Р = const). В этом случае объем
диэлектрика остается электронейтральным,
а на его поверхности появляются заряды —
на передней (по отношению к Р) положи-
положительные, на задней — отрицательные. Созда-
Создаваемая ими напряженность будет направлена
против поляризованности Р.
При поляризации через произвольную
площадку As в объеме диэлектрика (вклю-
(включая его границу) в направлении нормали к по-
поверхности проходит заряд
Aq = n(As(l) cos в)q0 = PnAs = (P • As),
Рис. 35 A8)
где As(l) cos 0 — объем тонкого цилиндриче-
цилиндрического слоя, молекулы которого при поляризации пересекают площадку
(рис. 35). Проинтегрировав по любой замкнутой поверхности, найдем

3.6] Электростатика диэлектриков 89
полный связанный заряд, вышедший из охватываемого ею объема, что
означает появление внутри объема связанного заряда
= -1 Р . ds или divP = -/B, A9)
где ds = n ds направлен, как обычно, в сторону внешнего пространства.
Для поверхностной плотности связанного заряда из A8) получим:
<тсв = Р„. B0)
> Электрическое смещение. Макроскопическая напряженность
электрического поля в диэлектрике определяется как результат усред-
усреднения микроскопической напряженности Е (сильно меняющейся на
межатомных расстояниях) по малому объему, содержащему достаточ-
достаточно много молекул: Е(г) = (Емикро). Напряженность поля определяется
как связанными, так и сторонними, нанесенными на диэлектрик извне,
зарядами:
= — (Св + Св)' B1)
Так как распределение связанных зарядов заранее не известно,
удобно ввести новую величину, которую называют электрическим сме-
смещением:
D = ?0E + P. B2)
Из уравнений A9), B1) следует, что электрическое смещение опреде-
определяется только сторонними зарядами:
D ds = Св B3)
(теорема Гаусса для электрического смещения). В дифференциальной
форме это уравнение имеет вид
divD = pCT.
> Изотропный диэлектрик. Поляризованность Р в данной точке
диэлектрика возникает под воздействием электрического поля и опре-
определяется его напряженностью Е. Для не очень сильных полей Р зави-
зависит от Е линейно, а в изотропном диэлектрике, кроме того, Р || Е:
Р = ?0^Е, B4)
где к — диэлектрическая восприимчивость вещества. Для электриче-
электрического смещения в однородном диэлектрике получим:
D = еоеЕ, B5)
где е = 1 + к — диэлектрическая проницаемость вещества.

90 Электродинамика [ Гл. 3
> Условия на границе раздела диэлектриков. На границе раз-
раздела двух диэлектриков выполняются следующие условия для танген-
тангенциальных (касательных) и нормальных компонент:
Е1т = Е2т, D2n-Dln = ac\ P2n - Р1п = -асв B6)
(нормаль п проведена из первой среды во вторую). Если стороннего
заряда на границе нет, то нормальные компоненты смещения равны
друг другу. Первое условие получается из условия потенциальности
поля Е (работа по замкнутому контуру равна нулю), второе и третье —
из формул B3) и A9). В случае изотропного диэлектрика имеем:
Е\т = Е2т, S\E\n — <S2^2n5 D\n = ?>2n5 = -• B7)
Видно, что на границе диэлектрических сред происходит преломление
линий напряженности. (Отметим, что линии электрического смеще-
смещения проходят через границу непрерывно, в отличие от линий напря-
напряженности, которые частично заканчиваются на отрицательном поля-
поляризационном заряде или начинаются на положительном.)
> Вычисление полей в присутствии диэлектриков. Уравнения
для Е и D вместе с условием связи между ними в данном веществе B5)
и граничными условиями B7) однозначно определяют поле во всем про-
пространстве по известному расположению сторонних зарядов. Отметим
некоторые свойства решения:
1. Из уравнений A9) и B3) и формулы Р = D, которая
является следствием B4) и B5), для однородного диэлектрика получим
рсв = -?—*рст. B8)
Следовательно, в отсутствие стороннего объемного заряда в результате
поляризации будет возникать только поверхностный связанный заряд.
(Если диэлектрик неоднородный, т. е. е зависит от координат, то объем-
объемный связанный заряд возникает и в отсутствие объемного стороннего
заряда.)
2. Если границы однородного диэлектрика совпадают с эквипотен-
эквипотенциальными поверхностями того поля Eq, которое создают сторонние
заряды в отсутствие диэлектрика, то всем граничным условиям удо-
удовлетворяет решение
Е(г) = *?>. B9)
Пример 1. Если точечный заряд q окружить сферическим слоем из
диэлектрика (внутренний радиус Ri, внешний — ife), то вне диэлектрика

3.6] Электростатика диэлектриков 91
напряженность поля не изменится, а внутри
4тг?о? г е 4тгг
Ц.
4тгЯ2
Связанные заряды на поверхностях равны друг другу: q%* = — q{B = g
Пример 2. Рассмотрим шар из однородного диэлектрика, равномерно
заряженный сторонним зарядом с объемной плотностью р. Напряженность
поля в отсутствие диэлектрика определена в примере 3 из разд. 3.4. В при-
присутствии диэлектрика напряженность при г < R уменьшится в е раз:
Нетрудно проверить, что сгсв4тг/2 = —pCB — 7rR , т.е. полный связанный
заряд, как и должно быть, равен нулю.
Пример 3. Если в однородное поле Ео перпендикулярно напряженности
поместить пластину диэлектрика, у которого е меняется от е\ на одном конце
до ?2 на другом, то получим
D = е0 Ео = const, Е = —^-, Р = D- , рсъ = -— = —$-;-,
е(х) ? dx el dx
а? = Р2 = D?2~l aT = -Pi = D?l~l
Легко проверить, что полный связанный заряд равен нулю.
Пример 4. Если в однородное поле Ео внести шар из однородного
диэлектрика, то он поляризуется однородно (Р = const). Действительно,
равномерная поляризация соответствует сдвигу на малый вектор 1 двух
равномерно заряженных шаров; как было показано в примере 2 из разд. 3.5,
при этом внутри шаров возникает однородное поле с напряженностью
Ei = — pl/Зео = —(<7l/V)/3eo = —P/3so- Полное поле в диэлектрике при
этом равно Е = Ео + Ei = Ео — Р/Зво- Из этого уравнения и условия
Р = (е — 1)боЕ находим
Е, РЕо.
? + 2' ? + 2
При этом выполняются все граничные условия.
> Механизмы поляризации. Различают три механизма поляриза-
поляризации диэлектриков.
1. Ориентпационный механизм поляризации полярных диэлектри-
диэлектриков. Молекулы полярного диэлектрика (полярные молекулы) обла-
обладают постоянным дипольным моментом ро в отсутствие поля (Н2О,
НС1 и др.). Вследствие теплового движения, в отсутствие поля все
направления дипольного момента равноправны, и средний дипольный
момент равен нулю. Внешнее поле стремится установить дипольные

92 Электродинамика [ Гл. 3
моменты молекул вдоль Е (см. разд. 3.3). В результате конкуренции
ориентирующего действия поля и теплового движения возникает сред-
средний дипольный момент (р), который в слабом поле (роЕ <С кТ)
пропорционален Е и убывает с ростом температуры.
В газообразных диэлектриках, в соответствии с распределением
Больцмана (см. разд. 2.5), вероятность ориентации р пропорциональна
expf — —^ 1, где Wn = — (р • Е). Видно, что во внешнем поле средний
дипольный момент должен быть направлен вдоль Е и пропорционален
-р=-], где f(x) — некоторая функция, равная нулю при х = О
и единице при х —> ос ( что соответствует сильному полю, когда все
диполи почти параллельны Е). При малых х (слабое поле) f(x) « jx,
2
(р) ~ ТттттЕ! — средний дипольный момент пропорционален Е и обрат-
гъ 1
но пропорционален Т. Расчет дает для j значение 1/3, т. е. Р = - —^-Е,
следовательно, для диэлектрической проницаемости получим
1 ЗеокТ
(формула Девая — Ланжевена).
2. Электронный (деформационный) механизм поляризации непо-
неполярных диэлектриков. В отсутствие внешнего поля дипольный момент
неполярной молекулы равен нулю (Н2, O2, N2 и т.д.), т.е. наименьшей
потенциальной энергией обладает такое состояние молекулы, при ко-
котором центр отрицательного заряда (электронного облака) совпадает
с центром положительного. При включении внешнего поля центры
положительного и отрицательного зарядов смещаются, и возникает
сила, стремящаяся вернуть их в положение равновесия; при малом
смещении / эта сила пропорциональна /: F = —/31 (квазиупругая сила).
В положении равновесия </Е = /31, т. е. возникающий под действи-
действием поля (индуцированный) дипольный момент р = q$\. оказывается
пропорциональным напряженности поля: р = аво~Е. Определенный
таким образом коэффициент а называют поляризуемостью молекулы.
Поляризуемость диэлектрика равна Р = пр = ns$aEi, где Е — поле,
действующее на одну молекулу. В газах это поле можно считать равным
среднему полю в диэлектрике, и для диэлектрической проницаемости
получим:
? = 1 + х=1 + an.
В плотных газах, жидких и твердых диэлектриках надо учитывать от-
отличие поля, действующего на молекулу, от среднего поля в диэлектрике
(второе включает в себя поле самой молекулы, а первое — нет).
Рассмотрим однородный кристаллический диэлектрик с неполярными мо-
молекулами. Чтобы найти локальное поле, действующее на данную молекулу,

3.7] Конденсаторы 93
рассмотрим сферу, центр которой совпадает с этой молекулой. Если молеку-
молекулы расположены правильным образом (например, в вершинах кубического
кристалла), то поле молекул, находящихся внутри сферы, в ее центре равно
нулю. Следовательно, локальное поле в данной точке равно ЕЛОк = E+Ei, где
Е — макроскопическое среднее поле в диэлектрике (равное сумме внешнего
поля и поля зарядов на внешней поверхности диэлектрика), a Ei — поле
зарядов на внутренней поверхности полости. Из примера 4 следует, что
Ei = P/3s0, и тогда Р = пеоа(Е + Р/Зео), откуда
~ па
1 ~ ~з~
Учитывая, что Р = ео(е — 1)Е, получим
па е — 1 па
е — 1 = , или = —.
па' е + 2 3
~ ~3~
Этот результат известен как формула Клаузиуса — Масотти.
3. Ионная поляризация в твердых диэлектриках, обладающих кри-
кристаллической решеткой. Под действием поля подрешетка положитель-
положительных ионов смещается целиком в одну сторону, подрешетка отрицатель-
отрицательных ионов — в другую.
> Сегнетоэлектриками называют вещества (например, сегнетову
соль), в которых ниже температуры Тс, называемой температурой
Кюри, небольшие области — домены — спонтанно поляризованы до на-
насыщения (все диполи ориентированы параллельно). Сегнетоэлектрики
по своим свойствам являются электрическими аналогами ферромаг-
ферромагнетиков: они имеют аномально большую диэлектрическую проницае-
проницаемость, зависящую от Е и Т, проявляют при поляризации гистерезисные
свойства, превращаются в обычные диэлектрики при нагревании выше
температуры Кюри (подробнее см. разд. 3.13).
3.7. Конденсаторы
> Электроемкость конденсатора. Конденсатором называется си-
система из двух изолированных друг от друга проводников, один из кото-
которых заряжен зарядом +</, другой — зарядом — q. Проводники называют
обкладками конденсатора, заряд q — зарядом конденсатора, разность
потенциалов между положительной и отрицательной обкладками U —
напряжением на конденсаторе. Напряжение на конденсаторе пропор-
пропорционально его заряду:
U = ig, C0)
где С — электроемкость (или просто емкость) конденсатора.
> Простые конденсаторы. Конденсатор называют простым, если:
а) электрическое поле сосредоточено в ограниченной области простран-
пространства между его обкладками (т. е. можно считать, что все силовые

94 Электродинамика [ Гл. 3
линии начинаются на положительной обкладке и заканчиваются на
отрицательной); б) все пространство, в котором сосредоточено поле,
заполнено однородным диэлектриком.
Пример 1. Плоский конденсатор. Конденсатор называется плоским,
если его обкладками служат две параллельные пластины площадью S, рас-
расстояние между которыми мало по сравнению с их размерами (d <С y/~S).
Поле между пластинами можно считать однородным всюду, кроме самых
краев. Напряженность поля найдем с помощью формулы A7): Е = q/{eqsS).
Напряжение на конденсаторе U = Ed, а его емкость равна
С = ^. C1)
а
Пример 2. Сферический конденсатор. Конденсатор называется
сферическим, если его обкладками служат две концентрические сферы
с радиусами R\ и R2. Напряженность поля между обкладками: Е =
0
где г — расстояние до центра. Напряжение вычисляется по формуле
U = /я2 Е(г) dr, а емкость равна
_
R2- Ri
При R2 —>- oo это выражение переходит в емкость уединенной сферы (см.
разд. 3.5).
Пример 3. Цилиндрический конденсатор. Конденсатор называ-
называется цилиндрическим, если его обкладками служат два концентрических
цилиндра радиусов R± и R2 и длиной / У%> R2 — R±. Напряженность меж-
между обкладками равна Е = -. Напряжение вычисляется по формуле
U = /я2 E(r) dr, а емкость равна
С = \n(R2/Ri)'
> Составные конденсаторы. Соединяя обкладки простых кон-
конденсаторов, получим составной конденсатор. Емкость составного
конденсатора определяется фор-
С\ мулой C0) и выражается через
емкости его компонентов.
Ci C2 i Параллельное соединение. Все
—| ^—^— \— обкладки соединены между собой
q —q q —q и образуют обкладки составного
конденсатора (рис. 36, а). В этом
^ случае имеем
Рис.36 U = U{, <7 = V]<7;, С = У^ Cj.
2. Последовательное соединение. Обкладками составного конден-
конденсатора служат обкладки крайних конденсаторов (рис. 36, б), полный
заряд на каждой паре внутренних обкладок равен нулю. Имеем

3.8] Энергия электростатического поля 95
3. Во многих случаях можно рассчитать емкость составного кон-
конденсатора, шаг за шагом заменяя последо-
последовательно и параллельно соединенные кон-
конденсаторы на эквивалентную емкость. Ее-
Сь\
I
с2 а
в
ли же схему нельзя свести к параллель-
параллельным — последовательным элементам, то
можно воспользоваться методом узловых
потенциалов.
Пример 4. Рассмотрим схему на рис. 37.
Примем срл = 0, тогда срв = U. Потенци- ' ' 2
алы (pi и (f2 найдем из системы уравнений, Р г 47
выражающих условие электронейтральности
в узлах 1 и 2 (полный заряд трех обкладок, подходящих к каждому узлу,
должен быть равен нулю):
(<?>i — и)Сз + (<^i ~~ ф2)Съ + (fiCi = О,
(у>2 - U)Ca + O2 - ч>\)Сь + V2C2 = 0.
Решив уравнения, найдем заряд составного конденсатора q = Ci(fi + С2У2
и емкость С = q/U.
3.8. Энергия электростатического поля
> Энергия системы зарядов. Энергия взаимодействия системы
зарядов определяется как работа внешних сил, необходимая для со-
создания этой системы, или как работа, совершаемая силами поля при ее
уничтожении. Энергия взаимодействия двух точечных зарядов равна
энергии одного заряда в поле, создаваемом другим зарядом:
Энергия взаимодействия системы точечных зарядов равна
w = Е wa = \H wiJ = \Т.чМп)- C2)
i>j гфз i
Здесь (f(ri) — потенциал, создаваемый всеми остальными зарядами
в той точке, где находится г-й заряд. Если переписать эту формулу
для заряда, непрерывно распределенного по поверхности или объему
в ограниченной области пространства, то получим:
W = \ \ <р(т)р(т) dV + \\ <р(т)<т(т) ds. C3)
V S
Хотя формула C3) получена формальным обобщением C2), между ними
есть принципиальные различия. В формуле C2) (p(ji) — потенциал, созда-
создаваемый остальными зарядами, а в C3) ip(r) — потенциал всех зарядов
в точке г (вклад элемента объема или поверхности при уменьшении размеров
стремится к нулю). Но самое главное — C2) учитывает только энергию
взаимодействия, после разнесения точечных зарядов далеко друг от друга

96 Электродинамика [ Гл. 3
остается собственное поле каждого заряда; формула C3) позволяет вычис-
вычислить полную энергию системы непрерывно распределенных зарядов (при
разделении системы на всё более мелкие части энергия стремится к нулю).
Пример 1. Вычислите энергию равномерно заряженного шара радиу-
радиусом R.
Решение. Подставляя в C3) потенциал поля шара (см. пример 3 из
разд. 3.4), получим
я
3 , а
2 J V 2Я3 2 R) 5 R
о
> Энергия уединенного проводника. Все заряды на проводнике
находятся при одинаковом потенциале, равном потенциалу проводни-
проводника. Из формулы C3) имеем
где С — электроемкость проводника (см. разд. 3.5). Это выра-
выражение получается и прямым расчетом работы электрического
поля при постепенном удалении всего заряда на бесконечность:
W = J (p(q) dq = С J^ ip dcp = -Сер2. Например, энергия уединенной
проводящей сферы равна
w= q2
где е — диэлектрическая проницаемость среды вокруг сферы.
> Энергия конденсатора. Из формулы C3) получим
w=<m__wi = q? = c\f_ q_ { ,
2 2 2 2 2С К ]
Поле в конденсаторе можно уничтожить, перенося заряд малыми пор-
порциями с одной обкладки на другую: W = §U(q)dq = С Jo U dU =
= -СU2. Например, энергия плоского конденсатора равна
W = -^-(Edy = -^—Sd. C6)
> Плотность энергии электрического поля. При полевом под-
подходе надо говорить не об энергии взаимодействующих зарядов, а об
энергии окружающего их электрического поля. Объемная плотность
энергии электрического поля w = dW/dV в пустом пространстве
зависит только от напряженности поля:
e0E. C7)
Это выражение верно для любого распределения зарядов (его можно
получить, рассмотрев однородное поле плоского конденсатора).

3.8] Энергия электростатического поля 97
Исходя из уравнений поля (см. разд. 3.4), формулу C3) можно
преобразовать к виду
W = \\e0E2dV, C8)
где интегрирование ведется по всему пространству.
Например, при вычислении энергии заряженного шара (пример 1) по
формуле C3) интегрирование производилось по объему шара, однако C8)
показывает, что только часть энергии поля заключена внутри шара, а часть —
в окружающем шар пустом пространстве. Формулы C3) и C8) позволяют
вычислить полную энергию поля во всем пространстве только если: а) от-
отсутствуют точечные заряды и заряды, распределенные по линии; б) заряды
распределены по конечной области пространства. Однако C8) позволяет вы-
вычислять энергию, сосредоточенную в конечной области пространства, даже
если полная энергия бесконечна.
В случае диэлектрика плотность энергии оказывается в е раз боль-
больше:
w = \е0еЕ2 = \ED = \е0Е2 + \ео(е - 1)Е2. C9)
Первый член в последнем выражении представляет собой непосред-
непосредственно энергию электрического поля в диэлектрике, а второй (рав-
(равный -Е • Р) — работу, совершаемую полем над молекулами при его
включении. Это выражение можно обобщить на случай, когда Р (и D)
не пропорциональны Е (сегнетоэлектрики, сильные поля). Для этого
надо рассмотреть зарядку плоского конденсатора, заполненного таким
диэлектриком:
D
о
> Закон сохранения энергии и вычисление сил. Для вычис-
вычисления сил, действующих на заряженное или поляризованное тело
в электрическом поле, надо рассмотреть медленное изотермическое
изменение его положения. При этом работа внешних сил плюс работа
источников равна изменению энергии поля. Так как тело находится
в механическом равновесии, то работа внешних сил равна работе силы,
действующей со стороны поля, с обратным знаком.
Пример 2. Рассмотрим плоский конденсатор (отключенный от источ-
источника), который заполнен жидким или газообразным диэлектриком. Найдите
силу, действующую на обкладку конденсатора.
Решение. При увеличении расстояния между обкладками на dx энер-
энергия увеличится на -EDS dx, а работа равна F dx. Следовательно, сила
притяжения равна F = -EDS = -Eq, где -Е — напряженность в ди-
диэлектрике, создаваемая одной обкладкой. Если диэлектрик представляет
собой твердую пластину, то между диэлектриком и обкладкой существует
4 А. И. Черноуцан

98 Электродинамика [ Гл. 3
4 / воздушный промежуток, изменение энергии равно
1 111
-?qE2S dx, а сила F = -?qE2S = -qE0, где -#о —
напряженность, создаваемая одной пластиной в воздушном
промежутке.
Пример 3. Вычислите силу, которая втягивает пластину
из диэлектрика в пространство между обкладками плоского
конденсатора.
Решение. Будем считать, что размеры пластины
совпадают с размерами обкладок, а толщина пластины
чуть меньше, чем расстояние b между ними. Будем
также считать, что конденсатор подключен к источнику,
Рис. 38 который поддерживает на нем постоянное напряжение U.
Уменьшим на dx расстояние, на которое пластина
вдвинута в конденсатор (рис. 38). Энергия поля в объеме dV = ab dx
изменится на dW = ( -sqE2 sosE2 1 ab dx (a — ширина пластины,
E = U/b — напряженность поля), заряд на пластинах изменится на
dq = Aaadx = (eoE — eoeE)adx, работа источника 8AUCT = U dq в два
раза больше изменения энергии поля. Записав закон сохранения энергии
F dx + 5АпСТ = dW, получим F = -ео(е — 1)аЬЕ2. Заметим, что нам
удалось вычислить силу, возникающую вследствие искривления поля
у краев конденсатора, хотя расчет энергии производился без учета краевых
эффектов.
3.9. Постоянный ток
> Сила тока. Плотность тока. Электрическим током называет-
называется упорядоченное движение электрических зарядов. Конвекционным
током называют движение зарядов, связанное с перемещением в про-
пространстве заряженного тела. Ток проводимости в веществе осуществ-
осуществляется свободными зарядами (носителями тока) —электронами в ме-
металлах, электронами и дырками в полупроводниках, ионами в электро-
электролитах. За направление тока принимается направление движения поло-
положительных зарядов. Заряд, проходящий за время dt через площадку
ds = n ds внутри проводника в направлении нормали п, определяется
средней скоростью свободных зарядов (v):
dq = qon(v) • ds dt = j • s dt, D0)
где qo — заряд носителей тока, п — их концентрация, a j = qon(v) —
плотность тока. Силой тока I называется заряд, проходящий через
сечение проводника в единицу времени:
dq = Idt = dt Г j - ds, D1)
где интегрирование производится по поперечному сечению. Для линей-
линейного (S = const) проводника j = const, и D1) приобретает вид: / = jS.
Ток называется постоянным, если / = const.

3.9] Постоянный ток 99
Уменьшение заряда внутри замкнутой поверхности равно dqo^ = — dt § j • ds.
В дифференциальной форме закон сохранения заряда принимает вид:
— = —divj. В случае постоянного тока §} • ds = 0 (divj = 0), т.е. линии
тока непрерывны и направлены вдоль проводника.
> Закон Ома в дифференциальной форме. Для поддержания
тока в веществе на свободные заряды должна действовать постоянная
сила F электромагнитной природы, которую можно характеризовать
напряженностью Е = F/^o- Как только эта сила исчезает, за ничтожно
малое время средняя скорость свободных зарядов обращается в нуль.
При не очень больших значениях Е плотность тока в изотропном
проводнике должна быть пропорциональна Е:
j = аЕ = ±Е, D2)
где а — удельная проводимость вещества, р — удельное сопротивле-
сопротивление. Из закона сохранения заряда следует, что если р = const, то
§~E-ds = р§5 • ds = 0 (divE = 0), т.е. в однородном проводнике
линии напряженности непрерывны, а в проводе постоянного сечения
они параллельны поверхности провода.
> Закон Джоуля — Ленца в дифференциальной форме. При
протекании тока по проводнику работа, совершенная полем Е над
свободными зарядами, полностью переходит в энергию теплового дви-
движения при их соударениях с ионами. Объемная плотность тепловой
мощности тока равна работе поля над зарядами в единице объема за
единицу времени:
^Тепл = n(v> • F = qon(v) • Е = j • Е = аЕ2 = pj2. D3)
> Однородный участок цепи. Сопротивление. Если на участ-
участки цепи протекание тока обеспечивается только электростатическим
(кулоновским) полем (т.е. pj = Екул), то участок цепи называется од-
однородным. В однородном (р = const) проводнике § Е • ds = р § j • ds = 0,
и в соответствии с теоремой Гаусса (см. разд. 3.4) заряд, создающий по-
поле, расположен только на поверхности. В проводе постоянного сечения
эквипотенциальные поверхности совпадают с поперечными сечениями
провода. Сила тока, протекающего в направлении от сечения 1 к сече-
сечению 2, пропорциональна разности потенциалов ipi — ip2 (закон Ома для
однородного участка цепи):
кул.(Д => (Pl-(P2 = IR. D4)
Если / < 0, то ток протекает от 2 к 1. Здесь R = §1(p/S)dl —
сопротивление проводника, измеряется в омах (Ом). Для однородного
линейного проводника R = pl/S. Удельное сопротивление зависит

100 Электродинамика [ Гл. 3
от температуры; в широких пределах можно пользоваться линейной
зависимостью р = роA + at), где ро — удельное сопротивление при
0°С, а — температурный коэффициент сопротивления. Для металлов
а « 1/273 (т.е. р ~ Т), для полупроводников а < 0.
> Сторонние силы. ЭДС. Хотя на отдельном участке цепи ток
может поддерживаться электростатическими силами, полная работа
этих сил в замкнутой цепи равна нулю. Следовательно, для компен-
компенсации тепловых потерь в цепи должны действовать сторонние силы
неэлектростатической природы,
1 ~ ~ 1+ полная работа которых отлична от
нуля, т.е. должны присутствовать
©12 = — © G12 = © источники тока (рис. 39). Эти
силы имеют электромагнитную
природу: IJtop = <7oECTOp, и их работа по переносу пробного заряда q
пропорциональна q:
2
Aq(l -> 2) = q jECTOp • d\ = q?12 = ±q?, D5)
l
где 8 называют электродвижущей силой источника (ЭДС), знак «+»
соответствует случаю, когда при движении от 1 к 2 источник проходит-
проходится в направлении действия сторонних сил (от отрицательной обкладки
к положительной), знак « —» — противоположному случаю. Мощность
сторонних сил (мощность источника) равна
(работа сторонних сил над всеми зарядами проводника за время dt
равна работе по переносу заряда I dt с одного конца проводника на
другой).
> Закон Ома для неоднородного участка цепи. На неоднород-
неоднородном участке цепи действуют как электростатические, так и сторонние
силы. Дифференциальный закон Ома D2) принимает вид
j = i(EK^ + ECTOp), D7)
а закон Ома для участка цепи записывается так:
2 2
Если / < 0, то ток протекает от 2 к 1. Величину U\2 — (</?i ~ ^2) + ?12?
равную работе полной силы по переносу единичного заряда между
сечениями 1 и 2, называют напряжением на участке цепи; для одно-
однородного участка напряжение равно разности потенциалов. Закон Ома
утверждает, что на любом участке цепи IR = Ui2-

3.9] Постоянный ток 101
> Закон Джоуля — Ленца для участка цепи. Тепловую мощ-
мощность тока на участке цепи можно найти с помощью формулы D3):
Ртепл =]wSdl = \pfSdl = I2 L| = I2R. D9)
1 1 1
> Закон Ома для неразветвленной цепи. В неразветвленной
замкнутой цепи / = const; сложив уравнения D8) для всех участков
цепи, получим:
/?Я4 = ??,-. E0)
В случае источника с внутренним сопротивлением г, замкнутого на
внешнее сопротивление R, имеем: / = ? /(R + r); разность потенциалов
на клеммах источника равна у?+ — ср- = IR = ? — Ir, ток короткого
замыкания источника (R = 0) равен /кз. = ? /г. Закон Ома E0) выра-
выражает закон сохранения энергии для неразветвленной цепи: мощность
сторонних сил равна мощности тепловых потерь на сопротивлениях
цепи.
Полезная мощность источника тока. Если источник служит для
передачи энергии во внешнюю цепь, то полная (затраченная) мощность равна
мощности сторонних сил: РПолн = ?11 потерянная мощность — тепловым
потерям на внутреннем сопротивлении: Рпотер = /V. Для полезной мощности
получим: Рполезн = ?1 — 1 г = /А(р, где Л(р — разность потенциалов на
клеммах источника, Рполезн максимальна при / = ?/Bг).
Если на участок цепи подается разность потенциалов ср± — ср2 и на
участке включено устройство, совершающее работу против внешних сил
(мотор), то полная мощность: РПОЛн = (ipi — ^2)/, потерянная мощность:
Рпотер = I2R (R — сопротивление обмотки мотора), полезная мощность:
Рполезн = (ifi — 4>i)I — I2R = —?12/ = ?1- Величины ? и I зависят от
скорости вращения ротора мотора; максимальная Рполезн достигается при
> Расчет разветвленной цепи. Правила Кирхгофа. Для нахо-
нахождения токов в различных участках разветвленной цепи надо произ-
произвольным образом обозначить неизвестные токи и придать им произ-
произвольные направления, после чего воспользоваться одним из следующих
методов:
1. Метод узловых потенциалов. В качестве неизвестных принима-
принимают потенциалы узлов цепи (один из потенциалов принимают равным
нулю). С помощью D8) выражают токи через потенциалы, затем для
7V — 1 узла записывают закон сохранения заряда: ^ U = 0 (алгебраи-
(алгебраическая сумма токов, сходящихся в узле, равна нулю). Найдя ipi, из D8)
находим токи.
2. Правила Кирхгофа. В этом методе неизвестными являются сами
токи. Сначала записывают для 7V — 1 узла уравнения ^ 1{ = 0 (первое
правило Кирхгофа). Затем выбирают произвольный замкнутый кон-
контур, обходят его в произвольном направлении и, суммируя D8) для

102 Электродинамика [ Гл. 3
каждого участка, получают уравнение ^ ЦЩ = ^2 ?ij (второе правило
Кирхгофа). Повторяя эту процедуру необходимое число раз, получают
систему уравнений для токов.
> Эквивалентные сопротивления и источники. Несколько со-
соединенных между собой сопротивлений Щ можно заменить одним
эквивалентным сопротивлением R.
1) Последовательно соединенные сопротивления: R = ^ Ri.
2) Параллельно соединенные сопротивления: R~x = ^ R~l.
3) В общем случае для вычисления эквивалентного сопротивления
надо использовать методы расчета разветвленных цепей.
Несколько соединенных источников с параметрами <^, г^ можно
заменить одним эквивалентным источником с параметрами ?, г.
1) Последовательное соединение: ? = ^^Ь r = S ri-
2) Параллельное соединение: ? = ^?^~г / ^ г, г = ^г~х.
3) В общем случае для вычисления эквивалентных ? и г надо
использовать методы расчета разветвленных цепей.
> Классическая электронная теория металлов. Проводимость
металлов осуществляется обобществленными валентными электрона-
электронами. В классической электронной теории Друде — Лоренца газ элек-
электронов считается классическим газом, концентрация которого равна
концентрации атомов металла, а температура — температуре метал-
металла. Ток проводимости рассчитывается в предположении, что элек-
электроны приобретают скорость упорядоченного движения при свобод-
свободном движении и полностью теряют ее при каждом столкновении
с ионами кристаллической решетки. Кроме того, предполагается, что
|(v)| <$C (v) ~ ykT. Средняя скорость упорядоченного движения равна
(v) r»j ат/2 = еЕт/Bте), где среднее время между столкновениями г
выражается через среднюю длину свободного пробега и среднюю ско-
скорость теплового движения: г = Л/ (v). С учетом D0) получим:
/ ч е2п\ „ 2me(v)
J = en<v> = 2^МЕ' т"е- р = ^Чх
(при более тщательном анализе получается такой же ответ, но без
двойки в числителе; однако для оценочной модели это несущественно).
Обсуждение результатов классической электронной теории.
1. Теория объясняет рост р при повышении температуры, но предсказы-
предсказывает зависимость р ~ у/Т, а наблюдается р ~ Т.
2. Теория успешно объясняет закон Видемана — Франца: для всех метал-
металлов произведение коэффициента теплопроводности к (см. разд. 2.9) и удель-
удельного сопротивления пропорционально Т (произведение >ср содержит толь-
только (vJ).
3. Длина свободного пробега электронов, вычисленная из формул клас-
классической электронной теории, оказывается на несколько порядков больше

3.10] Магнитное поле. Сила Лоренца и закон Ампера 103
межатомного расстояния, что противоречит основным представлениям тео-
теории.
4. Классическая электронная теория предсказывает электронный вклад
в молярную теплоемкость -R (см. разд. 2.5). Экспериментально вклад элек-
электронов в теплоемкость оказывается ничтожно малым.
3.10. Магнитное поле. Сила Лоренца
и закон Ампера
> Магнитная индукция. Сила Лоренца. Магнитное поле — од-
одна из двух составляющих электромагнитного поля (см. разд. 3.2).
Магнитное поле действует на движущиеся заряженные частицы, токи
и магнитные моменты. Источниками магнитного поля являются дви-
движущиеся заряженные частицы, токи, магнитные моменты и перемен-
переменные электрические поля. Характеристикой магнитного поля является
вектор магнитной индукции В. Для определения В можно исполь-
использовать выражение для силы, действующей на заряженную частицу
в электромагнитном поле:
F = qE + qv xB, E1)
Силу Е^ = qv xB, действующую на заряженную частицу со стороны
магнитного поля, называют силой Лоренца. (Иногда силой Лоренца,
или обобщенной силой Лоренца, называют полную электромагнитную
силу E1).) Сила Лоренца перпендикулярна скорости частицы, т.е.
работу не совершает.
Для определения магнитной индукции В с помощью формулы E1) надо:
1) измерить силу, действующую на неподвижную частицу, чтобы отде-
отделить действие электрического поля;
2) найти направление скорости v, для которого при постоянной v вели-
величина магнитной силы максимальна;
3) по величине силы найти модуль магнитной индукции: В = Fma^/(qv);
4) по направлению Ь^пах и v найти направление В с помощью правила
буравчика.
Магнитную индукцию удобно также определять по вращательному мо-
моменту, с которым магнитное поле действует на маленький виток с током. На
виток с током действует только магнитное поле.
В СИ магнитная индукция измеряется в тесла (Тл).
Пример 1. Рассмотрим движение нерелятивистской частицы массой т
с зарядом q в однородном магнитном поле с индукцией В. Пусть в неко-
некоторый момент времени скорость частицы v направлена под углом а к В.
Сила Лоренца перпендикулярна как к v (т. е. v = const), так и к В (т.е.
сохраняются проекции скорости г;ц и v± на направление вектора индукции
и на перпендикулярную к нему плоскость). В проекции на перпендикуляр-
перпендикулярную плоскость частица движется по окружности, радиус которой можно
найти из второго закона Ньютона: qv±B = mv\jR. Период вращения

104
Электродинамика
[Гл. 3
Т = 2ttR/v± = 2тгт/qB не зависит от скорости. Результирующее движение
происходит по спирали радиусом R с шагом h = v\\T = 27rmv cos a/(qB).
> Закон Ампера. Сила, действующая на элемент тока в магнитном
поле, равна сумме сил Лоренца, действующих на движущиеся свобод-
свободные заряды:
dF = qo[{v)x B]dN = n<7o[(v)x В] dV = j xB dV = I d\ xB. E2)
При выводе силы Ампера, действующей на элемент объема dV с плот-
плотностью тока j и на линейный элемент d\ с током /, использовалась связь
плотности тока со средней скоростью свободных зарядов D0). Для
вычисления полной силы, действующей на объем с распределенным
током j(r) или на протяженный участок провода с током, надо произ-
произвести интегрирование. Например, на прямой участок провода длиной 1
с током / в однородном магнитном поле с индукцией В действует сила
/1 х В. Сила, действующая в однородном поле на любой замкнутый
контур с током, равна нулю: F = § I d\ х В = / (| d\) x В = 0.
> Магнитный момент контура с током. Магнитным моментом
контура с током называется векторная величина рт, равная
В
Рт
= / nds,
E3)
где интегрирование ведется по лю-
любой поверхности, натянутой на кон-
контур, а направление нормали опреде-
определяется направлением движения бу-
буравчика при вращении его по току.
В случае плоского контура
'Fa
mg
Магнитный момент контура, так же
как и дипольный момент электри-
электрического диполя (см. разд. 3.1 и 3.3),
Рис. 40 определяет магнитное поле контура
на больших расстояниях вдали от него и описывает поведение малень-
маленького витка с током в магнитном поле.
Пример 2. Рассмотрим прямоугольный контур, длины сторон которого
равны а и 6, подвешенный за сторону а в однородном вертикальном маг-
магнитном поле с индукцией В (рис. 40). При включении тока силой / контур
отклонится на угол /3, при котором момент силы тяжести уравновешивается
моментом сил Ампера mg-b sin /3 = I Bab cos ft, или tg/3 = 21Ba/'(mg).
Обратите внимание, что вращательный момент, действующий на контур со
стороны магнитного поля, равен М = /S х В = pm x В. Аналогичное
выражение было получено для вращательного момента, действующего на
электрический диполь в электрическом поле (см. разд. 3.3).

3.11] Вычисление магнитной индукции 105
3.11. Вычисление магнитной индукции
> Закон Био — Савара — Лапласа. Магнитная индукция, созда-
создаваемая в точке А элементом тока / dl, равна
03 = ^1^1, E4)
где г — радиус-вектор, проведенный от элемента тока к точке Л,
/io = 4тг • 10~7 Гн/м — магнитная постоянная. Это выражение можно
переписать для магнитной индукции элемента объемного тока jdV,
элемента поверхностного тока ids или, разделив на число свободных
частиц в элементе тока, для нерелятивистской частицы qv:
(Поверхностной плотностью тока называют силу тока, приходящуюся
на единицу длины перпендикулярного току отрезка: dl — % dl.) Для
вычисления магнитной индукции, создаваемой конечным объемом, по-
поверхностью или проводом, надо произвести интегрирование (принцип
суперпозиции для магнитной индукции).
> О системах единиц в электромагнетизме. Формулы будут
приводиться в СИ. Для перехода к гауссовой системе (СГС) в большин-
большинстве случаев достаточно заменить одновременно В на В/с (и поток Ф
на Ф/с) и /io на 4тг/с2. Если в формуле присутствует кулоновская кон-
константа к, ее надо заменить на единицу, а электрическую постоянную ?q
на 1/Dтг). Отметим, что произведение /io^o равно 1/с2.
Пример 1. Вычислите силу магнитного взаимодействия двух частиц
с зарядами q± и #2, скорости которых в некоторый момент равны vi = V2 = v
(v <C с) и направлены перпендикулярно соединяющей их линии.
Решение. Магнитная индукция, создаваемая первой частицей в точке,
где находится вторая частица, равна В = ^- (г — расстояние между
частицами) и направлена перпендикулярно v и г. Сила Лоренца в случае од-
одноименных зарядов направлена в сторону частицы 1 и равна F = ~—.
4тг г
2
Отношение магнитной силы к электрической равно llqSqv2 = —«-.
с
Пример 2. Магнитное поле в центре кругового тока. Найдите
магнитную индукцию, создаваемую круговым контуром радиусом R с током
/ в центре контура.
Решение. Магнитная индукция, создаваемая элементом дуги с угловым
размером dtp, равна
IRdcp
и направлена вдоль оси (в сторону движения буравчика при его вращении
по току). Магнитная индукция, создаваемая в центре окружности всем кру-
говым током, равна В = .
2R

106
Электродинамика
[Гл. 3
Пример 3. Найдите магнитную индукцию кругового тока в точке А на
его оси, находящейся на расстоянии у от центра витка (рис. 41).
Решение. Вектор В направлен вдоль оси у, а вклад элемента дуги
с угловым размером d(p равен
dBy = dB sin a = ^-
4тг
IRdcp
R
R)
После интегрирования по (р получим
uqIR
D = .
На большом расстоянии от контура {у
магнитная индукция
uqIR uo 2/(тгЯ2)
2у3 4тг у3
выражается через магнитный момент
pm = /S аналогично тому, как напряженность
электрического поля выражается через электрический момент диполя (см.
пример 4 из разд. 3.3, случай г || р). Можно показать, что и в произвольной
точке г магнитная индукция плоского маленького витка с током равна
Рис. 41
В =
E6)
Пример 4. Найдите магнитную индукцию, создаваемую прямым отрез-
отрезком провода в точке Л, положение которой относительно отрезка задается
расстоянием у до прямой и углами а,\ и а.2 (рис. 42).
Решение. Вклад в В элемента dx равен dB = s- sin а и на-
4тг г
правлен перпендикулярно плоскости, проходящей через отрезок и точ-
точку А. Интегрировать удобно по уг-
А лу он. после подстановки г = у / sin он,
и замены переменной: х = —^/ctga,
dx = у da/ sin2 а. В результате по-
получаем
В = (cos ai — cos аг). E7)
4тг?/
Полагая аа = 0, ol<z = тг, находим
магнитную индукцию бесконечного
провода с током:
В = ^-. E8)
Если с помощью E7) рассчитать магнитную индукцию в центре прямо-
прямоугольного контура с током, то получим
В =
Но Sly
4тг
ab
где а и b — длины сторон контура.

3.12] Циркуляция и поток вектора магнитной индукции 107
3.12. Циркуляция и поток вектора
магнитной индукции
> Теорема о циркуляции. Из закона Био — Савара — Лапласа
можно вывести утверждение, что циркуляция магнитной индукции
вдоль любого замкнутого контура определяется алгебраической сум-
суммой токов, охватываемых этим контуром (т. е. током, проходящим через
натянутую на контур поверхность):
Г Г
<Ь В • d\ = /io/охв = А*о I j • ds, E9)
где положительное направление нормали определяется движением бу-
буравчика при его вращении в направлении обхода контура.
> Теорема Гаусса для магнитного поля. Поток вектора магнит-
магнитной индукции (магнитный поток) через любую замкнутую поверхность
равен нулю:
". В • ds = 0. F0)
Это означает, что линии магнитной индукции всюду непрерывны, т. е.
не существует магнитных зарядов, на которых бы начинались или
оканчивались линии поля. Магнитный поток в СИ измеряется в веберах
(Вб).
Полезно отметить, что магнитный поток через поверхность, натя-
натянутую на заданный контур, не зависит от формы этой поверхности.
Поэтому можно говорить о потоке через контур, не указывая поверх-
поверхность.
Пример 1. Поле соленоида. Соленоидом называется длинная ци-
цилиндрическая катушка из тонкого плотно намотанного провода. Соленоид
характеризуют количеством витков п,
намотанных на единицу длины. Иде-
альной моделью соленоида называют
тонкую бесконечно длинную цилиндри-
ческую поверхность с поверхностным
током плотностью г = п/, текущим
перпендикулярно образующей. Нетруд-
но убедиться, что магнитная индукция
в идеальном соленоиде всюду направле-
на параллельно образующей (для этого
надо рассмотреть вклад любых двух симметричных элементов тока). Вне
соленоида поле отсутствует. Из теоремы о циркуляции и теоремы Гаусса
следует, что внутри соленоида В = const. Чтобы найти величину В, надо
применить теорему о циркуляции к прямоугольному контуру, одна сторо-
сторона которого проходит вдоль образующей внутри цилиндра, а другая — вне
(рис. 43): Bl = fiQil. Получим, что магнитная индукция внутри соленоида
равна
В = fioi = fionl. F1)
/
/
/
/
1
I
1
\
\
\
\
\
\
»
1
I
I
/
/
/
Рис.
I
43
X \
1
1
I
= nl
\
\
\
\
i
i
f
/
/

108
Электродинамика
[Гл. 3
г < R
r>R
Рис. 44
Рис. 45
Пример 2. Поле толстого провода. Найдем магнитное поле беско-
бесконечного прямого провода радиусом Я, по которому протекает ток / (рис. 44).
Линии индукции имеют вид окружностей. Выбирая окружность радиусом г
в качестве контура для теоремы о циркуляции E9), при г > R получим
ВBтгг) = fiol. Аналогично при г < R имеем ВBтгг) = fio 1(тгг2'/'тгR2). Из
этих равенств находим магнитную индукцию
\^ZZ при г > Я,
при г < R.
Пример 3. Поле плоскости с током. Рассмотрим ток, текущий по
бесконечной плоскости (ж, у) в направлении оси у с постоянной плотностью г.
Магнитная индукция над плоскостью при z > 0 направлена вдоль ж, а при
z < 0 — противоположно х (в этом можно убедиться, рассмотрев вклад двух
линий тока, расположенных симметрично по отношению к данной точке).
Выберем прямоугольный контур, одна сторона которого проходит над плос-
плоскостью в направлении х, а другая — симметрично ей под плоскостью (рис. 45).
Из теоремы о циркуляции получим: 2В1 = Ltoil, т. е. В = — Ltoi.
2
> Перемещение контура с током в магнитном поле. При пере-
перемещении или деформации контура с постоянным током / в постоянном
магнитном поле работа силы Ампера, действующей на участок конту-
контура, равна
6A = dF-dr = I[d\ х В] dr = /В [dr x dl] = /В • ds,
где dr — перемещение участка контура dl, ds — элемент площади,
заметенный этим участком при его перемеще-
перемещении (рис. 46). Суммируя вдоль всего контура,
получим, что механическая работа магнитно-
магнитного поля выражается через изменение магнит-
магнитного потока Ф через контур:
5Аме^ = ЫФ. F2)
Рис. 46
Это значит, что контуру с током 1 в посто-
постоянном магнитном поле можно сопоставить потенциальную функцию

3.12] Циркуляция и поток вектора магнитной индукции 109
Wu = — 1Ф, изменение которой (с обратным знаком) равно работе силы
Ампера:
Амех = -AWn, \?П = -1Ф. F3)
Для случаев однородного поля или маленького плоского витка форму-
формула F3) принимает вид:
Wn = -PmB, F4)
где рт — магнитный момент контура с током (см. разд. 3.10). Посколь-
Поскольку это выражение совпадает с потенциальной энергией электрического
диполя (см. разд. 3.3), то такой же вид должны иметь выражения для
вращательного момента, действующего на магнитный момент, и для
силы, действующей на него в неоднородном поле:
тз ^ дВ дВ дВ дВ /*сч
M = pmxB, F = рт— =Ртх— +р __ + Pmz F5)
on ox oy oz
где вектор п параллелен вектору рш. Равновесная ориентация с мини-
минимальной энергией соответствует положению рт || В; ориентированный
таким образом виток втягивается в область более сильного магнитного
поля.
> Уравнения Максвелла для постоянного магнитного поля.
В дифференциальной форме это уравнения
rotB = /ioJ, divB = 0,
а в интегральной — уравнения E9) и F0).
> Векторный потенциал. Второе из уравнений Максвелла удовле-
удовлетворяется, если индукцию магнитного поля искать в виде В = rotA.
Векторный потенциал А определен неоднозначно: А' = А + grad%,
где х — произвольное скалярное поле, порождает такое же поле В, что
и поле А (калибровочное преобразование для векторного потенциала).
Это обстоятельство позволяет упростить уравнение для векторного
потенциала, которое получается после подстановки В = rotA в первое
уравнение Максвелла: graddivA — Л А = /ioj. Выбором подходящего
скалярного поля х можно добиться выполнения условия divA = 0. Для
векторного потенциала получаем уравнение
Л А = -/iOj.
Уравнение для каждой из проекций А математически тождественно
уравнению для скалярного потенциала в электростатике (см. разд. 3.4),
следовательно, решение этих уравнений имеет вид
¦j(r')dV
.J Ip-
Используя это выражение, можно, например, вычислить поле малень-
маленького витка с током (см.E6)), а также доказать закон Био — Савара.

110 Электродинамика [Гл. 3
3.13. Магнитное поле в веществе
> Намагниченность вещества. Вещество считается намагничен-
намагниченным, если оно создает внутри себя и в окружающем пространстве
магнитное поле в отсутствие токов проводимости. Источником магнит-
магнитного поля намагниченного вещества (магнетика) являются магнитные
моменты его атомов и молекул (молекулярные токи). В отсутствие
внешнего магнитного поля микроскопические магнитные моменты ли-
либо отсутствуют (в диамагнетиках), либо ориентированы хаотически
(в парамагнетиках), и создаваемое ими магнитное поле равно нулю
(кроме случая постоянных магнитов, см. ниже ферромагнетики). При
помещении во внешнее магнитное поле вещество намагничивается, т. е.
возникает магнитный момент объема вещества. Степень намагничен-
намагниченности в данной точке вещества характеризуют намагниченностью J,
равной полному магнитному моменту в расчете на единицу объема:
J= =п(Р)
=п(Рт), F6)
где п — концентрация молекул. Для построения макроскопических
уравнений поля в магнетике можно упрощенно считать, что все
молекулы в объеме AV имеют одинаковый магнитный момент
(рш) = J/n = /qs, т.е. могут быть представлены одинаковыми
микроскопическими витками с током.
> Намагниченность и макроскопические молекулярные то-
токи. При описании собственного магнитного поля огромное число ори-
ориентированных микроскопических витков (магнитных моментов) можно
заменить распределенными по поверхности и объему макроскопиче-
макроскопическими молекулярными токами. Проще всего представить себе такую
замену в случае однородно намагниченного цилиндра, когда молеку-
молекулярные витки с током ориентированы вдоль его оси. Внутри цилиндра
токи различных витков будут ском-
скомпенсированы, а по поверхности будет
течь некомпенсированный поверхност-
поверхностный ток. Магнитная индукция этого то-
тока Всоб будет внутри цилиндра направ-
направлена в ту же сторону, что и намагни-
Рис 47 ченность J.
Если рассмотреть произвольный
замкнутый контур, то его участок rfl, расположенный внутри
магнетика, пронизывает те витки, центры которых попали в объем
dV = s • d\ (рис. 47). На этом участке вклад в охватываемый контуром
молекулярный ток (пересекающий натянутую на контур поверхность)

3.13] Магнитное поле в веществе 111
равен Iqu dV = n/os • d\ = J • d\. Производя интегрирование, получим
-di = i:™. F7)
В дифференциальной форме имеем: rot J = jM(WI- Из этих уравнений
можно получить выражение для плотности тока на поверхности маг-
магнетика:
1мол = J X П, F8)
где п — внешняя нормаль к поверхности магнетика.
> Напряженность магнитного поля. Макроскопическая индук-
индукция магнитного поля в магнетике определяется как результат усред-
усреднения микроскопической В, сильно меняющейся на межатомных рас-
расстояниях, по малому объему, содержащему достаточно много молекул:
В(г) = (Вмикро). Индукция поля определяется как молекулярными,
так и сторонними токами (т. е. немолекулярными — токами проводимо-
проводимости, конвекционными токами):
в + СвЛ)- F9)
Так как распределение молекулярных токов обычно не известно, удоб-
удобно ввести новую величину, называемую напряженностью магнитного
поля:
Н = —-J, G0)
которая определяется только сторонними токами:
Н • d\ = IZB G1)
(теорема о циркуляции для напряженности). В дифференциальной
форме имеем: rotH = jCT. В СИ напряженность измеряется в А/м.
> Условия на границе раздела магнетиков. На границе раздела
двух магнетиков выполняются следующие условия для тангенциаль-
тангенциальных (касательных) и нормальных компонент:
B2n = Bln, Hi х п - Н2 х n = iCT, Ji x n - J2 x n = iMOJ1 G2)
(нормаль п проведена из первой среды во вторую, |Нх п| = НТ). Если
стороннего тока на границе нет, то второе условие можно записать
в виде Н\т = Н^т- Первое условие получается из теоремы Гаусса F0)
для вектора В, второе — из G1), третье — из F8). Для граничных
условий наблюдается формальная аналогия между Н и Е, а также
между В и D (см. разд. 3.6).
> Изотропный магнетик. Намагниченность J в данной точке маг-
магнетика возникает под воздействием магнитного поля и определяется
его индукцией В. Для не очень сильных полей J зависит от В линейно,

112 Электродинамика [Гл. 3
а в изотропном магнетике, кроме того, J || В. В этом случае векторы
J и Н пропорциональны В и друг другу, и по историческим причинам
(в силу аналогии между граничными условиями для Е и Н) магнитная
восприимчивость определяется соотношением
Mfe)B- G3)
Из формулы G0) получим:
В = /iO(l + Х)Н = »оцП, G4)
где \i — магнитная проницаемость вещества. В парамагнетиках
X > 0, в диамагнетиках % < 0, в обоих случаях \\\ <С 1 (слабые
магнитные свойства). В ферромагнетиках % ^> 1.
Объемная плотность молекулярного тока пропорциональна объем-
объемной плотности стороннего тока: jMOJ1 = XJCT; если объемных сторонних
токов нет, то при намагничивании возникают только поверхностные
молекулярные токи.
Граничные условия на границе двух изотропных магнетиков имеют
вид
B ^ ;
Если границы однородного магнетика всюду касаются линий индукции
поля Во, которое было до внесения магнетика, то всюду в магнетике
В = /iB0.
Пример 1. Длинный цилиндр из парамагнетика помещен в однород-
однородное магнитное поле, индукция которого Во параллельна его оси. Найдите
магнитную индукцию, напряженность магнитного поля и намагниченность
внутри цилиндра.
Решение. Всюду внутри цилиндра (кроме его краев) имеем: магнитная
индукция В = /хВо, напряженность магнитного поля Н = Но = Во///о,
намагниченность: J = (fi — l)Bo//io-
Пример 2. По бесконечному цилиндрическому проводу круглого сече-
сечения из материала с магнитной проницаемостью /j, > 1 течет постоянный
ток с плотностью j. Найдите напряженность поля, магнитную индукцию
и намагниченность и рассчитайте поверхностную и объемную плотности
молекулярного тока.
Решение. Молекулярный ток в объеме цилиндра имеет плотность
jMOJ1 = (jjl — l)j. Напряженность Н можно найти с помощью теоремы о цирку-
циркуляции G1); она равна Н = 7/Bтгг) при г > R и Н = Iг/BтгR2) при г < R
(см. пример 2 из разд. 3.12). Магнитная индукция равна В = jjlqH при г > R
и В = fio/iH при г < R] она испытывает скачок на поверхностном молеку-
молекулярном токе. Намагниченность равна J = (fi — l)Ir/BnR2) (вне цилиндра
J = 0). Линии магнитной индукции представляют собой концентрические
окружности, а Н и J параллельны В. Поверхностный молекулярный ток

3.13] Магнитное поле в веществе 113
равен i = J х п; он равен по модулю гмол = (// — 1)//BттЯ) и направлен про-
противоположно j. Полный молекулярный ток равен нулю: jmonirR2 = iMOJI27rR.
Пример 3. На сердечник из ферромагнетика (/i ^> 1) в виде тора со
средним радиусом R намотана обмотка с большим числом N витков с током
силой /. В сердечнике сделана узкая поперечная прорезь шириной Ь. Найдите
магнитную индукцию в прорези.
Решение. Магнитная индукция непрерывна на границах прорези, поэто-
поэтому В имеет одинаковое значение всюду на оси сердечника. Чтобы найти В,
запишем теорему о циркуляции для напряженности: NI = —b -\ 2ttR.
Получим: В =
> Механизмы намагничивания. Магнитные моменты атомов
и молекул создаются: а) движением электронов по замкнутым орбитам
(орбитальные магнитные моменты); б) собственными магнитными
моментами электронов, связанными с внутренним механическим
моментом — спином (спиновые магнитные моменты). Магнитный
момент каждого типа пропорционален своему
механическому моменту: рт = — g(e/2m)~LJ где
безразмерный множитель g называют гиромаг-
гиромагнитным отношением. Для орбитального мо-
момента g = 1, для спинового момента g = 2.
В диамагнетике магнитные моменты всех
электронов атома (молекулы) в отсутствие маг-
магнитного поля компенсируют друг друга. При
включении магнитного поля на каждый магнит-
магнитный момент начинает действовать вращатель-
вращательный момент, под действием которого происходит
вращение магнитного момента вокруг направления магнитного поля
(ларморовская прецессия):
_ = Рт х В = -g—L х В = (g—В) х L.
Вектор L (и рш) совершает вращение с угловой скоростью
сол = ge~B/2m (рис. 48). Такое вращение приводит к появлению у ка-
каждого электрона дополнительного магнитного момента Арт, направ-
направленного против В (независимо от направления исходного рш).
В парамагнетике магнитные моменты электронов в атоме не ком-
компенсируют друг друга даже в отсутствие магнитного поля. На слабый
диамагнитный механизм намагничивания накладывается более силь-
сильный ориентационный механизм: в присутствии поля ориентация маг-
магнитного момента по полю оказывается энергетически более выгодной.
В слабых полях (ртВ ^С кТ) средний магнитный момент пропорциона-
пропорционален магнитной индукции, в сильных полях происходит насыщение, все

114 Электродинамика [Гл. 3
магнитные моменты повернуты вдоль поля, и намагниченность прак-
практически не меняется. (Ориентационный механизм намагничивания па-
парамагнетиков аналогичен ориентационному механизму поляризации
полярных диэлектриков, см. разд. 3.6. В частности, остается верным
вывод об обратно пропорциональной зависимости восприимчивости от
температуры.)
> Ферромагнетиками называются вещества, в которых существует
спонтанная намагниченность в макроскопических (больших по срав-
сравнению с межатомными расстояниями) областях — доменах. Размеры
доменов (~ Ю~5 -^ 10~4 м) малы по сравнению с размером образца.
В пределах каждого домена спиновые магнитные моменты ориентиро-
ориентированы параллельно друг другу, что является результатом специального
квантового (обменного) взаимодействия между ними. В отсутствие
магнитного поля домены ориентированы таким образом, что средняя
намагниченность вещества равна нулю. При включении магнитного
поля размеры доменов, направленных вдоль поля, увеличиваются, на-
направленных против поля — уменьшаются. При увеличении поля начи-
начинается поворот доменов как целого в направлении поля. В сильных
полях домены ориентированы вдоль поля, т.е. наступает насыщение
(намагниченность достигает максимального значения JH, называемого
намагниченностью насыщения).
Зависимость J от Н носит нелинейный характер (рис. 49), т. е. маг-
магнитная проницаемость, определяемая
формулой J = (/л - 1)Н, зависит от Я
и достигает громадных значений ц ~
~ 105 -г-106. При снятии внешнего поля
в веществе наблюдается остаточная
намагниченность JOCT. Напряжен-
Напряженность Нк магнитного поля, полностью
размагничивающего ферромагнитный
образец, называется коэрцитивной
силой. Ферромагнетики, обладающие
большой Як, используются для
Риг 4Q
^ изготовления постоянных магнитов.
Зависимость J(H) при прямом и обратном намагничивании до
насыщения называется петлей гистерезиса.
При нагревании выше температуры Кюри вещество теряет ферро-
ферромагнитные свойства (спонтанная намагниченность доменов исчезает)
и становится парамагнетиком. В точке Кюри происходит фазовый
переход второго рода.
> Эффект Холла. При помещении проводника с током в попереч-
поперечное (перпендикулярное току) магнитное поле в проводнике возникает
поперечное электростатическое поле, направленное перпендикулярно
магнитной индукции (рис. 50). Это поле возникает в результате смеще-
смещения упорядоченно движущихся свободных зарядов под действием силы

3.14] Электромагнитная индукция 115
Лоренца, которое продолжается до тех пор,
пока сила Лоренца не будет уравновешена
электрической силой: </o(v) x В = — </оЕ.
Домножив на концентрацию свободных за-
зарядов п, выразим Е через плотность тока.
В результате получим Е = j x В. Вид-
go ^
но, что измерение величины и направления Рис. 50
напряженности в эффекте Холла позволяет
определить как концентрацию свободных зарядов (в случае свободных
зарядов одного типа), так и их знак.
3.14. Электромагнитная индукция
> Закон электромагнитной индукции. При перемещении или де-
деформации контура с током в постоянном магнитном поле силы Ампера,
направленные на каждом участке перпендикулярно току, согласно F2)
совершают механическую работу 5А± = / AФ. Так как полная работа
силы Лоренца над любой движущейся частицей равна нулю, то такая
же по величине, но обратная по знаку работа совершается магнитным
полем (тангенциальной компонентой силы Лоренца) над движущими-
движущимися по контуру свободными зарядами, что приводит к возникновению
в контуре дополнительной ЭДС индукции:
Аф Аф
6А\\ = -ЫФ = -A(И)^=?Aд, ? = -^- G5)
Из принципа относительности Эйнштейна следует, что ЭДС ин-
индукции должна возникать и при помещении неподвижного контура
в изменяющееся со временем магнитное поле. Рассмотрим, например,
сближение с постоянной скоростью замкнутого контура и постоянного
магнита. В инерциальной системе отсчета (ИСО), связанной с маг-
магнитом, создаваемое им поле не зависит от времени, и возникновение
ЭДС в контуре объясняется действием силы Лоренца. В другой ИСО,
связанной с контуром, наблюдается такая же ЭДС, но в неподвижном
проводнике она не может быть вызвана магнитными силами. Следова-
Следовательно, в изменяющемся со временем магнитном поле должно возни-
возникать электрическое поле. Так как работа этого поля при обходе контура
должна быть отлична от нуля, то это поле не является электростатиче-
электростатическим: его называют вихревым электрическим полем. Итак, независимо
от причины, по которой меняется магнитный поток через контур, в нем
возникает ЭДС индукции, равная

116 Электродинамика [Гл. 3
Я2
Рис. 51
(закон Фарадея). Средняя ЭДС индукции за конечное время At равна
?ср = —АФ/At. Прошедший по контуру за это время заряд равен
q = J / dt = J(?/R) dt = —(АФ/R), где R — сопротивление контура.
Правило Ленца. Направление ЭДС определяется ее знаком; напомним
(см. разд. 3.12), что контур должен быть ориентированным: положительное
направление нормали к поверхности при вычислении Ф и положительное
направление обхода контура для определения знака ЭДС должны быть свя-
связаны правилом буравчика. Знак « —» в формуле G6) соответствует правилу
Ленца, которое утверждает, что ЭДС индукции должна иметь такое направ-
направление, чтобы магнитное поле текущего в этом направлении тока создавало
магнитный поток противоположного знака по сравнению с тем изменением
потока, которое является причиной возникновения ЭДС. Правило Ленца
тесно связано с законом сохранения энергии.
> Движение участка контура. При движении элемента контура d\
со скоростью v работа силы Лоренца по переносу пробного заряда q
вдоль d\ равна 8 А = q\y x В] • d\ = qd?. ЭДС, наводимые при
произвольном движении участка и при поступательном движении в од-
однородном поле, равны соответственно:
? = J[v х В] • Л, ? = [v х В] • 1, G7)
где 1 — вектор, соединяющий начало и конец участка. Если концы дви-
движущегося проводника разомкнуты, то между ними возникает разность
потенциалов, равная ЭДС (в каждой точке проводника электростати-
электростатическая сила уравновешивается силой Лоренца).
Пример 1. Перемычка длиной / с сопротивлением г движется со ско-
скоростью v по двум горизонтальным рельсам, помещенным в вертикальное
магнитное поле (рис. 51). Найдите силу тока через перемычку.
Решение. Предположим, что рельсы замкнуты с одной стороны от
перемычки сопротивлением R\, а с другой — сопротивлением R2. Чтобы
найти ток через перемычку при ее движении со скоростью v, используя G7),
вычислим ЭДС в перемычке: 8 = Bvl. Тот факт, что ЭДС локализована
в движущейся перемычке, позволяет изобразить эквивалентную схему и най-
найти силу тока: / = 8/(г + Я), где R = R1R2/(R1 + R2).
> Уравнения для вихревого электрического поля. Уравнение
для вихревого поля в интегральной форме получается при записи зако-
закона Фарадея G6) для неподвижного контура в переменном магнитном
поле:
"E.dl=-^[B.ds. G8)

3.14] Электромагнитная индукция 117
Так как циркуляция напряженности электростатического поля по за-
замкнутому контуру равна нулю, то такому же уравнению удовлетворяет
полное электрическое поле. Дифференциальная форма этого уравне-
уравнения имеет вид
rotE = -f. G9)
Уравнения G8), G9) представляют собой одно из уравнений Максвелла
(в интегральной и дифференциальной формах).
> Квазистационарное приближение. Если токи и поля меняются
не очень быстро, то можно пренебречь запаздыванием процессов по
времени. Сказанное означает, что переменное магнитное поле в любой
точке системы определяется (по формулам Био — Савара — Лапласа)
токами в этот же момент времени; электростатическое поле определя-
определяется распределением зарядов в этот же момент времени, а вихревое
электрическое поле вычисляется по изменяющемуся магнитному полю
с помощью G8), G9). Именно в этом приближении рассчитываются
цепи переменного тока. Для выполнения этого приближения надо,
чтобы характерное время изменения токов г было велико по сравне-
сравнению, во-первых, с временами локальных релаксационных процессов
(например, временем установления равновесного распределения заряда
на проводнике еор), и, во-вторых, со временем запаздывания т3 = 1/с
(I — характерный размер системы). Последнее условие означает, что мы
пренебрегаем током смещения в уравнениях Максвелла (т.е. считаем,
что rotB = /ioj)-
Пример 2. Оценим время г перераспределения заряда на проводни-
проводнике. Будем считать, что где-то в проводнике образовался объемный заряд.
Убывание заряда внутри произвольного объема подчиняется уравнению
dQ I • i 1 t r, 1 Я f f \
-гг = -<VJnds = (bEnds = = , откуда q = q0 exp , т.е.
at j p } sop V eopJ
r = sop.
> Самоиндукция и взаимная индукция. Рассмотрим неподвиж-
неподвижный контур с током. Предположим, что ток / в этом контуре изменя-
изменяется со временем. Создаваемая этим током магнитная индукция будет
меняться со скоростью, пропорциональной dl/dt. Следовательно, воз-
возникающее в каждой точке пространства вихревое поле тоже пропорци-
пропорционально dl/dt. Это поле создает в контуре ЭДС самоиндукции:
?C = -L% (80)
где L называется коэффициентом самоиндукции или индуктивностью
контура. Индуктивность измеряется в СИ в генри (Гн). Величину
Фс = Ы называют собственным магнитным потоком контура. С уче-
учетом (80) получим:

118 Электродинамика [Гл. 3
Эта формула оказывается верной и в том случае, когда изменяется не
только /, но и L.
Заметим, что определение L как коэффициента пропорциональности
между потоком и током встречается с трудностями: в случае линейного
провода собственный поток бесконечен, а для провода конечной толщины
обычное определение потока не годится, так как неясно, как выбрать контур.
Пример 3. Индуктивность соленоида. Рассмотрим соленоид дли-
длиной / и площадью S (I ^> V~S), по которому течет ток с поверхностной
плотностью i = (N/l)I, где N — число витков, / — ток в обмотке. Магнит-
Магнитное поле в соленоиде однородно, его индукция (в приближении идеального
соленоида) согласно формуле F1) равна В = fiofii. При изменении тока
циркуляция вихревого поля вычисляется так: (рЕ • d\ = — S = —fiofiS —,
I СИ Ъ (jib
c adi N uquS dl
а ЭДС на всей длине обмотки равна сс = —NfiofiS— = . Для
dt I dt
индуктивности и собственного потока получим:
L=^^, ФС = Ы = ЫВБ. (82)
Пример 4. Так как ЭДС самоиндукции пропорциональна скорости из-
изменения тока, то наличие в контуре индуктивности препятствует слишком
быстрым изменениям тока. Предположим, что последовательно соединенные
сопротивление R и катушку индуктивностью L замкнули на источник с по-
постоянной ЭДС, равной 8. Нарастание тока от нуля до /о = 8 / R происходит
за конечное время и подчиняется уравнению 8 — L(dl/dt) = IR, решение
которого имеет вид / = /о[1 — ехр(—tR/L)]. Характерное время нарастания
тока равно т = L/R.
Если имеется два неподвижных контура, то изменение тока одного
контура вызовет в другом пропорциональную dl/dt ЭДС взаимной
индукции:
?>i\ — —L21—J-, ?\2 — —Li2—j—, (83)
где Li2 и L21 называются коэффициентами взаимной индукции; для
них оказывается верна теорема взаимности: L\2 = L21 (в неферромаг-
неферромагнитной среде). Магнитный поток через контур 1, создаваемый током
контура 2, определяется как Ф12 = L^h- Эта величина оказывается
определенной и для двух линейных токов.
В квазистационарном приближении можно использовать для векторного
потенциала такую же калибровку, как и в магнитостатике (см. раздел 3.12).
Магнитный поток можно записать в виде:
Ф = \ В ds = I rot A ds = J) A dl.
Для Ф±2 получаем
dh,
4тг П2
откуда видно, что выражение для Ь\ч симметрично по индексам 1,2.

3.14] Электромагнитная индукция 119
> Энергия контура. Энергией контура с током называется работа
внешних сил и источников при создании тока (или работа вихревого
поля при его уничтожении). Работа источника против ЭДС самоин-
самоиндукции контура вычисляется так:
(84)
При последовательно полевом подходе энергия должна быть связа-
связана не с током в контуре, а с магнитным полем. Зависимость плотности
энергии от магнитной индукции проще всего установить в случае длин-
длинного соленоида, в котором поле однородно:
W 1 ll0llN2S I2 /дод/ДЛ2 1 В2 ВН
V SI I 2 \ I 2LJLQLJL 2LJLQLJL 2
=^- (85)
В случае нелинейной зависимости В от Н для плотности энергии
получается выражение:
W г
Используя теорему взаимности (L12 = ?21), можно получить обоб-
обобщение выражения (84) для нескольких контуров:
сю
О
L2/2 . L12 + L21
(86)
Здесь <l>i — полный поток для г-го контура. Видно, что энергия токов
включает в себя энергию каждого тока и энергию их взаимодействия.
С помощью уравнений магнитного поля можно показать, что это вы-
выражение всегда преобразуется к виду:
\^V. (87)
> Закон сохранения энергии и вычисление сил. При медлен-
медленном изотермическом изменении расположения тел и контуров с током
суммарная работа внешних сил и источников тока идет на изменение
энергии магнитного поля и на выделение джоулевой теплоты. При этом
работа внешних сил над каждым телом равна работе сил, действующих
на тело со стороны магнитного поля. Если токи поддерживаются посто-
постоянными, то надо учитывать только дополнительную работу источников
против ЭДС индукции, а работа исходной ЭДС равна выделяющейся
теплоте, и в законе сохранения энергии они сокращаются.

120 Электродинамика [ Гл. 3
Пример 5. Рассмотрим два контура с токами 1\ и /2, которые поддер-
поддерживаются постоянными. Запишем закон сохранения энергии при медленном
смещении первого контура. Согласно (86) изменяется только энергия вза-
взаимодействия токов, равная W\2 = L12I1I2 = Ii^i2 = /1Ф12, где Ф±2 —
поток в первом контуре, создаваемый вторым током. В то же время по-
потенциальная функция контура с током во внешнем поле равна \УП = — 1Ф,
см. F3). Кажущееся противоречие объясняется, если учесть дополнительную
работу источников против ЭДС индукции в каждом контуре. Эта работа
равна 1\AФ\2 + /2^21 = h dL\2 /2 + /2 (IL21 /1, что в два раза больше, чем
изменение энергии поля dW±2 = /1/2 dh\2-
3.15. Уравнения Максвелла
> Ток смещения. Для обобщения уравнений электромагнитного по-
поля в вакууме на переменные поля необходимо изменить только одно
из написанных ранее уравнений (см. разд. 3.4, 3.12); три уравнения
оказываются верными в общем случае. Однако теорема о циркуляции
для магнитного поля в случае переменных полей и токов оказывается
неверным. В соответствии с этим законом ток Jj • ds должен быть
одинаковым для любых двух натянутых на контур поверхностей; если
заряд в объеме между выбранными поверхностями меняется, то
это утверждение вступает в противоречие с законом сохранения
заряда. Например, при зарядке конденсатора
(рис. 52) ток через одну из указанных
поверхностей равен / = dq/dt, а через
другую (проходящую между пластинами) —
нулю. Чтобы снять указанное противоречие,
Максвелл ввел в это уравнение ток
смещения, плотность которого пропорциональна скорости изменения
электрического поля:
JCM = f- (88)
В диэлектрической среде плотность тока смещения равна:
•>см = ?ож + ж- (89)
Первый член представляет собой плотность тока смещения в ваку-
вакууме, второй — плотность реального тока, обусловленного движением
связанных зарядв при изменении поляризованности. Ток смещения
через поверхность равен d<l>D/dt, где Фр — поток вектора D через
поверхность. Введение тока смещения снимает противоречие с зако-
законом сохранения заряда. Например, при зарядке плоского конденсато-
конденсатора ток смещения через поверхность, проходящую между пластинами,
/см = S(dD/dt) = S(da/dt) = dq/dt, равен току, текущему по
подводящим проводам.

3.15] Уравнения Максвелла 121
> Система уравнений Максвелла в вакууме. После введения
тока смещения система уравнений Максвелла в дифференциальной
форме принимает вид:
<9В
1) rotE = - —, 2) rotB =^7
3) dWE = p/e0, 4) divB = 0.
Система уравнений Максвелла в интегральной форме:
-ds, 2)
3) |E-ds= —\pdV, 4)
J во J
Плотности заряда и тока связаны соотношением
выражающим закон сохранения заряда (это уравнение является след-
следствием уравнений Максвелла).
> Решение уравнений Максвелла в виде запаздывающих потен-
потенциалов. Первому и четвертому уравнениям Максвелла можно удовлетво-
удовлетворить, если искать поля в виде
дА
В = rot А, Е = —gradcp .
ot
Скалярный и векторный потенциалы определены с точностью до калибро-
калибровочного преобразования:
А' = A + gradx, ч> = Ч> ~ ~^-
С помощью калибровочного преобразования можно упростить уравнения для
потенциалов, порождаемые вторым и третьим уравнениями Максвелла. Для
этого на потенциалы накладывают требование, чтобы они удовлетворяли
калибровке Лоренца:
В этом случае уравнения для потенциалов удовлетворяют уравнению Далам-
бера:
1 д2А . Л 1 д2(р р
В отсутствие правой части уравнение Даламбера превращается в волновое
уравнение (см. гл. 4). В присутствии источников (токов и зарядов), зависящих
от времени, уравнения Даламбера имеют решения в виде запаздывающих
потенциалов:

122 Электродинамика [ Гл. 3
Потенциалы в данной точке определяются значениями зарядов и токов
в остальных точках пространства, но в предшествующие моменты времени,
с учетом «запаздывания», т. е. времени, которое необходимо световому сигна-
сигналу, чтобы доставить в данную точку информацию о значении тока и заряда
в удаленной точке пространства.
> Уравнения Максвелла в среде имеют вид:
дифференциальная форма интегральная форма
4) divB = O,
и служат для определения четырех величин Е, D, В, Н. К уравнени-
уравнениям Максвелла в среде надо добавить материальные уравнения связи
между D, Е и Н, В, характеризующие электрические и магнитные
свойства среды. Для изотропных линейных сред эти уравнения имеют
вид:
D = ?о?Е, В = /io/iH.
Из уравнений Максвелла можно получить граничные условия для
Е, D, В, Н (см. разд. 3.6, 3.13).
> Закон сохранения энергии для электромагнитного поля.
Из уравнений Максвелла можно вывести следующее уравнение для
любого объема К, ограниченного поверхностью S:
Первый член описывает скорость изменения энергии электромагнит-
электромагнитного поля в рассматриваемом объеме. В общем случае для плотности
энергии электромагнитного поля оказываются верными формулы, по-
полученные ранее для постоянного электрического и магнитного полей.
Второй член представляет собой мощность работы поля над частицами
в рассматриваемом объеме; он равен скорости изменения кинетической
энергии частиц. Из закона сохранения энергии следует, что третий
член имеет смысл потока электромагнитной энергии (наружу) через
ограничивающую объем замкнутую поверхность. Плотность потока
энергии в данной точке пространства (вектор Пойнтинга) определя-
определяется векторами Е и В в этой же точке:
S = — Е х В = Е х Н. (90)

3.15] Уравнения Максвелла 123
Последнее выражение справедливо и для плотности потока электро-
электромагнитной энергии в веществе. Плотность энергии в среде имеет вид:
w = ^Е D + ^B Н. (91)
Пример 1. Рассмотрим зарядку плоского конденсатора с круглыми
пластинами, расположенными на расстоянии Ь. Скорость изменения
энергии в цилиндре радиусом г (меньше размеров пластин) равна
— (-еоеЕ2)(тгг2Ь) = тгг2ЬЕ . Напряженность магнитного поля найдем
dt Л dt
из второго уравнения Максвелла: НBтгг) = (тгг ) (справа стоит
ток смещения). Получаем, что скорость притока энергии через боковую
поверхность цилиндра: 5Bтгг6) = НЕBтггЬ) = Етгг Ь—— равна скорости
do
изменения энергии в объеме.
> Релятивистские свойства полей. При переходе из одной инер-
циальной системы отсчета (ИСО) в другую изменяются как источники
электромагнитного поля (плотности заряда и тока), так и сами поля,
но уравнения Максвелла сохраняют свой вид. Проще всего выглядят
формулы преобразования для источников р и j = pv (р — плотность
движущегося заряда). Если обозначить за ро плотность заряда в ИСО,
в которой j = v = 0, то с учетом сокращения продольных размеров
(см. разд. 1.11) получим
1
7 =
л/1 - v2/c2
Сравнивая с 4-вектором энергии-импульса, видим, что (j, pc) образуют
4-вектор, т.е. преобразуются друг через друга так же, как (г,с?), по
формулам преобразования Лоренца. Зная, как преобразуются источ-
источники поля, можно найти формулы для преобразования Е, В. Они
выглядят так:
е;|=Ец, e^ = 7(Ei + vxb),
в;|=Вц, b'± =
где V — скорость системы отсчета К1 относительно системы К', преоб-
преобразования записаны для компонент полей, параллельных и перпенди-
перпендикулярных V. Инвариантами этих преобразований являются скалярные
величины Е • В и Е2 - с2В2:
Е В = Е' В7, Е2 - с2В2 = {Е'J - с2{В'J. (93)

124 Электродинамика [ Гл. 3
При V ^ с формулы преобразования полей принимают следующий
упрощенный вид:
Е' = Е + V х В В/ = В V х Е. (94)
с2
Пример 2. Магнитное поле нерелятивистской частицы. Рассмот-
Рассмотрим частицу, которая движется относительно ИСО К с постоянной нере-
нерелятивистской скоростью v. В ИСО К'', связанной с движущейся частицей,
имеется только электрическое поле Е' = kqr'/г' . Для перехода в ИСО К
надо записать формулы преобразования (94) с V = —v. Учитывая, что
в нерелятивистском пределе длины отрезков не меняются, получим (для
момента, когда частица проходит в К через начало координат):
, _ 1 qr vxE' _ uoq v x r
И/ И/ о" , -D Ту — о .
4тг?0 г6 с2 4тг г6
При выводе этих формул было использовано равенство 1/с2 = /loSo.
Пример 3. Поляризация диэлектрика при движении в маг-
магнитном поле. При движении диэлектрика с нерелятивистской скоростью
перпендикулярно линиям индукции магнитного поля происходит его поля-
поляризация. В ИСО, связанной с диэлектриком, существует поперечное элек-
электрическое поле Е' = v х В. Характер поляризации диэлектрика зависит от
его формы.
Пример 4. Электрическое поле релятивистской частицы. Рас-
Рассмотрим частицу, которая движется относительно ИСО К с постоянной
релятивистской скоростью v. В ИСО К', связанной с движущейся частицей,
имеется только электрическое поле Е' = kqr jr . Для перехода в ИСО К
следует использовать формулы преобразования (92) с V = —v. Запишем
ответ для момента времени, когда частица в ИСО К проходит через начало
координат, для точки, лежащей в плоскости (ж, у). При переходе от коорди-
координат (ж', у') к координатам (ж, у) надо учесть, что х = jx, у' = у (координаты
точки измеряются в К одновременно с прохождением частицы через начало
координат). В результате получим
Видно, что вектор Е коллинеарен вектору г. Однако на одном и том же
расстоянии от заряда поле в точке, расположенной на линии его движения,
меньше, чем в точке, расположенной на перпендикуляре к скорости. Магнит-
Магнитное поле в той же точке определяется выражением:
D = V X ? = V X H =
с2 с2 4тг [Gа02+у2]3/2
Отметим, что рассмотренное электрическое поле не является потенциаль-
потенциальным.

Глава 4
КОЛЕБАНИЯ И ВОЛНЫ
4.1. Гармонические колебания. Сложение
колебаний
> Общие определения. Колебаниями называют такое изменение
состояния системы, при котором параметры состояния меняются со
временем по периодическому или почти периодическому закону. Если
колебания происходят без внешних воздействий, за счет отклонения си-
системы от устойчивого положения равновесия, то их называют свободны-
свободными или собственными. Если колебания происходят под воздействием
внешнего периодического воздействия, то их называют вынужденны-
вынужденными. Колебания характеризуются периодом Т и частотой и = 1/Т
(измеряется в герцах: Гц).
> Гармонические колебания. Колебания величины х называют
гармоническими, если она меняется со временем t по закону:
х = A cos(u>t + </?о), A)
где А — амплитуда колебаний, ср = (uit + сро) — фаза колебаний, сро —
начальная фаза, и = 2тг/Т — циклическая, или круговая, частота
колебаний. Первая и вторая производные величины х по времени
х = -Аи> sin(u>t + </?о) = Аи> cos(u>t + </?0 + тг/2),
B)
х = —Auj2 cos(ojt + (fo) = Auj2 cos(ojt + </?o + тг)
совершают гармонические колебания с такой же частотой, но с ампли-
амплитудами и А и о; Л и со сдвигом по фазе на тг/2 и тг соответственно.
Пример 1. Если известны начальные (при t = 0) значения величины х:
ж@) = хо и ее производной: ж@) = vo, то можно определить амплитуду
и начальную фазу колебаний. Из уравнений хо = A cos <^о и г^о = —о; Л sin cpo
находим А = y^Xq + (vq/ujJ и tg <^o = —vq/(ujxq).
> Уравнение гармонических колебаний. Как видно из B), если
величина х изменяется по закону гармонических колебаний A), то она
удовлетворяет уравнению гармонических колебаний:
х + и2х = 0. C)
Верно и обратное утверждение: если уравнение движения физической
системы, состояние которой определяется одной величиной х, удалось

126 Колебания и волны [ Гл. 4
при некоторых условиях (обычно — при малых значениях х) привести
к дифференциальному уравнению х + jx = 0, где j — положительная
постоянная, то х изменяется по закону A) с и = y/j (параметры Аи ipo
определяются начальными условиями, см. пример 1).
Если при изменении состояния физической системы квадратичная
функция
it l '2 , 1 2 / \ (л\
Ь = — fix -\—кх (/^5Х—положительные константы) D)
остается постоянной: Е = const, то х изменяется по закону A) при
uj = \J'i<lц. Действительно, продифференцировав D) по времени,
получим уравнение fix + кх = 0, которое является уравнением гар-
гармонических колебаний. Обычно величина Е пропорциональна энергии
колебательной системы при малых ж, поэтому такой подход называют
энергетическим методом определения частоты колебаний.
> Комплексная экспонента и векторная диаграмма. Форму-
Формула Эйлера exp(iip) = cosy? + isimp позволяет рассматривать закон
гармонических колебаний A) как действительную часть комплексной
экспоненты x(t) = Rex, где
х = Aexp(iu>t), E)
а А = A exp(icpo) называется комплексной амплитудой колебаний. Та-
Такой подход особенно удобен при рассмотрении систем, которые описы-
описываются линейными уравнениями, так как в этом случае действительная
и мнимая части преобразуются независимо друг от друга.
Закон гармонических колебаний A) может быть получен как проек-
проекция на ось х радиуса-вектора величиной Л, который равномерно враща-
вращается против часовой стрелки с постоянной угловой скоростью и от на-
начального углового положения у?о (в этом случае угол с осью х меняется
по закону ср = сро + uit). Такой подход называется методом векторных
диаграмм; он особенно удобен при сложении гармонических колебаний,
так как позволяет сложение функций заменить наглядным сложением
векторов (проекция суммы векторов равна сумме проекций).
> Сложение гармонических колебаний одного направления.
Сумма двух гармонических колебаний одинаковой частоты, амплитуды
которых равны А\ и А<ь, а начальные фазы — ipi и </?2, представляет
собой гармоническое колебание такой же частоты, амплитуда и началь-
начальная фаза которого могут быть найдены методом векторных диаграмм
(рис. 53):
А2 = А\ + А\ + 2А\А2 cos (у? 2 — ^i)?
А\ sin cpi + A2 sin (f2
A\ COS if\ + A2 COS if2

4.1] Гармонические колебания. Сложение колебаний 127
(параллелограмм на векторной диаграмме вращается с угловой скоро-
скоростью и как одно целое). Разность фаз колебаний одинаковой частоты
не меняется со временем; такие колебания называются когерентными.
При (f2 — ^fi = =Ь2ттг амплитуда максимальна: А = А\ + А<ь, а при
</?2 — </?i = ±Bга + 1)тг — минимальна: Л = |Ai — A<i\.
При сложении некогерентных колебаний с различными частотами
параллелограмм на векторной диа-
диаграмме деформируется со временем,
модуль результирующего вектора
и угловая скорость его вращения
меняются, т.е. движение не является
гармоническим колебанием. Однако
при сложении колебаний с близкими
частотами (Ли = \и± — o^l <С
<С u)i,uJ) на промежутке времени,
малом по сравнению с временем когерентности тког = 2-к/Ли,
колебания можно считать приблизительно когерентными. Колебания
происходят с циклической частотой и = (и\ + и 2)/2, а их амплитуда
периодически (с периодом 2тг/Ло;) изменяется от А\ + А^ до | Ai — А^ .
Такие колебания называются биениями, и^ = Ли — циклической
частотой биений, а период изменения амплитуды Т§ =
периодом биений. Если А\ = А^ = Л, то
2— ti;i \
tj c
Биения представляют собой один из примеров модулированных
колебаний, т.е. колебаний, происходящих по закону гармонических
колебаний A), в котором один из параметров периодически изменяется
со временем с периодом, значительно превышающим период основных
колебаний. Различают амплитудную, частотную и фазовую модуляции.
Произвольное периодическое колебание с периодом Т может быть
разложено в ряд Фурье по гармоническим колебаниям с частотами
ип = пBтг/Т). Такое разложение называется гармоническим анали-
анализом периодического колебания, а члены разложения — первой (основ-
(основной), второй, третьей и т.д. гармониками периодического колебания.
Непериодические колебания имеют, как правило, непрерывный спектр
частот и могут быть представлены в виде интеграла Фурье по гармо-
гармоническим колебаниям всех частот от нуля до бесконечности. Периоди-
Периодические колебания имеют линейчатый спектр частот, однако не любые
колебания с линейчатым спектром являются периодическими.
> Сложение взаимно перпендикулярных гармонических ко-
колебаний. Если точка движется по плоскости таким образом, что ее
проекции на оси ж, у совершают гармонические колебания, то гово-
говорят о сложении взаимно перпендикулярных гармонических колебаний.

128 Колебания и волны [ Гл. 4
При сложении колебаний одинаковой частоты х = А\ cos(ojt + ipi)
и у = А2 cos(ut + Ф2) траекторией точки является наклонный эллипс:
х у 2ху , . 2/
—о Н о ~Л 7~ COS (у? 2 ~ ty^l) = sin (^2 ~ (fl)-
А\ Аъ Л\Л2
Такое движение называют эллиптически поляризованными колебания-
колебаниями. При (f2 — Ф1 — B?тг + 1)тг/2 оси эллипса совпадают с осями коорди-
координат. При (f2 — (pi = т,тг эллипс вырождается в прямую; такое движение
называется линейно поляризованными колебаниями. Движение точки
может происходить по часовой стрелке (при 2ттг < </?2 — (/?i < 2ттг + тг)
или против часовой стрелки; в этих случаях говорят о правой или левой
эллиптической поляризации.
При сложении взаимно перпендикулярных колебаний с различны-
различными, но кратными частотами результирующее движение происходит
по траекториям, называемым фигурами Лиссажу. По виду фигуры
Лиссажу можно установить отношение частот.
4.2. Свободные незатухающие колебания
> Свободные механические колебания. Если смещение консер-
консервативной механической системы из положения устойчивого равновесия
описывается одним параметром ж, то при малых х потенциальная
энергия имеет вид
d3En\ >cx2
) + *
=0 + *' F)
т. е. при малых отклонениях от устойчивого равновесия система совер-
совершает гармонические колебания. Потенциальную энергию колебатель-
колебательной системы принято отсчитывать от положения устойчивого равнове-
равновесия (ЕП = 0 при х = 0). Обобщенная сила Fx = —dEu/dx при малых х
пропорциональна смещению: Fx = —кх. (Если х — линейная коорди-
координата, то обобщенная сила — проекция силы на направление смещения;
если х — угол отклонения (/?, то Fx — вращательный момент М.)
Если механическая система представляет собой материальную точ-
точку или поступательно движущееся тело, то кинетическая энергия имеет
вид Ек = -тпх2. Уравнение движения
тх = —кх G)
имеет такой же вид, как для груза на пружине. Действующую на тело
возвращающую (т. е. направленную в сторону положения равновесия)
силу называют при малых х квазиупругой силой: Fx = —кх, а коэффи-
коэффициент к— эффективной жесткостью. Циклическая частота и период

4.2]
Свободные незатухающие колебания
129
Рис. 54
колебаний имеют вид:
Рис. 55
(л) = \l —,
(8)
Точка совершает гармонические колебания: х = Ao,os(ut + </?о), а ее
кинетическая и потенциальная энергии — гармонические колебания
с частотой 2oj:
Ек =
Еп =
где ?7 = -ти2 А2 = -яА2 — полная механическая энергия, которая
Z Z
пропорциональна квадрату амплитуды. Средняя кинетическая энергия
равна средней потенциальной энергии.
Пример 1. Потенциальная энергия жидкости в U-образной трубке
(рис. 54) при смещении жидкости на х увеличивается на Amgx =
= (pSx)gx = BpgS)x2/2 (p — плотность жидкости, S — сечение трубки),
а кинетическая энергия равна тх /2. Следовательно, циклическая частота
колебаний равна си = ^j2pgS/т.
Пример 2. В одной из ранних моделей атома водорода (модель Томсона)
положительный заряд предполагался равномерно распределенным по шару
радиусом Я, равным радиусу атома, а электрон располагался в центре шара.
Найдем частоту колебаний электрона при смещении его из положения рав-
равновесия. Сила притяжения при смещении на г равна Fr = —ke2r/Rs (см.
разд. 3.4), поэтому при смещении на г < R будут происходить гармонические
колебания с частотой uj = y/ke2/(mR3).
Пример 3. Физический маятник. Физическим маятником называ-
называется твердое тело с горизонтальной неподвижной осью вращения, не про-
проходящей через его центр масс. При отклонении маятника от положения
равновесия на малый угол а (рис. 55) возникает момент силы тяжести,
5 А. И. Черноуцан

130 Колебания и волны [ Гл. 4
равный М = — mgd sin a (^ — расстояние от центра масс до оси враще-
вращения), стремящийся вернуть маятник в положение равновесия. Уравнение
вращательного движения твердого тела имеет вид: 1а. = — mgd sin а, где
/ — момент инерции тела относительно оси вращения. При малых углах
отклонения а <С 1 это уравнение превращается в уравнение гармонических
колебаний относительно угла а: а + (mgd/ 1)а = 0. Циклическая частота
и период колебаний маятника равны
ш = y/mgd/I, T = 2тг у/1/(mgd).
Например, для однородного стержня длиной /, подвешенного за один из
своих концов, получим / = m/2/3, d = 1/2, Т = 2ny/2l/Cg). Приведенной
длиной L физического маятника называется длина такого математического
маятника, период которого Т = 2тгу/L/g равен периоду данного физиче-
физического маятника: L = I /(md). (Для однородного стержня, подвешенного за
конец, L = 21/3.) Точка, находящаяся на расстоянии L от оси подвеса и лежа-
лежащая на прямой, проходящей через центр масс перпендикулярно оси подвеса,
называется центром качаний. Если подвесить тело на оси, проходящей через
центр качаний параллельно прежней оси, то период колебаний, а значит,
и приведенная длина маятника не изменятся.
Обобщенной силой в данном примере является момент силы тяжести.
Частоту можно определить и энергетическим методом, найдя зависимость
потенциальной энергии от угла отклонения: Еп = mgd(l—cos а) и mgda2/2.
Для полной энергии получим: Е = -1а2 -\--mgda2, откуда находим частоту
колебаний.
Гармонические колебания являются изохронными, т. е. их период
не зависит от амплитуды. Дело в том, что в уравнении гармонических
колебаний х + jx = 0 коэффициент j имеет размерность с~2, и по
соображениям размерности период не может зависеть ни от чего, кро-
кроме 7- Колебания большой амплитуды перестают быть гармоническими,
а значит, и изохронными — возникает зависимость периода от амплиту-
амплитуды. Однако в некоторых специальных случаях даже малые колебания
могут не быть изохронными. Это происходит тогда, когда в формуле F)
для разложения Еп по х вторая производная обращается в нуль. Такая
ситуация возникает, например, при отклонении груза, прикрепленного
к середине недеформированной пружины с закрепленными концами,
в перпендикулярном пружине направлении. Потенциальная энергия
при малых х пропорциональна ж4, и уравнение движения имеет вид:
х + jx3 = 0. Размерность 7 в этом случае м~2с~2, и период колебаний
Т ~ гу~1/2А~1 обратно пропорционален амплитуде.
> Колебательные системы с несколькими степенями свобо-
свободы. Если смещение системы из устойчивого положения равновесия
характеризуется N независимыми параметрами х\, ..., ждг, то при
произвольном малом начальном отклонении зависимость Xi(t) не бу-
будет гармоническим колебанием. Однако любое движение может быть
представлено в виде суммы N специальных движений, называемых

4.2]
Свободные незатухающие колебания
131
нормальными колебательными модами, в каждом из которых все Х{ со-
совершают гармонические колебания с некоторой циклической частотой,
характеризующей данную моду. В общем случае все N частот могут
быть различными.
Пример 4. Связанные маятники. Рассмотрим два одинаковых
математических маятника длиной /, грузы которых соединены недефор-
мированной пружиной жесткостью к (рис. 56).
Нормальные моды данной системы позволяет
угадать симметрия системы. Гармонические коле-
колебания возникают при: а) одинаковом отклонении
маятников в одну сторону (х± = жг) и б) при
одинаковом отклонении маятников в разные
стороны (хг = — Х2)- В первом случае: uji = y/g/l,
во втором: о;2 = л/(#/0 + B/г/ггг). Если отклонить
в сторону только первый маятник, что соответствует Рис 56
начальным условиям (жю,Ж2о) = (^>0), то такое
отклонение можно представить в виде суммы двух нормальных отклонений:
I
к
(л,о) = [\а,\а
-А,—А]. Это значит, что движение первого
маятника будет совершаться по закону: х\ = -Acos(ujit) + -Acos(uj2t),
а второго маятника — по закону: Х2 = -Acos(ujit) — -Acos(uJt). Если
к/т <С g/l, то частоты ил и ui2 будут близки: Auj и ш±——, и при
g/l
наложении двух колебаний с близкими частотами будут наблюдаться биения
(см. разд. 4.1): через время Тб/2 = тг/Ло; второй маятник раскачается,
а первый остановится, еще через такое же время энергия снова перейдет
к первому маятнику, и т. д.
> Свободные колебания в электрическом контуре. Колеба-
Колебательным контуром называется замкнутая цепь, состоящая из конденса-
конденсатора емкостью С и катушки индуктивностью L
(рис. 57). Процессы в колебательном контуре, -^
как и в цепях переменного тока, исследуются
в области частот, где выполняется условие ква-
зистационарности (см. разд. 3.14), т. е. uj ^C
^С с//, где I — характерные размеры систе-
системы (в этом приближении, в частности, можно
не учитывать излучение контура). Закон Ома
для участка цепи, содержащего индуктивность,
при выбранном правиле знаков для обхода кон-
контура и для заряда конденсатора имеет вид: Рис. 57
IR = ((/?i — (?2) + ?, где R — сопротивление
проводов и катушки. С учетом соотношений: I — q (верного при вы-
выбранных знаках), q = ((f2 — <pi)/R и ? = —LI имеем IR = —(q/C) — LI.

132 Колебания и волны [ Гл. 4
Отсюда получим
Если сопротивление контура пренебрежимо мало (что соответствует
R <С л/L/C), то заряд на конденсаторе изменяется по гармоническому
закону q = qm cos(ut + сро) с циклической частотой и периодом, рав-
равными
и = 1/л/ГС, Т = 2tt\/LC. A0)
Ток в контуре изменяется по гармоническому закону с амплитудой
/m = ojqm с опережением по фазе на тг/2. Энергия контура
2 ^ 2С
переходит из электрической в магнитную и обратно: в момент макси-
максимальной зарядки конденсатора она равна W = q2n/BC), а когда заряд
конденсатора равен нулю, то W = L/^/2. Для зависимости магнитной
и электрической энергии от времени верны такие же соотношения, как
для кинетической и потенциальной энергий при механических колеба-
колебаниях.
4.3. Затухающие и вынужденные колебания
> Затухающие колебания. Если в колебательной системе происхо-
происходят потери энергии, то амплитуда колебаний уменьшается со временем.
Если потери энергии механических колебаний определяются силой вяз-
вязкого трения, которая при малых скоростях пропорциональна скорости,
то уравнение движения тих = —кх — Ьх приводится к линейному
дифференциальному уравнению
? + 2/3? + а^ж = 0, A1)
которое называется уравнением затухающих колебаний. Здесь
/3 = = 6/Bт) — коэффициент затухания, ио — циклическая
частота собственных колебаний в отсутствие затухания (при /3 —>¦
—У 0). Решение этого уравнения удобно искать в виде экспоненты:
х = Лехр(—jt). Подставляя в A1), получим для j квадратное
уравнение: j2 — 2Cj + oj2, =0. Если /3 < и>о, то уравнение имеет
два комплексно сопряженных решения: 71,2 = /3 =Ь гл/oj2, — /З2,
которые приводят к одинаковым ответам, поэтому можно взять
любое. Применяя формулу Эйлера (см. разд. 4.1), получим:
x(t) = Аое'^ cos(ut + <р0), со = у^2-/32, A2)
где постоянные Aq и сро определяются начальными условиями.

4.3]
Затухающие и вынужденные колебания
133
Функция A2) принимает нулевое значение через равные промежут-
промежутки времени Т = 2тг/сс? (рис. 58), поэтому и и Т условно называют
частотой и периодом затухающих колебаний. Если /3 <С wo, то на
каждом временном интервале Т <С т <С /З колебания можно считать
гармоническими, a A(t) = Лоехр(—/3t) имеет смысл амплитуды коле-
колебаний на этом интервале. Поэтому A(t) называют (при любом /3 < uio)
зависящей от времени амплитудой затухающих колебаний. За время
г = C~г амплитуда убывает в е раз. Убывание амплитуды за период,
равное A(t)/A(t + Т) = ехр(/ЗТ), на-
называют декрементом затухания, а ло- х J,
гарифм декремента
Л = 1п
A(t)
= /ЗТ A3)
t
Рис. 58
называют логарифмическим декремен-
декрементом затухания. Величина 1/А пока-
показывает, за сколько полных колебаний
амплитуда уменьшается в е раз.
Если /3 > соо (сильное затухание), то квадратное уравнение для
имеет два действительных положительных корня: 71,2 =
и общее решение
x(t) =
A4)
имеет неколебательный (ангармонический) характер (параметры
Ai, A2 определяются начальными условиями).
> Затухающие электрические колебания. Сравнивая уравнение
колебаний в электрическом контуре (9) с уравнением затухающих ко-
колебаний A1), находим выражения для коэффициента затухания и ло-
логарифмического декремента затухания:
2L'
R
A5)
Условие слабого затухания А ^С 1 имеет вид: R ^С у/L/C (величи-
(величину \J'hiС называют волновым сопротивлением контура).
> Вынужденные механические колебания. Движение системы
под воздействием внешней периодической силы называют вынужден-
вынужденными колебаниями, саму внешнюю силу называют вынуждающей си-
силой. Из уравнения движения тх = —KX — bx+Fx(t) получим уравнение
вынужденных колебаний:
х + 2f3x + ojqX = f(t), A6)
где принято обозначение f(t) = Fx(t)/m.
Общее решение такого неоднородного (с отличной от нуля правой
частью) уравнения может быть представлено в виде суммы частного

134
Колебания и волны
[Гл.4
(т. е. любого) решения неоднородного уравнения и общего решения
однородного уравнения. (Общее решение должно содержать свободные
параметры, позволяющие удовлетворить любым начальным услови-
условиям.) Однородное уравнение представляет собой уравнение затухающих
колебаний, его общее решение (формулы A2) и A4)) экспоненциально
затухает за время г ~ 1//3. Затухание собственных колебаний означает
окончание переходного режима установления колебаний и наступление
режима установившихся вынужденных колебаний, характеристики
которого определяются функцией f(t) и параметрами /3, шо, но не
зависят от начальных условий.
Частное решение уравнения A6) будем искать в виде установивших-
установившихся колебаний. Так как любая периодическая сила Fx(t) может быть
разложена в ряд Фурье, то естественно исследовать установившиеся
вынужденные колебания под действием гармонической вынуждающей
силы f(t) = Fx(t)/m = (Fo/m) cos fit.
1 / \ Будем искать их в виде гармонических ко-
колебаний такой же частоты, но со сдвигом
по фазе:
х = A cos(fit + ф). A7)
Подставляя A7) в уравнение A6), находим
А =
0
0
—тг
2^
i
и
i
i
i
_ i4^
i
п
2/3/2
A8)
Рис. 59
При п — О получим <р = О
и А = Fo/(mujQ) = Fo/x, что соответ-
соответствует статическому смещению тела вслед за медленно меняющейся
силой. При Q —У оо имеем А —>¦ 0 и </?—>¦ —тг. Графики A(f2) и ip(f2)
приведены на рис. 59.
> Резонанс. Максимальное значение амплитуды установившихся ко-
колебаний достигается при резонансной частоте /2Р = д/cJq — 2/32 =
= л/и2 — /З2 и равно Лтах = A(f2p) = Fo/Bm/3uj), где о; = д/cjq — /З2 —
циклическая частота затухающих колебаний. При /3 ^С и)о зависи-
зависимость A(f2) содержит резкий и узкий максимум при резонансной ча-
частоте, которая в этом пределе близка к собственной частоте колебаний
системы. Это явление называется резонансом, а кривые зависимости
A(f2) — резонансными кривыми. Характеристики максимумов (при
Р <^С ojq): отношение Лтах к статическому отклонению А@) равно
оо/BР) = тг/Л (Л— логарифмический декремент затухания); величину

4.3]
Затухающие и вынужденные колебания
135
Q = тг/Л называют добротностью колебательной системы. Шири-
Ширина максимума на уровне Лтах/\/2 равна коэффициенту затухания:
Амплитуда установившихся колебаний скорости достигает макси-
максимального значения F0/Bmf3) при п — и>0. При резонансе колебания
скорости происходят в фазе с колебаниями возмущающей силы.
Рассмотрим процесс установления колебаний при частоте вынужда-
вынуждающей силы, равной резонансной частоте (предполагается, что /3 <С и>о).
Если в начальный момент смещение и скорость точки равнялись нулю,
то в рассматриваемом пределе начальным условиям удовлетворяет
решение:
Лтах sin cot +
sin cot = Л
и — е~^ь J si
sin cot.
х ^ А
Полученная зависимость изображена на рис. 60. При t <С 1//3
амплитуда растет пропорционально времени: A(t) ~ Amaxi^t =
= Fot/Bmoj); затухание на этом
этапе влияния не оказывает. От-
метим, что время установления
колебаний велико по сравнению
с периодом: 1/E > 2tt/uj. Если
частота Q близка к о;, но отли-
отличается от нее, то движение на
начальном этапе t С 1//3 пред-
представляет собой сумму колебаний
с близкими частотами. Если вы-
полнено условие и ^> \?2 — и\^>
1//3, то в процессе установ-
установления колебаний происходят явно выраженные биения (амплитуда
колебаний возрастает почти до 2Лтах и уменьшается почти до нуля
с периодом Тб = 2tt/|J? - ш\).
Резонанс при произвольном периодическом воздействии. Если
период внешнего воздействия Fx(t) кратен периоду собственных колебаний
системы Т = 2тг/о;, то в разложении Fx(t) в ряд Фурье может присутство-
присутствовать гармоника с частотой си. Если добротность колебательной системы ве-
велика, то под действием этой гармоники могут возникнуть гармонические ко-
колебания заметной амплитуды. Например, для раскачивания качелей можно
подталкивать их на каждом размахе (тогда резонансную частоту будет иметь
первая гармоника), можно — через раз (будет работать вторая гармоника),
и т.д.
> Вынужденные электрические колебания. Если в колебатель-
колебательный контур (см. разд. 4.2) включить переменную ЭДС ?(?), то вынуж-
вынужденные колебания будут описываться таким же дифференциальным
уравнением, как и для механической системы:
A9)

136 Колебания и волны [ Гл. 4
где q — заряд на конденсаторе, /3 = R/BL) — коэффициент затухания,
ujq = 1/y/LC — циклическая частота собственных колебаний контура.
Рассмотрим установившиеся колебания под действием гармонического
воздействия ?(t) = ?q cos J??. Колебания заряда происходят по закону
q(t) = q0 cos(?2t + (/?), где для амплитуды </о и сдвига по фазе р верны
выражения A8). Однако в электрической цепи интерес представляют
не колебания заряда, а колебания тока / = </, которые происходят по
закону / = /о cos(J2? — ср±) с амплитудой и сдвигом по фазе, равными
. B0)
Максимум амплитуды колебаний тока (резонанс) достигается при
значении J?p = и>0 = 1/y/LC и равен Io(f2p) = ?o/R. При резонансе
колебания тока происходят в фазе с колебаниями ЭДС.
Колебания напряжения на сопротивлении, конденсаторе и катушке
индуктивности описываются следующими формулами:
UR = IR = I0Rcos(m-<pA
Коэффициенты пропорциональности между амплитудами тока
и напряжения называют: хс = l/(f2C) — емкостным сопротивлени-
сопротивлением, xl = QL — индуктивным сопротивлением. Величину х = хь — %с
называют реактивным сопротивлени-
сопротивлением цепи, сопротивление R — активным
сопротивлением (в том смысле, что
= *°z только на нем рассеивается энергия),
величину z = VR2 + х2 — полным
сопротивлением. Формулу B0) можно
переписать в виде: /о = ?o/z,
tgipi = x/R. Все эти соотношения
рис 51 становятся очень наглядными при
использовании векторных диаграмм
(рис. 61). При резонансе х = 0, т.е. колебания напряжений на емкости
и на индуктивности компенсируют друг друга и сопротивление цепи
превращается в активное сопротивление R.
> Мощность на участке цепи. Действующим, или эффективным,
значением переменного тока (напряжения, ЭДС) называется такое
значение постоянного тока, при котором на активном сопротивлении

4.4] Упругие волны 137
выделяется за период такое же количество теплоты, как при перемен-
переменном токе (т. е. среднеквадратичное за период значение):
т
I2Rdt =
\
д
о
Для синусоидального тока /д = /о/л/2, UA = [/о/л/2. Если сдвиг фазы
между током и напряжением равен (р, то средняя за период мощность
равна
т
Р = — Uo cos(?2t) Io cos(?2t — <р) dt = -Uolocosp = /д?/д cos</?.
о
Для реактивного сопротивления средняя мощность равна нулю.
4.4. Упругие волны
> Основные определения. Если непрерывная среда обладает упру-
упругими свойствами, то движение точек в одном месте среды (в источ-
источнике) приводит к распространению этого движения с определенной
скоростью в виде упругой волны. Волновое движение среды описывают
функцией ?(r, i), задающей смещение частицы среды от равновесного
положения г в момент времени t. (Частицей среды называют доста-
достаточно маленький макроскопический, т. е. содержащий большое число
атомов и молекул, элемент среды.) Упругая волна может распростра-
распространяться в трехмерной среде, двухмерной среде (упругая мембрана)
и одномерной среде (упругий стержень, натянутая жесткая нить, столб
воздуха). Простейший вид волны— плоская волна, в которой функция
? = ?(ж, i) меняется только в одном направлении и зависит от коорди-
координаты х. Если при этом вектор ? перпендикулярен направлению распро-
распространения волны, то волна называется поперечной, а если параллелен —
продольной.
Среда называется однородной, если все ее точки эквивалентны, изо-
изотропной, если в ней равноправны все направления, упругой, если воз-
возникающие силы зависят только от смещения (деформации), линейной,
если силы пропорциональны деформациям. В абсолютно упругой среде
механическая энергия волны не рассеивается (не превращается во внут-
внутреннюю). Если среда обладает только объемной упругостью, то в ней
могут распространяться только продольные волны (жидкость, газ), ес-
если она обладает также упругостью формы, то возможны и поперечные
(сдвиговые) волны. В линейной среде распространение волн описыва-
описывается линейными дифференциальными уравнениями, и осуществляется
принцип суперпозиции: если два независимых источника вызывают две
разных волны ^(г,^) и ?2(г?0? т0 совместное действие источников
вызовет волну ?(r, t) = ^(r, t) + ^l1*? О- Такое же утверждение верно

138 Колебания и волны [ Гл. 4
и для одного источника, движение которого можно разложить на два
движения. Поскольку любую функцию времени можно представить
в виде интеграла Фурье по гармоническим функциям, то волновое
движение линейной среды можно разложить на гармонические вол-
волны. Через произвольную точку гармонической волны можно провести
единственную поверхность постоянной фазы, которая называется вол-
волновой поверхностью. Волновая поверхность, совпадающая с передним
краем волнового возмущения, называется фронтом волны.
> Уравнение плоской гармонической волны. Если в источнике
смещение происходит по закону ?@, t) = ?m coso;?, то в точках с коор-
координатой х смещение происходит по такому же закону, но с запаздыва-
запаздыванием на x/v, где v — скорость распространения волны:
*- -j-xj =
= ^mcos(cxjt- kx), B1)
где Л = 27tv/uj = vT — длина волны, k = и/v = 2тг/Л — волно-
волновое число. Длина волны представляет собой кратчайшее расстояние
между точками, совершающими синхронные колебания (разность фаз
Лср = 2тг); длина волны представляет собой пространственный период
профиля гармонической волны в любой момент времени. Разность фаз
между произвольными точками волны равна Лср = 2тг(ж2 — х\)/\.
В уравнении B1) предполагается, что потери энергии на расстоянии х
пренебрежимо малы; небольшое рассеивание энергии можно учесть
эмпирически, введя в B1) множитель ехр(—jx), где j — коэффици-
коэффициент затухания волны. Если ввести волновой вектор к, направленный
перпендикулярно фронту волны в сторону ее распространения, то B1)
принимает вид, инвариантный по отношению к выбору системы коор-
координат:
?M)=?racosM-k-r), f(r,t)=^»e<(wt-k-p). B2)
Последняя форма записи уравнения бегущей волны использует форму-
формулу Эйлера; физический смысл имеет только действительная часть Re ?.
Если скорость волны не зависит от частоты (отсутствует дисперсия),
то плоское волновое возмущение любой формы распространяется без
искажения формы.
> Сферические и цилиндрические расходящиеся волны. Если
волна распространяется от точечного (сферического) или линейного
(цилиндрического) источника изотропно по всем направлениям, то
волновые поверхности будут иметь соответственно форму сфер или
круговых цилиндров. В этих случаях уравнения расходящихся волн

4.4] Упругие волны 139
в отсутствие потерь энергии имеют следующий вид:
?(r, t) = — cos(ut — кг) (сферическая волна),
?(??,, ?) = —^L cos(o;? — klZ) (цилиндрическая волна),
где г = л/х2 + у2 + z2, 1Z = \/х2 + ?/2. Убывание амплитуды проис-
происходит вследствие возрастания площади волновой поверхности; закон
сохранения энергии требует, чтобы поток энергии оставался постоян-
постоянным (напомним, что энергия колебаний пропорциональна квадрату
амплитуды; также см. ниже).
> Волновое уравнение. Непосредственной подстановкой можно
убедиться, что смещение гармонической волны ?(r, t) удовлетворяет
уравнению
0+0+0^0- - *=*?• <*>
которое называется волновым уравнением. Если скорость гармониче-
гармонической волны не зависит от частоты (зависимость и от к является ли-
линейной, т.е. отсутствует дисперсия), то такому же уравнению удовле-
удовлетворяет любая суперпозиция плоских волн. Верно также и обратное
утверждение: если уравнение движения частицы среды удалось приве-
привести к B3), то волновые возмущения данной среды распространяются
со скоростью v.
В одномерном случае общее решение уравнения B3) имеет вид
? = fi(x-vt) + f2(x + vt), B4)
где Д и /2 — произвольные (дифференцируемые) функции. Первое
слагаемое описывает распространение плоского сигнала fi(x) со ско-
скоростью v без изменения формы в направлении положительных х,
а второе слагаемое — распространение сигнала /2 (х) со скоростью v
в направлении отрицательных х.
Пример 1. Упругий стержень. Силы, возникающие при продольных
упругих деформациях стержня, подчиняются закону Гука: а = Ее, где
а = F/S — напряжение в данной точке стержня (среды), е — (относитель-
(относительная) деформация Л1/1, ^ — модуль Юнга. Деформация в точке с координа-
?(ж + dx) — ?(ж) д?
той х выражается через частную производную: е = ~ -;—.
ах ох
Сила, действующая на частицу среды размером Ах и массой Am = р Ах S,
равна а(х + Ах) — а(х). Уравнение движения частицы среды имеет вид:
дх2 Е dt2 '
Следовательно, скорость распространения волн в упругом стержне равна
v = л/ЕIр. С такой же скоростью распространяется продольная волна
в упругой среде.

140
Колебания и волны
[Гл.4
Пример 2. Натянутая струна. По струне, сила натяжения кото-
которой равна Т, может распространяться поперечная волна. Пусть профиль
струны в данный момент задается функцией ?(ж,?) (рис. 62). Получим
уравнение движения частицы среды размером Ах в предположении «плав-
«плавной» волны: д^/дх <С 1. Вертикальная проекция силы натяжения равна
F±(x) = Tsina и Т(д$,/дх) (а —угол наклона струны); вертикальная сила,
действующая на частицу среды раз-
разAxf
мером Лх и массой Am = piAxS,
равна F±(x + Ax) — F±(x) (pi —ли-
—линейная плотность струны). Уравнение
движения частицы среды имеет вид
дх2 Т dt2 '
следовательно, скорость распростра-
нения волн в струне равна v = у/Т/pi
Пример 3. Воздушный столб в цилиндре. Объемная упругость
газа (или любой термодинамически простой среды) характеризуется объ-
объемным модулем упругости К = — V(dp/dV) = р(др/др). Значение К
зависит от условий, при которых происходит объемная деформация газа. Для
звуковых колебаний (у > 16 Гц) можно пренебречь теплообменом между
разными частицами среды и считать К адиабатическим модулем упругости:
/Сад = — V (dp/dV) . Изменение давления в данной точке цилиндра равно
(при малых деформациях) Ар(х) = —K(dV/V) = —К(д$>/дх); сила, дей-
действующая на частицу воздушной среды размером Ах и массой Am = р Ах S,
равна AF = [Ар(х) — Ар(х + Ax)]S. Уравнение движения частицы среды
имеет вид
дх2 К dt2 '
следовательно, скорость распространения волн в воздушном цилиндре равна
v = у/ КI p = у/др/др. (Эти выражения верны для любой термодинамиче-
термодинамически простой среды: для реального газа, для жидкости.) Для звуковых волн
в идеальном газе получим: К = 7Р> v = л/трТр — л/l^T/р,, где 7 ~~
показатель адиабаты (см. разд. 2.2).
> Объемная плотность энергии. Плотность потока энергии.
Плотности кинетической и потенциальной энергии в данной точке
плоской упругой продольной волны равны
Для бегущей волны произвольной формы ? = f(x ± vt) выполняет-
выполняется соотношение (д^/dtJ = v2(d^/дхJ. Учитывая, что для упругой
продольной волны v2 = Е/р, получим, что плотности кинетической
и потенциальной энергии в каждой точке бегущей волны равны друг
другу. Это утверждение верно для бегущей волны любой природы.
В случае гармонической плоской волны B1) объемная энергия волны

4.4] Упругие волны 141
и ее среднее по времени значение имеют вид:
w = wK + wn = рио2^ sin2(o;? — kx), (w) = -puo2^.
A
Плотность потока энергии {вектор Умова) в данной точке бегущей
волны равна
U = wu, B5)
где и — скорость переноса энергии. Для бездисперсионной среды u = v,
где v — скорость распространения волны, входящая в волновое уравне-
уравнение B4). Для гармонической бегущей волны B1) и = v, где v — фазовая
скорость волны: v = uj/k. Энергия, переносимая бегущей волной через
площадку ds за единицу времени (поток энергии), равна d<?> = XJ • ds.
Модуль среднего по времени значения модуля вектора Умова (его
иногда называют интенсивностью волны) для гармонической плоской
волны равен / = |(U)| = v(w) = -pvoj2^. В случае произвольной
А
(в том числе стоячей) продольной упругой волны можно использовать
выражение для U через мощность упругих сил (на единицу площади):
где а = Е д^/дх — напряжение в данной точке среды (см. пример 1).
Для поперечной волны в струне (пример 2) поток энергии имеет ана-
аналогичный вид:
~ ±~ЬЧ ~ ~ ~дх~ЬЧ'
> Дисперсия. Групповая скорость. Зависимость скорости гармо-
гармонической волны от частоты или длины волны называется дисперсией,
а среда, в которой наблюдается это явление, называется диспергиру-
диспергирующей. В диспергирующей среде несинусоидальный бегущий импульс
меняет свою форму в процессе движения, поскольку гармонические
волны, входящие в его разложение Фурье, перемещаются с разной
скоростью. Скорость переноса энергии, входящая в выражение B5) для
вектора Умова, определяется в этом случае как скорость движения
центра импульса (или как скорость точки, в которой деформация
максимальна) и называется групповой скоростью волнового пакета
(в отличие от фазовой скорости синусоидальной волны v = и/к).
Конечный импульс размером Ах называют волновым пакетом по той
причине, что в его разложение в интеграл Фурье по гармоническим
волнам входит конечная группа волн, спектральная ширина которой
определяется соотношением: Ах • Ak ~ 1. Групповая скорость такого
импульса равна
duj Л dv

142
Колебания и волны
[Гл.4
где v = uj/к — фазовая скорость волны. Точки максимумов («горбы»)
внутри волнового пакета перемещаются с фазовой скоростью v, а оги-
огибающая этих максимумов — со скоростью игр (рис. 63).
Понятием групповой скорости волнового пакета можно пользовать-
пользоваться только в том случае, если его спектральная ширина столь мала, что
зависимость и (к) можно считать линейной.
Для иллюстрации рассмотрим волну, являющуюся суперпозицией всего
двух бегущих волн близких частот и одинаковой амплитуды:
? = ?m cos[(u; + Au;)t - (к + Лк)х] + ?т cos[(u; - Au)t - (к - Лк)х] =
= 2?т cos(Auj t — Лк х) cos(ust — кх).
Отсюда видно, что огибающая волн имеет пространственный период Ах =
= 2тг/Лк и перемещается со скоро-
| »' игр стью и = Леи /Лк.
i
Пример 4. Групповая скорость
может быть как меньше, так и боль-
больше фазовой. Фазовая скорость волн
на поверхности жидкости для длин-
(гравитационных) волн зави-
от длины волны по закону
/g\/2n, а для коротких
Рис. 63
ных
сит
V ¦
(капиллярных) волн — по закону
v = л/2тгаIрХ. Подставляя в форму-
формулу B6), находим, что групповая скорость в первом случае равна игр = v/2,
а во втором — игр = 3v/2. Видно, что групповая скорость может сильно
отличаться от фазовой.
> Интерференция волн. Две волны называются когерентными,
если в любой точке пространства они создают когерентные колебания,
разность фаз которых не меняется со временем (см. разд. 4.1). Источ-
Источники когерентных волн называются когерентными источниками. При
сложении некогерентных волн средняя по времени энергия результи-
результирующего колебания равна сумме их средних энергий. При сложении
когерентных волн, колебания частиц в которых происходят в одном
или близких направлениях, может наблюдаться явление интерферен-
интерференции, т. е. устойчивое во времени ослабление колебаний в одних точках
пространства и усиление — в других. Если точка находится на рассто-
расстоянии 7*1 от одного из когерентных источников и на расстоянии r<i — от
другого, то разность фаз между колебаниями в этой точке равна
- kr2) = 2тг
2 - (у?2о - Ую) = 2^Гу
Здесь Aipo — разность фаз между колебаниями источников,
Л = (г2 — П.) — разность хода волн. Условие максимума ре-
результирующих колебаний: Лср = ±2тгт, условие минимума —

4.4]
Упругие волны
143
Atp = ±2тг
где т — порядок интерференционного
максимума (минимума). В случае синфазных источников (Aipo = 0)
эти условия принимают особенно простой вид:
А = ±тА (максимум), А = ±(т — -)Л (минимум).
Рис. 64
Пример 5. Рассмотрим два линейных когерентных источника цилиндри-
цилиндрических волн, которые находятся на расстоянии Л/2
друг от друга. В точках, расположенных вдали от
источников, разность хода волн определяется толь-
только направлением излучения и равна А = -Acos#
(рис. 64). В случае синфазных источников излу-
излучение ослаблено в направлении в = 0 и усилено
в направлении в = тг/2, а в случае источников, со-
совершающих колебания в противофазе (А<ро = тг), —
наоборот.
> Стоячие волны. Собственные колеба-
колебания. Важным примером интерференции явля-
является стоячая волна, возникающая при сложении двух одинаковых
плоских бегущих волн, распространяющихся навстречу друг другу:
? = ?m cos(u;t — кх) + ?т cos(u;t + кх) = 2?т cos kx cos ut. B7)
Амплитуда колебаний точек волны А(х) = 2?mcos&x периодически
меняется от нуля (в узлах волны) до 2?т (в пучностях волны). Рас-
Расстояние между соседними узлами равно Л/2. Колебания точек меж-
между двумя узлами происходят в фазе, но по разные стороны узла —
в противофазе. В узлах равна нулю амплитуда колебаний скорости,
но максимальное значение имеет амплитуда колебаний деформации
д^/дх. В пучностях, наоборот, отсутствуют деформации, но с мак-
максимальной амплитудой происходят колебания скорости. Средняя по
времени энергия имеет одинаковое значение во всех точках стоячей
волны. Вектор Умова равен нулю как в узлах, так и в пучностях,
а в промежуточных точках периодически меняет свое направление.
Если конец стержня, совершающего колебательное движение, жест-
жестко закреплен, то смещение точек конца стержня равно нулю; если
конец стержня свободен, то равна нулю деформация. В первом случае
граничное условие имеет вид ?|ж=о = 0, а во втором — д^/дх\х=о = О,
где значение х = 0 соответствует концу стержня. (Такие же условия
возникают для колебаний воздуха в цилиндрической трубке в случае
закрытого или открытого конца трубки. Для поперечных колебаний
натянутой струны из примера 2 возможен только первый вариант, когда

144
Колебания и волны
[Гл.4
Рис. 65
конец струны закреплен.) Если все точки конечного стержня совер-
совершают гармонические колебания с одной частотой, то такое движение
называют собственными колебаниями стержня. Если сделать мыслен-
мысленный разрез бесконечно длинного стержня в том месте, где находится
узел стоячей волны, то будет удовлетворяться граничное условие для
закрепленного конца, а если в том месте, где пучность, — то для свобод-
свободного. Следовательно, свободные колебания стержня длиной / в случае
двух свободных или двух закрепленных концов должны удовлетворять
условию / = -гаА, или ит = 7rmv/l (спектр собственных колебаний,
т = 1,2, ...), ав случае одного закрепленного конца — условию
/ = - | гп — - ) Л, или иот = тг ( т — - I v/I. Собственное колебание
с наинизшей частотой называется основным колебанием, все остальные
собственные колебания — обертонами или гармониками.
> Отражение бегущей волны. Рассмотрим отражение бегущего
импульса от конца стержня. Если конец стержня закреплен, то гра-
граничному условию ?|ж=о = 0 и начальным условиям (один набегающий
импульс) удовлетворяет суперпозиция набегающего импульса и точно
такого же по форме бегущего ему навстречу импульса, в котором сме-
смещения точек имеют противоположное направление (рис. 65, а). Если
же конец стержня свободен, то граничному условию д^/дх\х=о = О
удовлетворяет бегущий навстречу импульс смещений такого же знака
(рис. 65, б). В случае бегущей волны отражение от свободного конца
происходит без изменения фазы, при этом образуется стоячая волна
с пучностью на конце стержня. Отражение от закрепленного конца
происходит с изменением фазы на тг, при этом образуется стоячая волна
с узлом на конце стержня.
> Эффект Доплера в акустике. При движении источника и (или)
приемника волн относительно среды, в которой распространяется вол-
волна, регистрируемая частота отличается от излучаемой (если изменяет-
изменяется расстояние между источником и приемником). Направим ось х от
приемника к источнику. Если источник излучает звук с частотой i/q

4.5]
Электромагнитные волны
145
Рис. 66
и движется вдоль оси х со скоростью V™ (рис. 66), то расстояние
между соседними максимумами волны, распространяющейся вдоль х
со скоростью v в направлении приемника, будет равно Л = vTq + v*To,
а ее частота равна v/X:
" = "о-^-й. B8)
Если приемник неподвижен, то он зарегистрирует именно эту частоту.
Если приемник движется со скоростью г?", то интервал времени между
приходом соседних максимумов равен Т' = X/(v + г>"), а частота
принимаемого сигнала равна 1/Т":
B9)
Эффект Доплера наблюдается в том случае, когда изменяется рассто-
расстояние между источником и приемником.
4.5. Электромагнитные волны
> Свойства электромагнитных волн. Электромагнитной вол-
волной называется распространение возмущений электромагнитного поля
в пустом пространстве или в среде в отсутствие источников. Суще-
Существование электромагнитных волн следует из теории Максвелла (см.
разд. 3.15), в которой утверждается, что переменное электрическое
поле порождает переменное магнитное поле, а переменное магнитное
поле порождает переменное электрическое поле. В случае однородной
изотропной среды уравнения Максвелла имеют вид
l)rotE = -f,
3) divD = 0,
C0)
4) divB = 0,

146 Колебания и волны [ Гл. 4
где D = ??оЕ, В = /i/igH. Для электромагнитного поля, зависящего
только от координаты х, получаем уравнения:
дНу _ 8EZ
dHz 8EZ _ дНу
C1)
В этом случае уравнения для продольных компонент имеют вид
дЕх/дх = dEx/dt = 0, дНх/дх = dHx/dt = 0, т.е. все продольные
компоненты поля являются постоянными величинами.
Нетрудно убедиться, что поперечные компоненты электромагнит-
электромагнитного поля подчиняются волновому уравнению:
Лп д2Еу d2Hz
/ЛИ/у — SSq/jL/jLq Ту— , L\riz — SSq/jL/jLq -r—
ot ot
(таким же уравнениям подчиняются Ez и Ну). Из этих уравнений
следует, что электромагнитные возмущения в среде распространяются
со скоростью
1 се
п
C2)
где с = 1/^Sofio «3-108 м/с — скорость электромагнитных волн
в вакууме, а п = у/ё/7— показатель преломления среды.
Рассмотрим плоскую электромагнитную волну определенной часто-
частоты (монохроматическую плоскую волну), распространяющуюся вдоль
оси х: Еу = Eoycos(ujt - kx), Ez = EOz cos(u;t - kx + ip). Из C1)
получаем: Hy = —^/ееъ/ццъ Ez, Hz = y/eeo/'/jl/jlo Ey. Из этих формул
можно получить свойства плоской бегущей электромагнитной волны:
1) Электромагнитная волна поперечна.
2) Так как Е • Н = 0, то Е _L Н. Векторы (Е, Н, к) образуют
правую тройку векторов (т. е. направление вектора Е х Н совпадает
с направлением распространения волны).
3) Величины векторов Е и Н в каждый момент времени связаны
соотношением <sjee§ Е = у//л/ло Н (Е = vB).
От разности фаз ср зависит характер поляризации волны. При
ср = =Ьттг волна оказывается плоскополлризованной, т. е. вектор Е
совершает колебания в одной плоскости (эту плоскость называют плос-
плоскостью поляризации волны), а при иной разности фаз — эллиптически
поляризованной или (при ip = ±(т + -]7ги при Eqx = Еоу) —
поляризованной по кругу (см. разд. 4.1).

4.5] Электромагнитные волны 147
> Энергия электромагнитных волн. Объемная плотность энер-
энергии электромагнитной волны вычисляется по формуле
\Е2 + 1ццН2 = ееЕ2 = ццН2
W = -SSoE + -LLLLqH = ??0E = LLLLoH = -EH.
A A v
В случае монохроматической плоскополяризованной волны имеем
W = ??()Eq COS2(ut — kx), (w) = -??oEq.
Для эллиптически поляризованной волны:
w = ??о [EQycos2(u;t - кх) + EQZcos2(u;t - кх + у?)],
/ v 1
Для волны, поляризованной по кругу (Еоу = Eqz =
if = -7г±тгт), плотность энергии не меняется со временем: w =
А
Плотность потока энергии в электромагнитной волне определяется
вектором Пойнтинга (см. разд. 3.15):
который направлен в сторону распространения волны. Интенсивно-
Интенсивностью электромагнитной волны называется модуль среднего по време-
времени вектора Пойнтинга:
/= |(S> I =v(w).
> Давление волны. В соответствии с теорией относительности, по-
поток энергии электромагнитного поля в вакууме означает существова-
существование импульса электромагнитного поля. Объемная плотность импуль-
импульса электромагнитного поля равна (по модулю) w/c, поток импульса
равен S/c, его модуль равен w. При отражении или поглощении вол-
волны происходит изменение импульса волны, что должно проявляться
в давлении волны на препятствие. При нормальном отражении плоской
волны давление равно р = (w)(l + R), где R — доля отраженной энер-
энергии (коэффициент отражения). В рамках электродинамики давление
волны объясняется действием магнитного поля волны на ток, возбуж-
возбуждаемый на отражающей поверхности электрическим полем волны.
> Излучение плоского тока. Простейшим примером системы, со-
создающей переменные поля и излучающей плоскую электромагнитную
волну, является переменный по времени плоский ток. Рассмотрим ток
в плоскости (x,z), направленный вдоль z и изменяющийся по закону

148
Колебания и волны
[Гл.4
Z/
/
I /
i
A
/
/
л
/
f
У
%z = iocoso;^ (рис. 67). Из закона плоско-
плоского тока для узкого контура, охватывающе-
охватывающего ток, получим Bx@,t) = =b-/iO^o cosuit,
где знак « —» соответствует полю спра-
справа от плоскости (для малых у > 0),
знак « + » — слева от плоскости. Исполь-
Используя связь между Е и В в плоской
волне, получим Ez@,t) = — Ае cos cot, где
1
Ае = т:/^ос^о = ^о/B?ос)- Электрическое
поле направлено против тока, его работа над
током отрицательна, т. е. ток отдает волне
рис ^ энергию. Поле вдали от плоскости имеет
вид E(y,t) = —Ае cos(ujt — ку) при у > 0
и Е(у, t) = — Ае cos(u;t + ку) при у < 0.
> Излучение волн движущимися зарядами. Излучение элек-
электромагнитных волн происходит при движении зарядов с ускорением.
Простейшая излучающая система — электрический диполь, диполь-
ный момент которого быстро меняется со временем (осциллятор, или
вибратор Герца). Так как электромагнитные воз-
возмущения распространяются со скоростью с, то
поле излучения на расстоянии г в момент време-
времени t определяется движением зарядов в диполе
в момент t' = t — г/с. Поле излучения выглядит
достаточно просто только в волновой зоне, т. е. на
расстояниях, больших как по сравнению с разме-
размерами диполя, так и по сравнению с Л = ст, где
г — характерное время изменения дипольного
момента (в случае гармонических колебаний Л —
длина волны). Электрическое и магнитное поле
в волновой зоне перпендикулярны радиусу-вектору г, проведенному от
диполя к точке наблюдения:
о Г(р X г) X rl , , ,
Рис. 68
Е=
В =
t-r/c'
Взаимное расположение векторов Е, Н и г изображено на рис. 68.
Решение уравнений Максвелла в виде запаздывающих потенциалов (см.
разд. 3.15) позволяет написать выражения для потенциалов в точке г в мо-
момент времени t. Например, векторный потенциал имеет вид:
_ цо qv(t - г/с) _ цо p{t -r/с)
4тг г 4тг г
При вычислении В = rotA главную роль в волновой зоне играет член, возни-
возникающий при дифференцировании аргумента р, что приводит к приведенному

4.5] Электромагнитные волны 149
выше выражению для В. Аналогичные, но более громоздкие вычисления
можно провести и для электрического поля.
Убывание полей с расстоянием происходит по закону 1/г. Вектор
Пойнтинга в волновой зоне направлен вдоль г; в направлении, состав-
составляющем угол 6 с вектором р, он равен:
_ 1 sin2fl / ... ч2
Поток энергии через замкнутую поверхность есть не что иное, как
мощность излучения диполя:
77 •• 2
Р= \ SFJnr2 sin 6 d6 = -r^—Щг.
J 4тг?0 Зс
о
Считая, что движется только один из зарядов диполя, получим фор-
формулу для мощности излучения ускоренно движущейся частицы:
C3)
Зс3
которая оказывается пропорциональной квадрату ее ускорения.
Линейным гармоническим осциллятором называется электриче-
электрический диполь, момент которого изменяется по гармоническому закону:
р = р0 cosojt. Зависимость интенсивности излученной волны от угла в
имеет вид
8тгс3г2
Зависимость 1F) при г = const (диаграмма направленности) изоб-
изображена на рисунке 69). Средняя по време-
времени мощность излучения такого осциллято-
осциллятора
пропорциональна четвертой степени его
частоты. Рис. 69
Пример 1. Свободный электрон в поле плоской электромагнитной
волны с амплитудой Eq совершает вынужденные колебания с ампли-
амплитудой А = eEo/(muj2) (уравнение движения электрона имеет вид:
тх = — еЕо cos cut). Видно, что мощность излучения свободного электрона
в поле электромагнитной волны не зависит от частоты, а сечение рассеяния
(отношение мощности излучения к интенсивности падающей волны)
равно а = — = iy—г- ~ 10~30 м2. Другая ситуация возникает, когда
/ 3 т с
в поле электромагнитной волны попадает атомный электрон, собственная
частота ojq колебаний которого велика по сравнению с частотой падающей
(световой) волны. Амплитуда колебаний в этом случае (см. разд. 4.3) равна

150 Колебания и волны [ Гл. 4
А = еЕо/'(racdo), т.е. почти не зависит от о;. В этом случае мощность
излучения и сечение рассеяния света пропорциональны ш , что дает
качественное объяснение голубому цвету неба (голубой свет рассеивается
сильнее).
Пример 2. Если представить, что электрон в атоме совершает
собственные колебания с частотой о;о, то энергия колебаний равна
2.2 dW ке2ш%А2
W = тси0А , а мощность излучения равна Р = = о—.
at 3c°
dW ке2и2 __.
Получаем = о"*^, следовательно, энергия атома изменяется по
dt Зтс
закону W = Wo exp(—t/r), где г = 3mcs/(ke2uj2) ~ 10~9 -=-10~10 с называют
временем высвечивания атома.
> Эффект Доплера для электромагнитных волн в вакууме.
Главное отличие от акустического эффекта Доплера (см. разд. 4.4)
состоит в том, что отсутствует система отсчета, связанная со средой,
в которой распространяется волна. Поэтому соотношение между ча-
частотой излучения i/q (измеренной в системе отсчета источника КИ)
и зарегистрированной частотой v (измеренной в системе отсчета прием-
приемника Кп) может зависеть только от их относительной скорости. Пусть
в Кп источник движется со скоростью v, направленной под углом в
к радиусу-вектору, проведенному от приемника к источнику. Повторяя
рассуждения, приведенные в разд. 4.4, получим
V —
(w/c)cos0'
где щ — частота источника, измеренная часами системы Кп. Переходя
к собственному времени (То = 7^о? или ^о = ^о/т? см- разд. 1.11),
получим
j[l + (v/c)cos9] l + (v/c)cos9' У }
Видно, что вследствие преобразования времени наблюдается не
только продольный, но и поперечный эффект Доплера (при движении
источника перпендикулярно направлению на приемник).
Полезно посмотреть на эф-
' фект Доплера с иной точки зре-
зрения. Поскольку фаза колебания
в данной точке волны (cot — kr)
должна быть инвариантна по
отношению к переходу в другую
систему отсчета, то (к, о;/с)
представляет собой 4-вектор
у'у/ \ нулевой длины (к2 — со2/с2 = 0).
Й (К К ) Если в системе Кп ось х
направить параллельно скорости
источника Vй (рис. 70), то в этой

4.5] Электромагнитные волны 151
системе отсчета кх = —к cos 9 = — (со/с) cos 9. Применяя для перехода
к системе Ки преобразования Лоренца, имеем: uso/c = j[(uj/c) — kx(v/c)],
или ujo = j[w + uj(v/с) cos 9]. Выражая о;, приходим к C5). Этот метод
позволяет, записав преобразования Лоренца для волнового вектора к,
получить формулы для явления аберрации света, имеющего важное значение
в астрономии.
> Шкала электромагнитных волн. В зависимости от способов
излучения и регистрации электромагнитных волн, в шкале частот и
или длин волн в вакууме Л = с/и выделяют несколько диапазонов
с условными (перекрывающимися) границами:
1. Радиоволны (Л > 0,05 мм).
2. Оптическое (световое) излучение A0 нм < Л < 1 мм):
а) инфракрасное (ИК) излучение G70 нм < Л < 1 мм),
б) видимый свет C80 нм < Л < 770 нм),
в) ультрафиолетовое (УФ) излучение A0 нм < Л < 380 нм).
3. Рентгеновское излучение @,01 пм < Л < 100 нм).
4. Гамма-излучение (гамма-лучи) (Л < 0,1 нм).

Глава 5
ОПТИКА
5.1. Геометрическая оптика. Фотометрия
> Основные законы геометрической оптики. Оптика занима-
занимается изучением электромагнитного излучения оптического (светового)
диапазона (см. разд. 4.5) явлений, возникающих при его распростра-
распространении в пространстве и взаимодействии с веществом. Геометрическая
оптика отвлекается от волнового характера и от поляризации свето-
светового излучения, оперируя понятиями световых лучей, указывающих
направление распространения света, и узких световых пучков, образо-
образованных световыми лучами.
Основные законы геометрической оптики перечислены ниже.
1. Закон прямолинейного распространения света.
2. Закон независимости световых пучков. Энергия в каждом пучке
распространяется независимо от других пучков; освещенность поверх-
поверхности, на которую падает несколько пучков, равна сумме освещенно-
стей, создаваемых каждым пучком в отдельности.
3. Закон отражения света. Отраженный луч лежит в плоскости
падения, образуемой падающим лучом и нормалью к поверхности в точ-
точке падения; угол падения равен углу отражения. Все углы отсчитыва-
ются от нормали.
4. Закон преломления света. Преломленный луч лежит в плоскости
падения; отношение синуса угла падения а\ к синусу угла преломле-
преломления «2 зависит от длины волны, но не зависит от угла падения (закон
Снеллиуса):
sin gq _ _ п^ ^ч
sin OLi n\'
Постоянная величина п<ь\ называется относительным показателем
преломления второй среды относительно первой, который равен отно-
отношению (абсолютных) показателей преломления каждой из сред (по-
(показателей преломления среды относительно вакуума). С точки зрения
волновой оптики абсолютный показатель преломления указывает, во
сколько раз фазовая скорость световой волны данной частоты меньше,
чем скорость этой волны в вакууме:
v = с/п, п = л/JIs « у/е B)
(см. разд. 4.5). Если п^ < п\, то при а\ > апред, где sin апред = п<ь\ < 1,
наблюдается полное отражение света, т. е. отсутствует преломленный

5.1] Геометрическая оптика. Фотометрия 153
луч. При распространении луча света в среде с постепенно меняющим-
меняющимся вдоль некоторой оси показателем преломления (в слоистой среде)
удобно использовать формулу A) в виде nsina = const, где а — угол
с указанной осью. Видно, что а постепенно меняется, т.е. происходит
искривление луча.
К перечисленным законам геометрической оптики следует добавить
принцип обратимости световых пучков.
Законы геометрической оптики действуют тогда, когда оказыва-
оказываются несущественными явления интерференции, дифракции и поля-
поляризации. Это происходит в тех случаях, когда амплитуда волны и ее
первые пространственные производные мало меняются на длине вол-
волны. Эти условия нарушаются на границе тени, вблизи геометрической
точки схождения лучей (фокуса), при прохождении света через узкие
диафрагмы, при распространении света в средах с резко меняющимся
показателем преломления или с большим поглощением. Например, при
прохождении света через круглую диафрагму с диаметром d (для
отверстия неправильной формы под d надо понимать минимальный
поперечный размер) пучок света расплывается за счет дифракции на
расстоянии / r»j d2/X; на расстояниях, малых по сравнению с /, можно
пользоваться законами геометрической оптики.
С законами геометрической оптики тесно связаны принцип Гюйген-
Гюйгенса (волновое построение Гюйгенса) и принцип Ферма. Принцип Гюй-
Гюйгенса опирается на абстрактно-волновые представления и позволяет
построить в каждой точке вспомогательную волновую поверхность,
нормаль к которой указывает направление луча света. Для построения
волновой поверхности в момент времени t + At все точки волновой
поверхности в момент времени t рассматриваются как источники вто-
вторичных световых волн. Огибающая сферических волновых поверхно-
поверхностей вторичных волн образует новую волновую поверхность основной
волны.
Принцип Ферма является одним из примеров вариационных прин-
принципов, играющих в физике большую роль. Он утверждает, что время
распространения света по истинной траектории является экстремаль-
экстремальным (обычно — минимальным или максимальным) по сравнению со
всеми воображаемыми близлежащими траекториями. Более точно —
это время не меняется (в первом порядке малости) при малом искаже-
искажении траектории. Время прохождения света через среду с переменным
(или кусочно-переменным) показателем преломления удобно выражать
через оптическую длину пути L:
t = —-r- = —, L = \ndl. C)
1 c/n с ' v 7

154 Оптика [ Гл. 5
Это понятие оказывается полезным и при изучении интерференции.
Принципы Гюйгенса и Ферма позволяют получить основные законы
геометрической оптики, но не позволяют выйти за ее пределы.
Одной из важных задач геометрической оптики является построе-
построение изображений, формируемых оптическими системами, и изучение
их свойств. Изображением называется точка схождения лучей, прошед-
прошедших оптическую систему. Система отражающих и преломляющих сфе-
сферических (и плоских) поверхностей, перпендикулярных к некоторой
оси, формирует изображение точечного источника лучами, падающими
под малым углом к оси {параксиальное приближение). Ось системы
называют оптической осью; точку схождения параллельного оси пучка
лучей — фокусом системы; перпендикулярную оси плоскость, про-
проведенную в фокусе, — фокальной плоскостью. Теоретический предел
размеров изображения и разрешающей способности оптических систем
определяется дифракцией света. Важное для дальнейшего свойство
изображений: оптические длины всех лучей от источника до изобра-
изображения одинаковы, т. е. оптическая система не изменяет разности хода
лучей.
> Фотометрия. Излучение в данной точке пространства в данном
направлении характеризуется интенсивностью лучистого потока I:
AФ = I cos в dsdfi, D)
где AФ — лучистый поток (энергия, переносимая в единицу времени
через площадку ds лучами, заключенными в телесном угле d?2); в —
угол между выделенным направлением и нормалью к площадке. Про-
Произведение cos в ds называется видимой величиной площадки в данном
направлении. Объемная плотность лучистой энергии и = dW/dV
равна
и =
= -\ldn. E)
В случае изотропного излучения и = 4тг//с. Интенсивность / и плот-
плотность и можно подвергнуть спектральному разложению по частотам
или длинам волн:
LXJ LXJ LXJ
и = uv dv — \ иш du = \ u\ dX.
Приравнивая энергию, заключенную в соответствующих друг
другу спектральных интервалах, можно найти связь между раз-
различными спектральными представлениями. Например, приравняв
uvdv — и\ dX, с учетом Л = с/и получим
uy =

5.1] Геометрическая оптика. Фотометрия 155
Аналогично можно произвести разложение по двум взаимно перпенди-
перпендикулярным поляризациям.
Определенные выше энергетические характеристики используют при
объективном описании излучения. Фотометрические, или световые, ха-
характеристики учитывают восприимчивость глаза к световому излучению.
Лучистый поток измеряют в ваттах, а соответствующую ему фотометриче-
фотометрическую единицу называют световым потоком и измеряют в люменах (лм).
Чтобы перейти к световому потоку, надо лучистый поток умножить на
световую эффективность г\ (измеряется в лм/Вт), которая для длины волны
До = 555 нм равна щ = 625 лм/Вт, а для других длин волн равна щУ\, где
V\ — кривая видности, или относительной спектральной чувствительно-
чувствительности глаза (Va = 1 при А = 555 нм и падает до нуля при приближении
к границам видимого диапазона). Для пересчета от произвольного лучистого
потока к световому потоку можно использовать формулу Фсв = щ Ф\У\ d\.
Аналогичным образом происходит пересчет от остальных энергетических ха-
характеристик к световым и наоборот (например, от интенсивности излучения
к интенсивности света).
Для характеристики точечного источника используют энергетиче-
энергетическую силу источника, определяемую как лучистый поток в данном
направлении в расчете на единичный телесный угол: йФ — J dfl. Све-
Световая характеристика — сила света источника — определяется через
световой поток. Единица силы света кандела является основной едини-
единицей СИ (лм = кандела х ср, где ср — стерадиан). Если не происходит
поглощения или рассеяния излучения, то на расстоянии г от источника
в том же направлении интенсивность излучения равна
г2"
Поток лучистой энергии, приходящийся на единицу площади осве-
освещаемой поверхности, называется энергетической освещенностью. Со-
Соответствующая световая величина называется просто освещенностью
Е и измеряется в люксах (лк). Если излучение точечного источника
падает под углом в к нормали, то
Е = -^ cos#.
г
Для протяженных источников, т.е. для излучающей поверхности,
вводят энергетическую яркость в данном направлении Во (световая
характеристика— яркость). Энергетическая сила источника, соответ-
соответствующего площадке ds, равна
dJ = Bq cos 0 ds, или dФ = Во cos в ds dft, F)
где в — угол между нормалью к излучающей поверхности и направле-
направлением излучения. Источник, у которого Во не зависит от направления,

156 Оптика [ Гл. 5
"<l A ds'
at > I
/ г
ds
Рис. 71 Рис. 72
называется ламбертовским источником. Ламбертовский источник лю-
любой формы кажется равномерно ярким (например, диск Солнца). Энер-
Энергетическая светимость R (световая характеристика— светимость)
определяется как полный лучистый поток в телесном угле 2тг в расчете
на единицу площади излучающей поверхности:
R = \вв cos OdQ. G)
Для ламбертовского источника R = тгВ.
Пример. Освещенность, создаваемая светящейся поверхностью S на
некотором участке освещаемой поверхности ds', равна сумме вкладов от
всех участков ds. Телесный угол, под которым ds' видна от ds, равен
cos 9' ds'/r2 (рис. 71). Для светового потока, посылаемого в этот телесный
угол, имеем Be cos в ds (cos в' ds'/r2). Так как cos в ds/r2 равен телесному
углу сШ, под которым излучающий участок виден от точки освещения, то
dE = Вв cos 0' du.
Например, при освещении ламбертовским диском маленькой площад-
площадки, расположенной на оси диска и ориентированной перпендикулярно оси
(рис. 72), dfl = 2тг sin в'd9', и после интегрирования получим Е = тгВ sin2 0o,
где во — угол полураствора конуса, под которым диск виден от освещаемой
площадки.
5.2. Интерференция света
> Когерентность световых волн. При наложении световых волн,
обладающих очень высокой частотой колебаний, можно наблюдать
только усредненную по времени энергию колебаний, которую харак-
характеризуют интенсивностью колебаний I = (Е2). При сложении двух
колебаний Е = Ei + Е2 получим / = h + /2 + /12, где /i2 = 2(Ei • Е2)
называют интерференционным членом. Если lyi — 0, то пучки света
называют некогерентными. Волны, поляризованные во взаимно пер-
перпендикулярных направлениях, всегда некогерентны. Монохроматиче-
Монохроматические волны являются когерентными только в том случае, если остается
постоянной их разность фаз (т. е. их частоты совпадают) и если они
параллельно (или почти параллельно) поляризованы. При наложении

5.2] Интерференция света 157
таких волн
/ = /х + /2 + 2л
где Л у? — разность фаз колебаний в данной точке. В частном случае
при /i = 12 = /о имеем / = 2/qA + cos Aip). Для синфазных колебаний:
2 J, для колебаний в противофазе: / =
> Интерференция двух волн. При наложении двух плоских волн
Е\ — Ею cos(u;t — ki • г) и Е2 = Е2$ cos(o;? — k2 • г) получим
Aip = (ki —кг) -г. Поверхности постоянной разности фаз представляют
собой плоскости, перпендикулярные вектору (ki — кг). Расстояние
между соседними плоскостями с максимальной интенсивностью равно
л
|ki-k2| ksm(a/2)
где а — угол между векторами ki и k2. При малых а получим Ах ~
~ Х/а. Если в области перекрытия волн поставить плоский экран,
параллельный (ki — кг), то на нем будут наблюдаться параллельные
чередующиеся темные и светлые полосы.
При наложении сферических волн от двух синфазных точечных
источников условие максимума интенсивности ттг-ro порядка имеет вид
г2 — 7*1 = тХ (это уравнение гиперболоида вращения с осью, проходя-
проходящей через источники). При размещении экрана параллельно этой оси
получим светлые и темные полосы в виде гипербол. Если расстояние до
экрана D велико по сравнению с расстоянием d между источниками,
то в центре экрана получим равноотстоящие почти параллельные поло-
полосы. Расстояние между полосами будет такое
же, как в опыте Юнга, где интерференция
создается двумя параллельными линейными
источниками когерентного света. Если х —
расстояние от некоторой точки экрана до его
центра (рис. 73), то г\ — D2 + (х + d/2J,
r\ — D2 + (x — d/2J, и при d,x < D получим
для разности хода А = г\ — r2 ~ xd/D « ах, где а « d/D — угол, под
которым источник виден из центра экрана. Интенсивность меняется
от 4/ при А = ах = тпХ до нуля при А = (тп + -)А. Расстояние между
полосами равно Ах = Х/а = XD/d.
На большом расстоянии от двух синфазных линейных источни-
источников (ri,7*2 ^> d) можно написать г2 — r\ « dsinO, где в — угол
между нормалью к плоскости источников и направлением наблюде-
наблюдения интерференции (приближение Фраунгофера). Амплитуды колеба-
колебаний в интерферирующих волнах можно считать одинаковыми, т.е.
/ = 2/о[1 + cos(A*dsin0)]. Максимумы интерференции наблюдаются
под углами, удовлетворяющими соотношению sin в = mX/d.

158 Оптика [ Гл. 5
Уточним, на каком расстоянии от источников можно пользоваться при-
приближением Фраунгофера. Выразим r<i по теореме косинусов:
г2 = (г? + d2 -2dnsmOI/2
(угол в треугольнике равен 90° — в) и, разложив до второго порядка по d/ri,
получим
Г2 — r\ ~ <i sin в -\ sin2 в.
Поправкой можно пренебречь, если d2/n <С А. Получаем, что приближение
Фраунгофера работает в том случае, если расстояние г от точки наблюдения
до источников подчиняется соотношению
г» у- (9)
Отметим, что это неравенство более сильное, чем просто условие г У?> d.
> Интерференция большого числа волн. Рассмотрим интерфе-
интерференцию от N одинаковых синфазных источников,
расположенных на одной прямой на расстоянии d
друг от друга. На большом расстоянии от источ-
источников (г ^> (Nd)/А) в направлении в происходит
сложение N колебаний одинаковой амплитуды Ло,
причем разность фаз между соседними колебани-
г >*^ \ ями равна ф — Bтг/Л)с? sin ^. Результирующую
амплитуду А найдем из уравнений (см. вектор-
Рис. 74 НуЮ диаграмму на рис. 74): Ао = Дsin(<^/2),
А = Д sinGV0/2). Исключая радиус описанной окружности Д, по-
получим:
> Интерференция от естественных источников света. Излуче-
Излучение естественных (тепловых) источников света состоит из множества
цугов волн, спонтанно испущенных возбужденными атомами при их
высвечивании, т. е. при возвращении в нормальное состояние. Длитель-
Длительность цуга ~ 10~10 -г- 10~8 с, он содержит 106 -г- 108 колебаний. Сле-
Следовательно, два разных естественных источника некогерентны даже
при выделении в их излучении узкой спектральной полосы, поскольку
разность фаз колебаний очень быстро и хаотически меняется в каждой
точке наблюдения. Для наблюдения интерференции надо излучение от
одного источника расщепить на два или несколько пучков и заставить
их попадать в точку наблюдения различными путями. При этом будет
происходить интерференция каждого из цугов с самим собой, и условие
максимума или минимума будет одновременно выполняться для всех
цугов одной частоты, испущенных из одной и той же точки источника.
Удобно ввести оптическую разность хода пучков
Г Г
— \П2 dl — \п\ dl,

5.2] Интерференция света 159
где интегрирование ведется вдоль линии, которую данный пучок прохо-
проходит от точки излучения до точки интерференции. Условие максимума:
А — т\; условие минимума: Л = I т + - I Л, где т называется
порядком интерференции.
Приведем классические примеры получения двух когерентных ис-
источников.
1. Опыт Юнга (упоминался выше). Солнечный свет падает на
очень узкую щель в первом экране, вследствие дифракции расходится
и падает на две узкие щели во втором экране. Опять же из-за дифрак-
дифракции после этих щелей свет расходится и образует перекрывающиеся
когерентные пучки.
2. Зеркала Френеля. Свет от ярко светящейся щели падает на два
зеркала, скрещенных под углом почти 180°. Близко расположенные
мнимые изображения щели образуют два когерентных источника.
3. Бипризма Френеля. Свет от ярко освещенной щели преломляется
в двух стеклянных призмах с малыми преломляющими углами, сло-
сложенных своими основаниями. В результате преломления образуются
два близко расположенных мнимых изображения щели.
4. Билинза Бийе. Собирающая линза разрезается пополам и по-
половинки слегка раздвигаются. Билинза освещается узкой щелью, па-
параллельной линии разреза. Каждая половинка линзы формирует свое
действительное изображение щели.
5. Зеркало Ллойда. Свет от узкой щели отражается от зеркальной
плоскости, образуя мнимое изображение щели. Интерферируют свет
от самой щели и от ее изображения.
> Влияние размеров источника. Пространственная когерент-
когерентность. Разность хода лучей в данной точке экрана имеет определенное
значение только в случае точечного источника. При переходе от одной
точки протяженного источника к другой разность хода меняется. Если
разность хода изменится на Л/2, то условие максимума превратится
в условие минимума, т. е. наложение интерференционных картин от
разных участков протяженного источника приводит к смазыванию
общей интерференционной картины.
Рассмотрим, например, плоский источник. Предположим, что
первый из интерферирующих лучей исходит от источника под
углом а\ к его нормали, а второй — под уг-
углом «2 • Пусть эти лучи лежат в одной плоскости
с нормалью, а углы излучения почти одина- ai
ковы для всех точек источника (рис. 75). При
переходе от одного конца источника к другому
длина пути первого луча изменится на /sinc^i,
второго — на / sin а^ (I — размеры источника
в плоскости лучей),а разность хода изменится Рис. 75

160 Оптика [Гл.5
на /(sin«2 — sinc^i). Условие сохранения интерференционной картины
(условие пространственной когерентности) принимает вид
/| sin а,2 — sin ol\\ < А/2.
Пример 1. В опыте Юнга / — ширина щели в первом экране,
а± = —«2 = 6/BL), где b — расстояние между щелями во втором экране,
L ^> b — расстояние между экранами; получим: 2l(b/2L) < Л/2, т.е.
/ < XL/Bb). Перепишем эту формулу в виде: b < Х/Bф), где ф = I/L —
угловые размеры источника, или угол расхождения падающих на две щели
лучей. Например, при прямом освещении щелей Солнцем ф и 0,009 рад,
Л ~ 500 нм, т.е. расстояние между щелями должно быть меньше 0,06 мм.
Именно поэтому надо сначала солнечный свет пропускать через узкую щель.
> Влияние немонохроматичности света. Временная коге-
когерентность. Нарушение монохроматичности складывающихся волн
может привести к смазыванию картины интерференции. Предполо-
Предположим, что частоты излучаемых волн лежат в узком спектральном ин-
интервале Ли. Сильное искажение картины интерференции происходит
в том случае, если разность хода А превышает некоторое критиче-
критическое значение LK, которое называют длиной когерентности; LK имеет
смысл длины цуга волн, испускаемого атомом в одном акте излучения
(напомним, что устойчивая интерференция происходит при сложении
цугов в одном из разделенных пучков с соответствующими им цугами
в другом пучке).
Время тк = LK/c, которое называют временем когерентности,
имеет смысл длительности цуга волн. В соответствии с общими свой-
свойствами преобразования Фурье, спектральная ширина волнового пакета
связана с его длительностью соотношением Ли At ~ 2тг.
Пример 2. «Оборванная» синусоида A(t) sino;o^, где А = const в интер-
интервале —т/2 < t < т/2 и А = 0 вне этого интервала, имеет разложение Фурье
sin[-(o;-a;o)r] 2n
шал ~ -^ , ширина которого равна Леи ~ —.
(ш - шо)т т
Получаем, что спектральная ширина интерференции связана с дли-
длительностью когерентности соотношением Ли ~ 2тг/тк. Максимальный
порядок спектра, в котором можно наблюдать интерференцию, можно
оценить как N ~ тк/Т = и/Ли = Х/ЛХ. Полезно отметить, что
именно в этом порядке сольются полосы соседних порядков:
GV + 1)Л = 7V(A + 5X)
(задний край полосы порядка 7V + 1 совпадает с передним краем полосы
порядка N). Длину когерентности часто выражают через SX:

5.2] Интерференция света 161
> Интерференция в тонких пленках. Рассмотрим интерферен-
интерференцию лучей, отраженных от передней и задней поверхностей тонкой
пленки (рис. 76). Будем считать фронт волны плоским, т.е. источник
достаточно удаленными. Так как фронт преломленной волны пер-
перпендикулярен лучу, то луч 1 в точке D и луч 2 в точке D' имеют
одинаковые фазы. Значит, оптическая разность хода лучей в точке D
равна n(D'C + CD). Кроме того, к разности хода надо добавить Л/2,
что позволит учесть изменение фазы на тг при отражении от среды
с большим показателем преломления (на границе воздух — пленка
в точке D). После преобразований получим:
Л
Л = 2dn cos ф + - = 2dVn2 -sin20,
где d — толщина пленки, п — ее показатель преломления, 0 и ф — углы
падения и преломления. Условие максиму-
максимума для наблюдения в отраженном свете
Л = т\ выполняется для определенных
длин волн. Для очень тонких пленок усло-
условию максимума удовлетворяют одна или
две длины волны из видимого диапазона,
и пленка оказывается окрашенной. Уело- и
вию максимума для наблюдения в отра- w
женном свете соответствует для той же "
длины волны условие минимума для на- р 7fi
блюдения в проходящем свете (отражений
на границе воздух — пленка не происходит). Как всегда при интерфе-
интерференции, энергия не увеличивается, а перераспределяется.
Рассмотрим теперь два важных случая.
1) Полосы равной толщины. Если лучи падают под почти посто-
постоянным углом, например нормально, а толщина пленки меняется, то
линии постоянной толщины есть линии постоянной разности хода. При
освещении монохроматическим светом эти линии будут видны в виде
темных или светлых полос. При наблюдении в белом свете (при усло-
условии малой толщины пленки) линии будут цветными. Интерференция
происходит вблизи поверхности пленки (интерференционная картина
локализована на поверхности).
2) Полосы равного наклона. Толщина пленки постоянна, освеще-
освещение ведется рассеянным светом от удаленного источника. Меняя угол
наблюдения, мы будем получать то условие максимума, то миниму-
минимума. Интерференционная картина локализована на бесконечности (или
в фокальной плоскости линзы). Для очень тонких пленок свет может
быть не монохроматичным, наблюдение под данным углом выделяет
ту длину волны, для которой выполнено условие максимума.
6 А. И. Черноуцан

162 Оптика [Гл.5
Пример 3. Кольца Ньютона. Если плосковыпуклую линзу положить
на поверхность стеклянной пластинки (рис. 77) и освещать монохромати-
монохроматическим светом, падающим нормально, то на воздушном промежутке будут
наблюдаться полосы равной толщины, имеющие
форму окружностей. Толщина промежутка
равна d и y/R2 + г2 — R и г2/BЯ), где
г — радиус окружности. Условие минимума
имеет вид 2d + (А/2) = I т -\— 1 Л, или
Гщ = VmXR. В центре картины будет темное
пятно.
р 77 > Принципы голографии. Голография
используется для записи объемного изобра-
изображения предмета. Предмет освещается светом лазера, обладающим
очень высокой степенью когерентности, и попадает на фотопластинку.
Информацию о форме предмета несет зависимость фазы предметной
волны от положения на пластинке. Если на пластинку одновременно
со светом, отраженным от предмета, послать отраженный от зеркала
опорный лазерный луч, которым освещается предмет, то в результате
интерференции образуется волна, амплитуда и интенсивность которой
будут зависеть от фазы предметной волны. Так как почернение
фотопластинки пропорционально интенсивности, то на ней сохранится
информация о фазе волны. Освещая проявленную пластинку светом
того же лазера, можно восстановить исходный сигнал.
При записи интерференционного сигнала в объеме толстой про-
прозрачной фотопластинки возникает объемная голограмма, которая несет
информацию как о форме предмета, так и о длине волны лазерного
сигнала. При освещении голограммы белым светом волны других ча-
частот гасят друг друга за счет интерференции, и возникает изображение
предмета, освещенного монохроматическим лазерным светом. Если
в одной пластинке записать три голограммы от лазеров с различными
длинами волн, то при освещении белым светом возникает объемное
цветное изображение.
> Излучение Вавилова — Черенкова. При движении частицы
в среде со скоростью К, превышающей фазовую скорость v = с/п
света в этой среде, возникает излучение электромагнитных волн под
определенным углом к направлению движения частицы. Элементарное
объяснение этого явления совершенно аналогично объяснению возник-
возникновения ударной волны при движении со сверхзвуковой скоростью.
При прохождении частицы возникает излучение возбужденных ею ато-
атомов среды. Разность хода волн, излученных возбужденными атомами

5.3]
Дифракция
163
В
в направлении 0 из положений А и В
(рис. 78), равна
Л = v — — L cos 0 = L ( — — cos # J.
Если V < v, то для любого угла в
можно подобрать такое L, что излучение
точек Л и В гасит друг друга (Л = А/2).
При V > v то же самое относится к любому
углу, не равному во = arccos(v/V/) (можно
добиться Л = ±А/2). Однако в направлении во все точки излучают
волны с одной и той же фазой, т.е. происходит взаимное усиление
излучения.
Рис. 78
5.3. Дифракция
> Принцип Гюйгенса — Френеля. Дифракцией называются от-
отклонения от закона прямолинейного распространения света. Прибли-
Приближенный расчет интенсивности света после препятствий или отверстий
в экране опирается на принцип Гюйгенса — Френеля, который дополня-
дополняет геометрическое построение Гюйгенса (см. разд. 5.1) условием интер-
интерференции вторичных лучей. Согласно этому принципу, все точки про-
произвольной поверхности, окружающей источники волн, являются источ-
источниками когерентных вторичных волн, а амплитуда колебаний волны
в произвольной точке вне этой поверхности может быть получена как
результат интерференции вторичных волн. Обычно в качестве такой
поверхности выбирают фронт волны, тогда источники вторичных волн
синфазны. Амплитуда вторичной волны пропорциональна амплитуде
первичной волны и площади участка поверхности:
(П)
где Eq — (комплексная) амплитуда первичной волны в точках фронта,
а — угол между направлением излучения и нормалью к поверхности,
г — расстояние от фронта вторичных источников до точки наблюдения,
К (а) — медленно убывающая функция (К(тт) = 0).
Рассмотрим дифракцию на отверстиях различной формы в плоском
экране для случая нормального падения плоской монохроматической
волны.
Круглое отверстие радиусом ROTB, точка наблюдения В лежит
на оси отверстия на расстоянии / от его центра (рис. 79). В качестве
поверхности вторичных волн выберем участок фронта в плоскости
отверстия. Разобьем фронт на тонкие круговые сегменты, засекая на
нем из точки В окружности отрезками, длины которых составляют

164
Оптика
[Гл.5
2-я зона
Центр
Рис. 79
1-я зона
Рис. 80
3-я зона
/ + 5r, / + 25r, . . . Er <C ROtb)- Поскольку оптическая длина пути при
переходе от сегмента к сегменту испытывает постоянное приращение
5г, то одинаковым будет и приращение фазы колебаний; кроме того,
амплитуды колебаний от отдельных круговых сегментов, вычисленные
по формуле A1), также равны. Действительно, из г2 = R2 + l2 получаем
RSR = г8г и 8S/r = 2тт5г = const (SS = 2ttR5R). Следовательно,
векторная диаграмма складывающихся колебаний (рис. 80) имеет вид
медленно закручивающейся спирали (с учетом медленного уменьшения
К (а)). Из соображений симметрии можно сделать вывод, что спираль
сходится к центру окружности. Сумма всей спирали соответствует
свободному распространению света в отсутствие экрана.
Часть поверхности от центра до точек, где г\ — I + А/2, называется
первой зоной Френеля,, от края первой зоны до r<i — 1 + \ — второй зоной
Френеля, и т.д. Видно, что если открыть только первую зону Френе-
Френеля, а все остальное закрыть экраном, то амплитуда колебаний будет
в 2 раза больше, чем в отсутствие экрана, а интенсивность — в 4 раза
больше. Если открыть две первые зоны, то амплитуда и интенсивность
в точке В будут близки к нулю, и т. д. Наоборот, если закрыть экраном
небольшое число центральных зон Френеля, то это почти не скажется
на интенсивности колебаний в точке В — она будет почти такой же,
как и в отсутствие экрана (этот парадоксальный факт известен под
названием «пятно Пуассона»).
Если изготовить препятствие сложной формы, закрывающее зоны Френе-
Френеля через одну (все четные зоны или все нечетные), то в точке наблюдения бу-
будет происходить многократное увеличение интенсивности. Такое устройство,
фокусирующее свет подобно линзе, называется зонной пластинкой и находит
многочисленные применения.
Радиус ттг-й зоны Френеля найдем из теоремы Пифагора
г2 = R2 + /2, подставляя г = I + А (А ^ I — разность хода между

5.3]
Дифракция
165
Рис. 81
краем и центром отверстия):
R(A) = V21A.
Рис. 82
A2)
Если подставить Л = ттгЛ/2, найдем радиус т-й зоны Френеля:
Rm = л/тттТЛ.
Приведем также формулу для случая падения на отверстие сферической
волны, испускаемой точечным источником, лежащим на оси отверстия на
расстоянии а от его центра:
J2alA ImalX
При а —>- оо это выражение переходит в A2).
Число открытых отверстием зон Френеля равно т = R^TB/IX.
Следовательно, при I <С RqTB/А открыто много зон Френеля и интен-
интенсивность света в точке наблюдения мало отличается от интенсивности
падающей волны, т. е. дифракционные эффекты на оси отверстия вы-
выражены слабо (работает приближение геометрической оптики). В об-
обратном пределе I ^> R^TB/X открыта только малая часть первой зоны
Френеля, т. е. все колебания в точке наблюдения складываются в одной
фазе (приближение Фраунгофера).
Для круглого отверстия расчет дифракции для точек наблюдения,
лежащих в стороне от оси, оказывается сложным. Ниже мы вернемся
к этой задаче, но уже для дифракции Фраунгофера. Однако решение
задачи дифракции для всех точек наблюдения оказывается возможным
для отверстия в форме длинной щели.
Отверстие в виде щели шириной 6, точка наблюдения В лежит
в плоскости, отстоящей от экрана на расстояние /. В этом случае фронт надо
разбивать не на круговые, а на прямолинейные тонкие сегменты (рис. 81)
одинаковой ширины 8х. Главное отличие состоит в том, что площади сег-
сегментов пропорциональны не R5R, а просто 5х. При этом, как и раньше,

166
Оптика
[Гл.5
выполняются тождества г2 = х2 + /2, х5х = г?г, следовательно,
~ Sr/x, и амплитуды колебаний при удалении от точки О убывают. Это
приводит к тому, что радиус кривизны векторной диаграммы становится
все меньше, и она приобретает форму спирали, которая носит название
«спирали Корню» (рис. 82). На этой спирали откладывают значения пара-
параметра v = ху/2/1Х, пропорционального (при х ^ I) длине дуги спирали,
отсчитанной от центра. Поскольку разность хода равна Л = г — / и х2/21,
то Л = v2 — . Расстояние между конечными точками спирали F± и F^
равно амплитуде Aq колебаний в отсутствие преграды, т. е. амплитуде па-
падающей волны. Если края щели находятся на расстояниях х\ и Х2 от
точки О, то вычисляем соответствующие значения tii и «2, затем находим
на спирали соответствующие точки и, соединяя их, определяем амплитуду.
Таким образом можно получить ди-
дифракционную картину от щели не
только в центре экрана, но и в стороне
от центра. Случай b <С vlX соот-
соответствует дифракции Фраунгофера
(открыта малая часть спирали); слу-
случай b ^> л/ТХ соответствует прибли-
приближению геометрической оптики. При
этом вблизи краев щели наблюдает-
наблюдается дифракционная картина, соответ-
соответствующая дифракции на полуплоско-
Рис. 83 сти (рис. 83); точно напротив края
щели (точка Р) амплитуда OFi рав-
равна половине амплитуды падающей волны Aq (интенсивность — в четыре раза
меньше /о), ширина дифракционного размытия ~ л/ТХ.
Методом зон Френеля удается исследовать дифракционную кар-
картину от щели графически, с помощью спирали Корню, полученной
численным расчетом. Простое аналитическое описание дифракции от
щели удается получить в приближении Фраунгофера.
> Дифракция Фраунгофера от щели. Дифракцией Фраунгофе-
Фраунгофера называют дифракцию в параллельных лучах, когда разность фаз
вторичных волн, исходящих от различных точек рассматриваемого
участка волнового фронта, можно найти в предположении их парал-
параллельности. В этом приближении дифракционная картина упрощается
и можно рассчитывать интенсивность света в разных точках экрана.
Приближение Фраунгофера действует в двух случаях: во-первых, если
лучи света после дифракции собираются линзой в ее фокальной плоско-
плоскости, и, во-вторых, если экран удален от дифракционного отверстия на
достаточно большое расстояние г ^> R2/\, где R — размер источника
(см. обсуждение условия Фраунгофера в разд. 5.2, формула (9)).
Рассчитаем в приближении Фраунгофера дифракцию плоской мо-
монохроматической волны на щели шириной Ь. Ограничимся изучени-
изучением нормального падения волны на экран с щелью; в этом случае

5.3]
Дифракция
167
все точки щели являются источниками вторичных синфазных волн.
Разобьем плоскость щели на большое число N одинаковых узких
полосок (рис. 84). Амплитуда света от
каждой полоски равна Eq/N, где Eq — ам-
амплитуда света, посылаемого щелью в на-
направлении в = 0 (в этом случае все
полоски излучают свет синфазно). При
излучении в направлении, составляющем
угол в с нормалью, разность фаз меж-
между излучением соседних полосок рав-
равна Sip = Bтг/X)(b/N) sin в, разность
фаз между крайними полосками равна Рис. 84
ip = B7r/ANsin# = NSip. Используя вы-
выражение A0) для интерференции N источников, получим амплитуду
излучения щели в направлении в (sin Sip надо заменить на Sip):
где р = 2к^
A3)
Интенсивность излучения, равная/1 = /q sin2 (cp/2)/(ср/2J, а также
характерные векторные диаграммы изображены на рис. 85. Условие
минимумов излучения имеет вид:
6 sin в = тА
(т =
A4)
Условие максимумов: 6sin# « (т + -)А (т = 1, 2, . . .). Максимумы
интенсивности относятся как /о : 1\ : /2 . . . ~ 1 : A,5тгJ : B,5тгJ . . .
Максимальный порядок спектра определяется условием т ^ 6/BА).
> Дифракция Фраунгофера на круглом отверстии. Разреша-
Разрешающая способность оптических приборов. В случае дифракции на
круглом отверстии распределение интенсивности имеет вид концентри-
концентрических темных и светлых кругов вокруг центрального светлого пятна.
Распределение интенсивности при малых углах в с осью отверстия вы-
выражается через функцию Бесселя первого порядка: / = /q J2(
А
Рис. 85
2А
b sin в

168
Оптика
[Гл.5
где D — диаметр отверстия. Внешне угловое распределение интенсив-
интенсивности мало отличается от случая дифракции на щели; первый минимум
соответствует углу в\ = 1,22 X/D.
Угол 01 можно считать углом дифракционного расширения пучка
света. Расплывание пучка будет слабым на расстояниях /, удовлетво-
удовлетворяющих условию: 1в\ <С D, или / <С D /А. Это неравенство является
условием применимости геометрической оптики (см. разд. 5.1).
При наблюдении в оптический прибор (линза, телескоп) двух близ-
близких точек они будут изображаться на экране в виде маленьких дифрак-
дифракционных кружков. Условно считается, что изображения точек нераз-
неразличимы, если они сблизились настолько, что центральный максимум
одного кружка совпал с первым минимумом другого (критерий Рэлея).
Следовательно, угловое разрешение таких приборов выражается фор-
формулой
п 1 99_
"min — -1-1^^ г-* •
Этот предел возможного разрешения прибора накладывается волновой
природой света и не может быть превзойден никакими техническими
усовершенствованиями.
> Дифракционная решетка. Дифракционной решеткой называет-
называется последовательность из большого
числа N одинаковых параллельных
щелей (рис. 86). Ширину каждой
щели обозначим 6, а расстояние
между соответствующими точками
(например, центрами) соседних
щелей, которое называют периодом
решетки, обозначим d (d = l/N,
где / — ширина решетки). Каждая
>| ^. ^^CSnX P Щель излучает в направлении в
>| ^^ - ^""^Ч ^ свет, амплитуда которого Е\
определяется выражением A3).
р r>g Разность фаз между соседними
щелями равна 5 = Bтг/\)dsin6,
и для вычисления итоговой амплитуды можно опять воспользоваться
формулой A0) для суммы колебаний N независимых источников:
„ „ sm(Nd/2) т т sin
sm(S/2) ' si
где
о d .
= 27r-sm
А
Главные максимумы дифракционной решетки определяются условием
ds'mO = mX. A5)

5.3] Дифракция 169
В направлении главных максимумов интенсивность излученной волны
/ = N2I\ полностью определяется интенсивностью излучения от-
отдельной щели в этом направлении. Если главный максимум окажется
вблизи минимума /i(#), определяемого условием 6sin# = mA, то этот
максимум окажется подавленным. Максимальный порядок спектра
определяется условием т ^ d/ X.
Между каждыми двумя главными максимумами дифракционная
картина содержит 7V — 1 минимум и N — 2 добавочных максимума.
Минимумы определяются условиями dsinO = (т + n/N)X
(п = 1, 2, . . ., N — 1). Интенсивность добавочных максимумов
гораздо меньше, чем главных, и при большом числе штрихов их
можно не учитывать.
При падении света на решетку под углом во Ф О условие главных
максимумов приобретает вид:
d(sinO -sinOo) = m\. A6)
Для грубых решеток (d ^> Л) эффективным оказывается использо-
использование скользящих лучей (во ~ тг-/2), для которых условие главных
максимумов приобретает вид: dcos6oF — во) = тА. Видно, что роль
эффективного периода в этом случае играет малая величина d cos #o-
> Дифракционная решетка как спектральный прибор. Свой-
Свойства любого спектрального прибора определяются его угловой диспер-
дисперсией, дисперсионной областью и разрешающей способностью.
Угловой дисперсией называется производная Dm = dOm/d\, где
вш — положение главного максимума ттг-го порядка. Из условия глав-
главного максимума получим
ш d cos в '
Дисперсионной областью называется максимальная ширина
ЛХ спектрального интервала, при которой еще нет перекрытия
спектров соседних порядков. Из уравнений dsin# = m(A + Z\A)
и d sin в = (m + 1)A имеем ЛХ = X/m. Видно, что для исследования
широких участков спектра надо применять низкие порядки.
Разрешающей способностью называется отношение R = A/JA, где
5Х — наименьшая разность длин волн, которые может разрешить спек-
спектральный прибор. Две линии считаются разрешенными, если максимум
одной линии попал на минимум другой (критерий Рэлея). Из уравнений
ds'me = (т + 1/N)X и dsme = т(Х + 8Х) получим 5Х = X/(mN), т.е.
R= A = mN.
оХ

170 Оптика [Гл.5
> Дифракция рентгеновских лучей на кристалле. Длина вол-
волны рентгеновских лучей сравнима с расстоянием между атомами кри-
кристаллической решетки, которая для падающих лучей представляет
собой пространственную дифракционную решетку. Условие дифрак-
дифракционных максимумов состоит в одновременном выполнении трех урав-
уравнений A6) для трех взаимно перпендикулярных кристаллических осей
(условия Лауэ):
di(cosa — cos^o) = ^iA, ^(cos /3 — cos/3o) = П2А,
d3(cos7 - cos70) = n3A,
где a, /3, 7 —углы с осями, связанные условием cos2 a+cos2/3+cos2 7 =1.
Эти три уравнения нельзя одновременно удовлетворить при произволь-
произвольно выбранном направлении падающего луча и заданной длине волны.
Это значит, что при облучении кристалла монохроматическими, но
рассеянными рентгеновскими лучами (т. е. имеющими всевозможные
направления) возникают дифракционные максимумы во вполне опре-
определенных направлениях. Анализ получающихся лауэограмм позволяет
получать информацию о строении кристалла. Дифракционные мак-
максимумы отсутствуют, если А/2 превышает все периоды решетки; для
видимого света кристалл можно считать однородной средой.
Отражение рентгеновских лучей от поверхности кристалла можно
также рассматривать как интерференцию лучей, отраженных от систе-
системы последовательных атомных плоскостей в кристалле. По аналогии
с интерференцией в тонких пленках (см. разд. 5.2), разность хода
между лучами, отраженными от соседних плоскостей, равна dsin#,
где в — угол между падающим лучом и атомной плоскостью (не с нор-
нормалью!), a d — межплоскостное расстояние. (Отметим, что показатель
преломления рентгеновских лучей мало отличается от единицы, см.
разд. 5.5.) Отражение наблюдается только в направлениях дифракци-
дифракционных максимумов, удовлетворяющих условию Вульфа — Брегга:
= mA,
где т = 1, 2, . . . — порядок дифракционного максимума.
5.4. Поляризация света. Формулы Френеля
> Поляризованный и естественный свет. Плоская волна назы-
называется линейнополяризованной или плоскополяризованной, если коле-
колебания вектора Е происходят в одной плоскости, перпендикулярной
фронту волны (ее называют плоскостью поляризации волны). Моно-
Монохроматическая плоская волна либо линейно поляризована, либо по-
поляризована по эллипсу или по кругу (см. разд. 4.5). Эллиптически

5.4] Поляризация света. Формулы Френеля 171
поляризованная волна представляет собой сумму двух взаимно пер-
перпендикулярных плоских волн, между колебаниями которых имеется
разность фаз. Естественный свет, испущенный нагретыми телами,
является неполяризованным, поскольку направление колебаний векто-
вектора Е в каждой точке быстро и хаотически меняется. Смесь естествен-
естественного и поляризованного света называется частично поляризованным
светом.
Поляризатором называется устройство, на выходе из которого свет
линейно поляризован в определенной плоскости, называемой плоско-
плоскостью пропускания поляризатора. Причина в том, что поляризатор пол-
полностью поглощает свет, поляризованный перпендикулярно плоскости
пропускания. Если естественный свет пропустить через поляризатор,
то он станет линейно поляризованным, а его интенсивность уменьшится
в два раза (если нет поглощения в плоскости пропускания поляризато-
поляризатора). Если линейно поляризованный свет интенсивностью /о пропустить
через поляризатор, плоскость пропускания которого составляет угол а
с плоскостью колебаний световой волны, то интенсивность прошедшей
волны будет составлять
/ = /0 cos2 a
{закон Малюса). Объясняется это тем, что линейно поляризованный
свет с амплитудой Eq представляет собой сумму двух линейно поля-
поляризованных волн: волна, поляризованная в плоскости пропускания (ее
амплитуда равна Eq cos а), пройдет через поляризатор без изменений,
а вторая волна будет поглощена.
> Отражение и преломление волн. Формулы Френеля. Интен-
Интенсивность и поляризация отраженной и преломленной волн зависят от
того, как поляризована падающая волна. Запишем граничные условия
на поверхности раздела двух сред:
Здесь нижние индексы т, п обозначают тангенциальную и нормальную
компоненты, а верхние индексы г, г, d соответствуют падающей, отра-
отраженной и преломленной волнам. Кроме того, необходимо учитывать
соотношения между электрическим и магнитным полями в плоской
электромагнитной волне (см. раздел 4.5). Для плоской монохромати-
монохроматической волны
Е1 = E[oexp[i(ut -k1-!-)],
Ег =
Ed =

172
Оптика
[Гл.5
соотношения для волновых векторов (рис. 87) имеют вид:
Ll _ LT _ Ld
/Си — /Си — /Си
ИЛИ
k\ sin а = к\ sin /3 = &2 sin ф,
где &i = ami/с, к<± — uri2/c. Полу-
Получаем закон отражения /3 = а и закон
преломления ni sin a = П2 sin -0.
Особого внимания заслуживает слу-
случай, когда свет падает из оптически более
плотной среды (п\ > П2) под углом а,
большим предельного угла апр полного отражения (sin anp = П2/П1). В этом
случае к\ sin a > &2, и &^_ оказывается мнимым: kj_ =
Рис. 87
где \kj_\ = —уп\ sin2 ol — n\. Это означает, что амплитуда прошедшей волны
экспоненциально затухает на расстоянии S ~ 1/|&^_|, а амплитуда отражен-
отраженной волны равна амплитуде падающей.
Амплитуды прошедшей и отраженной волн зависят от поляризации
падающей волны. Приведем результат для отраженных волн:
= -El
{формулы Френеля). Здесь первая формула относится к волне, поля-
поляризованной в плоскости падения (ее удобно выводить из граничных
условий для Е), а вторая — к волне, поляризованной в перпендику-
перпендикулярной плоскости (ее удобнее выводить из граничных условий для Н).
Видно, что при угле падения, удовлетворяющем условию а + ф = тг/2,
волна, поляризованная в плоскости падения, отражаться не будет. Так
как в этом случае sin ф = cos а, то угол падения, при котором отражен-
отраженная волна будет линейно поляризованной перпендикулярно плоскости
падения (угол Брюстера), удовлетворяет соотношению:
tga = п.
Качественное объяснение состоит в том, что в этом случае направление
колебаний диполей (указаны на рисунке), возбужденных во второй
среде волной, поляризованной в плоскости падения, оказывается па-
параллельным направлению отраженной волны (отраженный и прелом-
преломленный лучи взаимно перпендикулярны). Но осциллятор не излучает
волну в направлении своих колебаний (см. разд. 4.5).

5.4] Поляризация света. Формулы Френеля 173
В случае нормального падения различие между поляризациями
пропадает:
П\ + П2
Видно, что при отражении от оптически более плотной среды (п2 > п-\)
фаза колебаний сменяется на противоположную (точнее, к фазе добав-
добавляется тг). Впрочем, это свойство видно и непосредственно из формул
Френеля: при а > ф происходит изменение знака колебаний.
Отношение потока отраженной энергии к потоку энергии падающей
называется коэффициентом отражения. При нормальном падении он
равен
Р (ni -п2J
(т + п2)
Коэффициент пропускания равен D = 1 — R (закон сохранения энер-
энергии).
Отметим, что если коэффициент отражения равен отношению объемных
плотностей энергии отраженной и падающей волн:
R = (ErIЕ1J, то при расчете коэффициента про-
пропускания надо учесть как различие в скоростях
волн в разных средах, так и (для падения под уг-
углом) изменение поперечной площади за счет пре-
преломления: Sd IS1 = cos ф/ cos а (рис. 88). В итоге
_ v2(EdJcosif;
vi(E1J cosa '
(Поток энергии равен произведению объемной
плотности энергии на скорость волны и на пло- Рис. 88
щадь поперечного сечения.)
Коэффициенты R и D зависят только от относительного показа-
показателя преломления n<i\ = uijn\ двух сред. Коэффициент отражения
обычно невелик; например, при п^х = 1,5 получим R — 0, 04.
Пример. Просветление оптики. Коэффициент отражения стекол
в оптических приборах невелик (несколько процентов). Тем не менее важной
задачей является уменьшение отражения для определенных длин волн. Для
этого на поверхность наносят прозрачную пленку с показателем преломления
7т/ = л/п (п — показатель преломления стекла) и толщиной Л/Dп/). Оптиче-
Оптическая разность хода между лучами, отраженными от поверхностей пленки,
равна Л/2 (изменение фазы при отражении учитывать не надо, так как
оно происходит у каждого из лучей), а коэффициенты отражения на этих
поверхностях будут близки друг к другу (см. формулу A7)). В результате
произойдет почти полное гашение отраженного света.
> Оптически анизотропные среды. В случае сред, обладающих
анизотропией, векторы Е и D в общем случае уже не параллельны
друг другу. Линейная связь между ними носит тензорный характер,

174 Оптика [Гл.5
т. е. каждая из компонент вектора D выражается в виде линейной ком-
комбинации всех трех компонент вектора Е. Существуют три взаимно пер-
перпендикулярные оси, называемые диэлектрическими осями кристалла,
для которых D || Е: Di = e^EiEi (i = 1,2,3). Значения Si называ-
называются главными диэлектрическими проницаемостями кристалла. Мы
рассмотрим только случай одноосных кристаллов, у которых две из
трех Si равны друг другу (е = е±). Выделенная ось (е = ?ц) называется
оптической осью кристалла.
При распространении в одноосном кристалле плоской волны вво-
вводят главное сечение кристалла — плоскость, проходящую через опти-
оптическую ось и вектор нормали п к фронту волны. Оказывается, что
распространение линейно поляризованной световой волны зависит от
направления ее поляризации. Волна, поляризованная перпендикуляр-
перпендикулярно главному сечению, называется обыкновенной. Скорость распростра-
распространения такой волны v± = с/\/s± не зависит от направления; колебания
векторов Е и D направлены одинаково; направление распространения
энергии (т. е. вектора Пойнтинга S = Е х Н) перпендикулярно фронту
волны. Волна, поляризованная параллельно главному сечению, назы-
называется необыкновенной. Скорость ее распространения зависит от угла
между п и оптической осью (при угле тг/2 между ними она равна
v\\ = с/д/ejj"). Колебания векторов Е и D происходят в разных направ-
направлениях, вектор Пойнтинга S = Е х Н не перпендикулярен к фронту
волны (нормаль к фронту волны параллельна D х Н). Разница между
обыкновенным и необыкновенным лучами исчезает только при распро-
распространении света параллельно оптической оси.
При падении света на поверхность кристалла он разделяется на
обыкновенный и необыкновенный лучи, линейно поляризованные пер-
перпендикулярно друг другу и имеющие разные показатели преломления
(явление двулучепреломления). Закону преломления (см. разд. 5.1)
подчиняется направление распространения фронта необыкновенной
волны, сам же луч может выйти из плоскости падения. Даже при
нормальном падении луча на кристалл, вырезанный под углом к опти-
¦ I I I I ческой оси, происходит пространственное
? ? f f f разделение лучей (рис. 89). Положения
фронтов указаны черточками, положе-
положение оптической оси — стрелкой. Необык-
Необыкновенный луч поляризован в плоскости
чертежа, обыкновенный — перпендику-
перпендикулярно ей.
Для получения и анализа поляризо-
поляризованного света используют поляризацион-
р с оп ные призмы (николи), разрезанные под
углом к распространению лучей таким
образом, что обыкновенный луч испытывает на плоскости разреза
4
/
/ /
Необ.
т
ч
Об.

5.4] Поляризация света. Формулы Френеля 175
полное отражение и уходит в сторону, а необыкновенный луч прохо-
проходит прямо. Другой способ получения поляризованного света основан
на различии в поглощении обыкновенного и необыкновенного лучей
в некоторых веществах. При пропускании света через дихроичную
пластину (пластинку турмалина, поляроид) обыкновенный луч погло-
поглощается, и наружу выходит линейно поляризованный необыкновенный
луч.
Для анализа характера поляризации света изучают зависимость ин-
интенсивности от ориентации николя. Если интенсивность не меняется, то
свет либо естественный, либо поляризован по кругу. Чтобы различить
эти случаи, используют пластинку в четверть волны, или компенса-
компенсатор. Толщина пластинки d подобрана так, чтобы разность хода между
обыкновенным и необыкновенным лучами Л = An d равнялась А/4.
Сдвиг фаз между взаимно перпендикулярными колебаниями станет
равным либо нулю, либо тг, и круговая поляризация превратится в ли-
линейную.
> Вращение плоскости поляризации. При распространении
в некоторых веществах (их называют оптически активными) линейно
поляризованного света происходит вращение плоскости поляризации.
Угол поворота пропорционален толщине пластины: % = а/, где а —
вращение на единицу длины. В зависимости от направления поворота
различают право- и левовращающие вещества. Пример — пластинка
кварца, вырезанная перпендикулярно оптической оси (кварц
бывает как лево-, так и правовращающим). В растворах оптически
активного вещества в неактивном растворителе а пропорционально
концентрации. Молекулы активных веществ обладают асимметрией
по отношению к правому и левому вращению по типу спирали.
Явление вращения плоскости поляризации можно охарактеризовать
как круговое двойное лучепреломление. Волны, поляризованные по
кругу в разные стороны, распространяются с разными скоростями,
т. е. разность фаз между ними меняется. Сумма двух таких колебаний
представляет собой линейное колебание, направление которого зависит
от разности фаз.
> Искусственная анизотропия. При помещении многих изотроп-
изотропных тел в однородное электрическое поле у них возникает одноосная
анизотропия с оптической осью, ориентированной параллельно на-
напряженности поля {электрооптический эффект Керра). Разность фаз
между обыкновенным и необыкновенным лучами при распространении
света перпендикулярно Е пропорциональна квадрату напряженности:
где / — толщина слоя вещества, а В называется постоянной Керра.
Искусственная анизотропия возникает в тех случаях, когда поляри-
поляризуемость молекул вещества зависит от их ориентации по отношению

176 Оптика [Гл.5
к полю. Аналогичный эффект возникает при помещении некоторых
веществ в магнитное поле (эффект Коттона — Мутона). Он описыва-
описывается соотношением Лср = 2тгС1В .
При помещении неактивных веществ в сильное магнитное поле
может возникнуть оптическая активность для света, распространяю-
распространяющегося параллельно вектору В (магнитное вращение плоскости поля-
поляризации). Угол поворота на единицу длины в этом случае (для диа-
и парамагнетиков) пропорционально величине магнитной индукции:
а = RB, где R называется постоянной Верде.
5.5. Дисперсия и поглощение света
> Классическая модель диспергирующей среды. При распро-
распространении в веществе электромагнитной волны заряженные частицы
среды приходят в вынужденное колебательное движение. Амплитуда
этих колебаний и их сдвиг по фазе по отношению к колебаниям на-
напряженности поля волны зависят от соотношения частоты волны и
и частоты собственных колебаний частиц ujq (cm. разд. 4.3). Резуль-
Результирующее волновое возмущение можно рассматривать как результат
интерференции исходной волны и волн, излученных частицами среды
(такой подход называют молекулярной оптикой). Однако в случае од-
однородной среды можно получить частотные характеристики волны по-
полуфеноменологически, учитывая возникающую при смещении частиц
поляризованность, вводя зависящие от частоты диэлектрическую вос-
восприимчивость и проницаемость и вычисляя показатель преломления.
Затухание волны, т. е. преобразование энергии колебаний в тепловую
энергию, учитывается введением полуэмпирических коэффициентов
затухания осцилляторов; диэлектрическая проницаемость и показа-
показатель преломления становятся при этом комплексными числами.
Рассмотрим сначала среду из одинаковых осцилляторов. Уравнение
движения заряженной частицы имеет вид
где Е — поле, действующее на частицу (в оптическом диапазоне игра-
играют роль только электроны). В неплотных газах можно не учитывать
отличие локального поля от среднего, т. е. считать, что на электроны
действует непосредственно поле волны Е = Еоехр[г(о;? — к • г)].
Решение уравнения движения ищем в виде ? = ?0 ехр(гс^), и после
подстановки получим
?Е
т(оио — lo + 2ij3uj)
(в комплексной записи автоматически учитывается сдвиг фаз). Сме-
Смещение частиц приводит к появлению у молекул дипольных моментов

5.5]
Дисперсия и поглощение света
177
Рис. 90
р = е^, т.е. к появлению поляризованности Р = TVp (TV — кон-
концентрация). Из соотношения Р = ео(е — 1)Е находим комплексную
диэлектрическую проницаемость
Ne2
A8)
Показатель преломления тоже будет мнимый: л/г = п — ix, причем че-
через действительную часть выражается фазовая скорость волны, а через
я — коэффициент затухания:
Е = Eq expf х) exp[i(ut — кх)\.
A9)
Чтобы найти п(оо) и я(оо), надо в равенстве е = (п — гкJ приравнять
действительные и мнимые части. Вдали от собственной частоты (при
\uj — о;о| ^> Р) получим
Ne2
г = пл = 1 +
Зависимости n{uj) и k(oj) качественно изображены на рис. 90 (по —
значение п при и —у 0, которое называют статическим). Там, где
поглощение невелико, показатель преломления возрастает с частотой
(нормальная дисперсия). В узкой области сильного поглощения наблю-
наблюдается аномальная дисперсия.
Аналогичная ситуация возникает возле каждой собственной ча-
частоты (cjoi и ооо2 на рис. 90). Например, в инфракрасной области
спектра наблюдаются полосы поглощения и аномальной дисперсии,
связанные с колебаниями ионов. Полосы поглощения в ультрафиолето-
ультрафиолетовой (иногда — в видимой) областях спектра объясняются колебаниями
электронов на внешних оболочках атомов (оптических электронов).
В рентгеновской области спектра частота волны и велика по сравнению
со всеми собственными частотами и зависимость п(оо) определяется

178 Оптика [Гл.5
колебаниями электронов, которые можно считать свободными:
2 1 Ne2
7тгво^
Коэффициент преломления рентгеновских лучей мало отличается от
единицы. Такая же формула верна для волны, распространяющейся
в разреженной плазме, содержащей свободные электроны.
Фазовая скорость волны в плазме (а также справа от полосы поглощения
в диэлектрике) оказывается больше скорости света в вакууме (п < 1).
Однако здесь не содержится противоречия с теорией относительности, так
как групповая скорость волны и = doj/dk (см. разд. 4.4) будет при этом
меньше с. Убедимся в этом для волны в плазме. Используя соотношение
k2 = ui2n2(uj)/c2 и уравнение B0), получим:
2, ,, , Ш d(jJ 2
с к ак = из аси => = с .
к dk
Значит, в этом случае и = пс < с.
У полярных молекул (например, воды) широкая полоса аномаль-
аномальной дисперсии находится в области сантиметровых радиоволн, где ам-
амплитуда вращательных колебаний диполей, стремящихся повернуться
вслед за напряженностью поля, сильно зависит от частоты. Именно
в этой области происходит уменьшение п = у/е от большого статиче-
статического значения (для воды no ~ 9) к высокочастотному значению (для
воды п « 1,3).
Формула A8) верна только при п, близких к единице, когда можно
пренебречь отличием поля, действующего на молекулу, от среднего
поля в веществе. Обобщением на случай плотных газов и жидкостей
является формула Лорентц — Лоренца:
п2 - 1 Ne2
j2 -о;2)'
которая следует из формулы Клаузиуса — Масотти (раздел 3.6). При
изменении плотности вещества величина
1 п2 -1
Г = ту ,
/?п2 + 2'
которая называется удельной рефракцией, должна оставаться постоян-
постоянной.
> Рассеяние света. Ослабление волны. Интенсивность волны
в среде уменьшается не только из-за поглощения света, но и вследствие
его рассеяния. Рассеяние объясняется излучением света атомными ос-
осцилляторами, которое происходит по всем направлениям (см. разд. 4.5).
Однако в идеально однородной среде свет, рассеянный молекулами,
находящимися на расстоянии Л/2 друг от друга, испытывал бы полное
интерференционное гашение, и ослабление за счет рассеяния в этом
случае отсутствовало бы. Рассеяние наблюдается на малых инородных

5.6] Тепловое излучение 179
частицах (тиндалевское рассеяние в мутных средах) и на неоднород-
ностях, возникающих вследствие флуктуации плотности (рэлеевское
рассеяние).
Интенсивность света, рассеянного на неоднородностях, размеры
которых малы по сравнению с длиной волны, пропорциональна Л~4
(закон Рэлея, см. также разд. 4.5). Этим объясняется голубой цвет неба
(рассеянный солнечный свет) и желто-красный цвет солнца (проходя-
(проходящий свет). Степень поляризации рассеянного естественного света за-
зависит от угла рассеяния; свет, рассеянный под углом тг/2, оказывается
полностью поляризованным. Качественное объяснение состоит в том,
что в этом направлении излучают только осцилляторы, направление
колебаний которых перпендикулярно направлению рассеяния. Рассея-
Рассеяние на неоднородностях, больших по сравнению с длиной волны, слабо
зависит от частоты; этим объясняется белый цвет облаков.
Рэлеевское рассеяние на флуктуациях плотности или концентра-
концентрации зависит от температуры. При приближении к критической точке
средние размеры флуктуации резко возрастают и наблюдается белое
помутнение жидкости, называемое критической опалесценцией.
Ослабление пучка света при не очень большой интенсивности про-
происходит по экспоненциальному закону (закон Бугера):
Т Т „ — (хх
1 = 70е ,
где коэффициент ослабления а равен сумме коэффициента поглоще-
поглощения, который выражается через мнимую часть показателя преломле-
преломления (см. формулу A9)), и коэффициента рассеяния, который описывает
ослабление волны из-за рассеяния.
5.6. Тепловое излучение
> Равновесное тепловое излучение. Излучение электромагнит-
электромагнитной (лучистой) энергии телом за счет энергии хаотического (теп-
(теплового) движения его молекул называется тепловым излучением.
Свойства теплового излучения определяются материалом тела и его
температурой. Если из любого материала сделать замкнутую по-
полость и поддерживать температуру ее стенок постоянной, то система
(стенка + излучение) придет в состояние термодинамического равнове-
равновесия, и в объеме полости установится равновесное тепловое излучение.
Важнейшая особенность равновесного излучения состоит в том, что его
свойства полностью определяются температурой стенок и не зависят от
их материала. Это утверждение является следствием второго начала
термодинамики. Кроме того, равновесное излучение однородно и изо-
изотропно.

180 Оптика [Гл.5
Основные характеристики как излучения с поверхности тела, так
и излучения в объеме были введены в разд. 5.1. Излучение с по-
поверхности характеризуется энергетической яркостью В и энергетиче-
энергетической светимостью R, равной количеству лучистой энергии, излученной
с единицы поверхности за единицу времени по всем направлениям (т. е.
в телесный угол 2тг). Вводятся также спектральные разложения энер-
энергетической светимости гл, rw, 7V, например, R = Jo r\ dX] величины г
называются излунательными способностями тела. Излучение в объ-
объеме характеризуется интенсивностью лучистого потока / и объемной
плотностью лучистой энергии п, а также их спектральными разложе-
разложениями. В случае изотропного излучения они связаны соотношением
и = 4тг//с. Освещенность Е определяется как полный лучистый поток
через единичную площадку со всех направлений (из телесного угла 2тг);
в случае изотропного излучения выполняются соотношения
Е = тг/ = -си.
4
Спектральные плотности освещенности Е обозначим е\, ev и еш. Пе-
Пересчет от одной спектральной характеристики к другой обсуждается
в разд. 5.1.
> Поглощательная способность. Закон Кирхгофа. Поглоща-
тельной способностью тела называется доля падающей лучистой энер-
энергии, поглощенная телом (для узкого интервала длин волн или частот):
Тело, для которого ал = 1 во всем спектральном интервале, называет-
называется абсолютно черным телом. Моделью черного тела может служить
замкнутая полость с небольшим отверстием; почти все лучи, попадаю-
попадающие в полость через отверстие, в результате многократных отражений
от внутренних стенок оказываются поглощенными. Тело, у которого
а\ = const < 1, называют серым.
Так как равновесное излучение находится в равновесии с поверхно-
поверхностью, то для любого спектрального интервала количество поглощенной
лучистой энергии, равное ел^л dX, должно быть равно количеству
излученной энергии, равному r\ dX. Поскольку характеристики равно-
равновесного объемного излучения не зависят от свойств конкретного тела,
то отношение излучательной способности любого тела к его погло-
щательной способности оказывается универсальной функцией длины
волны и температуры (закон Кирхгофа):
г^ = ех{Т) = \сих{Т). B1)
Поскольку для абсолютно черного тела поглощательная способность
равна единице, то стоящая справа функция есть не что иное, как

5.6] Тепловое излучение 181
излучателъная способность абсолютно черного тела, которую обозна-
обозначим г^:
Видно, что излучательная способность абсолютно черного тела и его
энергетическая светимость не зависят от способа его изготовления; они
связаны с объемной плотностью энергии соотношениями
г*х(Т) = \сих(Т), R*(T) = \cu(T). B2)
При одной и той же температуре абсолютно черное тело обладает самой
большой излучательной способностью и энергетической светимостью.
Например, для серого тела R = aR*. Отметим, что поскольку рав-
равновесное излучение изотропно, черное тело является ламбертовским
источником (см. разд. 5.1).
> Законы Стефана — Больцмана и Вина. Излучательная спо-
способность абсолютно черного тела при данной температуре стремится
к нулю при малых и больших Л и достигает максимального значе-
значения при некоторой длине волны Аш, которая зависит от температу-
температуры. Площадь под кривой г*х равна энергетической светимости R*(T).
Применение к равновесному излучению в полости общих соотношений
термодинамики позволило получить для него ряд общих соотноше-
соотношений. (Температура равновесного теплового излучения считается равной
температуре стенок.) Закон Стефана — Больцмана утверждает, что
энергетическая светимость абсолютно черного тела пропорциональна
четвертой степени температуры:
Я* = аТ\ B3)
где а = 5,67 • 10~8 Вт • м~2К~4 — постоянная Стефана — Больцмана.
Для вывода B3) надо воспользоваться выражением для давле-
давления изотропного излучения р = и/3 (см. разд. 2.5) и формулой
dU\ гг f др\
—— =1[ —— — р, которая является следствием второго начала
dVjT \дТ)у
термодинамики (разд. 2.3). Подставляя U = u(T)V, придем к уравнению
4и = du/dT, откуда получим и ~ Т4. Кроме того, из формулы для
давления и из первого начала термодинамики @ = d(uV) -\—и dV^j можно
о
для равновесного излучения вывести уравнение адиабатического процесса:
uV4/3 = const. Отсюда с учетом и ~ Т4 получим VT3 = const.
Если рассмотреть медленное адиабатическое изменение объема из-
излучения, заключенного в сосуд с зеркальными стенками, и применить
к отражению света от движущегося зеркала формулу эффекта Доплера

182 Оптика [Гл.5
(см. разд. 4.4, 4.5), то удается доказать формулу Вина:
или Г*=Т5/2(ЛГ)> B4)
где fi(x) — неизвестные функции, вид которых не может быть установ-
установлен в рамках термодинамики. Аналогичные выражения для г^ имеют
вид
г*и = lj^^lj/T) или г*и = Т3<р2(и>/Т). B5)
Из формулы Вина B4) (или B5)) можно вывести закон Стефана —
Больцмана B3). Кроме того, из этих формул следует закон смещения
Вина, выражающий зависимость положения максимума функции г^
(или г и) от температуры:
\mT = b (cjm/T = b1), B6)
где b = 2,9 • 10~3 м • К — постоянная Вина. Например, при уменьшении
температуры в два раза положение максимума функции г^ (или иш)
становится в два раза ближе к началу координат, а сам максимум стано-
становится в восемь раз ниже (рис. 91);
площадь под графиком уменьшает-
уменьшается при этом в 16 раз.
> Формула Рэлея — Джинса.
Рэлей и Джине предприняли по-
попытку получить вид функции иш
в рамках классической статисти-
статистической физики. Они рассмотре-
рассмотрели излучение в полости как ан-
ансамбль стоячих электромагнитных
волн, случайным образом обмени-
обменивающихся энергией со стенками
и между собой. С точки зрения ста-
статистики, каждая независимая стоячая волна, имеющая некоторую
частоту колебаний, эквивалентна осциллятору с такой же частотой.
Вычисление энергии сводится к двум независимым вопросам:
1) Какое число dg осцилляторов (стоячих волн) приходится на
интервал частот du? Ответ должен выражаться в виде функции G(lj),
которую называют плотностью состояний: dg = VG{u) du;, где V —
объем сосуда.
Для вычисления G(w) можно рассмотреть сосуд в форме прямоугольного
параллелепипеда со сторонами Lx, Ly, Lz. Граничные условия (например,
требование, чтобы на границах находились узлы стоячих волн) приводят
к условиям k^L^ = т^тг (? = x,y,z). Следовательно, в пространстве
волновых векторов допустимые состояния соответствуют узлам решетки
со сторонами тг/L^ и объемом ячейки S = 7rs/(LxLyLz) = tts/V. Объем
/^-пространства, соответствующий изменению величины волнового вектора

5.6] Тепловое излучение 183
от к до к + dk, равен -(Атгк2 dk) (объем сферического слоя, отсекаемый
8
первым квадрантом). Разделив на объем ячейки, получим число простран-
пространственно различных колебаний в интервале dk: dg = V %~. Необходимо
также учесть дополнительные степени свободы (в случае электромагнит-
электромагнитных волн — два возможных состояния поляризации), которые для общности
учтем дополнительным множителем j.
Найдем число состояний на единицу объема:
^ = 7^4?. B7)
Эта формула получена из граничных условий и имеет очень общий
характер и многочисленные применения. Для перехода к и надо учесть
соотношение к = uj / с. Окончательно получим
G(w) = 4^- B8)
7Г С
2) Чему равна средняя энергия одного осциллятора?
Классическая физика дает следующий ответ (см. разд. 2.2): ка-
каждому осциллятору, независимо от его частоты, надо приписать две
степени свободы, и в соответствии с теоремой о равнораспределении
энергии, средняя энергия каждого осциллятора должна быть равна кТ,
где к — постоянная Больцмана.
В результате таких рассуждений классическая физика приводит к
формуле Рэлея —Джинса:
п, г^(i Лит1 ^ /оп\
иш — Lr{UJ)Kl — 2 з ' \^У)
7Г С
Опыт показывает, что формула Рэлея — Джинса хорошо выполняется
на малых частотах (при и <С ojm), но абсолютно неверна на больших
(рис. 91). Действительно, хотя B9) удовлетворяет требованиям, нала-
налагаемым на любую возможную функцию иш формулой Вина B5), но
сразу видно, что полученная функция не имеет максимума; она моно-
монотонно возрастает, и интеграл J^ u^du;, т.е. полная энергия излучения,
равен бесконечности! Эта ситуация стала одним из признаков глубокого
кризиса классической физики и была названа современниками ультра-
ультрафиолетовой катастрофой.
> Формула Планка. Теорема о равнораспределении энергии являет-
является следствием того, что классическая энергия осциллятора, пропорцио-
пропорциональная квадрату его амплитуды, может принимать любые, в том числе
очень маленькие значения. Согласно квантовой гипотезе Планка энер-
энергия осциллятора (отсчитываемая от минимального значения) может
принимать только дискретные значения, кратные некоторой величине,
зависящей от частоты осциллятора:
?п(<л))=П?1(<л)), П = 0,1,... C0)

184 Оптика [ Гл. 5
Для вычисления средней энергии можно использовать формулу Макс-
Максвелла— Больцмана (см. разд. 2.5), согласно которой вероятность состо-
состояния с энергией е пропорциональна exp[—e/(kT)]. Получаем
Ряд в знаменателе есть просто сумма геометрической прогрессии, а чис-
числитель получается из знаменателя дифференцированием по 1/(кТ).
Проведя вычисления, имеем
Сравнение с формулой Вина B5) показывает, что S\ = S\(iS) должна
быть пропорциональна и:
?i(uj) = Ни), C2)
где h = /г/Bтг) = 1,05 • 10~34 Дж • с — универсальная постоянная.
Постоянную h называют постоянной Планка, h также называют посто-
постоянной Планка или иногда просто «аш с чертой»; первую удобно исполь-
использовать с частотой, а вторую — с циклической частотой: s\ = hv = huj.
Так как энергия кванта пропорциональна частоте осциллятора, то при
данной температуре колебания высоких частот возбуждаются с очень
малой вероятностью и их вклад в энергию излучения оказывается
ничтожно малым. Это разрешает проблему ультрафиолетовой ката-
катастрофы.
После подстановки C2) в формулу для средней энергии получим
формулу Планка для спектральной плотности энергии:
hoo Г / hoo
График этой функции приведен на рис. 91. Запишем формулу Планка
также в переменных v и Л:
8тг/ш3 Г (hu\ Л'1 8тг/гсГ / he 1
. C4)
При huj ^C kT формула Планка переходит в формулу Рэлея — Джин-
Джинса B9). Из формулы Планка можно получить выражения для постоян-
постоянных Стефана— Больцмана и Вина через универсальные постоянные:
7г к , _ оЛГ he
а = о-ч? 6^0,345^-.
60 с2 Я3 А;

5.7]
Световые кванты
185
Формула Планка очень хорошо согласуется с экспериментом во всем
диапазоне частот.
5.7. Световые кванты
> Фотоэффект. Внешним фотоэффектом называют вырывание
электронов из вещества под действием света. Для изучения фото-
фотоэффекта используют вакуумную лампу с холодным катодом (в этом
случае термоэлектронную эмиссию можно не
учитывать). Облучая катод светом фиксиро-
фиксированной частоты и интенсивности, снимают
вольтамперную характеристику лампы (зави-
(зависимость тока от анодного напряжения). По
вольтамперной характеристике (рис. 92) узна-
узнают: а) число электронов, вырываемых из като-
катода в единицу времени (оно выражается через
ток насыщения: N = IHajC/e) и б) максималь-
Рис. 92
eU3i
ную кинетическую энергию вырываемых электронов; она выражается
через задерживающее напряжение, т. е. анодное напряжение, при ко-
котором ток обращается в нуль:
1 2 тт
-mv = ef/зад.
При этом напряжении даже самые быстрые электроны не могут доле-
долететь до анода.
Первый закон фотоэффекта: количество электронов, вырываемых
светом из металла в единицу времени, пря-
прямо пропорционально интенсивности световой
волны. г)
Второй закон фотоэффекта: максималь-
максимальная кинетическая энергия фотоэлектронов
линейно возрастает с частотой света и не за-
зависит от интенсивности света. Если частота
света меньше определенной для данного ве-
вещества минимальной частоты i/m, то фото-
фотоэффект не наблюдается (красная граница фо-
фотоэффекта). Экспериментально было обна-
обнаружено, что зависимость е?/зад от ^ для дан-
данного металла имеет вид наклонной прямой, ис'
причем наклон прямых, построенных для разных металлов, оказался
одинаковым (рис. 93).
Классическая волновая теория света не смогла объяснить второй
х) Законы фотоэффекта были открыты Столетовым.

186 Оптика [Гл.5
закон фотоэффекта. Кроме того, в рамках этой теории выглядела
необъяснимой безинерционностъ фотоэффекта — полное отсутствие
задержки между началом облучения и возникновением тока.
> Кванты света. Объяснение законов фотоэффекта было дано Эйн-
Эйнштейном. Он опирался на квантовую гипотезу Планка (разд. 5.6), но
пошел гораздо дальше, предположив, что кванты световой энергии
поглощаются целиком отдельными электронами. Это означает, что
в процессе поглощения свет ведет себя как локализованная частица
(ее назвали фотоном) с энергией
Ev = hi/ = hu = hc/X. C5)
Как любая безмассовая частица, движущаяся со скоростью света,
квант света — фотон — обладает импульсом
pv = Еи/с = hi//с = /г/Л. C6)
Связь между энергией и импульсом безмассовой частицы дается тео-
теорией относительности (см. разд. 1.11).
Квантовые свойства света проявляются при испускании, поглоще-
поглощении и рассеянии света. В явлениях, связанных с распространением
света, проявляются его волновые свойства. Свет обладает двойствен-
двойственной природой (корпускулярно-волновой дуализм). Такие же свойства
проявляют все элементарные частицы.
Фотоэффектом (актом фотоэффекта) называется поглощение фо-
фотона какой-нибудь частицей, например электроном. В результате фото-
фотоэффекта квант света исчезает, а электрон приобретает дополнительную
энергию. Если фотоэлектрон вылетает из вещества, то наблюдается
внешний фотоэффект; если остается внутри, то имеет место внут-
внутренний фотоэффект. При внутреннем фотоэффекте электроны могут
переходить из связанного состояния в свободное, в результате чего
увеличивается число носителей тока и, следовательно, уменьшается со-
сопротивление. Фотоэффект используется при создании фотоэлементов,
фотореле и т. д.
Пример 1. Может ли происходить фотоэффект на свободном электроне?
Решение. Нет, не может, так как при этом не могут одновременно выпол-
выполняться законы сохранения энергия и импульса. Это становится очевидным,
если перейти в инерциальную систему отсчета, в которой электрон после
фотоэффекта покоится. До фотоэффекта в системе были квант света и дви-
движущийся электрон, а после фотоэффекта — только неподвижный электрон,
т. е. энергия не сохраняется.
Поглощая квант света, электрон приобретает энергию hi/. При вы-
вылете из металла энергия каждого электрона уменьшается на определен-
определенную величину, которую называют работой выхода Лвых (работа, кото-
которую необходимо затратить, чтобы удалить электрон из металла; работа
выхода зависит от рода вещества). Максимальная энергия электронов

5.7] Световые кванты 187
после вылета (если нет других потерь) имеет вид
-mv2 — hv - Лвых C7)
(уравнение Эйнштейна). Если hv < Лвых, то внешний фотоэффект не
происходит. Следовательно, красная граница фотоэффекта равна
vrn = /iBbIX//i.
Из C7) видно, что наклон прямых на графике е?/зад от ^ (рис. 93)
равен /г, а отрезок, отсекаемый прямой от оси ординат, равен работе
выхода.
Энергию фотонов и работу выхода принято выражать во внеси-
внесистемных единицах — электронвольтах (эВ). Один эВ равен энергии,
приобретенной электроном при прохождении им разности потенциа-
потенциалов — 1 В: 1 эВ = 1,6022 • 10~19 Дж. Если, например, задерживающее
напряжение равно —3,5 В, то максимальная кинетическая энергия
электронов равна 3,5 эВ.
Пример 2. Существование работы выхода означает, что на границе
металла возникают силы, удерживающие электрон внутри металла. Как
объяснить притяжение электрона к электронейтральному металлу?
Решение. Заряженная частица притягивается наведенными на поверх-
поверхности проводника зарядами противоположного знака. Сила притяжения вы-
вычисляется с помощью метода электростатических изображений (разд. 3.5).
Вылетающие и возвращающиеся электроны образуют возле поверхности
отрицательно заряженное облако, а заряды на поверхности металла — поло-
положительно заряженный слой. Между заряженными слоями существует нену-
ненулевая средняя напряженность поля, направленная наружу.
> Граница рентгеновского спектра. Если электроны разогнать
в вакуумной трубке, к электродам которой приложено напряжение
в несколько киловольт, то при ударе электронов об анод возникает
тормозное рентгеновское излучение. Исследование спектра этого из-
излучения показывает, что в нем отсутствуют длины волн, меньшие неко-
некоторого значения Лк, которое обратно пропорционально приложенному
к трубке напряжению. Этот факт находит естественное объяснение
в квантовой оптике. Энергия излученного фотона не может превысить
кинетическую энергию электрона: he/А ^ е?/, откуда получим
Теоретическое значение коэффициента пропорциональности между Лк
и 1/U хорошо согласуется с экспериментом.
> Давление света. Давление света было предсказано Максвеллом
на основе электромагнитной теории и измерено Лебедевым. Установка
Лебедева состояла из легкого стержня, подвешенного в вакууме на

188 Оптика [Гл.5
тонкой нити. По краям стержня были закреплены две тонких пла-
пластинки—одна отражающая, другая поглощающая. Освещая пластинки
и измеряя закручивание нити, он вычислял световое давление.
Электромагнитная теория давала следующее объяснение световому
давлению: электрическое поле электромагнитной волны вызывает в ме-
металле ток, на который действует сила Ампера со стороны магнитного
поля волны; эта сила направлена в сторону распространения волны
и является причиной светового давления. Гораздо проще выглядит
объяснение давления на языке световых квантов: фотоны, каждый
из которых обладает импульсом C6), поглощаются или отражаются,
передавая свой импульс веществу. При отражении фотона переданный
импульс в два раза больше, чем при поглощении (см. также разд. 4.5).
> Эффект Комптона. При взаимодействии фотона со свободным
электроном процесс поглощения фотона запрещен законами сохране-
сохранения, но может происходить рассеяние фотона. Если первоначально
электрон покоился, то в результате взаимодействия он приобретет
некоторую скорость. Закон сохранения энергии требует, чтобы энергия
фотона уменьшилась на величину кинетической энергии электрона, что
означает, что должна уменьшиться его частота. В то же время с точки
зрения волновой теории частота рассеянного света должна совпадать
с частотой падающего. Это явление называется эффектом Комптона,
оно было обнаружено при рассеянии рентгеновских лучей и сыграло
важную роль в утверждении квантовых представлений.
Рассеяние фотона на электроне можно рассматривать как упругое
соударение двух частиц, подчиняющееся законам сохранения энергии
и импульса:
рс + тс2 = р'с + Е'е, р = р' + ре',
где р и р' — начальный и конечный импульсы фотона,
р^ и Е'е — импульс и энергия электрона отдачи (рис.94). Выразим
энергию и импульс электрона от-
отдачи и подставим в соотноше-
соотношение #е'2 - ре/2с2 = т2с4 (см.
разд. 1.11). После преобразова-
преобразований имеем
тс(р — р') = рр'A — cos#),
где в — угол рассеяния фотона
Рис д4 (угол между векторами рир').
Выразив из уравнения C6) им-
импульсы падающего и рассеянного фотона: р = /г/Л, р' = /г/Л', получим
формулу для зависимости приращения длины волны от угла рассеяния:

5.8]
Принцип работы лазеров
189
Вынужденное
поглощение
Спонтанное
излучение
/vu
Вынужденное
излучение
Рис. 95
Величина Лс = h/mc = 2,43 • 10~12 м называется комптоновской
длиной волны электрона. Энергия фотона с длиной волны Лс равна
энергии покоя электрона тс2. Максимальный эффект соответствует
рассеянию фотона на угол в = тг.
> Число фотонов в равновесном излучении. Формулу Планка
C3) для плотности энергии равновесного теплового излучения можно
записать на языке световых квантов следующим образом:
где Ни — энергия одного кванта, G(oo) = и2/тг2с3 — плотность состоя-
состояний, а
^ = njr1 C8)
имеет смысл числа фотонов в состоянии с определенной частотой uj.
5.8. Принцип работы лазеров
> Спонтанные и вынужденные переходы. Коэффициенты
Эйнштейна. Рассмотрим атом, находящийся в поле равновесного из-
излучения. Если атом находится в состоянии с энергией Е{, то под воздей-
воздействием излучения он может перейти в состояние с большей энергией Ej,
поглотив при этом световой квант с частотой и = (Ej — E{)/h (рис.95).
Такой процесс называют вынужденным (индуцированным) поглощени-
поглощением. Вероятность такого перехода в единицу времени пропорциональна
плотности энергии излучения на частоте uj\
Обратный переход, из состояния с большей энергией в состояние с мень-
меньшей энергией, связан с рождением и излучением кванта частоты и. Он
может происходить двумя способами. Первый тип переходов называ-
называется спонтанным излучением, он происходит и в отсутствие внешнего
излучения (при иш = 0), и его вероятность от иш не зависит
реп — А ..

190 Оптика [Гл.5
Второй тип переходов называется вынужденным излучением, он про-
происходит под воздействием кванта частоты и. Вероятность перехода
в единицу времени, как и для вынужденного поглощения, пропорци-
пропорциональна иш:
Введенные таким образом коэффициенты Bij, Bji и Aji называются
коэффициентами Эйнштейна, они не зависят от температуры излуче-
излучения.
> Равновесие между атомами и излучением. Пусть в объеме,
заполненном равновесным излучением при температуре Т, находятся
одинаковые атомы. Будем считать, что установилось тепловое равно-
равновесие между атомами и излучением, при этом среднее число атомов
в состоянии % равно Л^, а в состоянии j равно Nj. Эти числа при
температуре Т связаны между собой соотношением Больцмана:
Nj = N.e-(Ei-
В состоянии равновесия число переходов из ъ в j должно быть равно
числу обратных переходов:
NiBijUu = NjiAji + Вции). C9)
Из соотношения Больцмана следует, что при Т —> ос Ni/Nj —> 1.
Учитывая, что при этом иш —у ос, получаем, что Bij = Bji.
Выразим из C9) иш:
(мы учли, что Ni/Nj = exp(hoj/kT)). Видно, что мы фактически выве-
вывели формулу Планка для равновесного излучения. Отношение Aji/Bji
может быть получено из условия, что при высоких температурах дол-
должна быть верна классическая формула Рэлея — Джинса:
Посмотрим на это соотношение с иной точки зрения. Учитывая C8)
для числа квантов с определенной частотой, запишем D0) в виде
Следовательно, отношение вероятности вынужденного излучения к ве-
вероятности спонтанного излучения равно числу квантов частоты uj.
Можно сказать иначе: вероятность вынужденного излучения в расчете
на один квант равна вероятности спонтанного излучения. Видно, что
спонтанное и вынужденное излучение должны быть одной природы.

5.8]
Принцип работы лазеров
191
Объяснение (качественное) состоит в том, что даже в отсутствие в си-
системе световых квантов в полости существуют так называемые нулевые
колебания электромагнитного поля данной частоты (энергия осцилля-
осциллятора в квантовой механике равна Ни i TV Ч— ]). Именно эти колебания
и являются причиной спонтанных переходов.
> Инверсная заселенность уровней. В каждом акте вынужден-
вынужденного излучения происходит образование нового кванта, причем рож-
рожденный квант имеет такую же фазу, как квант, вызвавший это излу-
излучение. Иначе говоря, вместо одного кванта в системе появляются два
когерентных кванта. Каждый из этих квантов может в свою очередь
вызвать появление нового когерентного кванта и т. д. Таким образом
может происходить усиление когерентного излучения. Однако вновь
рожденные кванты поглощаются атомами, находящимися в более низ-
низком из двух энергетических состояний. В равновесном состоянии число
атомов в нижнем состоянии (населенность нижнего уровня) выше,
чем в верхнем. Следовательно, поглощение будет превалировать над
вынужденным излучением, и усиление оказывается невозможным.
Для того, чтобы усиление когерентного луча стало возможным, на-
надо создать метастабильное состояние, обладающее инверсной населен-
населенностью уровней. Тогда усиление потока J квантов будет происходить
по формуле
или J(x) = J@)e°
D1)
где rij, rii — концентрации атомов, а — сечение вынужденного погло-
поглощения или излучения, 7 — a(nj ~ пг) — коэффициент квантового
усиления среды.
Для создания инверсной населенности используются различные
методы накачки. Самыми распространенными являются трехуров-
трехуровневые и четырехуров-
четырехуровневые схемы (рис.96). 3
В трехуровневой схеме
(рубиновый лазер)
происходит интенсивная
накачка с нижнего
уровня 1 на широкий ко-
роткоживущий уровень
3, с которого происходит
заполнение долгоживу-
щего (метастабильного)
уровня 2. Необходимо
Рис. 96
добиться, чтобы населенность верхнего рабочего уровня 2 превысила
населенность нижнего рабочего уровня 1. Трудность состоит в том,
что изначально населенность уровня 2 много меньше населенности

192 Оптика [Гл.5
уровня 1, и требуется интенсивная накачка. Этого недостатка лишена
четырехуровневая схема, в которой нижний рабочий уровень 2
содержит вначале так же мало атомов, как уровень 3. Заполнение
уровня 3 происходит с уровня 4, на который происходит накачка
с основного уровня 1. По этой схеме работает неодимовый лазер.
> Элементы устройства лазеров. Чтобы использовать явление
квантового усиления когерентного света для создания квантового ге-
генератора, надо обеспечить создание положительной обратной связи —
луч должен усиливать сам себя. Для этого на торцах образца помещают
зеркала (или наносят зеркальные покрытия). Одно из зеркал делают
полупрозрачным, что обеспечивает выход лазерного луча из системы.
Чтобы происходило усиление начального луча лучом, отраженным от
двух зеркал, должно выполняться условие
2Ln = тХ/2,
где п — показатель преломления, L — расстояние между образцами
(длина образца), т — целое число. Чтобы могла происходить гене-
генерация, полный коэффициент усиления луча на всем замкнутом пути
должен быть больше единицы:
где 7 ~~ коэфициент квантового усиления (см. D1)), a Ri, R2 — коэф-
коэффициенты отражения зеркал.

Глава 6
КВАНТОВАЯ МЕХАНИКА. АТОМНАЯ
ФИЗИКА
К началу XX века в классической физике накопились противоречия,
для полного разрешения которых потребовалось изменить основные
представления о пространстве и времени (теория относительности Эйн-
Эйнштейна, гл. 1) и о законах движения частиц на атомных масштабах
(квантовая механика). Первые квантовые представления появились
в самом начале века (формула Планка для теплового излучения и Эйн-
Эйнштейна для фотоэффекта, гл.5), однако квантовая механика как за-
замкнутая наука сложилась только к концу 20-х годов.
6.1. Строение атома. Модель Бора
Теория атома должна была в первую очередь объяснить накоплен-
накопленные экспериментальные факты по спектрам излучения разреженных
газов (т.е. отдельных атомов).
Атомные спектры представляют собой отдельные очень узкие линии
(линейчатые спектры), расположение которых характерно для каждого
элемента. Было замечено, что любая частота представляет собой разность
каких-нибудь двух термов: итп = Тт — Тп, так что элемент можно харак-
характеризовать не набором частот, а набором термов. Для водорода Тп = Ru/n2,
где Ни — постоянная Ридберга (для частоты). Спектральные линии, для
которых один из термов фиксирован, называют спектральной серией. На-
Например, в спектре атома водорода выделяют серию Пашена (п = 1), серию
Бальмера (п = 2) и т. д.
Однако в начале XX века отсутствовали даже ясные представления
о структуре атома, т. е. о массивном ядре и электронных орбитах. Более
привлекательной казалась модель Томсона, в которой масса и положи-
положительный заряд равномерно распределены по объему атома, а электроны
заключены внутри этого положительного облака, как изюм в пудинге.
> Ядерная модель атома была установлена в опытах Резерфорда
по рассеянию а-частиц на атомах тонкой золотой фольги (проведенных
его сотрудниками Гейгером и Марсденом в 1911 г.). Было обнаружено,
что часть частиц отклоняется на большие углы и даже летит в обратном
направлении. Таких частиц было немного (примерно одна из 8000
частиц рассеивалась на угол больше 90°), но само наличие таких частиц
вступало в противоречие с моделью Томсона.
7 А. И. Черноуцан

194 Квантовая механика. Атомная физика [ Гл. 6
Для оценки можно считать, что в модели Томсона максимальное отклоне-
отклонение испытывают частицы, пролетающие вблизи края атома (шара радиусом
R ~ 10~10 м), где напряженность электрического поля максимальна (см.
раздел 3.4, пример 3). Формула для угла отклонения частицы кулоновским
полем была выведена в разделе 1.6 (пример 4):
где А = 2Ze2/47rso (Z = 79), Ек ~ 5 т 7 МэВ — кинетическая
энергия а-частиц, b — прицельный параметр. Взяв для модели Томсона
b ~ R ~ 10~ м, получим, что максимальное отклонение а-частиц ~ 0, 01°.
Учет многократного рассеяния увеличивает угол отклонения, но при
толщине пленки d ~ 10~ -=-10 м вероятность рассеяния даже на несколько
градусов оказывается ничтожно малой.
Резерфорд показал, что результаты экспериментов прекрасно опи-
описываются формулой для углового распределения а-частиц, рассеянных
на точечном кулоновском центре с зарядом Ze.
Пример 1. Формула Резерфорда. Рассмотрим тонкую мишень, на
единицу площади которой приходится No = nd ядер (п — объемная концен-
концентрация ядер, d — толщина мишени). Считая, что каждая частица взаимодей-
взаимодействует только с одним ядром, получим, что в интервал углов (в, 0-\-d0) рассе-
рассеются те частицы, у которых прицельный параметр по отношению к какому-
нибудь ядру лежит в интервале [b(9), b(9 + d0)\. Доля частиц, рассеянных
в этот угол, равна полной площади таких колец вокруг всех ядер, приходя-
приходящихся на единицу площади мишени:
— = N02irbdb = N02irb — de.
N d9
Учитывая, что телесный угол равен dQ = 2тг sin 6d6, получим
dN ЛТ udb dQ
N " dOsinO'
Выражая b из формулы A) для рассеяния а-частиц на кулоновском центре
Ze, получаем формулу Резерфорда:
dN ( Z2 V
N \8ire0EKJ sin4@/2)' V J
Многочисленные опыты подтвердили прекрасное согласие этой формулы
с экспериментальными данными. (Отметим, что коэффициент при NodQ
называют дифференциальным сечением рассеяния; подробнее см. раздел 8.4.)
Атом с порядковым номером Z состоит из тяжелого ядра с зарядом
+Ze, в поле которого находятся электроны. Атом, у которого число
электронов не равно Z, называется ионом. Минимальная энергия,
необходимая для удаления электрона и образования иона, называется
энергией ионизации.
Ядерная модель находится в неразрешимом противоречии с основ-
основными представлениями классической физики. Электроны притягива-
притягиваются к ядру, значит, они не могут покоиться, а должны двигаться
вокруг ядра (поэтому ядерную модель иногда называют планетарной).
Но при движении с ускорением электрон излучает электромагнитные

6.1] Строение атома. Модель Бора 195
волны и за время порядка 10~10 с должен излучить всю энергию
и упасть на ядро (см. раздел 4.5). В рамках классической физики атом
не может быть устойчивым.
> Модель Бора. Полуклассическая модель Бора описывает свойства
атома водорода и водородоподобных ионов (один электрон в поле ядра
Ze). В основе модели лежат постулаты Бора:
1) Электроны могут двигаться только по определенным стационар-
стационарным орбитам, в соответствии с классическими уравнениями движения,
но без излучения энергии.
2) Момент импульса может при этом принимать только дискретные
значения Ln = nh. Для круговых орбит правило квантования прини-
принимает вид
mvnrn = nh. C)
Число п называют главным квантовым числом.
3) Излучение или поглощение квантов электромагнитного излуче-
излучения происходит только при переходе с одной стационарной орбиты на
другую:
huo = Еп - Еш. D)
> Атом водорода. Для движения электрона по круговой орбите из
правила квантования C) и уравнения движения
7 2 2
ke vn , ч
—Г = т— E)
Г2п ГП
находим скорость электрона на n-й орбите и ее радиус:
i 2 21-2
ke n n
Vn = — , Гп = 25
пп тке
а также энергию электрона
_ mvn ke2 _ ke2 _ R , .
где
R = m^2 ) « 13,6 эВ G)
— постоянная Ридберга (для энергии электрона). Состояние с номе-
номером п = 1 и энергией Е\ — —R — —13,6 эВ называется основным
состоянием атома, остальные значения соответствуют возбужденным
состояниям. Время жизни возбужденных состояний порядка 10~8 с.
Радиус орбиты электрона в основном состоянии атома водорода назы-
называют воровским радиусом и обозначают ао:
тке2

196
Квантовая механика. Атомная физика
[Гл.6
Энергия ионизации атома водорода равна \Ei\ = R.
Спектр излучения атома водорода:
где Rx =
туке )
4тг chs
(8)
= 1,097 • 107 м 1 — постоянная Ридберга (для
обратной длины волны), п\ — номер начального состояния, n<i —
номер конечного состояния электрона (рис. 97). Линии водорода
с П2 = 1 и п\ — 2,3,. . . образуют
п серию Лаймана (ультрафиолето-
оо вая область), линии с п^ — 2
4 и п\ = 3,4,... — серию Бальмера
3 (видимая область), с n<i — 3 —
серию Пашена (инфракрасная
область), далее следуют серии
Брэкета, Пфунда и т. д.
> Водородоподобные ионы.
Учет движения ядра. Формулы,
полученные для атома водорода,
легко обобщаются на случай
водородоподобного иона — одного
электрона в поле заряда Ze. Надо
просто во всех формулах заменить
е2 на Ze1. Постоянная Ридберга при
этом умножается на Z . Например,
в случае одноэлектронного иона
гелия Не+ энергия электрона
1 принимает значения Еп = —4R/n2.
рис д7 Видно, что энергия с номером 2п
совпадает с энергией электрона
в атоме водорода с номером п. Это означает, что переход, например,
с четвертого уровня на второй должен соответствовать такой же
частоте, как переход со второго уровня атома водорода на первый.
Анализ спектров показывает, что все соответствующие уровни иона
гелия лежат ниже уровней атома водорода примерно на 0,04%.
Это отличие объясняется конечностью массы ядра: происходит
движение как электрона, так и ядра вокруг их общего центра масс.
Учесть движение ядра проще всего заменой массы электрона т на
приведенную массу \i (см. раздел 1.7). Это приводит к умножению
всех значений энергии и частот на множитель М/(т + М), где М —
масса ядра. Для атома водорода повышение энергии самое большое.
По этой же причине уровни энергии электронов в более тяжелых
изотопах лежат ниже (изотопический эффект). Например, уровни
1
п
2"
4"
6"
о -
О
10"
12"
\ Е
, эВ
Серия Па-
Пашена
м
Серия
Бальмера
Серия
Лаймана

6.2] Элементы квантовой механики 197
дейтерия лежат немного ниже уровней водорода, а уровни трития —
немного ниже уровней дейтерия.
> Условие квантования Бора — Зоммерфельда. Обобщением прави-
правила квантования орбит является условие квантования Бора — Зоммерфельда:
(9)
где q, p — обобщенные координата и импульс. Если в качестве обобщенных
координат для движения в центральном поле взять угол (р и момент импульса
L, то получим правило квантования Бора. В случае одномерного движения
условие квантования (9) принимает вид
х2
у/2т(Еп - U(x)) dx = 2тгпН.
XI
где Ж1, Х2 —точки поворота, в которых импульс обращается в ноль. Напри-
Например, в случае осциллятора U(x) = muj x /2, и после вычисления интеграла
получаем
Еп = nhoj,
что с точностью до слагаемого Ни;/2 (нулевые колебания) совпадает с точным
ответом, даваемым квантовой механикой.
Теория Бора не является последовательно квантовой теорией. Она
не описывает тонкую структуру водородоподобных атомов и свойства
многоэлектронных атомов, начиная с атома гелия.
6.2. Элементы квантовой механики
> Корпускулярно-волновой дуализм. Волны де Бройля. Дви-
Движущаяся частица вещества может проявлять волновые свойства. Со-
Соответствующие длина волны, волновой вектор и циклическая частота
определяются формулами де Бройля:
где р — импульс частицы, Е — ее релятивистская энергия.
Важным аргументом в пользу волн де Бройля было то обстоятельство,
что с учетом определения A0) правило квантования Бора (формула C))
принимает вид условия существования замкнутой стоячей волны: 2тггп = пХ
(на длине орбиты укладывается целое число волн де Бройля).
Фазовая скорость волны де Бройля свободной частицы, имеющей
скорость v, равна с2/v, ее групповая скорость равна v. (Фазовая ско-
скорость не является наблюдаемой величиной.)
С частицей связывается комплексная волновая функция ф(т), име-
имеющая статистический смысл. Квадрат модуля волновой функции равен
плотности вероятности обнаружения частицы в данной точке простран-
пространства:
dP = \i/j(r)\2dV. A1)

198 Квантовая механика. Атомная физика [ Гл. 6
Явления интерференции и дифракции при распространении частиц
и их детектировании возникают благодаря принципу суперпозиции:
если реализуются состояния ф\ иф2, то реализуется и их суперпозиция
ф = с\ф\-\-С2ф2- Волновые свойства частиц были впервые обнаружены
в опытах по дифракции электронов на кристаллах в 1927 г. {опыты
Дэвиссона — Джермера).
> Соотношения неопределенностей Гейзенберга. Измерение
координат частицы и проекций ее импульса носит статистический ха-
характер. Неопределенности в измерениях этих величин связаны соотно-
соотношениями
Импульс и координата не могут одновременно принимать точные зна-
значения, понятие классической траектории теряет свой смысл.
Например, состояние электрона с определенным импульсом рх задается
волновой функцией в виде плоской волны:
1 А х
у/2тгЕ Ть
При этом электрон оказывается полностью делокализованным в простран-
пространстве. Чтобы узнать, какова неопределенность в измерении импульса для
электрона с локализованной волновой функцией ф(х), надо разложить эту
функцию в интеграл Фурье по волновым функциям с определенным импуль-
импульсом:
1 Г i
-. \ ехр{-рх х)(р{рх) dpx.
V2<Kh .
Вероятность того, что при измерении рх результат будет лежать в интервале
{рх,Рх + dpx), определяется квадратом фурье-образа \tp{px)\2dpx. В соот-
соответствии с общими свойствами преобразования Фурье, ширины функции и ее
фурье-образа связаны соотношением Ах- А{рх/К) ^ - (см. также раздел 5.2,
обсуждение временной когерентности).
Соотношение неопределенностей для времени и энергии имеет вид:
AEAt ^ П, A3)
где АЕ — неопределенность энергии состояния, At — время жизни
частицы в этом состоянии.
Пример 1. Невозможность локализации электрона в ядре. Ес-
Если предположить, что электрон заключен внутри ядра размером г ~
~ 10~ м, то неопределенность его координаты будет порядка размеров
ядра, а неопределенность импульса Ар ~ h/r. Принимая, что среднее значе-
значение импульса порядка его неопределенности, для энергии получаем оценку:
Е = р2/2т ~ 10~8Дж и 105МэВ, что на много порядков превосходит энер-
энергию связи электрона в атоме.
Пример 2. Оценка энергии основного состояния атома водорода.
Считая, что неопределенность координаты порядка среднего размера атома,
а неопределенность импульса порядка среднего импульса, получим связь

6.2] Элементы квантовой механики 199
между импульсом и радиусом:
h
р ~ —.
г
Подставляя р(г) в выражение F) для энергии электрона, получим энергию
как функцию одного параметра — радиуса орбиты:
Е ~ ту - к —.
2mr r
Это выражение принимает минимальное значение, равное (с точностью до
безразмерного множителя) энергии основного состояния, при значении г,
равном боровскому радиусу.
Критерий применимости классического описания. Понятием тра-
траектории можно пользоваться в том случае, если неопределенность координа-
координаты Ах мала по сравнению с характерными размерами области движения Я,
а неопределенность импульса Лр мала по сравнению с импульсом р. Другими
словами, должно выполняться неравенство pR ^> H. Кроме этого критерия,
можно сравнивать с h другие комбинации параметров системы, имеющие
размерность момента импульса: (импульс х длина) или (энергия х время).
> Уравнение Шредингера. Зависимость от времени волновой
функции частицы в силовом поле U(r) описывается временным урав-
уравнением Шредингера:
В состоянии с определенной энергией Е {стационарном состоянии)
волновая функция имеет вид
^М) = ^(г)ехр(-ф). A5)
Пространственная часть волновой функции стационарного состояния
подчиняется стационарному уравнению Шредингера:
Аф + ^(Е-и)ф = 0. A6)
Волновая функция свободной частицы (U = 0) в состоянии с опреде-
определенным импульсом р записывается так:
Плотность потока вероятности определяется выражением
A7)
и в случае свободной частицы с импульсом р = mv равна S = v|i0(r)|2.
Изменение вероятности обнаружить частицу в некоторой области опре-
определяется потоком вероятности через границу этой области.

200 Квантовая механика. Атомная физика [ Гл. 6
Решения стационарного уравнения Шредингера A6), описывающие
связанные состояния частицы в потенциальном поле, должно удовле-
удовлетворять следующим условиям:
1) Функция и ее первые производные должны быть непрерывны.
2) Функция должна быть нормированной: J|^|2rfV = 1. Эти два
условия могут быть удовлетворены только при определенных значени-
значениях энергии Ei, ^2, ... (дискретность энергетических уровней).
3) В одномерном случае решения действительны и невырожде-
невырождены, т. е. каждому значению энергии Еп соответствует одна функция
фп(х). Функция фп обращается в ноль в п — 1 точках (узлах волно-
волновой функции). Если потенциальная энергия является четной функ-
функцией (U(—x) = U(x)), то волновые функции с нечетными номерами
(в том числе волновая функция основного состояния) будут четны-
четными (ip2n+i(~x) = 102n+i(^)M а с четными номерами — нечетными
Среднее значение физической величины g(r), являющейся функци-
функцией координат, вычисляется по формуле:
где ф(т) — нормированная волновая функция.
Пример З.Яма с бесконечными стенками. Если потенциальная
энергия имеет вид
{О, при 0 ^ х ^ L;
оо, при х < 0 или х > L,
то волновая функция обращается в ноль на краях ямы, при х = 0 и х = L.
Уравнение Шредингера A6) принимает вид
d ф 1т
dx2 ft2
и имеет решения
фп(х) = у — sin кпх, кп = ——.
у Li Li
На ширине ямы укладывается целое число полуволн де Бройля. Энергия
П2к2п п2тг2П2 _
п-го уровня равна Ьп = = s-. Видно, что волновые функции
2т 2mL
с нечетными номерами симметричны относительно центра ямы, а с четны-
четными — антисимметричны.
Пример 4. Яма с конечными стенками. Если потенциальная энергия
имеет вид (рис. 98)
[О, при 0 ^ х ^ L;
U = ( Uo > 0, при х > L;
^оо, при х < О,
то уравнение Шредингера внутри ямы записывается так же, как

6.2]
Элементы квантовой механики
201
в предыдущем примере, а вне ямы, при х > L, принимает вид
2т .
Локализованные (связанные) состояния
должны иметь энергии в интервале
0 < Е < Uq. Волновая функция
обращается в ноль при х = 0, равна
фх(х) = As'm(kix) внутри ямы
и ф>2(х) = Бехр(—&2ж) + Сехр(&2ж)
вне ямы, где к\ = \j2mE /Я,
Рис. 98
к2 = л/2т(ио — Е)/Н. Из условия конечности и интегрируемости волновой
функции получаем G = 0. Условия непрерывности волновой функции
фАЬ) = ф
и ее гладкости
ах
ах
после исключения
x = L , „
коэффициентов Л и В приводят к уравнению для допустимых значений
энергии: к,2 = — /cictg&iL.
Корни можно искать графически, как точки пересечения графика
= —k\L ctg k\L с окружностью (kiLJ + (k2LJ = 2mUoL2/h2 в области
0, &2^ ^ 0 (рис. 99). Новые связанные состояния возникают при
условии E = Uo, kiL = 7r(n + 1/2); при UqL2 <тг2Н2/8т (очень «узкая» или
очень «мелкая» яма) связанные состояния отсутствуют.
Отметим, что волновая
функция связанного состояния
отлична от нуля при х > L
(рис. 98). По классическим
представлениям проникновение
частицы под потенциальный
барьер невозможно, так как при
Е < Uq кинетическая энергия
в этой области отрицательна.
В квантовой механике веро-
вероятность обнаружить частицу
под барьером отлична от
нуля, хотя и экспоненциально
быстро спадает при удалении от
границы барьера.
-1
^y = k2L I
—-«*^/ /г/
У V
2/
7Г
/
/
/
1
1
1
1
= — x ctga?
^\ I
V
/
/ Зтг
/ —
' 2
2тг
AjiL
Рис. 99
Пример 5. Гармонический осциллятор. Потенциальная энергия
гармонического осциллятора: U(x) = тио2х2/2. Энергии стационарных со-
состояний равны Еп = (п + 1/2) /го;, волновые функции стационарных состоя-
состояний выражаются через специальные функции — полиномы Эрмита. Энергия
основного состояния равна Ни;/2 (энергия нулевых колебаний).
После перехода к безразмерным переменным с помощью замены
E' =
вид
hex;
-s, ж =
уравнение Шредингера для осциллятора принимает
= о.

202 Квантовая механика. Атомная физика [ Гл. 6
При ? —>- оо членом е в скобках можно пренебречь, и мы получаем асимптоти-
асимптотическое при больших ? поведение волновой функции: ф ~ ехр(—? /2). Будем
искать волновую функцию в виде ф = ехр(—?2/2)у>(?), для у? получаем
уравнение
Представляя <р(?) в виде ряда: (р = ао + ai? + . . ., после подстановки
в уравнение получим серию рекурентных соотношений: 2а2 + (s — 1)ао = О,
баз + (е — 3)ai = 0, . . ., (п + l)(n + 2)an+2 + (s — 2п — 1)ап = 0, . . . Волновая
функция ф(?) удовлетворяет условию конечности только в том случае, если
ряд для у>(?) содержит конечное число членов (в противном случае у>(?)
при ? —>• оо растет как ехр(? )). Ряд можно оборвать при условии, что он
содержит либо только нечетные степени (для этого надо положить ао = 0),
либо только четные (ai = 0). Условие обрыва ряда позволяет получить
допустимые значения энергии: еп = 2п+1, или Еп =Huj (n + 1/2) (п = 0,1,. . .).
Как и в предыдущем примере, волновые функции стационарных состо-
состояний осциллятора отличны от нуля в той области, где энергия осциллятора
меньше его потенциальной энергии. Вероятность обнаружить частицу в за-
запрещенной области экспоненциально быстро спадает при углублении в эту
область.
Отметим, что в основном состоянии энергия осциллятора равна не нулю,
а Низ/2; эту энергию называют энергией нулевых колебаний. Наличие такой
энергии является неизбежным с точки зрения соотношения неопределенно-
неопределенностей: частица не может находиться в нижней точке ямы и иметь нулевой
импульс.
Как и любая квантовая система, осциллятор может излучать или по-
поглощать фотоны, переходя с одного уровня на другой. Анализ вероятностей
таких переходов показывает, что они могут происходить только между сосед-
соседними уровнями; иначе говоря, для переходов между уровнями осциллятора
действует правило отбора: An = ±1. Это значит, что осциллятор излучает
фотоны только одной частоты из.
Пример 6. Отражение от барьера. Покажем, как вычисляется веро-
вероятность отражения падающих частиц от препятствия (барьера). Рассмотрим
барьер простейшей формы, имеющей вид ступеньки высотой Uq (рис. 100):
{0, при х ^ 0;
[/о, при х > 0.
Уравнение Шредингера запишем в виде
(см. пример 4)
ф" + к\ф = 0, при х < 0;
U
Рис. 100
где к\ = у2тЕ/Я, к2 = л/2т(Е — Uo)/h.
Решение этого уравнения должно описывать падающую и отраженную вол-
волны при х < 0 и прошедшую волну при х > 0:
[ Aexp(ikix) + В ехр(—ik±x), при х < 0;
ф{х) = I
I Cexp(z&2#), при х > 0.

6.2]
Элементы квантовой механики
203
(Временную часть exp(—iEt/h) волновой функции мы опустили.) Плотности
потока вероятности (формула A7)) падающей, отраженной и прошедшей
волн равны Si = \A\2(hki/m), S2 = \B\2(hki/m) и S3 = \С\2(Пк2/т).
Следовательно, коэффициенты отражения и прохождения равны
R = S2/Si = \B/A\2, D = S3/Si = (k2/ki)\C/A\2. Условия непрерывности
волновой функции и ее производных при х = 0 дают
. В Ci if-, В \ Су
откуда получаем
R =
- k2
k2
D =
A8)
При Е > Uq числа к\ и к2 действительны, и коэффициенты R и D отличны
от нуля, причем R+ D = 1. Отметим, что в классической физике отражения
частиц при Е > Uq не происходит, т. е. R = 0. В квантовой физике R не
только отличен от нуля, но при Е — Uq ^С Uq получаем к2 ^С &i, т. е. D —»¦
—? 0, R —ь 1. Еще более удивительный чисто квантовый эффект получим при
[/о < 0 (формально A8) остается верным, но к2 > ki): в пределе ?7 <^ |[/о
получаем &i <С Л^2, т. е. R —>- 1 (!).
При ?7 < Uq (Uq > 0) решение остается формально верным, если
положить &2 = in, где х = у/2?тг([/о — Е)/Н. В этом случае Я = 1,
а решение при х > 0 представляет собой действительную экспоненту
|<0|2 = |G|2 ехр(—2х,х)\ глубина проникновения частиц в классически запре-
запрещенную область равна 1/2>с.
Пример 7. Туннельный эффект. При падении на потенциальный
барьер волны де Бройля, соответствующей свободной частице с энергией,
меньшей высоты барьера, существует отличная от нуля вероятность обна-
обнаружить частицу по другую сторону барьера. Прозрачностью барьера на-
называется отношение интенсивности (плотности
потока вероятности) прошедшей волны и волны
падающей. Прозрачность потенциального барье-
барьера (рис. 101) дается формулой
х2
D =
и * Х\ * Рис-
Частица мож:ет оыть обнаружена под оарьером,
в области, запрещенной для движения в классической механике.
> Операторы физических величин. Любой наблюдаемой физи-
физической величине в квантовой механике сопоставляется эрмитов (само-
(самосопряженный) оператор, действующий на волновые функции. Физиче-
Физическая величина G имеет определенное значение А<^ только в состояниях,
являющихся собственными функциями оператора G:
причем измеряемое значение физической величины в любом из этих
состояний совпадает с собственным значением оператора G. Система

204 Квантовая механика. Атомная физика [ Гл. 6
собственных функций эрмитова оператора является полной — любая
функция может быть представлена в виде линейной суперпозиции
этих функций. Если состояние является суперпозицией собственных
функций с разными А: ф = ^С{ф{, то вероятность получить при
измерении значение Л^ равна \С{\ , а среднее значение величины G
в этом состоянии равно
2 \ A9)
Оператор координаты имеет вид хф = хф, оператор проекции им-
импульса— рх = —г/i—, оператор энергии (гамильтониан) определяется
выражением:
H = ^- + U = -^-A + U. B0)
2т 2т v '
Уравнения Шредингера A4) и A6) принимают вид
гП^ = Нф и Нф = Еф, B1)
т. е. стационарные состояния являются собственными функциями га-
гамильтониана, а энергии этих состояний — соответствующими собствен-
собственными значениями.
Физические величины А и В соизмеримы (могут одновременно
иметь определенные значения), если они коммутируют: ЛВ — В Л = 0.
В случае координаты и проекции импульса
xpx-pxx = ih. B2)
Пример 8. Принцип неопределенности. Операторный подход. На
языке квантовых операторов принцип неопределенности становится точным
математическим утверждением. Неопределенностью физической величины
в состоянии ф называют AG = у ((G — (G)J) (в собственном состоянии
оператора G неопределенность равна нулю). Степень несоизмеримости двух
физических величин А и В определяется их коммутатором С = АВ — В А,
что выражается неравенством
АААВ>\\{С)\.
Важное утверждение квантовой механики состоит в том, что физи-
физическая величина сохраняется со временем, если ее оператор коммути-
коммутирует с гамильтонианом. Действительно,
где дф/dt выражена с помощью уравнения Шредингера B1)
(а дф*/dt — с помощью сопряженного уравнения).

6.2] Элементы квантовой механики 205
Пример 9. Квантовый осциллятор. Операторный подход. Комму-
Коммутационные соотношения позволяют получить важные результаты чисто ал-
алгебраическим способом. Найдем собственные значения и собственные функ-
функции гамильтониана, описывающего квантовый осциллятор:
- р2х тш2х2
исходя только из коммутационного соотношения B2) между координатой
и импульсом. Перейдем к безразмерным операторам с помощью замен:
причем р = —г —. Ьезразмерныи гамильтониан имеет вид
dq
а безразмерные операторы координаты и импульса подчиняются соотноше-
соотношению
qp-pq = г.
Введем операторы «повышения» и «понижения»:
а+ = q — гр, а~ = q + гр,
для которых верны тождества
о+о"=Л-1, о"о+ = Л + 1, [а+а~] = -2.
Собственные значения Л и собственные функции ф\ оператора А = а+а~
обладают следующими свойствами:
1) Собственные значения неотрицательны (Л ^ 0). Собственное значение
обращается в ноль в том и только в том случае, если Ъ,~фо = 0.
1 ^_
2) Если ф\ — нормированная собственная функция с Л > 0, то —-j=a фх —
V А
нормированная собственная функция с Л' = Л — 2, а д+фх — норми-
рованная собственная функция с Л = Л + 2.
Из этого следует, что собственными значениями оператора А являются
целые четные числа, оператора h — нечетные числа, оператора энергии —
значения Еп = Нои(п -\—). Основное состояние (п = 0) подчиняется урав-
уравнению а~фо = 0, или = —qфo. Получаем фо(д) = \ — exp(—q2/2).
dq \ 7Т
Все остальные функции могут быть получены последовательным действием
оператора повышения: ф\ = —^=(q — d/dq)фo, фч = —^=(q — d/dq^\ и т.д.
V2 V3
Перейдем к рассмотрению трехмерного уравнения Шредингера.
Это уравнение гораздо сложнее, чем одномерное, но в некоторых слу-
случаях может быть сведено к трем одномерным уравнениям методом
разделения переменных. Проиллюстрируем этот метод на трехмерном
осцилляторе.
Пример 10. Трехмерный квантовый осциллятор. Разделение
переменных. Уравнение Шредингера для трехмерного осциллятора имеет

206 Квантовая механика. Атомная физика [ Гл. 6
вид
Аф+2-^(Е-^)ф = 0. B3)
Потенциальная энергия осциллятора уникальна: будучи сферически симмет-
симметричной, она в то же время является суммой трех членов, каждый из которых
зависит только от одной координаты и совпадает с потенциальной энергией
одномерного осциллятора (Ux = muj2x2/2 и т.д.). Это позволяет искать
решение в виде
ф(г) = ф1{х)ф2{у)ф^).
Подставив ф в уравнение B3) и разделив его на ф, получим
д2фг _ 2гп \ ( 1 д2ф2 _ 2т п \ ( 1 д2<ф3 _ 2ш „ \
i дх2 П2 х) + \ф2 ду2 h2 V + \фг dz2 h2 z) +
Поскольку от х зависит только первый член, он должен быть константой,
которую мы обозначим 2mEi /h . Получившееся уравнение совпадает с урав-
уравнением для одномерного осциллятора, следовательно, Е\ может принимать
только значения huj(n\ -\—). То же самое относится и к двум остальным
членам. Поскольку Е = Е\ + Е^ + Ез, для энергии трехмерного осциллятора
получаем
3
ЕП1,п2,п3 = hw(n + -),
где п = m + П2 + пз, а т, П2, пз принимают значения 0,1,2,.. .. Видно,
что основное состояние (п = 0) не вырождено, уровень с п = 1 вырожден
трехкратно, с п = 2 — шестикратно, с п = 3 — десятикратно и т. д.
Операторная запись позволяет придать методу разделения переменных
более компактную форму. Уравнение Шредингера B3) принимает вид
(Hi + Я2 + Нз)фгф2фз = Ефгф2фз-
Разделив на фхфъфг-, получим
Hii/>i H2ip2 Нзфз _ р
Фг Ф2 Фз
От х зависит только первый член, он равен Ei, и т. д.
Однако общий подход к решению уравнения Шредингера в сфери-
сферически симметричном поле состоит в использовании закона сохранения
момента импульса (углового момента). Такой подход позволяет про-
произвести разделение переменных (по сферическим координатам) для
любого сферически симетричного потенциала.
> Оператор углового момента. Оператор орбитального углового
момента (момента импульса) электрона L относительно т. О опреде-
определяется соотношениями
Lx = ypz - zpy, Ly = zpx - xpz, Lz = xpy - ypx, B4)

6.2] Элементы квантовой механики 207
а оператор квадрата момента — соотношением L2 = L\ + L2y + L\.
Проекции момента не коммутируют друг с другом:
[LxLy] = ihLZj [LyLz] = ihLXj [LZLX] = ihLyj B5)
т.е. не могут одновременно принимать определенные значения. Одна-
Однако каждая из проекций коммутирует с квадратом импульса, поэтому
можно говорить об общих собственных функциях операторов Lz и L2.
Собственные значения могут быть найдены чисто алгебраическим
путем, из коммутационных соотношений B5). Общие собственные
функции операторов L2 и Lz могут отвечать только следующим соб-
собственным значениям:
причем / — целое или полуцелое неотрицательное число, а при заданном
/ число т может принимать 2/ + 1 значений: т = — /, — / + 1, . . ., / — 1, /.
Перейдем к безразмерным операторам: Lx = Шж, Ly = Шу, Lz = hlz,
удовлетворяющим коммутационным соотношениям [lxly] = Hz и т.д. Введем
операторы «повышения» и «понижения»:
' ~~ 1>Х ~Т~ 1>1у) I/ = {ж Ъ^У")
удовлетворяющие соотношениям:
[TzT+]= Г+, [Tzr] = -r, T+r = Р-^+?, г?+ = Р-^-?.
Если ф является собственной функцией операторов / и lz с собственными
значениями А и /i, то I ф будет собственной функцией этих операторов
с собственными значениями Л, /j, + 1, а 1~ф — собственной функцией с соб-
собственными значениями Л, /i — 1. Минимальное значение /ii и максимальное
fi2 удовлетворяют уравнениям:
Л — fii + fii = 0, Л — /^2 — /^2 = 0.
Отсюда следует, что /ii = —/^2, причем /12 — /^i = 2/^2 = / — целое число. Для
собственного значения оператора / получаем Л = /(/ + 1).
Видно, что максимальное значение проекции углового момента
Ы меньше его модуля Нл/1A + 1). В векторной модели угловой мо-
момент изображают в виде вектора, образую-
образующего фиксированный угол с осью z и враща-
вращающегося вокруг этой оси. При этом проекции ^~~~~~~
Lx и Ly не имеют фиксированных значений, ^\~
что отражает несоизмеримость Lz с Lx и Ly. _ Х^
На рис. 102 изображен случай / = 1.
Чтобы увидеть, какие собственные значе-
значения может иметь орбитальный угловой мо-
момент, определяемый формулами B4), удобно
произвести переход к сферическим координа-
координатам. Орбитальный момент является функци- Рис. 102
ей только угловых переменных, причем коммутирующие операторы Lz

208 Квантовая механика. Атомная физика [ Гл. 6
и L2 принимают вид
z
B7)
^9 ?-9 ^Г ^Г *- О ( • п О \ 1G
L = -й Л. где А — ——--р— [sin 0-^-: Н 5 9-
' sin (9 дв V <90/ sin (9 д<р
Для дальнейшего важно, что оператор А совпадает с угловой частью
оператора Лапласа, записанного в сферических координатах:
- \Л. B8)
Собственные функции могут быть представлены в виде произведения
функций отдельных угловых переменных: ф^т = О^ш@)Фш(ср). Урав-
Уравнение для Ф
—ih m = тНФш
имеет решение Фш = A exp(im(p), которое является однозначной функ-
функцией угла (/? только при целых значениях т. Следовательно, в случае
орбитального момента реализуются только целые значения чисел I и т.
Число / называют орбитальным квантовым числом, а число т — маг-
магнитным квантовым числом (используют обозначение mi). Полуцелые
значения реализуются в случае собственного углового момента— спина
(используют обозначения s и ms).
Уравнение для собственных функций оператора А имеет реше-
решение в виде известных в математической физике шаровых функций
Yim(9j Ц>) = Фт((р)&т1(^) с собственными значениями —/(/ + 1). (Функ-
(Функции в (в) имеют вид специальных функций — присоединенных функций
1 • /З
Лежандра). Например, Фт(ф) = —j= • егтф, вю(в) = y-cos#,
л/2тг ' V 1
/з" . [ъ
@i,±i = "FA/7sin^' ®2,о = у ^Ccos 0 — 1). Каждая из функций
нормируется на единицу: J^ Ф2 dip = 1, J^ в2 sin в d6 = 1. Шаровые
функции образуют полную систему функций угловых переменных —
любая функция переменных в, ср может быть разложена по шаровым
функциям.
> Сложение угловых моментов. Оператор суммы двух моментов
L = Li + L2, значения которых характеризуются квантовыми чис-
числами 1\ и /2 (т. е. L\ и L\ имеют собственные значения hy/l\{l\ + 1)
и hy/^ih + 1)) характеризуется квантовым числом /, которое может
принимать следующие значения: \h — h\ ^ I ^ h + h- Максимальное

6.2] Элементы квантовой механики 209
значение соответствует параллельному расположению моментов, ми-
минимальное — антипараллельному. Оператор L2 не коммутирует с опе-
операторами L\z и L2zi поэтому собственные функции операторов L2
и Lz не являются собственными функциями L\z и L2z (но являются
собственными функциями L2 и L2,).
> Движение в центральном поле. В этом случае потенциальная
энергия U(г) зависит только от модуля г. Поскольку операторы орби-
орбитального момента Lz и L2 коммутируют с?2 и р2, то они коммутируют
и с гамильтонианом. Следовательно, как и в классической механике,
при движении частицы в центральном поле сохраняются величина
углового момента и его проекция на ось z. Волновая функция любого
состояния ф(г,0,ср) может быть разложена по общим собственным
функциям Фе,1,ш1 трех коммутирующих операторов Я, Lz и L2, со-
соответствующих трем одновременно измеримым физическим величи-
намзнергии, проекции орбитального момента и его величине. Будем
использовать разделение переменных, т. е. искать собственные функ-
функции в виде: Фе,1,пц = Д#,/(г)ФтД<рH/?Ш|@). Записывая гамильтониан
в сферических координатах и учитывая B7) и B8), получим
Я = ^— (г2—) + -^-2 +{/(г). B9)
Уравнение Шредингера в форме B3) после действия гамильтониана
B9) на функцию Фе,1,пц превращается в уравнение для радиальной
части волновой функции Re,i(t)'-
W МГ 9r)RE'' + {^г + U(r))RE, = EREtl. C0)
Как и в классической механике (см. раздел 1.6), к потенциальной
энергии добавляется центробежная энергия К21A + 1)/2тг2. Видно,
что магнитное квантовое число не входит в уравнение для допустимых
значений энергии. Каждому уровню энергии соответствует два кван-
квантовых числа: орбитальное число I и радиальное число пг = 0,1, 2, . . .,
нумерующее допустимые дискретные значения энергии. Уровень EUri
оказывается B/ + 1)-кратно вырожденным по значениям магнитного
квантового числа т/.
> Магнитный момент. В классической физике движущаяся по
замкнутой траектории заряженная частица обладает магнитным
моментом. Величина и направление магнитного момента полностью
определяют как собственное магнитное поле движущегося заряда, так
и его взаимодействие с внешним магнитным полем (см. раздел 3.3).
Для орбитального движения отношение магнитного момента
электрона к механическому равно —е/2т. Следовательно, проекция
орбитального магнитного момента на ось z принимает значения

210 Квантовая механика. Атомная физика [Гл. 6
\iz = —{e/2m)hmi = —/i^m/, а величина орбитального магнитного
момента равна \1в\/Щ + 1), где цв — eh/2m « 9,274 • 10~24 Дж/Тл
называется магнетоном Бора. В общем случае соотношение между
магнитным и механическим моментами записывается в виде:
jaz = g[e/2m)Lz (или (цг/цв) = g(Lz/h)), где безразмерный мно-
множитель g называют гиромагнитным отношением. Для орбитального
момента g\ — 1, для спинового g^ = 2.
При помещении атома в магнитное поле с индукцией В,
направленное вдоль оси z, у электрона возникает добавочная
энергия взаимодействия магнитного момента с магнитным полем:
ЛЕ = —{izB — /llbtuiB. Видно, что в магнитном поле должно
сниматься вырождение по магнитному квантовому числу т/ —
вместо одного уровня возникает 21 + 1 эквидистантных уровней,
расстояние между которыми пропорционально магнитному полю.
При этом каждая спектральная линия должна расщепляться на три
равноудаленных линии (с учетом правил отбора, обсуждаемых ниже,
изменение т/ при переходе между уровнями может быть только
Ami = 0,=Ы). Этот эффект носит название простого (нормального)
эффекта Зеемана. Наличие у электрона собственного (спинового)
магнитного момента приводит к сильному усложнению картины
расщепления линий в магнитном поле.
> Атом водорода в квантовой механике. Для потенциальной
энергии U(г) = —ке2/г уравнение C0) имеет следующие решения:
1) Возможные значения энергии определяются формулой
R
где R — постоянная Ридберга (см. G)). Величину п = nr + I + \
называют главным квантовым числом. Видно, что энергия электрона
определяется только главным квантовым числом. Одному и тому же
главному квантовому числу п соответствуют состояния с различными
значениями /:/ = 0,1,...,п — 1. Полное вырождение каждого уровня
п-1
энергии составляет ^ {21 + 1) = п2. Дополнительное вырождение
/=о
является специальным свойством кулоновского потенциала. Отметим,
что энергетические уровни совпадают с теми, которые получались
в полуклассической теории Бора (раздел 6.1), однако бросаются в глаза
важные отличия: в теории Бора в основном состоянии (п = 1) орби-
орбитальный момент равен L = /г, а в квантовой теории момент основного
состояния равен нулю.
2) Радиальные функции имеют вид Rnj = rle~r/na°РПг(г), где
Рпг(г) — многочлен степени пг = п — I — 1, а ао = К2/тке2 —

6.2]
Элементы квантовой механики
211
радиус первой электронной орбиты в теории Бора (боровский ра-
радиус). Например, i?i?o =
1
/<2о Г>
5 ^2,0 —
-г/2а0 (о _
B
—ехр(—г/2ао). Радиальные функции нормированы
в0
t2,l =
на единицу: J^° /22r2 <ir = 1. Вероятность обнаружить электрон
на расстоянии от ядра, лежащем в интервале (г, г + dr), равна
dP = J |^|2dV = R2(r)r2 dr. В основном состоянии наиболее
(r,r-\-dr)
вероятное расстояние от электрона до ядра равно боровскому радиусу
а0.
Электронное состояние обозначают латинской буквой, указываю-
указывающей на значение орбитального квантового числа («s» для I = 0, «р»
для I = 1, «d» для / = 2, «/» для / = 3, далее по алфавиту), перед
которой указывают значение главного квантового числа. Например,
3d соответствует электрону с п = 3 и / = 2.
> Спектры щелочных металлов. В случае щелочных металлов
(Li, Na,...) состояние атома определяется состоянием электрона
на внешней оболочке. Этот
электрон находится в цен-
центрально-симметричном поле
ядра и Z — 1 электронов на
внутренних оболочках. Радиус
внешней оболочки заметно больше
радиусов внутренних оболочек
(rn ~ п2), поэтому в основной
области существования внешнего
электрона электрическое поле
совпадает с полем заряда -he.
Искажение поля внутренними
электронами оказывает большее
Е,
о
-1™
-2-
влияние на состояния с меньшим
орбитальным числом /, так
как при малых г ф(г) ~ г1.
Для уровней энергии i?n?/, где
п = пг + / + 1 — главное квантовое
число, используют выражение
R
где ai < 0 — ридберговская
поправка. Например, для Li
ао = —0,41 и «1 = —0,04, а для
Naai = -0,88.
-3
-4-
-5™
Диффузная
серия
Резкая
серия
Главная
серия
Рис. 103

212 Квантовая механика. Атомная физика [Гл. 6
Отличие поля, в котором движется электрон, от кулоновского может быть
в первом приближении учтено добавлением к потенциальной энергии члена
А/г2. Эта добавка учитывает сразу два эффекта: во-первых, экранирующее
поле электронного «остова», и, во-вторых, поляризацию остова самим
внешним электроном, которая приводит к появлению у остова небольшого
дипольного момента, направленного в каждый момент времени в сторону
этого электрона. Член А/г2 можно присоединить к центробежной энергии
(см. формулу C0)) и записать оба члена вместе как центробежную энергию
с переопределенным V = I -\- оц.
Для построения спектра надо принять во внимание, что главное
квантовое число п наинизшего состояния внешнего электрона равно
номеру оболочки, в которой находится этот электрон (для лития п = 2,
для калия п = 3 и т. д.). Кроме того, необходимо учитывать правило
отбора для орбитального числа /: Л1 = =Ы. На рис. 103 приведена схема
спектральных линий атома Li и указаны названия первых основных
серий.
> Спин электрона. Ряд экпериментальных фактов указывает на
то, что для описания состояния электронов в атоме недостаточно
трех квантовых чисел, связанных с его пространственным движением.
К этим фактам относятся:
1) Мультиплетная (тонкая) структура спектральных линий щелоч-
щелочных металлов. Например, самая интенсивная из линий главной серии —
резонансная линия, соответствующая переходу в основное s-состояние
из первого возбужденного р-состояния, имеет вид ярко выраженного
дублета.
2) Сложный (аномальный) эффект Зеемана. Расщепление атомных
линий в магнитном поле не описывается простым эффектом Зеемана,
связанным с магнитным моментом орбитального движения.
3) Результаты опытов Штерна — Герлаха по измерению магнитных
моментов атомов водорода A921). Пучок атомов водорода направлялся
в область сильно неоднородного магнитного поля, где на них действова-
действовала сила nz(dB/dz). Проекция орбитального момента fiz = т^в может
иметь 2/ + 1 различных значений. Атомы с электронами в s-состоянии
не должны испытывать отклонения; если имеется доля атомов с элек-
электронами в р-состоянии, то они должны разделиться на три пучка.
Было обнаружено, что пучок атомов разделяется на два, отклоняемых
магнитным полем в разные стороны на одинаковые расстояния.
Вывод: электроны обладают внутренним угловым моментом (стш-
ном), не связанным с движением электрона по орбите. Проекция спина
на ось z может иметь два значения, из чего следует, что спиновое
квантовое число s должно быть равно 1/2 (поскольку 2s + 1 = 2).
Величина спинового момента равна h\ -(- + 1) = —prh. Проекция
у z z A
спинового момента на ось z равна hms, где ms = ±- — магнитное

6.2] Элементы квантовой механики 213
спиновое число. Напомним, что полуцелое значение углового момента
не противоречит перестановочным соотношениям.
Так как проекция спина может принимать два значения, то теперь
набору квантовых чисел п, / соответствует 2B/ + 1) различных состо-
состояний, а квантовому числу п соответствует 2п2 состояний.
Измерение величины отклонения атомов в магнитном поле позволя-
позволяет установить значение собственного магнитного момента. Оказалось,
что собственный момент электрона обладает аномальным гиромагнит-
гиромагнитным отношением gs = 2: отношение спинового магнитного момента
к механическому равно не е/2т, а е/т. Проекция магнитного момента
на ось z принимает значения (e/m)hms = ±/i#. Аномальное значе-
значение гиромагнитного отношения подтверждается результатами опытов
Эйнштейна —де Гааза A914), в которых исследовались магнитомеха-
нические эффекты (образование механического момента при намагни-
намагничивании железного образца).
Внутренним магнитным моментом — спином — обладают все эле-
элементарные частицы. Спин протона, нейтрона и /i-мезонов равен 1/2,
спин фотона равен 1, спин тг-мезонов равен 0.
> Тонкая структура спектральных линий. Тонкая структура
линий водородоподобных атомов и щелочных металлов объясняется
взаимодействием спинового магнитного момента с орбитальным. По-
Появление такого взаимодействия проще всего понять в системе отсчета,
связанной с электроном. В этой системе отсчета движущееся ядро
создает магнитное поле, с которым взаимодействует спиновый магнит-
магнитный момент. С учетом спин-орбитального взаимодействия сохраняются
(коммутируют с гамильтонианом) следующие операторы: полный угло-
угловой момент J2, его проекция Jz и величина орбитального момента L2.
Положение уровней En^j определяется тремя квантовыми числами:
n, /, j. (В многоэлектронных атомах для квантовых чисел углового
момента используют прописные буквы L, S, J. Для спектроскопи-
спектроскопических обозначений орбитального момента используют буквы S, Р,
Z), F, . . . В щелочных металлах состояние атома определяется одним
электроном, и можно использовать как прописные, так и строчные
буквы.) Вырождение каждого уровня составляет 2j + 1 состояний
с различными значениями проекции полного момента. При заданном /
полный момент может принимать два значения: j = (I ± -), при / = 0
получается только одно значение j = -. Следовательно, s-уровни не
расщепляются (синглетные уровни), а уровни с / > 0 расщепляются
на два близких уровня (дублетные уровни). При построении спектров
надо учитывать правила отбора: Л1 = =Ы, Aj = 0, =Ы. Например, при
переходе с дублетного р-состояния в нижнее синглетное s-состояние
возникает две линии (дублеты главной серии), расстояние между кото-
которыми уменьшается с ростом п, а при переходе с синглетных s-уровней

214 Квантовая механика. Атомная физика [Гл. 6
на нижний р-уровень возникают дублеты резкой серии, имеющие оди-
одинаковое расщепление. При переходе с дублетного d-состояния в ниж-
нижнее дублетное р-состояние возникают три линии (сложные дублеты
диффузной серии). Величина расщепления уменьшается с ростом как
орбитального, так и главного квантовых чисел, но быстро возрастает
при переходе к атомам с большим порядковым номером.
В атоме водорода и водородоподобных ионах спин-орбитальное вза-
взаимодействие частично компенсируется релятивистскими поправками,
и окончательный ответ для уровней энергии не содержит зависимости
от орбитального квантового числа:
где а = ке2/Не « 1/137 называется постоянной тонкой структуры.
Дополнительное вырождение по орбитальному квантовому числу яв-
является специфической особенностью кулоновского потенциала.
6.3. Структура и спектры сложных атомов
> Самосогласованное поле. При переходе к многоэлектронным
атомам задача описания атомных состояний существенно усложняет-
усложняется. В общем случае необходимо рассматривать волновую функцию,
зависящую от координат и спиновых переменных всех электронов,
и учитывать взаимодействие электронов не только с ядром, но и друг
с другом. Однако хорошее описание дает приближение самосогласо-
самосогласованного поля, в котором каждый электрон движется в усредненном
поле ядра и остальных электронов. Потенциал самосогласованного
поля (р(г) описывается уравнением Томаса-Ферми, позволяющим по-
получить энергетически наиболее выгодное распределение электронов
в пространстве вокруг атома.
Решение уравнения Шредингера для электрона в самосогласован-
самосогласованном поле позволяет получить стационарные состояния, энергия кото-
которых Eni зависит от главного квантового числа и орбитального кванто-
квантового числа. Первым делом необходимо выяснить структуру основного
(обладающего наименьшей энергией) состояния атома. Какие одно-
электронные состояния занимают электроны в основном состоянии?
На первый взгляд может показаться, что наиболее выгодно поместить
все электроны в наинизшее состояние Is. Однако такое распределение
электронов оказывается невозможным вследствие принципа запрета
Паули, связанного со свойством тождественности частиц.
> Тождественность частиц. Принцип Паули. Принцип тож-
тождественности частиц в квантовой механике приобретает значительно
более сильный смысл, чем в классической. В классической физике
частицы одинаковы, но отличимы друг от друга: при перестановке

6.3] Структура и спектры сложных атомов 215
двух электронов возникает состояние, которое надо учитывать как
новое, не зависящее от начального. В квантовой механике частицы тож-
тождественны, т. е. абсолютно неотличимы: состояние, возникающее при
перестановке частиц, тождественно совпадает с начальным состоянием.
Это значит, что |^A,2)|2 = \фB,1)|2. Возникают две возможности:
либо волновая функция симметрична относительно состояний частиц,
т. е. -0A, 2) = фB,1), либо антисимметрична, т. е. -0A, 2) = —фB,1).
Частицы первого типа называются бозонами, частицы второго типа —
фермионами. В теории элементарных частиц доказывается, что к бозо-
бозонам относятся частицы с целым спином, а к фермионам — частицы с по-
полуцелым спином. Если волновая функция строится из одночастичных
волновых функций, то в случае бозонов она должна быть симметризо-
вана, а в случае фермионов — антисимметризована. Например, в случае
двух бозонов с одночастичными состояниями фх и •фч волновая функ-
функция имеет вид ^(ri, Г2) = —/=[^1 (г 1)^2A*2) + ^2A*1)^1 (гг)], а в случае
v 2i
двух фермионов ^(гьг2) = -^[^i(ri)^2(r2) - ^2(ri)^i(r2)].
Электроны являются фермионами, т.е. система нескольких элек-
электронов описывается антисимметричной (по состояниям частиц) волно-
волновой функцией. В такой системе (как и в системе любых тождествен-
тождественных фермионов) действует принцип запрета Паули: два электрона не
могут находиться в абсолютно одинаковых квантовых состояниях;
действительно, волновая функция такого состояния должна быть тож-
тождественно равна нулю.
> Таблица Менделеева. Для описания электронной структуры
основного состояния атома с порядковым номером Z надо расположить
Z электронов по различным квантовым состояниям с наименьшей
энергией. Для подсчета электронных состояний можно выбрать любой
набор независимых квантовых чисел одного электрона, например, как
в случае щелочных металлов, n, /, j и rrij. Однако удобнее не учитывать
спин-орбитальное взаимодействие и использовать числа п, /, т/ и ms
для электрона в центрально-симметричном самосогласованном поле.
(Для полного описания термов основного и возбужденного состояний
придется выбрать набор квантовых чисел, описывающих состояние
всего атома и относящихся к сохраняющимся величинам.)
Все электроны, имеющие одинаковое главное квантовое число п,
относятся к одному электронному слою. Максимальное число элек-
электронов в п-м слое равно 2п2. Слой с п = 1 называется /С-слоем,
с п = 2 — L-слоем и далее по алфавиту. Все электроны в данном слое
с фиксированным числом / образуют электронную оболочку с 2B/ + 1)
электронами. Электроны данного слоя с большим значением / имеют
большую энергию, благодаря возрастающему вкладу центробежной

216 Квантовая механика. Атомная физика [Гл. 6
энергии. Состояние электрона обозначается номером главного кван-
квантового числа, за которым следует буква, соответствующая его орби-
орбитальному числу. Если атом содержит несколько электронов из одной
оболочки, то справа вверху указывается число электронов. Приведем
электронные конфигурации ряда атомов:
if-слой:
ХН —Is, 2Не-Ь2;
L-слой:
3Li-ls22s, 4Be-ls22s2, 5B-ls22s22p,
6C-ls22s22p2, 7N-ls22s22p3, 8O- Is22s22p4,
9F-ls22s22p5, 10Ne-ls22s22p6;
две оболочки М-слоя:
nNa- [К, L]3s, 12Mg- [К, L]3s2,
13A1 - [K, L]3s23p, 14Si - [K, L]3s23p2, 15P - [K, L]3s23p3,
s-оболочка TV-слоя:
19K - [K, L]Ss2Sp4Sj 20Ca- [K, L]Ss2Sp4s2;
ti-оболочка М-слоя:
21Sc - [K, L]3823/3(i482, 22Ti - [K, L]3823/3(i2482;
и т.д.
Видно, что начиная с номера 19 нарушается последовательное за-
заполнение слоев — энергия s-электронов TV-слоя оказывается меньше,
чем энергия d-электронов М-слоя. Химические свойства элементов
определяются числом электронов во внешнем слое, поэтому возника-
возникает периодичность химических свойств. Например, благородные газы
гелий 4Не, неон 10Ne, аргон 18Аг, криптон 36Кг, ксенон 54Хе и радон
86Rn отличаются тем, что на них заканчивается заполнение р-оболочек
и они обладают большой энергией ионизации. У следующих по номеру
атомов (литий, натрий, калий, рубидий, цезий и франций) имеется за-
заполненная р-оболочка и один электрон в s-оболочке следующего слоя.
Эти атомы образуют группу щелочных металлов и обладают малой
энергией ионизации.
Отметим, что полные угловой и магнитный моменты любой запол-
заполненной оболочки равны нулю.

6.3] Структура и спектры сложных атомов 217
> Термы сложных атомов. В легких и средних атомах спин-орби-
спин-орбитальное взаимодействие для отдельных электронов невелико, и сложе-
сложение моментов происходит по следующей схеме. Орбитальные моменты
электронов складываются в полный орбитальный момент L, который
характеризуется квантовым числом L, а спины электронов складыва-
складываются в полный спиновый момент S (квантовое число S). В свою очередь
орбитальный и спиновый моменты складываются в полный момент
атома J. Такая схема носит название нормальной LS-связи, или связи
Рассела-Саундерса. Число L всегда целое, а число S целое, если в обо-
оболочке четное число электронов, и полуцелое, если нечетное. Отметим,
что складывать нужно только моменты электронов в незаполненной
оболочке.
В тяжелых атомах сложение моментов происходит по схеме, называемой
jj-связью. Сначала складываются угловой и магнитный моменты каждого
отдельного электрона (j = 1 + s), а потом уже происходит сложение элек-
электронных угловых моментов (J = ^ jj).
В случае нормальной связи сохраняются полный момент (величина
и проекция), величины орбитального и спинового моментов. Каждый
терм характеризуется квантовыми числами L, S и J и в отсутствие
магнитного поля B J + 1)-кратно вырожден. При заданных L, S кван-
квантовое число J может принимать 2S + 1 значений от L — S до L + S,
поэтому число 2S + 1 называют мулътиплетностъю терма. Отличие
между энергиями термов из одного мультиплета определяется срав-
сравнительно слабым спин-орбитальным взаимодействием. Спектральные
обозначения термов: орбитальное квантовое число атома изображается
с помощью прописной буквы S, P, D, F, G и далее по алфавиту (в отли-
отличие от одноэлектронных состояний, где используются строчные буквы).
Справа внизу указывается число J, которое выделяет данный терм из
мультиплета, а слева вверху указывается мультиплетность терма 2S+1.
(Следует иметь в виду, что при L < S реальная мультиплетность терма
равна 2L + 1, но принято указывать 2S + 1.) Например, терм 2Рз/2
соответствует квантовым числам L = 1, S = 1/2 и J = 3/2. Кроме того,
на схеме спектральных переходов, где надо изображать возбужденные
состояния, указывают главное квантовое число возбужденного элек-
электрона (наименьшее число равно номеру слоя, к которому принадлежит
незаполненная оболочка).
При сложении спиновых и орбитальных моментов электронов мож-
можно получить различные квантовые числа. Чтобы узнать, какие кван-
квантовые числа соответствуют основному состоянию атома, используют
эмпирические правила Хунда. Первое правило: у терма с наименьшей
энергией значение S максимально, и при этом значении S максимально
значение L. (Сначала определяют максимально возможные ms и т/,,
а потом по ним определяют S и L.) Второе правило: J = \L — S\,

218 Квантовая механика. Атомная физика [Гл. 6
если оболочка заполнена менее чем наполовину, и J = L + S в об-
обратном случае. Смысл первого правила Хунда заключается в том, что
если у электронов одинаковые спиновые состояния, то у них разные
пространственные состояния, что соответствует меньшей энергии вза-
взаимодействия между электронами. Например, у углерода для оболочки
2р2 полный спин равен S = 1, а орбитальное число не может иметь
максимальное значение L = 2, так как в этом случае у двух электронов
были бы одинаковые квантовые числа т/ = 1; следовательно, L = 1,
а так как два электрона заполняют меньше половины р-оболочки,
в которой 6 мест, то J = \L — S\ = 0. Основной терм атома углерода
3Ро- Проверьте, что основной терм атома азота 4*§з/2-
> Правила отбора. При построении схемы спектральных линий
и выяснении мультиплетности линии излучения необходимо использо-
использовать как мультиплетность термов, так и правила отбора для переходов
между термами. Правила отбора для излучательных переходов могут
быть получены путем вычисления вероятности перехода между состо-
состояниями. Однако смысл правил отбора можно понять исходя из закона
сохранения момента, с учетом того, что спин излученного фотона ра-
равен 1.
Правило отбора для числа J: A J = 0, =Ы, но запрещен переход
между двумя состояниями с J = 0. Правило отбора для числа mj\
Amj = 0, =Ы. Правило отбора для квантового числа S: AS = 0. Пра-
Правило отбора для квантового числа L:Z\L = 0,±1,ho запрещен переход
между двумя состояниями с L = 0. В атомах с одним электроном
в незаполненной оболочке переходы с AL = 0 запрещены.
Правило отбора для спинового числа связано с тем, что магнитное
поле электромагнитной волны слабо взаимодействует с магнитным мо-
моментом электрона (воздействие на орбитальный момент определяется
электрическими силами). Например, в атомах с двумя электронами
наблюдаются независимые серии для состояний с S = 0 (синглетные
термы) и для состояний с S = 1 (триплетные термы). В случае гелия
при описании данных используют исторически возникшее представле-
представление о двух видах гелия: парагелий (S = 0) и ортогелий (S = 1).
> Характеристические рентгеновские спектры. При бомбарди-
бомбардировке анода электронной лампы энергичными электронами (с энер-
энергиями ~ 102 -г- 104 эВ) наблюдается рентгеновское излучение двух
видов. Тормозное излучение связано с излучением рентгеновских кван-
квантов непосредственно электронами. Характерной особенностью этого
излучения является коротковолновая граница спектра (см. раздел 5.7)
и плавное распределение интенсивности излучения по спектру. На этом
фоне выделяется ряд интенсивных узких линий характеристического
излучения. Такое излучение возникает при выбивании электрона, при-
принадлежащего одному из внутренних электронных слоев, после чего на

6.3] Структура и спектры сложных атомов 219
освободившееся место переходит электрон с более высокого слоя и излу-
излучается рентгеновский квант. Если выбивается один из двух электронов
if-слоя, то для рентгеновских линий используются обозначения: Ка
для перехода электрона из L-слоя, Кр для перехода электрона из М-
слоя и т. д. Если выбивается электрон из L-слоя, то спектральные линии
обозначаются La, L^ и т.д.
Для электронов внутренних слоев поле ядра почти не экранировано.
Поэтому, в отличие от электронов внешних слоев, энергия внутрен-
внутренних электронов должна сильно зависеть от порядкового номера яд-
ядра. Можно ожидать, что энергия этих электронных уровней должна
описываться формулой для водородоподобных атомов, с поправкой на
экранирование: Еп = R(Z - 5J/n2. Однако такой подход не дает хоро-
хорошего описания экспериментальных фактов, и эмпирическую поправку
на экранирование вносят прямо в формулу для спектральных линий.
Например, для линии Ка получим
где экранировочная поправка а для легких атомов примерно равна еди-
единице. Этот закон был открыт в 1913 г. Мозли, который сформулировал
его как закон линейной зависимости y/v для частоты характеристиче-
характеристической линии от порядкового номера Z. Закон Мозли позволил уточнить
порядковые номера многих элементов в таблице Менделеева.
Поскольку рентгеновский спектр определяется внутренними обо-
оболочками атома, то он не зависит от того, является атом изолиованным
или входит в состав молекулы или кристалла. Поэтому анализ состава
вещества с помощью характеристических рентгеновских спектров об-
обладает высокой универсальностью.
Аналогично оптическим рентгеновские спектры обладают тонкой
структурой, вызванной расщеплением уровней энергии внутренних
электронов. Однако в этом случае работает не нормальная LS-связь,
a j j-связь. Например, электрон на L-слое может иметь / = 0, и тогда
j = 1/2, или / = 1, и в этом случае возможны два варианта: j = 1/2
или j = 3/2. Следовательно, L-оболочка распадается на три линии,
различие в энергиях которых определяется спин-орбитальным взаи-
взаимодействием. /С-слой содержит только один уровень, М-слой — пять
уровней и т. д. При анализе спектров надо учитывать правила отбора:
А1 = =Ы, Aj = О, =Ы. Например, Ка линия распадается на две линии:
Kai и Ка2, переход с уровня с / = 0 отсутствует.
Изучение поглощения рентгеновского излучения позволяет непо-
непосредственно увидеть положение уровней энергии электронов на внут-
внутренних оболочках. При увеличении частоты коэффициент поглощения
плавно убывает, но при частоте, равной ui = Ei/h, где Е{ —энергия
ионизации электрона с одного из внутренних уровней, наблюдается

220
Квантовая механика. Атомная физика
[Гл.6
резкое его возрастание, связанное с тем, что открывается дополнитель-
дополнительный канал поглощения. В соответствии с вышесказанным наблюдаются
один пик на энергии /С-слоя, три пика на энергии L-слоя, пять пиков
на энергии М-слоя и т. д.
> Атом во внешнем магнитном поле. В достаточно слабых маг-
магнитных полях (В < 1 Тл) энергия взаимодействия электрона с магнит-
магнитным полем мала по сравнением со спин-орбитальным взаимодействием,
и магнитное расщепление термов мало по сравнением с расстоянием
между термами мультиплета. В этом случае наблюдается сложный
(аномальный) эффект Зеемана, т. е. уровень энергии расщепляется на
2J + 1 подуровней с разными квантовыми числами mj, причем рассто-
расстояние между подуровнями пропорционально величине магнитного поля
и зависит от квантовых чисел L, S и J. Величина смещения подуровня
выражается формулой ЛЕ = gjmjfiBB, где цв — магнетон Бора, а
bJ - ^ ' 2J(J + 1)
называют фактором Ланде.
Сложный характер эффекта Зеемана в слабых полях объясняется ано-
аномальным значением спинового магнитного момента, для которого гиро-
гиромагнитное отношение равно 2. В результате полный магнитный момент
ji = (L + 2S) оказывается не пропорционален полному моменту J. В век-
векторной модели магнитный момент можно представить быстро вращающимся
вокруг сохраняющегося вектора полного момента, и в результате усреднения
должна остаться только проекция магнитного момента на полный момент:
_ (цЛ) _ е (L + 2S)(L + S)
J J2 2т J2
Выражая (LS) = -(J2-L2-S2) и заменяя J2 на J(J + 1), L2 на L(L + 1) и S2
, где gj —фактор Ланде, выражение
на S(S + 1), получаем Дг =
2т
для которого приведено выше.
Отметим, что даже при отличных от нуля S, L и J фактор Ланде
может обращаться в ноль (S = 3/2, L = 2, J = 1/2) и даже быть
отрицательным (S = 5/2, L = 3, J = 1/2).
Эти эффекты являются чисто квантовыми
и не имеют классических аналогов.
Чтобы получить расщепление спек-
спектральных линий в магнитном поле, надо
учесть правила отбора. Например, уровень
2Р3/2 расщепится на 4 уровня с фактором
4
1/2 Ланде -, а синглетный уровень S\/2 — на
о
— 1/2 два уровня с фактором Ланде 2 (рис. 104),
Рис. 104 но будет наблюдаться не 8 линий, а 6, так
Р* /2
\
#1/2 ^
1
f )
f V
3/2
1/2
-1/2
-3/2

6.4] Элементы физики молекул 221
как переходы с mj = 3/2 на mj = —1/2 и с mj = —3/2 на mj = 1/2
запрещены правилом отбора Amj — О, =Ы.
Простой эффект Зеемана (расщепление одной линии на три) наблю-
наблюдается при переходе между уровнями, у которых g± = g2 = g. В этом
случае Аи = gAmjB/h, где Amj = О, =Ы. Такая ситуация возникает
не только при переходе между двумя синглетными уровнями (S = О,
g = 1), но и в некоторых других случаях.
При помещении атома в сильное магнитное поле (когда магнит-
магнитное расщепление термов гораздо больше расстояния между терма-
термами мультиплета) тонкую структуру уровней можно не учитывать,
т.е. можно пренебречь спин-орбитальным взаимодействием. Уровень
с квантовыми числами m/,, ms смещается в магнитном поле на
АЕ = цвВ{ть + 2ms)- Изменение частоты излучения составляет
НАи = {1вВ(Ать + Arris)' С учетом правил отбора Ams = О,
ArriL = О, =Ы получаем, что происходит расщепление каждой линии на
три — две смещенных и одну несмещенную; следовательно, в сильном
магнитном поле эффект Зеемана становится простым. Это явление
носит название эффекта Пашена-Бака.
6.4. Элементы физики молекул
Молекулой называется связанное состояние электронейтральной
системы, состоящей из ядер нескольких атомов и окружающих их
электронов. Молекулы из двух атомов называются двухатомными, из
трех и более атомов — многоатомными. Молекулу с недостаточным или
избыточным числом электронов называют молекулярным ионом.
Мы ограничимся рассмотрением простейших двухатомных
систем — молекулы водорода Н2 и молекулярного иона водорода Hj.
> Классификация движений и уровней энергии молекулы.
Молекула, подобно атому, является микроскопической системой и обла-
обладает дискретными уровнями энергии, соответствующими ее основному
и связанным возбужденным состояниям. Однако, в отличие от атома,
кроме электронной энергии, отвечающей возможным состояниям элек-
электронов в поле неподвижных ядер, в молекуле существуют еще два вида
движения: колебательное движение, связанное с изменением рассто-
расстояния между ядрами, и вращение молекулы как целого относительно
некоторой оси. Энергию молекулы (отсчитанную от основного состо-
состояния) можно считать равной сумме энергий, отвечающих указанным
движениям:
Е = Еэл + ^кол + ^вр- C1)
Существует ярко выраженная иерархия этих энергий: Еэл ^> Екол ^> Евр.
Еэл для внешних электронов порядка нескольких эВ, Екол порядка
10~2 эВ, ^вр порядка 10~4 эВ. Отношение Екол/Еэл, также как

222
Квантовая механика. Атомная физика
[Гл.6
J
к
4
о
1
0
— 5
4
о
О
0
1
Вращательные
^ уровни
^^*"*^ Электронные
уровни
\^
\
\
/ \
/ \
* \
Колебательные \
уровни \
R
Рис. 105
Рис. 106
и отношение Евр/Екол, по порядку величины равно д/ш/М, где
m — масса электрона, а М — масса ядер, т. е. для тяжелых молекул
иерархия энергий усиливается.
В первом приближении все три энергии квантуются независимо,
каждому из них соответствует своя система дискретных уровней. Энер-
Энергетический спектр молекулы представляет собой совокупность далеко
отстоящих электронных уровней, более близко расположенных колеба-
колебательных уровней и еще более близких вращательных уровней. Система
уровней схематически изображена на рисунке 105 для двух соседних
электронных уровней, где буквами v и J обозначены колебательные
и вращательные квантовые числа.
Волновая функция молекулы может быть представлена в виде про-
произведения волновых функций трех видов движений. Каждая из этих
функций, так же как соответствующие значения энергий, получаются
решением соответствующих уравнений Шредингера. Сначала решают
уравнение Шредингера для электронов при заданном расстоянии R
между ядрами; эта энергия зависит от R как от параметра. Энер-
Энергия взаимодействия между ядрами равна сумме электронной энергии
и энергии кулоновского отталкивания ядер. Для одних электронных
уровней эта энергия имеет вид потенциальной ямы (кривая а на
рис. 106), для других (кривая Ь) — вид монотонной зависимости. Для
первого случая связанное состояние существует, для второго отсут-
отсутствует. Для основного электронного состояния энергия взаимодействия
имеет вид потенциальной ямы, а глубина этой ямы имеет смысл энергии
диссоциации молекулы. (Более точно, энергия диссоциации D меньше

6.4] Элементы физики молекул 223
глубины ямы на энергию нулевого колебательного уровня, отсчитан-
отсчитанную от глубины ямы, которая равна Ни/2.)
После того, как рассчитана зависимость энергии взаимодействия
между ядрами от расстояния /2, решают задачу о колебаниях вбли-
вблизи дна получившейся потенциальной ямы и о вращении молекулы
с расстоянием между ядрами, равным среднему равновесному рассто-
расстоянию Ro.
> Электронная энергия. Теория химической связи. Начнем со
случая молекулярного иона Н^~. Потенциал двух протонов для движе-
движения единственного электрона обладает в этом случае цилиндрической
симметрией по отношению к оси молекулы, но не обладает сферической
симметрией, свойственной атому водорода. В этом случае сохраняет-
сохраняется проекция углового момента на ось молекулы, но модуль углового
момента не сохраняется. Уровни энергии характеризуются значением
модуля магнитного квантового числа т/, которое обозначают буквой Л:
Л = \mi\ = 0,1, .... Состояния электрона с Л = 0,1, 2, ... обозначают
буквами сг, тг, ($,... и называют молекулярными орбиталями. С учетом
спина сг-состояние дважды вырождено, а состояния с Л > 0 вырождены
четырехкратно. В сг-состоянии электронная плотность сосредоточена
в области между ядрами, ядра притягиваются к электронному облаку
и таким образом реализуется притяжение между ядрами, описывае-
описываемое потенциальной ямой а на рис. 106 (при малых R преобладает
отталкивание между ядрами). Энергия диссоциации Hj равна 2,65 эВ.
Для тг-электронов электронная плотность имеет вид двух облаков,
расположенных между ядрами симметрично относительно некоторой
плоскости, проходящей через ось молекулы, причем в самой плоскости
электронная плотность равна нулю.
В молекуле водорода химическая связь осуществляется не одним,
а двумя электронами, которые притягиваются к ядрам, но отталкива-
отталкиваются друг от друга. Как для любых фермионов, волновая функция двух
электронов должна менять знак при их перестановке. Если спиновая
волновая функция симметрична по отношению к перестановке частиц
(спины параллельны, т. е. S = 1), то координатная —антисимметрична,
и наоборот. Меньшей энергией обладает состояние с антипараллельны-
антипараллельными спинами (S = 0) и симметричной координатной волновой функцией.
В этом состоянии достаточно велика вероятность пребывания электро-
электронов в пространстве между ядрами и ядра притягиваются к располо-
расположенному между ними электронному облаку.
Таким образом, химическая связь осуществляется двумя электрона-
электронами с антипараллельными спинами. Зависимость потенциальной элек-
электростатической энергии от расстояния между ядрами имеет вид кри-
кривой а на рис. 106. Энергия диссоциации молекулы водорода равна
4,5 эВ; это меньше удвоенной энергии диссоциации молекулярного иона
Н2~ вследствие электростатического отталкивания между электронами.

224 Квантовая механика. Атомная физика [ Гл. 6
Для электронов с параллельными спинами зависимость энергии от рас-
расстояния между ядрами имеет вид кривой b на рис. 106, т. е. связанное
состояние не образуется.
Такой механизм носит название ковалентной (гомеополлрной) хи-
химической связи. Он осуществляется не только в молекуле водорода, но
и любой парой внешних электронов сложных атомов, соединяющих-
соединяющихся в молекулу. Для двухатомных молекул, состоящих из различных
атомов, возможен другой механизм, который носит название ионной
(гетерополярной) химической связи, когда один из атомов отдает часть
внешних электронов другому атому, имеющему свободные места во
внешней оболочке. В результате образуются два иона, которые на
больших расстояниях притягиваются по закону Кулона, а при сближе-
сближении на малые расстояния начинают отталкиваться. Возможны также
промежуточные случаи между ковалентной и ионной связями.
Обменная энергия. Различие в энергиях симметричного и антисиммет-
антисимметричного состояний имеет общий характер и является следствием так называ-
называемого обменного взаимодействия — чисто квантового явления, смысл кото-
которого сводится к следующему. Будем конструировать координатную волновую
функцию двух электронов в поле двух ядер из одноэлектронных волновых
функций ipa(ri) и грр(г2). Эта функция может быть как симметричной, так
и антисимметричной (в зависимости от вида спиновой функции):
) (^(
Средняя потециальная энергия в этих состояниях равна
р р
J J
где U — потенциальная энергия взаимодействия электронов между собой
и с ядрами. Первый член соответствует обычному классическому взаимо-
взаимодействию электронных облаков и ядер. Второй член называется обменной
энергией, он отличен от нуля только в том случае, если волновые функции
электронов перекрываются. В случае молекулы водорода обменная энергия
отрицательна, и поэтому состояние с симметричной координатной волновой
функцией имеет меньшую энергию.
Обменная энергия проявляется во многих квантовых системах, в частно-
частности, она отвечает за различие энергий синглетного и триплетного состояний
электронов в атоме гелия.
Для приближенных расчетов химической связи обычно используют
один из двух методов. В методе электронных пар в качестве исходных
одночастичных волновых функций ф{т\) и ф(т2) используют атомные
волновые функции электронов, локализованные возле первого и второ-
второго ядер. При сближении ядер волновые функции начинают перекры-
перекрываться, обменная энергия возрастает и образуется связанное состоя-
состояние. В методе молекулярных орбиталей электроны последовательно

6.4] Элементы физики молекул 225
заполняют свободные а, тг, S молекулярные состояния с различными
спинами, образуя замкнутые электронные оболочки.
> Колебательные и вращательные спектры. Энергия взаимо-
взаимодействия между ядрами, приведенная на рис. 106, имеет минимум
при R = Rq. Возле этой точки энергия может быть разложена в ряд
и представлена в виде
U(R) = U(Ro) + \k(R - R0J + . . .,
где k = d2U/dR2\R_R —квазиупругая постоянная. Циклическая ча-
частота малых колебаний молекулы возле положения равновесия рав-
равна икол = y/k//i, где ц = mim2/'(гп\ + 777,2) — приведенная масса
двухатомной молекулы. Квантовая механика дает для разрешенных
значений энергии осциллятора значения
Е - U(Ro) = huKOJl(v + i), v = 0,1, 2,....
При учете отброшенных членов в U(R), существенных при больших v,
расстояние между уровнями начинает уменьшаться.
Вращательные уровни энергии молекулы получаются как собствен-
собственные значениия оператора
Я = |, C2)
где L — оператор углового момента, / — момент инерции молекулы
относительно центра масс. Вращающуюся систему с постоянным мо-
моментом инерции, описываемую гамильтонианом C2), называют рота-
ротатором. Разрешенные значения энергии ротатора
Частоту излучения или поглощения получаем из соотношения
Ни; = АЕЭЛ + АЕКОЛ + АЕвр, C3)
где первый член соответствует переходу между различными электрон-
электронными уровнями, второй — изменению колебательного состояния, а тре-
третий — изменению состояния вращения.
Если электронное состояние при переходе не меняется (АЕЭЛ = 0),
то наблюдается либо чисто вращательный спектр (если АЕКОЛ = 0),
либо колебательно-вращательный спектр. Для чисто вращательных
и колебательно-вращательных переходов действуют правила отбора
Sv = =Ы, AJ = ±1.
8 А. И. Черноуцан

226
Квантовая механика. Атомная физика
[Гл.6
J
4
4о;в
Зо;в
J
3
2
1
О
3
2
1
О
О ш школ-ивр кол о;кол + о;вр
Рис. 107 Рис. 108
При чисто вращательных переходах (АЕЭЛ = 0 и АЕКОЛ = 0)
изменение вращательной энергии равно
АЕвр = E(J + 1) - E(J) = у (J + 1).
Видно, что вращательные переходы образуют систему близких рав-
равноотстоящих спектральных линий о;вр, 2о;вр, . . ., где о;вр = h2/1
(рис. 107). Вращательные линии могут быть разрешены только при-
прибором с очень высокой разрешающей способностью, но обычно вос-
воспринимаются как сплошная полоса. Чисто вращательные переходы
соответствуют поглощению в далекой инфракрасной области (сотни
и тысячи мкм).
Колебательные переходы (при АЕЭЛ = 0) наблюдаются при погло-
поглощении в близкой инфракрасной области (несколько мкм). Так как при
этом обычно АЕв
0, то наблюдается не линия, а колебательно-
вращательная полоса. С учетом правил отбора получим
±
где п = 1, 2,. . .,
т. е. расстояние между соседними линиями в центре полосы равно 2о;вр
(рис. 108).
Учет ангармоничности колебаний приводит к усложнению характера
колебательно-вращательных спектров. Кривая потенциальной энергии
(рис. 106) при увеличении R — Ro становится несимметричной. Это приводит
в первую очередь к смещению колебательных уровней — с увеличением v
колебательные уровни сближаются. Кроме того, в состоянии с большим v

6.4] Элементы физики молекул 227
среднее расстояние между атомами оказывается больше, следовательно,
момент инерции с увеличением v возрастает, а сиър уменьшается. Это
приводит к тому, что линии в колебательно-вращательной полосе перестают
быть равноотстоящими.
Если же АЕЭЛ ф О, то наблюдаются электронные спектры испус-
испускания и поглощения в видимой и ультрафиолетовой областях. Каждо-
Каждому электронному переходу соответствует система колебательно-враща-
колебательно-вращательных полос. В отличие от колебательно-вращательных переходов,
при переходах с изменением электронного состояния правило отбора
Av = =Ы не выполняется, т.е. возможны переходы между уровнями
с любыми значениями колебательных квантовых чисел. Следователь-
Следовательно, будет наблюдаться не одна колебательно-вращательная полоса,
а серия полос, отстоящих друг от друга на сокол.
Отметим, что двухатомные молекулы с нулевым дипольным мо-
моментом (например, N2, СЬ) не обладают колебательно-вращательными
спектрами. Именно поэтому такие молекулы не поглощают в инфра-
инфракрасной (ИК) области спектра, и поглощение воздухом ИК излучения
определяется наличием в нем молекул Н2О и СО2.

Глава 7
КВАНТОВАЯ ТЕОРИЯ КРИСТАЛЛОВ
Несмотря на то, что законы квантовой механики действуют на
атомных масштабах, они оказывают влияние и на макроскопические
свойства газов, жидкостей и твердых тел. Квантовая механика и кван-
квантовая статистика — статистика тождественных частиц — позволили
правильно и непротиворечиво описать тепловые, магнитные и многие
другие свойства больших ансамблей частиц. Особое место здесь при-
принадлежит квантовой теории кристаллов, позволившей снять ряд нераз-
неразрешимых противоречий классической теории, количественно описать
электромагнитные свойства разных классов веществ, дать объяснение
сверхпроводимости и сверхтекучести и т. д.
7.1. Элементы квантовой статистики
Квантовая статистика изучает статистические свойства больших
ансамблей тождественных частиц — фермионов и бозонов. Статистика
классических частиц, т. е. частиц, отличимых друг от друга, называется
статистикой Максвелла — Больцмана (см. раздел 2.5). Статистика
фермионов, т. е. тождественных частиц, которые не могут занимать
одинаковые состояния, называется статистикой Ферми — Дирака.
Статистика бозонов, т.е. тождественных частиц, число которых в лю-
любом состоянии не ограничено, называется статистикой Бозе — Эйн-
Эйнштейна.
> Статистические распределения. Статистика каждого типа опи-
описывается своим статистическим распределением частиц по состоя-
состояниям. Статистическое распределение показывает, какое среднее число
частиц находится в данном состоянии при условии, что система пре-
пребывает в состоянии теплового равновесия. Важнейшее свойство всех
распределений состоит в том, что они представляют собой функцию
одного параметра —энергии частицы г): (N) = f(s).
В квантовой механике понятие состояния отдельной частицы можно счи-
считать вполне определенным, правда, при некоторых условиях. Чтобы уровни
энергии были дискретными, система должна быть локализована в конеч-
конечной области пространства. Обычно считают, что система заперта в ящике
х) Далее энергия одной частицы будет обозначаться е, а энергия системы
Е.

7.1] Элементы квантовой статистики 229
достаточно большого объема V. Кроме того, понятие одночастичного со-
состояния с определенной энергией предполагает отсутствие межчастичного
взаимодействия. Можно обойти последнюю трудность с помощью введения
самосогласованного внешнего поля, в которое включено усредненное поле
остальных частиц.
Для ансамбля классических частиц вводят понятие элементарной ячей-
ячейки фазового пространства. Фазовое пространство — это пространство трех
координат и трех импульсов. В классической физике каждому состоянию
соответствует одна точка фазового пространства. В этом случае элемен-
элементарную ячейку, соответствующую одному состоянию, вводят для удобства
статистического описания, и она может иметь произвольный (достаточно
маленький) объем. В квантовой механике состояние частицы нельзя изобра-
изображать точкой в фазовом пространстве, так как имеются неопределенности в ее
положении и импульсе, связанные между собой соотношениями Гейзенберга
ЛхЛрх ~ h и т. д. Видно, что отдельному состоянию должен соответствовать
объем AxAyAzApxApyApz ~ h3. Более точный анализ показывает, что
объем элементарной ячейки равен Bтг/г) . Чтобы узнать, сколько состояний
содержится в конечной области фазового пространства, надо ее объем разде-
разделить на объем элементарной ячейки. Такой подход, в котором элементарный
объем одного состояния для классической частицы выбирается из квантовых
соображений, называется квазиклассическим.
> Микроскопические и макроскопические состояния. Стати-
Статистический вес. Задать микроскопическое состояние (микросостоя-
(микросостояние) системы — значит определить в данный момент состояние всех ее
частиц. В классической физике надо определить координаты и импуль-
импульсы всех частиц, т. е. положение всех частиц в фазовом пространстве,
в квазиклассическом рассмотрении — распределение частиц по элемен-
элементарным ячейкам фазового пространства объемом Bтг/гK, в квантовой
механике — распределение частиц по состояниям с определенной энер-
энергией (для движения в самосогласованном поле). Для удобства изложе-
изложения объединим два последних случая и будем называть состояния ча-
частиц с определенной энергией также ячейками. За счет взаимодействия
между частицами и внешних воздействий микросостояние системы
все время изменяется, и наблюдаемыми являются только усредненные
характеристики, через которые определяется макросостояние.
Чтобы определить макросостояние количественно, разобъем всё
множество ячеек на ящики. Каждый ящик содержит большое количе-
количество ячеек с очень близкими значениями энергии, лежащими в узком
энергетическом интервале (е,е + Ле). Обозначим число частиц в г-м
ящике через Л^. Будем считать, что макросостояние задается набором
чисел Ni, т.е. все микросостояния, обладающие одинаковым набором
этих чисел, принадлежат к одному макросостоянию.
Без ограничения общности будем рассматривать систему частиц,
заключенную в ящик с жесткими теплонепроницаемыми стенками, т. е.
с фиксированной полной энергией. Почему без ограничения общности?

230 Квантовая теория кристаллов [ Гл. 7
Нас будут интересовать в первую очередь свойства равновесного макросо-
макросостояния, а в этом случае энергия большого ансамбля частиц определена
с очень высокой степенью точности при любых внешних условиях. Например,
для системы N частиц в термостате относительное отклонение от средней
энергии составляет 1/y/N. Поясним это на примере идеального газа. Если
средняя энергия одной частицы равна (s), а среднеквадратичное отклонение
от средней энергии 5е = у/{(е — (s)J), то средняя энергия системы равна
(Е) = N(e), а среднеквадратичное отклонение равно
(мы учли, что отклонения энергий разных частиц от среднего независимы
друг от друга).
> Основной постулат статистической физики для системы
с фиксированной энергией гласит, что все доступные ей микросостоя-
микросостояния (т. е. имеющие данное значение полной энергии) реализуются с оди-
одинаковой вероятностью. Этот постулат тесно связан с так называемой эр-
годической гипотезой, утверждающей, что в процессе своей эволюции
во времени система проходит через все допустимые микросостояния.
Главный вывод из основного постулата следующий: большую часть
времени система находится в тех макросостояниях, которым соответ-
соответствует наибольшее число микросостояний. Число микросостояний, со-
соответствующее данному макросостоянию, называется его статисти-
статистическим весом и обозначается Q. Макросостояние с максимальным Q
называется равновесным. В соответствии с постулатом Больцмана (см.
раздел 2.5) энтропия системы в данном макросостоянии связана с ее
статистическим весом:
Отклонения от равновесного состояния называются флуктуацилми.
Отметим, что в связи с огромным числом частиц в системе большие от-
отклонения чрезвычайно маловероятны, т. е. практически наблюдаемы-
наблюдаемыми являются лишь небольшие флуктуации. Если изначально система
находилась в сильно неравновесном состоянии, то в процессе эволюции
она должна переходить от макросостояний с меньшим статистическим
весом (меньшей энтропией) к макросостоянием с большей энтропией,
приближаясь к равновесному состоянию (второе начало термодинами-
термодинамики).
> Равновесное макросостояние. Чтобы определить, какое распре-
распределение частиц по ящикам {A^i, N2 . . .} является равновесным, надо
вычислить f2(Ni, N2 . . .) или S/k = In Q и найти максимум этого
выражения (при условии ^SiNi = Е и ^ Ni = N). Выражения для
статистического веса и энтропии существенно различны для частиц
с разным типом статистического поведения. Приведем выражения для
статистического веса (gi обозначает число ячеек в г-м ящике):

7.1] Элементы квантовой статистики 231
для статистики Максвелла — Больцмана
/v, N\
для статистики Бозе — Эйнштейна
и для статистики Ферми — Дирака
NiHgi-NiY/
г
Равновесное состояние { Л^}, соответствующее максимуму статисти-
статистического веса при условии, что Е и N фиксированы, находится с по-
помощью метода неопределенных множителей Лагранжа. (Надо найти
максимум выражения (S/к) — а^2 Ni — /3^2eiNi, считая все Ni неза-
независимыми. Множители Лагранжа затем определяются из уравнений
^2 Ni = N,^2siNi = Е.) Получаются следующие выражения:
для статистики Максвелла — Больцмана
для статистики Бозе — Эйнштейна
AT. — ёг
и для статистики Ферми — Дирака
Среднее число частиц в одной ячейке получается делением этих выра-
выражений на g{.
Физический смысл множителей а и /3 можно выяснить из
термодинамических соображений. Условие максимума выражения
(S/k) - aN - РЕ запишем в виде TdS/kT - fidE - adN = О
и сравним с термодинамическим тождеством TdS — dU — fidN = О,
верным для изменений состояния при постоянном объеме. Получим
/3 = 1/кТ, а = fi/кТ, где \i — химический потенциал.
Окончательно квантовые распределения принимают вид:
Распределение Бозе — Эйнштейна:
Ji. (I)

232 Квантовая теория кристаллов [ Гл. 7
Распределение Ферми — Дирака:
1- B)
Химический потенциал ц для системы с фиксированным числом
частиц N вычисляется из уравнения
где f(?i) — соответствующее распределение (Бозе — Эйнштейна или
Ферми — Дирака). Если же число частиц в системе не фиксировано,
то химический потенциал надо положить равным нулю.
При е — ц ^> kT оба квантовых распределения переходят в класси-
классическое распределение Максвелла — Больцмана
(N) = Ае~?1кТ. C)
Это связано с тем, что среднее число частиц в ячейке мало, и правила
запрета и тождественность частиц становятся несущественными.
Обычно наименьшее возможное значение энергии (энергия низшего
уровня) принимается равным нулю.
> Свойства распределения Бозе — Эйнштейна.
1) Химический потенциал бозонов не может быть положительным:
2) При Т —У О химический потенциал стремится к нулю, и при Т = О
равен нулю.
3) При Т = О все частицы находятся в низшем энергетическом
состоянии при ? = 0. При температурах конечных, но достаточно
маленьких в низшем энергетическом состоянии находится конечная
доля всех частиц. Это явление называется бозе — эйнштейновской
конденсацией, а ансамбль макроскопического числа частиц в низшем
состоянии — бозе — эйнштейновским конденсатом. Конденсация бозо-
бозонов начинается при некоторой критической температуре (температуре
конденсации). Это явление играет важную роль для объяснения таких
явлений как сверхтекучесть и сверхпроводимость.
4) Примером распределения Бозе — Эйнштейна является формула
Планка для распределения фотонов по энергиям (раздел 5.6). Число
фотонов не фиксировано, поэтому /i = 0.
> Свойства распределения Ферми — Дирака.
1) Химический потенциал ферми-газа может быть как положитель-
положительным, так и отрицательным. При низких температурах химический
потенциал положителен. Химический потенциал газа фермионов при
Т = 0 называют энергией Ферми и обозначают ?р-

7.2]
Электронный газ в металле
233
2) При Т = О зависимость среднего числа частиц в ячейке (N) от
энергии имеет вид резкой ступеньки: для ? < sf ячейки заполнены ча-
частицами ((N) = /f(^) = 1), а для г > sf ячейки свободны (/f(^) = 0).
3) При низких температурах (kT <С ?f) зависимость /f(^) имеет
вид сглаженной ступеньки (рис. 109). Ширина размытия по порядку
величины равна кТ. При ? = ц среднее число частиц равно 1/2.
Распределение частиц по энергиям при кТ <С ?f радикально отли-
отличается от классического, в этом случае газ называют вырожденным.
При кТ ^> sf газ фермионов почти не отличается от классического.
Более конкретные свойства ансамбля бозонов или фермионов
зависят от физических свойств
рассматриваемой системы,
в первую очередь от вида
функции G(e), характеризу-
характеризующей количество состояний
Ag, приходящихся на узкий
интервал энергий Ае в расчете
на единицу объема:
^f = G{e)As. D)
1,0
/f
0,5
0
, , , , 1 , , , , 1 , , , ,
0,02! !
од
Г I
Распределение '
Ферми при
разных кТ/?f
i
0 0,5 1,0 1,5 2,0
Рис. 109
Эту функцию называют энерге-
энергетической плотностью состоя-
состояний или просто плотностью состояний (сравните с разделом 5.6).
Через плотность состояний выражаются, например, число частиц в еди-
единице объема:
= ^=\f{e)G(e)de E)
п
и энергия частиц в единице объема:
F)
7.2. Электронный газ в металле
Классическая электронная теория проводимости металлов исхо-
исходила из представления, что электроны в металле можно рассматри-
рассматривать как классический идеальный газ (раздел 3.9). Одна из главных
трудностей, с которыми столкнулась эта теория, состояла в том, что
она предсказывала электронный вклад в теплоемкость равным теп-
лоемкости одноатомного идеального газа Сэл = ^kN, где N — чис-
ло свободных электронов. Именно на такую величину должны были

234 Квантовая теория кристаллов [ Гл. 7
бы отличаться теплоемкости металла и диэлектрика с аналогичными
кристаллическими решетками. Однако эксперимент показал, что элек-
электронная теплоемкость при комнатных температурах много меньше kN
(примерно в 100 раз) и изменяется пропорционально температуре. Эти
и некоторые другие факты находят свое естественное объяснение в
теории Зоммерфелъда, которая рассматривает электроны в металле
как квантовый газ фермионов.
> Плотность состояний электронного газа. Будем считать, что
внутри металла электроны свободны и что работа выхода электронов
из металла равна бесконечности, т.е. рассматривать их как частицы
в потенциальной яме с бесконечными стенками. Граничные условия
для волновых функций фх = Asinkxx имеют вид kxLx = тгп, где
Lx — размер потенциальной ямы (т. е. размер образца металла) вдоль
оси ж, кх — проекция волнового вектора, связанного с импульсом элек-
электрона соотношением к = р/Й, п — целое положительное число (см.
раздел 6.2). Граничные условия для волнового вектора тождественно
совпадают с теми, которые возникают при рассмотрении электромаг-
электромагнитных колебаний в замкнутой полости (раздел 5.6). Поэтому плот-
плотность состояний в этом случае имеет такой же вид:
dg_ _ k2dk
7
где V — объем сосуда, а)- множитель, учитывающий внутренние
степени свободы. В случае электронов j = 2 учитывает две возможные
проекции спина. Для перехода к импульсу электронов надо заменить
к2 dk на р2 dp/H3:
2
dg_ _ p2 dp
V • 4тгр2 dp
V
Перепишем эту формулу в виде
Видно, что для определения числа состояний надо объем фазового простран-
пространства разделить на объем элементарной ячейки Bтг/г) .
Для перехода к энергии е = р2 /2т надо заменить р = у/2гпё,
р dp = m de:
dg
=
> Энергия Ферми электронов. При Т = 0 заполнены все уровни
энергии от нуля до ? — ef- Чтобы связать энергию Ферми с концентра-
концентрацией электронов п, надо выразить полное число электронов в единице

7.2] Электронный газ в металле 235
объема и приравнять к концентрации
?F fo™^/2,-3/2
J
= п-
о
Выразим отсюда энергию Ферми:
Импульс электронов с энергией Ферми определяется соотношением
sF = p2F/2m и равен
pF = hCir2nI'3. (8)
Поверхность в импульсном пространстве, образуемая состояниями
с е = eFj называется поверхностью Ферми. В случае свободных элек-
электронов поверхность Ферми представляет собой сферу радиусом pp.
Плотность уровней на поверхности Ферми равна
dn 3 п
Средняя энергия электронов при Т = 0 равна
eF eF
Г
sG(s)ds ел/г de
J q
/ v _ _0 _ _0 _ 2_
\G(e)de \y/ede
о о
При Т > 0 химический потенциал /i надо находить из уравнения
n= \fF{e)G(e)de.
При повышении температуры /i постепенно уменьшается, но при
kT ^C ?f отличается от sf весьма незначительно (\/л — ер\/ер ~
~ [кТ/ер]2). При некоторой температуре Tq (A;To ^ <Sf химический
потенциал обращается в ноль, а при больших температурах ц < О
(см. рис. 109 , химический потенциал находится по графику, при ? = ц
Me) = 0,5).
Для удобства определения температурной области, в которой газ
электронов является вырожденным, вводят температуру Ферми, опре-
определяя ее соотношением кТр = ?f- При Т ^С Тр газ электронов
является вырожденным. Для большинства металлов Тр составляет
несколько десятков тысяч градусов, т. е. при комнатных температурах
газ электронов в металлах является сильно вырожденным.

236 Квантовая теория кристаллов [ Гл. 7
> Электронная теплоемкость металлов. В случае сильно вы-
вырожденного газа в тепловом движении участвуют только электроны,
энергия которых отличается от энергии Ферми на величину порядка
кТ. Только такие электроны могут перейти в свободное состояние
с энергией, большей ер. Доля таких электронов ~ кТ/sf = Т/Тр,
изменение их энергии ~ кТ. Следовательно, при повышении темпера-
температуры от нуля до Т энергия вырожденного электронного газа возрастает
на ~ к NT2 /Тр, а вклад электронов в теплоемкость Се\ ~ kN(T/Tp)
изменяется пропорционально температуре. (Точный расчет дает вы-
выражение Сei = GT2/2)kN(T/TF).) Число свободных электронов, при-
приходящихся на один моль металла, зависит от валентности; например,
в случае одновалентного металла N ~ TVa-
> Электропроводность и теплопроводность металлов. Теория
переноса дает следующие выражения для коэффициентов электропро-
электропроводности (раздел 3.9) и электронной теплопроводности (раздел 2.9):
пе2Х 1„ , *
C()X
Здесь Л — длина свободного пробега, Cei — теплоемкость электронов
в единице объема металла. В столкновениях с ионами принимают
участие только электроны, находящиеся вблизи поверхности Ферми,
поэтому (v) ~ vp = рр/гп, т.е. средняя скорость почти не зависит
от температуры. Тем не менее закон Видемана — Франца остается
верным: отношение к/а ~ (v) Cei/n для металлов оказывается ли-
линейной функцией температуры. Однако в отличие от классического
электронного газа, где Ce\jn от температуры не зависит, a (v) ~
~ Т, в теории Зоммерфельда линейная зависимость от температуры
определяется электронной теплоемкостью.
Теория Зоммерфельда не может объяснить зависимость электро-
электропроводности чистых металлов от температуры, так как в этой теории,
как и в теории Друде классического электронного газа, длина свобод-
свободного пробега является чисто эмпирическим параметром. Зависимость
длины свободного пробега от температуры объясняется в теории, учи-
учитывающей периодичность поля кристаллической решетки и взаимодей-
взаимодействие электронов с тепловыми колебаниями решетки (с фононами).
> Формула Ричардсона — Дэшмана. Теория Зоммерфельда поз-
позволяет объяснить температурную зависимость тока термоэлектронной
эмиссии с поверхности металла. Поверхность металла могут покинуть
только те электроны, для которых p2/2m > sf + А, где А — работа
выхода электрона из металла (ось z перпендикулярна к поверхности).
Опуская вычисления, приведем ответ
j = CT2exp(-A/kT),

7.3] Теплоемкость кристаллической решетки. Фононы 237
где С = —2~~з = 120 А/(м2 -К2) — постоянная, одинаковая для всех
металлов. п
7.3. Теплоемкость кристаллической решетки.
Фононы
> Закон Дюлонга и Пти. Классическая статистическая физика
предсказывает, что вклад колебаний кристаллической решетки в мо-
молярную теплоемкость должен быть равен 3R. Действительно, каж-
каждый атом решетки может совершать три независимых колебания око-
около положения равновесия, а каждой колебательной степени свободы
соответствует средняя энергия кТ. Энергия колебаний всех атомов
равна 3NkT = 3vRT, и молярная теплоемкость решетки должна не
зависеть от температуры и равняться SR. Действительно, молярная
теплоемкость многих диэлектриков при комнатной температуре оказы-
оказывается близкой к 3R (закон Дюлонга и Пти). Однако при уменьшении
температуры во всех случаях наблюдается существенное уменьшение
теплоемкости, и при низких температурах она стремится к нулю как
Т3. Объяснение такому поведению решеточной теплоемкости дает
квантовая теория.
> Теория Эйнштейна. Эйнштейн рассматривал колебания атомов
в узлах кристаллической решетки как 37V независимых друг от друга
одинаковых квантовых осцилляторов. Средняя энергия такого осцил-
осциллятора равна (см. раздел 5.6)
При кТ ^> Ни молярная теплоемкость системы квантовых осциллято-
осцилляторов равна 3/2, а при Т —> 0 экспоненциально стремится к нулю. Теория
Эйнштейна объяснила уменьшение теплоемкости при понижении тем-
температуры, но не по закону Т3.
> Упругие волны. Трудности теории Эйнштейна связаны с тем, что
в качестве элементарных возбуждений (нормальных колебательных
мод) рассматривались упругие колебания невзаимодействующих ос-
осцилляторов одинаковой частоты. На самом деле благодаря взаимодей-
взаимодействию между соседними атомами в кристалле распространяются упру-
упругие волны различных частот и длин волн. Элементарные возбуждения
представляют собой волны с определенными значениями частоты uj
и волнового вектора к. Для подсчета числа колебаний с различными
энергиями удобно перейти к рассмотрению стоячих волн, для которых
атомы на границе кристалла считаются неподвижными. Средняя энер-
энергия, приходящаяся на одну волну с частотой о;, дается формулой (9).

238 Квантовая теория кристаллов [ Гл. 7
Чтобы рассчитать число различных волн в интервале du, надо решить
две задачи:
1) Найти число независимых колебаний, приходящихся на элемент
объема d3k в пространстве волновых векторов. Эта задача решается
исходя из граничных условий. Общее число независимых колебаний
должно быть равно числу степеней свободы 37V.
2) Найти закон дисперсии, т. е. зависимость о;(к). Для решения этой
задачи надо записать уравнения движения отдельных атомов с учетом
их взаимодействия с соседними атомами. Теоретический расчет возмо-
возможен только в рамках достаточно простых моделей, однако для общего
случая удается установить некоторые важные закономерности.
Для длин волн, больших по сравнению с межатомными расстояния-
расстояниями (ка <С 1), хорошо работает континуальное приближение, в котором
среду можно считать сплошной. В этом случае уравнения движения ча-
частиц сводятся к волновому уравнению, и закон дисперсии для звуковых
волн имеет вид:
oj = vk, A0)
где v — скорость распространения звуковой волны (для простоты мы
пренебрегаем различием между продольными и поперечными волна-
волнами). Плотность состояний для звуковых волн в /^-пространстве рассчи-
рассчитывается так же, как и для электромагнитных волн (раздел 5.6):
f = 7^- (И)
Множитель 7 B случае звуковых волн равен трем, он учитывает на-
наличие двух продольных волн и одной поперечной. Основной вклад
в энергию дают волны с Ни ~ к^Т', где кв — постоянная Больцмана (ве-
(вероятность образования волны с Ни ^> квТ экспоненциально мала); сле-
следовательно, вклад звуковых волн (для которых ка ^ 1 или и <С v/а)
будет основным при условии к^Т <С Hv/a, т.е. при достаточно низких
температурах. Наоборот, при высоких температурах вклад в энергию
от каждой элементарной волны равен квТ, и энергия определяется
только общим числом степеней свободы.
> Теория Дебая. Чтобы получить правильное значение теплоемко-
теплоемкости как при высоких, так и при низких температурах в рамках простой
модели, Дебай предположил, что закон дисперсии A0) и плотность
состояний A1) верны для всех к вплоть до некоторого максимального
значения ко и соответствующей частоты и о, выше которых плотность
состояний обращается в ноль. Дебаевская частота и о выбирается та-
таким образом, чтобы полное число состояний равнялось 37V, что обеспе-
обеспечивает выполнение закона Дюлонга и Пти при высоких температурах.

7.3] Теплоемкость кристаллической решетки. Фононы 239
Плотность числа состояний в модели Дебая имеет вид:
ПРИ Ш < ^D\
За;2 duo
G(u)du =
1 0, при и >
Чтобы учесть различие между поперечными и продольными волнами,
3 / 1 2 \
можно определить среднюю скорость соотношением —g = ( —3 Н—з~ ) •
Дебаевскую частоту найдем из уравнения
Г За;2 do;
\ 1 Л3
Получаем
Шо = (^2n)l'3v, kD = (бтг2»I/3. A2)
Энергия колебаний решетки в модели Дебая дается выражением
j-, f hujG(uj) duj
о
Чтобы разделить области высоких и низких температур, удобно ввести
температуру Дебая с помощью соотношения
/Сб i /) — liU]j . \^"^)
Вводя безразмерную переменную х = Ни/квТ, получим
TD/T
При Т ^> Т^>, раскладывая экспоненту, получим Екр = Зк
т. е. закон Дюлонга и Пти. При Т ^С То интегрирование можно распро-
распространить до бесконечности, и он становится равным тг4/15. Получаем,
что энергия колебаний кристаллической решетки пропорциональна Т4,
а для теплоемкости получаем закон Т3:
12
Пример 1. Вычислите энергию нулевых колебаний кристаллической
решетки в модели Дебая.
Решение. Эта энергия равна
ujd Td/T
F _ Г xfe Г( w _ 9 Nk т _ Nk т ( т у Г xdx
0-^-Ш{Ш)Ш-- D- В D\Td) J ех_г-
о о

240
Квантовая теория кристаллов
[Гл.7
Пример 2. Вычислите энергию колебаний одномерной кристаллической
решетки в модели Дебая (только для продольных колебаний).
Решение. Для плотности состояний получим
{duo
— L, при со < ujd]
0, при ш > ojd,
где L — длина цепочки. Поскольку полное число состояний равно N, то
UJD = 7Г V = —V.
L а
A4)
Для энергии кристалла получаем
duo
При Т <С То энергия колебаний пропорциональна Т2.
> Одномерная цепочка. Закон дисперсии. Чтобы понять, к ка-
каким последствиям приводит дискретность в распределении массы,
рассмотрим бесконечно длинную цепочку атомов. Пусть масса атома
т, расстояние между соседними атомами в состоянии равновесия а,
между соседними атомами действует упругая сила с жесткостью х.
Уравнение движения s-vo атома имеет
вид
6" = "§F+1-26 + 6-0,
где 6 ~~ смещение s-vo атома из
положения равновесия, соо = у/х/т.
Будем искать решение в виде
6 = Aexp[i(ksa - uot)]. Для связи
тг/а 2тг/а между uj и к получим соотношение:
Wmax
Л
/
/
UOD
\
—тг/а
0
Первая зона
Бриллюэна
Рис. 110
к
о , . ка
ио = 2а;0| sm —
A5)
Скорость звуковой волны (ка ^С 1)
равна v = ujocl, а соответствующая этой скорости дебаевская частота
равна тгс^о = тг/2а;тах (о;тах = 2ljq). Отметим, что мы получили
периодическую функцию с периодом 2тг/а (рис. 110).
> Первая зона Бриллюэна. Выясним, какие значения к
соответствуют физически различным состояниям. Если рассмотреть
значения волнового вектора, отличающиеся на 2тгп/а: к' = к + 2тгп/а,
то мы получим не только одинаковые значения ш, ной тождественные
функции: 6(&') = 6(&) * expB7rms) = 6W- Следовательно, все
физически различимые состояния описываются волновыми векторами,
лежащими в интервале (—тг/а < к ^ тг/а). Этот интервал носит
название первой зоны Бриллюэна.
На границе зоны бегущая волна превращается в стоячую:

7.3]
Теплоемкость кристаллической решетки. Фононы
241
Лехр[г( — as — oji)\ = Аехр(—iujt){—l)s. Соседние атомы колеблются
в противофазе, узлы волны находятся между атомами. Отметим, что
на границе зоны обращается в ноль групповая скорость волны:
duo
~dk
ka
~2~
A6)
где o;max = 2loq — значение частоты на границе зоны Бриллюэна.
> Число состояний в зоне Бриллюэна. Введем дискретность
значений к с помощью периодических граничных условий: ?s = ?s+yv,
re TV — число атомов в цепочке. Получаем следующие значения к: О,
. 2тг , 4тг Ntt т лт
±—-, ±—-,..., ——, где L = Na — длина образца. В зоне Ьриллюэна
Lj Lj Lj
помещается ровно TV различных значений А;, т.е. в рамках зоны Брил-
Бриллюэна исчерпываются все степени свободы (мы рассматривали только
продольные волны).
Число состояний в расчете на единичный интервал к (плотность
состояний) равно G(k) = Ь/2тт. В одномерной модели Дебая плотность
состояний G(u) также постоянна: G(u) = 2G(k)/v, где v = uioa —
скорость волны при и —У 0. (Дебаевская частота в этом случае равна
ojd = (кIa)v = 7гооо = (тг/2)о;тах, см. рис.110 ). Однако если исходить
из закона дисперсии A5), то получим
„, ч , о L dk L duo
Giu) аи = 2-——аи = .
2тг dui тг vg
С помощью A5) и A6) получим
На границе зоны Бриллюэна плотность состояний G(u) обращается
в бесконечность.
> Двухатомная цепочка. Оптические ветви. Если элементарная
ячейка содержит несколько разных атомов, то кроме звуковых вет-
ветвей, для которых и ~ к при к —> 0, появля-
появляются оптические ветви, на которых и оста-
остается конечной для всех к в зоне Бриллюэна.
Например, для продольных колебаний в це-
цепочке из чередующихся атомов массами mi
и ?7i2 получаются две ветви, изображенные на
рис. 111. При малых к (вблизи центра зоны)
звуковая ветвь соответствует отклонениям раз-
разных атомов в одном направлении, а оптическая
ветвь — отклонениям в противоположные сто-
-тг/а 0 к
Рис. 111
роны. В общем случае, когда ячейка содержит р различных атомов,
имеется 3 звуковых ветви и Зр — 3 оптических.

242 Квантовая теория кристаллов [ Гл. 7
> Фононы. Подобно тому, как колебаниям электромагнитного поля
и электромагнитным волнам соответствуют квантовые частицы — фо-
фотоны, так и элементарным колебаниям решетки в виде бегущих волн
ставят в соответствие частицы, импульс и энергия которых связаны
с волновым вектором и частотой соотношениями р = Кк и е = Ни). Эти
частицы называют фононами. Поскольку энергия фононов является
периодической функцией их импульса, что не характерно для обычных
частиц, то их принято называть квазичастицами, а вместо импульса
используют термин квазиимпульс. Фононы подчиняются статистике
Бозе — Эйнштейна с ц = 0, поскольку число фононов в системе не яв-
является фиксированным. Фононы могут рассеиваться на примесях и де-
дефектах кристалла, а также взаимодействовать с другими частицами,
например, с электронами и фотонами. Фонон может также распасться
на два фонона (за счет нелинейных эффектов, которые надо учитывать
только для достаточно энергичных фононов).
Во всех этих процессах выполняются законы сохранения энергии
и импульса. Нетривиальной особенностью фононов является то, что
в конечном состоянии в законе сохранения импульса может присут-
присутствовать фонон не в первой зоне Бриллюэна. Если перейти к соответ-
соответствующему фонону из первой зоны, то в законе сохранения импульса
возникает дополнительный импульс /iG, описывающий сдвиг этой зо-
зоны Бриллюэна по отношению к первой. Этот импульс соответствует
движению кристалла как целого (которое невозможно обнаружить
экспериментально, так как масса кристалла очень велика). Например,
в одномерном случае G = 2тгп/а, что соответствует одинаковому
смещению всех узлов решетки.
Процессы рассеяния фононов определяют их длину свободного про-
пробега, через которую выражается фононная теплопроводность:
C
где Ссг ~ Т3 — объемная теплоемкость решетки, v — скорость звука.
С ростом температуры длина свободного пробега быстро уменьшается.
7.4. Электроны в периодическом поле.
Энергетические зоны
В рамках теории Зоммерфельда, в которой электроны в металле
рассматриваются как свободный газ фермионов, удается объяснить
некоторые факты, в первую очередь поведение электронной теплоемко-
теплоемкости. Однако многие явления не находят в этой теории объяснения. Это
в первую очередь вопрос о происхождении металлов, полупроводников

7.4]
Электроны в периодическом поле. Энергетические зоны
243
Рис. 112
и диэлектриков и описание их свойств. Для выяснения этих вопро-
вопросов необходимо учесть взаимодействие электронов с кристаллической
решеткой, образующей для электронов периодическое внешнее поле.
Взаимодействие электронов с периодическим полем решетки приводит
к появлению в их спектре разрешенных энергетических зон, разделен-
разделенных между собой запрещенными зонами, т.е. интервалами энергии,
в которых нет электронных уровней. Существование кристаллов раз-
различного типа соответствует различному характеру заполнения энерге-
энергетических зон электронами.
> Происхождение зон из атомных уровней. Проследим за по-
поведением электронных уровней энергии при постепенном образовании
кристалла из изолированных атомов. Пусть вначале N атомов находят-
находятся на таком расстоянии друг от друга, что волновые функции электро-
электронов не перекрываются. В этом случае каждый невырожденный уровень
отдельного атома можно в системе N атомов считать TV-кратно вырож-
вырожденным, если же атомный уровень имеет вырождение р, то в системе
N атомов его вырождение будет равно pN. Начнем сближать атомы до
расстояния, соответствующего равновесному кристаллу. В результате
взаимодействия между перекрывающимися электронными облаками,
относящимися к отдельным атомам, из одного уровня возникнет N
очень близко расположенных уровней, заключенных в полосе шириной
ЛЕ (рис. 112). Ширина полосы определяется энергией взаимодей-
взаимодействия между соответствующими электронами соседних атомов, она
не зависит от числа атомов. Для внешних оболочек взаимодействие
сильное (волновые функции существенно перекрываются), и ширина
полосы большая, для внутренних оболочек ширина маленькая. Число
уровней в каждой полосе столь велико, что спектр можно считать
непрерывным. Такие энергетические полосы называют разрешенными
зонами, а имеющиеся между полосами интервалы энергии, в которых
отсутствуют электронные уровни — запрещенными зонами.

244
Квантовая теория кристаллов
[Гл.7
Го Г
Рис. 113
> Классификация кристаллов. Определяющую роль для типа
проводимости кристалла имеет характер заполнения электронами (при
Т = 0) верхней разрешенной зоны (выше которой все разрешенные
зоны пустые). Зоны, лежащие ниже верхней, полностью заполнены
электронами. Электроны в этих зонах при Т = 0 не могут принимать
участия в проводимости, поскольку отсутствуют свободные состояния,
куда они могли бы перемещаться при включении внешнего поля. Верх-
Верхняя зона, происходящая из внешней атомной оболочки, может быть
заполнена электронами либо частично, либо полностью. Если эта зона
заполнена частично, то кристалл является металлом (или полуметал-
полуметаллом, если число электронов в этой зоне очень мало). Эту зону называют
зоной проводимости. Энергия Ферми металла находится внутри зоны
проводимости, электроны, находящиеся в этой зоне, образуют множе-
множество свободных носителей, принимающих участие в проводимости при
любой, сколь угодно низкой температуре. Свойства этих электронов
имеют много общего с электронным газом в модели Зоммерфельда
(если энергию отсчитывать от нижней границы зоны), но есть и важные
различия, которые мы обсудим ниже.
Атомы щелочных металлов содержат во внешней s-оболочке два
электронных состояния (соответствующих разным проекциям спина),
только одно из которых занято электроном. Поэтому зона проводи-
проводимости содержит 27V свободных мест, только половина из которых
заполнена (см. рис. 112 для лития). У редкоземельных металлов оба
s-состояния внешней оболочки заняты электронами, но проявляется
другой механизм образования незаполненной зоны: полоса энергий,
происходящая из s-оболочки и содержащая 27V мест, перекрывается
с полосой, происходящей из р-оболочки, которая содержит 67V мест.
Образованная таким образом разрешенная зона содержит 87V мест, из
которых только 27V заполнены электронами (см. рис. 113 для берил-
бериллия).
Если верхняя зона при Т = 0 полностью заполнена электронами,
то при Т = 0 кристалл является диэлектриком. При Т > 0 прово-

7.4] Электроны в периодическом поле. Энергетические зоны 245
димость такого кристалла определяется шириной ЛЕ запрещенной
зоны, лежащей между заполненной зоной (ее называют валентной
зоной) и ближайшей свободной зоной (которую в этом случае назы-
называют зоной проводимости). За счет теплового движения электроны
могут переходить из валентной зоны в зону проводимости. При квТ <С
<С ЛЕ концентрация электронов в зоне проводимости экспоненциально
мала (~ ехр(—ЛЕ/квТ)). При квТ ~ ЛЕ концентрация электронов
в зоне проводимости становится заметной и быстро возрастает с ро-
ростом температуры (проводимость становится заметной уже при квТ ~
~ 0,1ЛЕ). В этой области температур кристалл ведет себя как чистый
полупроводник. Обычно полупроводниками называют кристаллы, про-
проводимость которых становится заметной при комнатной температуре.
Одновременно с появлением отрицательных носителей заряда —
электронов в зоне проводимости, в чистом полупроводнике возника-
возникает такое же количество положительных носителей — вакантных мест
в валентной зоне, которые называют дырками.
Проводимость чистых полупроводников, связанную с появлением
одинакового количества электронов и дырок, называют собственной.
Добавление примесей приводит к нарушению симметрии между поло-
положительными и отрицательными зарядами. При добавлении примеси,
валентность атомов которой выше, чем валентность атомов кристалла,
возникают избыточные электроны, которые слабо связаны с атомами
примеси и становятся свободными при температурах, при которых пе-
переходы между зонами еще отсутствуют. Этим избыточным электронам
соответствуют донорные уровни, расположенные в запрещенной зоне
вблизи нижней границы зоны проводимости. Электроны с этих уровней
переходят в зону проводимости, а поскольку в валентной зоне при этом
не образуются вакансии, проводимость в этой области температур осу-
осуществляется преимущественно электронами. Такие примесные полу-
полупроводники называют полупроводниками п-типа. В полупроводниках
р-типа валентность примеси меньше, чем валентность атомов кристал-
кристалла, что приводит к появлению вакантных позиций, переход электронов
на которые начинается при достаточно низких температурах. Этим ва-
вакансиям соответствуют пустые уровни энергии (акцепторные уровни),
расположенные вблизи верхней границы валентной зоны. Переход на
эти уровни электронов валентной зоны приводит к образованию дырок
без появления электронов в зоне проводимости.
Хотя для обозначения зон уместно использовать квантовые числа
отдельного атома, состояние электрона внутри разрешенной зоны опи-
описывается совсем другим квантовым числом — квазиимпульсом, которое
изменяется квазинепрерывно и отражает трансляционные свойства
уравнения Шредингера и волновой функции.

246 Квантовая теория кристаллов [ Гл. 7
> Волны Блоха. Квазиимпульс электрона. Волновая функция
стационарного состояния электрона в бесконечно протяженном перио-
периодическом потенциале может быть записана в виде
ф(г) = eik>(r), A7)
где </?(г) — периодическая функция координат (с такими же периоди-
периодическими свойствами, что и потенциальная энергия электрона). Это
утверждение носит название теоремы Блоха, а вектор ftk называют
квазиимпульсом электрона. Векторы к и р для электрона в кристалле
в некотором смысле аналогичны волновому вектору и импульсу сво-
свободного электрона в модели Зоммерфельда. Поясним теорему Блоха
и смысл этих понятий в одномерном случае.
Пусть период одномерной решетки равен а, такой же пери-
периодичностью будет обладать потенциальная энергия электрона:
U(x + а) = U(x). Легко убедиться в том, что если ф(х) — решение
стационарного уравнения Шредингера, то ф(х + а) также является
решением этого уравнения. Следовательно, ф(х + па) = Т(па)ф(х),
причем дискретная функция Т(х) (определяемая при х = па) обладает
следующими свойствами: |Т(па)| = 1, Т(па) = [Т(а)]п. Получаем
Т(х) = егкх, а функция (р(х) = е~гкХ/ф(х) является периодической
функцией х: (р(х + а) = (р(х).
Для каждого заданного значения к из уравнения Шредингера для
ф(х) получается дифференциальное уравнение второго порядка для
(р(х) с граничным условием (р(а) = </?@). Это уравнение имеет ре-
решение только при дискретных значениях Еп(к). Если перейти от к
к к' = к + 2тг/а, то получим такое же уравнение для (р(х) и такие
же значения энергии ?V, как для числа к. Вывод: энергия является
периодической функцией к с периодом G = 2тг/а, и волновые функ-
функции для значений к, отличающихся на G, идентичны. Следовательно,
можно привести все электронные состояния к первой зоне Бриллюэна.
На краях зоны находятся экстремумы (минимумы или максимумы)
Е(к), что обеспечивает непрерывность и гладкость этой функции при
переходе из зоны в зону (рис. 114). В центре зоны (при к = 0) также
обычно находится экстремум Е(к).
Обсуждавшееся выше деление кристаллов на металлы и диэлектри-
диэлектрики (при Т = 0) хорошо поясняется зависимостью Е(к) в рамках зоны
Бриллюэна (рис. 114). Левый рисунок соответствует диэлектрику, сред-
средний— металлу (или полуметаллу) в случае перекрытия зон, правый —
металлу в случае частично заполненной зоны.
> Число состояний в зоне Бриллюэна. При изменении к в пре-
пределах первой зоны Бриллюэна энергия n-го уровня Еп(к) изме-
изменяется в пределах n-й разрешенной зоны. Если учесть конечность
кристалла (с помощью, например, периодических граничных усло-
условий), то в рамках первой зоны Бриллюэна к принимает N значений:

Электроны в периодическом поле. Энергетические зоны
247
7Г
а
0
к
Рис
б
. 114
7Г
а
0, ±2tt/L, ±4tt/L . . ., тг/а, где L = Na. Следовательно, n-я зона со-
содержит TV уровней En(ki). С учетом спина получим 27V электронных
состояний.
> Динамика электрона в кристалле. Энергетический спектр
электронов в верхних зонах (валентной зоне и зоне проводимости) несет
в себе информацию о взаимодействии электронов с кристаллической
решеткой. Если использовать этот спектр при вычислении групповой
скорости электрона
_ duj _ 1 de _ de , ,
Vg ~~dk~ h~dk ~ ф' [ }
то можно записать уравнения движения в форме, учитывающей дей-
действие на электроны только внешних сил. Это уравнение имеет вид
обычного закона Ньютона
^Е-F
dt ~ '
A9)
где F — внешняя сила (не учитывающая взаимодействие с решеткой),
ар — квазиимпульс электрона.
Для пояснения приведем выражение для скорости изменения энергии
электрона
de de dp dp
dt ~ dp dt ~ Ve dt '
которая должна быть равна мощности внешней силы Fvg.
В качестве примера применения уравнений движения A8) и A9)
рассмотрим поведение электрона, который находится в пустой энерге-
энергетической зоне (где нет других электронов), при действии на него посто-
постоянной силы. Будем считать, что этот электрон не испытывает столкно-
столкновений с другими электронами, фононами и дефектами решетки, и что
в начальный момент электрон покоился. В модели Зоммерфельда сво-
свободный электрон двигался бы с постоянным ускорением, удаляясь от
точки начала движения. В зонной теории электрон вначале находится
в центре зоны (при р = 0), затем его импульс линейно возрастает, но

248 Квантовая теория кристаллов [ Гл. 7
скорость при этом изменяется иначе. Сначала она возрастает, затем при
приближении к краю зоны Бриллюэна уменьшается, и на краю зоны
обращается в ноль. В этот момент происходит «переброс» на левый
край зоны (если мы хотим оставаться в рамках первой зоны Бриллю-
Бриллюэна), и скорость электрона меняет знак. К тому моменту, как импульс
электрона окажется снова в центре зоны, его скорость опять обратится
в ноль, и электрон окажется в прежнем месте. Движение электрона
имеет характер колебаний. Во избежание недоразумений отметим, что
электроны в металле не могут проделать такой цикл, так как между
соударениями они не успевают отойти далеко от поверхности Ферми
и приблизиться к краю зоны.
> Эффективная масса. В центре и на краях зоны dejdp = О,
значит, энергию вблизи этих точек можно приближенно записать в виде
\d2e
(р
Ро
где ?о5 Ро —энергия и квазиимпульс центра (или края) зоны. Если во
всех случаях отсчитывать импульс и энергию от вершины параболы,
то это соотношение можно записать единым образом:
6~ 2m*
где
1 _ d2e
т* dp2
B0)
РО
а определенная таким образом величина т* называется эффективной
массой электрона. Для скорости электрона получим привычное соот-
соотношение
р
Отметим, что определенная уравнением B0) эффективная масса элек-
электрона у дна энергетической зоны положительна, а у верхнего края зо-
зоны — отрицательна. Как мы видели, у верхнего края зоны под действи-
действием внешней силы скорость электрона не увеличивается, а уменьшается.
Определение B0) для т* действует не только у краев зоны. Действитель-
Действительно, в любой точке можно записать
dvg d de d?e dp
dt ~ dt dt ~ dp2 dt '
Fm
dt dt
Эффективная масса является важной динамической характеристи-
характеристикой электрона в кристалле. Эффективная масса электрона может быть

7.4] Электроны в периодическом поле. Энергетические зоны 249
как больше его настоящей массы, так и меньше ее (иногда в несколько
десятков раз). Эффективная масса стоит на месте обычной массы
в выражении для электропроводности: а — е2пт/т* и во многих
других физических формулах. Особенно удобна эффективная масса
для описания свойств полупроводников, где концентрация электронов
в зоне проводимости (и дырок в валентой зоне) невелика. В анизотроп-
анизотропных кристаллах эффективная масса зависит от направления движения
электрона в кристалле.
Несмотря на то, что отдельному электрону вблизи верхней границы
зоны надо приписать отрицательную эффективную массу, отсутствие
такого электрона в полностью заполненной валентной зоне оказывает-
оказывается эквивалентным присутствию одиночной частицы с положительной
массой и положительным зарядом. Как уже отмечалось выше, такие
носители заряда называются дырками.
> Поверхность Ферми электронов в металле. В зонной теории
поверхность Ферми электронов не является простой сферой с радиу-
радиусом pp. Эта поверхность может иметь слож-
сложную форму, определение которой является
важнейшей проблемой физики металлов. На-
Напомним, что при комнатных температурах
электроны металла находятся в сильно вы-
вырожденном состоянии (квТ <С ?f), и осо-
особую роль играют электроны вблизи поверх-
поверхности Ферми. Поверхность Ферми обычно
изображают в пределах первой зоны Брил-
люэна, но более наглядным является изобра-
изображение периодической связной поверхности, рис ^^
захватывающей несколько зон Бриллюэна.
На рис. 115 изображены поверхность Ферми и границы зоны Бриллю-
Бриллюэна для меди; аналогично выглядит поверхность Ферми для серебра,
золота и других элементов этой группы. На рисунке хорошо видны
переходы в соседние зоны Бриллюэна. (Объемные изображения поверх-
поверхностей Ферми для большинства элементов таблицы Менделеева можно
найти на сайте http: //www. phys.uf 1. edu/f ermisurf асе.)
> Свойства полупроводников. Различие между диэлектриками
и собственными полупроводниками определяется шириной запрещен-
запрещенной зоны Л между заполненной (при Т = 0) валентной зоной и пустой
зоной проводимости. К полупроводникам принято относить кристаллы,
у которых Л < 3 эВ. Например, у германия Л = 0,67 эВ, у кремния
Л = 1,11 эВ. Концентрация носителей тока у полупроводников на мно-
много порядков меньше, чем у металлов, и сильно меняется при добавлении
примесей даже в ничтожных концентрациях.

250 Квантовая теория кристаллов [ Гл. 7
Положение энергии Ферми в собственных полупроводниках опре-
определяется условием равенства концентрации электронов в зоне про-
проводимости и концентрации дырок в валентной зоне. При к^Т <С Л
энергия Ферми находится очень близко к середине запрещенной зоны.
(Отклонение от середины зоны возникает вследствие того, что эф-
эффективная масса электронов у дна зоны проводимиости отличается от
эффективной массы дырок у потолка валентной зоны). Концентрация
носителей заряда вычисляется из распределения Ферми, зависимость
концентрации от температуры определяется в первую очередь мно-
множителем ехр(—А/2квТ), где Л/2 — расстояние от уровня Ферми до
границы зоны.
Концентрация электронов в зоне проводимости вычисляется по формуле
оо оо
fF(e)G(e)de = \ е~(?-?1р)/квТ G(e)de =
о
где во — энергия дна зоны проводимости, е' = е — ео — энергия, отсчитанная
от дна зоны (учтено, что квТ <С во — ?f)-
Таким же образом зависит от температуры собственная проводи-
проводимость полупроводников:
а —
У примесного полупроводника энергия Ферми смещена к грани-
границе той зоны, где находятся основные носители заряда. У полупро-
полупроводников n-типа с донорной про-
проводимостью уровень Ферми распо-
расположен вблизи дна зоны проводи-
проводимости, у полупроводников р-типа
с акцепторной проводимостью —
вблизи верхней границы валентной
чистый n-типа р-типа зоны (Рис- 116)- ПРИ низких темпе-
ратурах число примесных носите-
носителей в зоне сильно зависит от тем-
температуры, и проводимость быстро растет с увеличением температуры.
Затем примесные уровни «истощаются», т.е. на донорных урвнях не
остается электронов (или на акцепторных уровнях — свободных мест),
и проводимость медленно уменьшается. (Так же как и у металлов,
уменьшается длина свободного пробега за счет роста числа фононов
в системе.) При более высоких температурах число носителей заряда
начинает снова возрастать, так как вступает в силу механизм собствен-
собственной проводимости. Энергия Ферми при этом приближается к середине
запрещенной зоны.

7.4]
Электроны в периодическом поле. Энергетические зоны
251
еЛ(р Зона проводимости
i
Энерг
Ферми
Валентная зона
п-типа ' р-типа
Рис. 117
При приведении полупроводника n-типа в контакт с полупроводни-
полупроводником р-типа возникает р-п переход. В результате диффузии основных но-
носителей в соседний полупроводник в об-
области перехода появляется контактная
разность потенциалов, причем потен-
потенциал полупроводника n-типа оказыва-
оказывается выше. Контактная разность потен-
потенциала препятствует движению основ-
основных носителей заряда. Разность потен-
потенциалов между полупроводниками воз-
возникает такой величины (рис. 117), что
энергии Ферми полупроводников ста-
становятся одинаковыми (условие равенства химических потенциалов).
В состоянии равновесия диффузионный ток основных носителей через
потенциальный барьер равен дрейфовому току неосновных носителей,
которому контактная разность потенциалов не препятствует.
При наложении внешнего поля в прямом направлении (положитель-
(положительный полюс к полупроводнику р-типа ток основных носителей увели-
увеличивается в exp(eUIквТ) раз, так как барьер уменьшается на eU (U —
приложенное напряжение). При включении обратного поля ток прямых
носителей уменьшается (барьер возрастает). На ток неосновных носи-
носителей приложенное напряжение влияния не оказывает. Вольт-амперная
характеристика р — n-перехода определяется выражением
1 = 10{ееи'к*т -1),
где /о — ток основных носителей в отсутствие поля (равный встречному
току неосновных носителей).

Глава 8
ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ
Представление о том, что практически вся масса атома сосредо-
сосредоточена в положительно заряженном ядре ничтожно малых размеров,
возникло в результате опытов Резерфорда (см. гл.6). Поскольку раз-
размеры ядер оказались на пять порядков меньше размеров атомов, то
в рамках атомной физики ядро можно считать точечным кулоновским
центром. В действительности ядро представляет собой сложное об-
образование сильно взаимодействующих частиц (от нескольких единиц
до нескольких сотен), подчиняющееся законам квантовой механики
и квантовой статистики. Ядра могут испытывать радиоактивные пре-
превращения, вступать в ядерные реакции, распадаться на части и объ-
объединяться с другими ядрами. Характерные энергии в этом ядерном
мире — миллионы электронвольт, и именно поэтому в атомных про-
процессах с энергиями в десятки (максимум — сотни) электронвольт ядра
выступают как стабильные объекты.
8.1. Основные свойства ядер
> Состав ядра. Атомное ядро состоит из частиц, которые называют
нуклонами — протонов и нейтронов.
Протон — положительно заряженная частица с зарядом е и массой
тр = 1836,15те, где те — масса электрона. Нейтрон — электриче-
электрически нейтральная частица с массой, немного большей массы протона:
тп = 1838,68те. В свободном состоянии нейтрон нестабилен — за
время, равное в среднем 15,5 минут он превращается в протон с испуска-
испусканием электрона и антинейтрино: п —У p + e + v. Спин обеих частиц равен
1/2, т.е. они являются фермионами. Не только протон, но и нейтрон
обладают отличными от нуля магнитными моментами: цр = 2, 793/ля,
1лп = —1? 91/^я, где ця = eh/2mp — так называемый ядерный магнетон
(/ля = /i^/1836,15). Наличие у нейтрона магнитного момента явля-
является косвенным свидетельством того, что нуклоны должны обладать
внутренней структурой, включающей более элементарные заряженные
частицы.
Состав ядра задается двумя целыми числами: зарядовым числом Z,
равным числу протонов в ядре, и массовым числом Л, равным полному
числу нуклонов в ядре. Число нейтронов может быть найдено как
N = А — Z. Зарядовое число совпадает с номером элемента в таблице
Менделеева и определяет его физико-химические свойства, поскольку

8.1] Основные свойства ядер 253
они зависят от заряда ядра и почти не зависят от его массы. Зарядовое
и массовое числа указывают слева от символа элемента: ^Х, например,
|Не, ^С. Поскольку указание символа элемента однозначно определяет
его порядковый номер, т.е. зарядовое число Z, то нижний индекс
иногда не указывают CНе, 13С).
Конкретные атомы с числом нуклонов в ядре Л и числом протонов
Z, вместе с электронной оболочкой, содержащей Z электронов, назы-
называют нуклидами. Все нуклиды с одинаковым Z называют изотопами
данного элемента. Изотопам водорода 1Н, 2Н и 3Н, ядра которых
наиболее существенно отличаются друг от друга, присвоили названия
обычный водород (иногда используют название протий), дейтерий и
тритий, а ядрам дейтерия и трития — названия дейтрон (d) и тритон
(t).
Изотопы могут быть как стабильные, так и радиоактивные. Радио-
Радиоактивные изотопы характеризуют типом радиоактивности (су-распад
и /3-распад) и временем жизни. (Подробнее о радиоактивных пре-
превращениях будет рассказано ниже.) Многие радиоактивные изотопы
встречаются в природе — если они обладают очень большим временем
жизни B35U, 232Th и другие) или постоянно образуются в результате
распада таких долгоживущих ядер (например, 223Fr). He существует
стабильных изотопов для Z = 43 (технеций), Z = 61 (прометий) и для
всех элементов с Z > 83 (начиная с полония). У остальных элементов
есть от одного до девяти (у олова Sn) стабильных изотопов, в среднем
примерно по три. Разные стабильные (или долгоживущие) изотопы
имеют различную распространенность, наблюдаемая атомная масса
возникает как усреднение по нескольким изотопам. Например, атомная
масса природного хлора 35, 5, в нем содержится 76 % 35С1 и 24 % 37С1.
Нуклиды, имеющие одно и то же массовое число Л, называют
изобарами (пример: ЩАг — ^Са). При ^-распадах происходят переходы
между изобарами. Отметим, что если какой-то нуклид стабилен, то обе
его ближайшие изобары ^-активны.
Среди стабильных и долгоживущих ядер чаще всего встречаются
четно-четные (с четным числом протонов и четным числом нейтронов),
а реже всего — нечетно-нечетные (всего четыре устойчивых: 2Н, |Li, ^B
и V4N).
На рис. 118 изображена зависимость N от Z для устойчивых нук-
нуклидов. Видно, что у первых 15-20 элементов наблюдается примерное
равенство между числом протонов и числом нейтронов (Z ~ ^/2).
С дальнейшим увеличением порядкового номера намечается явная
тенденция к превышению числа нейтронов над числом протонов (на-
(например, единственный стабильный изотоп висмута 28°39Bi).
> Спин и магнитный момент ядра. Спином ядра / называют
полный угловой момент ядра, который является результатом сложения
как спинов, так и орбитальных моментов отдельных нуклонов. У ядер

254
Элементы ядерной физики
[Гл.8
N
120
100
oU
60
40
20
/
Стабильные
ядра
Г
F
/
/
г
/
J
j
N = Z
20
40
Рис. 118
60
80 Z
с четным числом нуклонов спин целый, с нечетным — полуцелый.
У ядер с четным числом как протонов, так и нейтронов спин основного
состояния равен нулю. Это означает, что угловые моменты отдельных
нуклонов компенсируют друг друга. Отметим однако, что в основном
состоянии дейтрона / = 1.
У ядер с отличным от нуля спином имеется обычно и магнитный
момент. Магнитные моменты ядер очень малы (порядка ядерного маг-
магнетона), но их взаимодействие с орбитальным движением электронов
приводит к сверхтонкой структуре электронных уровней, которая
поддается наблюдению.
> Размеры и форма ядер. Распределение нуклонов по объему
ядра было установлено в многочисленных экспериментах по рассея-
рассеянию быстрых электронов и нуклонов. (Дебройлевская длина волны
рассеиваемых частиц должна быть мала по сравнению с размерами
ядра.) В опытах по рассеянию электронов, испытывающих только
электромагнитное взаимодействие, устанавливается пространственное
распределение заряда ядра (т.е. распределение протонов), а в опытах
по рассеянию нейтронов — пространственное распределение всех нук-
нуклонов. Выяснилось, что эти распределения отличаются мало, и далее
мы будем говорить только о распределении нуклонов.

8.1] Основные свойства ядер 255
Оказалось, что большинство ядер имеют форму, близкую к сфери-
сферической. Для ядер с достаточно большим числом нуклонов (Л > 12)
можно выделить внутреннюю область, в которой концентрация нукло-
нуклонов постоянна, и небольшой переходный слой, в котором концентрация
падает до нуля. Если принять за радиус ядра то расстояние от его
центра, на котором концентрация уменьшается в два раза, то получится
следующая зависимость от массового числа:
R ~ Ro • Л1/3 фм, A)
где Ro = 1, 2 -г 1, 4 фм; использована принятая в ядерной физике вне-
внесистемная единица ферми: 1 фм = 10~15 м. Видно, что концентрация
нуклонов внутри ядра остается примерно одинаковой для всех ядер.
Пример 1. Оцените среднюю концентрацию нуклонов в ядре и среднюю
плотность ядерного вещества.
Решение. Средняя концентрация нуклонов равна п = A/(-irR3) ~
о
~ 1,0 т 1,5 • 1044 м~3. Этой концентрации соответствует плотность
р = М • п ~ 2 • 1017 кг/м3, где М — масса нуклона.
Отметим, однако, что у многих ядер наблюдается заметное отклоне-
отклонение в распределении частиц от сферической симметрии (это отклонение
особенно существенно у возбужденных состояний, но есть и в основном
состоянии). Например, у простейшего составного ядра — дейтрона—
распределение заряда в основном состоянии отличается от сферическо-
сферического. (Этот факт свидетельствует о нецентральном характере ядерных
сил).
> Энергия связи ядра. Измеренные с достаточной точностью массы
ядер оказались меньше, чем суммы масс составляющих их нуклонов.
Проявляющаяся здесь неаддитивность массы является прямым след-
следствием формулы Эйнштейна для связи массы и энергии покоя (см.
раздел 1.11). Между нуклонами действуют силы притяжения, удер-
удерживающие их в ядре несмотря на сильное (на столь малом расстоя-
расстоянии) кулоновское отталкивание, и для разделения ядра на нуклоны
необходимо совершить положительную работу. Величину этой работы
называют энергией связи ядра:
Есв = (Zmp + Nmn - тя)с2, B)
где N = Л — Z — число нейтронов в ядре. Именно благодаря огромной
величине ядерных взаимодействий (по сравнению, например, с атом-
атомными и химическими, имеющими чисто электромагнитную природу)
это уменьшение массы оказалось доступно прямому измерению.
Сделаем несколько замечаний по поводу записи формулы B).
1. В ядерной физике массы ядер и частиц выражают либо в энерге-
энергетических единицах, либо в атомных единицах массы. В первом случае
указывают значение энергии покоя тс2, выраженное в электронволь-
тах. Например, массы электрона, протона и нейтрона в этих единицах

256 Элементы ядерной физики [ Гл. 8
равны те = 0,511 МэВ, тр = 938,28 МэВ, тп = 939,55 МэВ. При
использовании энергетических единиц многие формулы записываются
короче. Например, формула B) принимает вид:
Есв = Zmp + Nmn - тя. C)
Отметим, что 1 кг = 5, 61 • 1029 МэВ, 1 МэВ = 1, 78 • 100 кг.
Атомная единица массы (а.е.м.) определяется как 1/12 мас-
массы нуклида (не ядра!) углерода 12С. Именно в а.е.м. обычно
приводятся в справочных таблицах массы нуклидов. Например,
те = 5,486 • 10~4 а.е.м., тр = 1,007276 а.е.м., тп = 1,00898 а.е.м..
Отметим, что 1 а.е.м. = 931,50 МэВ = 1,660 • 107 кг.
2. В связи с тем, что в таблицах обычно приводят не массы ядер,
а массы нуклидов, формулу C) удобно переписать в следующем виде:
Есв = ZMH + Nmn - Ma, D)
где М\\ — масса атома водорода, а Ма — масса атома (нуклида), соот-
соответствующего данному ядру. Первый член в этой формуле отличается
от первого члена в C) на Zme; на столько же отличается масса нук-
нуклида Ма от массы ядра тя, если пренебречь энергией электрического
взаимодействия электронов и ядра.
3. В таблицах часто указывают не массу нуклида, а так называемый
дефект массы Z\a = Ма - А (где Ма выражена в а.е.м.). Например,
дефект массы нуклида 12С равен нулю, дефект массы атома водорода
0,007825 а.е.м., дефект массы нуклида 3Не 0,016030 а.е.м. Энергия
связи может быть выражена через дефекты масс:
Есв = ZAH + NAn - Ай. E)
> Зависимость энергии связи от состава ядра. Оказывается,
в первом, грубом, приближении энергия связи возрастает прямо про-
пропорционально числу нуклонов в ядре, т. е. его массовому числу А. Для
проведения как качественного анализа, так и численных расчетов удоб-
удобно пользоваться удельной энергией связи, определяемой как ? = Есв/А.
На рис. 119 изображена примерная зависимость е от массового числа
А. Оставаясь примерно равной 8 Мэв/нуклон, удельная энергия связи
сначала (при А < 16) быстро возрастает, потом продолжает плавно
расти и при А ~ 60 (в области железа) проходит через максимум
8,8 МэВ/нуклон, после чего плавно убывает до 7,6 МэВ/нуклон для
последнего природного нуклида 238U. Отметим, что благодаря возрас-
возрастанию е при малых А оказывается энергетически выгодным слияние
легких ядер, а благодаря убыванию е при больших А энергетически
выгодным оказывается деление тяжелых ядер. Энергию, выделяющу-
выделяющуюся при делении тяжелых ядер, называют атомной, а при слиянии
легких ядер— термоядерной. Термоядерная энергия в расчете на один
нуклон в несколько раз превышает атомную.

8.1]
Основные свойства ядер
257
е, МэВ
t
Ш ¦
50
100 150
Рис. 119
200
Хотя ядерным силам и ядерным моделям посвящен следующий
раздел, коротко отметим следующее.
1. То, что удельная энергия связи оказывается для большинства
ядер примерно постоянной и равной своему среднему значению, сви-
свидетельствует о том, что ядерные силы короткодействующие и обла-
обладают свойством насыщения (каждый нуклон взаимодействует только
с несколькими ближайшими соседями).
2. Уменьшение ? при малых Л объясняется возрастанием поверх-
поверхностных эффектов, которые зависят от относительной доли поверх-
поверхностных частиц.
3. Уменьшение удельной энергии связи при больших А объясняется
возрастанием относительного вклада кулоновской энергии.
4. Для легких элементов максимальная энергия связи для нуклидов
с фиксированным Л (изобар) соответствует Z ~ Л/2. (Именно поэто-
поэтому такие нуклиды обычно оказываются ^-стабильными.) Это явление
называется эффектом симметрии. Сдвиг в сторону большего про-
процентного содержания нейтронов, наблюдающийся при увеличении Л,
объясняется возрастанием роли кулоновского отталкивания протонов.
5. Удельная энергия связи четно-четных ядер оказывается в среднем
больше, чем у четно-нечетных ядер, а у последних — больше, чем
у нечетно-нечетных ядер. Это объясняется эффектом спаривания оди-
одинаковых нуклонов в ядрах. Объединение двух одинаковых нуклонов
в пару с нулевым спином дает выигрыш примерно в 1 МэВ.
6. Самыми устойчивыми (т. е. обладающими наибольшей е) среди
всех четно-четных ядер оказываются так называемые магические ядра,
у которых число протонов или число нейтронов оказывается равным
одному из магических чисел: 2, 8, 20, 28, 50, 82, 126. (Особенно ста-
стабильны дважды магические ядра, у которых магическими являются
9 А. И. Черноуцан

258 Элементы ядерной физики [ Гл. 8
и число протонов, и число нейтронов.) Существование магических ядер
свидетельствует об оболочечной структуре ядер, подобной структуре
атомов.
8.2. Ядерные силы. Модели ядер
> Свойства ядерных сил. Между нуклонами в ядре действуют
ядерные силы притяжения, которые в сотни раз превышают электро-
электромагнитные силы отталкивания между протонами. Именно эти силы
обеспечивают устойчивость ядер. Перечислим некоторые (наиболее
важные) особенности ядерных сил.
1. Ядерные силы являются короткодействующими с радиусом дей-
действия го ~ 2,0 т 2,5 фм. При удалении нуклонов на расстояние,
превышающее радиус действия, ядерное взаимодействие быстро исче-
исчезает. При сближении нуклонов на расстояние, в несколько раз меньшее
радиуса действия, притяжение сменяется сильным отталкиванием.
Пример 1. Зная массу дейтерия, можно вычислить энергию связи
простейшего ядра — дейтрона. Она равна 2,22 МэВ. По этой энергии связи
оцените глубину потенциальной ямы, соответствующей ядерному взаимодей-
взаимодействию между двумя нуклонами.
Решение. Во-первых, систему из двух взаимодействующих частиц мас-
массой М заменим одной частицей с приведенной массой т = М/2. Будем
для простоты считать, что потенциальная энергия представляет собой яму
радиусом R = 2,3фм глубиной Uq. Величину Uq найдем из условия, что
энергия основного состояния в этой потенциальной яме должна быть равна
Е\ = —2,2 МэВ. Для сферически симметричной волновой функции основно-
основного состояния уравнение Шредингера имеет вид:
где U = —Uq при г < R и U = 0 при г > R. После замены \Р(г) = ггр(г)
придем к уравнению
решение которого было получено в разделе 6.2. Опуская дальнейшие вы-
вычисления, приведем ответ: для получения правильной энергии основного
состояния глубина ямы должна быть около 29 МэВ. (Если радиус ямы
принять равным 2 фм, то ее глубина получится около 35 МэВ.)
Отметим, что такая величина притяжения соответствует только
состоянию системы двух нуклонов, в котором их полный спин равен
единице. В состоянии с нулевым спином притяжение примерно вдвое
слабее, и связанное состояние отсутствует. Именно поэтому не суще-
существует стабильного образования из двух нейтронов или двух протонов
(по принципу Паули две тождественные частицы не могут обладать
параллельными спинами).
Зависимость ядерных сил от расстояния между нуклонами окон-
окончательно не установлена. Для обработки экспериментальных данных

8.2] Ядерные силы. Модели ядер 259
с одинаковым успехом используют различные модельные зависимости.
Наибольшее теоретическое обоснование имеет формула Юкавы:
U {г) = Ае-^—. F)
2. С короткодействием ядерных сил тесно связано присущее им
свойство насыщения. Каждый нуклон внутри ядерного вещества вза-
взаимодействует с определенным числом ближайших соседей. (Нуклоны
у поверхности ядра имеют меньшее число соседей.) Именно поэтому
энергия связи ядра растет пропорционально числу нуклонов, а средняя
плотность ядра остается постоянной. Если бы ядерные силы были
дальнодействующими (как, например, кулоновская сила), то каждый
нуклон взаимодействовал бы со всеми остальными, и энергия связи
росла бы быстрее. Например, электрическая энергия шара с зарядом
Ze и радиусом R пропорциональна Z2/R (смотри раздел 3.8).
3. Ядерные силы обладают свойством зарядовой независимости:
они не зависят от того, какие нуклоны вступают во взаимодействие
(р — р, р — п или п — п).
4. Ядерные силы не являются центральными. Об этом свидетель-
свидетельствует, в частности, несферичность распределения заряда в основ-
основном состоянии дейтрона. Если бы взаимодействие было строго цен-
центральным, орбитальный момент импульса сохранялся бы и в основном
состоянии был бы точно равен нулю, что соответствует сферически
симметричной волновой функции.
5. Ядерные силы зависят от направления спинов. (Смотри выше
о взаимодействии нуклонов в дейтроне.)
> О природе ядерных сил. Современная физика рассматривает
любое фундаментальное взаимодействие как результат обмена части-
частицами — носителями взаимодействия. Ядерное взаимодействие между
нуклонами осуществляется за счет обмена тг-мезонами (пионами) —
частицами со спином, равным нулю и массой т^, примерно в 200 раз
большей, чем у электрона.
Вокруг одиночного нуклона непрерывно рождаются и умирают так
называемые виртуальные пионы. Их называют виртуальными, потому
что они существуют столь короткое время, что благодаря соотношению
неопределенностей время-энергия {At • АЕ ~ Н) возможно изменение
энергии системы на величину ~ т^с2. Для виртуальных частиц не
выполняется обычное соотношение между энергией и импульсом —
они обладают различными (и различно направленными) импульсами
со средним значением т^с и за время жизни пролетают в среднем
расстояние с At ~ Н/т^с, равное комптоновской длине тг-мезона.
Иногда образно говорят, что одиночный нуклон окружен «шубой» из

260 Элементы ядерной физики [ Гл. 8
тг-мезонов, радиус которой равен их комптоновской длине. При сбли-
сближении двух нуклонов на расстояние Rq их мезонные шубы начина-
начинают перекрываться, и часть виртуальных пионов, рожденных одним
нуклоном, поглощается другим. Как показал Юкава A935 г.), после
усреднения по импульсам виртуальных пионов возникает притяжение
с потенциальной энергией, описываемой формулой F) с го = Н/т^с.
В то время тг-мезоны еще не были открыты, и Юкава предсказал их
существование и оценил их массу по радиусу ядерного взаимодействия,
(тг-мезоны были открыты в космических лучах только в 1947 г.)
Отметим здесь же, что переносчиками электромагнитного взаимодей-
взаимодействия являются виртуальные фотоны. Масса фотонов равна нулю, и поэтому
электромагнитное взаимодействие является дальнодействующим (Ro = оо,
и формула Юкавы F) приводит к кулоновскому взаимодействию). Слабое
взаимодействие осуществляется обменом очень массивными VK-бозонами
и поэтому его радиус гораздо меньше, чем у ядерного. Отметим также, что со-
современная теория считает, что фундаментальными переносчиками сильного
взаимодействия являются глюоны, осуществляющие взаимодействие между
кварками, из которых состоят все сильно взаимодействующие частицы (см.
раздел 8.6).
> Ядерные модели. Отметим сразу, что к настоящему моменту не
создано универсальной модели ядер, которая позволила бы в рамках
единого теоретического подхода рассчитывать различные ядерные ха-
характеристики. Каждая модель наиболее успешно объясняет отдельные
свойства ядер, а другие свойства либо вообще не объясняет, либо делает
это слишком сложно и неубедительно. В ряду этих моделей особое
место занимает микроскопическая модель ядра, которую ее создатель
академик А.Б.Мигдал назвал теорией конечных ферми-систем. Эта
модель опирается на теорию квантовой ферми-жидкости, успешно при-
применившей методы квантовой теории поля к статистическому ансамб-
ансамблю взаимодействующих фермионов. Главные достижения микроско-
микроскопической модели состоят в сравнении и едином обосновании внешне
совершенно различных теоретических моделей (ее иногда называют
«моделью ядерных моделей»).
Остальные модели можно условно разделить на две группы — кол-
коллективные и одночастичные. В первую группу входят, например, тео-
теория бесконечной ядерной материи и капельная модель ядра. Во вторую
группу входят теории, рассматривающие движение отдельных нукло-
нуклонов либо в плоской потенциальной яме конечной глубины (ядерный
ферми-газ), либо в некотором эффективном потенциале (оболочечные
модели). В развитых вариантах оболочечных моделей учитывается
спаривание одинаковых нуклонов.
Отметим также появление моделей, объединяющих черты двух
указанных групп. Внутренняя часть ядра, соответствующая полностью
заполненным внутренним оболочкам, рассматривается как капля ядер-
ядерной жидкости, в поле которой движутся внешние нуклоны.

8.2] Ядерные силы. Модели ядер 261
Капельная (гидродинамическая) модель рассматривает ядро как за-
заряженную каплю ядерной жидкости, обладающую поверхностным на-
натяжением. Эта модель описывает основные черты зависимости энергии
связи от А и Z, поверхностные колебания ядер, особенности деления
тяжелых ядер.
Модель ядерного ферми-газа позволяет объяснить эффект симмет-
симметрии (примерное равенство Z и N в легких ядрах) и отклонение от него
в тяжелых ядрах, а также вычислить глубину эффективной потенци-
потенциальной ямы.
Как протоны, так и нейтроны рассматриваются в этой модели
как две подсистемы тождественных фермионов, свободно движущихся
в потенциальной яме. На каждом уровне могут находиться две тожде-
тождественных частицы с разными спинами. Чем больше нуклонов данного
вида находится в ядре, тем больше их энергия ферми. Если энергии
ферми нейтронов и протонов заметно отличаются друг от друга, то
будет происходить превращение одного нуклона в другой с понижением
общей энергии (либо п —У р + е~ + г/, либо р —У п + е+ + и). Следо-
Следовательно, в стабильном ядре энергии ферми должны быть примерно
равны друг другу. Если пренебречь кулоновским взаимодействием, то
минимум общей энергии будет соответствовать примерно одинаково-
одинаковому числу нейтронов и протонов. Эта ситуация соответствует легким
ядрам. В тяжелых ядрах кулоновское взаимодействие протонов играет
все большую роль, и выравнивание энергий ферми наступает при числе
нейтронов большем, чем число протонов.
Пример 2. Исходя из рассчитанной в Примере 1 средней концентрации
нуклонов в ядре, оцените глубину потенциальной ямы, в которой они нахо-
находятся.
Решение. Для оценки пренебрежем кулоновским взаимодействием.
Средняя кинетическая энергия нуклонов одного вида равна (см. разд. 7.2)
Кср = \ef = ^2C7Го2J/3 ~ 20 МэВ/нуклон,
5 5 2М
где п\ ~ 0,6 • 1044 м~3 — концентрация нуклонов одного вида, равная
половине концентрации нуклонов. Средняя удельная энергия связи равна
примерно 8 МэВ/нуклон; она может быть рассчитана как разность между
глубиной ямы и средней кинетической энергией. Получаем, что глубина ямы
должна составлять примерно 30 МэВ. Как мы увидим ниже, эта оценка,
видимо, сильно занижена.
> Эмпирическая формула для энергии связи. На основе капель-
капельной и газовой моделей можно записать достаточно простую эмпириче-
эмпирическую формулу для энергии связи ядра, которую называют формулой
Вейцзеккера A935 г.):
Z2 (A-2ZJ 6(Z,N) /hT4
« Щ^ а ^ G)

262 Элементы ядерной физики [ Гл. 8
где S(Z, N) равна —1 для четно-четных ядер, 0 для четно-нечетных
ядер и 1 для нечетно-нечетных ядер. Коэффициенты ai подбираются
из экспериментальных данных, в настоящее время приняты следую-
следующие значения: ах = 15,75 МэВ, а2 = 17,8 МэВ, а3 = 0,71 МэВ,
а4 = 23,7 МэВ, аъ = 34 МэВ.
Первые три члена соответствуют представлениям капельной моде-
модели. Первый член отражает примерную пропорциональность энергии
связи числу нуклонов; коэффициент а± можно понимать как энер-
энергию связи, приходящуюся на один нуклон в воображаемой ядерной
материи с «выключенным» электрическим взаимодействием. Второй
член описывает «поверхностное натяжение» ядерной капли (нуклоны
на поверхности ядра находятся в особых условиях), а третий член — ее
электростатическую энергию.
Четвертый член обусловлен эффектом симметрии, который нахо-
находит свое объяснение в модели ядерного ферми-газа. Он имеет минимум
при N = Z, поскольку наблюдаемое отклонение от полной симметрии
при увеличении Л связано с кулоновской энергией, а она уже учте-
учтена третьим членом. Пятый член отражает скачкообразное изменение
энергии связи при переходе от данного ядра к ядрам с соседними
значениями А или Z.
Интересно отметить заметное отличие коэффициента а\ от сред-
среднего значения удельной энергии связи е ~ 8 МэВ. Дело в том, что е
уже включает в себя кулоновскую и поверхностную энергии. Если при
оценке глубины ямы в Примере 2 вместо е подставить а\, она окажется
равной rsj 40 МэВ.
Формула Вейцзеккера позволяет с неплохой точностью (~ 10~4)
рассчитывать энергии связи многих, особенно тяжелых, нуклидов,
энергию а-распада, энергии деления и синтеза и многое другое. Однако
объяснить существование магических ядер, вычислить спины и магнит-
магнитные моменты удается только в рамках оболочечной модели.
> Оболочечная модель ядра (Гипперт-Майер и Йенсен, 1949 г).
В этой модели считается, что каждый нуклон движется в самосогласо-
самосогласованном поле, созданном остальными нуклонами. Потенциальную энер-
энергию этого поля подбирают так, чтобы получить наилучшее согласие
с опытными данными для широкого диапазона ядер.
Главное отличие от электронов в атоме заключается в том, что для
нуклонов гораздо большую роль играет спин-орбитальное взаимодей-
взаимодействие, вклад которого может достигать 10 — 15%. Кроме того, обыч-
обычная для электронов нормальная связь Рассела-Саундерса (LS-связь,
при которой сначала складываются отдельно спины и орбитальные
моменты всех частиц, а потом полный спин складывается с полным
орбитальным моментом) оказывается пригодной только для самых
легких ядер, а для большинства ядер действует jj-связь, в которой

8.3] Радиоактивность 263
складываются спин и орбитальный момент каждого нуклона. Уров-
Уровни нуклонов характеризуются квантовыми числами / (обозначаются
буквами s, р, d, /, g,. . .), j (равный / — - или / + -, указывается
правым нижним индексом), rrij и числом п, которое нумерует уровни
с заданным / и может принимать значения 1, 2, 3,. ... Каждому уровню
соответствует 2j +1 состояний. Уровни энергии нуклонов оказываются
разбитыми на группы (оболочки), расстояние между которыми заметно
превышает интервал между уровнями внутри группы. Магические
числа соответствуют полному заполнению очередной оболочки:
1; 1^1/2 B нуклона);
II: 2р3/2, 2р!/2 F нуклонов, всего 8);
III: 1^5/2, 2si/2? 1^з/2 A2 нуклонов, всего 20);
IV: I/7/2 (8 нуклонов, всего 28);
V: 2р3/2, 1/б/2Э 2pi/2, l#9/2 B2 нуклона, всего 50);
VI: 1#7/2> 24/2, 2d3/2j 3si/2j 1Лц/2 C2 нуклона, всего 82);
VII: l/ig/2j 2/7/2, 2/5/2, Зрз/2, 3pi/2j 1*13/2 D4 нуклона, всего 126).
Нуклонные состояния заполняются в указанном в данной схеме поряд-
порядке. С ее помощью удается также получить правильные значения спинов
почти всех ядер.
8.3. Радиоактивность
Радиоактивностью называют самопроизвольное (спонтанное) ис-
испускание ядром одной или нескольких частиц, сопровождающееся его
превращением в другое ядро (или переходом в другое состояние).
Изначальное радиоактивное ядро (нуклид) называют материнским,
а образовавшиеся ядра— дочерними.
Основные виды радиоактивности — а-, /3- и 7-распады. Несмотря
на различие физических процессов, связанных с этими распадами,
протекание их во времени описывается одним и тем же законом.
> Закон радиоактивного распада. Поскольку акт радиоактивного
распада является случайным, то можно считать, что за малое время dt
распадется доля ядер, пропорциональная dt. Если за N(t) обозначить
число нераспавшихся ядер к моменту времени t, придем к уравнению
^ = -Adt, (8)
где коэффициент пропорциональности Л называют постоянной распа-
распада. Решение уравнения (8) имеет вид:
N = Noe~x\ (9)
где TVo — число ядер при t = 0. Это соотношение носит название закон
радиоактивного распада.

264 Элементы ядерной физики [ Гл. 8
Число ядер, распадающихся в единицу времени, называют актив-
активностью радиоактивного образца:
A=^=XN = Aoe^, A0)
dt v '
где Aq — начальная активность образца. Активность в расчете на еди-
единицу массы называют удельной активностью. Активность измеряют
в бекерелях A Бк соответствует одному распаду в секунду) или в кюри
AКи = 3,7-1010Бк).
Кроме постоянной Л, распад характеризуют периодом полураспа-
полураспада 7\/2, равному времени, за которое распадается половина ядер
(N = No/2). Из (9) находим
Т _ _1п2 _ 0,693
Естественно также ввести среднее время жизни ядра т. Вероят-
Вероятность того, что ядро распадется в интервал времени (t,t + dt) равна
dN/N0 = XNdt/N0 = \e~xtdt, откуда
t.\e-xtdt= 1 = ^ = 1,44T1/2. A2)
Пример 1. Разберем пример на вычисление активности образца. Период
полураспада изотопа igSr около 28 лет. Чему равна активность m = 1 г
образца?
Решение. Активность равна произведению постоянной распада
Л = ln2/Ti/2 на число ядер N = Na(tti/ /jl), где /i = 90 г/моль. Получаем
А = 5, 2 • 1012 с = 140 кюри.
> Альфа-распад. При а-распаде образуются ядро 4Не (в этом слу-
случае его называют а-частицей) и дочернее ядро с порядковым номером
Z — 2 и массовым числом А — 4:
?Х-> ?:2y+2 Не, A3)
где X — символ материнского ядра, Y — дочернего. Альфа-распад на-
наблюдается только у тяжелых ядер (в основном с А > 209).
Энергия, выделяющаяся при а-распаде, равна
Q = ^х - та - тпу, A4)
где массы ядер выражены в энергетических единицах. Отметим, что
вместо масс ядер можно подставлять массы нуклидов (массы электро-
электронов сокращаются) или их дефекты масс.
Энергию распада можно также выразить через энергии связи ядер:
Q = ECBY + ЕСВа — ЕСВх
и через удельные энергии связи:
Q = (A- 4)sY + 4sa - Аех = 4(sa - eY) - А(ех - eY).

8.3] Радиоактивность 265
Поскольку у дочернего и материнского ядер четности как Z, так и N одина-
одинаковы, то их удельные энергии связи мало отличаются (см. формулу Вейцзек-
кера G)), и энергия распада становится положительной при г < га ~ 7 МэВ.
Как мы видели, в области наибольшей устойчивости ядер е ~ 8 МэВ
и уменьшается до 7 МэВ при А и 140. В этой области есть несколько а-
активных редкоземельных элементов с N ^ 84 (на 2 больше магического
числа 82, т. е. у дочернего ядра большая энергия связи) и энергией а-частиц
2-1-4,5 МэВ. Однако главная область а-активности лежит при А ^ 210
и Z ^ 84, с энергией а-частиц 4 -=- 9 МэВ.
То, что наблюдается распад с вылетом ядра 4Не, а не с вылетом
других легких ядер или отдельных нуклонов, объясняется аномаль-
аномально большой энергией связи ядра 4Не. Например, а-распад ядра 232U
сопровождается выделением 5,4 МэВ энергии, а для испускания этим
ядром протона ему надо сообщить 6,1 МэВ энергии.
Вследствие закона сохранения импульса ядро испытывает отдачу
и уносит часть энергии, поэтому регистрируемая энергия а-частиц
меньше энергии реакции Q. Предполагая, что материнское ядро покои-
покоилось, запишем закон сохранения импульса ра = ру через кинетические
энергии дочернего ядра и а-частицы:
таКа = туКу
Выразив Ку и подставив в закон сохранения энергии
Ka + KY = Q,
получим
0
где А — массовое число материнского ядра. Поскольку обычно А > 210,
то кинетическая энергия а-частицы составляет более 98 % энергии
распада.
Поскольку среднее время жизни большинства а-активных ядер
велико, то они распадаются из основного состояния. Кроме того, вслед-
вследствие очень резкой зависимости постоянной распада от энергии вылета-
вылетающих частиц наиболее интенсивным оказывается переход на основной
уровень материнского ядра. Поэтому в большинстве случаев все а-
частицы данного распада имеют одинаковые энергии. В ряде случаев
наблюдаются а-частицы, соответствующие переходам на низколежа-
щие (вращательные) уровни, что приводит к небольшому размытию
су-спектра. Кроме того, для некоторых самых короткоживущих ядер
возможен распад из возбужденных состояний материнского ядра и на-
наблюдаются су-частицы с энергиями, заметно превышающими основное
значение (например, у изотопов полония ^Ро и ^/Ро наряду с «обыч-
«обычными» вылетают а-частицы с энергиями до 10,5 МэВ).

266
Элементы ядерной физики
[Гл.8
> Теория а-распада. Некоторые особенности а-распада долгое
время выглядели весьма загадочно. Это в первую очередь необык-
необыкновенно сильная зависимость периодов полураспада от энергии а-
частиц. В основной области а-активности (Л ^ 210) а-частицы
с энергией заметно меньшей 4 МэВ вообще не наблюдаются (их
периоды полураспада слишком ве-
ве2°4
р ур
лики), для 28°24РЬ К
4 МэВ
17
и 7\/2 = 1,4 • 10 лет, а для
Ка « 9 МэВ и Ti/2 = 3 • 10 с.
Кроме того, было непонятно, как а-
частица вообще может вылететь из
ядра. Вне ядра ее кулоновская по-
потенциальная энергия
2(Z-2)e2
достигает максимума на границе яд-
ядра при г = R = гоЛ1/3 (см. форму-
Рис. 120 лу A)), а внутри ядра она попадает
в отрицательную потенциальную яму ядерных сил. Следовательно,
она оказывается запертой потенциальным барьером (рис. 120), высота
которого Uq ~ 25 -г- 30 МэВ заметно превышает энергию а-частиц
4 Ч- 9 МэВ. Альфа-частица может преодолеть этот барьер только бла-
благодаря квантовому туннельному эффекту (см. раздел 6.2). Теория а-
распада как туннельного перехода была разработана в 1928 г. Гамовым,
Кондоном и Герни и объяснила все его основные особенности.
Чтобы вычислить постоянную распада Л, надо умножить вероятность
р образования а-частицы внутри ядра (принимается р ~ 1) на число ее
соударений с барьером и ~ v/2R (v — скорость а-частицы) и на коэффициент
прохождения барьера
D~exp{-|
Именно коэффициент прохождения дает резкую (экспоненциальную) зависи-
зависимость постоянной распада (и периода полураспада) от энергии вылетающей
частицы Ка.
> Бета-распад. Бета-распадами называют такие радиоактивные
превращения ядер, в которых протон переходит в нейтрон (или
наоборот) и участвуют электроны (или позитроны) и нейтрино (или
антинейтрино). К основным типам /3-распада относятся:
а) Электронный ^"-распад:
+ е~ + и A5)
(пример — распад трития \Н —у |Не + е + v).

8.3] Радиоактивность 267
б) Позитронный /3+-распад:
^X^_1Y + e+ + i/ A6)
(пример — распад искусственного радиоактивного изотопа азота ^N —у
->¦ ^С + е+ + v).
в) Электронный захват
в"+ЙХ^Й-1^ + ^ A7)
(пример — реакция е~ +\ В ->• gLi + v). При электронном захвате
ядро поглощает электрон из атомной оболочки, причем обычно из
/С-оболочки, поэтому этот процесс часто называют /^-захватом (но
наблюдается и L-захват). Электронный захват сопровождается харак-
характеристическим рентгеновским излучением.
Важным отличием /3-распадов от других видов радиоактивности явля-
является то, что они являются не внутриядерными (затрагивающими сразу всё
ядро), а внутринуклонными процессами. Это значит, что элементарный акт
такого процесса состоит в превращении одного нуклона в другой. Схемы
таких превращений для перечисленных процессов таковы:
а) п —у р + е~ + и\
б) р —у п + е+ + и\
в) е~ + р —у п + v.
В свободном пространстве может самопроизвольно идти только первый
процесс (распад нейтрона). Однако в ядре новый нуклон попадает в окру-
окружение других нуклонов, в процессе его рождения происходит перестройка
всего ядра, и энергетическая возможность распада определяется массами не
нуклонов, а ядер (начального и конечного).
Самопроизвольный распад является разрешенным энергетически,
если сумма масс начальных частиц больше суммы масс конечных ча-
частиц. Для ^-распадов это условие имеет вид:
ш\ > ту + те (Р~ и /3+-распады);
ш\ + те > ту (электронный захват).
Удобно переписать эти формулы через массы нуклидов. Например, для
/^"-распада надо подставить шх = Мх — Zmej ту = My — (Z + 1)те
и условие распада примет вид:
Мх > My (/3~-распад).
Для других распадов получаем
Мх > My + 2те (/3+-распад);
Мх > My (электронный захват).
Отметим, что последние два распада приводят к одинаковым дочерним
ядрам, т.е. являются конкурирующими. Однако электронный захват
энергетически выгоднее.
Формула Вейцзеккера G) позволяет найти параметры (Z, А)
ядер, наиболее устойчивых к ^-распадам. Поскольку в этих распадах
массовое число А не меняется, надо сравнить массы (энергии связи)
всех изобар. Рассмотрим, к примеру, нечетное А (четно-нечетные ядра,

268
Элементы ядерной физики
[Гл.8
Нечетное А
Четное А
Е
а б в
Рис. 121
Л(А, Z) = 0). Минимизируя энергию ядра Е = Zmp + (A — Z)mn — ECB
по Z, найдем Z@, соответствующее наибольшей ^-устойчивости
(рис. 121,а). Изобары с Z < Zp надо исследовать на /3~-распад,
а с Z > Z@ — на /3+-распад и электронный захват. Для нечетных
А получится две ветви E(Z) (рис. 121,6), верхняя — для нечетно-
нечетных, а нижняя — для четно-четных ядер. Ядра на верхней
ветви обычно неустойчивы для переходов на нижнюю ветвь, но
существуют четыре ^-устойчивых ядра, которым соответствует
ситуация, изображенная на рис. 121,в.
Бета-активных нуклидов гораздо больше, чем су-активных (у каж-
каждого элемента есть ^-активный изотоп). Период полураспада зависит
от энергии (чем больше выигрыш в энергии, тем меньше 7\/2), хотя не
так сильно, как у а-распада. Кроме того, чем больше структура конеч-
конечного ядра отличается от начального (например, чем больше разность их
спинов), тем медленнее происходит распад. Иногда переход в основное
состояние дочернего ядра оказывается маловероятным, и в результате
/3-распада образуется ядро в возбужденном состоянии.
Нейтрино (точнее, одна из трех модификаций — электронное ней-
нейтрино) представляет собой очень легкую (возможно безмассовую) ней-
нейтральную частицу со спином 1/2, которая участвует только в слабых
взаимодействиях. Именно поэтому она чрезвычайно слабо взаимодей-
взаимодействует с веществом и ее очень трудно зарегистрировать. Например, для
нейтрино с энергией 100 МэВ длина свободного пробега в воде порядка
1016 км (т.е. около 100 световых лет). Прямое экспериментальное до-
доказательство существования нейтрино было получено только в 1956 г.,
когда появилась возможность использовать мощный поток нейтрино,
возникающих при делении урана в ядерном реакторе. (Регистрирова-
(Регистрировались реакции захвата антинейтрино V + р —> п + е+.) Теоретическое
же утверждение о существовании нейтрино было сделано В.Паули
еще в 1930 г., причем в довольно драматической ситуации, возникшей
вследствие именно «невидимости» нейтрино.

8.3] Радиоактивность 269
Считалось достоверно установленным, что в fi~-распаде рождаются
только две частицы — дочернее ядро и электрон. В этом случае, как при
любом двухчастичном распаде (например, а-распаде) неподвижного яд-
ядра, продукты распада должны иметь определенные энергии. В пренебре-
пренебрежении кинетической энергией дочернего яд-
ядdN/dE
pa энергия электрона должна быть равна
Л = тх — тпу — тпе = Мх — My. Одна-
ко в 1914 г. Дж.Чедвик установил, что /3-
спектры непрерывны. Оказалось, что распре-
распределение электронов по энергиям имеет вид,
приведенный на рис. 122, причем усреднен-
усредненная по этому распределению энергия элек- О
тронов равна всего Л/3. Ситуация выгляде-
выглядела столь парадоксально, что в 1924 г. Н.Бор гис. Izz
предположил, что в микропроцессах может нарушаться закон сохранения
энергии! В 1929 г. было замечено, что в некоторых /3-распадах нарушается
закон сохранения момента импульса. Например, в распаде §з°В1 —у Ц°Ро-\-е~
спины ядер равны 1 и 0, а электрон уносит полуцелый спин. Выходом из
тупика явилось предположение Паули о существовании нейтрино. В 1934 г.
Э.Ферми, основываясь на этом предположении, создал теорию слабого вза-
взаимодействия и рассчитал активности /3~-распадов и спектры вылетающих
электронов. В 1936 г. Н.Бор признал теорию Ферми и отказался от предпо-
предположения о несохранении энергии.
> Радиоактивные семейства. Большинство природных радиоак-
радиоактивных элементов принадлежат к четырем радиоактивным семей-
семействам, все элементы которых получаются последовательными распада-
распадами из одного родительского нуклида и заканчиваются на каком-нибудь
стабильном элементе. Семейство распада тория имеет массовые числа
4п, начинается с 29302Th и заканчивается на 28°28РЬ. Семейство распада
нептуния (А = An + 1) начинается с 29337Ne и заканчивается на 28°39Bi.
Семейство распада урана (А = An + 2) начинается с 29328U и заканчива-
заканчивается на 28°26РЬ. Наконец, семейство актиния (А = An + 3) начинается с
29325U и заканчивается на 28°27РЬ. (Первые три члена последнего семейства
были открыты позже.) Приведем для примера последовательность
элементов в семействе тория:
90 Тп У 88 Ка у 89 Ас у 90 Тп у 88 Ка у 8б Rn у 84 Ро у
Элемент ^Bi может распадаться путем а- и ^-излучения, поэтому на
этом элементе последовательность распадов разветвляется.
> Гамма-распад. Гамма излучение наблюдается при переходах воз-
возбужденного ядра на более низкие энергетические уровни без изменения
А и Z, но с испусканием 7-квантов- После испускания одного или

270 Элементы ядерной физики [ Гл. 8
нескольких фотонов ядро оказывается в основном состоянии. Посколь-
Поскольку значения энергии ядра дискретны, то спектр 7~излУчения также
дискретен. Возбужденные ядра образуются в ^-распадах, если распад
в основное состояние оказывается запрещенным. Например, /3~-распад
ifNa, имеющего спин / = 4, происходит не в основное состояние i|Mg,
спин которого / = 0, и не на первый возбужденный уровень (/ = 2),
а на второй уровень с / = 4, после чего ядро последовательно испускает
два 7-кванта с энергиями 2,7 МэВ и 1,4 МэВ и оказывается в основном
состоянии.
Свободный нуклон не может испускать 7-кв^нт5 поскольку это про-
противоречило бы законам сохранения энергии и импульса. Однако внутри
ядра импульс перераспределяется между всеми нуклонами, и излуче-
излучение становится возможным. Следовательно, в отличие от /3-распада
излучение 7-квантов является не внутринуклонным, а внутриядерным
процессом.
Кулоновский барьер не препятствует 7-излучению, и поэтому время
жизни 7-активных ядер обычно мало A0~7 -г- 10~15 с). Однако в тех
случаях, когда переход в основное состояние сильно затруднен, на-
наблюдаются долгоживущие возбужденные состояния, называемые изо-
изомерами. Время жизни изомеров может достигать нескольких часов
и даже больше. Некоторые свойства изомеров (например, вероятности
^-распадов) могут заметно отличаться от основных состояний.
Конкурентным 7-распаду является процесс, называемый внутрен-
внутренней конверсией, при котором возбужденное ядро передает избыток
энергии одному из электронов атомной оболочки. Спектр вылетающих
электронов, в отличие от спектра ^-электронов, является дискретным.
Кроме того, внутренняя конверсия сопровождается характеристиче-
характеристическим рентгеновским излучением.
> Измерение дозы излучения. Поглощенная доза излучения опреде-
определяется как энергия, поглощенная единицей массы, и выражается в греях
A Гр = Дж/кг). Для характеристики рентгеновского и гамма-излучения по
производимой ими ионизации сухого воздуха вводится экспозиционная доза
излучения, равная сумме зарядов всех ионов одного знака, образующихся
под действием электронов, возникших в облучаемом воздухе массой 1 кг
(выражается в Кл/кг или в рентгенах: 1 рентген = 2, 58 • 10~4 Кл/кг ).
Чтобы оценить биологическое воздействие излучения на живой орга-
организм, вводят коэффициент качества излучения Q, который показывает, во
сколько раз данное излучение опаснее, чем рентгеновское, при одинаковых
поглощенных дозах. Для бета-излучения Q = 1, для протонов с энергией
меньше 10 МэВ Q = 10, для тепловых нейтронов с энергией меньше 20 кэВ
Q = 3, а для нейтронов с энергией 0,5-10 МэВ Q = 10, для альфа из-
излучения с энергией меньше 10 МэВ Q = 20, для тяжелых ядер Q = 20.
Эквивалентная доза излучения равна произведению поглощенной дозы на
коэффициент качества. Она выражается в зивертах A Зв равен одному грею
при Q = 1). Используется также бэр (биологический эквивалент рентгена):
1бэр = 0,013в.

8.3] Радиоактивность 271
> Эффект Мессбауэра. Если энергия налетающего фотона совпа-
совпадает с энергией перехода системы из основного состояния в возбуж-
возбужденное, то вероятность поглощения такого фотона резко возрастает.
Это явление называют резонансным поглощением. Зависимость веро-
вероятности поглощения от энергии имеет вид острого пика с шириной,
равной ширине возбужденного уровня АЕ {АЕ ~ h/ At, где At —
время жизни возбужденного состояния). Естественная схема резонанс-
резонансного поглощения использует в качестве излучателя и поглотителя
одинаковые атомы. Такая схема используется в оптике, где излуче-
излучение и поглощение определяются электронными переходами. Однако
наблюдение резонансного поглощения ядерных 7-квантов встречается
с серьезными затруднениями. Дело в том, что при излучении 7-кванта
атом испытывает значительно большую отдачу и уносит больше энер-
энергии, чем при излучении оптического фотона. Это приводит к более
существенному уменьшению частоты излученного фотона, и его по-
поглощение оказывается маловероятным (тем более, что при поглощении
часть энергии фотона теряется на кинетическую энергию отдачи атома,
и энергия поглощаемого фотона должна быть не меньше, а больше
энергии возбужденного уровня).
Импульс отдачи ядра равен импульсу фотона: р = Ни;/с, а энергия ядра
равна
Для резонансного поглощения сдвиг энергии фотона (равный энергии ядра
Ея) должна быть не больше ширины уровня АЕ. Однако Нои > 104 эВ,
а тяс2 < 2 • 1011 эВ, поэтому Ея > 10~3 эВ. В то же время обычное значение
для ширины возбужденного уровня АЕ ~ 10~8 -т- 10~7 эВ. Видно, что
отдача ядра приводит к уменьшению энергии 7~кванта5 на много порядков
превышающему ширину возбужденных ядерных уровней.
В 1958 г. Р.Мессбауэр обнаружил, что при низких температурах
на изотопе ^/Ir наблюдается резонансное поглощение. Суть явления,
называемого эффектом Мессбауэра, состоит в том, что как при из-
излучении, так и при поглощении 7-квантов ядрами атомов, образую-
образующих кристаллическую решетку, импульс отдачи может восприниматься
всем кристаллом как целым (точнее — группой атомов в количестве
N ~ 108). Это значит, что энергия отдачи становится ничтожно ма-
малой (тя в A8) надо заменить на массу кристалла), и выполняются
условия для резонансного поглощения. Появляется возможность фик-
фиксировать изменения энергии 7-квантов порядка ширины уровня, т.е.
АЕ ~ 10~8 эВ. Здесь важна не величина АЕ (у электронных уровней
она того же порядка), а ее отношение к энергии фотонов, характе-
характеризующее относительную погрешность измерений. Поскольку энергия
ядерных 7-квантов составляет 104 -г- 108 эВ, то точность измерений
с помощью эффекта Мессбауэра достигает 10~12 -^ 10~16.

272 Элементы ядерной физики [ Гл. 8
Одним из первых применений эффекта Мессбауэра было измерение гра-
гравитационного красного смещения в поле тяжести Земли (Паунд и Ребка,
1960 г.). Суть явления состоит в том, что при движении фотона в поле тя-
тяготения его энергия должна изменяться. Относительное изменение частоты
и энергии должно быть равно
АЕ m-yAip A(p
Ь т^с с
где т1 — масса кванта, Аср — изменение гравитационного потенциала. Если
разместить мессбауэровские излучатель и приемник на одной вертикали на
расстоянии h друг от друга, то Аср = gh. При h = 30 м относительное
изменение частоты Auj/uj = АЕ/Е = 3 • 10~15 находится в пределах
точности метода.
Для измерения сдвига частоты используют эффект Доплера. При непо-
неподвижных излучателе и приемнике резонансное поглощение отсутствует из-
за гравитационного смещения. Перемещая приемник по вертикали, подби-
подбирают скорость v так, чтобы снова возникло резонансное поглощение. Тогда
Auj/uj = v I с.
8.4. Ядерные реакции
Ядерной реакцией называется процесс вида
o + ^X-^^'Y + 6, A9)
где а — начальная (налетающая) частица, ^Х — начальное ядро (ядро
мишени), ^,Y — конечное ядро, b — конечная (вылетающая) частица.
Часто используют символическую запись
АХ(а, b)A'Y, B0)
а для обозначения типа процесса — совсем краткую запись (а, Ь). Если
Ь = а (и X = У), то такой процесс называют рассеянием. Если конечное
ядро Y оказывается при этом в таком же состоянии (основном), как
и начальное X, то рассеяние называют упругим.
Для того, чтобы реакция A9) могла происходить, необходимо,
чтобы выполнялись законы сохранения электрического заряда и ряда
других зарядов (лептонного, барионного и др.), о которых пойдет речь
в следующей главе. Кроме того, состояния частиц на выходе реакции
связаны с состояниями начальных частиц законами сохранения энер-
энергии, импульса и момента импульса.
Ядерные реакции сопровождаются перестройкой ядра, т. е. могут
происходить только при сближении вступающих в реакцию частиц до
расстояния, меньшего радиуса ядерного взаимодействия го ~ 10~15 м.
> Выход и сечение реакции. Рассмотрим поток падающих частиц
(а) определенной энергии, падающий на неподвижную мишень ядер
X. Для начала рассмотрим тонкую мишень толщиной Ах с числом
ядер на единицу площади Nq = uqAx (no — объемная плотность ядер

8.4] Ядерные реакции 273
мишени). Выходом ядерной реакции называют долю падающих частиц
(а), вступивших в данную реакцию (т. е. вероятность данной реакции):
Ясно, что выход реакции w пропорционален Nq. Коэффициент про-
пропорциональности имеет размерность площади и называется сечением
реакции:
W = aN0 *=*»-. B2)
Сделаем несколько замечаний относительно определения сечения
реакции.
1. В разд. 2.9 для обсуждения явлений переноса было введено
эффективное сечение упругого рассеяния молекул, по смыслу ана-
аналогичное сечению реакции. Кроме того, понятие дифференциального
сечения упругого рассеяния понадобилось нам при анализе опытов
Резерфорда (разд. 6.2).
2. В формуле B2) вместо N можно поставить поток частиц (число
частиц за единицу времени) или плотность потока J (поток на единицу
площади), вид формулы не изменится, поскольку в ней стоит относи-
относительное число частиц.
3. В случае тонкой мишени можно считать, что каждая налетаю-
налетающая частица взаимодействует только с одним ядром мишени, поэтому
можно рассмотреть взаимодействие падающих частиц с одним ядром.
Поскольку число упавших на мишень частиц равно N = JSt (J —
плотность потока, S — площадь мишени), a NqS — полное число ядер
мишени, получаем, что сечение можно определить, как отношение чи-
числа частиц, вступивших за единицу времени в реакцию с одним ядром,
к плотности потока частиц.
3. Выход и сечение реакции вводятся для любого выделенного ре-
результата взаимодействия. При заданном входном канале (а+Х) обычно
есть несколько выходных каналов (Y + Ь). Например, результатом бом-
бомбардировки ядер gLi протонами могут быть Ihi+p (упругое и неупругое
рассеяние), а-\-а, |Ве + 7 и т- Д- Некоторые каналы закрыты при низких
энергиях. Вообще надо заметить, что одно из общих утверждений
квантовой механики состоит в том, что всякий процесс, не запрещенный
ни одним законом сохранения, обязательно реализуется (может быть,
с малой вероятностью). В частности, среди возможных каналов всегда
есть упругое рассеяние.
4. Чтобы описать зависимость конечного результата рассеяния от каких-
либо непрерывных параметров (обычно от угла вылета и энергии частицы),
вводят различные дифференциальные сечения. Их определяют как отноше-
отношение числа реакций, в результате которых заданный параметр (например, угол
в) лежит в определенном узком интервале (например, 0, в + d6), к числу
падающих частиц N, числу частиц мишени на единицу площади No и ширине

274 Элементы ядерной физики [ Гл. 8
интервала:
da dN
dO NNod9
da dN
dQ
(?2 — телесный угол, dQ = sin 9d9d(p). Интегрируя дифференциальное сече-
сечение по всем возможным значениям параметра (параметров), получим полное
сечение реакции.
5. Сечение приобретает более наглядный смысл, если частицы счи-
считать классическими, а взаимодействие между ними столь короткодей-
короткодействующим, что их можно заменить шариками радиусов R\ и /22, ПРИ
соприкосновении которых происходит реакция. Тогда а = ir(Ri + R2J
(такая модель используется в теории явлений переноса). Эта модель
имеет некоторое отношение к действительности в случае большой энер-
энергии падающих частиц, когда дебройлевская длина волны Л мала по
сравнению с радиусом ядра R (и отсутствует кулоновское взаимодей-
взаимодействие). В этом случае
а~7гЯ2~1(Г30-10-28м2. B3)
Для медленных частиц (Л ^> R) сечение резко возрастает, так как оно
определяется не радиусом ядра, а дебройлевской длиной волны:
а ~ тгА2.
Однако эта оценка относится только к нейтронам, так как медленная
заряженная частица не сможет преодолеть кулоновское отталкивание
и приблизиться к ядру.
Оценка B3) показывает, почему ядерные сечения выражают в бар-
нах A барн = 10~28м2).
6. Если мишень не тонкая, то по мере проникновения вглубь мишени
интенсивность пучка уменьшается, и сечение реакции выражается че-
через ее выход более сложно, чем в B2). Это можно сделать при условии,
что известно полное сечение процессов, приводящих к ослаблению пуч-
пучка. Самая простая ситуация возникает в случае, если рассматриваемая
реакция — единственно возможная. Тогда для каждого тонкого слоя
можно записать
— = -andx, B4)
где N — число частиц в пучке, дошедших до слоя с координатой ж,
ndx — число атомов мишени в слое толщиной dx (на единицу площади),
п — объемная концентрация атомов, знак (—) отражает тот факт, что
прореагировавшие частицы выбывают из пучка. Решение уравнения
B4) имеет вид
N = N0-e-anx, B5)

8.4] Ядерные реакции 275
где TVo — начальное число частиц в пучке. Величина а = an называется
коэффициентом поглощения. Легко убедиться в том, что средняя длина
свободного пробега равна
I = — B6)
an
(см. разд. 2.9).
Пример 1. Вычислить длину свободного пробега нейтрино в железе,
если сечение взаимодействия нейтрино аи и 10~19 барн = 10~47 м2.
Решение. Концентрация атомов железа равна п = р • Д/а//^,
где Na — число Авогадро, р = 7,8 • 103 кг/м3 — плотность железа,
a /j, = 58 • 10~3 кг/моль — молярная (атомная) масса железа. Получаем
/ = 1/{па) = 1,2- 1018 м2, что составляет примерно 130 световых лет.
> Механизмы ядерных реакций. Так же как нет пока универ-
универсальной ядерной модели, объясняющей все свойства ядер, так не суще-
существует единой теории ядерных реакций. Особенности различных типов
реакций в разных энергетических интервалах описываются в рамках
различных моделей (или, как их называют, механизмов) ядерных ре-
реакций. Коротко остановимся на некоторых из них.
Механизм прямых реакций (С.Батлер, 1953 г.) призван объяснить
некоторые особенности реакций, протекющих при высоких энергиях,
например, резкую анизотропию (максимальная вероятность вылета
вперед), почти полную передачу энергии вылетающему фрагменту
и т. д. К таким процессам относятся, например, реакции срыва (d,p),
(d,n) и реакции подхвата (р, d), (n, d). В прямых реакциях налетаю-
налетающая частица взаимодействует не с ядром в целом, а с отдельным его
фрагментом, нуклоном или небольшой группой нуклонов, передавая
ему энергию в течение малого (ядерного) времени 10~21 -г- 10~22 с.
(Такое время характерно для реакций, протекание которых опре-
определяется только ядерными силами. Ядерное время оценивают как
тяд = 2R/v ~ 10~23 ~ Ю~21 с, где v ~ 107 -^ 108 м/с —скорость нукло-
нуклона.)
Механизм составного ядра (Н.Бор, 1936 г.) объясняет многие осо-
особенности реакций, протекающих при низких энергиях. Это, во-первых,
большая (по ядерным масштабам) продолжительность многих реакций
(г ~ 10~16 -г- 10~12 с, что на много порядков больше ядерного времени
тяд ~ 10~22 с). Во-вторых, симметричность (в системе центра масс)
вылета частиц вперед-назад (а иногда даже полная изотропность).
В-третьих, резонансный характер реакций — их сечения имеют резкие
максимумы при некоторых значениях энергии. Суть механизма состав-
составного ядра состоит в том, что реакция протекает в два этапа:
a + X^C*^Y + 6. B7)
На первом этапе материнское ядро X захватывает падающую части-
частицу и образуется составное ядро (компаунд-ядро) С в возбужденном

276 Элементы ядерной физики [ Гл. 8
состоянии (на что указывает звездочка). Энергия возбуждения вы-
вычисляется как сумма энергии связи частицы (а) в ядре С (равной
Еа^с = тх + та — ^с) и начальной кинетической энергии К (в системе
центра масс):
#возб = #а,С + К. B8)
Процесс захвата частицы и распределения избыточной энергии между
нуклонами составного ядра продолжается короткое время ~ тяд. После
этого составное ядро распадается одним из возможных способов (с раз-
разной вероятностью): либо избыточная энергия случайным образом кон-
концентрируется на одной частице (нуклоне или группе нуклонов) и она
вылетает из ядра, либо излучается 7-квант, либо ядро делится. Все эти
процессы гораздо медленнее ядерных, что и объясняет медленность
реакций, протекающих с образованием составного ядра.
Симметрия вылета продуктов распада объясняется тем, что состав-
составное ядро успевает «забыть», с какой стороны прилетела падающая
частица. Резонансный характер сечения реакции связан с тем, что
вероятность захвата частицы (а значит, и сечение всего процесса) резко
возрастает, если Е^озб в B8) совпадает с одним из дискретных уровней
энергии составного ядра. Этим значениям соответствуют дискретные
значения кинетической энергии К, через которую, как мы увидим
ниже, выражается энергия падающей частицы.
Механизм составного ядра успешно объяснил тот факт, что реакции
с разными начальными частицами могут приводить к сходным конеч-
конечным результатам. Например, реакции n + ^N, JH+^C, fH+^C, fH+^C,
|He + ^B и |He + ^B идут с образованием одного и того же составного
ядра ^N , и если у них окажутся одинаковые энергии возбуждения, то
они будут иметь одинаковые выходные каналы.
При больших энергиях возбуждения спектр составного ядра ста-
становится практически непрерывным, и успешно работает статистиче-
статистическая модель распада, или модель испарения. В этой модели составное
ядро рассматривается как капля горячей жидкости с температурой
Т = Евозб/к (к — постоянная Больцмана), а вылет частицы — как ис-
испарение с ее поверхности. В рамках этой модели становится понятным,
почему в этой области энергий угловое распределение вылета частиц
становится изотропным (в системе центра масс).
> Энергия реакции. Закон сохранения энергии для произвольной
ядерной реакции можно записать в виде
^гщ+^К{=^т'{+^К'{ B9)
(массы — в энергетических единицах). Энергией реакции Q называют
приращение кинетической энергии (или убыль массы):

8.4] Ядерные реакции 277
где Л — дефект массы (см. разд. 8.1). Отметим также, что энергию ре-
реакции можно выразить через энергии связи ядер (Q = ^ Е'сщ — ^ ECBi),
но только в том случае, если число протонов сохраняется (если заряды
несут только протоны ядер). Реакции с выделением энергии (Q > 0)
называют экзоэнерзетическими, а реакции с Q < 0 — эндоэнергетиче-
скими. Иногда энергию реакции указывают прямо в ее записи, напри-
например, n + 10B -^ 7Li + 4He + 2, 79 МэВ или ^He + ^N -^ ^О + ^Н-1, 2 МэВ.
Поскольку последнее выражение в C0) не зависит от системы от-
отсчета, то энергия реакции равна приращению кинетической энергии
в любой СО, в том числе в системе центра масс (СЦМ):
Если в реакцию вступают падающая (нерелятивистская) частица мас-
массой т и неподвижная частица мишени массой М, то кинетическую
энергию системы в СЦМ можно связать с кинетической энергией па-
падающей частицы Кт:
Кинетическая энергия в СЦМ выражается через приведенную массу
/j, = тМ/(т + М) и относительную скорость частиц vOTH = vi — V2:
~~ 2 ~~ т + М 2
(см. разд. 1.7). Мы учли, что относительная скорость не зависит от системы
отсчета, а в лабораторной системе отсчета частица мишени покоится.
> Порог реакции. Эндотермическая реакция может идти только
в том случае, если кинетическая энергия налетающей частицы пре-
превышает некоторое минимальное значение, которое называют порогом
реакции. Порог реакции Кпор не совпадает с |Q|, поскольку вследствие
закона сохранения импульса конечная кинетическая энергия в лабора-
лабораторной системе не равна нулю, и Кпор = \Q\ + К' (см. C0)). Однако
в СЦМ на пороге реакции частицы в конечном состоянии покоятся
(К' = 0), и начальная кинетическая энергия равна \Q\ (см. C1)). Из
C2) получаем
пор Мх Мх '^''
В случае, когда падающая частица и продукты распада нельзя считать
нерелятивистскими, порог эндотермической реакции т-\- М —>• mi+m2 + . . .
можно выразить через ее энергию |Q| = (mi + 1712 + . . .)с2 — (га + М)с2
следующим образом. Величина Е2 —р2с2, где Е,р — энергия и импульс
системы, во-первых, сохраняется в реакции и, во-вторых, не меняется при
переходе в другую СО. Приравняем начальное значение этой величины
в лабораторной СО к конечному значению, но вычисленному в СЦМ (где

278 Элементы ядерной физики [ Гл. 8
[Кпор + (га + М)с2]2 — р2с2 = (mi + rri2 + . . .Jс4-
Учитывая, что импульс мишени М равен нулю, для частицы т запишем
р2с2 = (Кпор + тс2J - т2с4 = Кпор(Кпор + 2тс2).
После преобразований получим
(т + МJс2 + 2МКпор = (mi + т2 + . . .Jс2,
откуда
_(mi+m2 + ...)(m + M) 2_|^т + М | \Q\ \
Эту формулу можно применять и в случае, когда падающая частица пред-
представляет собой 7~квант5 надо только положить т = 0. Пороговая энергия
фотона равна
(Ш1+Ш2 + ...J_М2 / |Q| Ч
Snop = ^м с =IOIA + ^?J- C5)
8.5. Ядерная энергетика
Поскольку максимальной удельной энергией связи обладают сред-
средние ядра (с Л ~ 50 -г- 60), то как деление тяжелых ядер, так и слияние
(синтез) легких ядер должно сопровождаться выделением энергии.
Энергию, выделяющуюся при делении, принято называть атомной,
а при синтезе — термоядерной. Появление в середине прошлого века
атомных и термоядерных (водородных) бомб, в которых названные
реакции протекают в неуправляемом режиме, поставило под угрозу
само существование человечества. В то же время управляемое по-
получение энергии на атомных электростанциях играет большую роль
в энергетике многих стран (хотя и сопряжено с серьезными экологи-
экологическими рисками). Решение проблемы управляемого термоядерного
синтеза дало бы людям практически неисчерпаемый и экологически
безопасный источник энергии. Кроме того, реакции синтеза являются
главным источником энергии Солнца и других звезд.
> Деление ядер. Как для качественного понимания многих особен-
особенностей деления, так и для получения количественных оценок можно
использовать капельную модель ядра и связанную с ней формулу
Вейцзеккера G). Для качественного понимания можно рассматривать
деление на два одинаковых осколка. При делении происходит уменьше-
уменьшение кулоновской энергии, но зато увеличивается поверхностная энер-
энергия. Отношение соответствующих членов в G) зависит от параметра
к = Z2/Л, от него же зависит вероятность деления. Несложно прове-
проверить, что деление становится энергетически выгодным при
^ > щ « 18. C6)

8.5]
Ядерная энергетика
279
ЛЕ
Рис. 123
Подстановка реальных значений Z и А показывает, что деление выгод-
выгодно уже для ядер из области ниобия — палладия, т. е. начиная с А ~ 100.
Однако самопроизвольное (спонтанное) деление наблюдается только
у очень тяжелых ядер (сЛ~ 250).
Причина заключается в том, что хотя состояние из двух осколков
обладает меньшей энергией, для перехода в это состояние ядро долж-
должно преодолеть значительный потенциальный барьер. При постепенной
деформации ядро проходит через промежуточные состояния, облада-
обладающие большей энергией, чем начальное состояние. На рисунке 123 схе-
схематически изображена зависимость энергии деформированного ядра
от условного параметра 7, выражающего степень деформации. Высоту
барьера, равную превышению максимальной промежуточной энергии
над начальной энергией ядра, называют энергией активации Е&КТ. При
сообщении ядру энергии возбуждения, превышающей Е&кт, оно быстро
делится на два осколка. Энергия активации уменьшается с ростом
Z IА и обращается в ноль при
>
50.
C7)
В отсутствие барьера ядро мгновенно делится на два осколка без сооб-
сообщения дополнительной энергии.
За счет квантового туннельного эффекта спонтанное деление из
основного состояния может происходить и при Z2/А < ^2, но барьер
должен быть невысоким, иначе вероятность деления будет очень мала.
Например, для 29328U Z2/А = 35,5, что заметно меньше ^2, и период по-
полураспада 29328U по отношению к спонтанному делению 7\/2 ~ Ю16 лет
на 6 порядков превышает 7\/2 этого элемента по отношению к а-
распаду. Напротив, для искусственно синтезированного ядра cZ = 107

280 Элементы ядерной физики [ Гл. 8
и А = 261 Z2/А = 43,9, и период его полураспада по отношению к спон-
спонтанному делению 7\/2 ~ 10~3 с, что сопоставимо с 7\/2 по отношению
к а-распаду.
Удельная энергия связи ядер с А ~ 240 примерно на 0,9 МэВ
меньше, чем у осколков деления. Это значит, что при каждом акте
деления высвобождается примерно 200 МэВ. Более 80% этой энергии
уносится в виде кинетической энергии осколков. Остальная энергия
приходится на излучение осколками нейтронов и 7- и /3-частиц.
При делении чаще всего образуются осколки неравных масс. Легкие
осколки группируются вокруг Кг, а тяжелые — вокруг Хе. Это объяс-
объясняется тем, что числа нейтронов в этих ядрах близки к магическим
числам 50 и 82.
Поскольку в тяжелых ядрах доля нейтронов значительно выше, чем
в средних, дочерние ядра обладают избыточным числом нейтронов.
Сразу же после деления дочерние ядра испускают 2 — 3 нейтрона
с кинетической энергией ~ 2 МэВ, после чего происходит несколько
^-распадов, которые доводят осколки до стабильного состояния. Ис-
Испускание нейтронов продуктами распада играет решающую роль для
возникновения цепной реакции деления.
Важное значение для управляемой цепной реакции имеют так называ-
называемые запаздывающие нейтроны. Они возникают в том случае, когда в ре-
результате достаточно медленного /3-распада осколка деления образуется воз-
возбужденное состояние ядра с малой энергией отделения нейтрона, после чего
происходит почти мгновенное его испускание. Запаздывание определяется
временем /3-распада и может достигать десятков секунд.
При сообщении ядру достаточно большой энергии возбуждения
(в несколько МэВ) оно начинает совершать колебания, при которых
его форма периодически переходит от сжатой формы к вытянутой.
Даже если энергия возбуждения меньше энергии активации, вероят-
вероятность деления возбужденного ядра значительно выше, чем в основном
состоянии. Конкурентным процессом является излучение энергии воз-
возбуждения в виде 7-квантов. Получить ядро в возбужденном состоянии,
имеющем заметную вероятность деления, можно путем облучения его
различными частицами. Наиболее эффективным является облучение
нейтронами, для которых отсутствует кулоновский барьер и которые
могут приблизиться к ядру, обладая любой, в том числе очень малой
(порядка 1 кэВ) кинетической энергией.
Главным механизмом деления природных изотопов урана 235U и
238U является захват нейтронов с образованием составных ядер 236U и
239U в возбужденном состоянии. Важное значение имеет тот факт, что
235U делится любыми, в том числе тепловыми, нейтронами (с энергией
меньше 0,5 кэВ), a 238U — только быстрыми нейтронами (с энергией
порядка 2 МэВ). Причина состоит в том, что составное ядро 236U

8.5] Ядерная энергетика 281
является четно-четным, и при одной и той же энергии нейтронов его
энергия возбуждения оказывается больше, чем у четно-нечетного 239U.
Энергию возбуждения составного ядра можно найти из уравнения
тп + Кп + МА = МА+1 + #возб,
где Кп — кинетическая энергия нейтрона (мы пренебрегли кинетической
энергией составного ядра). Получаем
#возб = {тп + Мл - Ma+i} + Кп = еа+1 + Кп,
где ?а+1 — энергия связи нейтрона в составном ядре. Составное ядро будет
делиться в том случае, если Еъозь окажется больше энергии активации. Для
239U ^акт = 7,1 МэВ, а ?а+1 = 5,5 МэВ, и требуется Кп не меньше 1,6 МэВ.
Для 236U sa+i =6,8 МэВ больше Еакт = 6,5 МэВ, и это ядро будет делиться
любыми нейтронами.
Сечение захвата медленных нейтронов определяется их дебройлев-
ской длиной волны, которая может быть гораздо больше радиуса ядра.
Сечение захвата тепловых нейтронов с энергией 0,025 кэВ в сотни раз
больше, чем сечение захвата быстрых нейтронов с энергией 1 МэВ,
поэтому возможность деления тепловыми нейтронами имеет столь
большое значение.
> Цепная реакция. Возможность осуществления самоподдержива-
самоподдерживающейся реакции деления (цепной реакции) возникает вследствие того,
что при делении ядра одним нейтроном осколки деления испускают
два-три нейтрона, которые могут в свою очередь вызвать деление
других ядер. Проблема состоит в том, что некоторые из образовав-
образовавшихся нейтронов выбывают из цепной реакции — либо поглощаются,
не вызывая деления, либо уходят из системы через ее границу.
Определим коэффициент размножения нейтронов как отношение
числа нейтронов в следующем поколении к числу нейтронов в преды-
предыдущем:
Для возникновения цепной реакции необходимо, чтобы к был больше
единицы. Для работы реактора в стационарном режиме надо поддер-
поддерживать к равным единице.
С увеличением размеров системы доля нейтронов, уходящих через
ее границу, стремится к нулю. Поэтому, если в бесконечной ядерной
среде к ж > 1, то для конечной системы определенной формы условие
к > 1 будет выполняться, если масса этой системы превышает неко-
некоторую критическую массу. Критическую массу можно уменьшить,
если окружить активную область оболочкой, отражающей нейтроны.
Например, для чистого 235U критическая масса 47 кг (шар диаметром
17 см), но если прослоить 235U полиэтиленовыми пленками и окружить

282 Элементы ядерной физики [ Гл. 8
оболочкой из бериллия, то критическая масса снизится до 250 г (диа-
(диаметр 3 см). Далее мы сосредоточимся на цепной реакции в ядерной
среде бесконечных размеров.
Любое ядерное топливо, затраты на получение которого не превы-
превышают разумных пределов, содержит высокий процент 238U. Например,
природный уран содержит 99,3 % 238U и всего 0,7 % 235U. Хотя 238U тоже
может делиться нейтронами, но вероятность этого мала (а для нейтро-
нейтронов с энергией меньше 1,6 МэВ равна нулю), а остальные нейтроны
поглощаются 238U без деления, с испусканием 7-квантов (радиационный
захват (п, 7))- В то же время вероятность деления ядер 235U (а также
233U и 29349Ри) достаточно высока — 85-90 %, причем они могут делиться
как быстрыми, так и медленными нейтронами.
Процесс сильного обогащения урана (т. е. заметного увеличения
содержания 235U) является дорогостоящим и используется для созда-
создания зарядов атомных бомб (где экономический фактор не является
существенным) и производства горючего для бридеров — реакторов на
быстрых нейтронах (о них будет сказано ниже).
Главный способ получения цепной реакции состоит в использовании
медленных (тепловых) нейтронов. Нейтроны, рожденные при делении
ядер, имеют среднюю энергию ~ 2 МэВ. При этой энергии сечения
захвата нейтронов ядрами 235U и 238U одного порядка. Однако для
тепловых нейтронов ситуация кардинально меняется. Для 238U сечение
захвата остается небольшим («2,8 барн), а для 235U резко возрастает
и составляет « 650 барн (что гораздо больше геометрического сече-
сечения), причем большая часть (84%) поглощенных нейтронов вызывает
деление (сечение деления 550 барн).
Легко сосчитать, что для тепловых нейтронов сечение деления
«среднего» ядра природного урана составляет 550 х 0, 007 = 3,9 барн,
а сечение радиационного захвата —2, 8 + 100x0, 007 = 3, 5 барн. Видно,
что запас нейтронов не очень большой (при каждом делении рождается
в среднем 2,5 нейтронов, но почти половина из них теряется), поэто-
поэтому для осуществления цепной реакции приобретает большое значение
уменьшение потерь нейтронов в процессе их замедления. Наилучшим
замедлителем с точки зрения механики должен был быть водород (вхо-
(входящий в молекулы обычной воды), так как при упругом ударе наиболь-
наибольшая передача энергии происходит при одинаковых массах сталкиваю-
сталкивающихся частиц (см. раздел 1.5). Однако атом водорода легко поглощает
нейтроны AН + п —> 2Н + 7), и поэтому используют дейтерий (входящий
в состав тяжелой воды), углерод или бериллий. Чтобы уменьшить
поглощение замедляемых нейтронов ядрами 238U, ядерное горючее не
перемешивают с замедлителем (гомогенная структура), а чередуют
пласты горючего с пластами замедлителя (гетерогенная структура).
Попав в пласт замедлителя, нейтрон успевает полностью замедлиться,
не рискуя быть поглощенным, и затем возвращается в область реакции.

8.5] Ядерная энергетика 283
Если бы в цепной реакции участвовали только нейтроны деления, то
такой реакцией было бы очень сложно управлять. Действительно, время
жизни одного поколения нейтронов деления составляет ~ 10~3 с. Если
коэффициент размножения случайно возрастет до, скажем, к = 1,005, то
за 1 с число нейтронов будет возрастать в 150 раз, т. е. реакция приобретает
взрывной характер. Устойчивость управляемой реакции придают запазды-
запаздывающие нейтроны, о которых шла речь выше. Хотя их доля невелика (~
~ 0,75%), среднее время жизни поколения нейтронов оказывается равным
~ 0,1 с, и в приведенном примере число нейтронов возрастает за 1 с не в 150,
а только в 1,5 раза.
Трансурановые элементы. Единственным природным делящим-
делящимся элементом является 235U, но его запасы невелики. Хотя реакторы
на быстрых нейтронах требуют значительного обогащения урана (до
15 %) и обладают сравнительно небольшой мощностью, их особая роль
состоит в том, что их можно использовать для производства нового
ядерного горючего (поэтому их называют бридерами — «размножи-
«размножителями»). Например, радиационный захват нейтронов 238U, столь па-
пагубный для цепной реакции, приводит к образованию искусственного
трансуранового элемента 29349Ри:
29fU +
f|U -
flNe-
n -> f|U +
> 29fNe + e"
-»¦ flPu + e
¦75
" + ^;
T1/2
= 2,
= 2,
3
3
мин
дня.
Плутоний практически устойчив (период полураспада 24000 лет) и хо-
хорошо делится нейтронами любых энергий. Его легче отделять от 238U,
поскольку у них разные химические свойства.
> Реакции синтеза. Термоядерная энергия Солнца и звезд.
Как уже отмечалось, в области легких ядер удельная энергия связи е
с ростом А увеличивается (см. рис. 119). Это значит, что реакции сли-
слияния двух легких ядер с образованием более тяжелого ядра (реакции
синтеза) должны идти с выделением энергии. Поскольку рост е(А) при
малых А круче, чем спад при больших Л, в реакциях синтеза может
выделяться гораздо больше энергии (в расчете на один нуклон), чем
в реакциях деления.
Два ядра могут слиться только в том случае, если они сблизятся до
расстояния, на котором начинают действовать ядерные силы, чему пре-
препятствует кулоновское отталкивание. Для преодоления кулоновского
барьера ядра должны обладать большими кинетическими энергиями.
Если разогреть вещество до высокой температуры, то могут возникнуть
условия для возникновения самоподдерживающейся реакции — выде-
выделение энергии будет компенсировать ее потери (например, в виде из-
излучения). Именно поэтому реакции синтеза называют термоядерными.

284 Элементы ядерной физики [ Гл. 8
Термоядерные реакции являются источником энергии Солнца и других
звезд.
Отметим, что температуры, при которых возможно протекание тер-
термоядерных реакций, столь велики, что вещество оказывается в состоя-
состоянии полностью ионизованной плазмы.
Пример 1. Требуется оценить температуру, при которой будет проис-
происходить слияние двух протонов в дейтрон.
Решение. Для возникновения реакции протоны должны сблизиться до
расстояния, равного двум радиусам действия ядерных сил го ~ 2 • 10~ м
(см. раздел 8.2). Из закона сохранения энергии
^К ло
4тг?0 2г0
находим кинетическую энергию Ек ~ 0,1 МэВ, после чего по классической
о
формуле Ек = — кТ оцениваем температуру Т ~ Ю9 К.
Температура в центре Солнца примерно на два порядка меньше по-
полученной величины. Это значит, что средней энергии ядер недостаточно
для реакции синтеза. И все же реакция идет, причем излучаемая Солн-
Солнцем мощность колоссальна, ~ 4-1026 Вт. Дело в том, что в соответствии
с распределением Максвелла некоторая (весьма малая) часть частиц
обладает энергией, заметно превышающей среднее значение. Кроме
того, благодаря квантовому туннельному эффекту в реакцию могут
вступать ядра, энергия которых меньше кулоновского барьера. Все это
означает, что в реакцию вступает ничтожная часть сталкивающихся
ядер. Именно поэтому удельное энерговыделение Солнца в единицу
времени столь мало, ~ 10~4 Вт/кг, однако благодаря колоссальной его
массе полная излучаемая мощность столь велика.
Термоядерная энергия Солнца выделяется в двух циклах реакций —
углеродном и водородном. В результате каждого из этих циклов про-
происходит превращение четырех протонов в ядро гелия (с испускани-
испусканием позитронов, фотонов и нейтрино), с общим энерговыделением ~
~ 25 МэВ. Для протекания углеродного цикла необходимо присутствие
ядер углерода, которые играют роль катализатора, так как в результате
цикла опять восстанавливаются. Приведем реакции этого цикла:
}Н + ^С -)• V3N + г,
V3N -»¦ ^С + е+ + щ
iH + i|C -> V4N + т,
JH + V4N -»• ^О + 7;
е+
|
Не.

8.5] Ядерная энергетика 285
Водородный цикл содержит три разных реакции, но первая и вторая
реакции за цикл происходят дважды (всего — пять реакций):
}Н
{Н
При температурах до 1,5 • 107 К больший вклад в энерговыделение
дает водородный цикл, при более высоких температурах —углеродный
цикл. Для Солнца оба цикла играют одинаково важную роль, в менее
ярких звездах преобладает водородный, в более ярких — углеродный.
В звездах-гигантах важную роль играют другие циклы (гелиевый
и неоновый).
> Управляемый термоядерный синтез. Если бы человечество на-
научилось управлять термоядерными реакциями, оно получило бы в свое
распоряжение практически неисчерпаемые источники энергии. В отли-
отличие от реакций, протекающих в недрах звезд, энергию надо извлекать
из небольшого количества термоядерного горючего с максимальной
эффективностью. Для этого надо нагреть вещество до температуры,
при которой вероятность слияния ядер при столкновениях будет до-
достаточно высока. Кроме того, надо научиться удерживать полученную
раскаленную плазму достаточно долгое время и извлекать выделившу-
выделившуюся энергию, преобразовывая ее, например, в электрическую.
Главная техническая трудность состоит именно в удержании плаз-
плазмы. Наиболее перспективный способ — помещение плазмы в магнитное
поле определенной конфигурации (магнитную ловушку). В установках
токомак плазму пытаются удерживать магнитным полем, которое
создается током, протекающем через саму плазму (этот же ток сна-
сначала участвует в разогреве плазмы). Удержанию плазмы в течение
достаточно долгого времени препятствуют различного вида неустой-
неустойчивости, которые возникают и быстро развиваются в горячей плазме,
находящейся в магнитном поле.
Для каждой реакции существует характерная температура 7q, до
которой надо нагреть плазму для наиболее эффективного извлечения
энергии. Второй характерный параметр — минимальное время г удер-
удержания этой плазмы, требуемое для получения выигрыша в энергии
(точнее, произведение пт концентрации плазмы на время).
К сожалению, реакция слияния двух протонов, наиболее привлека-
привлекательная с точки зрения запасов топлива (водород входит в состав воды),
обладает столь малым сечением, что не может рассматриваться как
основа для управляемого синтеза (хотя и протекает в недрах Солнца).

286 Элементы ядерной физики [ Гл. 8
Столь же привлекательно выглядят дейтерий-дейтериевые реакции
2Н + 2Н -* ?>Не + п + 3, 25 МэВ,
2Н + 2Н -+ ?Н + }H + 4, 03 МэВ,
так как дейтерий составляет 0,015 % от общих запасов водорода. Ха-
Характеристики этой реакции: 7q ~ 109 К, пт > 1022 с/м3. Однако
наиболее перспективным ближайшим кандидатом является дейтерий-
тритиевая реакция
2Н + 3Н -+ |Не + п + 17, 6 МэВ,
которая обладает заметно большим энергетическим выходом и лучши-
лучшими критическими параметрами: 7q ~ 2 • 108 К, пт > 1020 с/м3, что
компенсирует трудности, связанные с производством трития.
8.6. Элементарные частицы
В этом разделе мы приведем краткие сведения справочного ха-
характера о классах элементарных частиц, квантовых числах, законах
сохранения и кварковой структуре адронов.
> Фундаментальные взаимодействия. Превращениями и распа-
распадами элементарных частиц управляют три фундаментальных взаимо-
взаимодействия — сильное, электромагнитное и слабое (гравитационное вза-
взаимодействие в этих процессах несущественно). Чем слабее взаимодей-
взаимодействие, тем медленнее протекают определяемые им процессы. Сильное
взаимодействие имеет радиус действия 10~15 м, характерное время
определяемых им процессов 10~23 с. Сильное взаимодействие скреп-
скрепляет нуклоны в атомные ядра. Электромагнитное взаимодействие —
дальнодействующее (радиус действия — бесконечность), характерное
время определяемых им процессов не менее 10~20 с. Один из полигонов
этого наиболее нам знакомого взаимодействия — управление атомными
электронами, т.е. всем разнообразием веществ и химических реакций.
Слабое взаимодействие имеет радиус действия 10~18 м, характерное
время определяемых им процессов (в которых обычно участвуют ней-
нейтрино) не менее 10~10 с. Именно слабое взаимодействие управляет
реакцией слияния двух протонов, столь важной в энергетике Солн-
Солнца, и разнообразными ^-распадами. Слабое взаимодействие — самое
универсальное из трех, оно присутствует всегда, но является определя-
определяющим только при отсутствии других взаимодействий.
Фундаментальные взаимодействия осуществляются путем обмена
специальными частицами, которые относятся к классу фундаменталь-
фундаментальных векторных бозонов (спин всех этих частиц равен единице). Пе-
Переносчики взаимодействия рождаются одной из взаимодействующих

8.6] Элементарные частицы 287
частиц и поглощаются другой. Рождаемые частицы являются вирту-
виртуальными, для них не выполняется соотношение Е2 — р2с2 = т2с4,
что допускается принципом неопределенности AEAt ~ /г, если время
их жизни мало. Если масса переносчиков отлична от нуля, то радиус
взаимодействия равен их комптоновской длине волны К/тс (подроб-
(подробнее см. раздел 8.2). Переносчиком электромагнитного взаимодействия
является безмассовая частица фотон — хорошо знакомый нам квант
электромагнитного поля. Переносчиками слабого взаимодействия яв-
являются тяжелые промежуточные бозоны VK+, W~ и Z, массы которых
почти 100 ГэВ. Переносчиками сильного взаимодействия являются
глюоны — кванты восьми глюонных полей, осуществляющие взаимо-
взаимодействие между кварками. (В ранней тг-мезонной теории ядерных сил,
описанной в 8.2, переносчиками сильного взаимодействия считались
тг-мезоны). Масса глюонов равна нулю, но в отличие от фотонов они
взаимодействуют друг с другом и с кварками и не могут удалиться
дальше чем на 10~15 м.
Теперь мы приступим к описанию различных классов элементарных
частиц. Отметим несколько общих свойств.
1) Частицы могут быть как стабильными (электрон, протон, ней-
нейтрино), так и нестабильными. В последнем случае указывают время
жизни частицы (или ширину энергетического интервала АЕ = h/At),
а также каналы распада. Частицы, время жизни которых ~ 10~23 с,
называют резонансами. Частицы, время жизни которых много больше
этой величины, называют квазистабильными.
2) Частицы могут быть либо составными (состоять из других ча-
частиц, как нуклоны из кварков), либо быть (на доступных сегодня
энергиях) безструктурными (фотон, электрон, нейтрино, кварки). В по-
последнем случае их называют истинно элементарными (или фундамен-
фундаментальными) частицами.
3) Частица может быть либо бозоном (целый спин), либо фермионом
(полуцелый спин).
4) Почти каждой частице соответствует античастица, у которой все
заряды (не только электрический) имеют противоположный знак. Ан-
Античастица электрона— позитрон, античастица протона — антипротон,
античастица нейтрона — антинейтрон. Если частица совпадает со своей
античастицей, ее называют истинно нейтральной (например, фотон
или тг°-мезон).
5) Все частицы делятся на сильно взаимодействующие адроны (ба-
рионы и барионные резонансы, мезоны и мезонные резонансы), лепто-
ны (фермионы, не участвующие в сильном взаимодействии) и фунда-
фундаментальные бозоны (переносчики взаимодействий).
> Адроны, кварки и глюоны. Адронами называют все частицы,
участвующие в сильном взаимодействии. Адроны делятся на два боль-
больших класса— барионы (адроны с полуцелым спином, т. е. фермионы) и

288 Элементы ядерной физики [ Гл. 8
мезоны (адроны с целым спином, т.е. бозоны). К барионам относятся,
например, нуклоны, к мезонам — тг-мезоны.
Адроны — весьма многочисленный класс (открыто более 400 адро-
нов). Стройная классификация адронов и понимание многих их свойств
пришло только после появления в 60-х годах гипотезы о кварковой
структуре адронов, в соответствии с которой все адроны состоят из
фундаментальных частиц, называемых кварками. Спин всех кварков
равен 1/2, т.е. они являются фермионами. Всего существует шесть
разновидностей (или ароматов) кварков: и, d, s, с, b и t (от англий-
английских слов up, down, strange, charm, bottom, top). Массы кварков равны
mu « 5 МэВ, md « 7 МэВ, ms « 150 МэВ, тс « 1, 3 ГэВ, mb « 4, 3 ГэВ,
nit ~ 175 ГэВ. Самое необычное свойство кварков состоит в том, что
они имеют дробные электрические заряды. Кварки п, с и t называют
верхними, их заряд равен +2/3, кварки d, s и b называют нижними, их
заряд равен —1/3 (в единицах элементарного заряда).
Все барионы состоят из трех кварков, а все мезоны — из кварка
и антикварка. Нуклоны состоят из легких кварков и и d: протон содер-
содержит два n-кварка и один d-кварк (р = uud), нейтрон — два d-кварка
и один n-кварк (n = ddu). Из этих же кварков состоят тг-мезоны:
тг+ = ud, тг~ = du, 7г° представляет собой квантовую суперпозицию
двух состояний: тг° = (ии + dd)/y/2. Видно, что тг+ и тг~ являются
античастицами друг друга, а тг° совпадает со своей античастицей.
Частицы, содержащие s-кварк, называют странными, содержащие с-
кварк — очарованными.
Отметим сразу же, что на первый взгляд массы адронов заметно
больше суммы масс образующих их кварков. Но масса любой связанной
системы должна быть меньше суммы масс образующих ее частей на
величину энергии связи. Дело в том, что кварки внутри адронов окру-
окружены облаком виртуальных глюонов («одеты» в глюонную «шубу»).
Массы «одетых» кварков примерно на 350 МэВ больше массы «голых»
кварков.
Барионы, в состав которых входят более тяжелые кварки, чем и и d,
называются «гиперонами». Из кварков n, d, s можно составить шесть
гиперонов со спином 1/2: Л° (uds, m « 1120 МэВ), i7+, X70, U~ (uus,
uds, dds, m « 1200 МэВ), S°, E~ (uss, dss, m « 1320 МэВ). Распад
всех этих гиперонов определяется слабым взаимодействием, поэтому
время их жизни г ~ 10~10 с (кроме Х^-гиперона, распад которого
определяется электромагнитным взаимодействием, г ~ 10~20 с). Вме-
Вместе с протоном и нейтроном эти гипероны образуют октет (восьмерку)
барионов со спином 1/2. (Ниже мы поясним, чем отличаются Л° и Е°).
Далее идет декуплет (десятка) барионов со спином 3/2, причем сре-
среди них присутствуют барионы, состоящие из трех одинаковых кварков,
например, Л", Z\°, Z\+, Z\++ (ddd, udd, uud, uuu, m « 1230 МэВ). Са-
Самым тяжелым из декуплетаявляется /2~-гиперон (sss, m « 1670 МэВ).

8.6] Элементарные частицы 289
Отметим, что элементарные частицы, имеющие одинаковый кварковый
состав и отличающиеся только значением спина (или других квантовых
чисел), очень часто носят разные названия, как, например, нейтрон
и Л°-гиперон.
Перейдем к описанию мезонов. Кроме трех тг-мезонов, существуют
еще шесть мезонов со спином и орбитальным моментом, равными нулю,
которые содержат s-кварк: четверка /С+, К0, К0, К~ (us, ds, sd, su,
m « 500 МэВ) и два истинно нейтральных мезона rj и rjf (разные
квантовые суперпозиции состояний ий, dd и ss). Далее идет девятка
мезонов со спином S = 1, среди которых три р, четыре /С*, о;0 и (р°.
Все эти мезоны (а также г}') относятся к резонансам (г ~ 10~23 с).
Большим событием было открытие в 1974 г. первой очарованной
частицы J/-^-мезона (т = 3,1 ГэВ), представляющей собой одно из
состояний чармония се (чармоний обладает «скрытым очарованием»).
Затем были открыты другие очарованные мезоны (например, D^~ = cd,
D° = ей, Df = cs) и очарованные барионы (например, Л+ = udc),
а также более тяжелые «красивые» адроны, содержащие 6-кварк.
Цвет. Существование барионов, состоящих из трех одинаковых
кварков, противоречит принципу Паули, поскольку два из них должны
иметь одинаковые направления спинов. Более того, Л2~-гиперон имеет
спин 3/2, т.е. все три его s-кварка могут находиться в одинаковых
состояниях (когда проекция спина гиперона максимальна). В чем же
дело? Оказалось, что существует не один, а три кварка с одним и тем
же ароматом. Различие между ними описывается дополнительным
квантовым числом, которое может принимать три значения. Было
предложено называть это число цветом (цветовым зарядом), и при-
приписать ему значения R (красный), G (зеленый) и В (синий). Соот-
Соответственно, антикварки обладают цветами R, G, В (антикрасный,
антизеленый, антисиний). Следовательно, всего существует 18 кварков
и 18 антикварков. Смесь всех трех цветов считается бесцветной (белой).
Пара кварк-антикварк обладает «скрытым» цветом.
Цветовые заряды кварков являются источниками глюонных полей
(подобно тому как электрический заряд является источником элек-
электромагнитного поля). Кванты этих полей глюоны (от слова glue —
клей) осуществляют сильное взаимодействие. (Электромагнитное вза-
взаимодействие осуществляется путем обмена фотонами — квантами элек-
электромагнитного поля.) И глюоны, и фотоны являются безмассовыми
частицами, обладают спином 1 и отрицательной четностью (см. ниже).
Однако фотоны электрически нейтральны, а глюоны «окрашены», т. е.
сами участвуют в сильных взаимодействиях. Каждый глюон несет два
цветовых заряда: один цвет и один антицвет. Всего существует восемь
разных глюонов, шесть явно окрашенных (gRQ, Erb-> Qgw &gb-> 8вю
gBq) и два глюона со скрытым цветом.
10 А. И. Черноуцан

290 Элементы ядерной физики [ Гл. 8
В соответствии с законом сохранения цветового заряда при испуска-
испускании и поглощении глюона кварк должен изменять свой цвет. Например,
при испускании красным R кварком глюона RG он становится зеленым
G, но аромат его при этом не меняется:
ur -+ uG + gRQ-
(Аромат кварков может меняться только в слабых взаимодействиях,
т. е. при испускании W- или Z-бозонов.)
Поскольку глюоны обладают цветовым зарядом, они могут сами
испускать и поглощать глюоны и испытывать сильное взаимодействие
друг с другом. Изучением сильного взаимодействия как результата
излучения и поглощения глюонов кварками и глюонами занимается
квантовая хромодинамика (названная так по аналогии с квантовой
электродинамикой, изучающей электромагнитное взаимодействие как
результат обмена фотонами). Одно из главных утверждений квантовой
хромодинамики — невозможность существования свободных окрашен-
окрашенных объектов. В свободном виде могут существовать только такие
комбинации цветовых зарядов, которые в целом цветового заряда не
несут. Например, свободные адроны могут быть только в «белом»
состоянии, три его кварка в каждый момент времени имеют разные
цвета. (Правда, каждый кварк непрерывно меняет свой цвет, испуская
и поглощая виртуальные глюоны, как испущенные другим кварком,
так и рожденные в окружающей его «глюонной шубе» — облаке вирту-
виртуальных глюонов. Но полный цветовой заряд адрона остается белым.)
То же относится и к мезонам. Например, тг+-мезон является квантовой
суперпозицией трех цветовых состояниях u^d^ ucd^, uedg. Каждое
из этих состояний обладает скрытым цветом, но их суперпозиция яв-
является «белой».
Почему же нельзя разделить белый объект на два цветных (напри-
(например, удалить один из кварков из мезона или адрона)? Во-первых, обмен
цветными глюонами приводит к взаимодействию, потенциал которого
растет с расстоянием не медленнее, чем линейно (сила взаимодействия
не убывает). Возможное объяснение состоит в том, что глюонное поле
не рассеяно по всем направлениям (что соответствовало бы кулоновско-
му потенциалу), а сосредоточено в узкой «трубке» (струне), соединяю-
соединяющей кварки. Следовательно, для разделения кварков надо было бы за-
затратить бесконечно большую энергию. На самом деле, при удалении их
на расстояние, превышающее 10~15 м, глюонная струна «рвется», рож-
рождается пара кварк-антикварк и удаляемый кварк превращается в белый
мезон. При попытке получить два цветных объекта мы снова получа-
получаем два белых. (Отметим, что при больших энергиях разлетающихся
кварков каждый из них превращается не в один мезон, а в несколько
адронов — возникает так называемая «адронная струя». Наблюдение
адронных струй стало важным аргументом в пользу существования

8.6] Элементарные частицы 291
кварков.) Таким образом квантовая хромодинамика объясняет неудачу
всех попыток обнаружить свободные кварки или выбить их адронов,
хотя само существование кварков внутри адронов было подтверждено
экспериментами по рассеянию на адронах электронов высоких энергий.
Такое поведение кварков было названо «конфайнментом» (от англий-
английского confinement— заточение).
> Лептоны. Фундаментальные фермионы. Лептонами называ-
называются фермионы, не участвующие в сильных взаимодействиях. Суще-
Существует три пары лептонов: электрон е~ и электронное нейтрино г/е,
мюон /л~ и мюонное нейтрино г/д, тау-лептон т~ и тау-нейтрино vT.
Спин всех лептонов равен 1/2. У каждого заряженного лептона есть
античастица: е+, /i+ и т+. Окончательно не установлено, являются ли
нейтрино истинно нейтральными частицами или у них есть античасти-
античастицы—антинейтрино г/е,^и^/г. Лептоны являются фундаментальными
частицами — у них не обнаружено никакой структуры. Эксперимен-
Экспериментально установлено, что каждый заряженный лептон участвует в сла-
слабых взаимодействиях в паре со своим нейтрино, например:
п—> ре~ие, тг+ —у /i+^M, т+ —у ите+ие.
Массы мюона и тау-лептона равны 106 МэВ и 1784 МэВ. Эти ча-
частицы нестабильны: мюон распадается по каналу /л~ —у е~г/ег/д, время
жизни 2 • 10~6 с, более тяжелый тау-лептон распадается по многим
каналам, время жизни 5 • 10~13 с. Для нейтрино можно указать только
верхние границы масс: mVe < 30 эВ, т^ < 0, 5 МэВ, т„т < 150 МэВ.
Шесть лептонов и шесть кварков образуют класс фундаменталь-
фундаментальных фермионов, из которых «сделаны» все остальные элементарные
частицы. Особую роль играют фундаментальные фермионы «первого
поколения» и, d, i/e, e~, из которых составлены нуклоны и атомы
и которые определяют ход почти всех наблюдаемых в природе про-
процессов. Фундаментальные фермионы второго (с, s, v^ fi~) и третьего
(t, d, i/t,t~) поколений получают искусственно в мощных ускорителях.
Однако только изучение всей совокупности фундаментальных частиц
дает возможность понять устройство и эволюцию нашего мира.
Все процессы в мире элементарных частиц сводятся к взаимодей-
взаимодействиям между фундаментальными фермионами, осуществляемыми пу-
путем обмена несколькими фундаментальными векторными бозонами
(фотоном, глюонами, тремя промежуточными бозонами). Всеми этими
процессами управляют законы сохранения.
Напомним, что переносчик электромагнитного взаимодействия —
фотон — может испускаться или поглощаться только заряженными
частицами, при этом ни заряд, ни цвет, ни аромат частицы не меняются.
Переносчики сильного взаимодействия — глюоны — могут испускаться
или поглощаться кварками и глюонами, при этом может меняться цвет
кварка, но его заряд и аромат не меняются.
ю*

292 Элементы ядерной физики [ Гл. 8
Слабые взаимодействия осуществляются за счет испускания и по-
поглощения промежуточных векторных бозонов VK+, W~ и Z°. При по-
поглощении или испускании заряженного бозона заряженным лептоном
он превращается в соответствующее нейтрино (и наоборот, нейтрино
превращается в соответствующий ему заряженный лептон). Универ-
Универсальность слабых взаимодействий проявляется в том, что векторные
бозоны испускаются и поглощаются не только лептонами, но и квар-
кварками. (Отметим, что в отличие от глюонов промежуточные бозоны не
обладают цветом, т.е. не участвуют в сильных взаимодействиях.) При
испускании или поглощении заряженного бозона верхний кварк пре-
превращается в нижний или наоборот. Существенно, что любой верхний
кварк (п, с, t) может превращаться в любой из нижних кварков (ti, s,
Например, распад нейтрона п —у ре ve сводится к распаду d-кварка
d —у ue~ve, который описывается как превращение d-кварка в п-кварк
с испусканием VK+-6o3OHa, который затем превращается в пару e~De.
Открытие в 1974 г. промежуточных бозонов, существование и свойства
которых были предсказаны так называемой «стандартной теорией электро-
электрослабого взаимодействия» Вайнберга-Глэшоу-Салама (см. ниже), было важ-
важным событием физики элементарных частиц. Открытие было сделано на
специально созданных протон-антипротонных коллайдерах (ускорителях на
встречных пучках). При столкновении один кварк и один антикварк превра-
превращались в промежуточный бозон, а оставшиеся два кварка каждой частицы
превращались в мощные адронные струи. За время ~ 10~ с рожденный
бозон распадался либо на кварк+антикварк, либо на два лептона (например,
электрон+антинейтрино). Удалось обнаружить именно электроны, рожден-
рожденные в распаде W~-бозона (при этом отбирались только те процессы, где
закон сохранения импульса нарушался на величину импульса, унесенного
нейтрино, который равен импульсу электрона). Чтобы оценить сложность
событий, отметим, что в первой серии опытов из миллиарда событий были
отобраны только шесть надежных.
> Характеристики частиц и законы сохранения. Все характе-
характеристики частиц можно разбить на две группы: геометрические характе-
характеристики, связанные со свойствами пространства-времени (масса, спин,
пространственная четность), и внутренние квантовые числа, отражаю-
отражающие симметрию фундаментальных взаимодействий (заряд, барионный
заряд, лептонный заряд, изоспин, странность, очарование и некоторые
другие).
С каждой из этих характеристик связан какой-нибудь закон со-
сохранения, и имеет смысл их обсуждать совместно. Некоторые законы
сохранения считаются абсолютно точными, другие — приближенными,
верными для определеного класса реакций. Некоторые из приближен-
приближенных законов сохранения нарушаются только слабыми взаимодействия-

8.6] Элементарные частицы 293
ми (в процессах, определяемых слабыми взаимодействиями), другие —
и слабыми, и электромагнитными взаимодействиями. Законы сохране-
сохранения позволяют предсказать возможность или невозможность распадов
и реакций, понять, какие времена им соответствуют, предсказать су-
существование новых частиц и указать условия их рождения. Отметим,
что в квантовой теории действует принцип «возможно все, что не
запрещено законами сохранения», что делает применение этих законов
особенно эффективным.
Масса частицы и сохранение энергии-импульса. Масса частицы т
является ее важнейшей характеристикой. Все элементарные частицы
имеют различные массы. Соотношение Эйнштейна связывает массу
частицы с ее энергией покоя.
Законы сохранения энергии и импульса является следствием од-
однородности времени и пространства. Они играют важную роль при
анализе реакций. Из закона сохранения энергии, например, следует, что
распад нестабильной частицы может идти только по таким каналам,
где сумма масс рожденных частиц меньше массы исходной частицы.
Другой пример: закон сохранения импульса запрещает аннигиляцию
электрон-позитронной пары с образованием одного 7-кванта (в системе
центра масс импульс пары равен нулю). Законы сохранения энергии
и импульса позволяют вычислить порог произвольной реакции (не за-
запрещенной другими законами сохранения). Такой расчет был выполнен
в разделе 8.4 (см. формулу C4)).
Пример 1. Вычислить пороговую энергию 7"кванта Для рождения
электрон-позитронной пары на покоящемся протоне.
Решение. Отметим, что рождение фотоном электрон-позитронной пары
невозможно в пустом пространстве (см. выше), но может происходить в поле
третьей частицы. В данном примере речь идет о реакции j-\-p —>¦ е~ +е -\-р.
Положив в формуле C4) т = О, М = тр, mi+m2 +. . . = 2те+тр, получим
2тр \ тпр)
(см. также C5), где |Q| = 2mec2).
Спин частицы I и закон сохранения момента импульса. Спин ча-
частицы определяет, какой статистике она подчиняется — Ферми-Дирака
(полуцелый спин) или Бозе-Эйнштейна (целый спин). Спин адрона
складывается из спинов и орбитальных моментов составляющих его
кварков. Спин частицы задает единственное выделенное направление
в системе отсчета, где она покоится.
Закон сохранения момента импульса является следствием изотроп-
изотропности пространства. Применение этого закона для анализа реакции
затрудняется тем, что спины складываются по правилу сложения мо-
моментов. Например, полный угловой момент системы двух частиц со
спином 1 может быть равен нулю. Однако легко установить, является

294 Элементы ядерной физики [ Гл. 8
полный момент целым или полуцелым. Этого часто достаточно, чтобы
закрыть возможность какой-либо реакции. Пример: безнейтринный
распад нейтрона на две частицы — протон и электрон — запрещен
законом сохранения момента импульса.
Четность. Четность (точнее, пространственная четность) части-
частицы Р является чисто квантовым понятием. Она показывает, как ведет
себя волновая функция частицы при пространственной инверсии —
замене х —У — х, у —У —y,z —У —z. Возможны два результата: волновая
функция не меняется (положительная четность, Р = +1) или изме-
изменяет знак (отрицательная четность, Р = —1). Четность — внутренняя
характеристика частицы (как заряд, спин и др.). Электрон, протон,
нейтрон имеют четность Р = 1, а фотон и тг-мезоны — четность Р = — 1.
Четность любого кварка равна +1, четность антикварка —1. Четность
составной частицы (в состоянии с нулевым орбитальным моментом)
равна произведению четностей составляющих ее частиц.
Долгое время предполагалось, что пространственная четность дол-
должна сохраняться во всех реакциях. Дело в том, что закон сохранения
четности является следствием утверждения об инвариантности про-
процессов относительно пространственной инверсии, или, что то же самое,
относительно зеркального отражения, так как инверсия сводится к от-
отражению и повороту (например, отражению относительно плоскости
XY и повороту на 180° относительно оси Z). Считалось очевидным, что
все процессы в обычном и «зазеркальном» мирах должны подчиняться
одним и тем же физическим законам. Однако впоследствии было уста-
установлено, что это утверждение неверно для процессов, определяемых
слабыми взаимодействиями. Нарушение четности было предсказано
Ц. Ли и Ч. Янгом в 1956 г. и чуть позже подтверждено в опытах By
Цзянь-сун. В этих опытах было показано, что при /3-распаде электроны
испускаются преимущественно в направлении, противоположном спи-
спину ядра. Поскольку при отражении спин ядра изменяет свое направле-
направление, то в зазеркальном мире электроны испускаются преимущественно
в направлении спина.
В этом же опыте наблюдается нарушение еще одной симметрии (ее на-
называют зарядовой, или С-симметрией) — относительно замены всех частиц
на античастицы. Получалось, что в «антимире» позитроны будут вылетать
преимущественно в направлении спина. Однако если произвести оба преоб-
преобразования — пространственное отражение и замену частиц античастицами —
то процесс опять перейдет сам в себя. Некоторое время считалось, что та-
такая «комбинированная» СР-симметрия является абсолютно точной. Однако
затем были обнаружены слабые процессы, протекающие с нарушением СР-
симметрии. В настоящее время абсолютно точной считается только СРТ-
симметрия, где вместе с описанными преобразованиями одновременно про-
производится отражение времени. Эта симметрия следует из основных свойств
пространства и времени и строго доказывается в квантовой теории поля (так

8.6] Элементарные частицы 295
называемая СРТ-теорема). Этой симметрии достаточно для доказательства
равенства масс и времен жизни частицы и античастицы.
Лептонные заряды Le, L^, LT. Экспериментально установлено, что
в любых процессах разность между числом лептонов и числом антилеп-
тонов данного вида сохраняется. В соответствии с этим были введены
три лептонных заряда— Le, L^ и LT. Для е и ve считается Le = 1,
соответственно для их античастиц Le = —1, а для всех остальных
частиц Le = 0. Точно так же поступают с двумя другими зарядами.
Лептонные заряды сохраняются во всех процессах (при доступных
в настоящее время энергиях).
Оставшиеся законы сохранения относятся к миру адронов. Вве-
Введенные эмпирически, они находят естественное объяснение в рамках
кварковой модели.
Барионный заряд В. Экспериментально установлено, что в любых
процессах сохраняется разница между числом барионов и числом ан-
тибарионов. Соответственно каждому бариону стали приписывать ба-
барионный заряд ?? = 1, антибарионам В = — 1, всем мезонам В = 0.
Барионный заряд сохраняется во всех процессах (при доступных
в настоящее время энергиях).
Если приписать всем кваркам заряд В = 1/3 (а антикваркам
В = —1/3), то закон сохранения барионного заряда сводится к сохране-
сохранению числа кварков (точнее, разности между числом кварков и числом
антикварков).
Странность. Когда были открыты первые гипероны, выяснились
некоторые странные особенности их поведения. Во-первых, хотя рож-
рождение гиперонов происходило при столкновениях нуклонов высоких
энергий, т.е. с участием сильных взаимодействий, они распадались
за времена ~ 10~10 с, соответствующие слабым взаимодействиям.
Во-вторых, гипероны никогда не рождались поодиночке. Например,
при столкновении протонов Л°-гиперон рождался только совместно
с /С+-мезоном или i7+-rHnepoHOM, но никогда с /С"-мезоном или Е~-
гипероном.
Для объяснения этих особенностей этим частицам было приписано
новое квантовое число странность S, которое сохраняется в сильных
и электромагнитных взаимодействиях, а в слабых взаимодействиях
может изменяться на =Ы. Для объяснения экспериментов частицам Л°,
X70, U~ и К~ была присвоена странность S = — 1, ^-гиперонам —
странность S = —2, /2~-гиперону — странность S = —3.
В кварковой модели адронов носителем странности считается кварк
аромата s (ему приписывается S = — 1, для всех остальных кварков
S = 0). Медленность распадов, связанных с изменением странности,
объясняется тем, что изменение аромата кварка s —У и может проис-
происходить только в слабых взаимодействиях, при испускании W"-бозона
или поглощении И/+-бозона.

296 Элементы ядерной физики [ Гл. 8
Очарование С', красота Ь. Совершенно аналогично странности вво-
вводятся квантовые числа очарование (charm) (с-кварку приписывается
G = 1), красота (beuty) F-кварку присваивается 6 = 1). Последнему,
самому тяжелому, ^-кварку соответствует квантовое число t (truth —
истинность). Аналогично странности, квантовые числа С, 6 и ? сохра-
сохраняются в сильных реакциях, но могут изменяться в слабых реакциях.
Изотопический спин Т . Изотопический спин был введен в ядерной
физике и сыграл важную роль в классификации основных и возбужденных
состояний ядер. Введение этого необычного квантового числа (которому
нет аналога в классической физике) отражает предположение о зарядовой
независимости ядерных сил, т. е. о тождественном совпадении этих сил
в парах п — п, п — р, р — р в одинаковых пространственных и спиновых
состояниях. Для описания зарядовой независимости вводят вектор изото-
изотопического спина Т, который имеет для обоих нуклонов значение Т = 1/2, но
разную проекцию: Tz = 1/2 для протона и Tz = —1/2 для нейтрона. Таким
образом, два нуклона образуют изотопический дублет. Ядерное взаимодей-
взаимодействие считается независимым от «направления» вектора Т, т. е. с точностью
до электромагнитного взаимодействия пространство изотопического спина
изотропно (свойства системы не меняются при вращении вектора Т).
Сложение изотопических спинов в системе из нескольких нуклонов про-
производится по тем же правилам, что и сложение угловых моментов. Ядра
с одинаковым числом нуклонов (изобары) и с одинаковыми значениями Т
образуют ядерный мулътиплет из ТТ + 1 ядер (с разными Tz, т. е. разными
зарядами), все члены которого обладают близкими свойствами. Например,
ядра ^С, ^В (в возбужденном состоянии) и ^Ве образуют изотопический
триплет с Т = 1, а 2Не является изотопическим синглетом (Т = 0). В основ-
основном состоянии ядро имеет минимально возможное значение Т при заданной
проекции Tz (которая вычисляется по его составу); например, основное
состояние ^В имеет Т = 0.
Изотопический спин играет важную роль в мире элементарных частиц,
в частности, для классификации адронов. Барионы и мезоны разбиваются
на мультиплеты с близкими свойствами, причем число частиц в мультиплете
связано с изотопическим спином соотношением N = 2Т + 1. Так, три тг-
мезона образуют триплет с Т = 1, К0- и /С+-мезоны — дублет с Т = 1/2,
три 17-гиперона — триплет с Т = 1, четыре Л-гиперона имеют Т = 3/2,
Л°-гиперон — единственный член синглета с Т = 0. Члены мультиплета
различаются между собой проекцией изотопического спина Tz.
В модели кварков наличие мультиплетов объясняется тем, что и- и d-
кварки обладают близкими массами и различаются только зарядами. Этим
кваркам приписывается значение Т = 1/2, причем для n-кварка Tz = 1/2,
а для d-кварка Tz = —1/2. Для остальных кварков принимается Т = 0.
Изотопический спин адронов вычисляется по правилам сложения угловых
моментов. Так, например, дублет /С-мезонов имеет кварковый состав u^s

8.6] Элементарные частицы 297
и ds. При сложении двух изотопических спинов 1/2 может получиться или
изотопический спин Т = О (TZ = 0), или изотопический спин Т = 1 (Тг = — 1,
Тг = 0, Tz = 1). Первому состоянию соответствует гиперон Л° = uds
(изотопический синглет), а изотопический триплет образуется гиперонами
Е~ = dds, U° = uds, Е+ = uus.
В реакциях, определяемых сильными взаимодействиями, действует закон
сохранения изотопического спина — сохраняются иТ,иТ2. Электромагнит-
Электромагнитные и слабые взаимодействия нарушают закон сохранения Г, но Т2 в элек-
электромагнитных взаимодействиях сохраняется, а нарушается только слабыми
взаимодействиями. Дело в том, что для изменения Tz должно произойти
превращение и- или с/-кварка в другой кварк, что возможно только при
слабых взаимодействиях (при поглощении или испускании заряженного W-
бозона).
> Электрослабое взаимодействие. В стандартной теории элек-
электрослабого взаимодействия оба взаимодействия — слабое и электро-
электромагнитное, вместе со своими векторными бозонами, возникают в рам-
рамках единого подхода. Изначальными (или, как их называют, затра-
затравочными) частицами, осуществляющими единое электрослабое взаи-
взаимодействие, считаются четыре векторные безмассовые частицы, две
нейтральные и две заряженные. В реальном мире симметрия между
этими частицами оказывается спонтанно нарушенной, и три из этих
частиц приобретают массу (промежуточные бозоны), а одна остается
безмассовой (фотон). Многие выводы теории (в частности, значения
масс промежуточных бозонов) получили экспериментальное подтвер-
подтверждение. Значение константы слабого взаимодействия оказалось боль-
больше, чем электромагнитного, а причиной медленности слабых процессов
по сравнению с электромагнитными является большая масса W- и Z-
бозонов (~ 100 ГэВ). При энергиях, гораздо больших, чем эти массы,
симметрия восстанавливается (массами можно пренебречь), и работает
единое симметричное электрослабое взаимодействие.
> Великое объединение. После блестящего успеха теории элек-
электрослабого взаимодействия были созданы теории, позволяющие объ-
объединить все три фундаментальных взаимодействия — сильное, слабое
и электромагнитное (эти теории были названы «великое объедине-
объединение»). Граничной энергией для этого объединения является немысли-
немыслимая величина Е ~ 1015 ГэВ. При этой энергии константы трех взаимо-
взаимодействий становятся равны друг другу. При больших энергиях все три
взаимодействия выступают вместе — как универсальное симметричное
взаимодействие. Носителями этого взаимодействия являются 24 век-
векторных бозона — восемь глюонов, три промежуточных бозона, фотон
и сверхтяжелые Х- и У-бозоны с массами ~ 1015 ГэВ. Эти бозоны несут
как электрический заряд D/3 у X и 1/3 у У), так и цветовой (с учетом
трех цветов и античастиц получаем 12 частиц). При поглощении или

298 Элементы ядерной физики [ Гл. 8
испускании Х- или У-бозона кварк может превратиться в лептон или
наоборот. Следовательно, участие этих бозонов во взаимодействиях
приводит к нарушению законов сохранения барионного и лептонного
зарядов (но закон сохранения электрического заряда остается незыб-
лимым!). В результате с очень малой вероятностью (из-за больших
масс X, Y) может происходить распад протона с превращением его
в позитрон (и несколько тг-мезонов). Предсказанное теорией время
жизни протона лежит в пределах г ~ 1030 -г- 1035 лет. В настоящее
время поиски распадов протона (в больших массах воды, помещенных
в глубокие шахты для исключения фона) дает границу г > 1032 лет.

Список литературы
1. Бейзер А. Основные представления современной физики. — М.: Атомиз-
дат, 1973. - 548 с.
2. Белонучкин В. Е., Заикин Д. Л., Кингсеп Л. С. и др. Задачи по общей
физике. — М.: Физматлит, 2002.
3. Дубровский И. М., Егоров Б. В., Рябошапка К. П. Справочник по физи-
физике. — Киев: Наукова думка, 1986. — 558 с.
4. Енохович А. С. Справочник по физике. — М.: Просвещение, 1978. — 512 с.
5. Иродов И. Е. Задачи по общей физике. — М.: Лаборатория Базовых Зна-
Знаний, 2001. — 432 с.
6. Иродов И. Е. Задачи по квантовой физикее. — М.: Лаборатория Базовых
Знаний, 2001. — 216 с.
7. Иродов И. Е. Волновые процессы. Основные законы. — М.: Лаборатория
Базовых Знаний, 1999. — 256 с.
8. Иродов И. Е. Физика макросистем. Основные законы. — М.: Лаборатория
Базовых Знаний, 2001. — 200 с.
9. Иродов И. Е. Квантовая физика. Основные законы. — М.: Лаборатория
Базовых Знаний, 2001. — 272 с.
10. Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. —
248 с.
11. Иродов И. Е. Основные законы электромагнетизма. — М.: Высшая школа,
1991. - 288 с.
12. Калашников С. Г. Электричество. — М.: Наука, 1985. — 576 с.
13. Кикоин Л. К., Кикоин И. К. Молекулярная физика. — М.: Наука, 1976. —
480 с.
14. Киттель Ч., Найт В., Рудерман М. Механика. — М.: Наука, 1975. —
480 с.
15. Киттель Ч. Элементарная физика твердого тела. — М: Наука, 1965. —
368 с.
16. Кошкин Н. И., Ширкевич М. Г. Справочник по элементарной физике. —
М.: Наука, 1988. — 256 с.
17. Курс физики / Под ред. Папалекси Н. Д., т. 1, 2. — М.: Гостехиздат, 1948.
18. Кухлинг X. Справочник по физике. — М.: Наука, 1982. — 520 с.
19. Лансберг Г. С. Оптика. — М.: Наука, 1976. — 926 с.
20. Матвеев А. И. Механика и теория относительности. — М.: Высшая шко-
школа, 1986. - 320 с.
21. Матвеев А. И. Молекулярная физика. — М.: Высшая школа, 1981. —
400 с.
22. Матвеев А. Н. Электричество и магнетизм. — М.: Высшая школа, 1983. —
463 с.
23. Наумов А. И. Физика атомного ядра и элементарных частиц. — М.: Про-
Просвещение, 1984 — 384 с.

300 Список литературы
24. Окунь Л. Б. a, /3,j, . . . , Z. Элементарное введение в физику элементар-
элементарных частиц. — (Библиотечка «Квант», выпуск 45). М.: Наука, 1985. —
112 с.
25. Орир Дж. Физика, т. 1, 2. — М.: Мир, 1981.
26. Парселл Э. Электричество и магнетизм. — М.: Наука, 1971. — 448 с.
27. Савельев И. В. Курс физики. Т. 1. Механика. Молекулярная физика. —
М.: Наука, 1989. - 350 с.
28. Савельев И. В. Курс физики. Т. 2. Электричество и магнетизм. — М.:
Наука, 1989. - 496 с.
29. Савельев И. В. Курс физики. Т. 3. Квантовая физика. — М.: Наука,
1989. - 301 с.
30. Сивухин Д. В. Механика. — М.: Физматлит, 2002. — 576 с.
31. Сивухин Д. В. Термодинамика и молекулярная физика. — М.: Физматлит,
2002. - 592 с.
32. Сивухин Д. В. Электричество. — М.: Физматлит, 2002. — 688 с.
33. Сивухин Д. В. Оптика. — М.: Физматлит, 2002. — 752 с.
34. Сивухин Д. В. Атомная физика. — М.: Физматлит, 2002.
35. Стрелков С П. Механика. — М.: Наука, 1975. — 560 с.
36. Таблицы физических величин, справочник / Под ред. И. К. Кикоина. —
М.: Атомиздат, 1976. — 1008 с.
37. Фейнман Р., Лейтон Р., Сэндс. М. Фейнмановские лекции по физике,
т. 1-9. - М.: Мир, 1965-1967.
38. Физика микромира. Маленькая энциклопедия. — М.: Советская энцикло-
энциклопедия, 1980. — 528 с.
39. Физическая энциклопедия / Под ред. А. М. Прохорова, Т. 1-4. — М.: Сов.
энциклопедия, 1988-1995.
40. Физический энциклопедический словарь / Под ред. А. М. Прохорова. —
М.: Сов. энциклопедия, 1983. — 928 с.
41. Хайкин С Э. Физические основы механики. — М.: Наука, 1971. — 752 с.
42. Яворский Б. М., Детлаф А. А. Справочник по физике. — М.: Наука,
1985. - 512 с.
43. Яворский Б. М., Детлаф А. А. Справочник по физике для инженеров
и студентов вузов. — М.: Наука, 1974. — 942 с.

Приложения
Основные физические постоянные
Название
Боровский радиус
Гравитационная постоянная
Комптоновская длина волны
протона
Комптоновская длина волны
электрона
Коэффициент в законе Био-
Савара
Коэффициент в законе Кулона
Магнетон Бора
Магнитная постоянная
Магнитный момент протона
Магнитный момент электрона
Масса нейтрона
Масса протона
Масса электрона
Отношение масс протона и элек-
электрона
Постоянная Авогадро
Постоянная Больцмана
Постоянная Вина
Постоянная Планка
Обозначение
h2
а0 — 2
теке
7
\ h
лсР —
трс
Асе —
тес
МО
4тг
* = /
4тг?о
eh
1
МО - 2
Pmpi fJ'p
Рте •> Me
тп
тр
ГПе
гпр
ГПе
NA
к = R/NA
b
h
Значение
5,2918- 101 м
6,6720- 101 Н-м2/кг2
1,3214-Ю-15 м
2,4263- 102 м
10 Гн/м
9,00-109 м/Ф
0,9274 • Ю-23 Дж/Тл
1,2566 • 10"8 Гн/м
1,4106 • 106 Дж/Тл
9,2848 • 10~24 Дж/Тл
1,6750- 107 кг
1,6726- 107 кг
9,1095- 101 кг
1836,15
6,0220 • 1023 моль
1,3807 -103 Дж/К
2,8978-Ю-3 м-К
6,6262-Ю-34 Дж-с

302
Приложения
Постоянная Планка
Постоянная Ридберга для энер-
энергии
Постоянная Ридберга для и
Постоянная Ридберга для из
Постоянная Ридберга для Л
Постоянная Стефана — Больц-
мана
Скорость света в вакууме
Удельный заряд электрона
Удельный заряд протона
Универсальная газовая постоян-
постоянная
Электрическая постоянная
Элементарный заряд
Энергия покоя нейтрона
Энергия покоя протона
Энергия покоя электрона
R-
Ru
R
Rx
а
h
i 2 4
тек е
~ 2П2
= R/2nh
cu = R/h
= R/2irch
60 с2 Я3
с
-e/rrie
е/тр
R
so
е
тпс2
трс2
тес2
1,0546-Ю-34 Дж-с
13,605 эВ
3,2898 • 1015 с
2,0671 • 1016 с
1,0974- 107 м
5,6703-Ю-8 Вт/(м2 -К4)
2,9979 • 108 м/с
-1,7588- 1011 Кл/кг
0,9579 • 108 Кл/кг
8,3144 Дж/(моль- К)
8,8542 • 102 Ф/м
1,6022 • 109 Кл
939,57 МэВ
938,28 МэВ
0,51100 МэВ
Греческий алфавит
А, а -
в,р
Г,у-
А,5-
Е,е-
Z,C-
н,л
0,е
- альфа
— бета
- гамма
- дельта
эпсилон
- дзета
— эта
— тета
i,t
К,к
А,Х-
М,
N,
О,о-
п,
— йота
— каппа
— ламбда
[1 — МЮ
v — ню
\ — кси
- омикрон
п — пи
р,
/ j (У
т,
ф,
х,
ф,
П, со
р
Т
ф
1
V
-ро
- сигма
— тау
ипсилон
— фи
— хи
— пси
- омега

Приложения
303
Десятичные приставки
Множи-
Множитель
ю18
ю16
ю12
ю9
106
103
ю2
ю1
Приставка
наимено-
наименование
экса
пета
тера
гига
мега
кило
гекто
дека
обозначение
Э
П
т
г
м
к
г
да
Множи-
Множитель
ю-1
ю-2
10
10
10"9
ю-12
106
ю-18
Приставка
наимено-
наименование
деци
санти
МИЛЛИ
микро
нано
пико
фемто
атто
обозначение
д
с
м
мк
н
п
ф
а
Массы легких нуклидов
Z
0
1
2
3
4
5
Нуклид
п
гН
2Н
Зн
3Не
4Не
6Li
7Li
7Ве
8Ве
9Ве
10Ве
юв
ПВ
М — А, а.е.м
0,00867
0,00783
0,01410
0,01605
0,01603
0,00260
0,01513
0,01601
0,01693
0,00531
0,01219
0,01354
0,01294
0,00930
Z
6
7
8
9
10
11
12
Нуклид
пс
12С
18С
13N
14N
15N
1б0
i60
17О
19p
20Ne
23Na
24Na
24Mg
M — А, а.е.м
0,01143
0
0,00335
0,00574
0,0037
0,00011
0,00307
-0,00509
-0,00087
-0,00160
-0,00756
-0,01023
-0,00903
-0,01496

304
Приложения
Элементарные частицы
Q — электрический заряд, L — лептонный заряд, / — спин, Р — четность,
В — барионный заряд, S — странность, С — очарование, Т — изотопический
спин, Тz — проекция изотопического спина
1. Лептоны (/ = 1/2, В = 0)
Частица
ит,ит
е-,е+
т-,т+
Масса,
МэВ
<8эВ
<0,27
<31
0,51100
105,66
1784
Q
0
0
0
Tl
=Fl
Tl
±1
0
0
±1
0
0
0
±1
0
0
±1
0
0
0
±1
0
0
±1
Время
жизни, с
2,197-Ю
2,95-10-13
Основные
каналы
распада
е~ иеи^
е ve и т;
2. Кварки
Кварк
и
d
s
с
b
t
Q
+2/3
-1/3
-1/3
+2/3
-1/3
+2/3
/
1/2
1/2
1/2
1/2
1/2
1/2
Т
1/2
1/2
0
0
0
0
Tz
+1/2
-1/2
0
0
0
0
в
1/3
1/3
1/3
1/3
1/3
1/3
s
0
0
-1
0
0
0
с
0
0
0
1
0
0
b
0
0
0
0
-1
0
t
0
0
0
0
0
1
m, ГэВ
0,005
0,075
0,150
1,5
5
175
3. Фундаментальные бозоны
Частица
Фотон, 7
Z0
W+, W"
Масса, ГэВ
0
91,19
80,15
1Р
\~
1
1
Ширина, ГэВ
Стабилен
2,49
2,25

Приложения
305
4. Некоторые барионы и барионные резонансы (L = 0, ?? =
Час-
Частица
Р
п
Л
Е+
и0
S~
А~
Л°
л+
Л++
Q-
"с
Л?
Л?
Квар-
ковый
состав
uud
udd
uds
uus
uds
dds
uss
dss
ddd
udd
uud
uuu
sss
udc
ddc
dsc
ssc
udb
Масса,
МэВ
938,27
939,57
1115,6
1189,4
1192,5
1197,4
1314,9
1321,3
1232
1672,4
2285
2453
2469
2706
5620
Ip
1/2+
1/2+
1/2+
1/2+
1/2+
1/2+
1/2+
1/2+
3/2+
3/2+
1/2+
1/2+
1/2+
1/2+
1/2+
S
0
0
-1
-1
-1
-1
-2
-2
0
0
0
0
-3
0
0
-1
-2
0
С
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
b
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-1
T
1/2
1/2
0
1
1
1
1/2
1/2
3/2
3/2
3/2
3/2
0
0
1
1/2
0
0
1/2
-1/2
0
1
0
-1
1/2
-1/2
-3/2
-1/2
1/2
3/2
0
0
-1
-1/2
0
0
Время
жизни, с
(ширина,
МэВ)
>5-1032 лет
889
2,63-10-10
0,799-10-10
7,4-Ю-20
1,48-НГ10
2,90-100
1,64-НГ10
A15)
0,82-100
1,9-НГ13
?
ю-13
?
1,0-Ю2

306
Приложения
5. Некоторые мезоны и мезонные резонансы (L = О, В = 0)
Частица
7Г+,7Г-
7Г°
п
я'
к+,к-
р+,р~
р°
к*+,к*~
D+,D~
D°,D°
Dt,D~
В+,В~
В°,В°
J/ф
Г
Кварко
вый
состав
ud, du
ии, dd
ии, dd,
ии, dd,
u!t, us
dl, ds
ud, du
uu, dd
uu, dd,
uu, dd,
u^s, us
ds, ds
dc, dc
uc, uc
cs, cs
ub, ub
db,db
cc
(чармо-
ний)
bb
Масса,
МэВ
139,57
134,97
548,8
957,2
493,65
497,67
768,3
781,95
1019,4
891,8
1869,3
1864,5
1968,8
5278,8
2980
3096,9
9460,3
Q
±1
0
0
0
±1
0
±1
0
0
0
±1
0
±1
0
±1
±1
0
0
0
0
Ip
0"
o-
o-
(Г
(Г
(Г
1"
1"
1"
1"
1"
1"
(Г
(Г
0"
0"
0"
0"
1"
1"
s
0
0
0
0
±1
±1
0
0
0
0
±1
±1
0
0
±1
0
0
0
0
0
с
0
0
0
0
0
0
0
0
0
0
0
0
±1
±1
±1
0
0
0
0
0
b
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
±1
±1
0
0
0
T
1
1
0
0
1/2
1/2
1
1
0
0
1/2
1/2
1/2
1/2
0
1/2
1/2
0
0
0
Tz
±1
0
0
0
±1/2
±1/2
±1
0
0
0
±1/2
±1/2
Tl/2
Tl/2
0
±1/2
±1/2
0
0
0
Время
жизни, с
(ширина,
МэВ)
2,603-НГ8
8,4-НГ17
@,0012)
@,208)
1,237-Ю"8
0,892-Ю0
5,17-Ю"8
A49,1)
(8,43)
D,41)
D9,8)
10,6-НГ13
4,2-Ю3
4,4-Ю3
1,6-НГ12
1,5-Ю2
A0)
@,068)
@,052)

Приложения
307
Некоторые астрономические постоянные
Название
Стандартное ускорение свободного
падения
Масса Земли
Плотность Земли (средняя)
Радиус Земли (средний)
Расстояние от Земли до Луны (сред-
(среднее)
Расстояние от Земли до Солнца
(среднее)
Масса Солнца
Радиус Солнца (средний)
Масса Луны
Радиус Луны
Обозначение
g
М3
рз
—
—
Me
Re
Мл
Rл
Значение
9,8067 м/с2
5,976 • 1024 кг
5,52 • 103 кг/м3
6378 км
3,844- 108 м
1,496 • 1011 м
1,99- 1030 кг
6,96-108 м
7, 35 • 1022 кг
1,74- 106 м

Предметный указатель
Абсолютно черное тело 180
Абсолютное будущее 43
Абсолютное прошлое 43
Адиабатическая оболочка 50
Адроны 287
Активность радиоактивного образца
264
Альфа-распад 264
Амплитуда колебаний 125
Ароматы кварков 288
Атом
— во внешнем магнитном поле 220
— водорода 195
в квантовой механике 210
Атомная единица массы 256
Барионный заряд 295
Барионы 287
Бета-распад 266
Биения 127
Билинза Бийе 159
Бипризма Френеля 159
Бозе-эйнштейновская конденсация
232
Бозон 215, 228
Боровский радиус 195
Вектор
— Пойнтинга 122
— Умова 141
Векторная диаграмма 126
Векторные бозоны 286
Великое объединение 297
Взаимная индукция 118
Взаимосвязь энергии и массы 44
Вибратор Герца 148
Виртуальные частицы 259, 287
Водородный цикл термоядерных ре-
реакций 284
Водородоподобные ионы 196
Волна
— в воздушном столбе 140
— в натянутой струне 140
— в упругом стержне 139
— гармоническая 138
— плоская 137
— плоскополяризованная 146
— поляризованная по кругу 147
— поперечная 137
— продольная 137
— стоячая 143
— эллиптически поляризованная 147
Волновая
— зона 148
— поверхность 138
— функция 197
Волновое
— сопротивление контура 133
— уравнение 139
— число 138
Волны
— Блоха 246
— де Бройля 197
— сферические и цилиндрические
139
Восприимчивость
— диэлектрическая 89
— магнитная 112
Вращение
— вокруг неподвижной оси 10
— плоскости поляризации 175
магнитное 176
Время
— высвечивания атома 150
— когерентности 127, 160
— релаксации 48
Вымораживание степеней свободы
63
Вынужденное (индуцированное) по-
поглощение 189
Вырожденный ферми-газ 233
Высвечивание атома 150, 158
Выход ядерной реакции 273
Вязкость 73, 74
Газ
— разреженный 75
— ультраразреженный 75
Гамильтониан 204
Гамма-распад 269
Гармоники 135, 144
Гауссова поверхность 83
Геометрическая оптика 152

Предметный указатель
309
Гипероны 288
Гиромагнитное отношение 210
Гироскоп 39
— тяжелый 40
Гироскопическое приближение 39
Главное квантовое число 210
Главные
— диэлектрические проницаемости
174
— максимумы дифракционной ре-
решетки 168
Глюоны 260, 287, 289
Голография 162
Гравитационная и инертная массы
30
Граница рентгеновского спектра 218
Давление
— волны 147
— света 187
Дальнодействие и причинность 14
Движение
— в центральном поле 22, 26, 209
— вращательное 10
— инфинитное 24
— по окружности 8, 9
— поступательное 10
— реактивное 18
— твердого тела
с неподвижной точкой 37
плоское 10, 37
— финитное 24
Двулучепреломление 174
Двухфазная система 68
Дебаевская частота 238
Действующее напряжение 136
Дейтерий 253
Дейтрон 253
Декремент затухания 133
Деление ядер 278
Дефект массы 256
Диаграмма направленности излуче-
излучения 149
Диамагнетики 110, 112
Динамика электрона в кристалле 247
Диполь
— во внешнем поле 81
— электрический 77
Дипольный момент 77
Дискретность уровней энергии 200
Диспергирующая среда 141, 176
Дисперсионная область 169
Дисперсия 138, 141
— света
аномальная 177
нормальная 177
Дифракционная решетка 168
— как спектральный прибор 169
Дифракция
— рентгеновских лучей на кристалле
170
— Фраунгофера на круглом отвер-
отверстии 167
— Фраунгофера от щели 166
Дифференциальные сечения реак-
реакций 273
Дихроичная пластина 175
Диэлектрик
— изотропный 89
— неполярный 92
— полярный 91
Длина
— волны 138
— когерентности 160
Добавочное давление под искрив-
искривленной поверхностью 71
Добротность (колебательной систе-
системы) 135
Домены 93, 114
Дырки 245, 249
Емкость
— (электроемкость) проводника 85
— конденсатора 93
Естественные переменные 60
Жесткость эффективная 128
^Жидкость перегретая 66
Закон
— Ампера 104
— Био-Савара-Лапласа 105
— Бугера 179
— Видемана- Франца 102
— Видемана-Франца 236
— всемирного тяготения 30
— Дальтона 63
— Джоуля-Ленца 99
— Дюлонга и Пти 237
— движения 7

310
Предметный указатель
— Кеплера
второй 26, 32
первый 32
третий 32
— Кирхгофа 180
— Кулона 76
— Малюса 171
— Мозли 219
— Ньютона
второй 14
первый 12
третий 14
— независимости световых пучков
152
— Ома 99
для неоднородного участка цепи
100
для неразветвленной цепи 101
для однородного участка цепи
99
— отражения света 152
— прямолинейного распространения
света 152
— Релея 179
— радиоактивного распада 263
— Снеллиуса 152, 172
— Стефана-Больцмана 181
— смещения Вина 182
— сохранения
импульса 17
механической энергии 22
момента импульса 28, 293
электрического заряда 76
энергии 293
энергии для электромагнитного
поля 122
— Фарад ея 116
— Фика 74
— фотоэффекта
второй 185
первый 185
— электромагнитной индукции 115
Законы
— геометрической оптики 152
— Кеплера 32
Запаздывающие нейтроны 280
Запаздывающие потенциалы 121
Заряд
— пробный 78
— точечный 76
— электрический 76
— элементарный 76
Заряды
— свободные 85, 98
— связанные 88
Звуковые ветви 241
Зеркала Френеля 159
Зеркало Ллойда 159
Зона
— валентная 245
— проводимости 244
Зоны Френеля 164
Излучательная способность абсо-
абсолютно черного тела 180
Излучение
— Вавилова-Черенкова 162
— вынужденное 190
— движущегося заряда 148
— плоского тока 147
— спонтанное 189
Изменение механической энергии 22
Изобары 253
Изотермический модуль всесторон-
всестороннего сжатия 49
Изотермы
— реального газа 66
Изотермы газа Ван-дер-Ваальса 67
Изотопический эффект 196
Изотропный магнетик 111
Импульс 13, 16
— и энергия в СТО 44
— релятивистский 44
— силы 13
Инвариантность 16
Инверсная заселенность уровней 191
Индуктивность (коэффициент само-
самоиндукции) 117
Индуктивность соленоида 118
Интеграл Фурье 127
Интенсивность
— волны 141
— лучистого потока 154
— пучка 73
— электромагнитной волны 147
Интервал 43
— времениподобный 43
— пространственноподобный 43
Интерференция 142
— большого числа волн 158

Предметный указатель
311
— в тонких пленках 161
— двух волн 157
Искусственная
— анизотропия 175
Истинно нейтральная частица 287
Источники
— поля 14
Калибровка
— Лоренца 121
Калибровочное
— преобразование 109, 121
Капельная (гидродинамическая) мо-
модель ядра 261
Капиллярные
— явления 72
Квазиимпульс 242
— электрона 246
Квазиклассическое приближение
229
Квазистационарное
— приближение 117
Квазичастицы 242
Квант света 186
Квантовая хромодинамика 290
Квантовое число
— главное 210
— магнитное 208, 209
спиновое 212
— орбитальное 208
— радиальное 209
— спиновое 212
Квантовый
— генератор (лазер) 192
— осциллятор 201, 205
Кварки 260, 288
Кварковая структура адронов 288
Кипение 70
Классификация кристаллов 244
Классическая электронная теория
металлов 102
Когерентность
— временная 160
— пространственная 159, 160
— световых волн 156
Когерентные
— волны 142
— источники 142
— кванты 191
Колебания
— вынужденные 133
механические 133
электрические 135
— гармонические 125
— затухающие 132
электрические 133
— изохронные 130
— когерентные 127
— линейно поляризованные 128
— модулированные 127
— свободные 125
в электрическом контуре 131
— систем с несколькими степенями
свободы 130
— собственные 125
в упругом стержне 139
— эллиптически поляризованные 128
Количество
— вещества 47
— теплоты 49
Кольца Ньютона 162
Компенсатор 175
Комплексная
— амплитуда 126
— экспонента 126
Комптоновская длина волны 189
Конденсатор 93
— плоский 94
— сферический 94
— цилиндрический 94
Конденсаторы составные 94
Континуальное приближение 238
Конфайнмент кварков 291
Корпускулярно-волновой дуализм
197
Коэрцитивная сила 114
Коэффициент
— вязкости 74
— диффузии 74
— затухания 132
волны 138
— качества излучения 270
— квантового усиления 191
— ослабления волны 179
— отражения 173
— поверхностного натяжения 70
— поглощения 275
— полезного действия замкнутого
цикла 53
— размножения нейтронов 281

312
Предметный указатель
— теплопроводности 74
Коэффициенты
— взаимной индукции 118
— Эйнштейна 190
Краевой угол 72
Красная граница фотоэффекта 185
Кривая
— видности 155
— возгонки 69
— парообразования 69
— плавления 69
— сосуществования фаз 68
Критерий Рэлея 168
Критическая
— масса 281
— опалесценция 179
Критический объем 66
Критическое давление 66
Лазер 191
Ламбертовский
— источник 156
Ларморовская прецессия 113
Лауэограммы 170
Лептоны 291
Линейчатые спектры 193
Локальное равновесие 48
Лоренцов 4-вектор 44
Лоренцов четырехмерный вектор 44
Лучистый поток 154
Магические ядра 257
Магнетон Бора 210
Магнитная индукция 103
Магнитный момент 209
— ядра 253
Масса 13
Материальная точка 7
Мезоны 288
Метастабильные состояния 66
Метод
— векторных диаграмм 126
— узловых потенциалов 101
— электростатических изображений
87
Механизм
— прямых ядерных реакций 275
— составного ядра 275
Механизмы
— намагничивания 113
— поляризации 91
Микроскопическая модель ядра 260
Модель
— атома
планетарная 194
Томсона 193
ядерная 194
— Бора 195
— испарения (ядра) 276
— ядерного ферми-газа 261
Момент
— импульса 25
— инерции 35
— магнитный 103, 110
— силы 24
Мощность
— механическая 19
— на участке цепи 101
Мультиплетность уровней 217
Мюон 291
Намагниченность 110
Направление неравновесных процес-
процессов 48
Напряжение 93
— задерживающее 185
Напряженность
— магнитного поля 111
— поля тяготения 31
— электрического поля 78
Начало термодинамики
— второе 53
— первое 50
— третье 59
Начальные условия 9
Нейтрино 268, 291
Необыкновенная волна 174
Неравенство Клаузиуса 56
Никол ь 174
Нормальные колебательные моды
131
Носители тока 98
Нуклиды 253
Нуклоны 252
Нулевые колебания 197, 202
Нутация земной оси 39
Обертоны 144
Оболочечная модель ядра 262
Объемная плотность энергии волны
140

Предметный указатель
313
Обыкновенная волна 174
Одноосный кристалл 174
Оператор орбитального углового мо-
момента 206
Операторный подход 204
Операторы физических величин 203
Оптическая длина пути 153
Оптически
— активные среды 175
— анизотропные среды 173
Оптические ветви 241
Опыт Юнга 157
Опыты
— Дэвиссона-Джермера 198
— Резерфорда 193
Освещенность 155
— энергетическая 155
Основное
— уравнение кинетической теории
идеального газа 60
Основное состояние атома 195
Основной
— закон релятивистской динамики
46
— постулат статистической физики
230
Основные положения молекуляр-
но=кинетической теории 47
Остаточная намагниченность 114
Ось
— вращения 10
мгновенная 11
— оптическая 154
Относительность движения 10
Отражение
— бегущей волны 144
— и преломление света 171
Пар
— насыщенный 66
— переохлажденный 66
Парадокс
— близнецов 42
— Гиббса 58
Параксиальное приближение 154
Парамагнетики 110, 112
Параметры
— термодинамические 47
Первая зона Бриллюэна 240
Перемещение 7
— контура с током в магнитном поле
108
Период
— дифракционной решетки 168
— колебаний 125
Период полураспада 264
Петля гистерезиса 114
Пластинка в четверть волны 175
Плечо силы 24
Плоскость
— падения 152
— поляризации 146
— поляризации волны 170
— пропускания поляризатора 171
Плотность 17
— вероятности 64, 197
— заряда
линейная 77
поверхностная 77
пространственная 77
— потока
вероятности 199
энергии волны 147
— состояний 182, 233
электронного газа 234
энергетическая 233
— тока 98
Плотность энергии электрического
поля 96
Поверхность Ферми 235
— электронов в металле 249
Поглощательная способность 180
Поглощенная доза излучения 270
Подход
— статистический 47
— термодинамический 47
Показатель
— адиабаты 52
— преломления
абсолютный 152
относительный 152
Поле 14
— внешнее стационарное 14
— диполя 81
— заряженного шара 84
— заряженной нити 83
— заряженной плоскости 83
— однородное 15
— отрезка 79
— плоскости с током 108

314
Предметный указатель
— потенциальное 20
— силовое 14
— системы зарядов 79
— соленоида 107
— толстого провода 108
— точечного заряда 78
— центральное 14
— электрическое 78
— электромагнитное 77
— электростатическое 78
Полезная мощность источника тока
101
Полное отражение света 152
Полосы
— равного наклона 161
— равной толщины 161
Полуметалл 244
Полупроводник
— п-типа 245
— р-типа 245
— чистый 245
Поляризатор 171
Поляризационная призма 174
Поляризация диэлектрика 88
Поляризованность 88
Поляризуемость молекулы 92
Порог ядерной реакции 277
Порядок интерференции 159
Постоянная
— Больцмана 58, 62
— Верде 176
— Керра 175
— Планка 184
— Ридберга 193, 195, 196
— распада 263
— тонкой структуры 214
— электрическая 77
Постулаты
— Бора 195
— СТО 40
Потенциал
— векторный 109
— поля
системы зарядов 80
точечного заряда 80
тяготения 31
— проводника 85
— электростатического поля 79
Потенциальная функция контура с
током в магнитном поле 108
Потенциальная энергия 20
— заряда в электростатическом поле
80
Потенциальные кривые 23
Поток вектора напряженности 82
Правила
— Кирхгофа 101
— отбора 210, 218
— Хунда 217
Правило
— Ленца 116
— Максвелла 67
Преломление линий напряженности
90
Преобразования
— Галилея 16
— Лоренца 41
Прецессия гироскопа 40
Приближение Фраунгофера 157
Приведенная
— длина(физического маятника) 130
— масса 29
Принцип
— Гюйгенса 153
— Гюйгенса-Френеля 163
Принцип единственности 87
— запрета Паули 215
— относительности
Галилея 15
Эйнштейна 40
— соответственных состояний 68
— соответствия 40
— суперпозиции
полей 30
— Ферма 153
Принцип суперпозици
— полей 79
Принцип суперпозиции
— (для волн) 137
— (для волновых функций) 198
Проводимость собственная 245
Проводник
— во внешнем электрическом поле 86
Проводящий шар в однородном поле
87
Промежуточные бозоны 287
Проницаемость
— диэлектрическая 89
— магнитная 112
Просветление оптики 173

Предметный указатель
315
Простые термодинамические систе-
системы 48
Протий 253
Протон 252
Процесс
— Джоуля-Томсона 51
— изобарный 52
— изотермический 52
— обратимый 48
— политропный 52
Путь 7
Пучности (стоячей волны) 143
Работа
— выхода 236
— механическая 19
Равновесное макросостояние 230
Равнодействующая 14
Радиационный захват 282
Радиоактивность 263
Радиоактивные семейства 269
Радиус-вектор 7
Разность хода
— волн 142
— оптическая 158
Разрешающая
— способность 169
оптических приборов 167
Распределение
— Бозе-Эйнштейна 231
— Больцмана 65
— Максвелла 63
— Максвелла-Больцмана 65, 232
— Ферми-Дирака 232
Рассеяние 272
— света 178
рэлеевское 179
— тиндалевское в мутных средах 179
Реакции
— экзоэнергетические 277
— эндоэнергетические 277
Реакции связей 15
Реакции синтеза 283
Резонанс 134
Резонансами 287
Резонансное поглощение 271
Релятивистские свойства полей 123
Ридберговская поправка 211
Ряд Фурье 127
Самодиффузия 74
Самоиндукция 117
Самосогласованное поле 214, 229
Сверхтонкая структура 254
Свет
— естественный 170
— поляризованный 171
— частично поляризованный 171
Светимость 156
— энергетическая 156
Световой поток 155
Световые
— лучи 152
— пучки 152
Свободная энергия 59
Свободные оси 38
Свободный симметричный волчок 39
Связанные маятники 131
Связанные состояния 200
Связь
— Рассела-Саундерса 217
— силы с потенциальной энергией 21
Сегнетоэлектрики 93
Серое тело 180
Сечение реакции 273
Сила 13
— Ампера 104
— возвращающая 128
— Кориолиса 34
— квазиупругая 128
— Лоренца 103
— обобщенная 128
— поверхностного натяжения 71
— равнодействующая 14
— реактивная 18
— результирующая 14
— света источника 155
— сухого трения 15
— тока 98
— тяжести 15
— упругости 15, 20
— центробежная 34
Силовые линии 83
Силы
— инерции 33
— консервативные 20
— неконсервативные 20
— природы 15
— сторонние 100
Сильное взаимодействие 286
Система

316
Предметный указатель
— консервативная 20
— материальных точек 16
замкнутая 16
— отсчета 7
— центра масс 16
Системы отсчета инерциальные 12
Скорости
— космические 33
— релятивистские 40
Скорость 8
— вторая космическая 33
— групповая 141
— первая космическая 33
— переносная 11
— средняя (среднеарифметическая)
65
— средняя квадратичная 62
— угловая 9
— фазовая 141
Слабое взаимодействие 286
Сложение
— гармонических колебаний 126
взаимно перпендикулярных 127
одного направления 126
— скоростей 10
в СТО 43
— угловых моментов 208
— угловых скоростей 11
Смачивание 72
Смесь идеальных газов 63
Собственное время 42
Соединение проводников 86
Соизмеримость физических величин
204
Сокращение длины 42
Соотношение Больцмана 190
Соотношения неопределенностей
Гейзенберга 198
Сопротивление
— активное 136
— емкостное 136
— индуктивное 136
— проводника 99
— реактивное 136
Состав ядра 252
Состояние
— квазиравновесное 48
— равновесное 48
Спектральное разложение света 154
Спектральные серии 196
Спектры щелочных металлов 211
Специальная теория относительно-
относительности Эйнштейна (СТО) 40
Спин 212
Спин ядра 253
Спонтанные и вынужденные перехо-
переходы 189
Среднее время жизни ядра 264
Статистика
— Бозе-Эйнштейна 228
— Максвелла-Больцмана 228
— Ферми-Дирака 228
Статистические распределения 228
Статистический вес 58, 230
Статистический смысл энтропии 58
Стационарное состояние 199
Степени свободы 7
Странность 295
Таблица Менделеева 215
Твердое тело 10
Тело однородное 17
Температура 49, 54
— в кинетической теории газов 61
— Дебая 239
— Кюри 93, 114
— кипения 70
— Ферми 235
Температурный коэффициент
— давления 49
— объемного расширения 49
— сопротивления 100
Теорема
— Блоха 246
— взаимности 118
— Гаусса 82
для магнитного поля 107
— — для электрического смещения
89
— Ирншоу 84
— Кёнига 20
— Карно 54
— Нернста 59
— о циркуляции 107
— о взаимно перпендикулярных осях
36
— о главных осях инерции 38
— о кинетической энергии 20
— о равнораспределении энергии по
степеням свободы 62

Предметный указатель
317
— Штейнера 36
Теория
— Дебая 238
— Зоммерфельда 234
— конечных ферми-систем 260
— Эйнштейна 237
Тепловое излучение 179
— равновесное 179
Теплоемкость 50
— молярная 52
— при постоянном давлении 52
— при постоянном объеме 51
— удельная 52
Теплообмен 49
Теплопроводность 74
Теплопроводность металлов 236
Теплота фазового перехода 69
Термодинамика поверхностного слоя
71
Термодинамическая шкала темпера-
температур 54
Термодинамический потенциал
Гиббса 60
Термы 193
— сложных атомов 217
Тождественность частиц 214
Ток
— проводимости 98
— смещения 120
Токомак 285
Тонкая структура спектральных ли-
линий 212, 213
Тормозное рентгеновское излучение
187
Точки поворота 24
Траектория 7
Трехфазная система 69
Тритий 253
Тритон 253
Тройная точка 69
Туннельный эффект 203
Углеродный цикл термоядерных ре-
реакций 284
Угловая дисперсия 169
Угол Брюстера 172
Удар
— неупругий 23
— упругий 23
Удельная
— активность 264
— рефракция 178
— теплота перехода 69
Удельная проводимость 99
Удельная энергия связи 256
Удельное сопротивление 99
Удельный
— объем 69
— термодинамический потенциал 60
Узлы (стоячей волны) 143
Ультрафиолетовая катастрофа 183
Уравнение
— Ван-дер-Ваальса 48, 67
— гармонических колебаний 125
— Даламбера 121
— движения 14
— Клапейрона-Клаузиуса 69
— Клапейрона-Менделеева 48
Уравнение Майера 52
— Мещерского 18
— Пуассона 52
— Пуассона (для потенциала) 85
— плоской гармонической волны 138
— процесса 49
— состояния 48
калорическое 50
термическое 50
— Циолковского 18
— Шредингера 199
временное 199
стационарное 199
— Эйнштейна для фотоэффекта 187
Уравнения
— Максвелла
в вакууме 121
в магнитостатике 109
в среде 122
в электростатике 84
— состояния канонические 60
— Эйлера 39
Уровни
— акцепторные 245
— донорные 245
Ускорение 8
— кориолисово 12
— нормальное 8
— свободного падения 31
— тангенциальное 8
— центростремительное 9
Условие

318
Предметный указатель
— Вульфа-Брегга 170
— квантования Бора-Зоммерфельда
197
Условия
— Лауэ 170
— на границе раздела диэлектриков
90
— на границе раздела магнетиков
111
— равновесия фаз 68
Устойчивость 24
Учет движения ядра 196
Фаза 68
— начальная 125
Фазовый переход
— второго рода 70
— первого рода 69
Фактор Ланде 220
Фермион 215, 228
Ферромагнетики 110
Фигуры Лиссажу 128
Физический маятник 129
Флуктуации 230
Фокальная плоскость 154
Фокус оптической системы 153
Фононы 242
Форма ядер 254
Формула
— Больцмана 58
— барометрическая 65
— Вейцзеккера 261
— Вина 182
— Дебая-Ланжевена 92
— Клаузиуса-Масотти 93
— Лапласа 71
— Лорентц-Лоренца 178
— Планка 183
— Ричардсона-Дэшмана 236
— Рэлея-Джинса 182
Формулы
— де Бройля 197
— Френеля 172
Фотометрические характеристики
световой волны 155
Фотометрия 154
Фотон 186
Фотоэффект 185
— внешний 185
— внутренний 186
Фотоэффектом 186
Фронт волны 138
Фундаментальные взаимодействия
286
Характеристические рентгеновские
спектры 218
Химический потенциал 60, 231
Цвет (квантовое число) 289
Центр
— масс 16
Центр качаний (физического маят-
маятника) 130
Центр тяжести 25
Центробежная энергия 209
Цепная реакция 281
Цикл Карно 53
Циркуляция магнитной индукции
107
Цуг волн 158
Чармоний 289
Частота колебаний 125
— круговая 125
— циклическая 125
Четность 294
Четырехмерный вектор энергии-
импульса 44
Числа
— магические 257
Число
— Авогадро 47
— зарядовое 252
— массовое 252
— степеней свободы молекулы 62
— ударов о стенку 61
Шкала электромагнитных волн 151
эдс
— самоиндукции 117
ЭДС взаимной индукции 118
Эквивалентные сопротивления и ис-
источники 102
Эквипотенциальные поверхности 83
Электрическое
— смещение 89
Электрическое поле

Предметный указатель
319
— вихревое 115
— релятивистской частицы 124
Электродвижущая сила источника
(ЭДС) 100
Электромагнитное взаимодействие
286
Электронная
— оболочка 215
— теплоемкость металлов 236
Электронный захват 267
Электропроводность металлов 236
Электрослабое взаимодействие 292,
297
Электростатическая индукция (яв-
(явление) 86
Элементарная ячейка фазового про-
пространства 229
Энергетическая сила источника 155
Энергетические зоны
— запрещенные 243
— разрешенные 243
Энергетический метод (определения
частоты) 126
Энергия
— внутренняя 22, 45, 49
газа Ван-дер-Ваальса 55
идеального газа 51, 55, 62
— ионизации 194
— кинетическая 19
— конденсатора 96
— контура с током 119
— механическая 22
— покоя 45
— потенциальная 20
— релятивистская 45
— связи ядра 255
— системы зарядов 95
— точки во внешнем потенциальном
поле 20
— уединенного проводника 96
— Ферми 232
электронов 234
— электромагнитных волн 147
— эффективная потенциальная 27
— ядерной реакции 276
Энтальпия 51
Энтропия 56
— газа Ван-дер-Ваальса 57
— идеального газа 57
— перехода 69
— смешения 58
Эргодическая гипотеза 230
Эффект
— Доплера
для электромагнитных волн 150
— Доплера в акустике 144
— Зеемана
аномальный 212
нормальный 210
— Керра 175
— Комптона 188
— Коттона-Мутона 176
— Мессбауэра 271
— Пашена-Бака 221
Эффект симметрии 257
— спаривания 257
— Холла 114
Эффективная масса 248
Эффективное сечение 72
Ядро
— дочернее 263
— материнское 263
Яма
— с бесконечными стенками 200
— с конечными стенками 200
Яркость 155
— энергетическая 155

Учебное издание
ЧЕРНОУЦАН Алексей Игоревич
КРАТКИЙ КУРС ФИЗИКИ
Редактор И.Н. Жетвина
Оригинал-макет: В. В. Дядичев
Оформление переплета: А.А.Логунов
ЛР№ 071930 от 06.07.99
Подписано в печать 25.07.02. Формат 60x90/16
Бумага офсетная. Печать офсетная
Усл. печ. л. 20. Уч.-изд. л. 21. Тираж: 3000 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3.
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72.
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv
KBN 5-9221-0292-3
9 785922 102926