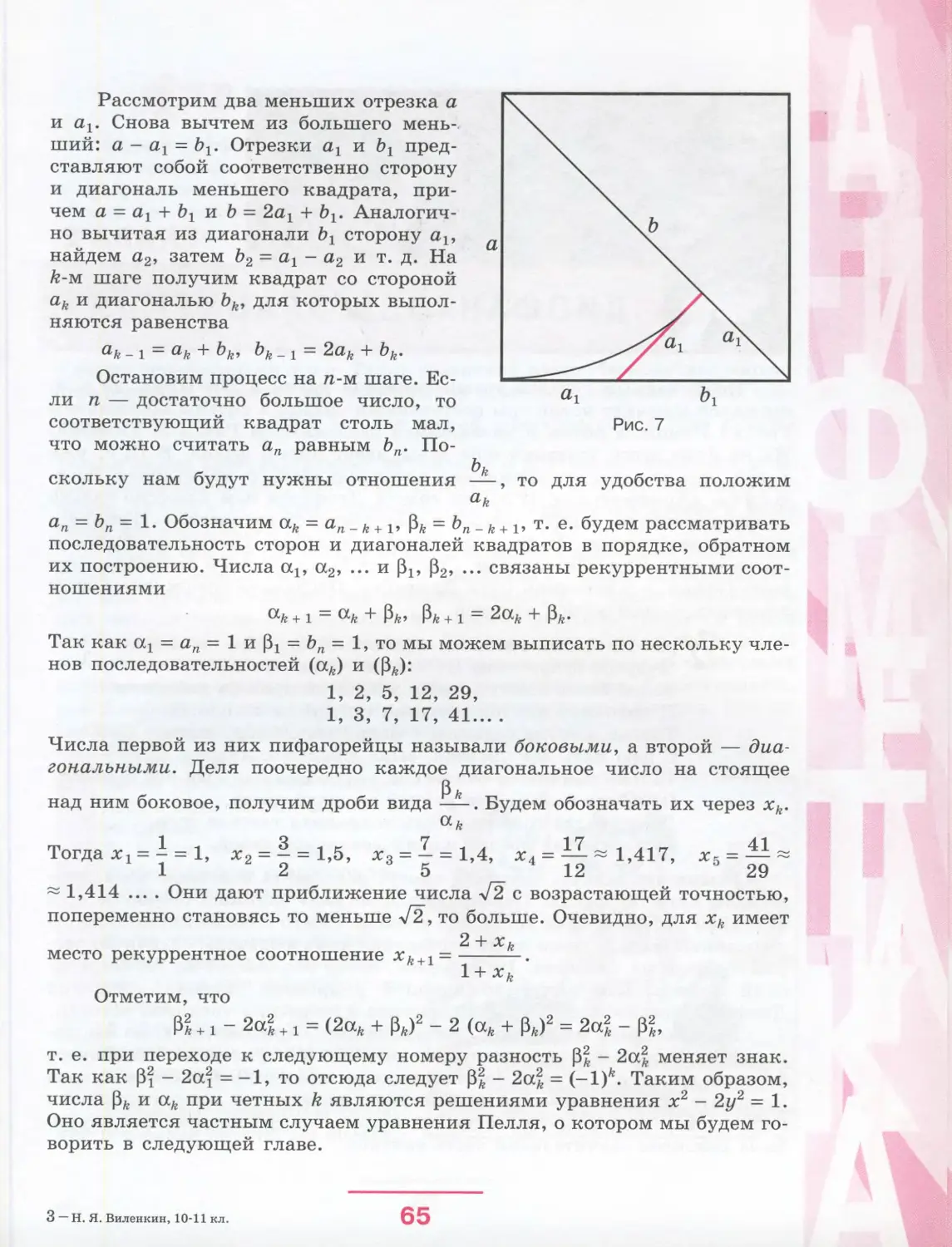
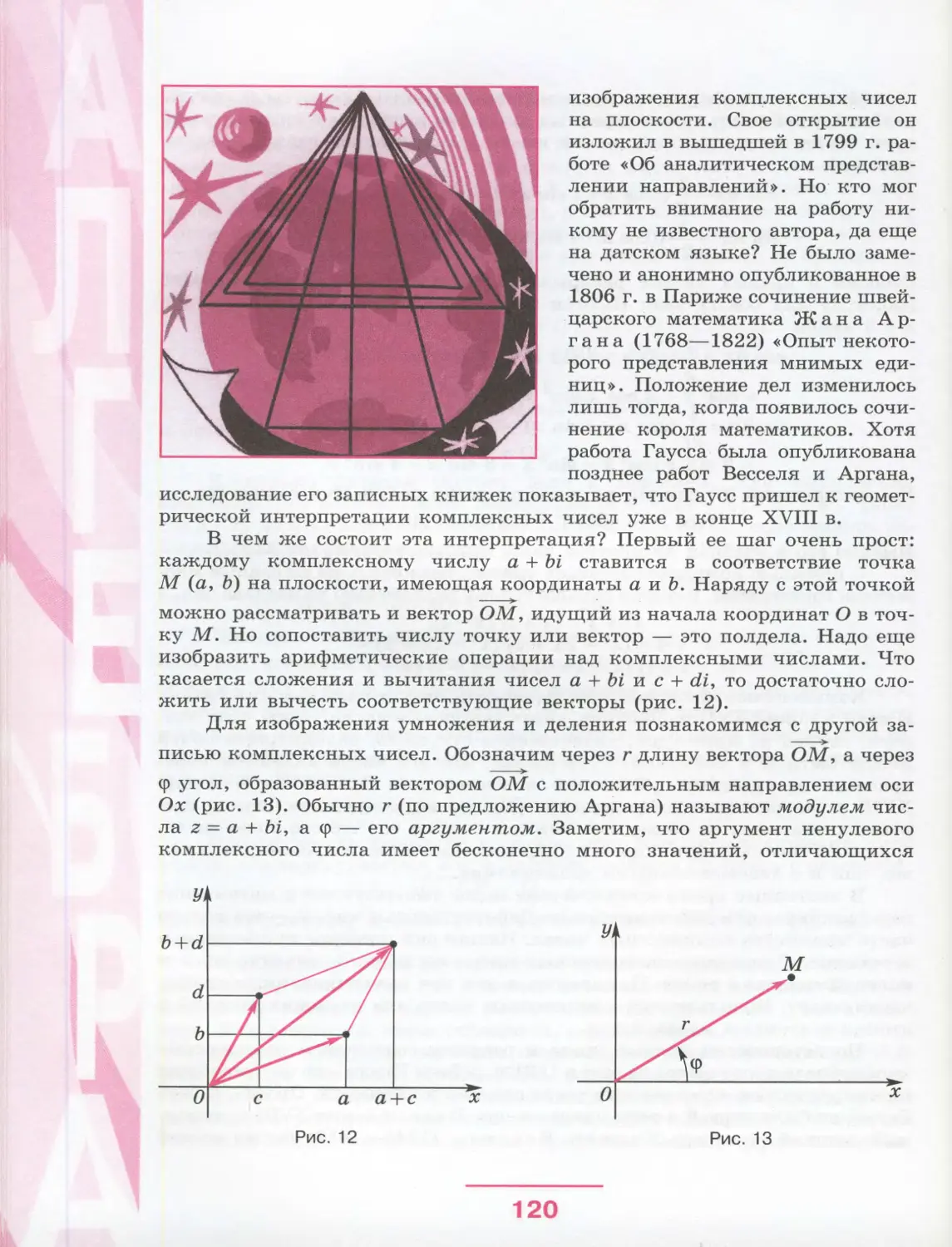
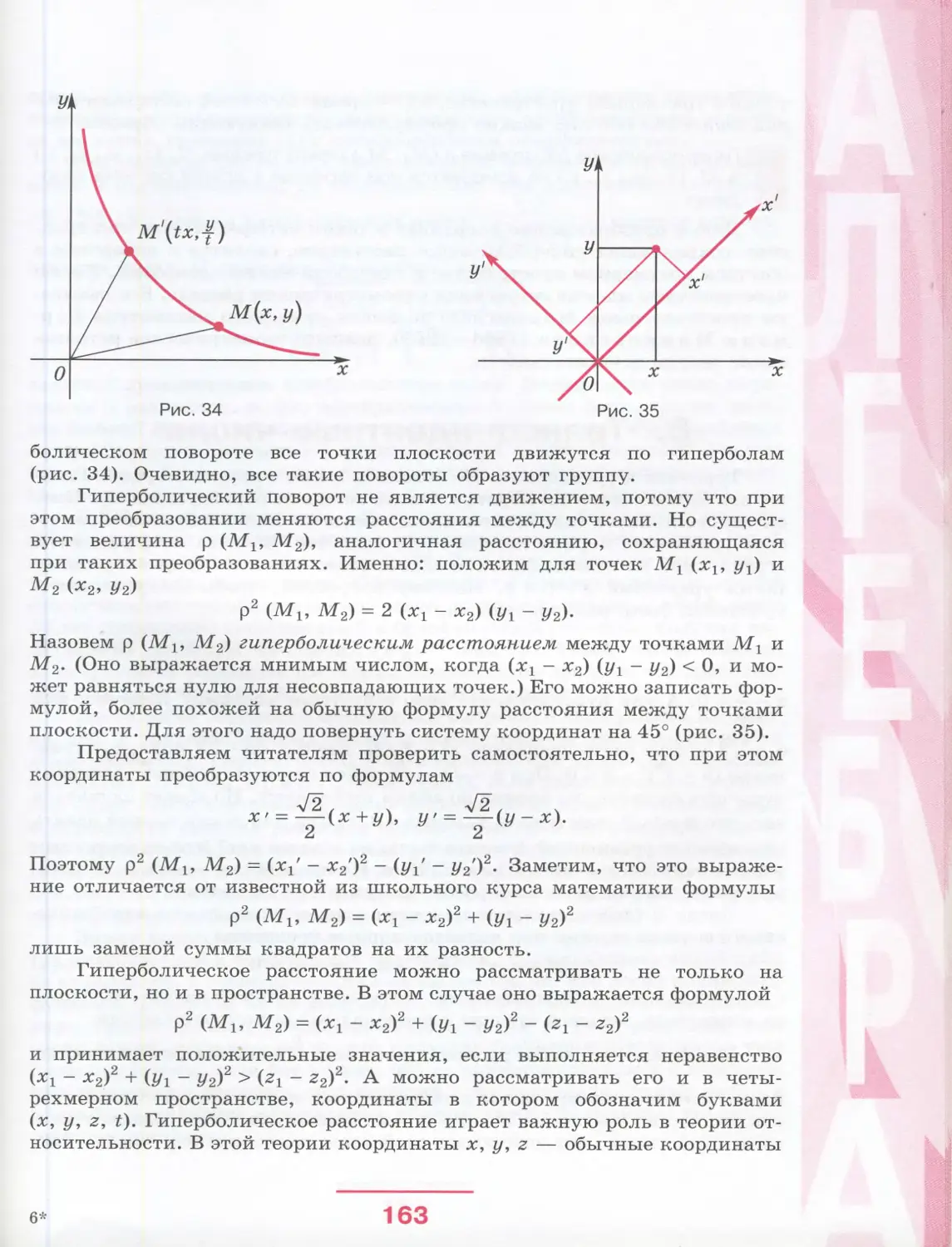
Автор: Виленкин Н.Я. Шибасов Л.П. Шибасова 3.Ф
Теги: общее школьное образование общеобразовательная школа математика учебные пособия и учебники по математике геометрия алгебра
ISBN: 978-5-09-016545-7
Год: 2008
Н.Я. Виленкин
Л.П. Шибасов
З.Ф. Шибасова
За страницами учебника математики
За страницами
учебника
математики
10
Арифметика.
Алгебра
ПРОСВЕЩЕНИЕ
Дж. НЕПЕР
(1550-1617)
П. ФЕРМА
(1601 - 1665)
Л. ЭЙЛЕР
(1707- 1783)
Число - это продукт нашего разума ...
пространство - это реальность,
лежащая вне нашего разума,
которой мы не можем приписывать
свои законы.
к. Гаусс
Числа не управляют миром,
но показывают, как управляется мир.
И.-В. Гете
Н. Я. Виленкин
Л. П. Шибасов
3. Ф. Шибасова
За страницами
учебника
математики
Арифметика
Алгебра
Пособие для учащихся
10—11 классов
Москва
«Просвещение»
2008
УДК 373.167.1:51
ББК 22.1я72
В44
Виленкин Н. Я.
В44 За страницами учебника математики : арифметика. Ал-
гебра : пособие для учащихся 10—11 кл. / Н. Я. Вилен-
кин, Л. П. Шибасов, 3. Ф. Шибасова. — М. : Просвещение.
2008. — 192 с.: ил. — ISBN 978-5-09-016545-7.
Книга адресована учащимся старших классов, желающим расширить и
углубить знания по всем разделам математики. Изложение новых математи-
ческих понятий опирается на школьный курс и сопровождается интересны-
ми историческими фактами. Книга погружает учащихся в мир современной
математики, рассказывает о роли ученых-математиков в развитии мировой
науки. Теоретические сведения дополнены разнообразными задачами.
УДК 373.167.1:51
ББК 22.1я72
Учебное издание
Виленкин Наум Яковлевич,
Шибасов Лев Петрович,
Шибасова Зинаида Федоровна
За страницами учебника математики
АРИФМЕТИКА. АЛГЕБРА
Пособие для учащихся 10—11 классов
Зав. редакцией Т. А. Бурмистрова
Редактор Л. Н. Белоновская
Младший редактор Е. А. Андреенкова
Художники А. В. Щетинцева, О. П. Богомолова
Художественный редактор О. П. Богомолова
Компьютерная графика: Г. М. Дмитриев
Технический редактор Н. В. Лукина
Корректор Е. В. Павлова
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000.
Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать с оригинал-макета 20.08.07.
Формат 70x90'/i6. Бумага офсетная. Гарнитура Школьная. Печать офсетная. Уч,-
изд. л. 13,61+0,5 форз. Тираж 5000 экз. Заказ № 17959 <д-гз>.
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Открытое акционерное общество «Смоленский полиграфический комбинат».
214020, Смоленск,ул. Смольянинова, 1.
ISBN 978-5-09-016545-7 © Издательство «Просвещение», 2008
© Художественное оформление.
Издательство «Просвещение», 2008
Все права защищены
Дорогие читатели!
аждый раздел математики, изучается он в школе или в
вузе, вырос из решения каких-то задач, возникавших в
практической деятельности человека или в недрах самой
науки. В предлагаемых книгах мы познакомим вас с за-
дачами, лежащими у истоков различных областей ма-
тематики или способствовавшими их развитию. Одни
задачи имеют солидный возраст, исчисляющийся тысяче-
летиями, другие — сравнительно молоды: им всего лишь
несколько веков или даже десятилетий. История многих
из них поистине драматична, овеяна тайнами и леген-
дами. Но все эти задачи замечательны тем, что в процес-
се их решения появлялись новые математические по-
нятия, выковывались новые математические методы.
В повествование вплетены рассказы и предания о круп-
ных и интересных открытиях, включены краткие биогра-
фии творцов математики.
Нашей целью не является полное и строгое изложе-
ние материала, позволяющее изучить какой-либо вопрос;
многие темы изложены на популярном или просто озна-
комительном уровне, хотя в книгах достаточно много
строгих определений, теорем и доказательств, которые,
надеемся, не отпугнут настоящих любителей математики.
Если кто-то из читателей, заинтересовавшись описанной
проблемой, потянется к специальной литературе, вот то-
гда наша цель будет достигнута.
Это новое издание трех книг под тем же названием.
Впервые оно вышло десять лет назад и состояло из
двух книг: первая (авторы Н. Я. Виленкин, Л. П. Шиба-
сов, 3. Ф. Шибасова) охватывала разделы «Арифметика»,
«Алгебра» и «Геометрия»; вторая (авторы Л. П. Шиба-
сов, 3. Ф. Шибасова) содержала разделы «Математиче-
ский анализ», «Теория вероятностей», «Старинные и
занимательные задачи». В настоящее время издание вы-
ходит в трех книгах, в связи с чем последний раздел пере-
несен во вторую книгу и объединен с разделом «Геомет-
рия».
За прошедшие десять лет в математике были полу-
чены новые результаты. Стараясь учесть их, мы внесли
соответствующие добавления. Исправлены замеченные
неточности и опечатки, упрощены отдельные доказатель-
ства, заменены и добавлены некоторые упражнения. Но в
1*
3
целом содержание радикальных изменений не претер-
пело.
В первую книгу, предлагаемую вашему вниманию,
входят разделы «Арифметика» и «Алгебра». Они разбиты
на главы, главы — на пункты, нумерация формул в каж-
дой главе своя, а рисунков сквозная. В конце разделов
предлагаются упражнения, также содержащие историче-
ские сведения. Не все упражнения одинаковой сложно-
сти. Некоторые из них аналогичны задачам, решенным в
тексте, другие требуют известного напряжения, упорства,
может быть, обращения к дополнительной литературе. Не
спешите сразу заглядывать в ответ. Для удобства работы
с книгой в конце приведен список использованной лите-
ратуры (далеко не полный), предметный и именной ука-
затели.
Мы благодарим всех читателей, высказавших свои за-
мечания и пожелания, и просим в дальнейшем направ-
лять их по адресу издательства: 127521, Москва, 3-й про-
езд Марьиной рощи, 41.
Приглашаем наших читателей войти в прекрасный
мир математики, погрузиться в ее проблемы и прикос-
нуться к неразгаданным тайнам.
Л. П. Шибасов, 3. Ф. Шибасова
ЧАСТЬ
ПЕРВАЯ
АРИФМЕТИКА
/// нтерес к изучению чисел возник у людей в глубокой древности.
9г и вызван он был не только практической необходимостью. При-
влекала необычайная, магическая сила Числа, которым можно выразить
количество любых предметов. Неожиданные и в то же время естествен-
ные свойства натуральных чисел, обнаруженные древними математика-
ми, удивляли их своей замечательной красотой и вдохновляли на новые
исследования.
За два тысячелетия до новой эры в Древнем Египте и Вавилоне были
созданы достаточно совершенные формы записи чисел. Решались задачи
практического содержания, в связи с чем сложились правила арифмети-
ческих действий. Вавилоняне составляли таблицы квадратов, кубов це-
лых чисел, таблицы обратных величин и т. п. Но наиболее значительные
результаты в области изучения свойств чисел были получены в Древней
Греции начиная с VI в. до н. э.
Несомненно, древнегреческие ученые во время путешествий в Египет
и Вавилон знакомились с имевшимися там достижениями. Однако в от-
личие от египтян, более склонных к измерениям, и от вавилонян,
тяготевших к вычислениям, греческие ученые отдавали предпочтение
теоретическим вопросам. Более того, решение задач практического содер-
жания считалось в Древней Элладе делом, недостойным истинного учено-
го, — этим должны заниматься купцы и ремесленники. Такой взгляд
объясняется в значительной степени тем, что большинство древнегрече-
ских ученых, а они были и математиками, и философами, и политиками
одновременно, принадлежало к имущему классу: им не надо было забо-
титься о хлебе насущном и ради него заниматься «недостойным ремес-
лом». Арифметику — науку о числах они ставили гораздо выше логи-
стики — науки о вычислениях.
Наивысшего расцвета учение о натуральных числах достигло в шко-
ле знаменитого философа и математика Пифагора Самосского
(ок. 580 — ок. 500 до н. э.). Этого необычного ученого еще при жизни по-
читали как полубога и чудотворца. До нас дошло мало биографических
сведений о Пифагоре. Известно, что по политическим мотивам он оставил
свой родной остров Самос. Предполагают, что он совершил путешествие в
Египет и Вавилон, где приобщился к тайнам жрецов. Вернувшись, он
6
поселился в Кротоне — греческом городе на юге Италии — и основал там
тайное общество, ставшее одновременно и политической организацией, и
философско-научной школой. Члены общества давали обет вести строгий
образ жизни, очищать души занятиями музыкой и математикой. Тради-
ции школы Пифагора хранились его учениками и последователями в те-
чение нескольких веков. В этой школе и созрело философско-мистиче-
ское учение, получившее название «пифагореизм».
Если другие древние философы считали основой всего сущего мате-
риальные стихии — огонь, воду, землю, воздух — и объясняли свойства
всех явлений природы сочетанием этих стихий, то пифагорейцы провоз-
гласили основным принципом всего мироздания число и объясняли свой-
ства всех предметов и явлений, исходя из их арифметической структуры.
Они создали оригинальную арифметику, где каждое число играло свою
роль. Натуральными числами обозначались и боги, и космос, и люди, и
их взаимоотношения. Естественно, что изучению натуральных чисел пи-
фагорейцы уделяли особое почтительное внимание, при этом они обнару-
жили массу интересных свойств. И хотя о результатах пифагорейцев мы
знаем по ссылкам на них более поздних авторов, можно с уверенностью
сказать, что они изучали делимость чисел, разработали теорию пропор-
ций, нашли различные виды средних: арифметическое, геометрическое и
гармоническое, рассматривали числа четные и нечетные, простые и со-
ставные, многоугольные и пирамидальные, дружественные и совершен-
ные и т. д. Полученные ими результаты настолько глубоки и серьезны,
что, отряхнув их от мистики, мы изучаем и используем их и по сегод-
няшний день. Почти все вопросы, которые мы будем обсуждать в этой
главе, в той или иной мере связаны с именем Пифагора и его последовате-
лей.
Пифагорейцы, подметив какое-либо свойство, считали необходимым
его доказать. Именно им мы обязаны введением в математику доказа-
тельств. Велики их заслуги и в области геометрии, но об этом мы будем
говорить в соответствующем разделе. А сейчас обратимся к натуральным
числам и их свойствам.
1. Системы счисления
В старых книгах по арифметике, кроме четырех основных действий,
упоминается и пятое — нумерация. Пожалуй, нумерация (счисление) бы-
ла одной из первых проблем, с которой столкнулись люди при построе-
нии арифметики. Ведь чтобы работать с числами, надо прежде научиться
называть их и записывать.
Процесс возникновения и развития различных систем счисления
был долгим и сложным. Каждая цивилизация разрабатывала и использо-
вала ту форму счета и записи чисел, которая была достаточно приспособ-
лена к решению стоящих перед ней задач.
Привычная нам запись десяти цифр, как и сама позиционная деся-
тичная система счисления, пришла к нам из Индии, где она зароди-
лась около V в. н. э. Правда, начертание тех цифр только отдаленно
7
напоминает современное. Видоизменяясь с течением веков, они распро-
странились сначала в арабские страны, а позже в результате арабских за-
воеваний в Европу. Поэтому современные цифры не совсем оправданно
называют арабскими.
Мы сейчас настолько свыклись с десятичной системой, что не заме-
чаем величия этого достижения человеческой мысли. Она проста и удоб-
на как все гениальное. Тем не менее принята она была не сразу: сказыва-
лись и вековые традиции, и отсутствие единой формы записи цифр, и
разобщенность ученых разных стран.
Важную роль в распространении десятичной системы в Европе
сыграла «Книга абака» Леонардо Пизанского (ок. 1180 — после
1240), вышедшая в свет в 1202 г. В ней автор показывает преимущества
новой формы записи чисел, которую он называет индийской, по сравне-
нию с распространенной в то время римской нумерацией, описывает пра-
вила действий над числами в новой записи и приводит очень много задач
практического содержания. Труд по тем временам был грандиозным; до-
статочно сказать, что в печатном виде он насчитывал 460 страниц. Автор
его известен в истории математики еще и под вторым именем — Фибо-
наччи. Объясняется происхождение имен ученого очень просто.
Леонардо родился в городе Пизе, откуда его первое имя. Отцом его
был писарь по прозвищу Боначчи — добряк, по-итальянски «сын Бонач-
чи» произносится как «фи боначчи» — от слияния этих слов и возникло
его второе имя. Отец Леонардо работал в Алжире в качестве торгового
представителя города Пизы. Там и обучался будущий ученый арифмети-
ке. Способный юноша превзошел ожидания отца, готовившего его к ком-
мерческой деятельности. По торговым делам он вместе с отцом часто бы-
вал в завоеванных арабами странах Средиземноморья, где основательно
изучил арабскую математику. Его «Книга абака» представляла собой ма-
тематическую энциклопедию того времени. В отличие от предшествую-
щих авторов, адресовавших аналогичные работы в основном ученому ми-
ру, Леонардо обратился к широкому кругу торговых и деловых людей.
Но для них книга оказалась трудновата. В полной мере она была оценена
только последующими учеными.
Интересные задачи из «Книги абака» и оригинальные методы их ре-
шения разошлись в XV—XVI вв. по многочисленным европейским кни-
гам. И десятичная система, постепенно пробивая себе дорогу, получила в
Европе повсеместное распространение и признание только в эпоху Воз-
ррждения.
С записью чисел в десятичной системе все мы хорошо знакомы.
В ней используются лишь десять цифр 0, 1, 2, ..., 9, причем каждая из
них имеет разный смысл в зависимости от занимаемой позиции. Напри-
мер, в записи числа 4784 последняя четверка означает 4 единицы, а пер-
вая — 4 тысячи. Такая система счисления называется позиционной. Лю-
бое натуральное число п представимо в виде
п = ak • 10* + ak_ j • 10* ”1 + ... + а, • 10 + а0, (1)
где а0, аг, ..., ak — одна из цифр 0, 1, ..., 9 и ak Ф 0. Но вместо этой гро-
моздкой записи используют более компактную: n = akah_l, ..., а^а^.
8
Особую роль здесь играет число 10 — основание десятичной системы
счисления. Иногда записывают п = (aAafc_ 1...а1а0)10, когда нужно именно
указать основание, ведь основанием позиционной системы счисления мо-
жет быть любое число q > 1.
Цифрами 7-ичной системы являются 0, 1, q - 1. Чтобы записать
произвольное число п в g-ичной системе, его представляют в виде
^ = bmqm + bm_1qm-1 + ... + b1q + b0, (2)
где b0, ..., Ьт принимают значения 0, 1, ..., q - 1, причем Ьт =£ 0. Отсюда
(bmbm_1, ..., — искомая запись.
Выбор человечеством десятичной системы счисления объясняется
наличием у людей 10 пальцев — первого подручного счетного прибора.
Мы настолько привыкли к этой системе, что даже не сомневаемся в одно-
значности представления числа в виде (1). Но уже при записи числа в
g-ичной системе счисления такая мысль естественно возникает. Пока-
жем, что и здесь все обстоит благополучно. Предположим, что некоторое
число п имеет два представления:
п = bmqm + bm_1qm~1 + ... + bxq + b0 = akqk + ак_^к~' + ... + axq + a0,
причем k < tn. Тогда
bmqm + bm_1qm~1 + ... + bYq - (akqk + ak _ Aqk - 1 + ... + a^) = a0 - b0.
Левая часть делится на q, значит, на q делится и разность а0 - Ьо, что воз-
можно лишь при а0 = Ьо. Поделив полученное равенство на q, запишем
его в виде
bmqm ' + ... + b2q - (akqk " 1 + ... + a2q) = ax - bx.
Откуда снова аг = b} и т. д. На (k + 1)-м шаге придем к равенству
bmqm~k + bn_1qm~k~1 + ... + bk + 1q = 0, а значит, bm = bm _ х = ... = bk + , = 0.
Таким образом, разложение (2) единственно.
Запишем, например, число 132 в троичной, пятеричной, семеричной
и двенадцатеричной системах счисления:
132 = 1 • З4 + 1 • З3 + 2 • З2 + 2 3 + 0 = (11220)3,
132 = 1 • 53 + 0 • 52 + 1 • 5 + 2 = (1012)5,
132 = 2 • 72 + 4 7 +_6 = (246)7,
132 = 11 • 12 + 0 = (110)12.
В последнем примере над числом 11 поставлена объединитель-
ная черточка, с тем чтобы не перепутать его с числом (110)12 =
= 1 • 122 + 1 12 + 0 = 156.
Конечно, 132 — число небольшое, и представить его в виде (2) для
различных q можно было устно. А как прийти к этому представлению
побыстрее, если число достаточно велико? Приглядимся вниматель-
но к равенству (2). Если разделить п на q, то в частном получим
bmqm 1 + bm~iqm~2 + ... + b1( а в остатке — Ьо. Разделив найденное част-
ное вновь на q, получим остаток Ьг и т. д. Последовательность остатков,
выстроенных справа налево, и даст g-ичную запись числа п. Воспользо-
вавшись этим правилом, представим число 4784 в восьмеричной системе.
Сначала произведем последовательное деление углом:
9
_4784 | 8
40 _598 | 8
_ 78 56 _74 | 8
72 _38 72 9 18
_64 32 2 8 1
64 6 1
0
Отсюда 4784 = (11260)8 = 1 • 84 + 1 • 83 + 2 • 82 + 6 • 8 + О. Последнее pa-
венство показывает, как от восьмеричной записи перейти к десятичной.
Попытайтесь самостоятельно вывести правило перевода числа из д-ичной
системы в р-ичную.
Аналогично записывают в q-ичной системе счисления и дробные чис-
ла. Здесь используют представление
Р #2 ak
-=а0 + — + — —= (а0, аха2 ... ak) .
г q q2 qk
Например, = 1 + — + -1— + — = (1,672)я; справа стоит так называемая
256 8 82 83 « н
систематическая дробь в 8-ричной системе счисления — аналог деся-
тичной дроби. Покажем на примере, каким образом переводится обык-
13
новенная дробь в </-ичную. Запишем дробь — в 12-ричной системе. За-
17
метим, что 13 = (11)12, 17 = (15)12, а теперь поделим числитель на
знаменатель:
11,0 115
10 5 0,733...
50
45
5...
13
17
(И)12
(15)12
= (0,733...)12.
Самой простой из систем счисления является двоичная, для запи-
си чисел здесь используются всего две цифры: 0 и 1. Но при этом
теряется компактность: даже сравнительно небольшие числа выгля-
дят в этой системе довольно внушительно. Так, запись числа 76 =
= 1 • 26 + 0 • 25 + 0 • 24 + 1 23 + 1 • 22 + 0- 2 + 0 = (1001100)2 содержит
семь разрядов, а числа 276 = 1 • 28 + 0 • 27 + 0 • 26 + 0 • 25 + 1 • 24 +
+ 0 • 23 + 1 -22 + 0- 2 + 0 = (100010100)2 уже девять разрядов. Такая гро-
моздкость является основным недостатком двоичной системы счисле-
ния. По этой причине она не получила бы большого распространения, не
появись электронные вычислительные машины (ЭВМ), которые работа-
ют на элементах, находящихся в двух устойчивых состояниях (ток про-
пускается или нет). Тем самым они могут легко моделировать две циф-
ры: 1 и 0. Но не только в вычислительной технике используется двоичная
система. Она бывает удобна и при решении некоторых задач. Рассмотрим
одну из них.
10
Задача (о системе разновесов). Определить наименьшее число
гирь, с помощью которых можно уравновесить любой груз массой не
более N граммов при условии, что груз и гири кладутся на разные ча-
ши рычажных весов. (Естественно, подразумевается, что масса груза
выражается целым числом граммов.)
Ясно, что гири в 1 г и 2 г необходимы: ими можно взвесить груз, не
превосходящий 3 г, но уже для следующего веса придется брать новую ги-
рю, масса которой не может превышать 4 г. Выгодно взять именно четы-
рехграммовую гирю: вместе с ней удастся уравновесить все целые веса,
меньшие 8 г. Легко сообразить, что если 2" ~1 < N < 2п, то потребуется п
гирь массой 1, 2, 22, ..., 2"1 граммов. Докажем это утверждение индук-
цией по п. При п = 1 оно очевидно; предположим его верность при п = т:
все грузы р, меньшие 2т, можно взвесить т гирями в 1, 2, 22, ...,
2т~1 граммов. Рассмотрим груз массой р < 2т + 1. Если при этом р < 2т, то
достаточно т гирь. В случае 2т < р < 2т + 1 груз массой р - 2т снова меньше
2т, значит, для его взвешивания хватит т гирь, а для груза в р граммов
остается добавить гирю массой 2т граммов. Утверждение доказано.
Какие гири конкретно кладутся на чашу весов для уравновешивания
груза р N, определяется ненулевыми коэффициентами записи чис-
ла р в двоичной системе счисления. Например, в случае р = 43 имеем
43 = 1 • 25 + 0 • 24 + 1 • 23 + 0 • 22 + 1 • 2 + 1 • 2°, а значит, для взвешива-
ния груза в 43 г потребуется четыре гири массой 32, 8, 2 и 1 г.
Эта задача для различных фиксированных значений N стала попу-
лярной после того, как появилась в книге французского математика и по-
эта Баше де Мезириака «Приятные и занимательные задачи»
(1612). На практике же при взвешивании на рычажных весах продавец
часто кладет гири на обе чаши весов. В такой более естественной поста-
новке задача встречалась еще за четыре столетия до Баше в «Книге аба-
ка» Леонардо Пизанского. Скорее всего, и Леонардо не сам придумал
ее. Судя по содержанию, задача эта имеет более древнюю историю и воз-
никла в голове какого-то пытливого и сообразительного купца.
При ее решении Леонардо исходил из того, что любое целое число
представимо в виде суммы или разности степеней тройки, т. е. он факти-
чески записывал число в виде
N = bn _ j • 3" - 1 + ... + Ьг • З2 + Ъг • 3 + Ьо.
Только у него в отличие от записи в троичной системе счисления
коэффициенты принимали значения не О, 1, 2, а 0, 1, —1. Установим
связь между этими записями: слагаемое 2 • Зт представим в виде
(3 - 1) • Зт = Зт + 1 - Зт и придем к записи, в которой коэффициент 2 за-
менен на —1, а коэффициент следующего разряда увеличен на 1. Если пе-
ред слагаемым З"1 стоит знак «—», то гиря весом Зт кладется на ту же ча-
шу весов, на которой находится груз. Выясним, например, какие гири
потребуются для взвешивания таким образом груза в 43 г. Так как
43 = 1 • З3 + 1 • З2 + 2 • З1 + 1 • 3° = 1 • З3 + 1 • З2 + (3 - 1) З1 + 1 • 3° =
= 1 • З3 + (3 - 1) • З2 - 1 • З1 + 1 • 3° = 1 З4 - 1 • З3 - 1 З2 - 1 • З1 + 1 • 3°,
то на пустую чашу весов нужно положить гири в 81 г и 1 г, а три осталь-
ные гири (27, 9, 3 г) — на ту чашу, где находится груз. Очевидно,
11
с помощью этого набора гирь можно взвесить любой груз от 1 до 121 г,
так как (11111 )3 = 121. (Двойка в записи присутствовать не может в соот-
ветствии с нашей договоренностью.)
Леонардо в «Книге абака» решает свою задачу для груза от 1 до 40 г.
Поскольку с помощью k гирь можно уравновесить любой груз массой
3fc — 1
№: 1 + 3 + З2 + ... + З*1 =-----,
2
то приходим к неравенству
Наименьшее k, для которого оно выполняется, равно 4. Таким образом,
достаточно четырех гирь массой 1, 3, 9 и 27 г.
2. Признаки делимости
Простые числа являются теми кирпичиками, из которых с помощью
умножения строят все остальные числа. Вот и попытаемся представить
числа в виде произведения составляющих их кирпичиков.
Сначала напомним, что число р > 1 называется простым, если оно
делится только на себя и на 1. Число же, имеющее больше двух различ-
ных делителей, называют составным. К числу 1 на протяжении многове-
ковой истории развития математики отношение было неоднозначное: не-
которые древние математики вообще не считали единицу числом, другие
относили к простым. Ее считали простым числом даже в XVIII в. Но сей-
час в целях стройности теории чисел (науки о целых числах) единицу
считают числом особого рода, не относя ее ни к простым, ни к составным.
Процесс разложения натуральных чисел на простые множители зна-
чительно упростится, если мы будем знать признаки делимости хотя бы
на некоторые простые числа. Итак, перед нами стоит следующая задача:
натуральное число записано в десятичной п = ak...ala0 или в некоторой
q-ичной п = (ak...a1a0)q системе. Как по этой записи определить, делится
ли оно на простое число р? Некоторые признаки делимости всем хорошо
знакомы. Постараемся расширить круг знакомств.
В основе теории делимости лежит утверждение, доказанное выдаю-
щимся французским ученым Блезом Паскалем (1623—1662). Чи-
татели, вероятно, сразу вспомнили закон гидростатики, носящий имя
Паскаля, его опыты по атмосферному давлению, единицу давления, на-
званную его именем. Но этот блестящий физик имеет не меньше заслуг
перед математикой. Его необычайное математическое дарование прояви-
лось очень рано. А уже в шестнадцатилетнем возрасте он написал иссле-
дование по теории конических сечений — кривых, получающихся в сече-
нии конуса плоскостью. Тщательно изучив известные тогда части книги
древнегреческого ученого Аполлония Пергского (III в. до н. э.) об
этих сечениях, он сумел восстановить содержание остальных частей со-
чинения, считавшихся утраченными. Позже они были найдены, и
12
предвидение Паскаля подтвердилось. Помимо геометрии, Паскаль зани-
мался комбинаторикой, а также вместе с другим французским математи-
ком П. Ферма заложил основы теории вероятностей. Значительный
вклад он внес и в создание основ математического анализа. В 1642 г. Пас-
каль сконструировал счетную машину, производящую операции сложе-
ния и вычитания чисел.
Несмотря на замечательные научные успехи, Паскаль главным де-
лом своей жизни считал богословские исследования. Он принимал актив-
ное участие в спорах между иезуитами и янсенистами — представителя-
ми двух направлений в католическом богословии. Его «Письма
провинциала», направленные против иезуитов, считаются одним из луч-
ших сатирических произведений французской литературы. После победы
иезуитов Паскаль подвергся преследованиям. Под влиянием своих бого-
словских убеждений он надолго отошел от науки. Но однажды, чтобы за-
глушить нестерпимую боль (он часто и тяжело болел), Паскаль выполнил
в течение ночи научное исследование о свойствах циклоиды (о ней будет
рассказано в геометрическом разделе). С именем Паскаля мы еще неодно-
кратно встретимся на страницах этой книги.
В работе «Особенности делимости чисел» Паскаль доказал следую-
щую теорему:
Пусть натуральное число п > 1 записано в g-ичной системе так:
n = akqk + ak_1qk-1 + ... + a^q + а0;
обозначим через rs остаток от деления qs на р > 1 (s = 1, ..., k) и соста-
вим новое число
m = a/lrk + ak_1rk_1 + .., + а^ + ао,
тогда числа тип имеют одинаковые остатки при делении на р.
Для доказательства этого утверждения рассмотрим разность
п - т = ak (qk - rk) + ak _ ! (qk - 1 - rk _ i) + ... + а2 (q2 - r2) + ax (q - Tj).
Так как rs — остаток от деления qs на р, то qs — rs делится на р при лю-
бом s, следовательно, и вся сумма, стоящая в правой части равенства, де-
лится на р. Это и означает, что остатки от деления чисел п и т на р оди-
наковы. Утверждение доказано, и из него вытекает, что
I числа п и т делятся на число р или не делятся на него одновременно.
Если число п достаточно громоздкое, то т сравнительно небольшое и про-
верить его делимость на р гораздо легче. Выведем с помощью теоремы Па-
скаля признаки делимости на некоторые простые числа. Иногда мы бу-
дем для удобства записывать число т так:
т = akrk + ... + ахт\ + аого,
считая r0 = 1.
Известные читателям признаки делимости на 3 (и на 9) следуют из
того, что для этих значений р при любом з имеем rs = 1 (10 = 9 + 1,
102 = 99 + 1, 103 = 999 + 1, ...). Значит,
число п = ак...а0 делится на 3 (или на 9), если на 3 (соответственно
на 9) делится число т = ak + ... + а1 + а0 — сумма цифр числа п в деся-
тичной записи, и только при этом условии.
13
Точно так же доказывается аналогичный признак в g-ичной си-
стеме:
п = (ak...a0)q делится на д-1 в том и только в том случае, если
т = ak + ... + а0 делится на q - 1.
Например, число (463573)8 делится на 7, так как сумма его цифр
равна (28)10 = 4 • 7, а это число делится на 7. Таким признаком делимости
на 7 было бы удобно пользоваться, если бы мы вели вычисления в восьме-
ричной системе счисления. Однако эта система (а точнее говоря, тесно
связанные с ней двоичная и шестнадцатеричная системы счисления) при-
меняется лишь в ЭВМ. В десятичной же системе счисления признак дели-
мости на 7 выглядит сложнее. Мы получим его ниже.
Для вывода некоторых признаков делимости удобно записать чис-
ло п в системах счисления с основанием, являющимся степенью 10, т. е.
положить q = 10z. Например, при Z = 2, т. е. в системе с основанием 100,
числа будут иметь вид
п = bk • 100* + ... + bx 100 + Ьо,
где все коэффициенты bs — двузначные числа. Из этого представления
легко получить признак делимости на 11.
Остатки от деления чисел 100, 1002, ..., 100®, ... на 11 равны 1. В самом
деле, 100 = 9 11 + 1, 10000 = 9-11-101 + 1, 1000000 = 9 • 11 • 10 101 + 1
и т. д. Здесь т = bk + ... + b0-, напоминаем, что все bs — двузначные числа.
Получаем следующий признак делимости на 11:
I Число п = ah...a0 делится на 11 в том и только в том случае, если на 11
делится сумма, получаемая следующим образом: десятичную запись
числа п разбивают на группы по две цифры справа налево (самая ле-
вая группа может состоять и из одной цифры) и все полученные числа
складывают.
Например, число 4092 делится на 11, так как 40 + 92 = 132 и
1 + 32 = 33, а 33 делится на 11 (здесь признак делимости применен
дважды).
Иногда бывает удобно использовать не только положительные, но и от-
рицательные остатки. Целое число г будем называть приведенным остат-
ком от деления а на Ь, если а = b d + г, причем | г | <
&
.2.
Ъ
.2.
— целая
часть числа Например, 19 = 5- 3 + 4, 4>2 =
5
.2.
следовательно, 4 не яв-
, где
ляется приведенным остатком; перепишем равенство в виде 19 =
= 5 • 4 + (—1), здесь |—11 = 1 < — , т. е. —1 — приведенный остаток.
Легко видеть, что теорема Паскаля остается верной, если использо-
вать приведенные остатки. Выведем на ее основе более простой признак
делимости на 11.
Поскольку 10 = 11 - 1, 102 = 9-11 + 1, то приведенные остатки от
деления степеней числа 10 на 11 будут такими: 1,-1, 1 — 1, ... (первым
записан r0 = 1).
14
Число п = ак...а0 делится на 11 в том и только в том случае, если на 11
делится знакочередующаяся сумма пг = а0 - at + а2 - ... + (-1)* ак.
Аналогичный признак делимости на q + 1 верен для любой д-ичной
системы счисления. Например, число п = (аА...а0)12 делится на 13 = (11)12
в том и только в том случае, если на 13 делится знакочередующаяся сум-
ма а0 - ал + а2 - ... + (-1)A ak. Это утверждение вытекает из равенства
<72 = (<7 - 1) (9 + 1) + 1-
Чтобы получить признаки делимости на 7 и на 13, пригодные для де-
сятичной системы, положим q = 103 = 1000 и р = 1001 = 103 + 1. Так как
1000 = 1001 - 1, то остатки от деления на 1001 степеней тысячи 1000°,
10001, 10002, ... принимают значения 1, -1, 1, —1, ... . Поэтому получаем
такой результат: числа п = (bk...b0) и т = b0 - bY + b2 - ... + (-l)ft bk имеют
одинаковые остатки при делении на 1001. Здесь Ьо, ..., bk — трехзнач-
ные числа. Но 1001 = 7 • 11 • 13, следовательно, равны остатки и при
делении п и пг на 7, 11 и 13. Значит, признаки делимости на 7 и
на 13 формулируются так:
Число п = ак...а0 делится на 7 (соответственно на 13) тогда и только
тогда, когда на 7 (соответственно на 13) делится знакочередующаяся
сумма
ТП — &2&1&0 — ••• •
(Сформулируйте словесно способ получения такой суммы.)
Очевидно, аналогичный признак справедлив и для числа 11, но для
него мы уже знаем более простые признаки. В g-ичной системе счисления
такой же вид имеет признак делимости на q2 - q + 1. Здесь по аналогии
нужно взять
р = qs + 1 = (q + 1) (g2 - q + 1).
Чтобы получить признак делимости на 37, заметим, что
999 = 9 • 111 = 27 • 37. Поэтому остатки от деления чисел 1, 1000,
10002, ... на 37 равны 1.
Число ak...a0 делится на 37 в том и только в том случае, если на 37 де-
лится сумма а2а1а0 + а3а4а3 + asa7a6 + ....
Обратим внимание на формулировки признаков делимости. Они со-
держат словосочетания «тогда и только тогда», «в том и только в том слу-
чае», «если ..., и только при этом условии». Можно записать общую схе-
му таких формулировок: «Предложение А выполняется тогда и только
тогда, когда выполняется предложение В» (А <=> В). Теоремы такого типа
содержат два
11) «Если
вытекает
для А.
2) «Если В, то А» (В => А) — выполнение В достаточно для выполне-
ния А, т. е. В — достаточное условие для А.
Теоремы, содержащие условие, являющееся одновременно необходи-
мым и достаточным, в математике называют критериями (от греч. «кри-
утверждения:
А, то В» (А => В) — из выполнимости А с необходимостью
выполнение В, поэтому В называют необходимым условием
15
терион» — средство для решения). Критерий устанавливает признак, по
которому отбирается все, что нужно, и ничего лишнего.
Признак делимости на 7, 11 и 13 используется в следующем число-
вом фокусе. Предложите своим друзьям загадать трехзначное число и
приписать к нему его же еще раз. Попросите их разделить полученное
шестизначное число на 7 (хотя бы с помощью карандаша). Несмотря на
недоверие к вашей просьбе, это число на 7 разделится нацело. Затем
предложите полученное число разделить на 11, а результат — на 13.
К удивлению друзей, они получат в результате загаданное число. Этот фо-
кус вы, вероятно, уже разгадали.
С этим же признаком связан более сложный фокус. Вы предлагаете ко-
му-либо задумать трехзначное число и сообщить вам остатки от деления
этого числа на 7, 11 и 13. Чтобы угадать по этим остаткам а, b и с задуман-
ное число, надо образовать сумму 715а + 3645 + 924с и вычесть из нее наи-
большее кратное числа 1001, не превосходящее этой суммы. Полученная
разность и даст задуманное число. Например, если остатки от деления рав-
ны соответственно 5, 6 и 3, то сумма 715 • 5 + 364 • 6 + 924 • 3 = 8531, а
наибольшее кратное числа 1001, меньшее этой суммы, равно 8008. Вычи-
тая его из числа 8531, получим в ответе 523.
Для объяснения этого фокуса разложим участвующие в нем числа на
множители: 715 = 5 • 11 • 13, 364 = 4 7 • 13, 924 = 3 • 4 • 7 • 11, кроме того,
вычислим их сумму 715 + 364 + 924 = 2 • 1001 + 1. Обозначим искомое чис-
ло через х. Так как х - а кратно 7, то 715 (х — а) делится на 1001. Анало-
гично на 1001 делятся 364 (х - Ь) и 924 (х - с), откуда и их сумма
715 (х - а) + 364 (х - Ь) + 924 (х - с) = (2х • 1001 + х) - (715а + 3645 + 924с)
кратна 1001. Поэтому обе последние скобки при делении на 1001 дают оди-
наковые остатки. Остаток первой скобки, учитывая неравенство х < 1001,
равен х. Поэтому остаток второй скобки совпадает с задуманным числом х.
3. Каноническое разложение
В конце предыдущего пункта мы уже встретились с разложением чи-
сел на простые множители и могли заметить, что порядок следования
множителей в каждом из разложений не имеет значения. Например,
364 = 2- 2- 7-13 = 7- 2-13-2ит. д.; переставляя множители, можно
получить двенадцать представлений этого числа в виде произведения про-
стых чисел. Но других разложений числа 364 на простые множители не
существует. Это утверждение является частным случаем следующей тео-
ремы, которую ввиду ее особой важности для решения многих числовых
проблем называют основной теоремой арифметики.
Любое натуральное число п > 1 можно записать в виде произведения
простых чисел, при этом два его разложения на простые множители
отличаются друг от друга лишь порядком следования множителей.
На первый взгляд теорема кажется очевидной, на самом деле доказа-
тельство ее не совсем легкое. Приводить его мы не будем и отметим, что
вообще доказательства многих предложений теории чисел, несмотря на
16
их кажущуюся простоту, невозможно провести без привлечения доста-
точно развитого математического аппарата.
Итак, порядок записи простых множителей в разложении числа не-
существен, но все же неудобно, если они расставлены как попало. Поэто-
му расположим их в порядке возрастания и воспользуемся обозначением
степени. В результате мы придем к разложению
п = р? Р22 — Pakk- (3)
Здесь />1 < р2 < ... < рк — простые числа, а1; а2, ..., аА — натуральные чис-
ла. Такое разложение называют каноническим (от греч. «канон» — пра-
вило, норма).
У каждого составного числа есть одно и только одно такое разложе-
ние. Например, 364 = 22 • 7 13. Для простых чисел считают, что они са-
ми для себя являются каноническими разложениями, а у числа 1 канони-
ческого разложения нет.
Докажем, используя каноническое разложение, лемму, которая
нам неоднократно понадобится в дальнейшем.
Если произведение двух взаимно простых натуральных чисел является
квадратом, то и каждый множитель является квадратом.
Напомним, что два натуральных числа называются взаимно просты-
ми, если они не имеют общих множителей, отличных от 1.
Запишем канонические разложения чисел а и Ь:
Из взаимной простоты а и b следует, что в этих произведениях нет совпа-
дающих множителей. По условию леммы ab = с2. Значит, равенство
дает представление числа с в виде произведения степеней различных
простых чисел. По основной теореме арифметики такое представление
единственно с точностью до порядка множителей. Но его можно получить
по-другому: взять каноническое разложение числа с и возвести его в
квадрат, т. е. умножить все показатели на 2. Из этих рассуждений выте-
кает, что все показатели 04, ..., aft, Р15 ..., р; четные, а значит, числа а и Ъ
являются квадратами.
Для решения многих задач бывает удобно записывать канониче-
ское разложение числа несколько иначе, включив в него еще все простые
числа, меньшие рк и не вошедшие в разложение (3), взяв их с нулевым
показателем. При таком условии разложение числа 364 примет вид
364 = 22 • 3° • 5° • 7 • 11° • 13.
Нулевые показатели часто применяют, когда имеют дело одновре-
менно с двумя или большим количеством чисел; в этом случае в канони-
ческое разложение каждого из них включают все простые множители за-
данных чисел. Например,
364 = 22 • 5° • 7 • 11° • 13, 715 = 2° • 5 • 7° • 11 • 13.
Прежде чем рассмотреть некоторые задачи, связанные с делимостью
натуральных чисел, введем для краткости обозначение п : т, которое чи-
тается так: «га делится на т».
Используя канонические разложения, можно ответить на вопрос,
тт ос 1 «2 ~ а k
делится число п на т или нет. Пусть п = рг 1 -р2 •... - pk ,
т = Pi 1 />2 2 ‘ •••' Рьк • Легко видеть, что га : гаг в том и только в том слу-
чае, если для всех s = 1, 2, ..., k выполняются неравенства as > ps. На-
пример, число 5040 = 24 • З2 • 5 • 7 делится на 360 = 23 • З2 • 5 • 7°, так
как для соответствующих показателей имеем 4>3, 2 = 2, 1 = 1, 1>0.
Теперь выясним, как найти наибольший общий делитель (НОД) и
наименьшее общее кратное (НОК) двух чисел. Очевидно, НОД (га, гаг) =
= р р^2 •• р^к , где ys — наименьшее из двух чисел as и Ps для всех
8=1, ..., k. Аналогично НОК (га, гаг) = р°' • р^2 •... • р^к , здесь 3S — наи-
большее из as и Ps. Например, из разложений 360 = 23 • З2 • 5 • 7° и
1575 = 2° • З2 • 52 • 7 получаем
НОД (360, 1575) = З2 5 = 45,
НОК (360, 1575) = 23 • З2 • 52 • 7 = 12600.
Заметим, что 45 • 12600 = 360 • 1575. Это не случайно.
Предлагаем читателям доказать, что для любых двух натуральных
чисел га и т выполняется равенство
НОД (га, гаг) • НОК (га, пг) = п пг. (4)
С помощью канонических разложений натуральных чисел можно ре-
шать и более сложные задачи. Например, найти сумму всех делителей
натурального числа п; обозначают ее о (га). Легко найти о (га) для неболь-
ших натуральных чисел, например о (12) =1 + 2 + 3 + 4 + 6+12 = 28. Но
при достаточно больших числах отыскание всех делителей, а тем более их
суммы становится затруднительным. Совсем другое дело, если известно
каноническое разложение числа: га = р“* •.../>“* . Его делителями яв-
ляются все числа т = р^1 •... • р^ к , для которых 0 Ps < as, s = 1, ..., k.
Ясно, что о (га) представляет собой сумму всех таких чисел при различ-
ных значениях показателей ри Р2, ..., РА. Этот же результат мы получим,
раскрыв скобки в произведении
(1 + pt + ... + )(1 + р2 + ••• + Рг*2 ) ••• (1 + Ра + ••• + Ра * )•
По формуле суммы конечного числа членов геометрической прогрессии
приходим к равенству
>-> но —------------------• • •------ •
Pi-1 Рг-1 Ра-1
24 — 1 З3 — 1 52 — 1
По этой формуле о (360) --------------------- 1170.
2 — 1 3 — 1 5 — 1
Формулу для вычисления значений функции о (га) вывел замеча-
тельный английский математик Джон Валлис (1616—1703) — один
18
из основателей и первых членов Лондонского королевского общества
(Академии наук). Он был первым из английских математиков, начав-
ших заниматься математическим анализом. Ему принадлежат многие
обозначения и термины, применяемые сейчас в математике, в частности
знак оо для обозначения бесконечности. Валлис вывел удивительную фор-
мулу, представляющую число п в виде бесконечного произведения:
я = 2 2 4 4 2k 2k
2 1 3 3 5 "' 2 Ze — 1 2 Ze -ь 1 " ‘
Д. Валлис много занимался комбинаторикой и ее приложениями к теории
шифров, не без основания считая себя родоначальником новой науки —
криптологии (от греч. «криптос» — тайный, «логос» -— наука, учение). Он
был одним из лучших шифровальщиков своего времени и по поручению
министра полиции Терло занимался в республиканском правительстве
Кромвеля расшифровкой посланий монархических заговорщиков.
С функцией о (га) связан ряд любопытных задач. Некоторые из них
не удается решить даже с использованием формулы (5). Например, не
иначе как подбором можно найти числа, для которых о (п) есть квадрат
некоторого натурального числа. Такими числами являются 22, 66, 70,
81, 343, 1501, 4479865. Вы можете это проверить сами. Приведем еще
две задачи, сформулированные в 1657 г. Пьером Ферма.
1. Найти такое т, для которого о (zn3) — квадрат натурального числа
(Ферма нашел не одно решение этой задачи).
2. Найти такое т, для которого о (т2) — куб натурального числа.
Читатели могут убедиться, что одним из решений первой задачи яв-
ляется т = 7, а второй — т = 43098.
4. Великий мастер индукции
Одним из крупнейших математиков XVIII в. был Леонард Эйлер
(1707—1783). Он родился в швейцарском городе Базеле, где в 15 лет окон-
чил университет, а в 17 лет получил степень магистра. Во время обучения в
университете Эйлер брал уроки у одного из самых известных математиков
того времени И о г а н н а Бернулли (1667—1748) и подружился с его сы-
новьями Даниилом (1700—1782) и Николаем (1695—1726). В 1726 г.
Николай и Даниил были приглашены для работы в только что созданную
Петербургскую академию наук. Через год по их рекомендации туда же был
приглашен и двадцатилетний Эйлер. Этот выбор оказался одним из самых
удачных для России. Работы Эйлера и Даниила Бернулли по математике и
ее приложениям выдвинули Петербургскую академию наук в число луч-
ших в Европе. (К сожалению, Николай, проработав в нашей северной сто-
лице лишь 9 месяцев, умер от лихорадки.)
С момента появления в России и до конца своих дней Эйлер неразрыв-
но связал свою научную деятельность с Петербургской АН. Даже когда
из-за осложнившегося политического положения он прервал в 1741 г. рабо-
ту в России и 25 лет работал в Берлине, его тесная связь с Петербургом не
19
прекращалась. Он издавал здесь свои труды, присылал научные книги и
приборы, руководил стажировкой русских математиков. Непосредственная
работа Эйлера в Петербургской АН состояла из двух периодов — 14-летнего
первого и 17-летнего второго, который был оборван только смертью.
Научная продуктивность Эйлера была удивительной: им опубликовано
около 850 работ, многие из которых — солидные монографии. Работать он
мог сутками напролет в любой обстановке, даже если дети играли у него на
коленях. Невероятна была и скорость, с которой он производил вычисле-
ния. Однажды он за три дня выполнил срочное вычисление, на которое дру-
гие академики требовали месяц (говорят, что речь шла о составлении горо-
скопа по заказу императрицы). Однако такое перенапряжение не прошло
даром — вскоре после этого Эйлер ослеп на один глаз. Во второй период
жизни ученого в Петербурге от чрезмерного переутомления перестал видеть
и второй его глаз. Лучший окулист Петербурга сделал ему операцию. Нуж-
но было некоторое время не утруждать глаза. Но без вычислений Эйлер не
представлял себе жизни. Начав раньше времени вновь напрягать зрение, он
навсегда лишился возможности видеть. После этого он стал диктовать свои
труды сыновьям. Однако сыновья не справлялись с таким огромным объе-
мом работы, и был приглашен секретарь. Но и совместными усилиями они
едва успевали записывать вычисления Эйлера.
В творчестве Эйлера переплетались исследования как в области не-
прерывной, так и в области дискретной математики. В каждом из этих
направлений Эйлер выступал как математик, вырабатывающий общие
методы решения задач. Самые остроумные преобразования и искусные
подстановки возникали у него совершенно естественно. Такой дар дается
природой только гениям. Именно они легко проникают из одной области
науки в другую, находят связи, скрытые от глаз других, легко обнаружи-
вают новые задачи и методы их решения.
Нет такого направления классической математики, где бы Эйлер не
сказал своего слова. Его работы либо открывали новую область математи-
ки, либо питали ее в течение долгого времени. Именно поэтому Лаплас
сказал: «Читайте, читайте Эйлера: это наш общий учитель», а Гауссу
принадлежат слова: «Изучение работ Эйлера остается наилучшей школой
в различных областях математики, и ничто другое не может это заме-
нить». Впрочем, временами у математиков от восхищения вырывались и
более крепкие выражения. Один из них в письме своему коллеге писал:
«Этот дьявол Эйлер» — достижения Эйлера казались ему превосходящи-
ми человеческие возможности.
Насколько велик был авторитет Эйлера в науке, характеризует сле-
дующий эпизод. Княгиня Екатерина Романовна Дашкова, назначенная
Екатериной II президентом Петербургской АН, отправляясь на первое за-
седание академии, где должна была председательствовать, заехала за
Эйлером. Поддерживая великого слепца под руку, Екатерина Романовна
вошла с ним в зал. Один нескромный академик поспешил занять место
рядом с председательским. Тогда Дашкова сказала: «Господин Эйлер!
Займите любое место в зале. С этого момента оно станет первым».
Почти в любой области математики сейчас используются функции,
формулы, подстановки, интегралы, связанные с именем Эйлера. Познако-
20
мимся с функцией, носящей его имя. Она, так же как и функция о (п), свя-
зана с делителями числа п и тоже нам понадобится в дальнейшем.
Функция Эйлера определяется следующим образом. При п = 1 она
равна 1, а для любого натурального числа п, большего 1, функция Эйлера
равна количеству натуральных чисел, меньших п и взаимно простых с п.
Обозначают ее <р (п). Пусть п = 12. Взаимно простыми с числом 12 и мень-
шими его являются числа 1, 5, 7 и 11. Поэтому ф (12) = 4. Совсем просто
найти <р (р), если р — простое число. В этом случае взаимно простыми с р
будут все натуральные числа от 1 до р — 1, и потому <р (р) = р — 1. Это ра-
венство можно переписать так: ф (р) = р 1 - — . Более сложные рассуж-
k Р)
дения показывают, что для п = р“* •... • р“* .
ф(п)=п|1----— I | 1-—|...|1---— |. (6)
V Pl J \ Р2 J k Pk )
Здесь в каноническое разложение включены лишь те простые числа ps,
для которых as Ф 0.
Например, из разложения 504 = 23 • З2 • 7 следует, что
ф (504) = 504-(1-|Д1-|Д1-у^ = 144.
Получить этот результат непосредственным подсчетом было бы не-
легко.
Функция Эйлера часто встречается в различных математических за-
дачах, и мы в этом еще сможем убедиться. А пока выведем одно ее свой-
ство: если числа п и т взаимно простые, то ф (пт) = ф (п) • ф (т). Други-
ми словами, функция ф сохраняет операцию умножения. Это свойство
называют мультипликативностью (от лат. multiplicatio — умножение).
Итак, покажем мультипликативность функции ф.
В силу взаимной простоты чисел п = р“‘ •... • р“* и т = q^1 •... -q^ 1
каноническое разложение их произведения пт имеет вид
a 1 ot ь Bi Р 1
пт = Pj 1 •...-pk -q^1 ...-qt .
Значит,
откуда и следует равенство ф (тп) = ф (п) • ф (т).
Например, ф (72 • 175) = 2880 = 24 • 120 = ф (72) • ф (175).
Докажите сами мультипликативность функции о (п).
Эйлер обладал удивительной способностью открывать новые соотноше-
ния для натуральных чисел, изучая свойства некоторых первых чисел.
Лишь потом ему (далеко не всегда!) удавалось найти строгие доказательства
угаданных свойств. С интересными и разнообразными результатами Эйлера
21
мы встретимся еще и в этой главе, и во многих последующих. А пока при-
ведем замечательное тождество, к которому великий мастер пришел с помо-
щью индукции. Оно связано с суммой делителей натурального числа.
Эйлер заметил, что для любого п выполняется равенство
о (п) = о (п - 1) + ст (п - 2) - а (п - 5) - о (п - 7) +
+ а (п - 12) + о (п - 15) — ст (п - 22) - ст (п — 26) +
+ ст (п - 35) + о (п - 40) - ст (и. - 51) — ст (га — 56) + .... (7)
Здесь числа 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 56, ... попеременно
3k2-k 3/г2+/г
выражаются формулами--------и — ----, где k = 1, 2, ..., а знаки чере-
дуются так, что после двух положительных слагаемых идут два отрица-
тельных. Суммирование ведется до тех пор, пока аргументы функции о
неотрицательны; если последнее значение аргумента окажется нулем, то
считается, что ст (0) = п.
Эйлеру не удалось сразу найти доказательство формулы (7), но он
свел его к доказательству равенства
(1 - х) (1 - х2) (1 - X3) (1 - х4) (1 - X5) (1 - X6) ... =
= 1 - X - X2 + X5 + X7 - X12 - X15 + х22 + х26 - X35 - х40 + ..., (8)
справедливость которого установил через год. В этом равенстве произве-
дение и сумма бесконечны. Его называют сейчас тождеством Эйлера.
Следует заметить, что многие математические исследования не дают
сиюминутной пользы, но через некоторое время выясняется их ценность.
В XIX в. обнаружилась фундаментальность тождества Эйлера: оно сыграло
важную роль в создании теории эллиптических функций. Еще почти через
полтора столетия оно оказалось причастным к развитию теории групп Ли.
Вот что пишет сам Эйлер по поводу наблюдений, приведших его к за-
мечательным открытиям: «...в теории чисел, которая все еще не совер-
шенна, наши самые большие надежды мы можем возлагать на наблюде-
ния; они непрерывно будут вести нас к новым свойствам, которые позже
мы будем стараться доказать. Этот вид знания, которое подкрепляется
только наблюдениями и все еще не доказано, следует тщательно отличать
от истины; оно, как мы обычно говорим, приобретается индукцией... мы
должны пользоваться таким открытием как возможностью более точно
исследовать эти открытые свойства и доказать их или опровергнуть; в
обоих случаях мы можем научиться кое-чему полезному».
5. Метод математической
индукции
Не всегда из наблюдения за некоторым количеством первых нату-
ральных чисел можно сделать верный вывод. Для примера рассмотрим
многочлен f (п) = re2 - п + 41 и начнем придавать аргументу п значения,
равные 1, 2, 3, 4, 5 и т. д. В результате будем иметь
f (1)= 41, f(2)= 43, f (3)= 47, f (4)= 53, f (5)= 61.
22
Каждое из полученных значений представляет собой простое число.
Отсюда можно предположить, что при любом натуральном п значение
многочлена f (п) есть простое число. Эта гипотеза выдерживает испыта-
ние для всех п от 1 до 40. Но уже f (41) = 412 — составное число. Таким
образом, наше предположение неверно.
От такого рода ошибок предостерегал Эйлер: «Однако мы видели
случаи, когда простая индукция вела к ошибке. Поэтому мы должны
проявлять большую осторожность, чтобы не принять за истинные такие
свойства чисел, которые мы открывали путем наблюдения и которые под-
крепляются одной лишь индукцией». Такую индукцию (от лат. induc-
tio — наведение) часто называют неполной. Мы еще будем иметь возмож-
ность убедиться в том, что и выдающиеся математики на основании не-
полной индукции делали неверные выводы. Как указывал Эйлер, этот
метод хорош лишь для того, чтобы угадать результат, который в дальней-
шем надо строго доказать. И не всегда математикам удавалось найти
нужное доказательство. А иногда его просто нет, как в рассмотренном на-
ми примере. Чтобы убедиться в этом, нам пришлось перебрать 41 число, в
других же случаях удача поджидает исследователя в очень длинном ряду
кропотливых и громоздких вычислений.
Если же свойство подмечено верно, то для его доказательства, как
правило, применяется метод математической индукции. (Термин «мате-
матическая индукция» появился впервые в 1838 г. в одноименной статье
де Моргана в Британской энциклопедии.) Состоит он в следующем:
|Если некоторое утверждение справедливо при п = 1 и из предположе-
ния, что оно верно при n = k, вытекает его справедливость и при
п = k + 1, то данное утверждение выполняется для любого натурально-
го числа.
Метод математической индукции был, по-видимому, впервые (1665)
разработан Б. Паскалем. Сейчас он широко применяется в математике
для доказательства самых разнообразных тождеств, неравенств и других
утверждений. Мы еще не раз обратимся к нему в этой книге. А пока дока-
жем с его помощью некоторые предложения о делимости натуральных
чисел.
Покажем, что сумма кубов любых трех последовательных целых не-
отрицательных чисел делится на 9. Поскольку
(п - I)3 + п3 + (л + I)3 = Зл (л2 + 2),
то достаточно доказать делимость на 3 числа л (л2 + 2) для произвольного
натурального л. При л = 1 это так. Предположим, что утверждение верно
в случае л = k, и выведем отсюда делимость на 3 числа л (л2 + 2)
при л = k + 1. Это следует из равенства (k + 1) ((А + I)2 + 2) =
= k (fe2 + 2) + 3 (k2 + k + 1), здесь первое слагаемое правой части делится
на 3 по предположению.
Задачи на делимость натуральных чисел часто предлагаются на ма-
тематических олимпиадах. Многие из них легко доказываются именно
методом математической индукции. Приведенный пример убеждает в его
удобстве.
23
Рассмотрим еще одно утверждение:
При любом натуральном п число 23" +1 делится на Зп + 1.
Докажем его. Для п = 1 число 2з1 + 1 = 9 делится на З1 +1 = 9. Пусть
наше утверждение верно для п = k, т. е. (23* + 1): 3* + 1. Перейдем к
п = k + 1:
23* + 1 + 1 = 23*'3 + 1 = (23*)3 + 1 = (23* + 1)((23*)2 - 23‘ +1).
Первый множитель в этом произведении делится на 3* + 1 по предпо-
ложению, осталось показать, что ((23 )2 -23 + 1): 3. В самом деле,
(23* )2 - 23* + 1 = (23* + I)2 - 3 • 23* ; эта разность, очевидно, делится на 3,
поскольку делимость на 3 уменьшаемого вытекает из предположения.
Итак, (23*+1 + 1)!3*+2.
я Докажите, что сумма 11п + 2 + 122л + 1 делится на 133.
В дальнейшем нам неоднократно понадобится формула, носящая на-
звание «бином Ньютона». Она настолько знаменита, что даже в та-
ком далеком от математики литературном произведении, как роман
М. А. Булгакова «Мастер и Маргарита», один из спутников Воланда час-
то повторяет: «Подумаешь, бином Ньютона!» Слово «бином» означает
«двучлен», образовалось оно от латинских слов bis — дважды, nomen —
часть, член. Формула показывает, как натуральную степень двучлена
представить в виде суммы степеней его слагаемых. Это для некоторых
показателей умели делать еще в X в. арабские математики. А они заимст-
вовали свой способ у индийцев. Ньютон нашел разложение в сумму ра-
циональной степени двучлена (при этом получается бесконечный ряд сла-
гаемых), но тем не менее за формулой закрепилось его имя.
Бином Ньютона имеет вид
(а + Ъ)п = ап +С1пап~1Ь + ... + С* ank Ьк + ... + C"~1abn~1 +bn , (9)
где п — натуральное число, С1п , С2п, ..., С^-1— числовые коэффициен-
ты, которые вычисляются следующим образом:
. п(п - 1) (п - 2)... (п - k + 1)
С к =--------------------------. (10)
k!
Через /г! (читается «fe-факториал») обозначено произведение
1 • 2 • 3 • ... k. Термин «факториал» (от лат. factor — множитель) впер-
вые появился (1800) у французского математика Луи Арбогаста
(1759—1803). Обозначение k\ ввел немецкий математик Кретьен
Крамп (1760—1826). Иногда применяют более компактную запись фор-
мулы (9):
(а + Ъ)л = ^Cknan"bk.
k = 0
24
п
Здесь знак означает суммирование по всем целым k от 0 до п. Коэф-
k = о
фициенты С* называются биномиальными. Они присутствуют во многих
математических соотношениях. Формулу (10) мы выведем в разделе, по-
священном теории вероятностей, а сейчас отметим, что из нее вытекает
следующее свойство биномиальных коэффициентов:
с^+с^с^. (11)
Формулу бинома Ньютона (9) легко доказать методом математиче-
ской индукции. Заметим сначала, что она верна при п = 1 (в этом случае
имеем а + b = а + Ъ). Предположим, что она верна при п = k. Чтобы дока-
зать ее справедливость при п = k + 1, надо умножить обе части формулы
(9) при п = k на а + Ъ, привести подобные члены в правой части равенства
и воспользоваться соотношением (11). Предлагаем читателям проделать
это самостоятельно.
Иногда подмечают свойство, верное лишь для чисел, больших неко-
торого определенного числа т. В этом случае доказательство методом ма-
тематической индукции начинают с п = т + 1.
Докажем в качестве примера такое утверждение:
Сумма внутренних углов произвольного (необязательно выпуклого)
В п-угольника равна л (п - 2).
Для п. = 3 утверждение известно. Пусть оно верно для п = k, и дока-
жем его для п = k + 1. В любом (fe + 1)-угольнике найдутся хотя бы две
смежные стороны, образующие угол, меньший развернутого. (Докажите!)
Проведем диагональ через концы этих сторон. В результате (k + ^-уголь-
ник разобьется на треугольник и fe-угольник. Сумма углов (k + ^-уголь-
ника равна л + л (k - 2) = л (k - 1).
6. Гениальный дилетант
Математикой занимаются не только профессионалы. Эта наука все-
гда притягивала внимание многих любителей. И иногда достижения
людей, обращавшихся к ней в часы досуга, не уступали достижениям
профессиональных ученых. Одним из самых выдающихся любителей ма-
тематики был французский юрист Пьер Ферма (1601 —1665).
Родился он в провинциальном городке Бомоне на юге Франции в
семье торговца кожами. Университетское образование получил в Тулузе,
где и провел почти безвыездно всю свою жизнь. Здесь он дослужился до
высокого поста советника городского парламента. (В то время во Фран-
ции парламентами называли окружные судебные органы.) Высшим чи-
новникам судебных органов предписывалось вести уединенный образ
жизни, чтобы иметь в округе меньше знакомых и, следовательно, быть
более объективными при решении различных вопросов. Ферма неукосни-
тельно следовал этим советам и зарекомендовал себя исключительно че-
стным человеком и большим знатоком своего дела. Замкнутый образ
25
жизни оставлял много свободного от юриспруденции времени, которое
Ферма отводил разным своим увлечениям. Зная многие современные ему
и древние языки, а также литературу, он занимался филологическими
исследованиями, сочинял стихи на латинском, французском и испанском
языках. Но наибольшее время он отдавал математике. И здесь достиже-
ния «дилетанта» поставили его в один ряд с самыми выдающимися мате-
матиками всех времен.
Ферма открыл метод отыскания экстремумов и усовершенствовал
способ вычисления площадей — эти исследования стали началом матема-
тического анализа. Параллельно с Декартом он создал аналитическую
геометрию (его результаты даже стали известны в Европе раньше резуль-
татов Декарта). Из задач, обсуждавшихся в его переписке с Паскалем,
выросла теория вероятностей. Он сформулировал основной принцип гео-
метрической оптики. Несмотря на все эти замечательные открытия, о ко-
торых мы еще будем говорить в соответствующих разделах, имя Ферма
чаще связывают с теорией чисел — областью математики, изучающей це-
лые числа. Она была его главной любовью.
Еще в 1575 г. был опубликован первый перевод на латинский язык
уцелевших книг «Арифметики» древнегреческого математика Диофанта.
Богатство содержавшегося в ней теоретико-числового материала было на-
столько велико, что привлекло внимание многих ученых. В 1621 г.
«Арифметика» Диофанта была переиздана Баше де Мезириаком, снаб-
дившим книгу своими комментариями. Именно такой том и принадле-
жал Ферма. Почему мы так подробно говорим об этой книге? Дело в том,
что Ферма не опубликовал ни одной печатной работы и о результатах его
научных трудов мы знаем лишь из оставшихся после него бумаг, записей
на широких полях диофантовой «Арифметики» (к сожалению, эти поля
были недостаточно широки) и из переписки с другими учеными. Записи
на полях «Арифметики» оказались бесценными. В них Ферма сформу-
лировал ряд утверждений, ставших фундаментальными в современной
теории чисел. Многие из утверждений приведены без доказательства.
В задачах, которые ставил Ферма в письмах европейским ученым, рас-
крывались новые тайны натуральных чисел. Надо отметить, что он сумел
выделить основные направления в теории чисел и определить перспекти-
вы ее развития: в течение всех последующих веков решение задач Ферма
и доказательство его утверждений оставались в центре внимания ученых.
Ферма переписывался со многими ведущими математиками своего
времени: Паскалем, Декартом, Валлисом, Робервалем, Торричелли и др.
Особенно обширна была его переписка с жившим в Париже ученым-мона-
хом Мареном Мерсенном (1588—1648). Мерсенн был разносторон-
ним ученым (получил ряд результатов в теории чисел, определил ско-
рость звука в воздухе, предложил схему зеркального телескопа) и
прекрасным организатором. Он возглавлял кружок ученых, который впо-
следствии преобразовался в Парижскую академию наук. Мерсенн быстро
схватывал идеи, умел выделять наиболее важные открытия. Кроме того,
он имел репутацию исключительно честного человека, которому можно
доверить свои еще не опубликованные результаты. Благодаря этим ка-
чествам и обширной переписке со многими учеными Мерсенн стал
26
своеобразным центром европейской научной информации. Сообщение ему
о научных открытиях было равносильно их публикации. Сети научных
журналов, которая ныне дает ученым возможность сообщить научному
миру о результатах своих исследований, в то время еще не существовало.
Писать каждому ученому о своих открытиях непосредственно было хло-
потно и не вполне безопасно. Слишком часто возникали споры о приори-
тете: случалось, что ученый, получивший письмо с решением какой-то
задачи, сам размышлял над ней или уже успел решить ее. Поэтому дея-
тельность Мерсенна была необходима всему научному сообществу Европы.
После смерти Мерсенна почетную миссию посредничества между уче-
ными стал выполнять бывший юрист Тулузы королевский библиотекарь
Пьер де Каркави (ум. в 1684 г.). Ферма в письме (1654) к Каркави
просит его и Паскаля позаботиться о посмертном издании своих работ. Но
Паскаль умер раньше Ферма, а одному Каркави не под силу было выпол-
нить просьбу друга. Его переписка оказалась разбросанной по всей Европе,
и искать ее в частных архивах или библиотеках, куда родственники ученых
могли передать деловую переписку, было делом почти безнадежным.
Впервые за издание работ Ферма взялся его старший сын Самю-
эль-Клемент (1630—1690). В 1670 г. он переиздал диофантову «Ариф-
метику» с замечаниями отца на полях. Издание называлось «Шесть книг
арифметики александрийца Диофанта с комментариями К. Г. Баше и заме-
чаниями П. де Ферма, тулузского сенатора». А в 1679 г. сын опубликовал
важнейшие результаты Ферма, содержащиеся в письмах Робервалю, Мер-
сенну и другим математикам. Конечно, это была только часть научного на-
следия Ферма, но и она послужила развитию математики.
Замечательный результат содержался в письме (1640) Ферма фран-
цузскому математику Ф р е н и к л ю де Бесси (1605—1675). В дальней-
шем он получил название малая теорема Ферма.
Если р — простое число и а — любое натуральное число, то разность
ар - а делится на р.
Например, если а = 8 и р = 5, то получаем число 85 - 8 = 32760, де-
лящееся на 5.
Доказательства этой теоремы не было ни в письме к Френиклю, ни в
бумагах, оставшихся после Ферма. Лишь через сорок с лишним лет эту
теорему доказал крупнейший немецкий философ и математик Готфрид
Вильгельм Лейбниц (1646—1716). При этом он использовал бином
Ньютона.
Проведем доказательство теоремы методом математической индук-
ции по а. Для а = 1 имеем 1Р - 1 = 0, 0 : р. Предположим, что (ар - а) р,
и выведем отсюда делимость на р разности (a+iy1 — (a + 1). Применяя
разложение по формуле бинома Ньютона, получим
(a + IX - (а + 1) = (ар +С1рар~1 + ... +Cpp~la + 1) - (а + 1) =
= (ар -а) + (С* ар-1 + ... +С£-1а).
Так как число р простое, то во всех коэффициентах С*, где 1 С k р - 1,
в числителе есть простой множитель р, а в знаменателе его нет (см.
27
формулу (10)). Поэтому все эти коэффициенты, а с ними и вторая скобка
делятся на р; первая скобка делится на р по предположению. Тем самым
малая теория Ферма доказана.
Само название «малая» подсказывает, что есть и большая теорема
Ферма, или, как ее еще называют, Великая. Но о ней речь пойдет в сле-
дующей главе.
Так как ар - а = а (ар~ 1 — 1), то при условии, что аир взаимно про-
сты, из малой теоремы Ферма следует делимость на р разности ap l — 1.
Число ------- называется частным Ферма. Интересно, делится ли оно
Р
на р? Проверка для простых чисел, меньших 1000, дала отрицательный
ответ, и известный советский математик Дмитрий Александрович
Граве (1863—1939) высказал предположение, что так будет для всех
простых чисел. Однако вскоре выяснилось, что, хотя 1093 — простое
2 1092 _ 1
число, частное Ферма —— делится на 1093. (Предупреждал же Эйлер,
что индукция может подвести!)
Через 100 лет после того, как Ферма высказал свою теорему, Эйлер
обобщил ее на случай, когда делитель не является простым. Он доказал, что
при взаимно простых числах а и т разность ач’(,п) - 1 делится на т.
Здесь <р (т) — та самая функция Эйлера, о которой мы говорили в
п. 4. Например, если а = 5, т = 6, то ф (т) = 2 и разность 52 - 1 = 24 де-
лится на 6.
Это и в самом деле обобщение малой теоремы Ферма, поскольку
Ф (?) = Р — 1 Для простого р.
В связи с утверждением малой теоремы Ферма возникает естествен-
ный вопрос: что можно сказать о делимости на т разности ат — а в слу-
чае, когда т — составное число? Этим вопросом интересовались еще
древнекитайские математики более двух с половиной тысяч лет тому
назад. Правда, не в такой общей постановке: они рассматривали только
случай а = 2. Если попробовать проверять делимость 2т — 2 на т для раз-
ных составных т, то окажется, что по крайней мере для составных чи-
сел, меньших 300 (а их более двух сотен), ответ будет отрицательным. Эта
проверка породила у древнекитайских математиков уверенность в том,
что числа вида 2т — 2 при составном т не делятся на т. Если бы речь
шла не о математическом утверждении, а о физическом опыте, то вывод
был бы, скорее всего, верен — закономерность, повторяющаяся более чем
в двухстах опытах, практически всегда имеет место. Но в математике так
рассуждать нельзя. Здесь даже миллиона опытов недостаточно для окон-
чательного решения вопроса. И действительно, оказалось, что существует
составное число 341 = 11 • 31, для которого 2341 - 2 делится на 341. Что-
бы убедиться в этом, воспользуемся тождеством
2341 - 2 = 2 (2340 - 1) = 2 ((210) 34 - 1) =
= 2 ( 210 - 1) ((2 1 0)33 + (210)32 + ... + 1).
Из него следует делимость числа 2341 - 2 на 210 - 1 = 1023 = 3 341, а
потому и на 341.
28
Оказывается, совокупность составных чисел т, для которых 2т - 2
делится на т, бесконечна. Среди них только в 1950 г. было найдено чет-
ное число 161038. Затем нашли и другие четные числа: 215326, 2568226,
14374226. А потом было доказано, что и четных составных чисел т, для
которых 2т — 2 делится на т, бесконечно много. Аналогичный результат
был получен для чисел вида Зт - 3.
Замечательное свойство было обнаружено у составного числа
561 = 3 • 11 • 17. Оказывается, для любого п, взаимно простого с этим
числом, разность га561 - п делится на 561.
Рассмотрим еще один интересный вопрос, ответ на который позволя-
ет дать малая теорема Ферма. Обратим обыкновенную дробь — в десятич-
Р
ную, получится бесконечная периодическая дробь. Связана ли длина пе-
риода этой дроби с числом р?
Этим вопросом еще в школьные годы заинтересовался немецкий ма-
тематик Карл Фридрих Гаусс (1777—1855). Об этом великом уче-
ном, которого при жизни называли королем математиков, мы расскажем
в алгебраическом разделе. Сейчас же отметим только, что Гаусс, как и
Эйлер, отличался удивительной способностью быстро и неутомимо вычис-
лять. В одном из писем к немецкому астроному И. Энке он пишет, что
«очень часто употреблял свободные четверть часа, чтобы то там, то здесь
просчитать хилиаду» (т. е. найти простые числа в какой-нибудь тысяче
натуральных чисел). Не знаем, как читатели, а авторы не взялись бы за
четверть часа найти все простые числа, например от 1800000 до 1801000,
а Гаусс в «свободное время» нашел все простые числа, меньшие 3000000
(на это он затратил по меньшей мере 750 часов). Конечно, ЭВМ справи-
лась бы с этой задачей значительно быстрее, но ведь во времена Гаусса не
было даже приличных ручных арифмометров!
Изучая вопрос о длине периода десятичной дроби, Гаусс брал одно за
другим простые числа р и подсчитывал количество цифр в периоде деся-
тичной дроби, равной —. Он сразу подметил, что длина периода является
Р
делителем числа р - 1. Например, для дроби — = 0,333... длина периода
3
равна 1, а 1 — делитель числа 2 = 3-1. У дроби — = 0,142857142857...
7
период имеет длину би 7-1=6. Длина периода дроби = 0,090909...
равна 2, а 2 — делитель числа 10 = 11 - 1. Объясняется это следующим
образом.
По малой теореме Ферма для любого простого числа р, отличного от
2 и 5, разность 10р“х — 1 делится на р. Значит, 10р-1 имеет вид тр + 1.
Но тогда — •10₽| = — (тр + 1) = т + —, т. е., переместив в десятичной
Р Р Р
дроби, равной —, запятую на р — 1 шагов вправо, получим число с той же
Р
29
самой дробной частью. А это может быть при условии, что р — 1 кратно
длине периода. У дробей — = 0,500... и — = 0,200... длина периода равна 1,
2 5
поэтому для р, равного 2 или 5, подмеченное Гауссом свойство тоже спра-
ведливо.
Из доказательства видно, что в десятичной системе счисления длина
периода дроби — (р * 2; 5) равна наименьшему из чисел к, для которых
(10* - 1) = р. Р
Аналогичная ситуация имеет место и в других системах счисления.
Именно, пусть q — некоторое натуральное число, ар — простое. Если
любую дробь вида —, знаменатель которой взаимно прост с q, записать
Р
в виде бесконечной периодической g-ичной дроби, то длина периода будет
делителем числа р — 1. Покажите, что в g-ичной системе длина периода
дроби — равна наименьшему из чисел k, для которых (qk — 1) • р.
Р
Гаусс заинтересовался вопросом: найдется ли для данного простого
- 1
числа р такая система счисления, что в ней длина периода дроби — в точ-
Р
ности равна р — 1? И сам доказал, что ответ на этот вопрос положитель-
ный: такие системы найдутся и даже с основаниями q, меньшими р.
Основания этих систем называют первообразными основаниями по отно-
шению к р. Правда, теорема Гаусса ничего не говорит о том, как искать
такие основания. Поэтому надо взять числа 2, 3, ..., р - 1, записать дробь
1 ,
— в системах с такими основаниями, а потом выбирать те, в которых ее
Р
период имеет длину р - 1. Теорема Гаусса гарантирует нам, что этот по-
иск не окажется, как говорится, поиском черной кошки в темной комна-
те, в которой кошек отродясь не бывало.
Обозначим найденное первообразное основание через q. Из малой те-
оремы Ферма вытекает, что (g₽-1 - 1) : р. Поскольку длина периода дро-
би — в q-ичнои системе равна р - 1, то это наименьшее из чисел k, для ко-
Р
торых (qk — 1) : р. Теперь теорему Гаусса можно сформулировать
так:
Для каждого простого р найдется такое число q<p, что qk - 1 не де-
лится на р ни при каких k <р - 1.
Найдем, например, первообразное основание для р = 17. Основание 2
не годится, потому что уже 28 дает при делении на 17 остаток 1, т. е.
(28 - 1) : 17 и длина периода дроби — в двоичной системе равна 8, а не
17
16. Но основание 3 нас уже устроит. Чтобы убедиться в этом, нужно най-
ти остатки от деления чисел 3, З2, ..., З16 на 17. Результаты приведены в
таблице, где в верхней строке стоят показатели степеней числа 3, а в
нижней — соответствующие остатки.
30
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
3 9 10 13 5 15 11 16 14 8 7 4 12 2 6 1
В нижней строке содержатся все числа от 1 до 16. Оказывается, это
общий факт.
Если q — первообразное основание для простого числа р, то остатки
от деления q, q2, ..., qp~1 на р все разные и принимают значения
1, 2, ...,р-1.
На самом деле всего остатков р — 1, среди них нет нулевых, посколь-
ку q и р взаимно просты. Если бы какого-то числа 1, 2, ..., р - 1 не было
среди остатков, тогда другой остаток встретился бы дважды, напри-
мер остаток от деления qm и qm + l на р. Но тогда бы разность
qm + l _ qm = qm (ql — 1) делилась на р, откуда на р делился бы множитель
(ql — 1) при I < р - 1, что противоречит первообразности основания q.
Другими первообразными основаниями для р = 17 являются числа
10, 5, 11, 14, 7, 12, 6. Заметим, что, как и основание 3, они стоят на не-
четных местах второй строки таблицы.
7. Семейные проблемы
Давно известно, что простых чисел бесконечно много. Еще Евклид
(ок. 365 — ок. 300 до н. э.) в своих «Началах» доказал это утверждение.
Мы повторим доказательство Евклида, немного видоизменив его. Пусть
Р — конечное множество простых чисел, занумеруем их pt, рг, ..., рп.
Рассмотрим число q = рг р2 • ... • рп + 1, для него возможны два вариан-
та: либо q — простое, при этом ясно, что оно не принадлежит Р, либо
q — составное, тогда оно имеет простой делитель, который не может сов-
падать с р2, ..., рп, поскольку q на них не делится. Итак, для любого
конечного набора простых чисел всегда найдется простое число, не вхо-
дящее в него. Отсюда вытекает бесконечность множества всех простых
чисел.
Многие ученые занимались простыми числами, но и сегодня далеко
не все известно о них. Неизвестно, например, сколько простых чисел
можно записать одними единицами. Пока найдены пять таких чисел: они
состоят из 2, 19, 23, 317 и 1031 единиц. Отметим, что количество единиц
в записи таких чисел само должно быть простым числом. Ведь если
п = km, то число, состоящее из п единиц, делится на числа, состоящие из
k и из т единиц. Например, 111111 = 111 • 1001 = 11 • 10101.
Любопытно, что для любого простого числа р, отличного от 2 и 5,
найдется записываемое только с помощью единиц число, делящееся на р.
Если р Ф 3, то таким свойством обладает, например, число, состоящее из
(р — 1) единицы. В самом деле, мы знаем, что если р отлично от 2 и 5, то
10₽ 1 - 1 делится на р. Число 10р 1 - 1 записывается с помощью (р - 1)
девятки. Так как р отлично и от 3, то, разделив 10р 1 - 1 на 9, получим
31
частное, записанное с помощью (р - 1) единицы, делящееся на р. (На
р = 3 число 11 не делится, но делится, например, 111.)
Иногда можно взять и менее (р - 1) единицы. Например, число
111111 делится на 13. Еще Гаусс пытался выяснить, конечна или нет
совокупность простых чисел р, для которых число из k единиц (k < р - 1)
не делится на р. Ответ на этот вопрос до сих пор неизвестен.
Есть в теории простых чисел и такая интересная проблема: конечна
или нет совокупность близнецов — так называют пары простых чисел,
разность между которыми равна 2. Примерами близнецов служат 3 и 5,
5 и 7, 11 и 13, 17 и 19, 29 и 31. Чем дальше мы продвигаемся вперед по
натуральному ряду чисел, тем реже встречаются простые числа, а уж
совсем редко — близнецы. И до сего дня неизвестно, а не оборвется ли
последовательность этих чисел. Пока же упорные поиски отдельных
энтузиастов приводят к открытию новых и новых близнецов, достаточно
далеко расположенных в натуральном ряду. С помощью ЭВМ были най-
дены такие близнецы: 9 • 2211 - 1 и 9 • 2211 + 1.
Кроме близнецов, в последовательности простых чисел существует
аналогичная тройня (3, 5, 7). Оказывается, она единственная. На самом
деле, в тройке (п — 2, п, п + 2) одно из чисел всегда делится на три (в чем
легко убедиться), в то же время оно должно быть простым, а поэтому рав-
но 3.
Итак, две пары близнецов, исключая пары (3, 5) и (5, 7), могут нахо-
диться друг от друга самое меньшее на «расстоянии», равном 4. Это, на-
пример, пары (5, 7) и (11, 13) или пары (11, 13) и (17, 19). Они определя-
ют четверку (п - 4, п - 2, п + 2, п + 4) простых чисел. Таких четверок на
достаточно большом отрезке числового ряда не так уж и мало. Например,
среди первых 10 миллионов натуральных чисел их насчитывается 899.
Одной из них является четверка
(2863308731, 2863308733, 2863308737, 2863308739).
И уж если мы не знаем, бесконечно ли множество близнецов, то тем
более неизвестно, бесконечно ли множество четверок простых чисел ука-
занного вида. (И у людей близнецы встречаются редко, а четверни — по-
разительное событие.)
Долгое время шел поиск критерия простоты числа р, т. е. такого
признака, по которому можно было бы безошибочно определить принад-
лежность произвольно взятого числа к семейству простых. В 1770 г. анг-
лийский математик Э. Варинг сформулировал гипотезу своего ученика
Джона Вильсона (1741—1793):
Для того чтобы число р было простым, необходимо и достаточно, что-
бы число (р - 1)! + 1 делилось на р.
Через три года она была доказана французским ученым Жозефом
Луи Лагранжем (1736—1813). Но этот признак мало что дает для
практики, потому что числа вида ге! очень быстро растут с возрастани-
ем п, и потому проверка делимости (р — 1)! + 1 на р требует слишком
больших вычислений.
32
Имеется довольно много необходимых условий простоты числа (т. е.,
по существу, свойств простого числа), но до сих пор нет удобного для при-
менения достаточного условия. Как мы видели, утверждение малой тео-
ремы Ферма является необходимым условием простоты числа р, но недо-
статочным. Ферма сформулировал и другой (доказанный впоследствии
Эйлером) необходимый признак простоты числа р:
Любое простое число р, имеющее вид 4п + 1, может быть единствен-
ным образом представлено в виде суммы квадратов двух натуральных
чисел.
Например, 5 = I2 + 22, 13 = 22 + З2, 17 = I2 + 42, ... . Но признак этот
тоже не является достаточным: числа 25 = З2 + 42, 45 = З2 + 62 имеют
единственное представление в виде суммы двух квадратов, но не являют-
ся простыми. Зато уж число вида 4п + 1, имеющее два таких разложе-
ния, наверняка составное:
221 = 52 + 142 = 102 + II2 и 221 = 13 • 17.
8. Генераторы простых чисел
Простые числа так причудливо расположены в натуральном ряду, что
у математиков не было надежды вывести формулу, которая давала бы все
такие числа и никакие другие. Поэтому попытались достичь более легкой
цели — найти формулу, подставляя в которую вместо п одно за другим на-
туральные числа получать каждый раз простое число. Одну из первых
таких формул предложил Ферма. Она имела вид Fn = 22" +1. В письме к
Паскалю (1654) он писал: «Последовательное квадрирование двух при уве-
личении на единицу всегда простое число — это свойство, за истинность ко-
торого я ручаюсь». Числа Fn получили название чисел Ферма.
Такой сложный вид показателя Ферма выбрал не случайно: число
2* + 1 при k Ф 2п является составным. На самом деле, если число k нечет-
но, k = 2т + 1, то имеет место разложение
2* + 1 = 22m + 1 + 1 = (2 + 1) (22т - 22"1-1 + ... - 2 + 1).
Таким же образом доказывается, что 2к + 1 является составным
числом, если у числа k есть хоть один нечетный множитель. И только
когда k является произведением двоек, т. е. k = 2", можно надеяться на
простоту числа 2* + 1.
Однако то был один из редчайших случаев, когда интуиция подвела
Ферма. При п = 0, 1, 2, 3, 4 действительно получаются простые числа 3,
5, 17, 257, 65537. Но значения п = 5 Ферма не проверял, иначе он обна-
ружил бы, что число 232 + 1 = 4294967297 делится на 641. Разглядел это
Эйлер. В настоящее время с помощью ЭВМ проверено, что при п = 6, 7, 8,
9, 10, 11, 12, 13, 14, 15, 16, 18, 19, 21, ... числа Ферма Fn составные. Бо-
лее того, предполагают, что они являются составными для всех п, боль-
ших 4; но определенных результатов здесь не получено. К числам Fn мы
еще вернемся в алгебраическом разделе. С ними связан вопрос о решении
уравнений, к которым приводит задача на построение правильных
2 ~ Н. Я. Виленкин, 10-11 кл.
33
многоугольников. (Таким образом, здесь в один узел сплетаются нити из
трех различных клубков — арифметики, алгебры и геометрии.)
После неудачи с числами Ферма стали искать другие генераторы
10я -7
простых чисел. Так, формула Рп =-----дает простые числа для п от 2
3
до 8 включительно (проверьте это, используя таблицу простых чисел). Но
при п = 16m + 9 (т = 0, 1, 2, ...) числа Рп делятся на 17. В самом деле,
10iem+9 7 (1016m+9 - 109 ) + (109 — 7) 1016m—1 9 109-7
3 3 3 3
1016-1
Первое слагаемое кратно числу-------, которое делится на 17 по ма-
3
лой теореме Ферма; делимость второго слагаемого проверяется непосред-
ственно.
Стремление ученых найти формулу общего члена последовательно-
сти, состоящей из одних только простых чисел, понятно. Дело в том, что,
хотя простых чисел бесконечно много, указать конкретно достаточно
большое простое число нелегко. Но, к сожалению, все предлагаемые фор-
мулы давали осечку.
Не удались попытки записать желанную формулу и в виде много-
члена. Мы уже видели в п. 5, что многочлен f (п) = п2 - п + 41 прини-
мает простые значения для всех п = 0, 1, 2, ..., 40. Но f (41) = 412 —
составное число. Еще больше простых чисел дает многочлен
g (п) = п2 - 79п + 1601 — они получаются при всех целых п от 0 до 79.
Но при п = 80 значение многочлена равно 412. Неизвестно, бесконечно
ли множество простых значений многочленов f (п) и g (п).
В дальнейшем попытки отыскать формулу для простых чисел в виде
многочленов были оставлены в связи с результатами Эйлера и Гольдба-
ха — немецкого ученого, судьба которого (как и судьба Эйлера) оказалась
связанной с Россией.
Христиан Гольдбах (1690—1764) в возрасте 35 лет был при-
глашен в Петербургскую академию наук, где в течение 15 лет исполнял
обязанности конференц-секретаря. Затем он перешел на дипломатиче-
скую работу и со временем получил весьма высокий чин тайного советни-
ка (по данной Петром Великим «Табели о рангах» выше этого были лишь
чины действительного тайного советника и канцлера). Математикой в
этих обстоятельствах он стал заниматься меньше и особо крупных дости-
жений не имел. Но у Гольдбаха был дар подмечать различные математи-
ческие закономерности. В своей переписке с Эйлером он выдвигал раз-
личные проблемы, привлекая к ним внимание великого ученого. Об
одной из этих проблем мы будем говорить в конце главы.
А сейчас сформулируем теорему Гольдбаха — Эйлера.
Никакой многочлен f (п) с целыми коэффициентами не может прини-
мать только простые значения.
До сих пор неизвестно, существует ли хоть один многочлен f (п)
с целыми коэффициентами степени выше первой, удовлетворяющий
34
ослабленному требованию, состоящему в том, чтобы среди его значений
было бесконечно много простых.
Этот же вопрос рассматривался и по отношению к арифметическим
прогрессиям (многочленам первой степени). Конечно, легко привести
примеры прогрессий, не содержащих ни одного простого числа:
4, 6, 8, ..., 2 + 2п, ...;
6, 9, 12, .... 3 + Зп, ...;
6, 10, 14, ..., 2 + 4п, ....
С другой стороны, простейшая прогрессия — натуральный ряд — содер-
жит все простые числа. А в последовательности нечетных чисел отсутст-
вует лишь простое число 2. Спрашивается: каким свойством обладают
прогрессии, содержащие бесконечное множество простых чисел? Прежде
чем давать ответ, рассмотрим еще одну прогрессию {4п + 3}. Заметим, что
каждое нечетное число, начиная с 5, записывается либо как 4п + 1, либо
как 4п + 3. Ясно, что произведение двух чисел первого вида имеет тот же
вид. Поэтому любое составное число типа 4п + 3 должно иметь по край-
ней мере один простой множитель этого же вида. Пользуясь этим замеча-
нием, покажем, что прогрессия {4п + 3} содержит бесконечно много про-
стых чисел. Доказательство проведем методом Евклида. Предположим,
что множество простых чисел вида 4п + 3 конечно. Обозначим эти числа
Pi, ..., pk, и пусть Р = 4 (/>! • ... pk) + 3. По сделанному выше замечанию
это число должно иметь хоть один простой делитель того же вида. Но все
такие делители по нашему предположению содержатся в наборе из чисел
Pi, ..., рк, а Р ни на одно из них не делится. Полученное противоречие по-
казывает, что наше предположение было неверным.
Таким же способом доказывается, что прогрессия {6п + 5} содержит
бесконечно много простых чисел. Эти утверждения являются частным
случаем теоремы, сформулированной в 1788 г. французским математи-
ком Адриеном Мари Лежандром (1752—1833):
Если числа а и d взаимно просты, то в арифметической прогрессии с
первым членом а и разностью d содержится бесконечно много про-
стых чисел.
Доказана она была методами математического анализа только через
50 лет немецким ученым Леженом Дирихле (1805—1859) и носит
теперь его имя.
9. Много ли простых чисел
в миллиарде?
Большое ли число миллиард? Оно настолько часто встречается в раз-
личных экономических сводках и статистических данных, что мы не за-
думываемся над тем, как оно велико. А ведь если задаться целью досчи-
тать до миллиарда, то понадобится более 95 лет при условии, что каждое
2*
35
число произносится всего за 1 секунду, что ежедневно на эту работу за-
трачивается 8 часов, что нет ни выходных, ни каникул. Сколько же про-
стых чисел в первом миллиарде натуральных? Оказывается, более пяти-
десяти миллионов, точнее, 50847534. Это немало, если учесть, что
каждое второе натуральное число делится на 2, каждое третье — на 3,
каждое пятое — на 5 и т. д. Дальше в натуральном ряду простые числа
встречаются пореже, можно даже указать отрезок длиной опять же хоть в
миллиард чисел, не содержащий ни одного простого. Правда, с этой
целью надо отойти от начала натурального ряда очень далеко. В самом
деле, для любого п > 2 числа п! + 2, п\ + 3, ..., п\ + п являются составны-
ми: первое из них делится на 2, второе — на 3, ..., (га - 1)-е — на п. По-
этому, начав с числа (109 + 1)! + 2, наверняка можно отсчитать ровно
миллиард идущих подряд составных чисел. Но это страшно далекие от
начала натурального ряда числа. Чтобы хоть в какой-то степени соста-
вить представление о росте п\, скажем только, что 10! больше трех мил-
лионов, а 13! уже больше шести миллиардов. Так что хоть поредение про-
стых чисел в натуральном ряду и наблюдается, но оно очень медленное.
Есть ли здесь закономерность? Этот вопрос не давал покоя математикам.
Неудачи в поисках формул заставили ученых подойти к проблеме с дру-
гой стороны. Если нет точной формулы, то, может быть, обратиться к
усреднению? Чтобы понять, что это такое, рассмотрим простой опыт.
Если бросить монету один раз, то нельзя предсказать, выпадет орел
или решка. Но при 10000 бросаний количество выпавших орлов не слиш-
ком отклонится от среднего значения 5000. Иными словами, усреднение
позволяет выявить закономерность там, где ее на первый взгляд нет.
Лежандр, много занимавшийся теоретико-числовыми проблемами,
применил эту идею к решению вопроса о распределении простых чисел.
Обозначим через п (га) количество простых чисел, не превосходящих п, и
л(га)
назовем отношение ---- средней плотностью распределения простых
п
чисел на отрезке натурального ряда от 1 до п. Приведем таблицу, в кото-
рой указаны количество простых чисел и их средняя плотность на отрез-
ке от 1 до 10s (где 8=1, 2, ..., 9).
п 10 102 103 104 105 106 107 108 109
п (п) 4 25 168 1229 9592 78498 664579 5761455 50847534
л(га) п 0,4 0,25 0,17 0,123 0,096 0,078 0,066 0,058 0,051
На основании табличных данных Лежандр стал подбирать функцию,
которая мало отличалась бы от---. Не надо думать, что он шел путем про-
га
стого подбора, — нет, он применял специально разработанные им методы.
В результате кропотливого исследования он пришел к выводу, что такой
1 п
функцией является --------------, откуда л (га) ~------------. Здесь
In га-1,08366 In га-1,08366
36
через In п обозначен натуральный логарифм числа п, т. е. логарифм по
( 1 V
основанию е. (Иррациональное число е = lim 1 н— приближенно равно
°о к п )
2,7182818284.) ’
Поисками подходящих выражений для л (га) занимался и 15-летний
Гаусс. Изучая таблицу простых чисел, он выдвинул гипотезу, что тг (га) при
достаточно больших га мало отличаются от п . Но это приближение было
In га
достаточно грубым. Уже в пожилом возрасте в письме к Энке он предложил
другое выражение для л (га), а именно сумму ——I—-—I-... -I——. Ее мож-
1п 2 In 3 In га
но заменить так называемым интегральным логарифмом
Li га
п ,
г dx
", In х
(Читатели, еще не знакомые с понятием интеграла, узнают о нем в
11 классе.) Правда, письмо Гаусса было опубликовано почти через 10 лет
после его смерти и не оказало влияния на решение данной проблемы.
Еще более точное приближение получил выдающийся немецкий матема-
тик Бернхард Риман (1826—1866). Оно имеет вид
n(ra)«f^.Li(V^).
k = i *
Здесь суммирование ведется по всем натуральным k, а ц (й) — так назы-
ваемая функция Мёбиуса (она равна нулю, если k делится на квадрат
простого числа, в остальных случаях ц (k) = (— l)d, где d — количество
простых множителей числа k; считают п (1) = 1). Это выражение дает
удивительно хорошее приближение для л (га). Например, при га = 109 по
формуле Римана имеем л(га)~ 50847455.
Значительный вклад в решение проблемы распределения простых
чисел внес замечательный русский ученый Пафнутий Львович
Чебышев (1821—1894). Он родился в селе Окатово (ныне Калужской
области). Родители прочили сыну военную карьеру, но из-за поврежде-
ния ноги они направили его учиться в университет в Москву. По оконча-
нии университета Чебышев получил степень магистра и был приглашен в
Петербургский университет на преподавательскую должность. Одновре-
менно он вел большую научную работу в Академии наук. В 1859 г. был
избран академиком.
Именно Чебышев стал основателем и многолетним руководителем
Петербургской математической школы. После смерти Эйлера в Петербур-
ге в течение многих лет не было математиков, имевших мировую извест-
ность. Только в 1828 г. в Петербург из Франции вернулся Михаил
Васильевич Остроградский (1801—1862), учившийся в Харьков-
ском университете, но исключенный из него за вольнодумство и вынуж-
денный впоследствии заканчивать образование в Париже. Научные ис-
следования Остроградского относятся к области математической физики,
37
где он получил ряд блестящих результатов, носящих его имя. Слава уче-
ного была настолько велика, что провинциальные помещики, отправляя
своих детей учиться в университет, говорили им: «Становись Остроград-
ским». Остроградский был избран членом Нью-Йоркской академии, Ту-
ринской академии, Национальной академии деи Линчеи в Риме, чле-
ном-корреспондентом Парижской академии наук. Несмотря на большие
научные достижения и широкую педагогическую деятельность, Остро-
градский не стал основателем математической школы — его ученики
(И. А. Вышнеградский, Н. П. Петров, Д. И. Журавский и др.) работали в
основном в области механики.
Заслуга создания математической школы в Петербурге принадле-
жит Чебышеву. Воспитанниками этой школы были Егор Иванович
Золотарев (1847—1878), Александр Николаевич Коркин
(1837—1908), Александр Михайлович Ляпунов (1857—1918),
братья Марковы — Андрей Андреевич (1856—1922) и Вла-
димир Андреевич (1871—1897), Георгий Феодосьевич Во-
роной (1868—1908), Владимир Андреевич Стеклов (1864—
1926) и многие другие замечательные русские математики. На чае-
питиях, которые устраивал Чебышев для бесед с математиками, бывала и
Софья Васильевна Ковалевская (1850—1891) — первая рус-
ская женщина-математик, которая была вынуждена изучать науки за ру-
бежом, так как в те времена в русские университеты женщины не допус-
кались.
Характерной чертой Петербургской математической школы был инте-
рес к конкретным задачам, которые по мере их решения становились ис-
точниками новых глубоких теорий. Например, исследования Чебышева по
наилучшему приближению функций многочленами выросли из задач тео-
рии механизмов, преобразующих вращательное движение в поступатель-
ное. Научные интересы ученых Петербургской математической школы вос-
ходили к кругу интересов Эйлера и касались математического анализа,
теории чисел, непрерывных дробей. Кроме того, они занимались теорией
вероятностей, математической физикой. Для них было характерно чувство
связи между различными областями математики. Результаты, полученные
в интегральном исчислении, находили применения в теории чисел и теории
вероятностей, непрерывные дроби были орудием исследования и в теории
ортогональных многочленов, и в теории чисел, и в теории моментов.
Большое внимание уделяли ученые Петербургской математической
школы приложениям математики. Например, Ляпунов исследовал вопрос о
формах равновесия вращающихся жидкостей, с помощью которых хотел уз-
нать, какими могут быть формы планет и как возникли их спутники. Во-
просами прикладной математики занимался и сам Пафнутий Львович. По-
сле поражения России в Крымской войне 1853—1856 гг. была поставлена
задача усовершенствования артиллерийских орудий, нужно было увеличить
точность попадания ядер и их пробивную способность. С этой целью ядра
были заменены на цилиндрические снаряды с твердыми наконечниками.
Но эти снаряды «кувыркались» при полете. Для разрешения возникших
проблем обратились к Чебышеву. Тот обосновал математически, что гладко-
ствольные орудия не дадут желаемого результата. Именно нарезные стволы
38
увеличивают точность попадания и устойчивость полета снаряда. Чебышев
и в зрелом возрасте сохранил детское стремление к конструированию. Им
было создано более сорока новых механизмов, многие из которых демонст-
рировались на международных выставках в Париже и Чикаго.
Для исследования вопроса о распределении простых чисел Чебышев
использовал элементарные соображения о делимости чисел. Но сделал
это он с таким мастерством, что сумел доказать утверждение:
Если предел произведения тг(п)-^-^ существует, то этим пределом
п
может быть только единица.
Через год он нашел, что при достаточно больших значениях п вы-
полняются неравенства
0,92129 < л (п) • — < 1,10555.
п
Окончательно равенство lim л(п)-^-^- = 1 было доказано в 1896 г.
оо п
независимо друг от друга французским математиком Жаком Адама-
ром (1865—1963) и бельгийским математиком Шарлем-Жаном де
Ла Валле-Пуссеном (1866—1962). Их методы были основаны на
результатах Римана.
10. Совершенные
и дружественные числа
В «Маленьком принце», замечательной сказке французского писате-
ля А. де Сент-Экзюпери, Лис спрашивает Маленького принца:
— А на той планете есть охотники?
— Нет.
— Как интересно! А куры
есть?
— Нет.
— Нет в мире совершенст-
ва! — вздыхает Лис.
Можно поспорить с Лисом.
Но пифагорейцы, жившие две с
половиной тысячи лет тому назад,
тоже считали совершенство ред-
ким явлением и обозначали его
числами, удовлетворяющими до-
вольно жесткому условию. Чис-
ло называлось совершенным, если
оно равнялось сумме всех своих
собственных делителей, т. е.
делителей, отличных от самого
числа. Примерами совершенных
39
чисел являются 6 = 1 + 2 + Зи28 = 1 + 2 + 4 + 7 + 14. Вспомним, что значе-
ние о (га) равно сумме всех делителей числа п, получим следующее утвер-
ждение:
Число п совершенно в том и только в том случае, если а (га) = 2га.
Совершенные числа весьма почитались в Древнем мире. Например,
египетская мера длины «локоть» содержала 28 «пальцев»; самым почет-
ным местом на пирах у римлян было шестое; во многих обществах число
членов равнялось 28. Даже сейчас, следуя древней традиции, некоторые
академии по уставу состоят из 28 действительных членов.
Пифагорейцы нашли правило, облегчавшее поиск совершенных
чисел. У Евклида в «Началах» оно формулируется так:
Если от единицы откладывать сколь угодно последовательно пропор-
циональных чисел в двойном отношении до тех пор, пока вся их сово-
купность сложенная не сделается первым (в нашей терминологии про-
стым) числом и вся совокупность, умноженная на последнее число,
произведет что-то, то возникающее число будет совершенным.
Иначе говоря, (1 + 2 + 22 + ... + 2*“ г) • 2* "1 = (2* — 1) • 2**1 является
совершенным числом, если число 2к - 1 простое.
Мы приведем доказательство, отличное от евклидова. Воспользуемся
формулой (5, с. 18), выражающей о (га) с помощью канонического разло-
жения числа га. По этой формуле при га = 2* " 1 (2* - 1) = 2* ~ 1 р получаем
2* —1 р2-1 .
о (п) = ---— = (2* — 1) (р + 1) =
2-1 р-1
= (2* - 1) 2* = 2 • 2* ’1 (2* - 1) = 2га.
Поэтому число га совершенно. Верно и обратное утверждение:
Всякое четное совершенное число имеет вид 2*-1(2*-1), где
2к - 1 — простое число.
Его высказал французский философ и математик Рене Декарт
(1596—1650), а доказал Эйлер. Приведем это доказательство.
Пусть га — четное совершенное число. Тогда га можно представить в
виде га = 2к 1 I, где k — натуральное число, большее единицы, а I — не-
четное число. Число I не может быть единицей, так как при I = 1 мы име-
ли бы о (га) = о (2* ’) = 2к - 1 Ф 2п, что противоречит совершенству чис-
ла га. Далее, 2" 1 и ( взаимно просты, а потому из мультипликативности
функции о (га) следует, что
ст (га) = о (2* “ ’) • ст (Z) = (2к - 1) • ст (Z).
Поскольку га — совершенное число, то выполняется условие:
ст (га) = 2га = 2к • I. Сравнивая два выражения для ст (га), получим
(2к - 1) • ст (Z) = 2к • I. В этом равенстве числа 2к - 1 и 2к взаимно просты, а
потому на 2к — 1 делится число Z. Значит, существует нечетное число s,
такое, что Z = (2к — 1) • s и о (Z) = 2к S. Если бы число s не равнялось 1, то
мы имели бы о (Z) = о ((2* - l)s)> 1 + « + (2к - 1) + (2к — 1) s = 2к s + 2к,
откуда следует ложное неравенство ст (Z) 5= ст (Z) + 2к. Значит, s = 1, и
40
потому I = 2* - 1, а <7 (Z) = 2*, откуда о (Z) = Z + 1, а это означает, что
Z — простое число. Тем самым гипотеза Декарта доказана.
Итак, мы можем сформулировать критерий совершенства четного
числа:
Четное число совершенно тогда и только тогда, когда оно имеет вид
п = 2к ~1 (2* - 1), где 2* - 1 — простое число.
В связи с доказанным критерием поиск четных совершенных чисел
сводится к выяснению вопроса: для каких k число Mk = 2k - 1 является
простым? Числа такого вида изучал М. Мерсенн, тот самый патер Мер-
сенн, которому доверяли свои труды все европейские математики. Сами
числа так и называются с тех пор числами Мерсенна. Он установил, что
для простоты Mk число k должно быть простым.
В самом деле, если бы это было не так, то k имело бы вид k = ab, где
о>1иЬ>1. И было бы справедливо разложение
2k - 1 = 2а6 - 1 = (2а - 1) (2а(6~1) + 2а (ь~2) + ... + 1),
из которого следует, что 2* — 1 — составное число. Таким образом, про-
стота k является необходимым условием простоты Mk. Обратное утверж-
дение неверно: существуют простые k, для которых Мк не является про-
стым числом. Например, Мп = 211 - 1 = 2047 = 23 • 89. Отметим, что
множитель 89 имеет вид 89 = 8-11 + 1, а множитель 23 имеет вид
23 = 2 • 11 + 1. Вообще все простые делители числа Мерсенна Мк = 2к — 1
имеют вид р = 2rk + 1, где г —- натуральное число. Это облегчает поиск
таких делителей.
Простыми являются числа Мерсенна М2 = 3, М3 = 7, М5 = 31, М7 =
= 127, М13 = 8181, М17 = 131071. Им соответствуют совершенные числа
6, 28, 496, 8128, 33550336, 8589869056, из которых лишь первые четыре
были известны в древности. Простыми являются и числа Мерсенна М19,
М31, М61, М8д (возводить двойку в 89-ю степень довольно утомительное
занятие: результат содержит 27 цифр).
Поиск простых чисел Мерсенна был облегчен после того, как фран-
цузский математик Франсуа Люка (1842—1891) нашел необходимое
и достаточное условие простоты чисел Mk.
Число Mk (k > 2) просто в том и только в том случае, если оно является
делителем (fe - 1)-го числа Люка.
Эти числа определяются так: первое из них равно 4, = 4, а
(п + 1)-е определяется формулой Ln + l = L2n — 2. По этой формуле получа-
ем L2 = 14, L3 = 194, L4 = 37634. С помощью своего критерия Люка в
1876 г. установил простоту числа М127, и 76 лет этот рекорд не был по-
бит.
Положение изменилось, когда были созданы первые электронные
вычислительные машины и математики получили возможность не только
проводить на них вычисления государственной важности, но и решать во-
просы, относящиеся к чистой математике. Конечно, поиск простых чисел
Мерсенна с помощью ЭВМ имеет примерно то же отношение к ручному
поиску, как ловля рыбы океанским тралом к рыбалке с удочкой. Поиск
шел все быстрее, рекорды падали один за другим. С 1952 г., когда стали
41
использовать ЭВМ, найдено 31 из 43 известных простых чисел Мерсенна.
Наибольшим из них является ЛГ3()402457, оно обнаружено в 2005 г. (после
50 суток непрерывной работы мощного компьютера) и содержит более
9 млн цифр. Поиск простых чисел Мерсенна, а значит, и четных совер-
шенных чисел продолжается. Создан международный проект «Поиск
больших простых чисел Мерсенна с использованием Интернета». Основан
фонд на сумму более полумиллиона долларов для четырех удачников, ко-
торые первыми найдут простые числа Мерсенна с количеством цифр соот-
ветственно более 1 млн, 10 млн, 100 млн и 1 млрд. Первый из четырех
денежных призов уже выплачен за 38-е простое число Мерсенна, содер-
жащее более двух миллионов цифр. И кто знает, какое наибольшее число
будет ходить в чемпионах тогда, когда вы прочтете эту книгу. А ведь ког-
да-то Мерсенн сказал, что не хватит и вечности, чтобы узнать, является
ли простым 20-значное число!
До сих пор неизвестно, есть ли наибольшее среди простых чисел
Мерсенна, или последовательность таких чисел столь же бесконечна, как
и последовательность простых чисел. Есть и другие вопросы, касающиеся
совершенных чисел и не решенные до сих пор. Например: существует ли
хотя бы одно нечетное совершенное число? Пока доказано, что среди не-
четных чисел, меньших 1О300, совершенных нет.
Известны многие свойства, которыми должны обладать нечетные со-
вершенные числа при условии их существования. Еще Эйлер показал, что
эти числа имеют вид N = (4k + 1)4Р +1 • p^ai • р^а2 ... • р^ак , где 4k + 1, рг,
р2, ..., pk — различные простые нечетные числа. В настоящее время уста-
новлено, что запись нечетного совершенного числа содержит не менее 300
цифр, а само число имеет более 36 простых делителей (необязательно раз-
личных), один из которых больше 1О20. Многое известно о нечетных про-
стых числах, неизвестно лишь одно — существуют ли они вообще?
Долгое время поиск простых чисел Мерсенна (тем самым и четных
совершенных чисел) или вопросы, связанные с нечетными совершенными
числами, интересовали только чи-
стых математиков, тех самых, о
которых представители приклад-
ной математики рассказывают та-
кой анекдот.
Однажды воздухоплаватели,
летевшие на воздушном шаре, по-
теряли ориентировку и, восполь-
зовавшись моментом, когда шар
опустился до 15 м над земной по-
верхностью, крикнули находив-
шемуся внизу человеку: «Где мы
находимся?» После трехминутно-
го размышления тот ответил:
«На воздушном шаре». Порыв вет-
ра поднял шар вверх, и один из
воздухоплавателей сказал: «Это,
42
несомненно, был чистый математик». «Почему ты так думаешь?» — спро-
сил его другой. «А потому, что его ответ был результатом размышления, он
оказался безукоризненно верным и совершенно бесполезным».
Числа Мерсенна тоже были долгое время абсолютно бесполезными,
как, впрочем, и совершенные числа. Но в настоящее время простые числа
Мерсенна положены в основу защиты электронной коммерции и элект-
ронной почты, а также используются в области криптографии и в других
приложениях математики. Как тут ни вспомнить слова Эйлера: «Из всех
проблем, рассматриваемых в математике, нет таких, которые считались
бы в настоящее время более бесплодными и бесполезными, чем пробле-
мы, касающиеся природы чисел и их делителей. В этом отношении ны-
нешние математики сильно отличаются от древних, придававших гораздо
большее значение исследованиям такого рода... Математика, вероятно,
никогда не достигла бы такой высокой степени совершенства, если бы
древние не приложили столько усилий для изучения вопросов, которыми
сегодня многие пренебрегают из-за их мнимой бесплодности...»
Изучая соотношения чисел и их делителей, пифагорейцы обнару-
жили, что два числа 220 и 284 обладают замечательным свой-
ством: сумма собственных делителей числа 220 = 22 • 5 • 11 равна
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284. В свою оче-
редь, 284 = 22 • 71. Для него соответствующая сумма равна
1 + 2 + 4 + 71 + 142 = 220. Эта связь между числами, скорее всего, не
очень удивила древних математиков. Вероятно, они увидели в этом еще
одно подтверждение своей философии и объявили эту пару чисел симво-
лом дружбы. С тех пор два числа тип, такие, что каждое из них рав-
но сумме собственных делителей другого, называются дружественны-
ми. Из определения вытекает равенство о (т) = о (п) = т + п.
Общий закон образования дружественных чисел неизвестен. Но су-
ществуют формулы, которые при некоторых условиях дают пары таких
чисел. Арабский математик Сабит ибн Курра (836—901) показал, что
числа m = 2k-p-qv\n = 2k-r дружественные, если р, q и г — простые
нечетные числа вида р = 3 • 2*“1 - 1, q = 3 • 2к - 1, г = 9 • 22к~1 - 1.
Докажем это утверждение. Сначала найдем сумму собственных дели-
телей числа т. Поскольку р и q — простые нечетные числа, получим
2*+1 _ 1
о (т) - т =------- (р + 1) (q + 1) - 2kpq =
2 — 1
= 2к (pq + 2р + 2q + 2) - (pq + р + q + 1) =
= 2k (9 • 22k -1 + 9 • 2к -1 - 1) - 9 • 22k “1 = 2h (9 • 22h -1 - 1) = 2k • r = n.
Нами использованы равенства
p<7 = 9 • 22/г ’ 1 - 9 • 2"1 + 1 и p + (/ = 9 • 2* ’ 1 - 2.
Аналогично для числа п имеем
о (л) - п = (2* + 1 - 1) (г + 1) - 2кг = 2к (г + 2) - г - 1 =
= 2к (9 22к -1 + 1) - 9 • 22к -1 = 2к (9 22к ~ 1 - 9 • 2к ~ 1 + 1) = 2kpq = т.
Утверждение доказано. Рассмотрим частные случаи.
43
Значение k = 1 не годится, так как при этом р — 2 является четным
простым числом. При k = 2 (тогда р = 5, q = 11, г = 71) получаем пару 220
и 284. При k = 3 число г = 9 • 25 — 1 = 297 = 27-11 составное — условия
предложения не выполняются. П. Ферма и Р. Декарт переоткрыли ре-
зультат Сабит ибн Курры и, пользуясь этим правилом, нашли еще две па-
ры дружественных чисел: Ферма — пару 17296 и 18416, отвечающую
значению k = 4, а Декарт — пару 9363584 и 9437056 (k = 7). Как стало
недавно известно, эти две пары за три века до них нашли арабские мате-
матики. Позже (1749) Л. Эйлер привел еще 61 пару дружественных чи-
сел. В настоящее время благодаря применению ЭВМ найдено около
1100 таких пар. Приведем первые 12 пар дружественных чисел:
220 И 284 12285 И 14595
1184 и 1210 17296 и 18416
2620 и 2924 63020 и 76084
5020 и 5564 66928 и 66992
6232 и 6368 67095 и 71145
10744 и 10856 69615 и 87633
Интересно, что следующей за первой парой была открыта восьмая,
а вторую пару нашел (1866) 16-летний итальянец Н. Паганини — тезка
великого скрипача. Ее не заметили математики, открывшие к тому вре-
мени более 60 пар дружественных чисел. Обратим внимание на то, что
четность дружественных чисел одной пары одинакова. До сих пор неизве-
стно, конечно ли множество пар дружественных чисел и существуют ли
пары с числами разной четности. И по настоящий день находят новые па-
ры дружественных чисел. Так, в 1972 г. нидерландский математик Хер-
ман де Риле открыл пару, состоящую из 152-значных чисел, одно из ко-
торых имеет 800, а другое — 3200 различных делителей.
Очевидно, совершенные и дружественные числа укладываются в сле-
дующую схему. Сложим все правильные делители некоторого числа, по-
лучим второе число; найдем сумму всех его правильных делителей, полу-
чим третье число; найдем далее сумму всех правильных делителей
третьего числа и т. д. Может оказаться, что на некотором шаге получится
исходное число, т. е. цепочка замкнется. Если замкнутая цепочка состо-
ит из одного звена, то это число совершенное; если из двух звеньев, то об-
разующие ее числа дружественные; если более чем из двух, то все числа
этой цепочки называются общительными. Известна цепочка из пяти об-
щительных чисел: 12496, 14288, 15472, 14536, 14264. Но пока не найде-
но ни одной цепочки, состоящей из трех звеньев. А вот цепочка из 28 зве-
ньев существует, она начинается с числа 14316.
11. Фигурные числа
В Древней Греции применялась буквенная запись чисел, неудобная
при вычислениях. Поэтому пифагорейцы часто изображали числа камеш-
ками или точками на песке. На этом пути они пришли к понятию фигур-
ных чисел.
44
Рассмотрим последовательность правильных треугольников, со-
ставленных из точек (рис. 1). Так как левую нижнюю точку тоже счи-
тают треугольником, то на рисунке изображено 5 членов этой последо-
вательности. Сопоставим каждому треугольнику число, выражающее
количество точек в нем. Получим числовую последовательность 1, 3, 6,
10, 15, ... . Это и есть треугольные числа. Если обозначить их Ф3 (п),
где п — номер числа в последовательности, то из рисунка хорошо вид-
но, что Ф3 (1) = 1, Ф3 (2) = 1 + 2, Ф3 (3) = 1 + 2 + 3, Ф3(4) = 1 + 2 + 3 + 4,
Ф3 (5) =1 + 2 + 3 + 4 + 5ит. д.
Очевидно, тг-е треугольное число является суммой п первых нату-
ральных чисел, т. е.
п(п + 1)
Ф3 (п) = 1 + 2 + ... + п =—---.
Аналогично рассматриваются последовательности квадратов (рис. 2).
Подсчитывая количество точек в них, приходим к квадратным числам
Ф4 (1) = 1, Ф4 (2) = 1 + 3, Ф4 (3) = 1 + 3 + 5, Ф4 (4) = 1 + 3 + 5 + 7
и т. д. Здесь тоже подмечаем, что п-е квадратное число есть сумма п пер-
вых нечетных чисел, т. е.
Ф4 (n) = 1 + 3 + 5 + ... + (2п - 1) = п2.
А теперь возьмем последовательность правильных пятиугольников
(рис. 3) и получим последовательность пятиугольных чисел'.
п(3п — 1)
Ф5 (п) = 1 + 4 + 7 + ... + (Зп - 2) = —---.
2
Очевидно, этим способом можно получить любые многоугольные
(или, как их еще называют, фигурные) числа. О таких числах писал еще
ученик Сократа и Платона Филипп Опунтиус. Общее определение много-
угольных чисел было дано лишь во II в. до н. э. Гипсиклом Алек-
сандрийским.
Число называется k угольным, если оно является одной из сумм чле-
нов арифметической прогрессии с первым членом 1 и разностью k — 2.
Используя формулу суммы п членов арифметической прогрессии,
находим й-угольное число с номером п:
45
2 + (n-l)(k-2)
Фк W =-------------п.
(12)
2
Много внимания уделено таким числам в сочинении «Изагог», или
«Вступление к арифметике», написанном в I в. н. э. александрийским уче-
ным Никомахом из Гераеы. Эта книга долгое время играла ту же
роль при изучении арифметики, как «Начала» Евклида для изучения гео-
метрии, а слова «считает, как Никомах Герасский» были большой похвалой.
Никомах доказывает в «Изагоге» теорему:
Всякое многоугольное число равно сумме многоугольного числа пре-
дыдущего названия, но занимающего в ряду то же место, и треуголь-
ного числа, занимающего предыдущее место.
В наших обозначениях она записывается следующим образом:
ФА(«) = Фй-1(п) + Ф3(п-1). (13)
Доказательство этого равенства предоставляем читателям.
В «Изагоге» доказано еще одно интересное утверждение:
Если разбить ряд нечетных чисел на группы, число членов которых воз-
растает как натуральный ряд, то сумма чисел каждой группы будет
равна кубу числа членов каждой группы.
Для решения этой задачи запишем
последовательность нечетных чисел,
разбив ее на группы, как указывает Ни-
комах:
1; 3, 5; 7, 9, 11; 13, 15, 17, 19;
21, 23, 25, 27, 29; ... .
Обратимся к рисунку 4. Каждое нечет-
ное число — это разность двух квад-
ратов. Вслед за Никомахом проведем
линии, разделяющие соседние группы
нечетных чисел. Точки каждой группы
составляют Г-образную фигуру, кото-
рую пифагорейцы называли гномоном.
Слово «гномон» в переводе с греческого
языка означает «распознаватель». (Сна-
чала это был распознаватель времени:
простейшие солнечные часы состояли
из двух перпендикулярных планок; затем — распознаватель перпендику-
лярности; позже — любая фигура Г-образной формы.)
Найдем число точек n-го гномона. В его основании ровно п точек.
Поскольку любой гномон является разностью соседних квадратов, то ис-
комое число равно
(1 + 2 + ... + п)2 - (1 + 2 + ... + (и - I))2 =
п2 (п + I)2 (и - I)2 п2 ,
=----------------------= п 3 .
4
Утверждение Никомаха доказано.
4
46
Поскольку все гномоны, начиная с
единицы (вырожденного гномона), образуют
в совокупности квадрат, получаем замеча-
тельное тождество
I3 + 23 + ... + n3 = (1 + 2 + ... + п)2.
Такие геометрические рассуждения по-
зволяют получить и другие соотношения.
Например, из рисунка 5 вытекает совсем
простое равенство Ф3 (п.) + Ф3 (п - 1) = п2.
Оно является частным случаем формулы
(13) при k = 4.
Фигурные числа обладают многими за-
мечательными свойствами. Вы сами можете
доказать, например, утверждения:
Г1. Всякое четное совершенное число является треугольным.
2. Шестиугольное число с номером п является треугольным числом с
номером 2п - 1.
Хотя фигурными числами начали заниматься еще на заре развития
теоретической математики, еще совсем недавно они были предметом
математических исследований весьма крупных ученых. Среди них сле-
дует назвать Огюстена Луи Коши (1789—1857) — известнейшего
французского математика XIX в. Ему принадлежат фундаментальные
исследования по математическому анализу, дифференциальным уравне-
ниям, теории упругости, геометрии и другим областям математики. Но
одной из первых работ Коши было исследование, посвященное фигур-
ным числам.
Задача, которой занимался Коши, восходит к Диофанту. Дио-
фант, по-видимому, был уверен, что любое натуральное число можно
представить в виде суммы не более четырех квадратов (например,
39 = 52 + З2 + 22 + I2). Баше де Мезириак подметил это свойство и
указал его в своих комментариях к «Арифметике» Диофанта. Изучая
этот замечательный труд, Ферма сформулировал более общее утверж-
дение:
I Всякое натуральное число является суммой не более трех треугольных
чисел, не более четырех квадратов, не более пяти пятиугольных чисел
и т. д.
В дальнейшем многие математики, в том числе и Эйлер, пытались до-
казать как утверждение де Мезириака, так и более общее утверждение Фер-
ма. Только через полтора столетия Лагранжу удалось доказать, что догадка
Баше справедлива. При этом он использовал некоторые соотношения, изве-
стные еще Эйлеру. Неясно, почему Эйлеру не удалось довести задачу до
конца. Утверждение Ферма о представимости натуральных чисел в виде
суммы фигурных было доказано лишь в 1815 г. Коши, только начинавшим
свою научную деятельность (до этого он работал инженером).
47
12. Шары в пространстве
Никомах рассматривал не только плоские фигурные числа, но и про-
странственные. У него встречаются кубические числа тя и числа т2 (т + Z)
и т2 (т — I), названные им соответственно балкообразными и кирпичеоб-
разными.
К слову сказать, отсюда видно, что
кирпичи в древности имели в основании
квадрат, а их высота была меньше сторо-
ны этого квадрата.
Изучал Никомах и пирамидальные
числа. С ними имели дело и пифагорейцы.
Чтобы представить себе эти числа, уло-
жим на плоскости шары в виде правиль-
ного треугольника (рис. 6), причем число
шаров в каждой стороне треугольника
равно п. (Шары здесь берем вместо точек
для большей наглядности.) На этот слой
шаров положим следующий, располагая
шары второго слоя в углублениях между
шарами нижнего слоя. Продолжим этот процесс до тех пор, пока в верх-
нем слое не окажется один шар. Уложенные таким образом шары образу-
ют правильный тетраэдр — треугольную пирамиду, все грани кото-
рой — правильные треугольники.
Найдем число шаров в построенном тетраэдре. Их число в т-м слое,
т (т + 1)
считая от вершины, равноФ3 (т) =-------. Поэтому общее число шаров
равно
Ф3 (1) + Ф3 (2) + ... + ф3 (ц) = 1-2 + 2_3 + ... + -П(П + 1)
Обозначим это число через Ф33) (га). Верхний индекс указывает на
размерность пространства, в котором укладываются шары. (Для плоского
случая индекс р = 2 мы не употребляли.) С помощью метода математиче-
ской индукции можно доказать, что
(31 га (га + 1) (га + 2)
ф‘3) (га) = —------—--------
3 ' ’ QI
(14)
Назовем числа Ф*3’ тетраэдрическими. Интересно, что существует
единственный тетраэдр, из шаров которого можно выложить два одина-
ковых тетраэдра; число шаров такого тетраэдра равно 20. Наименьший
же тетраэдр, из шаров которого составляются два неравных тетраэдра, со-
держит 680 шаров:
Ф^3) (15) = 680 = 120 + 560 = Ф^3) (8) + Ф^3) (14)
Шары можно сложить и в виде правильной четырехугольной пира-
миды, выкладывая каждый слой в виде квадрата. Число шаров в такой
пирамиде равно
48
Ф43) (га) = I2 + 22 + ... + n2,
где n — число шаров в стороне квадрата основания. Значение этой суммы
было известно уже Архимеду (ок. 287—212 до н. э.) . Он доказал, что
2 „ о п (п + 1)(2га +1)
1 + 2 + ... + п =-------—-------, и использовал это равенство при вы-
числении объемов различных тел и площадей фигур. Числа
п (п+ 1)(2га + 1)
ф4 (^) =------------------- (15)
О I
называют пирамидальными.
Индийский математик V в. н. э. Ариабхатта, в честь которого
был назван первый индийский спутник, вывел формулу для га-го тетраэд-
рического числа, исходя из вида пирамидального числа и учитывая свой-
ство треугольных чисел:
Ф*3>(ге) = I2 + 22 + ... + п2 =
= Ф3 (1) + (Ф3 (1) + Ф3 (2)) + ... + (Ф3 (га - 1) + Ф3 («)),
откуда
п(п + 1)(2га + 1)
2 (Ф3 (1) + Ф3 (2) + ... + Ф3 (га - 1)) + Ф3 (тг) = —-
6
а значит,
Ф^ (71) = Ф3 (1) + Ф3 (2) + ... + Ф3 (тг) =
1 ( га(га + 1)(2га + 1) га(га + 1)'| п(п + 1)(га + 2)
~ 21 6 2 2
В связи с изучением пирамидальных чисел возникает такой вопрос:
можно ли из шаров, составляющих правильную четырехугольную пира-
миду, выложить на плоскости квадрат, т. е. существует ли пирамидаль-
ное число, являющееся квадратным: Ф2 (га) = Ф4 (ттг)? Английский мате-
матик Джордж Ватсон (1886—1965) в 1918 г. показал, что равенство
I2 + 22 + ... + га2 = тга2 выполняется лишь при га = тга = 1 (квадрат и пира-
мида состоят из одного шара) и при га = 24, тга — 70.
Формально можно было бы строить из шаров пирамиды с основания-
ми в виде правильных пятиугольников, шестиугольников и т. д. Но при
k > 4 невозможно на правильный га-угольник, сложенный из шаров, уло-
жить новый слой из меньшего числа шаров, имеющий ту же форму, при-
том так, чтобы шары лежали плотно и не скатывались. Поскольку греки
мыслили геометрически, они не стали рассматривать такие пирамиды и,
следовательно, числа вида
Ф<3) (га) = Ф, (1) + ФА (2) + ... + ФА (га)
при k > 4, хотя и для таких сумм можно вывести различные формулы.
Не возникало у древних греков и мысли о другом обобщении фигур-
ных чисел, а именно об обобщении на большее число измерений. Конк-
ретное мышление древнегреческих математиков не допускало возможно-
сти четырехмерного пространства и тем более пространств высшей
размерности. Но в труде александрийского математика Паппа, жившего
49
во второй половине III в. н. э., есть удивительное высказывание: «Не су-
ществует ничего, что заключало бы больше, чем три измерения. Однако
незадолго до нас стали позволять себе выражаться подобным образом, не
указывая, впрочем, при этом на что-либо сколь-нибудь вразумительное».
Из этого замечания видно, что кто-то из живших в III в. ученых пре-
одолел вековой запрет и стал использовать геометрическую терминоло-
гию там, где раньше это было строжайшим образом запрещено. Кто же
был этот гениальный провидец? Мы думаем, что из известных нам уче-
ных той эпохи есть лишь один, к кому могли бы относиться слова Пап-
па, — это живший также в Александрии Диофант, которого по праву
можно считать основателем двух ветвей математической науки: теории
чисел и алгебры. В своей «Арифметике» Диофант рассматривает не толь-
ко квадраты и кубы чисел, но и четвертые, пятые и шестые степени. Вме-
сте с единицей (т. е. нулевой степенью) и самим числом (первой сте-
пенью) эти степени образуют лестницу из семи ступеней, а число 7
считалось священным еще у древних вавилонян. Но если Диофант гово-
рит о высших степенях чисел, то весьма вероятно, что именно он обра-
щался и к высшим размерностям пространства. Возможно, о связанных с
такими многомерными пространствами фигурных числах шла речь в
утраченных книгах «Арифметики», и, может быть, они потому и не до-
шли до нас, что никто из читавших и переписывавших их не понял, о чем
Диофант ведет речь. Или их уничтожили по причине вредоносности? Воз-
можно, по той же причине до нас дошел лишь фрагмент работы Диофанта
«О многоугольных числах», в котором о многомерных обобщениях фи-
гурных чисел ничего не сказано.
Впервые о многомерных аналогах фигурных чисел говорится в руко-
писи индийского математика Н а р а й а н ы, жившего в XIV в. Индийские
математики тяготели больше к арифметике и алгебре, чем к геометрии, и
не были связаны в своих работах необходимостью наглядно представлять
числа в виде геометрических фигур. Чтобы познакомиться с результата-
ми Нарайаны, введем функцию
(р) ,, 'i(n + l)...(n + p-l)
3 ( ’ 1-2-...р ~Сп+Р-1-
(16)
Ясно, что Ф*р) (1) = 1, а Ф*р) (О) = О. Простой подсчет показывает, что имеет
место равенство
Ф 6” (п) = ф <р) (п - 1) + Ф3<^ - ” (м),
применяя которое получим
ф‘₽_1)(1) + ... + Ф‘р-1)(п) =Ф<₽)(1) + (Ф<р) (2) -Ф*р)(1)) + ... +
+ (Ф*р) (п) - Ф'₽) (п - 1)) = ф(3р> (п).
Эту формулу для р = 1, 2, 3 знали древние греки, для р = 1, 2, 3, 4 — ки-
тайские математики XIII в. Нарайана получил ее для произвольного р.
Похожую формулу знал работавший во Франции математик Леви бен
Гершон (1288—1344). Но его работы, написанные на малознакомом
европейским ученым древнееврейском языке, остались незамеченными.
50
Лишь в XVII в. формулу получили европейские математики Б. Паскаль,
Дж. Валлис, В. Оутред.
Мы видели, что формула Ф3 (п) = Ф3 (1) + ... + Ф3 (п) задает число
шаров в правильном тетраэдре с ребром п. Аналогично Ф.1/'1 (п) равно чис-
лу шаров в правильной р-мерной пирамиде с ребром п. Такую пи-
рамиду называют р-мерным симплексом (simplex с латинского означа-
ет «простой», р-мерный симплекс является простейшим р-мерным
многогранником: любой многогранник можно сложить из симплексов,
как многоугольник из треугольников). Поэтому ф|р) (п) можно назвать
р-мерным симплициалъным числом. Иногда эти числа называют
(р + 1)-угольными индекса п. Такое название нельзя считать удачным,
поскольку Ф3<₽> (и) является обобщением не произвольного фигурного, а
лишь треугольного числа.
13. Степенные суммы
В многомерных пространствах существуют аналоги и для кубов.
В составленном из шаров «кубе» р-мерного пространства содержится ров-
но пр шаров, где п — число шаров в ребре такого «куба» (мы ставим ка-
вычки, чтобы подчеркнуть, что этот «куб» расположен в многомерном
пространстве и представить его себе наглядно при р > 3 мы не можем).
Из р-мерных «кубов» можно сложить «пирамиду» в (р + 1)-мерном
пространстве. Это аналог четырехугольной пирамиды трехмерного про-
странства. Число шаров в этой «пирамиде» равно 1₽ + 2Р + Зр + ... + пр.
Будем называть эту сумму степенной и обозначать
Sp (п) = 1₽ + 2Р + ... + пр.
При р = 1 «куб» превращается в отрезок, «пирамида» — в треуголь-
п(п +1)
ник, число шаров в котором S (п) = 1 + 2 + ... + п =--- выражается
2
п-м треугольным числом. При р = 2 роль «куба» играет квадрат, а «пира-
миды» — самая натуральная четырехугольная пирамида, и число шаров
в ней
S2 (п) = I2 + 22 + ... + п2 =
п (п + 1) (2п + 1)
6
является ге-м пирамидальным числом. При р = 3 «кубом» является обыч-
ный куб трехмерного пространства. Соответствующую «пирамиду» мы
уже представить не можем, поскольку она находится в четырехмерном
пространстве, тем не менее мы знаем количество шаров в ней. Оно выра-
жается суммой
S3 (п) = I3 + 23 + ... + п3 =
п2 (п + I)2
4
как уже доказано методом Никомаха.
51
Впрочем, формулу для S2 (п) мы не доказали, позаимствовав ее у
Архимеда. Выведем ее, используя тождество (k + I)3 = k3 + 3kz + 3k + 1.
Из него следует, что
£((/г + 1)3-/г3) = 3 £/г2+з£/е+Х1.
/г = 1 k = 1 k = l k = 1
Отсюда
s2(n)=((fe+i)3-£3)-£fe-|£i.
k=l 6k=l k = l k=l
Рассмотрим суммы, стоящие в правой части равенства:
у ((k + I)3 - й3) = (23 - I3) + (З3 - 23) + (43 - З3) + ... +
Аг = 1
по о о Д тг(тг + 1) Д
+ ((га + I)3 - га3) = (и + I)3 - I3, у/г = S(n) = —-£1 = га.
Л=1 k=1
Поэтому
с , V г,2 1« , -,лЗ 1Л гг(п + 1) п га(га + 1)(2га + 1)
S2(ra)= £й2 =-((га + 1)3-1)--------- =--------------.
*=i d z о о
Аналогично можно вывести формулу для 83 (га), не прибегая
к гномонам и геометрическим построениям, но используя тождество
(й + I)4 = й4 + 4й3 + 6й2 + 4й + 1 и формулы для S (га) и S2 (п). Читатели
могут это проделать самостоятельно. Формула для произвольной степен-
ной суммы выводится следующим образом. По биному Ньютона имеем
(й + iy + 1 - kp+1 = cj, + 1kp + с^^-1 + C3 + 1kp~2 + ... + Cpp+1k + 1.
Просуммируем обе части этого равенства по й от 1 до га и выразим из него
сумму р-х степеней, учитывая, что коэффициент перед этой суммой равен
С1р+1=Р+ 1:
Sp(n)=^kp =
k=l
= -^—y((k + i)p + 1-kp + 1-c2+1kp-1-c3+1kp-2-...-cp+1k-i).
n
Так как ^((/г 4- 1/*+ 1 - kp + J) = (n + I/7 + 1 - 1, то окончательно имеем
k=i
Sp (ra) = —l— ((n + ly*41 - ra - 1 - C2+ 1S ! (n) -
p +1
-C3p + 1Sp_2(n)-...-Cpp + 1S (n)). (17)
Пользуясь этой формулой, можно найти выражение для Sp (га), если
известны S (га), S2 (га), ..., Sp_r (п). Поскольку мы знаем S (га), S2 (га) и
S3 (п), то нетрудно подсчитать, что
52
,га1 _ ,4 . о4 . + „4 _ «(« + 1) (2п + 1) (Зп2 + Зп - 1)
30
_ , ч ,ч , п2 (п +1)2 (2п2 + 2п -1)
S5 (п) = I5 + 25 + ... + п5 =----------------------------
и т. д.
Если раскрыть в формуле (17) скобки, то сумма Sp (п) окажется вы-
раженной в виде многочлена от п. Строение этих многочленов изучал вы-
дающийся швейцарский математик Якоб Бернулли (1654—1705),
который в труде «Искусство предположений» (1713) доказал, что они
имеют следующий общий вид:
„ , > с;8,»'-' с’в2п--’
s" ’ 77Т + Т +---2----+----4----
^СрВ3пр~а ^СрВ4пр~7
(18)
Приглядимся повнимательнее к правой части равенства. Первые три по-
казателя степеней п равны р + \, р м. р - 1, а затем они убывают с каждым
шагом на две единицы. Сумма конечна: последний показатель равен еди-
нице, если р четно, и равен двум, если р нечетно. Числа С7 , С2,
Ср, ... — биномиальные коэффициенты.
Особый интерес представляют входящие в формулу (18) коэффици-
енты Вх, В2, В3, В4, ... . Их называют числами Бернулли. Встречаются
они во многих вопросах математического анализа и теории чисел. Для их
нахождения положим в этой формуле п = 1. Учитывая, что Sp (1) = 1, по-
лучим
1 = ^—+ ^ + -С1В. + -С2В2 + ^С®В3 +-С1В. +..., (19)
р+1 22р14₽26р38₽ > v г
т. е. сумма всех коэффициентов в многочлене Sp (п) равна единице. Пусть
теперь р = 2. Так как С7 =2, С2 = С| = ... = 0, то в (19) останутся
лишь три слагаемых, откуда В; = —. Рассматривая затем равенство (19)
6
при р = 4, 6, 8, ..., найдем последовательно числа В2 = ——, В3 = -~,
В4 = ——, .... Можно доказать, что вообще знаки чисел Бернулли череду-
30
ются.
С именами Якоба Бернулли, открывшего эти числа, его младшего
брата Иоганна (учителя Эйлера) и других представителей необычайно
богатого талантами рода Бернулли мы еще встретимся в последующих
главах.
53
14. Проблемы Варинга
и Гольдбаха
В п. 11 мы познакомились с задачей о представлении натурального
числа в виде суммы не более чем четырех квадратов, которая была поло-
жительно решена Лагранжем в 1770 г. В том же году английский мате-
матик Эдвард Варинг (1734—1798) высказал утверждение, что вся-
кое натуральное число может быть представлено в виде суммы не более
4 квадратов, или 9 кубов, или 19 четвертых степеней и т. д.
Например, для числа 17 имеем
17 = З2 + 22 + 22 = 42 + I2,
17 = 23 + 23 + I3,
17 = 24 + I4.
Это утверждение получило название гипотезы или проблемы Варин-
га, которую можно более строго сформулировать следующим образом:
Для любого показателя п > 2 найдется такое число k, зависящее толь-
ко от п, что всякое натуральное число N может быть представлено в
виде суммы
N = х " + х " + ...+ х " ,
где Xj, xk принимают значения 0, 1,2, ....
Если все xlt ..., xk отличны от нуля, то число слагаемых в правой ча-
сти равно k, в противном случае их меньше чем k. Важно, что k не зави-
сит от самого числа N, иначе утверждение было бы очевидным: мы запи-
сали бы N = 1" + 1" + ... + 1" (N слагаемых).
В течение долгого времени ученые не могли решить проблему Варин-
га. Сделать это удалось лишь в 1909 г. выдающемуся немецкому матема-
тикуДавиду Гильберту (1862—1943). Он показал, что гипотеза Ва-
ринга верна, правда, данная им оценка числа k = k (п) была довольно
грубой. Гильберт занимался этой проблемой в течение почти двух лет, со-
средоточив на ней все свое внимание. Такой стиль работы был в характе-
ре ученого. Приступив к какой-либо задаче, он не переключался ни на
что другое, даже если на решение уходили годы.
Своими фундаментальными результатами в различных областях ма-
тематики, высокой требовательностью к строгости изложения Гильберт
снискал себе огромный научный авторитет среди современников. Вместе
с тем его исследования оказали существенное влияние на дальнейшее
развитие почти всех разделов математической науки.
«Кто из нас не хотел бы приоткрыть завесу, за которой скрыто наше
будущее, чтобы хоть одним взглядом проникнуть в предстоящие успехи
нашего знания и тайны его развития в ближайшие столетия?» — так на-
чал Д. Гильберт свой доклад на Втором международном математическом
конгрессе, состоявшемся в Париже в 1900 г. В этом докладе, сделанном
на рубеже нового столетия, Гильберт сформулировал 23 проблемы, реше-
ние которых, на его взгляд, могло бы значительно стимулировать даль-
нейшее развитие науки. Гильберт оказался провидцем — его проблемы
54
определили в значительной степени направление развития математи-
ки XX в.
После решения Гильбертом проблемы Баринга математики стреми-
лись уточнить границы k (п). Наилучший результат получил советский
математик Иван Матвеевич Виноградов (1891 —1983) — пито-
мец Петербургской математической школы, основанной Чебышевым. На-
учные интересы Виноградова лежали в области аналитической теории чи-
сел — ветви математики, изучающей целые числа методами анализа.
Здесь он явился продолжателем дела всей замечательной плеяды петер-
бургских математиков, получивших, начиная с Эйлера, значительные
результаты в теории чисел. Виноградов создал оригинальный метод три-
гонометрических сумм, с помощью которого решил ряд теоретико-число-
вых проблем. В частности, в 1934 г. он улучшил результат Гильберта в
решении проблемы Варинга, указав более точные границы для k (п). За
большие научные заслуги Виноградов был избран членом многих ино-
странных академий. С 1932 г. он возглавил Физико-математический ин-
ститут Академии наук, основанный в 1920 г. замечательным русским ма-
тематиком Владимиром Андреевичем Стекловым. В 1934 г. от этого
института отделился Математический институт, получивший имя Стек-
лова, и Виноградов стал его директором. Эту ответственную и почетную
должность он бессменно занимал до конца своей жизни.
Решение проблемы Варинга и улучшение оценки для числа слагаемых
были получены в результате использования методов математического ана-
лиза, т. е. привлечения более сложного математического аппарата по срав-
нению с тем, в котором сформулирована сама проблема. Но математики
всегда стремились решать арифметические задачи методами самой арифме-
тики. Поэтому параллельно шел поиск решения проблемы Варинга «эле-
ментарными» методами, хотя название «элементарные» совсем не говорит
об их простоте. Такое решение было найдено в 1942 г. советским математи-
ком Юрием Владимировичем Л и н н и к о м (1915—1972).
Познакомимся теперь с проблемой, носящей имя Гольдбаха, кото-
рый в письме к Эйлеру в 1742 г. высказал гипотезу: «...каждое число,
большее чем 2, есть сумма трех простых чисел». (Аналогичную законо-
мерность столетием раньше подметил Р. Декарт, но опубликованы эти за-
писи были лишь в начале XX в.) В ответном письме Эйлер соглашается с
гипотезой и утверждает, что для этого достаточно доказать свойство, под-
меченное ранее самим Гольдбахом: «Каждое четное число есть сумма
двух простых чисел» (единицу они относили к простым числам). Напри-
мер, 2 = 1 + 1, 3=1 + 1 +1, 4 = 2 + 2 = 3 + 1, 5 = 2 + 2+1 = 3+1 + 1,
6 = 3 + 3 = 5 + 1, 7 = 3 + 2 + 2 = 3 + 3 + 1, 8 = 5 + 3 = 7+1, 9 = 5 + 2 + 2 =
= 3 + 3 + 3 = 5 + 3 + 1 = 7+1 + 1. Поскольку сейчас единицу не считают
простым числом, то гипотеза Гольдбаха звучит так:
Любое натуральное число, большее 5, представимо в виде суммы трех
простых чисел.
Утверждение Эйлера звучит так:
Каждое четное натуральное число, начиная с 4, можно представить в
виде суммы двух простых чисел.
55
Покажем, что гипотеза Гольдбаха вытекает из утверждения Эйлера.
Для этого рассмотрим произвольное натуральное число: оно может быть
четным 2п или нечетным 2п + 1. Так как, по Эйлеру, 2 (п - 1) = р1 + р2, то
2п = р} + р2 + 2 и 2п + 1 = р, + р2 + 3. Получаем предложение Гольдбаха.
Оказывается, верно и обратное. Пусть 2п — произвольное четное число. По
гипотезе Гольдбаха имеем 2 (п + 1) = рг + р2 + р3. Одно из трех слагаемых,
например р3, четное. Тогда р3 = 2 и 2п = Р\ + р2, т. е. из справедливости ги-
потезы Гольдбаха для четных чисел вытекает утверждение Эйлера.
Подтверждение гипотезы Гольдбаха для нечетных чисел ничего не
дает для четных. Естественно ожидать, что четный случай окажется бо-
лее трудным по сравнению с нечетным. Гипотеза Гольдбаха для четного
случая (а с ней и утверждение Эйлера) до сих пор не доказана и не опро-
вергнута. Нечетному случаю повезло больше.
Сначала английские математики Г о т ф р и Харди (1877—1947) и
Джон Литлвуд (1885—1977) показали (1923) возможность представ-
ления достаточно большого нечетного числа в виде суммы трех простых.
При этом они исходили из верности некоторого результата, не доказанно-
го до сих пор. Затем (1930) советский математик Лев Генрихович
Шнирельман (1905—1938) доказал, что всякое натуральное число,
большее единицы, есть сумма не более С простых чисел. Правда, он ука-
зал довольно большое значение для числа слагаемых: С = 800000. В даль-
нейшем усилиями математиков постоянная С постепенно уменьшалась: в
1936 г. она была доведена до 67, а в 1950 г. — до 20.
И только в 1937 г. Виноградов доказал гипотезу Гольдбаха для всех до-
статочно больших нечетных чисел п (таких, что In (In n) > 60368; позже
граница была уменьшена). Из полученного результата следует только, что
достаточно большое четное число записывается в виде суммы четырех про-
стых. В 1957 г. опять-таки Виноградовым доказана следующая теорема:
Любое достаточно большое четное число можно записать в виде сум-
мы двух слагаемых, каждое из которых имеет не более трех простых
множителей.
Трудности решения проблемы Гольдбаха, по-видимому, связаны с тем,
что сама проблема формулируется в аддитивной форме (использующей опе-
рацию сложения), а связана с понятием простого числа, которое формули-
руется в мультипликативной форме (на основе операции умножения).
Значение проблем Варинга и Гольдбаха для математики заключается
не в самих утверждаемых фактах. Ведь от того, что мы, допустим, докажем
представимость числа в виде суммы трех простых, мало что изменится.
Проблемы эти играют в истории математики существенную роль, посколь-
ку в процессе их решения разрабатываются новые методы, способствующие
созданию мощного аппарата теории чисел. Например, Шнирельман в связи
с решением проблемы Гольдбаха ввел в математику понятие плотности чис-
ловой последовательности, которое оказалось полезным для решения и дру-
гих теоретико-числовых и алгебраических вопросов.
Гольдбаху принадлежит еще одна гипотеза (1743): всякое нечетное
число есть сумма удвоенного квадрата и простого числа. Многие при-
меры подтверждают это предположение: 5 = 2 • I2 + 3; 13 = 2 • I2 + 11 ==
56
= 2 • 22 + 5; 31 = 2 • l2 + 29 = 2 • 22 + 23 = 2 • З2 + 13. Но нашлись числа,
в частности 5777 и 5993, которые не представляются в таком виде. На са-
мом деле легко убедиться, что разность между любым из этих чисел и
удвоенным квадратом последовательных чисел от 1 до 54 (так как
2 • 542 < 5993 < 2 • 552) не является простым числом. Таким образом, эта
гипотеза Гольдбаха оказалась неверной. Однако и она не была бесполезной
для математики. Сам автор гипотезы писал Эйлеру в том же письме, в кото-
ром сформулировал свою знаменитую проблему: «Я считаю небесполезны-
ми и такие предложения, которые весьма вероятны, хотя и недостает их на-
стоящего доказательства, ибо если даже они затем окажутся ложными, они
могут дать повод к открытию какой-либо новой истины».
Именно так обстояло дело в данном случае. В 1923 г. Харди и Литл-
вуд ослабили гипотезу Гольдбаха, высказав предположение:
Достаточно большое нечетное число есть сумма двух квадратов и про-
стого числа.
Доказано оно Линником в 1960 г.
Отметим еще одно наблюдение Гольдбаха — число 4п4 + 1 при п > 1
составное: 4n4 + 1 = (2п2 + 2п + 1) (2п2 - 2п + 1). В то же время числа ви-
да п2 + 1 могут быть как простыми (22 + 1 = 5, 42 + 1 = 17, 102 + 1 = 101),
так и составными (82 + 1 = 65, 122 + 1 = 145). До сих пор неизвестно, ко-
нечно ли множество простых чисел вида п2 + 1.
Сколько же загадок хранит в себе натуральный ряд — эта бесконеч-
ная вереница чисел! Работы здесь хватит и современным, и будущим ма-
тематикам.
15. Кролики, коровы и телки
Читатели, конечно, помнят, как герои жюль-верновского «Таинствен-
ного острова» сумели получить за несколько посевов громадный урожай
пшеницы, вырастив его из одного-единственного зернышка, которое зате-
рялось в кармане Герберта Брауна.
Напомним, как планировал этот
урожай Сайрус Смит: «...посадив
это зернышко, мы при первом сбо-
ре урожая снимем восемьсот зе-
рен, которые при втором сборе да-
дут шестьсот сорок тысяч зерен,
при третьем — пятьсот двенадцать
миллионов, а при четвертом —
свыше четырехсот миллиардов зе-
рен...»
Сайрус Смит добавил при
этом, что размножение пшеницы
ничто по сравнению с маком и та-
баком, у которого один корень да-
ет триста шестьдесят тысяч се-
мечек.
57
Здесь мы встречаемся с тем,
что математики называют геомет-
рической прогрессией. Напомним,
что так называют последователь-
ность чисел Ъх, Ъ2, ..., Ъп, ..., каж-
дый последующий член которой
получается из предыдущего умно-
жением на одно и то же число
q 0, называемое знаменателем
прогрессии. С геометрическими
прогрессиями люди сталкивались
уже давно. Они упоминаются и
в древневавилонских законах, на-
чертанных в XVIII в. до н. э. по
приказу царя Хаммурапи на ка-
менной стеле, и в законах Афин и
Рима, и в Русской Правде. Обыч-
но в этих законах речь шла либо о возрастании долга (в случае, когда про-
центы начисляются не только на основную сумму долга, но и на уже вырос-
шие проценты), либо о размножении скота. О том, насколько быстр этот
рост, видно из примера с зернышком пшеницы. Но это, скажет читатель,
бывает только в научно-фантастических романах. Оказывается, нет — та-
кой рост бывал и в жизни и приводил к серьезным последствиям. Завезен-
ные в Австралию кролики так быстро размножились, что стали националь-
ным бедствием.
Но бывают случаи размножения по более сложному закону, чем гео-
метрическая прогрессия. Один из них рассмотрен Леонардо Пизанским в
«Книге абака». Приведем его задачу: «Некто поместил пару кроликов в
некотором месте, огороженном со всех сторон стеной, чтобы узнать,
сколько пар кроликов родится при этом в течение года, если природа кро-
ликов такова, что через месяц пара кроликов производит на свет другую
пару, а потомство кролики приносят со второго месяца своего рождения.
Сколько пар кроликов в один год от одной пары рождается?» Решим эту
задачу.
В начале первого месяца была одна пара, в начале второго — две пары.
Причем одна из них зрелая, т. е. способная через месяц принести потомст-
во, вторая нет. Поэтому в начале третьего месяца будет три пары, две из
них уже зрелые. Затем станет пять пар (три пары были и две — новое по-
томство), причем только три из них зрелые, и т. д. Составим таблицу.
Начало месяца 1 2 3 4 5 6 7 8 9 10 11 12 13
Число зрелых пар 1 1 2 3 5 8 13 21 34 55 89 144 233
Число всех пар 1 2 3 5 8 13 21 34 55 89 144 233 377
58
Обозначим п-е число во второй строке через ип. Мы видим, что
Uj =1, и2 = 1, и3 = 2, и4 = 3, и5 = 5 и т. д.
Закон образования элементов последовательности 1, 1, 2, 3, 5, ... та-
ков: каждое последующее число равно сумме двух предыдущих.
Поэтому достаточно знать первые два члена этой последовательно-
сти, чтобы найти все ее дальнейшие элементы.
Естественно рассматривать бесконечную последовательность их, и2,
и3, ..., ип, ..., образованную по этому принципу. Элементы ее называют
числами Фибоначчи. Для нее
и3 = и2 + их, и4 = и3 + и2, и5 = и4 + и3 и т. д.;
вообще для произвольного номера п=1, 2, ... имеем ип + 2 = ип + 1 + ип.
Итак, чтобы вычислить (л + 2)-й член этой последовательности, нужно
вернуться к (га + 1)-му и га-му, но для нахождения (га + 1)-го нужно сде-
лать еще шаг назад и т. д.; попятное, или возвратное, движение продол-
жается до тех пор, пока не придем к первым двум членам. Такое возврат-
ное движение в математике принято называть рекуррентным (от лат.
recurrere — возвращаться назад). А последовательность, для которой су-
ществует формула, позволяющая найти га-й член по известным предыду-
щим, называется рекуррентной или возвратной.
Мы уже встречались в этой главе с рекуррентными последовательно-
стями: это числа Люка, степенные суммы, числа Бернулли. Читатели, не-
сомненно, вспомнили и более простые последовательности такого ти-
па — арифметическую и геометрическую прогрессии. В арифметической
прогрессии каждый следующий член получается из предыдущего прибав-
лением одного и того же числа d — разности прогрессии: an + l = ап + d, а
в геометрической — умножением на одно и то же число q — знаменатель
прогрессии: bn + l = bnq.
Вернемся к числам Фибоначчи. Рекуррентное соотношение ип + 2 =
= ип + 1 + ип, которому подчиняются члены этой последовательности, яв-
ляется линейным. В общем виде такое соотношение может быть записано
следующим образом:
хп + k = а4хп + fe _ ! + а2хп + k _ 2 + ... + akxn. (20)
Здесь а4, ..., ak — постоянные коэффициенты, хп — общий член рекур-
рентной последовательности. Число k называют порядком соотношения
(20). Оно показывает, сколько предыдущих членов надо знать для вычис-
ления xn + h. Например, соотношение Фибоначчи имеет второй порядок,
рекуррентные формулы для арифметической и геометрической прогрес-
сий — первый порядок.
Соотношение (20) позволяет выразить произвольный член хп после-
довательности без обращения к предыдущим. Для этого составляют урав-
нение
А? = аД*'1 + а2А?~2 + ... + «й, (21)
называемое характеристическим для (20), и находят его корни. Если
корни Zj, ..., Aft уравнения (21) различны, то искомая формула для хп
имеет вид
хп = сДД + сД2“ + ... + сД*". (22)
59
Здесь числа Cj, ck определяются заданием первых k членов последова-
тельности. Верность полученного результата проверяется непосредствен-
ной подстановкой. Может случиться, что среди корней характеристиче-
ского уравнения есть равные между собой, например Х.4 = Х2 = ••• = Кп-
Тогда в выражении (22) надо заменить сумму с4Х" + ... + ст \пт на
(Cj + с2п + ... + стпт) к".
Применим описанный метод к выводу формулы для чисел Фибонач-
чи. Здесь ип + 2 = ип +! + ип. Запишем соответствующее характеристиче-
ское уравнение Х2 = Л.+ 1. Его корнями являются числа А. 4 + и
1 — -/5
Л2 =------. Поэтому члены последовательности, удовлетворяющей дан-
ному рекуррентному соотношению, имеют вид
Чтобы найти с} и с2, воспользуемся тем, что первые два члена этой после-
довательности нам известны: и1 = 1, и2 = 1. В результате приходим к сис-
теме
Из нее находим сх = — с2 =-, и поэтому
Эта формула называется формулой Бине по имени получившего ее
французского математика Жака Бине (1786—1856). Заметим, что чис-
-/5 + 1
ло------ встретится нам в геометрическом разделе, когда мы будем го-
ворить о золотом сечении.
Свойства чисел Фибоначчи можно получить либо из рекуррентного
соотношения ип + 2 = ип + 4 + ип, либо с помощью формулы Бине. На-
пример, чтобы доказать, что каждое третье из чисел Фибоначчи четное,
удобнее пользоваться рекуррентной формулой. В самом деле, так как
и1 ~ и2 ~ 1> то ясно, что сумма и3 этих чисел четна. Поэтому и4 = и3 + и2
нечетно как сумма четного и нечетного чисел, а и5 = иЛ + и3 нечетно как
сумма нечетного и четного чисел. Но тогда и6 = и5 + и4 снова четно как
сумма двух нечетных чисел. Продолжая это рассуждение дальше, видим,
что четность чисел Фибоначчи идет в таком порядке: н, н, ч, н, н, ч, ... .
Аналогично показывается, что каждое четвертое число Фибоначчи делит-
ся на 3, а каждое шестое — на 4 и т. д. Вообще числа, делящиеся на d,
60
встречаются периодически. Далее из равенства ип + 2 = ип + 1 + ип следует,
что НОД (ип + 2, ип +,) = НОД (ип + р ип). Пятясь таким образом назад,
придем к НОД (u2, щ) = НОД (1, 1) = 1, а потому каждые два соседних
числа Фибоначчи взаимно просты.
В то же время доказать, что сумма квадратов двух соседних чисел
Фибоначчи снова является числом Фибоначчи, проще с помощью форму-
лы Бине. В самом деле, из этой формулы следует, что
Поэтому
Числами Фибоначчи описываются некоторые количественные соот-
ношения в растительном мире. Например, семечки в корзинке подсолну-
ха расположены по спиралям, закрученным в двух направлениях. Анало-
гично расположены цветки в соцветии ромашки, чешуйки на многих
шишках и т. д. При этом количество спиралей разных видов выражается,
как правило, соседними числами Фибоначчи. Например, у ромашки
количество спиралей, идущих в разных направлениях, может равняться
13 и 21, а у крупных подсолну-
хов — 55 и 89.
Числа Фибоначчи оказались
связанными со многими задача-
ми геометрии и математического
анализа, в частности с задачей о
нахождении оптимальной страте-
гии поиска приближенного экст-
ремума функции на данном ин-
тервале. С помощью этих чисел
была решена одна из важных
математических проблем — 10-я
проблема Гильберта, о чем будет
рассказано в следующей главе.
Через полтора века после на-
писания «Книги абака» на дру-
гом конце мира — в далекой
Индии, уже упоминавшийся на-
ми математик Нарайана написал
61
книгу «Биджаганита» (что означает «искусство вычислений»), в которой
решил задачу, похожую на задачу Леонардо о кроликах.
Найти число коров и телок, происходящих от одной коровы в тече-
ние 20 лет, при условии, что корова в начале каждого года прино-
сит телку, а телка дает такое же потомство в начале года, достигнув
трех лет.
Задачу Нарайаны тоже можно решить, составив рекуррентное соот-
ношение. Но здесь в начале тг-го года надо различать следующие числа:
число хп коров, которые в это время принесли потомство (число ново-
рожденных телок тоже равно хп) , число уп телок, которые принесут по-
томство через год, число гп телок, которые принесут потомство через
два года. Общее число голов в стаде равно 2хп + уп + гп. В силу условия
задачи эти числа связаны следующей системой соотношений:
Хп + 1 = Хп + Уп, уп + 1 = 2п, 2п + 1 = Хп.
При этом х4 = 1, г/х = 0, = 0, и потому х2 = 1, х3 = 1. Пользуясь этими
равенствами, можно исключить из системы уп, yn + i, г„, гп + 1 и получить
одно рекуррентное соотношение хп + 3 = хп + 2 + хп. Находить формулу для
хп с помощью характеристического уравнения нецелесообразно, так как
такое уравнение А3 = А2 + 1 имеет только один действительный корень.
Лучше вычислять непосредственно х4 = х3 + хг = 2, х5 = х4 + х3 = 3 и т. д.
Получаем последовательность 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88,
129, 189, 277, 406, 595, 872. Значит, все стадо через 20 лет будет состоять
из 2 • 872 + 595 + 406 = 2745 голов.
Однако сам Нарайана решал эту задачу иначе, используя введенные
им р-симплициальные числа ФдР>(п) (см. п. 12). Его решение таково:
1. Корова приносит 20=Ф*1)(20) телок первого поколения.
2. Первая телка первого поколения дает 17 телок второго поколе-
ния, вторая — 16 и т. д. Всего будет (17 + 16 + 15 + ... + 1) телок второго
поколения. Но эта сумма равна Ф*2)(17).
3. Учитывая потомство телок второго поколения, находим: число те-
лок третьего поколения равно Ф*2) (14) + Ф*21 (13)+ ... +Ф*2) (1). Эта сум-
( о \ & & °
ма равна Фд ’ (14).
4. Продолжая процесс, получаем, что численность всего стада через
20 лет будет равна
1 + Ф*1’ (20) + Ф*2) (17) + Ф<3) (14) + ф‘4) (11) + Ф*5) (8) + Ф*6) (5) + Ф*7) (2) =
= 1 + 20 + 153 + 560 + 1001 + 792 + 210 + 8 = 2745.
Как показали исследования историков математики, за тысячу лет до
Фибоначчи в работах Теона Смирнского уже содержались рекуррентные
последовательности. Но там речь шла не о размножении кроликов или
коров, а о вычислении отношения диагонали квадрата к его стороне. По-
скольку этот результат тесно связан с историей развития понятия числа,
то естественно начать с нее.
62
16. Великая тайна пифагорейцев
Древние знали лишь натуральные числа 1, 2, 3, 4, которые им
были нужны для счета предметов. Как же они обходились без нуля и без
отрицательных чисел? Все дело в том, что вычисления в древности произ-
водились на счетных досках: в Греции и Риме — это «абак», в Ки-
тае — «суан-пан». Да и у нас до появления микрокалькуляторов исполь-
зовались счеты. А для работы на них нужны только натуральные числа.
Знак нуля потребовался лишь при записи чисел в позиционной си-
стеме счисления для указания пропущенного разряда. Поэтому и по-
явился он впервые у вавилонян, располагавших 60-ричной системой
счисления. В вавилонских табличках нуль изображался в виде сдвоенно-
го угла д<. От вавилонян нуль перешел к греческим астрономам, за-
писывавшим его в виде кружка (по первой букве греческого слова
O'U&v — ничто). Дальнейший путь этого знака традиционный: из Греции
в Индию, затем в арабские страны, а позже в Европу. Заметим, что ин-
дийцы называли нуль словом «сунья» (пустое), арабы перевели его соот-
ветствующим словом «ас-сыфр». В латинском языке это слово оставили
почти без изменения. От латинского cifra и образовалось наше «цифра».
Кажется вполне естественным, что вслед за натуральными числами
должны были появиться отрицательные. Ведь нет ничего проще, чем обо-
значить долг, возникающий в процессе товарообмена, отрицательным
числом. История же рассудила иначе: раньше, чем отрицательные, воз-
никли рациональные числа. И способствовали этому вопросы измерений.
Ведь для измерений нужны лишь положительные числа. А поскольку ре-
зультаты не всегда выражались целыми числами единиц измерения, ста-
ли использовать различные доли этой единицы. Так появились положи-
тельные рациональные числа. Правда, древние греки не считали их
числами, а говорили о них лишь как об отношении натуральных. Пифа-
горейцы были уверены в том, что с помощью натуральных чисел можно
выразить все свойства окружающего мира и все измерить. И вдруг они
обнаруживают, что отношение диагонали квадрата к его стороне невоз-
можно выразить с помощью натуральных чисел.
Это открытие было как гром среди ясного неба. Подрывалась основа
философских взглядов пифагорейцев, их лозунг — «Весь мир есть число»
становился несостоятельным. Поэтому открытие несоизмеримости диаго-
нали квадрата с его стороной хранилось ими как великая тайна. Говорят
даже, что Гиппаса Месопотамского, разгласившего ее, изгнали из сообще-
ства пифагорейцев. Но тем не менее недостаточность натуральных чисел
стала явной, нужно было срочно искать выход из сложившейся кризис-
ной ситуации.
Нашел его великий древнегреческий ученый Евдокс Книдский
(ок. 406 — ок. 355 до н. э.). Идея Евдокса заключалась в следующем. По-
скольку длины отрезков не всегда выражаются рациональными числами,
то надо обратиться к самим отрезкам. Он назвал отрезки величинами и
стал рассматривать отношения величин, показав, что для них выполня-
ются все естественные числовые свойства. Тем самым Евдокс фактически
63
расширил множество рациональных чисел до множества действитель-
ных. Однако еще более двух тысячелетий математики не считали величи-
ны числами. Тем не менее работать с ними начали уже античные матема-
тики, предъявлявшие к формулировкам, построениям и доказательствам
требования высокой точности. Использование отношений величин заста-
вило их обратиться к геометрической форме изложения. Стала развивать-
ся геометрическая алгебра, базирующаяся на геометрических объектах:
отрезках, прямоугольниках и т. п.
Геометризация математики сдерживала появление отрицательных
чисел. Ведь для выражения длин, площадей или объемов они не нужны.
Поэтому потребность в отрицательных числах в Европе долго не возника-
ла. Не так обстояло дело на Востоке. В Китае отрицательные числа по-
явились еще до новой эры. В «Математике в девяти книгах» (ок. II в. до
н. э.) они встречаются в условиях некоторых задач и в промежуточных
вычислениях. Из Китая отрицательные числа, по-видимому, попали в
Индию, а оттуда к арабам. Но всюду они употреблялись лишь эпизоди-
чески.
В Европе отрицательные числа впервые появились у Диофанта, кото-
рый отошел от геометрических доказательств. В «Арифметике» он даже
формулирует правила действий над ними: «Недостаток, умноженный на
недостаток, дает наличие; недостаток же, умноженный на наличие, дает
недостаток». Но и у Диофанта отрицательные числа играют вспомога-
тельную роль: они используются лишь в промежуточных вычислениях;
условие задачи и ответ всегда даются в положительных числах. И не про-
слеживается какого-либо влияния этого трактата на развитие математи-
ки в Европе в последующее тысячелетие. В Средние века к отрицатель-
ным числам вновь обратился Леонардо Пизанский, толковавший их как
долг. Еще долго на отрицательные числа смотрели как на досадную необ-
ходимость, возникающую при вычислениях. Лишь с середины XVII в.,
когда их стали изображать на числовой оси, отрицательные числа обрели
права гражданства. А теперь обратимся к результату Теона Смирнского.
Несоизмеримость диагонали квадрата с его стороной показала, что
отношение этих двух величин (число V2) нельзя записать в виде отноше-
ния двух натуральных чисел. А если взять бесконечную последователь-
ность таких отношений? Другими словами, найти приближение числа 4~2
рациональными числами.
Такую задачу поставил перед собой греческий математик Теон
Смирнский, живший во II в. н. э. Как видим, в начале новой эры древ-
негреческие ученые уже интересовались практическими вопросами, в том
числе и приближениями, чего раньше они себе никогда не разрешали.
Правда, в этом вопросе у них были предшественники: еще вавилоняне
для практических целей находили приближения квадратных корней из
произвольных чисел. Но у Теона как истинного представителя греческой
математики было иное, чисто геометрическое решение этой задачи.
Пусть а — сторона квадрата, Ь — его диагональ, тогда 42 = —.
а
Вычтем из диагонали сторону, получим а1 = Ъ - а (рис. 7).
64
Рис. 7
Рассмотрим два меньших отрезка а
и ctj. Снова вычтем из большего мень-
ший: а - at = Ьг. Отрезки at и Ьх пред-
ставляют собой соответственно сторону
и диагональ меньшего квадрата, при-
чем а = ах + fej и b = 2в1 + Ьг. Аналогич-
но вычитая из диагонали Ь} сторону а1г
найдем а2, затем Ъ2 = а1 - а2 и т. д. На
fe-м шаге получим квадрат со стороной
ak и диагональю bk, для которых выпол-
няются равенства
ak -1 = ak + bk, bk_! = 2ak + bk.
Остановим процесс на n-м шаге. Ес-
ли п — достаточно большое число, то
соответствующий квадрат столь мал,
что можно считать ап равным Ъп. По-
скольку нам будут нужны отношения —— , то для удобства положим
ак
ап = bn= 1. Обозначим a* = ап _ k + х, Р* = bn _ k + x, т. e. будем рассматривать
последовательность сторон и диагоналей квадратов в порядке, обратном
их построению. Числа ах, а2, и Pi, Р2, ••• связаны рекуррентными соот-
ношениями
a* + i = <4 + рА, P* + i = 2а* + р*.
Так как а! = ап = 1 и рх = bn = 1, то мы можем выписать по нескольку чле-
нов последовательностей (а*) и (Р*):
1, 2, 5, 12, 29,
1, 3, 7, 17, 41... .
Числа первой из них пифагорейцы называли боковыми, а второй — диа-
гональными. Деля поочередно каждое диагональное число на стоящее
над ним боковое, получим дроби вида . Будем обозначать их через xk.
a-k
Тогда х, = - = 1, х2 = — = 1,5, х3 = — = 1,4, х4 = — ~ 1,417, х5 = — =
1 1 2 2 3 5 4 12 5 29
~ 1,414 .... Они дают приближение числа V2 с возрастающей точностью,
попеременно становясь то меньше V2, то больше. Очевидно, для х* имеет
2 + х*
место рекуррентное соотношение х* + 1 =----.
1 + х*
Отметим, что
P2 + i - М + 1 = (2а* + Р*)2 - 2 (а* + Р*)2 = 2а? - Р|,
т. е. при переходе к следующему номеру разность Р* - 2а* меняет знак.
Так как р2 - 2а2 = -1, то отсюда следует Р* - 2а* = (-1)*. Таким образом,
числа Р* и а* при четных k являются решениями уравнения х2 - 2у2 = 1.
Оно является частным случаем уравнения Пелля, о котором мы будем го-
ворить в следующей главе.
3 — Н. Я. Виленкин, 10-11 кл.
65
ГЛАВА 2
ДИОФАНТОВЫ УРАВНЕНИЯ
Необычайный расцвет древнегреческой науки в IV—III вв. до н. э.
сменился к началу новой эры постепенным спадом в связи с завоеванием
Греции Римом, а потом и начавшимся разложением Римской империи.
Но на фоне этого угасания еще вспыхивает яркий факел. В III в. уже
новой эры появляется сочинение александрийского математика Дио-
фанта «Арифметика». О жизни самого Диофанта нам известно только
из стихотворения, содержащегося в «Палатинской антологии». В этой ан-
тологии содержалось 48 задач в стихах, собранных греческим поэтом и
математиком VI в. Метродором. Среди них были задачи о бассейне, о ко-
роне Герона, о жизненном пути Диофанта. Последняя оформлена в виде
эпитафии — надгробной надписи.
pax Диофанта гробница покоит: дивись ей — и камень
V Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругою он обручился.
С нею пять лет проведя, сына дождался мудрец.
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе.
Тут и увидел предел жизни печальной своей.
Решив эту задачу, читатели смогут расставить основные вехи жиз-
ненного пути Диофанта. Трактат «Арифметика» занимает особое место в
античной математике не только по времени своего появления, но и по со-
держанию. Большую его часть составляют разнообразные задачи по тео-
рии чисел и их решения. Но, главное, автор использует не геометриче-
ский подход, как это было принято у древних греков, — решения
Диофанта предвосхищают алгебраические и теоретико-числовые методы.
К сожалению, из 13 книг, составлявших «Арифметику», до нас до-
шли лишь первые 6, а остальные погибли в перипетиях тогдашнего
бурного времени. Достаточно сказать, что через 100 лет после смерти
Диофанта понесла невосполнимый урон знаменитая александрийская
библиотека, содержавшая бесценные сокровища древнегреческой науки:
была сожжена значительная часть свитков.
66
1. В ответе только целые числа
Задачи диофантовой «Арифметики» решаются с помощью уравне-
ний, а проблемы решения уравнений относятся скорее к алгебре, чем
к арифметике. Почему же мы говорим о них в этом разделе? Дело
в том, что задачи эти имеют специфические особенности. Но прежде
чем говорить о них, рассмотрим вполне современную простенькую з а-
дачу.
| Ученик купил ручки и тетради на сумму 17 р. Какими способами он
может расплатиться, имея в наличии монеты по 2 р. и 5 р.?
Для ответа на этот вопрос достаточно решить уравнение 2х + 5у = 17
с двумя неизвестными х и у. Такие уравнения имеют бесконечное множе-
ство решений. В частности, полученному уравнению отвечает любая пара
( 17 — 2х\
чисел вида х, -------- . Но для нашей практической задачи годятся
\ 5 )
только целые неотрицательные значения х и у. Поэтому приходим к та-
кой постановке задачи: найти все целые неотрицательные решения урав-
нения 2г + 5г/ = 17. Ответ содержит уже не бесконечно много, а всего
лишь две пары чисел (1, 3) и (6, 1).
Теперь скажем об особенностях диофантовых задач. Во-первых, они
сводятся к уравнениям или системам уравнений с целыми коэффициента-
ми. Как правило, эти системы неопределенные, т. е. число уравнений в
них меньше числа неизвестных. Во-вторых, решения требуется найти
только целые, часто натуральные. Для выделения таких решений из
всего бесконечного их множества приходится пользоваться свойствами
целых чисел, а это уже относится к области арифметики. Кстати сказать,
сам Диофант находит рациональные решения своих задач. Вот не-
сколько задач из его «Арифметики».
1. Найти два числа так, что-
бы их произведение находи-
лось в заданном отношении к
их сумме.
2. Найти три квадрата так,
чтобы сумма их квадратов то-
же была квадратом.
3. Найти два числа так, что-
бы их произведение делалось
кубом как при прибавле-
нии, так и при вычитании их
суммы.
4. Для числа 13 = 22 + З2 най-
ти два других, сумма квадра-
тов которых равна 13.
Приведем диофантово реше-
ние последней задачи. Он полага-
3*
67
ет первое число (обозначим его через А) равным х + 2, а второе число В
равным 2х - 3, указывая, что коэффициент перед х можно взять и дру-
8
гой. Решая уравнение (х + 2)2 + (2х - З)2 = 13, Диофант находит х = —, от-
5
. 18 D 1
куда А = —, В = -.
5 5
Воспользуемся указанием Диофанта и возьмем произвольный коэф-
фициент перед х в выражении для В. Пусть снова А = х + 2, а В = kx — 3,
о , 2(3й-2)
тогда из уравнения (х + 2) + (kx - 3) = 13 получаем х =----. Отсю-
k2 + 1
2 (k2 +3fe-l) 3/г2-4/г-3
да А =-------------, В =----------
k2 + 1 k2 + 1
Теперь становятся понятны рассуждения Диофанта. Он вводит очень
удобную подстановку А = х + 2, В — 2х — 3, которая с учетом условия
22 + З2 = 13 позволяет понизить степень квадратного уравнения. Можно
было бы с тем же успехом в качестве В взять 2х + 3 или еще проще х ± 3,
но тогда получаются отрицательные значения для В, чего Диофант не до-
пускал. Очевидно, k = 2 — наименьшее натуральное число, при котором
А тл В положительны. И хотя Диофант приводит решение задачи в конк-
ретных числах, чувствуется, что он владеет общим методом.
Современной постановкой диофантовых задач мы обязаны Ферма.
Именно он поставил перед европейскими математиками вопрос о реше-
нии неопределенных уравнений только в целых числах. Надо сказать,
что это не было изобретением Ферма — он только возродил интерес к по-
иску целочисленных решений. А вообще задачи, допускающие только це-
лые решения, были распространены во многих странах в очень далекие
от нас времена.
Примерно в то же время, когда жил Диофант, далеко на Востоке, в
Китае, были популярны задачи на деление с остатком и задачи о птицах.
Приведем в качестве примера одну задачу из древнего китайского сбор-
ника.
Найти число, которое при делении на 3 дает остаток 2, при делении на
5 — остаток 3, а при делении на 7 — остаток 2.
Интересно, что эта задача с теми же числовыми данными почти че-
рез тысячелетие встречается в «Книге абака» Леонардо Пизанского.
Рассмотрим решение этой задачи китайским математиком С у н ь-
цзы (III или IV в.):
«При делении на 3 остаток есть 2, поэтому возьмем 140. При деле-
нии на 5 остаток есть 3, поэтому возьмем 63. При делении на 7 остаток
есть 2, поэтому возьмем 30. Сложив их вместе, получим 233. Из этого вы-
чтем 210 и получим ответ». (Вспомните числовой фокус, рассмотренный в
главе I п. 2.)
Разберем решение Сунь-цзы. Сначала он подбирает число 140, крат-
ное 5 и 7, которое при делении на 3 дает остаток 2. Конечно, это не наи-
меньшее натуральное число с такими свойствами: можно было бы взять
68
число 35. Но это не столь важно для решения задачи. Затем берется число
63, кратное 3 и 7, дающее при делении на 5 остаток 3. Аналогично нахо-
дится число 30. Очевидно, для числа 233 = 140 + 63 + 30 выполняют-
ся все условия задачи, а потому они выполняются для числа вида
п — 105Z + 233. В свою очередь, 233 = 2 • 105 + 23, поэтому все натураль-
ные решения можно записать формулой п = 105fe + 23, где k = 0, 1, ... .
При k = 0 из нее получаем наименьшее натуральное решение 23.
Древние математики находили в большинстве случаев одно, реже не-
сколько решений неопределенных задач и в основном подбором.
Правда, за этим подбором, как правило, стояла система, разгадав ко-
торую мы, вооруженные современной символикой, можем записать все
искомые решения уравнения. В нынешней математике существует целое
направление, занимающееся исследованиями диофантовых уравнений,
поиском способов их решений. Называется оно диофантовым анализом
или диофантовой геометрией, поскольку использует геометрические
способы доказательств.
Наиболее изучены диофантовы уравнения первой и второй степени.
Остановимся сначала на уравнениях первой степени. Так как решение
линейного уравнения с одним неизвестным не представляет интереса, то
обратимся к уравнениям с двумя неизвестными. Мы рассмотрим два ме-
тода их решения: с помощью алгоритма Евклида и с помощью цепных
дробей.
2. Алгоритм Евклида
Можно найти наибольший общий делитель натуральных чисел а и Ъ,
не раскладывая эти числа на простые множители, а применяя процесс деле-
ния с остатком. Для этого надо разделить большее из этих чисел на мень-
шее, потом меньшее из чисел на остаток при первом делении, затем остаток
при первом делении на остаток
при втором делении и вести этот
процесс до тех пор, пока не прои-
зойдет деление без остатка (так
как остатки убывают, то это на ка-
ком-то шаге случится). Последний
отличный от нуля остаток и есть
искомый НОД (а, Ь).
Чтобы доказать это утверж-
дение, представим описанный про-
цесс в виде следующей цепочки
равенств: если а > Ь, то
а = bq0 + г15
Ь = г±дг + г 2,
Г1 = г2д2 + гз, (1)
rn-i = rnqn
69
Здесь r1; rn — положительные остатки, убывающие с возраста-
нием номера. Из первого равенства следует, что общий делитель чи-
сел а и Ъ делит и общий делитель Ь и г1 делит а, поэтому
НОД (а, Ь) = НОД (Ъ, т\). Переходя к следующим равенствам системы (1),
получаем
НОД (а, Ь) = НОД (Ь, гх) = НОД (гх, г2) =
= ... = НОД (гп_ J, г„) = НОД (г„, 0) = гп.
Утверждение доказано. Приведенный способ нахождения НОД носит
название метода последовательного деления с остатком или алгоритма
Евклида, поскольку впервые он был изложен в его «Началах».
Само слово «алгоритм» имеет арабское происхождение. Algorith-
mus — латинизированная форма имени замечательного узбекского ма-
тематика и астронома IX в. ал-Хорезми. Он познакомил арабов с ин-
дийской десятичной системой счисления, которая потом пришла в
Европу. Сначала алгоритмом (алгорифмом) называлась сама десятич-
ная система, а позже — определенная совокупность операций, выполне-
ние которых в указанном порядке приводит к решению поставленной
задачи.
Обратимся снова к системе (1). Из первого равенства, выразив оста-
ток rj через а и Ь, получим r\ = а — bq0. Подставляя его во второе равенст-
во, найдем г2 = b (1 + q'oQi) — аЧ\- Продолжая этот процесс дальше, мы
сможем выразить все остатки через а и Ь, в том числе и последний:
гп = Аа + ВЬ. В результате нами доказано предложение:
Если d — наибольший общий делитель натуральных чисел а и Ь, то
найдутся такие целые числа А и В, что d = Аа + ВЬ.
Заметим, что коэффициенты А и В имеют разные знаки; если
НОД (а, b) = 1, то Аа + ВЬ = 1. Как найти числа А и В, видно из алгорит-
ма Евклида.
Перейдем теперь к решению линейного уравнения с двумя неизвест-
ными. Оно имеет вид
ах + Ъу = с. (2)
Возможны два случая: либо число с делится на d = НОД (а, Ь), либо нет.
В первом случае можно разделить обе части уравнения на d и свести зада-
чу к решению в целых числах уравнения агх + Ъху = сх, коэффициенты
а , Ь г,
которого Я1 = — и £>!= — взаимно просты. Во втором случае уравнение
d d
не имеет целочисленных решений: при любых целых х и у число ах + by
делится на d и поэтому не может равняться числу с, которое на d не де-
лится.
Итак, мы можем ограничиться случаем, когда в уравнении (2) коэф-
фициенты а и Ь взаимно просты. На основании предыдущего предложе-
ния найдутся такие целые числа х0 и у0, что ах0 + by0 = 1, откуда пара
(сх0, су0) удовлетворяет уравнению (2). Вместе с ней уравнению (2) удов-
летворяет бесконечное множество пар (х, у) целых чисел, которые можно
найти по формулам
х = сх0 + bt, у = су0 — at. (3)
70
Здесь t — любое целое число. Нетрудно показать, что других целочислен-
ных решений уравнение ах + by = с не имеет. Решение, записанное в виде
(3), называется общим решением уравнения (2). Подставив вместо t конк-
ретное целое число, получим его частное решение.
Найдем, например, целочисленные решения уже встречавшегося
нам уравнения 2х + 5у = 17. Применив к числам 2 и 5 алгоритм Евклида,
получим 2 • 3 - 5 = 1. Значит, пара сх0 = 3 17, су0 = — 1 • 17 удовлетворя-
ет уравнению 2х + 5г/ = 17. Поэтому общее решение исходного уравнения
таково:
х = 51 + 5#, у = —17 - 2t,
где t принимает любые целые значения. Очевидно, неотрицательные ре-
шения отвечают тем t, для которых выполняются неравенства
Г 51+5#>0,
[—17—2# > 0.
51 17
Отсюда найдем-----t =5-----. Этим неравенствам удовлетворяют числа
5 2
-10, —9. Соответствующие частные решения запишутся в виде пар:
(1, 3), (6, 1).
Применим этот же метод к решению одной из древних китайских за-
дач о птицах.
Задача. Сколько можно купить на 100 монет петухов, кур и цыплят,
если всего надо купить 100 птиц, причем петух стоит 5 монет, кури-
ца — 4, а 4 цыпленка — одну монету?
Для решения этой задачи обозначим искомое число петухов через х,
кур через у, а цыплят через 4г (из условия видно, что число цыплят дол-
жно делиться на 4). Составим систему уравнений
f х + у + 4г = 100,
[5х + 4у + z = 100,
которую надо решить в целых неотрицательных числах. Умножив пер-
вое уравнение системы на 4, а второе — на (-1) и сложив результа-
ты, придем к уравнению -х + 15г = 300 с целочисленными решениями
х = —300 + 15#, z = #. Подставляя эти значения в первое уравнение,
получим у = 400 - 19#. Значит, целочисленные решения системы име-
ют вид
х = -300 + 15#, у = 400 — 19#, z - #.
Из условия задачи вытекает, что
-300 + 15# > 0,
400-19# > 0,
# » 0,
откуда 20=£#^21 —, т. е. # = 20 или # = 21. Итак, на 100 монет мож-
19
но купить 20 кур и 80 цыплят, или 15 петухов, 1 курицу и 84 цыпленка.
71
Задачи о птицах и задачи на
деление с остатком из Китая по-
степенно распространились в Ин-
дию и на Ближний Восток. Впро-
чем, наверняка указать, где эти
задачи возникли впервые, доволь-
но сложно. Интерес к ним объ-
ясняется запросами практики.
В хозяйственной деятельности че-
ловека встречается много задач,
допускающих только целые ре-
шения. Большую роль в постанов-
ке задач на деление с остатком
сыграли календарные расчеты, в
которых для вычисления различ-
ных дат надо было отыскивать
промежутки времени, содержащие
целое число лет, месяцев, недель,
суток. С течением времени такого типа задачи проникли в Европу.
Рассмотрим задачу на деление с остатком из средневекового евро-
пейского сборника.
Крестьянка несла на базар корзину яиц. Неосторожный всадник, обго-
няя женщину, задел корзину, и все яйца разбились. Желая возместить
ущерб, он спросил у крестьянки, сколько яиц было в корзине. Она от-
ветила, что числа яиц не знает, но когда она раскладывала их по 2, по
3, по 4, по 5 и по 6, то каждый раз одно яйцо оставалось лишним, а
когда она их разложила по 7, лишних яиц не осталось. Сколько яиц не-
сла крестьянка на базар?
Пусть число яиц равно х. Так как х - 1 делится на 2, на 3, на 4, на 5,
на 6, то оно делится на их наименьшее общее кратное 60. Значит, х имеет
вид 60г/ + 1. Поэтому для ответа на вопрос задачи надо решить в нату-
ральных числах уравнение 60г/ + 1 = 7z. С помощью алгоритма Евклида
находим у0 = —2, г0 = -17, откуда все целочисленные решения уравнения
имеют вид у = -2 + 7t, z = -17 + 60i, где t — любое целое число. Наи-
меньшее положительное решение получаем при t = 1. В этом случае у = 5,
г = 43. Итак, крестьянка несла на базар 301 яйцо. Можно было бы найти
ответ и подбором—достаточно перебрать числа 1, 61, 121, 181, 241 и 301
и выбрать из них делящееся на 7.
3. Цепные дроби
Второй метод решения диофантовых уравнений первой степени по
своей сути не слишком отличается от рассмотренного в предыдущем
пункте, но он связан еще с одним интересным математическим понятием.
Речь идет о непрерывных или цепных дробях. Чтобы определить их,
вновь обратимся к алгоритму Евклида.
72
Из первого равенства системы (1) вытекает, что дробь — можно запи-
b
сать в виде суммы целой части и правильной дроби: — = q0 + —. Но — = —,
b b b b
b г2
и на основании второго равенства той же системы имеем — = q j ч-. Зна-
П Н
чит, — = q о Ч-----. Далее получим — = q 0 ч-------.
Продолжим этот процесс до тех пор, пока не придем к знаменателю qn.
В результате мы представим обыкновенную дробь — в следующем виде:
9г +
Чп
Эйлер назвал дроби такого вида непрерывными. Приблизительно в то же
время в Германии появился другой термин — цепная дробь. Так за этими
дробями и сохранились оба названия. Ввиду громоздкости развернутой
записи цепной дроби применяют компактную запись [q0; qt, q2, ..., </„].
В качестве примера представим дробь — в виде цепной:
40 = 1+ 9_ = 1 + J_ = 1 + _J_ =
31 31 31 0,4
-- о ч-
9 9
1 + —1— = 14--1-= [1; 3, 2, 4].
О I 1 О . 1
Если оборвать дробь [б/0; qt, q2, ..., qn] на знаменателе qk, то останется
р
дробь [</0; qx, q2, ..., qk]. Обращая ее в обыкновенную, получим ——. Это
Qk
выражение называют k-й подходящей дробью для исходной цепной дроби.
Посмотрим, как вычисляются подходящие дроби:
Ро 9 о Pi ,1 9o9i + l
— = —; — = 9 о ;
Qo 1 Qi Qi 9i
Рг 1 92(9o9i + 1) + 9o 9гЛ + -?о
—— = 9о +-----=----------------=--------- и т. д.
Q2 q1 + ^L_ 9г91 + 1 92Qi+Qo
1 9г
73
Вообще имеют место рекуррентные соотношения
Рк + 1 = Qk +1 • Pk + Pk - i и Qk + 1 = qk+iQk + Qk-i-
Докажем, что для любого k = 1, 2, п имеет место формула
Pk-iQk-PkQk 1 = (-1Л (4)
Для этого воспользуемся методом математической индукции. В самом де-
ле, для k = 1 имеем P0Q| _ PiQo - QoQi _ (7o9i + 1) = -1 = (-1)1- Предполо-
жим, что формула (4) верна для номера k, и перейдем в левой части (4)
к номеру k + 1. Используя рекуррентные соотношения, получим
рkQk + i ~ Рк + iQk — рк (qk + iQk + Qk -1) -
- (qk + Л + _ j) = -Pk _ A + PkQk -1 = (- D*+1 •
Таким образом, формула (4) доказана для любого натурального к. Из
нее, в частности, вытекает, что числа Pk и Qk взаимно просты.
Используем отмеченные нами свойства цепных дробей для решения
уравнения (2). Коэффициенты а и Ь взаимно просты. Разложим — в цеп-
b
ную дробь. При этом — = ——.
b Qn
Поскольку обе дроби несократимы, то а = Рп, b = Qn. По свойству (4)
имеем ЬРп _ , - aQn _ х = (-1)". Умножив обе части этого равенства на
(-1)" с, получим (-1)" + laQn _ щ + (-1)" ЬРп „ гс = с, откуда видно, что пара
чисел х0 = (~l)n + 1cQn _ j, у0 = (-1)" сРп _ ] представляет собой решение
уравнения (2). Общее решение (2), как мы знаем, запишется в виде
х = (-l)n + 1cQ„_1 + bt, у = (-1)" сР„_! - at,
где t принимает целые значения. Приведем примеры.
17 1
1) Рассмотрим уравнение 17х+13у=5. Поскольку — = 1-1-----, то
13 3 + -
4
Р л
п = 2, — = -, откуда х0 = -5 • 3 = -15, у0 = 4 • 5 = 20 и общее решение
Qi з
имеет вид х = -15 + 131, у = 20 - 171.
2) Для уравнения 63х - 100у = 90 имеем
— = [1; 1, 1, 2, 2, 1, 3],
63
т. е. п = 7, Р6 = 27, Q6 = 17, поэтому х = 90 • 27 + 1001, у = 90 17 + 631.
Иногда на распространенных в позднее Средневековье математи-
ческих турнирах предлагалось решить (конечно, в натуральных числах)
какое-нибудь уравнение типа (2) при довольно больших значениях коэф-
фициентов. Получить такое решение подбором, не имея общей форму-
лы, — задача весьма утомительная. Так во втором примере даже наи-
меньшее натуральное решение х = 30, у = 18 (оно получается из общего
при 1 = -24) найти подбором довольно затруднительно.
74
Мы познакомились с разложением в цепную дробь обыкновенной
дроби, т. е. рационального числа. Но надо сказать, что в виде цепной дро-
би можно записать любое действительное число. Только конечными цеп-
ными дробями здесь уже не обойтись. Найдем разложение в непрерывную
дробь числа 72. Из равенства 72-1 = —^— =---------т= получаем
42 + 1 2 + (Т2-1)
72 = 1-1--------, т. е. число 72 записывается в виде бесконечной перио-
дической цепной дроби [1; 2, 2, ...].
Оказывается, квадратичные иррациональности (т. е. числа вида
a + b4c, где а, Ъ, с — рациональные числа, а 4с не является рациональ-
ным), и только они, раскладываются в бесконечные периодические цеп-
ные дроби. На этот факт впервые указал Эйлер, строгое его доказательст-
во дал Лагранж.
В качестве примера рассмотрим периодическую цепную дробь
х = [0; 2, 3, 2, 3, ...]. Для нее выполняется равенство х =---, отку-
2 + ———
3 + х
да число х является корнем квадратного уравнения 2х2 + 6х — 3 = 0, т. е.
-3 ± 715 „ „ -3 + 715
х =--------. Так как х > 0, то х = ----.
2 2
Из утверждения Эйлера — Лагранжа вытекает, что иррациональные
числа, не представимые в виде квадратичной иррациональности, изобра-
жаются бесконечными непериодическими цепными дробями. Интересное
разложение нашел первый президент Лондонского королевского обще-
ства лорд У. Броункер (1620—1684):
1
2 +---------
2+ 25
2 + ^-
2+ ...
Не менее замечательные представления в виде непрерывных дробей
имеют числа е и In 2:
4
9
1+ 16-
, , 25
75
Приведенные разложения поражают своей закономерностью и в ка-
кой-то мере объясняют исключительность этих чисел. Конечно, можно
было бы дать их компактную запись. Для этого нужно представить полу-
ченные дроби в виде цепных с единицами в числителе, но тогда потеряет-
ся удивительная красота формул.
Цепные дроби обладают следующим важным свойством:
|Если действительное число а записать в виде непрерывной дроби, то
подходящая дробь —— дает наилучшее приближение числа а среди
Qk
всех дробей, знаменатели которых не превосходят Qk.
Именно в процессе поиска наилучшего приближения значений квад-
ратных корней итальянский математик Пиетро Антонио Каталь-
ди (1552—1626) пришел в 1613 г. к цепным дробям, с чего и началось
их изучение. Правда, они встречались почти на 40 лет раньше в
«Алгебре» другого итальянского математика — Рафаэля Бомбелли
(ок. 1526—1572). Но Катальди выделил цепные дроби в отдельный тип,
выявил некоторые их свойства, в частности показал, что цепная дробь за-
ключена между соседними подходящими дробями.
Современное обозначение непрерывных дробей предложил выдаю-
щийся нидерландский ученый Христиан Гюйгенс (1629—1695).
Читатели в основном знают Гюйгенса как физика — основателя волновой
теории света. Но он был и замечательным математиком, удивительным
изобретателем и конструктором. К тому же он писал неплохие стихи, в
чем у нас еще будет возможность убедиться.
Гюйгенс разработал теорию упругого удара, описал форму Земли,
установил (независимо от Гука) точки таяния льда и кипения воды, об-
наружил кольцо Сатурна и один из его спутников при помощи сконст-
руированного им «воздушного» телескопа (без трубы). Он построил пер-
вые маятниковые часы и применил их к определению долготы на море,
изобрел пружинный регулятор (балансир) карманных часов. Решая
практические задачи, Гюйгенс не удовлетворялся простой прикидкой, а
всегда обращался к строгой математической теории. Работая над маят-
никовыми часами, он с помощью геометрических рассуждений вывел
закон колебания физического маятника. Эту задачу перед ним поставил
М. Мерсенн. В то время Гюйгенсу было только 15 лет. Через три деся-
тилетия он снова вернулся к этой задаче и полностью решил ее.
К цепным дробям Гюйгенс был вынужден обратиться (1680) при по-
строении планетария в Париже. Он хотел получить наилучшие при-
ближения для отношений периодов обращения планет. Эти отношения и
отношения чисел зубцов соответствующих связанных между собой шесте-
рен планетария должны были совпадать. Но числа зубцов шестерен по
техническим причинам не могут быть очень большими. Необходимо было
так их подобрать, чтобы полученные отношения как можно меньше отли-
чались от истинных. Гюйгенс обратился к цепным дробям и с их помо-
щью нашел решение стоящей перед ним задачи. При этом он детально
изучил теорию цепных дробей.
76
Гюйгенсу принадлежит решение ряда важных задач математическо-
го анализа. Хорошо разбираясь в методах зарождавшегося тогда диффе-
ренциального и интегрального исчисления, он тем не менее предпочитал
проводить доказательства геометрическими методами, пользуясь строгим
языком древних греков. Безупречность и ясность рассуждений были его
коньком.
В заключение вернемся к цепным дробям и отметим их преиму-
щество и недостаток по сравнению, например, с десятичными. Удобст-
во заключается в том, что их свойства не связаны ни с какой системой счис-
ления. По этой причине цепные дроби эффективно используются в
теоретических исследованиях. Но широкого практического применения
они не получили, так как для них нет удобных правил выполнения арифме-
тических действий, которые имеются для десятичных дробей.
4. Пифагоровы тройки
Читателям, несомненно, хорошо знакомо уравнение
2.2 2
X+ у - г*.
(5)
Да, конечно, это записана знаменитая теорема Пифагора. Если х и
у — длины катетов прямоугольного треугольника, а г — длина его гипо-
тенузы, то равенство (5) утверждает:
Площадь квадрата, построенного на гипотенузе, равна сумме площа-
дей квадратов, построенных на катетах.
И наверное, читатели не раз слышали о том, что результат этот более
чем за тысячу лет до Пифагора был известен египтянам и вавилонянам.
В практических целях они использовали обратное предложение: если
числа х, у и г связаны соотношением (5), то треугольник с такими сторо-
нами является прямоугольным.
С именем Пифагора теорему связывают потому, что он, по-видимо-
му, впервые доказал ее. Существует даже легенда, что в связи с этим со-
бытием Пифагор принес в жертву богам гекатомбу (сто быков). В коммен-
тариях V в. к «Началам» Евклида об этом сказано скромнее: «Если
послушать тех, кто любит повторять древние легенды, то придется ска-
зать, что эта теорема восходит к Пифагору; рассказывают, что он в честь
этого открытия принес в жертву быка». Однако нидерландский матема-
тик Б. Л. Ван дер Варден, автор замечательной книги «Пробуждающаяся
наука», пишет: «...этот рассказ совершенно неправдоподобен, ибо, как
известно, Пифагор был непримиримым противником убоя и жертвопри-
ношения животных, а в особенности крупного рогатого скота». К тому же
Пифагор верил в переселение душ. Однажды, увидев, как били собаку, он
остановил обидчика: «Перестань ее бить, в этой собаке живет душа моего
друга: я узнал его по голосу». Так что ясно, что легенда о гекатомбе
77
совершенно лишена основания. А теорема независимо от того, кто и когда
ее доказал, была и остается одним из самых гениальных человеческих от-
крытий и одним из наиболее часто используемых геометрических утвер-
ждений.
Причина, по которой фундаментальная геометрическая теорема по-
пала в эту главу, естественна: ведь уравнение (5) — это диофантово урав-
нение второй степени. Сейчас мы займемся поиском его решений. Удобно
записывать их в виде троек чисел (х, у, z). Вообще говоря, уравнению (5)
удовлетворяет бесконечно много решений. Но нас будут интересовать
только натуральные. Другими словами, наша задача состоит в том, чтобы
найти общий вид троек натуральных чисел (х, у, г), удовлетворяю-
щих (5). Такие тройки называются пифагоровыми (так же как и соответ-
ствующие прямоугольные треугольники).
Заметим, что если два числа из такой тройки имеют общий дели-
тель, то на него делится и третье число. Поделив их все на общий дели-
тель, вновь получим пифагорову тройку. Значит, от любой пифагоровой
тройки легко перейти к пифагоровой тройке, числа которой попарно вза-
имно просты. Такую тройку называют примитивной. Очевидно, для ре-
шения поставленной нами задачи достаточно найти общий вид примитив-
ных пифагоровых троек.
Ясно, что в примитивной пифагоровой тройке два числа не могут
быть четными, но в то же время все три числа не могут быть нечетными
одновременно. Остается один вариант: два числа нечетные, а одно четное.
Покажем, что z не может быть четным числом. Предположим противное:
z = 2т, тогда х и у — нечетные числа: х = 2k + 1, у = 21 + 1. В этом слу-
чае сумма х2 + у2 = 4 (fe2 + k + I2 + I) + 2 не делится на 4, в то время
как z2 = 4m2 делится на 4. Итак, четным числом является либо х, ли-
бо у. Пусть х = 2и, у и z — нечетные числа. Обозначим z + у = 2v,
г — у = 2w.Числа v и w взаимно простые. На самом деле, если бы они име-
ли общий делитель d > 1, то он был бы делителем и для z = v + w, и для
у = v — w, что противоречит взаимной простоте у и г. Кроме того, о
и w разной четности: иначе бы у и z были четными. Из равенства
х2 = (z + у) (z - у) следует, что и2 = vu>.
Поскольку v и w взаимно просты, а их произведение является квад-
ратом, то каждый из множителей является квадратом (гл. I, п. 3).
Значит, найдутся такие натуральные числа р и q (будем считать
р > q), что и = р2, w = q2. Очевидно, числа р и q взаимно просты и
имеют разную четность. Теперь имеем z = р2 + q2, у = р2 - q2, откуда
х2 = (р2 + q2)2 - (р2 - q2)2 = ^p2q2.
В результате мы доказали следующее утверждение:
ЕДля любой примитивной пифагоровой тройки (х, у, г) найдутся взаим-
но простые натуральные числа р и q разной четности (р > q), такие, что
х = 2Р<7, у = р2 — q2, z=p2 + q2. (6)
Легко видеть, что справедливо и обратное утверждение: при тех же
условиях, наложенных на р и q, числа х, у, г, полученные по форму-
лам (6), образуют примитивную пифагорову тройку. Итак, способ нахож-
78
дения примитивных решений уравнения (5) найден. Все остальные его
натуральные решения имеют вид:
х = 2kpq, у = k (р2 - q2), z = k (р2 + q2),
где k — произвольное натуральное число.
Кстати сказать, еще вавилоняне знали, что таким способом получа-
ются стороны прямоугольного треугольника.
Заметим, что взаимная простота и разная четность для чисел р и q
нужны для того, чтобы тройка (х, у, г) по формулам (6) получалась при-
митивной. Если же р и q — произвольные натуральные числа (р > q), то
эти формулы тоже задают пифагорову тройку, но уже необязательно при-
митивную. Теперь рассмотрим задачу.
Дано произвольное натуральное число т > 2. Существует ли пифаго-
ров треугольник, одна из сторон которого равна т?
Если потребовать, чтобы заданную длину т имел катет, то для любо-
го т ответ положительный. Докажем это. Пусть сначала т — нечетное
число. Положим р = W + 1, q = ——-. Получаем пифагорову тройку
2 2
т2 -1 9 9 т2 + 1
х = 2qp =----, у = р - q = т, z = р + q =----.
Убедитесь в том, что полученная тройка (х, у, г) примитивная.
В случае четного т, положив р = q = 1, придем к тройке
[ тг 1 т2 л 'i
т,------1, --+ 1 .
у 4 4 )
Приведем примеры. Для т = 7 имеем треугольник с катетами
х = 24, у = 7 и гипотенузой г = 25. В случае т = 3 тройка (4, 3, 5) задает
наименьший пифагоров треугольник (он же получается и при т = 4).
Этот треугольник называют египетским, поскольку считается, что с его
помощью египтяне строили прямые углы. Числу т = 18 отвечает прямо-
угольный треугольник со сторонами х = 18, у = 80, z = 82.
Сложнее выяснить, для каких натуральных т существует пифагоров
треугольник с гипотенузой т. Так как в этом случае т должно быть крат-
но числу г = р2 + q2, где р и q имеют разную четность, то необходимо най-
ти вид чисел z > 2, представимых в виде суммы двух квадратов разной
четности. Обозначим р = 2r, q = 2s + 1, тогда р2 + q2 = 4 (г2 + s2 + s) + 1.
Значит, число z имеет вид 4Z + 1. Однако не всякое число вида 4Z + 1 рас-
кладывается в сумму двух квадратов. Например, число 9 = 4 • 2 + 1 так
разложить невозможно. Но если число 4Z + 1 простое, то оно представимо
в виде суммы двух квадратов, причем единственным способом (об этом го-
ворилось в гл. I п. 7).
Пифагоров треугольник с заданной гипотенузой т существует только
при условии, что в каноническом разложении числа т встречается
простой множитель вида 4Z + 1.
79
Рассмотрим примеры.
1. Пусть т = 17 (здесь 17 = 4 • 4 + 1). Из равенства 17 = 42 + I2 нахо-
дим р = 4, q = 1, х = 2pq = 8, у = р2 - q2 = 15. Тройка (8, 15, 17) задает пи-
фагоров треугольник.
2. У числа т = 39 = 3 13 второй простой множитель 13 = 4 • 3 + 1
имеет необходимое представление 13 = З2 + 22, откуда р = 3, q = 2, а зна-
чит, 2pq = 12, р2 - q2 = 5, р2 + q2 = 13. Умножив полученные числа на 3,
придем к тройке (36, 15, 39).
3. Числа 9 и 49 не могут выражать длину гипотенузы пифагорова
треугольника. Хотя 9 = 4 • 2 + 1 и 49 = 4- 12 + 1, но их простые множи-
тели не представляются в виде 41 + 1.
5. Вокруг теоремы Пифагора
С теоремой Пифагора связано много других разнообразных диофан-
товых уравнений. Найдем, например, пифагоровы треугольники, у кото-
рых один катет длиннее другого на 1. Здесь надо решить в натуральных
числах уравнение
х2 + (х + I)2 = у2. (7)
Пифагоров треугольник со сторонами 3, 4, 5 удовлетворяет этому требо-
ванию. Следовательно, числа х1 = 3, у{ = 5 дают наименьшее натуральное
решение уравнения (7). Остальные его решения получаются из рекур-
рентных соотношений, которые мы приводим без доказательства:
*n + i = Зх„ + 2уп + 1, уп + 1 = 4хп + Зуп + 2.
Из них находим х2 = 20, = 29; хч=119, г/о = 169; хл = 696,
г/4 = 985; х5 = 4059, у5 = 5741 и т. д.
Проверьте сами, что если пара чисел (хп, уп) удовлетворяет уравне-
нию (7), то ему удовлетворяет и пара (хл + 1, рл + 1).
Уравнение (7) можно переписать так: 2х (х + 1) + 1 = у2. Похожий
вид имеет уравнение х (х + 1) = у2. Однако в отличие от (7) оно не имеет
ни одного решения в натуральных числах. В самом деле, числа х и х + 1
взаимно просты, а потому их произведение может быть полным квадра-
том лишь в случае, когда х и х + 1 — полные квадраты, т. е. когда х = и2,
х + 1 = v2. Но это невозможно, так как разность квадратов двух натураль-
ных чисел всегда больше 1.
Рассмотрим теперь аналоги уравнения (5) в трехмерном пространст-
ве. Укажем все прямоугольные параллелепипеды, у которых целочислен-
ны и длины ребер и длина диагонали. Для этого надо найти все натураль-
ные решения (х, у, г, £) диофантова уравнения
х2 + у2 + г2 = t2.
По аналогии с пифагоровыми тройками они выражаются формулами
х = 2kpxq, у = 2kp2q, г = k (q2 - р\ - р22), t = k (q2 + р2х + р22),
где k, рх, р2, q — натуральные числа и q2 > р2 + pl-
80
Доказано также, что существует бесконечно много прямоугольных
параллелепипедов, у которых длины ребер и длины диагоналей всех бо-
ковых граней выражаются целыми числами. Иными словами, система
уравнений
х2 + у2 = и2, х2 + z2 = V2, у2 + z2 = w2
имеет бесконечное множество натуральных решений. Одно из них, на-
пример, такое: х = 44, у = 117, z = 240. Однако неизвестно, существует ли
прямоугольный параллелепипед, у которого целочисленны и все ребра и
диагонали всех боковых граней и диагональ самого параллелепипеда,
т. е. имеет ли хоть одно решение в натуральных числах система уравне-
ний
х2 + у2 = и2, х2 + z2 = V2, у2 + z2 = w2, х2 + у2 + z2 = t2.
Иногда возникающие в геометрии задачи приводят к системам урав-
нений, решения которых выражаются очень большими числами. Допус-
тим, надо найти прямоугольный параллелепипед, у которого сумма пло-
щадей трех граней, имеющих общую вершину, равна площади квадрата с
целочисленной стороной, а объем — объему куба с целочисленным реб-
ром. Эта задача сводится к системе диофантовых уравнений
ху + xz + yz = u2, xyz = v3.
Ее наименьшее натуральное решение имеет вид
х = 1663780814400, у = 252782198228, г = 3474741085973.
На древневавилонских клинописных таблицах встречается задача:
Разделить трапецию прямой, параллельной основаниям, на две равно-
великие части. При каких (натуральных) длинах оснований и делящего
отрезка это возможно?
Обозначим через х, г, у соответст-
венно длины меньшего, большего осно-
вания и делящего отрезка, hY и h2 —
высоты получаемых при этом трапе-
ций (рис. 8). Из условия задачи имеем
ht У+ 2 у+ z 1 ( hi )
откуда следует, что — =---и------= — -----1-1 . Исключив из этой си-
Л2 х+у x + z 2 [h2 )
стемы отношение ——, приходим к диофантову уравнению х2 + г2 = 2у2.
h2
81
Естественно, вавилоняне записывали эту формулу словесно. Как они к
ней пришли и как находили решение, нам неизвестно. Мы же можем по-
ступить следующим образом. Преобразуем уравнение к виду (5)
(z + х)2 + (z - х)2 = (2г/)2.
Воспользуемся формулами натуральных решений уравнения Пифагора:
z + х = 2kpq,
z- х = k(p2 — q2),
2у = k(p2 + q2)',
X = |((p+g)2 -2p2),
2 = ^p+q)2-2q2),
y = ^p2+q2)-
Здесь p, q — натуральные числа разной четности, р > q. При этом отно-
hY у + z р
шение высот трапеции равно — =-------= —. Взяв в качестве k четное
й2 х+у q
число, получим все натуральные решения исходной задачи.
Например, при k = 2, p = q+ X имеем
х = 2q2 - 1, у = (q + l)2 + q2, 2 = 2 (q + l)2 - 1.
Выпишем найденные тройки (х, у, г) для q = 1, 2, 3, 4:
(1, 5, 7), (7, 13, 17), (17, 25, 31), (31, 41, 49).
Именно эти тройки и фигурируют в вавилонских табличках.
Интересно, что вавилоняне рассматривали еще деление трапеции и
на четное число попарно равновеликих полос (площади различных пар
различны). При этом в качестве решений возникали уже не тройки, а
разной длины отрезки той же самой последовательности
1, 5, 7, 13, 17, 25, 31, 41, 49, 61, 71, ... .
Последовательность эта впервые встречается в клинописных текстах, в
связи с чем и называется вавилонской. Это одна из первых числовых по-
следовательностей, отличных от натурального ряда, которые рассматри-
вали древние математики. По возрасту с ней может поспорить только гео-
метрическая прогрессия.
6. Уравнение Пелля
Начало истории уравнения, о котором ниже пойдет речь, теряется в
глубине веков. Возможно, оно возникло в связи с задачей о приближен-
ном извлечении квадратного корня.
Пусть натуральное число а не является квадратом. Легко видеть, что
4а не выражается отношением натуральных чисел, т. е. не существует
82
( A2
X I X I
такой обыкновенной дроби — что — = а. Другими словами, если нату-
У \У)
ральное число а не является точным квадратом, то уравнение х2 - ау2 = О
не имеет решения в натуральных числах. Попытаемся в этом случае вы-
разить отношением натуральных чисел приближенно. Если Уа — то
У
х2 - ау2 ~ 0. Самое близкое к нулю натуральное число — это единица.
Поэтому дело сводится к решению в натуральных числах диофантова
уравнения
х2 - ay2 = 1,
(8)
которое носит (как мы увидим ниже, неоправданно) название уравнения
Пелля.
При а = 2 решения этого уравнения, как мы видели в конце первой
главы, нашел Теон Смирнский в процессе построения последователь-
ных приближений числа V2. Для некоторых значений а решения
уравнения (8) были получены индийским математиком Брахмагуп-
той (VII в.), а для любых а — тоже индийским математиком Бхаска-
рой (XII в.). Однако их метод решения долго оставался неизвестен евро-
пейской науке. В XVII в. этим уравнением заинтересовался Ферма. Най-
дя его натуральные решения, он предложил всем математикам Франции,
Англии и Голландии попробовать свои силы на конкретных примерах
для а = 61, 109, 149. Английские математики приняли вызов Ферма, но
из-за небрежности переводчика они неправильно поняли постановку за-
дачи и в качестве ответа дали решение в рациональных числах.
р
А в этом случае оно элементарно: положим х = 1-1—у, тогда
2 2
1 + —у + ^-—у2-ау2 = 1, откуда
У q2
2pq р2 +aq 2
У =-------, х =---------.
aq2 - рг aq2 - р2
Когда же Ферма разъяснил постановку задачи, то Дж. Валлис сооб-
щил, что задача решена Броункером. Позже Валлис поместил это реше-
ние в своей «Алгебре».
В следующем столетии «Алгебру» Валлиса прочел Эйлер. У него
осталось впечатление, что решение принадлежит Пеллю, другому анг-
лийскому математику, которого Валлис упоминал в своих работах. Эйлер
и назвал уравнение (8) уравнением Пелля. С легкой руки Эйлера за ним
так и закрепилось это название, хотя Пелль к этому уравнению никакого
отношения не имел. По справедливости его следовало бы назвать уравне-
нием Бхаскары или уравнением Ферма.
По-видимому, умел находить решения этого уравнения при любом а
и великий Архимед. Недаром он послал в Александрию Эратосфену сле-
дующий стихотворный вызов:
83
// колько у Солнца быков, найди для меня, чужестранец
(Ты их, подумав, считай, мудрости если не чужд),
Как на полях Тринакрийской Сицилии острова тучных
Их в четырех стадах много когда-то паслось.
5 Цветом стада различались: блистало одно млечно-белым,
Темной морской волны стада другого был цвет.
Рыжим третье было, последнее пестрым. И в каждом
Стаде была самцов множеством тяжкая мощь,
Все же храня соразмерность такую: представь, чужестранец,
f О Белых число быков в точности было равно
Темных быков половине и трети и полностью рыжим;
Темных число быков четверти было равно
Пестрых с прибавленной пятой и также полностью рыжим;
Пестрой же шерсти быков так созерцай число:
/5 Части шестой и седьмой от стада быков серебристых
Также и рыжим всем ты их число поравняй.
В тех же стадах коров было столько: число белошерстых
В точности было равно темного стада всего
Части четвертой и третьей, коль сложишь ты обе их вместе,
20 Темных число же коров части четвертой опять
Пестрого стада равнялось, коль пятую долю добавишь
И туда же быков в общее стадо причтешь.
Те же, чья пестрая шерсть, равночисленным множеством были
Рыжего стада частям пятой и с нею шестой.
25 Рыжих коров же считалось количество равным полтрети
Белого стада всего с частию взятой седьмой.
Сколько у Солнца быков, чужестранец, коль точно ты скажешь,
Нам раздельно назвав тучных быков число,
Так же раздельно коров, сколько каждого цвета их было,
50 Не назовет хоть никто в числах невеждой тебя,
Все ж к мудрецам причислен не будешь. Учти же, пожалуй,
Свойства такие еще Солнца быков числа.
Если быков среброшерстых ты с темными вместе смешаешь
Так, чтобы тесно они стали бы в ширь и в длину
35 Мерою равной, тогда на обширных полях Сицилийских
Плотным квадратом они площадь большую займут,
Если же рыжих и пестрых в одно смешаешь ты стадо,
Лесенкой станут они, счет с единицы начав,
Так что фигуру они треугольную нам образуют;
40 Цвета иного быков нам нет нужды добавлять.
Если ты это найдешь, чужестранец, умом пораскинув,
И сможешь точно назвать каждого стада число,
То уходи, возгордившись победой, и будет считаться,
Что в этой мудрости ты все до конца превзошел.
Переведем условия задачи на язык алгебры. Если X, У, Z, Т означа-
ют соответственно числа белых, черных, рыжих и пестрых быков, а х, у,
84
z, t — числа коров того же цвета, то приходим к следующей системе
(в скобках указаны номера строк, приводящих к соответствующим урав-
нениям):
X = [- + -]y + Z (строки 10—11),
y = f- + -lr + Z (строки 12—13),
7, = f- + llx + Z (строки 14—16),
1б 7J
х = ^ + ^(У+у) (строки 17—19),
у = [ — + — |(Т+£) (строки 20—22),
к 4 5 J
i = [ — + — |(Z + z) (строки 23—24),
\ 5 6 )
z = + у ^(Х + х) (строки 25—26),
X + У = □ (строки 33—36),
Z + Т = А (строки 37—39).
Итак, имеем 7 уравнений с 8 неизвестными, причем эти неизвестные
должны удовлетворять двум последним условиям: число X + У — квад-
ратное, a Z + Т — треугольное. После довольно громоздких преобразова-
ний эта система приводится к уравнению Пелля с коэффициентом а =
= 4729494. А окончательный ответ для общего числа быков и вовсе не-
правдоподобен: это число порядка 7766 • ю206541.
Возможно, Архимед сочинил эту задачу в период своего увлечения
большими числами, когда писал сочинение об исчислении числа песчи-
нок во Вселенной. Но тому числу далеко до численности стада быков
Солнца. Чтобы выписать все 8 чисел, составляющих ответ задачи, пона-
добилось бы 660 страниц при условии, что на каждой странице записано
2500 цифр. Архимед, несомненно, знал о том, что посылает своему оппо-
ненту фактически неразрешимую задачу.
Как же отыскиваются решения уравнения Пелля в натуральных чис-
лах? Сначала, как и для любого диофантова уравнения, надо найти наи-
меньшее натуральное решение. Для небольших значений коэффициента а
это можно сделать подбором, но при больших а подбор становится затруд-
нительным, и здесь на выручку приходят цепные дроби. Используется
разложение в цепную дробь числа Уа. Как получить такое разложение,
покажем на примере.
Представим в виде цепной дроби число УЗ. Для этого преобразуем
разность
^3 _1 = (Уз-1)(Уз + 1) = 2 = 1 = 1
Уз +1 Уз +1 Уз+ 1 г + Уз -1 ’
2 2
85
где 0 < -/3 — 1 < 1. Поделив на 2 обе части полученного равенства, найдем
V3-1 1 „
----— =----------. Следовательно,
2 2 +-Уз - 1
1 +---------
2+(л/3-1)
откуда V3 = [1; 1, 2, 1, 2, ...].
Аналогично строится цепная дробь для любого конкретного чис-
ла 4а. Как уже говорилось в п. 3, цепная дробь в этом случае является
периодической.
Теперь мы просто сформулируем окончательный результат, не при-
водя доказательств, которые принадлежат Ж. Лагранжу (1769).
Пусть s — длина периода непрерывной дроби [<?0; qr, q2, ...] = Va.
Л-i
Если s четно, то находят подходящую дробь -------= [q0; q1, ..., 9s_j].
Qs-i
В этом случае наименьшее натуральное решение уравнения (8) имеет вид
x = Ps_1, y = Qs_r. Если же з нечетно, то надо положить x = P2s-i»
Р2 s-1
У = Q23-1. где --= [<7о5 91» •••» 92s -11-
4<2s-l
Пусть теперь (х0, у0) — какое-либо решение уравнения (8), тогда
Хд - ауд = 1 или (х0 + у0 4а) (х0 - у0 4а) = 1, откуда при любом натураль-
ном п имеем (х0 + у0 4а)п (х0 - у0 4а)п = 1. Возведя обе скобки в ге-ю сте-
пень по формуле бинома Ньютона и приведя подобные члены, придем к
равенству (х„ + уп 4а) (х„ — уп 4а) — 1. Из него видно, что при любом п
пара (хл, уп) также является решением (8). Учитывая, что хп + уп 4а =
= (х0 + у0 4а)п л хп - уп 4а = (х0 - у0 4а)п, получаем формулы
х„ = | ((х0 + г/о -JaY + (хо ~ Уо Va)"),
Уп = ~Ц= ((*о + У о у/а)п - (х0 - у0 4а)п).
24а
Как показал Эйлер, если (х0, у0) — наименьшее натуральное реше-
ние уравнения Пелля, то эти формулы дают все его натуральные реше-
ния.
Рассмотрим в качестве примера уравнение х2 — Зу2 = 1. Разложе-
ние 43 в непрерывную дробь нам известно:
43 = [1; 1, 2, 1, 2, ...].
Л 12
Здесь s = 2, и поэтому находим подходящую дробь — = 1 + — = —, от-
Qi 11
куда х0 = 2, у0 = 1 — наименьшее решение уравнения в натуральных чис-
лах. Правда, этот результат был очевиден с самого начала. Остальные ре-
шения вычисляются по формулам
86
x„ = -((2 + V3)re+(2-V3)n),
2
j/n = -i=((2 + V3)n-(2-V3)n).
2V3
К решению уравнения Пелля сводится более общее диофантово урав-
нение
х2 ау2 = с. (9)
Именно если (х*, у*) — какое-нибудь из решений этого уравнения, а
(хп, уп) — произвольное решение соответствующего уравнения Пелля
2 2 ч
х - ay = 1, то числа
х = х*х„ + ау*уп и у = у*хп + х*уп
удовлетворяют уравнению (9). Читатели могут в этом убедиться непосред-
ственно проверкой. Правда, нельзя быть уверенным, что таким образом
будут получены все решения этого уравнения. Часто для этого нужно
знать не одно решение (х*, у*), а некоторый конечный набор и «размно-
жить» их с помощью указанных формул.
Решать уравнения типа (9) умел Ферма. По крайней мере по поводу
уравнения 2х2 + 7967 = у2 он писал (1657): «Я нашел общее правило, что-
бы решать такое уравнение, если оно возможно, или чтобы определить
его невозможность. И это — во всех случаях и для всех чисел».
Все рассуждения проходят лишь для натурального а, не являющего-
ся точным квадратом. В противном случае уравнение (9) может иметь
лишь конечное множество решений. То же самое относится и к уравне-
нию х2 + ау2 = с, где а — любое натуральное число. Предлагаем читате-
лям доказать оба утверждения.
Закончим наше знакомство с уравнением Пелля задачей.
Найти общий вид чисел т, являющихся одновременно и треугольными
— К и квадратными.
2 2(2+1) „
Решим в натуральных числах уравнение у =--------. Подстановкой
2
г = t - — оно приводится к виду t2 - 2у2 = —. Так как t — полуцелое число,
2 4
положим t = . В результате приходим к уравнению Пелля х2 - 8у2 = 1.
Сначала найдем его наименьшее решение (х0, у0). Так как
V8 = 2-/2 = [2; 1, 4, 1, 4, ...], то длина S периода полученной цепной дро-
Ps_1 Р1 13
би равняется 2. Поэтому вычислим ----= — = 2 + — = —, откуда х0 = 3,
Qs-i Qi 11
у0 = 1. Теперь обратимся к формулам общего решения (х„, уп). Нас инте-
ресует только
_ (3 + 2-/2)" -(3-2-/2)" _ (1 + V2)2" -(1-V2)2"
Уп 2V8 4V2
87
Искомое число тп — у2 имеет вид
(1 +V2)4n +(1-V2)4" -2
Этот результат был получен Эйлером. При п = 1, 2, 3, 4 находим т = 1,
36, 1225, 41616.
Обобщением уравнения Пелля на случай третьей степени ах3 + у3 = 1,
где а не является кубом натурального числа, занимался советский матема-
тик Борис Николаевич Делоне (1890—1980). Он установил, что та-
кое уравнение может иметь не более одного (не считая очевидного решения
х = 0, у = 1) целочисленного решения.
7. Великая теорема Ферма
Перейдем теперь к одной из самых знаменитых задач диофантова
анализа, получившей название Великой теоремы Ферма.
Начнем с истории возникновения этой теоремы. На полях «Арифме-
тики» Диофанта против того места, где рассматривается уравнение
х2 + у2 = г2, П. Ферма (ок. 1630) написал: «Наоборот, невозможно разло-
жить ни куб на два куба, ни биквадрат на два биквадрата и вообще ника-
кую степень, большую квадрата, на две степени с тем же показателем.
Я открыл этому поистине чудесное доказательство, но эти поля для него
слишком малы». Так родилась эта замечательная теорема:
При п > 2 уравнение
хп + уп = z" (10)
не имеет натуральных решений.
Предоставляем читателям возможность доказать, что из этого утверж-
дения вытекает отсутствие и рациональных решений уравнения (10) при
п > 2.
Несмотря на внешнюю простоту формулировки теоремы, над ее до-
казательством трудились многие поколения математиков более трех сто-
летий. Весьма вероятно, что и сам Ферма не нашел строгого доказательст-
ва этой теоремы, Иначе бы он предложил ее кому-нибудь из европейских
математиков в качестве задачи. Он имел такое обыкновение, когда знал
решение. Но ни в одном из известных нам писем Ферма не предлагал ни-
кому доказать отсутствие натуральных решений уравнения (10) для лю-
бого показателя п > 2. Хотя частный случай п — 4, правда, в иной форму-
лировке встречался. Речь идет о следующем утверждении:
Площадь пифагорова треугольника не может быть квадратом.
Мы не будем приводить доказательство этого утверждения, но пока-
жем, что из него действительно вытекает отсутствие натуральных реше-
ний уравнения
x4+t/4 = z4. (11)
88
Докажем это методом от противного: предположим, что уравне-
ние (11) имеет натуральное решение (х0, у0, z0). Обозначим уд = q, Zg = р и
подставим в уравнение (11), получив Хд = Zg - уд = р2 — q2. Числа р и q за-
дают пифагоров треугольник с катетами х = 2pq, у = р2 — q2 и гипотенузой
р2 + q2. Площадь этого треугольника равна S = pq (р2 - q2) = Zg • уд • Хд,
т. е. представляет собой квадрат натурального числа, чего не может быть.
Таким образом, уравнение (11) не имеет натуральных решений.
Предложение об отсутствии пифагорова треугольника с площадью,
выраженной квадратным числом, Ферма доказал на полях «Арифмети-
ки» Диофанта. При этом он воспользовался методом бесконечного спус-
ка, изобретением которого очень гордился. В чем же заключается этот
метод? К примеру, надо доказать, что какое-то уравнение не имеет нату-
ральных решений. И пусть из предположения, что у данного уравнения
все же есть решение в натуральных числах, можно вывести, что у него
есть еще меньшее, тоже натуральное решение. Тогда из существования
этого меньшего решения делается вывод о существовании еще меньшего
решения и т. д. Но так как натуральные числа не могут неограниченно
уменьшаться, то сделанное предположение неверно и решения данного
уравнения в натуральных числах не существует.
Применим метод бесконечного спуска к более общему, чем (11),
уравнению
x4 + y4 = z2. (12)
Если мы покажем, что у этого уравнения нет натуральных решений, то
их и подавно нет у уравнения х4 + у4 = (z2)2.
Предположим, что существует натуральное решение (х, у, г) уравне-
ния (12), причем тройка (х, у, г) примитивная. Тогда (х2, у2, z) является
примитивной пифагоровой тройкой. Следовательно, найдутся такие вза-
имно простые числа р и q разной четности, р > q, что х2 = 2pq, у2 = р2 - q2,
z = р2 + q2. Но из равенства q2 + у2 = р2 и взаимной простоты р и q следует,
что (у, у, р) — примитивная пифагорова тройка. Значит, снова найдутся
взаимно простые натуральные числа а и Ь, такие, что q = 2ab, у = а2 - Ь2,
р = а2 + Ь2. В результате имеем х2 = 2pq = 4а6 (а2 + Ь2), т. е. число
4а& (а2 + &2) является квадратом. При этом легко показать, что число
а2 + Ь2 взаимно просто с а и Ъ. Но тогда каждое из чисел а, Ъ, а2 + Ъ2 явля-
ется квадратом: а = а2, b = р2, а2 + Ь2 = у2. При этом а4 + р4 = у2, т. е. трой-
ка (а, р, у) снова является примитивным решением уравнения (12). С по-
мощью цепочки неравенств
у < у2 = а2 + Ъ2 = р < р2 + q2 = z
убеждаемся, что у< z. Применяя метод бесконечного спуска, приходим к
выводу, что уравнение (12) не имеет решений в натуральных числах.
Прежде чем говорить о попытках доказательства Великой теоремы
Ферма, сделаем некоторые общие замечания.
Если уравнение (10) для п > 2 имеет натуральные решения, будем по
аналогии со случаем п = 2 записывать их в виде троек (х, у, z). И здесь,
как и при п = 2, достаточно указать примитивные тройки. Далее, если
уравнение xpk + урк = zpk имеет решение (х0, у0, z0), то тройка (Хд, yg, Zg)
89
является решением уравнения хр + ур = zp. Отсюда следует, что теорему
Ферма достаточно доказать для всех простых нечетных показателей и для
71 — 4, поскольку любой показатель п > 2 имеет либо простой нечетный
множитель, либо множитель 4.
Естественно было начать доказательство теоремы Ферма с наимень-
шего показателя п = 3. Сам Ферма в письме своему другу Пьеру Каркави
писал, что знает, как вывести методом бесконечного спуска отсутствие
натурального решения уравнения х3 + г/3 = z3. Через сто с лишним лет до-
казательство этого случая теоремы нашел Эйлер. Однако его доказатель-
ство в корне отличается от доказательства Ферма, насколько можно су-
дить по его письму к Каркави. Эйлер использовал разложение суммы
кубов х3 + у3 = (х + у) (х + еу) (х + £2у), где через £ обозначено комп-
—1 + i >/~3 .
лексное число--------(о комплексных числах речь пойдет в следующем
2
разделе). Далее он работал с числами вида а + Ыу[3, где а и b — целые
числа, используя для них свойства, аналогичные свойствам натуральных
чисел. Надо заметить, что это было неправомерно, но после построения
строгой теории чисел вида a + biV3 доказательство Эйлера с небольшими
поправками осталось справедливым.
После Эйлера долгое время не было новых успехов в области доказа-
тельства Великой теоремы Ферма. Интерес к этой проблеме пробудился
вновь благодаря результатам, полученным в этом направлении одной из
первых женщин-математиков Нового времени француженкой Софи
Жермен (1776—1831). Изучив математику самостоятельно, она под
мужским именем Леблан вела переписку с ведущими учеными Европы,
которые высоко ценили математические способности господина Леблана
и были приятно удивлены, когда «обман» раскрылся.
Гаусс в связи с этим писал Софи Жермен из Геттингена: «Склон-
ность к абстрактным наукам вообще, а к таинствам чисел в особенно-
сти, — исключительно редкое качество... Но когда особа женского пола,
которой на этом тернистом пути, в соответствии с нашими обычаями и
предрассудками, приходится сталкиваться с неизмеримо большими, чем
мужчинам, трудностями, все же добивается успеха в преодолении этих
препятствий и проникает в самые темные области исследований, — она,
несомненно, должна обладать самым доблестным мужеством, совершенно
необычайными личными качествами и высшей одаренностью».
Наряду с математикой С. Жермен занималась исследованиями и по
теории упругости. За работу в этой области ей была присуждена (1811)
премия Парижской АН. Это была первая премия, которую Парижская
АН выдала женщине. Отметим еще один факт из биографии С. Жермен:
во время оккупации Германии наполеоновской армией она обратилась к
генералу, командующему французскими войсками в Геттингене, с прось-
бой благосклонно отнестись к Гауссу, поскольку такие люди принадле-
жат мировой науке.
Что же сделала Жермен для доказательства теоремы Ферма? В пись-
ме Лежандру (1828) она сообщила, что доказала следующее утвержде-
ние:
90
Если р и 2р + 1 простые, то в тройке (х, у, z), являющейся решением
уравнения хр + ур = zp, хотя бы одно из чисел делится на р.
Другими словами, среди троек чисел, не делящихся на р, решений
нет. Лежандр опубликовал этот результат в своей «Теории чисел», назвав
его теоремой Жермен.
Сам Лежандр и одновременно с ним Дирихле доказали невозмож-
ность решения в натуральных числах уравнения х5 + у5 = z5. Позже
(1839) французский ученый Габриель Ламе (1795—1870) доказал те-
орему Ферма для п = 7, а в 1847 г. он сделал доклад на собрании Париж-
ской академии наук, в котором изложил решение проблемы для любого
показателя п. Присутствовавший на заседании академик Жозеф Л и у-
билль (1809—1882) тотчас же указал на изъян в его рассуждении. Дело
в том, что Ламе неправомерно перенес на комплексные числа, возникаю-
щие при решении уравнения хр = 1, некоторые утверждения, кажущиеся
естественными для натуральных чисел, в частности основную теорему
арифметики.
Чтобы почувствовать, что метод аналогий при переходе к новым
классам не всегда проходит, рассмотрим множество чисел вида a + bJH
при целых а и Ь. Естественно, все целые числа включаются в это множе-
ство, так как любое целое число а можно записать как а + 0-V3. В этом
множестве число 2 (которое среди обычных целых чисел является про-
стым) раскладывается на множители:
2 =(73 + 1)(73-1).
Еще более необычным выглядит равенство
1 = (2 + V3)(2- V3).
А если рассматривать числа вида а + by]-5, где а и b — целые, то здесь
число 6 раскладывается на множители двумя способами:
6 = 2-3=(l + V^5)(l-T=5).
Обсуждение работы Ламе привлекло к себе внимание Коши, который
изучил вопрос о разложении комплексных чисел специального вида на про-
стые множители и изложил его в ряде статей, соперничая с Ламе. Но не ему
было суждено прояснить возникшую ситуацию в новых классах чисел.
Спас положение с проблемой однозначности разложения чисел на простые
множители немецкий математик Эрнст Куммер (1810—1893).
Математические интересы Куммера имели широкий диапазон. Он за-
нимался вопросами геометрии, анализа, теоретической механики. Но
главной его заслугой является создание теории алгебраических чисел. Ее
методы оказали влияние на все последующее развитие алгебры и теории
чисел. Куммер поступил следующим образом: он расширил рассматривае-
мые классы комплексных чисел, дополнив их новыми элементами, кото-
рые назвал идеальными. В получившихся таким образом множествах
основная теорема арифметики уже выполнялась.
Чтобы проиллюстрировать идею Куммера, обратимся к числам вида
а + Ьу/-5. Добавим к этому множеству идеальные элементы А = V2,
91
В =---——, С =----——, которые будут использоваться лишь в связанном
V2 у/2
состоянии: А2 = 2, АВ = 1 + V—5, АС = 1 — V —5, ВС = 3. В результате един-
ственность разложения на множители числа 6 восстановлена: 6 = А2ВС.
Два способа, которые возникали раньше, объясняются различной группи-
ровкой множителей: (А2) (ВС) = 2-3, (АВ) (АС) = (1 + V—5)(1 — V-5).
Надуманность идеальных чисел кажущаяся, их отсутствие в рас-
сматриваемом множестве объясняется ограниченным набором элементов
в нем. Ведь нас не смущает, что среди целых чисел нет рациональных, а
среди рациональных — иррациональных и т. д. Сам Куммер сравнивал
идеальные числа с химическими элементами, которые в природе сущест-
вуют лишь в связанном состоянии. На основе идеальных чисел Куммера в
дальнейшем возникло понятие идеала — одно из важнейших понятий со-
временной алгебры.
С помощью своей теории Куммер доказал теорему Ферма для
всех показателей, не превосходящих 100. Постепенно верхняя граница
отодвигалась под натиском ученых, и за полтора столетия она достигла
числа 125000. Но и при этом находились отчаянные любители, пытавши-
еся найти контрпример, т. е. тройку (х, у, г), удовлетворяющую уравне-
нию (10). Охладить пыл таких энтузиастов должен был результат
Грюнерта (1856):
Если тройка (х, у, г) является решением уравнения хп + уп = гп при не-
котором показателе п, то должны выполняться неравенства х > п,
у > п, г> п.
В самом деле, так как г > х, то z = х + а, где а — натуральное
число. По формуле бинома Ньютона имеем хп + уп = (х + а)п =
— хп + пхп ~ га + ... + ап, и потому выполняются неравенства уп > пхп " ха >
>пхв. Аналогично доказывается, что xn>nyni. Следовательно,
(z/")n > ппхп D > пппп - ("“D2 ; и потому у2п ~ 1 > и2"’1, откуда у > п. Та-
ким же образом доказывается, что х > п. Тогда и подавно z > х > п.
В начале XX в. проблема Ферма привлекла к себе внимание не толь-
ко специалистов, но и любителей математики. Это было связано с тем,
что в 1907 г. немецкий астроном П. Вольфскель, сам всю жизнь безу-
спешно пытавшийся доказать теорему, учредил премию в сумме ста ты-
сяч марок тому, кто найдет ее доказательство. Чтобы получить премию,
нужно было опубликовать доказательство и получить признание его вер-
ности от Геттингенского математического общества не менее чем через
два года. В Геттингенский университет посыпались различные «доказа-
тельства», отличавшиеся крайней безграмотностью. Правда, инфляция,
последовавшая за Первой мировой войной, свела к минимуму эту пре-
мию, а заодно и число желающих доказать теорему.
У Артура Порджеса есть научно-фантастический рассказ, в котором
профессор математики Саймон Флэгг заключил с чертом договор, что от-
даст ему свою душу, если тот за 24 часа докажет теорему Ферма. Черт,
проявив свои дьявольские способности, проштудировал за сутки сначала
92
всю элементарную математику, затем массу областей высшей математи-
ки, но решить задачу не смог. Однако проблема настолько затянула даже
черта, что автор оставляет его углубившимся вместе с ученым в изучение
этой мучительной и заманчивой задачи.
После того как Гильберт решил проблему Баринга, он говорил, что
смог бы решить и проблему Ферма, но не хочет резать курицу, которая
несет золотые яйца. Дело в том, что проценты с капитала, завещанного
Вольфскелем, шли Геттингенскому математическому обществу, которое
выдавало из них премии математикам, получившим результаты в облас-
ти проблемы Ферма. Например, немецкий математик Виферих получил
премию за следующий результат: если р — простое число и 2Р — 2 не де-
лится на р2, то в решении (х, у, z) уравнения хр + ур = zp хотя бы одно из
трех чисел делится на р. Работавший в Геттингене русский математик
Мириманов доказал, что в утверждении Вифериха число 2Р — 2 можно за-
менить числом 3₽ - 3. И он тоже получил премию.
В середине 50-х гг. прошлого столетия японский математик Юта к а
Т а н и я м а высказал некоторую гипотезу в теории алгебраических кри-
вых. В 1986 г. было показано, что из гипотезы Таниямы, если она верна,
вытекает утверждение теоремы Ферма. Над этой гипотезой размышляли
многие ученые, но только один из них, английский математик Эндрю
Уайлс, проявив необыкновенное упорство, сумел доказать ее справед-
ливость. Впервые он услышал о Великой теореме Ферма в десятилетнем
возрасте и загорелся желанием доказать ее. Через 30 лет ему удалось осу-
ществить свою мечту. Судьба была благосклонна к Уайлсу: тема диссер-
тации оказалась связанной с классом кривых, для которых была выска-
зана гипотеза Таниямы. Семь лет он упорно трудился над поставленной
задачей, храня свои исследования в секрете. Ему пришлось подключить
к решению проблемы методы, работающие в самых различных облас-
тях математики. И титанические усилия были вознаграждены. В июне
1993 г. Э. Уайлс на конференции в Кембридже выступил с доказательст-
вом гипотезы Таниямы. При проверке этого доказательства группой экс-
пертов были обнаружены пробелы. Но через полтора года Уайлс вместе со
своим учеником Р. Тейлором сумели эти пробелы ликвидировать.
Конечно, методы доказательства этой теоремы чрезвычайно далеки
от тех, которые мог использовать Ферма. Так что неизвестно, то ли его
посетило гениальное озарение, то ли он просто ошибся. Хоть и редко, но
бывало, что и он анонсировал неверные результаты. Так, в письме Мер-
сенну (1641) он сформулировал два утверждения:
1. Ни одно из простых чисел вида 12fe ± 1 не является делителем ни
одного из чисел вида Зл + 1.
2. Ни одно из простых чисел вида 10/г ± 1 не является делителем ни
одного из чисел вида 5” + 1.
Из этих утверждений верно только одно относительно чисел вида
(12/г — 1). Остальные опровергаются следующими примерами:
(35+1)-61, (5®+1);521, (57 + 1) : 29.
Практическое значение самого утверждения теоремы Ферма весьма
мало. Факт ее доказательства интересен, скорее, с исторической точки
93
зрения как доказательство проблемы, волновавшей математиков много
веков. Ценность этой теоремы заключается в том, что в длительном про-
цессе поиска ее доказательства были разработаны принципиально новые
методы, появились новые понятия, созданы новые области математики.
Это и дало основание назвать теорему Великой. Называют ее и Большой
теоремой Ферма в отличие от Малой, о которой мы говорили в предыду-
щей главе. Кроме того, эта теорема долго оставалась последней из утвер-
ждений Ферма, доказательство которой не поддавалось усилиям матема-
тиков. В связи с этим ее иногда называют Последней теоремой Ферма.
Под таким названием она может встретиться читателям в различной ли-
тературе.
Интересно, что и сейчас, когда теорема уже доказана, находятся лю-
ди (их называют «ферматисты»), одержимые идеей получить элементар-
ное доказательство. Но, как убеждает вся история теоремы, едва ли кому
из них повезет.
8. Обобщения
Многие математики пытались обобщить теорему Ферма на случай
большего числа переменных. Например, Эйлер был уверен, что уравнение
х" + Х2 + ... + х" = гп
при любом показателе имеет натуральные решения. В случае п = 3 это
так: З3 + 43 + 53 = 63, о чем знал еще Диофант. Для п = 4 уверенность
Эйлера была подтверждена в 1911 г.:
304 + 1204 + 2724 + 3154 = 3534.
Вместе с тем Эйлер высказал предположение, что уравнение
х" + х£ + ... + х"_ г = z", п > 2,
не имеет натуральных решений. Ясно, что для п = 3 оно верно — это как
раз случай теоремы Ферма, доказанный Эйлером.
В 1940 г. было даже высказано более общее по сравнению с гипоте-
зой Эйлера утверждение: «При 2 < k < п уравнение х” + xf + ... + xnk =
= z" не имеет натуральных решений».
Но в 1966 г. Леон Лендер и Томас Паркин нашли пример
275 + 845 + НО5 + 1355 = 1445,
опровергающий предположение Эйлера, а вместе с ним и последнее
утверждение в общем виде.
В то же время уравнение х" + х£ + ... + xjj = z” +1 всегда имеет беско-
нечно много натуральных решений.
Для доказательства рассмотрим k произвольных целых чисел сц,
а2, ..., ak. Покажем, что совокупность чисел г = а" + ... + а£, х,-=
— аг (а" + ... + а£), 1=1, ..., k является решением данного уравнения.
В самом деле,
х" + х2 + ... + xnk = (а" + а2 + ... + а£)" (а" + а2 + ... + а£) =
= (а? + ... + a^n + 1 = zn+1.
94
Поиски решения теоремы Ферма и других аналогичных проблем по-
ставили перед математиками вопрос о том, как узнать, имеет ли данное
уравнение решение. Недаром среди 23 знаменитых проблем (см. гл. I,
п. 14) Гильберт сформулировал следующую: «Указать метод, при помощи
которого можно после конечного числа шагов установить, разрешимо ли
произвольное уравнение с целыми коэффициентами во множестве целых
чисел».
Решить проблему долгое время не удавалось. Появилось предполо-
жение, что метода, о котором говорил Гильберт, не существует. Однако
для доказательства этого факта нужно было иметь точное определение то-
го, что такое этот метод и какими средствами его можно получить. В се-
редине 50-х гг. в трудах английского математика Алана Тьюринга
(1912—1954) были выработаны необходимые определения, которые легли
в основу теории алгоритмов. Сразу после этого была доказана неразре-
шимость некоторых алгоритмических проблем. В 50-е гг. группа амери-
канских математиков получила существенные результаты на пути отри-
цательного решения проблемы Гильберта. Окончательное ее решение
удалось найти советскому математику Ю. В. М а т и я с е в и ч у (род. в
1947 г.), который «элементарными» методами, используя свойства чисел
Фибоначчи, доказал (1970) отсутствие алгоритма разрешимости произ-
вольного диофантова уравнения.
Математиков интересовал и такой вопрос: можно ли по виду дио-
фантова уравнения сказать, имеет оно бесконечно много рациональ-
ных решений или нет? В начале прошлого века были известны два
обширных класса уравнений, обладающих бесконечным множеством та-
ких решений. В 1922 г. английский математик Луиз Морделл
(1888—1972) выдвинул гипотезу: остальные типы уравнений могут
иметь лишь конечное число рациональных решений. Доказана она бы-
ла в 1983 г. 29-летним нидерландским математиком Г. Фалтингсом.
Из его результатов вытекало, что уравнение хп + уп = гп может иметь
не более конечного числа примитивных решений. В свое время это
было значительным шагом на пути доказательства Великой теоремы
Ферма.
Завершая арифметический раздел, подведем некоторые итоги и
чуть-чуть заглянем вперед.
При отборе материала для данного раздела мы старались не пропус-
тить задач, ставших классическими, — тех задач, решение которых при-
вело к появлению и развитию понятий, связанных с числами. Наряду с
арифметическими мы рассматривали задачи и проблемы теории чисел.
Здесь надо уточнить, что линия раздела между этими двумя областями
математики весьма условна. Арифметика изучает числа (любые), их свой-
ства, приемы вычислений; теория чисел занимается в основном целыми
числами.
Теория чисел в виде отдельной области математики начала оформ-
ляться, собственно, с работ Ферма, хотя теоретико-числовые задачи,
как мы видели, решались с древнейших времен: ведь основным источни-
ком для исследований Ферма служила диофантова «Арифметика». По су-
ществу, труд этот представляет собой монографию по теории чисел.
95
Вообще у древних греков бытовало другое (по сравнению с современным)
подразделение.
Науку о способах вычислений они называли логистикой. Арифмети-
кой же греки именовали науку о свойствах чисел (не будем забывать, что
числа они изучали только натуральные). Так что арифметика древних
греков в нынешнем понимании была теорией чисел.
Только в эпоху Возрождения элементы теории чисел и практика вы-
числений объединились под общим названием «Арифметика», и почти
сразу от нее стала отпочковываться теория чисел. Конечно, с тех пор тео-
рия чисел неузнаваемо разрослась вглубь и вширь. Достигнуты значи-
тельные успехи в области изучения целых чисел, возникли разные новые
направления. Связаны эти направления, с одной стороны, с привлечени-
ем для решения задач методов других математических дисциплин, на-
пример математического анализа, теории вероятностей. В результате в
ней появились такие области, как аналитическая теория чисел, вероятно-
стная теория чисел. С другой стороны, изменился взгляд и на сам пред-
мет исследования: возникла теория алгебраических чисел, теория транс-
цендентных чисел и т. д.
А чем же занимается современная арифметика? Ее интересуют самые
разнообразные числовые множества, операции в них, аксиоматическая
структура этих множеств. Здесь арифметика очень близко соприкасается с
алгеброй. В настоящем разделе речь шла в основном о целых, рациональ-
ных числах и немного об иррациональных. Рассматривая Великую теорему
Ферма, мы затронули алгебраические расширения множества рациональ-
ных чисел.
С другими расширениями понятия числа мы встретимся в «Алгебре».
А в геометрическом разделе будем говорить об аксиоматике, причем приме-
нительно не только к геометрии, но и к любой математической теории вооб-
ще, в частности к арифметике. Мы узнаем, какую исключительную роль
играет система аксиом арифметики, какой ответственный груз несет она на
себе. Вернемся мы к арифметическим задачам и во второй книге в разделе
«Старинные и занимательные задачи». Там пойдет речь о старинных спосо-
бах решения некоторых элементарных задач. Так что оставляем мы различ-
ные числовые проблемы ненадолго. Новые встречи с ними ожидают нас
уже в следующем разделе.
Упражнения
1. Покажите, что в возрастающей арифметической прогрессии с четным
числом членов сумма второй половины больше суммы первой поло-
вины на число, кратное квадрату половины числа членов (результат
Гипсикла).
2. Обобщите результат Гипсикла на случай, когда складываются квадраты
членов арифметической прогрессии с четным числом членов.
96
3. Пусть сумма (n + 1) подряд идущих членов арифметической прогрес-
сии равна сумме п членов, следующих за ними. Покажите, что первая
О
сумма начинается с числа, кратного п.
4. Замените в предыдущей задаче члены арифметической прогрессии их
квадратами и найдите, с какого числа начинается первая сумма.
5. Докажите, что не существует (2п + 1) последовательных натуральных
чисел, таких, что сумма кубов первых п + 1 из них равнялась бы сумме
кубов последних п чисел.
6. Используя определение совершенного числа, представьте единицу в
виде суммы различных единичных дробей, знаменателями которых яв-
ляются все делители данного числа.
7. Разделим последовательность натуральных чисел на группы, число
членов которых растет как натуральный ряд чисел:
1; 2,3; 4,5,6; 7,8,9,10; 11,12,13,14,15;....
(п2 + 1)п
Покажите, что сумма S„ чисел п-и группы равна -------------, а
Si + 83 + ... + S2m_1 = т4.
8. Найдите сумму
I3 + З3 + 53 + ... + (2n - I)3.
9. Покажите, что числа Мерсенна, и только они, записываются в двоич-
ной системе счисления с помощью одних только единиц.
10. Докажите, что числа вида 4m- 1 не представимы в виде суммы двух
квадратов.
11. Почему все числа Ферма Fm при т> 1 оканчиваются цифрой 1?
12. Решите уравнение
60х + 16 = 1 Зу
(Бхаскара привел его минимальное натуральное решение: х = 11,
У = 52).
13. Покажите, что произведение длин сторон пифагорова треугольника
делится на 60.
14. Найдите все пифагоровы треугольники, площади которых равны их пе-
риметру.
15. Докажите, что любая пифагорова тройка, члены которой составляют
арифметическую прогрессию, подобна египетской (3, 4, 5).
16. Пусть А, В, С — точки на координатных осях пространственной прямо-
угольной системы координат с началом в точке О. Докажите стерео-
метрический аналог теоремы Пифагора:
q2 । q2 i q2 _____ q2
&OAB + &OAC + &OBC — & ABC’
где S — площадь соответствующего треугольника.
4 —Н. Я. Виленкин, 10-11 кл.
97
17. Треугольник называется героновым, если его площадь и длины всех
сторон выражаются натуральными числами. Покажите, что любой пи-
фагоров треугольник является героновым.
18. Найдите общий вид героновых треугольников, длины сторон кото-
рых — последовательные натуральные числа (результат Герона).
19. Если два пифагоровых треугольника с равными катетами приложить
друг к другу этими катетами, получим геронов треугольник. Покажите,
что не всякий геронов треугольник можно так получить.
20. В какой степени простое число р < п встретится в каноническом разло-
жении числа п\ на простые множители?
ЧАСТЬ
ВТОРАЯ
АЛГЕБРА
Если спросить выпускника средней школы, чему его учили на уро-
ках алгебры, то в ответ почти наверняка можно услышать: «Решать урав-
нения». Той же точки зрения на содержание алгебры придерживаются и
современные ученые. Французские математики Александр Гротен-
дик (род. в 1928) и Жан Дьедонне (род. в 1906) в статье «Элементы
алгебраической топологии» пишут: «Можно утверждать, что решение по-
линомиальных уравнений послужило исторически источником алгебры и
что со времени вавилонян, индусов и Диофанта и до наших дней оно оста-
ется одной из ее основных целей».
Разница в мнениях школьников и ученых состоит, пожалуй, лишь в
том, что те добавили не совсем понятное слово «полиномиальных». Оно
означает попросту «многочленных». Такие уравнения, как
sin3 х + 1g2 х = 1 или 10 *2 - 4 • 10х + 5 = 0,
к алгебре отношения не имеют. А вот уравнение у/ х + у = х 2 + 4, хоть и со-
держит квадратный корень, является алгебраическим, так как его можно
переписать в виде х + у - (х2 + 4)2 = 0, а выражение х + у - (х2 + 4)2 —
многочлен от х и у. Правда, в школе решают и не алгебраические уравне-
ния, но они относятся скорее к математическому анализу.
Итак, цели алгебры оставались неизменными на протяжении тыся-
челетий — решались уравнения: сначала линейные, потом квадратные,
затем кубические, а там и уравнения еще больших степеней. Но форма, в
которой излагались алгебраические результаты, менялась до неузнавае-
мости.
1. Истоки алгебры
Древние египтяне излагали свои алгебраические познания в число-
вой форме. В дошедших до нас папирусах решаются задачи практическо-
го содержания: вычисляются площади земельных участков, объемы сосу-
дов, количество зерна и т. д. Все задачи с конкретными числовыми
данными. Но в некоторых из них уже проскальзывает теоретический ин-
терес. Вот, например, задача из папируса Кахуна (ок. XVIII—XVI в.
до н. э.). Мы приводим ее в современных обозначениях.
100
о
« Найти два числа х и у, для которых х2 + у2 = 100 и х : у = 1: —
4
В папирусе она решена методом «ложного положения». Именно: ес-
з / л 2
ли положить х = 1, то у = — и х2+у2= — . Но по условию задачи
4 \ 4 )
х2 + у2 = 102, следовательно, в качестве х надо брать не 1, а 10: —= 8.
4
Тогда у = 6.
Числа в условиях задач подбирались так, чтобы получались «хоро-
шие» ответы (желательно натуральные или рациональные). Других чисел
древние не знали. Как же они избегали «плохих» ответов? Чтобы выяс-
нить это, вернемся к рассмотренному выше примеру.
Щ Найдем решение системы в общем виде
х2 + у2 = а,
х :у = т : п.
Так как у = — х и х 2------= а, то х = I-----.
т т2 \ т2 + п2
Таким образом, решение в рациональных числах возможно лишь в
случае, когда дробь ----- представляет собой квадрат рационального
т2 + п2
числа. Для этого достаточно, чтобы а было квадратом натурального чис-
ла, а т и п. были пропорциональны длинам катетов пифагорова (египет-
ского) треугольника. Именно так египтяне и поступали, приходя к этим
условиям, скорее всего, путем проб и ошибок.
Довольно значительные успехи в развитии алгебры были достигнуты
в Древнем Вавилоне. Там решались уравнения первой, второй и даже от-
дельные уравнения третьей степени. Но эти достижения еще нельзя на-
звать наукой, поскольку общей
теории не было. Правда, способы
решения конкретных уравнений
дают основание считать, что вави-
лоняне владели и общими прави-
лами нахождения корней уравне-
ний первой и второй степени. Все
задачи и их решения излагались
в словесной форме. В одной из
клинописных табличек встреча-
ется такая задача: «Я вычел из
площади сторону моего квадрата,
это 870». Нетрудно догадаться,
что речь идет о квадратном урав-
нении х2 - х = 870. Решение его
в табличке рекомендуется искать
следующим образом:
101
«Ты берешь 1, число. Делишь пополам 1, это —. Умножаешь i на —,
2 2 2
это —. Ты складываешь (это) с 870, и это есть 3^81, что является квадра-
4 4
59 1 59
том для —. Ты складываешь —, которую ты умножал, с —, получаешь
2 2 2
30, это сторона квадрата». (Все числа в табличке записаны в 60-ричной
системе счисления, мы приводим их в десятичной записи.)
Запишем указанные действия в привычных нам обозначениях:
f I ]2 + 870 = 3481 = f 59 V ,
l2j 4 I2 )
1 59
откуда х = —I---- = 30. Читатели, конечно, узнали формулу вычисления
2 2
корня приведенного квадратного уравнения. Это уравнение имеет еще
1 59
один корень, отрицательный: х =-----= -29. Но, во-первых, с отрица-
2 2
тельными числами древние не имели дела, во-вторых (как мы бы сейчас
сказали), этот корень не удовлетворяет условию задачи.
Совсем другой вид приняла алгебра в Древней Греции. Как уже гово-
рилось в арифметическом разделе, со времени кризиса, вызванного от-
крытием несоизмеримых отрезков, у древних греков вся математика при-
обрела геометрическую форму. Любые утверждения и доказательства
имели право на существование только в случае, если они давались на гео-
метрическом языке.
Например, соотношение, которое мы
записываем в виде формулы (а + ft)2 =
= а2 + 2ab + ft2, в «Началах» Евклида форму-
лируется так: «Если отрезок АВ разделен
точкой С на два отрезка, то квадрат, постро-
енный на АВ, равен двум квадратам на от-
резках АС и СВ вместе с удвоенным пря-
моугольником на АС и СВ». После этого
дается довольно длинное доказательство это-
го факта на геометрическом языке (рис. 9).
Древнегреческие математики работали
не с числами, а с отрезками. Поэтому найти
неизвестное для них означало построить ис-
комый отрезок. Посмотрим, как они решали
задачу, приводящую к квадратному урав-
нению.
Построить прямоугольник, периметр которого равен данному отрезку
2р, а площадь — данному квадрату ft2.
Эта задача сводится к системе уравнений
х+у = р,
ху = ft2
102
или к равносильному ей квадратному урав-
нению
рх - х2 = Ь2.
Левую его часть можно преобразовать следу-
2
ющим образом: рх - х2 =
Р
2
= рх (при ЭТОМ
Р
2
Для нас равенство очевидно. Но ученые то-
го времени еще не имели буквенной сим-
волики, к тому же единственно верным
они считали геометрическое доказательст-
во. На рисунке 10 показано, как древние
греки устанавливали это равенство: сумма
площадей двух заштрихованных прямо-
of Р
угольников равна 21 — х
квадрат со стороной х присутствует в этих
прямоугольниках дважды). Следовательно,
площадь заштрихованного гномона (Г-об-
разной фигуры) равна рх - х2. С другой
стороны, эта площадь равна разности пло-
щадей двух квадратов: одного — со сто-
р
роной —, другого — со стороной
2
Равенство доказано!
Теперь исходное уравнение принимает вид
Рис. 10
2
Р
2
Р
2
Отсюда ясно, как построить отрезок х (рис. 11). Надо построить пря-
Р
моугольный треугольник с катетом b и гипотенузой —; второй его катет
2
Р Р
имеет длину----х, а поэтому х — разность двух отрезков с длинами — и
2 2
р
— ~х. Геометрический подход к математике отражал, по-видимому,
определенные черты духовной жизни древних греков. Греки создали не-
превзойденные скульптуры, удивительные по своему совершенству хра-
мы и другие архитектурные сооружения, пропорции которых строго
математически выверены. Это стремление к красоте, гармоничности, со-
размерности, вероятно, способствовало геометризации математики.
Геометрический путь, несомненно, был гениальной находкой антич-
ных математиков. Но, к сожалению, он сдерживал развитие алгебры.
Ведь геометрически можно выразить лишь первые степени (длины), квад-
раты (площади) и кубы (объемы), но не высшие степени неизвестных. Да
103
и неизвестные в такой ситуации должны быть положительными числами.
При выполнении действий использовался принцип однородности: не раз-
решалось, например, складывать числа а и Ьс. На самом деле число а
означало отрезок (точнее, его длину), Ьс — прямоугольник (его площадь)
со сторонами Ь и с. Но нельзя же складывать отрезок с прямоугольником!
Наконец, алгебраические преобразования приходилось заменять геомет-
рическими построениями, часто очень громоздкими. Чтобы построить не-
известное, нужно было быть подлинным виртуозом — это шло на пользу
геометрии, но не алгебре. Алгебраические методы, ростки которых воз-
никли в более ранних цивилизациях, в Древней Греции не получили раз-
вития.
Выделение алгебры в самостоятельную ветвь математики произошло
в арабских странах, куда после распада Римской империи переместился
центр научной деятельности. К концу VIII в. в результате захватниче-
ских войн арабы покорили почти все страны Средиземноморья, а на вос-
токе их владения простирались до самой Индии, заняв даже часть ее тер-
ритории. Многие арабские халифы для укрепления своего могущества и
славы поощряли развитие наук. В Багдаде, новой столице халифата,
основанной в конце VIII в., создаются хорошие условия для работы уче-
ных. Здесь открыто много библиотек, построен Дом мудрости, при нем
оборудована прекрасная обсерватория. Сюда съезжаются ученые из раз-
ных стран. Арабские математики на первых порах усердно изучают тру-
ды древнегреческих авторов и достижения индийских ученых.
В Доме мудрости работал выдающийся узбекский ученый первой по-
ловины IX в. ал-Хорезми. О самом ученом мы знаем лишь то, что ска-
зано в его полном имени Мухаммед ибн Муса ал-Хорезми ал-Маджуси,
что означает Мухаммед сын Мусы из Хорезма из рода магов (жрецов). Но
сохранилось несколько его сочинений по арифметике, алгебре, астроно-
мии, географии и календарным расчетам. В арифметическом трактате он
изложил «индийское исчисление», открыв тем самым для арабов деся-
тичную систему счисления. Но наиболее значительным является его
трактат по алгебре. Здесь ал-Хорезми, по-видимому, впервые разработал
правила преобразования уравнений. Уравнения у него, конечно, были с
числовыми коэффициентами и выражались в словесной форме. Но на
этих конкретных примерах он показывает способы решения основных ти-
пов линейных и квадратных уравнений. Квадратные уравнения различа-
лись по типу вне зависимости от знака дискриминанта, как сейчас. Дело
было тоже в знаках, но совсем в другом смысле. Арабы еще не рассматри-
вали отрицательных чисел, и поэтому у них, например, уравнения
ах2 + Ъх = с vl ах2 + с = Ьх относились к разным типам. В греческих тра-
дициях ал-Хорезми строго геометрически обосновывает свои способы.
Любое другое уравнение должно было быть преобразовано к одному из
рассмотренных видов с помощью двух операций: 1) восполнение — пере-
несение отрицательных членов уравнения в другую часть; 2) противопо-
ставление — приведение подобных членов. Сам трактат так и называл-
ся — «Краткая книга о восполнении и противопоставлении». В XII в.
труд ал-Хорезми был переведен на латинский язык и долгое время оста-
вался в Европе основным руководством по алгебре. Арабское название
104
операции восполнения «ал-джебр» и дало название области математики,
связанной с искусством решения уравнений.
Вслед за ал-Хорезми решению уравнений посвящают свои труды
многие арабские ученые. В XI в. известный поэт, астроном и математик
Омар Хайям описал геометрическое решение уравнений третьей сте-
пени. Занимался кубическими уравнениями и его современник арабский
энциклопедист ал-Бируни. В XV в. в знаменитой Самаркандской об-
серватории, основанной внуком Тимура Улугбеком, работал замечатель-
ный математик и астроном ал-Каши. Он изучал уравнения четвертой
степени. Корни уравнений третьей и четвертой степеней все они строили
при помощи пересечения парабол, гипербол, окружностей. Таким спосо-
бом решали задачи и греческие геометры. Но арабов, чья математика тя-
готела к вычислениям, интересовало и численное значение корней. Мно-
гие ученые пытались найти правило вычисления корней кубического
уравнения, но потерпели неудачу. Вот что по этому поводу писал Омар
Хайям: «Доказательство этих видов в том случае, когда предмет задачи
есть абсолютное число, невозможно ни для нас, ни для кого из тех, кто
владеет этим искусством. Может быть, кто-нибудь из тех, кто придет по-
сле нас, узнает это».
2. Алгебра обретает язык
Сейчас мы настолько свыклись с записью, например, линейного
ах + b = 0 или квадратного ах2 + Ьх + с = 0 уравнения, что не задумыва-
емся, как много символов надо было ввести, чтобы получить ее. Это и
буква для обозначения неизвестного, и буквы для коэффициентов, и зна-
ки действий, и знак равенства. Возникла буквенная символика сравни-
тельно недавно, но она сразу позволила исследовать уравнения, записать
общие формулы для корней, вывести различные соотношения, помогаю-
щие упростить или преобразовать нужным образом алгебраические выра-
жения.
Зачатки буквенной символики появились еще в Древней Греции. На-
пример, Евклид обозначал отрезок двумя буквами, а Архимед в некото-
рых случаях — одной (такие обозначения сохранились и до наших дней).
Но операции над буквами не производились — древнегреческие матема-
тики, мыслящие геометрическими образами, не могли на это решиться.
Первым, кто порвал с вековыми традициями и сделал шаги к алгебраиче-
ской символике, был Диофант. Следует иметь в виду, что Диофант жил в
египетском городе Александрии, где переплетались различные культу-
ры — греческая, вавилонская, арабская, иудейская и многие другие, ку-
да приезжали индийские купцы. Поэтому он не был так скован запрета-
ми светил древнегреческой науки.
Диофант обозначал неизвестное в уравнении буквой g (по последней
букве слова «арифмос» — число; от него произошло название «арифмети-
ка»), квадрат неизвестного — знаком Av (по первым двум заглавным бук-
вам слова «дюнамис» — степень, сила); куб неизвестного — знаком К4
(от «кубос» — куб); равенство — сочетанием io (по первым двум буквам
105
слова «изос» — равный); свободный член — буквой М (от «монас» —
единица); вычитание — знаком Л. Слагаемые он записывал одно за дру-
гим: сначала все положительные, затем отрицательные после знака Л;
числовые коэффициенты шли после неизвестного и его степеней. Напри-
мер, многочлен х3 - 2х2 + 10х - 3 в записи Диофанта выглядел бы так:
К',а.фЛ\£$Мч
(здесь а = 1, [3 = 2, у= 3, т = 10), а уравнение х3 = 2 — х следующим обра-
зом:
X'vai’oAipA<;a.
Конечно, современному читателю эти обозначения непривычны, но Дио-
фант и его последователи отлично понимали, что здесь написано.
Александрийские ученые, подвергшиеся в IV в. н. э. религиозным
гонениям со стороны фанатичных христиан, рассеялись по всему миру.
По-видимому, некоторые из них добрались до Индии: недаром у индий-
ских математиков встречаются обозначения, похожие на диофантовы.
Здесь зерна математической мысли упали на благодатную почву, и уже в
работах Брахмагупты и Бхаскары вводятся особые знаки для разных не-
известных. Это первые слоги слов, обозначавших разные цвета. Появля-
ются у них знаки и для обозначения всех арифметических операций,
квадратного корня и степеней до 9-й включительно. Например, уравне-
ние Зх2 +10х-8 = х2+1 Брахмагупта записал бы так:
йа ва 3 йа 10 ру 8
йа ва 1 йа 0 ру 1
Здесь «йа» означает неизвестное, «ва» — его квадрат, «ру» — свободный
член, точка над числом означает его вычитание. Поскольку обозначения
были первыми слогами соответствующих слов, то алгебра у индийцев из-
лагалась в простой для запоминания стихотворной форме.
В арабских странах обозначения Диофанта и индийцев не были вос-
приняты. Здесь применяли довольно пространные словесные формули-
ровки алгебраических соотношений. Европейские ученые, перенявшие
алгебру у арабов, тоже долгое время пользовались словесной записью.
Арабское название неизвестного «шай» — вещь было переведено на ла-
тынь словом res с тем же значением. По-итальянски оно звучит cose, в
Германии его стали произносить как coss. Этим словом в XV в. стали име-
новать алгебру, а алгебраистов — коссистами.
Для обозначения степеней неизвестного пользовались словами censo
(квадрат), cubo (куб), censo de censo (квадрат квадрата). Для обозначения
названий следующих степеней применялся либо принцип сложения пока-
зателей, либо принцип их умножения. Второй путь менее удобен, так как
уже пятую степень нельзя выразить через квадраты и кубы. Поэтому та-
кие степени назывались surdus — глухие или relato — отношения. Заме-
тим, что в начале XV в. ал-Каши применял принцип сложения показате-
лей как более естественный.
Постепенно в словесную ткань алгебраических сочинений начинают
проникать сокращенные обозначения неизвестных и их степеней, а потом и
106
буквы. Они встречаются уже у немецкого математика Жордана Немо-
рария (ум. в 1236 г.), работавшего в Парижском университете (языковых
трудностей у него не возникало, так как все лекции читались на латыни).
Но знаков действий у Неморария еще не было. Они появляются в тру-
дах французского математика Никола Шюке (ок. 1445 — ок. 1500) и
итальянского ученого Луки Пачоли (ок. 1454 — ок. 1514).
Пачоли был монахом, членом ордена Святого Франциска. В то время
многие молодые люди, желавшие заниматься наукой, принимали мона-
шеский постриг. Пачоли преподавал математику в крупнейших итальян-
ских городах и был большим другом великого художника и ученого Лео-
нардо да Винчи. В изданной им в 1494 г. «Сумме знаний» — первой
печатной книге по алгебре — неизвестное обозначается со (от cosa), его
квадрат — се (censo), куб — си (cubo), четвертая степень — се се, пя-
тая — p°r° (primo relate—первое отношение) и т. д., свободный член — п°
(питего — число). Пачоли использовал обозначения и для операций сло-
жения — р (plus) и вычитания — т (minus).
Знаки р и th применял и Шюке, но степени неизвестного он обозна-
чал иначе — просто приписывал их показатели к коэффициентам. На-
пример, современные символы 5, 5х, 5х2 у него имели бы вид 5°, 51, 52, а
равенство 8х3 7х-1 = 56х2 он записывал так: «83, умноженное на 71'т,
дает 562». Таким образом, Шюке использовал уже отрицательные и нуле-
вые показатели. Следует отметить, что сокращения р и т встречались за-
долго до Пачоли и Шюке в купеческих конторских книгах. Там они слу-
жили для обозначения прибыли и убытка. Знаки же «+» и «-» впервые
появились у немецкого математика, уроженца чешского города Хеба,
Яна Видмана (род. в 1460 г.) в книге «Быстрый и красивый счет для
всего купечества» (1489).
Было бы заблуждением думать, что буквенные обозначения, раз про-
никнув в алгебру, начали неуклонно совершенствоваться. Нет, их разви-
тие шло волнообразно: обозначения то улучшались, то забывались вовсе.
Наряду с ними долго существовала словесная запись. В трудах математи-
ков разных стран рождались различные обозначения одних и тех же ве-
личин и операций. К примеру, Бомбелли — итальянский ученый, кото-
рый первым рассмотрел цепные дроби, записывал различные степени
неизвестного через 1, 2, 3, .... Голландский ученый Симон Стевин
(1548—1620), введший в употребление десятичные дроби, изменил обо-
значения Бомбелли на @, (2), (§), ....
Интересна история современного обозначения корня, а также самого
названия «корень». С древних времен в уравнениях, как правило, фигури-
ровали как неизвестное, так и его степени, т. е. неизвестное являлось осно-
вой возникающих соотношений. Индийцы называли его «мула» — корень
(дерева), основание, начало; арабы — «джизр» — корень, основание квад-
рата, а европейцы, сохранив смысл, перевели его на латынь. Так появилось
название radix (по-латыни «корень»), отсюда —радикал. Сначала обозна-
чение корня сократили до Rx, затем до строчной буквы г. В дальнейшем
буква г трансформировалась в знак J. Декарт объединил его с горизонталь-
ной чертой, которую ставили над подкоренным выражением, в результате
107
появился современный знак у/ . Относительно квадратных корней допол-
нительных указаний не делали, кубические же корни Виет обозначал 4С, а
Стевин — V®- Жирар ввел современную запись , ....
Важный вклад в совершенствование алгебраической символики внес
французский математик Франсуа Виет (1540—1603). Виет, как и
Ферма, был по образованию юристом и служил при дворе короля Генри-
ха III. Но по настоянию герцогов Гизов, возглавлявших католическую ре-
акцию, он был отстранен от должности. Де Гизы подозревали Виета в
симпатиях протестантам, которых во Франции называли гугенотами (он
был хорошо знаком с их идейным вдохновителем Генрихом Наварр-
ским — будущим королем Генрихом IV). В дальнейшем Виет вернулся ко
двору и помог Генриху IV в расшифровке важной переписки между его
противниками внутри страны и испанцами.
Укреплению математического авторитета Виета способствовало сле-
дующее событие. В ноябре 1594 г. нидерландский посланник, находясь
на приеме у Генриха IV, сказал, что во Франции, по-видимому, нет выда-
ющихся математиков, поскольку ученый его страны ван Роумен
(1561—1615), бросивший научный вызов лучшим математикам своего
времени, не назвал ни одного француза. «У меня есть математик, — отве-
тил король, — и весьма выдающийся. Позовите Виета». Получив из рук
посланника письмо ван Роумена, Виет тут же написал одно из решений
содержащегося в нем уравнения 45-й степени! Уравнение имело вид
х45 - 45х43 + 945х41 - ... - З795х3 + 45х = J7 - |В * * * * * * 15~3л^ .
V 4 V 8
В правой части ученый сразу же узнал длину стороны правильного
15-угольника, вписанного в единичную окружность. Эта сторона опирает-
ся на дугу в 24°. А по коэффициентам левой части уравнения установил,
что х — хорда — части этой дуги. На другой день Виет указал еще 22 по-
45
ложительных корня этого уравнения. Имелось еще 22 отрицательных ре-
шения, но они тогда не рассматривались.
В свою очередь Виет предложил Роумену задачу Аполлония о по-
строении окружности, касающейся трех данных окружностей. Тот смог
ее решить лишь с использованием конических сечений. Виет же в работе,
где он себя назвал Apollonius Gallus (галльский, т. е. французский Апол-
лоний), решил ее с помощью циркуля и линейки. (О задаче Аполлония
будет рассказано подробно в следующем разделе.) После этого Роумен
стал ревностным почитателем таланта Виета.
Ф. Виет первым начал обозначать буквами не только неизвестные,
но и коэффициенты уравнений. В работе «Введение в аналитическое ис-
кусство» (1591) он обозначил неизвестные прописными гласными буква-
ми латинского алфавита, а коэффициенты — согласными. Показателей
степеней он не писал, заменял их словами. Например, уравнение
А3 + ЗВ А = D у Виета выглядело следующим образом:
A cubus + В planum in А 3 aequatur D solido.
108
В этой записи слово aequatur означает «равно» (от него же слова «эква-
тор», «эквивалентность» и др.), а слова planum (плоский) и solido (телес-
ный) вставлены потому, что большой приверженец древнегреческой уче-
ности Виет хотел, чтобы все члены уравнения имели одну и ту же
размерность, — иначе в его глазах равенство не имело смысла. Пользуясь
своими обозначениями, он получил важные соотношения между коэффи-
циентами и корнями алгебраических уравнений, которые сейчас называ-
ются формулами Виета.
Дальнейший вклад в формирование алгебраических обозначений
внесли английские математики Роберт Рекорд (1510—1558), кото-
рый ввел знак «=» для обозначения равенства (он писал, что ничто не мо-
жет быть более равно, чем параллельные отрезки одинаковой длины),
Томас Гарриот (1560—1621), впервые применивший знаки
«<» — «меньше» и «>» — «больше» и обозначивший неизвестные и коэф-
фициенты уже строчными буквами латинского алфавита, Вильям
Оу тред (1574—1660), придумавший знак «х» умножения чисел. Обо-
значение операции умножения точкой ввел Г. Лейбниц, у него же впер-
вые появился знак деления в виде двоеточия.
Для того чтобы алгебраические обозначения приняли современный
вид, не хватало только удачного обозначения для степени. Оно появилось
в 1637 г. в «Геометрии» Р. Декарта. В этой книге Декарт ввел обозначе-
ния, которыми мы пользуемся и поныне: для неизвестных — последние
буквы алфавита х, у, г, ..., а для коэффициентов — первые а, Ъ, с, ... .
Любопытно отметить, что, несмотря на неоспоримые преимущества де-
картовых обозначений, некоторые математики еще долгое время исполь-
зовали устаревшие к тому времени обозначения Виета.
Удачные обозначения вообще играют важную роль в математике. По
этому поводу Лейбниц писал: «Следует заботиться о том, чтобы обозна-
чения были удобны для открытий. Это большей частью бывает, когда
обозначения коротко выражают и как бы отображают интимнейшую сущ-
ность вещей. Тогда поразительным образом сокращается работа мыс-
ли...» Успехи алгебры за прошедшие три с половиной века убедительно
показывают, что обозначения Декарта были удачны.
3. Седьмая операция
Если начать вести счет, как в Средние века, с нумерации, то седьмая
операция над числами после четырех арифметических действий и возве-
дения в степень — это извлечение корня. От остальных шести она отли-
чается одной неприятной особенностью — не всегда выполняется. Точнее
говоря, извлечение квадратных и кубических корней всегда имело на-
глядный смысл: найти сторону квадрата по его площади или сторону ку-
ба по его объему. Но ответ не всегда выражался натуральным или рацио-
нальным числом. Приходилось разрабатывать специальную технику
работы с корнями.
При этом возникли две проблемы — научиться преобразовывать вы-
ражения, содержащие корни, и научиться с достаточной точностью
109
вычислять приближенное значение корня. В решении первой задачи зна-
чительных успехов достиг древнегреческий философ и математик Т е э-
тет (ок. 410—368 до н. э.). Сведения о нем сохранились в диалогах
Платона (428—348 до н. э.) — великого древнегреческого философа
(большинство его произведений написано в форме диалога). Теэтет жил в
Афинах, был членом академии Платона. Вслед за Архитом Тарент-
с к и м (ок. 428—365 до н. э.) и Ф е о д о р о м из К и р е н ы (V в. до н. э.),
доказавшими иррациональность квадратных корней из чисел 3, 5, 6, ...,
17, Теэтет доказал это утверждение относительно корней из любых нату-
ральных чисел, не являющихся целыми квадратами. Но он не остановил-
ся на этом, а стал изучать различные выражения, которые можно соста-
вить из натуральных чисел с помощью арифметических операций и
извлечения квадратного корня. Разумеется, исследования были облечены
в геометрическую форму. Если перевести результаты Теэтета на совре-
менный язык, то окажется, что он рассматривал выражения вида а ± у[Ъ,
± у/Ъ, у/а + уГЬ .
Более сложные преобразования ему не понадобились. Дело в том, что
он искал способы построения правильных многогранников, вписанных в
сферу (о них речь пойдет в геометрическом разделе). А для этого нужно
было выразить ребро многогранника через радиус описанной около него
сферы и найти соотношения между некоторыми другими связанными с
многогранниками отрезками. При этом возникали только указанные ир-
рациональные выражения. По той же причине он не рассматривал и ку-
бических иррациональностей, хотя, по свидетельству Платона, знал о
них.
Теэтет вывел некоторые формулы, связывающие изученные им ирра-
циональности. В частности, он использовал утверждение, которое в со-
временных обозначениях имеет вид
I---у= I а + -J аI 2 - b | а - Ja2 - Ъ
yla±y[b = , --------± , ---------.
V 2 V 2
С его помощью он умел упрощать иррациональные выражения. Так, по
этим формулам имеем л/2 + у/~3 = -(-/б ± V2).
2
Преобразованиями выражений, содержащих корни, занимались и
последующие математики. Безусловно, такие преобразования чрезвычай-
но полезны. Запись иррациональных выражений с помощью корней ис-
пользуется во многих теоретических исследованиях. Но при решении
практических задач нужны числовые (рациональные) результаты, поэто-
му приходится обращаться к приближенным вычислениям корней. Эти-
ми вопросами занимались еще древние вавилоняне. Они нашли простой
метод приближенного вычисления квадратных корней, известный нам из
«Метрики» древнегреческого ученого Герона (I в. н. э.).
Заключается он в следующем. Любое натуральное число представи-
мо в виде произведения двух множителей а Ь. Например, 14 = 7 • 2,
13 = 13 • 1. Возьмем в качестве первого приближения среднее арифмети-
ческое множителей а и Ь:
110
_ a + b
1- 2
Вычислим отношение у, = — =-----.
xt a + b
Число ---- называется средним гармоническим чисел а и Ь. (Про-
а + Ъ
верьте, что обратная ему величина равна среднему арифметическому чи-
сел, обратных а и Ъ.)
Покажем, что у} й Jab < х1 или
2 ab ~ /—г а + Ь
-----С V ао <-----
а + Ь 2
(1)
Среднее геометрическое двух положительных чисел заключено между
их средним гармоническим и средним арифметическим.
В самом деле, из неравенства (а — Ъ)2 > 0 следует (а -Г Ь)2 > 4аЬ, от-
куда
4а2Ь2
(а + Ъ)2
С ab,
—г ' а + Ь
ab <---- и
2
что и требовалось доказать. Таким образом, х1 — приближение корня с
избытком, а — с недостатком.
Теперь найдем среднее арифметическое и среднее гармоническое чи-
сел хх и ур
хх+У1 Х1у1 2х±у±
х2= ------, У 2 = --- = ------•
2 х2 хг + уг
Из неравенств (1) получаем
Следовательно, уг С у2 С Jab < х2 < хт. Продолжая этот процесс, получим
две последовательности. Первая последовательность хп, состоящая из
приближений Jab с избытком, убывает, а вторая уп из приближений Jab
с недостатком возрастает. Другими словами, с увеличением номера точ-
ность приближения квадратного корня повышается.
Конечно, вавилоняне так не рассуждали. Они находили, в лучшем
случае, значения х2 и у2 и убеждались на многочисленных примерах, что
полученные числа достаточно хорошо приближают искомый корень.
Применим описанный алгоритм к вычислению V14 = V7 -2:
%! = 4,5, = 3,(1); х2 = 3,80(5), у2 ~ 3,678832;
х3~ 3,742194, у3 ~ 3,741121; х4 ~ 3,741657, у4 ~ 3,741657.
Таким образом, с точностью до 0,000001 число 3,741657 можно при-
нять за приближенное значение корня V14.
Античные ученые не могли опуститься до практических вычисле-
ний, поэтому они не интересовались приближениями корней. Методы
приближенных вычислений были развиты арабами. Они позаимствовали
у индийских математиков прием извлечения квадратного и кубического
111
корней, основанный на формуле возведения двучлена во вторую и третью
степени. Возможно, этот способ извлечения корней имеет более древнее
китайское происхождение. Интересовались они и корнями более высоких
степеней. В работе «Ключ арифметики» (1427) ал-Каши приводит способ
приближенного вычисления корня любой степени. В наших обозначени-
ях он может быть записан формулой
Пу1ап + Ь ~ а +-------.
(а + 1)п-ап
А теперь вернемся к решению уравнений.
4. Математический турнир
В феврале 1535 г. жители итальянского города Болоньи оказались
свидетелями необычайного зрелища. К зданию Болонского университета
направлялись торжественные процессии с герольдами и знаменами. Сту-
денты и профессора, ученые-монахи и пышно одетые дворяне стремились
поскорее занять места в аудитории — ведь в университете должен был со-
стояться турнир! Состязаться собрались математики.
В то время ученые часто соревновались в решении трудных задач. От
исхода этих состязаний зависела их научная репутация и даже право за-
нимать кафедру. Каждый университет старался заполучить к себе побе-
дителей таких турниров.
Болонцы надеялись на быструю победу своего «бойца» — Антонио
Марио Фиоре. Правда, сам Фиоре не слишком славился своими матема-
тическими открытиями. Но он был одним из ближайших учеников изве-
стного алгебраиста Сципиона дель Ферро (1465—1526), который
перед смертью открыл ему великую тайну — правило решения кубиче-
ского уравнения. С тех пор Фиоре побеждал очень легко — он давал сво-
им противникам задачи, сводящиеся к кубическим уравнениям. И сопер-
ники сдавались без боя — ведь даже в знаменитой книге Луки Пачоли
«Сумма знаний», содержащей все сведения о тогдашней алгебре, говори-
лось четко и определенно: общего правила для решения кубических урав-
нений нет.
Уравнениями третьей степени занимался сам Архимед, изучали их и
другие ученые, но никому не удалось отыскать общего метода. Ходили,
впрочем, темные слухи, что испанский математик Паоло Вальмес решил
даже уравнение четвертой степени, но, когда он рассказал об этом печально
известному инквизитору Томасу Торквемаде, тот счел, что это противоре-
чит воле Бога, и приказал сжечь Вальмеса на костре. Неизвестно, насколь-
ко справедливы были эти слухи, но то, что в конце XV — начале XVI в. на-
чался упадок испанской науки, вызванный преследованиями и казнями
еретиков, это несомненно. Из страны изгонялись ученые, заподозренные
либо в склонности к мусульманству или иудейству, либо в том, что их
взгляды расходились с мнением инквизиторов. Центр развития науки пере-
местился в Италию. Но еще через столетие и там начался разгул рели-
гиозных преследований — на костре был сожжен философ Джордано
112
Бруно (1548—1600), подвергнут угрозам пытки и домашнему аресту ве-
ликий математик и механик Г а л и л е о Галилей (1564—1642). Их обви-
нили в приверженности учению Николая Коперника (1473—1543).
Но это случилось намного позже турнира в Болонье.
На этот раз «жертвой» Фиоре должен был стать Никколо Тар-
талья (ок. 1500—1557) — главный консультант по математическим
расчетам венецианского арсенала. Фиоре был тем более уверен в победе,
что Тарталья не был признан официальной наукой. Все свои знания, на-
чиная с азбуки, он приобрел, занимаясь самообразованием. У его матери
хватило средств лишь для оплаты нескольких первых уроков грамоты, на
которых Никколо ознакомился с полутора десятком букв, остальные он
разгадал сам. Да и выступать на диспуте Тарталье было трудно — он заи-
кался с тех пор, как в детстве был ранен в гортань при взятии француза-
ми его родного города Брешии. Отец Никколо погиб, заслонив сына сво-
им телом. Настоящая фамилия ученого была Фонтане, а Тарталья — его
прозвище, означающее по-итальянски «заика» (в итальянских комедиях
масок одним из действующих лиц всегда являлся заика Тарталья; вспом-
ните знаменитую пьесу-сказку Карло Гоцци «Принцесса Турандот»).
Тарталья занимался многими вопросами математики, в частности
комбинаторикой (знал формулы для числа сочетаний), геодезией, форти-
фикацией, баллистикой. Ему было известно, что снаряд, выпущенный из
артиллерийского орудия с заданной скоростью, пролетит наибольшее рас-
стояние, если его выпустить под углом 45° к горизонту. Это открытие он
под большим секретом сообщил герцогу Урбинскому, чтобы тот использо-
вал его для эффективного ведения огня при ожидавшемся нападении ту-
рецкого флота на Венецию.
Тарталья хорошо понимал, какой удар его репутации нанесет пора-
жение на турнире. Он знал, что его коллеги не испытывают к нему боль-
шой любви: характер у него был тяжеловатый. Один из современников
Тартальи написал о нем даже так: «Этот человек по натуре своей был так
склонен говорить только дурное, что даже хуля кого-нибудь, считал, что
дает о нем лестный отзыв». Оставался единственный выход из этого отча-
янного положения — самому найти формулу для решения кубического
уравнения. Ведь все задачи, полученные им через нотариуса от Фиоре,
были связаны с решением таких уравнений.
После длительных размышлений, мучительных неудачных попыток
и бессонных ночей он получил желанную формулу для решения уравне-
ний вида х3 + ах = Ъ, где а и Ъ — положительные числа (именно к ним и
сводились задачи Фиоре). Поэтому 12 февраля 1535 г. стало черным днем
болонской математики — Тарталья решил за два часа все задачи, предло-
женные ему соперником, а Фиоре не сумел решить ни одной из при-
думанных Тартальей задач. (Вообще в математике хорошо устроенная го-
лова лучше, чем хорошо меблированная, — способность к решению
трудных проблем важнее обширности знаний.) Через день после турнира
Тарталья нашел способ решения уравнения вида х3 = ах + Ь. Напомним,
что тогда использовались лишь положительные числа и это уравнение
считалось отличным от предыдущего. Правда, и привычной нам записи
уравнений тогда еще не было: их записывали в словесной форме.
113
Ученые до сих пор обсуждают, каким именно путем пришел дель
Ферро к правилу решения кубического уравнения. Мы опишем один из
возможных подходов к этой задаче. Есть предположение, что дель Ферро
хотел найти такие числа х и у, при которых выполняется равенство
3^а + Ур = х + у[у. Легко видеть, что тогда У а - У[3 = х - y/у. Если обе час-
ти любого из этих равенств возвести в куб и приравнять рациональные
части, то придем к уравнению
х3 + Зух = а, (2)
кубическому относительно х. Чтобы найти его решение, сложим исход-
ные равенства, а затем перемножим их. В результате получим
2х = Уа + УР +У<х-Ур ,
' г/ = х2+зУр^г.
Подставив выражение для у в (2), придем к уравнению
х3 +3(х2 + Ур -а2 )х =а, которое легко преобразуется к виду
(2х)3 + ЗУР-а2 -(2х) = 2а. (4)
Его решение выражается первым равенством системы (3). Этот корень и
нашел дель Ферро. Для уравнения вида
х3 + рх +<7=0,
сравнивая его коэффициенты с коэффициентами уравнения (4), найдем
2
формуле
2
<7
2
. Поэтому один из его корней вычисляется по
з
4.3
2
3
Ч
2
Р
3
Ч
2
Р
3
(5)
К сожалению, эта формула часто приводит к неудобным для вычис-
лений выражениям. Например, в случае уравнения х3 + 15х - 16 = 0 она
дает действительное решение х = У8 +V189 -УУ189-8. Но достаточно
внимательно взглянуть на заданное уравнение, чтобы угадать один его
корень х = 1. Других действительных корней оно не имеет, так как
х3 + 15х - 16 = (х - 1) (х2 + х + 16) и дискриминант второго множителя
отрицателен. Значит, формула дает именно этот корень, в чем можно убе-
.------------------------------ ( у[2Л ± 1V
диться, установив равенство V189 ±8 = ------
I 2 J
Совсем плохо обстоят дела в случае, когда уравнение имеет три дей-
ствительных корня. Так, корнями уравнения х3 — 7х + 6 = 0 являются
числа 1, —3 и 2, а по формуле (5) получается
х = з/-3 + J- + 3/-3- •
V V 27 V V 27
Для вычисления х нужно извлекать квадратный корень из отрицательно-
100 -
го числа —, а такая операция в области действительных чисел невы-
полнима.
114
В дальнейшем этот случай для кубического уравнения получил на-
звание неприводимого.
В странном положении оказался Тарталья: он знал значения всех
трех корней, но ни один не мог вычислить по своей формуле. Он долго
пытался разобраться во всех возникших трудностях и отложил из-за это-
го издание книги о своих открытиях. Такую книгу написал другой уче-
ный— Джироламо Кардано (1501—1576), и формулу (5) называют
не формулой дель Ферро или Тартальи, а формулой Кардано. Так бывает
довольно часто — ведь и Америка названа не в честь открывшего для ев-
ропейцев этот материк Христофора Колумба, а в честь Америго Веспуч-
чи, который первым дал описание новой земли.
В отличие от Тартальи Кардано происходил из обеспеченной семьи.
Его отец был юристом, но сын не пошел по стопам отца и окончил меди-
цинский факультет университета в Падуе. В начале своей карьеры он за-
нимался в основном медициной, проявив незаурядные диагностические
способности. Затем он увлекся другими науками, во многих из которых
достиг значительных успехов. Популярными были его книги по филосо-
фии и этике; помимо математики, он сделал открытия в области физики
и техники. Упомянем лишь о подвеске, состоящей из двух валов, предло-
женной им для экипажа короля Испании Карла V. Эту систему подвески,
позволяющую карете занимать горизонтальное положение, теперь назы-
вают карданом. Правда, еще раньше Леонардо да Винчи в «Атлантиче-
ском кодексе» предложил для судового компаса использовать такую под-
веску, и есть предположение, что Кардано с работой Леонардо был
знаком. О жизни Кардано можно было бы написать авантюрный роман,
не уступающий по своей занимательности лучшим образцам этого жанра.
Там были и убийства, и тюремное заключение, и даже согласно легенде
добровольная смерть от голода в 75 лет, вызванная желанием подтвер-
дить истинность составленного им гороскопа.
Кардано был вспыльчивым человеком, увлекался азартными игра-
ми. Но даже этот порок он использовал во благо науки: в 1526 г. он вы-
пустил «Книгу об игре в кости»,
где рассмотрел некоторые вопро-
сы комбинаторики и теории веро-
ятностей. Кардано долго вына-
шивал план написать книгу о
новейших достижениях алгебры
под названием «Великое искусст-
во». Он хорошо понимал, что луч-
шим украшением задуманной им
книги было бы описание способа
решения кубического уравнения.
Узнав, что Тарталья владеет этим
искусством, Кардано обратился к
нему с просьбой раскрыть секрет.
Сначала Тарталья категорически
отказался сделать это, но после
ряда настойчивых просьб и клятв
115
сохранить все сведения в тайне он поделился своим достижением, офор-
мив его в виде стихотворения.
Время шло, а Тарталья все не публиковал сделанного им открытия.
И тогда Кардано включает его в свою книгу. Каково же было возмущение
Тартальи! Правда, решение было приведено со ссылкой на него и дель
Ферро. Но это не меняло сути дела: тайна раскрыта, клятва нарушена,
а главное, его планы издания собственной книги сорвались. Тарталья
обрушивает на автора «Великого искусства» град упреков. В защиту
Кардано выступил его талантливый ученик Людовико Феррари
(1522—1565), который вызвал Тарталью на публичный диспут. Красноре-
чие молодого человека и его незаурядные математические способности
позволили ему выйти победителем в этом поединке. Поражение Тартальи
сильно подорвало его авторитет в научном мире, а за ним и материальное
положение.
Справедливости ради следует отметить, что в «Великом искусстве»
многие результаты принадлежали самому Кардано. Он рассмотрел общее
кубическое уравнение и ввел подстановку, приводящую его к виду, ре-
шенному Тартальей; он первым уравнял в правах положительные и отри-
цательные корни уравнений и обратил внимание на мнимые корни.
В книге содержался еще один новый результат — метод решения уравне-
ния четвертой степени, полученный Феррари.
Поясним его на примере решения уравнения х4 + 8х3 + 11 = 68х,
приведенного в «Алгебре» Бомбелли. Добавив к обеим частям уравнения
16х2 и перенеся свободный член вправо, перепишем уравнение следую-
щим образом:
(х2 + 4х)2 = 16х2 + 68х - 11.
А теперь введем еще одно неизвестное t и добавим к обеим частям уравне-
ния выражение t2 — 2 (х2 + 4х) t. Получим
(х2 + 4х - О2 = (16 - 2t) х2 + (68 - 8£) х - (11 - t2).
Левая часть уравнения является квадратом. Найдем такое значение t,
при котором квадратный трехчлен от х, стоящий в правой части, тоже
является полным квадратом. Как известно, для этого нужно, чтобы диск-
риминант квадратного трехчлена равнялся нулю, т е. чтобы выполнялось
равенство (34 — 4£)2 + (16 — 2t) (11 - t2) = 0. Раскрыв в нем скобки, при-
дем к кубическому уравнению t3 - 147t -I- 666 = 0. Если решать его по
формуле (5), получим отрицательное число -6760 под знаком квадратно-
го корня. Поэтому попытаемся подобрать целый корень этого уравнения.
Нетрудно проверить, что одним из его корней является число 6. (Позже
мы расскажем, как облегчить поиск целых корней.) Вернемся к нашему
уравнению. При t = 6 оно принимает вид
(х2 + 4х - 6)2 = (2х + 5)2.
Значит, х2 + 4х — 6 = ± (2х + 5). Решая оба получившихся квадратных
уравнения, найдем четыре корня данного уравнения:
х1>2 =-l±V12, х3.4 = -3±Л0.
Из этого примера видно, что Феррари сводит решение уравнения 4-й
степени к решению одного кубического и двух квадратных уравнений.
116
5. Гибрид из мира идей
Общие методы решения уравнений 3-й и 4-й степеней стали первыми
математическими результатами нового времени после многовекового за-
стоя. А неприводимый случай для кубического уравнения привлек вни-
мание ученых к квадратным корням из отрицательных чисел.
Конечно, с такими корнями математики сталкивались не впер-
вые — ведь они часто возникают при решении квадратных уравнений.
Правда, от этой неприятной ситуации античные математики были защи-
щены диоризмами — так в Древней Греции называли ограничения, на-
кладываемые на условия задачи.
Например, для уравнения х2 - рх + Ь2 = 0 они полагали, что сторо-
на b квадрата не превосходит половины отрезка р. И при нахождении ре-
шения по известному правилу
под знаком корня получали неотрицательное число.
Таким образом, от квадратных корней из отрицательных чисел мож-
но было «отмахнуться»: если они вдруг появлялись, значит, коэффициен-
ты шагнули через границу дозволенной области и уравнение просто не
имеет корней (действительных). Но для кубических уравнений такие
рассуждения не проходят. В неприводимом случае решение по формуле
Кардано — Тартальи содержит квадратный корень из отрицательного
числа, тем не менее уравнение имеет корни — полный набор, и все дейст-
вительные.
Здесь скрывалась какая-то непостижимая связь между действитель-
ными числами и удивительными корнями из отрицательных чисел. Эту
связь пытался понять Тарталья. Много размышлял над ней и Кардано.
В своем «Великом искусстве» Кардано привел следующую задачу:
। Найти два числа, сумма которых равна 10, а произведение равно 40.
Соответствующая этой задаче система уравнений не имеет действи-
тельных решений. Кардано назвал ее корни софистическими.
Разобрался в проблеме корней кубического уравнения итальянский
математик и инженер Рафаэль Бомбелли, почитатель и последователь
Кардано. Он начал действовать с корнями из отрицательных чисел так,
как оперируют с обычными числами, учитывая, что (-/-I)2 = —1. При та-
ком подходе формула Кардано — Тартальи давала действительный ко-
рень для любого кубического уравнения. В результате работ Бомбелли и
его последователей математики оказались перед загадочным фактом. Хо-
тя квадратные корни из отрицательных чисел не имели никакого смысла
и, по мнению большинства ученых, просто не существовали, применение
их приводило к правильным результатам. Пришлось, скрепя сердце,
допустить такие корни в науку. Но поскольку они не имели никакого
реального истолкования, их стали называть мнимыми числами.
117
Прежде чем познакомиться с операциями над этими числами, вве-
дем некоторые понятия и обозначения. Обозначим через г число особого
вида, обладающее тем свойством, что i2 = —1. Так как мы не хотим отка-
зываться от обычных чисел, нам придется иметь дело с произведения-
ми Ы и с суммами вида а + Ы, где а и b — действительные числа. В такой
сумме есть и действительная часть а, и чисто мнимая часть Ы. Поэтому
числа вида а + Ы называют комплексными (от лат. complexus — связь,
сочетание). Действовать с ними будем как с многочленами от буквы I, не
забывая только, что I2 = — 1.
Например,
(1 - 4i) + (6 + 7г) - (-3 + г) = 10 + 2г = 2 (5 + г);
(3 + 5г) (2 - 7г) = 6 - 21г + Юг - 35г2 = 41 - 11г.
Ясно далее, что
г3 = г2-г = -г, г4 = (г2)2 = (-1)2 = 1,
и потому
г4" + k = (г4)" ik = ik.
Несколько сложнее обстоит дело с делением. Для выполнения
этой операции воспользуемся равенством (а + Ы) (а — Ы) = а2 + Ь2. Число
z = а — Ы называется сопряженным числу г = а + Ы. Из полученного ра-
венства следует, например, что
7-2г (7—2г)(3 —4г) 13-34г п
-----=---------------=--------= 0,52 — 1,36г.
3 + 4г (3 + 4г)(3 — 4г) 25
Заметим, что в неприводимом случае формула (5) содержит сумму ку-
бических корней из комплексно-сопряженных чисел х = ^Ja + Ы + '^Ja - bi.
И хотя в XVI в. не было известно, как с такими выражениями обращаться,
Бомбелли каким-то чудом сообразил, что кубический корень из комплекс-
ного числа вновь является комплексным числом, причем комплексная со-
пряженность сохраняется. Поэтому сумма таких корней есть действитель-
ное число. Например,
>/2 + 11г + V2 - 11г = (2 + г) + (2 - г) = 4.
Прозорливость Бомбелли вызывает еще большее восхищение, если
учесть, что через столетие, когда Лейбниц сообщил Гюйгенсу о равенстве
тот очень удивился и сказал, что в этом кроется нечто для нас непости-
жимое.
Комплексные числа на длительное время превратились во что-то та-
инственное, но полезное для решения математических проблем. Поэтому
математики, хотя и не верили в их реальность, привыкали с ними рабо-
тать. Как говорится, глаза страшатся, а руки делают.
Большая заслуга в изучении комплексных чисел принадлежит Аб-
рахаму де Муавру (1667—1754), родиной которого была Франция.
Но, будучи по религиозным убеждениям гугенотом (протестантом), он был
вынужден перебраться в Англию, когда в 1685 г. Людовик XIV отменил
Нантский эдикт, предоставлявший гугенотам свободу вероисповедания.
118
Муавр искал формулы, позволяющие выразить косинусы и синусы
двойной, тройной и других кратных дуг через косинусы и синусы самой
дуги. Найденные им соотношения имеют в современной записи следую-
щий вид:
cos пх = — ((cos х + i sin х)п + (cos х - i sin x)n),
1 (6)
sin nx = — ((cos x + i sin x)n - (cos x - i sin x)n).
2i
Степени в правых частях раскрываются с помощью бинома Ньютона
(формулу для cos пх знал Ньютон задолго до Муавра). Например, для
п = 3 имеем
cos Зх = — (cos х + i sin х)3 + (cos х - i sin х)3 =
= cos3 х - 3 cos x sin2 x = 4 cos3 x - 3 cos x,
sin 3x = — (cos x + i sin x)3 —— (cos x — i sin x)3 =
2i 2i
= 3 sin x cos2 x - sin3 x = 3 sin x - 4 sin3 x.
Из соотношений (6) для sin пх и cos пх легко получается тождество
(cos х + i sin х)п = cos пх + i sin пх.
Именно его в учебной литературе чаще называют формулой Муавра.
С помощью комплексных чисел удалось разложить на линейные мно-
жители многочлены, которые раньше такому разложению не поддавались:
х2 + 1 = (х + i) (х - I),
х4 + 4 — (х2 + 2х + 2) (х2 — 2х + 2) =
= (х + 1 + i) (х + 1 — i) (х — 1 + 0 (х — 1 — О-
Комплексные числа помогли вычислить многие сложные интегралы.
И если в конце XVII в. Лейбниц писал: «Мнимые числа — это чудо ана-
лиза, гибрид из мира идей, двойственная сущность, находящаяся почти
между бытием и небытием», утверждал, что эти числа являются «пре-
красным и чудесным убежищем божественного духа», то к концу
XVIII в. Лагранж спокойно заявил: «Одним из важнейших шагов, сде-
ланных анализом за последнее время, я считаю то, что его более не за-
трудняют мнимые величины и что вычисления с ними производятся так
же, как и с действительными величинами».
В настоящее время комплексные числа используются в математике
гораздо шире, чем действительные. Действительные числа — это только
часть множества комплексных чисел. Нашли они широкое применение и
в технике. С помощью комплексных чисел исследуется течение воды и
полет самолетов и ракет. Применяются они при вычерчивании географи-
ческих карт. Используются комплексные числа для изучения явлений в
атомах и атомных ядрах и т. д.
Но исторически полные права и реальное содержание комплексные
числа обрели после выхода в свет в 1831 г. работы Гаусса, где он предложил
интерпретировать комплексные числа как точки плоскости. Правда, работа
Гаусса не была первой в этом направлении. В самом конце XVIII в. скром-
ный датский землемер Каспер Вессель (1745—1818) нашел способ
119
изображения комплексных чисел
на плоскости. Свое открытие он
изложил в вышедшей в 1799 г. ра-
боте «Об аналитическом представ-
лении направлений». Но кто мог
обратить внимание на работу ни-
кому не известного автора, да еще
на датском языке? Не было заме-
чено и анонимно опубликованное в
1806 г. в Париже сочинение швей-
царского математика Жана А р-
гана (1768—1822) «Опыт некото-
рого представления мнимых еди-
ниц». Положение дел изменилось
лишь тогда, когда появилось сочи-
нение короля математиков. Хотя
работа Гаусса была опубликована
позднее работ Бесселя и Аргана,
исследование его записных книжек показывает, что Гаусс пришел к геомет-
рической интерпретации комплексных чисел уже в конце XVIII в.
В чем же состоит эта интерпретация? Первый ее шаг очень прост:
каждому комплексному числу а + Ы ставится в соответствие точка
М (а, Ь) на плоскости, имеющая координаты а и Ъ. Наряду с этой точкой
можно рассматривать и вектор ОМ, идущий из начала координат О в точ-
ку М. Но сопоставить числу точку или вектор — это полдела. Надо еще
изобразить арифметические операции над комплексными числами. Что
касается сложения и вычитания чисел а + Ы и с + di, то достаточно сло-
жить или вычесть соответствующие векторы (рис. 12).
Для изображения умножения и деления познакомимся с другой за-
писью комплексных чисел. Обозначим через г длину вектора ОМ, а через
Ф угол, образованный вектором ОМ с положительным направлением оси
Ох (рис. 13). Обычно г (по предложению Аргана) называют модулем чис-
ла г = а + bi, а ф — его аргументом. Заметим, что аргумент ненулевого
комплексного числа имеет бесконечно много значений, отличающихся
120
друг от друга на число, кратное 2л. Для числа z = 0 аргумент не опреде-
лен вовсе. Очевидно, г = | z | = -Ja2 +b2 , а = г cos ф, b = г sin ф, и потому
имеет место равенство
z = а + Ы = г (cos ф + i sin ф).
Запись комплексного числа z в таком виде называют его тригонометри-
ческой формой в отличие от записи z = а + Ы, которую называют алгебра-
ической формой. Например, для z = 1 + i найдем | z | = V2 ,ф = — + 2лт, по-
4
этому , . , . , X
1 + i = V2 cos — + 2 пт + i sin — + 2nm
1 I 4 ) I 4 ))
Часто из всех значений аргумента выбирают наименьшее по абсолютной
величине, называя его главным значением аргумента, и записывают
кратко z х
, , . /77 ( Л , . . Л
1 +1 = V2 cos —I-1 sin — .
I 4 47
Теперь, если имеем два комплексных числа
z = г (cos ф + i sin ф), w = R (cos ф + i sin ф),
то их произведение
zw = rR (cos ф + i sin ф) (cos ф + i sin ф) =
= rR (cos (ф + ф) + i sin (ф + ф)).
Мы видим, что при умножении комплексных чисел их модули перемно-
жаются, а аргументы складываются. Разумеется, при делении модули де-
лятся, а аргументы вычитаются, т. е.
— = — (cos (ф - ф) + i sin (ф - ф)), w Ф О.
w R
Итак, чтобы построить вектор, изображающий произведение zw,
нужно вектор ОМ, отвечающий числу г, растянуть в R раз и повернуть на
угол ф; аналогично поступают при изображении частного.
Возведение комплексных чисел в степень с натуральным показате-
лем выполняется по правилу
(г (cos ф + i sin ф))ге = rn (cos пф + i sin пф),
которое при г = 1 превращается в формулу Муавра. По этому правилу
Z Z х\5 Z _ _ X
(1 + i)5 = I у[2 cos — + i sin — = 4-/2 cos — + i sin —— = -4 - 4i.
I V 4 47/ I 4 4 7
Несколько сложнее выполняется извлечение корня из комплексных
чисел. Ясно, что при этом из модуля извлекается корень соответствую-
щей степени, а аргумент делится на показатель корня. Но надо еще учи-
тывать, что аргумент определен неоднозначно. В связи с этим существуют
п различных значений корня n-й степени из любого комплексного числа,
не равного нулю. Все они задаются формулой
------=-=---V Фо + 2тг/г .. Фо + 2пй'|
J Г (cos ф + ISin ф ) = V г COS----h ISin----- ,
v In n
121
k = 0, 1
n — 1, (p0 — главное значение аргумента <р. Так, например,
- + 2л/г - + 2л/г
4 , • 4
COS----------1- I sin------
3 3
, где k = О,
2,
6
имеет три значения а0 = \
л , . . л
cos----h i sin —
12 12
Зл , . . Зл )
----h I sin ,
4---4 )
, Zi =
22 =
17 л , . . 17 л
-----F I Sin--- .
12 12 ;
Точки z0, zx, z2 являются вершинами правильного треугольника,
вписанного в окружность радиуса *У2 с центром в точке О (рис. 14). Вооб-
ще все корни n-й степени из комплексного числа г лежат в вершинах пра-
вильного n-угольника, вписанного в окружность радиуса n-J\ z\ с центром в
начале координат. Так что достаточно построить один корень, а затем
разделить соответствующую окружность на п равных частей, начиная с
построенного корня.
6. Корни из единицы
Интересная ситуация возникает при извлечении корня в случае, ко-
гда г — действительное число, в частности при z = 1. Пока мы находимся
на прямой (среди действительных чисел), корень п-й степени из 1 имеет
всего либо одно значение 1, либо два ±1 в зависимости от четности п. Но
когда мы выходим в плоскость, этот корень уже принимает п различных
значений, определяемых равенствами
„ 2 л/г , . . 2 л/г , п , л
Ek = cos--1- г sin-, k = 0, 1, ..., п — 1.
п п
Все они лежат в вершинах правильного n-угольника, вписанного в единич-
ную окружность (рис. 15). При любом п одна из вершин многоугольника
122
е0=1, при четном п противоположная вершина е п = — 1. Из формулы
. а
Муавра видно, что еА = (£х) , т. е. е0 £„_] являются степенями корня Ех.
Остановимся еще на некоторых любопытных свойствах этих корней.
Так как при умножении степеней с одинаковым основанием показа-
тели этих степеней складываются, то произведение двух корней степе-
ни п из единицы снова является корнем того же вида: Ек • £z = Ек + (. Надо
только иметь в виду, что если k + I равно п или больше п, то индекс k + I
заменяется остатком от деления его на п. Получается, что операция умно-
жения корней п-й степени из единицы связана с арифметикой остатков, о
которой будет говориться в п. 8 настоящей главы. Только умножение при
этом превращается в сложение.
Введем теперь операцию над корнями n-й степени из единицы, соот-
ветствующую умножению в арифметике остатков:
ел ° е< = ем-
Мы ее обозначили кружком, чтобы не путать с умножением £/; • ez = Ек + (.
Например, при п = 17 получим £13 ° £6 = £10 и е12 ° е7 = £16, так как остаток
от деления произведения 13 • 6 = 78 на 17 равен 10, а произведения
12 • 7 = 84 на 17 равен 16. В возникающей арифметике корней n-й сте-
пени из единицы можно определить и операцию, соответствующую воз-
ведению в степень, — она сводится к многократному применению опера-
ции °. Пусть снова п = 17, имеем (е6)2 = £6 ° £6 = е2, (е5)3 = £5 ° £5 ° £5 = £6-
Корень е0 = 1 играет в такой арифметике роль нуля, а £, — роль единицы:
ведь 1 о Ek = е0 ° Ек = £0 . к = Ео = 1 И £х ° Ek = £х . к = Ек.
Мы не знаем, в какой момент Гауссу пришла в голову мысль о том,
что арифметика корней степени п из единицы имеет прямое отношение к
его школьным занятиям по превращению обыкновенных дробей в деся-
тичные периодические дроби. Он заметил, что если п — простое число, то
среди корней найдется такой, который при возведении в степень по ново-
му правилу дает все без исключения корни из единицы, кроме лишь са-
мого числа 1. Такой корень называется первообразным. Например, при
п = 17 первообразным корнем является £3 (посмотрите на таблицу, приве-
денную на с. 31, в которой выписаны остатки от деления на 17 степеней
тройки). Как мы узнаем вскоре, это был великий момент в жизни Гаусса,
определивший всю его дальнейшую судьбу.
7. Математика или филология?
Необычайная математическая одаренность Гаусса проявилась уже в
раннем детстве. Казалось бы, этим предопределялся его жизненный путь,
тем более что влиятельный покровитель — сам герцог Брауншвейгский
Карл Вильгельм Фердинанд взялся решить все материальные проблемы,
связанные с обучением вундеркинда. Но способности Гаусса были разно-
образны, и его влечение к лингвистическим проблемам было не слабее,
чем к математике. Поэтому он поступил на филологический факультет
Геттингенского университета, продолжая параллельно заниматься ма-
тематикой. Следует отметить, что способности к изучению иностранных
123
языков Гаусс сохранил до преклонных лет — в 60-летнем возрасте он вы-
учил трудный для иностранцев русский язык, чтобы в подлиннике про-
читать работы Лобачевского по неевклидовой геометрии (кроме того, он с
удовольствием читал произведения русских поэтов и прозаиков). Надо
было выбирать, какой же из двух наук посвятить свою жизнь.
Ответ на мучившие гениального юношу сомнения пришел 30 марта
1796 г. Проснувшись утром этого дня, Гаусс вдруг понял, что из свойств
корней из единицы, размышлениям о которых он предавался в последнее
время, вытекает решение геометрической задачи о построении циркулем
и линейкой правильного 17-угольника — задачи, которую математики не
могли решить более двух тысячелетий! О своем открытии он сообщил в
короткой заметке, помещенной 1 июня того же года в «Йенском листке».
Еще древнегреческие геометры умели строить циркулем и линейкой
правильные треугольник и пятиугольник, а тем самым и пятнадцатиуголь-
ник. К тому же они знали, как разделить угол пополам, поэтому могли по-
строить любой правильный n-угольник, для которого п имело вид 2* + 1,
2* • 3, 2* • 5 или 2к 15, где k = 0, 1, ... (например, правильный четырех-
угольник, шестиугольник, десятиугольник и т. д.). Об этих построениях
мы расскажем подробнее в геометрическом разделе. Но ни правильного се-
миугольника, ни правильного девятиугольника древние геометры строить
не умели. Поэтому они были уверены, что, кроме указанных правильных
многоугольников, никакие другие построить циркулем и линейкой нельзя.
Гаусс подошел к задаче о построении циркулем и линейкой с другой
стороны. Он выяснил сначала, при каком условии задача на построение
вообще разрешима с помощью этих двух инструментов. Оказалось, что
это возможно лишь тогда, когда длина искомого отрезка выражается че-
рез единицу с помощью четырех арифметических действий и извлечения
квадратного корня. В этом случае говорят, что искомая величина выра-
жается в квадратных радикалах (доказательство этого утверждения бу-
дет дано в следующем разделе).
Мы уже знаем, что корни n-й степени из 1, т. е. корни уравнения
zn - 1 = 0, изображаются на комплексной плоскости вершинами правиль-
ного n-угольника, вписанного в единичную окружность. Поэтому вопрос
о том, можно ли построить циркулем и линейкой правильный «-уголь-
ник, свелся к чисто алгебраической проблеме: выражаются ли корни п-й
степени из 1 в квадратных радикалах.
Разумеется, уравнение zn - 1 — 0 всегда имеет корень Eq = 1. Но нас ин-
2nk
тересуют как раз другие корни этого уравнения, т. е. числа е к = cos-1-
п
+ tsin^^, где ЮО-1. Поскольку гп - 1 = (z - 1) (z"-1 + ... + г + 1),
п
то интересующие нас числа ек, являются корнями уравнения
2п.-1 + 2п-2+ ,„ + г+1=0. (7)
Очевидно, для построения всех корней достаточно найти корень £Р
Тогда, откладывая последовательно на единичной окружности, начиная с
точки 1, дуги, равные дуге е^, мы получили бы все вершины правиль-
ного вписанного n-угольника. Но если мы найдем какой-то другой корень,
124
например е3, то сможем ли построить все
остальные вершины правильного мно-
гоугольника? Для случая п = 5 ответ
утвердительный; читатели не раз реша-
ли эту задачу, вписывая в окружность
пятиконечную звезду единым росчерком
карандаша (не отрывая его от бумаги и
не проходя дважды по одному отрезку,
рис. 16). Но в случае п = 9 ситуация ме-
няется: аналогичные действия приводят
к правильному треугольнику, но не к
девятиугольнику (рис. 17). Объясняется
это тем, что в первом случае число п про-
стое, а во втором — составное.
Оказывается, при простом п можно
построить все вершины правильного
n-угольника, вписанного в единичную
окружность, зная любую его вершину
Е0-
Итак, при простом числе п доста-
точно выразить в квадратных радика-
лах хотя бы один корень уравнения (7).
Далее если мы можем построить
циркулем и линейкой корни т-й и 1-й
степеней из единицы, где т и I — вза-
имно простые числа, то это можно сде-
лать и для корней степени ml. Доста-
1 1 А В
точно — записать в виде — = 1—
ml ml т I
(существование таких целых чисел А и
В, что А1 + Вт = 1, следует из алгорит-
ма Евклида). Остается выяснить: при
каком простом р корень р-й степени из
1 выражается в квадратных радикалах? Рассмотрим сначала примеры,
решая уравнение z2 + z + 1 = 0, находим £х 2 =
задача сводится к решению уравнения четвертой
Если р = 3, то,
= - — ± - — . При р = 5
2 2
степени z4 + z3 + z2 + z
+ 1=0. С этой целью делим обе его части на z2 и
вводим подстановку z + — = w. В результате приходим к уравнению
Z
w2 + w - 1 = 0, из
которого находим 2 =-----------• Осталось решить два
2
+ V5 1 —x — -V -J
----и z -I— =------. Их корни соответственно рав-
2 z 2
= — (V5 + l±iV10-2V5).
4
уравнения z + — =
z
НЫ £ ! 4 = — (-/б — 1 ± I V10 + 2-/б ), £ 2 з
4
125
Интересна идея подстановки, при-
ведшей уравнение 4-й степени к квад-
ратному. Ведь корнями квадратного
уравнения являются числа и>г = + е4
и w2 = е2 + е3. Каждое из них представ-
ляет собой сумму сопряженных корней
(е4 = £i, £3 = £^). Поскольку комплекс-
но-сопряженные числа имеют одинако-
вые действительные части и противопо-
ложные мнимые, то корни £4 и е4, а
также корни е2 и £3 симметричны отно-
сительно оси Ох (рис. 18).
Та же идея группировки комплекс-
но-сопряженных корней заложена в
подстановках, позволивших Гауссу вы-
разить в квадратных радикалах корни
17-й степени из 1. Но самое главное, как удачно сгруппировать корни
уравнения г16 + zls + ... + z + 1 = О? Размышляя над этим вопросом, Гаусс
открывает неожиданную его связь с первообразными корнями из 1. Оста-
новимся на решении этого уравнения.
Выразим номер каждого корня Ek, 1 < k < 16, в виде степени тройки
(3 — номер первообразного корня). Получим нумерацию этих корней, за-
даваемую таблицей (см. табл, на с. 31).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
ез е9 е10 е13 е5 е15 е11 е1б е14 е8 е7 е4 е12 е2 бб е.
В верхней строке таблицы записаны показатели степени, в которую
возводится число 3, а в нижней — соответствующие корни. Сложим те-
перь отдельно все корни, стоящие под четными номерами верхней стро-
ки, и отдельно — под нечетными. Получим
Ло — е9 + е13 + е15 + е16 + е8 + е4 + е2 + е1»
Л1 = ез + ею + 65 + £ц + е44 + £7 + е12 + е6.
(На рисунке 19 сопряженные корни со-
единены вертикальными хордами.)
При этом выполняются соотношения
"По + Hi = _1 и По ’ П1 = ~4, которые не-
сложно проверить, учитывая, что
£417 = 1. Это значит, что Г|о и щ являют-
ся корнями квадратного уравнения
х2 + х - 4 = 0, и потому (из рисунка
легко видеть, что г]0 > щ) выражаются
формулами Т| 0 =
Но в т]0 и rjj по восемь слагаемых.
126
Аналогичным приемом приходим к подстановке
Т0 = Е13 + £16 + е4 + Е1> Т1 = е9 + Е15 + е8 + е2>
Т2 ~ Е3 + е5 + Е14 + е12> Т3 = Е10 + £11 + Е7 + Е6-
При этом т0 и оказываются корнями квадратного уравнения с более
сложными коэффициентами х2 — ~ х — 1 = 0. Значит,
т0 = 1(717 -1 + 734-2717), т1= 1(717-1- 734-2717).
4 4
Далее, т2 и т3, в свою очередь, корни квадратного уравнения
х2 — тцх -1 = 0, откуда
т2 = -(-V17 - 1 + V34 + 2/17 ), т3 = 1(-Т17 - 1 - 734 + 2717 ).
4 4
Подстановка Pj = е16 + е15 р2 = £13 + £4 приводит к уравнению
х2 - тох + т2 = 0, один из корней которого
р! = - (717 - 1 + 734-2717) + - 717+3717-7170 + 38717" .
8 4
Так как е16 = Ej-1, то задача решена — корень выражается через нату-
ральные числа с помощью арифметических операций и извлечения квад-
ратных корней, а потому правильный 17-угольник строится с помощью
циркуля и линейки!
Приглядимся внимательнее к рассуждениям Гаусса. Сначала он
объединяет все корни уравнения хп - 1 = 0, кроме £0, в две равные груп-
пы т]0 и гц, затем каждую из них вновь делит на две равные части и так
до тех пор, пока не приходит к уравнению, содержащему лишь два кор-
ня. Такую процедуру можно совершить лишь тогда, когда число корней
Си е2, ..., £„~1 равно степени двойки: п — 1 = 2®. Вспомним теперь, что
мы рассматриваем случай простого показателя п. А как мы уже убеди-
лись раньше (см.: «Арифметика», гл. I, п. 8), число п = 2s + 1 может
быть простым лишь при з = 2* (k = 0, 1, 2, ...). Таким образом,
п = 22 +1, т. е. является простым числом Ферма. Позже Гаусс доказал
следующий критерий:
1 Разделить окружность циркулем и линейкой на п равных частей воз-
можно тогда и только тогда, когда
n = 2m-pi • ... -рп
где т = 0, 1, 2, ..., plt ..., рг — различные между собой простые числа
Ферма.
В настоящее время нам известны лишь пять простых чисел Ферма:
3, 5, 17, 257, 65537. И хотя мы не знаем, есть ли еще и другие, тем не ме-
нее всегда можно установить, является произвольное простое число р чис-
лом Ферма или нет. Так, 7, 11, 13, 19, 23 не являются числами Ферма.
Поэтому на такое число равных частей разделить окружность циркулем и
127
линейкой нельзя. Несмотря на разложение 9 = 3-3, где 3 — простое чис-
ло Ферма, разделить окружность на 9 равных частей тоже нельзя — ведь
по теореме Гаусса в разложении должны участвовать лишь различные
простые числа Ферма.
Немецкий математик Фридрих Ришелло (1808—1875) дал опи-
сание построения правильного 257-угольника, оно заняло 80 страниц
(есть сведения, что это выполнил и сам Гаусс). Для 65537-угольника та-
кую работу проделал О. Гермес, затративший на поиски 10 лет жизни, но
его решение не опубликовано и хранится в чемодане солидных размеров в
Геттингенском университете.
Результат Гаусса важен для математики не столько фактом решения
древней задачи, сколько идеей группировки корней уравнения. Именно
эта идея, как мы увидим ниже, стала основной в вопросе решения алгеб-
раических уравнений в радикалах.
День 30 марта 1796 г. определил судьбу Гаусса. Он твердо решил
стать математиком и начал вести дневник, в который заносил свои раз-
мышления. «На его страницах... — писал выдающийся немецкий мате-
матик Феликс Клейн (1849—1925), — перед нами проходит гордели-
вый ряд великих открытий, сделанных в арифметике, в алгебре и в
анализе... Странно и почти трогательно видеть между этими следами не-
удержимо рвущегося гения проявления добросовестной, доходящей до
мелочей ученической работы, от которой не освобождены и такие люди,
как Гаусс». Говоря о величии достижений Гаусса, Клейн сравнивает его с
высочайшей вершиной Баварских Альп: «Купола, постепенно уходящие
вверх с востока на запад, венчаются исполинским гигантом, который,
круто обрываясь, переходит в долины новой формации, в которые еще на
многие десятки километров вдаются его отроги и стекают его воды, несу-
щие с собой новую жизнь».
Математики обычно весьма сдержанны в проявлении своих эмо-
ций, особенно в печатном виде, так что зря таких слов не говорят. Фун-
даментальной важности новые идеи Гаусс внес и в алгебру, и в геомет-
рию, и в математический анализ, и в высшую арифметику, которую
считал царицей математики, а саму математику Гаусс называл царицей
наук. Но, кроме математики, он занимался астрономией, где придумал
способ вычисления орбит малых планет по немногим наблюдениям
(в частности, нашел орбиту Цереры после того, как открывший эту пла-
нету астроном Пиацци потерял ее в ярких лучах Солнца). Занимаясь
картографической съемкой Ганноверского королевства, он фактически
создал высшую геодезию, а на основе этой практической работы — тео-
рию поверхностей. Занимался Гаусс и теорией электромагнетизма. Вме-
сте с физиком В. Вебером он ввел абсолютную систему электромагнит-
ных единиц.
И хотя многообразна была его деятельность во всех областях матема-
тики и ее приложений, Гаусс до конца жизни сохранил воспоминание о
первой победе. Перед смертью он высказал пожелание, чтобы на его мо-
гильном камне был изображен правильный 17-угольник. Это не удалось
выполнить, но воздвигнутый Гауссу памятник в Брауншвейге стоит на
17-угольном постаменте.
128
8. Золотая теорема
Не прошло и десяти дней после решения Гауссом проблемы построе-
ния правильного 17-угольника, как он нашел решение другой трудней-
шей задачи, с которой не удалось справиться гигантам математической
мысли Ферма и Эйлеру. Прежде чем рассказывать об этой задаче, остано-
вимся подробнее на разработанной Гауссом арифметике сравнений (или,
как ее еще называют, арифметике остатков, или арифметике вы-
четов).
Начнем с определений. Выберем произвольное натуральное чис-
ло т и зафиксируем его, далее все целые числа будем делить на т и сравни-
вать остатки от деления. Если два числа а и Ъ имеют одинаковые остатки
от деления на т, то говорят, что они сравнимы по модулю т, и пишут:
а = b (mod т).
Например, 8 = 23 (mod 5), так как при делении на 5 числа 8 и 23 да-
ют остаток 3. Если а = Ъ (mod т), то а называют вычетом числа Ъ по мо-
дулю т — ведь а можно получить из Ъ вычитанием числа, кратного т.
Из нашего примера видно, что 8 — вычет числа 23 по модулю 5. Правда,
чаще берут наименьшие неотрицательные вычеты (наименьшие неотри-
цательные остатки). Так, 3 — вычет чисел 8 и 23 по модулю 5. Иногда бе-
рут вычеты, наименьшие по абсолютной величине (приведенные остат-
ки), таким вычетом по модулю 5 для 8 и 23 является число (-2).
Сравнения обладают свойствами, аналогичными свойствам ра-
венств:
1) а = a (mod m);
2) если а = b (mod т), то b = a (mod т);
3) если а = b (mod т) и b = с (mod т), то а = с (mod т).
Кроме того, сравнения можно почленно складывать и почленно умно-
жать: если а = b (mod т) и с = d (mod т), то а + с = b + d (mod т) и
ac = bd (mod т). В частности, к обеим частям сравнения можно доба-
вить одно и то же целое число и обе части сравнения можно умножить
на одно и то же число.
Несколько сложнее обстоит дело с делением: делить обе части срав-
нения al = Ы (mod т) на I можно лишь в случае, если I взаимно просто с
т. В противном случае надо еще разделить т на НОД (I, т). Например,
из того, что 42 = 18 (mod 8), вытекает сравнение 7 = 3 (mod 4). Ясно, что
если т — простое число, то обе части сравнения можно делить на любое
число I Ф 0.
В одном арифметика сравнений сильно отличается от обычной: может
случиться, что а £ 0 (mod т) и b 0 (mod т), но ab = 0 (mod т). Например,
2^0 (mod 6), 3 0 (mod 6), но 2 • 3 = 0 (mod 6). Положение исправляется,
если т — простое число. В этом случае сравнение ab = 0 (mod т) может вы-
полняться только тогда, когда либо а = 0 (mod т), либо b = 0 (mod т). По-
этому чаще рассматривают сравнения по простому модулю.
Многие результаты, о которых шла речь в первом разделе, можно
сформулировать на языке сравнений. Например, малая теорема Ферма
5-Н. Я. Виленкин, 10-11 кл.
129
состоит в том, что если р — простое число, то для всех значений а имеем
ар = a (mod р). А теорема Вильсона (критерий простоты числа р) бу-
дет выглядеть так:
Число р просто тогда и только тогда, когда (р - 1)! = -1 (mod р).
Разумеется, для сравнений можно строить не только арифметику, но
и алгебру, в частности решать сравнения вида Р (х) = 0 (mod р), где
Р (х) = аохп + ... + ап _ ,х + ап — многочлен, ар — простое число. Многие
теоремы обычной алгебры оказываются верны и для таких сравнений.
Например, сравнение степени п имеет не более п корней; сравнение
Р (х) Q (х) = 0 (mod р) сводится к решению сравнений Р (х) = 0 (mod р) и
Q (х) = 0 (mod р) и т. д. Решение сравнения первой степени ах = Ъ (mod р)
эквивалентно решению диофантова уравнения ах + ру = Ь. Сложнее об-
стоит дело со сравнениями второй степени. Наиболее простое из них
х2 = a (mod р) (оно равносильно диофантову уравнению х2 + ру = а).
Но даже для того, чтобы решить уравнение х2 = а, надо уметь извле-
кать квадратные корни. А эту операцию, оставаясь в действительной об-
ласти, можно проделывать только с неотрицательными числами. Поэто-
му, если мы хотим научиться извлекать квадратные корни из вычетов,
надо знать, какие из них «положительные», а какие «отрицательные».
Здесь не поможет использование приведенных остатков, хотя одни из
них положительные, а другие — отрицательные: никакого отношения
к извлечению квадратных корней это не имеет. Например, сравнение
х2 = 2 (mod 7), как легко можно проверить, имеет решение х = 3 (mod 7).
Нетрудно убедиться также, что сравнение х2 = -3 (mod 7) имеет решение
х = 2 (mod 7). А вот сравнение х2 = 3 (mod 7) вовсе не имеет решений (по-
чему?).
Чтобы прояснить этот вопрос, познакомимся с новыми понятиями.
Число а называется квадратичным вычетом (соответственно невыче-
том) по модулю р, если сравнение х2 = a (mod р) имеет (соответственно не
имеет) решения. Квадратичные вычеты в арифметике вычетов по моду-
лю р играют роль положительных чисел, а невычеты — роль отрица-
тельных чисел. Иными словами, «положительны» те ненулевые вычеты,
из которых можно извлечь квадратный корень по модулю р (либо само а,
либо какой-то из его вычетов, т. е. число вида pt + а, является квадра-
том).
Числа 0 и 1 являются квадратичными вычетами по любому модулю,
так как О2 = 0 (mod р) и I2 = 1 (mod р). По модулю 5 квадратичными вы-
четами являются 0, 1 и 4, а невычетами — 2 и 3, так как никакое число
вида 5t + 2 или 5t + 3 не может быть квадратом. По модулю 7 квадратич-
ными вычетами являются 0, 1, 2, 4, а невычетами — 3, 5 и 6. Другими
словами, квадрат любого числа при делении на 7 дает остатки 0, 1,2, 4,
но никогда не дает остатков 3, 5, 6.
К сожалению, данное определение «положительности» и «отрица-
тельности» вычетов не слишком удобно — мы хотели узнать, решается
ли сравнение х2 = a (mod р), а нас отсылают именно к нему. О том, какие
остатки дают квадраты при делении на простые числа, задумывались уже
Ферма и Эйлер. Но окончательный ответ на этот вопрос удалось найти
130
только юному Гауссу. Чтобы сформулировать эти результаты, используем
символ — Лежандра. Дадим его определение.
IP 7
Пусть р — простое нечетное число. Для любого квадратичного выче-
I а I «
та а по модулю р положим — =1; если же а является квадратичным
невычетом, то — = —1. Можно показать, что для символа Лежандра
невычетом, то — = —1. Можно и
I Р J
выполняется следующее равенство:
ab
Р
6
Р
Ферма, разбирая различные примеры, догадался, что числа вида х2 + 1
делятся на простые числа вида 4/г + 1 и не делятся на 4k - 1. Используя
символ Лежандра, это утверждение можно записать очень коротко:
р -1
= (-1) 2
Доказательства этой теоремы Ферма не оставил, и первым ее доказал
Эйлер в 1747 г. Размышляя дальше на эту тему, Эйлер угадал, что число
2 является квадратичным вычетом только для простых чисел вида 8k ± 1,
а для чисел 8k ± 3 — квадратичным невычетом. И здесь символ Лежанд-
ра позволяет перейти к более краткой формулировке:
2^
Р
= (-1) 8
Доказать это утверждение Эйлер не смог, удалось это сделать лишь Ла-
гранжу. Анализируя большой числовой материал, Эйлер сформулировал
(1772) гипотезу, которая выражается с помощью символа Лежандра.
Для любых двух нечетных простых чисел р и q выполняется равенство
р - 1 я - 1
= (-1) 2 2
Это замечательное утверждение, которое носит название квадратич-
ного закона взаимности, и доказал юный Гаусс. Он назвал эту теорему
золотой и привел в дальнейшем 6 различных ее доказательств. Золотая
теорема позволяет довольно легко установить, является данное число
квадратичным вычетом по модулю р или нет. Рассмотрим примеры.
Выясним, имеет ли решение сравнение х2 = 31 (mod 73), т. е. являет-
ся ли число 31 квадратичным вычетом по модулю 73.
5*
131
Для этого вычислим символ Лежандра
Следовательно, уравнение х2 = 31 (mod 73) не имеет решений.
А вот у уравнения х2 = 37 (mod 61) они есть, поскольку
О доказанной им теореме Гаусс отозвался так: «Я случайно натолкнулся
на одну изумительную арифметическую истину, и так как она не только
показалась мне прекрасной сама по себе, но и навела на мысль, что она
связана и с другими выдающимися фактами, я со всей энергией взялся за
то, чтобы выяснить принципы, на которых она основывается, и получить
строгое ее доказательство. После того как это желание, наконец, осущест-
вилось, прелесть этих исследований настолько увлекла меня, что я уже
не мог их оставить».
Продолжая исследования, связанные с квадратичным законом вза-
имности, Гаусс обобщил его на случаи уравнений х3 = a (mod р) и
х4 = a (mod р).
Различными обобщениями золотой теоремы ученые занимались и в
дальнейшем. Фундаментальные результаты в этом направлении получил
ученик Б. Н. Делоне советский математик Игорь Ростиславович
Шафаревич (род. в 1923 г.). Математическое дарование Шафаревича
раскрылось очень рано: в 17 лет он экстерном окончил Московский уни-
верситет, в 19 лет был уже кандидатом, а в 30 лет — доктором физи-
ко-математических наук. В 35 лет его избирают членом-корреспондентом
АН СССР. За работы по алгебраической теории чисел Шафаревич награж-
ден Ленинской премией.
9. Дама с собачкой
После успешного решения уравнений 3-й и 4-й степени математики,
естественно, пытались найти формулы корней уравнений 5-й и более вы-
сокой степени. Но все их попытки приводили к неудачам. Лишь через два
столетия будет доказано, что таких формул нет, а в то время возникали
сомнения: может быть, как для решения квадратных уравнений не хвата-
ло действительных чисел, так и для решения уравнений более высокой
132
степени недостаточно комплексных? Или все-таки можно надеяться, что
произвольное алгебраическое уравнение п-й степени
Zn + CjZ"-1 + ... + Сп _ jZ + сп = О
с комплексными коэффициентами имеет хотя бы один комплексный ко-
рень? А сколько всего оно может иметь корней?
Считается, что первыми сформулировали положение о числе корней
такого уравнения Жирар и Декарт. Французский математик Альберт
Жирар (1595—1632) в молодости вынужден был покинуть родную Ло-
тарингию из-за гонений на протестантов. Большую часть своей жизни он
провел в Голландии. Там и вышла в 1629 г. главная его книга «Новые от-
крытия в алгебре». Она содержала много оригинальных результатов, из-
ложенных доступным языком. Среди них предложение: «Все уравнения
алгебры получают столько решений, сколько их показывает наименова-
ние высшей величины». Книга привлекла внимание ученых, но несрав-
ненно больший резонанс имела вышедшая позже «Геометрия» Декарта.
Об этом произведении, влившем в математику новые жизненные силы,
мы будем говорить в следующем разделе. В ней Декарт, в частности,
сформулировал утверждение, что количество действительных и мнимых
корней алгебраического уравнения п-й степени может достигать значе-
ния п. Правда, еще за двадцать с лишним лет до Жирара немецкий мате-
матик Петер Роте (умер в 1617 г.) высказал аналогичное утвержде-
ние, но его скромная работа осталась незамеченной.
В XVIII в. утверждение приняло более четкую форму: количество ком-
плексных корней алгебраического уравнения равно его степени (каждый ко-
рень считается столько раз, какова его кратность). Появились первые по-
пытки его доказательства, в частности, в работах Эйлера и французского
математика, механика и философа Ж а н а Лерона Даламбера (1717—
1783), но они оказались не вполне строгими. Например, Эйлер рассуждал
так: если zx, z2, ..., z„ — корни уравнения, то это уравнение можно записать
в виде (z - Zj) (z - z2) ... (z - z„) = 0. Отсюда Эйлер вывел обобщенные фор-
мулы Виета, связывающие корни уравнения с его коэффициентами. По
этим формулам он восстановил корни уравнения и считал доказанным тот
факт, что уравнение п-й степени имеет ровно п корней. Позже Гаусс указал
на порочный круг рассуждений Эйлера: сначала существование корней
предполагается, а затем из полученных формул этот факт выводится.
Сам Гаусс в своей докторской диссертации (1799) дал строгое доказа-
тельство теоремы, которая в настоящее время приводится в следующей
формулировке:
Всякое алгебраическое уравнение с комплексными коэффициентами
имеет хотя бы один комплексный корень.
В дальнейшем Гаусс дал еще три доказательства этой теоремы, полу-
чившей название основной теоремы алгебры многочленов. Одно из них
мы приведем чуть ниже, а сейчас покажем эквивалентность приведенной
формулировки следующему утверждению:
Уравнение п-й степени с комплексными коэффициентами имеет ровно
п корней.
133
Для этого нам потребуется теорема, носящая имя французского
математика Этьенна Безу (1730—1783) (хотя ее формулировка встре-
чалась уже у Декарта):
Если число z0 является корнем уравнения Р (z) = 0, то многочлен Р (z)
делится без остатка на г - z0.
На самом деле, если при делении получается остаток, то он может
быть только некоторым числом г, а тогда выполняется равенство
Р (z) = (г - z0) Q (z) + г. Подставляя вместо z значение z0, получим слева
нуль (поскольку zQ — корень уравнения Р (г) = 0), а справа г. Значит,
г = 0 и Р (z) делится на z - z0 без остатка.
А теперь, если гх — корень многочлена Р (z) = cozn + cxzn ~ 1 + ... + сп,
получаем разложение Р (z) = (z - z}) Q (г). Затем аналогично поступаем с
многочленом Q (z) и через п шагов приходим к разложению
Р (z) = с0 (г - zx) (г - г2) ... (z - гп).
Таким образом, уравнение Р (г) = 0 имеет п корней г1( г2, , zn, которые
называют также корнями многочлена Р (г). Если среди корней есть рав-
ные, то полученное нами разложение записывается в виде
•P(z) = c0(2-z1)*1 ...(z-zm)km,
где kr + ... + km = п (это равенство напоминает каноническое разложение
натурального числа).
Интересно, что, когда коэффициенты многочлена Р (z) — действи-
тельные числа, многочлен можно разложить на множители с действи-
тельными коэффициентами. Возможно, не все они будут первой степени.
Дело в том, что такие многочлены вместе с каждым комплексным корнем
z0 = а + Ы обязательно имеют сопряженный с ним корень z0 = а — Ы.
А произведение (z - z0) (z - z0) = (z - a - bi) (z - a + bi) после раскрытия
скобок принимает вид (z — а)2 + b2 = z2 — 2az + а2 + b2. В этом квадратном
многочлене уже нет никакой мнимости.
Когда-то выдающийся немецкий математик Карл Густав Якоб
Якоби (1804—1851) сказал своим ученикам: «Господа, для гауссовской
строгости у нас нет времени». У нас нет не столько времени, сколько мес-
та, чтобы изложить во всей полноте рассуждения Гаусса, и потому мы
ограничимся рассказом об идее одного из предложенных им доказа-
тельств основной теоремы алгебры многочленов.
Выберем на плоскости точку и начертим какую-нибудь замкнутую кри-
вую. Может случиться, что выбранная точка лежит вне кривой (рис. 20, а),
134
а может случиться, что кривая несколько раз обходит вокруг точки
(рис. 20, б). Можно доказать следующее утверждение:
Как бы мы ни деформировали незамкнутую кривую, следя лишь за тем,
чтобы она не разорвалась и ни разу не прошла через данную точку,
число ее обходов вокруг этой точки не изменится.
Хотя это предложение кажет-
ся очевидным, его доказательство
довольно сложно, даже определить
точно, что означают слова «кривая
ни разу не обходит заданную точ-
ку» совсем не просто. Но эти труд-
ности относятся уже не к алгебре,
а к другой ветви математики, на-
зываемой топологией. Иногда это
утверждение шутливо называют
«дама с собачкой». Представим се-
бе, что дама, прогуливающая со-
бачку, идет вокруг площади. Ког-
да она один раз обойдет всю
площадь, собачка, которая дви-
жется более сложным маршрутом,
обегая даму с разных сторон, все
же, по сути дела, тоже обежит
площадь один раз (рис. 21).
Итак, примем утверждение об обходах точки за истинное и выведем
из него основную теорему алгебры. Заметим, что если свободный член
уравнения
2п + CjZ'1 “ 1 + ... + Сп _ jZ + Сп = 0
равен нулю, то и доказывать нечего — уравнение имеет корень 2 = 0. Бу-
дем считать, что сп Ф 0. При очень малых значениях | г | выражение
| zn + ... + сп _ jZ | = | 2 | • | 2п ~ 1 + ... + сп _! | мало по сравнению с | сп |. Поэто-
му когда точка г описывает окружность малого радиуса г с центром в на-
чале координат, точка w = Р (г) = 2п + c1z”~ 1 + ... +сп_12 + сп описывает
замкнутую кривую, расположенную вблизи от точки сп (рис. 22).
Рис. 21
Ук
0
Рис. 22
х
135
Совсем иной будет картина, если точка z снова описывает окруж-
ность с центром в начале координат, но уже очень большого радиуса R.
Из равенства
Р(г)= zn ( 1 + — + ... + — 'I
I 2 Zn )
видно, что отклонение кривой w = Р (г) — «собачки», от кривой со = zn —
«дамы», мало по сравнению с Rn (при больших значениях I z | все слагае-
мые в скобке, кроме 1, малы по модулю). Значит, эти кривые можно де-
формировать друг в друга вдали от начала координат, и потому число об-
ходов, которые они делают вокруг точки О, одинаково. Сколько же
обходов делает кривая w = zn? При возведении в степень п числа
z = г (cos <р + i sin ф) аргумент ф умножается на п, и потому, пока точка z
обходит точку О один раз, точка zn успевает обойти ее п раз.
Итак, мы видим, что, когда радиус окружности, описываемой точ-
кой г, возрастает от очень малых до очень больших значений, число обхо-
дов, совершаемых точкой w = Р (z) вокруг начала координат, меняется от
нуля до п. А это может быть лишь при условии, что путь точки W при
этой деформации ровно п раз проходит через точку О, т. е. многочлен
Р (г) обращается в нуль п раз. Это и значит, что уравнение п-й степени
имеет ровно п корней. (Мы здесь не останавливаемся на некоторых
осложнениях, связанных с возможным совпадением корней.)
10. Целые корни
Мы уже встречались с уравнением х3 — 147х + 666 = 0 при иллюстра-
ции метода Феррари. Решение его по формуле Тартальи имеет вид
х = V-333 + iV6760 + V-333-iV6760.
Это числовое выражение слишком громоздкое, и работать с ним неудоб-
но. В то же время мы знаем, что данное уравнение имеет действительный
корень х = 6, который получается по указанной формуле, если воспользо-
ваться равенством (3 + 2-/10Z)3 = -333 ±iV6760. Установить же его, не
зная заранее ответа, задача нелегкая. И вообще, как угадать корень урав-
нения и среди каких чисел его искать? Поставим общую задачу:
Найти рациональные корни алгебраического уравнения с рациональ-
ными коэффициентами.
В первую очередь заметим, что после умножения обеих частей такого
уравнения на общий знаменатель для всех коэффициентов получим урав-
нение с целыми коэффициентами. Получившееся уравнение
аохп + аххп ~ 1 + ... + ап = О,
вообще говоря, не является приведенным, т. е. коэффициент а0 может
быть не равным единице. Чтобы перейти к приведенному уравнению,
умножим обе части полученного уравнения на множитель а0"-1, по-
сле чего положим аох = у. В результате получается приведенное уравне-
ние с целыми коэффициентами уп + Ь1уп~1 + ... + Ьп = О. Оно не может
136
иметь дробных корней. В самом деле, если бы несократимая дробь —
q
(q Ф 1) была его корнем, то выполнялось бы равенство
откуда рп = — q (b}prl^ 1 + ... + bnqn ~ 1). Здесь правая часть делится на q, а
левая нет, следовательно, такое равенство невозможно.
Итак, общая задача свелась к следующей: найти целые корни приве-
денного уравнения
хп + арх11 ~1 + ... + ап = О (8)
с целыми коэффициентами. Решение этой задачи основано на следующей
теореме:
К Любой целый корень уравнения (8) является делителем свободного
члена этого уравнения.
В самом деле, если целое число а удовлетворяет уравнению (8), то
выполняется равенство ап = - а (ап ~ 1 + с^а" ~ 2 + ... + ап _ г). Так как пра-
вая часть этого равенства делится на а, то и ап делится на а. Например,
целые корни уравнения Xs - 2х2 - 5х - 12 = О надо искать среди делите-
лей числа —12, т. е. среди чисел ±1, ±2, ±3, ±4, ±6, ±12. Подставляя эти де-
лители один за другим в заданное уравнение, видим, что единственным
целым корнем является число 4. Поэтому многочлен х3 - 2х2 - 5х - 12
делится без остатка на х — 4. Остается решить уравнение х2 + 2х + 3 = О,
которое имеет два корня х2 3 = -l±i-/2. Итак, все три корня найдены.
Можно подобрать и комплексные корни уравнения (8) вида а + bi,
где а и Ъ — целые числа. В предыдущем пункте говорилось, что вместе с
корнем г0 = а + Ы это уравнение имеет и сопряженный корень z0 = а - Ы.
Рассуждения, аналогичные проведенным выше, показывают, что в этом
случае свободный член уравнения должен делиться на произведение
zozo = (а + Ы) (а - Ы) = а2 + Ь2. Поэтому сначала надо найти делители сво-
бодного члена, представимые в виде суммы двух квадратов, а затем и са-
ми корни.
Читатели легко могут доказать, что сумма квадратов двух целых чи-
сел либо делится на 4, либо при делении на 4 дает остатки 1 и 2. Следова-
тельно, среди делителей свободного члена надо отобрать лишь числа ука-
занного вида. Затем для каждого из отобранных делителей найти все
разложения в сумме двух квадратов. При этом нельзя упускать из виду,
что разложению d = а2 + Ь2 соответствуют четыре «подозрительных» чис-
ла а + Ы, - а + bi, b + ai, — b + ai и четыре им сопряженных. Есть ли среди
них корни уравнения (8), выясняют непосредственной подстановкой.
Найдем, например, решения вида а + Ы уравнения
х4 - 6х3 + 26х2 - 42х + 91 = 0.
Его свободный член имеет положительные делители 1, 7, 13, 91. Из
них остатки 0, 1 или 2 при делении на 4 дают лишь числа 1 и 13.
137
Эти делители имеют следующие разложения в сумму двух квадратов:
1 = О2 + I2, 13 = 22 + З2. Нам осталось путем подстановки проверить, есть
ли корни среди чисел 1, —1, i, 2 + 3i, —2 + 3i, 3 + 2i, —3 + 2i. Проверка по-
казывает, что уравнению удовлетворяет число 3 + 2i, а следователь-
но, и сопряженное с ним число 3 — 21. Мы нашли корни х4 2 = 3 ± 21.
Значит, многочлен х4 — 6х3 + 26х2 - 42х + 91 делится на произведение
(х — 3 — 21) (х — 3 + 21) = х2 — 6х + 13. Выполнив деление, приходим к
уравнению х2 + 7 = О, откуда находим еще два корня х3 4 = ±г-/Т.
11. Симметрия в алгебре
Вернемся к разложению многочлена на линейные множители
Р (х) = аохп + a4xn _ 1 + ... + ап _ хх + ап =
= а0 (х - хО (х - х2) ... (х - х„).
Напомним, что х4, ..., хп — корни многочлена Р (х); они могут быть как
действительными, так и комплексными. Если раскрыть скобки в правой
части этого разложения и сравнить коэффициенты при одинаковых сте-
пенях х слева и справа, то получим
ai
х1 + х2+... + хп =-,
а0
. . . а2
XjX2 + Х1Х3 + ... + Хп_1Хп =-,
а О
Л з
x4x2x3 + х4х2х4 + ... + х„ _ 2х„ _ 1Х„ =-, (9)
а 0
/ "1 \п Ч
Х1х2...хп = (-1)п-.
«о
Эти соотношения для п < 5 вывел Виет. Поэтому равенства (9) назы-
вают формулами Виета. При п = 2 они принимают вид
а1
х4 + х2 =—— ,х4х2 =-----,
а0 а0
хорошо знакомый читателям.
Посмотрим внимательно на левые части равенств (9). Они являются
многочленами от п переменных х4, ..., хп, причем каждый из этих много-
членов обладает замечательным свойством: как бы мы ни меняли буквы
х15 ..., хп местами, каждый раз получается многочлен, тождественно рав-
ный исходному. Например, поменяем в многочлене х4 + х2 + х3 + х4 мес-
( X, Ху Хо Xa
тами переменные по схеме или, как пишут короче,
\Х2 х4 х, х3 )
произведем перестановку | ^ |. (Чаще для обозначения переста-
у zj 4 1 о у
новок используют только вторую строку. Удобство записи, содержащей
138
две строки, выяснится в дальнейшем при определении произведения пе-
рестановок.) Получится многочлен х2 + х4 + х4 + х3, который отличается
от заданного лишь порядком слагаемых. Эта же перестановка переводит
одночлен х1х2х3х4 в тождественно равный ему одночлен х2х4х1х3. По-
лученный результат неудивителен — эти многочлены являются симмет-
рическими, т. е. не изменяющимися при любых перестановках вхо-
дящих в них переменных. Помимо приведенных выше, интересным
примером симметрических многочленов являются степенные суммы.
Sfi = х4 + х2 + ... + х„. В арифметическом разделе мы уже встречались с
частным случаем степенных сумм (гл. I, п. 13). В самом деле, если поло-
жить х4 = 1, х2 = 2, ..., хп = п, то получим сумму Sk = 1* + 2k + ... + nk, ко-
торую мы там обозначили через Sk (п).
Симметрические многочлены, записанные в левых частях ра-
венств (9), называются элементарными и обозначаются так:
Х4 + Х2 + ... + Хп = Gj,
хгх2 + ... + X„_jXn = о2,
х^х2...хп — о„.
Если теперь взять какой-либо многочлен Р (о1; ..., о„) и заменить в нем
все переменные на их выражения по формулам (10), то получится
симметрический многочлен от х4, ..., хп. Например, из многочлена
of - Зо1о2 при п = 3 получаем симметрический многочлен
(Xj + Х2 + Х3)3 — 3 (х4 + Х2 + Х3) (Х]Х2 + х4х3 + х2х3) =
— х4 + х2 + х3 — Зх4х2х3.
Основная теорема теории симметрических многочленов утверждает,
что этим способом можно получить любой симметрический многочлен от
Xj, х2, ..., хп. Проверьте, например, что при п = 2 выполняются следую-
щие равенства:
xf + х2 = of - 2о2,
X3 + Х2 = О3 - ЗО4О2,
х4 + х2 = of - 4ofo2 + 2о2.
Если же п = 3, то имеют место такие соотношения:
xf + х2 + х3 = of - 2о2,
xf + х2 + х3 = о3 - Зо^з + Зо3,
xf + х2 + х3 = of - 4ofo2 + 2о2 + 4охо3.
Из формул Виета вытекает, что основную теорему о симметри-
ческих многочленах можно сформулировать следующим образом:
Любой симметрический многочлен от корней х4, ..., х„ приведенного
алгебраического уравнения х" + а4хп~1 + ... + ап = 0 является много-
членом от коэффициентов этого уравнения.
Симметрические многочлены применяются для решения разнообраз-
ных задач школьной математики. Приведем примеры.
139
Задача 1. Решим систему уравнений
X + у = 5,
х4+у4 = 97.
Так как левые части уравнений системы являются симметрическими
многочленами от х и у, то их можно выразить, используя формулы (10),
через ох = х + у и о2 = ху. Удобнее взять разные буквы: и = х + у, v = ху.
В результате система примет вид
и = 5,
и4 - 4u2v + 2v2 = 97.
Подставляя значение и = 5 во второе уравнение, получим
2v2 — 100t> + 528 = 0, и потому рх = 6, v2 = 44. Задача свелась к решению
двух систем уравнений
х + у = 5,
ху = 6;
х + у = 5,
ху = 44,
откуда
xi — 2, j/i — 3; х2 — 3, у2 — 2;
х3,4 = |(5 ± iV151), уз. 4 = |(5 + i V151).
Л L
К За дач а 2. Составим квадратное уравнение, корни которого были
бы кубами корней уравнения х2 - 7х + 11 = 0.
Обозначим корни уравнения х2 — 7х + 11 = 0 через х, и х2. По форму-
лам Виета имеем х1+х2=7и ххх2 = 11. Корни уравнения, которое требу-
ется составить, имеют вид ух = xf, у2 = х2. Поэтому коэффициенты иско-
мого уравнения таковы:
Р = - (У1 + Уг) = - (*i + х%), q = угу2 = xfxf.
Но xf + х2 = (Xj + х2) ((хх + х2)2 - Зххх2) = 7 (72 - 3 • 11) = 112, а
xfx2 = (XjX2)3 = 1331.
Поэтому р = — 112, у = 1331 и требуемое уравнение имеет вид
у2 - 112у + 1331 = 0.
Задача 3. Для неотрицательных а и Ь докажем неравенство
«3 + Ь3 -Ла + Н3
2 " I 2 J ’
Рассмотрим разность
з , з з
-------( a-+b 1 =1(а3-3о1о2)-1о? = 1о1(о2-4о2).
2 I 2 ) 2 1 8 1 8 1
Из неотрицательности а и b следует, что ох > 0. Кроме того, of — 4о2 яв-
ляется дискриминантом квадратного уравнения х2 — охх + о2 = 0. Он не-
отрицателен, поскольку квадратное уравнение имеет действительные
корни а и Ъ. Тем самым неравенство доказано.
140
В знаменитом спектакле Художественного театра «Синяя птица»,
поставленном по пьесе Э. Метерлинка, артисты идут, взявшись за руки, и
поют
ы дружной вереницей
* г Идем за синей птицей.
Но синяя птица остается неуловимой, и спектакль заканчивается про-
буждением главных героев — мальчика Тильтиля и девочки Митиль. Си-
няя птица стала синонимом недоступной мечты.
Такой же погоней за неуловимым призраком стали для математиков
попытки найти способ решения уравнений высших степеней. Но для ал-
гебры эти устремления оказались очень плодотворными. Формула не бы-
ла найдена, поскольку таковой не существует вообще! Но были получены
гораздо более ценные результаты, направившие развитие алгебры в новое
русло.
1. В погоне за синей птицей
После того как Феррари решил уравнение 4-й степени, начались по-
иски формулы корней уравнения 5-й степени, т. е. уравнения вида
х5 + ajX4 + а2х3 + азх2 + а4х + «5 = 0. (1)
Формула должна была дать решение этого уравнения в радикалах, т. е.
выразить корни уравнения через его коэффициенты с помощью четырех
арифметических действий и извлечения корня. Многие математики по-
святили этой проблеме долгие годы напряженного труда.
Бесплодность их поисков ослабила интерес к задаче, тем более что к
концу XVII в. почти все математики были захвачены новой бурно разви-
вающейся областью знаний — анализом бесконечно малых. Его методы
позволяли найти приближенные значения корней любого уравнения с на-
перед заданной точностью. Поэтому задача отыскания формулы корней
перестала быть актуальной. Но давно уже сказано, что не хлебом единым
141
жив человек. Хотя эта проблема утратила свой практический интерес,
находились энтузиасты, продолжавшие поиск решения в радикалах урав-
нений пятой и более высоких степеней.
Одним из них был немецкий барон Эренфрид Вальтер фон
Чирнгауз (1651—1708), который, впрочем, занимался не только ал-
геброй, но и математическим анализом, а еще строил заводы для изготов-
ления невиданных тогда больших оптических линз и зеркал, был одним
из изготовителей знаменитого саксонского фарфора. Предки барона жили
в северных областях Чехии и носили фамилию Черноус.
ai
Чирнгауз, произведя замену х = у----, свел уравнение (1) к более
5
простому уа + Ь2у3 + Ь3у2 + Ь4у + Ь5 — 0, не содержащему слагаемого с чет-
вертой степенью неизвестного. Пытаясь сделать то же самое со всеми дру-
гими степенями неизвестного, меньшими пятой, он рассмотрел более
сложную подстановку х = сгу3 + с2у2 + с3у + с4, подбирая специальным об-
разом коэффициенты сх, с2, с3, с4. Однако все меньшие степени ему иск-
лючить не удалось. Как показал позднее шведский любитель математи-
ки, профессор истории Лундского университета Эрланд Самуэль
Бринг (1736—1798), этим методом можно свести уравнение пятой сте-
пени лишь к уравнению у5 + ру + q = 0. Освободиться же от слагаемого ру
никак не удается.
И тогда в битву вступила «тяжелая артиллерия» — проблемой реше-
ния уравнения пятой степени в 30-е гг. XVIII в. занялся величайший из
математиков этого века Леонард Эйлер. Он заметил, что уравнения вто-
рой, третьей и четвертой степеней сводятся к уравнениям более низкой
степени, которые он назвал aequato resolvens — разрешающими уравне-
ниями-, сейчас их называют резольвентами. Опираясь на то, что решение
кубического уравнения получается в виде х = уСА + \ГВ, он применил к
уравнению х4 = ах2 + Ьх + с аналогичную подстановку х = \Га + Vfi + Vc.
И новый способ решения уравнения четвертой степени был получен!
Вдохновленный этим успехом, Эйлер предпринял попытку решить урав-
нение n-й степени с помощью подстановки х = \ГА+\Гв + ...+ п4с, где
число слагаемых равно п — 1. Как и у Чирнгауза, метод дал осечку при
п = 5 — уравнение пятой степени устояло. Не помогли и подстановки бо-
лее сложного вида. Единственным существенным успехом было открытие
способа решения так называемых возвратных уравнений. Это урав-
нения, у которых коэффициенты членов, равноудаленных от начала и
от конца, одинаковы. Например, возвратное уравнение пятой степе-
ни имеет вид ах5 + Ьх4 + сх3 + сх2 + Ьх + а = 0, шестой степени — вид
ах6 + Ьх5 + сх4 + dx3 + сх2 + Ьх + а = 0.
Для возвратных уравнений Эйлер доказал несколько предложений.
Во-первых, уравнение нечетной степени имеет корень —1; в результате деле-
ния такого уравнения на х + 1 вновь получается возвратное уравнение уже
четной степени. Во-вторых, уравнение четной степени вместе с корнем х = а
содержит и корень х = — (нулевого решения возвратное уравнение не
а
142
имеет). Таким образом, подстановка у = х + — позволяет уменьшить степень
х
уравнения в два раза. Надо отметить, что такую подстановку при решении
возвратных уравнений применял (1730) уже Муавр.
В качестве примера рассмотрим уравнение
х4- —х3-11х2- —х + 1 = 0.
10 10
Разделим обе его части на х2 и введем подстановку х Ч— = у. Так как
х
/ 1 \ 27
у2 = х ч— = х2 + 2 ч----, то получаем уравнение у2---у - 13 = 0. Из
I х) х2 Ю
него находим уг = — — ,У2 = ~- Осталось решить уравнения
2 5
,1 5 1 26
х 2 х 5
В результате имеем Xj = -2, х2 =-, х3 = 5, х4 = —.
2 5
Некоторые уравнения сводятся к возвратным при помощи подста-
новки х = lz. Для этого достаточно, чтобы коэффициенты уравнения
аохп + аххп ~1 + ... + ап = 0
удовлетворяли условию akln ~ k = ап_ klk, 0 k п, т. е. ak = ап~ kl2k ~ ".
у. 4 у. 3 лл 2
Например, уравнение —------— + — х + 4 = 0 подстановкой х = 2г
приводится к возвратному 4г4 — 2г3 + 2г2 - 2г + 4 = 0. Вы можете его ре-
шить самостоятельно.
Издавна было известно, что допускают понижение степени уравне-
ния вида аох2п + а1х2п ~ 2 ч- ... ч- ап _ 4х2 + ап = 0.
Здесь достаточно сделать подстановку у = х2. При этом корни таких
уравнений обладают следующей симметрией: вместе с корнем а у них
есть противоположный ему корень — а.
Исследования Эйлера наводили на мысль, что существует какая-то
связь между возможностью понизить степень уравнения и симметриями
его корней. Однако пролить свет на этот вопрос удалось не ему, а другому
выдающемуся математику XVIII в. — Жозефу Луи Лагранжу.
Лагранж был правнуком французского офицера, поступившего в ар-
мию сардинского короля, и родился в итальянском городе Турине. Учил-
ся он в туринском артиллерийском училище, но еще до получения дипло-
ма об окончании стал преподавать в нем математику. С 17 лет Лагранж
начал исследования в области математического анализа, а в 18 лет всту-
пил в переписку с Эйлером, одобрившим и поддержавшим юного матема-
тика. Жизнь в Италии, где каждый шаг любого человека и каждое его
высказывание контролировались неусыпной святейшей инквизицией и
каждый ученый должен был помнить о судьбе Джордано Бруно и Галилео
Галилея, не слишком нравилась молодому ученому. Он мечтает пере-
браться во Францию: там в эти годы выходит знаменитая «Энциклопедия
143
наук, искусств и ремесел», во главе которой стоят великие философы
Ж. Даламбер и Д. Дидро; там же Алексис Клеро в возрасте 18 лет избран
в Академию наук за свои математические открытия. Но мечте Лагранжа
перебраться на родину своих предков не скоро было суждено осущест-
виться.
А пока он вместе с друзьями организует научное общество (позже
оно будет преобразовано в Туринскую АН), публикует в журнале этого об-
щества свои результаты. Мемуар, посвященный создававшемуся в те го-
ды вариационному исчислению, получил высокую оценку Эйлера. По его
представлению Лагранж в возрасте 23 лет был избран иностранным чле-
ном Берлинской академии наук, а в 30 лет стал директором ее физи-
ко-математического отделения. В Берлин он был приглашен по рекомен-
дации Эйлера, возвращавшегося в Россию. И только в 1787 г. Лагранж
переехал в Париж, где стал действительным членом Парижской акаде-
мии наук (прежде он был ее иностранным членом). Здесь он преподавал в
Политехнической и Нормальной школах, работал в комиссии по созда-
нию метрической системы мер и вел активную исследовательскую рабо-
ту. По свидетельству современников, Лагранж был необычайно скромен и
равнодушен к каким-либо почестям.
Помимо вариационного исчисления, этому выдающемуся ученому
принадлежат значительные результаты в теории чисел и алгебре, в облас-
ти дифференциальных уравнений, в теоретической и небесной механике,
в сферической астрономии, в картографии и многих других разделах ма-
тематики и ее приложений. Крупнейшим трудом Лагранжа стала книга
«Аналитическая механика», в которой он подвел итог исследованиям в
этой области за XVIII столетие и показал, что все вопросы этой науки сво-
дятся к решению дифференциальных уравнений.
Характерной чертой творчества Лагранжа было стремление к глубо-
кому теоретическому анализу изучаемых им вопросов. С полным правом
он мог бы сказать о себе словами Б. Л. Пастернака:
'о всем мне хочется дойти
До самой сути:
В работе, в поисках пути,
В сердечной смуте.
Во всем, что он делал, Лагранж искал глубинные корни, то, что можно
назвать истинной философией данного вопроса. В этом отношении инте-
ресно сравнить его со старшим современником — Эйлером. Несмотря на
небольшую разницу в возрасте, Лагранж уже принадлежал следующему
поколению ученых, которые занялись вопросами обоснования различных
разделов математики. И если Эйлер превосходил Лагранжа в изобрета-
тельности, в выдумке новых методов решения разнообразных задач,
то Лагранж был более строг в доказательствах, глубже проникал в суть
изучаемой проблемы. Например, если Эйлер дал алгоритм решения
уравнения Пелля, то Лагранж доказал существование такого реше-
ния (без этого метод Эйлера оставался необоснованным). Они часто зани-
мались одинаковыми задачами, но, несмотря на некоторое творческое со-
перничество, между ними установились добрые отношения.
144
Вопросом решения алгебраических уравнений Лагранж занялся во
время отдыха от сложнейших размышлений о дифференциальных урав-
нениях и их приложениях к теоретической физике. В результате прове-
денных исследований он установил связь между разрешимостью таких
уравнений в радикалах и перестановками их корней.
Чтобы понять идею Лагранжа, вспомним формулы Виета, выражаю-
щие элементарные симметрические многочлены от корней уравнения сте-
пени п через его коэффициенты. Очевидно, решение самого уравнения
равносильно решению системы, составленной из соотношений Виета. Но
задача при этом не упрощается, поскольку решение системы сводится к
исходному уравнению. Лагранж пришел к мысли, что надо рассматри-
вать не только симметрические многочлены, которые не меняются ни при
какой перестановке корней, но и многочлены, меняющиеся только при
некоторых перестановках. На этом пути можно найти резольвенту —
вспомогательное уравнение, по корням которого определяются корни
данного уравнения. Обратимся к примеру.
Рассмотрим многочлен у = х4х2 + х3х4 от корней уравнения четвер-
той степени. Он не изменяется при следующих перестановках:
1) I 9 i ч л I — здесь меняются местами хх и х2;
f JL о 4 у
2) ( 1 о j о I — меняются местами х3 и х4;
f 1 ZL 4 О у
3) I 1 2 | — переставляются xt и х3, х2 и х4.
I о 4 1 А у
Кроме того, можно по-разному комбинировать друг с другом эти пе-
рестановки. В результате получаются следующие 8 перестановок, сохра-
няющих неизменным многочлен х4х2 + х3х4:
fl 2 3 4Л fl 2 3 4'1 fl 2 3 4Л f 1 2 3 4Л
fl 2 3 4j’ 1,2 1 3 4j’ fl 2 4 3/ (,2 1 4 3J’
fl 2 3 4^ fl 2 3 4A fl 2 3 4) f1 2 3 4)
1,3 4 1 2 J’ (,3 4 2 1)’ 1,4 3 1 2 J’ 1,4 3 2 1J’
Обычно перестановку конечного числа элементов записывают в одну
строку, например перестановку 3) обозначают так: (3, 4, 1, 2); а запись
в две строки, которую мы применили, называют подстановкой. Но посколь-
ку между этими записями нет существенной разницы, мы сочли возмож-
ным и для обозначения в две строки оставить название «перестановка».
Общее число перестановок из 4 букв равно 4! = 1 2 • 3 • 4 = 24. Так
как 8 из них не изменяют многочлена х4х2 + х3х4, то при всевозможных
перестановках получатся лишь 24 : 8 = 3 различных многочлена:
У1 = х4х2 + х3х4, у2 = х4х3 + х2х4 и у3 = х4х4 + х2х3.
Образуем теперь многочлен от t вида:
F (t) = (t - yi) (t - у2) (t - у3) =
= (t — XjX2 - х3х4) (t - х4х3 - х2х4) (t - х4х4 — x2x3).
При любой перестановке корней х1г х2, х3, х4 в этом многочлене разве что
переставляются множители, а поэтому сам многочлен не изменяется.
145
Следовательно, не будут меняться коэффициенты при различных степе-
нях t. Значит, эти коэффициенты — симметрические многочлены от кор-
ней х4, х2, х3, х4 уравнения
х4 + а4х3 + а2х2 + а3х + а4 = О.
В силу основной теоремы о симметрических многочленах коэффициенты
многочлена F (Г) запишутся в виде многочленов от а1, а2, а3, а4. Поэтому
по корням кубического уравнения F (t) = 0 можно восстановить корни х4,
х2, х3, х4 исходного уравнения 4-й степени.
Лагранж в «Размышлениях об алгебраическом решении уравнений»
(1771—1773) доказал теорему:
Пусть Xj, х2, ..., хп — корни уравнения
х" + ajXn _ 1 + ... + ап_ 4х + ап = О
и пусть число у — значение некоторого многочлена от этих корней;
пусть, далее, при всевозможных перестановках корней х4, ..., х„ этот
многочлен принимает лишь k различных значений, тогда у является
корнем уравнения F (г) = О степени k, коэффициенты которого — мно-
гочлены от коэффициентов а4, ..., ап исходного уравнения.
Зная корни многочлена F, можно восстановить корни исходного
уравнения. Многочлен F и является резольвентой данного уравнения.
Лагранж показал, что для уравнения тг-й степени резольвента имеет
(п-1)!
степень, равную--------где <р (п) — функция Эйлера. При п = 3 выраже-
<Р (п)
(п- 1)!
ние--------равно 1, при п = 4 оно равно 3, а при п = 5 равно 6. Значит,
<р(п)
кубическое уравнение сводится к линейному, уравнение 4-й степени — к
кубическому, а вот уравнение 5-й степени — к уравнению 6-й степени,
т. е. степень резольвенты не уменьшается по сравнению со степенью ис-
ходного уравнения, а увеличивается.
Получив этот результат, Лагранж написал: «Весьма сомнительно, что-
бы методы, которые мы рассмотрели, могли дать общее решение уравнения
пятой степени». И заключил свой мемуар следующими пророческими сло-
вами: «Вот, если я не ошибаюсь, истинные принципы решения уравнений и
анализ, наиболее пригодный, чтобы привести к решению; как мы видели,
все сводится к некоторому исчислению комбинаций, с помощью которого
получают a priori1 результаты, которые следует ожидать».
Исследованиями Лагранжа теория алгебраических уравнений была
поставлена на правильные рельсы: все до тех пор известное получается с
единых позиций, покончено с кустарным рассмотрением частных случа-
ев, четко выделены трудности. И главное, указывается роль перестановок
корней. Именно эта идея позволила в дальнейшем полностью закрыть
проблему разрешимости алгебраических уравнений в радикалах. Но это
уже было сделано в следующем столетии.
1 Латинское сочетание a priori означает буквально «от предшествующего»,
т. е. до проведения опыта.
146
2. Любимцы богов
Латинская поговорка гласит, что боги рано забирают к себе своих
любимцев. Дальнейшая история решения алгебраических уравнений под-
тверждает эту невеселую мысль. Два молодых гения решили вопрос, сто-
явший перед математиками почти 300 лет, и оба рано ушли из жизни.
Норвежец Нильс Хенрик Абель родился в 1802 г. в небольшой
деревушке. Первоначальные школьные успехи в математике у Нильса
были не слишком большими. Но, когда он учился в старших классах, в
школу пришел новый учитель математики Б. М. Хольмбое, который пер-
вым заметил и выпестовал математический талант юноши. Под его руко-
водством Нильс стал продвигаться вперед с быстротой, отличающей ге-
ния. С особенным интересом изучал он работы Лагранжа. Еще не
закончив школу, молодой математик пытался решить общее уравнение
5-й степени. После нескольких недель напряженной работы ему показа-
лось даже, что нужная формула найдена. Но, применяя ее к конкретным
уравнениям, он понял, что где-то в рассуждения закралась ошибка.
Учась в университете, он вернулся к этим исследованиям и в 22 года по-
лучил выдающийся результат.
На этот раз Абель не ставил перед собой цель отыскать формулу кор-
ней уравнения пятой степени. Он задался вопросом: может ли вообще су-
ществовать такая формула? Преодолев большие трудности, он доказал,
что такой формулы не существует: общее уравнение 5-й степени неразре-
шимо в радикалах. Тем самым проблема, над которой столь долго бились
математики, была полностью решена. Чтобы сделать поскорее получен-
ный результат достоянием математиков, Абель за свой счет отпечатал
брошюру с доказательством на французском языке, который был тогда
самым распространенным в математике. Из-за отсутствия средств ему
пришлось сократить изложение и предоставить читателям возможность
додумать детали рассуждения. Неудивительно, что лишь немногие мате-
матики смогли полностью разобраться в содержании этой работы. Вскоре
выяснилось, что за четверть века до Абеля аналогичный результат полу-
чил итальянский ученый Паоло Руффини (1765—1822). И хотя до-
казательство Руффини было неполным, все же теорему о неразрешимости
уравнений пятой степени в радикалах теперь называют теоремой Руффи-
ни — Абеля.
Итак, формулы решения произвольного уравнения 5-й степени
не существует. Тем не менее отдельные виды уравнений 5-й и более
высоких степеней решаются в радикалах. Например, уравнение
х5 + х4 + х3 + х2 + х + 1 — 0. В качестве примера уравнения, неразрешимо-
го в радикалах, годится уравнение Xs + 2х + 2 = 0. Но как это устано-
вить? Вопрос о том, как определить, разрешимо ли вообще данное уравне-
ние в радикалах, пока оставался открытым.
Результат, полученный Абелем, выдвинул его в ряды первых ма-
тематиков мира. Окончив университет в Осло, он получил стипендию
для образовательной поездки за границу. В это время немецкий инже-
нер и математик А в г у с т Леопольд Крелль (1780—1855) основал
147
«Журнал чистой и прикладной математики». Благодаря своим личным
качествам он сумел привлечь к участию в своем журнале маститых уче-
ных и одаренную молодежь. В первом номере журнала Крелля было опуб-
ликовано пять работ Абеля. Продолжал он печататься и в последующих
номерах. Результаты Абеля открыли новые направления в математике.
Он развил теорию специальных интегралов и положил начало изучению
так называемых эллиптических функций (в дальнейшем и интегралы, и
функции стали называться абелевыми). Абель первым рассмотрел урав-
нение, содержащее интеграл, доказал теорему об области сходимости сте-
пенного ряда, носящую теперь его имя.
Но на родине эти работы не принесли автору заслуженного успеха.
После возвращения домой он вынужден был давать частные уроки. Нуж-
да преследовала его. Ухудшилось и без того слабое здоровье: развился ту-
беркулез. Тем не менее он продолжал усиленно заниматься математикой.
Через год Абель наконец получил должность доцента в университете и в
том же году был избран в Королевское общество Норвегии. Но вскоре он
сильно простудился, болезнь обострилась, и молодой ученый скончался в
1829 г. в возрасте 26 лет. «Он работал не для себя, а лишь для науки, ко-
торую горячо любил, — писал журнал Крелля, — давайте же воздадим
должное памяти человека, который отличался столь огромным талантом
и столь необычайной душевной чистотой. Давайте почтим в его лице од-
ного из тех редких людей, которых природа раз в столетие создает на на-
шей земле».
Ф. Клейн, характеризуя творчество Абеля — этого «математика ми-
лостию Божьей», сравнивает его с блистательным Моцартом. В «Лекциях
о развитии математики в XIX столетии» он пишет: «...дух Абеля облада-
ет силой, позволяющей ему подыматься ввысь и, обозревая все окрест, в
полете, на первый взгляд не требующем никаких усилий, достигать еще
более общих целей».
Еще в более раннем возрасте оборвалась жизнь другого юного ге-
ния — французского математика Эвариста Галуа. «У меня нет времени...
У меня нет времени!» Эти слова, нацарапанные майской ночью 1832 г",
почти неразборчивыми каракулями на листке бумаги, кричат о самой
удивительной и трагической судьбе, которая когда-либо выпадала на до-
лю ученого. В глазах окружающих он был недоучившимся студентом, из-
гнанным из Подготовительной школы, участником тайных революцион-
ных кружков, недавним арестантом. Но сам он знал, что создал новый
мир в математике, открыл пути, по которым пойдут будущие исследова-
тели. Однако, чтобы это свершилось, нужна была одна малость — успеть
записать новые идеи, чтобы они дошли до современников и потомков.
А стрелки часов неуклонно продвигались вперед, приближая момент,
когда он должен будет выйти на линию огня и начать смертельную дуэль
с какими-то малоизвестными ему людьми, с которыми неожиданно
вспыхнула ссора. Сколько талантливейших людей от Парижа до Кавказа
уносила эта мода на дуэли, с которой безуспешно боролись короли и
императоры.
Эварист Галуа родился в 1811 г. в небольшом городке близ Па-
рижа. В 12 лет он поступил в Парижский лицей Людовика Великого, где
148
стал одним из лучших учеников. Вначале он был увлечен изучением
древних языков, но растущая страсть к математике постепенно завладела
всем его временем. Эварист приступил к самостоятельному изучению ра-
бот Лагранжа, Эйлера, Гаусса. В 16 лет он решил, что нашел формулу
корней общего уравнения 5-й степени, сделав ту же ошибку, что и Абель.
Попытка поступить в одно из лучших учебных заведений Евро-
пы — знаменитую Политехническую школу — окончилась неудачей, и он
был вынужден вернуться в опостылевший ему лицей. Но тут ему повезло.
Эварист попал в класс учителя Ж. Ришара, который был в курсе современ-
ных достижений науки и стремился расширить кругозор учащихся.
В 17 лет Галуа получил первый научный результат. Одна его заметка была
послана в известный научный журнал и вскоре увидела свет. Другую рабо-
ту он послал в Парижскую академию наук, но она была там затеряна. По-
вторная попытка поступить в Политехническую школу тоже оказалась не-
удачной: предложенный им оригинальный способ решения труднейшей
задачи не был понят экзаменаторами. В бумагах Галуа сохранилась такая
запись: «Почему экзаменаторы задают кандидатам только запутанные во-
просы? Может показаться, что они боятся быть понятыми теми, кого спра-
шивают. Откуда взялась эта злосчастная манера нагромождать в вопросах
искусственные трудности? Неужели кто-нибудь думает, что наука слишком
проста? А что из этого получается? Ученик заботится не о том, чтобы полу-
чить образование, а о том, чтобы выдержать экзамены...» Вряд ли можно
сказать, что эти слова устарели сегодня...
Через несколько дней после провала на вступительном экзамене на
Эвариста свалилась новая, неизмеримо большая беда. Его отец, затрав-
ленный политическими противниками, клерикалами и иезуитами, по-
кончил жизнь самоубийством.
В феврале 1830 г. Галуа был зачислен в Подготовительную шко-
лу — ничтожную и бледную тень прежней Нормальной школы, создан-
ной Наполеоном и упраздненной Бурбонами в 1826 г. В ней готовились
будущие преподаватели. Во время обучения в этой школе он опубликовал
еще три научные работы и представил рукопись на конкурс в Академию
наук. Но она, как и первая, бесследно там исчезла. В июле 1830 г. Галуа
сделал попытку присоединиться к народным массам, восставшим против
режима Бурбонов. Это привело к столкновению с директором школы и
через некоторое время к исключению из нее. Юноша начал давать уроки
математики и продолжал научные исследования. Свою очередную работу
он снова послал в Парижскую академию. Но продолжал он и революци-
онную деятельность, за что был арестован и заключен в тюрьму. В тюрь-
ме Эварист не переставал заниматься математикой. Здесь он узнал, что
рукопись его возвращена из Академии наук с письмом, где сказано, что
его «рассуждения недостаточно ясны, недостаточно развернуты и не дают
возможности судить, насколько они точны...». Дело было в том, что Га-
луа явился провозвестником новой математики, в которой идеи важнее
формул, а для математиков, воспитанных на формальных преобразовани-
ях, такой метод рассуждений был недоступен.
Вскоре после освобождения из тюрьмы Галуа был убит на дуэли, по
некоторым данным, подстроенной полицией. В ночь перед дуэлью он
149
написал письмо своему другу Огюсту Шевалье, в котором изложил свои
результаты и попросил опубликовать их. Просьба была выполнена, но ра-
бота осталась не замеченной математиками. Лишь через 14 лет на нее об-
ратил внимание Ж. Лиувилль. Он изучил другие работы Галуа и опубли-
ковал их в основанном им «Журнале чистой и прикладной математики».
Только после этого результаты Галуа были признаны научным миром.
Сейчас общеприняты термины «поле Галуа», «группа Галуа», «кого-
мологии Галуа». И когда, читая какую-нибудь научную работу, встреча-
ешь сокращение Gal, не надо долго размышлять о его смысле: буквы Gal
означают Galois (Галуа) — имя гениального юноши, построившего фунда-
мент современной алгебры.
... п
... kn
означает перестановку, при
3. Группа перестановок
В повседневной жизни мы часто употребляем слово «группа», имея в
виду совокупность каких-либо объектов. Начиная с работ Галуа, оно ста-
ло использоваться и в математике, но здесь оно означает не любое собра-
ние объектов, а лишь такое, для которого выполняются определенные
свойства. Что это за свойства, мы сейчас узнаем. Пока лишь отметим, что
в исследованиях Абеля и Галуа, посвященных проблеме разрешимости
алгебраических уравнений в радикалах, использовались свойства групп
перестановок корней уравнений.
Напомним, что запись (
k2
которой число 1 переходит в число kx, число 2 — в k2, ..., а число п пере-
ходит в kn, где kr, ..., kn — те же числа 1, 2, ..., п, взятые в другом поряд-
ке. Две перестановки а = | 1 ••• п | и Ь = ( 3 ? ••• п | можно
«2 ••• «п ) U1 12 1п )
выполнить последовательно одну за другой (сначала а, затем Ь) следую-
щим образом: берут число 1 и смотрят, в какое число kx оно переходит
при перестановке а. Затем находят, в какое число переходит kr при пере-
становке Ь. Получающееся число записывают под цифрой 1. Аналогично
выясняют, в какие числа переходят числа 2, 3, ..., п. Результат последо-
вательного выполнения двух перестановок а и Ь называют их произведе-
нием и обозначают Ьа (именно в таком порядке).
Найдем, например, Ьа, если
(1 2 3 4) . _ (1 2 3 4"|
1^3 4 2 1J’ 1 3 2/
Так как при перестановке а число 1 переходит в 3, а при перестанов-
ке Ъ число 3 переходит в 3, то при Ьа число 1 переходит в 3. Таким же
образом находим, что 2 переходит в 2, далее 3 переходит в 1, а 4 — в 4.
Значит,
150
В то же время ab = л . , т. е. произведение перестановок не
\ 1 о Л 4 у
обладает переместительным (коммутативным) свойством. Но оно облада-
ет сочетательным (ассоциативным) свойством. Иными словами, если а, Ъ,
с — три перестановки, то с (ba) = (cfe) а. Кроме того, среди перестановок
есть похожая на единицу тождественная перестановка
2 ... n'l
6 [1 2 ... п /
Сходство этой перестановки с числом 1 заключается в том, что для любой
перестановки а выполняются равенства
ае = еа = а.
Наконец, для каждой перестановки а есть обратная к ней переста-
новка о'1, такая, что
аа1 = а~га = е.
Чтобы написать ее, достаточно поменять местами в перестановке а верх-
нюю и нижнюю строки, после чего расположить столбцы в порядке воз-
„ , „ fl 2 3 4k
растания чисел верхней строки. Например, обратной к 3 4 । I будет
перестановка
2 3 4 П
1 2 3 4J
т. е.
1 2 3 4)
4 12 3)
. Легко проверить,
что для
любых двух перестановок выполняется равенство
(аЬ)-1 = Ь'а\
Так, когда обуваются, то сначала надевают носки, а потом туфли; при об-
ратной же операции (т. е. разувании) действия выполняются в обратном
порядке — сначала снимают туфли, а потом носки.
Обозначим множество всех перестановок чисел 1, 2, ..., п через Sn.
Мы, во-первых, определили в множестве Sn операцию умножения, убеди-
лись, что она ассоциативна. Во-вторых, множество Sn содержит единицу.
И наконец, в-третьих, вместе с каждым элементом Sn содержит ему об-
ратный. Множество, обладающее тремя указанными свойствами, в мате-
матике называют группой. Таким образом, Sn является группой. А по-
скольку под действием ее элементов (перестановок) симметрические
многочлены от п переменных остаются неизменными, то Sn называют
симметрической группой (отсюда и обозначение). Число элементов груп-
пы называют ее порядком. Порядок симметрической группы Sn равен п!,
в частности, порядок группы S3 равен 3! = 1 • 2 • 3 = 6, а порядок S4 равен
4! = 1 • 2 • 3 • 4 = 24.
Если взять не все множество Sn, а только какую-то его часть (под-
множество), то может оказаться, что для двух перестановок этой части их
произведение в нее не входит. Может случиться и так, что какая-то пере-
становка входит в выбранную часть, а обратная к ней не входит. Но если
перестановки выбираются не произвольно, а отражают симметрию неко-
торого многочлена, то таких неприятностей не будет. Рассмотрим, напри-
мер, перестановки переменных х15 ..., хп, оставляющие неизменным мно-
гочлен
151
lCi<j«n
(произведение всех разностей xL — Xj,
для которых i < j). Ясно, что все такие
перестановки образуют группу. Обозна-
чим ее Ап. При перестановках, не во-
шедших в эту группу, многочлен Dn
меняет знак на противоположный.
В связи с этим многочлен Dn называют
знакопеременным, а группу Ап — зна-
копеременной группой. Решение урав-
нений 2, 3 и 4-й степени тесно связано
с этой группой.
Подмножество в группе, само об-
разующее группу относительно той же
операции, называется подгруппой дан-
ной группы. Так что Ап является под-
группой Sn. Она содержит ровно половину перестановок из S„, а поэтому
ее порядок вдвое меньше порядка Sn. В Sn, помимо элементов подгруппы
Ап, имеется еще ровно столько же перестановок, но они группы не обра-
зуют, так как среди них нет единичной (тождественной) перестановки.
Еще один вид групп перестановок возникает при решении задачи о
построении правильных многоугольников. Они состоят из таких переста-
новок чисел 1, 2, ..., п, при которых не меняется их порядок, если они за-
писаны на окружности (рис. 23). Например, при п = 4 к числу таких пе-
рестановок относятся
e = fl 2 3 4) fl 2 3 4)
[1 2 3 4/ [2 3 4 1/
,=fl 2 3 4) fl 2 3 4)
1^3 4 1 2p [4123/
Так как эти перестановки связаны с вращением окружности, то со-
стоящую из них группу называют циклической (от греч. «кюклос» —
круг). Интересно, что а2 = b, as = с, а4 = е, т. е. все элементы группы яв-
ляются степенями одного из них. Именно это свойство является характе-
ристическим для циклической группы и положено в основу определения
такой группы. Из этого определения легко видеть, что любая цикличе-
ская группа коммутативна:
ат • ak = ат + к = ак + т = ак • ат.
Приведем еще два примера циклических групп в S4:
fl 2 34) , fl 2 3 4)
[1 2 3 4/ [2 4 13/
, = fl 2 3 4) fl 2 3 4)
' [4 3 2 1/ 8 [3 1 4 2/
где d2 = f, d3 = g, d4 = e;
152
= f1 2 3 4Л , _(1 2 3 4)
е Ц 2 3 4/ (3 4 2 1)’
,(1234) (1 2 3 4)
(2 1 4 3/ m 4 3 1 2 J ’
где k2 = I, ks = m, k4 = e.
Очевидно, все три указанные циклические группы являются под-
группами S4, но не являются подгруппами А4. В нее входят только пере-
становки Ъ, f, I и е. Интересно, что они тоже образуют группу (проверьте),
ее обозначают В4. Поскольку Ь2 = /2 = Z2 = е, то В4 имеет три циклические
подгруппы 2-го порядка. Обозначив одну из них через С4, получим следу-
ющую цепочку:
S4 2 А4 и В4 D С4.
Исследования Лагранжа, о которых говорилось выше, были основа-
ны на следующей теореме, называемой ныне теоремой Лагранжа:
Если Н — подгруппа в группе перестановок G, то порядок группы G
делится на порядок подгруппы Н.
Правда, сам Лагранж не употреблял слова «группа», а формулиро-
вал утверждение в иных терминах. Проблему разрешимости уравнения в
радикалах Лагранж свел к отысканию подгрупп группы Sn, сохраняю-
щих некоторые многочлены.
Утверждение, доказанное Абелем, гласит:
I Уравнение
аохп + a-jx" _ 1 + ... + ап = О (2)
разрешимо в радикалах, если каждый его корень xk выражается в виде
рациональной функции rk (х) от одного фиксированного корня, допус-
тим х4, причем для любых k и т выполняются равенства
rk (fm (*i)) = rm (гк (xj).
Напомним, что рациональной функцией называется частное двух
многочленов. Из условия теоремы ясно, что функции (х), ..., гп (х) со-
ставляют группу относительно операции образования сложной функции,
причем группа эта коммутативна. Сейчас коммутативные группы называ-
ют еще абелевыми.
В случае уравнения деления круга
хп -1 + хп ~ 2-г ... + х-г 1 = О (3)
рациональными функциями являются rk (х) = xk, так как xk = rk (х4) =
=х4. Они образуют циклическую группу порядка п. По теореме Абеля
уравнение (3) разрешимо в радикалах (необязательно квадратных) при
любом п. Рассмотрим частный случай этого уравнения при п = 5:
х4 + х3 + х2 + х + 1 = 0.
Покажем, что утверждение Абеля связано с перестановками его кор-
ней. Сопоставим каждой из функций г4 (х) = х, г2 (х) = х2, г3 (х) = х3 и
г4 (х) = х4 перестановку корней уравнения по правилу
153
Для простоты вместо самого корня будем записывать его номер. Тогда
, , fl 2 3 41 . . fl 2 3 41 ,
Г1(«)«-*Ц 2 3 4j е, г2(х)^»^2 4 г 3j-d,
,, fl 2 3 4)_„ , ч fl 2 3 41 .
3 ( ) ^ 1,3 1 4 2J ё’ Г4 [4 3 2 1)
В результате получили знакомую нам циклическую подгруппу симметри-
ческой группы S4.
Однако исследования Абеля выделили лишь некоторый класс урав-
нений, разрешимых в радикалах. Их называют абелевыми. А как найти
все такие уравнения? Ответ на этот вопрос дал Галуа.
Имеем произвольное алгебраическое уравнение (2) с рациональными
коэффициентами. Будем считать, что его левую часть невозможно разло-
жить на множители более низкой степени так, чтобы коэффициенты
остались рациональными (иначе наше уравнение свелось бы к более про-
стым уравнениям). Каждому такому уравнению сопоставляется некото-
рая группа перестановок его корней — подгруппа в Sn. Описать ее можно
следующим образом. Найдем все рациональные соотношения между кор-
нями уравнения. Рассмотрим группу всех перестановок корней, при кото-
рых эти соотношения переходят друг в друга или не меняются. Эту груп-
пу называют группой Галуа данного уравнения. Пусть для нее можно
построить цепочку подгрупп (обладающих специальными свойствами)
так, что каждая следующая является подгруппой предыдущей и заверша-
ющая эту цепочку подгруппа содержит только тождественную переста-
новку. В этом случае группу называют разрешимой.
Мы не можем дать строгого определения группы Галуа и разреши-
мой группы ввиду недостаточности нашего знакомства с группами. Заме-
тим только, что любая подгруппа разрешимой группы тоже является раз-
решимой. Критерий Галуа гласит:
I Алгебраическое уравнение разрешимо в радикалах в том и только в
том случае, если его группа Галуа разрешима.
В теории групп доказывается разрешимость симметрической группы
<S4. Соответствующая цепочка подгрупп для нее имеет вид
S4 з А4 d В4 эС4 з {е}.
Отсюда сразу вытекает, что любое уравнение степени п 4 разрешимо в
радикалах: его группа Галуа является одной из подгрупп группы S4.
А вот для п 5 группа Sn неразрешима, поэтому уравнения пятой и более
высоких степеней в общем случае неразрешимы в радикалах. Тем не ме-
нее имеются отдельные виды таких уравнений, составляющие исключе-
ние из общего правила (их группы Галуа являются разрешимыми под-
группами в S„). Например, абелевы уравнения. Каждое из них имеет
своей группой Галуа конечную коммутативную (абелеву) группу, а они
154
все разрешимы. Разрешимы и все конечные циклические группы как ча-
стный случай абелевых, поэтому разрешимо в радикалах уравнение (3).
В настоящее время построена теория, позволяющая для данного
уравнения с числовыми коэффициентами найти его группу Галуа и тем
самым ответить на вопрос о его разрешимости в радикалах. Если ответ
положительный, то для решения уравнения в рамках общей теории Галуа
составляют резольвенты Лагранжа, при этом существенно используются
первообразные корни из единицы.
4. Чем измеряют симметрию
Симметрия господствует в окружающем нас мире. Многочисленные
примеры симметрии поставляет нам живая природа — флора и фау-
на (рис. 24). Вид симметрии живого организма (зеркальная, осевая,
Рис. 24
поворотная) определен способом его существования и принципом мини-
мальности (экономности). Труднее разглядеть образы симметрии в неживой
природе. Но и здесь ей подчинено устройство и небесных тел, и кристаллов,
и молекул. Оно тоже не случайно, а обусловлено физическими законами.
Человек живет среди симметричных предметов, созданных его рука-
ми. Это дома и машины, мебель и книги, и... почти все предметы нашего
обихода. Своей соразмерностью радуют глаз замечательные произведения
искусства и великолепные архитектурные сооружения. Но в строительстве
и технике, да и при изготовлении предметов быта симметрия используется
не только из соображений красоты и удобства. Пропорциональность и урав-
новешенность всех частей сооружения являются основой его прочности.
Немецкий математик Герман Вейль (1885—1955) писал: «Симмет-
рия является той идеей, посредством которой человек на протяжении веков
пытался постичь и создать порядок, красоту и совершенство». Но относится
ли симметрия к ведению математики? Можно ли измерить симметричность
155
Парфенона или выразить числом
симметричность морской звезды?
На первый взгляд это кажется пу-
стым занятием.
Однако не будем торопиться
с ответом и вновь обратимся к
группам.
Сначала понятие группы свя-
зывали только с перестановками
корней уравнений. Но затем обна-
ружили, что перестановками мож-
но охарактеризовать симметрию
многоугольников и многогранни-
ков. Это и понятно: ведь для зада-
ния симметрии достаточно ука-
зать, какая вершина переходит в
какую. Приведем примеры.
Сначала рассмотрим равнобедренный треугольник; на рисунке 25 его
вершины занумерованы. Этот треугольник имеет одну ось симметрии.
Симметрия его относительно этой оси определяется перестановкой
его вершин. Очевидно, а2 = е, где е — тождественная пере-
3
3
а =
1 2
2 1
становка, оставляющая вершины на месте. В самом деле, выполняя по-
следовательно два раза отражение от оси, мы возвращаемся в исходное
состояние. Таким образом, осевая симметрия описывается циклической
группой 2-го порядка.
Правильный треугольник обладает тремя осями симметрии — это
прямые, содержащие высоты треугольника (рис. 26). Его осевые симмет-
рии определяются следующими перестановками вершин:
156
Каждая из этих перестановок задает циклическую группу 2-го по-
рядка а1 2 = Ь2 = с2 = е.
Кроме осевых симметрий, правильный треугольник обладает двумя
поворотными симметриями вокруг центра О на 120° и на 240° против ча-
совой стрелки. Они задаются перестановками
Легко видеть, что d2 = f, — выполнение двух последовательных поворо-
тов на 120° дает поворот на 240°. Еще один поворот на 120° — и мы воз-
вращаемся в исходное положение: <73 = е. Итак, поворотные симметрии
правильного треугольника описываются циклической группой 3-го по-
рядка, состоящей из перестановок d, f, е. Далее, так как ab = be = са = d,
ba = cb = ас = f, то все шесть перестановок a, b, с, d, f, е образуют группу.
Ее называют группой, симметрии правильного треугольника. Она совпа-
дает с симметрической группой S3.
У прямоугольника имеются лишь две оси симметрии (рис. 27), с ко-
торыми связаны перестановки
а =
1 2 3 4А
2 1 4 3J
Ъ =
и
1 2 3 4Л
4 3 2 1/
причем а2 = Ь2 = е. Повороту прямоугольника вокруг центра на 180° отве-
чает перестановка с = [д । 2 ) ’ легко виДеть> что °2 = е> т- е- группа
симметрии прямоугольника имеет три циклические подгруппы второго
порядка.
Квадрат обладает четырьмя осевыми симметриями (рис. 28), задава-
емыми перестановками
_ f 1 2 3 4) ,=fl 2 3 4'|
а V2 1 4 3J’ ^4 3 2 1J’
_fl 2 3 4) ,_(1 2 3 4)
С 1^3 2 1 4J’ Ц 4 3 2/
157
Ясно, что а2 = b2 = с2 = d2 = е. А еще у квадрата имеются четыре по-
воротные симметрии вокруг центра О против часовой стрелки на углы,
кратные Они описываются перестановками:
„ = f 1 2 3 4Л ,2=fl 2 3 4^
' t2 3 4 1J’ ' I3 4 1 2)’
f3 = fl 2 3 4^ fi_e_(l 2 3 4^
1 {4 1 2 3)’ 1 {1234)'
Таким образом, группа симметрии квадрата содержит четыре цикличе-
ские подгруппы второго порядка и одну циклическую подгруппу четвер-
того порядка. Она явно не совпадает с S4.
Мы видим, что группа симметрии фигуры полностью характеризует
все ее симметрии, при этом, чем большее число элементов содержит эта
группа, тем более симметрична фигура. У окружности, например, она со-
держит бесконечное множество элементов: любая прямая, проходящая
через центр окружности, является ее осью симметрии; поворот на произ-
вольный угол вокруг центра переводит окружность в себя.
Исходя из теории групп русский кристаллограф Евграф Степа-
нович Федоров (1853—1919) и немецкий математик Артур Шенф-
лис (1853—1928) независимо друг от друга дали в 1890 г. классифика-
цию кристаллических решеток. Оказалось, имеется 17 плоских (так на-
зываемых «федоровских групп») и 230 пространственных. Этот результат
имеет, с одной стороны, важное значение для изучения кристаллов.
С другой стороны, он оказался первым связующим звеном теории групп с
физикой.
Мы познакомились пока только с группами перестановок из п эле-
ментов и группами симметрии многоугольников. Но большинство извест-
ных нам числовых множеств с существующими в них операциями также
являются группами. Так, все рациональные числа без нуля образуют
группу относительно операции умножения. Группа с операцией умноже-
ния называется мультипликативной. Если в качестве операции взять
сложение, то соответствующую группу называют аддитивной. В адди-
тивной группе вместо единичного элемента рассматривают нуль, а вместо
обратного — противоположный. Множество целых чисел, а также мно-
жество всех рациональных чисел образуют аддитивные группы. Отно-
сительно операции сложения образуют группы и множество всех дей-
ствительных чисел, и множество всех комплексных чисел. Но чтобы
рассматривать эти множества как мультипликативные группы, надо (по-
добно случаю рациональных чисел) удалить из них нуль, поскольку для
него нет обратного элемента.
Конечно, пока мало толку в том, что мы увидели в знакомых множе-
ствах групповые структуры. Смысл в этом, несомненно, был бы, если бы
групповой подход позволил вывести какие-то свойства этих множеств, о
которых мы до этого не догадывались. Так оно и есть на самом деле. В на-
стоящее время теория групп столь глубоко развита, что с ее помощью
удается вывести массу новых свойств известных нам множеств. Но для
158
знакомства с этими свойствами надо иметь более солидную подготовку по
теории групп. Сегодня почти каждая область математики обращается к
теории групп, без нее нельзя себе представить современную теоретиче-
скую физику. Но мы не имеем возможности рассматривать все ее прило-
жения. Остановимся лишь на группах геометрических преобразований
плоскости.
5. Группы в геометрии
1. Движения. Простейшими преобразованиями плоскости, при ко-
торых все фигуры сохраняют свою форму и размеры, являются движе-
ния. Вы, конечно, знакомы с ними из школьного курса геометрии. В ма-
тематике движения стали рассматривать сравнительно недавно, во вто-
ром тысячелетии нашей эры. Впервые их использовали при решении гео-
метрических задач арабские математики Ибн ал-Хайсам (XI в.) и
Насирэддин Туси (XIII в.). В Европе это произошло в работах фран-
цузских энциклопедистов. В школьном курсе геометрии движения тоже
нужны для доказательства теорем и решения задач. А сейчас мы посмот-
рим на них с другой точки зрения.
Зададим на плоскости прямоугольную систему координат. Напом-
ним, что переносом на вектор I (а, Ь) называется такое преобразование
плоскости, при котором каждая точка М (х, у) переходит в точку
Mi (*1> У1)> где Xj = х + а, ух = у + Ь.
Вот здесь мы и встанем на новую точку зрения: переносы на всевоз-
можные векторы сами образуют множество. Элементы этого множества
можно складывать. Суммой двух переносов на векторы I (а, Ь) и т (с, d)
будем считать результат их последовательного выполнения, т. е. перенос
на вектор I + т. Ясно, что сложение обладает переместительным и сочета-
тельным свойствами. В множестве всех переносов есть нуль — это пере-
нос на нулевой вектор О — и для переноса на вектор I есть противополож-
ный перенос на вектор — I. Все это означает, что совокупность переносов
образует коммутативную группу относительно операции сложения. По-
скольку мы уже знакомы с более сложной терминологией, то можем ска-
зать, что переносы плоскости образуют аддитивную абелеву группу.
Другим простейшим видом движения плоскости является поворот
(вращение) вокруг фиксированной точки, например начала координат.
В результате поворота на угол <р точка М переходит в точку Мг, такую,
что вектор ОМ] равен по абсолютной величине вектору ОМ и образует с
ним угол <р (положительным, как обычно, считается угол, задающий вра-
щение против часовой стрелки). В множестве всех вращений вокруг нача-
ла координат можно выполнять сложение — последовательное выполне-
ние поворотов. Нулем здесь является поворот на нулевой угол; вращение
на угол —ф противоположно вращению на угол ф. Так что и повороты об-
разуют аддитивную абелеву группу.
159
А теперь возьмем какой-нибудь поворот вокруг точки О и любой пе-
ренос и выполним их последовательно друг за другом. Ясно, что получен-
ное преобразование тоже является движением. Только здесь важно, в ка-
ком порядке выполнены исходные преобразования. Чтобы убедиться в
этом, рассмотрим точку М на оси абсцисс и произведем сначала ее пере-
нос по горизонтали на вектор I, а затем поворот на угол — (рис. 29). В ре-
2
зультате точка М перейдет в точку Мх, лежащую на оси ординат. Если
теперь, наоборот, сначала произвести поворот на угол — (при этом точ-
2
ка М переместится на ось ординат), а затем перенос на вектор I, то полу-
ченная в результате точка М2 не совпадет с точкой Мг, поскольку уже не
будет лежать на оси ординат.
Преобразование, полученное комбинацией поворота и переноса, на-
зывается движением первого рода. В частности, любой поворот — это
движение первого рода; можно считать, что он скомбинирован с нулевым
переносом. То же относится и к произвольному переносу. Движения пер-
вого рода также образуют группу, но уже не коммутативную.
Если обратиться к множеству симметрии относительно всевозмож-
ных прямых на плоскости, то оно группы не образует, поскольку после-
довательное выполнение двух симметрий относительно различных пря-
мых уже не является осевой симметрией (рис. 30).
Покажите, что последовательное выполнение симметрии относитель-
но двух параллельных прямых есть перенос, а относительно пересекаю-
щихся — поворот вокруг точки их пересечения.
Преобразование, представляющее собой комбинацию движения пер-
вого рода и осевой симметрии, называется движением второго рода
(в нем присутствие осевой симметрии обязательно). Движения второго ро-
да, естественно, группы не образуют из-за обязательного присутствия осе-
вой симметрии. Совокупность же всех движений плоскости и первого, и
второго рода снова образует группу.
2. Аффинные преобразования. Впервые об аффинных преобразова-
ниях один из авторов этой книги услышал на лекции по аналитической
160
Рис. 31
М.
м'<
____
I
Рис. 32
геометрии, которую читал юным первокурсникам профессор Б. Н. Дело-
не. Это был очень оригинальный человек, великолепный геометр, стре-
мившийся к геометрической наглядности во всех вопросах, которыми он
занимался, и в то же время весьма известный альпинист, прививший лю-
бовь к путешествиям в горы многим своим ученикам. Чтобы объяснить
новое понятие, Борис Николаевич нарисовал на доске кошку, а рядом
изобразил ту же кошку, но уже меньшей высоты и значительно раздав-
шуюся в ширину (рис. 31). «Вот это и есть аффинное преобразова-
ние», — сказал он, и с тех пор все его слушатели навсегда запомнили
основное свойство такого преобразования — сохранять родственные чер-
ты. Ведь латинское слово affinis означает родство по жене.
Впрочем, через несколько минут студенты услышали более точное
определение: «Аффинным преобразованием плоскости называют взаим-
но однозначное отображение этой плоскости на себя, при котором каждая
прямая переходит в прямую». Разумеется, любое движение является аф-
финным преобразованием. Но преобразованием того же типа является и
сжатие плоскости к некоторой прямой. Остановимся на нем подробнее.
При сжатии (растяжении) к прямой I образ М' любой точки М плос-
кости лежит на перпендикуляре ML, опущенном из М на I, причем вы-
полняется равенство M’L — kML (рис. 32). Положительное число k назы-
вается коэффициентом сжатия (при k > 1 будет растяжение). Если
теперь точки М, Р nN лежат на одной прямой, то их образы (точки М',
Р’, N’) тоже лежат на одной прямой, причем если Р лежит между М и N,
то Р' лежит между М’ и ЛГ', т. е. сжатие к прямой является аффинным
преобразованием.
Оказывается, любое аффинное преобразование можно получить пу-
тем последовательного выполнения сначала движения плоскости, а затем
сжатия к двум взаимно перпендикулярным прямым. Этого мы доказы-
вать не будем, а выведем одно из важнейших свойств аффинного пре-
образования:
При аффинном преобразовании параллельные прямые переходят в па-
раллельные прямые.
В самом деле, если бы это было неверно, то нашлись бы параллель-
ные прямые и 12, такие, что их образы 1{ и 12 пересекались бы в некото-
рой точке М’. Эта точка была бы образом точки М, лежащей как на
6 —Н. Я. Виленкин, 10-11 кл.
161
прямой Z1; так и на прямой 12. Но такой точки нет из-за параллельности 1Г
и 12. Значит, утверждение истинно. Отсюда следует, что параллелограмм
при аффинном преобразовании переходит в параллелограмм. Если вспом-
нить, что диагонали параллелограмма делятся точкой их пересечения по-
полам, то получаем важный вывод:
При аффинном преобразовании середина отрезка переходит в сере-
дину образа этого отрезка.
ношение отрезков, лежащих на
Можно показать, что вообще аффинное преобразование сохраняет от-
одной или на параллельных прямых.
Применим изложенные результа-
ты, чтобы доказать теорему о точке пе-
ресечения медиан треугольника. Для
этого заметим сначала, что с помощью
двух сжатий (растяжений) к перпен-
дикулярным осям можно превратить
любой треугольник в равносторонний
(рис. 33). А поскольку при этом середи-
ны отрезков переходят в середины их
образов, то медианы перейдут в медиа-
ны. Поэтому достаточно доказать теоре-
му для равностороннего треугольника, а
потом вернуться к исходному, применив
обратные преобразования. Кстати, об-
ратным преобразованием к сжатию с ко-
эффициентом k является растяжение с коэффициентом —. В равностороннем
k
же треугольнике медианы совпадают с биссектрисами; пересечение их в од-
ной точке следует из свойства биссектрисы угла. И еще: в равностороннем
треугольнике медианы делятся точкой пересечения в отношении 1:2, сле-
довательно, это свойство верно и для медиан произвольного треугольника.
Совокупность всех сжатий к произвольной фиксированной прямой
образует группу. Поскольку движения плоскости тоже составляют груп-
пу, то и аффинные преобразования образуют группу. С частным случаем
аффинного преобразования, подобием, читатели знакомы из школы. По-
этому мы на нем не будем останавливаться, а перейдем еще к одному ин-
тересному виду преобразований плоскости.
3. Гиперболические повороты. Если поворачивать плоскость вокруг
точки О, то эта точка останется на месте, а все остальные будут описы-
вать окружности. Существует похожее преобразование плоскости, при
котором точки движутся по гиперболам. Чтобы описать его, выберем на
плоскости прямоугольную систему координат и зададим положительное
число t. Назовем гиперболическим поворотом с параметром t такое
преобразование плоскости, при котором точка М (х, у) переходит в точ-
( У У
ку М' tx, — . Так как при этом преобразовании не изменяется про-
V *)
изведение координат, а уравнение ху = с задает гиперболу, то при гипер-
162
болическом повороте все точки плоскости движутся по гиперболам
(рис. 34). Очевидно, все такие повороты образуют группу.
Гиперболический поворот не является движением, потому что при
этом преобразовании меняются расстояния между точками. Но сущест-
вует величина р (Мх, М2), аналогичная расстоянию, сохраняющаяся
при таких преобразованиях. Именно: положим для точек Мх (xlt уг) и
М2 (х2, у2)
р2 (Mv М2) = 2 (xt - х2) (yj - у2).
Назовем р (Mt, М2) гиперболическим расстоянием между точками М} и
М2. (Оно выражается мнимым числом, когда (Xj - х2) - у2) < 0, и мо-
жет равняться нулю для несовпадающих точек.) Его можно записать фор-
мулой, более похожей на обычную формулу расстояния между точками
плоскости. Для этого надо повернуть систему координат на 45° (рис. 35).
Предоставляем читателям проверить самостоятельно, что при этом
координаты преобразуются по формулам
V2, , . V2, .
х' = —(х+у), У' = — (у-х).
Поэтому р2 (М1( М2) = (х/ - х2')2 - (у/ - у2')2- Заметим, что это выраже-
ние отличается от известной из школьного курса математики формулы
р2 (М15 М2) = (Xj - х2)2 + (yj - у2)2
лишь заменой суммы квадратов на их разность.
Гиперболическое расстояние можно рассматривать не только на
плоскости, но и в пространстве. В этом случае оно выражается формулой
р2 (М1; М2) = (Xj - х2)2 + (У! - у2)2 - (2| - 22)2
и принимает положительные значения, если выполняется неравенство
(Xj — х2)2 т (у; — у2)2 > (2j — г2)2. А можно рассматривать его и в четы-
рехмерном пространстве, координаты в котором обозначим буквами
(х, у, 2, t). Гиперболическое расстояние играет важную роль в теории от-
носительности. В этой теории координаты х, у, 2 — обычные координаты
6*
163
точки в трехмерном пространстве, a t — время. Основной постулат тео-
рии относительности можно сформулировать следующим образом:
Гиперболическое расстояние р (М1э М2) между точками Мг (х15 г/1; z1( tj
и М2 (х2, у2, z2, t2) не изменяется при переходе к другой системе коор-
динат.
Любое преобразование координат в таком четырехмерном простран-
стве, сохраняющее гиперболическое расстояние, сводится к поворотам в
обычном трехмерном пространстве и гиперболическим поворотам. С этим
пространством мы еще встретимся в геометрическом разделе. Его называ-
ют пространством Минковского по имени немецкого математика Гер-
мана Минковского (1864—1909), давшего геометрическое истолко-
вание теории относительности.
6. Трансцендентные числа
Вернемся к уравнениям. Но подойдем к ним с другой стороны. Рань-
ше нас интересовали их корни, а теперь поставим обратную задачу. Име-
ем действительное (или комплексное) число а. Надо найти алгебраиче-
ское уравнение, корнем которого оно является. Если на коэффициенты
ограничений не накладывать, то задача более чем элементарная: одно из
таких уравнений х — а = 0. Поэтому потребуем, чтобы коэффициенты
уравнения были рациональными.
тт Р
Для рационального числа а = — подходит то же самое уравнение
Ч
р
х----= 0. А как будет обстоять дело с другими числами? Конечно, для
Q
а = ‘УЗ можно взять уравнение х4 - 3 = 0, для а = 5 - V3 подходит урав-
нение (5 - х2)4 -3 = 0. При а = V5 - V3 найти соответствующее уравнение
чуть-чуть сложнее, но вполне по силам школьнику. Но может случиться
так, что а = In 2, или а = sin 1, или а = З1^2 . Как для таких корней искать
подходящие уравнения? А может быть, их и вовсе нет? Этими вопросами
ученые заинтересовались еще в XVIII в. Но прежде чем говорить об исто-
рии решения указанных вопросов, введем определение.
Число а (действительное или комплексное) называется алгебраиче-
ским степени п, если оно является корнем уравнения
хп + с^х" 1 + ... + ап _ хх + ап = 0
(4)
с рациональными коэффициентами, левую часть которого нельзя разложить
на множители меньшей степени с рациональными коэффициентами.
р
Мы видели, что любое рациональное число — является алгебраическим
первой степени; число i также алгебраическое, но уже второй степени, так
как это корень уравнения х2 + 1 =0. Алгебраические числа обладают мно-
гими свойствами, аналогичными свойствам рациональных чисел. Так,
164
сумма, разность, произведение и частное двух алгебраических чисел вновь
являются алгебраическими числами. Более того, алгебраическими являют-
ся все корни уравнения (4) с алгебраическими коэффициентами.
Эти свойства для многих чисел помогают определить их принадлеж-
ность к алгебраическим, не отыскивая для них уравнений. Например,
__ 6 ^2
У7 — V5 +3 — сумма алгебраических чисел;-----------частное алгебра-
V2V6+ 7
ических чисел. И даже такой «монстр», как
1з/1_ 17 I 19 + Уб
11 V 2 7 ,__ гу’
11/3-V2 V 15-1Д|3
является произведением алгебраических чисел. Вообще если число выра-
жается в радикалах, то оно алгебраическое. А может быть, других чисел
нет вообще? И если поискать получше, то для любого числа всегда найдется
соответствующее уравнение с рациональными коэффициентами? Ученые
были уверены, что это не так, т. е. существуют и неалгебраические числа.
Их назвали трансцендентными (от лат. transtendere — превышать).
Л. Эйлер в первом томе «Введения в анализ бесконечно малых»
(1744) высказал предположение о трансцендентности чисел вида logo b
почти при всех рациональных а и Ъ. Ж. Лиувилль более чем через столе-
тие после выхода в свет труда Эйлера доказал с помощью цепных дробей
существование трансцендентных чисел и привел примеры. Еще через
30 лет совершенно неожиданный и более сильный результат получил вы-
дающийся немецкий математик Георг Кантор (1845—1918). Исходя
из результатов созданной им теории множеств, он доказал, что трансцен-
дентных чисел гораздо больше, чем алгебраических.
После работ Лиувилля математики направили свои усилия на поис-
ки новых трансцендентных чисел и доказательство трансцендентности
давно известных. Первую брешь в этом направлении пробил французский
математик Шарль Эрмит (1822—1901). Этот замечательный ученый
благодаря своим крупным научным достижениям, педагогическому дару
и скромности снискал уважение современных ему математиков, всегда
был окружен большим числом талантливых учеников и последователей.
Последние 10 лет своей жизни он возглавлял Парижскую АН. На Втором
конгрессе математиков, где Эрмит из-за болезни не мог присутствовать,
он был заочно избран Почетным председателем конгресса.
Эрмит чрезвычайно плодотворно работал в самых различных облас-
тях классической и современной математики. Трудно назвать какой-либо
из ее разделов, в котором не осталось бы его имени. Его носят полиномы,
функции, формулы, пространства, ... . В 1873 г., используя методы ана-
лиза, Эрмит доказал трансцендентность числа е. Этот результат был
очень важен, несмотря на то, что примеры трансцендентных чисел уже
были приведены, хотя бы потому, что те примеры строились с помощью
определенного алгоритма, под который е не подпадало. А еще число е
давно было в обиходе математиков, поэтому важно было знать, что оно из
себя представляет.
165
Используя метод Эрмита, немецкий математик Карл Линдеман
(1852—1939) показал трансцендентность некоторого вида действитель-
ных чисел, в том числе и л. Тем самым было доказано, что число л нельзя
связать с рациональными числами никакими алгебраическими соотноше-
ниями. Отсюда немедленно следовала неразрешимость древней задачи
квадратуры круга циркулем и линейкой. (Об этой задаче, возникшей бо-
лее 25 веков тому назад, мы подробно расскажем в геометрическом раз-
деле.) Затем немецкий математик Карл Вейерштрасс (1815—1897)
доказал трансцендентность чисел sin а и cos а почти для всех алгебраиче-
ских а. Было выяснено, что генераторами трансцендентных чисел явля-
ются тригонометрические и логарифмические функции, тем самым под-
твердилось предположение Эйлера.
Но математики хотели найти генераторы таких чисел среди более про-
стых функций, в частности степенных, тем более что алгебраические числа
определяются с помощью степенных функций. По этой причине Д. Гиль-
берт среди своих знаменитых проблем сформулировал следующую:
Доказать, что любое число вида ар, где а — алгебраическое число, от-
личное от 0 и 1, а р — алгебраическое число не ниже второй степени,
является трансцендентным.
Сначала было неясно, как подступиться к решению этой проблемы.
Лишь через три десятилетия советский математик Александр Оси-
пович Гель фонд (1906—1968) разработал метод, с помощью которого
решил ее для случая, когда р является квадратичной иррационально-
стью. Дальнейшее продвижение в доказательстве гипотезы Гильберта
шло с использованием метода Гельфонда. Наконец, в 1934 г. самому
Гельфонду и независимо от него немецкому математику Т. Шнейдеру
удалось полностью решить проблему. Теперь уже смело можно утверж-
дать, что числа б^2, 32‘, (л/т — V3 )трансцендентные.
7. Случай на мосту
Как много разных вопросов возникло в связи с поисками общих ме-
тодов решения алгебраических уравнений! Как много различных направ-
лений в математике родилось из размышлений над этими вопросами!
Прежде чем была доказана основная теорема алгебры многочленов, уче-
ных посещала мысль: может быть, надо расширить множество комплекс-
ных чисел, чтобы выразить все корни уравнений высших степеней. Но,
оказалось, для решения алгебраических уравнений этого не требуется.
Однако мысль о расширении множества комплексных чисел, однажды
появившись, не исчезла, тем более что этому способствовало геометриче-
ское истолкование комплексных чисел. На самом деле действительные
числа изображаются точками прямой, комплексные — точками плоско-
сти... Может быть, добавить к комплексному числу еще какое-нибудь
«мнимое» слагаемое и выйти в пространство?
Долго над этой проблемой размышлял Уильям Гамильтон
(1805—1865), ирландский математик, необычайные разносторонние способ-
166
ности которого проявились очень рано. К 12 годам он изучил дюжину язы-
ков, знал наизусть Гомера. В 10 лет освоил «Начала» Евклида, а в
13 лет — «Всеобщую арифметику» Ньютона. В 22 года Гамильтон стал про-
фессором Дублинского университета и директором обсерватории со званием
королевского астронома Ирландии. До самых последних лет он писал стихи.
Его научная работа связана с дифференциальными уравнениями и механи-
кой. Именем Гамильтона названы дифференциальные уравнения определен-
ного типа, оператор, группа, вариационный принцип в механике. Но наибо-
лее известным его открытием считается обобщение комплексных чисел.
Думать здесь Гамильтону было над чем. Ведь если добавить к комп-
лексным числам еще одну мнимую единицу j (j2 = -1), получим числа ви-
да z = а + bi + cj, где а, Ь, с — действительные числа. Их можно склады-
вать и вычитать естественным образом как многочлены от i и j, умножать
на действительные числа. Трудность возникала при перемножении таких
чисел: неизвестно, куда отнести произведение ij. Положим, например,
ij = 0, откуда и ji = 0. Но тогда найдутся отличные от нуля числа, про-
изведение которых равно нулю: (ai + bj) (bi - aj) = - ab + ba = 0. Та-
кие числа называются делителями нуля. Следовательно, в таком мно-
жестве нельзя делить. Ведь при делении обеих частей равенства
(ai + bj) (bi - ay) = 0 на один из множителей левой части получим равенст-
во нулю второго множителя, а они оба отличны от нуля. Когда же строят
обобщение какого-нибудь множества чисел, стараются сохранить наибо-
лее естественные его свойства. Для действительных чисел одним из таких
свойств является деление, а оно не сохраняется при этом обобщении. По-
этому указанное обобщение не могло удовлетворить Гамильтона.
Но в 1843 г. он догадался, как обойти эту трудность. Причем про-
изошло это не за письменным столом, где, как правило, одерживают свои
победы ученые, а совсем в неожиданном месте. Гамильтон с супругой, бе-
седуя, шли по набережной королевского канала. Вдруг его осенила
мысль, что все затруднения отпадут, если взять не две мнимые единицы,
а три, но отказаться от основы основ алгебры — принципа коммутативно-
сти. Он сразу сообразил, какими
должны быть правила умноже-
ния в алгебре новых чисел:
i2=y2 = fe2=_l,
ij = -ji = k,
jk = - kj = i,
ki = - ik = j,
где i, j, k — мнимые единицы.
В момент озарения супруги шли
по мосту, и, говорят, Гамильтон в
восторге от своего открытия перо-
чинным ножом вырезал на де-
ревянных сваях моста формулу
умножения мнимых единиц. По-
зже он писал об этом счастливом
моменте: «Казалось, замкнулась
167
электрическая цепь и вспыхнула искра, пришел вестник многих долгих
лет неуклонной работы мысли».
Так как запись числа с тремя мнимыми единицами q = а + bi + cj + dk
содержит 4 слагаемых, а четыре на латыни quater, то новые числа получи-
ли название кватернионов. Впоследствии английский математик Артур
Кэли (1821—1895) построил еще более общие числа, содержащие уже
8 слагаемых. Они были названы числами Кэли или октавами (от лат. oc-
to — восемь). К сожалению, умножение октав не удовлетворяет не только
переместительному закону, но и сочетательному.
Мы замечаем интересную закономерность: комплексные числа полу-
чаются удвоением действительных. В самом деле, любое комплексное
число г = а + Ы можно рассматривать как пару (а, Ь), кватернионы — в
виде удвоения комплексных:
а + bi + cj + dk = (а + bi) + (с + di) j = zr + z2j.
Аналогично строятся октавы как удвоение кватернионов: X = qr + q2I,
где qlt q2 — кватернионы, I — новая мнимая единица, для которой
I2 = — 1. Возникает вопрос: можно ли ввести другие числа, обобщающие
комплексные, но без процедуры удвоения? Оказывается, можно. Рассмот-
рим число вида и = а0 + а1е1 + ... + _ 1еп _ х, где а0, ап_ х — действи-
тельные числа, ех, ..., еп_1 — новые единицы, которых нет среди дейст-
вительных. Теперь нужно знать, как с этими числами работать, т. е.
определить для них арифметические операции. Сложение, вычитание и
умножение на действительное число вводятся естественным образом.
Чтобы определить умножение таких чисел друг на друга, надо задать таб-
лицу умножения мнимых единиц ekem, где 0 < k, т С п.
Получаемые при этом числа называются гиперкомплексными. Остает-
ся определить в этом множестве деление. И вот здесь нас ждет главная не-
приятность. Не при всех значениях п деление возможно, т. е. система ги-
перкомплексных чисел (как мы уже убедились на примере п = 3) не всегда
является системой с делением. Деление возможно лишь в случае п = 2, 4, 8,
т. е. в множествах комплексных чисел, кватернионов и октав. В общем слу-
чае системы гиперкомплексных чисел малоинтересны. Ведь в них нельзя
даже решить линейные уравнения их = и или хи = и. Эти уравнения различ-
ны, так как в общем случае умножение гиперкомплексных чисел не облада-
ет переместительным свойством.
Наблюдательные читатели, наверное, обратили внимание на одну осо-
бенность — все вновь вводимые единицы г, j, k, ... берутся такими, что их
квадраты равны -1. А почему не 1 или 0? Ответ заключается в пробле-
ме делимости. Рассмотрим для примера числа вида z = а + be, где а,
Ъ — действительные числа, е2 = 1. Они называются двойными числами.
В этом множестве имеются делители нуля: (1 + е) (1 — е) = 0. Покажите, что
для числа 1 + е нет обратного, т. е. такого г, для которого (1 + е) z = 1. Де-
лители нуля имеются и в множестве так называемых дуальных чисел: г =
= а + be, е2 — 0. В самом деле, имеем (ае) (be) = 0. Поэтому в множествах
двойных и дуальных чисел отсутствует деление. Но и эти числа иногда ис-
пользуют в математике.
168
Мы видели, как расширились владения алгебры в XIX столетии.
Комплексные числа не только утвердились, но и получили обобщения.
Вопрос о разрешимости уравнений в радикалах оказался связанным с
группой перестановок корней уравнения. От изучения группы перестано-
вок перешли к изучению групп симметрии многоугольников. Была обна-
ружена групповая структура различных числовых множеств. Постепенно
понятие группы отделилось от элементов, из которых она составлена, и
само стало предметом изучения. Алгебра вступила в современный этап
своего развития. Современная алгебра изучает различные алгебраические
операции, отвлекаясь от природы объектов, над которыми эти операции
производятся. Такой абстрактный подход к изучению операций, их
свойств, взаимосвязей оказался очень плодотворным. Он позволил алгеб-
раическим методам проникнуть не только в различные области математи-
ки, но и в физику, кибернетику, экономику...
8. Векторы
На кватернионы возлагались большие надежды. Однако они не
оправдались, и сейчас кватернионы сравнительно редко встречаются в
научной литературе. Но они привели к становлению векторного исчисле-
ния — области математики, богатой своими приложениями в различных
областях науки и практики.
Понятие вектора появлялось в математической литературе и до Га-
мильтона — изображали же векторами комплексные числа Бессель, Ар-
ган и Гаусс. Но именно Гамильтон подразделил величины на скалярные и
векторные и ввел термин вектор. Его работы послужили началом век-
торной алгебры.. Вектором Гамильтон назвал мнимую часть кватернио-
на, т. е. bi + cj + dk. Название становится понятным, если перейти к
геометрическому истолкованию таких чисто мнимых кватернионов. По
аналогии с геометрической интерпретацией комплексных чисел каждо-
му кватерниону Ы + cj + dk поставим в соответствие точку М (Ъ, с, d)
в пространстве, а с ней и вектор с началом в точке О (О, О, 0) и концом
в точке М. Сложению чисто мнимых кватернионов соответствует сло-
жение векторов, а умножению — сразу две операции, а именно скаляр-
ное и векторное умножение векторов. Если перемножить кватернионы
(Ър + ср + djfe) и (b2i + c2j + d2k), то получим
bxb2i2 + bxc2ij + bxd2ik + cxb2ji + c1c2j2 + 4- dxb2ki +
+ dxc2kj + dxd2k2 = - (feib2 + cic2 + did2) +
+ (cxd2 - dxc2) i + (b2dx - bxd2) j + (bxc2 - b2cx) k.
Слагаемое bxb2 + cxc2 + dxd2 называют скалярным произведением
векторов Zj = (&j, cx, dj) и l2 = (b2, c2, d2), а слагаемое (cxd2 — dxc2) i +
+ (b2di - bxd2) j + (fe1c2 — b2cx) k — их векторным произведением.
Векторы оказались удобным средством изображения различных физи-
ческих величин, имеющих направление (скорость, ускорение, сила, элект-
рическая напряженность и др.). По этой причине векторы на плоскости и в
трехмерном пространстве стали изучать и в школе. Являются они
169
незаменимым средством в таких областях науки, как аэро- и гидродинами-
ка, теоретическая механика, электродинамика и т. д. В этих науках прихо-
дится иногда рассматривать векторы большей размерности, чем три.
Многомерные векторы впервые стал изучать Герман Грасман
(1809—1877), немецкий ученый, обладавший разнообразными даровани-
ями: он был выдающимся математиком, филологом, изучал богословие и
философию. Если гуманитарные науки Грасман изучал в Берлинском
университете, то математикой он стал заниматься самостоятельно не-
сколько позже. Сдав дополнительный экзамен, Грасман получил долж-
ность учителя математики в гимназии своего родного города Штеттцин.
В этой должности он проработал до конца жизни. Хотя в математике он
был самоучкой, здесь ему принадлежат значительные достижения. Он
первым рассмотрел многомерные пространства, построил гиперкомплекс-
ные числа, ввел скалярное произведение векторов. Недаром многие поня-
тия в математике носят его имя.
Может показаться странным, зачем ученые рассматривают много-
мерные векторы, а тем более обращаются к многомерным пространствам.
Ведь окружающий нас мир трехмерен. Правда, иногда его считают четы-
рехмерным, добавляя временную координату: но это делается лишь для
удобства рассуждений. А уж большее число измерений нигде не может
встретиться. На самом же деле именно запросы практики заставляют об-
ращаться к многомерным пространствам. Рассмотрим пример.
Допустим, требуется описать движение точки. Для этого нужно задать
6 чисел, 3 из которых — координаты точки, остальные — координаты век-
тора скорости. Если же механическая система состоит из п не связанных
между собой точек, то приходится вводить уже 6п координат. Получаемое
при этом пространство в классической механике называют фазовым.
Да и в самой математике иногда приходится выходить в пространст-
ва больших размерностей. Пусть в плоскости расположены две фигуры,
симметричные относительно некоторой оси. Чтобы совместить их, надо
произвести вращение вокруг оси
симметрии, т. е. выйти из плос-
кости в пространство. Аналогич-
но зеркально симметричные тела
переводятся друг в друга лишь
путем выхода в 4-мерное про-
странство. Этот факт впервые от-
метил (1827) немецкий мате-
матик Август Фердинанд
Мёбиус (1790—1868), а англий-
ский писатель Г. Уэллс использо-
вал его в фантастическом расска-
зе «История Платнера». У его
героя после возвращения из
4-мерного пространства сердце
оказалось с правой стороны.
Многомерные векторы у Грас-
мана задавались в виде наборов,
170
состоящих из п чисел, взятых в определенном порядке. К сожалению, его
изложение векторной алгебры было сложным и малодоступным. Сейчас эта
часть математики благодаря многочисленным практическим приложениям
подробно разработана и стала достаточно прозрачной. Познакомимся с ней
на примере.
Пусть мебельная фабрика выпускает продукцию четырех видов: сту-
лья, столы, шкафы и диваны. Чтобы сообщить, сколько какой продукции
выпустила фабрика в январе, достаточно указать 4 числа, порядок кото-
рых существен. Допустим, первое из них означает число выпущенных в
январе стульев, второе — столов, третье — шкафов, а четвертое — дива-
нов. Получаем четырехмерный вектор а = (а15 а2, а3, а4). Фабрика может
выпустить не четыре наименования продукции, а 10 или 20 различных
наименований, которые запишутся в виде 10- или 20-мерного вектора.
В общем случае рассматривается n-мерный вектор а = (а1; а2, ..., ап), где
п — произвольное натуральное число (в зависимости от рассматриваемой
ситуации). Числа аг, ..., ап называются координатами вектора. Они
также могут принимать различные значения. В нашем примере они явля-
ются натуральными числами, в другом могут быть рациональными и т. д.
Мы в дальнейшем будем рассматривать векторы с действительными коор-
динатами.
Сумма двух векторов дает новый вектор, который определяет выпуск
продукции фабрикой за два месяца. Разность векторов указывает, на
сколько изменилось количество изделий, выпускаемых фабрикой за вто-
рой месяц по сравнению с первым. Увеличение всех видов продукции в Л,
раз задает умножение вектора а на число X:
Л.П — (Л.П|, ...,
Рассмотрим еще один вектор Ь = (Ьг, ..., Ьп), составленный из стоимостей
каждого из произведенных фабрикой изделий: стул стоит Ьх рублей,
стол — Ъ2 рублей, .... Тогда скалярное произведение (а, Ъ) векторов а и Ь,
равное а1Ь1 + а2Ь2 + ... + апЪп, выражает общую стоимость всей продук-
ции, произведенной предприятием за месяц.
Если мы хотим иметь данные не за один месяц, а за k месяцев сразу,
то для этого достаточно составить таблицу
а11 а12 ••• а1п
_ а21 а22 ••• а2п
,аА1 ak2 ••• а kn j
Здесь в первой строке указано количество изделий, выпущенных фабрикой
в первый месяц, в следующей строке — продукция второго месяца и т. д.
Прямоугольные таблицы из чисел в математике называют прямоугольными
матрицами (у нас выписана матрица размера k х п, содержащая k строк, п
столбцов), а числа, входящие в таблицу, — элементами матрицы. Матри-
цу записывают в виде таблицы, заключенной в круглые скобки.
171
Пусть имеются два предприятия, выпускающие одинаковые изде-
лия. Продукция первого из них в течение k месяцев задается матри-
цей А, продукция второго — матрицей В. Чтобы описать совместный вы-
пуск продукции обоими предприятиями, надо сложить две матрицы:
а И а12 ••• а1п Ьц &12 ... i ’in '
А= а 21 0-22 ••• а2п + &21 ^22 ••• 2п —
Ski ak2 ••• akn J Ski ^к2 ••• bkn ,
аи + Ъц al2 + &12 ••• oln+bln '
= а21 + ^21 а22 + ®22 ... а2п +b2n
Skl+^kl o.k2+bk2 • • • О-кп 4" ^kn /
Аналогично определяется вычитание матриц.
Умножение матрицы на число А. производится по правилу
Ллц ^#12 .. ХаХп '
ХА = Ад21 Ха 22 • • А.а2 „
ХаЛ2 • • • ^а1т >
Легко видеть, что совокупность всех матриц размера k х п относительно
операции сложения образует группу. В ней роль нуля играет нулевая
матрица (матрица, состоящая из нулей), а противоположной для матри-
цы А является матрица
-А = (-1) • А.
Предположим теперь, что нас интересует вопрос: на какую сумму
фабрика выпустила изделий в первом, втором, ..., k-м месяце? Для этого
матрицу А, определяющую выпуск п видов изделий за k месяцев, надо
умножить на вектор b = (Ьг, Ь2, .... Ьп), составленный из стоимостей этих
изделий; его координаты удобно записать в виде столбца. Тогда
а11 а12 • • п г bl
а21 0-22 •• а2п i>2 = «2
akl ак2 • • • ^kn , J Sn ,
где = anbi + а12Ь2 + ... + alnbn, с2 = a2lbY + а22Ь2 + ... Л-а2пЪп, ..., ск =
= akibv + ak2b2 + ... + aknbn. Аналогично определяется умножение матрицы
размера k х п на матрицу размера п х т:
all a21 a12 0-22 • • ^ln •• “2n ^21 £>12 ^22 •• b2m = CJ rt bo 1- 1—1 c12 c22 • • 1 m •• C2 m
Sn 1 an2 • • ^kn 7 ЬП2 • • ^nm ck2 •• C km ?
172
Здесь Су = апЬ1} + ai2b2j + ... + alnbnj, 1 =£ i =% k, 1 < j С т. Другими словами,
элемент Су матрицы произведения равен скалярному произведению i-й
строки первой матрицы на у-й столбец второй матрицы. Очевидно, только
для квадратных матриц одинакового размера произведение вновь будет
матрицей того же размера.
9. Как решить систему
Рассмотрим совокупность квадратных матриц размера п х п, или,
как говорят, матриц га-го порядка:
а11 а12 «1п
а21 а22 ••• а2п
& п.2 О'пп '
Среди них имеется так называемая единичная матрица
О '
О
Покажите, что для любой матрицы А имеет
= Е А = А. Обратной к матрице А называется
которой А • А-1 = Е.
Например, для матрицы третьего порядка
место равенство А •Е =
такая матрица А-1, для
обратной
1 -2
О 1
° О
является А 1
. Проверьте это самостоятельно.
О
О
.0
Но не для каждой матрицы существует обратная. Так, у матрицы
2-11 (12-11
нет обратной. Нет ее и у матрицы
. Убедитесь в
этом сами.
Как узнать, имеет ли данная матрица обратную? Оказывается, кри-
терием является наличие отличного от нуля определителя; сама матрица
в этом случае называется невырожденной (в противном случае — вырож-
денной).
Определителем матрицы А называется число А, равное сумме
S (-1)* аи • a2j • ... • апг, где сумма берется по всем перестановкам из чисел
1, 2, ..., га, a t — число таких перестановок, которые приводят набор
173
(i, j, ..., г) к натуральному порядку (1, 2, n). Определитель матрицы
обычно записывают следующим образом:
«И «12 ... «1П
д = а21 а22 ••• а2п
& п1 п 2 • • • & пп
Читателям предлагается проверить, что:
а) ДЛЯ п = 2 Д = aii а21 а12 а22 — а11 а22 ~ а12а21 ;
б) для п = 3
а11 а12 а13
Д = а21 а22 а23 =
а31 а32 а33
— а11а22а33 + а13а21а32 + а12а23а31 ~ а13а22а31 ~ а12а21а33 ~ а11а23а32-
Существует простое для запоминания правило вычисления опреде-
лителя матрицы 3-го порядка: сначала вычисляется произведение чисел,
стоящих на главной диагонали а11а22а33, затем чисел, расположенных в
вершинах двух треугольников, имеющих сторону, параллельную главной
диагонали (рис. 36). После этого перемножаются числа побочной диаго-
нали а13а22а31 и числа, находящиеся в вершинах треугольников со сто-
роной, параллельной побочной диагонали (рис. 37). Эти произведения
умножаются на -1. Сумма всех шести найденных таким образом чисел
равна определителю матрицы.
Интересно, что модуль определителя 2-го порядка равен площади па-
раллелограмма, образованного векторами Zj = (ап, а12) и 12 = (а21, а22), а
модуль определителя 3-го порядка — объему параллелепипеда, построен-
ного на векторах Zj = (йц, Oi2> а1з)> Z2 = (a2i, а22, ^гз) и Z3 = (®31> ^32> ^зз)‘
174
Теперь ясно, что матрица 2-го порядка является вырожденной, если зада-
ющие ее векторы параллельны, а 3-го порядка — если все три вектора,
задающие матрицу, лежат в одной плоскости.
Вырожденные матрицы не имеют обратных; более того, среди них
(a 0W0 (П (О О') m ,
есть делители нуля, например, К q II с j = I 0 q I - -*ак что °®Раш'ать'
1 2
-1 О
и В =
реместительным свойством. Например, для А —
ся с матрицами нужно осторожно. Произведение матриц не обладает пе-
'3 1 '
- -2
\2 ;
2 6
1
2
имеем А - В =
4 -3^
-3 -1J
, но В • А =
. Совокупность всех невырож-
денных матриц порядка п образует группу относительно операции умно-
жения. Как мы только что видели, эта группа не коммутативна.
В настоящее время создано целое матричное исчисление, где подроб-
но изучаются матрицы и их свойства. Матричные модели лежат в основе
балансовых расчетов в экономике, на их основе строится линейное про-
граммирование и т. п.
А когда матрицы появились в математике? Впервые их стали ис-
пользовать китайские ученые. В «Математике в девяти книгах» (ок. II в.
до н. э.) имеется задача: «Если из зерна 5 снопов хорошего урожая уба-
вить 1 доу 1 шэн, то это соответствует количеству зерна 7 снопов плохого
урожая. А если из зерна 7 снопов хорошего урожая убавить 2 доу 5 шэн,
то это соответствует количеству зерна 5 снопов плохого урожая. Спраши-
вается, сколько зерна получается из каждого снопа хорошего и плохого
урожаев». (При решении задачи следует учесть соотношение мер объема:
1 доу = 10 шэн.)
Если обозначить искомые величины через х и у, то условие задачи
записывается в виде системы
5х-11 = 7г/,
7х —25 = 5у,
откуда
5х-7у = 11,
7 х - 5у = 25.
Китайские математики вместо полученной системы составляли таблицу,
записывая коэффициенты уравнений в столбцы (расположенные справа
7 5
налево): —5 —7. Затем они умножали первый столбец на 5 и вычи-
25 11
тали из полученного столбца семь раз второй столбец:
35 5 30 5 0 5
-25 -7 -18 -7 -> . .. -> 24 -7
125 11 114 11 48 11.
Из первого столбца полученной матрицы 48 q они находили у = = 2, из
11 + 7-2
второго X = - 5.
5
175
Такой метод решения системы линейных уравнений в Китае полу-
чил название «фан-чен» — буквально «выстраивание чисел по клеткам».
Приведенная задача интересна еще и тем, что здесь впервые в истории
математики в условии встречаются отрицательные числа.
Метод «фан-чен» приводит к последовательному исключению неиз-
вестных, знакомому читателю из школы. На самом деле первое уравне-
ние системы умножается на 5, а второе — на —7, полученные выражения
складываются и записываются на месте второго уравнения. В результате
система принимает вид
[5х-7г/ = 11,
(о + 24;, = 48, °ТКУДа!' = 2“Х'5-
О достижениях китайских математиков ученые Европы узнали не-
давно. Поэтому указанный метод решения системы уравнений в настоя-
щее время связывается с именем Гаусса, переоткрывшего его в 1849 г.
Идея нумерации элементов матрицы по строкам и столбцам восходит
к Г. Лейбницу, обозначившему в письме (1693) к французскому матема-
тику Гийому де Лопиталю (1661 —1704) систему трех уравнений
следующим образом:
10 + Их + 12г/= 0,
20 + 21х + 22г/ = 0,
30 + 31х + 32г/ = 0.
(Обратите внимание на коэффициенты: это не конкретные числа, а обо-
значения!)
В этом же письме Лейбниц изложил способ решения системы линей-
ных уравнений с помощью определителей. Правда, десятилетием раньше
такой метод нашел японский математик Кова Секи (1642—1708). Но
оба эти результата не стали достоянием математиков Европы. Лишь в
1750 г. он был переоткрыт швейцарским математиком Габриелем
Крамером (1704—1752) и получил название правила Крамера. Разбе-
рем его на примерах.
1. Решим систему двух уравнений
Зх-5г/ = 1,
2х + Зг/ = 2.
Сначала вычислим определитель, составленный из коэффициентов
неизвестных; его называют определителем системы.
А =
= 3 3 - 2 (-5)= 19.
Заменим в этом определителе первый столбец свободными членами урав-
нений системы и найдем новый определитель
А1
1 -5
2 3
= 3 + 10 = 13.
Заменяя далее в А второй столбец свободными членами, вычислим еще
один определитель
2 2 =6-2 = 4.
176
Ai 13 Д2 4
Решение системы находим по формулам х - , у = = —
2. Решим систему трех уравнений с тремя неизвестными
х - у + г = 1,
2х + Зу - 2z = 2,
х + у + 3 г = -4.
Вычислим определитель системы
= 9 + 2 + 2- 3 + 2 + 6 = 18.
Затем вычислим следующие определители:
1 -1
2 3
—4 1
Ai
А 2
A3
= 9 + 2- 8 +12+ 2 + 6 = 23;
111
2 2 -2 = 6 - 8 - 2 - 2 - 6 - 8 = -20;
1-4 3
1-1 1
2 3 2 =-12 - 2 + 2 - 3 - 2 - 8 = -25.
11-4
Д1
Откуда х = --
А
23 Л2
— ’ У - —
18 А
10 Аз
—, г =--
9 А
25
18’
10. Алгебра Буля
Вероятно, многим из читателей знакома книга Э. Л. Войнич «Овод».
До замужества автора этой книги звали Этель Лилиан Буль. Отцом писа-
тельницы был английский ученый Д ж о р д ж Буль (1815—1864), осно-
воположник математической логики. Ему удалось осуществить мечту
многих поколений математиков и философов. О возможности механизи-
ровать не только вычисления (этой цели служил еще абак), но и рассуж-
дения ученые задумывались очень давно. Испанский рыцарь Раймон
Люллий пытался построить машину, вращая колеса которой можно из
правильных утверждений (посылок) делать правильные выводы. С ее по-
мощью он надеялся убедить мусульман перейти в христианство. Однако
эта попытка не увенчалась успехом, да и машина не оправдала надежд
изобретателя.
Через несколько столетий о возможности превратить логические рас-
суждения в вычисления мечтал Лейбниц. Он надеялся, что когда-нибудь
при возникновении споров между людьми они скажут: «Перейдем к вы-
числениям» — и таким образом смогут разрешить все возникшие пробле-
мы. Английский писатель Джонатан Свифт в третьей книге своих
177
бессмертных «Путешествий Гулливера» подверг мечты о механизирован-
ных рассуждениях жестокой насмешке (впрочем, он смеялся и над опти-
ческими исследованиями Ньютона). Знаменитый сатирик оказался не
прав. Желанное исчисление было построено в XIX столетии.
Познакомимся с ним, конечно, в современном виде. Назовем выска-
зыванием любое утверждение, о котором можно сказать лишь одно из
двух — либо оно истинно, либо ложно. Например, высказываниями яв-
ляются утверждения: «Дважды два — четыре», «Сейчас здесь идет
дождь». «Если 2x2 = 5, то существуют ведьмы», «Суворов победил в
битвах при Фокшанах и Рымнике», «Всякий треугольник правильный»
и т. п. (А вопросы и восклицания высказываниями не являются.)
Из нескольких заданных утверждений, можно получить более слож-
ные. Это делается с помощью союзов «и», «или», «либо ..., либо ...», «ес-
ли ..., то ...», а также отрицания «не». Чтобы такое построение новых
высказываний из данных имело однозначно определенный смысл, надо
каждому из союзов придать точно определенный смысл. Это делается с
помощью следующих таблиц:
«А и В» «А или В» «не А»
\в а\ и Л
и и Л
Л Л Л
\в а\ и Л
и и и
Л и Л
А И Л
не А Л и
В этих таблицах буква «И» означает «истинно», а «Л» — «ложно».
Из первой таблицы видим, что если высказывание А и высказывание В
истинны, то истинно и высказывание «А и В». В остальных случаях это
высказывание ложно. Из второй таблицы высказывание «А или В» лож-
но лишь в случае, когда ложны и А, и В. Наконец, «не А» ложно, если А
истинно, и наоборот. Как в обычной алгебре слова, применявшиеся для
обозначения арифметических операций, были заменены знаками, так и
здесь союзы «и», «или» и отрицание «не» заменяются соответственно
знаками л, v и —> (или чертой сверху). Поэтому запись (А л В) v С означа-
ет: «А и В, или не С».
Операция замены А на А называется отрицанием, получения А л В
из А и В — конъюнкцией, а получения A v В — дизъюнкцией. Для этих
операций при всех А, В, С выполняются свойства:
1) А л А = А; 2) А л В = В л А; 3) (А л В) л С = А л (В л С);
4) A v А = А; 5) A vB = B v А;
6) (A v В) v С = A v (В v С); 7) (A v В) л С = (А л С) v (В л С);
8) (А л В) v С = (A v С) л (В v С); 9) А = А;
10) Av В = А л В; 11) А л В = A v В.
178
Кроме того, справедливы равенства
Й = Л, И А А = А, Л_л А = Л, H_v А = И,
Л v А = А, А л А = Л, A v А = И,
где через «И» обозначено заведомо истинное высказывание, а через
«Л» — заведомо ложное.
Множества, наделенные алгебраическими операциями, для кратко-
сти называют просто алгебрами. Перед нами алгебра высказываний.
С помощью перечисленных тождеств можно преобразовать любые
выражения, правильно составленные из высказываний А, В, С, ... и зна-
ков операций v, л, Законы преобразований таких логических выраже-
ний были найдены Булем в 1847 г., и потому алгебру высказываний на-
зывают булевой алгеброй. Она во многом напоминает обычную, но
некоторые ее законы имеют иной вид. Например, в булевой алгебре (на
основании свойств 1 и 4) нет ни степеней, ни коэффициентов; в ней два
распределительных закона, выражающиеся тождествами 7 и 8.
Иногда удобно истинному высказыванию сопоставить число 1, а
ложному — число 0. Тогда конъюнкцию А л В лучше записывать в виде
произведения А • В, а дизъюнкцию A v В — в виде суммы А + В. (Надо
только иметь в виду, что при этом 1 + 1 = 1.)
Законы булевой алгебры исполь-
зуются при конструировании элект-
рических цепей и вычислительных
устройств. При этом высказываниями
являются предложения типа «Ток по
участку ... проходит», операция отри-
цания сводится к замене включенных
рубильников на выключенные и об-
ратно, конъюнкция соответствует по-
следовательному соединению, а дизъ-
юнкция — параллельному. Разберем,
например, пойдет ли ток по цепи, изображенной на рисунке 38. Для этой
цепи по участкам В, С, Е ток проходит, а по участкам A, D, F нет. Нам
надо вычислить значения выражения
(А А (С V D)) V (В A (Е V F)),
если A, D, F соответствует 0, а В, С, Е соответствует 1. По правилам
0+1 = 1, 0-1 = 0, 1-1 = 1 получаем (0 • (1 + 0)) + (1 • (1 + 0)) = 0+1 = 1.
Таким образом, по цепи ток пойдет.
Булеву алгебру можно составить не только из высказываний или из
электрических проводов и рубильников, но и из множеств. Под множест-
вом в математике понимают любую совокупность объектов (элементов),
такую, что о любом объекте можно сказать, принадлежит он этому мно-
жеству или нет. Например, можно говорить о множестве учителей, пре-
подающих в данном классе, множестве всех тигров в лесах полуострова
Индостан, множестве всех простых чисел, множестве всех кругов на
плоскости и т. д.
Если элемент а принадлежит множеству А, то пишут а & А, если
же он не принадлежит А, то пишут а е А. Множество В называется
179
подмножеством А (обозначают В с А), если любой элемент Ь из В при-
надлежит А.
Приведем примеры. Множество всех учеников данного класса явля-
ется подмножеством множества учеников данной школы. Множество всех
квадратов на плоскости — подмножество множества всех параллелограм-
мов на той же плоскости. Множество всех простых чисел — подмножество
множества всех натуральных чисел. Множество может не содержать ни од-
ного элемента (например, множество круглых квадратов или жителей на
Луне). Такое множество называют пустым и обозначают 0. Пустым явля-
ется множество действительных корней уравнения х2 + 1 = О.
Определим для множеств три операции — пересечение, объединение и
дополнение. Пересечением множеств А иВ называется множество, состоя-
щее из всех элементов, которые одновременно входят в А и в В. Например,
если А — множество ромбов, а В — множество прямоугольников, то их пе-
ресечением является множество квадратов, потому что фигура, одновремен-
но являющаяся ромбом и прямоугольником, есть квадрат. Пересечение
множеств А и В обозначают А П В. Объединением множеств А и В называ-
ют множество, состоящее из всех элементов, которые принадлежат хотя бы
одному из этих двух множеств. Обозначают его A U В. Например, если
А — множество всех натуральных чисел, дающих при делении на 3 оста-
ток 1, а В — чисел, дающих при делении на 3 остаток 2, то A U В — мно-
жество натуральных чисел, не делящихся на 3. Наконец, если В — подмно-
жество А, то дополнением к В в А называют множество всех элементов
из А, не принадлежащих В. Например, дополнением к множеству простых
чисел в множестве натуральных является множество, состоящее из 1 и всех
составных чисел. Мы будем в дальнейшем рассматривать лишь множества,
являющиеся подмножествами некоторого универсального множества U.
В этом случае дополнения берутся в множестве U.
При выполнении операций пересечения и объединения подмножеств
множества U вновь получаются подмножества U. Таким образом, возникает
алгебра таких подмножеств. Ее законы совпадают с законами алгебры вы-
сказываний с той лишь разницей, что операцию дизъюнкции высказыва-
ний заменяет объединение множеств, конъюнкции — пересечение мно-
жеств, а отрицания — дополнение к множеству. Причина такой аналогии
проста. Возьмем какой-нибудь элемент х из множества U. Тогда каждому
подмножеству А множества U соответствует высказывание: «Элемент х
принадлежит множеству А». При этом операции над множествами превра-
щаются в операции над высказываниями.
Булеву алгебру можно построить и из более простого материа-
ла — обычных натуральных чисел. С этой целью возьмем какое-нибудь
натуральное число, например 60, и обозначим через U множество всех его
делителей (в нашем случае — множество, состоящее из чисел 1, 2, 3, 4, 5,
6, 10, 12, 15, 20, 30, 60). В качестве операций в U возьмем образование
НОД (а, Ъ) и НОК (а, Ъ), а роль операции отрицания будет играть переход
, 60 тт
от делителя а к делителю —. Читателям предоставляется возможность
d.
проверить, что при этом получается булева алгебра.
180
Упражнения
1. Решите задачу индийского
математика Ариабхатты
«о встрече» двух небесных
тел, движущихся навстречу
друг другу или в одном на-
правлении, т. е. найдите, че-
рез какое время они встретят-
ся, если известны их скорости
и расстояния между ними.
2. Решите задачу индийского
математика Бхаскары: «Один
имеет 300 монет и 6 лошадей,
другой имеет 10 лошадей, но
у него недостает 100 монет.
Оба одинаково богаты. Како-
ва цена лошади?»
3. Покажите, что уравнение х3 - Зх - 1 = 0 не имеет целых решений.
_ , 2nk , . . 2nk
4. Покажите, что любая натуральная степень числа cos--------г ism----
п п
удовлетворяет уравнению х" = 1.
5. Решите уравнение х3 = 15х + 4 (результат Бомбелли).
6. Решите уравнение х3 + 10х = 6х2 + 4 (результат Кардано).
7. Найдите корни уравнения х3 + 26х= 12х2 + 12 (результат Кардано).
8. Найдите все корни уравнения х7 - х6 - х + 1 = 0.
9. Докажите следующие свойства возвратных уравнений:
1) возвратные уравнения не имеют нулевых корней;
2) если х0 — корень возвратного уравнения, то тоже его корень;
х0
3) при нечетной степени возвратного уравнения число х = -1 является
корнем этого уравнения;
4) если Р (х) = 0 — возвратное уравнение нечетной степени, то урав-
Р (х)
нение------= 0 вновь является возвратным.
х +1
10.
Из предыдущего упражнения выведите метод решения возвратного
уравнения (результат Эйлера).
Если уравнение Р (х) = О нечетной степени, то нужно перейти к урав-
Р(х)
нению-----= 0; в случае четной степени уравнения нужно применить
х +1
подстановку t = х + — .
х
181
11. Докажите коммутативность группы S2-
12. Покажите, что группа S3 не является коммутативной.
13. Пусть о1 = х + у, о2 — ХУ> Sn = хп + уп. Выведите рекуррентную формулу
&п - °1®п-1 — ^2^п-2-
14. Используя предыдущую формулу, найдите
х5 + у5, хв + у6, х7 + у7.
15. Найдите серию целочисленных решений уравнения
х2 + у2 = z3.
16. Найдите серию целочисленных решений уравнения
х2 + у2 = z4.
17. Покажите некоммутативность произведения кватернионов.
18. Используя теорему Гаусса, докажите следующий критерий:
Разделить циркулем и линейкой окружность на п равных частей можно
тогда и только тогда, когда функция Эйлера ф (п) является степенью
числа 2.
Ответы и решения
АРИФМЕТИКА
„ 2а + (п -l)d
1. Сумма первой половины Sn =-----------— п, сумма второй половины
равна S2n — S„, откуда их разность S2n - 2Sn = n2d.
2. Как и в предыдущем случае, найдем разность Q2n ~ 2Qn> где Qn =
= ^(a2 + d(k- I)2 + 2ad (k - 1)) = n (a2 + d2 (n - 1) (2n - l)/6 + ad (n - 1)). Она
k = i
равна dn2 (2a + d (2n — 1)).
3. Из равенства a + a + d + ... + a + nd = a + (n + l)d+... + a + 2nd находим
a = n2d.
4. После преобразования получим (a - n (2n + 1) d) (a + nd) = 0; случай
a = -nd тривиальный, остается a = n (2n + 1) d.
5. От противного: пусть (x — n)3 + ... + (x - I)3 + x3 = (x + l)3 + ... + (x + n)3,
тогда x2 (x - 3 (n + 1) n) = —--—, чего не может быть: левая часть равенства
должна быть положительной, но тогда х > Зп (п + 1) и левая часть больше
9n2 (п + I)2.
6. Например, для чисел 6 и 28 имеем l = i+ X+ A,l = — + —+ i + i + i.
6 3 2 28 14 7 4 2
, г, - п(п + 1) п(п-1) .
7. Последнее число n-и группы равно —-------, а первое равно -----+ 1,
2 2 2
- = +1^П , откуда Si 4- S3 + ... + S2m - 1 =
следовательно, S,
п(п + 1 + п -1)
У (2k2 - 2k + 1) (2k - 1)
)2 2
4£й3-6уЛ2+4£/г_щ
т2 (т + I)2
/? = 1 /г = 1 /г = 1 /г = 1
— т (пг + 1) (2т + 1) + 2т (т + \) - т - т4.
8. Искомая сумма равна I3 + 23 + З3 + 43 + ... + (2n)3 - (23 + 43 + 63 + ... +
+ (2н)3) = S3 (2п) - 23S3 (п) = п2 (2п2 - 1).
9. Mk = 2k - 1 = 2к - 1 + 2* - 2 + ... + 2 + 1 = (1, ..., 1)2.
10. Очевидно, (2k)2 + (2т + I)2 = 4 (k2 + т2 - т) + 1 Ф 4п - 1.
11. Fm=42m- + 1, а четная степень четверки оканчивается цифрой 6.
12. х = 131 - 80, у = 601 - 368.
13. Произведение длин сторон кратно числу
П = 2pq (р2 - q2) (р2 + q2), а оно делится на 3, 4 и 5.
14. Из равенства S = Р следует
pq (Р2 ~ Q2) k2 = 2р (р + q) /гили q (р - q) k = 2.
Перебирая все варианты, найдем (6, 8, 10) и
(5, 12, 13).
15. Решая уравнение a2 + (a + d)2 = (а + 2d)2,
находим а = 3d; получаем тройку (3d, 4d, 5d).
16. По формуле Герона (рис. 39) имеем
Ч2 _ а + Ь + с а + b - с а + с - b Ь + с - а _
авс 2 2 2 2
_(а + Ь)2-с2 с2-(а-Ь)2
4 4
2
183
_ ab + z2 ab- z2 = (ab)2 - z4 _ f xy)2 + (xz)2 + ( уг\2
2 2 4 I2JI2JI2J'
17. В пифагоровом треугольнике длина одного из катетов — четное число,
следовательно, его
18. Площадь
площадь — целое число.
треугольника со сторонами х - 1, х, х + 1 равна
Поэтому х = 2а и а2 - 1 = 3d2, откуда х = 2а = (2 + V3 )л + (2 --Уз )”. Например,
(3, 4, 5), (13, 14, 15), (25, 26, 27).
19. Египетский треугольник, являясь героновым, не может быть получен
приложением двух пифагоровых. Легко показать, что тем же свойством обладает,
например, геронов треугольник (65, 119, 180).
20. В произведении п( = 1 2 • 3 ... • п через р шагов встречаются множите-
ли, делящиеся на р; их число равно
п
.Р
(квадратные скобки означают целую часть
п
.Р2 .
числа). Среди них имеется
множителей, делящихся на р2, и т. д. Итак, в ка-
ноническом разложении п! число р встретится а =
п + _п_
.pj Lp2
+ ... раз.
АЛГЕБРА
1 S S
У1+ V2 ’ V1-V2
2. 100 монет.
3. Целыми решениями могут быть лишь ±1, но они не удовлетворяют уравне-
нию.
4. Пусть w^cos^ + isin^, тогда (<вА)т = coj*"1. Так как <0j— корень
п п
уравнения хп = 1, то и ot>ikm тоже корень этого уравнения.
5. х = 'У 2 + 11г + 2 — 1 li; поскольку (2 ± г)3 = 2 + 11г, то х = (2 + г) + (2 - г) =
= 4. Из равенства (х - 4) (х2 + 4х + 1) = 0 находим два других корня: х2> 3 = -2 + 43.
6. После замены х = t + 2 уравнение примет вид t (t2 - 2) = 0, откуда Ц = 0,
t2 з = ±42; xj = 2, х2, 3 = 2 ± 42.
7. Пусть х = t + 4, тогда уравнение запишется так: i3 — 22t - 36 = 0, откуда
t = 318+10/ /19+з18_10 Я9 так как 18±10z^9=L1 m то
V 3V3V з V з з V з V v з }
t = (-1 - г /1?) + f-i + г /И 1 = -2 следовательно х. - 2 Остается решить уравне
ние х2 — 10х + 6 = 0; х2, з = 5 ± -/T9.
8. xj = 1 — корень уравнения, поэтому (х — 1) (х6 - 1) = 0, или
(х - 1) • (х2 - 1) (х4 + х + 1) = 0, откуда х2 3 = ±1, х4 5 = -1 ± i х6 7 = i ± i —.
2 2’22
9. а) Если бы х = 0 было корнем уравнения, то ап = 0, откуда а0 = ап = 0, че-
го не может быть, б) Пусть хд — корень уравнения; рассмотрим многочлен
( 1 V fl V"1 «0+ ajx0+ ... + anx"
fl 0 - 4- Al 4- ... 4- fl л = --------------.
xj
184
Так как xq * О, а уравнение возвратное, то дробь обращается в нуль, т. е. — ко-
*0
рень уравнения, в) Если степень уравнения нечетная, то число его коэффи-
циентов четное; подставив в левую часть уравнения число х= — 1, полу-
чим -ао + а1 - а2 + ... - ап _ 1 + ап = О, т. е. х = -1 — корень уравнения, г) Пусть
х = —1— корень уравнения Р (х) = 0, обозначим частное от деления Р (х) на
(х + 1) через Ь\хп _ 1 + Ь2Хп ~2 + ... + Ьп. Тогда (х + 1) (&jxn ” 1 + ... + Ьп) = bixn +
+ (bi + b2) хп " 1 + (Ь2 + Ьз) хп ~ 2 + ... + (Ьп _ 1 + Ъп) х + bn = Р (х). Из возвратности
Р (х) следует bi = Ьп, b2 = bn_ i, ... .
10. Если степень уравнения Р (х) = О нечетная, то х = -1 —его корень и
Р(х) _ „ „
уравнение —-—- = О вновь возвратное, но уже четной степени. Если xq — корень
х + 1
уравнения четной степени, то и -1- — его корень, следовательно, хо+ —------ко-
х0 *о
рень уравнения. Чтобы его найти, понижают степень 2т уравнения (деля все его
члены на х") и вводят подстановку t = х + —.
X
11. Группа S2 состоит из элементов е
. Очевидно, ае = еа.
и а
12. Это видно, например, из равенств
1 2 3U1 2 3)(1 2 3)
312JL213J Ц 3 2)
1 2 3V1 2 3> = fl 2 3)
2 1 зДз 1 2) U 2 1)'
13. S„ = X" + уп = (X + у) (Хл - 1 + уп - !) - Ху (хп~2 + уп~2) = G1S„ _ J - C2Sn _ 2.
14. S5 = <Д + 50102 (<*2 - of), S6= of -6ofo2 + 9o2o2-2o2,
S7=of - 7oio2(of-2of o2 + of).
15. Из равенства
(m2 + n2)3 = (| m + in |2)3 = | (m + in)3 |2 = | m3 + 3m2ni - 3mn2 - n3i |2 =
= (m3 - 3mn2)2 + (3m2n - n3)2
находим x = m3 - Зтп2, у = 3m2n - n3, z - m2 + n2.
16. Так как (m2 + n2)4 = | (m + in)4 |2 = | m4 + 4m3ni - 6m2n2 - 4mn3i + n4\2 =
= (zn4 - 6mV + zi4)2 + (4m3n - 4mn3)2, to x = m4 — 6mV + n4, у = 4m3n - 4mn3,
z = m2 + n2.
17. ij = (ij) (ijji) = (ij)2 (ji) = k2 (ji) = -ji.
18. Если окружность можно разделить на п равных частей, то по теореме Га-
усса п = 2mpiP2...pr, где pi, р2, ..., рг — различные простые числа Ферма. Так
как все сомножители взаимно простые, то ф (п) = ф (2т) ф (pi) • ... • ф (рг). Но
Ф (2т) = 2т~ 4, ф(22“ +1) = 22‘, поэтому ф (п) является степенью числа 2. Обратно:
пусть ф (п) = 2е. Если среди простых множителей числа п имеется нечетное число
qa, то ф (qa) = qa ~ 1 (q — 1). Правая часть является степенью числа 2 лишь при а = 1
и q = 2( + 1. Простым число q может быть только в случае t = 2s (см. с. 33). Таким
образом, если п имеет простые нечетные множители, то все они — различные чис-
ла Ферма в первой степени.
Литература
Болл У. Математические эссе и развлечения / У. Болл, Г. Кок-
сетер. — М.: Мир, 1974.
Болтянский В. Г. Пифагоровы тетраэдры / В. Г. Болтянский //
Квант. — 1986. — № 11. — С. 29—30.
Вайнтроб А. Ю. Доказательство гипотезы Морделла /
А. Ю. Вайнтроб, А. Б. Сосинский // Квант. — 1984. —
№ 3. — С. 19.
Ван дер Варден Б. Л. Пробуждающаяся наука / Б. Л. Ван
дер Варден. — М.: Физматгиз, 1959.
ВарпаховскийФ. П. О решении десятой проблемы Гиль-
берта / Ф. П. Варпаховский, А. Н. Колмогоров // Квант. —
1970. — № 7. — С. 38—44.
Вейль Г. Симметрия / Г. Вейль. — М.: Наука, 1968.
Виленкин Н. Я. За страницами учебника математики/
Н. Я. Виленкин, Л. П. Шибасов, 3. Ф. Шибасова. — М.: Про-
свещение, 1996.
Воробьев Н. Н. Числа Фибоначчи / Н. Н. Воробьев. — М.: На-
ука, 1984.
Гарднер М. Крестики-нолики / М. Гарднер. — М.: Мир, 1988.
Гарднер М. Математические головоломки и развлечения /
М. Гарднер. — М.: Мир, 1971.
Гарднер М. Математические досуги / М. Гарднер. — М.: Мир,
1972.
Гарднер М. Математические новеллы / М. Гарднер. — М.: Мир,
1974.
Гельфонд А. О. Решение уравнений в целых числах /
А. О. Гельфонд. — М.: Наука, 1983.
Гиндикин С. Г. Рассказы о физиках и математиках/
С. Г. Гиндикин. — М.: Наука, 1985. — Вып. 14. — (Биб-
лиотека «Квант»),
Глейзер Г. И. История математики в школе / Г. И. Глейзер. —
М.: Просвещение, 1981—1983.
Декарт Р. Геометрия / Р. Декарт. — М.; Л.: ГОНТИ, 1938.
Депман И. Я. История арифметики / И. Я. Депман. — М.: Про-
свещение, 1965.
Депман И. Я. За страницами учебника математики / И. Я. Деп-
ман, Н. Я. Виленкин. — М.: Просвещение, 1989.
Диофант. Арифметика / Диофант. — М.: Наука, 1974.
Евклид. Начала / Евклид. — М.: ОГИЗ, 1948—1950. — Т. 1—3.
Живые числа: пять экскурсий / В. Боро, Д. Цагир, Ю. Рольфе
и др. — М.: Мир, 1985.
Кантор И. Л. Гиперкомплексные числа / И. Л. Кантор, А. С. Со-
лодовников. — М.: Наука, 1973.
Клейн Ф. Элементарная математика с точки зрения высшей /
Ф. Клейн. — М.: Наука, 1987. — Т. 1—2.
Колосов А. А. Книга для внеклассного чтения по математике /
А. А. Колосов. — М.: Учпедгиз, 1963.
Курант Р. Что такое математика / Р. Курант, Г. Роббинс. —
М.: ОГИЗ, 1947.
186
Маркушевич А. И. Возвратные последовательности/
А. И. Маркушевич. — М.: Наука, 1983.
Никифоровский В. А. В мире уравнений / В. А. Никифо-
ровский. — М.: Наука, 1987.
Оре О. Приглашение в теорию чисел / О. Оре. — М.: Наука,
1980. — Вып. 3. — (Библиотека «Квант»).
Постников М. М. Теорема Ферма / М. М. Постников. — М.:
Наука, 1978.
Радемахер Г. Числа и фигуры / Г. Радемахер, О. Теплиц. —
М.: Наука, 1966.
Рыбников К. А. Возникновение и развитие математической
науки / К. А. Рыбников. — М.: Наука, 1987.
Савелов А. А. Плоские кривые / А. А. Савелов. — М.: Наука,
1960.
Фаермарк Д. С. Задача пришла с картины / Д. С. Фаермарк. —
М.: Наука, 1974.
Фомин С. В. Системы счисления / С. В. Фомин. — М.: Наука,
1987.
X и н ч и н А. Я. Три жемчужины теории чисел / А. Я. Хинчин. —
М.: Наука, 1979.
Хинчин А. Я. Цепные дроби / А. Я. Хинчин. — М.: Наука,
1978.
Чистяков В. Д. Старинные задачи по элементарной математи-
ке / В. Д. Чистяков. — Минск: Вышэйшая школа, 1978.
Шибасов Л. П. От единицы до бесконечности / Л. П. Шиба-
сов. — М.: Дрофа, 2006.
Юшкевич А. П. История математики в Средние века /
А. П. Юшкевич. — М.: Физматгиз, 1961.
Яглом И. М. Почти простые числа / И. М. Яглом // Квант. —
1981. — № 9. — С. 16—19.
Предметный указатель
Алгоритм 70
— Евклида 70
Аффинные преобразования 161
Бином Ньютона 24
Биномиальные коэффициенты 25
Близнецы 32
Булева алгебра 179
Варинга проблема 54
Виета формулы 138
Высказывание 178
Вычет 129
Гармоническое среднее 111
Геометрическая прогрессия 58
Гиперболический поворот 162
Гиперболическое расстояние 163
Гипотеза Гольдбаха 55
— Эйлера 55
Гномон 46
Группа 151
— абелева 153
— аддитивная 158
— Галуа 154
— знакопеременная 152
— мультипликативная 158
— симметрий 157
— симметрическая 151
— циклическая 152
Движения 159
— второго рода 160
— первого рода 160
Деление с остатком 69
Делители нуля 167
— собственные 39
Дизъюнкция 178
Диоризмы 117
Диофантов анализ 69
Диофантова геометрия 69
Дополнение множества 180
Дроби непрерывные 73
— подходящие 73
— систематические 10
— цепные 73
Индукция математическая 23
— неполная 23
Каноническое разложение 17
Кватернионы 168
Комплексное число 118
— —, алгебраическая форма 121
— —, аргумент 120
— —, главное значение аргумен-
та 121
— —, модуль 120
— —, сопряженное 118
— —, тригонометрическая форма 121
Конъюнкция 178
Координаты вектора 171
Корень многочлена 134
— первообразный 123
Крамера правило 176
Критерий 17
— Вильсона простоты числа 32, 130
— Галуа 154
— Гаусса 127
— Люка 41
Лежандра символ 131
Логарифм интегральный 37
— натуральный 37
Матрица вырожденная 173
— квадратная 173
— невырожденная 173
— прямоугольная 171
Метод бесконечного спуска 89
Минковского пространство 164
Многочлен знакопеременный 152
— симметрический 139
— элементарный симметрический 139
Множество 179
— пустое 180
Мультипликативность 21
Неопределенные уравнения 67
Неприводимый случай 115
Объединение множеств 180
Октавы 168
Операция восполнения 104
— противопоставления 104
Определитель матрицы 173
— системы 176
190
Основная теорема алгебры 133
— — арифметики 16
— — о симметрических многочле-
нах 139
Отрицание 178
Первообразное основание 30
Перенос 159
Пересечение множеств 180
Пифагоровы тройки 78
Поворот 159
Подгруппа 152
Подмножество 180
Позиционная система счисления 8
Последовательность вавилонская 82
— возвратная 59
— рекуррентная 59
Порядок группы 151
Приведенный остаток 14, 129
Примитивные тройки 78
Произведение векторное 169
— скалярное 169
Радикал 107
Резольвента 142
Решение уравнений в радикалах 141
Симплекс 51
Сравнение по модулю 129
Средняя плотность распределения
простых чисел 36
Степенные суммы 51, 139
Сумма делителей числа 18
Теорема Абеля 153
— Безу 134
— Гаусса 30
— Гольдбаха — Эйлера 34
— Дирихле 35
— Жермен 91
— Лагранжа 146, 153
— Паскаля 13
— Пифагора 77
— Ферма Великая 88
— — малая 27
Тетраэдр 48
Тождество Эйлера 22
Треугольник геронов 97
— египетский 79
Тройки пифагоровы 78
— примитивные 78
Уравнение возвратное 59, 142
— - Пелля 83
— характеристическое 59
Условие достаточное 15
— необходимое 15
Факториал 24
Ферма признак простоты числа 33
— частное 28
Формула Бине 60
— Муавра 119
Функция Мёбиуса 37
— рациональная 153
— Эйлера 21
Числа Бернулли 53
— боковые 65
— гиперкомплексные 168
— двойные 168
— диагональные 65
— дружественные 43
— дуальные 168
— квадратные 45
— Кэли 168
— Люка 41
— Мерсенна 41
— мнимые 118
— многоугольные 45
— общительные 44
— пирамидальные 49
— пятиугольные 45
— симплициальные 51
— совершенные 39
— тетраэдрические 48
— трансцендентные 165
— треугольные 45
— Ферма 33
— Фибоначчи 59
— фигурные 45
Число алгебраическое 164
— е 37
— простое 12
— составное 12
Элементы матрицы 171
Содержание
АРИФМЕТИКА
Глава 1. Натуральные
числа...................... 6
1. Системы счисления .... 7
2. Признаки делимости ... 12
3. Каноническое разложе-
ние ................... 16
4. Великий мастер индук-
ции ................... 19
5. Метод математической
индукции............ 22
6. Гениальный дилетант ... 25
7. Семейные проблемы ... 31
8. Генераторы простых чи-
сел..................33
9. Много ли простых чисел
в миллиарде?............35
10. Совершенные и дружест-
венные числа............39
11. Фигурные числа.........44
12. Шары в пространстве. . . 48
13. Степенные суммы.....51
14. Проблемы Варинга
и Гольдбаха.............54
15. Кролики, коровы
и телки................ 57
16. Великая тайна пифаго-
рейцев .................63
Глава 2. Диофантовы
уравнения..................66
1. В ответе только целые
числа................67
2. Алгоритм Евклида .... 69
3. Цепные дроби...... 72
4. Пифагоровы тройки. ... 77
5. Вокруг теоремы
Пифагора................80
6. Уравнение Пелля......82
7. Великая теорема
Ферма...................88
8. Обобщения...............94
Упражнения.................96
АЛГЕБРА
Глава 1. Наука о решении
уравнений...................100
1. Истоки алгебры.......—
2. Алгебра обретает
язык...................105
3. Седьмая операция.....109
4. Математический тур-
нир ....................112
5. Гибрид из мира идей. . . 117
6. Корни из единицы . . . .122
7. Математика или фило-
логия? .................123
8. Золотая теорема......129
9. Дама с собачкой......132
10. Целые корни.........136
11. Симметрия в алгебре . . .138
Глава 2. Зарождение совре-
менной алгебры..............141
1. В погоне за синей пти-
цей ....................141
2. Любимцы богов............147
3. Группа перестановок . . .150
4. Чем измеряют симмет-
рию ....................155
5. Группы в геометрии . . .159
6. Трансцендентные числа . 164
7. Случай на мосту..........166
8. Векторы..................169
9. Как решить систему . . .173
10. Алгебра Буля............177
Упражнения..................181
Ответы и решения........183
Литература..............186
Именной указатель.......188
Предметный указатель . . . .190
192
Н. АБЕЛЬ
(1802-1829)
Ж. ЛАГРАНЖ
(1736- 1813)
П. Л. ЧЕБЫШЕВ
(1821 - 1894)
И. М. ВИНОГРАДОВ
(1891 - 1983)
С. В. КОВАЛЕВСКАЯ
(1850- 1891)
Алгебра щедра. Зачастую она дает
больше, чем у нее спрашивают.
Ж. Даламбер
Природа говорит языком математики:
буквы этого языка - ... математические
фигуры.
Г. Галилей
В мире нет места для некрасивой
математики.
Г. Харди
Интересные исторические факты,
рассказы о крупных открытиях в области математики,
сведения из жизни ученых-математиков
содержат книги:
уб Н.Я. Виленкин, Л.П. Шибасов, З.Ф. Шибасова
За страницами учебника математики, 10 -11
Арифметика. Алгебра
Н.Я. Виленкин, Л.П. Шибасов, 3. Ф. Шибасова
За страницами учебника математики, 10 -11
Геометрия. Старинные и занимательные задачи
Л.П. Шибасов, З.Ф. Шибасова
За страницами учебника математики, 10 -11
Математический анализ. Теория вероятностей
ИЗДАТЕЛЬСТВО