Автор: Карпушина Н.
Теги: математика основы математики математическая логика математический анализ история науки исследования
Год: 2013
Текст
Занимательная математика:
гимнастика для ума или
искусство удивлять?
Н. М. Карпушина
В
Н
Е
Ф
О
Р
М
А
Т
А
ВНЕ ФОРМАТА
Н. М. Карпушина
Занимательная математика:
гимнастика для ума или искусство удивлять?
«НАУКА И ЖИЗНЬ»
Москва 2013
4
ББК 22.12
83.3
УДК 51-78
Ответственный редактор Е. Л. Лозовская
Макет, оформление обложки, верстка З. А. Флоринская
Корректор Ж. К. Борисова
На обложке — картина М. Эшера «Иной мир», 1947 г.
Н. М. Карпушина
ВНЕ ФОРМАТА
Занимательная математика: гимнастика для ума или искусство удивлять?
— М.: АНО Редакция журнала «Наука и жизнь», 2013. — 288 с.
Книга охватывает обширный круг вопросов: от малоизвестных стра-
ниц истории науки и биографий ее популяризаторов до увлекательных
исследований свойств чисел и фигур и применений математики на
практике. В ней наглядно показано, как законы математики проявля-
ются в природе, издавна используются в живописи и архитектуре, не
говоря уже о повседневной жизни. И все это разбавлено множеством
занимательных задач и головоломок — незаменимой пищей для ума,
без которой немыслимо ни одно издание подобного рода. Эта книга для
тех, кому не чужда математика, кто любит всякие загадки и интеллекту-
альные развлечения и не прочь побывать в роли исследователя.
Издано при финансовой поддержке Федерального агентства по печати
и массовым коммуникациям в рамках Федеральной целевой программы
«Культура России (2012—2018 годы)»
ISBN 978-5 -904129-07-1
© Н. М. Карпушина, текст, 2013
© АНО Редакция журнала «Наука и жизнь», 2013
© З. А. Флоринская, оформление, обложка, 2013
5
СОДЕРЖАНИЕ
Увлечь читателя математикой .......................................... 10
Неформально о главном.................................................. 12
ЧАСТЬ ПЕРВАЯ
Житейская математика
ГЛАВА 1. КАК МЫ ВИДИМ
Что такое угол зрения ..................................................... 14
Опыт с монетами ............................................................ 15
Почему рельсы сходятся ................................................. 16
Острый глаз ................................................................... 17
Под одним углом ............................................................ 18
Параллакс: знакомство с явлением ................................... 20
Вид из окна вагона ......................................................... 21
ГЛАВА 2. ОТ ТЕОРИИ — К ПРАКТИКЕ
Доверяй, но проверяй! .................................................. 23
Наука о видении одним глазом ........................................ 24
На службе у живописи .................................................... 26
Между небом и землей.................................................... 27
Простейшие угломеры .................................................... 29
Недоступные расстояния................................................. 31
В зрительном зале .......................................................... 33
ГЛАВА 3. НЕПОСТИЖИМЫЙ СЛУЧАЙ
Любимчики фортуны ...................................................... 35
Заветная шестерка ......................................................... 36
«Бесплатная» лотерея..................................................... 38
Народная игра ............................................................... 39
Непростительный промах ................................................ 40
Доводы рассудка ........................................................... 42
Словарик ....................................................................... 44
к
ГЛАВА 4. ВСЯКАЯ ВСЯЧИНА
Потеря времени ............................................................. 45
Все на праздник колбасы! ............................................... 46
Кофейное топливо ......................................................... 47
Расплата за лишний вес .................................................. 47
По закону золотого сечения? ........................................... 47
Бесполезная реклама ..................................................... 48
История одного долга ..................................................... 48
Размер крыла ................................................................ 49
Рекордсмен поневоле ..................................................... 49
Вода из воздуха ............................................................. 50
Карта-невидимка ........................................................... 50
Булочник-мошенник ....................................................... 50
Ответы........................................................................ 52
6
ЧАСТЬ ВТОРАЯ
Неожиданная математика
ГЛАВА 1. «ЕСТЬ ТАКОЙ ЗАКОН ПРИРОДЫ...»
Дельный совет от удава .................................................. 56
Надежная опора ............................................................ 57
Сколько ножек нужно столику? ........................................ 58
Полезные конструкции ................................................... 59
ГЛАВА 2. В ПОИСКАХ СЕМИЦВЕТИКА
Дивные творения природы .............................................. 61
Тrientalis, он же троичник, он же седмичник ...................... 62
Цветочные мотивы вокруг нас ......................................... 63
Геометрия орнамента ..................................................... 65
И все-таки он делится! ................................................... 66
ГЛАВА 3. СЕКРЕТЫ ДРЕВНИХ ЗОДЧИХ
Эффект иррадиации ....................................................... 69
Прямые или кривые? ...................................................... 71
Устойчивее и выше ........................................................ 72
По законам перспективы ................................................ 73
Оригинальные находки ................................................... 74
ГЛАВА 4. СТРАННОСТИ КАРТИН
Загадка Леонардо .......................................................... 76
Нереальные объекты ...................................................... 78
Нарушая соразмерность .................................................. 79
Стоит или падает? .......................................................... 80
Запрещенное изображение ............................................. 81
Два в одном .................................................................. 82
Ответ .......................................................................... 84
ЧАСТЬ ТРЕТЬЯ
Числа и фигуры
ГЛАВА 1. ВОЛШЕБСТВО И МАГИЯ В КВАДРАТЕ
Из глубины веков ........................................................... 86
В западном искусстве ..................................................... 89
В европейской науке ...................................................... 91
Вопросы, вопросы... ..................................................... 92
Проще простого ............................................................. 94
Нет предела совершенству! ............................................. 95
Делим на части .............................................................. 98
ГЛАВА 2. В КРУГЕ ФРАНКЛИНА
Из простых чисел ..........................................................100
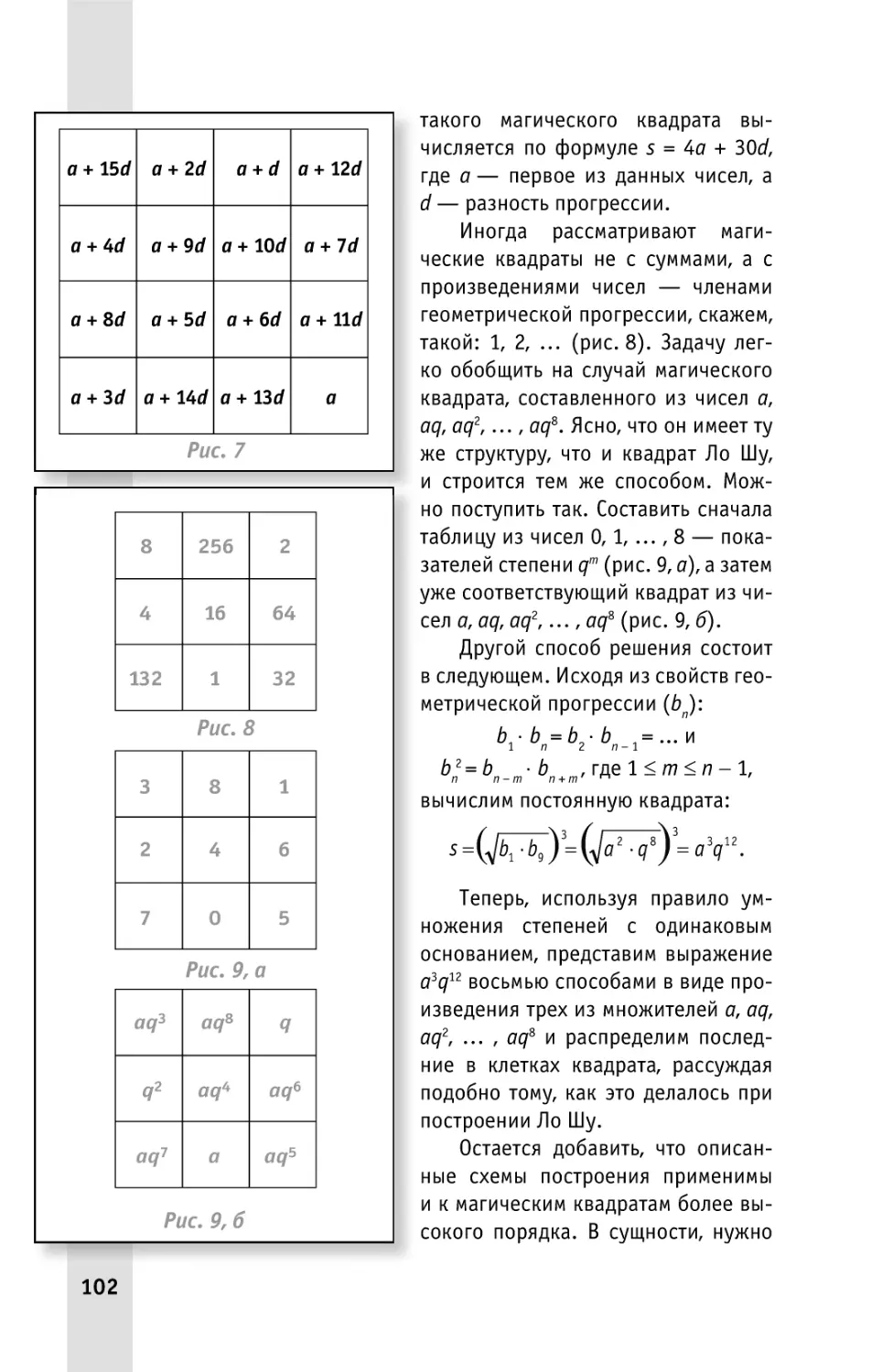
Прогрессии в квадрате ..................................................101
7
Занятные образцы .........................................................103
Двенадцать, сто восемьдесят, триста шестьдесят... ............105
От прямоугольника Нарайаны до куба Эйлера ...................108
В задачах и головоломках ..............................................110
Гимнастика для ума .......................................................112
Ответы.......................................................................114
ГЛАВА 3. ПАЛИНДРОМЫ И «ПЕРЕВЕРТЫШИ»
СРЕДИ ПРОСТЫХ ЧИСЕЛ
Задом наперед ..............................................................115
Игры цифр ...................................................................116
Примечательные пары ...................................................118
Числовой конструктор ...................................................119
Еще несколько фигур.....................................................121
ГЛАВА 4. ЗАМЕЧАТЕЛЬНЫЕ «СМИТЫ»
Невероятное везение профессора Смита ..........................124
Диковинки среди смитов................................................125
Заключенные в квадрат..................................................127
Продолжим эксперимент! ..............................................129
Такие простые закономерности... ...................................130
ГЛАВА 5. СООБЩЕСТВО РЕПЬЮНИТОВ
Увлечение Бернулли ......................................................132
Магия единицы .............................................................133
Вопросы делимости .......................................................134
Усложняем задачу .........................................................136
Закономерности разложения ..........................................137
Простота и периодичность .............................................139
Череда вопросов...........................................................140
Ответы.......................................................................142
ГЛАВА 6. ПОД ЗНАКОМ СИММЕТРИИ
Генератор палиндромов .................................................143
В игру вступают степени ................................................144
Семейство «12...n...21» .................................................145
Дальнейшие исследования .............................................147
Ответы.......................................................................149
ГЛАВА 7. ПОДЛИННАЯ ИСТОРИЯ ПАУКА И МУХИ
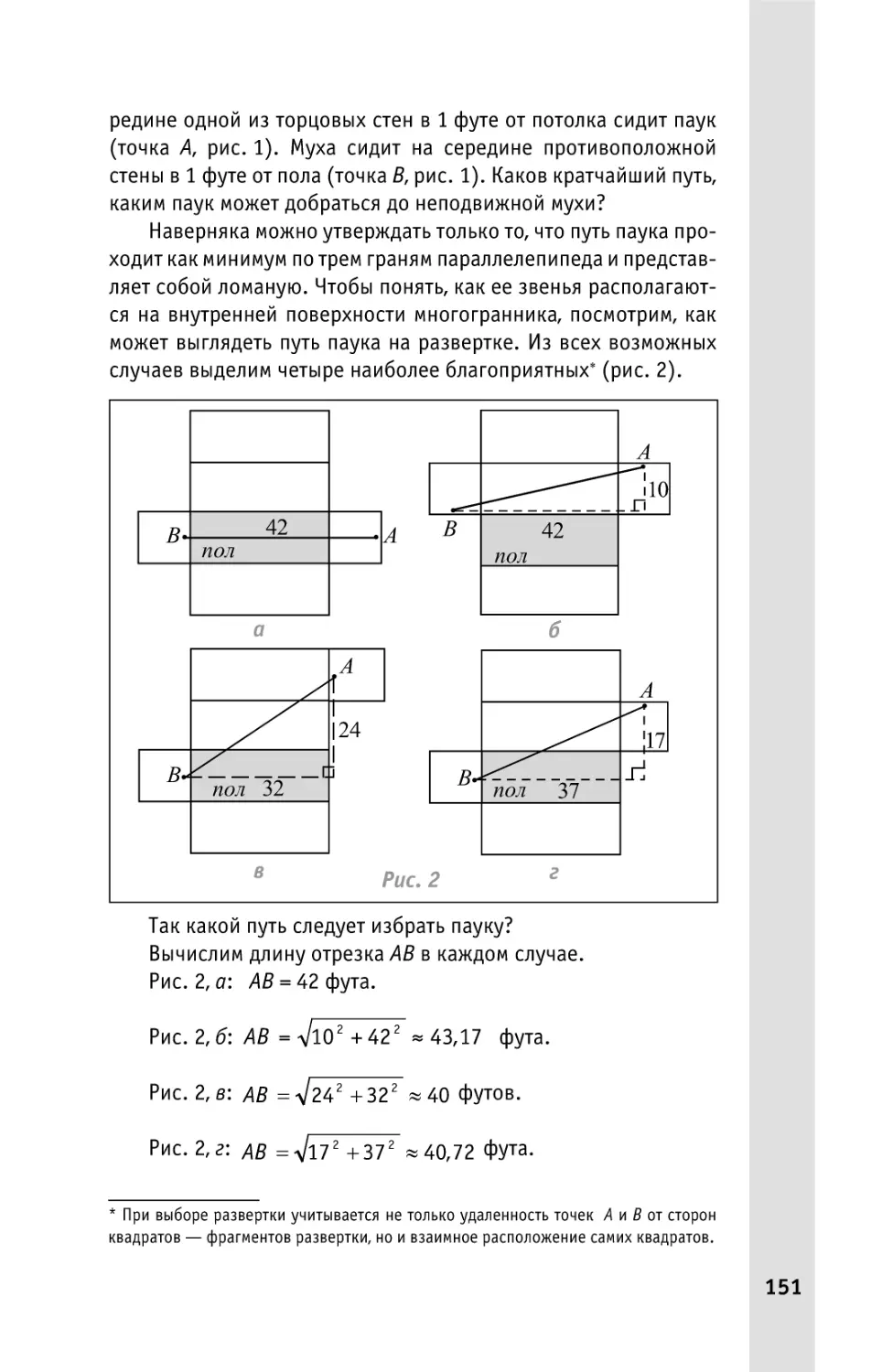
Внутри параллелепипеда................................................150
В стиле вольной интерпретации ......................................152
Из угла в угол ...............................................................153
Круговой путь ...............................................................155
Петля, дуга, окружность .................................................157
На цилиндрической поверхности ....................................159
Pourquoi pas? ...............................................................161
Ответы.......................................................................163
8
ЧАСТЬ ЧЕТВЕРТАЯ
Исторические зарисовки
ГЛАВА 1. РЕШЕТЧАТОЕ УМНОЖЕНИЕ
Наследие индусов .........................................................167
Как же он действует? .....................................................168
Палочки Непера ............................................................169
Машина Шиккарда.........................................................171
ГЛАВА 2. ВО ВЛАСТИ СЕЧЕНИЙ
Триада Менехма ..........................................................173
Поперек конуса ............................................................174
Древняя рогулька..........................................................175
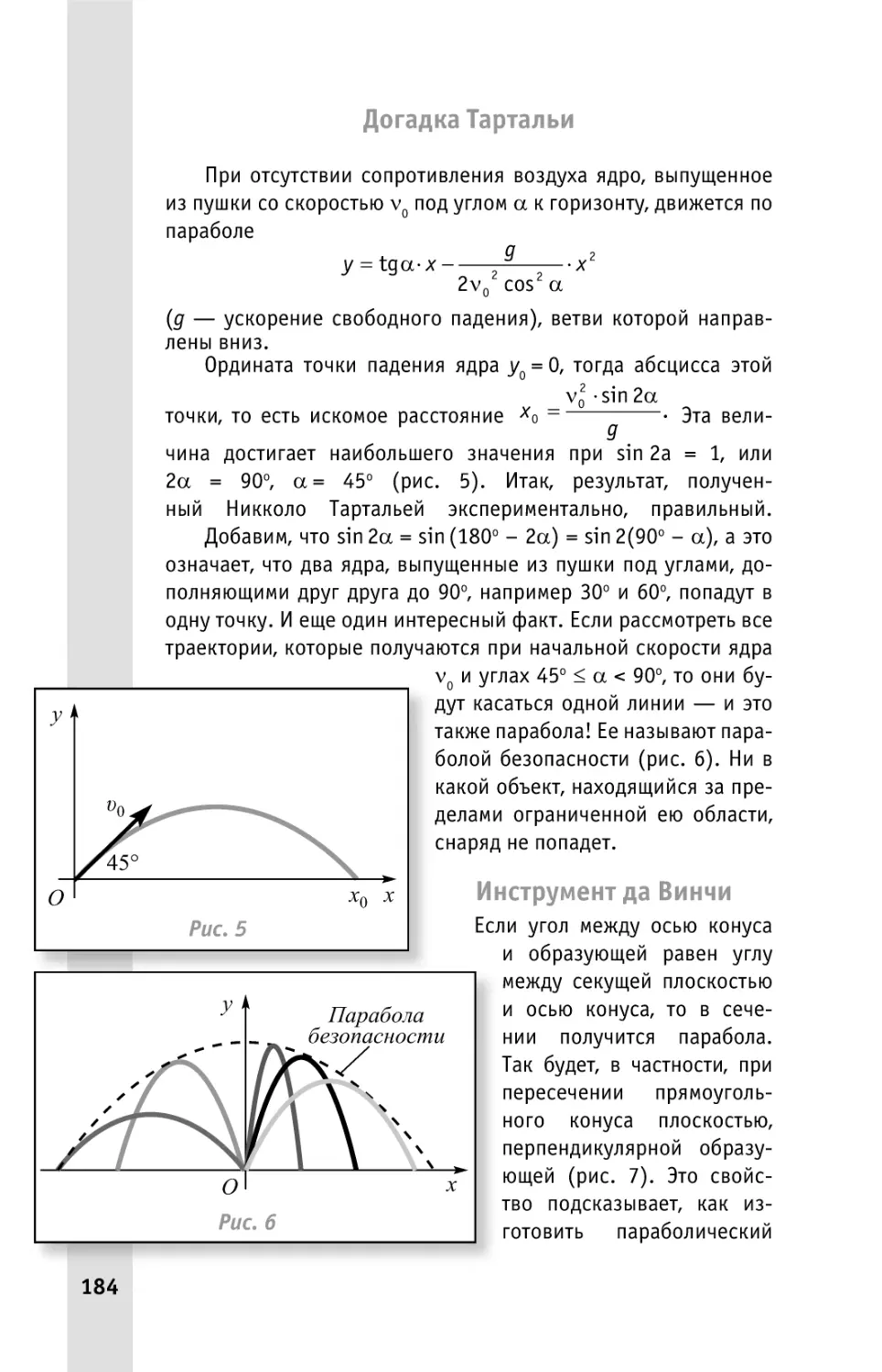
Догадка Тартальи ..........................................................176
Инструмент да Винчи .....................................................177
Стеклорез-циркуль ........................................................179
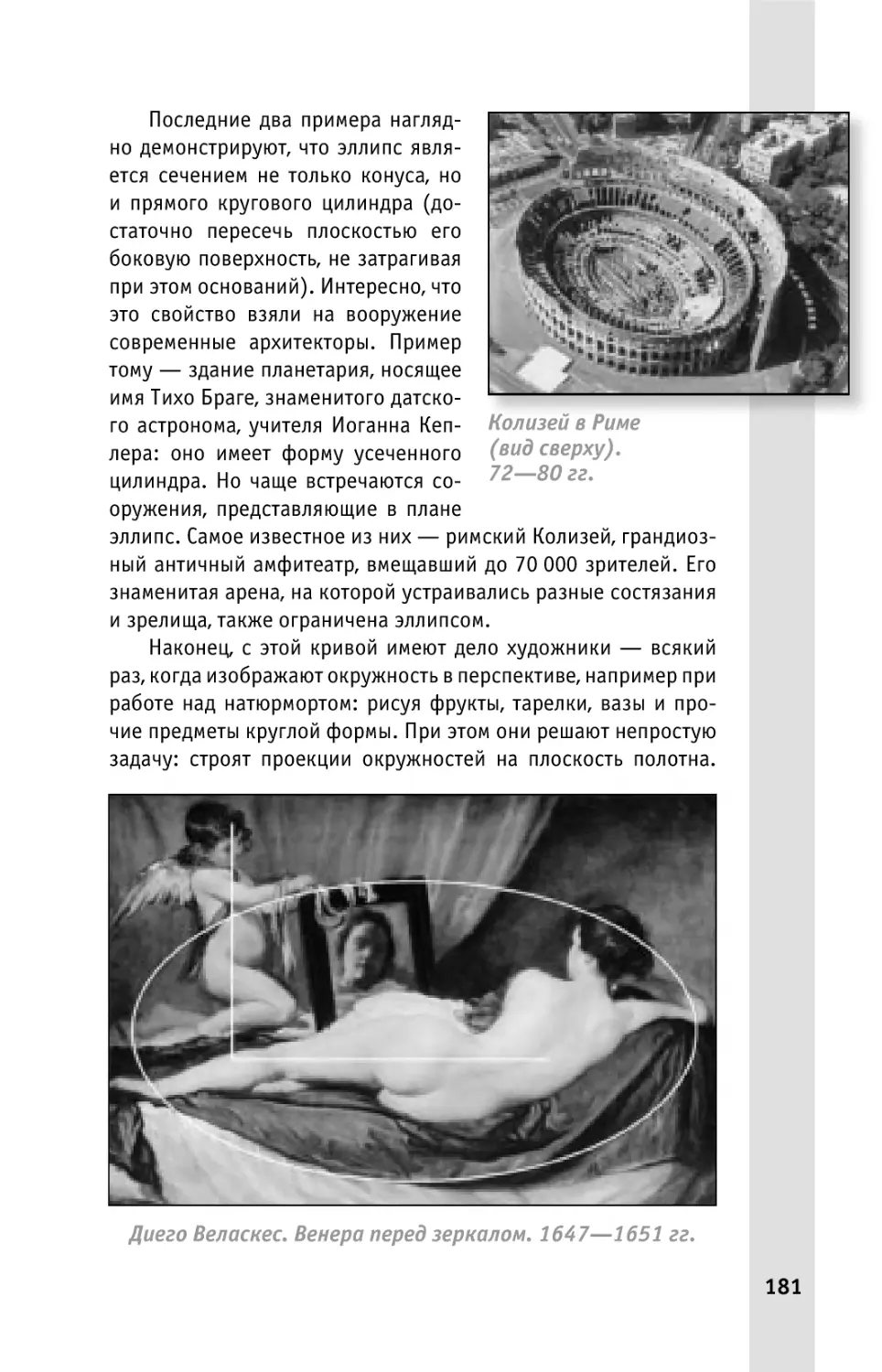
Вездесущий эллипс .......................................................180
Ответы.......................................................................183
ГЛАВА 3. ПОСТИГАЯ ЗАКОНЫ ВСЕЛЕННОЙ
Когда на помощь приходит геометрия ..............................187
Законодатель неба ........................................................189
Природа затмения .........................................................190
Первый гелиоцентрист...................................................192
Как Эратосфен измерил Землю........................................193
Далеко ли до Луны? .......................................................194
На фоне звезд ..............................................................195
Вечные спутники...........................................................196
ГЛАВА 4. LIBER АBACI
Книга-энциклопедия .....................................................198
Заслуги и достижения Леонардо Пизанского ....................200
Универсальный задачник ...............................................202
Знакомые задачи из трактата Фибоначчи..........................203
Опередивший время ......................................................210
ЧАСТЬ ПЯТАЯ
Творцы занимательной науки
ГЛАВА 1. ДАРОВИТЫЙ МИСТЕР ДОДЖСОН
Человек-загадка ...........................................................212
Родом из детства...........................................................213
В стенах Крайст-Черч ....................................................215
Поклонник эпистолярного жанра ....................................218
Из писем к детям...........................................................219
Раз задачка, два задачка... .............................................221
Талантливый фотограф и страстный театрал .....................222
9
Неутомимый выдумщик и изобретатель ............................224
Лингвист-экспериментатор.............................................226
Как превратить косу в бант? ...........................................229
ГЛАВА 2. ТАЛАНТЛИВЫЙ ПОПУЛЯРИЗАТОР КЭРРОЛЛ
О пище для ума .............................................................231
Как избавиться от праздных мыслей ................................233
Utile dulci! ...................................................................234
Математик и логик.........................................................237
Диаграммы и фишки ......................................................239
Задачи на силлогизмы ...................................................241
От диаграмм – к формулам .............................................241
ГЛАВА 3. ЯКОВ ПЕРЕЛЬМАН: ШТРИХИ К ПОРТРЕТУ
Проба пера...................................................................244
Я.П. и другие... ............................................................245
Благодарный ученик......................................................247
У истоков новых изданий ...............................................249
Сколько шкаликов в трех бочках? ....................................250
На ниве просвещения ....................................................251
В жанре занимательной науки ........................................253
За работу! ....................................................................255
В стенах ДЗН ................................................................257
Сколько весит кирпич?...................................................258
Фома неверующий.........................................................260
«Уважаемый профессор Перельман!» ..............................261
ГЛАВА 4. ТОТ САМЫЙ МАРТИН ГАРДНЕР
И это все о нем .............................................................265
Репортер, редактор, автор... ........................................266
...и ведущий раздела в научном журнале .........................266
Журналист, мыслитель, критик ........................................268
Корифей занимательной математики ...............................269
Секрет успеха ...............................................................270
Писатель и его читатель .................................................271
Математика и игра.........................................................272
Пять простых, но каверзных задач ...................................273
В знак благодарности ....................................................275
Десять зарисовок из жизни мастера ................................277
Ответы.......................................................................283
Именной указатель .......................................................284
Предметный указатель .................................................285
10
Увлечь читателя математикой
Математика — это поэзия на языке формул и логики. Ис-
следуя коллективное рациональное, она знакомит нас с красо-
той безупречных рассуждений и бесконечностью. Вот почему
многие математики — «очарованные странники» в фантас-
тическом и причудливом многомерном мире, в системе коор-
динат которого привычные «трехмерные» ценности не имеют
значения. Вот почему Григорий Перельман, доказавший гипо-
тезу Пуанкаре, отказался от награды в миллион долларов. Вот
почему другой известный математик — Дмитрий Меньшов так
рассказывал о рождении Московской математической школы:
«В 1914 году я поступил в Московский университет. В том году
Дмитрий Федорович Егоров и Николай Николаевич Лузин орга-
низовали семинарий для студентов, он был посвящен числовым
рядам. В 1915 году мы занимались функциональными рядами,
а в 1916 году — ортогональными рядами. А потом наступил
1917 год. Это был очень памятный год в нашей жизни, в этот год
произошло важнейшее событие, повлиявшее на всю дальней-
шую нашу жизнь: мы стали заниматься тригонометрическими
рядами». Похоже, он даже не заметил Первую мировую войну
и Октябрьскую революцию! В его жизни «тригонометрические
ряды» были гораздо важнее...
Увы, завороженных «царицей всех наук» становится все
меньше. И этому есть много причин, главная из которых — не-
хватка «проводников» в прекрасный сад математики, тех не-
многих, кто может увлечь неофита ее незримым совершенством,
то есть популяризаторов этой науки. Хороших педагогов-ма-
тематиков (а они тоже популяризаторы!) много меньше, чем
хороших математиков. И уж совсем немного тех, кто может
увлекательно писать о математике. Знаменитых математиков
сотни, знаменитых популяризаторов математики — единицы.
А ведь именно они воспитывают будущих Перельманов! Приве-
ду только один пример: Эндрю Уайлс, доказавший легендарную
теорему Ферма, увлекся ею в десятилетнем возрасте, прочитав
какую-то научно-популярную книжку. Именно тогда он поклял-
ся, что обязательно решит эту проблему.
Неудивительно, что талантливые популяризаторы матема-
тики появляются крайне редко. Тем ценнее каждое новое имя.
11
Одно из них, Наталья Карпушина, стоит на обложке этой заме-
чательной книги. Я давно знаю этого автора и всегда с удоволь-
ствием читаю описания ее увлекательных путешествий в мир
математики и математиков. Многие из них печатались в жур-
налах «Математика в школе» и «Математика для школьников»,
в редакции которых я имею честь состоять, а также в журнале
«Наука и жизнь». Поэтому я не понаслышке знаю, какой интерес
вызывают подобные материалы как у школьников, так и у пре-
подавателей. И это не удивительно. Описывать тысячу и один
способ решения тригонометрических уравнений могут многие,
увлечь же тригонометрией или любым другим разделом мате-
матики — лишь редкие счастливцы. У Натальи это получается!
Каждое ее математическое «приключение» — идет ли речь о
загадках Леонардо да Винчи или причудах Льюиса Кэрролла
— написано легко и в то же время подробно, со знанием дела.
Я, как и тысячи благодарных читателей, получил огромное
удовольствие от предыдущей книги автора «Любимые книги
глазами математика». Она была высоко оценена как специалис-
тами, так и рядовыми любителями научно-популярной литерату-
ры. Не сомневаюсь, что и новая книга Натальи Карпушиной бу-
дет иметь столь же счастливую судьбу, а сотни юных читателей,
быть может, благодаря ей полюбят математику на всю жизнь.
И, кто знает, возможно, кто-то из них решит очередную «про-
блему тысячелетия» и прославит отечественную науку.
Сергей Николаевич ФЕДИН,
заместитель главного редактора
журналов «Математика в школе»
и «Математика для школьников»,
кандидат физико-математических наук
12
НЕФОРМАЛЬНО О ГЛАВНОМ
В основу книги легли эссе, статьи и заметки для детей,
знакомых с математикой не понаслышке, и для взрослых, еще
не успевших позабыть эту науку. Для тех, кто неравнодушен к
математике, но и не обременен специальными знаниями, а по-
тому особо восприимчив к любым неожиданностям и вообще
ко всему новому. И конечно, для тех, кто любит всякого рода
загадки и головоломки и не отказался бы попробовать себя в
роли исследователя.
Многие затронутые в книге вопросы, попавшие однажды в
поле зрения, и для меня оказывались внове. Не раз приходи-
лось начинать работу буквально с чистого листа, не имея ника-
кого представления о конечном результате. Состояние неопре-
деленности рождало внутренний диалог в духе беседы Алисы с
Чеширским Котом.
«Скажите, пожалуйста, куда мне отсюда идти?
— А куда ты хочешь попасть?
— Мне все равно, только бы попасть куда-нибудь.
—
Куда-нибудь ты обязательно попадешь. Нужно только
достаточно долго идти».
Всякий раз, запасясь терпением и положившись на интуи-
цию, приходилось куда-нибудь идти — искать ответы на самые
разные вопросы. И если исходным пунктом всегда была мате-
матика, то конечный пункт был непредсказуем. Порой начатые
изыскания приводили к неожиданным находкам и открытиям.
Каждая глава, подобно пазлу, складывалась из множества раз-
розненных примеров, историй и зарисовок. И когда все части,
наконец, удавалось собрать воедино и обозреть картину цели-
ком, впору было удивиться: «Ай да математика! Ай да наука!
Неисповедимы пути твои!»
Книга охватывает обширный круг вопросов: от малоизвест-
ных страниц истории науки и биографий ее популяризаторов до
увлекательных исследований свойств чисел и фигур и примене-
ния математики на практике. И все это разбавлено множеством
занимательных задач и головоломок — незаменимой пищей
для ума, без которой немыслимо ни одно издание такого рода.
13
Всего в книге пять частей:
ЖИТЕЙСКАЯ МАТЕМАТИКА,
НЕОЖИДАННАЯ МАТЕМАТИКА,
ЧИСЛА И ФИГУРЫ,
ИСТОРИЧЕСКИЕ ЗАРИСОВКИ,
ТВОРЦЫ ЗАНИМАТЕЛЬНОЙ НАУКИ.
В первой, второй и четвертой частях основное внимание
уделено связям математики с разными областями знаний и
сферами деятельности. Мы оценим знакомые явления с точки
зрения математики, посмотрим, как ее законы проявляются в
природе, издавна используются в живописи и архитектуре, не
говоря уже о повседневной жизни, и конечно, обратимся к ис-
тории науки. Третья часть книги — «самая математическая»,
поскольку содержит больше всего оригинальных задач и ин-
теллектуальных развлечений, не требующих, однако, каких-то
особых познаний и доступных даже школьнику. Наконец, пятая
часть — дань уважения и признательности трем выдающимся
популяризаторам науки, представляющим разные эпохи и на-
правления в жанре занимательной математики: Льюису Кэр-
роллу, Якову Перельману и Мартину Гарднеру. Каждому из них
посвящена не одна публикация. Однако в большинстве своем
это лишь формальные жизнеописания. За их пределами оста-
лось, пожалуй, самое любопытное: круг интересов и увлечений
писателей (выходящий далеко за рамки науки и ее популяриза-
ции), их творческая кухня и малоизвестные житейские истории,
в которых все трое предстают перед нами, что называется, без
глянца. Восполним этот пробел хотя бы отчасти.
Как говорил один из героев Анатоля Франса, чтобы пере-
варить знания, надо поглощать их с аппетитом. Так пусть же
отменный умственный аппетит никогда не покидает тебя, чита-
тель!
Автор
14
ЧАСТЬ ПЕРВАЯ
Житейская математика
ГЛАВА 1
Как мы видим
—
Взгляни-ка на дорогу. Кого ты там видишь?
—
Никого, — сказала Алиса.
—
Мне бы такое зрение! — заметил Король с
завистью. — Увидеть Никого! Да еще на таком
расстоянии!
Л. Кэрролл. Алиса в Зазеркалье
Почему чтобы разглядеть детали висящей на стене
картины, мы подходим к ней ближе? Отчего устремляю-
щиеся вдаль рельсы кажутся пересекающимися в вообра-
жаемой точке? И можно ли разглядеть спичечную головку
с расстояния 10 м? Ответить на эти вопросы помогает
наука геометрия, проясняющая некоторые особенности
зрительного восприятия.
ЧТО ТАКОЕ УГОЛ ЗРЕНИЯ
Еще Евклид в сочинении «Оптика» говорил: мы видим пред-
мет, когда на него попадают исходящие из глаза и распростра-
няющиеся по прямым линиям лучи зрения. Они образуют «пира-
миду зрения» с вершиной в глазу и основанием на поверхности
рассматриваемого предмета. Среди множества всех касающихся
предмета лучей зрения выделяют два, которые проходят через
его крайние точки (как правило, это концы отрезка, являюще-
гося высотой). Они образуют угол, под которым предмет виден
целиком, — угол зрения (рис. 1). Как и всякий плоский угол, он
измеряется в градусах, минутах, секундах или в радианах.
По отношению к наблюдаемому объекту употребляют так-
же термин угловой размер. Так поступают, в частности, в аст-
15
рономии. Например, фраза «Угловой
размер Луны равен 0,5 » означает,
что под углом в полградуса земной
наблюдатель видит диаметр лунного
диска.
Рассматривая один и тот же
предмет из различных точек, мы ви-
дим его под разными углами. Иначе
говоря, угловой размер предмета оп-
ределен неоднозначно (в отличие от
линейных размеров: длины, ширины
и высоты). Его величина зависит от
удаленности предмета от глаза, в чем
легко убедиться экспериментально.
Угловой размер предмета определя-
ют при помощи специальных прибо-
ров. Например, в геодезии для изме-
рений на местности используют теодолит, а в астрономии для
нахождения высоты светил над горизонтом — секстант.
ОПЫТ С МОНЕТАМИ
Попробуйте сравнить на глаз видимый размер двух
одинаковых монет, удаленных от глаза на 50 см и на 1 м. Во
сколько раз вторая монета кажется меньше? Запомните ответ,
проверим его позже, а пока разберемся, почему чем дальше от
глаза находится предмет, тем меньше по размеру он кажется.
Физик объяснил бы это так: угол, под которым виден предмет,
уменьшается при его удалении от глаза, и изображение предме-
та на сетчатке занимает меньше места (рис. 2). Математика та-
кой ответ вряд ли устроит — его нужно обосновать. Почему же
уменьшается этот угол,
а вместе с ним и размер
изображения на сетчат-
ке?
ПустьАВиАС—изо-
С
бражения на сетчатке
Рис. 1
Рис. 2
B
C
h
h
L
S
Рис. 3
* Для простоты изложения поверхность сетчатки изображена плоской, а не сфери-
ческой и один из лучей зрения выбран так, что он перпендикулярен высоте пред-
мета.
16
предмета высотой h, удаленного от глаза на расстояния S и
SL
соответственно, тогда < и АВ < АС (рис. 3). Действительно,
С
поскольку
<
=
=
тоtg <tg,откуда
<
(так как мы имеем дело с острыми углами, а для малых углов
вообще можно считать tg = и tg = ) и, кроме того,
АВ<АС.
Вернемся к вопросу, с которого начали. И опыт, и рас-
суждения подсказывают, что углы, под которыми видны
монеты, а значит, и размеры изображений на сетчатке должны
отличаться, как и расстояния монет от глаза, в два раза. В самом
деле,еслиS=2
S L,то
=
Поэтому вторая монета кажется
вдвое меньше первой. Более того, при изменении расстояния в
другое число раз результат будет аналогичным, поскольку, как
мы убедились, величина угла зрения обратно пропорциональна
расстоянию до предмета.
От величины угла зрения зависит также, насколько деталь-
но можно рассмотреть предмет. Чем больше этот угол, тем круп-
нее изображение каждого фрагмента на сетчатке глаза, оно
«захватывает» все больше нервных окончаний, благодаря чему
мы начинаем различать в предмете подробности, которых не
видели раньше. Поэтому, чтобы разглядеть детали висящей на
стене картины или мелкий шрифт на странице книги, нужно уве-
личить угол зрения, подойдя к холсту ближе (приблизив текст
к глазам). А если предмет слишком мал, чтобы рассмотреть его
как следует невооруженным глазом, придется воспользоваться
лупой или другим оптическим прибором, который позволит уви-
деть его под бо́льшим углом.
о
ПОЧЕМУ РЕЛЬСЫ СХОДЯТСЯ
По мере удаления предмета от глаза мы сначала переста-
ем различать его детали, затем очертания, наконец, наступает
момент, когда предмет становится настолько мал, что воспри-
нимается как точка. Вспомните часто наблюдаемую зрительную
иллюзию: две «убегающие» вдаль параллельные линии, напри-
мер железнодорожные рельсы или края шоссе, кажутся сходя-
щимися в некоторой точке на горизонте. При этом сама точка
представляется нам бесконечно удаленной и недосягаемой.
Такое же впечатление создают ряды объектов, расположенных
17
по краям прямолинейной дороги: фонарные или телеграфные
столбы, деревья аллеи, опоры свода станции метро. Зрение
словно пытается убедить нас, что вопреки законам геометрии
параллельные прямые пересекаются.
Все дело в рассмотренной выше особенности зрительного
восприятия. Объект (шпала), находящийся на различных рас-
стояниях от наблюдателя, виден под разными углами зрения.
При удалении вдоль параллельных прямых (рельсов) его угло-
вой размер уменьшается, что приводит к видимому уменьшению
расстояния между линиями (оно определяется величиной шпа-
лы). Очевидно, когда угол зрения достигает некоторой «крити-
ческой» величины, глаз перестает различать удаляющийся объ-
ект как тело, имеющее размеры, и прямые «сливаются» для него
в одну точку. Иначе говоря, существует предельное значение
угла зрения — наименьшее значение, при котором глаз спосо-
бен видеть раздельно две точки.
ОСТРЫЙ ГЛАЗ
Так и есть. Для здорового глаза при нормальном освещении
это значение равно примерно 1 . Под таким углом с расстояния
1,7 м видна типографская точка диаметром всего 0,5 мм. А вот
разглядеть спичечную головку размером 2,5 мм с расстояния
18
10 м невозможно: угол зрения достигает предельного значения
уже на расстоянии 8,5 м.
Способность человеческого глаза различать две близко
расположенные точки называют остротой зрения. Ее опре-
деляют как отношение 1 к предельному значению угла зрения
испытуемого. Считается, что нормальная острота зрения равна
единице. Однако у некоторых людей она достигает 1,5—2 еди-
ниц и более. Они в буквальном смысле слова обладают острым
глазом и видят окружающий мир «дальше и глубже», чем обыч-
ный человек.
Отменным зрением могли бы похвастаться древние охотни-
ки и воины, основным оружием которых на протяжении многих
столетий был лук. Славой искусных лучников пользовались в
разное время древнеегипетские, скифские, русские, английские
воины. Известно, например, что последние с расстояния 100 м
могли попасть стрелой в стрелу с древком толщиной всего 1 см.
Только люди с очень острым зрением способны разглядеть на
таком расстоянии мишень столь малого диаметра.
Необычайно острым зрением обладали и тульские мастера
—
герои сказа Николая Лескова «Левша», подковавшие аглиц-
кую блоху. По легенде, мастера изготовили для блохи крошеч-
ные подковки и выбили на них свои имена. А особо отличился
Левша: он сделал к подковкам такие маленькие гвоздики, что
их и в микроскоп нельзя было разглядеть. И, кстати, именно ос-
тротой зрения Алисы, увидевшей на дороге Никого, восхитился
Белый Король.
ПОД ОДНИМ УГЛОМ
На практике приходится сравнивать относительные разме-
ры сразу нескольких находящихся в поле зрения предметов.
Если последние удалены от глаза на одно и то же расстояние
и расположены достаточно близко друг от друга, их сравнить
легко. В этом случае мы редко ошибаемся в своей оценке: более
высокий предмет виден под бо’ льшим углом, поэтому и кажется
выше.Всамомделе,еслиH>h,тоtg <tg, <
(рис. 4).
Сложнее провести подобную оценку, когда предметы находятся
на различных расстояниях от глаза.
Часто можно наблюдать под одним и тем же углом зрения
предметы разного размера (рис. 5). В этот момент их видимые
размеры кажутся одинаковыми, в чем легко убедиться на
19
простом опыте. Если выстроить
по росту несколько матрешек и
смотреть на них со стороны самой
маленькой фигурки, а затем начать
медленно отходить назад, не
изменяя направления взгляда, то
можно наблюдать, как матрешки
будут постепенно
«сливаться»,
загораживая одна другую. Наконец,
на некотором расстоянии будет
видна только одна из них — та, что
расположена ближе остальных. Если
теперь сместить фигурки в стороны
так, чтобы все они были полностью
видны, матрешки будут казаться
одного размера.
Аналогичный
опыт
легко
провести с любыми имеющимися под рукой предметами
(наибольшего визуального эффекта удастся достичь, если взять
предметы одинаковой формы, скажем, спичку и карандаш или
орех и апельсин). Тогда достаточно сравнить их линейные
размеры. Результат будет таким же.
Похожее явление можно наблюдать и в природе. Так, во
время полного солнечного затмения Луна целиком закрывает
собой Солнце, и размеры их кажутся одинаковыми, поскольку
оба тела видны с Земли под одним углом. Случается подобное
и с некоторыми двойными звездами. Если плоскости орбит
входящих в их состав звезд проходят через нашу планету, то
при «полном затмении» главной звезды менее ярким спутником
они обе оказываются видны земному наблюдателю под одним
углом. Правда, последний настолько мал, что даже в самые
мощные телескопы нельзя разглядеть звезды в форме дисков,
как мы видим ту же Луну или Солнце. Поэтому о наступлении
«полного звездного затмения» можно судить по уменьшению
блеска (видимой яркости) звезды, которая в этот момент словно
игриво подмигивает нам.
Во всех рассмотренных примерах мы имеем дело с подоб-
ными фигурами либо соответствующими отрезками (высотами,
диаметрами) различных по форме фигур. Поэтому можно ут-
верждать, что если два предмета видны под одним углом зре-
ния, то их линейные размеры отличаются во столько же раз, во
H
h
L
Рис. 4
Рис. 5
20
сколько раз отличаются расстояния
до предметов (рис. 6):
.
=
Это равенство позволяет не
только сравнить расстояния, а
также относительные размеры двух
объектов, наблюдаемых под одним
углом зрения, но и найти любую из
входящих в него величин по трем
остальным.
ПАРАЛЛАКС: ЗНАКОМСТВО С ЯВЛЕНИЕМ
Возьмите карандаш и держите его перед собой на вытя-
нутой руке. Посмотрите на него сначала правым, потом левым
глазом. Что вы заметили? Теперь отодвиньте руку немного в
сторону и, продолжая удерживать ее в поле зрения, повторите
опыт, попеременно закрывая то один, то другой глаз. Опять тот
же эффект? Карандаш словно перескакивает с одного места на
другое! Почему?
Это явление поясняет рис. 7, на котором точки L и P обоз-
начают зрачки глаз, а точки В и С — видимые положения конца
С
карандаша: при изменении точки наблюдения (сначала была Р,
затем стала L) изменяется видимое положение рассматривае-
мого объекта (с В на С), что и приводит к эффекту перескаки-
СС
вания.
Видимое изменение положения предмета вследствие пере-
мещения глаза наблюдателя из точки А в точку В называется па-
раллактическим смещением, или просто параллаксом (от греч.
parаllaxis — отклоне-
ние), а длина отрезка
АВ — его базисом.
Параллакс характе-
ризуется величиной
угла между лучами
зрения, направлен-
ными на предмет из
точек А и В (рис. 8).
Если в качестве бази-
са выбрано расстоя-
ние между зрачками
BC
••
••
LP
Рис. 8
Рис. 7
H
h
l
L
Рис. 6
21
глаз человека, говорят о параллаксе зрения, имея в виду разли-
чие в восприятии предмета левым и правым глазом.
ВИД ИЗ ОКНА ВАГОНА
Как вычислить угол ? Представьте, что, сидя в поезде, вы
движетесь из точки А в точку В и наблюдаете из окна вагона
за некоторым объектом, например за домом, расположенным на
пригорке в точке С. Дом виден из точек А и В под углами и
к направлению движения (см. рис. 8). Углы АСВ и равны как
вертикальные, а из теоремы о внешнем угле треугольника сле-
дует, что АСВ =
, откуда =
.
Какими свойствами обладает параллакс? Иначе говоря,
от чего зависит величина угла ? Попробуем ответить на воп-
рос, продолжив наше воображаемое путешествие. Из окна
вагона видно множество объектов,
удаленных от поезда на различные
расстояния. Кажется, что предметы
перемещаются с разными скоростя-
ми (на самом деле, конечно, это мы
проносимся мимо них), и чем дальше
находится предмет, тем медленнее
он «движется». Почему?
Рис. 9 иллюстрирует, как для
одного и того же базиса АВ при из-
менении положения луча зрения, на-
правленного из точки А на объекты
Си
С D, изменяется соответствующий
угол между направлением движения
и лучом зрения, выходящим уже из
точкиВ.Таккак 2<
1
,то2<
1
,то
есть параллактическое смещение бо-
лее удаленного объекта меньше.
Еще ярче проявляется обнару-
женная закономерность при наблю-
дении за проплывающим над голо-
вой облаком или за солнцем — оно
кажется словно застывшим на небе.
Итак, чем дальше от движущегося
наблюдателя находится предмет,
тем меньше его параллакс, то есть
2
C
1
2
1
2
1
2
D
1
2
1
Рис. 9
Рис. 10
22
видимое перемещение в пространстве. Таким образом, парал-
лакс является важным показателем удаленности предметов,
поэтому он широко используется в геодезии и астрономии для
измерения недоступных расстояний.
Разберемся, как влияет на параллактическое смещение
увеличение длины базиса. Из рис. 10 ясно: если АВ2 > АВ
1
,то
2
1
, поэтому 2
1
. Таким образом, при увеличении базиса
параллакс увеличивается. Это приводит к тому, что видимые ка-
кое-то время объекты «выпадают» из поля зрения движущегося
наблюдателя, а их место занимают новые.
А теперь попробуйте ответить на такие вопросы. Можно ли
утверждать, что любые два объекта, расположенные на прямой,
параллельной базису АВ, имеют одинаковый параллакс? Если
смотреть одним глазом на вытянутый перед собой палец руки,
медленно поворачивая при этом голову из стороны в сторону,
то можно заметить, что палец перемещается в противополож-
ном движению головы направлении относительно фона удален-
ных предметов. Как вы это объясните?
Мы обсудили лишь некоторые особенности восприятия гла-
зом окружающего мира и дали им геометрическое толкование,
ограничившись примерами из повседневной жизни. Между тем
закономерности зрения издавна широко используются на прак-
тике. Об этом расскажем подробнее дальше.
23
ГЛАВА 2
От теории — к практике
—
Все страньше и страньше! — воскликнула
Алиса. От изумления она совсем забыла, как нужно
говорить.
Л. Кэрролл. Алиса в Стране чудес
Мы раскрыли лишь несколько секретов зрения и изложили
«теорию вопроса» с точки зрения геометрии. Но даже этих
знаний вполне хватит как для объяснения многих наблю-
даемых явлений и оптических иллюзий, так и для решения
самых разных задач, связанных с понятием угла зрения.
ДОВЕРЯЙ, НО ПРОВЕРЯЙ!
С давних пор человек не только поражался обманам зрения,
но и сознательно прибегал к некоторым из них в своей деятель-
ности. Немало примеров тому имеется в искусстве — архитек-
туре и живописи. Большой интерес к оптическим иллюзиям
проявляли в разное время и представители естественных наук,
в частности физики и астрономы, которых всегда волновала
надежность визуальных наблюдений. Сами ученые создали не-
мало обманчивых картинок, наглядно демонстрирующих, сколь
ограничены возможности человеческого глаза.
Вот несколько классических образцов зрительных иллюзий,
связанных с геометрическими фигурами. Взгляните на Т-образ-
ную фигуру (рис. 1), состоящую из двух отрезков. Сравните их
на глаз. Вам кажется, что вертикальный отрезок длиннее гори-
Подробнее об этом см. в главе «Секреты древних зодчих» второй части книги.
Рис. 1
Рис. 2
Рис. 3
24
зонтального? На самом деле они равны, в чем легко убедить-
ся, воспользовавшись циркулем или линейкой. А что скажете о
длинах диагоналей параллелограммов (рис. 2)?
Приведем пример зрительной иллюзии другого рода. Перед
вами изображение каркаса куба (рис. 3). С какой стороны вы
смотрите на фигуру: сверху или снизу? А может быть, сбоку?
При длительном наблюдении происходит удивительная транс-
формация: кажется, что грани куба все время меняют свое по-
ложение! При этом взгляд фиксируется то на одной, то на дру-
гой грани.
Причины одних зрительных иллюзий давно установлены,
других — до конца не выяснены до сих пор. Так, на восприятие
длины и кривизны линий значительное влияние оказывают их
положение, размеры фигур, в которые они включены, и наличие
прилегающих или пересекающих линий. Например, длину го-
ризонтального отрезка глаз всегда оценивает точнее, чем вер-
тикального, который выглядит больше, чем есть на самом деле.
При визуальном сравнении диагоналей параллелограммов на
рис. 2 кажется, что у левого параллелограмма диагональ коро-
че, хотя она такая же, как у правого. В данном случае свойство
всей фигуры мы ошибочно переносим на ее элемент.
Иллюзия с кубом имеет иное объяснение. Дело в том, что
любое изображение может быть истолковано по-разному, одна-
ко зрительная система человека отдает предпочтение наиболее
привычной и вероятной интерпретации. Для данного изобра-
жения куба равновероятны сразу несколько таких интерпрета-
ций, поскольку оно не содержит точных признаков того, какие
точки находятся ближе (выше) других. Поэтому наша зритель-
ная система и колеблется в выборе решения: видимые образы
периодически сменяют друг друга.
Вспомните, как обычно избавляются от этой зрительной
иллюзии и добиваются однозначности в восприятии рисунка
куба. Невидимые ребра, то есть те из более удаленных ребер,
что заслонены от взгляда передней гранью куба, выделяют осо-
бо — пунктиром, тем самым придавая изображению глубину.
НАУКА О ВИДЕНИИ ОДНИМ ГЛАЗОМ
Вопросы изображения на плоскости пространственных фи-
гур с давних пор волновали не только геометров, но и художни-
ков, стремившихся научиться рисовать трехмерные объекты на
25
двумерном холсте. Как писал Леонардо да Винчи (1452—1519),
«первое намерение живописца сделать так, чтобы плоская по-
верхность показывала тело рельефным и отделяющимся от этой
плоскости».
Художники хотели вызвать у зрителя ощущение пространс-
тва, находящегося за плоскостью картины. Последняя должна
была играть роль своеобразного окна, в котором окружающий
мир представал бы таким, каким мы его видим сквозь прозрач-
ное стекло. Для этого необходимо было найти метод изображе-
ния объемных тел, который не только отражал бы их структуру
и взаимное расположение в пространстве, в том числе удален-
ность от наблюдателя, но и учитывал бы механизмы работы че-
ловеческого глаза. Таким методом стала линейная перспектива
(от лат. perspicio — ясно вижу), которую иногда справедливо
называют наукой о ви’ дении одним глазом.
Разработанная в соответствии с особенностями зритель-
ного восприятия, линейная перспектива позволяет изобра-
зить видимый предмет наиболее реалистично. При взгляде на
картины, написанные по ее законам, возникает ощущение, что
рассматриваешь трехмерную сцену. Как же создается столь по-
разительная иллюзия пространства? Вспомним: чем дальше от
глаза находится предмет, тем меньше он кажется. Учитывая эту
особенность зрения, художник рисует на заднем плане предме-
ты и человеческие фигуры меньшего размера, чем на переднем,
создавая впечатление их разной удаленности и добиваясь тем
самым глубины изображения. Визуальный эффект усиливают
сходящиеся в воображаемой точке параллельные линии.
Перспектива рассчитана на фиксированную точку зрения,
поэтому, чтобы полнее ощутить ее действие, следует рассмат-
ривать картину с определенной позиции. Причем одним глазом,
который, как советовал зрителю Леонардо да Винчи, должен
находиться на таком же расстоянии от полотна, той же высоте и
смотреть в том же направлении, что выбрал для себя художник,
делая набросок.
А вот самому художнику, желающему видеть, насколько его
картина соответствует предмету, срисованному с натуры, Леонар-
до рекомендовал сравнивать изображение на холсте с отражени-
ем предмета в зеркале, поскольку последнее «содержит в себе
истинную [объемную, трехмерную] картину на [плоской] повер-
хности; и совершенная картина, исполненная на поверхности ка-
кой-либо плоской материи, подобна поверхности зеркала».
26
Также Леонардо описал перспектограф — приспособление
для построения перспективного изображения предметов и лю-
дей, позже получившее известность благодаря гравюрам Дюре-
ра. На стекле с квадратной сеткой художник вычерчивал види-
мый образ (разделенный на фрагменты), чтобы затем перенести
его на разграфленную бумагу; при этом дополнительно он мог
использовать окулярную шкалу, как в оптическом приборе.
НА СЛУЖБЕ У ЖИВОПИСИ
С точки зрения геометрии линейная перспектива — это
способ изображения фигур, основанный на применении цен-
трального проектирования. Рассмотрим задачу на построение
перспективного изображения, или центральной проекции,
фигуры (от лат. projectio — бросание вперед). Пусть выбра-
на плоскость проекций , на которой строится изображение, и
задан центр проекции — точка О, ей не принадлежащая. Тогда
произвольная точка М фигуры будет проецироваться в точку М’
А. Дюрер. Перспектограф. 1525 г.
27
пересечения прямой ОМ с плоскостью . Ясно, что при разных
положениях плоскости
получатся различные изображения
одной и той же фигуры.
В живописи плоскость проекций (полотно картины) обычно
находится между центром проекции (глазом художника) и объ-
ектом, так что точка М’ оказывается между точками
’
ОиМ.При
этом плоскость перпендикулярна предметной плоскости , на
которой располагаются изображаемые объекты.
Итак, каждому художнику, пишущему в реалистической ма-
нере, приходится решать геометрическую задачу на построение
центральной проекции объектов
на картинную плоскость. Очевид-
но, что точки основания картины
(лежащие на линии пересечения
плоскостей и ) проецируются в
себя. На рис. 4 показано, как по-
лучается изображение произволь-
ной точки М плоскости (цифры
1—4 указывают порядок проведе-
ния прямых).
Если точка К не лежит в пред-
К
метной плоскости, то сначала из
нее опускают перпендикуляр на
(отрезок КМ на рис. 4), затем для
его основания выполняют постро-
ения 1—3. Наконец, проводят прямую КО, пересечение которой
с плоскостью и есть изображение точки К.
Вообще, построение центральной проекции фигуры — за -
дача не простая. Она рассматривается в одном из разделов при-
кладной математики — начертательной геометрии, изучающей
пространственные фигуры при помощи построения их изобра-
жений на плоскости проекций. Начертательная геометрия ши-
роко применяется в инженерном деле, строительной практике,
в архитектуре и живописи.
МЕЖДУ НЕБОМ И ЗЕМЛЕЙ
Находясь на открытом пространстве, на равнине или в море,
можно наблюдать вокруг доступную взору часть земной повер-
хности. Ее граница — линия, визуально разделяющая небо и
землю, называется видимым горизонтом. Всякий раз при по-
Рис. 4
28
пытке приблизиться к ней в
любом направлении, линия
перемещается вместе с нами,
оставаясь недосягаемой. Что
это: еще одна зрительная ил-
люзия?
На этот раз нет. Линия
горизонта не только сущес-
твует, но и имеет вполне оп-
ределенную форму и длину.
Из-за ограниченности поля
зрения взору доступна лишь
ее небольшая часть, которую
глаз воспринимает как пря-
мую. На самом деле эта линия
—
замкнутая кривая. Она состоит из точек касания выходящих
из глаза в разных направлениях лучей зрения с земной поверх-
ностью, а все такие точки образуют окружность (рис. 5).
А вот то, что линия горизонта находится на уровне глаз
—
на высоте h, нам только кажется, она всегда расположена
ниже. Обман зрения объясняется тем, что рост человека нич-
тожно мал по сравнению с размером видимого участка земли,
который можно считать плоским. Поэтому угол между лучами
зрения, один из которых параллелен плоскости земли, а другой
ее касается (см. рис. 5), столь мал, что неуловим для глаза.
Желая обозреть окрестности, мы взбираемся на близлежа-
щий холм или горку, уверенные, что оттуда дальше видно. Так и
есть, но почему? Этому имеется простое геометрическое объяс-
нение. Дальность видимого горизонта, то есть расстояние d от
d
глаза до линии горизонта, можно вычислить по теореме Пифа-
гора:
+
=
+
=
Поскольку высота h чрезвычайно мала по сравнению с ра-
диусом Земли — R, слагаемым h2 можно пренебречь и считать
=
Отсюда следует, что чем выше над землей расположена
точка наблюдения, тем дальше и больше вокруг из нее видно.
В частности, значение d зависит от роста. Например, если Гул-
d
ливер мог видеть окружающую территорию в радиусе 3 миль, то
Рис. 5
29
перед жителями Лилипутии и Бробдингнега она простиралась
в радиусе 0,9 мили и 10,4 мили соответственно. В реальности
разница, конечно, не столь велика и заметна глазу.
Полученная формула позволяет не только оценивать даль-
ность горизонта , но и судить о том, какая величина растет быс-
трее и насколько: h или d. С увеличением высоты подъема в k
раз дальность горизонта увеличивается в k раз, что гораздо
k
медленнее, чем может показаться поначалу. Так, если h станет
больше в два раза, то d увеличится почти наполовину, а если
d
h
возрастет в сто раз, то d — только в десять.
d
Интересно, что просчет в оценке расстояния вызван не обма-
ном зрения, а интуицией. Она же является причиной другой рас-
пространенной ошибки: большинству людей кажется, что площадь
круга, ограниченного линией горизонта, измеряется сотнями, а то
и тысячами квадратных километров. Однако это не так. Для стоя-
щего на равнине человека среднего роста площадь обозреваемо-
го участка земли составляет примерно 70 км2
. Ивтомивдругом
случае доверять следует, конечно, математическим расчетам.
ПРОСТЕЙШИЕ УГЛОМЕРЫ
Обратимся теперь к астрономическим наблюдениям.
В древности высоту небесных светил (угол между направлени-
ем на светило и плоскостью истинного горизонта) и угловые
расстояния (углы между любыми двумя видимыми объектами)
определяли при помощи примитивных инструментов, принцип
действия которых основан на понятии угла зрения.
Один таких инструментов — посох Якова, предшественник
современного секстанта. Он состоял из стержня и скользящей по
нему поперечной рейки. На стержень были нанесены деления,
которые соответствовали разным углам (для разметки требовал-
ся транспортир). Наблюдатель подносил один конец посоха к
глазу, другой направлял в сторону светила и затем перемещал
рейку до тех пор, пока два ее конца не касались линии горизон-
та и светила (рис. 6), после чего оставалось «снять показания»
— посмотреть, какому делению на стержне соответствует рейка.
Посох Якова легко сделать своими руками, он вполне годится
для приближенного измерения углов в любой плоскости.
* Расчет делается чисто геометрический, не учитывающий физических факторов,
которые на практике могут по-разному влиять на дальность видимого горизонта.
30
Еще проще изготовить инструмент, при помощи которого ин-
женер Сайрес Смит, герой романа Жюля Верна «Таинственный
остров», нашел высоту звезды Альфа Южного Креста. Достаточ-
но взять две планки и скрепить их концы с одной стороны. По-
лучится конструкция вроде циркуля с раздвижными ножками.
Направив одну ножку на горизонт, а другую на светило, легко
определить нужный угол. Зафиксируем его (для чего прикре-
пим к двум планкам третью, поперечную) и измерим транспор-
тиром. Задача решена.
Оценить угловое расстояние можно вообще без каких-либо
приспособлений. Угломером послужит кисть руки, если, ко-
нечно, знать некоторые углы. Например, ноготь указательного
пальца вытянутой перед собой руки мы видим под углом при-
мерно 1о
, кулак — под углом 10о
, а промежуток между концами
расставленных большого пальца и мизинца — под углом 22о
(рис. 7). При том же положении руки угол между широко рас-
ставленными средним и указательным пальцами составляет 8о
,
а между большим и указательным — 16о
.
Рис. 7
Рис. 6
10°1
°2
2
°
31
НЕДОСТУПНЫЕ РАССТОЯНИЯ
Особенности зрения издавна использо-
вались для определения недоступных для
непосредственного измерения длин и рас-
стояний. Вот несколько примеров.
В древнекитайском трактате «Математи-
ка в девяти книгах» разбирается такая за-
дача. Требуется найти глубину x колодца по
x
известной длине H шеста, ширине d колодца
d
и отрезку l, отсекаемому лучом зрения на-
блюдателя на границе колодца (рис. 8). Ка-
кой формулой выражается глубина колодца?
Так как отрезки d и
d l видны под одним углом,
то верно равенство
,
H
x
H
l
d
откуда
.
)
(
l
l
d
H
x
В одном из русских руководств по прак-
тической геометрии описан следующий способ определения
расстояния до вершины башни. Квадрат ABCD со стороной CD,
разделенной на n равных частей — единичных отрезков, де-
ржат так, чтобы луч зрения от глаза наблюдателя (точки А) до
вершины башни (точки M) проходил через сторону AD (рис. 9).
Затем на вершину башни смотрят из точки B, находят точку пе-
ресечения прямой BM со стороной CD квадрата (точку K) и соот-
KK
ветствующее ей деление k. Тогда из подобия прямоугольников
треугольников ABM и CKB следует, что
AM:n=n:k,тогда
k
AM=n
2
:k.
А как определить примерную высоту стоящего неподалеку
столба (вышки, дерева), не имея при себе никаких инструментов
и приспособлений? Можно
поступить так. Отойти от
столба на расстояние, на
котором большой палец
вытянутой вперед руки
закроет его полностью, то
есть их видимые разме-
ры станут одинаковыми, и
подсчитать при этом чис-
ло сделанных шагов. Для
взрослого человека сред-
d
x
l
H
Рис. 8
C
B
D
A
K
M
Рис. 9
32
нее расстояние от глаза до большого пальца вытянутой руки
составляет 60 см, длина пальца — 7 см, а длина шага — 65 см.
По этим данным легко вычислить высоту столба.
Еще один способ нахождения недоступного расстояния ос-
нован на измерении углов и применении тригонометрии. Рас-
смотрим такую задачу. Лесничий следит за пожарами с распо-
ложенной на холме наблюдательной вышки. Известны высота
вышки и холма — h и H. Лесничий заметил огонь под углом к
горизонту (рис. 10). На каком расстоянии S от места наблюде-
S
ния возник пожар? Ответ прост. Поскольку
+
=
,то
+
=
Чтобы узнать расстояние между удаленными объектами,
скажем, деревом и домом, расположенными в точках C и
CD
(рис. 11), воспользуемся параллак-
сом. Пусть базис АВ равен a. Его
можно измерить непосредственно,
какиуглы ,
1
и2
. Теперь найдем
углы 1и
2
. Из треугольника ABC по
C
теореме синусов выразим сторону
ВС, а из треугольника
СС
BCD, в котором
СВD =
1
2
, по той же теореме вы-
числим искомое расстояние CD:
,
sin
)
sin(
2
2
1
BC
CD
1
sin
sin
a
BC
.
h
H
S
Рис. 10
D
1
2
2
1
Рис. 11
33
В ЗРИТЕЛЬНОМ ЗАЛЕ
Напоследок такой житейский пример. Покупая билеты в те-
атр, мы стараемся выбрать места в центе зрительного зала или
хотя бы в середине ряда кресел, поскольку из опыта знаем, что
с этих мест будет хорошо видна вся сцена. На самом деле такой
выбор имеет вполне научное объяснение. В зале с параллельны-
ми рядами кресел зрители, сидящие на одном ряду, видят сцену
под разными углами (рис. 12). Другое дело,
когда места располагаются на дуге окруж-
ности (рис. 13). Как известно из геометрии,
вписанные углы, опирающиеся на одну дугу,
равны. В таком случае отовсюду сцена будет
просматриваться в горизонтальной плоскости
под одним углом, то есть зрители будут нахо-
диться в одинаковых условиях, хотя и смотрят
на происходящее с разных точек.
Имеет значение также величина угла зре-
ния. Чем ближе к сцене, тем больше этот угол,
и наоборот. Для мест в середине каждого
ряда его легко вычислить, зная ширину сцены
и расстояние до нее. Комфортным для про-
смотра считается угол, не превышающий 53о
,
оптимальным — 35—40
о
. Если с первого ряда
сцена видна под углом 60о
, то с последнего
— под углом всего 30о
. Так что хорошие места,
действительно, находятся в центральной час-
ти зала. Добавим, что четче всего различаются
глазом предметы, расположенные в пределах
угла зрения 10—15°, поэтому увидеть одинаково хорошо про-
исходящее в разных уголках сцены не получится.
Итак, самой подходящей формой для распределения мест в
зрительном зале является дуги окружности. Ее придумали и ис-
пользовали при строительстве театра под открытым небом еще
древние греки. В центре античной постройки размещалась ор-
хестра — площадка круглой формы, на которой выступали хор
и танцоры. Две трети ее окружал театрон — ряды для зрите-
лей, располагавшиеся дугообразно один над другим по склону
холма. На другой стороне находилась скена — помещение для
хранения реквизита и переодевания актеров. К ней примыкал
проскений — площадка, на которой шло представление. Си-
Рис. 12
Рис. 13
34
дящие на одном ряду зрители видели ее под равными углами.
Добавим, что форма, выбранная для театрона, также улучшала
акустику театра. Ряды скамеек отражали звук в направлении ау-
дитории, и каждое произнесенное актерами слово было слышно
одинаково хорошо отовсюду.
С понятием угла зрения можно встретиться не только на
практике или в разных науках и искусствах. Оно давно и прочно
вошло в обиход и укоренилось в русском языке в качестве фра-
зеологизма. Угол зрения — это определенный взгляд на то или
иное явление, особая позиция или мнение.
Театр в Эпидавре. IV век до н. э.
35
ГЛАВА 3
Непостижимый случай
—
В жизни ведь еще лотерея есть. Я вот всегда
лотерейный билет покупаю!
—
Ну и как, выиграла что-нибудь?
—
А как же! Два раза по рублю!
Из разговора героев фильма
«Москва слезам не верит»
«Лотерея — организованная игра на счастье, при которой
распределение выгод и убытков зависит от случайного
извлечения того или иного билета или номера» (Энцикло-
педический словарь Брокгауза и Ефрона). Игра эта давно
приобрела массовый характер и стала неотъемлемой
частью современной жизни. И хотя она все больше расши-
ряет свои возможности, многие люди по-прежнему видят в
ней лишь способ обогащения. Пусть и не бесплатный, и не-
надежный. С другой стороны, людям иногда везет — это
факт. Так играть или нет? И если не играть, то почему?
ЛЮБИМЧИКИ ФОРТУНЫ
Известный способ быстро раз-
богатеть — выиграть в мгновенной
лотерее. Как правило, шансы приоб-
рести счастливый билет очень малы.
Тем более невероятной выглядит
история работницы нью-йоркского
гастронома Валери Вильсон, которая
заполучила главный приз дважды.
В 2002 году она выиграла миллион
долларов в лотерее Cool Million, имея
шансы 1 : 5 200 000. А четыре года спустя, приняв участие в
лотерее Jubilee, стала обладательницей второго миллиона. На
этот раз шансы на выигрыш оценивались как 1 : 705 600. Каков
же был ее шанс выиграть главный приз в обеих лотереях?
Его нетрудно подсчитать:
1:(5200000 705600)=1:3669120000000,
или примерно один из 3,7 триллиона. Шанс и в самом деле нич-
36
тожно мал, в чем можно убедиться, если представить себе дру-
гую лотерею.
Допустим в ней участвуют все жители Земли — 7 млрд че-
ловек. Выпущенные по такому случаю 3,7 триллиона билетов со
стираемым защитным слоем, из которых лишь один выигрыш-
ный, распределены между ними поровну. По правилам лотереи
в регулярном еженедельном розыгрыше каждый участник ис-
пользует один билет. Конечно, первый же открытый билет мо-
жет оказаться выигрышным. Однако в самом неблагоприятном
случае ожидание выпадения счастливого билета растянется на
10 лет!
Надо сказать, в истории американских лотерей (коих мно-
жество, и проводятся они постоянно) было всего несколько слу-
чаев с повторным выигрышем призов, превышающих миллион
долларов. Правда, все они касались обычных лотерей, в кото-
рых джекпот, как правило, куда больше главного приза в мгно-
венной лотерее. Примечательно также, что один из самых круп-
ных выигрышей — 254 млн долларов — достался в 2007 году
84-летнему пенсионеру, чья фамилия оказалась... Вильсон. Вот
и не верь после этого в совпадения.
А рекордсменкой по количеству крупных выигрышей явля-
ется Джоан Гинтер из Лас-Вегаса. За 17 лет она побеждала в
различных лотереях четыре раза — последний в 2010 году — и
«заработала» таким образом более 20 млн долларов. Согласно
расчетам, с учетом имевшихся каждый раз шансов выиграть, по-
добное достижение возможно лишь в одном случае из 36 1024
,
или 36 септиллионов, на фоне которых меркнут даже 3,7 трил-
лиона, или 3,7 1012
!
Как остроумно и верно заметил по этому поводу один аме-
риканский профессор математики, специалист в области теории
вероятностей, случай сей поразительный, однако у вероятности
нет памяти! И что характерно, шансы Джоан выиграть в очеред-
ной лотерее точно такие же, как и у любого другого игрока. Ины-
ми словами, они есть всегда, пусть и крошечные. Должно быть,
перед покупкой очередного билета подобные мысли посещают
(более того — обнадеживают) многих любителей лотерей.
ЗАВЕТНАЯ ШЕСТЕРКА
«Случилось невероятное!» — так прокомментировал ди-
ректор болгарской лотереи «6 из 42» выпадение в двух тира-
37
жах подряд одинаковых выигрышных чисел: 4, 15, 23, 24, 35 и
42. Произошли эти события в сентябре 2009 года, с разницей
всего в четыре дня. В простое совпадение никто, включая оче-
видцев, тогда не поверил. Однако тщательная проверка, прове-
денная под личным контролем министра спорта, в чьем ведении
находится лотерея, фактов махинаций не выявила. Почему же
все усомнились в том, что одна и та же выигрышная комбинация
чисел выпала два раза подряд случайно?
Сделаем простой расчет. Всего способов выбрать шесть из
сорока двух различных чисел имеется
)!
6
42
(!6
!
42
6
42
C
.
786
245
5
6
5
4
3
2
1
42
41
40
39
38
37
Значит, вероятность выпадения единственно возможного выиг-
рышного набора чисел в любом тираже равна
=
той же числовой комбинации в двух тиражах подряд возникли
из-за того, что вероятность этого события крайне мала, всего
(1,9 10 7)
2
= 3,61 1014
.
Заметим, что в подобных лотереях повторное выпадение
выигрышного набора чисел изредка все же происходит (в той
же Болгарии такое было пару раз), правда, не в двух тиражах
кряду. А вот интересно, что предприняли бы организаторы ло-
тереи, если бы числа выпали дважды да еще в одном и том же
порядке? И кстати: чему равна вероятность такого двойного
совпадения?
Между тем если в первый раз шесть чисел не угадал ник-
то, то во второй на них поставили сразу 18 человек! Надежды
тех, кто рассчитывал на крупный
выигрыш, не оправдались: при-
зовую сумму пришлось делить на
всех. Словно желая опровергнуть
законы теории вероятностей, на-
кануне следующего тиража многие
всерьез обсуждали, не поставить
ли на те же шесть чисел снова, ведь
не исключено, что они выпадут и в
третий раз!
38
Если одни игроки в лотерею рассчитывают победить благо-
даря якобы придуманной ими системе угадывания чисел (рано
или поздно она, возможно, и даст результат — по законам все
той же теории вероятностей), то другие придерживаются при-
митивных стратегий. Ставишь, например, всегда на один и тот
же набор чисел и ждешь, когда он выпадет (если вообще вы-
падет). Поступавшему так американцу Крису Хоффману, люби-
телю лотереи «5 из 39», можно сказать, крупно повезло: ждать
пришлось всего-то 15 лет! О том, сколько средств он потратил за
это время на покупку билетов, а главное, покрыл ли все расходы
выигрыш в размере 150 тысяч долларов, история умалчивает.
«БЕСПЛАТНАЯ» ЛОТЕРЕЯ
Кстати, о потраченных деньгах. В середине 1990-х годов
в США проводилась «почтовая лотерея». В ней разыгрывался
денежный приз в размере 5 млн долларов, а шанс получить его
составлял 1 из 200 млн. От участников требовалось всего ниче-
го: сделать ставку и отправить ее по почте. Разрешалось делать
сколько угодно ставок, но с условием — высылать их по одной.
Стоит ли участвовать в такой «бесплатной» лотерее?
При таких условиях, конечно, не стоит. И вот почему. Зная
вероятность выигрыша и его сумму, легко подсчитать ожидае-
мый выигрыш игрока (среднюю сумму выигрыша, приходящую-
ся на один билет):
=
доллара, или 2,5 цента.
Однако расходы на отправку письма куда больше! Иначе
говоря, ожидаемый выигрыш во много раз меньше вложенной
игроком суммы, и их разность выражается числом отрицатель-
ным. Так что, если тратиться на пересылку многократно, очень
скоро придется подсчитывать убытки.
Как тут не вспомнить рассказ нашего классика Антона Пав-
ловича Чехова «Житейские невзгоды»? Если бы его герой сразу
прикинул, во сколько ему обойдется покупка выигрышного би-
лета внутреннего займа, участвовавшего в денежной лотерее,
то всерьез призадумался, нужен ли он ему вообще.
Кому же выгодна «почтовая лотерея»? Ответ очевиден: поч-
товой службе США. По самым скромным подсчетам, при благо-
приятном развитии событий доход с отправленных писем дол-
жен был превзойти заявленный приз как минимум в десять раз.
39
НАРОДНАЯ ИГРА
А в России свой любопытный
опыт имеется. Так, у нас прижились
лотереи с вещевыми призами. Неда-
ром их часто называют «народными».
Вот лишь один из примеров. Чего
только не придумывают транспорт-
ники, чтобы заставить пассажиров
платить за проезд! Весной 2010 года
в Барнауле проводилась стимулиру-
ющая лотерея «Счастливый билет».
В ней разыгрывались номер и серия
разовых проездных билетов на трам-
вай и троллейбус. Призы выдавались
«натурой»: подарочными картами ги-
пермаркета электроники, месячными
проездными на городской транспорт
и тому подобным. Стоит ли говорить,
что за три недели проведения лоте-
реи число «зайцев» резко сократилось, а доходы транспортни-
ков (при скромных в общем-то затратах) ощутимо возросли!
Бывает, сам процесс игры захватывает не меньше, чем же-
лание получить приз, особенно когда возможность выигрыша
заложена в каждый билет. Об этом заявляют, например, орга-
низаторы моментальной Всероссийской жилищной лотереи.
А дальше, как и положено в рекламе: «Не верите? Не хотите
рисковать? Все еще сомневаетесь? Тогда мы идем к вам!» И не
просто так, а с разумным предложением потренироваться для
начала на виртуальных лотерейных билетах.
Правила игры просты. В билете девять строк (этажей), по
два игровых окна в каждой; в одном из них спрятано «счастли-
вое число», равное сумме выигрыша (она указана на защитном
слое). Задача проста — угадать это число, открыв только одно
окно в строке. Таким образом, двигаясь построчно снизу вверх,
можно по желанию открыть от одного до девяти окон. При пер-
вой же неудаче игра прекращается, билет считается невыигрыш-
ным. Так насколько справедливо заявление организаторов?
Ясно, что вероятность выбора «счастливого числа» на каж-
дом шаге одна и та же — она равна одной второй — и по ходу
игры убывает в геометрической прогрессии:
40
=
=
=
А какова средняя сумма выигрыша, приходящаяся на один
билет? Если сделать всего один шаг из девяти, то она составит
=
если два шага, то
=
если три,
то
=
и далее будет только уменьшаться
(из-за того что вероятность выигрыша убывает значительно
быстрее, нежели растет призовая сумма), а проигрыш, напротив,
будет увеличиваться.
Сколько ни тренируйся, а предугадать исход игры в каждом
конкретном случае невозможно. А вот сесть за компьютер
все же стоит. Если достаточно долго экспериментировать с
виртуальными билетами и фиксировать результаты, можно
заметить, как проявит себя «закон больших чисел» — с
увеличением количества испытаний частота появления события
(выпадения крупного денежного приза) приближается к его
вероятности, а последняя, как мы убедились, невелика.
Имея билет на руках, благоразумно ограничиться
угадыванием чисел во второй-третьей строках и скромным
выигрышем. Очевидно, так же рассуждают многие участники
лотереи. А на что всегда рассчитывают ее устроители? Как и в
случае любой другой азартной игры — на человеческие слабости
и неумение вовремя остановиться. Поэтому уже на билетах
следующей партии «по многочисленным просьбам игроков»
была выделена строка с несгораемой суммой (на седьмом
этаже), а также добавилось новое правило: если на пятой или
шестой строке окажется открыто окно с символом «+», игра
закончится, а вы получите утешительный приз — 50 рублей.
Устроителям лотереи в изобретательности не откажешь, не так
ли? Как думаете, стали ли правила честнее и возросла ли после
этих нововведений продажа билетов?
НЕПРОСТИТЕЛЬНЫЙ ПРОМАХ
Допускают ли организаторы лотерей просчеты? Не пове-
рите, но и такое случается. Следующая история произошла в
одном американском штате 20 лет назад. Карточки очередного
тиража лото «6 из 44» продавались по 1 доллару, в то время как
41
призовой фонд составлял на тот мо-
мент 27,9 млн долларов, и почти все
они приходилось на джекпот.
Несколько инвесторов сообра-
зили, что смогут хорошо заработать,
выкупив и заполнив карточки всеми
возможными комбинациями шести
из сорока четырех чисел. Они учли
дополнительные расходы и риски (в
частности, изучив статистику преды-
дущих розыгрышей, выяснили: в 120 случаях победителей не
оказалось, в 40 был один победитель, еще в 10 — два) и заодно
оценили прибыль. Для осуществления задуманного привлекли
две с половиной тысячи мелких инвесторов из разных стран, а
также группу людей для работы с карточками лото. В итоге из-
за нехватки времени удалось использовать всего 70% карточек
от запланированного числа, но и этого хватило, чтобы выиграть
главный приз. А ведь повезло!
В чем заключался финансовый просчет организаторов
лотереи, побудивший инвесторов пойти на сговор? И каковы
были, по подсчетам последних, общий ожидаемый выигрыш и
прибыль с одного вложенного доллара? (Второстепенными рас-
ходами можно пренебречь.)
Просчет был в том, что организаторы лотереи продавали
карточки лото по невыгодной для себя цене. На самом деле ее
следовало увеличить в четыре раза. Действительно, для гаран-
тированной победы нужно заполнить
)!
6
44
(!6
!
44
6
44
C
052
059
7
6
5
4
3
2
1
44
43
42
41
40
39
карточки. Призовой фонд — 27,9 млн долларов. Значит, карто-
чка должна стоить хотя бы
27 900 000 : 7 059 052 3,95 доллара*.
Неудивительно, что цена 1 доллар показалась инвесто-
рам очень привлекательной. В идеале доход с нее составляет
2,95 доллара.
* В данном примере «мелкие» выигрыши, по сути, не влияющие на ответ, в расчет не
принимались.
42
Как показывают расчеты, ожидаемый выигрыш равен
+
+
+
млн
долларов, а прибыль с одного вложенного доллара
доллара.
Даже с учетом всех затрат доход оказался бы огромным!
Нетрудно догадаться, чем закончилась эта история. Узнав,
что главный приз достался группе инвесторов, устроители ло-
тереи поначалу не хотели выплачивать выигрыш. Но после не-
продолжительных юридических пререканий были вынуждены
признать, что причин для отказа нет. В итоге им пришлось доро-
го заплатить за собственный промах. Случай исключительный и
довольно поучительный.
ДОВОДЫ РАССУДКА
Так стоит ли участвовать в лотереях в надежде быстро раз-
богатеть? Стоит ли полагаться на случай в погоне за легкими
деньгами? Повезет или нет — большой вопрос. В лотереи ре-
гулярно играют миллионы людей по всему миру, а побеждают
единицы. Но в одном можно не сомневаться — в любой лотерее
всегда выигрывают организаторы.
Никаких надежных стратегий угадывания чисел в лото или
выявления счастливого билета в мгновенной лотерее не сущес-
твует, кроме как заполнить все карточки или скупить все биле-
ты. Но это возможно лишь при условии, что игроки объединят
усилия, и имеет смысл делать, только если призовой фонд зна-
чительно превышает стоимость всех билетов, а на это рассчиты-
вать не приходится.
В лотерее типа «почтовой» устроители и игроки решают
две обратные задачи: первые подбирают комбинацию, которую
не угадает никто, а вторые ее старательно отгадывают, — и на-
блюдать за этим «состязанием» все же интереснее, чем за слу-
чайным выпадением чисел в лото. Каковы шансы на успех у тех
и других в теории? А на практике? Как ни странно, разные: не
секрет, что никак не связанные между собой участники нередко
ставят на одни и те же комбинации, а любого рода совпадения
и повторы на руку организаторам: почти всегда можно просчи-
тать наиболее вероятный «круг» таких комбинаций.
43
Устроители лотереи заинтересованы в том, чтобы в ней
участвовало как можно больше людей. При подходящем ожида-
емом выигрыше и приемлемой цене на билеты всякий призовой
фонд быстро окупится за счет проданного количества билетов
(о том, какая их доля приходится на тот или иной выигрыш, иг-
рокам, конечно, неведомо). На продажу влияют и размер при-
зовых, и вероятность выигрыша, а ее можно варьировать, изме-
няя правила игры. Так, если эта вероятность достаточно велика
(в таком случае выигрыш всегда небольшой) или, напротив,
слишком мала, продажа лотерейных билетов падает. Одним сло-
вом, успех лотереи во многом зависит от умения устроителей
отыскать ту «золотую середину» между величиной призовых и
шансом выиграть, которая обеспечила бы им крупный доход.
И этим искусством они прекрасно владеют, будучи знакомы и с
психологией любителей азартных игр, и с основами теории ве-
роятностей.
И наконец, главный довод рассудка, не только подтверж-
денный многовековым опытом, но и научно обоснованный: во
всякой азартной игре каждый раз все решают везение и случай,
но чем больше играешь, тем больше проигрываешь.
44
СЛОВАРИК
Сочетание — выборка k элементов из
k
n имеющихся (k ≤
k n),
при которой их порядок неважен. Число всевозможных
сочетаний из n элементов по k обозначается
k
и
вычисляется по формуле
=
,гдеn!=123...n.
Случайное событие — событие (результат, исход испытания),
которое объективно может произойти или не произойти в
данном испытании.
Вероятность события A — число, выражающее меру
объективной возможности наступления случайного
события A; определяется как отношение числа m исходов
испытания, благоприятствующих этому событию (влекущих
за собой его наступление), к числу n всех равновозможных
исходов, то есть равно .
Случайная величина — переменная величина X, которая может
XX
принимать то или иное значение в зависимости от случая.
Математическое ожидание (или среднее значение) случайной
величины X, принимающей конечное число значений
XX
x1x,x
2
,...,x
n
, — число, равное сумме произведений этих
значений на соответствующие им вероятности p1
,p
2
,...,p
n
,
то есть x1p
1
+ x2p
2
+...+xnp
n
.
Математическое ожидание выигрыша игрока в лотерее
определяется как сумма произведений возможных
выигрышей на вероятности их выпадения.
Минимальная цена билета в лотерее равна математическому
ожиданию выигрыша игрока.
45
ГЛАВА 4
Всякая всячина
Есть многое на свете, друг Горацио,
Что и не снилось нашим мудрецам.
У. Шекспир. Гамлет
С недавних пор моя авторская копилка стала пополнять-
ся забавными задачками. Они лишены ряда недостатков,
присущих задачам из школьного учебника с их далекими от
жизни и порой устаревшими сюжетами, искусственными
условиями, «удобными» числами и предсказуемым ответом.
В копилку попадают задачки на реальные сюжеты, которые
обладают поистине бесценными качествами, — при всей своей
простоте и доступности они нетривиальны и никогда не повто-
ряются. Сюжеты эти берутся из повседневной жизни и личного
опыта, научно-популярных книг и журналов, интернет-публи-
каций и прочих полезных источников. Поэтому цифры и факты
в таких задачках самые что ни на есть настоящие. И данные в
условии могут оказаться в избытке (задача содержит лишнюю
для решения, но небесполезную и просто любопытную инфор-
мацию, обеспечивающую «полноту картины») или недостатке
(приходится добирать сведения из доступных источников), и
вопрос звучать необычно, и ответ на него быть неочевидным
и на удивление содержательным. Решая эти задачки, придется
не только производить расчеты, но и «фильтровать» условия,
оценивать результаты и выбирать подходящий ответ. Зато ка-
кой отличный повод порассуждать и разобрать по косточкам
описанную ситуацию, потренировать критическое мышление и
проверить бдительность!
ПОТЕРЯ ВРЕМЕНИ
Проведенное недавно в Англии исследование деятельности
4000 сотрудников из 150 организаций показало, что 77% опро-
шенных, придя на работу, первым делом проверяют свою элек-
тронную почту. Выяснилось также, что в течение рабочего дня
каждый сотрудник получает в среднем 34 электронных письма,
46
47% которых не имеют отношения к работе. Сколько бесполез-
ных, с точки зрения работодателя, писем ежедневно получают
сотрудники всех этих организаций и как много времени тратят
на их просмотр, если для прочтения одного письма требуется не
менее 1 минуты? Велика ли потеря рабочего времени в пересче-
те на одного человека?
ВСЕ НА ПРАЗДНИК КОЛБАСЫ!
В XVI веке жители Кёнигсберга на Новый год любили от-
мечать праздник Длинной колбасы. Впервые он был устроен в
1520 году. Изготовленная мясниками колбаса имела длину все-
го 41 локоть. С каждым разом ее размер становился все больше
и больше и в 1601 году достиг рекордных 1005 локтей! На изго-
товление гигантской колбасы пошел 81 свиной окорок, потро-
ха, 18 фунтов перца и другие специи. В начале праздника 103
подмастерья, выйдя с постоялого двора мясников, под музыку
важно прошествовали с колбасой по городу (вернее, по трем
городам, из которых состоял в то время Кёнигсберг), неся ее на
плечах и раздавая по дороге как новогоднее угощение: герцогу
и его советникам, трем бургомистрам, пивоварам, священни-
кам... Закончилось шествие на постоялом дворе пекарей. В за-
вершение праздника состоялись народные гулянья с поеданием
остатка колбасы.
В наше время мясники из разных стран соревнуются в про-
изводстве колбасы, чтобы только попасть в знаменитую Книгу
рекордов Гиннесса. Самая большая — длиной более 600 м —
свиная колбаса современности была изготовлена в 2005 году
в городе Льеж. Интересно, удалось ли бельгийским колбасных
дел мастерам превзойти достижение прусских коллег?
47
КОФЕЙНОЕ ТОПЛИВО
Как-то раз индийский химик М. Мисра заметил, что остав-
ленный в чашке недопитый кофе через некоторое время затя-
нулся радужной пленкой, похожей на нефтяную. Выяснилось,
что это масло, содержащееся в зернах кофе. Вместе с японс-
кими и американскими коллегами химику удалось выделить
это масло из кофейной гущи и получить на его основе горючее
для дизеля, которое оказалось вдвое дешевле бензина. Извес-
тно, что за день пилотная установка, перерабатывая 20—25 кг
отходов молотого кофе, дает 4 л жидкого топлива. Как много
топлива можно было бы изготовить из отходов кофе, которого
за год в мире потребляется более 7 млн тонн, и сколько таких
аппаратов потребовалось бы, чтобы выполнить всю работу за
тот же период?
РАСПЛАТА ЗА ЛИШНИЙ ВЕС
Большинство американцев име-
ют избыточную массу тела. В сред-
нем взрослый житель США весит
больше нормы на 14 кг, подросток —
на 3,6 кг, а ребенок — на 1,4 кг. Это
приводит не только к проблемам со
здоровьем, но и, например, к значи-
тельному перерасходу бензина при
поездках. Подсчитано, что ежегод-
ный общий автомобильный пробег
населения США составляет 3 трил-
лиона километров. Средний расход
горючего на 1 кг груза — 0,0045 л на 100 км. Оцените, сколько
литров бензина тратится каждый год на перевоз лишнего жира
по дорогам США.
ПО ЗАКОНУ ЗОЛОТОГО СЕЧЕНИЯ?
Какие только свойства не приписывает производитель
собственной продукции, расписывая ее достоинства! Недавно
купила литую сковороду «нового поколения». Приготовленная
в ней еда гораздо вкуснее и полезнее, уверял изготовитель,
поскольку корпус сделан из специального пищевого сплава
48
алюминия с кремнием, к тому же согласно принципу золотого
сечения — стенки имеют толщину 4 мм, а дно 6,3 мм, что обес-
печивает исключительные термоаккумулирующие свойства
посуды. Чудо-сковорода в самом деле оправдала ожидания.
Вот только золотое сечение здесь ни при чем. Почему?
БЕСПОЛЕЗНАЯ РЕКЛАМА
Многие полагают, что спам (нежелательные рекламные
электронные письма) неэффективен, но даже не подозревают
насколько! Недавно группа американских компьютерщиков
проанализировала результаты одной рекламной кампании. За
26 дней ее проведения с 75 869 компьютеров крупной сети спа-
мовой рекламы было разослано 350 млн сообщений о новом ле-
карственном препарате. Результат оказался плачевным — всего
28 покупок этого средства. Определите КПД спамовой рассылки
и сравните его с КПД обычной рекламной кампании (когда ин-
формация рассылается по запросу или же заинтересованным в
товаре людям), который достигает 2,15%.
ИСТОРИЯ ОДНОГО ДОЛГА
В августе 1825 года, находясь в ссылке в Михайловском,
Александр Пушкин послал своему другу Петру Вяземскому шу-
точную деловую бумагу для предъ-
явления дяде поэта. Как и поло-
жено, написана она была в стиле
официальных документов того вре-
мени. «1811 года дядя мой Василий
Львович... взял у меня взаймы 100
рублей ассигнациями, данных мне на
орехи покойной бабушкой моей Вар-
варой Васильевной Чичериной и по-
койной тетушкой Анной Львовною.
...Так как оному прошло уже более
10 лет без всякого с моей стороны
взыскания или предъявления, и как
я потерял уже все законное право
на взыскание вышеупомянутых 100
рублей (с процентами за 14 лет, что
составляет более 200 рублей), то
49
униженно молю его высокоблаго-
родие, милостивого государя дядю
моего заплатить мне сии 200 рублей
по долгу христианскому — получить
же оные деньги уполномочиваю кня-
зя Петра Андреевича Вяземского,
известного литератора». А интерес-
но, какой процент годовых разумел
Пушкин, подсчитывая сумму дядюш-
киного долга?
РАЗМЕР КРЫЛА
Все птицы делятся на две
группы. Одни умеют летать, и
их подавляющее большинство.
Другие этой способности лиши-
лись в ходе эволюции. Впрочем, они от этого не страдают:
у пингвинов, например, крылья превратились в ласты, и они мо-
гут «летать в воде» — отлично плавать и нырять, а страусам до-
стались мощные ноги, и эти птицы отменные бегуны. Чем мень-
ше весит птица, тем легче ей оторваться от земли и тем меньшая
подъемная сила требуется в полете. А какую роль играет в этом
вопросе размер крыльев? Как известно, у мелких птиц крылья
по сравнению с телом небольшие и короткие, а у крупных, на-
оборот, широкие и длинные. Почему природа распорядилась
именно так? Какие законы на это повлияли?
РЕКОРДСМЕН ПОНЕВОЛЕ
«Кто зарабатывает в одну минуту больше всех?» — заметка
с таким названием была опубликована в газете «Русский спорт»
сто лет назад, в 1911 году. В ней сообщалось: «Американский
миллиардер Пирпонт Морган получает в минуту 125 франков,
а известный адвокат Бельмас за процесс, длившийся 30 ча-
сов, получил гонорара 500 000 франков, или по 277 франков
в минуту. Хирург Дуайен за операцию, длившуюся 10 минут,
получил 100 000 франков, или по 10 000 франков в минуту.
Гонорары певцов также значительны: Шаляпин зарабатывает
около 350 франков в минуту, Карузо — 500 франков. Профес-
сиональные спортсмены могут получать еще больше. Так, негр
50
Джонсон за победу в боксе над чемпионом мира Джефрисом
получил 1 500 000 франков. Борьба их длилась 18 минут, что
дает 83 000 франков в минуту. Честь и слава спорту!» С пос-
ледними словами трудно не согласиться, а вот с другими выска-
зываниями можно поспорить. Это что же выходит, миллиардер
зарабатывает меньше остальных?! Так ли это на самом деле?
А если нет, то в чем подвох?
ВОДА ИЗ ВОЗДУХА
Всего 2% содержащейся в воздухе воды собрано в обла-
ка, остальные 98% приходятся на невидимый пар. При этом
1 км3 воздуха содержит от 10 до 40 т воды. Несколько лет назад
одна израильская фирма разработала технологию извлечения
этой скрытой влаги. Воздух прогоняется через поглотитель,
захватывающий только водяной пар. При нагреве поглотителя
пар выделяется, а затем охлаждается для конденсации воды.
Разработка пользуется большим спросом у покупателей из Аф-
рики, Индии, Австралии и других мест, жители которых испы-
тывают острую нехватку пресной воды. Небольшие, размером
с персональный компьютер, установки позволяют добывать
10—30 л воды в сутки, а крупные — 25 м3. Польза изобретения
очевидна. А насколько выгодно такое производство воды из
воздуха, если на получение 1 л требуется около 0,3 кВт/ч элек-
троэнергии?
КАРТА-НЕВИДИМКА
Желая продемонстрировать возможности современной
микролитографии (формирование миниатюрных рисунков на
поверхности твердого тела), с помощью которой планируется
делать микросхемы для фотонных компьютеров будущего, бель-
гийские ученые изготовили на кремниевой пластинке самую ма-
ленькую карту мира — ее масштаб 1 : 1012
. Можно ли разглядеть
на этой карте невооруженным глазом линию, изображающую
земной экватор, или без лупы никак не обойтись?
БУЛОЧНИК-МОШЕННИК
О знаменитом математике Анри Пуанкаре (1854—1912) бы-
тует такая история. Долгое время он регулярно покупал хлеб у
51
одного булочника. Однажды ученый
заподозрил, что хлеб весит меньше,
чем было указано на этикетке. При-
обретя несколько буханок, Пуанка-
ре взвесил их и убедился в своей
правоте. Он пожаловался властям
на нечистого на руку булочника, и к
тому были приняты меры. Но ученый
на этом не успокоился и решил про-
вести эксперимент. В течение года
он ежедневно взвешивал купленные
буханки и удостоверился, что их вес
увеличился и почти не отличался
от нормы. Однако, проанализиро-
вав собранные данные, Пуанкаре
пришел к неутешительному выводу:
булочник продолжает обманывать
покупателей, просто тот пошел на
хитрость — стал продавать ему бу-
ханки побольше, рассчитывая усыпить бдительность ученого.
Стоит ли говорить о том, как поразился мошенник, когда поли-
ция навестила его вновь! Каким образом математику удалось
уличить булочника в обмане?
52
ОТВЕТЫ
Потеря времени
Посторонних электронных писем за день набирается ог-
ромное количество — 63 920. На их просмотр сотрудники всех
организаций регулярно тратят как минимум 1065 ч 20 мин ра-
бочего времени. Если исходить из этой цифры, то на одного
человека приходится примерно четверть часа. Оказывается,
это не так много. Аналогичные исследования, проведенные в
разных странах, выявили, что гораздо больше рабочего вре-
мени нерационально тратится служащими по другим поводам:
на неформальное общение с коллегами, разговоры по телефо-
ну, блуждание по интернету, перекуры, чаепития, опоздания и
преждевременный уход с работы. Суммарный итог — полдня
простоя!
Все на праздник колбасы!
Прусский локоть равнялся примерно 67 см. Значит,
сделанная мясниками Кёнигсберга свиная колбаса дости-
гала в длину 673 м, то есть значительно превосходила по
размеру аналогичную колбасу, изготовленную в Льеже в
наши дни, хотя и имела более рыхлую консистенцию. Так
что ее по праву можно было бы занести в Книгу рекордов
Гиннесса.
Кофейное топливо
Согласно расчетам, за 1 год из отходов кофе можно было
бы изготовить до 1,4 млрд литров жидкого топлива. Для этого
потребовалось бы примерно 960 000 установок по их перера-
ботке.
Расплата за лишний вес
Нетрудно подсчитать, что каждый лишний килограмм
приводит к расходу дополнительных 144 млн литров бензи-
на. Общий его годовой перерасход составит не менее 2 млрд
литров и не более 8 млрд — при условии, что в автомобиле
находится один или четыре взрослых соответственно. Более
точную, «усредненную» оценку можно получить, рассмат-
ривая такие типичные ситуации: в машине либо взрослый с
53
двумя детьми, либо два взрослых. В таком случае на перевоз
лишних килограммов ежегодно тратится от 2,7 до 4 млрд литров
бензина.
По закону золотого сечения?
Принцип золотого сечения предполагает наличие отношения
длин двух отрезков, равное числу Ф 1,618..., например деление
отрезка на соответствующие части или отношение длины прямо-
угольника к ширине. Даже если взять в этом качестве отношение
толщины дна сковороды к толщине стенок, получится число 1,575,
а вовсе не Ф. Возможно, найденная пропорция и «обеспечивает
термоаккумулирующие свойства посуды», но с золотым сечением
она не связана. Нахваливая свой товар, производитель слишком
увлекся раскрученной идеей и красивыми словами.
Бесполезная реклама
КПД спамовой рассылки составляет всего
(28 : 350 000 000) 100% = 0,000008%.
Это почти в 270 000 раз меньше КПД обычной рекламной
кампании. Это ли не показатель неэффективности спама?!
История одного долга
Должно быть, поэт имел в виду сложные проценты, начисля-
емые с одолженной дяде суммы в размере 100 рублей. Вычис-
лим процент годовых, считая долг равным 200 рублям:
100 (1 + 0,01p)14
= 200, откуда p 5,2%.
А вот если бы речь шла о простых процентах, взимаемых
ежегодно с исходной суммы, процент годовых был бы больше,
а именно
(200 100) : 14 7,1%.
Размер крыла
Вес птицы зависит от ее размеров, а подъемная сила крыла
определяется его площадью и рядом других параметров. При
увеличении линейных размеров птицы в k раз ее вес возрастет в
k
k3 раз, а площадь крыла — только в k2 раз. В природе все долж-
но развиваться сбалансированно, поэтому разница была ком-
пенсирована отчасти за счет увеличения размера крыльев. По
данным орнитологов, более 85% видов птиц весят меньше 2 кг,
а масса летающих птиц, как правило, не превышает 12—15 кг
(рекордсмен — африканская большая дрофа, чей вес достигает
54
19 кг). Самой крупной известной науке летающей птицей в ис-
тории Земли признан аргентавис, обитавший в Южной Америке
6—8 млн лет назад. Этот похожий на грифа гигант весил около
70 кг и имел размах крыльев до 7 м.
Рекордсмен поневоле
Если бы вопрос звучал так: «Кто сумел заработать в одну
минуту больше всех?», ответ был бы: «Боксер». Но на вопрос
«Кто зарабатывает в одну минуту больше всех?» правильный
ответ: «Миллиардер». Ведь только финансист увеличивает свой
капитал непрерывно (ежеминутно). Для представителей осталь-
ных профессий расчет заработка сделан с учетом конечного и
непродолжительного отрезка времени. О том, как обстояли дела
все остальное время, умалчивается. Так при неравных условиях
проведения «состязания кошельков» победителем заочно был
объявлен боксер.
Вода из воздуха
Для маленькой установки ежедневный расход электро-
энергии составляет 3—9 кВт/ч, для большой — 7500 кВт/ч. Это
много да к тому же стоит недешево. Для сравнения: затратив
всего 1 кВт/ч электроэнергии, можно выткать 10 м ситца, вы-
печь 88 буханок хлеба, вспахать участок земли площадью 2,5
сотки или же целую неделю пользоваться энергосберегающей
лампой мощностью 20 Вт, включая ее ежедневно на семь часов.
Разработки в этом направлении ведутся и в других странах. Так,
недавно российские инженеры создали устройство для получе-
ния влаги из воздуха на основе технологии, при которой вода
конденсируется, а воздух при этом не охлаждается. Благодаря
этому потребление энергии удалось сократить до 0,2 кВт/ч на
1 л. Новое устройство годится не только для выработки воды,
которую легко сделать питьевой, но и для осушения влажных
помещений, низкотемпературной сушки древесины и т.п.
Карта-невидимка
Нетрудно подсчитать, что длина экватора на этой микрокарте
составляет 40 10 6 м, или 40 мкм (такую же в среднем толщину
имеет человеческий волос). Расстояние, на котором здоровый
глаз перестанет видеть его как отрезок и будет воспринимать
как точку, оценивается в 13—13,5 см — при предельном угле
зрения 1 . Между тем расстояние наилучшего зрения (от глаза
55
до ближайшей точки, на которой тот может сфокусироваться)
для взрослого человека с нормальным зрением почти вдвое
больше — 25 см. Так что разглядеть на микрокарте экватор, не
говоря уже о мелких деталях, без лупы или другого оптического
прибора с многократным увеличением не получится. Достойна
упоминания также трехмерная кар-
та мира, изготовленная в 2010 году
фирмой IBM: она выполнена на под-
ложке из полимерного материала
размером всего 22 11 мкм в масш-
табе вдвое меньшем, чем микрокарта
бельгийцев.
Булочник-мошенник
В этой житейской истории не
обошлось без теории вероятностей,
с которой булочник, очевидно, не
был знаком. Иначе он знал бы, что
при случайном выборе буханок хлеба их вес будет варьировать
в соответствии с нормальным законом распределения, то есть
отклоняться от наивероятнейшего значения (от нормы веса —
например, 1 кг) вполне определенным образом. Характер этого
отклонения наглядно демонстрирует колоколообразная кривая
нормального распределения, или кривая ошибок, показанная
на рисунке. Симметрия графика говорит о том, что появления
буханок хлеба, вес которых отличается от нормы на одно и то
же число граммов, скажем 50, как в сторону увеличения, так и в
сторону уменьшения, равновероятны. Если бы булочник каждый
раз давал Пуанкаре первую попавшуюся буханку, как обычно и
происходит в действительности, то количество одних и других
буханок было бы практически одинаковым. Однако математи-
ку слишком часто доставался хлеб, весивший больше нормы, и
очень редко — весивший меньше нормы. Это «расхождение по-
казателей» и позволило Пуанкаре сделать вывод, что продавец
по-прежнему мошенничает.
56
ЧАСТЬ ВТОРАЯ
Неожиданная математика
ГЛАВА 1
«Есть такой закон природы...»
На подоконнике сидели три мухи. Вспугнутые хозяй-
кой, они взлетели. Какова вероятность, что ровно
через минуту мухи окажутся в одной плоскости?
И. Шарыгиин. Математический винегрет
Сколько гвоздей достаточно взять, чтобы надежно ук-
репить на стене зеркало? На каком велосипеде кататься
безопаснее: на трехколесном или двухколесном? Почему
чашки весов подвешивают на трех нитях? И наконец, что
объединяет эти вопросы с упомянутой задачей про мух?
ДЕЛЬНЫЙ СОВЕТ ОТ УДАВА
В сказке Григория Остера «Зарядка для хвоста» мартышка
учила слоненка делать зарядку. Каждый раз, когда она коман-
довала «Ноги вместе!», слоненок падал. Этой сценой заинтере-
совался проползавший мимо удав.
«— Сначала я ставлю ноги вместе, — рассказал слоненок.
— А потом падаю. Хоть мне и не хочется.
— Ты ставишь их вместе все? — переспросил удав, который
пока еще ничего не понял, но уже кое-что начал подозревать.
— Ты ставишь вместе все четыре ноги?
— Да, — сказал слоненок. — Все.
—
Все четыре ноги ставить вместе нельзя! — воскликнул
удав. — От этого всегда падают. Это есть такой закон приро-
ды...
— А сколько можно? — спросила мартышка.
—
Только некоторые! — охотно объяснил удав, который
в глубине души считал себя большим специалистом по ногам.
57
— Например, только задние. Или только передние.
— И тогда не падают? — спросил слоненок.
— Тогда стоят! — подтвердил удав».
О каком таком законе природы говорил удав?
Должно быть, он имел в виду известную аксиому геометрии:
через любые три точки, не лежащие на одной прямой, проходит
плоскость, и притом только одна. Из аксиомы следует, что ус-
тойчивое положение объекта на земле достигается при опоре на
три точки при условии, что они не лежат на одной прямой. Выхо-
дит, удав дал слоненку дельный совет — ставить вместе только
две ноги из четырех, то есть опираться на три конечности.
НАДЕЖНАЯ ОПОРА
Отмеченный факт человек давно использует на практике.
Пример тому «Медный всадник» — памятник Петру I работы Эть-
ена Фальконе в Санкт-Петербурге. По замыслу скульптора Петр
должен был восседать на вздыбленном коне. Но тогда монумент
имел бы всего две точки опоры (копыта задних ног коня), что
не гарантировало его устойчивости после отливки. Чтобы спра-
виться с этой проблемой, Фальконе утяжелил нижнюю часть
памятника, сделав ее стенки толще,
чем у верхней (ведь чем ниже распо-
лагается центр тяжести, тем предмет
устойчивее), и включил в компози-
цию деталь, сыгравшую конструктив-
ную роль. Этой деталью стала змея:
в изгиб ее тела упирается хвост коня
(третья точка опоры), и часть нагруз-
ки переносится на туловище змеи.
С действием упомянутой аксио-
мы мы часто сталкиваемся в повсед-
невной жизни. Обычно это происхо-
дит, когда требуется зафиксировать
положение какого-нибудь предмета
в пространстве. Например, чтобы
зеркало на стене висело неподвиж-
но, его нужно укрепить в трех точках,
а чтобы дверь на двух петлях не от-
крывалась от сквозняка, ее закрыва-
ют на ключ, тем самым однозначно
Э. Фальконе.
Памятник Петру I.
Открыт в 1782 г.
58
определяя ее положение. Теперь понятно, почему кататься на
трехколесном велосипеде безопаснее, чем на двухколесном, и
почему чашки весов подвешивают на трех нитях. С задачей про
мух (в эпиграфе к этой главе) тоже все ясно: в любой момент
времени они определяют в пространстве некоторую плоскость
(и даже бесконечно много плоскостей — всякий раз, когда ока-
зываются на одной прямой). Так что, «вырвавшись» из одной
плоскости, мухи тут же попадают в другую.
СКОЛЬКО НОЖЕК
НУЖНО СТОЛИКУ?
У тещи Ипполита Матвеевича Во-
робьянинова, мадам Петуховой, из
романа И. Ильфа и Е. Петрова «Две-
надцать стульев», как известно, был
мебельный гарнитур, а в нем — один
примечательный предмет, о котором
мы узнаем из следующего разговора
героев:
«— Ипполит, — повторила теща,
—
помните ли вы наш гостиный гар-
нитур?
— Какой?..
—
Тот... Обитый английским
ситцем...
—
Помню, отлично помню... Ди-
ван, дюжина стульев и круглый сто-
лик о шести ножках».
Согласитесь, столик с шестью
ножками — вещица в самом деле
редкая! И зачем, интересно, их столь-
ко понадобилось? Разве что ради
красоты? Изготовить такой столик не-
просто да и сидеть за ним неудобно, а
главное — налицо явный перерасход
материала: ножек вдвое больше, чем
необходимо на самом деле!
Как известно, на практике ме-
бель круглой формы часто делают
опирающейся именно на три ножки,
Четыре точки могут
и не лежать в одной
плоскости
Столик на четырех
ножках часто менее
устойчив, чем на трех
59
причем их концы располагают в вершинах равностороннего
треугольника, — оптимальное решение с точки зрения геомет-
рии. Во-первых, так обеспечивается устойчивое положение
предмета на поверхности пола, которая, кстати, не всегда быва-
ет ровной; во-вторых, учитываются его форма, а также симмет-
рия всей конструкции.
Теперь легко понять, почему стол с четырьмя ножками за-
частую бывает менее устойчив, чем с тремя. Оказывается, че-
тыре произвольно взятые точки необязательно попадут в одну
плоскость. Если пол неровный или одна из ножек чуть короче
других, конец ножки может «зависнуть» над полом. Сам по себе
стол будет находиться в равновесии, опираясь на остальные
ножки, но стоит на него облокотиться, и он пошатнется. Чтобы
вернуть столу устойчивость, придется выровнять длину всех но-
жек, подложив что-нибудь под самую короткую из них.
ПОЛЕЗНЫЕ КОНСТРУКЦИИ
О том, что три точки опоры делают предмет устойчивым
даже на неровной поверхности, знали еще в древности, о чем
свидетельствуют известные в разных культурах трехногие пред-
меты. Один из них — трипод — сосуд на трех ножках (горшок,
чан, котел, кубок, чаша), служивший для различных целей:
приготовления пищи, хранения запасов и др. У некоторых на-
родов он назывался треножником
и использовался как домашняя, а
также ритуальная утварь. Позже так
стали именовать всякую подставку
на трех ножках. А примитивный и,
вероятно, самый древний тренож-
ник, которым и сегодня пользуются в
походе туристы, готовя пищу на огне,
представляет собой конструкцию из
трех шестов, скрепленных наверху и
упирающихся в землю свободными
концами.
Человек давно изобрел разно-
го рода складные, легкие и удобные
для транспортировки трехногие при-
способления. Все они по-прежнему
выполняют, в сущности, одну и ту
Жертвенный
треножник.
Китай. XVI—XVII вв.
60
же функцию — фиксируют положение размещенного на них
предмета в пространстве, занимая устойчивое положение на
плоской поверхности. Некоторые треножники получили даже
собственное название. Например, станок, на который худож-
ник помещает при рисовании картину, называется мольбертом,
а устройство для установки кино- и фотоаппарата при съемке,
геодезических, астрономических и прочих приборов при работе
с ними — штативом.
Образ треножника продолжает вдохновлять мастеров и ди-
зайнеров. Вот лишь два современных «изобретения» — бокал-
треножник и вешалка для верхней одежды, сделанная из... вил.
Выглядят предметы довольно забавно и необычно, но это не ме-
шает им отвечать своему основному назначению.
И. И. Фирсов.
Юный живописец.
1760-е гг.
Бокал-треножник
(автор — Мартин
Баптист)
Вешалка из трех
вил (автор —
Давид Ольшевски)
61
ГЛАВА 2
В поисках семицветика
То была блестящая и оригинальная импровизация.
О. Уайльд. Портрет Дориана Грея
Помнится, героиня сказки Валентина Катаева, девочка
Женя, получила в подарок чудо-цветок, исполнявший лю-
бые желания. Он походил на ромашку и имел семь разно-
цветных лепестков, за что его и прозвали семицветиком.
Цветов, подобных ромашке, предостаточно, и лепестков у
них бывает разное число, но отчего-то автор остановил
выбор именно на семи. Интересно, был ли у того цветика
реальный прообраз? Может, цветка с семью лепестками
в природе и не найти?
ДИВНЫЕ ТВОРЕНИЯ ПРИРОДЫ
Цветы издавна считаются символом красоты и совершенс-
тва. По словам известного математика Германа Вейля (1885—
1955), человек на протяжении веков пытался постичь и то и
другое посредством идеи симметрии. Как истинный ученый, он
считал, что цветы достойны внимания исследователя, потому
что обладают свойством поворотной симметрии, весьма распро-
страненной в мире растений. Биологи с математиком соглас-
ны: характер симметрии в строении
цветка служит одним из его сущест-
венных признаков.
Свойственная большинству цве-
тов поворотная симметрия n-го
порядка проявляется в том, что
цветок совмещается сам с собой
при повороте вокруг своей оси на
любой из углов
=
гдеn>1,k=1,2,...,
k
n. Что это оз-
начает в простейшем случае, когда
располагающиеся по кругу лепес-
тки образуют один слой? А вот что:
Цветок триллиума
(n=3)
62
всякий раз при повороте на угол
каждый лепесток встает
на место соседнего и после n таких перемещений в одном на-
правлении занимает исходное положение. Таким образом,
порядок поворотной симметрии цветка определяется, по сути,
числом его лепестков в венчике (а у некоторых растений —
строением околоцветника либо прицветника).
Например, для цветка молочая n = 2, он совмещается сам
с собой при повороте на углы 180о и 360о
. Для триллиума и
ириса n = 3, а подходящие углы поворота — 120о
, 240о
, 360
о
.
Нередко встречаются цветы с поворотной симметрией 4-го
порядка (сирень, чистотел), 6-го (лилия, шафран), 8-го (космея,
сангвинария) и более высокого порядка, но особенно часто
— 5 -го (герань, лютик).
Не странно ли, что из этого стройного ряда выпадает
семицветик? Природа явно отдает предпочтение цветам с другим
числом лепестков, в частности кратным 3, 4 или 5. А может,
семицветик и вовсе не был ею предусмотрен? Известно ведь,
что в неживой природе у безупречно симметричных кристаллов,
из которых состоят все твердые тела, поворотная симметрия
7-го порядка принципиально невозможна, а в животном мире
из всех видов симметрии преобладает зеркальная; поворотная
встречается куда реже и опять же другого порядка...
ТRIENTALIS, ОН ЖЕ ТРОИЧНИК, ОН ЖЕ СЕДМИЧНИК
И все-таки семицветик нашелся! В малочисленном роду
Trientalis семейства первоцветных всего-то три вида, из них два
встречаются на территории нашей страны. Вот он — похожий
на звездочку белоснежный цветок многолетнего травянистого
растения седмичник европейский, или Тrientalis europaea. Воо-
чию полюбоваться этим обитателем елового леса можно в пери-
од цветения, приходящийся на май—июль.
Вероятно, русское название (седмичник) произошло от сло-
ва «седмь» — семь да так и закрепилось за диковинным расте-
нием: одиночный цветок с семью лепестками в природе — явле-
ние и впрямь редкостное! И даже исключительное, если учесть,
что у данного растения к тому же 7 чашелистиков и 7 тычинок, в
завязи выделяются 7 частей, а плод (коробочка) раскрывается
7-ю створками и нередко содержит 7 семян. Даже листьев — и
тех зачастую бывает 7! Любопытно, что в толковом словаре
63
В. Даля упоминаются и другие названия этого растения. В наро-
де его прежде величали и семитычинником, и троичницей. Если
первое название указывает на число тычинок цветка, то второе
(от лат. triens — третья часть), говорит о другой особенности
растения: длина его цветоножки составляет примерно треть от
длины стебля.
Остается добавить, что цветки с семью лепестками встреча-
ются и у некоторых других видов, например у печеночницы бла-
городной, но чаще лепестков бывает все-таки шесть или восемь.
ЦВЕТОЧНЫЕ МОТИВЫ ВОКРУГ НАС
Итак, в природе поворотная симметрия 7-го порядка —
большая редкость. Быть может, она свойственна творениям рук
человеческих? Логично было бы поискать подходящие образцы
в декоративном искусстве: прикладном (в вышивке, росписи,
резьбе, чеканке) и монументальном, связанном с архитектурой
(в витражах, мозаике, рельефах и пр.). Здесь симметрия гос-
подствует как ни в каком другом виде искусства. Свидетельс-
тва тому — художественные изделия и памятники зодчества,
созданные разными народами в различные эпохи. Поворотная
симметрия четко прослеживается в круглом и круговом орна-
ментах, которыми украшают одежду и предметы быта, фасады и
интерьеры домов и других зданий.
Цветки печеночницы
(n=6,7,8)
Цветок седмичника
(n=7)
64
Во все времена одним из наиболее
популярных орнаментальных мотивов
был растительный, навеянный челове-
ку самой природой. Растения для ор-
намента выбирались разные: египтяне
часто изображали лотос и папирус,
греки и римляне — листья аканта, ев-
ропейцы эпохи Средневековья — три-
листник и т.д.
Вот несколько примеров. Во-пер-
вых, каменные цветы. Это не только
декоративные вазы и чаши вроде тех,
что изготовлял герой сказов Павла
Бажова Данила-мастер, но и фонтаны
в парках, и венчающие колонны капи-
тели. Во-вторых, украшающие потолки
и стены рельефные орнаменты и гип-
совые розетки. В-третьих, роскошные
стеклянные витражи готических собо-
ров: нередко их узор имеет «цветочное
происхождение». Плоский цветочный
орнамент встречается в росписи блюд
и подносов, аппликации на одежде, ри-
сунке плитки и паркета.
Капитель (n = 8)
Розетка (n = 6)
Витраж в соборе
Парижской Богоматери
(n=12)
Узор паркета (n = 10)
Орнамент на гербе (n = 7)
65
И что же мы видим? В декоративных элементах преоблада-
ет поворотная симметрия порядка n, равного или кратного 3, 4
либо 5, но никак не 7. Похожая картина наблюдается и в других
случаях. Поворотная симметрия 7-го порядка не нашла отраже-
ния ни в оригинальной форме окон, ни в строении колонн, ни в
конструкциях куполов и сводов, ни в общей планировке соору-
жений. Выходит, семицветик — диковинка не только в природе,
но и в искусстве!
И все же не бывает правил без исключений. Подтверждени-
ем тому служит орнамент с поворотной симметрией 7-го поряд-
ка, обрамлявший герб Республики Грузия (1918—1921).
ГЕОМЕТРИЯ ОРНАМЕНТА
Почему же семицветик такая
редкость? Очевидно, все дело в осо-
бенностях конструирования рисун-
ка. Должно быть, секрет кроется в
геометрии построений. Правила пос-
троения эскиза круглого орнамента
можно описать на языке геометрии.
Для простоты ограничимся создани-
ем плоского узора. Его легко полу-
чить, вращая вокруг заданной точки
исходный элемент и копируя его. Та-
кова общая идея.
Сначала нужно, вооружившись
инструментами, разделить круг на n
равных секторов и в одном из них
выполнить образец рисунка. Затем
повторить его в остальных частях,
поворачивая каждый раз на угол
=
. Если бы мы захотели сде-
лать эскиз семицветика, то первым
делом пришлось бы разбить круг на
семь равных секторов.
Проще говоря, в основе созда-
ния рисунка орнамента лежит зада-
ча о делении круга на равные части,
которая сводится к разбиению на
α
Создание круглого
орнамента
(n=8,
= 45°)
Построение
правильного
2n-угольника (2n = 8)
66
равные дуги ограничивающей круг окружности. Она известна
также как задача на построение правильного многоугольника
с заданным числом сторон и традиционно решается при помо-
щи циркуля и линейки. Эта задача, кстати, стоит в одном ряду
с тремя знаменитыми задачами древности: квадратурой круга,
трисекцией угла и удвоением куба. И попала она туда не толь-
ко благодаря своей многовековой истории, но и потому, что не
всегда разрешима с помощью упомянутых инструментов.
Еще со времен Пифагора греческие ученые проявляли ин-
терес к правильным многоугольникам и развивали искусство
их точного построения. Впоследствии эти знания были систе-
матизированы Евклидом и изложены в IV книге «Начал». При
помощи циркуля и линейки древние геометры умели строить
правильные n-угольники c числом сторон, равным 3, 4, 5, 6, 8,
10, 15. При этом использовалась окружность, описанная около
многоугольника.
Одни из указанных фигур можно получить на основе дру-
гих. Так, имея квадрат, легко построить правильный восьми-
угольник: достаточно разделить пополам каждую из четырех
дуг, на которые вершины квадрата разбивают описанную около
него окружность. Всего на окружности будут отмечены восемь
точек — вершин искомой фигуры. Остается последовательно
соединить их отрезками.
Умея строить правильный n-угольник, нетрудно получить
правильный 2n-, затем 4n-, 8n- и вообще всякий правильный
(2k n
k )-угольник, повторяя процедуру деления необходимое чис-
ло раз. Отсюда следует, что достаточно решить исходную задачу
для правильных многоугольников с нечетным числом сторон.
А вот правильный n-угольник, для которого n = km, а числа
k и m взаимно просты (не имеют общих делителей, кроме 1),
можно построить на основе двух правильных многоугольников
— с числом сторон k и
k m, вписанных в одну окружность. В «На-
чалах» Евклида приводится решение этой задачи для пятнадца-
тиугольника (15 = 3 5).
И ВСЕ-ТАКИ ОН ДЕЛИТСЯ!
Но во многих случаях ни первый, ни второй способ не годится,
как, впрочем, и другие. Скажем, правильный девятиугольник был
бы построен, если бы удалось разделить на три равные части
каждую из дуг, на которые разбивают описанную окружность
67
вершины равностороннего треугольника. Однако точно
это сделать нельзя: при помощи циркуля и линейки задача
неразрешима (доказано, что трисекция угла 120о невозможна).
Безуспешными оказались и попытки решить задачу для ряда
других значений n, в том числе n = 7. Неизвестно было даже,
осуществимо ли такое построение в принципе.
Ответ на вопрос, занимавший геометров почти 2300 лет, был
дан только в XIX веке. Сначала Карл Фридрих Гаусс, прозванный
королем математиков, показал, что при помощи циркуля и ли-
нейки правильный n-угольник с нечетным числом сторон можно
построить, если n — простое число вида
+ или является
произведением различных простых чисел указанного вида.
А позже Пьер Ванцель доказал: других правильных многоуголь-
ников, для которых эта задача разрешима, не существует.
Отметим, что при n = 3, 5, 15 задача покорилась еще древним
грекам, при n = 17 — все тому же Гауссу. Но она так и останется
невыполнимой для n = 7, 9, 11, 13 и
многих других чисел. Выходит, пос-
троить при помощи двух основных
инструментов снежинку, трилистник
или пятиконечную звезду можно, а
вот нарисовать «правильный» семи-
цветик не получится.
Что ж, деваться некуда. Придет-
ся пожертвовать этой самой «пра-
вильностью». Точность, которую так
ценят математики, — это, конечно,
хорошо, но в действительности до-
стигнуть ее бывает сложнее, чем ка-
жется. Скажем, разделить круг на 3,
4 или 6 равных секторов — задача
нетрудная, но с делением на 5 частей
справится уже далеко не каждый.
Другое дело — освоить для прак-
тических нужд какой-нибудь более
простой и, что важно, пригодный в
разных ситуациях приближенный
* Пьер Лоран Ванцель (1814—1848) — французский математик, известный тем, что
доказал невозможность ряда построений с помощью циркуля и линейки, в том числе
удвоение куба и трисекция угла.
C
AB
D
Приближенный метод
деления окружности
наnчастей(n=7)
68
метод решения задачи. Главное, чтобы он обеспечивал доста-
точно точный результат.
Вот один из подходящих методов деления окружности
на n частей, для которого при n ≤ 10 погрешность построе-
ния не превышает 1%. На диаметре AB окружности постро-
им равносторонний треугольник ABC, разделим основание
CC
AB на n равных частей. Затем проведем из вершины C через
C
вторую точку деления луч до пересечения с окружностью
— получим точку D. Тогда дуга AD составит n
1 часть окружности,
а хорда AD будет стороной правильного n-угольника.
Применим этот метод в случае n = 7. Две точки деления —
A и D уже есть, отметим при помощи циркуля остальные пять
точек (раствор циркуля, которым делаются засечки на окруж-
ности, берем равным AD). Наконец, соединим каждую из семи
точек с центром окружности. Заготовка для семицветика готова,
дело за малым — придумать и нарисовать узор из лепестков!
69
ГЛАВА 3
Секреты древних зодчих
Самым ценным из пяти чувств, по-видимому, явля-
ется зрение, и следует прежде всего проверить, в
какой мере мы можем доверять ему.
М. Клайн. Математика. Поиск истины
Нередко зрение обманывает нас, и мы видим то, чего в
действительности не существует. Объясняется это
оптическими иллюзиями — ошибками зрительного воспри-
ятия. С давних пор люди учились преодолевать их,
а иногда даже использовать. И, надо сказать,
значительно в этом преуспели.
ЭФФЕКТ ИРРАДИАЦИИ
Ошибки восприятия, свойственные человеческому глазу,
умели исправлять еще древние зодчие, когда создавали раз-
ные архитектурные формы. Оптический обман зачастую связан
с выбором точки наблюдения, особенностями окружающего
фона или освещенностью. Чтобы скорректировать искажения,
мастера прибегали к оптическим поправкам еще на стадии
проектирования сооружения. Они сознательно нарушали гео-
метрию строения: изменяли пропорции, отклоняли элементы от
вертикали или горизонтали, искривляли их контуры и т.п. С по-
мощью таких приемов зодчим удавалось «перехитрить» зрение.
Иногда, напротив, оптические иллюзии специально создавали и
усиливали. Считается, что более всех преуспели в этом искус-
стве греки: они научились придавать архитектурным формам
особую пластичность и выразительность.
Давно подмечено, что светлые предметы на темном фоне
кажутся больше, чем есть на самом деле, а темные на светлом,
наоборот, меньше. В оптике это явление называется иррадиа-
цией . Римский архитектор и инженер Марк Витрувий, живший
в I веке до н. э., образно выразил ее суть так: при сочетании
* Иррадиация — зрительное восприятие трехмерных объектов и плоских фигур на
контрастном фоне, при котором происходит оптический обман: наблюдаемый пред-
мет кажется иного размера, чем есть на самом деле.
70
темного и светлого свет «пожирает»
мрак. Действительно, в белой одеж-
де человек выглядит полнее, нежели
в черной, а ветви деревьев в лучах
солнца заметно «истончаются».
Знакомые с этой иллюзией ар-
хитекторы Древней Греции шли на
хитрость — делали колонны своих
построек разной толщины. Примером
тому служит знаменитый Парфенон
—
главный храм Афинского Акропо-
ля, построенный в 447—438 годах
до н. э. Его создатели, архитекторы
Иктин и Калликрат, учли, что для угло-
вых колонн фоном будет яркое небо
Эллады, а для остальных темным фоном послужит святилище хра-
ма. Поэтому сделали угловые колонны более широкими и умень-
шили расстояние между ними и соседними колоннами. Благодаря
этим «поправкам» издали все колонны выглядели совершенно
одинаково, а разница между ними обнаруживалась только при
непосредственном измерении.
Разные по толщине колонны
Парфенона на фоне яркого неба
кажутся одинаковыми
Энтазис и утонение
греческой колонны
в храме Афины
в Пестуме
71
ПРЯМЫЕ ИЛИ КРИВЫЕ?
Древнегреческие зодчие знали и о том, что вертикальные
и горизонтальные прямые при значительной длине кажутся не
параллельными. Чтобы колонны здания визуально не расходи-
лись, их при установке на основание (стилобат) слегка наклоня-
ли внутрь, тогда, как отмечал Витрувий, сооружение выглядело
цельным и прочным как монолит. Чтобы колонны не казались
вогнутыми, их немного утолщали на уровне трети высоты. При-
ем этот получил название энтазис (от греч. entasis — напряже-
с
ние, усиление). Кроме того, колонны сужали кверху, как говорят
архитекторы, утоняли, зрительно удлиняя их и делая менее мас-
сивными. Наглядным примером служит коллонада храма Афины
в Пестуме, возведенного в конце VI века до н. э.
С эффектом «провисания» горизонтальных линий боро-
лись с помощью другого приема — искривления прямых, или
курватуры (от лат. curvatura — изгиб, кривизна). Так, ступени
Парфенона были слегка изогнуты, а само здание стояло на вы-
пуклой каменной платформе — тем самым сглаживалась иллю-
зия «проседания» пола. Лежащая на капителях колонн горизон-
тальная балка (архитрав) в центральной части была уже, чем по
краям, а издали выглядела абсолютно ровной.
Вероятно, подобные секреты были известны не только
древним грекам. Например, строители Стоунхенджа (древней-
шего каменного сооружения на территории Англии) при обра-
ботке камней делали их поверхность выпуклой с разных сторон.
Благодаря такой форме стыки каменных столбов и уложенных
Камни Стоунхенджа издали выглядят прямоугольными,
но это оптический обман
72
на них плит визуально выпрямляют-
ся (возникает иллюзия их перпенди-
кулярности), а сами камни кажутся
прямоугольными.
УСТОЙЧИВЕЕ И ВЫШЕ
Оптические иллюзии, видимо,
были знакомы и русским зодчим.
Один из примеров тому — Троицкий
собор в Троице-Сергиевой лавре,
сооруженный в 1422—1423 годах в
честь основателя монастыря препо-
добного Сергия Радонежского. Его
наружные стены имеют заметный
наклон к центру здания, благодаря
чему усиливается впечатление устой-
чивости строения. Служащий опорой
купола барабан со щелевидными ок-
Оптические поправки делают
Троицкий собор более устойчивым
и устремленным ввысь
Находясь в храме,
зритель часто
преувеличивает его
высоту. Интерьер
Благовещенского
собора
73
нами сужается кверху. Этот прием зрительно вытягивает храм, и
он выглядит выше, чем есть на самом деле.
В православном храме возникает и другая иллюзия — свя-
занная с восприятием замкнутого пространства. Внутри пост-
ройка кажется значительно выше, нежели есть в действитель-
ности. Достигается такой эффект не без помощи оптических
поправок. При возведении Троицкого собора, например, были
наклонены внутрь стены выше арок порталов и столбы, слу-
жащие опорами свода (пилоны). Еще больший эффект высоты
создают крутые линии арок и сводов, имеющие вид дуг окруж-
ности и кривых, близких к параболе. Взгляните на снимок, сде-
ланный в Благовещенском соборе Московского Кремля.
ПО ЗАКОНАМ ПЕРСПЕКТИВЫ
При строительстве монументальных
сооружений чаще всего архитекторам
приходилось бороться с кажущимся ис-
Кампанила
Джотто
спроектирована по
законам обратной
перспективы
Колокольня Ивана Великого
как будто падает назад
74
кажением их размеров с изменением расстояния, то есть в пер-
спективе. Если, например, взглянуть на высокое здание снизу,
создается впечатление, что в верхней части оно гораздо уже,
чем у основания, и отклонено назад. Пример тому — колоколь-
ня Ивана Великого, построенная в начале XVI века. Эффект ее
«падения» ощущается даже на фотографии. Более того — его
запечатлел на своей картине «Вид на Соборную площадь Мос-
ковского Кремля» художник Джакомо Кваренги (1744—1817),
рисовавший колокольню с натуры и смотревший на нее с другой
точки.
Один из приемов устранения оптической иллюзии, связан-
ной с перспективой, предложил известный итальянский живо-
писец эпохи Возрождения Джотто ди Бондоне (1267—1337).
Проектируя кампанилу (колокольню) при кафедральном соборе
Санта-Мария дель Фьоре во Флоренции, он сделал ее в верхней
части шире, чем у основания, то есть прибегнул к обратной пер-
спективе. При строительстве эту часть еще больше увеличили,
придав всему сооружению монументальность.
Древние греки использовали такой прием: отклоняли эле-
менты верхней части постройки от вертикального положения.
Например, фронтон устанавливали под углом, наклоняя немного
вперед, подобно тому как вешают картины в музеях. А скульпто-
ры делали фигуры, украшавшие здания, более рельефными, и
это сглаживало визуальный эффект их уменьшения при взгляде
с земли. Принимались во внимание и точки наблюдения: каж-
дая статуя создавалась с учетом места, которое ей отводилось
во всей композиции.
ОРИГИНАЛЬНЫЕ НАХОДКИ
Иногда античные архитекторы использовали иллюзию пер-
спективы не для сглаживания, а, наоборот, для усиления того
или иного визуального эффекта. Например, в портике (крытой
галерее перед входом в здание) с двойным рядом колонн внут-
ренние колонны делали более тонкими по сравнению со сто-
ящими впереди, зрительно удаляя их. Тем самым создавалось
впечатление большей глубины пространства.
Другое оригинальное изобретение греков состояло в том,
что внутреннюю колоннаду в храмах они возводили иногда
двухэтажной. В Парфеноне, например, это было сделано не
столько для красоты, сколько для достижения иллюзии боль-
75
шей высоты статуи богини Афины, установленной в святилище.
На фоне двухэтажного сооружения она смотрелась крупнее,
чем есть, и оттого выглядела более торжественно и величес-
твенно.
Наконец, снимок Парфенона зафиксировал еще одну опти-
ческую иллюзию. Когда взгляд «скользит» по колоннаде, запол-
ненное ею пространство зрительно удлиняется, отчего здание
кажется больше. По той же причине мы склонны преувеличи-
вать размеры построек, украшенных орнаментами и скульптур-
ными композициями — даже они помогают добиться нужного
зрительного эффекта.
Рассмотренные примеры свидетельствуют о том, что древ-
ние архитекторы и строители не только знали об особеннос-
тях человеческого зрения и порожденных ими иллюзиях, но и
применяли эти знания для создания определенных образов и
впечатлений, которым мы, зрители, легко поддаемся. Система
оптических поправок, придуманная зодчими, лишний раз де-
монстрирует их высочайшее мастерство в сложном искусстве
архитектуры.
Окруженная колоннадой статуя Афины
выглядит настоящим колоссом.
Реконструкция святилища Парфенона
76
ГЛАВА 4
Странности картин
Чтобы представить привычное
Крупным планом,
Нужно уметь обычное
Сделать странным.
П. Хейн
Порой мы видим на картинах то, чего не может быть в
действительности, каким бы правдоподобным ни казалось
изображение. Это происходит, когда художники допуска-
ют ошибки, связанные с нарушением законов геометрии.
В одних случаях несоответствия бросаются в глаза, в
других и вовсе незаметны, но вызывают у нас ощущение
чего-то необычного и даже странного, и бывают они как
случайными, так и допущенными намеренно — с целью
привлечь внимание или поразить воображение зрителя.
ЗАГАДКА ЛЕОНАРДО
Перед вами эскиз картины «Поклонение волхвов» Леонар-
до да Винчи (1452—1519), который исследователи творчества
знаменитого художника эпохи Возрождения считают превос-
ходным образцом построения линейной перспективы. В самом
деле, набросок заднего плана выверен с математической точ-
ностью — взгляд так и скользит по прямым линиям, устрем-
ляющимся к центральной точке схода , и фиксируется на ней.
Но приглядитесь к колоннам у левого края рисунка. Ничего
странного не замечаете? Колонны изображены с нарушением
той самой перспективы, которая так восхищает всех в рисунке
Леонардо. Колонна, что опирается на ступеньку, показана сразу
на двух планах: переднем (у основания) и заднем (на уровне
капители). Да и вторая колонна стоит явно не на месте.
Истинная причина допущенной художником «ошибки» так
и останется для нас загадкой. В то время уже сложившийся
* Центральная (главная) точка схода — точка на горизонте, расположенная против
глаз наблюдателя, в которой сходятся все прямые линии, перпендикулярные плос-
кости изображения.
77
мастер, Леонардо вряд ли допустил просчет по неведению, тем
более что налицо «отвлекающий маневр» — взгляд зрителя
волей-неволей сосредотачивается в центре рисунка. Другое
дело — работа начинающего художника, вчерашнего учени-
ка. Взгляните на «Благовещение», самую раннюю из известных
картин да Винчи. На ней допущено несколько ошибок. Наибо-
лее явная — рука Девы Марии не может достать книгу, лежащую
на аналое: он стоит ближе к зрителю, чем к самой Деве. Как
следствие — ее правая рука длиннее левой, пропорции фигуры
нарушены.
Леонардо да Винчи. Поклонение волхвов. Эскиз. 1481 г.
Леонардо да Винчи. Благовещение. Ок. 1472—1475 гг.
78
НЕРЕАЛЬНЫЕ ОБЪЕКТЫ
Невозможную фигуру, или геомет-
рически противоречивое изображение,
подобное колоннам на эскизе Леонар-
до, представляет собой конструкция на
знаменитой литографии «Бельведер»
голландского художника-графика Ма-
урица Эшера (1898—1972). По этой кар-
тине, написанной почти через 500 лет
после «Поклонения волхвов», можно
судить о направлении имп-арт (от англ.
impossible — невозможный и art — ис-
кусство) в так называемом оптическом
искусстве — оп-арте. Вариации на ту
же тему можно видеть и в работах сов-
ременных художников, создающих па-
радоксальные фигуры — объекты, ко-
торые кажутся реальными, однако не
могут существовать в действительности.
Изображая различные предметы, авторы
намеренно нарушают законы геометрии
и добиваются тем самым неожиданных
визуальных эффектов — создают пора-
зительные оптические иллюзии.
Вот лишь один пример — «Натюр-
морт в окне» бельгийского художника и
дизайнера Жоса де Мея (1928—2007).
Верхняя и нижняя половины «оконной
рамы», если рассматривать их по отде-
льности, выглядят как нормальные, но
соединенные вместе образуют невоз-
можный объект. Дело в том, что они
показаны с различных точек, в разной
перспективе, и это приводит к неверно-
му расположению одной части относи-
тельно другой. А теперь взгляните еще
раз на картину Леонардо да Винчи «Бла-
говещение». Каменный парапет справа
удивительным образом сливается со
стеной дома, и его верхняя часть будто
М. Эшер.
Бельведер. 1958 г.
Жос де Мей.
Натюрморт
в окне. 1997 г.
79
вывернута в пространстве: линии
краев в какой-то момент, неулови-
мый для глаза, превращаются из па-
раллельных прямых в скрещивающи-
еся. Что это: результат неудачного
эксперимента или очередная загад-
ка художника? Как бы то ни было, но
перед нами еще одна невозможная
фигура.
НАРУШАЯ СОРАЗМЕРНОСТЬ
А вот «Портрет знатной генуэз-
ской дамы и ее сына» кисти знаме-
нитого фламандского портретиста
Антониса ван Дейка (1599—1641).
Герои картины производят совер-
шенно разное впечатление. Из-за
сильной диспропорции женщина
выглядит нереально. У нее огромный
для человека рост, несоразмерно ма-
ленькая голова и, судя по положению
рук и ног, проблемы с телосложени-
ем. Кажется, что портрет дамы соб-
ран по частям и они плохо подогна-
ны одна к другой. В фигуре мальчика
ничего подобного не наблюдается,
она воспринимается совершенно ес-
тественно.
Не менее странное впечатление
производит картина «Возвращение
с рынка» французского живопис-
ца Жана Батиста Шардена (1699—
1779), признанного мастера бытово-
го жанра. Женщина на ней выглядит
чересчур высокой и нескладной, а ее
правая рука неестественно длинной.
И если остальные части фигуры по
отдельности имеют правильные про-
порции, то при соединении прояв-
ляется несоответствие их размеров.
Ван Дейк. Портрет
знатной генуэзской
дамы и ее сына. 1626 г.
Ж. Б. Шарден.
Возвращение с рынка.
1739 г.
80
Просчет Шардена можно было бы
счесть случайностью, если бы он не
обнаружился и на некоторых других
полотнах художника.
СТОИТ ИЛИ ПАДАЕТ?
Нарушение перспективы и про-
порций — наиболее частые ошиб-
ки, встречающиеся в произведениях
живописи. Но глаз замечает и другие
неточности.
Например, на картине «Ужин в
Эммаусе», написанной предположи-
тельно итальянцем Джованни Бел-
лини (ок. 1430—1516), сцена тра-
пезы выглядит очень реалистично.
Тщательно прорисованы позы, лица
и одеяния людей, детали интерьера,
еда и посуда. А вот ножки стола явно
не на месте. Через их концы, как вер-
Дж. де Кирико.
Пророк. 1915 г.
Дж. Беллини. Ужин в Эммаусе.
1490-е гг.
81
хние — со стороны столешницы, так и нижние — упирающие-
ся в пол, можно мысленно провести по прямой линии, которые
окажутся параллельны. Это означает, что все ножки расположе-
ны в одной плоскости. Такой стол крайне неустойчив, он упадет
при первой же попытке установить его на пол. Следовало бы
развернуть пары ножек (достаточно одну, а лучше обе — из со-
ображений симметрии конструкции) в пространстве, скажем на
90о
, чтобы они располагались в параллельных плоскостях.
Любопытно, что эта ошибка встречается и на полотнах дру-
гих живописцев, например в картине «Пророк» Джорджо де Ки-
рико (1888—1978), одного из основоположников сюрреализ-
ма. Хотя тут, пожалуй, все зависит от нашей договоренности.
Если сочтем, что мольберт падает, то художник не ошибся. Если
решим, что мольберт твердо стоит на полу, то это такой же вы-
мысел автора, как и вся композиция.
ЗАПРЕЩЕННОЕ ИЗОБРАЖЕНИЕ
Пример «ошибки» иного рода,
свидетельствующий об оригиналь-
ном авторском замысле, — знаме-
нитая картина-загадка «Портрет
Эдварда Джеймса» бельгийского ху-
дожника-сюрреалиста Рене Магрит-
та (1898—1967). У этой работы есть
и другое название — «Воспроизве-
дение запрещено». Герой картины
—
известный в свое время английс-
кий коллекционер и меценат, друг и
покровитель Магритта — смотрит на
себя в зеркало, но, вопреки закону
отражения (симметрии относитель-
но плоскости), вместо лица видит
свой затылок.
С точки зрения геометрии это
невозможно, значит, такое «воспро-
изведение» действительно запре-
щено. Правда, это касается только
героя портрета: и каминная полка, и
лежащая на ней книга отражаются в
зеркале правильно. Ошибка допуще-
Рене Магритт.
Портрет Эдварда
Джеймса. 1937 г.
82
на Магриттом, конечно, намеренно. В его стиле было сочетать в
своих работах вещи, в реальности не сочетаемые, изображать
персонажей со спины, закрывать или заменять их лица различ-
ными предметами.
ДВА В ОДНОМ
Не менее интересна для изучения картина-перевертыш
Сальвадора Дали (1904—1989) «Лебеди, отраженные в слонах»,
в которой мы также сталкиваемся с нарушениями законов сим-
метрии. С одной стороны, лебеди на воде — самостоятельная
часть картины, а с другой — они словно срослись с деревьями.
Самое удивительное, что их отражение — фигуры слонов, сто-
ящих на земле. Перевернем картину «вверх ногами» и увидим
лебедей, которые, отразившись «в обратную сторону», вновь
превращаются в слонов.
С точки зрения геометрии такое взаимно обратное превра-
щение объектов объясняется проявлением закона зеркальной
симметрии. Но присмотритесь к группе лебедей. Три птицы от-
ражаются в воде правильно, а четвертая, будто завалившаяся
набок, нет. Не потому ли, что по замыслу автора этот лебедь от-
ражается в другой зеркальной плоскости и последняя располо-
жена под углом к первой? В реальности такое, конечно, было бы
невозможно, а в воображении художника-сюрреалиста вполне.
Сальвадор Дали. Лебеди, отраженные в слонах. 1937 г.
83
Напоследок еще одна картина-загадка. Перед вами полотно
нидерландского живописца Дирка Баутса (ок. 1415—1475) на
известный библейский сюжет — помазание Христа женщиной
при посещении им дома Симона*
.
Здесь сразу несколько за-
метных глазу ошибок и несоо тветствий. Попробуйте отыскать
нарушения в изображении фигур и предметов, делающие кар-
тину менее реалистичной и больше похожей на коллаж. На этой
картине также есть деталь, лишняя с точки зрения геометрии.
Какая именно?
* В Евангелии от Луки Симон — фарисей (член иудейской секты), в дом которого
был приглашен на трапезу Иисус Христос во время странствий по Галилее.
Дирк Баутс. Христос в доме Симона. 1440 г.
84
ОТВЕТ
Картина Дирка Баутса — настоящая головоломка. На ней
можно обнаружить немало «ошибок», несоответствий и даже
невозможных объектов.
В глаза бросается нарушение пропорций. Так, у монаха
справа голова несоразмерна кистям рук — выглядит слишком
большой (1). Странно смотрятся руки человека рядом с ним
—
кажется, они вообще разной длины (2). Это можно было бы
объяснить выбранным ракурсом, если бы позы и жесты людей
выглядели более естественно и согласованно. Имеются пробле-
мы с линейной перспективой. Персонажей, стол и предметы на
нем, детали помещения, стены и пол, даже колонны и пейзаж
вдали — все это мы видим с разных точек, в разной перспекти-
ве (например, стол изображен в прямой перспективе, а рисунок
пола — в обратной). Создается впечатление, будто их рисова-
ли порознь, и после соединения в одно целое они оказались не
связаны друг с другом. Отсюда — эффект коллажа.
Слева неверно изображены части проема, к которым крепят-
ся основание и капитель декоративной колонны (3): линии их
верха и низа должны быть соответственно параллельны, однако
1
2
3
4
4
5
5
85
они скрещиваются, превращая всю конструкцию в невозможную
фигуру. Линии основания самой колонны излишне искривлены,
а вот колонна на заднем плане такого изъяна лишена.
Наконец, недостатком, опять-таки с точки зрения геомет-
рии, можно назвать «перебор» ножек у изображенного на пе-
реднем плане стола. Если вверху они скреплены перекладиной,
что характерно для столов подобной конструкции, то внутрен-
ние подпорки (4) — лишние. На гладком полу стол будет стоять
и без них за счет имеющихся параллельных опор (5), поскольку
две параллельные прямые однозначно задают плоскость и фик-
сируют ее положение в пространстве.
86
ЧАСТЬ ТРЕТЬЯ
Числа и фигуры
ГЛАВА 1
Волшебство и магия в квадрате
Я не знаю ничего более прекрасного в арифметике,
чем эти числа, называемые некоторыми планетны-
ми, а другими — магическими.
Пьер де Ферма в письме Мерсенну
Магические квадраты давно стали развлечением для одних
и предметом изучения для других. Им посвящено множес-
тво статей, заметок и монографий. Редкая книжка по
занимательной математике обходится без этой голово-
ломки-долгожительницы: сегодня, как и столетия назад,
она привлекает к себе пристальное внимание.
ИЗ ГЛУБИНЫ ВЕКОВ
«В незапамятные времена, научившись считать, люди поз-
нали меру количества — число. Вглядываясь в сочетания чисел,
они с изумлением увидели, что числа имеют какую-то самосто-
ятельную жизнь, удивительную и полную тайны; тайны необъ-
яснимой и поэтому загадочной и многозначительной... Ока-
залось, что, располагая числа правильными рядами, один под
другим, в случае удачи можно, складывая их слева направо и
сверху вниз, каждый раз получать одно и то же число. Наконец,
кто-то придумал разделить числа линиями так, что каждое из
них оказалось в отдельной клетке, как птицы в доме птицелова.
Так посвященные увидели квадрат, населенный числами, неиз-
вестно что сулящий его владельцу, но, конечно, обладающий
магической силой» .
* Гуревич Е. Я. Тайна древнего талисмана. — М.: Наука, 1969.
87
Священные, волшебные, загадочные, таинственные, совер-
шенные... Как только их не называли! Привлекающие естест-
венной красотой, наполненные внутренней гармонией, такие
доступные, но по-прежнему непостижимые, скрывающие за ка-
жущейся простотой множество тайн. Знакомьтесь: магические
квадраты — удивительные представители воображаемого мира
чисел.
Магическим квадратом n-го порядка называется квадрат-
ная таблица размером n n, заполненная натуральными числа-
миот1доn2
, суммы которых по всем строкам, столбцам и обеим
диагоналям одинаковы. Различают магические квадраты чет-
ного и нечетного порядка (в зависимости от четности n). Поля
таблицы, в которые записывают числа, называются клетками
магического квадрата, а сумма чисел, стоящих в любой строке,
столбце или на диагонали, — его постоянной.
Магические квадраты возникли в глубокой древности в Ки-
тае. Вероятно, самым «старым» из дошедших до нас магических
квадратов является таблица Ло Шу (ок. 2200 до н. э.). Она име-
ет размер 3 3 и заполнена натуральными числами от 1 до 9.
В этом квадрате сумма чисел в каждой строке, столбце и на
диагонали равна 15 (рис. 1, а). Согласно одной из легенд, про-
образом Ло Шу был узор из связанных черных и белых точек
(рис. 1, б), украшавший панцирь огромной черепахи, которую
встретил однажды на берегу реки Ло мифический прародитель
китайской цивилизации Фуси. Жители Поднебесной считали
таблицу Ло Шу священной, у них даже не возникала мысль о со-
ставлении аналогичных квадратов большего размера, поэтому
последние стали появляться только спустя три тысячелетия.
492
357
816
аб
Рис. 1
88
Из Китая магические квадраты
распространились сначала в Индию,
затем в Японию и другие страны.
На Востоке их считали волшебными,
полными тайного смысла символами
и использовали при заклинаниях. На
рис. 2 изображен один из магических
квадратов 4-го порядка, известный
еще древним индусам. Он интересен
тем, что сохраняет свойство быть ма-
гическим после последовательной
перестановки строк (столбцов). На-
звание «магические» квадраты полу-
чили от арабов, которые усмотрели
в их свойствах нечто мистическое
и потому принимали квадраты за
своеобразные талисманы, защищав-
шие тех, кто их носит, от многих не-
счастий. К удивительным квадратам
проявляли интерес и средневековые
арабские математики, приводившие
их в качестве примеров в своих со-
чинениях.
Древние греки были знакомы
с простейшим (3-го порядка) маги-
ческим квадратом. В одном из араб-
ских манускриптов конца VIII века
упоминается его автор (который на
самом деле лишь открыл заново то,
что было известно за много веков до
него) — философ-новопифагореец
Аполлон из Тиана, живший в начале
нашей эры. В средневековой Евро-
пе, как и на Востоке, магическим квадратам часто приписывали
различные мистические свойства. Неудивительно, что они поль-
зовались особой популярностью у прорицателей, астрологов и
врачевателей. Бытовало даже поверье, что выгравированный на
серебряной пластине магический квадрат защищает от чумы.
Европейцев с волшебными числовыми квадратами в начале
XV века познакомил византийский писатель и языковед Мос-
хопулос. Его работа была первым специальным сочинением на
712114
213811
163105
96154
Рис. 2
Рис. 3
89
эту тему и содержала примеры магических квадратов разного
порядка, составленных самим автором. С именем Мосхопулоса
связывают также оригинальный метод построения магических
квадратов нечетного порядка. В нем заполнение клеток табли-
цы числами от 1 до n2 происходит согласно ходу коня на шах-
матной доске — в виде буквы Г (отсюда другое название — ме-
тод коня). Алгоритм построения довольно прост и сводится к
трем правилам.
1. Если n делится на 3, запишем 1 в среднюю клетку ниж-
ней строки таблицы, в остальных случаях клетку можно выбрать
произвольно.
2. Запишем числа по порядку, двигаясь ходом коня вверх
и вправо. Как только выйдем за пределы квадрата, перенесем
число внутрь его, пользуясь правилом: если число оказалось
справа от квадрата, сместим его на n
клеток влево, а если над квадратом,
то на n клеток вниз. Если же число
попало в клетку, расположенную
иначе, например на линии диагона-
ли, выполним последовательно оба
эти переноса.
3. Если клетка, куда следует за-
писать число n + 1, занята, смещаем
это число на четыре клетки выше по
отношению к числу n.
Применим этот алгоритм в слу-
чаеn=5(рис.3).
В ЗАПАДНОМ ИСКУССТВЕ
В начале XVI века знаменитый
немецкий художник Альбрехт Дю-
рер привнес магический квадрат в
искусство, изобразив его на гравюре
«Меланхолия» (рис. 4).
Квадрат Дюрера имеет размер
4 4 и составлен из чисел, сумма ко-
торых в каждой строке, столбце и на
диагонали равна 34. Оказывается, 34
равны и суммы других четверок чи-
сел: расположенных в центре, в уг-
Рис. 4
90
ловых клетках,
по бокам цент-
рального квад-
рата (рис. 5, а),
а также обра-
зующих четыре
равных квад-
рата, на которые можно разделить
исходный квадрат (рис. 5, б). А вот
числа 15 и 14 в нижней строке квад-
рата указывают на дату создания
гравюры — 1514 год.
Отметим попутно еще несколь-
ко свойства квадрата Дюрера. Сум-
мы четверок чисел из клеток, от-
меченных ходом шахматного коня
(рис. 5, в), одинаковы и равны пос-
тоянной квадрата, например 16 + 11 + 1 + 6 = 34. Нетрудно ви-
деть, что суммы квадратов чисел, стоящих в крайних столбцах,
равны:
162+52+92+42
= 132+82+122+12
= 378.
Для наборов чисел из средних столбцов имеем:
32+102+62+152
=2
2
+112+72+142
= 370.
Сложив найденные суммы, получим 748 = 2 11 34.
И вновь о себе напоминает постоянная квадрата! Аналогичным
образом связаны четверки чисел, размещенных построчно.
А вот для чисел, расположенных по бокам центрального квадра-
та (см. рис. 5, а), выполняются такие равенства:
Рис. 6
Рис. 5, a
Рис. 5, б
Рис. 5, в
91
* Клод Гаспар Баше де Мезириак (1581—1638)
—
французский математик и поэт, автор книг по
занимательной математике.
32+52+122+142
=2
2
+82+92+152
=1134,
33+53+123+143=23+83+93+153=2
2
342
.
Другой пример использования магического квадрата в за-
падном искусстве — изображение Ло Шу на гравюре, украша-
ющей трактат немецкого ученого-иезуита Атанасиуса Кирхера
«Аритмология» (1665), рис. 6. Обращение к этой фигуре, веро-
ятно, было связано с содержанием трактата, ибо две его части
посвящены магическим квадратам, и с интересом автора ко все-
му, что связано с Китаем. Он, конечно, знал и о происхождении
Ло Шу, и об особом отношении к этому числовому квадрату.
В ЕВРОПЕЙСКОЙ НАУКЕ
В середине XVI века в Европе по-
явились первые сочинения, в кото-
рых магические квадраты предстали
как объекты математического иссле-
дования, тем самым было положено
начало их новой жизни. Затем пос-
ледовало множество других работ, в
том числе таких известных матема-
тиков, как Штифель, Баше, Паскаль,
Ферма, Эйлер, Гаусс. Так, Баше де
Мезириак описал простой графи-
ческий способ построения квадратов
нечетного порядка, известный также
как метод террас (он не раз переот-
с
крывался и, вероятно, был изобретен
в древности). Проиллюстрируем его
на примере построения магического
квадрата 5-го порядка.
Числа от 1 до 25 запишем по-
следовательно в клетках по диаго-
нали по пять в ряд, как показано на
рис. 7, а.
Выделим в центре квадрат разме-
ром 5 x 5 (основу будущего магичес-
кого квадрата). Затем каждое число,
Рис. 7, б
Рис. 7, а
92
расположенное в не его, перенесем внутрь —
к противоположной стороне квадрата, сме-
щаясь при этом на пять клеток по горизон-
тали либо по вертикали (рис. 7, б).
Магический квадрат готов (рис. 7, в),
его постоянная равна 65.
В XVI—XVII веках составлением маги-
ческих квадратов занимались с таким же
увлечением, с каким сегодня придумывают
и разгадывают сканворды. Любопытно, что
именно в одной из книг Баше де Мезириака
магические квадраты впервые предстали как
математическая забава. Примерно в то же время Пьер де Ферма
разработал общий метод построения квадратов четного поряд-
ка, а Френикль де Бесси вычислил и построил все различные
квадраты 4-го порядка. Дальнейшее развитие теории магичес-
ких квадратов оказалось связано с развитием теории чисел и
комбинаторики.
В наше время магическими квадратами интересуются не
только специалисты, но и любители математических игр и раз-
влечений. Известно множество оригинальных задач и голо-
воломок, связанных с необычными фигурами из чисел. В них
привлекают, прежде всего, простота, наглядность и изящность
построений. Для успешного решения таких задач требуются не
особые знания, а умение подмечать числовые закономернос-
ти. Эти головоломки не только доставляют удовольствие, но и
служат прекрасной гимнастикой для ума, в чем читатель скоро
убедится сам.
ВОПРОСЫ, ВОПРОСЫ...
Возникают самые разные вопросы, связанные с магически-
ми квадратами. На одни из них ответы давно найдены, на другие
только предстоит найти. Остановимся подробнее на некоторых
проблемах.
Как уже отмечалось, квадрат 3-го порядка является самым
простым (не считая тривиального случая, когда n = 1 и рассмат-
ривается всего одно число). А почему не существует магическо-
* Бернар Френикль де Бесси (1605—1675) — французский математик, известный
работами в области теории чисел.
Рис. 7, в
93
го квадрата 2-го порядка? Квадрат размером 2 2 должен был
бы состоять из чисел 1, 2, 3 и 4, а его постоянная — равняться
5. У такого квадрата по две строки, столбца и диагонали. Итого
шесть. Чтобы квадрат стал магическим, надо представить число
5 в виде суммы двух из данных чисел шестью различными спо-
собами, при этом порядок слагаемых не учитывается, а сами они
не должны повторяться ни в какой сумме. Но это сделать не-
возможно! Ведь таких комбинаций всего две: 1 + 4 и 2 + 3. Как
ни расставляй числа в клетках таблицы, их сумма будет равна 5
либо в каждой строке, либо в обоих столбцах, либо на диагона-
лях (рис. 8), но никак не одновременно.
Рассматривая магические квадраты разного порядка, мы
указывали их постоянные, которые, как легко догадаться, од-
нозначно определяются размером соответствующей таблицы.
Конечно, при наличии квадрата для небольших значений n
заветную сумму можно вычислить непосредственно. Но даже
нескольких приведенных выше примеров достаточно, чтобы по-
нять: с увеличением n она быстро растет. А что делать в том слу-
чае, когда квадрат еще не построен? Или если нужно проверить,
является ли данный квадрат магическим? Да и как составить
сам квадрат, не зная его постоянной?
Выведем общую формулу, позволяющую вычислить ее для
квадрата любого порядка. Пусть в таблице размером n n рас-
полагаются натуральные числа от 1 до n2
. Их сумма S равна
S
.
2
)
1(
...
3
2
1
2
2
2
n
n
n
Обозначим постоянную магического квадрата буквой s, тогда
+
=
=
+
=
Покажите, что число s является натуральным при любом
n 3. Подумайте также над тем, будет ли магическим квадрат,
1
4
2
3
1
3
4
2
1
2
3
4
Рис. 8
94
полученный из некоторого магического квадрата в результате
увеличения всех его чисел на какое-либо натуральное число, и
почему? Изменится ли ответ, если операцию сложения заменить
умножением?
С давних пор математики стремились решить две основные
задачи, связанные с магическими квадратами: найти общий ме-
тод их построения и описать все возможные магические квадра-
ты. Первая задача достойна подробного рассмотрения, которое
выходит за рамки нашего рассказа. Отметим лишь, что основы
математической теории построения магических квадратов были
заложены французскими учеными в XVII веке. Позже она стала
излюбленной темой исследований многих авторов. И хотя для
каждого вида квадрата были найдены свои способы решения
задачи, пока не известен общий, пригодный для квадратов лю-
бого порядка метод их построения. Вторая задача также до сих
пор не решена. Отчасти это связано с тем, что с увеличением
n число магических квадратов стремительно растет. Доказано,
что для n = 4 существует 880 различных (не переходящих друг в
друга при поворотах и отражениях) магических квадратов, для
n 5 их число оценивается примерно в 35 млн, а для больших
значений n вообще не найдено.
ПРОЩЕ ПРОСТОГО
Не менее удивительно то, что существует всего один маги-
ческий квадрат 3-го порядка! Общее число квадратов, которые
можно составить из девяти чисел,
9!=1 2 ... 9 =362880.
Среди них есть такие, которые получаются один из другого
при помощи поворота на 90о
, 180о
, 270о вокруг центра квадра-
та или в результате осевой симметрии относительно всякой из
четырех осей квадрата. Если найден один магический квадрат,
то каждый из семи квадратов, полученный из него любым из
указанных способов, не следует рассматривать как новый вари-
ант искомого квадрата. Как известно, от перестановки мест сла-
гаемых сумма не меняется. В данном случае важна сумма, а не
порядок расстановки слагаемых. Так что все восемь квадратов
представляют по сути один квадрат. Отбросив все «ложные» ва-
рианты, получим интересующее нас число расстановок чисел в
таблице размером 3 3, а именно 362 880 8 = 45 360, и только
одна из комбинаций соответствует магическому квадрату!
95
Как же ее найти? Оказывается, это не такая уж сложная за-
дача. Для начала представим число 15 в виде сумм троек нату-
ральных чисел от 1 до 9. Получим восемь комбинаций.
1+5+9
2+6+7
1+6+8
3+4+8
2+4+9
3+5+7
2+5+8
4+5+6
Теперь тройки чисел надо разместить соответствующим об-
разом в клетках квадрата. Замечаем, что число 5 входит сразу
в четыре суммы. Значит, содержащая его клетка должна нахо-
диться на пересечении четырех прямолинейных рядов. В квад-
рате размером 3 3 этому условию удовлетворяет только одна
клетка — центральная (рис. 9, а). Нетрудно сообразить: любые
два числа, попавшие в одну тройку с числом 5, должны разме-
щаться симметрично относительно центра квадрата.
Осталось выяснить, как именно располагается конкретная
числовая пара: по горизонтали, вертикали или по диагонали?
Будем рассуждать так же, как и раньше. Каждое четное число
встречается сразу в трех суммах, поэтому четные числа должны
попасть в клетки, лежащие на пересечении трех рядов, то есть
в углах таблицы (рис. 9, б). Наконец, каждое из оставшихся не-
четных чисел входит в суммы дважды, их место — в средних
клетках по краям квадрата (рис. 9, в). Следуя найденным при-
нципам, легко распределить все девять чисел. Одно из решений
показано на рис. 1, еще семь вариантов того же квадрата пост-
ройте сами.
НЕТ ПРЕДЕЛА СОВЕРШЕНСТВУ!
Среди множества магических квадратов некоторые выделя-
ются особыми свойствами: числа, из которых они составлены,
Рис. 9, а
Рис. 9, б
Рис. 9, в
96
удовлетворяют различным допол-
нительным условиям. Так, у изобра-
женного на рис. 10, а магического
квадрата 5-го порядка суммы пяте-
рок чисел в клетках, расположен-
ных на «разломанных» диагоналях
(клетки закрашены одним и тем же
цветом), равны постоянной магичес-
кого квадрата — числу 65. Квадрат
с таким свойством называется совер-
шенным. Таковым является и ранее
упомянутый древнеиндийский квад-
рат.
Легко убедиться в том, что квад-
рат останется совершенным, если
подвергнуть его таким преобразо-
ваниям, как поворот и симметрия.
Оказывается, существуют и другие
преобразования, сохраняющие это
свойство. Например, квадрат оста-
нется совершенным после того, как
его верхнюю строку переставить
вниз или левый столбец перенести
к правой стороне (либо наоборот,
нижнюю строку поместить сверху, а
правый столбец — слева). Отметим
другое, вытекающее отсюда свойс-
тво: если расположить рядом два
одинаковых квадрата так, чтобы у
115
8
24
17
91821125
12 21
19
10
3
20413226
2371651
4
115
8
24
17
91821125
12 21
19
10
3
20413226
2371651
4
115
8
24
17
91821125
12 21
19
10
3
20413226
2371651
4
Рис. 10, а
Рис. 11
Рис. 12
Рис. 10, б
97
них была общая сторона, получится своеобразный паркет, в
котором числа, оказавшиеся в любой группе клеток размером
5 5, образуют совершенный квадрат (рис. 10, б). Более того,
если замостить этим паркетом плоскость и выделить в любом ее
месте квадрат 5-го порядка, он окажется магическим.
Некоторые магические квадраты отличаются симметрич-
ным рисунком. Рассмотрим следующий квадрат 5-го порядка
(рис. 11). Что интересного можно заметить в расстановке обра-
зующих его чисел? Во-первых, четные и нечетные числа распо-
лагаются симметрично как относительно центра квадрата, так и
относительно каждой из четырех его осей симметрии.
Во-вторых, суммы пар чисел, занимающих центрально-сим-
метричные клетки, одинаковы и вдвое больше числа, стояще-
го в центре (рис. 12). Можно сказать иначе: число, стоящее в
центральной клетке квадрата, есть среднее арифметическое
любой пары чисел из центрально-симметричных клеток. И это
не случайно. Натуральные числа 1, 2, ... , 25 являются членами
арифметической прогрессии. Как известно, суммы членов, рав-
ноудаленных от концов такой прогрессии, равны:
а1+аn
=а
2
+аn 1
=....
Но именно по этому принципу построены все двенадцать
пар чисел:
1+25=2+24= ... = 12+14=26=n
2
+1.
Наконец, оставшееся число 13 — непарное и помещается
в центре квадрата. Кроме того, это единственное из двадцати
пяти чисел, совпадающее с номером своей клетки (если прону-
меровать все клетки по порядку построчно сверху вниз).
Аналогичными свойствами обладают таблица Ло Шу и
квадрат Дюрера. Вообще квадрат, в котором любые два числа,
расположенные симметрично относительно его центра, дают в
сумме одно и то же число, называется симметрическим. Причем
неважно, какого он порядка: четного или нечетного. Неверно
было бы говорить, что именно симметрия строения является
основным признаком магического квадрата. Вместе с тем она
часто определяет его свойства и широко используется при пос-
троении магических квадратов.
Укажем, наконец, еще одну интересную особенность вы-
бранного для примера магического квадрата. Все пятерки чи-
сел, стоящих на его «разломанных» диагоналях (рис. 13), яв-
ляются членами арифметических прогрессий с одной и той же
разностью d = 5, совпадающей с порядком квадрата (кстати, их
98
суммы обладают таким же свойством). Найдите на рис. 13 еще
две пятерки расположенных рядом чисел, из которых можно
составить арифметические прогрессии с разностями d1 и d2
, от-
личными от 1. Как связаны между собой числа d,d d
1
и d2?
ДЕЛИМ НА ЧАСТИ
Многими интересны-
ми свойствами обладает
магический квадрат 8-го
порядка, изображенный
на рис. 14. Его можно раз-
бить на четыре пары пря-
моугольников размером
4 x 2 каждый, расположен-
ных симметрично относи-
тельно центра квадрата (на рисунке они закрашены одним и тем
же цветом). Суммы пар чисел в соответствующих столбцах та-
ких прямоугольников одинаковы и равны 57 или 73 (например,
1+56=54+3,46+27=25+48),чтодаетвсумме130.Аесли
составить из полученных чисел прямоугольную таблицу, они
распределятся в ней симметрично (рис. 15). Значит, в исходном
квадрате можно выделять квадраты меньшего порядка, у кото-
рых сумма всех чисел одинакова. Какие, например?
Рис. 13
Рис. 15
Рис. 14
99
Можно также разделить исходный
квадрат на четыре равные части —
квадраты размером 4 x 4. Возьмем для
примера левый верхний квадрат. Сло-
жим числа, расположенные симметрич-
но относительно его горизонтальной, а
также вертикальной осей симметрии.
Суммы снова повторяются и закономер-
но распределяются в таблицах (рис. 16),
«скрывая в себе» числа 130 и 260. Ана-
логичными свойствами обладают и ос-
тальные три квадрата, причем с каждым
связан свой набор из восьми чисел,
принадлежащих множеству
{43, 47, 51, 55, 56, 58,
72, 74, 75, 79, 83, 87}.
Легко видеть, что сумма двух любых
чисел, равноудаленных от его концов,
равна 130, а сумма четверок чисел —
260. В очередной раз убеждаемся: как
ни крути, а в итоге все равно придем к постоянной квадрата! И
наконец, еще одна задачка из той же серии. Каким образом со
всеми этими квадратами связана пара чисел 33 и 97; четверка
чисел 62, 64, 66 и 68?
Все отмеченные закономерности — проявление особеннос-
тей «внутреннего строения» исходного магического квадрата,
которое подчинено закону центральной симметрии. Выделяя в
этом квадрате другие фигуры и складывая числа построчно или
каким-либо иным способом, можно обнаружить еще немало его
свойств.
Рис. 16
100
ГЛАВА 2
В круге Франклина
Бенджамин Франклин... признавался, что, будучи
служащим Законодательного cобрания штата
Пенсильвания, он скрашивал скучные часы на службе
составлением причудливых магических квадратов и
даже магических кругов.
О. Оре. Приглашение в теорию чисел
Помимо классических магических квадратов существуют
и нетрадиционные квадраты, например составленные из
чисел определенного вида. К тому же известны другие
магические фигуры с не менее любопытными свойства-
ми, чем те, что были рассмотрены в предыдущей главе.
Встречаются даже «эсклюзивные экземпляры»,
носящие имена своих создателей.
ИЗ ПРОСТЫХ ЧИСЕЛ
Для начала рассмотрим магические квадраты из простых
чисел. Получить их нелегко: постоянную s нельзя вычислить
по формуле, применявшейся для классического магического
квадрата, поскольку числа не являются членами арифметичес-
кой прогрессии, и это осложняет поиски. Принято считать, что
первый такой квадрат с минимальной постоянной s = 111 пост-
роил из девяти чисел Генри Дьюдени (рис. 1). Но вот незадача
67143
133761
31737
17 113 47
895929
715101
569 59 449
239 359 479
269 659 149
Рис. 1
Рис. 2
Рис. 3
* Генри Эрнест Дьюдени (1857—1930) — английский математик, классик жанра за-
нимательной математики, автор множества увлекательных задач и головоломок.
101
— число 1 не является простым! Для случая n = 3 правильное и
единственно возможное решение головоломки привел Мартин
Гарднер — это квадрат с постоянной s = 177 (рис. 2).
Еще два квадрата из простых чисел изображены на
рис. 3, 4. Любопытно, что все подобранные числа заканчи-
ваются цифрами 9 и 7 соответственно. У первого квадрата
сумма чисел, стоящих в каждой строке, столбце и на обеих
диагоналях, равна 1077, у второго — 798. А вот квадрат
на рис. 5 состоит только из простых однозначных и двуз-
начных чисел. Его постоянная равна всего 120. Труднее
построить магический квадрат из первых n2 простых чисел.
В начале XX века было доказано, что наименьший такой
квадрат имеет размер 12 x 12. Правда, при его составлении
было сделано исключение: число 2 заменено единицей.
Как думаете, почему это было необходимо?
ПРОГРЕССИИ В КВАДРАТЕ
Другая задача — на построение магических квадратов из
членов арифметической прогрессии. На рис. 6, к примеру, изоб-
ражен квадрат из первых шестнадцати нечетных чисел, полу-
ченный на основе квадрата Дюрера (хотя подошел бы и любой
другой). А как построить аналогичный квадрат из любых шес-
тнадцати последовательных членов произвольной арифмети-
ческой прогрессии, все числа в которой натуральные? Какова
формула постоянной s такого квадрата?
Задача эта не такая уж сложная. Достаточно записать чис-
ла «в общем виде», воспользовавшись формулой n-го члена
арифметической прогрессии, и расставить их в том же поряд-
ке, что использовался в квадрате Дюрера (рис. 7). Постоянная
Рис. 4
Рис. 5
Рис. 6
102
такого магического квадрата вы-
числяется по формуле s = 4a + 30d,dd
где а — первое из данных чисел, а
d — разность прогрессии.
d
Иногда рассматривают маги-
ческие квадраты не с суммами, а с
произведениями чисел — членами
геометрической прогрессии, скажем,
такой: 1, 2, ... (рис. 8). Задачу лег-
ко обобщить на случай магического
квадрата, составленного из чисел a,
aq,qq aq2
,... , aq8.Ясно,чтоонимеетту
же структуру, что и квадрат Ло Шу,
и строится тем же способом. Мож-
но поступить так. Составить сначала
таблицуизчисел0,1, ... , 8 —пока-
зателей степени qm (рис. 9, а), а затем
уже соответствующий квадрат из чи-
сел a, aq,qq aq2
, ... , aq8(рис.9,б).
Другой способ решения состоит
в следующем. Исходя из свойств гео-
метрической прогрессии (bn):
b1b
n
=b
2
bn–1
=...и
bn
2
=b
n–m
bn+m
,где1mn1,
вычислим постоянную квадрата:
()( )=
=
=
Теперь, используя правило ум-
ножения степеней с одинаковым
основанием, представим выражение
a3q12
восьмью способами в виде про-
изведения трех из множителей a, aq,qq
aq2
, ... , aq8 и распределим послед-
ние в клетках квадрата, рассуждая
подобно тому, как это делалось при
построении Ло Шу.
Остается добавить, что описан-
ные схемы построения применимы
и к магическим квадратам более вы-
сокого порядка. В сущности, нужно
Рис. 9, б
Рис. 7
Рис. 8
Рис. 9, а
103
свести задачу к более простой — построению квадрата разме-
ромn n.
ЗАНЯТНЫЕ ОБРАЗЦЫ
Среди магических квадратов встречаются совсем уж не-
обычные, если не сказать редкостные. Так, для некоторых
значений n 8 построены квадраты, не утрачивающие своего
главного свойства при замене всех чисел их квадратами. Бо-
лее того, известны удивительные квадраты
(32-го и 64-го порядка), которые остаются
магическими после возведения каждого их
числа и в квадрат, и в куб!
А вот квадрат-перевертыш (рис. 10, а)
—
из чисел, запись которых не теряет смыс-
ла при повороте квадрата на 180о вокруг
центра. Так, число 18 превращается при этом
в 81, 99 — в 66 и т. д., занимая клетку, цен-
трально-симметричную исходной. Получив-
шийся в итоге квадрат показан на рис. 10,
б. Он обладает такими же свойствами, что и
данный.
Впрочем, не перестают удивлять даже
хорошо изученные квадраты. К примеру, для
трехзначных чисел, у которых цифры совпа-
дают построчно с числами квадрата на рис.
11, выполняется равенство
2762 + 9512 + 4382
= 6722+1592+8342
.
Таким же свойством обладают числа,
получающиеся при прочтении квадрата по
столбцам и по диагоналям (главной и лома-
ным). Выходит, и этот квадрат — перевер-
тыш, да еще какой!
И еще одна любопытная фигура (рис. 12).
Ее составил Бенджамин Франклин , большой
любитель этой головоломки. Его знаменитый
квадрат 16-го порядка полумагический: сум-
ма чисел в каждой строке и каждом столбце
Рис. 10, а
Рис. 10, б
Рис. 11
* Бенджамин Франклин (1706—1790) — американский
просветитель, государственный деятель, ученый.
104
равна 2056, а на диагоналях — не равна (отличается от нее на
128). Но за что же автор назвал свой квадрат «самым магичес-
ким из всех магических квадратов, когда-либо составленных
магом»? Надо полагать, за его особые свойства.
Так, выделяя симметричные узоры из четырех, восьми или
шестнадцати чисел, мы будем получать одни и те же суммы: 514,
1028 и 2056, то есть четверть постоянной квадрата, половину
и саму постоянную. К примеру, восемь чисел из клеток, смеж-
ных с четырьмя угловыми, при сложении дают 1028. А вот сум-
ма чисел из клеток, образующих симметричную «лесенку» (на
рис. 12 выделена цветом), равна 2056. Эта «лесенка» ведет себя
подобно разломанным диагоналям: она может перемещаться по
квадрату вверх-вниз и переходить через его края, сохраняя при
этом указанное свойство. Не изменяется оно и при поворотах
«лесенки» на 90о
, 180о и 270о и последующих сдвигах вправо-
влево. Но главная особенность квадрата Франклина в том, что в
любом квадрате размером 4 х 4, находящемся внутри его, сумма
чисел одинакова и равна 2056 (рис. 12). Догадайтесь, чему рав-
на сумма чисел во всяком выделенном квадрате размером 2 х 2?
Рис. 12
105
А может, сумеете объяснить, откуда взялись все перечисленные
свойства?
ДВЕНАДЦАТЬ, СТО ВОСЕМЬДЕСЯТ,
ТРИСТА ШЕСТЬДЕСЯТ...
Не менее сильное впечатление производит другая хитроум-
ная фигура, составленная Бенджамином Франклином, — маги-
ческий круг. В основе его лежит конструкция из малого круга
и примыкающих к нему восьми колец с общим центром. Прове-
денные радиусы делят ее на восемь секторов, а каждое кольцо
—
на восемь одинаковых частей (рис. 13). Такое разбиение
дает8 8=8
2
ячеек, словно подчеркивая принадлежность кру-
га Франклина к магическим фигурам.
В центре малого круга записано число 12, а в ячейках — це-
лые числа от 12 до 75. Выбор их не случаен, а вполне обосно-
ван. Очевидно, по замыслу автора, постоянная магической фи-
гуры должна было быть непременно связана с кругом. А какое
Рис. 13
106
целое число подходило для этого больше всего? Конечно, 360
— именно столько градусов в ограничивающей круг окружнос-
ти! И как раз указанные числа в различных комбинациях давали
в сумме 360. Кроме того, на практике с кругом оказалось тесно
связано число 12 (вспомним хотя бы циферблат часов). Оно
идеально подошло на роль ключевого числа, без которого, как
мы увидим далее, не обошлась ни одна важная сумма. Остава-
лось заполнить ячейки, с чем Франклин отлично справился, до-
бившись строгого порядка и симметрии в расположении чисел
и их отдельных групп.
Укажем некоторые свойства построенной магической фи-
гуры. Если сложить все числа в любом из колец и прибавить к
найденной сумме 12, получится 360. Таким же свойством об-
ладают и числа каждого сектора. Вообще, если мы хотим, что-
бы постоянная магического круга равнялась 360, без девятого
слагаемого никак не обойтись. Действительно, 360 8 = 2880, а
сумма чисел от 12 до 75 равна
(12+75) 32=2784=348 8.
Прибавим к ней 96 = 12 8 и сразу получим желаемый ре-
зультат. Теперь понятно, как оказалось в центре круга число 12.
Распределение чисел по ячейкам четко продумано с учетом
симметрии фигуры. Объединяя числа в группы и затем склады-
вая, будем получать одинаковые суммы. Рассмотрим, к примеру,
соседние кольца — восьмое и седьмое (нумеруем их, двигаясь
от центрального круга) и пары чисел в ячейках одного сектора.
Суммы этих чисел будут чередоваться через одну:
73+15=88,14+72=86,
25+63=88,30+56=86ит.д.
Выпишем такие суммы для всех пар соседних колец:
88и86,79и95,86и88,88и86,
86и88,95и79,88и86.
Каждый раз при сложении они дают 174, а вместе с чис-
лом 6 = 12 : 2 — половину постоянной круга Франклина, то есть
180. Теперь, двигаясь вдоль каждого кольца по часовой стрел-
ке, попробуем сложить соседние числа. Для внешнего кольца
получим:
73+14=87,14+25=39,25+30=35ит.д.
Оказывается, наборы из восьми сумм чередуются через
кольцо и выглядят так:
87, 39, 55, 71, 87, 103, 119, 135;
87, 135, 119, 103, 87, 71, 55, 39.
107
Сложив всякие два числа из этих наборов, стоящие на оди-
наковых местах, и прибавив к результату 6, снова получим 180.
И в этом тоже есть своя числовая магия, связанная уже с полу-
окружностью.
Следующее свойство вытекает из двух предыдущих. Сумма
чисел из любых четырех ячеек с общей вершиной и половины
числа из центрального круга равна 180, например:
12+27+61+74+12:2=180.
Подобным свойством, очевидно, обладают и другие четвер-
ки чисел, в частности занимающих центрально-симметричные
ячейки колец с нечетными номерами:
26+29+61+58+12:2=180,
36+19+68+51+12:2=180ит.д.
Магический круг Франклина покрыт сеткой из 24 окруж-
ностей (рис. 14). Они разбиты на одинаковые группы по шесть
концентрических окружностей, сдвинутые вверх, вниз, влево
и вправо относительного центра. Сумма чисел, заключенных
между двумя любыми соседними окружностями, при сложении
с числом 12 дает 360. Кроме того, окружности одного радиуса
Рис. 14
108
образуют центрально-симметричную фигуру, напоминающую
цветок. Одна из таких фигур показана на рис. 14. Она включа-
ет в себя числа из первых трех колец круга Франклина и, буду-
чи разбита на пары и четверки чисел, о которых шел разговор
выше, унаследовала его «магические свойства» (это касается и
других аналогичных фигур). Примечательно также, что в преде-
лы каждой окружности попали 12 чисел (не считая помещенно-
го в центре круга), а соответствующая постоянная равна сумме
уже знакомых нам чисел 12, 174 и 348 (проверьте!).
ОТ ПРЯМОУГОЛЬНИКА НАРАЙАНЫ ДО КУБА ЭЙЛЕРА
И наконец, еще несколько магических фигур. Перед вами
составленный индийским математиком XIV века Нарайаной ма-
гический прямоугольник размером 4 x 8 (рис. 15). У него сумма
чисел в любой строке равна 132, суммы чисел из каждого стол-
бца, а также стоящих на диагоналях двух квадратов размером
4 x 4, на которые можно разбить прямоугольник, равны 66.
Следующая фигура — магический треугольник из первых
девяти натуральных чисел (рис. 16). У него равны не только сум-
мы четверок чисел на сторонах, но и суммы их квадратов — 20 и
126 соответственно. Можно выделить на рисунке разные, в том
числе равные, фигуры (равнобедренный треугольник, правиль-
ный шестиугольник, прямоугольник, трапецию и др.) и рассмот-
реть суммы чисел, расположенных в их вершинах. Оказывается,
они также связаны тем или иным образом. Так, сумма чисел в
вершинах исходного т реугольника S258
= 15 вдвое меньше суммы
чисел в вершинах правильного шестиугольника S961374
= 30. Для
равнобедренных треугольников S126
= 9,S
753
= 15,S
984
=21,а15
— среднее арифметическое чисел 9 и 21. Для прямоугольников
Рис. 16
Рис. 15
109
S7963
= 25, S9134
= 17,S
1746
= 18, что при сложении дает утроенную
постоянную исходной фигуры. К тому же суммы часто повторя-
ются, например: S569
= S9614
= 20, S418372
=S
56149
= S9682
= 25.
А вот магический шестиугольник 3-го
порядка, составленный из чисел от 1 до 19
(рис. 17). В нем пять рядов и десять диаго-
налей (по пять в каждом направлении), все
пятнадцать сумм чисел одинаковы. Посто-
янная шестиугольника
=
+
+
+
=
Интересно, что магический шестиуголь-
ник 3-го порядка существует в единствен-
ном экземпляре (с точностью до поворотов
и отражений), как и его «младший брат»
квадрат. Более того, нельзя построить такой
шестиугольник никакого другого порядка!
Наконец, можно рассматривать трех-
мерные магические фигуры. Вот, скажем,
правильный октаэдр, на ребрах которого
размещены числа 1, 2, ..., 12 (рис. 18). Они
разбиты на шесть пар чисел, каждая из ко-
торыхдаетвсумме13(5и8,1и12ит.д.).
Если составить из этих пар различные чет-
верки, шестерки, восьмерки чисел, их сум-
мы будут кратны 13.
Другой пример — магический куб, пространственный ана-
лог магического квадрата. Подобный куб размером n n n
должен быть заполнен натуральными числами от 1 до n3, сум-
мы которых в каждой строке и каждом столбце произвольного
Рис. 17
Рис. 18
18 23
1
22
3
17
21
624
20
7
15
91
419
13 21
8
41
226
11
25
6
27
5
10
Рис. 19
Верхний слой
Средний слой
Нижний слой
110
слоя, а также на любой из четырех диагона-
лей куба одинаковы. Покажите, что его пос-
тоянная вычисляется по формуле
=
+
Например, для n = 3 постоянная s = 42.
Один из магических кубов 3-го порядка пос-
троил Леонард Эйлер. На рис. 19 показано,
как распределены в слоях куба натуральные
числа1,2, ... , 27.
В ЗАДАЧАХ И ГОЛОВОЛОМКАХ
Остановимся подробнее на примерах
задач, тесно связанных с магическими фигу-
рами и представляющих жанр заниматель-
ной математики.
Латинские квадраты. Головоломку
на построение классического магичес-
кого квадрата можно решить с помощью
латинских диагональных ортогональных
квадратов. Латинский квадрат — это таб-
лица размером n n с числами от 1 до n,
размещенными так, что в каждой строке
и каждом столбце они встречаются по од-
ному разу. Если к тому же различны все
числа на обеих диагоналях, квадрат назы-
вается диагональным. Два латинских квадрата ортогональны,
если при наложении одного на другой все пары получившихся
двузначных чисел различны. Так вот, если k и
km—числаиз
клеток с одинаковым номером первого и второго латинских
диагональных ортогональных квадратов соответственно, то
число р из такой же клетки искомого магического квадрата
вычисляется по формуле р = n(k — 1) + m. На рис. 20 изобра-
жен магический квадрат 4-го порядка, полученный указанным
способом.
Карты и домино. В книгах по занимательной математике
не редкость задачи на составление магических квадратов из
игральных карт и домино. В этом случае числа заменены до-
стоинством карты или количеством точек на костяшках домино.
Рис. 20
111
Если из 9 карт получится всего один квадрат — размером 3 3
с постоянной s = 18 (рис. 21), то из 28 костяшек домино гораздо
больше, если располагать их по-разному на плоскости и варьи-
ровать порядок и постоянную квадрата (на рис. 22 изображен
квадрат 4-го порядка с минимальной постоянной s = 5). Доба-
вим, что аналогичную задачу можно решать, на-
пример, со спичками, раскладывая их на разграф-
ленном поле (на рис. 23 показан полумагический
квадрат: число спичечных головок в каждой его
строке и столбце одинаково — 4).
Игральные кости. В различных играх, в том
числе азартных, издавна используются игральные
кости в виде правильных многогранников. Самая
популярная кость представляет собой куб с граня-
ми, пронумерованными числами от 1 до 6 так, что
для любой пары противолежащих
граней сумма чисел равна 7. Можно
также п ронумеровать г рани п равиль-
ного многогранника так, что суммы
чисел на гранях, сходящихся в каж-
дой вершине, будут одинаковыми.
Нетрудно доказать, что подходящая
кость должна иметь форму октаэдра,
а постоянная равняться 18. Один из
способов нумерации показан на рис.
24. Еще два попробуйте отыскать са-
мостоятельно.
Кросс-суммы. Сродни магичес-
ким квадратам головоломка на пос-
Рис. 22
Рис. 23
Рис. 24
Рис. 25
Рис. 21
112
троение фигур из пересекающихся рядов чисел с одинаковыми
суммами (по аналогии с кроссвордами их называют кросс-сум-
мами). Обычно числа располагают вдоль линий какой-либо
симметричной фигуры, причем те из них, что оказываются на
пересечении нескольких линий, включаются во все суммы, с
ними связанные. Пример — шестиконечная звезда на рис. 25:
сумма четырех чисел на любом ее луче равна 26. А как нужно
расставить числа в кружках, чтобы 26 была равна также сумма
всех чисел в вершинах звезды?
ГИМНАСТИКА ДЛЯ УМА
Напоследок три оригинальные головоломки.
Раздели поровну (из немецкого рукописного сборника
XIII века).
В Кёльне было три брата, у них имелось девять сосудов с ви-
ном. Первый сосуд был емкостью в одну кварту, второй содер-
жал две кварты, а каждый следующий одной квартой больше,
так что последний сосуд вмещал девять кварт. Как разделить
вино поровну между тремя братьями, не смешивая содержимо-
го сосудов? Сколько решений имеет задача?
Головоломка оксфордского студента (из сборника Г. Дью-
дени «Кентерберийские головоломки»).
Герои книги Дьюдени — паломники, которые, встретившись
по воле случая в одной харчевни, желая скоротать время, пред-
лагают друг другу решить занимательные задачи.
Когда молчаливого и задумчи-
вого оксфордского студента убеди-
ли задать головоломку своим това-
рищам по путешествию, он сказал:
«Я тут как-то размышлял над стран-
ными и таинственными талисманами,
охраняющими от чумы и прочих зол.
В них замешаны магические квадра-
ты. Глубока тайна подобных вещей,
а числа таких квадратов воистину
можно назвать великими. Но та не-
большая загадка, которую я приду-
мал накануне для всей компании, не
настолько трудна, чтобы ее нельзя
было решить, вооружившись нена-
Рис. 26
113
долго терпением». Сту-
дент изобразил квадрат
(рис. 26) и сказал, что его
надо разрезать на четыре
части (вдоль прямых или
ломаных), из которых
можно было бы сложить
магический квадрат. Как
это сделать?
Играем в «очко»
(из книги Б. Кордемско-
го «Математические за-
влекалки»).
Дан квадрат раз-
мером 8
8 (рис. 27).
Разместите на его белых
клетках костяшки доми-
но так, чтобы суммарное
количество точек вдоль
каждой строки, каждого столбца, двух диагоналей, а также в че-
тырех вершинах квадрата составило «очко», то есть равнялось
21. Одна костяшка уже заняла свое место. Как разместить ос-
тальные?
Рис. 27
114
ОТВЕТЫ
Раздели поровну. Составим из чисел 1, 2, ... , 9, обознача-
ющих емкость сосудов с вином, простейший магический квад-
рат (Ло Шу). Рассмотрим тройки чисел в столбцах. Тогда один
брат должен получить сосуды емкостью в 3, 4 и 8 кварт, другой
— 1, 5 и 9 кварт, а третий — емкостью 2, 6 и 7 кварт. Поскольку
каждому брату может достаться любая из этих троек сосудов,
возможно шесть решений. Еще столько же решений получим,
взяв тройки чисел в строках.
Головоломка оксфордского студента. Решение показано
на рис. 28.
Играем в «очко». Решение
показано на рис. 29.
Рис. 28
Рис. 29
115
ГЛАВА 3
Палиндромы и «перевертыши»
среди простых чисел
Палиндромы издавна интересовали тех, кто любит
играть со словами и числами, возможно, из-за до-
ставляемого глубокого эстетического удовольствия
от симметрии, которой обладают.
М. Гарднер. Математический цирк
В переводе с греческого палиндром — «бегущий вспять».
По сути, это осмысленный набор символов, который не
изменяется при прочтении наоборот. Палиндромы встре-
чаются не только в языке — в форме слов или фраз,
но и в математике — в виде формул и выражений типа
a+b=b+aиxy2yy y
2
yy x, а впервые мы сталкиваемся
2
с ними при знакомстве с числами.
ЗАДОМ НАПЕРЕД
Числовой палиндром — это натуральное число, которое чи-
тается одинаково слева направо и справа налево. Иначе говоря,
отличается симметрией записи (расположения цифр), причем
число знаков может быть как четным, так и нечетным. Палинд-
ромы встречаются в некоторых множествах чисел, удостоенных
собственных названий: среди чисел Фибоначчи — 8, 55 (6-й и
10-й члены одноименной последовательности); фигурных чи-
сел — 676, 1001 (квадратное и пятиугольное соответственно);
чисел Смита — 45454, 983389. Указанным свойством обладает
также всякий репдиджит, например 3333333, в частности репь-
юнит .
Палиндром можно получить как результат операций над
другими числами. Так, в книге «Есть идея!» известного попу-
ляризатора науки Мартина Гарднера в связи с этой задачей
упоминается «гипотеза о палиндромах». Возьмем любое нату-
ральное число и сложим его с обращенным числом, то есть за-
* Число Смита — составное число, сумма цифр которого равна сумме цифр его
простых делителей. Репдиджит — натуральное число, в записи которого все цифры
одинаковые. Репьюнит — натуральное число, записанное с помощью одних только
единиц. Подробнее об этих числах см. в главах 4—6.
116
писанным теми же цифрами, но в обратном порядке. Продела-
ем то же действие с получившейся суммой и будем повторять
его до тех пор, пока не образуется палиндром. Иногда доста-
точно сделать всего один шаг (например, 312 + 213 = 525), но,
как правило, требуется не менее двух. Скажем, число 96 по-
рождает палиндром 4884 только на четвертом шаге. В самом
деле:
96+69=165,
165+561=726,
726 + 627 = 1353,
1353 + 3531 = 4884.
А суть гипотезы в том, что, взяв любое число, после конеч-
ного числа действий мы обязательно получим палиндром.
Можно рассматривать не только сложение, но и другие опе-
рации, включая возведение в степень и извлечение корней. Вот
несколько примеров того, как при их помощи из одних палинд-
ромов получаются другие:
=
+
=
+
2122
– 1212
= 44944 – 14641 = 30303,
11 101 12321 = 1111 12321 = 135531 101 =
= 1244421 11 = 11 101 1112
= 13688631,
,
11
...
11
21
...
78987
...
12
единиц
9
==
×
+
+
+
+
+
+
+
+
ИГРЫ ЦИФР
До сих пор мы рассматривали в основном составные
числа. Теперь обратимся к числам простым. В их бесконечном
множестве имеется немало любопытных экземпляров и даже
целые семейства палиндромов. Только среди первых ста
миллионов натуральных чисел насчитывается 781 простой па-
линдром, причем двадцать приходятся на первую тысячу, из них
четыре числа однозначные — 2, 3, 5, 7 и всего одно двузначное
—
11. С такими числами связано немало интересных фактов и
красивых закономерностей.
Во-первых, единственным простым палиндромом
с четным числом цифр является 11. Другими словами,
117
произвольный палиндром с четным числом цифр, бо’ льшим
двух, является числом составным, что нетрудно доказать
на основе признака делимости на 11. Во-вторых, первой и
последней цифрой любого простого палиндрома может быть
только 1, 3, 7 или 9. Это следует из известных признаков
делимости на 2 и на 5.
Любопытно, что все простые двузначные числа, записанные
с помощью перечисленных цифр (за исключением 19), можно
разбить на пары чисел-«перевертышей» (взаимно обращенных
чисел) вида ab
__
иba
__
, где цифры a и b различны. Каждая
из них, независимо от того, какое число стоит на первом месте,
читается одинаково слева направо и справа налево:
13и31,17и71,37и73,79и97.
Заглянув в таблицу простых чисел, мы обнаружим анало-
гичные пары, в записи которых присутствуют и другие цифры,
в частности среди трехзначных чисел подобных пар наберется
четырнадцать.
Кроме того, среди простых трехзначных палиндромов встре-
чаются пары чисел, у которых средняя цифра отличается всего
на единицу:
181 и 191, 373 и 383,
787 и 797, 919 и 929.
Аналогичная картина наблюдается и у бо’ льших простых чи-
сел, например:
94849 и 94949,
1177711 и 1178711.
Простые числа-палиндромы могут «задаваться» разными
симметричными формулами, которые отражают особенности их
записи. Это хорошо видно на примере пятизначных чисел:
— 96269,
— 18181,
— 3 3533,
— 79997.
Кстати, простые многозначные числа вида
встречаются, очевидно, только среди репьюнитов. Таких чисел
известно пять. Примечательно, что у каждого из них количество
цифр выражается простым числом: 2, 19, 23, 317, 1031. А вот
среди простых чисел, у которых все цифры, кроме центральной,
118
—
единицы, был обнаружен палиндром весьма внушительной
длины — в нем 1749 цифр:
Вообще, среди простых чисел-палиндромов встречаются
удивительные экземпляры. Вот лишь один пример — числовой
гигант
А интересен он тем, что содержит 11811 цифр, которые
можно разбить на три палидромические группы, причем в каж-
дой группе количество цифр выражается простым числом (5903
или 5).
ПРИМЕЧАТЕЛЬНЫЕ ПАРЫ
Любопытные палиндромические закономерности просмат-
риваются и в группах простых чисел, в записи которых присутс-
твуют определенные цифры. Скажем, только цифры 1 и 3, при-
чем в каждом числе. Так, двузначные простые числа составляют
упорядоченные пары 13 — 31 и 31 — 13, из шести трехзначных
простые сразу пять чисел, среди которых есть два палиндрома:
131 и 313, а еще два числа образуют пары «переверты-
шей»: 311 — 113 и 113 — 311. Во всех этих случаях со-
ставленные пары наглядно представляются в виде чис-
ловых квадратов (рис. 1).
Своими свойствами они напоминают магический и ла-
тинский квадраты. Например, у среднего квадрата сумма
чисел, стоящих в каждой строке и в каждом столбце, равна
444, на диагоналях — 262 и 626. Сложив числа из всех
клеток, получим 888. И что характерно, каждая сумма —
палиндром. Даже просто выписывая без пробела несколь-
ко чисел из одной таблицы, получим новые палиндромы:
3113, 131313131 и т.д. Какое наибольшее число можно
составить таким способом? Будет ли оно палиндромом?
Есливкаждуюизпар311—113и113—311доба-
вить 131 или 313, образуются четыре палиндромические
тройки. Запишем одну из них в столбик:
311
131
113
Рис. 1
119
Как видим, и сами числа, и нужная их комбинация дают о
себе знать при прочтении в разных направлениях. Кроме того,
расположение цифр симметрично, а их сумма в каждой строке,
каждом столбце и на одной из диагоналей выражается простым
числом — 5.
Надо сказать, рассмотренные числа интересны и сами по
себе. Например, палиндром 131 является простым циклическим
числом: при любых последовательных перестановках первой
цифры на последнее место оно порождает простые числа —
311 и 113. Можете ли вы указать другие простые палиндромы,
обладающие таким же свойством?
А вот пары чисел-«перевертышей» 13 — 31 и 113 — 311
при возведении в квадрат дают также пары «перевертышей»:
169 — 961 и 12769 — 96721. Любопытно, что даже суммы их
цифр оказались связаны хитрым образом:
(1+3)2
= 1+6+9,
(1+1+3)2
= 1+2+7+6+9.
Добавим, что среди натуральных чисел имеются и дру-
гие пары «перевертышей» с подобным свойством: 103 — 301,
1102 — 2011, 11113 — 31111 и др. Чем объясняется отмечен-
ная закономерность? Чтобы ответить на этот вопрос, нужно по-
нять, что особенного в записи указанных чисел, какие цифры и
в каком количестве могут в ней присутствовать.
ЧИСЛОВОЙ КОНСТРУКТОР
Из простых чисел-палиндромов, располагая их опреде-
ленным образом, скажем, построчно, можно составлять сим-
метричные фигуры, отличающиеся оригинальным рисунком из
повторяющихся цифр. Вот, например, красивая комбинация из
простых палиндромов, записанных с помощью 1 и 3 (кроме пер-
вого, рис. 2). Особенность этого числового треугольника в том,
что один и тот же фрагмент повторяется трижды, не нарушая
симметрию рисунка:
1
131
13331
1333331
131333131
13331113331
Рис. 2
120
Легко видеть, что общее количество строк и столбцов —
число простое (17). К тому же простые числа и суммы цифр:
выделенных жирно фрагментов (17); каждой строки, за исклю-
чением первой (5, 11, 17, 19, 23); третьего, пятого, седьмого и
девятого столбцов (7, 11) и «лесенки» из единиц, образующих
«боковые стороны» треугольника (11). Наконец, если двигать-
ся параллельно указанным «сторонам» и складывать по отде-
льности цифры третьего и пятого рядов (рис. 3), получим еще
два простых числа (17, 5).
1
131
13331
1333331
131333131
13331113331
Рис. 3
Продолжая построение, можно сконструировать на основе
данного треугольника более сложные фигуры. Так, еще один
треугольник с аналогичными свойствами нетрудно получить,
двигаясь с конца, то есть начать с последнего числа, вычеркивая
на каждом шаге две одинаковые симметрично расположенные
цифры и переставляя или заменяя другие — 3 на 1 и наобо-
рот. При этом сами цифры следует выбирать с таким расчетом,
чтобы образующееся в итоге число оказалось простым. Объеди-
нив обе фигуры, получим ромб с характерным узором из цифр,
скрывающим в себе немало простых чисел (рис. 4), в частности
сумма выделенных жирно цифр равна 37.
1
131
13331
1333331
131333131
13331113331
313111313
1311131
13331
313
1
Рис. 4
Другой пример — треугольник, полученный из исходного
после добавления к нему шести простых палиндромов (рис. 5).
121
Фигура сразу привлекает внимание своим изящным обрамлени-
ем из единиц. Ее окаймляют два простых репьюнита одинако-
вой длины: 23 единицы составляют «основание» и еще столько
же — «боковые стороны» треугольника.
1
131
13331
1333331
131333131
13331113331
1313311133131
133133111331331
13311131113111331
1113313311133133111
111133133111331331111
11111111111111111111111
Рис. 5
ЕЩЕ НЕСКОЛЬКО ФИГУР
Можно составлять из чисел многоугольные фигуры c оп-
ределенными свойствами. Пусть требуется построить фигу-
ру из простых палиндромов, записанных с помощью 1 и 3, у
каждого из которых крайние цифры — единицы, а сумма всех
цифр и общее количество единиц в строке — простые чис-
ла (исключение — однозначный палиндром). Простым чис-
лом должно выражаться и общее количество строк, а также
цифр 1 либо 3, встречающихся в записи. Вот одно из реше-
ний задачи (рис. 6).
3
131
13331
1333331
13331113331
133111331
113111311
131111131
1133331333311
133133111331331
13311131113111331
Рис. 6
122
Конечно, не обязательно ограничиваться двумя цифрами и
требовать наличия в записи каждого используемого числа всех
указанных цифр. Скорее, наоборот: ведь именно их необычные
сочетания придают своеобразие узору фигуры, в подтверждение
чему приведем несколько примеров красивых палиндромических
зависимостей (рис. 7—9).
3103013103013
31030303013
310131013
3103013
31013
313
3
Рис. 7
911090119
9110119
91019
191
19991
9919199
919191919
Рис. 8
7
757
75557
787
78887
7778777
727
72227
7722277
772222277
Рис. 9
Теперь, вооружившись таблицей простых чисел, вы и сами
сконструируете фигуры вроде предложенных нами. А напосле-
док еще одна диковинка — треугольник, буквально пронизан-
ный вдоль и поперек палиндромами (рис. 10). В нем 11 строк из
простых чисел, а столбцы образованы репдиджитами. И главное:
ограничивающий фигуру палиндром 193111111323111111391
— число простое!
123
2
30203
133020331
1713302033171
12171330203317121
151217133020331712151
1815121713302033171215181
16181512171330203317121518161
331618151217133020331712151816133
9333161815121713302033171215181613339
11933316181512171330203317121518161333911
Рис. 10
124
ГЛАВА 4
Замечательные «смиты»
—
Мой дорогой Гарднер, — заметил доктор
Матрикс покровительственным тоном, — не
существует ни одного числа, которое не обладало
бы необычными свойствами. Взять хотя бы номер
вашей комнаты в лиссабонском отеле...
М. Гарднер. От мозаик Пенроуза
к надежным шифрам
В былые времена у кондуктора в автобусе всего за пята-
чок можно было купить «счастливый билетик», помогав-
ший в исполнении желаний. Так в народе прозвали проезд-
ной билет с шестизначным номером, у которого совпадали
суммы первых трех и последних трех цифр. Многие склады-
вали цифры забавы ради, не подозревая, что из такого вро-
де бы пустячного занятия можно извлечь немалую пользу.
НЕВЕРОЯТНОЕ ВЕЗЕНИЕ ПРОФЕССОРА СМИТА
История науки знает немало примеров случайных открытий.
Кто не слышал предание о том, как Архимед, принимая ванну,
открыл закон о телах, погруженных в жидкость, или байку о Нью-
тоне, который, наблюдая за падением с дерева яблока, придумал
теорию тяготения? Сколько раз пытливые умы находили источ-
ник озарения в живой природе! А как много блестящих идей
посетили ученых во сне! Д. И. Менделееву приснилась периоди-
ческая таблица элементов, а Ф. Кекуле — структурная формула
бензола. Но иногда важное открытие, сделанное специалистом,
запоминается куда меньше, чем нехитрая закономерность, под-
меченная человеком, вовсе ее не искавшим, да и вообще дале-
ким от науки. Каким-то непостижимым образом та находит его
сама. И чем необычнее обстоятельства, сопутствующие этому
событию, тем более яркое впечатление оно производит.
Один из примечательных случаев такого рода произошел
30 лет назад с любителем чисел, наблюдательным профессором
психологии Гарольдом Смитом, которому (без всякого преувели-
чения) крупно повезло: он сумел войти в историю математики,
не имея к ней, в сущности, никакого отношения. А счастливым
125
для Смита оказался... номер собственного телефона! Как-то
профессор заметил, что этот номер, выражающийся составным
семизначным числом 4 937 775, обладает любопытным свойс-
твом — сумма цифр номера равна сумме цифр всех его простых
делителей:
4937775=3 5 5 65837,
4+9+3+7+7+7+5=42,
3+5+5+6+5+8+3+7=42.
Быть может, этот факт так и остался бы в разряде числовых
курьезов, не вмешайся в историю родственник Смита — мате-
матик, профессор одного из американских университетов Аль-
берт Виланский. Он опубликовал в 1982 году заметку об обна-
руженном свойстве, а обладающие им составные числа назвал
именем Смита. Тогда же Виланский предположил, что таких
чисел существует бесконечно много. И оказался прав: вскоре
эту гипотезу доказал его коллега. Так было положено начало
исследованию весьма интересного множества чисел. Самое
удивительное, что изучение чисел Смита, или просто «смитов»,
началось с семизначного (!) числа, но еще поразительнее то, что
их не открыли гораздо раньше. Даже любой школьник знает:
2+2=4,иэтоникакойнекурьез!
ДИКОВИНКИ СРЕДИ СМИТОВ
Числа Смита обладают многими замечательными свойства-
ми. Мы не станем на них останавливаться, заметим только, что
смиты тесно связаны с другими известными математикам чис-
лами, через которые могут выражаться: с репьюнитами и про-
стыми числами Мерсенна*
. В семействе смитов найдется немало
настоящих диковинок! Одни числа отличаются красивым соче-
танием цифр: 654, 44733, 67067. Другие — их повторяемостью:
666, 1111, 4444444444. Третьи — симметрией записи (палинд-
ромностью): 3663, 22522, 864468. А разве не радует глаз разло-
жение некоторых смитов на множители?
3663=3 1221=33 111,
864468 = 2 432234 = 111 7788,
.
100001
44444
101010101
44
11
...
11
4
44
...
44
10
цифр
10
* Простые числа Мерсенна — простые числа вида — Mp = 2p – 1, где — p также
простое число.
126
К изюминкам множества смитов можно смело отнести и де-
сятизначные числа, у которых все цифры различные. Укажем
наименьшее и наибольшее из них:
1023465798и9876542103.
А вот семизначное число 1 346 269 привлекает внимание
тем, что это самый маленький смит, встречающийся в знамени-
той последовательности Фибоначчи (31-й ее член). Не редкость
смиты и среди фигурных чисел, учение о которых восходит еще
к пифагорейцам. Так, смит 121 — квадратное число, 378 — тре-
угольное, а 22 — пятиугольное.
Кроме того, во множестве смитов имеются примечательные
пары чисел, отличающихся друг от друга всего на 1. Вероятно,
по аналогии с числами-близнецами (простыми числами, отли-
чающимися на 2), их прозвали братьями Смита. Наименьшую
такую пару составляют числа 728 и 729. Для примера именно
она выбрана потому, что каждый из «братьев» интересен сам по
себе. Первый — сумма двух смитов, второй — квадрат смита:
728=706+22,729=272
, то есть они оба порождены числами
Смита. Сколько всего существует таких пар, пока неизвестно.
Возможно, бесконечно много. Зато, как показали исследования,
по мере углубления в нескончаемое семейство смитов в нем
можно обнаружить также тройки, четверки, пятерки и шестерки
последовательных чисел. В частности, наименьшая тройка вы-
глядит так: 73 615, 73 616 и 73 617.
Надо сказать, некоторые члены этого семейства образуются
из других его представителей более простыми путями. Иногда
бывает достаточно записать рядом (без пробела) два смита. Та-
ким способом из чисел 22 и 27 получаются четырехзначные числа
Смита 2227 и 2722. В ином случае в запись исходного смита-па-
линдрома добавляются нули. Например, числа 22 и 535 порож-
дают смиты 202 и 50305. Нередко нужный результат достигается
простой перестановкой цифр (как в тройке смитов 319, 391, 913)
или благодаря симметрии их расположения, приводящей к пов-
тору цифр в образующихся числах (454, 45454, 454454).
В этом удивительном множестве выделяют также числа, у ко-
торых сумма цифр выражается числом Смита. Им даже дали собс-
твенное название — суперчисла Смита. Таким свойством облада-
ют,кпримеру,числа202(2+0+2=4)и778(7+7+8=22).
Особо ценятся среди смитов рекордсмены по числу
цифр, присутствующих в их записи. К ним относится, в час-
тности, исполин 9R1031
(1069882
+ 3 1034941
+ 1)1476
103913210
,
127
где R1031
—
наибольший из известных простых репьюнитов.
В этом числе Смита насчитывается 107 060 074 цифры! С тру-
дом верится — так компактно оно «упаковано» с помощью
степеней. А знаете, сколько времени потребовалось бы, чтобы
записать это число полностью? Даже при непрерывной работе
с высокой скоростью письма 90 цифр в минуту на это ушло бы
2 года и 3 месяца!
ЗАКЛЮЧЕННЫЕ В КВАДРАТ
В книге Мартина Гарднера «От мозаик Пенро-
уза к надежным шифрам» приведен магический
квадрат третьего порядка, составленный из чисел
Смита (рис. 1). Его магическая постоянная равна
822 и является, по словам автора, наименьшей из
возможных для такого квадрата. Все указанные в
клетках числа — четные. Разделив каждое из них
на 2, получим новый магический квадрат с пос-
тоянной, равной 411 (рис. 2). Примечателен он
тем, что состоит из девяти простых чисел; согла-
ситесь, неплохое наблюдение автора. Но если бы
дело было только в обнаруженном им свойстве...
Ведь известны и другие магические квадраты, со-
ставленные из простых чисел. Однако нас сейчас
интересуют вовсе не они, а числа Смита. Какое
отношение имеют они к получившейся таблице?
Приглядитесь внимательнее, и вы заметите,
что суммы некоторых ее чисел дают числа Смита.
Так, в простейшем случае 11 + 47 = 58.
Разность магической постоянной 411 и чис-
ла 137 из центральной клетки равна другому
представителю семейства смитов — числу 274.
Это означает, что сумма любых двух простых чисел, занимаю-
щих центрально-симметричные клетки квадрата, оказывается
числом Смита:
11+263=83+191=47+227=101+173=274.
А вот еще один любопытный факт: суммы пар чисел, сто-
ящих вдоль линий, параллельных главным диагоналям, также
равны числам Смита. Действительно:
11+83=94,83+263=346,
263+191=454,191+11=202.
Рис. 1
Рис. 2
128
Все пять смитов есть
в исходной таблице и,
что характерно, красиво
располагаются в ее уг-
ловых клетках и в цент-
ре (см. рис. 1), в то вре-
мя как сами слагаемые
размещаются в средних
клетках по сторонам вто-
рой таблицы (см. рис. 2).
Если собрать все девять
чисел в новую таблицу
(рис. 3), они образуют
двойной симметричный
узор (рис. 4).
К тому же теперь на-
глядно видно, как просто
и разумно связаны между
собой тройки чисел, вхо-
дящих в каждое из четы-
рех последних равенств
(рис. 5, 6).
Можно также рас-
сматривать суммы трех
или более чисел второго
квадрата, при выборе ко-
торых логично руководс-
твоваться симметрией их
расположения, к приме-
ру, относительно главной
диагонали. Возьмем для определенности диагональ квадрата,
идущую из левого нижнего в правый верхний угол. Она дает три
числа: 101, 137 и 173. Добавим к ним еще четыре: 47, 263, 227
и 83 (рис. 7).
Оказывается, их различные комбинации приводят к разным
числам Смита. Скажем, каждая из троек 47, 263, 173 и 227, 83,
173 при сложении дает 483:
47+263+173=227+83+173=483.
Рис. 3
Рис. 4
Рис. 5
Рис. 6
Рис. 7
Рис. 8
129
ПРОДОЛЖИМ ЭКСПЕРИМЕНТ!
Весьма любопытная картина вырисовывается при игре с
четверками чисел. Легко заметить, что смит 483 получается так-
же при сложении 346 и 137 (оба числа встретились в рассмот-
ренных магических квадратах, см. рис. 1 и 2). Тогда смит 346
можно представить в виде разности 483 и 137:
(47+263+173)–137=(227+83+173)–137=346.
Аналогично 483 = 382 + 101, откуда 382 = 483 – 101, или
(47+263+173)–101=(227+83+173)–101=382.
Пойдем дальше: 274 = 411 – 137, где 411 есть магическая
постоянная второго квадрата, а значит, выполняются равенства
(47+263+101)–137=(227+83+101)–137=274.
Итак, задействовав возможные пары чисел главной диа-
гонали этого квадрата, удалось «сконструировать» три числа
Смита, присутствующие в исходном квадрате: 346, 382 и 274.
И если в первый раз такой результат мог быть случайностью,
а во второй — простым совпадением, то в третий раз начи-
нает проявляться вполне определенная закономерность. А
какой истинный любитель математики откажется ее прове-
рить?
Если теперь ограничиться рассмотрением чисел 47, 263,
83 и 227, нетрудно получить хотя и не столь очевидные, но уже
вполне ожидаемые и даже предсказуемые результаты:
227+83–263+47=94,
227+83–47+263=526,
47+263–227+83=166,
47+263–83+227=454.
И вот перед нами еще четыре смита из исходного квадрата.
Любопытно, что они занимают такие же клетки, что и числа вто-
рого квадрата, из которых получены. Мозаика почти сложилась,
осталось всего ничего — выразить еще два смита: 22 и 202. А в
том, что эта задача разрешима, сомнений не осталось.
Воспользуемся тем, что уже известно. Ближайший к чис-
лу 22 смит из составленного Гарднером магического квадрата
— число94;22=94 –72,или
(227+83–263+47)–(173–101)=22.
Аналогично 202 = 166 + 36, или
(47+263–227+83)+(173–137)=202.
Впрочем, в этом случае можно обойтись и четверкой чисел:
202=303 –101=47+83+173–101.
130
Между тем попытки выразить аналогичным образом число
22 приводят к еще одному открытию: оказывается, смиты из
исходной таблицы можно получить из четверок чисел, занима-
ющих соседние центрально-симметричные клетки второй таб-
лицы (рис. 8), например:
58–36 =(47+11)–(263–227)=22,
58+36=(47+11)+(263–227)=94,
(173+83)–(191–101)=166,
(173+83)+(191–101)=346.
Получается изящная головоломка: как, имея набор простых
чисел, составить простейший магический квадрат из составных
чисел Смита, да еще и с наименьшей постоянной?
ТАКИЕ ПРОСТЫЕ ЗАКОНОМЕРНОСТИ...
Поразмышляв немного, вы обнаружите и, возможно, обос-
нуете немало интересных закономерностей, связывающих числа
Смита. А начать можно с чего-нибудь совсем простого. Скажем,
58–36 =22,а58+36=94,откуда58=(22+94):2,следователь-
но, смит 58 — среднее арифметическое смитов 22 и 94. В свою
очередь 94 — среднее арифметическое 22 и 166, а вот число 22
— среднее геометрическое смитов 4 и 121, поскольку
.
121
4
11
2
22
Или другой пример. Выпишем по порядку первые пятнад-
цать чисел Смита и выделим из них каждое второе:
4, 22, 27, 58, 85, 94, 121, 166,
202, 265, 274, 319, 346, 355, 378.
Посмотрите, как интересно они связаны:
22=58–6
2
= 94–2 62
= 166–4 6
2
,
22=265–1 35
= 319–11 33
= 355–111 3.
А вот еще одно наблюдение. Оно касается многозначных
чисел Смита, у которых всего два простых множителя.
22=2 11=22+0, 2+1+1=2+2+0=4,
58=2 29=22+36, 2+2+9=2+2+3+6=13,
85=5 17=22+63, 5+1+7=2+2+6+3=13,
94=2 47=22+72, 2+4+7=2+2+7+2=13.
Как видим, если такое число представить в виде суммы двух
слагаемых, причем одно из них 22 (смит), то сумма цифр его
множителей такая же, как и сумма цифр слагаемых, и равна
либо 4, либо 13.
131
Оказывается, аналогичным свойством обладают и трехзнач-
ные числа Смита, при этом повторяется слагаемое 202 (снова
смит!), а суммы цифр равны 4, 13 или 22. Например:
355=5 71=202+153(суммацифр—13),
778=2 389=202+576(суммацифр—22).
Любопытно также, что у всех ключевых чисел (4, 13, 22, 202)
сумма цифр равна наименьшему смиту, а два из них (22 и 202)
— суперчисла Смита.
Можно изучать самые разные группы смитов и даже отде-
льных представителей этого семейства, открывая все новые и
новые их свойства. Чем, например, примечательна тройка 27, 58
и 85? Что общего у чисел 4, 121 и 10 201? А какое отношение к
смитам имеет число 31?
Пожалуй, доктор Матрикс прав, полагая, что не существует
ни одного числа, которое не обладало бы какими-нибудь не-
обычными свойствами. И представители многочисленного се-
мейства смитов лишь подтверждают это.
132
ГЛАВА 5
Сообщество репьюнитов
Почти дожив до голубых седин,
Я понял арифметике назло,
Что у людей простейшее «один»
Поистине сложнейшее число.
И. Фоняков
В разное время эти числа привлекали внимание многих
известных математиков, среди которых были даже Эйлер
и Гаусс. Но только полвека назад этими числами занялись
всерьез. Более того, дали им собственное название —
репьюниты, а такое случается не часто.
Что же это за числа? Чем они так интересны?
УВЛЕЧЕНИЕ БЕРНУЛЛИ
У известного математика и астронома Иоганна III Бернул-
ли, представителя прославленной династии швейцарских уче-
ных , было хобби — раскладывать на множители многозначные
числа, записанные с помощью одних только единиц. Он даже
опубликовал в 1773 году в «Трудах Берлинской Королевской
академии» таблицу простых делителей первых тридцати та-
ких чисел. Несмотря на некоторые допущенные ошибки и тот
факт, что задача была решена не полностью (в правильности
разложения на простые множители нескольких чисел Бернулли
сомневался), надо признать: работа им была проделана по тем
временам огромная. Особенно если учесть, в каких условиях, в
отсутствие вычислительных средств, она велась и с какими ог-
ромными числами имел дело математик. Достаточно упомянуть,
что тогда наибольшим известным простым числом было
231
– 1 =2147483647.
Между тем некоторые из рассмотренных Бернулли чисел
имеют куда бо’льшие простые делители, среди которых рекорд-
сменом является 20-значное число
57 336 415 063 790 604 359.
* Бернулли Иоганн III (1744—1804) — внук знаменитого математика Иоганна
Бернулли, известен трудами в области теории вероятностей и теории чисел.
133
Это делитель числа
, которое, по предположению
математика, было простым, чего он проверить не мог. Как не мог
проверить и другие свои гипотезы. Например, являются ли про-
стыми числа
и
.
Лишь спустя шестьдесят пять лет после опубликования таб-
лицы Бернулли было найдено разложение на множители числа
из 11 единиц, еще через сорок — из 17 и столько же времени
понадобилось, чтобы доказать, что 19-значное число из единиц
— простое (как и полагал Бернулли).
МАГИЯ ЕДИНИЦЫ
И в самом деле, есть что-то неуловимо притягательное в не-
прерывной череде единиц
1 11 111 1111 11111...
Некая внутренняя гармония и порядок, скрывающиеся за
ее внешней простотой. В памяти всплывает еще одна вереница
единиц, порожденная цепной дробью
+
+
+
+
которая равна знаменитому числу Фидия, или в более компак-
тной записи
+
Бесконечная периодическая последовательность непол-
ных частных этой непрерывной дроби переходит в себя при
чтении задом наперед, то есть обладает свойством палиндром-
ности.
А вот еще одна, не менее красивая и завораживающая фор-
мула:
+
+
+
просто и так непостижимо глубоко — иррациональная величи-
на бесконечно выражается через самую что ни на есть рацио-
нальную единицу.
134
А вспомните, как ладно обрамляют единицы арифметичес-
кий треугольник Паскаля!
1
11
121
1331
14641
15101051
1615201561
С их чередой мы встречаемся и в оригинальной гипотезе
Гильбрайта (она звучит так: если выписать в первой строке пос-
ледовательные простые числа, во второй — разности последо-
вательных простых чисел, в третьей — модули разностей пос-
ледовательных чисел второй строки и т.д., то в каждой строке,
начиная со второй, первым числом будет 1):
2357111317
122424
10222
1200
120
12
1
Но вернемся к числам, записанным с помощью одних только
единиц. Чем длиннее становится цепочка цифр, тем больше зага-
док таят в себе сами числа, тем интереснее их изучать. Недаром
они продолжают занимать пытливые умы ученых. Спустя два века
после обнародования таблицы Бернулли эти числа даже удосто-
ились имени — репьюниты (от англ. repeated unit — повторен-
ная единица), а математики по-прежнему ищут их разложения на
простые множители и открывают все новые и новые свойства, о
некоторых из которых наш дальнейший рассказ.
ВОПРОСЫ ДЕЛИМОСТИ
Репьюнитов существует бесконечно много, в десятичной
системе счисления они задаются формулой
=
Можно определить их рекуррентно:
R1
=1,R
n+1
= 10Rn+1, n N.
135
Как уже отмечалось, среди репьюнитов встречаются про-
стые числа. Примечательно, что количество единиц в их записи
выражается простым числом (а вот из того, что n — простое, не
следует, что Rn
— простое, например R3
=3
37). Действительно,
еслиn=km(k>1,
k m>1),точисло
=
делится
на числа
=
и
=
Верно и обратное.
Иначе говоря, R
m
делит Rn тогда и только тогда, когда m делит
n (это легко доказывается на основе известного в алгебре ут-
верждения: am
–
1 делит an
– 1 тогда и только тогда, когда m
делит n при условии, что am 1). Например:
n=4
1111 = 11
101,
n=6 111111=11
10101 = 111 1001,
n = 8 11111111 = 11 1010101 = 1111 10001,
n = 9 111111111 = 111 1001001.
Как видим, при делении без остатка одного репьюнита на
другой частное является палиндромом, записанным с помощью
единиц и нулей, и либо эти цифры чередуются (при делении на
11), либо нули группируются между единицами по (m – 1) штуке
(при делении на Rm
, m > 2), не нарушая симметрии в записи чи-
сел. Чем это объясняется?
Заметим, что если число n представимо в виде произведения
km несколькими различными способами, то Rn можно записать
в виде произведения
×
вдвое бо’ льшим числом разных
способов. Скажем, n = 12 = 2 6 = 3 4, репьюнит R12
делится
на R2
,R
3
,R
4
,R
6
, получаются такие его разложения на множи-
тели:
11 10101010101,
111 1001001001,
1111 100010001,
111111 100001.
А вот каждый множитель в разложении 12 показывает,
сколько раз цифра 1 встречается в записи стоящего на таком
же месте, что и он сам, делителя репьюнита R12
.
Например,
12 = 3 4, во второй строке у 111 три единицы, а у 1001001001
— четыре.
136
Если числа k и
k m взаимно просты и делят n, то репьюнит
Rn делится на Rk m
. Это наблюдается и в случае, когда k пред-
k
ставимо в виде степени с натуральным показателем. Так, число
R30 делится не только на репьюниты R2
,R
3
,R
5
, ноинаR6
,R
10
,R
15
,
а число R32
—
на R2
,R4,R8,R
16
. А на какие репьюниты делится
число R111111?
Еслиkи
k m взаимно просты и делят n, то Rn делится на про-
изведение Rk Rm
. И вот еще одно любопытное наблюдение:
с увеличением n проявляется периодичность в записи цифр
частного, к которым добавляется 9. К примеру, при k = 2,
k m=3
(заметьте:
, 6 = 2 3 = km). Какова природа подме-
ченной закономерности? Иначе говоря, какие особенности
«строения» делимого и делителей влияют на конечный ре-
зультат?
УСЛОЖНЯЕМ ЗАДАЧУ
Возникает логичный вопрос: а существуют ли репьюниты,
кратные степеням других репьюнитов — Rk
m
(k>1,
k m>1)?Ока-
зывается, существуют. Можно доказать, что номер n наименьше-
го репьюнита, делящегося нацело на Rk
m
, вычисляется по фор-
мулеn=kRk
m–1
. Так, в простейшем случае k = m = 2 это будет
репьюнит R22
. Очевидно, что с увеличением k и
k mчислоцифрв
искомом репьюните стремительно растет. Например, при k = 2 и
k
m=3оноравно242,априk=3и
k m=4 —уже4102893!Раз-
ница громадная: если запись (без пробелов) всех цифр числа
уместилась бы на нескольких строчках, то запись
репьюнита
заняла бы 16 тетрадей в клетку объемом
96 листов каждая!
×
×
=
×
×
=
×
×
=
×
×
×
=
×
×
=
×
×
=
137
Примечательно, что частным от деления
числа R22 на R2
2
= 121 является почти палин-
дром
9182736455463728191
с поразительно простым и легко запоминаю-
щимся порядком цифр: если разбить их, начи-
ная со второй, на пары и представить данное
число в виде суммы
9182736455463728190 + 1,
взору явится череда первых десяти чисел,
кратных 9, выписанных в порядке возраста-
ния!
А теперь составим таблицу из получаю-
щихся на каждом шаге деления, кроме пос-
леднего, неполного частного l и остатка r.
1111=9 121+22,221=1
,
121+100ит.д.
И что мы видим? Среди всех возможных
остатков от деления на 112 оказались «вы-
браны» те, которые можно выразить через
11.Эточиславида11n,гдеn=2,3, ..., 10,или
100–11n,гдеn=0,1, ..., 8;оничередуют-
ся друг с другом и упорядочены в первом случае по возраста-
нию, во втором — по убыванию. Соответствующие им неполные
частные располагаются в обратном порядке, а их совокупность
представляет собой почти полный список возможных остатков
от деления на 11.
ЗАКОНОМЕРНОСТИ РАЗЛОЖЕНИЯ
Если Rm
— наименьший репьюнит, делящийся на число a, то
следующий репьюнит, кратный a, должен содержать 2m единиц,
далее идет репьюнит из 3m единиц и т.д., а все подходящие ре-
пьюниты имеют вид
гдеk>1.
k
В случае, когда a — простое число, начинает проясняться
картина с разложением чисел из единиц на простые множители,
более того — иногда его можно предугадать.
Например, 111 = 3 37, поэтому и на 3, и на 37 делится каж-
дый третий репьюнит.
138
111=3 37,,
1111 = 11 101,
11111 = 41 271,
111111=3 7 11 13 37,,
1111111 = 239 4649,
11111111 = 11 73 101 137,
111111111 = 3
2
37 333 667.
Теперь понятно, как искать каноническое разложение сле-
дующего репьюнита. Поскольку он делится на 11 и 11111, среди
его простых делителей будут числа 11, 41 и 271. Разделив на
них данный репьюнит, получим
.
111141
...
11
10
271 9091
Остается выяснить, является ли последний множитель прос-
тым числом. Если да, то разложение завершено, а если нет, то
деление нужно продолжить.
Сложнее обстоит дело с 11-м репьюнитом; у него всего два
простых делителя, но оба — многозначные числа:
×
=
Неудивительно, что в свое время Иоганн III Бернулли испы-
тал трудности в решении этой задачи!
Зато каноническое разложение числа из 12 единиц получа-
ется без труда, когда известны аналогичные разложения деля-
щих его репьюнитов:
×
×
×
×
×
×
=
А вот какая игра цифр наблюдается непосредственно в про-
цессе деления (взять хотя бы повторяющиеся в определенном
порядке последние цифры делителей или одинаковые комби-
нации цифр):
3
37037037037
37
5291005291
3711
481000481
371113
37000037
37111337
1000001
371113371019901
Кто бы мог подумать, что за разложением на множители чи-
сел из единиц порой скрывается такая закономерная красота!
Все же задача на нахождение простых делителей репь-
юнитов по-прежнему трудоемка и сложна, и неудивитель-
139
139
но: зачастую количество цифр в записи делителей исчис-
ляется многими десятками. С еще большими проблемами
сталкиваются математики при отыскании простых репью-
нитов. После выхода в свет таблицы Бернулли их было об-
наружено всего четыре. Доказано, что простыми являются
числа R19
,R
23
,R
317
и R1031
.
ПРОСТОТА И ПЕРИОДИЧНОСТЬ
Упомянем еще об одном любопытном факте: оказыва-
ется, для любого простого числа p, отличного от 2 и 5, су-
ществует репьюнит, делящийся на p (числа 2 и 5 исключаем,
поскольку последняя цифра делимого — 1). Так, для p = 3
это число 111. Для любого другого p подойдет, например,
репьюнит
.
Это следует из малой теоремы Ферма:
если p — простое число и a не делится на p, то
ap–1
– 1 делится на p. Согласно этой теореме число
×
=
=
×
делится на p 2; 5, откуда следует, что при p 3 множитель
делится на p.
Заметим, что репьюнит
должен быть кратен
наименьшему репьюниту Rm
, делящемуся на p (в случае, когда
m p – 1), так что для некоторых p можно указать репьюнит
из m < p – 1 единиц. Здесь m — длина периода числа p, то есть
количество цифр в периоде десятичной дроби, равной . На-
пример, для p = 7 наименьшим делящимся на него репьюнитом
будет R6, так как
)
142857
(,0
7
1
цифр
6
, адляp=41—репьюнитR5
,
поскольку
=
Итак, задача на нахождение наи-
меньшего репьюнита, делящегося на простое p > 5, по сути
сводится к вычислению длины периода числа p.
Интересные свойства обнаруживаются и при изучении ре-
пьюнитов, номера которых выражаются простыми числами. Из-
вестно, что число 3 делит репьюнит R3. А существуют ли простые
p 3, делящие Rp? Оказывается, нет. Всякое p > 5 делит репью-
нитRp–1
, а два последовательных репьюнита взаимно просты
140
(в противном случае разность Rn
–
Rn–1
= 10n–1
делилась бы на
p > 5, чего быть не может).
Другой пример. Все простые делители числа R5 имеют оди-
наковую длину периода (m = 5). Аналогичная картина наблюда-
ется в случае R7 (m = 7) и R11 (m = 11). Можно ли утверждать, что
при p 3 каждый простой делитель репьюнита Rp имеет длину
периода, равную p? Почему?
ЧЕРЕДА ВОПРОСОВ
Знание рассмотренных свойств также поможет в решении
задач, связанных с делимостью репьюнитов и разложением их
на простые множители. Вот для начала несколько несложных
упражнений.
1. Какой формулой задается число k единиц в репьюнитах,
k
делящихся на 17?
2. Покажите, что любой репьюнит, делящийся на 7, делится
ина13.
3. Приведите примеры других пар простых чисел, для кото-
рых верно свойство, аналогичное рассмотренному в задаче 2.
4. Существуют ли репьюниты, делящиеся на тройку простых
чисел 11, 13 и 17?
5. Приведите пример другой тройки последовательных про-
стых чисел, делящих репьюниты. Как найти наименьший репью-
нит, кратный всем трем числам?
6. Найдите наименьший репьюнит, делителями которого яв-
ляются простые числа 7, 13 и 19.
7. Разложите на множители число
11
...
11
18
.
8. Чему равен остаток от деления на 41 репьюнита
?
9. Делится ли репьюнит
на 239?
10. Число a делит репьюниты
11
...
11
18
и
11
...
11
24
. Будет ли
оно делить 111 и
11
...
11
12
?
Вообще, числа из единиц вызывают немало вопросов. На
одни из них ответы давно получены, на другие пока нет. Вот
лишь несколько примеров.
Верно ли, что если число a делит репьюниты Rn и Rm
, тоa
делит и Rk, где
kk
k — наибольший общий делитель чисел
k
mиn?
Верно ли, что при любом натуральном n числа R2n
иR2n+2
;R2n+1
141
и R2n + 3 взаимно просты? Как найти наименьший репьюнит, де-
лящийся на репьюниты Rk и
k Rm в случае, когда числа k и
k mне
являются взаимно простыми? Какова длина периода числа Rk
и что он собой представляет (как устроен)? Может ли репью-
нит быть степенью некоторого натурального числа, в частности
степенью другого репьюнита? Как найти наименьший репьюнит,
делящийся на квадрат данного простого числа? Существуют ли
простые числа, квадраты которых делят репьюниты с номерами,
выражающимися простыми числами?
142
ОТВЕТЫ
1.k =16
kn,nN.
3. 73 и 137; 41 и 271 (это числа с одинаковой длиной пери-
ода:m=8впервойпареиm=5 —вовторой).
4. Да. Периоды чисел 11, 13 и 17 равны 2, 6 и 16 соответс-
твенно. Наименьшее общее кратное 2, 6 и 16 (то есть самое
маленькое число, которое делится на все эти числа) равно 48,
поэтому подойдет любой репьюнит с номером, кратным 48.
5.31,37и41.Числа37и41спериодамиm=3иm=5со-
ответственно делят репьюниты из 3n и 5n единиц, в частности
репьюнит из 15 единиц — наименьший, который делится также
на 31 (период числа 31 равен 15). Для любой другой тройки
последовательных простых чисел номер наименьшего репьюни-
та, кратного всем трем числам, совпадает с наименьшим общим
кратным их периодов.
Интересно также рассмотреть различные обобщения за-
дачи. Можно ли, например, снять ограничение с количества
рассматриваемых простых делителей? Не требовать, чтобы они
были последовательными простыми числами?
6.R
18
. Периоды чисел 7, 13 и 19 равны 6, 6 и 18 соответс-
твенно, а наименьшее общее кратное 6 и 18 равно 18.
7.
×
×
×
×
×
×
×
=
8. 4. На 41 делятся репьюниты вида
, в част-
ности
. Число
можно представить в виде суммы
+
×
+
=
+
значит, остаток от
деления
на 41 равен 4.
9.Да.2009=7
2
41, поэтому
делится на
×
=
а значит, и на 239.
10. 111 — не обязательно, а
будет.
143
ГЛАВА 6
Под знаком симметрии
Расшифруйте: «He spoke from 2222222222 people».
Я представил это в виде: «He spoke from 22 to 2 to
2 : 22 to 2222 people».
М. Гарднер. Математический цирк
Одно из замечательных свойств репьюнитов — порождать
целые семейства палиндромов. Оно лежит в основе многих
головоломок и фокусов с числами, поначалу ставящих в ту-
пик многих. Но стоит только подметить цифровую законо-
мерность и обобщить результаты наблюдений, как нужное
свойство будет открыто и задача решится в уме. Одна,
другая, третья... и вот вы уже щелкаете их как орехи!
ГЕНЕРАТОР ПАЛИНДРОМОВ
Репьюниты, а также числа-палиндромы, в запись которых
помимо 1 входит 0, при выполнении над ними различных ариф-
метических операций порождают целые вереницы красавцев-
палиндромов. Простейший пример тому — многозначные числа,
в записи которых все цифры одинаковые (их называют репдид-
житами, от англ. repeated digit — повторенная цифра):
×
=
,где1n9,m N.
А любопытен он тем, что такого вида палиндромы могут
быть какой угодно длины (длина числа — общее количество
цифр в его записи): от двузначных коротышек до многозначных
чисел-гигантов.
Заметим, что даже из такого простенького примера мож-
но извлечь пользу — усмотреть нехитрый способ построения
цепочки палиндромов вида n...n. А начинается она с девяти-
значного (по количеству цифр, которые могут использоваться в
записи) репьюнита 111111111. Данное число делится на 9, пос-
кольку на 9 делится сумма его цифр, да как примечательно:
111111111 = 9 12345679,
чему есть простое объяснение (какое?). Дальнейшее — су-
щие формальности: умножаем результат сначала на 2, затем на
3, 4, ..., 9 и получаем девять палиндромов-репдиджитов.
144
1 9 12345679 = 111111111
2 9 12345679 = 222222222
3 9 12345679 = 333333333
............................................
9 9 12345679 = 999999999
Конечно, за основу можно было взять любой другой репью-
нит с оригинальным разложением на множители. Это сказалось
бы только на длине чисел-палиндромов.
Не менее эффектно выглядит, например, следующая число-
вая пирамида.
1 11 101 10001 = 11111111
2 11 101 10001 = 22222222
3 11 101 10001 = 33333333
............................................
9 11 101 10001 = 99999999
Вот уж где действительно вовсю царствуют нули и еди-
ницы!
В ИГРУ ВСТУПАЮТ СТЕПЕНИ
Большего цифрового разнообразия в записи чисел-палин-
дромов легко добиться, перейдя к рассмотрению степеней. Вы-
пишем несколько первых степеней чисел 11, 101 и 111:
110= 1
1010 =
1
1110 =
1
111
=
11
1011
=
101
1111
=
111
112
=
121
1012
=
10201
1112
=
12321
113
= 1331
1013
=
1030301
1113
= 1367631
114 = 14641
1014 = 104060401
Любопытные семейства палиндромов, не так ли? Вам ни-
чего не напоминают числа, составляющие левую пирамиду?
А если записать так?
1
11
121
1331
14641
Оказывается, можно было обойтись и без умножения. Край-
ние цифры всех выписанных степеней — единицы, а чтобы по-
лучить остальные цифры каждого следующего числа, начиная с
третьего, достаточно сложить две цифры предыдущего, стоящие
над ним (левее и правее).
145
112
=
121 (1+1=2),
113= 1331(1+2=3,2+1=3),
114
= 14641(1+3=4,3+3=6,3+1=4)
У чисел, образующих среднюю пирамиду, те же самые циф-
ры «разбавлены» нулями.
Наконец, при записи степеней числа 111 нужно сложить
сначала по две, а затем по три цифры предыдущего числа.
1112
=
12321 (1+1=2, 1+1+1=3)
1113
= 1367631(1+2=3, 1+2+3=6, 2+3+2=7)
Ясно, что при увеличении показателя степени всего на 1,
во всех трех случаях симметрия в записи получающихся чисел
нарушается. Но это еще не повод останавливаться в своих изыс-
каниях. Можно комбинировать исходные числа или поиграть с
другими числами, сконструированными из нулей и единиц и
приводящими к новым цепочкам палиндромов. Вот лишь один
пример — на построение чисел вида
Любое из них можно получить в результате умножения двух
палиндромов:
и
,
1
00
...
00
1
N
n
n
,
причем первое число в списке будет простым.
Попробуйте построить аналогичные рассмотренным фигу-
ры и поискать интересные закономерности в записи образую-
щих их чисел, например вида:
а) 11 101m
, гдеm=0,1,2,3,4;
б)
1
00
...
00
1
m
n
, гдеm=0,1,2,3,4иn 2;
в)
, гдеm=0,1,2,3иn N;
г)
1
00
...
100
...
11 11
n–2
n
, гдеn 2.
СЕМЕЙСТВО «12...n...21»
И снова к репьюнитам. Легко получить множество красивых
палиндромов, умножая одинаковые или разные по длине числа
из единиц. При этом в структуре палиндромов будут прослежи-
ваться четкие закономерности. Так, у квадратов первых девяти
146
репьюнитов цифры в записи упорядочены сначала по возраста-
нию, а затем по убыванию.
12
=
1
112
=
121
1112
=
12321
...............................................
1111111112
= 12345678987654321
Как видим, добавление к записи репьюнита единицы уве-
личивает длину каждого нового палиндрома на две цифры, при
этом их общее число остается нечетным. А вот центральная
цифра n в числе 12...n...21 показывает, сколько единиц в по-
родившем его репьюните. Механизм образования палиндрома
поясняет следующий пример на умножение:
1111
1111
1111
+ 1111
1111
1111___
___
1234321
Будет ли эта закономерность проявляться и дальше? Если
да, то как долго? А если нет, то почему?
Сформулировав подмеченное свойство репьюнитов в общем
виде, легко (без всяких вычислений) ответить на самые разные
вопросы, касающиеся палиндромов вида 12...n...21, где 1 n 9,
например такие.
1. Какой формулой задается число k цифр в числе
=
,где1n9?
2. Может ли палиндром 12...89098...21 быть квадратом ре-
пьюнита?
3. Какая цифра в записи числа
=
стоит на вось-
мом месте? На каких по счету местах стоят цифры 4 и 2?
4. Сколько цифр в записи каждого из чисел =
и b = 2 11112? Какие цифры в ней отсутствуют?
5. Квадрат какого репьюнита является 11-значным палинд-
ромом и что это за число?
6. Чему равны сумма и произведение цифр квадрата репь-
юнита 1111?
147
7. Чему равен квадратный корень из числа 123454321?
8. Какие репьюниты являются делителями числа
12...78987...21?
9. Какие из палиндромов вида 12...n...21, где 1 n 9,
кратны наименьшему простому репьюниту?
10. При каком x верно равенство 111
x
x
+11
x
x
– 21 = 12421?
x
ДАЛЬНЕЙШИЕ ИССЛЕДОВАНИЯ
Затем можно перейти к изучению произведений репьюнитов
разнойдлины.Приn<mи1 n 9произведениеRm R
n
является
палиндромом. В нем, как нетрудно подсчитать, m + n – 1 цифра,
причем первые n цифр — это 1, 2, ..., n. В середине n повторяется
m–n+1раз.Итак,
.
21
...
...
...
12
1
1
n
m
n
m
n
m
n
n
R
R
Например:
R8R
7
= 12345677654321,
=
×
Другой пример. Сколько единиц в наименьшем репьюните,
делящемся на R11
2
? Ответ легко подсчитать в уме. Речь идет о
репьюните с номером
=
×
=
то есть о числе из
единиц.
Не менее увлекательно изучать и отдельные числа-палинд-
ромы, отличающиеся красивыми разложениями на множители,
вроде таких:
2468642 = 22 112211 = 1111 2222 =
= 2 1234321=2 121 10201=
= 2 11112
=21121012
.
Предлагаем несколько любопытных задач-исследований
на эту тему.
1. Представьте разными способами в виде произведения
чисел-палиндромов и их степеней каждый из палиндромов:
888000888; 1122332211; 133126621331.
2. Произведением каких двух репьюнитов является палин-
дром
148
3. Произведением каких трех репьюнитов является палин-
дром 135787531?
4. Сколько цифр содержится в записи числа
×
=
Сколько восьмерок входит в запись числа
×
=
Какие цифры отсутствуют в записи числа
×
=
Какой вид имеют палиндромы, получающиеся в результа-
те умножения двух чисел вида
и
n+1
11
...
11
,где1 n9?
Сколько цифр в самом большом палиндроме из этого списка?
8. Верно ли, что число
=
×
делится без
остатка на каждый их первых десяти репьюнитов? Найдите
наибольший палиндром, являющийся его делителем.
9. Укажите все пары репьюнитов, для каждой из которых
произведением чисел, составляющих пару, будет 11-значный
палиндром. Чему равен наименьший; наибольший из этих па-
линдромов? Решите задачу для 111-значного палиндрома.
Обобщите ее для палиндрома, в котором
цифр.
10. Проверьте справедливость данных формул, предвари-
тельно выяснив, при каких n и k с их помощью можно получить
k
многозначные палиндромы:
Rn+1
2
= 10Rn
2
+R2n+1
,
Rn
2
= 10n–k Rk
2
+Rn+k Rn–k
,
kk
Rn+1
2
=R
2n+1
+10 R2n–1
+102 R
2n–3
+...
... +10n–1
R3+10n R
1
.
149
ОТВЕТЫ
Семейство «12...n...21»
1.k =2
kn–1,1n9.
2. Нет.
3. На 8-м месте стоит цифра 8. Цифра 4 стоит на 4-м и 12-м
местах, а цифра 2 — на 2-м и 14-м.
4.Вчисле =
цифр 13, отсутствуют 0, 8 и 9.
Вчислеb=2 11112цифр7,отсутствуют0,1,3,5,7и9.
5. 12345654321 = 111111
2
.
6.Суммацифр—2 (1+2+3)+4=16,апроизведение
— 4 (3!)2
= 144.
7. 11111.
8.R
3
иR9
.
9. 121, 1234321, 12345654321, 123456787654321.
10.Приx=2.
x
Дальнейшие исследования
2. R3 и R12323
.
3. 11, 1111 и 11111.
4. 105 цифр.
5. 993 восьмерки.
6.Цифры0,8и9.
7. 12...nn...21; 18 цифр.
8. Нет. 11223344544332211.
9. Это пары (Rn
,R
12–n
), где n = 1, 2, ..., 6; наименьшим
будет палиндром
а наибольшим — 12345654321.
(Rn
,R
112–n
), где n = 1, 2, ..., 9; наименьшим будет палиндром
, а наибольшим —
В общем случае
приk>2этопарывида(
k
Rn
,R
m
),гдеn=1,2, ..., 9и
=
150
ГЛАВА 7
Подлинная история паука и мухи
Тише едешь — дальше будешь.
Русская пословица
Геометрические задачи с участием насекомых и пауков
— не редкость. Это связано не только с желанием авто-
ров заинтересовать читателя неожиданным сюжетом, но
и с тем, что крошечные создания природы очень подходят
на роль «подвижных точек»: они могут легко переме-
щаться в пространстве, описывая на поверхности фигур
причудливые линии. Уже одного этого достаточно, чтобы
привлечь внимание пытливого геометра.
ВНУТРИ ПАРАЛЛЕЛЕПИПЕДА
Среди задач на изучение траекторий самой известной явля-
ется задача о пауке и мухе. В ней хищнику-пауку надо отыскать
путь к своей жертве, неподвижно сидящей в указанной точке
поверхности многогранника или другого тела. Причем не ка-
кой-нибудь путь, а самый короткий, быстрее всего ведущий к
цели. Примечательно, что каждый автор, будь то собиратель
головоломок или признанный мастер этого жанра, предложил
собственную версию задачи о пауке и мухе, сохранив и зало-
женную в ней идею, и общий подход к решению. Любопытно
сравнить вариации на тему этой красивой задачи, придуманные
известными авторами, а заодно посмотреть, в каких направле-
ниях развивался ими классический сюжет и какие новые инте-
ресные исследования мог бы породить.
А начнем, пожалуй,
с такого примера — из
книги Генри Дьюдени
«200 знаменитых голо-
воломок мира». Внутри
прямоугольной комна-
ты, имеющей 30 футов
вдлинуипо12футовв
ширину и высоту, на се-
30
1
2
1
2
Рис. 1
A
B
151
редине одной из торцовых стен в 1 футе от потолка сидит паук
(точка A, рис. 1). Муха сидит на середине противоположной
стены в 1 футе от пола (точка B, рис. 1). Каков кратчайший путь,
каким паук может добраться до неподвижной мухи?
Наверняка можно утверждать только то, что путь паука про-
ходит как минимум по трем граням параллелепипеда и представ-
ляет собой ломаную. Чтобы понять, как ее звенья располагают-
ся на внутренней поверхности многогранника, посмотрим, как
может выглядеть путь паука на развертке. Из всех возможных
случаев выделим четыре наиболее благоприятных (рис. 2).
Так какой путь следует избрать пауку?
Вычислим длину отрезка AB в каждом случае.
Рис.2,а: AB=42фута.
Рис. 2, б:
17
,
43
42
10
2
2
≈
+
=
AB
фута.
Рис. 2, в:
+
=
футов.
Рис. 2, г:
+
=
фута.
* При выборе развертки учитывается не только удаленность точек A и B от сторон
квадратов — фрагментов развертки, но и взаимное расположение самих квадратов.
B••
A
42
B
A
•
•
42
10
B•
•
A
32
24
B•
•
A
37
17
Рис. 2
a
б
в
г
152
Итак, кратчайший путь имеет длину 40 футов и пролегает
сразу через пять граней параллелепипеда, или три стены, по-
толок и пол комнаты. Выходит, пауку придется передвигаться
по замысловатой пространственной ломаной. Как же она вы-
глядит?
Исследование первое. Причудливая ломаная
Нарисуйте параллелепипед и, опираясь на рис. 2, в, изоб-
разите эту ломаную на его внутренней поверхности. Постройте
также соответствующую кратчайшему пути паука ломаную, ко-
торая проходит через: а) три грани; б) четыре грани параллеле-
пипеда. Какая из построенных ломаных плоская и почему?
Впрочем, «за кадром» остался еще один важный вопрос,
не прозвучавший в задаче Дьюдени. Это вопрос о количестве
ее решений. Нетрудно исправить это упущение, а для полноты
картины следует рассмотреть пути, пролегающие через разное
число граней. Будет ли решение в каждом случае единственным
или имеется несколько ломаных минимальной длины, проходя-
щих через разные тройки (четверки, пятерки) граней данного
многогранника? На последнее предположение наталкивает
симметрия параллелепипеда, а также центрально-симметрич-
ное расположение паука и мухи, выбранное автором, конечно,
неслучайно.
Исследование втрое. Подсчет числа путей
Сколько всего существует кратчайших путей паука в слу-
чае, когда они пролегают через: а) три грани; б) четыре грани;
в) пять граней параллелепипеда?
В СТИЛЕ ВОЛЬНОЙ ИНТЕРПРЕТАЦИИ
До сих пор мы обсуждали некоторые вопросы, естественно
возникающие по мере изучения описанной в задаче ситуации.
Если хотите, «углублялись» в ситуацию, не выходя при этом за
рамки задачи, а лишь расширяя их в двух возможных направ-
лениях.
А ведь головоломку Дьюдени легко видоизменить, варьи-
руя лишь исходные данные. Скажем, задать иное начальное по-
ложение паука и мухи: посадить их в противоположных углах
комнаты, разместить на полу и на потолке и т.п. Можно указать
новые числовые данные: размеры комнаты или расстояния па-
153
ука и мухи от потолка и пола. Наконец, вместо прямоугольного
параллелепипеда рассмотреть другие пространственные фигу-
ры, в том числе тела вращения, скажем цилиндр. Ведь иссле-
довать передвижения паука по цилиндрической поверхности
не менее интересно, чем наблюдать за его перемещениями по
многограннику!
А чтобы помочь пауку найти кратчайшую дорогу к цели,
можно воспользоваться проверенным способом: развернуть
поверхность на плоскость, начертить отрезок с концами в на-
чальной и конечной точке пути, затем свернуть поверхность,
придав ей первоначальную форму. Тогда на ней будет видна
искомая траектория — некоторая кривая или ломаная.
Ну, а теперь перейдем к «вольным интерпретациям» знаме-
нитой задачи, предложенным в разное время несколькими ав-
торами — классиками занимательной математики.
ИЗ УГЛА В УГОЛ
Следующая задача — из книги Е. И. Игнатьева «В царстве
смекалки». На потолке в углу C комнаты сидит паук, а на полу в
C
противоположном углу K спит муха (рис. 3). Какой путь должен
K
избрать паук, чтобы добраться до
мухи по кратчайшему расстоянию?
Как видим, паук и муха перемес-
тились в вершины параллелепипеда,
служащего моделью комнаты, одна-
ко по-прежнему расположены сим-
метрично относительно его центра.
А это, наряду с симметрией самого
многогранника, позволяет упростить
решение: вместо шести ребер — AB,
AD, BE,EE FG,G EG,G DF, которые может пересечь траектория паука, до-
FF
статочно рассмотреть три последние. Возможные кратчайшие
пути, пересекающие ребра FG,G EG и
G DF, показаны на рис. 4, 5.
FF
Пусть длина, ширина и высота комнаты равны a, b, c соот-
c
ветственно. Найдем длины отрезков CK,KK C
1
CKи
K C2CC K:
* Игнатьев Емельян Игнатьевич (1869—1923) — русский математик и популяризатор
науки.
EG
BC
KF
AD
Рис. 3
+
+
+
=
+
+
=
154
Подкоренные выражения отличаются только последним
слагаемым. Произведения 2ab, 2bс, 2
сс aс могут принимать раз-
с
личные значения при разных значениях a, b и c. Иначе говоря,
длина кратчайшего пути зависит от размеров комнаты и при оп-
ределенном их соотношении любой из трех отрезков CK,KK C
1
CK,KKC
2
CCK
может служить траекторией паука.
Возможнытрислучая.Еслиa>bиa>c,то2
cc
aс>2bcи
c
2ab > 2bc, поэтому кратчайшим будет путь
cc
C2CC K. Аналогично рас-
сматриваем два других случая. Если b > a и b > c, то самым ко-
c
ротким будет путь C1C K. Если c >
c aиc>
c b, то пауку следует выбрать
путь CK. Итак, маршрут минимальной длины должен пересекать
самое длинное из ребер FG,G EG,G DF.
Данная задача порождает самые разные вопросы. Вот не-
которые из них. Как выглядит на внутренней поверхности па-
раллелепипеда, служащего моделью комнаты, кратчайший путь
паука из угла C в угол
C
K (см. рис. 3), если между собой равны два
K
из трех измерений комнаты? (Рассмотрите все случаи.) Сколько
всего кратчайших путей паука существует в случае, когда ком-
ната имеет форму куба? Какими свойствами обладает ломаная
линия, изображающая траекторию? Как определить положение
точки пересечения траектории паука с ребром параллелепипе-
G
F
C
K
c
ab
F
D
1
K
2
EG
c
b
()
()
b
c
a
Рис. 4
Рис. 5
+
+
+
=
+
+
=
+
+
+
=
+
+
=
155
да, зная размеры многогранника, и все ли три размера (длину,
ширину, высоту) для этого необходимо знать?
Исследование третье. «Удобное» положение
В комнате, имеющей форму прямоугольного параллелепи-
педа размером a b c (
c a ≥ b ≥ c), кратчайший путь паука из
угла C в угол
C
K (ломаная
K
CMK) пролегает по задней стене и по-
KK
толку (рис. 6).
а) В каком отношении точка M
делит общую для задней стены и
потолка сторону (ребро EG)? б) При
каком соотношении размеров ком-
наты точка M окажется серединой
этой стороны? Верно ли, что в таком
случае точка M будет равноудалена
от вершин углов C и
C K? в) Чему равны
KK
расстояния от точки M до ближайших
к ней углов комнаты (вершин парал-
лелепипеда), а также до паука и до
мухи?
КРУГОВОЙ ПУТЬ
В книге Гуго Штейнгауза « Математический ка-
лейдоскоп» история паука и мухи разыгрывается
уже на поверхности куба. Как и в задаче Дьюдени,
хищник и его жертва сидят на противоположных
гранях многогранника, однако их исходное по-
ложение не привязано к каким-то определенным
точкам, а может быть произвольным. Если паук и
муха находятся в точках P и M соответственно, то
кратчайший путь паука на развертке многогранни-
ка будет пролегать по отрезку PM (рис. 7).
Однако самого автора, кажется, больше занимает другой
вопрос: как будет выглядеть путь мухи, если она захочет обойти
все грани куба, дабы удостовериться в отсутствии паука и как
можно скорее вернуться на прежнее место? Оказывается, кру-
говой путь мухи на развертке куба также пролегает по прямой
EG
B
C
K
F
A
D
M
b
c
a
Рис. 6
P
M
Рис. 7
* Гуго Дионисий Штейнгауз (1887—1972) — польский математик, педагог и попу-
ляризатор науки.
156
и, как ясно из рис. 8, его длина будет
одной и той же, из какой бы точки ни
начала движение муха.
Штейнгауз указывает и другие
любопытные свойства кратчайших
круговых дорог на поверхности куба.
Например, такое: всякое семейство
параллельных дорог покрывает ров-
но половину поверхности многогран-
ника (рис. 9), а всего таких семейств
насчитывается четыре. Упоминает он
и о том, что у мухи всегда имеются на
выбор две кратчайшие дороги. Через
каждую точку M на поверхности куба проходят сразу две плос-
кие простые замкнутые ломаные одинаковой длины из шести
звеньев каждая, причем их звенья, проходящие через точку M,
пересекаются под прямым углом (рис. 10).
Траектория мухи, представляющая собой шестиугольник,
и сама по себе является интересным объектом для изучения.
С одной стороны, получившуюся фигуру можно исследовать как
выпуклый многоугольник, весьма богатый свойствами, а с дру-
гой — рассмотреть как фигуру, получающуюся при пересече-
нии поверхности куба плоскостью. Это позволит, в частности,
понять, как вычислить длину кратчайшего кругового пути на
поверхности куба и как построить этот путь на заданном изоб-
ражении многогранника.
Исследование четвертое. Геометрия траектории
Нарисуйте отдельно траекторию мухи — шестиугольник.
Какими свойствами обладает этот шестиугольник? Как вычис-
лить его периметр (а стало быть, длину кругового пути мухи),
зная длину ребра куба?
•
•
Рис. 8
Рис. 9
M
Рис. 10
157
Исследование пятое. Правильный шестиугольник
При каком условии искомый шестиугольник будет правиль-
ным? Можно ли в этом случае указать местоположение мухи на
поверхности куба (точное положение точки M на его грани)?
Если можно, то будет ли оно определено однозначно?
Решение задачи на построение кратчайшего кругового пути
мухи, приведенное на рис. 10, станет очевидным, если заметить,
что траектория на развертке куба параллельна диагоналям его
граней (см. рис. 8, 9). Значит, каждая сторона шестиугольника
будет изображаться как отрезок, параллельный одной из диа-
гоналей той грани куба, в плоскости которой он лежит. Так что
достаточно знать, в какой точке сидит муха. А если еще будет из-
вестно, параллельно какой из двух диагоналей квадрата попол-
зет насекомое, мы получим единственно возможное решение.
Исследование шестое. Новые построения
Решите задачу Штейнгауза при условии, что муха сидит:
а) в центре грани; б) в вершине; в) на ребре куба (рис. 11).
Сколько круговых путей возможно в каждом случае?
ПЕТЛЯ, ДУГА, ОКРУЖНОСТЬ
Автор «Математического калей-
доскопа» рассматривает также за-
дачу на отыскание кратчайшего пути
бдительной мухи, пролегающего по
конической поверхности. Интуиция
подсказывает, что насекомое должно
двигаться по окружности, лежащей в
плоскости, параллельной плоскос-
ти основания конуса (окружность ,
рис. 12).
•
M
•
M
M
•
Рис. 11
M
Рис. 12
158
Но это не так. На самом деле
муха опишет на поверхности конуса
петлю, которая имеет излом в исход-
ной точке M (рис. 12). Если бумаж-
ную модель конической поверхности
разрезать по образующей, проходя-
щей через точку M, и разложить на
столе, то развертка будет иметь фор-
му кругового сектора.
Возможны два случая.
Если угол сектора меньше 180о
,
кратчайший путь мухи на развертке
будет пролегать по отрезку MM1
,а
вовсе не по дуге с концами в точках
MиM1
, соответствующей окружности
(рис. 13, а). Если же угол сектора
равен или больше 180о
, мухе придет-
ся подняться по отрезку образующей
на вершину S конуса, осмотреться по
S
сторонам и спуститься обратно тем
же путем (рис. 13, б).
Исследование седьмое. Поиски формулы
Выведите формулу для вычисления длины кратчайшего
кругового пути мухи на конической поверхности, если образую-
щая конуса равна d, длина окружности его основания равна
d
l,а
расстояние от вершины конуса до точки, в которой сидит муха,
равно m. Предложите разные способы решения.
Заметим, что если вместо кони-
ческой поверхности рассмотреть
сферу (которую, кстати, нельзя раз-
вернуть и разложить на плоскости
без искажения длин кривых), то
кратчайший круговой путь насекомо-
го пройдет по большой окружности.
А вот в задаче о пауке и мухе крат-
чайший путь паука на сфере должен
пролегать по меньшей из двух дуг
большой окружности, проходящей
через точки P и M, и он будет опре-
делен однозначно (рис. 14).
M
M1
S
M
M1
S
а
Рис. 13
M
•
•
P
•
Рис. 14
б
159
НА ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ
Вернемся к истории хищника и его жертвы. Для полноты
картины следует посмотреть, как развивались бы в ней события,
случись они на цилиндрической поверхности. Конечно, авторы,
писавшие в жанре занимательной математики, не оставили их
без внимания.
Перед нами одно из
продолжений истории о
пауке и мухе, описанное
в книге Ч. Б. Таунсенда
«Звездные головолом-
ки» (сама задача, прав-
да с несколько иным
сюжетом, встречается
еще у Дьюдени). По
стеклянному цилинд-
ру высотой 4 дюйма и
с длиной окружности
6 дюймов ползет паук.
Сейчас он находится на расстоянии 1 дюйма от нижнего края
цилиндра (точка P). Напротив, на внутренней стороне, всего в
1 дюйме от верхнего края, сидит муха (точка M, рис. 15). Пауку
нужно отыскать кратчайший путь, чтобы добраться и сцапать
жертву. Что это за путь и чему равна его длина?
Представим, что нам удалось разрезать цилиндрическую
поверхность по образующей и разложить на плоскости. Полу-
чился прямоугольник размером 6 4 дюйма. И хотя благодаря
прозрачности материала мы видим обе отмеченные точки, одна
из них, пусть это будет точка P, находится на обратной сторо-
не развертки (рис. 16). Чтобы добраться до мухи, паук снача-
ла должен переползти через ближайший край цилиндра на его
внутреннюю поверхность. Но в какой именно точке? По сути,
это и есть главный вопрос задачи и ключ к решению.
Поскольку путь паука на развертке состоит из двух отрез-
ков, не лежащих на одной прямой, то есть является ломаной,
исходная задача сводится к другой хорошо известной со вре-
мен древних греков задаче о нахождении на заданной прямой
* Чарлз Барри Таунсенд — современный американский собиратель и автор занима-
тельных задач, игр и головоломок, посвятивший им более двух десятков книг.
M
M
(
)
6
4
P
P
Рис. 15
Рис. 16
160
такой точки, сумма расстояний от которой до двух данных точек,
лежащих в одной полуплоскости относительно этой прямой, ми-
нимальна .
А эта задача решается с помощью осевой симметрии: в дан-
ном случае достаточно построить точку Q, симметричную P от-
носительно нижней стороны развертки, и провести отрезок MQ,
тогда точка N пересечения его с нижней стороной развертки —
искомая. Итак, кратчайший путь паука пролегает по ломаной
PNM (рис. 17), причем одно ее звено расположено на лицевой
стороне развертки цилиндра, а другое — на оборотной.
Чему же равна длина найденного пути?
Изусловияследует,чтоMR=3+1=4дюйма,RQ=6:2=3дюйма
(рис. 18), тогда
=
+
=
=
+
=
+
дюймов.
Исследование восьмое. Иные возможности
В решении сказано, что паук должен перебраться на внут-
реннюю поверхность цилиндра через его ближайший край. Со-
гласны ли вы с этим требованием? Быть может, если паук сразу
поползет по направлению к противоположному краю цилиндра,
то обнаружит и другой путь к мухе, ни в чем ни уступающий пер-
вому? Попробуйте построить сначала на развертке, а затем на
* Ее прототипом является задача древнегреческого математика и механика Герона
Александрийского (I век н. э.): доказать, что из всех лучей, падающих из одной дан-
ной точки и отражающихся в другую данную точку, минимальны те лучи, которые от
плоских зеркал отражаются под равными углами.
Q
N
M
•
•
•
P
Рис. 17
P
•
6
4
Q
N
M
•
•
3
3
1
R
Рис. 18
161
изображении цилиндра все возможные в данной задаче крат-
чайшие траектории паука.
И еще пара задач, навеянных последней головоломкой.
Исследование девятое. Двойной расчет
Допустим, у паука появилась еще одна жертва — вторая
муха сидит на одной образующей с первой, на расстоянии
1 дюйма от нижнего края цилиндра (положение паука и первой
мухи не изменилось). Найдите самый короткий путь, которым
паук может добраться сначала до одной, а затем до другой жер-
твы. Чему равна его длина? Имеет ли значение, какую жертву
паук выберет первой? Если нет, то почему? А если имеет, то на
каком расстоянии от нижнего края цилиндра следовало бы по-
местить паука, чтобы перед ним не стояла проблема выбора?
Исследование десятое. Туда и обратно
Пусть паук и муха сидят снаружи и внутри (соответственно)
того же стеклянного цилиндра напротив друг друга на расстоя-
нии 2 дюймов от краев. На этот раз паук должен доползти самым
коротким путем до своей жертвы, а затем вернуться кратчайшим
путем, но уже другим, в исходную точку. Какое расстояние при-
дется преодолеть пауку и сколько вариантов пути у него будет
на выбор?
POURQUOI PAS?
Как видим, остроумная выдумка математика, а быть может,
и просто любителя математики, некогда придумавшего задачу о
пауке и мухе, имела далеко идущие последствия. Ее идея ока-
залась столь красива и плодотворна, а решения столь просты
и изящны, что задача эта популярна по сей день: разные ее ва-
рианты можно встретить не только на страницах книг по зани-
мательной математике, но и в сборниках задач по геометрии, и
даже в школьных учебниках.
...И все-таки интересно было бы знать, выбирает ли паук
на самом деле из всех возможных путей к своей жертве самый
короткий? Способен ли он решить подобную задачу, четко ори-
ентируясь в пространстве? А почему бы собственно, нет? Умеют
же находить самый короткий путь к цели некоторые насекомые.
Пчелы, например. Экспериментально было установлено, что
если перед ульем поместить туннель, изогнутый под прямым уг-
162
лом, а в его конце поставить чашку с сиропом, то пчела из всех
возможных направлений к ней выберет то, которое соответс-
твует кратчайшему пути от улья до чашки. А путь этот, как легко
сообразить, пролегает по гипотенузе треугольника, катетами ко-
торого служат отрезки туннеля. Впрочем, примеры проявления
математического гения некоторых насекомых столь необычны и
интересны, что достойны самостоятельного исследования.
163
ОТВЕТЫ
Подсчет числа путей
а), в) 2 пути; б) 4 пути.
«Удобное» положение
Рассмотрим фрагмент развертки паралле-
лепипеда — две грани, через которые проходит
кратчайший путь паука (рис. 19).
а)EM:MG=
G EK:K GC=
Cc:
cb.
б) Точка M будет серединой отрезка EG, когда
G
b=c,атакжекогда
c
a=b =c.Вобоихслучаяхтре-
угольники EKM и GCM равны, поэтому KM = CM.
в) Ближайшими к точке M являются трехгран-
ные углы с вершинами в точках E и
E G. Требуется
найти длины отрезков ME и
E MG.
+
=
=
+
=
+
=
Расстояния от точки M до мухи и до паука найдем по теоре-
ме Пифагора.
+
+
=
+
+
=
Искомый шестиугольник по-
казан на рис. 20, а. У него три
пары параллельных сторон, а сто-
роны, идущие через одну, равны.
Прямые, содержащие три равные
стороны, попарно пересекаясь,
образуют равносторонний тре-
угольник со сторонами, параллельными оставшимся сторонам
шестиугольника (рис. 20, б). Отсюда следуют другие свойства
шестиугольника, в частности такие. Все его углы равны — по
120о
. Из трех диагоналей, выходящих из любой вершины, две
b
c
KaF
EG
M
Рис. 19
Рис. 20
а
б
164
равны и образуют угол 60о
, а третья диагональ параллельна
двум сторонам шестиугольника и делит его на две равнобед-
ренные трапеции (см. рис. 20, а). Если соединить вершины шес-
тиугольника через одну, получится правильный треугольник.
Кроме того, у получившегося шестиугольника три оси симмет-
рии и около него можно описать окружность (см. рис. 20, б).
Периметр шестиугольника равен утроенной диагонали гра-
ни куба (см. рис. 9, 10). Если ребро куба обозначить буквой a, т о
этот периметр равен
Правильный шестиугольник
Получившийся шестиугольник будет правильным, если
окажутся равны все его стороны. В таком случае его вершины
должны совпадать с серединами ребер куба. Следовательно,
муха может сидеть в любой точке любой стороны квадрата с
вершинами в серединах произвольно выбранной грани куба.
Новые построения
a) Траектория мухи — равносторонний треугольник
(рис. 21, а). Из точки M муха может направиться к любой из
четырех вершин грани, а из этой вершины перейти на любую из
двух соседних граней, значит, всего получится восемь путей. Од-
нако пути, проходящие через одну и ту же тройку вершин куба,
пусть и взятых в разном порядке, выглядят одинаково, поэтому
можно считать, что различных траекторий существует четыре.
Из каждой вершины куба видны сразу три его грани, поэтому
прохождение через три указанные вершины многогранника
позволит мухе обозреть всю его поверхность.
•
•
M
M
•
M
Рис. 21
абв
165
б) Одна из траекторий изображена на рис. 21, б. Всего раз-
личных траекторий мухи три.
в) Одна из траекторий изображена на рис. 21, в. Всего раз-
личных траекторий мухи две.
Поиски формулы
Требуется найти длину отрезка
ММ1 (см. рис. 22). Обозначим угол
MSM1 сектора буквой .
Если ≥ 180°, то ММ1
= 2m. Если
< 180°, то
=
(рис. 22), где =
o
Иные возможности
Ограничение
можно
снять. Рассмотрев анало-
гично симметрию относи-
тельно верхней стороны
развертки, получим еще
один возможный путь пау-
ка (рис. 23). Ломаная PRM
состоит из звеньев такой
же длины, что и ломаная
PNM, поскольку четырех-
угольник MNPR — парал-
лелограмм. Одна из траекторий пау-
ка на цилиндрической поверхности
изображена на рис. 24, она состоит
из двух кривых, соединяющихся в
точке N (пунктиром показаны линии
на внутренней поверхности цилин-
дра). Еще два различных решения
получим, направив паука в другую
сторону: на рис. 24 паук повора-
чивает направо, однако с таким же
успехом может двигаться и налево;
в определенном смысле ситуации
симметричны.
S
H
m
MM
1
2
Рис. 22
R
N
•
P
M
•
N
M
P
Рис. 24
QN
R
P
M1
M2
•
•
Рис. 25
Рис. 23
166
Двойной расчет
Пусть паук находится в точке P, а мухи — в точках M1 и M2
.
Выполним необходимые построения на развертке. Из четырех
возможных путей (рис. 25) кратчайшим является PQM2M
1
. Его
длина равна
6,5
2
5,1
1
2
2
2
2
1
2M
M
PQ
дюйма.
Как видим, для паука существенно, какую из мух он выберет
на закуску, а какую оставит на десерт. А вот если бы паук на-
чинал движение из точки, равноудаленной от краев цилиндра,
то есть находящейся в двух дюймах от них, это не имело бы для
него никакого значения,
выбирать пришлось бы не
мух, а лишь направление
движения.
Туда и обратно
Траектория
паука
представляет собой за-
мкнутую пространствен-
ную линию, причем, в за-
висимости от того, в какую
сторону поползет паук из
точки M, она может вы-
глядеть по-разному (рис.
26—28, а). На развертке
мы увидим либо простые
незамкнутые
л
оманые
(см. рис. 26, б и 27, б), либо
ромб (см. рис. 28, б).
Вычисления п оказыва-
ют, что длина пути паука в
обаконцаравна10 дюймам.
А благодаря симметрии
цилиндра и в
заимному
положению точек M и P у
паука будет на выбор сра-
зу двенадцать вариантов
пути.
N
P
M
R
•
•
P
R
2
1,5 N
M
•
P
R
2
1,5 N
M
N
R
•
•
P
M
•
•
R
P
M
N
M
N
P
R
3
4
Рис. 26
Рис. 28
а
б
Рис. 27
а
б
а
б
167
ЧАСТЬ ЧЕТВЕРТАЯ
Исторические зарисовки
ГЛАВА 1
Решетчатое умножение
—
А ну-ка проверю, помню я то, что знала, или нет.
Значит так: четырежды пять — двенадцать, че-
тырежды шесть — тринадцать, четырежды семь...
Л. Кэрролл. Алиса в Стране чудес
Чтобы освоить умножение многозначных чисел, нужно
знать таблицу умножения и уметь складывать числа.
По сути, вся сложность заключается в том, как правильно
разместить промежуточные результаты умножения (час-
тичные произведения). Стремясь облегчить вычисления,
люди придумали множество способов умножения чисел.
За многовековую историю математики их набралось
несколько десятков.
НАСЛЕДИЕ ИНДУСОВ
Индусы, с давних времен применявшие десятичную систему
счисления, предпочитали устный счет письменному. Они изоб-
рели несколько быстрых способов умножения, которые позже
заимствовали арабы, а уже от них эти способы перешли к евро-
пейцам. Те, однако, ими не ограничились и разработали новые, в
частности тот, что изучается в школе, — умножение столбиком.
Этот способ известен с XV века, в следующем столетии он прочно
вошел в употребление у математиков, а сегодня используется
повсеместно. Но является ли этот способ умножения лучшим?
На самом деле существуют и другие, в наше время забытые спо-
собы умножения, ничуть не хуже, например способ решетки.
Этим способом пользовались еще в древности, в Средние века
он широко распространился на Востоке, а в эпоху Возрождения
168
— в Европе. Его именовали также ин-
дийским, мусульманским или «умно-
жением в клеточках». А в Италии его
называли джелозия или «решетчатое
умножение» (в переводе с итальянс-
кого gelosia — решетчатые ставни),
—
за внешнее сходство получавшей-
ся при умножении фигуры из чисел со
ставнями-жалюзи, которыми украша-
ли окна венецианских домов.
Суть этого нехитрого способа
умножения поясним на примере. Вы-
числим произведение 296 73. На-
рисуем таблицу с квадратными клет-
ками, в которой будет три столбца и
две строки, — по количеству цифр в
множителях. Разделим клетки попо-
лам по диагонали. Над таблицей за-
пишем число 296, а с правой стороны
вертикально — число 73. Перемно-
жим каждую цифру первого числа с
каждой цифрой второго и запишем
произведения в соответствующие
клетки, располагая десятки над диа-
гональю, а единицы под ней. Циф-
ры искомого произведения получим
сложением цифр в косых полосах.
При этом будем двигаться по часо-
вой стрелке, начиная с правой нижней клетки: 8, 2 + 1 + 7 и т.д.
Запишем результаты под таблицей, а также слева от нее. (Если
при сложении получится двузначная сумма, укажем только еди-
ницы, а десятки прибавим к сумме цифр из следующей полосы.)
Осталось прочитать ответ: 21 608. Итак, 296 73 = 21 608.
КАК ЖЕ ОН ДЕЙСТВУЕТ?
Способ решетки ни в чем не уступает умножению столби-
ком. Он даже проще и надежнее, при том, что количество вы-
полняемых действий в обоих случаях одинаковое. Во-первых,
работать приходится только с однозначными и двузначными
числами, а ими легко оперировать в уме. Во-вторых, не требу-
296
608
7
3
2
1
1
4
6
3
4
2
0
6
2
7
1
8
Умножение способом
решетки. Илл. из
первой печатной
книги по арифметике.
1478 г.
169
ется запоминать проме-
жуточные результаты и
следить за тем, в каком
порядке их записать.
Память разгружается, а
внимание сохраняется,
поэтому
вероятность
ошибки уменьшается. К
тому же способ решетки
позволяет быстрее полу-
чить результат. Освоив его, вы сможете убедиться в этом сами.
Почему способ решетки приводит к правильному ответу?
В чем заключается его «механизм»? Разберемся в этом с помо-
щью таблицы, построенной аналогично первой, только в ней
множители представлены как суммы 200 + 90 + 6 и 70 + 3.
Как видим, в первой косой полосе стоят единицы, во второй
—
десятки, в третьей — сотни и т.д. При сложении они дают
в ответе соответственно число единиц, десятков, сотен и т.д.
Дальнейшее очевидно.
10000
10000
+ 1500
100
8
21608
Иначе говоря, в соответствии с законами арифметики про-
изведение чисел 296 и 73 вычисляется так:
296 73=(200+90+6) (70+3)=
= 14000+6300+420+600+270+18=
= 10000+(4000+6000)+(300+400+600+200)+
+(20+70+10)+8=21608.
ПАЛОЧКИ НЕПЕРА
Описанный способ умножения лежит в основе простого и
оригинального счетного прибора — палочек Непера. Его изоб-
рел в начале XVII века Джон Непер, шотландский барон и лю-
битель математики, который наряду с профессионалами зани-
мался усовершенствованием средств и методов вычисления. В
истории науки он известен, прежде всего, как один из создате-
лей логарифмов.
10 000
6 000
4 000
600
70
8
300
20
400
10
200
200
90
6
15
70
3
1
ДЕСЯТКИ
ТЫСЯЧ
10
ТЫСЯЧИ
СОТНИ
10
ДЕСЯТКИ
8
ЕДИНИЦЫ
170
Прибор состоит из десяти линеек,
на которых размещена таблица умно-
жения. В каждой клетке, разделенной
диагональю, записано произведение
двух однозначных чисел от 1 до 9: в
верхней части указано число десят-
ков, в нижней — число единиц. Одна
линейка (левая) неподвижна, осталь-
ные можно переставлять местами, вы-
кладывая нужную числовую комби-
нацию. При помощи палочек Непера
легко умножать многозначные числа,
сводя эту операцию к сложению.
Так, чтобы вычислить произведе-
ние 296 и 73, нужно умножить 296 на
3 и на 70 (сначала на 7, затем на 10)
и сложить полученные числа. При-
ложим к неподвижной линейке три
другие — с цифрами 2, 9 и 6 навер-
ху (они должны
образовать число
296). Теперь за-
глянем в третью
строку (номера
строк указаны на
крайней линей-
ке). Цифры в ней
образуют уже зна-
комый нам набор.
Джон Непер
(1550—1617)
Палочки Непера,
впервые
описанные
в сочинении
Д. Непера
«Рабдология».
1617 г.
171
Складывая их, как в способе решетки, получим
296 3 = 888. Аналогично, рассмотрев седьмую строку, най-
дем, что 296 7 = 2072, тогда 296 70 = 20 720. Таким образом,
296 73=20720+888=21608.
Палочки Непера применялись и для
более сложных операций — деления и из-
лечения квадратного корня. Этот счетный
прибор не раз пытались усовершенствовать
и сделать более удобным и эффективным в
работе. Ведь в ряде случаев для умножения чисел, например с
повторяющимися цифрами, требовалось несколько комплектов
палочек. Такая проблема решалась заменой линеек вращающи-
мися цилиндрами с нанесенной на поверхность каждого из них
таблицей умножения в том же виде, как ее представил Непер.
Фактически вместо одного набора палочек получалось сразу
девять. Подобные ухищрения в самом деле облегчали и уско-
ряли расчеты, однако не затрагивали главный принцип работы
прибора Непера. Так способ решетки обрел вторую жизнь, про-
длившуюся еще несколько столетий.
МАШИНА ШИККАРДА
Ученые давно задумывались над
тем, как переложить непростую вы-
числительную работу на механичес-
кие устройства. Первые успешные
шаги в создании счетных машин уда-
лось осуществить только в XVII сто-
летии. Считается, что раньше других
подобный механизм изготовил не-
мецкий математик и астроном Виль-
гельм Шиккард. Произошло это в
1623 году. По иронии судьбы об этом
знал лишь узкий круг лиц, и столь по-
лезное изобретение более 300 лет не
было известно миру. Поэтому оно не
повлияло на последующее развитие
вычислительных средств. Описание
и эскизы машины Шиккарда были
обнаружены всего полвека назад в
архиве Иоганна Кеплера, а чуть поз-
0
6
2
7
1
8
Вильгельм Шиккард
(1592—1635)
172
же по сохранившим-
ся документам была
создана ее действу-
ющая модель.
По сути, ма-
шина
Шиккарда
представляет собой
ш естиразрядный
механический каль-
кулятор, выполняю-
щий сложение, вы-
читание, умножение
и деление чисел.
В ней три части:
множительное уст-
ройство, суммиру-
ющее устройство
и механизм для сохранения проме-
жуточных результатов. Основой для
первого послужили, как нетрудно
догадаться, палочки Непера, свернутые в цилиндры. Они крепи-
лись на шести вертикальных осях и поворачивались с помощью
специальных ручек, расположенных наверху машины. Перед
цилиндрами располагалась панель с девятью рядами окошек по
шесть штук в каждом, которые открывались и закрывались бо-
ковыми задвижками, когда требовалось увидеть нужные цифры
и скрыть остальные.
В работе счетная машина Шиккарда оказалась очень про-
ста. Чтобы узнать, чему равно произведение 296 73, нужно
установить цилиндры в положение, при котором в верхнем ряду
окошек появится первый множитель: 000296. Произведение
296 3 получим, открыв окошки третьего ряда и просуммиро-
вав увиденные цифры, как в способе решетки. Точно так же,
открыв окошки седьмого ряда, получим произведение 296 7,
к которому припишем справа 0. Остается сложить найденные
числа на суммирующем устройстве.
Придуманный некогда индусами быстрый и надежный
способ умножения многозначных чисел, много веков приме-
нявшийся при расчетах, ныне, увы, забыт. А ведь он мог бы
выручить нас и сегодня, если бы под рукой не оказалось столь
привычного всем калькулятора.
Модель счетной
машины Шиккарда
173
ГЛАВА 2
Во власти сечений
Бросая в воду камешки, смотри на круги, ими образу-
емые, иначе такое бросание будет пустою забавою.
Козьма Прутков. Мысли и афоризмы
Как выглядел простейший циркуль? Что такое коники
Аполлония и как их получить? Какую форму имел в плане
знаменитый римский Колизей? Как устроен стеклорез?
Кто из ученых стоял у истоков науки баллистики? И поче-
му живописцы прошлого были неравнодушны к эллипсу?
ТРИАДА МЕНЕХМА
Античные геометры изучали самые разные плоские кривые.
Особого их внимания удостоились конические сечения: эллипс,
парабола и гипербола. Все это — линии пересечения прямо-
го кругового конуса плоскостями, не проходящими через его
вершину и наклоненными под разными углами к образующей.
Интерес к коническим сечениям проявился у греков в связи со
знаменитыми задачами древности: об удвоении куба, квадрату-
ре круга и трисекции угла. Когда стало ясно, что построением
прямых и окружностей дело не ограничится, математики попро-
бовали решить эти задачи, определяя точки пересечения кри-
вых. Выбор пал на конические сечения.
Их открыл в IV веке до н. э. Менехм, пересекая разного вида
конусы (остроугольный, прямоугольный и тупоугольный) плос-
костью, перпендикулярной образующей. В итоге ему удалось
свести решение задачи об удвоении куба к нахождению точек
пересечения двух парабол. Более столетия конические сечения
не имели собственных названий, указывали лишь способ полу-
чения кривых (например: эллипс — «сечение остроугольного
конуса»). В истории науки они известны также как «триада Ме-
нехма». Свойства эллипса, параболы и гиперболы изучали мно-
гие ученые, в числе которых были Архимед и Евклид. Однако
наиболее важные результаты касательно конических сечений
получил Аполлоний Пергский в III веке до н. э. Он разработал
их общую теорию, которую изложил в труде «Коника» (отсюда
174
другое название кривых — коники), в восьми книгах, где рас-
смотрел почти 400 теорем. Аполлоний первый получил все три
линии как сечения одного и того же конуса. Он же ввел их сов-
ременные названия: термины парабола, гипербола и эллипс.
Они происходят от греческих слов «приближение», «избыток»
и «недостаток». Кстати, того же происхождения литератур-
ные термины: парабола (иносказательная история) гипербола
(образное преувеличение), элипсис (пропуск несущественных
слов в фразе).
Долгое время конические сечения не находили должного
применения, пока ими всерьез не заинтересовались астрономы
и физики. Выяснилось, что эти линии встречаются в природе
(самый замечательный пример тому — траектории небесных
тел) и графически описывают многие физические процессы
(здесь лидирует гипербола: вспомним хотя бы закон Ома и за-
кон Бойля–Мариотта), не говоря уже об их применении в меха-
нике и оптике. На практике, в частности в технике и строитель-
стве, чаще приходится иметь дело с
эллипсом и параболой.
ПОПЕРЕК КОНУСА
Эллипс и его частный случай
окружность, параболу и гиперболу
легко получить экспериментально.
На роль конуса вполне подойдет,
например, вафельный рожок для
мороженого. Мысленно проводим
одну его образующую и разрезаем
рожок под разными углами к ней.
Задача — сделать всего четыре по-
пытки и получить на срезах все воз-
можные конические сечения. Еще
проще провести опыт с карманным
фонариком: в зависимости от его
положения в пространстве конус
света даст на стене комнаты пятна
разной формы. Граница каждого
пятна — какое-то коническое сече-
ние. Поворачивая фонарик в вер-
тикальной плоскости, вы увидите,
Конические сечения:
окружность (1),
эллипс (2),
парабола (3),
гипербола (4)
1
2
3
4
175
как одна кривая сменяет другую: окружность вытягивается в
эллипс, затем он превращается в параболу, а она, в свою оче-
редь, в гиперболу.
Математик решает ту же задачу теоретически, сравнивая
два угла: — между осью конуса и образующей и — между
секущей плоскостью и осью конуса. И вот результат: при <
в сечении получится эллипс или окружность, при =
— пара-
бола, а при > — ветвь гиперболы. Если считать образующие
прямыми, а не отрезками, то есть рассмотреть неограниченную
симметричную фигуру из двух конусов с общей вершиной, станет
понятно, что эллипс — замкнута кривая, парабола состоит из од-
ной бесконечной ветви, а гипербола
— из двух.
ДРЕВНЯЯ РОГУЛЬКА
Простейшее коническое сечение
можно начертить, воспользовавшись
ниткой и булавкой. Достаточно при-
вязать один конец нитки к булавке,
воткнутой в бумагу, а другой — к
карандашу и натянуть. Сделав пол-
ный оборот, карандаш очертит ок-
ружность. А можно воспользоваться
циркулем: меняя его раствор, легко
нарисовать целое семейство окруж-
ностей. По легенде, этот инструмент
изобрел Талос, племянник и ученик
Дедала, но на самом деле он был
известен задолго до греков. Изоб-
ражения циркуля — не редкость на
старинных картинах и фресках, гра-
вюрах и обложках книг. Этот инстру-
мент можно увидеть также в руках
музы Урании — покровительницы
астрономии и Бога-Творца — Вели-
кого Геометра.
А самый древний из найденных
археологами циркулей представляет
собой металлическую рогульку (то
есть имеет фиксированный раствор).
Урания. Римская
копия греческой
скульптуры.
IIIвекдон.э.
176
Им наносили простейший орнамент на
изделия из дерева, керамики, кости и
т.д. Чтобы хоть как-то разнообразить
узор из одинаковых линий, мастера
вполне могли пользоваться набором
рогулек. Еще лучше, если бы под рукой
был один инструмент, рисующий сразу
несколько окружностей разного радиу-
са. Подумайте, как могла бы выглядеть
его простейшая конструкция? И вот еще
одна геометрическая головоломка: как
одним раствором циркуля описать ок-
ружности разного радиуса? Попробуйте
найти несколько решений.
ДОГАДКА ТАРТАЛЬИ
Еще Аристотель в IV веке до н. э.
интересовался траекторией метатель-
ных снарядов. Философ полагал, что она
состоит из двух отрезков — наклонного
и вертикального — и связывающей их
дуги окружности. Представления эти,
конечно, далеки от истины. В XVI столе-
тии, в эпоху активного развития военно-
го дела, тем же вопросом применитель-
но к огнестрельному оружию занимался
итальянский ученый-самоучка Никколо
Тарталья (tartaglia — заика). Он про-
славился не только как математик и ин-
женер, но и как автор первых научных
трудов по баллистике.
Работая в венецианском арсенале
«консультантом по расчетам», Тарталья
первый исследовал траекторию ядра и
дальность его полета в зависимости от
угла наклона ствола пушки к горизонту.
Кстати, этот угол он предложил опреде-
лять при помощи квадранта, помещен-
ного в ствол орудия. Но этот способ не
прижился: слишком уж уязвимым стано-
Титульный лист
книги Никколо
Тартальи «Новая
наука» — первого
сочинения по
баллистике. 1537 г.
Сотворение мира.
Миниатюра XIII в.
177
вился артиллерист-измеритель в момент вражеской атаки. На
основе многочисленных наблюдений Тарталья пришел к выво-
ду: траектория снаряда — кривая линия, а наибольшая даль-
ность его полета соответствует углу наклона пушки 45°. Правда,
строго обосновать этот результат в то время было невозможно.
Это удалось сделать лишь сто лет спустя, когда Галилей от-
крыл законы падения тел. Согласно его теории, выпущенный под
углом к горизонту снаряд движется по параболе при условии,
что сопротивлением воздуха можно пренебречь. Истинная тра-
ектория, конечно, от нее отличается. Используя результат Гали-
лея, покажите, что дальность полета ядра будет максимальной,
если оно вылетает из пушки под углом 45о к горизонту, как и
указал Тарталья. Как определить расстояние до точки падения
снаряда?
ИНСТРУМЕНТ ДА ВИНЧИ
Ответы на вопросы, занимавшие Никколо Тарталью, почти
на полвека раньше его дал Леонардо да Винчи, который изучал
Измерение угла наклона ствола пушки при помощи
оружейного квадранта. Гравюра XVI в.
178
различные траектории и виды сложного движения в природе
и технике. В записных книжках художника имеется немало на-
бросков, сделанных на основе наблюдений. Полет птиц, водо-
ворот, распространение света и звука, круги на воде, движе-
ние мяча и снаряда... Во всех случаях его особо интересовала
геометрия траекторий: углы падения и отражения, кривые и
прочие линии движения тел, а также зависимость их формы
от различных параметров. Неудивительно, что Леонардо пред-
восхитил результаты Тартальи. Взгляните на один из рисунков
художника: из него ясны и траекто-
рии снарядов (семейство кривых,
близких к параболе), и угол наклона
ствола пушки, обеспечивающий яд-
рам дальний полет.
Леонардо часто доводилось де-
лать всякие построения и измерения,
для которых требовались специаль-
ные инструменты. Вот как описыва-
ет мастера за работой Дмитрий Ме-
режковский в романе «Воскресшие
боги»: «Стоя на коленях, рядом с
Венерой, вынул он циркуль, угломер,
полукруглую медную дугу, наподобие
тех, какие употреблялись в матема-
тических приборах, и, с выражением
того же упорного, спокойного и про-
никновенного любопытства в холод-
Да Винчи. Пушки с разрывными ядрами. 1490 г.
Да Винчи.
Параболический
циркуль. Ок. 1500 г.
179
ных, светло-голубых глазах и тонких, плотно сжатых губах, начал
мерить различные части прекрасного тела...»
В рукописях да Винчи содержатся упоминания о самых раз-
ных чертежных инструментах. Считается, что некоторые из них
сконструировал он сам. Одно из изобретений Леонардо — уст-
ройство для рисования параболы (этот кривой художник заин-
тересовался, изучая труды Архимеда и свойства параболичес-
ких зажигательных зеркал). Подобный инструмент, известный
еще грекам, описал арабский математик X—XI веков ас-Сид-
жизи. Это был совершенный циркуль: с помощью него чертили
эллипс, параболу и гиперболу, то есть все виды конических се-
чений. Попробуйте объяснить принцип работы устройства Ле-
онардо, уяснив роль каждой детали
и установив, какому элементу конуса
она соответствует.
СТЕКЛОРЕЗ-ЦИРКУЛЬ
Самый простой способ построе-
ния эллипса, безо всяких инструмен-
тов, рассматривается в одном араб-
ском трактате IX века. Он сродни
способу рисования его ближайшей
родственницы — окружности и ос-
нован на определении эллипса как
множества всех точек плоскости, для
каждой из которой сумма расстоя-
ний до двух данных точек постоянна.
Нужно прикрепить лист бумаги к кар-
тону двумя иголками, привязать к ним
нитку, длина которой больше рассто-
яния между иголками, и натянуть ее
карандашом. Если провести каран-
дашом по бумаге, сохраняя нитку на-
тянутой, и вернуться в исходную точ-
ку, конец его опишет эллипс. Однако
такое построение не всегда надежно
и практично. Например, очертить на
земле клумбу эллиптической формы,
используя колышки и веревку, или
вырезать в доске отверстие, вбив в
A
B
M
Построение эллипса при
помощи нитки, иголок
и карандаша
Эллиптический циркуль.
При движении ползунов
по прорезям точка M
описывает эллипс
180
дерево пару гвоздиков и нарисовав эллипс, всегда можно. А как
быть, если требуется изготовить зеркало такой же формы?
Придется воспользоваться специальным стеклорезом на
присосках, механизм работы которого основан на действии
простого чертежного инструмента, известного как эллиптичес-
кий циркуль. Устройство состоит из крестовины с двумя одина-
ковыми перпендикулярными прорезями. По ним перемещаются
ползуны А и В (один — по вертикали, другой — по горизонта-
ли), к которым шарнирами прикреплена линейка, а на ее конце
—
в точке М закреплен карандаш (в стеклорезе его заменяет
режущий ролик). При движении линейки конец карандаша опи-
сывает эллипс. Докажите это — выведите уравнение получаю-
щейся кривой.
ВЕЗДЕСУЩИЙ ЭЛЛИПС
Вообще с эллипсом мы встречаемся постоянно. Взять, к при-
меру, работу дизайнеров. Одни любят украшать ландшафт цвет-
никами, фонтанами и искусственными водоемами эллиптической
формы. Другие часто выбирают ее для предметов интерьера.
Столешница, абажур, рама для картины, рисунок ковра, декора-
тивное блюдо, циферблат часов — и тот может иметь очертания
эллипса. Даже просто наклонив кружку с водой или разрезав по-
полам батон колбасы, мы увидим эту замечательную кривую.
Планетарий им. Тихо Браге в Копенгагене. Открыт в 1989 г.
181
Последние два примера нагляд-
но демонстрируют, что эллипс явля-
ется сечением не только конуса, но
и прямого кругового цилиндра (до-
статочно пересечь плоскостью его
боковую поверхность, не затрагивая
при этом оснований). Интересно, что
это свойство взяли на вооружение
современные архитекторы. Пример
тому — здание планетария, носящее
имя Тихо Браге, знаменитого датско-
го астронома, учителя Иоганна Кеп-
лера: оно имеет форму усеченного
цилиндра. Но чаще встречаются со-
оружения, представляющие в плане
эллипс. Самое известное из них — римский Колизей, грандиоз-
ный античный амфитеатр, вмещавший до 70 000 зрителей. Его
знаменитая арена, на которой устраивались разные состязания
и зрелища, также ограничена эллипсом.
Наконец, с этой кривой имеют дело художники — всякий
раз, когда изображают окружность в перспективе, например при
работе над натюрмортом: рисуя фрукты, тарелки, вазы и про-
чие предметы круглой формы. При этом они решают непростую
задачу: строят проекции окружностей на плоскость полотна.
Колизей в Риме
(вид сверху).
72—80 гг.
Диего Веласкес. Венера перед зеркалом. 1647—1651 гг.
182
Живописцы прошлого использовали эллипс как одну из базо-
вых фигур при создании композиции картины. Сначала мастера
придумывали общую геометрическую схему, а затем вписыва-
ли в нее различные элементы. При этом они преследовали не-
сколько целей: сделать композицию более отчетливой, разбить
пространство картины на фрагменты, удобные для просмотра,
управлять движением взгляда зрителя, акцентируя внимание на
важных деталях, и, в конечном счете, создать привлекательный
зрительный образ. Для этих целей прекрасно подходил эллипс:
он заставлял взгляд плавно и неспешно блуждать по картине и
в то же время удерживал внутри очерченной им области. Эти
функции эллипс незримо выполняет, например, на полотне зна-
менитого испанского художника Диего Веласкеса «Венера пе-
ред зеркалом». В композиции использована еще одна фигура
— в виде буквы L. У нее иная задача: направлять взгляд зрителя
на главный объект (фокусную точку картины) — зеркало.
Даже беглое знакомство с коническими сечениями показы-
вает, насколько богата и интересна их история и многообразны
приложения. Недаром в разные времена ими интересовались
не только ученые, инженеры, строители, но и представители
разных искусств.
183
ОТВЕТЫ
Древняя рогулька
Инструмент для построения двух и более окружностей раз-
ного радиуса, очевидно, должен представлять собой циркуль с
несколькими ножками, число, местоположение и длину которых
можно при необходимости изме-
нить. Две простейшие конструкции
показаны на рис. 1.
Построить окружности разного
радиуса циркулем с фиксированным
раствором можно так. Сначала про-
вести линию на бумаге, как это де-
лается обычно, а затем приподнять
конец циркуля и опе-
реть, скажем, на ку-
бик, а другим концом
описать на бумаге
еще одну окружность,
меньшего
разме-
ра (рис. 2). Второй
способ — начертить
окружность на по-
верхности фигуры, в
сечении которой она
может получиться: на поверхности
шара, конуса (рис. 3) или иного под-
ходящего тела вращения.
С помощью таких нехитрых при-
емов и приспособлений легко на-
нести рисунок из концентрических
или пересекающихся окружностей
и дуг, например, на глиняную посу-
ду. Подобные узоры (их называют
циркульными) встречаются на мно-
гих древних сосудах, на поверхнос-
ти видны даже отметки от острия
циркуля (рис. 4, на фото — гречес-
кая амфора, изготовленная в X веке
до н. э.).
Рис. 1
Рис. 2
Рис. 4
Рис. 3
184
Догадка Тартальи
При отсутствии сопротивления воздуха ядро, выпущенное
из пушки со скоростью 0 под углом к горизонту, движется по
параболе
2
2
2
0 cos
2
tg
x
g
x
y
(g — ускорение свободного падения), ветви которой направ-
лены вниз.
Ордината точки падения ядра y0
= 0, тогда абсцисса этой
точки, то есть искомое расстояние
.
2
sin
2
0
0
g
х
Эта вели-
чина достигает наибольшего значения при sin 2a = 1, или
2=90
о
,
=
45о (рис. 5). Итак, результат, получен-
ный Никколо Тартальей экспериментально, правильный.
Добавим, что sin 2 = sin (180о
–
2 ) = sin2(90о
–
),аэто
означает, что два ядра, выпущенные из пушки под углами, до-
полняющими друг друга до 90о
, например 30о и 60о
, попадут в
одну точку. И еще один интересный факт. Если рассмотреть все
траектории, которые получаются при начальной скорости ядра
0 и углах 45о
<90
о
, тоонибу-
дут касаться одной линии — и это
также парабола! Ее называют пара-
болой безопасности (рис. 6). Ни в
какой объект, находящийся за пре-
делами ограниченной ею области,
снаряд не попадет.
Инструмент да Винчи
Если угол между осью конуса
и образующей равен углу
между секущей плоскостью
и осью конуса, то в сече-
нии получится парабола.
Так будет, в частности, при
пересечении прямоуголь-
ного конуса плоскостью,
перпендикулярной образу-
ющей (рис. 7). Это свойс-
тво подсказывает, как из-
готовить параболический
y
O
45°
0
x0x
y
O
x
Рис. 5
Рис. 6
185
циркуль. Конструкция должна иметь
две ножки: неподвижную, опорную
(представляет ось конуса), и враща-
ющуюся, составляющую с ней угол
45о (играет роль образующей, а точ-
нее, ее отрезка от вершины конуса
до линии сечения). Первая ножка
—
фиксированной длины, вторая
—
переменной; по сути, это тру-
бочка, в которой свободно скользит
стержень, рисуя параболу. Такова и
конструкция Леонардо, которую он
укрепил на треноге.
Во Флоренции в Музее истории
науки имеется действующая модель
циркуля, изготовленная по эскизу да
Винчи в 2001 году (рис. 8). Парабола
чертится на листе бумаги на наклон-
ной плоскости, параллельной одной
из «ног» треноги, причем в два шага:
сначала одна ветвь, затем другая, на-
чиная с вершины. Стержень соскаль-
зывает вниз под тяжестью собствен-
ного веса и веса прикрепленного на
нитке груза.
Добавим, что конструкция со-
вершенного циркуля аналогична той,
что придумал Леонардо, но более мо-
бильна: она позволяет варьировать
углы между осью конуса и образую-
щей и между секущей плоскостью и
осью конуса. Иными словами, всегда
можно наклонить опорную ножку к плоскости листа под опреде-
ленным углом и выбрать раствор циркуля так, чтобы начертить
то или иное коническое сечение. Однако на практике удобнее
пользоваться стационарной моделью и изменять положение се-
кущей плоскости.
Стеклорез-циркуль
Пусть AM = a, BM = b, точка M имеет координаты (x; y). Тогда
AB=a –b,MN =y,yyKM=x(рис.9).Треугольники
x
AOB и MNB по-
45
Рис. 7
Рис. 8
y
O
A
M
N
BD
C
K
x
Рис. 9
186
добны, поэтому AO : MN = BO : BN (*), где
2
2
x
a
a
b
a
AO
a
b
a
x
BO
)
(.
Подставим в равенство (*) длины всех отрезков и преобра-
зуем его к виду
.
1
2
2
2
2
b
y
a
x
Получившееся уравнение задает эллипс с полуосями a и b
(на рис. 9 это отрезки OD и OC). В стеклорезе им соответствуют
CC
расстояния от режущего ролика до шарниров на ползунах. Эти
расстояния можно изменять, задавая тем самым размер и форму
описываемого эллипса.
187
ГЛАВА 3
Постигая законы Вселенной
Великий архитектор Вселенной все более представ-
ляется нам чистым математиком.
Д. Джинс. Загадочная Вселенная
Однажды Оскар Уайльд, рассуждая о единстве искусств
заметил, что все они несут в себе нечто общее и говорят
на одном языке, хотя и разными голосами. Но разве не спра-
ведливы эти слова по отношению к наукам, среди кото-
рых особое место занимает математика? Ведь она тесно
связана со всеми областями естествознания. Обратимся за
примерами хотя бы к древнейшей науке — астрономии.
КОГДА НА ПОМОЩЬ ПРИХОДИТ ГЕОМЕТРИЯ
Еще древние греки начали изучать связи математики с при-
родой, стремясь найти во всех ее проявлениях порядок, гармо-
нию и совершенство: начиная со строения человеческого тела
и заканчивая движением небесных светил. Их труды только ук-
репляли веру людей в то, что в основе построения Вселенной
лежат математические принципы. Невозможно постичь тайны и
оценить красоту природы, не понимая ее языка. А говорит при-
рода на языке фигур и формул (о чем писали еще Леонардо да
Винчи и Галилей). Он универсален, ибо точен и лаконичен.
«Всю природу и изящные небеса символически отража-
ет искусство геометрии», — написал однажды Иоганн Кеплер
(1571—1630), знаменитый немецкий астроном и математик.
Именно он на основе результатов длительных астрономических
наблюдений, проводившихся еще его учителем Тихо Браге, вы-
вел законы движения планет, которые имеют точное математи-
ческое описание.
Первый закон описывает траекторию планет. Как извест-
но, еще античные ученые провозгласили догмат о равномерном
движении небесных тел по окружностям, господствовавший в
астрономии вплоть до Нового времени: планета В движется с
постоянной скоростью по малому кругу, а его центр, точка А,
равномерно движется вокруг Земли (рис. 1).
188
Пытаясь создать модель движения
планет, Кеплер пришел к выводу, что каж-
дая из них вращается по эллипсу, в одном
из фокусов которого находится Солнце
(рис. 2). Свойства эллипса подробно описал
еще древнегреческий математик Аполлоний
Пергский (ок. 260—170 до н. э.), рассмотрев
его как разновидность конических сечений.
Эллипс — это плоская замкнутая кри-
с
вая, для каждой точки которой сумма рас-
стояний от нее до двух данных точек F1F и F2FF (фокусов) постоян-
на (рис. 4). По сути, эллипс — это «сплюснутая» окружность.
Степень «сплюснутости» характеризуется эксцентриситетом
эллипса — числом = F
1
FO:AO,0 < <1.Сувеличением эллипс
вытягивается все больше, а при = 0 превращается в окруж-
ность. У большинства планет эксцентриситет орбиты невелик.
У Земли, например, всего 0,0167.
Примечательно, что в древности теория конических сече-
ний использовалась в науке довольно ограниченно: при реше-
нии некоторых задач на построение и кубических уравнений.
Она оказалась востребована только в XVII веке и в дальнейшем
нашла широкое применение в астрономии и механике, а также
послужила отправной точкой для создания аналитической и
проективной геометрии. Но не будь эта теория заранее разра-
ботана, фундаментальные законы природы, возможно, не были
бы своевременно открыты, а история науки и человечества мог-
ла бы пойти по иному пути развития.
Законы Кеплера явились итогом обобщения многолетних
астрономических наблюдений, а их универсальность и истин-
ный физический смысл раскрыл Исаак Ньютон (1643—1727),
показав, что они являются следствиями закона всемирного
O
F1
F2
F1
22
A
Рис. 2
Рис. 3
Рис. 4
A
B
Рис. 1
189
тяготения. В частности, рассматривая задачу о движении двух
материальных точек, между которыми существует сила притя-
жения, Ньютон средствами математики получил следующее ре-
шение: если одна из точек неподвижна, то траектория другой
(относительно первой) будет иметь форму эллипса, параболы
или гиперболы.
ЗАКОНОДАТЕЛЬ НЕБА
На вопрос о характере движения планет отвечает второй
закон Кеплера: каждая планета вращается в плоскости, прохо-
дящей через центр Солнца, и ее радиус-вектор за одинаковые
промежутки времени описывает равные площади (рис. 5). Ра-
венство S1
=S
2
достигается при различных длинах дуг, значит,
планета движется по орбите неравномерно: чем ближе к свети-
лу, тем быстрее, и наоборот.
С помощью этого закона и простых геометрических сооб-
ражений удалось, например, объяснить движение планет в на-
правлении, перпендикулярном плоскости эклиптики (проходя
вблизи эклиптики, планеты отклоняются от нее на небольшие
угловые расстояния). Еще Клавдий Птолемей (ок. 87—165)
считал, что орбиты планет лежат в разных плоскостях. Однако
он заблуждался, полагая, что все эти плоскости проходят через
центр Земли. Ошибался и Николай Коперник (1473—1543), ука-
зывая в качестве общей точки центр земной орбиты. И только
Кеплер совместил эту точку с Солнцем и сделал важный вывод:
плоскость планетной орбиты пересекает плоскость эклиптики
A
B
S1
S2
S1=S2
* Радиус-вектор планеты — отрезок, соединяющий ее с Солнцем, его длина постоян-
но изменяется в некоторых пределах из-за формы орбиты планеты.
** Эклиптика (от греч. ekleipsis — затмение) — большой круг небесной сферы, по
которому происходит видимое годичное движение Солнца. Плоскость эклиптики
совпадает с плоскостью земной орбиты.
Рис. 5
Рис. 6
190
по прямой, проходящей через Солнце. Отрезок прямой, соеди-
няющий Землю с планетой, наклонен к плоскости земной орби-
ты (рис. 6), поэтому планета видна на небе то выше, то ниже
эклиптики (за исключением точек A и B).
Наконец, Кеплер вывел закон, позволяющий вычислять от-
носительные расстояния планет от Солнца. Квадраты периодов
обращения Т1ТТ и Т2ТТ любых двух планет относятся как кубы их
средних расстояний а1 и а2 от Солнца:
.
3
2
3
1
2
2
2
1
a
a
T
T
Этот закон справедлив и для других небесных тел, движу-
щихся по эллиптическим орбитам. Иногда его записывают в
виде T2TT = k a3, где k — постоянная, одинаковая для всех пла-
k
нет. Позже Ньютон уточнил закон Кеплера, включив в него мас-
суСолнца—Mимассыпланет—m
1
и m2:
.
)
(
)
(
3
2
3
1
2
2
2
2
1
1
a
a
T
m
M
T
m
M
Уже современники Кеплера смогли убедиться в справедли-
вости открытых им законов, хотя многие и считали их случай-
ными догадками, установленными путем подбора величин. Но
возможно ли было тогда оценить по достоинству труды велико-
го ученого? Законы, носящие сегодня его имя, нашли широкое
применение в первую очередь в самой астрономии, а за Кепле-
ром утвердилась слава «законодателя неба».
ПРИРОДА ЗАТМЕНИЯ
Законы движения небесных тел позволяют решать самые
разные задачи и объяснять многие явления вроде изменения
картины звездного неба и смены времен года. Например, пер-
вый закон Кеплера объясняет наличие двух видов солнечного
затмения: полного, когда видна только солнечная корона, и
кольцевого, при котором заметен край солнечного диска в фор-
ме кольца. Оба явления возможны потому, что Луна движется
вокруг Земли, а Земля, в свою очередь, вокруг Солнца по эллип-
су, и расстояния между ними периодически изменяются.
Где и при каких условиях наблюдается солнечное затмение
и какова его природа? В этих вопросах также помогает разо-
браться геометрия.
191
Освещаемая Солнцем сферичес-
кая Луна отбрасывает в пространс-
тво тень в форме сходящегося кону-
са, которая окружена расходящимся
конусом полутени (рис. 7). Полное
затмение будет видно в тех районах
Земли, которые попадут в область
лунной тени. Значит, необходимо,
чтобы ее конус пересекал земную
поверхность. Иными словами, имел
форму усеченного конуса. Его мень-
шее основание и есть та зона на
планете, находясь в которой можно
видеть удивительное природное яв-
ление «в полной красе». Иначе будет
наблюдаться кольцевое затмение.
Кстати, сравнивая среднее расстоя-
ние S между телами со средней высо-
S
той h конуса лунной тени, мы нашли
бы,чтоS>
S h, и пришли к выводу, что
полных солнечных затмений вообще
не бывает.
Итак, полное затмение наступает при попадании Земли в
лунную тень, когда Луна в точности закрывает собой солнечный
диск. Такое случается, если во время новолуния* Луна находит-
ся вблизи эклиптики и все три тела выстраиваются в одну линию
(при несоблюдении этого условия затмение будет частичным).
В этот момент с Земли видимые размеры Луны и Солнца кажут-
ся одинаковыми. Почему? Ответ прост: центр Луны попадает на
прямую, проходящую через центр Солнца и глаз находящегося
на Земле наблюдателя, и стороны его угла зрения касаются по-
верхности Луны и Солнца, то есть оба тела оказываются видны
под одним углом (рис. 8).
Полюбоваться уникальным явлением было бы невозможно,
если бы размеры Луны и Солнца, а также расстояния от этих тел
до Земли не связывало простое математическое соотношение.
Какое? С точки зрения геометрии мы имеем дело с подобием,
точнее говоря, с гомотетией, центр которой совпадает с глазом
Рис. 7
* Новолуние – фаза, в которой Луна находится между Солнцем и Землей и обращена
к нашей планете неосвещенной стороной.
r
l
L
R
=
Рис. 8
Геометрия полного
солнечного затмения
192
наблюдателя. Отсюда сле-
дует,чтоL:l=R:r(*).
На языке «угловых
размеров» механизм за-
тмения можно объяснить
так. Изменение расстояний
между телами приводит
к изменению их угловых
размеров. Когда угловые
размеры Луны и Солнца
совпадают, наблюдается
полное затмение, а когда первый меньше второго — кольцеоб-
разное (рис. 9).
ПЕРВЫЙ ГЕЛИОЦЕНТРИСТ
Первым, кто попытался с помощью геометрии определить
относительные расстояния Солнца и Луны от Земли, а также их
относительные размеры (приняв за единицу измерения радиус
Земли), был выдающийся древнегреческий астроном Аристарх
Самосский (ок. 320—250 до н. э.).
Первую задачу он решил, наблюдая за сменой фаз Луны.
В фазе четверти, когда Луна видна на небе в форме полукруга,
Солнце, Луна и Земля располагаются в вершинах прямоугольно-
го треугольника. Измерив угол между первыми двумя телами,
Аристарх вычислил угол, под которым с Солнца виден радиус
лунной орбиты (рис. 10). Он нашел его равным 3° (в действи-
тельности его величина приблизительно 9’). По расчетам уче-
ного, Солнце находилось от Земли в 19 раз дальше, чем Луна
(на самом деле почти в 400 раз дальше). Ошибка, конечно, ве-
лика, но вполне объяснима большой погрешностью измерения
угла: было трудно точно уловить момент наступления нужной
фазы Луны, к тому же древние изме-
рительные инструменты были далеки
от совершенства.
Решение второй задачи основа-
но на применении пропорции (*).
Аристарх обобщил результаты на-
блюдений солнечных затмений, как
свои собственные, так и сделанные
другими астрономами, и пришел к
>
Рис. 9
Рис. 10
Геометрия кольцеобразного
солнечного затмения
193
следующему выводу. Если видимые
размеры Луны и Солнца почти оди-
наковы, а Солнце отстоит от Земли
в 19 раз дальше, чем Луна, то и его
диаметр в 19 раз больше лунного
(рис. 11).
А как соотносятся размеры Зем-
ли и Солнца? На основе знаний о
лунных затмениях Аристарх рассчитал, что Земля примерно в 3
раза больше Луны. Во сколько раз в таком случае диаметр Сол-
нца больше диаметра Земли и чему равно отношение объемов
этих тел? Давайте подсчитаем. По данным Аристарха, диаметр
Солнца в 19 : 3 ≈ 6,3 раза больше диаметра Земли. Тогда по за-
конам подобия объем Солнца должен превышать объем Земли в
6,3
3
≈ 250 раз. А теперь сравним результаты, полученные древ-
ним астрономом, с современными данными. На самом деле
Земля больше Луны в 3,67 раза. Искомые числа равны соответс-
твенно400:3,67≈109и1093≈1300000.
Разница огромная, но отнюдь не умаляющая главного до-
стижения Аристарха Самосского. Сопоставив относительные
размеры Земли и Солнца, античный ученый за 18 веков до Ко-
перника сделал на их основе правильный вывод: именно Солн-
це является центром, вокруг которого вращаются планеты, а не
наоборот, благодаря чему известен в истории науки как первый
гелиоцентрист.
КАК ЭРАТОСФЕН ИЗМЕРИЛ ЗЕМЛЮ
Сегодня каждому школьнику известно, что длина окружнос-
ти Земли равна примерно 40 000 км. Но мало кто знает, что ее с
ошибкой всего в 1% вычислил еще в 240 году до н. э. Эратосфен
Киренский (ок. 276—194 до н. э.), знаменитый ученый-энцик-
лопедист и хранитель Александрийской библиотеки. Для срав-
нения: по оценкам Аристотеля (384—322 до н. э.) длина земной
окружности была в 1,6 раза больше. Неизвестно, как получил
свой результат Аристотель, а вот о методе, примененном Эра-
тосфеном, сведения сохранились. Как же он справился со столь
сложной по тем временам задачей?
В день летнего солнцестояния, в полдень, когда в Сиене (се-
годня это город Асуан, известный своей плотиной) Солнце было
в зените, Эратосфен, находясь в Александрии, расположенной
.
.
.
ZS
Dc:D =SZ:LZ
L
Рис. 11
194
севернее Сиены почти
на одном с ней мериди-
ане, измерил угол между
воткнутым в землю вер-
тикальным шестом и лу-
чом, проходящим через
вершину шеста и конец
отбрасываемой им тени
(рис. 12): 1 7°12'.
Падающие на землю
солнечные лучи можно считать параллельными, поэтому 1 =
2. Расстояние между городами равно длине дуги окружности,
соответствующей центральному углу 7°12', или одной пятидеся-
той части окружности. В эпоху Эратосфена это расстояние было
известно и оценивалось путешественниками примерно в 5000
стадиев. Следовательно, длина окружности земного шара по
меридиану в 50 раз больше — 250 000 стадиев, или 39 625 км
(предположительно 1 стадий 158,5 м). Так Эратосфен приме-
нил геометрию по ее прямому назначению, то есть к измерению
Земли. Полученный им результат оставался непревзойденным
почти 2000 лет.
ДАЛЕКО ЛИ ДО ЛУНЫ?
Астрономам приходится не только
сравнивать относительные размеры
тел, но и вычислять их линейные раз-
меры. Для близких к Земле объектов
можно воспользоваться проверенным
способом: призвать на помощь дав-
нюю и верную помощницы астрономии — тригонометрию, пред-
лагающую простое решение поставленной задачи. Зная рассто-
яние D до небесного тела и измерив его угловой радиус (угол,
под которым виден с Земли радиус R тела), легко вычислить пос-
ледний в линейных единицах: R = D sin (рис. 13).
На основе этого равенства можно решить и обратную зада-
чу: найти D по известным R и . Вычислим, например, среднее
расстояние от Земли до Луны и радиус Луны, если ≈ 16',
≈ 57',
RЗ 6380 км (рис. 14). Получим:
D=RЗ:sin57' ≈ 380 000км,
RЛR =D sin16' ≈ 1750км.
1
2
Рис. 12
D
R
Рис. 13
195
То же расстояние
можно определить гео-
метрически и с помо-
щью метода триангу-
ляции. Нужно одно-
временно
измерить
в двух точках земной
поверхности углы 1 и
2 (рис. 15), и, зная уда-
ленность точек друг от друга, средс-
твами тригонометрии вычислить ис-
комое расстояние.
Угол, под которым из центра све-
тила виден радиус Земли, перпенди-
кулярный лучу зрения, называют го-
ризонтальным параллаксом светила
(на рис. 14 это угол ). Его величина
может заметно «колебаться» и зависит от расстояния светила
до Земли. Так, минимальный и максимальный горизонтальные
параллаксы Луны равны примерно 53' и 61', что дает в среднем
57'. Таким образом, задача на вычисление расстояний, по сути,
сводится к задаче на измерение углов.
НА ФОНЕ ЗВЕЗД
Однако этот способ не подходит для
звезд: расстояния до них чрезвычайно ве-
лики по сравнению с радиусом Земли, а угол
, наоборот, ничтожно мал и не поддается
измерению. В таком случае рассматривают
годичный параллакс, вызванный вращением
сс
Земли вокруг Солнца. С его помощью мож-
но установить расстояния до сравнительно
близких к нам звезд. Годичный параллакс
характеризуется углом р, под которым со
звезды видна большая полуось земной ор-
биты (она играет роль базиса), перпендику-
лярная лучу зрения (рис. 16).
Итак, расстояние до звезды опреде-
ляется по ее видимому смещению на фоне
значительно более удаленных звезд, фикси-
1
2
D
R
R
Рис. 14
Рис. 15
P
Рис. 16
196
руемому при ее наблюдении с разных точек
земной орбиты. При этом с Земли кажется,
что звезда описывает на небе крошечный
эллипс (рис. 17).
Поскольку выбранный базис ничтожно
мал по сравнению с расстоянием до звезды,
не имеет значения, откуда отсчитывать это
расстояние: от Земли или от Солнца. Угол p
также очень мал, его величина оценивается
десятыми и сотыми долями секунды дуги.
Поэтому можно считать, что расстояние D до
звезды обратно пропорционально ее годич-
ному параллаксу, то есть D = 1 : p.
Оно выражается в парсеках . Ближайшая
к Земле звезда (за пределами нашей систе-
мы) Проксима Центавра находится от нее на
расстоянии D 1,31 пк, или 4 1013
км, что в
270 000 раз дальше, чем Солнце. Свет от нее до Земли идет более
четырех лет! Остальные звезды находятся гораздо дальше.
ВЕЧНЫЕ СПУТНИКИ
В заключение — об одной красивой конфигурации тел в
Солнечной системе, возможность существования которой тео-
ретически обосновал еще в XVIII веке французский математик
и астроном, один из создателей небесной механики Жозеф Луи
Лагранж (1736—1813).
Решая задачу о движении трех тел, связанных силами при-
тяжения, он показал, что такая система устойчива, если тела на-
ходятся в вершинах правильного треугольника, вращающегося
вокруг центра масс системы с постоянной угловой скоростью.
Задача намного упрощается, когда массы тел значительно раз-
личаются. Если в одной вершине расположить тело А, в другой
—
гораздо менее массивное тело В, а в третьей — малое тело
С, то оно окажется в «точке равновесия». При воздействии на
тело С внешней силы, пытающейся сместить его, возникает при-
тяжение со стороны тела В, заставляющее вернуться его в ис-
ходное положение, и конфигурация сохраняется.
* 1 парсек (от слов «параллакс» и «секунда») — расстояние до воображаемой звез-
ды, годичный параллакс которой равен 1’’; равно 30,9 1012
км.
Рис. 17
197
В начале XX века выяснилось,
что такой равносторонний треу-
гольник, а точнее, сразу два, реаль-
но существует в Солнечной систе-
ме. Эти треугольники образованы
Солнцем, Юпитером и двумя груп-
пами астероидов, которые дви-
жутся по орбите Юпитера — одна
впереди него на 60о
, а другая на-
столько же позади (рис. 18) — и
имеют такой же период обращения
вокруг Солнца, что и сама плане-
та. Наиболее крупные астероиды
получили имена героев Троянской
войны, описанной в «Илиаде» Го-
мера. Опережает Юпитер группа
«греков», а догоняет — группа
«троянцев». Так и следуют друг за
другом эти вечные спутники.
Подобные астероиды ныне известны и у других планет —
Марса и Нептуна. А совсем недавно, в 2010 году, «троянец» диа-
метром всего 300 м был обнаружен у Земли. Заметить подобные
объекты очень сложно из-за их малого размера, к тому же для
земного наблюдателя их орбиты находятся слишком близко к
Солнцу. Но можно распознать астероиды на снимках из космо-
са. Так что скоро, надеются ученые, по соседству с нашей пла-
нетой будут открыты и другие «троянцы».
«
»
«
»
60°
60°
Рис. 18
198
ГЛАВА 4
Liber аbaci
—
«Либер абачи», — повторил Фило. — Если не
ошибаюсь, учебник арифметики?
—
Вот именно, и, смею вас заверить, замечатель-
ный, — с жаром подхватил Мате. — Среди матема-
тических книг того времени нет ему равных!
Э. Александрова, В. Левшин.
Искатели необычайных автографов
В 1202 году появилась на свет знаменитая «Книга аба-
ка» (Liber аbaci) Леонардо Пизанского, более известного
как Фибоначчи — сын Боначчи (то есть Добряка — так
прозвали его отца), крупнейшего европейского математи-
ка Средневековья. Этот объемный труд стал настоящей
энциклопедией математических знаний того времени и
сыграл важную роль в их распространении в странах
Западной Европы в следующие столетия.
КНИГА-ЭНЦИКЛОПЕДИЯ
Liber abaci, или трактат по арифметике (именно так мож-
но истолковать название, поскольку под абаком Леонардо по-
нимал не счетную доску, а арифметику), написана на латыни и
считается первым сочинением такого рода, автор которого был
христианином. В предисловии к своей книге Фибоначчи вспоми-
нает, как возник ее замысел и что этому предшествовало: «Отец
мой, родом из Пизы, служил синдиком на таможне в Бужи, в Аф-
рике, куда он меня взял с собою для изучения искусства считать.
Удивительное искусство считать при помощи только девяти ин-
дусских знаков мне так понравилось, что я непременно захотел
познакомиться с тем, что известно об этом искусстве в Египте,
Греции, Сирии, Сицилии и Провансе. Объехав все эти страны, я
убедился, что индусская система счисления есть самая совер-
шенная... Изучив основательно эту систему и все к ней относя-
щееся, прибавив свои собственные исследования и почерпнутое
из «Начал» Евклида, я решился написать это сочинение».
Работа Фибоначчи отличалась полнотой охвата и глубиной
изложения. В ней подробно разъяснялись не только азы на-
199
уки о числах и действиях над ними,
но и основы учения об уравнениях,
то есть алгебры. Кроме того, в Liber
abaci имелось большое количество
задач с практическим содержанием,
иллюстрировавших различные при-
емы решения, как арифметические
(тройное правило, правило товари-
щества, метод ложного положения
и др.), так и алгебраические, при-
водящие к одному или нескольким
уравнениям.
Само изложение было словес-
ным, лишенным привычных для сов-
ременного читателя символов и фор-
мул, а решение примеров и задач,
носивших, как мы говорим сегодня,
частный характер, сводилось к опи-
санию действий, которые следовало
применить в той или иной конкрет-
ной ситуации, и нередко сопровож-
далось разъяснениями или коммен-
тариями автора.
Книга была адресована не только ученым мужам, но и более
широкому кругу читателей: купцам, счетоводам, продавцам, чи-
новникам. В предисловии отмечалось, что автор написал свой
труд, «дабы род латинян не прибывал более в незнании изла-
гаемых в нем вещей». Однако для многих из тех, кому предна-
значалась Liber abaci, книга оказалась трудновата, поэтому, не-
смотря на популярность и доработанное автором издание 1228
года , не получила того широкого распространения, которого
заслуживала.
Зато трактат Леонардо приобщил к достижениям индийских
и арабских математиков европейских ученых и оказал сущест-
венное влияние на дальнейшее развитие алгебры и теории чи-
сел. Liber abaci была востребована математиками эпохи Возрож-
дения и Нового времени, сумевшими оценить ее по достоинству,
ведь книга отличалась не только богатством и разнообразием
Леонардо Пизанский
(Фибоначчи).
Ок. 1170–1240 гг.
*
До нас Liber abaci дошла как раз во втором варианте. Ее первое печатное изда-
ние, (объемом 459 страниц) появилось на родине математика, в Италии, в середине
XIX века.
200
рассмотренных в ней примеров и методов, но и строгостью, до-
казательностью изложения.
На протяжении нескольких столетий по труду Фибоначчи
ученые знакомились с двумя важнейшими разделами математики
—
арифметикой и алгеброй и черпали из него задачи и ориги-
нальные методы решения, благодаря чему уже в XV—XVI веках
те разошлись по многочисленным итальянским, французским,
немецким, английским, а позже и русским рукописям, печатным
книгам и учебникам. Некоторые задачи или их аналоги можно
обнаружить и в «Сумме арифметики» Пачоли (1494), и в «При-
ятных и занимательных задачах» Баше де Мизириака (1612), и
в «Арифметике» Магницкого (1703), и даже в «Алгебре» Эйлера
(1768).
ЗАСЛУГИ И ДОСТИЖЕНИЯ ЛЕОНАРДО ПИЗАНСКОГО
Каково же было содержание написанной Фибоначчи кни-
ги-энциклопедии, в которой насчитывалось целых пятнадцать
глав? Оказывается, в ней рассматривался весьма обширный
круг вопросов:
индусская система нумерации;
правила действий над целыми числами;
дроби и смешанные числа;
разложение чисел на простые множители;
признаки делимости;
учение об иррациональных величинах;
способы приближенного вычисления квадратных и куби-
ческих корней;
свойства пропорции;
арифметическая и геометрическая прогрессии;
линейные уравнения и их системы.
Наконец, отдельная глава была посвящена квадратным
уравнениям и геометрическим задачам на применение теоремы
Пифагора.
Как мы помним, основную часть сведений автор кропот-
ливо собирал, путешествуя по разным странам как купец,
кое-что почерпнул из трудов Евклида, а по сути — из насле-
дия античных математиков. Особую ценность представляло
подробное изложение малоизвестной в то время в Европе
индусской, или десятичной, системы счисления и новых ме-
тодов вычисления, которые позволяли заметно упростить
201
всевозможные расчеты и успешно решать большой круг за-
дач. Преимущества их Фибоначчи показал, сравнив разные
нумерации (индусскую и римскую, бывшую тогда в употреб-
лении), а также виды счета, включая счет на пальцах и на
абаке.
Надо сказать, отдельные случаи использования этой сис-
темы встречались и ранее. С Востока ее привозили паломники,
ученые, купцы, посланники и военные. Наиболее древний ев-
ропейский манускрипт, в котором упоминаются придуманные
индусами цифры, относится еще к концу X века. Однако десяти-
чная система счисления очень медленно проникала в западные
страны и получила там широкое распространение лишь в эпоху
Возрождения.
Отметим также, что именно благодаря Фибоначчи европей-
цы познакомились с общими правилами решения квадратных
уравнений, описанными в трактате ал-Хорезми.
Но Леонардо Пизанский был не только автором-составите-
лем энциклопедии Liber abaci. В ней математик отразил и ре-
зультаты собственных научных изысканий. В частности, в этом
труде он впервые:
сформулировал правило для нахождения суммы членов
произвольной арифметической прогрессии;
рассмотрел возвратную последовательность, в которой
каждое число, начиная с третьего, равно сумме двух предшес-
твующих ему чисел;
ввел термин «частное» для обозначения результата деления;
описал способ приведения дробей к общему знаменателю
с помощью нахождения наименьшего общего кратного знаме-
нателей (более рациональный, чем использовали арабские ма-
тематики).
Кроме того, Фибоначчи самостоятельно разработал ряд ал-
гебраических приемов решения задач, исследовал некоторые
уравнения высших степеней, сводящиеся к квадратным, вывел
приближенную формулу для вычисления кубического корня и
первым среди европейских ученых подошел к введению отри-
цательных чисел и их толкованию как долга, что по тем време-
нам являлось огромным достижением.
202
УНИВЕРСАЛЬНЫЙ ЗАДАЧНИК
Немалую ценность Liber abaci придавало наличие в ней
множества разнообразных задач, одни из которых были
заимствованы из арабских и прочих источников, а другие
придуманы самим автором. Большую группу составляли
арифметические и алгебраические примеры: на выполне-
ние простейших действий над числами, извлечение корней,
решение уравнений или систем. В другую группу входили
сюжетные задачи, в том числе связанные с житейскими си-
туациями: на смешение, определение стоимости или коли-
чества купленного товара, раздел имущества и разного рода
финансовые расчеты между людьми (задачи коммерческой
арифметики) и т.п.
Например, к задачам на смешение относились два вида
задач «на сплавы»: на определение пробы сплава, сделан-
ного из других сплавов известного состава и количества,
и на выяснение того, сколько каждого из данных сплавов
потребуется, чтобы получить сплав нужной пробы. А одной
из типичных задач коммерческой арифметики была задача
на раздел некоторой суммы денег пропорционально долям
участников.
В трактат Фибоначчи вошли также текстовые задачи на вос-
произведение определенного действия, например нахождение
числа по его части. Вот одна из них. Четвертая и третья части
дерева находятся под землей и составляют 21 фут. Чему равна
длина всего дерева?
Некоторые из затронутых в труде Леонардо вопросов в
разное время привлекали внимание ученых-математиков и не
раз упоминались в более поздних сочинениях. Так произошло,
в частности, с популярной в Средние века задачей на отыска-
ние наименьшего набора различных гирь, с помощью которого
можно уравновесить любой груз с целочисленной массой, не
превосходящей заданного числа.
Но наиболее известной по сей день остается задача о
размножении кроликов, впервые появившаяся именно в Liber
abaci. Ее решение привело Фибоначчи к открытию едва ли не
самой знаменитой числовой последовательности
1,1,2,3,5,8,13, ... (*).
Позже она была названа его именем и породила множество ис-
следований.
203
ЗНАКОМЫЕ ЗАДАЧИ ИЗ ТРАКТАТА ФИБОНАЧЧИ
А теперь поговорим подробнее о некоторых задачах из
Liber abaci, с которыми должны легко справиться (в отличие
от первых читателей книги Леонардо) и нынешние школьники.
Задачи эти интересны не только, а иногда и не столько своими
решениями или конкретным математическим содержанием. Во
многом они любопытны с исторической точки зрения, посколь-
ку имеют свою биографию, выдержали испытание временем,
«прижились» и благополучно дошли до наших дней. К тому же,
рассматривая предложенную кем-то задачу, никогда не быва-
ет лишне ознакомиться с чужим рассуждением и сравнить его
с собственным решением. Тем более, когда читателя и автора
разделяют столетия, а то и тысячелетия!
Неизвестное число
Найти число,
20
19 которого равны квадрату самого числа.
О твет:
20
19.
Ответ очевиден каждому, кто знаком с понятием квадрата
числа. Решая задачу с помощью уравнения
,
20
19
2
x
x
полу-
чим еще одно удовлетворяющее условию задачи число — 0.
Автор же, очевидно, имел в виду число, отличное от нуля,
что вообще-то неудивительно. Во времена Леонардо Пизанского
нуль не признавался как корень уравнения, то есть как число.
Впрочем, это не мешало некоторым математикам и до и после Фи-
боначчи выполнять простейшие операции с нулем, который вос-
принимался ими в качестве символа, обозначавшего «ничто».
Размножение кроликов
Некто поместил пару кроликов в некоем месте, огорожен-
ном со всех сторон стеной, чтобы узнать, сколько пар кроликов
родится при этом в течение года. Природа кроликов такова, что
через месяц пара кроликов производит на свет другую пару, а
рождаются кролики со второго месяца. Сколько пар кроликов
будет через год?
Ответ: 377пар.
204
Даже одной этой задачи хватило бы Фибоначчи, чтобы оста-
вить след в истории науки. Именно в связи с ней сегодня чаще
всего и упоминается имя ученого. Решая задачу о размножении
кроликов, Леонардо описал бесконечную числовую последова-
тельность (an), любой член которой, начиная с третьего, выра-
жается через предыдущие члены:
a1
= 1,a
2
= 1,a
n+2
=a
n+1
+an
, гдеn 1.
Для математиков она является прежде всего классическим
примером рекуррентной последовательности, элементы кото-
рой, числа Фибоначчи, обладают многими весьма интересными
и нашедшими неожиданные применения свойствами. Из них
широко известно следующее: предел отношения an + 1
кanпри
неограниченном возрастании n устремляется к числу Ф ≈ 1,618,
выражающему закон божественной пропорции.
Что же касает-
ся ответа в задаче о
кроликах, то он сов-
падает с 13-м чле-
ном
построенной
Леонардо последо-
вательности 1, 2
,3
,
5,8 , ... — числом377.
Здесь каждое число,
начиная со второго,
показывает, сколько
всего пар кроликов
будет насчитываться
к началу очередного
месяца. Заметим, что
Фибоначчи рассматривал свою зада-
чу для взрослой пары кроликов. Если
решать ее для новорожденной пары,
получится последовательность (*).
В этом случае ровно через год количество животных увеличится
до 233 пар особей.
Добавим, что в работах других математиков встречаются раз-
личные вариации на тему задачи о кроликах. Так, спустя полтора
столетия после Фибоначчи индийский математик Нарайана рас-
сматривал задачу о размножении коров: найти число коров и те-
лок, происходящих от одной коровы в течение 20 лет, при условии,
что корова в начале каждого года приносит телку, а телка, достиг-
Схема размножения
кроликов из задачи
Фибоначчи
205
нув трех лет, дает такое же потомство в начале года. Если решать
ее, составляя рекуррентное соотношение, придем к формуле
an
=a
n–1
+an–3
, гдеn 4,
и последовательности
1,1,1,2,3,4,6,9,13, ... .
Интересно, что обнаруженная Фибоначчи числовая зако-
номерность реализуется в реальных процессах размножения, а
именно у медоносных пчел. Известно, что и матка, и рабочая
пчела имеют двух родителей, а трутень — только одного (мат-
ку). Если построить семейное древо трутня и подсчитать число
его родителей, прародителей, прапрародителей и так далее, по-
лучится в точности ряд чисел из задачи о кроликах.
Сколько предметов?
Семь старух отправляются в Рим. У каждой по семь мулов,
каждый мул несет по семь мешков, в каждом мешке по семь хле-
бов, в каждом хлебе по семь ножей, каждый нож в семи ножнах.
Сколько всего предметов?
Ответ: 137 256 предметов.
Перед нами хорошо известная, встречающаяся у разных на-
родов задача-шутка, как ее часто называют историки математи-
ки, полагая, что в былые времена она была всего лишь нехитрой
забавой для учеников. А ведь эта восходящая еще к древним
египтянам задача, вернее ее решение, служит прекрасной на-
глядной иллюстрацией построения геометрической прогрессии
и нахождения суммы первых n ее членов по известному перво-
му члену и знаменателю.
Напомним задачу из папируса Ахмеса . У семи лиц по семь
кошек, каждая кошка съедает по семь мышей, каждая мышь съе-
дает по семь колосьев ячменя, из каждого колоса может вырас-
ти по семь мер зерна. Как велики числа этого ряда и как велика
их сумма? Задача из трактата Фибоначчи отличается от нее, по
сути, лишь тем, что в ней суммируются не пять, а шесть чисел:
.
256
137
6
)1
7(
7
7
...
7
7
6
6
2
6
S
* Папирус Ахмеса (или папирус Ринда) — древнеегипетская математическая
рукопись (ок. XX—XVIII веков до н. э.), названная по имени ее составителя пис-
ца Ахмеса. Содержит условия и решения 84 задач по арифметике и геометрии.
206
Оптимальный разновес
Выбрать пять гирь так, чтобы с их помощью можно было
взвесить любой груз массой от 1 до 30 целых весовых единиц.
При взвешивании все гири разрешается класть только на одну
чашу весов.
Ответ: надо взять гири с массами 1, 2, 4, 8 и 16 весовых
единиц.
Затронутый в задаче вопрос равносилен вопросу о пред-
ставлении натурального числа n 30 в виде суммы не более
пяти различных натуральных чисел из набора m1
,...,m
5
, не пре-
восходящих n:
n=a
1
m1+a2 m
2
+a3 m
3
+a4 m
4
+a5 m
5
,
где каждый из множителей a1
,...,a
5
равен 1 или 0 (гиря либо
кладется на чашу весов, либо нет). Но тогда естественно перей-
ти к двоичной системе счисления:
n=a
5
24+a4 23+a3 22+a2 2
1
+a1 20.
Таким образом, в набор должны входить гири, массы кото-
рых выражаются числами 1, 2, 4, 8 и 16.
Данную задачу часто связывают с именем Баше де Мези-
риака (приведена им в одной из книг по занимательной мате-
матике), однако она встречается еще у Фибоначчи. Вероятно,
и тот не сам ее придумал. Настоящим автором этой вызванной
практическими потребностями задачи мог быть какой-нибудь
сметливый торговец, которому частенько приходилось взвеши-
вать товар. Любопытно, что ею интересовался даже Д. И. Мен-
делеев в бытность свою директором Главной палаты мер и ве-
Старинные разновесы
207
сов. В наше время задача о разновесе приводится как пример
применения двоичной системы счисления.
В Liber abaci содержался также более сложный вари-
ант рассмотренной задачи. В нем разрешается класть гири
на обе чаши весов, а значит, надо будет думать не только о
выборе гирь, но и о том, куда и в каком количестве их до-
бавлять. Ясно, что в данном случае каждое из чисел ai мо-
i
жет принимать три различных значения (гиря добавляется
либо на свободную чашу весов, либо на чашу с грузом или
вообще не используется), поэтому приходится обращаться
уже к троичной системе счисления. Решив задачу для n 40,
Леонардо получил в ответе набор гирь массами 1, 3, 9 и 27
весовых единиц.
Оба варианта задачи интересны еще и тем, что найденные
числа являются членами геометрических прогрессий со знаме-
нателями q = 2иq = 3 соответственно. А к системе из пяти гирь,
упоминающейся в первой задаче, можно прийти, рассматривая
неравенство
30 1+2+22+...+2m–1
, или30 2m
–1.
Его наименьшее натуральное решение m = 5.
Идеальные с точки зрения математики наборы гирь никогда,
однако, не применялись на практике. Пользоваться такими раз-
новесами — дело хлопотное. Только представьте: всякий раз
вместо того, чтобы проворно взвесить товар, продавец подби-
рает нужную числовую комбинацию и переставляет туда-сюда
гири. Это долго и утомительно, к тому же раздражает нетерпе-
ливого покупателя. Какая уж тут торговля!
Птицы у колодца
Две башни, одна высотой 40
футов, а другая — 30 футов, рас-
положены на расстоянии 50 футов
одна от другой. К находящемуся
между ними колодцу слетают од-
новременно с обеих башен две
птицы и, двигаясь с одинаковой
скоростью, одновременно прибы-
вают к колодцу. На каком рассто-
янии от каждой башни находится
колодец?
Ответ: 18футов, 32фута.
40
30
AxK 50 xB
Чему равны длины
отрезков AK и KB?
208
Решение сводится к применению теоремы Пифагора и на-
хождению корня уравнения
x2+402
= (50–x)2+302
.
Аналоги этой задачи встречаются в более ранних источ-
никах. Например, в одном из трактатов иранского математика
Х—XI веков ал-Караджи имеется задача с несколько иным сю-
жетом. На разных берегах реки напротив друг друга растут две
пальмы. Высота одной 20 локтей, а высота другой 30 локтей.
Ширина реки 50 локтей. На верхушке каждой пальмы сидит пти-
ца. Обе птицы, увидев в реке рыбу, разом летят к ней по прямой
линии и одновременно достигают поверхности воды в точке на
прямой, соединяющей основания пальм. Определить длину пу-
тей, которые пролетели птицы, и место их встречи.
История с имуществом
Если первый человек получит от второго 7 денариев, то ста-
нет в пять раз богаче второго, а если второй человек получит от
первого 5 денариев, то станет в семь раз богаче первого. Сколь-
ко денег у каждого?
Ответ:
17
2
7и
17
14
9 денариев.
Обозначив буквами x и
x y количество денег, имеющихся у
y
первого и у второго человека, получим систему
),
5
(7
5
)7
(5
7
x
y
y
x
из которой найдем искомые числа. Такой способ решения на-
прашивается сам собой, поскольку в задаче говорится о двух
неизвестных.
А вот Леонардо Пизанский в своих рассуждениях ограни-
чился одним неизвестным, назвав его по давно укоренившейся
среди математиков традиции «вещью». Приняв имущество вто-
рого человека за вещь и семь денариев, то есть за (x + 7), он вы-
разил имущество первого как (5x – 7) и в дальнейшем пришел к
x
линейному уравнению x + 12 = 7(5
x
x–12).
x
Попутно заметим, что в трактате Фибоначчи содержатся
аналогичные задачи и с бо’льшим числом людей.
Куропатки, голуби и воробьи
30 птиц стоят 30 монет. Куропатки стоят по 3 монеты, голуби
по 2, а пара воробьев — по монете. Сколько птиц каждого вида?
Ответ: 3 куропатки, 5 голубей, 22 воробья.
209
Из-за большого количества неизвестных данную задачу
вполне логично решать алгебраически. Если число куропаток,
голубей и воробьев обозначить буквами x,x y,yy z соответственно,
z
то решение сведется к нахождению тройки натуральных чисел,
удовлетворяющих системе уравнений
.
30
2
2
3
30
z
y
x
z
y
x
Исключив z и выразив затем
z
x через
x
y, получим
yy
x=6 –0,6
x
y.
Единственное возможное значение y равно 5, тогда
y
x=3,
x
z=22.
z
Интересно, что данную задачу автор Liber abaci рассмат-
ривал как задачу на сплав достоинства 1, который должен по-
лучиться из трех целочисленных количеств достоинством 3, 2
и . Эта же задача, но с чуть измененными числовыми данными
(стоимость птиц разного вида выражается обратными числами:
0,5 и 2) разбиралась еще в одном сочинении Леонардо.
Симметричная система
Решить систему уравнений
.
5
10
x
y
y
x
y
x
Ответ:
).
5
5
5;5
5
15
(
имеет не одно, как указал Фибоначчи, а два решения; второе
—
).
5
5
15
;5
5
5(
В Liber abaci приведены разные способы ее решения.
Во-первых, «стандартный» в нашем понимании: с помощью
подстановки y = 10 – x. Исключаем y и сводим задачу к реше-
y
нию квадратного уравнения
.
10
200
5
100
2
x
x
Во-вторых, посредством замены. Пусть
,
z
x
y
тогда приходим
к уравнению
,
1
)
5
(z
z
из него определяем z. С другой стороны, y
= 10–
y
x, тогда
xx
,
10
x
x
z
откуда легко найти x, а затем уже вычислить
x
y.
210
Идея первого способа решения выглядит, конечно, про-
зрачнее и привычнее, однако решать так систему технически не
проще, чем вторым способом. А в подобных задачах, как извес-
тно, простота вычислений, особенно если те связаны с корнями,
играет не последнюю роль.
ОПЕРЕДИВШИЙ ВРЕМЯ
Как отмечают историки науки,
Liber abaci не просто выделяется, а
резко возвышается над средневе-
ковой литературой по арифметике
и алгебре. Прежде всего, благодаря
фундаментальности изложения и
многообразию рассмотренных в ней
методов и задач. Уровень сочинения
оказался столь высок, что осилить
и воспользоваться изложенными
в нем сведениями смогли главным
образом ученые-математики, отчас-
ти современники Леонардо и в еще
большей мере — представители по-
следующих поколений.
Фактически лишь спустя три сто-
летия после выхода в свет Liber abaci
стало заметно ее влияние на работы
других авторов. С появлением труда
Фибоначчи европейские ученые эпо-
хи Средневековья, бывшие зачастую
философами-схоластами или духов-
ными лицами, для кого математика
не была основным занятием, стали
уделять больше внимания алгебре и затрагивать в своих иссле-
дованиях ее новые вопросы. Однако первых серьезных резуль-
татов удалось достичь только в эпоху Возрождения, в первой
половине XVI столетия, когда группа итальянских математиков
(Сципион дель Ферро, Никколо Тарталья, Джераломо Кардано,
Лодовико Феррари) получила общее решение кубических урав-
нений, положив тем самым начало высшей алгебре.
Выходит, как ученый Леонардо Пизанский не только превзо-
шел, но и на многие десятилетия опередил западноевропейских
Памятник Фибоначчи
в городе Пизе
211
математиков своего времени. Подобно Пифагору, привнесшему
в греческую науку сведения, некогда полученные от египетских
и вавилонских жрецов, Фибоначчи во многом способствовал
передаче приобретенных им в молодости математических зна-
ний индусов и арабов в западноевропейскую науку и заложил
фундамент для ее дальнейшего развития.
212
ЧАСТЬ ПЯТАЯ
Творцы занимательной науки
ГЛАВА 1
Даровитый мистер Доджсон
Нам кажется, что вот он, наконец, Льюис Кэрролл;
мы глядим пристальнее — и видим оксфордского
священника. Нам кажется, что вот он, наконец,
достопочтенный Доджсон; мы глядим присталь-
нее — и видим волшебника и чародея.
В. Вулф. Льюис Кэрролл
Первая биография Чарлза Лютвиджа Доджсона (Льюиса
Кэрролла) появилась в 1898 году, вскоре после его кон-
чины, и основывалась на личном архиве. Считается, что
ее автор — племянник писателя, преподобный Стюарт
Коллингвуд — создал идеализированный портрет своего
знаменитого дяди. Но именно на эту работу ориентирова-
лись все последующие биографы Кэрролла. Вот уже столе-
тие внимание к его персоне не ослабевает, а достоверные
ответы на многие вопросы до сих пор не получены.
ЧЕЛОВЕК-ЗАГАДКА
Со времени выхода в свет «Алисы в Стране чудес» о писате-
ле Льюисе Кэрролле и его творчестве было опубликовано мно-
жество работ: очерков, статей, исследований, монографий, книг,
а саму сказку в своих сочинениях комментировали, цитировали
или просто упоминали не только коллеги автора по цеху, но и
многие известные ученые. Сегодня имя Льюиса Кэрролла зна-
комо даже тем, кто не читал его книг. А вот жизнь профессора
математики и священнослужителя Чарлза Лютвиджа Доджсона,
как ни парадоксально, изучена куда меньше, и это несмотря на то,
что она тщательно документировалась в личных дневниках, пере-
213
писке, воспоминаниях друзей и зна-
комых. Выясняется, что в биографии
этого человека имеется немало белых
пятен и противоречий, а происходив-
шие события нередко переплетаются
в ней с домыслами исследователей.
Даже для многих из тех, кто был
хорошо знаком с достопочтенным
мистером Доджсоном, он во многом
остался человеком-загадкой. А тот,
подробно рассказывая о внешней
стороне собственной жизни, отнюдь
не спешил раскрывать свои секреты,
ни словом не обмолвился о личных
переживаниях и привязанностях, о
мечтах и несбывшихся надеждах, ни
разу не упомянул о взглядах на науку
и литературу. Нельзя даже с уверен-
ностью сказать, как он «уживался» с
Льюисом Кэрроллом и как относился
к нему на самом деле, как серьезный
и сдержанный на проявление эмоций профессор математики
ладил с веселым и неугомонным, вечно выдумывающим что-то
сказочником. Человека, который был бы столь знаменит и вмес-
те с тем столь неизвестен, как мистер Доджсон, еще поискать.
Сохранившиеся документы и свидетельства вкупе с замет-
но разнящимися мнениями и оценками биографов позволяют
говорить о том, что Доджсон имел весьма обширный круг инте-
ресов, был личностью незаурядной и одаренной во многих от-
ношениях. Но только читая произведения самого автора: книги,
научные работы, статьи, заметки, эссе, письма к детям, можно
составить о нем некоторое представление как о писателе, поэте
(чьи стихи давно вошли в антологию английской поэзии), уче-
ном, оригинальном мыслителе, изобретателе, преподавателе,
воспитателе... и найти в его обширном наследии что-то инте-
ресное и полезное для себя.
РОДОМ ИЗ ДЕТСТВА
Чарлз Лютвидж Доджсон родился 27 января 1832 года в де-
ревушке Дэрсбери (графство Чешир на западе Англии) в семье
25-летний Доджсон
(Льюис Кэрролл).
Фото Р. Саути
214
приходского священника и был старшим из сыновей. Поначалу
мальчик рос и воспитывался дома вместе с остальными детьми.
Отец, человек религиозный и университетски образованный,
обучал их не только закону Божьему, но и языкам, и основам
естественных наук.
В детстве Чарлз был бойким и развитым ребенком, любил
изобретать разные игры и развлечения и выступал в семье ини-
циатором всяческих затей. Так, однажды он придумал игру в же-
лезную дорогу с подробными правилами езды и задействовал в
ней все семейство. В весьма юном возрасте мальчик проявил
интерес к театральным постановкам, рисованию и сочинитель-
ству, что говорит о нем как о натуре увлекающейся и творчес-
кой. Нередко, переодевшись фокусником, маленький Чарлз по-
казывал собравшимся на представление зрителям необычные
номера и трюки. Став постарше, мальчик стал писать пьесы для
домашнего театра марионеток, который ему помог соорудить
деревенский плотник, и сам же их потом разыгрывал.
Позже, уже в период ученичества, Чарлз начал «издавать»
для младших братьев и сестер несколько журналов (да так ув-
лекся, что продолжал делать это почти четверть века): как автор
придумывал забавные истории, оригинальные загадки и юмо-
ристические стихи, записывал их, иллюстрировал, после чего
оформлял и переплетал подготовленные материалы. В одном
из журналов юноша «опубликовал» свою знаменитую задачу
о часах: «Какие часы лучше: те, что показывают точное время
один раз в году, или те, что показывают точное время дважды
в сутки?» А много лет спустя Доджсон подготовил рукописный
вариант своей первой сказки, снабдив текст 37 рисунками, в по-
дарок Алисе Лидделл, по просьбе которой рассказанная неког-
да ей и ее сестрам история о необыкновенных приключениях
маленькой девочки под землей была подробно записана им и
впоследствии легла в основу «Алисы в Стране чудес».
...В 1843 году семья Доджсонов перебралась в деревушку
неподалеку от Ричмонда. Вскоре вольная домашняя жизнь Чарл-
за закончилась: его отдали в небольшую частную школу. А через
два года он поступил в знаменитый Рэгби — элитную мужскую
школу-пансион. Бытовавшие там атмосфера и порядки не при-
шлись мальчику по душе, зато учеба давалось юному Доджсону
легко, причем наибольшее внимание он уделял математике и
классическим языкам. Уже тогда Чарлз стал проявлять особый
интерес к слову и логическим тенденциям в языке, позже на-
215
шедший отражение в сочинениях Льюиса Кэрролла. Так, один из
наставников будущего писателя отмечал, что при чтении вслух
тот с удивительным хитроумием подменял предписанные прави-
лами грамматики окончания существительных и глаголов более
точными аналогами или подходящими формами собственного
изобретения. И по признанию педагогов, подобные «отклоне-
ния от нормы» были всегда логически оправданны.
Однажды, вот так же играючи словами, молодой Доджсон,
тогда только начинавший писательскую карьеру, придумал
себе псевдоним Льюис Кэрролл, под которым прославился еще
при жизни и впоследствии вошел в историю мировой литера-
туры. Дело было так. Чарлз предложил одному журналу свою
поэму «Одиночество» (1856), которую подписал инициалами
Б.Б. Издатель попросил его подыскать настоящий псевдоним.
Но и второй предложенный вариант — Дэрс (от названия де-
с
ревушки Дэрсбери) ему не понравился. Тогда Доджсон решил
поэкспериментировать с собственным именем и придумал на
его основе сразу четыре псевдонима: Эдгар Катвеллис,сс Эдгар
У. Ч. Вестхилл (получены перестановкой букв), Луис Кэрролл
и, наконец, Льюис Кэрролл (он «перевел» Charles Lutwidge на
латынь — Carolus Ludovicus, поменял
местами слова, а затем «перевел» их
обратно на английский язык), из ко-
торых издатель выбрал последний,
самый благозвучный и легко запоми-
нающийся.
В СТЕНАХ КРАЙСТ-ЧЕРЧ
Бо’льшая часть жизни Чарлза Лю-
твиджа Доджсона (без малого пол-
века) связана с одним из старейших
учебных заведений Британии — Ок-
сфордом. В возрасте 19 лет он пос-
тупил в Крайст-Черч (Christ Church
College, колледж Христовой церкви),
в 22 года получил степень бакалав-
ра, в 25 — стал магистром матема-
тики, а в 29 — принял сан диакона.
Доджсон остался здесь преподавать
математику и логику. Долгие годы
Так я выгляжу, когда
читаю лекции.
Автошарж
216
он занимал должность профессора, был членом ученого совета
колледжа и одним из хранителей местной библиотеки. Здесь же
работал над сочинениями по математике и логике и творил под
именем Льюиса Кэрролла.
Но мало кто знает, что на заре своей профессиональной
карьеры Доджсон, возможно, подумывал о ее завершении. Не-
удачной оказалась его попытка поработать учителем в школе
для мальчиков, и через месяц он покинул учебное заведение
—
раз и навсегда. Не блестяще обстояли дела и в университе-
те. Довольно быстро Доджсон устал от лекций и студентов и,
разочарованный результатами, записал в дневнике: «Тяжелый
и неблагодарный это труд — навязывать знания неохочим лю-
дям в ущерб тем, у кого есть желание учиться». Но откуда было
взяться интересу у студентов? Им запомнилась сухая и небреж-
ная манера, с которой молодой преподаватель их поучал, не
выказывая никакого внимания к волновавшим их вопросам, его
угрюмость и отсутствие чувства юмора. Однако позже в пере-
писке с детьми, эссе и других сочинениях перед нами предстает
совсем другой преподаватель Доджсон — живой, заинтересо-
ванный и толковый педагог.
С годами в университете мистер Доджсон прослыл чело-
веком чопорным и педантичным, имел репутацию эксцентрика
и чудака, отличался независимостью взглядов и поведения,
Вид на Крайст-Черч колледж в Оксфорде
217
участвовал во всех тамошних делах и спорах, по любому пово-
ду печатал и распространял за свой счет брошюры и памфлеты
(от него не раз доставалось даже ректору Крайст-Черч Генри
Лидделлу). И все же, какой бы активной ни казалась деятель-
ность Доджсона, в стенах колледжа он вел одинокий и строго
упорядоченный образ жизни: лекции, ланч, занятия, прогулка
по окрестностям, обед и снова занятия... Жизнь его протекала
размеренно и спокойно, и, если верить дневнику, была «на удив-
ление свободна от всяких волнений и бед». В 50 лет Доджсон,
к тому моменту известный писатель и вполне обеспеченный че-
ловек, перестал преподавать и занял должность куратора Клу-
ба преподавателей в надежде, что новое занятие заставит его
«вылезти из скорлупы» и не жить затворником, занимающимся
только собой. Целых 10 лет он решал хозяйственные вопросы:
заведовал винным погребом и продовольственными припасами,
командовал поварами и слугами, а заодно следил за настроени-
ями и времяпровождением коллег — членов клуба. Однако с
любимой наукой Доджсон и не думал расставаться! Еще в 1881
году он писал: «Отныне я буду располагать всем своим време-
нем... надеюсь, смогу совершить нечто полезное с помощью мо-
его пера — отчасти на поприще обучения математике, отчасти
придумывая невинные развлечения для детей». Так и вышло:
в этот период появились на свет знаменитые книги автора по
логике и занимательной математике.
А каким запомнился наш герой окружающим? Как отмечали
многие, Чарлз Лютвидж был человеком деликатным, утончен-
ным, мягким, добрым; не любил привлекать к себе внимание,
избегал знакомств и двух слов не мог связать в светской бе-
седе. Спокойнейший и самый застенчивый из взрослых людей
после Дядюшки Римуса, как метко охарактеризовал его Марк
Твен после встречи у общих знакомых. Общению со взрослыми
Доджсон предпочитал дружбу с детьми, в присутствии которых
оживлялся и превращался из замкнутого, робкого человека в
интересного и оригинального рассказчика. «Дети — это три
четверти моей жизни», — писал он. И этим многое сказано. Со
своими юными друзьями он отправлялся на прогулки, ходил
в театр, переписывался, иногда приглашал их в гости. Для их
развлечения писатель всегда имел под рукой разные игрушки:
заводных животных, музыкальные шкатулки и т.п., а нередко
сам придумывал игры и загадки, показывал фокусы или сочи-
нял забавные истории. Живое и непосредственное общение
218
с детьми раскрепощало его, стимулировало в нем творческое
начало, давало простор фантазии и импровизации и во мно-
гом способствовало рождению лучших произведений писателя
Льюиса Кэрролла.
ПОКЛОННИК
ЭПИСТОЛЯРНОГО ЖАНРА
Вопреки устоявшемуся мнению,
круг знакомств Доджсона был ши-
рок и разнообразен; в него входили
люди самого разного возраста и рода
деятельности. Писатель вел обшир-
ную переписку с родными, друзьями,
коллегами и читателями, скрупулезно
фиксируя каждое письмо в специаль-
ном журнале. В другом журнале он
регистрировал официальную кор-
респонденцию, приходившую на имя
преподобного Ч. Л. Доджсона. Чуть
ли не ежедневно он отправлял пачку
посланий. По оценкам исследовате-
лей, их насчитывалось около 100 000,
сохранилось более 4000 писем, из
них было опубликовано 1305. Неуди-
вительно, что писатель, большой пок-
лонник эпистолярного жанра, посвя-
тил последнему брошюру «Восемь или девять мудрых слов о том,
как писать письма», где поведал о некоторых его секретах.
Несколько важных штрихов к портрету Доджсона добавляет
его переписка с детьми, которую отличает не имеющий анало-
гов, уникальный в своем роде и такой узнаваемый кэрролловс-
кий стиль изложения. Каких только писем здесь нет! «Дразнил-
ки», «ворчалки», письма-небылицы, загадки, советы...
В общении с детьми мистер Доджсон выступал в роли их
наставника и старшего друга. Это был человек, любящий детей,
знающий и понимающий их натуру, иногда даже позволяющий
себе немного побыть ребенком. Судя по тому, как много времени
Доджсон посвящал юным созданиям (поначалу — собственным
братьям и сестрам, а позднее — родным племянникам, детям
коллег и друзей, маленьким читателям своих произведений и
Приглашение
на крокет.
Илл. Д. Тенниела из
«Алисы в Стране
чудес»
219
поклонникам творчества постарше),
эта роль была для него едва ли не
самой желанной. «Одна из главных
радостей моей — на удивление счас-
тливой — жизни проистекает из при-
вязанности моих маленьких друзей»,
— признался однажды писатель. Де-
тям всегда было интересно общаться
с ним, а тот мог ответить на любой их
вопрос и старался уделить должное
внимание каждому ребенку.
ИЗ ПИСЕМ К ДЕТЯМ
Как правило, желая выразить
симпатию юному адресату, автор
подписывал свое послание «Твой
любящий [или — преданный] друг
Ч. Л. Доджсон», реже использовал
для этого имя Льюис Кэрролл. При-
мечательно также, что мистер Кэр-
ролл... оказался героем нескольких
писем. Так, однажды Доджсон упо-
мянул о нем как об очень близком
друге, с которым никогда в жизни не разлучался, а в другой раз
назвал его своим другом-писателем, престранным человеком и
большим любителем нести всякую чепуху. Самокритично и, как
всегда, иронично.
Так или иначе незримое присутствие Кэрролла ощущает-
ся практически в каждом письме. Многие послания написаны
в шутливой манере и содержат забавные примеры, зарисов-
ки, любопытные наблюдения, курьезные истории и небылицы
(«почти все мои высказывания сильно преувеличены», — за -
метил в одном из писем Доджсон). Очевидно, автор специаль-
но придумывал их для развлечения юных читателей и, как это
часто бывало, играл словами. Вот, например, как он объяснял в
одном из писем-небылиц «древнее происхождение» некоторых
выражений: «Все делалось очень просто в те давние дни. Если у
кого-то было много денег, он просто клал их в банку, закапывал
ее под забором, говорил: “У меня деньги в банке” — и больше
ни о чем не беспокоился. А как путешествовали в те далекие
Фрагмент письма-
ребуса Джорджине
Уотсон
220
времена! Вдоль дорог тогда стояли шесты. Люди влезали на них
и старались удержаться на самой верхушке как можно дольше,
а потом (обычно это происходило очень скоро) падали оттуда.
Это и называлось путешествовать».
В другом письме читаем: «А вот загадка: как сделать пре-
восходную фотографию? Ответ: сначала снять восход, а потом к
восходной фотографии приставить “пре-”». «Разъяснил — как
по полкам разложил!» как сказал бы искушенный лингвист
Шалтай-Болтай .
Даже укоризна или наставление адресату (равно как и
собственные извинения или оправдания) звучат из уст воспи-
тателя Доджсона забавно и вместе с тем трогательно, если не
сказать по-детски. Вот, например, фрагмент одного из писем-
«ворчалок»: «Передай, пожалуйста, Джуди (с приветом от меня,
который я посылаю ей с большой неохотой), что я могу забыть,
но не могу простить ее в высшей степени бессердечное по-
ведение вчера в моих апартаментах. Ты не присутствовала при
этом, и я не стану терзать твою чувствительную натуру описа-
нием содеянного ею. Но когда-нибудь я с ней расквитаюсь.
Она придет ко мне едва живая от жажды, и я достану бутылку
великолепного холодного лимонада. Затем я открою бутылку,
налью пенящийся лимонад в большой бокал, поставлю его на
таком расстоянии от нее, чтобы она могла дотянуться, и выпью
лимонад на ее глазах сам, доставив тем самым ей несказанное
удовлетворение. Ей не оставлю ни капли!»
Письма Доджсона содержат и ответы на самые разные воп-
росы детей, и полезные советы, которые он так любил давать.
Встречаются в них и «глубокомысленные высказывания» вроде
следующих: «По каким-то причинам люди, которые не сущес-
твуют, гораздо приятнее в обращении, чем те, которые сущес-
твуют»; «Женщины обладают сверхъестественной интуицией
—
способностью, гораздо более тонкой, чем способность к
здравому суждению»; «Мысли, которые приходят задним чис-
лом, всегда самые лучшие. Я настолько убежден в этом, что поч-
ти все мои мысли теперь уходят мне в голову задним числом.
Мыслей, которые приходили бы мне в голову передним числом,
у меня, как правило, не бывает».
* Поскольку многие примеры писателя построены на словесной игре, которую при
дословном переводе не удается передать, переводчикам книг Льюиса Кэрролла
приходилось подбирать подходящие примеры в русском языке.
221
РАЗ ЗАДАЧКА, ДВА ЗАДАЧКА...
И уж, конечно, математик и преподаватель Доджсон не упус-
кал случая предложить ребенку в качестве интеллектуального
развлечения загадку, головоломку, логическую игру или задач-
ку (в том числе и собственного сочинения), очень ненавязчиво,
как бы между делом. Так, обращаясь к одной девочке с просьбой
поздравить с днем рождения их общую знакомую, Доджсон пи-
сал: «Что и говорить, 21 год — возраст весьма юный... Подумать
только, что в прошлом году я был вдвое, а еще раньше — втрое
старше Лили! Когда именно я был втрое старше Лили, попытай-
ся решить сама. Для тех, кто любит такие вещи, это прекрасная
арифметическая задача!»
В письме к другой девочке содержится следующая геомет-
рическая головоломка: «У некоего джентльмена... в гостиной
было только одно окно — квадратное окно высотой в 3 фута и
шириной в 3 фута. У джентльмена очень болели глаза, а окно
пропускало слишком много света, поэтому... он послал за стро-
ителем и попросил того переделать окно так, чтобы оно пропус-
кало вдвое меньше света. Но при этом джентльмену непремен-
но хотелось, чтобы окно оставалось квадратным и имело 3 фута
в высоту и 3 фута в ширину. Как удалось строителю удовлет-
ворить требования заказчика? Использовать занавеси, жалюзи,
цветные стекла и тому подобные ухищрения он не мог».
А вот одному молодому человеку Доджсон предложил ра-
зобраться с классическим алгебраическим софизмом, давно не
дававшим покоя автору. «Если каждая из величин x и
x увотде-
у
льности равна 1, то ясно, что 2 (x2
–
у2)=0ичто5 (x–
x у)=0.
Следовательно, 2 (x2
–
у2)=5 (x–
x у). Разделив теперь обе
части этого уравнения на (x –
x у),мыполучим2 (x+
x у)=5.Но
(x+у)=1+1=2.Следовательно,2 2 =5.Стехпор,какэтот
тревожный факт стал мне известен, я потерял покой и сплю не
более 8 часов за ночь и ем не чаще трех раз в день. Надеюсь, вы
проявите ко мне жалость и объясните, в чем тут дело».
Надо также сказать, что профессор Доджсон как человек,
который всерьез изучал математику и всю жизнь ее преподавал,
мог дать (и не раз давал на страницах своих книг) полезные со-
веты тем, кто только приступил к постижению этой сложной на-
уки. Встречаются они и в переписке с детьми. К примеру, одной
юной особе, безуспешно пытавшейся решить задачи из знаме-
нитых кэрролловских «Узелков», он рекомендовал следующее:
222
«Если ты упорно и достаточно долго пытаешься что-то по-
нять и тебе это так и не удается, отложи то, что ты изучаешь,
в сторону. Подожди до следующего утра и, если тебе и тогда
не станет ясно то, что ты хотела понять, и у тебя нет человека,
который мог бы объяснить непонятное место, оставь это мес-
то совсем и обратись к тому разделу математики, который тебе
понятен». «Никогда не оставляй нерешенную трудность на по-
том. Я имею в виду: не углубляйся в книгу дальше до тех пор,
пока не преодолеешь трудность. ...В этом отношении математи-
ка полностью отличается от многих других предметов. Если ты
пропустишь какую-нибудь математическую трудность, то вско-
ре пожнешь плоды своей небрежности: тебе встретится какое-
нибудь другое доказательство, опирающееся на пропущенное
тобой утверждение, и ты будешь все глубже и глубже увязать
в трясине». «Продолжай работу лишь до тех пор, пока голова
остается совершенно ясной. Как только ты почувствуешь, что
мысли твои начинают мешаться, остановись и отдохни, ибо в
противном случае тебя ожидает заслуженная кара: ты никогда
не выучишь математику! Поверь мне!»
ТАЛАНТЛИВЫЙ ФОТОГРАФ И СТРАСТНЫЙ ТЕАТРАЛ
У мистера Доджсона были и другие любимые занятия, кото-
рым он предавался в свободное время. В юности, иллюстрируя
свои первые сочинения, Чарлз мечтал стать художником. Как-
то, уже по окончании колледжа, он даже отправил несколько
рисунков в известную газету, но их не опубликовали. Тогда мо-
лодой человек решил попробовать себя в зарождавшемся в то
время искусстве фотографии и всерьез увлекся им, проявил в
этом деле немалый художественный талант и безупречный вкус
и добился больших результатов. Будучи любителем, Доджсон
не уступал в мастерстве иным профессионалам; более того,
спустя столетие он был признан специалистами одним из луч-
ших фотографов XIX века. Он снимал не только своих друзей и
коллег, но и священнослужителей, политиков, а также многих
знаменитостей. Среди них поэт Альфред Теннисон, писатель и
теоретик искусства Джон Рескин, живописец и поэт Данте Габ-
риэль Россетти, физик Майкл Фарадей, биолог Томас Гексли, ак-
триса Эллен Терри. Но особенно хорошо у него получались де-
тские и групповые портреты, которые он в большом количестве
рассылал друзьям. Кстати, о том, как работалось фотографам во
223
времена Доджсона и с какими труд-
ностями приходилось сталкиваться,
можно узнать из его юмористическо-
го рассказа «Фотограф на съемке».
С малолетства Чарлз Лютвидж
сохранил любовь к театру и часто
приходил сюда в зрелые годы. Из-
за этого увлечения он даже не сразу
принял важный для себя сан диакона
(по существовавшей тогда традиции
преподаватель Крайст-Черч должен
был иметь духовное звание). Посе-
щение театра священнослужителем,
мягко говоря, не приветствовалось,
но расставаться с любимым заняти-
ем Чарлз не хотел. Его притягивали
атмосфера спектакля и развиваю-
щееся на сцене действие, заворажи-
вала игра актеров. Мистер Доджсон
интересовался самыми разными те-
атральными жанрами и был не просто любителем, но и цени-
телем этого вида искусства. Говорят, впоследствии, наблюдая
за постановкой собственных сказок о приключениях Алисы, он
проявил тонкое понимание сценических законов.
Доджсон любил общаться с актерами, долгие годы под-
держивал дружеские отношения с известной актрисой Эллен
Терри, прославившейся ролями в пьесах Шекспира. А из вос-
поминаний писателя известно, что, находясь в единственной в
жизни заграничной поездке, а она состоялась в 1867 году, он
не забывал о своем увлечении. Путешествуя по России вместе с
другом и коллегой Генри Лиддоном, он посетил два театра — в
Москве (Малый театр) и Нижнем Новгороде и восторженно от-
зывался об игре русских актеров. Даже незнание чужого языка
(программка — и та упорно изучалась в антрактах с карманным
словарем в руках) не помешало мистеру Доджсону оценить по
достоинству их высокое мастерство. Любопытно, что наиболь-
шее впечатление на него произвели провинциальные артисты.
«Я никогда не видел актеров, которые бы так полно отдавались
происходящему на сцене и обращали так мало внимания на
происходящее в зале», — отметил позже Доджсон в «Русском
дневнике». О том, что он был заядлым театралом, говорит и такой
Эмми Хьюз.
Фото Ч. Доджсона
224
факт: по подсчетам исследователей, только по поводу актерской
игры в сохранившихся записях писателя содержатся 870 коммен-
тариев.
НЕУТОМИМЫЙ ВЫДУМЩИК И ИЗОБРЕТАТЕЛЬ
Всю жизнь наш герой проявлял интерес к игре и тягу к изоб-
ретательству. Чарлза Доджсона можно было бы смело назвать
человеком изобретающим (а его верного спутника Льюиса Кэр-
ролла — человеком играющим, ибо таково было его обычное
состояние). На счету мистера Доджсона немало оригинальных
находок и открытий, хитроумных приспособлений и устройств,
о которых он мог бы сказать, подобно Белому Рыцарю: «Это мое
собственное изобретение!»
Хотя почему подобно? По мнению исследователей, создан-
ный писателем комичный образ — не что иное, как шарж на
самого себя. «Мой ум работает, не переставая, — говорил Бе-
лый Рыцарь. — Чем ниже моя голова, тем глубже мои мысли!»
Должно быть, и самому Доджсону, уделявшему много времени
активным умственным занятиям, думалось и творилось лучше
всего тогда, когда удавалось увидеть мир перевернутым; а если
требовалось, он и сам мог поставить все с ног на голову. Этому
он пытался учить и других. Как справедливо заметил Г. К. Чес-
тертон, величайшее достижение Кэрролла состоит отчасти в том,
что он учил стоять на голове не только детей, но и ученых.
Мистер Доджсон постоянно искал способы сделать что-ни -
будь по-новому или усовершенствовать давно известные вещи.
Некоторые изобретения, о которых он упомянул в дневнике,
были признаны непрактичными, если не сказать бесполезными;
у кого-то они вызовут лишь недоумение или улыбку. Зато другие
оказались вполне пригодными и со временем вошли в широкое
употребление (кое-какие из них даже были открыты заново).
Впрочем, судите сами. Чарлз Лютвидж Доджсон придумал:
заменитель клея для заклеивания конвертов, приклеива-
ния мелких предметов к книжкам и пр. (это была бумага, сма-
занная клеем с обеих сторон);
дорожные шахматы (в них фигуры держались на доске
за счет небольшого выступа, соответствующего углублению в
клетке);
никтограф (так он назвал специальную доску, на которой
можно было писать в темноте);
225
упрощенный способ денежных переводов (его суть тако-
ва: отправитель заполняет два бланка перевода и один посы-
лает по почте — в нем содержится номер-код, который должен
назвать адресат, чтобы получить деньги);
систему запоминания чисел (с ее помощью сам он выучил
число до 76-го знака);
трюк с календарем (способ определения в уме дня недели
для любой названной даты);
правила проверки делимости чисел на 17 и 19;
символы для обозначения синуса и косинуса угла —
и
;
знаки для обозначения логических операций (вместо об-
щепринятых сегодня , и использовал †, и Р);
Алиса и Белый Рыцарь.
Илл. Д. Тенниела из «Алисы в Зазеркалье»
226
оригинальные методы решения силлогизмов и соритов;
массу головоломок, занимательных и логических задач.
Большой интерес Доджсон проявлял к всевозможным иг-
рам и развлечениям, в особенности связанным со словами.
К примеру, он составлял анаграммы и сочинял акростихи, из ко-
торых самым известным является стихотворение, завершающее
«Алису в Зазеркалье». В нем писатель вспоминает лодочную
прогулку с сестрами Лидделл, на которой было положено нача-
ло дилогии о приключениях Алисы:
Ах, какой был яркий день!
Лодка, солнце, блеск и тень,
И везде цвела сирень.
И
Сестры слушают рассказ,
СС
А река уносит нас...
Из первых букв каждой строки складывается имя Алиса
Плэзнс Лидделл.
Мистер Доджсон любил сочинять новые правила для ста-
рых, хорошо известных игр (кстати, сам он предпочитал шах-
маты, триктрак, крокет и бильярд, в который даже предложил
играть... на круглом столе), а также придумал несколько интел-
лектуальных развлечений с числами и словами. Им посвящены
в общей сложности два десятка изданных писателем брошюр.
ЛИНГВИСТ-ЭКСПЕРИМЕНТАТОР
Со школы Чарлз Лютвидж Доджсон проявлял интерес к
языкам и, если бы не отдал предпочтение математике, мог стать
незаурядным лингвистом. По мнению некоторых специалистов,
у Доджсона «было не только безупречное чувство языка, но и
умение проникнуть в его сущность, была своя (вероятно, интуи-
тивная) лингвистическая концепция».
Надо сказать, его интересы касались таких важных разделов
лингвистики, как этимология, семантика и словообразование.
Сочиняя произведения, писатель часто экспериментировал со
словами и их значениями: придумывал неологизмы, переделы-
вал известные выражения, каламбурил, прибегал к алогизмам
и т.д. Считается, что игра с языком — основа метода Кэррол-
ла; она придает неповторимое своеобразие его речи, в которой
сдержанность и лаконичность сочетаются с динамичностью и
выразительностью. Эта игра, нашедшая отражение в диалогах
227
и размышлениях героев, была очень важна для автора сама по
себе, так как определяла поступки героев и развитие сюжета в
целом. Результаты этих экспериментов ярко отражены, в част-
ности, в обеих сказках об Алисе.
Например, названия предметов, которые довелось изучать в
школе Черепахе Квази, построены на каламбурах. «Сначала мы,
как полагается, Чихали и Пищали, — говорит Алисе Черепаха.
—
А потом принялись за четыре действия Арифметики: Сколь-
жение, Причитание, Умиление и Изнеможение». Кроме того, в
этой школе преподавали Рифы Древнего мира, Грязнописание,
Хливкие шорьки.
Илл. Д. Тенниела из «Алисы в Зазеркалье»
228
Мимические опыты, Триконометрию, Физиономию, Латунь и
Драматику.
А вот как забавно рассуждает еще один участник этого раз-
говора — Грифон: «Занятия почему так называются? Потому
что на занятиях мы у нашего учителя ум занимаем... А как все
займем и ничего ему не оставим, тут же и кончим. В таких слу-
чаях говорят: “Ему ума не занимать”».
Корневая игра и игра с омонимами вообще очень характер-
ны для стиля Кэрролла. Вот еще один эпизод из сказки, в нем
Грифон рассказывает Алисе о разных рыбах: треску’ так назы-
у
вают потому, что от нее тре’ску много, среди ее друзей — ста-
у
ричок Судачок, с которым они с утра до ночи судачат, Щука, что
любит всех щучить, и во всем сомневающийся Сом.
Результатом иной словесной игры писателя являются при-
думанные им слова-бумажники, смысл которых пытался разъ-
яснить Алисе Шалтай-Болтай. Они составлены из фрагментов
нескольких слов («Раскроешь [бумажник], а там два отделения!
Так и тут — это слово раскладывается на два!») и допускают
разные прочтения. Например, хливкие — означает хлипкие
и ловкие; шорьки — это помесь хорька, ящерицы и штопора;
пырялись — значит прыгали, ныряли, вертелись; хрюкотали —
хрюкали и хохотали (или летали); ну а зелюки — не кто иные,
как зеленые индюки!
А вспомните, какие смешные имена получили в результате
«склеивания» двух слов с общей частью зазеркальные насеко-
мые — Баобабочка, Стрекозел и Бегемошка! И вместе с именами
обрели необычные качества. Оказалось, что зазеркальная Бао-
бабочка — вся деревянная и питается стружками и опилками;
бородатый и рогатый Стрекозел вечно норовит с кем-нибудь
пободаться и предпочитает есть траву и отруби; а толстые и
неповоротливые Бегемошки — прекрасные летуны и любители
лягушек и мелкой рыбешки.
Игра писателя по-своему логична и вовсе не бессмысленна,
как может показаться на первый взгляд. Она сродни словесной
игре детей, которую можно наблюдать, когда те фантазируют
или пытаются подобрать в разговоре подходящее слово. Ов-
ладевая языком, ребенок старается осмыслить происхождение
слова и, следуя собственной логике, нередко заменяет одну его
часть другой, более понятной и правильной, с его точки зрения.
Кстати говоря, переводчики Кэрролла считают одной из причин
истинной оригинальности автора его умение слышать слова так,
229
как их слышат дети, — во всем богатстве первоначальных связей,
не успевших еще стереться от повседневного употребления.
КАК ПРЕВРАТИТЬ КОСУ В БАНТ?
В менее известных широкому читателю заметках, эссе и ста-
тьях Ч. Л. Доджсона можно найти любопытные утверждения и
правила, касающиеся «законов словообразования». Так, одно
из них гласит, что корень любого слова всегда можно извлечь,
а согласно другому слова одинаковой длины всегда равны. Эти
«правила» легли в основу двух придуманных писателем игр со
словами, о которых стоит рассказать подробнее.
Одна из самых известных и по сей день популярных игр
Доджсона называется Дублеты, или «Словесные звенья». Вот
что пишет о ней сам автор: «Правила игры достаточно просты.
Предлагаются два слова, состоящих из одинакового числа букв.
Игра заключается в том, чтобы выстроить цепочку слов от од-
ного слова к другому, таких, чтобы каждое слово в цепочке
отличалось от предыдущего только одной буквой. Перестав-
лять буквы не разрешается, каждая буква должна оставаться
на своем месте. ...Два задаваемых слова я называю дублетом,
промежуточные слова — звеньями, а всю последовательность
слов — цепочкой». Например, БАНТ можно превратить в КОСУ,
составив такую цепочку слов:
БАНТ—рант—рана—раса—роса—КОСА.
В состязании побеждает тот, чья цепочка содержит на-
именьшее число звеньев.
Другая словесная игра Доджсона называется Миш-маш:
«Суть этой игры состоит в том, что один игрок предлагает “ядро”
(две или несколько букв, идущих подряд), а другой пытается
найти “законное” слово (слово, используемое в обычной речи и
выражаемое несобственным именем существительным в имени-
тельном падеже единственного числа), которое содержало бы
предложенное партнером ядро». Вот пример:
ЯДРО
ЗАКОННОЕ СЛОВО
жн
жнец
ифу
центрифуга
у
гемо
бегемот
Игроки могут подбирать разные слова с заданным «ядром».
Ясно, что чем оно сложнее, тем интереснее играть. Сам автор в
230
письме двоюродному брату предлагал, в частности, такие хит-
роумные сочетания букв: лстр, оап, еел, вчи (фрагменты слов
— полстраницы, фотоаппарат, змеелов и певчий).
Математика, логика, лингвистика, педагогика, фотография,
театр, изобретательство... Несмотря на обширный круг интере-
сов и многогранный талант, Чарлз Лютвидж Доджсон просла-
вился как писатель и поэт. Одной только дилогии о приключе-
ниях Алисы в Стране чудес и Зазеркалье ему хватило бы, чтобы
войти в историю мировой литературы. Но неутомимый мистер
Доджсон, чей ум работал неустанно, постоянно сочинял стихи и
прозу, придумывал задачи и головоломки, корпел над научными
трудами. И так более сорока лет. Поток публикаций не исся-
кал. В английском «Справочнике по Льюису Кэрроллу» (1979)
значатся 326 изданий его работ, из них 286 прижизненных.
В их числе — книги по символической логике и занимательной
математике, в которых раскрывается еще один редкостный дар
их автора. Но эта тема заслуживает отдельного разговора.
231
ГЛАВА 2
Талантливый
популяризатор Кэрролл
Кэрролл — это мир, мир со своей логикой, мир со
своей математикой, который очень непросто
открывается.
Из выступления Ю. Данилова
на Секции книги в московском Доме ученых
Интерес к занимательной математике Чарлз Доджсон
проявлял всегда. Он был мастером загадок и логических
парадоксов, придумывал их для больших и маленьких и
часто облекал в форму забавных рассказов. Читателям
было над чем призадуматься! Писателя Льюиса Кэрролла
по праву можно назвать самобытным популяризатором
науки — на его счету не один сборник хитроумных
задач и головоломок.
О ПИЩЕ ДЛЯ УМА
В России книги Кэрролла по логике и занимательной мате-
матике известны благодаря переводам Юлия Данилова. Эти и
другие сочинения писателя можно смело рекомендовать педа-
гогам, воспитателям и родителям: они содержат массу полезных
примеров и историй, что называется, на любой случай. Берите
и пользуйтесь! Как верно заметил в связи с этим Ю. Данилов,
Льюис Кэрролл еще никого и никогда не подводил. Из работ ав-
тора хочется выделить эссе. В них содержатся дельные советы,
а писатель раскрывается, как ни в каких других своих произве-
дениях. Ограничимся лишь одним примером.
Будучи человеком, склонным к интеллектуальным занятиям,
Доджсон был убежден, что наш разум нуждается в пище для раз-
мышлений не меньше, чем организм — в регулярном питании.
Свое мнение по этому поводу он изложил в любопытном эссе
«Пища для ума». В нем звучит риторический вопрос: почему,
всячески заботясь о теле, мы так мало внимания уделяем разуму?
Неужели первое гораздо важнее второго? «Отнюдь!» — утверж-
дает Доджсон и предлагает несколько важных «правил питания
ума» (аналогичных правилам рационального питания тела).
232
Прежде всего, он рекомендует
позаботиться о том, чтобы наш ум
регулярно получал полезную и раз-
нообразную пищу в надлежащем ко-
личестве, не переедал и не потреб-
лял много ее сортов сразу. К тому же
следует соблюдать интервалы меж-
ду приемами духовной пищи, давая
кратковременные передышки разу-
му. А следующий совет просто бес-
ценен для любого ученика: для того
чтобы эта пища полностью усвоилась,
надо тщательно ее пережевывать, то
есть обдумывать, и раскладывать
в голове «по полочкам», чтобы при
необходимости с легкостью можно
было найти ответ на интересующий
вопрос.
Далее автор дает полезные со-
веты относительно того, как нужно
правильно читать книги, являющиеся
одним из основных источников пищи
для ума. В частности, он справедливо
замечает, что торопливое «проглатывание» книг не приводит ни
к чему хорошему, в голове остается только «горсть многообеща-
ющих фактов», а действительно нужный факт среди этого хлама
безнадежно теряется. (Знакомая ситуация! С проблемой «каши
в голове» у учеников приходилось иметь дело всем педагогам.
Вероятно, с ней не раз сталкивался и профессор Доджсон...)
А может быть, вы хотите выяснить, каким «умственным
аппетитом» обладает тот или иной человек? Тогда дайте ему
«булочку для ума» — краткий, хорошо написанный, но мало-
увлекательный трактат на какую-нибудь популярную тему.
И если ваш подопечный прочтет его с неподдельным интере-
сом и сосредоточенным вниманием, а затем сумеет ответить на
любой вопрос по содержанию, то ум его работает превосходно.
Если же человек вскоре отложит трактат в сторону или заметит:
«Я не могу читать такие глупые книги! Нет ли у вас второго тома
“Загадочного убийства”?», можете считать, что с умственным
пищеварением у него не все обстоит благополучно. Вот такой
простой и действенный совет.
Ни дня без книги.
Шарж на Кэрролла.
Худ. Г. Фернисс
233
КАК ИЗБАВИТЬСЯ ОТ ПРАЗДНЫХ МЫСЛЕЙ
Мистер Доджсон полагал, что активные умственные заня-
тия вроде решения головоломок или математических задач
—
прекрасный способ избавиться от навязчивых мыслей, лег-
ко овладевающих праздным умом, и лучшее лекарство от более
тягостных мук разума. Писатель и сам не раз прибегал к этому
средству в часы бессонницы.
Часть задач, которые он, лежа в постели, придумывал и тут
же решал без помощи карандаша и бумаги, выполняя все вы-
кладки в уме, впоследствии вошла в сборник «Полуночные зада-
чи» (1893). В предисловии говорится, что книга предназначена
людям с обыкновенными математическими способностями, вре-
мя от времени испытывающим потребность занять чем-нибудь
свой ум. Автор ставил целью не только дать читателям пищу для
размышлений, но и поощрить их собственным примером, а по-
тому решения всех задач привел в первозданном виде, не внося
специально улучшений в проделанную в уме часть работы.
В сборник включены 72 задачи разного уровня сложности
(часть их по силам и школьникам), относящиеся к различным
разделам математики: арифметике, алгебре, планиметрии, сте-
реометрии, теории вероятностей, тригонометрии и др. В пре-
дисловии Доджсон также рассказывает о том, как создавал не-
которые задачи. Так, размышляя одно время над «геометрией
частично правильных тел», он пришел к выводу: в отличие от
случая с правильными телами, число которых вызывающе мало,
ничто не мешает строить новые частично правильные тела.
И вот, вернувшись как-то раз ночью к этой мысли, он придумал
(по сути — мысленно сконструировал) десятигранник, поверх-
ность которого состояла из двух квадратов и восьми равносто-
ронних треугольников, а затем поставил себе задачу — вычис-
лить его объем.
Результатом игры разума профессора Доджсона стала сле-
дующая оригинальная задача: «Два равных квадрата лежат в
различных горизонтальных плоскостях так, что центры их рас-
положены на одной вертикали и стороны одного параллельны
диагоналям другого. Расстояние между плоскостями выбрано
так, что, соединив соседние вершины квадратов, мы получим
восемь равносторонних треугольников. Вычислить объем тела,
ограниченного квадратами и треугольниками». Остается доба-
вить, что на ее создание и решение автор потратил две ночи.
234
UTILE DULCI!
Любителям головоломок и занимательных задач придется
по душе другая, не менее известная, книга писателя — «Исто-
рия с узелками» (1885), призывающая читателя соединить при-
ятное с полезным. Первоначально она была опубликована по
частям в журнале The Monthly Packet, а затем вышла отдельным
изданием. Книга представляет собой сборник новелл (десять
«Узелков» с задачами), героям которых приходится искать вы-
ход из затруднительных положений и ответы на самые разные
вопросы. В свою очередь читателю предлагается помочь им в
этом.
В «Узелке IV», к примеру, рассказана следующая курьезная
история. Пятеро рыбаков-туземцев собирались продать капита-
ну взявшего их на борт судна мешки с деньгами своего острова,
тяжеловесными, но малоценными. Тот был готов заплатить по
5 шиллингов за фунт веса и даже оценил «на глаз» стоимость
всех пяти мешков в 10 фунтов. Однако по вине матросов ры-
баки лишились мешков. Желая возместить им убытки, капитан
спросил, каков был вес каждого мешка, и выяснил, что тузем-
цы взвешивали их сразу по две или по три штуки. Вот незадача!
А вернее — самая настоящая задача! Итак, первый и второй
мешки вместе весили 12 фунтов, второй и третий — 13,5 фун-
та, третий и четвертый — 11,5 фунта, четвертый и пятый —
8 фунтов, а первый, третий и пятый — 16 фунтов. Сколько весил
каждый мешок?
Ко многим из рассмотренных задач даны не только подроб-
ные решения и их анализ, в том числе вариантов, присланных
читателями журнала, но и авторские комментарии, не менее лю-
бопытные, чем сами «Узелки». В частности, по поводу задачи
об определении веса мешков Доджсон справедливо замечает:
«Как ясно с первого взгляда любому алгебраисту, [эта задача]
сводится к решению системы линейных уравнений. Однако она
без труда решается и с помощью одной лишь арифметики, и по-
этому использование более сложных методов я считаю дурным
тоном».
Читатель с отменным «умственным аппетитом» конечно же
заметит, что писатель не озвучил другой важный вопрос: сколь-
ко на самом деле должен был заплатить туземцам капитан?
И, поразмышляв немного, придет к выводу, что это не случайно.
Доджсон нашел отличный способ привлечь к нему наше внима-
235
ние — грамотно разбросал по тексту числовые подсказки. Кста-
ти, вычисления показывают, что настоящая стоимость мешков
не 10 фунтов (или 200 шиллингов), а всего 6,75! Будем считать
переплату компенсацией морального вреда потерпевшим ту-
земцам.
Всякому, кто однажды откроет эту или другие книги писате-
ля, нужно быть готовым к тому, что такой специалист по «булоч-
кам для ума», как мистер Доджсон, может сознательно ввести
читателя в заблуждение или допустить ошибку. Вспомним хотя
бы его знаменитую задачу «Обезьяна и груз», вызвавшую в свое
время многочисленные споры о том, какое ее решение считать
единственно правильным: «Через блок, прикрепленный к потол-
ку, переброшен канат. На одном конце каната висит обезьяна,
к другому прикреплен груз, вес которого в точности равен весу
обезьяны. Предположим, что обезьяна начала взбираться вверх
по канату. Что произойдет при этом с грузом?» Ученые коллеги
Доджсона давали самые разные ответы и всерьез обсуждали их,
Илл. А. Б. Фроста из «Истории с узниками»
236
чем только позабавили автора. На самом деле ответ зависит от
дополнительных условий, вводимых при решении*
.
А вот задачка для маленьких: «Кошка съедает мышку за 1 ми-
нуту. За сколько времени кошка съест 60 000 мышек?» Не спеши-
те браться за карандаш. Лучше представьте себе армию мышек,
окружившую кошку, тогда правильный ответ станет очевиден.
Или вот такая детская загадка:
Ровно два фунта весила палка,
И хоть пилить мне ее было жалко,
Семь раз отмерив, я на восьмой
По меткам прошелся острой пилой.
Все восемь восьмушек по весу равны
И внешне похожи, как капли воды.
Но возникает вопрос непростой:
Сколько же весу в восьмушке такой?
Если думаете, что четверть фунта, то это неверно, уверяет ав-
тор, и с ним трудно не согласиться, узнав ответ. В чем подвох?
Или другой яркий пример — из
«Алисы в Зазеркалье». Уже на пер-
вых страницах книги автор нарушил
главный закон, действующий в За-
зеркалье. Оказавшись в отраженной
комнате, Алиса попыталась прочесть
лежавшую на столе книгу, но смогла
сделать это только после того, как
поднесла ее к зеркалу. Между тем
описанная ситуация теоретически
была бы возможна лишь в том случае,
когда девочка, пройдя сквозь стек-
ло, совершенно не изменилась, что,
как видим, и произошло в наруше-
ние известных законов симметрии.
По воле автора, разумеется. Так что
не стоит особо удивляться или пос-
пешно упрекать мистера Доджсона в
оплошности. Возможно, тот допустил
ее в надежде, что «радость открытия
ошибок и испытанное при этом чувс-
Что произойдет с грузом,
когда обезьяна полезет вверх?
* Эта задача была включена в вышедший в 1957 году сборник 400 лучших задач,
опубликованных в журнале American Mathematical Monthly в 1918—1950 годах.
237
тво интеллектуального превосходства над автором в какой-то
мере вознаградят счастливца [читателя] за потерю времени и
беспокойство» (так считал сам писатель).
МАТЕМАТИК И ЛОГИК
Говорят, когда королева Виктория, прочитав «Алису» Кэр-
ролла, захотела ознакомиться с другими книгами именито-
го автора, ей принесли стопку... его математических трудов.
История вполне правдоподобная, если учесть, что Доджсон
посвятил жизнь математике и ее преподаванию, а первую на-
учную работу опубликовал еще в 1858 году. Она называлась
«Алгебраический разбор Пятой книги Евклида» и вышла под
псевдонимом Преподаватель колледжа. Все последующие на-
учные труды автор подписывал настоящим именем, не желая,
вероятно, отождествлять математика Доджсона с сочинителем
Кэрроллом.
Однако по иронии судьбы талантливый писатель Кэрролл
оказался лучшим математиком, чем профессор Доджсон (книги
Кэрролла, созданные в жанре занимательной математики, широ-
ко известны и переиздаются до сих пор), был куда удачливее в
своих начинаниях и получил мировое признание. Сегодня даже
в самых авторитетных энциклопедиях мы не найдем статьи об
ученом Ч. Л. Доджсоне. В лучшем случае в них указывается, что
Чарлз Доджсон — настоящее имя английского писателя Льюиса
Кэрролла, и имеется скромная приписка — «математика и логи-
ка», но никак не наоборот.
Доджсон не оставил сколь-нибудь заметного следа в ис-
тории математики (среди причин этого называют его скромное
математическое образование, недостаточное для того, чтобы
«двигать науку», переживавшую в XIX веке период бурного раз-
вития, и изолированность от широкого круга ученых). В наше
время о его научном наследии упоминают разве что биогра-
фы. В числе наиболее солидных работ автора обычно называ-
ют «Конспекты по плоской алгебраической геометрии» (1860),
«Элементарное руководство по теории детерминантов» (1867)
и книгу «Евклид и его современные соперники» (1879), кото-
рую сам Доджсон считал основным трудом своей жизни (в ней
критиковались авторы новых учебников геометрии, пришед-
ших на смену «Началам» Евклида). Признавая, что эти и другие
работы написаны необычно и включают любопытные задачи,
238
историки науки отмечают традици-
онность их содержания и элемен-
тарный уровень изложения.
Больший интерес представляют
сочинения Ч. Л. Доджсона по логи-
ке. Бытует мнение, что достижения
автора в области математической ло-
гики скорее опережали свое время,
чем отставали от него. Кто-то видит
в нем талантливого ученого-само-
учку, разработавшего собственную
систему логики, творившего в оди-
ночку и вынужденного изобретать
многое заново, и полагает, что на-
ходки Доджсона так и остались недо-
оцененными и невостребованными.
А возможно, непонятыми. Мало про-
читать его работы, в них нужно еще
разобраться. Как бы там ни было, в
современных учебниках по истории
логики не упоминаются ни сам автор,
ни его сочинения.
Между тем Доджсон одним из
первых разработал символический и
графический методы решения логических задач (на силлогизмы,
соритов). А некоторые из придуманных им задач до сих пор вос-
хищают не только любителей головоломок, но и специалистов в
области логики. К числу достижений Доджсона относят также
два парадокса — «Аллен, Браун и Карр» (1894) и «Что черепаха
сказала Ахиллу» (1895), опубликованных в солидном философ-
ском журнале Mind. На протяжении следующего столетия оба
парадокса не раз обсуждались на страницах этого издания.
Мы можем познакомиться с идеями Доджсона благодаря
книгам «Логическая игра» (1887) и «Символическая логика»
(1896), первая из которых является фактически упрощенным
вариантом второй. Кстати, автором обеих значится Льюис Кэр-
ролл. «Символическая логика» адресована прежде всего уча-
щимся. И не как учебник, а в качестве источника умственного
развлечения. На тот случай, если работа попадет в руки пре-
подавателей, Доджсон предусмотрительно включил в нее соот-
ветствующее «Приложение».
Обложка книги
«Логическая игра».
Издание 1991 г.
239
Понимая, сколь трудной может оказаться книга для юных
читателей, в обращении к ним автор признается, что стара-
тельно избегал в работе все трудные вопросы, недоступные
их пониманию. Кроме того, многое из содержания книги было
неоднократно испытано им в непосредственном общении
со знакомыми подростками, которые проявили живой инте-
рес к предмету. Для тех, кто захочет разобраться во всем сам,
Доджсон дает несколько советов и правил по работе с книгой.
И наконец, главный аргумент автора: овладев описанными в
«Символической логике» методами, читатель получит в свое
распоряжение не только увлекательное, но и полезное, резуль-
тативное интеллектуальное развлечение. «Методы эти поз-
волят вам обрести ясность мысли, способность находить собс-
твенное, оригинальное решение трудных задач, выработают у
вас привычку к систематическому мышлению и, что особенно
ценно, умение обнаруживать логические ошибки и находить
изъяны и пробелы тех, кто не пытался овладеть увлекательным
искусством логики. Попытайтесь. Вот все, о чем я прошу вас».
А материала для этой интереснейшей умственной забавы в
книге предостаточно.
ДИАГРАММЫ И ФИШКИ
Для решения логических задач Доджсон разработал метод
диаграмм, позволяющий графически представлять суждения
разного типа. Он напоминает метод Джона Венна (английского
логика, современника писателя, с которым тот был знаком), но
более нагляден и удобен в работе. Суть своего метода Доджсон
объясняет на примере двух-
буквенной диаграммы — как
указано на рис. 1, разбирая
сначала конкретные, а затем
абстрактные суждения.
Изобразим в виде квад-
рата класс всех рассматри-
ваемых в задаче предметов,
а буквами обозначим разные
признаки (видовые отличия),
позволяющие разбить его на
подклассы. Пусть, напри-
мер, выбран класс «книги»
Рис. 1
а
б
240
и указаны признаки: x — «старые»,
x
x — «новые», y — «английские»,
y
y — «иностранные». Тогда четыре
различных класса книг (назовем их
согласно выделенным признакам —
xy,yyxy,xyи
y x y ) можно распределить
в клетках диаграммы так (рис. 1).
Будем расставлять в клетках
фишки двух цветов: белые и чер-
ные. Если белая фишка окажется
внутри клетки, то это означает «клетка занята» (в выбранном
классе есть по крайней мере один предмет), а если на границе
между клетками, то — «по крайней мере одна клетка занята».
Черная фишка в клетке означает «клетка пуста» (в данном
классе нет ни одного предмета). Тогда каждое суждение (от-
ношения или существования) о книгах можно представить на
диаграмме, задав то или иное положение фишек. Например,
суждениям «Некоторые английские книги новые» и «Ни одна
старая книга не существует» соответствуют следующие диа-
граммы (рис. 2).
Такова элементарная задача, которую можно решать с по-
мощью двухбуквенной диаграммы. Доджсон рассматривает так-
же обратную задачу — на нахождение одного или нескольких
суждений, отвечающих заданной позиции фишек. Итак, про-
стейший вариант предлагаемой им логической игры состоит в
решении задач указанных типов. В нее могут играть двое. Для
этого одному человеку потребуется проверочная таблица с 28
возможными вариантами расположения фишек и перечнем от-
вечающих им высказываний, а другому — чистая диаграмма и
фишки двух цветов.
Прежде чем браться за более сложные задачи, необходи-
мо научиться работать с несколькими суждениями. С помощью
своего метода автор разъясняет юному читателю, как устроено
двойное суждение, какие суждения являются эквивалентными,
обратными, каким образом обратить суждение и т.д., тща-
тельно раскладывая «по полочкам» обильную пищу для ума.
Так, диаграмма на рис. 2, б соответствует суждению «Ни один
б
x
не существует», а если фишки рассматривать порознь, то двум
другим — «Ни один xy не существует» и «Ни один
y
xy не сущес-
твует». А значит, первое суждение — двойное и эквивалентно
двум последним.
Рис. 2
аб
241
ЗАДАЧИ НА СИЛЛОГИЗМЫ
При решении задач на силло-
гизмы (вывод умозаключений из
двух суждений-посылок, истинных
или ложных, возможно даже про-
тиворечащих здравому смыслу) ав-
тор использует уже трехбуквенные
диаграммы, построенные по анало-
гичным принципам. К разбитому на
четыре части квадрату добавляется
внутренний квадрат. Ему приписы-
вается признак m, а внешней полосе
—
признак m . В итоге получаются
восемь клеток, в которых размеща-
ются классы с признаками xym, xym
и т.д. (рис. 3).
В «Символической логике» под-
робно рассматриваются задачи двух
типов: 1) на вывод заключения из
двух суждений отношения, приня-
тых за истинные посылки, и 2) на
проверку правильности и полноты
заключения данного силлогизма.
В работе обсуждаются общие прави-
ла решения, а также приводится гра-
фическое представление каждой разобранной задачи.
Например, диаграммы на рис. 4 иллюстрируют решение
задачи на вывод умозаключения из суждений «Все кошки
знают французский язык» и «Некоторые цыплята — кошки»
(m — «кошки», x — «знающие французский язык»,
x
y — «цып-
y
лята»). Сначала суждения-посылки отображаются на трехбук-
венной диаграмме (рис. 4, а), а затем информация переносится
на двухбуквенную диаграмму (рис. 4, б), согласно описанным
в книге правилам. С нее и «считывается» правильный ответ:
«Некоторые цыплята знают французский язык».
ОТ ДИАГРАММ — К ФОРМУЛАМ
Метод индексов позволил Доджсону записывать суждения
и силлогизмы в виде кратких формул и упростить тем самым ре-
xy
m’
xy
m
xy’
m
x’y
m
x’ y’
m
xy’
m’
x’y
m’
x’ y’
m’
Рис. 3
Рис. 4
аб
242
шение многих логических задач. Этот метод лишен наглядности,
зато более подготовленному читателю позволит сразу, без пос-
троения диаграмм, выводить заключения из посылок, имеющих
такую же индексную форму. Одним словом, решение ряда логи-
ческих задач автор свел к оперированию несколькими получен-
ными им формулами.
В их записи Доджсон использовал собственные символы
для некоторых логических операций и типов высказываний, в
частности суждения вида «Некоторые xy существуют» и «Ни
y
один x не существует» он обозначает как
x
xy1 и x0 соответствен-
но, используя в качестве индексов 1 и 0. Так, запись xy1 † m0
означает «Некоторые xy существуют, и ни одно
y
m не сущест-
вует», а силлогизм о кошках и цыплятах сводится к формуле
m1x
0
†ym1Рxy1
.
Освоившим метод индексов Доджсон предлагает поупраж-
няться в решении соритов, которым посвящена отдельная глава
«Символической логики». Речь идет о задачах со следующей
общей формулировкой: «Даны три или более суждения отно-
шения. Приняв их за посылки, установить, какое заключение
(если таковое существует) из них следует». Разумеется, задачи
подобраны определенного типа и доступны тем, кто только на-
чинает изучать логику.
Решать сориты Доджсон рекомендует либо методом отде-
льных силлогизмов, либо методом подчеркивания (оба сводят-
ся к оперированию формулами). И замечает, что, придумывая
свои задачи, располагал посылки в случайном порядке, чтобы
дать читателям возможность поупражняться в построении це-
почек правильных силлогизмов, выбирая в качестве первого
звена любую посылку. Одним словом, верный своим принципам,
усложнил им и без того непростую задачу. А преданные чита-
тели по сей день продолжают ломать голову над тем, какой же
правильный вывод следует из диковинных посылок автора:
Ни один терьер не блуждает среди знаков Зодиака.
То, что не блуждает среди знаков Зодиака, не может быть
кометой.
Только у терьера хвост колечком...
243
ЛИТЕРАТУРА
1. Кэрролл Л. История с узелками / Пер. с англ. Ю. А. Данилова.
— 3-е изд., испр. — М.: Мир, 2000.
2. Кэрролл Л. Логическая игра / Пер. с англ. Ю. А. Данилова.
— М.: Наука, 1991.
3. Кэрролл Л. Приключения Алисы в Стране чудес. Сквозь
зеркало и что там увидела Алиса, или Алиса в Зазеркалье /
Пер. с англ. Н. М. Демуровой. — 2-е изд., стер. — М.: Наука,
1991.
4. Падни Д. Льюис Кэрролл и его мир. — М.: Радуга, 1982.
5. Демурова Н. М. Картинки и разговоры: Беседы о Льюисе
Кэрролле. — СПб.: Вита Нова, 2008.
244
ГЛАВА 3
Яков Перельман: штрихи к портрету
—
У вас поразительная способность замечать
мелочи, — сказал я.
—
Просто я понимаю их важность.
А. Конан Дойл. Знак четырех
23 сентября 1899 года в «Гродненских губернских ведомос-
тях» вышел очерк «По поводу ожидаемого огненного дож-
дя», подписанный двумя буквами — Я. П. За парой литер
скрывался ученик реального училища неполных
17 лет от роду, никому тогда неизвестный, а ныне
признанный классик жанра занимательной науки, автор
более тысячи научно-популярных статей и заметок, свы-
ше ста книг и брошюр и почти двух десятков
учебных пособий Яков Перельман.
ПРОБА ПЕРА
Внушительный писательский багаж Перельмана накопился
за многолетний стаж творческой работы на поприще популяри-
зации целого ряда наук. А началось все с выхода в свет упо-
мянутой публикации. За несколько месяцев до этого события
Якову попалась на глаза книжка некоего магистра Махина; в
ней утверждалось, что в ноябре 1899 года наступит конец света,
одним из предзнаменований которого станет «обильное выпа-
дение звезд», предсказанное на конец года учеными мужами.
Юноша обложился книгами по астрономии и вскоре смог найти
научное объяснение предстоящему небесному явлению. Позже
ему пришла в голову мысль написать научно-популярный очерк
о причинах звездопадов, истории их наблюдений и значении для
жителей Земли, а заодно развенчать в статье нелепые выдумки
«магистра». Единственным человеком, кому Яков рассказал об
этом, была мать, и она поддержала идею сына. Через два месяца
очерк был готов, выверен с научной точки зрения и отправлен в
редакцию газеты «Гродненские губернские ведомости».
Статья впечатляла эрудированностью автора и досто-
верностью материала, привлекала читателя доступностью и
245
живостью изложения, а потому вы-
звала интерес. В ней, в частности,
отмечалось, что звездопад — явле-
ние периодическое, а вызывающий
его метеорный поток имеет приме-
чательную особенность: раз в 33
года падающие звезды появляются
в таком количестве, что образуют
настоящий огненный дождь, еще в
древние времена наводивший ужас
на народные массы. Говорилось
также, что человечество наблюдает
его с 902 года, трижды в столетие,
и последние наблюдения астроно-
мов относятся к 1833 и 1866 годам.
Никаких гибельных последствий
для людей явление, протекающее в
верхних слоях атмосферы, не несет,
и «роскошным небесным фейервер-
ком» можно любоваться совершен-
но безопасно. Дабы избавить чита-
телей от последних сомнений, автор
указывал, в какое время и в какой
части неба предстоит удивительное
природное явление, и давал его под-
робное описание.
Статья редакции очень понравилась и была опубликована
спустя всего два месяца, а ее автору, господину Я. П., был вы-
плачен неплохой гонорар — 7 рублей 31 копейка серебром (для
сравнения: после смерти мужа его бывший работодатель пожа-
ловал вдове Перельман пенсию в размере 8 рублей в месяц).
Я. П. И ДРУГИЕ...
Но почему, собственно, Я. П.? Зачем начинающему авто-
ру вообще понадобился псевдоним? Казалось бы, чего уж тут
скромничать? На самом деле причина тому была иной. Нам
трудно в это поверить, но по существовавшим в те времена по-
рядкам учащимся и студентам запрещалось печататься в газе-
тах и журналах под угрозой исключения из учебного заведения.
Кстати, это объясняет, почему о подготовке статьи не знали даже
Начинающий писатель
Яков Перельман. Он же
Рельман, Сильвестров,
Цифиркин и Недымов
246
любимые школьные учителя Якова Е. Н. Бунимович и А. А. Маз-
лумов. Так что принятое юношей решение было вынужденным
и вполне оправданным.
Впоследствии многие статьи и очерки Перельман подпи-
сывал просто и лаконично — Я. П. Однако известны и другие
псевдонимы автора. Ни много ни мало — целых 11! Об одной
из причин их появления уже говорилось. С 1901 года студент
Петербургского Лесного института Яков Перельман начал пери-
одически публиковаться в журнале «Природа и люди» , а став в
1904 году ответственным секретарем редакции этого издания, с
завидной частотой печатал в нем свои материалы. За годы ра-
боты в редакции на страницах журнала появилось более пяти-
сот статей, очерков и заметок Я. И. Перельмана, основная часть
которых была посвящена самым разным вопросам из области
астрономии, физики, математики и техники. Писал он очерки и
на «лесные» сюжеты; их названия говорят сами за себя: «Орга-
ны чувств у растений», «Почему птицы летят правильным стро-
ем?», «Насекомые в янтаре», «Красота в природе». Так вот, из-
за такого обилия публикаций их автору пришлось использовать
несколько псевдонимов.
Упомянем лишь некоторые из них: П. Я-в, П. Рельман, Я. Лес-
ной, П. Сильвестров (от лат. silvestrum — лесной), Цифиркин и
даже... Я. Недымов. Первые два псевдонима, очевидно, про-
изводные от имени. Третий и четвертый содержат слово «лес-
ной», что, должно быть, указывает на название оконченного
Перельманом института и полученное когда-то звание лесово-
да I разряда. Весьма оригинальное применение этому званию,
если учесть, что Яков Исидорович не работал по профессии
(за исключением одного эпизода: в 1916—1917 годах он служил
в петроградском Особом совещании по топливу, где предложил
с целью экономии дефицитного топлива перевести стрелку ча-
сов на час вперед).
Что касается следующего псевдонима — Цифиркин, то он
прекрасно подходит автору «Занимательной арифметики» и
других книг, в которых тот мастерски оперирует сухими циф-
рами. Перельман знал, как можно заставить цифры говорить:
только путем неожиданного сравнения.
* Еженедельный научно-популярный журнал, выпускавшийся в 1889—1918 годах
известным российским издателем П. П. Сойкиным. В нем публиковались видные
ученые, путешественники и литераторы того времени.
247
Так, для того чтобы мы могли составить представление об ог-
ромности миллиарда, автор привел следующий наглядный при-
мер: «В одном кубометре содержится кубических миллиметров
ровно миллиард (1000 1000 1000). Попробуем подсчитать,
какой высоты получился бы столб, если бы все эти крошечные
миллиметровые кубики были поставлены один на другой. Итог
получается поразительный — 1000 км!» А дабы мы «прочувс-
твовали», что такое биллион, автор сделал такое сравнение:
«Волос, увеличенный по толщине в биллион раз, был бы раз в
8 шире земного шара, а муха при таком увеличении была бы в
70 раз толще Солнца!» Как видим, в своих примерах Перельман
умело опирался на уже имеющиеся у читателя представления о
том, что такое кубометр, миллиметровый куб, каков размер зем-
ного шара и т.д., и достигал поразительного эффекта, вызывая у
него неподдельное удивление.
Наконец, псевдоним Я. Недымов звучит, прямо скажем, не-
ожиданно и может слегка озадачить неподготовленного чита-
теля. Однако как раз причина его появления на свет не вызы-
вает сомнений: дело в том, что под псевдонимом Осип Дымов
работал в свое время известный беллетрист и драматург Осип
Перельман, старший брат Якова. Так вот, одно время они оба
публиковались в журнале «Природа и люди». Что ж, в чувстве
юмора Перельману-младшему, призывавшему не путать его с
автором О. Дымовым, не откажешь!
БЛАГОДАРНЫЙ УЧЕНИК
Но вернемся немного назад, к периоду ученичества Пере-
льмана, и вспомним о некоторых из тех, без чьего участия он не
стал бы тем самым «доктором занимательных наук», которого
все мы знаем. В училище и в институте любимыми педагогами
Якова Перельмана были преподаватели математики (Е. Н. Буни-
мович и А. С. Домогаров) и физики (А. А. Мазлумов и Д. А. Ла-
чинов), которые сумели привить ему интерес к точным наукам и
научили видеть необычное в обычном. Многое перенял у своих
учителей Перельман и всегда вспоминал их с благодарностью.
Е. Н. Бунимович получил приличное образование: окончил
Петербургский университет. Суть его педагогического метода
заключалась в том, чтобы сделать изложение математики ув-
лекательным и доступным, не нарушая его научной строгости.
Учитель стремился развивать в подопечных любознательность
248
и всячески побуждал их к самостоятельному мышлению. На
занятиях он часто привлекал примеры из истории науки, пред-
лагал задачи, требовавшие догадки или рассуждений, учил ре-
бят вычислять изящно. Многое из услышанного и увиденного
на уроках Бунимовича его талантливый ученик позже перенес
в свои книги по занимательной арифметике, алгебре и геомет-
рии, и уже не одно поколение педагогов успешно пользуется
этим багажом. Числовые загадки египетских пирамид, задача о
Диофанте, история вычисления числа , приемы быстрого счета,
квадратура круга, трисекция угла, простые способы измерения
недоступного расстояния...
Показательна следующая история, произошедшая на одном
из уроков Бунимовича. Однажды он вывел учеников на улицу и
предложил определить высоту подвеса уличного фонаря. Кто-
то из ребят откликнулся: «Это очень просто! Надо взять лестни-
цу и рулетку...» На что учитель воскликнул: «Браво! Стало быть,
и к Луне тоже будем приставлять стремянку?» Затем Бунимович
показал, как измерить высоту или удаленность предмета при по-
мощи двух картонных прямоугольников и спички. Практические
задачи, наблюдения и опыты, попытки обобщить полученные
результаты и дать им строгое научное объяснение... Так еще
в школьные годы закладывался фундамент глубоких знаний и
началось формирование будущего популяризатора науки Якова
Перельмана.
Упомянем еще об одном его
увлечении. Все свободное от заня-
тий время Яков посвящал чтению,
посещая две библиотеки, а также
читальню при книжном магазине,
куда одних только газет и журналов
доставлялось более 60 (здесь ему
однажды и попала в руки та самая
брошюра магистра Махина, которая
побудила подростка впервые взять-
ся за перо). Читал он много, а глав-
ное систематично. Не последнюю
роль в этом сыграла мать, педагог
по профессии: она составила об-
ширный список литературы, которую
необходимо было освоить в строгой
последовательности. Яков даже вел
Измерение высоты
дерева при помощи
книжки и карандаша.
Илл. из «Заниматель-
ной геометрии»
249
дневник «Прочитанное», куда заносил отзывы на понравившие-
ся ему книги и где цитировал последние. Стоит ли говорить, что
среди прочитанного было немало книг научного содержания?
Кстати говоря, в библиотеке Я. И. Перельмана за несколь-
ко десятилетий собралось более 10 тысяч томов на нескольких
языках (сам он знал их пять), в основном — труды классиков
науки, ее популяризаторов, беллетристов, комплекты десятков
журналов. Встречались и раритеты: «Арифметика» Магницкого,
первые русские учебники по математике и физике. Несколько
шкафов занимали одни только библиографические карточки и
вырезки из разных изданий.
В институте высшую математику и механику преподавал
другой любимый наставник Перельмана — молодой профессор
А. С. Домогаров. Это был настоящий знаток своего предмета и
прекрасный педагог. Глубокий анализ Домогаров ставил выше
механического умения оперировать математическим аппара-
том, а «элегантные вычисления» предпочитал каноническим
(нередко более громоздким) решениям. Математику профес-
сор считал «царицей всех наук», полагал, что она помогает
формированию у человека правильного мировоззрения, и был
убежден — со временем она приникнет во все отрасли знания.
Большое внимание на лекциях Домогаров уделял историческим
экскурсам и рассказам о жизни великих математиков.
Он поощрял студентов, которые не ограничивались в пос-
тижении его предмета одним учебником, а привлекали допол-
нительные источники, в том числе по истории науки. К таким
студентам относился и Яков Перельман. Профессор Домогаров
считал, что после института тому следует остаться на кафедре
математики. Однако к этому времени Перельман приобрел опре-
деленный авторский и редакторский опыт и всерьез думал о ка-
рьере журналиста, а потому отказался от лестного предложения,
как, впрочем, и от других заманчивых предложений (например,
от должности главного лесоустроителя в имениях миллионера
Кочубея, владельца огромных лесных угодий в Курской губер-
нии). И как показало время, сделал правильный выбор.
У ИСТОКОВ НОВЫХ ИЗДАНИЙ
Многие слышали, что Яков Исидорович как автор сотрудни-
чал в разных изданиях, среди которых «Наука и жизнь», «Знание
—
сила» и «Техника — молодежи». Менее известно, что Пере-
250
льману обязаны появлением на свет
сразу два издания: сборник расска-
зов и повестей «Мир приключений»
и журнал «В мастерской природы».
Сборник «Мир приключений»
выпускался в качестве приложения
к журналу «Природа и люди». По за-
думке Я. И. Перельмана его основу
составляли лучшие произведения за-
рубежных мастеров приключенчес-
кого, детективного и научно-фантас-
тического жанров, в частности таких
известных авторов, как Л. Буссенар,
А. Конан Дойл, Э. По и Г. Уэллс.
Работа Перельмана состояла в от-
боре подходящих сочинений и ре-
дактировании их переводов, кое-что
он переводил сам. Первый сборник
появился в 1910 году и имел огром-
ный успех, позволивший выходить
приложению еще почти десятилети-
епосле закрытия журнала, вплоть до
1928 года.
В 1919 году, вскоре после за-
крытия журнала «Природа и люди»,
по предложению Якова Исидоровича стал издаваться научно-
популярный журнал «В мастерской природы», а сам Перельман
вошел в состав редколлегии. Новое издание было призвано вос-
питывать у читателей любознательность и интерес к активному
изучению природы, руководить их научной самодеятельностью
в области естествознания, наполнять досуг полезными заняти-
ями и увлечениями. Среди его авторов были видные отечест-
венные ученые: К. Э. Циолковский, Н. А. Морозов, Н. А. Рынин,
А. Е. Ферсман и др. Более полутора сотен статей и заметок на-
писал для журнала сам Яков Исидорович, проработавший в нем
до 1929 года.
СКОЛЬКО ШКАЛИКОВ В ТРЕХ БОЧКАХ?
Скажем теперь несколько слов о другом интересном опы-
те Я. И. Перельмана. В начале 20-х годов прошлого века он
Обложка журнала
«В мастерской
природы»
251
написал серию брошюр, в которых пропагандировал декрет от
1918 года о введении в стране новой метрической системы мер
и весов и убеждал широкие массы в необходимости скорейшего
перехода на нее. На простых примерах и задачах автор пока-
зывал преимущества использования (очевидные нам, но не ма-
лограмотным выходцам из простого народа — современникам
Перельмана) новых единиц измерения веса, длины, объема —
килограмма, метра, литра и их производных перед устаревшими
— пудом, аршином, четвериком и т.д.
Так, десять мер емкости: гарнец, четверик, осьмина, четверть
(для сыпучих тел) и бочка, ведро, штоф, бутылка (винная и пив-
ная), чарка, шкалик (для жидких тел) заменялись всего двумя:
литром и миллилитром. Попробуйте-ка быстро подсчитать,
сколько шкаликов содержится, к примеру, в трех бочках, если:
1 бочка = 40 ведрам,
1 ведро = 10 штофам,
1 штоф = 2 пивным бутылкам,
1 пивная бутылка = 5 чаркам,
1 чарка = 2 шкаликам.
Другое дело, когда вычисления делаются в литрах: задача
решается в одно действие!
Опыт автора оказался успешным. Первая же брошюра серии
— «Новые и старые меры. Метрические меры в обиходной жиз-
ни, их преимущества. Простейшие приемы перевода в русские»
(1920) получила высокую оценку специалистов Главной палаты
мер и весов и выдержала пять изданий массовыми тиражами.
НА НИВЕ ПРОСВЕЩЕНИЯ
Вообще, начало 1920-х годов отмечено в жизни Перельмана
плодотворной научно-педагогической деятельностью и написа-
нием по заданию Наркомпроса РСФСР учебных пособий по ма-
тематике и физике для школы. Это был сложный период, когда
ощущалась острая нужда в квалифицированных кадрах, а новых
учебников, соответствующих времени и произошедшим в стра-
не переменам, почти не было.
В своих пособиях Я. И. Перельман, учитывая специфику
читательской аудитории, старался представить материал на-
глядно и доходчиво, сделать научные истины убедительными
и в то же время легко запоминающимися. Этих же принципов
252
он придерживался, препо-
давая в 1918—1923 годах
математику и физику в раз-
личных учебных заведени-
ях. Приобретенный педаго-
гический опыт вскоре очень
пригодился Перельману как
автору серии книг по «зани-
мательным наукам».
Среди его пособий
по математике выделим
«Новый задачник по гео-
метрии»,
первое издание
которого появилось в де-
кабре 1922 года, а второе,
значительно пополненное и
составившее основу после-
дующих изданий, — уже в сентябре 1923 года. Наряду с хорошо
известными учебными задачами в него включены задачи исто-
рические; на литературные сюжеты; посвященные любопытным
научным фактам и другие (позже многие из них благополучно
«перекочевали» в книги по занимательной математике). Глав-
ной особенностью пособия являлось обилие задач на примене-
ние геометрии в естествознании, технике и на практике. В час-
тности, в книге немало заданий, в которых требуется объяснить
принцип работы какого-то прибора либо то, как с его помощью
выполнить необходимые измерения или построения. Некото-
рые задачи и сегодня можно встретить на страницах школьных
учебников геометрии.
Немалый интерес представляют также задачи, сформулиро-
ванные в том виде, в каком они возникли в реальной жизни (сам
Перельман называл их реальными, не переведенными на услов-
ный язык математических схем). Многие задачи — на чисто жи-
тейские сюжеты, что делает их понятными и привлекательными
для читателя любого возраста и круга интересов. Вот несколько
примеров.
1. Квадратный пол измерили метром, но впоследствии об-
наружилось, что метр, которым пользовались при обмере, на
5
1 см короче истинного. Как нужно изменить полученную ранее
величину площади пола, чтобы результат был верен?
Какой самовар остынет быстрее?
253
2. Очищено 6 кг картофеля. Средний поперечник картофе-
лины 4 см, средняя толщина срезаемого слоя — 1 мм. Сколько
приблизительно весит очищенный картофель?
3. Какая жестянка вместительнее: в форме ящика высотой
20 см и основанием размером 8 10 см или же цилиндрическая
высотой 16 см и шириной 12 см?
4. Два полных самовара, большой и малый, одинаковой
формы, нагреты одинаково. Какой остынет быстрее?
5. Взрослый и ребенок, одинаково одетые, стоят на морозе.
Кому из них холоднее?
Остается добавить, что имеющий в книге предметный ука-
затель дает представление о том, откуда черпался материал и
каких вопросов он касался. Вот, к примеру, список объектов на
букву «Т» (упоминаются в 60 из 828 задач).
Телега
Тиски параллельные
Телескоп
Токарное дело
Тело человеческое
Толстой Лев
Температура
Точильный станок
Тень
Труба водопроводная
Термометр
Трубка стеклянная
Течение воды
Туман
В ЖАНРЕ ЗАНИМАТЕЛЬНОЙ НАУКИ
Первая книга Я. И. Перельмана — «Занимательная физи-
ка» вышла в свет сто лет назад, в далеком 1913 году и, как ни
странно, была издана не сразу. Работа над ней началась за пять
лет до того и длилась почти два года. Издатель П. П. Сойкин,
пролистав рукопись, поначалу усомнился: разве может быть за-
нимательной физика — наука строгая? Не замахнулся ли автор
на освященные веками школьные традиции? Не ополчатся ли
против него учителя физики и чиновники из министерства про-
свещения? Тем не менее Сойкин пообещал прочитать рукопись.
Но окончательное решение о публикации принял лишь два года
спустя.
Книга Перельмана быстро получила огромное читательское
признание и похвальные рецензии, книгопродавцы наперебой
заказывали допечатку тиража, а окрыленный успехом автор
взялся написать ее продолжение. Уже в 1916 году вышло вто-
рое издание «Занимательной физики» в двух частях. Этому тру-
254
ду, в каждом последующем издании
выходившему обновленным и допол-
ненным новыми примерами, было
уготовано завидное долголетие. Так
было положено начало целой се-
рии научно-популярных сочинений
в жанре занимательной науки. Они
не раз переиздавались, давно стали
классическими, по сути — визитной
карточкой писателя Я. И. Перель-
мана, и в полной мере раскрыли его
талант.
Для нас особый интерес пред-
ставляют четыре книги: «Занима-
тельная геометрия» (1925), «За-
нимательная арифметика» (1926),
«Занимательная математика» (1927)
и «Занимательная алгебра» (1928).
Ни одна из них не нуждается в пред-
ставлении. Отметим лишь, что все
книги построены по единому за-
мыслу и написаны в одном стиле.
Каждая книга — не только кладезь
полезных теоретических и практи-
ческих сведений, любопытных ис-
торических зарисовок и миниатюр,
математических развлечений, но и своеобразный сборник за-
нятных упражнений и задач-новелл на оригинальные сюжеты.
Сам Яков Исидорович подчеркивал, что его сочинения из серии
«Занимательная наука» — не учебные руководства, а книги для
вольного чтения. Их цель — собрать воедино и закрепить име-
ющиеся у читателей сведения по предмету и, что еще важнее,
внушить им охоту и воспитать вкус к занятию наукой матема-
тикой.
А пополнить досуг юных математиков, в том числе и тех, кто
успел уже почувствовать вкус к этой науке, были призваны дру-
гие перельмановские книги, создававшиеся в тот же период,
что и основные произведения. Среди них наиболее известны
«Живая математика. Математические рассказы и головоломки»
(1934), «Для юных математиков. Первая сотня головоломок»
(1925), «Для юных математиков. Вторая сотня головоломок»
Обложка 22-го
издания первой части
«Занимательной
физики»
255
(1925). По сути это сборники занимательных задач, вопросов,
опытов, игр и фокусов, как заимствованных из других сочи-
нений этого жанра, так и придуманных самим Перельманом.
Тематика задач очень разнообразна. Среди разделов книги
—
«Искусное разрезание и сшивание», «Вес и взвешивание»,
«Неожиданные подсчеты», «Геометрические силуэты» и др.
Многие задачи в свое время предлагались читателям журна-
лов «Природа и люди» и «В мастерской природы». По словам
автора, цель книг — дать материал для приятной умственной
гимнастики, для тренировки сообразительности и находчивос-
ти. Несмотря на то что некоторые задачи не назовешь чисто
математическими, они были включены в сборники как облада-
ющие хорошим потенциалом для развития логики (некоторые
головоломки, затруднительные положения), наблюдательнос-
ти (обманы зрения), воображения и геометрической интуиции
(игры со спичками, «Танграм», построение фигур одним рос-
черком).
ЗА РАБОТУ!
Популяризацией науки задолго до Перельмана занимались
многие авторы — ученые и литераторы; первые общедоступ-
ные сочинения такого рода появились еще в середине XVI века.
Но Яков Исидорович достиг в этом деле огромного мастерства,
сумев точно «нащупать» его секреты и выработать собственный
неповторимый стиль изложения. Когда однажды Перельмана
спросили о предшественниках, тот ответил: «Я многому научил-
ся у них, но пишу не так, как они».
к
А все потому, что автор сохранил в себе способность удив-
ляться и подмечать в обыденных вещах и явлениях то, чего не
видят (а если и видят, то проходят мимо, не останавливаясь)
большинство людей, и обладал редким даром увлекательно
рассказывать об этом другим. Яркое и образное изложение,
отточенный и ясный слог, неожиданные повороты мысли, про-
никновение в самую суть явлений, отсутствие каких бы то ни
было назиданий, доверительная беседа с уважаемым читателем
—
все это составляющие перельмановского стиля. Поставив
перед собой однажды очень трудную задачу — сделать строгое
научное изложение интересным, доступным и наглядным, Пе-
рельман прекрасно с ней справился, памятуя, должно быть, об
услышанном когда-то от Е. Н. Бунимовича высказывании Блеза
256
Паскаля: «Предмет математики настолько серьезен, что полез-
но, не упуская случая, сделать его немного занимательным».
Даже строгие критики сочинений Перельмана не находили в
них искажений научных фактов, зато признавали, что тот со-
здал новый вид учебного пособия — «доступного миллионам
людей, остроумного, доказательного, даже веселого и вместе с
тем научающего».
Яков Исидорович Перельман разработал собственную ме-
тодику, позволившую ему в ясной и занятной форме знакомить
читателя с интересными научными фактами. Некоторое пред-
ставление о его взглядах можно составить, прочитав авторские
предисловия к книгам. Более подробно он писал об этом в 1939
году в статье «Что такое занимательная наука», где также рас-
крыл секрет популярности и неувядаемости своих книг и дал
нам ключ к пониманию сути его творческого метода.
Характеризуя занимательную науку как одно из направле-
ний в популяризации знаний, Перельман отмечал, что развле-
кательный элемент в ней призван «забаву ставить на службу
обучению». Она не берется популяризировать все на свете, а
сосредоточивает внимание на основах науки и восполняет про-
белы школьного образования. Назначение занимательной на-
уки состоит в том, чтобы углубить и оживить уже имеющиеся
у читателя знания, научить сознательно распоряжаться ими и
побудить к разностороннему их применению.
Я. И. Перельман за работой
257
В сущности, специфика жанра занимательной науки, а так-
же работы самого автора-популяризатора отражена в ответах
Перельмана на следующие ключевые вопросы.
Какую цель преследует автор? Преодолеть косность ру-
тинного мышления и разбудить работу мысли читателя.
Каким образом? Подстрекая его любознательность и
обостряя интерес, ибо там, где присутствует интерес, широко
открыты врата для новых восприятий, новых знаний.
Что для этого нужно сделать? Для начала — привлечь
внимание к хорошо известным предметам. Затем показать их
в новом свете, раскрыть незнакомые стороны, продолжая при
этом удерживать внимание читателя (а это куда сложнее, чем
его завоевать!), иначе все усилия пропадут даром, как бы увле-
кательна ни была сама по себе излагаемая тема.
С помощью каких приемов это достигается? Их нако-
пилось немало: использование неожиданных сопоставлений;
привлечение примеров и задач из художественной литературы;
экскурсы в историю науки; использование математических игр,
фокусов, головоломок и других развлечений; обсуждение жи-
тейских ситуаций и др.
В книгах Перельмана любой читатель найдет массу инте-
ресного и полезного. И это не только нестареющие примеры и
задачи, но и более ценный багаж — оригинальные идеи, даю-
щие большой простор творчеству. Так что при желании каждый
может попробовать себя в роли автора.
В СТЕНАХ ДЗН
Рассказывая о Якове Исидоровиче, нельзя не упомянуть
еще об одном интересном его начинании, о замечательном де-
тище мастера — Доме занимательной науки, который открылся
в Ленинграде 15 октября 1935 года. Так назывался культурно-
просветительский центр, созданный по инициативе Перельмана
с целью пропаганды естественно-научных и технических зна-
ний. Фактически это была попытка «овеществления» занима-
тельной науки и создания ее своеобразной кунсткамеры. Про-
тотипом «Дома» послужил Павильон занимательной науки, в
котором размещалось всего около 20 экспонатов. Он распахнул
двери для посетителей еще летом 1934 года. Успех экспозиции
был велик: только за первый месяц здесь побывало более 30
тысяч человек. А уже осенью началось сооружение стендов и
258
изготовление оборудования для залов будущего Дома занима-
тельной науки.
В четырех его отделах — астрономии, математики, физики и
географии — располагалось несколько сотен различных экспо-
натов (многие — действующие), макетов, приборов, схем. Все
они погибли во время блокады, сохранились лишь описания
некоторых. Так вот, этот уникальный в своем роде музей очень
быстро стал любимым местом ленинградских школьников, а
книга отзывов была полна восторженных записей юных посе-
тителей (кстати, даже она служила местной достопримечатель-
ностью: когда кто-то садился за стол, на котором лежала книга,
та сама раскрывалась, а когда вставал — захлопывалась; чистая
физика, никаких фокусов!).
Во-первых, там ребят в увлекательной форме знакомили с
достижениями науки и техники, о которых упоминал Перельман.
Большинство выставленных в этом центре экспонатов словно
сошли со страниц его книг и обрели самостоятельную жизнь.
Более того, со многими экспонатами дети встречались в школе:
слышали о них от учителя или читали в учебнике. Вот только
почему-то учитель рассказывал иначе, а в книге было написано
совсем по-другому...
Во-вторых, в залах «Дома» не было табличек с предупреж-
дениями вроде «Руками не трогать!», напротив, надписи гласи-
ли: «Трогайте!» Как-то один из сотрудников заведения посето-
вал: «От рук школьников экспонаты часто выходят из строя!»
Перельман утешил его: «Это же очень хорошо, что ломают! Стало
быть, интерес к экспонату не угасает. Если перестанут ломать,
значит, он перестал впечатлять. Делайте экспонаты рукоупор-
ными, вот и все!»
В-третьих, экскурсовод часто задавал школьникам разные
замысловатые вопросы или предлагал самим объяснить какое-
то явление. А зал математики вообще был превращен в поле для
самостоятельной работы. В нем размещалось около 80 крупных
экспонатов, более 100 озадачивавших посетителей матема-
тических игр, головоломок, приборов и таблиц. Заглянем туда
хотя бы на пару минут.
СКОЛЬКО ВЕСИТ КИРПИЧ?
Входом в зал служила дверь, оформленная в виде переплета
знаменитой «Арифметики» Л. Магницкого. Ряд стендов был пос-
259
вящен известным математическим
задачам. Так, сразу за входной две-
рью располагалось красочное панно
с иллюстрацией к древнеиндусской
задаче о лотосе («Над озером тихим,
с полфута над водой высился лото-
са цвет...») — озеро, цветок в воде,
рыбак в лодке, его нашедший... Тут
же приводилось ее геометрическое
решение.
А какой удивительный потолок
был в этом зале! Темно-синего цвета,
весь усыпанный небольшими желты-
ми кружками, а означал он... один
миллион — наглядный и осязаемый,
состоящий из отдельных единиц
(кружков). Под потолком тянулся
гипсовый фриз из первых 707 цифр,
входящих в запись числа . Тут же на полу лежали разлинован-
ные листы картона. Школьники с завидным упорством бросали
на них иголки, подсчитывали количество пересечений иголок с
линиями на картоне, делили на него число бросков и получали
в частном число . Вот так интересно проходило знакомство со
знаменитой задачей Жоржа Бюффона.
По всему залу размещались «отгадчики»: после несложных
манипуляций они могли правильно назвать ваше имя, возраст
и даже фамилию любимого писателя. Были здесь и экспонаты
«с подвохом». Например, на столе стояли в равновесии весы:
на одной чаше лежал кирпич, а на другой — полкирпича и ки-
лограммовая гиря. Рядом красовалась табличка с надписью
«Кирпич весит килограмм и еще полкирпича. Сколько весит
кирпич?» Прочитав вопрос, многие посетители, не задумываясь,
восклицали: «Полтора килограмма!» И конечно, ошибались.
Была среди экспонатов и доска Гальтона — конструкция
для наглядной демонстрации закона Гаусса (нормального рас-
пределения). Она представляла собой ящик в прозрачном фут-
ляре, в заднюю стенку которого в шахматном порядке были вби-
ты гвоздики без шляпок, нижнюю часть делили вертикальные
рейки, а вверху крепилась воронка. В воронку тонкой струйкой
засыпалась горсть пшена. Опускаясь вниз, крупинки всю дорогу
хаотично прыгали за стеклом, укладываясь в итоге в удивитель-
Илл. к задаче
Бюффона из
«Занимательной
геометрии»
260
ном порядке: через их верхнюю границу пролегала симметрич-
ная колоколообразная кривая. Опыт повторяли снова и снова, и
всякий раз результат поражал посетителей.
ФОМА НЕВЕРУЮЩИЙ
Большое впечатление производили экспонаты, служившие
неожиданными иллюстрациями к числам-великанам из «Занима-
тельной арифметики». О потолке мы уже упоминали. А вот другое
оригинальное толкование миллиона. На одном из стендов висел
увеличенный листок календаря с датой 15 октября 1935 года,
надпись рядом гласила: «От начала нашей эры до открытия Дома
занимательной науки не прошло еще одного миллиона дней».
Самый «коварный» экспонат в «Доме» — и тот посвящался
миллиону. Это был механизм из зубчатых колес и шести цифер-
блатов со стрелками. Чтобы стрелка на последнем цифербла-
те совершила полный оборот, первую шестеренку требовалось
повернуть миллион раз. Табличка предупреждала: «Если у Вас
есть немного свободного времени, вращайте рукоятку. Пока Вы
совершите миллион оборотов, пройдет 11 суток. Имейте в виду,
что этот срок взят из расчета, что Вы будете вращать ее днем и
ночью, без сна, отдыха и перерыва на еду. Желаем успеха, убеж-
дайтесь, сколь велик миллион». И что вы думаете: нашелся Фома
неверующий, который задумал проверить это на себе и вертел
рукоятку шесть часов кряду! Узнав об этом, Перельман поинте-
ресовался: «Неужели
хотите докрутить до
конца?» Посетитель
махнул рукой: «И кто
только выдумал этот
аппарат! Решил на
пари попробовать,
авось удастся. Кручу,
кручу с самого утра,
а только до седьмой
тысячи
оборотов
добрался...»
Достопр имеча-
тельностей в зале
математики
были
десятки! Экспози-
Модель доски Гальтона
261
ция отлично справлялась со своей задачей: скучная, по мне-
нию многих, наука приобретала здесь все новых и новых по-
читателей. Кто бы отказался хоть раз побывать на экскурсии в
таком удивительном месте? Надо признать, даже современные
компьютерные технологии при всех возможностях и простоте в
использовании пока не в состоянии заменить живого и непос-
редственного общения ребят с математикой. Недаром создате-
ли современных «Домов науки» пошли по тому же пути, который
выбрал когда-то Перельман.
Однако закончим наш рассказ. Чем же занимался в Доме за-
нимательной науки сам Яков Исидорович? Прежде всего, он был
бессменным научным руководителем центра. Вскоре после от-
крытия его сотрудники стали «экспортировать» занимательную
науку: помогали устраивать аналогичные уголки в районных
Домах пионеров, читали лекции в школах, воинских частях и на
предприятиях. А еще в самом центре работало несколько де-
сятков кружков, регулярно проводились олимпиады, конкурсы
и диспуты. Дважды в неделю Перельман принимал посетителей,
приходивших за консультацией по самым разным вопросам. Кто
только не переступал порог его кабинета: рабочие, изобретате-
ли, врачи, учителя, военные, артисты... и, конечно, школьники!
При этом Яков Исидорович не изменил своей любимой
профессии: он был составителем и редактором серии научно-
популярных брошюр, выпускавшихся «Домом» и служивших до-
полнением основной экспозиции. В серию вошли, в частности,
давно ставшие библиографической редкостью книжки «Дваж-
ды два — пять! Математические софизмы» (1939), «Алгебра
на клетчатой бумаге» (1940), «Магические квадраты» (1940),
«Квадратура круга» (1941), «Быстрый счет. Тридцать простых
приемов устного счета» (1941). Всего было издано 30 брошюр
(карманного формата, по 10—16 страниц) тиражом от 30 до 200
тысяч каждая. Остается сказать, что за шесть лет существования
центр посетили более полумиллиона человек.
«УВАЖАЕМЫЙ ПРОФЕССОР ПЕРЕЛЬМАН!»
Наконец, добавим еще один штрих к портрету мастера, бес-
конечно преданного любимому делу и своему читателю. Как
известно, Яков Исидоровия Перельман не сделал никаких на-
учных открытий или изобретений, не имел каких-либо ученых
степеней и званий. Так ведь не в них писательское счастье, не
262
они приносят автору известность,
читательскую любовь и благодар-
ность! За высокий профессионализм
и верность Перельмана науке, за
умение дарить людям радость от об-
щения с ней этого человека уважали
и ценили и ученые мужи, и простые
рабочие.
Обычно в предисловии к своим
книгам Яков Исидорович указывал
домашний адрес, на который мог
прислать письмо любой читатель.
Ежемесячно Перельман получал де-
сятки писем с вопросами от людей
самого разного возраста и рода де-
ятельности, а нередко с приглашени-
ями выступить перед трудящимися
—
от коллективов различных пред-
приятий. И вот что интересно: обра-
щаясь к автору, читатели часто назы-
вали его не иначе как «профессор
Перельман». В их глазах тот давно
заслужил это почетное звание.
На какие
только
вопро-
сы не приходилось отвечать Пе-
рельману! Так,
обыкновенный
школьник
интересовался
при-
нципами реактивного движения и устройством ракеты
К. Э. Циолковского. Хирурги просили сообщить, какая марля
быстрее останавливает кровотечение из ран: с мелкой сеткой
или с крупной? Автор научного труда по гидравлике консульти-
ровался о причинах шумов в трубопроводе. А одна домохозяй-
ка непременно хотела знать, как правильно замазывать окна на
зиму — обе рамы или одну? И каждый считал Перельмана зна-
током в интересовавшем его деле и доверял ему как большому
специалисту. Для самого автора переписка служила важным
источником пополнения книг новыми материалами.
Случались и курьезы. Был период, когда Перельман полу-
чал массу писем от изобретателей «вечных двигателей». Один
особо настойчивый корреспондент буквально завалил его со-
общениями, что машина вот-вот заработает, не хватает самой
Мнимый
вечный двигатель,
устроенный
ради рекламы.
Илл. из «Заниматель-
ной физики»
263
малости — денег на шестеренки. Поначалу писатель терпели-
во разъяснял таким изобретателям их заблуждения. Но вскоре
поток писем стал настолько велик, что Перельман опубликовал
брошюру «Возможен ли вечный двигатель?» и стал рассылать
ее вместо ответов.
В «Занимательной физике» Яков Исидорович вспоминал,
как пресловутый механизм доставил ему однажды немало хло-
пот с собственными подопечными. Его ученики-рабочие были
так поражены выставленным в витрине часового магазина «веч-
ным двигателем», незаметно приводившимся в действие элект-
рическим током, что не внимали никаким доводам о невозмож-
ности такого устройства. «Выручило меня то, что в выходные
дни ток тогда не подавался. Зная это, я посоветовал слушателям
сходить к витрине в эти дни. Они последовали моему совету.
— Н у что, видели двигатель? — спросил я.
—
Нет, — ответили мне сконфуженно. — Его не видно:
прикрыт газетой...
Закон сохранения энергии вновь завоевал у них доверие и
более уже не утрачивал его».
Много писем Перельман получал из-за рубежа. С ними так-
же связано несколько забавных историй. Например, один швед-
ский пастор собрался написать «Занимательное богословие» и
интересовался, как лучше исполнить свой замысел. «Вот уж ни-
как не предполагал, что подам повод для насаждения мракобе-
сия», — рассказывал со смехом Перельман. А пастору ответил
так: «Разумеется, вы вольны сочинить свое “Занимательное бо-
гословие”. Но прошу Вас учесть, что я в своей работе придержи-
ваюсь исключительно научных фактов. Сумеете ли Вы, опираясь
только на Библию, а не на факты науки, написать свою книгу?»
Однажды на вопрос, не опасается ли он потока читатель-
ских писем, Яков Исидорович ответил: «Я жду этого потока!
Плохо, очень плохо, если он иссякнет. Стало быть, меня переста-
ли читать... Это было бы ужасно!» Время показало, что опасения
«профессора Перельмана» были совершенно напрасными. Его
читали, читают и еще долго будут читать.
264
ЛИТЕРАТУРА
1. Перельман Я. И. Веселые задачи. — М.: Астрель — АСТ —
Транзиткнига, 2005.
2. Перельман Я. И. Занимательная алгебра. — Д.: ВАП, 1994.
3. Перельман Я. И. Занимательная арифметика. — М.: Триада
— Литера, 1994.
4. Перельман Я. И. Новый задачник по геометрии. — 4 -е изд.
— М.-Л., ГосИздат, 1925.
5. Мишкевич Г. И. Доктор занимательных наук: Жизнь и
творчество Якова Исидоровича Перельмана. — М.: Знание,
1986.
265
ГЛАВА 4
Тот самый Мартин Гарднер
А кто-нибудь в детстве компьютер из спичечных ко-
робков для крестиков-ноликов делал? Или «кошачьи
колыбельки» из ниток плел? Помню, в пионерлагере
гарднеровский тессеракт вместо страшилки на
ночь рассказывал (с приукрашениями).
Из переписки на интернет-форуме
Когда-то он мечтал стать физиком, но не сложилось. Учился
на философском факультете, а выбрал карьеру журна-
листа. В науке был любителем и самоучкой, однако сумел
добиться признания у профессионалов. Его самая популярная
книга посвящена знаменитой литературной сказке. И все же
во всем мире его знают и ценят прежде всего как лучшего
популяризатора математики за последние полвека.
ИЭТОВСЕОНЕМ
«Книги Гарднера — бестселлеры»; «С жадностью читала его
книги в детстве и сейчас перечитываю своим детям с не мень-
шим удовольствием»; «Таких популяризаторов науки за всю ис-
торию человечества по пальцам одной руки пересчитать мож-
но»; «Этот человек для многих из нас сделал больше, чем все
школы и институты»; «Его книги во многом сформировали меня
и привели в профессию. Дали тот самый первотолчок»; «На-
стоящий педагог был. Все мое школьное детство прошло среди
книг Мартина Гарднера. Именно он заложил в меня те основы,
которые стали базой для дальнейшего понимания математики.
Я очень благодарен Вам, Учитель...»
Так откликнулись взрослые обитатели Рунета на известие о
кончине 22 мая 2010 года Мартина Гарднера, человека, имя ко-
торого знакомо миллионам людей по всему миру, на чьих книгах
выросло не одно поколение читателей. Патриарх современной
занимательной математики, определивший ее лицо, наполнив-
ший новым содержанием и максимально приблизивший к серь-
езной науке, — так отзывались о нем специалисты.
Кем же вы были, мистер Гарднер? Почему вашими книга-
ми зачитывались и обычные школьники, и маститые ученые?
266
За что вас так ценили и любите-
ли математики, и профессионалы?
В чем главный секрет вашего успеха?
РЕПОРТЕР, РЕДАКТОР, АВТОР...
Мартин Гарднер родился 21 ок-
тября 1914 года в Талсе (штат Окла-
хома, США). После школы поступил
в Чикагский университет, который
окончил в 1936 году со степенью ба-
калавра философии. Там же учился в
магистратуре, но обучение не завер-
шил и степень магистра не получил.
Да и цели такой не преследовал, а
помышлял о карьере писателя. Уже в
середине 1930-х годов Гарднер стал
редактором и автором студенческого
журнала и опубликовал свою первую
брошюру — о фокусах, интерес к ко-
торым проявлял с детства. Позже работал репортером газеты в
Талсе и сотрудником пресс-центра университета в Чикаго.
В годы Второй мировой войны Мартин служил во флоте пи-
сарем (секретарем на судне), а по окончании службы вернулся
к прежней работе. Тогда же Гарднер написал свой первый юмо-
ристический рассказ и продал его журналу «Эсквайр» (Esquire).
Поняв, что может побыть какое-то время свободным журналис-
том, он оставил работу в университете и пару лет жил на гонора-
ры за публикации в «Эсквайре». Здесь, в частности, был напеча-
тан «Нульсторонний профессор» (1947) — дебютный рассказ
Мартина Гарднера в жанре фантастики. В 1947 году Гарднер пе-
ребрался в Нью-Йорк и вскоре стал редактором и постоянным
автором нового детского журнала «Шалтай-Болтай» (Humpty
Dumpty Magazine). Он придумывал всякие забавы, сочинял ув-
лекательные истории и стихи для детей 5—8 лет и вскоре заво-
евал определенную популярность.
...И ВЕДУЩИЙ РАЗДЕЛА В НАУЧНОМ ЖУРНАЛЕ
Как-то на досуге Гарднер написал статью о флексагонах —
многоугольниках, сложенных из полосок бумаги и проявляющих
Мартин Гарднер
у памятника героям
Кэрролла в Нью-Йорке
267
необычные свойства при перегибании. Она попала в редакцию
Scientific American, старейшего авторитетного научно-популяр-
ного журнала в США , была опубликована в декабре 1956 года и
вызвала у читателей живой отклик.
«Как-то утром один из наших сотрудников, — сообщалось
в одном письме, — занимаясь от нечего делать складыванием
гексагексафлексагона, не заметил, как кончик его галстука по-
пал внутрь этой игрушки. При каждом последующем перегиба-
нии галстук несчастного все больше и больше втягивался внутрь
флексагона. После шестого перегибания исчез сам сотрудник.
Разумеется, мы тут же начали лихорадочно перегибать флекса-
гон, но так и не обнаружили никаких следов нашего товарища,
зато мы нашли шестнадцатую поверхность гексагексафлексаго-
на. Возникает вопрос: должна ли вдова исчезнувшего сотруд-
ника получить компенсацию за все время его отсутствия или же
мы можем с полным основанием сразу считать его умершим?
Ждем вашего совета».
Статья так понравилась издателям журнала, что Гарднеру,
весьма далекому в то время от науки, предложили стать посто-
янным ведущим раздела математических развлечений. Купив и
изучив несколько книг по занимательной математике, он напи-
сал вторую статью — об одном фокусе с отгадыванием чисел.
Ее оказалось достаточно для официального утверждения Гар-
днера в должности ведущего нового раздела. Последний по-
лучил название «Математические игры» (Mathematical Games;
примечательно, что его первые буквы совпали с инициалами
будущего автора — M. G.).
Так Мартин Гарднер стал вести постоянную колонку в
известном журнале и очень успешно делал это на протяжении
25 лет — до 1982 года, пока не «вышел в отставку». Однако тво-
рить и радовать читателей он не перестал и еще четверть века
продолжал активно заниматься литературной деятельностью
Scientific American («Ученый американец») издается с 1845 года. На его страницах
специалисты из разных областей науки делятся своими открытиями и теориями с
широкой публикой. Выходит не только в США, но и в других странах (в России под
названием «В мире науки»).
О ее содержании можно судить, в частности, по книгам «Математические голово-
ломки и развлечения», «Математические досуги», «Математические новеллы»; в них
вошли многие материалы из Scientific American за период с 1956 по 1973 год. Отде-
льные статьи публиковались также в журналах «Наука и жизнь», «Знание — сила»,
«Математика в школе», «Квант».
268
и периодически писать статьи и за-
метки. Кстати, последняя книга Гар-
днера вышла в свет, когда ему было
95 лет.
ЖУРНАЛИСТ,
МЫСЛИТЕЛЬ, КРИТИК
На вопрос о своей профессии
Гарднер отвечал: «Думаю, что я жур-
налист, пишущий по вопросам мате-
матики и естественных наук, а также
другим интересующим меня вопро-
сам». А волновало этого человека
многое. Прежде всего, проблемы фи-
лософии (которая, считал он, откры-
вает доступ ко всем наукам и знани-
ям) и религии. Затем — псевдонаука
и разоблачение всякого рода обман-
щиков и шарлатанов. Он много писал
о научных фикциях и домыслах, раз-
венчивал предрассудки, критиковал
магов, экстрасенсов и пр. Его первая
книга на эту тему — «Причуды и за-
блуждения во имя науки» (1957)
—
была очень популярна и за полвека не раз переиздавалась
на Западе. Долгое время Гарднер вел рубрику «Записки сторон-
него наблюдателя» в журнале Skeptical Inquirer, где печатались
результаты расследований различных паранормальных явле-
ний . Эти его статьи легли в основу нескольких книг.
Немалый интерес Мартин Гарднер проявлял к искусству и
литературе. Он известен, в частности, как комментатор произ-
ведений Г. К. Честертона и Л. Кэрролла. Его «Аннотированная
“Алиса”» (1960; дополненные издания — 1990 и 1999 годы)
давно признана классикой «кэрроллианы» и является самым из-
Сказки Л. Кэрролла
с биографическим,
литературным
и научным
комментариями
М. Гарднера.
Издание 1999 г.
* Расширенное издание книги «Во имя науки» (1952).
** Skeptical Inquirer («Исследователь-скептик») — официальное издание Комитета
по научным исследованиям паранормальных явлений (CSI), выходит с 1976 года.
Среди учредителей CSI были Мартин Гарднер, писатель-фантаст и популяризатор
науки Айзек Азимов, философ-гуманист Пол Куртц, иллюзионист и разоблачитель
разного рода мистификаций Джеймс Рэнди.
269
даваемым произведением писателя (надо заметить, Гарднер во-
обще имел особое отношение к творчеству Кэрролла: он не раз
привлекал примеры из его книг, рассказывал о самом авторе и
придуманных им играх и головоломках). Кроме того, перу Гард-
нера принадлежит ряд литературных эссе и критических статей.
А вот своими любимыми работами он считал фундаментальный
труд по философии «Почемучки философского писаки» (1983)
и отчасти биографический теологический роман «Полет Питера
Фромма» (1973).
На счету Мартина Гарднера около семи десятков книг и
несколько сотен статей и заметок в газетах и журналах. И это
не считая рассказов и эссе, рецензий и отзывов, предисловий
и комментариев к сочинениям других авторов. Все упомянутые
выше книги продолжают переиздаваться на Западе. Увы, Гард-
нер-мыслитель, борец с лженаукой, критик и беллетрист прак-
тически не знаком российскому читателю. Всего один сборник
его статей разных лет «“Когда ты была рыбкой, головастиком
—
я...” и другие размышления о всякой всячине» был издан в
России — в 2011 году.
КОРИФЕЙ ЗАНИМАТЕЛЬНОЙ МАТЕМАТИКИ
Зато Мартин Гарднер хорошо известен у нас как один из луч-
ших популяризаторов науки математики, автор многочисленных
задач, головоломок, игр и прочих развлечений, оригинальных
новелл и эссе, затрагивающих едва ли не все разделы совре-
менной математики. Все это можно найти в его замечательных
книгах , которых у нас вышло (в разных переводах) полтора де-
сятка. Наибольшей популярностью по сей день пользуется се-
рия книг издательства «Мир», среди них — «Этот правый, левый
мир» (1967), «Математические досуги» (1972), «Математичес-
кие новеллы» (1974), «Есть идея!» (1982), «Крестики-нолики»
(1988), «Машина времени» (1990), «От мозаик Пенроуза к на-
дежным шифрам» (1993).
Работы Гарднера — это своеобразный курс общедоступной
математики, показанной во всей ее красе и многообразии. Ка-
кие только проблемы не освещались автором! Благодаря ему
многие впервые узнали об игре «Жизнь» и сюрреальных числах
* По просьбе старого друга Дональда Кнута, известного математика и специалиста в
области программирования, все свои книги по математике и архив (статьи, рабочие
материалы и пр.) Гарднер передал Стэнфордскому университету.
270
Конуэя, познакомились с мозаиками Пенроуза и фракталами
Мандельброта, столкнулись с топологическими опытами и па-
радоксами комбинаторики и массой других интересных вещей.
«Тема, которая объединяет все книги моей серии, — говорил
М. Гарднер, — занимательная математика, то есть математика,
излагаемая в игровом духе».
И действительно, на страницах его книг серьезная наука
легко уживалась с развлечениями, а сложные идеи делались
доступными и «прозрачными». Ах этот гарднеровский стиль,
такой незамысловатый и неотразимо привлекательный, прони-
занный тонким юмором и изящной импровизацией! Ах этот без-
упречный слог и дар убеждения, эта парадоксальность мысли и
безграничная фантазия автора!
СЕКРЕТ УСПЕХА
Свой талант излагать сложные вещи простым и живым
языком Мартин Гарднер объяснял отсутствием у него глубоких
знаний. «Недостаточность» математического образования он
расценивал как преимущество: только лично пройдя через все
сложности постижения нового, он мог обойти их и в доступной
форме донести до непосвященного читателя главное. И делал
это мастерски, попутно прививая читателю интерес и любовь к
математике.
Добавим, что Гарднер постоянно занимался самообразова-
нием. Он не только изучил курс математики, но и пополнял, и
углублял свои познания, как только сталкивался с новой инте-
ресной для себя проблемой. А потому всегда был в курсе всего
того, что происходило в сфере его научных интересов. Как-то
Гарднера спросили, что его восхищает больше всего. «Больше
всего я восхищаюсь, когда учусь чему-то новому и значительно-
му, — ответил он. — И нет лучшего способа изучить что-либо,
чем начать писать об этом!»
Мартин Гарднер вел обширную картотеку. Поначалу он со-
бирал выписки и вырезки из журнальных статей, газетных со-
общений и книг («под ножницы» шли даже раритетные изда-
ния!), наклеивал их на картонные листы и хранил в коробках
для обуви. Позже он обзавелся металлическими ящиками, куда
помещал заметки и вырезки по темам. С годами накопленные
материалы заняли 20 больших шкафов. В распоряжении писа-
теля имелась также домашняя библиотека, содержавшая все
271
нужные для работы книги, что избавляло его от необходимости
посещать публичные библиотеки и позволяло экономить драго-
ценное время.
За каждой гарднеровской заметкой стояли упорный труд и
огромная исследовательская работа: тщательный сбор матери-
ала, его основательный анализ и полное усвоение и, наконец,
обстоятельное и доступное изложение. Одному из друзей писа-
тель признался, что подготовка колонки для Scientific American
оставляет ему для остальных занятий лишь несколько дней в
месяц. А ведь он непрерывно вел ее четверть века! Для Гардне-
ра с его широким кругом интересов этого было слишком мало,
именно нехватка времени для других дел послужила основной
причиной его ухода из журнала.
ПИСАТЕЛЬ И ЕГО ЧИТАТЕЛЬ
Многие публикации Мартина Гарднера — плод творческо-
го содружества писателя с огромной читательской аудиторией.
Он не только вел переписку с разными людьми, но и давал им
слово на страницах журнала и собственных книг. Среди его по-
мощников и соавторов были как именитые ученые-математики,
так и никому неизвестные любители, впервые приобщившиеся
к научному творчеству. Кстати, именно энтузиасты-любители
составляли основную армию почитателей Гарднера и, соревну-
ясь в решении предложенных им задач, порой выдавали более
Мартин Гарднер в кабинете
272
ценные и оригинальные результаты, нежели получали профес-
сионалы . Читатели задавали автору вопросы, высказывали по-
желания, предлагали для обсуждения новые темы. Тот отвечал,
вносил в статьи уточнения и дополнения, писал продолжение.
И попутно усовершенствовал с каждым новым изданием свои
книги.
Снова и снова Гарднер возбуждал у читателя интерес (бла-
го для этого располагал целым арсеналом средств), приглашал
к раскрытию тайны и самостоятельному исследованию. Более
того — старался научить его искусству оригинального, «не-
линейного» мышления, и не рассказом, а показом, пользуясь
проверенным временем способом: вовлекал читателя в игру и
делал соучастником.
Несмотря на огромную популярность Гарднер не был чело-
веком публичным, почти не бывал на конференциях и собраниях
единомышленников, нечасто давал интервью. Лишь единицам
поклонников его таланта посчастливилось видеть и слышать
Гарднера лично. Он предпочитал общаться с людьми через свои
публикации, любил тишину и уединение, самым приятным делом
для него было почитать книгу или постучать по клавишам пи-
шущей машинки. За счастье почитал способность зарабатывать
на жизнь работой, приносившей ему огромное удовольствие, и
шутил: «Я ничего не умею делать. Я все время развлекаюсь и
очень рад, что мне за эти развлечения еще и платят».
МАТЕМАТИКА И ИГРА
В деле популяризации математики Гарднер ставил игру едва
ли не на первое место. Да и саму математику отождествлял с ней.
В предисловии к «Крестикам-ноликам» он говорит: «Подобно
другим естественным наукам, математика представляет собой
игру, в которую мы играем с окружающим миром, со Вселенной.
Самые лучшие математики и самые хорошие преподаватели —
это, очевидно, люди, которые прекрасно разбираются в ее прави-
лах, а также получают удовольствие от самого процесса игры».
Далее автор вспоминает случай, произошедший с извест-
ным математиком и логиком, популяризатором этих наук Рэй-
мондом Смаллианом на занятии по геометрии. Желая подвес-
* Одна из историй такого рода (ее героиня — простая домохозяйка) описана в ста-
тье Д. Шаттшнайдер «Хвала любителям» из сборника «Математический цветник»
(М.: Мир, 1983), подготовленного к 65-летию Мартина Гарднера.
273
ти учеников к пониманию теоремы Пифагора, тот начертил на
доске прямоугольный треугольник и по квадрату на каждой
его стороне, а потом сказал: «Представьте, что эти квадра-
ты сделаны из кованого золота и вам предлагают взять себе
либо один большой квадрат, либо два маленьких. Что вы вы-
берите?» Мнения разделились примерно пополам, возникла
оживленная дискуссия. Каково же было удивление учеников,
когда он объяснил им, что никакой разницы нет! «Именно
это чувство радостного удивления и отличает всех великих
математиков, точно так же как лучших преподавателей мате-
матики отличает способность передать его своим ученикам,
—
писал Гарднер. — И не знаю лучшего способа осущест-
вить это, чем с помощью игр, загадок, парадоксов, фокусов
и прочих веселых атрибутов так называемой “занимательной
математики”».
Была и другая причина, в силу Гарднер высоко ценил игру.
Писатель интересовался природой математического творчества,
нестандартного мышления и внезапных озарений, приводящих
к открытиям, и особенно — процессом поиска оригинальных,
простых и красивых решений математических задач. В этом по-
иске именно игре он отводил важную психологическую роль.
В предисловии к книге «Есть идея!» читаем: «Тот, кто умеет на-
ходить нестандартные решения, при встрече с головоломкой
или трудной задачей испытывает радость, сравнимую с той,
которая знакома любителям бейсбола или шахмат. Дух игры,
по-видимому, предрасполагает к озарениям, позволяющим на-
ходить оригинальные решения».
ПЯТЬ ПРОСТЫХ, НО КАВЕРЗНЫХ ЗАДАЧ
Нет лучшего способа проверить это на себе, как поломать
голову над задачами автора. Вот несколько примеров. Все за-
дачи решаются в уме и имеют неожиданно легкие и изящные
решения, если отыскать к ним правильный подход. Немного во-
ображения, логики, нехитрых рассуждений — и ключ к реше-
нию будет найден!
Сколько серег?
Среди жителей одной африканской деревни 800 женщин,
3% из них носят по одной серьге, половина из оставшихся 97%
носит по две серьги, а другая половина вообще не носит серег.
274
Сколько серег можно насчитать в
ушах у всего женского населения де-
ревни?
Украденные гайки
Мистер Грин снял колесо с лоп-
нувшей шиной и хотел заменить его
запасным колесом. Он не заметил,
как белочка стащила у него четы-
ре гайки, которыми ступица колеса
крепится к оси. Обнаружив пропажу,
мистер Грин не растерялся и сумел
прикрепить к оси запасное колесо,
чтобы доехать до ближайшей стан-
ции техобслуживания. Как ему уда-
лось это сделать?
Тетраэдр из конверта
Как разрезать запечатанный
конверт так, чтобы из него можно
было сложить правильный тетраэдр?
Попробуйте найти самое простое ре-
шение, требующее всего одного раз-
резания.
Таксист и дама
Одна дама остановила такси и попросила отвезти ее домой.
По дороге она без умолку болтала и довела шофера до крайнего
исступления. «Прошу прощения, мадам, — сказал он. — Я не
слышу ни слова из того, что вы говорите. Я глух, а мой слуховой
аппарат, как назло, весь день не работает». Тогда дама смолкла.
Но когда она вышла у подъезда своего дома и машина скрылась
за углом, вдруг сообразила, что шофер солгал. Как она об этом
догадалась?
Кто же прав?
Внутри цилиндрической башни высотой 100 м ходит лифт, а
снаружи имеется винтовая лестница, образующая с вертикалью
постоянный угол 60°. Однажды мистер и миссис Пицца подня-
лись на лифте на смотровую площадку, расположенную на вер-
шине башни. Их сын Томато решил идти наверх пешком. Когда
Как укрепить колесо?
Илл. Д. Синклера
из «Классических
головоломок»
275
он добрался до смотровой площадки,
вид у него был не блестящий. «Не-
мудрено, что ты устал, сынок, — за-
метил мистер Пицца.
—
Ведь тебе
пришлось проделать путь в четыре
раза больший, чем нам, и все пеш-
ком». «Ты ошибаешься, папа, — отве-
тил Томато. — Я прошел лишь вдвое
больший путь, чем проехали вы». Так
кто же прав: отец или сын?
В ЗНАК БЛАГОДАРНОСТИ
Гарднеровские статьи и книги
пользовались неизменным успехом у
миллионов читателей по всему миру,
а сам автор сумел завоевать автори-
тет у профессионалов. Даже критики
смотрели на Гарднера как на серьез-
ного ученого, хотя он никогда им не
был (да и не стремился к этому), од-
нако был влюблен в науку и, по сути,
посвятил ей жизнь. Основную часть наград Гарднер получил от
научных обществ, а лучшие похвалы в свой адрес услышал от
ведущих математиков своего времени, со многими из которых не
только был знаком, но и поддерживал дружеские отношения.
Обладая исключительным интеллектом и широчайшей эру-
дицией, будучи одаренным и увлеченным человеком, Мартин
Гарднер развил в себе редкий талант заинтересовывать и вести
за собой других. Хотя Гарднер и был математиком-самоучкой,
его личность и деятельность оказали влияние на многих специ-
алистов. Нередко автор черпал темы для своих статей из науч-
ных публикаций. В свою очередь, его статьи не раз становились
стимулом к проведению серьезных исследований. Для одних
материалы Гарднера служили источником знаний, для других
— источником вдохновения. В знак уважения и признательнос-
ти группа ученых из США, Канады, Англии и ряда других стран
посвятила ему сборник статей по занимательной математике —
«Математический цветник» (1981).
Еще при жизни профессионалы по достоинству оценили
вклад Гарднера в дело популяризации науки. В частности, в
Эмблема конференции
Gatherings for Gardner
276
1987 году он был награжден премией Американского матема-
тического общества (American Mathematical Society) — союза
профессиональных математиков США. Также Гарднер являл-
ся почетным членом Математической ассоциации Америки
(Mathematical Association of America) — сообщества препода-
вателей математики колледжей и университетов США. Кстати,
эта организация до недавнего времени занималась переизда-
нием его книг по занимательной математике, написанных на ос-
нове статей в Scientific American, и даже выпустила в 2005 году
компакт-диск со всеми книгами знаменитой серии.
В 1993 году друзья Мартина Гарднера провели в его честь
конференцию Gatherings for Gardner, или G4G, в Атланте (штат
Джорджия, США). Она собрала любителей головоломок, загадок,
фокусов и прочих развлечений — всего того, что так занимало
всю жизнь Гарднера. Спустя три года мероприятие повторили
(кстати, оба раза на нем побывал и сам виновник события).
С тех пор конференция проводится на постоянной основе и ста-
ла доброй традицией. А ныне ее границы расширились. С 2010
года в память о выдающемся популяризаторе науки Мартине
Гарднере в день его рождения в разных уголках мира любите-
ли игр и головоломок устраивают себе настоящий праздник для
ума, и к нему может присоединиться каждый.
Постер «с секретом», извещающий о мероприятии
в честь Мартина Гарднера в 2011 г.
277
ДЕСЯТЬ ЗАРИСОВОК ИЗ ЖИЗНИ МАСТЕРА
Будущим исследователям только предстоит осмыслить фе-
номен Гарднера, этому человеку посвятят множество публика-
ций, но что бы о нем ни говорили и ни писали, у каждого из нас
все равно будет свой Мартин Гарднер — писатель, мыслитель,
критик, творец занимательной науки. А пока мы можем вспом-
нить еще несколько фактов и любопытных историй из биогра-
фии этого неординарного человека.
Хобби длиною в жизнь
Еще будучи ребенком, Мартин увлекся фокусами, с которы-
ми его познакомил отец. Студентом он иногда подрабатывал на
рождественские праздники, развлекая ловкими трюками поку-
пателей универмага. Гарднер был хорошо знаком с миром про-
фессиональных фокусников и иллюзионистов, многих знал лич-
но. На основе предоставленных ими материалов он подготовил
несколько брошюр о фокусах (первые публикации появились
еще в 1940-е годы). Однако на эту тему Гарднер писал не только
для специалистов. Много лет спустя он рассказал в своих кни-
гах по занимательной математике о трюках с числами, а также с
картами, монетами, кольцами и прочими предметами как о раз-
новидности головоломок и дал им научное обоснование.
Магия на всю жизнь стала хобби Мартина. В его доме хра-
нилась коллекция всяких хитроумных приспособлений и конс-
трукций для фокусов, а личную биб-
лиотеку украшала полная подборка
книг Л. Ф. Баума о волшебной Стране
Оз, которым он, кстати, посвятил не-
сколько публикаций. Гарднер с удо-
вольствием показывал трюки друзь-
ям и знакомым и с детским восторгом
воспринимал любой новый фокус,
ведь тот всегда таил в себе загадку!
История с флексагонами
Об этих фигурах Гарднер впервые
узнал от любителя магии Рояла Хита.
Как-то Мартин был у Хита в гостях, и
тот показал ему большой гексафлек-
сагон (6-угольный флексагон), сде-
Развернутый
гексафлексагон
278
ланный из ткани. Услышав, что головоломку еще до войны приду-
мала группа из Принстонского университета (в нее входили три
аспиранта — А. Стоун, Б. Таккермен, Р. Фейнман, будущий знаме-
нитый физик, и молодой преподаватель математики Д. У. Тьюки),
Гарднер решил написать о заинтересовавшей его «игрушке» ста-
тью и отправился в Принстон, где взял интервью у Тьюки.
Публикация в Scientific American имела огромный успех:
американцы поголовно увлеклись складыванием флексаго-
нов. Со временем головоломка стала популярна во всем мире, а
Гарднеру удалось собрать целую коллекцию гексафлексагонов
(ныне хранится в Стэнфорде).
Несостоявшийся физик
Когда-то Мартин мечтал стать физиком (любовь к точным
наукам ему привил учитель физики — М. Е. Херст, которому Гар-
днер впоследствии посвятил одну из своих книг) и даже решил
поступать в Калифорнийский технологический институт, но для
этого нужно было сначала получить... гуманитарное образо-
вание. Так он оказался в Чикагском
университете, где всерьез заинтере-
совался философией и распрощался
с планами стать физиком.
И все же давнее школьное ув-
лечение нашло свое отражение в
творчестве Гарднера: в его книгах
нередко можно встретить описание
всяких физических явлений и опы-
тов, не говоря уже о занимательных
задачах. На русском языке не раз из-
давались научно-популярные книги
автора «Теория относительности для
миллионов» (1965) и «Этот правый,
левый мир» (1967), посвященная
симметрии и асимметрии в природе,
искусстве и науке.
«Если бы я был
математиком...»
В одном интервью Гарднера
спросили, чем бы он занимался, если
бы стал профессиональным мате-
Обложка 2-го издания
книги «Этот правый,
левый мир»
279
матиком. Писатель признался: «Топология очаровывает меня,
потому что имеет дело с основополагающими свойствами про-
странства». О давнем интересе Гарднера к топологии говорит
тот факт, что ей был посвящен один из первых его рассказов —
«Нульсторонний профессор», в котором автор даже попытался
объяснить несведущему читателю, что же это за наука такая и
какие задачи в ней рассматриваются. Впоследствии Гарднер не
раз возвращался к этой теме в своих математических эссе и за-
метках. Наконец, из всех видов головоломок и фокусов больше
всего он любил топологические (трюки с платками, шнурами,
гибкими лентами и кольцами — вроде тех, что показывают в
цирке).
Любовь к Евклиду
Одно время семейство Гарднеров проживало на улице Евк-
лида (Euclid Avenue). Возможно, это лишь совпадение, в кото-
рое, однако, верится с трудом. Но уж точно не случайно одну из
своих героинь Гарднер назвал мисс Евклид. Кстати, она препо-
давала геометрию.
Вот вам пара вопросов из тех, что мисс Евклид предлагала
своим ученикам. Чему равен угол между диагоналями смежных
граней куба, выходящими из одной вершины? Как при помощи
линейки измерить длину диагонали куба? И помните: никаких
вычислений!
Фаллер, Грот и доктор Матрикс
Иногда Мартин Гарднер творил под вымышленными име-
нами. Одно из них — Урия Фаллер (намек на Ури Геллера, ко-
торого писатель считал мошенником). Под этим псевдонимом
были опубликованы книги «Признания экстрасенса» (1975) и
«Дальнейшие признания экстрасенса» (1980). В них раскрыва-
лись секреты необъяснимых «достижений», продемонстриро-
ванных обладателями сверхъестественных способностей. Име-
нем Джордж Грот оказалась подписана статья «Игра Гарднера
с Богом» (1983) в журнале The New York Review of Books («Нью-
Йоркский обзор книг») — критический отзыв на сочинение
«Почемучки философского писаки»... самого автора. Большой
он, однако, был оригинал!
Один из любимых персонажей Гарднера — остроумный
доктор Матрикс, знаменитый нумеролог, давний друг писателя.
На Западе Гарднера часто ассоциировали с его героем. Нашему
280
читателю доктор Матрикс знаком по
книге «От мозаик Пенроуза к надеж-
ным шифрам».
В жанре пародии.
И не только!
Среди работ Мартина Гарднера
по литературе особый интерес пред-
ставляют подробные комментарии
к произведениям знаменитых писа-
телей: его аннотированные «Алиса»
и «Охота на Снарка» (1960, 1962)
Л. Кэрролла, «Поэма о старом моря-
ке» (1965) С. Т. Кольриджа, «Неве-
дение отца Брауна» и «Человек, ко-
торый был четвергом» (1987, 1999)
Г. К. Честертона, «Волшебник из
Страны Оз» (2000) Л. Ф. Баума. Так-
же он подготовил к выпуску несколь-
ко сборников стихов, в том числе
«Ночь перед Рождеством» (1991) —
коллекцию продолжений, пародий и
подражаний одноименной балладе
К. К. Мура.
Кстати, о пародии. Гарднер все-
рьез интересовался этим жанром. Более того, работал в нем под
разными псевдонимами. Так, пародию на одну из собственных
книг он подписал именем Нитрам Рендраг. А несколько лет на-
зад вышла книга «Любимые поэтические пародии Мартина Гар-
днера». В ней собраны оригинальные стихотворные произве-
дения и искусные подражания им известных писателей. Среди
авторов значится и Арманд Т. Рингер, он же — неповторимый
Мартин Гарднер. Вы уже догадались, как родился каждый псев-
доним?
Мистификатор
В апреле 1975 года Scientific American напечатал ста-
тью Мартина Гарднера о шести наиболее важных открытиях
1974 года, не получивших, однако, широкой огласки по раз-
ным причинам. Например, в ней говорилось, что Леонардо да
Винчи, известный своими изобретениями, придумал туалет с
Обложка книги
«Любимые поэтичес-
кие пародии Мартина
Гарднера». 2002 г.
281
клапанным смывным устройством,
в подтверждение чему приводился
считавшийся утраченным рисунок
Леонардо из его работы по теоре-
тической и прикладной механике.
К тому же автор подробно освещал
«историю вопроса» и самой находки
и даже приводил ссылки на источни-
ки. Рассказ выглядел столь правдо-
подобно, что не вызвал сомнений у
читателей, никто не обратил внима-
ния ни на пародийные имена его ге-
роев, ни на абсурдность открытия, ни
на дату публикации. Вероятно, свою
роль сыграл и авторитет журнала.
На деле громкая сенсация ока-
залась... первоапрельской шуткой
Гарднера. О том, как родилась ее
идея, что в статье было вымыслом, а
что правдой, о других пяти «научных
открытиях» и главное о том, как от-
реагировали читатели на мистифи-
кацию автора, можно узнать из его
книги «Путешествие во времени».
Мы же приведем подлинный набро-
сок да Винчи — вероятный прототип
«рисунка Леонардо».
Самое удивительное, что и сегод-
ня находятся те, кто верит в историю
про смывной механизм Леонардо,
пересказывает ее в статьях о сантех-
нике и даже объясняет, почему столь
полезное изобретение мастера так и
не было воплощено в жизнь!
Знаменитые головоломщики
Как известно, Мартин Гарднер писал о таких признанных
мастерах головоломок, как Л. Кэрролл, С. Лойд, Г. Э. Дьюдени
и Р. М. Смаллиан. Первые трое — основоположники этого жан-
ра, а последний, современник Гарднера, прославился своими
логическими задачами и парадоксами, в частности на сюжеты
Тот самый
«рисунок Леонардо».
Автор — А. Равиелли
Леонардо да Винчи.
Размышляющий
старик и зарисовки
движения воды.
Ок. 1513 г.
282
из кэрролловской «Алисы». Из этих
четверых только двое имели непос-
редственное отношение к матема-
тике. Дьюдени был талантливым са-
моучкой, а Лойд всерьез занимался
шахматами и даже одно время вел
шахматную страничку в приложении
к журналу Scientific American.
Но мало кто знает, что благода-
ря Мартину Гарднеру состоялся еще
один замечательный головоломщик.
Речь идет об американском писате-
ле и любителе математики Стивене
Барре. Его интерес к математике, в
особенности к топологическим экс-
периментам, во многом стимулиро-
вался вниманием и поддержкой со
стороны Гарднера. Российскому чи-
тателю Барр известен по книге «Рос-
сыпи головоломок», первое издание
которой вышло еще в 1978 году.
Портреты в подарок
Узнаете? Это портреты Мартина
Гарднера. Первый — работа профес-
сора математики Фэн Чунг Грэхем,
знавшей Гарднера лично. Второй
—
подарок писателю от художника
Кена Ноултона. Мозаичный портрет
Гарднера сложен из 330 костяшек
домино. Согласитесь, мастерская ра-
бота!
Мартин Гарднер.
Худ. Ф. Ч. Грэхем.
Акварель. 2009 г.
Мартин Гарднер.
6 комплектов домино.
Худ. К. Ноултон. 1993 г.
283
ОТВЕТЫ
Сколько серег? 800 серег.
Украденные гайки. Мистер Грин снял по одной гайке с
каждого из трех оставшихся колес и прикрепил этими
гайками четвертое колесо. Три гайки способны достаточно
точно и надежно удерживать колесо во время поездки на
небольшое расстояние.
Тетраэдр из конверта. С двух сторон
конверта у одного и того же края
начертим равносторонний треугольник.
Разрежем конверт по пунктирной линии
AB, параллельной двум его краям. Правая
часть не нужна, а левую перегнем по
сторонам нарисованного треугольника
с каждой стороны конверта, затем
совместим точки А и В. Тетраэдр готов!
Таксист и дама. Таксист высадил даму у подъезда ее дома.
Если бы он был глухой, то не услышал бы, куда нужно
ехать.
Кто же прав? Прав Томато. Винтовую лестницу можно
«развернуть» в гипотенузу прямоугольного треугольника
(в данном случае, разрезав поверхность цилиндра по
винтовой линии, получим два равных прямоугольных
треугольника) с острым углом 30° и меньшим катетом 100 м.
У такого треугольника гипотенуза равна 200 м.
ЛИТЕРАТУРА
1. Гарднер М. Есть идея! / Пер. с англ. Ю. А. Данилова. — М.:
Мир, 1982.
2. Гарднер М. Классические головоломки / Пер. с англ. Н. А.
Чупеева. — М.: АСТ, Астрель, 2007.
3. Гарднер М. Математические головоломки и развлечения /
Пер. с англ. Ю. А. Данилова. — 2-е изд. испр. и доп. — М.:
Мир, 1999.
4. Гарднер М. Математические новеллы / Пер. с англ. Ю. А.
Данилова. — М.: Мир, 1974.
284
А
Ал-Караджи 208
ал-Хорезми 201
Аполлон из Тиана 88
Аполлоний Пергский 173, 174,
188
Аристарх Самосский 192, 193
Аристотель 176, 179, 193
Архимед 124, 176, 177
ас-Сиджизи 179
Б
Барр С. 282
Баутс Д. 83, 84
Баше де Мезириак 91, 92, 200,
206
Беллини Дж. 80
Бернулли Иоганн III 132, 133,
138
Браге Т. 181, 187
В
Ван Дейк А. 79
Ванцель П. 67
Вейль Г. 61
Веласкес Д. 182
Венн Д. 239
Верн Ж. 30
Виланский А. 125
Витрувий 69, 71
Г
Галилей Г. 177, 187
Гарднер М. 115, 127, 265—273,
275—282
Гаусс К. 67, 91
Д
Да Винчи (см. Леонардо
да Винчи)
Дали С. 82
Данилов Ю. 231
Де Кирико Дж. 81
Де Мей Жос 78
Дель Ферро С. 210
Джотто ди Бондоне 74
Доджсон Ч. 212—222, 226,
229—242
Дьюдени Г. 100, 112, 150, 152,
155, 159, 281, 282
Дюрер А. 26, 89
Е
Евклид 14, 66, 173, 198, 200
И
Игнатьев Е. И. 153
Иктин 70
К
Калликрат 70
Кардано Дж. 210
Кваренги Дж. 74
Кекуле Ф. 124
Кеплер И. 171, 181, 187—190
Кирхер А. 91
Коперник Н. 189, 193
Кордемский Б. 113
Кэрролл Л. 212, 213—216,
218—221, 224, 226, 231, 237,
269, 281
Л
Лагранж Ж. 196
Леонардо да Винчи 25, 26,
76—78, 177—179, 185, 187,
189, 280, 281
Леонардо Пизанский
(см. Фибоначчи)
Лойд С. 281, 282
М
Магницкий Л. 249, 258
Магритт Р. 81, 82
Менделеев Д. И. 124, 206
Менехм 173
Мосхопулос 88, 89
Н
Нарайана 108, 204
Непер Д. 169, 170
Ньютон И. 124, 188—190
П
Паскаль Б. 91, 256
Пачоли Л. 200
Перельман Я. И. 244—258,
260—263
Пифагор 64, 211
Птолемей Клавдий 189
Пуанкаре А. 50, 51, 55
Пушкин А. 48, 49
С
Смаллиан Р. 273, 281
Смит Г. 124
ИМЕННОЙ УКАЗАТЕЛЬ
285
Т
Талос 175
Тарталья Н. 176—178, 184,
210
Таунсед Ч. 159
Твен М. 217
Ф
Фальконе Э. 57
Ферма П. 91, 92
Феррари Л. 210
Фибоначчи 198—211
Франклин Б. 103, 105, 106
Френикль де Бесси 92
Ч
Честертон Г. 224
Ш
Шарден Ж. 79
Шиккард В. 171
Штейнгауз Г. 155—157
Штифель М. 91
Э
Эйлер Л. 91, 110, 200
Эратосфен Киренский 193, 194
Эшер М. 78
А
Аксиома о трех точках, задающих
плоскость 57—59
В
Вероятность
в лотерее 37, 39
случайного события 44
Высота светила 29
Г
Гипотеза Гильбрайта 134
Горизонт видимый 27
Д
Дальность видимого горизонта 28
Деление окружности на равные
части
приближенный метод 68
с помощью циркуля и линейки
65, 66
Доска Гальтона 259
З
Задача
Герона 160
Жоржа Бюффона 259
из папируса Ахмеса 205
на силлогизмы 241
на сориты 242
о пауке и мухе 150
о размножении кроликов
202—205
о разновесах 206, 207
Закон больших чисел 40
Закон Гаусса 259
Законы Кеплера 187—190
Затмение солнечное 19, 190—192
Золотое сечение 48, 53
И
Имп-арт 78
Иррадиация 69
К
Квадрант 176
Книга абака (Liber abaci) 198, 199,
201, 202
Конические сечения (коники)
гипербола 173—175
парабола 173—175
применение 174, 177, 180, 181, 188
эллипс 173—175, 188
Кривая нормального распределе-
ния 55
Курватура 71
Л
Латинский квадрат 110
Лотерея 35
М
Магический квадрат
ЛоШу 87
метод коня 89
метод террас 91
постоянная 87, 93
симметрический 97
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ*
* Для каждого объекта (понятия, утверждения) указаны страницы в книге, где дает-
ся его описание либо он рассматривается в связи с решением какой-то задачи.
совершенный 96
n-го порядка 87
Магические фигуры (именные)
квадрат Дюрера 89
квадрат Франклина 103
круг Франклина 105
куб Эйлера 110
прямоугольник Нарайаны 108
Математическое ожидание
выигрыша в лотерее 44
случайной величины 44
Машина Шиккарда 172
Метод диаграмм 239
Метод индексов 241
Метод триангуляции 195
Н
Нарушение пропорции 77, 79, 84
Невозможная фигура 76, 78, 79
О
Оптическая иллюзия
в архитектуре 69—75
в геометрии 23, 24
в живописи 25
в жизни 16
Оптическая поправка 69
Орнамент
примеры 64, 175
построение 65
Острота зрения 18
П
Палиндром
гипотеза о палиндромах 115
простой 116
фигуры из чисел 119—123
числовой 115
Палочки Непера 169, 170
Парабола безопасности 184
Параллакс
в астрономии 195
определение и свойства 20—22
применение на практике 32
Перспектива
в архитектуре 74
в геометрии 26
в живописи 25, 26
ошибки 76, 78, 84
Перспектограф 26
Поворотная симметрия 61
Подобие (применение) 19, 31, 53,
191, 193
Последовательность
рекуррентная (возвратная) 201,
204, 205
Фибоначчи (см. числа Фибоначчи)
Посох Якова 29
Предельный угол зрения 17, 54
Проценты 48, 49, 53
Р
Репдиджит 115, 143
Репьюнит 115, 134
С
Секстант 15
Случайная величина 44
Случайное событие 44
Сочетание 44
Способ решетки 167, 168
Т
Теодолит 15
Теория вероятностей (примене-
ние) 35—42, 55
Треугольник Паскаля 134
Три знаменитые задачи древности
66, 173
Триада Минехма (см. конические
сечения)
Тригонометрия (применение) 16,
32, 194, 195
У
Угловое расстояние 29
Угловой размер 14
Угол зрения 14
Ф
Фи (число Фидия) 53, 133
Флексагон 264
Ц
Циркуль
параболический 179, 184, 185
совершенный 179, 185
эллиптический 180
Ч
Числа
взаимно обращенные 117
Мерсенна простые 125
Смита 115, 125
Фибоначчи 115, 126
фигурные 115, 126
циклические 119
Э
Эклиптика 189
Энтазис 71
286
www.nkj.ru
• можно заказать по почте subscribe@nkj.ru
• приобрести в интернет-магазине www.nkj.ru/shop
• или в редакции по адресу: г. Москва, Мясницкая ул., д.24/7, стр. 1
в любой день недели с 9 до 18.30
научно-популярный журнал
КНИГИ СЕРИИ
«Библиотека журнала «Наука и жизнь»
Отпечатано в соответствии с предоставленными материалами
в ООО «ИПК Парето-Принт», г. Тверь, www.pareto-print.ru
Подписано в печать 12.12.2012.
Заказ 7331/12 Формат 60х90/16 Бумага офсетная
Печать офсетная
П еч.л. 20.5
Тираж 2000 экз.
Редакция журнала «Наука и жизнь»
Телефон: (495) 624-18-35, факс: (495) 625-05-90
101000, Москва, Мясницкая ул., д. 24/7, стр. 1
E-mail: mail@nkj.ru
www.nkj.ru
Н. М. Карпушина
ВНЕ ФОРМАТА
Занимательная математика:
гимнастика для ума или искусство удивлять?
Карпушина
Наталья Михайловна —
ру
преподаватель математики, редактор
журнала «Математика в школе», кандидат
педагогических наук; автор сборника
«Любимые книги глазами математика.
Занимательные задачи и познавательные
истории для взрослых и детей» (2011),
множества научно-популярных статей
и заметок в журналах «Наука и жизнь»,
«Математика в школе»,
«Математика для школьников».