Некоторые
физические
постоянные
Более полный список физических постоянных
с точностью до четвертой значащей цифры
приведен в приложении А
Скорость света с 3,00 • 108 м/с
Ускорение свободного падения g 9,8 м/с2
Гравитационная постоянная G 6,67 • 10й
Н м7кг2

Сооружения, изображенные на передней и задней сторонах
обложки, разделяет почти 4000 лет. Стоунхендж (на передней
стороне обложки книги) был построен в 1900 г. до н.э. в Англии
учеными того времени. Национальная лаборатория им. Э. Ферми
(на последней стороне обложки показано здание центральной
лаборатории) создана учеными США в 1970 г. н.э.
[Фотография Стоунхенджа выполнена Престоном Лионом, а
фотография лаборатории-фотографическим отделом Национальной
лаборатории им. Э. Ферми.]
Энрико Ферми, 1901-1954.

PHYSICS Jay Orear
Cornell University
MacmiUan Publishing Co., Inc.
New York
Collier Macmillan Publishers
London

ДЖ.ОРИР
ФИЗИКА
В 2-Х ТОМАХ
2
Перевод с английского
под редакцией
Е.М. ЛЕЙКИНА
МОСНВА
'МИР 1981

3
Орир Дж.
0-66 Физика: Пер. с англ.-М.: Мир, 1981.-288 с,
ил-Т. 2.
Новая книга известного американского физика Дж. Орира-это вводный курс
физики, -читаемый автором студентам Корнеллского университета. С большим
педагогическим мастерством автор в доступной форме излагает открытия последних
лет в физике. Учебник прекрасно иллюстрирован, в нем приводится большое число
примеров и упражнений. На русском языке книга выпускается в двух томах. В т. 2
вошли главы, посвященные электромагнитному излучению и волнам, оптике,
квантовой механике, атомной и ядерной физике, физике твердого тела, астрофизике и физике
элементарных частиц.
Предназначена для преподавателей и студентов, а также для всех, кто желает
пополнить свои знания в области физики.
°ЙЩГ¥165"81' Ч* * 1704020000 ББК 22.3
Редакция литературы по физике
Copyright © 1979, Jay Orear
© Перевод на русский язык, «Мир», 1981

ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ
И ВОЛНЫ
Эта и три последующие главы
посвящены электромагнитным волнам и оптике.
Настоящую главу мы начнем с
рассмотрения бегущих электромагнитных волн, а
затем перейдем к бегущим волнам на струне.
В табл. 18-2 представлена система
четырех уравнений, на которых основано
описание всех электрических явлений,
происходящих с постоянными токами,
покоящимися или равномерно движущимися
зарядами. Совокупность этих четырех уравнений
называется максвелловскими уравнениями
(для случая электростатики и
магнитостатики).
§ 1. Ток смещения
Перейдем теперь к рассмотрению более
общего случая меняющихся во времени
токов и движущихся с ускорением зарядов.
Приведенные в табл. 18-2 уравнения
следует видоизменить таким образом, чтобы
они учитывали изменение электрического
и магнитного полей. Эта задача
наполовину решена в предыдущей главе. Мы там
показали, что если магнитное поле
меняется, то, согласно закону Фарадея, возникает
электрическое поле:
§E-ds = -j®* гДе фв = |93-^А
-магнитный поток, охватываемый
замкнутым контуром. В следующем параграфе
мы увидим, что в случае меняющегося
электрического поля в правой части
уравнения, выражающего закон Ампера,
должен присутствовать аналогичный член
(1/с2) (d/dt) ФЕ. Добавляя этот член
соответственно к уравнениям II и IV в табл. 18-2,
мы получаем уравнения Максвелла,
записанные в наиболее общем виде. Именно
в этом виде они используются для
описания любых электромагнитных явлений.
Мы увидим далее в этой главе, что при
включении, выключении, а также любом
изменении тока во времени уравнения
Максвелла предсказывают испускание
электрического и магнитного полей,
распространяющихся в пространстве со
скоростью v = с.
На рис. 20-1 приведен пример, который
показывает, почему в закон Ампера нужно
добавить дополнительное выражение
(l/c2)(d/dt)<5>E. Конденсатор с пластинами
круглой формы заряжается током J,
который переносит заряды с левой пластины
на правую. Магнитное поле в точке
Р можно вычислить, проведя через нее
окружность радиусом г и
воспользовавшись законом Ампера. На рис. 20-1,а через
ограниченную этой окружностью
плоскость протекает ток I. Согласно закону
Ампера (18-2),
§ ».& = 47c-4-Jj-dA.
С с
По окружности
Из рис. 20-1,а следует, что Jj'dA = I.
Таким образом,
^•2кг = 4тс-?-/,
с2
^ = —^-— (в точке Р).
<г г
Однако закон Ампера должен выполняться
для любой поверхности, опирающейся на
ту же окружность, в частности и для такой
поверхности, как S' на рис. 20-1,6. Но
в этом случае мы имеем J j • dA = 0 (по-
S'
скольку через поверхность S' ток не прохо-

342 гл- 20- ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
(Г~)
Рис. 20-1. Через конденсатор с круглыми
пластинами течет ток /. а-электрическое поле
между пластинами конденсатора; ток / пересекает
плоскую поверхность 5, ограниченную
штриховой линией; б-изогнутая поверхность 5',
опирающаяся на ту же линию, не пересекается
током /.
;ит); тогда, согласно закону Ампера,
93. ds = 0, а это противоречит
предыдущему результату, справедливость которого
доказана. Опираясь на аналогичные
примеры, Максвелл в 1860 г. пришел к выводу
о том, что выражение для закона Ампера,
приведенное в гл. 18, некорректно в случае
переменного электрического поля. Вместе
с тем Максвелл обнаружил, что
некорректность записи можно устранить, добавив
к правой части уравнения выражение
(l/c2)l(dE/dt)-dA. В корректной форме
закон Ампера запишется следующим
образом:
§*.*-*** ll.dA + ± jf.4А.
Теперь мы покажем, что это уравнение
приводит к одному и тому же значению
поля & в точке Р, независимо от вида
поверхности интегрирования S или S'. Для
участка поверхности S', расположенного
между пластинами конденсатора,
E = 4nk0Q/Ac.
Таким образом, дифференцируя это
выражение по t, имеем
дЕ 4кк0 dQ 4пк0
dt ~ ~Аг dt~ ~ Аг
Интегрирование по поверхности S' дает
-J.
5Е
dt'
dA = 4nk0I,
и, следовательно, добавленное Максвеллом
выражение принимает вид
1
^L.dA = ±-{4nk0I),
dt с2
приравнивая которое к интегралу $*B-ds,
мы получаем правильный результат. Итак,
записанный Максвеллом в корректной
форме закон Ампера имеет вид
fe-A-^Jj-iA+^Jf.^. (20-2)
Первый член в правой части представляет
собой реальный ток, протекающий через
поверхность, ограниченную замкнутым
контуром. Второй член также можно
интерпретировать как ток. Максвелл назвал
его током смещения.
Пример 1. Определим поле 0£ как функцию
г между пластинами конденсатора (рис. 20-2).
Решение: Запишем уравнение (20-2) для контура,
показанного на рис. 20-2 штриховой линией:
.(bar)
а ! (дЕ\
(яг*), й9=__—
г дЕ
2ст dt
Подставляя вместо dE/dt его выражение (20-1),
находим
(20-1) * ' (*^\ ИЛ
2с2 V nR2 ) c2R2

§ 2. УРАВНЕНИЯ МАКСВЕЛЛА В ОБЩЕМ ВИДЕ 343
Рис. 20-2. Конденсатор с круглыми
параллельными пластинами, через который
«протекает» ток 1С. Силовые линии магнитного поля
88 представляют собой окружности с центром
на оси конденсатора.
Следует заметить, что этот результат совпадает
с выражением (18-4) для магнитного поля
внутри сплошного стержня радиусом R, по
которому течет ток 1С. Магнитное поле 0И то же, что
и в случае, когда зазор между пластинами
конденсатора заполнен проводником.
§ 2. Уравнения Максвелла в общем виде
Получив выражения для закона Фара-
дея и тока смещения в законе Ампера, мы
можем записать четыре уравнения
Максвелла в наиболее общем виде, как это
сделано в табл. 20-1. С помощью этих
уравнений можно найти поля Е и 93 для любых
точек пространства и любого момента
времени, если известны координаты и
скорости создающих поля зарядов. Таким
образом, известны поля ЕиФв месте
расположения каждой частицы и
соответственно силы, действующие на каждую из
частиц: F = qE + q\ х 23. В свою очередь
это позволяет вычислить координаты
и скорости взаимодействующих
заряженных частиц в будущем. Тем самым
электромагнитная теория в принципе
достигает поставленной цели, а именно
позволяет вычислять координаты и скорости
для любой системы взаимодействующих
заряженных частиц. Максвелл обнаружил
также, что излучаемое поле обладает
энергией и импульсом.
Напомним, что эти уравнения были
получены в гл. 16-19 (т. 1) с помощью закона
Кулона и специальной теории
относительности. Поэтому систему этих четырех
уравнений можно рассматривать как
релятивистскую форму записи закона Кулона.
Действительно, использование высшей
математики позволяет переписать все четыре
уравнения Максвелла в виде единого
тензорного уравнения.
Уравнения Максвелла
Таблица 20-1
Система единиц МКС с исполь- Система единиц МКС с
использованием к0 зованием е0 и ц0 (система СИ)
Система единиц СГС
(или гауссова)
I. Теорема Гаусса
§E-dA = 4Kk0$pdV
§E-dA = —$pdV
е0
И. Закон Фарадея
dt
§E-ds = -
dA
$E.</s= -
dt
•dA
III. Отсутствие магнитных зарядов
<j>©.</A = 0 |©.</A = 0
IV. Модифицированный закон Ампера
м
ЫА +
дЕ
§<B-ds = [i0$ydA +
dt
•dA
+ Цое0
~dT'dA
§E-dA=4n$pdV
$©.</А = 0
1
+ —
с
dt
-dA
}-dA +
дЕ
dt
dA

344 гл- 20- ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
Уравнения Максвелла справедливы как
в вакууме, так и в среде при условии, что
выражения для р и j включают
внутриатомные заряды и токи (а также магнитные
моменты). Эти уравнения справедливы для
поверхностей и контуров любой формы
и имеют единственное решение для Е и
93 при данном распределении заряда и
тока (р и j). Свойство единственности
позволяет отыскивать решение, угадывая его
вид. Подставляя затем это решение в
уравнения Максвелла, можно проверить, что
угаданное решение действительно
удовлетворяет им. Если выбранное
математическое выражение удовлетворяет уравнениям
Максвелла, каковы бы ни были
поверхности и контуры интегрирования, то оно
представляет собой искомое решение.
В следующем параграфе мы применим
теорему единственности в задаче о
плоском синусоидальном токе.
Максвелл не только сумел описать все
электрические явления с помощью четырех
Рис. 20-3. Шкала спектра электромагнитных
волн.
простых уравнений, но и предсказал такие
следствия этих уравнений, которые прежде
вряд ли связали бы со свойствами
электричества. В 1864 г. он показал, что ускоренно
движущийся заряд должен испускать
электрическое и магнитное поля,
распространяющиеся^ пространстве со скоростью
и = l/]Ai0£o = с- Эти электрическое и
магнитное поля излучения взаимно
перпендикулярны, а также перпендикулярны
направлению распространения волны. Он также
показал, что в излучаемой волне Е = сМ
(в системе единиц СГС Е = В) и что поле,
излучаемое ускоряющимся зарядом,
обладает энергией и импульсом. Если заряд
совершает колебания, то частота волны
совпадает с частотой его колебаний.
Максвелл предположил, что свет представляет
собой электромагнитные волны
определенного диапазона частот [(4-7) 1014 Гц] и что
должны существовать электромагнитные
волны с более высокими и более низкими
частотами во всем диапазоне значений. На
рис. 20-3 приведен спектр
электромагнитных волн.
Мы видим, что Максвелл не только
раскрыл великую тайну природы света, но
и предсказал, что колебания заряда в
резонансном контуре будут приводить к
испусканию электромагнитных волн, которые
можно обнаружить. Таким образом, он
предсказал возможность радиосвязи
задолго до того, как были открыты радиоволны.
Благодаря столь замечательному синтезу
разнообразных физических явлений эта
работа Максвелла считается величайшим
достижением классической физики.
Несомненно, Максвеллу удалось достичь в
электромагнетизме того же, что сделал
Ньютон в теории тяготения. Однако значение
работы Максвелла еще выше, поскольку
в большинстве физических явлений
преобладают электромагнитные, а не
гравитационные взаимодействия. Максвелл
разработал законченную релятивистскую
теорию электромагнитных взаимодействий, не
отдавая себе полного отчета в этом. По
существу он впервые создал теорию поля,
которая устраняет проблемы,
обусловленные взаимодействием на расстоянии.
§ 3. Электромагнитное излучение
Уже из простого рассмотрения
уравнений Максвелла видно, что электрическое
и магнитное поля могут существовать
и после того, как источники будут
выключены. Разумеется, покоящиеся заряды или
Частота, Гц
104 105 106 107 108 109 ю10 ю11 ю12 1013 10м ю15 ю16 ю17 ю18 ю19
-ТвЬ-Ми
W
Полоса Корот .
радио- кие Диа-
вещания волны ,ldiUH
Радиоволны-
кроволны-^
* ИК-
излуче!
ние m и
-УФ-
1злучение IРент-
1 генов-
ское-
излу-
Видимый чение
свет
Гамма-
излучение

§ 3. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ 345
постоянные токи создают постоянные поля
(поле Е описывается законом Кулона, а
поле ©-законом Ампера). Однако
переменный ток или движущийся с ускорением
заряд создают меняющееся магнитное
поле; иными словами, дЪ/dt ф 0. В этом
случае в соответствии с уравнением II (см.
табл. 20-1) электрическое поле возникает,
даже если повсюду р = 0. При этом
производная dE/dt отлична от нуля, вследствие
чего в соответствии с уравнением IV она
должна давать вклад в поле 93 далее после
выключения источника тока. Естественно,
что этот вклад в 93 имеет дЪ/dt Ф 0, в
результате чего появляется дополнительный
вклад в поле Е, и т.д. Это похоже на то,
как собака гоняется за собственным
хвостом. Если энергия электромагнитного
поля не расходуется, то процесс
продолжается бесконечно, а электромагнитное
возмущение, как мы вскоре увидим,
распространяется в пространстве со скоростью,
определяемой коэффициентами
пропорциональности в уравнениях Максвелла. Собака
беспрестанно гонится за своим хвостом,
и граница области, в которой она
кружится, раздвигается со скоростью и = с.
ИЗЛУЧЕНИЕ ПЛОСКОГО ТОКА
Рассмотрим поверхностный ток #,
текущий по бесконечной плоскости yz в
отрицательном направлении оси у (рис. 20-4).
•Р
Величина ^/-это поверхностный ток на
единицу длины (в данном случае вдоль
оси z). Даже в случае переменного тока
магнитное поле вблизи плоскости можно
вычислить, интегрируя по прямоугольному
контуру, охватывающему ток, как показано
на рис. 20-5. Пусть а-ширина, а
Ъ-высота прямоугольника. Нас интересует поле
93 на расстоянии а/ 2 от плоскости. Если
а стремится к нулю, то к нулю стремится
В
п
У
У
У
У
т
4*
dx
»
Вид сверху
Рис. 20-5. Вид сверху элемента тока,
изображенного на рис. 20-4. Контурные интегралы
берутся соответственно по часовой стрелке
вокруг тока и вокруг точки Р.
и площадь прямоугольника; тогда в
уравнении (20-2) можно пренебречь членом
J (дЕ/dt) -dA. Поскольку ток # направлен за
плоскость чертежа, обход контура
совершается по часовой стрелке. При этом
уравнение (20-2) запишется в виде
§
с2 с2 *°9
или
Рис. 20-4. Прямоугольный элемент бесконечной
пластинки с поверхностным током #'.
4тг/сл
Отсюда находим
2ti/cq
08 = —jr <& (поле вблизи плоского тока).
С (20-3)

346 ГЛ. 20. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
Это выражение совпадает с (18-5) для
случая постоянного тока #. Однако теперь
ток $ может изменяться во времени и
полученный результат справедлив лишь в
непосредственной близости от источника.
Поле в точке Р, расположенной на
некотором расстоянии от источника, можно
вычислить, интегрируя по двум взаимно
перпендикулярным прямоугольным
контурам, включающим точку Р (один из этих
контуров показан на рис. 20-5). Поскольку
математические выкладки в этом случае
довольно громоздки, мы вынесли их в
приложение к настоящей главе. Запишем лишь
окончательные результаты:
дЕ,
дх
L. —
дх
д2@2 1 д2
дх2
дг2
(волновое уравнение)
(20-5)
Равенство (20-5)-это знаменитое
дифференциальное уравнение, называемое
волновым уравнением. В § 6 мы изучим его
более подробно. Решение этого уравнения
представляет собой бегущую волну,
которая распространяется ют источника со
скоростью и = с. Уравнение (20-4) содержит
дополнительную информацию, которая
состоит в том, что величина сопутствующего
электрического поля равна Е = с£8 и что
поля Е и 93 взаимно перпендикулярны.
Эти решения подробно анализируются
в следующих двух параграфах.
§ 4. Излучение плоского
синусоидального тока
Предположим, что поверхностный ток на
рис. 20-4 имеет вид
/ = /0COS0)t,
причем ток #0 течет в направлении,
противоположном оси у. Такой
синусоидальный ток легко возбудить с помощью
электрической схемы, описанной в § 5
гл. 19. Определим 0B(x,t) для всех
значений х и L При малых х решение дается
выражением (20-3):
_ . ч 2пк0 ^
Sz(x,t) = —— </0COSG)t.
В случае больших значений х мы
попытаемся «угадать» решение, которое
совпадало бы при малых х с уже известным
решением, и покажем, что оно удовлетворяет
волновому уравнению (20-5). В этом случае
«угаданное» решение будет единственным
для рассматриваемого источника тока.
Такое решение, совпадающее при малых х
с уже известным решением, имеет
следующий вид:
■ М) =
2я/сп
-^/ocoscof г
(20-6)
Подставляя это решение в левую часть
уравнения (20-5), имеем
(20-4) *^ /«y&kjj^^
дх
>(«-7*)!
00
а в правой части
1 д2
с2 dt2
•=-г(-ю2)
2пка
#о cos (соГ х ) = -
от
Мы видим, что при использовании
выражения (20-6) обе части уравнения
совпадают. Кроме того, при х -► 0 это
выражение дает fflz = (27ifc0/c2)(/0cosa)t. Таким
образом, это решение удовлетворяет так
называемым граничным условиям и,
следовательно, является единственным
решением данной задачи.
В §6 мы покажем, что функция
cos со (t — х/с) описывает
монохроматическую волну, распространяющуюся вдоль
оси х со скоростью с, причем длина этой
волны X = 2тгс/со.
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ИЗЛУЧЕНИЯ
Теперь, зная ^, мы можем вычислить Е,
подставив решение для & в уравнение
(20-4):
lh-£[*ooMeH)]-

§ 4. ИЗЛУЧЕНИЕ ПЛОСКОГО СИНУСОИДАЛЬНОГО ТОКА 347
Рис. 20-6. Плоская электромагнитная волна,
распространяющаяся вправо со скоростью и =
= с. Волна испускается синусоидальным
поверхностным током </, текущим в плоскости yz.
, sin со t —
Еу = (o^0^sin(olt - — jdx =
= СУ&о cos со [t -
+ const.
Постоянная интегрирования равна нулю,
поскольку заряды, создающие постоянное
электрическое поле, отсутствуют.
Следовательно,
2тг/сп
/Ocoso) г
ev = cm
с \ с
(поле излучения). (20-7)
За положительное направление тока #0
выбрано направление, противоположное
оси у. Поэтому положительные знаки
величин Еу и @lz означают, что вблизи
источника поле Еу направлено противоположно
току $. Удобно запомнить это
следующим образом. Посмотрим, что происходит
на верхнем и нижнем «краях» элемента
плоского тока. Положительные заряды
будут накапливаться на нижнем «крае», а
отрицательные на верхнем. Силовые линии
поля идут снизу вверх, т.е.
противоположно направлению токаЧ
1] Если бы направление поля совпадало
с направлением тока, электрическое поле
совершало бы над зарядами положительную работу.
Энергия тогда передавалась бы от поля току,
и происходило бы поглощение, а не излучение
электромагнитной волны. В нашем случае
наоборот: направления поля и тока
противоположны, т.е. происходит излучение
электромагнитной волны-Прим. перев.
Мы показали, что Е = с& (в системе
единиц СГС Е = В), а также, что
электрическое и магнитное поля взаимно
перпендикулярны. (Чтобы продемонстрировать,
что Ez = 0, можно вычислить интеграл
$E-ds по прямоугольному контуру на
рис. 20-5.) Полученное решение для Е и
93 справедливо для любого контура
интегрирования и является единственным. На
рис. 20-6 показаны силовые линии
электрического и магнитного полей для случая
синусоидального плоского тока.
*Пример 2. Лампа-вспышка мощностью 3 Вт
дает пучок света квадратного сечения размером
10 х 10 см2 (рис. 20-7). Этот пучок падает на
полированную металлическую пластину и
отражается от нее. Отраженный свет мощностью
3 Вт излучается поверхностным током
$ = —COS ЮГ,
zo
где z0^- ширина пучка по оси z. Найдем ток /0
в амперах (10- полный ток, текущий по
поверхности пластины), Е0 в вольтах на метр и В0
в гауссах.
Решение: Пучок сечением 10 ~2 м2
распространяется ежесекундно на 3 • 108 м. Следовательно,
энергия пучка 3 Дж заключена в объеме, равном
3 • 106 м3. Тогда
dU
ЗДж
3•106 м3
= 10_6Дж/м3.
Из формулы (19-10) видно, что эта энергия
распределяется поровну между электрическим

348 ГЛ' 20- ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
Зеркало
Пучок
<Ы
Вследствие непрерывности электрического поля
излучения £изл в пластине на каждый электрон
проводимости действует сила еЕтл. Эта сила
обеспечивает передачу энергии от генератора
электронам проводимости. Пренебрегая
омическими потерями, вычислим мощность,
потребляемую от генератора участком пластины
площадью 1 м2.
Решение: Выделим участок пластины размером
y0z0. Электрическая мощность, приходящаяся на
единицу площади,
Р
~А
VI (iWo)(/zo)
Уо*о
Уо20
: ЕИЗЛ<У •
Используя выражение ^изл = (2пк0/с2)#,
получаем
Рис. 20-7. Световой пучок квадратного сечения,
падающий на зеркало справа и отражающийся
от него. Отраженный пучок создается
индуцированным током $.
и магнитным полями; поэтому
Поскольку Е2 = Eq/2, то
Е20 = 8я/с0-Ю-6Дж/м3,
Е0 = ]/8я(9.109).10-6В/м = 475 В/м,
®0 = ^ = TWT= 1'58'10"бТ'
откуда получаем
Бо = 1,5810-2Гс.
Используя формулу (20-7), находим
сЕ0 (3-108)(475)
2пк0 2тг(9-109)
А/м = 2,52 А/м
/о = *оЛ = (0Д м>(2'52 А/м) = °'252 А-
*Пример 3. Генератор переменного тока
подключен к большой металлической пластине
и создает в ней поверхностный ток ^ocoswt.
Р
~Л
2пкп
~ -^ИЗЛ^]
ИЗЛ^ИЗЛ'
Эта энергия излучается в виде электрического
и магнитного полей (см. § 1 гл. 21). Усредняя
полученное выражение по времени, находим,
что для бегущей электромагнитной волны
Мощность на единицу площади
4пкп
*Пример 4. Найдем эффективное сопротивление
участка пластины размером 1 х 1 м2 в
примере 3.
Решение:
V
R = — =
I
Еу0
$4
Поскольку у0 = z0 = 1 м, то
R =
2пкп
= 2п-
9-109
3-Ю8
-Ом = 188,5 Ом.
В реальных случаях ток, текущий по каждой
поверхности металлической пластины, равен #/2.
Поэтому эффективное сопротивление участка
каждой поверхности вдвое превышает
вычисленное нами значение, а именно
с е0с
= 377 Ом.
Эта величина называется импедансом
свободного пространства.

§ 5. НЕСИНУСОИДАЛЬНЫЙ ТОК
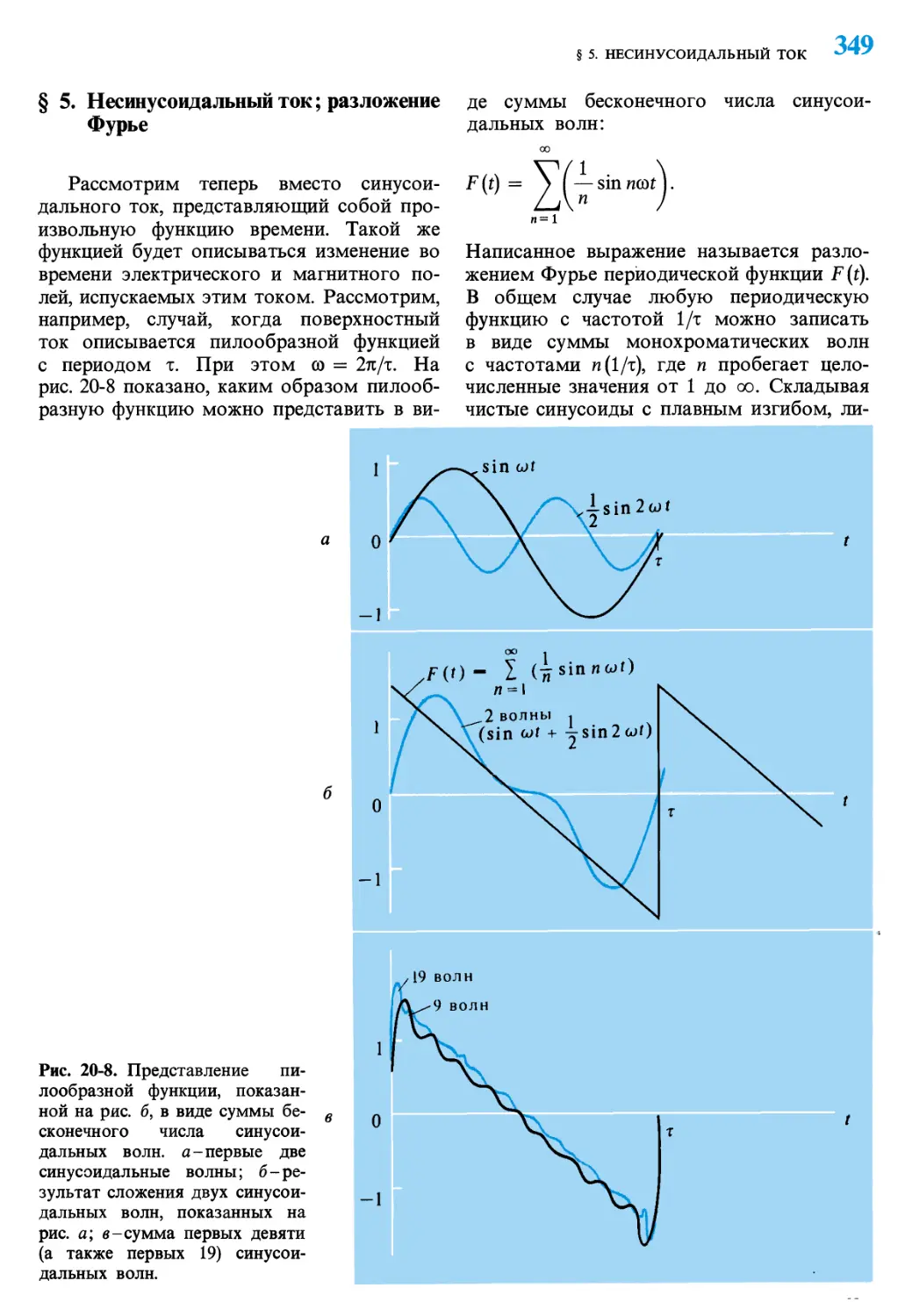
§ 5. Несинусоидальный ток; разложение
Фурье
Рассмотрим теперь вместо
синусоидального ток, представляющий собой
произвольную функцию времени. Такой же
функцией будет описываться изменение во
времени электрического и магнитного
полей, испускаемых этим током. Рассмотрим,
например, случай, когда поверхностный
ток описывается пилообразной функцией
с периодом т. При этом со = 2тг/т. На
рис. 20-8 показано, каким образом
пилообразную функцию можно представить в
виде суммы бесконечного числа
синусоидальных волн:
00
F(t) = \ { — sinncoM.
Написанное выражение называется
разложением Фурье периодической функции F(t).
В общем случае любую периодическую
функцию с частотой 1/т можно записать
в виде суммы монохроматических волн
с частотами и (1/т), где п пробегает
целочисленные значения от 1 до оо. Складывая
чистые синусоиды с плавным изгибом, ли-
,sin o)t
Рис. 20-8. Представление
пилообразной функции,
показанной на рис. б, в виде суммы
бесконечного числа
синусоидальных волн, а-первые две
синусоидальные волны;
б-результат сложения двух
синусоидальных волн, показанных на
рис. а; в-сумма первых девяти
(а также первых 19)
синусоидальных волн.

350 ГЛ. 20. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
шенные прямолинейных участков, можно
получить абсолютно прямые линии с
редкими изломами. Разумеется, чтобы
получить строго прямые линии с резкими
изломами, требуется бесконечное число
синусоид.
Для генерации пилообразной
электромагнитной волны поверхностный ток
должен иметь вид
-•o£(j*
sin пШ , где со =
2тг
Каждому члену этой суммы отвечает
решение, определяемое выражениями (20-6)
и (20-7). Поскольку уравнения Максвелла
линейны относительно Е9 & и ,/, полное
решение равно сумме отдельных решений.
<=0,
включение тока
j_
300
600
900
1200
1500 м
t = lxl0_t> с,
выключение тока
1-й импульс
и(=0
r = 3xl0"6c,
включение'тока
1-й импульс
Mi til I
1 I т i I Г1
u( = c)
r = 4xl0~6c,
выключение тока
2-й импульс
1-й импульс
/L
V
ц( = с)
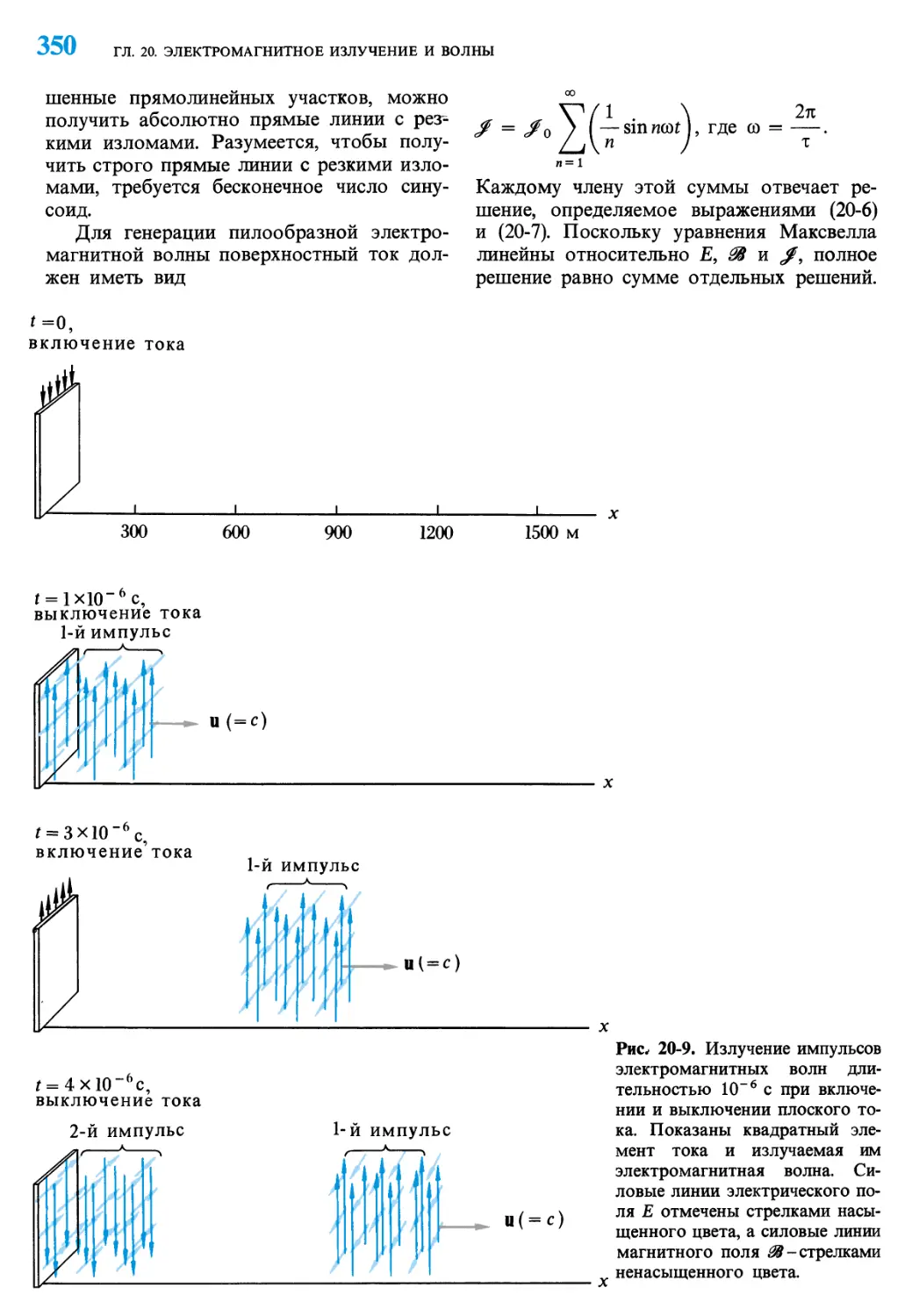
Рис* 20-9. Излучение импульсов
электромагнитных волн
длительностью 10"6 с при
включении и выключении плоского
тока. Показаны квадратный
элемент тока и излучаемая им
электромагнитная волна.
Силовые линии электрического
поля Е отмечены стрелками
насыщенного цвета, а силовые линии
магнитного поля ^-стрелками
. ненасыщенного цвета.

§ 6. БЕГУЩИЕ ВОЛНЫ
Это называется принципом суперпозиции.
Полное решение записывается в виде
е = cm =
Поскольку все волны, отвечающие
отдельным членам суммы, распространяются
вдоль оси х с одной и той же скоростью
и = с, они всегда будут суммироваться
так, как показано на рис. 20-8. Таким
образом, поле в любой точке пространства
повторяет пилообразную зависимость тока
от времени и лишь запаздывает
относительно него на время .х/с.
В общем случае любую периодическую
функцию, описывающую ток, можно
записать в виде1*
00
f = У Ansm(rmt + <ря).
Решение будет иметь ту же зависимость
от времени:
Е = с0В =
= —^~/ Ап*™\ n®[t - — J + ф„ .
В качестве последнего примера
рассмотрим поля, возникающие при резком
включении и выключении тока (т.е.
прямоугольные импульсы или волны). Этот
случай иллюстрируется на рис. 20-9. Даже
если источник генерирует единственный
импульс, мы можем воспользоваться
рассмотренным выше методом. В приложении
2 гл. 21 показано, что отдельный импульс
можно записать в виде бесконечной суммы
чисто монохроматических волн или
интеграла Фурье. Принцип суперпозиции по-
прежнему выполняется, и решение
сохраняет характерные особенности, а именно
Е = Ш, причем Е и 93 взаимно
перпендикулярны, перпендикулярны направлению
распространения и удаляются от источни-
1} При условии, что среднее значение
функции равно нулю -Прим. перев.
ка со скоростью и = с. Кроме того, в
любой точке пространства, например на оси
х, зависимость полей от времени такая же,
как и у источника, но с запаздыванием по
времени на величину х/с.
§ 6. Бегущие волны
Мы начнем рассмотрение с бегущих
волн на струне, поскольку их легче
наглядно представить, нежели электромагнитные
волны. Для бегущих волн любого
происхождения, включая и электромагнитные,
описываемые выражением (20-7),
определения и математический аппарат одни и те
же.
Если один из концов длинной
натянутой струны совершает гармонические
колебания, то по струне будет
распространяться синусоидальная волна (рис. 20-10). Мы
докажем, что скорость распространения
волны по струне определяется натяжением
Ти массой струны ц, приходящейся на
единицу ее длины. Скорость вертикального
движения точки на струне мы обозначим
через v, а скорость волны, т.е. скорость
перемещения гребня волны но струне,
обозначим через и.
Прежде всего убедимся в том, что
волна, бегущая со скоростью и в
положительном направлении оси х, описывается
выражением
У\х>4 = Уо^об—(х - ut)
{бегущая волна). (20-8)
Для любого фиксированного момента
времени t косинус в правой части записы-
(2%х \
— h ф ), где
ф-некоторый угол. Заметим, что при увеличении
х на X фаза 2пх/Х + ф возрастает на 2тг.
Следовательно, в выражении (20-8) X
представляет собой длину волны (волна
повторяется через промежуток X). Можно
показать, что величина и-это скорость волны,
соответствующая скорости перемещения ее
гребня. Когда в выражении (20-8) фаза
[(2тгД)(х — ut)~\ обращается в нуль, у(х91)
достигает максимума, т.е. мы имеем
гребень волны (гребень 1 на рис. 20-10).
Условие того, чтобы волна имела в данной точ-

Гребень 1
Гребень 2
Гребень 1
Гребень 2
Гребень 1 т Гребень 2
Гребень 1
Гребень 1
Рис. 20-10. Бегущая по струне
волна. Смещение струны в
точке х = 0 меняется по закону
У = Уоcos ©*• Показаны
последовательные состояния струны
через интервалы в 1/8 периода.
Гребень волны сдвигается
вправо на расстояние (5/8) А,.

§ 6. БЕГУЩИЕ ВОЛНЫ 353
ке гребень, записывается в виде
2тг
—(х - т) = 0.
В этом случае
х = ut или и = x/t,
где х-положение гребня в момент
времени t. По определению x/t характеризует
скорость гребня, и она, как только что мы
показали, равна и.
Скорость гребня волны и есть скорость
распространения волны, или просто
скорость волны Ч
Теперь, когда мы убедились, что
выражение (20-8) описывает синусоидальную
волну, распространяющуюся со скоростью и,
это выражение можно переписать, введя
величину со. Заметим прежде всего, что
где
Xf = и (скорость волны),
(20-9)
т.е. длина волны, умноженная на частоту,
равна скорости волны. Действительно,
произведение длины волны (X) на число
колебаний в секунду (/) есть путь,
проходимый волной за одну секунду, т.е. и.
Перепишем теперь соотношение (20-9)
следующим образом:
X X
—(2nf) = и или со = и.
2ttv "" 2тг
2тг
к = -— (волновое число),
X
со
— = и (скорость волны).
(20-10)
(20-11)
Следует заметить, что для любого
фиксированного значения х у = у0 cos (cot — ф),
где ф-некоторый угол. Это значит, что
каждая точка струны совершает в
поперечном направлении простые гармонические
колебания.
Пример 5. Бегущая волна имеет вид у =
= cos(i4x + Bt). Какова скорость волны?
Решение: Сравнивая вид волны с выражением
(20-8), мы можем написать А = 2п/Х и В =
= —2пи/Х. Следовательно, В/А= —и, т. е.
скорость волны равна — В/А. Если А и В
положительны, то волна распространяется в
отрицательном направлении оси х.
Теперь мы можем выразить скорость
волны на струне через Т и ц. Рассмотрим
элемент струны Ах, концы которого
образуют малые углы осх и ос2 с осью
х (рис. 20-11). Под малыми мы понимаем
Заменяя в выражении (20-8) скорость и на
(Х,/2я)со, получаем
у (х, t) = у0 cos I —— X — СОМ =
2тг
= уоcos I ®t ^~х
Обычно используется обозначение к =
= 2п/Х. Величину к называют волновым
числом. Тогда последнее выражение
можно записать в виде
у(х,г) = у0 cos (cot — /ос),
1J Ее называют также фазовой скоростью.-
Прим. перев.
*s&T
^^ а2
т
Рис. 20-11. Силы, действующие на элемент
струны Ах.
углы, для которых справедливо
приближенное равенство sin а # а # ду/дх.
Результирующая сила, действующая на элемент
струны в вертикальном направлении, равна
^Рез = Т&1 — Та2 • Эта сила равна произве-

ГЛ. 20. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
дению массы элемента струны \х(Ах) на его
вертикальное ускорение д2у/дг. (Запись
dy/dt означает, что при
дифференцировании по времени независимая переменная
х остается постоянной.) Таким образом,
Fpe3 = Тс*!
Та2 = (цАх)^,
Да д2у
T~Kx~ = [i~dt2~9
да _ ц д2у
дх~ Т dt2 '
Подставив а = ду/дх в левую часть
последнего выражения, получим
д2у _ \i д2у
дх2 " Т dt2
(волновое уравнение для
струны), (20-12)
Это уравнение известно под названием
волнового уравнения для струны. Скорость
волны можно определить, подставив
в (20-12) соответствующие производные
функции у(х, t\ определяемой выражением
(20-8):
д2у (2%
= -у°{-х
дх
д2у
~дЧ2~
(2%
cos——(х - ut), (20-13)
2тг
= - Уо[-^~и) cos—(х - ut). (20-14)
Подставим в левую часть уравнения (20-12)
выражение (20-13), а в правую
часть-выражение (20-14). Тогда
[I / 2ки ч 2
откуда находим
и =
— (скорость волны на струне).
* (20-15)
Мы не только вывели формулу для
скорости волны, но и показали, что выражение
(20-8) для бегущей волны является
решением уравнения (20-12). Тем самым мы
доказали, что монохроматическая волна
распространяется по струне со скоростью, не
зависящей от амплитуды и частоты волны.
Пример 6. На струне гитары длиной 30 см
и массой 100 г укладывается ровно половина
длины волны. Каким должно быть натяжение
струны, настроенной на частоту 262 Гц (нота
«до» первой октавы)?
Решение: Из формулы (20-15) находим Т:
Т= [ш2,
где ц = (0,1 кг)/(0,3 м) = 0,333 кг/м. Скорость
и можно определить из соотношения и = Xf:
и = (0,6 м) (262 Гц) = 157,2 м/с.
Таким образом,
Т= (0,333 кг/м) (157,2 м/с)2 = 8,2-103Н.
Это довольно сильное натяжение для такой
легкой струны. Поэтому струны музыкальных
инструментов обычно изготавливают из прочных
металлических сплавов.
Подставив в уравнение (20-12) вместо
[i/T отношение 1/м2, получим
д2у 1 д2у
дх2
и2 dt2
(волновое уравнение).
(2046)
Следует заметить, что по виду это
уравнение совпадает с (20-5) с точностью до
замены @tz на, у, а, с на и. Уравнение (20-16)
известно как волновое уравнение, и оно
справедливо для всех видов бегущих волн:
электромагнитных, звуковых, крутильных,
волн в жидкости, волн,
распространяющихся по стержням, по струнам и
пружинам. Мы уже показали, что выражение
2я / х
у = у0 cos —— (х — ut) = у0 cos со it
(20-17)
является решением волнового уравнения
и справедливо при любых значениях со.
Электрическое поле
йу =
2пк0
ч cos со it —
испускается синусоидальным
поверхностным током с амплитудой #0. Оно
представляет собой бегущую волну, которая
распространяется вдоль оси х со
скоростью и — с; длина этой волны X = 2тгс/со.

§ 7. ПЕРЕНОС ЭНЕРГИИ ВОЛНАМИ
Изложенная в этом и следующем
параграфе теория волн является совершенно
общей и применима к любым видам волн.
§ 7. Перенос энергии волнами
Воздействуя рукой на конец длинной
натянутой струны и заставляя ее
вибрировать, мы совершаем работу, которая
проявляется в виде кинетической и
потенциальной энергии отдельных элементов
струны. С течением времени начинают
колебаться все более и более удаленные
элементы струны. Энергия, сообщаемая
одному концу струны, переносится со
скоростью волны и может быть принята
Конец струны
Рис. 20-12. Конец струны оттягивается вверх,
чтобы возбудить бегущую волну.
и поглощена на другом ее конце. Скорость
переноса энергии можно найти, вычислив
силу, с которой мы тянем струну вверх
и вниз. Для этого запишем соотношение
для мощности Р = F • v [см. выражение
(.6-3), т. 1] и применим его к струне на
рис. 20-12:
p = Tv = Т
sin а,
полагая» v = dy/dt. Угол а всегда мал,
поэтому sin а ж — ду/дх. Следовательно,
Р = -Г!
dt
а поскольку у = у0 cos со (t — х/и), то
dt
= — j'o00 sincol t
дх
со
и
и мы можем записать выражение
Р = Tyl sin2cot
и
для мгновенного значения мощности Р,
передаваемой в момент времени t в точке
х = 0. Среднее значение мощности должно
быть вдвое меньше, так как sin2 Ш = 1/2:
й Т®2 2 , Л
Р = ——у о (средняя мощность, перено-
и симая по струне). (20-18)
Среднее значение переносимой
мощности называется интенсивностью
волны (см. § 6 гл. 11, т. 1). Интенсивность
волны пропорциональна квадрату ее
амплитуды. Интенсивность волн в
трехмерном пространстве, таких, как звуковые
и электромагнитные волны, равна средней
мощности, переносимой через единицу
поверхности фронта волны. То, что для волн
любого вида интенсивность
пропорциональна квадрату амплитуды,
подтверждается предыдущим выводом о том, что
энергия, переносимая электромагнитной
волной, пропорциональна Е2. В следующей
главе мы найдем коэффициент
пропорциональности, связывающий ток # с
излучаемой мощностью.
Пример 7. Длинный металлический провод с
линейной плотностью ц = 4 г/см
характеризуется натяжением Т=5 103Н. К одному из
его концов подключен вибратор мощностью
10 Вт, настроенный на «до» первой октавы
(частота 262 Гц). К другому концу провода
присоединен поглотитель энергии, от которого волна
не отражается. Определим скорость и длину
волны, а также величину максимального
поперечного смещения точек провода.
Решение: Скорость волны
5 • 103 Н
0,4 кг/м
= 112 м/с.

ГЛ. 20. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
Длина волны
и 112 м/с
~7 262 с"1
0,427 м.
Из (20-18) находим максимальное поперечное
смещение у0:
1
со
2иР_= 1
Т ~2я(262)
/2 (112) (10)
5103
4,06 • 10~4 м = 0,406 мм.
Основные выводы
В случае переменных токов в правую
часть выражения для закона Ампера
следует добавить еще один член. При этом
закон Ампера приобретает вид
fe.Ae**L/ +
1 <1ФЕ
с" с" dt
Поскольку I и ФЕ можно записать как
интегралы по замкнутым поверхностям, мы
имеем
IV $».& = ^|УйА + 1|
с J с J
дЕ
—iA.
dt
Это уравнение и три других составляют
систему четырех уравнений Максвелла:
I <j> Е • dA = 4пк0 J р dV (теорема Гаусса),
с [дЪ
II <)>E-ds = — — -dA (закон Фарадея),
III <р 33 • dA = 0 (отсутствие магнитных
зарядов).
Эти четыре уравнения полностью
определяют поля, создаваемые системой
движущихся (в том числе и с ускорением)
зарядов. Из них следует, что ускоренное
движение зарядов приводит к излучению
электромагнитного поля,
распространяющегося со скоростью с = 3 • 108 м/с,
причем Е = с£8 и поля Е и 33
перпендикулярны друг другу и направлению
распространения волны.
Мы рассмотрели конкретный пример
вертикальных колебаний поверхностных
зарядов на бесконечной плоскости и
показали, что в этом случае поля Е и &
удовлетворяют волновому уравнению
д2у 1 д2у
дх
т- ~7Х
dt
у, где у = Еу или
Решение этого уравнения в случае
синусоидального поверхностного тока $ —
= ^оcos ю*, когда ^о течет в
отрицательном направлении оси у, записывается
в виде
Еу = i
2пк0
i cos со It —
Это бегущая волна, распространяющаяся
от плоскости со скоростью и = с.
Если поверхностный ток оказывается
периодическим, но не синусоидальным, то
его можно разложить в ряд Фурье по
синусоидальным волнам. Тогда в любой
фиксированной точке поле излучения
2% ка
е = ст = —-#{?\
с
где f = (t — х/с)- время запаздывания.
Между частотой /, длиной волны X
и скоростью и имеет место соотношение
Xf = и, которое можно также записать
в виде со//с = и.
Решением волнового уравнения
d2y 1 d2y
(волновое уравнение)
dx2 и2 dt2
является смещение у (например, точек
струны), которое записывается в виде
следующей функции от х и t:
у = у0 cos (cot - кх) (бегущая волна).
Скорость бегущей по струне волны равна
и = ]/Т/\х, где Г-натяжение, а ц-линейная
плотность струны. Среднее значение
мощности, переносимой по струне, равно
о Та2 2
* = -**•
Приложение. Вывод волнового уравнений
Чтобы найти магнитное поле ffl в точке
Р на рис. 20-5, мы воспользуемся
прямоугольным контуром интегрирования вокруг
точки Р, показанным на том же рисунке.

ПРИЛОЖЕНИЕ. ВЫВОД ВОЛНОВОГО УРАВНЕНИЯ 357
Если интегрировать по контуру в
направлении против часовой стрелки, то вектор
dA будет направлен за плоскость чертежа
в отрицательном направлении оси у. Тогда
Е • dA = —EydA= —Eybdx. В этом
случае уравнение (20-2) принимает вид
$в.Ав0+1[
ЗЕ
dt'
dA
или
+ d38x)b - 0В2Ъ = -
1 дЕу
с2 dt
(Ъ dx),
где £9 = £9Z на левой стороне и £9 =
= £9Z + d£9z на правой стороне
прямоугольного контура. (Верхняя и нижняя его
стороны не дают вклада в фЗЗ-ds.)
Таким образом,
Т
tJ<E+
dE)
Рис. 20-13. Вид сбоку на элемент плоского
тока, изображенный на рис. 20-4.
dx
1
t = const
1
dt
1
= ~P~
.ЁЬ.
dEv
dt
dt
(20-19)
dx
В левой части этого уравнения стоит
частная производная, поскольку время t
считается постоянным, а на рис. 20-5 дано
мгновенное изображение, соответствующее
этому моменту времени.
Из второго уравнения Максвелла
можно получить еще одно соотношение между
полями 09 и Е. Возьмем уравнение II из
табл. 20-1 и проинтегрируем в
направлении против часовой стрелки по
прямоугольному контуру вокруг точки Р в
плоскости ху (рис. 20-13):
|E.*--|f-.iA,
(Ey+dEy)h-Eyh =
dEv = —т-^dx,
y dt
dEv
dt
- (h dx),
dx
dt
dx
dt '
(20-4)
Нам нужно вычислить поле ffi в точке
Р. Мы имеем два совместных уравнения
с двумя неизвестными (092 и Еу).
Продифференцировав первое уравнение по х,
а второе по t, можно исключить из них Еу.
Дифференцируя уравнение (20-19) по х,
получаем
д /д38.
dx\ dx
d2m
~dx~2
dx
1^3
c2 dt
1 d2Ey
c2 dxdt'
(20-20)
Теперь продифференцируем уравнение
(20-4) no t:
dEv
dt \ dx
d2E^
>L\ -
dxdt
dt
d2®,
~~de
d№z
~dt
Подставим это выражение в правую часть
уравнения (20-20):
(20-5)
а2^2
dx2
д20&г _
1
с2
1 д2.
d2mz
dt2 \
**.
dx2
dt2

358 гл- 20- ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ И ВОЛНЫ
Упражнения
1. Запишите уравнения Максвелла в табл. 20-1
через магнитный поток Фд, электрический
поток Фд, ток / и заряд Q.
2. Используя спектр электромагнитных волн
на рис. 20-3, укажите, каким участкам
соответствуют следующие длины волн: 1 м,
1 см, 1 мкм, 0,5 мкм и 1 А = 10"10 м.
3. Предположим, что поле Е на рис. 20-5
изменяется по закону Е = Е0 cos Ш и направлено
на читателя из плоскости чертежа.
Вычислите J (д Е/д t) • d\ по площади
прямоугольника, пересекающего линии тока. Ответ
запишите через а, Ь, Е0 й со.
4. Чему равен J Е • ds по прямоугольному
контуру на рис. 20-5?
5. Постройте график функции
1 °° 1
У= Е -sinих = X ?TZTsin(2J + 1)х-
По нечет, п п j = 0 Ч "•" 1
6. Справедливо ли выражение (20-7) для
отрицательных значений х, т.е. для
электромагнитной волны, распространяющейся влево
от плоскости на рис. 20-4? Если оно не
справедливо, то какие нужны изменения,
чтобы описать Еу и 88z для отрицательных
значений х?
7. Определите направление вектора Е х ©
в случае выражения (20-7).
8. Найдите скорость и бегущей волны у =
= sin(^x — Bt).
9. Струна из материала с линейной
плотностью 10 г/м колеблется с частотой 30 Гц.
Каким должно быть натяжение струны, если
длина волны равна 20 см?
10. По струне бежит волна у = sin (at — bx).
Найдите выражения для а и Ъ через X и /
11. Повторите решение примера 6 для случая
настройки струны на ноту «до» второй
октавы:/= 2(262) Гц.
12. В темперированном музыкальном строе
каждая октава имеет 12 полутонов, причем
отношение частот двух соседних полутонов
всегда одинаково. Найдите это отношение.
13. Синусоидальный поверхностный ток с
частотой 100 МГц течет по большой
плоскости. Амплитуда излучаемого электрического
поля равна 5 В/см.
а) Чему равна амплитуда тока в амперах на
метр?
б) Какова амплитуда поля $8 в теслах?
14. Найдите расстояние в длинах волн между
соседними максимумами интенсивности
в электромагнитной волне.
15. Чему равны граничные значения длин волн
видимого света в ангстремах (1 А =
= 10"10 м)? {Указание: Используйте
рис. 20-3.)
16. Минимальная и максимальная частоты,
воспринимаемые человеческим ухом, равны
соответственно ~ 20 Гц и ~ 15 000 Гц. Какие
соответствуют им длины волн в воздухе?
Скорость звука в воздухе 330 м/с.
Задачи
17. Через конденсатор на рис. 20-2 за время At
протекает ток /с. Вычислите в пространстве
между пластинами конденсатора на
расстоянии г от его оси
а) поле Е и
б) поле 0&.
Ответ запишите через R, г, Е и At.
18. Подковообразный электромагнит
включается в момент времени t = 0. Предположим,
что магнитный поток линейно возрастает во
времени, т. е. Ф = Kt t. Каковы величина
и направление поля Е между полюсами
магнита? Ответ запишите через Kv t, г и R.
( У^Г' \
6 О
,\ А
19. Предположим, что обмотка электромагнита
в задаче 18 содержит N витков. Ток в ней
изменяется во времени по линейному
закону: I = К2 t. Чему равна индуктивность
обмотки? Ответ запишите через Kv К2 и N.
20. Подставьте в волновое уравнение (20-5)
величину Bz = B0cos(kx - Ш). Определите,
чему должно быть равно отношение ю/Й
21. Подставьте в уравнение (20-5) выражение
Bz =/(х — ut). При каком значении и это
выражение будет решением уравнения
(20-5)?
22. Подставьте в уравнение (20-5) выражение
В2 = Вх cos ©! (t — х/с) + B2cos ю2 (* — х1и)'
При каком значении и это выражение будет
решением уравнения?

ЗАДАЧИ 359
23. Две параллельные пластины расположены
на расстоянии Х/2 друг от друга, где X =
= 2яс/ю. По каждой из пластин течет
поверхностный ток # - «/о cos ®t- Чему
равно поле 08!
~ФР
а) На расстоянии х от второй пластины?
б) Посередине между пластинами?
24. Предположим, что на рис. 20-7
металлическое зеркало заменено решеткой из
вертикальных проводников (каждый диаметром
ОД см), находящихся на расстоянии 2 см
друг от друга.
а) Если на решетку падает волна, описанная
в примере 2, то чему равен
индуцированный в каждом проводнике ток?
Считайте, что /пров равен произведению $ на
диаметр проводника.
б) Если проводники медные (удельное
сопротивление меди р = 1,72 • 10"8 Омм),
то каковы потери мощности в каждом
проводнике?
в) Какая доля энергии светового пучка
теряется в решетке?
25.* Внутри германиевой пластинки толщиной
1 мм от генератора переменного тока
создается электрическое поле £Внутр =
=400coscot В/м. Частота со/2я = 109 Гц.
Найдите электрическое поле излучения, если
удельное сопротивление германия р =
= 0,5 Ом-м. Чему равно отношение*поля
излучения к полю внутри пластинки?
26. Предположим, что $ = £^ sin cor +
+ 2^ cos cor. Нам нужно получить $ в
виде $ = «/о sin (см + (р).
* Для решения задач 25, 28 и 29, строго
говоря, необходимо найти решение уравнения (20-5)
в виде двух волн с учетом граничных условий.
Автор же, очевидно, предполагает
использование просто соотношения между напряженностью
поля и величиной тока в пластине-Прим. перев.
а) Найдите соотношение между ^0 и # v
б) Найдите фазу ср.
[Указание: #0sm((ut + ср) = (</0cos<p)sincor +
27. Предположим, что $ = Ах sin cot + А2 cos cor.
Требуется записать $ в виде $ =
= «/о sin (см + ф).
а) Найдите соотношение между $$ и Аи
А2.
б) Найдите выражение для ср через А± и А2.
28. Тонкая пластинка толщиной х0> длиной у0
и шириной z0 изготовлена из материала с
удельным сопротивлением р. К пластинке
приложено переменное напряжение V0 cos cor.
Покажите, что в точке Р электрическое поле
излучения дается выражением
2пк0 х0 Х7 / . .
Яизл = — — V0 cos (юг - кх\
х « у0 и х0 « X.
V0 cos (ot (~)
29. В условиях задачи 28 найдите среднюю
мощность:
а) рассеиваемую единицей площади
пластинки
(Указание: Используйте выражение Р =
= V2/R.);
б) излучаемую единицей площади.
{Указание: Используйте уравнение
dV 8я/с0 8я/с0 '}
30. Чему равна скорость волны,
представляющей собой решение уравнения
д2у
дг дх2
д2у

взаимодействие излучения
с веществом
В этой главе мы займемся изучением
взаимодействия электромагнитной волны
с веществом. Мы рассмотрим четыре
различных случая: плохой проводник,
хороший проводник, диэлектрик и плазму.
Оказывается, плохой проводник частично
поглощает энергию и импульс волны,
и это позволяет оценить количество
энергии и импульса, переносимого
электромагнитной волной. Хороший проводник
отражает электромагнитную волну со 100%-ной
эффективностью. Через диэлектрик, такой,
как газ, волна распространяется, не
испытывая поглощения; однако
распространение волны в этом случае происходит
медленнее, нежели в пустоте. С другой
стороны, в плазме существуют волны,
распространяющиеся быстрее, чем в пустоте.
Эти кажущиеся парадоксы разрешаются
при микроскопическом подходе, с учетом
атомного строения вещества. Наконец, мы
рассмотрим излучение колеблющегося
точечного заряда.
§ 1. Энергия излучения
В примере 3 гл. 20 мы видели, что
колебания тока приводят к потерям энергии,
причем потери мощности, приходящиеся
на единицу площади, составляют
с2 Е&/4пк0, где Е и ^-поля в излучаемой
электромагнитной волне. Эта энергия
должна куда-то деваться. Мы считаем, что она
уносится излучаемыми электрическим
и магнитным полями. Если бегущая
электромагнитная волна уносит от источника
некоторую энергию, то, поставив на
пути плоской волны поглощающую
пластинку, можно уловить эту энергию. Пусть
материал пластинки обладает конечной
электропроводностью; это позволит нам
определить полное количество джоулева тепла,
выделившегося в пластинке. Согласно
закону сохранения энергии, полное
количество выделившегося тепла соответствует
энергии электромагнитной волны,
прошедшей через пластинку. В гл. 16 мы
показали, что поле само по себе обладает
энергией, причем полная электростатическая
энергия системы равна величине Е2/$пк0,
проинтегрированной по всему
пространству. Точно так же в гл. 18 было
установлено, что магнитная энергия, запасенная
в единице объема, составляет с2&2/$пк0.
Если эта энергия действительно заключена
в самом поле, то джоулево тепло,
выделившееся в поглощающей пластинке, должно
быть равным сумме этих двух величин.
На рис. 21-1 изображена
электромагнитная волна, падающая на
прямоугольный элемент пластинки бесконечных
размеров. Если плотность
индуцированного тока равна j, то в прямоугольном
элементе будет наводиться ток I = jz0 Ах.
Разность потенциалов между верхним
и нижним краями V = Еу0. Следовательно,
энергия, теряемая в единицу времени,
—- = IV = (jz0Ax){Ey0) = jE{y0z0Ax\
at
где у0 z0 Ах - объем элемента пластинки.
Таким образом, мы показали, что
теряемая в единице объема внутри проводника
мощность равна jE. Если на проводящую
пластинку падает монохроматическая
плоская электромагнитная волна, то при этом
не только выделяется тепло со скоростью
jE Вт/м3, но и в соответствии с формулой
(20-7) индуцированный ток j сам излучает
электромагнитные волны. Пусть Д£-поле,
излучаемое индуцированным током j. На
рис. 21-1 показано поле излучения для
тонкой пластинки толщиной Ах. Будем обо-

§ 1. ЭНЕРГИЯ ИЗЛУЧЕНИЯ 361
'Ёл
А * *
ипад
АЕ
а
Ах
И"
АЕ
Рис. 21-1. Падающая волна
Епад распространяется вправо
и попадает на пластинку,
индуцируя в ней ток, который в
правую и левую стороны от
пластинки излучает свое
собственное поле АЕ.
значать поле падающей плоской волны
через £Пад. Эквивалентный поверхностный
ток </=;Ах. Следовательно, в
соответствии с (20-7) можно записать
2тг к0 А
АЕ = -;Ах.
(21-1)
Знак минус указывает на то, что вне
пластинки поле АЕ направлено
противоположно току j. Пусть AS-потери мощности на
единицу поверхности. В случае тонкой
пластинки толщиной Ах
AS =
1 dU
= jEAx.
У о zo dt
Подставим сюда вместо величины Ах ее
выражение, полученное из (21-1); тогда
■с
AS =
2пкп
-ЕАЕ.
(21-2)
Рассмотрим теперь стопку таких тонких
пластинок. Для каждой из них поле АЕ,
излучаемое вправо, всегда направлено
противоположно результирующему полю,
которое порождает излучение, и таким образом
уменьшает результирующее поле на
величину АЕ. Излучаемое влево поле АЕ
обусловлено слабым отражением волны. Если
электропроводность а достаточно низка,
так что поле Е на расстоянии в одну длину
волны внутри проводника почти не
уменьшается, то отраженные волны
компенсируют друг друга. Это объясняется тем, что
для любой отраженной волны найдется
волна, отраженная от более глубоких слоев,
которая на обратном пути окажется
сдвинутой по фазе на Х/2. (Горб одной из волн
придется на впадину другой, и
результирующая амплитуда окажется всюду равна
нулю.) В целом отраженные волны погасят
друг друга. Мы воспользовались условием,
что проводник не очень хороший. Это мо-
. жет быть графит или ионизованный газ.
Позже мы обсудим случай хорошего
проводника вроде серебра. Если стопка
пластинок бесконечно толстая, то поле Епад
поглотится целиком, и полную мощность,
излучаемую с единицы поверхности,
можно найти, проинтегрировав выражение
(21-2): '
S =
2пк0
,2
j EdE =
47ifc0 пад
4тг/с0
Излучаемая единицей поверхности
мощность характеризуется вектором Пойнтин-
га. Его величина обозначается S.
Поскольку направление потока энергии
определяется векторным произведением Е х
х 93, то для вектора S мы имеем
ЕхЖ (вектор Пойнтинга).
(21-3)
4ти/с0
Пример 1. Рассмотрим ту же
лампу-вспышку мощностью 3 Вт, что и в примере 2 гл. 20,
дающую пучок света квадратного сечения 10 х
х 10 см2. Вычислим величину S, а также поле
Е0, для чего воспользуемся формулой (21-3)
и соотношением 88 = Е/с.
Решение: Поскольку S-мощность,
приходящаяся на единицу поверхности, то
= 300 Вт/м2.
S =
(ОД м)2

362 ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
Заменяя в формуле (21-3) 0В = Е/с, получаем
-2 Е с зт
S =
4я/с0 с 4я/с0
Поскольку Е2 = £о/2, мы имеем
с
S =
8я/с0
откуда
Е 2
*0 =
8я/с0
5 = 475В/м.
Этот результат совпадает с полученным в
примере 2 гл. 20.
Наконец, проверим, не противоречит ли
наш результат для S полученному ранее
выражению для энергии единицы объема
поля. Рассмотрим плоскую волну,
падающую на площадку А. Согласно
определению S, поток энергии за время dt
dU = SA dt,
где dt/-энергия, заключенная в объеме
dV = Adx. Но dt = dx/c, поэтому
dx S
dU = SA = —dV,
с с
или
dU =
dV
Используя формулу (21-3), получаем
dU
~dV
4тг/сп
-Em\
Заменим E на ci
dU
~dV
?2 (cmf
8тг k0 8тг k0
а затем cffi на E:
dU _ E2 c2i
~dV~ +
8л k0 8тг k0
В правой части последнего равенства
первое слагаемое-это плотность энергии
электрического поля, а второе-магнитного
поля. Предшествующее рассмотрение
показывает, что количество тепла,
выделяющееся в рассмотренной нами
поглощающей пластинке, численно равно
полученным выше значениям для энергии
электрического и магнитного полей. О
взаимном гашении отраженных волн
свидетельствует черный цвет графита (графит не
отражает падающее на него
электромагнитное излучение). То, что падающая
волна поглощается, следует из
непрозрачности достаточно толстого слоя графита.
§ 2. Импульс излучения
Покажем теперь, что плоская волна на
рис. 21-1 сообщает пластинке толщиной
Ах не только энергию, но и импульс.
Рассмотрим прямоугольный элемент
бесконечной пластинки площадью y0z0
(рис. 21-2). Поскольку ;Е ^-количество
джоулева тепла, выделяющегося в единице
J
aft
В
Ах
Рис. 21-2. Падающая волна наводит в
пластинке ток / = jz0Ax. На этот ток действует
магнитная сила Fm = /у0 х ©.
объема за время dt, то количество тепла,
выделяющегося в элементе пластинки
объемом y0z0Ax, равно
dU = (jEdt)(y0z0Ax).
Заменим £ на с^:
dU = cjzoAxyo0Sdt.
Ток через рассматриваемый элемент
пластинки
I = j (z0 Ах),
поэтому
dU = cly0 i
'dt.

§ 2. ИМПУЛЬС ИЗЛУЧЕНИЯ 363
На элемент тока длиной у0,
перпендикулярный падающему магнитному полю,
действует сила Fm = /у0 х 93 в
направлении Ех$, которое совпадает с
направлением падающей волны. Заменяя 1у0£8 на
Fm, получаем
dU = cFw dt.
Импульс, сообщаемый элементу
пластинки, dp = Fm dt, или
dU = cdp, (21-4)
Рис. 21-3. Радиометр. Свет, отраженный
посеребренной поверхностью каждой лопасти,
передает вдвое больший импульс по сравнению со
светом, поглощенным зачерненной
поверхностью. Вследствие этого лопасти на снимке
должны вращаться по часовой стрелке. Однако
в действительности они вращаются в обратном
направлении! Это объясняется наличием более
сильного физического эффекта, а именно тем,
что вблизи зачерненной поверхности
остаточный газ нагревается больше, что приводит
к более высокому давлению на эту поверхность.
Если же сосуд откачать до более высокого
вакуума, то направление вращения изменится на
противоположное.
dp = —dU.
с
Как и прежде, проинтегрировав по
толщине пластинки х, мы получим р = U/c.
Таким образом, сообщаемый пластинке
импульс равен величине 1/с, умноженной на
энергию, рассеиваемую в пластинке.
Поле излучения обладает не только
энергией, но и импульсом. В любом
элементе объема dVnonn излучения
заключена энергия
Е2
dU = -n-dV,
4пк0
а его импульс равен энергии, деленной на
величину с. Иными словами, элемент
объема dОхарактеризуется вектором импульса
(с учетом соотношения dU = SdV/c)
Мы видим, что поле излучения, которое
испускается движущимся с ускорением
зарядом, представляет само по себе
физическую реальность. В каждой точке
пространства оно имеет энергию и импульс,
и их можно измерить. Энергию вы можете
измерить, поместив руку в пучок света:
Большая часть света поглотится рукой
и превратится в тепло. Из-за малости
величины 1/с измерить импульс светового
пучка довольно трудно (рис. 21-3).
Пример 2. Предположим, что свет от яркой
лампы мощностью 100 Вт фокусируется на
отражающей лопасти радиометра. С какой силой
свет давит на лопасть?
Решение: Импульс пучка света дается
выражением (21-4)
1
dp = —dU.
с
Поскольку при отражении направление света
меняется, передаваемый лопасти импульс
оказывается в два раза больше по величине:
2
dPnon = —dU.
с

364 ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
Таким образом, давление на лопасть
_ ^Рлоп _ 2 dU 2_
dt с dt ~ 3 • 108
= H100)H
= 6,67 • 10"7 Н.
Столь малая сила даже при ничтожном трении
с трудом приводит лопасть в движение Ч
Физическая реальность поля станет еще
более ощутимой при изучении квантовой
теории и свойств фотонов в гл. 24. Мы
увидим, что излучение состоит из
физических частиц, называемых фотонами,
которые столь же реальны, как электроны
и протоны. Каждый фотон обладает
энергией U = hf и импульсом р = hf/c, где
/-частота волны, a h-очень маленькое
число, называемое постоянной Планка.
§ 3. Отражение излучения от хорошего
проводника
Как уже отмечалось, в случае высокой
проводимости а электромагнитная волна
поглощается не полностью, а частично
отражается. В этом легко убедиться,
рассматривая предельный случай а = оо
(сверхпроводник). Напомним,' что электрическое
поле внутри сверхпроводника должно
всегда обращаться в нуль (в противном случае
неограниченно возрастал бы ток).
Следовательно, индуцированный поверхностный
ток оказывается таким, что поле излучения
АЕ = — £пад.- При этом внутри пластинки
результирующее поле Е = Ета + АЕ = 0.
Слева от пластинки оно не будет
обращаться в нуль, поскольку его
существование обусловлено двумя
монохроматическими волнами одинаковой интенсивности,
бегущими в противоположных
направлениях. В этих условиях слева от пластинки
на рис. 21-4 образуется стоячая волна с
узлами и пучностями. Стоячие волны мы
обсудим в § 1 гл. 22.
1} Существование светового давления было
экспериментально доказано П. Н. Лебедевым.—
Прим. перев.
Пример 3. Какова на рис. 21-4 величина
индуцированного поверхностного тока, а также
величина и направление магнитного поля А©,
создаваемого этим током?
Решение: В соответствии с выражением (20-7)
мы имеем
АЕ = сАт =
2пк0
ДЕ
lit
/
АЕ
I I
Пластинка
Рис. 21-4. Падающая волна наводит в
сверхпроводящей пластинке ток $, который излучает
поле АЕ, равное по величине £пад.
откуда
с с
-АЕ =
2% кп
2пкп
Мы записали индуцированный поверхностный
ток через величину электрического поля
падающей волны. Магнитное поле А&, создаваемое
током $, получаем из первого выражения:
Направление поля А© вблизи тока $
определяется правилом правой руки и иллюстрируется-
на рис. 20-5. Справа от тока поле направлено от
читателя за плоскость чертежа, слева-на
читателя. В обоих случаях векторное произведение
АЕ х А©, характеризующее направление
распространения волны, направлено от тока $.
Наконец, последний результат: величина $
совпадает с током в источнике,
генерирующем £пад.

§ 5. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ
Мы завершили рассмотрение
взаимодействия излучения с веществом,
содержащим свободные электроны. Излучение
приводит к появлению электрического тока
и связанных с ним эффектов. В следующем
параграфе мы обсудим вещества, в
которых не имеется свободных электронов.
Такие вещества называются
диэлектриками или изоляторами.
§ 4. Взаимодействие излучения
с диэлектриком
Внешние электроны атомов
диэлектрика связаны с атомом не жестко и под
влиянием внешнего поля испытывают
смещение. Постараемся вычислить величину
такого смещения.
Воспользуемся моделью атома,
близкой к той, которая принята в современной
квантовой теории. Согласно этой модели,
внешний электрон рассматривается в виде
шарового облака радиусом R. Мы будем
предполагать плотность заряда
постоянной. В соответствии с уравнением (16-3)
при смещении подобного шарового заряда
на расстояние у от центра атома возникает
возвращающая сила, пропорциональная у.
Вследствие этого электронное облако
совершает гармонические колебания
относительно центра атома [уравнение (16-3а)].
Центр атома представляет собой
атомное ядро, окруженное облаком внутренних
электронов, прочно связанных с ядром.
Сила, действующая на внешнее электронное
облако, дается выражением [см. (16-3а)]
^атом = -та&у, (21-5)
где со0/2я- частота собственных колебаний
атомного электрона.
Если на электронное облако действует
поле Епад падающей волны, то
результирующая сила запишется в виде
F = F 4- ( — е) Е
± рез ± атом ^ V с/ ■'-'пад >
откуда получаем следующее уравнение:
d2y 2 с
Для обозначения смещения мы
использовали здесь вместо х величину у,
поскольку нами будет рассматриваться
случай, когда Епад направлено вдоль оси у.
Падающую волну на расстоянии х от
источника мы обычно записывали как Епад =
= Е0 cos со (t — х/с). Поэтому написанное
выше уравнение принимает вид
d2y 2 еЕ0 ( х\
—— = - Щу — COS СО U .
аг т \ с J
Запишем решение этого
дифференциального уравнения:
У=~ , f" 2, C0S<» б--)' (21-6)
т (coo — or) \ с/
Данное решение можно проверить
подстановкой в исходное уравнение.
Таким образом, мы показали, как
взаимодействует отдельный атом с излучением.
Теперь мы рассмотрим множество таких
атомов, из которых состоит твердая
пластинка или слой газа.
§ 5. Показатель преломления
Пусть на плахтинку толщиной Ах,
состоящую из атомов, модель которых мы
рассмотрели в предыдущем параграфе,
падает плоская волна. Попробуем
догадаться, что при этом произойдет. В
соответствии с формулой (21-6) электрическое
поле падающей волны Епад вынудит
атомные электроны совершать
гармонические колебания. Любой колеблющийся
электрон должен сам по себе излучать
электромагнитную волну. Как и в случае
пластинки из проводника, возникают
отраженная и прошедшая волны, но только
теперь потери на джоулево тепло в
пластинке отсутствуют. Вся энергия сохраняется
в форме электромагнитного излучения;
таким образом, пластинка оказывается
прозрачной. Более того, если заимствовать
известный из оптики результат, то окажется,
что электромагнитная волна (или свет) рас-
пространяегся внутри пластинки со
скоростью и < с. Отношение с/и = п
называется показателем преломления. У
большинства твердых сред показатель
преломления равен приблизительно 1,5; это
означает, что скорость света замедляется
в них примерно на 33%. В табл. 21-1 при-

366 ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
Таблица 21-1
Некоторые показатели преломления
(^ = 5,9-10"7 м—желтая линия натрия)
Вещество
Показатель
преломления
Воздух 1,0003
Сероуглерод 1,63
Алмаз 2,42
Стекло (тяжелый флинт) 1,89
Стекло (легкий флинт) 1,58
Стекло (цинковый крон) 1,52
Полиэтилен 1,52
Плавленый кварц 1,46
Сапфир 1,77
Хлористый натрий 1,53
Вода 1,33
ведены показатели преломления некоторых
широко используемых веществ.
Как это может быть, чтобы
электромагнитная волна распространялась со
скоростью и < с? Из уравнений (20-5) и (20-7)
следует, что поля £и ^ должны
описываться волновым уравнением, в которое
входит скорость волны с. Это безусловно
так с микроскопической точки
зрения-поле излучения движущейся с ускорением
заряженной частицы распространяется со
скоростью и = с. Парадокс устраняется,
если мы обратим внимание на то, что поле
внутри пластинки не совпадает с полем
излучения отдельной частицы (или плоского
тока, генерирующего падающую волну).
Поле внутри пластинки представляет
собой суперпозицию поля падающей волны
и полей излучения всех атомных
электронов. Каждое из полей в отдельности будет
распространяться со скоростью и = с, но
результирующее поле, вероятно, может
распространяться так, как если бы его
скорость уменьшилась. Используя формулу
(21-6), мы покажем, что поле излучения
каждого из атомных электронов запаздывает
по фазе на 90° относительно поля
падающей волны, которая приводит в движение
эти электроны. Можно ожидать, что
в этом случае испущенная результирующая
волна будет запаздывать по фазе
относительно падающей. Оказывается, что
скорость результирующего волнового фронта
меньше, чем и = с, хотя индивидуальные
волны распространяются с и = с.
Выведем формулу для показателя
преломления в случае пластинки на рис. 21-5.
Этот вывод можно выполнить за пять
этапов следующим образом:
1. Зададим электрическое поле
падающей волны.
2. Вычислим скорость,
приобретаемую атомными электронами в
пластинке под действием
электрического поля падающей волны.
3. Используя эту скорость (или
плотность электронного тока),
вычислим испускаемое электронами
вторичное излучение.
4. Просуммируем падающую и
вторичные волны для получения
результирующей испускаемой
волны.
5. Свяжем фазу испускаемой волны
с показателем преломления.
1. Падающая волна
Электрическое поле падающей волны
зададим в виде [см. (20-7)]
£пал = Ег, cos со ( t |.
Рис. 21-5. Падающая волна
Епад наводит в пластинке
плотность тока j, излучение
которого вносит вклад в
результирующую волну Е'.
'пад
♦ И
Вакуум
Ах
И
Пластинка
♦ МЕ'
I
Вакуум

§ 5. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ
2. Скорость электронов
Дифференцируя (21-6) по времени,
получаем выражение для скорости слабо
связанных внешних электронов:
eE0w
-sin со
dy ^_
dt т (coo - со2)
собственных
х
где со0-частота сооственных колебаний
электронов. Плотность тока в пластинке
j = yi( — e)Vy9 Где У1 -число колеблющихся
атомных электронов в единице объема.
Используя приведенное выше выражение для
Же2соЕ0 . /, х
- sin со [ t
m(coo - ю2)
3. Излучение, испускаемое атомными
электронами
Поле излучения у пластинки,
создаваемое электронами пластинки, в
соответствии с (20-7) запишется в виде
АЕ =
2тг
-k0jAx,
где знак минус указывает на то, что ток j
и создаваемое им поле излучения имеют
противоположные направления. Таким
образом, подставляя сюда выражение для
j, имеем
АЕ =
2пк0 Г
с L
91е2соЕ0
т (соо — ю2)
х sin со I t j
Ах.
перпозицию поля падающей волны и поля,
испускаемого атомными электронами:
Е = Епад + АЕ.
Заменяя АЕ выражением (21-7), получаем
Е = Е0 cos 0 + АЕ0 cos ( 0
где 0 = со (t — х/с). Хотя 0 и увеличивается
во времени, обе монохроматические волны
сохраняют постоянную разность фаз,
равную я/2 радиан. Используя метод фазовых
диаграмм, описанный в приложении 1, эти
две волны нетрудно сложить. В данный
момент времени t первая волна
представляет собой проекцию на ось х вектора Е0
(рис. 21-6). Вторая волна является
проекцией на ось х вектора АЕ0, составляющего
у = sin CJt
y2 = 0,5sin(wr-f )
Перепишем это выражение в виде
АЕ = AEn cos (cot — кх
(ух + У2)
где
2тг/с091е2со
cm (cOq —to)
(21-7)
(21-8)
4. Результирующая волна
Результирующее электрическое поле
испускаемой волны представляет собой су-
Рис. 21-6. а-фазовая диаграмма для случая
сложения двух монохроматических волн Е0 cos 0
и A£ocos(0 — я/2); б-непосредственное
сложение двух монохроматических волн, сдвинутых
по фазе на 90°.

ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
угол —я/2 с первым вектором. Из
рис. 21-6, а видно, что результирующий
вектор Е'0 сдвинут по фазе относительно
падающей волны на угол
Ф = АЕ0/Е0.
При выводе этого выражения мы
воспользовались малостью углов, предположив,
что АЕ0/Е0 « 1.
5. СООТНОШЕНИЕ МЕЖДУ
СДВИГОМ И ПОКАЗАТЕЛЕМ
ПРЕЛОМЛЕНИЯ
ФАЗОВЫМ
Падающая волна проходит через
пластинку за время t = Ах/с, тогда как волна,
распространяющаяся со скоростью и =
= с/и, затрачивает большее время f =
= п(Ах/с). Результирующий волновой
фронт при прохождении пластинки
задержится на At = (п — 1)Ах/с. Это
соответствует фазовому сдвигу
Г Ах~|
Ф = со At = со \ (п — 1) .
Поскольку ф = АЕ0/Е0, то
ДИСПЕРСИЯ
Полученный нами результат
обеспечивает правильную зависимость от частоты
падающего света со (рис. 21-7). В примере
1 гл. 16 мы показали, что для типичных
атомов со0 > со, причем со относится к
видимой области спектра. Этому
соответствует показатель преломления больше
1 или скорость волны меньше с. Кроме
того, при переходе частоты света из красной
области спектра в фиолетовую показатель
преломления увеличивается и возрастает
отклонение светового луча призмой, т.е.
имеет место нормальная дисперсия.
Именно благодаря этому призма разлагает
пучок белого света в спектр.
со (и — 1)-
Ах АЕП
Яо
Подставляя выражение (21-8) для А£0 и
решая относительно и, находим
2пк0У1е2
/7=1 +
2—^2\" (показатель
преломления). (21-9) строенная в соответствии с формулой (21-9).
т(шо - со2)
Рис. 21-7. Кривая нормальной дисперсии, по-
Это показатель преломления пластинки.
Следует заметить, что Ах не входит
в окончательный результат. Это не
является неожиданным, поскольку толстую
пластинку можно представлять в виде набора
тонких, в каждой из которых повторяется
один и тот же процесс. Напомним также,
что мы использовали приближение,
согласно которому поле падающей волны
меняется слабо, т.е. (п — 1)«1. В случае
больших п поле Епад внутри пластинки
следует заменить на результирующее поле.
Это усложняет расчеты, и мы не приводим
их здесь.
Пример 4. Используя формулу (21-9) и данные
табл. 21-1, вычислим показатель преломления
воздуха для ультрафиолетового излучения с
^ = 3,0-10"7м в предположении, что ю0 =
= 7,5- 1015 с"1.
Решение: Перепишем формулу (21-9) в виде
п2— 1
а>о-<*>1
Из табл. 21-1 находим для воздуха nt = 1,0003,
причем Wj = 27СС/Л.! = 3,19
линия натрия). Тогда
101
(желтая

§ 6. ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ 369
ш2 = -^- = 6,28.1015 с-1, где Х2 =
= 3,0- 10" 7м.
Таким образом,
п2- 1 (7,5-1015)2
1,0003 - 1 (7,5 • 1015)2
п2 = 1,00082.
- (3,19- 1015)2
- (6,28 1015)2
= 2,74,
Используя уравнения Максвелла и
упрощенную атомную модель
проводников и диэлектриков, мы смогли рассчитать
многие из наблюдаемых в природе общих
свойств света и электромагнитного
излучения.
§ 6. Электромагнитное излучение
в ионизованной среде
В плазме или ионизованном газе
электроны свободны и со0 = 0. Полагая в (21-9)
со0 = 0, имеем
2пк0У1е2
п = 1 -
mar
Эта формула справедлива в случае, когда
средний свободный пробег электрона
превышает величину умакс = еЕ0/ты2. Такой
случай реализуется при распространении
радиоволн в ионосфере и космическом
пространстве. Внимательный читатель
должен обратить внимание на то, что здесь
мы имеем п < 1, иными словами, скорость
волны превышает скорость света с. Однако
хорошо известно, что ни сигнал, ни
частица не могут распространяться быстрее
света. В действительности отдельные частицы
света (фотоны) всегда движутся со
скоростью и = с. Здесь же мы рассматриваем
результирующее поле, обусловленное
суперпозицией большого числа фотонов,
испускаемых многочисленными электронами.
Свойства фотонов мы обсудим в гл. 24.
МОДУЛЯЦИЯ И ГРУППОВАЯ СКОРОСТЬ
Решивший ниспровергнуть Эйнштейна
читатель мог бы предложить увеличивать
и уменьшать амплитуду электромагнитной
волны, распространяющейся в
ионизованном газе, и создавать тем самым
модуляцию электромагнитной волны. С помощью
такой модуляции могла бы быть
закодирована информация (например, с
использованием азбуки Морзе), и тогда сигналы
передавались бы быстрее света. Однако
модулированная волна уже не будет
монохроматической. Эту волну можно было бы
разложить по Фурье на группы
монохроматических волн с различными частотами.
Каждая из монохроматических волн
действительно распространяется со скоростью
и > с, но в приложении 2 показано, что
огибающая сигнала при этом
распространяется со скоростью, называемой
групповой скоростью vg, которая может
существенно отличаться от скоростец
монохроматических составляющих, и в данном
случае vg < с. В приложении 2 получена
формула
dco , 2%
„,-_ где*=х.
* Пример 5. Какова групповая скорость в
обычном диэлектрике, для которого имеет место
формула (21-9)? Всегда ли она меньше с?
Решение: Запишем к как функцию от со:
со с со
— = и = —, к = —п.
к п с
Формулу (21-9) можно представить в виде
2пк0У1е2
п — 1 -
Тогда
с
Г 2 J' 1At Л"
СОо — <° т
мы имеем
Гц л )
\1 ' ai-a2)'
а дифференцируя, получаем
dk
1 A cog + ш2
—i
da с с (cog-со2)2
Используя соотношение
dk/dw = l/vg,
находим
1 ! Г oog+oo2 "1
— 1 + л-j—2 2П- . 21-ю
Таким образом, v < с.

370 ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
Следовательно, в соответствии с формулой
(21-10) vg всегда меньше с, если только ю0 > со
или со0 < со. Это справедливо и в случае, когда
со0 = 0, например при распространении
радиоволн в ионосфере. Мы показали, что vg меньше
скорости света даже в том случае, когда
скорость волны превышает с.
* Пример 6. Через каждые 3,6 с пульсар
излучает импульс радиоволн. Этот импульс можно
регистрировать только радиотелескопами. Если
радиоприемник перестроить с частоты 150 МГц
на частоту 240 МГц, то импульс будет
появляться на 1,3 с раньше. Каково расстояние до
этого пульсара, если в межзвездном
пространстве плотность электронов 91 = 0,03 см-3?
Решение: Обозначим расстояние до пульсара
через £>. Разница во времени
D D
At = .
\ %
Используя (21-10) при со0 = 0, запишем
выражение для величины l/v :
vg с I со2 J
Тогда
At =
DA f 1
oof
Отсюда находим время, за которое
радиоимпульс от пульсара дойдет до Земли:
D mAt4n2
(к-
с 2пк091е2
2тс(9,М(Г31 кг)(1,3 с)
=(9-109 Н.м2/Кл2)(0,03.106 м"3)(1,6.10-19
Кл)2
1
1
'Г-
L(150.106)2c"2 (240.106)2 с
= 3,97- 1010с = 1260 лет.
Таким образом, свет от пульсара доходит до
Земли за 1260 лет, т.е. расстояние до пульсара
составляет 1260 световых лет.
Этот пример иллюстрирует новый
независимый метод определения
астрономических расстояний, но он годится лишь для
пульсаров (вращающихся нейтронных
звезд). К счастью, этот новый метод
астрономы могут проверить и откалибровать
с помощью старого, поскольку один из
пульсаров можно наблюдать визуально
(см. рис. 30-8).
§ 7. Поле излучения точечных зарядов
До сих пор мы изучали поле излучения,
испускаемого большим числом зарядов,
которые совершают совместные
колебания, образуя ток. Допустим, что в единице
объема находится 91 зарядов. Если каждый
заряд q колеблется по закону у = у0 sin cot,
то плотность тока j = 91 q соу0 cos cot и ток
в слое толщиной Ах
# — j Ах = (91 q соуо &*)cos cot-
Тогда, используя выражение (20-7), поле
излучения можно записать в виде
2тг/с,
— 9lq Ах соуо cos (®t — кх). (21-11)
Е,=
Но предположим теперь, что вместо
распределения зарядов мы имеем
отдельный заряд q, колеблющийся по закону
у = у0 sin cot. С помощью уравнений
Максвелла можно показать, что на расстоянии
г от заряда q поле излучения дается
выражением
£ = /с0 q(°2y° sinco(t--)sin9, (21-12)
где 0-угол, который составляет вектор
ускорения с радиус-вектором г (рис. 21-8).
Замечая, что ускорение а = — со2 у0 sin cot,
имеем
Е= -к
4
0 Т~
aH)si
sin0 (излучение mo-
ценного заряда);
(21-13)
Рис. 21-8. Направление поля излучения Е,
создаваемого точечным зарядом q, движущимся
с ускорением а.

§ 7. ПОЛЕ ИЗЛУЧЕНИЯ ТОЧЕЧНЫХ ЗАРЯДОВ 371
здесь a(t — г/с) -ускорение в момент
времени t — г/с. Вектор Е направлен по
нормали к радиус-вектору г. Формула (21-13)
справедлива не только для колеблющегося
заряда, но и для любого движущегося
заряда при условии, что его скорость v « с.
Направление поля 93 перпендикулярно
Е и г. Как и прежде, £8 = Е/с. Следует
заметить, что при вычислении поля на
расстоянии г от точечного заряда мы должны
использовать значение ускорения в более
ранний момент времени t — г/с. Это
значение ускорения обозначается как a(t — г/с).
Если бы это было не так, то, измеряя поле
в точке Р, мы могли бы сказать, что
происходит в этот же момент времени с
зарядом. Однако это противоречило бы
условию, согласно которому сигналы не могут
распространяться со скоростью v > с. Мы
можем судить лишь о состоянии заряда
в котором он находился в более ранний
промежуток времени t — г/с.
*Пример 7. Какую мощность излучает заряд q,
движущийся с ускорением а?
Решение: Излучаемая с единицы площади
мощность характеризуется вектором Пойнтинга [см.
(21-3)]. Полную мощность можно найти,
проинтегрировав по поверхности сферы величину
S =
4пкп
4пкп
4пк
АтУ
4пкп
-Е2 =
ко4а • Л2 ,
—— sine = /с,
0 4пс3г2
sin2 е.
Полная мощность излучения
At 7
где элемент поверхности dA = 2nr2 sin QdQ.
Таким образом,
sin20 2яг2 sin е<Ю =
*Пример 8. Каково поле излучения
электрического диполя р = р0 sin cot? Какую среднюю
мощность излучает этот диполь?
Решение: Пусть отрицательный заряд диполя
— q расположен в начале системы координат,
а положительный заряд q-ш оси z, причем его
координата меняется по закону z = z0 sin cot.
Тогда p0 = qz0, а ускорение
— orzn sin cor =
00 Po • ,
—Sill CD*.
Подставляя это выражение в (21-13), находим
поле излучения
'--^-■^-(-т)]
-*о
<о2р0 sin 6
■к>
sinG =
(21-15)
Отсюда мы видим, что поле излучающего
диполя спадает с расстоянием по закону 1/г, в то
время как в случае статического диполя поле
уменьшается как 1/г3.
Чтобы ответить на второй вопрос, запишем
, выражение (21-14):
3 с3
где а* обозначает среднее значение функции
((u4Po/q2)sin2(ot. Поскольку среднее значение
sin2 cot равно 1/2, то
p = U*C
(21-16)
Следует заметить, что при постоянной
амплитуде колебаний мощность излучения возрастает
пропорционально четвертой степени частоты.
Пример 9. Пусть в точке расположения
свободного электрона радиопередатчик, работающий
на частоте 500 кГц, создает поле
электромагнитного излучения Е0 = 10 мВ/см. Каковы
будут амплитуда колебаний и максимальная
скорость электрона? Какую среднюю мощность
излучает электрон?
— Kq
q2a2
~2?~
sin39 d% =
-±k Ч a2
5 С
(21-14)
Решение: Полагая в выражении (21-6) со0 = 0,
находим амплитуду:
У о =
еЕ0 (1,6-НГ 19Кл) (1,0 В/м)
moo2 ~ (9,1Ы0-31кг)(27г.5-105с-1)2
= 1,78 -10 " 2 м.

372 ГЛ- 2L ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
В случае простых гармонических колебаний
максимальная скорость электрона
и0 = юуо = (2тс• 5• 105 с-1)(1,78.10"2м) =
= 5,58-104 м/с.
Для того чтобы найти среднюю мощность
излучения Р, вычислим дипольный момент р0
и подставим его в (21-16):
/?0=в3;о=(156.10-19Кл)(1,78.10-2м) =
= 2,85-10"21Кл.м,
P = ifc/i^ = 8j79.10-32BT.
3 с5
АТОМНЫЕ ПЕРЕХОДЫ
Если проанализировать спектр
излучения атома с помощью идеального
спектрометра, обладающего бесконечно большим
разрешением, то окажется, что излучение
сосредоточено при определенных
дискретных значениях частот или в
определенных «линиях». Каждая из этих линий
обладает естественной шириной А/.
С помощью формулы (21-16) можно
оценить время жизни возбужденного
состояния атома, которое связано с
естественной шириной линии атомного
спектра. Воспользуемся приближением,
согласно которому сила, связывающая
излучающий электрон с центром атома,
аналогична силе, действующей со стороны пружины
с коэффициентом упругости к = т&\. При
этом частота излучения f0 = со0/2тг и р0 =
= ех0. В § 4 гл. 11 мы установили, что
полная механическая энергия
колебательной системы Е = focjj/2 = тсо^оА гДе
х0- амплитуда колебаний. В соответствии
с (21-16) скорость, с которой излучается
энергия,
dt ~ 3 ко[еХ°> с3 '
В этом случае
dE 2 е2 а>1
-т = Jk°^dt-
Интегрируя обе части этого выражения,
получаем
Е = Е0е-"\ где х= 2 2 .
2к0е щ
Вычислим среднее время жизни т атомного
перехода, при котором испускается желтый
свет (/= 6 1014Гц):
3 (9,1Ы(Г31НЗ-108)3
Т 2(9-109)(1,6.10-19)2(2ti)2(6.1014)2 С"
= 1,13-10"8 с.
Несмотря на то что при вычислениях мы
пользовались классическим приближением,
полученный результат почти совпадает
с правильным результатом, даваемым
квантовой механикой. Ширину желтой
спектральной линии можно получить из
формулы (21-17), приведенной в
приложении 2:
Асо » — или А/ж .
т 2тгт
Относительная ширина линии
-^~_^~2,35. 10"8.
/о 2тс/0т
В следующем примере в аналогичных
расчетах мы используем боровскую
модель атома водорода и оценим, сколько
времени потребуется электрону, чтобы
излучить энергию, сравнимую с его энергией
связи.
Пример 10. В боровской модели атома
водорода электрон движется по круговой орбите
радиусом R = 0,53-10" 10 м. С какой скоростью
электрон излучает энергию (в единицах эВ/с)? За
какое время в этих условиях будет испущена
энергия 7 эВ, составляющая примерно половину
энергии связи электрона?
Решение: Ускорение электрона можно найти
с помощью закона Кулона:
ma = °~R*9
Подставляя это выражение в (21-14), находим
скорость излучения энергии:

ПРИЛОЖЕНИЕ 1.. МЕТОД ФАЗОВЫХ ДИАГРАММ
dU _ 2 . е2
dt
2
3 к° с3 [k°~mR2
/с,
3 ■* с3т2Д4
= ^(9.109)3 х
х (1,6-КГ19)6 дж/с =
(3-10-8)3(9,П-10-31)2(0,53.10-10)4 А '
= 4,61-Ю-8 Дж/с = 2,88-1011 эВ/с.
Время, за которое излучается 7 эВ энергии,
равно
At--
АС/
<*С//Л 2,88-1011
с = 2,43-10-п с.
Мы видим, что, согласно классической
физике, электрон, движущийся по круговой орбите
вокруг протона, быстро излучит значительную
часть имеющейся у него энергии. Более
детальный расчет показывает, что электрон будет
двигаться по спирали и через ~ 10" п с упадет
на протон (см. задачу 21). Современная
квантовая механика свободна от этой трудности,
поскольку электронное облако стационарно; его
ускорение равно нулю.
Основные выводы
Плотность энергии электромагнитной
волны дается выражением
е2 + (cm)2
8л/с0
Поток энергии через единицу площади
в единицу времени равен
S =
4тг/с0
Ех 93.
Эта величина называется вектором Пойн-
тинга и характеризует потери мощности,
приходящиеся на единицу площади в
среде, поглощающей волну.
Бегущая электромагнитная волна,
несущая энергию АС/, несет также и импульс
АС//С.
Плоская электромагнитная волна,
попадая на поверхность проводника,
индуцирует в нем поверхностный ток, благодаря
которому происходит отражение
падающей волны.
Если электромагнитная волна с
частотой со проникает в диэлектрик., то внешние
электроны атомов колеблются с той же
частотой и испускают вторичные
электромагнитные волны, сдвинутые по фазе на
90° относительно падающей волны.
Вследствие этого скорость волны и оказывается
меньше, чем с. Показатель преломления
определяется как п = с/и и в непроводящей
среде (не слишком, плотной) дается
выражением
2пк0У1е2
т\щ — от)
где со0-частота собственных колебаний
атома. Увеличение п с ростом частоты
со называется нормальной дисперсией.
Волновой пакет распространяется с
эффективной скоростью
dco
vn =
dk '
называемой групповой. В среде,
обладающей дисперсией, поскольку п зависит от со,
vg отличается от и. Групповая скорость vg
остается меньше с даже в том случае,
когда и > с.
Отдельный точечный заряд q,
движущийся с ускорением a(t), испускает
электромагнитную волну
Е = - к
О 2
С Г
а\ t
sinG.
Приложение 1. Метод фазовых диаграмм
В этом приложении мы изложим метод
суммирования двух или нескольких
монохроматических волн, сдвинутых по фазе
друг относительно друга. Разумеется, для
того чтобы разность фаз сохранялась
постоянной, частоты этих волн должны быть
одинаковыми. Таким образом, нужно
вычислить сумму
S(t) = A1cos((ot + фх) + А2 cos (cot + ф2).
Она также представляет собой
монохроматическую волну, имеющую ту же частоту
со:
S(t) = S0 cos (cor + cps).

ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
Теперь нам остается записать величины S0
и ф5 через А19 А2, (р1 и ф2.
Это нетрудно сделать, если заметить,
что на рис. 21-9 проекция вектора на ось
х равна А х cos (со £ + фх), т.е. первой из
У
х
Рис. 21-9. Проекция вращающегося вектора At
на ось х представляет собой одну из двух
монохроматических волн, которые образуют
сумму S.
двух волн. На этом рисунке вектор длиной
А1 составляет угол 0 = сог + фх с осью х.
С увеличением времени t вектор вращается
против часовой стрелки, и в любом случае
нас интересует его проекция на ось х.
Построим теперь второй вектор длиной А2
под углом 02 = cot + ф2. Угол между
вторым и первым векторами всегда равен
ф2 — фА. Таким образом, у нас имеется
сумма двух проекций на ось х. Чтобы най-
У
V/yA2
\ а А?2
Рис. 21-10. Векторная сумма S = Ах + А2,
определяемая длиной S0 и углом фа.
ти решение, заметим, что сумма проекций
на ось х равна проекции на эту ось вектора
суммы. Длина этого вектора Ах + А2
определяет амплитуду S0 результирующей
монохроматической волны. На рис. 21-10
показано, как все получается: нужно
построить векторы Ах и А2, один из которых
составляет с осью х угол ф1? а другой-
угол ф2. Тогда длина их векторной суммы
равна S0, а угол между S и осью х
будет фг
Приложение 2. Волновые пакеты
и групповая скорость
ВОЛНОВЫЕ ПАКЕТЫ
В предыдущем приложении мы
занимались сложением монохроматических волн,
имеющих одинаковые частоты. В
настоящем приложении мы будем складывать
монохроматические волны с различными,
но близкими частотами. В этом случае
с течением времени волны будут все
больше «разбегаться» по фазе друг
относительно друга. Рассмотрим простейший случай
сложения двух одинаковых
монохроматических волн, частота одной из которых
равна ©19 а другой -со2 (рис. 21-11).
Используем обозначения со = (сох + со2)/2 и Асо =
= (со2 — coJ/2. Тогда сумма
S(t) = cos(co + Aco)t + cos(co - A(6)t.
Это выражение можно преобразовать с
помощью известного в тригонометрии
правила сложения косинусов:
cos А + cos Б =
= 2cos(A^cos(^t^.
Таким образом,
S(t) = 2cosAcotcosco£ = A(t)cos(5t,
где A (t) = 2cos (Aco)t - огибающая или
функция модуляции (белая кривая на
рис. 21-11). В данном случае огибающей
является монохроматическая волна с
меньшей частотой.
Складывая большое число
монохроматических волн с несколько различными
частотами, можно получить функцию моду-

ПРИЛОЖЕНИЕ 2. ВОЛНОВЫЕ ПАКЕТЫ И ГРУППОВАЯ СКОРОСТЬ 375
cos w2r
Рис. 21-11. я-две
монохроматические волны с несколько
различными частотами,
находившиеся в фазе в начале
координат, по мере того как они
удаляются от начала
координат, оказываются
последовательно то в противофазе, то
снова в фазе; б-сумма двух
монохроматических волн.
(COS (л)Л + cos w2/)
Огибающая
ляции любой формы. В качестве примера
можно рассмотреть отдельный импульс,
который играет важную роль в волновых
процессах. Такой импульс выглядит
наподобие центрального всплеска на рис. 21-11
и называется волновым пакетом.
Посмотрим, как с помощью набора близких по
частоте монохроматических волн можно
построить волновой пакет. Используя
представленную на рис. 21-11,6 картину,
можно подавить соседние всплески
колебаний, добавив третью монохроматическую
волну с частотой со и амплитудой, равной
высоте всплеска [отметим, что A(t) меняет
знак у чередующихся всплесков]. Такая
монохроматическая волна добавится к
центральному всплеску и окажется сдвинутой
по фазе на 180° в области соседних
всплесков (рис. 21-12). Функция G(co)
характеризует относительные интенсивности трех
суммируемых монохроматических волн.
Для того чтобы подавить следующий
набор всплесков, можно добавить две
монохроматические волны cos (со — Асо/2) t и
cos (со + Дсо/2)£ с соответствующими
амплитудами, как показано на рис. 21-13.
Добавление еще двух монохроматических
волн вряд ли повлияет на центральный
всплеск, но их сумма будет сдвинута по
фазе на 180° относительно следующих
всплесков.
В действительности для формирования
отдельного волнового пакета, не
сопровождающегося дополнительными
всплесками, приходится складывать бесконечно
большое число монохроматических волн
с близкими частотами. Соответствующая
ситуация иллюстрируется на рис. 21-14; на
этом рисунке функция G(co) характеризует
относительные амплитуды отдельных
монохроматических компонент. Такая
функция G(co) называется гауссовой и
записывается в виде
G(co) = e"((0"^/2(Aa))2,
где Асо-среднеквадратичное (или стандарт-
Рис. 21-12. а -сумма трех
монохроматических волн;
б-относительное распределение
амплитуд.
G(w)
ACl>

ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
G(o»
Рис. 21-13. а-сумма пяти монохроматических
волн; б-относительное распределение
амплитуд.
G(o»
А-
Рис. 21-14. а-сумма бесконечного числа
монохроматических волн; б - относительное
распределение амплитуд; G(со)-гауссова функция со
средним значением, равным со, и
среднеквадратичным отклонением Лео.
ное) отклонение величины со относительно
со. Мы будем называть Асо разбросом
частот. Для того чтобы найти сумму
бесконечно большого числа монохроматических
волн, необходимо вычислить интеграл
JG(co)coscordco.
Этот интеграл можно вычислить,
используя следующий табличный интеграл:
Je
-(со-ш)2/2(Дсо)2
cos т dco =
= y^Acoe-(t2/2)(Aw)2coscof.
Мы видим, что в правой части этого
равенства записана монохроматическая
волна cos cot, промодулированная гауссовой
огибающей e~(t /2)(Лсо). Среднеквадратичное
отклонение для этой функции равно At =
= 1/Асо и называется шириной волнового
пакета:
д^ s —« (ширина волнового пакета),
(21-17)
Дсо
Таким образом, разброс частот
монохроматических компонент в точности равен
обратной величине ширины волнового
пакета. Функция G(co) называется фурье-
образом волнового пакета.
ГРУППОВАЯ СКОРОСТЬ
Можно также просуммировать бегущие
волны с различными частотами. При этом
мы получим интересный результат,
заключающийся в том, что скорость
распространения огибающей может значительно
отличаться от скорости волны, с которой
распространяются монохроматические
компоненты. Вследствие этого скорость
перемещения волнового пакета как целого
может существенно отличаться от
скорости распространения входящих в его
состав монохроматических волн. Скорость
волнового пакета, или огибающей,
называется групповой скоростью. Почему
огибающая может распространяться с иной
скоростью, можно показать на примере
двух монохроматических волн, показанных
на рис. 21-11, с близкими частотами и
длинами волн. Суперпозицию двух таких
бегущих волн можно записать в виде
y(x,t) = cos [(со + Aco)t — (k + А/с)х] +
+ cos [(со — Aco)t - (k — A/c)x],
где k = 2к/Х-среднее волновое число. На
рис. 21-15 представлены две такие волны
в зависимости от х для четырех
последовательных моментов времени t В данном
случае огибающая перемещается вправо
вдвое быстрее каждой из
монохроматических компонент. Применяя для cos А +
+ cos В тригонометрическую формулу
сложения, получаем
у (х, t) = 2 cos [(Асо) г — (А/с) х] cos (cot — kx).
Мы видим, что огибающая записывается
в виде А(х, t) = 2 cos [(Асо) t — (А/с)х]. Она

УПРАЖНЕНИЯ
штттт:..
лллм-^wwvvvv- ;,.„
у\ллллдлллллллллл
тллмллллллллллллл ,
VVWVvwxaa/vvvvk '
VWWWWVWWW
AM/VWVWWWWW
Рис. 21-15. Две монохроматические волны j>i и
у2, движущиеся вправо с несколько
отличающимися скоростями. В этом случае огибающая
суммы ух + У 2 распространяется вправо
с удвоенной скоростью. Приведены четыре
последовательных положения (см. сверху вниз),
соответствующие моментам времени tv ..., t4.
Стрелками показаны положения горбов в
разные моменты времени.
имеет максимум при
(Aco)t - [Ак)х = О,
т.е. при
х Асо
Т = ~Кк'
Эта величина представляет собой скорость
перемещения горба огибающей: именно
так определяется групповая скорость.
Если мы имеем набор
монохроматических волн с близкими частотами, причем
со является функцией от к, так что со =
= со (/с), то групповая скорость
определяется следующим образом:
vg = —— (групповая скорость), (21-18)
Наиболее характерный пример
распространения с групповой скоростью-это
прохождение света через диэлектрик (см. пример
5). Другое весьма важное применение
понятия групповой скорости связано с
квантовой механикой, в которой частицам
сопоставляются волновые пакеты. Скорость
частицы совпадает с групповой скоростью
волнового пакета, а не со скоростями
отдельных компонент; эти скорости обычно
сильно различаются.
Упражнения
1. Напишите выражение для величины вектора
Пойнтинга сначала через 8#, /с0 и с, а затем
через е0, |х0, Е и ^.
2. Космический корабль массой 1 т
приводится в движение с помощью пучка света.
Насколько увеличится скорость корабля после
работы двигателя в течение суток, если
мощность пучка 10 кВт (влиянием
гравитационных сил можно пренебречь)?
3. Космический корабль можно заставить
двигаться с помощью давления солнечных
лучей. Предположим, что для этого на
корабле имеется парус, изготовленный из алю-
минированного майлара плотностью
2 г/см3. Если поток солнечного излучения,
падающего на Землю, составляет
1,35 кВт/м2, то какую толщину должен
иметь парус, чтобы сила светового давления
уравновесила силу гравитационного
притяжения Солнца?
4. Падающий на Землю солнечный свет
обеспечивает S = 1,35 кВт/м2. Чему равны
соответствующие среднеквадратичные
значения Е и ^?
5. Максимальное значение магнитного поля,
создаваемое колеблющимся диполем на
расстоянии 1км, равно 10 ~15 Т. Найдите
а) максимальное значение электрического
поля,
б) максимальное значение вектора
Пойнтинга и
в) среднюю мощность, излучаемую
диполем.
6. Свободный электрон находится в
переменном электрическом поле, амплитуда
которого равна 0,1 В/м. Чему равна амплитуда
колебаний электрона
а) при / = 1 кГц?
б) при / = 100 МГц?
7. В упражнении 6 вычислите
соответствующие скорости электрона.
8. Чему равен угол q> в градусах на
рис. 21-6,6?
9. Чему равен показатель преломления
воздуха для ИК-излучения с X = 2 мкм (см.
пример 4)?

378 ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
10. Предположим, что молекулы воздуха при
действии на них света с частотами fx и /2
начинают колебаться, причем молекулы
приобретают дипольный момент р =
= p0(sm<o1t + sinco20- Если/2 соответствует
голубому свету, а /х- красному, то каково
отношение соответствующих энергий
излучаемого света? Приведите численный ответ.
Задачи
11. На космическом корабле массой 1 т
установлен парус из алюминированного майлара
площадью 100 х 100 м2. Парус может
ориентироваться в любом направлении.
Космический корабль первоначально
движется по круговой орбите радиусом 105 км.
Поток мощности солнечного излучения
равен 1,35 кВт/м2.
а) Какой примерно выигрыш в энергии за
один оборот космического корабля можно
было бы получить за счет светового
давления?
б) Сколько приблизительно времени
понадобится космическому кораблю, чтобы
добраться до Луны за счет светового
давления, создаваемого Солнцем?
12. Допустим, что плохо проводящая пластинка
на рис. 21-1 имеет удельное сопротивление
р. На какой толщине пластинки поле
падающей волны £Пад уменьшится вдвое?
Запишите ответ через р, к0 и с (плохая
проводимость означает, что эта толщина
эквивалентна большому числу длин волн).
13. Все излучение от дуговой лампы
мощностью 1 кВт собирается в пучок кругового
сечения радиусом 10 см.
а) Если пучок направить на зеркало, то
с какой силой он будет давить на зеркало?
б) Чему равен индуцированный
поверхностный ток $ (в А/м)?
в) Какова плотность энергии в пучке (в
Дж/м3)?
14. Частица с массой т колеблется под
действием внешней силы F0coscor вдоль оси у.
а) Найдите зависимость у от t.
б) Запишите выражение для амплитуды
в зависимости от F0, со и т.
15. На частицу массой m действует
результирующая сила вида
[ рез
= - ку + FB1
а) Определите зависимость у от £, если
^внеш = -F0sinWf,
б) зависимость у от t, если FBHeilI = F0 cos со*.
в) Какова частота собственных колебаний
со0 в отсутствие внешней силы FBHem?
г) Если частота вынуждающей силы со
больше со0, будет ли внешняя сила в фазе или
противофазе относительно смещения?
16. Каков в примере 6 сдвиг во времени
прихода сигнала при перестройке приемника с
частоты 150 МГц на частоту 160 МГц?
17. Предположим, что в примере 6 расстояние
до пульсара известно и составляет 1500
световых лет. Какой должна быть средняя
плотность электронов в межзвездном
пространстве, чтобы получился наблюдаемый
сдвиг во времени?
18. Предположим, что электрон проводимости
находится в электрическом поле Е =
= Е0 cos oof, где Е0 = 100 В/м и /= 100 Гц.
Какова амплитуда его колебаний?
19. Электромагнитная волна .Епад падает на
тонкую плохо проводящую пластинку,
которая излучает поле АЕ = — 0,01 £пад- В этом
случае амплитуда прошедшей волны равна
(1-0,01) £Пад> а амплитуда отраженной
0,01 £пад. Рассмотрим две такие
пластинки, расположенные на расстоянии Х/4
друг от друга (см. рисунок). Какими в этом
случае будут результирующие прошедшая
и отраженная волны? Заметим, что, когда
отраженная от пластинки 2 волна достигает
пластинки 1, ее фаза будет отличаться на
180° от фазы отраженной волны,
покидающей пластинку 1.
пад
А А
Пластинка Пластинка
1 2
20. Какова скорость электрона в задаче 18?
21. Рассмотрим классическую модель атома
водорода, согласно которой электрон
движется по круговой орбите радиусом jR =
= 0,53-Ю-10 м. Сумма кинетической и
потенциальной энергий электрона
E = K + U= -к0^-= -13,6 эВ.
а) Какая энергия излучается за один
оборот? Дайте числовой ответ в электронволь-
тах.
Получите следующие равенства:
б) dE/dt = - (2/3)(k30e6)/(m2c3R%
в) dE/dR = k0e2/2R2 и
г) dR/dt = - (4/3)(k2e*)/(m2c3R2).
д) Когда электрон достигает R = 10" 15 м,
он падает на протон. Сколько ему для этого
понадобится времени, иными словами, како-

ЗАДАЧИ *7"
во «время жизни» классического атома
водорода? Воспользуйтесь соотношением
R2
t = ${dt/dR)dR.
Ri
22. Чему равна в примере 6 разность с — vg для
частоты 150 МГц?
23. Покажите, что для электромагнитного
излучения, распространяющегося в
ионизованной среде,
..,[-(-
2пк091е2\2-
mor
Л г2
24. Используя метод фазовых диаграмм,
покажите, что
sin cot + sin (cot + ф) + sin (cot + 2(p) =
=(1 + 2 cos cp) sin (cot + cp).
25. Квадрупольный излучатель можно
представить как два диполя р, расположенные на
расстоянии z0 друг от друга (см. рисунок),
при условии, что z0« X. Диполи излучают
в противофазе. Если верхний диполь
колеблется по закону р = pocos ю*» то его поле
излучения
С)
Ех = к0 -V~sm 0 cos со [ t •
В случае нижнего диполя
Е2 = к0—-—sin 0 cos
K'-vH
Какой вид имеет результирующее поле
излучения обоих диполей? Запишите
результат через со, с, г, 0 и квадрупольный момент
Q0 = p0z0. [Указание: k(r2 — rt) « /czocos0.]
26. Заряд Q движется с ускорением а вдоль оси
z. В нештрихованной системе заряд
находится в точке, показанной на рисунке для
t = 0. Какова величина и направление
действующей на заряд q силы, обусловленной
полем излучения заряда б?
27. Повторите решение задачи 26 для случая,
когда заряд Q распределен по кольцу
радиусом R = rsin0.
28. Повторите решение задачи 26 для случая
равномерного распределения заряда Q
внутри шара радиусом R.
±пВ?
29. Повторите решение задачи 26 для случая
малой массы т и однородного шара массой
М. Предположим, что гравитационная сила

ГЛ. 21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С ВЕЩЕСТВОМ
пропорциональна а/г по тем же
соображениям, что и электрическая сила. Покажите,
что результирующая сила, действующая на
т, записывается в виде
F = ma[(4n/3)Gp(R2/c2)~].
Р -
М
|яЯ3
(Замечание: В гл. 30 мы покажем, что для
нашей Вселенной множитель (4я/3) Gp(R2/с2)
может оказаться близким единице (в этом
случае R-радиус, а р-средняя плотность
Вселенной). При этом мы получим F = та\
Это объяснение инертной массы носит
название принципа Маха.)
30. Дипольная антенна длиной 1(1«Х)
подсоединена к генератору переменного тока.
Генератор подводит заряд q = q0cosa)t.
В этом случае ток в максимуме /0 = щ0.
Предположим, что заряды колеблются
между краями диполя. В этом случае р0 = q0l.
I
а) Покажите, что поле излучения
Е= V-^coswU )sin0.
б) Используя соотношение Р = I2R,
покажите, что эффективное сопротивление на
выходе генератора равно R =
= (2/3)(/с0/с)(/с/)2 = (/с/)2 20 Ом. (В случае / =
= Х/2 заряд q0 перемещается в среднем на
расстояние / =0,61 Х/2. Таким образом,
полуволновая дипольная антенна имеет R =
= 72 Ом.)

ИНТЕРФЕРЕНЦИЯ ВОЛН
В предыдущей главе мы рассмотрели
эффекты, создаваемые отдельным
источником электромагнитных волн, независимо
от того, был ли этим источником
переменный поверхностный ток или
колеблющийся электрический заряд. В данной
главе мы займемся изучением явлений,
создаваемых двумя или несколькими
источниками волн, колеблющимися с определенной
фазой относительно друг друга. При этом
амплитуда результирующей волны
оказывается равной сумме отдельных амплитуд.
Данное явление называется
интерференцией волн. Интерференция свойственна не
только электромагнитным волнам, но
и волнам любого другого вида. При
описании интерференции любых видов волн
применяется один и тот же
математический аппарат, поскольку как механические
волны (типа волн, распространяющихся по
натянутой струне и рассмотренный в § 6
гл. 20), так и электромагнитные волны
удовлетворяют одним и тем же волновым
уравнениям.
§ 1. Стоячие волны
При полном отражении бегущей волны
сумма падающей и отраженной волн
порождает стоячую волну. В § 3 гл. 21 мы
показали, что электромагнитная волна,
падающая на идеально отражающую
поверхность, индуцирует поверхностный ток #.
Этот ток излучает поле £', направление
которого в непосредственной близости от
отражающей поверхности в любом случае
противоположно направлению Епад. На
рис. 22-1 в отраженной волне
электрическое поле равно Е', а магнитное поле 93'.
Следует заметить, что вектор Е' х ЗУ,
соответствующий направлению
распространения волны, смотрит в отрицательном
направлении оси х. Если падающая волна
имеет вид Епад = Е0 cos (cot — кх), то в
левую сторону от отражателя должна
излучаться волна Е'лев = — £0 cos (cot + /ос), а в
правую Еправ = — Ео cos (art — кх). Эти
волны удовлетворяют условию, согласно
которому повсюду справа от отражателя
Е = £пад + Я'прав = 0- Слева от отражателя
результирующее электрическое поле
запишется в виде
& = -^пад г -С/лев =
= Е0 [cos (cot — кх) — cos (cot + /ос)].
Чтобы преобразовать это выражение,
воспользуемся тригонометрическим
соотношением
(В + А\ . ( В - А
cos А — cos В = 2sin( -
Ism
Л 2
Тогда
Е = 2 E0sin cot sin кх = A(t) sin кх,
(22-1)
\
»'
»,
Рис. 22-1. Падающая волна (Епад и ©п
индуцирует поверхностный ток $, который излучает
волну (Е' и ©'), распространяющуюся влево.

/-0
-I
>-4т
Рис. 22-2. Функция,
описываемая выражением (22-1), в
последовательные моменты времени.
Физически она соответствует
монохроматической волне,
распространяющейся вправо и
отражающейся в точке х = 0.

§ 1. СТОЯЧИЕ волны 383
где A (t) = 2Е0 sin cot. На рис. 22-2
построены графики этой функции для
последовательных значений t. Стоячая волна
представляет собой определенную
функцию от х (в данном случае sin /ос), значения
которой возрастают и убывают во
времени по гармоническому закону.
Следует заметить, что если кхп = пп,
где п- положительное или отрицательное
целое число, то возникает узел, т.е. Е = О
при любых г. Узлы располагаются в
точках
х„ =
пп
пп X
(2п/Х) = "У
(п-любое целое число). Соседние узлы
отстоят друг от друга на расстоянии,
равном полуволне.
Пример 1. Микроволновый генератор (см.
рис. 22-3) излучает вправо плоские
электромагнитные волны, которые затем отражаются
обратно. Точки Pt и Р2 соответствуют
положениям двух соседних минимумов интенсивности
и отстоят друг от друга на расстоянии 5 см.
Чему равна частота/ микроволнового генератора?
Решение: Поскольку расстояние между двумя
последовательными узлами равно половине
длины волны, то X = 10 см. Таким образом,
с 3,00-108 м/с
j ~~Х ~ ОДм
= 3000 МГц.
3,00-109 Гц =
Генератор
рх рг
Отражатель
Рис. 22-3. Микроволновый генератор излучает
вправо электромагнитные волны, которые
отражаются назад. В точках Р1 и Р2 наблюдаются
узлы.
СТОЯЧИЕ ВОЛНЫ НА СТРУНЕ
Закрепленный конец натянутой струны
ведет себя как идеальный отражатель. При
этом отраженная волна, как и в случае
электромагнитных волн, распространяется
в направлении, противоположном
падающей. Поэтому в любом случае смещение
у конца струны равно нулю. В точке х = 0
функция
у = у0 [cos (cot — kx) — cos (cot + /ос)] =
= 2y0 sin cot sin kx
всегда имеет нулевое значение. На
рис. 22-4 иллюстрируются стоячие волны,
возникающие на струне длиной L.
Поскольку на обеих концах струны
расположены узлы, на рис. 22-4,а, б, в и г мы имеем
соответственно Ь=Х/2, 2(Х,/2), 3(Х/2)
и 4(Х/2). Такие чисто стоячие волны
называются резонансами. Они удовлетворяют
следующим соотношениям:
п -у- = L или Хп = (стоячие волны).
(22-2)
Звучание струнных музыкальных
инструментов основано на стоячих волнах,
возбуждаемых щипком струны. Аналогично
звучание духовых музыкальных инструментов
основано на стоячих волнах воздушного
столба.
Пример 2. На колеблющейся струне длиной
12 см узлы расположены на расстоянии 4 см
друг от друга. Скорость распространения волны
и = 30 м/с. а) Определим частоту колебаний,
б) перечислим все возможные низшие
резонансные частоты и в) найдем натяжение струны
при условии, что ее масса равна 24 г.
Решение: а) Расстояние между узлами Х/2 =
= 4 см и, следовательно, X = 0,08 м. Тогда
и 30 м/с
X ~ 0,08 м
/ =
375 Гц.
б) Резонансные длины волн удовлетворяют
условию Хп = 2L/n. Таким образом,
^i
2(12 см)
1
: 24 см, Х2
2(12 см)
2
12 см.
Соответствующие частоты fy — и/Х1 = 125 Гц,
/2 = и/Х2 = 250 Гц, а /3 совпадает с / в случае а.

ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
Рис. 22-4. Первые четыре резонанса
колеблющейся струны, а -на струне укладывается
полволны, г-на струне укладываются две длины
волны. [С любезного разрешения Центра по
развитию образования.]
в) Натяжение находим с помощью
формулы (20-15):
Т= \хи2 = (0,2кг/м)(30м/с)2 = 180 Н.
§ 2. Интерференция волн, излучаемых
двумя точечными источниками
Рассмотрим два электрических диполя
Sx и S2, колеблющиеся в фазе в
направлении оси z (рис. 22-5). Пусть дипольный
момент каждого из диполей р = р0 cos cot.
Тогда в соответствии с (21-15)
электрическое поле в точке Р запишется в виде
Е = Ех + Е2 =
= Е0 cos (кг\ — cot) + Е0 cos (кг2 — cot),
Рис. 22-5. а -два точечных источника 5Х и S2 на
расстоянии d друг от друга; б-те же источники
в увеличенном масштабе. Разность хода
r2 — ri ~ dsinQ.

§ 2. ИНТЕРФЕРЕНЦИЯ ВОЛН, ИЗЛУЧАЕМЫХ ДВУМЯ ТОЧЕЧНЫМИ ИСТОЧНИКАМИ 385
где
г к0®2р0
^0 — 2 *
Поскольку оба источника колеблются
в фазе, для нахождения суммы двух волн
можно воспользоваться методом фазовых
диаграмм (см. приложение 1 гл. 21), как
показано на рис. 22-6. Оба вектора Ех и Е2
имеют одну и ту же длину Е0. Угол ф
между векторами равен разности фаз полей
Е2 и Еь собственно
Ф = (к>г2 — ю0 ~~ (k>ri — ю0 = к(г2 — ri)-
Векторная сумма, равная Е', характеризует
амплитуду результирующего поля.
Применяя правило косинусов к равнобедренному
Рис. 22-6. Фазовая диаграмма для случая двух
диполей с разностью фаз ср.
/
VV/V
о А А
2d d
Рис. 22-7. Интерференционная картина от двух
источников. Приведена зависимость
интенсивности от sin 0.
треугольнику на рис. 22-6, получаем
Е'2 = El + El + 2£gcoscp =
= 2Eg(l + coscp).
Интенсивность J волны пропорциональна
квадрату амплитуды. Поэтому
/ = 2/0[1 +cosk(r2-r1)].
Из прямоугольного треугольника на
рис. 22-5, б видно, что разность хода равна
г2 — rx = d sin 0, если расстояние до экрана
достаточно велико. Это условие, согласно
которому разность хода равна d sin 0,
называется приближением Фраунгофера. В этом
случае
/ = 21 о [1 + cos {kd sin 0)] (интерференция
волн от двух
источников),
(22-3)
На рис. 22-7 построена функция,
описываемая выражением (22-3). Максимум
интенсивности наблюдается всякий раз, когда
kd sin 0 = п2п или
sm0 = (условие максимума). (22-4)
d
В этом случае разность хода, которая в
соответствии с рис. 22-5 равна dsin0,
составляет пХ. Разумеется, на экране мы ожидаем
максимума интенсивности в том месте, где
гребень одной волны совпадает с гребнем
другой. Это может быть только в случае,
когда разность хода равна целому числу
длин волн. Если же разность хода
составляет половину длины волны или (п +
+ 1/2) А,, то гребень одной волны
совпадает с впадиной другой волны, и мы будем
иметь минимум интенсивности.
Геометрическое место таких минимумов
интенсивности называется линией узлов. На
рис. 22-8 иллюстрируется
интерференционная картина волн, образующихся на
поверхности воды.
Пример 3. Два динамика расположены на
расстоянии 2 м друг от друга и воспроизводят
один и тот же музыкальный тон на частоте
1000 Гц. В 4 м от них находится слушатель
(рис. 22-9). На какое расстояние слушатель
должен удалиться от центральной линии, чтобы
достичь первого узла интерференционной
картины? Скорость звука 330 м/с.

386 ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
Рис. 22-8. Интерференционная
картина от двух .источников,
создаваемая на поверхности воды
с помощью двух
синхронизованных вибраторов. [С
разрешения Центра по развитию
образования.]
Решение: Первый узел наблюдается, когда
разность хода достигает Х/2 или когда
r2- rt = Х/2.
Если 0 < 30°, то с хорошей точностью разность
хода равна dsin0. В этом случае sin0 = X/2d.
Чтобы найти длину волны, воспользуемся
соотношением Х = u/f:
Х =
330 м/с
1000 Гц
0,33 м,
sin0 =
0,33 м
2(2 м)
: 0,0825, j/ = Z)tge = 0,33 м.
Таким образом, если слушатель переместится
в любую сторону примерно на одну треть
метра, то он обнаружит узел на частоте 1000 Гц
(в том же месте будут находиться узлы на
частотах 3000, 5000, 7000 Гц). В обычной комнате
из-за значительного отражения от стен
интенсивность звука в узлах не спадает до нуля.
Однако интерференционный эффект вполне
ощутим, если через стереофоническую систему
воспроизводить чисто синусоидальную волну
и при этом перемещаться по комнате.
Рис. 22-9. Динамики в примере 3.
§ 3. Интерференция волн от большого
числа источников
Предположим, что наблюдатель
расположен под углом 0 относительно нормали
к линии, соединяющей N равномерно
размещенных источников (рис. 22-10). Для
наблюдателя разность фаз между соседними
источниками равна ф = к(г2 — гг) =
= Ы sin 0. На рис. 22-11 приведена фазовая
диаграмма для случая N источников.
Используя прямоугольный треугольник на

§ 3. ИНТЕРФЕРЕНЦИЯ ВОЛН ОТ БОЛЬШОГО ЧИСЛА ИСТОЧНИКОВ 387
Рис. 22-10. N синхронизованных источников на
расстоянии d друг, от друга.
и возведем результат в квадрат:
sin2(N(p/2)
/ = Jo-
sin2 (ф/2)
(22-5)
здесь /0-интенсивность, обусловленная
отдельным источником, а ф = /cdsinG. На
рис. 22-12 показано распределение
интенсивности, построенное в соответствии
с (22-5). Следует заметить, что при ф -► 0
мы имеем sm(N<p/2) -► АГф/2, a sin (ф/2) -►
-► ф/2; при этом соотношение (22-5)
записывается в виде
I
Io (ф/2)2 " N 7°-
Таким образом, интенсивность волн,
создаваемых N источниками, оказывается
в N2 раз больше интенсивности,
создаваемой отдельным источником.
Рис. 22-11. а-фазовая диаграмма в случае
N источников, изображенных на рис. 22-10;
концы векторов располагаются на окружности
радиусом R; б-диаграмма для первого
источника.
рис. 22-11, а, получаем
Е/2 = JRsin(JVq>/2).
Из прямоугольного треугольника на
рис. 22-11,6 имеем
EJ2 = R sin (ф/2).
Разделим первое из этих соотношений на
второе:
Е _ sin(JVq>/2)
El sin (ф/2)
Пример 4. В небольших городах США не
допускается работа широковещательных
радиостанций в ночное время, поскольку сотни таких
станций мешали бы друг другу. (Ночью
ионосфера располагается на значительной высоте, так
что благодаря отражению от нее возможен
прием сигналов от станций, удаленных на большие
расстояния.) Однако радиостанция WTKO
вблизи г. Итака (шт. Нью-Йорк, США) продолжает
широковещательные передачи и ночью,
поскольку она снабжена антенной системой,
которая посылает относительно сильный сигнал
в направлении города и очень слабый сигнал
в остальных направлениях. В этой системе
используются 4 дипольных излучателя,
расположенные в ряд в направлении Итаки, причем

ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
sine
Рис. 22-12. Интерференционная картина от
шести расположенных в ряд источников.
Зависимость интенсивности I от sin 0 описывается
формулой (22-5).
каждый последующий излучатель сдвинут по
фазе относительно соседних на 90°. Расстояние
между соседними излучателями d = Х/4. Как
в этом случае интенсивность зависит от угла
0 (рис. 22-13)?
Решение: В данном случае ф = kdsind — я/2,
а не /cdsinG; поэтому
Ф = к — sin0
4
|->.-ч.
Распределение интенсивности дается
выражением (22-5), причем N = 4 и ф = (я/2) (sin 0 — 1):
1 = 1
sin2 [я (sin 0 - 1)]
0 sin2 [(я/4) (sin 0 - 1)]
Зависимость интенсивности / от 0,
соответствующая этому выражению, приведена на
рис. 22-13,6.
§ 4. Дифракционная решетка
Процарапав параллельные штрихи на
плоской стеклянной пластинке, можно
изготовить систему из N щелей. Полоски
стекла между штрихами будут вести себя
подобно отдельным щелям. Если
направить на эти щели параллельный пучок
монохроматического света от отдельного
источника (рис. 22-14), то мы получим
N источников, колеблющихся в фазе. Для
этого случая распределение интенсивности
на экране дается выражением (22-5):
/ = /г
sin2[JV((p/2)]
sin2((p/2)
, где ф = /cdsinO.
Интенсивность принимает значение I =
= N2I0 в тех случаях, когда знаменатель
обращается в нуль или когда
Ф„ = 2пп,
или
kd sin 0„ = 2пп,
т.е.
sm6„ = и — .
(22-6)
(22-7)
Итака
Четыре \
излучателе
Другие
направления
Направление
на Итаку
и озеро
Рис. 22-13. а-ориентация 4-х
дипольных излучателей
радиостанции WTKO в направлении
на г. Итаку; б-зависимость
интенсивности излучения I от
угла 0.

§ 4. ДИФРАКЦИОННАЯ РЕШЕТКА 389
От источника
К экрану
02
.J—0
4rf sin д
Рис. 22-14. а-участок дифракционной решетки
в увеличенном масштабе; б-соответствующее
распределение интенсивности на экране.
При других углах 0 интенсивность I
приблизительно равна 10, т.е. примерно в N2
раз меньше. В типичных дифракционных
решетках величина N составляет несколько
тысяч. Параллельные световые лучи за
решеткой можно сфокусировать с помощью
линзы и получить четкое изображение
линий на экране, как показано на рис. 22-14.
С помощью этого рисунка нетрудно
получить условие (22-7). Для того чтобы все
параллельные лучи находились в фазе,
разность хода для каждой пары соседних
лучей должна составлять пХ. Поскольку
эта разность хода равна dsinG, мы
получаем
dsinG = пХ, или sinG = nX/d.
Спектральная линия, отвечающая длине
волны X, будет наблюдаться под углом,
определяемым соотношением sinG = X/d.
Изображение второго порядка для этой
линии будет соответствовать sinG = 2X/d,
третьего порядка-sinG = ЗХ/d и т.д.
Пример 5. Рассмотрим выпускаемую
промышленностью решетку с 13400 штрихами на дюйм
(2,54 см). Предположим, что мы смотрим сквозь
эту решетку на свечение натрия. Ионизованные
атомы натрия испускают свет о практически
одной длины волны X = 5893 А (1 А = 10"10 м).
Под каким углом будет видна за решеткой эта
желтая линия?
Решение: Расстояние между штрихами решетки
равно
2,54 см
d = -^гт^г = W •10 м-
13400
Используя формулу (22-7), находим
sin 0j = —
X 5893 • 10"
d 1,90 • Ю-6
2Х
sin 02 = —- = 0,62,
а
ЗХ
sin 03 = —- = 0,93,
= 0,31, 0! = 18,1°,
02 = 38,3°,
03 = 68,5°.
Если источник света линейный, то эти три
линии будут наблюдаться по обе стороны от
прямого луча под углами ±18,1, +38,3 и +68,5°.
РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ
В идеальном спектроскопе свет с
определенной длиной волны Х0 должен
наблюдаться в виде спектральной линии нулевой
ширины. Однако дифракционная решетка
вносит приборную ширину АХ0, которую
мы сейчас вычислим.
Распределение интенсивности,
создаваемое источником света с длиной волны Х0,
дается выражением (22-5). На рис. 22-15
приведено это • распределение в виде
кривой 1. На этом рисунке А0О -разность
между угловыми положениями максимума
и первого нуля интенсивности. Назовем
эту разность приборной шириной. Величи-

390
ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
Рис. 22-15. Распределение интенсивности,
создаваемое дифракционной решеткой, в случае
двух источников, различающихся по длине
волны на АХ0; кривая 1 -источник с длиной волны
Х0; кривая 2-источник с длиной волны Х0 +
+ AV
на А0О соответствует такому сдвигу фаз
Аф0, при котором в числителе выражения
(22-5) угол АГф/2 меняется на 180°.
Следовательно,
ЛГАф0/2 = я,
или
Аф0 = 2n/N.
Дифференцируя выражение ф0 = /cdsin0o,
получаем Аф0 = /cdcos0oA0o. Определяя
отсюда А0О, имеем
А0 2К
0 Nkd cos 0О '
А6° = А^ё/ (22"8)
Угловую шкалу спектрометра можно
также проградуировать в длинах волн. Нас
интересует величина АА,0, соответствующая
этой приборной ширине линии. Ее можно
найти, используя соотношение sin 0 = X/d,
которое дает АХ = dcosGAG.
Воспользовавшись выражением (22-8) для А0, мы
получим следующую формулу для
приборной ширины линии:
АХ0 = X0/N.
(22-9)
Предположим теперь, что источник
испускает свет с двумя определенными
длинами волн Х0 и Х0 + АХ,. Если АХ = АХ0,
где АХ0- величина, определяемая
формулой (22-9), то на экране обе эти линии
окажутся не полностью разделенными. Такой
случай иллюстрируется на рис. 22-15, на
котором кривая 1 -это распределение
интенсивности, отвечающее Х0, а кривая
2-распределение интенсивности,
отвечающее Х0 + АХ0. Следовательно, если две
линии находятся друг от друга на
расстоянии, равном приборной ширине линии
АХ = X/N, то максимум одной из них
расположится на краю другой; при этом
линии должны слиться воедино. Если же
АХ окажется больше X/N, то обе линии
удастся разрешить. Отношение X к такому
критическому значению АХ называется
разрешающей способностью (или
разрешающей силой). Разрешающая способность
дифракционной решетки равна просто
полному числу ее штрихов N.
Пример 6. Известнаяо линия натрия D с
длиной волны X = 5893 А в действительности
представляет собой две отдельные линии с длинами
волн 5890 и 5896 А. Можно ли с помощью
дифракционной решетки, параметры которой
приведены в примере 5, разрешить эти линии?
Решение: Необходимая разрешающая
способность
X
~АХ
5893
982.
Разрешающая способность дифракционной
решетки равна полному числу штрихов. Для
рассматриваемой решетки длиной 2,54 см
(1 дюйм) с плотностью штрихов 13400 на дюйм
разрешающая способность составляет 13400,
что примерно в 13 раз превышает найденное
выше значение минимально необходимого
разрешения.

§ 5. ПРИНЦИП ГЮЙГЕНСА 391
§ 5. Принцип Гюйгенса
В действительности, для того чтобы
наблюдать интерференционные эффекты,
необязательно иметь отдельные источники
света. С помощью единственного
источника и экрана с отверстиями в нем можно
получить большое количество источников.
На рис. 22-16 изображены плоские волны
на поверхности воды (от единственного
источника), падающие на экран с двумя
отверстиями. Волны, выходящие из этих
отверстий, ведут себя так, как если бы они
испускались двумя источниками,
находящимися на месте отверстий и
колеблющимися в фазе.
воды сформулировал без доказательства
следующий принцип: Когда волновой фронт
проходит одно или несколько отверстий,
каждый элемент волнового фронта ведет
себя так, как если бы он стал
источником излучения. На первый взгляд это
может показаться странным, поскольку в
отверстиях не имеется каких-либо
источников тока. Действительно, токи должны
индуцироваться в любом месте экрана, за
исключением отверстий. Покажем теперь,
что математически поле, излучаемое
источниками тока, заполняющими отверстие
в экране, совпадает с полем волны,
падающей на экран с отверстиями. Обозначим
Рис. 22-16. Волны на
поверхности воды, возбуждаемые
единственным вибратором и
падающие на экран с двумя
отверстиями.
Известным опытом по получению
интерференции электромагнитных волн,
аналогичной изображенной на рис. 22-16
интерференционной картине на воде,
является опыт с двумя щелями и источником
света, как показано на рис. 22-17. Две
узкие щели освещаются единственным
источником света. Распределение интенсивности
света на экране описывается формулой
(22-3) и представляет собой такую же
картину, как если бы щели были заменены
источниками. Впервые такой эксперимент
выполнил Томас Юнг в 1803 г.
В XVIII столетии Христиан Гюйгенс на
основе опытов с волнами на поверхности
поле, излучаемое индуцированными в
экране токами через Еэкр. Тогда справа от
экрана результирующее поле запишется в виде
Ярез = Япад + Дэкр > (22-10)
где Епад-поле, создаваемое самим
источником (при отсутствии экрана). Это
равенство соответствует физической ситуации,
при которой возникает наблюдаемая
интерференционная картина. Теперь закроем
отверстия дополнительными экранами
(заглушками), размеры которых совпадают
с размерами отверстий. Пусть Еотв-поле,
излучаемое токами, наведенными в
заглушках, закрывающих отверстия в экране.

392 ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
У
I
Источник I
Экран с Экран
двумя щелями
а
Рис. 22-17. а-схема опыта по интерференции
света от двух щелей (источником может быть
либо лазер, либо единственная щель,
освещаемая монохроматическим светом лампы; экран
имеет две щели на рсстоянии d друг от
друга); б-распределение интенсивности, полученное
на фотопленке, расположенной у второго
экрана. [С любезного разрешения Центра по
развитию образования.]
Для случая экрана с заглушками имеем
Ярез = Япад + Яэкр + ^отв = 0 (справа ОТ
экрана).
Следовательно,
-^отв -^пад "т" -^экр >
I -^отв I == I -С'пад г -С<экр | .
Мы видим, что правая часть этого
равенства совпадает с полем, соответствующим
реальной физической ситуации [(22-10)],
а левая часть свидетельствует о том, что
эта ситуация математически эквивалентна
распределению интенсивности излучения,
создаваемому источниками тока,
расположенными в отверстиях и испускающими
излучение независимо друг от друга. Мы
продемонстрировали, что если каждый
элемент прошедшего за экран волнового
фронта рассматривать как новый точечный
источник излучения, то распределение
интенсивности будет таким же, как и в случае
экрана и отдельного источника. Однако
наше рассмотрение требует небольшой
поправки, связанной с краевыми эффектами,
которыми мы будем пренебрегать.
(Проведенное нами доказательство предполагает,
что индуцированные токи могут
пересекать края отверстий, разграничивающие
экран и заглушки.)
Мы «доказали» принцип Гюйгенса для
случая падения плоской волны на плоский
экран. Принцип Гюйгенса можно
применить для волновых фронтов произвольной
формы при отсутствии экрана. При этом
каждая точка волнового фронта
рассматривается как источник новой волны.
Такое рассмотрение приводит к правильному
результату, когда речь идет о форме
фронта вторичных волн. Однако при этом не
всегда удается получить правильные
значения амплитуды волны.
§ 6. Дифракция на отдельной щели
Параллельный пучок
монохроматического света, падая на отдельную щель
шириной а, создает на удаленном экране
интерференционную картину, как показано на
рис. 22-18. Подобная интерференция,
возникающая от одной щели или от края
экрана, называется дифракцией. При этом
лучи света «дифрагируют» (отклоняются)
от своего первоначального направления.
С помощью построения на рис. 22-19
легко определить угол 0, под которым
наблюдается первый минимум
интенсивности. В соответствии с принципом Гюйгенса
мы можем рассматривать щель как
последовательность новых источников Sb S2, ...
..., SN. Если разность фаз между волнами,
испускаемыми из точки Sx и из центра щели,
составляет 180°, то эти волны погасят друг
друга (лучи 1 и 2 на рис. 22-19). Также
погасят друг друга волны, одна из которых

§ 6. ДИФРАКЦИЯ НА ОТДЕЛЬНОЙ ЩЕЛИ 393
Рис. 22-18. а-распределение интенсивности на
удаленном экране при дифракции на отдельной
щели; б-изображение на фотопленке,
помещенной в плоскости экрана. В качестве источника
света использовался неон-гелиевый лазер.
создается источником S2, а
другая-следующим источником, расположенным
ниже за лучом 2. Аналогично луч из S3 и
последующие лучи будут попарно гасить
друг друга. Разность хода между лучами
Интенсивность для произвольного угла
0 получается в результате суммирования
вкладов всех бесконечно малых источников
'(рис. 22-20). Соответствующие векторы
образуют дугу окружности, для которой
результирующая разность фаз
Ф = /casinG (разность фаз лучей 1 и 3).
Результирующую амплитуду Л можно
найти из прямоугольного треугольника:
sin
Ф
Л/2
откуда
Л = 2Д sin (Ф/2).
(22-12)
Длина дуги равна Л0; это
результирующая амплитуда для угла 0°. Она равна
радиусу R, умноженному на угол Ф в
радианах:
ЯФ = А0.
Отсюда находим
R = А0/Ф.
Падающий
волновой
фронт
Рис. 22-19. Излучение от
отдельной щели. Лучи 1 и 3 идут
от краев, а луч 2 исходит из
центра щели.
т!
1:
1
а ;
Препятствие
1 и 2 равна (а/2) sin 0. Для того чтобы
получить разность фаз между ними 180°, эта
разность хода должна составлять Х/2.
Угол, соответствующий первому
минимуму интенсивности, определяется из
равенства
а • л X
- sin 6i = -,
2 1 2'
X
sinGi = - (условие минимума интенсив-
а ности для отдельной щели).
(22-11)
Подставим эту величину в (22-12):
sin (Ф/2)
Л = Ап
Ф/2
Возводя это выражение в квадрат,
получаем распределение интенсивности:
'sin (Ф/2) I2
Ф/2 J '
(22-13)
/ = /о
где Ф = /easinG.
Эта функция изображена на рис. 22-18.
Последовательные минимумы наблюдают-

394
ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
Рис. 22-20. Вектор А представляет собой
векторную сумму сигналов от N источников,
изображенных на рис. 22-10. Ф-разность фаз между
первым и последним источниками.
Чтобы найти минимум величины у, нужно
положить dy/du = 0. Таким образом,
XD
= 0,
откуда
u0x\/XD.
-D-
т
У
i
Экран
ся при Ф/2 = шг, или при
/casinG . _ X .
= итг, или sin 0МИН = и — (и ^ 1).
2 а
Это условие совпадает с тем, которое
мы получили выше, а именно с условием
(22-11). Следует отметить, что центральный
максимум в два раза шире вторичных
максимумов.
Пример 7. Параллельный пучок света падает
на широкую щель шириной и, как показано на
рис. 22-21. При этом на экране возникает
полоса света шириной у = и. Если щель постепенно
сужается, то полоса света сокращается, пока не
начинают преобладать дифракционные эффекты
и полоса снова становится шире. При какой
ширине щели и0 на экране наблюдается самая
узкая полоса света?
Решение: За счет дифракции полоса света на
экране уширяется на величину
X
Удиф ~ 9мин D ~ — D.
и
Таким образом, полная ширина полосы света
будет
XD
у « и Н .
Рис. 22-21. Параллельный пучок света, проходя
щель шириной и, образует на экране полосу
шириной у.
§ 7. Когерентность и некогерентность
До сих пор мы изучали
интерференционные эффекты, создаваемые
источниками, которые находятся в фазе
относительно друг друга (или с некоторым
постоянным соотношением фаз). Такие
источники называются когерентными.
Когерентные источники радиоволн можно
получить, запитав две или несколько антенн
от одного и того же генератора.
Когерентные же источники света, как мы
показали в § 5, можно получить, освещая
одним и тем же точечным источником света
пару или большее число щелей или
отверстий. Кроме того, можно создать
когерентные пучки света, используя
полупрозрачные зеркала, как в интерферометре
Майкельсона (см. рис. 8-4).
Однако в случае, когда оба плеча
интерферометра имеют разную длину,
интерференционная картина может исчезнуть,
если разность хода превысит некоторую
величину AL0, соответствующую разности

§ 7. КОГЕРЕНТНОСТЬ И НЕКОГЕРЕНТНОСТЬ 3"5
времен At0 = AL0/c. Величина AL0
называется длиной когерентности, a At-
временем когерентности. Если свет от
источника в интерферометре (независимо
от того, используется ли свечение лазера
или газового разряда) проанализировать
с помощью спектрометра высокой
разрешающей способности, то мы обнаружим
резкую линию с естественной шириной (на
шкале частот) А/. Эта ширина связана
с временем когерентности At0
соотношением
2nAfAt0 ж 1.
Это соотношение совпадает с (21-16) и
интерпретируется аналогичным образом.
Высококачественный источник
монохроматического света независимо от того, идет ли
речь о лазере или о свечении атомов, ведет
себя подобно генератору, средняя частота
f0 которого случайным образом меняется
в интервале от f0 — Af до f0 + Af. В
соответствии с (21-16) две чисто
синусоидальные волны, разнесенные по частоте на
величину Af, будут оставаться в фазе на
протяжении времени At ж 1/(2тгА/).
Наиболее узким линиям атомных спектров
соответствует At0 ~ 10"8 с. В лазере дрейф
частоты оказывается меньше, и поэтому
время когерентности больше.
Из квантовой механики мы знаем, что
свет представляет собой фотоны,
испускаемые один за другим различными
атомами. Лазер излучает фотоны, которые
находятся в фазе друг с другом (см. § 6
гл. 26). Во всех прочих источниках света
относительные фазы фотонов случайны,
и в этом случае говорят, что фотоны
некогерентны. Однако на интервале времени
At0 # 1/(2яА/) (Af- наблюдаемая ширина
линии) любая пара таких фотонов будет
поддерживать друг с другом постоянное
фазовое соотношение. Эти фотоны ведут
себя подобно волновым пакетам длиной
AL0 = cAt0 я c/(2kAJ).
ИНТЕРФЕРОМЕТРИЯ ИНТЕНСИВНОСТИ
От двух независимых и некогерентных
источников света можно наблюдать
интерференционную картину, если эту картину
удастся зарегистрировать за промежуток
времени меньше чем At0 = 1/(2тгА/).
В большинстве случаев интенсивности
оказываются слишком слабыми, чтобы их
можно было измерить. Однако существует
метод, развитый в 1956 г. Хэнбери
Брауном и Твиссом. В этом методе
используется эффективное усреднение большого
числа измерений, каждое из которых
выполнено за промежуток времени короче чем
1/(27г А/)- Ухищрение состоит в том, что на
«экране», на котором должна наблюдаться
интерференционная картина,
устанавливают два раздельных детектора.
Регистрируемые этими детекторами интенсивности
/х и 12 мгновенно перемножаются (это
достигается с помощью быстрой
электроники и благодаря использованию в качестве
детекторов фотоэлектронных
умножителей). На рис. 22-22 детектор 1 расположен
в точке Рх под углом 0 = 0. Детектор 2,
помещенный в точке Р2, используется для
т*
*Л
Рис. 22-22. Sj и S2 -независимые источники.
Детекторы измеряют интенсивности в точках Р1 и
Р2 в один и тот же момент времени.
проведения серии измерений при близких
значениях 0. Источники Sx и S2 являются
независимыми и некогерентными. Если
расстояние d между ними неизвестно, то
его можно определить, измерив величину
hi2, усредненную по всем значениям
разностей фаз между Sx и S2. Это можно
показать, воспользовавшись формулой (22-3)
для интенсивности каждого из детекторов.
Если на протяжении промежутка времени
более короткого, чем At0, разность фаз
между источниками света равна ф, то
детектор 1 измерит интенсивность
1Х = 2/0 (1 + cos ф).

396 ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
В случае детектора 2 имеется
дополнительная разность фаз ф0 = /cdsinG, так что
/2 = 2/0[1 +С08(ф + ф0)].
Усреднение по времени можно
осуществить, беря среднее по всем возможным
значениям ф:
_ |/1(ф)/2(ф)#
hi2=JJ =
Л/,
2я
2я
О
(1 + cosc|>) [1 + COS((j) + ф0)] d$ =
о
2J2 С
° ' [1 + COS ф + COS((|> + фо) +
+ cos ф cos (ф + ф0)] ^ф.
Поскольку значения со8ф и со8(ф + ф0)
бывают одинаково часто как
положительными, так и отрицательными, то
интегралы от соответствующих членов
обратятся в нуль. Таким образом,
ат2 2я
/1/2 = —— Г2тс 4- f cos ф (cos ф cos фо—
71 0
— sin ф sin фо) ^ф] =
III
= (2ТГ + 7ГС08фо) =
71
= 2/о [2 + cos (kd sin 9)]. (22-14)
На рис. 22-23 приведена соответствующая
кривая. Мы видим, что два некогерентных
источника создают интерференционную
картину! Несмотря на этот расчет,
некоторые физики в 1956 г. поначалу не
поверили в возможность наблюдения
интерференции от некогерентных источников1}. (В
1} Этих физиков можно в какой-то степени
оправдать, поскольку объяснение этого явления
с позиций квантового рассмотрения света
оказывается весьма непростым делом. Однако
корректное применение квантовой механики
к двум фотонам также приводит к результату,
описываемому формулой (22-14).
6/:
2/п
2d
sin в
2 d
Рис. 22-23. Произведение интенсивностей,
зарегистрированных двумя детекторами, в
зависимости от угла между ними.
некоторых учебниках с этим можно
встретиться и по сей день.) Однако затем с
помощью радиотелескопов были выполнены
эксперименты, которые позволили
измерить расстояние между компонентами
двойной звезды и даже определить
диаметры некоторых близких звезд.
Осуществление таких экспериментов - весьма
сложное дело, поскольку в условиях очень
высокого временного разрешения шумы
фотоумножителя оказываются сравнимы
с полезным сигналом2).
Пример 8. Две антенные чаши радиотелескопа
настроены на частоту 1000 МГц и направлены
к двойной звезде, которая находится на
расстоянии 100 световых лет. Произведение
интенсивностей измеряется при нескольких значениях
расстояния между антеннами; соответствующие
результаты' приведены на рис. 22-24. Каково
расстояние между компонентами двойной
звезды?
Решение: Угол между двумя детекторами в
случае первого минимума равен
0 =
3 км
3 км
100 св. лет
= 3,18- Ю-15.
9,42 • 1014 км
2) В последние годы были получены
обнадеживающие теоретические и
экспериментальные результаты по применению этого
метода в физике элементарных частиц для изучения
того, как протекают в пространстве и времени
процессы рождения адронов при высоких
энергиях- Прим. перев.

§ 7. КОГЕРЕНТНОСТЬ И НЕКОГЕРЕНТНОСТЬ 397
Ыг
менной оптики. Следующую главу мы
начнем с рассмотрения одного примера из
современной оптики, а именно голографии.
6 км
Рис. 22-24.
Из выражения (22-14) следует, что первый
минимум наблюдается в том случае, когда 0 = X/2d,
откуда находим
d =
X
~2Q
5,0-
0,30 м
2(3,18
Ю-3
ю-15;
св. лет.
= 4,72 • 1010 км
Последние два десятилетия
ознаменовались значительным расширением области
приложения оптики, которое
сопровождалось появлением радиотелескопов,
микроволновой техники, инфракрасных
детекторов, лазеров, квантовых детекторов,
голографии, быстрой электроники, ЭВМ и т.п.
Все эти разработки легли в основу совре-
Рис. 22-25. а-часть крупнейшего в мире
радиотелескопа в Аресибо на острове Пуэрто-Рико.
Чаша отражателя диаметром 1000 футов
разместилась в естественной горной выемке.
Отраженный сигнал фокусируется на подвижную
антенну, которая поддерживается на высоте 500
футов над чашей с помощью трех вышек,
каждая размером с памятник Вашингтону (высота
памятника 555 футов); б-студентка из Корнелл-
ского университета в специальной обуви для
выравнивания отражающей поверхности.
Показана лишь небольшая часть чаши.
(Обсерватория в Аресибо принадлежит Национальному
центру астрономических и ионосферных
исследований и используется Корнеллским
университетом по контракту с Национальным научным
фондом.)

398 ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
Основные выводы
В результате интерференции бегущей
волны с волной, отраженной от конца
струны (или зеркала, если речь идет об
электромагнитной волне), образуется
волна, амплитуда которой записывается в
виде У = (Уо sin cot) sin кх. Эта волна имеет
узлы в точках хп = п(Х/2). Длина стоячей
волны, образующейся в закрепленной на
обеих концах струне длиной L, равна Хп =
= 2L/n.
Колеблющиеся в фазе два точечных
источника, каждый из которых излучает с
интенсивностью /0, создают
интерференционную картину, интенсивность в которой
изменяется по следующему закону: I =
= 21 о [1 + cosk(r2 - rj)], где (г2 - г^-раз-
ность хода. На очень больших
расстояниях от источников г2 — rl = dsinG,
где d-расстояние между ними. Условие
максимума интенсивности записывается
в виде sinG = nX/d.
Для расположенных в ряд N точечных
источников
sin2 (N6/2)
В случае дифракционной решетки с N
«щелями» соотношение sinG = nX/d
определяет угловое положение спектральной
линии с длиной волны X. Две спектральные
линии, различающиеся на АХ, могут быть
разрешены, если
АХ 1
~Y ^ ~N'
Принцип Гюйгенса утверждает, что
каждую точку волнового фронта можно
рассматривать как новый источник волн.
Дифракционная картина от отдельной
щели шириной а описывается выражением
г _ г sin2 \ка sin G/2]
° [fai sin G/2]2
Это распределение интенсивности имеет
минимумы, когда
sinG = rik/a, где п-целые числа.
Если естественная ширина
спектральной линии равна А/, то время
когерентности составляет At0 = l/(2nAj), а длина
когерентности AL0 = cAt0. Измеряя
произведение интенсивностей излучения от двух
некогерентных источников в течение
промежутка времени, не превышающего At0,
мы получаем среднее значение этого
произведения в следующем виде:
7777 = 211 [2 + cos (kd sin G)].
Упражнения
1. Как направлены Е' и 2У на рис. 22-1 в
непосредственной близости от отражающей
поверхности справа от нее?
2. Перепишите условие (22-2), заменив Хп на кп.
3. Предположим, что на рис. 22-5 Ех =
= E0cos(kr1 — ш) и Е2 = 2Е0cos(kr2 — cot)-
Как зависит / от 10 и 0?
4. Чему равна на удаленном экране разность
фаз между волнами, испущенными из St и
S3 на рис. 22-14? Запишите ответ через X,
d и 0.
5. Скорость распространения волны по струне
с закрепленными концами равна 2 м/с.
Расстояние между узлами стоячих волн 3,0 см.
а) Какова частота колебаний?
б) Сколько раз в секунду струна
вытягивается в прямую линию без каких-либо
видимых следов волн?
6. Пусть S1 и S2-источники, испускающие (в
фазе) синусоидальные звуковые волны и
находящиеся на расстоянии 3 м друг от друга.
Sx S2 Р
#-* Зм »- • -* 6 м *- •
а) Перечислите три различные длины волн,
для которых в точке Р волны будут
погашать друг друга (деструктивная
интерференция).
б) Перечислите три различные длины волн,
для которых в точке Р волны будут
усиливать друг друга (конструктивная
интерференция).
в) Какова низшая частота, при которой
в точке Р волны гасят друг друга?
Скорость звука 330 м/с.
7. Каким условиям должна удовлетворять
разность Dj — £>2 (см. рисунок), чтобы в точке
Р наблюдался интерференционный
максимум или минимум? Предполагается, что
фаза волны не меняется при отражении.
Отражающая поверхность
Источник

ЗАДАЧИ 399
8. В предыдущем упражнении фаза волны при
отражении меняется на 180°. Каково теперь
условие минимума интенсивности в точке
Р?
9. На решетке с 2000 штрихов/см происходит
дифракция света с длиной волны 5000 А.
Экран расположен в 3 м от решетки. На
каком расстоянии находятся на экране
изображения нулевого и первого порядка?
10. Свет падает по нормали к отражательной
дифракционной решетке (в такой решетке
штрихи нанесены на зеркало) и дифрагирует
под углом 0 к ней (см. рисунок).
1
О
16. Предположим, что диполи на рис. 22-5
сдвинуты по фазе на 180°. Как зависит / от 0?
17. В задаче 16 покажите, что в случае, когда
d«X, I*I0k2d2 sin2 0.
18. Решите задачу 16 для случая двух диполей
р0, колеблющихся в направлении оси у
с разностью фаз 180°; d « X. Обозначая угол
между радиус-вектором г и осью у через 0,
покажите, что
k0p0®3d . / г
Е = sin 20 cos со (t —
2c3r I с
19. Предполагая, что на рис. 22-6 Е1 Ф Е2,
напишите выражение для Е через Ev Е2 и 0.
20. Видимые части спектра второго и третьего
порядка от дифракционной решетки будут
частично перекрываться. Какая длина волны
в спектре, полученном в случае N = 3,
совпадает с положением линии X = 7000 А
в спектре с N = 2?
На дифракционную решетку свет с длиной
волны X падает не под прямым углом, а под
углом 0j к ней (см. рисунок). Запишите
условие максимума интенсивности через Qv 02,
X и d.
21
К экрану
а) Найдите разность хода, ответ запишите
через 0 и d.
б) Под каким углом 0 наблюдался бы
максимум интенсивности?
11. Сколько штрихов должна иметь
дифракционная решетка, чтобы ширина линии,
отвечающей типичному атомному переходу,
была бы естественной (см. стр. 372)?
12. Чему равна в примере 6 приборная ширина
А0О каждой из D-линий натрия? Ответ дайте
в градусах.
Сколько штрихов должна иметь
дифракционная решетка, чтобы она могла
полностью разрешить D-линии натрия?
Покажите, что
13.
14,
sin2 (ЛГф/2)
sin2№/2)
= 2(1 + созф), N = 2.
Задачи
15. Предполагая, что на рис. 22-1 падающая
волна имеет вид £пад = Е0 sin (юг - be),
найдите выражение для стоячей волны Е =
= ^пад + ^лев •
>f
К экрану
22. Повторите решение в примере 3 для ноты
«до» первой октавы (частота 262 Гц).
Получите точное решение без использования каких-
либо приближений. (Чтобы найти численные
значения, можно использовать метод проб
и ошибок.)
23. Некоторый атомный переход имеет время
жизни т = 2- 10"4 с. Соответствующая ему
длина волны излучения равна 4000 А.
Какова естественная ширина линии АХ и сколько
штрихов должна иметь дифракционная
решетка, чтобы измерить эту ширину линии?

400 ГЛ. 22. ИНТЕРФЕРЕНЦИЯ ВОЛН
24. Сигнал от радиопередатчика поступает на
две антенны, расположенные друг от друга
на расстоянии, равном половине длины
волны. Необходимо, чтобы излучение под
углом 30° было минимальным (см. рисунок).
Какой должна быть фаза ф между
сигналами в обеих антеннах, чтобы в этом
направлении интенсивности взаимно
компенсировались?
в четырех динамиках? Мы увидим, что
некоторой направленности можно добиться,
комбинируя при записи из четырех
исходных сигналов с различными фазами два
сигнала, а затем воспроизводя записанные
два сигнала с различными фазами. Пусть Lf
и Rf- исходные сигналы соответственно
с левого и правого передних микрофонов, а
Lb и Rb-сигналы с левого и правого задних
микрофонов. В квадратной матричной
системе эти сигналы комбинируются таким
образом, что для амплитуды на левой
дорожке записи мы имеем
U = Lf
S,Q
130°
s2o
25. Покажите, что интерференционная картина
от трех щелей дается выражением
/ = /0(1 + 2cosc|>)2, где ф = /cdsinG.
26. На рис. 22-22 добавьте третий
некогерентный источник (см. иллюстрацию к
задаче). Пусть фх-случайная разность фаз
между St и S2, ф2-между S2 и S3i а ф0 =
= /cdsinG.
а) Покажите, что /х = /0 [3 + 2со8ф! +
+ 2соБф2 + 2соз(ф2 — фх)].
б) Найдите выражение для 12.
в) Покажите, что IJ2 = /о [6 + (1 + 2совф0)2],
т. е. эта величина соответствует
интерференционной картине от трех когерентных
источников (щелей) плюс постоянный
член.
27. В стереофоническом приемнике имеются
два независимых сигнала. Как можно
воспользоваться этими сигналами, чтобы
получить квадрафоническую направленность
-Lh +
Дь
1/2 1/2
здесь через ±j обозначены фазовые
сдвиги + 90° любой записанной
монохроматической волны; иными словами, если
напряжение сигнала Lb равно V0 cos art, то в
выражении для Lt оно запишется в виде
(1/]/2) V0 cos (cor - 90°). Амплитуда на
правой дорожке записи равна
Я,
*/ +
V*
1
Затем в стереофоническом усилителе сигнал
Lt подается на левый передний динамик, а
Я,-на правый передний динамик. Сигнал
L'b = (//|/2)Lt - (l/\/2)Rt подается на левый
задний динамик, a R'b = {l/\/2)Lt — (j/y2)Rt-
на правый задний динамик.
а) Если имеется единственный источник
монохроматической волны Lf = V0 cos art,
то каким будет отношение интенсивно-
стей сигналов от четырех динамиков?
Чему равны (L})2, (Я})2, (L'b)2 и (jRJ,)2, если
Lf= F0cosort и Rf= Lb= Rb= 0?
Повторите решение задачи, если
единственным источником сигнала является
б) микрофон Rf,
в) микрофон Lbi
г) микрофон Rb.
28. При атомном переходе испускается свет
с длиной когерентности AL0.
а) Найдите выражение для естественной
ширины линии АХ через X и AL0.
б) Свет от источника падает на
дифракционную решетку длиной у0 см. Каким
должно быть минимальное число 91 штрихов
на одном сантиметре решетки, чтобы
наблюдать естественную ширину линий?
Ответ запишите через X, т и у0 (т-время
жизни возбужденного состояния).

ОПТИКА
В настоящей главе речь пойдет о
различных электромагнитных явлениях,
которые наиболее характерны для диапазона
частот, соответствующих видимому свету.
Разумеется, все, что обсуждается в этой
главе, применимо к явлениям как в
микроволновом, так и в инфракрасном и
ультрафиолетовом диапазонах электромагнитных
волн. В § 5 мы приведем даже пример,
в котором длина волны в 10"10 раз
отличается от световой.
С более общей точки зрения любое
изучение волновых явлений подразумевает
изучение и оптики, или того, что мы
называем физической оптикой в
противоположность геометрической. В этом смысле мы
были бы вправе назвать физической
оптикой гл. 21 и 22, а также те разделы гл. 20,
в которых рассмотрены волновые
процессы.
В настоящей книге наряду с
классической оптикой мы излагаем и современную
оптику, т.е. те вопросы, которые получили
развитие в последние 10-20 лет.
§ 1. Голография
Голография, которая стала развиваться
в шестидесятые годы, представляет собой
одно из многочисленных применений
лазера. В своем обычном виде голограмма
выглядит наподобие фотографического
негатива. Однако негатив этот обладает одним
замечательным свойством. Хотя он сам по
себе является плоским, но если его
рассматривать в монохроматическом свете, то
мы увидим парящее в пространстве перед
или за негативом полное трехмерное
изображение реального предмета. По
сравнению со стереоскопическим голографиче-
ское изображение имеет то преимущество,
что в какую бы сторону мы ни
перемещались, разглядывая голограмму, в наше
поле зрения будет попадать
соответствующая часть изображения, как если бы мы
разглядывали реальный предмет. Еще одна
замечательная особенность голограммы
состоит в том, что изображение на негати-
Рис. 23-1. Участок
топографического негатива (очень
сильное увеличение).
V
V \
Ч

402
ГЛ. 23. ОПТИКА
Рис. 23-2. Студенты
рассматривают голографический негатив,
освещенный
монохроматическим светом. Они (а также
и фотокамера) видят полное
трехмерное изображение,
парящее в пространстве. [С
любезного разрешения
Нью-Йоркского музея голографии.]
ве совершенно не похоже на предмет,
который виден парящим в пространстве.
Негатив скорее похож на множество
перекрывающихся друг с другом отпечатков
пальцев, как на рис. 23-1. Несмотря на то что
ни одна из частей негатива не повторяется
где-либо в другом месте, любой из его
участков, помещенный в пучок
монохроматического света, воспроизведет трехмерное
изображение, но уже с худшим оптическим
разрешением. Ни при экспозиции негатива,
ни при воспроизведении трехмерного
изображения не используются линзы.
Принцип голографии представляет
собой наглядную иллюстрацию волновой
природы света и того, в чем состоит
отличие когерентного света от некогерентного.
Чтобы получить голографический негатив
(голограмму), предмет освещается пучком
от когерентного источника света-обычно
от лазера. При этом на пленку попадает
отраженный предметом свет, а также с
помощью зеркала направляется часть
первоначального светового пучка, как это
показано на рис. 23-3. Если падающий на
фотографическую пленку свет когерентен,
то на ней возникает определенная
интерференционная картина. Если же свет
некогерентен, то пленка засвечивается
равномерно. Необходимая длина когерентности
составляет 2L, где L-расстояние от предмета
до зеркала на рис. 23-3
Если пленку проявить и осветить
аналогичным световым пучком, то
восстановится и первоначальный волновой фронт
в месте расположения пленки в момент ее
экспозиции. Вследствие принципа
Гюйгенса восстановленный фронт волны будет
перемещаться в направлении глаза
наблюдателя точно так же, как это происходило
бы с фронтом исходной волны. Но каким
образом с помощью изображения на
пленке удается восстановить волновой фронт
с правильными значениями амплитуд
и фаз вдоль всей его поверхности, если
пленка чувствительна лишь к
интенсивности света? На этот вопрос можно
ответить, используя следующее упрощенное
математическое описание принципа
голографии.
Зеркало
Предмет
Фотопленка
Рис. 23-3. Способ получения голограммы. На
фотопленку попадают как отраженный от
предмета лазерный свет, так и опорный пучок от
зеркала.

§ 1. ГОЛОГРАФИЯ 403
Предположим, что пленка расположена
в плоскости yz. Тогда в этой плоскости
амплитуду отраженной предметом световой
волны можно записать в виде
Е = а(у,z)cos [cot + ф {у,z)]. (23-1)
Если, проявив пленку, мы сможем
воспроизвести это поведение амплитуды, то
у глаза возникнет ощущение, что он видит
исходный предмет. Допустим теперь, что,
имея такое распределение амплитуды
волны на пленке, мы освещаем ее плоской
волной от того же лазера. Тогда
распределение электрического поля по плоскости
пленки примет вид
Ерез = £0 cos cot + a cos (cot + ф), где а =
= a(y,z) и ф = ф (у, z).
Поскольку интенсивность
пропорциональна квадрату амплитуды поля, мы имеем
I = /0 cos2 cot + 2Е0а cos cot cos (cot + ф) +
+ a2 cos2 (cot + ф).
Усреднение по времени квадрата косинуса
дает 1/2. Следовательно, для среднего
значения интенсивности мы получим
выражение
_ J Q2
I = -у + E0a[cos§ + cos(2cot + ф)] + —^-,
в котором применено тригонометрическое
тождество cos A cos В = (1/2) cos (В — А) +
+ (1/2) cos (В + А). Среднее значение
cos(2cot + (|)) равно нулю; поэтому
I = Кх + Е0 а (у, z) cos ф (у, z), где Кг =
Следует отметить, что в случае
использования источника света с длиной
когерентности, превышающей 2L, удается
сохранить информацию о распределении фазы
$(y,z) по пленке. Почернение пленки
пропорционально 7. Если направить на
негатив такой же лазерный пучок
интенсивностью Г cos2 cot, то сразу же за негативом
мы получим
I = Г cos2 cot [1 - К2(КХ + Е0асозф)].
Соответствующее электрическое поле
пропорционально квадратному корню из
этого выражения:
E = E,coscot[l - (KiK2 + К2Е0а cos ф)У12 »
« К3 cos cot + IK^a cos cot cos ф,
где
_ 1 ^2^1 тх v _ K2E0
a3 = i — и A4 = —.
Воспользуемся снова соотношением
2cos A cos В = cos (A - B) + cos [A + В);
тогда
E « X3 cos cot +
+ K4a (y, z) cos [cot + ф (y, z)] +
+ K4a (y, z) cos [cot - ф (y, z)] =
__ /Прямой свет\ «. /Свет, отражен-V
— ( от лазера J 4( ный предметом )
к / Свет от предмета \
41 с обращенной фазой )'
Вклад первого члена регистрируется
глазом как прямой лазерный свет, второго-в
виде света, отраженного предметом, как
если бы предмет действительно
находился в своем первоначальном положении
[см. (23-1)]; третий член проявляется в
виде еще одного реального изображения.
Пример 1. Имеется голограмма очень
маленького шарика, находящегося на расстоянии х0 =
= 50 см от фотопленки (рис. 23-4). Амплитуда
света, отраженного точечным предметом,
записывается в виде Е = Е1 cos (cot — kr\ а
амплитуда опорного пучка-в виде Е0 cos (cot — kx0).
Каково распределение интенсивности на пленке,
если X = 6400 А?
Решение: Максимумы интенсивности имеют
место, когда разности фаз отраженного и
опорного пучков кратны 2я, т.е.
кг — кх0 = 2пп.
Отсюда находим
г — х0 = пХ,
Vyi+xl = пХ + х0,
уп = ]/2пХх0+п2Х2 « 0,08 ]/п см.

404 ГЛ 23- ОПТИКА
Шарик
Опорный
пучок
Фотопленка
Рис. 23-4. Свет от лазера, отраженный
маленьким шариком, и опорный пучок попадают на
фотопленку.
Распределение интенсивности представляет
собой концентрические окружности радиусами
0,08, 1,13, 1,39, 1,6 мм и т.д.
Хотя голографию изобрели в 1949 г.,
она оставалась вещью в себе до начала
шестидесятых годов и получила широкое
распространение лишь с изобретением
лазера. В настоящее время голография
представляет собой одно из главных
направлений в оптических исследованиях. В
шестидесятые годы были развиты различные
аспекты теории и разработаны новые
методы. Голография по-прежнему остается
новым полем деятельности для нас,
и трудно предвидеть ее окончательные
практические применения. В настоящее
время ведутся исследования и разработки
по применению голографии в медицине.
Например, по получению оптических
голограмм глаза, обеспечивающих единое
трехмерное изображение хрусталика и
сетчатки, или акустических голограмм тела,
которые могут иметь важное
преимущество по сравнению с двумерными
рентгенограммами. К другим применениям
голограммы относятся исследования и
разработки по созданию кассетной
видеозаписи, запоминающих
электронно-вычислительных устройств, а также таких способов
испытания материалов, которые не
вызывают разрушения этих материалов.
§ 2. Поляризация света
В любой момент времени световая или
электромагнитная волна иного диапазона
представляет собой в каждой точке
пространства взаимно перпендикулярные поля
Е и 93. За направление поляризации волны
выбрано направление Е. Плоскость
поляризации определяется как плоскость,
содержащая вектор Е и вектор направления
распространения волны. Следовательно,
направление поля 93 перпендикулярно
плоскости поляризации. Электромагнитное
излучение, у которого направление поля
Е остается неизменным, называется пло-
скополяризованным (или
линейно-поляризованным) излучением. В пучке света
некогерентного источника направление
электрического поля хаотически меняется,
оставаясь, однако, перпендикулярным
направлению распространения света. Такой
пучок называется неполяризованным.
КРУГОВАЯ (ЦИРКУЛЯРНАЯ)
ПОЛЯРИЗАЦИЯ
Предположим, что два когерентных
пучка света совмещаются с помощью
полупрозрачного зеркала, как это показано
на рис. 23-5. Пучок 1 поляризован
вертикально (вектор ЕА расположен в плоскости
ху), а пучок 2-горизонтально (вектор Е2
расположен в плоскости xz). Будет ли
результирующий пучок неполяризованным,
если разность фаз ф между пучками равна
нулю и Ех = Е2? А если ф = я/2?
Чтобы ответить на первый вопрос,
запишем обе волны как Е^ = Ег cos (cot—кх)

§ 2 ПОЛЯРИЗАЦИЯ СВЕТА
Полупрозрачное
зеркало
Рис. 23-5. Два пучка поляризованного света
смешиваются с помощью полупосеребренного
зеркала. Поле Е2 направлено на читателя из
плоскости чертежа параллельно оси z.
О (Е2)
2'О
Рис. 23-6. Проекция на плоскость yz полей,
показанных на рис. 23-5.
и Е2 = Е2о cos (cot — /сх), причем
направления полей £1о и Е2о образуют
прямой угол (рис. 23-6). Мы видим, что
вектор результирующего электрического поля
всегда расположен в плоскости, которая
составляет угол а с вертикалью, причем
tga = Е2о/Е1о. Если Е1о = £2о, то a = 45°.
Следовательно, результирующий пучок
света является плоскополяризованным,
причем плоскость поляризации составляет
угол 45° с вертикалью.
Если два пучка сдвинуты по фазе на
90°, то при х = 0 мы имеем
Еу= Elocos(ot и Ez= E2ocos((ot — тг/2).
На рис. 23-7 показано расположение
векторов Ех и Е2 в последовательные моменты
времени. Как видно из рисунка,
результирующий вектор Е остается постоянным по
величине и вращается по часовой стрелке
вокруг оси х, совершая один оборот за
период колебаний Т. Такая поляризация
называется левой круговой. Если вектор
Е вращается против часовой стрелки
(когда смотрят по направлению
распространения пучка), то поляризация называется
правой круговой.
В некоторых отношениях свет с
круговой поляризацией ведет себя как неполяри-
зованный. Однако если смешать пучки
одинаковой интенсивности, один из
которых имеет левую, а другой - правую
круговую поляризацию, то в результате мы
получим плоскополяризованный пучок.
Ясно, что это не может произойти, если
использовать неполяризованный свет.
Круговая поляризация встречается и в природе.
Оказалось, что отдельные фотоны имеют
круговую поляризацию.
ПОЛЯРИЗАТОРЫ
Большинство источников испускает
некогерентный, неполяризованный свет.
Пучок неполяризованного света можно
поляризовать, если пропустить его через
поляризатор. Экран, изготовленный из тонких
параллельных проволочек, является
прекрасным поляризатором для микроволн,
Рис. 23-7. Электрическое поле
в плоскости yz в
последовательные моменты времени для
случая, когда пучок 2 отстает
по фазе от пучка 1 на я/2.
Результирующее поле Е
вращается по часовой стрелке. Еу и Ez
имеют одинаковые амплитуды.
'=0
/
— ч
Е, еГЧ
t=7T t =jT
/
Е^Е,
1-iT

406 ГЛ. 23. ОПТИКА
U
/-0
Рис. 23-8. Электромагнитная
волна с вертикальной
поляризацией, падающая на экран из
параллельных проволочек,
а-экран с вертикальными
проволочками отражает волну;
б-экран с горизонтальными
проволочками не отражает волну,
и она проходит через экран без
ослабления.
как это видно из рис. 23-8. Если пучок
микроволнового излучения поляризован
вертикально и проволочки также натянуты
вертикально, как на рис. 23-8, а, то в
каждой проволочке индуцируется ток J. Как
разъяснялось в § 3 гл. 21, индуцированный
ток излучает поле АЕ = — Е^д. Поэтому
справа от поляризатора результирующее
поле Е = Епад + АЕ = 0. Следовательно, при
такой ориентации поляризатор ведет себя
аналогично идеальному отражателю,
который не пропускает пучок. Если же
проволочки перпендикулярны Епад, то
вертикальным токам «негде» индуцироваться.
Поэтому не возникает дополнительного
излучения, и падающая волна проходит
без искажений.
Примем за ось поляризатора на
рис. 23-8 перпендикуляр к линии, в
направлении которой расположены проволочки.
Из рис. 23-9 видно, что если ось
поляризатора составляет угол а с направлением
Епад» то поляризатор будет излучать поле
АЕ под прямым углом к оси. Поскольку
АЕ компенсирует составляющую Епад
в этом направлении, то результирующее
поле Е' будет представлять собой
составляющую поля Епад, параллельную оси и,
следовательно,
Е' = -Епад cos а,
или
Г = /падсоз2а.
(23-3)
В случае идеального поляризатора
интенсивность пропорциональна cos2oc, где ос-
угол между плоскостью поляризации света
и осью поляризатора. Поляризатор
пропускает максимум интенсивности в том
случае, когда его ось направлена вдоль
плоскости поляризации. Любое излучение
после прохождения поляризатора
оказывается плоскополяризованным в направлении
оси поляризатора.
На этом же принципе основано
действие светового поляроидного фильтра.
Поляроид изготавливают из специально
ориентированной пластмассы, которая
состоит главным образом из длинных
параллельных цепочек молекул, вдоль которых
может течь электрический ток.
Следовательно, поляроид представляет собой ми-
Ось поляризатора
Проволочки
V Ег=(Епад + ДЕ)
Рис. 23-9. а-вид в поперечном сечении пучка
(пучок входит в плоскость чертежа); вектор
вертикальной поляризации пучка составляет угол
а с осью поляризатора из прямолинейных
проволочек, которые излучают поле АЕ;
б-результирующее поле Е' за проволочками.

§ 2. ПОЛЯРИЗАЦИЯ СВЕТА 407
кроскопическую разновидность
поляризатора с параллельными проволочками. Ось
поляроидного фильтра, разумеется,
перпендикулярна молекулярным цепочкам.
В случае неполяризованного света
составляющие поля Е, параллельные
молекулярным цепочкам, поглощаются. После
прохождения поляроидного фильтра в
пучке остаются лишь те составляющие поля
Е, которые параллельны оси поляроида.
Если за первым поляроидом поместить
второй, причем таким образом, чтобы их
оси были взаимно перпендикулярны, как
показано на рис. 23-10, а, то пучок
полностью поглотится и из второго
поляроида по существу свет не выйдет.
Если теперь между двумя скрещенными
поляроидами поместить третий, как
показано на рис. 23-10,6, то свет снова
появится там, где его прежде не было! Каким
образом дополнительный поляроид «со-
Ось
'ч!*
Рис. 23-10. а-два взаимно перпендикулярных
поляроида полностью гасят свет; б-свет
появляется, когда между ними помещают третий
поляроид.
здает» свет? Чтобы объяснить это,
предположим, что на средний поляроид падает
свет, интенсивность которого равна /0 =
= ^пад/2. За вторым поляроидом свет
будет поляризован под углом а и иметь
интенсивность Г = J0 cos2 а. Ось последнего
поляроида составляет угол я/2 — а с
плоскостью поляризации света.
Следовательно,
/" = Г cos2 [ -^— а ) =
= (J0 cos2 а) cos2 ( а j = -j- sin2 2а.
Это выражение имеет максимальное
значение при а = 45°, причем в случае
идеальных поляроидов окончательная
интенсивность составляет 1/8 от /пад.
* Пример 2. Поляризованный
монохроматический свет падает на двойную щель (рис. 23-11).
Свет поляризован в направлении вектора j + к
(т.е. в направлении оси, проходящей посередине
между осями у и z). Если в щелях нет
поляроидов, то мы наблюдаем на экране стандартную
интерференционную картину от двух щелей.
Затем щель 1 закрывают поляроидом с
горизонтальной осью, а щель 2-поляроидом с
вертикальной осью. Пусть /0 - интенсивность света на
экране в случае, когда открыта либо щель 1,
либо щель 2 (каждая со своим поляроидом).
В точках экрана а, Ь, с и d разности хода
таковы, что величина к{гх — г2) равна
соответственно 0, я/2, п и 2я. Каковы интенсивности
и поляризации света в этих точках?
Решение: Электрическое поле от щели 1
записывается в виде j£0cos(oot — кгх\ а поле от щели
2-в виде кЕ0 cos (юг — кг2); следовательно, в
точке а мы имеем (будем считать, что г2 = гх)
Е = }Е0 cos (cot - krx) + k£0 cos (cot - kr2).
Таким образом, E = y2E0cos((Dt — kr{). Это
поле направлено под углом 45° к вертикали.
Направление поляризации задается вектором j+k.
Будем считать, что оно соответствует углу +45°.
Интенсивность Е2 = 2£ocos2(cot — кг), что в два
раза превышает интенсивность от одной щели.
В точке d оба косинуса оказываются в фазе,
и мы получаем то же, что и в точке а.
В точке с оба косинуса сдвинуты на угол
180°, и
Е = j£0cos cot - k£0 cos cot.

408 ГЛ. 23. ОПТИКА
'пад
Вертикальный
поляроид
Горизонтальный
поляроид
Экран
Рис. 23-11. Устройство для
получения интерференции от двух
щелей. Щели 1 и 2
закрываются соответственно
горизонтальным и вертикальным
поляроидами.
Таким образом, Е = |/2£0coscot, и поляризация
направлена вдоль вектора j — к. Припишем
этому направлению угол —45°. (Мы определили
момент времени t = 0 как время, когда
амплитуда от щели 1 максимальна.) В данном случае
интенсивность снова вдвое больше
интенсивности от одной щели, однако направление
поляризации перпендикулярно поляризации в точках
a Yi. d.
В точке Ъ обе волны сдвинуты по фазе на
90°, и мы вновь имеем ту же ситуацию, что и на
рис. 23-7, а именно волну с круговой
поляризацией, у которой Е2 = Eq. Поскольку
усреднение по времени дает в случае одной щели Ё?=
— Eq/2, средняя интенсивность также вдвое
превышает интенсивность от одной щели.
Мы показали в данном примере, что
интенсивность распределена по экрану равномерно,
но поляризация из плоской под углом +45°
становится круговой, затем снова плоской под
углом —45°, опять круговой, потом плоской
под углом + 45° и т. д. по мере перемещения по
экрану.
* Пример 3. а) Предположим, что в примере
2 непосредственно перед экраном располагается
еще один поляроид с горизонтально
направленной осью. Каким тогда будет распределение
интенсивности по экрану?
б) Пусть в примере 2 непосредственно
перед экраном помещен поляроид, ось которого
направлена под углом +45° (в направлении
оси, идущей посередине между осями у и z).
Каким будет теперь распределение интенсивности?
Решение: а) В произвольной точке экрана на
расстоянии г от щели 1 мы имеем Е =
= j£0cos (Ш - кг) и Е2 = El cos2 (cor - кг).
Таково распределение интенсивности от одной
щели 1 (в отсутствие поляроида). Свет от щели
2 поглощается поляроидом и не может попасть
на экран. Если же на экране появляется свет, то
мы знаем, что он пришел от щели 1.
б) В точках а и d экрана излучение
поляризовано в плоскости, параллельной оси
поляроида, а в точке с-в плоскости, перпендикулярной
оси поляроида. Интенсивность равна 2/0 в
точках and, нулю в точке с и /0 в точке Ъ. Это
классическая интерференционная картина от
двух щелей, при которой каждая из щелей сама
по себе обеспечивает интенсивность 10/2.
Из примеров 2 и 3 следует, что, зная
ориентацию поляроида перед экраном,
можно сказать, через какую из щелей
прошел свет. В зависимости от того,
горизонтальна или вертикальна ось поляроида,
можно утверждать, что свет прошел через
щель 1 или щель 2. Однако если ось
поляроида ориентирована под углом + 45° или
— 45°, то информация о поляризации света
в щели утрачивается и уже нельзя
выяснить, через какую из щелей прошел свет.
В случае ±45° мы имеем классическую
интерференционную картину от двух щелей,
однако при горизонтальной и
вертикальной ориентациях интерференционная
картина исчезает.
ПОЛЯРИЗАЦИЯ ПРИ ОТРАЖЕНИИ
Почти каждому доводилось наблюдать,
что поляроидные стекла уменьшают
интенсивность солнечного света,
отраженного поверхностью воды, песка, стекла,
дороги и т.п. Неполяризованный солнечный
свет после отражения приобретает
поляризацию. При этом, если ось поляроида
перпендикулярна плоскости поляризации
отраженного света, отражение гаснет.
В приложении 1 показано, что если угол
падения Qx светового пучка на
отражающую поверхность связан с показателем

§ 3. ДИФРАКЦИЯ НА КРУГЛОМ ОТВЕРСТИИ
преломления п соотношением tg д1 = п, то
в этом случае отраженный свет будет
иметь 100%-ную поляризацию, причем
вектор электрического поля будет
перпендикулярен плоскости, содержащей падающий
и отраженный лучи.
Пример 4. Показатель преломления воды равен
1,33. Под каким углом полностью исчезает
отражение от поверхности воды, если
использовать поляроид? Как направлена при этом ось
поляроида-горизонтально или вертикально?
Решение: В данном случае tg0Х = 1,33, т.е.
0t = 53°. Поскольку свет будет поляризован
горизонтально, ось поляроида должна быть
направлена вертикально. В этом случае, если
Солнце стоит над горизонтом под углом 37°,
поляроид погасит его отражение от гладкой
поверхности воды.
гралом
$ cos [kr{Q)~]dA.
По апертуре
Это крайне сложный интеграл. Его
вычисление дает функцию, хорошо известную
физикам, инженерам и математикам и
называемую функцией Бесселя первого рода
Jl (х). Эта функция, график которой
приведен на рис. 23-13, записывается в виде
•М*)'
- sin [ х — — ) для х > 5.
гас \ 4
Интенсивность излучения в направлении
под углом 0 мы получим, если проинтегри-
JiOO
§ 3. Дифракция на круглом отверстии
Рассмотрим теперь вместо щели
шириной а круглое отверстие диаметром а.
Согласно принципу Гюйгенса, чтобы
получить результирующую амплитуду, нужно
просуммировать волны, испущенные всеми
участками этой круговой апертуры. Вклад
каждой из волн в приближении Фраунго-
фера составляет cos кг dА, где г-радиус-
вектор, показанный на рис. 23-12, и dA-
элемент площади внутри апертуры.
Амплитуда излучения под углом 0 дается инте-
Рис. 23-13. График функции Бесселя первого
порядка.
Пучок
света
Дифрагированный
волновой
фронт
Экран с отверстием
руем эту функцию по апертуре и результат
возведем в квадрат:
1 = 1о
•■МФ/2)"
Ф/4
, где Ф = /casinG. (23-4)
Следует заметить, что это распределение
аналогично тому, которое мы получили
для случая щели [см. формулу (22-13)]:
' sin (Ф/2) ~»2
Ф/2
Г sin (Ф/2) I2
Рис. 23-12. Дифракция на круглом отверстии В слУчае °ДН0Й Щели пеРвый минимум
диаметром а. Каждый элемент площади dA вно- имеет место под углом 9МИН, удовлетворяю-
сит вклад в амплитуду волны, испускаемую под шим условию sin 0МИН = Х/а. В случае кру-
углом 0. говой апертуры первый минимум соответ-

410 ГЛ. 23. ОПТИКА
ствует Jx (х) = 0. Как видно из рис. 23-13,
первый нуль этой функции Бесселя
расположен при х = 3,84; таким образом,
Ф^/2 = 3,84
или
(l/2)/casin0MHH = 3,84,
sin Ом™ = 1,22 Х/а.
(23-5)
Вычисленное по формуле (23-5)
значение отличается от случая одной щели всего
на 22%. На рис. 23-14, а приведена
фотография дифракционной картины на
круглом отверстии, а на рис. 23-14,6 показано
соответствующее распределение
интенсивен
е i,o
0,1
S 0,01
0,001
Расстояние от центра
Рис. 23-14. а-фотография дифракционной
картины, создаваемой монохроматическим светом
на круглом отверстии; б-распределение
интенсивности, описываемое формулой (23-4).
ности, вычисленное по формуле (23-4).
Картина дифракции прсдставляе! собой
светлый центральный диск, окруженный
слабыми кольцами.
Используя результаты настоящего
раздела, вычислим в следующем параграфе
разрешающую способность телескопа
и микроскопа. Затем применим
полученные результаты к супермикроскопам
физики элементарных частиц -
современным ускорителям частиц высоких
энергий - и продемонстрируем использование
этих приборов для определения размеров
и формы ядерных частиц.
§ 4. Оптические приборы и их
разрешающая способность
В § 4 гл.' 22 мы уже исследовали
разрешающую способность спектрометра. Она
характеризует способность прибора
воспроизводить две спектральные линии
с близкими длинами волн все еще как две
раздельные линии. Аналогичный смысл
имеет разрешающая способность
телескопа или микроскопа: насколько близко
расположенные друг к другу два точечных
источника света можно еще различать как
два отдельных источника. Из-за вносимой
спектрометром приборной ширины линии
(в случае дифракционной решетки эта
ширина равна АХ = X/N) две спектральные
линии, расположенные слишком тесно,
могут слиться в одну линию. Аналогично
в телескопе или микроскопе два чересчур
близких точечных источника сольются
в один, поскольку оптический прибор
делает точечный источник похожим на
крошечный диск или световое пятно с
круговыми дифракционными кольцами.
Действительно, мы имеем здесь дело с
дифракционной картиной, которая
аналогична изображенной на рис. 23-14.
ТЕЛЕСКОП
Для того чтобы понять, почему с
помощью телескопа нельзя получить
точечное изображение точечного источника,
объясним сначала хотя бы кратко, как он
работает. Рассмотрим схематически
изображенный на рис. 23-15 телескоп, в
который рассматривают находящиеся на

§ 4. ОПТИЧЕСКИЕ ПРИБОРЫ И ИХ РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ
411
Линза
>в*
От источника А
Рис. 23-15. Изображения двух
точечных источников А и В
в телескопе. Эти изображения
(А' и В') расположены в
фокальной плоскости.
t«
0"f
*<*°ч"
н»*а
Круговая
апертура
Фокальная
плоскость
очень большом расстоянии от него два
точечных источника А и В. В телескоп входит
объектив-линза (или вогнутое зеркало)
с фокусным расстоянием F. Линза (или
вогнутое зеркало) фокусирует параллельные
лучи в точку, расположенную на
расстоянии F от линзы. Это расстояние
называется фокусным. Если угол между лучами А
и В равен а (см. рис. 23-15), то расстояние
между их изображениями равно у0 = Fa.
В астрономических телескопах эти
изображения непосредственно регистрируются на
пленке, расположенной в фокальной
плоскости. Изображения можно также
наблюдать в окуляр. Это тоже линза с фокусным
расстоянием /, расположенная на
расстоянии / справа от фокальной плоскости.
В этом случае кажущийся угол между А
и В будет
а' =
Уо_
f
Fa
Увеличение М определяется как
(увеличение телескопа).
a' F
М = — = -
а /
Хотя подходящим выбором фокусных
расстояний увеличение можно сделать сколь
угодно большим, в действительности оно
ограничивается разрешающей
способностью. Разрешающая способность
определяется как минимальный угол оСмин
между лучами от двух точечных источников,
при котором их изображения удается
различить как два световых пятна.
Значение радиуса Rd центрального
светового пятна от отдельного точечного
источника можно определить с помощью
рис. 23-16. В соответствии с выражением
(23-5) первый минимум в дифракционной
картине от круговой апертуры дается
соотношением
sin 0мин ~ 0МИН ~ 1,22Х/а.
Радиус соответствующего диска
^d = F0MHH = F(l,22V«).
Если изображения двух точечных
источников отстоят друг от друга не меньше чем
на Rd, их можно различить как два диска.
Таким образом, величина у0 (или Fa)
должна быть больше, чем jRd, т.е.
(23-6) Fa>l,22Ftya, a> l,22tya.
Рис. 23-16. Круговая апертура
перед линзой создает в
фокальной плоскости
дифракционную картину.
От точечного
источника
Ь-
Фокальная
плоскость

ГЛ. 23. ОПТИКА
Разрешающая способность дается
выражением
и<мт=1>22Х/а.
(23-7)
Пример 5. Угол между двумя звездами
составляет 10" 6 рад.
а) Можно ли разрешить эти звезды с
помощью 100-дюймового оптического телескопа
(т.е. с диаметром апертуры 2,54 м)?
б) Предположим, что эти звезды излучают
также радиосигналы на частоте 400 МГц.
Можно ли их разрешить с помощью корнеллского
радиотелескопа (Аресибо, Пуэрто-Рико),
имеющего 1000-футовую апертуру (1 фут = 30,5 см)?
Решение: а) Круговая апертура 100-дюймового
телескопа обеспечивает угол дифракции бмин =
= 1,22Х/а, где а = 2,54 м. Для света с длиной
волны X = 5-10"7 м
^. 10~7
емин= 1,22^4~ = 2,4-Ю-7 рад.
Угловое расстояние между звездами в 4 раза
превышает это значение, так что телескоп
должен разрешить свет от этих звезд (при условии,
что в атмосфере отсутствует турбулентность).
б) В случае радиотелескопа а = 305 м.
Поскольку
Х =
с _ 3,00 -108 м/с
= 0,75 м,
= 3-10"3рад.
/ 4-108с
мы имеем
а _ 1 22 °'75
Таким образом, чтобы разделить обе звезды,
нам потребовалось бы в 3000 раз более высокое
разрешение. (На практике это достигается
использованием сигналов от радиотелескопов,
отстоящих друг от друга на расстоянии свыше
1200 км.)
МИКРОСКОП
В оптическом микроскопе с большим
увеличением в качестве объектива
используется линза с коротким фокусным
расстоянием F. Предмет располагается от
линзы на расстоянии, примерно равном
F (рис. 23-17). Плоскость изображения
находится от линзы на значительно большем
расстоянии D. Поскольку лучи,
проходящие через центр линзы, ею не
отклоняются, увеличение М = А'В'/АВ (рис. 23-17,6).
Таким образом, М = D/F. Как и в случае
телескопа, в плоскости изображения
можно поместить фотопластинку либо
наблюдать изображение через окуляр.
Свет от источника А, выходящий из
круглой апертуры под углом 0МИ„ ж 1,22Х/а,
фокусируется в плоскости изображения
и образует первый минимум
интенсивности. Радиус светового диска равен
величине этого угла, умноженной на расстояние D:
а
Если а-угол,, под которым из объектива
микроскопа видны два точечных источника
света, то расстояние между их
изображениями равно у = Da и условие,
определяющее разрешающую способность, т. е.
минимальный угол а, под которым эти два
источника еще видны раздельно,
запишется в виде
X
Doc,™ = 1,22—Д
а
X
Омин = 1,22 — .
Линза
Точечный .объектив
источник
л
Круговая
апертура
Плоскость
изображения
*А
-Z)-
4
Два точечных
источника
Рис. 23-17. В микроскопе
короткофокусная линза
фокусирует изображение в плоскости,
расположенной на расстоянии
D от линзы.

§ 5. ДИФРАКЦИОННОЕ РАССЕЯНИЕ 413
Последнее выражение в точности
совпадает с формулой (23-7) для телескопа.
В случае микроскопа больший интерес
представляет оценка минимального
расстояния, на котором удается разрешить
два точечных источника. Обозначим его
через dMm. Поскольку dMm = 0Cm„„F, мы
имеем
4ин = U22XF/a.
Отношение a/F называется числовой
апертурой. Иммерсионные объективы высокого
качества имеют, как правило, a/F» 1,2.
В этом случае
Мы приходим к выводу, что с
помощью микроскопа нельзя разрешить
малые предметы, если они расположены
друг от друга на расстоянии, меньшем, чем
длина световой волны. Использование
в микроскопе голубого света позволяет
несколько повысить его разрешающую
способность. Еще лучшего разрешения можно
добиться, используя ультрафиолетовое или
рентгеновское излучение. В следующем
разделе мы покажем, как на ускорителях
частиц высоких энергий удается получить
предельное разрешение. До сих пор
удалось достичь наилучшего разрешения
порядка 1/10 радиуса протона или 10"16 м1}.
РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ
ЛАЗЕРНОГО ПУЧКА
На стр. 411 мы показали, что если
параллельный световой пучок фокусируется
на экране линзой с фокусным расстоянием
F и апертурой а, то образуется
дифракционный диск радиусом Rd = l,22XF/a.
Поскольку практически максимальный размер
апертуры достигает значения а ^ F, мы
имеем jRd « X. Это означает, что даже при
наличии идеально параллельного
светового пучка свет можно сфокусировать лишь
до пятна размером порядка длины свето-
1} В действительности к началу 1980 г.
изучение структуры ряда элементарных частиц
было проведено вплоть до расстояний 10"18 м,
что соответствует в 100 раз более высокой
предельной разрешающей способности -Прим. ред.
вой волны. Поскольку лазер дает
параллельный световой пучок, всю энергию
излучения лазера можно сконцентрировать
в области, имеющей площадь примерно
(6-10~7 м)2 или 4-10"13 м2. Тем самым
достигается исключительно высокая
плотность энергии, которая способна
обеспечить получение чрезвычайно высоких
температур. В этом состоит важное
преимущество лазеров по сравнению с другими
источниками света. До изобретения
лазеров все источники света представляли
собой протяженные источники типа дуги или
нити накаливания диаметром один
миллиметр или около этого. Если линза
располагается вблизи такого источника, то чтобы
собрать значительную долю излучаемой
им энергии, она должна давать
изображение, соизмеримое с размером источника.
Таким образом, до тех пор пока не
появились лазеры, не существовало способов
получения плотностей энергии, которые
превышали бы плотность энергии источника
света.
Пример 6. Испускаемый лазером свет
представляет собой параллельный пучок кругового
сечения диаметром 5 см. Длина волны света
равна 6328 А. Если этот пучок направить на
теневую сторону поверхности Луны, то каким
будет размер светового пятна на этой
поверхности? Расстояние до Луны D = 3,84 • 108 м.
Решение:
а
1^(6328>10-1Ом)(3,84.108м)
= 1,22 — = 5,9 км.
0,05 м
Вскоре после изобретения лазеров такое пятно
лазерного светового пучка наблюдалось на
Луне с помощью больших телескопов.
§ 5. Дифракционное рассеяние
Соотношение sin0MHH = 1,22Х/а можно
использовать для определения неизвестных
размеров крошечного отверстия (узкой
диафрагмы). Если за отверстием поместить
экран, то мы увидим на экране
дифракционную картину (см. рис. 23-12). Пусть
Rd- расстояние от центра картины до
первого минимума, a D- расстояние от отвер-

414 ГЛ. 23. ОПТИКА
стия до экрана. Тогда
D а
Отсюда находим выражение для а:
U22KD
Таким образом, простое измерение jRd
позволяет оценить поперечные размеры
узкой диафрагмы.
Аналогичный метод можно также
использовать для измерения размеров
крошечной сферы или непрозрачного диска.
Нетрудно видеть, что дифракционная
картина от непрозрачного диска будет
совпадать с картиной от круглого отверстия.
В случае круглого отверстия мы прибегали
к принципу Гюйгенса и провели
вычисления, в предположении, что отверстие само
по себе является протяженным источником
света. В случае непрозрачного диска
благодаря индуцированным в нем токам мы уже
имеет готовый протяженный источник.
При этом дифракционная картина будет
совпадать с изображенной на рис. 23-14;
в центре также будет яркое пятно,
соответствующее пучку, падающему под углом 0°.
Пример 7. Пучок света от лазера с длиной
волны X = 6328 А освещает стеклянную пластинку
(рис. 23-18), покрытую порошком ликоподия
(споры сферической формы). На экране в 5 м
от лазера виден красный диск с первым темным
кольцом, расположенным на расстоянии 19 см
от центра диска. Каков диаметр споры
ликоподия?
Решение:
D 19 см ао 1Л_3 1,22А,
0-н=5ОО^ = 38'10 3Pa* = ^->
1,22Х, _ 1,22 • 6328 -НГ^м _
а 38-10"3 3810"3
= 2,03.1(Г5м.
Каким образом можно измерить
поперечник сферы, если он значительно меньше
длины световой волны? Можно
попытаться использовать более коротковолновое
излучение, например рентгеновское или
гамма-излучение. Вместо такого излучения
Стекло Экран
Споры
Рис. 23-18. Споры ликоподия на стеклянной
пластинке создают на экране дифракционную
картину.
можно использовать и любой другой вид
плоских волн при условии, что X < а,
а диск (или сфера) сильно поглощает их.
Любая плоская волна, из которой
вследствие поглощения удален круговой участок
волнового фронта, должна воспроизвести
дифракционную картину с распределением
интенсивности, описываемым функцией
[Л(Ф/2)/(Ф/4)]2.
Теперь нам следует обратиться к
самому поразительному и революционному
представлению в физике. Вне всяких
сомнений установлено, что любую
движущуюся частицу можно представить в виде
плоской волны с длиной X = h/p, где h =
= 6,63• 10"34 Дж-с, а р-импульс
частицы. Эта сумасшедшая идея была
выдвинута в 1924 г., а в 1927 г. она была впервые
подтверждена экспериментально. Волновая
природа вещества является центральной
темой остальных глав книги. Пока же
давайте примем ее на веру (в следующих
главах содержатся соответствующие
доказательства). В этом случае пучок протонов
с энергией 19 ГэВ (19 • 109 эВ) можно
представить в виде плоской волны с длиной
волны X = 0,65 • 10"16 м. Эта величина
значительно меньше поперечника (~ 10"14 м)
атомных ядер. Таким образом, если
соотношение X = h/p справедливо, то,
«освещая» свинцовую фольгу пучком протонов
с энергией 19 ГэВ, мы должны наблюдать
дифракционную картину. Такой
эксперимент нетрудно выполнить с помощью
пучка протонов от ускорителя частиц высоких
энергий. На рис. 23-19 приведены
результаты такого эксперимента, которые можно
было бы рассматривать как еще одно
доказательство волновой природы вещества.

§ 5. ДИФРАКЦИОННОЕ РАССЕЯНИЕ 415
дает
sin 0МИН = 1,22 —.
мин ра
Поскольку а = 2R, мы имеем
h
J sin Эмин = 0,61
Рис. 23-19. Результаты изучения рассеяния
протонов с энергией 19 ГэВ на ядрах 207'2РЬ.
Показана зависимость числа рассеянных протонов от
угла рассеяния. Сплошная кривая описывает
классическую дифракционную картину с
распределением интенсивности (2Ji(kRQ)/kRQ)2 для
случая плоских световых волн с такой же
длиной волны, рассеиваемых на диске радиусом
Я = 7,5- 1(Г15 м.
С другой стороны, принимая
справедливость представлений о волновой природе
вещества, их можно использовать для
определения размеров и толщины
поверхностного слоя ядра свинца.
Независимо от того, из каких частиц
состоит пучок - фотонов (т. е. частиц света)
или протонов,-решение волнового
уравнения оказывается тем же самым, что и
в классической задаче о дифракции
световой волны на непрозрачном диске
радиусом R. Это означает, что формула (23-5)
применима и к протонам высоких энергий:
необходимо лишь заменить X на h/p, что
pR
(23-8)
Картина дифракции протонов наблюдается
при измерении числа упруго рассеянных
протонов в зависимости от угла 0. На
рис. 23-19 точками отмечены результаты
измерений, выполненных для 30 различных
значений углов в интервале от 0,11 до
1,03°. Сплошная кривая-стандартное
распределение интенсивности, характерное
для дифракции света на непрозрачном
диске в случае, когда длина волны света
совпадает с длиной волны протонов.
Отклонения экспериментальных точек от
плавной кривой не связаны с какими-либо
нарушениями представлений о волновой
природе вещества. Дело в том, что ядро
свинца не во всем схоже с непрозрачным
(черным) диском, имеющим резкие края.
Черный диск с частично прозрачным
краем приводит к более гладкому
распределению, которое согласуется со всеми
экспериментальными точками. В
действительности приведенные на рис. 23-19
экспериментальные данные можно использовать
для определения как радиуса ядра свинца,
так и толщины поверхностного слоя.
Радиус R находим из формулы (23-8):
R = 0,61 ^—. (23-9)
psin9MHH
Из рис. 23-19 следует, что 0миН
соответствует 0,3°; подстановка этого значения^
в (23-9) дает для радиуса ядра свинца R =
= 7,5.10"15м.
Дифракционная картина возникает
даже при рассеянии протонов на протонах.
Однако в этом случае она еще сильнее
отличается от случая черного диска с резким
краем, поскольку у протона прозрачность
возрастает, начиная от самого центра.
Эффективный радиус протона можно
получить, измеряя ширину центрального
максимума. «Оптический» радиус, определяемый
из дифракции протонов на протонах, равен
1,Ы0~15м. А что можно сказать
относительно внутренней структуры протона?

416 гл- 23- ОПТИКА
Нет ли у протона, подобно атому, жесткой
«непрозрачной» сердцевины? Наложение
черного диска или сердцевины на
полупрозрачный диск больших размеров должно
давать сложную дифракционную картину:
центральный максимум будет
определяться наложением двух максимумов
различной ширины. До сих пор такой эффект
обнаружить не удалось. Верхний предел
размеров предполагаемой сердцевины
можно получить с помощью формулы
(23-9), подставляя в нее наибольшее из
достигнутых до настоящего времени
значений величины psinG.
Рассеяние протонов на протонах
изучалось в Брукхейвенской национальной
лаборатории (США) при максимальной энергии
частиц ускорителя. Содержащая водород
мишень облучалась пучком протонов
с энергией 32 ГэВ. Рассеянный протон
и протон отдачи вылетают под углом 15°
к направлению пучка, и каждый из них
имеет половину энергии частицы в пучке.
В этом случае рс sin 0 = 4 ГэВ или
psinG = 2ДЗ-10"18 кг-м/с. Подставляя это
значение в (23-9), получаем R = 0,19- 10~15м.
На самом деле сердцевина, имеющая
в два раза меньшие размеры, уже
давала бы заметный центральный максимум.
Следовательно, мы приходим к выводу,
что размер сердцевины протона не может
быть больше 0,1 -10" 15 м. Таким образом,
ускоритель Брукхейвенской лаборатории
и другие ускорители частиц высоких
энергий вполне можно рассматривать как
супермикроскопы, позволяющие измерять
размеры вплоть до долей ферми (фер-
ми-единица длины, равная 10" 15 м).
Разрешающая способность этих приборов
в миллиард раз выше, чем у лучшего
оптического микроскопа. Для того чтобы
исследовать структуру протона с
разрешающей способностью лучше 0,1 -10" 15 м,
необходимо использовать ускорители на еще
более высокие энергии Ч
1} По-видимому, наивысшая разрешающая
способность получена в экспериментах на
встречных пучках протонов, где происходит
рассеяние частиц, движущихся навстречу друг
другу. При этом достигаются энергии,
эквивалентные примерно 2000 ГэВ, т. е. в 70 раз выше
тех, которые использует в своем примере
автор -Прим. перев.
§ 6. Геометрическая оптика
Длина световой волны настолько мала
по сравнению с размерами большинства
оптических приборов, что
интерференционные эффекты обычно не проявляются.
Волновой цуг или последовательность
световых волн распространяется вдоль
прямой линии, перпендикулярной волновому
фронту. Любая такая прямая, идущая
вдоль направления распространения
световых волн, называется световым лучом.
Мы покажем, что световые лучи
подчиняются законам отражения (от зеркал)
и преломления (в прозрачных средах,
например в линзах). Используя эти два
закона и обычные правила евклидовой
геометрии, можно построить математическое
описание или геометрическую картину рас-
&g& v
Проводник
4§N> /1
к
0
&
Рис. 23-20. а-три последовательных положения
волнового фронта падающей волны с углом
падения 0пад; в проводнике индуцируется
поверхностный ток $ {у\ максимумы которого
отвечают пересечению волнового фронта с
поверхностью проводника; б-поле излучения,
создаваемое лишь током $ (у).

§ 6. ГЕОМЕТРИЧЕСКАЯ ОПТИКА 417
Пучок
света
т
—v\
Центр
кривизны
Фокус
U
Вогнутое
зеркало
Рис. 23-21. а -параллельные лучи света,
падающие на вогнутое зеркало радиусом СР;
б-человеческий глаз, расположенный в центре
кривизны вогнутого зеркала, составленного из
плоских зеркал, увидит себя во всех зеркалах.
Лучи от предмета возвращаются обратно
к предмету.
пространения световых лучей. Такое
математическое описание световых лучей
представляет собой самостоятельный раздел
и носит название геометрической оптики.
Поскольку в данном случае новыми
физическими принципами являются лишь
законы отражения и преломления света,
рассмотрим их подробно, остальные же
вопросы обсудим лишь кратко.
ЗАКОН ОТРАЖЕНИЯ
Согласно закону отражения, угол, под
которым световой луч падает на
отражающую поверхность, равен углу отражения.
Угол падения определяется как угол между
падающим пучком и перпендикуляром
к отражающей поверхности.
Следовательно, угол между волновым фронтом и
отражающей поверхностью также представляет
собой угол падения 0пад.
Как видно из рис. 23-20, а, падающее
электрическое поле индуцирует
поверхностный ток $ (у, t\ который меняется с у по
синусоидальному закону. В случае проводника
поверхностный ток оказывается таким, что
поле внутри проводника всегда равно
нулю. Это означает, что излучаемое током
вправо поле в точности должно
компенсировать Епад- Следовательно, как видно из
рис. 23-20,6, E'R = - Епад и 0к = епад.
Условия симметрии требуют, чтобы E'L = E'R
и G'l = ®'r • (Физическая картина не
изменяется, если на рис. 23-20, б поменять
местами правое и левое.) Таким образом, мы
доказали, что в случае проводящей
поверхности амплитуда отраженной волны
сохраняется прежней, но ее составляющая вдоль
поверхности меняет свое направление на
противоположное.
В качестве применения закона
отражения покажем, каким образом вогнутое
зеркало выполняет функции фокусирующей
линзы. Хорошо известно, что простая
линза или увеличительное стекло фокусирует
параллельный пучок световых лучей в точ-

ГЛ. 23. ОПТИКА
Предмет
1
Изображение! \0
VI
и
Рис. 23-22. Образование
изображения вогнутым зеркалом.
С помощью лучей 1 и 2
строится графически положение
изображения.
ку, называемую фокусом. Подобным же
образом ведет себя и вогнутое зеркало.
Например, вогнутым зеркалом для бритья
можно прожечь дыру в листе бумаги,
направив зеркало на солнце и поместив
бумагу в фокусе. Как видно из рис. 23-21, а,
фокусное расстояние вогнутого зеркала
равно половине его радиуса кривизны. На
этом рисунке из пучка параллельных лучей
выбран произвольный луч АР. Пусть
0-угол между этим лучом и нормалью
к зеркалу СР. Заметим, что СР- радиус
кривизны зеркала. В соответствии с
законом отражения угол A PC должен быть
равен углу FPC; тогда треугольник FPC
должен быть равнобедренным. Следовательно,
стороны CF и FP равны друг другу, и
длина любой из них равна приблизительно
половине расстояния между точками С и Р,
или радиуса кривизны.
На рис. 23-22 показано, как можно
графически построить изображение предмета
(в данном случае стрелки), если известно
положение фокуса F. Проведем из конца
стрелки луч 1 параллельно оси зеркала,
а луч 2-в центр зеркала. Изображение
конца стрелки располагается в точке
пересечения этих лучей. Все прочие лучи,
исходящие из конца стрелки, также пройдут
через эту же самую точку изображения или
вблизи нее. Вогнутое зеркало можно
использовать для получения изображения
удаленного предмета. Изображение можно
увеличить с помощью короткофокусной
линзы или окуляра. Такое устройство
представляет собой телескоп, и его
увеличение равно отношению фокусных
расстояний (см. рис. 23-6). В астрономических
телескопах фотопластинки помещают
непосредственно в фокусе большого вогнутого
зеркала. Этот широко распространенный
тип телескопов был изобретен Ньютоном
и называется отражательным телескопом.
ЗАКОН ПРЕЛОМЛЕНИЯ (ЗАКОН СНЕЛЛА)
Закон преломления утверждает, что при
переходе из одной прозрачной среды
в другую световой луч меняет свое
направление. Например, если луч света попадает
из воздуха в воду или стекло, то он
отклоняется в сторону нормали. Рассмотрим
рис. 23-23 и покажем, почему на границе
Среда 1
Рис. 23-23. Два последовательных положения
волнового фронта, когда волна пересекает
поверхность раздела стекло-воздух.
меняется направление распространения
волны. На рисунке изображены два
последовательных положения участка волнового
фронта АВ и А'В'. Пусть Хх -длина
световой волны в среде 1, а Х2-в среде 2; тогда
А1 — —f~ И Л2 — "у •
(23-10)
Из прямоугольного треугольника ABB'
находим
sinGi =
АВ' '
а из прямоугольного треугольника А'АВ'
sinG, =
АВ'

ОСНОВНЫЕ выводы 419
Разделим первое соотношение на второе:
sin 0Х Хг
sin02 Х2
Подставим сюда вместо Хг и Х2 их
отношение, полученное из (23-10); тогда
sinGi
sin0„
с/и2
с/щ
В § 5 гл. 21 было показано, что с/и-это
показатель преломления среды.
Следовательно,
sinGi
sinG?
«i
(закон Снелла),
где п1 и п2 -показатели преломления
соответственно среды 1 и 2.
ЛИНЗЫ
С помощью закона Снелла
[соотношение (23-11)] можно рассчитать оптические
свойства линз. Так же как и вогнутое
зеркало, собирающая линза отклоняет пучок
параллельных лучей и фокусирует их на
расстоянии F от линзы. Расстояние F
называется фокусным расстоянием линзы.
Положение изображения можно
определить графически путем построения,
показанного на рис. 23-24. Проведем сначала
луч 1 параллельно горизонтальной оси.
Линза отклонит его таким образом, что он
пройдет через фокус F. Затем через центр
линзы проведем луч 2. Пересечение этих
лучей дает точку, в которой располагается
изображение. С помощью рис. 23-24
можно получить количественное соотношение
между расстояниями до предмета s и до
изображения s'. Заметим, что треугольник
АВО подобен треугольнику А'В'О. Из
подобия этих треугольников находим
АВ' _ s'
АВ ~ "7"
(23-12)
Кроме того, треугольник POF подобен
треугольнику A'B'F, так что
А'И
РО
s' -f
f '
(23-13)
Поскольку РО = АВ, левые части в
формулах (23-12) и (23-13) равны друг другу.
Приравнивая между собой правые части,
получаем
(23-11) ^ = ^^11^
s f f S S
Это соотношение между расстояниями
до предмета и изображения называется
формулой тонкой линзы. Необходимо
договориться, в каких случаях следует
считать величины s, s' или f положительными,
а в каких-отрицательными. Обычно при
решении какой-либо задачи оптические
элементы располагают таким образом,
чтобы свет проходил через линзу слева
направо. Тогда величина s' считается
положительной, если изображение расположено
справа от линзы, и отрицательной, если
оно расположено слева от нее. В случае
рассеивающей линзы величина / является
отрицательной. Величина s будет
отрицательной, если выходящие из линзы лучи
сходятся в мнимом предмете (это может
быть мнимое изображение, созданное
слева предшествующей линзой).
Основные выводы
Голограмма-это фотографическое
изображение интерференционной картины,
создаваемой отраженным от предмета
светом лазера и опорным пучком. При
Рис. 23-24. Предмет АВ
расположен на расстоянии s от линзы
с фокусным расстоянием /.
Изображение А'В расположено
на расстоянии $'.

420 ГЛ. 23. ОПТИКА
прохождении через голограмму
монохроматического света происходит
восстановление первоначального волнового фронта
отраженного света.
Плоскость поляризации
электромагнитной (световой) волны содержит вектор Е.
Поляризатор, состоящий из параллельных
проволочек (или вытянутых цепочек
молекул), будет пропускать лишь
составляющую поля Е, перпендикулярную
направлению проволочек. Свет, отраженный от
среды с показателем преломления п под
углом 0Х, удовлетворяющим условию
tg0x = п, имеет 100%-ную поляризацию.
Это называется законом Брюстера.
Монохроматический свет, проходя
через круглое отверстие диаметром а,
образует дифракционную картину, первый
минимум в которой (или темное кольцо)
соответствует углу 0МИН,
удовлетворяющему условию suiOmhh = 1,22Х/а.
Увеличение телескопа М = F/f, т.е.
увеличение равно отношению фокусных
расстояний объектива и окуляра. Угловая
разрешающая способность телескопа (а также
микроскопа) определяется как осмин =
= 1,22Х/а, где а-диаметр объектива.
Минимальное расстояние, которое
разрешается микроскопом, равно DocMHH ~ X. Свет от
лазера можно сфокусировать в пятно
таких размеров, однако для других
источников света сделать этого не удается.
Можно наблюдать дифракционное
рассеяние пучка протонов высоких энергий на
ядре радиусом R. Первый минимум в
дифракционной картине соответствует 0МИН =
= 0,61 h/pR, где h -постоянная Планка,
а р- импульс протонного пучка.
Геометрическая оптика основана на
законе отражения (угол падения равен углу
отражения) и законе преломления (закон
Снелла). Согласно закону Снелла,
отношение синусов угла падения и угла отражения
обратно пропорционально отношению
показателей преломления:
sin©! п2
sin02 пх
Вогнутое зеркало или собирающая
линза сводят пучок параллельных лучей в
фокус. Расстояние от зеркала (или линзы) до
фокуса называется фокусным расстоянием
и обозначается буквой F. Если предмет
находится на расстоянии s от линзы, то на
расстоянии s' от нее образуется его
перевернутое изображение, причем
1 1 _ 1
7 + У~ Т'
Приложение. Закон Брюстера
Если пучок света падает под углом дг
на непроводящую среду, то часть света
отражается под тем же углом, а часть
преломляется, согласно закону Снелла, под
углом 02:
sin©!
. _ = п.
sin02
Отраженный свет может испускаться
только благодаря колебаниям электронов
атомов непроводящей среды. Благодаря
наличию в формуле (21-13) множителя sin0
электроны не испускают излучения в
направлении своего движения. Если
падающий свет поляризован, как показано на
рис. 23-25, то электроны будут колебаться
Падающий
ЛУЧ Отраженный
луч
*пад I
Преломленный
луч
Рис. 23-25. Изменение поляризации при
отражении. Отраженный и преломленный лучи
взаимно перпендикулярны, т.е. направление
поля Е' совпадает с направлением отраженного
луча.

ЗАДАЧИ 421
в направлении Е\ В этом случае свет не
будет отражаться, поскольку отраженный луч
оказался бы направленным вдоль
направления движения электронов. Однако если
падающий свет на рисунке поляризован
перпендикулярно плоскости чертежа, то
отражение допустимо. На рис. 23-25 мы
имеем 0Х + 02 = я/2. Подставляя в закон
Снелла вместо 92 величину я/2 — 01?
получаем
sinGi
= и, или
sin (я/2 - 0Х)
tg0x = п (закон Брюстера).
(23-12)
Мы видим, что если неполяризованный
свет падает под углом Брюстера, то
отраженный свет должен быть поляризован
перпендикулярно плоскости страницы. Это
условие возникновения полной
поляризации при отражении называется законом
Брюстера.
Упражнения
1. Начертите диаграмму, аналогичную
приведенной на рис. 23-7, для случая Еу =
= Е0 cos cot и Ez = 2Е0 cos (cot — я/2). Это
случай эллиптической поляризации (конец
вектора Е описывает эллипс с отношением
осей 2:1).
2. Волна с правой круговой поляризацией
складывается с волной левой круговой
поляризации, причем обе волны имеют
одинаковые амплитуды и частоты и
распространяются вдоль оси х. В любом случае, когда
вектор Е волны 1 ориентирован в
положительном направлении оси + у, также
ориентирован и вектор Е волны 2. Опишите
поляризацию результирующей волны.
3. Повторите упражнение 2 для случая, когда
векторы Е обеих волн ориентируются вдоль
оси у в противоположных направлениях.
4. Расстояние до ближайшей звезды 4
световых года. Каким должен быть ее диаметр,
чтобы его можно было измерить с
помощью 200-дюймового телескопа (1 дюйм =
= 2,54 см)?
5. Предположим, что по орбите вокруг звезды,
удаленной на 10 световых лет, вращается
очень большая планета, которую можно
увидеть в 200-дюймовый телескоп. На
каком расстоянии от звезды должна
находиться эта планета, чтобы их можно было
разрешить?
6. Параллельный пучок лазера диаметром
1 см фокусируется линзой с фокусным
расстоянием 10 см. Каковы размеры пятна,
если X = 6400 А?
7. Повторите упражнение 6 для пучка
диаметром 1 мм.
8. Недавно было установлено, что при
упругом рассеянии протонов на протонах в
области высоких энергий минимум в
распределении интенсивности отвечает величине
поперечного импульса рассеянного протона
1,1 ГэВ/с, т.е. рсsin0 = 1,1 ГэВ. Каким
должен быть радиус эквивалентного протону
черного диска, дающего минимум в том же
месте?
9. Рассмотрим расположенные один за другим
два поляроида. Ось поляроида Л
вертикальна (т. е. он не поглощает вертикально
поляризованный свет). Ось поляроида В
ориентирована под углом 45°.
В
иВ
а) Чему равна интенсивность /, если
вертикально поляризованный свет падает на
поляроиды слева?
б) Чему равна интенсивность /', если
вертикально поляризованный свет падает на
поляроиды справа?
10. Предмет расположен между фокусом и
центром кривизны вогнутого зеркала. Будет ли
изображение перевернутым? Какова его
величина по сравнению с размером предмета?
11. Расстояние предмета до вогнутого зеркала
меньше фокусного расстояния. Увидите ли
вы его изображение в зеркале? Если да, то
будет оно больше или меньше предмета?
Не будет ли изображение перевернутым?
(Может быть, все обстоит точно так же, как
бывает, когда вы смотритесь в вогнутое
зеркало для бритья?)
12. Луч света падает на пластинку из стекла
под углом 60° относительно нормали к
пластинке. Если п = 1,5, то под каким углом
луч выйдет с другой стороны пластинки
(поверхности пластинки параллельны друг
другу)?
Задачи
13. Голограмма в примере 1 освещается светом
с X = 4800 А. На каком кажущемся
расстоянии за плоскостью голограммы находится
изображение?
14. Повторите расчеты, проведенные в конце
§ 1 настоящей главы для волнового фронта
восстанавливающей волны, но с
использованием в качестве голограммы позитива, а не

422 ГЛ. 23. ОПТИКА
негатива. В этом случае интенсивность света
за голограммой имеет вид
/ = I'cos2(ut( 1 + —-acoscH.
15. Вертикально поляризованный свет с
интенсивностью /0 проходит 9 идеальных
поляроидов. Ось первого поляроида составляет
10° с вертикалью, ось второго повернута
еще на 10° и т. д.; ось девятого поляроида
повернута на 90°. Чему равна
результирующая интенсивность?
16. Повторите решение задачи 15 для случая 90
поляроидов при условии, что оси соседних
поляроидов повернуты на 1°.
17. Вертикально поляризованный свет от лазера
падает на экран с двумя горизонтальными
щелями. Если одна из щелей закрыта,
интенсивность в любой точке экрана равна /0.
Вертикальная
поляризация
\/^f/\ Щель 1 (+45°)
1 чУЧ1 Щель2(-45°)
Вид на щели от экрана
а) Чему равна интенсивность в точках
экрана, где г2 — rt = 0?
б) Чему равна интенсивность в точках
экрана, где г 2 — rt = Х/2Ч
Закроем теперь щель 1 поляроидом,
ориентированным под углом + 45°, а щель 2
закроем поляроидом, ориентированным под
углом — 45°. Чему равна интенсивность
в точках, где
в) г2 -гх =0?
г) г2-Г1= Х/4?
д) r2-rl= Х/21
Поместим теперь в дополнение к
поляроидам на щелях ориентированный
вертикально поляроид перед экраном. Чему равна
интенсивность в точках экрана (за
вертикальным поляроидом), где
е) j-2 - гх = 0?
ж) г2 — rt = Х/21
18. Предположим, что диаметр звезды виден
под углом 10" 7 рад.
а) Можно ли измерить диаметр этой звезды
с помощью оптического телескопа?
б) Можно ли измерить диаметр методом
интерферометрии интенсивности?
Расстояние до звезды предполагается известным'
(см. пример 8 в гл. 22).
19. Какое минимальное расстояние можно
разрешить с помощью электронного
микроскопа, в котором используется пучок
электронов с кинетической энергией 1000 эВ?
20. Существует еще один метод оценки
среднего радиуса элементарной частицы,
пригодный даже в тех случаях, когда не удается
наблюдать первый минимум. Он
заключается в измерении кривизны или скорости
спада центрального максимума. Оказалось, что
при малых углах распределение
интенсивности рассеяния протонов на протонах
уменьшается по закону 1 — Ар\, где А =
= 10(ГэВ/с)"2. При малых значениях
аргумента функцию Бесселя можно
аппроксимировать функцией
11 ' 2 16
В этом случае
Ф
•МФ/2П 1 Ф2
__|*1__ ГДет =
= kR sin 0 и р± = р sin 0.
Какому значению R (в м) соответствует А =
= 10(ГэВ/с)"2?
21. Допустим, что у протона существует
жесткая сердцевина радиусом 10~14см. Пусть
протоны с энергией 200 ГэВ
взаимодействуют в основном с сердцевиной.
а) Под каким углом будет наблюдаться
первый дифракционный минимум?
б) Если протон не имеет сердцевины и
ведет себя как поглощающий диск с R =
= 10"13 см, то под каким углом будет
наблюдаться первый дифракционный
минимум?
22. Камера-обскура представляет собой черный
ящик длиной 10 см с крошечным
отверстием, играющим роль линзы. Какой диаметр
Узкая
диафрагма
Фотопленка

отверстия обеспечивает наибольшую
резкость изображения?
23. Две линзы с фокусными расстояниями
соответственно F и —F расположены на
расстоянии D друг от друга, причем D < F.
Если слева на линзы падает параллельный
пучок света, то будет ли он
фокусироваться, и если да, то в каком месте?
Н
24. Повторите решение задачи 23 для случая,
когда пучок падает на линзы справа.
25. Докажите, что если две тонкие линзы с
фокусными расстояниями Ft и F2 поместить
рядом, то эта система будет вести себя
аналогично линзе с фокусным расстоянием
F = 1—=—.
Ft+F2
26. Рыба находится на глубине ОР (см.
рисунок). Чему равна кажущаяся глубина ОР\
если для воды п = 1,33?
ЗАДАЧИ 423
27. Показатель преломления пластинки
ориентированного пластика равен щ для света,
поляризованного в направлении ориентации
пластика, и п± для света, поляризованного
нормально ориентации.
а) Если внешние электроны
преимущественно колеблются вдоль направления
ориентации пластика, то какая из величин будет
больше, «|| или их?
б) Если через такую пластинку проходит
поляризованный свет, вектор Е которого
составляет угол 45° с направлением
ориентации пластика, то плоскость поляризации
света оказывается повернутой на 90°. Такая
пластинка называется полуволновой. Какой
должна быть толщина х0 этой пластинки?
Ответ запишите через /, с, Wj_ и пц.
Свет от
рыбы
Вода
i
о
•р

ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
§ 1. Классическая и современная
физика
Физические явления и описывающие их
законы принято разделять на классические
и современные. Современная физика
опирается на возникшее в конце 20-х гг.
представление о волновой природе вещества
и обязательно включает новую
фундаментальную постоянную, открытую Планком
в 1900 г. (Чтобы объяснить спектр
излучения нагретых тел, Планк предположил, что
осцилляторы могут излучать свет лишь
порциями с энергией Е = hf, где/-частота
осциллятора, a h-постоянная Планка.)
Согласно такому определению
современной физики, все, что мы излагали до
сих пор, соответствует классической
физике (исключение составляет § 5 гл. 23,
посвященный дифракционному рассеянию).
Однако в этой главе будет показано, что
всем элементарным частицам присущи
волновые свойства, которые значительно
влияют на их поведение, особенно на
небольших расстояниях. Не уяснив
предварительно волновой природы вещества,
невозможно было бы разобраться ни в строении
атомов и молекул, ни в свойствах
элементарных частиц, ни в таких разделах
физики, как ядерная физика, астрофизика и
физика твердого тела. Вытекающие из
представлений о волновой природе вещества
основные положения и математический
формализм составляют предмет квантовой
механики. В этой и следующей главах мы
дадим основные понятия квантовой
механики. Остальные главы посвящены ряду
важных приложений, которые не только
помогут нам разобраться в изучаемых
явлениях, но и окажутся полезными для
более глубокого понимания самой
квантовой механики.
Прежде чем излагать совершенно
новые представления квантовой теории,
вернемся назад и перечислим те достижения,
которые были получены в классической
физике, а также ее возможные недостатки.
С помощью законов Ньютона нам удалось
объяснить законы падения тел, полет
снарядов, движение искусственных спутников
Земли, движение планет и другие случаи
макроскопического движения. Кроме того,
ньютоновская механика дала нам законы
сохранения энергии, импульса и момента
импульса.
Согласно представлениям химиков
XIX в., вещество построено из молекул
и атомов. Вместе с законами Ньютона эти
представления легли в основу
кинетической теории тепла, которая раскрыла нам
таинственное содержание понятия тепла.
Более века тому назад, используя понятие
заряда и основные законы теории
электричества, Максвелл дал объяснение
многообразным электрическим и магнитным
явлениям. Венцом достижений
классической физики стала созданная в 1870 г.
Максвеллом теория света (и оптика) как
математическое следствие его уравнений.
Следующим этапом было возникновение
трудностей в теории эфира при объяснении
отрицательных результатов опыта Май-
кельсона - Морли, что в свою очередь
послужило поводом к созданию в 1905 г.
специальной теории относительности. Лишь
с течением времени уравнения Максвелла
стали рассматриваться как необходимое
релятивистское следствие закона Кулона
(их можно вывести из этого закона).
Поразителен был переворот,
произведенный Эйнштейном в наших
представлениях о пространстве и времени.
(Действительно, как могут два движущихся
по-разному наблюдателя получить одинаковые
значения скорости одного и того же
светового импульса?) Однако мы увидим, что
волновая природа вещества, корпускуляр-
но-волновой дуализм и их следствия
окажутся еще более удивительными и
противоречащими здравому смыслу, чем
эйнштейновский постулат о постоянстве скоро-

§ 2. ФОТОЭФФЕКТ 425
сти света во всех инерциальных системах
отсчета.
Волновая природа вещества
качественно проявляется в том, что каждой частице
присущи свойства волны и, наоборот,
любые волны имеют свойства,
характерные для частиц. В качестве первого
примера, демонстрирующего это свойство
волн, мы приведем фотоэффект, теорию
которого Эйнштейн разработал в 1905 г.
§ 2. Фотоэффект
В конце XIX столетия был открыт
электрон. Вскоре после этого обнаружили, что
электроны вылетают с некоторых
металлических поверхностей, когда на эти
поверхности падает свет (рис. 24-1). Со времени
дифракционных экспериментов Юнга на
Свет
Металлическая
пластинка
Рис. 24-1. Нейтральный электроскоп,
соединенный с металлической пластинкой. При
освещении пластинки светом из нее выбиваются
фотоэлектроны, и листочки заряжаются
положительно.
Поэтому можно было ожидать, что
электрон, расположенный вблизи поверхности,
покинет металл, как только амплитуда его
колебаний А превысит некоторое
критическое значение. Из волновой теории света
мы имеем следующие выводы: 1)
электроны не будут вылетать из металла, до
тех пор пока Е0 не превысит
определенного критического значения; 2) энергия
испущенных электронов возрастает
пропорционально Eq и 3) если величину Е0 (а значит,
и интенсивность) поддерживать
постоянной, а частоту света со увеличивать, то
число испускаемых электронов должно
уменьшаться.
Однако экспериментальные
наблюдения опровергли все эти предсказания:
1. Пороговой интенсивности
обнаружено не было. Число вылетающих
электронов оказалось строго пропорциональным
El при любой сколь угодно малой
интенсивности.
2. Энергия электронов оказалась не
зависящей от величины Е0.
3. Обнаружена зависимость энергии
электронов от частоты. Оказалось, что
существует пороговая частота/0, причем при
частотах, превышающих пороговую,
энергия выбитых электронов линейно
увеличивается с ростом частоты. Фактически
кинетическая энергия электронов менялась
в интервале от нуля до некоторого
значения Кмакс и не было электронов с энергией
больше Кмакс. На рис. 24-2 приведена
найденная из опыта зависимость Кмакс от
частоты /
двух щелях не было сомнений в том, что
свет представляет собой волны. Эти
представления позволяли объяснить
фотоэффект. Амплитуда колебаний свободного
электрона в переменном электрическом
поле Е = EQ cos cot в соответствии с
выражением (21-6) записывается в виде
еЕ0
А =■
шаг
Рис. 24-2. Зависимость максимальной
кинетической энергии испущенных металлом электронов
от частоты света.

426 ГЛ. 24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
В 1905 г. Эйнштейн (хотя ему еще не
были известны все эти экспериментальные
факты) дал правильное объяснение
фотоэффекта. Ученый высказал весьма
смелую по тем временам мысль. Он
предположил, что свет представляет собой
совокупность квантов, каждый из которых
обладает энергией Е = hf где
й-постоянная Планка. Эйнштейн также
предположил, что эти кванты света (теперь их
называют фотонами) ведут себя подобно
материальным частицам и что при
столкновении с электроном в металле фотон может
поглотиться, а вся его энергия перейдет
к электрону. Даже самому Планку это
казалось крайне странным. Каким образом,
подчиняясь, как известно, законам
интерференции волн, свет мог в то же самое
время состоять из частиц? Ведь тогда в опыте
с двумя щелями частица света проходила
бы либо через одну, либо через другую
щель и, следовательно, не была бы в
состоянии создать интерференционную
картину.
И все же теория Эйнштейна сумела
объяснить экспериментальные факты.
Предположим, что для удаления
поверхностного электрона из металла
необходимо затратить энергию W0. Тогда, поглотив
фотон с энергией hf и вылетев с
поверхности, электрон будет иметь энергию hf—
— W0. Это и есть максимально возможная
кинетическая энергия:
^макс = hf- W0 (фотоэффект). (24-1)
Данное соотношение согласуется с
экспериментальной прямой, изображенной на
рис. 24-2. Эйнштейн предсказал, что наклон
прямой должен быть равен постоянной
Планка h. Его теория фотоэффекта
выдержала это трудное испытание. Наклон
действительно оказался равен
h = 6,63 • 10"34 Дж • с (постоянная
Планка)
(единицей измерения постоянной Планка
является джоуль • секунда или кг-м2-с-1).
Величина W0 называется работой
выхода и зависит от свойств данного металла.
Свободный электрон вне металла
испытывает вблизи его поверхности притяжение.
Если электрон сначала покоился, то,
проникнув в металл, он приобретет
кинетическую энергию U0. Иными словами, мы
утверждаем, что систему электрон и
металл можно представить в виде
потенциальной ямы глубиной U0, как
схематически показано на рис. 24-3. В гл. 28 мы
увидим, что внутри металла внешние
атомные, электроны оказываются
свободными (т.е. они не связаны с
определенными атомами) и их кинетическая
энергия может меняться от нуля до Kf.
Величина Kf называется энергией Ферми.
Если электрону с энергией Ферми
сообщить дополнительно энергию W0, то его
энергии К = Kf + W0 едва хватит на то,
чтобы покинуть металл. Иными словами,
когда он вылетит из металла, энергия
электрона станет равной К = 0. Из рис. 24-3
видно, что W0 + Kf = U0 или
W0 = U0- Kf.
Схематическая иллюстрация фотоэффекта
представлена на рис. 24-4. Первоначально
электрон находится на уровне с энергией
Поверхность
-и.
К
-В
нутрией наружи-
Потенциальная
энергия
Рис. 24-3. Потенциальная яма,
в которой находятся электроны
внутри металла, ^-граничная
кинетическая энергия
«свободного» электрона в металле.

§ 3. ЭФФЕКТ КОМПТОНА 427
JlJlZ
-"о
Рис. 24-4. Электрон с энергией — W0 поглощает
фотон и переходит на более высокий уровень.
Kf (этот уровень показан на рисунке
штриховой линией). После поглощения фотона
с энергией hf электрон переходит на более
высокий энергетический уровень,
обозначенный на рисунке сплошной зеленой
линией. При этом энергия электрона вне
металла оказывается равной hf — W0. Это
и есть максимально возможная энергия,
которую может иметь испущенный
электрон: Кмакс = hf — W0. Если же электрон
находится на более низком уровне (ниже
штриховой линии) и поглощает фотон той
же энергии, то энергия электрона вне
металла будет меньше Кмакс.
Пример 1. В случае цезия работа выхода равна
1,8 эВ. Какова максимальная длина волны
света, который способен выбить из металла
электрон с кинетической энергией 2 эВ?
Решение: Из выражения (24-1) находим частоту
J " h "
Тогда
с he
J -К-макс "Г vVq
_ (6,63 • 10 " 34 Дж ■ с) (3 • 108 м/с) _
(3,8эВ)(1,6-10-19Дж/эВ) ~
= 3,27-10" 7м.
§ 3. Эффект Комптона
Используя классическую
электродинамику, в гл. 21 мы показали, что свет,
переносящий энергию Е, должен обладать
импульсом р = Е/с. Следовательно, и
световой квант с энергией Е = hf должен иметь
импульс р = hf/c. Если заменить f/c на 1/Х,
то
р = т- <24"2)
Эйнштейн предсказал, что световые кванты
или фотоны будут вести себя подобно
материальным частицам с импульсом р =
= h/X. В случае фотоэффекта этот
ничтожный импульс передается всему образцу
металла и испущенному из него электрону.
Импульс, приобретенный металлом в
таких условиях, слишком мал и не поддается
измерению; однако при столкновении
фотона со свободным электроном величину
передаваемого импульса уже можно
измерить. Этот процесс-рассеяние фотона на
свободном электроне-называется
эффектом Комптона. Впервые он был
экспериментально подтвержден А. Комптоном
в 1923 г. Этот эффект аналогичен
соударению биллиардных шаров.
Выведем теперь соотношение,
связывающее длину волны рассеянного фотона
с углом рассеяния и длиной волны фотона
до соударения. Пусть фотон с импульсом
р и энергией рс сталкивается с
неподвижным электроном, энергия покоя
которого тс2. После соударения импульс
фотона становится равным р' и направлен под
углом 0, как показано на рис. 24-5.
Импульс электрона отдачи будет равен р'е,
а полная релятивистская энергия Е'е. Здесь
мы используем релятивистскую механику,
поскольку скорость электрона может
достигать значений, близких к скорости
света. Согласно закону сохранения энергии,
полная начальная энергия равна полной
энергии после соударения; таким образом,
рс + тс2 = р'с + EJ,
(р-р'+тс)2=(Е'е/с)2. (24-3)
Закон сохранения импульса дает
Р - Р' = Ре-

428 ГЛ. 24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
Возводя обе части в квадрат:
р2 - 2р р' + р'2 = р'2е
и вычитая последнее равенство из (24-3),
имеем
т2с2 - 2рр' + 2ртс - 2р'тс + 2pp'cos0 =
Из (9-11) мы видим, что правую часть
здесь можно заменить на т2с2:
т2с2 — 2р' (р + тс — р cos 0) + 2ртс = т2с2,
До
6\/\/Ч •
^— е~
Фотон
После
Фотон Р
0
^ /\*
\
\
\
\
\
%
к
Рис. 24-5. Эффект Комптона. Соударение
фотона со свободным электроном.
откуда находим
1 +—(1 - cos6)
тс
Воспользовавшись тем, что р = h/X,
получаем
1 = 1
Х' Х + — (1-COS0)'
тс
или
X' - X = (1 - cosO) (эффект Комп-
тс
тона).
(24-4)
В своем опыте Комптон использовал
рентгеновское излучение с известной
длиной волны и обнаружил, что у рассеянных
фотонов увеличивается длина волны в
соответствии с предсказаниями по формуле
(24-4).
Эффект Комптона, фотоэффект и
множество других экспериментов с участием
света и атомов подтвердили, что свет
действительно ведет себя так, как если бы он
состоял из частиц с энергией hf и
импульсом h/X.
§ 4. Корпускулярно-волновой дуализм
Если бы в первых же экспериментах со
светом были обнаружены эффект
Комптона и фотоэффект, то все были бы
убеждены в том, что свет представляет собой
поток фотонов, которые ведут себя
подобно всем добропорядочным частицам. При
таком положении вещей наблюдение
интерференционной картины от двух щелей
должно было бы вызвать изумление.
Действительно, как могут частицы
обнаруживать свойства, присущие классическим
волнам? Ведь частица может пройти только
либо через одну, либо через другую щель.
Интерференцию фотонов друг с другом
можно исключить, уменьшив
интенсивность света настолько, чтобы средний
интервал времени между испусканием
фотонов значительно превышал время пролета
фотонов от источника света до экрана.
Если экран удален от источника на 3 м, то
время пролета составит t = L/c = 10" 8 с.
Поэтому выберем интенсивность
источника порядка Ю-11 Вт, что
соответствует испусканию менее 108 фотонов в
секунду.
Закрыв щель В, мы получим
распределение интенсивности, соответствующее
одной щели А, как показано на рис. 24-6.
Для регистрации отдельных фотонов,
когда они попадают на экран, можно
использовать фотоумножитель. Если открыта
только щель В, то получается идентичная,

§ 5. ВЕЛИКИЙ ПАРАДОКС 429
Рис. 24-6. Распределение
интенсивности, обусловленное
фотонами, прошедшими через щель
Л (либо через щель В).
&
^А^
Экран
От щели А
но немного сдвинутая картина (см. тот же
рисунок). Но, как было показано в гл. 23,
в случае, когда открыты обе щели,
распределение интенсивности света на экране
отнюдь не будет суммой распределений,
обусловленных каждой щелью в
отдельности; возникает интерференционная картина
Юнга от двойной щели. Таким образом,
мы приходим к парадоксу - свет обладает
одновременно свойствами, характерными
как для волн, так и для частиц.
В 1927 г. благодаря обнаружению
волновых свойств у электрона этот парадокс
стал еще более значительным! В
действительности еще за три года до этого Луи де
Бройль в своей диссертации на соискание
ученой степени доктора философии
предположил, что соотношение (24-2)
справедливо не только для фотонов, но и вообще
для всех частиц, а именно:
P = -h£ = 1i/ для любых частиц
К
(соотношение де Бройля), (24-5)
Де Бройль предположил, что пучок частиц
любого сорта будет создавать на
подходящей двойной щели интерференционную
картину, характерную для опыта Юнга
с двумя щелями. В то время гипотеза де
Бройля выглядела безумной и вряд ли
уместной для соискания степени доктора
философии. Лишь три года спустя наука
пережила огромное потрясение -
эксперимент подтвердил гипотезу де Бройля.
Потрясение было обусловлено тем, что
казалось невозможным, чтобы такие частицы,
как электроны, представляли собой в одно
и то же время и частицы, и волны. В
следующем параграфе мы продемонстрируем,
каким образом современные данные
приводят к полному крушению представлений,
основанных на «здравом смысле» и
повседневном опыте.
§ 5. Великий парадокс
Парадокс можно устранить,
предположив, что отдельный фотон после
прохождения через щели Л и В способен
расщепляться и интерферировать с самим собой.
Однако парадокс усиливается, если
заменить пучок фотонов на пучок электронов.
В природе никогда не наблюдалось
половины или части электрона. Независимо от
того, находится детектор за щелью А или
В, электрон всегда обнаруживается
целиком. В этом сущность атомизма,
справедливого для всех элементарных частиц,
включая фотоны. С этой точки зрения мы
приходим к выводу, что отдельный
электрон может пройти лишь через одну из
двух щелей на рис. 24-7. Следовательно,
распределение электронов на экране
должно быть суммой распределений для
каждой из щелей в отдельности. Хотя логика
эта кажется безукоризненной,
распределение, характерное для (Л + В), не имеет
места! Вместо этого мы видим стандартную
интерференционную картину для двух
щелей, изображенную на рис. 24-8.
Не происходит ли крушения чистой
логики? Ведь все это выглядит так, как если
бы 100 + 100 оказалось равным нулю.
Предположим, что в точке Р1 на рис. 24-8
находится счетчик Гейгера, регистрирую-

430 ГЛ. 24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
Электронный
пучок
А
Экран
Открыта только щель А
Открыта только щель В
Открыты обе щели
Распределение
электронов
Только В
А + В
Только А
Рис. 24-7. Распределение
интенсивности электронов согласно
классической физике.
щий ежесекундно 100 электронов, когда
открыта любая из щелей А или В. При этом,
когда открыты обе щели одновременно,
счетчик перестает регистрировать
электроны. Это значит, что точка Рх попадает
в интерференционный минимум (г2 — гх =
= Х/2). Если сначала открыть только щель
А, а затем постепенно открывать щель В,
то в соответствии со здравым смыслом мы
вправе ожидать, что скорость счета по
мере открывания щели В будет постепенно
увеличиваться от 100 до 200 отсчетов в
секунду. Однако вместо этого мы
наблюдаем уменьшение скорости счета от 100 до
нуля. Каким образом открывание щели
В может повлиять на электроны, которые,
казалось бы, прошли через щель А? Более
того, если счетчик Гейгера поместить
в точку Р2, то по мере открывания щели
В скорость счета будет постепенно
увеличиваться от 100 до 400 отсчетов в секунду,
когда вторая щель полностью открыта.
Таким образом, 100 + 100 = 400.
Единственный способ объяснения этих
парадоксальных результатов состоит в
создании математического формализма,
совместимого с атомизмом и всегда
правильно предсказывающего наблюдаемые
интерференционные явления. При этом
следует позаботиться о его внутренней
непротиворечивости.
\
Классическое
распределение
\
Наблюдаемое
распределение
Рис. 24-8. Распределение
интенсивности электронов согласно
квантовой теории.

§ 5. ВЕЛИКИЙ ПАРАДОКС 431
ВОЛНОВАЯ ФУНКЦИЯ
Математический формализм, с
помощью которого устраняется парадокс,
ставит в соответствие каждой частице
амплитуду вероятности \|/(x,j;,z,t), которая
представляет собой функцию координат
и времени. Вероятность обнаружить частицу
в произвольный момент времени t в любой
точке х, у, z пропорциональна |\|/(х, у, z9 t)\2,
т.е. интенсивности. Квадрат модуля
используют потому, что \|/, вообще говоря,
комплексная функция. Формально она
обладает свойствами классических волн,
и поэтому ее часто называют волновой
функцией.
Если событие может произойти
несколькими взаимно исключающими
способами (как, скажем, при прохождении
частицы через одну из щелей А или В), то
амплитуда вероятности этого события
представляет собой сумму амплитуд
вероятностей каждого из способов:
v|/ = vj/i + v|/2 (принцип суперпозиции).
Это утверждение совпадает с правилом
сложения амплитуд волн в оптике. В
рассмотренном выше примере ^г описывает
волну, проходящую через щель А, а
\|/2-через щель В. На экране обе волновые
функции перекрываются и дают
классическую интерференционную картину от двух
щелей, причем направление на п-й
максимум определяется выражением sin0„ =
= nX/d [см. формулу (22-4)].
Этот формализм, составляющий основу
волновой или квантовой механики,
возможно, оставит у читателя тревожное
ощущение, * что более глубокое понимание
ускользнуло от него. Но это не так. Ничего
более фундаментального нет. Возможно,
читателя утешит высказывание Ричарда
Фейнмана, удостоенного в 1965 г.
Нобелевской премии за приложение квантовой
механики к электродинамике. В своих
«Лекциях по физике»1} Фейнман пишет:
1] См. 3-е издание русского перевода:
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские
лекции по физике. Вып. З.-М.: Мир, 1965,
с. 217 -Прим. перев.
«Быть может, вам все еще хочется выяснить:
«А почему это? Какой механизм прячется за
этим законом?» Так вот: никому никакого
механизма отыскать не удалось. Никто в мире не
сможет вам «объяснить» ни на капельку больше
того, что «объяснили» мы. Никто не даст вам
никакого более глубокого представления о
положении вещей. У нас их нет, нет представлений
о более фундаментальной механике, из которой
можно вывести эти результаты».
Пример 2. На рис. 24-9 в точке Р находится
счетчик Гейгера. Амплитуда волны, прошедшей
через щель А и достигшей точки Р, в условных
единицах равна \|/д = 2, а в случае щели В мы
^ А
Пучок I
| Рис. 24-9.
имеем \|/в = 6. Если открыта только щель А, то
в точке Р ежесекундно регистрируется 100
электронов.
а) Сколько электронов регистрируется
ежесекундно, если открыта только щель В?
б) Если открыты обе щели и происходит
конструктивная интерференция, то сколько будет
ежесекундно регистрироваться электронов?
в) То же, но в случае деструктивной
интерференции.
Решение: Отношение интенсивностей волн
\|/в/\|/Д = 36/4 = 9. Следовательно, через щель
В проходит ежесекундно в 9 раз больше частиц,
чем через щель А, т.е. 900 электронов.
В случае «б» полная амплитуда волны \|/ =
= \|/д + Фв> или v|/ = 8. Поскольку \|/2 = 16\|/\,
то в точке Р будет регистрироваться 1600
электронов в секунду.
В случае «в» \|/д и \|/в должны иметь
противоположные знаки, чтобы ослаблять друг друга.
Следовательно, \|/ = 2 — 6 = — 4. Теперь \|/2 =
= 16, т.е. в 4 раза больше \|/\. Это
соответствует регистрации 400 электронов в секунду.
Пример 3. Каким будет распределение
интенсивности в интерференционном опыте с двумя
щелями, если щель В пропускает в 4 раза
больше электронов, чем щель А.
Решение: Имеем \|/2в = 4\|/\ или \|/в = 2\|/д.
Полная интенсивность в максимуме пропорцио-

432 ГЛ. 24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
нальна (\|/д + *|/в)2 или
/макс = (Фа + 2>А)2 = 9v|/2A-
Интенсивность в минимуме равна
/мин = (Фа - 2\|/А)2 = Фа-
Следовательно, отношение /МаксДмин = 9.
Распределение интенсивности описывается
выражением / = /А [5 + 4cos/c(rB - гА)], где гА
и гв - расстояния от экрана до щелей А и
В соответственно.
Изложенный формализм порождает
ряд недоуменных вопросов, требующих
дальнейшей физической интерпретации.
Допустим, что мы выпускаем электроны
поодиночке. Тогда, согласно волновым
представлениям, каждому электрону
сопоставляется цуг волн, или волновой пакет,
расщепляющийся поровну между двумя
щелями. Однако, поместив за щелью
А счетчик Гейгера, камеру Вильсона или
иной детектор частиц, мы увидим, что
через щель никогда не проходит половины
электрона. В этом сущность атомизма,
который совместим с гипотезой о том, что
интенсивность волны за щелью А
характеризует вероятность найти электрон
(целиком!) в этом месте. Более того, если
детектор поместить за щелью А, то
интерференционная картина сгладится и получится
классический результат. Наличие детектора
изменяет результат, превращая
интерференционную картину (рис. 24-8) в
классическую (рис. 24-7). Многие физики, включая
Эйнштейна, пытались придумать такой
опыт, в результате которого можно было
бы, не нарушая интерференционной
картины, установить, через какую именно
щель прошла данная частица; однако все
эти попытки потерпели неудачу. Один из
таких экспериментов описан в примере 3
в гл. 23. В этом эксперименте нужно было
установить, через какую щель проходят
фотоны. Для этого можно менять
ориентацию поляроида, расположенного у экрана.
Однако всякий раз при соответствующем
повороте поляроида картина
интерференции на двух щелях будет превращаться
в картину, характерную для одной щели.
Но что же все-таки представляют собой
«волны», отвечающие электронам? На
этот вопрос следует ответить так же, как
в случае фотонов. Электромагнитные
волны свободно распространяются в пустом
пространстве. В отличие от механических
волн в этом случае не существует среды,
совершающей колебательное движение.
Волновая функция \|/ не является
непосредственно наблюдаемой величиной, и в этом
смысле ничто не совершает
колебательного движения. Проблемы квантовой
механики решаются с математической точки
зрения аналогично задаче о волнах в
жидкости или другим классическим волновым
проблемам. Классические волны и волны,
отвечающие частицам, подчиняются
математическим уравнениям одного и того же
типа. Но в классическом случае амплитуда
волны непосредственно наблюдаема, а
\|/ нет.
Электронная-
пушка
^LVJ /40 кВ
1—* Диафрагма
Двойная -
щель
Электростатические ■
линзы для
увеличения
изображения
— Линза
— Фраунгофера
(
-о Экран
— Фотопластинка
Рис. 24-10. Экспериментальная установка Йёнс-
сона для наблюдения интерференционной
картины от двух щелей в случае электронов. [См.
С. Jonsson, Zs. Phys., 161, 1961.]

§ 6. ДИФРАКЦИЯ ЭЛЕКТРОНОВ 433
§ 6. Дифракция электронов
Эксперимент по дифракции электронов
на двух щелях сложно осуществить,
поскольку характерная длина волны
электронов [см. (24-5)] оказывается много меньше
длин волн видимого света. Подлинную
картину интерференции электронов на двух
щелях удалось зафиксировать на
фотопластинке в эксперименте, выполненном
К. Йёнссоном в 1961 г. Схема этого экспе-
Рис. 24-11. а-интерференционная картина от
двух щелей в случае электронов; каждое из
зерен негатива образовано отдельным
электроном; б-для сравнения приведена
интерференционная картина от двух щелей в случае света
(см. рис. 22-17); на этом фото каждое из зерен
негатива образовано отдельным фотоном.
[Фото на рис. а получено проф. К. Йёнссоном,
Тюбингенский университет.]
римента приведена на рис. 24-10, а
полученные результаты воспроизведены на рис.
24-11, а.
В том месте, где электрон попадает на
пластинку, образуется черное пятно.
Приведенная фотография-это результат
попадания большого числа электронов от
двойной щели. Для сравнения на рис. 24-11,6
показана интерференционная картина,
полученная при дифракции света на двух
щелях. С помощью генератора случайных чи-
Рис. 24-12. Результаты моделирования
эксперимента с двумя щелями. Распределения отвечают
экспозициям с малым числом электронов: а-27
электронов; 6-70 электронов; в-735
электронов.
сел, удовлетворяющих распределению
вероятностей вида sin2x, можно
смоделировать распределение на рис. 24-11, а,
полученное в условиях малой интенсивности.
На рис. 24-12, а воспроизведено попадание
27 электронов на фотопластинку. Рисунки
24-12,6 и в отвечают попаданию 70 и 735
электронов соответственно.
Гипотеза де Бройля впервые была
подтверждена на опыте двумя американскими

434 ГЛ. 24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
физиками К. Дэвиссоном и Л. Джермером,
наблюдавшими в 1927 г. различные типы
дифракции электронов. Любопытно, что
в этом опыте, как и в ряде других,
имевших исключительно большое значение для
физики, великое открытие было сделано
«случайно». Дэвиссон и Джермер не
ставили своей целью поиски дифракции
электронов. Поначалу они даже не имели
представления о ней. В 1926 г. Дэвиссон повез
в Англию, на Международную
конференцию в Оксфорд некоторые полученные им
предварительные данные. Европейские
ученые обратили его внимание на то, что эти
результаты можно скорее
интерпретировать как дифракцию электронов, нежели
классическое рассеяние, которое он изучал.
А спустя несколько месяцев Дэвиссон
и Джермер получили результаты, которые
недвусмысленно демонстрировали
волновую природу электронов и позволили
определить величину постоянной Планка
с точностью около 1%. Они исследовали
рассеяние медленных электронов от
поверхности монокристалла металла.
Упорядоченные ряды атомов на поверхности
металла действовали подобно штрихам
тонкой дифракционной решетки. Длина волны
электронов была найдена по известной
величине расстояния между атомами.
На рис. 24-13 показано схематически
устройство для наблюдения дифракции
электронов от поверхности кристалла.
Детектором частиц может служить
люминесцентный экран. Значение угла 0, под
которым наблюдается максимум
интенсивности, позволяет найти постоянную Планка.
Как видно из рис. 24-13,6, разность хода
AD = d sin 0 в первом максимуме
интенсивности должна быть равна длине волны h/p.
Следовательно,
h , . л
— = asinG,
Р
откуда
h = pdsinG.
Вскоре после появления в 1924 г.
гипотезы де Бройля английский физик Томпсон
приступил к систематическому
исследованию дифракции электронов. В его
экспериментах электроны с высокой энергией
пропускались через тонкую металлическую
Электронная
пушка
Детектор
Кристалл
Волновые
фронты
Поверхность^]
кристалла
д£> Кристалл
d о о
Рис. 24-13. а-прибор для
наблюдения дифракции
электронов от поверхности кристалла;
б-участок поверхности
кристалла при сильном увеличении.

УПРАЖНЕНИЯ 435
фольгу. Поскольку длина волны
рентгеновских лучей почти та же, что и у
электронов, Томпсон надеялся получить картину
дифракции электронов, сходную с уже
известной дифракционной картиной
рентгеновского излучения. В 1928 г. он получил
ряд дифракционных картин для
электронов, весьма похожих на дифракционную
картину в случае рентгеновских лучей.
Интересно, что здесь «случайность» оказалась
более счастливой, чем тщательное
изучение и обдуманный подход. Разумеется, это
не может служить для читателя
концепцией научного метода, однако таковы уж
пути развития науки. Опыт Дэвиссона
и Джермера является хорошим примером
истинно научного подхода. Если
экспериментатор, пусть даже случайно, обнаружит
непонятный ему эффект, то следует
тщательно разобраться в нем, пока не будет
достигнута полная ясность.
В настоящее время подробно изучены
интерференционные картины, создаваемые
не только электронами, но и нейтронами,
протонами и даже целыми атомами.
Например, приведенное на рис. 23-19
распределение представляет собой
интерференционную картину, создаваемую протонами
высокой энергии. Волновая природа
вещества сейчас твердо установлена и
всесторонне проверена. Никаких отклонений от
теории пока обнаружить не удавалось.
Основные выводы
Планк предположил, что свет
квантован, и каждый квант света-фотон-имеет
энергию Е = hf. Эйнштейн дал объяснение
фотоэффекту, предположив, что энергия
электрона, выбитого фотоном с
поверхности металла, может достигать Кмакс =
= hf— W0, где W0- работа выхода для
данного металла. Работа выхода в
конкретном металле зависит от глубины U0
потенциальной ямы и максимальной
кинетической энергии Kf электронов
проводимости: W0= U0-Kf.
Фотон обладает импульсом р = h/X;
при столкновении фотона со свободным
электроном часть его энергии и импульса
передается электрону. Если длина волны
фотона после столкновения %', то из
законов сохранения энергии и импульса имеем
следующее соотношение для эффекта
Комптона:
X' - X = —(1 - cos0).
тс
Не только фотоны, но и все частицы
имеют длину волны X = h/p. Волновая
природа пучка электронов с импульсом
р проявляется в интерференционной
картине, которая возникает при прохождении
пучком двойной щели. Если на
поверхность металла под прямым углом падает
пучок электронов, то в направлении,
определяемом углом sin Q = h/(pd) (где
d-межатомное расстояние), будет наблюдаться
дифракционно рассеянный пучок.
Волновые свойства частицы можно
описать с помощью волновой функции \|/.
Вероятность найти частицу в любой
момент времени t в любой точке
пространства х, у, z пропорциональна
интенсивности волны |\|/ (х, у, z, t)\2. Если событие может
произойти несколькими взаимно
исключающими способами, то амплитуда
вероятности события будет представлять
собой сумму отдельных амплитуд
вероятностей: \|/ = \|/! + \|/2.
Упражнения
1. Какова длина волны (в ангстремах) фотона
с энергией 1 МэВ?
2. Запишите выражение для инертной или
релятивистской массы фотона через h, X и с.
3. Если релятивистская масса фотона 10"15 г,
то каков его импульс в системе СИ? Чему
равна его длина волны?
4. Связь энергии с длиной волны фотона
удобно записывать в виде X = К/Е. Найдите
численное значение постоянной К, если X
измеряется в ангстремах, а Е-ъ
электрон-вольтах.
5. Электрон и фотон имеют каждый
кинетическую энергию 1 эВ. Каковы длины волн
каждой из частиц?
6. Выразите кинетическую энергию
нерелятивистского электрона через его массу, длину
волны и постоянную Планка h.
7. Каждый металл характеризуется порогом
фотоэффекта А,0 (излучение с длиной волны,

ГЛ. 24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА
превышающей Х0, не может вырвать
электрон). Каково значение Х0 в случае меди,
если для нее работа выхода равна 4,4 эВ?
8. Пороговая чувствительность сетчатки
человеческого глаза к желтому свету составляет
1,7-10"18 Вт. Какому числу ежесекундно
попадающих на сетчатку фотонов это
соответствует?
9. Выразите длину волны свободного
электрона через Е, h, т и с, где Е-полная
релятивистская энергия.
10. Напишите выражение для кинетической
энергии релятивистского электрона через
его длину волны.
11. Допустим, что в опыте с двумя щелями
в некоторой точке экрана амплитуды волн,
прошедших через щели А и В, равны
соответственно + 3 и +5, а скорость счета,
если открыта только щель А, составляет 60
отсчетов в секунду.
а) Какова скорость счета, если открыта
только щель В?
б) Какова скорость счета, если открыты обе
щели?
в) Какой будет скорость счета, если обе
щели открыты, а амплитуды волн имеют
разные знаки?
12. Предположим, что в опыте по дифракции
электронов на трех одинаковых щелях
детектор электронов расположен в точке, куда
все три волны приходят в фазе.
а) Какова скорость счета от трех щелей,
если каждая из них в отдельности
обеспечивает 100 отсчетов в секунду?
б) Если интенсивность пучка от электронной
пушки увеличится в два раза, во
сколько раз возрастет скорость счета от трех
щелей?
13. Если удвоить и амплитуду и частоту
плоской электромагнитной волны, то во
сколько раз изменится плотность потока фотонов
[число фотонов/ (м2 • с)] ?
Задачи
14. Электрон притягивается к электрически
нейтральному куску металла. Силу
притяжения можно представить в виде
потенциальной ямы глубиной — U0. Рассмотрим
электрон с наибольшей энергией внутри металла
(т.е. на уровне Ферми), Пусть эта энергия
в металле равна К = 6 эВ. Поглотив фотон
с энергией 7 эВ, электрон вылетает из
металла с энергией К = 5 эВ, Будем считать,
что электрон не испытывает столкновений
с другими электронами.
а) Чему равна работа выхода в электрон*
вольтах для этого металла?
б) Какова величина U0 в электрон-вольтах?
в) Найдите отношение длины волны
электрона после вылета из металла к
длине волны до того, как он поглощает
фотон?
15. Фотон с длиной волны X сталкивается с
покоящимся свободным электроном. После
соударения длина волны фотона равна Х\
а направление его движения меняется на
противоположное (угол рассеяния 180°).
а) Каким после соударения будет импульс
электрона в зависимости от X и Х'1
б) Чему равна кинетическая энергия
электрона после соударения? Приведите
ответ для релятивистского случая, выразив
его через X и X'.
16. Фотон с энергией Е » тес2 испытывает
обратное рассеяние на покоящемся электроне.
Чему равна (в МэВ) энергия фотона
после рассеяния?
17. Фотон с энергией Е»Мрс2 испытывает
обратное рассеяние на покоящемся протоне.
Чему равна (в МэВ) энергия фотона после
рассеяния?
18. Фотон с энергией 100 кэВ испытывает комп-
тоновское рассеяние на угол 90°.
а) Какова его энергия после рассеяния?
б) Чему равна кинетическая энергия
электрона отдачи?
в) Определите направление движения
электрона отдачи.
19. Пусть Е0 -начальная энергия фотонов,
испытывающих комптоновское рассеяние.
Покажите, что кинетическая энергия электрона
отдачи дается выражением
(l-cose)£0
1 - cos 0 + тс2/Е0 '
20. Допустим, что при комптоновском
рассеянии угол между направлением движения
налетающего фотона и направлением вылета
электрона отдачи равен ф. Найдите
выражение для ф через X и V.
21. Тепловые нейтроны находятся в
температурном равновесии со средой при
комнатной температуре. В этом случае кТ =
= 0,025 эВ. Какова средняя кинетическая
энергия теплового нейтрона? Чему равна
его длина волны?
22. На две очень тонкие щели, расположенные
друг от друга на расстоянии 10 мкм, падает
пучок электронов с энергией 1 эВ, В 10 м
от щелей находится экран. Каково
расстояние между соседними минимумами на
экране?
23* На рис. 24-13 изображена поверхность
кристалла с взаимно перпендикулярными
цепочками атомов; расстояние между
соседними атомами равно 1,5 А по оси у и 2,0 А по
оси z. На поверхность кристалла падает пу-

ЗАДАЧИ 437
чок электронов с энергией 90 эВ. Расстояние
от кристалла-мишени до экрана 10 см. На
люминесцентном экране образуются пятна,
как показано на рисунке. Каково расстояние
между точками по осям у и z? В каких
направлениях будут перемещаться эти точки
при увеличении энергии пучка?

КВАНТОВАЯ МЕХАНИКА
§ 1. Волновые пакеты
В основе квантовой механики лежит
соотношение де Бройля р = h/X. Однако
импульс принято выражать не через длину
волны Х9 а через волновое число к = 2п/Х:
h 2% _ h
2п X In
Величина h/2n встречается столь часто,
что для нее введено специальное
обозначение Ь («аш» перечеркнутое):
р = Ш (соотношение де Бройля). (25-1)
Рассмотрим движущуюся вдоль оси х
частицу, длина волны которой в точности
равна Х0. Волновое число частицы к0 = 2п/Х0.
Можно ли в качестве волновой функции взять
\|/ = A cos (k0x - art)? В этом случае
распределение вероятностей имеет вид |\|/|2 ~
~ cos2 (k0x — cot), т. е. в любой момент
времени t на оси х нашлись бы точки, в
которых невозможно было бы обнаружить
частицу, тогда как в действительности ее
можно с равной вероятностью найти в
любой точке на оси. Поэтому в качестве
волновой функции следует взять \|/ = A el(/c°x_a)t).
Хотя сама \|/ опять-таки представляет собой
волну, распространяющуюся в
положительном направлении оси х,
| v|/12 = v|/*\|/ = (AQ-i{koX - fflt)) (Ae+ i{k°x ~ ю°) =
= A2.
Мы видим, что использование
комплексной волновой функции разрешает
указанное выше затруднение и дает
равномерное распределение вероятностей по оси х.
Из формулы Эйлера
ei(p = cos ф + i sin ф (формула Эйлера)
следует, что мнимая и действительная
части функции \|/ являются
монохроматическими волнами:
Re (\|/) = A cos (k0x — cot) и
Im (\|/) = A sin (k0x — cot).
Мы показали, что если импульс
частицы имеет определенное значение, то она
с равной вероятностью может находиться
в любой точке пространства. Иначе
говоря, если импульс частицы точно известен,
то мы ничего не знаем о ее
местонахождении. Однако в большинстве физических
ситуаций бывает известно, что частица
находится в определенной области
пространства. Рассмотрим, например, следующую
волновую функцию в момент времени t =
= 0:
\|/ (х, 0) = А ехр ( - -*—) exp (ik0x). (25-2)
На рис. 25-1, а приведена действительная
часть этой волновой функции, а на
рис. 25-1,6 показано соответствующее
распределение вероятностей:
Следует заметить, что более чем в 50%
случаев частицу можно обнаружить в
интервале от х = — ох до х = + ох.
Функция ехр ( — х2/ 2а2) представляет собой
известное распределение Гаусса; здесь
gx -среднеквадратичное отклонение,
которое мы будем называть
неопределенностью величины х и обозначать Ах. Такая
локализованная волна называется
волновым пакетом. Хотя изображенная на
рис. 25-1, а волна не является чисто
монохроматической, как было показано в
приложении 2 гл. 21, подобный волновой пакет
можно представить в виде суммы
монохроматических волн. Для иллюстрации это-

§ 2. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ 439
го рассмотрим волновой пакет в момент
времени t = О и подберем подходящую
суперпозицию монохроматических волн типа
exp(iTcx). Для этого необходимо найти
коэффициенты Вп в следующем
выражении:
ехр(*7с0х) =
^ = ехр \--п
\ 4а2
= 2XexP(*V).
Воспользуемся следующим
математическим тождеством:
Qxp(ik0x) =
ехр -
4а2
= -рг- I ехр [ — а2 (к — к0)2~\ ехр (ikx) dk.
l/тг (25-4)
(Вычисление интеграла в правой части
можно найти в любом курсе
математического анализа.) Сравнивая формулу (25-3)
с (25-4), получаем
Ке(Ф)
1*\л
-б*
Рис. 25-1. Волновой пакет в виде распределения
Гаусса, а-зависимость действительной части
волновой функции от х; б-зависимость
квадрата модуля волновой функции или плотности
вероятности от х.
В этом выражении содержится бесконечное
число монохроматических волн. Поэтому
мы перейдем от суммирования к
интегрированию:
4а2
\|/ = ехр I - — I ехр (ik0x) ■■
= $B(k)Q\p(ikx)dk.
5(/c) = -f-exp[-a2(/c-7c0)2].
уп
Наконец, заменим к на pj%
воспользовавшись соотношением де Бройля (25-1):
§ 2. Принцип неопределенности
На рис. 25-2 представлены
распределения по импульсам для случая двух
волновых пакетов различной ширины. Сле:
дует отметить, что чем уже волновой
пакет, тем шире распределение по
импульсам. Поскольку вероятность найти частицу
в состоянии, описываемом волновой
функцией В (к) ехр (ikx), пропорциональна
квадрату ее амплитуды, вероятность
различных значений импульса определяется
функцией
|Я(#- -^-ехр|
r_j^4]. (25.5)
L 2(^/2ax)2J
Мы видим, что \В(р)\2 также является
распределением Гаусса для р и его можно
переписать в виде
,,„,.. 4-р[-^].
(25-6)-
или «неопределенность» величины р.
Сравнивая выражения (25-5) и (25-6), получаем
(25-3) стр = П/2сх, страх = */2.
(25-7)

440 rJI 25- КВАНТОВАЯ МЕХАНИКА
B(p)
В(р)
Рис. 25-2. Функция
распределения В(р) по импульсам
(наверху) и соответствующий ей
волновой пакет (внизу). Ширина
волнового пакета на рис. а
вдвое превышает его ширину на
рис. б. В обоих случаях заметим,
что произведение <зхор одно
и то же.
Таким образом, в случае волновой
функции в виде распределения Гаусса
произведение ширины волнового пакета на
ширину функции распределения по импульсам
равно fr/2. В других случаях это
произведение может быть больше Й/2, но оно
никогда не будет меньше h~/2. В общем случае
мы имеем
АхАр>Й/2 (принцип неопределенности).
(25-8)
Принцип неопределенности утверждает,
что если частица локализована в
пространстве со среднеквадратичным отклонением
Ах, то ее импульс не имеет
определенного значения, а характеризуется
распределением \В(р)\2 с «шириной» Ар. Физически
это означает, что невозможно
одновременно точно определить значения координаты
и импульса частицы.
Пример 1. Допустим, что в случае волнового
пакета распределение по импульсам имеет вид
прямоугольника, как показано на рис. 25-3, а:
0, к < (к0 - а),
В(к)=^ Л, (к0-а)<к<(к0 + а),
0, к > (к0 + а).
В(к)
А
О-
К~а kQ к0+а
W2
Рис. 25-3. а-прямоугольное
распределение по импульсам; б-
распределение по координатам,
или волновой пакет,
соответствующий распределению на
рис. а.

§ 2. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ
441
Конденсорная
линза
Фотоны
Найдем \|/(х) и произведение Ах Ар
(Ах-полуширина распределения вероятностей
координаты, измеренная на уровне половины
максимального значения, и Ар-то же самое для
импульса).
Решение: Используя формулу (25-3), находим
ко-a Llx Jk0-a
= — {ехр[>(/со + а)] - expRx(/c0-a)]} =
= 2^sinox_e*oX
X
. . |2 л л2 sin2 ах
|v|/|2=442 —.
xl
Эта функция уменьшается вдвое при ах =
= 1,39. Следовательно,
аАх = 1,39.
Поскольку а = А/с = Ар/% то
(Ар/Й)Ах = 1,39.
Таким образом,
АхАр= 1,39Й.
Если известно, что частица покоится, то
неопределенность ее импульса Ар = 0.
Можно было бы думать, что с помощью
микроскопа удастся определить положение
частицы и тем самым ниспровергнуть
принцип неопределенности. Но микроскоп
позволит определить положение частицы
в лучшем случае с точностью до длины
волны используемого света (см. § 4 гл. 23).
Следовательно, Ах # X. Но поскольку
Ар = 0, то произведение Ах Ар также
должно быть равно нулю и принцип
неопределенности нарушится! Так ли это? Давайте
подойдем к этому с позиций квантовой
механики. Мы пользуемся светом, а
квантовая теория утверждает, что свет состоит из
фотонов с импульсом р = h/X. Чтобы
обнаружить частицу, на ней должен
рассеяться или поглотиться по крайней мере один
из фотонов пучка света, собранного кон-
денсорной линзой (рис. 25-4).
Следовательно, частице будет передан импульс,
достигающий h/X. Таким образом, в момент
Рис. 25-4. Взаимодействие в микроскопе
фотонов с частицей.
наблюдения положения частицы с
точностью Ах » X неопределенность ее
импульса Ар ^ h/X. Перемножая эти
неопределенности, получаем
h
Ах Ар ^ X— = %
X
что согласуется с (25-8). Этот пример
иллюстрирует внутреннюю
непротиворечивость квантовой механики. Физики вместе
с математиками усердно искали
противоречий, но ничего обнаружить не удалось.
СКОРОСТЬ ВОЛНОВЫХ ПАКЕТОВ
В гл. 21 мы выяснили, что волновой
пакет распространяется не со скоростью
волны и = со//с, а с групповой скоростью
vg = da/dk [см. (21-17)]. Согласно
соотношению де Бройля, Ш = Е и Ш = р для
всех частиц. Заменим в выражении Е =
= р2/2т величину Е на Ш, а р на Ш; тогда
2т
Продифференцируем это выражение по к:
^ Лео ^Ъ2к
dk т '

442 ГЛ. 25. КВАНТОВАЯ МЕХАНИКА
~dk =
V„ = V.
Ш р _
т т
Таким образом, представление
локализованной частицы в виде волнового пакета
приводит к верному классическому
результату. Волновой пакет (как ему и надлежит)
перемещается с такой же скоростью, как
и частица.
РАСПЛЫВАНИЕ ВОЛНОВОГО ПАКЕТА
Рассмотрим две частицы, одна из
которых имеет скорость vg, а
другая-скорость vg + Avg. В момент времени t = 0 их
координаты совпадают, а спустя
промежуток времени t частицы расходятся на
расстояние
Ах — (Av)t.
(25-9)
Покажем, что отдельному волновому
пакету свойствен разброс значений групповой
скорости Avg9 который в соответствии
с (25-9) должен приводить к увеличению
ширины Ах. Оценим величину Avg. Мы
имеем
Avg = ^АР.
Используя результат предыдущего раздел
ла, мы можем вместо v написать v:
A dV A l А
Ava = —— Ар я — Ар.
dp т
(25-10)
Начальное значение Ар ограничено,
согласно принципу неопределенности, величиной
Й/Ах0, где Ах0-неопределенность
начального положения или ширина исходного
волнового пакета. Подставляя эту величину
в (25-10), получаем
Avnx
1
П
9 т\ Ах(
Подстановка
в (25-9) дает
Ах :
последнего выражения
mAxn
Это уширение растет пропорционально t
и складывается с начальной шириной Ах0.
Как мы вскоре увидим, подобного «рас-
плывания» волнового пакета можно
избежать, только поместив частицу в
потенциальную яму. На рис. 25-5 показано, как
деформируется волновой пакет с течением
времени, а на рис. 25-6-к чему приводит
столкновение волнового пакета,
описывающего свободную частицу, с потенциальным
барьером.
Чтобы получить количественное
представление о скорости расплывания
волнового пакета в случае свободной частицы,
рассмотрим свободный электрон,
локализованный в начальный момент времени
в области Ах0 = 10"10 м (типичный
размер атома). Спустя одну секунду мы будем
иметь
Ах =
*
-г =
10"
тАх0 ' 9- КГ31 • 10"10
= 1,1 • 106м = 1100 км.
Мы видим, что уже через одну секунду
электронное облако окажется по своим
размерам больше штата Техас. Хотя
квантовая теория позволяет точно определить
поведение волновой функции в будущем,
если она известна в начальный момент
Re(tfr)
/ПРИ
При Г = 0
Более
поздние
значения
/ _
Рис. 25-5. Гауссов волновой
пакет в два последовательных
момента времени. Пакет движется
вправо с групповой скоростью,
которая совпадает со
скоростью частицы.

§ 2. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ 443
Aju _Ai /к_
280 320 II 440
_Jl _JL _Jl
480 560 800
Рис. 25-6. Столкновение гауссова волнового
пакета с потенциальным барьером прямоугольной
формы. Для удобства плотность вероятности
и потенциальный барьер (показан цветной
линией) построены на одной и той же оси (высота
пакета относительно величины барьера не имеет
определенного значения). Средняя энергия
волнового пакета равна половине высоты барьера.
Ширина пакета растет со временем (время
указано числами в левой верхней части каждого
рисунка). [Из статьи: A.Goldberg, Н.М. Schey,
J. L. Schwartz, Amer. Journ. Phys., 177, March
1967.]
времени, однако это мало чем может
помочь, поскольку волновая функция очень
быстро расплывается по всему
пространству.
Квантовая механика позволяет выйти
из одного затруднения философского
плана, с которым столкнулась классическая
физика. В период господства классической
физики считалось, что если в некоторый
момент времени t0 известны точные
значения координат и скоростей всех частиц во
Вселенной, то, используя точные
физические законы, в принципе можно полностью
описать картину прошлого и будущего.
Вселенная при этом представлялась
единым гигантским механизмом.
Основываясь на подобных аргументах, некоторые
философы могли бы прийти к выводу, что
все действия человека (ведь даже люди
состоят из протонов, нейтронов и
электронов) полностью предопределены. При
этом, разумеется, учитывалось, что
подобные расчеты будущего или прошлого
никогда не удастся осуществить из-за
бесконечно большого числа частиц во
Вселенной. Но все-таки , подобные аргументы
доставляли беспокойство тем, кто хотел
бы верить в свободу воли.
Из принципа неопределенности следует,
что существует более серьезное
препятствие, чтобы можно было выполнить такие
расчеты, и, таким образом, классический
детерминизм больше не «довлеет» над
физиками. Однако это не означает, что мы
вправе взывать к квантовой механике как
к доказательству существования свободы
воли.
Нам встречались и другие примеры,
в такой же степени опровергающие
классический детерминизм. Скажем, согласно
общепринятой интерпретации квантовой
теории, нет способа установить, каким из
электронов был поглощен фотон при
фотоэффекте. Мы можем лишь вычислить
вероятность поглощения фотона данным
электроном. Это же относится и к месту
попадания отдельного электрона на экран
(см. рис. 24-8). Интерференционная
картина характеризует лишь вероятность
обнаружить электрон в данной точке экрана. То
же самое справедливо и для распада
радиоактивного ядра, например урана. Не
существует способа определить момент
времени, когда произойдет распад данного
ядра урана. Согласно квантовой теории,
все, что нам вообще может быть
известно-это только вероятность, с которой
в данный интервал времени может
произойти распад. Предсказываемые
вероятности можно затем сопоставить со
средними значениями по многим
наблюдениям.
Мы видим, что, когда речь идет
о взаимодействиях и структуре
микрочастиц, представления квантовой теории
коренным образом отличаются от
классических. Если же, как мы считаем, квантовая
теория верна, то нельзя надеяться, что
с помощью классической физики можно
изучить явления микромира и строение
вещества.

444 ГЛ- 25- КВАНТОВАЯ МЕХАНИКА
§ 3. Частица в ящике
Рассмотрим частицу, заключенную
в одномерный ящик с абсолютно
отражающими стенками, расстояние между
которыми равно L. Справа от стенки в точке
х = О (рис. 25-7) происходит наложение
двух волн, распространяющихся в
противоположных направлениях. В этом случае
y\f(x,t) = Bd
ikx - i(nt
-Be
ikx-
- ikx — i<ut .
= B(Qikx-Q
Мы выбрали знак минус в силу того, что
\|/ должна обращаться в нуль при х = О
(\|/ обращается в нуль за стенкой и должна
Стенка
Это равенство имеет место, когда kL = пи,
где п- целое число. Мы видим, что разре-
о"0
Рис. 25-7. Частица отражается от левой стенки
ящика, имеющего длину L.
быть непрерывной). Используя известную
формулу
sin кх =
21
перепишем \|/(х, t) в виде
ty(x,t) = 2iBQ-l(0tsmkx.
Пусть А = 2Bi, а \|/ (х) - волновая функция,
зависящая только от координат; тогда
\|/ (х) = A sin кх.
(25-11)
Функция \|/(х) должна обращаться в нуль
при х = L по той же причине, что и при
х = 0. Подставляя в (25-11) вместо х
величину L, получаем
0 = sin (Щ.
Рис. 25-8. Первые четыре стоячие волны,
соответствующие частице в ящике; на нижнем
рисунке-плотность вероятности для частицы в
состоянии с п = 4.

§ 3. ЧАСТИЦА В ЯЩИКЕ
445
шены только такие значения волнового
числа кп, которые удовлетворяют
равенству
кп = nn/L.
(25-12)
Тем самым мы потребовали, чтобы в
ящике укладывалось целое число полуволн,
что совпадает с условием возникновения
стоячей волны на струне:
L = п(Х/2).
На рис. 25-8 изображены волновые
функции \|/„(х) = A sin (nn/L)x для п = 1, 2, 3, 4.
Соответствующие значения импульса
записываются в виде
Рп = **„
или, с учетом (25-12), как
рп = п (тсЙ/L).
(25-13)
Этим импульсам соответствуют значения
кинетической энергии
Е =
Рп
2т
= п
п2П2
2mL2
(25-14)
Следует заметить, что наинизшая
возможная энергия п2Ъ2/2тЬ2 отвечает п = 1,
а соответствующая волновая функция
представляет собой в точности половину
синусоиды. Эта энергия называется
энергией основного состояния. В квантовой
механике частица в ящике не может иметь
энергию меньше п21г2/2тЬ2, вследствие
того что \|/ в ящике должна быть ненулевой
функцией; в классической же физике
частица может иметь нулевую энергию.
Чтобы получить представление о
масштабе этих энергий, рассмотрим электрон,
заключенный в ящик с размерами,
типичными для атома (10~10 м или 1 А).
В этом случае
„ п2П2
(3,14)2(1,05. 10"34)
34\2
2mL2 2(9,11 • 1(Г31)1(Г20
=* (5,97 -КГ18 Дж)п2 = (31,Зп2) эВ.
На рис, 25-9 представлены четыре низших
уровня энергии. Энергия Ех сравнима по
величине с кинетической энергией
электрона в атоме водорода.
Е4
500 эВ
Е,
Е2
Я,
0
Рис. 25-9. Четыре низших энергетических
уровня электрона, находящегося в ящике шириной
10"10 м. Стрелкой показан переход,
обсуждаемый в примере 2.
Пример 2. Допустим, что в ящике с линейным
размером L = 10"10 м в состоянии с п = 2
находится электрон, который может испустить
фотон и перейти в состояние с наименьшей
энергией. Чему равна длина волны фотона?
Решение: Из закона сохранения энергии
следует, что энергия фотона
Дж,
¥ =
Е2-
откуда
/=
и
X =
1,79
с
-Ег
• 10"
~h
3
= 4Е
17
. ю8
L"Sl =
1,79
2,70-1016 с"1
- = 1,11 •
10"8
• 10
м =
/ 2,7 • 1016
111 А.
В этом примере фотон принадлежит
ультрафиолетовой области спектра
электромагнитного излучения, в которой как
раз и расположены наиболее интенсивные
лиции спектра водорода. Поскольку
энергия электрона в ящике может принимать
лишь определенные дискретные значения,

446 ГЯ 25. КВАНТОВАЯ МЕХАНИКА
*>^К
-£-J
Л/(х)
Рис. 25-10. а-четыре низших энергетических
уровня в случае потенциальной ямы с
бесконечно высокими стенками; б-четыре низших
энергетических уровня в случае потенциальной ямы,
образованной силой электростатического
притяжения.
Пример 3. Предположим, что ящик настолько
мал, что энергия частицы в нем сравнима с тс2.
Найдем точное релятивистское значение
энергий Еп частицы.
Решение: В этом случае следует
воспользоваться релятивистским соотношением
ф1
-полная энергия частицы, включая энер-
„2
где Еп
гию покоя тс2. Поскольку для релятивистских
частиц также справедливо соотношение де
Бройля, последнее выражение с учетом (25-13)
для рп можно переписать в виде
Еп = с
и ——+mV.
Пример 4. Предположим, что частица с
энергией Е находится в потенциальной яме,
показанной на рис. 25-11. Эта потенциальная яма та же,
что и на рис. 25-10, а, отличаясь от нее лишь
тем, что начало отсчета энергии сдвинуто на
величину V1. Таким образом, внутри ямы
потенциальная энергия равна Uv (В данной задаче
величина U1 отрицательна.)
а) Чему равна вторая производная d2y\r/dx2
волновой функции частицы, находящейся в яме?
энергии (или длины волн) испускаемых
электроном фотонов также должны
составлять дискретный набор значений. Такой
«свет», проанализированный
спектроскопом, имел бы линейчатый спектр, как
и спектр излучения атомов. На самом деле
электрон, заключенный в ящике, является
лишь очень грубой моделью атома
водорода. Ящик представляет собой
прямоугольную потенциальную яму, тогда как
в атоме водорода электрон движется в
потенциальной яме, образуемой кулоновским
полем и показанной на рис. 25-10. Однако
в обоих случаях качественное поведение
оказывается сходным. Поскольку элБктрон
должен описываться стоячей волной,
существует лишь определенный набор
возможных волновых функций \|/„ и
соответствующих им энергий Еп.
Рис. 25-11. Потенциальная яма с бесконечно
высокими стенками, аналогичная яме на
рис. 25-10, а, но со смещенной энергетической
шкалой.

§ 4. УРАВНЕНИЕ ШРЕДИНГЕРА
447
б) Каков набор энергий Еп?
Решение: а) В общем случае волновая функция
частицы в яме имеет вид
\|/ = Л sin (/ос + ф),
где импульс р можно получить из соотношения
Е = р2/2т + Ux:
p = ]/2m(E-Ul)
к =
(2т
2 (Е-U,).
Следовательно, вторая производная \|/ имеет
вид
—- = — к2 Л sin (кх + ф) = — к2 \|/,
dx2
d2ty
~dxT~
2т
(Е- l/Оф.
(25-15)
б) Набор значений кинетической энергии
дается выражением (25-14); только нужно
заменить LHa 2х0 и учесть, что Кп = (Еп — Ux).
Таким образом,
К=п2
п2Ъ2
2mL2
и,
п2Ъ2
2т(2х0)2 '
, п2П2
§ 4. Уравнение Шредингера
До сих пор мы имели дело со
свободными частицами, которые обладают
определенным импульсом и,
следовательно, определенной длиной волны. В более
общем случае на частицу могут
действовать внешние силы, характеризуемые
потенциальной энергией взаимодействия
U(x). При этом, поскольку полная энергия
Е =
2т
+ U(x)
(25-16)
сохраняется постоянной, возрастание
потенциальной энергии U с х будет
сопровождаться уменьшением импульса р и
соответствующим увеличением длины волны.
Таким образом, волновой функции должна
U(x)
Рис. 25-12. а-с ростом х потенциальная
энергия U(x) возрастает, а К уменьшается;
б-соответствующая волновая функция \|/(х), длина
волны которой увеличивается с х;
в-аппроксимация функции С/(х), приведенной на рис. а,
ступенчатой функцией.
отвечать меняющаяся длина волны. На
рис. 25-12,6 изображена волновая функция,
у которой длина волны увеличивается
с ростом х. Точный вид волновой функции
\|/(х) с меняющейся длиной волны можно
найти, решая дифференциальное уравнение,
называемое уравнением Шредингера.
Найдем это уравнение для случая,
когда U (х) аппроксимируется ступенчатой
функцией, приведенной на рис. 25-12, е. Из
примера 4 известно, что в области Ux
волновая функция \|/(х) удовлетворяет
уравнению (25-15):
d2y\f
1х^~
^(E-U^.

448 ГЛ. 25. КВАНТОВАЯ МЕХАНИКА
Поскольку это уравнение справедливо
и для U29 ^з> •••> Uj9 а любую функцию
U (х) можно представить в виде набора
маленьких «ступенек», то Ul можно заменить
на U(x):
12
dx2
Это известное стационарное уравнение
Шредингера для одного измерения. Оно
применимо к нерелятивистским системам
при условий, что распределение
вероятностей не меняется со временем; иными
словами, оно справедливо в случаях, когда
функции имеют вид стоячих волн. [Суще- б
ствует также нестационарное (или
зависящее от времени) уравнение Шредингера,
применяемое при решении задач, в
которых волновой пакет изменяется во
времени]. Мы рассмотрим несколько задач,
относящихся к частице в потенциальной
яме. Для нахождения стационарных
состояний (стоячих волн) мы используем
стационарное уравнение- Шредингера.
ГРАНИЧНЫЕ УСЛОВИЯ
Если частица заключена в
потенциальной яме, то вероятность найти ее вне ямы
обращается в нуль; следовательно, в этом
случае граничное условие состоит в том,
что вероятность найти частицу при
больших значениях |х| обращается в нуль. Как
будет показано в следующем параграфе,
этому граничному условию удовлетворяют
лишь определенные значения Е (будем
обозначать их Еп) и соответствующие \|/„.
Значения Еп называются собственными
значениями, а соответствующие волновые
функции-собственными функциями.
§ 5. Потенциальные ямы конечной
глубины
В § 3 мы рассматривали частицу в
ящике, который представлял собой
потенциальную яму с бесконечно высокими
стенками. В данном параграфе с помощью
уравнения Шредингера мы решим задачу
о движении частицы в потенциальной яме
со стенками конечной высоты U0
d4 2т Г17 rr/^n.ir (стационарное а
ТТ = " -tfT Iе - u WJ * уравнение
Шредингера).
(25-17)
U(x)
-•-Область 1^—Область II*-
Рис. 25-13. а-потенциальная яма глубиной U0
и первый энергетический уровень;
б-соответствующая волновая функция.
(рис. 25-13). Нам нужно найти волновые
функции \|/„ и энергии Еп9 которые
удовлетворяли бы граничному условию, такому,
что \|/(х) -► 0 при больших |х|. На первый
взгляд может показаться, что при \х\ > х0
функция \|/(х) должна обращаться в нуль,
поскольку в этой области величина Е — U
отрицательна, и это соответствовало бы
отрицательным значениям кинетической
энергии, запрещенным в классической
механике (К = Е - U). Однако в области II
на рис. 25-13 уравнение Шредингера
можно записать в виде
dx2
Это уравнение имеет решения
v|/n = е кх и е+юс,
где
к =
/2m(U0-E)
Н2
(25-18)

§ 5. ПОТЕНЦИАЛЬНЫЕ ЯМЫ 449
Заметим, что в случае, когда
кинетическая энергия отрицательна, знаки второй
производной d2^f/dx2 и функции \|/
совпадают и функция изгибается в сторону от
оси х, в то время как в случае
положительной кинетической энергии (например,
в области I) \|/ (х) изгибается в направлении
к оси х, как и синусоида. На рис. 25-14
кривая Ъ иллюстрирует поведение волно-
Область 1
Область И
Кривая а
Кривая с
Рис. 25-14. Кривая Ь совпадает с приведенной
на рис. 25-13,6. Кривая а соответствует случаю,
когда Е несколько меньше Ev а кривая с-когда
Е несколько больше Ev
вой функции \|/ при правильном выборе
значения Е. Если энергия Е выбрана чуть
меньше, то в области I \|/(х) будет
изгибаться медленнее (кривая а). Если же Е
выбрать несколько больше, то \|/ (х) будет
соответствовать кривой с. Правильное
поведение, иллюстрируемое кривой Ъ,
описывается функцией
\|/„ = А&-*Х (в области IIJ
v|/i = Bcoskx (в области \),
где
к = ]/2тЕ/П2.
При х = х0
^i(^o) = *l>ii(*o) или Bcoskxo = Ае~хх°.
При х0 одинаковы также и наклоны обеих
кривых, так что
-кВ sin кх0 = -хАе~хх°.
Разделив это соотношение на предыдущее,
получим
к tg кх0 = х.
Это трансцендентное уравнение можно
решить для первого энергетического уровня
Ev Используя формулу (25-18), его можно
привести к более простому виду:
tg кх0 = — =
Uo
- 1 .
Определим величины
Уо =
Тогда
tgj>
2т ТТ
и у = кх0 •
'И>
- 1.
(25-19)
Уравнение (25-19) может иметь
несколько корней в зависимости от величины у0.
Интересно сравнить потенциальную яму
конечной глубины с бесконечно глубокой
потенциальной ямой шириной 10"10 м
(х0 = 0,5 • 10"10 м). Повторим вычисления
для электрона, находящегося не в
бесконечно глубокой яме (такие вычисления
были проделаны в § 3), а в яме глубиной
800 эВ. Для U0 = 800 эВ мы имеем
_ ]/2mU0
Уо - щ *о -
^2(9,M0-31)(800.1,6.10-*9) ^QZ =
= 7,27.
При этом уравнение (25-19) имеет три
положительных корня; обозначим их уи
Уз, у5. Найти эти корни можно либо
графически, либо методом итераций, либо
методом «проб и ошибок». Корни имеют
значения ух = 1,38, уъ =4,11 и у5 = 6,69.
Поскольку к = у/х0 и Е = (Ък)2 /2т,
получаем
Е1 = 28,8 эВ, Еъ = 256 эВ, Е5 = 678 эВ.

450 ГЛ. 25. КВАНТОВАЯ МЕХАНИКА
Следует заметить, что для п = 2 и 4
волновые функции в области I имеют вид
\|/i = В sin кх. Сшивая граничные условия
при х = х0, имеем
Bsinkxo = Ае~хх°,
кВ cos кх0 = - хАе~хх°.
Разделив одно соотношение на другое,
получим
ctg/oc0 = — x/fc,
ctg
(25-20)
2тЕ
fi2
Е
- 1,
или
ctgy =
Уо
- 1.
В случае у0 = 7,27 существуют два
положительных корня: у2 = 2,75 и у4 = 5,44.
Соответствующие энергии Е2 = 115 эВ и
£4 = 447 эВ (напомним, что они получены
для электрона в потенциальной яме конеч-
эВ
:ь
700
600
500
400
300
200
100"
0
Рис. 25-15. Энергетические уровни электрона
в яме шириной 10"10 м. Сплошные линии
соответствуют потенциальной яме глубиной
800 эВ, а штриховые-потенциальной яме с
бесконечно высокими стенками (то же, что и на
рис. 25-9).
ной глубины). На рис. 25-15 показаны все
эти уровни энергии, а на рис. 25-16—
первые три волновые функции.
Рис. 25-16. Сплошные линии-стоячие волны
низшего порядка, соответствующие энергиям
Ev Е2, Еъ на рис. 25-15. Штриховые
линии-соответствующие волновые функции в
потенциальной яме той же ширины, но с бесконечно
высокими стенками.
В гл. 29 при изучении ядерной физики
мы увидим, что общее решение задачи
о частице, находящейся в прямоугольной
потенциальной яме конечной глубины,
имеет практическое значение.
Короткодействующие ядерные силы, действующие
между нейтроном и протоном, можно
приближенно представить в виде
прямоугольной потенциальной ямы, а затем с
помощью формулы (25-20) вычислить
энергию связи дейтрона и его размеры (т.е.
волновую функцию дейтрона).

§ 6. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР 451
Пример 5. Предположим, что функция \\tt на
рис. 25-13,6 уменьшается вдвое при х = х0, т.е.
*M*o) = *
*i (0) 2 '
Найдем выражение для Et в зависимости от \
т и х0.
c/W
Решение: Поскольку i^
1
cos кх0 = —,
кх0=-,
п
Зх0
| / 2mEx тг
|/ И2 Зх0 '
я2 И2
"* 18тх02 '
= Bcosfoc,
§ 6. Гармонический осциллятор
Следующим приложением уравнения
Шредингера будет решение задачи о
движении частицы массой т под действием
гармонической силы F = — кх (здесь
к -коэффициент упругости, а не волновое
число). В гл. 11 (т. 1), посвященной
простому гармоническому движению, мы
установили, что потенциальная энергия U(x) =
= кх2/2 = т(02Клх2/2. В классической
физике такая частица совершает гармонические
колебания с угловой частотой сокл = j//c/m,
а ее энергия может принимать любое
значение, в том числе равное нулю. (Здесь
и далее нижний индекс «кл» означает
«классическая».) Как мы убедимся, в
квантовой механике наличие граничных
условий при больших | х | приводит к тому, что
разрешен лишь набор энергий Еп = (п —
— 1/2)Йсокл, где п-целое положительное
число.
Прежде чем обратиться
непосредственно к уравнению Шредингера, проделаем
приближенные расчеты. Они
проиллюстрируют основные методы квантовомеханиче-
ских вычислений. Попробуем решить эту
задачу по аналогии с задачей о частице
-*,
о 0
Рис. 25-17. а-потенциальная энергия
гармонического осциллятора; б-стоячая волна третьего
порядка (сплошная линия-точное решение;
штриховая линия-приближенное решение).
в ящике. Из рис. 25-17 видно, что длина
ящика L— 2х0, где х0 - максимальное
смещение, или амплитуда колебаний. В случае
стоячей волны п-го порядка на отрезке
длиной L уложится п полуволн:
пХп/2 = 2х0,
или
К = 4х0/и.
Среднее значение импульса
-_ h= h = h
X 4х0/п 4х0'
Средняя кинетическая энергия
^ = р2 = n2h2
2т Ъ2тх%
Полная энергия Е в два раза превосходит
эту величину:
Е =
n2h2
16mxl

452 ГЛ. 25. КВАНТОВАЯ МЕХАНИКА
она также равна максимальному значению
потенциальной энергии:
Перемножая два последних равенства,
получаем
n2hWKU
Е2 =
или
£ =
32
2 ]/2
пШ(дкп.
В пределах точности наших «вычислений»
можно считать, что тг/2|/2 ъ 1; тогда
Еп « ийсйкл, где п = 1, 2, 3, ....
Мы покажем, что точные вычисления
приводят к следующим значениям энергии:
Еп = (п - 1/2) Йсокл, где п = 1, 2, 3, ....
Выполним теперь с помощью
уравнения Шредингера точные вычисления.
Подставляя в уравнение Шредингера величину
U = (1/2) тсо2лх2, получаем
d2\|/ 2т Л 1 2 2».
(25-21)
Поскольку нам надо отыскать решение
с меняющейся длиной волны, попытаемся
применить функцию Гаусса. То, что мы
«угадываем» решение, а затем проверяем,
годится ли оно, оправданно и служит
общепринятым способом отыскания решений
дифференциальных уравнений. Таким
образом, запишем волновую функцию
в виде
i|/(x) = e"flX\
Чтобы проверить, удовлетворяет ли эта
функция уравнению (25-21), мы должны
взять вторую производную и подставить
ее в левую часть уравнения. Вторая
производная
d2y\f
dx2
■= -2ae"flX +4aVe-flX .
Подстановка в уравнение (25-21) дает
(-2a + 4aV)e"flx2 =
2m / р * 2 2 \ -ах2
ft2 V 2
2а + (4а2)х2 = - ——+
2т£ /т2со2
Й2 V Й
х .
Приравнивая коэффициенты при х2, имеем
4а2 = ^
а =
тсок
2Й
Из сравнения свободных членов вытекает
следующий результат:
- 2а = -2тЕ/П2,
EJb2a = Ъ2 тсокл = faoKJI
т т 2Н 2
Мы видим, что функция Гаусса является
решением, но лишь при условии, что
Е = -Шкл.
В этом случае
х|/1(х) = е-(тЮкл/2й)х2.
Путем подстановки в уравнение (25-21)
читатель может убедиться, что решением,
соответствующим стоячей волне второго
порядка, будет
\|/2(х)
= хе~(та)кл/2й)х2
Эта функция является решением только,
когда Е = ЗШкл/2. Следует заметить, что
расстояние между двумя соседними
уровнями равно Е2 — Ех = Йсокл. Это
относится и к более высоким уровням,
которые описываются выражением. Еп =
= (п- 1/2)7кокл.
Отсюда мы видим, что гармонический
осциллятор испускает фотоны, частота
которых совпадает с частотой колебаний
классического осциллятора в случае, когда
переход происходит между соседними
уровнями.

УПРАЖНЕНИЯ 453
Основные выводы
Волновая функция свободной частицы,
импульс которой в точности равен р0,
имеет вид v|/(x,t) = А ехр [i(k0x — cot)], гДе
^о = Ро/Ъ-
Если частица локализована в
пространстве, причем ее вероятность описывается
распределением Гаусса, то v|/(x,0) =
= ехр [ — x2/4<j2~\ Qlk°x. Соответствующее
распределение по импульсам В (к) =
— (Ъх1)/к) ехР [— ®1 (& — ^о)2]> причем
v|/(x,0) = $B(k)Qikxdk.
Среднеквадратичное отклонение
распределения по координатам равно ах,
а распределения по импульсам ар = й/2ах.
Для любого волнового пакета <jx<jp ^ Й/2
(принцип неопределенности).
Групповая скорость любого волнового
пакета в квантовой механике совпадает
с классической скоростью частицы:
vg = da/dk = р/т = v. Волновой пакет с
первоначальной шириной Ах0 расплывается
по закону Ах га (Н/тАх0) L
Частице, заключенной в ящике длиной
L, соответствуют стоячие волны только с
Хп = 2L/n или кинетические энергии
En = n2n2ti2/2mL2.
В случае «ямы» переменной глубины
U = U(x) волновая функция удовлетворяет
стационарному уравнению Шредингера
Граничному условию \|/ -► 0 при х -► ± оо
удовлетворяют лишь определенные
собственные функции \|/„ (х) и собственные
значения Еп.
В случае прямоугольной потенциальной
ямы конечной глубины волновая функция
имеет вид \|/ = В cos (кх + (р) внутри ямы и
Л^е"** + А2олх вне ее, где х =
= ]/2m(U0 -E)fh2. Сшивая волновую
функцию \|/ и ее производную dty/dx на
границе ямы, мы получаем условия на
допустимые значения Е.
Если U(x) = т(02Клх2/2 представляет
собой потенциальную энергию
гармонического осциллятора, то собственные
значения энергии записывают в виде Еп =
= (п — 1/2) Йсокл, где п-целое
положительное число. Первые две собственные
функции имеют вид
Упражнения
1. Если \|/ = ехр [/(/ex — со£)] + ехр [i(kx + cot)],
то чему равно \|/*\|/?
00
2. Вычислите х= j хехр(— х2/2а2)dx.
-00
3. Пусть \|/ = exp[i(/c0 + A/c)x] + exp[i(/c0 — А/с)х].
а) Чему равно \|/*\|/?
б) Если Ах-полуширина центрального
волнового пакета, на уровне половины
максимальной высоты, то чему равно
произведение Ах Ар, где Ар = Ъ А/с?
4. Если Е = Ш = тс2+р2/2т, то каковы
фазовая и групповая скорости соответствующе-
• го волнового пакета (ответ запишите через
с и классическую скорость и)?
5. При t = О размер волнового пакета
электрона Ах0 = 1 мкм. Каким будет его размер
при t = 1 с?
6. Размер Ах0 волнового пакета электрона
таков, что спустя каждую секунду он
увеличивается на Ах0. Найдите Ах0.
7. Электрон заключен в одномерный ящик
длиной L = 4-10"10 м.
а) Чему равна энергия Е2 (в эВ)?
б) Найдите длину волны фотона,
испускаемого при переходе Е4 -> Е2.
8. Если в примере 4 положить Ut = — 20 эВ,
а х0 = 5-10-11 м, то каковы при этом будут
значения Ех и К^ для электрона?
9. Найдите правильное релятивистское
выражение для энергии в примере 4.
10. Предположим, что волновая функция \\fx на
рис. 25-13,6 при х = х0 уменьшается в три
раза, т. е.
+i(x0)/+i(0) = l/3.
Найдите выражение для Ех в зависимости
от % т и х0.
11. В момент времени t = О функция |\|/(х)|2
волнового пакета представляет собой
распределение Гаусса со среднеквадратичным
отклонением <j0. Волновой пакет перемещается
вдоль оси х со скоростью v0.

454 ГЛ. 25. КВАНТОВАЯ МЕХАНИКА
а) Огибающая волновой функции
представляет собой также гауссову функцию.
Найдите ее среднеквадратичное отклонение.
б) Определите В(к\ где ф(х) = $B(k)Qikxdk.
Выразите ответ через т, % а0, к и v0.
Задачи
12. Если функция ф = е* + М)х "(а)° + Аю)^ +
+ ei[(*o-Afc)x-(fflo-Affl)0) то чему.равно ф*ф?
13. Приведите выражение фх = ^е^-Ь /42е1(р2 к
виду ф = Ле1(р. Найдите выражения для Л и
Ф в зависимости от Аи A2i q>i и ф2.
14. Пусть Я(/с) имеет вид, показанный на
рисунке.
В(к)
о
(к0-а)
(к0+а)
а) Чему равна вероятность того, что
импульс р = % (к0 + а/2) сравним по
величине с импульсом р =Ш01
б) Что представляет собой волновая
функция ф(х)?
в) Чему равно произведение АхАр, если Ах
и Ар-полуширины на половине
максимальной высоты?
15. Докажите, что для величины х,
распределенной по закону Гаусса, х2 = ст2; иными
словами, докажите равенство
оо
j х2ехр(- x2/2a2)dx
j ехр( — x2/2o2)dx
о
16. Какова вероятность обнаружить частицу
с импульсом в интервале Й(к0 + а/2) > р >
>Ъ(к0- а/2), если В (к) имеет вид,
показанный на рисунке к задаче 14?
17. Если Е = ]/р2с2 + т2с* = Асо, то чему равна
групповая скорость vg = dw/dk!
18. Расплывание волнового пакета описывается
выражением
Ах =
Ш
\mAxo
+ (Ахо)2
где Ах0- ширина пакета при t = 0, когда все
монохроматические составляющие
находятся в фазе. Пусть в момент времени t -
= 0 Ах0 = 10 ~10 м для электрона 1 и
Ах0 = 10"9м для электрона 2. Через какой
промежуток времени волновые пакеты этих
электронов будут иметь одну и ту же
ширину?
19. Предположим, что электрон находится в
потенциальной яме, описанной в примере 4,
причем х0 = 10" 14 м и С/х = 0. Вычислите
а) нерелятивистские значения энергий Е1 и
Е2 и
б) релятивистские значения этих энергий.
20. Предположим, что электрон захвачен
атомным ядром диаметром 2-Ю"15 м.
Какой была бы энергия электрона в основном
состоянии? Используйте приближение
одномерной прямоугольной потенциальной ямы.
21. Используя метод проб и ошибок, вычислите
Ех и Е2 для электрона в потенциальной яме
глубиной U0 = 200 эВ и шириной 2х0 =
= 10-10м.
22. Предположим, что ф3 {х0)№3 (0) = - 1/4 (см.
рисунок). Найдите выражение для Еъ через
% т и х0, считая, что в области I
функция ф3 представляет собой синусоиду.
23. Частица массой т находится в одномерной
потенциальной яме, изображенной на
рисунке. Чему равна Еи если на участке 0 - хх
функция фх воспроизводит 1/6 периода
синусоиды (60°)?
и.
и\
0
">
0
-и2-
1
1
*1 ;
[
л
и
Е\
х2

ЗАДАЧИ 455
24. Подставьте в уравнение Шредингера с
потенциалом U(x) = кх2/2 функцию \|/(х) =
— ах2
= хе .
а) Какова величина а?
б) Чему равно соответствующее
собственное значение энергии?
25. Уравнение Шредингера для частицы массой
т записывается в виде
а) Найдите наинизшую собственную
функцию y\f1(x).
б) Чему равно соответствующее
собственное значение энергии Ех в зависимости
от % т и /с?
26. Потенциальную энергию, обеспечивающую
связь протона с нейтроном в дейтроне,
можно аппроксимировать прямоугольной
потенциальной ямой, как показано на рисунке.
Глубина такой ямы 29 МэВ, а радиус г0 =
= 2,3- Ю-15 м. Обозначим волновую функ-
-29 МэВ
U(r)
цию и(г). Внутри ямы она имеет вид
и (г) = sin кг, где -—— = Е — U.
2М
Приведенная масса системы
протон-нейтрон равна М = 8,36-10" 28 кг. Найдите
численное значение энергии Е (в МэВ). Это
и будет энергия связи дейтрона. [Указание:
Можно использовать соотношение (25-20).]
Решение трансцендентного уравнения
можно найти методом проб и ошибок,
используя обычный микрокалькулятор.
27. Подставляя волновую функцию \|/ =
= х ехр [ — тсох2/(2Й)] в уравнение
£--£«.-«,*
где £/ = (1/2)тсЛс2
найдите энергию Е.
28. Волновой пакет \|/ (х, t) составлен из чисто
монохроматических волн:
^(x9t)^^A(k)ti{kx-^dk9
где
(к - кр)2
А(к) = е 2а2 .
Чему равна полуширина распределения
вероятности по х при t = 0?

АТОМ ВОДОРОДА
§ 1. Приближенная теория атома
водорода
В предыдущей главе мы решили задачу
о частице массой т, заключенной в
потенциальной яме вида U = кх2/2. В таком
потенциале, имеющем форму параболы,
частица совершает простое гармоническое
движение. Теперь мы рассмотрим
потенциальную яму, в которой потенциальная
энергия меняется обратно
пропорционально расстоянию. Потенциал такого типа
отвечает гравитационным или
электростатическим силам взаимодействия двух частиц.
В случае атома водорода потенциальная
энергия взаимодействия электрона и
протона имеет вид U = — к0е2/г, где
г-расстояние между частицами.
Сначала найдем приближенное решение
задачи; для этого аппроксимируем
потенциал ямой прямоугольной формы точно
так же, как мы это сделали при
рассмотрении гармонического осциллятора. Такой
подход, состоящий в выполнении сначала
простых приближенных вычислений,
поможет получить более наглядное
представление об атоме водорода и избежать
несущественных математических подробностей.
Наша цель - объяснить существование
и характер стоячих электронных волн
в случае атома водорода и их зависимость
от фундаментальных констант h, т и е. Мы
надеемся понять, почему разрешены лишь
определенные энергетические уровни и как
зависит их положение от фундаментальных
констант и величины квантового числа п.
В этих приближенных расчетах мы
используем потенциальную яму,
изображенную на рис. 26-1. Как видно из рисунка,
электрон, находящийся на уровне с
энергией Е, в соответствии с представлением
классической физики может удаляться на
максимальное расстояние jR0. В качестве
оценки среднего удаления R возьмем
величину R 0/2. Глубину U0 эквивалентной
прямоугольной _ямы определим как значение
U при х = R, т.е. U0 = k0e2/R. В случае
стоячей волны п-го порядка в пределах
этой прямоугольной ямы (штриховая
линия на рис. 26-1) уложится п полуволн.
Таким образом,
л% = 2Д0,
или
К =
4Д0
г— Г
:U*Aj^s^A
о г
Рис. 26-1. Потенциальная яма для электрона
в атоме водорода. Эквивалентная
прямоугольная яма, используемая в приближенных
вычислениях, показана штриховой линией.
Допустим, что средний импульс электрона
приблизительно равен импульсу де Брой-
ля, т.е.
h _ hn
Рп
4Д0
Тогда средняя кинетическая энергия
Р2п _ h2n2
2т Ъ2тЯ1 '
К

§ 2. УРАВНЕНИЕ ШРЕДИНГЕРА В ТРЕХ ИЗМЕРЕНИЯХ 457
Из рис. 26-1 следует, что
к0е2
К = -Е =
Яо
(26-1)
Сравнивая это выражение с предыдущим,
получаем
к0е2 h2n2
До 32т Rl
откуда находим
R0'
h2n2
An2 Ъ2
32к0те 32 к0те
(26-2)
В § 3 мы увидим, что «размер» п-й
гармоники волновой функции близок к
найденному значению, а именно
к0те2
Подставляя (26-2) в правую часть
выражения (26-1), получаем приближенное
решение для энергетических уровней:
р _ 16 ,2 те4 1
7Г
2П2 п2
Точный результат записывается в виде
_ Цте4
2П2п2 '
что на 38% меньше предыдущей величины,
полученной нами с использованием
довольно грубого приближения. Однако
наше решение в действительности дает
правильную зависимость от т, е, Ъ и
квантового числа и, а также позволяет
разобраться в том, что происходит.
§ 2. Уравнение Шредингера в трех
измерениях
Двумерные стоячие волны можно
возбудить в заполненной жидкостью кювете
прямоугольной формы. При постукивании
или вибрации в ней возбуждаются стоячие
волны, причем линии узлов располагаются
во взаимно перпендикулярных
направлениях, как показано на рис. 26-2. Амплитуда
волны записывается в виде
\|/ = A sin кхх sin куу,
где
71 71
К = -г-пх и ку = — пу;
bY Ljv
(26-3)
она удовлетворяет граничному условию
\|/ = 0 при х = Lx или у — Ly.
Рис. 26-2. Изображенный художником бак с
водой, покрытой рябью в двух измерениях. Длина
бака Lx, ширина Ly\ изображены стоячие волны
с w = 3 и w = 2.
Пример 1. Найдем выражение для
энергетических уровней частицы массой т в трехмерном
ящике с линейными размерами Lxi Ly и Lz.
Решение: Кинетическая энергия частицы
К
р1 + р2у + р1
2т
В соответствии с соотношением де Бройля
имеем
Рх = Ъкх, ру = Ъку, pz = %kz.
Следовательно,
K = ^-(kl + k2y+kl).
2т
Используя соотношение (26-3), получаем
Ъ2п2 '"2 «2 ~2"
К = Е„
2т
пх п; и:
~jT ~7l г 2
-L*v -L(V Л^~
Мы видим, что в трехмерном пространстве
собственные значения энергии и
соответствующие им собственные функции зависят от трех
квантовых чисел.
Пример 2. Электрон находится в ящике
кубической формы размером с атомное ядро (L =
= 4-10~15 м). Чему равна минимальная
кинетическая энергия электрона?

458 ГЛ. 26. ATOM ВОДОРОДА
Решение: Используя (26-3), мы можем написать
Кх — j пх, Ку— j nyi Kz— j nz.
Состоянию с наинизшей энергией отвечает пх =
= пу- nz= 1; следовательно,
k2= k1 — k2= -^—
кх — ку — kz — _ ^ ,
L2
р2 = ^2 = Й2(Л2 + к2 + fc2) = Зй2 / М
На всякий случай воспользуемся
релятивистской формулой для кинетической энергии:
К = ]/с2р2+т2с*-тс2 =4,2%Л0~11 дж = 267 МэВ.
По-видимому, мы не ошиблись, применив
релятивистскую формулу, поскольку полученное нами
значение более чем в 500 раз превосходит
энергию покоя электрона.
Этот пример демонстрирует, почему
электрон не может находиться внутри атомного ядра.
Мы не знаем в природе сил, величина которых
обеспечила бы связь электронов, обладающих
столь большой эьергией, с группой протонов и
нейтронов. Заметим, что электростатическая
потенциальная энергия электрона на поверхности
ядра составляет лишь 10 МэВ, а никак не 270 МэВ.
В примерах 1 и 2 волновая функция
частицы имеет вид
\|/ = A sin кх х sin ку у sin к2 z.
Беря частные производные от этого
выражения по х, получаем
—— = hvA cos /cv х sin kv v sin К z
дх y
(символ д/дх означает дифференцирование
по переменной х при постоянных у и z) и
л2 |
—т" = — к\А sin кх х sin kv у sin k„z =
дх2 у
Аналогично имеем для производных по
остальным координатам. Таким образом,
d2y\f дЦ d2y\f
дх2
+
ду2
dz2
= - /c2v|/.
Следует заметить, что если потенциальная
энергия постоянна и равна U0, то
/с2 = ^(£-гу0).
/г
Как и в случае одномерной задачи,
обобщим уравнение Шредингера на случай
меняющейся потенциальной энергии U(x, у, z):
дх2 ду2 dz2 ъ2
-№-с/)Ф
{стационарное уравнение Шредингера
в трех измерениях). (26-4)
Во многих прикладных задачах
потенциальная энергия зависит только от
расстояния г = ух2 + у2 + z2 до начала
координат. В этих случаях уравнение
Шредингера удобнее переписать в сферических
координатах, которые связаны с
декартовыми, как это следует из рис. 26-3,
Рис. 26-3. Декартовы (х, у, z) и сферические
(г, 0, ф) координаты точки Р.
соотношениями
х = г sin 0 cos ф,
у = г sin 9 sin ф,
z = rcos0.
Перейти в уравнении (26-4) от координат х,
у и z к сферическим координатам довольно
просто, но приходится выполнять
громоздкие вычисления. Поэтому запишем
окончательный результат:
г2 дг
+
1
г2sine ео\ ев
+
1 02\|/
r2sin20 д<р2
«-^№
U)y\>.
(26-5)

§ 3. СТРОГАЯ ТЕОРИЯ АТОМА ВОДОРОДА 459
§ 3. Строгая теория атома водорода
Чтобы получить уравнение Шредингера
для атома водорода, в уравнение (26-5)
нужно подставить U = — к0е2/г. В
качестве решения попробуем для начала взять
просто экспоненциальную функцию \|/ =
= е"г/а. Подставляя ее в (26-5) и замечая,
что частные производные 3\|//30 и 3\|//3ф
обращаются в нуль, имеем
1 д ( 2d(Q-r/a)
1 д
>-г/а\ _
--£(-+т>~"
.1 (г2 2г\ 2т ( к0е2\
~ 1 "
а2\
-ш-
2тЕ
И2 _
-
/2тк0е2\\
{ V )г-
Приравнивая члены, содержащие 1/г,
(2\ (2тк0е2\
W ( *2 У
находим
а = -
л_
(26-6
к0те2
а приравнивание друг другу свободных
членов, т.е.
Г 1"
у _
=
2т Е
1i2 j
дает
Я= -
п2
2т а2
Подставляя сюда выражение (26-6) для а,
получаем окончательный результат:
Е~ к° 2Ъ2
(26-7)
Таким образом, простая экспоненциальная
функция действительно является решением,
если а и Е принимают значения,
определяемые выражениями (26-6) и (26-7).
Подстановка численных значений т, к0, е и
t дает
Е = - 21,8-НГ19 Дж= -13,6эВ.
Это и есть минимальное количество
энергии, необходимое для удаления электрона
из атома водорода. По определению эта
энергия называется энергией связи:
(Энергия связи) = — Е = (Энергия,
необходимая для удаления электрона).
Согласно этому определению, энергия
связи электрона в металле совпадает с
работой выхода W0, так как наивысший
энергетический уровень на рис. 24-3
расположен именно при Е — — W0.
Следует заметить, что при г = а
амплитуда волны уменьшается в е раз по
сравнению с максимальным значением. (В этой
точке Q~r/a = 1/е.) Поэтому данное
значение R выбирается в качестве радиуса
атома водорода. Используя (26-6), получаем
R =
k0me
= 5,3- КГ11 м
(радиус атома
водорода).
(26-8)
Функция \|/ = е~г/а не имеет узлов и
представляет собой стоячую волну
низшего порядка, следовательно, энергия Е =
= — кЪте4/2Ъ2 соответствует низшему
уровню. Обозначим ее Е1. Волновые
функции для следующих двух энергетических
уровней записываются в виде
+»-'1-i
-г/2а
*3 = ( 1 " ^ +
2г2
За 27а2
■г/За
Графики всех этих функций приведены на
рис. 26-4. То, что эти функции
действительно являются решениями уравнения (26-5),
можно проверить непосредственной
подстановкой. Они удовлетворяют уравнению
(26-5) при условии, что Е2 = EJ4 и Е3 =
= Et/9 (см. пример 3).

460 ГЛ. 26. АТОМ ВОДОРОДА
Следовательно,
2 5 г
аг 4а2 8а3
2тк0е2
%2г
2т
к0е
тЕ
. + 7Г-
2а J afi2
1 2 3 4 5х10~шм
Приравнивая друг другу члены, содержащие 1/г,
получаем
2 _ 2т/с0е2
откуда, как и прежде, имеем а = Тг2/к0те2. Из
сравнения членов при г следует
1 _ тЕ
~ "8^"""^"'
П2
Е =
8а2т
Подставляя сюда Ъ2/к0те2 вместо а,
окончательно получаем
ко те4 1
Е= - — = -- (13,6 эВ).
4 2И2 4К
Рис. 26-4. Волновые функции атома водорода,
соответствующие п = 1, 2, 3 и / = 0.
Пример 3. Покажем, что функция \|/2 = (1
г/2а)&
-г/2а
является решением уравнения
Шредингера для атома водорода, и найдем
энергию Е2 соответствующего уровня.
Решение: Вычислим первую производную
дг 2а
Затем найдем
д /,#2\_
дг \ дг )
г2 дг{ дг
('
-
=
2а,
\е-г/2а
1 д
2a~~fr
(-1
Ur2-
5
?2-ку"2°}
8аэ
-г 12а
В соответствии с (26-5) последнее выражение
равно - (2т/П2)(Е + k0e2/r)y\i.
Можно показать, что энергетическим
уровням
Яи=-
1
к 2
те
(энергетические
уровни атома водорода),
(26-9)
где п- целое положительное число,
отвечают решения в виде стоячих волн;
величина п называется главным квантовым
числом. Однако для полного описания
трехмерной стоячей волны необходимы еще
два квантовых числа. Эти числа
характеризуют момент импульса частицы; мы их
рассмотрим в следующем параграфе.
§ 4. Орбитальный момент импульса
Предположим, что волновой пакет с
волновым числом к движется по окружности
радиусом R, как показано на рис. 26-5.
Такой пакет имеет момент импульса
относительно оси z, равный Lz = Rp = R (Щ. На
дуге s (рис. 26-5) волновую функцию
пакета можно записать в виде
*'
J(ks-
(nt) _ i(kR(p-(ut)

§ 4. ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА 461
Волновой
пакет
Рис. 26-5. Волновой пакет, движущийся по
окружности радиусом R. Длина дуги s = Дф.
Поскольку \|/ (ф = 0) и \|/ (ф = 2тг)
измеряются в одной и той же точке
пространства, их значения совпадают, т.е.
е**(0) _ QikR(2n)
ИЛИ
1 = ei2KkR
Последнее соотношение может
выполняться, только если kR- целое число (его
обычно обозначают mt):
kR = т{.
Умножим обе части этого равенства на ft:
ft/cR = mfi.
Таким образом,
Lz = mfi.
Соответствующая волновая функция имеет
вид
ikRy — Ш /т,ф - iat
Следовательно, мы показали, что если
волновая функция частицы содержит
множитель вида eim,(p, то у такой частицы будет
составляющая момента импульса вдоль
оси z, равная Lz = mfi. Существует и более
строгое доказательство этого утверждения,
однако оно несколько выходит за рамки
нашей книги. Мы видим, что момент
импульса квантуется, т.е. составляет целое
кратное ft; иными словами, L2 может
принимать значения 0, ± ft, ± 2ft, ± 3ft и т. д.
До сих пор мы рассматривали решения
уравнения (26-5), которые являются только
функцией от г. Между тем существуют
и другие решения, зависящие также от 0
и ф. В наиболее общем виде решение
записывается следующим образом:
vlW> е> ф) = *»М® иДе)Фт/(ф),
где
Фт/(Ф) = е^.
Из приведенного выше рассмотрения
следует, что волновой функции i|/„,/, т,
должна соответствовать составляющая
момента импульса по оси z, равная mft.
В случае и = 2 нам уже известно решение
вида
*2>o,o = (l-t-)e-r/2a-
Однако наряду с ним существуют и другие
решения:
v|>2,i,i =re-r/2asin0el,<p,
v|/2>lo = re~r/2acos0,
v|/2,i,-i =re-r/2asin0e-l4p.
Эти решения можно проверить, подставляя
их непосредственно в уравнение (26-5). На
рис. 26-6 приведены контурные диаграммы
электронной плотности, отвечающие
волновым функциям с п = 2. Заметим, что
при п = 2 квантовое число / может
принимать два значения: 0 или 1; при / = 1
квантовое число тх пробегает три значения1*:
1, 0 и — 1. В соответствии с (26-9) всем этим
четырем функциям отвечает один и тот же
энергетический уровень Е2 = (1/4) (13,6 эВ).
Вообще говоря, каждой волновой функции,
или собственной функции, соответствует
свой единственный энергетический уровень,
или собственное значение. Однако куло-
новский потенциал обладает особым
свойством: всем собственным функциям с
одним и тем же квантовым числом
1} Квантовое число / принято называть
орбитальным квантовым числом, а тг-магнитным
квантовым числом-Прим. перев.

462
ГЛ. 26. АТОМ ВОДОРОДА
2-й максимум
2J,0
Рис. 26-6. Распределения электронного облака
|\|/|2 в плоскости xz для волновых функций
атома водорода с п = 2. Показаны контурные линии
равной вероятности (значения соответствующих
вероятностей указаны числами). Максимальная
вероятность выбрана равной 1. Масштаб осей
х и z соответствует ангстремам (1А = 10"10 м).
п соответствует единственное собственное
значение энергии. Можно показать, что
значение квантового числа / никогда не
превосходит п — 1, а квантовое число т1
Таблица 26-1
Возможные комбинации п, I и т, для случая и = 3
п
3
3
3
3
/
0
1
1
1
щ
0
1
0
-1
2
1
0
-1
-2
пробегает ряд целочисленных значений от
- / до + Z.
Рассмотрим теперь в качестве примера
случай п = 3, чтобы показать, какие
комбинации можно составить из этих трех
квантовых чисел. Из табл. 26-1 мы видим,
что возможно всего девять различных
комбинаций. Таким образом, имеется
девять различных волновых функций,
зависящих от г, 0 и ф, причем всем им отвечает
одна и та же энергия Е3 = - (1/9) (13,6 эВ).
Пример 4. Сколько имеется различных
волновых функций в случае п = 4?
Решение: Возможные значения / равны 0, 1, 2, 3.
Из табл. 26-1 следует, что значениям / = 0, 1
и 2 соответствуют девять волновых функций.
Дополнительному значению / = 3 отвечает еще
семь функций cw, от — 3 до +3. Полное число
функций 7 + 9 = 16.
Заметим, что значения проекции
момента импульса на ось z меняются от — Ш до
+ Ш. Если экспериментально измерять
величину момента импульса относительно
произвольной оси, то максимальное
значение будет равно Ш. Физически это
означает, что полный момент импульса
электрона, описываемого волновой функцией
с квантовым числом /, равен Ш и что его
проекция на ось z характеризует
ориентацию волновой функции, или орбитали. Все
эти факты получили экспериментальное
подтверждение. Отношение т1 к /
представляет собой угол между осью z и
направлением момента импульса частицы.
Кинетическая энергия вращательного
движения твердого тела К = L2/2I, где
/-момент инерции. Если измерять эту
энергию, то, согласно квантовой теории
(это подтверждается и экспериментом),
К =
/(/+1)^2
2/

§ 4. ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА 463
Таблица 26-2
Ненормированные радиальные и угловые функции, используемые при построении полных
волновых функций ФиДи, для атома водорода (р = г/а)
Я„,,(Р)
©/,m,= ©/,-m,
^10
Я30
Rn,n-\
Q~p
К>-
ре-«2
3 + 21 )е
«-('-!)•■*
р2е"р/3
р(и-1)е-р/И
©00
©10
©11
©20
©21
©22
в„
('-*♦£
1
cosG
sinG
3cos20-l
sin 0 cos 0
sin20
sin'0
Отсюда следует, что L = Ь у I (I + 1).
Таким образом, в измерениях, связанных
с энергией, нужно полагать L = Й ]//(/+1),
а при измерениях момента импульса L =
= Ы1\
Используя табл. 26-2 и выражение
+^Я1М.ф) = ^,(г)01Я((О)е
im{<p
можно построить различные волновые
функции. На рис. 26-7 построены
контурные диаграммы |\|/|2 в плоскости xz.
Следует заметить, что при больших п
распределение |\|/|2, отвечающее / = (и — 1),
концентрируется на окружности радиусом
п2а с центром на оси z. В сущности это
и есть предсказанная Бором орбита, с той
лишь разницей, что, согласно современным
представлениям, электрон равномерно
«размазан» по круговой орбите.
НОРМИРОВКА ВОЛНОВЫХ ФУНКЦИЙ
Определим величину | \|/12 dx dy dz как
относительную вероятность того, что
частица заключена в элементе объема dxdydz.
Эту величину можно рассматривать также
п В действительности Ъ2 1(1 + 1)
определяет квадрат величины момента импульса,
тогда как Ш представляет собой максимальное
значение проекции момента импульса на
выбранное направление-Прим. перев.
как абсолютную вероятность, если она
удовлетворяет условию
Ш №\2dxdydz = l.
По всему
пространству
Это условие нормировки однозначно
определяет коэффициент пропорциональности,
на который умножается данная волновая
функция. Поскольку до сих пор мы имели
дело лишь с относительными
вероятностями, мы не рассматривали нормировку
волновых функций.
СРЕДНЕЕ ЗНАЧЕНИЕ
Предположим, что волновая функция
частицы представляет собой суперпозицию
нескольких собственных функций. Иными
словами, пусть волновая функция
^М = EflA(*)>
j
где каждая из \|/;- представляет собой
нормированную собственную функцию,
которая отвечает собственному значению
энергии Ег В соответствии, с основным
постулатом гл. 24 мы знаем, что вероятность
найти частицу в состоянии,
характеризуемом волновой функцией vj/y, дается
квадратом амплитуды ау Таким образом,
вероятность найти частицу в состоянии с энер-

v3,2,21
464 ГЛ. 26. ATOM ВОДОРОДА
|^3,2,1|2
гией Ej равна \а}\2. При этом среднее
значение энергии можно записать в виде
<E> = Z\aj\2Ej.
J
Такое среднее значение энергии дает серия
повторных измерений, произведенных над
частицей, которая каждый раз находится
в одном и том же начальном состоянии
\|/(х). То же самое справедливо для любой
другой физической величины, в частности
Рис. 26-7. То же, что и на
рис. 26-6, но для случая двух
волновых функций атома
водорода с п = 3.
для момента импульса; следовательно
<Lz> = Z\aj\2Lj.
J
*Пример 5. Атом водорода в состоянии с п = 2
и / = 1 имеет Lz = % а волновая функция
записывается в виде \|/(г,0,ф) = R2 р1©! д(0)е*ф.
Предположим, что мистер Штрих находится
в штрихованной системе координат, ось z'
которой повернута на угол а относительно оси z.

§ 5. ИСПУСКАНИЕ ФОТОНОВ 465
Какую величину <Ц> измерит мистер Штрих?
Указание: Проделав некоторые
тригонометрические преобразования, можно показать, что
011(0)е,чр = —(cosа + l)0n(0')e,v -
1/2 01о(0) +
+ —(cosa - 1)0!-! (вОе"'
(см. задачу 28).
Решение: В штрихованной системе координат
исходная волновая функция имеет следующий
вид:
v|/ (г, 0, ф) = a^i (г, 6', ф') + а2ф2 (г, 0', ф') +
+ а3\|/з(г,0,,ф'),
где
cos а + 1 sin a cos а — 1
ах = , а2 = т=~> аз = •
2 1/2 2
Функция \|/! содержит 0ц(6')е'ф', следовательно,
14 = Й; \|/2 отвечает L^ = 0, а \|/3 соответствует
Li = — % Таким образом,
<14> = в?(+Л) + в1(0) + в1(-й) =
s(cas«+iy(+>) +
+ (cos^-l)^(_7_) = (cosa)7.
Квантовая физика дает тот же результат, что
и классическая физика.
§ 5. Испускание фотонов
После того, как было написано
уравнение Шредингера, квантовая механика стала
применяться в теории электромагнитных
взаимодействий, в результате чего
возникла квантовая электродинамика.
Подробное рассмотрение этой теории выходит за
рамки нашей книги. Нам лишь
понадобится установленный квантовой
электродинамикой факт, что заряженная частица
может поглощать или испускать отдельные
фотоны и что теория позволяет точно
рассчитать соответствующие амплитуды
вероятностей поглощения или испускания.
СПОНТАННОЕ ИЗЛУЧЕНИЕ
Рассмотрим заряженную частицу,
закрепленную на пружинке с коэффициентом
упругости, которому соответствует частота
собственных колебаний со0 = У к/т. Если
пружину растянуть, а затем отпустить, то
прикрепленная к ней заряженная частица
в соответствии с классической физикой
будет излучать на частоте со0. На языке
квантовой механики это означает, что частицу
из основного состояния перевели на более
высокий энергетический уровень. Согласно
квантовой механике, электрон,
находящийся на энергетическом уровне выше
основного, может с определенной вероятностью
испустить фотон и перейти на более
низкий энергетический уровень. Такой процесс
называется спонтанным излучением. Если
у атома водорода два уровня различаются
по энергии на несколько электронвольт,
то амплитуда вероятности перехода между
этими уровнями оказывается такой, что
типичное время, необходимое для процесса
испускания фотона, составляет порядка
10"8 с (см. § 7 гл.21 и § 7 настоящей
главы). Если фотон испускается в результате
перехода между уровнями с энергиями Еп>
и Еп9 то его энергия hf= Еп> — Еп. Частота
такого фотона /= {Еп> — En)/h.
Таким образом, если атом имеет
четыре различных энергетических уровня, как
показано на рис. 26-8, то возможны шесть
различных переходов с более высоких
уровней на более низкие. При этом
излучаемый атомом «свет» будет
характеризоваться шестью различными частотами. Ес-
■*4
Рис. 26-8. Шесть возможных переходов между
четырьмя энергетическими уровнями.

466 ГЛ. 26. АТОМ ВОДОРОДА
ли анализировать это излучение
спектроскопом, то можно увидеть шесть
спектральных линий. В нормальных условиях
атомы находятся в основном состоянии
и не излучают света. Однако если газ,
состоящий из этих атомов, нагревается, или
в нем происходит электрический разряд, то
вследствие столкновений некоторые атомы
приобретут энергию и перейдут на уровни
с более высокой энергией. Именно эти
относительно немногочисленные атомы в
состояниях с более высокой энергией и
испускают фотоны.
Согласно современной теории, фотоны
представляют собой элементарные
частицы со спином 1 (L = Ш). Поэтому при
испускании фотона квантовое число атома
/ изменяется по меньшей мере на единицу.
СПЕКТР АТОМА ВОДОРОДА
Поскольку мы располагаем
количественным соотношением для
энергетических уровней атома водорода, можно
рассчитать весь его спектр. Пусть энергия
более высокого возбужденного уровня
равна
ЕП' = — к0
1
а энергия более низкого уровня
,-, к20 те4 1
£„ = — -
2П2 п2
Тогда частоты, соответствующие
различным спектральным линиям, можно
записать в виде
/=
к I те4,
4пП3
1
(26-10)
2П2 ri*
Серия спектральных линий, отвечающая
п = 1, называется серией Лаймана. Все
линии этой серии расположены в
ультрафиолетовой области спектра
электромагнитного излучения. При п = 2 возникает другая
серия линий, называемая серией Бальмера.
Спектр атомарного водорода приведен на
рис. 26-9, а, а некоторые из
соответствующих переходов между уровнями показаны
с помощью диаграмм энергетических
уровней на рис. 26-9,6. На этих диаграммах по
горизонтали принято откладывать
состояния с различными значениями момента
импульса.
Пример 6. Какие длины волн соответствуют
линиям серии Бальмера? Сколько линий
расположено в видимой части спектра?
Серия Лаймана (N= 1)
Серия Бальмера (#= 2)
(I N= ~ 7,6,5, 37
1000 А 2000 А 3000 А 4000А 5000 А 6000 А 7000 А
эВ
о
-5
-10
-13,6
/=0
/-1
/=2
/-3
/=4
Серия Бальмера
/ / ' /^Серия Лаймана
III
Рис. 26-9. а -возможные линии
водородного спектра вплоть до
X = 7000 А; б-переходы,
отвечающие серии Лаймана
(штриховые линии со
стрелками) и серии Бальмера
(сплошные линии со стрелками).

§ 6. ВЫНУЖДЕННОЕ ИЗЛУЧЕНИЕ 467
Решение: Энергии испускаемых фотонов
вычисляем по формуле
hf= 13,6 эВ (0,25 - 1/и'2), где ri = 3, 4, 5... .
Таким образом, первым четырем линиям
спектра соответствуют следующие значения
энергии:
Л/i = 13,6 (j ~j) = ^89эВ'
hf2 = 13,6^--^ = 2,55 эВ,
hf3 = 13,6^-^-) = 2,86 эВ,
hfA = 13,6^-^ = 3,02 эВ.
При очень больших п имеем
hf„ = 13,6^-1- о) = 3,40 эВ,
_ с _ he _ (6,63-10" 34) (3,00-108) _
Х~1~~¥~ ¥ "
19,9.10-26Дж.м _ 12,4.10-7эВ-м
" ¥ " ¥ '
Следовательно,
Х1 = 656 нм; Х2 = 486нм; ^3 = 443 нм; Х4 =
= 411 нм; Хт = 365 нм.
Спектр содержит бесконечное число линий,
сходящихся при п -► оо к значению Х^ = 3650 А,
которое отвечает близкой ультрафиолетовой
области. Xt (6560 А) расположена в красной
области видимого спектра, Х2-в синей, а ^3_в
фиолетовой. Х4 попадает на границу между
видимой и ультрафиолетовой областями спектра.
ПОГЛОЩЕНИЕ
Если излучение со сплошным спектром,
как, например, излучение нагретого до
красного свечения тела, проходит через
холодный газ, то находящиеся в основном
состоянии атомы газа будут переходить
в одно из возбужденных состояний и
поглощать при этом фотоны определенной
энергии. В случае холодного водорода
поглощаться будут фотоны,
соответствующие серии Лаймана. Если исследовать
сплошной спектр излучения, прошедшего
через газ, то в нем обнаружится отсутствие
фотонов с энергиями Е2 — Е19 Е3 — Е19
£4 — Ех и т.д. Отсутствие фотонов с
этими энергиями проявляется на
спектрограмме в виде темных линий. Процесс, при
котором в результате облучения образца
вещества светом возбуждаются более
высокие энергетические уровни атомов,
называется оптической накачкой.
§ 6. Вынужденное излучение
Согласно квантовой электродинамике,
наряду с процессами спонтанного
излучения и поглощения имеет место процесс,
называемый вынужденным (или
стимулированным) излучением. Допустим, что атом
находится в возбужденном состоянии Еп>
и может испустить фотон с энергией Еп> —
— Еп. Оказывается, что если такой атом
поместить в поле внешнего излучения,
которое уже содержит фотоны с энергией
Еп> — Еп, то вероятность испускания
атомом фотона увеличится. Это явление
ускорения атомных переходов возбужденных
атомов под действием «света» называется
вынужденным излучением. Более того,
возникающий в результате вынужденного
излучения фотон оказывается точно в фазе
с внешним фотоном, стимулировавшим
это излучение атома, и летит в том же
направлении.
В качестве классического аналога этого
явления можно вновь рассмотреть
прикрепленную к пружине заряженную частицу.
Пусть коэффициент упругости пружины
отвечает частоте собственных колебаний
со0. Если теперь эту частицу поместить во
внешнее электрическое поле Е = Е0 cos cot,
то она будет совершать колебания с
частотой со и излучать. Чем ближе со и со0, тем
больше амплитуда колебаний [см.
выражение (21-6)]. Следует заметить, что частота
излучения совпадает не с со0, а с частотой
со внешнего поля.
ЛАЗЕР
Предположим, что мы имеем образец,
содержащий атомы (или молекулы),
большинство которых находится в
возбужденном состоянии Еп>. Такой образец можно

468 ГЛ. 26. ATOM ВОДОРОДА
приготовить различными способами: с
помощью оптической накачки, за счет
соударений с потоком электронов и соударений
с другими возбужденными атомами, а
также используя спонтанное излучение атомов
с переходом в данное возбужденное
состояние с более высоких уровней и т.п.
3 возбужденных атома
Первый фотон
Первый фотон
Фотон, испущенный
первым атомом
Проследим теперь за фотоном, который
был испущен первым. Пролетая через газ,
этот фотон стимулирует вынужденное
излучение у встречных атомов. Если образец
поместить между двумя зеркалами, то
процесс принимает характер цепной реакции
и идет до тех пор, пока не излучат все
атомы (рис. 26-10). При этом все фотоны
оказываются в фазе друг с другом. Если
одно из зеркал сделать частично
отражающим (полупрозрачным), то выходящий
наружу свет является когерентным. Он
представляет собой непрерывную
монохроматическую электромагнитную волну, как и
в случае электромагнитного излучения
радиопередатчика. Для того чтобы процесс
вынужденного испускания преобладал над
процессом поглощения, большая часть
атомов должна находиться в
возбужденном состоянии. На рис. 26-11 приведена
схема такого процесса для случая гелий-
неонового лазера; в состоянии Еп>
находится больше атомов, чем в состоянии Еп.
До разработки лазера в 1960 г. все
доступное человечеству излучение в
инфракрасной, видимой и ультрафиолетовой
областях спектра было некогерентным, т.е.
фазы отдельных фотонов имели случайные
1
£ WW
Фотон, испущенный
вторым атомом
2
•
Рис. 26-10. Вынужденное излучение в лазере,
а-первый фотон падает на возбужденный атом;
б-атом испускает фотон, который падает на
другой возбужденный атом; г-три фотона
испытали отражение и готовы «подцепить»
четвертый фотон.
эВ
20
10
или
Я = 6328 А
Рис. 26-11. Три энергетических уровня атома
неона. В гелий-неоновом лазере атомы неона
переходят в возбужденное состояние Еп>
вследствие столкновений с возбужденными атомами
гелия. Переход в состояние Еп обусловливается
вынужденным излучением. Затем благодаря
столкновениям со стенками атомы неона
быстро переходят в основное состояние.

§ 7 БОРОВСКАЯ МОДЕЛЬ АТОМА 469
значения относительно друг друга. Как
было отмечено в § 4 гл. 23, с помощью
когерентного светового пучка можно получить
на больших расстояниях пятно
значительно меньших размеров; с момента
появления первого лазера достигнуты
значительные успехи в технологии, что
позволило создать лазеры как импульсного, так
и непрерывного действия, использующие
газообразное, жидкое или твердое
вещество, с длинами волн излучения в
инфракрасной, видимой или ультрафиолетовой
областях спектра.
§ 7. Боровская модель атома
Современная модель атома,
рассматриваемая в настоящей главе, была создана
в 1926 г. вскоре после появления уравнения
Шредингера. Однако за тринадцать лет до
этого Нильс Бор создал теорию, которая
прекрасно объясняла весь спектр водорода,
а также легла в основу физической модели
устойчивого атома.
Рис. 26-12. Нильс Бор на лыжах в
Лос-Аламосе. [Фото печатается с любезного разрешения
г-жи Лауры Ферми.]
Хотя, как известно, теория Бора
устарела, однако она столь проста, а ее
историческое значение так велико, что мы изложим
ее здесь. Кстати, символы боровской
теории употребляются и по сей день
(рис. 26-13). Бор считал, что возможные ор-
Рис. 26-13. а-традиционные символ атома;
б-боровская модель водородоподобного атома.
биты электронов аналогичны классическим
круговым орбитам планет, и пытался
найти правило, которое допускало бы лишь
определенные значения энергий электрона
или радиусов орбит. Он придумал
правило, согласно которому численное значение
момента импульса должно быть целым
кратным постоянной Й:
mvR = nK. (26-11)
Следует заметить, что боровский постулат
отличается от наших современных
представлений о свойствах атома водорода
в двух отношениях. Во-первых, мы знаем,
что понятие классической орбиты теряет
смысл применительно к электрону,
состояние которого характеризуется стоячей
волной. Во-вторых, теперь нам известно, что
момент импульса равен не пЪ, а Ш, т.е.
в любом случае он меньше боровского
значения. Таким образом, то
обстоятельство, что теория Бора правильно
описывает спектр энергетических уровней атома
водорода, является лишь счастливой
случайностью. В том, что правильный ответ
может оказаться следствием неправильных
рассуждений, нет ничего не обычного.
Такое случается и с великими мира
сего.
Проследим теперь за вычислениями,
проделанными Бором для нахождения
энергетических уровней электрона в поле
ядра с зарядом Ze. Согласно постулату
Бора (26-11), радиус п-й орбиты
Rn = n —. (26-12)

470 ГЛ. 26. АТОМ ВОДОРОДА
Приравняем центростремительную силу
силе электростатического притяжения:
mv2 k0Ze2
Rn Rn
-a
KZe2
„2 =^L
R„
KZe2
= — U (потенциальная
энергия),
mR„
(26-13)
(26-14)
Подставляя сюда вместо Rn выражение
(26-12), получаем
2 k0Ze2
ml п
Й \ '
v =
k0Ze2
(26-15)
Энергии уровней определяются
соотношением
Еп = (1/2) mv2 + U
или [после замены в соответствии с (26-13)
U = - mv2]
Еп = —mv2 + (— mv2) = ——mv2.
Возводя в квадрат правую часть
выражения (26-15) и подставляя полученное
выражение вместо v2, окончательно находим
Еп=-к1^^\=-1ъМ^\эЪ.
2t2 п
(26-16)
Эту величину можно также выразить через
R, подставив (26-14) в выражение Е =
= — (1/2) mv2, что дает
Е = -
fcpg2
2R„
(26-17)
Соотношение (26-16) следует и из
современной квантовой теории [см.
соотношения (26-7) и (26-9)]. Боровская модель дает
также простой ответ на вопрос о размерах
атома. Формулу для Rn получаем
подстановкой выражения (26-15) в (26-12):
Rn = n2
k0Zme2
(26-18)
Это выражение согласуется с формулой
(26-8) для среднего радиуса электронного
облака.
Однако серьезным недостатком модели
Бора является то, что она оказалась
неспособна объяснить спектры атомов, начиная
с атома гелия, вокруг ядра которого (Z =
= 2) вращаются два электрона. Несмотря
на сложность проблемы трех
взаимодействующих частиц, квантовая механика
позволяет рассчитать энергетические уровни
атома гелия. В последнее время на
основании современной теории с помощью
быстродействующих ЭВМ спектр гелия
просчитан с высокой точностью. Данные
эксперимента подтвердили результаты
этих расчетов. Физики и химики убеждены,
что современная квантовая механика
в принципе способна описать все спектры
атомов и свойства химических соединений.
*Пример 7. Докажем, что полученное в теории
Бора значение радиуса (Rn = п2а) согласуется
с расчетами на основе волновых функций атома
водорода при I = п — 1. Определим «средний»
радиус как расстояние, на котором
распределение вероятностей достигает максимума.
Решение: Распределение вероятностей дается
выражением | \|/„tlI_ j_ \2dV, где dV =
= 4nr2dr - элемент объема. Следовательно,
распределение вероятностей как функция от г
пропорционально величине
r2[Kn-Ar)Vdr.
Используя табл. 26-2, можно написать, что
(1? \2 ~ *2п ~ 2(* ~ 2г/па
Обозначим распределение вероятностей через
Р(г):
р(г) = г2»е"2г/иа.
Эта функция имеет максимум, когда dP/dr — 0:
dP
2пг2
- 2г/па
■ Irjna

ОСНОВНЫЕ ВЫВОДЫ 471
Приравняв нулю это выражение и сократив на
экспоненциальные множители, получим
2ПГ2"-1 г2п = О,
па
„2пг2п - 1 Jin
Время перехода определяется следующим
образом:
3 m2c3R2 '
-!£«-!(
,4 Не4
dR =
Заметим, что полученный результат справедлив
для любых целых значений и, включая п = 1,
соответствующего волновой функции основного
состояния.
СТАБИЛЬНОСТЬ ОРБИТ
Используя теорию Бора и формулу для
излучения точечного заряда, можно
вычислить время, за которое совершается
переход с орбиты радиусом Rn> на орбиту
радиусом Rn. В соответствии с (21-14)
скорость потери энергии можно записать в
виде
dE 2, е2 2 F , е2
— = -к0 — а2, где а=—=к0—-2-
dt 3 сй т mR
dE 2 } з е"
dt 3 к° т2сзЛ4
(26-19)
Нам понадобится также величина dE/dR,
которую можно получить дифференцируя
выражение
„2
Е= -к0
откуда
2R
dE__, е2
dR-ko2R2'
Теперь вычислим di/dR:
(26-20)
dt =( dt\ dE
dR \dEjdR'
С учетом (26-19) и (20-20) получаем
dt
dR
2 ,з е6
3 ° mV*4
3 m2c3R2
~4 к20е4 '
к0
2R2
4к20е
2 „4
Rl - R\
(26-21)
Для первой линии серии Бальмера Rn. =
= R3 = 0,477 нм, a Rn = R2 = 0,212 нм.
Таким образом,
(9,Ц.10-31кг)2(3.108м/с)3
1 " 4(9-109 Н-м2/Кл2)2(1,6.10" 19 Кл)4 Х
х [(4,77.10-10м)3 -
- (2,12.10-10м)3] = 1,04-10" 8 с.
Как и целый ряд других следствий теории
Бора, этот результат хорошо согласуется
с точным квантовомеханическим расчетом,
в котором не используется классическая
физика.
Пример 8. Используя формулу (26-21),
вычислим время, за которое электрон атома
водорода, находящегося в основном состоянии в
модели Бора, упадет на протон. Радиус протона
R = 10"15м.
Решение: Положим в (26-21) Rn> = Rt =
= 0,53-10" 10 м (начальный радиус) и Rn = г =
= 10" 15 м (конечный радиус):
t =
4к20е'
-[(0,53.10-1Ом)3 -(Ю"15м)3] =
= 1,57-10" п с
Это означает, что если бы электрон на боров-
ской орбите, отвечающей основному состоянию,
излучал в соответствии с классической физикой,
то атомы водорода испытывали бы коллапс за
время Ю-11 с. Бор нашел выход из этого
затруднения, постулировав, что электроны в
основном состоянии не излучают.
Основные выводы
Уравнение Шредингера в трех
измерениях записывается следующим образом:
2т
Т2
a2v|/ дЦ дЦ
дх2 ду2 dz2
_2-(Е-и^.

472 ГЛ. 26. АТОМ ВОДОРОДА
В случае, когда \|/ (х, у, z) зависит только от
г, это уравнение принимает вид
В случае атома водорода U =
= — /с0 (в2/г). При этом решением,
соответствующим состоянию с низшей
энергией Ех = - к0(те4/2П2) = - 13,6 эВ,
является функция ^ = ехр(— г/а), где
а = Ъ/(к0те2)- радиус. Собственные
значения энергии Еп = (-13,6/п2) эВ.
Соответствующие им решения могут зависеть от
углов 0 и ф. Зависимость волновой
функции от угла ф имеет вид exp(im^), где
L2 = тхЪ-проекция момента импульса на
ось z. Зависимость от угла 0
характеризуется значением квантового числа /,
причем L— Ш- максимальное значение
величины Lz; иными словами, mt может быть
любым целым числом в пределах от — /
до + /. Квантовое число / может
принимать целочисленные значения от 0 до
и-1.
При п' > п возможен спонтанный
переход с уровня Еп> на уровень Еп,
сопровождающийся испусканием фотона. Энергия
фотона hf= Еп> — Еп. Если фотон с такой
частотой / сталкивается с атомом в
состоянии Еп, то фотон может поглотиться,
а атом при этом перейдет из начального
состояния Еп в состояние Еп>. Если
газообразный водород нагрет и часть атомов
находится в возбужденных состояниях
с более высокой энергией, то энергии
фотонов в спектре излучения запишутся
в виде
й/=13'6(-^-^)эВ-
Фотон может стимулировать
возбужденные атомы испускать кванты с той же
частотой и фазой. Таким образом,
совокупность атомов, находящихся в
подходящем возбужденном состоянии, позволяет
получить пучок когерентного света. На
этом принципе основано действие лазера.
Боровская модель дает правильные
значения энергетических уровней и радиусов
орбит атома водорода. В ее основе лежит
гипотеза, что электрон движется по
классической орбите, для которой mvR = rih.
Упражнения
1. Повторите вывод формулы (26-2) для
электрона в поле ядра с зарядом Ze.
2. Допустим, что электрон покоится у
поверхности ядра урана (Z = 92). Какую энергию
надо затратить, чтобы удалить электрон на
бесконечность, если радиус ядра составляет
5,5- 1(Г15 м?
3. Электрон находится в ящике кубической
формы. Если L увеличить на 1%, то площадь
поверхности ящика возрастет на 2%,
а объем-на 3%. Как изменятся энергии
уровней, отвечающих стоячим волнам (в
процентах)?
4. Положите в уравнении (26-5) U = — к0 Ze2/r
и попытайтесь отыскать решение в виде
\|/! = е~г/а. Какие в этом случае получатся
значения а и Е!
5. Сколько будет различных волновых
функций в случае п = 5?
6. Какая минимальная энергия может быть
поглощена атомом водорода в основном
состоянии?
7. Чему равен боровский радиус Не+ в
основном состоянии?
8. Найдите для основного состояния атома
водорода в боровской модели:
а) кинетическую энергию (в эВ);
б) потенциальную энергию (в эВ);
в) энергию связи (в эВ);
г) энергию, необходимую для удаления на
бесконечность электрона, который
находится от протона на расстоянии боров-
ского радиуса.
9. Атомы газообразного водорода находятся
в состоянии с п = 5. Сколько всего линий
будет в спектре излучения этого газа?
10. В спектре поглощения элемента X
наблюдаются следующие три линии: fl =
= 2,2 • Ю15.Гц, /2 = 3,0 • 1015 Гц и /3 =
= 3,5- 1015 Гц.
а) Будут ли эти линии присутствовать
в спектре излучения этого элемента?
б) Перечислите частоты трех других линий
в спектре излучения.
11. В спектре Не+ найдите линию с той же
длиной волны, что и в спектре водорода.
Чему равна эта длина волны?
12. Мю-мезоатом состоит из ядра с зарядом
Z и мюона (частица в 207 раз тяжелее
электрона, обозначается ц) в основном
состоянии.
а) Чему равна энергия связи
отрицательного мюона (ц~), захваченного протоном?
б) Чему равен соответствующий радиус
боровской орбиты с п = 1?

ЗАДАЧИ 473
в) С какой энергией испускается фотон при
переходе из состояния с п = 2 в основное
состояние?
13. Напишите в явном виде волновую функцию
Фз,2,-2(г, 9> ф) Для водорода.
14. Проведите нормировку волновой функции с
п = 1, т.е. положите \|/ = Се~г/а, а затем
вычислите
Jv|/v|,*^K= 1 или C2\Q-2rladV = 1.
15. Используя формулу (26-21), вычислите
время перехода из состояния с п = 4 в
состояние с п = 3.
16. Определите длины волн, соответствующие
первым четырем линиям в спектре
поглощения водорода.
Задачи
17. Рассмотрим электрон, находящийся в
трехмерном кубическом ящике размером L =
= 10"10 м. Чему равны энергии (в эВ)
четырех низших уровней? Сколько состояний
отвечает каждому энергетическому уровню?
Напишите волновые функции для каждого
состояния.
18. Ящик имеет размеры Ly = L2 = 2LX.
Выразите энергии трех низших уровней через пх,
пу, nz, т,% и Lx. Напишите соответствующие
собственные функции. Заметьте, что
второму энергетическому уровню отвечают две
различные собственные функции.
19. Подстановкой в уравнение (26-5) покажите,
что функция \|/(г, 0, ф) = (re"r/2a)(sin 0) (е»Ф)
является решением в случае атома
водорода. Какие получатся при этом значения а
и Е?
20. Подстановкой в уравнение (26-5) покажите,
что функция
V Ъа 27а2 J
также является решением в случае атома
водорода.
21. Найдите среднее значение функции 1/г в
основном состоянии атома водорода,
принимая во внимание, что
r/ jy\,*y\,dV
22. С помощью соотношения (26-21) вычислите
время перехода из состояния с п = 4 в
состояние с п = 3. Чему равно отношение
АХ/Х для этой спектральной линии? Каким
должно быть расстояние между штрихами
дифракционной решетки длиной 5 см, чтобы
она могла разрешить естественную ширину
линии?
23. Используя боровскую модель, вычислите
радиус орбиты, по которой электрон
движется вокруг нейтрона.
24. Легкая частица с массой т и
положительным зарядом q движется по круговой
орбите радиусом R вокруг тяжелой частицы,
имеющей массу М и заряд — Q. Пусть
между этими частицами действуют лишь
электростатические силы.
а) Найдите выражение для потенциальной
энергии заряда q через его массу т и
скорость V.
б) Чему равна полная энергия Е в
зависимости от т и v?
в) Используя постулат Бора о квантовании
момента импульса, найдите выражение
для v через R, т, Ъ и п.
г) Запишите квантованные радиус R и
энергию Е через т, %, Q, q и п.
25. Рассмотрим воображаемый элемент Q,
атомы которого имеют валентность +1.
Пусть энергия связи внешнего электрона
равна 3,2 эВ. Известно также, что энергии трех
возбужденных уровней этого электрона
составляют — 1,0, — 1,4 и — 2,0 эВ.
а) Какова энергия основного состояния
в эВ?
б) Перечислите все линии в спектре
излучения этого элемента. Найдите энергии
соответствующих фотонов в эВ.
26. а) Какова вероятность того, что в атоме
водорода электрон находится в области
г > а, где а-радиус боровской орбиты?
б) Какова вероятность того, что электрон
находится в области г < 10"15 м?
(Протон следует считать точечным зарядом.
Это приводит к правильному значению
вероятности обнаружить электрон внутри
протона.)
27. Предположим, что \|/ является функцией
только от г. Пусть и{г) = г\|/. Напишите
радиальное уравнение Шредингера в трех
измерениях для функции и.
28. В примере 5 использовались следующие
уравнения преобразования координат при
переходе из штрихованной в нештрихован-
ную систему:
{х = х' cos a — z' sin a,
У = У>
z = x' sin a + z' cos a.
Пусть нормированные угловые функции
имеют вид 0n = l/3/4sin0 и @10= 1/3/2cos0.

474 ГЛ. 26. АТОМ ВОДОРОДА
Запишите 011(0)е,(р как функцию
а) от х, у и z,
б) от х', у' и z',
в) от 0' и ср'.
г) Чему равны коэффициенты av а2 и аъ
в выражении
0ii(0)eI<p = a, 0ii(0')e/<p' + a2®io(0') +
+ a30i-1(0')e-I'(p'?

27
АТОМНАЯ ФИЗИКА
§ 1. Принцип запрета Паули
Как видно из периодической системы
элементов (см. табл. 27-2) и из рис. 27-1,
периоды повторения химических и
физических свойств элементов образуют
последовательность чисел 2, 8, 8, 18, 18, 32.
В 1925 г. Вольфганг Паули предложил
простое правило, которое автоматически
объясняло наличие групп из 2, 8, 18 и 32
видим, что числа 2, 8 и 18 являются
прямым следствием принципа запрета,
а также квантовомеханического правила,
согласно которому — /^тг^+/иО^
</<и— 1. В§3 мы объясним, почему
«оболочки» с 8 и 18 электронами
повторяются. В момент своего возникновения
принцип Паули явился новым постулатом,
который в то время нельзя было вывести
из общих положений.
10 20 30 40 50 60 70 80 90
Рис. 27-1. а-Зависимость ионизационного
потенциала элементов от атомного номера Z;
б-зависимость атомного объема от Z.
элементов. Паули постулировал, что одну
электронную орбиталь, или стоячую волну,
могут занимать не более двух электронов.
Следовательно, в состоянии с п = 1 могут
находиться два электрона. Состоянию с
п = 2 отвечают 4 орбитали: (и, /, т,) =
= (2, 0, 0), (2, 1, 1), (2, 1, 0) или (2, 1, - 1).
Таким образом, в состоянии с п = 2 могут
находиться 8 электронов. Итак, мы
получили числа 2 и 8. Число 18 можно
получить, сложив 5 орбиталей с / = 2 и 4
орбитали с / = 0 и 1. Эти девять орбиталей
могут быть заняты 18 электронами. Мы
СПИН ЭЛЕКТРОНА
Однако годом позже было обнаружено,
что у каждого электрона имеется
собственный момент импульса, или спин, равный
Ьсоб=Ь/2. Следует заметить, что он
составляет половину обычного значения
орбитального момента. Это похоже на то, как
если бы электрон представлял собой сферу,
вращающуюся вокруг собственной оси
с постоянным моментом Й/2. Этот
собственный момент, или спин, невозможно
ни уменьшить, ни увеличить. Он одинаков
у всех элементарных частиц данного типа.
Вскоре после того, как был открыт
спин электрона, Паули и Дирак разработа-

476 rJI 27< АТ0МНАЯ ФИЗИКА
Рис. 27-2. Вольфганг Паули,
1900-1958. [Фото печатается
с любезного разрешения
Американского института физики.]
ли релятивистскую теорию частиц со
спином 1/2 и с радостью обнаружили, что
условие релятивистской инвариантности
приводит к волновым функциям электрона,
которые автоматически удовлетворяют
принципу запрета Паули. Это означало,
что принцип запрета не был взят с
потолка! У частицы со спином 1/2 проекции ее
спина на ось z могут принимать лишь
одно из двух значений (+ 1/2)Й или ( — 1/2)Й.
Эта величина проекции спина
необходима для полной характеристики
состояния электрона. Если состояние
электрона задано таким образом, то принцип
запрета утверждает, что в данном
состоянии может находиться не более одного
электрона. Поскольку при данном
орбитальном числе возможны две ориентации
спина, то равнозначна следующая
формулировка принципа Паули: на данной орби-
тали может находиться не более двух
электронов.
§ 2. Многоэлектронные атомы
Имея на вооружении уравнение Шре-
дингера и принцип Паули, можно
«рассчитать» свойства всех элементов, не
обращаясь к результатам химических опытов.
Действительно, уже в 1929 г. Дирак сказал:
«Все фундаментальные физические законы,
необходимые для построения
математической теории большей части физики и всей
химии, уже известны». С помощью
современных быстродействующих ЭВМ были
рассчитаны электронные плотности и
энергии связи более тяжелых, чем водород,
атомов. Таким способом можно вычислять
скорости химических реакций и изучать
структуру молекулярной связи, как это
иллюстрируется на рис. 27-3. Впрочем, для
большинства относящихся к химии задач
использование вычислительных машин
нецелесообразно; гораздо легче провести
непосредственные измерения. (На решение

§ 2. МНОГОЭЛЕКТРОННЫЕ АТОМЫ 477
2LiF
юА
Рис. 27-3. Три различные химические реакции.
Плотности электронов в начальном и конечном
состояниях вычислены на ЭВМ А. Уолом. На
каждом последующем контуре плотность
электронов уменьшается вдвое. Промежуточные
стадии химической реакции представлены на
рис. 27-6. [Заимствовано из статьи: Arnold
С. Wahl, Scient. Amer. (April 1970).]
некоторых типичных задач с помощью
ЭВМ могут потребоваться годы.)
Принцип Паули позволяет определить
положение каждого электрона в атоме.
Рассмотрим, например, лишенное
электронов ядро неона (Z = 10). Если оно
приобретает один электрон, то последний
быстро переходит на орбиталь с и = 1. То же
справедливо и для второго электрона. Оба
этих электрона целиком заполняют
орбиталь с и = 1. Если теперь добавить
остальные восемь электронов, то они
целиком заполнят четыре возможные орбитали с
п = 2: (/, m,) = (0S/p), (1, 1), (1, 0) или (1, -1).
Перейдем теперь к описанию структуры
атомов, начиная с водорода, на
основе квантовой теории. Не прибегая к
детальным расчетам, мы сможем вычислить
валентность и сделать грубые оценки
ионизационных потенциалов, а также
предсказать размеры и форму атомов.
Z = 1 (ВОДОРОД)
Структура этого атома обсуждалась
в предыдущей главе. Единственный
электрон находится в состоянии с п = 1,
энергия которого равна — 13,6 эВ. Таким
образом, энергия связи, или энергия ионизации,
равна 13,6 эВ. Ускоренный разностью
потенциалов в 13,6 В, электрон едва-едва
может ионизовать атом водорода. Это
минимальное напряжение, необходимое для
ионизации атома, называют
ионизационным потенциалом. Таким образом,
ионизационный потенциал водорода равен
13,6 В. На рис. 27-1, а изображена
зависимость ионизационных потенциалов
различных элементов от атомного номера Z.
Отметим периодичность, отвечающую
числам 2, 8, 8, 18, 32.

478 ГЛ. 27. АТОМНАЯ ФИЗИКА
Z = 2 (ГЕЛИЙ)
Рассмотрим сначала ион гелия Не + ,
состоящий из ядра гелия и единственного
электрона. Любое ядро с атомным
номером Z и единственным электроном
аналогично атому водорода, с той лишь
разницей, что сила электростатического
взаимодействия увеличивается в Z раз. Стоячие
волны сохраняют прежний вид, но
постоянная к0 умножается теперь на Z. При
этом по-прежнему имеет место формула
(26-16):
(koZfme4 Z2
(27-1)
в выражении для R^} постоянная а теперь
равна а = ~И/к0 Zme2, а не 1г/к0 те2. Из-за
присутствия множителя Z2 ионизационный
потенциал Не+ будет равен 4-13,6 или
54,4 В. Это подтверждается
экспериментом.
Если в окрестности Не+ поместить
второй электрон, то он первоначально
«видит» заряд, равный Z — 1. Однако, после
того как этот электрон попадает на
оболочку с п = 1, половину времени он будет
находиться к ядру ближе первого
электрона и будет «видеть» при этом заряд ядра
Z. Если взять просто среднее этих
величин, то мы получим Z — 1/2. Таким
образом, для электрона в атоме гелия
эффективный заряд ядра должен быть равным
Z = 1,5е. Обобщая формулу (27-1), мы
имеем
Еп1= -13,6^эВ,
где 2эфф зависит как от п, так и от /. На
основании такой оценки 2эфф следует
ожидать, что ионизационный потенциал гелия
составит примерно (1,5)2 • 13,6 или 30 В.
В действительности из-за наличия
положительной потенциальной энергии,
обусловленной отталкиванием двух электронов,
следовало бы ожидать более слабой связи.
В случае гелия экспериментально
найденное значение ионизационного потенциала
равно 24,6 В. Это самый большой из
ионизационных потенциалов всех элементов.
Вследствие значительного
ионизационного потенциала, а также из-за того, что
на оболочке с п = 1 отсутствует место для
третьего электрона, гелий химически
крайне инертен. Химические силы не в
состоянии обеспечить энергию в 24,6 эВ, чтобы
мог образоваться положительный ион
Не +. Если попытаться образовать
отрицательный ион гелия Не", то
дополнительный электрон должен оказаться в
состоянии с п = 2. Соответствующая стоячая
волна достаточно удалена как от ядра с
зарядом + 2е, так и от отрицательных
зарядов обоих электронов в состоянии с п = 1.
Следовательно, результирующий заряд
в центре волны с п = 2 равен нулю, и не
будет потенциала, способного удержать
волну с п = 2; иными словами, в случае
п = 2 2эфф « 0. Следовательно, гелий не
образует молекул ни с одним из
элементов. Его и другие атомы с заполненными
оболочками называют благородными (или
инертными) газами. Некоторые из более
тяжелых благородных газов образуют
специальные соединения.
Пример 1. Ионизационный потенциал гелия
24,6 В. Чему равна полная энергия связи гелия,
т.е. какую энергию надо затратить, чтобы
разделить атом гелия на ядро и два свободных
электрона?
Решение: Для удаления первого электрона
требуется 24,6 эВ, а для удаления второго 13,6 Z2
или 54,4 эВ. Сумма этих значений даст полную
энергию связи, равную 79 эВ.
Z = 3 (ЛИТИЙ)
Дважды ионизованный литий, Li++,
имеет водородоподобный спектр, у
которого энергии уровней в (З)2 = 9 раз больше,
чем у водорода. Спектр однократно
ионизованного лития подобен спектру гелия, но
с 2эфф # 3 — 1/2, а не 2 — 1/2 как в случае
гелия. В силу принципа Паули третий
электрон в нейтральном атоме лития должен
находиться на оболочке с п = 2. Для этого
электрона 2эфф будет несколько больше
единицы. Таким образом, ионизационный
потенциал лития, по-видимому, будет
несколько больше чем 13,6/и2 = 13,6/22 =
= 3,4 В. Экспериментальное значение
равно 5,4 В, что соответствует 2эфф = 1,25.
Второй ионизационный потенциал, со-

§ 2. МНОГОЭЛЕКТРОННЫЕ АТОМЫ 479
ответствующий удалению второго
электрона, составляет 75,6 В. Таким образом,
в соединениях литий всегда должен
обнаруживать валентность + 1 (т.е. терять
один электрон) и никогда не будет
обнаруживать валентность +2 (т. е. терять два
электрона).
Каким квантовым числом / обладает
внешний электрон атома лития? Согласно
предыдущему изложению, состояния с п =
= 2, I = 0 и и = 2, I = 1 должны иметь
одну и ту же энергию. Однако, как следует
из рис. 27-4, состоянию с / = 0 будет
отвечать более сильная связь, чем состоянию с
/ = 1. Это обусловлено тем, что волновая
функция электрона в состоянии с меньшим
моментом импульса (/ = 0)
концентрируется ближе к ядру по сравнению с волновой
функцией состояния с большим значением
момента импульса. В действительности
волновые функции \|/ всех электронов с / >
> 0 обращаются в нуль при г = 0.
Для электронной волны,
сосредоточенной вблизи ядра, 2эфф ж Z, тогда как для
/=1
*и /=2
Рис. 27-4. Волновые функции атома водорода
в состояниях с и = 3, / = 0, 1 и 2. Заметим, что
только в случае / = 0 волновые функции не
обращаются в нуль в начале координат.
удаленной от ядра волны 2эфф » 1.
Следовательно, для волны с / = 0 2эфф больше, чем
для волны с / = 1. Это и объясняет,
почему 2эфф зависит не только от п, но и от /.
Этот эффект может вызывать
значительные различия в энергиях подоболочек
с / = 0 и 1=1 или / = 2. Действительно,,
в случае Z = 19 (калий) эффект
оказывается настолько сильным, что энергетический
уровень с п = 4 и / = 0 располагается
ниже уровня с и = 3 и 1 = 2. В табл. 27-1
приведен порядок следования
энергетических уровней. Другая интерпретация этого
эффекта основана на том, что орбиты
с большими значениями моментов
импульса оказываются более круговыми и,
следовательно, более удалены от ядра, чем
орбиты с меньшими моментами импульса.
Поэтому состояния с меньшими / связаны
более сильно.
Z = 4 (БЕРИЛЛИЙ)
Согласно принципу Паули, в
состоянии с и = 2 и / = 0 могут находиться два
электрона. Поскольку Z^ для близкой
к ядру электронной волны оказывается
в данном случае больше, чем у лития,
более высоким будет и ионизационный
потенциал. Если в случае лития значение
ионизационного потенциала равно 5,39 В, то
в случае бериллия эксперимент дает 9,32 В.
Однако второй ионизационный потенциал
в случае бериллия оказывается ненамного
больше, поскольку второй электрон
находится также в состоянии с п = 2. Поэтому
в соединениях валентность бериллия равна
+ 2.
Z = 5 (БОР), Z = 6 (УГЛЕРОД), Z = 7 (АЗОТ),
Z = 8 (КИСЛОРОД), Z = 9 (ФТОР) И Z = 10
(НЕОН)
Эти атомы образуются при заполнении
состояний с / = 1 в оболочке с п = 2.
Поскольку значению / = 1 отвечают три
различных значения mv на подоболочке (п =
= 2, / = 1) могут разместиться 6
электронов. В состоянии с п = 2 в атомах бора,
углерода и азота находятся соответственно
три, четыре и пять электронов, что
соответствует валентностям +3, + 4 и +5.
Существует вполне объяснимая причина,

480 ГЛ. 27. АТОМНАЯ ФИЗИКА
почему в атомах бора все три электрона с
и = 2 (или все четыре электрона в атомах
углерода) ведут себя одинаково при
образовании химических соединений. Это
связано с процессом гибридизации, который мы
обсудим в § 6.
Кислород и фтор обнаруживают новое
явление, называемое электронным
сродством (или сродством к электрону).
Отдельный атом фтора может приобрести
дополнительный электрон и превратиться
в стабильный ион F". Соответствующая
этому дополнительному электрону волна
частично «видит» большой эффективный
заряд 2Эфф, и электрон оказывается
связанным с энергией 3,6 эВ. Таким образом,
валентность фтора равна — 1. Сродство
к электрону при образовании О"
составляет 2,2 В. В химических соединениях
кислород и азот имеют валентности
соответственно — 2 и — 3. У неона все состояния
с п = 2 заняты, т.е. оболочка заполнена.
Поскольку электронные волны,
отвечающие п = 2, частично расположены очень
близко к ядру (в данном случае 2эфф
достигает 10), то ионизационный потенциал
оказывается весьма высоким (21,6 В).
Таким образом, следует ожидать, что неон,
как и гелий, является химически инертным.
§ 3. Периодическая система элементов
Если продолжить предыдущее описание
элемента за элементом, то мы сразу же
обнаружим, что их свойства очень сходны со
свойствами уже перечисленных элементов.
ОТ Z = 11 (НАТРИЙ) ДО Z = 18 (АРГОН)
Согласно принципу Паули,
одиннадцатый электрон натрия должен занять
состояние с п = 3, для которого Z-эфф « 1
и которое отвечает волне гораздо больших
размеров, нежели состояние неона с п = 2.
Следовательно, теория предсказывает, что
всякий раз, когда внешний электрон
попадает на орбиталь с более высоким
квантовым числом п, размер атома будет
значительно увеличиваться. Как видно из
рис. 27-1,6, такое резкое увеличение
размеров наблюдается для Z = 3, 11, 19, ... .
В последовательности из восьми
элементов-от натрия до аргона-заполнение
состояний с и = 3, I = 0 и п = 3, 1=1
происходит совершенно аналогично
предшествующим восьми элементам. Поэтому
химические свойства этих элементов
оказываются весьма похожими на свойства
соответствующих элементов предыдущей
восьмерки. В этом и заключается объяснение
«периодической системы» химических
элементов. Пока мы объяснили наличие
периодов, соответствующих числам 2, 8, 8.
Посмотрим теперь, почему следующему
периоду соответствует число 18.
ОТ Z = 19 (КАЛИЙ) И ДАЛЕЕ
Мы могли бы предположить, что
внешний электрон следующего элемента
окажется в состоянии с п = 3 и / = 2. Однако,
как указывалось при обсуждении лития
(Z = 3), в случае волн с п = 4, / = 0
величина Z^ существенно больше, чем в
случае волн с п = 3, / = 2, поскольку волна с
/ = 0 концентрируется в области г = 0, где
эффективный заряд максимален. Для
волны с п = 4, / = 0 мы имеем Z^ = 2,26
и энергию связи 13,6Z^/42= 4,34 эВ, в то
время как для волны с п = 3, 1 = 2
величина Z^ несколько меньше 1,7, чему
соответствует энергия связи меньше 4,34 эВ.
Если бы девятнадцатый электрон оказался
в состоянии с п = 3, / = 2, то он очень
скоро перешел бы в состояние с п = 4, / = 0,
которому отвечает меньшая энергия, и при
этом испустил бы фотон с энергией,
равной разности энергий обоих состояний.
При переходе к Z = 21 (скандий)
состояние с п = 4, / = 0 оказывается
заполненным, так что при размещении двадцать
первого электрона возникнет конкуренция
между состояниями и = 3, 1 = 2 и п = 4,
/ = 1. Как и следовало ожидать, более
низким оказывается состояние с п = 3,
поэтому в скандии начинают заполняться десять
состояний с / = 2 оболочки п = 3. Затем
заполняются следующие шесть состояний
с п = 4, / = 1. Таким образом, всего
имеется 2+10+6=18 состояний с близкими
энергиями. На рис. 27-5 приведены эти 18
состояний, отвечающие изменению Z от 19
до 36 (см. на рисунке группу
периодичности 4). На этом рисунке показаны
относительные расположения энергетических
уровней атомов в зависимости от кван-

§ 3. ПЕРИОДИЧЕСКАЯ СИСТЕМА ЭЛЕМЕНТОВ 4о1
товых чисел пи/. Эти энергетические
уровни получаются, если взять «голое» ядро
с большим атомным номером и
поочередно добавлять к нему электрон за
электроном. При этом можно было бы измерять
энергию, выделяющуюся при переходе
каждого электрона на наинизший
возможный уровень. Таким способом удалось
бы выявить относительное расположение
энергетических уровней для всех
внутренних электронов.
Мы ожидаем, что при любом данном
значении п энергия уровней будет
скачкообразно увеличиваться с ростом
/ (рис. 27-5). Именно это и наблюдается
экспериментально. Следует заметить
также, что непосредственно после чисел
электронов 2, 10, 18, 36, 54 и 86 имеют место
особенно большие скачки энергии. У
элементов с атомными номерами Z = 2, 10,
18, 36, 54 и 86 оболочки заполнены, так что
внешние электроны связаны особенно
прочно. Этими элементами являются
благородные газы Не, Ne, Ar, Кг, Хе и Rn.
Значения квантовых чисел и энергий уровней
для каждого электрона любого из
элементов можно предсказать заранее.
В табл. 27-1 представлены предсказанные
электронные конфигурации атомов.
Соответствующая периодическая система
элементов приведена в табл. 27-2. Элементы
в одной группе (колонке) обладают
одними и теми же валентностями и
аналогичными химическими свойствами.
На этом мы и завершим
«теоретическое» рассмотрение химии атомов.
Вычисления с помощью ЭВМ точных значений
ионизационных потенциалов и
электронного сродства требуют крайне громоздких
расчетов. Однако в нашем распоряжении
имеется теория, и подобные расчеты
в принципе выполнимы. Таким образом,
Группа /_0 /=1 /«2 /=3
периодич- Aj-cocToVp -cocto4W.cocto-\//-coctoA
ности ^яния Дяния 7\яния /\яния )
Рис. 27-5. Относительные
расстояния между энергетическими
уровнями электронов в атомах
с высоким Z (показаны не
в масштабе). Состояния с
одинаковыми главными
квантовыми числами п соединены
штриховыми линиями. Заметим, что
с ростом / энергии уровней
увеличиваются. Состояния
образуют группы периодичности
с числом электронов 2, 8, 8, 18,
18, 32, 32.
' J электрона]
л =6
"[электронов
л=5
л=4
2/ 8 v 2/"
рлектронов] г
(электрона)
*п=2
~п = \

482
ГЛ. 27. АТОМНАЯ ФИЗИКА
Электронные конфигурации атомов 1}
Таблица 27-1
г
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
31
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
Символ
Н
Не
Li
Be
В
С
N
О
F
Ne
Na
Mg
Al
Si
P
S
CI
Ar
К
Ca
Sc
Ti
V
Cr
Mn
Fe
Co
Ni
С
Zn
Ga
Ge
A*
Se
Br
Kr
Rb
Sr
Y
Zr
Nb
Mo
Tc
Ru
Rh
Pd
Ag
Cd
In
Sn
Sb
Основная
конфигурация
Is
Is2
[He] Ъ
Ъ2
2s22
2s22p2
ls22p3
2s22p4
b22p*
b22p*
[Ne] 3s
3s2
3s23p
3s23p2
3s23p3
3s23p4
3s23p5
3s23pe
[Ar] 4*
As2
3d4s2
3d24s2
3d34s2
3d54s
3d54s2
3d*4s2
3d74s2
3d4s2
3d104s
3dl04s2
3d104s24p
3dw4s24p2
3dl04s24p3
3d104s24p4
3dl4s24pb
3d™4s24p*
[Kr] 55
5s2
4d5s2
4d25s2
4d45s
4d*5s
4dbSs2
4d75s
4d*Ss
4d™
4d105s
4dl0Ss2
4dl05s25p
4d105s25p2
4d105s25p3
Энергия
ионизации,эВ
13,595
24,581
5,390
9,320
8,296
11,256
14,545
13>614
17418
21,559
5,138
7,644
5.984
8,149
10,484
10,357
13,01
15,755
4,339
6,111
6,54
6,83
6,74
6,76
7,432
7,87
7,86
7,633
7,724
9,391
6,00
7,88
9,81
9,75
11,84
13.996
4,176
5,692
6,377
6,835
6,881
7,10
7,228
7,365
7,461
8,33
7,574
8,991
5,785
7,342
8,639
Z
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
Символ
Те
I
Xe
Cs
Ba
La
Ce
Pr
Nd
Pm
Fm
Eu
Gd
Tb
Dy
Ho
Er
Tm
Yb
Lu
Hf
Та
W
Re
Os
Ir
Pt
Au
Hg
Tl
Pb
Bi
Po
At
Rn
Fr
Ra
Ac
Th
Pa
U
Np
Pu
Am
Cm
Bk
Cf
Es
Fm
Mv
No
Lw
Ku
Основная
конфигурация
4d105s25p4
4d105s25p*
4d105s25pe
[Xe] 65
652
5d6s2
4/5d6s2
4f36s2
4f462
4/*6s2
4/6652
4/7652
4f5d6s2
4f>6s2
4f106s2
4/U652
4/12652
4/13652
4/14б52
4f145d6s2
4fl45d4s2
4f145d36s2
4f145d46s2
4f145d*6s2
4P45d4s2
4f145d4s2
4P45d4s2
[Xe,4/145</10] 65
652
6s26p
6s4p2
6s26p3
6s26p4
6526/>5
6s4pe
[Rn]75
752
bdls2
6d27s2
Spddls2
5p6dls2
5f46dls2
5f*ls2
Sfls2
Sfbdls2
spedls2
5pQls2
5f"ls2
5/1275
5p3ls2
5p4ls2
5f46d7s2
Sp46d2ls2
Энергия Л
ионйзации,эВ
9,01
10,454
12,127
3,893
5,210
5,61
«,54
5,48
5,51
5,6
5,67
6,16
6,74
6,82
6,22 j
6,15
7,0 j
7,88
7,98
7,87
8,7
9,2
8,88
9,22
10,434
6,106
7,415
7,287
8,43
10,745
5,277
6,9
4,0
J
l) Символами s, p, d, f обозначаются соответственно
значения / = 0, 1, 2, 3. Например, конфигурация для кислорода
(Z = 8) представляет собой [Не] 2s22p4. Элемент, указанный в
квадратных скобках, означает, что внутренние оболочки
заполняются, как и в данном элементе (в нашем случае как у Не).
Выражение 2522р4 означает, что имеются два электрона в
состоянии 2s и четыре электрона в состоянии 2р. Запись 2р
соответствует п = 2, 1=1.
всю химию можно получить из простои
теории - квантовой механики электронов со
спином 1/2. В § 5 и 6 мы
проиллюстрируем подход к решению на ЭВМ задачи об
образовании молекул из атомов.

§ 4. РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ 483
Периодическая система элементов
Таблица 27-2
Электронное
состояние
Is
2s, 2р
3s, Зр
4s, 4р, 3d
5s, Sp, Ad
6s, 6p, 5d
Is, lp, 6d
IA
3
Li
6,941
11
Na
22,990
19
К
39,10
37
Rb
85,47
55
Cs
132,91
87
Fr
(223)
HA
4
Be
9,012
12
Mg
24,31
20
Ca
40,08
38
Sr
87,62
56
Ba
137,34
88
Ra
226,03
III В
21
Sc
44.96
39
Y
88,91
57*|
La
138,91
89t /
Ac \
(227) I
IVB
22
Ti
47,90
40
Zr
91,22
( 72
Hf
178,49
104
(Ku)
| (261)
VB
23
V
50.94
41
Nb
92,91
73
Та
180,95
105
(Ha)
(260)
VIB
24
Cr
52,00
42
Mo
95,94
74
W
183,85
106
1
H
1,008
VIIB ,
25
Mn
54,94
43
Tc
98,91
75
Re
186,2
26
Fe
55,85
44
Ru
101,07
76
Os
190,2
— VIII—
27
Co
58,93
45
Rh
102,91
77
Ir
192,22
N IB
28
Ni
58,71
46
Pd
106,4
78
Pt
195.09
29
Cu
63,55
47
Ag
107,87
79
Au
196.97
IIB
30
Zn
65,37
48
Cd
112,40
80
Hg
200,59
IIIA
5
В
10,81
13
Al
26,98
31
Ga
69,72
49
In
114,82
81
Tl
204.37
IVA
6
С
12,011
14
Si
28,09
32
Ge
72,59
50
Sn
118,69
82
Pb
207,2
VA
7
N
14,007
15
P
30,97
33
As
74,92
51
Sb
121,75
83
Bi
208,98
VIA
8
0
15,9994
16
S
32,06
34
Se
78,96
52
Те
127,60
84
Po
(210)
VIIA
9
F
18,998
17
a
35,453
35
Br
79,90
53
126,90
85
At
(210)
2
He
4,003
10
Ne
20,18
18
Ar
39,95
36
Kr
83,80
54
Xe
131,30
86
Rn
(222)
* Ланта.ниды
58
\ Ce
140,12
\ 90
Th
, 232,04
59
Pr
140,91
91
Pa
231,04
60
Nd
144,24
92
U
238,03
61
Pm
(147)
93
Np
237,05
62
Sm
150,4
94
Pu
(244)
63
Eu
151^6
95
Am
(243)
64
Gd
157,25
65
Tb
158,93
96
Cm
(245)
97
Bk
(247)
66
Dy
162,50
98
a
(249)
67
Ho
164,93
99
Es
(249)
68
Er
167,26
69
Tm
168,93
100
Fm
(255)
101
Md
(256)
70
Yb
173,04
102
No
(254)
71 (
Lu \
174,97?
103 j
U 1
(257) )
Пример 2. Какие, по вашему мнению, значения
п и / отвечают внешним электронам недавно
открытого 106-го элемента? Какова электронная
конфигурация этого элемента?
Решение: Седьмой период начинается с Z = 86.
Согласно рис. 27-5, восемьдесят седьмой и
восемьдесят восьмой электроны находятся на
оболочке Is2 (п = 7, / = 0). Затем еще 14 электронов
занимают состояние 5/14 (л = 5, / = 3) почти
с той же энергией. Оставшиеся 4 электрона
образуют конфигурацию 6d4 (п = 6, / = 2). На
рис. 27-4 все эти уровни расположены очень
близко друг к другу, так что не совсем ясно,
какой из них должен заполняться раньше. Из
табл. 27-1, в которой приведены
количественные данные, видно, в каком порядке эти
уровни возникают с ростом Z. Основываясь на
данных этой таблицы, можно полагать, что
электронная конфигурация представляет собой
заполненную оболочку Rn, за которой следует
конфигурация 5/146d47s2.
§ 4. Рентгеновское излучение
В предыдущем параграфе мы показали,
что в любом атоме два первых электрона
образуют электронную конфигурацию
гелия (гелиевый кор). Энергия связи этих
электронов равна 13,6 Z^ эВ. Благодаря
экранирующему действию электронов с
/ = 0 атомы с более высокими атомными
номерами имеют 2эфф # Z - 2. В атомах
с очень большим атомным номером
энергия связи двух электронов, принадлежащих
оболочке с п = 1, заметно превышает
10000 эВ, тогда как энергия связи внешних
электронов составляет всего несколько эВ.
Если образец данного элемента поместить
в электрическую дугу или разрядную
трубку, то его атомы начнут терять внешние
электроны и допустимые квантовые
переходы окажутся порядка нескольких
электрон-вольт, а характеристический спектр
будет содержать линии соответствующих

ГЛ. 27. АТОМНАЯ ФИЗИКА
длин волн. Поскольку фотону с энергией
1 эВ отвечает длина волны X = 12 390 А,
характеристический спектр типичного
элемента будет состоять из линий в
инфракрасной, видимой и ультрафиолетовой
областях.
А теперь допустим, что у атома удален
внутренний электрон. В этом случае
внешний электрон мог бы «спрыгнуть вниз»
и заместить внутренний электрон; при
этом испустился бы фотон с энергией,
в тысячи раз превышающей обычную.
Длина волны этого фотона была бы в
сотни или тысячи раз короче длины волны
видимогоо света. Такие фотоны с А, в
интервале 0,1А<А,<100А называют
рентгеновским излучением. Но как удалить
внутренний электрон? Оказывается, очень
просто. Надо бомбардировать образец
пучком электронов, кинетическая энергия
которых превосходит энергию связи
внутренних электронов. Из приведенного ниже
примера мы увидим, что пучок электронов
с энергией 1650 эВ (или выше) способен
вырвать из алюминия электроны,
находящиеся на оболочке с п = 1. Согласно
принятой для рентгеновского излучения
терминологии, электроны с п = 1 называются
электронами К-оболочки.
Пример 3. Какова максимальная энергия
рентгеновского излучения алюминия и свинца?
Вычислим значения энергии и длин волн фотонов.
Решение: Максимальная энергия
рентгеновского излучения отвечает переходу свободного
электрона (с нулевой энергией) на вакантное
место в К-оболочке. Алюминий имеет Z = 13;
тогда hf= 13,6(13 - 2)2 эВ = 1,65 кэВ.
Соответствующая длина волны X = 7,5 А.
В случае свинца Z = 82. Поэтому hf =
= 13,6 (80)2 эВ = 87 кэВ и X = 0,14 А
Этот пример иллюстрирует весьма
надежный метод определения значений Z
у вновь открытых элементов. Он
заключается в измерении длины волны
высокоэнергетического (жесткого) рентгеновского
излучения, испускаемого неизвестным
образцом при бомбардировке его
электронами.
Поскольку длины волн рентгеновского
излучения сравнимы с межатомными
расстояниями в твердых телах, его с успехом
можно применить для определения
структуры твердых тел. В предыдущих главах
вы уже видели, что расположенные
периодически атомные плоскости действуют
подобно штрихам дифракционной
решетки. Таким образом, если известна длина
волны рентгеновского излучения, то,
измеряя углы дифракции, можно определить
межатомные расстояния (см. § 6 гл. 24).
§ 5. Связь в молекулах
Рассмотрим два различных механизма,
обеспечивающие два типа связи атомов
в молекулах (ионную и ковалентную).
ИОННАЯ СВЯЗЬ
Если два нейтральных атома
постепенно сближать друг с другом, то в случае
ионной связи наступает момент, когда
внешний электрон одного из атомов
предпочитает присоединиться к другому атому.
Атом, потерявший электрон, ведет себя как
частица с положительным зарядом + е,
а атом, приобретший лишний электрон,—
как частица с отрицательным зарядом
-е. Потенциальная энергия
электростатического взаимодействия между ними U =
= —k0e2/R, где R-расстояние между
центрами двух ионов.
В качестве примера рассмотрим
образование молекулы фторида лития LiF. Так
как энергия ионизации лития 5,4 эВ, а
электронное сродство фтора 3,6 эВ, то
результирующая энергия, необходимая для того,
чтобы удалить электрон лития и
присоединить его к фтору, составляет 5,4 эВ —
— 3,6 эВ = 1,8 эВ. Если оба атома
находятся на расстоянии R = 8 А друг от
друга, то k0e2/R =1,8 эВ. Следовательно, на
расстояниях, меньших чем 8 А, внешний
электрон лития, перейдя к атому фтора,
окажется в состоянии с меньшей энергией.
Этот процесс виден на рис. 27-6, на
котором приведены контуры электронной
плотности, полученные путем расчета на ЭВМ
полных электронных плотностей обоих
атомов. В нижней части рисунка приведена
результирующая энергия системы. Следует
заметить, что, когда атомы сближаются на
расстояние R = 8 А (конфигурация Ъ на

§ 5. СВЯЗЬ В МОЛЕКУЛАХ 485
рис. 27-6), внешний электрон атома лития
переходит к атому фтора. В конфигурации
h на рисунке энергия начинает расти
благодаря отталкиванию внутренних
электронов обоих атомов. Минимум энергии
достигается на расстоянии R = 1,5 А, на
котором результирующая энергия связи
составляет 4,3 эВ (конфигурация д на
рисунке).
КОВАЛЕНТНАЯ СВЯЗЬ
Еще один очень распространенный тип
молекулярной связи, встречающийся
у большинства органических соединений,
носит название ковалентной связи. Кова-
лентная связь образуется, когда электроны
обобществляются двумя атомами.
Простейшим примером ковалентной связи
является молекула водорода. Рассмотрим
сначала ионизованную молекулу водорода
Hj. Она состоит из двух протонов,
окруженных электронным облаком. В
присутствии двух протонов энергия связи
электрона оказывается, разумеется, больше,
чем при наличии только одного протона.
С другой стороны, электростатическое
отталкивание протонов стремится разорвать
связь. Однако вследствие тенденции
электронной волны концентрироваться в
области между протонами, преобладающим
оказывается электростатическое
притяжение электрона к обоим протонам. В Щ
энергия связи атома водорода с ионом
водорода составляет 2,65 эВ; иными словами,
требуется затратить (2,65 + 13,6) эВ, чтобы
ион HJ полностью диссоциировал на два
протона и электрон.
Согласно принципу Паули, на орбите,
где находится первый электрон, имеется
Рис. 27-6. Вычисленные на ЭВМ зависимости
полной электронной плотности лития и фтора
от расстояния R между этими атомами. В
нижней части рисунка приведена результирующая
энергия как функция от R. В каждой
последующей конфигурации электронная плотность
уменьшается вдвое (в конфигурации е она
уменьшается до 3%). Заметим, что в
конфигурации b внешний электрон атома лития
«перескочил» к атому фтора. [Вычисления выполнены
А. Уолом и опубликованы в Scient. Amer. (April
1970).]
т
к
и
о.
4>
X
О
' 1
"0
-1
-2
-3
-4

место еще для одного электрона. Такая
система из двух электронов и протонов
представляет собой нейтральную молекулу
водорода. Из-за электростатического
отталкивания двух электронов их волновая
функция оказывается несколько более
размытой, чем волновая функция
единственного электрона в Н2+. В нейтральной
молекуле водорода энергия связи двух
атомов составляет 4,48 эВ. На рис. 27-7
приведены вычисленные с помощью ЭВМ
контуры электронной плотности и энергии
связи двух атомов Н в зависимости от
расстояния между ними.
Атомы углерода обычно образуют
соединения с ковалентной связью. Атом
углерода имеет тенденцию обобществить
четыре дополнительных электрона, с тем
чтобы заполнить ими свою оболочку с
п = 2, / = 1. Простейшим примером
является молекула СН4 (метан),
изображенная на рис. 27-8. Как и в молекуле
водорода, электронные волны стремятся
сконцентрироваться главным образом
между положительными зарядами, где они
вносят наибольший вклад в энергию связи.
Поскольку четыре электронных облака
взаимно отталкиваются, конфигурация
с наименьшей энергией соответствует их
максимальному удалению друг от друга
(рис. 27-8). Конфигурация электронных
волн в молекулах определяется уравнением
Шредингера, а также условием, что энергия
уровней должна быть по возможности
минимальной.
§ 6. Гибридизация
Мы видим, что при образовании
молекул четыре электрона атома углерода с
п = 2 способны «растекаться» и играть
равноценную роль, благодаря чему
углерод приобретает валентность, равную 4.
Но как это может быть, когда первые два
электрона с п = 2 более сильно связаны на
заполненной подоболочке с / = 0? Точно
Рис. 27-7. Ковалентная связь. Два водородных
атома исследуются таким же образом, как и на
рис. 27-6. Обратите внимание, как электроны
стремятся заполнить пустую оболочку другого
атома. [Вычисления выполнены А. Уолом
и опубликованы в Scient. Amer. (April 1970).]

§ 6. ГИБРИДИЗАЦИЯ 487
Рис. 27-8. а-относительные
ориентации ядра углерода и
четырех ядер водорода
(протонов) в молекуле СН4; б -
четыре электронных облака,
или лепестки,
простирающиеся от ядра углерода и
окутывающие протоны; каждый
из лепестков содержит по
два электрона с ковалентной
связью.
(-i+J-k)
(-i-J+k)
Направление =
-(l + J+k)
так же, почему бор (Z = 5) с единственным
электроном в состоянии с / = 1 имеет
валентность 3, а не 1? Ответ заключается
в том, что атомы в молекулах не
тождественны изолированным атомам. В
изолированном атоме существует различие
между электронами в состояниях с 1 = 0и
/ = 1. В § 2 указывалось, что электроны с
/ = 0 в действительности связаны более
сильно, чем электроны с / = 1. Однако
молекулы-это не просто сумма атомов.
Например, в молекуле СН4 кроме ядра
углерода имеются еще 4 центра
сосредоточения положительного заряда. Решение
уравнения Шредингера в виде стоячих волн для
системы из пяти атомных ядер
оказывается более сложным и для основного
состояния приводит к конфигурации, показанной
на рис. 27-8.
Хотя стоячие волны, описывающие
четыре внешних электрона, выглядят
совершенно иначе, чем стоячие волны в
атоме, их можно формально представить в
виде суперпозиции водородоподобных
стоячих волн (см. пример 5 в гл. 26).
Действительно, любую стоячую волну можно
разложить в ряд по водородоподобным
волновым функциям. В случае атома
углерода энергии связи четырех внешних
электронов одинаковы и соответствуют
энергии связи электрона на уровне с п = 2;
следовательно, можно ожидать, что
электронные стоячие волны являются
комбинацией главным образом функций \|/2, о, о»
*|>2, i,i> *1>2,1,0 и \|/2,1,-1. Комбинации,
приводящие к изображенным на рис. 27-8
распределениям, записываются в виде
^i ="2"(5 + Рх + Ру + Рм)>
f* =у(5 + Рх- Ру" Pzl
^3 =y(s -Vx + Pf-Pb
^4 =у(5 ~ Px ~ Py + Pzl
где s= - \|/2,о,сь
Px = (1/1/2) M/2,l,l + V|>2, l,-l),
py = (l/l^)(v|/2tlfl-v|/2,1,_1)
Pz = 4/2,1,0-
На рис. 27-9 показана комбинация
функций v|/2,o,o и v|/2, i,i, приводящая
к электронному облаку, вытянутому
в одном направлении. На этом рисунке
v|/Sp= *1>2, о, о + *1>2,1, 1 • Заметим, что, за
исключением небольшой центральной
области, волновая функция \|/2 0 0
отрицательна в любом направлении, тогда как \|/2, i, i
положительна в положительном
направлении оси z и отрицательна в обратном.
Следовательно, \|/2, о, о и ^2, i, i имеют
противоположные знаки в "положительном
направлении оси z, что приводит к их
взаимному ослаблению, тогда как в
отрицательном направлении они усиливают
друг друга. Сложение волновых функций
отдельных атомов, приводящее к
образованию направленных лепестков,
называется гибридизацией. Электронное облако на

488 гл- 27- АТОМНАЯ ФИЗИКА
Рис. 27-9. ф2,0,о + Фг. l.i = *v КонтУРы
электронной плотности. Заштрихованная область
соответствует максимуму электронной
плотности (в пределах 40%). Знаки « + » и « — »
указывают полярность волновой функции, до того
как она возведена в квадрат. [С любезного
разрешения проф. Дж. Джерхолда.]
рис. 27-9 называется sp-орбиталью, а
четыре облака на рис. 27-8 называются sp3-op-
биталями.
Учитывая это, получаем следующее выражение:
^2рх =
2r „-Tit
]fla
]/la
-г/а
cosGv
где 0х-угол между вектором г и осью х. Это
выражение по виду аналогично выражению для
^2, 1, о = (r/a)e~r,2acos 0Z, где 0Z-обычный
полярный угол. Мы видим также, что ф2рх сим_
метрична относительно оси х, тогда как ф2рг
симметрична относительно оси z. Следовательно,
ф2рх имеет форму гантели, ориентированной
вдоль оси х.
*Пример 4. Из табл. 26-2 и рис. 26-7 гл. 26
видно, что волновая функция ф2рг = фг, i, о имеет
форму гантели, ось которой направлена вдоль
оси z. Требуется показать, что функция
ЬР = —г Mb1,1 + Фг, 1, - О
х /2
соответствует той же форме гантели, но ось
которой направлена вдоль оси х.
Решение: Используя табл. 26-2, можно написать
Фа
-e-r/flsin0(el4p + e-i<p).
]/2а
Поскольку coscp = (е1(р + е~1(р)/2,
ф2Р = г- е"^ sin 0 cos ср.
у2а
Из рис. 27-10 следует, что sin 0 = р/r и cos ф =
= х/р, и произведение этих величин дает х/г.
Рис. 27-10. Радиус-вектор г точки Р составляет
угол 0Z с осью z и угол Qx с осью х (р-проекция
вектора г на плоскость ху).

Основные выводы
Физические и химические свойства
элементов обнаруживают поразительное
сходство в группах из 2, 8, 8, 18, 18, 32, 32
элементов. Группы, содержащие 2, 8, 18, 32
элемента, можно получить на основе
стоячих электронных волн или орбиталей
атома водорода и принципа Паули, согласно
которому в данном состоянии может
находиться лишь один электрон. Поскольку
у электронов имеется собственный момент
импульса, равный Й/2, каждой орбитали
соответствуют два разрешенных
состояния.
Свойства элементов, такие, как
валентность и ионизационный потенциал, можно
объяснить с помощью некоторых
полуколичественных рассуждений, используя во-
дородоподобные стоячие волны с
энергиями связи (13,6/n2)Z^ эВ, где Zm-
«средний» заряд центральной части атома, в
поле которого находится рассматриваемый
электрон.
При данном п электроны с более
высокими / расположены дальше от ядра и
«видят» меньший заряд 2эфф и, следовательно,
связаны слабее. Поэтому энергетические
уровни с более высокими / группируются
с уровнями, соответствующими более
высоким п, но меньшим /, так что количество
элементов в группах образует
последовательность чисел 2, 8, 8, 18, 18, 32, 32.
Рентгеновское излучение представляет
собой фотоны, энергия которых выше
100 эВ и которые испускаются тяжелыми
атомами при отсутствии у них внутренних
электронов. Внешние электроны быстро
переходят на более низкие орбиты и
заполняют свободное состояние. Электрон на К-
оболочке имеет энергию около 13,6 х
х (Z — 2)2 эВ; это максимальная энергия,
которую может иметь рентгеновское
излучение.
Атомы удерживаются в молекулах за
счет либо ионной, либо ковалентной связи.
В случае ионной связи потенциальная
энергия системы, состоящей из
положительного и отрицательного ионов, U я — k0 e2/R,
где R-расстояние между центрами ионов.
В случае ковалентной связи атомы
обобществляют одни и те же внешние
электроны.
ЗАДАЧИ 489
Упражнения
1. С помощью рис. 27-1 определите
межатомное расстояние в жидком натрии.
Проделайте то же для калия.
2. Сколько электронов отвечает главному
квантовому числу п = 4 в тяжелом атоме,
таком, как, например, атом урана? Сколько
у него электронов с п = 5?
3. Какие линии в спектре иона Li++ можно
обнаружить глазом?
4. Какова величина Z3$$ для внешнего
электрона в ионе F ~ ? (Воспользуйтесь
измеренным значением электронного сродства.)
5. Некоторые линии в спектре Не+
соответствуют видимой области. Найдите их длины
волн.
6. Какова величина гэфф для электронов в ионе
Li+ ? (Воспользуйтесь измеренным
значением энергии связи.)
7. Найдите максимальную энергию
рентгеновского излучения, испускаемого ураном.
8. Длина волны рентгеновского излучения,
имеющего максимальную энергию и
испускаемого неизвестным образцом, составляет
2,16 А. Каков атомный номер Z элемента,
входящего в состав образца?
9. Сколько энергии надо затратить, чтобы
разделить молекулу водорода Н2 на два
свободных протона и два свободных
электрона?
10. Какая электронная конфигурация ожидается
для элемента с номером 107?
Задачи
11. Дополните рис. 27-5 данными о восьмой
группе периодичности. Сколько элементов
будет в этой группе?
12. Результирующая энергия связи молекулы
LiF равна 4,3 эВ. Чему равна молярная
теплота образования этого вещества?
13. В принятой для рентгеновского излучения
терминологии восемь электронов с п = 2
находятся на L-оболочке.
а) Вычислите 2эфф для 2р-электрона с
L-оболочки. (Считайте, что 25-электроны
находятся внутри.)
б) По той же терминологии при переходе
2р-электрона на К-оболочку возникает
-Ка-линия спектра. Определите длины
волн, отвечающие Ка-линиям в спектрах
алюминия и свинца.
14. Пусть состояние атома водорода
соответствует п = 10, 1 = 9. Каково отношение
вероятности найти при фиксированном г
электрон под углом 70° к той же вероятности
для угла 90° ? Можно воспользоваться
таблицей 26-2. Изобразите форму электронного

490 ГЛ. 27. АТОМНАЯ ФИЗИКА
облака. Углы отсчитываются от оси, вдоль
которой направлен момент импульса.
15. Покажите, что волновая функция \|/2Ру =
= (1/1/2) (\|/2,1,1 — \|/2,1, -1) имеет фо£му
гантели, как и \|/2} i, о» но вытянутую вдоль
оси у, а не вдоль оси z.
16. а) Найдите выражение для \|/2, i, i через ]fiPx
И V|/2p,-
б) Как запишутся волновые функции \|/ь \|/2,
\|/3 и \|/4, приведенные в § 5, через \|/2,0,о>
♦2.1.1. ^2,1,0 И \|/2,1,-1?
17. Измеренные длины волн Ка-линий в случае
А1 и РЬ соответственно равны 8,3 и .0,17 А.
Найдите 2эфф для 2р-электронов атомов А1
и РЬ.
18. В HJ протоны находятся на расстоянии
друг от друга 1,06 А. Каким было бы это
расстояние, если бы протоны связывал
мюон ц~ (масса которого в 207 раз больше
массы электрона)?
19. Свойства элементов повторяются в группах,
содержащих 2, 8, 8, 18, 18, 32, 32, ...
элементов. Сколько элементов было бы в
следующей группе, начиная с Z = 119? (Ядра
считаются стабильными.)

КОНДЕНСИРОВАННЫЕ СРЕДЫ
Если достаточно сильно охладить
вещество (элемент или соединение),
находящееся в газообразном или жидком состоянии,
то оно переходит в твердое состояние,
характеризующееся относительным
постоянством взаимного расположения атомов1*.
Раздел физики, изучающий свойства
твердых тел и жидкостей и происходящие
в них явления, называется физикой
конденсированных сред или физикой твердого
тела и в настоящее время представляет
собой одну из основных областей физических
исследований.
Физика конденсированных сред
занимается не только глубоким изучением
сущности явлений, но и использует
результаты этого изучения для предсказания новых
явлений, которые вряд ли иначе были бы
обнаружены.
Большинство элементов и соединений
обнаруживают под микроскопом
кристаллическую структуру. Зерна поваренной
соли (NaCl) под микроскопом имеют вид
идеальных кубиков. Многие твердые
вещества, хотя внешне и не похожи на
кристаллы, в действительности состоят из
множества мельчайших кристалликов (это
так называемая поликристаллическая
структура). Механизм, связывающий
атомы в молекулы, может приводить
к образованию безграничных твердых
периодических структур, которые можно
рассматривать как сверхмолекулы. Подобно
ионным и ковалентным молекулам,
существуют ионные и ковалентные кристаллы.
Некоторые твердые тела существуют
благодаря еще одному, третьему типу сзязи,
а именно металлической связи, которая не
1} Исключение составляет гелий,
остающийся жидким даже при Т = О К. Твердая фаза
гелия образуется только при р > 25 алы-Прим.
перев.
имеет аналога в двухатомных молекулах.
Мы рассмотрим все три типа связи, уделив
особое внимание металлам и
полупроводникам. Обсудим также квантовомеханиче-
ские явления в больших масштабах, такие,
как сверхпроводимость,, сверхтекучесть
и автоэлектронная эмиссия. В § 5 мы
попытаемся дать представление о том, какое
влияние на современную технику и
цивилизацию оказала физика полупроводников.
В дополнение к общей теории мы обсудим
ряд конкретных применений
полупроводников: полупроводниковые диоды,
транзисторы, светодиоды, твердотельные лазеры,
фотоэлементы, солнечные батареи, термис-
торы, интегральные схемы и т. д. Без
глубокого понимания теории твердого тела
эти и ряд других важных приложений
были бы просто невозможны.
§ 1. Типы связи
ИОННАЯ связь
Подобно ионным и ковалентным
молекулам, существуют ионные и ковалентные
кристаллы. На рис. 28-1 изображена
структура ионного кристалла NaCl. Отметим,
что ближайшими соседями у каждого иона
Na+ являются шесть ионов С1~. Этому
пространственному расположению ионов
Na+ и С1~ отвечает наименьшая энергия
(т.е. при образовании такой конфигурации
выделяется максимальная энергия), чем
и объясняется то, что при охлаждении
ниже точки плавления NaCl и многие другие
вещества стремятся образовывать чистые
кристаллы. С ростом температуры
тепловая кинетическая энергия в конечном счете
оказывается достаточной, чтобы
преодолеть связь в правильном кристалле, и
кристалл расплавляется.

492
ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
0,95
<t
\1
Na+
3,*А С1"
0,95А^ Щс
49
^
Na+
С1-
Рис. 28-1. Кристаллическая структура NaCl.
Положения центров атомов Na и С1 отмечены
кружками, а-расположение центров атомов;
б-расположение самих атомов.
КОВАЛЕНТНАЯ СВЯЗЬ
В предыдущей главе мы показали, что
углерод, имеющий валентность 4, охотно
образует ковалентные связи с четырьмя
электронами других атомов. Примером
такой связи может служить молекула СН4
(см. рис. 27-8). Разновидностью твердого
углерода с наиболее сильной связью
является алмаз (рис. 28-2). Если четыре
атома водорода (см. рис. 27-8) заменить
атомами углерода, то получится
элементарная ячейка кристаллической структуры
алмаза (рис. 28-2). Структуры,
аналогичные алмазу, образуют при
кристаллизации и другие четырехвалентные элементы,
такие, как германий, кремний и олово. Для
валентных электронов кристалла германия
были вычислены контуры постоянной
плотности заряда. Из рис. 28-3, а мы
видим, что электронные облака концентри-
Рис. 28-2. Кристаллическая структура алмаза.
Каждый атом имеет по четыре ближайших
соседа.
руются посередине между каждой парой
атомов германия, образуя ковалентные
связи.
МЕТАЛЛИЧЕСКАЯ СВЯЗЬ
Допустим теперь, что один из
валентных электронов перешел на более
высокий энергетический уровень. Можно
ожидать, что его волновая функция станет
более размытой. Но при этом электрон
окажется ближе к соседним атомам.
Поскольку остовы (коры) этих атомов
обладают положительным зарядом и
притягивают электрон, то они будут еще больше
размывать электронную волновую
функцию, что приведет к перекрытию ее с
соседней. В результате такого эффекта
волновая функция окажется равномерно
размытой по всему кристаллу (с некоторыми
сгущениями вблизи каждого
притягивающего атомного остова). На рис. 28-3, б
приведены контуры плотности заряда для
состояний с более высокой энергией.
Заметим, что плотность заряда в возбужденном
состоянии изменяется не более чем в
3 раза, причем минимумы находятся
посередине между любой парой атомных
остовов, тогда как на рис. 28-3, а заряд четко
локализован между каждой парой атомных
остовов, а его плотность изменяется в 28
раз, что характерно для ковалентной связи.

§ 1. типы связи
Рис. 28-3. а-контуры
плотности отрицательного заряда,
усредненного по состояниям
валентного электрона в кристалле
германия; б-то же для
следующих возбужденных состояний.
[С любезного разрешения проф.
М. Коэна.]
Отсюда можно заключить, что, как только
валентный электрон в кристалле германия
переходит на следующий более высокий
энергетический уровень, он ведет себя как
свободный электрон (т.е. электрон
проводимости). В германии, для того чтобы
поднять валентный электрон на следующий
более высокий уровень, необходима
энергия 0,72 эВ. Иначе говоря, между
валентным состоянием и состоянием
проводимости имеется энергетическая щель
шириной 0,72 эВ. Такие вещества называются
полупроводниками, поскольку при
нормальных условиях они имеют
незначительное количество электронов проводимости.
В § 4 мы вернемся к изучению германия
и других полупроводников.
В кристаллах, построенных из
одновалентных атомов (таких, как Li, Na, К),
плотность заряда распределяется
аналогично тому, как это показано на
рис. 28-3,6. Кристаллы с таким типом
связи называются металлами. Металлическая
связь возникает, когда атомы сближаются
на расстояние, меньшее размеров облака
внешних электронов. Вследствие принципа
Паули такая конфигурация приводит к
возрастанию энергии внешних электронов.
Однако в случае металлов эта энергия
будет все же меньше, чем если бы атомы
находились на больших расстояниях друг от
друга.
Если атомы сближаются настолько, что
их внутренние заполненные оболочки
соприкасаются, то соседние ядра попадают
в пределы области, занимаемой облаком
внешних электронов у свободного атома.
В таком случае внешний электрон будет
притягиваться соседними ядрами, что
приведет к возрастанию его энергии связи и
к еще большему увеличению размеров
соответствующего облака. Это позволяет
электрону приближаться к удаленным
соседям, которые в свою очередь еще больше
«размывают» электронное облако. В
конечном итоге волновая функция каждого
из внешних электронов равномерно
распределяется по всему кристаллу!
Нетрудно видеть, что квантовая теория
вполне разумно объясняет, почему
металлы проводят электричество, а другие
вещества не проводят (или почти не прово-

494 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
дят). То, что в металлах приходится по
крайней мере один «свободный» электрон
на каждый атом, обусловлено отчасти
волновой природой электронов. Эти
«свободные» электроны, или электроны
проводимости, не связаны с каким-то
определенным атомом и могут свободно
перемещаться по металлу в любом направлении.
В ионных и ковалентных кристаллах
внешние электроны связаны
(локализованы); поэтому такие кристаллы обычно не
проводят электричество. Их называют
изоляторами. Тот факт, что в кристаллах
чистых металлов могут существовать
свободные электроны, следует рассматривать
как квантовомеханическое явление в
больших масштабах. С точки зрения
классической физики каждый электрон
принадлежал бы своему собственному атому.
§ 2. Теория свободных электронов
в металлах
В первом приближении силы
притяжения, действующие со стороны ядра на
внешний электрон, можно усреднить
и представить в виде постоянного
потенциала притяжения: обозначим его U0. На
рис. 28-4 приведена эта усредненная
потенциальная энергия, имеющая вид
потенциальной ямы. Каждый внешний электрон
описывается стоячей волной, ограниченной
Внутри
Снаружи
О ♦
-Щх)
ш
-%
Заполненные
* энергетические
уровни
Рис. 28-4. Потенциальная энергия внешнего
электрона при его переходе через поверхность
металла приближенно показана сплошной
линией. На рисунке также приведены уровень
Ферми Kf и работа выхода W0.
размерами этой потенциальной ямы. Мы
видим теперь, что приведенный в гл. 25
гипотетический пример электрона в ящике не
выглядит столь уж надуманным. В этом
приближении металл объемом К можно
рассматривать как ящик того же объема К,
содержащий п свободных электронов.
Согласно принципу Паули, в каждом из
состояний, описываемых выражением (25-11),
может находиться не более двух
электронов. Все п электронов стремятся заполнить
низшие энергетические состояния, образуя
так называемый ферми-газ. Такой газ
обладает интересными свойствами,
необычными с точки зрения классической
физики, на которые впервые обратил внимание
Энрико Ферми. Данные п электронов
заполнят все энергетические состояния от
низшего до состояния с кинетической
энергией Kf, называемого уровнем Ферми.
Величина Kf должна зависеть от п и объема
К. Мы сейчас покажем, что она зависит
только от отношения 91 = и/К,
определяющего число электронов проводимости
в единице объема. Кинетическая энергия
частицы, заключенной в ящике, называется
ее энергией Ферми.
Расчеты упростятся, если выбрать ящик
в форме куба объемом L3. Если в этот
ящик поместить один-единственный
электрон, то он быстро излучит избыток
энергии и перейдет на низший энергетический
уровень. На тот же уровень перейдет
и второй электрон. Согласно принципу
Паули, третий электрон будет вынужден
занять следующий, более высокий, т. е.
второй энергетический уровень. Пятый
электрон займет третий энергетический
уровень и т.д. Если в ящике имеется всего
и электронов, то уровню Ферми отвечает
энергия уровня с номером и/2. Как
указывалось в § 2 гл. 26, уровни энергии в
трехмерном ящике зависят от трех квантовых
чисел пх, пу, п2, причем
2Lpx
2LPy
«* = — • ",- h ■
i 9.
-(и* + Пу + nl).
и* =
h '
Р* =
AV
Пусть pf- импульс электрона на уровне
Ферми. Тогда pf- максимально возможное
значение рх любого из и электронов в ящи-

§ 2. ТЕОРИЯ СВОБОДНЫХ ЭЛЕКТРОНОВ В МЕТАЛЛАХ 495
ке. В этом случае максимальное значение
пх, соответствующее заполненному
состоянию, равно (nx)f = ILpJh; то же самое
имеем для пу и п2. Чтобы получить полное
число заполненных состояний, нам надо
сосчитать все возможные комбинации из
трех чисел пх, пу и nz, каждое из которых не
превышает значения 2Lpf/h. Такой подсчет
был бы крайне утомительным, но можно
воспользоваться рис. 28-5. На этом
рисунке для удобства пх, пу и nz отсчитываются
через интервалы 1 см соответственно
вдоль осей х, у и z. При этом любое
возможное состояние (или набор трех целых
чисел) изображается точкой в
пространстве. Эти точки образуют кубическую
решетку с ребром ячейки, равным 1 см.
Заметим, что число таких кубических ячеек
равно числу точек. Теперь воспользуемся
тем, что заполненные состояния находятся
>(1/8)(4/3)яД3=(я/6)
Рис. 28-5. Верхний квадрант сферы радиусом
R = (2L/h)pf.
внутри области радиусом R = 2Lpf/h.
Тогда полное число заполненных состояний
будет численно равно количеству
кубических ячеек, ограниченных сферической
поверхностью, показанной на рис. 28-5.
Поскольку объем, ограниченный этой
поверхностью, равен 1/8 объема сферы, мы
можем написать
Полное число состояний =
2Lp/\
Pf
3h3
Поскольку в каждом состоянии йаходятся
два электрона, полное число электронов
_ SnVp/
3h3
(28-1)
где V = L3-объем ящика.
Из (28-1) получаем следующее
выражение для pf:
/З/?3 /?\1/3 /
р _ / \ (граничный импульс
f \ 8тс У) Ферми). (28-2)
Подстановка этого результата в
выражение Kf= pj/2m дает
f 8m 1 %
2/3
(граничная энергия
Ферми). (28-3)
Эта величина не зависит ни от конкретной
формы, ни от объема данного образца
металла. Она зависит лишь от того,
насколько плотно «упакованы» свободные
электроны.
Пример 1. Литий имеет плотность 0,534 г/см3.
Каково значение граничной энергии Ферми в эВ
у электронов проводимости лития?
Решение: Атом лития имеет лишь один
внешний электрон; следовательно, 91 равно числу
атомов в 1 см3. Поскольку атомная масса лития
6,94, то
91 = (0,534 г/см3) (6,02 х
х 1023 атом/моль) ( -т^-Л—г-
7 \ 6,94 г/\
= 4,63 • 1022 *™ = 4,63 • 1028 3JieKt3poH .
Используя соотношение (28-3), получаем
= 7)55-10-19Дж = 4,7эВ.

496
ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
* Пример 2. Найдем выражение для средней
кинетической энергии К в зависимости от Kf.
Полная энергия Ферми в образце, содержащем п
электронов проводимости, равна пК.
Решение: Если dn-число электронов, импульсы
которых находятся в интервале dp, то по
определению средняя кинетическая энергия
-_ \Kip)dn
Дифференцирование выражения (28-1) дает
8тг Vp2dp
dn — -= .
Таким образом,
\КрЧр S(p2/2m)p4p
К=-
\p2dp
[Р3/3]&
\1'
1 [P5/5ff
2т р}/3
-ь
* Пример 3. Если плотность электронов
чрезвычайно высока (как в случае некоторых
астрономических объектов), то практически все
электроны будут ультрарелятивистскими;
иными словами, Е = К = рс. Чему в этом случае
равна энергия Kfi выраженная через % и
какова средняя кинетическая энергия К ?
Решение: Релятивистское значение граничной
энергии Ферми получаем умножением обеих
частей выражения (28-2) на скорость света с:
Kf = cPf = c^j'\
_ jKdn J{cp)p4p _ tf/4
" J A» ~ \v4p ~°~йЛ'
w
Потенциальная энергия электрона
внутри металла имеет приблизительно вид,
показанный на рис. 28-4. За нулевую мы
выбрали энергию покоящегося свободного
электрона вне металла. Энергетические
уровни электронов ферми-газа обозначены
тонкими горизонтальными линиями,
начинающимися при — Uо и заполняющими
интервал энергии Kf от дна
потенциальной ямы. При этом минимальная энергия,
необходимая для удаления электрона из
металла, равна величине U0 — Kf9
определяемой как работа выхода W0 (см. § 2
гл. 24, посвященный фотоэффекту):
W0 = U0- Kf.
Хотя кинетическая энергия электрона на
уровне Ферми равна Kf, его полная
энергия
Ef = Kf+U = Kf + (-U0) =
= - (U0 - К,),
Ef = - W0.
Следовательно, на энергетической шкале
уровень Ферми соответствует величине
— W0. В действительности строго
определенное значение работы выхода
имеется только при температуре
абсолютного нуля. При температуре Т К
электроны находятся в тепловом равновесии,
поэтому к их энергии Ферми добавляется
еще некоторая тепловая энергия. В гл. 13
мы показали, что средняя тепловая
энергия, приходящаяся на одну частицу
идеального газа, составляет (3/2) к Т. В ферми-газе
тепловую энергию могут иметь лишь
частицы, кинетическая энергия которых
близка к Kf. Таким образом, кинетическая
энергия некоторой части электронов будет
чуть больше Kf; при комнатной
температуре кТ = 0,025 эВ, в то время как
величины Kf и W0 оказываются порядка
нескольких эВ.
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
Стоит только соединить два разных
металла, как между ними возникает разность
потенциалов, называемая контактной.
Поскольку нам теперь известно, что такое
уровень Ферми, это явление можно
объяснить, используя диаграммы
потенциальных ям. Рассмотрим два различных
металла А и В (рис. 28-6, а). Пусть уровень
Ферми в металле А составляет — 2 эВ, а
в металле В — 3 эВ; при этом
потенциальная энергия электронов внутри металла
А равна -4 эВ, а внутри металла В
— 6 эВ (все эти величины измеряются
относительно энергии покоящегося
электрона, находящегося вне металла). На
рис. 28-6,6 показано, что происходит сразу
после того, как оба металла были
приведены в соприкосновение. Электроны из ме-

£,эВ
§ 3 ЭЛЕКТРОПРОВОДНОСТЬ
497
А
V
-1
-2
, -з
-4
-5
-6
В
ь- J
-6 ^
f-fTu
-6
Рис. 28-6. При соединении двух различных
металлов электроны переходят из одного металла
в другой, пока уровни Ферми не станут
одинаковыми, как показано на рисе.
талла А могут перейти в металл В, где
имеются свободные состояния с более
низкой энергией. Но как только электроны
перейдут в металл В, он быстро
приобретет отрицательный заряд по отношению
к А. Теперь уже, чтобы отрицательный
электрон мог попасть в отрицательно
заряженный металл В, требуется совершить
большую работу; это означает, что
диаграмма потенциальной энергии металла
В сместится вверх относительно
диаграммы металла А. Это смещение будет
происходить до тех пор, пока уровни
Ферми не сравняются (рис. 28-6, в). Такое
равновесие достигается после того, как очень
небольшая часть электронов проводимости
перейдет из А в В. Из рис. 28-6, в следует,
что разность потенциальных энергий AU
равна исходной разнице в уровнях Ферми;
таким образом, если уровни Ферми двух
металлов различаются на 1 эВ, то при
соединении этих металлов между ними
возникает разность потенциалов 1 В.
§ 3. Электропроводность
В идеальной кристаллической решетке
металла, как мы показали, внешние
электроны ведут себя подобно свободным
электронам в ящике. Поскольку эти
электроны могут переносить электрический
ток, следует ожидать, что электрическое
сопротивление идеального металла
должно быть равным нулю. Однако в
реальных металлах всегда присутствуют
примеси и дефекты решетки, с которыми
свободный электрон может
взаимодействовать и терять при этом свою энергию.
Электрическое сопротивление (измеряется
в омах) зависит от средней длины
свободного пробега электрона между
столкновениями с примесями или дефектами.
Основываясь на этой теории электрического
сопротивления, нетрудно вывести закон
Ома по аналогии с выводом в § 2 гл. 17.
Согласно закону Ома, сопротивление
зависит лишь от температуры и совсем не
зависит от величины тока. В соответствии
с формулой (17-5) удельное сопротивление
можно записать в виде
Р =
е2Ш
Отсюда нетрудно показать, что с ростом
температуры электрическое сопротивление
увеличивается. Естественным источником
дефектов решетки является колебательное
движение атомов, которое существует
всегда, поскольку кристалл не находится при
температуре абсолютного нуля. Поэтому
с ростом температуры средняя длина
свободного пробега L должна уменьшаться.
Отсюда можно сделать вывод, что
сопротивление чистого металла будет тем боль-

498 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
ше, чем интенсивнее тепловое движение
атомов. Согласно теории, при стремлении
температуры к абсолютному нулю
сопротивление чистого кристалла должно
стремиться к нулю. Это подтверждается
экспериментом.
СВЕРХПРОВОДИМОСТЬ
То, что при температуре абсолютного
нуля чистый металл может иметь равное
нулю сопротивление, т. е. бесконечно
большую проводимость, не следует путать
с другим квантовомеханическим явлением,
а именно со сверхпроводимостью. Явление
сверхпроводимости состоит в том, что при
температурах, на несколько градусов
превышающих абсолютный нуль,
проводимость становится бесконечно большой.
В действительности лишь очень небольшое
число металлов и металлических сплавов
обладает этим удивительным свойством.
У каждого сверхпроводника есть
критическая температура, выше которой металл
ведет себя как обычный проводник, а ниже
переходит в сверхпроводящее состояние.
Насколько известно, максимальная
критическая температура составляет около 20 К.
Если в сверхпроводнике создать
круговой ток, то он будет течь до тех пор, пока
система охлаждения не выйдет из строя.
Известны случаи, когда такие токи
сохранялись в лаборатории на протяжении
нескольких лет. Квантовомеханическое
объяснение сверхпроводимости представляет
собой одну из актуальных теоретических
проблем физики твердого тела. В
последнее время в понимании этого одного из
наиболее замечательных явлений были
достигнуты значительные успехи.
В двух словах теория заключается в
следующем. Ниже определенной температуры
преобладающую роль начинает играть не
тепловое движение решетки, возмущающее
электрон, а возмущение самой решетки
электроном проводимости. При этом
возмущение решетки электроном А повлияет
на движение электрона В, вследствие че,го
между электронами А и В возникнет
эффективная сила притяжения. В некоторых
веществах эта сила превосходит силу
электростатического отталкивания.
Следовательно, если оба электрона движутся
в одном и том же направлении (существует
результирующий ток), то этому будет
соответствовать состояние с наинизшей
энергией, причем электроны должны и далее
оставаться в этом состоянии, поскольку
для них не существует состояний с более
низкой энергией. Отсюда мы делаем
вывод, что будет существовать вечный
результирующий ток в направлении движения
электронов.
В настоящее время разрабатывается ряд
интересных проектов практического
применения сверхпроводимости. Мы обсудим
три из них: 1) магниты, создающие
сильные поля, 2) линии электропередач
с малыми потерями и 3)
высокоскоростные транспортные устройства.
Уже создано множество
электромагнитов со сверхпроводящими обмотками.
Эти магниты обеспечивают поля до
~ 100000 гаусс (10 тесла) при полном
отсутствии электрических потерь в обмотках.
Имеются лишь затраты энергии на
охлаждающие системы.
Как было показано в § 4 гл. 19,
основные потери энергии в линиях
электропередачи составляют I2R.
Сверхпроводящие линии передач постоянного тока
будут свободны от потерь электроэнергии,
поскольку в них R = 0. На рис. 28-7
показан сверхпроводящий кабель,
сконструированный для передачи переменного тока
мощностью 4 • 109 Вт. Такой кабель
должен быть дешевле традиционного
подземного кабеля и обеспечивать более низкие
потери энергии. Если когда-либо
пустынный район США будет использован для
снабжения страны энергией, получаемой
здесь из солнечных лучей, то для передачи
ее из этого района на очень большие
расстояния потребуются сверхпроводящие
линии электропередачи. Когда стоимость
солнечной энергии станет сравнима со
стоимостью энергии, производимой
атомными или тепловыми станциями,
окончательное решение проблемы может
быть получено на основе использования
солнечной энергии и сверхпроводящих
линий электропередачи. При этом возникает
ряд экономических вопросов, как,
например, необходимость в больших
количествах жидкого гелия, идущего на
охлаждение. В настоящее время газообразный

Наружная
стальная
трубка
Вакуум
§ 4. ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ 499
Сверхизоляция
Гелиевые
трубки
Азотопроводы
Изолирующая
пластинка
Радиационный
экран
Прокладка
Азотопроводы
Распорка
Опора
проводника
Внутренний
проводник
Диэлектрик
Внешний
проводник
Гелий
Гелиевая
трубка
ромежуточный
провод
Рис. 28-7. Сечение полугибкого
сверхпроводящего кабеля переменного тока. Кабель с
внешним диаметром 4,7 см рассчитан на напряжение
275 кВ. Рисунок дает представление о
разработках, ведущихся в ряде лабораторий. С помощью
одного из таких кабелей можно передавать
мощность 4 • 109 Вт.
гелий выпускают в атмосферу, и он в
конечном счете покидает Землю (тепловые
скорости молекул гелия сравнимы со
второй космической скоростью). На Земле
запасы гелия весьма ограниченны, и в
настоящее время не существует приемлемой
программы его сбережения. Если бы
органы государственного планирования
заглянули подальше в будущее, то, вероятно,
уже сейчас были бы приняты меры для
сохранности гелия.
В заключение обсудим не менее важный
вопрос о применении сверхпроводимости
на транспорте. Один из проектов
высокоскоростного наземного транспорта для
перевозки пассажиров требует, чтобы
транспортное средство парило над
дорогой. В этом случае возможны скорости до
500 км/ч. Предположим, что каждый
пассажирский вагон снабжен сверхпроводящими
обмотками, расположенными поблизости
от полотна «дороги» из проводящего
материала. Тогда, как только вагон достигнет
определенной скорости, между током,
наводимым в полотне дороги, и током
в сверхпроводящих обмотках возникнет
сила отталкивания, достаточная для того,
чтобы вагон оказался парящим в воздухе.
В настоящее время такие системы
разрабатываются главным образом в Японии
и ФРГ (рис. 28-8). Развитие эффективного
высокоскоростного общественного
транспорта необходимо, чтобы положить конец
ненужной трате ограниченных мировых
запасов бензина на личные автомобили.
§ 4. Зонная теория твердых тел
До сих пор при описании состояний
электрона в металле мы пренебрегали
периодическим изменением потенциальной

ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
ЧУ
Рис. 28-8. Поезд, разрабатываемый
западногерманской фирмой АЭГ-ББС-Сименс, в
представлении художника. Показаны сверхпроводящие
обмотки, обеспечивающие «парение» в воздухе
и одновременно направляющие движение, а
также обмотки индукционного мотора. Отметим,
что рельсы проложены вдоль всей трассы. [С
любезного разрешения Исследовательских
лабораторий Сименса, Эрланген, ФРГ.]
энергии электрона, связанным с его
взаимодействием с атомными остовами. Мы
предполагали, что дно потенциальной ямы
(рис. 28-4) плоское и не имеет
периодических углублений. Если же учесть такие
периодические изменения потенциальной
энергии, то окажется, что возможные
значения энергии образуют ряд зон. Почему
это так происходит, мы объясним на
следующих примерах.
В качестве первого примера
рассмотрим две одномерные прямоугольные
потенциальные ямы глубиной U0 и шириной
х0. Они соответствуют эффекту, который
дают два последовательно расположенных
атомных остова. Мы покажем, что
первоначальный энергетический уровень
основного состояния, существовавший в каждой
из ям, превратится в «зону» с двумя
значениями энергии. В случае же п
последовательно расположенных прямоугольных ям
основному состоянию будет
соответствовать зона, содержащая п энергетических
уровней. В соответствии с (25-14) энергии
уровней в отдельной прямоугольной яме
можно записать приближенно в виде
г ~ "2 h2
Еп^—^——, где L-ширина ямы.
L 8т
Если теперь, как показано на рис. 28-9, а,
соединить две ямы в одну, но с удвоенной
шириной (L = 2х0), то мы получим
4*0 8т '

§ 4. ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ 501
*1
1
8тхо
и £9
Smxl '
На рис. 28-9,6 яма «двойной ширины»
поделена на две соседствующие
одинаковые ямы. Заметим, что энергии,
отвечающие волновым функциям y\f1 и \|/2,
сблизились друг с другом. На рис. 28-9,в обе
ямы раздвинуты настолько, что стоячие
волны в каждой из них по существу
совпадают с низшей стоячей волной в
отдельной яме; следовательно,
Si
£2 =0,0813 U0
Е. =0,0204 U0
-*о-
Е7 =0,0750 U0
\
0 Е. =0,0543 U*
Е2 =0,0683 1/0
"К *
Е2 =0,0682 Un
*У<—У'
Рис. 28-9. а -первые два энергетических уровня
в прямоугольной яме шириной 2х0
составленной из двух ям шириной х0 каждая; показаны
также соответствующие стоячие волны. U0 =
= 50И2/тхо; б-две ямы, изображенные на
рисунке я, раздвигаются на расстояние х0/10;
заметим, что энергетические уровни сближаются;
в-при удалении двух ям на достаточно
большое расстояние друг от друга оба
энергетических уровня почти сливаются, а волновая
функция в пределах каждой ямы практически
совпадает с волновой функцией основного состояния
в случае отдельной ямы,
8тХо
Таким образом, мы показали, что при
сближении двух ям, изобоаженных на
рис. 28-9,в, уровни энергии, отвечающие х)^
и \|/2, раздвигаются. Состояние с
наинизшей энергией в случае отдельной ямы
превращается в два состояния с различными
энергиями в случае двух ям, причем чем
меньше расстояние между ямами, тем
сильнее раздвинуты соответствующие
энергетические уровни.
Повторим это рассмотрение для случая
четырех ям, расположенных друг за
другом (рис. 28-10). Ямы на рис. а можно
рассматривать как одну яму, но учетверенной
ширины (L = 4х0). В этом случае энергии
уровней даются выражением
п2 h2
Е =
16 8тхо
Если ямы несколько раздвинуть
(рис. 28-10,6), то зона, содержащая четыре
энергетических уровня, станет уже. На
рис. 28-10,в ямы разнесены на столь
большое расстояние, что соответствующие
энергии почти совпадают с энергией
основного состояния в случае отдельной ямы.
Этот результат нетрудно обобщить на
случай п расположенных друг за другом ям.
При этом в окрестности исходного уровня
должна образоваться зона из п
энергетических уровней. Увеличение числа п не
приводит к изменению ширины зоны при
условии, что расстояние между ямами
остается тем же самым. В образцах
твердого тела типичные значения п
оказываются порядка 1023, так что образованную
энергетическими уровнями зону можно
считать сплошной.
В случае реальных твердых тел
одномерную прямоугольную яму следует
заменить трехмерной потенциальной ямой
атома. При сближении п атомов каждое

502 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
ил
Е2 =0,0224^
4Х,
Е. =0,0894 U,
^^^0,0503 t/Q;
Е] =0,0056 U0
ил
Н-хЛ
£4=0.0805 UQ
X
Е2=0,0600 UQ
£,=0,0495^
Рис. 28-10. а-яма шириной 4х0,
составленная из четырех ям
шириной х0 каждая; показаны
четыре первых энергетических
уровня; б-расстояние между
ямами х0/10; в-расстояние
между ямами х0; в этом случае
все четыре энергетических
уровня почти сливаются.

§ 4. ЗОННАЯ ТЕОРИЯ ТВЕРДЫХ ТЕЛ 503
атомное состояние будет превращаться
в зону, содержащую п соответствующих
энергетических уровней. Чем ближе атомы
расположены друг к другу, тем шире зоны
(рис. 28-11).
Пример 4. Предположим, что имеется цепочка
из 100 прямоугольных ям шириной х0 = 1А
и глубиной U0 = 378 эВ.
а) Пусть расстояние между ямами также
равно 1А. Найдите кинетические энергии первых
100 уровней.
о б) Пусть расстояние между ямами равно
0,1 А. Найдите энергии первого, пятидесятого
и сотого уровней.
Решение: Глубина ямы та же, что и в случае
рис. 28-10, для которого U0 = 50h2/mxl =
= 378 эВ. В вопросе «а» расстояние между
ямами такое же, как и на рис. 28-10,в, где зона,
отвечающая основному состоянию (первые 100
энергетических уровней), соответствует
К « 0,068 Uо = 25,7 эВ. В вопросе «б»
расстояние между ямами такое же, как в случае
рис. 28-10,6. При этом зона простирается от
0,0495 Uо до 0,0805 U0 или от 18,7 до 30,4 эВ.
Следовательно, Kt = 18,7 эВ, а Кюо = 30,4 эВ.
Уровень К50 лежит приблизительно посередине
между Кх и Кюо\ таким образом, К50«
* 24,5 эВ.
Для металлической связи характерно
столь близкое расположение
потенциальных ям, что зона, в которой
находится внешний электрон, перекрывается с
другими зонами. Это справедливо для
энергетических зон металлического натрия,
изображенных на рис. 28-11. Как и в модели
свободных электронов, в металле в данном
случае имеется неограниченное число
свободных состояний, которые может занять
внешний электрон.
В некоторых ковалентных- кристаллах,
например в кремнии и германии,
расстояние между атомами таково, что зоны,
содержащие валентные электроны
(валентные зоны), не перекрываются.
Оказывается, что у кремния заполненная
валентная зона и следующая за ней более
высокая пустая зона разделены
запрещенной зоной шириной 1,09 эВ. В случае
германия ширина соответствующей
запрещенной зоны составляет 0,72 эВ. Для того
чтобы через кремний и германий мог
протекать электрический ток, в пустой зоне
должно иметься некоторое количество
электронов. При комнатной температуре
количество электронов, попавших в эту
зону проводимости за счет теплового
движения, невелико. Проводимость германия
и кремния значительно ниже, чем у обыч-
Е,*Е^Ез«Е~о,№ио
Рис. 28-10 (продолжение).

504 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
-10
«
Я
о.
w -20
-30
3d
-Наблюдаемое
значение R,
Л0=3,67А
2,
10
15
Рис. 28-11. Энергетические зоны натрия в
зависимости от межатомного расстояния R. Зона 2s
располагается при —63,4 эВ, а зона Is-при
— 1041 эВ. Обе эти зоны еще уже, чем зона 2р.
[Воспроизводится из статьи: J. С. Slater, Phys.
Rev, 45, 794 (1934).]

§ 5. ФИЗИКА ПОЛУПРОВОДНИКОВ
505
Следующее
возбужденное
состояние
Валентная
зона
т
Рис. 28-12. Схематическое сравнение валентной
зоны и зоны проводимости; а -проводник,
б - полупроводник, в-диэлектрик. На рис. в
ЕА » к Т.
ного металла. Поэтому эти кристаллы
называют полупроводниками. Если же
ширина запрещенной зоны кристалла слишком
велика, так что теплового движения
недостаточно для ее преодоления, то такой
кристалл называется диэлектриком
(рис. 28-12). При абсолютном нуле чистые
кристаллы диэлектриков и даже
полупроводников обладали бы бесконечно
большим сопротивлением.
На рис. 28-3, а приведены контуры,
отвечающие значениям квадрата средней
волновой функции валентной зоны германия,
а контуры на рис. 28-3, б-квадрату средней
волновой функции зоны проводимости.
§ 5. Физика полупроводников
В данном параграфе мы не только
обсудим основные свойства
полупроводников, но и попытаемся дать представление
об их необъятных практических
применениях, совершивших революцию в
электронике и многочисленных областях
современной техники.
При тепловом возбуждении электрона,
находящегося в валентной зоне германия,
он освобождает состояние в валентной
зоне и переходит в зону проводимости,
образуя там заполненное состояние.
Незаполненное состояние, или вакансия,
образующееся при этом в валентной зоне,
называется дыркой. На рис. 28-13 показаны
электрон, перешедший в зону
проводимости, и образованная им дырка. В
присутствии внешнего электрического поля
ближайший к дырке электрон в валентной
зоне попадает в нее, оставляя при этом
новую дырку, которую заполнит следующий
соседний электрон, и т.д. Таким образом
дырка будет перемещаться в направлении,
противоположном направлению движения
электронов, и вести себя как носитель
положительного заряда. Любая дырка может
рассматриваться как электрон
проводимости с положительным зарядом.
Если углубиться в статистическую
механику несколько больше, чем это
позволяют рамки нашей книги, то можно было
Электрон
проводимости
нэ-
Рис. 28-13. а-возбужденный электрон из
валентной зоны, в которой осталась дырка,
перешел в зону проводимости; б-иное
представление ситуации, показанной на рис. а.

506 гл- 28- КОНДЕНСИРОВАННЫЕ СРЕДЫ
бы показать, что вероятность перехода
электрона в результате теплового
возбуждения с верхнего края валентной зоны
в зону проводимости пропорциональна
е-Е^кт, (28-4)
где Ед-ширина запрещенной зоны. Для
германия при комнатной температуре
{кТ= 0,026 эВ) имеем EJkT ъ 29.
Несмотря на то что у германия и кремния при
комнатной температуре имеется
небольшое число электронов в зоне
проводимости, они несравненно лучше проводят ток,
чем такой диэлектрик, как алмаз, у
которого Ед « 7 эВ. При температуре Т ~ 30 К
и кремний, и германий также становятся
диэлектриками.
В полупроводнике электрон,
попадающий за счет теплового возбуждения
в зону проводимости, в конечном счете
столкнется с дыркой и возвратится назад
в валентную зону. При этом скорость
уменьшения числа электронов
проводимости пропорциональна N~N+, где N~-
число термически возбужденных
электронов, a N+ — число дырок. Выше мы
показали, что скорость рождения пар
пропорциональна ехр ( — EJkT). В тепловом
равновесии эти скорости одинаковы, так
что
N~N+ ~ ехр(- EJkT).
В чистом полупроводнике N~ = N+ и,
следовательно,
ЛГ ~ехр(-£д/2/сГ).
Поскольку электропроводность а
пропорциональна числу N ", она будет очень
быстро увеличиваться с ростом температуры.
Пример 5. Кремниевый образец нагревают от
0 до 10°С. Во сколько раз возрастет его
электропроводность ?
Решение: Отношение
ЛГ' _ ехр(-£д/2/сГ) _
ЛГ ~ &xp(-EJ2kT) ~
=ехр[!Кт-Ф)}
Таким образом, поскольку ЕА = 1,1 эВ =
= 1,76 -10 ~ 19 Дж, мы имеем
ЛГ' _ Г 1,76-Ю-19 / 1 1 Y1 _
ЛГ ~ СХР|_ 2(1,38-10" 23) \273" ~ ~283/J "
= 2,28.
ТЕРМИСТОР
Из примера 5 следует, что при
повышении температуры на каждые 10 К
сопротивление образца из чистого кремния
уменьшается вдвое. Поэтому чистый кремний
можно использовать в качестве очень
чувствительного электронного датчика
температуры. Такое устройство (изготовленное
из чистого полупроводника) называется
термистором.
ЛЕГИРОВАНИЕ ПОЛУПРОВОДНИКОВ
Если при выращивании кристалла
германия в расплав добавляется небольшое
количество мышьяка (с валентностью 5),
то последний внедряется в решетку
кристалла, и четыре из его пяти валентных
электронов образуют четыре необходимые
ковалентные связи. Оставшийся пятый
электрон занимает состояние,
расположенное чуть ниже края зоны проводимости1*,
так что незначительное тепловое
возбуждение может перевести этот электрон в зону
проводимости. Следовательно, электронов
проводимости будет почти столько же,
сколько атомов мышьяка. Обычно
электронов проводимости оказывается
намного больше, чем электронов, попавших в
зону проводимости из валентной зоны
благодаря тепловому движению. Такой
полупроводник называется полупроводником
п-типа (п означает, что носители заряда
являются отрицательными).
Германий можно легировать также
галлием (с валентностью 3). В этом случае
атом галлия в решетке кристалла при
формировании четырех валентных связей
будет присоединять соседний электрон. В
результате атом галлия будет создавать
1] Так называемый донорный уровень.—
Прим. перев.

§ 5. ФИЗИКА ПОЛУПРОВОДНИКОВ 507
дырку, и мы получим полупроводник р-ти-
па (р означает, что носители заряда
являются положительными).
р-И-ПЕРЕХОДЫ
Если между двумя образцами из
полупроводников р- и п-типа создать контакт,
то, как указывалось в § 2, электроны будут
переходить из образца п-типа в образец
в обоих образцах. Ниже мы обсудим ток,
возникающий благодаря дыркам, а потом
рассмотрим, как образуется ток
отрицательных носителей заряда.
Фактически будет существовать
небольшой ток /0, вызванный перемещением
дырок и текущий в обоих направлениях через
переход. Величина дырочного тока,
протекающего, как показано на рис. 28-15,6,
Уровень
Ферми
л-тип
Уровень
Ферми
Рис. 28-14. Диаграммы потенциальной энергии
полупроводников р- и w-типа до того, как они
были приведены в контакт, е V0- расстояние
между уровнями Ферми.
р-типа, а дырки-в обратном направлении,
пока в образцах не сровняются уровни
Ферми. При этом образец р-типа,
получивший дополнительные электроны, станет
более отрицательным, а образец и-типа —
более положительным. Между образцами
устанавливается контактная разность
потенциалов, равная разности исходных
уровней Ферми, которая в свою очередь
близка к ширине запрещенной зоны Ед.
(Из рис. 28-14 можно видеть, что уровни
Ферми близки наивысшим энергетическим
электронным состояниям, которые
заполняются при абсолютном нуле.) Обозначим
контактную разность потенциалов через
V0. Тогда после того как два образца будут
приведены в контакт друг с другом,
электрический потенциал V (но не
потенциальная энергия) принимает вид, как показано
на рис. 28-15,а. На рис. 28-15,6 изображены
соответствующие плотности носителей
отрицательного и положительного зарядов
N
р -тип
л
п -тип
Рис. 28-15. а-зависимость электрического
потенциала от х в случае образцов, показанных на
рис. 28-14, когда они приводятся в контакт;
контактная разность потенциалов равна V0;
б-распределение концентрации носителей
зарядов обоих знаков вдоль оси х.

508 гл- 28- КОНДЕНСИРОВАННЫЕ СРЕДЫ
справа налево, пропорциональна
концентрации дырок N+ в образце и-типа. При
пересечении дырками поверхности
контакта они будут ускоряться разностью
потенциалов V0. Таким образом, /лев = CN+, где
С - коэффициент пропорциональности.
Аналогично ток дырок слева направо
пропорционален произведению N+ на долю
дырок, которые могут преодолеть
потенциальный барьер. Эта доля
определяется с помощью статистической
механики и в соответствии с (28-4) равна
ехр (— е V0/k Т). Следовательно,
Inp2iB = CN+pQxp(-eV0/kT).
Поскольку /лев = /прав = /0, мы имеем
N+n = N+pexp(-eV0/kT)
I0 = CN+pexp(-eV0/kT).
Приложим теперь к р-и-переходу
внешнее напряжение V (рис. 28-16). Тогда
разность потенциалов между образцом и-типа
и образцом р-типа станет равной V0 — V
и ток, текущий направо, можно записать
в виде
/прав = CJV+exp l-e(V0 - V)/kT] =
= [CN+P Qxp(-eV0/kT)~] ехр (eV/kT) =
= I0Qxp(eV/kT).
Текущий налево ток по-прежнему равен /0,
поскольку величина N* не изменилась;
следовательно, результирующий ток равен
/ = /,
-7 -l*(tfYlkT-\\
прав -«лев — *0 \* 1)
(ток в р-п-переходе)<
(28-5)
Этот результирующий дырочный ток течет
в образец и-типа, где дырки в конечном
итоге аннигилируют с электронами
проводимости. Потери электронов при
аннигиляции пополняются за счет тока
электронов из внешнего источника напряжения,
как показано на рис. 28-16. На рис. 28-17
приведена зависимость I от V, вычисленная
по формуле (28-5). Следует заметить, что
Ш-
hr
ф
Рис. 28-16. а-напряжение, приложенное к
p-w-переходу в прямом направлении; б-общее
схематическое представление р-и-перехода.
Рис. 28-17. Зависимость тока / от напряжения
V, соответствующая выражению (28-5). В
первом приближении положительное напряжение
V вызывает большой ток, а отрицательное
почти не создает тока.
при положительном напряжении ток, как
правило, во много раз превосходит
величину /0, в то время как при обратном
напряжении максимальный ток равен /0.
Устройство, обладающее такой
нелинейной характеристикой, называется диодом.
Главнейшей частью любого
радиоприемника с амплитудной модуляцией (AM)
является диодный детектор, которым
обычно служит р-п-переход. Такое применение

§ 5. ФИЗИКА ПОЛУПРОВОДНИКОВ
р-и-перехода мы подробно опишем в
приложении к данной главе.
Мы не стали рассматривать ток
электронов проводимости, обусловленный
концентрациями N~ и N~ отрицательных
носителей, поскольку все выкладки в этом
случае абсолютно те же, что и
выполненные нами выше, и приводят к тому же
результату, а именно к формуле (28-5).
Если принять во внимание наличие
отрицательных носителей заряда, то /0
представляет собой максимальный ток,
создаваемый носителями обоих знаков, при
обратном напряжении.
Пример 6. Предположим, что p-w-переход
находится при 0°С и при прямом напряжении ОД В
его сопротивление равно 10 Ом. Каково
сопротивление перехода, если поменять полярность
напряжения?
Решение: В соответствии с (28-5) сопротивление
перехода обратно пропорционально величине
\exp(eV/kT) — 11. Следовательно, отношение
сопротивления в обратном направлении к
сопротивлению в прямом направлении при значении
приложенного напряжения Vx запишется в виде
Кобр \&хр(еУ1/кТ) - 1|
Япрям ~ |ехр(-вК1//сТ)-1| '
где eVx = ОД эВ, а /сТ= (1,38 • 10 " 23) (273) Дж =
= 0,0236 эВ. Таким образом,
"^ = 4,237, и
Добр = |ехр(4,237)-1[
Япрям |ехр(-4,237)-1|
откуда находим
R = 692 Ом.
СОЛНЕЧНЫЕ БАТАРЕИ
Если на область перехода между двумя
образцами п- и р-типа направить свет, то
электроны будут поглощать фотоны
и переходить из валентной зоны в зону
проводимости. Каждый такой фотон
создает пару электрон-дырка. Под
действием электрического поля (рис. 28-15,а)
вновь образованные дырки будут
перемещаться в образец р-типа, а электроны-в
образец п-типа. Эти дополнительные
носители заряда могут перемещаться по
замкнутой внешней цепи. Таким образом, свет
можно преобразовывать непосредственно
в электрическую энергию. Кремниевый
элемент солнечной батареи ведет себя как
обычная электрическая батарейка
напряжением ~ 0,5 В, причем КПД
преобразования солнечного света в электричество
достигает 15%. Солнечные батареи
используются в качестве источников энергии на
космических, кораблях. Если стоимость
солнечных батарей удастся сделать
сравнимой со стоимостью обычных
электростанций (см. пример 1 в гл. 1), то их можно
будет также использовать для получения
электроэнергии и на Земле. Поэтому важно
быстрыми темпами развивать дешевое
производство полупроводников для
солнечных батарей, и в этом направлении уже
прилагаются серьезные усилия.
ФОТОДИОДЫ
Если к элементу солнечной батареи
приложено обратное напряжение, то под
действием света слабый в обычных
условиях ток /0 сильно возрастает, так как при
этом образуются дополнительные
носители заряда. Фототок пропорционален
количеству фотонов, падающих на
фотоэлемент. Такое устройство, чрезвычайно
чувствительное к интенсивности падающего
на него света, используется во многих
приборах для регистрации изменений
интенсивности света.
СВЕТОДИОДЫ
Ярко-красные светящиеся точки в
индикаторных устройствах
микрокалькуляторов, наручных часов и т.п. создаются
устройствами, называемыми светодиода-
ми. Они представляют собой крошечные
диоды, к которым прикладывается
достаточно высокое прямое напряжение. При
этом электроны проводимости рождают
при столкновениях пары электрон-дырка,
а последующая рекомбинация электрона
с дыркой приводит к испусканию фотона
с энергией Ед. Чтобы получить красный
свет, величина hfx ЕА должна быть около

510
ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
+|ь
п
Эмиттер
* Р
'База
Коллектор
v—
Диод
-р—»4*-л-
Рис. 28-18. а-общепринятое схематическое
представление транзистора; б-схема
соединения полупроводников и- и р-типа; в-изменение
потенциала внутри транзистора; если
напряжение Vb отсутствует, то контактная разность
потенциалов между базой и эмиттером равна V0.
2 эВ. Такую ширину запрещенной зоны
обеспечивают кристаллы арсенида галлия.
Если светодиоды эксплуатируются при
достаточно больших значениях токов, то
эффективность преобразования
электрической энергии в видимый свет
приближается к 100%. Эти устройства сродни
твердотельным лазерам.
ТРАНЗИСТОР
На рис. 28-18 представлен р-и-р-пере-
ход. Соответствующее устройство
называется транзистором. Его можно
рассматривать как р-и-переход (рис. 28-16),
к которому справа добавлена область
р-типа (называемая коллектором). На
рис. 28-18 к «диодной части» приложено
прямое напряжение V0, что приводит
к большому дырочному току из левой
области р-типа (называемой эмиттером)
в область п-типа (база). «Секрет»
транзистора состоит в том, что база
изготавливается настолько тонкой, чтобы большая
часть дырок диффундировала через нее
в коллектор. К коллектору прикладывается
отрицательное по отношению к базе
напряжение, чтобы усилить движение к нему
носителей положительного заряда (дырок).
В типичном транзисторе лишь ~ 1% тока
эмиттера отводится в электрическую цепь
базы. Остальные 99% тока идут в цепь
коллектора через вывод с. Отношение тока
коллектора к току базы называется
коэффициентом усиления по току Р:
Р = у- (коэффициент усиления
I
по току).
В типичных транзисторах, имеющих Р =
= 100, небольшой входной ток в цепи
базы позволяет управлять в 100 раз
большим выходным током в цепи коллектора.
Следовательно, транзисторы можно
использовать для усиления, т. е. для
преобразования малых сигналов в большие.
Например, ток Ibe на рис. 28-18 может
представлять собой слабый ток в антенне
радиоприемника. В этом случае ток 1се
должен повторять изменения во времени
тока Ibe, но быть в 100 раз больше.
Следует заметить, что и-р-и-транзисторы
имеют те же характеристики, что и

§ 6. СВЕРХТЕКУЧЕСТЬ
р-и-р-транзисторы, но они отличаются
тем, что в случае и-р-и-транзисторов
основными носителями зарядов являются
электроны, а не дырки.
ИНТЕГРАЛЬНЫЕ СХЕМЫ
Появление множества недорогих
твердотельных приборов привело к перевороту
в области электроники. Разработка же
интегральных схем произвела в этой области
вторую революцию. Мы ушли бы
значительно в сторону, если бы увлеклись
обсуждением множества остроумных и сложных
методов изготовления полупроводниковых
диодов и триодов. Однако идея
построения интегральных схем настолько
интересна и почти неправдоподобна, что ее стоит
рассмотреть. Даже для электронных
микрокалькуляторов требуются тысячи
транзисторов, соединенных в сложные схемы.
Однако все эти транзисторы вместе с их
многочисленными электрическими цепями
и соединениями умещаются на тонкой
плате площадью около 1 см2. Лучшим
достижением в настоящее время являются 20 000
твердотельных элементов, размещенных на
площади около 0,4 см2. (Это уже
соизмеримо с плотностью нейронов в человеческом
мозге.)
Соединительные «провода» настолько
малы, что их можно увидеть только в
микроскоп. Тонкие слои кристалла наносятся
на плату с помощью оптических масок
(схема уменьшается фотоспособом и
проецируется на светочувствительную маску).
Если такая многоэлементная интегральная
схема содержит 10 000 транзисторов и
продается за 10 долларов, то стоимость
одного транзистора составляет всего десятую
долю цента, т. е. 0,001 доллара.
Производство интегральных схем обходится в
тысячу раз дешевле, чем производство
вытесненных ими вакуумных приборов. При
этом на несколько порядков величины
были улучшены такие характеристики, как
вес, габариты, надежность и потребляемая
мощность.
ДРУГИЕ УСТРОЙСТВА
Множество твердотельных устройств
нашло ценное практическое применение.
Поскольку наша книга предназначена для
того, чтобы дать общие представления
о предмете, мы не имеем возможности
обсудить все такие устройства. Поэтому
перечислим лишь некоторые из них-это
туннельные диоды, кремниевые
выпрямители, стабилитроны (диоды Зенера),
полевые транзисторы, твердотельные лазеры,
термоэлектрические устройства и т.д.
§ 6. Сверхтекучесть
Сверхтекучесть жидкого гелия-это еще
одно необычное квантовомеханическое
явление, имеющее место при температуре,
близкой к абсолютному нулю. Если
газообразный гелий охлаждать, то при
температуре 4,2 К он сжижается.
Дальнейшее охлаждение уже жидкого гелия
приводит к тому, что при температуре
2,2 К его свойства резко меняются1}. При
этом происходят макроскопические
явления, совершенно не укладывающиеся
в рамки обычных представлений.
Например, сосуд, частично заполненный этой
странной модификацией жидкого гелия
(называемой сверхтекучим гелием II)
и оставленный незакрытым, вскоре
опорожняется сам собой. Объясняется это тем,
что жидкий гелий поднимается по
внутренней стенке сосуда (независимо от ее
высоты) и переливается наружу. По той же
причине может происходить и обратное
явление (рис. 28-19). Если пустой стакан
частично погрузить в жидкий гелий, то он
быстро заполнится гелием до того же
уровня, что и уровень жидкости снаружи.
Если далее понижать температуру ниже
2,2 К, то количество свертекучей
компоненты увеличивается. При абсолютном
нуле должна остаться лишь сверхтекучая
компонента.
Другим необычным свойством чистой
сверхтекучей жидкости является то, что
она не передает усилия на другие тела.
Бьющий из брандспойта под большим
давлением поток такой жидкости не смог бы
опрокинуть даже поставленную на ребро
монету. Жидкость свободно обтекала бы
монету, не оказывая на нее никакого уси-
1} Это относится к изотопу 4Не. Гелий-3
ведет себя как обычная жидкость-Прим. перев.

512 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
Пустой
стакан
11
1
Г 1
li il
[f
Жидкий гелий II
Рис. 28-19. Стрелками показана поверхностная
пленка жидкого гелия II, перетекающая в
пустой сосуд. Поверхность действует как сифон.
лия. Сверхтекучая компонента жидкого
гелия имеет нулевую вязкость. Но почему
все-таки вязкость равна нулю? Как
и сверхпроводимость, любопытные
свойства жидкого гелия сейчас интенсивно
изучаются. Значительных успехов удалось
достичь в теоретическом объяснении
сверхтекучести. Атомы гелия не подчиняются
принципу Паули, так как их спин равен
нулю1}. Частицы с нулевым спином могут
находиться в одном и том же состоянии
в любом количестве; эти частицы
подчиняются так называемой статистике Бо-
зе- Эйнштейна. Все атомы сверхтекучего
гелия находятся в основном состоянии.
Чтобы такая жидкость имела отличную от
нуля вязкость, ее атомы должны
совершать переходы в состояния с более
высокой энергией, а энергии для этого у них
нет.
§ 7. Проникновение сквозь барьер
ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ
Если к металлу приложить
электрическое поле, которое стремится вырвать
электроны из металла, то появляется
устойчивый ток электронов, покидающих
1} Это относится только к изотопу 4Не,
тогда как спин атома 3Не равен 1/2. То, что
атомы 3Не и 4Не подчиняются разным
статистикам, проявляется в коренном различии их
свойств при низких температурах-Прим. перев.
металл. Потенциальная энергия,
обусловленная постоянным электрическим полем
Е, равна U = — еЕх. На рис. 28-20,а
приведен результирующий потенциал, в
котором движется электрон проводимости.
Можно видеть, что избежать «заточения»
в металле могут лишь те
немногочисленные электроны, энергия теплового
движения которых превышает W.
Это явление называется термоэлектронной
эмиссией. Можно ожидать, что небольшое
увеличение температуры приведет к
значительному возрастанию эмиссии
электронов, так как вероятность того, что
тепловая энергия электрона равна W,
пропорциональна ехр(— W'/kT). Вот почему
специально подогревают катоды электронных
ламп. Однако даже если катоды охладить
до абсолютного нуля, электроны все равно
будут испускаться! Но это совершенно
иное явление; мы его рассмотрим в
следующем разделе.
АВТОЭЛЕКТРОННАЯ ЭМИССИЯ
Установлено, что слабый электронный
ток продолжает течь с катода даже при
очень низких температурах, когда
отсутствуют электроны с тепловыми энергиями,
достигающими W. Это явление
называется автоэлектронной эмиссией и
представляет собой важное следствие квантовой
механики, ниспровергающее классические
представления. Оно представляет собой
квантовомеханическое свойство проникать
сквозь потенциальный барьер. Впервые
с проникновением сквозь барьер мы
столкнулись при изучении прямоугольной
потенциальной ямы со стенками конечной
•высоты в гл. 25. Оказалось, что в
запрещенную с точки зрения классической
физики область волновая функция проникает,
уменьшаясь по мере распространения по
экспоненциальному закону. В
рассматриваемом случае мы имеем дело с
потенциальным барьером высотой W
(рис. 28-20). Согласно классической физике,
электрон, кинетическая энергия которого
равна Kf внутри металла, в точке хх
должен иметь нулевую кинетическую энергию.
Благодаря тому что со стороны атомов
металла на электрон действуют силы
притяжения, он возвратится из этой точки
обратно на прежнее место. Классическая

§ 7. ПРОНИКНОВЕНИЕ СКВОЗЬ БАРЬЕР
физика запрещает электронам проникать
даже на небольшие расстояния внутрь
барьера. В области между точками хх и х2
кинетическая энергия электронов оказалась
бы отрицательной, что недопустимо с
точки зрения классической физики. Однако из
чаши.
На самом деле пример проникновения
сквозь потенциальный барьер можно найти
и в классической физике. Поскольку
уравнение Шредингера и уравнения для
световых волн или волн в жидкости имеют
Энергия
К
-ил
Рис. 28-20. а-та же диаграмма
потенциальной энергии, что
и на рис. 28-4, но при наличии
внешнего электрического поля;
б-волновая функция электрона,
находящегося внутри ямы на
уровне Ферми.
уравнения Шредингера следует, что
электронная волна существует и в этой
области. Как видно из рис. 28-20,6, она должна
изгибаться в направлении к оси х.
Заметим, что с некоторой вероятностью
электрон можно обнаружить и вне металла.
Согласно квантовой механике, вероятность
проникновения сквозь барьер при каждом
столкновении с ним данного электрона
должна составлять Фвнеш/^нутр-
Классическим примером потенциального барьера мог
бы служить маленький стеклянный шарик,
катающийся внутри чаши. Если шарик
выпустить у края чаши, то он будет
кататься туда-сюда и никогда не выберется из
нее. Однако, согласно представлениям
квантовой механики, имеется, хотя и очень
небольшая, вероятность (порядка одного
шанса на 10(1°29)) того, что шарик исчезнет из
один и тот же вид, можно ожидать, что
проникновение через барьер вполне
возможно в оптике. Поверхность стеклянной
пластины представляет собой барьер для
света, пытающегося выйти из нее наружу.
Если свет падет на поверхность под углом
больше критического (такие углы
запрещены законом Снелла), то свет не
может пройти сквозь барьер и,
следовательно, полностью отразится назад в стекло
(рис. 28-21,а). Однако если вблизи этой
пластинки поместить другой кусок стекла
(на расстоянии одной или двух длин волн,
как показано на рис. 28-21,6), то часть
света преодолеет барьер и станет
распространяться во второй стеклянной пластинке. На
рис. 28-22 показано аналогичное явление,
наблюдаемое при возбуждении волн в
ванне с вибратором.

514 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
Воздух
Полностью
отраженный
пучок
Падающий
пучок
Пучок,
прошедший
через
воздушный
барьер
Рис. 28-21. Проникновение света сквозь барьер.
При помещении второй стеклянной пластинки
рядом с первой часть света может проникнуть
из первой пластинки во вторую.
Основные выводы
В кристаллах с ковалентной связью
облака валентных электронов имеют форму
«лепестков», связывающих соседние ядра.
В случае металлической связи не имеется
такой локализации электронных облаков-
Рис. 28-22. Иллюстрация того, как волны
проникают сквозь барьер в ванне с вибратором,
а-волны испытывают полное отражение от
щели в воде; б и в-по мере того как щель
сужается, образуется прошедшая волна,
интенсивность которой возрастает с уменьшением щели.
[С любезного разрешения Центра по развитию
образования.]

ПРИЛОЖЕНИЕ. РАЗЛИЧНЫЕ ПРИМЕНЕНИЯ р - W-ПЕРЕХОДА 515
волновые функции валентных электронов
как бы расплываются по всему металлу.
Максимальная кинетическая энергия
электронов проводимости дается выражением
h2 /3 \2/3
J Sm\n J
где 91 -число атомов в единице объема.
Величина Kf называется граничной энергией
Ферми. Электроны проводимости
находятся в потенциальной яме, средняя глубина
которой равна U0. Работа выхода W0 =
= \U0\ -К,.
Если два различных металла привести
в соприкосновение друг с другом, то
возникнет кратковременный ток небольшой
величины, выравнивающий уровни Ферми.
При этом образуется контактная разность
потенциалов, которая по величине равна
разности работ выхода этих металлов.
Величина электропроводности
пропорциональна средней длине свободного
пробега электронов проводимости между
столкновениями. С понижением
температуры средняя длина свободного пробега
увеличивается и у некоторых проводников
(называемых сверхпроводниками)
становится бесконечно большой, прежде чем
температура достигнет абсолютного нуля.
Если имеется цепочка из п одинаковых
атомов, расположенных через равные
промежутки, то энергетический уровень
отдельного атома расщепляется и образует
зону из п близко расположенных
энергетических уровней. В случае металлической
связи зона, отвечающая основному
состоянию валентных электронов, либо
неполностью заполнена, либо перекрывается
с незаполненной зоной, отвечающей
уровню с более высокой энергией.
Валентная зона полупроводников
заполнена полностью и отделена
запрещенной зоной (энергетической щелью) от
следующей незаполненной зоны (называемой
зоной проводимости). Число термически
возбужденных валентных электронов,
попадающих в зону проводимости,
пропорционально ехр(-ЕдДТ). Легирование
полупроводника приводит к тому, что в нем
могут образовываться избыточные либо
электроны проводимости (полупроводник
и-типа), либо дырки (полупроводник р-ти-
па). При создании контакта между
полупроводниками р- и п-типа образуется р-п-
переход. Если к этому переходу приложить
внешнее напряжение V, то через переход
будет протекать ток I0\_Qxp(eV/kT) — 1].
Прибор, называемый р — и-р-транзи-
стором, можно рассматривать как р-п-
переход (эмиттер - база) с коллектором
р-типа, присоединенным к базе. В этом
случае малый ток в цепи базы 1Ъ позволяет
управлять большим током коллектора 1С.
При этом коэффициент усиления по току
Р = Ic/Ib может достигать ~ 100.
Электроны проводимости можно
извлекать с поверхности холодного металла,
приложив сильное электрическое поле. Это
явление называется автоэлектронной
эмиссией, и его можно объяснить
проникновением сквозь потенциальный барьер, при
котором волновая функция
экспоненциально затухает внутри барьера.
Приложение. Различные применения
р-гс-перехода (в радио и телевидении)
Неотъемлемой частью любого радио-
или телевизионного устройства является
диодный детектор. Обычный диодный
детектор представляет собой
последовательное соединение резистора R и диода на
р-и-переходе (рис. 28-23). В § 5 мы
показали, что сопротивление диода сильно
зависит от знака приложенной к нему
разности потенциалов: в одном направлении
сопротивление почти равно нулю, а в
другом очень велико. Любой элемент схемы,
обладающий этим свойством, называется
диодом. Из рис. 28-23 следует, что если
в цепи диода с резистором приложить
напряжение в прямом направлении, то диод
по существу эквивалентен короткозамкну-
тому участку цепи, и на резисторе R
возникает положительное напряжение. Если же
прикладывается отрицательное
напряжение, то сопротивление диода оказывается
много больше R и большая часть
отрицательного напряжения падает не на резисто-

516 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
Напряжение
вА
•W
Вход
ф
Напряжение
в В
Выход
_1
/VA/
Рис. 28-23. Диодный выпрямитель. К входной
клемме А приложено переменное напряжение.
На выходной клемме В все отрицательные
полупериоды напряжения «обрезаны».
ре, а на диоде. Заметим, что, хотя напряже- можно использовать для зарядки конден-
ние на клемме А отрицательно на протя- сатора. Такая схема называется диодным
жении полупериода, на клемме В оно выпрямителем (рис. 28-24); с помощью
никогда не бывает отрицательным и его диодного выпрямителя напряжение пере-
Переменное
напряжение
на входе
ЛА/4
Вход
Постоянное
напряжение
на выходе
Рис. 28-24. Диодный выпрямитель при наличии
конденсатора С. В отсутствие конденсатора
выходное напряжение имело бы вид, показанный
штриховой линией.

ПРИЛОЖЕНИЕ. РАЗЛИЧНЫЕ ПРИМЕНЕНИЯ р - И-ПЕРЕХОДА 517
менного тока можно преобразовывать
в постоянное напряжение. Во всех
действующих радио- и телеустройствах
имеются диодные выпрямители, преобразующие
переменный ток в постоянный.
Напряжение
на выходе
детектора I
I
Рис. 28-26. Напряжение, снимаемое с диодного
детектора (кривая белого цвета). Заметим, что
выходное напряжение повторяет
первоначальный звуковой сигнал с небольшими
высокочастотными пульсациями. Кривая зеленого
цвета-высокочастотный сигнал с отсеченными
отрицательными полупериодами.
РАДИО
Радиостанция с AM излучает
электромагнитные волны постоянной частоты,
лежащей в радиовещательном диапазоне.
Частоты радиовещательного диапазона
изменяются от 0,5 до 1,6 МГц. Амплитуда
ТЕЛЕВИДЕНИЕ
В телевидении видеосигнал также
представляет собой высокочастотные
колебания, промодулированные по амплитуде.
Поэтому телевизионный приемник очень
похож на радиоприемник, с той лишь
разницей, что видеосигнал используется для
управления интенсивностью электронного
пучка, который падает на экран
телевизионной трубки (кинескопа). Напряжение
выходного видеосигнала прямо
пропорционально яркости передаваемого
изображения. В интервалы времени между двумя
последовательными строками развертки
видеосигнал содержит импульсы,
запускающие генератор развертки, который
выдает следующую строку. На рис. 28-28,а
-10
-Эг
03
Рис. 28-25. Зависимость радиочастотного
напряжения (кривая зеленого цвета) от времени.
Радиочастотная (или высокочастотная)
электромагнитная волна промодулирована по
амплитуде чисто синусоидальной волной (кривая белого
цвета) с частотой 1000 Гц (звуковая волна). Для
наглядности частота несущей волны на рисунке
значительно уменьшена.
V
Антенна
Динамик
Рис. 28-27. Блок-схема радиоприемника с AM.
электромагнитной волны модулируется
передаваемым звуковым сигналом. В
качестве примера на рис. 28-25 изображена
электромагнитная волна, промодулирован-
ная чистым музыкальным тоном на
частоте 1000 Гц. В радиоприемнике этот слабый
сигнал улавливается антенной, усиливается
высокочастотным усилителем (УВЧ), а
затем подается на диодный детектор.
Напряжение на выходе диодного детектора
повторяет первоначальный звуковой сигнал
с частотой 1000 Гц, как показано на
рис. 28-26. Этот звуковой сигнал
усиливается усилителем низкой частоты (УНЧ)
и подается на динамик. На рис. 28-27
приведена блок-схема радиоприемника с AM.

518 ГЛ. 28. КОНДЕНСИРОВАННЫЕ СРЕДЫ
Рис. 28-28. Передача изображения буквы N
с помощью видеосигнала при использовании
9 строк развертки, а-изображение на экране
кинескопа; б-форма соответствующего
видеосигнала, управляющего интенсивностью
электронного пучка.
Видеосигнал
ОПТ
дг
mm
IT
[ШЛЛ
W
пппп
1Г
пплл
1Г
Синхронизирующий импульс
горизонтальной развертки
пгшл ппл
1Г
1Г
тг
показана последовательность передачи
изображения буквы «N», а
соответствующий видеосигнал-на рис. 28-28,6.
Блок-схема телевизионного приемника, включая
блоки развертки, приведена на рис. 28-29.
Коммерческое телевидение в США
работает на 525 строках при 30 кадрах
в секунду. (В СССР, Франции и ряде
других стран принят иной стандарт-625 строк
и 24 кадра в секунду-Прим. перев.)
Управляющая
сетка
электронной
Ьпушки
К-Горизонтальные
отклоняющие
катушки
Вертикальные
отклоняющие
катушки
Электронный
пучок
Рис 28-29. Блок-схема телевизионного
приемника.

ЗАДАЧИ 519
Упражнения
1. Глубина потенциальной ямы металла
составляет 11 эВ, а работа выхода 4 эВ.
а) Найдите полную энергию электронов на
уровне Ферми.
б) Насколько увеличивается кинетическая
энергия электрона при его
проникновении в металл?
2. Сколько электронов проводимости
приходится на 1 грамм натрия? Сколько
электронов проводимости в 1 грамме германия,
легированного мышьяком в пропорции три
части мышьяка на миллион частей
германия?
3. Электрон с кинетической энергией 3 эВ
попадает в металл; при этом его кинетическая
энергия увеличивается до 8 эВ. Какова
глубина потенциальной ямы?
4. Если значения работы выхода двух
металлов равны соответственно 2,8 эВ и 3,2 эВ, то
какая возникнет контактная разность
потенциалов, когда эти металлы приводятся в
соприкосновение друг с другом? Какой из
этих металлов будет иметь более высокий
потенциал?
5. Металл А имеет U0 = 4 эВ и Kf = 3 эВ,
а металл В U0 = 3,5 эВ и Kf = 2 эВ. Какова
будет контактная разность потенциалов,
если эти металлы привести в
соприкосновение? Какой из металлов будет иметь более
высокий потенциал?
6. Интенсивность солнечного излучения на
поверхности Земли равна 2 кал-мин-1 см-2.
Какой должна быть площадь солнечной
батареи с КПД = 15%, чтобы создать ток
мощностью 100 Вт?
7. Рассмотрим воображаемый металл А. При
поглощении Металлом фотонов с энергией
7 эВ испускаются фотоэлектроны с энергией
3 эВ. Плотность электронов проводимости
такова, что внутри металла они имеют
кинетические энергии вплоть до 5 эВ. Найдите
а) положение уровня Ферми,
б) работу выхода,
в) глубину потенциальной ямы,
г) кинетическую энергию, которую теряет
электрон, вылетая с поверхности металла,
д) порог фотоэффекта в эВ.
8. Сосуд диаметром 1 см содержит гелий II,
причем высота столба жидкости равна 5 см.
Через сколько времени после удаления
крышки вытечет вся жидкость? Скорость
вытекания 50 см/с, толщина пленки 10"5 см.
9. В некотором металле потенциал сил
притяжения электронов равен U0. Вне металла
длина волны электрона равнао 10 А, а в
металле она уменьшается до 4 А. Каково
значение U0 в эВ?
10. Повторите решение в примере 5 в случае
германия.
11. Повторите решение в примере 6 в случае,
когда напряжение равно 1 В.
12. Повторите решение в примере 6 для
температуры 100 °С.
13. Какой должна быть ширина запрещенной
зоны полупроводника, из которого
изготовлен светодиод, светящийся зеленым светом
(X = 500 нм)?
14. Считая, что мозг человека содержит 1010
нейронов, определите приближенную толщину
интегральной схемы, в которой плотность
размещения твердотельных элементов
соизмерима с плотностью нейронов в мозге.
15. Чему равна частота горизонтальной
развертки в американском телевидении?
Задачи
16. Если в кристаллической решетке атом
удерживается силой, пропорциональной его
смещению, то по какому закону будет
увеличиваться среднее смещение с температурой?
Считая коэффициент упругости равным х,
найдите выражение для
среднеквадратичного смещения атома через х, Т и другие
необходимые величины.
17. Вычислите плотность состояний р в
фазовом пространстве (элемент этого
пространства записывается в виде dx dy dz dpxdpydpz).
Величина p определяется формулой dn =
= р dx dy dz dpxdpydpz. (Указание:
Р/ р/
^dpxdpY(Ip= = J 4np2dp = (4/3) np}.)
о о
18. Если для свободных электронов в белом
карлике справедливо соотношение pf=mc,
то чему равно отношение K/Kfl Здесь
следует воспользоваться точным выражением
для кинетической энергии К = ]/с2р2 + т2с4 —
— тс2.
19. Используя рис. 28-11, найдите, при каком
расстоянии между атомами натрий становится
проводником. Чему равна соответствующая
плотность в г/см3?
20» Масса Солнца 2,0 • 1030 кг. Допустим, что оно
неожиданно сжалось в сферу диаметром
5 км, имеющую однородную плотность.
а) Считая число протонов, нейтронов и
электронов одинаковым, определите
максимальную кинетическую энергию
электрона и нейтрона в эВ. Чему равна
полная кинетическая энергия всех частиц в
Дж?
б) Чему будет равна полная кинетическая
энергия, если протоны и электроны
превратятся в нейтроны?

520 гл- 28- КОНДЕНСИРОВАННЫЕ СРЕДЫ
21. В литии работа выхода равна 2,36 эВ, а
плотность лития 0,534 г/см3. Вычислите U0.
22. Если бы величина U0 на рис. 28-9,а
оказалась бесконечно большой, то чему были
бы равны Ei и E2i записанные через
Ъ2/тхо! Сравните полученную величину со
значением, приведенным на этом рисунке.
23. С помощью изложенного в гл. 25 метода
определения уровней энергии найдите Et
(рис. 28-9,в) в потенциальной яме конечных
размеров.
24. Во сколько раз возрастет сопротивление
цилиндра из чистого германия, если его
температуру понизить с 300 до 30 К?
25. Какое количество примеси мышьяка
потребуется для того, чтобы удвоить
электропроводность легированного им германия? В
чистом германии число электронов
проводимости можно считать равным ехр( — EJ2kT).
26. Повторите решение в примере 4 для
случая, когда цепочка составлена не из 100, а
из 200 прямоугольных ям. Все остальные
величины прежние. Чему будет равна энер-
-~"~гия первого, пятидесятого, сотого и
двухсотого энергетического уровня?
27. Предположим, что потенциальная энергия
взаимодействия электрона с отрицательно
заряженным шариком радиусом 10"4 см
изменяется так, как показано ниже на рис. а.
Волновая функция электрона внутри
шарика приведена на рис. б. Найдите
W
а) длину волны электрона внутри шарика,
б) скорость электрона внутри шарика,
в) вероятность вылета электрона наружу при
каждом соударении с поверхностью,
г) среднее время жизни электрона до
вылета из шарика при отсутствии потерь
энергии.
28. В небольшом холодном катоде 1018
электронов ежесекундно сталкиваются с
поверхностью, ограничивающей область большого
электрического поля. При прохождении через
барьер волновая функция электрона
ослабляется в 103 раз. Найдите величину тока
автоэлектронной эмиссии в амперах.
29. К точке А в схеме, показанной на
рисунке, приложено переменное напряжение.
Нарисуйте зависимость напряжения в точке В от
времени.
Щх)

ЗАДАЧИ 521
30. Рассмотрим цепь, составленную из трех
резисторов и двух идеальных диодов. Чему
равны токи в резисторах сопротивлением
2, 3 и 4 Ом? Вычислите ток в резисторе
сопротивлением 4 Ом, если полярность
батареи поменяется на обратную.
31. Плотность состояний ферми-газа равна 91 =
= (8/ 3) п (pj/ h3). Найдите выражение для
среднего импульса р через граничный импульс
Pf
32. Выведите формулу для Kf в двумерном
пространстве. В этом случае 91
представляет собой число частиц на единицу площади.
33. Повторите решение предыдущей задачи для
случая ультрарелятивистских частиц.

ЯДЕРНАЯ ФИЗИКА
Эта глава посвящена главным образом
описанию свойств и строения атомных
ядер. Мы рассмотрим также различные
применения ядерных взаимодействий,
такие, как использование радиоизотопов,
ядерные реакторы, работающие на
реакциях деления и синтеза, а также атомное
оружие. Рассмотрение ядерной физики
будет вестись по аналогии с атомной
физикой. Обсудим сначала основной закон
действия сил и попытаемся предсказать
размеры, энергии связи, моменты импульсов,
энергии уровней и другие характеристики
различных ядер. Некоторые практические
приложения связаны с мощной индустрией,
в которую вкладываются многие
миллиарды долларов, и имеют крайне важное
значение для будущего человеческой
цивилизации.
ТЕРМИНОЛОГИЯ
Любое атомное ядро состоит из
протонов и нейтронов, связанных между собой
ядерными силами (сильным
взаимодействием). Поскольку нейтроны и протоны
имеют почти одну и ту же массу и весьма
сходные свойства, их обычно называют
нуклонами. Сложные ядра называют также
нуклидами (термины «ядро» и «нуклид»
равнозначны). Ядра (нуклиды), имеющие
одинаковое число протонов, но различные
числа нейтронов, называются изотопами.
У легких и средних ядер число протонов
и нейтронов примерно одинаково.
Суммарное число протонов и нейтронов
называется массовым числом и обозначается
символом А. Число нейтронов равно A-Z,
где Z-атомный номер или число
протонов в ядре. Величина А данного
атомного ядра очень близка к атомной массе
самого атома. Для обозначения
конкретного ядра используется символ атома с
указанием сверху массового числа. Например,
14С-это изотоп углерода, ядро которого
состоит из 6 протонов и 8 нейтронов.
Атомная масса ядра 12С выбрана в точности
равной 12. Таким образом, шкала атомных
масс основана на массе 12С.
§ 1. Размеры ядер
Наиболее прямым методом измерения
размеров ядер и распределения в них
массы, по-видимому, является метод,
аналогичный оптическому, но при этом
должны использоваться длины волн,
значительно меньшие размеров ядра. Этот
метод, называемый дифракционным
рассеянием, мы рассматривали в § 5 гл. 23.
В качестве коротковолнового излучения
можно применять пучки протонов или
нейтронов высоких энергий. С помощью
дифракционного рассеяния, а также других
методов установлено, что у всех ядер, за
исключением самых легких, средний
радиус дается выражением
R *(1,2-10-15 м)А113. (29-1)
В ядерной физике и физике элементарных
частиц столь часто встречается единица
длины 10"15 м, что ей дали специальное
название-ферми. 1 ферми=1 фм = 10~15 м.
Дифракционное рассеяние позволяет
получить сведения не только о размерах, но и
о распределении материи внутри ядра.
Пример 1. Чему равна массовая плотность
и плотность числа частиц ядерного вещества?
Решение: В ядре объемом (4/3)nR3 число
нуклонов в единице объема
(4/3) nR3 (4/3)я [(1,2-10"15 м) A1/3Y
= 1,38-1044 м-3. (29-2)
Таким образом, умножая это значение на массу

§ 1. РАЗМЕРЫ ЯДЕР 523
нуклона, получаем массовую плотность
р = 9ШР = (1,38 • 1044) (1,67 • 1(Г27) кг/м3 =
= 2,3.1017кг/м3.
Следовательно, один кубический
сантиметр ядерного вещества имеет массу
230 млн. тонн. Заметим, что плотность
ядерного вещества не зависит от размеров
ядра, поскольку объем ядра
пропорционален массовому числу А.
РАССЕЯНИЕ ЭЛЕКТРОНОВ
ЭНЕРГИЙ
ВЫСОКИХ
Второй метод, позволяющий изучать
распределение ядерного вещества, основан
на использовании электронов высоких
энергий. Поскольку сила, действующая на
электрон при его прохождении через ядро,
определяется зарядом ядра, то по
рассеянию электронов на ядре можно изучить
распределение электрического заряда или
распределение протонов внутри ядра. На
рис. 29-1 приведены распределения зарядов
внутри ядер углерода и золота,
измеренные этим методом. Покажем теперь,
что если заряд сконцентрирован в центре
ядра, то электроны будут отклоняться на
большие углы, чем если бы этот же заряд
был равномерно распределен по объему
сферического ядра.
Если электрон высокой энергии
проходит на расстоянии Ъ от ядра с зарядом Ze,
Золото
5 фм
Рис. 29-1. Распределение плотности заряда (в
единицах 1019 Кл/см3) в ядрах углерода и
золота, полученное посредством изучения рассеяв
ния электронов. [Согласно Хофштадтеру (R. Hof-
stadter, Ann. Rev. Nucl. Sci., 7, 231 (1957).]
то он испытывает отклонение на угол
0 (рис. 29-2). Согласно закону Кулона, чем
ближе электрон к ядру, тем больше
действующая на него сила, и, следовательно,
больше угол, на который он отклоняется.
Можно рассчитать зависимость 0 от Ъ.
Однако если электрон проникает внутрь ядра,
то он уже не испытывает большой куло-
новской силы (см. рис. 16-3). В случае
заряженной сферической оболочки
максимальный угол отклонения соответствует
Ъ = R, т. е. радиусу сферы. Это происходит
+ Ze
т
в APV
/
Ядро
Рис. 29-2. Рассеяние электрона с импульсом
р на атомном ядре с зарядом Ze.

524 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
из-за того, что поле_ внутри такой
оболочки равно нулю. В данном случае радиус
можно определить, измеряя 9макс.
Необходима лишь формула, связывающая 0 с Ъ.
Ниже приводится приближенный вывод
этой формулы.
Пусть Ару- изменение импульса
электрона за счет действия кулоновской силы.
Согласно ньютоновскому определению
силы,
Ару = \Fydt = e\Eydt = е\Еу —.
Для малых углов отклонения ds я dx, и,
следовательно,
Apv ~-\Evdx = ±—гfEv2nbdx.
Заметим, что 2nbdx-3TO площадь
цилиндрического пояса dA. Тогда изменение
импульса можно записать в виде
Ap^^b~v
§E-dA,
где интеграл берется по поверхности
цилиндра радиусом Ь, на оси которого
находится ядро. Для вычисления интеграла
воспользуемся теоремой Гаусса [см.
формулу (15-7), согласно которой <j>E-dA =
= 4тг/с0<2внутр]. Таким образом, поскольку
полный заряд внутри цилиндра равен Ze,
мы имеем
Ар а _ . 4nknZe =
2nbv
bv
Из рис. 29-2 следует, что Ару = р tg 0.
Подставляя это соотношение в предыдущее
выражение, находим
ptg0:
2k0Ze2
bv
k0Ze2
b*pvtgQ/2'
С помощью более сложных вычислений
можно показать, что строгая формула,
справедливая для всех значений 0,
записывается в виде
Ъ =
k0Ze2
p»tg(e/2)
(29-3)
Если бы заряд ядра был распределен по
поверхности сферы радиусом R, то радиус
ядра можно было бы вычислить, положив
в формуле (29-3) 0 = 0макс; тогда
R =
k0Ze2
Pl>tg(0MaKc/2)
До сих пор мы пользовались классической
механикой. Учет волновой природы
электрона показывает, что небольшое
рассеяние происходит и на углы, превышающие
9Макс- В случае равномерно заряженного
шара электроны, проникшие внутрь ядра,
будут испытывать действие силы,
создаваемой внутренним зарядом, и,
следовательно, электроны будут отклоняться на угол,
несколько превышающий 0макс. Поэтому
угол 0макс следует рассматривать как
размытый предел. Однако если измерить
форму и размеры этого «размытия», то затем
путем расчетов можно установить
распределение заряда внутри ядра. Такие расчеты
можно выполнить как в случае рассеяния
электронов на ядрах, так и при рассеянии
на протонах, причем результаты не
обнаруживают у протона заряженной
сердцевины.
Пример 2. Электрон с энергией 10 ГэВ
«нацелен» в край ядра свинца (R = 7,5 фм). Каким
будет классический угол рассеяния электрона 0?
Решение: Из формулы (29-3) найдем tg (в/2)
и вместо v подставим скорость света с; тогда
tg(G/2)
k0Ze2
pcb
(29-4)
Поскольку энергия равна рс = 10 ГэВ =
= 1,6-10"10 Дж, а Ъ = 7,5-10~15 м, получаем
tg(6/2):
(9-109)(82)(l,6-lQ-19)2
:(1,6.10-1О)(7,5.10-15):
= 0,0157,
0 = 1,80°
Из этого примера видно, что если бы
у ядра свинца весь заряд был распределен
по его поверхности, то, согласно
классической физике, электроны с энергией 10 ГэВ
не могли бы рассеиваться на углы больше,
чем 0макс = 1,8°.

Пример 3. Повторим решение в примере 2 для
случая, когда водородная мишень
бомбардируется электронным пучком с энергией 10 ГэВ.
Если радиус протона R = 1 ферми, то каким
будет соответствующий угол рассеяния?
Решение: Подставляя в формулу (29-4) значения
Z = lHb = 10~15M, имеем
tg(0/2) = ^- = 0,00144,
pcR
откуда
0 = 0,17°.
Из этого примера мы видим, что если
при рассеянии электронов с энергией
10 ГэВ на протонах в угловом
распределении обнаруживается спад при углах,
превышающих 0,17°, то радиус протона
должен быть равен приблизительно 1 фм.
Такие эксперименты проводились в 60-е
годы и показали, что среднеквадратичный
радиус распределения заряда в протоне
составляет 0,8 фм.
Пример 4. Если бы треть заряда протона была
сконцентрирована в его сердцевине радиусом
Rc ~ 0,1 фм, то каким оказался бы
соответствующий угол 6макс в случае электронов с
энергией 10 ГэВ?
Решение: В формуле (29-4) заряд
частицы-мишени нужно заменить на е/Ъ. Полагая в этой
формуле Ъ = 10"16 м, находим (0макс)с = 0,55°.
Заметим, что это значение примерно в 3 раза
превосходит полученное в примере 3.
Пример 4 демонстрирует, что если бы
у протона была заряженная сердцевина, то
рассеяние происходило бы на большие
углы, чем это наблюдается на опыте.
В гл. 31 мы узнаем, что протон состоит,
по-видимому, из трех субъядерных частиц,
называемых кварками. Однако вряд ли эти
кварки располагаются в центре и ведут
себя подобно сердцевине протона.
СЕЧЕНИЕ ПОГЛОЩЕНИЯ НЕЙТРОНОВ
Площадь и, следовательно, радиус
атомного ядра можно определить еще
одним, третьим способом, если пластинку,
§ 1. РАЗМЕРЫ ЯДЕР 525
Рис. 29-3. Пучок нейтронов, падающих на
пластинку площадью А.
содержащую исследуемые атомы,
бомбардировать нейтронами высоких энергий
(рис. 29-3). До тех пор пока нейтрон не
сталкивается с ядром, он движется через
пластинку по прямой. Поэтому число
нейтронов, выбывающих из пучка,
пропорционально площади ядра. Если длина волны
нейтрона много меньше размеров ядра, то
эффективная площадь поперечного сечения
ядра а = tlR2, где R-радиус ядра.
Вероятность потери нейтрона равна
отношению полной площади, занятой
ядрами, к общей площади пластинки:
Вероятность = ——,
где Na- полное число атомов в пластинке,
а-эффективная площадь каждого
атомного ядра и А-площадь пластинки. Пусть
91 = NJAx- число атомов в единице
объема, где х-толщина пластинки. Тогда для
пластинки толщиной dx вероятность
потери нейтрона равна Wlodx. Если АГ-число
нейтронов в пучке после прохождения ими
толщины х, то изменение величины N
равно числу частиц в пучке, умноженному на
вероятность У1Ых:
dN = - NKcjdx,

526 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
Интегрируя обе части последнего
равенства, получаем
In АГ = — У1ах + const,
а после потенцирования имеем
N = ЛГПаДехр(- Wax),
где АГпад- число падающих нейтронов (N =
= ЛГпад при х = 0). Таким образом, сечение
записывается в виде
1 , -^пад
(29-5)
Пример 5. Предположим, что на рис. 29-4
нейтронный детектор регистрирует 10000
нейтронов в минуту. При наличии медной пластинки
Пучок
нейтронов
Детектор
нейтронов
Медная
пластинка
Рис. 29-4. Медная пластинка, помещенная на
пути пучка нейтронов, приводит к уменьшению
скорости счета с N до N'.
толщиной 2 см скорость счета снижается до
8950 отсчетов в минуту. Чему равно нейтронное
сечение меди и каков соответствующий радиус?
Решение: Число ядер в единице объема можно
найти, используя значения массовой плотности
р = 9,0 г/см3 и атомной массы меди 63,5:
^ = 9,0 г/см (6>02>102з атом/моль) =
63,5 г/моль
= 8,53-1022 атом/см3.
Подстановка этого значения в формулу (29-5),
а также х = 2 см и NnSLJJN = 1,117 дает
a = 0,65-10"24 см2.
Обычно ядерные сечения имеют порядок
величины Ю-24 см2. Поэтому, как это часто
случается в ядерной физике, это значение стало
играть роль единицы измерения, и ей было
присвоено специальное название-барн (Ю-24 см2 =
= 1 барн). Записывая a = nR2, получаем
71Д2=0,65.10-24см2,
R = 4,55 фм.
§ 2.Фундаментальные силы,
действующие между двумя нуклонами
Основная цель физики состоит в
объяснении всех физических явлений на основе
небольшого числа простых
фундаментальных законов. Поскольку материальные
тела построены из электронов и ядер, мы
старались до сих пор изучать основные
типы взаимодействий между электронами,
ядрами и фотонами. Этот подход, как мы
видели в предыдущей главе, позволяет
достигнуть значительных успехов. Он
обеспечивает исчерпывающее (хотя и с
использованием сложных вычислений) объяснение
строения вещества и соответствующих
взаимодействий. Действительно,
современная квантовая электродинамика настолько
совершенна, что в области атомной физики
она дает результаты с точностью,
значительно превышающей ту, которую может
обеспечить эксперимент. До сих пор не
удавалось установить расхождение теории
с экспериментом, несмотря на то что
погрешность некоторых экспериментальных
результатов не превышала одной
десятимиллионной (10 "7).
С другой стороны, квантовая
электродинамика не может объяснить структуры
атомных ядер, которые, как теперь
известно, состоят из протонов и нейтронов.
Чтобы объяснить, почему протоны внутри
ядра столь прочно связаны, требуется
ввести фундаментальные силы нового типа.
Для преодоления электростатического
отталкивания протонов эти силы должны
быть больше электростатических. Они
называются ядерными силами (или сильным
взаимодействием). Как видно из рис. 29-5,
глубина потенциальной ямы,
соответствующей ядерным силам, на порядок
больше потенциальной энергия
электростатического отталкивания двух протонов.
Если не учитывать довольно слабое
электростатическое отталкивание, то сильное
взаимодействие протона с протоном,
протона с нейтроном и нейтрона с нейтроном
будет в любом из этих случаев одним
и тем же. Это взаимодействие называется
нуклон-нуклонным. Потенциальную
энергию взаимодействия двух нуклонов можно
грубо описать кривой, показанной на
рис. 29-5, хотя детальный вид этого взаи-

§ 2. ФУНДАМЕНТАЛЬНЫЕ СИЛЫ МЕЖДУ ДВУМЯ НУКЛОНАМИ 527
U
20
10
Рис. 29-5. Диаграмма
потенциальной энергии
фундаментального нуклон-нуклонного
взаимодействия.
- Отталкивание
кле<
Притяжение
модействия пока неизвестен. На этом же
рисунке для сравнения приведена
потенциальная энергия электростатического
взаимодействия двух протонов, равная
к0е2/г (штриховая линия). Специфической
особенностью ядерных сил является то,
что потенциальная кривая на рис. 29-5 для
этих сил справедлива, лишь если спины
нуклонов параллельны; если же спины анти-
параллельны, то ядерные силы
оказываются примерно вдвое слабее. Глубину
потенциальной ямы на рис. 29-5 можно
определить, как мы увидим в дальнейшем, из
величины энергии связи дейтрона (2Н, ядро
тяжелого изотопа водорода). Более
детальные сведения о форме потенциала
дают опыты по рассеянию протонов и
нейтронов на протонах.
В атомной физике единственным
атомом, легко поддающимся анализу, был
атом с одним протоном и одним
электроном, т.е. атом водорода. Аналогичная
ситуация имеет место и в ядерной физике:
простейшее ядро, поддающееся анализу,
состоит из одного протона и одного
нейтрона, т.е. представляет собой дейтрон.
В дейтроне протон и нейтрон связаны друг
с другом с энергией 2,22 МэВ. Эта
величина получается из измеренных значений
масс или энергий покоя протона, нейтрона
и дейтрона, которые равны соответственно
938,21; 939,50 и 1875,49 МэВ. Энергия связи
ядра определяется суммой масс отдельных
нуклонов за вычетом массы ядра. В случае
дейтрона энергия связи равна тр + тп —
- md = 2,22 МэВ.
Как и в случае атома водорода, энергия
связи которого равна 13,6 эВ, эту величину
можно было бы рассчитать, исходя из
известного закона действия сил между двумя
частицами. Задача заключается в том,
чтобы найти волновую функцию низшего
порядка, соответствующую кривой
потенциальной энергии на рис. 29-5. В первом
приближении эту потенциальную энергию
можно представить в виде «прямоугольной
ямы» радиусом г0 = 2,3-10~15 м. Такая
яма изображена на рис. 29-6, а. Энергия Е,

528 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
СО
2
S
и
О.
<L>
ас
Г)
Энергия
связи
я 4л—
-ю
-20
-с/
I 1
5хЮ"*13см
Г"
1 Е = -2,22 МэВ
-и
S
и
а*
X
>»
•е
CQ
О
X
о
00
Х10 ,5м
Рис. 29-6. а-приближенное
изображение потенциальной ямы,
отвечающей взаимодействию
нейтрона с протоном;
б-низшая волновая функция,
соответствующая энергетическому
уровню Е= -2,22 МэВ.
отвечающая стоячей волне низшего
порядка, приведенной рис. 29-6,6, показана на
рис. 29-6, а штриховой линией.
Теперь можно заняться вычислениями.
Выберем для расчета положение низшего
энергетического уровня Е, исходя из
известной глубины потенциальной ямы;
с другой стороны, зная величину | Е |
(измеренное значение энергии связи), можно
вычислить глубину ямы. В действительности
впервые был выполнен именно последний
расчет, и мы поступим аналогичным
образом. Будем исходить из того, что известны
энергия связи и радиус действия ядерных
сил г0. Наша цель-получить из этих
данных сведения о глубине потенциальной
ямы, которая характеризует величину
ядерных сил.
Как и в случае атома водорода,
воспользуемся трехмерным уравнением
Шредингера. Для волновой функции низшего
порядка, которая не зависит от 0 и ф,
трехмерное уравнение Шредингера
записывается в виде [см. (26-5)]
2 dy\f\ _ 2ц
dr
= - -Z- (E - t/)i|/.
(29-6)
В этом уравнении г означает
относительное смещение, т.е. расстояние между
протоном и нейтроном. Затем (см. в § 2 гл. 11,
т. 1) мы должны использовать
приведенную массу двух частиц ц. Массы протона
и нейтрона почти одинаковы, обозначим
эти массы М; тогда \х = М/2. Определим
функцию и (г) = п|/(г):
~dr~
1 du
г dr
и
Производя замену в уравнении (29-6),
уравнение Шредингера можно записать в более
простом виде:
[ d ( du
-— г и } =
2dr\ dr
nr г

§ 2. ФУНДАМЕНТАЛЬНЫЕ СИЛЫ МЕЖДУ ДВУМЯ НУКЛОНАМИ 529
ИЛИ
d2U
М,
^<«-о>.-о.
(29-7)
В области I величина Е — U постоянна
и положительна, и решением уравнения
оказывается синусоидальная волна. Таким
образом,
sin/cr cos/cr
\|/ = А (- В , где к =
-1/
(В-и).
Поскольку при г = 0 функция v|/ должна
быть конечной, мы имеем В = 0 и
щ = A sin fcr, где fe =
2(£-[/) =
2(Uo
\Е\).
В области II уравнение (29-7) принимает
вид
^--2\Е\ип = 0.
dr2 П2
Решение этого уравнения записывается
в виде
ии = Be , где К =
>■
Следует заметить, что аналогичное
решение получается и для функции \|/2 на
рис. 25-16. Решение для Е мы получаем
путем сшивания значений щ и щъ а также их
производных на границе между областями
I и И. Таким образом, имеем [см. (25-20)]:
ctg/cr0 = - К/к, (29-8)
или
tgx = — х/Кг0, где х = kr0.
Подставляя численные значения г0 =
= 2,3 • 10" 15 м и | Е | = 2,22 МэВ,
получаем
Хг0 = ^-1/м|Е| = 0,53,
так что
tgx = - х/0,53.
Это уравнение можно решить графически,
построив на одном графике функции tg х и
— х/0,53 и найдя точки, в которых
значения этих функций совпадают. Оказывается,
что х = 1,85. Используя
микрокалькулятор, решение можно также найти методом
проб и ошибок. Поскольку
х = kr0 = 1,85,
мы получаем
1,85
к =
2,3-10-
'м
= 8,04-1014 м-1. (29-9)
Заменим величину к ее выражением и
возведем обе части этого выражения в
квадрат; таким образом,
|f([/o-|£|) = (8,04.1014)2M-2.
Отсюда
U0- \Е\ =
_ (8,04)2-1028-(1,05.10-34)2
— 27 ДЖ —
1,67-10
= 4,27-10"12Дж = 26,7 МэВ,
или
U0 = \E\ + 26,7 МэВ = 28,9 МэВ.
Мы видим, что в соответствии с
измеренным на опыте значением энергии связи
дейтрона глубина потенциальной ямы,
характеризующей взаимодействие нейтрона
с протоном, должна иметь величину около
29 МэВ.
Пример 6. В рассмотренной выше модели
дейтрона плотность вероятности максимальна при
г = 0. Во сколько раз плотность вероятности
(или плотность массы) уменьшится при г = г0?
Решение: В области I решение уравнения Шре-
дингера имеет вид и (г) = r\|/ (г) = A sin кг,
откуда
sin кг sin кг
ф(г) = А = кА
г кг

530 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
\|/ (г0) к A (sin кг0)/ кг 0 sin кг0
\|/(0) = Ы = /сг0
Воспользовавшись формулой (29-9), получим
\|/(r0) sin 1,85
-^-т- = — = 0,52,
Ф(0) 1,85
или
Ж0)|2 °'7-
Мы видим, что в случае дейтрона 25% функции
распределения вероятностей находится за
пределами радиуса действия ядерных сил.
Пример 7. Предположим, что ядерные силы
таковы, что они едва-едва обеспечивают связь
протона и нейтрона в дейтроне, т. е. энергия
связи | Е | близка к нулю. Какой в этом случае
была бы глубина потенциальной ямы?
Решение: При Е -> 0 величина К в формуле
(29-8) обращается в нуль. Тогда
ctg/cr0 = - К/ к = 0.
В этом случае кг0 = я/2, или к = я/2г0, и мы
имеем
откуда
1 / кп\2
U0= = 3,08-10" 12Дж = 19,2 МэВ.
M\2r0J
§ 3. Строение тяжелых ядер
Большую плотность нуклонов в
тяжелых ядрах можно объяснить следующим
образом. Пусть первоначально имеется
множество свободных нуклонов, и
расстояние между соседними нуклонами равно s.
Будем теперь понемногу сближать
частицы, т.е. уменьшать s. Как только s
окажется меньше 2,5 • 10 ~ 13 см, нуклоны
внезапно почувствуют сильное притяжение
своих соседей и их энергия связи
соответственно возрастет. С другой стороны, как
было показано в гл. 28, при более плотном
сгущении свободных электронов их
средняя кинетическая энергия также должна
возрасти вследствие принципа Паули [см.
(28-3)]. Поскольку протоны и
нейтроны-это частицы со спином 1/2, они тоже
должны подчиняться принципу Паули.
Таким образом, влияние этого принципа
будет сказываться в снижении энергии
связи, по мере того как s уменьшается. К
счастью, силы нуклон-нуклонного
притяжения оказываются как раз настолько
большими, насколько это необходимо,
чтобы обеспечить «золотую середину»,
а именно существование такого значения s,
при котором энергия связи достигает
максимума (если бы нуклон-нуклонные силы
оказались на 30% слабее, то
преобладающим оказалось бы влияние принципа
Паули и ядер вообще не существовало бы).
Значение s, при котором энергия связи
максимальна, и определяет размеры ядер.
Из эксперимента найдено s=l,9-10"13 см,
что согласуется с (29-2).
Рассмотрим теперь отдельный нейтрон
внутри тяжелого ядра. На нейтрон
действует сила притяжения, усредненная по
всем остальным нуклонам внутри ядра.
Аналогичная ситуация уже встречалась
нам в гл. 28, когда речь шла о потенциале,
в котором свободный электрон находится
внутри металла. На рис. 29-7 показан
усредненный потенциал, в котором
находится рассматриваемый нами нейтрон. При
этом глубина ямы, соответствующей
средним и тяжелым ядрам, составляет около
42 МэВ. Добавление большего количества
нуклонов не приводит к увеличению
результирующей силы, дейстэующей на
данный нуклон, поскольку, как отмечалось
выше, он притягивается лишь
ближайшими соседями. В действительности в эту
потенциальную яму «набито» около А/2
нейтронов. Вследствие принципа Паули они
занимают различные состояния или
энергетические уровни вплоть до уровня
Ферми. Величину уровня Ферми можно
записать в виде [см. (28-3)]
h2 /3 \2/3
"'-тик*) ' (29"10)
где 91 -число нейтронов в единице объема,
что составляет примерно половину
плотности ядерных частиц, которая в
соответствии с (29-2) достигает 0,7-1044м~3. Та-

§ 3. СТРОЕНИЕ ТЯЖЕЛЫХ ЯДЕР 531
Рис. 29-7. Усредненная
потенциальная энергия ядра, которую
«ощущает» нейтрон в ядре
радиусом R. Занятые уровни
указаны сплошными линиями,
а свободные, или возбужденные,
уровни-штриховыми линиями.
Показана также энергия связи
нейтрона (энергия, необходимая
для удаления нейтрона).
-ю:
-20-
-зо.
-40:
-50 МэВ
R
z—*—
Энергия связи
L
ким образом,
(6,62.10"
34\2
К
-.0,7.1044)2/3 Дж =
'' 8(1,67-10" 27)Vti
= 5,4.10_12Дж = 33,8 МэВ.
Мы видим, что наиболее высокий занятый
нейтронами энергетический уровень
расположен приблизительно на 34 МэВ выше
дна потенциальной ямы, или примерно на
8 МэВ ниже нулевой энергии.
Следовательно, для того чтобы удалить отдельный
нейтрон из типичного ядра, потребуется по
меньшей мере 8 МэВ энергии. Глубина
ямы и величина уровня Ферми у
оставшегося ядра останутся прежними. Поэтому
для удаления второго нейтрона
потребуется еще 8 МэВ. В конечном счете можно
сказать7 что в средних ядрах энергия связи,
приходящаяся на один нуклон, или удель-
Рис. 29-8. Экспериментальная
зависимость удельной энергии
связи (энергии связи,
приходящейся на один нуклон) от
массового числа А.
I
as
(Т)
50 ЮО 150
Массовое число А
200

532 гл- 29. ЯДЕРНАЯ ФИЗИКА
ная энергия связи составляет 8 МэВ.
Глубина потенциальной ямы более легких
ядер не будет оставаться одной и той же,
поскольку среднее число ближайших
соседей уменьшается и, как следствие, удельная
энергия связи оказывается меньше 8 МэВ.
В случае более тяжелых ядер
существенным оказывается дополнительный
вклад в полную энергию ядра,
обусловленный электростатической
потенциальной энергией, которая пропорциональна
Z2/R; поэтому у этих ядер удельная
энергия связи также должна быть меньше
8 МэВ. На рис. 29-8 приведены
экспериментальные данные, подтверждающие эти
предсказания. Наше обсуждение касалось
только нейтронов; на протоны в ядре
действуют такие же ядерные силы,
соответствующие потенциальной яме глубиной
U0 = 42 МэВ. Однако в случае протонов
дно ямы поднимается на несколько МэВ
благодаря электростатической
потенциальной энергии, которая пропорциональна
k0Ze2/R.
Предположим, что ядро радиусом
К первоначально содержало одинаковое
число нейтронов и протонов. В этом
случае диаграммы потенциальной энергии для
протонов и нейтронов имели бы вид,
показанный на рис. 29-9, и наиболее высокая
энергия протона оказалась бы на
несколько МэВ выше максимальной энергии
нейтрона.
В § 5 мы увидим, что, если бы так оно
и было, протон превратился бы в нейтрон
с испусканием позитрона и нейтрино.
Таким образом, рассматриваемая модель
потенциальной ямы предсказывает, что в
тяжелых ядрах должно быть в конечном
счете больше нейтронов, чем протонов.
Например, ядро 238U содержит 146
нейтронов и 92 протона.
Приводимый ниже количественный
пример дает представление о том, почему
отношение числа нейтронов к числу
протонов превышает единицу и почему это
отношение увеличивается с ростом массового
числа А.
* Пример 8. Каким, согласно модели
потенциальной ямы, должно быть число протонов Z
в ядре с массовым числом Л = 51?"
Решение: Пусть в случае нейтронов глубина
потенциальной ямы U0 = 42 МэВ, а в случае
протонов она равна U0 — k0(Z - l)e2/R.
Предположим, что энергия нейтрона,
находящегося на наиболее высоком уровне, равна £п,
а соответствующая энергия протона равна Ер.
Тогда
Еп = Ер,
Uо - (К,)п = С/0 - /со (Z д1)в2~ (Kf)p
R
О О
ж.
<К/К
(к,
■/'п
-ия
Рис. 29-9. Диаграммы
потенциальной энергии нейтронов
и протонов в ядре радиусом R.
Если число протонов и
нейтронов в ядре одинаково, то для их
энергий Ферми мы имеем
(Kf)n < (Kf)pi т. е. ч протоны с
наиболее высокой энергией
будут превращаться в нейтроны с
испусканием пар
позитрон-нейтрино.

§ 3. СТРОЕНИЕ ТЯЖЕЛЫХ ЯДЕР
h2 / 3 (Л - Z) \2/3 _
U° ~ ~Ш\п (4/3)яД3 /
- л _ ъ g2(Z - Ц _ h2 (3 Z У/3
0 ° К 8MU (4/3)tlR3/
Используя значение R = 4,45 -Ю-15 м,
вычисленное по формуле (29-1), уравнение в числах
относительно Z (все величины в МэВ) можно
написать в виде
42 - 3,87(51 - Z)2/3 = 42 - 0,324(Z - 1) -
- 3,87Z2/3,
или
0,324(Z - 1) - 3,87[(51 - Z)2/3 - Z2/3] = 0.
Решение этого уравнения можно быстро найти
методом проб и ошибок с помощью
микрокалькулятора. Мы получим Z = 21,7. Это
значение почти совпадает с тем, которое имеет
элемент ванадий сЛ = 51 hZ = 23. Существует
также радиоактивный изотоп титана с Л = 51 и
Z = 22.
Мы видим, что упрощенная модель
ядра в виде прямоугольной ямы вполне
надежно предсказывает отношение числа
протонов в ядре к числу нейтронов, а
также значения энергии связи. Можно
предсказать и другие результаты, например
значения энергий возбужденных состояний
(на рис. 29-7 они показаны штриховыми
линиями). Расстояние между
энергетическими уровнями можно вычислить, если
взять логарифм от обеих частей равенства
(29-10) и результат затем
продифференцировать :
АЕ __ 2 ДЖ
~Ё~ ~У"1гГ
Если к ядру, содержащему 20 нейтронов,
добавить еще один нейтрон, то мы
получим AW/9i = 0,05 и Д£/£^0,03; отсюда
Е ж 0,03 х 34 МэВ = 1,1 МэВ. Это
типичное расстояние между низшими
энергетическими уровнями в легких и средних
ядрах. В случае более тяжелых ядер АУ1/91
и, следовательно, расстояние между
уровнями оказываются меньше.
ОБОЛОЧЕЧНАЯ МОДЕЛЬ
Каждому энергетическому уровню
нейтрона на рис. 29-7 соответствует стоячая
волна, или орбиталь, с определенной
энергией и моментом импульса. Это относится
как к занятым уровням, так и к уровням
с более высокой энергией, т.е. к
возбужденным состояниям. Нуклонные орбита-
ли будут «стабильны» и иметь
определенную энергию только в том случае, если
средний свободный пробег нуклона в
ядерном веществе значительно превысит
размеры ядра. Благодаря принципу Паули
средний свободный пробег действительно
оказывается значительно больше 10" 15 м.
Если нет свободного состояния, в которое
мог бы перейти рассеянный нуклон, то
столкновений в обычном смысле не может
происходить: состояние с подходящим
импульсом, в которое ему надлежит перейти,
уже занято.
На рис. 29-10 приведены результаты
расчета энергетических уровней с
соответствующими моментами импульса, которые
отвечают допустимым стоячим волнам
в потенциальной яме, показанной на рис.
29-7. Энергии уровней вычислены с учетом
того факта, что действующая на нуклон
сила оказывается больше, если спин и
орбитальный момент импульса направлены
в одну сторону. Сумма спина и
орбитального момента импульса представляет
собой полный момент j. Ядро, у которого
заполнена оболочка с и = 5, ! = 4 и j = 9/2,
содержит 50 нейтронов (либо 50 протонов).
Кроме того, как видно из рис. 29-10, эта
оболочка и следующая оболочка с более
высокой энергией разделены большим
энергетическим промежутком. Поэтому
можно ожидать, что ядра с 50 нейтронами
(А — Z = 50) или 50 протонами (Z = 50)
окажутся сильно связанными и особенно
стабильными. Рис. 29-11 наглядно
иллюстрирует это обстоятельство: для того
чтобы перевести ядро, содержащее 50
нейтронов, в ближайшее возбужденное
состояние, необходима энергия свыше 2 МэВ,
тогда как соседним ядрам для этого нужна
гораздо меньшая энергия. Еще один
пример более сильной связи ядер с
магическим числом 50 заключается в том, что
у олова (Z = 50) имеется 10 стабильных

534 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
изотопов, больше чем у любого другого
элемента. Кроме того, ядра с 50
нейтронами или 50 протонами значительно более
широко распространены в природе, , чем
ядра с 51 нейтроном или протоном.
N I
Число
нуклонов Полное
в число
J оболочке нуклонов
<Т>
4 0
5 2
6 4
5 2
7 6
6 4
5 3
4 1
7 6
4 1
5 3
6 5
3 0
6 5
4 2
4 2
5 4
5 4
3 1
3 1
4 3
1/2
3/2
7/2
5/2
11/2
9/2
5/2
1/2
13/2
3/2
7/2
9/2
1/2
11/2
3/2
5/2
7/2
9/2
1/2
3/2
5/2
2
4
8
6
12
10
6
2
14
4
8
10
2
12
4
6
8
10
2
4
6
126
120
118
104
100
92
82
80
68
64
58
50
40
38
34
4 3 7/2
2 0 1/2
3 2 3/2
3 2 5/2
2 1
2 1
1/2
3/2
2
4
28 —
20 —
18
14
8 —
6
1 0 1/2
Приведенные на рис. 29-11
экспериментальные результаты согласуются с
теоретическими расчетами, согласно которым
ядра с числами нейтронов (или протонов) 2,
8, 20, 28, 50, 82 или 126 связаны более
прочно. Эти числа называются магическими;
они аналогичны числам, соответствующим
заполненным оболочкам в атомной
физике, со значениями 2, 10, 18, 36, 54 и 86 (см.
рис. 27-1).
§ 4. Альфа-распад
По причинам исторического характера
ядро 4Не называют альфа-частицей (ос-ча-
стицей). Установлено, что многие тяжелые
ядра с Z > 82 (Z = 82 имеет свинец)
испытывают радиоактивный распад с
испусканием альфа-частицы. Поскольку в альфа-
частице удельная энергия связи
оказывается больше, чем в тяжелых ядрах, альфа-
распад энергетически вполне возможен.
Например, образец урана 238U испускает
альфа-частицы с периодом полураспада
4,5 • 109 лет. Самопроизвольно происходит
ядерная реакция
238U - 234Th + 4Не + 4,2 МэВ.
Спустя 4,5-109 лет половина ядер 238U
распадается. Разность масс 238U и
продуктов его распада составляет 4,2 МэВ.
Диаграмма потенциальной энергии
альфа-частицы и конечного ядра на рис. 29-12
позволяет получить представление о том,
почему происходит альфа-распад. На этом
рисунке Ed-кинетическая энергия
вылетающей альфа-частицы. Первоначально
альфа-частица находится в области I и
может быть описана стоячей волной с
амплитудой \|/ВНутр. Однако из-за проникновения
сквозь барьер (см. § 7 гл. 28) в области
Рис. 29-10. Относительное расстояние между
энергетическими уровнями ядер с учетом спин-
орбитального взаимодействия (сила больше,
если спин и орбитальный момент параллельны).
Как и у атома водорода, каждый
энергетический уровень или «оболочка» распадается на
подоболочки, соответствующие различным
квантовым числам тх. В правой колонке
приведено полное число нуклонов, необходимое для
заполнения этих подоболочек. Магические числа
отмечены стрелками.

§ 4. АЛЬФА-РАСПАД 535
126
Рис. 29-11. Экспериментальные
значения энергий возбуждения
для ядер с четным числом
протонов и нейтронов. Линии
соединяют ядра с одинаковым
числом протонов.
X
82
ад 1
40
80 120
160
Число нейтронов
Еа
0
I
-</о ^
^ //-* 2Ze2
^ч^^^
II
Рис. 29-12. а - потенциальная
энергия взаимодействия
ос-частицы и остаточного ядра с
зарядом Ze; величина
£а-кинетическая энергия ос-частицы на
больших расстояниях от ядра;
б-соответствующая волновая
функция.

ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
вдали от ядра имеется небольшой «хвост»
волновой функции с амплитудой \|/ВНеш.
Следовательно, вероятность вылета альфа-
частицы в момент ее соударения с
барьером можно записать приблизительно
в виде
U \2
увнутр
Число таких столкновений в 1 с составляет
приблизительно v/2R, где v- скорость
альфа-частицы в области I. Таким образом,
вероятность испускания альфа-частицы
в единицу времени запишется в виде
dt
2R |v|/ внутр
Определим величину
_ 2R |\|/ внутр
(29-11)
V |\|/внеш|2 '
Тогда из (29-11) и (29-12) получаем
dpr = J_
dt т*
(29-12)
В образце, содержащем п ядер, число
распадов в секунду (т.е. скорость уменьшения
п) равно
dn dpr _ /1
dt dt \x
Отсюда находим
dn 1 ,
= dt,
П T
£--Я*
Интегрирование дает
t
In n = h const.
T
Потенцируя обе части последнего
равенства, получаем
п = const х е
■t/x
Если п0- число ядер при t = 0, то
-г/т
(29-13)
N
о
о
X
Рис. 29-13. Кривая
радиоактивного распада. Зависимость
числа нераспавшихся атомов от
времени на протяжении четырех
периодов полураспада.

§ 4. АЛЬФА-РАСПАД
537
Это закон радиоактивного распада. На
рис. 29-13 представлена соответствующая
этому закону кривая распада.
Период полураспада Г определяется как
такое значение времени t, для которого
п = и0/2. Подставляя эту величину
в (29-13), получаем
по - Г/т
Т = П° '
2 = ег/\
Логарифм этого выражения дает
Т
In 2 = —,
т
откуда
Т= 0,693т.
Заменяя т на Т, формулу (29-13) можно
записать в виде
п = „0 е-ода^= «о (е-П'/Г= "о (|)'/Г. * = "^*
Если в формулу (29-12) подставить т =
= 1,4Т, то мы получим формулу для
периода полураспада
1,4R |\|/,
внутр
7^
(29-14)
Пример 9. Чему равно среднее время жизни
ядра до распада? Ответ нужно выразить через
параметр т.
Решение: Рассмотрим образец, содержащий
вначале п0 радиоактивных ядер, и найдем
среднее взвешенное t с весовым множителем и:
\tndt J
ьср
\ndt
Jexp(- t/x)dt
_b2e-^(-t/T-l)To _т
Мы видим, что параметр т, определенный как
величина, обратная скорости распада
отдельного ядра, представляет собой среднее время
жизни.
Пример 10. Пусть в ядре 238U альфа-частица
сталкивается с потенциальным барьером 5 • 1020
раз в секунду и \|/ВнешЛ|/Внутр = Ю-19.
а) Какова вероятность распада этого ядра в
1 с?
б) Каково среднее время жизни этого ядра?
Решение: Согласно (29-11), скорость распада
dPr / ЧИСЛО \ /у\,внеш\2
— « I столкн. х I I =
«* V В 1 С / ЧУвнутр/
= (5 1020)(10-38) = 510"18 с"1.
Таким образом,
Aprx5-10-18At.
Поскольку At = 1 с,
Дрг«5-НГ18.
Среднее время жизни можно получить, обращая
соотношение dpjdt = 1/т:
1
5-10"
= 2-1017с =
= 6,5-109 лет.
Следовательно, период полураспада Т-
= 0,693 т = 4,5 • 109 лет.
Формула (29-14) иллюстрирует
применение квантовой механики для объяснения
радиоактивности. Современная квантовая
механика дает столь же исчерпывающее
объяснение альфа-распада и других видов
радиоактивных превращений, как и в
случае других явлений. Природа вероятности
такова, что если в силу редкой случайности
данное ядро уцелело на протяжении
большого числа периодов полураспада, то эта
предыстория ни в коей мере не влияет на
вероятность распада в будущем. Это же
имеет место и при бросании монеты. Если
у вас пять раз подряд выпала решетка,
вероятность шестой раз выпасть решетке по-
прежнему остается равной половине. Мы
не имеем возможности предсказать, когда
произойдет распад данного ядра.
Вероятность распада ядер одного сорта всегда
одна и та же независимо от их возраста.
Например, половина ядер радиоактивного
изотопа с периодом полураспада 1 год
распадается за первый год, однако то или
иное ядро, избежавшее распада в первый

ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
год, по-прежнему будет иметь вероятность
1/2 распасться на протяжении второго года.
Если же ядро сохранится на протяжении
двух лет, его вероятность распада на
третий год снова будет равна 1/2.
§ 5. Гамма- и бета-распад
ГАММА-РАСПАД
Если ядро возбуждено и находится
в состоянии с более высокой энергией (на
одном из уровней, показанных на рис. 29-7
штриховыми линиями), то оно может
самопроизвольно перейти на более низкий
энергетический уровень, испустив при этом
фотон (см. § 5 гл. 26). Расстояние между
энергетическими уровнями ядер составляет
порядка 1-2 МэВ. Поэтому энергия
фотонов, испускаемых атомными ядрами,
оказывается в сотни и тысячи раз выше
энергии фотонов, испускаемых атомами.
Такие фотоны с высокой энергией,
испускаемые ядрами, называются
гамма-квантами.
Возбужденные состояния ядер можно
получить, используя нейтроны низких
энергий. К примеру, попадая в образец
238U, медленный нейтрон, оказавшись
в пределах радиуса действия ядерных сил,
испытает ядерное притяжение со
стороны атомного ядра. В этом случае вполне
вероятно, что нейтрон будет поглощен
ядром, в результате чего образуется 239и*
в возбужденном состоянии. (Звездочка
наверху справа в символе элемента
обозначает возбужденное состояние.) Такое
возбужденное ядро возвращается в основное
состояние, испуская один либо
последовательно несколько гамма-квантов.
Подобные процессы изображают в обозначениях
ядерных реакций следующим образом.
n + 238U-»239U*,
239u*_>239TJ + у.
БЕТА-РАСПАД
Свойства радиоактивного излучения
были изучены вскоре после открытия
радиоактивности в 1896 г. Оказалось, что
существуют три различных вида излучений,
а именно альфа, бета и гамма. После
многолетних исследований было
обнаружено, что альфа-излучение состоит из ядер
гелия, а гамма-излучение-это фотоны
с высокой энергией. Было установлено, что
бета-излучение состоит из электронов или
позитронов. При распаде некоторые ядра
испускали электроны, а
другие-позитроны. Более тщательные исследования
обнаружили, что испускание электронов
или позитронов всегда сопровождается
испусканием нейтрино или антинейтрино.
Нейтрино-это элементарная частица
с электрическим зарядом, равным нулю,
и нулевой массой покоя. Нейтрино имеет
такой же спин, как и электрон.
Пример 11. Используя принцип
неопределенности, покажем, что электрон не может
находиться внутри атомного ядра.
Решение: Неопределенность величины импульса
электрона должна быть равна по меньшей мере
П 1,05-1(Г34 _.
Ар « — « —— кг • м • с =
F Ах 10"15
= ^ОЗ-КГ^кг-м.с-1 = 197МэВ/с.
В соответствии с формулой (9-11) полная
энергия электрона с таким импульсом должна быть
равна
Е = |/(тес2)2 + (ср)2 = l/(0,51)2 + (197)2 МэВ =
= 197 МэВ,
где тес2 = 0,51 МэВ. Чтобы электрон с
кинетической энергией 197 МэВ удержать в связанном
состоянии, необходимо обеспечить еще
большую электростатическую энергию связи.
Однако электростатическая энергия связи равна
k0Ze2/R, что для любых ядер меньше, чем
10 МэВ.
Современная теория бета-распада
основана на теории, разработанной Энрико
Ферми в 1931 г. Ферми предположил, что
протон или нейтрон могут испускать пару
электрон-нейтрино благодаря в сущности
тому же механизму, что и при испускании
фотона заряженной частицей. Пара элек7
трон-нейтрино рождается благодаря
слабым взаимодействиям, подобно тому как
фотон рождается за счет
электромагнитных взаимодействий. До того как
происходит бета-распад, внутри ядра нет ни
электрона, ни нейтрино.
Простейшим примером бета-распада
является превращение свободного нейтро-

§ 6. ДЕЛЕНИЕ ЯДЕР
на в протон с периодом полураспада 12
мин:
п -* р + е~ + v,
где символ v обозначает антинейтрино.
(То, в чем состоит отличие v от v, мы
рассмотрим в гл. 31). Оказалось, что масса
покоя нейтрона больше массы покоя
протона на 1,3 МэВ; поэтому полная энергия
испускаемой пары электрон-нейтрино
составляет 1,3 МэВ; 0,5 МэВ идет на массу
покоя электрона и 0,8 МэВ остается на
кинетическую энергию, которую делят между
собой электрон и нейтрино.
Из рис. 29-9 можно видеть, что в
типичном ядре нейтрон с наивысшей энергией
располагается почти на том же
энергетическом уровне, что и протон с наивысшей
энергией. В таком ядре закон сохранения
энергии запрещает нейтронам
превращаться в протоны. Если же к ядру добавляется
нейтрон, энергетический уровень которого
оказывается более чем на 0,5 МэВ выше
наиболее высокого энергетического уровня
протонов, то становится возможным
рождение пары электрон-нейтрино и может
произойти бета-распад. В качестве примера
рассмотрим бомбардировку нейтронами
ядер 238U. Выше мы показали, что при
этом в результате поглощения нейтрона
образуется 239U. У этого изотопа урана
энергия наивысшего энергетического
уровня нейтрона на 1,8 МэВ выше, чем для
протона. Следовательно, пара электрон —
нейтрино будет испускаться с
кинетической энергией 1,3 МэВ. Наблюдаемый
период полураспада составляет 24 мин:
239и _> 239Np + е- + у.
Нептуний также оказывается
нестабильным относительно бета-распада:
239Np _^ 239pu + е- + -
с периодом полураспада 2,35 суток. В
случае этого двухступенчатого процесса два
наивысших нейтронных уровня
освобождались, а два протонных энергетических
уровня заполнялись, так что у
образующегося ядра 239Ри наивысшие протонный
и нейтронный уровни оказались близкими
друг к другу. Следовательно, для ядра
плутония 239Ри бета-распад запрещен. Однако
это ядро способно испытывать
альфа-распад с периодом полураспада 24000 лет.
Как мы увидим в следующем разделе, еще
более важным свойством 239Ри является
его малое время жизни относительно
деления, вызванного нейтронами.
§ 6. Деление ядер
Как видно из рис. 29-8, с ростом
значения А удельная энергия связи
увеличивается вплоть до А я 50. Это поведение можно
объяснить сложением сил; энергия связи
отдельного нуклона усиливается, если его
притягивают не один или два, а несколько
других нуклонов. Однако в элементах со
значениями массового числа больше
А ж 50 удельная энергия связи постепенно
уменьшается с ростом А. Это
свидетельствует о том, что ядерные силы
притяжения являются короткодействующими
(радиусом действия порядка размеров
отдельного нуклона). За пределами этого радиуса
преобладают силы электростатического
отталкивания; иными словами, если два
протона удаляются друг от друга более
чем на 2,5-10" 15 м, то силы оказываются
силами отталкивания, а не притяжения.
Следствием такого поведения удельной
энергии связи в зависимости от А является
существование двух процессов - синтеза
и деления ядер. Рассмотрим вначале, что
произойдет, если сблизить электрон и
протон. В этом случае высвобождается
энергия 13,6 эВ и масса атома водорода
оказывается на 13,6 эВ меньше суммы масс
свободного электрона и протона. Точно
также масса или энергия покоя двух легких
ядер превышает массу их соединения. Если
их удастся соединить, то они сольются
с выделением энергии, которое
соответствует разности масс. Этот процесс
называется синтезом ядер. В § 7 мы увидим,
что эта разность масс может превышать
0,5%. С другой стороны, если тяжелое
ядро расщепляется на два более легких
ядра, то их масса будет меньше массы
родительского ядра на 0,1%. Таким образом,
у тяжелых ядер существует тенденция к
делению на два более легких ядра с
выделением энергии. Энергия атомной бомбы
и ядерного реактора представляет собой
энергию, высвобождающуюся при делении
ядер. Энергия водородной бомбы-это

ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
энергия, выделяющаяся при ядерном
синтезе. Альфа-распад (см. § 4) можно
рассматривать как сильно асимметричное
деление, при котором родительское ядро
М расщепляется на маленькую
альфа-частицу и большое остаточное ядро М'.
Альфа-распад возможен только в том случае,
если в процессе
М -+ М' + а
масса М оказывается больше суммы масс
М' и альфа-частицы. В этом случае ядро
будет радиоактивным и может
претерпевать альфа-распад. Оказывается, что у всех
ядер с Z > 82 (свинец) М > М' + Ма. При
Z > 92 (уран) полупериоды альфа-распада
оказываются значительно короче возраста
Земли. Вот почему такие элементы не
встречаются в природе. Однако их можно
создать искусственно. Например, плутоний
(Z = 94) можно получить из урана в
ядерном реакторе. Эта процедура стала
настолько обычной, что обходится всего в 15
долларов за 1 г. До сих пор удалось
получить элементы вплоть до Z = 106, однако
гораздо более дорогой ценой и, как
правило, в ничтожных количествах. Можно
надеяться, что в конце концов радиохимики
научатся получать, хотя и в небольших
количествах, новые элементы с Z > 106.
Если бы массивное ядро урана удалось
разделить на две группы нуклонов, то эти
группы нуклонов перестроились бы в ядра
с более сильной связью, причем в процессе
перестройки выделилась бы энергия.
Таким образом, спонтанное деление ядер
разрешено законом сохранения энергии.
Однако потенциальный барьер
встречающихся в природе ядер настолько высок, что
вероятность спонтанного деления
оказывается даже меньше вероятности альфа-
распада. Например, период полураспада
ядер 238U относительно спонтанного
деления составляет 8-Ю15 лет. Это более чем
в миллион раз превышает возраст Земли.
С другой стороны, если нейтрон
сталкивается с таким ядром, то оно может
возбудиться и перейти на более высокий
энергетический уровень вблизи вершины
электростатического потенциального барьера,
в результате чего возрастет вероятность
деления. Кроме того, ядро в возбужденном
состоянии может обладать значительным
моментом импульса и приобрести
овальную форму. Участки на периферии ядра
легче проникают сквозь барьер, поскольку
они частично уже находятся за барьером;
поэтому, когда ядро принимает овальную
форму, роль барьера еще больше
ослабляется. При захвате ядром 235U или
239Ри медленного нейтрона образуются
состояния с очень короткими временами
жизни относительно деления. Разность
масс ядра урана и типичных продуктов
деления такова, что в среднем при делении
урана высвобождается энергия 200 МэВ.
Масса покоя ядра урана 2,2• 105 МэВ;
следовательно, в энергию превращается около
0,1% этой массы, что равно отношению
200 МэВ к величине 2,2 • 105 МэВ.
Рис. 29-14. а-в каждой мышеловке
установлено по два шарика для пинг-понга;
мышеловка представляет собой ядро 235U, а шарики-
это нейтроны, испускаемые при делении ядер;
б - моментальный снимок спустя несколько
секунд, после того как в мышеловки был брошен
дополнительный шарик (нейтрон); в течение
нескольких секунд шла цепная реакция.

§ 6. ДЕЛЕНИЕ ЯДЕР
541
Поскольку в 1 г любого вещества
содержится тс2 = 9-Ю13 Дж, деление 1 г урана
сопровождается выделением ~9-1010Дж.
Это почти в 3 млн. раз превосходит
энергию 2,9 • 104 Дж, получаемую при
сжигании 1 г угля. С другой стороны, 1 г
урана обходится значительно дороже 1 г угля.
Однако стоимость 1 Дж энергии,
полученной сжиганием угля, оказывается в 400 раз
выше, чем в случае уранового топлива.
В 1974 г. в США выработка 1 кВт-ч
энергии обходилась в 1,7 цента на
электростанциях, работающих на угле, ив 1,05 цента
на ядерных электростанциях.
Предполагается, что в северо-западных районах
США ядерная энергия будет успешно
конкурировать с природным горючим, в то
время как в угледобывающих областях
производство энергии, основанное на угле,
будет экономичнее ядерной энергетики.
Благодаря цепной реакции процесс
деления ядер можно сделать
самоподдерживающимся. При каждом делении вылетают
2 или 3 нейтрона. Если одному из этих
нейтронов удастся вызвать деление
другого ядра урана, то процесс будет
самоподдерживающимся (рис. 29-14). Совокупность
делящегося вещества, удовлетворяющая
этому требованию, называется
критической сборкой. Первая такая сборка,
названная ядерным котлом, была построена Эн-
рико Ферми на корте для игры в сквош1}
на территории Чикагского универститета.
На мемориальной бронзовой доске,
укрепленной на одной из стен корта, написано:
«Здесь 2 декабря 1942 г. человек впервые
осуществил самоподдерживающуюся
цепную реакцию и этим положил начало
управляемому получению ядерной
энергии». В Чикагском университете имеется
также монумент, посвященный этому
событию (рис. 29-15).
Массу 235U и 239Ри можно также
сделать надкритической. В этом случае
возникающие при делении нейтроны будут
вызывать несколько вторичных делений.
Поскольку нейтроны движутся со скоростями,
1} Сквош-игра в мяч с ракеткой, сходная
с теннисом. Корт для сквоша представляет
собой бетонную коробку, лишенную потолка
и одной из стен -Прим. перев.
Рис. 29-15. Скульптура «Атомный век»
(выполнена Генри Муром и приобретена Чикагским
университетом) в память об овладении
атомной энергией.
превышающими 108 см/с, надкритическая
сборка может полностью прореагировать
(или разлететься) быстрее чем за тысячную
долю секунды. Такое устройство
называется атомной бомбой. Сферу из плутония
переводят в надкритическое состояние
обычно с помощью взрыва. Подкритиче-
скую сферу из плутония окружают
химической взрывчаткой. При ее взрыве
плутониевая сфера подвергается мгновенному
сжатию. Поскольку плотность сферы при
этом значительно возрастает, скорость
поглощения нейтронов оказывается выше
скорости потери нейтронов за счет их
вылета наружу. В этом и заключается
условие надкритичности.

542 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
Взрыв атомной бомбы можно сделать
достаточно эффективным (большая часть
плутония прореагирует, а не разлетится).
Энергии химических превращений таковы,
что 1 т тринитротолуола (ТНТ)
высвобождает 109 кал, или 4 • 109 Дж. При взрыве
атомной бомбы, расходующей 1 кг
плутония или 235U, высвобождается около
8-Ю13 Дж энергии, что почти в 20000 раз
больше, чем при взрыве 1 т ТНТ. Такая
бомба называется 20-килотонной бомбой.
Современные бомбы мощностью в
мегатонны в миллионы раз мощнее обычной
ТНТ-взрывчатки. Но дело не только в том,
что это в миллионы раз более мощное
энерговыделение, но и в том, что каждый
грамм израсходованного плутония или
урана порождает почти грамм
радиоактивных продуктов деления, обладающих
огромной радиоактивностью.
Независимо от того, «сжигается»
урановое горючее быстро, как в бомбе, или
медленно, как в ядерном реакторе,
возникающая при этом радиоактивность
представляет собой серьезную проблему.
Значительная часть стоимости ядерных
реакторов обусловлена тщательно
разработанными средствами безопасности для
предотвращения аварий и обработки
радиоактивных отходов. Хотя в случае
редких аварий, таких, как нарушение системы
водяного охлаждения или неисправность
управляющих стержней, ядерный реактор
не взорвется наподобие атомной бомбы,
однако при этом могут расплавиться
соответствующие детали, в результате чего
произойдет утечка радиоактивности в
окружающую среду. Для обеспечения
безопасности используемые в
промышленности ядерные реакторы снабжаются
аварийной системой охлаждения активной зоны
и заключаются в герметичные баки,
рассчитанные на высокое давление.
Надежные оценки вероятностей возникновения
аварий на реакторе и возникающих при
этом потерь представляют собой весьма
сложную задачу. Многие считают, что
большую опасность для человечества
представляет не радиоактивность, создаваемая
ядерными электростанциями, а загрязнение
от обычных электростанций на угле.
Имеется также проблема длительного
хранения радиоактивных продуктов деления.
Более косвенная опасность,
обусловленная использованием ядерной энергии,
которая обычно не упоминается в этой
связи, таится в ее распространении среди
небольших государств, что может привести
к дальнейшему распространению ядерного
оружия и, как возможное следствие,
к ядерной войне. Если бы мир отказался
от получения ядерной энергии, это,
вероятно, уменьшило бы и опасность
возникновения ядерной войны. Ожидается, что
ядерная энергия поможет обеспечить мировые
потребности в энергии, когда добыча
нефти будет уже не в состоянии
удовлетворить спрос на нее. Согласно прогнозам,
нехватка нефти в мире обострится примерно
к 1990 г., причем в течение последующих
20 лет запасы ее полностью истощатся.
Примерно к этому же времени,
по-видимому, истощится и горючее на обогащенном
изотопе 235U, необходимое США для
работы ядерных реакторов на обычной воде.
Однако переход к реакторам на тяжелой
воде, использующим горючее,
вырабатываемое с помощью меньшего количества
реакторов-размножителей (бридерных
реакторов или бридеров), может на
неопределенный срок продлить пригодность
делящегося ядерного горючего.
§ 7. Синтез ядер
Из рис. 29-8 мы видим, что масса или
энергия покоя двух легких ядер
оказывается больше, чем у суммарного ядра. Если
бы эти ядра можно было привести в
соприкосновение, то результирующее ядро
имело бы меньшую массу и
высвободилась бы энергия, равная разности масс.
Например, если бы удалось соединить два
дейтрона и получить ядро гелия, масса
которого меньше суммарной массы двух
дейтронов на 24 МэВ, то удалось бы
высвободить энергию синтеза в количестве 24 МэВ.
Таким образом, при объединении двух
дейтронов с образованием гелия в энергию
превращается 0,6% их первоначальной
массы покоя. Если бы этот процесс синтеза
удалось использовать для производства
энергии, то он оказался бы примерно в
6 раз эффективнее процесса деления урана.
Более того, в воде озер и океанов имеются
неограниченные запасы недорогого дейте-

§ 7. СИНТЕЗ ЯДЕР 543
рия, чего нельзя сказать о других видах
топлива. Мировые запасы газа и нефти
будут исчерпаны в последующие несколько
десятилетий. Даже запасов угля и урана
хватит в лучшем случае на несколько
столетий. Серьезным препятствием на пути к
получению энергии в неограниченных
количествах из «морской воды» является
закон Кулона. Электростатическое
отталкивание двух дейтронов при комнатной
температуре не позволяет им сблизиться
до расстояний, на которых сказываются
короткодействующие ядерные силы
притяжения.
Пример 12. Предположим, что для преодоления
электростатического отталкивания два дейтрона
должны сблизиться до 10" 14 м. Какова при
этом высота электростатического
потенциального барьера в МэВ?
Решение:
= 2,3-КГ14 Дж = 0,14МэВ.
Пример 13. Пусть энергия каждого дейтрона
равна (Ъ/2)кТ. До какой температуры нужно
нагреть дейтроны, чтобы преодолеть
потенциальный барьер?
Решение: Из примера 12 мы знаем, что два
дейтрона должны иметь энергию 0,14 МэВ, или
каждый из них 0,07 МэВ. Таким образом,
(3/2)кТ= 0,07 МэВ = 1,15-10" 14 Дж,
откуда
Т= 5,6 108 К.
Из этого примера мы видим, что если
бы удалось нагреть дейтерий до
температуры ~ 5 • 108 К, то в нем осуществилась
бы реакция синтеза. Благодаря тому что
имеется возможность проникновения сквозь
барьер, нет необходимости в создании
столь высоких температур. Для
получения управляемой термоядерной энергии
и для инициирования термоядерного
взрыва водородной бомбы достаточно
температуры около 5 • 107 К. Ядерные реакции,
требующие для своего осуществления
температур порядка миллионов градусов,
называются термоядерными. Мгновенные
температуры, развивающиеся при взрыве
атомной бомбы, оказываются достаточно
высокими, чтобы поджечь термоядерное
горючее.
Для этого вместо жидкого дейтерия
в качестве горючего используется
соединение LiH, причем только с изотопами 6Li
и 2Н (дейтерий вместо водорода). Изотоп
6Li поглощает нейтроны, возникающие
в реакции
2Н + 2Н -> 3Не + п;
таким образом,
n + 6Li -> 3Н + 4Не.
Затем тритий (3Н) вступает в реакцию
2Н + 3Н -+ 4Не + п.
В результате происходит выгорание
дешевого дейтерида лития-6 (6Li2H),
сопровождающееся образованием 3Не, 4Не и
нейтронов. Начавшись, термоядерные реакции
сопровождаются выделением энергии,
и этим обеспечивается поддержание
высоких температур, пока большая часть
вещества быстро не «выгорит». В этом случае
происходит то, что мы называем взрывом
водородной бомбы. Термоядерное горючее
для водородной бомбы (дейтерид лития-6)
крайне дешево, и не имеется ограничений
на его количество при использовании в
отдельной бомбе. Проводились испытания
бомб мощностью 60 мегатонн (с ТНТ-эк-
вивалентом 6 • 107 т).
Энерговыделение при взрыве чисто
термоядерной водородной бомбы можно
почти удвоить (при этом стоимость ее
увеличится не намного) за счет использования
оболочки из 238U. В этом случае нейтроны,
возникающие в результате термоядерных
реакций, вызывают деление ядер 238U, что
приводит к увеличению числа нейтронов,
бомбардирующих 6Li, и т.д. Поэтому
в большинстве взрывов водородных бомб
энерговыделение, обусловленное делением
ядер, оказывается таким же, как и
получаемое в процессе синтеза, и сопровождается
опасными выпадениями радиоактивных
продуктов деления.

544 ГЛ- 29- ЯДЕРНАЯ ФИЗИКА
УПРАВЛЯЕМЫЙ СИНТЕЗ
Для того чтобы с помощью ядерного
синтеза можно было получить полезную
энергию, термоядерные реакции должны
быть управляемыми. Необходимо найти
способы создания и поддержания
температур во много миллионов градусов. Одна
из технических проблем связана с тем, что
высокотемпературный газ, или плазму,
нужно удерживать таким образом, чтобы
не расплавились стенки соответствующего
объема. На решение этой технической
задачи уже затрачены и затрачиваются
огромные усилия. Плазму пытаются
изолировать от стенок с помощью сильных
магнитных полей. Задача заключается
в том, чтобы удержать плазму в
изолированном состоянии в течение достаточно
продолжительного времени и при этом
выработать мощность, превышающую ту,
которая была затрачена на запуск
термоядерного реактора. Достигнутое до сих пор
время удержания оказывалось в лучшем
случае раз в 50 меньше необходимого. Ряд
специалистов считают, что эта проблема
будет успешно решена до конца нашего
столетия. На рис. 29-16 показана
предполагаемая схема конструкции реактора.
Электростанция, работающая на
термоядерной реакции, из-за отсутствия в ней
продуктов деления должна иметь
значительно меньшую радиоактивность по
сравнению с ядерными реакторами. Однако
в термоядерных установках испускается,
Модули
воспроизводства
Плазма
Защита
Тороидальные
катушки
Защита
Рис. 29-16. Предполагаемая конструкция
термоядерного реактора с магнитным удержанием.
Магнитное поле создается сверхпроводящими
обмотками. Такой реактор рассчитан на
выработку мощности ~750 МВт. Конструкция
разработана в Ок-Риджской национальной
лаборатории. [С любезного разрешения Д. Штейнера
из Ок-Риджской национальной лаборатории.]
а затем захватывается большое число
нейтронов, что, как правило, приводит к
образованию радиоактивных изотопов.
Поэтому вокруг камеры с плазмой
предполагается создавать оболочку («бланкет») из
лития. В этом случае нейтроны будут
производить тритий (изотоп 3Н с периодом
полураспада 12 лет), который можно
использовать в дальнейшем как горючее.
Еще одна возможность основана на том,
чтобы окружать камеру с плазмой ураном
или торием; при этом воспроизводится
делящееся горючее для ядерных реакторов.
Если такой способ обеспечит производство
дешевой энергии, то термоядерные
электростанции в конечном счете могут
оказаться такими же источниками
радиоактивности, как и нынешние способы
получения атомной энергии. Сходное устройство
называется гибридным реактором. В таком
реакторе нейтроны, возникающие в
результате синтеза, производят ядерную энергию
с использованием 238U. Энергия
вырабатывается одновременно как за счет
синтеза, так и за счет деления. Все до сих пор
предлагавшиеся проекты реакторов,
основанных на процессе синтеза, являются
малообещающими с точки зрения
экономической выгоды по сравнению с
конкурирующим производством энергии на основе
минерального горючего.
Другой возможностью овладения
термоядерной энергией является поиск
практических путей использования энергии,
выделяющейся при взрыве водородных бомб.
Изучались возможности получения энергии
при взрывах небольших водородных бомб
в глубоких подземных полостях
многократного использования. Такой способ мог
бы, вероятно, составить конкуренцию
с экономической точки зрения методам
магнитного удержания.
Миниатюрный вариант этого способа
связан с использованием значительно
меньших по габаритам (диаметром
гораздо меньше 1 см) «водородных бомб».
Маленькую таблетку с термоядерным
горючим можно подвергнуть быстрому сжатию
и таким образом нагреть до высокой
температуры, направив на нее импульсы от
группы мощных лазеров. Вместо лазерных
пучков можно использовать пучки
электронов или тяжелых ионов. Для получения

УПРАЖНЕНИЯ 545
подходящей мощности достаточно
расходовать несколько таблеток в минуту.
В природе существует еще один
механизм удержания, обеспечивающий
непрерывное выделение термоядерной
энергии,-это гравитационное удержание.
Однако, чтобы обеспечить достаточно сильное
гравитационное поле, потребуется масса
порядка солнечной. Как мы увидим в
следующей главе, источниками энергии в
звездах, безусловно, являются термоядерные
реакции.
Основные выводы
Размеры ядер можно определить,
используя дифракционное рассеяние при
высоких энергиях, а также упругое рассеяние
электронов или поглощение нейтронов.
Оказалось, что радиус ядра R«(1,2 х
х 10"15 м)Л1/3.
Если электрон «нацелен» в край ядра,
имеющего заряд Ze и радиус R, то,
согласно классической механике, его угол
отклонения определяется соотношением
♦ М . Ze2
tg\V °Wv'
Фундаментальное взаимодействие
между двумя нуклонами можно приближенно
описать прямоугольной ямой радиусом
R = 2,3.10"15 м и глубиной 29 МэВ (в
случае, когда спины нуклонов
параллельны). В таком потенциале низшей ну-
клонной стоячей волне соответствует
уровень с энергией Е = — 2,22 МэВ, что
представляет собой экспериментальное
значение энергии связи дейтрона.
В ядрах с большим числом нуклонов
эффективная глубина ямы увеличивается
примерно до 42 МэВ. Подстановка в
формулу для энергии Ферми Kf известного
значения плотности нейтронов дает Kf =
= 34 МэВ. Соответствующий
энергетический уровень Е = Kf + U = (34 - 42) МэВ =
= — 8 МэВ. Протон с наивысшей энергией
будет находиться в ядре несколько
выше этого энергетического уровня, так что
энергия, необходимая для удаления протона
или нейтрона из типичного ядра средней
массы, составляет 8 МэВ. Эта модель
потенциальной ямы с учетом наблюдаемого на
опыте спин-орбитального взаимодействия
лежит в основе оболочечной модели ядра,
из которой мы получаем значения
магических чисел: 2, 8, 20, 50, 82, 126 для
наиболее сильно связанных ядер.
Характеристики альфа-распада можно
получить, используя представление о кван-
товомеханическом проникновении сквозь
кулоновский барьер. Среднее время жизни
т относительно альфа-распада дается
выражением
^2Д|^/внутр|2
V №внеш|2'
Если первоначально имеется п0
радиоактивных ядер, то спустя время t число
ядер п = п0 ехр ( — t/x).
Ядро в возбужденном состоянии может
самопроизвольно испускать фотон точно
так же, как это происходит в случае
возбужденного атома. Этот процесс называется
гамма-распадом. Бета-распад имеет
аналогичное квантовомеханическое объяснение,
с той лишь разницей, что вместо фотона
испускается пара электрон - нейтрино.
Производство плутония основано на
облучении 238U нейтронами, ведущем
к образованию изотопа 239U, который
в результате бета-распада превращается
в 239Np, а затем после еще одного бета-
распада в 239Ри. При поглощении
нейтрона с малой энергией оба изотопа 235U
и 239Ри испытывают деление. Продукты
деления характеризуются более сильной
связью (на ~ 1 МэВ на нуклон),
благодаря чему в результате деления
высвобождается примерно 200 МэВ энергии.
Энергия выделяется также при синтезе
двух легких ядер, таких, как 2Н, 3Н или
6Li. Для сближения двух положительно
заряженных ядер до области действия
ядерных сил притяжения, способных
превратить их в более сильно связанное ядро
больших размеров, требуются чрезвычайно
высокие температуры (~ 108 К).
Упражнения
1. Допустим, что нейтрон состоит из
сердцевины радиусом Rc = 0,1 фм и зарядом + е,
окруженной заряженным облаком,
имеющим радиус 1 фм и заряд — е. На какой
угол 0макс отклоняются при рассеянии на
сердцевине электроны с энергией 10 ГэВ?

546 ГЛ. 29. ЯДЕРНАЯ ФИЗИКА
2. Чему равна электростатическая
потенциальная энергия двух протонов, расположенных
на расстоянии 1 фм друг от друга?
3. Каково расстояние между соседними
нуклонами, если в кубическом сантиметре
вещества содержится 1,38 • 1044 нуклонов?
(Предполагается, что нуклоны образуют
кубическую решетку.)
4. Найдите электростатическую
потенциальную энергию протона на поверхности ядра
меди.
5. С помощью рис. 29-10 найдите магическое
число, которое следует после магического
числа 126.
6. Какое в примере 10 использовалось
значение v средней скорости альфа-частицы
внутри ядра?
7. Если период полураспада радия 1600 лет, то
какая доля образца радия распадается по
прошествии 3200 лет?
8. Что продолжительнее-3 периода
полураспада или 2 средних времени жизни?
9. Какой процент радиоактивного образца
распадается на протяжении одного времени
жизни? А на протяжении двух времен
жизни?
10. Рассмотрим образец, содержащий 1000
радиоактивных ядер с периодом полураспада
Т. Сколько приблизительно атомов
останется спустя Т/21
11. Солнце имеет массу 2-Ю30 кг, распределен-
* ную со средней плотностью 1,4-103 кг/м3.
Каким был бы диаметр Солнца, имеющего
ту же массу, но плотность ядерного
вещества?
12. В термоядерной бомбе 18 кг взрывчатки
могут обеспечить энерговыделение,
эквивалентное взрыву 1 млн т ТНТ. Из 1 т ТНТ
высвобождается 109 кал. Сколько граммов
термоядерной взрывчатки превращается в
энергию ?
13. Тяжелое ядро X содержит 204 нуклона и
характеризуется удельной энергией связи
8 МэВ. Допустим, что энергия покоя
свободного протона или свободного нейтрона
равна 940 МэВ.
а) Найдите энергию покоя ядра X.
б) Ядро X испускает ос-частицу (с энергией
связи 28 МэВ) и превращается в ядро
с удельной энергией связи 8,1 МэВ.
Найдите кинетическую энергию, которая
выделяется в этом процессе.
14. Энергии покоя трития и гелия-3 равны
соответственно Мс2(3Н) = 2805,205 МэВ и
Мс2(3Не) = 2804,676 МэВ. Энергия покоя
электрона 0,511 МэВ. Будет ли тритий
испытывать бета-распад и если да, то какой будет
энергия р-частиц?
Задачи
15. Если радиус звезды R = 2 GM/c2, то свет не
сможет покинуть ее-звезда представляет
собой черную дыру. Рассмотрим звезду,
радиус которой удовлетворяет этому
соотношению, а плотность равна плотности
типичного атомного ядра. Чему равны
радиус и масса этой звезды? Сравните
полученную массу с массой Солнца.
16. Покажите, что если толщина пластинки
х мала, то сечение столкновения нейтронов
дается выражением
где А -площадь пластинки и Na-число
атомов в ней.
17. Нейтронное сечение меди равно 0,65 барн.
На какой толщине пучок нейтронов
ослабится в е раз?
18. Допустим, что U0 = 25 МэВ, а энергия
связи дейтрона равна 2,2 МэВ. Используя
соотношение (29-8), найдите г0-радиус
эффективной прямоугольной ямы.
19. В некотором тяжелом ядре ос-частица
соударяется 1022 раз в секунду с потенциальным
барьером И фвнутр/Фвнеш = Ю14.
а) Какова вероятность распада этого ядра
в течение 1с?
б) Чему равны среднее время жизни и
период полураспада?
20. Образец радиоактивного материала
содержит 1012 радиоактивных атомов. Если
период их полураспада равен 1 ч, то сколько
атомов распадается за 1 с?
21. Рассмотрим следующую фотоядерную
реакцию:
у + 63Cu - 63Cu*, 63Си* - 62Ni + р.
Предположим, что фотон с энергией 13 МэВ
поглощается протоном на уровне Ферми
(см. рисунок ниже, на котором приведена
потенциальная кривая протона в 63Си).
а) Чему равна энергия вылетающего
протона?
б) Грубо оцените число соударений этого
протона с потенциальным барьером
в секунду.
в) Если \|/Внешн/Фвнутр^ Ю~8, то чему при-
близительно равно время жизни
промежуточного состояния?
г) Пусть энергия фотона 12 МэВ. Будет
время жизни длиннее или короче?
д) Чему равен энергетический порог этой
фотоядерной реакции? (Какова
минимальная энергия фотона, поглощение
которого приводит к испусканию протона?)

ЗАДАЧИ 547
22. Допустим, что в трехмерном пространстве
потенциальная энергия зависит только от
расстояния г (см. рисунок). Постройте
функции u(r) = п|/(г), отвечающие двум низшим
энергетическим уровням в этой яме.
23. Начертите и(г) и \|/(г) для случая,
рассмотренного в примере 7.
24. Какая доля дейтрона сосредоточена в
области радиусом г0? [Указание: Эта доля равна
^0 со
( $y\r2r2dr)/( { \|/2r2dr).]
О о
25. Повторите решение в примере 8 в случае
А = 60. Чему равно отношение числа
протонов к числу нейтронов?
26. Повторите решение в примере 8 в случае
А = 40. Чему равно отношение числа
протонов к числу нейтронов?
27. Сколько граммов урана расходуется
ежедневно для производства 1000 МВт
электроэнергии? (КПД преобразования 30%.)
28. Ежегодное потребление электроэнергии
в США составляет примерно 2-Ю12 кВт-ч.
КПД преобразования тепла в
электроэнергию составляет 30%.
а) Сколько для этого приходится ежегодно
сжигать тонн угля (или нефти)? Сколько
потребовалось бы тонн урана, если бы
соответствующие электростанции были
ядерными?
б) Если бы электроэнергия извлекалась из
подземного взрыва водородной бомбы
мощностью 1 Мт, то сколько бы
потребовалось ежедневно взрывов?
29. Число ядерных бомб, имеющихся в
настоящее время в США, оценивается примерно
в ЗЗООО. Допустим, что каждая бомба
содержит около 2 кг 239Ри. Этот плутоний был
изготовлен в ядерных реакторах для
военных целей, в которых при каждом
процессе деления образуется один нейтрон,
обеспечивающий реакцию n + 238U -> 239U.
а) Сколько килограммов продуктов деления
образовалось в этих реакторах?
б) Допустим, что производство ядерной
энергии в США для промышленных
целей достигло на протяжении 30 лет 10%
от уровня современного производства
электроэнергии. Сколько килограммов
продуктов деления образовалось в
созданных для этого реакторах?

АСТРОФИЗИКА
Мы попытаемся здесь разобраться
в том, как могли возникнуть звезды и
планеты, откуда берется огромная энергия,
излучаемая звездами, и, наконец, что
происходит со звездой, когда иссякнет источник
ее энергии. Мы увидим, что звезда может
возникнуть в процессе гравитационного
сжатия облака холодного водорода
соответствующей массы и что основным
источником излучаемой звездой энергии
является термоядерная реакция
превращения водорода в гелий.
Пример 1. Как долго просуществовало бы
Солнце на химической реакции горения? А за
счет превращения водорода в гелий? Масса
Солнца 2-Ю30 кг, а мощность его излучения
41023 кВт.
Решение: При сгорании углерода (типичная
химическая реакция) выделяется 7,9 • 106 Дж
энергии в расчете на 1 кг С02. Умножив эту
величину на массу Солнца, получим 1,6-1037 Дж.
Поскольку по определению мощность Р = E/t,
t =
1,6-1037 Дж
4-Ю26 Вт
4-Ю1
1250 лет.
Следовательно, если бы Солнце состояло из
смеси углерода с кислородом, а источником его
энергии было горение углерода, то спустя 1250
лет оно погасло бы. При превращении водорода
в гелий высвобождается энергия, составляющая
0,7% энергии покоя исходного количества
водорода. Таким образом, Е = (7-10" 3)Мс2 =
= 1,3 • 1045 Дж. Отсюда
Е 1,3 • 1045
1 = -^ = л <„<ук С = Ю лет>
Р 4-Ю26
что приблизительно в 20 раз превосходит
настоящий возраст Солнца.
Когда в звезде исчерпываются запасы
ядерного горючего, она может сжаться
еще сильнее и превратиться в белый
карлик, нейтронную звезду или стать черной
дырой. В этой главе мы расскажем о таких
объектах и вычислим приближенно их
размеры и массу. Соответствующие
вычисления помогут нам понять основные
свойства этих гигантских материальных
объектов. Оказывается, законы физики, в основе
которых лежат явления микромира,
применимы и к астрономическим объектам. Мы
встретим такие поразительные примеры
единства науки, как описание нейтронной
звезды в виде гигантского «атомного»
ядра, которое по своим размерам в ~ 1056
раз превосходит обычное атомное ядро.
§ 1. Источник энергии звезд
Большинство космологических теорий
исходит из того, что прародителем и звезд,
и планет является в основном
газообразный водород. В недрах звезд, как мы
покажем ниже, происходит образование
тяжелых элементов - вплоть до железа.
Полагают, что при взрывах сверхновых звезд
возникают еще более тяжелые элементы.
При формировании планет, таких, как
Земля, происходит отбор преимущественно
тяжелых элементов, так как
гравитационное поле оказывается недостаточно
сильным, чтобы оно могло удержать более
легкие элементы, находящиеся в
газообразном состоянии и стремящиеся улетучиться.
Образование звезды начинается с процесса
сжатия облака холодного водорода под
действием сил гравитационного
притяжения. По мере более тесного сближения
атомов водорода друг с другом их
кинетическая энергия (или температура) возрастает.
В нагретом газе развивается давление,
которое препятствует дальнейшему
гравитационному сжатию. Однако вследствие
электромагнитного излучения происходят
потери тепловой энергии газа, и сжатие

§ 1. ИСТОЧНИК ЭНЕРГИИ ЗВЕЗД 549
продолжается до тех пор, пока в игру не
вступит новый источник энергии. Таким
источником энергии являются
термоядерные реакции, и, как мы увидим, они
начинаются в звездах при температуре около
107 К.
Теперь у нас достаточно сведений,
чтобы, зная массу Солнца (Мс = 2 • 1030 кг),
«вычислить» его радиус. Для
упрощения вычислений будем считать, что
массовая плотность Солнца постоянна. В
действительности плотность в центре звезды
значительно превышает плотность на
периферии. Однако предположение о
постоянстве плотности дает результат,
правильный по порядку величины и даже
точнее. Гравитационное сжатие
газообразного водорода массой 2 • 1030 кг
происходит до тех пор, пока давление,
обусловленное термоядерным нагревом, не
уравновесит гравитационное давление. В примере
3 гл. 12 было показано, что
гравитационное давление в центре однородного шара
радиусом R равно Р = pgR/2, где д =
= GMq/R2- величина ускорения
свободного падения на поверхности шара. Таким
образом,
Р = (l/2)pGMc/R.
Из формулы (12-10) (см. гл. 12, т. 1)
следует, что тепловое давление
где тр-масса протона. Приравнивая эти
давления, получаем
кТ_ 1 GMC
mp~2 R '
откуда
GMC mp
R =
2кТ
(30-1)
Р =
_ркТ
В случае Т ~ 1Q1 К мы имеем /сТ~
~ 1,38-Ю-16 Дж. Таким образом,
^ (6,67-10"''Им-кг"2)(2-1030кг)
2(1,38-10-16Дж)
х(1,67.10~27кг) = 8.108м.
Измерения дают R = 7 • 108 м.
Следовательно, по порядку величины результаты
этих расчетов и эксперимента хорошо
согласуются между собой.
Если исходная масса невелика, то
гравитационное сжатие продолжается до тех
пор, пока атомы не приходят в
соприкосновение друг с другом. В конечном счете
образуется планета, такая, как'Земля. Если
же исходная масса значительно больше
и достигаются столь высокие давления
и плотности, что волновые функции
отдельных атомов перекрываются, то
возникает плазма и результирующий радиус
будет определяться выражением (30-8),
которое мы получим ниже. К этому классу
Рис. 30-1. Схематическое
представление протон-протонного
цикла. Из шести протонов
образуются 4Не + 2р + 2е+ +
+ 2v + 2у.

ГЛ. 30. АСТРОФИЗИКА
относится Юпитер - планета достаточно
больших размеров. В таких случаях
гравитационные силы компенсируются кванто-
вомеханическим давлением плазмы. (Кван-
товомеханическое давление мы
рассмотрим в § 4 настоящей главы.)
Можно показать, что если исходная
масса превосходит величину, равную 0,08
массы Солнца, то температура окажется
достаточно высокой, чтобы начали
протекать следующие термоядерные реакции:
p + p->D + e++v,
р + D -+ 3Не + у,
3Не + 3Не -> 4Не + р + р
[здесь D-дейтерий (2Н)].
Последовательность этих трех реакций называется
протон-протонным циклом и схематически
показана на рис. 30-1. Это основной
механизм выделения энергии на Солнце
и других водородных звездах. В результате
этой последовательности реакций 4
протона превращаются в ос-частицу, 2 позитрона,
2 нейтрино и 2 фотона с общей
кинетической энергией около 26 МэВ. Заметим, что
первая из реакций с образованием пары
позитрон-нейтрино представляет собой
пример слабого взаимодействия. Эта
реакция аналогична превращению протона
в радиоактивном ядре в нейтрон и пару
электрон-нейтрино (один из видов бета-
распада).
Пример 2. Какая температура необходима,
чтобы протоны приблизились друг к другу на
расстояние 5-Ю"15 м?
Решение: Если энергия каждого протона (3/2)/сТ,
то полная кинетическая энергия двух протонов
составляет ЪкТ. Приравнивая эту энергию
величине к0е2/Я, получаем
Т=-^— = 1,1-109 К.
3/сД
Однако, даже если температуры будут меньше
этого значения на один или два порядка, в
центре звезды имеется достаточное число протонов
с энергией выше средней, чтобы
поддерживалась реакция.
Таким образом, мы показали, что при
гравитационном сжатии облака холодного
водорода температура должна стать выше
107 К, прежде чем начнется
протон-протонный цикл.
§ 2. Гибель звезд
Пример 1 показывает, что Солнце,
образовавшееся около 4,5 • 109 лет назад,
к настоящему моменту времени прошло
лишь небольшую часть своего жизненного
пути. А нет ли звезд, у которых уже
полностью израсходован запас ядерного
горючего? Звезды с большими массами
имеют более высокую температуру, и,
следовательно, водород в них выгорает
быстрее. На небе сверкает множество звезд,
которые вследствие большей массы
обладают большей яркостью и синеватым
блеском, свидетельствующим о более высокой
их температуре. Такие звезды могут
израсходовать весь свой водород быстрее чем за
1010 лет (возраст Вселенной). Когда запас
водорода исчерпан, такая звезда,
продолжая светить, начинает сжиматься. При
этом одна часть высвобождаемой по мере
уменьшения радиуса звезды
гравитационной энергии расходуется на излучение,
а другая-идет на нагревание внутренних
областей звезды до более высокой
температуры Т. Когда достигается температура,
необходимая для дальнейших
термоядерных превращений гелия с образованием
углерода, кислорода и неона, сжатие и
нагревание прекращаются. При наличии
достаточного времени этот процесс будет
продолжаться до тех пор, пока большая
часть вещества внутри звезды не
превратится в изотоп железа 56Fe. Ядро этого
изотопа железа оказывается самым
устойчивым, и поэтому любые последующие
ядерные реакции будут идти не с
выделением, а с поглощением энергии.
Когда в звезде с сердцевиной из железа
исчерпывается запас термоядерного
горючего, устраняется и один из факторов
(тепловое давление), препятствующих
дальнейшему сжатию. Для звезд малой массы
существует другое препятствие, а именно
квантовомеханическое давление (см. § 4).
В достаточно же массивных звездах
процесс сжатия может не только
продолжаться, но, ускоряясь, принимает форму
катастрофического коллапса. Рассматривалось

§ 3. ЧЕРНЫЕ ДЫРЫ
несколько различных механизмов такого
коллапса; однако вопрос о том, какой из
них приводит к возникновению сверхновых
звезд, пока остается открытым. Тем не
менее можно получить условия, налагаемые
на величину массы и радиуса звезды.
§ 3. Черные дыры
Если нет других видов сил
отталкивания или внутреннего давления, то звезда
будет продолжать сжиматься. Однако
существует предельный радиус jR0,
называемый радиусом Шварцшильда или
горизонтом, за пределами которого звезду уже
нельзя увидеть. При R < R0 любые
испущенные звездой частицы (даже фотоны)
будут возвращаться обратно к звезде. Для
такой звезды невозможно сообщение
с внешним миром. Это иллюстрируется на
рис. 30-2, в, на котором показаны
траектории фотонов, возвращающихся обратно
к звезде. При этом фотоны могут даже
удалиться на некоторое расстояние от
звезды, однако им не суждено уйти на
бесконечно большое расстояние, если только
R не превышает jR0.
Значение R0 можно оценить, вычислив
потенциальную энергию фотона в
гравитационном поле звезды, с поверхности
которой он испускается. Эта потенциальная
энергия имеет вид U = —GMm/R, где
т = s/c2 - гравитационная масса фотона с
энергией ё, а М-масса звезды. Согласно
закону сохранения энергии, на больших
расстояниях от звезды энергия фотона
уменьшится на величину GMm/R. Таким
образом, если ё < GMm/R, то фотон не
сможет оказаться на бесконечно большом
расстоянии от звезды. Условие для пре-
Рис. 30-2. Три звезды с
одинаковыми массами, но
различными радиусами, а и б-радиусы
звезд больше, чем R0 (R0 =
= 2GM/c2); в-радиус звезды
меньше, чем R0, и
гравитационное поле оказывается настолько
сильным, что ни один фотон не
может покинуть звезду. В
каждом случае показаны
траектории фотонов, испускаемых с
поверхности звезды под углами 0,
30 и 60°.
дельного значения радиуса R
записывается в виде
GMm GM ё
откуда находим
GM
с
В этих расчетах мы не использовали
общую теорию относительности. Однако,
когда гравитационная энергия сравнима
с полной энергией системы, вычисления
должны проводиться на основе общей
теории относительности.
Более точная формула записывается
в виде
2GM
R0 = —г— (горизонт). (30-2)
с
Отсюда следует, что в случае, когда М =
= Мс, т. е. в случае Солнца (масса
2 • 1030 кг), мы имеем R0 = 3 км. Если
звезда коллапсирует до размеров, меньших
или равных величине 2GM/c2, то ни свет,
ни частицы, испущенные такой звездой, не
смогли бы достичь Земли или любого
другого удаленного объекта. Тем не менее эти
объекты будут по-прежнему испытывать
на себе влияние гравитационного поля
такой звезды. В самом деле, гравитационная
масса такой звезды практически не
уменьшается, и частицы (в том числе и фотоны)
могут безвозвратно «провалиться» в
направлении звезды - отсюда и название
«черная дыра». Но хотя «дыра» и «черна»
сама по себе, приблизившееся к ней извне
облако газа, прежде чем достигнет гори-
-ЬН 0-
о

552 ГЛ. 30. АСТРОФИЗИКА
Рис. 30-3. Черная дыра в
изображении художника на
передней стороне обложки журнала
"The New York Times Magazine"
от 14 июля 1974 г., в котором
появилась большая статья по
этому вопросу. [Copyright 1974
by The New York Times
Company. Воспроизводится
с разрешения.]
зонта 2GM/c2, начнет сжиматься и
нагреваться, а следовательно, будет и излучать.
На рис. 30-3 изображена черная дыра, как
ее представляет себе художник.
§ 4. Квантовомеханическое давление
Рассмотрим еще одно не менее важное
явление, которое сродни силам
отталкивания и при больших плотностях
обусловливает высокое давление и большие
кинетические энергии частиц (даже при низкой
температуре). Согласно принципу Паули,
частицы со спином 1/2 (скажем, электроны,
протоны, нейтроны), находящиеся в ящике,
не могут одновременно занимать
состояния с одним и тем же значением импульса.
Поэтому даже при нулевой температуре
частицы не покоятся, а распределены по
состояниям с импульсами вплоть до
значения pf9 называемого граничным
импульсом Ферми. Если в объеме V находится
п таких частиц, то расстояние между
частицами по порядку величины равно (V/n)113.
Если бы частица была локализована
в пределах такого расстояния, то в
соответствии с соотношением
неопределенностей Гейзенберга импульс этой частицы
был бы определен с точностью ~ h/(V/n)1/3.
Точное же значение pf дается формулой
(28-2):
/ 3 nV'3
р/-*(^т) • (30-3)
С увеличением плотности n/V
кинетическая энергия (граничная энергия Ферми) Kf
частицы с импульсом pf возрастает и это
приводит к увеличению давления.
Характер связи между энергией Kf и импульсом
pf зависит от того, является частица с
массой покоя т релятивистской или нет.
Точное выражение для энергии записывается
в виде
Kf = ]/c2p2f + rn2c*-mc2.
(30-4)

§ 5. БЕЛЫЕ КАРЛИКИ 553
Если pf « тс, то частица является
нерелятивистской, и
К =А = ^(1Л2'3 ДМ)
f 2т Ы\к V)
В соответствии с формулой (12-7) (см.
т. 1) произведение давления на объем
определяется выражением
Ру=п^- = \пК.
8 примере 2 гл. 28 показано, _что средняя
кинетическая энергия частицы К = (3/5) Kf.
Таким образом,
рк-у"(тк')
откуда
_ 2 nKf h2 П\2/3/п\"/3
Р ~J~~V~ ~~Шп~\п) \V) '
Это и есть квантовомеханическое давление
нерелятивистского ферми-газа.
В ультрарелятивистском случае pf » тс
и граничная энергия Ферми дается
выражением
1 /3 п\1/3
Kf = pfc = -hc^--)j . (30-6)
Полная кинетическая энергия всех частиц
в этом случае равна (3/4) nKf, как показано
в примере 3 гл. 28.
§ 5. Белые карлики
Вычислим теперь полную энергию
холодной «выгоревшей» звезды и установим,
что эта энергия Е является функцией
радиуса R. Даже полностью израсходовав
свое ядерное горючее, такая звезда
продолжает излучать и сжиматься до тех пор,
пока не будет достигнуто минимальное
значение энергии E(R). Полная энергия
системы складывается из общей энергии
всех частиц (пК = (3/5)nKf) и
гравитационной потенциальной энергии U. Из примера
9 гл. 16 известно, что потенциальная
энергия сферической оболочки массой М равна
U = — GM2/2R. В случае однородного
твердого шара U = — (3/5)GM2/R.
Рассмотрим звезду, состоящую из
атомов с массовым числом А. Пусть п-
полное число нуклонов в ней. Тогда в звезде
имеется п/А ядер, каждое из которых
состоит из Z протонов и A-Z нейтронов.
Положим х = Z/A и будем считать, что в данном
случае х ~ 1/2. Полная масса звезды
М » птр, где тр-масса протона. Полное
число электронов (а также протонов) пе =
= хп. Мы увидим, что в звезде достаточно
малой массы, сжимающейся после полного
израсходования термоядерного горючего,
энергии электронов (и ядер) будут
оставаться нерелятивистскими. В этом случае
квантовомеханическая кинетическая
энергия электронов (Kf)e и ядер дается
соотношением (30-5); однако вкладом в энергию
ядер можно пренебречь по сравнению
с энергией электронов, так как масса
частицы входит в знаменатель выражения
(30-5). Если звезда остыла настолько, что
тепловой энергией можно пренебречь по
сравнению с квантовомеханической, то
полная энергия звезды равна
— 3 3 GM2
E(R) = пеКе + U = уиДКД - j—^-
при условии, что плотность звезды
является однородной. Используя соотношение
(30-5), в котором мы сделали замену т на
те, п на хп и положили V = (4/3) яЯ3,
получаем в явном виде
л/т 3 хп h2 ( 9 \2/3
v } 5 R2 8тД 4тг2 )
_3G^. (30-7)
5 R
График этой функции представлен на
рис. 30-4.
Таким образом, даже после полного
выгорания ядерного топлива звезда
продолжает светить и сжиматься, и,
следовательно, ее полная энергия Е(К) должна
непрерывно уменьшаться. При данном
радиусе R минимальное значение энергии E(R)
будет достигнуто, когда звезда остынет
настолько, что можно будет пренебречь
тепловой энергией и использовать
соотношение (30-7). Это минимальное значение
энергии Е (R) можно найти, построив зави-

554
ГЛ. 30. АСТРОФИЗИКА
Гравитационная энергия - (-1/Л)
Рис. 30-4. Два вклада в
энергию белого карлика. Верхняя
сплошная кривая-полная
кинетическая энергия электронов,
а нижняя-гравитационная
потенциальная энергия;
штриховая кривая-сумма этих
энергий, имеющая минимум при
R = Rmuu •
симость E(R), как показано на рис. 30-4,
или решая уравнение dE/dR = 0. Решение
дает
^мин
xh2
4mP \ 4тс
2/3
1
Gnm2
ЭР
£0-8)
Если подставить это значение в (30-7), то
оказывается, что гравитационная энергия
связи — U в два раза превосходит
кинетическую энергию [первый член в
соотношении (30-7)]. Белые карлики-это звезды,
которые, продолжая остывать, сжались почти
до размера, определяемого формулой
(30-8). Для типичного белого карлика,
масса которого приблизительно на 15%
меньше массы Солнца (п = 1057 и х = 1/2),
формула (30-8) дает Дмин » 8000 км, что
соответствует плотности р » 3 • 106 г/см3.
Мы видим, что размеры белого карлика
близки к размерам Земли, однако его
масса в миллион раз больше. Планету
Юпитер тоже можно считать белым карликом.
Дело в том, что выражение (30-8)
справедливо независимо от того, достаточно ли
велика масса для возникновения
термоядерной реакции или нет. Вместе с тем
масса должна быть достаточно большой,
чтобы электронный газ был фермиевским1*
(т.е. плазмой). Выражение (30-8)
иллюстрируется графиком на рис. 30-5; из рисунка
видно, что эта формула хорошо
согласуется со значениями массы и радиуса
Юпитера.
Если соотношение (30-7) справедливо, то
звезда не может сжиматься меньше
размеров, определяемых формулой (30-8). При
этом jR ~ п~1/3, а энергия, приходящаяся
на один электрон, возрастает
пропорционально п4/3. С увеличением п соотношение
(30-7) перестанет быть справедливым в
силу того, что энергия отдельного электрона
становится сравнима с энергией покоя
тес2. Если в (30-7) использовать точное
релятивистское выражение для (Kf\, то мы
получим зависимость R от массы,
приведенную на рис. 30-5. В случае
ультрарелятивистского электронного газа вместо
формулы (30-5) для граничной энергии
Ферми нужно использовать формулу (30-6),
а формулу (30-7) следует заменить соотно-
1} Такой газ еще называют «морем
Ферми»-Ярим, перев.

§ 5. БЕЛЫЕ КАРЛИКИ
Рис. 30-5. Зависимость радиуса
R, соответствующего
минимальной сумме энергии Ферми
электронов и гравитационной
энергии, от массы звезды.
Предполагается, что плотность
звезды однородна. При расчетах
этой зависимости
использовалось точное релятивистское
выражение для энергии Ферми.
В случае малых масс такой же
результат можно получить с
помощью нерелятивистской
формулы (30-8). Заметим, что
предельная масса в случае, когда
электроны становятся
ультрарелятивистскими, дается
выражением (3-10).
R~M~m
п0тр
10"3Л/Г 0,0ШС 0,1 Лёс ьол/с\ юл/с
Масса звезды
шением
3 хп he
\1/3 3 ^
-хп) G
п2т\
4^'У "Т"~?Г'
(30-9)
Заметим, что в этом соотношении оба
члена имеют одинаковую зависимость от R
и что при достаточно большой массе птр
второй член будет преобладать. Если
п превысит некоторое критическое
значение икр, то энергия Е (R) будет непрерывно
убывать с уменьшением радиуса. Без
наличия тепловой энергии и соответствующего
давления стабильная конфигурация не
может существовать ни при каком значении
радиуса. Поэтому достаточно массивные
звезды имеют возможность продолжать
сжиматься, испуская излучение
(окончательную судьбу звезды мы рассмотрим
в следующих параграфах).
Соотношение (30-9) основано на
предположении об однородной плотности (в
действительности плотность больше в
центре звезды, чем на периферии) и
справедливо, строго говоря, лишь для
ультрарелятивистских электронов. Тем не менее,
определив значение п, при котором оба
слагаемых в (30-9) становятся
одинаковыми, мы можем получить оценку
критического значения пкр. Таким образом,
запишем это условие
3 хпкр he ( 9 V/3 3 п2 т2р
4 R 2 \4п2 7 5 R
откуда
_ (125тг)1/2
fie у2
Gm2) '
Следует заметить, что в это выражение
входит безразмерная величина
п0 =
be Y/2
Gml
= 2,4-105
(30-10)
Получение точного значения икр требует
привлечения численных методов
интегрирования и приводит в конечном счете
к следующей формуле: пкр = 0,7 (х/0,5)2и0.
Соответствующая критическая масса пкртр
называется пределом Чандрасекара или
предельной массой и представляет собой
максимальную массу белого карлика, при
которой он, продолжая остывать,
переходит в холодное стабильное состояние с
конечными значениями радиуса и плотности.
Эта масса лишь на 40% превышает массу
Солнца Мс = 0,49потр.
Заметим, что величина п0 не зависит от
массы электрона те, несмотря на то что
в случае белого карлика преобладает
кинетическая энергия электронов. Это
обусловлено тем, что в ультрарелятивистском
пределе в соответствии с (30-6) энергия не
зависит от массы. С другой стороны, как
мы покажем в примере 3, плотность рг,
при которой граничный импульс Ферми
равен pf = тес, должна зависеть от массы
электрона те.

556
ГЛ. 30. АСТРОФИЗИКА
Пример 3. Какова плотность рг белого карлика,
если граничный импульс Ферми электрона pf =
= тес?
Решение: Из формулы (30-4) находим
отношение
V 3~{h
Заменяя в этом выражении ие на хп, a pf на тес
и умножая затем обе части этого выражения на
тр, получаем
откуда в случае pf = mec находим
8тгтр/тес\3 0,97 • 106
Рг =
Зх \ h
г/см3. (30-11)
Для х = 1/2 плотность такой звезды будет
около 2 • 106 г/см3.
§ 6. Нейтронные звезды
Предположим, что белый карлик, масса
которого почти равна массе Солнца,
может быть сжат внешними силами. Если бы
значение х удалось уменьшить от ~ 1/2
почти до нуля, то, как мы увидим,
возможно состояние с существенно меньшим
значением полной энергии и при значительно
меньших R. В соответствии с формулой
(30-7) такие предполагаемые внешние силы
должны сначала совершить работу.
Однако с некоторого момента времени энергия
электронов станет столь высокой, что
начнется превращение протонов в нейтроны
за счет слабого взаимодействия:
e~+p->n + v.
Эта реакция называется обратным бета-
распадом; для ее осуществления нужны
электроны высоких энергий, а как вытекает
из (30-6), высокие энергии достижимы, если
плотность достаточно велика. Детальный
процесс превращения обычного вещества
в обогащенную нейтронами субстанцию
оказывается весьма сложным, однако
расчеты показывают, что при плотностях р >
> 1011 г/см3 будет больше нейтронов, чем
протонов. Таким образом, в этом случае
мы имеем дело с «нейтронной звездой», но
нам еще надо найти равновесные значения
R и х для заданного полного числа
нуклонов, причем ир = пе = хп. В случае
нейтронных звезд мы имеем дело с
плотностями, намного превосходящими величину
рг, определяемую выражением (30-11);
электроны оказываются здесь
ультрарелятивистскими, и для них справедлива
формула (30-6). Между тем нейтроны, масса
которых намного превосходит массу
электронов, останутся нерелятивистскими до
тех пор, пока плотность мала по
сравнению с эквивалентным значением (30-11)
для случая нейтронов, которое равно
_ 8тш1р
1Рг)п - 3 (1 - X)
ГПрС
h
6-Ю15
1 -х
т/см3
(30-12)
Если плотность звезды меньше этого
значения, то для нейтронов справедлива
формула (30-5); энергией протонов можно
вовсе пренебречь, поскольку они составляют
малую долю общего числа нуклонов.
Поэтому, чтобы получить E(R, х), мы просто
добавим к выражению (30-9) полную
кинетическую энергию нейтронов:
E(iR.v) ^ Энергия нейтронов +
+ Энергия электронов +
+ Гравитационная энергия
= 3(1 -х)п h2
~ 5 R2 8тр
Ъхппс( 9 \
4 R 2 \4к2 J
_9_
_4тт2
у/з
(1-
3
5
- х)п\
2 2
Gnzm;
R
2/3
+
(30-13)
Величины R и х, отвечающие
минимуму этого выражения при данной массе
звезды М = пшр, можно определить из
графика или решая совместную систему
уравнений
дЕ дЕ
— = 0и—= 0.
3R дх
Благодаря тому что величина х невелика,
решение этих уравнений с хорошей
точностью можно отыскать с помощью
следующих двух простых операций. Сначала
в уравнении dE/dR = 0 положим х = 0

§ 6. НЕЙТРОННЫЕ ЗВЕЗДЫ 557
и отсюда найдем R. Затем подставим это
значение R в уравнение дЕ/дх = 0 и
определим х. Подстановка х = 0 в уравнение
dE/dR = 0 дает
к2 ( 9 \2/3 1
R = — 1-^п) ——т. (30-14)
4тр \4п2 ) Gnml v ;
Это выражение очень похоже на (30-8),
однако численное значение в данном случае
оказывается меньше, в силу того что в
знаменателе вместо массы электрона стоит
масса протона. Следовательно, радиус
нейтронной звезды должен быть примерно
в 1000 раз меньше радиуса белого карлика.
Например, в случае звезды, масса которой
равна массе Солнца, п = 1,2 • 1057, и из
формулы (30-14) мы получаем R = 12,6 км,
а плотность 2,4-1014 г/см3. Если в
результате сжатия диаметр звезды, имеющей
массу Солнца, уменьшится примерно до
25 км, то ее плотность окажется почти
такой же, как у атомного ядра. Наконец,
чтобы определить величину х, т.е. долю
протонов в этом гигантском «атомном
ядре», подставим в уравнение дЕ/дх = 0
значение R = 12,6 км и разрешим его
относительно х. В итоге получим х = 0,005.
Мы видим, что в этом гигантском «ядре»
около 99,5% нуклонов являются
нейтронами. Обычные атомные ядра не содержат
электронов; в нейтронной же звезде около
0,5% всех частиц составляют электроны.
При выводе выражения для Е (R, х) мы
не учли влияния ядерных сил. В
действительности, поскольку плотность звезды
сравнима с плотностью атомного ядра,
ядерные силы должны быть
значительными. Однако для звезд, массы которых
составляют от половины до одной массы
Солнца, ядерные силы отталкивания и
притяжения компенсируют друг друга; точные
расчеты дают значения R и х, весьма
близкие к тем, которые мы нашли путем
приближенного расчета.
Пример 4. Какой была бы частота вращения
Солнца, если бы его радиус уменьшился до
R = 20 км без изменения момента импульса?
В настоящее время период вращения Солнца
равен 27 суткам, что соответствует частоте
/ = 4,3 • 10 7 с \ а радиус Солнца R =
= 1,4 • 106 км.
Решение: Обозначим момент инерции Солнца
через /. Тогда момент импульса дается
выражением
L = /со = /'со',
откуда
/
СО' = "СО.
/'
Таким образом, частота вращения
= 2,1 • 103 об/с.
Коллапс, ведущий к превращению
гаснущей звезды в нейтронную, представляет
собой катастрофу (она называется
сверхновой), сопровождающуюся выбросом
огромных газовых облаков, которые
уносят значительную часть момента импульса.
Однако на основании результата,
полученного в примере 4, можно было бы
ожидать, что частота вращения вновь образо-
вавщ<щс_я нейтронной звезды будет
составлять десятки оборотов в секунду. Если на
поверхности такой звезды имеются
возмущения наподобие солнечных пятен, то
испускаемое ими излучение будет походить
на гигантский луч от прожектора
колоссального маяка. Примером может служить
нейтронная звезда в центре Крабовидной
туманности; эта звезда вращается со
скоростью 30 оборотов в секунду. На
рис. 30-6 показано облако газа, оставшееся
после взрыва сверхновой, который
наблюдался в 1054 г. Взрыв был настолько
ярким, что его можно было наблюдать даже
днем. Наблюдения с помощью
оптического и радиотелескопа показывают, что
звезда в центре туманности вспыхивает и
гаснет 30 раз в секунду, как видно из
рис. 30-7. Нейтронные звезды такого типа
называют пульсарами. Когда в 1967 г.
с помощью радиотелескопа обнаружили
первый пульсар, было совершенно неясно,
какой механизм может обеспечить
испускание регулярных импульсов радиоизлучения

558 ГЛ. 30. АСТРОФИЗИКА
Рис. 30-6. Фотография Крабо-
видной туманности,
демонстрирующая распределение
выброшенного из нее облака газа. [С
любезного разрешения
руководства Калифорнийского
технологического института.]
с такой большой частотой. Это было
совершенно новое и неожиданное
астрономическое явление. Одной из первых попыток
найти объяснение была гипотеза LGM4
Но уже на следующий год, когда был
открыт второй пульсар, от этой гипотезы,
основанной на существовании внеземной ци-
1} LGM-аббревиатура выражения "little
green men" что переводится как «маленькие
зеленые люди», т.е. инопланетяне-Ярим, перев.
вилизации, которая ищет с нами связи,
пришлось отказаться.
Ключевая проверка гипотезы
вращающейся нейтронной звезды основана на том,
что энергия вращения звезды должна
уменьшаться в соответствии с излучаемой
звездой энергией. Выполненные недавно
измерения обнаружили наличие
замедления, соответствующего этим
предсказаниям.

§ 7. КРИТИЧЕСКАЯ МАССА ЧЕРНЫХ ДЫР 559
NP 0532 -|
/ ч
/ \
Л
I , I I L
0,1 0,2 0,3 0,4
Рис. 30-7. Фотографии центральной области
Крабовидной туманности, полученные при
короткой экспозиции. Положение родительской
нейтронной звезды указано яркими метками.
Сигналы с большой яркостью от этой звезды
нанесены на диаграмме. Изменению фазы на 0,1
соответствует 1/300 с. [Фото получено в Китт-
Пикской обсерватории.]
§ 7. Критическая масса черных дыр
Мы показали, что даже без учета
ядерных сил плотность нейтронной звезды,
имеющей массу Солнца, сравнима с
плотностью обычного ядерного вещества, в
котором характерная энергия Ферми на один
нейтрон равна около 40 МэВ. Более
массивные звезды имеют более высокую
плотность, и кинетическая энергия нейтронов
в них может достигать 939
МэВ-величины, которая соответствует их энергии
покоя. Если плотность превосходит
значение (рг)п, определяемое формулой (30-12),
то при вычислении энергии Ферми для
нейтронов надо пользоваться
релятивистским соотношением (30-6). Сейчас мы оце-
V
0,§
»,0
Фаза
ним верхний предел массы, при которой
нейтронная звезда остается устойчивой,
и сделаем это аналогично случаю белых
карликов; звезды с массой выше
критической должны превращаться (если только
они прежде не растратят своей массы)
в черные дыры.
Самую грубую оценку критической
массы можно получить, если положить
х = 0, пренебречь ядерными силами и
общей теорией относительности и
рассмотреть в рамках специальной теории
относительности одни лишь нейтроны.
В случае ультрарелятивистских
нейтронов для расчета Е(К) можно
воспользоваться выражением (30-9), полагая в нем
х = 1 (поскольку в данном случае все
частицы-это нейтроны). Полученная таким
образом оценка критической массы
отличается лишь множителем 1/х2, т. е. в 4 раза
от найденной ранее критической массы
белого карлика (в случае которого х = 1/2).
Она совпадает по порядку величины с
п0тр, причем п0 определяется формулой
(30-10). Были проделаны и более точные
расчеты с учетом ядерных сил и общей
теории относительности.

560 ГЛ. 30. АСТРОФИЗИКА
Привлечение в данном случае общей
теории относительности дает сравнительно
небольшой эффект, что вполне понятно.
Учет ядерных сил также приводит лишь
к незначительным изменениям, однако
в настоящее время свойства этих сил
изучены еще недостаточно, и различные
варианты вычислений приводят к значениям
критической массы в диапазоне 0,7-4
солнечных масс.
§ 8. Обзор экспериментальных данных
В предшествующих параграфах мы
занимались главным образом
теоретическим рассмотрением нейтронных звезд,
белых карликов и черных дыр,
представляющих собой три различных возможных
результата эволюции звезд. Однако в
настоящее время на основании лишь
теоретических соображений нельзя
сколько-нибудь надежно предсказать, какая из этих
возможностей реализуется и при каких
условиях. Нам лишь известно, что в
конечном счете любая из звезд должна
превратиться либо в белый карлик, либо
в черную дыру, либо в нейтронную звезду.
Можно достаточно надежно оценить
скорость, с которой гибнут звезды в нашей
Галактике; оказывается, что это одна или
несколько звезд в год. (Очень грубую
оценку можно получить, разделив полное'число
звезд на возраст Галактики: результат
с точностью до множителя 5 будет
совпадать с приведенной выше оценкой.) Белые
карлики составляют категорию звезд,
существование которых не вызывает
сомнений. Они весьма многочисленны (около
10 % звезд нашей Галактики), и по крайней
мере ближайшие из них можно подробно
изучать. Анализ статистических данных
показывает, что белые карлики остывают
в соответствии с тем, как это
предсказывает теория, и что большинство звезд
гибнет, проходя обычно через стадию белых
карликов.
Рождение сверхновых звезд
чрезвычайно заметно и является крайне редким
событием (примерно одна сверхновая на
сотню погибающих звезд). Сам факт
существования сверхновых и выброса оболочки
газа бесспорен, однако то, что происходит
с центральной частью исходной звезды,
пока неясно. Теоретически
предсказываются две возможности: образование
нейтронной звезды и черной дыры. За последнее
время о нейтронных звездах накоплено
большое количество косвенных, но вместе
с тем достаточно убедительных данных.
Большая часть этих данных связана с
открытием пульсаров в 1967 г., которые
представляют собой источники импульсов
радиошума, повторяющихся регулярно
через определенные интервалы времени. Эти
интервалы между импульсами весьма
малы (вплоть до 0,03 с). Поэтому трудно
представить себе, что это излучение дает
какой-либо иной видимый объект, а не
нейтронная звезда. Разработаны
исключительно подробные теории пульсаров,
которые по разному объясняют механизм
излучения; однако все теории сходятся на
том, что источником излучения является
вращающаяся нейтронная звезда и что
энергия этого излучения черпается из
кинетической энергии вращения звезды. Один
из пульсаров обнаружен в остатках
известной сверхновой (Крабовидная туманность),
взрыв которой наблюдался в 1054 г., и его
вспышки можно наблюдать в видимой
части спектра. До настоящего времени
обнаружено около 70 пульсаров.
С помощью установленных на ракетах
и искусственных спутниках детекторов
совсем надавно было обнаружено несколько
компактных источников рентгеновского
излучения. Излучение этих источников
быстро меняется во времени, что
свидетельствует о малости объектов - порядка
размеров нейтронной звезды, или же о
наличии вещества вблизи черной дыры (в
случае объектов больших размеров
различие времен прихода света от различных
участков объекта полностью смазало бы
быстрые изменения интенсивности
излучения). Большинство этих изменений во
времени носит случайных характер; однако
в ряде случаев они оказываются
достаточно регулярными, так что их удается
детально изучить. В шести или семи случаях
результаты свидетельствуют о
существовании двойной системы, состоящей из
компактного источника рентгеновского
излучения и более или менее ординарной звезды,
вращающихся друг относительно друга.

ОСНОВНЫЕ выводы 561
В двух случаях (Her Х-1 в созвездии
Геркулеса и Cen Х-3 в созвездии Центавра) по
доплеровскому сдвигу была измерена
орбитальная скорость рентгеновского
источника, который, по-видимому, является
пульсаром; в третьем же случае (Cyg Х-1
в созвездии Лебедь) измерения доплеров-
ского сдвига позволили найти скорость
ординарной (или оптической) звезды. К
сожалению, пока не удалось одновременно
определить скорости обоих партнеров
пары.
Тем не менее в каждом из трех случаев
можно сделать некоторые оценки массы
рентгеновского источника (правда, лишь на
основе нескольких предположений).
Наиболее ясным является случай рентгеновского
источника Her Х-1, у которого масса,
вероятно, составляет примерно (0,6 ± 0,2)
солнечной массы, т.е. вполне приемлемую
величину для нейтронной звезды. В этом
случае имеется много данных в отношении
как рентгеновского источника, так и
оптического партнера, причем все данные
свидетельствуют о том? что источником
рентгеновского излучения является поверхность
нейтронной звезды, которую
бомбардирует вещество, извергаемое ординарной
звездой. В созвездии Лебедь обнаружен
рентгеновский источник Cyg Х-1, масса
которого по оценкам составляет 5Мс.
Поскольку эта величина превосходит
критическую массу стабильной нейтронной звезды,
источником рентгеновского излучения,
вероятно, является черная дыра, или, скорее,
ее окрестность (если только правильны
предположения, при которых получена эта
оценка). Разумеется, сама по себе дыра
«черна», однако извергаемое обычной
звездой вещество, падая и «проваливаясь»
в черную дыру, будет ускоряться
гравитационным полем и подвергаться сжатию.
В такой модели испытывающее сжатие
вещество разогревается и излучает в
процессе падения рентгеновское излучение.
Однако излучение происходит лишь до тех пор,
пока это вещество не достигает
критического радиуса jR0, определяемого
формулой (30-2). В 1978 г. в созвездии Скорпиона
была обнаружена вторая двойная звезда,
аналогичная по своим свойствам Cyg Х-1
из созвездия Лебедь. Эту черную дыру
назвали Sco V-861. Кроме того, есть
свидетельство того, что огромная черная дыра
находится в центре галактики М-87.
Приводящий к образованию
нейтронной звезды или черной дыры
гравитационный коллапс представляет собой
катастрофу, на последних стадиях которой
радиус звезды уменьшается со скоростью,
близкой к скорости света. Согласно общей
теории относительности, вещество звезды,
испытывающее в процессе коллапса
ускорение, должно испускать импульс
гравитационного излучения аналогично тому, как
излучает электромагнитные волны
ускоренно движущийся заряд. Из теории
следует, что в земных условиях можно
построить детектор гравитационных волн,
который обладал бы достаточной
чувствительностью для регистрации такого
коллапса (или сверхновой). В настоящее время
уже работает несколько опытных образцов
таких детекторов гравитационных волн
и разрабатываются детекторы с более
высокой чувствительностью. С помощью
этих детекторов, возможно, удастся
регистрировать происходящие в центре нашей
галактики взрывы сверхновых или
столкновения с черными дырами, что вряд ли
удалось бы обнаружить иными методами.
Основные выводы
В звезде массой М гравитационное
давление уравновешивается тепловым
давлением; это обстоятельство приводит к
соотношению
Энергия, обеспечивающая тепловое
давление, выделяется за счет уменьшения в
процессе сжатия гравитационной
потенциальной энергии, однако, как только
температура станет выше 107 К, возникает
термоядерный протон-протонный цикл, и
медленное сжатие приостанавливается.
После того как термоядерное горючее
полностью израсходовано, снова
происходит гравитационное сжатие, пока кванто-
вомеханическое давление не уравновесит
давление гравитационных сил. В случае
белого карлика квантовомеханическое
давление создается за счет фермиевской энер-

562 ГЛ. 30. АСТРОФИЗИКА
гии электронов [давление равно Р =
= (2/5)nKf/V~\. Иногда этот
окончательный этап сжатия протекает столь
бурно, что большая часть протонов и
электронов превращается в нейтроны - образуется
нейтронная звезда, в которой квантовоме-
ханическое давление создается нейтронами,
а также небольшим числом уцелевших
электронов. В таком случае радиус звезды
составляет около 10 км, а плотность
оказывается сравнима с плотностью
атомных ядер. Радиус же белого карлика
достигает ~ 104 км, а его плотность
приблизительно в 106 раз больше плотности
Земли. Пока электроны нерелятивистские,
радиус белого карлика меняется
пропорционально М~1/3, причем предельная
масса, когда электроны становятся
релятивистскими, оказывается порядка 1,4Мо
По той же причине (нейтроны
становятся релятивистскими) предельная масса
нейтронной звезды составляет ~ 3 Мс.
Коллапс звезды, масса которой превышает
~ ЗМС, должен приводить к образованию
черной дыры, если только вся масса
звезды участвует в коллапсе. После того
как радиус звезды достигнет значения
R0 = 2GM/c2, ни одному фотону или иной
частице не удастся вырваться из области
«звезды». Сигналы из черной дыры не
могут достичь удаленного наблюдателя,
однако ее гравитационное поле будет
проявляться.
Поскольку нейтронная звезда,
называемая также пульсаром, наследует момент
импульса своей «родительской звезды»,
она вращается с частотой несколько
оборотов в секунду и любое ее излучение
обладает той же периодичностью или
частотой повторения импульсов. Некоторые
нейтронные звезды, а возможно, и
некоторые из черных дыр имеют в качестве
партнера ординарную звезду. Часть газа
из внешней оболочки ординарной звезды
может всасываться черной дырой, испуская
при этом характерное рентгеновское
излучение. Наблюдения рентгеновских
источников представляют собой, пожалуй, лучшее
из экспериментальных доказательств
существования черных дыр.
Упражнения
1. Поток падающей на Землю солнечной
энергии равен 1,4 кВт/м2. Какова полная
мощность излучения Солнца? Расстояние от
Земли до Солнца 1,5-1011 м.
2. Допустим, что планета Юпитер находится
в процессе формирования на стадии
сжатия. Какова должна быть ее температура
в центре, вычисленная по формуле (30-1)?
Масса и радиус Юпитера равны
соответственно 6-1024кг и 7,2-104 км.
3. В ходе протон-протонного цикла каждый
протон высвобождает около 6 МэВ
кинетической энергии. Если производительность
Солнца равна 4-Ю23 кВт, то какое число
протонов ежесекундно участвует в
термоядерных превращениях?
4. Для того чтобы материальная частица,
расположенная на горизонте, смогла покинуть
черную дыру, ее начальная скорость
должна быть равна скорости света.
Воспользуйтесь нерелятивистским выражением для
начальной скорости и найдите R0.
5. Будем считать, что вся видимая часть
Вселенной-это черная дыра радиусом Ru =
= 1010 световых лет. Какой в таком случае
должна быть средняя плотность р, чтобы
величина Ru достигла 2GMu/c2? Найдите
численное значение р. (На самом деле величина
наблюдаемой плотности весьма
неопределенна, но она могла бы быть равна этому
найденному значению.)
6. С помощью формулы (30-7) найдите
выражение для dE/dR, приравняйте его нулю
и разрешите относительно R.
7. Если радиус белого карлика уменьшается
в 2 раза, то во сколько раз возрастает
энергия Ферми отдельного электрона?
8. Чему равно отношение «критической»
плотности нейтронной звезды к плотности
атомного ядра? [Воспользуйтесь формулой
(30-12).]
9. Найдите с помощью формулы (30-13)
выражение для dE/dR, приравняйте его нулю
и разрешите относительно R, положив х = 0.
Задачи
10. Допустим, что при сжатии огромного
облака водорода массой М излучается небольшое
количество энергии; иными словами; мы
предполагаем, что уменьшение
гравитационной потенциальной энергии равно приросту
кинетической энергии. Пусть кинетическая

ЗАДАЧИ 563
энергия равна (3/2)пкТ, a U = -(3/5) GM2/R.
Найдите выражение для R через Т, М и тр.
11. Выведите формулу для критического
значения угловой частоты шкр вращающегося
однородного шара массой М и радиусом R.
(Если со > сокр, то шар разлетается на куски.)
Рассмотрите элемент массы Am,
расположенный на экваторе. (Ответ: сокр = j/GM/Я3.)
12. Предполагая, что в процессе
гравитационного сжатия момент импульса Солнца не
меняется, и используя закон сохранения
момента импульса, найдите минимальный
радиус, до которого могло бы сжаться
Солнце. Воспользуйтесь результатом предыдущей
задачи.
13. Предположим, что Вселенная представляет
собой шар радиусом R, а ее средняя
плотность р = 10"28 г/см3. Какова должна быть
скорость в зависимости от R, чтобы можно
было вылететь за пределы Вселенной? При
каком значении R эта скорость станет
равной скорости света? (Интересно заметить,
что ответ близок к скорости разбегания
галактик, находящихся на расстоянии R.
Кроме того, соотношение между р, G и Ru
совпадает с соотношением, полученным в
упражнении 5.)
14. Повторите вывод уравнения (12-7) (см. гл. 12,
т. 1) и покажите, что для релятивистских
частиц PV = (1/3)npv. (Указание: Fх = Apx/At
и № = ^7 = М>7 = (1/3)ри.)
15. Используя уравнение, полученное в
предыдущей задаче, покажите, что квантовомеха-
ническое давление, обусловленное энергией
Ферми ультрарелятивистских частиц,
записывается в виде
<"т(Г»*"
16. Какой должна быть плотность белого
карлика, чтобы кинетическая энергия
электронов стала равной 1 МэВ? Положите х = 1/2.
17. В ящике находится 91 фотонов в единице
объема с частотой /0. Чему равно давление?
18. Используя формулу (30-8), найдите плотность
белого карлика как функцию его массы.
Затем подставьте найденное значение в
выражение (30-11) вместо р и разрешите его
относительно п. (Это еще один путь для
оценки предельной массы белого карлика.)
19. Если протоны в Солнце находятся при
температуре Т = 107 К, то какова доля
протонов, энергия которых превышает величину
/с0е2/2Д, где R = 10 фм? Функцию
распределения вероятностей можно использовать в
виде ехр(-Я//сТ).

ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Основная цель физики-дать
объяснение всем физическим явлениям исходя из
небольшого числа простых,
фундаментальных принципов. Поскольку любое
вещество построено из элементарных частиц,
бесчисленные физические явления и
свойства вещества можно в принципе
объяснить с помощью нескольких простых
свойств небольшого числа элементарных
частиц.
В поисках элементарных частиц человек
первоначально установил, что все
соединения состоят из «элементарных» молекул.
Затем оказалось, что молекулы построены
из «элементарных» атомов. Спустя
столетия было обнаружено, что «элементарные»
атомы построены из «элементарных» ядер
и вращающихся вокруг них по орбитам
электронов. Эти последовательные
попытки выяснить, что же является истинно
элементарным, похожи на «шелушение»
луковицы. Более поздним этапом этого
процесса «шелушения» обычного вещества
явилось открытие того, что все атомные ядра
построены из протонов и нейтронов.
Достигли ли мы наконец сердцевины
луковицы? Не окажется ли, что протоны
и нейтроны состоят из еще более «мелких»
элементарных частиц? До недавнего
времени протоны и нейтроны считались
элементарными частицами, не обладающими
внутренней структурой. Считая протоны,
нейтроны, электроны и фотоны основными
строительными блоками, из которых
построено обычное вещество, как это
объяснялось в гл. 28 и 29, на этом можно было
®J) с Jfefcr Шхк Si mc s IHa tjasin с
^^ II II \/ Л О Л П7С
JULY 18, 1976
Cover
By the beautiful sea in the early 1920's. "The thing that is so wonderful about Coney
Island is that for so many, many years . . . it has sturdily refused to pander
to good taste." Page 10.
Photograph from Nathan's Famous Collection
Russell Baker
4 Sunday Observer
Net loss
7 Bargain with terrorists?
Is America's no-negotiating policy a deterrent
or an invitation to murder?
Sheldon L. Glashow
8 The bunting of the quark
Are the physicists close to a breakthrough in their
search for the ultimate structure of matter? That remains
to be seen—but, then, so does the quark.
Gilbert Millstein
10 Coney Island forever
"They've been writing Coney off for 50 years, but here
.Рис. 31-1. Неуловимый кварк
появляется в журнале «Тайме».
[Copyright 1976 by The New
York Times Company.
Печатается с разрешения.]

бы и поставить точку. Но поскольку
главная цель нашей книги в том, чтобы
осветить все существенные стороны
физической реальности, нам следует предварить
ее завершение вопросом: не существует ли
каких-то иных физически реальных
фундаментальных частиц, которые не
встречались бы в окружающем нас веществе?
Ответ представляет собой решительное да!
С 1933 г. физики открыли свыше 200 новых
элементарных частиц. И появляются все
более убедительные аргументы в пользу
того, что большинство из этих 200 частиц
построено из четырех субчастиц,
называемых кварками. Однако до сих пор ни
одну из частиц еще не удалось расщепить на
составляющие ее кварки, а о кварках уже
пишут в популярных журналах (рис. 31-1).
В следующих параграфах мы
познакомимся с некоторыми из новых частиц.
Модель кварков рассматривается в § 6. В
заключение мы дадим сводку известных
законов сохранения.
§ 1. Слабое взаимодействие
Новые элементарные частицы в
большинстве нестабильны - они распадаются,
превращаясь в другие элементарные
частицы с меньшей массой. Прежде чем
обсуждать свойства новых частиц,
необходимо более подробно познакомиться с
бета-распадом и тем, что называется
слабым взаимодействием. Это взаимодействие
можно рассматривать как всеобщую
эпидемию, поразившую в одинаковой степени
все частицы. Оно стремится превратить
в конечном счете все элементарные
частицы в электроны и нейтрино.
Исторически электроны, образующиеся при таком
распаде, получили название р-частиц.
Поскольку в бета-распаде всегда
участвуют нейтрино, их описание является
весьма существенным. Нейтрино-это
элементарная частица, не имеющая
электрического заряда и массы покоя1 \ Более того,
нейтрино взаимодействует с веществом на-
1} Вопрос о величине массы покоя нейтрино
окончательно не решен. Время от времени
появляются экспериментальные данные,
свидетельствующие о том, что масса нейтрино может
оказаться отличной от нуля. Такой результат
имел бы важные последствия для наших
представлений не только о строении микромира, но
и о свойствах Вселенной-Прим. перев.
§ 1. СЛАБОЕ ВЗАИМОДЕЙСТВИЕ 565
Рис. 31-2. Р. Фейнман во время визита в Кор-
неллский университет. Проф. Р. Фейнман
удостоен Нобелевской премии за свой вклад в
современную квантовую электродинамику и
теорию универсального взаимодействия Ферми.
[Фото выполнено Чиу.]
столько слабо, что оказывается почти
ненаблюдаемым. Если представить себе, что на
Землю падает пучок, содержащий 1012
нейтрино, то все они, за исключением
одного, прошли бы через земной шар без
всяких последствий. До сих пор эта частица
все еще кажется плодом воображения.
Однако нейтрино отнюдь не мистификация,
придуманная теоретиками.
Экспериментальные и теоретические доказательства
столь убедительны, что никто из
компетентных ученых не сомневается в
существовании нейтрино.
1958 год ознаменовался значительным
прогрессом в понимании природы слабого
взаимодействия. Было высказано
предположение о существовании специфического
взаимодействия, способного превращать
частицы в электроны и нейтрино. Теория
этого взаимодействия, названного
универсальным взаимодействием Ферми, была

566 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
разработана Р. Фейнманом и рядом
других ученых. Новая теория, например, точно
предсказывает время жизни мюона.
Одним из примеров слабого
взаимодействия является бета-распад свободного
нейтрона:
п->р + е~ + ve,
который происходит с периодом
полураспада 12 мин и сопровождается выделением
энергии 1,3 МэВ. Поскольку масса покоя
электрона составляет 0,5 МэВ, то избыток
энергии 0,8 МэВ выделяется в виде
кинетической энергии электрона и антинейтрино
(символом ve обозначено антинейтрино,
сопровождающее рождение электрона). В § 3
мы обсудим вопрос о том, в чем состоит
различие между нейтрино и антинейтрино.
Следует заметить, что кинетическая
энергия 0,8 МэВ может распределяться
между образующимися в результате распада
электроном и нейтрино любым способом.
Поэтому, если распадается большое число
нейтронов, то в этом случае удастся
обнаружить электроны с любыми
кинетическими энергиями от нуля до 0,8 МэВ. Если бы
нейтрон распадался только на протон
и электрон, то последний всегда уносил бы
всю кинетическую энергию 0,8 МэВ.
Энергию электрона можно определить
экспериментально, измеряя радиус кривизны его
траектории в магнитном поле (рис. 31-3).
Оказывается, что Р-частицы редко
приобретают максимально возможную
кинетическую энергию. Исторически дело
обстояло так, что именно «исчезновение»
кинетической энергии послужило
первопричиной «изобретения» нейтрино.
Чтобы избежать нарушения закона
сохранения энергии, в 1930 г. В. Паули
предположил, что недостающая энергия
уносится нерегистрируемой легкой
нейтральной частицей. Вскоре после этого Э.
Ферми назвал эту частицу нейтрино
(нейтральная малютка) и разработал теорию бета-
распада, сходную с современной, более
универсальной теорией слабого
взаимодействия, названной теорией универсального
взаимодействия Ферми.
Доказательство существования
нейтрино как продукта распада было вполне
убедительным. Однако физикам хотелось
иметь дополнительные подтверждения, ос-
Рис. 31-3. След электрона в жид-
ководородной пузырьковой
камере. След закручен в
однородном магнитном поле,
направленном на рисунке из плоскости
чертежа. Радиус кривизны
уменьшается по мере того, как
скорость электрона в жидком
водороде уменьшается. [С любезного
разрешения группы Альвареса,
Лаборатория излучения им. Лоу-
ренса, Калифорнийский
университет.]

§ 1. СЛАБОЕ ВЗАИМОДЕЙСТВИЕ 567
Рис. 31-4. Схематический
разрез нейтринного детектора в
защите ядерного реактора.
Каждый из трех баков (I, II
и III) содержит примерно по
1400 л жидкого сцинтиллятора
и снабжен ПО
фотоэлектронными умножителями (ФЭУ).
Позитроны, образующиеся в
результате реакции v + р -> п + е+,
создают в жидком сцинтилля-
торе характерные световые
вспышки. [С любезного
разрешения руководства Лос-Аламо-
ской научной лаборатории и
д-ра Ф. Рейнеса.]
нованные на наблюдении прямого
взаимодействия под действием пучка нейтрино.
Согласно теории Ферми, антинейтрино
с энергией, достаточной для компенсации
разности масс, должны вызывать
следующую реакцию:
ve + р->п + е+,
где е+ - позитрон (положительно
заряженный электрон). Однако вероятность
прямого взаимодействия нейтрино
предсказывалась близкой к нулю. Наблюдать
эту реакцию можно было единственно при
наличии исключительно интенсивных
пучков антинейтрино. Такая возможность
была обеспечена развитием техники ядерных
реакторов. Каждый процесс деления
в ядерном реакторе сопровождается нет
сколькими бета-распадами и,
следовательно, испусканием нескольких антинейтрино.
Для осуществления подобного
эксперимента необходимо иметь ядерный реактор
высокой мощности и детектор огромных
размеров. Этот эксперимент был осуществлен
группой физиков из Лос-Аламоса. При
этом использовался детектор,
схематически показанный на рис. 31-4. Результат
был таков, что в 1956 г. впервые удалось
«поймать» неуловимое нейтрино.
По сравнению с ядерными реакторами
ускорители частиц высоких энергий
позволяют получать пучки нейтрино с гораздо
более высокой энергией, но с меньшей
интенсивностью. К счастью, сечение
нейтринного взаимодействия линейно возрастает
с энергией, и в течение нескольких
последних лет на пучках нейтрино высоких
энергий удалось зарегистрировать тысячи
случаев нейтринных взаимодействий.
ЗАКОН СОХРАНЕНИЯ БАРИОНОВ1)
Поскольку свободный нейтрон
распадается благодаря слабым
взаимодействиям, можно было бы предполагать, что
и свободный протон будет также
испытывать распад. Однако тщательные
измерения показали, что свободные протоны
стабильны. Этот факт, а также наблюдение за
процессами с участием сильно
взаимодействующих частиц привели к установлению
закона сохранения барионов. К барионам
относятся протон, нейтрон и примерно
половина всех сильно взаимодействующих
частиц. Закон сохранения барионов
утверждает, что в замкнутой системе разность
полного числа барионов и полного числа
антибарионов сохраняется неизменной.
И поскольку протон самый легкий из
барионов, ему не во что распадаться. Ба-
1} Этот вопрос подробно рассматривается
в статье: Гелл-Манн М. и др. УФН, 1980, т. 130,
№ 3, с. 459-Прим. перев.

568 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
рионы обладают полуцелыми спинами,
а именно: (1/2)Й, (3/2)% (5/2)й и т.п.
§ 2. Ускорители частиц высоких энергий
Только рассмотрение способов
получения и регистрации новых элементарных
частиц убеждает нас в том, что эти частицы
не являются всего лишь плодом богатого
воображения.
Под ускорителем частиц высоких
энергий мы будем подразумевать установку,
обеспечивающую получение пучков
протонов или электронов с энергиями свыше
1 ГэВ (109 эВ). За исключением
единственного в мире линейного ускорителя, все
остальные ускорители частиц высоких
энергий представляют собой синхротроны.
В синхротроне частицы циркулируют
внутри вакуумной тороидальной камеры,
расположенной между полюсами
кольцеобразного магнита (рис. 31-5). Частицы
ускоряются при прохождении области
электрического поля, создаваемого ВЧ-ге-
нератором. Радиус кривизны можно
вычислить, приравняв центростремительную
силу mv2/R магнитной силе ev@l\
mv
~R
R =
P_
R
Таким образом, если поддерживать
величину 31 пропорциональной импульсу р, то
частицы будут удерживаться на
траектории с постоянным радиусом кривизны
и оставаться в центре тороидальной
вакуумной камеры.
Пример 1. В синхротроне радиусом R имеются
четыре прямолинейных промежутка длиной
L каждый. Пусть период высокочастотного
генератора соответствует периоду обращения
частиц. Найдите выражение для
соответствующего магнитного поля через R, L и частоту
генератора /.
Решение: Период обращения
Длина пути 2nR + 4L 1
V V f '
Т =
откуда находим
v = (2nR + 4L)f.
Подставляя это выражение для v в формулу
(31-1), получаем
Myv
eR
М Г
= —(2nR + 4L)f\ 1
eR L
(2nR+4L)2f2 "1-1/2
-P-
(31-1)
Для поддержания в синхротронах этого
соотношения между величиной магнитного поля и
частотой генератора используются ЭВМ.
Рис. 31-5. Старый корнеллский
электронный синхротрон с
удаленной тороидальной
вакуумной камерой. Ускоряющее
электрическое поле создается в
полости справа.

§ 2. УСКОРИТЕЛИ ЧАСТИЦ ВЫСОКИХ ЭНЕРГИЙ
Многие из первоначальных
исследований по изучению новых частиц
проводились в Брукхейвенской национальной
лаборатории (США) на протонном синхротроне
с энергией 3 ГэВ и на протонном
синхротроне (называемом также беватроном)
в Беркли (США) с энергией 6,2 ГэВ.
В г. Дубне вблизи Москвы ускоритель,
аналогичный беватрону, рассчитан на
энергию 10 ГэВ.
В начале шестидесятых годов были
введены в действие два протонных
синхротрона на энергию 30 ГэВ, один в Брукхейвене
(США), а другой в международной
лаборатории ЦЕРНа в предместьях Женевы
(Швейцария). В Советском Союзе вблизи
Серпухова под Москвой построен
аналогичный ускоритель, рассчитанный на вдвое
более высокую энергию.
В настоящее время крупнейший
ускоритель частиц высоких энергий находится в
Национальной лаборатории им. Э. Ферми
близ Чикаго (шт. Иллинойс, США). Это
протонный синхротрон на энергию 500 ГэВ
(рис. 31-6). На снимке видно здание
линейного ускорителя, в котором протоны
ускоряются до энергии 200 МэВ, а
затем поступают в бустерный
(предварительный) синхротрон и приобретают
энергию 8 ГэВ. После этого протоны вводятся
в основной кольцевой магнит, длина
окружности которого превышает 6 км.
В основном кольце протоны ускоряются
от 8 до 500 ГэВ. В 1976 г. в ЦЕРНе был
введен в строи аналогичный ускоритель на
энергию 400 ГэВ. Его размеры столь
грандиозны, что он «не уместился» в
Швейцарии и частично оказался на территории
Франции.
Пример 2. Чему равна максимальная энергия
протонов в ускорителе Национальной
лаборатории им. Э. Ферми, если магнитное поле в
максимуме достигает 20 кГс, a R = 800 м?
Решение: Из формулы (31-1) получаем
следующее выражение для р:
Таким образом,
рс =
= (1,6 • Ю-19) (2,0) (800) (3 • 108) Дж =
= 4,8- 1011 эВ =480 ГэВ.
Поскольку эта энергия значительно превышает
энергию покоя протона 0,94 ГэВ,
релятивистская энергия практически совпадает с рс [см.
формулу (9-11)].
Крупнейший электронный синхротрон
находится в Корнеллском университете
(США) и сообщает пучку электронов
энергию 12 ГэВ. Электроны с энергией 20 ГэВ
обеспечивает линейный ускоритель Стен-
фордского центра (СЛАК, США),
достигающий почти двухкилометровой длины.
Рис. 31-6. Общий вид
ускорителя на 500 ГэВ в Национальной
лаборатории им. Э. Ферми,
расположенной в 30 милях к
западу от Чикаго. [С любезного
разрешения отдела фотографий
Национальной лаборатории
им. Э. Ферми.]

570 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
В синхротронах электроны в процессе
ускорения проходят путь длиной около
2000 км, и при этом для их ускорения
требуются гораздо меньшие электрические
поля, чем в линейных ускорителях.
Существует иной способ достижения
эффективных высоких энергий. Он связан
с использованием соударений частиц во
встречных пучках. В ЦЕРНе протонный
синхротрон на энергию 28 ГэВ
используется для введения ускоренных частиц
попеременно в два пересекающихся кольца и
накопления в них частиц. В области
пересечения при соударениях частиц имеют место
взаимодействия, эквивалентные
взаимодействиям в обычном ускорителе на энергию
1500 ГэВ; однако число взаимодействий
в единицу времени весьма мало. В Брук-
хейвенской национальной лаборатории
сооружается система со встречными пучками
протонов на энергию 400 ГэВ каждый.
Накопительные кольца со встречными
пучками электронов и позитронов имеются
в Новосибирске, Риме, Гамбурге1}, Стен-
форде; накопительные кольца на энергию
18 ГэВ имеются в Гамбурге и строятся
в Стенфорде; в Корнеллском университете
сооружается накопительное кольцо на
энергию 8 ГэВ.
Без существования ускорителей мы бы
не имели возможности изучать
фундаментальные свойства и взаимодействия
элементарных частиц. Большинство
элементарных частиц было открыто с помощью
ускорителей на высокие энергии.
Стоимость новых ускорителей может достигать
100 млн. долларов, однако строить их
необходимо, если мы хотим добиться успеха
в области знания, на которой в конечном
счете основаны все физические науки.
1} На накопительных кольцах в Гамбурге
в последние годы был сделан ряд выдающихся
открытий; получены экспериментальные
подтверждения существования кварков, открыты
два новых типа кварков и глюоны, обнаружен
тяжелый лептон и ряд других новых частиц.
Подробнее с результатами этих исследований
можно познакомиться в статьях, публикуемых
в журналах «Природа» и «Успехи физических
наук».-Ярил*, перев.
§ 3. Антивещество
Из релятивистской квантовой теории
частиц со спином — 1/2 следует не только
принцип Паули, но и существование
античастиц. Античастица должна иметь в
точности ту же массу, что и соответствующая
ей частица, но противоположный
электрический заряд. Кроме того, античастица
может аннигилировать с соответствующей ей
частицей. В этом случае обе массы покоя
непосредственно превращаются в
энергию-в форме других частиц, например
фотонов. Первой античастицей, с которой
довелось познакомиться человеку, был
позитрон, открытый в 1933 г. в камере
Вильсона при регистрации космических лучей.
Первый позитрон обнаружили случайно,
хотя существование этих частиц
предсказывалось уже релятивистской квантовой
теорией. Позитрон, или положительный
электрон, имеет ту же массу, что и
электрон, но противоположный электрический
заряд. Тормозясь в веществе, позитрон
быстро аннигилирует с электроном и
превращается, как правило, в два фотона:
е + + е ~ -► 2у.
При этом каждый из фотонов должен
иметь энергию 0,51 МэВ, которая равна
массе покоя электрона. Позитроны легко
возникают в так называемом процессе
рождения пар (при соударении с ядром
фотон с высокой энергией превращается в
пару электрон-позитрон):
у -► е+ + е~.
Эта реакция служит одним из множества
примеров прямого превращения энергии
в массу покоя. Как указывалось в § 1,
и электроны и позитроны могут возникать
в результате бета-распада. При
бета-распаде вместе с позитроном всегда образуется
нейтрино.
Античастица протона называется
антипротоном или отрицательным протоном р.
Обычно античастицы обозначаются
символом частицы с черточкой наверху. Таким
образом, р-это антипротон, а
п-антинейтрон. Антиэлектрон (позитрон) должен был
бы обозначаться как ё~, однако его
принято обозначать е + . После открытия
в 1933 г. позитрона многим физикам стало

§ 3. АНТИВЕЩЕСТВО 571
ясно, что должен также существовать и
антипротон. В соответствии с теорией
антипротоны могли бы рождаться при
бомбардировке ядер протонами с кинетической
энергией 6 млрд. эВ. В этом случае одна
из реакций рождения антипротонов имела
бы вид
D + p -> р + р + р + р.
Энергия 6 ГэВ непосредственно
превращается в энергию покоя пары
протон-антипротон.
Возможность открыть антипротон
была одним из главных аргументов,
приведших Комиссию по атомной энергии США
к решению построить
беватрон-протонный синхротрон на высокие энергии,
размещенный в Беркли (шт. Калифорния).
Беватрон ускорял протоны до энергии
6,2 ГэВ, которой едва-едва хватало для
рождения пары протон-антипротон. В
1955 г.-на втором году работы беватро-
на-был открыт антипротон. Еще через год
был открыт антинейтрон п. Поскольку
нейтрон электрически нейтрален, то
нейтральным должен быть и антинейтрон.
Однако антинейтрон быстро аннигилирует
либо с нейтроном, либо с протоном.
Продуктами аннигиляции антинуклонов обыч-
р + р -2тг+ + 2я~+ тг°
Рис. 31-7. Антипротон в жидко-
водородной пузырьковой
камере останавливается и
аннигилирует с протоном. Продуктами
аннигиляции являются пять
пионов: два положительных,
два отрицательных и один
нейтральный. Один из
положительных пионов также
тормозится и останавливается,
распадаясь при этом на |х +, который
в свою очередь останавливается
и распадается на позитрон. [С
любезного разрешения группы
жидководородной пузырьковой
камеры Лаборатории излучения
им. Лоуренса.]

572 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
но являются пионы (см. § 5). На рис. 31-7
показано, как антипротон, который
попадает в пузырьковую камеру, наполненную
жидким водородом, замедляется до полной
остановки и аннигилирует с одним из ядер
водорода. На этом снимке масса покоя
антипротона и протона превращается в
пять пионов:
р + р -► 71+ + К+ + П~ + П~ + 7Е°.
Возникает вопрос: почему все атомы
водорода построены из положительных
протонов и отрицательных электронов,
а не из отрицательных протонов
(антипротонов) и положительных электронов
(позитронов)? Такой «обращенный» атом
водорода называется антиводородом.
Вещество, построенное из антинуклонов и
орбитальных позитронов, называется
антивеществом. Из общих соображений симметрии
следовало бы ожидать, что половина
атомов во Вселенной должна была бы
представлять собой антивещество. Трудно
понять, почему положительный заряд должен
иметь преимущество над отрицательным.
С другой стороны, если бы на Земле или
даже в нашей Галактике имелось бы
антивещество, то оно не могло бы
просуществовать очень долго. Антивещество
довольно скоро аннигилировало бы; при
этом выделилась бы энергия, почти в 1000
раз более эффективно, чем при взрыве
водородной бомбы. В настоящее время
имеются предположения о том, что
некоторые галактики, возможно, состоят из
антивещества, однако в пользу этого до сих
пор не получено достаточных
доказательств.
Как уже упоминалось, античастицей
нейтрино является антинейтрино v. В
соответствии с теорией фотон должен быть
тождествен своей античастице. С учетом
античастиц список рассмотренных нами до
сих пор элементарных частиц возрос до
девяти: у, v, v, е~, е+, р, р, п, п.
СИММЕТРИЯ АНТИЧАСТИЦ
Предположим, что в процессе
физического эксперимента все частицы внезапно
превратились в соответствующие
античастицы. Не скажется ли это на результате
эксперимента? До 1957 г. физики
предполагали, что античастицы должны
подчиняться в точности тем же физическим
законам, что и соответствующие им частицы.
В принципе не должно существовать
способа, позволяющего определить, построена
физическая система из обычного вещества
или антивещества. Мы будем называть
этот краеугольный принцип симметрии
симметрией античастиц. В теоретической
физике его обычно называют
инвариантностью относительно зарядового
сопряжения. Зарядовое сопряжение-это
математическая операция, которая заменяет все
частицы соответствующими
античастицами и оставляет все остальное без
изменений. При зарядовом сопряжении атом
водорода переходит в антиводород. Принцип
симметрии античастиц, например,
предсказывает, что спектр излучения
газообразного антиводорода должен точно
совпадать со спектром обычного водорода.
Поскольку античастицы создать непросто
(еще никогда не удавалось получить
антиводород), нелегко поддаются
экспериментальной проверке и некоторые явления,
связанные с симметрией античастиц.
Действительно, в 1957 г. физики были
потрясены, узнав, что слабые
взаимодействия нарушают симметрию античастиц.
В § 7 мы обсудим вопрос о
происхождении этого нарушения.
§ 4. Сохранение лептонов
Слабые взаимодействия вызывают
распады тяжелых частиц не только с
испусканием электрона и нейтрино, но в
некоторых случаях вместо этих частиц
возникают мюон и нейтрино. Мюон-это
элементарная частица, тождественная с
электроном во всех отношениях, за
исключением массы покоя. Ей суждено иметь
массу покоя в 207 раз больше электронной.
Мюон следует рассматривать как тяжелый
электрон. В 1975 г. появилось сообщение
о том, что существует еще один тяжелый
электрон с массой примерно в 20 раз
больше мюонной1*. Но никому неведомо, поче-
1} В настоящее время свойства этого
третьего, самого тяжелого электрона, так
называемого т-лептона, уже хорошо изучены -Прим. перев.

8 4. СОХРАНЕНИЕ ЛЕПТОНОВ 573
му должно быть именно два или три сорта
«электронов».
Мюоны не так уже необычны. Они
были открыты в 1936 г. в космических лучах.
Действительно, космические лучи,
достигающие уровня моря, состоят главным
образом из мюонов и электронов в
соотношении 4 к 1. Подобно тому как
е+-античастица электрона е~, так и \х+
является античастицей мюона ц~. Почему
обычное вещество не содержит наряду с
электронами также и мюонов, объясняется
тем, что благодаря слабым
взаимодействиям мюоны могут распадаться,
превращаясь с периодом полураспада 1,5 • 10"6 с
в электроны:
Ц"-^и + е~ +ve.
Следует заметить, что возникающим
при распаде нейтрино приписываются
индексы е и [I. Это обусловлено следующим.
В 1963 г. группой физиков на брукхейвен-
ском синхротроне было обнаружено, что
существует нейтрино двух различных
типов: уц, связанное с мюоном, и ve,
связанное с электроном. Нейтрино уц можно
рассматривать как нейтральную
разновидность мюона, а уе-как нейтральную
разновидность электрона; их можно было бы
обозначать соответственно ц° и е°. Класс
частиц, к которому относятся мюоны,
электроны и соответствующие им
нейтрино, называют лептонами. Лептоны
участвуют в слабых взаимодействиях.
Установлено, что во всех процессах рождения
лептоны возникают парами. Это привело
к установлению нового закона сохранения,
а именно к закону сохранения лептонов.
В действительности же имеются два
независимых закона сохранения лептонов-
один для электронов и один для мюонов.
Электрону е~ и его нейтрино ve
приписывается электронное лептонное число (или
«заряд») + 1, а соответствующим
античастицам е+ и ve-электронное лептонное
число — 1. В любой замкнутой системе
полное число лептонов электронного
семейства должно сохраняться. Например,
при распаде нейтрона
n-»p + e~+ve
лептонное число
(0) - (0) + (1) + (-1).
Поскольку суммарное лептонное число до
распада равно нулю, то суммарное
лептонное число и в правой части уравнения,
описывающего распад нейтрона, также
должно быть равно нулю. Мы видим, что
так оно и есть. Аналогично при
бета-распаде с испусканием позитрона нейтрино
должно иметь противоположное лептонное
число. Поскольку лептонное число
позитрона равно — 1, нейтрино должно иметь
лептонное число + 1 и, следовательно, это
должно быть ve, а не ve.
В качестве последнего примера
сохранения лептонов рассмотрим распад мюона
[X ~ -+ уц + е" + ve,
в котором мюонное лептонное число
(1) -► (1) + (0) + (0), электронное
лептонное число (0) -► (0) + (1) + ( - 1).
Первоначально мюонное лептонное число равно
+1. Это число сохраняется, если при
распаде возникает нейтральный мюон уц.
Электрический заряд сохраняется
благодаря испусканию электрона, однако для
сохранения электронного лептонного числа
должно также испускаться антинейтрино ve.
Пример 3. При соударении
высокоэнергетического положительного мюона и электрона они
могут превратиться в два нейтрино: \х+ + е~ -> 2v.
Какого типа эти нейтрино?
Решение: Одно нейтрино должно иметь
мюонное лептонное число — 1, такое же, как \i +.
Следовательно, это уц. Другим нейтрино является
ve, у которого электронное лептонное число
такое же, как и у атомного электрона.
В заключение отметим, что хорошо
известны восемь лептонов, а именно \х~, vp
е~, ve и их античастицы ц+, уц, е+, ve. Эти
частицы парами участвуют в слабых
взаимодействиях. Кроме того, существуют
тяжелый т-лептон с массой покоя около
1,8 ГэВ и соответствующее ему нейтрино
с нулевой массой покоя: т", vT и их
античастицы т+, vT.

574 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
§ 5. Адроны
Если лептоны-это частицы,
участвующие в слабых взаимодействиях, то
адроны-частицы, участвующие в сильных или
ядерных взаимодействиях. Для
электромагнитных взаимодействий не
существует таких разграничений, и в этих
взаимодействиях участвует любая заряженная
частица, а также фотон.
Электромагнитные взаимодействия присущи как
заряженным лептонам, так и заряженным адро-
нам.
Среди адронов лучше всего изучены
протоны и нейтроны. Однако начиная
с 1947 г. было открыто множество других
нестабильных адронов. Из последних 21
частица (см. рис. 31-10) обладают
достаточно большими периодами полураспада
и оставляют видимые следы в ядерных
фотоэмульсиях или пузырьковых камерах.
У большинства из этих 21 частицы
периоды полураспада оказываются порядка
10"10 с. За это время частица, движущаяся
со скоростью v = с, пролетает путь длиной
3 см. Несмотря на наличие среди частиц
определенных объединений и групп, их
количество может показаться чрезмерным
и заставить нас заподозрить, не скрывается
ли за ними нечто более элементарное
и простое. Это безусловно центральная
проблема, с которой столкнулись ныне
физики. Таким образом, мы достигли в этой
книге передовых позиций в наших знаниях
и представлениях об устройстве
физического мира. В оставшихся разделах
предпринята попытка познакомить читателя с
сегодняшними «пионерскими»
исследованиями в области строения вещества.
Существуют два типа адронов - мезоны
и барионы. Мезоны имеют спин 0, 1, 2 или
другие целые значения. Спины барионов
являются полуцелыми, а именно 1/2, 3/2,
5/2 и т. п. Барионы подчиняются закону
сохранения барионов, и конечным продуктом
их распада всегда оказывается протон или
антипротон. У всех барионов, таких, как
протон и нейтрон, барионное число равно
+ 1, а у всех антибарионов, таких, как р
и п, барионное число равно — 1. В
замкнутой системе суммарное барионное число
остается неизменным. Мезоны имеют
нулевое барионное число.
МЕЗОНЫ
Известны два долгоживущих мезона—
пион и К-мезон (или каон). Масса пиона
равна около 1/7 массы протона, а масса К-
мезона-примерно половине массы
протона.
Пионы имеют равный нулю спин и
могут быть заряжены положительно,
отрицательно или быть электрически
нейтральными (соответственно тс", п+ и я0). Пион
71 "-это античастица пиона п +. Как
и фотон, я0 тождествен своей античастице.
Теоретически проще понять существование
пионов, нежели мюонов. В самом деле,
пион был предсказан Юкавой еще
в 1936 г., за 11 лет до его обнаружения.
Юкава предпринял попытку объяснить
ядерные силы по аналогии с квантовоэлек-
тродинамическим описанием
электрических сил. В квантовой электродинамике
существование электрических сил
объясняется тем, что электрический заряд
непрерывно испускает и поглощает виртуальные
кванты (фотоны). Чтобы объяснить
существование ядерных сил, больших по
величине, но с малым радиусом действия,
Юкава ввел виртуальные кванты нового типа.
Квантовая теория дает соотношение
между массой этих новых частиц (квантов)
и радиусом действия ядерных сил. Это
соотношение можно грубо оценить,
воспользовавшись принципом неопределенности.
Если радиус действия виртуальных
квантов R, то, согласно принципу
неопределенности,
R Ар # %
где Ар-неопределенность импульса,
которая по порядку величины составляет m^v.
Следовательно,
(Шл v)Rx%
или
гщ ж fi/Rv.
Эта величина имеет наименьшее значение,
когда v = с. В этом случае масса
гщ « fi/Rc
и ее предсказываемое значение хорошо
согласуется с измеренным значением массы

§ 5. АДР0НЫ 575
пиона. Помимо правильного значения
массы пиона Юкава также установил, что
пионы должны сильно взаимодействовать
с нуклонами. Например, пионы легко
рождаются в процессе соударения нуклонов.
При этом кинетическая энергия нуклонов
непосредственно превращается в массу
покоя пионов. Примерами процессов
рождения пионов могут быть следующие:
р + р -► р + П + 7Г + ,
р + П -> р+р+ 71",
у + р -► П + 7Г + ,
Y + Р -> Р + я0.
Чтобы произошло рождение пиона,
энергия протонов должна быть равной
нескольким сотням миллионов эВ. Пучки
таких протонов удавалось получать еще на
старых протонных
ускорителях-синхроциклотронах.
Впервые пион был обнаружен в 1947 г.
в космических лучах при анализе следов
космических частиц в ядерных
фотоэмульсиях (рис. 31-8). А годом позже на
синхроциклотроне в Беркли (США) были зареги-
Рис. 31-8. След, оставляемый в ядерной
фотоэмульсии останавливающимся пионом. Видна
последовательность распадов п+ -> ц+ + уц
и затем |i+ -> е+ + уц + ve (нейтрино
невидимы). Так же как и под действием света,
зерна фотоэмульсии приобретают способность к
проявлению при попадании на них заряженной
частицы.
стрированы первые «созданные руками»
человека пионы. Благодаря слабым
взаимодействиям заряженные пионы обычно
распадаются следующим образом:
71+ -* Ц+ + Уц,
71" -► Ц" + Уц
с периодом полураспада 1,8 • 10"8 с.
Нейтральный пион распадается гораздо
быстрее на два фотона благодаря
электромагнитным, а не слабым взаимодействиям.
Период полураспада тг° равен примерно
10~16 с. Распад тг + , а также распад \х +
можно встретить на снимках, полученных
с помощью пузырьковой камеры,
например на рис. 31-7. Один из двух к + -мезонов
останавливается в жидком водороде, а
затем распадается, в результате чего
возникает видимый след ц+ и невидимое
нейтрино. Пройдя путь длиной 1,1 см, \х+
также останавливается и в свою очередь
распадается, создавая видимый след е +
и два невидимых нейтрино.
В действительности мюон был открыт
почти тогда же, когда Юкава предсказал
существование пиона. Поскольку массы
мюона и пиона близки, физики довольно
долго принимали мюон за частицу Юкавы.
Но незадолго до открытия пиона
большинство физиков поставили крест на мюо-
не (возможно, и на идее Юкавы),
поскольку мюон, вопреки предсказаниям Юкавы,
никогда не участвовал в сильных
взаимодействиях.
р-мезон. Существует родственная пиону
частица, называемая р-мезоном. Эта
частица также встречается в трех зарядовых
состояниях, однако ее спин равен 1 в отличие
от пиона, спин которого равен 0. Кроме
того, р-мезон примерно в 5 раз тяжелее
пиона. Поскольку р-мезон является сильно
взаимодействующей частицей, он может
и рождаться, и распадаться благодаря
сильным взаимодействиям. Эти частицы
легко рождаются в соударениях протонов
или пионов с протонами. Если пион или
протон с большой энергией пролетает
сквозь атомное ядро, то в среднем до
взаимодействия он проходит 3 • 10~15 м. На
это уходит время
D 3. 1(Г15м 4Л „
v 3 • 108 м/с

576 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Следовательно, чтобы произошло сильное
взаимодействие, нужно примерно 10"23 с.
Распад благодаря сильным
взаимодействиям занимает такой же промежуток
времени; поэтому период полураспада
р° -* тг+ + тг" составляет примерно
10"23 с.
К-мезон. На первый взгляд К-мезон
сходен с р-мезоном. Точно так же, как
существуют р + -, р°- и р"-мезоны,
имеются К+-, К0- и К "-мезоны. К-мезоны
рождаются в результате сильных взаимодействий.
Масса К-мезона сравнима с массой р-ме-
зона, и он также распадается на два пиона:
К0 -► я+ + тг". Однако период
полураспада К-мезона составляет 10"10 с, а не
10"23 с, что должно быть в случае сильно
взаимодействующих частиц! Как может
сильно взаимодействующая частица не
распадаться благодаря сильным
взаимодействиям, если продукты ее распада-это
опять-таки сильно взаимодействующие
частицы? В момент открытия К-мезонов
в 1950 г. это казалось, мягко выражаясь,
странным. Поэтому физики назвали их
странными частицами и затем
предположили, что существует новый закон
сохранения-сохранение странности. К-мезонам
было приписано новое квантовое число S,
названное странностью. К + - и К°-мезоны
имеют S = +1. Закон сохранения
странности утверждает, что в замкнутой системе
суммарная странность сохраняется во всех
сильных и электромагнитных
взаимодействиях, но не в слабых взаимодействиях.
Таким образом, при распаде К°-мезона
странность не сохраняется:
К0 -> к+ + тс",
странность: (+1) -> (0) + (0).
Мы видим, что до распада странность
была равна + 1, а после распада она стала
нулевой. Следовательно, этот распад
должен происходить за счет слабых
взаимодействий, которые примерно в 1013 раз
слабее сильных. Это означает, что
ожидаемое время жизни 10~23с должно возрасти
в 1013 раз. Таким образом, это согласуется
с измеренным значением времени жизни
~ 10"10с.
ГИПЕРОНЫ (СТРАННЫЕ БАРИОНЫ)
Теперь нам предстоит выяснить, каким
образом К-мезоны могут рождаться за счет
сильных взаимодействий. В 1950 г. были
открыты новые бар ионы тяжелее протона
со временем жизни также порядка 10"10 с.
Например, Л°-гиперон с массой 1116 МэВ,
распадающийся с периодом полураспада
2-10"10 с на протон и пион:
Л0-+р+7Г.
Л°-гиперону приписывается странность S =
= — 1, что объясняет его большое время
жизни. Однако следует заметить, что Л° и
К0 в совокупности имеют равную нулю
полную странность и могут совместно
рождаться в результате сильных
взаимодействий при столкновении пионов с протонами:
я" +р-+Л° + К°
странность: (0) + (0) -* (-1) + (1).
Таблица 31-1
Категории элементарных частиц
Адроны
(сильно взаимодействующие
частицы)
Лептоны
(слабо взаимодействующие
частицы)
Фотон у
(электромагнитное
взаимодействие)
Барионы
Мезоны
Электронное семейство е, ve
Мюонное семейство ц, vM
Тау-лептонное семейство т, vT
Гипероны А, £, S, Q
(странные)
Нуклоны п, р, А
(не странные)
(странные) К
(не странные) тс, р

§ 5. АДР0НЫ 577
Этот «трюк» с совместным или
ассоциативным рождением для сохранения
странности разъясняет нам, каким образом в
результате сильных взаимодействий легко
рождаются пары странных частиц.
Родившись, каждая из странных частиц, однако,
может распадаться лишь за счет слабых
взаимодействий. На рис. 31-9 приведена
фотография следов, наблюдаемых в
жидководородной пузырьковой камере в процессе
тГ+р-+Л° + К0.
Помимо Л°-гиперона известны еще три
типа гиперонов (странных барионов) со
временем жизни порядка 10"10 с. Это Е-ги-
перон (сигма-гиперон со странностью S =
= —1), S-гиперон (кси-гиперон со
странностью S = —2) и ^-гиперон
(омега-гиперон со странностью S = — 3). Поскольку
квантовые числа любых античастиц
должны иметь противоположные знаки по
отношению к квантовым числам частиц, то
в случае Л°-гиперона должно быть S = +1.
1ГэВя-
л + Р — Л + К"
Рис. 31-9. Ассоциативное рождение Л-гиперона
и К-мезона в жидководородной пузырьковой
камере. В камеру попадает я "-мезон с
энергией 1 ГэВ от беватрона, который затем
сталкивается с протоном, в результате чего
образуются Л и К0. [С любезного разрешения
группы жидководородной пузырьковой камеры
Лаборатории излучения им. Лоуренса.]

578 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
При этом странность сохраняется в
следующей реакции:
р + р -* Л° + Л°.
«РЕЗОНАНСЫ»
В последние годы было открыто
множество новых мезонов и барионов,
непосредственно распадающихся за счет
сильных взаимодействий. Первый такой
барион был открыт Ферми с сотрудниками
в начале 50-х годов. Он называется А и на
160 МэВ тяжелее протона и пиона вместе
взятых. Как и Л, он распадается на протон
и пион, но со временем полураспада не
10~10 с, а 10~23 с. Поэтому странность
этой частицы должна быть равна 0.
За последние годы обнаружены десятки
новых частиц с временами жизни 10 " 22 —
10"23 с. Все они распадаются
благодаря сильным взаимодействиям и
исторически были названы резонансами.
Большинство этих вновь открытых
частиц объединяется в соответствии с их
квантовыми числами в группы по 9 или 10
частиц (см. следующий параграф). Вполне
возможно, что протон и пион не более
элементарны, чем любой из адронов, и что
каждый адрон представляет собой лишь то
или иное состояние или уровень энергии
сильно взаимодействующей материи. До
сих пор было обнаружено свыше 200 таких
частиц.
Поскольку интенсивность слабых
взаимодействий примерно в 1013 раз уступает
сильным, времена жизни частиц,
распадающихся благодаря слабым
взаимодействиям, составляют 1013 • 10~23 « 10~10 с.
Все заряженные частицы на рис. 31-10
распадаются за счет слабых
взаимодействий или же стабильны. Мы уже
отмечали, что некоторые адроны распадаются не
за счет сильных взаимодействий, а
благодаря слабым взаимодействиям в силу
законов сохранения, таких, как сохранение
странности, препятствующих распаду при
сильных взаимодействиях.
§ 6. Кварки
Во введении к этой главе мы
упоминали, что многие из известных элементарных
частиц могут быть построены из
субчастиц. В 60-е годы была разработана кварко-
вая модель адронов. Простейший вариант
этой модели основан на существовании
трех фундаментальных частиц, называемых
кварками, и трех соответствующих
античастиц, или антикварков. Все барионы
рассматриваются как комбинации трех
кварков в состояниях с определенным момен-
Относи-
тельная
Тип масса Спин
кК"
щ
т
\&
V-
®
Рис. 31-10. Таблица «долгожи-
вущих» элементарных частиц.
Частицы располагаются слева.
Их «отражения» в
соответствующие античастицы
расположены справа. Стабильные
частицы обведены кружками.

§ 6. КВАРКИ 579
том импульса (моментом количества
движения). Мезоны представляют собой
комбинации кварка и антикварка. Смелым
шагом в теории явилось предположение
о том, что эти фундаментальные частицы
имеют дробные электрический заряд и ба-
рионное число. Предполагаемые квантовые
числа приведены в табл. 31-2. В
теоретической физике не существует каких-либо
запретов на дробную величину заряда.
Таблица 31-2
Квантовые числа трех кварков (у антикварков
квантовые числа имеют те же значения, но
противоположные знаки)
— 1,-2 или — 3, поскольку антикварк s
не входит в состав барионов. Всего
имеется лишь десять комбинаций из трех
кварков w, d и s, приведенных в п. «б»
табл. 31-3; поэтому, согласно теории,
каждое семейство барионов содержит десять
частиц.
Теория не только предсказывает
известные семейства барионов и мезонов, но
и дает грубые оценки масс, вероятностей
превращений и магнитных моментов адро-
нов. По существу все эти предсказания
согласуются с экспериментальными
данными.
Имеются и другие важные
теоретические результаты, относящиеся к
взаимодействиям электронов и нейтрино высоких
энергий с протонами и нейтронами,
которые также выдержали
экспериментальную проверку. Однако крайне загадочным
кажется то, что частицы с дробным
зарядом никогда не наблюдались на опыте.
Если сложной частице типа атомного ядра
сообщается достаточно большая энергия,
то она расщепляется на составные части.
Однако распад протона на кварки никогда
не наблюдался, даже если протону сообща-
Таблица 31-3
Девять комбинаций кварк-антикварк, которые сопоставляются мезонам со спином 0 и 1 (п. а) и
десять комбинаций из трех кварков, которые сопоставляются барионам со спином 3/2 (п. б)
Кварк
и
d
s
Заряд
2/3
-1/3
-1/3
Спин
1/2
1/2
1/2
Барионное
число
1/3
1/3
1/3
Странность
0
0
-1
Следует заметить, что если кварк и
антикварк находятся в состоянии с одним
и тем же моментом импульса, то
существует именно 9 различных комбинаций,
приведенных в п. «а» табл. 31-3. (Следует
а
Мезоны
б
Барионы
Г од-комбинации :
J it (спин нуль)
[ ТТ (спин единица)
Г #ад-комбинации:
|Ш (спин 3/2)
ud us du ds
к+ K+ п- К0
р+ к+*Р- К0*
иии uud uus ddd
А++А+ Е+ Д~
sd
К°
к°*
ddu
А0
SU
К"
К~*
dds
2Г
555
Q"
dd
к0
Р°
55W
7?0
UU
Л
СО
ssd
s"
S5
Л
Ф
uds
Z°
заметить, что все перечисленные в таблице
частицы обнаружены и детально изучены.)
Таким образом, теория предсказывает
существование группы из девяти мезонов
с равным нулю спином и определенными
значениями заряда и странности. Среди
множества мезонов имеются лишь девять
мезонов со спином нуль, и их квантовые
числа в точности совпадают с
предсказанными теорией. Согласно теории, мезоны
могут иметь значения странности,
определяемые s- или s-кварками, т. е. странность,
равную только -1, 0 или 1. В случае
барионов предсказываются значения S = О,
ли энергию, в сотни раз превышающую
его энергию покоя. Существуют разумные
объяснения этому, основанные на
утверждении о том, что образование свободных
кварков невозможно (невылетание
кварков)1*.
1} Внешне это похоже на то, как столь же
безуспешны попытки отделить северный полюс
постоянного магнита от южного. Разламывая
пополам магнитный стержень, мы вновь
получаем два целых магнита, а не отдельные
магнитные полюса. Совершенно неясно, имеет ли
подобная аналогия под собой более глубокое
основание-Прим. перев.

S80 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
ОЧАРОВАННЫЕ КВАРКИ
В 1963 г., для того чтобы лучше понять
поведение адронов в процессах,
обусловленных слабыми взаимодействиями, было
постулировано существование четвертого
кварка с новым квантовым числом,
получившим название «чарм» - очарование.
Роль квантового числа чарма С аналогична
роли квантового числа странности S. Оба
они сохраняются в процессе сильных
взаимодействий и могут нарушаться слабыми
взаимодействиями. Вплоть до 1974 г.
теория с очарованным кварком
рассматривалась как довольно экстравагантная. В
случае ее справедливости должен был бы
существовать целый набор новых мезонов
и барионов, как показывает пример 4.
Очарованный кварк должен был иметь С = 1,
S = 0, 2 = 2/3 и В = 1/3, а также спин,
равный 1/2.
Пример 4. Сколько можно предсказать
различных очарованных мезонов (С = + 1) со
спином 0 на основе модели кварков? Каковы их
заряды и остальные квантовые числа?
Очарованный кварк будем обозначать символом с.
Решение^ Возможны следующие комбинации из
с и q: сщ cd и cs. Поскольку заряд кварка с
равен 2/3, а антикварка и равен — 2/3, то мезон,
состоящий из комбинации см, имеет заряд Q =
= 2/3 + (- 2/3) = 0. У этого мезона S = 0,
и он называется D0. Комбинации cd отвечает
заряд Q = 2/3 + 1/3 = 1 и странность S = 0. Это
D+-мезон. В случае комбинации cs мы имеем
(2 = 2/3 + 1/3=+! и S = - 1. Это Р+-мезон.
Наконец, в 1974-1975 гг. было
обнаружено несколько новых мезонов с массой
покоя, превышавшей 3 ГэВ. Эти частицы
проще всего объяснялись комбинацией се
(с - очарованный кварк). Как и все
известные до того времени частицы, эти
новые тяжелые мезоны имели С = 0.
Однако они с трудом распадались на мезоны,
состоящие из обычных кварков, и поэтому
их времена жизни оказались больше, чем
у других нестранных адронов. Но
истинные доказательства справедливости
теория с очарованными кварками
получила лишь в 1976 г., когда окончательно
было доказано существование очарованных
мезонов и барионов, предсказанных
задолго до этого. Массы всех очарованных
частиц превышают 1,8 ГэВ, поскольку масса
кварка с составляет ~ 1,5 ГэВ, а массы
трех остальных кварков ~ 0,5 ГэВ.
В 1977-1978 гг. история повторилась.
Было установлено существование долгожи-
вущего мезона с гораздо большей массой
(9,46 ГэВ). Полученные данные указывают
на то, что он представляет собой
комбинацию ЪЪ из новых кварка и
антикварка. Новый кварк назвали кварком Ъ (первая
буква в англ. слове beauty, что значит
«прелестный»). Электрический заряд этого
пятого кварка равен —1/3. Такой кварк
должен порождать новое семейство частиц
с массами выше 5 ГэВ и новым квантовым
числом, предварительно названным
«прелестью».
§ 7. Несохранение четности
«Ну как, хочешь жить в зеркале, Китти?
Интересно, дадут ли там тебе молоко?
Впрочем, не знаю; можно ли пить зеркальное
молоко?»
Льюис Кэррол «Алиса в Зазеркалье»^
В этом параграфе мы узнаем, что
Льюис Кэррол был прав-зеркальное
молоко, если не губительно, то уж, во всяком
случае, несъедобно. Кроме того, мы
увидим, что слабые взаимодействия приводят
к нарушению не только закона сохранения
четности, но и симметрии античастиц,
обсуждавшейся в § 3. Сохранение четности
представляет собой математическую
формулировку свойства симметрии,
называемого инвариантностью относительно
отражений. Такая инвариантность означает, что
зеркальное отображение любого
физического явления само представляет реальное
физическое явление. Принцип сохранения
четности утверждает, что если физик сле-
1} Льюис Кэррол «За зеркалом и что там
увидела Алиса», перев. с англ., София,
1961-Прим. перев.

§ 7. НЕСОХРАНЕНИЕ ЧЕТНОСТИ 581
дит за зеркальным изображением хода
реального эксперимента, не зная при этом,
что он смотрит в зеркало, то не
существует способа, с помощью которого по
результатам эксперимента можно было бы
утверждать, что он получил их глядя в
зеркало. Иными словами, математическое
описание всех фундаментальных законов
физики не должно зависеть от того,
выбрана правая или левая система отсчета. Одно
из следствий сохранения четности состоит
в том, что эксперимент не в состоянии
помочь рассеянному ученому определить,
какая из его рук правая. Использовать для
этого сторону тела, в которой
расположено сердце, было бы надувательством. Это
все равно, что вручить ему перчатку с
нашивкой «левая».
В действительности же молекулы его
тела, и в этом смысле все живое на Земле,
эквивалентны перчаткам с метками.
Возникающие в организмах белковые молекулы
построены из аминокислот, которые все
имеют левовинтовую структуру.
(Исключение составляют антибиотики типа
пенициллина, которые содержат определенную
долю правовинтовых аминокислот.
Считается, что подобная структура делает их
губительными для бактерий и объясняет
их использование в качестве
антибиотиков.) С другой стороны, химики могут
синтезировать правовинтовые белки, и, как
следует из сохранения четности,
химические свойства этих белков в точности
совпадут со свойствами естественных
разновидностей. Единственное различие их будет
в том, что одни представляют собой
зеркальное изображение других (рис. 31-11).
Зеркало
Правый винт
Изображение
Зеркальное
изображение
правого винта
(левый винт)
Рис. 31-11. Правый винт и его зеркальное
отражение.
Тот факт, что в биосфере Земли молекулы
воспроизводятся всегда с одной и той же
зеркальной симметрией, тогда как те же
молекулы образуются в результате
химического синтеза всегда в виде однородной
смеси лево- и правовинтовых
разновидностей, может показаться загадочным.
Возможное объяснение состоит в том, что
первоначальные формы жизни на Земле были
как лево-, так и правовинтовыми. При
этом животные и растения одного типа
могли быть несовместимы с другим типом
и, возможно, губительны для них. В конце
концов в борьбе за существование один
тип взял верх над другим.
По причинам, изложение которых
выходит за рамки настоящей книги,
сохранение четности запрещает распад К-мезонов
как на два, так и на три пиона. К-мезонам
не возбраняется распадаться одним или
другим способом, но не обоими. Однако
экспериментально наблюдались оба типа
распадов. Это заставило Ли и Янга
в 1956 г. серьезно усомниться в
«самоочевидности» того, что природа не должна
отдавать предпочтения левого перед правым
или наоборот. Ли и Янг предположили,
что слабые взаимодействия действительно
нарушают «священный» принцип
сохранения четности. Они предложили также
некоторые конкретные эксперименты для
проверки своей гипотезы. Сейчас мы подробно
обсудим один из этих экспериментов. Им
будет распад тг+ -мезона, который
происходит вследствие слабых взаимодействий:
7Г+ -+\1+ + V.
Ли и Янг предположили, что спины мюона
и нейтрино, возникающих при распаде,
могли бы ориентироваться
преимущественно вдоль направления движения этих
частиц.
Мы продемонстрируем сейчас, что в
таком случае будет нарушаться
инвариантность относительно отражений. Условно
будем сопоставлять спину движение в
экваториальной плоскости частицы и
изображать частицы в виде вращающихся сфер.
Ли и Янг предполагали, что распад тг +
всегда выглядит так, как показано на рис.
31-12,а, а именно \х+ и v вращаются в
противоположные стороны, поскольку их

582 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
"dD dD"
Эксперимент
Зеркало
Изображение
Рис. 31-12. а-распад п+ -мезона; б-зеркальное
отражение этого распада.
спины должны в сумме давать равный
нулю спин исходного пиона. На рис. 31-12,6
изображено отражение этого распада
в зеркале. Заметим, что в зеркале сферы
кажутся вращающимися в
противоположных, направлениях. «Участок» экватора
ц+ или v на рис. а описывал бы левовин-
товую линию, а на изображении в зеркале
(рис. б)~правовинтовую. Картина,
изображенная на рис. 31-12, а, впервые
наблюдалась в 1957 г. с помощью мюонов,
полученных на циклотроне. Отраженный
в зеркале эксперимент (рис. 31-12,6)
никогда не встречался в природе. Таким
образом, абсолютно очевидно, что четность не
сохраняется. Нейтрино всегда оказываются
левовинтовыми. Несохранение четности
впервые наблюдалось в опыте по
бета-распаду, выполненному By из Колумбийского
университета, и группой физиков
Национального бюро стандартов в Вашингтоне.
Теперь нам известно, что нейтрино всегда
подобны левому винту, а антинейтрино —
правому.
Все еще трудно поверить, что в самом
пространстве заложено предпочтение
левого перед правым. Однако доказательство
оказывается столь простым и ясным, что
каждый почти немедленно убеждается
в его справедливости. Таким образом,
чтобы определить, где у него левая рука,
рассеянному профессору необходимо лишь
взглянуть на любое нейтрино или на \х +,
образованные при распаде тг+ -мезона.
Здесь имеет место очевидный случай
отсутствия симметрии в законе природы.
Одна из причин всех волнений состоит в том,
что здесь впервые было обнаружено
нарушение основного принципа симметрии.
НАРУШЕНИЕ СИММЕТРИИ АНТИЧАСТИЦ
Применяя операцию зарядового
сопряжения к рис. 31-12, а, мы получим распад,
представленный на рис. 31-13, а. Заметим,
что при этом антинейтрино оказывается
левовинтовым. Однако из эксперимента
известно, что антинейтрино всегда право-
винтовое, как показано на рис. 31-13,6.
Этот рисунок иллюстрирует, как
происходит в действительности распад тг" -мезона.
Таким образом, мы имеем дело со
случаем, когда замена частиц
соответствующими им античастицами приводит к
результату, который не наблюдается в
природе. Это явное нарушение симметрии
античастиц.
Следует заметить, что если распад я+-
мезона отразить в зеркале (рис. 31-12, а)
и заменить частицы на соответствующие
"(Л) (©"
/л" V
а
"" б ~v
Рис. 31-13. а-распад, зарядово-сопряженный
с распадом п + -мезона; получен заменой частиц
на соответствующие античастицы;
б-наблюдаемый на опыте распад к "-мезона.

§ 7. НЕСОХРАНЕНИЕ ЧЕТНОСТИ 583
Рис. 31-14. Проф. Ли, работа
которого в соавторстве с проф.
Янгом привела к
ниспровержению сохранения четности.
Внимательное изучение
расположения пуговиц на пиджаке проф.
Ли обнаруживает, что перед
нами не зеркальное, а истинное
его изображение.
античастицы, то мы получим правильный
результат для распада я "-мезона (рис.
31-13,6). Таким образом, общая симметрия
сохранится. И по-прежнему рассеянный
профессор, оказавшийся в удаленной
галактике, не сможет определить, какая из
его рук правая, поскольку неизвестно,
построена его галактика из антивещества или
нет, и мы не могли бы предложить ему
способа, как ему отличить \х+ от ц~.
И наоборот, пока он не научится отличать
правое от левого, ему не удастся узнать,
содержат атомы вокруг него орбитальные
электроны или позитроны. Эта общая
симметрия названа теоретиками СР-инва-
риантностью. Интересно, на фотографии
рис. 31-14 мы видим истинное изображение
проф. Ли или зеркальное?
Позднее, в 1965 г. группа физиков,
работавшая на брукхейвенском синхротроне,
провела тщательные измерения способов
распада К°-мезона и обнаружила слабое
нарушение СР-инвариантности. Речь идет
о следующих вариантах распада:
К0
или
к°-
+ V + 71"
+ v + я"1
Оказывается, что несколько
предпочтительнее идет распад с образованием е + ,
нежели е ". И это не зависит от_того, был
ли исходной частицей К0 или К0. Таким
образом, теперь мы имеем абсолютный
способ определения правой руки у
профессора в удаленной галактике. Ему следует
соорудить ускоритель на высокие энергии
и получить на нем пучок К°-мезонов. Если
планета, на которой он находится,
построена из_антивещества, то пучок будет
содержать К°-мезоны. Но цри этом ему не
следует волноваться, поскольку мы
посоветуем проверить, какой из указанных выше
способов распада происходит чаще. Мы
сообщим ему, что в предпочтительном
способе распада электрон имеет
положительный электрический заряд. Затем наш
профессор сможет воспользоваться
распадом пиона того же знака, чтобы
определить, где у него левая рука. До сих пор
нарушение СР-инвариантности удалось
обнаружить лишь в распадах К°-мезонов.
Существование слабого нарушения
СР-инвариантности представляет собой загадку
для теоретиков.

584 ГЛ. 51. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
§ 8. Сводка законов сохранения
По сравнению с другими физическими
законами основные законы сохранения
в некотором смысле представляют собой
более сильные утверждения. Объясняется
это тем, что все, что может происходить,
действительно происходит, если нет
запрета со стороны закона сохранения.
Основываясь на законе сохранения, мы не можем
сказать, сколь часто будет происходить
какое-либо явление, хотя надежным
указателем здесь служит относительная величина
четырех фундаментальных
взаимодействий. Напомним, что электромагнитные
взаимодействия в 102 раз, а слабые
взаимодействия в 1013 раз менее вероятны, чем
сильные взаимодействия. Важно отметить,
что любая реакция или способ распада,
какие можно только себе вообразить, будут
происходить в природе при условии, что
нет запретов со стороны одного из
законов сохранения.
Некоторые из 14 законов сохранения
формулируются в форме принципов
симметрии. В квантовой механике для
каждого принципа симметрии всегда удается
найти математически эквивалентный закон
сохранения. Произошедшая недавно
внезапная утрата закона сохранения
четности и симметрии античастиц еще раз
предупреждает ученых, что и остальные
«неприкосновенные» законы физики также
могут нарушаться. Например, никогда не
удавалось в общем виде доказать
справедливость закона сохранения энергии.
Однако если бы обнаружилось
одно-единственное очевидное нарушение этого закона, то
мы имели бы абсолютное доказательство
несправедливости закона сохранения
энергии. Сделав это предостережение, мы
приведем окончательный список законов
сохранения. Для полноты представлены
также и законы, о которых не упоминалось
в тексте книги.
1. Сохранение полной энергии. При этом
должна учитываться масса (энергия)
покоя.
2. Сохранение полного импульса.
3. Сохранение полного момента импульса.
4. Сохранение электрического заряда.
5. Сохранение барионов. Нуклоны и
гипероны имеют барионное число +1,
а их античастицам соответствует
барионное число — 1. Этот закон
утверждает неизменность суммарйого ба-
рионного числа.
6. Сохранение лептонов. Этот закон
можно считать аналогом закона 5 для
легких частиц. У лептонов ve и е~
электронное лептонное число равно + 1,
а у их античастиц соответственно — 1.
Согласно данному закону, суммарное
электронное лептонное число должно
быть одним и тем же до и после
взаимодействия. Существует аналогичный, но
независимый закон сохранения мюон-
ного лептонного числа, а также тау-
лептонного числа.
7. Зарядовая независимость (или
сохранение изотопического спина). Этот закон
имеет место только для сильных
взаимодействий. Из-за существования
электромагнитных взаимодействий
результаты на основе этого закона
предсказываются с точностью около 1%.
По этому закону сила, действующая
между двумя протонами, такая же, что
и между протоном и нейтроном.
8. Сохранение странности (ассоциативное
рождение странных частиц). Данному
закону подчиняются сильные и
электромагнитные взаимодействия; однако
для слабых взаимодействий он не
имеет места. Благодаря этому закону
распад гиперонов и К-мезонов
происходит настолько медленно, что
позволяет увидеть их следы.
9. Симметрия античастиц. Этот закон
справедлив для сильных и
электромагнитных взаимодействий, слабые
взаимодействия ему не подчиняются.
10. Сохранение четности. Это справедливо
для сильных и электромагнитных
взаимодействий, исключение составляют
слабые взаимодействия.
11. СР-инвариантность. Этот закон
гласит, что если в зеркальном
изображении любого эксперимента все частицы
заменить соответствующими
античастицами, то новый эксперимент будет
вполне законным. Это, по-видимому,
справедливо для сильных и
электромагнитных взаимодействий, но в не-

§ 9. ПРОБЛЕМЫ БУДУЩЕГО 585
большой степени нарушается при
распадах нейтральных К-мезонов.
12. СРТ-инвариантность. Согласно этому
закону, если в зеркальном изображении
любого эксперимента все частицы
заменить соответствующими
античастицами и поменять на противоположные
все скорости и направления вращений,
то полученный в результате новый
эксперимент будет вполне реальным.
Предполагается, что этот закон
справедлив для всех взаимодействий.
13. Инвариантность относительно
обращения времени. Если в любом
эксперименте направления скоростей и
вращений у всех частиц заменить на
противоположные, то новый эксперимент будет
вполне законным. По-видимому, это
справедливо для сильных и
электромагнитных взаимодействий, но в
небольшой степени нарушается в случае
слабых взаимодействий, вследствие
того что СР-инвариантность несколько
нарушается, а СРТ-инвариантность не
нарушается.
14. Сохранение очарования. Этот закон
аналогичен закону сохранения
странности. Подобно тому как одни
адроны могут иметь квантовое число,
называемое странностью, другие
адроны обладают квантовым числом,
называемым «чармом», или
очарованием. Считается, что этот закон
справедлив для сильных и
электромагнитных взаимодействий и нарушается
в слабых взаимодействиях. Аналогично
сохрайяется «прелесть» тех адронов,
в состав которых входит кварк Ъ.
§ 9. Проблемы будущего
Использование термина
«элементарные» становится нелепым, когда мы
начинаем говорить более чем о 200
элементарных частицах. Пожалуй, было бы более
целесообразно толковать о частицах
четырех типов: фотоне, электронных лептонах,
мюонных лептонах и адронах. Разумно
надеяться на возможное сокращение в
будущем числа истинно элементарных
частиц. Способность элементарных частиц
к взаимным превращениям (совместимым
с законами сохранения) вселяет надежду на
существование единого общего поля,
различными «квантовыми состояниями»
которого и являются эти частицы. Теория
единого поля могла бы предсказывать
значения масс существующих «элементарных»
частиц. Кроме того, такая теория
позволила бы вычислить заряд электрона и
любые другие физические константы. В
настоящее время все физические константы,
такие, как с, е, h, те, тр и т. п.,
полностью независимы. Вообще говоря, по
мере приближения к истине в конечной
инстанции мы должны научиться вычислять
некоторые из этих постоянных с помощью
других. Например, энергию связи атома
водорода можно теперь вычислить с
помощью е, h и те. Еще один пример.
Теория универсального взаимодействия
Ферми позволяет вычислить время жизни
мюона через известное время жизни
нейтрона.
Достигнуты успехи в создании единой
теории слабых и электромагнитных
взаимодействий. В этой теории, хотя она и не
прошла еще окончательной проверки,
времена жизни мюона и нейтрона можно
выразить через заряд электрона.
Окончательная теория не только
снабдит нас способом вычисления заряда
электрона (или силы электромагнитных
взаимодействий), но и позволит объяснить
сильные, слабые и гравитационные
взаимодействия. Гравитационные взаимодействия
намного слабее даже слабых
взаимодействий. Известны безуспешные попытки
объяснить гравитацию с помощью
нейтрино. Возможно, в один прекрасный день
гравитацию удастся объяснить на основе
других, казалось бы, не связанных с ней
явлений. Среди нерешенных проблем
остаются такие, как вопросы о
происхождении, размерах и эволюции Вселенной. Не
имеется ли столько же галактик из
антивещества, сколько и из обычного
вещества?
Наши представления о свойствах
окружающего физического мира прошли
длинный путь со времен Аристотеля, когда
все вокруг объяснялось комбинацией
четырех основных элементов: Огня, Воды,
Воздуха и Земли. В настоящее время
квантовая электродинамика обеспечивает нам
всестороннее и удовлетворительное объяс-

586 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
нение строения обычного вещества.
Однако мы пока лишь скользим по поверхности
в своих попытках уяснить, что же является
действительно фундаментальным в
пестром разнообразии элементарных частиц
и присущих им взаимодействий.
Основные выводы
В любых взаимодействиях обычно
участвует пара электрон-ve или пара
мюон-уц. Как электрон е~, так и
нейтрино ve имеют электронное лептонное число
+ 1. Мюон ц~ и уц имеют мюонное
лептонное число + 1. Оба электронное
и мюонное лептонные числа строго
сохраняются, как и барионное число. Адроны
(сильно взаимодействующие частицы) с
полуцелыми спинами обладают барионным
числом, равным + 1. Адроны с целым
спином называются мезонами и имеют
нулевое барионное число. Всем элементарным
частицам соответствуют античастицы
с квантовыми числами противоположного
знака. Например, у антипротона барионное
число В=—1, а электрический заряд
С--1.
Пучки протонов и электронов высоких
энергий можно получить, ускоряя эти
частицы в синхротронах. В синхротронах
магнитное поле поддерживается равным $ =
= p/eRy где р-импульс частицы, а
Я-радиус кривизны траектории частицы в
тороидальной вакуумной камере.
При наличии достаточной энергии
сильные взаимодействия на протяжении
примерно 10"23 с могут приводить к
обильному рождению адронов, Адроны
распадаются на более легкие адроны за такой
же промежуток времени при условии,
что это возможно энергетически и не
запрещено другими законами сохранения,
такими, как сохранение заряда, барионного
числа и странности. Для распада странных
частиц требуется примерно в 1013 раз
больше времени в силу закона сохранения
странности, который не выполняется для
процессов, вызванных слабыми
взаимодействиями.
Все известные адроны объединяются
в регулярные группы, которые можно
объяснить существованием четырех
субчастиц, называемых кварками. Заряд кварков
Q = — 1/3 или + 2/3, а барионное число
В = 1/3. Мезоны состоят из кварка и
антикварка (qq), а барионы-из трех кварков
(qqq). «Обычные» частицы, такие, как
нуклоны, пионы и р-мезоны построены из и-
и ^-кварков. Странные частицы содержат
по крайней мере один s-кварк, а
очарованные частицы-один с-кварк.
Слабые взаимодействия нарушают не
только законы сохранения странности
и очарования, но также законы сохранения
четности и симметрии античастиц.
Элементарные частицы
взаимодействуют всеми возможными способами, если
только нет запретов, налагаемых одним
или несколькими законами сохранения.
В этой главе приведены 14 таких законов.
Упражнения
1. Чему равен период полураспада
антинейтрона? Каковы продукты его распада?
2. За альфа-распадом 238U следует два
последовательных бета-распада (с испусканием
е "). Чему равны значения Z и А у
конечного ядра-продукта?
3. Выберите из четырех типов нейтрино (ve, ve,
уц, \7Ц) то, которое подходит для каждой из
приведенных реакций:
а) ? + р->п + е+;
б) ? + п -> р + ц " ;
в) ? + п-»р + е~.
4. Предположим, что все продукты процесса
аннигиляции, изображенного на рис. 31-7,
в дальнейшем не взаимодействуют, но все
распадаются. Заряженные пионы сначала
, распадаются на мюоны, которые затем
также распадаются. Конечными продуктами
являются е*", е + , v, V и фотоны. Сколько
образуется каждой из этих частиц?
5. При захвате мюонов \х " протоном они
превращаются благодаря универсальному
взаимодействию Ферми в нейтрон и еще одну
частицу. Что это за частица?
6. Ниже приведен список запрещенных
способов распада. Для каждого из них.
перечислите законы сохранения, которые он
нарушает.
а) Л -► я + +Я"";
б) К+ ->я+ + п" + я0;
в) n->e" +р + v;
г) р-+п + е+ + v;
д) п->е+ + е" + v.
7. Установите, запрещены или нет
перечисленные ниже реакции. Если имеется запрет,
то укажите, с нарушением какого закона
сохранения он связан.

ЗАДАЧИ 587
а) Л -► р + тг°;
б)р + р->|1+ +е";
в) п->р + е" + ve;
г) p->n + e+ + ve;
д) Е+^Л° + я+.
8. Нарисуйте, как будет выглядеть на
фотографии следов, полученных с помощью
пузырьковой камеры, процесс К~+р->£" +
+ 7t+ в предположении, что К"
останавливается в камере, а £~ распадается на лету.
Магнитное поле направлено за плоскость
чертежа.
9. Изображение правого винта проецируется
на матовое стекло, и картина
воспроизводится также в виде правого винта. А если
взглянуть на экран с другой стороны, что
мы увидим, изображение правого или
левого винта?
10. Правый винт ввертывается в отверстие с
резьбой. Если смотреть со стороны отверстия,
то винт будет казаться правым или левым?
11. На рисунке вращающиеся сферы
отражаются в зеркале. Нарисуйте, как выглядит их
зеркальное изображение. Каким будет
изображение мюона ц+ в зеркале, право-
или левовинтовым?
Зеркало
12. Если ядра 60Со выстраиваются таким
образом, что их спины направлены вверх, то
вниз вылетает больше бета-частиц, чем
вверх. Нарисуйте зеркальное изображение
приведенного ниже рисунка.
Д Направление
U спина
@ е
I
а) Каким будет направление спина в
зеркальном изображении 60Со, если зеркало
расположено горизонтально?
б) Если зеркало расположено вертикально?
в) В каждом из этих случаев установите, как
движется электрон, параллельно или ан-
типараллельно направлению спина? Не
нарушает ли этот распад закона
сохранения четности? . Для определения'
направления спина всегда пользуйтесь
правилом правой руки.
13. Из эксперимента известно, что при распаде
остановившихся положительных (левовин-
товых) мюонов позитроны распада
вылетают преимущественно назад. Рассмотрим
случай, когда позитрон вылетает точно
назад, a ve и vM-вперед. Будет позитрон лево-
или право винтовым?
Задачи
14. Рассмотрите пучок частиц с полной
энергией Ebi падающих на покоящиеся частицы
мишени. Обе частицы имеют одинаковую
массу покоя т. В задаче 8 гл. 9 (т. 1
настоящей книги) было показано, что в системе
ц.м. энергия любой из этих частиц равна
Г тсЧ Д11/2
а) Рассмотрите два сталкивающихся пучка
протонов с энергиями 1000 ГэВ каждый.
Чему равна эквивалентная энергия
пучка Еь в условиях, когда пучок падает на
неподвижную протонную мишень?
(Имеются проекты для осуществления
подобного столкновения пучков
использовать ускоритель Национальной
лаборатории им, Э. Ферми.)
б) Покажите, что в случае электрон-пози-
тронных встречных пучков
эквивалентная энергия пучка е+ (для покоящихся
электронов в мишени) составляет Еъ =
= 3914F2 ГэВ (величина Е' измеряется
в ГэВ).
15. Предположите, что существуют т -лептон
и соответствующее ему нейтрино, vT. Этот
лептон в ряде случаев будет распадаться на
три мюона и два нейтрино. Определите эти
нейтрино.
16. Ядро плутония-239 (Z = 94) испытывает
альфа-распад, а ядро-продукт претерпевает
бета-распад (с испусканием е") и образует
ядро-продукт, которое в свою очередь
участвует в бета-распаде (е ~). Затем это
полученное в конечном счете ядро облучается
нейтронами и поглощает 4 нейтрона. Что при
этом образуется?

588 ГЛ. 31. ФИЗИКА ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
17. При распаде я+->ц++у энергия
нейтрино ср и кинетическая энергия мюона
черпаются из разности масс. Найдите р и
кинетическую энергию мюона в МэВ. При
вычислениях используйте для мюона
классическую механику.
18. Повторите решение задачи 17, но используя
при вычислениях для мюона
релятивистскую механику.
19. Какова максимальная энергия электрона,
образующегося в распаде ц~ -> е~ +v + v?
Предположите, что электрон
ультрарелятивистский, а его импульс р = Е/с.
20. Сколько должно существовать очарованных
барионов со спином 3/2? Каковы их заряды
и другие квантовые числа?
21. Радиус действия нуклон-нуклонных сил
составляет ~ 2 фм. Какую массу должна
иметь виртуальная частица, чтобы
обеспечить такой радиус действия?

Приложение А
Физические константы
Скорость света
Ускорение свободного падения
Гравитационная постоянная
Элементарный заряд
Постоянная Больцмана
Число Авогадро
Газовая постоянная
Масса электрона
Масса протона
Магнитная проницаемость
Диэлектрическая проницаемость
Кулоновская постоянная
Боровский радиус
Постоянная Планка
Давление 1 атм
Плотность воды
Плотность воздуха
Абсолютный нуль
с
9
G
е
к
No
R = N0k
те
тр
Но
£о
/с0 = 1/4яе0
k0/c2=[i0/4n
а
h
ft = h/2n
Ро
2,998 108 м/с
9,807 м/с2
6,672-10"п Н.м2/кг2
1,602-10" 19Кл
1,381-10"23 Дж/К
6,022-1023 (моль)"1
8,314 ДжДК-моль)
9,110-10"31 кг
1,673-10"27 кг
4тс10-7 Н/м
8,854-10"12 Ф/м
8,988-109Н-м2/Кл2
10"7 Нс2/Кл2
5,292-10" п м
6,626- ИГ34 Дж-с
1,055-Ю"34 Дж-с
1,013 105 Н/м2
1,00 103кг/м3
1,293 кг/м3
-273,16° С
Некоторые астрономические сведения
Солнце
Земля
Луна
Меркурий
Венера
Марс
Юпитер
Сатурн
Масса, кг
1,99 -1030
5,977-1024
7,36-1022
3,28-1023
4,82-1024
6,4-1023
1,90-1027
5,7-1026
Расе
Диаметр, км
1,39-106
1,27
3,48
5,14
1,26
6,86
1,44
104
103
103
104
103
105
1,2Ь 105
гояние от
Земли до Л\
Расстояние от
Солнца, км
1,49-108
-
5,8-107
1,08-108
2,28-108
7,78 • 108
1,43-109
шы = 3.80 105 км
Ускорение
свободного
падения на
поверхности
(Х0)
28,0
1,00
0,17
0,40
0,90
0,40
2,70
1,20

Приложение Б
Соотношения между единицами измерения
Единица
Метр
Килограмм
Секунда
Джоуль
Электронвольт
Ньютон
Ватт
Кельвин
Паскаль
м/с (скорость)
Х) Btu — британская
МКС (СИ)
1 м
1 кг
1 с
1 Дж
1,602 • 10" 19Дж
1 Н
1 Вт
1 К
1 Н/м2
1 м/с
тепловая единица.
2) psi — фунт-сила на квадратный дюйм.
сгс
100 см
103г
1 с
107 эрг
1,602-10"12 эрг
105 дин
107 эрг/с
1 К
10 дин/ см2
100 см/с
Британская
система
39,37 дюйм
2,205 фунт
1 с
9,48-КГ4 Btu1*
-
0,2248 фунт-сила
3,413 Btu/ч
1,8° F
1,45-Ю-4 psi2)
3,281 фут/с
Внесистемные
единицы
1010 А
0,2389 кал;
6,24-1018эВ
1,341-Ю-3 л.с.
9,869-10" 6атм
2,237 миля/ч
Единицы измерения электрических величин
Величина
МКС (СИ)
СГС (или гауссова)
Заряд (Q)
Ток (/)
Напряжение (V)
Магнитное поле (0£)
Электрическое поле (Е)
Кл (кулон)
А (ампер)
В (вольт)
1 Т (тесла)
1 В/м
2,998-109ед.СГСЭ
2,998-109ед.СГСЭ
3,336-10" 3ед.СГСЭ
104 Гс (гаусс)
3,336-10"5 ед.СГСЭ
Чтобы перейти от системы единиц СИ к гауссовой, нужно заменить ^ на В/с, е0
1/4я, |л0 на 4я/с2, а к0 положить равным 1.

Приложение В
Геометрия
(Площадь круга) = кг2
(Площадь поверхности шара) = 4пг2
(Объем шара) = (4/3) тгг3
(Объем сферической оболочки толщиной dr) = 4nr2 dr
Тригонометрия
sin 0 = у/г
cos 0 = х/г
tg 0 = у/х
sin(- 0) = - sin0
cos (— 0) = cos 0
sin2 0 + cos2 0 = 1
sin 5- 0 = cos0 sin20 = 2sin0cos0
cos 20 = 2cos2 0-1 = 1- 2sin2 0
e±ie = cos0 + isin0
sin (a ± P) = sin acos P ± cos asin P
cos (a jl P) = cos acos P ± sin asin P
sin a ± sin p = 2sin (^-y^-) cos ( ^^
a2 = b2 + c2 - 2bccosA
sin A sin В sin С
Биномиальное разложение

592 ПРИЛОЖЕНИЕ В
Квадратное уравнение
Решение квадратного уравнения
ах2 + Ъх + с = О
имеет вид
х —
-Ъ ± ]/b2 - 4ас
2а
Некоторые производные
d
dx
d
dx
d
dx
(au)
xn =
lnx
du
— a~v~
dx
nxn ~ 1
1
— —
X
d dv du
—— (uv) = u—— + v——
dx dx dx
dx
-еил = aeu-
Некоторые неопределенные интегралы
(с точностью до произвольной
постоянной)
\du= и
\xndx =
-, п Ф - 1
п + 1
\x~ldx = \пх
\Qaxdx=-Qax
J а
j sin axdx = cos ax
d .
—sin ax — a cos ax
dx
f cos ax dx = —sin ax
J a
—cos ax = — asinax
dx
Произведения векторов
A-B = \A\ |jB|cosa a—угол между векторами А и В;
А х В = п|Л| |B|sina
А-В = В-А п—единичный вектор, нормальный плоскости,
А • (В х С) = (А х В) • С содержащей векторы А и В.
Греческий алфавит
Альфа
Бета
Гамма
Дельта
Эпсилон
Дзета
А
В
Г
А
Е
Z
a
Р
У
5
6
С
Эта
Тэта
Йота
Каппа
Ламбда
Мю
Н
0
I
К
Л
м
л
0
1
к
X
И
Ню
Кси
Омикрон
Пи
Ро
Сигма
N
2
О
П
Р
Е
V
5
о
п
р
a
Тау
Ипсилон
Фи
Хи
Пси
Омега
Т
Т
Ф,
X
*Р
a
т
V
ф.
1
+
со

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ1)
Том 1
Глава 1
1. 235 миль. 3. К = Р2/2М. 5.
1-Р
1/1 -Р2
1 + Р
. 7. К,/^ = 1,53 = 3,375.
9. Шн = 1,66 • 10" 24 г/атом. 11. ехр [- In (1/х)] = exp (In х) = х.
13. t1/2 = (In 2) т = 0,693 т. 15. у = 1,745 м. 11. Е = - e2/(2R).
19. Е = ]/м1с2 + сV. 21. !? = ]/У/р~. 23. а) 3,87 г/с; б) 116-103 Вт = 116 кВт. Обычно
на нагревание дома тратится несколько киловатт мощности, автомобиль же
_с с_
2у2 8у4
27. а) Точность среднего значения для часов А равна 1,58 • 10"2 с;
б) точность среднего значения для часов В равна 1,58 • 10"2 с;
в) точность среднего значения измерений обоими часами А и В равна 1,12 • 10"2 с.
потребляет примерно в 30 раз больше. 25. v = с — ^-j — -^ +
31. sin (24) = 2 sin (A]/l - sin2 A). 33. 30%; C = 2,0-101.
Глава 2
1. 1 км/ч = 0,911 фут/с. 3. v = (t?! + v2)/2.
m - xxvx + x2v2
5. v = .
Xi + X2
7.
1} Здесь помещены ответы только к задачам и упражнениям, имеющим нечетную нумерацию.

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
11. Полное время равно 237 с = 3,94 мин. 13. Полное время равно 2828 с = 47 мин.
15. 1,225 м. 17. а = 118,52 м/с2 * 12,1 д. 19. h = 154,3 м. 21. v = 2х/Т - v0. 23. Мяч
будет подниматься вверх 2 с и падать также 2 с; полное время мяча в полете 4 с;
следовательно, бегущий опоздал на 0,5 с. 25. а) а = —2,5 м/с2; б) Т = 4 с. 27. v = 2,8 км/с, Т=
= 286 с = 4,76 мин. 29. Классическое приближение: v = 1,54 • 108 м/с; релятивистское
значение v = 1,37 • 108 м/с. 31. Т = 2,15 • 108 с = 6,84 года. 33. Цветочный горшок
пролетел 19,4_ м, прежде чем он достиг окна; следовательно, он упал с десятого
этажа. 35. v = (2/3)vv 37. v = At2/2.
Глава 3
I. С = В-А; Z = X-Y. 3. В cos 30° = 1,732 м. 5. F± = F, cos а. 7.0 = 15° или 75°.
9. Е" = Е/2 при 0' = в" = 45°; Е = 0,866Е при 0' = 30°; Е" = F/2 = 0,433Е при 0" = 60°.
II. Паром должен править к западу под углом 56,44° от направления на север.
Скорость его относительно берега 3,32 км/ч.
13. у = 3,82х - 0,098х2. УчЬЛ
30
20
10
0 Ю 20 30
15. а = 0/2. 17. h =V°S™ 0. 19. 490 м. 21. а) 4 ч; б) 4,167 ч; в) 4,0825 ч.
23. a) v = 7 м/с; б) 22,3 об/с. 25. 27,5 суток.
Глава 4
Л „ „, MXF ^ (MX + M2)F
1.^з = 0. 3. Т1==М1 + М2 + Мз;Т2 = М1 + М2 + Мз; результирующие силы:
<F*- - М1 + мГ+М3; (F2)- - М1 + мГ+М3; (F3)- = M1 + M2F+M3- 5- 1 1Ы(ФУНТ"
сила) = 32 паундаля; 1 Н = 7,226 паундалей; 1 слаг = 14,528 кг. 7. F = - 833 Н. 9.
Результирующая сила, действующая на плуг, равна нулю; при этом плуг движется с
постоянной скоростью. 11. 7,08-1015 об/с; v = 2,22• 106 м/с. 13. а) Т= 1,9456 с; б)
отношение периодов равно 0,9694; в) отношение периодов равно 0,841. 15. а) Сила Fpe3 =
= 100 Н и направлена под углом 0°; б) сила F^ = 500,5 Н и направлена под углом 37°.
17. а) а = F/(4M); б) F2 = 0,75F. 21. a) F = 58,8 Н; б) F = 70,8 Н; Т = 47,2 Н. 23. а) а =
= 0,333#; б) Т = 0,667Мд. 25. АР = Ft0. 27. а) М2 = 2М1; б) ускорение a2 = g/S и
направлено вверх. 29. Период равен 1,0035 с; 0 = 60°. 31. v = 4,11334 км/с; это значение
меньше орбитальной скорости 8 км/ч. 33. уотец = 0,0833 м/с; vao4b = 0,238 м/с.
35. а = arctg( -^-J. 37. v = 16,6 м/с. 39. a) а = 0,327 #; б) t? = 0,189 м/с.
х.м

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
Глава 5
1. 490 Н. 3. 1,87 года или 684 суток. 5. Нет; нет; да. 7. Остался бы неизменным.
9. а) Вверху; б) 490 м. 11. На 3,46• 108 м от центра Земли. Пассажиры должны
находиться в состоянии невесомости в течение всего времени, пока выключены ракетные
двигатели, т. е. практически в течение всего путешествия. (Это верно для невращающегося
космического корабля.) 13. 2,006-1030 кг. 15. 5,95-Ю-3 м/с2. 17. (4/9)n2Gp2R4. 19. В]/2
раз больше обычного веса водителя. 21. а) 264,6 Н; направлен вниз; б) 264,6 Н;
направлено вверх. 23. Радиус орбиты Луны уменьшился бы в 4 раза, а период
обращения-в 8 раз по сравнению с существующим. 25. F = 4n2mR/T2; a) R = 3,84 • 108 м;
Т = 27 суток = 2,33 • 106 с, так что F = 2,79 • 10_3 Н; б) R = 1,50 • 1011 м, Т = 1 год =
= 3,15-107 с, так что F = 4,58>10"2 Н. 27. Т =7071 с = 1,96 ч. 29. 4,73-ИГ5 рад =
= 2,70 • 10"3 град. 31. Т = 2тг]/R3/GM. 33. vjv2 = {RJR2)-112.
35. v2/vx = (a — b )/b. 37. Кажущийся вес равен Ътд.
39. Т=2п
'М L
~№~9
; тс/ТРЬ = 1,0005. 41. 2,0 года.
Глава 6
1. Это отношение составляет 6,27 • 10~4. 3. а) Работа равна нулю; б) совершается
отрицательная работа величиной 8,14 • 106 Дж. 5. 2,34 • 105 МВт. 7. F = - 2Ах. 9. Будет
использовано 5% комнатного кислорода. Поэтому для пополнения запаса кислорода
вентиляция не нужна, но она необходима для удаления неприятных запахов и
уменьшения концентрации молекул С02. П. Потенциальная энергия возрастает на
3-10"5 Дж. 13. v0 = 0,5 м/с. 15. AU = - кхЦЪ.
GmM (г2 R\ 3 ,
17. а) Нуль; б) U(r)=— _ _+_L *J
R32-Ri
GMm (R\ R\ 3 A /1 V
в) U(r) = —+—--Д2 ) + GMm[
^-^\2 R2 2 J \R2 rj
19. Масса должна пролетать 10,2 м независимо от величины начальной скорости. Если
движение началось из состояния покоя, то потребуется время t = 1,44 с; в общем случае
время полета зависит от начальной скорости.
21. а) - 2000 Н; б) 6 • 104 Вт; в) 4 км на 1 л.
23. a) U = - GM2m/r; б) U = - GM2m/R2.
Глава 7
1. v = \1——Хо, з. а) 0,045 с; б) 66,7-103 м/с2 = 6800#.
у 4 m
5. При соударении 8/9 энергии массы т1 передается массе т2. 7. vx = 0,983 v0.
9. АК/Ктч = 0,331. 11. 0,84 кг. 13. v = ]/gL(l -cosG). 15. FB= ISMg. 19. 0 = 90°.
23. a) V= ]/rgR/2; 6) h = jR/4. 25. 9,09.10"2.
27. a) 0,049 Дж; 6) 0,07 Дж; в) 2,0 м/с. 29. 319 Н.
31. )W = 12,25 м; амакс = 17,33 д.
33. a) high; б) v = ][gh\ в) а = v2/2L.
35. 8,4 л/ч; 70 кВт. 37. 4,52 м вправо; подъем на 0,204 м. 39. 316 м/с.

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
Глава 8
1. а) 0,1222 с; б) 0,012273 с; в) 6,67-10"3 с.
3. 94,9 км/с. 5. v = cj/l-L'/L. 7. а) 22,37; б) 4,026-10"7 с; в) 120,66 м.
9. (20 - 3,44)-10"13 м. 11. Близнецу А исполнится 100,08 лет, а близнецу В-
23,58 года. 13. у = j-^p
15. р увеличивается с ростом скорости.
19. Д*д - Д*в = 0. 21. х = ух' - yvf; t = yt - y(v/c2)x'.
Z«5. %2 — Xi —
yzfb0. 25. /7/= 1 - Э-
27. a) -4 • 10"7 c; 6) 5,333 • 10"7 с; в) 1,11 . 10"6 с
29. a) 1,484-10"12c; 6) (1 + 7,42)-КГ13; в) 7,42-10"13; 2,47-10"15.
Глава 9
1. ux = 4 x , t 2. 3. 0,0654 r. 5. 5,01%.
1 - Uxv/c2
7. 35,1-10"9 кг. 9. a) 117 МэВ; 6) 145 МэВ. 11. 0,75c.
13. 1,25. 15. Наибольшая величина p2/2m0.
17. a) E = mpc2 + K0; б) P = (1/с)]/к0(2трс2 + K0); в) v = Щ-..
19. ux= Ux~V .. 23. a) 93,8 МэВ; 6) 2,4-108 м/с; в) 1,67; г) 1,337.
1 — u'yVJC1
25. p = (1/c)\/k(2Mc2 + K). 27. Eb = 1918 ГэВ.
31. При малых t, v-+a0t; при больших t, v-+c.
33. a) F = ma(1 - w2/c2)" 1/2 + ma (w2/c2) (1 - u2/c2)~3/2; 6) F'y = (dpy/dt) [у + у (v/c2)ux ].
35. a) E/c2; 6) gh/c2. 37. 6) c/|/2.
Глава 10
1. со = b + 2ct0, a = 2c. 3. а) ш = co0 + a0t/2; б) ш = (0 - 0О)Д. 5. /2 = 36/x. Конечная
угловая скорость в 36 раз превышает начальное значение; то же верно для кинетической
энергии.
7. 10,7 с. 9. Р = /оссо. 11. F = (^RJ^RJMg.
13. Для маховика из плавленого кварца в 3,33 раза выше.
15. 66,67 см. 17. 49 Н.
21. А х В = \{AyBz - А2Ву) + ](AZBX - АХВ2) + к(АхВу - АуВх);
(АуВ2 - А2Ву)2 + (А2ВХ - АХВ2)2 + (АхВу - АуВх)2
(А2х+А1 + А22)(В2х + В2у+В2)
23. a) L=2M0R0v0; б) F = G(M20/4R20); в) F = M0v%/R0; г) R0 = b2/GM30. 25. (3/4)Mv2.
27. Отношение кинетической энергии вращения к полной кинетической энергии гантели
4 - (4уо/у) + (УНУ2)
составляет
4-(4Уо/у) + 2(У2о/У2)
29. а) 3,59 -1034 кг-м2/с; б) 6,0 -108 м; в) 53,3 суток.
31. I=M[(L/2-x)2 + L2/12l

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ 597
33. a) vA/2; б) L = (1/2)тг2сол; в) аА/6; г) (l/4)mr2co2 + (l/2)mv2A; д) (5/24)mr2co2 +
+ (l/4)mi&
37. Человек, прежде чем начнет скользить, сможет подняться по лестнице на расстояние
х = 0,741 L.
41. Т = (2т + ЗМ)^.
Глава 11
1. Амплитуда равна 1,5 см; период равен 4 с; максимальная скорость равна 0,75л см/с;
максимальное ускорение равно 0,375тг2 см/с2. 3. 2тг/А 5. 0,248 м.
7. 0,4яс. 9./=943d011c"1. 11. 6 дБ.
13. а) х = х0 cos
m
(t-ti
; б) v = -
—x0sin
m
-cos
V4
15. a) x = — x0sin( /— M; б) i> = —x0
17. a) x = Я0 cos со (t + - n) , у = jR0 cos со ft + j n
в) окружность.
■м.
r = я0; б) v = соД0;
21.
23.
d2xl
dt2
d2(Ax2)
dt2
= -k
mi + m2
m1m2
xx; T= 2ti
= -3-^Ax2. 25. r0 = (5a/b)
1/4
m
27. / = 27,57 Гц. 29. Разность между двумя звуковыми сигналами равна
201ё(К1-72)дБ.
Глава 12
I. 6,24 • 107 Н/м2. 3. 8,245 км. 5. Независимо от формы льда 10% его объема находятся
выше поверхности воды.
7. Ар = mv.
9. Объем составляет 10,2 л; плотность 3000 кг/м3.
II. а) 28,8 г; б) 28,8 г; в) 12 см2. 13. За неделю теряется 2,42 г. 15. 0,36°С.
17. АТ= 0,468°С.
19. а) А/е; б) 2е/3/с; в) 2Ne/3V; г) температура остается неизменной, а давление падает
в два раза.
21. а) отношение равно 1; б) 1/2. 23. 5 • 10"5 м. 25. d = RP/2S.
27. б) h = Л01п 2 = 5,50 км; в) 3,33 • 104 Н/м2.
31. у = 2,16 • 1010/jR3, если R измеряется в метрах.
Глава 13
1. -12,3 Дж. 3. а) ЛГо/2,016; б) ЛГ0/18; в) ЛГ0/180. 5. 3,68-103 молекул/см3.
7. 0,75кал/(г-К) для Не; 2,5кал/(г-К) для Н2; 5,28 калДг• К) для N2.
9. Cv = 10 калДмоль-К). 11. Тг/Тх = 0,488.
' •*• ■* одноат/ •* двухат = I * 1/ ' 2)
15. а) 9 кал/К; б) 6 кал/К, в пренебрежении колебательными степенями свободы.
17. RT\n[(V2-V0)/(V1-V0)l

598 ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
19. а) Р2 = 0,379 атм; Т2 = 207 К; б) W12 = 1,37-103 Дж; в) W 2Ъ = -1,19-Ю3 Дж;
г) 175 Дж; д) 207 К; е) 1,37-103 Дж.
21. а) 6; б) 1; в) ЗД; г) 4Д; д) Т= гтЦЪк.
23. а) Т2 = 7\ (Ка/КО; б) Рх (72 - Vx); в) (5/2) Я (Г2 - TJ; г) 73 = МТУГ^"1*.
25. 13,2 л. с. 27. a) Wab = 3,37 • 103 Дж, Wbc = 7,00 • 103 Дж, Wcd = 0; б) Qab = 8417 Дж
поглощается, Qbc = 7000 Дж выделяется, Qcd = 5047 Дж выделяется, Qda = 7397 Дж
поглощается; в) 8 = Qab + Qbc ~ 6da = 0,287.
Глава 14
I. Все величины AWV AQX и AQ2 отрицательны; соотношение AW = AQX — AQ2
продолжает выполняться.
3. 767 кВт. 5. 74 Дж. 7. 10 Дж. 9. AS = 0,10 кал/К.
II. 1/32. 17. 3,22-104 Дж; 32,2 Вт. 19. (Тх - Тъ)/Тх. 21. 1443 кал; AW = 1,75-105 Дж.
23. 35%. 25. 66,7°С.
27. а) Теплоемкость равна 0,214 кал/г-К; б) AS^ = -8,90 кал/К; ASW = 10,1 кал/К;
1,2 кал/К.
Глава 15

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ 599
г2 + Р/4
13- 2k0q {г2 _ /2/4)2 .
15. Результирующая электростатическая сила равна 1,86 • 10 64 Н. Она равна
гравитационной силе. Из сделанного предположения следует, что в случае нейтральных
элементарных частиц, например нейтронов, гравитационные силы должны быть равны нулю. Из
предположения также следует, что гравитационная масса урана-238 лишь в 92 раза
больше, чем масса атома водорода, а в действительности она больше в 238 раз.
17 E = lz.X)l X + R/2 I X~R/2 }
М \[(х + R/2)2 + Я2]3'2 [(х - К/2)2 + Я2]3'2/'
19. 2nk0G. 21. 2к0Х/у0. 23. Е = 3k0ql2/x4. 25. Обе производные равны нулю.
Глава 16
1. Е1=0,
1 »
F -к Ql
г2
17 Ь Ql+Q2
Лш— ^о :
г2
F k Q1 + Q2
rz
>
+ 6з
>
v1 = kl
vn= h
Vm= k0
Vlv=k0
Qa
r
+
Q.t
R2
+
0л
R3
Q1+Q2 ( Q3
r R3
Qi+Q2+Q3
3. Радиус сферы равен 0,5 м, заряд Q = 2,8-10"5 Кл.
5. Пусть для левого края левой пластины х = 0, тогда
Ег = 0; £п = 4пк0рх; Еш = 4пк0рх0; E1V = 4jtfe0p(2х0 + d-x); Еу = 0.
7. 1,13-10'и» ,.C-[j-+±+^]-1.
11. а) Нуль; б) нуль; в) Е = 1,8-ГО7 В/м.
13. 3,09-106 м/с. 15.400 В.
17. а) 4,28- КГ2 Кл; б) Е = 1,54-1013 В/м; F= 7,7-1010 В.
19. 1153 В. 21. 1,28.
29. а) 3,39-104 В/м; б) 1,13-Ш4 В/м; в) -3,39-10* В/м; г) 226 В.
33. а) 0,5 МэВ; б) 8-Ю"14 Дж; в) 2,88-Ю-15 м.

500 ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
35. а) 12 МэВ; б) -10 МэВ; в) 4МэВ; г) 6 МэВ.
А
37. С' = —
4пк0 (xi/x — хх + х0)'
39. Q1 = V0R1/k0; Q2=V0R2/k0.
Глава 17
1. / = 2,69 А. 3. р =.^_. 5. а) J = 80 А; б) Р = 640 Вт, т. е. в 6,4 раза больше, чем
в 100-ваттной лампе.
7. а) М = 0; б) т = 2- 10"5 Т.
/2m (d — h)
9. а) а = еЕ/т, направлено вверх; б) t = \ *-= '; в) F = -е\0 х 93 (направлена из
плоскости чертежа).
11. 1,05 мА. 13. I = Q/T= 4nR2v/T.
15. Rx = (1/2)(R12 + Д13 - Д23), R2 = (1/2)(Rl2 - Rl3 + Д23), R3 = (1/2) (R23 - Rl2 + Д13).
17. a) 100 Ом; 6) 300 Ом.
19. a) 93 направлено вертикально вверх; б) 0,4 Т или 4000 гаусс.
21. т = 58,5 те.
23. а) 1,13 • 106 Н/Кл; б) 1,41 • 106 Н/Кл; в) 2,82 • 10"3 Т или 28,2 гаусс, направлено за
плоскость чертежа.
25. а) 4 • 10"4 Т, направлено за плоскость чертежа; б)5-10~4Т;в)3-10~4 В/м,
направлено вниз.
27. ё = 10 В, г = 20 Ом.
29. а) * — ^ ; б) ё *2
rR1 + R:R2 + rR2 R1 + R2
Глава 18
I. &\ = ^ni = 4nk0e?/c2, 0B\\ = 0; ^ направлено из плоскости чертежа, ^ш направлено
за плоскость чертежа.
3. & = 4тт —j-(<#i + «/г)» направлено за плоскость чертежа, если г < R1; 0& =
с
— 4пк0(#2/с2, направлено за плоскость чертежа, если Rx < г < R2; & = 0, если г > R2.
5. Электрон движется с постоянной скоростью.
7. а) 4 • 10"6 Т; б) 1,2 • 10"4 Т. 9. 0,02 дин/см.
к0 r2-R\ kj
II. & = 0, когда г < R,; & = 2-f J —, когда Я< < г < Д2; ^ = 2-?-, ког-
с2 (R2-R2)r с2г
да г > R2.
13-ж = 2?^^Ку-^-]хТТ7]дляз;<К2-
п. я = аф* {[(* + |J + *]~9,а + [(А _ ху + * Js,aJ.
19. 2л
0 21. 0,467 Т.

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
601
23. a) L = — МсоД2; б) ц = — бсоД2; в) ц/L = Q/2M.
25. Ответ такой же, как и в случае пластин, расположенных в упражнении 2, за исключе-
к
нием того, что в области между пластинами поле М — An —^-jx0 и направлено из плоско-
с
сти чертежа.
Глава 19
I. AnR20B. 3. Против хода часовой стрелки.
5. ё = n2f&R2 sin cot, J = <f/£m.
7. 10"2Bt. 9. f=R/{2nL).
II. 6-10"5 T = 0,6 гаусс. 13. 4,58 • 10"7 гаусс. 15.
CDoQR co0
х/2. 17. P2. 19. 3,16 kB.
23. C =
i + e2
CO
co0
COo
CO
25. ® = 2-
kn N1
L = 2^rN2(R2-R1)\n(-±\
С Г С \ /<!
27. 3-Ю-3 Кл. 29. а) сторона b; б) сторона a.
R,
■; 6) £ = 0,2В/м. 33. 12,5 м/с. 37. Пусть L = 10"3 Г, тогда C =
= 25,33 пФ и Я = 36,3 Ом.
39. a) J = 0,4237 А; б) P = 17,95 Вт; в) максимальная мгновенная мощность в
конденсаторе равна 47,6 Вт.
41. 0,693 RC 43. / = f (1 - Q~Rt/L).
R
Глава 20
1. Ф£ = 4тг/с0е, <j>E-ds =
3. — aba Е0 sin cot.
5.
dO
Том 2
dt J с2 с2 dt
НФР
2я
Зя
7. В положительном направлении. 9. Т=36Н. 11. Г = 329,6 Н.
13. a) f = 2,65 А/м; б) ^ = 1,67 • 10"6 Т.
4knLAt г Е
15. От 400 до 700 нм. 17. а) Е = —Ц—; б) ® =
R2
2с2 At
19. L = NKX/K2. 21. u = с. 23. а) ® = 0; б) ® = 0.
25. £изл = 109,6 cos cot (В/м). Отношение равно 0,274.

602 ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
27. а) А = ]/Al + Al; б) <р = arctg(A2/A1).
29. а) —-, о) = —.
y0z0 2pyg y0z0 с ру0
Глава 21
_ съ®2
4тг/с0 ц0
3. Гравитационное притяжение уравновешивается при толщине 0,75 мкм. При меньшей
толщине паруса результирующая сила со стороны Солнца будет силой отталкивания.
5. а) Емакс = 3 • 1(Г7 В/м; б) SMaKC = 2,39 • 10"16 Вт/м2; в) Р = 1,00 • 10"9 Вт.
7. a) v = 2,79 • 106 м/с; б) v = 27,9 м/с. 9. п = 1,00025.
11. а) За один оборот энергия увеличивается приблизительно на 2-Ю7 Дж; б) примерно
1 год.
13. a) F = 6,61 • 10"6 Н; б) среднеквадратичное значение индуцированного тока 36,8 А/м;
в) 4,244 • 10"4 Дж/м3.
F F /
15. а) у = —г-sin cot; б) у = —г- cos cot; в) со0 = у к/т; г) в противофазе.
к — mar к — mar
17. 91 = 0,025 электрон/см3.
19. а) Епрош = 0,98Епад; Еотр = 2 • 10-4Епад; б) Епрош = 0,96Епад; Еотр = 1,98 • 10"4Enafl.
21. а) А17 = 4,39 • 10"5 эВ; д) t = 1,57 • КГ11 с.
/спОсо3
25. Е = Е, + Е2 = °% sin 26.
1 2 2с3г
27. Сила FniJl = —=—sin0 и направлена вдоль — z.
Глава 22
1. Е' направлено вдоль отрицательного направления оси у; 93'-вдоль отрицательного
направления оси z.
3. I = 5/0 + 4J0 cos (Ы sinG).
5. а)/= 33,3 Гц; б) 66,7 с"1.
7. Условие минимума: Dx — D2 = {п + 1/2)X.
9. 30 см. 11. JV = 4,25 • 107. 13. N = 982.
15. Е = - 2Е0 sin foe cos cot.
19. F2 = E2 + E\ + 2£jE2 cos (Ы sin0).
21. sinej + sine2 = nk/d.
23. AX = 4,24 • 10"19 м; необходимо 9,4 • 10й штрихов.
27. Результаты приведены в следующей таблице, но только числа в ней нужно умножить
на VI:
а)
б)
в)
г)
ц
1
0
1/2
1/2
щ
0
1
1/2
1/2
ц
1/2
1/2
1
0
RI,
1/2
1/2
0
1

Глава 23
1.
ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ 603
Г=0
1Т
Q л
\т
\
'2*0 *
JX
\
2 1
3. Плоскополяризованная волна в направлении оси z.
5. Ю-6 св. лет = 9,5 • 109 м.
7. Размер пятна равен 7,72-10"5 м. 9. а) / = /0/2; б) Г = /q/4.
11. Увеличенное, прямое; такое же изображение получается в зеркале для бритья.
13. 66,7 см. 15. /' = 0,759/0.
17. а) 4/0; б) нуль; в) /0, поляризация вертикальная; г) круговая поляризация; средняя
энергия совпадает со случаем «в»; д) /0> поляризация горизонтальная; е) /0; ж) нуль.
19. 0,389 нм. 21. а) 3,79-10~2 рад; б) 3,79 • 10 "3 рад.
23. F(F — D)/D, вправо от выпуклой линзы.
27. а) „„ > Я1; б) х0 - ^„Д^-
Глава 24
1. 0,0124 нм. 3. 3,0-КГ10 кг-м/с; Я,- 2,21-10
5. Хф0тон = 1,24.10"6м; к. - Ю1.1 п-9.
7. Х0 = 2816 нм. 9. X -
■24
^электрон
Ас
= 1,23 • 10"
м.
м.
|/я2 - mV '
11. а) 166,7 отсчет/с; б) 426,7 отсчет/с; в) 26,7 отсчет/с.
13. В 2 раза.

604 ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
17. 469 МэВ. 21. К = 0,0375 эВ, X = 6,35-10"9 м.
23.
3,42
(5,14; 3,85)
-4,79 см-
С ростом энергии пучка
точки на рисунке сближаются.
Глава 25
1. \|/*\|/ = 2(1 + cos2cot) = 4 cos2 cot.
3. \|/*\|/ = 4 cos2 Акх, АрАх = ^й. 5. Ах = 115т.
7. а) Е2 = 9,42 • 10"2 эВ; б) X = 438 нм.
4х2
11. а) 1/2 а0; б) В (к) = _^ехр[-а2(/с - mt>0/»)2].
1/71
13. ф = arctg
ГА^тср^ A2sm<p2
17.
dco
~d/T
рс
L^4iC0S91+ y42cos92J
2
- = V.
; i4 = ]/a\+ A\+ 2A1A2cos(91- ф2) .
19. a) Ex = 942,4 Мэв; E2 = 3770 МэВ; 6) E1 = 31,1 МэВ; E2 = 62,2 МэВ.
21. Ex = 22,76 эВ; E2 = 88,23 эВ.
23. E, = fc2/(72mx2). 25. a) iK (x) = exp [- (l/m/c /2ft)x2]; 6) Ex = (1/2)П]/к/т .
27. £ = (3/2)ftco.
Глава 26
7l2 ft2
I. R0 — .* .
8 k0mze
3. Энергия уменьшится на 2% в случае нерелятивистских частиц.
5. 25 различных стоячих волн.
7. Вдвое меньше радиуса водородного атома, или ДНе+ = 0,265 нм. 9. 10.
II. Переходу вНе+ сп = 4нап = 2 соответствует та же энергия фотона, что и перехо
ду в Н с и = 2 на и = 1. Длина волны 1215 нм.
13. v|/
3,2,-2-?
= -^е-г/3а8т20е-2/<р. 15. t = 4,7.10"8c.
17. Все волновые функции имеют вид
. . пхп . nvn . nz%
^п„Пу>пг = Sin — Sin -^Sm-£-.

ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ ®\ЗЭ
Ех = 112 эВ, \|/ = \|/!,i,i>
Е2 = 224 эВ, \|/ = vj/i' х' 2; \|f1§ 2t х и v|/2> lf х;
Е3 = 336 эВ, \|/ = \|flf 2f 2; \|/2,1э 2 и \|f2t 2f t;
E4 = 410 эВ, \|/ = \К, i, 3; *K, з, i и Фз, l, i-
19. a= j. 21. <->=-- -ту-.
23. Я = b2n2/GMnm2e = 1,2-1029 м для и = 1.
25. a) Ex = — 3,2 эВ; б) трем переходам в основное состояние отвечают hf = 1,2; 1,8
и 2,2 эВ; двум переходам в первое возбужденное состояние отвечают hf = 0,6 и 1,0 эВ;
одному переходу во второе возбужденное состояние отвечает hf = 0,4 эВ.
Глава 27
I. 3,40 • 10"10 м в случае натрия; 4,24 • 10"10 м в случае калия.
3. Переходы с п = 9, 10, 11, 12, 13 или 14 на п = 6; кроме того, сп = 5нап = 4;сп = 7
или 8наи = 5;си = 9-23наи = 6;си=12 или выше на п = 7; с п = 21 или выше на
п = 8.
5. 6560, 5411, 4859, 4541 и 4338 А. 7. 110 кэВ. 9. 31,7 эВ.
II. 50 элементов. 13. a) Z3^ = Z — 5; б) hf = 13,6 (z — 2)2 дает 8,68 А для
А1 и 0,185 А для РЬ.
17. 2эфф = 6,7 для 2р электронов в случае Al; z^ = 64,5 для 2р электронов в случае РЬ.
19. 50.
Глава 28
1. а) Е = К + U = -4 эВ; б) К = И эВ.
3. U0 = 5 эВ.
5. Контактная разность потенциалов 0,5 В; более высокий потенциал у металла А.
7. а) Е = -4 эВ; б) W0 = 4 эВ; в) U0 = 9 эВ; г) 9 эВ; д) 4 эВ.
9. U0 = 7,91 эВ. 11. Добр/Кпрям = 2,5 • 1018.
13. £д = 2,48 эВ. 15. 15750 Гц. 17. р = 1/h3.
19. 6,77 А; р = 124 кг/м3. 21. U0 = 7,06 эВ.
23. Е1 = 0,06833 U0.
Глава 29
1- 0макс=1,7°. 3. 2,0-10"15м. 5. 148. 7. 3/4.
9. 63,2% на протяжении 1 среднего времени жизни; 86,5% на протяжении 2-х средних
времен жизни.
11. Диаметр уменьшится в 5,47 • 104 раз и составит 25,4 км.
13. а) 190,128 ГэВ; б) К = 16 МэВ. 15. Я = 26,5 км; М = 1,78-1031 кг или 8,9 массы
Солнца.
17. 18,0 см. 19. а) 10"6 с"1; б) т = 106 с; Т= 6,93-105 с.
21. а) 5 МэВ; б) 8,4-1021 с"1; в) т = 1,2 мкс; г) длиннее; д) 8 МэВ.

606 ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ
23. U(r) $(г)
25. z = 25,3. 27. Около 3 кг в сутки.
29. а) ~ 66 т; б) около 800 т за 30 лет.
Глава 30
1. 3,96-1026 Вт. 3. 4,17-1038 протонов в секунду.
5. р = 1,8-10~26 кг/м3. 7. В 4 раза в нерелятивистском и в 2 раза в релятивистском
случае.
h2 ( 9п \2/3
9. R =
R = c/
4Gm3n \ 4тг2
. 13. v =
!—nGpR = (7,47 • 10"18 с"1)/*.
^TtGp = 4 • 1025 м = 4,26 • 109 световых лет.
17. Р = —9Mf0. 19. 6,5- 1020.
Глава 31
I. Т = 12 мин, п -► р + е+ + ve. 3. a) ve; б) уц; в) ve.
5. ц~ + р -> п + уц. 7. Нарушаются законы сохранения а) заряда; б) мюонного и
электронного лептонных чисел; в) электронного лептонного числа; г) энергии; д) энергии.
9. Левовинтовое.
II. На изображении в зеркале мюон \х+ -правовинтовой.
рм
Изображение
Зеркало
13. Позитрон распада-правовинтовой. 15. т -► \х+ + \х + ц + уц + vT.
17. Кц = 4,18 МэВ. 19. Ке = 52,6 МэВ. 21. тс2 - 100 МэВ.

Абсолютная температура 192-195
Авогадро гипотеза 202, 203
- число 203
Автоэлектронная эмиссия 512
Адиабатическое расширение 207-209
Адроны 574-578
Альфа-распад 533-538, 540
Ампер (А) 267, 296
Ампера закон 289-292
Анализ размерностей 15
Ангстрем 358, 389
Аннигиляция 143, 144, 231, 570
Антивещество 570-572, 583
Антиводород 572
Антинейтрино 539, 566
Антипротон 570
Античастицы 570-572
Аристотель 53, 74
Архимеда закон 190
Атвуда машина 62, 63, 67
Атом водорода 203, 247, 256, 457
- волновая функция 459, 461-463
- основное состояние 459
- радиус 459
- спектр 466, 467
Атомная бомба 539, 541
- масса 203, 523
Атомное ядро 522
размеры 524
- распределение заряда 523
структура 530-533
энергетические уровни 533, 534
энергия связи 531, 532
Атомные переходы 372
- часы 14, 133, 147
Атомный номер 522
- объем 475
Балъмера серия 466
Барионы 144, 576-579, 584
- сохранение 567
Барн 526
Барометр 188-190
Беватрон 569, 571
Белый карлик 520, 548, 553-556, 559
Бензиновый двигатель, см. Карно цикл
Бета-распад 143, 538, 539, 565, 573
Био-Савара закон 281, 295
Благородный (инертный) газ 478, 481
УКАЗАТЕЛЬ
Бозе-Эйнштейна статистика 512
Бойля закон 192
Болъцмана постоянная 192
Бор Нильс 469
Бора модель атома 106, 256, 469-471
- излучение 372, 373
стабильность орбиты 471
- постулат 469
Брюстера угол 420, 421
Валентная зона 505
Валентность 477
Валентные электроны 492
Ван де Граафа генератор 254
Векторы 37-41, 87-89
- произведение векторное 87-89
скалярное 88
- сложение 38
Великовский 12
Вероятность 222
- амплитуда 430, 431
- перехода 465
- распределение 438
Вес 59, 75-77
- кажущийся 76, 77
Вечный двигатель 98
второго рода 220
первого рода 220
Взвешенное среднее 27
Водородная бомба 539, 543, 544
Воздух 241
- электрический пробой 254
Волновая амплитуда 459
- функция 430, 446, 447, 463
Волновое уравнение 346, 354
- число 353
Волновой пакет 374-377, 437-441
- расплывание 441
- ширина 376
Волны 341
- бегущие 181
- гравитационные 148
- звуковые 181
- интенсивность 182, 183, 355, 431
- интерференция 381
- на поверхности воды 386
- скорость 353, 366
Вольт (В) 253
Время 13, 14, 128

УКАЗАТЕЛЬ
Время, замедление 124-127
- обращение 225
- постоянная 320
- собственное 125
Вселенная 148
Вынужденное излучение 467
Газовая постоянная 203
Галилей Галилео 124
Гальванометр 275
Гамма-распад 538
Гармоническая сила 172, 251
Гармонический осциллятор в квантовой n
нике 450-452
Гаусс (Гс) 280
Гаусса распределение 375, 376, 437, 451
- теорема 245, 524
Гауссова поверхность 238
Гейгера счетчик 431
Гелий 478
- атом 470
Гельмголъца катушки 303
Генератор переменного тока 305, 306
Геометрическая оптика 416-423
Гибридизация 480, 486-488
Гипероны 576
Голограмма 402, 404
Голография 401, 404
Горизонт см. Шварцшилъда радиус
Гравитационная постоянная 73
- энергия звезды 554
потенциальная 92, 93, 97
- сохранение 104
Гравитационное давление 549
- красное смещение 147
- поле 78-81, 246
Гравитационные волны 148
Гравитационный коллапс 548, 549, 561
Гравитация искусственная 77
Граничные условия 448
Групповая скорость 369, 370, 376, 377, 440
Гука закон 89, 100
Давление 187-192
- атмосферное 188, 189
Движение снаряда 42, 44
Де Бройль Луи 429
Де Бройля соотношение 429, 458
Дейтерий 543
Дейтрон 455, 530, 542
- энергия связи 527, 530
Деление ядер 144, 149, 539-542
- спонтанное 540
Детектор гравитационных волн 561
Дефекты кристаллической решетки 497
Джордано Бруно 74
Джоуль (Дж) 86
Дикке 79
Дина 55, 56
Диодный выпрямитель 516
- детектор 509
Диполь, излучение 371
- магнитный 294-296, 300
- электрический 244, 254, 296
Дипольная антенна 380
Дипольный момент 248
Дирак П.М. 475, 476
Дисперсия 368
Дифракционная решетка 388, 389
Дифракционное рассеяние 413-416
Дифракция
- второго порядка 389
- на двух щелях 392
круглом отверстии 409-413
отдельной щели 392-394
- электронов 434
Диэлектрическая проницаемость 232, 259-261
Длина волны 346, 351, 353
- когерентности 395, 402
Доплера эффект 130, 132
Дырки 505, 508
Дэвиссона и Джермера эксперимент 433
Дюлонга-Пти закон 206, 224
Единая теория слабых и электромагнитных
взаимодействий 584
Единицы измерения 590
Емкостное сопротивление 314. 315
Жидкий гелий 512
Закон всемирного тяготения 70-74
- равнораспределения энергии 196
- равных площадей 74, 75
Законы сохранения 584, 585
Закороченные цепи 272
Замкнутая петля с током 295
- система 64, 101
Зарядовое сопряжение 572
Заряд электрический 230
движущийся 275, 344
- индуцированный 260, 261
точечный 253
Заряженная пластина 251
- сфера 245-247
Заряженный провод 248, 250, 281
Затухающие колебания 180
Звезда нейтронная 548, 556-561
Звук 16, 23
- интенсивность 182
- скорость 16, 385
Земля 71, 72, 92, 94
- давление в центре 190
- магнитное поле 295, 297, 325
Значащие цифры 18
Идеальный газ 191
уравнение состояния 191
Излучение, импульс 374-377
- мощность 371
- точечного заряда 370-372
- электромагнитное 344-347
- энергия 363
Изображение оптическое 417, 418
Изотермическое расширение 207

УКАЗАТЕЛЬ 609
Изотоп 522
Изотопический спин 585
Импеданс 316
- свободного пространства 348
Импульс 52, 64, 90, 91, 102
- квантовомеханический 438
- релятивистский 140-143, 148, 149
- силы 102
- фотонов 427
- электромагнитного излучения 362-364
Инвариантность относительно отражений
Индуктивное сопротивление 315
Индуктивность 311, 312
- соленоида 311, 312
Индукция электрическая 241
Инерциальная система 53
Интегральные схемы 512
Интенсивность 182, 355, 385
Интерференция волн 381-391
- двойная щель 407, 408
Интерферометр 122
Интерферометрия интенсивности 395
Инфракрасное излучение 180
Ионизационный потенциал 477
Ионная связь 484, 485
Ионосфера 369, 370
Ионы 485
Кавендиш Генри 73
Калория 111, 197
Камера-обскура 422
Карно цикл (машина) 215-217
- - КПД 216, 217
Квадрупольный излучатель 379, 400
Квазары 132, 135
Квант света 426
Квантовая электродинамика 465, 585
Квантовомеханическое давление 550, 551
Кварки 564, 565, 578-580
Кеплер Иоганн 74, 75
Кеплера законы 74, 75
Кинетическая энергия 89-91
- вращательная 160, 168
- релятивистская 145
Кирхгофа правила 273
Ковалентная связь 485, 486
Когерентный световой пучок 402, 469
Колебания молекулярные 205
Колебательный контур 312, 313
Комптона эффект 427, 428
Конденсатор 257, 258
- КС-цепь 320, 321
Консервативные силы 91, 92, 98, 99, 107
Контактная разность потенциалов 496
Коперник Николай 74
Коронный разряд 254
Корпускулярно-волновой дуализм 428-432
Космические лучи 572
Космология 148
Коэффициент полезного действия (КПД)
бензиновый двигатель 211
тепловая машина 216, 217, 220
- усиления по току 511
Крабовидная туманность 557, 558
Красное смещение гравитационное 147
Кулон (Кл) 231, 232
Кулона закон 231, 277
К-мезон 574, 576
Магические числа 533, 534
Магнитная сила 274, 275
Магнитное поле 274, 275, 277, 289, 308
движущегося заряженного тела 291
Магнитный заряд 297
- поток 290, 309
Майкельсона-Морли опыт 120-123
Макроскопические величины 187
Макроскопическое приближение 92, ПО
Максвелл Дж. К. 342, 343
Максвелла уравнения 239, 300, 341
общий вид 343
Малые колебания 178, 179
Масса 13, 14, 55, 56, 74
- гравитационная 78, 79, 83, 146-148
- инертная 79, 83, 147
- определение 51, 52
- покоящегося тела 54
- релятивистская 54, 143-145, 146
Массовое число 523
Маховик 166, 167
Маятник
- баллистический 109
- конический 63, 64
- математический 63, 177, 183
- физический 176
Мезоны 574-576, 580
Мёссбауэра эффект 147
Мёссбауэровские часы 126, 133, 138
Металлическая связь 491, 492
Микроволны 383
Микроскоп 412, 413, 440
Микроскопическое приближение 92
Модуляция 369, 517
Молекула
- водорода 184, 205, 485, 486
- двухатомная 197, 204, 205
- неполярная 261
- полярная 260, 261
- потенциальная энергия 106
- частота колебаний 179, 180, 205
Молекулярная масса 203
- связь 476, 484-487
Моль 203
Момент импульса 75, 155
в квантовой механике 460, 461
Лазер 402, 403, 413, 414, 467, 469
Поймана серия 466, 467
Лебедев П. Н. 364
Легирование полупроводников 506
Ленца закон 309
580 Лептоны 572, 573, 584
Ли 581
Линейное распределение заряда 248
Линзы 419
Линия электропередачи 311, 312
Лоренца преобразования 128, 141, 148
Лоренцево сокращение 128, 129, 276
Лошадиная сила 86, 87

610 УКАЗАТЕЛЬ
Момент импульса звезды 557
молекулы 204
определение 155
- сохранение 156-159
- инерции 162, 163
- силы 157
Монохроматическая волна 346
Мощность 87, 112
- цепь переменного тока 317, 318
- электрическая 270, 310
Мюон 144, 572-575
Надкритическая масса 541
Напряжение переменное 306, 310, 314
Невесомость 61, 76
Нейтрино 532, 538, 565, 573
Нейтрон 140, 143, 522, 532, 556
- взаимодействие с протоном 529
- поглощение 526, 527, 538
- сечение 525
- распад 565-567
Нейтронная звезда 548, 556-561
Некогерентное излучение 468
Необратимый процесс 225
Нуклон 523
- фундаментальные силы 526, 529, 530
Ньютон Исаак 45, 53, 70-72
Ньютона законы 52, 53
Образование звезд 548
Обратимый процесс 209, 210
Обратное напряжение 509
Объектив 411, 412
Одновременность 129, 130
Однородность времени и пространства 64
Оккама бритва 11, 19
Ом Георг 268
Ома закон 268
Омметр 286
Оптическая накачка 468
Орбиталь 475
Орбитальный момент импульса 460, 461
Основное состояние атома 466
Основные типы взимодействий 11
Относительность 28
- общая теория 79, 146-148
- принцип 123, 124, 307
- специальная теория 119, 123-135, 267
Отражение волн 381
электромагнитных 364, 365
- закон 417-419
- поляризация 408
Отто цикл 210, 211, 217, 228
Очарованные частицы 580, 585
Ошибки
- систематические 18
- случайные 18, 24
Парадокс близнецов 132-134
Паскаля закон 187
Паули Вольфганг 475, 476, 566
Паули принцип запрета 475, 476, 530, 533, 552
Переменный ток 314
Переходный процесс 319
Периодическая система элементов 483
Периодичность элементов 475, 480
- группа 480
Период полураспада 126, 537
Пион 126, 144, 150, 574-577, 581, 582
Плазма 251, 369
- электромагнитное излучение 369
- удержание 544
Плазменная частота 251
Планк Макс 424, 426
Планка постоянная 299, 424, 426
Плоский ток 292
излучение 345
Плотность 13, 14, 55
- идеального газа 193
- тока 267, 291, 292
- электронного заряда 476
- энергии магнитной 314
Плутоний 539-542
Поверхностный заряд 240
Поглощение 463, 467
Позитрон 143, 532, 570
Пбйнтинга вектор 361, 363
Показатель преломления 365, 368, 369, 409, 419
Поле
- гравитационное 79, 80
- излучения 347, 360
- физическая реальность 364
Полное внутреннее отражение 513
Полупроводник 493
Поляризатор 405
Поляризация 404
- круговая циркулярная 404, 405, 407
- при отражении 408, 409, 421
- света 404, 405
Полярная молекула 260
Поляроид 406, 409
Поперечное сечение 525, 526
Порог слышимости 182
Последовательное соединение цепи 317
Постоянный магнит 291, 294, 297, 298
Потенциальная энергия 91-94, 100
гравитационная 92-94, 105
пружины 94
электрическая 252
Потенциальная яма 444-446
конечной глубины 447-450
Поток магнитный 290, 306
- самоиндукции 311
Правило многоугольника 38
- правой руки 154, 155, 278, 309
Предельная масса, см. Чандрасекара предел
Преломления закон 418, 419
Преобразования полей 281, 282
Приборная ширина линии 390
Приведенная масса 175, 528
Призма 368
Принцип неопределенности 443, 538, 573
- суперпозиции 232, 431
- эквивалентности 78, 79, 149
Принципы симметрии 64
Продукты деления 542, 547
Проникновение сквозь барьер 512, 513, 534
Простое гармоническое движение (ПГД) 173
энергия 177

УКАЗАТЕЛЬ 611
Протон 247, 521, 531
- пучок 414
- сердцевина 524
- структура 415, 416
Протонный синхротрон 416
Протонов рассеяние на протонах 415, 416
Протон-протонный цикл 549, 550
Пружина, потенциальная энергия 94
- сила 94, 99, 100
Птолемей 74
Пузырьковая камера 144, 571, 574, 577
Пульсар 370, 558-560
Пучок электронов 274, 484
р-п-переходы 507-509
я-мезон см. Пион
Работа 85-87, 89
- выхода 425, 426, 458, 496
- моля идеального газа 208
Равновесие 107
- тепловое 195, 196
Радиоактивность 538, 539
Радиоактивный распад 143, 442
- кривая 535
Радиоастрономия 396, 370
Радиометр 363
Радиопередатчик 371
Радиотелескоп 370, 396, 397, 557
Разность потенциалов 253
Разрешающая способность 389, 390, 410
лазерный пучок 413
телескоп 412
Ракета 105
- многоступенчатая 65, 68, 69
Распределение по импульсам 438
Рассеяние электронов высоких энергий 523-525
Реактор бридерный 542
- гибридный 544
- ядерный 23, 539-542, 567
Резонанс 316, 317
- частиц 578
Резонансная частота 313
Результирующая сила 57
Релятивистское сложение скоростей 139, 140
Рентгеновское излучение 428, 434, 483, 484
- звезды 560
р-мезон 575, 576
Самоиндукция 311, 312
- ЭДС 312
Сверхновая звезда 148, 548, 551, 557
Сверхпроводимость 498, 499
Сверхпроводящий кабель 498
Сверхтекучесть 511, 512
Свет 120-123
- давление
- Доплера эффект 130, 133
- красное смещение 131
- поляризация 404-406
- скорость 29, 120, 124, 277, 369
Световой луч 417-419
Светодиод 509
Свободное расширение газа 195
Сила 52
- взаимодействия 55
- внешняя 55
- выталкивающая 190, 191
- гармоническая 172
- гравитационная (тяжести) 51, 59, 70-72, 75, 89
- единицы измерения 55, 56
- консервативная 91, 92
- контактная 55, 56, 62
- магнитная 274-276
- трения 107
- упругая 89, 94
- центральная 157
- электрическая 230
- электромагнитная 51, 274
- электростатическая 232
Силовые линии 235, 236
Сильное взаимодействие 522, 526
Симметрия античастиц 572
Синтез ядер 539, 542-545
Скорость 25-28, 38-40
- волны 353, 366
- вторая космическая 104
- групповая 377
- дрейфа 268
- звука 16
- мгновенная 25, 26
- относительная 65
- первая космическая (орбитальная) 45
- постоянная 25
- предельная 34
- простое гармоническое движение (ПГД) 173
- света 29, 120, 124, 277, 369
- сложение 39
- средняя 26-28
- угловая 153
- центра масс 160
Снелла закон 418, 419
Современная оптика 401-404
Соленоид 293, 294
Солнечная энергия 95, 498, 509
Солнечные батареи 509
Сопротивление воздуха 17, 32, 56, 112, 113
- электрическое 268, 269
полное цепи 271
удельное 269, 497
Соударения 101-104
- неупругие 108-110
- упругие 102-104
Сохранение импульса 64, 65
момента 75, 156-158
релятивистского 141
- энергии 98-101, 107, 108, 114
Спектр 368, 446
- сплошной 467
Спектрометр 389, 390
Спин электрона 475, 476
Спонтанное деление 540
- излучение 465, 476
Спутник искусственный 45-47
стационарный 72
Среднее значение 463, 464
Среднеквадратичное значение 319
- отклонение 376, 438
Среднее время жизни 372, 537
Средняя длина свободного пробега 269, 497

612 УКАЗАТЕЛЬ
Степень свободы 196
вращательная 204
Стоячие волны 381, 383
двумерные 458
— квантовая механика 444, 447
трехмерные 457, 458
Странность 576, 577
- сохранение 584
Странные частицы 576, 577, 584
Струна, колебания 382, 383
Сферическое распределение заряда 245
СР-инвариантность 583-585
Твердое тело 153, 161
Телевидение 517
Телескоп 410-412
- отражательный 418
- увеличение 410-412
Температура 192-195
- термодинамическая шкала 221
Теорема о связи работы и энергии 90, 107
Тепло 197, 198
- Ъжоулевы потери 270
- механический эквивалент 198
Тепловое загрязнение 217
Тепловые насосы 218, 219
Теплоемкость 203-207
- при постоянном давлении 206, 207
объеме 203-206
Термистор 506
Термодинамика 187
- закон второй 219, 220
- - нулевой 195, 196
первый 202
Термометр 192-194
Термоэлектронная эмиссия 512
Термоядерная реакция 194, 543, 550
энергия 543
Тесла (Т) 277
Ток в р-и-переходе 507, 508
- смещения 342
Торий 569, 571
Точечный заряд 237, 253
движущийся 275, 276
Траектория 42, 43
Транзистор 510
Трансформатор 309-311
Трение 58-60, 86, 92, 111, 112
- коэффициент динамический 58
статический 58
Тринитротолуол (ТНТ) 542
Тритий 543
Турбулентность 211
Тяжелое ядро 530-533
Тау-лептон 573
Угловая скорость 153, 154
Уитстона мост 273, 274
Ультрафиолетовая область спектра 445
Уравнение состояния идеального газа 191
Уран 534
Ускорение 28-33, 39
- мгновенное 28
- постоянное 29
Ускорение, простое гармоническое движение 173,
174
- свободного падения 28, 29, 37, 47
- угловое 154
- центростремительное 44, 45, 63
Ускорители частиц высоких энергий 568-570
Фазовое пространство 519
Фарада (Ф) 257
Фарадея закон 282, 307, 308
Фейнман Ричард 431, 566
Ферми 416, 523
Ферми Энрико 494, 538, 541, 566, 578
Ферми граничная энергия 494, 495, 552-554
- граничный импульс 495, 552, 555, 556
- универсальное взаимодействие 564, 584
- уровень 494-496, 508, 531
Ферромагнитные материалы 300
Формула тонкой линзы 419
Фотодиод 509
Фотон 364, 395, 441, 484
- излучение 465-467
- масса гравитационная 551
Фотоэффект 425, 443
Франклин БенЪжамин 231, 268
Фраунгофера приближение 385, 409
Фурье интеграл 351
Фурье-образ 376
Фурье разложение 349
Холодильники 217
Хэнбери Брауна и Твисса метод 395
Центр масс 159-161
скорость 160
Центростремительное ускорение 44, 45, 63, 99
Цепная реакция 468, 540, 541
Цепь тока переменного 314
соединение параллельное 271
последовательное 316
постоянного 271
Чандрасекара предел 555
Частица в потенциальной яме конечной
глубины 448-451
ящике 444-447
Черная дыра 147, 546, 551, 552, 558, 559, 561
Четвертое измерение 128
Четность 581-585
Числовая апертура 413
Шварцшилъда радиус 551
Шредингера уравнение 447
в трех измерениях 457, 458, 528
стационарное 448
Эйнштейн Альберт 120, 123, 147, 425, 427
Эйнштейна уравнения 147
Эквипотенциальная поверхность 257
Эквивалентность массы и энергии 143
Электрическая индукция 241
- мощность 270, 310

УКАЗАТЕЛЬ 613
Электрический потенциал 253, 254
- ток 267
- амперовский 298
- единицы измерения 275
- релятивистское преобразование 283, 284
Электрическое поле 283, 306, 308, 309
Электродвигатель 307
Электродвижущая сила (ЭДС) 270, 305-308
- индуцированная 309
- магнитная 306
Электромагнитная волна 314, 404
- индукция 282
- сила 274
Электромагнитное поле 281
- энергия 313
Электрон 143, 251, 481
- заряд 258
- магнитный момент 299
- проводимости 267-269, 275, 494-497
- радиус 259
Электронвольт 87, 256
Электронная орбиталь 475
Электронное облако 247, 365, 373, 470, 487
- сродство 480
Электронные конфигурации атомов 482
Электронный микроскоп 422
Электропроводность 270, 506
Энергия 85-87
- в катушке индуктивности 313, 314
- внутренняя 107, 202
- внутриядерная ПО
- гравитационная 104
Энергия гравитационная потенциальная 93, 105
- закон сохранения 98-101, 114, 142, 202
- ионизации 258
- кинетическая 89-91, 109
- конденсатора 259, 260, 314
- магнитного поля 313, 314
плотность 315
- механическая 98-101
- молекулы 106
- основного состояния 445
- полная 106
- потенциальная 91-94, 100
- распределение зарядов 259
- релятивистская 142
- связи 459
ядерная 530, 531
- тепловая 197, 198
- химическая ПО
- электрического поля 258
плотность 259
Энтропия 222-224
Эрг 86
Этвеш 79
Юкава 575, 576
Ядерная фотоэмульсия 574
Ядерное вещество 522, 523
Ядерные силы 51, 522, 526, 574
Янг 581

ОГЛАВЛЕНИЕ
ТОМ 1
Предисловие редактора перевода 5
Предисловие к русскому изданию 7
Предисловие 7
1. ВВЕДЕНИЕ и
§ 1. Что такое физика? 11
§ 2. Единицы измерения 13
§ 3. Анализ размерностей 15
§ 4. Точность в физике 17
§ 5. Роль математики в физике 19
*§ 6. Наука и общество 21
Приложение. Правильные ответы, не содержащие
некоторых распространенных ошибок 22
Упражнения 22
Задачи 23
2. ОДНОМЕРНОЕ ДВИЖЕНИЕ ... 25
§ 1. Скорость 25
§ 2. Средняя скорость 26
§ 3. Ускорение 28
§ 4. Равномерно ускоренное движение 29
Основные выводы 33
Упражнения 33
Задачи 34
3. ДВУМЕРНОЕ ДВИЖЕНИЕ 36
§ 1. Траектории свободного падения 36
§ 2. Векторы 37
§ 3. Движение снаряда 42
§ 4. Равномерное движение по окружности .... 44
§ 5. Искусственные спутники Земли 45
Основные выводы 48
Упражнения 48
Задачи 49
4. ДИНАМИКА 51
§ 1. Введение 51
§ 2. Определения основных понятий 51
§ 3. Законы Ньютона 52
§ 4. Единицы силы и массы 55
§ 5. Контактные силы (силы реакции и трения)... 56
§ 6. Решение задач 59
§ 7. Машина Атвуда 62
§ 8. Конический маятник 63

ОГЛАВЛЕНИЕ 615
§ 9. Закон сохранения импульса 64
Основные выводы 65
Упражнения 66
Задачи 61
5. ГРАВИТАЦИЯ 70
§ 1. Закон всемирного тяготения 70
§ 2. Опыт Кавендиша 73
§ 3. Законы Кеплера для движений планет ... 74
§ 4. Вес 75
§ 5. Принцип эквивалентности 78
*§ 6. Гравитационное поле внутри сферы 79
Основные выводы 81
Упражнения 81
Задачи 82
6. РАБОТА И ЭНЕРГИЯ 85
§ 1. Введение 85
§ 2. Работа 85
§ 3. Мощность 87
§ 4. Скалярное произведение 87
§ 5. Кинетическая энергия 89
§ 6. Потенциальная энергия 91
§ 7. Гравитационная потенциальная энергия ... 92
§ 8. Потенциальная энергия пружины 94
Основные выводы 94
Упражнения 95
Задачи 96
7. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ 98
§ 1. Сохранение механической энергии 98
§ 2. Соударения 101
§ 3. Сохранение гравитационной энергии .... 104
§ 4. Диаграммы потенциальной энергии 106
§ 5. Сохранение полной энергии 107
*§ 6. Энергия в биологии ПО
§ 7. Энергия и автомобиль 111
Основные выводы 114
* Приложение. Закон сохранения энергии для системы
N частиц 114
Упражнения 115
Задачи 115
8. РЕЛЯТИВИСТСКАЯ КИНЕМАТИКА ш
*§ 1. Введение 119
*§ 2. Постоянство скорости света 120
*§ 3. Замедление времени 124
*§ 4. Преобразования Лоренца 127
*§ 5. Одновременность 129

616 ОГЛАВЛЕНИЕ
*§ 6. Оптический эффект Доплера 130
*§ 7. Парадокс близнецов 132
Основные выводы 134
Упражнения 135
Задачи 136
9. РЕЛЯТИВИСТСКАЯ ДИНАМИКА т
*§ 1. Релятивистское сложение скоростей 139
*§ 2. Определение релятивистского импульса . . . 140
*§ 3. Закон сохранения импульса и энергии .... 141
*§ 4. Эквивалентность массы и энергии 143
*§ 5. Кинетическая энергия 145
*§ 6. Масса и сила 146
*§ 7. Общая теория относительности 146
Основные выводы 148
* Приложение. Преобразование энергии и импульса 148
Упражнения 149
Задачи 150
10. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ... 153
§ 1. Кинематика вращательного движения .... 153
§ 2. Векторное произведение 154
§ 3. Момент импульса 155
*§ 4. Динамика вращательного движения 156
*§ 5. Центр масс 159
*§ 6. Твердые тела и момент инерции 161
*§ 7. Статика 163
*§ 8. Маховики 166
Основные выводы 167
Упражнения 168
Задачи 169
11. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ . . . 172
§ 1. Гармоническая сила 172
§ 2. Период колебаний 174
§ 3. Маятник 175
§ 4. Энергия простого гармонического движения 177
*§ 5. Малые колебания 178
*§ 6. Интенсивность звука 181
Основные выводы 183
Упражнения 183
Задачи 184
12. КИНЕТИЧЕСКАЯ ТЕОРИЯ 187
§ 1. Давление и гидростатика 187
§ 2. Уравнение состояния идеального газа .... 191
§ 3. Температура 192
§ 4. Равномерное распределение энергии .... 195
§ 5. Кинетическая теория тепла 197

ОГЛАВЛЕНИЕ 617
Основные выводы 198
Упражнения 199
Задачи 200
13. ТЕРМОДИНАМИКА 202
§ 1. Первый закон термодинамики 202
§ 2. Гипотеза Авогадро 202
§ 3. Удельная теплоемкость 203
§ 4. Изотермическое расширение 207
§ 5. Адиабатическое расширение 207
§ 6. Бензиновый двигатель 210
Основные выводы 211
Упражнения 212
Задачи 212
14. ВТОРОЙ ЗАКОН
ТЕРМОДИНАМИКИ 215
§ 1. Машина Карно 215
§ 2. Тепловое загрязнение окружающей среды . . . 217
§ 3. Холодильники и тепловые насосы 217
§ 4. Второй закон термодинамики 219
*§ 5. Энтропия 222
*§ 6. Обращение времени 225
Основные выводы 227
Упражнения 227
Задачи 228
15. ЭЛЕКТРОСТАТИЧЕСКАЯ СИЛА 230
§ 1. Электрический заряд 230
§ 2. Закон Кулона 231
§ 3. Электрическое поле 233
§ 4. Электрические силовые линии 235
§ 5. Теорема Гаусса 238
Основные выводы 241
Упражнения 242
Задачи 243
16. ЭЛЕКТРОСТАТИКА 245
§ 1. Сферическое распределение заряда 245
§ 2. Линейное распределение заряда 248
§ 3. Плоское распределение заряда 249
§ 4. Электрический потенциал 252
§ 5. Электрическая емкость 257
*§ 6. Диэлектрики 259
Основные выводы 261
Упражнения 262
Задачи 264

618 ОГЛАВЛЕНИЕ
17. ЭЛЕКТРИЧЕСКИЙ ТОК И
МАГНИТНАЯ СИЛА 267
§ 1. Электрический ток 267
§ 2. Закон Ома 268
*§ 3. Цепи постоянного тока 271
§ 4. Эмпирические данные о магнитной силе . . . 274
§ 5. Вывод формулы для магнитной силы .... 276
§ 6. Магнитное поле 277
§ 7. Единицы измерения магнитного поля .... 279
*§ 8. Релятивистское преобразование величин 93 и Е 281
Основные выводы 283
* Приложение. Релятивистские преобразования тока
и заряда 283
Упражнения 285
Задачи 285
18. МАГНИТНЫЕ ПОЛЯ 289
§ 1. Закон Ампера 289
§ 2. Некоторые конфигурации токов 291
§ 3. Закон Био-Савара 295
*§ 4. Магнетизм 297
§ 5. Уравнения МаксвелЛа для постоянных токов 300
Основные выводы 300
Упражнения 301
Задачи 302
19. ЭЛЕКТРОМАГНИТНАЯ
ИНДУКЦИЯ 305
§ 1. Двигатели и генераторы 305
§ 2. Закон Фарадея 307
§ 3. Закон Ленца 309
§ 4. Индуктивность 309
§ 5. Энергия магнитного поля 312
*§ 6. Цепи переменного тока 314
*§ 7. Цепи RC и RL 319
Основные выводы 321
* Приложение. Контур произвольной формы .... 322
Упражнения 323
Задачи 325
ТОМ 2
20. ЭЛЕКТРОМАГНИТНОЕ
ИЗЛУЧЕНИЕ И ВОЛНЫ 341
§ 1. Ток смещения 341
§ 2. Уравнения Максвелла в общем виде .... 343
§ 3. Электромагнитное излучение 344
§ 4. Излучение плоского синусоидального тока. . . 346

ОГЛАВЛЕНИЕ
619
§ 5. Несинусоидальный ток; разложение Фурье. . . 349
§ 6. Бегущие волны 351
§ 7. Перенос энергии волнами 355
Основные выводы 356
Приложение. Вывод волнового уравнения .... 356
Упражнения 358
Задачи 358
21. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ
С ВЕЩЕСТВОМ 360
§ 1. Энергия излучения 360
§ 2. Импульс излучения 362
§ 3. Отражение излучения от хорошего
проводника 364
§ 4. Взаимодействие излучения с диэлектриком. . . 365
§ 5. Показатель преломления 365
§ 6. Электромагнитное излучение в ионизованной
среде 369
§ 7. Поле излучения точечных зарядов 370
Основные выводы 373
Приложение 1. Метод фазовых диаграмм .... 373
Приложение 2. Волновые пакеты и групповая
скорость 374
Упражнения 377
Задачи 378
22. ИНТЕРФЕРЕНЦИЯ ВОЛН 381
§ 1. Стоячие волны 381
§ 2. Интерференция волн, излучаемых двумя
точечными источниками 384
§ 3. Интерференция волн от большого числа
источников 386
§ 4. Дифракционная решетка 388
§ 5. Принцип Гюйгенса 391
§ 6. Дифракция на отдельной щели 392
§ 7. Когерентность и некогерентность 394
Основные выводы 398
Упражнения 398
Задачи 399
23. ОПТИКА 401
§ 1. Голография 401
§ 2. Поляризация света 404
§ 3. Дифракция на круглом отверстии 409
§ 4. Оптические приборы и их разрешающая
способность 410
§ 5. Дифракционное рассеяние 413
§ 6. Геометрическая оптика 416
Основные выводы 419

620 ОГЛАВЛЕНИЕ
Приложение. Закон Брюстера 420
Упражнения 421
Задачи 421
24. ВОЛНОВАЯ ПРИРОДА ВЕЩЕСТВА 424
§ 1. Классическая и современная физика .... 424
§ 2. Фотоэффект 425
§ 3. Эффект Комптона 427
§ 4. Корпускулярно-волновой дуализм 428
§ 5. Великий парадокс 429
§ 6. Дифракция электронов 433
Основные выводы 435
Упражнения 435
Задачи 436
25. КВАНТОВАЯ МЕХАНИКА 438
§ 1. Волновые пакеты 438
§ 2. Принцип неопределенности 439
§ 3. Частица в ящике 444
§ 4. Уравнение Шредингера 447
§ 5. Потенциальные ямы конечной глубины . . . 448
§ 6. Гармонический осциллятор 451
Основные выводы 453
Упражнения 453
Задачи 454
26. АТОМ ВОДОРОДА 456
§ 1. Приближенная теория атома водорода . . . 456
§ 2. Уравнение Шредингера в трех измерениях . . . 457
§ 3. Строгая теория атома водорода 459
§ 4. Орбитальный момент импульса 460
§ 5. Испускание фотонов v. . 465
§ 6. Вынужденное излучение 467
§ 7. Боровская модель атома 469
Основные выводы 471
Упражнения 472
Задачи 473
27. АТОМНАЯ ФИЗИКА 475
§ 1. Принцип запрета Паули 475
§ 2. Многоэлектронные атомы 476
§ 3. Периодическая система элементов 480
§ 4. Рентгеновское излучение 483
§ 5. Связь в молекулах 484
§ 6. Гибридизация 486
Основные выводы 489
Упражнения 489
Задачи 489

ОГЛАВЛЕНИЕ 621
28. КОНДЕНСИРОВАННЫЕ СРЕДЫ 491
§ 1. Типы, связи 491
§ 2. Теория свободных электронов в металлах 494
§ 3. Электропроводность 497
§ 4. Зонная теория твердых тел 499
§ 5. Физика полупроводников 505
§ 6. Сверхтекучесть 511
§ 7. Проникновение сквозь барьер 512
Основные выводы 514
Приложение. Различные применения р-и-перехода
(в радио и телевидении) 515
Упражнения 519
Задачи 519
29. ЯДЕРНАЯ ФИЗИКА 522
§ 1. Размеры ядер 522
§ 2. Фундаментальные силы, действующие между
двумя нуклонами 526
§ 3. Строение тяжелых ядер 530
§ 4. Альфа-распад 534
§ 5. Гамма- и бета-распад 538
§ 6. Деление ядер 539
§ 7. Синтез ядер 542
Основные выводы 545
Упражнения 545
Задачи 546
30. АСТРОФИЗИКА 548
§ 1. Источник энергии звезд 548
§ 2. Гибель звезд 550
§ 3. Черные дыры 551
§ 4. Квантовомеханическое давление 552
§ 5. Белые карлики 553
§ 6. Нейтронные звезды 556
§ 7. Критическая масса черных дыр 559
§ 8. Обзор экспериментальных данных 560
Основные выводы 561
Упражнения 562
Задачи 562
31. ФИЗИКА ЭЛЕМЕНТАРНЫХ
ЧАСТИЦ 564
§ 1. Слабое взаимодействие 565
§ 2. Ускорители частиц высоких энергий .... 568
§ 3. Антивещество 570

622
ОГЛАВЛЕНИЕ
§ 4. Сохранение лептонов 572
§ .5. Адроны 574
§ 6. Кварки 578
§ 7. Несохранение четности 580
§ 8. Сводка законов сохранения 584
§ 9. Проблемы будущего 585
Основные выводы 586
Упражнения 586
Задачи 587
ПРИЛОЖЕНИЕ А 589
Физические константы 589
Некоторые астрономические сведения .... 589
ПРИЛОЖЕНИЕ Б 590
Соотношения между единицами измерения 590
Единицы измерения электрических величин 590
ПРИЛОЖЕНИЕ В 591
Геометрия 591
Тригонометрия 591
Биномиальное разложение 591
Квадратное уравнение 592
Некоторые производные 592
Некоторые неопределенные интегралы (с
точностью до произвольной постоянной) .... 592
Произведения векторов 592
Греческий алфавит 592
ОТВЕТЫ К УПРАЖНЕНИЯМ И ЗАДАЧАМ 593
УКАЗАТЕЛЬ 607

Уважаемый читатель!
Ваши замечания о содержании книги, ее оформлении, качестве
перевода и другие просим присылать по адресу: 129820, Москва,
И-110, ГСП, 1-й Рижский пер., д. 2, изд-во «Мир».

ДЖЕЙ ОРИР
ФИЗИКА
том 2
Научн. редактор А. КУКСЕНКО
Мл. научн. редакторы В. ЦЛАФ, В. АКСЕНОВА
Художник А. ШИПОВ
Художественный редактор Л. БЕЗРУЧЕНКОВ
Технические редакторы Л. ЧУРКИНА, Н. ТОЛСТЯКОВА*
Корректор Н. ЯКОВЛЕВА
И Б № 2755
Сдано в набор 03.12.80.
Подписано к печати 29.09.81.
Формат 70x1001/16.
Бумага офсетная № 1.
Гарнитура Тайме. Печать офсетная.
Объем 9,00 бум. л. Усл. печ. л. 23,40.
Уч.-изд. л. 23,23. Изд. № 2/0979.
Тираж 75000 экз. Зак. 954. Цена 1 р. 80 к.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2.
Можайский полиграфкомбинат Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полифафии и книжной торговли,
г. Можайск, ул. Мира, д. 3.

Постоянная Больцмана к
1,38 • 10"23 Дж/К
Число Авогадро Nc
Элементарный заряд е
mt
т,
Масса электрона
Масса протона
Постоянная Планка
Масса Земли
Масса Луны
Масса Солнца
Расстояние от Земли
до Луны
Радиус Земли R
h
М3
Мс
Электрические
постоянные:
к0=1/(4пе0)
к0 /с2={г0/4л
6,02 • 1023
1,60 • 10"19 Кл
9,1 • Ю-31 кг
1,67 • 10"27
6,63 • 10"34 Дж • с
5.98 • 1024 кг
7,36 1022 кг
1.99 • 1030 кг
3,80 105 км
6,35 • 103 км
9,00 • 109 Н • м2/Кл2
10=7 Н с7Кл2
8,85 10"12 Ф/м