Текст
СПРАВОЧНИК
ПО ПРИКЛАДНОМ
СТАТИСТИКЕ
<
HANDBOOK OF APPLICABLE MATHEMATICS
Chief Editor: Walter Ledermann
Volume VI: Statistics
PART A
Edited by Emlyn Lloyd University of Lancaster
A Wiley-lntersclence Publication
JOHN WILEY & SONS
Ch ichester-New Yor k-Br isbane-Toronto-S i ng<
СПРАВОЧНИК ПО ПРИКЛАДНОЙ СТАТИСТИКЕ
Под редакцией Э. Ллойда, У. Ледермана
ТОМ 1
Перевод с английского под редакцией Ю.Н. Тюрина
(©
МОСКВА "ФИНАНСЫ И СТАТИСТИКА" 1989
ББК 16.2.9
С74
Справочник по прикладной статистике. В 2-х т. Т. 1: Пер. с С74 англ. / Под ред. Э. Ллойда, У. Ледермана, Ю. Н. Тюрина. —М.: Финансы и статистика, 1989.— 510 с.: ил.
ISBN 5-279-00245-3.
В Справочнике освещены основные математико-статистические методы.
Том 1 включает введение в статистику, вопросы, связанные с выборочным распределением, точечным и интервальным оцениванием, общую теорию статистических критериев, дисперсионный анализ, планирование эксперимента.
Для широкой аудитории специалистов, разрабатывающих и использующих статистические методы.
0702000000 —131
010(01)-89
109-89
ББК 16.2.9.
ISBN 5-279-00245-3 (Т. 1, рус.)
ISBN 5-279-00244-5
ISBN 0-471-90274-8 (англ.)
©1984 by John Wiley & Sons Ltd.
© Перевод на русский язык, предисловие, «Финансы и статистика», 1989
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Математизация знания, получившая техническую базу в виде широкого распространения все более совершенных ЭВМ, привела к тому, что математико-статистические методы вошли в жизнь почти каждого специалиста. В связи с этим возникла массовая потребность быстро получать необходимые оценки и расчеты, не углубляясь в вычислительные детали и математические доказательства.
Ведущие издательства мира выпускают в помощь специалистам, имеющим дело с математическим аппаратом, многотомные энциклопедии и различного рода справочники. Каждое такое издание имеет определенные особенности и свой круг читателей. Некоторые издания предназначены в первую очередь для математиков и для использования содержащегося в них материала «внутри математики». Такова, например, вышедшая в нашей стране «Математическая энциклопедия». Другие предназначены для математиков-консультантов, к которым обращаются специалисты других отраслей знания (профессия, лишь недавно ставшая распространенной). Третьи адресованы тем, кто, не считая себя математиком, применяет или хотел бы применять математические методы в своей работе.
В справочной литературе такого рода большое внимание уделяется математической статистике. Количество посвященных ей изданий довольно значительно. Отметим из них лишь 14-томный справочник по статистике «Handbook of Statistics» (Amsterdam: North Holland), шесть томов которого уже вышли в свет, и 9-томную энциклопедию статистических наук «Encyclopedia of Statistical Sciences» (New York: Wiley).
К сожалению, на русском языке аналогичных изданий пока нет. Этот пробел отчасти восполнят готовящаяся издательством «Советская энциклопедия» многотомная энциклопедия по теории вероятностей и математической статистике, а также предлагаемый читателю «Справочник по прикладной статистике» под редакцией Э. Ллойда и У. Ледермана. Он предназначен для широкого круга читателей. Это перевод одного из шести томов, вышедших в серии «Handbook of Applicable Mathematics» издательства Wiley. В состав серии входят также тома, посвященные алгебре (I), теории вероятностей (II), численным методам (III), математическому анализу (IV), геометрии и комбинаторике (V). Справочник по прикладной статистике представляет собой шестой том серии. В русском переводе, как и в оригинале, он выходит в двух томах.
Слово «Applicable» в названии серии употребляется вместо традиционного «Applied», что довольно непривычно. Оно подчеркивает, что речь идет о математике, имеющей приложения за ее пределами. Необычность названия указывает на сугубо практическую направленность излагаемого материала.
В наших программах обучения математике уделяется явно недостаточное внимание статистическому подходу к явлениям природы и общества. Давно назрела необходимость пересмотра этих программ. Владение основами математической статистики нужно каждому экономисту, социологу, инженеру и естествоиспытателю. Функциональные связи, которыми оперируют математики, иногда не проявляются в «чистом виде». Они всегда осложнены случайными погрешностями и обстоятельствами, роль которых нельзя адекватно учесть вне статистического мышления и без соответствующего аппарата. Для студентов же, которые по роду своей профессии будут иметь дело с массовыми явлениями, необходимы не столько математические, сколько математико-статистические знания. Будущие специалисты чаще всего не вспоминают об аналитической геометрии или правилах дифференцирования, но остро чувствуют недостаток статистических знаний. В подобных случаях настоящий Справочник будет служить им надежным руководством.
Среди отечественных работ по математической статистике нет изданий, предназначенных для «пользователя» и по широте охвата проблем сопоставимых со Справочником. Круг затронутых в нем тем включает основные понятия, относящиеся к генеральной совокупности, случайному выбору, распределениям и их параметрам, точечному и интервальному оцениванию, статистическим гипотезам и возможностям их проверки. Отдельно рассматриваются широко применяемые методы оценивания — метод наименьших квадратов, метод наибольшего правдоподобия. В Справочнике обсуждаются также наиболее важные с точки зрения приложений статистические методы и модели: дисперсионный анализ линейных моделей, анализ временных рядов, анализ таблиц сопряженности и т. п. Отдельные главы посвящены важным методическим направлениям (например, последовательному анализу, непараметрическим методам, планированию эксперимента), научным концепциям (байесовскому подходу к статистическому выводу), конкретным приемам (фильтр Калмана и т. п.). В каждой теме авторы выделяют наиболее важное и ограничиваются им.
Справочник содержит большой фактический материал. Он дает возможность познакомиться со многими идеями, методами и правилами математической статистики, обходя утомительные математические доказательства. Работа с ним не требует специальной предварительной подготовки. Достаточно скромных знаний по высшей математике, матричной алгебре и теории вероятностей. Необходим лишь интерес к математической статистике.
Главы Справочника можно читать независимо друг от друга. Неизбежные при принятом в нем способе изложения повторы невелики. Работа с книгой не требует от читателя ежеминутного напряжения, хотя это отнюдь не «легкое чтение».
По характеру изложения материала Справочник под редакцией Э. Ллойда и У. Ледермана близок к широко известным и пользующимся большой популярностью «Справочнику по математике для инженеров и учащихся втузов» И. Н. Бронштейна и К. А. Семендяева (М.: Наука, 1986) и «Справочнику по математике» Г. Корна, Т. Корн (М.: Наука, 1984).
В «Справочник по прикладной статистике» включены только вполне разработанные и устоявшиеся методы. Из-за этого ряд развивающихся направлений математической статистики оказался незатронутым, например устойчивые (робастные) статистические выводы, ранговый статистический анализ, нестандартные модели регрессии, разведочный анализ данных, целенаправленное проектирование и т. д.
Сведения по вопросам, не охваченным Справочником, можно найти в трех книгах М. Дж. Кендалла и А. Стьюарта «Теория распределений» (М.: Наука, 1966), «Статистические выводы и связи» (М.: Наука, 1973), «Многомерный статистический анализ и временные ряды» (М.: Наука, 1976), а также в трехтомной работе С. А. Айвазяна, И. С. Енюкова, Л. Д. Мешалкина, вышедшей в издательстве «Финансы и статистика» (Прикладная статистика: Основы моделирования и первичная обработка данных. 1983; Прикладная статистика: Исследование зависимостей. 1985; Прикладная статистика: Классификация и снижение размерности, 1988).
Дополнительный интерес для читателя представляет то обстоятельство, что настоящий Справочник отражает своеобразие английской школы математической статистики, основы которой заложили Ф. Гальтон, К. Пирсон, Р. Фишер. Этой школе свойственно меньше следовать в русле господствующих идей теории принятия решений, а больше полагаться на здравый смысл и вероятностную интуицию.
Остается сделать несколько технических пояснений.
Материал Справочника условно разделен на шесть категорий: 1) определения; 2) теоремы, предложения, леммы, следствия; 3) уравнения и другие строчные формулы; 4) примеры; 5) рисунки и графики; 6) таблицы. Внутри каждого раздела элементы одной категории нумеруются последовательно. «Адрес» каждой выделенной категории состоит из трех цифр: номера главы, номера раздела и номера элемента (внутри раздела). Например, в разделе 5 гл. 3 мы можем найти строчную формулу (3.5.7), но также и лемму 3.5.7, за которой может последовать теорема 3.5.8. Ссылки заключены в квадратные скобки и содержат сведения о категории. Так, например, могут встретиться указания [см. (3.4.5)], что означает обращение к формуле (3.4.5), и [см. теорему 2.4.6]. Ссылки на другие тома серии «Handbook of Applicable Mathematics» построены по тому же принципу и, кроме того, снабжены номером тома (римская цифра).
7
В конце каждой главы приведена дополнительная литература. Составители Справочника стремились ограничиться немногими книгами и статьями. К этому списку были добавлены некоторые работы на русском языке, в том числе имеющиеся переводы книг, указанных в Справочнике.
Математико-статистические методы используются в самых различных областях. В экономике, например, широко применяется регрессионный анализ; в социологии и медицине проводятся выборочные обследования; все шире внедряются статистический контроль качества продукции, анализ социально-экономических данных с помощью многомерных статистических методов, методы планирования экспериментов в науке и технике.
Специалисты многих отраслей народного хозяйства остро нуждаются в справочных руководствах по прикладной статистике. Поэтому можно надеяться, что настоящий Справочник окажег им существенную практическую помощь.
С. А. Айвазян, Ю. Н. Тюрин
Глава I
ВВЕДЕНИЕ В СТАТИСТИКУ
1.1. СМЫСЛ ПОНЯТИЯ «СТАТИСТИКА»
В Оксфордском словаре английского языка приведено следующее разъяснение термина «статистика»: собранные и классифицированные числовые данные и сведения. Таким образом, можно говорить о статистике образования, финансовой статистике, статистике промышленности и т. д.
В том же словаре дается и другое разъяснение этого термина: в более старой трактовке статистика — один из разделов науки об управлении государством, сбор, классификация и обсуждение сведений о состоянии общества и государства. В настоящее время — наука, изучающая методы сбора и обраоотки фактов и данных, относящихся к человеческой деятельности и природным явлениям.
Итак, устаревшее определение, если его освободить от связи с государством, окажется не слишком отличающимся от современного толкования. Это «современное» определение удивительно старомодно, поскольку в нем не отражен ключевой аспект — интерпретация данных.
Определение, вполне приемлемое для большинства практических работников, можно сфбрмулировать, перефразировав приведенное в Оксфордском словаре: в настоящее время статистика — наука, изучающая методы сбора и интерпретации числовых данных. Здесь интерпретация данных рассматривается как существенный аспект.
Трудно дать краткое и в то же время исчерпывающее определение статистики — дисциплины с такой широкой и разнообразной областью приложения. Однако в первом приближении можно сказать, что главная цель статистики — получение осмысленных заключений из несет засованных (подверженных разбросу) данных.
* А вот определение из БСЭ. «Математическая статистика — раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. При этом статистическими данными называют сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками». (См.: БСЭ. — 3-е изд. — М.: Советская энциклопедия, 1974. — Т. 15. — С. 1428.) — Примеч. ред.
Действительно, исключая тривиальные ситуации, реальные данные всегда являются несогласованными, что требует применения статистических методов. Рассогласованность (разброс) между индивидуальными наблюдениями может быть, например, обусловлена ошибкой, как при считывании позиции указателя, когда он расположен между двумя делениями шкалы прибора. Изменчивость может быть также следствием флуктуаций во внешней среде, как, например, в случае мерцания звезд из-за флуктуаций в атмосфере, или следствием неравномерности работы электронного оборудования при передаче сообщений по радио или телеграфу. (В последнем случае для характеристики ситуации используется термин «шум».) Можно еще привести пример обследования части генеральной совокупности, индивидам которой присуща врожденная изменчивость измеряемой характеристики (например, рост двадцатилетних студентов мужского пола).
Чаще всего ситуация слишком сложна, чтобы ее можно было изучить на основе полного описания, отражающего все детали. Поэтому обычно применяется некоторая математическая модель явления. Она, по замыслу, должна воспроизводить его существенные черты и исключать те, которые предполагаются несущественными. Такая модель использует законы науки, приложимые к рассматриваемой ситуации, и обычно включает в себя детерминистские и стохастические (случайные) элементы. Последние в свою очередь представлены некоторой вероятностной моделью, необходимой для объяснения математической модели и проверки истинности того, что статистические выводы, строго говоря, применимы.
Пример 1.1.1. Молоко и вес детей. Рассмотрим, влияет ли регулярное потребление молока на физическое развитие школьников. Прежде чем попытаться получить ответ, мы должны решить, какое количество молока (полпинты в день?) должно быть взято, за какой период (год?), какого возраста дети (9^,-10 у лет?) и какой аспект
(или аспекты) их физического развития должен быть измерен (их вес?). Простой метод взвешивания детей до и после периода регулярного потребления молока непригоден, так как при этом невозможно отделить приращение веса, обусловленное потреблением молока, от того, которое произошло независимо от его потребления. Чтобы выявить эти составляющие, необходимо сравнить группу детей, находящихся на молочной диете, с контрольной группой детей с обычным режимом питания (который должен быть определен). Для отнесения детей к группе с молочной диетой и к контрольной группе можно было бы применить какой-либо из методов, предполагающих процедуры рандомизации, что позволило бы рассматривать индивидуальные изменения веса как реализации независимых случайных величин [см. II, определение 4.4.1]. В первом приближении, но с достаточной точностью эти изменения веса могли бы рассматриваться как нормально распределенные [см. II, раздел 11.4] со стандартным отклонением о и с математическим ожиданием для группы детей с обычным режи
10
мом питания и д2 для группы детей с молочной диетой. Здесь ци ц2 на — неизвестные параметры. Подходящие приближения для их значений, называемые «оценками», могли бы быть выведены из данных. Исходный вопрос «Ведет ли увеличенное потребление молока к возрастанию веса?» превращается в следующий: «Является ли различие между оценками gi и д2 значимым, т. е. достаточно ли оно велико, чтобы позволить нам учесть случайные эффекты и заключить, что g2 действительно больше, чем и если это так, то сколь значительно и насколько точно оценено различие?».
Это в принципе простой пример, но он иллюстрирует некоторые главные черты статистического вывода. Прежде всего сбор данных должен быть организован так, чтобы выполнялись требования теории вероятностей: обследование должно быть правильно спланировано, и выборочный метод должен соответствовать поставленной цели. Далее характеристики жизни детей, несущественные для исследования, необходимо исключить из рассмотрения. Тогда модель будет основана на упрощающем предположении, что при правильном планировании вариабельность может быть объяснена в терминах выбранного семейства распределений [см. II, гл. 4 и 11]. Выбор такого семейства (нормального в нашем примере) является результатом компромисса между сложностью реальности и простотой, необходимой для получения правильных количественных заключений с наименьшими вычислительными трудностями. Чтобы гарантировать истинность этого выбора, возможно, понадобятся дальнейшие исследования. В рассмотренном примере модель проста: наблюдениями является вес детей, а в качестве исследуемого эффекта взято различие между конечным и исходным весом. В хорошо разработанном эксперименте наблюдения могли бы быть выражены в виде более сложных функций переменных и/или параметров, предлагаемых или необходимых в данной области науки. Некоторые (или все) из этих переменных могли бы рассматриваться как подверженные случайному разбросу, что требует толковать их как случайные переменные. Могли бы быть подобраны подходящие семейства распределений и оценены соответствующие параметры. Затем, как и в вышеприведенном примере, следовала бы процедура, подтверждающая пригодность модели в целом.
Например, наблюдениями могло бы быть количество осадков, измеряемых в 20 соседних городах за каждый из 100 последовательных четвертьчасовых интервалов. Модель, основанная на радиометеорологии, могла бы связать осадки в данном месте как функцию времени с зарождением, ростом, распадом облачных масс. В качестве переменных тогда можно было бы использовать темп зарождения облачности (возможно, как двумерный пуассоновский процесс [см. II, раздел 20.1.7]) и параметры, описывающие форму облаков и скорость их роста и распада.
Пример 1.1.2. Эксперимент по определению смертельной дозы инсектицида. Другой пример, детально описанный в разделе 6.6, связан с оценкой смертности насекомых в зависимости от дозы применяе
11
мого инсектицида. Действие различных доз инсектицида измеряется числом насекомых, погибших после применения соответствующей дозы. При очень низкой дозировке насекомые не погибают, при очень высокой погибают все. В то же время при промежуточных дозах процент погибших насекомых, который подвержен экспериментальному разбросу и зависит от многих факторов, в среднем возрастает с увеличением дозы. Необходимо: а) подобрать правдоподобную параметрическую модель для описания «кривой роста» доли погибших насекомых в зависимости от дозировки; б) оценить параметры этой кривой и проверить, что результирующая кривая действительно является приемлемой моделью; в) получить значение дозировки, при которой погибает 50% насекомых (эта величина будет служить принятой мерой токсичности), вместе с оценкой ее надежности.
Приведенный пример показывает, что нам необходимы методы для получения хороших приближенных значений параметров («оценок»), характеризующих член выбранного семейства вероятностных распределений, а также методы для описания точности этих оценок. Оценка точности должна подсказать, являются ли различия в оценках параметров настолько значимыми, чтобы можно было говорить о различиях между действительными (неизвестными) значениями параметров. Она необходима также для того, чтобы проверить, дает ли избранное семейство распределений приемлемую модель для наблюдаемых данных. Таковы наиболее важные черты статистического вывода. Они детально описаны в последующих главах настоящего Справочника наряду с некоторыми другими подходами, основанными на них. Введение в статистический вывод содержится в работе [Barnett (1982), гл. 1].
1.2. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ, СТАТИСТИКА, ОЦЕНКА
Как было отмечено в разделе 1.1, при статистическом подходе вопросы, относящиеся к реальному миру, превращаются в какой-то мере эквивалентные им вопросы о свойствах вероятностных распределений в принятой статистической модели. Так, влияние молока на вес детей обсуждалось в терминах значения параметра в (или набора параметров) вероятностного распределения, описывающего прирост веса отдельных детей. В исследование было включено конечное число детей, и они, или, точнее, приросты их веса, образуют выборку. Эта выборка, скажем, объема п позволяет получить п единиц данных, а именно индивидуальные приросты веса xif х2.хп. Мы будем полагать, что
выборка — это тот набор данных, который только и доступен статистику. Следовательно, оценка значения неизвестного параметра О (для простоты полагаем, что параметр только один), которую может получить статистик, должна быть вычислена по определенному правилу из выборочных величин хь х2....хп, скажем,
О* = tn (xltx2.хп). (1.2.1)
12
Например, есть веские основания взять в качестве оценки 0* выборочное среднее
(*! 4- Х2 4- ... 4- Хп) / П.
Любая подобная комбинация наблюдаемых значений называется статистикой (итак, это расширяет значение слов «статистика» по сравнению с его нетехническим употреблением, когда оно означало сбор данных или фактов). Статистика — это число, вычисленное по выборке. Если оно используется как оценка величины параметра 0, то статистика должна быть в некотором смысле приближенным значением для 0. Вопрос в том, в каком смысле?
Пытаясь ответить на этот вопрос, мы должны вспомнить, что частное значение статистики, которое нам удалось получить по выборке приростов веса детей, могло бы измениться, если бы мы взяли другую группу детей. Действительно, если вывод, который мы надеемся получить, должен быть использован для более расширенной группы детей, чем та, которая включена в нашу выборку, существенно, чтобы эта выборка была извлечена из этой расширенной группы с помощью метода, включающего элементы случайного выбора. На вопрос о том, является ли наша оценка хорошей, можно ответить в терминах, относящихся к широкому классу оценочных правил (1.2.1), которые возникают в выборочных процедурах.
Пример 1.2.1. Контроль качества в промышленности. Пусть имеется партия из 10000 номинально идентичных изделий. Известно, что некоторые из этих изделий дефектны: их критические размеры лежат вне допустимых границ. Требуется оценить долю (скажем, 0) дефектных изделий в партии на основе результатов точного измерения размеров, проведенного на выборке из 20 изделий, взятых из партии.
Рассмотрим сначала процедуру формирования выборки. Предположим, что она организована следующим образом: 20 изделий должны быть выбраны «случайно», т. е. таким образом, чтобы при каждом акте выбора все изделия в партии имели бы одинаковый шанс быть отобранными. (Этого не всегда легко достигнуть, и практические способы различны в зависимости от объема партии и свойств изделий.) Так как в нашем случае партия очень велика по сравнению с объемом выборки, доля дефектных изделий в ней после извлечения выборки не будет существенно отличаться от исходной доли в. В этих условиях статистические свойства нашей выборки практически неотличимы от свойств выборки, полученной с помощью процедуры «случайного выбора с возвращением» [см. II, раздел 3.6.3]. Следовательно, с приемлемой степенью точности вероятность того, что наша выборка содержит г дефектных изделий, г = 0, 1, 2..19 или 20, определяется
по формуле биномиальной вероятности [см. II, раздел 5.2.2]:
С?) 0" (1 — 0)м’г. (1.2.2)
13
Обратимся теперь к оценке. Критерии для формулирования правил, позволяющих получать «хорошие» оценки, обсуждаются ниже (см. гл. 3); сейчас же мы будем основываться на интуитивном представлении о том, что доля дефектных изделий в выборке кажется разумным приближением к доле дефектных изделий во всей партии. Следовательно, мы принимаем в качестве оценки для 9 число 9*, определенное как
О* = /720, (1.2.3)
где г — число дефектных изделий в выборке (объема 20). Если наблюдаемое значение г = 8, то
9* = 0,40.
Выражение (1.2.3) есть специальный случай (1.2.1); оно дает некоторое правило для получения оценки из выборочных данных. Теперь согласно (1.2.2) значение г в (1.2.3) представляет собой реализацию [см. II, гл. 4] случайной переменной R, распределенной по биномиальному закону Bin (20,0) [см. II, раздел 5.2.2]. Следовательно, 9* есть реализация некоторой случайной величины, скажем Т, где
Т = R/20, (1.2.4)
ее возможные значения —
0,1/20,2/20...19/20,1.
Согласно (1.2.2) ее распределение вероятностей определяется формулой
Р(Т = /720) = P(R/20 = /720) =
= P(R = г)=(“ )9Г(1 — 0)2О Г, г = 0,1.20. (1.2.5)
В этом примере вопрос «Какова доля дефектных изделий в партии?» был заменен вопросом «Каково значение параметра 9 распределения вероятностей (1.2.2)?». Оценка 0*=О,4О рассматривается как реализация случайной величины Т, распределение которой приведено в (1.2.5). Случайную величину, реализацией которой является оценка, будем называть оценивателем (estimator). Соответствующее распределение вероятностей называется выборочным распределением оценки (или оценивателя). (Аналогичный смысл придается выборочному распределению любой статистики независимо от того, может ли она непосредственно использоваться как оценка.)
Приведенные рассуждения наводят на мысль, что вопрос «Является ли 0* хорошей оценкой 0?», можно рассматривать как сокращенную форму другого вопроса: «Высока ли вероятность того, что согласно выборочному распределению 0* его наблюдаемое значение близко к 0?». В примере, который обсуждался выше, мы можем, не-
* В русском языке нет специального названия для этой величины, поэтому здесь мы следуем английскому образцу. — Примеч. ред.
14
Вероятность
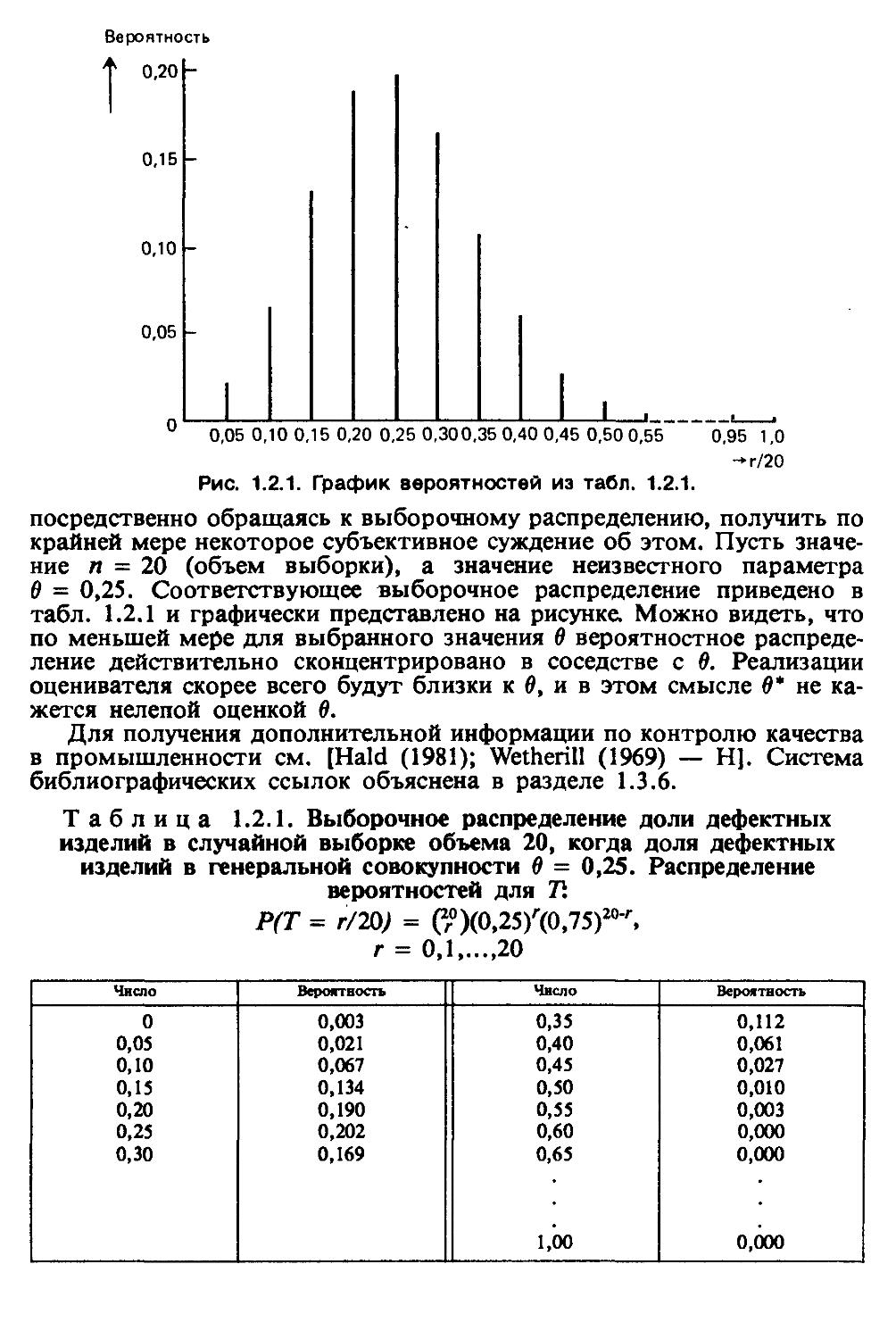
посредственно обращаясь к выборочному распределению, получить по крайней мере некоторое субъективное суждение об этом. Пусть значение п = 20 (объем выборки), а значение неизвестного параметра О = 0,25. Соответствующее выборочное распределение приведено в табл. 1.2.1 и графически представлено на рисунке. Можно видеть, что по меньшей мере для выбранного значения 6 вероятностное распределение действительно сконцентрировано в соседстве с 0. Реализации оценивателя скорее всего будут близки к 6, и в этом смысле О* не кажется нелепой оценкой 6.
Для получения дополнительной информации по контролю качества в промышленности см. [Hald (1981); Wetherill (1969) — HJ. Система библиографических ссылок объяснена в разделе 1.3.6.
Таблица 1.2.1. Выборочное распределение доли дефектных изделий в случайной выборке объема 20, когда доля дефектных изделий в генеральной совокупности 6 = 0,25. Распределение вероятностей для 71
Р(Т = г/20; = (2°)(0,25)г(0,75)20'г»
г = 0,1...20
Число Вероятность Число Вероятность
0 0,003 0,35 0,112
0,05 0,021 0,40 0,061
0,10 0,067 0,45 0,027
0,15 0,134 0,50 0,010
0,20 0,190 0,55 0,003
0,25 0,202 0,60 0,000
0,30 0,169 0,65 0,000
1,00 0,000
1.3. ТЕМА ЭТОЙ КНИГИ
Хотя термин «статистика» значительно шире, чем «прикладная теория вероятностей», концепции и методы статистики тесно связаны с концепциями и методами теории вероятностей. Возможно, идеальным было бы развитие теории вероятностей и статистики как единой интегрированной дисциплины. В серии «Handbook of Applicable Mathematics», однако, было решено посвятить один том (т. И) теории вероятностей и один том (т. VI) статистике. Это не означает, конечно, что том II целиком должен быть изучен перед попыткой обратиться к настоящему тому! Напротив, методы, изложенные здесь, чаще всего понятны читателю и реже требуются лишь отдельные сведения по основам теории вероятностей. Во всех случаях, когда такие сведения необходимы, даются ссылки на соответствующие разделы тома II. Аналогии-ю обсушл дело с ссылками на другие тома серии «Handbook of Applicable Mathematics».
Очевидно, что и теория вероятностей, и статистика имеют свой круг проблем. Одя&ко среди них есть общие для обеих этих дисциплин. Например, в нашем случае вопрос относительно независимости квадратичных форм нормально распределенных случайных величин, который мог бы прекрасно вписаться в том, посвященный теории вероятностей, в действительности был признан как имеющий большой интерес для статистики и рассмотрел в настоящем Справочнике. То же относится к центральным распределениям (см. раздел 2.8).
Тематика, охваченная Справочником, кратко представлена в разделах 1.3.1—1.3.5, в то время как в разделе 1.3.6 перечислены некоторые проблемы, не рассмотренные здесь.
Прежде чем приступить к краткому описанию содержания, необходимо сказать несколько слов о порядке изложения материала.
Одна из основных целей серии «Handbook of Applicable Mathematics» состоит в том, чтобы предоставить читателю удобный подбор математических процедур и результатов. Казалось бы, расположение материала в алфавитном порядке, как в энциклопедии, наилучшим образом соответствовало бы указанной цели. Однако такой порядок привел бы к большому числу довольно коротких и сильно взаимосвязанных разделов. Принимая в расчет частично упорядоченную структуру математики, издатели считают, что группирование материала в однородные по содержанию главы больше отвечает поставленной цели: это обеспечивает бблыпую непрерывность и осмысленность изложения, как в традиционных учебных курсах, а благодаря развитой системе перекрестных ссылок сохраняет и преимущество энциклопедии. Однако поскольку эта книга не является учебным пособием, расположение материала в ней достаточно произвольно, ссылки даются как на более поздние главы, так и на более ранние. В частности, гл. 2 содержит материал, относящийся к выборочным распределениям, которые связаны с тематикой, рассмотренной позднее. Каждая из других глав
16
представляет какую-либо одну важную тему. В одном или двух случаях было признано удобным разделить материал, относящийся к одной, главной, теме, на две главы.
Теперь рассмотрим кратко содержание Справочника.
1.3.1. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ. МЕТОДЫ, СВОБОДНЫЕ ОТ РАСПРЕДЕЛЕНИЯ
Статистик должен получить свои выводы, используя наличную выборку. Каждое наблюдение является реализацией случайной величины. Известно множество значений, которые может принимать случайная величина; некоторые из них имеют ббльшую вероятность появления, чем другие. Значение, которое наблюдалось, представляет собой реализацию. Вероятности возможных реализаций характеризуются распределением вероятностей случайной величины. В исключительных случаях вероятность реализации может быть указана в виде числа, определяемого из распределения вероятностей. Но обычно функции распределения вероятностей бывают заданы с точностью до одного-двух параметров, значения которых не известны. Это приводит к проблеме поиска таких комбинаций выборочных значений, которые бы давали наилучшее приближение для неизвестных параметров. Каждая такая комбинация есть статистика, и, как и любое наблюдаемое значение, статистика представляет собой реализацию некоторой случайной величины. Если х2 и х3 — независимые наблюдения из распределения Ы(д,а) с математическим ожиданием д и стандартным отклонением а (это параметры семейства нормальных распределений), то мы можем рассматривать Xi как реализацию случайной величины Xit х2 — как реализацию случайной величины Х2 и х3 — как реализацию Х3, где Х\, Х2 и Х3 — независимые случайные величины, распределенные согласно N (д, а). Мы можем назвать Xt случайной величиной, индуцированной хх, Х2 — индуцированной х2 и Х3 — индуцированной х3. Статистика х = (xt +х2+х3)/3, так называемое выборочное среднее, есть реализация случайной величины X = (Xi+X2+X3)/3, которая может рассматриваться как индуцированная х. Из свойств нормального распределения [см. II, раздел 11.4.5] следует, что распределение вероятностей для индуцированной случайной величины X есть Ы(д,(т/73). Это — выборочное распределение статистики х, которое с точностью до д и а позволяет судить о вероятностях различных значений реализаций X (конечно, одно из них есть значение статистики х, полученное по нашей выборке). В частности, соответствующая плотность вероятностей достигает максимального значения при д, и поэтому х представляет собой разумную оценку для д. С помощью выборочного распределения можно также получить и вероятность того, что наше значение х расположено от д на расстоянии, большем, чем заданное (в масштабе о).
Итак, выборочное распределение статистики позволяет судить, может ли предложенная статистика служить оценкой интересующего нас параметра.
(Здесь, как и всюду в книге, мы использовали соглашение об обозначениях, согласно которому случайные переменные обозначаются прописными латинскими буквами (например , X), а реализации этой случайной переменной — строчными латинскими буквами (например, X, ИЛИ Xi, ИЛИ А';).)
Выборочное распределение, таким образом, весьма важно. Поэтому в книге выделена глава, где сосредоточена информация о выборочных распределениях статистик, имеющих большое значение для практики.
Однако статистические процедуры, которые сильно зависят от выборочных распределений, могут быть подвергнуты критике, поскольку выборочные распределения статистик зависят от предположений относительно распределений, лежащих в основе самой вероятностной модели. Если эти предположения не выполнены, то конструкция в целом нарушается. На практике наиболее широко используемые процедуры являются устойчивыми (робастными), т. е. сравнительно нечувствительны к тем отклонениям от вероятностной модели, которые не выходят за пределы разумно допустимых.
Ясно, что наиболее устойчивыми среди всех процедур будут такие (если они существуют), которые эффективны без каких-либо предположений о распределении. Такие процедуры в самом деле существуют и называются свободными от распределения (или непараметрическими). Эти методы рассмотрены в гл. 14.
1.3.2. ОЦЕНКИ, ТЕСТЫ, РЕШЕНИЯ
Обманчиво короткий заголовок этого раздела соответствует тому, что в действительности составляет большую часть данной книги.
Проблема оценивания была схематично описана в разделе 1.3.1. Гл. 3 расширяет это описание и подводит к систематическому подходу, позволяющему находить хорошие оценки. В ней рассмотрены и графические методы представления информации, содержащейся в выборке, а также некоторые формальные критерии, например, оценка параметра должна иметь ту же физическую размерность, что и оцениваемый параметр, оценка должна быть связана с интересующим нас параметром, а нс с другими параметрами, оценка должна иметь возможно меньшую вариабельность (измеренную ее стандартным отклонением).
Оказывается, что в некоторых случаях можно сконцентрировать всю информацию относительно некоторого параметра, содержащуюся в выборке, в одной («достаточной») статистике. Эта концепция также обсуждается в гл. 3, в конце которой есть и короткий раздел, посвященный практическим приемам конструирования оценок, имеющих желательные свойства.
Ясно, что разумная процедура оценивания не должна ограничиваться лишь выбором приближенного численного значения для неизвестного параметра; она должна что-то говорить и о надежности этого приб-18
лижения. Хотя эти два аспекта единой проблемы оценивания тесно связаны, иногда удобно обсуждать их отдельно. Соответственно мы говорим о точечном оценивании и об интервальном оценивании. Гл. 4 в основном посвящена интервальному оцениванию. В ней рассматриваются: а) «доверительные интервалы», связанные с поведением статистик в повторных выборках, теория которых сильно зависит от выборочных распределений; б) правдоподобные интервалы, один из аспектов функции правдоподобия, которая позволяет среди всех возможных значений параметра выделить правдоподобные с учетом имеющихся данных (выборки); в) байесовские интервалы, сконструированные на основе подхода, при котором выборка рассматривается как средство для изменения и уточнения априорной информации, имеющейся в наличии до получения выборки (этот подход подробно обсуждается в гл. 15).
Поскольку в целом статистика как научная дисциплина основана на идее случайной изменчивости, каждая оценка подвержена ошибке; если получены две различные оценки параметра — одна при одном наборе условий, а другая при другом, — непосредственно не ясно, соответствует ли имеющееся между ними различие различию между параметрами. Например, параметром может быть вероятность определенного заболевания при приеме препарата А (одно условие) или препарата В (другое условие). Вопрос об их различии решается с помощью статистического критерия (теста) или критерия значимости; эта процедура описана в гл. 5.
Один из подходов к статистическим критериям (проверке гипотез) связан с именем Р. А. Фишера [см. Box (1978) — D], который рассматривает проверку гипотезы как пробный шаг в проведении научного исследования, позволяющий получить ученому объективный критерий, с помощью которого можно судить об истинности гипотезы. Другой подход связан в основном с именами Дж. Неймана и Э. Пирсона, которые рассматривают процедуру проверки гипотезы как правило, с помощью которого должен быть сделан выбор между одним способом действия и другим либо принято решение об истинности одной гипотезы в противовес другой. В обычной статистической практике реальные процедуры при этих двух подходах не очень различаются. Сравнительно недавно теория принятия решений стала самостоятельной дисциплиной, задачей которой является анализ потерь и выигрышей при принятии неправильных и правильных решений. Достижения этой дисциплины важны и полезны в теории оценивания, проверке статистических гипотез и в других областях. Эти вопросы обсуждаются в гл. 19.
Одна из частных проблем теории проверки статистических гипотез — оценка пригодности вероятностной модели, предложенной для объяснения данных. С достаточным основанием можно предположить, что некоторая последовательность нерегулярно возникающих событий (например, отсчетов счетчика Гейгера) представляет собой пуассоновский процесс (см. II, раздел 20.1). После того как интересующий нас
19
параметр оценен по имеющимся данным, возникает вопрос, насколько предложенная модель соответствует выборке. Являются ли выборочные значения действительно близкими к тем, которые можно ожидать, используя подогнанную модель? Наиболее широко применяемая для решения подобного вопроса процедура позволяет вычислить некоторую статистику, введенную Карлом Пирсоном, и воспользоваться критерием, основанным на ее выборочном распределении. Это пирсо-новский критерий согласия хи-квадрат (х2), описанный в гл. 7.
Существуют различные методы конструирования «точечных» оценок и определения их надежности. Наиболее полезен из них метод максимального правдоподобия, который обсуждается в гл. 6. Там же приведены и примеры его применения. Другой известный метод, который может рассматриваться либо как специальный случай метода максимального правдоподобия, либо как независимая процедура подгонки, — метод наименьших квадратов. Этот метод и более или менее систематизированный набор правил для проверки статистических гипотез (все это называется дисперсионным анализом или сокращенно ANOVA) описаны в гл. 8.
Те методы оценивания и проверки гипотез, о которых говорилось выше, предназначены для данных, представленных «фиксированной» выборкой. Это значит, что сначала была завершена процедура выбора, а затем ее результаты были подвергнуты обработке. В некоторых ситуациях порции данных поступают последовательно. Для подобных выборочных процедур разработаны специальные методы проверки гипотез. В этих методах доказательства в пользу интересующей нас гипотезы или против нее накапливаются одновременно с ростом выборки до тех пор, пока они не станут убедительными. Тогда выборочная процедура прерывается. Такие процедуры проверки гипотез называются последовательными. Они рассматриваются в гл. 13.
Сельское хозяйство, пожалуй, в наиболее сильной степени подвержено влиянию природной изменчивости. По этой причине в ранний период своего развития сельскохозяйственная наука встретилась с большими трудностями при сравнении различных сортов семян и удобрений. Важнейшая роль сельского хозяйства, немалая стоимость и большая продолжительность полевых исследований требуют эффективного планирования действий. Это обусловило развитие планирования сравнительных экспериментов, науки (или искусства), не ограниченной теперь только сельским хозяйством.
В гл. 9 дано введение в эту обширную дисциплину, а гл. 10 посвящена методам анализа данных, получаемых в результате таких экспериментов. Эти методы основаны на линейной модели, в которой предполагается, что отклик системы (например, урожай пшеницы) в зависимости от имеющихся стимулов (например, количества удобрения) представляет собой линейную функцию. Концепция линейности может быть, впрочем, успешно расширена до более сложных моделей, нелинейных, как в большинстве случаев применения дисперсионного анализа. Например, токсичность некоторых лекарственных пре-20
паратов является нулевой, если их доза не превышает пороговой величины; затем токсичность возрастает с увеличением дозы, сначала медленно, затем быстрее, потом снова медленнее. Прирост токсичности сходит на нет при приближении к стопроцентной смертельной дозе (см. пример 1.1.2). Иногда говорят, что кривая отклика, измеряющая при установленной дозе процент погибших в эксперименте животных, имеет S-образную форму. Можно найти преобразование, которое переводит ее в прямую линию. Так несколько неожиданно мы приходим к линейной модели, для которой может быть применен метод наименьших квадратов (усложненный, однако, различием в разбросе откликов).
Такое обобщение линейной модели обсуждается в гл. 11 и 12.
1.3.3. БАЙЕСОВСКИЙ ВЫВОД
Мы уже упоминали байесовскую статистику, названную так в честь английского математика 18-го столетия Р. Томаса Байеса [см. Pearson and Kendall (1970) — D]. Если говорить просто, при байесовском подходе параметр, который должен быть оценен, рассматривают как случайную величину. В этом случае его свойства следует описывать в терминах распределения вероятностей.
При выборочном контроле в промышленности, обсуждавшемся в примере 1.2.1, доля дефектных изделий в партии оценивалась с помощью значения некоторой статистики, основанной только на выборке из этой партии. Предположим теперь, что данная партия сама представляет собой одну из множества партий, относительно которых опытным путем установлено, что доля дефектных изделий в них (0) независимо изменяется от одной партии к другой известным образом: например, в 3% партий доля дефектных изделий 0 = 0,01, в 5% 0 = 0,025 и т. д. Значение 0 для исследуемой выборки можно рассматривать как реализацию некоторой случайной величины с известным (априорным) распределением вероятностей. Используя теорему Байеса [см. II, раздел 16.10], можно скомбинировать выборочную величину с априорным распределением, чтобы улучшить вероятностные характеристики оценки (ее апостериорное распределение). Это уменьшает неопределенность вывода о значении 0 для данной партии.
При «новейшем байесовском подходе» к статистическому выводу учитывают то обстоятельство, что всегда имеется некоторая априорная информация о неизвестном параметре, возможно, менее точная, чем в случае, описанном выше, но все же достаточная для получения априорного распределения, из которого конструируется апостериорное. Эти проблемы обсуждаются в гл. 15.
1.3.4. МНОГОМЕРНЫЙ АНАЛИЗ
Только в простейших ситуациях статистик имеет дело с единственной случайной величиной. Обычно каждый объект из выборки может
быть подвергнут нескольким различным измерениям, например, можно измерить рост, обхват талии, вес человека. В этом случае статистика интересует, ведут ли себя компоненты вектора наблюдений независимо друг от друга; если нет, то как можно описать их совместное поведение; являются ли некоторые из компонентов более информативными для разделения на классы и т. д. Классический подход к решению подобных задач обсуждается в гл. 17. В гл. 18 приведен обзор современного состояния этих проблем.
1.3.5. ВРЕМЕННЫЕ РЯДЫ
Последняя тема, которой мы коснемся в этом описании разделов статистики, охваченных книгой, связана с анализом последовательности наблюдений (каждое из них подвержено случайному разбросу), порождаемых источником, который сам изменяется, развивается или флуктуирует. Такими наблюдениями могут быть, например, ежедневные измерения уровня воды в Темзе на Марлоу, еженедельное количество дождевых осадков в Сан-Франциско, ежечасные замеры концентрации определенного химиката в камере повышенного давления для какого-нибудь химического процесса, ежемесячная статистика дорожно-транспортных происшествий и т. д. Вариации в данных представляют собой смесь в неизвестных пропорциях закономерных колебаний (таких, как, например, чистый синусоидальный сезонный эффект) с флуктуациями, подчиненными некоторому (неизвестному и, возможно, изменяющемуся во времени) рапределению вероятностей. Поведение системы в момент времени t может зависеть от ее поведения в более ранние моменты t—1, t—2, ... Целью изучения такой системы обычно служит предсказание (прогноз) ее поведения.
Теория временных рядов рассматривается в гл. 18. Важный мегод, известный как фильтр Калмана, описан в гл. 20.
1.3.6. БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ
Родственные темы в книге связаны системой перекрестных ссылок. Используются также ссылки на другие тома серии «Handbook of Applicable Mathematics». Отсылки за пределы Справочника организованы по-разному: внутри глав и для тома в целом.
Список книг (литература для дальнейшего чтения) для конкретной главы приведен в конце ее. Это позволяет получить дополнительную информацию. В тексте ссылки на эти работы выглядят так: [см. Barnett (1982), гл. 1].
В т. 2 Справочника приведен общий для обоих его томов список литературы. Он разбит на разделы: А — библиография; В — словари, энциклопедии, справочники; С — общие работы, охватывающие широкий круг вопросов; D — исторические и библиографические материалы; Е — руководства по статистическим таблицам; F — таблицы
22
случайных чисел, подчиненных конкретным распределениям; G — таблицы статистических функций; Н — специальные темы, не рассмотренные или кратко изложенные в Справочнике. Ссылки на эти источники в тексте обозначены так: [см. Kendall and Buckland (1971) — В].
1.3.7. ПРИЛОЖЕНИЕ: СТАТИСТИЧЕСКИЕ ТАБЛИЦЫ
Серьезное статистическое исследование предполагает интенсивное использование таблиц [см. список литературы, раздел GJ. Однако во многих случаях читатель обнаружит, что будет достаточным небольшое собрание таблиц в приложении. Это таблицы биномиального, пуассоновского, нормального распределений, распределения Стьюдента и распределения хи-квадрат, 5000 случайных цифр, 500 чисел, распределенных по стандартному нормальному закону, и диаграммы для определения доверительных интервалов параметров биномиального и пуассоновского законов.
1.3.8. ТЕМЫ, НЕ РАССМОТРЕННЫЕ В СПРАВОЧНИКЕ
Идеальная книга по статистике должна содержать сбалансированное описание теории и практики с охватом всех аспектов предмета. Она должна быть понятна читателям и иметь умеренный объем. Издатели считают, что этот идеал не был достигнут: в частности, некоторым темам отведено слишком много места, другим слишком мало, а иные не рассмотрены вовсе. Главный акцент в Справочнике сделан на интерпретацию данных. Практическим деталям сбора данных уделено меньше внимания: краткое введение в планирование сравнительных экспериментов содержится в гл. 9. Для получения более подробной информации о планировании, скажем, выборочных обследований, читатель должен обратиться к списку литературы [см. Arkin (1963); Barnett (1974); Cochran (1963); Deming (1950); Hanson, Hurwitz and Madow (1953); Stuart (1976); Yates (1960) — Н].
Другие темы постигла та же судьба либо потому, что они были сочтены слишком специальными, либо из-за близости их к границам рассматриваемой области, либо потому, что они являются предметом будущих публикаций в серии «Handbook of Applicable Mathematics». Сюда относятся основания и общие принципы нечеткого вывода, приложения математического программирования и методов оптимизации в статистике, анализ специальных типов данных, таких, как направленные данные или экстремальные значения, использование и возможности пакетов статистических программ, статистическое моделирование и метод Монте-Карло, выборочный контроль в промышленности и контроль качества. Работы, посвященные этим проблемам, можно найти в разделе Н списка литературы.
23
1.4. СОГЛАШЕНИЯ И ОБОЗНАЧЕНИЯ
Мы завершаем эту главу замечаниями, касающимися обозначений и других соглашений, которые используются в Справочнике. Некоторые из них стандартны, другие же требуют пояснения.
1.4.1. МАТЕМАТИЧЕСКИЕ СОГЛАШЕНИЯ
Логарифм: если не оговорено другое, log х всегда означает In х, т. е. loge х, натуральный логарифм, логарифм по основанию е.
Символ принадлежности к множеству: € : ^означает, что х — элемент множества (набора класса) Л [см. I, раздел 1.1].
Символ О', мы часто имеем дело со статистиками [см. определение 2.1.1], скажем tn, определенными по выборке объема п, некоторые свойства которой могут быть выражены в виде hn + en, где hn — некоторая функция, а еп — ошибка, которая изчезает с ростом п. Выражение еп = О(1тх), например, означает, что еп имеет тот же порядок, что и л'1, т. е. еп для больших значений п ведет себя, приблизительно как ап' для некоторой константы а. Аналогичный смысл имеет выражение О(п {/2) и т. д. [см. IV, определение 2.3.3].
1.4.2. СТАТИСТИЧЕСКИЕ И ВЕРОЯТНОСТНЫЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
1. Сокращения
ф. р. — (кумулятивная) функция распределения [см. II, разделы 4.3.2, 10.3].
distr ( ) — распределение ( ), как в distr (X) = distr (У), означает, что X и Y имеют общее распределение.
с. с. — степени свободы [см. раздел 2.5.4].
н. о. р. — независимые и одинаково распределенные, как в н. о. р. величины Xi, Х2,..., Хп.
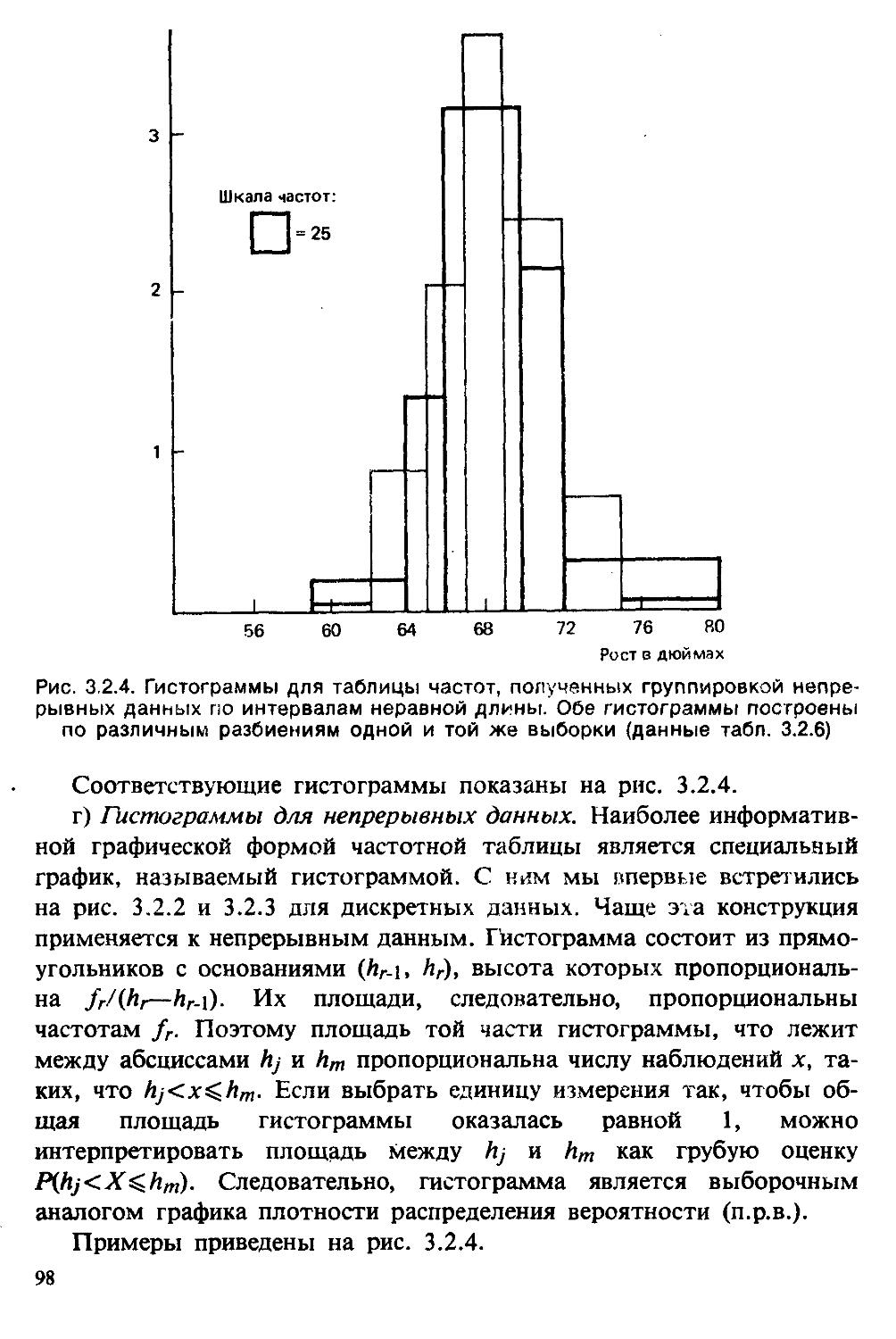
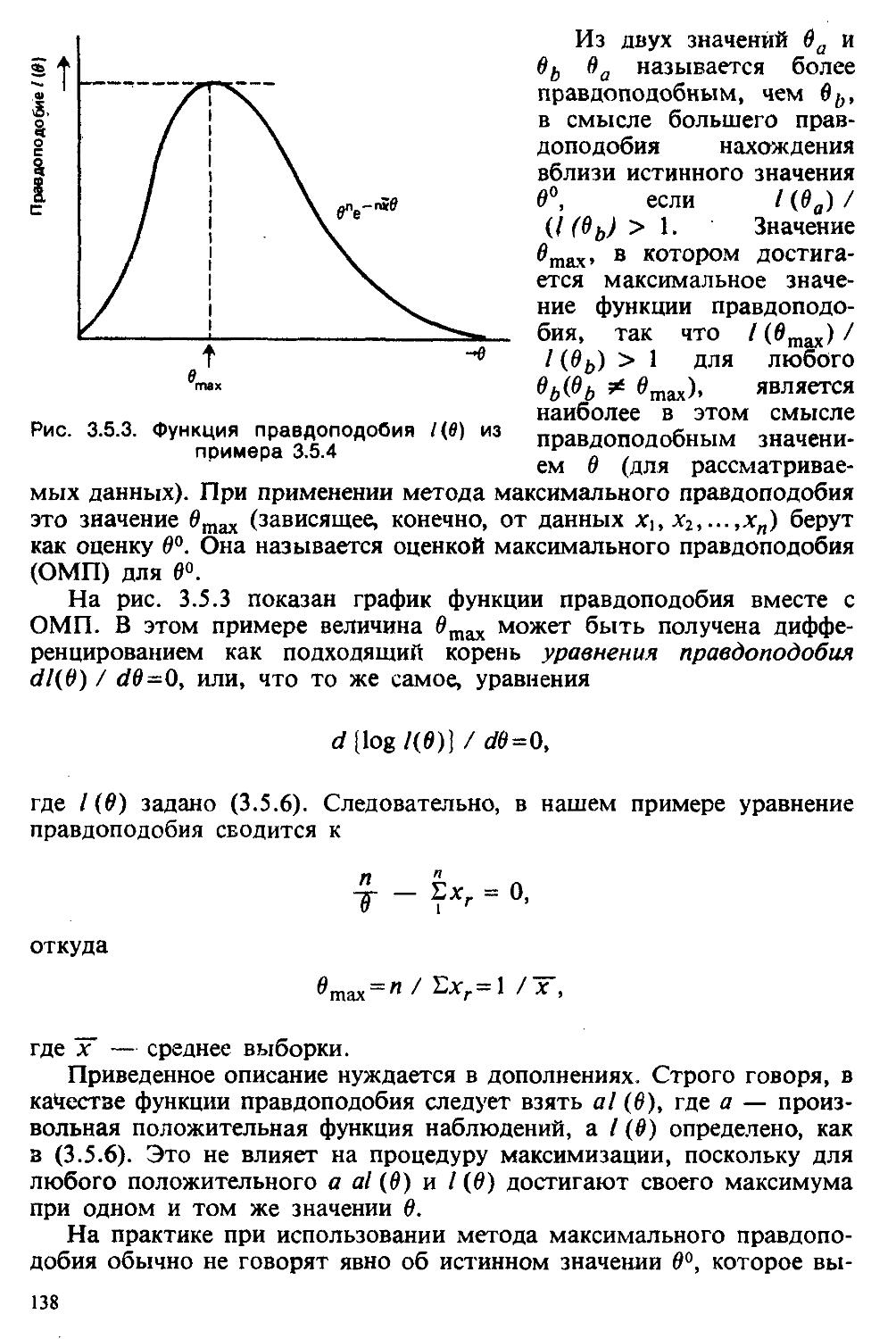
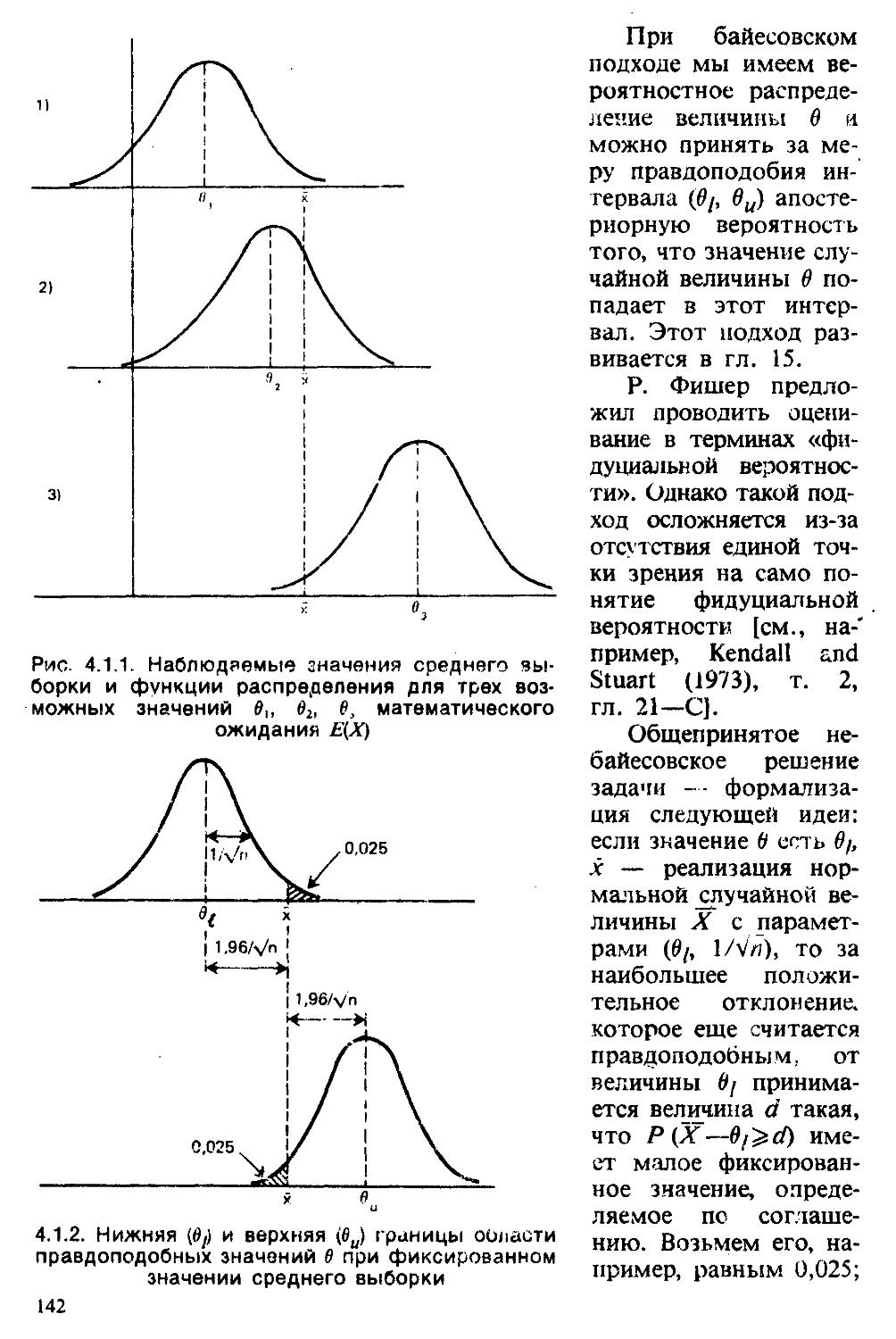
п. р. в. — функция плотности распределения вероятности, называемая также функцией частот. В этой книге мы используем выражение п. р. в. как для дискретных, так и для непрерывных распределений. Те, кто возражает против термина «плотность» для дискретного распределения, может интерпретировать п. р. в. как точечную (point) функцию распределения [см. II, разделы 4.3.1, 10.1].
с. в. — случайная величина, с. п. — случайная переменная [см. II, гл. 4].
~ (тильда) — распределено как. Итак, %~N(^,ct) означает, что распределение X есть нормальное с параметрами ц и ст. Некоторые читатели могут быть настроены против этого обозначения, потому что тильда используется в других разделах математики, например, для обозначения отношения эквивалентности [см. I, раздел 1.3.3], а также асимптотической эквивалентности [см. IV, определение 2.3.2]. Для других же удобство такого обозначения перевешивает возражения.
24
2. Обозначения стандартных распределений
Bernoulli (0) — распределение Бернулли с параметром (вероятностью) успеха 0, т. е. распределение с.в. R с п.р,в.
P(R = г) = 0Г(7—0)’“г, г = 0,1
[см. И, раздел 5.2.1].
Bin (п,0) — распределение с.в. R, для которой
P(R = г) = (”)0Г(7—0)л'г, г = 0,1.п
[см. II, раздел 5.2.2].
Gamma (а,0) — распределение с.в. X с п.р.в.
[х^Лех^]/^Г{а\ х>0.
Здесь а называют параметром масштаба, а 0 — параметром формы [см. II, раздел 11.3.1].
MVN — многомерное нормальное распределение [см. И, раздел 13.4].
N (д,а) — нормальное распределение с ожидаемым значением д и стандартным отклонением а. (Дисперсия есть а2. Некоторые авторы используют поэтому обозначения Normal (д.о3) или N (g,<?).) [См. И, И.4.]
Poisson (0) — распределение с.в. R, для которой
P(R = г) = ев07г!, г = 0,1,...
[см. II, раздел 5.4].
Uniform (a,b) — распределение с.в. X с п.р.в., задаваемой для каждого х как
f(x) =
г 1/(Ь—а), а^х^Ь; -
0 в противном случае
[см. И, раздел 10.7.1].
3. Соглашение об использовании прописных букв для обозначения случайных величин
Мы будем придерживаться следующей системы обозначений: прописные латинские буквы обозначают случайные переменные, а соответствующие строчные латинские буквы — их реализации (наблюденные значения). Итак, мы говорим о совокупности (хь х2,..., хп) наблюдений над с.в. X. В то же время иногда допустимы отклонения от этого правила, например использование F как имени соответствующего распределения.
Строгая приверженность к соглашениям — признак педантичности, и профессиональные статистики не всегда беспокоятся по этому поводу. Однако учащимся и тем, кто еще не стал специалистом, мы рекомендуем их придерживаться.
25
4. Обозначения для моментов и связанных с ними величин
Мы используем символ Е(Х) для обозначения математического ожидания (ожидаемого значения) или с.в. [см. II, гл.8]. Применяются также варианты Е, 8. Наше сокращение для дисперсии X есть var (АЭ; широко используются также символы V(x) и D(X). Для стандартного отклонения X мы используем s. d. (X), для ковариации X и Y — cov(X, У), для коэффициента корреляции между X и Y — согг (X, У), а для асимметрии X — skew (X) [см. II., гл. 9].
5. Нестандартные обозначения: индуцированные случайные величины, статистические копии
Совокупность взаимно независимых наблюдений х2,...,хп случайной величины X (т.е. выборку) можно рассматривать и как совокупность, составленную из наблюдения xt над некоторой случайной величиной Xit наблюдения х2 над некоторой случайной величиной Х2 и т.д., где Xi, Х2.Хп считаются статистическими копиями X. Это
значит, что они независимы и распределены одинаково, так же как распределена случайная величина X:
distr (Xj) = distr (Д')» j ~ 1,2,...и.
Утверждение «х есть реализация ( = наблюденное значение) X» может быть обращено. Итак, «X есть случайная величина, индуцированная х» означает, что выборочное распределение [см. гл. 2} х есть distr (АЭ« Так, статистика ~х = / п (среднее значение выборки),
которая принимает некоторое определенное численное значение для данной выборки, имеет выборочное распределение, которое может быть получено с помощью стандартных процедур из общего распределения Xj, а случайная величина, вероятностное распределение которой совпадает с этим выборочным распределением, является случайной величиной, индуцированной х~. Естественно обозначить ее символом X = i,Xj / п, где Хи X2t...,Xn — статистические копии X.
Говорить о выборочном распределении некоторой статистики, имея в виду вероятностное распределение соответствующей индуцированной случайной величины, столь же педантично по отношению к сказанному выше, сколь и использование различий в обозначениях между случайной величиной X и ее реализацией х\ в обоих случаях целью является ясность изложения.
6. Два смысла обозначения Р(А\К)'. вероятность А при условии К
Один смысл «Р(А\В)у> есть «условная вероятность предложения (события) А при условии, что предложение В истинно» [см. II, раздел 6.5]. Тогда Р(А\В) = Р(А пВ) / Р(В); обе вероятности Р(А) и Р(В) имеют смысл.
Однако мы часто используем Р(А\Н) в смысле «вероятность предложения А, вычисленная в предположениях Н», обычно сокращая это до «вероятность А при Н», где Н является гипотезой. Например, пусть А — предложение Х>х0, а X — нормально распределенная случайная величина N (д,1), где значение ц неизвестно и Н есть гипотеза, что д = 0.
26
Еще одна неоднозначность возникает при использовании выражений P(N = л|0) или ф(п|р), где N— случайная величина, распределение которой зависит от неизвестного параметра 0, a P(N = и|0) означает вероятность получить значение п в качестве наблюдения. Эта выроят-ность зависит от параметра 0. То же относится и к выражениям E(N]0) и т.д. На практике обычно ясно из контекста, какой смысл подразумевается.
7. Номенклатура для табличных значений: процентные точки
В статистической практике часто необходимы таблицы функций различных вероятностных распределений. Для некоторых наиболее употребительных распределений доступны таблицы, которые можно назвать прямыми. Например, в приложении 3 приведена обычная таблица функции Ф(ц), стандартного нормального интеграла (стандартной функции нормального распределения), а в приложении 5 — аналогичная таблица для функции распределения Стьюдента. Однако с целью экономии места таблицы даны в обратной форме. Так, для стандартного нормального распределения таблицы обратной формы содержат значения и в зависимости от Ф (вместо Ф(и) в зависимости от и), т.е. дается значение иа, такое, что 1—Ф(иа) = а, как, например, в приложении 4.
Для случайной величины Z значение такое, что
P(Z>za) = а
называют верхней ХЮа-процентной точкой распределенйя Z; величину такую что
P(Zcr3) = называют нижней процентной точкой; при этом
Ь = Zl~0-
Выражение «процентные точки» без уточнения «верхние» или «нижние» обычно означает «верхние процентные точки».
Процентные точки используются, например, в наиболее доступных таблицах распределения Стьюдента (но не в приведенных в Справочнике), а также в таблицах х2- и P-распределений [см. приложения 6,7].
Нижние процентные точки иногда называют квантилями (фракти-лями). Специальный случай — нижний и верхний квартили, которые являются соответственно 25%-ным и 75%-ным квантилями; медиана же есть 50%-ная точка.
1.5. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Соответствующие справочники и статистические энциклопедии приведены в разделе В списка литературы, учебные пособия — в разделе С, из них особый интерес представляет работа [Barnett (1982)]. Работы по истории вопроса можно найти в разделе D.
27
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Основы моделирования и первичная обработка данных. — М.: Финансы и статистика, 1983. — 471 с.
Айвазян С. А., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Исследование зависимостей. — М.: Финансы и статистика, 1985. — 487 с.
Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: Классификация и снижение размерности. — М.: Финансы и статистика, 1988. — 607 с.
Бикел П., Доксам К. Математическая статистика. Вып. 1 / Пер. с англ. — М.: Финансы и статистика, 1983. — 278 с.
Бикел П., Доксам К. Математическая статистика. Вып. 2 / Пер. с англ. — М.: Финансы и статистика, 1983. — 254 с.
Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы обработки данных / Пер. с англ.; Под ред. Э. К. Лецкого. —М.: Мир, 1980. — 510 с.
Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке: Методы планирования эксперимента / Пер. с англ.; Под ред. Э. К. Лецкого, Е. В. Марковой. — М.: Мир, 1981. — 516 с.
Закс Л. Статистическое оценивание / Пер. с нем.; Под ред. Ю. П. Адлера, В. Г. Горского. — М.: Статистика, 1976. — 598 с.
Кендалл М., Стьюарт А. Теория распределений / Пер. с англ.; Под ред. А. Н. Колмогорова. — М.: Наука, 1966. — 587 с.
Кендалл М.,Стьюарт А. Статистические выводы и связи / Пер. с англ.; Под ред. А. Н. Колмогорова. — М.: Наука, 1973. — 899 с.
Кендалл М.,Стьюарт А. Многомерный статистический анализ и временные ряды / Пер. с англ.; Под ред. А. Н. Колмогорова, Ю. В. Прохорова. — М.: Наука, 1976. — 736 с.
Химмельблау Д. Анализ процессов статистическими методами / Пер. с англ.; Под ред. В. Г. Горского. — М.: Мир, 1973. — 957 с.
Глава 2
ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
2.1. МОМЕНТЫ И ДРУГИЕ СТАТИСТИКИ
2.1.1. СТАТИСТИКА
Как уже объяснялось в гл. 1, если мы стремимся описать изменчивые и неопределенные черты природы, то разумно это сделать, пользуясь понятиями случайной величины и ее распределений вероятностей (см. II, гл. 4). При этом обычно постулируется, что эти распределения должны принадлежать к определенным семействам, предполагаемым в явном виде или подразумеваемым. Тогда одной из целей статистического исследования будет выделение того члена заданного семейства рассматриваемого распределения, с которым мы имеем дело, исключение (по крайней мере, условное) некоторых возможных членов в семействе или отрицание либо подтверждение принадлежности к постулированному семейству в целом. Эти цели могут быть достигнуты в результате проведения соответствующего анализа доступных данных. Оказывается, что основную роль в анализе играют комбинации величин, получаемых из имеющихся данных, каждая из которых называется статистикой. Эти комбинации, заслуживающие отдельного рассмотрения, зависят от природы распределений вероятностей, включенных в анализ, а также от характера выводов, которые пытаются получить.
Пример 2.1.1. Выборочная проверка. Рассмотрим набор (группу или партию) более или менее схожих предметов, состоящих из отдельных единиц, которые, однако, различаются по определенному признаку, измеряемому или наблюдаемому. Например, это могли бы быть обработанные бруски длиной номинально 50 мм. Действительная же длина их несколько меняется вследствие флуктуаций в процессе производства. Желательно оценить долю брусков, длина которых колеблется в заданном диапазоне, например между 49 и 51 мм. Такие бруски будем называть годными, в то время как остальные будут называться дефектными. По практическим соображениям оказывается неприемлемым проверить все бруски в партии. Вместо этого можно проверить выборку из брусков, определив заранее ее объем, например 100 штук. При этом потенциально доступная информация — размещение меток
29
«годный», «дефектный» на каждом из 100 проверенных брусков. Если бы выборка формировалась случайно (и были бы предприняты обычные предосторожности, чтобы гарантировать ее случайность), т. е. так, чтобы у каждого из различимых (неупорядоченных) подмножеств по 100 брусков были бы одинаковые шансы оказаться выбранным, то полной информации об этих 100 метках на брусках не потребовалось бы. При последующем анализе понадобилось бы только общее число дефектных единиц в выборке (например, четыре).
В этом примере статистикой является просто общее число дефектных единиц в выборке.
Для выборки объема s, извлеченной из партии объема Ь, содержащей d дефектных единиц (где d неизвестно), число дефектных единиц будет случайной величиной (скажем, 7?). Вероятность того, что в данной выборке окажется определенное число (например, г) дефектных единиц, равняется
P^=r;=(?;(fcr/;/fJ;r=O,l,...,min (5, d). (2.1.1)
Это элемент семейства гипергеометрических распределений [см. И, раздел 5.3]. Неизвестным параметром, с помощью которого идентифицируют члены семейства, является переменная d, относящаяся к партии в целом. Выводы относительно значения d должны основываться на статистике (в нашем примере равной четырем), т. е. на полном числе дефектных единиц в выборке [см. пример 2.1.1].
Пример 2.1.2 (продолжение). Использование упрощенных аппроксимирующих семейств распределений. Если бы в примере 2.1.1 объем партии был гораздо больше, чем объем выборки (например, Ь~ 10000, 5=100), то можно было бы с небольшой погрешностью заменить гипергеометрическое распределение (2.1.1) биномиальным (см. И, раздел 5.2.2):
P(R=r)=fi)pr(\-pf~r, г=0,1 s, p~d/b. (2.1.2) Полное число дефектных единиц в выборке по-прежнему оставалось бы подходящей статистикой.
Пример 2.1.3 (продолжение). Введенное в примере 2.1.1 семейство распределений предопределяется процедурой формирования выборки. Теперь предположим, что вместо того, чтобы пытаться оценить долю — т (49,51), скажем, брусков, длина которых х лежат в заданном интервале [х49Сл'С51), надо для всех пар значений и и v(u<v) оценить долю x(u,v) тех брусков, длина которых х принадлежит интервалу Эта задача эквивалентна следующей: будем считать измеренную длину х определенного бруска реализацией непрерывной случайной величины X [см. II, раздел 10.1] и оценим распределение вероятностей X. Это в свою очередь можно было бы интерпретировать следующим образом: постулируем для X нормальное распределение с математическим ожиданием g и стандартным отклонением о [см. II, раздел 11.4] и оценим значения параметров распределения д .и а. [Естественно подумать, что это несостоятельный постулат, так как в прин-30
ципе можно получить сколь угодно большие наблюдаемые значения |Af|, если величина X нормально распределена. В то же время длина наших брусков не может быть меньше нуля и практически не будет больше, чем например, 60 мм. Однако фактически предположение нормальности может оказаться вполне разумным, если стандартное отклонение будет малым [см. II, разделы 9.2 и 11.4.3], так как тогда становится пренебрежимо малой вероятность очень больших отклонений от среднего.] В этом случае подходящими статистиками были бы ухг и ^хгг [см. раздел 6.4.1] (при условии, что заданы длины хх,х2.хп
j 1
брусков в выборке объема «ил существенно меньше, чем объем партии).
Пример 2.1.4. Нестатическая ситуация. В примерах 2.1.1, 2.1.2 и 2.1.3 мы имели дело с выборками, взятыми из фиксированного распределения. Такие случаи можно назвать статическими. Рассмотрим нестатическую ситуацию. На пружине, закрепленной с одного конца, подвешен определенный груз х;. На результат измерения длины пружины у, влияют ошибки измерения. Процедура повторяется для / = 1»2.Веса хх,х2,..,хк считаются точно известными числами. Пе-
ременные такого типа часто называют неслучайными переменными. Соответствующие длины пружины содержат ошибки. Удобная модель: для каждого i будем рассматривать у, как реализацию нормально распределенной случайной переменной с математическим ожиданием [см. II, раздел 8.1] £'(У/) = а+ (jXj (закон Гука) и дисперсией [см. II, раздел 9.1] ог (одинаковой для всех z). Цель эксперимента состоит в том, чтобы оценить модуль упругости /3. Оказывается, что соответствующими этому случаю статистиками будут и ууху-
[см. пример 4.5.3]. Они представляют собой комбинации наблюдаемых значений yj случайных переменных и связанных с ними неслучайных переменных x-t.
Теперь суммируем результаты анализа рассмотренных примеров в виде следующего определения.
Определение 2.1.1. Статистика. Пусть ух,у2 ук обозначает множество наблюдаемых значений случайных ’ переменных, а Xj^r2...хт — множество (известных) значений связанных с ними не-
случайных переменных. Статистикой называется любая функция этих переменных, например ,h(ylt...yk\ xp...,xw), количественное значение которой может быть рассчитано, как только будут указаны выборочные значения уг и величины связанных с ними переменных xs.
В любой процедуре вывода могут быть использованы только статистики. Например, согласно теории оценивания надо указать, каким членом заданного семейства распределений порождена выборка. При этом требуется дать численное значение (оценку) каждому параметру, который содержится в математических формулах, определяющих семейство
31
[см. гл. 3]. Каждое такое численное значение должно быть статистикой. Практические правила оценивания сводятся к выбору статистик, наиболее подходящих для этой цели.
Статистики, которые строятся в теории оценивания и в теории проверки статистических гипотез, часто оказываются комбинациями простой системы статистик, известных как выборочные моменты и являющихся выборочными аналогами моментов генеральной совокупности.
2.1.2. МОМЕНТЫ
а) Моменты генеральной совокупности. Важным множеством постоянных величин, связанных со случайной переменной и ее распределением вероятностей, оказывается множество моментов генеральной совокупности [см. II, раздел 9.11]. Моментом порядка г(г=Ъ2,...) случайной переменной X называют величину
^Е(ХГ). (2.1.3)
Моментом первого порядка ц! будет просто математическое ожидание X, часто обозначаемое символом д:
д=д[=Е(Л). (2.1.4)
К моментам относят также и центральные моменты
р=Е(Х—цУ г=1,2,... (2.1.5)
Центральный момент первого порядка тождественно равен нулю. Центральным моментом второго порядка является дисперсия (мера изменчивости). Момент третьего порядка связан с асимметрией (мерой асимметрии). Коэффициент асимметрии X определен как
skew (X)=дз/дг72 (2.1.6)
Центральный момент четвертого порядка д4 связан с кривизной п.р.в. вблизи ее максимума. Для центральных моментов более высокого порядка нет непосредственной интерпретации.
Возможны очевидные обобщения на случай многомерных распределений. Например, для генеральной совокупности, каждый из членов которой обладает двумя интересующими нас признаками, такими, как рост и вес, обратимся к паре случайных переменных, например (А",У), реализации которых (xit уО,(хг, уг),... представляют пары (рост, вес) членов совокупности. Вероятностное поведение X и Y описывается их совместным распределением вероятностей.
Двумерные моменты (или моменты произведений) этого распределения задаются величинами
I^EfX'Y5), V=l,2.......
а центральные моменты определяются как дгд=£(<х-£/(У-д/}, t=E(X), n=E(Y). (2Л,7)
32
Наиболее важным среди этих смешанных моментов является ковариация, определяемая как
covfc>9=>41 j (Х—£)(у—ц)).
Ее нормированная версия
Q(X,Y^^/axaY (2.1.8)
называется коэффициентом корреляции corr(X,Y), величина которого при подходящих обстоятельствах будет мерой связи между X и Y. Здесь = var<A7, = var(Y).
б) Моменты выборки*. Выборочными аналогами теоретических моментов (моментов генеральной совокупности) являются моменты выборки. Для выборки (хх^сг,...х„) момент порядка г определяется как
т'= L х^/п, г=1,2,... . (2.1.9)
r j=i 1
Если выборка задается в виде таблицы частот, а именно, если Xi,x2,...,хк — список возможных различных наблюдаемых значений X, а — частоты, с которыми они появляются в выборке, то
шг'= £4Л7/Л> где k
п- Е fr
есть объем выборки.
Аналогично получаем центральные моменты выборки, известные также как моменты выборки относительно среднего, задаваемые в виде
mr= Е (Xj—xf/n, r=l, 2,..., (2.1.10)
y=i j
где
x =m\
есть среднее по выборке. Соответствующее выражение для таблицы частот имеет вид
т = I fi(x.—xf/n, r=l, 2,... . (2.1.11)
r j=i J J
Соотношение между моментами выборки относительно среднего и относительно начала отсчета. Моменты выборки тг относительно среднего связаны с соответствующими моментами т'г относительно начальной точки следующими соотношениями:
т2=т\—х2, т3 =т$—Зт& +2х3,
(2.1.12)
и т. д.
т4=/и4/—imjX + 6трс2—Зх4.
а
• В советской литературе часто употребляется термин «выборочные моменты» (см. также примечание на с. 39). — Примеч. ред.
33
Моменты выборки тр т'г порядка г являются оценками соответствующих моментов генеральной совокупности цг, ц,, хотя и не обязательно наилучшими.
В пункте в) обсуждается второй момент выборки.
в) Дисперсия выборки и стандартное отклонение выборки. Момент второго порядка выборки относительно среднего представляет собой один из вариантов дисперсии выборки. Однако более часто последняя определяется как
Л _
^=птг/(п-1)= Е (Xj—х)2/(п-\) (2.1.13)
или, эквивалентно, в случае таблицы частот
$*= T.fj(Xj—х)2/(п-1А п- Efj.
Положительное значение квадратного корня из этого выражения 5 называют стандартным отклонением выборки из наблюдаемой переменной.
Идея взять делитель в виде п—1 вместо п подкрепляется одним или несколькими из следующих аргументов:
1) смещение: s2 — несмещенная оценка дисперсии о2 генеральной совокупности; это означает, что среднее большого числа п выборочных значений приближается к о2, когда п становится сколь угодно большим [см. раздел 3.3.2]. В противоположность этому следует сказать, что s не является несмещенной оценкой а [см. раздел 2.3.5]*;
2) имеет смысл при л=1: когда п равно единице, s2 не определено. Именно это требуется от выборочной оценки ст2, так как при объеме выборки, равном единице, нет информации относительно изменчивости (разброса). Однако значение тг обращается в нуль. Это не слишком хорошая оценка для ст2;
3) «не раскачивайте лодку»: в стандартных процедурах оценивания и проверки гипотез и в соответствующих таблицах применяется делитель п—1 [см., например, раздел 2.5.5]; „ _
4) степени свободы: сумму квадратов Е (xj—х)г можно выразить в виде суммы квадратов п — 1 алгебраическилнезависимых переменных: другими словами, квадратическая форма Е (хг—х/ имеет п — 1 степеней свободы (или ранг порядка п — 1). В результате становится и логически привлекательно, и удобно по алгебраическим мотивам делить на (л—1).
г) Двумерные выборки. В выборке (хх,ух),(хг,уг), ...,(хп,у„), из двумерной генеральной совокупности, где хг обозначает, например, рост, а уг — вес г-го индивида в выборке, выборочная ковариация определяется как
* Несмещенность s2 означает, что Es2 = a (при этом Es^a2). Указанное авторами свойство при л-»00 обычно называют состоятельностью. —Примеч. ред.
34
тхл = х)(уг—у )/n = { nxу ) /и, (2.1.14)
где x ~'Exr/n и у ~Еуг/п. В случае таблицы частот это выражение заменяется на t
/и1Д = Lfr(xr—x)(yr—y)/n.
По причинам, аналогичным тем, которые перечислены применительно к выборочной дисперсии в пункте 1), более принята оценка ковариации /*1 л генеральной совокупности не в виде /им, а в виде
М = ^(Xi—x)(y,—у)/(п— Ц (2.1.15)
В общем случае смешанный момент порядка г, s для двумерной выборки записывается в виде
m^txr.ys./n, г,5= 1,2 (2.1.16)
а соответствующие центральные моменты в виде
тГг5 =^(х{-х)г(У1-у?/п. (2.1.17)
В особом случае, когда 5=0, г=0, оказывается, что
mr,o = i(Xf—xf/n, г — 1,2,...;
п _ (2.1.18)
mQJS ^(у~yf/n, 5=1,2,... .
Эти величины являются маргинальными центральными моментами порядка г для значений х и маргинальными центральными моментами порядка 5 для значений у. Для таблицы частот необходимо изменить эти формулы очевидным образом [ср. (2.1.10), (2.1.11)].
Коэффициент корреляции. Нормированная версия
r(x,y) =miti/y/(mi0m0l) (2.1.19)
выборочной ковариации называется выборочным коэффициентом корреляции (моментным), или (иногда) коэффициентом корреляции К. Пирсона. Она является оценкой коэффициента корреляции $(х,у) (2.1.8) генеральной совокупности. Отметим, что выражение
r(x,y) = Cj , /s(x)s(y), где 52<х> — выборочная дисперсия (2.1.13) значений х, а &(у) — выборочная дисперсия значений у, эквивалентно выражению (2.1.19).
2.2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ: ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
Выбрав определенную статистику, такую, как среднее выборки (среднее значение наблюдений), и отметив ее значение, мы вынуждены признать, что при повторении процедуры выборки численное значение
35
этой статистики во второй выборке будет, вероятно, отличаться от ее значения в первой выборке. Последовательность таких повторений породила бы последовательность числовых значений статистики; одни значения встречались бы чаще, другие — реже. Таким образом, мы можем представить совокупность значений вместе с распределением вероятностей среди них. Это и есть выборочное распределение статистики.
В примерах 2.1.1 и 2.1.2 рассматривалась статистика г — количество дефектных единиц в выборке. В примере 2.1.2 она трактовалась как реализация (т.е. наблюдение) случайной переменной R [см. II, гл. 4], которая имеет распределение Вт&д) [см. II, раздел 5.2.2]. В этом случае число обследованных брусков s является числом «испытаний», как это понимается для биномиального распределения, а р — неизвестной долей дефектных изделий в партии.
Статистика г является реализацией случайной величины R. Выборочное распределение статистики г оказывается распределением вероятностей (2.1.2) [см. II, раздел 4.3] соответствующей случайной переменной R. В примере 2.1.3 рассматривались статистики и Ех/, при этом хг были реализациями случайной переменной X, распределенной N(/x,a) [см. II, раздел 11.4].
С точки зрения обозначений удобно рассматривать xi как реализацию случайной переменной Jfpx2 — как реализацию случайной переменной Х2,... и, наконец, хп — как реализацию Хп, где случайные переменные XvX2,...,Xn — н.о.р. (т.е. взаимно независимые [см. II, раздел 4.4] и одинаково распределенные переменные). При этом их общее распределение — это распределение исходной случайной переменной X. Взаимная независимость [см. II, определение 4.4.1] наблюдаемых событий Ar=xp Х~х2,..., обеспеченная процедурой выборки, отражается в предположении взаимной независимости случайных переменных Хп а тот факт, что все наблюдения хг взяты из одного и того же распределения, отражается в приписывании всем Хг распределения X. О переменной Хг можно говорить как о статистической копии X [см. определение 2.2.1].
Определение 2.2.1. Статистические копии, индуцированные случайные переменные, случайная выборка. Говорят, что случайные переменные XVX2,... будут статистическими копиями заданной случайной переменной X, если Хг взаимно независимы и одинаково распределены, причем их общее распределение совпадает с распределением X. Множество независимых наблюдений (xY,x2,...,xk) переменной X называется случайной выборкой. По соображениям удобства можно считать xt наблюдением Xlt х2 — наблюдением Х2 и т. д. Эти случайные переменные XitX2,... индуцируются (порождаются) наблюдениями хрх2,... Аналогично статистика y=h(xitx2,...,xk) порождает случайную переменную Y=h(XltX2,...,Xk). (Определение, случайной выборки из конечной совокупности можно найти, например, в [II, раздел 5.3].)
36
В примере 2.1.3, таким образом, статистики i.xr и могут рассматриваться как реализации индуцированных случайных переменных соответственно ЁАГГ и ЁА^, где хрх2,...хл — статистические копии х. Теперь случайная переменная становится суммой п взаимно независимых переменных N(p,a) и поэтому сама оказывается распределенной нормально с математическим ожиданием ц и стандартным отклонением а/4п [см. раздел 2.5.3, а)]. Это распределение NQi,ff/Vn) будет выборочным распределением статистики t,xr. Подобным об-разом выборочным распределением статистики Ех* является распределение индуцированной случайной переменной ЕА^.
В примере 2.1.4 имелось к взаимно независимых случайных переменных Ур У2,..., Yk, распределения которых уже не были одинаковыми. Вместе с наблюдаемыми значениями уг переменной Уг у нас были неслучайные переменные хг, известные точно. Статистика t>xryr рассматривается как реализация случайной переменной ЁхгУг, являющейся взвешенной суммой независимых случайных переменных ........
Выборочным распределением статистики Ёх.у_ будет распределе-1 * ние вероятностей индуцированной случайной переменной ЕхгУг
В этом примере оказывается, что Yr — независимые нормально распределенные случайные переменные с параметрами E(Yr) = а + (5хг и v&r(Yr)- о2, г- 1,2,..., к. Отсуда вытекает [см. раздел 2.5.3] нормальность выборочного распределения переменной Ехгуг с ожиданием аЕхг + 0Ех* и дисперсией а2Ехг2.
В свете этих примеров можно дать формальное определение выборочного распределения.
Определение 2.2.2. Выборочное распределение статистики. Пусть УрУр..«»Ул представляют собой собрание данных, в которых yj для каждого j может рассматриваться как реализация случайной переменной Yj. Пусть xpx2,...,xm — множество неслучайных переменных, значения которых известны (сюда может входить, например, объем выборки). Пусть рассматриваемой статистикой будет
Л ,У2,. •. ,УЛ, Xj ,Х2,... tXffJ •
Выборочным распределением этой статистики называют распределение вероятностей индуцированной случайной переменной
й (^Ур У2, • • •, Ул, хрх2,... ,x^).
В этих выражениях уг могут быть скалярными или векторными величинами [см. I, разделы 5.1, 5.2]. В последнем случае Уг — векторные случайные переменные [см.П, раздел 13.3.1]. Аналогично переменные хс могут быть скалярными или векторными. Статистика Л
37
может быть скалярной функцией векторных аргументов или сама может быть вектором. Тогда и выборочное распределение оказывается многомерным распределением вероятностей [см. II, раздел 13.1]). Далее приводятся дополнительные примеры.
Пример 2.2.1. Выборочное среднее. Предположим, что хрх2,..., хп — случайная выборка [см. определение 2.2.1] из распределения Пуассона с параметром 6 [см. II, раздел 5.4]. Рассмотрим статистику х =(х} + х2 + ...+ хп)/п. Эта статистика, выборочное среднее, порождает случайную переменную
Х=(Хх + ...+Х„)/п, где Хп — взаимно независимые, одинаково распределенные переменные [см. раздел 1.4], подчиняющиеся распределению Пуассона с параметром (0). Распределение суммы Sn п независимых переменных, распределенных как PoissOn (в), будет следовать Poisson (л0) [см. II, раздел 7.2], так что
P(Sn =г)=е~пв(пд)г/г\, г=0,1,...,
откуда _
Р(Х = v) = P(Sn = nv) = e~n6(n0)v6/(nv)\, v = 0,1 /п, 2/n,... . _
Эта формула выражает выборочное распределение статистики х.
Пример 2.2.2. Случайная выборка из двумерного распределения. (Выборочное распределение статистики, имеющей векторное значение.) Предположим, что X является двумерной векторной случайной переменной, определяемой выражением Х = (Y,Z), где Y и Z — одномерные переменные, совместное распределение которых является двумерным нормальным распределением с параметрами E(Y) = X, E(Z)=ij., corr(Y,Z) = q, var(Y) = a2, varfZ> = а? [см. II, раздел 13.4.6]. Случайная выборка объема п из этого распределения будет состоять из п упорядоченных пар (yx.zx), (y2,z2),...,(yn,zn), представляющих собой независимые реализации пары (Y,Z). Статистика = (y,z), где У = Y.yx/n и z = £zx/n, позволяет сделать выводы относительно X и g. Чтобы обсудить выборочное распределение статистики x=(y,z) с векторными значениями, введем индуцированные двумерные случайные переменные Xj = (YX,ZX), Х2 = (Y2,Z2),..., Хп = (Yn,Zn), являющиеся статистическими копиями X в том смысле, что Хг взаимно независимы и для любого г Хг распределены так же, как X. Таким образом, пары (Yj,Zj) и (Yk,Zk) будут независимыми всегда, когда jV к, и для любых j Yj и Zj будут иметь такое же двумерное нормальное распределение, как Y и Z. Отсюда следует, что индуцированная случайная переменная X = (Y, ZJ^ имеет двумерное^ нормальное распределение с E(Y) = \, E(Z) = fj.t corr(Y,Z)=Q, var(Y)=a2/n, varfZ) =а?/л. Такое же распределение имеет и переменная х=(х,у).
Искусственные выборки: имитация. Опубликованные собрания независимых реализаций случайных переменных с определенным распределением обеспечивают возможность создания небольших моделируемых случайных выборок. Когда требуются выборки сравнительно 38
большого объема, такая процедура становится недостаточной и предпочтение отдается генерированию реализаций с помощью компьютера (моделирование на ЭВМ).
В разделе F списка литературы приведены работы, включающие таблицы случайных чисел, принадлежащих различным распределениям: числа с равномерным распределением см., например, в [RAND Corporation, (1955)]; числа с нормальным распределением см. в [Wold (1954)]; двумерные нормальные пары см. в [Fieller, Lewis and Pearson (1957)]; числа с экспоненциальным распределением см. в [Clark and Holtz (I960)] или в [Barnett (1965)]. Так как сумма чисел, подчиняющихся экспоненциальному закону, имеет гамма-распределение, моделируемые выборки гамма-переменных (и, следовательно, Х2-переменных) можно получить из «случайных чисел», следующих экспоненциальному закону.
Сведения о генерировании случайных реализаций можно найти в книге [Newman and Odell (1971)] (а также в работах, включенных в раздел F списка литературы или в [Abramowitz and Stegun, ed. (1970), section 26.8—D].
2.3. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАТИСТИК
Моменты [см. раздел 2.1.2] выборочного распределения [см. определение 2.2.2] статистики называют выборочными моментами этой статистики; аналогично вводятся центральные выборочные моменты. (Следует особо отметить, что выборочные моменты — это не то же самое, что моменты выборки [см. раздел 2.1.2, п. б)]*.
Определение 2.3.1. Выборочные моменты. Выборочным моментом порядка г статистики t является момент порядка г выборочного распределения t(r-\,2,...). Или, равнозначно, r-Й выборочный момент t есть
EfT), г=1,2.....
где Т — случайная переменная, порождаемая статистикой t [см. раздел 1.4.2,п.5)].
Центральный выборочный момент порядка г задается выражением
Е(Т-т)г. г =1,2...
где т~Е(Т).
Выборочный момент первого порядка называется выборочным ожиданием, выборочный момент второго порядка называется выборочной дисперсией и т. д. в соответствии с общепринятым употреблением названий моментов генеральной совокупности. Таким образом, можно говорить о выборочном ожидании среднего значения выборки: оно оказывается ожиданием выборочного распределения Х\
Стандартное отклонение не является моментом, однако оно имеет большое значение как связанная с ним статистическая величина.
* В советской литературе обычно не делают такого различия. Обычно и моменты выборки называют выборочными моментами. — Примеч. ред.
39
Определение 2.3.2. Выборочное стандартное отклонение. Стандартная ошибка. Выборочным стандартным отклонением статистики t называют стандартное отклонение (оно равняется положительному значению квадратного корня из дисперсии) выборочного распределения статистики t.
Соответствующая оценка стандартного выборочного отклонения статистики t называется стандартной ошибкой t [см. раздел 4.1.2].
Например, если в качестве статистики t берется выборочное среднее х выборки объема п из распределения, имеющего дисперсию о2, то выборочная дисперсия х будет равняться а2/п [см. (2.3.1)], и поэтому выборочное стандартное отклонение х будет равно a/yfn.
Стандартное отклонение выборки [см. (2.5.23)] является статистикой, у которой имеется свое выборочное распределение, и, следовательно, выборочная дисперсия и выборочное стандартное отклонение. Это выборочное распределение для нормально распределенной выборки обсуждается в разделе 2.5.4,д).
Именно выборочные моменты образуют объект изучения в настоящем разделе. Особый интерес представляют выборочное ожидание, выборочная дисперсия и выборочная асимметрия; они выражают соответственно математическое ожидание [см. II, раздел 8.1], дисперсию [см. II, раздел 9.2.1] и асимметрию [см. II, раздел 9.10.1] выборочного распределения статистик.
2.3.1. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ СРЕДНЕГО ЗНАЧЕНИЯ ВЫБОРКИ
Пусть xi,x2,...txn — совокупность п независимых наблюдений случайной переменной X. Среднее значение выборки х определяется как (jq 4-Xj + ... + xj/n, его выборочное распределение — это распределение индуцированной случайной переменной X = (Х{+ Х2 + ... + XJ/n, где Хг — статистические копии X [см. определение 2.2.1]. Простые вычисления показывают, что _
Е(Х)=Е(Х),
var<¥) = zi-1var6A7, (2.3.1)
skewfX) = n“,/2skew (X).
Статистика х вполне может претендовать на то, чтобы служить оценкой [см. раздел 1.3.2] параметра Е(Х). Ее выбдрочное ожидание (т. е. среднее, получаемое при бесконечных повторениях выборочной процедуры) тождественно равно величине искомого параметра (это свойство называется несмещенностью [см. раздел 3.3.2]). Ее выборочная дисперсия уменьшается при увеличении объема выборки; согласно неравенству Чебышева [см. II, раздел 9.5] отсюда следует, что при достаточно большом объеме выборки весьма вероятно, что значения х очень близки к Е(Х).
40
2.3.2. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ ДИСПЕРСИИ ВЫБОРКИ
В обозначениях раздела 2.3.1 дисперсия выборки v иногда определяется как —х)2/п, а иногда — как —ху-/п—1 [см. разделы
2.1.2,в), 2.5.4,г)]. Сначала мы воспользуемся первым определением. Выборочный момент первого порядка и центральные выборочные моменты v второго и третьего порядков имеют вид соответственно
E(V), var(V), Е{ V— E(V)}\
где V — случайная переменная, порождаемая v (таким образом, v является реализацией V): „ _
Х)2/п,
где X и Xit как в разделе 2.3.1. Аналогично выборочная асимметрия дисперсии выборки v равна:
skew(K> = Е {(V—E(V) )’/ {var(K) )3/2.
Вычислить E(V) достаточно просто, однако центральные моменты второго и третьего порядков требуют больше усилий. Результаты вычислений приводятся ниже, они выражены в терминах центральных моментов [см. II, раздел 9.1.1] цг переменной X:
gj = varfA) = Е(Х— fi)2 (где fi-E(X)), р^=Е(Х—ц)\ (=M’/2skew<¥)>, (2.3.2)
д4 = Е(Х— ц)* и т.д.
Получаем, что
E(V) = IV
..„/jz. _ _ 2(/Ч~2/4) + М4-3/4 = /1,-/4 +<?/ 1 \
' ' п т т п \пг)
£[ у Е(У)]У - ЗдзД4—6/4 + 2/4 / 1 \
(2.3.3)
skewf₽7 =
/4—3/12/4—6/4 + 2/4 / 1 \
6ч—/4Г2л,я 1л5/2Л
(Что значит О, см. раздел 1.3.1.) Отсюда следует, что v'=nv/(n—1>= = —х)г/(п—1) — несмещенная оценка [см. раздел 3.3.2] дисперсии
д2 генеральной совокупности и что выборочная дисперсия v', так же как дисперсия v, равняется л-‘(д4—pfy+Ofn-1), т. е. уменьшается с увеличением и.
Более детальное изложение этих результатов, а также полученных в разделах 2.3.3.—2.3.6 можно найти в книге [Cramer (1946) — С].
2.3.3. ВЫБОРОЧНАЯ КОВАРИАЦИЯ МЕЖДУ СРЕДНИМ ЗНАЧЕНИЕМ ВЫБОРКИ F И ДИСПЕРСИЕЙ ВЫБОРКИ v
Выборочная ковариация [см. II, раздел 9.6.1] между х и v задается _
covfX, V) = (2.3.4)
В частности, X и V будут некоррелированными в случае, когда распределение X симметрично, так как ач=О.
2.3.4. ВЫБОРОЧНЫЕ МОМЕНТЫ ДЛЯ МОМЕНТОВ ВЫБОРКИ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ
Для моментов выборки mk='L(xj—хУЧп при больших значениях к подробные вычисления становятся очень сложными. Для Лг= 3 выборочное ожидание задается в виде
Е{ ZfXi—Xf/n ) =(п—1)(п—2)ц3/п. (2.3.5)
В общем случае для £=2,3,...
Е { Ъ(Х(-Х)к/п} = цк+О(п~') (2.3.6)
и „ _
var ( L(X:—X)k/n ) =с(к,п)/п + О(п~>), (2.3.7)
где 1
с(к,п) = —2кцк_^ц {—ц2к+ArWj-r
2.3.5. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАНДАРТНОГО ОТКЛОНЕНИЙ ВЫБОРКИ
V n _ {$(xi—Xjr/n}, получим
Е№) = ^2 + О(п-‘) (2.3.8)
и 2
var(\fV) = —~2 + О(п~2)- (2.3.9)
2.3.6. ВЫБОРОЧНЫЕ МОМЕНТЫ КОЭФФИЦИЕНТА АСИММЕТРИИ ВЫБОРКИ
В соответствии с определением
skew (X)~Е(Х—ц)3/ {var(X) }3/2 (jl=E(X)),
коэффициента асимметрии случайной переменной X, определим коэффициент асимметрии выборки (xitx2.....xj из наблюдений за перемен-
ной X как
(= V' (ш23/ш1)), (2.3.10)
где
т3 - L(xi—x)3/n, т2 = —х)2/п.
1 1
Из этого определения следует, что выборочное ожидание g имеет вид skew<X)+O(h-9, (2.3.11)
а выборочная дисперсия g —
d(n)/n+O(n-3'2), (2.3.12)
42
где d(n) определяется с помощью соотношения
— 12дгМзМ5—24д1д4 + 9/*зД4 + 35дгДз + 36д25- (2.3.13)
Когда распределение X симметрично, последнее выражение сводится к 4/4/4—24^4 + 36/4. (2.3.14)
2.4. РАСПРЕДЕЛЕНИЯ СУММ НЕЗАВИСИМЫХ ОДИНАКОВО РАСПРЕДЕЛЕННЫХ ПЕРЕМЕННЫХ
Статистика встречается часто. Очевидно, что ее выборочным
распределением является распределение суммы 5И = ЁАГГ н.о.р. индуци-
1
рованных случайных переменных Xt.......Хп, которые определяются
как статистические копии случайной переменной X [см. „определение 2.2.1]. В табл. 2.4.1 и 2.4.2 приводятся распределения ЁХГ для различных случайных переменных X.
Таблица 2.4.1. Распределение сумм статистических копий X (X—дискретная). Эти распределения обсуждаются в (II, гл. 5]
Распределение X Распределение S„
Описание Описание
f(x)=P(X=x} fnM=P(Sn=x)
Бернулли Биномиальное (nj))
Л°)=1-Р ]о<п<1 Д1)=р (£)р’х(1—рГ,~х. х=0,1 п
Биномиальное (kj)) Биномиальное (nkj})
(x)px(l-p)k-x, 0<р<1,
х=0,1 к х=0,1,...,пк
Пуассона (0) Пуассона (л0)
е~в9х/х\, 0>О, х=1,2,... е-пв(п9)х/х1, х=0,1,2,...
Геометрическое Отрицательное биномиальное распределение (Паскаля)
pfX—pf, 0<р<1, ( х)У(1—р)х,
х=0,1,2,... х=0,1,2,..,
Отрицательное биномиальное Отрицательное биномиальное
( х)р"(1—р)х, а>0, 0<р<1, х=0,1,2,... CxV^l—РГ, х=0,1,2,...
Замечание. Для а>0 и х-0,1,...
(~х) = (—аХ—а—!)...(—а—х+ 1)/х! = х сомножителей
=коэффициенту при tx в разложении степенного ряда (1+0-а«
43
Таблица 2.4.2. Распределение сумм статистжеских копий
X (X— негрерывная). Эти распределения обсуждаются в [II, гл. 11]
Распределение X Распределение Sn
Описание /<х)=п.р.в. X от X Экспоненциальное <г~хё~х>0 Gamma (а,0) х>0 0*Т(а) N(/i,o) {—{х—ц)г/2аг) Равномерное (0,1) [ 1, 0<х<1; J’x>~ 10 в остальных случаях Описание /и<х>=п.р.в. Эрланга с п стадиями = Gamma (лд) a~nxf'~ie~x,*/(n—1>!, х>0 (если а=1, то 2Sn имеет распределение х2 с 2п степенями свободы) [см. раздел 2.5.4,а] Gamma (па,/9) уЛО-1_—Х/(3 X" е , х>0 0"“Г<ла) 1Ч(лд,<г/л) (2тл)^,/2а~*ехр {—(г—л/1)2/2ла2) £„/*)> 0<х<1, 7<х<2> А r-\<x<r, =(„-i)!/nW л—1 <х<п, где ' ♦ 1<х> = (—1У+К")(х— г)"-', г=0,1 л—1
2.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
Бдльшая часть статистической теории основана на поведении выборок из нормальных распределений. В этом разделе суммируются некоторые основные свойства нормальных переменных и связанных с ними статистик. Дополнительную информацию можно получить, обратившись, например, к работам [Hogg and Craig (1965), гл. 4, 13; Kendall and Stuart (1969), т. 1; Mood, Graybill and Boes (1974), гл. V, VI; Wilks (1961), гл. 8]. Указанные книги приведены в разделе С списка литературы.
44
р.5.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ [см. II, раздел 11.4]
Говорят, что случайная переменная X имеет распределение N(/4,ct) или нормальное распределение с параметрами (дцст): с математическим ожиданием ц и стандартным отклонением ст, если ее функция плотности вероятностей (п.р.в.) в точке х [см. II, раздел 10.1] имеет вид
f(x) = (27гЛ'/2ст 'ехр {— (х—ц)2/2о2). (2.5.1)
Эта функция показана на рис. 3.5.2.
2.5.2. РЕЗУЛЬТАТ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СТАНДАРТИЗАЦИЯ
Если
У= аХ+Ь,
где X — N(/4,ct), ст(ст#0) и b — постоянные, то Y также распределена нормально, но имеет параметры (стд+b, ст|ст|). Этот результат получается с помощью теоремы 10.7.1 из т. II серии «Handbook of Applicable Mathematics».
Если X — N (д,ст), то ее линейная функция
и=(Х—р.)/о (2.5.2)
определяет случайную переменную U, распределенную N (0,1). Это так называемая стандартная нормальная переменная. Ее функция плотности в точке и, обозначаемая обычно как ф(и) равна:
</>(ц) = (27г)-1/2ехр{—Гм2}, -«><„<- (2.5.3)
Для функции ф(ц) имеются подробные таблицы, так же как для стандартного нормального интеграла, т. е. ее функция распределения (ф.р.) Ф(д) задана в виде
Ф(и)=Р(С7^и) = J <t>(z)dz. (2.5.4)
--CW>
Таблица этой функции приведена в приложении 3.
С помощью результатов из раздела 2.5.1 таблицы Ф(и) могут использоваться для получения значений ф.р. любой нормальной переменной. Если X — то можно записать
X = oU + р.,
откуда P(X^x)=P(oU+ ц^х)~
= P{U^(x—(так как ст>0) (2.5.5)
= Ф[(х—J4)/CT|.
Таким образом, вероятность того, что X находится в заданном интервале (Xi,x2), выражается с помощью
Р(х^Х^х2)=Р(Х^хд-Р(Х^хд = п .
= Ф {(х2-^)/о}-Ф {(л,-^/а}.
2.5.3. ЛИНЕЙНЫЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
а) Линейные функции независимых нормальных переменных. Пусть
Y~ й\Х\ + а2Х2 +... + апХп + Ь,
где Хг — независимые нормальные величины с параметрами (/4г,аг), 1,2,...,/?. Тогда где
Х=«1^1 + а2у2 +... + апуп + Ь, ") (2 5 7)
о/2 = a 2 a2t + д2ст2 +... + а гпа2 J
(см. II, раздел 11.4.5).
Как следствие центральной предельной теоремы [см. II, раздел 11.4.2] получаем, что Y будет приближенно даже в случае, когда сами величины Хг не подчиняются нормальному распределению.
Наиболее важное применение результат (2.5.7) находит, когда все X— N(y,o). Тогда
Х=(а}+.Лап)^Ь, 'l (2 5 8)
а)2 = (а! +... + д„)а . )
б) Выборочное распределение среднего значения выборки. В частном случае, для которого справедлив последний результат, укажем распределение арифметического среднего X величин Хг. Если
X — (Х\ +Х2 +... + Хп)п, то распределение X—N(n,a/yfri). Этот важный результат дает нам выборочное распределение среднего значения х выборки из п наблюдений над нормальной случайной переменной X с параметрами (у.,о).
Ввиду важности среднего выборки в теории оценивания повторим замечание, которое следует за выражением (2.5.7) и касается приближения к нормальности. Оно сводится к тому, что распределение X приближенно N(/i,ct/V«) независимо (в широких пределах) от вида действительного распределения X [см. II, раздел 17.3].
в) Линейная функция коррелированных нормальных переменных. Предположим, что Х\,Х2,...,Хп имеют совместное многомерное нормальное распределение [см. II, раздел 13.4], для которого EPQ = /4r, var(Xr)^(j^ r=l,2,...,/?, и corr(Xr,A^)= Qrs, r,s = 1,2,...,/?. Тогда 46
Y— UjXj +t?2^2 + ••• + ^rr^n +
N(X,w), где
X—ffi/x.! + a2fi2 + ... + an(in + b,
2 vv (2.5.9)
w ^=^afljQijaiaj =
= Ea-ff* + 2EE<7 6r p,,(j.(T, = a Va.
i * * i j • J U * J
Здесь a -(aifa2,...,an) и V=(prsaras) — матрица ковариаций случайных величин Xl,X2,...,Xr [см. I, гл. 5 и 6].
г) Несколько линейных функций коррелированных переменных. Предположим, что Х\,Х2,...,Хп имеют совместное многомерное нормальное распределение, как и в разделе 2.5.3, в). Получим следующий основной результат для линейных функций. Пусть
Yr = anX\ + anX2 + ... + arnXn + br, r-l,2,...,n, (2.5.10)
где матрица коэффициентов А=(дг5) невырожденная [см. I, определение 6.4.2]. Тогда Y},Y2,...,Yn имеют многомерное нормальное распределение с
E(Yf) = annl+ar2ti2 + ...+arnnn + br, г=1,2,...,л, (2.5.11)
и матрицей ковариаций [см. II, определение 9.6.3], заданной в виде
AVA, (2.5.12)
где А'— транспонированная [см. I, раздел 6.5] матрица А, а V — матрица ковариаций Хг с элементами
Vr5=erACTP Г,5=1,2,...,77,
При ЭТОМ Qrs = Qsr для всех Г И S' И Qrr -1 для любого г.
Если вместо того, чтобы рассматривать все множество
п линейно независимых линейных функций от Х{,Х2,...,Хп, взять только подмножество Yx,Y2,---Xk (k<n) линейно независимых линейных функций, то это подмножество будет по-прежнему распределено по многомерному (^-мерному) нормальному закону с математическими ожиданиями вида (2.5.11). Его матрица ковариаций будет ведущей подматрицей размерности (kxk) [см. I, раздел 6.13] матрицы AVA из (2.5.12)
д) Независимые линейные функции коррелированных нормальных переменных. Пусть Х1,Х2,...,Хп подчиняются многомерному нормальному закону как в разделе 2.5.3,в) и пусть их ковариационная матрица V представлена в виде
VSS,
где S — невырожденная матрица [см. I, определение 6.4.2].
Пусть матрица А из раздела 2.5.3,г) теперь имеет вид
A=S-1
47
[см. I, раздел 6.4]. Тогда Yr, определенные с помощью линейного преобразования (2.5.11), в совокупности подчиняются многомерному нормальному закону с матрицей ковариаций
AVA =S (SS)(S ) =1,
где I — единичная матрица [см. I, раздел 6.2]. Отсюда следует, что в этом случае Yr — взаимно независимые стандартные нормальные переменные.
е) Независимые линейные функции независимых одинаково распределенных нормальных переменных. Результат при независимых Хг можно извлечь из пунктов в), г), д) раздела 2.5.3, взяв в качестве V диагональную матрицу [см. I, раздел 6.7]. Наиболее важен случай, когда Хг — одинаково распределенные независимые нормальные величины с общим математическим ожиданием, скажем д, и дисперсией ст2, так что дисперсионная матрица равна: V=o2l. Тогда, если линейные преобразования У,,У2,...,УЯ определяются в соответствии с (2.5.10), где матрица А — ортогональная, то ковариационная матрица переменных Yr примет вид ААст2 = 1ст2 и, таким образом, Yr остаются взаимно независимыми стандартными нормальными переменными.
Вообще, если строки матрицы А взаимно ортогональны [см. I, раздел 10.2], но не обязательно ортонормальны, т. е. произведение АА — диагональная матрица [см. I, раздел 6.7]
АА=diag(Z?b&2,... ,bn\
то Уг будут подчиняться многомерному нормальному распределению с матрицей ковариаций
CT2diag(Z>i,Z>i,--.,^2)-
Это означает, что Yr — взаимно независимые нормальные переменные с математическими ожиданиями, заданными выражением (2.5.11), и с дисперсиями, заданными в виде
var(Yr) = b2/}2, r=\,2,...,n-
В частности, любые к линейных функций (к^п)
Yj = ajxXl + ... + ajnXn + bj, j=l,2,...,k, (2.5.13)
независимых, одинаково распределенных переменных XitX2,...,Xn, общее распределение которых N(jx,ct), будут взаимно независимыми нормальными при условии, что
Eairajr=0 для i^j.
Тогда E{Yd, E(Y2) и т.д. указаны в (2.5.11), а дисперсии задаются выражениями
var( У,)=ст2Ест2,
(2.5.14) var(y2) = ст2Ест22 и т. д.
48
Рис. 2.5.1. Функция плотности вероятностей f/z) из формулы (2.5.16) для распределения х1 при различных значениях параметра числа степеней свободы
2.5.4. КВАДРАТИЧЕСКИЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
а) Распределение хи-квадрат. Суммы квадратов независимых стандартных нормальных переменных. Квадратичные формы от нормальных переменных. Одним из наиболее важных классов квадратических функций в выборочной теории является класс функций, которые сводятся к суммам квадратов независимых стандартных нормальных переменных. Пусть U],U2,...,UV — независимые стандартные нормальные переменные [см. II, раздел 11.4.1] и пусть
Kv = u} + u\ + ...+ U2- (2.5.15)
Эта величина называется случайной величиной х2 [см. II, раздел 11.4.11] с v степенями свободы (с.с.), или сокращенно — переменной Х2(р), или просто x2v. П.р.в. Kv в точке z равна:
4(Z)=Z(^ ^2/2"Т(±^), г>0. (2.5.16)
Это унимодальное распределение [см. II, раздел 10.1.3], достигающее максимального значения при z-v—1 [см. рис. 2.5.1], имеет следующее математическое ожидание, дисперсию и коэффициент асимметрии:
E(K)=v, var(/Q = 2p, skew(K„) = 2V2/V?.
Замечание. Выбор символа Кг обусловлен желанием обозначать прописными латинскими буквами случайные величины. На практике чаще всего употребляются обозначения х2> или х2(р)’ или X2-Символ х2 обычно используется для обозначения реализации или от
49
делоного значения переменной Kv. Контекст помогает избежать двусмысленности.
Итак, если Z — гамма-переменная с единичным параметром масштаба и параметром формы «, то 2Z — переменная х2 с числом с.с. г=2а или, что равнозначно, Gamma a-переменная является переменной (4*Х2(1?)) с J/ = 2of.
Выделим случай, когда р = 2. П.р.в. для него имеет вид Ш = z>0.
Таким образом, распределение хг оказывается экспоненциальным распределением с математическим ожиданием, равным 2.
Аддитивное свойство переменных хг- Сумма независимых случайных величин х2 является переменной х2- Одно важное и полезное свойство семейства х2 состоит в том, что оно замкнуто относительно сложения. Как видно из (2.5.15), справедливо следующее правило сложения: если С] и С2 — независимые переменные х2 с т и п степенями свободы (с.с.), то С! + С2 также будет переменной х2 с гп + п степенями свободы.
Это правило можно распространить и на суммы большего числа переменных.
Удобное обозначение: переменная кх2. Часто приходится иметь дело со случайной переменной Z, такой, что Z/k подчиняется распределению Хр- Тогда говорят, что Z является переменной кх2-
Квадратичные формы, имеющие распределение х2- Определение, данное в (2.5.15), можно переформулировать следуюгцим образом. Пусть u/=(t7i,[/2,...,t7|)), тогда [см. I, раздел 9.1] ии = Еи^ имеет распределение х2 с v степенями свободы. 1
Хорошо известно, что квадратичные формы, которые нельзя непосредственно выразить в виде сумм квадратов, можно путем преобразований свести к суммам квадратов преобразованных переменных [см. I, раздел 9.1]. Поэтому естественно задать вопрос, не могут ли такие формы иметь распределение х2- Основной ответ на этот вопрос, у которого много приложений, выражен в следующей теореме.
Теорема 2.5.1. Необходимые и достаточные условия для того, чтобы квадратичная форма от независимых стандартных нормальных переменных имела распределение х2- Пусть u=(t71,[/2,.,.,t7A.), где Ur — независимые, стандартные нормальные переменные. Пусть А=А обозначает симметрическую матрицу [см. I, раздел 6.7] с действительными неслучайными элементами. Неотрицательная квадратичная форма u'Au имеет распределение х2 тогда и только тогда, когда k2=k. В этом случае число степеней свободы равняется рангу (А)=следу (А) [см. I, разделы 5.6 и 6.2].
Пример 2.5.1. Выборочное распределение суммы квадратов выборки. Просто сумма квадратов стандартных нормальных случайных величин редко используется в качестве статистики, но связанная с ней статистика встречается часто и имеет большое значение. Это сумма квадратов отклонений наблюдений х\,х2,...,хп от среднего выборки х.
50
Такая величина
d2= Е(%(—х)2 часто называется суммой квадратов выборки. Когда наблюдения хг образуют выборку из нормальной генеральной совокупности с параметрами (д,ст) случайная величина (Р/о2 подчиняется распределению хи-квадрат с п—1 степенями свободы.
Чтобы увидеть, как это получается, рассмотрим Xi,x2,...,xn как реализации индуцированных случайных переменных XitX2,...,Xn, где Хг — статистические копии X, так что они являются взаимно независимыми N(n,o). Аналогично х рассматривается как реализация индуцированной случайной переменной (с.п.) X = 'ЕХг/п.
Тогда с.п., индуцированная d2 [см. определение 2.2.1], равна:
D2 = £(X:—X)2.
1 1
Далее Uj-iXj—n)/^ — стандартная нормальная случайная величина, /=1,2,...,п, a U ='LUi/n = (X—fi)/o, откуда
D2/<j2=£(U — U)2.
Хотя переменные UitU2,...,Un — взаимно независимы, переменные U\—U, U2—U ,...,Un—U — не являются независимыми, так как все они включают величину = В терминах вектора u =((/i,t72,
...,Un) имеем
D2/o2 — ЕС/—иС72 = ии—«(ul/и)2, 1 г
1 = (1,1,...,iy = и и—л (и 1)(1 и)/л2=u Au, где
А=1—117л.
При возведении в квадрат видно, что А=А2, обращаясь же к диагональным элементам А, а именно ((1—1/п),(1—1/л),...,(1—1/л)), видим, что tr(A) = n—1. Поэтому на основании теоремы 2.5.1 D2/o2 есть х2 с п—1 степенями свободы.
б) Независимость суммы квадратов и среднего в нормальных выборках. Результаты, обсуждавшиеся в примере 2.5.1, являются частью следующей теоремы.
Теорема 2.5.2. Ортогональное разложение Т,(ХГ—ц)2. Пусть Х}, Х2,...,Хп — независимые N(/t,or) и пусть X =LXr/n. Тогда
Е(Х— id2/о2 = Е(Х—X )2/ст2 + п(Х — цУ/а2
и оба члена в правой части взаимно независимые х2-переменные с п—1 и 1 степенями свободы.
51
Эта теорема — частный случай более общего результата, представленного в теореме 2.5.5 в разделе 2.5.8. Она необходима для понимания Z-статистики Стьюдента [см. раздел 2.5.5] и для дисперсионного анализа [см. гл. 8].
в) Таблицы распределения х2- Чтобы использовать результат, полученный выше, и другие, ему подобные, нужно иметь таблицу функции распределения (ф.р.), распределения х2 — для любого числа степеней свободы. Таблицы таких ф.р. существуют [см. список литературы], но наиболее доступные из них дают значения только в терминах процентных точек [см. раздел 1.4.2, п.7]. Вариант такой таблицы приведен в приложении 6. В ней содержатся значения величины Х2(а, v), такие, что
Р{Кр^х2М}=а (2.5.17)
для различных значений а.
В таблицах, приведенных, например, в [Pearson and Hartley (1966)— G] x2(q!,p) указаны для 100qi=0,1; 0,5; 1; 2,5; 5; 10; 25; 50; 75; 90; 95; 97,5; 99; 99,5 и для
r = l(l) 30(10)100.
Та же информация [см. указанную выше работу] содержится в таблице (табл. 7) интеграла вероятностей (т.е. непосредственно функции распределения х2, где приводятся значения
P(KV^X2) Для 1(1)30(2)70 и
X2 = 0,001 (0,001 )0,010(0,01 )0,1 (0,1 )2(0,2) 10(0,5)20(1 )40(2) 134.
Таблицы распределения х2 и неполная гамма-функция. Неполной гамма-функцией [см. Abramowitz and Stegun (1970) — G] называют функцию
G(x, a)-\e~‘ta-xdt/'T{a')> a>Q.
0
Из (2.1.15) следует, что
G(x, a)=P(Kv^k), v = 2a, k=2x.
Таблицы x2 u распределение Пуассона. Если случайная переменная R подчиняется распределению Пуассона [см. приложение 2] с параметром 0, то
P(R^c)=Ee~eei/jl =
е (2.5.18)
$P(Kv^k), v=2c, k=26.
К этому соотношению можно прийти, беря по частям [см. IV, раздел 4.3] интеграл, выражающий P(Kv^k). Этот интеграл равен:
f 2е-,ez/2dz/2cT(c) = J uc~,e~udu/r(c) =
28 9
=A(c,Q), = скажем,
= I[—wc-’e-M]o + (c— 1) Tuc~2e~~Udu] =
52
= 0<-ie-0/(c— 1)! + А (с— 1,0) =
= 0с-1е-о/(с—1)! + 0с-2е-е/^с_ 2)! + А (с—2,0)
и т.д., пока не будет получен требуемый результат.
Эго свойство используется в табл. 7 из упомянутой выше работы. Таблица применима как в случае распределения х2, так и в случае распределения Пуассона.
г) Выборочное распределение дисперсии выборки. В выборке Х],хг>...,хп из N(/i,a) дисперсию можно определить по-разному, а именно как п
E(xt—x)2/n ( = V0)
или как „
Е(х-х)2/(п-1) (=v>). (2.5.19)
Более употребительно второе определение, которое дает несмещенную [см. II, раздел 3.3.2] оценку ст2.
Рассмотрим более общую статистику
v=£(x —х)2/а(п), (2.5.20)
где делитель а(п) — произвольная функция п, т.е. объема выборки. Эта величина является реализацией случайной величины
£(Х—Х)2/а(п),
где Хг — независимые N(^,ct). Ее распределение можно получить на основании теоремы 2.5.1, согласно которой a(n)V/a2 есть х2-перемен-ная с п—1 степенями свободы. Таким образом, выборочная п.р.в. для i(x—x)2/a(n) в точке z равна:
{a(n)},n-wlz,n-'iv2exp{—a(n)z/2o1}
------ (2-5-21)
(z>0), « = 2,3,...,
где а(п)-п при определении v0 и а(п) = п—1 при несмещенной оценке v, (2.5.19). Отсюда следует, что
E(V)=(n-Wa(n) = ^71)<г!/Л’
И , ,
/Т7> ч/ п^/( / »2 (2(п—\)о*/п2, а(п) = п;
[2oV7«-l), <7^=я-1.
Итак, выборочная дисперсия несмещенной оценки v, параметра ст2, основанная на выборке объема п, равна:
2CTV(n—1). (2.5.22)
д) Выборочное распределение стандартного отклонения выборки. Стандартное отклонение выборки можно определить как
wn = ^(х-ху/а(п)), (2.5.23)
где а(п) — подходящий делитель. Применение метода максимального правдоподобия [см. раздел 6.4.1] приводит к а(п)-п, в то время как
для получения несмещенной оценки w2n параметра а2 величина а(п) должна равняться (л—1) [см. пример 3.3.5]. В обоих случаях wn оказывается смещенной оценкой а, занижающей значение ст. Далее показано, что для п ^2 выбор а(п) в виде
а(п) = п—у
приводит к оценке ст, которая оказывается почти несмещенной.
Пусть V определяется, как и раньше, и пусть Wn(>0) определяется как
\у — jzi/2. (2.5.24)
Тогда
Wn^\Z(Xr-Xy/a(n)\.
П.р.в. этой индуцированной случайной величины в точке W равна:
hn(w)=2wgn(w2), w>0,
где gn(z) задается формулой (2.5.21), отсюда [см. II, раздел 4.7]
Vw>= ^2exp(-a^wV2^) (w>0). (2.5.25)
Таким образом, момент порядка г переменной Wn равняется: г, г ( 2<? }г/2 ni<r+w— Е^~1 а(п) 1 Г[|(и-1)) г~1>2
Смещение. В частности,
Е(^ = спа,
(2.5.26)
где
(2.5.27)
Сп~ а(п) Г{ f f«-l)).
Когда а(п)-п—1, что соответствует дисперсии выборки в виде Е(х-—х)2/(п—1) (несмещенной оценке ст2), стандартное отклонение выборки, определенное как
имеет выборочное ожидание спо, где
(2.5.28)
Г{ \(п-1)| V л-1 •
(2.5.29)
Эта величина всегда меньше единицы. Поэтому оценка (2.5.28) будет смещенной оценкой ст. Величину смещения иллюстрирует табл. 2.5.1. В ней же представлены значения а(п), которые превращают (2.5.23) в несмещенную оценку ст, а именно
а0(п) = 2Г2(±п)/Г2 [ |(п-1)}. (2.5.30)
54
Таблица 2.5.1. Смещение оценок о
Объем выборки п Выборочное ожидание "Г" /1 Значения а„(п), такие, что ^1 Г'а,,(п) | — несмещенная опенка о ? /1— 5
5 0,9400 3,534 3,5
10 0,9727 8,515 8,5
25 0,9896 23,502 23,5
50 0,9949 48,502 48,5
100 0,9975 98,501 98,5
200 0,9987 198,501 198,5
Числа во втором столбце (с^) табл. 2.5.1 показывают, что при /7 — 10, например, делитель п—1, использованный в (2.5.24), приводит к оценке о, выборочное ожидание которой равняется 0,9727а. В третьем столбце (ао(п)) показаны значения делителя, необходимые для получения несмещенной оценки о.
Из таблицы можно увидеть, что значение «несмещенного» делителя очень близко к п—3/2 (ср. с последним столбцом). Отсюда следует, что оценка V {Е/х,—F)2//»—3/2)) является превосходным приближением 1 1
к несмещенной оценке о.
Выборочная дисперсия оценки (2.5.23) параметра о. Из выражения (2.5.26) следует, что выборочная дисперсия оценки wn параметра о, определенная в (2.5.23), равна:
<2-5-3|>
где сп определено в (2.5.27). При а(п)-п, п—1 или п—3/2 она приближенно равна о2/2п с ошибкой, имеющей порядок величины п~2. В табл. 2.5.2 приведены ее числовые значения при а(п)-п—1 и п—3/2 для некоторых значений п вместе с приближением о2/2п.
Таблица 2.5.2. Выборочная дисперсия оценки wn= х~у/а(п)\ в виде,
представленном в (2.5.31)
п Приближенное значение о'/2п Точные значения
а(п) = п— 1 а(п)~п—~
10 0,05 0,0539 0,0588
25 0,02 0,0207 0,0213
50 0,01 0,0101 0,0103
100 0,005 0,0050 0,0051
200 0,0025 0,0025 0,0025
55
Из таблицы видно, что смещенная оценка имеет несколько меньшую дисперсию, чем несмещенная, но приближение вида о2/2п чаще всего оказывается достаточно точным.
Вероятность того, что оценка укладывается в определенный интервал. Вычисления вероятностей, связанных со случайной переменной wn, определенной в (2.5.24), можно выполнять с помощью таблиц хи-квадрат [см. приложение 6], так как Кп_ {=a(nJW2/a2 распределена как х2 с п—1 с.с. Например, чтобы найти Р(0,98а 1,02а) при л = 25, нужно вычислить (взяв а(п)-п—1=24)
Кп_Л — (п— 1)И^/а2 = 24И^/а2, откуда
Р(0,98 W25/a 1,02) = Р {24(0,98)2 К24 24( 1,02)2} = = Р{ 23,05 ^К24^ 24,96).
(Для приложений такого рода недостаточны таблицы процентных точек, которые приведены в приложении 6. Пользуясь таблицами обычной функции распределения х2 из работы [Pearson and Hartley — G], находим, что вероятность равняется 0,115).
2.5.5. РАСПРЕДЕЛЕНИЕ СТЫОДЕНТА (/-распределение)
Предположим, что X — нормальная случайная величина с параметрами (д,а) [см. II, раздел 11.4.3], что xx,x2,...,xn —„выборка наблюдений над X, так что среднее значение выборки х =Ёхг/п служит оценкой д и что
s2^E(x—x)2/(n—l)
можно взять в качестве оценки а2 [см. раздел 2.5.4,г)]. Как обычно, переменные Xt,X2,...,Хп вводятся как статистические копии X, хг рассматриваются в качестве реализации Хг для г=1,2,...,л. Тогда х и а2 оказываются реализациями соответственно
X = ЕХг/п, S2=i(X—X)2/(n—\Y
Из раздела 2.5.4,в) следует, что п(Х— g)2/a2 и (п—1)52/а2 — взаимно независимые переменные, имеющие распределение х2 с одной и п—1 степенями свободы соответственно.
Стьюдент (У. Госсетт) ввел случайную величину
s/y/n
которая называется отношением Стьюдента* (биографические сведе-
* А также стьюдентовым отношением, стьюдентовой дробью, стьюдентовым t и т.д. — Примеч. ред.
56
ния приведены в [Pearson and Kendall (1970) — D]. Выборочное распределение этой величины, имеющее большое значение при статистическом подходе, называется распределением Стьюдента с п—1 степенями свободы. Можно видеть, что /, определенная выше, является реализацией случайной величины _______
Г= п1'2(Х — n)/S = ,
5/о такой, что
(X-цУ/(<У/п) _ К, S2/°2 Кп_х/(п-\)
где _
Кх=п(Х— fi)2/о2
И п _
кп_х =(п— l)S2/o2= £(Х —Х)2/а2.
Таким образом, К{ и Кп_х взаимно независимые переменные, имеющие распределения х2 с одной и п—1 степенями свободы соответственно, а переменная Стьюдента Т, определенная выше, равняется
Дадим более общее определение отношения Стьюдента и его распределения в следующем виде.
Определение 2.5.1. Отношение Стьюдента. Случайная переменная Tv, которую можно выразить в виде Г, = v'V'XVTf.), где X и Kv — взаимно независимые случайные величины, имеющие распределения X2 с одной и v степенями свободы соответственно, называется отношением Стьюдента с v степенями свободы, а его распределение называется распределением Стьюдента с v степенями свободы.
Поскольку числитель и знаменатель Г2 — взаимно независимые переменные, пропорциональные х2-переменным, оказывается достаточно простым делом вывести распределение Т2 и, следовательно, распределение ГДсм. раздел 2.5.6]. В результате получим, что п.р.в. отношения Стьюдента Tv с v степенями свободы в точке w равна:
+ р=1,2,..„
где
bv = Г { (р+ 1 )/2) /Г(р/2)7(^).
Существует много таблиц распределения Tv (один из вариантов приведен в приложении 5).
П.р.в. симметрична относительно начала. Она качественно напоминает п.р.в. стандартного нормального распределения, но отличается более «массивными» хвостами (т.е. медленнее убывает). Этот эффект сильнее выражен для меньших значений v [см. рис. 4.5.1]. В
* Не совсем точно. Из этого соотношения можно узнать лишь |Т|. Та же неточность содержится и в определении 2.5.1. — Примеч. ред.
57
Рис. 2.5.2. Функция плотности вероятностей F „ для типичных значений • тип
частном случае, когда г=1, она совпадает с распределением Коши [см. II, раздел 11.7], а для значений v, превышающих 40, она очень близка к стандартной нормальной плотности.
Первые моменты Тр равны:
E(Tv)=0,
var(7;)=l + 2/(p—2), г >2,
skew(TJ,)=0.
2.5.6. РАСПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ДИСПЕРСИЙ (^распределение)
a) F как взвешенное отношение х2-переменных. Дисперсионный анализ, наиболее широко применяемый по сравнению с другими статистическими методами, в большой мере зависит от возможности сравнения взаимно независимых сумм квадратов, которые пропорциональны х2-переменным. Основной статистикой в нем является реализация случайной величины
_ Кт/т т'п Кп/п ’ где Кт и Кп — взаимно независимые х2-переменные с т и п с.с. Ее распределение называется F-распределением с т и п степенями свободы. Символ F — дань Р. Фишеру. Сам Фишер, однако, предпочитал статистику z=-ylnF(,.
Из определения 2.5.1 следует, что Г2, квадрат отношения Стью-дента (с п степенями свободы), имеет F-распределение с 1 и п с.с. (Может возникнуть вопрос, почему статистики не пользуются более простой случайной переменной Кт/Кп7 Ответ заключается в том, что коэффициент п/т в определении Fmn играет роль удобного нормирующего коэффициента. Математическое ожидание Fmn близко к единице, точнее говоря, оно равно п/(п—2) для всех значений т и п (п>2)).
Распределение Fmn можно вывести прямым вычислением. Функция плотности вероятности Кт в точке z равна fm(z), определенной в (2.5.15), поэтому п.р.в. Кт/т в точке х есть
hm(x) = rnfm(rnx).
Аналогично, п.р.в. п/Кп в точке у равна:
gn(y) = ny~2fn(n/y).
Наконец, п.р.в. Fmtn=(Km/m)(n/KJ является сверткой [см. II, гл. 7] и £„(•), откуда плотность F п в точке z выражается как
58
a(m,n)z("'~2}/2/{1 + ^zV'"""1
где
z>0,
a(m,n) =
r\(m + n)/2) m . „,,‘2
Г(т/2)Г(п/2) ( n )
Типичная функция плотности вероятности показана на рис. 2.5.2. Ожидаемое значение и дисперсия даются выражениями
E(F„in) = n/(n-2), ">2,
И
var(Fw п) = 2п2(т + п—2)/т(п—2)2(п—4), п > 4.
Заметим, что математическое ожидание зависит только от п.
Функция распределения (ф.р.) Fmn табулирована во многих справочных изданиях, но только в виде процентных точек (квантилей). В нашей таблице (см. приложение 7) приведены верхние процентные точки хр(т,п), такие, что
р{рт,п^хр(т’п)\=Р
для р = 0,05; 0,01; 0,001, для т=1(1); 10; 12; 15; 20; 24; 30; 40; 60; 120;
••• и п= 1(1); 30; 40; 60; 120; -
В табл. 7 из [Pearson and Hartley (1966), приложение Т7] можно найти дополнительные значения для р=0,25; 0,10; 0,05; 0,025; 0,01; 0,005; 0,001.
В таблицах, как правило, приводятся значения х , только такие, что хр>1. Для получения значений хр<1 можно пользоваться соотношением
х}_р(п,т)= ‘
Оно позволяет найти значения нижних процентных точек. Например, нижнюю 5%-ную точку для F (20,10) находят как х095(20,Ю) = = 1/х0 05(Ю,20). Поскольку для верхней 5%-ной точки F (10,20) таблица дает значение 2,35, для нижней 5%-ной точки F (20,10) получаем 1/2,35 = 0,426.
Эти результаты следуют из
P=p\Fm,n>Хр(т>”)} =Р{пК^тКп>хр=(т,п)\ =
= тКп/пКт 1 /хр(т,п)) =
= р\рп,т^х/хр(т’П)\ =
= \—P{Fnm^\/xp(m,n)\ = = ^—p{pn,m>xs_p(n,m)}.
б) Связь между F-распределением и бета-распределением. Говорят, что с.в. Y имеет бета-распределение с параметрами (к,т), если ее плотность в точке у равна:
f(y;k,m)-yk-{(\—у)т~{/В(к,т), O^j’^l, (k>Q, m>Q),
где В(к,т) — бета-функция с параметрами к и т,
59
В(к,т)=\ик~\\—и)т~х -о
=X(k)V(m)/V(k+m)
[см. II, раздел 11.6].
Если U и V — независимые х2-переменные с 2к и 2т степенями свободы, а У= U/(U+ V), то У имеет бета-распределение с параметрами (к,т) [см. II, раздел 11.6.3]. Отсюда следует, что
т У _ U/2k к' 1—У V/2m
и поэтому переменная mY/k(\—Y) имеет ^^-распределение.
в) Аппроксимация для F-распределения, когда одна степень свободы гораздо больше, чем другая. Если Fmn имеет F-распределение с т,п степенями свободы, нетрудно установить, что
Hm P\Fmn>f}=P{femf\,
где, как обычно, х2-переменная имеет распределение х2 с 'т с.с. Практическим следствием из этого является то, что при п>т
P{Fm,n^f}=P(x^rnf).
В качестве иллюстрации в Примере 5.10.1 рассматривается проблема оценивания
^*2,13061 0,66 } .
Она возникает из-за того, что число степеней свободы оказывается гораздо больше, чем в любой из существующих таблиц. Используя приведенную выше аппроксимацию, получим
P{F2 ]30б) <10,66} =Р(х2^ 1,32) = 0,6 (приближенно) (интерполируя с помощью таблицы распределения хг)-
Аналогично если в переменной Fm т^>п, то
P{Fm,nZA=P(x2n^n/f).
2.5.7. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ВЫБОРКИ
Пусть (^гУЭЛхгхУг),.--,^^ — выборка из п наблюдений пары случайных переменных (X,Y), которые имеют совместное двумерное нормальное распределение с коэффициентом корреляции е[см. II, раздел 13.4.6]. Коэффициент корреляции выборки г определяется как
г=А/уЦВС), где
Л = Е {(Xj—х )(у —у)} = Хх^—пху,
60
р =0,7
Рис. 2.5.3. Функция плотности выборочного коэффициента корреляции для нормальных распределений с а) р=0; б) р=0,7
В= t(x—x)2= ^х]—пх2,
п п
С=Ш-7)2=Е^-«г2.
Выборочное распределение коэффициента корреляции выборки имеет п.р.в. в точке г, заданную в виде
уп—3
fn(r,Q) = -^^(i-Q2yn~')/2(i-r2yn-4>/2a(n,r,e), -1 <Г< 1,
где
a(n,r,o)= Е Г2[(л+$— 1)/2}(2@г/7$!
5 = 0
Выборочное ожидание г имеет вид [см. раздел 1.4]
q + О(п~‘)
(относительно О см. раздел 1.4), а выборочная дисперсия —
(1—е2)2/л + ОГл-3/2).
Функция плотности вероятностей унимодальна [см. II, раздел 10.1.3] (для л>4). На рис. 2.5.3 представлены некоторые типичные случаи.
Преобразование Фишера. Выборочные распределения коэффициента корреляции выборки считаются слишком сложными, чтобы ими пользоваться для практических целей (за исключением случая, когда р=0). Вместо них применяется следующее преобразование, найденное Р. Фишером. Пусть*
z = acrtanh г = у In уу, £=acrtanh q = yin .
* Приняты также обозначения arth г и th 'г.— Примеч. ред.
61
Тогда выборочное распределение z близко к нормальному с математическим ожиданием £+е/[2(л—1)] и дисперсией \/(п—3) [см. пример 5.2.2].
Когда q=0, это аппроксимирующее выборочное распределение становится нормальным с нулевым математическим ожиданием и дисперсией \/(п—3). Когда е=0, то точное выборочное распределение переменной г сводится к
fn(r; 0} = Ьп(\—г2Уп~^,г, -1 <r< 1,
где
Ьп = Г{(п-\)/2}/[^Г[(п-2)/2}].
Отсюда получаем, что выборочное распределение величины
(п—2)1/2r/V (1—г2)
является распределением Стьюдента с п—2 с.с. [см. также раздел 2.7.5 и пример 5.2.1]. В дальнейшем Г() обозначает гамма-функцию [см. IV, раздел 10.2].
Дополнительную информацию по этому вопросу можно найти в книге [Fisher (1970), т. VI — С].
2.5.8. НЕЗАВИСИМОСТЬ КВАДРАТИЧНЫХ ФОРМ. ТЕОРЕМА ФИШЕРА—КОКРЕНА. ТЕОРЕМА КРЕЙГА
При дисперсионном анализе, о котором говорилось в разделе 2.5.6 (а также в гл. 8 и 10), часто необходимо установить, будут ли определенные суммы квадратов взаимно независимыми. Главный критерий дает следующая теорема, известная как теорема Кокрена, или как теорема Фишера—Кокрена.
Теорема 2.5.3 (теорема Фишера—Кокрена). Пусть Ui,U2,...,Un — независимые стандартные нормальные величины. Пусть Qi,Qz,..., Qk — неотрицательные квадратичные формы от переменных Ui,U2,...,Un с рангами пх,п2,...,пк соответственно [см. I, раздел 5.6], такие, что
iu\ = Qx+Qi + ,...,Qk.
Qr будут взаимно независимыми х2-переменными тогда и только тогда, когда
п}+п2 + ... + пк = п.
В этом случае Qr имеет пг степеней свободы, г=\,2,...,к.
Далее приводятся две другие полезные теоремы.
Теорема 2.5.4. В обозначениях теоремы 2.5.3 предположим, что п
где Qi — х2 переменная с т с.с., a Q2 — переменная с неотрицательными значениями. Тогда Q2 имеет распределение х2 с п—т с.с. и независима от Qi.
62
Теорема 2.5.5. В обозначениях теоремы 2.5.3 предположим, что Q>Q\ и Q2 — неотрицательные квадратичные формы от переменных
U2,...,Un, такие, что
Q-Q\ +Q2,
причем Q и Q\ распределены как х2 с п с.с. и т с.с. соответственно.
Тогда Q2 распределена как х2 с п—т с.с. и независима от Q\.
Пример 2.5.2. Ортогональное разложение T,(Ur—д)2. Рассмотрим следующее алгебраическое тождество для независимых стандартных _____________________________________ п
нормальных переменных U2,...,Un (U =EUr/n): п — п _
Е U2 = п U2 + L(U-U )2 = 0, + Q2.
Ясно, что квадратичные формы Q} и Q2 неотрицательны. Очевидно, что ранг 0! равен 1, а ранг Q2 — п—1. Отсюда на основании теоремы 2.5.3 следует, что Q} и Q2 — взаимно независимые х2-переменные с 1 и п—1 с.с. соответственно. (Этот результат был установлен в примере 2.5.1.)
Иначе говоря, можно утверждать (причем в более простой форме), что, когда_£7 — нормальная переменная с параметрами (О, л-1/2), переменная Uni/2 будет стандартной нормальной. Откуда получим, что Qx-nU2 — х2-переменная с 1 с.с. Применение результатов теоремы 2.5.4 к указанному выше тождеству приводит к выводу, что 02 = П __
= E(Ur—U)2 — переменная, имеющая распределение х2 с п—1 с.с.
Соответствующий результат для н.о.р. нормальных случайных величин Xi, Х2,...,Хп с параметрами (^,ст) основан на тождестве п __ п _
Е(Х-р)2 = п(Х -р)2 + Ъ(Х -X )2
или, скажем,
0= 01 + 02-
Здесь 0/ст2 — х2-переменная с п с.с., а 01/ст2 — х2-переменная с 1 с.с., откуда, согласно теореме, 02/ст2 — переменная с распределением х2 с п—1 с.с., независимая от 0t. Этот результат важен для проверки значимости среднего выборки с помощью /-критерия Стьюдента [см. раздел 5.8.2].
Пример 2.5.3. Сравнение двух средних. Тождество р+ч р <7 па
Е (х,-хУ = |И(у—уУ + Eft,-?21 + У (у-ГУ
требуется для применения критерия Стьюдента при сравнении средних У и z двух независимых выборок [см. раздел 5.8.4], скажем
^2,---1Ур) и (zi, Z2,---,z4), из нормальных генеральных совокупностей с одинаковой дисперсией ст2, но, возможно, с неравными ожидаемыми значениями. В приведенном выше тождестве
63
(yr, r=l,2,...,p,
r lzr_p, r=p+l,p + 2,...,p + q, — p+q _ _
и x = E xr/(p + q) = (py + qz)/(p + q) — общее среднее.
Записав тождество в виде
Q=Q\ + 02»
легко увидеть, что Q/o2, QJo2 и Qe/o2 суть х2-переменные с числом степеней свободы
P + q— 1, (Р— l) + (q— 1) и 1*.
Отсюда следует, что 01 и Q2 не зависят друг от друга.
Приведенные выше теоремы полезны в случаях, когда квадратичная форма расщепляется на две или более квадратичные формы. Когда же этого нет, например, когда просто даются две квадратичные формы и возникает вопрос, являются ли они независимыми, главную роль может играть следующая теорема.
Теорема 2.5.6. Теорема Крейга. Пусть 0; и Q2 — квадратичные формы от независимых нормальных переменных Х}, Х2,...,Хп с параметрами (р,а), причем Q. соответствует матрица k, a Q2 — матрица В. Случайные величины 0! и 02 взаимно независимы тогда и только тогда, когда АВ = 0.
Пример 2.5.4. Независимость х и s2. Пусть хь х2,...,хп — случайная выборка из нормального распределения с параметрами (g,ст). Установленную в примере 2.5.2 выборочную независимость х=Ъхг/п и s2 = t(xr—х)2/(п—1) можно продемонстрировать с помощью теоремы 2.5.6: рассмотрим квадратичные формы 01=(ЕАГГ)2 и 02 = t>(X —Х)2 = п __ 1 1
= ЕХГ2—пХ2, в которых, как обычно, Хг — случайная переменная, индуцированная xr(r=l,2,...,n), а X — с.в., индуцированная х. Матрица А для 01 имеет вид 1Г/л, а для 02 матрица B I—1Г/л. (I — единичная матрица, Г = (1,Тогда АВ=11 (I—1Г/л> = 1Г—1(11)Г/л = = 11'—1Г (так как 1'1 = л> = 0, откуда следует, что 01 и 02 взаимно независимы. Предположим, что нас интересует, зависимы или нет линейная форма Z=EarA'r = aX и 02 = Е(Аг—X)2. Построим квадратичную форму Z2 = (a X)2 = Xaa Х = Х АХ, для которой матрица А равна аа'. Как и раньше, матрица В для 02 равна I—1Г/л. Тогда АВ= = аа(1—117и>=аа'—а(а/1)17л = аа/—ааГ (где а=аТ/и = Ъаг/п-<а). Элемент (r,s) в этой матрице равен ar(as—а). Он отличен от нуля для всех (r,s) за исключением случая, когда as = ot для всех 5, т.е. когда Z
* Надо добавить: при равенстве математических ожиданий исходных распределений. При неравных математических ожиданиях Q2/+ подчиняется нецентральному распределению х2. — Примеч. ред.
64
пропорционально выборочному среднему X. Таким образом, X не просто независима от S2; X (или линейная форма, пропорциональная X) оказывается единственной линейной формой от Хг, которая не зависит от S2. Например, в выборке объема 3 сумма Х}+Х2+Х3 независима от суммы квадратов выборки Е(ХГ—X)2, однако линейная комбинация Xi—2Х2+Х3 этим свойством не обладает.
2.5.9. РАЗМАХ И СТЬЮДЕНТИЗИРОВАННЫЙ РАЗМАХ
Размахом гп выборки наблюдений Л'ь х2,...,хп над случайной переменной X называется разность х(п)—x(d между наибольшим наблюдением Xfnj и наименьшим наблюдением х(1> [ср. с разделом 14.3]. Пусть Х(п) и A(d обозначают случайные переменные, порождаемые х(л) и х(1), тогда размах индуцирует случайную переменную
Rn~X{n)~X^'
Если, например, X распределена равномерно в области (0,а), то п.р.в. Rn в точке г равна:
h(r) = n(n—1)г"-2(а—г)/а", О^г^а,
с ожидаемым значением
E(R) = (n—l)a/(n + l) [см. II, раздел 15.5].
В приложениях математической статистики размах используется для оценки разброса в малых выборках. В случае выборки объема в два наблюдения размах в точности эквивалентен по информационному содержанию стандартному отклонению выборки. Когда п-2,
L(x—х у/(п— 1) = хд2,
поэтому стандартное отклонение равняется точно г2/^2\ таким образом, г2 можно считать оценкой <г/2. Для выборок объема больше 2, но не превышающего 10 или 12 наблюдений, размах оказывается хотя и не эффективной [см. определение 3.3.5 и пример 3.3.10], но вполне приемлемой оценкой для произведения стандартного отклонения о с известным множителем генеральной совокупности [см., например, Hald (1957), гл. 12 — С]. При увеличении объема выборки относительная эффективность оценки уменьшается, и ею не рекомендуется пользоваться, когда объем выборки превышает 12 [см. Davies (1957) — С]. Для нормальных выборок существуют таблицы выборочного распределения так называемого стандартизованного коэффициента гп/а размаха [см. например, Hald (1952) или Owen (1962) — С].
Стьюдентизированный размах. Для образования стандартизованного коэффициента размаха гп/о из обычного размаха гп выборки надо знать стандартное отклонение а генеральной совокупности. Когда о неизвестно (это бывает чаще всего), предлагается заменить его подходящей оценкой. Если в распределении имеется статистика v, которая не зависит от гп и такая, что v/ст2 распределена по закону х2 с т с.с., то подходящей оценкой а будет величина Vv/щ, а статистика 65
r^) называется стьюдентизированным размахом [ср. с определением 2.5.1]. Стьюдентизированный размах необходим при построении по методу Тьюки совместных доверительных интервалов для нескольких параметров [см. Graybill (1976), табл. Т7].
2.6. АССИМПТОТИЧЕСКОЕ ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ х И НЕЛИНЕЙНЫХ ФУНКЦИЙ ОТ х
Наиболее богатые результаты получаются в выборочной теории (как показано на примерах в разделе 2.5), когда в ее основе лежит нормальное распределение. Хотя на практике абсолютная нормальность никогда не встречается, выборочная теория нормального распределения может применяться с некоторой приемлемой степенью приближенности благодаря следующим результатам (и их многомерным обобщениям). Они во многих случаях формулируются в терминах асимптотической нормальности, которая определяется ниже.
Определение 2.6.1. Асимптотическая нормальность при больших значениях п. Говорят, что статистика sn, основанная на выборке объема л, асимптотически нормальна с математическим ожиданием ц и дисперсией vn, если
lim Р( Sn~>l =(2-тг)-|/2 j е(u^/2du = Ф(у),
где S„ — случайная величина, индуцированная sn [см. определение 2.2.1], а Ф — функция стандартного нормального распределения.
Это определение практически можно интерпретировать как утверждение, что при больших п распределение sn с разумной точностью аппроксимируемо с помощью нормального распределения с параметрами (/z,Vvn). Например, отношение Стьюдента с п степенями свободы асимптотически нормально с параметрами (0,1), что можно трактовать как распределенное N (0,1) с хорошей степенью приближения при п >40.
Теорема 2.6.1 (теорема Хинчина). Если (х\, х2,...,хп) — выборка из распределения, которое имеет конечное математическое ожидание ft, то выборочное среднее х сходится по вероятности к ц. [см. определение 3.3.1].
Это означает, что при больших значениях п маловероятно, чтобы х существенно отличалось от ц,.
Теорема 2.6.2 (теорема Линдеберга). Если (х{, х2,...,хп) — выборка из распределения с конечным математическим ожиданием цис конечной дисперсией а1, то выборочное распределение среднего значения выборки х будет ассиметрически нормальным с математическим ожиданием ц и дисперсией а2/п при растущих п.
66
Этот результат является частным случаем центральной предельной теоремы [см. II, раздел 17.3]. Его практическая интерпретация состоит в том, что при больших п выборочное распределение среднего значения выборки х хорошо аппроксимируется (в разумных пределах) нормальным распределением с параметрами (д,а/7л).
Теорема 2.6.3 (теорема Муавра—Лапласа). Если случайная переменная R имеет распределение Вш(л, в) [см. II, раздел 5.2.1], то R — асимптотически нормальна с математическим ожиданием пв и дисперсией п0(1—0) [см. II, раздел 11.4.7].
Среди приведенных здесь и подобных им теорем исключительную практическую важность имеет следующая теорема (она представлена в форме, предложенной в работе [Wilks (1961), гл. 9 — С].
Теорема 2.6.4. Асимптотическое выборочное распределение g(x). Если (Х\, х2,...,хп) — выборка из распределения, которое имеет конечное математическое ожидание ц и конечную дисперсию о2, a g(x) — определенная функция х, то при соблюдении условий, устанавливаемых ниже, выборочное распределение g(x) будет асимптотически нормальным с математическим ожиданием g(jT) и дисперсией [см. определение 2.6.1].
Условия, налагаемые на функцию g, состоят в том, что g'(x) должна существовать в некоторой окрестности х=ц и что ^(/х)#0.
На основании этого результата можно показать, например, что в выборках объема п из различных распределений соответствующие асимптотически нормальные выборочные распределения для выборочного среднего х или для определенной функции g(x) оказываются такими, как это показано в табл. 2.6.1.
Таблица 2.6.1
Распределение с.в. X g(x") Асимптотически нормальное выОо-рочное распределение с.в. g(x~j
математическое ожидание дисперсия
Распределение Пуассона с параметром 0[см. II, раздел 5.4] 2Vx 2<в 1/п
Gamma (0) (т.е. гамма-распределение с параметром формы в) [см. II, раздел 11.3.1] 2Ух 2V0 1/п
Bernoulli, (0) [см. II, раздел 5.2.2] sin—1(2x—1) sin-‘(20—1) 1/п
Геометрическое распределение с параметром в (т.е. с п.р.в. Р(Х=х)=(1—в)вх,~1 х=1,2,...) [см. II, раздел 5.2.3] log[x(l + VT— 1/х)) и',2? 5) 1/п
Равномерное распределение (—Ев, Ее) [см.II, раздел 11.1] vT21og(2r) V121og0 4/п
67
2.7. ПРИБЛИЖЕНИЕ ВЫБОРОЧНЫХ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ НЕЛИНЕЙНЫХ СТАТИСТИК. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
2.7.1. АППРОКСИМАЦИЯ
а) Функции одной случайной переменной. Внутреннее содержание понятия предела в математике состоит в том, что если последовательность {zn}, /7 = 1,2,..., сходится к пределу а при п— ««*. то zn должны стать приближенно равными а для всех достаточно больших значений п. Асимптотические результаты, описанные в разделе 2.6, которые будут справедливы в строгом смысле только в пределе, когда п-*-«•, оказываются приближенно верными для всех достаточно больших конечных значений п. К сожалению, нечасто встречаются случаи, когда легко сказать, насколько большими должны быть п, чтобы они стали «достаточно большими». На практике часто приходится использовать асимптотические результаты (или какие-либо результаты, основанные на них) в качестве приближения, когда п всего лишь умеренно большое или даже совсем не велико. Более того, может возникнуть необходимость в аппроксимациях выборочных распределений (или по крайней мере их математических ожиданий и дисперсий) для нелинейных функций от статистик, отличных от среднего значения выборки. Обычно в таких случаях возлагают надежду на грубые приближения к математическому ожиданию и дисперсии подходящей гладкой функции h(X) случайной переменной X, которые можно получить из нескольких первых членов (или даже из одного первого члена) разложения функции h(-) в ряд Тейлора [см. IV, раздел 3.6] в точке li-E(X). Такие аппроксимации имеют вид
(2.7.1)
var[h(X)] = {h^)]2a2
где /г=Е(Х) и <r2=varf.X>.
Эти аппроксимации часто берутся в простейшем варианте:
E[h(X)} =h(^ s.d[h(X)} = \h^)\o.
(2.7.2)
Так, например, при h(x) = l/X, имеем
Е(1/Х) = 1 /д, s.d(l /X) = а//?
Коэффициент вариации. Когда X — переменная с положительными значениями, ее изменчивость можно выразить в удобном виде с помощью коэффициента вариации (c.v.), определяемого как
68
c.v.(X)=s.d.(X)/E(X)=a/ti
[см. II, раздел 9.2.6].
Для функции h(X)=Xa аппроксимации (2.7.2) наиболее четко выражаются в терминах коэффициента вариации. Имеем
Е(Ха) = ца,
s.d.(Xa) = |а|/г“~1ст, поэтому
c.v.(Xa) = |a|c.v/A7
В частности,
c.v.(l/X; = c.v/X>.
Пример 2.7.1. Стандартное отклонение выборки. Предположим, что Y — нормальная переменная с параметрами (/х,а), и рассмотрим дисперсию выборки v-t(yr—у)2/(п—1) для выборки (уь у2,...^п). В
разделе 2.5.4 г) и д) показано, что порожденная (индуцированная) случайная величина V имеет математическое ожидание ст2 и дисперсию 2а4/(п—1). Для случайной переменной S=tzl/2, порожденной стандартным отклонением 5=v1/2 выборки, выражение (2.7.1) приводит к следующим приближениям для E(S) и varfS) после подстановки в (2.7.1) V вместо X, о1 вместо /л и 2а4/(п—1) вместо а2, если принять Л(/х) равным /х1/2:
E(S) = о+ 4-’-’) = 11-1 /4М-1) 1»,
varfS) = = <?/2(п-Г).
Точные значения (см. раздел 2.5.4] имеют вид
E(S)^o,
(== {(2п—3)/(2п—2)} для больших п),
^(S) = d<n)o\ d(n) = 1- Д ,
(= 1 /(2л—4) для больших п).
Аппроксимации (2.7.1) в этом случае оказываются довольно точными, как можно судить по некоторым численным значениям, представленным в табл. 2.7.1.
Таблица 2.7.1. Выборочное ожидание и дисперсия стандартного отклонения выборки из нормальной генеральной совокупности. Точные и приближенные значения
Объем выборки Математическое ожидание Дисперсия
точное приближенное точная приближенная
5 0,940а 0,938а 0,116а2 0,125 а2
10 0,973а 0,972а 0,054а2 0,056а2
69
Объем выборки Математическое ожидание Дисперсия
точное приближенное точная приближенная
20 0,987а 0,986а 0,026а2 0,028а2
50 0,995а 0,995а 0,010а2 0,0102а2
Не следует думать, что аппроксимации вида (2.7.1) всегда так •точны, как в этом случае. Менее благоприятные ситуации рассматриваются в [II, раздел 9.9].
б) Функции двух случайных переменных. Формулы (2.7.1) можно обобщить на случай двух переменных. Пусть h(Xi,X2) — заданная дифференцируемая функция случайных переменных Х{ и Х2, где
Е(Хд = 1м, Е(Х2) = ц2,
varfAF1) = о], var(X2)=0^ согг(Х{,Х2)= q.
Тогда
E{h(XuX2)]=h(iw2) (2.7.2)
и var {h(X\ ,Х2)} — Л2о^ + 2,hih2QO\<j2 +А2О2, (2.7.3)
где hj = d[h(ni,ii2)]/dnj, j=\,2.
Когда %i и Х2 некоррелированны (и тем более когда они независимы), приближение для дисперсии сводится к
уаг(Л(ХьХ2)] =Л?а| + Л^ (2.7.4)
Пример 2.7.2. Дисперсия произведения и частного. Для произведения Х\Х2 независимых случайных переменных формула (2.7.2) становится точной, в то время как формула (2.7.4) для дисперсии дает приближение
varfXjXa) =
Соответствующей приближенной формулой для коэффициента вариации [см. раздел 2.7.1] будет
{сх.(Х,Х2)}2 = {c.v/%1)}2+ (c.v/%2)}2.
В этом примере легко указать точные формулы:
Е(Х},Х2) = 1гщ2, var (Х{ ,Х2)=Е(ХхХ2У-(у^2у = =E(X2dE(Xl)-^22 = ~ (Рл + /ч)(Р2 + Мг)—М1М2 = = 0102 + g! (72 + /4<Г1,
70
откуда
[c.v.(X,X2)\2 = (c.v.(X,)!2+ (c.v.(X2))2 +
+ |c.v.(X,))2|c.v.(X2))2.
Для частного X\/X2 получаем приближения
Е(Х\ /Х2) = м 1 М2»
var(X,/X2) = (д2/^) {а?/д2 + а2,/^} и
{c.v.(^/%2))2 = [c.v.(X1)]2 + (c.v.(X2) }2.
Таким образом, приближения для коэффициентов вариации ХГХ2 и Х{/Х2 совпадают.
2.7.2. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ
а) Общая формула. Когда данные возникают из подсчета (например, сколько стерильных образцов?), их выборочное распределение обычно биномиальное или пуассоновское. Трудности анализа связаны не только с тем, что наблюдения дискретны, но и с тем, что выборочная дисперсия зависит от неизвестного параметра. Например, если наблюдаемые доли успехов в двух совокупностях равны гх/п\ и г2/п2, то сравнение соответствующих вероятностей успехов 0^ и 02 затрудняет зависимость выборочных дисперсий Г] и г2 от параметров 0} и 02. (Именно они равны Л101(1—0J и л202(1—02) соответственно.) Ситуация упростится, если будет найдено преобразование, превращающее все биномиальные случайные величины в новые переменные, которые имеют постоянную дисперсию; сказанное относится и к пуассоновским переменным. Преобразования, которые в известной степени ведут к такой идеальной ситуации, можно вывести с помощью (2.7.1). Если X имеет ожидаемое значение 0 и дисперсию ст2(0), a Y-h(X) — преобразование X, то
уаг<У> = сР(0){ /г(0)}2.
Подбирая h{0) так, чтобы
a(0)h'(0) = k (=const), можно добиться того, что varfX) станет постоянной (приближенно). Это произойдет, если
при этом дисперсия преобразованной переменной Y=h(X) приближенно равна к1.
б) Пуассоновские данные. Преобразования с помощью извлечения квадратного корня. Предположим, что X имеет распределение Пуассона с параметром 0, так что а2(0) = 0. Тогда (2.7.4) превращается в
Л(0) = ^0-1/2б70=<0 (£=±).
Это приводит к преобразованию х в
Vx (2.7.5)
Наблюдаемые величины х(, х2,... преобразуются в Vxi, Vx2,...; преобразованные данные имеют выборочную дисперсию, приближенно равную 1/4.
Точность аппроксимации можно определить путем прямого вычисления var(v'JV) по формулам
var(VX)=0—{£(<¥) )2,
£(<*)= Ё г=0,1,...).
Представления о точности аппроксимации дает табл. 2.7.2.
Таблица 2.7.2. Эффект стабилизации дисперсии с помощью преобразования квадратного корня пуассоновской случайной величины
е Дисперсия «преобразованной переменной X Дисперсия преобразованной переменной \Гх е Дисперсия «преобразованной переменной X Дисперсия преобразованной переменной Гх
0,2 0,2 0,164 2 2 0,390
0,4 0,4 0,272 5 5 0,287
0,6 0,6 0,334 10 10 0,259
0,8 0,8 0,381 20 20 0,255
1 1 0,402
Хотя на первый взгляд это преобразование не кажется особенно полезным в смысле достижения постоянной дисперсии, равной 0,25, на самом деле оно значительно уменьшает изменчивость дисперсии для значений параметра 0, которые меньше десяти, и поддерживает ее практически постоянной для больших значений.
Энскомб показал, что еще эффективнее преобразование
< 6¥+3/8) . (2.7.6)
В этом случае, например, при 0 = 2 дисперсия равняется 0,2315, что уже совсем близко к нашей цели — значению 0,25 [см. Wetherill (1981), гл. 8 — С].
в) Биномиальные данные. Преобразование арксинуса (или угловое преобразование). Если X следует распределению Бернулли с параметрами (0), то наблюдения хь х2,...,хп часто преобразуются в статистику х=г/п (г-хх +х2 + ...+хл), которая является обычной оценкой параметра 0. Выборочное распределение г— Binfn,0) с математическим ожиданием ц=п0 и дисперией а2=пв(1—0). Соответствующие значения для г/п — 0 и 0(1—0)/п. Попытаемся найти преобразование z=h(r/n) с постоянной выборочной дисперсией. С помощью (2.7.1) получим выражение
var/z> = {Л(0)) 20( 1 —0)/п,
72
у которого член в правой части будет постоянным (=£2), если
Это условие удовлетворяется, если принять*, что
/7(0) = 2A771/2sin-‘V0,
т.е. если взять
z=2A'/71/2sin-1Vr7w.
Эквивалентным и более удобным оказывается преобразование г в z/'lkJn, т. е. в
sin-1Vr7w. (2.7.7)
Эта случайная величина имеет выборочную дисперсию, приближенно равную 1/4л. Модификация
sin-1/^^8, (2.7.8)
м+1/4
предложенная Энскомбом, лучт’ле. Приближенная выборочная дисперсия для этой модификации равняется 1/(4л + 2) [см. Wetherill (1981), гл. 8 — С].
г) Стабилизация дисперсии отклика с помощью взвешивания. Если при проведении линейного регрессионного анализа [см. раздел 6.5] выясняется, что рассеяние значений отклика у на графике данных изменяется систематически с изменением переменной х, то дисперсию можно стабилизировать путем простой процедуры взвешивания. Например, если выборочное стандартное отклонение у(х), т.е. отклонение значений у, соответствующих значению х, возрастает пропорционально значению х, то переход от у(х) к взвешенным данным,
z(x)=y(x)/x, будет стабилизировать дисперсию.
2.7.3. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
Поскольку нормальные наблюдения сравнительно легко исследовать, йасто бывает полезным преобразовать данные в приближенно нормальные.
а) Логарифмическое преобразование. Положительные переменные с положительной асимметрией. Данные, которые могут принимать любые положительные значения, часто происходят из распределения с положительной асимметричной п.р.в. [см. II, раздел 9.10.1], напоминающего логарифмически нормальное распределение [см. II, раздел 11.5], гамма-распределение [см. II, раздел 11.3] или распределение х2 [см. II, раздел 11.4]. Если случайная переменная X распределена как логарифмически нормальная переменная, то ее логарифм будет нормальным (по определению). С помощью логарифмического преобразования можно добиться только приближенной нормальности для
* sin *x=arcsin х. — Примеч. ред.
73
Рис. 2.7.1. Графики ф.р. распределения х! и распределения xh на логарифмической вероятностной бумаге
случаев, когда оно применяется к случайным переменным, распределение которых лишь качественно напоминает логарифмически нормальное распределение. На рис. 2.7.1 изображены графики функции распределения (ф.р.) распределения х2 с различными значениями числа степеней свободы, а прямая линия соответствует ф.р. логарифмически нормального распределения (таким образом разграфленная бумага называется логарифмически вероятностной бумагой (ср. с разделом 3.2.2,а)).
б) Логарифмическое преобразование переменных, значения которых ограничены сверху или снизу. Преобразование Фишера для коэффициента корреляции. Если значения случайной переменной X заведомо лежат в интервале (а,Ь), то значения преобразованной переменной Y- In {(X— а)/(Х— Ь)} могут изменяться от —°° до+~- Тем самым не исключается, что Y может быть приближенно нормальной переменной.
Это преобразование рекомендуется в случае коэффициента корреляции. Коэффициент корреляции г, рассчитанный по выборке п пар (Xj^p из двумерной нормальной совокупности [см. II, раздел 13.4.6], а именно
[ {Н Eyj-CEjJVn} ] 1/2
[см. раздел 2.5.7], имеет значения, лежащие в интервале (—1, +1). Выборочное распределение г сильно скошено, его точная форма зависит от значения q коэффициента корреляции в исходной генеральной
74
совокупности. Преобразованная статистика [см. § 2.5.7] z=llnlt^(=tanh-1r> (2.7.9)
2 1—г
имеет почти нормальное выборочное распределение с математическим ожиданием
4-inp^ + 2 1—е
е 2(п—1)
и дисперсией
\/(п—3) (приближенно).
Это преобразование заметно упрощает вопрос о точности г как оценки е [см. пример 5.2.2].
в) Нормализующие преобразования распределения х2- Хотя для распределения х2 [см. раздел 2.5.4, а) и гл. 7] существует много таблиц, иногда удобнее работать с приближенно нормальной функцией от х2. Обычно для х2-переменной с v степенями свободы используются следующие два преобразования:
1) для v> 100 переменная
^=<(ад — V (2р—1) (2.7.10)
приближенно распределена по стандартному нормальному закону; это приближение неплохо действует также для 30<р^100. Большую точность дает вариант:
2) для р>30
Х= {(х2/^)1/3—(1— 2/9р)}/< (2/9р) — (2.7.11)
приближенно нормальная стандартная переменная.
Например, при р=40 вероятность того, что х2-переменная будет превышать 51,805, равняется 0,100; аппроксимация (2.7.11) дает 1—Ф(х), где х=(1,0900—0,9944)/0,0745= 1,283, откуда 1— Ф(^=0,998, т.е. ошибка составляет 0,2%. Аппроксимация (2.7.10), для которой у=40 считается слишком малым, дает приближенное значение 0,98, т.е. ошибка составляет 2%.
г) Преобразование с помощью интеграла вероятности. Пробиты. В принципе любая непрерывная случайная переменная поддается точной нормализации с помощью преобразования интеграла вероятности: если ф.р. X в точке х обозначить через F(x), то преобразованная переменная U-F(X) будет иметь равномерное распределение в области (0,1) [см. II, разделы 1.4 и 10.7]. Если обозначить ф.р. стандартной нормальной переменной в точке у через Ф(у) [см. II, раздел 11.4.1], то случайная переменная $(Y) будет равномерно распределена в области (0,1). Таким образом, преобразование X в Y, заданное соотношением
$(Y)=F(X) или
Y=$-'{F(X)}, (2.7.12)
75
Рис. 2.7.2. S-образная кривая
будет преобразовывать X в стандартную нормальную переменную.
Величина у=Ф~1(г) или чаще (чтобы избежать отрицательных значений)
у = 5 + Ф-‘^ называется пробитом z-
В разделах 2.7.4 и 6.6 описывается практическая реализация этой идеи. Подробное обсуждение ее применительно к исследованиям типа «доза — эффект» мож-
но найти в книге [Finney (1971)]. Другое преобразование такого же рода — преобразование типа «логит» можно найти в работе [Ashton (1972)]. В этом случае вероятность р заменяется на z=lnp/(l—р).
2.7.4. ПРЕОБРАЗОВАНИЯ, ВЫПРЯМЛЯЮЩИЕ ЗАВИСИМОСТЬ
В тех ситуациях, когда согласно принятой гипотезе наблюдения у(х) должны лежать на кривой q(x) (с’учетом случайных ошибок), прежде чем прибегнуть к более сложным методам оценивания, имеет смысл по виду наблюдений выяснить, согласуются ли точки на графике с этой гипотезой. На глаз легче обнаружить отклонения от прямой, чем от кривой, поэтому полезно преобразовать данные так, чтобы кривая q(x) превратилась в прямую линию.
Хорошим примером может служить использование этой идеи при проверке нормальности выборки. Пусть для каждого х у(х) обозначает долю наблюдений, которые меньше х или равны ему, a q(x) — нормальная ф.р. Существует специальная разграфленная бумага, называемая нормальной вероятностной бумагой, которая имеет такую шкалу, что q(x) становится прямой линией [см. раздел 3.2.2, г), а также II, раздел 11.4.8].
Другой пример — анализ данных типа «доза — эффект», когда, например, требуется оценить токсичность реагента. Этот препарат не оказывает воздействия, если он достаточно сильно разведен; он становится умеренно действенным ядом при низких концентрациях; его действие усиливается при увеличении концентрации, и в конце концов он становится способным убивать всю выборку. Общепринятой мерой токсичности является доза, убивающая 50% организмов. Ожидается, что процент смертности у(х) организмов, подвергающихся воздействию яда в увеличивающихся дозах х, лежит на кривой, вид которой показан на рис. 2.7.2. Ее иногда называют 5-образной, сообразной, сигмоидой. Удобной моделью для такой кривой оказывается нормальная функция распределения с параметрами (^,ст). В этом случае проблема оценивания токсичности сводится к проблеме оценки парамет
76
ров fi и о. Прямой подход к этой проблеме включает получение последовательных приближений, которые можно упростить, используя пробит-преобразование, спрямляющее кривую [см. раздел 6.6].
2.7.5. ПРЕОБРАЗОВАНИЕ ВЫБОРОЧНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПРИ Q=0 В СТЫОДЕНТОВУ ВЕЛИЧИНУ
Для полноты изложения приведем преобразование коэффициента корреляции нормальной выборки, о котором уже была речь в разделе 2.5.7. Оно сводится к следующему.
Если г обозначает коэффициент корреляции выборки, вычисленный, как указано в разделе 2.5.7, для выборки из п независимых пар (*j, Ji), (х2, у2),...,(jc„, Уп), где хг — наблюдения над нормально распределенной случайной переменной X, а уг — наблюдения над нормально распределенной случайной переменной Y, причем X и Y независимы, то выборочное распределение статистики
fn—2)1/2r/V (1—г2)
будет распределением Стьюдента с п—2 с.с. [см. пример 5.2.1].
2.7.6. ПРЕОБРАЗОВАНИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПЕРЕМЕННОЙ В ^-ПЕРЕМЕННУЮ
В соответствии со стандартной теорией преобразований [см. II, раздел 10.7], если с.в. X имеет ф.р. F(x), то ее функция
Y=F(X)
равномерно распределена в области (0,1) [см. II, раздел 11.1].
Это известное преобразование с помощью интеграла вероятностей [ср. с разделом 2.7.3, г)].
Возьмем случай, когда X имеет экспоненциальное распределение с математическим ожиданием 2. Функцией плотности вероятностей для него будет
х^О, а функцией распределения —
F(x) = l— е-х/2, х^О.
Из сказанного выше следует, что
1—е-*/2
является равномерно распределенной переменной в области (0,1).
Разумеется, и
Z=e~x/2(=1—Y)
также имеет равномерное распределение. Верно и обратное: если Z равномерно распределена на (0.,1) и
Х=— 21ogZ, то X — экспоненциально распределенная переменная с ожиданием, равным 2; это означает [см. раздел 2.5.4,а)], что X представляет собой х2-переменную с двумя степенями свободы.
Фишер использовал этот результат для объединения уровней значимости нескольких статистических критериев [см. раздел 5.9].
77
2.8. НЕЦЕНТРАЛЬНЫЕ ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
2.8.1. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ
Пусть
где Vr — нормальная переменная (дг,1) и V2,...,Vm взаимно независимы. Распределение Wm называется нецентральным распределением хи-квадрат с т степенями свободы и с параметром нецентральности *
1 т
Если Х=0, то это распределение сводится к обычному (центральному) распределению хи-квадрат [см. раздел 2.5.4, а)]. Альтернативное представление Wm имеет вид т т
wm = yur+^
где Ur — независимые стандартные нормальные переменные. Частный случай, когда т = \, может быть представлен в виде
где U — стандартное нормальное распределение. Параметр нецент-ральности Х=у^?
К фундаментальным свойствам этого распределения относятся следующие:
1) Е<И^=т+2Х;
2) var<H^=2^+4X);
3) производящая функция моментов Wm равняется:
E(expIFw0) = (1—20)-т/2ехр {2Х0/(1—20)}, 0 < 0 < ±;
4) п.р.в. Wm в точке w есть,,
/|Ч*Х)= Еg(k)h(w;\),
г=0
где gr(X) = е~хХ7г/ = п.р.в. распределения Пуассона с параметром X в точке г [см. II, раздел 5.4], и
hr(w;\) = {/2) /2“<'Т {a(r)}, w > О,
где
a(r)=-L(m + 2r),
такая, что hr — п.р.в. центрального распределения хи-квадрат с т + 2г степенями свободы [см. II, раздел 11.4.11];
* Параметром нецентральности чаще называют Ед2 [см., например, Л. Н. Большее, Н. В. Смирнов. Таблицы математической статистики. — М.: Наука, 1983.—С 18].—Примеч. ред.
78
5) если Wm, и Wm„ — независимые нецентральное переменные х2 с т'т" степенями свободы и с параметрами нецентральности X' и X" соответственно, то + — также нецентральная переменная х2
с т = т'+т" степенями свободы и параметром нецентральности X = .
Наиболее важное применение это распределение находит при рассмотрении функции мощности (или функции чувствительности) критериев дисперсионного анализа [см. раздел 5.3.1]. Дополнительную информацию по этому поводу можно найти в работе [Graybill (1976), гл. 4]. Таблицы нецентрального распределения хи-квадрат приведены в работе [Harter and Owen (1970), т. 1—GJ.
2.8.2. НЕЦЕНТРАЛЬНОЕ F-РАСПРЕДЕЛЕНИЕ
Нецентральным F-распределением с (т,п) степенями свободы и с параметром нецентральности X является распределение отношения nW/mZ, где W имеет нецентральное распределение х2 с т с.с. и параметром X [см. раздел 2.8.1], в то время как Z, которая не зависит от W, имеет обычное распределение х2 с п с.с.
Это распределение находит применение в тех же случаях, что и нецентральное распределение х2- Дополнительная информация и соответствующие таблицы можно найти в книге [Graybill (1976), гл. 4 и табл. Т 11]. Кроме того, таблицы приведены в [Harter and Owen (1974), т.2—G],
2.8.3. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
Нецентральным распределением Стьюдента с т степенями свободы и параметром X называется распределение отношения
L4-X
VfV/m)
где U — стандартная нормальная переменная, а V — (центральная) Х2-переменная с т степенями свободы, причем U и V взаимно независимы.
Так, например, в выборке (хь х2,...,х^ из N(^,ct) со средним х и дисперсией У = —х)2/(п—1) выборочное распределение статистики
t'-(x —ц + а)п1 /2/s
оказывается нецентральным распределением Стьюдента с п—1 с.с. и параметром
\-п1/28/а.
Наше заключение можно проверить, заметив, что t,_ (х—ц+8)/(р/>/п) _ l(x— n)/(a/yfn)} +\
S/a V(Erx;—F)2/a2l/Vrn—1)
79
Эта величина является реализацией {(U+ X)V7}/V(x*), где Х=6л1/2/а и v — n—1, так как выборочное распределение х нормально с парамет-п рами [см. раздел 2.5.3,6)], распределение переменной Е(х;—
—х)2/о2 — центральное распределение х2 с v=n—1 с.с. [см. пример 2.5.1], а числитель и знаменатель взаимно независимы [см. раздел 2.5.4, в)].
Применение этого распределения в случае чувствительности (или мощности) критериев значимости показано в разделе 5.3.2. Более подробная информация содержится в книге [Owen (1976)]. Соответствующие таблицы можно найти в работе [Resnikoff and Liebermann (1957) — G].
2.9. ПОЛИНОМИАЛЬНОЕ (МУЛЬТИНОМИАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ В ТЕОРИИ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ
2.9.1. БИНОМИАЛЬНОЕ, ТРИНОМИАЛЬНОЕ И МУЛЬТИНОМИАЛЬНОЕ (ПОРЯДКА т) РАСПРЕДЕЛЕНИЯ
1) Биномиальное распределение. Простым испытанием Бернулли считается статистический эксперимент, в котором возможны два исхода Ai и Аг (часто называемые успехом и неудачей). Пусть
Р(Ад=Рх, Р(А2)=р2, где
Р1+Рг = 1-
Важной случайной переменной оказывается полное число Rx появлений А2 в п независимых испытаниях; может возникнуть интерес к полному числу R2 появлений А2. Достаточно обсудить только одну из этих переменных, так как
7?1 +R2 = п.
Распределение Rx—Bin (п;Pi):
P(Ri =Л)=(^)pf'(l-Pi)n-fl, г,=0,1,...,л (0СР.С1).
Иногда предпочитают более симметричную запись:
Р<Г1’Г2)=
Г] =0,1,...,л; г2=0,1,...,п; гх+г2=п (2.9.1)
(O^pi^l, 0^р2^1, Pi+p2 = l).
Отметим, что появление двух символов гх и г2 в (2.9.1) не означает, что мы должны рассматривать это выражение как двумерную функцию. Формула дает нам одномерную вероятность того, что Rx=rx,
80
при этом г2=п—Г\, или одномерную вероятность события /?2 = г2, при ЭТОМ Г1 = п—Г2.
2) Триномиальное распределение. Очевидно, что при испытаниях, для которых возможны три исхода Ль А2 и Л3 с
P(A^ps, 5= 1,2,3,
И Р1+Рг+Рз = 1,
совместное распределение R} и R2 полного числа появлений событий Л1 и Л2 при п независимых испытаниях будет обобщением (2.9.1), а именно
Р(гъг2,г2)=
Г1!Г2!Г3!
Г1,г2,г2=0,1,...,п; гх+г2 + г3 = п (2.9.2)
(0^ps^l, 5= 1,2,3, Pi+p2+p3 = l).
Это дает выражения двумерных вероятностей P(7?i=ri, Р2=г2), при ЭТОМ Г3 — П—Г\—Г2, ИЛИ P(Rx-rx, R3=r3), При ЭТОМ Г2=П—Г\—г3, или, что аналогично, P(R2 = r2, R3 = r3).
3) Полиномиальное (мультиномиальное) распределение (порядка пг). Теперь предположим, что существует т возможных исходов испытания, назовем их Ль А2,...,Ат, и пусть
P(As)=ps, s=l,2,...,m, причем
р1+р2 + ...+рт = 1.
Пусть Rj обозначает полное число появлений исхода Лу в п независимых испытаниях, j=l,2,...,m. Тогда совместное распределение R\, - ,Rm-i будет иметь вид
P(h, г2,...,гт_х, Гт)= —^—^рг...р^
Г1.Г2....Гт.
rs=0,l,...,n, s=l,2,...,m, rl+r2 + ...+rm = n (2.9.3)
(0^ps^l, 5=1,2,...,щ, pl+p2 + ...+pm = l).
Это дает
P(Ri=rt, R2 = r2,...,Rm_l=rm_1) при rm = l—h— r2—...—rm_x или
P(Ri~fi> P2 — ^lf>yRm—2~^m—2’
C
Гх—Гг-...-Гт_2-Гт И Т.Д.
Таким образом, (2.9.3) задает вид распределения вероятностей любых т—1 из т случайных переменных Rlf R2,...,Rm, для которых Rx+R2 + ...+Rm = n. Оно называется полиномиальным распределением (порядка т) с индексом п и параметрами вероятности рх, р2,...,рт. Полиномиальное распределение с т = 2 — биномиальное, с т = 3 — триномиальное и т. д.
81
2.9.2. СВОЙСТВА ПОЛИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
а) Первые моменты. Математические ожидания:
E(Rj)=npj, 7=1,2....т.
Дисперсии:
var(/ty=npy(l—Pj), j=l,2 т.
Ковариации:
cov(Rj, Rk)=—npjpk, j,k=\,2,...,m, j*k.
б) Маргинальные распределения. Все маргинальные распределения также являются полиномиальными: в частности, маргинальное распределение /?у является биномиальным с параметрами <лу, р^, j=i,2,...,m; совместное маргинальное распределение Rj и Rk является триномиальным с параметрами (n;pj,pk), j,k=\,2,...,m(j^k) и т. д.
2.9.3. ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК УСЛОВНОЕ ОТ СОВМЕСТНОГО РАСПРЕДЕЛЕНИЯ НЕЗАВИСИМЫХ ПУАССОНОВСКИХ ПЕРЕМЕННЫХ
В выборочной теории иногда оказывается полезным следующий результат. Предположим, что Xit Х2,...,Хк — независимые пуассоновские переменные с параметрами ц2,...,цк соответственно. Тогда распределение переменных Xt +...+Хк — пуассоновское с параметром 1ц), ц= ца + ... + цк, а условное распределение Xit Х2,...,Хк при фиксированной сумме Xi+X2 + ...+Xk=x имеет вид
P(Xx=Xi,...,Xk=xk | Х\ 4-... +Хк =х) =
_ П<е~^дгг/хг.9 _ х! >хг
е-рцп/х! Т1(хг!) ц
В тривиальном случае, когда Ехг#х, эта вероятность равняется нулю, но когда Ехг=х, она совпадает с (2.9.3). Это показывает, что условное распределение — полиномиальное порядка к с индексом х и параметрами вероятности Р\, р2,...,рк, где р5 = (^/^), s=\,2,...,k.
2.9.4. ТАБЛИЦЫ ЧАСТОТ
Совместное выборочное распределение частот является полиномиальным.
Предположим, что выборка из п наблюдений над непрерывной случайной переменной представлена в виде таблицы частот [см. раздел 3.2.2, б)] следующим образом:
Номер ячейки 1 2 ... к
Частота /, /2 ••• fk
Границы ячеек не обязательно должны быть равноотстоящими; если 82
наибольшее и наименьшее наблюдения равняются d и d', то ячейками могли бы стать интервалы (aj, aJ+l), j=O,l,...,k— 1, значений х для любого разбиения
d=a0<ai <а2<... <ak=d'.
Наблюдаемое значение х располагается в ячейке с номером j, если aj_l^x<aJ, у =1,2...к.
Отсюда следует, что совместное выборочное распределение частот — полиномиальное порядка к с индексом п и параметрами
вероятности pit р2,...,рк:
pj=P(aj_i ^X<aj), j= 1,2....к.
(Аналогичные рассуждения с возможными модификациями вполне применимы, когда случайная переменная X дискретная).
2.10. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
В тексте даны ссылки на работы, приведенные в списке литературы в т. 2 Справочника. Дополнительная литература дается ниже.
Ashton W. D. (1972). The Logit Transformation with Special Reference to its Uses in Bioassay, Griffin.
Finney D. J. (1977). Probit Analysis, Third edition, Cambridge University Press.
Graybill F. A. (1976). Theory and Application of the Linear Model, Duxbury Press, Mass.
Owen D. B. (1968). A Survey of Properties and Applications of the Non-central t-dist-ribution, Technometrics 10, 445-478.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Крамер Г. Математические методы статистики /Пер. с англ.; Под ред. А. Н.
Колмогорова.—2-е изд., стереотипное.—М.: Мир, 1975.—Гл. 27—29.
Хан Г., Шапиро С. Статистические модели в инженерных задачах /Пер. с англ.; Под ред. В. В. Налимова.—М.: Мир, 1969.—396 с.
Хастингс Н., Пикок Дж. Справочник по статистическим распределениям /Пер. с англ.—М.: Статистика, 1980.—96 с.
Глава 3
ОЦЕНИВАНИЕ. ВВОДНОЕ ОБОЗРЕНИЕ
3.1. ЗАДАЧА ОЦЕНИВАНИЯ
Когда статистики говорят о проблеме оценивания, они обычно имеют в виду ограниченное толкование этого термина: полученные данные предполагаются наблюдениями из одного или нескольких определенных семейств вероятностных распределений, в которых элементы отличаются друг от друга значениями одного или нескольких параметров. Задача оценивания состоит в том, чтобы извлечь из данных наилучшее статистическое приближение для неизвестных значений параметров, отвечающих наблюдениям, а также объективную меру точности этого приближения.
Выбор семейства распределений, соответствующего обсуждаемой задаче, может быть в некоторых случаях обстоятельствами дела указан более или менее однозначно. Однако во многих ситуациях этот выбор далек от единственности. Когда идет речь об оценивании неизвестной доли дефектных изделий в большой партии по случайной выборке из нее определенного объема [см. пример 2.1.1], вполне ясно, что надо подсчитать число дефектных изделий в выборке, а из организации выбора следует, что оно является реализацией гипергеометрического распределения [см. II, раздел 5.3]. При известных условиях это распределение удовлетворительно приближается биномиальным распределением [см. II, раздел 5.2.2]. Если говорят о средней длине изделий в партии, надо работать с семействами распределений длин. Каких именно семейств? В обсуждаемом примере разумно предположить, что флуктуации длин обусловлены многими причинами, поэтому, помня о центральной предельной теореме (см. И, разделы 11.4.2 и 17.3], будем считать это распределение (хотя бы приблизительно) нормальным [см. II, раздел 11.4.3].
В других случаях может не быть ни физических, ни каких-либо причин для того, чтобы предпочесть одно семейство другому; единственной основой для выбора остается сама выборка. Подходящим может оказаться более одного семейства. Этот пример показывает, что теория оценивания для своей завершенности требует метода, который позволил бы решить, может ли подобранное распределение разумно описать имеющуюся выборку. Этот вопрос «согласия» обсуждается в гл. 7.
84
Очевидно, что любая оценка неизвестного параметра должна основываться на выборке. Функция наблюдений (называемая статистикой [см. определение 2.1.1]), которая будет служить оценкой, обычно выбирается с учетом многих требований. Существуют два основных подхода. При первом каждое значение статистики рассматривается как наблюдение над выборочным распределением этой статистики: берут в расчет не только реальное наблюдение, но и все возможные потенциальные наблюдения. При другом подходе свойства оценки обсуждаются исключительно в терминах действительно наблюдаемых величин. Это подход правдоподобия.
Более распространен и развит подход с выборочным распределением. На нем основаны несмещенные оценки с минимальной дисперсией, байесовские правила, теория решений и т. д. Этому подходу посвящена ббльшая часть настоящей книги. Методы правдоподобия описаны не столь детально [см. разделы 3.5.4, 4.13.1, 6.2.1].
Рассмотрим пример статистического вывода. Предположим, что у нас есть десять одинаково надежных, но разноречивых измерений x1,x2,...,x10 веса некоторого образца. Какова же величина, скажем д, его действительного веса? Статистический подход постулирует, что различия между наблюдениями появляются из-за случайных флуктуаций условий эксперимента и наблюдения рассматриваются как реализации [см. II, раздел 4.1] набора случайных переменных XY,X2,..^Xi0. Затем предлагается особое семейство вероятностных распределений, к которому принадлежат эти случайные переменные. С учетом наших знаний об экспериментальной процедуре может оказаться разумным остановиться, например, на нормальном семействе, т. е. счесть Хг независимыми случайными величинами с общим нормальным распределением. Никакой другой информации, кроме этих десяти наблюдений, принимать в расчет не следует. (Альтернативное мнение изложено в гл. 15, посвященной байесовским методам.) Тот конкретный член нормального семейства, который приложим к нашим данным, определяется параметрами (д,а) с неизвестными значениями, которые мы должны оценить. В нашем примере мы отождествляем параметр д с неизвестной «действительной величиной» веса; параметр а — это мера изменчивости в наблюдениях, порожденной измерительной техникой [см. II, раздел 11.4.3]. Следующим шагом будет нахождение комбинаций наблюдений Л(Х1,...,%ю), которую мы будем использовать как статистику [см. раздел 2.1], чье численное значение дает приближенное значение для д и другой статистики, служащей тем же целям для ст. Эти численные значения позволяют получить оценки для д и а.
По причинам, которые будут ясны позже, могут быть использованы такие статистики:
1 ю
М = hi(Xi...Xl0) = jQ Ехг = х (3.1.1)
85
и (среднее выборки)
ст=Л2(*1,*2 x10)=[s (хг—х)2/9]1/2=$ (3.1.2)
(стандартное отклонение выборки). (Здесь оценка параметра 0 обозначена как 0: мы будем также применять обозначения вроде 0* или ~0.) Оценивание и оценка. Численное значение оценки х, приведенной выше, можно рассматривать как реализацию индуцированной [см. определение 2.2.1] случайной величины
%=(%1+Л2 + ...+Х10)/10,
которая называется оценивателем, соответствующим оценке х *. Подобно этому оцениватель, соответствующий выборочному стандартному отклонению есть
5= [E(Jfr-X)2/9]1/2.
Эта мысль обобщена в следующем определении.
Определение 3.1.1. Оценка и оцениватель; стандартная ошибка. Оценка 0 параметра 0 по выборке х},х2,...,хп — это статистика [см. определение 2.1.1], скажем 0 = А (хьх2,...,хл), численное значение которой может быть использовано как приближение к неизвестной величине 0. Выборочное распределение § — это распределение случайной величины Т = h(XuX2,...,Xn), где Хг — случайные величины, индуцированные хг [см. определение 2.2.1]. Случайная величина Т — это оцениватель, соответствующий оценке 0. Какая-либо подходящая оценка стандартного отклонения Т называется стандартной ошибкой 0 [см. раздел 4.1.2].
В (3.1.1) и (3.1.2) есть два параметра ц и а, оцениваемых статистиками /2 = х и ст = S соответственно. Порождаемые ими случайные величины — это X = (*] +х2 + ...+хп)/п для выборки объема п и
S= [t(Xr — Х)2/(п — 1)]1/2.
X и S взаимно независимы [см. раздел 2.5.4, в)]; X распределена нормально с математическим ожиданием д и дисперсией ст2/п. Распределение S легче всего описать, сказав, что величина 9S2/«г2 распределена по закону хи-квадрат [см. раздел 2.5.4, а)] с 9 степенями свободы.
В каком смысле х хорошая оценка для д?_На этот вопрос можно ответить так: маловероятно, что реализация X сильно отличается от ц; для любого фиксированного положительного Д и для любого фиксированного X вероятность того, .что X лежит в интервале X ± Д, максимальна, если X = ц.
* В оригинале — estimator. Термин «оцениватель» возможен, но в литературе на русском языке он практически не употребляется. В дальнейшем термин «estimator» будем, по возможности, переводить как «оценка». — Примеч. пер
86
Это показывает, что оценка У удовлетворяет некоторым требованиям, предъявленным к хорошим оценкам ц. Мы не хотим этим сказать, что лучшей оценки не может существовать: если, например, и = й(Х1,...,хл) — такая статистика, что индуцированная переменная U с большей вероятностью лежит в_интервале д ±Д, чем X, то мы можем считать, что U лучше, чем X, оценивает д . Если бы неравенство
P(U € д ± Д) >Р(Х € д ± Д)
было справедливым для всех значений д и Д, то U была бы равномерно лучше, чем X, в соответствии с этим критерием.
Наши рассуждения приводят к идее о том, что свойством хорошей оценки должна быть высокая концентрация вероятности около истинного значения параметра. Мы скажем, что оценка Т имеет равномерно наибольшую концентрацию относительно 0, если для любой другой оценки Т
р(е — \1<т<е+х2)^Р(0 — Х!<г<0+х2) (зл.з)
для всех положительных Xi и Х2. К сожалению, оценок с таким свойством, как правило, не существует; приходится руководствоваться более скромными соображениями [см. раздел 3.3].
Возвращаясь к нашему примеру, включающему среднее нормальной выборки с параметрами (д,а) объема п, воспользуемся хорошо известным фактом, что с вероятностью 0,95 реализация х случайной переменной X окажется в интервале д±1.96ог/Тл [см. приложение 3 и 4].
Заменяя неизвестное а/7л ее оценкой i/Vw (стандартной ошибкой д), перефразируем сказанное выше: с высокой вероятностью значение х будет отстоять от д не более чем на 2$7Vn; потому неизвестное д будет лежать на расстоянии, не превышающем 2s/Vn, от значения У.
Это довольно грубое утверждение можно существенно уточнить, например, в терминах доверительных интервалов [см. пример 4.5.2]. Тем не менее оно интуитивно понятно. В статистической практике стандартная ошибка оценки широко применяется как мера точности этой оценки и как основа для более сложных мер.
Существуют разные мнения о том, какова должна быть эта мера. Некоторые статистики считают, что удовлетворительное решение (проблемы) дает байесовский подход [см. гл. 15]. В соответствии с этим подходом выборку не считают единственным источником информации и стремятся использовать также ту информацию, что была до проведения опытов (априорную), например уверенность в том, что значение д не меньше 100 г и не больше 400 г. В других случаях первичная информация может быть более содержательной. Как происходит прирост этой априорной информации? Предлагается мыслить неизвестное д как реализацию некоторой случайной переменной, имеющей какое-то априорное распределение. В свете же имеющихся на
87
блюдений это неизвестное значение надо рассматривать как реализацию другого — апостериорного — распределения, т. е. условного распределения ц при фиксированных значениях наблюдений.
С помощью теоремы Байеса [см. гл. 15] можно найти это вероятностное распределение возможных значений ц. С его помощью, используя значение х, можно строить вероятностные интервалы любого уровня для неизвестного ii (например, 0,95). Такие выводы — это как раз то, что хотелось бы получить. Есть конечно, определенная степень произвола в выборе априорного распределения. Более серьезная же трудность состоит в том, что для многих статистиков концепция априорного распределения в таких условиях неприемлема. Некоторые из них будут возражать не только против априорного распределения, как не имеющего объективного характера; они скажут, что с неизвестной величиной ii, являющейся константой, нельзя обращаться как со случайной переменной. И все же эти доводы не окончательны. В терминах нашего примера: если ст будет, скажем, равной 10 г, а х равным 125 г, то постулированное значение 200 г для ц надо рассматривать как неправдоподобное в том смысле, что неправдоподобно получить как реализацию значение 125 из нормального распределения N(ji,d) с ц = 200 и ст = 10. Даже Р. Фишер, убежденный противник байесовского подхода, принял подобную точку зрения и развил фидуциальный подход, определенным образом приписывающий вероятность возможным значениям ц, не привлекая идеи априорного распределения. Несмотря на редкостные аналитические способности Р. Фишера и его глубочайшую статистическую интуицию, теория фидуциального вывода так и не была представлена научному статистическому сообществу в достаточно убедительной форме. Она так и не стала частью принятого канона [см. Kendall and Stuart (1973), т. 2, гл. 21; Barnett (1982) — С].
Тем, кто не готов встать на точку зрения, согласно которой вероятность может быть приписана интервалам возможных значений величины ц, остается ограничиться стандартной техникой обращения с вероятностными утверждениями относительно х, которые дают возможность для косвенных вероятностных утверждений о ц, а именно:
1) доверительными интервалами и/или критериями значимости;
2) теорией статистических решений с предписанными значениями риска для возможных ошибок;
3) приписывая постулируемым значениям неизвестного ц степени относительной приемлемости, которая пропорциональна их правдоподобию. Эти концепции обсуждаются более детально в гл. 4. Соответствующая литература указана в разделе 3.6.
Точечное оценивание и интервальное оценивание Целью практической процедуры оценивания должен быть не только выбор отдельной статистики, численное значение которой будет обеспечивать требуемое приближение («оценку») искомых параметров, но и построение подходящей меры точности этой оценки. Таким образом, существуют два аспекта одной и той же задачи. Тем не менее часто удобнее обсуждать их порознь; в таком случае выбор статистики называется точечным оцениванием, а определение ее точности — интервальным оцениванием.
88
3.2. ИНТУИТИВНЫЕ ПРЕДСТАВЛЕНИЯ И ГРАФИЧЕСКИЙ МЕТОД
3.2.1. ВВЕДЕНИЕ
Интуиция подсказывает нам, что выборка подобна совокупности, из которой она взята. Это — основа теории оценивания. Чтобы использовать эту пока еще не определенную мысль, нужно уточнить методы описания выборок, в каком-то смысле аналогичные методам описания совокупности. Основные такие методы для совокупностей состоят в следующем:
1) прямое или косвенное описание полного распределения; прямое описание в терминах плотности или функции распределения [см. раздел 1.4.2, пункт 1)], косвенное в терминах одной из стандартных производящих функций [см. II, гл. 12];
2) описание отдельных свойств полного распределения, таких, как первые моменты [см. II, раздел 9.11], избранные процентные точки [см. раздел 2.5.4, в)] и т. д.
У всех этих объектов существуют выборочные аналоги. Выборочные аналоги производящих функций вероятностного распределения (плотности, моментов и т. д.) не нашли широкого применения и не будут далее обсуждаться в этой книге. Выборочные аналоги моментов распределения рассматривались детально в гл. 2. Темой настоящего раздела остаются выборочные аналоги плотности распределения (п.р.в.) и функции распределения вероятности (ф.р.). Мы продолжим их обсуждение в разделе 3.2.2.
3.2.2. ЧАСТОТНЫЕ ТАБЛИЦЫ, ГИСТОГРАММЫ И ЭМПИРИЧЕСКАЯ ф.р.
а) Дискретные данные. Частотная таблица — основной метод представления информации, содержащейся в выборке. Для дискретной одномерной случайной переменной [см. II, гл. 5] R, определенной, скажем, на неотрицательных целых числах, — это просто таблица, указывающая, сколько раз число г встречается в выборке г=0,1,2,...; или (что эквивалентно) указывающая отношение этого числа к объему выборки п. Эти числа называют соответственно частотой fr наблюдения г и относительной частотой fr/n наблюдения г. Накопленная частота сг — число наблюдений х, для которых х<г; эти величины, деленные на объем выборки п, называются относительными накопленными частотами сг/п.
89
Пример 3.2.1. Данные Резерфорда и Гейгера о числе а-частиц, испущенных радиоактивным источником за 7,5 с, содержатся в столбцах 1 и 3 табл. 3.2.1.
Таблица 3.2.1. Частотная таблица по данным Резерфорда и Гейгера
Номер временного промежутка г Число испущенных частиц Частота Л Относительная частота (%) 100/,/и Накопленная частота сг=Ь/ 0 Накопленная относительная частота (%) 100сг/л
1 2 3 4 5 6
0 0 57 2,19 57 2,19
1 1 203 7,78 260 9,97
2 2 383 14,69 643 24,65
3 3 525 20,13 1168 44,79
4 4 532 20,40 1700 65,18
5 5 408 15,64 2108 80,83
6 6 273 10,46 2381 91,30
7 7 139 5,33 2520 97,01
8 8 45 1,73 2565 98,35
9 9 27 1,04 2592 99,39
10 10 10 0,38 2602 99,77
11 11 4 0,15 2606 99,92
12 12—14 2* (f\l +/1Э +/14 = 2) 0,08* 2608 (=<•14) 100,00
Общее п 2608 100,00
Основные сведения, а именно частоты, приведены в столбце 3. Общая сумма по этой колонке равна объему выборки п (=2608). В таблицу, правда, не входят отдельно частоты /и, Лз,/м- Вместо этого приведена «группированная частота» /1г+/1з+./14 = 2, выделенная как 2* в столбце частот 3. Это принятая практика в частотных таблицах — объединять таким образом малые частоты. В этой таблице только одна сгруппированная частота, но вообще их может быть и несколько.
Выборочный аналог п.р.в. Столбец 4 табл. 3.2.1 содержит величины относительных частот, выраженные в процентах от общего п (=2608). (Отмеченное звездочкой число 0,08 — это группированная частота /12+/13+/14» выраженная в процентах от общего целого.) Таблица относительных частот — это выборочный аналог таблицы вероятностей [см. II, раздел 4.3.1] рассматриваемой случайной переменной R.
90
Накопленные частоты в столбце 5 являются частичными суммами столбца частот. Из-за группирования 12—14 пропадают значения ct2 и Си, но См остается. Наконец, в последнем столбце приведены значения сг в процентах от объема выборки. Естественно, последнее число здесь равно 100, поскольку 1ООЧ7о наблюдений удовлетворяют условию х^14. Этот столбец дает выборочный аналог ф.р. (функции вероятностей) [см. II, раздел 4.3.2] изучаемой случайной величины. (Столбец Г нужен только ради нумерации строк.)
В рассмотренном примере мы имеем дело с 13 частотами, скажем Zo, Zj,...,Zi2> где
Zr=fr, /•=0,1.11,
И
Z12 =/12 +/13 +/14-
Выборочное распределение [см. раздел 2.2] этого вектора с 13 компонентами — полиномиальное [см. II, раздел 6.4.2]. Следовательно, математическое ожидание [см. раздел 2.3.1] частоты zr равно итгг, г=0,1,...,12, где л=2608 — объем выборки, а тгг — вероятность того, что наблюдение попадает в ячейку г. Аналогично математическое ожидание относительной частоты zr/n равно ттг. В нашем примере, где R — число частиц, испущенных в случайно выбранный интервал времени продолжительностью в-7,5 с, мы получаем:
7Г0=Р(Я = 0),
7Г1 = P(R = 1),... ,7Г,, = P(R = 11),
7Г,2=Р(12^/?С 14).
В настоящем случае разумно предположить, что R имеет пуассоновское распределение [см. II, раздел 5.4]. Если бы частотная таблица не содержала никаких группированных частот, подходящей оценкой пуассоновского параметра X было бы значение среднего выборки. Объединение /г, /,з и /,4 в принципе усложняет задачу оценивания, но сгруппированные частоты столь малы по отношению к объему выборки (2 и 2608), что интуитивно ясно — влияние группировки частот на величину оценки будет незначительным. Подсчеты с применением метода максимального правдоподобия подробно описываются в примере 6.7.1.
Для наших целей с достаточной степенью точности мы вычисляем оценку, которая должна быть средним значением выборки, так, как будто каждое группированное наблюдение попадает в среднюю клетку, т. е. г=13. Оценка в этом случае равна 3,871.
91
Р(Я=г)=е-ХХг/г!, г=0,1,...,11;
/ ^14\
Р(12^/?<14) = е-М 12! + 13! + 14!/’
Х=3,871.
Ниже сопоставляются исходные частоты и их ожидаемые значения в случае выбранного модельного (пуассоновского) распределения. Это показано в табл. 3.2.2, где ожидаемые частоты округлены до ближайшего целого:
г
ТГг= <
причем
Видимое согласие между частотами и их ожидаемыми значениями служит хорошим подтверждением правильности выбора пуассоновского распределения. Такое же согласие обнаружилось бы и между относительными частотами и их ожидаемыми значениями тгг; это подтверждает, что относительные частоты служат естественным аналогом п.р.в. (Объективный критерий близости для наблюдаемого согласия рассмотрен в гл. 7.)
б) Столбцовые диаграммы и гистограммы для дискретных данных. Рассмотрим частотную таблицу, полученную на основе табл. 3.2.1 вычеркиванием строки, соответствующей ячейке 12. (Эту частотную таблицу мы получили бы, если бы не было зарегистрировано ни одного наблюдения, превышающего 11.) Такую частотную таблицу без группированных частот можно представить графически в виде столбцовой диаграммы, т. е. последовательностью вертикальных отрезков (ординат) длины fr с абсциссами г, г=0,1,...,11. Она представлена на рис. 3.2.1.
Для наглядности столбцы можно расширить до тех пор, пока они не станут касаться друг друга. Теперь частоту fr изображает прямоугольник высоты fr', центр его основания — абсцисса г, левая и правая границы основания — г —А- и г+у ^см‘ Рис- 3.2.2]. Высота столбца численно равна площади прямоугольника: шкала высот превращается в шкалу площадей, так что полная частота события г=6, г=7, г=8 представляется суммой площадей прямоугольников с центрами в г=6, г=7, г=8. Граф дает пример гистограммы для дискретных данных с равномерной группировкой.
92
Рис. 3.2.1. Столбцовая диаграмма для табл. 3.2.3
Теперь предположим, что некоторые отдельные частоты объединены в группы (переход от табл. 3.2.3 к табл. 3.2.4). Здесь объединены ячейки, соответствующие г=0 и г=1, равно как г=6 и г=7, а также г=8, 9, 10 и 11. Дополнительно включены данные для г=12, 13 или 14, которые уже были сгруппированы в исходной частотной табл. 3.2.1. Для этой новой частотной таблицы с неравномерной группировкой графическая интерпретация сохраняет, насколько это возможно, основные черты рис. 3.2.2. Графическое представление объеди
Рис. 3.2.2. Столбцовая диаграмма для табл. 3.2.3, столбцы которой расширены
93
ненных частот 57 и 203, соответствующих г=0 и г=1, должно наглядно изображать слияние отдельных прямоугольников для г=0 и г=1 в объединенный прямоугольник, высота которого равна среднему из отдельных высот. Кроме возможностей визуальной интерпретации, этот метод сохраняет удобную шкалу площадей рис. 3.2.3. Этот пример поясняет, как принятое ранее соглашение о том, как изображать гистограмму группированных дискретных данных, действует в случае неравномерной группировки. Гистограмма частотной табл. 3.2.4 показана на рис. 3.2.3.
Таблица 3.2.2. Сравнение частот с их ожидаемыми значениями
{см. пример 3.2.1]
Число испущенных частиц Частота Л Ожидаемая частота (округленно) Л1Г, Число испущенных частиц Частота Л Ожидаемая частота (округленно) пт.
0 57 54 7 139 140
1 203 211 8 45 68
2 383 407 9 27 29
3 525 525 10 10 11
4 532 508 11 4 4
5 408 394 12—14 1 1
6 273 254
Общее п =2608
Рис. 3.2.3. Гистограмма для табл. 3.2.4
94
Таблица 3.2.3
Число испущенных частиц, г 0 1 2 3 4 5 6 7 8 9 10 11 Общее
Частота, fr 57 203 383 525 532 408 273 139 45 27 10 4 2608
Таблица 3.2.4
Число испущенных частиц Частоты
0 или 1 2 3 4 5 6 или 7 8, 9, 10 или 11 12, 13 или 14 57 + 203 = 260 383 252 532 408 273 + 139=412 45+27+10+4=86 2
в) Непрерывные данные. Аналогичным образом, с чуть большей затратой труда, можно представить и непрерывные данные, т. е. наблюдения над непрерывной случайной величиной [см. II, раздел 10.1]. Чтобы образовать частотную таблицу по выборке из наблюдений над X, надо разделить отрезок (а, Ь) значений выборки на £ ячеек, или интервалов (Аг-1, hr), разделенных границами hr, г=\,2,...,к:
a=h0<hi<h2<...<h/c = b.
Первая, вторая ... ячейки есть интервалы (Ло, Л1), (Ль Л2) и т. д. Затем определяются частоты, т. е. количества наблюдений, попавших в различные ячейки:
fr — число наблюдений х, таких, что hr-i<x^hr, г=1,2.......к.
Таблицы иногда строят по другому правилу: частота fr равна количеству наблюдений, для которых hr-i<x<hr плюс половина числа наблюдений, которые (при принятой точности измерений) совпадали с Лг-1 или Лг. Примером может служить табл. 3.2.5.
Накопленные частоты определяются так:
сг= [число наблюдений х, таких, что x^hr]=f +fi +
r= 1,2,...,£.
95
Количество ячеек к и значения их границ hr в какой-то мере произвольны. В таблицах оно может быть результатом компромисса между требованиями экономии и точности. Часто размеры всех (или почти всех) интервалов группировки одинаковы, как в таблице, где рост измерен в дюймах, округленных до ближайшего целого числа. Неравные интервалы группировки тоже, впрочем, иногда оправданы. Например, в таблицах смертности от коклюша, где указан возраст умерших после достижения, скажем, 15 лет, многое зависит от возраста. Поэтому для возраста, превышающего 15 лет, оправданы широкие интервалы, например 5—10 лет. Напротив, высокая и заметно зависящая от возраста смертность малышей требует более узких интервалов: возможно, от 6 месяцев до 1 года.
Таблица 3.2.5. Частотная таблица, показывающая рост мужчин, интервалы группировки равные. Полуцелые частоты возникают, когда измерение попадает на границу интервала; по соглашению это увеличивает частоту интервала на 0,5 (воспроизведено с разрешения Macmillan Publishing Company. Statistical Methods for Research Workers. R. A. Fisher.
Copyright ©1970 University of Adelaida)
Границы интервалов (в дюймах) Центральная высота (в дюймах) Частота Граница интервалов (в дюймах) Центральная высота (в дюймах) Частота
(59,60) 59,5 1 (70,71) 70,5 137
(60,61) 60,5 2,5 (71,72) 71,5 93
(61,62) 61,5 1,5 (72,73) 72,5 52,5
(62,63) 62,6 9,5 (73,74) 73,5 39
(63,64) 63,5 31 (74,75) 74,5 17
(64,65) 64,5 56 (75,76) 75,5 6,5
(65,66) 65,5 78,5 (76,77) 76,5 3,5
(66,67) 66,5 127 (77,78) 77,5 1
(67,68) 67,5 178,5 (78,79) 78,5 2
(68,69) 68,5 189 (79,80) 79,5 1
(69,70) 69,5 137 1164
96
Примером частотной таблицы с неодинаковой шириной интервалов может служить табл. 3.2.6, полученная объединением ячеек табл. 3.2.4 (совместное выборочное распределение частот обсуждается в разделе 2.9.4).
Таблица 3.2.6. Таблица группированных частот с изменяющейся шириной интервалов. Данные взяты из табл. 3.2.5 и соответствуют разным способам выбора границ интервалов
Границы интервалов (в дюймах) Частота
1) (59,64) ' 45,5
(64,66) 134,5
(66,70) 631,5
(70,72) 230
(72,80) 122,5
1164
2) (59,62) 5
(62,65) 96,5
(65,67) 205,5
(67,69) 367,5
(69,72) 367
(72,75) 108,5
(75,80) 14
1164
97
Рис. 3.2.4. Гистограммы для таблицы частот, полученных группировкой непрерывных данных по интервалам неравной длины. Обе гистограммы построены по различным разбиениям одной и той же выборки (данные табл. 3.2.6)
Соответствующие гистограммы показаны на рис. 3.2.4.
г) Гистограммы для непрерывных данных. Наиболее информативной графической формой частотной таблицы является специальный график, называемый гистограммой. С ним мы впервые встретились на рис. 3.2.2 и 3.2.3 для дискретных данных. Чаще эта конструкция применяется к непрерывным данным. Гистограмма состоит из прямоугольников с основаниями (Лг-ь hr), высота которых пропорциональна fr/(ht—hr-i)- Их площади, следовательно, пропорциональны частотам fr. Поэтому площадь той части гистограммы, что лежит между абсциссами hj и hm пропорциональна числу наблюдений х, таких, что hj<x^hm. Если выбрать единицу измерения так, чтобы общая площадь гистограммы оказалась равной 1, можно интерпретировать площадь между hj и hm как грубую оценку P{hj<X^hm\ Следовательно, гистограмма является выборочным аналогом графика плотности распределения вероятности (п.р.в.).
Примеры приведены на рис. 3.2.4.
98
д) Выборочный аналог функции распределения; вероятностная бумага. Подобно тому как в примере 3.2.1 относительные частоты представляют собой естественный выборочный аналог п.р.в., накопленные относительные частоты в том же примере образуют естественный выборочный аналог ф.р. [сокращения приведены в разделе 1.4.2]. Относительная накопленная функция r.c.f. частот определена для hr и равна:
r.c.f. (hr)=Lfj/n, r=l,2,...,k.
Эту функцию называют также эмпирической функцией распределения. Редко привлекаемая в случае дискретных данных, она часто используется для непрерывных выборок как основа для глазомерных критериев и сравнений. С точностью до случайных колебаний эта функция совпадает (там, где она определена) с ф.р. F(x)=P(X^ х) наблюдаемой случайной величины X [см. II, раздел 10.1.1].
Есть полезный графический прием, позволяющий судить о степени этого совпадения. Он основан на следующей идее. Поскольку F(x) — неубывающая функция, можно выбрать такую неоднородную шкалу на оси ординат, что график F(x) как функции х превратится в прямую линию. С помощью обычной равномерно разлинованной бумаги можно построить на оси ординат новую, уже не равномерную шкалу. Каждой точке оси ординат с координатой у из подходящего набора (скажем, 0,01; 0,02; ...; 0,99) приписываем значение F(y) в качестве ее метки*. Затем строим график на этой, по-новому размеченной шкале. Если F(x) такова, что в ее явное выражение х входит в форме (х—Х)/а>, где X, ы — постоянные, то в указанном неравномерном масштабе график F(x) будет прямолинеен при любых X, со. Это очень удобно, поскольку график эмпирической функции распределения на таком планшете состоит из точек, лежащих вблизи прямой линии. Это позволяет (хотя и субъективно) каждому оценить на глаз, насколько хорошо ф.р. выборки приближается к гипотетической ф.р. [см. пример 3.5.1].
Бумага с подобной шкалой может использоваться для нормального (нормальная вероятностная бумага), логнормального (логарифмическая вероятностная бумага) и некоторых других распределений. Примеры работы с вероятностной бумагой приведены в книге [Hald (1952) — С].
* Правильно иначе: надо приписать метку «у» той точке оси ординат, расстояние которой от начала отсчега равно F~'(y). — Примеч. ред.
99
3.3. НЕКОТОРЫЕ ОБЩИЕ КОНЦЕПЦИИ И КРИТЕРИИ ОЦЕНОК
3.3.1. ВВЕДЕНИЕ. РАЗМЕРНОСТЬ, ЗАМЕНЯЕМОСТЬ, СОСТОЯТЕЛЬНОСТЬ, КОНЦЕНТРАЦИЯ
Раздел 3.2 начинался рассуждением по поводу основополагающего представления о том, что выборка подобна множеству, из которого она выбрана (генеральной совокупности). В этом разделе мы продолжим обсуждение ряда принципов, подсказанных интуицией, на этот раз тех, с помощью которых формируется отношение к статистикам, претендующим на роль оценок параметров данного распределения вероятностей.
а) Размерность. Первый из этих принципов может быть назван принципом правильной размерности. Он состоит в том, что когда 6 не является безразмерной величиной, но обладает физической размерностью, такой, как время или длина, оценка 6 должна иметь ту же физическую размерность, что и 6. Предположим, мы утверждаем, что последовательные моменты испускания частиц из радиоактивного источника образуют пуассоновский процесс с интенсивностью 6 [см. II, разделы 5.4, 11.2, 20.1]. Следовательно, последовательные промежутки между событиями распределены экспоненциально [см. II, раздел 11.2] с плотностью распределения 9е-0х в точке х, х> 0. Для заданной выборки Xi, х2,...,х„ таких интервалов статистика /(хь х2,...,хп), призванная оценивать 6, должна иметь ту же физическую размерность, что и в, т. е. (время) . Такой оценкой, например, будет n/Lxr — величина, обратная к среднему выборки. Среднее выборки как возможная оценка 6 в соответствии с этим критерием исключается из рассмотрения.
Когда размерность оценки не вытекает из определения очевидным образом, полезно проверить ее математическое ожидание.
Пример 3.3.0. Отрицательное биномиальное распределение. Если N — число испытаний Бернулли с параметром 0, требуемых для получения фиксированного числа успехов х, то
P(N= п) = ("-})0Х(1 _0)и-х
п=х, х+1, х+2,...,
где х — положительное целое и О<0<1 [см. II, раздел 5.2.4]. Спросим себя: будет ли UN возможной оценкой для 0? Оказывается, что Е(1/ N) имеет нужную размерность. Проще вычислить E[U(N— 1)}, чем E(UN). Находим, что
Е[1/(АГ— 1)} = Е 1 6)n~x=6/(x— 1)(х>2).
п=х п—1 х 1
100
Отсюда видно, что 1/(N—1) имеет правильную размерность и что (х—1)/(N—1) — несмещенная оценка 0 [см. раздел 3.3.2].
б) Заменяемость. Второй принцип — принцип заменяемости — состоит в следующем. Если оценка t(xif х2, ...» хп) базируется на случайной выборке (хь х2, ...» хп) равноточных наблюдений заданной случайной величины X, то порядок, в котором идут наблюдения, несуществен; оценка должна быть симметрической функцией наблюдений [см. I; раздел 14.16]. Примером могут служить широко известные ста-
— П J " — 7
тистики х =Ехг/п и sr = Е(хг—х ) /(и—1).
в) Состоятельность. Важным принципом является состоятельность. Это попытка формализовать идею о том, что оценка 0 параметра 0 должна быть, в каком-то смысле, ближе к 0, чем, скажем, к 20, 1/0, ехр(0) и т. д., или к какому-нибудь другому параметру ф. Эту идею легче высказать, чем формализовать. Р. Фишер, первый высказавший эту мысль, предложил следующую формализацию. Предположим, что выборочные данные собраны в частотную таблицу. Понятно, что случайно можно получить выборку, которая будет точной копией генеральной совокупности в том смысле, что частоты f, f2, ...» fk в выборке точно пропорциональны соответствующим вероятностям 7Г1, тг2, ..., кк в совокупности. В такой выборке значение оценки должно в точности совпадать с оцениваемым параметром. Следовательно, если оценка & обозначена через t(f, f2, ..., fk), то принцип состоятельности требует, чтобы
/(ля-], птг2, ..., птгк) = 0. (3.3.1)
к
Здесь л=Е/г обозначает объем выборки.
Пример 3.3.1. Состоятельность оценки параметра геометрического распределения. Рассмотрим случай, когда 0 — параметр геометрически расположенной переменной 5 с распределением вероятностей
P(S=$) = 7Г5 = 0(1—0)Ч 5=1,2.
[см. II, раздел 5.2.3]. Основываясь на выборке, в которой наблюдаемые значения $ встречаются с частотами fs, s=l,2,...,k, получим оценку максимального правдоподобия [см. раздел 3.5.4]:
0=1 /5 = л/Е$/$(л = ЕЛ).
В нашем случае /$=0 для s>k, следовательно,
0 = л/Е5/5.
Требование состоятельности в данной ситуации —
0=1/2р7г5 = 1/£’(5).
101
Поскольку £(S)=l/0, условие выполняется и § — состоятельная оценка 0по Р. Фишеру.
Эта привлекательная концепция, к несчастью, теряет изрядную долю своей простоты, когда мы пытаемся применить ее к непрерывным распределениям. Возможно, поэтому она не стала частью принятого канона. Вместо нее чаще всего используется близкий, но отличающийся критерий, также называемый состоятельностью, что создает некоторую двусмысленность.
Определение 3.3.1. Состоятельность оценки. Сходимость по вероятности. Оценка 0n-tn(Xi, *2,--,*Л), основанная на выборке из п наблюдений (п= 1,2,...) случайной величины X, рассматривается как элемент последовательности Л, 6,-.., в которой явная форма 1п как функции Xi, х2,...,хп точно установлена для каждого значения п. Соответственно мы рассматриваем последовательность случайных переменных ^n = tn(Xi, Х2,...,Х^), л =1,2,..., где Хг — независимые реализации X [см. определение 2.2.1]. § называют состоятельной оценкой 0, если при п сходится по вероятности к 0, т. е. если для всех сколь угодно малых Л>0
Р(0 —1 (3.3.2)
при п-* [см. IV, раздел 1.2]. Удобное и достаточное условие для этой сходимости состоит в тем, что
~ е I
(3-3.3) var(G„) 0 j
при п -*
Согласно этому определению состоятельная оценка имеет высокую вероятность быть почти равной параметру, который она оценивает, при условии, что выборка будет достаточно большой.
Пример 3.3.2. Состоятельность оценки дисперсии. Оценка дисперсии о2 нормального распределения, заданная (2.5.20), где а(п)-п — 1, обычно обозначаемая символом s2, имеет выборочное математическое ожидание а 2 и выборочную дисперсию 2а4/(л — 1), которая сходится к 0. Следовательно, г — состоятельная оценка для о2 (в смысле сходимости по вероятности).
Обсуждаемый принцип состоятельности основан на той мысли, что при достаточно больших объемах выборок выборочное распределение оценки должно иметь унимодальную плотность распределения вероятности [см. II, раздел 10.1.3] с высоким и, по возможности, узким пиком, максимум которого находится около 0 [см. рис. 3.3.1]. Если п возрастает, пик становится выше и уже, его максимум приближается к 0. Недостаток принципа состоятельности, описанного в разделе 3.3.1, заключается в том, что на практике обычно интересуются выборочным распределением оценки, основанной на выборке небольшого объема, и нет гарантий, что оценка, состоятельная в опи-102
Рис. 3.3.1. Выборочная плотность приемлемой оценки е
санном выше смысле, при небольших п будет иметь плотность вероятности, как на рис. 3.3.1. Для подобных выборок принцип состоятельности нуждается в дополнении. Таким дополнением может быть принцип высокой локальной вероятности.
г) Концентрация (высокая локальная вероятность). Оценка в для в должна с высокой вероятностью быть близкой к в. Вероятность больших отличий в от в должна быть малой. Поясним этот принцип.
Пример 3.3.3. Выборочное распределение х и $2 в нормальной выборке. В случае нормального распределения с параметрами (д, ст) [см. II, раздел 11.4.3] рассмотрим статистики
п tl=x = Ехг/п,
/2=52 = Е(хг — х)г/(п — 1)
как оценки для ц и ст2 соответственно. Они имеют следующие выборочные распределения [см. раздел 2.2]. Для Л выборочное распределение Ы(д, а/у/п), т. е. унимодальное, к тому же с модой ц. Мода определяет местоположение максимума, ширина которого (она измеряется выборочным стандартным отклонением) пропорциональна л~1/2. Таким образом, чем больше п, тем уже пик.
В случае t2 выборочное распределение (л—I^/ct2 является распределением хи-квадрат с п—1 степенями свободы [см. раздел 2.5.4, а)]; п.р.в. s2 в точке z задается формулой
(п— 1)(”- (л-3)/2 ехр[—(я— j )z/2o2]
2<'’-1>/2стл-1г[(л-1)/2]
(3.3.4)
[см. (2.5.21)]. Это унимодальное распределение с модой (1—2/(л—!))</ около желаемого значения ст2. Ширина пика, измеряемая стандартным выборочным отклонением и равная с/>/2/(л—1), уменьшается при возрастании п [см. (2.5.22)].
юз
Обе оценки удовлетворяют интуитивному требованию высокой локальной вероятности. Они и в самом деле принимаются как «лучшие» оценки для ц и ст2.
Требование концентрации оценки для в в окрестности в в смысле, подразумеваемом в начале раздела 3.3.1, г), вытекает из (обычно нереализуемой) концепции максимальной концентрации [см. раздел (3.1)]. Некоторых продвижений в реализации принципа максимальной концентрации можно ожидать при применении критерия минимальности среднего квадрата ошибки, который мы сейчас введем. Говорят, что оценка Т параметра в имеет минимальный средний квадрат ошибки, если для любой другой оценки Г для всех в выполняется соотношение
Е(Т—0)2^Е(Г—0)2.
К сожалению, не всегда существует оценка, имеющая минимальный средний квадрат ошибки. Интуитивно ясно, что одна оценка лучше другой, если она имеет меньший средний квадрат ошибки.
Если мы ограничимся несмещенными оценками (оценка Т параметра 6 называется несмещенной, если Е(Т) = 0 для всех 0), то средний квадрат ошибки превратится в дисперсию. Несмещенные оценки с минимальной дисперсией встречаются часто, и некоторые их свойства обсуждаются в разделе 3.2.2. Связанная с этим концепция эффективности рассматривается в разделе 3.3.3.
Осталось упомянуть еще один важный принцип. Некоторые статистики способны извлекать из данных больше информации, чем другие. Это приводит к принципу достаточности. Достаточной оценкой 0 называется статистика, в определенном смысле собирающая всю информацию с 0, которая содержится в выборке. Подробнее эта идея обсуждается в разделе 3.4.
3.3.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ И НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ
Принципы, обсуждавшиеся в разделе 3.3.1, дают нам представление о свойствах, которыми должна обладать хорошая оценка. Однако они не подсказывают способов найти такую оценку. Мы нуждаемся в сжатом описании требуемых свойств в форме конструктивных определений или, иначе, в общем методе, приводящем к оценкам с желательными свойствами. Такие методы изложены в разделе 3.5 и в гл. 6. В настоящем разделе мы ограничимся лишь приближением к «конструктивному определению».
Все требования, о которых говорилось в разделе 3.3.1, могут быть заменены требованием, чтобы «центр» выборочного распределения был близок к 0 и чтобы «разброс» выборочного распределения был как можно меньше. В этой формулировке «центр» не определен: он в принципе может быть модой [см. II, раздел 10.1.3], медианой [см. II, 104
раздел 10.3.3] или ожидаемым значением [см. II, раздел 10.4.1]. По соображениям простоты обычно выбирают ожидаемое значение. И вновь требование близости выборочного математического ожидания к 6 недостаточно определенно. В конце концов потребуем совпадения в и математического ожидания 0. Оценка 0 в таком случае называется несмещенной. Разброс выборочного распределения удобно измерять дисперсией. Итак, мы подошли к несмещенным оценкам с минимальной дисперсией.
Определение 3.3.2. Несмещенная оценка. Пусть 0=1(х\, х2,...,хп) — оценка в, основанная на данных, в которых хг — реализации случайной величины Хг, г=1,2,...,л. Она называется несмещенной оценкой 0, если при всех в
E[t{X\, Х2,...,Хг^] = 0.
Оценка, которая не является несмещенной, называется смещенной. Смещение Ьп(0) определяется соотношением
bn(0)=E[t(X„ Х2,...,Хп)]—0.
Несмещенная оценка с минимальной дисперсией может подчиняться дополнительным требованиям к форме ее функциональной зависимости от хг (таким, как линейность и т. п.).
Из этого следует, что свойство несмещенности не принадлежит к важнейшим в первую очередь из-за неинвариантности при функциональных заменах (кроме линейных). Предположим, что мы интересуемся некоторым технологическим процессом и оцениваем вероятность того, что X не превышает заданной величины х0, т. е. мы хотим оценивать значение F(x0, 0), где F — функция распределения X. Если 0 — несмещенная оценка 0, то F(x0, 0) в общем случае не будет несмещенной для F(x0, 0). Для подобных приложений, следовательно, несмещенность является бесполезной.
С тем же сталкиваемся и в следующей ситуации. Если в п испытаниях Бернулли с вероятностью успеха 0 зафиксировано г успехов, то оценка г/п — несмещенная для 0; однако п/r смещено относительно 1/0.
Наконец, несмещенные оценки — не обязательно более точные, чем п смещенные. Известный пример — несмещенная оценка s2 = S(.xj—х)2/(л—1) дисперсии генеральной совокупности. Средняя квадратичная ошибка смещенной оценки (л—^/(л-М) меньше, чем у s2.
Почему же тогда несмещенность приобрела такое важное значение для статистических правил? Причины — в математических удобствах, в линейности и состоятельности: оператор математического ожидания £"(•) имеет много свойств, облегчающих работу с ним; многие важные статистики являются линейными функциями наблюдений, а несмещенность инвариантна относительно линейных преобразований; независимые несмещенные оценки можно комбинировать и получать более точные несмещенные оценки.
105
Построение несмещенных оценок с минимальной дисперсией НОМД обычно связывают с понятием достаточности. Дополнительные сведения по этому поводу содержатся в разделе 3.4.
Следующие примеры относятся к минимизации дисперсии в определенных классах оценок (линейных, квадратичных и т. д.).
Пример 3.3.4. Линейная несмещенная оценка с минимальной дисперсией (ЛНОМД). Пусть (Xi, х2,...,х^) — случайная выборка наблюдений за переменной X, для которой Е{Х) = 6 и var(X) = ст2. Чтобы найти ЛНОМД для в, составим линейную функцию от наблюдений, скажем
л п
И- 'уИгХг + Ь.
Выборочное математическое ожидание [см. раздел 2.3] равно е£аг+ъ.
Чтобы оно в точности было равно в, т. е. 104-0, необходимо положить
£аг=\, Ь=0.
Последний шаг состоит в выборе аг, минимизирующем выборочную дисперсию ст2 Ед2. Легко видеть, что при условии Еяг=1, Еа* достигает своего минимального значения, когда ау-а2 = ... = ап = \/п. (Минимизация обсуждается в [IV, раздел 15.1.3].) Итак, §=Lxr/n=x является ЛНОМД для в. Общая теория ЛНОМД будет детально исследована при обсуждении метода наименьших квадратов в гл. 8, 10.
Пример 3.3.5. Квадратичная несмещенная оценка с минимальной дисперсией (КНОМД). Дисперсия а2 случайной переменной X имеет размерность X2- В соответствии с принципом правильной размерности [см. раздел 3.3.1, а)] мы требуем, чтобы оценка а2 тоже имела размерность X2. Простейшая такая функция — квадратичная форма [см. I, гл. 9] от значений выборки х2,...,хп, скажем
v=xQx,
где Х' = (Х], х2,...,хп), X — ег,о транспонирование и Q=(qrs) — симметрическая (дхд)-матрица [см. I, раздел 6.2]. Согласно принципу заменяемости [см. раздел 3.3.1, б)] v должна иметь вид
аЕх/ + 0S Exixj.
1
Выборочное математическое ожидание, следовательно, будет равно [см. II, раздел 9.2.1]:
ante2 + б2) + /?л(л—-1)02 = аист2 + [ал + 0л(л—1) ]02.
106
По свойству несмещенности оно должно быть равно ст2, откуда (кроме тех случаев, когда в — заведомый нуль)
ал-1, от + (3п(п—1)-0,
т. е.
а = 1/л, /?= — 1/л(л—1).
Следовательно, а и определяются однозначно принципами заменяемости и несмещенности. В этом частном случае применение принципа заменяемости фактически эквивалентно минимизации выборочной дисперсии [см. теорему 3.3.1]. Из этого следует, что КНОМД есть
~ ~ 2 ^xixj].
П 1 П-1 i^j
Преобразив это выражение, мы придем к уже известной нам оценке
з2 = Е(х/—х )2/(п— 1).
Пример 3.3.6 (продолжение). В особо простом случае, когда 0=0, принцип заменяемости применяется так же, а условие несмещенности становится проще: ап=1. Мы, следовательно, получаем оценку
Ех|/п + /ЗЕ 'LxjXi, 1 i*j
где 3 пока не определено. Вычисления показывают, что выборочная дисперсия этой статистики равна [-%~+п(п—1)/32]ст4. Это выражение обращается в минимум при /3=0. Таким образом, в данном случае п
КНОМД равна Exj/n; ее выборочная дисперсия — 2ст4/п.
Следующая теорема Халмоша связывает понятие несмещенной оценки с минимальной дисперсией и принцип заменяемости [см. раздел 3.2.1, б)].
Теорема 3.3.1. Симметричные оценки. Пусть х}, х2,...,хп — выборка взаимозаменяемых наблюдений X и g (Xi, х2,...,хп) — несмещенная оценка в параметра распределения X. Если g — несимметрическая п!
функция х, определим симметризацию g как g = Eg{(Xi, х2,...,хп)/п/, где gi(xit x2,...,x„)=g{Pi(xi, х2>...,хп)!, i=\,2,...,nl, для каждого i, х2,---,хг^ есть i-я (вне зависимости от порядка нумерации) из п!
перестановок [см. I, раздел 8.1] множества из п элементов (Xi, х2,...,хп). Мы примем за Р\ тождественную перестановку, т. е. gt =g. Тогда g несмещенная оценка в, а выборочная дисперсия g" меньше, чем у статистики g. Если g симметрическая функция, то g совпадает с g.
Это означает, например, что среди всех линейных несмещенных оценок математического ожидания 0 среднее по выборке будет наилучшей, т. е. будут иметь наименьшую дисперсию. (Общий вид линейной
107
оценки Ёагхг+Ь с произвольными коэффициентами а}, аг,...,ап, Ь. Выборочное математическое ожидание ее равно 0Еаг + 6, и для того, чтобы это выражение было равным 0, чего требует несмещенность, должно быть Ёаг=1 и Ь=0. Следовательно, несмещенная линейная
п _ п
оценка в есть ^агхг, Едг=1. Ее симметризация имеет вид х -Ехг/п, и согласно теореме Халмоша она имеет меньшую дисперсию, чем любая другая несмещенная линейная оценка Ёагхг+Ь [см. пример 3.3.4].) 1
3.3.3. ЭФФЕКТИВНОСТЬ. ГРАНИЦА КРАМЕРА—РАО
а) Неравенство Крамера—Рао: случайная выборка из одновременного однопараметрического распределения. Примеры 3.3.4, 3.3.5 и 3.3.6 показывают, как достичь минимальности выборочной дисперсии для оценки специальной функциональной формы. Однако они не дают ответа на вопрос, может ли оценка другой функциональной формы иметь меньшую дисперсию. Ответ можно получить из следующей теоремы, которая при весьма общих условиях указывает нижнюю границу для выборочной дисперсии несмещенной оценки.
Теорема 3.3.2. Нижняя граница для выборочной дисперсии несмещенной оценки. Пусть (хъ х2,...,хп) — выборка независимых наблюдений случайной переменной X, п.р. в. которой в точке х равна f(x, 0), где 0 — неизвестный параметр. Пусть 0n = tn(x}, х2,...,хп) — несмещенная оценка 0. Тогда при некоторых условиях регулярности f выборочная дисперсия vn оценки 0п удовлетворяет неравенству
vn^i/ln(0)=l/nl(0), (3.3.5)
где
1п(0) = п!(0)
и
I(0)=E{d\ogf(X,0)/d0]2=-E[d2\ogf(X, 0)/д02]. (3.3.6)
Р. Фишер назвал 1п(0) количеством информации в выборке, а 1(0) — количеством информации в отдельном наблюдении. Равенство в (3.3.5) достигается, если и только если
E31og/(xz, 0)/д0=п1(0)(0п—0). (3.3.7)
Из (3.3.5) следует, что при упомянутых условиях регулярности нижняя граница для выборочной дисперсии несмещенной оценки, основанной на п наблюдениях, пропорциональна 1/п.
108
Наиболее ранняя формулировка этой теоремы была предложена Фишером. Дальнейшее развитие и обобщения связаны с именами Фреше, Дюгю, Крамера, Рао. Не стоит привлекать имя Фишера к каждой статистической концепции или теореме, идущей от него: это неуместно, как и подобное упоминание Гаусса в анализе. На эту теорему обычно ссылаются, как на неравенство Крамера—Рао. (Отметим, что условие (3.3.7) выполнено, в частности, если
aiog/U 0)/Э0=/(0)И(х)—0].
В этом случае
log/U 0)=А (х) (I(e)d6— (07(0)йГ0+D(x)=А (х)В(0)+С(0)+D(x) ,(3.3.8) следовательно,
£ aiog/(xn 0)/Э0=/(0)ЕЛ(хг)—л0/(0)
и условие (3.3.7) превращается в
0л = ЕЛ(хг)/и
по требованию несмещенности оценки 0. О п.р.в. вида (3.3.8) говорят, что она принадлежит экспоненциальному семейству [см. раздел 3.4.2].)
Пример 3.3.7. Достижимость границы Крамера—Рао в случае биномиального распределения. Предположим, что X имеет распределение Бернулли [см. II, раздел 5.2.1] с параметром 0, так что п.р.в. X равна:
Лх, »)= Р.-*’ *°°] =(1-«)'Х=О,1.
< (7, X— 1 >
Тогда
log/(X 0) = (l-A)log(l-0)+Alog0,
dlogftX, 0)/Э0 = — (1 —Х)/(Д — 0)+Х/0=(%—0)/0(1—0)
и
a2log/'(X 0)/Э02 = — (1—Х)/(1 -0)2—Х/02.
Поскольку £’(Х) = 0, получаем
1п(0) = п [ 1 /(1 — 0) +1 /0] = п / 0( 1 — 0).
Нижняя граница, следовательно, равна 0(1—0)/л. Мы видим, что
Saiog/(x/, 0)/Э0= Цх,—0)/0(1— 0)= [Ех//л—0}/[0(1— 0)/«].
109
Это равно 1п(0)[§л—0}, если мы возьмем Bn-’Lxj/n (=г/п, скажем, где г=Ех/, т. е. числу успехов в выборке). Следовательно, граница Крамера—Рао достигается в этом примере на оценке г/п.
Пример 3.3.8. Граница Крамера—Рао для а2 в случае распределения N(0, о). Положим, что X нормально распределена с £(.¥)-О и var(A3 = 0. Тогда п.р.в. равна:
f(x, 0)~д0~1/2ехр(—х2/20), a=(2ir)~l/2, откуда
dlogf(X, 0)/Э0 = — 1 /20+Х2/202,
d2\ogflX, 0)/Э02 = 1 /202—-Х2/63.
Поскольку ДЛ)=0, то Е(Х2)=у&гХ=9, откуда
7„(0) - — п( 1 /202—-1 /02)=л/202.
Нижняя граница для выборочной дисперсии, следовательно, равна 202/л. Она достижима, поскольку
5Elog/(x{, 0)/Э0= Е(х-—#)/2#2 = /л(0)(0п—0], если мы возьмем §п = '£х1/п [см. пример 3.3.6].
Пример 3.3.9. Граница Крамера—Рао для с в распределении N(0, а). Предположим, как и в примере 3.3.8, что X нормально распределена с Е(Х)=О, но на этот раз параметр 0, подлежащий оценке, будет стандартным отклонением, т. е. чгх(Х)-Е{Х2)= О2. В этом случае
Дх, 0)=(2тг) ~ 1/20~4ехр(—х7202), откуда
diog/fx, 0)/Э0 =—1/0+Х2/03 и
cHog/fY, 0)/Э02 = 1/02—ЗЛ2/04, так что
Д(0)=2л/02.
Следовательно, нижняя граница Крамера—Рао равна Э2/2п. Она, однако, недостижима в условиях теоремы, поскольку
0Llog/'(Xb 0)/Э0=(Ex2 — пв2)/в3 =/„(0)[Ех?/2л0—20], что не имеет формы, требуемой (3.3.7).
но
Существуют модификации теоремы 3.3.2, применимые к смещенным оценкам. Например, теорема 3.3.3.
Теорема 3.3.3. Граница Крамера—Рао для смещенных оценок.
Предположим, в обозначениях теоремы 3.3.2, что 0* = 0* (Х|, х2,...,хп) — оценка 0 со смещением Ьп(0) [см. определение 3.3.2], т. е. с выборочным математическим ожиданием 0+Ьп(О)- Тогда выборочная дисперсия 0* не меньше, чем
[1 + dbn(0) /d0]2/In(O).
б) Достижимость границы Крамера—Рао. Эффективность оценки.
Определение 3.3.3. Эффективные оценки. Несмещенная оценка параметра 0 называется эффективной, если ее выборочная дисперсия равняется границе Крамера—Рао.
Эффективная оценка далеко не всегда существует. Более того, как показывают примеры 3.3.8 и 3.3.9, может существовать эффективная оценка параметра а2 и не существовать эффективной оценки о, ее квадратного корня. Это часть платы за удобство работы с математическим ожиданием.
Из (3.3.7) следует, что только в исключительных случаях семейство распределений допускает эффективное оценивание своих параметров. Когда эффективная оценка 0п существует, ее, несомненно, стоит использовать. В терминах критерия дисперсий лучшей оценки не существует (в условиях теоремы, конечно). Можно сказать, что другая несмещенная оценка, не являющаяся эффективной, скажем 0*, использует выборку менее эффективно, поскольку ее точность (измеряемая обратной величиной ее выборочной дисперсии) меньше, чем у эффективной оценки. Эффективность 0* можно определить как отношение va.r(0m)/ var(0Zj). Концепцию эффективности можно применять и тогда, когда эффективной оценки не существует. Вот общепринятое определение.
Определение 3.3.4. Эффективность оценки. Эффективностью несмещенной оценки 0п параметра 0, основанной на выборке объема п, называется
eff(0„)=
Уи(пйп) var(^)
где Тл(тш)-1//л(0) — нижняя граница Крамера—Рао [см. теорему 3.3.2].
Подобное употребление слов «эффективный», «эффективность» несколько сомнительно, поскольку не всегда малая выборочная дисперсия предполагает высокую точность. Даже если мы не будем обращать на это внимание, употребление слова «эффективность» при недостижимости границы Крамера—Рао двусмысленно, поскольку наилучшая оценка может иметь эффективность менее 100%. Поэтому чаще используется понятие относительной эффективности.
Определение 3.3.5. Относительная эффективность. Относительная эффективность двух несмещенных оценок 0*, 6** параметра 0, основанных на общей выборке, определяется как
var(0„**)/var(0„*);
эффективность 0* относительно 0** больше единицы, если var0„ < var0„ *.
Пример 3.3.10. Относительная эффективность среднего отклонения и выборочного стандартного отклонения как оценок о. В случае нормального распределения с параметрами (0, а) граница Крамера— Рао для выборочной дисперсии несмещенной оценки о, основанной на выборке объема п, равна (г*/2п. Эта граница недостижима, как показано в примере 3.3.9.
Среднее отклонение
< = (тг/2)1/2р |лг/| /п
является несмещенной оценкой и имеет выборочную дисперсию (тг—Itf/Zn, так что ее эффективность равна: 1/(тг—2)=0,88.
Стандартная оценка о2 равна:
s£ = £(Xi-х)2/(п-1).
С ее помощью мы находим несмещенную оценку а, заданную [см. (2.5.29)] соотношениями
2 Г(и/2)
Сп п—1 Г[(п—1)/2] '
Ее выборочная дисперсия равна (1—с2) а2 [см. (2.5.31)], а эффективность
О—сл)/2л.
В отличие от оценки среднего отклонения стл* эффективность зависит от объема выборки п.
Некоторые значения относительных эффективностей а* и (взятые из табл. 2.5.2) приведены ниже:
п 5 10 25 50
Эффективность ой Эффективность стл относительно on 0,86 1,02 0,93 0,94 0,97 0,90 0,99 0,88
112
в) Условия регулярности. Условия регулярности, при которых доказана теорема 3.3.2, как говорят, выделяют регулярный случай оценивания. Они обеспечивают справедливость тождества
а
де —
Г(х,, х2,...,xn)gn(Xi, х2....хп; e)dxi...dxn =
/(Xi, x2,...,xn) — gn(Xi, x2,...,xn; 3)dx{...dxn, ее
где
gn(X\, x2..xn\ &) = Tlf(Xi, в),
поскольку при доказательстве теоремы нужно провести это дифференцирование под знаком интеграла. Трудности возникают, если п.р.в. имеет угол или разрыв [см. IV, раздел 2.3] в точке, которая сама есть функция от в. Например, если
Ах, е)= [
g(x, еу, о^х^е, о, х>е,
мы имеем
< ж , е
J t(xtf(x> 3)dx= \t(x)g(x, 3)dx > О
и
— j i(x\f(x, 3)dx= — f/(x)g(x, 0)dx= де — ее о
0 oc
= \t(x)—dx+ t(e)g(e, e) * ( t(x) —Ax, eydx о ее de
[см. IV, раздел 4.7]. Аналогично и для многомерного интеграла наличие Ах, 3) как функции х таких точек разрыва, которые изменяются в зависимости от 3, — самый важный практический пример отступления от условий регулярности, требуемых теоремой.
Пример 3.3.11. Экстремальность равномерного распределения. Пусть X имеет непрерывное равномерное распределение на (0, в), т. е. его п.р.в. равна:
Ах, 3) =
О, х^О;
1/3, О<х^0;
о, х>е.
113
П.р.в. в точке и(0<и^д) наибольшего наблюдения Х(П) в выборке объема п равна пип~л/6п [см. II, пример 15.2.1], его математическое ожидание и0/(и+1). Следовательно, 0„* = (n+l)Xfn;/n — несмещенная оценка в. Однако применить концепцию эффективности к этой оценке невозможно, поскольку обсуждаемое распределение имеет разрыв в точке в и, следовательно, не удовлетворяет условиям теоремы. Фактически выборочная дисперсия в* равна пв2/(п + 2)(п +1)2, т. е. убывает гораздо быстрее при росте п, чем нижняя граница Крамера—Рао в случае регулярной оценки, — как п2, а не как п~1.
г) Неравенство Крамера—Рао для независимых векторных наблюдений однопараметрического многомерного распределения. Теорема 3.3.2 была высказана для независимой скалярной выборки (Ль х2 .v„) из однопараметрического распределения. Она остается
справедливой и в случае, когда каждое наблюдение хг в ее утверждениях понимается как векторное наблюдение, извлеченное из многомерной совокупности, как, например, из двумерного распределения пары (Y, Z) с п независимыми парами наблюдений (уь Zi), (уг, zd,...,(yn> Zn)-Случайная переменная X, упомянутая в теореме, заменяется парой (Y, Z) с совместной п.р.в. Ди z; 0) в точке (у, г), а наблюдение хг заменяется парой (yr. zr), г=1,2,...,п.
При условиях регулярности неравенство (3.3.5) остается верным при замене (3.3.6) на
In(f))==nE{d\ogf(Y, Z; 0)/Э0]2 = —n^logAK Z; 0)/дв2]. (3.3.9)
Граница достижима, если и только если
piog/Uc, у/; 0)/Э0=7«(0)(0л-0) (3.3.10)
аналогично (3.3.7). В обоих случаях вп должна быть несмещенной оценкой в.
Пример 3.3.12. Однопараметрическое триномиальное распределение. Пусть пара (Y, Z) подчиняется триномиальному распределению с параметрами (к; в, в) [см. II, раздел 6.4.1]:
Ли z; e)=P(Y^y, z=z)= —- ey^(\-2e)k-y-z-
yXzlQc—y—zY.
Отсюда
01og/-(K Z; в)/де= =
0 1—20 (3.3.11)
= [(Y+Z)/2k—0]/[0(l—20)/k]
114
и
02log/(Y, Z; 0)/d02=—(Y+Z)/62—4(k—Y—Z)/(l—20)2.
Поскольку E(Y)=E(Z) = k0, имеем
O2log/(X Z; 0)/d02] = 2£/0+4£/(l—20) = 2fc/0(l—20).
Для выборки из n nap (yb Zi)...(y«, Zn) независимых наблюдений (Y, Z) нижняя граница Крамера—Рао для выборочной дисперсии несмещенной оценки 0 равна:
1п(0)^0(1—20)/2пк.
Эта нижняя граница достигается для оценки л 1
0n = E(yi+Zi)/2kn= — (у +z),
поскольку в силу (3.3.11)
Edlog/Оъ Zi; 0)/д0=[ £(yi + Zi)/2k—п0]/{0(1 — 20)/£] =
= InWl Z(yi+Zi)/2kn-0] =Z„(0)(0„-0).
д) Неравенство Крамера—Рао для наблюдений, не являющихся независимыми и/или одинаково распределенными. Модифицировав неравенство Крамера—Рао, можно применять его и в случае, когда наблюдения не являются независимыми и/или неодинаково распределенными. Например, когда хг — реализации нормальной случайной величины Хг, для которой Е(Хг)=г0, г=\,2,...,п (упрощенная версия линейной регрессии). Пусть 0п определена, как в теореме 3.3.2. Неравенство Крамера—Рао тогда будет иметь вид
1/Z„(6>),
I где'
/„(0)=Ei01og gntX', X2)...,X„, 0)/00]2 = —£{02log gn(Xit X2.Xn; 0)/d02],
gn(ui, u2.un) — совместная п.р.в. случайной переменной (щ, и2,...,ип)
в точке (%,, Х2,...,Хп).
е) Обобщение неравенства Крамера—Рао на случай нескольких параметров. Информационная матрица. Пусть X имеет в точке х п.р.в. f(x; 0]...0k), a 0r — неизвестные параметры, и пусть х2,...рсп — выборка из п наблюдений X. (Здесь X и хг могут быть скалярами или векторами. Мы рассмотрим скалярную ситуацию. Добавления, которых требует векторная ситуация, обсуждались в разделе 3.3.3, г).)
115
, г, s = 1,2....к.
Функция правдоподобия [см. раздел 4.13.1] равна:
...Xi,...,x„)= nf(xr;6x.......вк).
Пусть 0* = 0* (Х\,...,хп) — несмещенная оценка 0Г, г=1,2.....к.
Аналогом количества информации 1п (0) в многопараметрическом случае служит информационная матрица 1(0), симметрическая кхк - матрица [см. I, раздел 6.7]; элемент равен:
-Е f 62log ...................*п) ] =
< derdes 3 (3.3.12)
= -пЕ ( ^2log/(%;01,02...........0.)
I
Аналогом выборочной дисперсии единственной оценки 0* в случае многих параметров служит выборочная матрица ковариаций V оценок 0* ...0А* , т. е. симметрическая (к х /г)-матрица, (г, $)-элемент которой
равен выборочной ковариации 0* и 0* (г, $ = 1,2,...,А:: когда г = s, элемент равен выборочной дисперсии 0*).
В этой ситуации аналогом неравенства Крамера—Рао (3.3.5) будет следующее: матрица
V — [ I (0)]'1 положительно полуопределена; это означает, что для каждого ненулевого (kxl) вектора X выполняется неравенство
Xх V X > X [ I (0) ]-'Х', т. е.
var (Xх 0*) X' [ I (0) j’1 X. (3.3.13)
(Уточнение: var (Xх 0*) означает выборочную дисперсию Xх 0*.)
Поясним смысл предыдущего неравенства. Выборочная дисперсия любой линейной комбинации оценок не меньше, чем дисперсия той же линейной комбинации случайных величин Z( , для которых матрица V0 = [ I (0)] -1 служит матрицей ковариаций.
var (0р var (Z;) = ,
var (а^+Ье*2 ) > var (a Z,+b Z2) = a2V?} + 2abV?2 + b2V?2
и т. д., где К?- — (i, j )-элемент матрицы V° = [ I (0)]'1.
Пример 3.3.13. Среднее и дисперсия нормального распределения.
Пусть X распределено нормально, Е ( X )- в} и var(X) = 02, т.е. п.р.в. X в точке х равна:
f(x; 0j, 02) = (2тг)-1/2 02~1/2 ехр [ -(х - 0,)2 / 202 ] .
Пусть 0* и 0* — несмещенные оценки 0j и 02, основанные на выборке П _
Xi, х2..хп объема п. (Так, мы можем взять 0* = Е хг / п=х и
0* = Е (хг — х)2 / (л—1).)
116
Имеем
log f(X; 02) = constant—log02—— 0j2/202,
откуда
d2 log/ / дв2 = —1/02, d2 Iog//d0,d02 = — (A — 0, ) / 022, d2 log/ / d022 = l/2022—(X- 0,)2. /402 . Взяв математические ожидания, найдем информационную матрицу I (0,, е2)-.
-п 0\
\ 0 1/202/
откуда [см. I, равенство (6.4.11)]
V° =[ I (0>, 02): = (в1/П ° V
\ 0 202 /п /
Интерпретация неравенства (3.3.13) для этого примера следующая. Для любой пары постоянных а, b и для любых несмещенных оценок 0* и 0* параметров 0,, 02 справедливо соотношение
/Л* КЛ* Ч / Кч/02/Л 0 \ / а
var (с/0, + Ьв2 ) (а, Ьц ) (
\0 — 2022 /nJ \b
= а2в2/п + 2Ь2 $1 /п.
В этом примере для оценок 0* = х и 0* = Ё(хг—Т)2/(и-1), V0 совпадает с ковариационной матрицей 0* и 02 , т. е. неравенство (3.3.13) превращается в равенство*.
Пример 3.3.14. Двухпараметрическое гамма-распределение. Положим, X имеет двухпараметрическое гамма-распределение [см. II, раздел 11.3.1] с п.р.в. в точке х
ffx; а, /3) = (х«-1е-^)//?«Г (а), х 0.
На основании (3.3.12) и равенства Е (Х) = а(3 найдем информационную матрицу, основанную на п наблюдениях:
I (а, \ 1/0 a/02J
где 4й (се) = <12 log Г (а)/<1а2 [см. Abramowitz and Stegun (1970) — G].
Обращая ее, получаем
*Это не так. В случае выборки из N (g, а2) дисперсия L (х2—х)2/(л—1) равна 2аЛ/(п—1). В обозначениях рассматриваемого примера это дает величину 202/(п—1), что превосходит указанную границу 292/(п). — Примеч. ред.
117
( | („ m >1 = V° = — / ~1/П13 \
1 1 dI -1/П0 ^(a)/n ) ’
где \ /
D=[a Ф'(а)-1: //32.
Например, если а=2 и 0=1, то ¥'(2)=0,045, D=0,29 и 1 / 6,90 —3,45 \
v - п 1—3,45 2,22 I
Следовательно, для несмещенных оценок а*, 0* var «* 6,90/л,
var 0* 2,22/п,
а для произвольных а и b
var (да*+ 60*) > 6,90д2 /п — 7,90д6/л+2,2262/и.
3.4. ДОСТАТОЧНОСТЬ
3.4.1. ОПРЕДЕЛЕНИЕ ДОСТАТОЧНОСТИ
В разделе 3.3.3 обсуждалась концепция эффективности как меры приближения выборочной дисперсии оценки к тому минимальному значению, которое может быть получено теоретически. Концепция достаточности принадлежит к тому классу идей, но представляется более глубокой.
Р. Фишер обнаружил, что в некоторых случаях можно собрать в единственной статистике всю информацию, содержащуюся в выборке относительно оцениваемых параметров (пользуясь словом «информация» в бытовом смысле). Такая статистика была названа достаточной оценкой данного параметра. (Существование достаточной статистики — даже в ограниченном классе распределений — имеет огромное теоретическое значение, как будет объяснено далее. С практической точки зрения это, возможно, менее важно, поскольку не всегда можно сделать выбор между двумя моделями распределения, одна из которых обладает достаточной статистикой, а другая нет.)
Пример 3.4.1. Достаточность наблюдаемой частоты как оценки биномиального параметра. Чтобы проиллюстрировать смысл достаточности, рассмотрим оценивание вероятности р выпадания «шестерки» на несимметричной игральной кости по данным о результате п бросаний этой кости. Интуитивно ясно, что п отдельных результатов в этой задаче неважны (т.е. не нужен учет по номерам успехов и неуспехов), а важно только общее число успехов (или доля успехов в п). Интуиция в данном случае правильна, поскольку, как показано ниже, общее число успехов является достаточной статистикой для оценивания параметра р.
Обозначим через х\,х2,...,хп последовательность результатов бросания кости, где Xj-1, если при j-м бросании был успех (т. е. выпала 118
«шестерка») и ху=0 — в противном случае, у-1, 2,...,л. Рандомизация [см. II, раздел 3.3], достигаемая встряхиванием кости в коробочке перед бросанием, обусловливает независимость [см, II, раздел 3.6.2]; поэтому мы можем рассматривать Xj как реализации индуцированной случайной величины Xj, j-\, 2,...,п, где Xif Х2..Хп — независимы и
одинаково распределены с общим распределением, заданным [см. II, раздел 5.3.1]:
Р(ХГ\) = р, Р(Х~0) = 1-р ;=], 2,..„л,
т.е. (3.4.1)
P(Xj=y) = рУ(\—ру-У, у~0, 1; у- 1, 2,...,п.
При заданном общем числе успехов (скажем, г0) условное совместное распределение [см II, 13.1.4] Xj имеет вид
P(Xi=yi, Х2=у2.....Хп = уп | Е Xj = r0) (уу=0 или 1, /=1, 2...д) =
(3.4.2)
=P(Xt=yi, Х2-у2,...,Хп = yti, ё йу-г0) / F I ё Л>г0).
Если теперь Е У/-^-. то числитель в (3.4.2) сократится до 1 •'
Р(Х}=У1, Х2=у2,...,Хп=уп), поскольку подразумевается, что
п
Е Xj-r0, и эта вероятность просто
Р (Л, = ух, Х2 =Хъ • • • ,Х„ -= У„) п
= П Р(Х:=у:) из независимости [см. II, раздел 4.4] I ' J
= П рУ<(\—ру-У; по (3.4.1)
7=1
П
=рго (1—р)"—'о, поскольку Ек=г0-п 1
Если же Еуу # г0, то числитель в (3.4.2) равен нулю, поскольку это вероятность невозможного события.
Знаменатель в (3.4.2) равен: л п
Р(ЪХ:=г0) = ( п ) р'0 (1—р)л—г°, поскольку Е%, имеет распределение ‘ /“о 1
Bin (п, р) [см. II, раздел 5.2.2].
Итак,
'О 1
0 в противном случае.
Отметим важную особенность этого результата^ условное распределение выборки при данном значении статистики Еху не зависит от р. Если значение этой статистики известно, любые дальнейшие заключения о р, принимающие в расчет это знание, должны основываться на условном распределении значений выборки; поскольку же р в нем
п
Р(Х,=у....Х„ =у„ | Е Xj=rot =
119
не участвует, никакие выводы о р из него извлечь невозможно, т. е. при заданном общем числе успехов нельзя извлечь из данных что-нибудь еще, относящееся к р. В этом смысле статистика Ё хг содержит всю информацию о р, которую можно извлечь из выборки. Вот в каком смысле статистика Ё хг является достаточной для р. (Это, конечно, совсем не значит, что отдельные выборочные значения хх, х2,...,хп бесполезны для других умозаключений. Рассуждения в примере основывались на предположении о том, что Xj независимы и одинаково распределены, что действительно имеет место при бросании костей. Может статься, что в других случаях взаимная независимость Xj окажется под сомнением. Для разъяснения, конечно, понадобится вся выборка (хь х2,...,хп) целиком.)
Те же доводы, что показали достаточность Ехг для р, покажут достаточность для р и таких статистик, как-у- Exf, a Y,xr + b и т. д. Фактически любая функция от Ехг достаточна*. В обсуждаемом случае интуитивно ясно, что приемлемой функцией будет Ехг /п доля успехов, поскольку это несмещенная оценка р. Далее [см. раздел 3.4.3] будет рассмотрен объективный критерий (теорема Рао—Блеквелла) для правильного выбора.
Приведем теперь формальное определение достаточности.
Определение 3.4.1. Достаточность. Пусть (непрерывные или дискретные) случайные величины (Xit Х2........Хп) имеют в точке
(хь х2..хп) п.р.в. fn(xx, х2.хп; в), где в — (скалярный) параметр, и
пусть 0* = 0*(х,,х2.хп) — статистика, основанная на наблюдениях
(хь х2,...,хп). Тогда 9* достаточна для 9, если для любой другой статистики 9 (х,, х2 хл) условное распределение 9 при данном 9* не зависит от 9. В частности, 9* достаточна для 9, если совместное условное распределение Xit Х2,...,Хп при данном 9* не зависит от 9 [см. также раздел 4.13.1.6)].
Пример 3.4.2. Достаточность выборочного среднего как оценки экспоненциального параметра. Пусть (xj,...,xn) — выборка наблюдений экспоненциальной случайной величины X, п.р.в. которой в х равна:
/(х; 9)=9е~вх, X > 0.
_ п
Тогда, х = Е Xj/n достаточна для 9. В терминах независимых одинаково распределенных переменных Х}, Х2,...,Хп, которые являются статистическими копиями X, так что ху представляют собой реализации %,(/'= 1,2,...,и), условное распределение выборки при данном значении х определяется условной п.р.в. в точке (wb и2.ип) случайного
п ______
вектора (Х{, Х2...Хп) при условии ЕXj = nx .
* Имеется в виду взаимно однозначная функция. — Примеч. ред.
120
Если Ему=лх , эта плотность равна
(пЯи ;0)) /«(тТ; 0), (3.4.3)
п 1 __
где g(z', 6) — п.р.в. Xj в точке z; если же пх , это нуль [см. пример 3.4.1]. Теперь [см. II, раздел 11.3.2]
g(z; 0)= (^)!0nzn-/e-0z
И п
хщи-, e)=ene~eLuj = = 0пе—пх0 ' 'Euj = rix'.
Таким образом, (3.4.3) сводится (в нетривиальном случае) к 0п<гпхв/{ -L-е^пху^е-пхв ] =(Л-1)!/(иТ)п1,
что не зависит от в. Следовательно, х~ достаточна для в.
Пример (3.4.3) (продолжение). В примере 3.4.2 было показано, что при заданных х1,...,хп с п.р.в. 6егвх среднее выборки Y является достаточной статистикой для 0. Из этого, однако, не вытекает, что Y — в каком-то смысле хорошая оценка для в. Фактически Y совершенно неприемлема как оценка для 0, поскольку она даже не имеет нужной размерности [см. раздел 3.3.1, а)]: Е(Х) = 1/0, так что, х~ имеет размерность вЛ, а не в. Что действительно следует из примера 3.4.2, так это то, что наилучшая возможная оценка 9 должна быть функцией Y. Ответа на вопрос, какая функция, концепция достаточности не дает; он должен быть получен с помощью других критериев (таких, как состоятельность [см.раздел 3.3.1]). В данном случае по соображениям размерности правомерно считать, что 1/х" может оказаться приемлемой оценкой. Действительно, распределение Z=t,Xj задается (3.4.4), откуда ожидаемое значение \/Х -n/Z равно:
J (л/г) g (z; &)dz-n9/(n—Y) о
[см. II, раздел 10.4.1]. Следовательно, (п—1)/пх~ — несмещенная [см. раздел 3.3.2] функция достаточной статистики Т, и с этой точки зрения — наилучшая возможная оценка 0. (Формальная процедура получения несмещенной достаточной статистики приведена в разделе 3.4.3.)
3.4.2. КРИТЕРИЙ ФАКТОРИЗАЦИИ И ЭКСПОНЕНЦИАЛЬНОЕ СЕМЕЙСТВО
В примерах 3.4.1, 3.4.2 и 3.4.3 показано прямое применение определения достаточности. Более прост подход с использованием критерия факторизации, который позволяет немедленно ответить на вопрос о существовании достаточной статистики. Этот критерий состоит в следующем.
-121
Теорема 3.4.1. Критерий факторизации для достаточности. Пусть х2,...,хл; в) — выборочная п.р.в. наблюдений хь х2,...,хп. Статистика в* = 6*(Xi, х2,...,хп) достаточна для в тогда и только тогда, когда fn может быть разложена в произведение вида
fn (*i, х2,...,хп; 6)=g {0*(хь х2,...,хп), 6) h (хь х2,...,хп), (3.4.4)
где сомножитель /?() не зависит от 6. (В частности, h(-) может быть постоянным.)
Пример 3.4.4. Критерий факторизации и распределение Бернулли. В примере 3.4.1. совместное распределение данных имеет п.р.в.
fn (х„ х2,...,хп-, / (1-0)л~^
(с заменой р в (3.4.1) на 0). Это выражение того же вида, что и (3.4.4), с 0* = Exy, g(0*, 0)=09*(1—в)п~в* и Л(Х], х2,...,хл) = 1. Следовательно, ЕХу достаточна для 0.
Для данных примера 3.4.2 совместная п.р.в. в точке (хн х2,...,хл) равна:
fn(xx, х2,... ,хл; 0) = 0Л е -eLxj’
что также имеет форму (3.4.4), если в ней положить 0* = Еху g(0*, 0) = 0ле^’ и А(х1,...,хл)=1.
Пример 3.4.5. Критерий факторизации и нормальное распределение. Для N (0, 1) п.р.в. выборки в точке (хь х2,...,хл) равна:
(2тг)л/2 ехр{—4 Е(х—0)2] =(2тг) ~п/2 ехр{ — 4 Е(х—х )2—4 п(х —
—0)2] =
=g(0*; 0) А(хь...,хл), где
0*=х\ g(0*;0)=(2?r)-л/2ехр{—4 л(0*—0)2j и h(xlf х2,...,хл)=ехр{ — 4 Е(ху—х )2}.
Отсюда следует, что статистика 0*=х" достаточна для в.
Подобным образом для нормального распределения с Е (А)=0 и var (Х) = 0 получаем, что /л(Х1,...,хл; 0) = (2тг0) -л/2ехр(—Ех2 / 0), откуда Ех) — достаточная статистика для дисперсии 0 (а следовательно, и для стандартного отклонения 01/2).
Пример 3.4.6. Критерий факторизации и гамма-распределение. Для однопараметрического гамма-распределения [см. II, раздел 11.3] с параметром формы 0, для которого п.р.в. в точке х равна
х^-1 е~х / Г(0), х>0,
122
получаем „
х2,...,х„; 0 = ( Пл»-') е-^j / Г”(0.
17 п
Здесь разложение на множители (3.4.1) достигнуто для 0* = ГЦ , достаточной статистики для в. 1
В теореме 3.4.1 не требовалось, чтобы х, были наблюдениями над независимыми и одинаково распределенными переменными. Для однопараметрических распределений, однако, обычно рассматривается ситуация, когда xt образуют случайную выборку из общего однопараметрического распределения, как в примерах 3.4.4, 3.4.5 и 3.4.6. При таких обстоятельствах и слабых ограничениях распределение, обладающее достаточной статистикой, должно принадлежать к экспоненциальному семейству распределений, определяемому следующим образом.
Определение 3.4.2. Экспоненциальное семейство. Однопараметрическое экспоненциальное семейство (или класс экспоненциального типа) одномерных распределений имеет в х следующую п.р.в.:
f(x, 0)=exp { А (х) В(6) + С(х)+D(6)), (3.4.5)
где А(х), В(в), С(х) и D(0) — произвольные функции указанных аргументов, ограниченные только тем, что f(x) — плотность распределения, т. е. f(x) должна быть неотрицательна и нормализована*. (Этот класс иногда называют классом Дармуа—Питмана—Купманса.)
При применении критерия факторизации из теоремы 3.4.1 к (3.4.5) можно увидеть, что распределение выборки можно записать в форме произведения:
fn(xi, х2,...,хп; 6)= { exp В(6) ZAfxJ+nDtd) } - { exp ЕСЦ) },
откуда статистика 0* = ЕЛ(х,) достаточна для 0.
Если к тому же ЕЛЦ) / п несмещенная оценка 0, то она удовлетворяет неравенству Крамера—Рао (3.3.5) [см. (3.3.8)]. Оценка ЕЛ(Х|) / п в таком случае несмещенная, эффективная и достаточная.
Примером экспоненциального семейства могут служить п.р.в. однопараметрического гамма-распределения с параметром формы 0 [см. пример 3.4.6]:
х*-1 е~х / Г(0)=ехр { (log (х))(0— 1)—х— logF(0) },
что имеет вид (3.4.5) с /4(x) = logx, 5(0) =0—1, С(х) = —х и £)(0) = log Г(0). Достаточная статистика 6* = '£A(xi) есть Е log Xj = log (П х}} или любая функция от нее в соответствии с примером 3.4.6, где установлено, что статистика ГЦ достаточна для 0.
В приведенных выше примерах рассмотрены биномиальное и отрицательное распределения.
Пример 3.4.6 а. Биномиальное распределение как член экспоненциального семейства. Если X — число успехов в фиксированном количестве п испытаний Бернулли с вероятностью успеха 0, то п.р.в. X в точке х равна:
* Т. е. ее интеграл по всей прямой должен быть равен 1. — Примеч. ред.
123
f(x;e, n)=(”} вх(1~е)п~х, x=0, (3.4.5a)
откуда
log/= log ( £ )+x log +И log (1—0).
Это выражение имеет фо£>му (3.4.5) с log ( ^ ^ = С(х), xlog {0/(1—0)} = =А(х) В(6) и п log (1—0)=Z)(0). Поэтому биномиальное распределение входит в экспоненциальное семейство, и статистика 0* = А(х)=х достаточна для 0 [см. пример 3.4.4].
Пример 3.4.6 б. Отрицательное биномиальное распределение принадлежит экспоненциальному семейству. Если по контрасту с ситуацией из примера 3.4.6а, N — число испытаний Бернулли (0), требующееся для достижения фиксированного числа х успехов, то N имеет отрицательное биномиальное распределение, для которого
Р (N=n)=f(n в^~х> п=х,х+1, х+2,... (3.4.56)
(ср. с примером 3.3.0). Здесь
log/= log (п~))+ п log-r-Ц +п log (1—0), \Х—1/ 1—и
и снова мы видим, сравнивая с (3.4.5), что плотность распределения вероятности принадлежит экспоненциальному семейству и п — достаточная статистика для 0.
Пример 3.4.6 в. Влияние усечения. Положим, что X — пуассоновская переменная с параметром в и что в выборке п наблюдений X значение Х=г встретилось пг раз, г=0,1,...,к и Lnr = n. Вероятность получения такой выборки равна:
Л . г к
fn(n0, пх,...,пк; 0) = П(е-(? 0Г / г\уг=е~пв 0»™' / П(г!)п'.
Поскольку это произведение имеет вид (3.4.4), где
0* = £глг, g (0*, 0) = е~в№гпг
и 0
Л = 1 / П (г!)%
то (сумма всех к наблюдавшихся значений) достаточна для 0.
Теперь предположим, что нулевые значения Х=0 были ненаблюдаемы, возможно, из-за ошибок эксперимента или неприспособленности оборудования; тогда X имеет усеченное пуассоновское распределение [см.II, раздел 6.7] с отсутствующим нулевым классом [см. II, пример 6.7.2]. Плотность распределения вероятности в точке х в этом случае будет равна:
Р (Х=Х) = 0(0) 0r !, r= 1, 2,..., 0(0) = е~° / (1—е~0).
124
Вероятность выборки равна:
П [ф (6) 6Г / г !}"' = { 0(0)0^ ГПг / П(Н)%
что также имеет вид произведения (3.4.4) с в* = ^гпг (та же статисти-1 к
ка, что и для неусеченного случая), g (6*, 6) = фп(6) 6'г и к к
А=1 / П (г!)"г. Следовательно, достаточна для 0.
Этот последний пример иллюстрирует общий результат об усечении X (непрерывной или дискретной) с п.р.в. f(x; в)=а/(6) ф(х, 0) и достаточной статистикой для 0. Оказывается, если наблюдаемы лишь значения X, удовлетворяющие условию а^Х^Ь, то у усеченного распределения тоже есть достаточная статистика для 0. Действительно, поскольку ffx, в) принадлежит к экспоненциальному семейству (3.4.5), усеченную п.р.в. можно представить в виде
/trunc(* д)/Х(0), а^х^Ь, где ь
Х(в) = \fMdx, а и, таким образом,
/Inl№(x,«) = । А(Х) B(6) + C(X) + D(^ 1 =
Л(Р)
= exp { А (х) В(0) + С(х) + D, (в) ], где
Dx (0)=Z>(0)—log Х(0).
Следовательно, /trunc (х, 0) тоже принадлежит экспоненциальному семейству и имеет достаточную статистику для 0.
3.4.3. ДОСТАТОЧНОСТЬ И НЕСМЕЩЕННАЯ МИНИМАЛЬНО ДИСПЕРСНАЯ ОЦЕНКА
а) Теорема Рао—Блеквелла. Различные критерии, фигурировавшие выше, дают возможность найти достаточную статистику 0*, когда она существует. Но, как выяснилось в примере 3.4.3,.остается открытой проблемой выбор подходящей функции от 0*, которая была бы разумной оценкой 0.
Почти тривиальный пример дает биномиальное распределение Bin (п, в). Если X имеет такое распределение, то наблюдаемое значение х переменной X достаточно для 0 [см. пример 3.4.6а]; как оценка эта статистика неприемлема: значение 0 должно заключаться между О и 1, между тем, если л = 20, то х может быть равным, скажем, 19.
125
Очевидное решение состоит в том, чтобы взять в качестве оценки не х, а х/п (несмещенную для в).
Подобные свойства проявляет и отрицательное биномиальное распределение. Если N имеет такое распределение, как в примере 3.4.66, то наблюдаемое значение п переменной N достаточно для 0, но как оценка п неприемлемо по соображениям размерности, как указывает соотношение E(N)=x/0. Преобразование, которому следует подвергнуть х дЛя получения приемлемой, т. е. несмещенной, оценки в, не столь очевидно, как в предыдущем случае. Но небольшое вычисление все-таки приводит к оценке (х-1)/(л-1), которая является несмещенной для в [ср. с примером 3.3.0].
Нельзя, однако, надеяться на то, что всякий раз удастся найти подходящие решения, как было в этой задаче. Следующая теорема предлагает регулярный метод.
Теорема 3.4.2 (теорема Рао—Блеквелла). ^Предположим, что s=s(Xt, x2,...,xj — достаточная, но смещенная оценка в, основанная на выборке (хь x2,...,xj наблюдений случайной величины X, а u(xt,..., хп) — несмещенная, но недостаточная оценка в. Пусть S=s(Xlt Х2,...,Хп) и U^u(Xi, Х2,...,Хп), где Х1г Х2,...,Хп — статистические копии X. Тогда условное математическое ожидание [см. II, раздел 8.9]
(s)=E((7/S=5)
является несмещенной достаточной оценкой 6 и
var { 0*(S) } ^var (U).
В качестве тривиальной иллюстрации действия теоремы рассмотрим выборку (X], х2,...,хп) наблюдений бернуллиевски распределенной переменной X. Статистика 5=Ёхг достаточна для в, но смещенная. Статистика х} несмещенная, но недостаточная. Статистика Рао—Блеквелла равна:
e*(s)=E (х, I Ехг=5) = Е (Ехг ! Ехг=5)= -1 5.
Эта оценка s/n — несмещенная и достаточная. Следующий пример более содержателен.
Пример 3.4.7. Применение теоремы Рао—Бреквелла. Пусть (Х1,...,хл) — случайная выборка наблюдений случайной переменной X с п.р.в. Дх)=02хг~Ч х>0. (Отметим, что Е(Х)=2/0.) Из формы п.р.в. п
выборки П/(х) = 02"(П х ) e~eLxJ следует (с учетом теоремы 3.4.1), что 1 л
5=5 (Xi,...,x„) = Ex/ достаточна для в. Поскольку выборочное математическое ожидание этой статистики равно 2 п/в, она неудовлетворительна по соображениям размерности. С другой стороны, оценка 126
u==u(xi,..>tx„)=l/x\ — несмещенная для так как ее математическое ожидание равно: j (х—1)(02 хе~вх) dx=6. Согласно теореме 3.4.2 оцен-® —1 л
ка 6* = 0*(s)=E (U J S=s) = Е (X i | ^Xr=s) — несмещенная и достаточная для в. Отметим, что условное распределение U при данном S=5 должно быть свободно от параметра в, по определению, достаточной статистики, и, таким образом, 0* — статистика. Чтобы вычислить ее, мы должны знать условное распределение Xi при п
заданном Ехг=$. Заметим, что Дх) — специальный случай гамма-распределения. Из свойства аддитивности гамма-функций [см. II, раздел 11.3.2] следует, что плотность вероятное t -юго распределения ^Хг в точке 5 равна:
gn(s) = e2n s2”-'1 e-°s / (2л—1)!, $>0.
п
Для того чтобы найти условное распределение Xi при данном LXr=s, п 1
нужно знать совместную п.р.в, скажем, й(х, 5), пары Хх и EAL. Оче-п 1
видно, что это то же самое, что и совместная п.р.в. Xi и ЕХ.в точке т? 2
(х, 5—х). Поскольку же Х} и ^Хг независимы,
А(х, s)-f(x) gn-i(s—х)~^гп x(s~x)2n'3 / (2л—3)!
п
Условная п.р.в. Xt в точке х при данном' 12Xr=s равна:
fc(x/s)=h(x, s) / gn(s) = (2n—1)(2л—2) x(s—х) 2п~3 / 5 2п~0<х<$.
Окончательно: искомой несмещенной функцией s будет $
0* (s)=E(U | 5)=£’(Х-1 j s)== Jx -1./;.^ | 5) dx= 1 о
= (2л-1).(2л.-.2_) j (s-x) 2л~3 dx= S2n~l о
= (2n—1) / s=(2n—1) / nx,
где x" -s / n — выборочное среднее. Очевидно, что это достаточная статистика, поскольку она является функцией* достаточной статистики 5. Несмещенность можно проверить и прямым вычислением:
со
Е [0*($)}=(2и—1)Е (5-1)=(2л-1) J 5-1 gn(s) ds=0.
__________ о
* Взаимно-однозначной. — Примеч. ред.
127'
б) Несмещенные оценки с минимальной дисперсией и достаточность. Теорема Рао—Блеквелла позволяет нам для в построить несмещенную достаточную оценку по достаточной оценке S и произвольной несмещенной оценке U:
0* (s)=E(U | S=s)
с дисперсией, не большей, чем var (L7). По соображениям концентрации [см. раздел 3.3.1,а], 0*, очевидно, лучше, чем U. Предположим, что кто-то работает с другой несмещенной оценкой Ux. Получит ли он иную и, возможно, лучшую несмещенную достаточную оценку 0? Ответ на этот вопрос отрицателен. При некоторых не слишком ограничительных условиях оценка Рао—Блеквелла 0* единственна и тем самым является НОМД для 0. Это следует из известного результата Рао: если существует полная достаточная статистика, то любая функция ее — несмещенная оценка ожидаемого значения с минимальной дисперсией. (Достаточная статистика называется полной, если ее любая функция, не равная нулю, с вероятностью 1 имеет ненулевое математическое ожидание.)
Пример 3.4.8. НОМД для биномиального и отрицательного биномиального параметров. Как мы убедились в разделе 3.4.5,а), если х — число успехов в п испытаниях Бернулли с параметром 0, то х/п — несмещенная достаточная оценка 0. Можно показать, что х — полная в смысле предыдущего определения. Из чего следует, что х/п является НОМД для 0. Аналогично если п — число испытаний до достижения фиксированного числа х успехов, то (х—-1) / (п—1) — НОМД для 0.
3.4.4. ДОСТАТОЧНОСТЬ В СЛУЧАЕ МНОГИХ ПАРАМЕТРОВ
Понятие достаточной статистики, введенное в разделе 3.4.1 для однопараметрического семейства распределений, может быть распространено на случай нескольких параметров. Расширение определения 3.4.1 состоит в следующем.
Определение 3.4.3. Совместная достаточность. Пусть случайные переменные Хи Х2,...,Хп (непрерывные или дискретные) имеют в (Хь х2,...,хп) п.р.в. fn{xx, х2,...,хп\ 01, 02,...,0Д где 0Ь 02,...,0к — параметры. Статистики 0у (xit х2,...,хп), j=\,2,...,m, совместно достаточны для 6j, если для произвольного набора т статистик 0; = 0у (хх,...,хп), j=l,2, т, условное совместное распределение 0Н 02,...,6т при данных 0Г, 0*,...,0W* не зависит от параметров 01, 02,...,0^. Эта совокупность статистик называется минимальной совместно достаточной, если т — минимальное целое число, для которого выполняется сказанное выше.
В частности, 0* совместно достаточны для 61у 62,...,6к, если условное совместное распределение Хх, Х2,...,Хп при данных 0* не зависит от 0Ь 02,...у6к.
128
Как и в однопараметрическом случае, прямое применение теоремы может оказаться трудоемким; обычно вместо этого легче пользоваться эквивалентной многопараметрической версией критерия факторизации из теоремы 3.4.1. Она состоит в следующем.
Теорема 3.4.3. Критерий факторизации. Пусть
х2,...,х^, 01,...,0д.),
как в определении 3.4.3. Совокупность статистик ву, j=l, 2,...,к, совместно достаточна для параметров в 6к, если и только если функция fn может быть разложена на множители следующего вида:
fп’• • ’>%П’ 0 •>••» 0jt)
(3.4.6)
= g(0*, 02*,-.,0л* ; 01, 02,...,0„) к(Хц х2,...,хп).
Пример 3.4.9. Совместная достаточность х" u~s~2 для параметров N(n, а). В случае когда Xj, J=l, 2,...,п, — независимые и одинаково нормально распределенные переменные с Е(Ау) = 01, var (Ау)=02, ф „ Л ______
обычные оценки для 0! и 02 есть 0i =х , 02 = Е(ху—х )2 / (п—1) (=s2, скажем). Оказывается, эти оценки совместно достаточны для 0j и 02. Чтобы убедиться в этом, представим п.р.в. выборки в следующей форме:
(2тг02)—ехр - 4- (х,—0i)2= Zt/2 J
(2тг02)—л/2 ехр---=1— { Е (х,—х")2+п(х'—0i)2} =
202 J
(2тг02)-л/2 ехр— 4- ( («— 1)52+л(х — 01)2), 202
т. е. в форме (3.4.6) с 0* =х", 02=$2 и Л(хь х2,...,х„)= 1. Следовательно, ~х и s2 совместно достаточны для 0] и 02. Пользуясь терминологией раздела 3.4.1, мы можем сказать, что х" и s2 вместе содержат всю информацию с 01 и 02, содержащуюся в выборке.
Как и в однопараметрическом случае, любая пара алгебраически независимых функций от 0*, 02 также является парой совместно достаточных статистик. В примере 3.4.8 эта пара уже обсуждалась, поскольку 0? и 02, по отдельности, несмещенно оценивают 0! и 02 соответственно.
129
3.5. ПРАКТИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ ОЦЕНОК. ВВЕДЕНИЕ
3.5.1. ГРАФИЧЕСКИЕ МЕТОДЫ
Если случайная величина X имеет двухпараметрическую ф.р. вида P(AXx)=F(x; 0,, 02)=H[(x—0J / 02)1. где 01 и 02 — параметры (01 называется параметром положения, а 02 — параметром масштаба), то можно придумать специально разграфленную бумагу со шкалой, не зависящей от 0{ или 02, на которой график F(x; 0„ 02) — прямая линия [см. раздел 3.2.2,г)]. Если изобразить на этой бумаге эмпирическую ф.р. [см. разделы 3.2.2,г), 14.2] выборки и множество точек окажется близким к прямой линии, то это может служить грубой проверкой предположения о том, что распределение выборки принадлежит семейству с функцией распределения F(x; 0lt 02). Прямая линия, проведенная «на глаз» по нанесенным точкам, позволяет получить приближенные значения для 0! и 02.
Из подобных распределений наиболее часто встречаются нормальное [см. II, раздел 11.4], логарифмически-нормальное [см. II, раздел 11.5] и распределение Вейбулла [см. II, раздел 1.9]. Графический метод такого типа полезен как предшественник более точных аналитических методов.
Пример 3.5.1. Использование нормальной вероятностной бумаги для оценивания ц и а. Следующая частотная таблица содержит данные об измерении роста 1456 женщин.
Рост (9 дюймах) X г Верхняя граница-интервала группировки Хг+ "Г Частота / г Накопленная частота число женщин, рост которых <*.+ 4-) Накопленная частота в % от целого
52,5 53 0,5 0,5 0,03
53,5 54 0,5 1 0,07
54,5 55 0 1 0,07
55,5 56 1 2 0,14
56,5 57 5 7 0,48
57,5 58 15 22 1,51
58,5 59 15,5 37,5 2,5
59,5 60 52 89,5 6,1
60,5 61 101 190,5 13,08
61,5 62 150 340,5 23,3
62,5 63 199 539,5 37,05
63,5 64 223 762,5 52,37
64,5 65 215 977,5 67,14
65,5 66 169,5 1147 78,78
66,5 67 151,5 1298,5 89,18
во
Рост (в дюймах) X 1 Верхняя граница интервала группировки •V-r Частота t г Накопленная частота (»число женщин, рост которых << + 4-) Накопленная частота в от целого
67,5 68 81,5 1380 94,78
68,5 69 40,5 1420,5 97,56
69,5 70 19,5 1440 99,90
70,5 71 10 1450 99,59
71,5 72 5 1455 99,93
72,5 73 0 1455 99,93
73,5 74 1 1456 100
воспроизведено с разрешения Macmillan Publishing Gompany. Statistical Methods for
Research Workers, 14 th edition, by Sir Ronald A. Fisher, copyright © 1970, University of
Adelaide (см. русский перевод: P. Ф и ш e p. Статистические методы для исследователей /
(Объект измерения ростом ровно 53 дюйма был занесен как 0,5 в клетку с центром 52,5 и как 0,5 в следующую клетку, так же объясняется наличие и других полуцелых частот.)
Эмпирическая ф.р. (т. е. значения накопленных частот, выраженных в процентах от целого, отложенные на нормальной вероятностной бумаге против соответствующих верхних границ клеток) показана па рис. 3.5.1. Прямая линия по точкам проведена на глаз. Точки лежат в разумной близости от этой линии, что показывает приблизительную нормальность распределения рассматриваемой совокупности (т. е. роста женщин).
Для нормального рас-
м Рос. в дюймах (zi пределения график может
Рис. 3.5.1. График эмпирической функции распределения (ф.р.) на нормальной вероятностной бумаге
быть интерпретирован с помощью стандартной
131
Рис. 3.5.2. Эскиз п.р.в.; отменены 50%-ная точка (А) и 95%-ная точка (В)
нормальной плотности, показанной на рис. 3.5.2. 50%-ная точка (64,6 дюйма) дает оценку ц, 95%-ная точка (69,0 дюйма) — оценку для + 1,645а. Следовательно, наш графический метод подтверждает приближенную нормальность выборки (с параметрами /*=64,6 дюйма, а=(69—64,6) / 1,645=2,76 дюйма).
3.5.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Как объяснялось в разделе 3.3.2, несмещенная (ограниченная) оценка с минимальной дисперсией параметра 0, основанная на выборке (Xi, х2.хп), есть функция h(Xi, х2,...,хп\ alt а2,...,ак), где коэффици-
енты а2,...,ак выбраны так, чтобы выборочное математическое ожидание было равно 0, и при этом условии выборочная дисперсия была бы минимальной. Выбор формы функции А(-) обычно основывается на соображениях размерности. В примере 3.3.4 параметр 0 был математическим ожиданием X, и линейная функция поэтому была приемлема. Пример 3.3.5 иллюстрирует использование функции, линейной по коэффициентам и квадратичной по наблюдениям.
Метод наименьших квадратов чаще всего применяют при линейной зависимости от коэффициентов. В этом случае он четко систематизирован и продуктивен. «Принцип наименьших квадратов» описан в гл. 8. (Это один из старейших и известных методов оценивания, его, например, использовал Лежандр в 1805 г.; широко известно также применение этого метода Гауссом в 1809 г. [см. Pearson and Kendall (1970), гл. 15 —D].) Связь между методом наименьших квадратов и несмещенной оценкой с минимальной дисперсией очевидна из следующего примера. Предположим, что для п точно известных нагрузок Х\, х2,...,хп наблюдались соответствующие прогибы У\, у2,....,уп стального бруса. Предполагается, что «уровни» хг нагрузок формируют часть предсказуемой картины эксперимента: они не являются «наблюдениями» в
132
нашем техническом смысле этого слова, так как не являются реализацией случайных величин. Напротив, прогибы уг представляют собой «наблюдения»: они неизвестны заранее; более того, цель эксперимента в том, чтобы наблюдать и измерять их с максимальной точностью, доступной техническому оснащению опытов. Физический подход предполагает, что в пределах рассматриваемых нагрузок и при отсутствии сшибок измерения искомое отклонение >'(х) — прогиб, вызванный нагрузкой х, выражается формулой
у(х) = Оо + 01Х+е2х2,
при определенном значении коэффициентов 0(, 02. Реально наблюдения удовлетворяют соотношениям
yr=0o + 0i хг + 02 х2г + ег, г=1,2,...,п,
где ег обозначает ошибку наблюдения. Согласно принципу наименьших квадратов оценки 0Г Для 0г, г-0,1,2, должны быть выбраны как значения (неизвестных) вг, которые минимизируют «сумму квадратов»
ег = Е1 (уг-60-~е} х-02 х^)2. (3.5.1)
С другой стороны, если мы решили использовать несмещенные оценки с минимальными дисперсиями, линейные по уг с произвольными функциями заданных нагрузок хг в качестве коэффициентов, то нам следует искать оценки вида:
§r=ar + L brsys, r=0,l,2.
Коэффициенты ar, brs определяются из условий: а) 0Г должна быть несмещенной оценкой 0Г (г=0,1,2); б) при условии а) выборочная дисперсия каждой из 0Ь 02 должна быть наименьшей.
Оказывается, для этого «линейного» случая (при описанных выше условиях) оценки наименьших квадратов 0Г и несмещенная оценка с минимальной дисперсией 0Г [см. раздел 3.5.2] в точности совпадают (коротко перечислим эти условия: 1) каждая ощибка ег имеет нулевое выборочное математическое ожидание; 2) все ошибки ег имеют одинаковую выборочную дисперсию; 3) ошибки не коррелированы).
Процесс минимизации суммы квадратов Ее2 хорошо организован алгоритмически и дает для оценки простые ясные выражения. В нашем примере легко видеть, что 0о, 0*, 0* являются (единственными) решениями следующей системы линейных уравнений [см. I, раздел 5.8]:
133
0о + 0* ^»xr + 02 Ex^ = E yr,
0o ilxr + 0* Ex; + 0* Ex; = Exr, yr, 0o ExJ + 0* Ex’ + 0* Ex; = Ex^ yr
Формально решение есть вектор в*=(0*> 0*, 0*), заданный линейной формой
(3.5.2)
**=Су,
где у' = СУ1, у2,...,уп} и С = В~‘ к с
Развитие этих идей, а также выборочные свойства 0* содержатся в теореме Гаусса—Маркова и в ее приложениях [см. гл. 8].
3.5.3. МЕТОД МОМЕНТОВ
Пусть (Xi, х2,...,х„) — выборка наблюдений случайной величины X, п.р.в. которой в точке х равна /(х; 01, 02,...,0^), где 0Г — неизвестные параметры. Пусть
n'r=E(Xr)=hr (0Ь 02,...,0Д г-1,2,..., (3.5.3)
— моменты X (относительно начала) [см. раздел 2.1.2], Здесь hr (•) — известные функции неизвестных параметров. Соответствующие моменты выборки есть
m'r = Е х*- / «, г=’,2............. (3.5.4)
Метод моментов основывается на интуитивном представлении о том. что моменты выборки приблизительно равны моментам генеральной совокупности. Моментные оценки 0™, г-1,2,...,А, находят приравниванием первых к моментов генеральной совокупности соответствующим моментам выборки и решением полученных уравнений
Аг(0;и, 0”....0f)-<, Г=1,2...к.
1
Этот метод прост в применении и, хотя ему недостает твердого теоретического обоснования, часто дает приемлемые результаты. Но опенки могут быть и очень низкой эффективности. Обычно этот метод предшествует методу максимального правдоподобия [см. раздел 3.5.4], который часто требует численного решения нелинейных уравнений. По этой причине метод моментов ранее был наиболее популярным, но при современных возможностях вычислений степень его распространенности существенно снизилась. Моментные оценки могут, однако, служить полезными и легко получаемыми первыми приближениями в итеративном процессе решения уравнений правдоподобия [см. пример 6.4.3].
Пример 3.5.2. Оценивание параметров нормального распределения ц и а методом моментов. В случае распределения N (д, а) имеем
ц\ =Е (Х)-ц
и
/2=£(^2)=о2+/*2.
Следовательно, уравнения моментов принимают вид
= п
и
(=х , скажем)
(д2)"'+(а2)/я = ExJ / л (=х 2, скажем).
Отсюда моментные оценки:
[кт=Х , (<Г2)(,И> = X 2—(У2) = (LXj — х ZXj) / п.
Как будет видно из раздела 6.4.1, моментные оценки в этом примере совпадают с оценками по методу наибольшего правдоподобия.
Пример 3.5.3. Оценивание параметров гамма-распределения с помощью моментов. В случае гамма-распределения с параметром формы а, параметром масштаба (3 и п.р.в.
/(х; а, 3)=ха"1 е~х/& / Г (а), х>0,
первые два начальных момента равны:
и
ц\ =Е (Х)= j xf(x; ct, 0)dx=a& сж, °
д2=£ (%2)= J х2/(х; a, 0)dx=a(a+1)/32.
О
135
Следовательно, моментные оценки ат, 0т выборки (х(, х2,...,хп) для а и /3 — это корни уравнений
а$=х (=Еху/л),
__ п 2
а(а + 1) /32=х 2 (= LXj / п), а именно
a<J”) = (x)2 / [Т2 — (X)2],
[Т2 — (х)2] /Т.
(3.5.5)
[Оценивание этих параметров обсуждается в примере 6.4.3.]
3.5.4. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Этот широко используемый и наиболее эффективный метод детально описан в гл. 6. В настоящем же разделе мы лишь кратко обсудим его.
М. Кендалл считает первой публикацией на эту тему статью Даниила Ёернулли, вышедшую в 1777 г. [см. Pearson and Kendall (1970), гл. 11 — Dj.
Начнем с простого примера.
Пример 3.5.4. Оценка максимального правдоподобия параметра экспоненциального распределения. Предположим, что X распределено экспоненциально с неизвестным математическим ожиданием, т. е. п.р.в. X принадлежит к однопараметрическому семейству:
с х>0;
/(*»= „
< 0 в противном случае.
Семейство возникает, когда в пробегает все положительные значения. То особое значение в (скажем, 0°), которое свойственно нашему X, неизвестно. Мы будем называть его истинным значением 0. Желательно оценить 0° по данным (хь х2,...,хп), состоящим из независимых наблюдений X. Имея в виду, что хг фиксированы, строим функцию
l(0) = l(0',xi, x2,...txn) = Uf(xi-, 0) =
= 0пе~^Хг, 0>О, (3.5.6)
136
как функцию свободной переменной 0, для которой наши данные служат известными и фиксированными коэффициентами. Она называется функцией правдоподобия данных [см. разделы 4.13.1, 6.2.1]. В нашем примере X — непрерывная переменная. Данные хх,хг,...,хп должны рассматриваться как конечные (ограниченные) приближения к бесконечным десятичным дробям, требуемым для точной записи действительных чисел, так что хг означает некоторое число, лежащее в интервале хг ± А, где h — размер измерительной сетки, скажем —1 мм, для хг, измеряемого в миллиметрах. При малых h такого порядка вероятность
Р(Х€хг ±4- h)
может быть заменена с необходимой точностью на
hf(xr\ 0), г=1,2,...,л.
Вероятность получения наблюдаемой выборки для данного значения 0 будет поэтому равной
п
hn Пф(хг\ 0).
Следовательно, для каждого фиксированного значения (скажем, 00 параметра численное значение правдоподобия пропорционально п
Пf(xr', 00, и мы можем, таким образом, принять за значение правдоподобия выражение (которое определяется с точностью до умножения на константу, т. е. функцию данных, не зависящую от 0)
п
n/Ur; 0),
где хг остаются фиксированными, а 0 — неопределенная переменная. Между вероятностью и правдоподобием есть существенная разница: вероятностные утверждения касаются множества возможных исходов при фиксированном значении 0. В утверждениях о правдоподобии, напротив, значения исходов фиксированы и рассматриваются все возможные значения 0. При подходящих условиях суммы вероятностей также являются вероятностями, но суммы правдоподобий не являются правдоподобиями и т. д.
Несмотря на эти различия, есть и общие свойства. Относительно большие правдоподобия соответствуют вероятным значениям 0 более, чем относительно малые, так как большие вероятности соответствуют сильно ожидаемым исходам более, чем малые вероятности.
137
Рис. 3.5.3. Функция правдоподобия Цв) из примера 3.5.4
Из двух значений ва и еь ва называется более правдоподобным, чем еь, в смысле большего правдоподобия нахождения вблизи истинного значения 0°, если I (0а) / (/ (вь) > 1. Значение 0тах, в котором достигается максимальное значение функции правдоподобия, так что I (0тах) / I (0b) > 1 для любого еь(вь * 0тах)» является наиболее в этом смысле правдоподобным значением 0 (для рассматривае
мых данных). При применении метода максимального правдоподобия
это значение 0тах (зависящее, конечно, от данных хь х2,...,хл) берут как оценку 0°. Она называется оценкой максимального правдоподобия (ОМП) для 0°.
На рис. 3.5.3 показан график функции правдоподобия вместе с ОМП. В этом примере величина 0тах может быть получена дифференцированием как подходящий корень уравнения правдоподобия dl{0) / dd=0, или, что то же самое, уравнения
d [log Z(0)} / de=0,
где I (0) задано (3.5.6). Следовательно, в нашем примере уравнение правдоподобия сводится к
п
Ёхг = 0,
откуда
0тЯу==И / ^хг=1 / X ,
где х* — среднее выборки.
Приведенное описание нуждается в дополнениях. Строго говоря, в качестве функции правдоподобия следует взять al (0), где а — произвольная положительная функция наблюдений, а I (0) определено, как в (3.5.6). Это не влияет на процедуру максимизации, поскольку для любого положительного дд/(0)и/(0) достигают своего максимума при одном и том же значении 0.
На практике при использовании метода максимального правдоподобия обычно не говорят явно об истинном значении 0°, которое вы
138
деляет определенное f (х, 0°) из рассматриваемого семейства плотностей заданного вида /(х, 0), в € Й (□ — пространство параметров, в примере 0= {0, 0 > 0})’. Вместо этого: 1) говорят (несколько вольно) о задаче оценивания параметра 0 плотности оаспределения вероятности /(х, 0), имея в виду под 0 истинное значение 0°; 2) одновременно говорят о функции правдоподобия 1(0), имея в виду под 0 переменную, чья область изменений — пространство параметров 42.
Процедура максимизации часто упрощается, если вместо функции правдоподобия использовать ее логарифм log (1(0)) — логарифмическую функцию правдоподобия, поскольку при этом нужно дифференцировать не произведение, а сумму; log I (0) достигает своего максимума при том же значении 0тах, что и / (0). (Нельзя, однако, думать, что максимум может быть найден дифференцированием в каждом случае. Контрпримеры см. в гл. 6.)
Когда (как в примере 3.5.3) уравнение правдоподобия имеет простое и ясное решение, можно исследовать выборочное распределение оценки непосредственно. Однако чаще решение может быть получено лишь в виде итеративной численной процедуры, и потому прямое изучение выборочного распределения невозможно. В соответствии с общей теорией [см. гл. 6] для подобных случаев возможны простые и эффективные аппроксимации.
Этот метод также применим при нескольких параметрах и когда наблюдения не обязательно независимы и одинаково распределены [см. гл. 6].
3.5.5. НОРМАЛЬНЫЕ ЛИНЕЙНЫЕ МОДЕЛИ, В КОТОРЫХ ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ И НАИМЕНЬШИХ КВАДРАТОВ СОВПАДАЮТ
Обычную задачу оценивания можно пояснить следующим примером. Предположим, что выход химического процесса линейно зависит от температуры, продолжительности остывания и количества присутствующих активаторов при неизбежных, конечно, ошибках эксперимента. Когда уровни контролируемых переменных представляют собой множества значений
tr (температуры), dr (продолжительности), аг (активации),
предполагается, что выход (переменная отклика) уг является реализацией нормально распределенной случайной величины Yr с
Е ( Yr) = 0Q + $1 tr + 02dr + 0jUr
и
var (Y г)-аг.
139
Здесь — неизвестные постоянные, которые отражают зависимость среднего выхода от изменений уровней, о2 — неизвестная, но постоянная дисперсия выхода.
Мы предполагаем, что для каждой комбинации уровней имеется одно наблюдение. (На практике их должно быть несколько; такое ограничение сделано ради упрощения записи.) Для данных .У), У2,... ,Уп функция правдоподобия пропорциональна
о~п ехр (yr—0o—6\tr—e2dr—03ar)2].
Это выражение максимально относительно переменных 6, когда
Е (у — 0О—Oitr—62dr—63ar)2
минимально. Следовательно, оценки максимального правдоподобия линейных параметров 0о, 01, 02, 0з совпадают в этом примере с оценками наименьших квадратов.
3.6. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Содержание этой главы раскрывает основу статистического исследования. Эта тема отражена в большинстве учебников по математической статистике. Мы особо рекомендуем следующие: [Barnett (1982); Fisher (1959); Kalbfleisch (1979); Kendall and Stewart (1973); Rao (1965); Zacks (1971) — С].
Глава 4
ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
4.1. ВВЕДЕНИЕ: ПРОБЛЕМА
4.1.1. СООБРАЖЕНИЯ, ОСНОВАННЫЕ НА ИНТУИЦИИ
В предыдущих раз дел .ох мы видели, что статистика l(xlt х2,...,хп), которая имеет допустимое выборочное распределение [см. раздел 2.2], может рассматриваться как оценка [см. раздел 3.1] параметра в плотности распределения случайной величины X [см. раздел 3.1].
Можно сказать, что доступная информация о значении параметра 6 содержится в выборочном распределении оценки, но ее трудно извлечь из-за того, что это распределение само зависит от неизвестного значения 6 (иная ситуация в случае байесовского подхода [см. раздел 15.4.2]).
Необходимо разработать метод, который позволил бы выразить вероятностную точность оценки с использованием лишь рассматриваемой статистики и без привлечения другой информации относительно истинного значения параметра. Естественным представляется следующий подход (в предположении, что такой метод существует).
Пример 4.1.1. Среднее выборки как оценка истинного значения. Предположим, что X — случайная величина, распределение которой N(0, 1). Среднее выборки х, определенное из выборки объема л, является реализацией случайной величины X [см. определение 2.1,1], которая распределена по закону N(0,_l/vn). Изменения значения 0 сдвигают плотность распределения X, не меняя ее формы. Из возможных значений 0 (соответствующих функций плотности) рассмотрим три с наблюдаемым значением х. Это показано на рис 4.1.1.
В случае I) наблюдаемое значение х лежит в зоне весьма малых значений плотности и с большой вероятностью значение 01 для величины 0 должно быть отвергнуто. То же относится и к 03 в случае 3). Напротив, в случае 2) наблюдаемое значение х лежит в зоне большой плотности вероятности, и гипотеза о значении 02 параметра 0 вполне совместима с наблюдениями. Очевидно, должны существовать значение 0/ между 0, и 02, а также значение 0W между 02 и 03 такие, что значения 0 между 0/ и 0М представляются правдоподобными, а значения 0 вне этого отрезка — неправдоподобными. Однако насколько правдоподобными? И в каком смысле правдоподобными?
141
Рис. 4.1.1. Наблюдаемые значения среднего выборки и функции распределения для трех возможных значений 02, в, математического ожидания Е(Х)
4.1.2. Нижняя (Oj) и верхняя (0и) границы области правдоподобных значений в при фиксированном значении среднего выборки
При байесовском подходе мы имеем вероятностное распределение величины О и можно принять за меру правдоподобия интервала (О/, вы) апостериорную вероятность того, что значение случайной величины 0 попадает в этот интервал. Этот подход развивается в гл. 15.
Р. Фишер предложил проводить оценивание в терминах «фи-дуциальной вероятности». Однако такой подход осложняется из-за отсутствия единой точки зрения на само понятие фидуциальной вероятности [см., на-' пример, Kendall and Stuart (1973), т. 2, гл. 21—С].
Общепринятое небайесовское решение задачи — формализация следующей идеи: если значение 0 есть х — реализация нормальной случайной величины X с параметрами (0/, 1/V/J), то за наибольшее положительное отклонение, которое еще считается правдоподобным, от величины 0/ принимается величина d такая, что Р (X—Qf^d) имеет малое фиксированное значение, определяемое пс соглашению. Возьмем его, например, равным 0,025;
142
тогда получим [см. приложение 4] J=l,96/V«. Отсюда
1,96/Тл.
Аналогично п - , < , г
0u=x+l,96/vn.
Эти рассуждения приводят в конце концов к понятию доверительного интервала, которое рассматривается в разделе 4.2.
4.1.2. СТАНДАРТНОЕ ОТКЛОНЕНИЕ
В примере 4.1.1 было рассмотрено нормальное (в, 1) распределение. Если бы мы рассмотрели вместо этого нормальное (0, а) распределение [см. II, раздел 11.4.3] с известным а, то мы пришли бы к выражению х±1,96ст/Тй для интервала правдоподобных значений величины 6, так как ст/7й — стандартное отклонение случайной величины х [см. определение 2.3.2]. Если же, напротив, значение ст не известно (а именно так чаще всего и бывает), этот интервал не может быть выражен в таком виде и возникает соблазн заменить неизвестное значение ст какой-нибудь оценкой а* величины ст и считать х±1,96ст*/Тл выражением для интервала правдоподобных значений (с 95Фо-ной вероятностью) величины в.
Аналогично, если вместо х для оценки 0 мы используем некую статистику х2,...,х„) для оценки параметра т, то мы приходим к интервалу t±2>lv(ty в качестве 95%-ного интервала для т, где Vр(0* — соответствующая оценка для стандартного выборочного отклонения /.
Эти идеи могут быть, конечно, сформулированы более строго. Цель настоящей главы — пояснить, как этого достигнуть. Они также проясняют значение величины Vw(?)*, которое называется стандартной ошибкой t [см. определение 2.3.2].
4.1.3. ИНТЕРВАЛЫ ВЕРОЯТНОСТИ
а) Интервалы вероятности для непрерывных случайных величин. Полная информация о проведении случайной величины X может быть получена только при известном законе ее распределения [см. II, разделы 4.3, 10.1]. Часто необходим более простой способ выражения изменчивости. Удобным обобщающим понятием является интервал вероятности, определенный следующим образом.
Определение 4.1.1. Пусть X имеет нейрерывное распределение, зависящее от известного параметра 0 (или нескольких таких параметров), и пусть а-а(0), b=b{0), а<Ь — такие числа, что для заданно-гор(0<р<1) Р^Х^р
или, иначе говоря, ь
]/(х, 0) dx~F(b, 0)—F(a, ff)^p, а
где /(х, 6) и F(x, 0) — плотность и функция распределения величины X соответственно. Тогда интервал (а, Ь) (который зависит от (в) назы-
143
Рис. 4.1.3. Интервал (а, Ь) — 100/>%-ный вероятностный интервал распределения, плотность которого задана графиком. Он является центральным 100р%-ным интервалом, если площади под графиком левее а и правее b равны между собой (и равны у(1—р))
вается интервалом вероятности уровня р или иначе 100р%-ным интервалом вероятности для X. (Отметим, что так как X — непрерывная случайная величина, определение не изменится, если выражение Р(а^Х^Ь) будет заменено на любое из Р(а<Х^Ь), Р(а^Х^Ь), Р(а<Х<Ь).)
Об интервале (а, Ь) можно сказать, что он содержит р-ю часть всего распределения в том смысле, что при большом чис
ле испытаний p-я часть чисел выборки будет попадать в него. Это утверждение иллюстрирует рис. 4.1.3 для унимодального распределения.
Смысл утверждения, подсказанный интуицией, заключается в том, что если р велико (скажем, 0,95 или 0,99), то можно быть «почти уверенным», что любая реализация X попадет в интервал (а, Ь). Здесь а и b — любые числа, такие, что a<b, F(b, в)—F(a, 9)=р (F(x, 6) — функция распределения X).
Если X — дискретная случайная величина, то такие а, Ь, вообще говоря, не могут быть определены точно, поэтому необходима соответствующая модификация определения {см. пример 4.1.3].
Пример 4.1.2. Интервалы вероятности для стандартного нормального распределения. Если X—N(/i, о) (т.е. С/=(АГ— ц)/а — N(0, 1)), то вероятностный интервал для U уровня 0,95 — это любой интервал (а', Ь'), такой, что
Ф(Ь')—Ф(У)=0,95,
где Ф(-) — функция стандартного нормального распределения. Примеры таких интервалов, полученных из таблиц Ф(-) [см. приложение 3, 4], следующие: 1) (—3,00, 1,66), 2) (—2,50, 1,71), 3) (—1,96, 1,96), 4) (—1,75, 2,33).
Соответствующие интервалы для Х(= ц+ oU):
1) (д—За, д+ 1,66а) 2) (д—2,5а, д+1,71а) 3) (д—1,96а, д+1,96а) 4) (д—1,75а, д + 2,33а) (длина 4,66а), (длина 4,21а), (длина 3,92а), (длина 4,08а).
Как видно из этих примеров, уровень интервалов вероятности однозначно не определяет их границ. Чтобы достигнуть однозначности, необходимо ввести дополнительные ограничения, а именно: 1) либо 144
интервал должен иметь минимальную длину, 2) либо он должен быть центральным или симметричным в том смысле, что
Р(Х^а)=Р(Х>Ь). (4.1.1)
Для симметричного унимодального распределения [см. II, раздел 10.1.13] эти условия эквивалентны. В случае унимодального несимметричного распределения можно определить наименьший вероятностный интервал с помощью условия равных ординат, т. е. для данного Р вероятностный интервал (а, Ь) будет кратчайшим, когда f(a, 6)=f(b, в), где/ft 0)=dF(x, 0)/dx — плотность распределения X. Таблицы плотностей распределения часто недоступны (в отличие от таблиц функций распределения), и поэтому приходится работать непосредственно с условием симметричности. В этом случае для вероятностного интервала уровня р значения а и b для примера 4.1.1 можно найти как нижнюю и верхнюю 100(1—ур)<7о-ные точки распределения X.
Пример 4.1.3. Вероятностные интервалы для Т-образного распределения. Экспоненциальное (показательное) распределение с плотностью 0-1ехр (—х/в) при х>0 [см. II, раздел 10.2.3] имеет монотонно убывающую плотность, и следовательно, условие равных ординат здесь не применимо. Ясно, впрочем, что в этом случае для любого р кратчайшим вероятностным интервалом уровня р будет интервал (0, Ь), где b выбирается из условия Р(Х^Ь)=р, что с учетом равенства р=1—ехр(—Ь/0) дает Z?=01og(l/(1—р)). Таким образом, кратчайшим 95%-ным вероятностным интервалом будет (0, 2,9960). Симметричным вероятностным интервалом уровня 0,95 будет интервал (а', Ь'), где для а' и Ь' выполняются соотношения
Р(Х^а ) = 1 — ехр(— а/в)=0,025,
Р(Х > Ь) = ехр(—Ь/0)=0,025,
откуда а' = 0,0780, Ь' = 3,690.
б) Вероятностные интервалы для дискретных случайных величин. Для непрерывной случайной величины X интервал (а, Ь) будет' интервалом вероятности уровня 100р%, если
Р(а^Х^Ь)=р, или, что равносильно,
Р(а<Х<Ь)~р.
Это действительно одно и то же, так как в непрерывном случае P(X=a)=P(X=b)~G. Однако это, вообще говоря, перестает быть верным при дискретном X. Возьмем, к примеру, в качестве X величину, распределенную по пуассоновскому закону. Пусть а, b — положительные целые числа. Тогда P(X=a)>Q, P(X=b)>Q и, что очевидно, Р(а<Х<Ь)<Р(а^Х^,Ь). Чтобы избежать неопределенности, в дискретном случае мы будем назыв'ать [а, Ь] замкнутым интервалом вероятности и уровня lOOpOfa для X, если
Р(а^Х^Ь)=р.
145
(Иногда для случайных величин, принимающих целые значения, удобнее говорить об открытых интервалах (а—1, Ь+1), для которых Р(а—1<Х<Ь+1)=р.)
Более серьезное осложнение для дискретных величин состоит в том, что хотя для данных а и Ь всегда можно вычислить р=Р(а^Х^Ь), отнюдь не для любого р можно найти соответствующий вероятностный интервал (а, Ь), а тем более центральный вероятностный интервал, для которого Р(а^Х^Ь)-р
Самое большое, что здесь можно сделать — это найти «почти симметричный» вероятностный интервал уровня не меньше 100р%, как можно более близкого к lOQp^fo. Для замкнутого вероятностного ин-
ея — случайная величина, распределенная биномиально (20, 0,4) [см. приложение I].)
г P(R<r)
1 0,0000
2 0,0005
3 0,0036
4 0,0160.. .Р(Я<4/=0,0160< 0,0250
5 0,0510.../¥Ж5Л=0,0510>0,0250
(слишком большое), отсюда q-4
г Р(>г)
14 0,0016
13 0,0065
12 0,012...Р(7?>12>=0,0210< 0,0250
11 0,0565...Р/Я> 11^0,0565 > 0,0250
(слишком маленькое), отсюда ги = 12
Pty С R С rj « P(R=4>+P(R « 5)+...+PfR=12)=0,963
г: 0 12 3 | [ 1 4 5 6 7 8 9 10 11 12 1 1 |_ [ 1 13 14 15 ... 20 1 1
Вероятность: 0,0160 1 0,0630 1 1 (вероятностный интервал)1 0,0210
Рис. 4.1.4. Приближенный квазицентральный 95%-ный вероятностный интервал биномиального (20,0,4) распределений
146
тервала этого вида с р-0,95 мы находим из таблиц распределения значение /•/ ,такое, что
Р(/?<г,К 0,025, при этом
Р(Я<г,+ 1) >0,025, а значение ги такое, что
P(R>ru) <0,025, при этом .
P(R>ru—\) >0,025*.
Тогда
P(r- <R<ru)=\ —P(R < rj)—P(R > rM) > 0,95.
Необходимо иметь в виду, что иногда таблицы дают значения вероятностей вида P(R~$tr) (так построены, например, таблицы биномиального распределения в приложении 1). Диаграмма типа изображенной на рис. 4.1.4 поможет разобраться в ситуации. Для иллюстрируемого случая (биномиальное распределение с л-20, р=0,4) квази-симметричный интервал уровня не менее 95% на самом деле является интервалом уровня 96,2%.
4.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
Оценка d=t(xA, x2,...,xrtJ параметра в есть реализация соответствующей случайной величины [см. определение 2.2.1] T~t(X}, Хг..А^А
поведение которой может быть описано в терминах ее распределения, т. е. в терминах выборочного распределения оценки. Это распределение, разумеется, будет зависеть от неизвестного значения 0.
Можно применить к этому распределению концепцию, развитую в разделе 4.1, и получить обобщенное описание поведения § на языке вероятностных интервалов, которые в свою очередь будут зависеть от 0, Даже принимая во внимание, что значение 0 неизвестно, эти сведения не бесполезны. Обычно все же требуется более прямая информация о точности оценки. Один из способов дать такую информацию состоит в придании точной формы (формализации) интуитивному подходу, продемонстрированному в примере 4.1.1, и в построении, если это возможно, интервала, который с заданной вероятностью содержит в. Поскольку понятие вероятности применимо только к случайным величинам и (исключая байесовскую точку зрения) О не является случайной величиной, видно, что это может быть достигнуто только в том случае, если концы интервала сами окажутся случайными величинами. Такие интервалы называются доверительными, а их конечные точки — доверительными пределами. Прежде чем перейти к формальным определениям, приведем простой пример (он может показаться несколько искусственным, так как основан на нормальном
* Авторы имеют в виду целочисленную случайную величину R. — Примеч. ред.
147
распределении, где общий вид распределения известен и единственным неизвестным параметром является математическое ожидание; однако его искусственность оправдана простотой и частой встречаемостью соответствующего выборочного распределения).
Пример. 4.2.1. Доверительные интервалы для математического ожидания нормального распределения при известном значении дисперсии. Пусть Хь хг,...хп — реализация случайной величины X, распределенной нормально с параметрами (в, 1)._Тогда статистика x-^Xj/n есть реализация случайной величины X, также распределенной по нормальному закону с параметрами (0, 1/у/п). Соответствующая стандартизованная случайная величина U~4n(X—0) распределена нормально с параметрами (0, 1). Так же, как в примере 4.1.2, можно построить симметричный вероятностный интервал для U уровня 0,95 (или любого другого); это будет интервал (—1,96, 1,96). Таким образом,
0,95 =Р(—1,961,96)=Р(—1,96$:<п(Х— 0)^1,96)= _
=Р(0—1,96/V^X ^0+1,96/Тй). (4-2Л)
Соотношение _
0— 1,96/Vw^% ^0+1,96А/й (4.2.2)
равносильно двум соотношениям:
Х>0- 1,96/Vn
И __ _ '
X ^0+1,96/Vn, выполняющимися одновременно, или соотношениями 0<Х + 1,96/Vw и __ _ '
0^Х— 1,96/х/й, или соотношению
X— 1,96/\Гп^9^Х + 1,96/V«. (4.2.3)
Равенство (4.2.1) поэтому может быть записано в «обращенном» виде: __ _ __
O,95=P(X—l,96/<h^0^X +1,96/VzM,
ему можно придать такой смысл: с вероятностью 0,95 случайный
интервал
(X — 1,96/Тй, X +1,96/7й)
(4.2.4)
«накрывает» (неизвестное) истинное значение 0. (Под случайным интервалом понимается интервал, границы которого — случайные величины.) Взяв х, наблюдаемое выборочное значение, за реализацию X, можно утверждать, что интервал
(х—1,96/Vw, x+l,96/Vn), (4.2.5)
границы которого (при фиксированном л) — известные числа, представляет собой реализацию случайного интервала (4.2.6) [ср. с примером 4.1.2]. Эта реализация называется доверительным интервалом для 0 с коэффициентом доверия 0,95, или, короче, 95%-ным доверительным интервалом для 0. Повторения выборочной процедуры будут
148
Рис. 4.2.1. Примеры доверительных интервалов для параметра 9 нормального (в, 1) распределения, построенных по выборке из 25 значений
давать новые значения элементам выборки Xi, х2,...,хп и, очевидно, другие реализации случайного интервала (4.2.6). При большом числе повторений этой процедуры в 95% случаев значение 0 будет попадать внутрь доверительного интервала. Иными словами, 95% всех реализаций доверительного интервала будут содержать неизвестную нам точку 0. В этом смысле можно «быть уверенным на 95%», что 0 будет внутри доверительного интервала, построенного по какой-то одной выборке объема л. Ситуация проиллюстрирована на рис. 4.2.1.
Доверительные интервалы для ц, когда X есть N(g, а) (при известном а). Стандартные обозначения для математического ожидания нормального распределения и его стандартного отклонения есть g и а соответственно. Если X распределена по нормальному закону с параметрами (g, а), симметричный 95%-ный доверительный интервал для g имеет вид
(х— 1,9 6 ст/Ул, x+l,96a/V,z). (4.2.6)
Теперь дадим формальное определение доверительного интервала и (в следующем разделе) формализацию процедуры, использованной в примере 4.2.1 для его построения.
Определение 4.2.1. Доверительный интервал, доверительные пределы. Доверительным интервалом параметра 0 распределения случайной величины X с уровнем доверия 100р%, порожденным выборкой (х}, х2.х^, называется интервал с границами w/x,, Хг,...^^ и w2(xt,
х2,...,х^), которые являются реализациями случайных величин W\ = = Х2,...,Х„) и W2 = w2(Xx, X2,...,X^, таких, что
PfW^^W^p.
Граничные точки доверительного интервала и и’2 называются доверительными пределами (здесь Хг — статистические копии X [см. определение 2.2.1]).
Так же, как в случае вероятностных интервалов [см. раздел 4.1.1], интерпретация доверительного интервала, основанная на интуиции, будет следующей: если р велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение 0.
149
4.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА С ПОМОЩЬЮ ОПОРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
В примере 4.2. i построение доверительного интервала (4,2.4) было основано на использовании уравнения (4.2.1), которое выражает свойства распределения величины \п(Х —6) (т. е. выборочного распределения величины ^ln(x- B)). Так как распределение VwA"—0) свободно от влияния параметра (а именно, это стандартное нормальное распределение), можно построить 95%-ный интервал вероятности (—1,96, 1,96), как это сделано в (4.2.1).-Поскольку случайная величина V зависит как от случайной величины X, реализацию х которой мы наблюдали, так и от неизвестного параметра 0, неравенства (4.2.2) можно было переписать в обращенной форме (4.2.3), где неизвестный параметр 0 заключен в интервал, границы которого определяются с помощью значения наблюдаемой случайной величины X ±1,96/Vw. Столь важная здесь величина уГп(х—0) — пример опорной случайной величины (pivot), которую мы сейчас и определим.
Определение 4.3.1. Опорная случайная величина. Пусть ль х2,...,лп — наблюдаемые значения случайной величины X, распределение когм-рой зависит от неизвестного параметра 0, и ti -h(x^ --- неко-
торая статистика. Случайная величина q(h, 0) называется опорной случайной величиной, если ее выборочное распределение не зависит от параметра 0.
Если в распоряжении имеется такая опорная переменная, то можно пользоваться следующей процедурой: опорная случайная величина q(h, 0) есть реализация случайной величины Q=q(H, 0), где H=h(X{, Х2,...,Хп). Здесь Xj, как всегда, — статистические копии X [см. определение 2.2.1]. Обозначим (не содержащую параметра) функцию распределения Q как G(q)=P(Q^.q) и построим симметричный 100р%-ный (например, 95%-ный) вероятностный интервал (а, Ь) для Q, т. е. интервал (а, Ъ) такой, что
G(a)^\—G(b)^{\~p)/2 (4.3.1)
(так же, как в (4.1.1)). Тогда мы имеем
=Р или
P{a^q(H, 0)^b\=p (4.3.2)
[ср. с (4.2.1)]. Затем решим относительно 0 неравенства q(H, 0)>а ? q(H, в)ЦЬ j
[ср. с (4.2.3)]. В результате йолучим соотношения 0^г(а, Н) (=Wi) ? 0>wl(b, Н)(=И\) j
[ср. с (4.2.4)]. Их можно переписать в виде
W^0^W2,
(4.3.3)
(4.3.4)
150
доверительным ин-
основе нашего по-
параметра показа-
причем последнее соотношение выполнено с вероятностью р [ср. с определением 4.2.1]. Таким образом, 100р%-ным тервалом для в будет
где h=h(Xi,x2...х„) — статистика, лежащая в
строения.
Пример 4.3.1. Доверительный интервал для тельного распределения. Пусть X — случайная величина, распределенная по экспоненциальному закону [см. II, раздел 10.2.3] с математическим ожиданием В, так что плотность распределения X в точке х есть 0~1ехр(—х/В), х>0. Из выборки (х}, х2,...,Хп) определяется (достаточная [см. раздел 3.4.1)] статистика h(X\, х2,...,х„)= Она является реализацией случайной величины Н- где % г статистические копии X. Н имеет гамма-распределение [см. II, раздел 11.3], плотность которого задается в виде В~nhn~h/e/(n—1)1, 6>0. Отсюда видно [см. II, раздел 10.7], что величина Q=H/B имеет плотность распределения qn~le~^/n\, q>0. Эта плотность не содержит параметра, и, следовательно, случайная величина q= ЁхДв является опорной для В. Можно построить симметричный 95%-ный вероятностный интервал для Q с помощью таблицы распределения х2 [см. приложение 6], так как 2Q имеет распределение х2 с 2л степенями свободы [см. раздел 2.5.4, а), п. 2].
Например, если п=10, то соответствующее распределение х2 имеет 20 степеней свободы, и согласно приложению 6 симметричный 95%-ный вероятностный интервал для 2Q есть интервал (9,591, 34,170). Соответствующий интервал для Q(=H/B) есть (4,795, 17,085), откуда
Р{ 4,795 ^Н/В^ 17,085} =0,95, или, что эквивалентно,
Р{4,7950^77^ 17,0850} =0,95 (4.3.5)
(ср. с (4.3.2), где л = 4,795, q(H, В)=Н/В, 6=17,085, р=0,95]. Обратив неравенства
Н/В>4,795, Н/В^ 17,085
[ср. с (4.3.3)], получим
В ^77/4,795 =0,208577( = 1Г2В(4.3.4)),
0 >77/17,085 =О,О585Я(= 1^6(4.3.4)), или
0,058577 ^0^ 0,208577, (4.3.6)
что выполнено с вероятностью 0,95. Таким образом, 95%-ный доверительный интервал для В — этот интервал (0,05856, 0,20856), где 6= Ё,хг—пх— 10х, в нашем случае х обозначает наблюденное выбо-1
рочное значение. Итак, доверительный интервал для неизвестного значения 0 (математического ожидания) есть (0,585х, 2,085х). При х, равном, скажем, 2,1, доверительным интервалом для 0 (с коэффициентом доверия 95%) будет (1,23, 4,38).
151
4.4. ИСТОЛКОВАНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА КАК МЕРЫ ТОЧНОСТИ ОЦЕНКИ НЕИЗВЕСТНОГО ПАРАМЕТРА
Надо отметить, что доверительный интервал для параметра распределения, найденный исходя из данной выборки, определяется выбором «рабочей статистики» h(xXi х2,...,х^. Если эта статистика является достаточной (как в примере 4.3.1), то, несомненно, вся информация, содержащаяся в выборке, будет извлечена. Но как выйти из положения, если простой достаточной статистики не существует? На интуитивном уровне очевидно, что необходимо использовать наилучшую из доступных статистик, например эффективную [см. определение 3.3.3] статистику, такую, как оценка наибольшего правдоподобия [см. разделы 3.5.4, 6.2.2]. Это, однако, приводит к некоторой неопределенности, и она возрастает, если по соображениям удобства берут другую подходящую статистику.
В обычной статистической практике выбор рабочей статистики определяется на самом деле соображениями удобства, традициями, доступностью соответствующих таблиц и т. д. Р. Фишер, вероятно, меньше доверял бы выводам, полученным таким путем, чем выводам, основанным на точных вероятностных соотношениях с использованием достаточной статистики. Однако практикующие статистики не склонны к большим беспокойствам по подобным поводам. Существует мнение, что коэффициент доверия данного интервала для параметра в следует рассматривать как число, которое получилось бы при многократном повторении процедуры выборки и вычисления по ней доверительного интервала с использованием данной рабочей статистики.
Для интерпретации доверительного интервала более важными являются такие факторы, как объем выборки и значение коэффициента доверия. В примере 4.2.1, где рассматривались доверительные интервалы для математического ожидания нормального распределения, было установлено, что симметричный 95%-ный доверительный интервал есть интервал (х—1,96/Тл, х + 1,96/Тл), длина которого 3,92/Тл. Для уровня доверия 0,99 соответствующий интервал — (х — 2,58/Ул, х -4-2,58/Vz?), его длина равна 5,16/Ул. Это подтверждает известный факт: за повышение значения уровня доверия приходится расплачиваться увеличением длины доверительного интервала. С другой стороны, точнее оценку можно получить по выборке большего объема. Длина доверительного интервала с фиксированным уровнем доверия будет убывать с увеличением объема выборки. В данном случае длина доверительного интервала пропорциональна л~|/2.
Рассмотренный пример не типичен: не всегда длина доверительного интервала зависит только от объема выборки и коэффициента доверия. Вообще говоря, она зависит также от используемой статистики. Так, в примере 4.3.1 100р%-ный доверительный интервал для математического ожидания в экспоненциального распределения, определенный по выборке объема п и выборочному среднему х в качестве 152
рабочей статистики, был получен с использованием по ходу дела вероятностного интервала
кр(\, п)х ^2пх/0^кр(2, п)х,
где доверительные пределы кр(1, п), кр(2, п) определяются при помощи распределения х2 с 2п степенями свободы из условия
P\x2dn)iкра, п)} = -тв-р)=Р1х2ап»кр(2, »)}.
(Уравнение (4.3.6) выражает этот результат для случая, когда л = 10, р=О,95.) Таким образом, доверительные пределы для в есть 2пх/ кр(2, п), 2пх/кр(\,п), а ожидаемая длина доверительного интервала — 2п0{\/кр(2, п)—\/кр(\,п)}. Значения коэффициента при р=О,95, р=0,99 (/1 = 5, 10, 15, 20) приведены в следующей таблице:
Объем выборки 'Уровень доверия
0,95 0,99
5 2,590 4,240
10 1,500 2,390
15 1,150 1,620
20 0,960 1,330
(Предшествующее обсуждение основано на сложившейся практике. Следует, однако, признать, что хотя практика и заставляет нас совершенствоваться, она сама не всегда совершенна и не всегда вполне оправданна. Измерять степень соответствия оценки 0* параметру 0 длиной доверительного интервала имеет смысл, когда 0 — параметр расположения и, следовательно, плотность распределения выборочной случайной величины имеет вид f(x—0). Замена значения параметра 0] на 0г сдвигает график плотности на расстояние 01 — 02. Если же 0 не является параметром положения, может оказаться разумным использовать иные способы оценки точности. Например, если 0 — параметр масштаба и плотность распределения имеет вид f(x/0), замена значения 0] на 02 эквивалентна умножению аргумента на 0{/02. Это подсказывает, что в качестве меры точности вывода о параметре 0, представленной доверительным интервалом (02, 0<), правильнее использовать отношение 0]/02, а не длину этого доверительного интервала.)
4.5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ПРИ НЕСКОЛЬКИХ ПАРАМЕТРАХ
Из числа вопросов, возникающих при переходе к доверительным интервалам для нескольких параметров, выделим следующие:
1) можно ли получить индивидуальные (отдельные) доверительные интервалы для каждого из параметров?
153
. 2) можно ли получить доверительные интервалы для различных комбинаций параметров, таких, как их сумма, разность, отношение и т. д.?
3) можно ли получить (многомерные) доверительные области для нескольких параметров сразу?
Эти и близкие им проблемы излагаются в гл. 8 в аспекте дисперсионного анализа. Вопросы 1) и 2) мы коротко обсудим в этом разделе. Более глубокое рассмотрение, затрагивающее также вопрос 3), содержится в разделе 4.9.
4.5.1. ИНДИВИДУАЛЬНЫЕ ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
Прежде всего мы приведем примеры индивидуальных доверйтель-ных интервалов для каждого из одномерных параметров, взяв дисперсию о2 и математическое ожидание семейства Г4(д, а) [см. пример 4.5.1], а также каждый из трех параметров, рассматриваемых в теории линейной регрессии [см. пример 4.5.3].
Пример 4.5.1. Доверительные интервалы для дисперсии (или для стандартного отклонения! Ы(д, а) распределения. Пусть (%i, Xi,...^^ — выборка из нормального (д, а) распределения. Тогда при х = Ехг/л статистика s2= Ё(хг—х}2/(п—\), несмещенная оценка а2, есть реализация случайной величины S^= Ё(ХГ—Х)2/(п—1>, где Хг — независимые Г4(д, а) случайные величины, а / - Ы(д, a/Vn). Тогда величина (л—IJSVo2 распределена по закону —1), т. е. по закону х2 с (л—1) степенями свободы [см. раздел 2.5.4, II, раздел 11.4.11].
Для нее мы можем построить симметричный 100/>%-ный вероятностный интервал (а, Ь), где а и Ь определяются так, чтобы
Лх2(л-1)^а)=Лх2(л-1)>*)=|-(1-р). (4.5.1)
Значения а и b могут быть найдены по таблицам распределения х2 [см. приложение 6]. Тогда с вероятностью р
а^(п— 1)&/о2^Ь,
или, что равносильно,
(л—DSV^a2 < (л—l)SV<z.
Это в свою очередь равносильно
{(л— 1 )S2/b ]1/2 С о < {(л—1 )S2/a}|/2.
ТЬким образом, 100р%-ные доверительные интервалы для а2 следующие: ((n—Y)s2/b, (n—Ytf/a), (4.5.2)
3 °' ({(л—1)№/г>}12, {(л—1)$2/л)|/2).
В этом примере наличие второго неизвестного параметра д ничуть не изменило нашего вывода [ср. с примером 5.8.6]. Данные, представленные в табл. 4.5.1, связаны с эффективностью двух разных видов снотворного [см. Fisher (1970)—С]. Пациенты принимали каждый из этих препаратов через промежутки времени достаточно большие, чтобы можно было считать его действие независимым.
154
Таблица 4.5.1. Перепечатано с разрешения Macmillan Publishing Company из книги Statistical Methods foi Research Workers, 14th edition, by Sir Ronald A. Fischer, copyright ^1970 University of Adelaide
Пациент Дополнительные часы сна Разность у Пациент Дополнительные часы сна Разность у
препарат А препарат В препарат А препарат В
1 0,7 1,9 1,2 6 3,4 4,4 1,0
'У Л. -1,6 0,8 7 4 7 3,7 5,5 1,8
3 —0,2 1,1 1,3 8 0,8 1,6 0,8
4 — 1,2 0,1 1,3 9 0,0 4,6 4,6
5 —0,1 -0,1 0,0 10 2,0 3,4 1,4
Числа в последнем столбце могут рассматриваться как независимые наблюдения (уг) над мерой сравнительной эффективности препаратов, за которую здесь взята разность их действия. Мы предполагаем, что уг — распределены нормально с параметрами (/4, а), и берем в качестве оценки для ст2 статистику
s2-=L(yr—y)2/(n~-l)
с л=10,7 = Еу/10=1,58,
9s2 = Uy ~У)2 = Ъугт—^у2 = 38,58—24,96 = 13,62.
Итак, оценки для а2 и ст есть s2 = 1,513 и 5=1,230 соответственно. Симметричный 95%-ный вероятностный интервал для х2 с 9 степенями свободы — (2,700, 19,023), следовательно, 95%-ный доверительный интервал для ст2—(13,62/19,023, 13,62/2,700), т. с. (0,716, 5,044). Соответствующий интервал для ст—(0,846, 2,246).
Пример 4.5.2. Доверительный интервал для математического ожидания нормального распределения.
а) Значение дисперсии известно. Этот случай рассмотрен в примере 4.2.1 для выборки (xt_,,х2,...,хп): 95%-ный доверительный интервал для р. есть x±l,96o/Vn, где х — среднее выборки.
б) Значение дисперсии неизвестно. Вот метод оценки «на скорую руку» с использованием стандартной ошибки: заменяем неизвестное значение ст в п. а) его оценкой s. В более общем случае предположим, то 0* — несмещенная оценка параметра 6 и выборочное распределение 0* приближенно нормальное; тогда, грубо говоря, 95%-ный доверительный интервал для 0 есть
0*±2s. е.(0*),
где s. е.(0*) означает стандартную ошибку 0* (т. е. подходящую оценку выборочного стандартного отклонения 0*). Это имеет некоторое отношение к методу наибольшего правдоподобия.
155
в) Значение дисперсии неизвестно. Вычисление точных доверительных интервалов с помощью распределения Стьюдента. Здесь возникает новое осложнение: мы ищем доверительный интервал для одного параметра (/а), когда значение другого неизвестно. Эта задача была блестяще решена на основе идеи Стьюдента, которая состоит в исключении а с помощью процесса, известного теперь как «стьюденти-зация». Если (xit Хг,...^^ — выборка из N(/a, а) и
х -Lxj/n, s2-lL(x— х)2/(п— 1),
то величина (х—д)А инвариантна относительно изменения значений а: если о заменить на o', то тем не менее
(х~—-g) _ (х~—ц)/а _ (х~—цУ/а
s s/a s/d
Удобнее использовать величину
'„„>=(*—/ОЛ^Л/й),
которую называют величиной Стьюдента с (л—1) степенями свободы. Она имеет не зависящее от параметра о выборочное распределение [см. раздел 2.5.5] и, следовательно, является опорной для g.
Это распределение симметрично, и если а — значение, которое tnне превосходит с вероятностью ~т(\—р), то 100р%-ный доверительный интервал для ц. есть
(х— as/'fn, х +as/\fn).
Значения а, соответствующие рассматриваемым р, могут быть найдены из таблиц [см. приложение 5, ср. с примером 5.8.2]. Если, например, л = 10, то число степеней свободы 9, и, взяв р=О,95, мы получим для а значение 2,262. Если взять те же исходные данные, что в примере 4.5.1, то мы будем иметь у = 1,58, $2=1,513, л = 10 и $/7л = 0,389. Таким образом, 95%-ный доверительный интервал для ц будет
1,58 ±2,262-0,389 или
1,58±0,88 = (0,70, 2,46). (4.5.3)
Это показывает, что разница в действии лекарств существует: добавочное время сна после приема препарата В превышает время после приема препарата А в среднем на 1,58 ч (или, более точно, на 1,58 ±0,88 (с 95%-ной точностью)). Численные значения, использованные здесь, показаны на графике распределения Стьюдента на рис. 4.5.1.
Интуитивный подход, продемонстрированный в примере 4.1.1, находит применение и здесь: нужно только заменить плотность нор-156
Рис. 4.5.1. Плотность распределения
Стьюдента с 9 степенями свободы
Рис. 4.5.2. ti — неправдоподобно большое отрицательное значение величины t = (х — n)/s/y[n) (ц — слишком сильно превосходит х). Аналогично t3 соответствует слишком малому значению д, t2 соответствует правдоподобному значению д
мального распределения из примера 4.1.1 на плотность распределения Стьюдента.
На рисунке 4.5.2 изображен график плотности распределения Стьюдента с 9 степенями свободы, при разных значениях, / = (х — — д)/($/7ТО) = (1,58 — д)/0,389, т. е. д = 1,58 — 0,389/. Значение t\ для t (и, следовательно, соответствующее значение д, а именно gi = 5,40 — 0,601) слишком маловероятно, чтобы можно было его принять. То же относится и к /3. Значение /2 лежит в зоне больших значений плотности, так что д2 = 1,58 — 0,389/2 совместимо с исходными данными. Условная граница между «приемлемыми» и «неприемлемыми» значениями (с 95%-ной точностью) определяется точками t, и tu на рис. 4.5.1, где /; — квантиль уровня 0,025 и tu — квантиль уровня 0,975 распределения Стьюдента с 9 степенями свободы. Эти значения следующие: tt = —2,262, tu = 2,262, а доверительный интервал — (д/, дм), где д/ = 1,58 + 0,389/, = 0,70 и ци - 1,58 + 0,389/м = = 2,46.
Пример 4.5.3. Простая линейная регрессия. Если пара случайных величин (%, У) имеет совместное распределение [см. II, раздел 13.1.1], то условное математическое ожидание E(Y\X - х) = g(x) [см. II, раздел 8.9] называется регрессией Y на X. Если g(x) линейна по х, скажем, g(x) = а1 + /З’х, то мы имеем простую линейную регрессию. Если наблюдаемое значение У,- соответствующее заранее заданному значению X = хг, есть уг, г = 1,2,..., п, то удобно переписать формулу для g(x) в виде
g(x) = а + fi(x — х),
157
п
где х = Lxr/n. Если условное распределение Y при фиксированном X = х — N(g(x), о) при любом х, то оценки наибольшего правдоподобия для а и 3 [см. пример 6.4.4] будут следующими:
a =J( = iyr/n),
0 = £yr (xr — X) /Е (xr — x)2,
а соответствующая несмещенная оценка для а2 равна:
s2 = Ej;2— naz — $2Е (xr — x)2. (4.5.4)
Легко видеть, что величины
tx = (d — а)/$1, где sf = s2 /n, и
t2 •= (3 -- $)/s2, где S2 = ^/£(хг — x)2,
будут иметь распределение Стьюдента [см. раздел 2.5.5] с п — 2 степенями свободы, в то время как величина (п — 2)s2/a2 имеет распределение х2 с п — 2 степенями свободы. Таким образом, 95%-ные доверительные интервалы для а, (3 и а2 будут следующими:
(d — f-S;, d + P$l),
(,? - t°s2, -- /%)
[ср. с примером 4.2.2] и
((л — 2)52/с2, (л — 2)s2/cx)
[ср. с примером 4.4.1], где /° — верхняя 2.5%-ная точка распределения Стьюдента с (п — 2) степенями свободы, а с, и сг — нижняя и верхняя 2,5%-ные точки случайной величины, распределенной по закону у2 с п — 2 степенями свободы [см. также пример 4.5.4 и раздел 5.8.5]. Численный пример и белее подробное обсуждение линейной регрессии содержатся в разделе 6.5.
4,5.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ФУНКЦИЙ ДВУХ ПАРАМЕТРОВ, ВКЛЮЧАЮЩИХ ОТНОШЕНИЕ ПАРАМЕТРОВ И ИХ РАЗНОСТЬ (ТЕОРЕМА ФЕЛЛЕРА)
В этом разделе будут рассмотрены наиболее известные и часто встречающиеся на практике доверительные интервалы для функций двух параметров. Такими примерами (для нормальных моделей) буду” следующие:
1) разность двух математических ожиданий [пример 4.5.4];
158
2) ордината а + 0хь линейной perpecv m при фиксированном значении х0 независимой переменной х [пример 4.5.5];
3) разность наклонов двух регрессионных прямых (пример 4.5.6];
4) отношение двух параметров, оцениваемых линейными функциями наблюдений (теорема Феллера) [пример 4.5.8].
Пример 4.5.4. Доверительные пределы для разности математических ожиданий двух нормальных величин с общей дисперсией. Пусть (xi, Хг...xj — выборка из NQib а) распределения и (у>, у2,
.... _?„) — выборка из N(/42, ст) распределения. Удобные оценки для и Ц2 — средние выборки х и у соответственно. Определяя s* и s2 по обычным формулам
“ Е (хг - х)‘/(п, - 1), s* = Е (у, - у)*/(пг - г;, (4.5.5) мы получим объединенную оценку s2 общего значения дисперсии в виде
(л. + л2 — 2)$2 = (л. — l)sf + (л2 — l)s*. (4.5.6)
Подходящей оценкой для выборочной дисперсии х будет s2/fli, а si/n1 — для у, так что оценка дисперсии х — у будет (s2/Hi + s2/n2). Таким образом,
t = 1(Х - У) - (ж - д2)] / [5 VQ; + ]
есть реализация случайной величины, распределенной по закону Стьюдента с Hi + п2 — 2 степенями свободы [см. пример 2.5.3]. Следовательно, как и в примере 4.5.2, интервал (а, Ь) есть центральный 95%-ный доверительный интервал для — д2 при
а = х — у — t^s
+
(4.5.7)
b = х- у 4 tosV (~ + ,
где /о — квантиль распределения Стьюдента с л, 4- л2 — 2 степенями свободы уровня 0,975 [ср. с примером 5.8.4]. С помощью данных, приведенных в табл. 4.5.1, мы покажем эту процедуру, рассматривая с иллюстративными целями столбцы, соответствующие препарату А и препарату В так, как будто они получены в эксперименте с разными и независимыми группами пациентов. Будем считать числа, соответствующие препарату А, значениями хг, а соответствующие препарату В — значениями уг. Применяя предыдущие формулы, получаем
х = 0,75, у - 2,33,
159
где «1 = л2 =Ю, и находим s2 из соотношений
18$2 = Е(хг — х)2 + Z(yr —у)2 = (Ех? — 10х2) + (Ej? — 10j>2) = = (34,43 — 5,62) + (90,37 — 54,29) = 64,88,
так что
s2 = 3,60 и 5 = 1,899.
Тогда
U+ £) =°’849-
Значения, соответствующие квантилям уровня 2,5% и 97,5% величины Стьюдента с 18 степенями свободы есть —2,101 и +2,101 [см. приложение 5], откуда 95%-ный доверительный интервал для /л — цг будет следующим:
—1,58 ± (2,101) • (0,849) = —1,58 ± 1,78 = (—3,36, 0,20).
Заметим, что 0 покрывается этим интервалом. Это значит, что данные не противоречат гипотезе, что /л = ц2. (Этот пример рассмотрен исключительно в иллюстративных целях. Предполагается, что хг и уг — наблюдаемые значения независимых случайных величин Хи Y, в то время как в действительности данные, показывающие эффективность различных препаратов, не могут считаться независимыми. Напротив, следует ожидать, что эти величины будут иметь положительную корреляцию и значение дисперсии var (X — У) (= var (X) — 2cov(JV, У) + + var(У) с cov (X, У) > 0) будет в действительности меньше оценки, полученной в предположении независимости величин X и У. Поэтому понятно, что истинный доверительный интервал (4.5.3), а именно 1,58 ± 0,88, короче, чем полученный в предположении независимости интервал 1,58 ± 1,78.)
Пример 4.5.5. Доверительные пределы для регрессии при данном значении х. В примере 4.5.3 регрессия
у = а + 3 (х — х)
оценена в точке х = х0 как
а + в(х0 — х).
Это — реализация нормально распределенной случайной величины с математическим ожиданием
а + 3 (х0 — х)
и дисперсией
160
1 (х0 — х)2
~п + Е(хг —х)2
где значение ст2 оценено через s2, как в (4.5.4). Необходимый нам 95%-ный доверительный интервал для а + 0(хо — х) будет тогда [см. пример 4.5.2]
а + 0(хо — х) ± /97)5 Vv , где
С 1 (Хо-Х)2 ]
V2 = S2 I — + ------— ( —
С п Е(хг —х)2 >
оценка дисперсии а + 0(хо— х) и t97 s — 97,5%-ный квантиль распределения Стьюдента с п — 2 степенями свободы.
Пример 4.5.6. Доверительные пределы для разности наклонов двух регрессионных прямых. Пусть у нас есть две выборки, таких, как в примере 4.5.3: одна из наблюдаемых значений уг и соответствующих значений хг независимой переменной, г = 1, 2, .... п, а другая из наблюдаемых значений у'г и значений независимой переменной х'г, г = 1, 2, ..., п'. Исходя из этого мы оцениваем линейные регрессии
а, + 0i(x — х), а2 + 02 (х' — х), принимая за оценки параметров величины
di = <7i, 01 = bi, а 2 = </2, 02 = bz.
Математическое ожидание Ь\ — bz есть 01 — 02, его дисперсия есть а2 / Е1 + а г / Е 2, где а2 и а2 — теоретические дисперсии случайных наблюдений, Ei = Е(хг— х)2, Ег = Е(х'г — х)2. Оценкой дисперсии bi — bz служит
v = $*/Е 1 + $*/Ег,
где s] соответствует s2 в (4.5.4), s22 определяется аналогично для х'г, у'г. Оценка v имеет п + п' — 2 степеней свободы.
Теперь, как в примере 4.5.2, 95%-ный доверительный интервал для 01 — 02 есть
bx — b2 ± Г97>5<v,
где t915 — 97,5%-ный квантиль распределения Стьюдента с п + п' — — 2 степенями свободы.
Пример 4.5.7. Доверительные пределы для отношения дисперсий двух нормальных величин. Метод, с помощью которого в примере 161
4.5.1 были получены доверительные пределы для дисперсии а2 нормального распределения, допускает обобщение на отношение о\/ о\ дисперсий двух нормальных случайных величин. Используя обозначения из примера 4.5.3, заметим, что
(Л! — (п2 — l)sz2/ff22— (4.5.8)
независимые реализации х2 с /и — 1 и пг — 1 степенями свободы. Отсюда видно, что отношение
есть реализация F-распределения [см. раздел 2.5.6] с (т — 1), (т — — 1) степенями свободы, т. е. F V1 с vi = пх — 1, v2 = п2 — 1. Обозначим через а и b 0,025- и 0,975-квантили (т. е. а — 2,5%-ная точка, Ъ — 97,5%-ная точка) [см. И, раздел 10.3.3] этого распределения. (Их можно найти, используя стандартные таблицы [см. пример, приведенный ниже]. Такая таблица представлена в приложении 7.) Теперь мы получим 95%-ный доверительный интервал для из неравенств (<\/(*\\
а \ ° 1 / * \ аг / (с вероятностью 0,95),
откуда
as22/s] о2/о] bs22/s].
Таким образом, доверительный интервал для о2/о] есть
(as2/s], bs\/s\), (4.5.9)
или же доверительный интервал для о\/а2 есть
(а1/252/5!, д1/252/5>), (4.5.10)
а для —
{s\/bs\, s\/as\}. (4.5.11)
Если нужный уровень доверия был бы равен, скажем, 0,99, то а и b нужно было бы искать как 0,005- и 0,995-квантили F-распределения.
Чтобы проиллюстрировать сказанное, возьмем П\ = 20, п2 = 30, и пусть = 1. 95%-ный доверительный интервал для а\/ получим, взяв а и b как квантили уровней 0,025 и 0,975 распределения Fj9 29. В опубликованных таблицах b называется верхней 2,5%-ной точкой. В нашем случае ее значение b = 2,40. Нижняя 2,5%-ная точка а в таблицах явно не содержится, так как ее значение совпадает с величиной, обратной к верхней 2,5%-ной точке распределения F2919
162
(обратите внимание на то, что числа степеней свободы здесь мы поменяли местами; то же самое будет иметь место и для 0,5%-ных точек [см. раздел 2.5.6]). В нашем случае 1/а = 2,23, а = 0,448. Таким образом, искомым доверительным интервалом для о\/а\ будет (0,448, 2,40).
То же можно проделать и для примера 4.5.4. Здесь п} = п2 = 10, = 28,81, 9s22 = 36,08, 1/а = Ь = 4,03, откуда 95%-ный доверительный интервал для а2 / а\ есть (0,311, 5,04), а для (сп / ст2) — (0,558, 2,24). Отметим, что этот интервал содержит единицу, и, следовательно, данные согласуются с гипотезой равных дисперсий.
Пример 4.5.8. Доверительные интервалы для отношений параметров, оцениваемых через линейные функции данных (теорема Феллера). В этой задаче мы имеем дело с отношением X = а/0, где а и (3 — параметры, относящиеся к двум нормальным распределениям с одинаковой дисперсией, из которых имеются выборки. Например, а и 0 могут быть математическими ожиданиями этих распределений, или коэффициентами наклона регрессионных прямых; или же, для регрессии у = «1 + X может быть значением х, при котором регрессия принимает значение у0; тогда х = (у0 — ai)/0i — отношение рассматриваемого здесь вида и т. д. Мы предполагаем, что а и Ь — несмещенные оценки а и (3, являющиеся линейными функциями наблюдений; выборочные оценки их дисперсий и ковариаций пусть Vn, v22 и V12 с f степенями свободы.
Рассмотрим величину ХЬ — а. Она распределена нормально с нулевым математическим ожиданием и дисперсией, имеющей оценку
v = X2v22 — 2Xvn + V]) (4.5.12)
с / степенями свободы. Величина
(ХЬ — a)/y[v (4.5.13)
имеет распределение Стьюдента с f степенями свободы, откуда с вероятностью 0,95
(ХЬ — а)2 С
где t95 — 95%-ная точка распределения Стьюдента с f степенями свободы.
Корни Xi, Х2 уравнения
(Xb — aY = t}5v (4.5.14)
являются границами доверительного интервала с коэффициентом доверия 95% для X = а/&. Квадратное уравнение относительно X можно переписать в виде
163
\2(bi — tiVn) — 2\(ab — r2v12) + (a2 — r2vn) = 0, (4.5.15), где t = t95. Это и есть результат Феллера.
Если, как это часто бывает в приложениях, v12 = 0, корни полученного уравнения могут быть выписаны в следующем виде, показывающем отклонение Xi и Х2 от «естественной» оценки а/b для а//3:
Х> _ а Г 1 ± V{(1 -^V22/^)(l _^Vu/a2)] х2 т L 1 — r2v22/&2
В последующем численном примере мы также приведем приблизительные доверительные пределы, полученные из приближенных формул примера 2.7.7, а именно для выборочной дисперсии а/Ь
(d2vH + <z2v22)/d4,
так что
Xi а Г Л/ (vn v22\ х2 s b L1 ± z ’ \ a2 + b2 / J •
(4.5.16)
Если, как, например, в разделе 6.6.6, рассматриваемое отношение есть X = —а/0, где а и /3 оцениваются через а и b соответственно, то нужно исследовать величину \Ь + а, анеХд — а. Математическое ожидание (—а/0)0 + а равно нулю, как и требуется. Величина v из (4.5.12) должна быть заменена на
X2v22 + 2Xvu 4- Vi,
и квадратное уравнение (4.5.15) — на уравнение
X2(d2 — t2v22) + 2X(ab — t2vi2) + (а2 — Z2vlf) = 0.
В качестве численного примера мы используем данные из примера 4.5.4. Для разности — ц2 средней эффективности двух параметров доверительные примеры уже найдены. За нее было принято добавочное время сна. Теперь же вместо разности рассмотрим отношение fii/fi2. Используя (4.5.15), получим
а = Д1 - У\ =0,75, b = Д2 = у2 = 2,33, а/b = 0,322,
Vn = v22 = 52/9 =3,605/9 = 0,401 и
Vj2 = 0.
Тогда
v = 0,401 (X2 + 1).
Значение /9$ равно 2,101. Квадратное уравнение (4.5.4) принимает вид
(2,33 X — 0,75)2 = (2,101)2 (0,401)(Х2 + 1).
164
Его корни
X) = —0,270, Х2 = 1,225.
Для сравнения по приближенной формуле (4.5.16) получаем
X) = —0,28, Х2 = 0,92.
(еще один численный пример приведен в разделе 6.6.6).
4.6. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ БЕЗ ИСПОЛЬЗОВАНИЯ ОПОРНОЙ ПЕРЕМЕННОЙ
В разделе 4.3 было показано, как построить доверительный интервал в случае одного неизвестного параметра с помощью опорной переменной. Такую переменную всегда можно найти, если функция распределения наблюдений F(x, 0) непрерывна по х. Заметим, что для случайного наблюдения выборочное распределение случайной величины F(Xj, 0) является равномерным на отрезке (0, 1) [см. II, раздел 10.2.1] по теореме о преобразовании с помощью интеграла вероятностей [см. II, теорема 10.7.2]. Это распределение не зависит от параметров. Отсюда ясно, что любая функция от величин F(xit 0), ..., F(xn, 0) будет опорной переменной. Такой, в частности, будет случайная величина tj.F(xr, 0), функцию распределения которой можно найти исходя из того, что величина q = —Е logF(xr, 0) есть реализация гамма-распределения с плотностью qn~{e'<1 /Г(л). Однако решение неравенств (4.3.3) может быть трудным, поэтому для подобных ситуаций желательно иметь альтернативный метод. Такой метод здесь будет рассмотрен.
Пример 4.6.1. Доверительные пределы для параметра формы гамма-распределения. Пусть случайная величина X имеет гамма-распределение с параметром сдвига X и параметр масштаба 1, т. е. плотность этого распределения есть
х\-1е-х/Г(Х), х > 0 (0 > 0),
так что Е(Х) = X [см. II, раздел 11.3].
Пусть имеется выборка хъ х2..хп. Как уже отмечалось, довери-
тельный интервал (если он может быть найден) будет существенно зависеть от выбора «рабочей» статистики. Опыт показывает, что лучше всего п
взять достаточную статистику. В нашем случае это Пх, — величина, 1 п
с которой трудно работать. Поэтому мы используем статистику у Это несмещенная оценка лХ, реализация случайной величины Y с плотностью распределения [см. II, раздел 11.3.2]
165
g(y, 9) = /-'г-'/Г(»), У > о, (в > О),
где 9 = пХ (так что E(Y) = 0 = лХ), и с функцией распределения
Р(У у) = G(y, 0) = ^~le~^z/r(0). в
При любом значении 0 можно найти центральный 95%-ный вероятностный интервал (у^, у2) для Y, взяв у{ и у2 так, чтобы
GOb 0) = 0,025, G(y2, 0) = 0,975
[см. раздел 4.1.3]. Например, для 0 = 2,0 и п = 10 получаем
G(j„ 2,0) = Р(У у,) = Р(2У 2у>) = Р[х2(4) 2у.]>
так как 2 У имеет распределение х2 с 4 степенями свободы [см. раздел 2.5.4, а)]. Из таблиц распределения х2 [см. приложение 6] видно, что 2yi = 0,484, откуда yt = 0,242. Аналогично у2 = 5,572. Можно провести вычисления для других значений 0 и получить результаты, как в табл. 4.6.1 (в которой значения yt и у2, соответствующие данному 0, обозначены как yi(0) и у2(0)).
Таблица 4.6.1. Значения У Ав) и j2(<0> такие, что Р[у|(6) Y = 0,95, где У имеет гамма-распределение с параметром 6( = 10Х)
в у АО) ЛИ») в >,(«) УА«)
1 0,0253 3,689 9 4,116 15,713
2 0,242 5,572 10 4,796 17,085
3 0,618 7,224 11 5,491 18,390
4 1,090 8,768 12 6,200 19,682
5 1,624 10,242 13 6,922 20,962
6 2,202 11,668 14 7,654 22,230
7 2,814 13,060 15 8,396 23,490
8 3,454 14,422
166
4.6.1. Графики функций /,(0), у2(в) из табл. 4.6.1; Yo — типичное значение величины У, при котором точка (0о, Уо) лежит между кривыми. Рисунок демонстрирует равнозначность условий /,(^о) < Уо Уг(во) и в'о в0 о
Таким образом, мы сумели получить те же результаты, что и с использованием опорной статистики в (4.3.5) из примера 4.3.1, и разница состоит лишь в том, что границы доверительных интервалов найдены по таблицам, а не с помощью явных формул. Теперь наша задача решить неравенство
Л(0) < Y ^у2(0)
(которое выполнено с вероятностью 0,95), т. е. получить эквивалентное (и выполненное с той же вероятностью) неравенство вида
Д.(У) 0 С а2(У).
Обе функции ji(0) и у2(0) непрерывные, монотонно возрастающие, как показано на рис. 4.6.1. Предложение Y у2(6) иллюстрируется расположением точки (0о, Уо), где Yo j2(0o), т. е. Уо лежит не выше графика у2(0). Так как график непрерывен и монотонен, функция j2(0) обратима [см. IV, раздел 2.7], т. е. существует единственное значение 00 = yi'iYo), такое, что Уо = у2(0Ь), которое можно найти, проведя горизонтальную прямую через точку (0О, Уо) и отметив абсциссу 0О точки ее пересечения с графиком. Так как функция возрастает, 0b 0О. Получаем, что предложение Уо у2(0о) эквивалентно предложению 0о 0'о, где 0'о(= 0Ь(Уо), скажем) = ^2*(Уо)« Аналогично, глядя на нижнюю кривую У1(0), находим, что предложение Уо ji(0) логически эквивалентно предложению
0о С 0о,
167
где 0'6(= 0'6(YO), скажем) = _ут‘(Уо)- Следовательно, предложение
У1 (0о) Yo Уг(0о)
(выполненное с вероятностью 0,95) эквивалентно предложению 0'о(Ко) < 00 0о(Уо),
которое, конечно, выполнено с той же вероятностью (см. рис. 4.6.1). Это имеет место для всех точек (0, У) в интервале (У1(0), Уг(0)) при любом значении 0. Из этого следует, что если случайная величина Y приняла значение у, то 95%-ным доверительным интервалом для 0 служит (0'оСУо), 0'6(Уо))-
Нижний предел 0'о = 0'о(Уо) определяется из условия
Р{У(0Ь) > Уо] = 0,025,
где Y(0'o) — гамма-распределенная случайная величина, имеющая параметр формы 0'о. Значение 0'о выбрано так, чтобы у0 служило верхней 0,025-критической точкой.
Верхний предел 0'6 = 0б(уо) определяется из условия
Р[ К(0 6) < = 0,025,
т. е. 0О — такое значение параметра, при котором у0 служит нижней 0,025-критической точкой.
Для заданного у0, например у0 = 6, можно найти значения 0'о и 0о из таблиц или графически, как на более подробном варианте рис. 4.6.1, построенном по точкам табл. 4.6.1 [см. рис. 4.6.2]. Из графика видно, что наблюденное значение у = 6 (отвечающее значению несмещенной оценки X* = 0,6 для X) порождает 95%-ный доверительный интервал (2,3, 11,7) для 0 = 10Х и 95%-ный доверительный интервал (0,23, 1,77) для X. (Область между верхним и нижним графиком называют доверительной полосой.)
Интуитивный подход, который обсуждался перед примером 4.3.1, здесь заключается в рассмотрении нескольких характерных типичных плотностей гамма-распределения, соответствующих разным значениям 0, как показано на рис. 4.6.3. Весьма малое значение 0i величины 0 на графике (1) и большое значение 03 на графике (3) представляются неправдоподобными в том смысле, что в каждом случае наблюдаемое значение статистики yi лежит в области малых значений плотности вероятности; в то же время 02 сочетается со значением у, так как у лежит в зоне больших значений этой плотности. Границы между «правдоподобными» и «неправдоподобными» значениями 0 могут быть приняты, как и ранее, равными 0и и 0[ так, чтобы (как показано на рис. 4.6.4)
P(Y > ус, 0и) = Р(У УС, 0/) = 0,025.
168
ic. 4.6.3. Плотности гамма-распределения, соответствующие различным зна^
Рис. 4.6.4. Плотности гамма-распределения с параметрами 0, и ди
169
Для у = 6 мы находим 0, и 0И, используя тот факт, что 20, — число степеней свободы такого распределения хи-квадрат, квантиль уровня 0,025 которого равна 12, а 20и — число степеней свободы такого распределения хи-квадрат, квантиль уровня 0,975 которого равна 12. Из таблиц распределения х2 [см. приложение 6] получаем, что 20и лежит между 23 и 24, а 20, — между 4 и 5. Интерполяция дает значения 0, = 2,3, 0и = 11,7, что согласуется с результатом, полученным ранее*.
4.7. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ ДЛЯ ПАРАМЕТРОВ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ
Теперь перейдем к примерам, в которых не только отсутствует опорная переменная, но есть и еще одна дополнительная сложность — распределение дискретно. Рекомендации по поводу того, как поступать в подобных условиях, содержатся в [Blyth and Hutchinson (1960); Clopper and Pearson (1934); Crow (1956); Eudey (1949); Pearson (1950); •Stevens (1950)].
Мы ограничимся рассмотрением биномиального и пуассоновского распределений. Есть два различных подхода, связанных с аппроксимацией. В первом случае исходное дискретное распределение приближенно заменяется непрерывным, во втором приближенная доверительная область строится на основе дискретного распределения.
Простейшая (но не всегда самая точная) аппроксимация — нормальная. Она удобна еще и потому, что для нормального распределения доверительные интервалы найти легко. Этот подход обсуждается ниже применительно как к биномиальному, так и к пуассоновскому распределениям [см. примеры 4.7.1, 4.7.2].
Более сложное семейство непрерывных распределений можно построить, считая, что наблюдаемая дискретная случайная величина представляет собой значения некоторой непрерывной случайной величины, записанные с ограниченной точностью. Аппроксимирующая случайная величина z поэтому может быть представлена в виде
Z = R 4- U,
где R — исходная дискретная (целочисленная) случайная величина, U — не зависящая от нее непрерывная величина со значениями на отрезке [—у]- Наделить U определенным распределением (например,
* Вывод основан на том, что распределения х2 входят в семейство гамма-распределений и снабжены доступными таблицами. — Примеч. пер.
170
равномерным) значит указать распределение аппроксимирующего Z (зависящее, конечно, от параметра 0 распределения R). Если, например, R имеет биномиальное распределение с параметрами (л, 6) и U — равномерное распределение на [—у yj, то наблюдаемое значение Z с 5 десятичными знаками можно получить, взяв реализацию г величины R и добавив к г —у число O-Sis2s3s4s5, где 5, — «случайные цифры» [см., например, RAND Corporation (1955) — Метод, основанный на этой идее, был развит в [Tocher (1950)].
Другой вид приближения связан с тем, что мы работаем с исходным дискретным распределением и получаем доверительные интервалы, не связанные с какими-либо аппроксимирующими распределениями, о которых, однако, мы можем сказать лишь то, что их уровень доверия не ниже заданного. Нельзя, например, получить 95%-ный доверительный интервал, можно лишь указать интервал, уровень доверия которого не меньше 95%. Этот подход развит в примерах 4.7.3 и 4.7.4.
Пример 4.7.1. Доверительные интервалы для параметра 0 Bin (л, 0) распределения; нормальное приближение. Хорошее непрерывное приближение биномиального (л, 0) распределения дает нормальное распределение; если R — случайная величина, распределенная Bin (л, 0), а X — величина, распределенная нормально, то имеет место приближенное равенство
P(R х) = Р(Х х), 0 х л, (4.7.1)
если х — Ы(д, ст),
д = Е(Х) = E(R) = п0 и
ст2 = var(A') = var (R) = л0(1 — 0)
[см. II, раздел 11.4.7], т. е. R распределена приблизительно нормально с параметрами (д, а). Может оказаться более удобным работать с величиной R/ п, которая является естественной оценкой 0; эта величина приближенно N(0, Vfl(l — 0)/п ).
а) Грубое приближение. Для М(д, а) распределения величины X 95%-ный доверительный интервал для д, основанный на наблюдаемом значении х, есть х ± 1,95ст. При самой грубой (но часто применяемой) процедуре в качестве х берут наблюдаемое значение величины R/n, т. е. р = r/л (р — наблюдаемое отношение числа успехов к общему числу испытаний), а в качестве ст — величину V(p(l — р)/п). Тогда приближенным выражением для 95%-ного доверительного интервала будет
р ± l,96V[p(l — р)/л] . (4.7.2)
171
Это без существенной потери точности может быть заменено на
р ± 2V[p(l — р)/п] . (4.7.3)
б) Более точное приближение. Если X — случайная величина N(/x, а), то с вероятностью 1 — а
—а (X — ц) / а а, где
Ф(а) = 1 — уа
(Ф, как обычно, — функция нормального распределения [см. приложение 3.4]). Итак, с вероятностью 1 — а
X /г + ао и X > /х — оа.
Поскольку R приближенно N(/x, а), причем р. = пд и ст2 = п0(1 — 0), можно утверждать с вероятностью примерно 95%, что
R л0 + <zV«0(l — 0) и
Л > л0 — а\/пе(1 — 0) .
В этом приближении 100(1 — а)%-ный доверительный интервал для 0 будет состоять из значений 0, удовлетворяющих неравенствам
г л0 + aVfl0(l — 0) и
г > и0 — а<и0(1 — 0) ,
т. е. интервал, граничные точки которого 01 и 02, представляет собой корни квадратного уравнения
(Г _ пву = агпе{\ — 0). (4.7.4)
Выражая это уравнение через р{ = г/п — наблюдаемая доля успехов), получаем
(1 + о2/и2)02 — (2р + о2/и)0 + рг = 0.
Корни этого уравнения есть
р + а2/2п ± oVp(l — р)/п + а2/4п2 .. - _ч
------------ (4.7.5)
’ 1 + а2/п
Для 95%-ного доверительного интервала (а = 0,05) а = 1,96 = 2, откуда 95%-ные доверительные пределы есть (приближенно)
р + 2/я ± 2V(p(l — р)/п + 1/л2) .. _
172
Например, если г = 8 и п = 20, то в результате этой процедуры получаем уравнение (4.7.4) в виде
(8 — 2О0)2 = (1,96)2 • 200(1 — 0).
Отсюда доверительный интервал есть (0,216, 0,617). Заменив в вычислениях 1,96 на 2, получим практически тот же ответ. Соответствующий интервал, найденный с помощью грубого приближения (4.7.2), будет (0,181, 0,619).
Пример 4.7.2. Доверительный интервал для параметра распределения Пуассона (нормальное приближение). Мы предполагаем, что величина X имеет распределение Пуассона с параметром 0; имеется выборка ее значений (хь х2, •••, хЛ); среднее выборки равно х. Тогда, если 0 не очень мало, то исходное распределение X приближается нормальным (0, V0) распределением, и выборочное распределение х приблизительно N(0, V0/«). В соответствии с рассуждениями в примере 4.7.1 приближенное выражение 100р%-ного доверительного интервала для 0 можно найти из предложения (выполняющегося с вероятностью 0,95):
х~ — 0
—а < -------- < а,
где а = Ф-1(у + у), так что доверительные пределы 01 и 02 есть корни уравнения
Г — 6>
V(fl/n) =а
ИЛИ
(х — 0)2 = ач/п. (4.7.7)
Если р = 0,95, то а = 1,96 ~ 2.
В качестве примера рассмотрим данные табл. 3.2.3. В течение 2606 интервалов времени, каждый по 7,5 сек, общее число радиоактивных частиц, испущенных неким источником, было 10070. Среднее число частиц за промежуток времени, таким образом, есть х = 10070/ 2606 = 3,864. Это оценка наибольшего правдоподобия для 0 по этой выборке. Ее точность выражается через 95%-ный доверительный интервал, полученный из квадратного уравнения (4.7.7):
(3,864 — 0)2 = (1,96)20/2606,
соответственно (0Ь 02) = 3,864 ± 0,049.
Эта оценка, как видим, имеет хорошую точность, что объясняется большим объемом использованной выборки.
173
Теперь перейдем к более глубокому изучению проблем, затронутых в примерах 4.7.1 и 4.7.2, принимая во внимание дискретность данных.
Пример 4.7.3. Доверительные интервалы для параметра 6 распределения Bin (л, 0) с учетом его дискретности. Пусть Xq — случайная величина, отвечающая испытанию Бернулли с вероятностью успеха 0, так что ее распределение имеет вид
P(Xq = х) = 0*(1 — х = 0,1; 0 < е < 1.
В выборке объема п (т. е. в серии из п испытаний) общее число успехов г = Ёх,- есть достаточная статистика. Мы возьмем ее в качестве рабочей статистики. Соответствующая (несмещенная) оценка для 0 есть 0 = г/ п. Статистика г является реализацией Bin (и, 0) распределения Re, для которого п. р. в. есть
P(Re = г) = 0 0'(1 — 9)п~г, г = 0,1, ..., п. (4.7.8)
Будем по возможности следовать тому, как мы поступали в примере 4.6.1 при непрерывном распределении.
Статистика г представляет собой реализацию биномиального распределения Re. Сначала необходимо построить, с наибольшей возможной точностью, 100р%-ный (скажем, 95%-ный) вероятностный интервал для Re при каждом значении 0(0 < 0 < 1). Поскольку распределение Re дискретно, симметричные вероятностные интервалы определены неоднозначно [см. раздел 4.1.3, б)]. Вместо них мы будем использовать квази-центральные ' вероятностные интервалы (г;(0), гм(0)) уровня не менее 95%, т. е. такие, что
< R, < г„(0)] » 0,95 (4.7.9)
И
P[R6 rz(0)] 0,025,
где rz(0) — наибольшее значение г, для которого P[Re г] 0,025, или, что эквивалентно, для которого P(Re > г) 0,975. Аналогично
PjP, > r„(«)j 0,025,
где гм(0) — наименьшее значение г, для которого P[Re г] 0,025 или P(Re < г) 0,975 [см. пример 4.1.4].
Теперь мы построим графики rz(0) и гм(0) как функций 0 [см. рис. 4.7.1] и постараемся их истолковать с точки зрения доверительной полосы. Чтобы показать, как можно построить функции rz(0) и гд(0), рассмотрим ситуацию, когда 0 = 0,45. Из таблиц биномиального распределения [см. приложение 1] получим следующие значения:
174
Г P(*o.4J < г)
0 0,00253 1,0000
=> 1 0,02325
2 0,09955 •
• • •
•
• • •
8 • 0,02740
=> 9 0,00451
10 1,0000 0,00035
Рис. 4.7.1. Графики функций ги(в) и rt(6), таких, что Re ги(0)] 0,95
Отсюда видно, что
>7(0,45) = 1, гм(0,45) = 9
(стрелки в таблице указывают значения вероятности, максимально близкие к 0,025, но не превышающие 0,025).
Действуя таким образом, нетрудно построить таблицы значений ги(0) и г/0); такая таблица приведена ниже для 0 = 0,10(0,05)0,90:
е е
0,10 4 0,55 2 9
0,15 5 0,60 3 10
0,20 6 0,65 3 10
0,25 6 0,70 4
0,30 7 0,75 5
0,35 8 0,80 5
0,40 0 8 0,85 6
0,45 1 9 0,90 7
0,50 1 9
175
Из этой, довольно грубой, таблицы нельзя извлечь точной информации о том, где происходят скачки ги(0) и однако такую информацию можно извлечь из более подробных таблиц биномиального распределения и их интерполяции.
Мы следовали, насколько это было возможно, построению 95%-ных вероятностных интервалов в примере 4.6.1 и соответствующих кривых j 1(0), ^2(0), изображенных на рис. 4.6.1. Таким образом, мы пришли к разрывным ступенчатым функциям, приведенным на рис. 4.7.1. Теперь мы покажем по аналогии с примером 4.6.1, что зона между этими кривыми есть доверительная полоса. К сожалению, эти рассуждения не могут быть просто повторены: при непрерывном распределении в примере 4.6.1 использовалась обратимость функции у 1(0), у2(0), а наши ступенчатые функции не имеют обратных. Это, однако, только малая часть возникающих трудностей. Как видно из рис. 4.7.2, при любом значении 0 утверждение
Г/(0) < г < гм(0)
(4.7.10)
Л’
г( (6}
г । । ।
_1____L
О' (г)
в" (г)
(заметьте, неравенства строгие) равносильно предложению
0'(г) < 0 С 0"(г), (4.7.11)
где 0(г) (равное, скажем, 0') — абсцисса правого конца горизонтального отрезка («ступеньки») гм(0), чья высота равна г, т. е.
ги(0/) = г.
Аналогично, 0"(г) (равное, скажем, 0") есть абсцисса левого конца ступеньки высоты г, т. е. той, для которой
(6. г)
г/0") = г.
Рис. 4.7.2. Из рисунка видно, что
Г/(0) < г < г„(0) * в'(г) < (в) С в"(г)
ступеньки, так как и то, и другое
ния 0 (6) и 0"(6), соответствующие
Поскольку предложения (4.7.10)
бых значениях г (реализации Re) и
(Необходимо отметить, что каждое из возможных значений г совпадает с высотой какой-нибудь - целые числа 0, 1,2,..., п.) Значе-г=. 6, показаны на рис. 4.7.1.
и (4.7.11) эквивалентны при лю-0(0 < 0 < 1), то
/>{г,(0) < Re < ru(«)] = />[«-(/?,) в «
176
где 0'(Re) и 0"(Re) — случайные величины, соответствующие 0'(г) и 0"(г). Вероятность в левой части не меньше 0,95 по построению, откуда
р[е-(Л,) s; о > о,95.
Итак, если г является реализацией Re, то интервал
(0 (г), 0 (г)) (4.7.12)
представляет собой квази-центральный доверительный интервал уровня не менее 95% (и ближайшего к 95%).
Существуют таблицы значений 0'(г) и 0"(г) для всех значений г и объемов выборки. Один из вариантов такой таблицы приведен в приложении 10. Таблица составлена для значений r/п, где г — наблюдаемое значение Bin (л, 0). Из нее видно, например, что если г = 8, п = 20, т. е. г/п = 0,40, то доверительный интервал есть (0,19, 0,64). (95%-ный доверительный интервал для тех же данных, вычисленный с помощью нормального приближения [см. пример 4.7.1], равен (0,18, 0,62) при использовании «грубого» метода и (0,22, 0,62) — при лучшем приближении.)
Пример 4.7.4. Доверительные интервалы для параметра распределения Пуассона. Чтобы построить доверительный интервал для параметра распределения Пуассона, можно применить метод, полностью аналогичный использованному в примере 4.7.3.
Если число событий R за данное время (или в данной области, объеме и т. д.) имеет распределение Пуассона с параметром 0 и его наблюденное значение равно с, то доверительные интервалы уровня не менее 100/?% могут быть найдены из таблиц 11 приложения (в этих таблицах р = 1,2а).
4.8. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ КВАНТИЛЕЙ, НЕ ЗАВИСЯЩИЕ ОТ ИСХОДНОГО РАСПРЕДЕЛЕНИЯ (РАСПРЕДЕЛЕННЫЕ СВОБОДНО)
В этой главе доверительные интервалы строились исходя из выборочного распределения рабочей статистики. Однако встречаются ситуации, когда доверительные интервалы можно построить, не затрагивая исходного распределения. Например, свободный от распределения доверительный интервал может быть построен для квантилей (иногда говорят — фрактилей, процентилей) данного непрерывного распределения. Квантиль уровня р, или р-квантиль функции распределения F(x, 0) есть такое %р, которое удовлетворяет уравнению
F(£p) = р, 0 < р < 1.
177
Пусть х(1), х(2), ..., х(л) — порядковые статистики [см. II, раздел 15.1] выборки объема п из заданного распределения, так что
Х(1) < х(2) < ... < х(л).
Выборочная плотность распределения х(г) есть
g(y) = [1 - ГО)]” ~ rf(y)/B(r, n — r + 1),
где В(и, у) — бета-функция [см. IV, раздел 10.2].
Теперь, если Х(г} — случайная величина, реализацией которой является х(г) и
Р{Х„ <$„) = ! g(y)dy,
-OD
то, делая замену и - F(y) и используя равенство и = F(£p) = р (откуда у = £р), получаем
р
j иг~ 1(1 — и)" ~ rdu/B(r, п — г + 1) = 1р(г, п — г + 1), о
так называемую неполную бета-функцию. Этот результат не зависит от функции распределения Г(х), т. е. свободен от распределения. С помощью соответствующего соотношения для совместного распределения порядковых статистик Х(г>) и (г < s) аналогичным образом можно показать, что интервал
(х(г), x(s)) (4.8.1)
(для г < s) является свободным от распределения доверительным интервалом для 1;р с коэффициентом доверия
1р(г, п — г + 1) - Ip(s, n-s+\). (4.8.2)
Значения 1р(и, у) содержатся в опубликованных таблицах неполной бета-функции [см. Thompson (1941) — G]. Они также могут быть вычислены на основе биномиальных таблиц, так как
IЛа, л — а + 1) = Е (")р«(1 -р)" — s=a xs/
(здесь в правой части — вероятность того, что значение биномиальной величины не меньше а).
Пример 4.8.1. Крайние по величине значения х(1) и х(10) выборки объема 10 являются граничными точками интервала (4.8.1) для медианы (квантиля £1/2) с уровнем доверия (4.8.2), а именно
/1/2(1, 10) - /1/2(10, 1) = 1 - 2/1/2(10, 1) = 1 - 2(4)1» = 0,998.
Аналогично интервал (х(2), х(9)) является доверительным интервалом для медианы, но с уровнем доверия Z1/2(2, 9) — А/г(^» 2) = 0,979.
178
4.9. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ МНОГОМЕРНОГО ПАРАМЕТРА
4.9.1. ТОЧНЫЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
Как видно из предшествующих разделов этой главы, теория доверительных интервалов для одного параметра развита неплохо. Теперь перейдем к двухпараметрическим семействам распределений. Среди них наиболее важным является нормальное (ц, а) распределение, для которого, как показано в примерах 4.5.1 и 4.5.2, отдельные доверительные интервалы для каждого из параметров строятся без особого труда. Это интервалы (/*,, ци) и (а;, аи) соответственно, где
Д/ = X + tQQ15s/<n, ци = х + tO915s/yfn,
— (п 1)1/2$/Хо,975» °и = 1)1/2,у/Хо,О25*
Здесь (исходя из выборки (хь х2, ..., х„))
х = Lxr/n, s2 = Е(хг — х )2/(л — 1),
tp — р-квантиль распределения Стьюдента с п — 1 степенями свободы, р — 0,025, 0,975 и
Х2р — р-квантиль распределения хи-квадрат с л — 1 степенями свободы, р = 0,025, 0,975.
Тогда с вероятностью 0,95 имеем
Д/ Ри
и с той же вероятностью а1 ° °и-
Отсюда, однако, не следует, что с вероятностью (0,95)2 одновременно
М/ ц ци И о аи
(попадание двумерного параметра в прямоугольник), так как индивидуальные доверительные интервалы построены с помощью величин (х —fi)/s и s/о соответственно, которые являются зависимыми.
Итак, даже для такого простого случая вопрос о построении совместной доверительной области для двух параметров не так прост. Нужно прежде всего уточнить,, что же мы имеем в виду под «совместной доверительной областью», какими свойствами она должна обладать и зачем она нужна на практике.
Следует сказать для начала, что теория таких областей есть, в сущности, переложение теории одномерного доверительного интервала. Для определения двумерной доверительной области нужно обратиться к такой случайной величине У, распределение которой зависит
179
от двух параметров а и 0, оцениваемых через а* и /3*, чтобы с вероятностью 95% для всех а, 13, действовало соотношение
(Л* — а)2 + (В* — /З)2 С 1.
Здесь а*, /3* — реализации случайных величин А*, В*. С помощью реализации Y определяемая 95%-ная доверительная область для (а, /3), а именно
(а* — а)2 + (/3* — /З)2 С 1, —
единичный круг на плоскости (а, (3) с
Рис. 4.9.1. Доверительная область для пары параметров (а, 0).
центром в (а*, 0*).
Вообще, для случайной переменной Y, распределение которой зависит от двух параметров а, (3, приемлемой доверительной областью для а и /3, основанной на оценках а*, /3*, может служить часть плоскости внутри замкнутой кривой С(а*, /3*), такой, что
Р[(а, /3) € С(Л*, В*)] = 0,95.
Такие области существуют, и это будет показано ниже [см. пример 4.9.1]. Мы построим совместные довери-
тельные области для параметров N(^, а) распределения. Прежде чем перейти к построению, скажем несколько слов о практическом применении подобных областей. Главная проблема, возникающая в ситуаци
ях с несколькими параметрами, состоит в оценке достоверности данного значения комбинации параметров, предпочтительно в терминах доверительных интервалов. В случае двух параметров (скажем, а и /3) их простейшая комбинация — сам параметр а (или /3). Мы немедленно приходим к тому разочаровывающему факту, что, вообще говоря, невозможно построить доверительный интервал для а с известным уровнем доверия исходя из 95 %-ной доверительной области для совокупности (а, /3)- Рассмотрим ситуацию, изображенную на рис. 4.9.1, где область, ограниченная кривой С, является 95 %-ной доверительной областью для (а, /3). Очевидный 95%-ный доверительный интервал для а есть (а,, а2) — проекция кривой С на ось а. Действительно, по определению доверительной области, утверждение, что (а, 0) лежит внутри С, выражается одним или несколькими неравенствами относительно А*, В*, а, &, совместная вероятность которых равна 0,95.
180
Этим неравенствам удовлетворяют все точки, лежащие внутри С. Если же (а, /3) лежит внутри С, то а лежит внутри проекции Са. Отсюда логически следует, что
Р[а 6 CJ 0,95
[см. II, теорема 3.4.5]. Итак, хотя (аь а2) является доверительным интервалом, его точный уровень не известен; можно лишь сказать, что он не меньше 95%.
Если нельзя построить точные доверительные интервалы для а и /3 исходя из знания двумерных доверительных областей, то и нельзя надеяться построить точные доверительные интервалы для комбинации параметров вида а + 2/3, а//3 и т. д. Методы, позволяющие получить доверительные интервалы уровня не менее заданного, однако, существуют [см., например, Scheffe (1953), (1970)].
Теперь перейдем к примерам построения двумерных доверительных областей.
Пример 4.9.1. 95%-ная доверительная область для (ц, а). Рассмотрим величины (X — /л)/о, S2/ а2, где, как обычно, X — случайная величина, порожденная статистикой х, и s2 — величина, порожденная s2 (обозначения те же, что и ранее). Тогда величина (X — — n)/(a/yfn) нормальна (0, 1), и (п—l)S2/a имеет распределение хи-квадрат с л — 1 степенями свободы. Более того, 5 и X статистически независимы [см. теорему 2.5.2].
Теперь, если и0 — 0,975-квантиль стандартного нормального распределения, то
Р{—и0 п'/2(Х — р)/а С «о] = 0,95, (4.9.1)
так что
Р(ц — иоа/у[п с X, ц + иоа/уГп X ] = 0,95.
Рис. 4.9.2. Заштрихованная клинообразная область — неограниченная доверительная область для пары (ц, а)
Отсюда следует с вероятностью 0,95, что клинообразная область на рис. 4.9.2 содержит точку (д, а). Таким образом, эта область является 95 %-ной совместной доверительной областью для (д, а). Но поскольку она не ограничена, из нее нельзя извлечь какой-либо пользы.
Аналогично мы имеем
181
Р[а2 (л — 1)52/ст2 Ь2] = 0,95, (4.9.2)
где а2 = х0025(л 1), Ь2 = Х*975(и — 1) — квантили уровней 0,025 и
0,975 распределения хи-квадрат с п — 1 степенями свободы, так что Р[(п — l),/2S/6 а (п — \)i/2S/a] = 0,95.
Отсюда следует, что на плоскости (д, а) полоса на рис. 4.9.3 содержит а с вероятностью 0,95. Эта полоса — двумерная доверительная область для а.
Так как X и S статистически независимы, утверждения (4.9.1) и (4.9.2) также независимы, откуда
Р{—и0 С л1/2(Х — д) и0
и а2 (п — l)S2/a2
Рис. 4.9.3. Заштрихованная полоса — неог- < М] = (0 95)2
раниченная доверительная область для а ’ ’
т. е. с вероятностью (0,95)2
Л
д — Uqo/^п X, д + uQo/y[n X
и ( . (4.9.3)
(л _ l)i/2S/ft а (п — l)i/2S/a. J
Это равносильно предложению, которое тоже выполнено с вероятностью (0,95)2 = 0,9025, что случайная область А(Х, S), определенная (4.9.3), содержит точку (д, а). Если мы заменим X и S их значениями х и s, то результирующая область А(х, $) будет 90,25%-ной доверительной областью для пары (д, ст). Эта область изображена на рис. 4.9.4.
Если мы хотим получить доверительную область уровня, скажем 0,95, то мы должны провести те же вычисления, взяв за м0 квантиль уровня 0,9875 стандартного нормального распределения (т. е. 2,24). При п = \\, а = 2,1 и b - 22,6 — квантили уровней 0,0125 и 0,9275 распределения х2 с 10 степенями свободы. (Чтобы пояснить, откуда взялось число 0,9875, отметим, что мы должны заменить вероятность 0,95 на р = V0,95 = 0,975 в каждом из равенств (4.9.1) и (4.9.2). Чтобы получить такие вероятности, нужно брать квантили нормального 182
Рис. 4.9.4. Заштрихованная фигура — пересечение областей рис. 4.9.2 и 4.9.3. Она является доверительной областью для пары (д, а)
Рис. 4.9.5. Границы интервала (а, Ь) — квантили уровней |(1—р) ид + |(1— р)=
= |(1 + Р)
распределения и распределения хи-квадрат уровней у (1 — р) и у(1 + р), как показано на рис. 4.9.5.)
4.9.2. ЭЛЛИПТИЧЕСКИЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ВЕКТОРА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДВУМЕРНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ. ПРИБЛИЖЕННЫЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
ДЛЯ ОЦЕНОК НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ
Согласно теории оценка наибольшего правдоподобия 0 параметра О часто оказывается распределенной приближенно нормально (0, а2в), где а2в — выборочная дисперсия. Если действовать не очень аккуратно, можно считать, что распределение величины (0 — 0)/ ад — стандартное нормальное и с вероятностью 0,95 ее значение попадает в интервал ± 1,96. Отсюда
0 ± \,96ав — приблизительный 95%-ный доверительный интервал для 0. В случае двух параметров, скажем,
е = (0>, 02), соответствующее приближенное распределение для оценки наибольшего правдоподобия § = (§it 02) — двумерное нормальное с вектором
183
математического ожидания 6 и ковариационной матрицей V, которую можно оценить по выборке [см. раздел 6.2.5, п. 3]. Желательно получить 95%-ную доверительную область хотя бы в грубом приближении. Можно рассуждать следующим образом: если
/ V1 с \
v = L J •
то выборочная дисперсия 0г равна vH а 02 равна v2. Можно, разумеется, построить отдельные 95%-ные доверительные интервалы
01 ± 1,96v^2, 02 ± l,96v'2 (4.9.4)
для 0] и 02. Этого недостаточно, поскольку (как отмечено в разделе 4.9.1) отсюда не следует, что с вероятностью (0,95)2 точка (0Ь 02) будет лежать в прямоугольнике (4.9.4). «Доверительное» утверждение для совокупности 0] и 02 можно установить следующим образом. Оговорка «приближенно» означает, что 0} и — оценки наибольшего правдоподобия и их распределение не является в точности двумерным нормальным. Если бы это распределение было нормальным в точности, оговорку следовало бы снять. Для любого вектора az = (alt а2) случайный вектор
«1 01 + «202
распределен нормально с ожиданием
«101 + «202
и дисперсией
a'Va = a2Vi + 2«i«2c + a22v2.
Поэтому 95%-ный доверительный интервал для
«10! + а20г
есть
«101 + а2§2 ± l,96V(«^Vi + 2«i«2c + a2v) . (4.9.5)
При другом подходе, позволяющем построить двумерную доверительную область для б, используется двумерный аналог центрального вероятностного интервала уровня 0,95 для одномерного нормального распределения, т. е. внутренность эллипса С, построенного так, чтобы плотность вероятности на его границе всюду была одинаковой и jj/(Xi, x2)dxidx2 = 0,95, С
raef — плотность двумерного N(0, V) распределения. Тогда с вероятностью 0,95,
S —е е с,
184
так что 95%-ная доверительная область для О есть эллипс С + 6 [результат переноса С на вектор ё).
Эллипс С можно построить следующим образом. Плотность двумерного N(0, V) распределения [см. II, раздел 13.4.6] равна
(2тг)~1/2 | V | _|/2ехр(—-L-x'V-’x).
Кривая С удовлетворяет уравнению
xV"‘x = b,
где b должно быть определено. Напишем V= ЕЕ и V = Е~’Х, так что Y имеет двумерное N(0, I) распределение [см. II, пример 13.4.8]. Под действием этого преобразования эллипс С переходит в круг
У У = b (или у2 + у\ = Ь),
где
у = Е~’х.
Остается найти b из уравнения
— \\e~^+y>2dy.dy2 = 0,95.
^1Г у2 +/. ь
Интеграл можно взять с помощью перехода к полярным координатам [см. IV, пример 6.2.3]. Уравнение при этом сводится к
1 — е~ь/2 = 0,95,
откуда
b = 5,991.
Итак, 95%-ной доверительной областью для (0Ь 02) служит внутренность эллипса
(х — 0)V~‘(x — = 5,991,
где
х' = (0Н f)2).
(То же и для 99%-ного доверительного интервала. В этом случае получаем уравнение 1 — е~ь/2 - 0,99, откуда Ъ = 9,210.) Итак, если
/ V1 с \ / a2. QO\O2\
V= ( ) = ( 2 ) ,
\ с v2 / \ QOia2 ff2 /
то [см. I, раздел 6.4]
, 1 / 1/о2, —
у—1 = ______ / 1 \
1 б2 ( —q/o,а2 l/ffj )
185
и уравнение имеет вид
(аг. — $,)* 2в
-----2---- - (х. - 0>)(х2 - 02) + (4.9.6)
° ! ° I ° 2
(хг - ё2у
+ ---— = 5,991 (1 - е2).
а2
Эта область является точной (но не единственной) 95 %-ной доверительной областью для 0, когда параметры (q, aif а2) известны точно. Если они определены приближенно, то и доверительная область, разумеется, будет приближенной.
Для линейной регрессии с независимыми нормально распределенными ошибками существует прямой способ построения точных доверительных областей — эллипсоидов для совокупности параметров (или их подмножества). Метод описан в разделе 8.3.2.
4.10. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ НА ОСНОВЕ БОЛЬШИХ ВЫБОРОК С ИСПОЛЬЗОВАНИЕМ ФУНКЦИИ ПРАВДОПОДОБИЯ
Когда выборка достаточно велика, становится возможным упростить приближение.
4.10.1. ФУНКЦИИ ПРАВДОПОДОБИЯ
Пусть X имеет плотность распределения f(x, 0). Исходя из выборки (Х), х2....хп) строят функцию правдоподобия [см. раздел 6.2.1]
И»; х„ *2.....х„) = ftf(xr, в). (4.10.1)
1 п
Логарифмической функцией правдоподобия будет Elog/(xr, 0), а ее производная по 0 [см. IV, раздел 4.5] есть
dlogZ п д
z(0; хь х2....хп) = = Е a# log/(xr, 0). (4.10.2)
Выборочное распределение этой функции — распределение индуцированной случайной величины п д ,
Z = z(0; Х„ Х2, Хп) = Е м k>gf(Xr, в), ' (4.10.^) где Хг — статистические копии X. Случайные величины 31og/(Arr, 0)/д0, г = 1, 2, ..., п также независимы и одинаково распределены и согласно центральной предельной теореме [см. II, раздел 17.3] их сумма Z асимптотически Нормальна. Чтобы как-то использовать этот факт, нам необходимо получить выражения для E(Z) и D(Z). Первое математическое ожидание равно нулю, так как 186
£'(31og/(X„ О)/д0] = J [ > log/(x,0)]/(x, O)dx = J
a f
= Ы e>)dx
в предположении, что f(x, в) удовлетворяет обычным условиям регулярности [см. IV, раздел 4.7]. Так как j f(x, 0)dx = 1, то 31og/(Arf, О)/дв имеет нулевое математическое ожидание, а потому E(Z) = 0.
Дисперсия величины 31og/*(A"r, 0)/д0 равна
f ^2 р"2> г Э1ое/(х 0)') 2
E[dlog/(Xr, ^)/^J = J I ~^Г~ J -Я*’ ^dx- (4-10-4)
Теперь
/ Slog/ \ 2 1 / df\ 2
' де ' ~ T2" ^~дё'
и далее
a2iog/ _ i / df\2 i a2/ ae2 f2 'её' + T ~de2’
откуда
/aiog/\2 _ i a2 a2iog/
' de ' ~ / ~di2 de2 ’
Интеграл в правой части (4.10.4) записывается в виде
(°° а2/ . (~ fa2iog/(x; m .
dx - I-----------— J/(x, &)dx.
-CZXZ»
При нужных условиях регулярности [см. раздел 3.3.3, в)] первый из этих интегралов преобразуется к виду (д2/д02) j f(x, 0)d0, откуда видно, что он равен 0, так как j f(x, 0)d0 = 1. Наконец, из (4.10.4)
f(d2\ogf(x, 6)^1
var[dlog/(Xr, 0)/д0] = - J [ J/(x, 0)dx =
= ~E[d2\ogf(Xr, 0)/д02] ,
и из (4.10.3)
г = 1, 2, ..., п, n^z = -iE[d2\ogf(xr, 0)/д02].
187
Положим по определению
varZ = (4.10.5)
где
7„(0) = —л£[Э21о&/(Х 0)/д02] — (4.10.6)
«количество информации» в выборке (3.3.6).
Итак, величина Z, определенная соотношением (4.9.2), имеет распределение, близкое к N(0,
4.10.2. ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ ПРОИЗВОДНОЙ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ ПРАВДОПОДОБИЯ
Из результатов раздела 4.10.1 следует, при обозначении и2 = что
Р(—l,96w < Z < l,96w) S 0,95,
(4.10.7) Р(—2,576w Z 2,576ш) == 0,99
и т. д., откуда легко получить приближенные доверительные интервалы для в с уровнями доверия 0,95, 0,99 и т. д. Это мы покажем в следующем примере.
Пример 4.10.1. Построение доверительного интервала для параметра в биномиального распределения с помощью функций правдоподобия. Рассмотрим случайную величину X, соответствующую испытанию Бернулли с вероятностью успеха 6 [см. II, раздел 5.2.1]; тогда функция вероятности X есть
/(х, 0) = 0*(1 — 0)1-*, х = 0, 1 (0 С 0 С 1).
Для выборки (Xi, х2, ..., хп) функция правдоподобия [см. (4.9.1)] имеет вид
/(0; X], х2, ..., хп) = П0Х/(1 — 0)1-х' = 0Г(1 — 0)п~г, г = Ех(.
Производная (4.10.2) логарифмической функции правдоподобия есть z(0; х,, х2, ..., хп) = -^log[0r(l — 0)п~г] =
= ~ [rlog0 + (п — r)log(l — 0)] =у - =
Это реализация случайной величины
Z = (Я — л0)/0(1 — 0)
(4.10.8)
188
[ср. с (4.10.3)]. Легко проверить, что E(Z) = 0. Это следует из того, что для величины R, распределенной Вт(л, 0), E(R) = п0.
Теперь необходимо обратиться к 1п(0). Имеем
log/PG 0) = *log0 + (1 — X)log(1 — 0),
откуда
Поскольку Е(Х) = 0, то
L дв2 -> 0 + 1 — 0 ~ 0(1 — 0)
Откуда, используя (4.10.5), находим, что
var(Z) = 7„(0) = л/0(1 — 0).
Это может быть проверено с помощью (4.9.8): так как величина R распределена Bin (л, 0), то var(7?) = л0(1 — 0),
откуда
var(Z) = п0(1 — 0)/{0(1 — 0)]2 = л/0(1 — 0).
Чтобы получить 95%-ный доверительный интервал для 0, используем (4.10.7); с вероятностью 0,95 (приближенно!)
—l,96Vn R — п& l,96Vn
V0(1 — 6) 0(1 — 0) " \'0(1 — в) ’
т. е.
(R — п0)2 3,842л0(1 — 0).
Итак, из выборки (хь х2.....хп), для которой Ех; = г (общее число
успехов), 95%-ный доверительный интервал, полученный с помощью процедуры, приведенной выше, есть (0М 0и), где 0Z и 0и равны соответственно меньшему и большему корням квадратного уравнения
(г — п0)2 = 3,842л0(1 — 0).
Например, если г = 6 и п = 20 (и, следовательно, оценкой для 0 будет г/п = 0,30), мы имеем уравнение
(6 — 200)2 = (3,842) (20)0(1 — 0), откуда
0/ = 0,138, 0и = 0,526 (4.10.9)
с той точностью, какую может обеспечить нормальное приближение (то, что биномиальное распределение можно приближенно считать нормальным, есть на самом деле частный случай общей центральной предельной теоремы [см. II, раздел 11.4.7]). «Грубый» вариант вычислений по предшествующей схеме будет таким: распределение вели-189
чины R приближенно нормальное с математическим ожиданием 200 и дисперсией 200(1 — 0). Заменяя 0 в выражении для дисперсии оценкой г/п(= 0,3), получаем значение дисперсии 4.2. Если распределение R считается N(2O0,2,O5), то 95%-ным доверительным интервалом для 0 будет г ± (1,96)(2,05)/(20), т. е. 0,30 ± 0,20, т. е. (0,10, 0,50) [ср. с (4.10.9)]. Эту оценку на базе выборки большого объема можно сравнить с точным выражением (0,12, 0,54) для 100р%-ного доверительного интервала для 0сг = 6ии = 2О, полученным в примере 4.7.1, где, однако, мы имели р 0,95.
4.10.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ (ПРИБЛИЖЕННО) НОРМАЛИЗУЮЩЕГО ПРЕОБРАЗОВАНИЯ
Иногда бывает, что статистика, имеющая «неудобное» распределение, может быть преобразована в другую статистику, имеющую распределение, хорошо поддающееся исследованию. Примером может служить выборочный коэффициент корреляции как оценка коэффициента корреляции двумерного нормального распределения [см. раздел 2.7.3, б)].
Пример 4.10.2. Приближенный доверительный интервал для коэффициента корреляции. Пусть q — коэффициент корреляции нормальной пары (X, У). По выборке (хь (х2, у2).....(х„, у„) оценим q
как
г = ^5 (xj — x^j — 7 — * )2£(л — у )2]1/2-
Чтобы выразить доверительный интервал для q через наблюдаемое значение г, воспользуемся тем, что если п велико (например п > 50), то величина
1 / 1 + г\
-•=тНт^7>
с достаточной точностью может считаться реализацией нормальной величины Z с E(Z) = ylog[(l + @)/(1 — е)] и var(Z) = 1/(л — 3). Благодаря этой аппроксимации можно считать, что с вероятностью 95%
Z — 1,96/<(л — 3) ylog-TZ7 z + 1,96/VTn — 3) .
Разрешая эти неравенства относительно q, найдем соответствующий 95%-ный доверительный интервал для q в виде
[(e-l)Z(e + 1), (b- l)/(ft + 1)],
190
где
1 + Г \ -3,92/V(n - 3)
1 — Г/ к
и
1 + Г A 3,92/V(n — 3) 1 - г/ е
Например, если г = 0,3 и п = 55, то а = 1,07 и b = 3,20; 95%-ный доверительный интервал для q есть (0,03, 0,52) [см. также пример 5.2.2].
4.11. ДОВЕРИТЕЛЬНАЯ ПОЛОСА ДЛЯ НЕИЗВЕСТНОЙ НЕПРЕРЫВНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
4.11.1. ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
Функция распределения F(x) непрерывной величины X определяется равенством
F(x) = Р(Х х), —< х < <-’•
На базе выборки из п наблюдений величины X очевидный аналог функции распределения F(x) определяется равенством
nFn(x) = [число наблюдений величины х, которые не превосходят х] = fr(X х). (4.11.1)
Символ fr(^<) означает частоту попадания наблюдений в множество Эта функция называется эмпирической функцией распределения.
Возможен также следующий эквивалентный вариант определения.
Определение 4.11.1. Порядковые статистики выборки. Пусть х(1), х(2), ...» х(п) (где x(ij < х(2) < ... <х(п)) — порядковые статистики [см. II, гл. 15] выборки из п наблюдений непрерывной случайной величины X. Эмпирическая функция распределения X есть
0, х < х(П,
k/n, xwCx<x(A.+ i), к = 1, 2 л—1,
" 1, х > \пУ
(4.11.2)
Пример 4.11.1. Порядковые статистики. Следующий набор четырехзначных десятичных чисел [см. II, раздел 5.1] есть случайная выборка из десяти наблюдений, записанных до четвертого знака непрерывного равномерного распределения [см. II, раздел 10.2.1]:
191
0,4754
0,7591
0,5566
0,5435
0,0392
0,0063
0,0666
0,1330
0,8572
0,6566
Располагая данные в порядке возрастания, мы видим, что порядковые статистики будут такими:
Г Х(г) Г Х(Г)
1 0,0063 6 0,5435
2 0,0392 7 0,5566
3 0,0666 8 0,6566
4 0,1330 9 0,7591
5 0,4754 10 0,8572
Эмпирическая функция распределения F10(x) задана табл. 4.11.1. График ее показан на рис. 4.11.1. Это ступенчатая функция [см. IV, определение 4.9.4], промежутки постоянства которой замкнуты слева и открыты справа [см. I, раздел 2.6.3]. Для сравнения покажем истинную функцию распределения F(x):
0, х < 0,
F(x) = ' х, 0 х 1,
1, х > 1.
192
Рис. 4.11.1. График эмпирической функции распределения Fl0(x) выборки из примера 4.11.1
Таблица 4.11.1
Значения x Значения x
x < : 0,0083 0 0,5435 s % x < ; 0,5566 0,6
0,0083 s J X < C 0,0392 0,1 0,5566 s S x < : 0,6566 0,7
0,0392 s $ X < : 0,0666 0,2 0,6566 s S x < Z 0,7591 0,8
0,0666 s S x < : 0,1330 0,3 0,7591 s % X < Z 0,8572 • 0,9
0,1330 s S x < C 0,4754 0,4 x ; > 0,8572 1,0
0,4754 s S x < i 0,5435 0,5
4.11.2. РАССТОЯНИЕ КОЛМОГОРОВА—СМИРНОВА МЕЖДУ ИСТИННОЙ (ТЕОРЕТИЧЕСКОЙ) И ЭМПИРИЧЕСКОЙ ФУНКЦИЯМИ РАСПРЕДЕЛЕНИЯ
При построении доверительной полосы для неизвестной функции распределения F(x) наиболее полезной мерой близости эмпирической функции распределения и истинной служит статистика Колмогорова—Смирнова dn, определяемая равенством
dn = dn(xar х(2)» •••> х(л)) = sup I Fn(x) — F(x) | , (4.11.3)
193
где sup означает точную верхнюю грань [см. I, раздел 2.6.3].
Для данной выборки эта статистика есть модуль наибольшего отклонения Fn(x) от F(x). На рис. 4.11.1 оно достигается при х = 0,1330, при этом Fn(x) = 0,4000 и F(x) = 0,1330, откуда dn = 0,2670.
Статистика dn является реализацией случайной величины
Dn — ^(2)> •••>
где Xj — случайные величины, соответствующие порядковым статистикам. (Здесь существуют определенные трудности, связанные с обозначениями. Согласно сложившейся практике функция распределения F(x) обозначается прописной буквой, например F. Это противоречит соглашению прописными буквами латинского алфавита обозначать случайные величины. Разумеется, двусмысленности можно избежать. С эмпирической функцией распределения картина не столь ясна. Здесь также существует традиция в обозначениях, как, например, в нашем случае Fn(x) в (4.11.2), (4.11.3). Для каждого х Fn(x) (несмотря на то, что буква прописная) есть реализация случайной величины
0, х < Хщ,
F<rv-)(x) = к/п, Х^х<Х(к+х), к = 1, 2,
.., п— 1 ,
(4.11.4)
1, X >
[ср. с (4.11.2)]. Здесь мы вынуждены использовать неуклюжее обозначение F^'Xx), чтобы различать случайную величину и ее реализацию Fn(x). На практике, однако, никто не пользуется символом Fjr,v,)(x); одно и то же обозначение Fn(x) применяется и для статистики (4.11.2), 41 для случайной величины, реализацией которой она является. А это всегда ясно из контекста.)
4.11.3. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СТАТИСТИКИ КОЛМОГОРОВА—СМИРНОВА. ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Легко видеть, что выборочное распределение dn [см. определение 4.11.1] не зависит от исходной функции распределения F(x). Чтобы убедиться в этом, рассмотрим преобразование X в Y = F(X). Функция распределения У есть G(y), заданная в точке у = F(x) соотношением
G(y) = P(Y^ у) = P[F(X) F(x)] = Р(Х х) = F(x) = у, так как F монотонно возрастает. Отсюда эмпирическая функция распределения У есть Gn(y), заданная равенством
194
nFn(x) = fr(X x) = fr[F(X) F(x)] = fr(Y y) = nGn(y), следовательно,
Fn(x) — F(x) = Gn(y) — y.
Теперь пусть Fn(x) — эмпирическая функция распределения, построенная по п реализациям случайной величины X, функция распределения которой есть F(x). Отсюда следует, что Gn(y) — эмпирическая функция распределения, построенная по п реализациям случайной величины Y = F(x), которая имеет равномерное распределение на (0, 1) [см. II, теорема 10.7.2]. Поэтому выборочное распределение Gn(y)—у определяется свойствами именно равномерного распределения и никоим образом не зависит от F(x). Имеем
P(Dn d) = P[sup | Fn(x) - F(x) | d] = x
= P[sup | Gn(y) — у | d] = скажем, Kn(d). (4.11.5) У
Это распределение табулировано [см., например, Owen (1962); Harter and Owen (1970), т. 1 — G]. Чтобы построить 95%-ные доверительные пределы, необходимо знать для каждого п значение d, такое, что Kn(d) = 0,95. Эти значения доступны [см. табл. 4.11.2] также и для 99%, 98%, 90% и т. д. Для п = 10, например, 95%-ное значение d есть 0,409, так что
P(D10 0,409) = 0,95.
Пример 4.11.2. Доверительная полоса для функции распределения.
Для выборки объема л = 10
0,95 = P(D10 0,409) = P(sup | Fl0(x) — F(x) | 0,409) =
х
= Р[ | F10(x) — F(x) | 0,409 для всех х] =
= P[Fio(x) — 0,409 F(x) F10 ’+ 0,409 для всех х].
Следовательно, неравенства для каждого х
F10(x) — 0,409 F(x) Fl0(x) + 0,409 (4.11.6)
определяют 95%-ную доверительную полосу для функции распределения F(x), которая считается неизвестной. Поскольку также
0 F(x) 1,
можно уточнить границы (4.11.6) до
/л(х) F(x) м„(х), (4.11.7)
195
где
/л(х) = max(0, Fn(x) — 0,409),
(4.11.8) и„(х) = min(l, Fn(x) + 0,409).
Для выборки из 10 наблюдений из примера 4.11.1 эмпирическая функция распределения Fn(x) была приведена в табл. 4.11.1. Доверительная полоса (по формуле (4.11.8)) приведена в табл. 4.11.2.
Таблица 4.11.2. Доверительная полоса (4.11.8)
Значения х 95%-ные доверительные пределы для F(x)
i 10 (*)
х < 0 0 0
0 х < 0,0083 0 0,409
0,0083 л- < 0,0392 0 0,509
0,0392 х < 0,0666 0 0,609
0,0666 sj х < 0,1330 0 0,709
0,1330 sj х < 0,4754 0 0,809
0,4754 «С х < 0,5435 0,091 0,909
0,5435 х < 0,5566 0,191 1
0,5566 х < 0,6566 0,291 1
0,6566 С х < 0,7591 0,391 1
0,7591 < х < 0,8572 0,491 1
0,8572 С х < 1 0,591 1
х > 1 1 1
Мы видим, что доверительная область безнадежно широка. Поэтому невозможно получить достаточно точную оценку функции распределения исходя из выборки малого объема. (Значение 0,409, решающее при п = 10, убывает до 0,294 при п = 20, до 0,242 при п = 30, до 0,210 при п = 40 и далее асимптотически при больших п как 1,36/Vn; все это относится к 95%-ному уровню доверия.)
196
Асимптотически при п -* распределение величины Dn (на практике при п > 40) имеет весьма “простой вид:
P(Dn < z/yfn) = Я(г), где
H(z) = 1 - 2Е (—z > 0. 5=1
(4.11.9)
Несколько значений H(z) (в процентах) приведены в табл. 4.11.3.
Таблица 4.11.3. Процентные точки распределения
Колмогорова—Смирнова (4.11.9)
H(z): 0,99 0,98 0,95 0,90 0,85 0,80
z: 1,63 1,52 1,36 1,22 1,14 1,07
Для выборки объема 100, например, 95%-ная доверительная область определяется неравенствами
шах{0, Fioo(x) — 0,136] < F(x) < min[l, F100(x) + 0,136].
Можно вычислить, что для построения 95%-ной доверительной полосы, ширина которой не превосходит 0,1, необходима выборка такого объема п, что
1,36/Vn = 0,05,
т. е. п приблизительно равно 740.
4.12. ТОЛЕРАНТНЫЕ ИНТЕРВАЛЫ
Задачей, во многом близкой к нахождению доверительных интервалов, является построение границ, между которыми лежит определенная доля (например, 0,99) генеральной совокупности. Такое утверждение, естественно, может быть сделано лишь с вероятностью р, где р = 0,95 или 0,99 и т. д. Например, исходя из выборки измерений роста мужчин (данные предполагаются нормально распределенными) необходимо указать числа х{ и х2, при которых рост 99% мужчин не меньше х{ и не больше х2 (с вероятностью 0,95). Такие границы называют толерантными пределами [см. Wilks (1961) — С].
197
Чтобы как-то сформулировать сказанное, определим 100р%-ные толерантные пределы для нормальной (д, а) величины с уровнем вероятности /3. Если бы ц и а были известны, мы могли бы найти центральный интервал (at, а2), содержащий р-ю часть вероятности. Границы ai и а2 удовлетворяют уравнению °2
j/(x; ц, o)dx = р, (4.12.1)
О,
где f(x; fi, а) означает плотность N(/x, а) распределения в точке х.
Можно извлечь ах и а2 из таблиц нормального распределения. Например, если р = 0,95, то
а} = д — 1,96а, а2 = ц + 1,96а.
Если же fi и а неизвестны, лучшее, что можно сделать, основываясь на выборке x]t х2, ..., хп, это заменить д ± 1,96а на х ± Xs„, где, как всегда, х = £xr/n, (п — l)s2 = L(xr — х)2, X — константа, которую необходимо определить. Конечно, нельзя утверждать, что
Ьг
J/(x; д, o)dx = р, (4.12.2)
ь,
так как Ь{ и Ь2 — статистики. Они являются реализациями случайных величин В{ = X — XS и В2 = X + XS, где X и S — случайные величины, соответствующие х и s. Утверждение (4.12.2) должно рассматриваться как реализация соотношения
X+XS
J /(х; д, a)dx = р.
x—xs
Теория толерантных интервалов предполагает схожие соотношения виДа х + х5
J /(х; ц, a)dx р.
x—\s
Нельзя гарантировать полную истинность этого соотношения, однако можно требовать, чтобы оно выполнялось с предписанной вероятностью, скажем, /3:
X +XS
p[J /(х; д, a)dx р] = 0. (4.12.3)
X—XS
Если мы сможем найти X для (4.12.3), то интервал (х — Xs, х + Xs) будет 100р%-ным толерантным интервалом уровня вероятности 0.
Такие значения X действительно могут быть найдены. Существуют таблицы значений X для различных значений 0, р и объемов выборки. 198
4.13. ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
4.13.1. ПРАВДОПОДОБИЕ
а) Функция правдоподобия и логарифмическая функция правдоподобия. Примеры, определения. Пример функции правдоподобия был приведен в разделе 3.3.4. Там же рассматривалось интуитивное обоснование метода наибольшего правдоподобия как метода оценивания неизвестного параметра [см. также раздел 4.10.1]. Подлинное же обоснование этого метода базируется на том, что выборочное распределение оценок наибольшего правдоподобия имеет желаемые свойства.
Однако есть возможность определить оценки наибольшего правдоподобия и их точность методом, не затрагивающим понятия выборочного распределения. Этот раздел кратко знакомит с этой точкой зрения. Мы будем рассматривать функцию /(0; х{, х2, ..., хп) как функцию в, считая величины (хн х2, ...» хп) фиксированными. Надо принять, что понятие вероятности относится к ситуации, когда наблюдения производятся над случайной величиной и нас интересуют вероятности их попадания в различные множества. При этом параметр в считается фиксированным (даже если он неизвестен). С другой стороны, понятие правдоподобия относится к случаю, когда результаты наблюдений известны и возможные значения 6 рассматриваются в свете этих данных.
Необходимо подчеркнуть, что несмотря на численное совпадение (или пропорциональность) значений правдоподобия и соответствующих плотностей вероятности, правдоподобие не является вероятностью и имеет совершенно другие свойства.
Пора сформулировать более общее определение правдоподобия, чем то, которое дано в (4.10.1).
Определение 4.13.1. Правдоподобие. Пусть (хь х2, ..., хп) — реализации случайных величин Хх, Х2, ..., Хп. Положим
rP(A”i =хь Х2-х2,..., Хп=хп), если X дискретны, g(*i, *2, •••,*„, 0) совмесТная плотность распределения (4.13.1) величин (JV], Х2, ..., Хп) в точке (хь х2, ..., х„),
^если X непрерывны.
Здесь в означает (скалярный) параметр совместного распределения случайных величин Хг, если это распределение зависит только от одного параметра; в случае нескольких параметров 0 — вектор. Функция правдоподобия 0 этих данных определяется как
199
1(0) = 1(0; xn) = ag(x1} x2, ..., xn; 0), 0 € Q, (4.13.2)
где Q — параметрическое пространство, т. e. множество возможных значений 0, а = a(xt, х2, ..., хп) — константа относительно 0, возможно, зависящая от наблюдений. Здесь хг фиксированы, и, следовательно, правдоподобие есть функция 0, а не наблюдений хь х2, ..., х„. Не имеют значения абсолютные величины правдоподобия. Мы будем иметь дело лишь с отношениями значений функции правдоподобия при разных 0. Так, значение l(0i) будет сравниваться с 1(02) с помощью отношения l(0i)/l(02), которое, очевидно, не зависит от множителя а в (4.13.2). На практике (4.13.2) часто заменяют его эквивалентом
l(0)^g(xt, х2, ..., хп; 0). (4.13.3)
Если хг — независимые, одинаково распределенные величины [см. раздел 1.4.2, п. 1], то выражение для функции правдоподобия принимает более простой вид:
/(0) = /(0; х2....х„)« П/(х,; 0), (4.13.4)
где f(x, 0) — п.р.в. X в точке х (включая случай дискретной величины X, когда f(x; 0) = Р(Х=х)).
Логарифм функции правдоподобия часто более удобен в работе, и поэтому вводится логарифмическая функция правдоподобия log/(0). Очевидно, что если 1(0) имеет в точке 0 максимум, то и log/(0) имеет максимум в этой точке.
Пример 4.13.1. Правдоподобие в пуассоновском случае. Пусть X' — величина, имеющая распределение Пуассона, с параметром (0) так, что
Р(Х=х) = е~*?7х!, х = 0,1, ... (0 > 0).
При выборке (%1, х2, ..., хп) функция правдоподобия принимает значение
1(0) = 1(0; Xl, х2, ..., х„) ~ ne~Wx.7 = у= 1 •’
= e~ne0n^/nXj! (пх = ёху),
~ e-"Vr, 0 > 0.
. 200
Рис. 4.13.1. Графики функции правдоподобия /(0); 0тах — значение 0, максимизирующее 1(0); 0', 0" — точки, в которых правдоподобие принимает равные значения
График 1(6) изображен на рис. 4.13.1. Отметим, что хотя величина X дискретна, функция правдоподобия 1(0) — непрерывная функция 0. Она имеет единственный максимум. Он достигается в точке 0тах, такой, что
[<//((!)/</«],_, = 0 = [dlog/(«)/<W],_, , max max
т. е.
(d/d0)(—п0 + их logfl) = О,
так что
0 — х
''max л •
Максимальное значение 1(0) пропорционально епх (х )пх, и правдоподобие любого другого значения 0 можно сравнить с ним, исследуя отношение
W/(0max) = е-п<в~хЧ0/х)пх.
Инвариантность. Предположим, что рассматривается нормальное распределение с нулевым средним и дисперсией а2 или, что то же самое, среднеквадратическим отклонением а. С чем нам следует работать — с правдоподобием а или с правдоподобием а2? Имеет ли значение этот выбор? Одно из привлекательных свойств функций правдоподобия состоит в том, что этот выбор не существен. При данных значениях совокупности наблюдений правдоподобия а и а2 равны. В этом заключается свойство инвариантности.
201
Пример 4.13.2. Правдоподобие функции от 9. Инвариантность. При данных (xi, х2, ..., х„) правдоподобие среднеквадратического отклонения N(0, ст) распределения есть
/,(ст) = (2тг)~"/2ст~" ехр {£ х2/2ст2] ,
в то время как правдоподобие дисперсии v( = ст2) есть
/2(у) = (27г)_"/2(т)~"/2ехр [—[Ex2/2v]] .
Очевидно, что это одно и то же. В этом примере ст2 — взаимно однозначная функция ст (по определению ст > 0, и поэтому ст = + Vct2, а не ст = ± У^2). Наши соображения приемлемы для любой взаимно однозначной функции: если правдоподобие 0 при фиксированных данных есть Ц(9) и ф - h(9), где Л(-) — взаимно однозначная функция, то правдоподобие ф есть
12(Ф) = 1А>г'(Ф)).
б) Правдоподобие и достаточность. Вся информация о 9, содержащаяся в выборке Xi, х2, ..., хп ( = х, скажем), отражена функцией правдоподобия /(0; х), и все выборки, дающие одно и то же правдоподобие, содержат одну и ту же информацию.
Если для любой пары 9\, 92 возможных значений параметра 9 отношение l(9i; х)/1(92; х) есть функция совокупности статистик 9\(х), 9\(х), ..., 9*(х) и оно не может быть представлено как функция меньшего числа таких статистик, то набор 9\, 9\, ..., 9* есть (минимально) достаточный для 9 [см. раздел 3.4].
Так, например, если X имеет распределение Пуассона, правдоподобие 1(9; х) принимает для выборки (Xi, х2, ..., хп) значение 1(9) = = fV/Пх/ и
КОд =
1(02) V 02 ’ ’
Следовательно, х — достаточная статистика для 9. Для выборки (Хь х2, ..., хп) из нормального распределения с параметрами (ц, ст) имеем
l(lM, <*1) Ml \ Г 1 f ( 1 1 \ „ 2 f 121 122 \
-------- = ( — ) ехр — — ( —-------= ) ---------) ^xi +
l(l22, <b) L 2 1 v а2 7 VCTi СТ27 '
202
откуда следует, что пара статистик Ех(, Ех) является минимальной достаточной статистикой для вектора 0 = (/z, ст).
4.13.2. ПРАВДОПОДОБНЫЕ ЗНАЧЕНИЯ И ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
а) Одинаково правдоподобные значения 0. Два значения 0', 6", для которых
1(6'; хь ..., х„) = 1(0"; Хх, ..., х„),
рассматриваются при данных значениях (хь х2, ..., х„) как одинаково правдоподобные (или одинаково неправдоподобные) приближения к неизвестному истинному значению 0; для дискретных данных равенство правдоподобий эквивалентно равенству
Р(Хх = xi, хп; 0') = Р(Хх = хь ..., хп = хп; 0").
Следовательно, вероятность получения именно тех значений, которые наблюдались, если истинное значение 0 есть 0\, равна вероятности получения этих значений, если истинное значение 0 есть 0'{ [см. 0' и 0" на рис. 4.13.1].
Эту аргументацию, оправдывающую рассмотрение значений 0' и 0" как одинаково правдоподобных, можно распространить с помощью предельного перехода и на случай непрерывных Хг.
б) Одно из значений 0 более правдоподобно, чем другие. Если
1(6\; Хх, х2, ..., х„) > 1(02; Хх, х2, ..., х„),
то значение 0х рассматривается в свете данных (хь х2, ..., хп) как более правдоподобное, чем 02, приближение к неизвестному значению 0, поскольку вероятность (или плотность вероятности) данных значений наблюдаемых величин будет больше при истинном значении 0, равном 0х, чем при 02. Таким образом [см. рис. 4.13.1], 0х более правдоподобно, чем 02, а 02 более правдоподобно, чем 03. При таком способе рассуждений наиболее правдоподобным будет значение 0тах. Это оценка наибольшего правдоподобия [см. гл. 6].
в) Недостаточно правдоподобные значения 0. Интервалы правдоподобия. Подход, развитый в предыдущих разделах, наводит на мысль, что значение 0, такое, что отношение 1(0)/1(0 тах) лишь немногим меньше единицы, является не намного менее правдоподобным, чем 0тах, в то время как значение 0, для которого 1(0)/1(0тъх) много меньше единицы, является, соответственно, много менее правдоподобным, чем 0тах. Мы можем, например, по соглашению установить следующий критерий неправдоподобия: любое значение 0, такое, что
W/^max) < 0,Ю,
203
будем считать неправдоподобным с уровнем правдоподобия 10%. Аналогично и для уровня правдоподобия 12,5% и т. д. Интервал (0t, 0и), такой, что
z(0)/z(0max) > 0,10, ot^o^ou,
будет рассматриваться как интервал, внутри которого с уровнем правдоподобия 10% любое значение 0 будет считаться правдоподобным приближением к неизвестному истинному значению 0. Для ббльшей аккуратности введем следующее определение.
Определение 4.13.2. Интервалы правдоподобия (один параметр). Для данных (Xi, х2, ..., х„), совместное выборочное распределение которых зависит от единственного параметра О, обозначим функцию правдоподобия через 1(6). Если существуют такие значения 0Z и ви, что
W/Z(0max) > 0,10 для 0/ =££ 0 =£5 ои, то интервал (0Z, 0Ы) называется 10%-ным интервалом правдоподобия для данной выборки (аналогично для интервалов других процентных уровней).
Если мы работаем с логарифмической функцией правдоподобия, важно заметить, что logZ(0) и 1(0) достигают своих максимальных значений в одной точке 0тах. В терминах логарифмической функции правдоподобия концы 0Z и 0М 0,10-интервала правдоподобия представляют собой корни уравнения
logZ(0) = log/(0max) + log(0,10).
Отметим, что в случае дискретной величины, распределение которой зависит от параметра, пробегающего континуум, как, например, Пуассоновское распределение, вычисление интервалов правдоподобия не вызывает тех трудностей, которые возникают при вычислении доверительных интервалов. Это показано в примере 4.13.3.
Пример 4.13.3. Интервал правдоподобия для параметра распределения Пуассона. В примере 4.13.1 функция правдоподобия выражалась как
1(0) ~ е~пв0п* , где О = х"
Границы 0Z, 0и 10%-ного интервала правдоподобия есть корни уравнения
е_„(й_Г)(0/-)Яг = 0>10
Например, если п = 10 и х = 2,4, придется решать уравнение
е-10(в-2,4)^/2>4)24 = 0>10
204
или, взяв логарифмы,
—100 + 24 + 241og0 — 241og2,4 = logO, 10, т. е.
100 — 241og0 = 5,29.
Корни (полученные приближенно) есть 1,5 и 3,6. Таким образом, для данной выборки наиболее правдоподобным значением 0 будет 2,4. Любые значения 0 в интервале (1,5 и 3,6) рассматриваются по соглашению как правдоподобные, а любые значения вне него — как неправдоподобные (уровня 10%).
Не все функции правдоподобия имеют горизонтальную касательную в точке максимума и не для всех существуют два значения 0Z и 0М, удовлетворяющие условиям определения 4.13.2. Рассмотрим пример.
Пример 4.13.4. Функция правдоподобия для семейства равномерных распределений. Предположим, что X распределена равномерно на интервале (0, 0), так что плотность распределения X есть
№; 0) =
г 1/0,
о
о х 0,
в другом случае.
Для выборки (Xi, х2, ..., хп) функцией правдрподобия будет
/(0) =
[ 1/0", 0
0 х, 0, 0 Хг 0,
в другом случае,
0 хп 0,
т. е.
/(0) =
' 1/0",
0
о ХМ 0, (т. е. 0 > х(и)),
в другом случае.
Здесь есть наибольшее наблюденное значение. График этой функции показан на рис. 4.13.2. В этом примере правдоподобие достигает максимума /тах, когда 0 = х(я), в точке, где кривая не имеет горизонтальной касательной.
В таком случае мы положим 0Z = х(л) и определим 0М (для уровня 10%) из уравнения
(х(л)/0)" = 0,10, т. е.
= 1о1'Хг
205
Рис. 4.13.2. Функция правдоподобия для верхней границы равномерного распределения
Рис. 4.13.3. Логарифмическая функция правдоподобия из примера 4.13.4
Например, если = 1,8 и п = 17, то 6и = 2,06.
Для количественного выражения интервалов правдоподобия не нужна глубоко разработанная теория выборочных расследований, подобная той, которая требуется для доверительных интервалов. В следующем Примере показано, что в некоторых случаях количественное определение доверительных интервалов связано со значительными вычислительными трудностями.
Пример 4.13.5. Пуассоновское распределение без нулевого значения. Пусть X имеет усеченное пуассоновское распределение без нулевого значения, так что его п.р.в. есть
Р(Х = г) = (—er/rl, г = 1, 2, ...
1 - е~в
206
[см. II, раздел 6.7]. Функция правдоподобия пропорциональна
/ ~в \п Л(0) = (—е—-в) 0s, 1 - е
О > о,
(4.13.5)
где 5 — сумма п значений X. (Это достаточная статистика для 6 [см. раздел 3.1].) Несколько минут несложных вычислений на карманном калькуляторе дадут таблицу значений логарифма величины (4.13.5), с помощью которой легко построить график логарифмической функции правдоподобия. Таблица 4.13.1 и рис. 4.13.3 иллюстрируют ситуацию, когда п - 20 и 5 = 40. Видно, что 0тах = 1,60 и что 10%-ный интервал правдоподобия для в есть (0,99, 2,39).
Таблица 4.13.1
в —log/, (в) в —log/, (9)
0,9 11,78 1,8 8,80
1,0 10,83 1,9 9,09
1,1 10,09 2,0 9,37
1,2 9,54 2,1 9,71
1,3 9,14 2,2 10,11
1,4 8,88 2,3 10,57
1,5 8,73 2,4 11,08
1,6 8,69 2,5 11,63
1,7 8,74 2,6 12,24
г) Интервалы правдоподобия для 0 и g(0). Из свойства инвариантности [см. пример 4.13.2] следует, что если (0/5 0М) есть 100р%-ный интервал правдоподобия для 0 при данных наблюдениях, то 100р%-ным интервалом правдоподобия для величины ф = g(0) при тех же наблюдениях будет (ф/, фи), где ф1 = g(0z) и фи = g(0M). (Здесь g(0) — любая взаимно однозначная функция 0.) Так, если в примере 4.13.2 10%-ный интервал правдоподобия для среднеквадратического отклонения о есть (1,2, 2,2), то соответствующий интервал для дисперсии ст2 есть (1,44, 4,84).
207
4.13.3. СИТУАЦИЯ С ДВУМЯ ПАРАМЕТРАМИ
Определение правдоподобия [см. определение 4.13.1] может быть обобщено на случай с несколькими параметрами, например с двумя, скажем, и 02. Символ 0 в определении 4.13.1 будем толковать как обозначение вектора (0Ь 02).
Пример 4.13.6. Нормальное распределение с двумя неизвестными параметрами. Пусть X — величина, распределенная по нормальному закону со средним g и дисперсией v. Правдоподобие /(g, v) пары (g, v) при данных Xi, х2, ..., х„ пропорционально
v_"/2exp [—Е (Xj — fi)2/2v] =
= v~"/2exp[ — ^[L(xj — x)2 + n(x — g)2]] =
= V n/1 exp — [a + n(fi — X )2] ,
где
a = E(x7 — x)2 - (w — l)s2 и n
X = EX:/n.
1 J
Рассмотрим случай, когда n = 10, x = 10, a = 20. Тогда логарифмическим правдоподобием будет
log/(pc, V) = — у n logv — у; — (g — X )2 -
, , 10 5(д — 10)2
= —5 logv------— —---------- .
° V V
Рис. 6.2.4 изображает линии уровня этой поверхности. Рис. 6.2.5 показывает ее рельеф.
Аналогом 10%-ного интервала правдоподобия из раздела 4.13.2, в) будет 10%-ная область правдоподобия, отмеченная на рис. 4.13.4 как 0,1/тах. Уровень логарифмического правдоподобия этой области будет, конечно, log/max — loge10. По соглашению, соответствующему 10%-ному уровню, все пары значений (g, v) внутри области будут рассматриваться как правдоподобные, а вне ее — как неправдоподобные. 208
4.14. БАЙЕСОВСКИЕ ИНТЕРВАЛЫ
С байесовской точки зрения [см. гл. 15] персональная оценка вероятности любого утверждения есть рациональная мера доверия к этому утверждению. Назначение вероятности каждому интервалу из множества Q возможных значений параметра равносильно взгляду на этот параметр как на случайную величину в том смысле, что вероятностные утверждения относительно этого параметра наиболее удобно могут высказываться в терминах его распределения вероятностей. Если назначение таких вероятностей происходит на основе знаний о параметре, имеющихся до проведения эксперимента, это приводит к концепции априорного распределения параметра с п.р.в., скажем, g\(0). Наблюдения (х,, х2, ...,х„), получаемые в ходе эксперимента, приводят затем к функциям правдоподобия £(0; хь х2, хп), определенной в разделе 4.13.1, и уточненные знания исследователя относительно 0 выражаются в терминах апостериорной п.р.в. g2(0 | Xi, х2, ..., хп), которая есть условное распределение [см. II, раздел 6.5] 0 при данных наблюдениях. По теореме Байеса [см. гл. 15] имеем
gi(0 | хь х2, ..., хп) = Agx(0)l{0-, хь х2, ..., хп), 0 € Q,
где А — нормирующая константа.
Так мы получаем для возможных значений 0 вероятностное распределение. В качестве оценки 0 мы можем выбрать либо моду (то значение, которое максимизирует апостериорную плотность распределения), либо математическое ожидание \0g2(0 \ х}, х2, xn)d0, либо значение, минимизирующее подходящую функцию потерь, и т. д. [см. гл. 15]. Неопределенность нашей оценки может быть выражена в терминах интервалов вероятности [см. раздел 4.1.3].
4.15. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Работы, на которые мы ссылались в разделе 3.6, вновь рекомендуются здесь. Применение функции правдоподобия рассмотрено в работе [Kalbfleisch (1979) — С], а байесовский подход — в работе [Lindley (1965) — С]. Ниже приведена литература, которую мы рекомендуем для усвоения материала этой главы.
209
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
В 1 у t h С. R. and Hutchinson D. W. (1960). Thbles of Neyman-shortest
Unbiased Confidence Intervals for the Binomial Parameter, Biometrika 47, 381.
В 1 у t h C. R. and Hutchinson D. W. (1961). • Thbles of Neyman-shortest
Unbiased Confidence Intervals for the Poisson Parameter, Biometrika 48, 191.
С 1 о p per C. J. and Pearson E. S. (1934). The Use of Confidence or Fiducial
Limits Illustrated in the Case of a Binomial, Biometrika 26, 404.
Crow E. L. and Gardner R.S. (1959). Thble of Confidence Limits for the Expectation of a Poisson Variables, Biometrika 46, 441.
E u d e у M. W. (1949). On the Treatment of Discontinuous Random Variables, Technical Report, No. 13, Statistical Laboratory, University of California, Berkeley.
Garwood F. (1936) Fiducial Limits for the Poisson Distribution, Biometrika 28, 437.
Crow E. L. (1956). Table for Determining Confidence Intervals for a Proposition in Binomial Sampling, Biometrika 43, 423.
Pearson E. £. (1950). On Questions Raised by the Combination of Tests Based on Discontinuous Distributions, Biometrika 37, 383.
Sc h e f f ё H. (1953). A Method for Judging all Contrasts in the Analysis of Variance, Biometrika 40, 87.
Scheff^ H. (1970). Multiple Testing Versus Multiple Estimation. Improper Confidence Sets..., Anais, of Math Statistics 41, 1.
Stevens W. L. (1950). Fiducial Limits of the Parameter of a Discontinuous Random Variable, Biometrika 37, 117.
Tocher K. D. (1950). Extension of Neyman-Pearson Theory- of Testing Hypothesis to Discontinuous Variables, Biometrika 37, 130.
Глава 5
СТАТИСТИЧЕСКИЕ КРИТЕРИИ
5.1. ЧТО ТАКОЕ КРИТЕРИЙ ЗНАЧИМОСТИ?
Критерии значимости (критерии проверки гипотез, иногда — просто тесты) — это, возможно, простейшие, но, конечно, наиболее широко используемые статистические средства. Обширна литература по этой тематике, но сколько-нибудь подробный обзор в подобной книге был бы неуместен. Мы ограничимся введением в основные понятия, несколькими иллюстративными примерами и изложением наиболее употребительных критериев. Другие, столь же общие критерии описываются в последующих главах при изложении соответствующих тем: например, используемые обычно в связи с дисперсионным анализом критерии рассмотрены в гл. 8 и 10. В настоящей главе лишь кратко упоминаются последовательные критерии, свободные от распределения критерии и критерии согласия, так как именно этим темам посвящены последующие главы.
Критерий значимости дает возможность статистику найти разумный ответ на вопрос, подобный следующему. В двух образцах стали, из которых один произведен методом А, а другой — методом В, средние пределы прочности неодинаковы. Указывает ли это обстоятельство на то, что производимая разными методами сталь различается по прочности, или же выявленное различие можно просто объяснить выборочными флуктуациями?
В этом примере поставлен вопрос, превосходит ли по прочности одна партия стали другую. Можно также задавать вопросы типа: «Превосходит ли по эффективности одно противогриппозное средство другое?», «Способствует ли отказ от курения снижению вероятности раковых заболеваний?», «Превосходит ли по воздействию одно удобрение другое при выращивании овощей?» и т. д.
В следующем разделе обсуждаются простые критерии проверки столь общих гипотез.
5.2. ВВЕДЕНИЕ В КРИТЕРИИ ПРОВЕРКИ ПРОСТОЙ НУЛЕВОЙ ГИПОТЕЗЫ ДЛЯ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ
В этом разделе вводятся основные понятия, относящиеся к простым критериям для дискретных распределений. Блестящее изложение этой темы содержится в [Kalbfleisch (1979) — С].
Непрерывные распределения обсуждаются в разделах 5.2.5 и 5.8.
211
5.2.1. ДВУХСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ. СОСТАВНЫЕ ЧАСТИ, ПРОЦЕДУРА И ИНТЕРПРЕТАЦИЯ
В следующем примере описан простой критерий, иллюстрирующий общий подход и основные понятия. В частности, вводятся ключевые понятия области значимости и уровня значимости. Рассмотрим исследование, в котором проводится сравнение частоты рождения мальчиков в индейских семьях английского города, в котором значительную долю населения составляют выходцы из Вест-Индии. Средняя частота по Великобритании составляет 52%. Исходные данные представляют собой упорядоченный по датам список всех новорожденных в индейских семьях за исследуемый год.
а) Вероятностная модель. Выбор подходящей вероятностной модели — это первый шаг при построении критерия. Мы примем простейшую возможную модель, а именно такую, когда рождения считаются взаимно независимыми испытаниями Бернулли [см. II, раздел 5.2.1], каждое из которых с одной и той же вероятностью, скажем р, приводит *к рождению мальчика. Для настоящего критерия эта модель в дальнейшем сомнению не подвергается. (Открытыми остаются такие вопросы, как возможность более частого появления новорожденных мальчиков у одной из возрастных групп матерей по сравнению с прочими, которые и сами могли бы составить содержание отдельного исследования; однако поскольку такая модель непосредственно не связана с критерием, то она и не обсуждается.)
Для формального описания модели пусть хг обозначает пол г-го ребенка, появившегося в последовательности п данных, причем для мальчика хг=1, а для девочки хг=0, так что обозначает общую численность мальчиков в выборке. Тогда при r= 1, 2,...,л значение хг представляет собой реализацию случайной величины Хг, имеющей распределение Бернулли [см. II, раздел 5.2.1]:
р(Л',=лг)=А1-/->)Ьл.
xr=0; 1,
а совместное распределение данных описывается формулой п
Р(Х=х, г=1, 2....п) =
' ' г= 1
Ex_z, ,п—
=Р Г(\—Р)
б) Сокращение данных. Статистика критерия. Работать одновременно с п составными частями информации неудобно. Стоит свести их в одну статистику, в связи с чем мы заменим исходную вероятностную модель, приведенную в п. а), сокращенной версией, а именно выборочным распределением этой статистики. Наиболее эффективное сокращение данных осуществляется с помощью достаточной для интересующего нас параметра (р) статистики, поскольку при таком сокращении информация не теряется. В нашей ситуации подходящей достаточной статистикой служит Ь0 = ^хг, т. е. зарегистрированная 212
численность мальчиков. Ее выборочное распределение, т. е. распределение соответствующей случайной величины В, реализацией которой и оказывается Ьо, имеет вид [см. II, раздел 5.2.2]
Р(В=Ь) = фрь(Д-р)п-ь,
(5.2.1) Ь=0, 1,...,и.
в) Нулевая гипотеза, нулевое распределение. Нужно ответить на вопрос: отличается ли величина р от среднего по Великобритании значения 0,52? Предпочтительнее иная формулировка этого вопроса, при которой он звучит так: согласованы ли данные с предположением, что р=0,52? Чтобы ответить на него, примем рабочую гипотезу, что величина р равна именно 0,52. Это предположение и называется нулевой гипотезой и обозначается так:
Н: р=0,52. (5.2.2)
Совместное распределение величин Хг, обусловленное этим предположением, получается, если подставить такое значение р в соотношение (5.2.1), что приводит к нулевому распределению Хг или распределению Хг при нулевой гипотезе Н, т. е.
Р(Хг=хп г=1, 2,...,я|Я>(0,52)^(0,48)л~Е\ Ехг=0, 1,...,л.
Нулевое распределёние статистики критерия получится, если взять (5.2.1) при отвечающем нулевой гипотезе значении р=0,52, т. е.
Р(В=Ь\Н) = $ ) (0,52)*(0,48)"-*,
(5.2.3) Ь=д, 1,...,л,
в нашем случае при п = 20.
В основе критерия лежит такая идея: если нулевая гипотеза и данные согласованы с довольно высокой степенью правдоподобия (в определяемом ниже смысле), то мы считаем, что она подтверждается данными; в противном же случае мы считаем, что гипотеза не согласована с данными, т. е. данные значимо отклоняются от гипотезы. То, что понимается под выражением «достаточно (или недостаточно) высокая степень правдоподобия», обсуждается ниже в п. д) и е).
В настоящем примере нулевая гипотеза оказывается простой: при ней значение параметра становится точно известным. (В пример входит только один параметр. При построении более «хитрых» критериев могли бы встретиться несколько параметров [см. раздел 8.3.3]. Тогда нулевая гипотеза называется простой, если она определяет значение всех параметров.)
Приведем пример критерия, для которого нулевая гипотеза сложная. Среди «1 новорожденных у матерей в возрасте 20—25 лет — Ь\ мальчиков, а среди новорожденных у матерей в возрасте 30—35 лет — Ьг мальчиков. Нужно проверить значимость различия частот Ь\/п\ и Ьг/п2. В этом случае нулевая гипотеза предполагает, что вероятность рождения мальчика одинакова для обеих групп. Однако это общее для обеих групп значение вероятности не определяется нулевой гипотезой, так что она не будет «простой». Этот и ему подобные критерии обсуждаются в разделе 5.4.1.
213
г) Альтернативная гипотеза. Цель критерия в том, чтобы усмотреть, можно ли считать данные согласованными с нулевой гипотезой или же они настолько сильно расходятся с ней, что даже опровергают ее. При этом важно знать, какое расхождение считать умеренным. В настоящем примере против Н можно выдвинуть так называемую альтернативную гипотезу вида
Н'р #0,52.
Таким образом, гипотеза Н отвергается для тех данных, в которых доля мальчиков существенно выше или существенно ниже, чем 0,52. В этом случае критерий называют двусторонним. (Пример одностороннего критерия приведен в разделе 5.2.3.)
д) Согласованность выборки с гипотезой Н. Исходный вопрос о согласованности л(=20) наблюдений с нулевой гипотезой (5.2.2) теперь можно заменить эквивалентным — о согласованности наблюденного значения д0(=5) с нулевым распределением (5.2.3). Это распределение унимодально, и для него близкая к центру область имеет высокую вероятность, тогда как его. хвосты — это области малой вероятности. Если значение В попало в имеющую высокую вероятность область, когда гипотеза Н на самом деле верна, то можно заключить, что выборка явно не опровергает гипотезу Н: она согласуется с Н. Однако если наблюдается крайнее, практически невероятное при Н значение Ъо, то это следует считать явным расхождением с Н.
Представленное здесь рассуждение — это обычное доказательство от противного в аристотелевой логике. В соответствии с ней, если из А следует В, то из не-В следует не-А для произвольных высказываний А и В. Статистический вариант этого принципа таков: если В — вероятностное следствие А, то не-А будет вероятностным следствием не-В. Возьмем в качестве суждения А высказывание «17 верна», а в качестве суждения В — «наблюденное значение Ь, вероятно, будет близким к моде нулевого распределения». Тогда статистический «закон исключенного третьего», или «принцип рассуждения от противного», утверждает, что гипотеза, вероятно, не верна, если наблюденное значение b удалено от моды нулевого распределения. Неясно только, какое крайнее значение b достаточно для отклонения гипотезы Н. Из вида исходного примера можно понять, что гипотеза Н отклоняется или для очень больших (близких к п) значений Ьо, или для очень малых (близких к нулю): критерий должен быть «двусторонним». Непонятно, однако, какие именно значения считать очень большими или очень малыми.
е) Области значимости, уровень значимости (вероятность значимости). Критическая область. Есть немало привлекательных подходов к определению значимости данного значения Ьо для отклонения Н. В качестве первой попытки можно было бы считать Ьо значимым в этом смысле, если вероятность Р(В=Ь0\Н) [обозначения см. в разделе 1.4.2] мала. Здесь, однако, возникает сложная ситуация: при достаточно большом объеме выборки вероятность Р(В=Ь\Н) обязательно 214
будет мала, каково бы ни было значение Ь. Следовательно, надо заменить вероятность одной точки Р(В=Ь\Н) эквивалентной мерой, которая стандартизована таким образом, что позволяет избежать осложнений. Добиться этого можно различными способами. Обычный путь состоит в том, что решение основывают на вероятности, которую Н приписывает специальному множеству возможных значений статистики критерия В, причем это множество выбирают так, что когда Н верна, то и его вероятность мала. Искомое множество состоит из всех значений, которые в известном смысле (см. ниже) еще более крайние, чем фактическое Ьо. Это множество называется областью значимости G(b0), а используемая для измерения значимости Ьо при отклонении гипотезы Н величина — это уровень значимости SL (Significance level), или SL(b0), определенный как вероятность принадлежности множеству области значимости, вычисленная в предположении, что справедлива нулевая гипотеза, т. е.
SL(bo) = P{B€G(6o)|//). (5.2.4)
Так определенный уровень значимости называют еще вероятностью значимости выборок, чтобы отличить от близкого понятия, используемого при подходе Неймана—Пирсона. Этот подход к проверке гипотез связан с теорией принятия решений. Он излагается в разделе 5.12.
Общая концепция, которую мы будем развивать, состоит в том, что выборка согласуется с нулевой гипотезой Н, когда вероятность значимости в определенном смысле велика, и не согласуется, когда эта вероятность мала [см. раздел 5.2.2].
Критическая область. Следует отметить, что специалисты по прикладной статистике часто не определяют область значимости и уровень значимости, отвечающий их данным. Вместо этого они находят условное множество значимости, которое при фактических наблюдениях имеет довольно низкий уровень значимости а (например, а=0,02) и тем самым обеспечивает высокую условную надежность отклонения (1—а) нулевой гипотезы [см. раздел 5.2.1, з]. Это условное множество значимости называется критической областью размера а. Вместо определения фактического уровня значимости своей выборки приверженцы такого подхода проверяют, не попадает ли статистика их критерия в критическую область. Если попадает, то говорят, что выборка на уровне а значима, а нулевая гипотеза отклоняется на уровне а; в противном случае говорят, что выборка на уровне а не значима.
Этот подход будет подробнее изложен в разделе 5.12.
Какие значения будут не менее крайними, чем Ьо? Определение области значимости осмысленно только тогда, когда разъяснена фраза «не менее крайние, чем». Для того чтобы осознать нетривиальность этого, предположим, что Ьо меньше, чем ожидаемое при Н значение. Например, при р=0,52 и п=20 ожидаемое значение равно 10,4, а наблюденное значение Ь=5 меньше его. Возможные значения, столь же или более крайние, чем 5, но меньшие (в том смысле, что они находятся на «нижнем хвосте») — это 5, 4, 3, 2, 1,0. Каково же соответствующее
215
множество на «верхнем хвосте»? Иначе говоря, как можно определить, что наблюдение Ь', которое больше, чем ожидаемое значение 10,4, столь же далеко (как большое наблюдение), сколь и b (но рассматриваемое как малое наблюдение)? Применяются такие методы.
Упорядочение по расстоянию. При таком подходе «большое» значение Ь\>Е(В\Н)) и «малое» b{<E(E\iI)) в равной степени значимы, если они одинаково отстоят от Е(В\Н)\ величины, отстоящие от Е(В\Н) дальше, чем любое из них, конечно, более значимы. Здесь Е(В\Н) обозначает математическое ожидание В при гипотезе Н, т. е. среднее ожидаемое значение распределения (5.2.3). Проблема сравнения обоих хвостов получает решение при следующем определении области значимости, порожденной наблюдением Ьо:
G(b.)= {b:\b—E(B\H)\ >\b0—E(B\H)\},
так что уровень значимости наблюдения Ьо равен
SL(bJ = P{B£G(b0)\H] =Р[[\В-Е(В\Н)\^Ь0-Е(В\Н)\]Н]. (5.2.5)
Участвующие в этом вычислении точки распределения В показаны на рис. 5.2.1.
Таким образом, если среди 20 новорожденных оказалось 5 мальчиков, г при нулевой гипотезе случайная величина В подчиняется биномиальному распределению Bin (20, 0,52) с пэпаметрами (20, 0,52), то Е(В|/7) = 10,4, а уровень значимости данных составляет
SL = P[{|B—10,4|>|5-10,4|}|77] = Р[{|В—10,4|>5,4}|//] = ^Р{В^5\Н]+Р{В>15,8\Н]=Р{В^5\Н}+Р{В>1Ь\Н] (5-2-6)
(см. рис. 5.2.1).
Из таблиц биномиального распределения [см. Приложение (Т1)] находим SL = 0,023.
Упорядочение по вероятности. Предположим вначале, что наблюдение Ьо случайной величины В «мало» в том смысле, что Ьо<Е{В\Н) (в представленном на рис. 5.2.1 примере b0 = 5, а Е (В|/7)=10,4, т. е. &о = 5 «мало»). При связанном с упорядочением по вероятности подходе значение Ьо сопоставляют с имеющим такую же вероятность, но «большим» значением Ь'о, если понимать «большое» в том смысле, что Ь'0>Е(В\Н), а равенство вероятностей рассматривают как условие
Р{В=Ь^\Н)=Р{В=Ь0\Н).
Может, однако, случиться, что при таком возможном значении Ьо точное равенство вероятностей не достигается. В нашем примере при &о = 5, когда при гипотезе Н распределение В оказывается биномиальным с параметрами (20, 0,52), возникает такая ситуация:
*0 (на нижнем хвосте) *0 (на верхнем хвосте)
Р(В=Ь0\Н)=0,00975 Р(В=15|/7)=О,02171 (>0,00975) Р(В=16|Я)=0,00735 (< 0,00975)
216
О
Наблюденное значение
9 10fl1
20
10,4 = = Е(В|Н)
Расстояние
5,4
5 6
Расстояние 5Л
"Равноотстоящая точка 15,8
Рис. 5.2.1. При гипотезе Н случайная величина В подчиняется биномиальному распределению с параметрами (20, 0,52), так что £’(В|/7) = 10,4. Значение 5 находится ниже Е(В\Н) на расстоянии 10,4—5=5,4. «Равноотстоящая» точка выше Е(В\Н} — это 10,4+5,4=15,8. Ближайшей к ней возможной реализацией, столь же крайней (или критической), как 5, служит 16. Множество точек, не менее крайних (или критических), чем наблюденное значение, — это (0,1,...,5) U (16,17,...,20).
Поэтому 15 — слишком малое, а 16 — слишком большое из возможных значений Ь'о, равновероятных с Ьо (см. рис. 5.2.2). В таком случае требование равенства вероятностей при Н значений Ьо и Ьо заменяется условием, что Ьо — наименьшее целое число, для которого
Р(В = Ь'о\Н) < Р(В= Ьо\Н). (5.2.7)
В рассматриваемом примере это приводит к значению &о = 16.
Порожденная наблюдением Ьо область значимости — это
G(b0)= {Ь’.Ь^ЬоПЛИ Ь^Ьо],
а уровень значимости наблюдения Ьо равен
SL=P(B^bo\H)+P(B^bo\H).
В нашем примере, когда из 20 новорожденных только 5 мальчиков, уровень значимости составляет
Р(В<5|Н)+Р(Р^16|Я)=0,023.
(Описанная процедура применима, когда наблюдение Ьо «мало». Если же оно «велико», то используется очевидная модификация.)
В этом примере величина SL одна и та же как при подходе, основанном на расстояниях, так и при подходе с применением «наименьших вероятностей». На самом деле оба подхода всегда приводят к одинаковым результатам, если нулевое распределение симметрично, и к почти одинаковым, когда нулевое распределение «почти» симметрично; различие возникает, только когда нулевое распределение имеет заметную асимметрию. В такой ситуации предпочтительнее упорядочение по вероятности.
217
0,02171
0,00975
0,00795
0 1 ... 4 5 6
"I I I
14 15 16 17 ... 20
Рис. 5.2.2. Часть биномиального распределения вероятностей с параметрами (20, 0,52), для которой Р(В=5)=0,00975
Упорядочение с помощью отношения правдоподобия. Для статистики критерия Ьо, представляющей собой реализацию биномиально распределенной случайной величины В с параметрами (п, р), функция правдоподобия для р [см. раздел 4.13.1] пропорциональна
1(р) = Рй°( 1 —р)п~Ьй.
В нашем случае Ъо = 5, а л=20, так что
1(р)=р\\-рГ,
а гипотеза Н состоит в том, что р=рн=0,52 и
/н=РМ1-Ря)15 = (0.52)5(0,48)>\
Когда р пробегает всю область (0^р^1), а величина Ьо фиксирована, максимум 1(р) достигается, если р принимает «наиболее правдоподобное» значение p=b0/n{=5/2Q=Q,25). Этот максимум равен:
Zmax = (O,25)5(O,75)15.
Отношение
X=zyzmax (5.2.8)
называется статистикой отношения правдоподобия. Ее значение для нашего примера равно
Х=(0,52/0,25)5(0,48/0,75)15 = 0,048.
При произвольном значении b случайной величины В статистика отношения правдоподобия принимает значение, скажем, Х(Ь), равное
X=№) ^р^-РнУ-"/ ("~=^ ) = (np„/i)» ((п-прнУ(п-Ь))
так что, когда л = 20, а ря=0,52, имеем
При основанном на отношении правдоподобия упорядочении значение b будет «более крайним» по сравнению с Ьо, если
\(b)<\(bo),
откуда область значимости — это
G(bo)={b:\(b)^\(bo)},
218
а уровень значимости равен
SLfb^PlBtGfbo)}.
(Это придает точную форму той мысли, что ожидаемое значение X должно быть большим, т. е. близким к единице, когда гипотеза Н верна, и малым, если Н неверна.)
Для удобства вычислений \(Ь) обычно заменяют на d(b)=—2\n\(b), и в этом случае областью значимости служит множество G^=W>W}.
В нашем примере возможные значения b и соответствующие значения d(b) связаны соотношением
d(b)=2Ып/7?/ пр^+2(п—Ь)\п {(п—Ь)/(п—прн)} = = 2dln(Z>/10,4) + 2(20—ft)ln(^=^-).
ь dfb) ь dfb) b dfb)
0 29 7 2,з 14 2,7
1 21 8 1,2 15 4,5
2 16 9 0,4 16 6,8
3 12 10 0,03 17 10
4 8,7 11 0,07 18 14
5 6,1 12 0,5 19 18
6 4,0 13 1,4 20 26
Наблюденное значение b0 = 5, a cf(5)=6,l. Меньшцм значениям 4, 3, 2, 1,0, отвечают значения d, не превосходящие 6,1; то же относится и к значениям 16, 17, 18, 19, 20. Таким образом, область значимости
G(5) = {0, 1, 2, 3, 4, 5, 16, 17, 18, 19, 20}= [b:b^5 или b> 16}.
Уровень значимости составляет
8Ь(5)=Р{В^5\Н}+Р{В>ЩН}.
Область значимости совпала с полученной при упорядочении по вероятности, а потому и критерий имеет тот же уровень значимости, т. е. 0,023. Это типичное явление для простых критериев такого вида. На самом деле метод отношения правдоподобия рассчитан на более сложные ситуации, в особенности на содержащие более одного параметра [см. раздел 5.5].
ж) Интерпретация уровня значимости. Степень доверия. В нашем числовом примере (5 из 20 новорожденных — мальчики) мы нашли, что SL=0,023. Как следует расценить это с точки зрения подтверждения или отклонения согласия данных с нулевой гипотезой
219
(5.2.2), в силу которой доля мальчиков среди всех выбранных новорожденных равна среднему по Великобритании значению 0,52? Если мы скажем, что это во многом — вопрос соглашения, наш ответ, возможно, вызовет разочарование. Однако на интуитивном уровне можно применить следующие рассуждения [см. раздел 5.3]. Если нулевая гипотеза Н верна, то неправдоподобно, что полученное значение статистики критерия заметно отличается от ожидаемого значения. Но, конечно, даже когда гипотеза Н верна, может оказаться, что в каком-то частном случае статистика критерия заметно отличается от своего математического ожидания; при этом уровень значимости будет мал. Однако и вероятность такого события тоже невелика. На самом деле при любом а вероятность получить уровень значимости, не превосходящий а, в точности равна а. Более строго [см. раздел 5.3], когда Н верна, то
P(SL^a) = a. (5.2.9)
Поэтому только в одном случае из тысячи значение SL окажется не более 0,001, когда верна гипотеза Н. Эта вероятность крайне мала. Разумно поэтому считать уровень значимости 0,001 достаточным доводом против принятия Н. В силу подобных причин на практике принята интерпретация уровней значимости в соответствии с приведенной ниже табл. 5.2.1. Из нее видно, что полученный в нашем числовом примере (5 мальчиков из 20 новорожденных) уровень значимости 2,3% достаточно низок, так что можно, не сомневаясь, отклонить нулевую гипотезу.
Если бы численность мальчиков составила для выборки 7, то основанный на подходе «равных расстояний» уровень значимости j\ оказался бы
Р[( |В-10,4| > |7—10,4|} |Я] = Р{ |В—10,4| >3,4|Я) =
= Р{В^7\Н] + Р{В^13,8\Н} = Р{В^7\Н} +Р[В^14\Н} =0,178.
Столь большое значение SL следует интерпретировать как согласие данных с нулевой гипотезой.
з) Степень недоверия. Отметим, что чем меньшее значение SL, тем сильнее это свидетельствует, в частности, против Н. Возможно, удобнее было бы принять прямое, а не косвенное измерение силы доводов против Н. Однако удобно это или нет, но уровень значимости слишком глубоко «укоренился», чтобы его можно было отбросить. Более того, с его помощью мы можем измерить то, что называется степенью недоверия к основной гипотезе Н. Она представляет собой дополнительную к уровню значимости величину:
степень недоверия к нулевой гипотезе Н~
= 1 — уровень значимости. (5.2.10)
Близкий к нулю уровень значимости интерпретируется как близость степени недоверия к 1, т. е. как очень сильный довод против Н. Близкий же к единице уровень значимости показывает, что степень недоверия близка к нулю, т. е. доводы против Н слабы, что фактически указывает на согласие выборки с нулевой гипотезой.
220
5.2.2. ТРАДИЦИОННАЯ ИНТЕРПРЕТАЦИЯ УРОВНЕЙ ЗНАЧИМОСТИ; ИСПОЛЬЗУЕМЫЕ НА ПРАКТИКЕ УРОВНИ ЗНАЧИМОСТИ;
КРИТИЧЕСКАЯ ОБЛАСТЬ
Традиционная интерпретация уровней значимости представлена в табл. 5.2.1. Это понятие обсуждается далее в разделе 5.3. Можно сказать, что эта схема отражает все оттенки возможного отношения к гипотезе со стороны статистика: от полной убежденности в ее ошибочности до признания того, что ясные доводы против нее вообще отсутствуют.
Т аблица 5.2.1. Традиционная интерпретация уровней значимости (SL)
SL Интерпретация
>0,10 Данные согласуются с Н.
=0,05 Возможна значимость. Есть некоторые сомнения в истинное-
ти Н.
=0,02 Значимость. Довольно сильный довод против Н.
=0,01 Высокая значимость. Гипотеза Н почти наверняка не под-
тверж дается.
Обратные таблицы. Точное вычисление уровня значимости зависит от возможности получить детальную информацию о функции распределения статистики критерия при нулевой гипотезе (здесь «при» означает «вычисляется в предположении, что нулевая гипотеза верна». Такое сокращение применяется часто). Из-за полиграфических ограничений таблицы могут дать меньше сведений, чем нужно статистику. Наиболее распространенным средством сокращения занимаемого таблицами места служит обратная табуляция с помощью процентилей (процентных точек [см. раздел 1.4.2]).
Практический эффект применения обратных таблиц состоит в том, что когда точная интерполяция невозможна, нельзя строго определить и уровень значимости данных, так что вместо этого приходится оперировать с неравенствами типа «уровень значимости лежит между 2,5 и 5%». Это не так плохо, как кажется, поскольку чаще всего простейшая интерполяция позволяет найти приближение (например, SL = 3%), которое оказывается достаточно точным во многих случаях.
Данные, значимые на уровне р. К сожалению, специалисты, применяющие статистические методы, часто вместо того чтобы отметить, что уровень значимости их данных лежит между 2,5 и 5%, сообщают лишь о том, что он менее 5%. Для этого используется выражение «данные значимы на уровне 5%» (аналогично и для других уровней). Подчеркнем, что в такой формулировке оно означает следующее: уровень значимости данных не более, чем 0,05 [см. также раздел 5.10].
Критическая область. Со сказанным выше тесно связан следующий способ описания статистического критерия: указать те значения статистики критерия, при которых уровень значимости в точности равен 100р%, например для р=1; 2,5; 5. Тогда совокупность точек, образующих множество значимости [см. раздел 5.2.1, е)] для такого специального наблюдения называется критической 100рЧъ-ной областью или областью отклонения гипотезы [см. раздел 5.10].
221
5.2.3. ОДНОСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ
В одной деревне в течение 1980—1981 гг. большую долю новорожденных — 25 из 35 — составляли девочки. Это сочли необычным явлением: в прессе давались разнообразные объяснения. Одно из них напоминало, что окрестности богаты кадмием, возможно, в виде микроскопических пылинок из ближайших каменоломен. Воздействие кадмия на организм отца повышает вероятность того, что новорожденный ребенок будет девочкой. Для проверки гипотезы о кадмии нужно было бы применить критерий значимости. Как и в разделе 5.1.2, при разумной вероятностной модели отдельные рождения рассматриваются как взаимно независимые испытания, в каждом из которых вероятность появления девочки неизменна. Соответствующая нулевая гипотеза Н утверждает, что р=0,48 (среднее по стране). Альтернативная гипотеза здесь гт „ 1п
Нс. р>0,48.
В данном примере вопрос о том, что р меньше 0,48, не представляет интереса.
Принимая, что вероятность рождения девочки равна р, вероятность появления последовательности У\, Уг,...уп новорожденных, где для девочки уг=1, а для мальчика уг=6, в выборке из п новорожденных составляет п
P(Yr=yr, г=1, 2...п)= ПрУг(1-ру-Уг=р^г(\-р)п-^ =
=р8(1—р)п~8, g=0, 1,...,л.
Здесь Yr — случайная величина, реализацией которой служит уг, а g=Xyr — общее число девочек в выборке. С помощью соответствующей достаточной статистики g произведем сокращение данных. Выборочное распределение статистики [см. II, раздел 5.2.2] имеет вид:
P(G=g) = (g)pS(i-p)n-g, g=0, 1...п.
При нулевой гипотезе распределение G задается формулой P(G=g\H„) = (2 )(0,48«0,52)”-г.
Поскольку мы интересуемся лишь тем, превосходит ли р значение 0,48, и этот вопрос возникает исключительно в связи с выборками, в которых число девочек не меньше ожидаемого значения G при Но (т. е. 0,48л), уровень значимости полученного значения g будет равен
SL=P{G>g\H0}.
Здесь не обязательно заботиться о нижнем хвосте распределения, и мы избегаем осложнений, описанных в разделе 5.2.2, е).
Для значений п и g (л = 35, g=25) уровень значимости равен:
35 /35\
Е 0 )(0,48)г(0,52)35-'=0,004.
Г=25
Эта вероятность очень мала, так что данные нужно считать весьма значимыми. Доводы против Но очень сильны. (Конечно же, нельзя считать, что это подтверждает гипотезу о влиянии кадмия*.)
* Приведенное рассуждение — только иллюстрация технического приема. Его нельзя считать серьезным обсуждением вопроса о влиянии внешних условий на вероятность рождения мальчиков и девочек. Среди большого числа деревень Англии непременно должны найтись такие, в которых в отдельные периоды соотношение полов среди новорожденных значительно отличается от 0,52:0,48. Поэтому первой реакцией на сообщение, которым открывается этот раздел, были предположения о случайных флуктуациях. Простейший способ решить, так ли это, — обратиться к статистике рождений за следующие годы. Если там будут отмечены значимые отклонения, тогда можно будет говорить об их неслучайном характере.—Примеч. ред.
222
5.2.4. КРИТЕРИИ О РАСПРЕДЕЛЕНИИ ПУАССОНА
Односторонние и двухсторонние критерии для проверки возможных отклонений параметра пуассоновского распределения от его гипотетического значения в принципе не отличаются от биномиальных критериев, описанных в разделах 5.2.2 и 5.2.4.
Рассмотрим эксперимент, в котором надо проверить, значимо ли превышает доля дефектной продукции в партии из п изделий требуемую норму 2%, если выборка объема 100 изделий из этой партии содержит 4 дефектных изделия. При нулевой гипотезе, согласно которой фактическая доля дефектных изделий равна 2®7о, число D дефектных изделий в выборке будет подчиняться гипергеометрическому распределению, в данном случае довольно хорошо аппроксимируемому [см. II, раздел 5.5] распределением Пуассона
P(D-r)=e~x\r/r\, r=0, 1,...
при Х=2. Здесь нужен односторонний критерий, так что уровень значимости данных равен:
SL=P(D^\H0)=P{D>4\D
подчиняется распределению Пуассона с параметром 2} =0,143 (из таблиц распределения Пуассона [см. приложение 2]). Это — большая вероятность. Результат не значим: данные согласуются с гипотезой относительно 2Q7o.
5.2.5. КРИТЕРИИ ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
До сих пор мы обсуждали только критерии для параметров дискретных распределений. Аналогичные методы применяются и для непрерывных распределений.
Пример 5.2.1. Значимость коэффициента корреляции. Пусть г обозначает выборочный коэффициент корреляции [см. раздел 2.5.7], полученный по извлеченным из двумерного нормального распределения [см. II, раздел 13.4.6] парам наблюдений (хь ух),...,(хп, коэффициент корреляции q неизвестен; таким образом,
г= {^Xjy—ИХ у } /V(Ех2—лх 2)(Еу?— пу2), где х = Еху/л, у =Еуу/л. Если нужно проверить, указывает ли наблюденное значение г на действительную коррелированность данных, то соответствующая нулевая гипотеза имеет вид:
Н: е=0.
Достаточно большое по абсолютной величине значение г будет стремиться опровергнуть нулевую гипотезу. На вопрос «Насколько большое?» легче ответить с помощью преобразования
При нулевой гипотезе выборочное распределение этой статистики есть распределение Стьюдента с п—2 степенями свободы [см. раздел 2.7.5]. Большие абсолютные значения г отвечают большим абсолютным значениям /, а поскольку выборочное распределение t симметрич-
223
но относительно точки О [см. раздел 2.5.5], то приведенные в разделе 5.2.J, п. е) соображения применительно к непрерывному распределению позволяют определить уровень значимости следующим образом: SL = P(T>\t\)+P(T^— |/|)=
= 2Р(Т> |/|),
где Т подчиняется распределению Стьюдента с п—2 степенями свободы, a t вы-
числяется в соответствии с (5.2.11) по выборочному ко-Рис. 5.2.3. Хвостовые площади, относящие- эффициенту корреляции г.
ся к примеру 5.2.1 Например, Фишер отмеча-
ет, что выборочный коэффициент корреляции между годовым урожаем пшеницы и осенним уровнем дождей за 20 лет составил в Восточной Англии г=—0,629. Соответствующее значение t (вычисленное по формуле (5.2.11) при л = 20) оказалось равным —3,433. Уровень значимости составляет 2Р(Т18 >3,433), где индекс 18 указывает число степеней свободы [см. рис. 5.2.3]. К сожалению, доступные таблицы значений функции распределения Стьюдента представляют собой разновидность обратных таблиц [см. раздел 5.2.2], что не позволяет легко вычислить нужную вероятность. Вместо вероятностей в таблицах приведены значения t,
которые должны соответствовать наперед заданным уровням значимости. Например, таблица Фишера в книге «Statistical Methods for Research Workers» содержит значения t, отвечающие величинам SL=0,01, 0,02, 0,05, 0,1, 0,2(0,1) 0,9*. Для 18 степеней свободы ближайшее табулированное значение — отвечающее SL- 0,01 и составляющее 2,878. Отсюда следует, что /=3,433 отвечает значение SL, которое меньше 0,01. Конечно, это значимо [см. табл. 5.2.1]: доверие к нулевой гипотезе заметно подорвано, а существование корреляции можно считать установленным. В этом примере то, что мы не смогли точно определить уровень значимости (а ограничились неравенством SL<0,01), не привело к большим неприятностям. Однако если бы выборочный коэффициент корреляции г оказался равным 0,468, чему соответствует /=2,25, то таблица показала бы только, что SL лежит между 0,05 (значение, соответствующее /=2,101) и 0,02 (значение, соответствующее /=2,552). Такой результат можно было бы сформулировать так: «значимость на уровне 5%, но не на уровне 2%». Следует всегда иметь в виду, что подобное многословие обусловлено исключительно структурой публикуемых таблиц и, грубо говоря, эквивалентно высказыванию, что SL равен 0,03 или 0,04 (если провести допускаемые таблицами интерполяции).
* 0,2 (0,1) 0,9 — сокращенное обозначение массива чисел, заключенных в диапазоне от 0,2 до 0,9 с шагом 0,1.—Примеч. пер.
224
Еще один момент, на который необходимо обратить внимание пользователям таблиц: в некоторых их вариантах (как, например, упомянутая выше таблица Фишера) предполагается, что проверяется двухсторонняя гипотеза, и дается соответствующее значение SL, т. е. 2Р(Т> |/|), тогда как в других таблицах приводится односторонняя вероятность Р(Т>|/|). Пользователь должен быть уверен, что он правильно понимает, о какой таблице идет речь.
Критерии для нормальных выборок обсуждаются в разделе 5.8. Однако следующий пример достоин особого внимания.
Пример 5.2.2. Значимость различия между выборочными коэффициентами корреляции. Предположим, что по двум выборкам объемом Л] и п2, извлеченным из двумерных нормальных совокупностей [см. II, раздел 13.4.6], получены выборочные коэффициенты корреляции Г] и г2, причем Г1#гг- Указывает ли это на то, что коэффициенты корреляции pi и обеих совокупностей различны? Соответствующая нулевая гипотеза
Н: q2 = q2, и вопрос сводится к тому, достаточно ли велико значение |г]—г?|, чтобы отклонить ее. Мы снова обратимся к преобразованию: известно,
с высокой степенью точности можно считать реализациями нормально распределенных случайных величин с математическими ожиданиями
„ 11 1 + б'
Г1 = —log-----,
2 1—Q2
J. 1 1 1 + б2 f2=±10g-------
2 1—q2
и дисперсиями 1/(И]—3) и 1/(л2—3) соответственно [см. раздел 2.7.3, б)]. Следовательно, при Н, т. е. при gn = q2, оказывается, что Zi—z2 будет реализацией нормально распределенной случайной величины с нулевым математическим ожиданием и дисперсией, равной примерно й)2={1/(Л1—3)+1/(л2—3)} [см. II, раздел 9.2]. Поэтому статистику Ui—z2)/o> можно считать наблюдением стандартной нормальной величины U [см. II, раздел 11.4.1]. Большие значения |zi—гг|/<» будут соответствовать неправдоподобным «хвостовым» значениям этого распределения, которые опровергают Но. При заданных Z\ и Z2 Уровень значимости равен:
SL=P(U> \Zi—Z2\/^+P(U< — |zi—Z2|/a?) = 27’(С7> |Zi— z2|/w),
* log — здесь и далее обозначает натуральный логарифм (по основанию е=2,718281828459045...), который часто в других изданиях обозначается как In.—Примеч. пер.
8 Заказ № 1123 225
если использовать соображения симметрии. Например, при г{=0,3, «1 = 10 и г2=0,6, л2 = 15 имеем Zi =0,31, z2=0,69, а o?=(l/7) + (l/12)= -0,226, так что о?=0,475 и |zi—z2|/<a=0,8, откуда
SL=2P((/> 0,8) = 0,42
из таблиц нормального распределения [см. приложение 4]. Эта вероятность большая. Различие между г, и г2 незначима. Поэтому здесь против нулевой гипотезы возражений не возникает.
5.2.6. ВЫБОР СТАТИСТИКИ КРИТЕРИЯ
Ниже приводится пример, в котором статистика критерия подбирается более явно, чем в примерах 5.2.1 и 5.2.2.
Пример 5.2.3. Проверка гипотезы о параметре экспоненциального распределения. Предположим, что имеется п реализаций х2,...,хп экспоненциально распределенной случайной величины X [см. II, раздел 11.2] с плотностью f(x)=0~ve~x/e(x>0). Нужно проверить нулевую гипотезу Н, в соответствии с которой 0-во, против односторонней альтернативы 0>0О. Функция правдоподобия имеет вид 0-ле~Ч/0, откуда s=Exz оказывается достаточной статистикой для 0 [см. раздел 4.13.1]. Это наводит на мысль, что $ или подходящее преобразование статистики s можно было бы использовать в качестве статистики критерия. Выборочное математическое ожидание s равно «0, так что $ измеряется в тех же единицах, что и 0, a s/n (=х — среднее выборки) будет хорошей оценкой 0: при Н большие значения s/n неправдоподобны, но они более вероятны, когда справедлива альтернатива. Итак, х — подходящая статистика критерия.
Чтобы найти уровень значимости, нужно знать выборочное распределение х. Плотность выборочного распределения определяется формулой [см. раздел 2.4]
g(s)-sn-le-s,9/{6n(n—1)’, s>0.
Таблицы соответствующей функции распределения не всегда доступны, но случайная величина z=2s/6 имеет плотность
Л(г)=(тз)”-'^!/2/(2Г(л)),
т. е. подчиняются распределению хи-квадрат с 2п степенями свободы [см. II, раздел 11.2.2, 11.4.11]. Таблицы соответствующей функции распределения вполне доступны. (Здесь Г<«> = («—1)!) Уровень значимости SL среднего выборки х —s/n равен
SL=P(X^x\H) =
(где X обозначает случайную величину, индуцированную статистикой X )
= P(S>s|H) =
(где 5=пХ)
=р(^2пх/е0), при этом x^=2S70o подчиняется распределению хи-квадрат с 2п степенями свободы.
226
С очевидными изменениями эти принципы применимы, когда альтернатива имеет вид 0<6О. Предположим, например, что суммарная продолжительность работы 18 электрических лампочек (допустим, что продолжительность подчинена экспоненциальному распределению) с номинальным сроком эксплуатации 100 часов составила 1500 часов. Здесь значение параметра в при нулевой гипотезе 0О= 100, а уровень значимости равен:
Лх236^ 3000/100) = Р(х236^ 30).
Стандартные таблицы распределения хи-квадрат [см. приложение (6)] дают
Р(х36^28,7) = 0,80, Р(х23б^31,1)=О,7О, (5.2.11а)
откуда
0,70<Р(Х236^30)<0,80, так что
0,20 <Р(х236< 30) <0,30.
В частности, уровень значимости превышает 0,20, следовательно, результаты не значимы. Данные не позволяют отвергнуть гипотезу, что средняя продолжительность работы лампочки равна 100 часам.
[В этом примере достаточны и неравенства (5.2.11а). Линейная интерполяция дала бы Р(х36<ЗО) = О,75. Однако если бы требовался более точный результат, то нужно было бы или воспользоваться более детальными таблицами, или применить подходящее преобразование, приводящее к случайной величине с более детально табулированным распределением. Наиболее известное из таких преобразований при р>30 [см. раздел 2.7.3, в)] дает следующее хорошее приближение с помощью стандартной нормально распределенной случайной величины U:
Ptfv>k) = P(U>u), где
и = (5.2.12)
/2/(9р) v ’
При f = 40 и Лг = 59,3, например, находим и= 1,956, так что обеспечиваемый приближением (5.2.12) уровень значимости равен 0,026. Точное же значение равно 0,025].
5.3. КРИТЕРИИ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ
Главное требование к качеству критерия состоит в том, чтобы он по возможности не отвергал истинную гипотезу, но зато с большой вероятностью отвергал бы ложную. До сих пор мы интуитивно верили, что наши критерии именно так и ведут себя. В этом разделе обсуждается объективное обоснование процедуры и уточняется, в каком смысле можно говорить, что один критерий превосходит другой.
227
5.3.1. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ
Чтобы не усложнять изложение материала математическими подробностями, сосредоточим внимание на простой ситуации, когда имеется вектор х=(х\, х2,...,хп) независимых наблюдений хг распределенной нормально с параметрами (в, 1) случайной величины, для которой проверяется нулевая гипотеза
Я(О):0-О (5.3.1)
против односторонней альтернативы 0>О. В этом примере возьмем среднее выборки х0 в качестве статистики критерия, а областью значимости будет служить совокупность G(xb) возможных значений среднего выборки, превышающих наше значение х0:
G(^) = {х: Е хг^пх0], (5.3.2)
где вектор х представляет выборку. Уровень значимости (скажем, Zo) статистики х0, как и в (5.2.4), равен
Zo = SL(xo)=P{X €G(^)|/7(0)] =Р{Х >Ло|% нормальна
с параметрами (0,1/7л)}. (5.3.3)
Здесь X обозначает случайную величину, индуцированную выборочным средним; она нормально распределена с параметрами (0, где 0=Е(Х), а при Н(0) и 0=0. В результате получаем
Zo=SL(xo)=1 -Ф(х07й), (5.3.4)
где Ф, как обычно, обозначает функцию стандартного нормального распределения [см. II, раздел 11.4.1]. Этот уровень значимости полностью определяется статистикой х&Гп, поэтому и сам он оказывается статистикой; мы подчеркнем это обстоятельство, называя его при необходимости статистикой уровня значимости. Сама же статистика представляет собой реализацию случайной величины уровня значимости Z=SL(X), т. е. _ _г_
Z=SL(%)=1—Ф(Х7й). (5.3.5)
Нелишне отметить, что хотя уровень значимости Zo статистики х0 по определению равен вероятности, вычисленной в предположении справедливости нулевой гипотезы
Я(0): £(.¥)=О
[см. (5.3.3)], выборочное распределение Zo, т. е. распределение Z, зависит от истинного (неизвестного) значения (скажем, 0) математического ожидания Е(Х). Это распределение (посредством функции распределения) определяется как
P(Z^z|0)=Q(z, 0)
(O^z^l).
Когда 0=0, т. е. верна нулевая гипотеза, имеем
_ Q(z, 0>P(Z^z|0) =
= Р{ 1—Ф(Х <л) Ф(Х <л) > 1 —z|EW=0 ] =
=P{XJn>u(z)\E(X)=Q} = \—Ф(и(гЛ [см. (5.3.5)]
(здесь Ф(м(гЛ = l-~z) =
228
(так как XFn при Е(Л)=О распределена по стандартному нормальному закону)
= Z O^z^l- (5.3.6)
Таким образом, когда верна гипотеза Н(0), уровень значимости имеет равномерное на (0, 1) выборочное распределение, а вероятность получить малое значение z уровня значимости (скажем, меньше 0,01) соответственно мала (для приведенного выше примера — это один шанс из ста). Тем самым шанс отклонить гипотезу //(0), когда она на самом деле верна, очень мал.
Таким образом, критерий описанного типа удовлетворяет первому из сформулированных в начале раздела 5.3 условий. Что же можно сказать о втором условии, т. е. будет ли критерий с высокой вероятностью отклонять ложную гипотезу? Чтобы ответить на этот вопрос, вычислим выборочное распределение уровня значимости для неопределенного значения 0. Вероятность того, что уровень значимости окажется не больше z, когда истинная величина Е(Х) равна 0 — это
Q(z, 0)=P(Z^z\0)=P{l^(X\Fn)^z\0} = =Р{А’Ул>Ф~1(1—z)|0] = (применяем (5.3.5)) (так как функция Ф монотонно возрастает)
= 1—Ф{ф-’(1— Z)—0>Гп}, (5.3.7)
поскольку X у/п—0Fn подчиняется стандартному нормальному распределению.
Чтобы интерпретировать это, полезно рассмотреть значения Q(z, 0) при фиксированной величине Z (скажем, Zo) и всех возможных допустимых значениях 0. (В «одностороннем» примере допустимые значения 0 — только неотрицательные.) Для выбранного фиксированного значения Zo уровня значимости среднего выборки х0 имеем
ZO = SL(X))=P{X нормальна с параметрами (0, 1/7л)} = (где п — объем выборки)
= 1—Ф(^\/л),
а значение Q{Zo, 0), определенное формулой (5.3.7), сводится к
eta, 0)=1-Ф((л5-0)<л), (5.3.8)
причем в силу (5.3.6)
Q(z0, 0) = 1 — Ф(х^п) = Zo-
Ниже будет показано, что значения функции Q(Zo, 0) измеряют, в какой степени процедура проверки, гипотез позволяет обнаружить отклонения 0 от гипотетического нулевого значения (т. е. различать значения параметра 0). По этой причине Q(z> 0) называется функцией чувствительности критерия. (На самом деле численно она совпадает с функцией мощности в теории Неймана—Пирсона проверки гипотез [см. раздел 5.10], но интерпретируется несколько иначе.)
Предположим, что нормальная выборка объема л = 20 привела к среднему выборки ль = 0,458. Известно, что исходное распределение
229
имело единичную дисперсию. Ожидаемое значение (в) — это неизвестный параметр, равный согласно нулевой гипотезе 0 = 0. Уровень значимости выборки при такой гипотезе составляет
z0 = SL(xo) = Р(Х 0,4581^ нормально распределена с параметрами (0, 1/720))= 1—Ф(0,458-4,472) =
(так как 720 = 4,472)
= 1— Ф(2,048) = 0,02.
Вот некоторые из вычисленных по формуле (5.3.8) типичных значений функции 0(0,02, 0):
0(0,02, 0)= 1—ф {(0,458—0)4,472}
в 0 0,2 0,4 0,6 0,8 1,0
0(0,02, 0) 0,020 0,125 0,398 0,737 0,937 0,992
Возникают следующие вопросы:
1) Значение 0(0,02, 0) равно уровню значимости 0,02. Это «малая» величина. Ее смысл таков: если бы нулевая гипотеза была верна (т. е. истинное значение было бы 0 = 0), то вероятность получения уровня значимости 0,02 или менее была бы в точности равна 0,02. Эквивалентно это можно выразить, сказав, что вероятность получить сильные доводы против Н(0) (силы 0,98) мала (фактически равна 0,02). При процедуре проверки невероятно получить сильные доводы против верной гипотезы.
2) 0(0,02, 1,0)=0,992. Это вероятность (весьма высокая) получить уровень значимости 0,02, когда нулевая гипотеза далека от истины (0=1,0, тогда как гипотеза 7/(0) утверждает, что 0=0). Уровень значимости 0,02 можно считать сильным доводом против гипотезы 77(0). Таким образом, видно, что критерий почти наверное обеспечивает сильные доводы против 77(0), когда Н(О) далека от истины.
3) То же относится, хотя и в меньшей степени, к ситуации, возникающей, когда 77(0) неверна, но ближе к истине, чем в п. 2); например, при 0 = 0,6.
4) Когда 77(0) еще ближе к истине, например, если 0=0,4, процедура приобретает некоторую неопределенность, поскольку только (грубо говоря) в 40% случаев она обеспечивает доводы против 77(0) силы 0,98 и, конечно, в 60% случаев таких доводов не будет.
Понятно, что критерий, который в большом числе случаев обеспечивает сильный довод против «только слегка ложных» гипотез и при котором невозможно получить сильные доводы против заведомо истинной гипотезы, будет чувствительным при различении близких к нулю значений 0. Тем самым функцию Q(Zo, можно назвать функцией чувствительности критерия.
230
Однако не все критерии одинаково чувствительны. Это можно показать с помощью критерия, статистика которого представляет собой среднее (скажем, х0) первого и последнего наблюдений в выборке без учета остальных наблюдений. Ясно, что этот критерий будет обладать теми же свойствами, что и основанный на среднем выборки критерий из предыдущего примера, когда объем выборки п=2. Следовательно, его функция чувствительности в силу (5.3.8) равна
Q'(z0, 0) = 1 —Ф(Хо<2—(9V2). (5.3.10)
Для того же, что и в (5.3.9), уровня значимости Zo = O,O2 ниже приведены значения функции Q'(Zo, 0)’
в 0 0,2 0,4 0,6 0,8 1,0 2,0 3,0
а(0,02, 0) 0,020 0,039 0,069 0,115 0,180 0,264 0,118 0,014
Этот критерий имеет тот же уровень значимости 0,02, что и критерий, основанный на выборке объема 20, функция чувствительности которого табулирована в (5.3.9). Но значения Q' меньше соответствующих значений Q. Это показывает, что для любых положительных 0, какова бы ни была степень ложности гипотезы, более правдоподобно, что она будет отклонена первым критерием, а не вторым (при котором используется лишь часть данных). Аналогичные результаты справедливы и для других уровней значимости z. (Тот факт, что QU, 0) < Q'(z, 0) при отрицательных 0, не относится к делу, поскольку односторонний критерий допускает лишь положительные конкури-
231
рующие значения параметра 0.) Вид функций чувствительности Q(z, 0) при фиксированной для обоих критериев общей величине уровня значимости z представлен на рис. 5.3.1. Функция чувствительности Q(z, 0) критерия при z-a принимает те же значения (но имеет иную интерпретацию), что и функция мощности W(0) критерия уровня а в теории Неймана—Пирсона [см. раздел 5.10].
5.3.2. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ОДНОСТОРОННЕГО КРИТЕРИЯ ДЛЯ ВЫБОРКИ ИЗ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ С ПАРАМЕТРАМИ (О, о), КОГДА ЗНАЧЕНИЕ а НЕИЗВЕСТНО
При изложении материала в разделе 5.3.1 мы стремились разъяснить принципы, составляющие содержание анализа чувствительности, по возможности без математических подробностей. Это удалось, поскольку речь шла о проверке гипотез относительно величины математического ожидания 0 распределения N(0, 1) — единственного нормального распределения, встретившегося в вычислениях. Теперь кратко наметим вычисления для более реальной ситуации, когда исходное распределение — N(0, о), а величина о неизвестна.
Определим Х}, Х2,...,Хп как независимые случайные величины, каждая из которых нормальна с параметрами (0, ст), и пусть
X=(Xit Х2,...,Хп), Х=£х,/п, a S2=E(Xr—Х)2/(п— 1).
Положим __
T = Xny2/S.
Мы проверяем гипотезу
Н(0): 0 = 0,
которая ничего не предполагает относительно о.
Пусть X], х2,...,хп — типичная реализация случайных величин Хг, п п
х=(х}, х2,...,хп), х = Lxr/n, s2=E(xr—х)2/(п—1), a t'=xny2/s. Предположим, что вектор наблюдений и соответствующие статистики для нашей выборки приняли значения х0, и /о=^л1/2/5,о- Тогда аь — оценка 0, a — оценка ст2; при этом t'Q — значение отношения Стьюдента. Если 0=0, то последняя величина представляет собой реализацию распределения Стьюдента с п—1 степенями свободы; ее значение будет с гораздо большей вероятностью находиться около нуля, чем увеличиваться (при условии, что 0=0), так что мы будем считать, что большие значения t' приводят к отклонению нулевой гипотезы.
Таким образом, в качестве области значимости выбирается множество вида
G(t0)= {x:Z ^t0}.
Уровень значимости (SL) вектора выборки х0 равен
Zo = P{T/£G(to)\0 = O]=P{T''^to\T' подчиняется распределению Стьюдента с (п—1) степенями свободы] = 1—^я_1(^о),
где ^„_x(t) обозначает функцию распределения Стьюдента с п—1 сте-232
пенями свободы, вычисленную в точке t. Так что случайная величина
Z уровня значимости равна:
Z=l-
[ср. с (5.3.5)], функция чувствительности — это
Q(z, 0) = P(Z<z\0)=P{*n_x(T'^-z|0) = Р{Т £)|0).
Здесь T=Xnl/2/S. Когда Е(Х)= 0, случайная величина (X—0)n1/2/S имеет распределение Стьюдента с п—1 степенями свободы, так что Т подчиняется нецентральному распределению Стьюдента с п—1 степенями свободы, а параметр нецентральности Х=Х(0, п) определя-
ется формулой
Х(0) = Х(0, п) = — 0п'/2/а
[см. раздел 2.8.3]. Обозначим функцию этого распределения в точке w
символом
так что
НП_Х{Ч Х(0)),
[ср. с (5.3.7)]. Когда 0 = 0, эта величина превращается в euo, o)=i-^_1(c'i(i-^o)),
поскольку Х(0) = 0, а нецентральное распределение Стьюдента с функ-
цией Нп_х {w, Х(0)} становится обычным «центральным» распределением Стьюдента, имеющим функцию распределения (и/ Таким
образом,
Q(z0, 0) = 1 — (1 —Zo) =Zo,
откуда Q(Zo, 0) представляет собой уровень значимости, как и в ранних примерах [ср. с (5.3.6)].
Например, 5^ = 0,458, so=UOO, л = 20 и t'o = 0,458^20 = 2,048, то уровень значимости равен
Р{Т>2,048|Т подчиняется распределению Стьюдента с 19 степенями свободы } =0,022
(из таблиц). Это малая величина; вероятность получить столь малое значение, если бы Н(0) была верна, составляет 0,022 и, что эквивалентно, сила доводов против //(0) равна 0,978. Поэтому результат не может быть следствием //(0); тем самым получен существенный довод против гипотезы, а значит, ее можно считать отвергнутой.
Вероятность получить довод силы 1—z против 7/(0), когда Е(Х) = 0, равна вероятности получения уровня значимости z или менее; эта вероятность выражается функцией Q(z, 0), численные значения которой можно найти в таблицах нецентрального распределения Стьюдента с п—1 степенями свободы и параметром нецентральности X. Поведение функции показано на рис. 5.3.1.
5.3.3. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ДВУХСТОРОННЕГО КРИТЕРИЯ
В разделе 5.3.1 применительно к выборке (xit х2,...,хп) из совокупности N(0, 1) обсуждался вопрос о значимости среднего выборки х в связи с нулевой гипотезой 0=0, когда альтернативой была односторонняя гипотеза 0>О.
233
Если бы при альтернативе параметр 6 мог бы принимать значения как <0, так и >0, то мы имели бы двухсторонний критерий. Так что теперь мы предполагаем, что альтернатива на самом деле двухсторонняя. В таком случае отвечающая (5.3.3) статистика уровня значимости равна
z0 = SL(^) = 2P{x > |^||
X нормальна с параметрами (0, 1)) =
=2(1- Ф(|ль|Л)|. (5-3.11)
Функция выборочного распределения Zo при 0=0 — это Q(z, O)=P(Z^z|0 = O), где Z — индуцированная Zo случайная величина, т. е.
Z=2{ 1—Ф(|Х |Vn)}.
Таким образом,
Q(z, 0)=Р[2{1—Ф(|Г|<п)}^|0=О]=Р{Ф(|Г|<п)>1—-|-z|0=O} = = Р{ |Х|7й>Ф-1(1— 4-z)|0=O) =2Р{Х<л^Ф-1(1—) = (считая величину х (для определенности) положительной)
_ =2[1-ф|ф-1(1—h))]=
(так как Х\/п нормальна с параметрами (0, 1))
=z, (O^z^l). (5.3.12)
Аналогичный результат был получен в разделе 5.3.1 для одностороннего критерия: когда нулевая гипотеза верна, уровень значимости имеет равномерное на (0, 1) выборочное распределение.
Выборочное распределение, когда параметр 0 не обязательно принимает нулевое значение, следующее:
P{Z^z\0}=Q(z, 0)=
= Р[2и-Ф(|Х|<й)}^|0] =
= Р{|Аг|^>Ф-1(1-4-£)|0} =
= Р{Х<л>Ф-1(1—2-z)|0) +P{XV7?^—Ф-41—4-z)|0} =
= 1 —Ф {Ф—1 (1 —yz)—&<п} + + 1— Ф{ф-1(1—4-г) + 0<л),
поскольку при Е(Х) = 0 случайная величина Х\п нормальна с параметрами (6^1, 1). Если теперь, как при односторонней альтернативе, зафиксировать значение z=z0, т. е. взять такое Zo, при котором справедливо соотношение (5.3.11), так что
1—2*го = Ф(|^|<й)
и 1
Ф-1(1—2^о)=
то функция Q(z0, 0) примет вид
Q(z0, 0) = 2—Ф{(|ль|—0)V«}—Ф{(|^1 + 0)^} (5.3.13)
234
Рис. 5.3.2. Функции чувствительности для двухстороннего критерия
Это соотношение представляет собой аналог (5.3.8) для двухстороннего критерия. График зависимости Q(z, 0) от 0 при фиксированном z приведен на рис. 5.3.2. Он показывает, что вероятность получить сильные доводы против гипотезы Ho:0 = Q, когда Е(Х)=0, возрастает при увеличении |0|. Анализ ситуации, когда дисперсия исходного распределения неизвестна, можно, как и в разделе 5.3.2, провести с помощью нецентрального распределения Стьюдента.
[При заданном уровне z функция чувствительности принимает те же значения, что и обсуждаемая в разделе 5.10 функция мощности, но они интерпретируются по-разному.]
5.4. КРИТЕРИИ ДЛЯ СЛОЖНЫХ НУЛЕВЫХ ГИПОТЕЗ
В предыдущем разделе обсуждались примеры, относящиеся к таким ситуациям, когда для заданной вероятностной модели нулевая гипотеза полностью определяла «нулевое распределение», или «распределение при нулевой гипотезе». Но обычно встречаются примеры, в которых это неверно. Тогда говорят, что нулевая гипотеза — сложная. Подобные ситуации возникают как для однопараметрических, так и для многопараметрических моделей. Примером первого типа служит сравнение биномиальных частот*, когда при нулевой гипотезе параметры pi и р2 биномиальных распределений равны. Примером нулевой гипотезы в многопараметрической ситуации служит такая: математическое ожидание нормального распределения равно нулю, а стандартное отклонение неизвестно и при гипотезе не уточняется (пример «мешающего параметра»).
* Этот пример фактически относится к двухпараметрической ситуации, поскольку совместное распределение пары наблюдаемых частот зависит от векторного параметра р2).—Примеч. пер.
235
5.4.1. УСЛОВНЫЕ КРИТЕРИИ: РАВЕНСТВО БИНОМИАЛЬНЫХ ЧАСТОТ; ОТНОШЕНИЕ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ ПУАССОНА
Стандартный способ, позволяющий преодолеть связанные со сложной нулевой гипотезой затруднения, состоит в том, чтобы работать с подходящей версией условного нулевого распределения. Лучше всего пояснить это примерами.
Пример 5.4.1. Критерий равенства биномиальных частот. При изучении зависимости вероятности появления ребенка мужского пола от возраста матери было отмечено, что в выборке из т новорожденных у матерей в возрасте от 20 до 25 лет оказалось х0 мальчиков, тогда как в выборке объема л, где возраст матери был заключен между 30 и 35 годами, число мальчиков составило у0 [ср. с разделом 5.2.1, в)]. За основу возьмем вероятностную модель, описываемую распределением Bin (т, pi) [см. II, раздел 5.2.2] для мальчиков, родившихся от более молодых матерей, и независимо [см. II, § 6.6] от них — распределение Bin (п, р2) для остальных, так что плотность совместного выборочного распределения* х0 и у0 в точке (х, у) равна
(х) $)р\ (У-Рх)т~хРУ1 (Д-Р1)п-у.
При нулевой гипотезе Н, т. е. при Р\=Рг (обозначим это общее значение р), эта плотность принимает вид
Ах, у)=(?) (Р)^^(1-рГ+я-^.
Понятно, что х+у будет достаточной статистикой для р [см. пример 3.4.1], так что условное совместное распределение х и у при заданном значении x+y=s не зависит от р. На самом деле условная плотность равна
8(Х> y'S)= PfS-s) ’ =
где случайная величина S индуцирована статистикой s.
Поскольку (при Н) случайная величина S подчинена распределению Bin (т + п,р), имеем
P(S=s) = (ms(l-p)n^n-s,
°ткуда (П
(*+>’=s)-
Здесь y~s—х, так что на самом деле получается одномерное распределение, которое можно представить в виде
h(x\s)=-~—j^’ х=0, l,...,min (т, s) (5.4.1)
* Здесь и далее для принимающих целочисленные значения случайных величин плотность понимается относительно «считающей» меры (вообще говоря, не конечной, а лишь ст-конечной), которая приписывает единичные массы точкам 0, 1, 2 —При-меч. пер.
236
Свободное от параметра (гипергеометрическое [см. II, раздел 5.3]) распределение и будет требуемой условной версией нулевого распределения. Полезно отметить, что оно описывает вероятность получить х дефектных изделий в выборке объема 5, извлеченной без возвращения из совокупности, содержащей т дефектных и п недефектных изделий. Таблицы гипергеометрического распределения доступны [см., например, Liebermann and Owen (1961)—G].
Биномиальное приближение. Гипергеометрическое распределение зависит от трех параметров: т, п и $, так что обычно таблицы оказываются громоздкими. Если s мало по сравнению с т и п, то вероятности не будут очень сильно отличаться от получаемых результатов для выборки с возвращением, так что в такой ситуации h(x\s) можно приблизить величиной b(x; s, р) — вероятностью (Bin (s, р)) с параметром р=т/(т + п), т. е.
h(x\s) == b(x; s, р) = (£)р*( 1 —рУ~\
(5.4.2) x=0, 1,р=т/(т + п),
если только
5«min п). (5.4.3)
Эти вероятности можно легко вычислить с помощью рекуррентных отношений _
b(x+1; s, р) = ()(~~ )b(x; s, р),
р/ (5.4.4)
х=0, l,...,s—1, либо получить из сравнительно компактных биномиальных таблиц [см. приложение 1].
Примером, когда биномиальное приближение (5.4.2) не применимо к гипергеометрическому распределению (5.4.1), может служить ситуация, при которой ш = 15, п = 20, 5=17. Значения /1(х|17) представлены в табл. 5.4.1.
Значение х()=10 лежит на верхнем хвосте, и вероятность столь же или более критических в этом направлении значений составляет А(1О) + Л(11) + ... + Л(15) = 0,0647. Используя «упорядочение по вероятности», как в разделе 5.2.1, п. е), можно видеть, что вероятность столь же или более критических, но в противоположном направлении (на нижнем хвосте), как х0, значений представляет собой сумму А(4) + Л(3) + ... + А(О), так как /1(4) — наибольшее из нижних значений, не превышающее А(10). Приведенная нижняя «хвостовая» сумма равна 0,0276. Поэтому уровень значимости составляет
SL =0,0647 + 0,276 = 0,0923.
Получена довольно большая вероятность, откуда следует, что результаты не значимы, т. е. данные не опровергают нулевую гипотезу относительно равенства pi -р2.
237
Таблица 5.4.1 Значения Л(х)=Л(х|17)
X h(x) X h(x) л h(x)
0 0,0000 6 0,1852 12 0,0016
1 0,0000 7 0,2620 13 0,0001
2 0,0004 8 0,2381 14 0,0000
3 0,0039 9 0,1389 15 0,0000
4 0,0233 10 0,0513 Полная масса
5 0,0834 11 0,0117 =0,9997
(Полная масса отлична от 1,0000 из-за ошибок округления.)
Пример 5.4.2. Критерий для проверки равенства параметров распределений Пуассона. Как и в предыдущем примере, нулевая гипотеза утверждает, что неизвестные параметры двух распределений Пуассона равны, и оказывается сложной, так что для ее проверки можно использовать условное нулевое распределение.
Предположим, что получены наблюдения х'2,...,хт пуассоновской случайной величины X [см. II, раздел 5.4) и у\, у2,...,у'т— другой пуассоновской величины Y. Пусть и 02 — соответствующие неизвестные параметры. Нужно проверить нулевую гипотезу, что 0i=02 (их общее значение обозначим 0). Для принятой вероятностной модели плотность* совместного выборочного распределения данных в точке (л-,, х2,...,хт; yit у2,...,уп) задается формулой
е-^,-^0! Ч02Е У((Пх,! )(Пуу!)).
Нулевая гипотеза
//:0,=02(-0)
проверяется против альтернативы 0154 02. Теперь мы должны выбрать статистику критерия [ср. с разделом 5.2.1, г)]. В данном случае она будет двумерной. Поскольку
51 = EXj И S2 = tyj — достаточные статистики [см. раздел 3.4] для 0! и 02, данные можно сократить и рассмотреть статистики
s'l-YXj и в2=£у/.
В результате совместное распределение данных можно заменить более простым, но эквивалентным выборочным распределением 51 и s2. Поскольку эти величины представляют собой суммы пуассоновских случайных величин, то они также подчиняются распределению Пуассона [см. табл. 2. 4.1] с параметрами тОх и л02 соответственно. Их совместное распределение имеет в точке (s,, s2) плотность
е~тв -"ЦтбдЧпбг)^/^! 52!).
* Плоз'ность по считающей мере на множестве (0, 1, 2...}—Примеч. пер. 238
При нулевой гипотезе (0!=02 = 0) эта плотность (плотность нулевого распределения) принимает вид
f(Si, s2) = e~(-m+n}efns'ns2ds'+sV(Sil s2!).
Теперь перейдем к условному распределению. Заметим, что s=S] +s2 служит достаточной статистикой для 0 при нулевом распределении, откуда свободное от параметра 0 условное распределение Si и S2 при заданном значении Si + S2 можно найти так:
P(S\—S\f S2—s2\S\+S2=s).
Поскольку (при Н) статистика Sj+S2 подчиняется распределению Пуассона с параметром (т + п)6, условное нулевое совместное распреде-
ление Si и S2
На самом s2=s—$i. Его
имеет вид
g(s15 52|s)= у
деле это распределение будет одномерным, так как плотность можно записать в виде
h(Sl\s)=
5i!52! т + п' 'm + n' =
= (s,)/^'( 1 —py~s', P = m/(m + n),
(5.4.5)
S2=S—51.
Это — распределение Bin(s, p) с известным параметром p=m/(m + n). Чтобы проверить значимость 5i = £xz- относительно нулевой гипотезы, нужно убедиться, лежит ли sj в имеющей относительно высокую вероятность области или же 5{ попадает в одну из двух маловероятных областей (т. е. лежит на одном из хвостов). Когда верно первое положение, можно считать, что данные согласованы с нулевой гипотезой 01 = 02; если же оно не выполняется, то гипотеза в той или иной степени отвергается. Процедура в точности совпадает с описанной в разделе 5.2.1.
Предположим, например, что данные х — это количество радиоактивных частиц, испущенных образцом А в т интервалах времени, каждый из которых продолжительностью в 10 секунд. Данные у получены аналогично в п интервалах времени для образца В, причем
/и = 20, Ех;=5^ = 15, л = 30,.Е^-=52 = 35. (5.4.6)
Условная выборочная плотность si в точке st при нулевой гипотезе равна
A(5i 150) = (с°)/А (1 —р)50-^ ,5! = 0, 1,... ,50,
причем р=т/(т + п)~20/50=0,4. Значение si = 15 лежит на нижнем хвосте этого распределения. Поскольку распределение не очень асимметрично, двухсторонний уровень значимости, вычисленный с помощью упорядочения по вероятности, будет примерно равен определенному с помощью упорядочения по расстоянию [ср. с разделом 5.2.1, е)], откуда
SL = P(Si^l5|s=5O) + P(Si^25|s=5O)
239
(так как значения 15 и 25 находятся на одинаковом расстоянии от ожидаемого значения 0,4-50=20). Применяя таблицы биномиального распределения при л = 50 и р=0,4, находим
SL = 0,19.
Данные не значимы. Нулевая гипотеза не отклоняется.
Пример 5.4.3. Проверка гипотезы об отношении параметров распределений Пуассона. Использованные в примере 5.4.2 принципы применимы и для проверки согласия данных с гипотезой, что параметры двух пуассоновских распределений относятся как к'Л. Если нулевая гипотеза есть ,, Л
Н-.в\ = к02, или, что эквивалентно,
H$i=ke, 02 = 0, где к — заданный множитель, то нулевое распределение (5.4.3) примет вид S2) = e-<km+^(kmyms^4(sx\ s2!),
т. е. статистика подчиняется пуассоновскому распределению с
параметром (кт + п)в, а условное совместное распределение (5.4.4) станет таким:
+*,
•У]. -Уз*
и сведется к выражению
h(sx\s) = (J)ps^l—p)s-s^ р=кт/(кт + п). (5.4.7)
Например, для данных (5.4.6) из примера 5.4.2 при Аг=1,5 имеем р= 30/60=0,5. Уровень значимости равен
SL = P(S> < 15|s=5O) + P(Sl ^35|s=5O).
так как точки 15 и 35 расположены на одинаковом расстоянии от ожидаемого значения 0,5-50=25, так что
SL- 0,003.
Эта вероятность очень мала; данные обладают высокой значимостью, а гипотеза 0Х = 1,56? безусловно отклоняется.
(Выбирать подходящую нулевую гипотезу следует так: в рассмотренном примере данные подсказывают, что 6Х составляет примерно половину от 02- Если бы мы оценивали 0, и д2 методом наибольшего правдоподобия [см. раздел 3.5.4 и пример 6.3.3], то получили бы 0Х ~s'/m = 0,75, 02=s2/n= 1,5, откуда 02 = 20j. .Не так уж сложно, приглядевшись к данным, заметить, что 02 = 20], а на этой основе сформулировать гипотезу, что 6?2 = 26?i, и проверить ее. Понятно, что результат проверки оказался бы «незначимым», т. е. в настоящих условиях оказывается, что данные согласуются с той гипотезой, которая и выдвинута самими данными. Можно было бы сказать, что данные согласуются с той гипотезой, которая согласуется с данными, но нельзя прийти к какому-то более глубокому суждению. Аналогично после тщательной проверки данных можно было бы выдвинуть не согласующуюся с ними гипотезу. Ситуация существенно отличается от той, при которой нулевая гипотеза выдвигается до проверки данных, поскольку в этом случае согласие или несогласие данных с гипотезой приводит к реальным выводам, из которых можно почерпнуть что-либо новое.
240
Из сказанного можно заключить, что при проверке значимости нулевую гипотезу следует формулировать независимо от используемых при ее проверке данных.)
5.4.2. КРИТЕРИИ НЕЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ 2x2. ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА
Таблица сопряженности представляет собой двумерный (или с двумя входами) массив частот, как в приведенном ниже примере, где анализируется успеваемость заданного числа (п) студентов а) по экзаменационным результатам в конце семестра и б) по проводимым в течение семестра испытаниям:
Экзаменационные оценки, %
<30 30—49 50—69 >70 Сумма
г Слабая «11 «12 «13 «14 Г\
Успевае- Удовлетвори-
мость при < тельная «21 «22 «23 «24 Г1
испытаниях Хорошая «3! И 32 «33 «34 Гз
Сумма Г] Сг Сз с4 п
1
Здесь, например, п23 — число студентов, получивших на экзаменах оценки в диапазоне 50—69 и показавших удовлетворительную успеваемость при испытаниях. Таблица содержит также суммы по строкам r2f г3 и суммы по столбцам сь с2, с3, с4, как и общее количество студентов п. Поскольку приведенные данные расположены (если не считать «суммы» по строкам и по столбцам) в 3 строках и в 4 столбцах, ее можно назвать таблицей сопряженности 3x4. Простейшие таблицы сопряженности — это таблицы 2x2 [см. также раздел 7.4.1]. Они могут быть построены разными способами, но, Возможно, наиболее важны те, которые приведены ниже в примерах.
а) Перекрестная классификация (например, школьники классифицируются по цвету волос и степени веснушчатости):
Светловолосые Темноволосые Сумма
Сильно веснушчатые «11 «12 Гх
Слабо веснушчатые «21 «22 г2
Суммы с. сг п
241
б) Две обработки (например, пациентам назначают или не назначают лекарство от ревматизма):
Боли уменьшились Боли не уменьшились Сумма
Назначен аспирин «и «!2
Назначено плацебо «21 «22 Г1
(пустая таблетка)
Сумма Ci п
в) Две совокупности (например, из двух совокупностей извлекаются выборки для выявления В-отрицательной группы крови, причем к первой относятся жители Эксетера, а ко второй — Эдинбурга):
В-отрицатсльная группа крови Прочие Сумма
Выборка по Эксетеру «и «12 Г\
Выборка по Эдинбургу «21 «22 Г1
Сумма С1 сг п
В частных случаях совокупность данных не обязательно принадлежит к одному и только к одному из таких типов*. К счастью, методы исследования во всех трех случаях одинаковы.
Представляет интерес вопрос о зависимости признаков, указанных в строках и в столбцах, т. е. в примере а): связан ли цвет волос со степенью веснушчатости или же он никак не влияет на нее (признаки независимы)? В примере б): облегчает ли аспирин ревматические боли либо, напротив, боли одинаковы как при приеме аспирина, так и при отказе от него? В примере в): содержат ли обе совокупности разные доли носителей В-отрицательной группы крови или же эти доли равны?
В примере в) мы интересуемся, отличается ли доля Р1индивидуумов с В-отрицательной группой крови в одной совокупности (где она встречается раз из извлечений) от соответствующей доли рг в другой (где выборочная частота составила Пц из г2). Если объемы выборок достаточно малы по сравнению с генеральными совокупностями, то к каждой из двух выборок применима биномиальная аппроксимация, а вопрос сводится к анализу значимости различия параметров Pi и р2 биномиальных распределений. Критерий (условный) для проверки этой гипотезы описан в примере 5.4.1.
* Эти примеры показывают, как могут возникать таблицы сопряженности 2x2.— Примеч. пер.
242
В примере б) с «двумя обработками» тем же способом проверяется, значимо ли отличается частота Лц/ri ослабления болей у пациентов, которым назначен аспирин, от аналогичной доли n2i/r2 в группе плацебо.
Пример а) правильной перекрестной классификации в принципе иной, но оказывается, что он поддается точно такому же анализу. Чтобы убедиться в этом, примем более общие обозначения, при которых таблица из примера а) заменится следующей:
в в Сумма
А «и «12 Г
А «21 «22 п—г
Сумма С и—с п
(Л служит обозначением для «не Л» и т. д.). Например, и)2 здесь обозначает частоту появлений индивидуумов «АВ », т. е. обладающих свойствами А и В . Предположим, что случайно выбранный индивидуум обладает свойством Л с вероятностью Р(Л) = а, а свойством В — с вероятностью Р(В}~(3, так что маргинальные вероятности двумерного распределения [см. II, раздел 6.3] следующие:
в в Сумма
А А Сумма 13 1-0 а 1—а
Соответствующая нулевая гипотеза (цвет волос не влияет на веснуш-чатость) состоит в том, что А и В статистически независимы [см. II, раздел 3.5), так что
Р(ЛВ) = Р(Л)Р(В)=аЗ
(отсюда Р(АВ ) = Р(А)Р(В )=а(1 — /3) и т. д.).
Таким образом, при нулевой гипотезе связанные с четырьмя, клетками таблицы 2x2 распределения вероятностей имеют вид:
в в
А А Pi: =(1— а)0 р|2 = а(1—0) Р22 = (1- «)(1- 0)
243
Для выборок объема п из определенной такими вероятностями совокупности совместное распределение частот /7ц, л12, п21, п22 в клетках будет мультиномиальным (или полиномиальным) [см. II, раздел 6.4.2) с функцией плотности вероятности
Л»„. »,2. л2„ ВД = ЛП, „|8"-г|, =
(П"+пх2 + п2х + п22 = п).
Понятно, что достаточной статистикой для параметра а служит г, а для параметра $ — с [ср. с примером 5.4.1]. Поэтому свободное от параметра условное распределение при фиксированных г и с получается таким:
g(nu, nl2, n2i, n22,\r, c)= ffi11’.-?!2.’. ”21’ ,
h(r, с)
Где h(r, с) — плотность совместного выборочного распределения г и с. Поскольку при HQ свойства А и В независимы, то
h(r, с)=(r)oir(1 —а)"-г(с)0е (1 — 0У- С.
Свободное от параметра условное нулевое распределение принимает вид
g(rtn, л12, и21, п22,\г, с)= п~ п { , /{<?) (?)}. (5-4-9)
Л|2! Л?2Н л22* 4 J
nn+ni2=r} n2i+n22 = c, r+c-b.
На самом деле это распределение одномерное, и (принимая в качестве переменной /7ц) его можно с помощью введенных в (5.4.8) обозначений записать следующим образом:
£(Лц|/; С) = (л (с—ли)/(с)>
Л 1 • , х (5.4.10)
лп=0, l,...,mm(r, с),
а нулевую гипотезу мы проверяем, вычисляя уровень значимости наблюденного значения пп при этом гипергеометрическом распределении. Следовательно, проверка сводится к точно такой же процедуре, что и При сравнении двух биномиальных вероятностей. Эта процедура описана в примере 5.4.1.
Предложенный Р. А. Фишером критерий часто называют точным критерием Фишера в отличие от более простого в вычислительном отношении критерия, основанного на распределении хи-квадрат и описанного в разделе 7.4.1. Эти вопросы изложены Фишером в книге [Fisher (1970), раздел 21.02—С]. При сравнении двух биномиальных частот в примере 5.4.1 был необходим двухсторонний критерий. Критерий независимости для таблиц 2x2 также предполагает двухстороннюю альтернативу. Однако возможно рассмотрение и односторонней ситуации. Для примера в) (две совокупности) уместен двухсторонний критерий, поскольку нулевая гипотеза об однородности совокупностей была бы противоречивой как в случае, когда доля эксетерцев с В-отри-цательной группой крови превышает долю эдинбуржцев, так и в случае, когда доля эдинбуржцев превышает долю эксетерцев.
244
Однако в примере б) (две обработки) «эффект», каким бы он ни был, оказывается односторонним, так как если бы данные опровергали нулевую гипотезу, то число пп в них было бы столь же мало или еще меньше, чем ожидаемое при нулевой гипотезе значение. Таким образом, уровень значимости здесь оказывается обычной «хвостовой» вероятностью
5 с)’
s:s^nlt
где g определена так же, как в (5.4.10).
Пример 5.4.4. Эффективность прививки от холеры. Ситуация, в которой нужен односторонний критерий, характеризуется следующими данными о числе членов некоторой общины, заболевших холерой после того, как им была привита противохолерная вакцина, и о численности непривитых и заболевших (данные Гринвуда и Юла):
Заболели Не заболели Сумма
Прошли прививку 5 1 625 1 630
Не прошли прививку 11 1 022 1 033
Сумма 16 2 647 2 663
Мы интересуемся эффективностью прививки для предупреждения инфекции, т. е. значимо ли мало число Лц=5 заболевших, несмотря на прививку. Примем обозначения, как в (5.4.8):
«и=5 «12 = 1625 г=1630
«21=11 «22= 1022 п—г= 1033
с= 16 л—с=2647 « = 2663
Уровень значимости нулевой гипотезы о бесполезности прививки в силу (5.4.1) составляет
£ & (£?)/(?)= £ (*?° )(,'«’)/(“«)•
Входящее в это выражение гипергеометрическое распределение удовлетворяет приведенным в (5.4.3) условиям применимости биномиального приближения (5.4.2), так что уровень значимости примерно равен
2 р= 1630/2663 = 0,6129,
?=1—р=0,3871.
Вычислим
Z>5 = (156)p5911=0,0112
и тогда, как в (5.4.4), найдем
Z>4 = (5/12)(q/p)Z>5 и т. д.,
245
откуда получаем уровень значимости
$£=0,015.
Это довольно малая величина (около одного шанса из 70), чтобы принять нулевую гипотезу. Вывод таков: количество заболевших среди прошедших прививку значительно меньше, чем среди прочих [ср. с примером 7.4.1, где к тем же данным применяется критерий хи-квадрат].
Пример 5.4.5. Преступность среОи близнецов. Известный пример таблицы 2x2 приведен в книге [Fisher (1970)—С]. Выборка содержит 30 преступников, у каждого из которых имеется брат-близнец. Эти 30 человек были подвергнуты перекрестной классификации, при которой один признак относился к природе близнецов (13 идентичных и 17 неидентичных), а другой — к виновности или невиновности брата (12 виновных, 18 — невиновных):
Брат виновен Брат невиновен Сумма
Близнецы идентичны 10 3 13
Близнецы неидентичны 2 15 17
Сумма 12 18 30
Перепечатано с разрешения Macmillan Publishing Company из книги «Statistical Methods for Research Workers», 14th edition, by Sir Ronald A. Fisher. Copyright ©1970 University of Adelaide.
По нулевой гипотезе преступность среди идентичных близнецов не будет значимо более частой, чем среди неидентичных. Подтверждается ли это данными? Здесь нам нужен односторонний вариант условного критерия. Условное нулевое распределение (5.3.10) принимает такой вид:
g(«uk с) =(«,,)( 12-л„ )/(1?)» «11=0, 1,...,12,
а уровень значимости равен сумме вероятностей, размещаемых согласно этому распределению в точках пи, не меньших наблюденного значения, т. е. в точках 10, 11, 12. Таким образом,
SL= ((1J)(Y) + (1? )(+ (Н )(>„’) 1 / G? ) =0,0005.
Получается, что данные имеют высокую значимость — нулевая гипотеза абсолютно отклоняется.
Рационализация труда при анализе таблиц 2x2. Представленные выше вычисления можно выполнить с помощью небольшого калькулятора. Но существует два альтернативных метода. Один из них ориентирован на использование таблиц Финни для проверки значимости в таблицах 2x2 [см. Pearson and Hartley, (1966), т. 1, табл. 38—G]. Другой связан с применением рассмотренного в разделе 7.4.1 приближения хи-квадрат. Конечно, таблицы Финни дают точный уровень значимости не для всех возможных таблиц 2x2, а только в случаях, когда 246
объемы выборки л ^60. При этом они позволяют судить о том, что SL меньше, чем 0,005, или заключен между 0,005 и 0,01, между 0,01 и 0,05, больше 0,05; немного меньше сведений приведено для п ^80.
Условные критерии для таблиц axb. Изложенные выше методы анализа таблиц 2x2 можно распространить и на таблицы а х Ь. Сводка точных условных критериев содержится в работе [Kalbfleisch (1979) т. II—С]. Часто достаточным оказывается применение изложенного в гл. 7 приближения хи-квадрат.
5.5. КРИТЕРИИ, СОДЕРЖАЩИЕ БОЛЕЕ ОДНОГО ПАРАМЕТРА. ОБОБЩЕННЫЕ КРИТЕРИИ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
Критерий отношения правдоподобия для проверки простой гипотезы был описан в разделе 5.2.1, е). Особенно полезно обобщение этой процедуры, когда имеется несколько параметров, а нулевая гипотеза уточняет значение или значения только части из них. Сначала проведем формальное описание процедуры, а затем проиллюстрируем ее примерами.
Предположим, что вероятностная модель данных содержит т параметров, обозначаемых 0=(0i, 02..0т). Пусть 0 — «параметриче-
ское пространство», т. е. множество всех допустимых значений 0. Предположим, что нулевая гипотеза уточняет значения к параметров (k<rri), но ничего не говорит об остальных. Мы обозначим ее так:
Н: 0€ЙЯ (ЙЯСЙ). (5.5.1)
Удобно назвать Йя суженным параметрическим пространством. (В частном случае может быть, что 0 — скалярный, или одномерный, параметр, а Йя содержит одну—единственную точку). Обозначим
х), (5.5.2)
функцию правдоподобия в точке 0 [см. раздел 4.3.1[ для вектора данных х. Ее наибольшее при изменении 0€ЙН значение (когда вектор х остается неизменным) —
1Н = № (5.5.3)
а наибольшее значение, когда 0 пробегает все несуженное пространство Й, — это
/max= max /(0-,х). (5.5.4)
Определим обобщенное отношение правдоподобия формулой
X=W=Z„//max, (5.5.5)
а область значимости для проверки Н, когда вектор данных равен х0, еСТЬ G(x0) = [х:Х(х) С Х(х0)) = {x:d(x) d(x9)},
ГДе d(x) = — 21пХМ, (5.5.6)
поскольку с последней величиной часто работать удобнее, и ее легче вычислять, чем X (х). Уровень значимости равен
SL(xq)=P{X^G(x.)\H). (5.5.7)
Проиллюстрируем это примером.
247
Пример 5.5.1. t-критерий Стьюдента. В этом примере нужно проверить гипотезу о математическом ожидании нормального распределения, когда стандартное отклонение неизвестно. Вектор данных — это х=(*1, х2,...,хп),
где Xj — реализации нормальной случайной величины с параметрами (g, ст), так что функция правдоподобия (5.5.2) пропорциональна
Z(g, ст; х) = ст-лехр { — ^(х~у.)1}.
Несуженное параметрическое пространство — это
fi:—<ж’ <g<<*>; ст>0.
Предположим, при нулевой гипотезе определяется значение g0 параметра g, но ничего не говорится о параметре ст, так что (5.5.1) принимает ВИД тт.
Н. ц =
а суженное параметрическое пространство будет таким:
fi/p №—Mo, fi-
Максимум функции правдоподобия по суженному параметрическому
пространству достигается при значении ст параметра ст, определяемом
формулой
ст 2=E(xz— nQy/n,
откуда
Л,= тах /(g0, o', х) = 1(ц0, о ", х)=ст ~пе ±п. а>0
Максимум функции правдоподобия по несуженному параметрическому пространству достигается при значениях g и ст параметров g и ст соответственно, выражаемых формулами
g=x = Ехг/и, а
ст2= Е(хг—х у/п, отсюда
Zmax =_..rnLa< а’ *> =
о>0
= /(g, д', х) = ог-пе~±п.
Таким образом,
Х = (ст /ст)-”•
Теперь имеем
(ст /ст)2= E(xz—g0)2/E(xz— хУ=
= 1 + п(х —g0)2/S (х{—х)2.
С помощью статистики
s2= Е(х—ху/(п— 1)
предыдущее выражение можно преобразовать к виду 1+№)}2/(л-1),
где
t(x)=n'/2(x—no)/s — (5.5.8)
статистика Стьюдента. (Отметим, что в этой ситуации s2 служит обычной оценкой параметра ст2.)
248
Область значимости G состоит из всех возможных векторов (Хл, х2,...,хп) размерности п, для которых величина Х = (ст/ст)-” оказывается меньше вычисленной по настоящим наблюдениям, т. е. для которых величина больше, чем значение |/(х0)|- Таким образом, уровень значимости равен
SLW=P(|71>kl |W),
где t — значение статистики Стьюдента (5.5.8), а Т — соответствующая случайная величина. Распределение Т имеет стандартный вид и детально представлено в таблицах [см. приложение 5], имеющих название «Распределение Стьюдента с п—1 степенями свободы» [см. раздел 2.5.5]. На интуитивном уровне критерий выглядит привлекательно. Он отличается от критерия, применяемого в ситуации, когда величина ст известна [см. раздел 5.8.1], только заменой неизвестного значения параметра ст оценкой ст и применением порождаемого такой заменой выборочного распределения [см. раздел 5.8.2]. Численная иллюстрация /-критерия (односторонняя версия) приведена в примерах 5.8.1 и 5.8.2.
Пример 5.5.2. Критерии отношения правдоподобия для параметров регрессии. Весьма важное для статистической теории обобщение примера 5.5.1 — в задачах линейной регрессии. Снова обозначим вектор данных х=(хь х2,...,хп), но на этот раз предположим, что наблюдение хг извлечено из нормального распределения с математическим ожиданием
E(Xr)=arXe, + аг202 + ... + агт0т, (5.5.9)
г=\,2,...,п (т<п),
где ars — заданные константы, a 6S — неизвестные параметры (называемые коэффициентами регрессии), и с дисперсией ст2 (также неизвестной, но общей для всех наблюдений). Нужно проверить гипотезу, которая уточняет значение какого-то набора коэффициентов регрессии.
Например, данные могли бы представлять измерения растяжения при различных температурах, а вероятностная модель задавала бы ожидаемое растяжение при температуре (в шкале Цельсия) в виде 0i+c02, где — ожидаемое при нулевой температуре растяжение, а в2— ожидаемое увеличение растяжения при нагревании на 1 градус; в этом случае (5.5.9) принимает более простой вид:
E(Xr) = 0i+cr62, г=1,2,...,п
(т. е. arl=l, ar2 = cn аг3 = ...=агт=0, г=1, 2,...,п), где сг указывает, при какой температуре проводится наблюдение величины Хг, принявшей значение хг. Например, можно было бы проверить гипотезу вида
Н\02=д
[ср. с (5.5.1)]. Для представленной в (5.5.9) ситуации выберем параметрическое пространство
249
и предположим, что нулевая гипотеза (5.5.1) состоит в том, что
Я:01=02 = ... = ^=о (к<т), (5.5.10)
так что суженное параметрическое пространство таково:
r er=o, r=i, 2,...л,
J s=k+l, к+2,...,т,
ст>0.
Статистика отношения правдоподобия вычисляется приблизительно так же, как в примере 5.5.1. Вместо /‘-отношения Стьюдента в качестве статистики критерия появляется F-отношение Фишера, т. е.
F= (^-w)(Stf-sn), (5.5.11)
(m—k)SQ
где SH — минимум суммы квадратов по суженному параметрическому пространству, т. е. минимум выражения
аг, к+1^к+\ •" агпРт^’
a Sn — минимум такой же суммы, но по полному параметрическому пространству, т. е. минимальное значение величины
... аг$к "• arrrftm)2’
Оказывается, что при Н выборочное распределение статистики F — это стандартное F-распределение с (п—т) и (т—к) степенями свободы, которое в таблицах обычно обозначается как Fn_m> т__к, а уровень значимости представляет собой вероятность ’ того, что соответствующая случайная величина (при Н) превосходит наблюденное значение F [см. раздел 2.5.6].
(Статистика (5.5.11) всегда обозначается F, и такое обозначение заставляет нас нарушать обычное соглашение, в силу которого прописная буква указывает на случайную величину, а соответствующая строчная — на ее реализацию.)
Некоторые иллюстрации приведены в гл. 8.
5.6. АППРОКСИМАЦИЯ УРОВНЯ ЗНАЧИМОСТИ КРИТЕРИЯ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ ДЛЯ БОЛЬШИХ ВЫБОРОК
Для описанной в разделе 5.5 процедуры проверки гипотезы выборочное распределение при Н статистики критерия
d(x)=—2\пХ(х)
вида (5.5.6) аппроксимируется распределением хи-квадрат с к степенями свободы, где к — число точно определяемых при нулевой гипотезе параметров. (Предполагается, что вероятностная модель удовлетворяет некоторым условиям регулярности.) На практике приближение может оказаться удивительно хорошим, как показывает следующий пример.
250
Пример 5.6.1. Таблица сопряженности 2x2. Рассмотрим таблицу сопряженности 2x2 для классификации по двум признакам [ср. с разделом 5.4.2] с частотами a, b, с, d в клетках, суммами г2 по строкам, Ci, с2 — по столбцам и объемом выборки п, т. е.
а b Г|
с d г2
С| с2 п
Соответствующие вероятности обозначим так:
Pit Pl2 Рю
Pit Р-22 P20
Pot P02 1
где Рю =Р\ 1 +P12, Pzo =Ри +Р111 Pv\—P\\+Pl\, Ро2~Р\2+Р22, а Рю +Р20 — ~Ро1+Ро2 = 1- Эти вероятности с помощью трех параметров а, (3, 6 представимы так:
a/3 + 0 (1—a)(3—6 a(l—/3)—в (1—a)(l—/3) + б a « 1
0 1-0 1
Функция правдоподобия [см. раздел 4.13] пропорциональна
/(а, 0, 0) = (а/3+0)°{а(1 — /?)—0]*((1 — а)0—(1— а)(1—(3) + 0}d. (5.6.1)
Предположим, мы хотим проверить гипотезу И относительно взаимной независимости признаков, т. е. что вероятность получить наблюдение в клетке (г, s) равна произведению p,ps, где рг — сумма двух вероятностей в клетках r-й строки, a qs — аналогичная сумма для х-го столбца. Эквивалентно можно записать гипотезу как
И: е=о.
Наибольшее значение /(а, /3, 0), когда а, (3, 0 изменяются в соответствии с Н, равно __
1н = 1(а , 0,0), где _ ~
а =Г'/п, /3 =с{/п,
251
так что
/я=(П Ci /п2)а(г i c2/n2)b(r2ci /n2)c(r2c2/n2)d.
В то же время при отсутствии ограничений наибольшее значение / равно „ „
4пах = 0),
где
а0+д=а/п, а(1—0)—д = Ь/п, (1—а)$—д = с/п, (1 — а)(1— (3)+d=d/n, так что
/тах = (a/ri)a(b/n)b(c/n)c(d/n)d.
Тогда статистика отношения правдоподобия (5.5.5) принимает значение abed
\ — / // — / г'с' \ / r‘cz \ / ггс\ \ / rici \
к-1н'1тах-{~гш) \~пЕГ) \~nc~) \~псГ)
Для упомянутых в примере 5.4.4 данных о преступности среди близнецов таблица была такой:
а= 10 Ь=3 г, = 13
с=2 d=15 г2 = 17
с, = 12 с2 = 18 л = 30
откуда и
г1с1/л = 5,2, Г]С2/л = 7,8, г2с1/л=6,8, г2с2/л=10,2,
—21пХ=14.
Поскольку нулевая гипотеза определяет значение только одного параметра, асимптотическая теорема (если бы ее можно было применять к столь малой выборке) утверждала бы, что при Н это значение 14 нужно считать реализацией распределения хи-квадрат с одной степенью свободы. При такой интерпретации, следовательно, уровень значимости будет равен
5£=Лх?>14)=Р(^>14),
где U — стандартная нормальная случайная величина (так как U2 подчиняется распределению xf). Поэтому уровень значимости
5£=Р(|(/|>3,7)=0,0002.
Полученный в примере 5.4.4 для условного критерия уровень значимости составил 0,0004. Таким образом, ошибка при приближении отношения правдоподобия с помощью асимптотики для больших выборок составляет всего 0,0002.
252
5.7. КРИТЕРИИ РАНДОМИЗАЦИИ
При анализе результатов эксперимента обычно принимается вероятностная модель, а исследование проводится в терминах ее параметров. Однако это не обязательно при специальном планировании эксперимента. Следующий пример представляет собой эскиз проведенного Фишером анализа известного опыта Чарльза Дарвина [см. Fisher, (1951), гл. III].
Пример 5.7.1. Сравнение двух обработок. В своей книге «Statistical Methods and Scientific Inference» Фишер обсуждает известный опыт, проведенный Чарльзом Дарвином для сравнения роста семян одного и того же растения, когда одна часть семян получена перекрестным опылением, а другая — самоопылением. Пятнадцать пар семян выращивались в сравнимых условиях в 15 горшочках, причем каждый горшочек содержал пару семян, из которых одно принадлежало к группе перекрестно опыленных, а другое — к группе самоопыленных. Для каждой пары полученных растений фиксировалось, насколько растение из первой группы выше растения из второй, что привело к следующим результатам:
Таблица 5.7.1. Разница в росте растений (восьмая доля дюйма)
49 23 56
-67 28 24
8 41 75
16 14 60
6 29 —40 (Сумма® 312)
Поскольку при тринадцати из пятнадцати сравнений перекрестно опыленное растение оказалось выше самоопыленного, то это довольно серьезный довод в пользу той точки зрения, что перекрестное опыление способствует более интенсивному росту, чем самоопыление. Задача состоит в определении, насколько сильны эти доводы.
Фишер рассуждал примерно так: в каждом горшочке два семени — самоопыленное и перекрестно опыленное. Одно из них посажено, скажем, на восточной стороне, а другое — на западной. Строго говоря, ни к каким выводам нельзя прийти, если невозможно считать, что самоопыленное или перекрестно опыленное семя помешается нд тойГ или иной стороне случайно, например с помощью подбрасывания монеты. Допустим, что это и было сделано. Теперь в качестве нулевой гщюте-зы предварительно примем, что систематического различия в возможностях роста нет. Тогда наблюдаемые различия следует приписать таким факторам воздействия окружающей среды, как плодородие почвы, атмосферные условия, солнце, луна и т. д.
253
В одном опыте, включавшем 15 пар растений, разности Zj^Xj—yj (где Xj — высота перекрестно опыленного растения в ьм горшочке, а у,— высота самоопыленного растения в том же горшочке) представлены в табл. 5.7.1.
В качестве подходящей статистики предлагается взять среднее значение этих разностей (или, что эквивалентно, сумму этих разностей).
Фактическое размещение семян (самоопыленное на восточной стороне, а перекрестно опыленное — на западной, или наоборот) было одним из 215 возможных, причем в силу рандомизации все они одинаково вероятны. Размещение, которое отличалось бы от фактического только положением семян в первом горшочке, при нулевой гипотезе привело бы к результатам, отличающимся от полученных на самом деле лишь тем, что вместо величины 49 для первого горшочка появилась бы величина —49, так что значение Ег,- оказалось бы 214. Аналогично можно найти 215 = 32 768 равновероятных значений для каждого из возможных размещений. Выполнив эти вычисления, находим, что в 863 случаях значение суммы было таким же или больше, чем фактически полученное, так что уровень значимости равен Р {сумма отклонений^ 312} =863/32 768=0,026, что показывает (цитируя Фишера) «существенное преимущество перекрестно опыленного семени..., так как только (примерно) в одном из 40 испытаний (т. е. с вероятностью 0,026) наблюдалось бы столь большое отклонение в правильном направлении»*.
5.8. СТАНДАРТНЫЕ КРИТЕРИИ ДЛЯ МОДЕЛИ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
В этом разделе описываются некоторые из обычно используемых критериев, когда исходная вероятностная модель нормальна. Для каждого случая уровень значимости можно интерпретировать в соответствии с табл. 5.2.1.
5.8.1. ЗНАЧИМОСТЬ ВЫБОРОЧНОГО СРЕДНЕГО, КОГДА ДИСПЕРСИЯ ИЗВЕСТНА
Выборка х=(х\, х2,...,хп) извлечена из совокупности, которая предполагается нормальной с неизвестным средним g, но с известной дисперсией, равной о» [см. II, раздел 11.4.3]. (Почти всегда нереально предполагать, что дисперсия известна. Описание процедуры в первую очередь служит введением в более часто реализуемую на практике процедуру с применением /-критерия, рассмотренного в разделе 5.8.2.) Чтобы проверить согласие данных с нулевой гипотезой Н:р.-цо (например, до=0), образуем статистику
u = (x—g0)/(a0/Vn), (5.8.1)
* Подробнее с этим методом можно познакомиться в книге: Маркова Е. В., М а с л а к А. А. Рандомизация и статистический вывод.—М.: Финансы и статистика, 1986.—Примеч. ред.
254
где х — среднее выборки (*i + ...+х_)/ •« Эта статистика служит реализацией случайной величины 17= (X—ц0)/(сп/п)[см. раздел 2.5.3, б)], где пХ =Xi + ...+Xn, а Хг — независимы^ нормальные случайные величины с параметрами (ц, ст0), так что X нормальна с параметрами (д, о0/уГп), a U нормальна с параметрами (д—до, 1)-
Если конкурирующая гипотеза — односторонняя, т. е.
Н': д>до, то уровень значимости статистики и равен SL=P(U^u)=l— Ф(и).
Однако при двухсторонней конкурирующей гипотезе, т. е.
уровень значимости равен
SL=P(U^\u\ или С/С—|ы|)= = 2{1—Ф(|д|)}.
(Ф обозначает стандартный нормальный интеграл*. В некоторых из опубликованных версий таблиц функции Ф [см., например, приложение 3] ее приводят для значений и, тогда как в других — для значения 1—Ф(и>.)
5.8.2. ЗНАЧИМОСТЬ СРЕДНЕГО, КОГДА ДИСПЕРСИЯ НЕИЗВЕСТНА. /КРИТЕРИЙ СТЬЮДЕНТА
Предполагается, что выборка х=(хь х2....хп) извлечена из нор-
мальной совокупности с неизвестными параметрами; при этом д обозначает математическое ожидание, а а2 — дисперсию. Нулевая гипотеза такова: ..
И-
Процедура состоит в вычислении следующих статистик: _ п
1) среднее выборки х -Lx^'n^
п 2 —2
2) дисперсия выборки $2= {}/(л—1)= п 1 п
= )/(/>-!),
после чего строится «отношение Стьюдента»
I t=(x—i)/(sHn) (5.8.2)
[ср. с (5.8.1)]. В соотношении (5.8.2) неизвестное значение и0 заменено его оценкой 5 [см. также пример 4.5.2].
При гипотезе Н статистика t оказывается реализацией случайной величины Тп_х, подчиняющейся распределению Стьюдента с п—1 степенями свободы.
Если конкурирующая гипотеза односторонняя —
И’- ii>hq ---------- м
* Т. е. Ф(и)= -7— J ехр(— Z2/2)dt.—Примеч. пер.
255
(так что значения х, которые меньше до, не представляют интереса или считаются фактически невозможными, а полученное по формуле (5.8.2) значение t обязано быть положительным), то уровень значимости равен
5£=Р(Тл_1>0. (5.8.3)
Если же конкурирующая гипотеза односторонняя, но в противоположном направлении, т. е.
Н': ц<цо,
то уровень значимости равен
SL=P(Tn_^t), (5.8.4)
a t принимает в этом случае отрицательное значение. В двухсторонней ситуации, когда конкурирующая гипотеза имеет вид
уровень значимости равен
5£=2Р(Гл_1>|ф. (5-8.5)
На самом деле опубликованные таблицы не содержат значений , >0 как функции от t. Наоборот, в них приводятся значения t как функции от pn_x(t) [см. приложение 5]. Тогда уровень значимости приходится определять посредством интерполяции [см. «Обратные таблицы» в разделе 5.2.2). Следует также иметь в виду, что в некоторых таблицах значение t приводится как функция от
Наиболее важна проверка гипотезы мо=О при выявлении «эффекта», когда данные представляют собой упорядоченные в содержательном смысле пары, как в следующем примере.
Пример 5.8.1. Сопоставление пар. Каждый из п образцов проволоки разламывают на два куска, для одного из которых (выбор производится случайно) измеряется нагрузка на растяжение при фиксированной низкой температуре, а для другого — при фиксированной высокой. Надо проверить, влияет ли разность температур на величину растяжения. Получены такие данные:
Номер образца 1, 2 ... п
Измерение при низкой температуре х{, х2... хп
Измерение при высокой температуре yt, у2-• • Уп
Разность Zi, z2... zn
Здесь zr—xr—yr, r=l, 2..n.
Анализируя не отдельно х и у, а величины z, мы принимаем во внимание только результаты сравнения частей одного и того же образца и тем самым исключаем лишние различия, которые могут обнаружиться при сравнении исходных образцов. Величины z считаются реализациями нормальной случайной величины, которая имеет нулевое математическое ожидание при нулевой гипотезе, утверждающей,
256
что температура не влияет на удлинение проволоки (так что здесь fio-O), а дисперсия ее неизвестна. Вычислим
Л z = Zzr/n,
S2 - (Ezr2—nz 2)/(п— 1)
и __ _ ’
t=z /(s/vn).
Проверку гипотезы проводят по /-критерию — одностороннему или двухстороннему, в зависимости от того, какой из них более подходит: например, если бы из основ техники было известно, что влияние, коль скоро оно может иметь место, должно было бы уменьшать требуемую силу нагрузки с повышением температуры, то следовало бы воспользоваться односторонним критерием, основанным на (5.8.4) с п—1 степенями свободы. Пусть л = 10 и t-—2,95; тогда односторонний критерий для нулевой гипотезы об отсутствии влияния против гипотезы об отрицательном влиянии дает уровень значимости
SL=P(T9C—2,95) = = Р(Т9> 2,95)=0,002 [см. приложение (9.5)].
Это обеспечивает сильный довод против нулевой гипотезы. (Отметьте роль предположений нормальности исходной вероятностной модели: /-критерий оказывается устойчивым (робастным) при умеренных отклонениях от нормальности, т. е. он не очень чувствителен к подобным отклонениям, так что для малых выборок, когда нет определенности в том, какова же природа исходного распределения, довольно безопасно применять /-критерий.)
Пример 5.8.2. Данные опыта Дарвина. Если проанализировать с этой точки зрения опыт Дарвина [см. пример 5.7.1], то мы должны представить 15 разностей высот из табл. 5.7.1 как 15 независимых реализаций Xi, x2,...,xi5 нормальной случайной величины с параметрами (д, и), где значение а неизвестно, а ц=0 при нулевой гипотезе. Для проверки этой гипотезы вычислим
t=x/(s/y[)5), где
х =314/15 = 20,933, а
14$2=Ex?—15*2=25814—6573,
5-2= 1374,35,
$=37,07, $/<15 = 9,572, так что
/=2,187.
При 14 степенях свободы уровень значимости для одностороннего критерия, если воспользоваться таблицами /-распределения из при-
257
ложения (5), равен 0,025, т. е. он принимает довольно малое значение, в силу чего нулевая гипотеза отклоняется. Таким образом, экспери-, мент обеспечивает достаточно сильный довод в поддержку предположения, что полученные перекрестным опылением растения оказываются более высокими, чем самоопыленные.
Можно было бы заметить, что полученный уровень значимости близок к величине (0,026), найденной с помощью метода рандомизации Фишера [см. пример 5.7.1]*.
5.8.3. КРИТЕРИЙ ФИШЕРА—БЕРЕНСА ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ
Мы располагаем двумя выборами (хь x2,...,xw) и (yt, у2,...,уп) объема т и п из нормальных совокупностей, имеющих математические ожидания /*1, ц2 и неизвестные дисперсии «И, oj соответственно. Надо проверить нулевую гипотезу, что Ц1=ц2, не предполагая, что aj-oj.
Вычислим средние выборок т п
х ='Exr/tn, у = ^у,/п 1 г 1
и дисперсии выборок
si = (Lx2r—тх2)/(т—1),
(5.8.6)
Тогда si/m и si/п — выборочные дисперсии х, у соответственно, а si/m+si/n — выборочная дисперсия х—у [см. II, раздел 9.2.5].
Вычислим статистику Фишера—Беренса
Уровень значимости основанного на этой статистике критерия зависит не только от т и л, но и от отношения si/si, входящего в таблицы
в виде
й . / SiMm \
0=arctg(~—
' s2/\n '
Этот уровень значимости можно найти с помощью интерполяции таблицы Сукхатма (Sukhatme) [см. Fisher and Yates (1974), табл. VI—G], где приведены 1%-ные и 5%-ные значения d для тип, равных 6, 8,
* Вместо /-критерия правильно было бы применить критерий знаковых ранговых сумм Уилкоксона, при котором не используются предположения о нормальности. См., например: Холлендер М., В у л ф Д. Непараметрические методы статистики.—М.: Финансы и статистика, 1983 — Примеч. ред.
258
12, 24 и «“», а также для 6, равного 0°, 15°, 30°, 45°, 60°, 75° и 90°. [Предупреждение. В таблицах Фишера и Йейтса обозначения sf и s? применяются для тех величин, которые мы обозначили как s\/m и $|/п.] Например, при ш = 20, г =29,233, $1 = 5,62 и и=10, _у~ = 27,562, $2 = 2,19 имеем Si/m+Sz/n=0,500.
<7=2,364
и
0 = arctg(l,133)=48,6°.
Соответствующие входы в таблице дают:
5^-ные точки
п 9=45“ 0=60”
т = 12 8 2,229 2,262
12 2,167 2,169
/и = 24 8 2,175 2,236
12 2,112 2,142
1°7о-ные точки
п 9=45° 9=60°
/п = 12 8 2,083 3,192
12 2,954 2,978
/г? = 24 8 2,988 3,158
12 2,853 2,938
Воспроизведено с разрешения Longman Group Ltd. из книги. R. A. Fisher, F. Yates. Statistical Tables for Biological, Agricultural and Medical Research, 1974.
Для нашей выборки (m=20, л =10, 0=48,6°) линейная интерполяция приводит к таким значениям:
5%-ная точка: 2,2.35
1%-ная точка: 2,971
Поскольку найденное значение лежит между этими величинами, его уровень значимости заключен между 0,01 и 0,05 и равен примерно 0,04.
Критерий Фишера—Беренса не часто применяют на практике, потому что даже когда неизвестные дисперсии и oi существенно различны, предположение, что они на самом деле равны, дает результаты, довольно близкие к получаемым по этому критерию, но при гораздо меньшем объеме вычислений [см. раздел 5.8.4].
259
5.8.4. /-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ (КОГДА ДИСПЕРСИИ РАВНЫ)
Пусть (хь x2,...,xw) и (Уь — выборки из нормальных рас-
пределений с неизвестными параметрами (jii, а) и (д2, <0- Отметим, что неизвестные дисперсии по предположению равны, а их общая величина обозначена а2. Для проверки нулевой гипотезы щ=м2 поступим так. Вычислим средние выборок т п
х = Lxr/m, у = £уг/п, выборочные суммы квадратов т
(т—1)5? = (Ех2—тх2),
(п—1)5? = ('Ey2—пуг)
[ср. с (5.8.6)] и результирующую оценку общей дисперсии
52 = {(^—1)52 + (я—1)52}/(ш + я—2). (5.8.7)
Тогда оценкой выборочной дисперсии х—у~ служит
S2( 1 + 1\ = ^?52, \ т п / тп
так что стандартное отклонение х—у равно sVi + -К=s>[(m + ri)/(mri}.
Это объясняет следующий шаг вычисления:
*~У уТ™ . (5.8.8)
При нулевой гипотезе эта статистика подчиняется распределению Стьюдента [см. раздел 2.5.5] с т + п—2 степенями свободы. Уровень значимости можно найти так же, как и в разделе 5.8.2, из таблиц t-распределения [см. также пример 4.5.5].
Для данных, которые исследовались с помощью критерия Фишера—Беренса в разделе 5.8.5, но при предположении, что дисперсии х=29,233, 5?=5,62,
7=27,562, 5? = 2,19,
откуда согласно (5.8.7) результирующая оценка дисперсии, равная 52, будет удовлетворять соотношению
2852 = (19-5,62) + (9-2,19).
Суммарная оценка общей дисперсии а2 равна 52=4,5175, а дисперсия разности средних оценивается величиной
s2(± + ±)=°,
Таким образом, значение t будет следующим: t=l^LL = 2 030 1 0,823
Уровень значимости этого (двухстороннего) критерия при 28 степенях свободы равен 0,051. (Заметьте, что эта величина близка к полученному в разделе 5.8.3 значению «примерно 0,04» по критерию Фишера— Беренса.)
260
ди = 20, п — 10,
5.8.5. /-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА РЕГРЕССИИ В ПРОСТОЙ ЛИНЕЙНОЙ МОДЕЛИ
Предположим, мы измеряем рост х и вес у каждого из п индивидуумов, так что получены данные (хь _>’]), (х2, у2),...,(х„, уп). Это может быть также ростом х отца и ростом у его старшего сына или температурой х, до которой нагревается сталь, и результирующим растяжением у и т. д. Наблюдения (хг, уг), г=1, 2,...,л, можно считать независимыми реализациями пары случайных величин (X, У). Часто полезно исследовать одно или оба условных математических ожидания E(Y\X-x), Е(Х\ Y-y). Они называются соответственно регрессией Y на Хи регрессией X на Y. Во многих ситуациях одна, а то и обе регрессии оказываются линейными функциями. В случае анализа взаимосвязи между ростом отцов (X) и ростом сыновей (У), напри-мер, регрессия £(Г|а-=х)
будет (при разумной аппроксимации) линейной функцией от х, скажем, E(Y\X=x)=a +fi'x
[см. примеры 4.5.3 и 4.5.4]. Если на плоскость нанести точки (хг, уг), г=1, 2,...,л, то получится полоса, указывающая линейный тренд. Чтобы оценить о/ и /3', удобнее представить уравнение прямой в виде п а + /3(х—х),
где х =Ехг/л, так что fi' = fi и а' = а—fix. Оценка а и fi методом наименьших квадратов [см. гл. 8] приводит к таким результатам: п
а=у(=Ъуг/п) (5.8.9)
для а и
b= Еуг(хг—х )/Е(хг—х )2 (5.8.10)
для fi. Если условное распределение У при заданном Х-х для каждого х можно считать нормальным с параметрами (д, а), то а и b представляют собой реализации независимы^ нормальных случайных величин с параметрами (а, oNri) и (fi, о/у/е(хг—х)2). В таком случае подходящей оценкой о2 служит
s2 = Е {у— a—b(xr~ X)) 2/(п—2)=
поскольку и
= {Еу2—пу 2—Ь2(Ех2г—пх2)) /(п~ 2),
а—а s/Vn
, Ъ-0 _
s/yll2(xr—х)2
(5.8.11)
(5.8.12)
(5.8.13)
оказываются независимыми реализациями распределения Стьюдента, причем каждая из них обладает п—2 степенями свободы. Поэтому с помощью распределения Стьюдента можно построить критерии значимости, позволяющие получить ответы на вопросы:
значимо ли а отличается от принятого значения а0 параметра а?
261
значимо ли b отличается от принятого значения /30 параметра /3?
Численные примеры и другие детали этих проблем рассматриваются в разделе 6.5.
Пример 5.8.3. Значимость коэффициента наклона. Часто приложение этой схемы связано с таким вопросом: влияют ли вообще значения х на значения у, т. е. не равно ли (3 нулю? Другими словами, не объясняется ли отличие b от нуля только случайными флуктуациями? Соответствующая нулевая гипотеза состоит в том, что в~0. Тогда [ср. с (5.8.13)] t______
t= Ь\^х~х)г (5.8.14)
реализация отношения Стьюдента с п--2 степенями свободы. Если альтернативная гипотеза состоит в том, что 0#О, то нужен двухсторонний Z-критерий, а уровень значимости выборки равен
2Р(Г>|ф,
где Т подчиняется распределению Стьюдента с п—2 степенями свободы, a t выражается по формуле (5.8.14), тогда как у находят из соотношения (5.8.11). Затем значимость оценки b интерпретируется с помощью полученной величины в соответствии с табл. 5.1.2.
Значимость а относительно нулевой гипотезы а-а» можно проверить аналогично и независимо против гипотезы а#а0, если вычислить _
oiQ)/(svn).
При нулевой гипотезе эта статистика подчиняется распределению Стьюдента с п—2 степенями свободы [ср. с разделом 5.8.2].
5.8.6. КРИТЕРИЙ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ
Пусть (Xi, х2,...,хт) — выборка, составленная из наблюдений случайной величины X, подчиняющейся нормальному распределению с параметрами (/ль aj, a (у, у2,— выборка из наблюдений нормальной случайной величины Y с параметрами (д2, а2). Согласуются ли данные с нулевой гипотезой Но, что а? = ст2 (и, скажем, равны общему значению а2)?
Определим следующие величины: /И х =Lxr/m, 1 г
Si = Е(л'г—х)2/(т—1)= {—хЕхг}/(т—1),
у = Еуг/л, п п п
s22 = Е(уг—у )2/(л—1)= (Еу2-уЕуг]/(л-1).
Тогда, если гипотеза /70 справедлива, то (т— 1)5?/л2 и (п—1)5; /а2
262
распределены независимо как -^{т—1) и х2(л—-1) соответственно [см. раздел 2.5.4] (как обычно, обозначение x2(v) относится к распределению хи-квадрат с v степенями свободы). Отсюда следует, что «дисперсионное отношение» [см. раздел 2.5.6]
$?/$2
оказывается реализацией случайной величины, подчиняющейся /^распределению с т—1 и п—1 степенями свободы, которое мы для краткости называем распределением F(m—1, п—1) [см. также пример 4.5.7].
1) Альтернативная гипотеза oi. При нулевой гипотезе значение sf/sj скорее всего будет близко к единице, а большие значения этого отношения неправдоподобны, тогда как при альтернативе более вероятны именно большие значения отношения. Соответствующая область значимости будет, таким образом, верхним хвостом F-pacnpe-деления, лежащим под значением s^/sl, а уровень значимости равен
SL=P{F(m—1, п
(При такой альтернативной гипотезе значения s\/si меньше 1 считаются согласующимися с нулевой гипотезой.) Кривая, изображающая плотность F-pacnpe деления, приведена на рис. 2.5.2.
2) Альтернативная гипотеза Здесь значение отношения si/si при альтернативе будет малым, так что уровень значимости равен
SL=P{F(m— 1, л—1)О|/*2}.
В опубликованных таблицах обычно эти нижние хвосты распределения не приводятся. Но все сводится к случаю 1), если поменять местами т и п, sf и si, так что уровень значимости будет равен*:
SL=P{F(n—1, т—1)>^А?}.
3) Двухсторонняя альтернатива ai^aj. В этой ситуации уровень значимости наблюденного отношения равен
2P{F(m—1, п—l)>5j/4}, если
SL =
2P[F(n— 1, т—-ly^si/si], если
Пример 5.8.4. Равенство двух дисперсий. В разделах 5.8.3 и 5.8.4 мы рассматривали выборки объема га = 20 и л =10 с выборочными дисперсиями $? = 5,62 и .si = 2,19, так что
Ai = 2,57.
* Здесь и далее фактически используется своеобразная симметрия семейства F-распределений: .
P{F(m, n)^J]=P{F\n, m)>y). — Примеч. пер.
263
Таким образом, уровень значимости этого отношения применительно к нулевой гипотезе о равенстве дисперсий против двухсторонней альтернативы равен:
SL = 2P[F(19,9)>2,57).
В таблицах F-распределения [см., например, приложение 7] не приводятся значения SL для таких значений s^/s2', в них содержатся значения статистики r=s'2/s"2 как функции от величины P(F>r), где г — большее из чисел sl/s2 и s2/si. Соответствующий раздел одной из наиболее подробных таблиц F-распределения дает приведенные в табл. 5.8.1 значения для F (15,9) и F (20,9). Интерполированные значения F (19,9), которые и требуются для нашего примера, приведены в последнем столбце этой таблицы, заключенном в скобки. (В опубликованных таблицах эти последние значения не содержатся.)
Видно, что наше значение дисперсионного отношения, равное 2,57, при 19 степенях свободы в числителе и 9 в знаменателе находится между отвечающими 0,100 и 0,050 процентными точками; это приводит к вероятности, примерно равной 0,080, так что получаемый при ее удвоении уровень значимости составляет 0,16. Поскольку это довольно высокое значение, данные следует считать незначимыми, т. е. согласующимися с нулевой гипотезой.
Подчеркнем, что этот критерий чувствителен к нарушениям предположения о нормальности.
5.8.7 ПРОВЕРКА РАВЕНСТВА НЕКОТОРЫХ СРЕДНИХ. ВВЕДЕНИЕ В ДИСПЕРСИОННЫЙ АНАЛИЗ
а) Введение. В разделе 5.8.4 обсуждалась проблема оценки значимости различия между средними двух выборок. Соответствующая вероятностная модель исходила из предположения, что обе выборки извлечены из нормальных совокупностей с общей дисперсией, но, возможно, с различными математическими ожиданиями, и проверялось, согласуются ли. данные с нулевой гипотезой о фактическом равенстве этих математических ожиданий. На практике эти две выборки могли бы быть измерениями каких-то сопоставимых величин, полученных в результате различных «обработок», а расхождение между математическими ожиданиями, если оно имеется, можно было бы приписать различию действия (эффекта) обработок. Например, измерения могли бы быть урожаями пшеницы, а две обработки соответствовали бы применению различных удобрений, так что одно из удобрений вносится на том поле, где собирают данные о первой выборке, а другое — на том, откуда поступают данные о второй выборке.
Но как сравнить три и более обработок? Один способ состоит в их попарном сравнении, когда для каждой пары применяются методы, рассмотренные в разделе 5.8.4. Это довольно обременительно и не может нас удовлетворить (не все пары будут независимыми), поэтому предпочтительнее обобщить двухвыборочную процедуру так, чтобы можно было ответить на вопрос: равны ли три (или более) математических ожидания?
264
Таблица 5.8.1. Значения s'2/s"2, имеющие установленный уровень значимости
Число степеней свободы в знаменателе 9 Число степеней свободы в числителе
15 20 (19)
Вероятность значений, превосходящих 0,100 2,34 2,30 (2,31)
0,050 3,01 2,94 (2,95)
0,025 3,77 3,67 (3,69)
0,010 4,96 4,81 (4,83)
0,005 6,03 5,83 (5,87)
б) Сравнение двух средних как дисперсионный анализ. На первый взгляд неясно, как обобщить соображения, высказанные в разделе 5.8.4. Чтобы увидеть, какие изменения необходимы для обобщения, рассмотрим альтернативную точку зрения относительно проведенного в разделе 5.8.4 анализа. Сначала в (5.8.8) избавимся от квадратного корня, для чего возведем правую часть в квадрат. Рассмотрим теперь связь между числителем и знаменателем. Для ее выражения применим следующие обозначения:
Z\ Х\, Zl -^*2, • • •
%т+\~У^’ %т + 2~ У2.%т + п~ У п>
так что вектор (Zi, Z2.zm+n) будет представлять собой объединение
двух выборок, т. е. [см. I, раздел 6.6] его можно разделить на такие части z/ = (x/|y/). Пусть
z= Е zr/(m + n) = (mx+пу)/(т+п).
Эта величина называется главным средним. Далее, справедливо алгебраическое тождество
zn+л т п
Е (г-Г)2 = Е(х-х)2+ЕО-у)2+ ^(х-уУ. (5.8.15)
' V— -----'
= w + b
Первый член в правой части называется суммой квадратов х-в, он пропорционален изменчивости* элементов первой выборки. (На самом деле он просто, равен увеличенной в (т— 1) раз выборочной дисперсии.) Второй член справа, равный сумме квадратов у-в, имеет такой же смысл для второй выборки. Сумма w этих двух членов образует меру изменчивости «внутри» выборок и называется внутривыбо-рочной суммой квадратов.
* Или выборочной дисперсии.—Примеч. ред.
265
Последний член справа, Ь, понятным образом измеряет различие между выборками и называется межвыборочной суммой квадратов. Наконец, стоящая слева величина называется полной суммой квадратов, она измеряет изменчивость совокупности данных в целом, а в силу тождества понятно, что полная сумма квадратов представляет собой сумму внутривыборочной и межвыборочной компонент.
Если две исследуемые выборки на самом деле не отличаются, проявившееся различие, обозначенное Ь, вызвано лишь случайными флуктуациями, которые и породили внутривыборочные изменения, обозначенные ж Фактически нетрудно увидеть, что выборочные математические ожидания будут следующими:
для ж {т+п—2) ст2, для Ь: ст2, где а2 — общая дисперсия наблюдений.
Однако, когда имеется реальное различие между совокупностями, так что их математические ожидания отличаются на величину 5, то выборочное математическое ожидание В увеличивается до
° т + п° •
Поскольку величина ст2 неизвестна, нужна подходящая процедура, позволяющая вычислить отношение b/w, или более удобную величину {т + п—2)b/w. Тоща при нулевой гипотезе числитель и знаменатель будут иметь одинаковые математические ожидания, но когда воздействия различны, математическое ожидание в числителе будет больше, чем в знаменателе.
Рассмотрим выборочное распределение величины {т + п—2)b/w. При нулевой гипотезе это F(1, т + п—2)-распределение. Уровень значимости данных относительно нулевой гипотезы об отсутствии различий в действии обработок против гипотезы о том, что эффект различия обработок есть, равен
SL=P[F{1, m+n—2)>{m+n—2)b0/w0}, (5.8.16)
где b0 и w0 обозначают наблюденные значения величин b и w, которые определены согласно (5.8.15).
Если сопоставить это с (5.8.8), то квадрат величины t в точности равен {т + п—2)b/w, причем явно это общее значение равно
(т + п—2)тп ___(х—у)2____
т + п Е(хг—х)2+Е(уг—у)2
Квадратный корень из случайной величины F(l, т+п—2) подчиняется распределению Стьюдента с т+п—2 степенями свободы. Тем самым (5.8.16) приводит точно к такому же уровню значимости, что и Z-критерий (5.8.8).
266
В чем же смысл проведенного анализа? Этот метод, основанный на тождестве для сумм квадратов (5.5.15), указывает способ обобщения на три или более выборок. Прежде чем продолжить, представим результаты анализа двух выборок в следующей таблице:
Источник изменчивости Сумма квадратов Число степеней свободы
Различия между выборками /7П _ т + п (х -у)1 1
Различия внутри выборок Е(хг-Л2+Е(,уг-Л2 т + п—2
Полная изменчивость Ыг-гУ т + л— 1
Таблица с подобным представлением арифметических значений входящих в тождество (5.8.15) членов, а также их делителей (т. е соответствующих значений числа степеней свободы той или иной суммы квадратов) и приведенной в первом столбце интерпретацией называется таблицей дисперсионного анализа.
Мы привели довольно обстоятельные рассуждения не только потому, что они играют основополагающую роль ври сравнении трех или более средних, что обсуждается ниже в пункте в), но и потому, что дисперсионный анализ имеет исключительно важное значение в статистических исследованиях [см. гл. 8, 10].
в) Ситуация при к выборках. Предположим теперь, что имеется к выборок, относящихся соответственно к к обработкам и имеющих объемы л,, л2,...,Л£, как в табл. 5.8.2 (где выборки представлены векторами данных). Тождество для сумм квадратов имеет вид
ЕЕ(х„—х )2 = ЕЕ(д'—х ,.)2 + (хх )2, (5.8.17)
5 Г “ S Г Л S
т. е.
полная
сумма квадратов
внутривыборочнаяХ + / межвыборочная сумма '1’
ч сумма .квадратов / \ квадратов ,
Таблица 5.8.2
Номер обработки
) 2 к
Данные Xi Х21 Ххк
Хц Х22 х2к
ХЛ,1 хпг2 хпкк
Суммы С ~ ^Хг\ С* = “,Хг2 Gk ~ ^хгк ^Xrs = G S г ГЛ
Число наблюдений пг пк п
Средние ct=x 1 с^хг ск=х.к X =g
267
Выборочное математическое ожидание w равно (п—к) а2, где п-^пк — полный объем наблюдений. Выборочное математическое ожидание b равно (к—1)а2, если нулевая гипотеза верна (т. е. если на самом деле воздействия к обработок не различаются), но оно будет больше этого значения, если нулевая гипотеза неверна (т. е., по крайней мере, некоторые из обработок приводят к различным эффектам). Итак, подходящей статистикой критерия служит f--{b/(k—1)}/{и>/(«—к)); ее большие значения (значимо превышающие единицу) указывают на реальный эффект обработок. Более точно, эта статистика имеет выборочное распределение F(k—1, п—к), а уровень значимости относительно нулевой гипотезы об отсутствии эффектов обработок равен
SL=P(F(k-~ 1, п—к)>/}.
Арифметические выкладки удобно представить в виде таблицы дисперсионного анализа [см. табл. 5.8.3].
Таблица 5.8.3. Анализ дисперсий внутри выборок и между ними
Источник изменчивости Сумма квадратов Число степеней свободы Статистика кригерия
Различия между выборками ь к—1 Г- - / J - к— 1 ' п~-к
Различия внутри выборок W п—к
Полная изменчивость ЕЕх* —пх1 S Г п—1 Распределение: F(k— 1, п—к)
Полная сумма квадратов определяется приведенным в таблице выражением. Величина b определяется формулой
b= Ел^х2. —лх2.,
a w можно получить, если вычесть b из полной суммы квадратов.
На практике вычисления оказываются менее сложными, чем представляется на первый взгляд. Надо вычислить суммы по столбцам Ci, С2,...,Ск, общую сумму G, средние по столбцам tj, с2..ск (где
Cj = Cj/rij, j=\, 2,...,к), общее среднее g=G/n и сумму квадратов, скажем, S, всех наблюдений. Тогда
полная сумма квадратов = 5—Gg, а
Ь=межвыборочная сумма квадратов=
= C|tj + С2с2 +... + Скск—Gg и м,=внутривыборочная сумма квадратов =
= S—(C?iC| + С2с2 +... + Скск).
268
Наконец, вычисляется f= [b/(k—l)]/[w/(n—к)} и с помощью распределения F(k—1, п—к) находится уровень значимости, который равен SL-P{F\k— 1, и—k)>f].
Можно предложить эквивалентное представление данных в виде таблицы частот [см. табл. 5.8.4]. Тогда указывает частоту отклика х, при применении обработки с номером j.
Таблица 5.8.4. Представление к выборок в виде таблицы частот
Номер обработки
1 2 к
V, «и Л<2 п'к
X, Отклик Л21 П 22
ха Па\ ”а2 ”ак
Полная сумма (т. е. все наблюдения) С2 = ?л/2хг С к - С=Е12П::Х: j i J
Число наблюдений л2 пк n
Среднее С, =Х, С-<2 ск~х.к g- X
Здесь х.\ = 'Enjlxi/ni и т. д., а х.. = LrijjXj/n. При таком подходе тождество для суммы квадратов принимает вид
(xi—x.y=E'Lnii (xj—xy+'Lnj(Xj~x..)2^w+b. (5.8.18) j i j j j j j j j ./
Сумма квадратов всех n наблюдений равна:
S= ^ЪП.:Х], j I
суммы Cj и средние ci по столбцам, а также полные сумма G и среднее g указаны в таблице; статистики b и w и уровень значимости (относительно гипотезы об отсутствии эффектов обработок) вычисляются так же, как для приведенной ранее таблицы с векторами данных.
Пример 5.8.5. Проверка эффектов обработок. Совокупности данных можно представить в виде таблицы частот [см., например, табл. 6.5.3]. Здесь «обработки» — температура; имеющая номер j обработка обозначена Xj. Отклики, ранее обозначавшиеся как xif х2 и т. д., в этой таблице обозначены У\, y2,...,y2s- Суммы Су и средние с,- по столбцам таковы:
j 1 2 3 4 5
CJ CJ 409,32 4,548 189,76 3,514 206,84 2,492 32,00 0,320 -208,21 —2,420
269
J CJ CJ 6 - 222,90 —1,627 —633,35 —4,623 —652,68 —6,660 2 -408,79 — /.713
G и g равны соответственно — 1264.13 и —1,536, тогда как величина 5=18143,70 Поэтому таблица дисперсионного анализа будет такой, как табл. 5.8.5.
Табл и ц а 5.8.5. Таблица диспеосионного анализа
Источник изменчивости Сумме квадратов Число степеней снободы Средний квадрат
Между массивами (Ь) 12,370 4—1 =8 Ь 1546,25 = pzi
Внутри массивов (w) 3,832 л—4 = 814 4,708=
Полная изменчивость 16,202 п—1=822 1
Таким образом, дисперсионное отношение равно 329. Вероятность получить такое или большее значение при /--распределении, конечно, ничтожно мала; тем самым показано, что гипотеза об отсутствии значимых различий между столбцами неразумна (что, конечно, было очевидно и вначале).
5.9. ПРОВЕРКА НОРМАЛЬНОСТИ
Поскольку понятие нормальности играет важную роль для многих статистических процедур, довольно важно иметь возможность проверить. что выборка значимо не отличается от нормальной, а используемые статистики имеют выборочные нормальные распределения.
Обоснованием перспективности этой проблемы может служить следующий принцип Фишера: «Отклонения от нормального вида, если только они не слишком заметны, можно обнаружить лишь для больших выборок; сами по себе они вносят малое отличие в статистические критерии и другие вопросы». Конечно, при изучении выборочных распределений статистик можно убедиться в гом, что одни из них более чувствительны, чем другие, к нарушениям предположений о нормальности. Именно таким оказывается рассмотренный в разделе 5.10 критерий Бартлетта для проверки равенства дисперсий.
Применение вероятностной бумаги Хотя исследование вопросов, связанных с чувствительностью, может оказаться сложным, довольно легко проверить, разумно ли считать, что данная выборка извлечена из нормального распределения. Первичную проверку можно быстро провести, нанося график выборочной функции распределения на веро-270
ятностную бумагу [см. раздел 3.2.2, г)]. Точки графика выборочной ф. р. из нормальной выборки будут лежать на прямой линии или близко к ней, тогда как для заметно не нормальной совокупности они будут приближаться к некоторой кривой. Пример 3.5.1 иллюстрирует вычисление выборочной ф. р., а на рис. 3.5.1 показан ее график на вероятностной бумаге.
Ниже описана более объективная процедура.
Проверка нормальности с помощью асимметрии и эксцесса. Коэффициент асимметрии (скажем, 71) случайной величины X равен
skew (АЗ = 71«£(Х—д)3/ {var(X)}3/-
[см. II, раздел 9.10], где
Р=Е(Х).
В обозначениях раздела 2.1 его можно выразить как 71 =ДзМ/2
[см. (2.1.5), (2.1.6)]. Для таких симметричных распределений, как нормальное, величина 7i равна нулю. Соответствующий выборочный коэффициент асимметрии равен
тз/т'£
где для выборки объема п
mr='Efj (Xj—xy/n, r=2, 3,...
J J
[см. (2.1.8)]. Фишер рекомендует некоторую модификацию такой оценки 7н а именно .
g\ —Ку К2, где . .
k3=m3/[( 1—4)( 1 ~i) h
а 1
k2 = m2/{l~4 )•
Здесь т2 и т3 можно найти, зная нецентральные моменты т2, т3, если воспользоваться (2.1.9).
Аналогично эксцесс (или стандартизованный четвертый момент) случайной величины X равен
72 = М4/Д2—3;
соответствующим выборочным аналогом служит т4/т2—3, а рекомендуемая оценка есть .
g2 = k4/kz2, где - _ _ .
Ar4 = m4/t(l-s|1)(l-4)(l-4))-3m22/{(l-i)(l—5-)).
Для нормального распределения можно считать, что gx и g2 имеют нормальные выборочные распределения*, причем математическое ожидание каждого из них равно нулю, а дисперсии определяются выражениями х , ..... ... ... ...
6и(л—1)/[(п4-3)(п4-1)(п—2)), 24л(и— I)2/ {(п 4- 5)(л + 3)(л—2)(п—3))
соответственно. Основанный на этих допущениях критерий нормальности представлен в примере 5.9.1.
* По поводу точности этого приближения см., например: Большее Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, 1983.—Табл. 4.7. — Примеч. ред.
271
Пример 5.9.1. Выборочные асимметрия и эксцесс. Имеются следующие данные о количестве осадков [см. Fisher (1970), раздел 14, табл. 3 — С]:
Уровень осадков, дюймы Частота Уровень осадков, дюймы Частота Уровень осадков, дюймы Частота
16 1 24 2 32 7
17 0 25 12 33 4
18 0 26 4 34 4
19 3 27 7 35 4
20 2 28 4 36 3
21 3 29 8 37 3
.22 0 30 9 38 0
23 3 31 6 39 1
л=90
Перепечатано с разрешения Macmillan Publishing Company.
Данные привели к таким значениям выборочных моментов:
т{ = 28,62, т2 =23,013, ди3=—24,909, т4 = 1403,656, откуда
Лг2—23,2715, к3 = —25,761, ^ =—162,487,
gi=—0,231 со стандартной ошибкой ±0,254, g2 =—0,302 со стандартной ошибкой ±0,503.
Поскольку и gi, и g2 по абсолютной величине оказались меньше соответствующих стандартных отклонений, ни одна из этих величин не значима. Следует считать, что данные согласованы с гипотезой о нормальности.
Проверка нормальности с применением х2. Критерий х2 описан в гл. 7, а применение процедуры к данным из примера 5.9.1 изложено в примере 7.4.1.
5.10. ПРОВЕРКА РАВЕНСТВА к ДИСПЕРСИЙ (КРИТЕРИЙ БАРТЛЕТТА)
Предположим, что имеется к выборок, причем каждая извлечена из нормального распределения; допустим, что они представлены следующим массивом:
Номер выборки
1 2 к
Данные Ju упД 712 Ун Упг2 У'к У2к Уп^к
Средние У л У.2 ... У.к
272
Чтобы проверить, одинаковы ли дисперсии к выбранных совокупностей, можно сначала использовать графический метод: выборочные ф. р., нанесенные на вероятностную бумагу, будут приближаться к параллельным прямым, если интересующие нас распределения нормальны и имеют одинаковые дисперсии.
Более объективной для нашего примера будет следующая процедура с применением критерия Бартлетта: для каждой выборки вычислим обычную оценку дисперсии*
= 1), >1, 2,...Л,
а также суммарную оценку**
к к
s1^ Е (л,—1)$?/ Е (л,—1).
у=1 J у=1 J
Критерий Бартлетта для проверки гипотезы о равенстве дисперсий таков:
w = {Е(лу—l)}log 52—l)log sj
(логарифмы в этой книге подразумеваются по основанию е). Для уровня значимости можно получить хорошее приближение, если воспользоваться, следуя Боксу, такими преобразованиями. Вычислим
Л = 3(Аг—1) /7у—Т )~Е(л;—1) 1»
f2 = (k+i)/A2, b=f2/(l—A+2/f2).
Тогда выборочным распределением статистики
f2w/{J\(b—w)}
будет (приближенно) F-распределение с j\ и f2 степенями свободы.
Пример 5.10.1. Равенство трех дисперсий. Применим критерий к следующим трем выборкам:
Номер выборки j Число степеней свободы л^—1 S2 J log s2
1 81 58,57 4,070
2 44 76,84 4,342
3 13 79,67 4,378
* Естественно, в предположении, что все объемы выборок «у>1.—Примеч. пер.
** Это оценка общего значения а2 дисперсии, когда нулевая гипотеза верна.— Примеч. пер.
273
Е(л.—1)=138 Е(л.-1)5?= ' E(zz.--l)logs? =
=9160,84 =577,632
$2=66,383, {Е(Лу—l))Iog 52=
= 578,971,
w= 1,339,
А = -’-(0,1120—0,0072) = 0,0175,
/1=2, /2 = 13061, 6=13291,
/2w/{/I(6-w)}=0,66.
При гипотезе «равных дисперсий» получается реализация F-pac-пределения с 2 и 13061 степенями свободы. При больших значениях v2 F-распределение с yt и v2 степенями свободы хорошо приближается распределением х2 с степенями свободы, если считать, что v\F — это и есть наблюденное значение* х2- Таким образом, при нулевой гипотезе F= 2x0,66 =1,32 — реализация случайной величины х2 с двумя степенями свободы, а уровень значимости составляет примерно 0,6. Это очень большая вероятность, так что данные согласованы с гипотезой «равных дисперсий».
Следует подчеркнуть, что этот критерий рассчитан на нормальные распределения и он не будет точным при заметно не нормальных распределениях. Поэтому (приближенную) нормальность исходных выборок нужно установить до применения критерия, а если уровень значимости гипотезы нормальности составит от 0,01 до 0,07, то при его интерпретации требуется осторожность. В рассмотренном выше примере уровень значимости довольно высок, что и обосновывает вывод о равенстве дисперсий**.
5.11. СОЧЕТАНИЕ РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ КРИТЕРИЕВ
Предположим, что в к независимых экспериментах относительно гипотезы //получены уровни значимости qx, Если некоторые
или все из них оказались неопределенными, то, быть может, вся совокупность данных, рассматриваемая как результат единого укрупненного эксперимента, окажется более информативной. Например, рассмотрим три отдельных эксперимента для выявления, будет ли некая добавка увеличивать прочность бетона, когда ь каждом случае при проверке гипотезы /-критерий оказался недостаточно убедительным и привел соответственно к уровням значимости 0,051; 0,038 и 0,046.
* Иначе говоря, если случайная величина Y имеет распределение Hp,, v2) с р, и v2 степенями свободы, а X подчиняется распределению х2 с степенями свободы, то при V2~*“ao распределения v,Y и X сближаются.—Примеч. пер.
** Если придерживаться точности, то здесь не столько обосновывается вывод о равенстве, сколько отклоняется вывод о неравенстве.—Примеч. пер. 5482-418 274
Сочетать эти уровни значимости можно при гаком рассуждении. При нулевой гипотезе выборочное распределение уровня значимости 5 — это равномерное распределение на (0,1) [см. соотношение (5.3.6)], отсюда —21og 5 подчиняется распределению хи-квадрат с 2 степенями свободы [см. раздел 2.7.6]. Семейство распределений хи-квадрат замкнуто [см. раздел 2.5.4], и отсюда следует, что если только уровни значимости 5,, s2,...,sft независимы, го величина
<7——2L'log sr
распределена как хи-квадрат с 2п степенями свободы. Тогда требуемый «комбинированный» уровень значимости равен вероятности превысить это значение д. Для нашего примера мы шмели:
Номер критерия SL -s — 21п 5 Число степеней свободы
1 0,051 5,952 2
2 0,038 6,540 2
3 0,046 6,158 2
Сумма 18,650 6
Вероятность того, что распределенная как хи-квадрат с 6 степенями свободы случайная величина превысит 18,6, равна 0,005. Таким образом, зпи не вполне определенных уровня значимости в сочетании дают довольно высокий уровень значимости 0,005. Поэтому гипотеза о неэффективности добавки решительно отвергается.
Этот критерий предложен Фишером [см. Fisher (1970), раздел 2.1.1—С].
5.12. ТЕОРИЯ НЕЙМАНА—ПИРСОНА
5.12.1. СХЕМЫ ВЫБОРОЧНОГО ОБСЛЕДОВАНИЯ
При повседневно повторяющемся процессе промышленного производства для анализа качества можно взять ежедневный выпуск продукции или проверять каждую поставку изделий, так что целая партия будет фигурировать в качестве выборки. Можно например, воспользоваться такой очень простой процедурой: возьмем 100 изделий, проверим их и подсчитаем число d дефектных в выборке. Если d<c (где с — заданное «число принятия», например с=2), то партия «принимается»; в противном случае она «отклоняется». Выражение «отклонить партию» имеет разный смысл. Это может означать буквальное отклонение, т. е. возврат партии поставщикам, или некоторое дальнейшее обследование для определения того, на сколько надо, например, снизить цену и т. д. При длительном применении этой процедуры будут
275
Рис. 5.12.1. График оперативной характеристики схемы выборочного обследования
приниматься партии наивысшего качества (но некоторые из них будут отклонены). Для определенности предположим, что анализируемая партия достаточно велика по сравнению с объемом выборки, так что число дефектных изделий в выборке достаточно хорошо представляется* случайной величиной, подчиняющейся биномиальному распределению с параметрами (л, 9) [см II, раздел 5.2.2], где 9 — неизвестная доля дефектных изделий в партии. Тогда вероятность принятия партии с уровнем качества 9 равна
А(0)=Р{ЯСс; Я-Bin (л, 0)} = = |(?) 9r (1— 9)п~г.
Эта функция, называемая функцией принятия или оперативной характеристикой процедуры, имеет график, похожий на изображенный на рис. 5.12.1. Если 01 — такое значение параметра 9, что партия с величиной 0^01 считается «хорошей», то вероятность принятия «хорошей» партии не ниже, чем А^). Эквивалентно вероятность отвергнуть хорошую партию не больше, чем 1—-A(0i). Можно установить сколь угодно малое значение (скажем, а) этой вероятности, если подходящим образом выбрать величины лис. Выбранные значения лис задают кривую, показывающую, что вероятность принятия партии низкого качества (т. е. с большой долей 0) мала; насколько именно мала — зависит, разумеется, от 0, л и с.
5.12.2. ТЕОРИЯ НЕЙМАНА-ПИРСОНА ПРОВЕРКИ ГИПОТЕЗ
В теории Неймана—Пирсона (или теории Н—П) проверки гипотез используются понятия повторного процесса решения «принять или отклонить», похожего на описанный в разделе 5.12.1. Как и в разделе 5.3, вектор данных х0 получают из семейства индексированных векторным параметром 0(0€О) распределений; причем это семейство образует вероятностную модель, с помощью которой описывается выборочная процедура.
* Биномиальное распределение рассмотрено также в разделе 5.4.1.—Примеч. пер.
276
Нулевая гипотеза //(0О) теперь предполагается простой и утверждающей, что векторный параметр 0 распределения выборки принимает значение 0О. С ней конкурирует альтернативная гипотеза Н(0), согласно которой 0 принимает значения в некотором подмножестве 12 (выделенном из множества (2). Как в разделе 5.3, выбирается статистика критерия 5(Ло)- Соответствующая случайная величина обозначается S, так что s(x0) служит реализацией S. В отличие от приведенного в разделе 5.3 рассуждения, основанного на «области принятия» Сг(.Го) с уровнем значимости
SL(xo) = Р | SC G(x0) | Я(0О)), (5.12.1)
определяемым наблюденной статистикой .г0, в теории Н—П применяется подходящим образом выбранное подмножество С(а) пространства наблюдений, называемое критической областью и обладающее свойством Р{5бС(а)|//(0о))=а, (5.12.2)
где а — наперед заданное постоянное число (например, а = 0,01), называемое уровнем значимости или размером критерия (либо размером критической области). Если значение х0 случайной величины X попало в эту наперед заданную критическую область, то нулевая гипотеза отклоняется, а альтернатива принимается. В противном случае Н(в0) принимается, а альтернатива отклоняется. Как и область значимости из раздела 5.3, критическая область выбирается так, чтобы приписываемая ей при Я(0О) вероятность была малой, а при Н(6) — большой, если значение 0 достаточно удалено от 0О.
Р)отклонить Н(в0), когда верна /7(0О)) = = Р{5€С(а)|Я(0о))=а -
наперед заданный уровень значимости. Его также называют ошибкой первого рода. Аналогично определим
Р{принять Я(0О), когда верна Н(6), 06(2) = =P{S6C(a)iH(0))=w(a, 0).
Величина 1—w (сб 0) называется ошибкой второго рода, отвечающей значению параметра 0. При данном а функция w(«; 0) называется функцией мощности уровня а для критерия. Как отмечено в разделе 5.3, она принимает те же значения, что и введенная там функция чувствительности G(a, 0), хотя их интерпретации различны. При описанном в разделе 5.3 подходе к проверке гипотез цель (статистического) критерия понимается как измерение силы обеспечиваемого статистикой довода против Н(0), чтобы статистик мог выдвинуть предварительное суждение о том, можно ли верить в гипотезу Й(0). С другой стороны, подход Н—П состоит в принятии решения — отклонить или не отклонить нулевую гипотезу. При изложенном в разделе 5.3 подходе уровень значимости оказывается функцией от наблюденной статистики (скажем, хь). Тогда естественно сравнивать значения функции G(x0, в) при различных 0, но при фиксированной величине х0 — при фактически наблюденной величине х0. В теории Н—П уровень значимости а (размер критерия) заранее фиксирован (скажем, равен 1 % или 5%), а мы вычисляем функцию мощности w(c6 0) при разных 0 и при одном заданном значении а.
277
Для иллюстрации рассмотрим тот же пример, что и в разделе 5.3, — когда вероятностной моделью процесса выбора служит распределение N(0, 1), а статистика критерия представляет собой среднее Г из п выборочных значений. Возьмем одностороннюю альтернативную гипотезу
W):0>O;
в качестве критической области примем верхний хвост выборочного распределения X при Я(0О), состоящий из всех таких значений х, для которых
х^с(а), где
Р[Х^с(а)\Н(0)}=а.
Тогда эта величина равна
Р{Х^с(а)\Х ~N(0, 1/Vn)) = 1—Ф(<ис(а)), откуда
7лс(а)-Ф-1(1—а).
Функция мощности равна
w(с/, = отклонить Н(О)\Н(в)} =
= Р[Х^с(а\ когда X~N(0, 1/7л)) =
= 1 —Ф(7дс(а)—в/п) =
= 1—Ф(ф-'(1—a)—0V«),
т. е. совпадает с функцией чувствительности (5.3.7). График этой функции представлен на рис. 5.12.2.
Более предпочтительным из двух критериев размера а при значении параметра в считается тот, у которого мощность в точке в выше. Критерий, мощность которого превосходит мощности всех прочих критериев того же размера при любых значениях в из (Г, называется равномерно наиболее мощным (критерием).
Может показаться, что теория Н—П обладает серьезным преимуществом перед подходом, рассмотренным в разделе 5.3: она позволяет найти вероятность ложного заключения, т. е. ошибочного отклонения //(0), как функцию от истинного значения параметра 0. Однако при этом требуется признание теории полностью, при котором уровень значимости определяется априори, а нулевая гипотеза отклоняется или принимается не на основе полученных данных или фактического значения статистики критерия, а в зависимости от того, попало ли вообще наблюденное значение в заданную критическую область. Конечно, при некоторых условиях так действовать можно. Но для большинства критериев статистическая практика состоит в подтверждении результатов эксперимента, для чего определяют уровень значимости найденного значения статистики, как в разделе 5.3, и дополнительно используют величину как меру силы довода против Я(0О)-278
Рис. 5.12.2. Функция мощности одностороннего
Такая процедура согласуется со следующей модификацией канонического варианта теории Н—П: вместо того чтобы работать с единственной критической областью С(а) фиксированного размера а (например, а=0,02), учитывается совокупность вложенных друг в друга критических областей различных разме-
критерия уровня а ров, например всех
возможных между 0,001
и 0,10; пусть а0 обозначает размер критической области, последней,
которая содержит полученное значение статистики критерия, т е. такой, что это значение лежит в С(а) при но не попадает в С(а) при а>а0. Тогда Н(0о) «точно» отклоняется на уровне а0; эквивалентно это можно выразить, сказав, что статистика имеет уровень значимости «о в смысле, который подразумевался в разделе 5.3. Если выражение «гипотеза Н(вп) отклоняется на уровне ап» интерпретировать как «вероятность получить уровень зн.'.чимссги (или менее.!, если бы гипотеза Н(0о) была верна, равна а:0», то i—а0 можно считать мерой силы довода против нулевой гипотезы.
Лемма Неймана—Пирсона. Жемчужиной теории Н—П считают лемму Неймана—Пирсона, согласно которой оптимальный критерий проверки простой нулевой гипотезы Н(в0) против простой альтернативы Н(61) представляет собой критерий отношения правдоподобия, рассмотренный в разделе 5.2. Оптимальность критерия понимается в том смысле, что ее мощность в точке не менее чем \ любого другого возможного критерия*.
Сложные гипотезы. Выше приведена простейшая схема теории Н—П. В действительности же эта теория имеет большие ответвления. Она позволяет работать со сложными гипотезами и оперировать спе
циальными средствами, называемыми рандомизированными критериями, которые дают возможность рассматривать дискретные вероятностные модели как объекты общей теории.
5.13. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
В этой главе изложены основы теории и практики статистического вывода. Этот материал в том или ином виде встречается во всех учеб
* При том же уровне значимости.—Примеч. пер.
279
никах математической статистики. Мы рекомендуем также работы, упомянутые в разделе 3.6. В частности, в книге [Kalbfleisch (1979)—С] уделено большое внимание работам, посвященным дискретным данным и условным критериям. Книга Фишера (в основном не математическая) — прекрасный источник для изучения многих статистических процедур. В ней рассматривается и теория Неймана— Пирсона, которая, однако, полнее представлена в других приведенных работах. Основная роль в ее изложении принадлежит, естественно, Нейману [см. Neyman (1937)]. Вопросам теории проверки статистических гипотез посвящена книга [Lehmann (1959)]. Для более глубокого понимания проблем, обсуждаемых в этой главе, можно обратиться к следующим работам:
Fisher R. А. (1951). The Design of Experiments. 6th edition, Oliver and Boyd.
Neyman J. (1937). Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability, Phil. Trans., A 236, 333.
Lehmann E. L. (1959). Testing Statistical Hypotheses. Wiley.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Леман Э. Проверка статистических гипотез /Пер. с англ.—М: Наука, 1985. — 500 с.
Нейман Ю. Вводный курс теории вероятностей и математической статистики /Пер. с англ.; Под ред. Ю. В. Линника.—М.:Наука, 1968.—448 с.
Глава 6
МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
6.1. ВВЕДЕНИЕ
Как было подчеркнуто в предыдущих главах [см., например, гл. 1 и 3], основная идея статистического анализа состоит в том, чтобы рассматривать имеющиеся данные как реализации случайных переменных. Существуют методы, для которых нет необходимости делать какие-либо предположения относительно исходных распределений случайных переменных [см. гл. 14]. Однако большинство статистических методов не является «свободным от распределения» и, как правило, основано на использовании определенных параметрических семейств распределений. В простейших ситуациях семейство распределений может быть указано на основе самой процедуры выборки; в общем же случае его приходится выбирать в определенной степени произвольно среди существующих параметрических семейств распределений, которые кажутся совместимыми с имеющимися данными.
Примером «простейшей ситуации» служит выборочное обследование, где выборка фиксированного объема извлекается из конечной совокупности объектов с некоторым неизвестным параметром 0, скажем, долей «бракованных» объектов. С определенной осторожностью в процессе выбора можно утверждать, что распределение вероятностей числа бракованных объектов в выборке будет принадлежать семейству гипергеометрических распределений [см. II, раздел 5.3]. При этом функция распределения вероятностей (ф.р.) зависит от неизвестного параметра 0. Наша задача заключается в том, чтобы по имеющейся выборке построить удовлетворительное приближение для истинного значения 0 (соответствующее приближенное значение называется оценкой 0), а также определить степень точности этого приближения.
Пример другого рода — задача измерения ежегодного потока воды в реке, проходящего через некоторую измерительную станцию. Эта величина неотрицательна и, как правило, положительно скошена [см. II, раздел 9.10] с неопределенной верхней границей. В качестве одного из возможных распределений измеряемого потока воды можно взять двухпараметрическое семейство гамма-распределений [см. II, раздел 11.3] или семейство логнормальных распределений. И в том и в другом
281
случае есть два параметра, значения которых неизвестны и их следует оценить на основании выборки (серии ежегодных наблюдений за ряд лет). Для подобных задач необходима процедура, с помощью которой можно было бы проверить, адекватно ли выбранное семейство распределений с оцененными параметрами имеющейся выборке [см. гл.7].
Задачу нахождения удовлетворительной статистики для неизвестного параметра иногда называют точечным оцениванием, а задачу описания точности такого оценивания — доверительным оцениванием. Эти названия нельзя считать в достаточной мере удовлетворительными. Они, скорее, несут на себе печать статистического жаргона. В данной главе рассматривается один из наиболее известных методов точечного оценивания — метод максимального правдоподобия. На его основе не только определяется оценка неизвестных параметров, но и вычисляется соответствующая степень точности этой оценки.
В разделе 6.2.1 вводится понятие функции правдоподобия, в разделе 6.2.2 объясняется суть метода максимального правдоподобия, основанного на максимизации функции правдоподобия, а в разделе 6.2.3 приводятся соображения в пользу этого метода. Свойства оценки максимального правдоподобия и соответствующие процедуры описаны в разделе 6.2.5. В разделах 6.3 и 6.4 рассматриваются некоторые примеры. В конце этой главы проводится анализ двух нетривиальных проблем: раздел 6.5 посвящен линейной регрессии, а раздел 6.6 — определению кривой «доза — эффект».
6.2. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
6.2.1. ФУНКЦИЯ ПРАВДОПОДОБИЯ И ЕЕ ЛОГАРИФМ
Данные могут быть представлены по-разному. Наиболее распространенными формами представления являются вектор данных и таблица частот. Вектор данных
-X=(JV}, х2,...,хп)
составлен из наблюдений хг, записанных в порядке их получения. (Каждое xt в свою очередь также может быть вектором. Например, хг может состоять из пары (ur, vr), где иг и vr — наблюдаемые характеристики (А и В) объекта г.) Если значения наблюдений представляют собой целые числа и если порядок получения экспериментальных данных несуществен, то вектор данных может быть записан в компактной форме в виде таблицы частот [см. раздел 3.2.2]. При
282
одномерных наблюдениях таблица частот имеет следующий вид (аналогично выглядит таблица, если начальное значение наблюдений равно 0):
Наблюдаемое значение 1 2 S... к Общее число
Частота п (1) п (2) ... ns... п (к) п
Как видно из таблицы, значение з наблюдалось п(ъ) раз (5=1,2.к),
максимальное значение наблюдений равно к, объем выборки составляет n=Ln(s).
Если данные являются реализацией непрерывной случайной переменной, наблюдения необходимо фиксировать с более высокой степенью точности. Например, данные могут быть представлены сгруппированной таблицей частот:
Наблюдаемое значение Xr±il/1
Частота п'У}
Здесь и(г) обозначает число наблюдений, попавших в интервал (хг—уЛ, хг+уЛ), h называется шириной интервала группировки. (В некоторых таблица^ ширина интервала группировки меняется в зависимости от хг [см. раздел 2.2.2].) В сгруппированных таблицах частот подобного типа часть информации теряется. Последствия потери информации, возникающие в процедурах оценивания, рассматриваются в разделе 6.5.
Правдоподобие и логарифмическое правдоподобие. Для нахождения оценки методом максимального правдоподобия необходимо прежде всего построить функцию правдоподобия [см. также разделы 3.5.4 и 4.13.1]. Для того чтобы понять, как это делать, рассмотрим сначала представление данных в векторной форме. Итак, предположим, что мы имеем выборку в виде п одномерных наблюдений Xi, х2..хп, которые образуют вектор данных x=(Xj, х2,...,х„). Будем
считать, что наблюдаемый вектор является реализацией случайного вектора АГ=(АГ), Х2,...,Хп) с некоторой функцией плотности распределения вероятности (п.р.в.), которую назовем функцией плотности выборки и обозначим
g(x; 0)=g(xi, х2,...,х„; 0Ь 0>,...,0р), 0=(0Ь ..., 0р)€О, (6.2.3)
283
где 0Ь в2,...,0р — неизвестные параметры, Й — «пространство параметров», г. е. множество значений, которые могут принимать неизвестные параметры, g — известная функция. Функция правдоподобия д для вектора данных х определяется как
/(0; x) = a(x)g(x; в), 0€(2, (6.2.4)
где а(х) — произвольный коэффициент, зависящий от данных, но не зависящий от параметров 0Г. Произвольный коэффициент в (6.2.4) может вызвать удивление у читателя, однако поскольку в контексте рассматриваемых проблем, как будет видно из дальнейшего, для нас важно лишь отношение /(0/, х) к /(02; х) при фиксированном векторе х, наличие коэффициента а(х) действительно становится несущественным. Он нужен лишь для упрощения вида функции правдоподобия и служит для устранения «неинформативных множителей» (т. е. не содержащих вектор параметров 0).
Функция правдоподобия, таким образом, является функцией параметров 0], 02,...,0^. Еще раз подчеркнем, что для нас важно изменение значения этой функции при изменении значений 0Г. Вектор данных х при этом остается неизменным. (В некотором смысле данная ситуация противоположна ситуации, связанной с вычислением вероятностей по известной ф.р., например, при нахождении доверительного интервала для х, где вектор параметров 0 известен и остается на протяжении всех расчетов фиксированным.)
Часто удобнее работать не с самой функцией правдоподобия, а с ее логарифмом (натуральным). Такая функция называется логарифмической функцией правдоподобия.
Простейшей и наиболее распространенной является ситуация, когда случайные величины Хг независимы [см. II, раздел 6.6.2] и одинаково распределены (н.о.р.). Тогда п.р.в. выборки имеет вид
п
g(x; 0) = П/(хг, 0), (6.2.5)
1
где f — общая п.р.в. случайных переменных Хг. Ниже приводятся примеры построения функций правдоподобия н.о.р. случайных величин для: а) однопараметрической ситуации (примеры 6.2.1, 6.2.2, 6.2.3) и б) двухпараметрической ситуации (пример 6.2.4). В примере 6.2.5 строится двухпараметрическая функция плотности для зависимых наблюдений (цепь Маркова).
Пример 6.2.1. Функция правдоподобия для распределения Пуассона. Допустим, Хг — н.о.р. [см. раздел 1.4.2, п. 1] и имеют распределение Пуассона с параметром 0. Выборочная п.р.в. (6.2.5) в этом случае принимает вид
П (е~еехг/хг\)=e-/J00/jF/Пхг!.
г~ 1
284
Рис. 6.2.1. Функция правдоподобия в для данных из нормального распределения с параметрами (в, 1) [см. пример 6.2.2]
Рис. 6.2.2. Логарифм функции правдоподобия ——п(в—Г)2 для 2 данных из нормального распределения N(0, 1)
Для построения функции правдоподобия в виде (6.2.4) естественно положить а(х)= 1/Пхг!, поскольку при этом ликвидируется несущественный для целей нашего анализа множитель 1/Пхг!. Функция правдоподобия тогда будет равна:
1(0- х)=е~пе0™ , 0>Q. (6.2.6)
График этой функции относительно 0 показан на рис 4.13.1.
Пример 6.2.2. Функция правдоподобия нормального распределения (дисперсия известна). Пусть случайная переменная X распределена по нормальному закону N (0, 1) (с математическим ожиданием 0 и дисперсией 1). Тогда совместная п.р.в. выборки (хь х2,...,хп) имеет вид
(2тг)~«/2ехр(——ё (Хг—0)2) — - <0 < «—
2 1
Функцию правдоподобия для данной выборки (хь х2,...,хп) можно выбрать в виде
ехр(— -Е(хг—0)2).
2 1
Поскольку
ё (хг—0)2 = ё (хг—х )2 + п(0—X )2,
285
Рис. 6.2.3. Логарифм функции правдоподобия /(0) = 0-" ехр(—Dr;/202), и=10, Ех2 = 20 [см.
пример 6.2.3]
Рис. 6.2.4. Линии уровня логарифма функции правдоподобия из примера 6.2.4 (масштаб не выдержан)
функция правдоподобия окончательно может быть записана так:
/(0)- ехр (—~п(0— х )2).
График этой функции представлен на рис. 6.2.1, график логарифма функции правдоподобия
In /(0) = — ~п(0 -.г)2 2
показан на рис. 6.2.2.
Пример 6.2.3. Функция правдоподобия нормального распределения (математическое ожидание известно). Если исходная случайная величина распределена по нормальному закону с нулевым математическим ожиданием и стандартным отклонением 0, го п.р.в. равна
(г^-^^-^хрС—х2/202'), 0>О.
а п.о.в выборки х(, х2,...,хп, равная произведению индивидуальных п.р.в., имеет вид
(27г)-«/20-лгехр(—LxJ/202).
Функцию правдоподобия 0 ДЛЯ выборки X), х2,...,хп, опуская постоянный множитель (2тг)-'!/2, тогда можно записать как
/(0) = 0-”ехр(—с/202),
286
Рис. 6.2.5. Объемное изображение логарифма функции правдоподобия из примера 6.2.4
где с=Ёх.2, а ее логарифм — как 1 *
In /(0) = — п In 0—с/202.
График функции (6.2.7) показан на рис. 6.2.3.
Пример 6.2.4. Двухпараметрическое нормальное распределение. Если X имеет нормальное распределение с математическим ожиданием д и стандартным отклонением а, то функция правдоподобия выборки (ЛГ|, х2,...,хл) пропорциональна
а~лехр[—Е(х,—д)2/2ст2], —а>0. (6.2.8)
л п _
Подставляя вместо Е(л>—д) эквивалентное выражение Е(х,—х) + + п(у.—х)2, где х обозначает среднее выборки, функцию правдоподобия можно записать в виде
/(д, о) = о~"ехр[—{а+п(ц—х)]/2а2],
где л -а=Е(Хг-х)2-
Логарифм функции правдоподобия тогда равен:
In / =const—л In а—{a+n(ji—х)2]/2<т2,
где в целях простоты const можно положить равной нулю. Другой вариант этого выражения может быть записан в терминах дисперсии т( = а2) :
1п/=— -±-п1пт—{а+п(ц—х)2} /2т.
287
Например, если
п= 10, х = 10, «=20,
то функция правдоподобия будет равна:
1п/=-51п7-1°-^-1())2. 7 7
Грубое представление о форме графика логарифма функции правдоподобия можно получить с помощью расчета значений 1п/ на сетке значений (/х, т) и построения соответствующих линий уровня (интерполяции на глаз). Такой способ наглядного представления показан на рис. 6.2.4; пространственный график поверхности логарифма функции правдоподобия представлен на рис. 6.2.5.
Пример 6.2.5. Марковская цепь. Рассмотрим последовательность t\, t2,...,tn «индикаторов» максимального уровня воды в реке в году г по отношению к некоторому фиксированному уровню (норме). Так, если /г=1, то максимальный уровень воды в году г превышает норму, если /7=0, то не превышает, г=1,...,л. Предположим, что tr являются реализациями случайных переменных 7Н Tz,...,Tn, образующих цепь Маркова [см. II, раздел 19.3] с матрицей вероятностей перехода, равной
0 1
0 г 1 1—а а Р i~P
0<а< 1,
О<0<1.
Вероятность того, что Tr=tr, г =1,...,л, равна
PiT,=t„ т2=г2....г„=г„)=дт,=г,)п'лт,+1=
= tr+{ | Tr = tr) = ir(a, /S)(l— а)«(0,0)ал(0,1)^(1,
где n(i, j) обозначает число переходов в выборке из состояния i в состояние j (i, j равно 0 или 1), тг(а, ^)=Р(Т} =tx). Если, например, последовательность данных имеет вид
оП 1 б о (Л о о оП 11 о, п=14,
то существуют три перехода от 0 к 1 (обозначено 0 1), поэтому л(0, 1) = 3. Аналогично л(0, 0)=4, и(1, 0) = 3 и л(1, 1) = 3. Таким образом, в данном случае мы имеем следующую таблицу числа переходов п (г, 5):
288
5=0 5=1
'll 'll — о 4 3 3 3
Рис. 6.2.6. Линии уровня функции правдоподобия (6.2.9.): /(а, /3)=(1— а)41а3/34(1— 0)2/(а + /3), О < а < 1, 0 </? < 1
Вероятность (абсолютная) PtTi=ti) может быть вычислена на основе предельного стационарного распределения [см. II, раздел 19.6]
P(T,=0)=/3/(a+/J),
Р(Т1 = 1)=а/(а + ^),
т. е.
Р(Т1=0=а</31-'/(а + |8), t=0, 1.
Для приведенной выше последовательности при Tj =0 функция правдоподобия будет иметь вид
/(а, £)=
0<а< 1, О<0< 1.
В другом примере с бдль-шим объемом выборки максимальный уровень реки фиксировался в течение 50 лет. Было отмечено 5 паводков. При этом в первом году превышения нормального уровня не отмечалось (Ti=0). Таблица частот перехода имеет вид
S 0 1
г ° 1 41 3 3 2 ’
289
Функция правдоподобия в этом случае будет равна:
/(а, /?) = (1-а)4,а334(1-3)2/(а + ^). (6.2.9)
Линии уровня поверхности, заданной этим уравнением, представлены на рис. 6.2.6; показаны линии уровня, соответствующие значениям функции /=(0,5, 1, 2, 4, и 5)-10—7 (продолжение примера см. в примере 6.2.7).
Вычисление функции правдоподобия по таблице частот. Если данные выборки представлены в виде таблицы частот (6.2.1), то частоты л (г) можно считать реализациями случайных переменных N(r), совместное распределение которых полиномиальное [см. II, раздел 6.4.2]. Поэтому (6.2.5) следует заменить на
Р[Мг)=л($), $=1,2,...Л} = [л!/Пл($)!]х
*, 1 (6.2.10)
х П [Ptxtr-l-h < X xs +
где п.р.в. X является общей п.р.в. для всех Хг, а именно f(x, 0). Поскольку нас интересует функция правдоподобия, комбинаторный множитель может быть опущен и в качестве функции правдоподобия можно взять величину, пропорциональную
ЩРСъ-уЛ <X^xs + уЛ)}^>.
Для дискретной случайной величины это выражение превращается в
1(0; х) = П[/(х* 0)}ЙЧ (6.2.11)
5=1
что представляет собой очевидное обобщение (6.2.5) на случай таблицы частот. Например, в случае таблицы частот для распределения Пуассона с параметром 0 функция правдоподобия (6.2.11) станет равной:
П(е-^/5!)и<5)=г-и^ /П($!)л<5>
5=1
[ср. с примером 6.2.1]. На практике коэффициент 1/П($!)л^) опускается. Таким образом, функцию правдоподобия можно записать в виде
1(0; х)=<г-п90п*,
что полностью совпадает с функцией правдоподобия для данных, представленных в векторной форме [см. пример 6.2.1].
Если в исходном виде непрерывные случайные переменные группируются в таблицу частот, как в (6.2.2), то функция правдоподобия будет равна:
/(О; х) = П№3+ -Ц, в) - F(xs-±-h, (6.2.12)
5=1 2 2 v '
где F(x, 0) — общая функция распределения вероятностей для Хг.
Затруднения, вызванные подобной группировкой, обсуждаются в разделе 6.5.2.
290
6.2.2. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Рассмотрим сначала однопараметрическую ситуацию. Функция правдоподобия 1(0; х), определенная выше, является функцией параметра 0 и вектора данных х. Оценкой максимального правдоподобия (о.м.п.) параметра 0 называют то значение параметра 0=0, которое максимизирует 1(0; х); соответствующий метод называют методом максимального правдоподобия. В большинстве случаев существует единственная оценка максимального правдоподобия, т. е. единственное значение 0€О, максимизирующее функцию правдоподобия [см. рис. 6.2.1 — 6.2.6]. Значение 0 (которое в многопараметрической ситуации может быть вектором) является функцией данных х, т. е. статистикой. Чтобы подчеркнуть зависимость 0 от х, оценку будем записывать в виде 0(х). Например, в рассмотренном примере, где хг — независимые наблюдения, подчиненные распределению Пуассона с параметром 0 > О, функция правдоподобия имеет вид е~пв0пх , где х — среднее выборки, и поэтому максимум этой функции достигается в единственной точке 0=х. [См. рис. 6.2.1]. Таким образом, о.м.п. 0(х)=х.
Статистические свойства оценки 0(х) полностью определяются исходной случайной переменной §(Х) [см. раздел 11.4.2], для которой эта оценка является реализацией. При только что рассмотренном пуассоновском распределении такой исходной случайной переменной слу-________ п жит X = 'ЕХг/п, где Хг — н.о.р. случайные величины, распределенные по закону Пуассона с параметром 0. Отсюда, в частности, следует, что, во-первых, Е0(Х)=Е(Х)=0, т. е. оценка 0 несме-щена [см. раздел 3.3.2], во-вторых, что va.r(0(X)) = 0/п, и в-третьих, что выборочное распределение л0=Ехг является пуассоновским с параметром и0[см. табл. 2.4.1]. Точность оценивания 0 с помощью 0 может быть описана разными способами. По-видимому, наиболее удовлетворительным является построение 95%-кого доверительного интервала для 0 на основе 0 [см. гл. 4].
Двухпараметрическая ситуация представлена в следующем примере.
Пример 6.2.6. Оценка максимального правдоподобия параметров нормального распределения. В примере 6.2.4 была построена функция правдоподобия 1(ц, а) нормального распределения, функция плотности которого пропорциональна (6.2.8). Соответствующая поверхность имеет вид гладкой горы с единственной вершиной [см. рис. 6.2.4 и 6.2.5]. На вершине, координаты которой обозначим через (д, о), касательная плоскость горизонтальна, поэтому, если записать / вместо /(д, о), условие максимума может быть выражено в виде следующих уравнений:
291
где производные вычислены в точке (д, а). Эти уравнения назовем уравнениями правдоподобия, их решение определяет точку максимума (fi, а). Поскольку
а/ дд ц дц
и аналогично din//да=(д1/да)/о, уравнения правдоподобия в эквивалентной форме могут быть записаны в виде
Э1п//Эд=0, Э1п//Эст=О.
Следует отметить, что дифференцирование, как правило, легче проводить для логарифма функции правдоподобия, т. е. последняя запись предпочтительней.
Из (6.2.8) имеем
л
1п/=— п In ст—Е (Xj—д)2/2ст2, поэтому
Э1п//дд=—Е(ху—цУа2, д\п1/да——п/а+ Е (Xj—д)2/ст3.
Приравнивая эти выражения к нулю, получаем оценку для fi и ст:
fi-x (среднее выборки) и
9=$(XJ-ry/n]''2.
Так, для данных из примера 6.2.4
fi—10, ст=1,41.
Вместо параметров д и ст можно взять параметры д и v-a2. Оценки максимального правдоподобия для д и v можно получить, подставляя в /(д, ст) вместо ст величину v1/2, после чего запишем условие максимума:
Э//Эд=О, dl/dv=Q.
Решением этих уравнений будут оценки
fi=x, v=L(Xj—x)z/n,
т. е. (ct)2 = v: о.м.п. для ст2 есть квадрат о.м.п. для ст. Свойство «инвариантности», как мы увидим позднее, широко используется далее.
Разумеется, далеко не всегда уравнения правдоподобия могут быть решены аналитически. Это следует считать, скорее, исключением. Как правило, уравнения необходимо решать численными методами, например, итеративно. Такая ситуация рассмотрена ниже.
292
Пример 6.2.7. Численное отыскание о.м.п. для двух параметров. Функция правдоподобия (6.2.9) из примера 6.2.5 приводит к следующим уравнениям правдоподобия:
г з 41 _ 1 а 1—а a+(i ’
< 4 2 1
3 1-3~
L
В качестве начального приближения для а и 3 можно взять значения «1 и Зь получаемые в результате сравнения матрицы вероятностей перехода с матрицей частот перехода. Эти матрицы соответственно имеют вид:
Сумма Сумма
1—а а -1 1 г 41 3 -1 44
3 1—3 J 1 L 3 2 J 5
поэтому «1 будет равно 3/44 = 0,068, а 31 равно 3/5=0,600. Применение итеративных методов или прямое вычисление функции правдоподобия 7(а, 3) в окрестности точки (0,068, 0,600) приводит к о.м.п.
а=0,066, 3 =0,607.
(Дальнейшее обсуждение см. в примере 6.4.4)
6.2.3. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ИНТУИТИВНАЯ АРГУМЕНТАЦИЯ
«Нет ничего проще, чем придумать метод оценивания», — писал Р. Фишер*. Этим он хотел сказать, как важно уметь различать удовлетворительные методы оценивания от неудовлетворительных. Существует довольно простой аргумент в пользу метода максимального правдоподобия. Процесс нахождения о.м.п. § равносилен выбору среди семейства плотностей /(х, &), 0€О, такой /(х, 0), которая для имеющегося набора данных х доставляет максимальную вероятность (точнее, плотность распределения вероятностей). Любое значение 0, отличное от 0, для которого 7(0; х)<7(0; х), приводит к меньшей вероятности по отношению к исходным данным, и поэтому оно менее удовлетворительно^ что может быть оценено относительным правдоподобием 7(0; х)/(7(0; х).
* Действительно, формально в качестве оценки может выступать любая статистика, т. е. любая функция наблюдений. — Примеч. пер.
293
Рис. 6.2.7. Типы функции правдоподобия
Точность оценивания должна зависеть как от самих данных, так и от природы выборочного распределения. Если мы приходим к функции правдоподобия с плоским максимумом, т. е. с малой кривизной в точке максимума, то значения 0, даже достаточно далекие от 9, будут приводить к относительному правдоподобию, близкому к единице. В этом случае $ имеет небольшую точность. Наоборот, высокую степень кривизны в точке максимума с интуитивной точки зрения следует связывать с относительно высокой точ
ностью оценивания. Поскольку кривизна [см. IV, определение 6.1.4] функции /(0; х) в точке максимума, для которого dl/dd-Q, равна dd/dO2, в качестве меры точности о.м.п. можно взять cPl/dO2. Как будет показано, более подходящей в этом отношении является не сама функция правдоподобия, а ее логарифм, и можно ожидать, что особую роль будет играть вторая производная d2ln//d02.
6.2.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ТИПЫ МАКСИМУМОВ
Типичные графики функции правдоподобия, зависящей от одного параметра, показаны на рис. 6.2.7.
На рис. 6.2.7, а) представлен «регулярный» случай: 1(0) является непрерывно дифференцируемой функцией 0 и ее максимум достигается в точке, для которой dl(0)/d0=Q. На рис. 6.2.7, б) максимум достигается в крайней точке пространства параметров О. Этот максимум не может быть найден путем дифференцирования и решения уравнения правдоподобия. Рис. 6.2.7, в) — аналог рис. 6.2.7, а), рис. 6.2.7, г) — аналог рис. 6.2.7, б) для случая, когда параметрическое пространство дискретно. Примеры этих ситуаций будут рассмотрены ниже*.
Следует с особой осторожностью выбирать метод для поиска максимума, адекватно соотносить его с видом функции правдоподобия. «Регулярный» случай наиболее типичен для практики. Здесь максимум
* Здесь не представлена еще одна довольно распространенная на практике ситуация, когда функция правдоподобия имеет несколько локальных максимумов. Уравнение правдоподобия тогда имеет несколько корней, о.м.п. соответствует глобальному максимуму. — Примеч. пер.
294
находят в результате дифференцирования функции правдоподобия. В условиях простой случайной выборки, т. е. когда наблюдения н.о.р. и п.р.в. имеет вид (6.2.5), т. е. функция правдоподобия пропорциональна ЦЯхг, 0), дифференцирование облегчается, если сначала перейти к логарифмам. Логарифм функции правдоподобия равен:
In/((?; х) = Eln/(xr, 0), (6.2.13)
при этом важно, что уравнение d\nl/d0=O имеет те же корни, что и уравнение правдоподобия. В принципе можно использовать логарифмы по любому основанию, на практике же чаще всего работают с основанием е (натуральные логарифмы). В этой главе запись In подразумевает натуральный логарифм [см. пример 6.2.6].
6.2.5. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ. СВОЙСТВА ФУНКЦИИ ПРАВДОПОДОБИЯ
а) Асимптотическое распределение производной логарифма функции правдоподобия. Основанная на интуиции аргументация для обоснования метода максимального правдоподобия подтверждается теоретическими исследованиями. В «регулярном» случае метод максимального правдоподобия приводит к оценке, которая при неограниченном увеличении объема выборки является асимптотически несмещенной [см. раздел 3.3.2], состоятельной [см. раздел 3.3.1, в)], эффективной [см. раздел 3.3.3, б)], а также асимптотически нормальной [см. II, раздел 13.4]. Более того, о.м.п. является минимальной достаточной статистикой [см. раздел 3.4] при условии, если такие статистики существуют. На практике это означает, что для конечных объемов выборок о.м.п. имеет достаточно малое смещение (или вообще несмещена) и ее точность не намного отличается от теоретически оптимальной.
Еще раз заметим, что при исследовании теоретических свойств о.м.п. мы будем работать не с самой функцией правдоподобия, а с ее логарифмом. Далее будем записывать функцию правдоподобия (6.2.4) одним из следующих способов:
1=1(0)=1(0; x)=l(0;xi, х2,...,хп);
для данного х эту величину можно считать реализацией случайной переменной
L=L(0)=L(0; X) = L(0; Xlf Х2,...,Хп).
Установим сначала следующее свойство:
Е[Э1п£(0)/Э0л]=О, г=1,...,р. (6.2.13а)
295
Это свойство вытекает из того, что
ainL ding(x g) дОг ~ дег ’
где g(x, 0) — совместная п.р.в. X,, Х2,...,Хп, т. е.
£[Э1п£/Э0г]= &gdx
(здесь j обозначает л-мерный бесконечный интеграл по всему выборочному пространству S [см. IV, раздел 6.4], a dx обозначает б/Х1...б/хл)« .В регулярном случае предыдущее выражение может быть переписано так:
\(dg/d0r)dx= -^-$gdx=0,
поскольку [gdr=l, a g — плотность распределений вероятностей.
Другое свойство производной логарифма dlnL/d0r, которое понадобится нам в дальнейшем, состоит в следующем.
Дисперсии и ковариации случайных переменных d\nL/d6r, г=\,2,...,р задаются формулами:
var(dlnL/d0r)=—E(d2lnL/d02),
(6.2.13 б) cov(dlnL/d0r, d\nL/d0s)=—E(d2lnL/d0rd6s).
Эти формулы следуют из соотношения
Е(д\пЬ/д0г)2 =— Е(Э21п£/Э02).
Для доказательства последнего равенства заметим, что
02lnL/002 = 02lng(X, 0)/Э02,
где g(x 0) — выборочная п.р.в. Тогда
Е(Э21п£/Э02)=Е[—g-2(0g/00r)2+g~l х
х (d2g/d02r)]=—E(01ng/0$2 + $(d2g/d02)dx,
где, как и прежде, интеграл берется по всему выборочному пространству. В регулярном случае
j(d2g/d02r)dx=(d2/d02)$gdx,
но последнее выражение равно нулю, так как \gdx=l. Таким образом, окончательно
£(02lnL/002)=— E(dlnL/d0r)2.
Первое тождество в (6.2.13 б) вытекает из этого равенства непосредственно. Второе может быть установлено аналогично.
296
Отметим важное асимптотическое свойство о.м.п.:
Совместное распределение случайных переменных д\пЬ(6)/д6г, г=1,2,...,р, приближенно нормально [см. II, ~ ... раздел 13.4] с нулевым математическим ожиданием и кова- (0.Z.14) риационной матрицей, задаваемой формулами (6.2.13 б).
Этот результат вытекает из того, что в случае н.о.р. наблюдений д\пЬ/двг представляет собой сумму н.о.р. случайных переменных dln/(X 0)/д0г с положительной дисперсией, и поэтому в соответствии с центральной предельной теоремой [см. II, раздел 17.3] величина d\nL/ddr асимптотически нормальна, т. е. для конечных объемов выборок распределение этой величины может быть удовлетворительно аппроксимировано законом нормального распределения. Многомерный вариант центральной предельной теоремы приводит к результату (6.2.14).
Однопараметрическая ситуация. В частном случае, когда существует лишь один неизвестный параметр 0, результат (6.2.14) может быть сформулирован так:
распределение случайной переменной d\nL(Q)/de приближенно нормально с нулевым математическим ожиданием и дис- (6.2.15) Персией /(0), задаваемой формулой г2(&)=—EltflnL^/dO2].
Из свойств нормального распределения следует, что с определенной точностью интервал
(—1,96т(0), 1,96т(0))
является центральным 95%-ным вероятностным интервалом [см. раздел 4.1.3] для d\nL/d0 [см. пример 4.5.2, б).
б) Доверительный интервал для оценивания параметра. Первый метод. В предыдущих разделах на основе метода максимального правдоподобия был предложен прямой эффективный подход для построения доверительного интервала для оцениваемого параметра. Однако нужно заметить, что на практике иногда используют более грубый, но достаточно удовлетворительный метод приближенного построения доверительного интервала. Этот подход будет описан в разделе 6.2.5.
Начнем с описания первого (прямого) метода. Ограничимся однопараметрическим случаем, для которого результат (6.2.14) может быть сформулирован так:
наблюдаемое значение d\nl/dQ (приближенно) с вероятностью 0,95 лежит в интервале
±1,967(0),
где т2(0)= — E{d2\nl/d6l) [см. пример 4.5.2, б)].
297
Если функция d\nl/dO взаимно однозначна по 6, то принадлежность значений этой функции интервалу ±1,96т(0) эквивалентна тому, что параметр 0 принадлежит интервалу (0Ь 02), где 02 и 0] — корни уравнений
d\nl/cto= ±1,96т(0).
Это утверждение приводит к следующему (первому) методу построения доверительного интервала для 0: интервал (0Ь 02), где 02 и 01 — корни уравнений
d\nl/d0= ±1,96т(0), (6.2.16)
является доверительным интервалом [см. раздел 4.2] для 0 с коэффициентом доверия, приближенно равным 0,95, а т(0) определяется по формуле (6.2.15).
Аналогично интервалы строятся с другими коэффициентами доверия. Этот метод построения доверительных интервалов проиллюстрирован далее в примерах.
Пример 6.2.8. Доверительный интервал для параметра экспоненциального распределения. Рассмотрим однопараметрическое экспоненциальное распределение [см. II, раздел 10.2.3] с плотностью f{x, &)=0ег~вх, 0>О. Заметим, что £(Х)=1/0, var(A)=l/02. Для данных х=(х,,...,хл) функция правдоподобия имеет вид
7(0; х)=0пе^-^г=eng-nOx,
а ее логарифм равен: 1п7=и1п0—пОх, откуда
din/ п _ — =~Г—ИХ • de е
Таким образом, уравнение правдоподобия имеет вид
7~т =0-
откуда находим о.м.п. 0=1/х.
Рассмотрим теперь случайную переменную d\nL/d0, она равна:
dlnL п -гт-
—— = ПЛ . de е
Поскольку Е(Х)=Е(Х)=1/0, в соответствии с (6.2.13 а)
rVC/lnLx п п п ^) = 7-7=0-
298
Дисперсия dlnL/dd в соответствии с (6.2.15) равна:
Поскольку var(x)= 1/02, это соответствует прямому вычислению 7^(0) на основе выражения d\nL/dO=n/0—rix.
Займемся теперь исследованием распределения величины d\TtL/d6. Из результата (6.2.14) вытекает, что эта величина приближенно распределена как N(0, Истинное распределение dlnL/dQ, как следует из предыдущей формулы, совпадает с распределением случайной величины п/0—ЁХГ. Но функция плотности распределения с.в. п г~1
Y=EXr в точке у равна 0пуп~ 1е~вУ/(п—1)! [см. раздел 2.4.2]. Это совпадает [см. II, раздел 11.3] с плотностью гамма-распределения с математическим ожиданием п/в, дисперсией п/62 и коэффициентом асимметрии, равным 2/7и. При средних и больших значениях п это распределение почти симметрично с эксцессом, равным 3(1+2/л), который приблизительно равен 3 (значение эксцесса, соответствующее нормальному распределению). Для средних объемов выборки распределение dlnL/df) близко к нормальному с математическим ожиданием, в соответствии с (6.2.13 а) равным 0, и дисперсией, в соответствии с (6.2.15) равной п/02.
Вернемся к точности оценивания параметра 0. Сначала построим точный 95%-ный центральный вероятностный интервал [см. раздел 4.1.3] для случайной величины ИЛ=20У=20ЕЛ>=20лАг. Поскольку плотность W в точке w равна (w/2)"‘1exp(—м/2)/2Г(п), случайная величина И/=20ЕА> имеет распределение х2[см. раздел 2.5.4, а)] с v=2n степенями свободы. На основе этого распределения можно найти (точно) W] и w2, отсекающие 2,5% площади соответственно от левого и правого хвоста ф.р. Так, допустим, объем выборки п=40. Тогда из таблиц распределения х2 с 80-ю степенями свободы находим, что W] =57,153 и w2= 106,629. С вероятностью, равной 0,95, можно утверждать, что
Wi < W^w2, т. е.
57,153 <80^0 < 106,629, а значит,
О,714/Х<0< 1,333/Х.
В терминах оценки 0=1/х можно утверждать, что с вероятностью, равной 0,95, интервал (0,714 0, 1,3330) накрывает истинное (неизвестное) значение параметра 0. Такой интервал называется доверительным [см. гл. 4]; 95%-ными доверительными границами для 0 являются 0,714 0 и 1,333 0.
299
Построенный доверительный интервал является точным*. Теперь воспользуемся тем, что в соответствии с (6.2.14) величина d\nL/d6 имеет распределение, близкое к нормальному с нулевым математическим ожиданием и дисперсией п/02. Поэтому d\nl/d6=n/6—пх можно считать реализацией нормальной переменной N(0, yfn/G), а yfn(\—0х)=у/п(1—6/в) — реализацией нормальной переменной N(O,1). Центральный 95%-ный доверительный интервал (0Ь 02) находится из решения неравенств
—1,96 ^1,96.
Для примера, как и ранее, положим п=40. Тогда
0Ь 2 = (1 ± 1,96/V4O)0=(1 ±0,310)0.
Итак, 95%-ным доверительным интервалом для 0, полученным на основе приближения (6.2.14) или, что эквивалентно, на основе (6.2.16), будет интервал
(0,6900, 1,3100).
Сравним его с точным интервалом
(0,7140, 1,3330).
Разница, как видим, не очень велика.
в) Аппроксимация выборочного распределения о.м.п. Вывод приближенного распределения и получение на его основе доверительного интервала (6.2.16) основаны на применении центральной предельной теоремы [см. II, раздел 17.3], и можно ожидать, что при больших п это приближение будет достаточно удовлетворительным. На практике, однако, часто необходимо распределение самой о.м.п., а не величины dlnL/df). Это распределение предлагается ниже.
Приближенное распределение о.м.п. 1) В однопараметрическом случае с функцией правдоподобия /(0; х) выборочное распределение о.м.п. приближенно нормально с математическим ожиданием 0 и дисперсией ш2, где
w2 =—l/E(<flnL/d02). (6.2.17а)
Здесь L обозначает случайную переменную, порождаемую /, т. е. 7=/(0; Xi, х2,...,хп), L=L(0-, Х{, Х2,...,Хп), где хг является реализацией Хг, Г= 1..п.
* В том смысле, что вероятность накрытия этим интервалом истинного значения в в точности равна 0,95. Ниже будет построен интервал с вероятностью накрытия, приблизительно равной 0,95. — Примеч. пер.
300
Приведенное выше выражение для ц>2 может быть оценено как
—\/(d2\nl/dd2). (6.2.17 6)
2) Если число неизвестных параметров 0Ь 02,...,0р больше одного, совместное выборочное распределение о.м.п. 0,, 02,...,0р асимптотически нормально [см. II, раздел 13.4] с математическим ожиданием 0ь 02,...,6р и ковариационной матрицей А1, где (г, $)-й элемент матрицы А равен
—E(d2\nL/d0rd6s), (6.2.17 в)
или приближенно
—d2\nl/d0rd0s, s, г=1.р.
Как правило, ш2 в п. 1 или элементы матрицы А в п. 2 зависят от неизвестных истинных параметров 0Ь 02,...,0р, поэтому для получения оценок этих величин необходимо вместо 0Г подставить соответствующие оценки этих параметров, например о.м.п. 0Г.
В двухпараметрическом случае ковариационную матрицу о.м.п. можно записать в виде
(Т? 6<Г1<т2
е<Т1<г2 а2
где а? — выборочная дисперсия 0Ь о? — выборочная дисперсия 02, а q — их выборочный коэффициент корреляции. Ее можно оценить как
- E(32lnL/30?)
_ E,(32lnL/30I302)
£,(Э21пЬ/д01д02)-|’1
E(32lnL/302) _
(6.2.17 г)
которая в свою очередь приблизительно равна
’ Э21п//Э0? 321п//301302Т1
_32ln//30,302 Э21п//302 _
(6.2.17 д)
где производные вычислены в точке (0ц 02). Эти формулы применяются в примерах 6.4.1—6.4.4.
Основания для предложенных приближений читателю могут показаться довольно поверхностными, однако, несмотря на это, в большинстве случаев эти приближения на удивление хороши.
301
г) Доверительные интервалы и области. Второй метод. Прямой метод построения приближенных доверительных интервалов был описан в разделе 6.2.5, п.б). Здесь мы рассмотрим второй, более грубый метод, основанный на формулах (6.2.17 а) — (6.2.17 д). Это наиболее распространенный метод для построения доверительных интервалов на практике.
Один оцениваемый параметр. При одном оцениваемом параметре в стандартное отклонение о.м.п. § находится на основе формулы (6.2.17 а), откуда
—1 /a>2 =E[(f\nL/dO2] « ct2In//d62 |
Поэтому приближенным 95%-ным доверительным интервалом для О можно считать
О ± 2w
[см. пример 4.5.2, 6)1.
Рассмотрим экспоненциальное распределение из примера 6.2.7. В этом случае
d2\nl/d62=— п/02,
поэтому
Ы » 6/4п,
а значит, 95%-ным доверительным интервалом для в будет 0 ± 20/Тл.
Многопараметрический случай. Ограничимся лишь двумя параметрами (0Ь 02), оцениваемыми, как и прежде, по методу максимального правдоподобия. Как следует из сказанного выше, о.м.п. (приближенно) распределена по двумерному нормальному закону с математическим ожиданием (0Ь 02) и ковариационной матрицей (6.2.17д). Рассмотрим две ситуации: в первой строится доверительный интервал для некоторой линейной комбинации параметров (что сводится к однопараметрической задаче), а во второй строится совместная довери-тельная область для 01 и 02.
1) Приближенным 95%-ным доверительным интервалом для линейной комбинации Ц101+а202 является интервал
«Л + «202 ± 1,96 + 2ахагс + ajv2,
где
V! с "
_ С v2_
оценка ковариационной матрицы (6.2.17д), см. (4.9.5)*.
* Это следует из того, что линейная комбинация нормально распределенных случайных величин имеет нормальное распределение. — Примеч. пер.
302
2) Допустим, теперь требуется построить совместную (двумерную) доверительную область для пары параметров (0Ь 02). Такой областью с приближенно 95%-ным уровнем доверия будет внутренность эллипса
-------+ =6(1—е2), ffl <7102 °2
где
(У? Р<У1<Т2
QOiOl 02
оцененная ковариационная матрица (6.2.17д). Более подробно об этом сказано в разделе 4.9.2. Точные уравнения для эллипсов приведены в примерах 6.4.3, 6.4.4.
6.2.6. ОЦЕНИВАНИЕ ФУНКЦИИ ПАРАМЕТРА в. СВОЙСТВО ИНВАРИАНТНОСТИ
При решении уравнений правдоподобия относительно параметра 0 нередко оказывается, что их проще решить относительно какой-либо функции от него, например 1п0, 1/0, и т. д. [см. пример 4.3.12]. В этом случае уравнение правдоподобия необязательно решать относительно 0. Обозначим эту функцию через ф и допустим, что ф=7(0) — взаимно однозначная дифференцируемая функция, т. е. с!ф/d0 и с^О/дф существуют и не равны нулю. Тогда, если через § и ф обозначить о.м.п. параметров 0 и ф, то
Ф = 7(0).
Например, если ф=1/0, то ф=1/§; если ф=1п0, то ф=1п0. Действительно, в регулярном случае функция правдоподобия относительно ф может быть записана как
Х(ф)=Х(7(0))=/(0),
откуда
d\^=(dl/d6)(d0^).
О.м.п. ф определяется как корень уравнения d\/dф-O. Но (dl/dfr)(d0/ /d$)=0 при ф=ф, т. е. когда 7(0) = ф. Поскольку по условию d0/d4>^O, последнее уравнение эквивалентно dl/dO=Q, откуда следует, что ф = 7(0). Доказанное свойство о.м.п. часто называется свойством инвариантности.
Между дисперсией v(0) о.м.п. 0, рассчитываемой по формуле (6.2.17а), и дисперсией у(Ф) оценки ф=7(0) можно установить приближенную зависимость. Двойное дифференцирование логарифма функции правдоподобия приводит к
б/2 In 7/ б/ф2 =(б/2 In 7/ б702)(б/0 / + (б71п 7/ б/0)(б/20 /б/ф2).
зоз
Поскольку d\nl/d0 =0 при 0 = 0, то
—l/v(0>(<fln//d02) | i = (d2\nl/d02) | ^0/б7ф)2« — [l/v(0)](d0/d</>)2, откуда окончательно получаем приближенную формулу*
v(0)«v(0)(^/d0)2, (6.2.18)
где v(0) и v(0) — дисперсии о.м.п. параметров ф и 0 соответственно, производная dф/dO рассчитывается при 0=0. Например, для ф=1/0 получим
v(<A) = 0‘2v(0).
При двух неизвестных параметрах 0] и 02 дисперсия функции ф от 01 и 02 приблизительно равна:
VW) = v(91)(gУ + 2cfl>„ ад( £)(£) + v№)( g )2, (6.2.19)
OU\ OV2 ^“2
где с(0ь 02) обозначает ковариацию между и 02.
6.3. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ В ОДНОПАРАМЕТРИЧЕСКОЙ СИТУАЦИИ
Пример 6.3.1. Распределение Бернулли. Вектор данных обозначим через х=(Х], х2.хл), где хг=0, если r-е испытание оказалось «неудач-
ным», и хг=1, если r-е испытание оказалось «удачным». Для случайной величины Хг п.р.в. равна:
Дхг,0)=^(1-0)1А »=0, 1,
поэтому функция правдоподобия имеет вид
/(0; х) = ^(1—0)ЛЛ О<0< 1, п
s=Y,xr — общее число удачных исходов в серии из п испытаний; случайная величина 5 в свою очередь является реализацией случайной величины, распределенной по биномиальному закону. Уравнение правдоподобия для этого примера следующее:
dlnl/dO =s/0— (п— $)/(1— 0) =(s—n0)/0(1—0), откуда находим решение, т. е. о.м.п. для 0:
§ = s/п=доля удачных исходов в серии из п испытаний.
* Эту формулу проще получить в результате разложения функции ф по 0 в ряд Тейлора до линейных членов: ф—Еф »(§—Её)(дф/(10), возведения в квадрат и взятия математического ожидания от обеих частей равенства. — Примеч. пер.
304
Приближенное значение дисперсии оценки 0, рассчитанное по формуле (6.2.17а), равно
—1 /Е[—S/О2—(п—£)/(!— 0)2],
где S распределено по биномиальному закону Вш(л, 0). С учетом этого предыдущее выражение равно
0(1—0)/л,
что в действительности в точности равно дисперсии 0. Оценкой дисперсии будет 0(1—6)/n=s(n—s)/n3.
Пример 6.3.2. Биномиальное распределение. Так называется распределение общего числа удачных исходов S в серии из п независимых испытаний Бернулли с вероятностью удачного исхода 0. Для случайной величины S п.р.в. равна:
Р(Х=5)=Д5, 0) = (2)0s(l-0)"-5, 5=0, 1.п.
После удаления множителя (”), не зависящего от 0, п.р.в. совпадает с п.р.в. из предыдущего примера. В действительности это неудивительно, поскольку в примере 6.3.1 s является достаточной статистикой для 0. Процесс поиска о.м.п. здесь полностью повторяется. Итак, о.м.п. для данного примера будет равна:
0 =s/n — доля удачных исходов в серии из п испытаний.
При построении приближенного доверительного интервала, основанного на формуле (6.2.15), функция правдоподобия может быть записана в виде
L(0)=/(0, S) = 0s(l— 0)n~s,
где S имеет биномиальное распределение с параметрами (п, в). Тогда ln£(0)=Sln0 +(п—S)ln(l— 0),
dlnL / d6 =S/e—(n—S) / (1 —0)=(S—пв) / [0(1—0)]
и
б/21п£/б702= —S/02—(л—S)/(l—0)2.
Поскольку Д5)=л0, выражение (6.2.15) для т2 сводится к
т2(0)=л/0(1—0).
305
Для построения 95%-ного доверительного интервала для 0, как было рекомендовано в разделе 6.2.5, п. б), необходимо решить следующие неравенства:
—1,96Vл/0(1—0) (5—л0)/0(1—0) l,96Vn/0(l—0).
Эти неравенства полностью совпадают с неравенствами, полученными в примере 4.7.1 при аппроксимации биномиального распределения нормальным.
Пример 6.3.3. Распределение Пуассона. Допустим, данные представлены в виде таблицы частот, т. е. известно, что х повторяется пх раз, х=0,1,2..к, причем каждое наблюдение является реализацией
случайной величины X с п.р.в.
Р(%=х)=е-^/х!, х=0,1,2,.. .
Функция правдоподобия 0 пропорциональна
П(е-е0*/х!)лх.
Опуская множитель 1/П(х!)"х, функцию правдоподобия можно записать в виде
/(0; х)=П (е^0*)«х=^0™, 0 > О, х=0 \
где обозначает общее число наблюдений, а х=Ехлх/л есть
среднее выборки. Далее находим х
1п/=—пО + пх 1п0.
Таким образом, о.м.п. является корнем уравнения
—п+пх/0 =0, откуда
0=х.
Аналогично
d\nL/d0 =—п + пХ /0,
где X — случайная переменная, порождаемая х, и d2\nL/d0~ = — пХ/02,
откуда с учетом того, что Е(х)=Е(Х)=0, по формуле (6.2.15) приходим к
1*(0)=п/0.
Для реализации метода, предложенного в разделе 6.2.5, б), необходимо решить неравенства
—1,96^— п + пх/0 1,96.
306
Отметим, что соответствующий 95%-ный доверительный интервал в точности совпадает с доверительным интервалом, построенным в примере 4.7.2 на основе аппроксимации пуассоновского распределения нормальным.
Математическое ожидание оценки О, рассчитанное по формуле (6.2.16), равно 6, а ее дисперсия равна 6/п. Для данного распределения это точное значение.
Пример 6.3.4. Геометрическое распределение. Обозначим через X число независимых испытаний в схеме Бернулли до первого «успеха» (включая его), вероятность «успеха» в одном испытании, как и прежде, будем обозначать через 6. Тогда
Р(Аг=х)=Дх, 0)=(1—0)*-10, х=1,2,...,0< 0 < 1.
Для каждого значения j обозначим через n(J) его частоту, т. е. число элементов выборки со значением J, у=1.к. Здесь к — максимальное
наблюденное значение. Тогда функцию правдоподобия для 0 можно записать как
/(0)=П [(1— 0y-10]«O) = (i—0)«Сг— 1)0лэ х = £jn(j), 7 = 1 1
откуда
1п/=л(х—1)1п(1—0) + л1п0
и уравнение правдоподобия d\nl/d6=Q примет вид
п(х—1)/(1— 0) + п/0=О.
Отсюда находим, что о.м.п. для 0 будет равна:
0 = 1/х.
Для данного примера расчет точного значения дисперсии оценки весьма затруднителен, поэтому здесь как раз уместно использование приближенной формулы. Для геометрического распределения, как легко проверить,
—d2 In l(X) / de = n(X—1) / (1 — 0)2 + n / 02.
Поскольку E(X}=E(X)=\/e, to
E(—fifln l(X) / dO)=n/02( 1 — 0).
В соответствии с (6.2.15) дисперсия о.м.п. приближенно равна 02(1—0)/л,
а ее оценка — 02(1—§)/п.
307
Если нас интересует параметр \/0 = ф, а не сам параметр 0 [см. раздел 6.2.3], то функцию правдоподобия удобнее записать в виде что приводит к о.м.п.
ф=х = 1/0.
Смещение этой оценки для 1/0 равно нулю, а приближение (6.2.15) ее выборочной дисперсии приводит к точному результату
ф(ф—1)/л=(1 — 0)/л02.
Пример 6.3.5. Отрицательно биномиальное распределение. Обозначим через X число независимых испытаний в схеме Бернулли до первых с «успехов», с=1,2,... (частный случай, когда с=1 соответствует геометрическому распределению). Тогда [см. II, раздел 5.2.4]
/(х, 0)=P(Ar=x) = gzJ)(l— 0У-С0С, х=с, с+1. О<0< 1.
Как и в предыдущем примере, легко найти о.м.п. для 0. Она равна:
9 =с/х
с приближенной дисперсией 02(1—&)/пс.
Пример 6.3.6. Выборка без возвращения из конечной совокупности. Этот пример характерен тем, что наблюдения здесь зависимы, а неизвестный параметр дискретен. Вектор данных x=(xHx2........хл)
представляет собой последовательность нулей и единиц; хг=0 означает, что г-й выбранный элемент совокупности «доброкачествен», а хг=1 — что этот элемент «дефектен» (в последующем выбранный элемент удаляется из совокупности), г=1, 2,..., п. Вся совокупность состоит из N элементов (N — неслучайная переменная), число дефектных элементов во всей совокупности неизвестно и равно 0. Совместное распределение Хг (случайная переменная, ее реализацию обозначаем через хг) удобно определить в терминах п.р.в. Х} и условной п.р.в. Хг для г=2,3,...,л при фиксированных Xs=xs, 5=1,2.....г—1. Для %,
п.р.в. равна:
/,(х„ 0)=0*.(l-0)1-*/N, х,=0, 1, 0=0,1..... N,
а условная п.р.в. Хг, г=2.л, равна:
fAXr, 9 I Л-,, Х1.
xs=0, 1, (s=l, 2.г).
Совместная п.р.в. Хг имеет вид
п g(x, 0)=/1(х1, 0)П fr(xr, 0 I Хь х2.х^.р,
308
она может быть переписана как
8(хв)=(^О/(^(3),
где п d=^xr= число дефектных элементов в выборке.
Опуская неинформативные множители, функцию правдоподобия можно записать в виде
l(6)=ei(N—ey./(0—d)!(N— 0—n+d)l, 0=0,1,...,7V.
Поскольку 0 принимает только целочисленные значения, максимум не может быть найден с помощью дифференцирования. Он определяется неравенствами
/(0)>/(0—1), /(0)>/(0 + 1),
которые приводят к оценке
0 = [(N+l)d/rt],
где [z] обозначает целую часть z. Таким образом, приближенно
§ =Nd/n.
Формула выборочной дисперсии приводится в следующем примере.
Пример 6.3.7. Гйпергеометрическое распределение. Вместо записи индивидуальных значений хг будем фиксировать лишь общее число дефектных элементов d в выборке (объем выборки равен п). Распределение вероятностей d хорошо известно [см. II, раздел 5.3],
«w «>=($)«)/(£).
Как видим, эта функция правдоподобия с точностью до Q) совпадает с функцией правдоподобия из предыдущего примера (аналогичное соответствие можно видеть и в примерах 6.3.1, 6.3.2)*.
Выборочную дисперсию § нельзя найти методами приближения, описанными в разделе 6.2.5, поскольку здесь параметрическое множество дискретно. Непосредственный расчет дисперсии оценки
0=Nd/n,
которая, кстати, является несмещенной, приводит к результату
ЛГ N— Г
* Это свойство функций правдоподобия связано с одним из фундаментальных понятий теории математической статистики — достаточными статистиками. — Примеч. пер.
309
Пример 6.3.8. Определение плотности распространения микроорганизмов методом разбавления. Применение метода Ньютона. Один из методов оценивания плотности распространения невидимых микроорганизмов в воде заключается в следующем. Производится п проб одинакового объема исследуемой воды. Каждая проба помещается в благоприятную среду, в которой вырастает до видимых размеров колония микроорганизмов, если хотя бы один такой микроорганизм присутствует в пробе. Так определяется наличие или отсутствие микроорганизмов в пробе. Опыты проводятся для неразбавленной воды (с=1), для двукратно разбавленной (с=2), а также для четырехкратно разбавленной (с=2 =4). Разбавление производится стерильной водой. Допустим, было произведено п = 5 проб, каждая объемом 1 см3, причем везде были обнаружены микроорганизмы. При двукратном разбавлении в каждом объеме раствора в двух случаях не было обнаружено микроорганизмов, а в трех их обнаружили. При четырехкратном разбавлении лишь в одном объеме раствора было замечено наличие микроорганизмов. Таким образом, мы имеем следующую таблицу:
Кратность разбавления Число проб с необнаруженными микроорганизмами Число проб с обнаруженными микроорганизмами
1 0 5
2 2 3
4 4 1
Обозначим через 0 плотность распространения микроорганизмов в исследуемой воде (число организмов в 1 см3). В качестве вероятностной модели распределения микроорганизмов естественно взять плотность распределения Пуассона, при которой число R микроорганизмов в 1 см3 пробы является случайной переменной, распределенной по закону Пуассона с параметром 0. Таким образом, вероятность того, что в пробе не будет микроорганизмов (7?=0), равна е’в, а вероятность, что они будут обнаружены, равна 1—е'в. Число S проб с необнаруженными микроорганизмами в выборке из 5 проб подчиняется биномиальному распределению с параметрами (п, р), где п = 5, В двукратно
разбавленных пробах необходимо 0 заменить на 0/2, а в четырехкратно разбавленных — на 0/4. Вероятность отсутствия микроорганизмов в s'], s2, s3 неразбавленных, двукратно и четырехкратно разбавленных пробах соответственно равна:
g(0-, s{, s2, s3) = n( )p^(l—Pr)5'Sr,
310
где
Pi=H, р2=е'0/2, р3=е-®/4.
Таким образом, если опустить неинформативный множитель, функция правдоподобия 9 для наших данных будет иметь вид
р?(1-Р1)5Рг(1-р2)3р|(1-р3),
или в терминах р-е'е/^
1(р) = (1-р4)’р4(1-р2)3р4 (1-р) =р8( 1 -р4)5( 1 -р2)3( 1 -р).
Найдем производную
d\xd/dp=(8—р—1р2—р3—35р4) / р(1 —р4).
Приравнивая ее к нулю, приходим к уравнению правдоподобия. Несколько вычислений производной позволяют заключить, что корень лежит между 0,60 и 0,61. Таким образом, в качестве первого приближения можно взять р' =0,605. Более точное значение корня уравнения правдоподобия можно получить, воспользовавшись итеративным методом Ньютона, по которому
п" = п'—( d}nl<P'WdP' ) dfXnlty') / dp'2 ''
В качестве оценки d2\nl(p')/dp'2 берем d2\nl(p)/dp2 = —1/var, где var задается выражением (6.2.15) и определяет приближенную дисперсию о.м.п. Тогда
р" «p' + var •dXnllp'j/dp'. (6.3.1)
Метод Ньютона дает достаточно высокую точность решения уравнений правдоподобия*.
Выражение d\nl/dp для нашего примера было выписано выше. Нетрудно показать, что l/var=—d2\nl/dp2 или
1 + 14р+3р2+ 140р3 /сПпЛ/1—5/А р(1-р4) ' ф
Вычисления по методу Ньютона приводят к следующим результатам:
первое приближение р' =0,605, din l/dp=0,0126, var=0,0126, второе приближение р"=0,6031.
* Для этого, однако, необходимо иметь хорошее начальное приближение. — Примеч. пер.
311
Последнее приближение достаточно точно, его и возьмем в качестве корня уравнения правдоподобия. Итак, о.м.п. параметра р=е_0/4 равна 0,6031. Для построения 95%-ного доверительного интервала, как следует из (6.2.16), необходимо решить уравнения
d\nl/dp= ± 1,96w, где
w2 = — (Pkil/dp2 | р=у>= 1/0,0126=(8,91)2.
Таким образом, эти уравнения сводятся к
d\nl/dp= ± 17,46;
его корнями являются
/>1=0,355, />2=0,760.
Поэтому 95%-ным доверительным интервалом для р будет (0,355, 0,760).
Оценка для в находится из соотношения в = —41пр, откуда 0 =2,023 с 95%-ным доверительным интервалом (1,10, 4,14).
Можно было бы воспользоваться более грубым методом построения доверительного интервала [см. раздел 6.2.5, п. г)], который основывается на том, что р имеет приближенно нормальное распределение с выборочной дисперсией, равной 0,0126=(0, И2)2. Поэтому доверительным интервалом для р будет р ± 1,96-0,122, т. е. (0,38, 0,82). Соответствующий интервал для 0 есть (0,79, 3,87).
При построении доверительного интервала для 0 можно было бы учесть, что выборочная дисперсия для 0 равна 4/р выборочной дисперсии для р, равной 0,0126. Из этих соображений приближенным 95%-ным доверительным интервалом для 0 будет (0,56, 3,48).
Пример 6.3.9. Нерегулярные случаи, а) Граница равномерного распределения. Если случайная величина X распределена равномерно на интервале (0, 0), то ее п.р.в. имеет вид
г 0'1, О^х^0,
f(x, 0)=
10 в другом случае.
Функция правдоподобия 0 для данных х=(хь х2,...,хп) равна:
0'п, 0 ^Xi, х2,...,хп ^0,
0 в другом случае,
п
1(0, x) = nf(xr, 0) = г= 1
312
т. е.
I 0 в другом случае, где *тах(*т]П) обозначает максимальное (минимальное) значение среди наблюдений. Тогда значение 6, максимизирующее функцию правдоподобия, равно 0=хтах- Заметим, что здесь в не является решением уравнения правдоподобия dl/dG-O.
б) Оценивание параметра сдвига экспоненциального распределения. В этом случае п.р.в. равна:
. ( е^х'°\ х^е,
10 в другом случае,
а функция правдоподобия имеет вид
Х1, ....хп^в, сеп$-*~\ xmin>0,
/(0; х) = (.0 в другом случае to в другом случае,
где xmin обозначает минимальное из наблюдений. Здесь, как и в предыдущем примере, о.м.п. находится не путем дифференцирования и решения уравнения правдоподобия, а на основе непосредственного анализа функции правдоподобия. Легко видеть, что о.м.п. равна “^rnirr
Формулы для вычисления приближенного значения выборочной дисперсии о.м.п., представленные в разделе 6.2.2, в нерегулярном слу- -чае неприменимы. Выборочные свойства о.м.п. теперь должны изучаться непосредственно. Так, в пункте а) о.м.п. имеет математическое ожидание, равное пв/(п + 1), и дисперсию пб2 / (п + 2)(п+1)2, за оценку последней можно взять пв2 / (и + 2)(и + 1)2.
6.4. ПРИМЕРЫ О.М.П. В МНОГОПАРАМЕТРИЧЕСКИХ СЛУЧАЯХ
Пример 6.4.1. Нормальное распределение. Если случайная величина X нормально распределена с параметрами (д, <т), то функция правдоподобия для ц и о по данным х=(хь Х2,...,х^ равна:
г 1 п
/(/г, а; х) = ст-лехр — —- £ (xr—ii) , Za r= 1
—< ц <о=., а>0.
(6.4.1)
313
Найдем производные по параметрам
din//др = Е(хг—р)/а2, d\nl/da = —п/а + Е(л>—g)2/a3.
Оценки максимального правдоподобия являются решением системы уравнений
Е(хг—м)-0, £(хг—р)2-ги?, откуда
р=х, a = (L(xr—х)2/п)1/2.
Далее находим
d2ln//d/? =—п/а2,
д21п1/дрда = —2Е(х>—р)/а3 =—2п(х—р)/а\
д2\п1/да2 - п / а2-—3'Е(хг-—р)2 / а, поэтому
Е(д2InL/др2) =—пЕ(Х)/ст2 = — пр/а2,
Е( d2lnL / дрда) = — 2пЕ(Х — р) / а3 = О,
Е(д2 InL / да2)=п/a2—3LE(xr—p)2 /а4 = п/ а2—3п / а2 = —2п / а2.
Таким образом, приближенной ковариационной матрицей D о.м.п., как следует из (6.2.17д), будет
о
а4/2п
Отсюда следует, что приближенными выборочными дисперсиями для р и а будут соответственно а2 / п и а4/2л, а ковариация между р и а приближенно равна нулю. Численные значения оценок дисперсии находятся по формулам
var(£)= а2/п, var(a2) = 2a4/n, cov(g, d2) = 0.
Если в качестве параметров взять р и 6 = а2, то р=х, в = a2=L(xr—х)2/п,
314
a jj _ в/п 0 ” ” a2/n О
- О 202/п J L о 2а4/п J
Таким образом,
var(g)=a2/n, var(a2) = 2a4/n, cov(g, ст2)=0.
Здесь g — несмещенная оценка, а а2 имеет небольшое смещение; точное математическое ожидание о2 равно (1 — 1/л)а2.
Пример 6.4.2. Логарифмически нормальное распределение. Положительная случайная переменная Y подчиняется логарифмически нормальному (логнормальному) распределению, если In Y=Х имеет нормальное распределение. Таким образом, У=ехр(Аг), где X распределено нормально с параметрами, скажем, ц и а [см. раздел 6.6.1]. Для случайной величины Y п.р.в. равна
—y^expf---------L- (Iny—g)2], у > О,
а\2тг 2а
а функция правдоподобия, если опустить множитель (1/Пуг), для g и а по данным y=(yit уг,...^^ имеет вид
/(g, у) — а-"ехр[— -Ц- E(lnyr—g)2], —.»> < g < .„, а > 0.
2а
Положим
lnj>r=xr, г=\,...,п.
Легко видеть, что тогда функция правдоподобия совпадает с (6.4.1). Отсюда следует, что метод максимального правдоподобия для логнормального распределения совпадает с методом максимального правдоподобия для нормального распределения с заменой наблюдения уг на его логарифм xr = lnyr.
Пример 6.4.3. Гамма-распределение. Допустим, имеется выборка объема п из двухпараметрического гамма-распределения с функцией плотности
/(х; а, (3) = (х«-1е-х/^)/(3«Г(а), х>0(а>0, /3 > 0),
где а — параметр формы, /3 — параметр масштаба [см. II, раздел 11.3.1]. Предположим, что данные представлены в векторной форме. Функция правдоподобия, как легко проверить, в этом случае равна
/(а, х) = (Пхг)«-1е-^/^-л«Г-л(а), г= 1
а ее логарифм
In / = (а—1 )Е 1пхг—/3~1 Ех,—па In/3—п 1пГ(а).
315
Уравнения правдоподобия имеют вид
Е1пхг—л1п/3—иГ(а)/Г(а) = 0, да
^-' = 0-2Ехг-ла/0=О.
Ор
Из второго уравнения следует, что
(8=х /а,
где а и 3 — о.м.п. параметров а и /3, а х — среднее выборки. Подставляя полученное соотношение в первое уравнение правдоподобия, приходим к нелинейному уравнению относительно а:
1пх— 1пх +1па—^(а) = 0, где
1пх = Е1пхг/л, ^(а) = Г(а)/Г(а).
Для иллюстрации рассмотрим выборку из гамма-распределения с параметрами а = (3=2. Каждое наблюдение было получено суммированием четырех последовательных независимых реализаций квадрата нормальной случайной величины с нулевым математическим ожиданием и единичной дисперсией [см. Barnett (1965) — F). Выборка имеет следующий вид:
5,6135 2,2197 5,8971 3,8243 6,5021
0,8590 3,5452 2,9483 2,0567 0,7797
1,0184 11,3595 2,1279 2,0924 4,1648
4,9673 0,3939 4,7217 2,9399 6,8468
5,6229 3,6467 6,0812 1,9336 4,4899
При этом
Е1пх = 27,59314, Ех = 96,1934, Ех2 = 517,5038,
1пх= 1,1037, х =3,8477, х2 = 20,702,
1пх =1,3475, 1пх—1пх=0,2438.
316
Метод максимального правдоподобия приводит к нелинейному уравнению относительно а:
Л(а)=0, где
Л(а) = 1па—^(а)—0,2438.
После того как значение а будет получено, оценку /3 находят из уравнения
/?=3,8477/а.
Метод моментов. Метод моментов заключается в приравнивании значения как функции от параметров к соответствующим выборочным моментам лт [см. (2.1.7)], г=1, 2,...,р, где р — число неизвестных параметров. При двухпараметрическом гамма-распределении метод моментов приводит к следующим уравнениям:
Дх)=х, £'(Л2)=х2,
что для гамма-распределения дает систему уравнений
= 3,8477, а/?2 + а2/?2 = 20,702.
Решением этой системы будут значения
а° = 2,52, 0°=1,53.
Они могут быть взяты в качестве начального приближения для итеративного процесса решения уравнений правдоподобия. Результаты подобного итеративного процесса, основанного на методе Ньютона — Рафсона (метод касательных), представлены в таблице:
Номер итерации а ^(а) Л(а) Лх(а) Поправка —Л(а)/h\a)
1 2,52 0,713 —0,32 0,49 —0,09 —0,36
2 2,160 0,521 0,0052 0,590 —0,123 0,042
3 2,202 0,5454 0,00013 0,5723 —0,1182 0,0011
4 2,203
317
Итак, d=2,203, откуда 3=1,747 (ср. с истинными значениями а =2, (8=2).
Точность оценивания определяется матрицей ковариации V о.м.п. а и 3, обратная к которой, как следует из раздела 6.2.5, а), имеет вид
V~~l=nE ’ М«) 1/3 -п
. 1/3 Х/З3—а/32 - . 1/3
откуда
к= х п з2 ' а/02 —1/3' г 2 ^1
аф'(а)—1 _ -1/3 ’Г(а) _
1/3 -
а/32 -
QO\<h.'
г
<Ъ J
Для нашей выборки а! =0,58, ст2 = 0,52, g =—0,67. В соответствии с разделом 4.9, на основе полученных величин можно построить приближенный 95%-ный доверительный интервал для а:
а€2,203± 1,96-0,58,
т. е.
а€(1,07, 3,34).
Аналогично строится приближенный 95%-ный доверительный интервал для 3:3€ 1,747 ± 1,96-0,52, т.е. 3^(0,73, 2,77). Совместное рассмотрение этих доверительных интервалов требует определенной осторожности, поскольку прямоугольник, построенный на основе этих интервалов, не будет накрывать истинное значение пары параметров (а, 3) с вероятностью (О,95)2 *.
Для построения совместной 95%-ной доверительной области [см. раздел 4.9.2] рассмотрим область, ограниченную эллипсом (4.9.6), т. е. в нашем случае
2,923 (а—2,203)2+4,443 (а —2,203) (3—1,747) +
+ 3,704(3—1,747)2 = 3,302. (6-4-2>
Этот эллипс показан на рис. 6.4.1. Заметим, что при а = 3 = 2 лева» часть (6.4.2), равная .0,354, меньше правой, значит, точка (2, 2) лежиз внутри доверительной области. Таким образом, построенный довери тельный эллипс накрывает истинное значение параметров (а, 3).
* Это будет иметь место, если а и 3 независимы, но как было подсчитано, q = = —0,67 #0. — Примеч. пер.
318
Рис. 6.4.1. 95%-ный доверительный эллипс для (а, 0) из примера 6.4.2. Уравнение этого эллипса задается в (6.4.2)
Пример 6.4.4. В случае марковской цепи, обсуждавшейся в примерах 6.2.5 и 6.2.7, параметры а и 0 матрицы вероятностей перехода
а 1—а
1-0 0 _
имеют функцию правдоподобия вида
/(а, 0)==(1—а)41а304(1—0)2/(а + 0).
В примере 6.2.7 было найдено достаточно удовлетворительное начальное приближение максимума функции правдоподобия (а, 0)=(0.068, 0,600). Вычисление значения функции /(а, 0) на сетке значений параметров в окрестности начального приближения привело к следующим результатам (/(а, 0)-1О7):
5 а 0,060 0,070 0,080
0,59 5,356 5,401 5,099
0,60 5,370 5,417 5,115
0,61 5,372 5,420 5,119
0,62 5,362 5,412 5,113
319
Как видно из этой таблицы, максимум функции правдоподобия достигается вблизи точки (0,070, 0,61). Дальнейшие расчеты на более мелкой сетке в окрестности найденного максимума привели к следующим результатам:
5 а 0,064 0,066 0,068
0,605 5,4405 5,4494 5,4420
0,606 5,4407 5,4496 5,4430
0,607 5,4409 5,4498 5,4427
0,608 5,4408 5,4495 5,4426
Отсюда следует, что с достаточной степенью точности можно считать, что максимум достигается в точке
а =0,066, 0=0,607
[ср. с рис. 6.2.6].
Для построения приближенной ковариационной матрицы необходимо обратить матрицу (6.2.17д), т. е.
— д21п//да2 д21п//дад0 "|
- аг1п//даа/з а21п//аз2 -I а=«,/М
которая для нашего примера равна:
~ 41 3 _ 1 . _ 1 “
(1—а)2 + а2 (а + /3)2’ (а + /3)2 _ Г 734 —2 1
_ 1 . 2 + -1 _ 1 I- —2 22 1 ’
L (а + 0)2’ (1-0)2 02 (а + «2
Обратная к ней будет следующая:
- 0,00136 0,00012 -
_ 0,00012 0,04528 _
т. е.
0'1=0,037, о2=0,213, е=0,015.
320
Приближенным 95%-ным доверительным эллипсом будет область, задаваемая уравнением
735(а—0,068)2—3,8(а—0,068) (0—0,607)4-22(0—0,607)2 = 6,
как в (4.9.6). Например, при подстановке в левую часть этого равенства значений а =0,1, 0=0,5 получим 1,02. Это значение меньше 6, поэтому соответствующая точка принадлежит 95%-ной доверительной области. Наоборот, при а=0,2 и 0=0,5 значение левой части равно 13,1, что превосходит 6, т. е. точка (0,2, 0,5) не принадлежит доверительной области. Другими словами, можно считать, что истинное значение параметров отличается от (0,2, 0,5) с 5%-ным уровнем значимости (ошибки).
6.5. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ
6.5.1. ПОНЯТИЕ «РЕГРЕССИЯ»
Читателя, не знакомого со статистикой, возможно, удивит использование в статистике термина «регрессия», который в обычном смысле понимается как «обратное движение, возврат к исходной точке или месту» [см. Oxford English Dictionary]. Этот термин в статистике был введен в XIX в. в связи с исследованием вопросов наследования физических характеристик человека. В качестве одной из характеристик был взят рост человека; при этом было обнаружено, что в целом сыновья высоких отцов, что неудивительно, оказались более высокими, чем сыновья отцов с низким ростом. Более интересным было то, что разброс в росте сыновей был меньшим, чем разброс в росте отцов. Так проявлялась тенденция возвращения сыновей к среднему росту, т. е. регресс. Этот факт был продемонстрирован вычислением среднего роста сыновей отцов, рост которых равен 56 дюймам, вычислением среднего роста сыновей отцов, рост которых равен 58 дюймам, и т. д.*После этого результаты были изображены на плоскости, по оси ординат которой откладывались значения среднего роста сыновей, а по оси абсцисс — значения среднего роста отцов. Точки (приближенно) легли на прямую с положительным углом наклона меньше 45°; важно, что регрессия была линейной.
Итак, допустим, имеется выборка из двумерного распределения пары случайных переменных (X, У). Прямая линия в плоскости (х, у) была выборочным аналогом функции
g(x)=E(Y \ Х=х).
* Описываемое исследование было проведено английским естествоиспытателем Ф. Гальтоном, им же был введен термин «регрессия». — Примеч. пер.
321
В теории вероятностей под термином «регрессия» и понимают эту функцию, которая есть не что иное, как условное математическое ожидание случайной переменной Y при «условии», что другая случайная переменная X приняла значение х. Если, например, пара (X, У) имеет двумерное нормальное распределение с f(x)=/ii, Е’(У)=д2> уаг(Л)=ст?» уаг(У) = с^, сог(Х У) = 2, то можно показать, что условное распределение У при Х=х также будет нормальным с математическим ожиданием, равным
E(Y I X=x)=/J2 +
(6.5.0)
и дисперсией
var(y | Ar=x)=af(l—e2)
(см. И, раздел 13.4.6]. В этом примере регрессия У на X является линейной функцией.
В общем случае регрессия одной случайной переменной на другую не обязательно будет линейной. Также не обязательно ограничиваться парой случайных переменных. Можно, например, рассмотреть совместное распределение трех случайных переменных (Х1г Х2, Х3), тогда регрессия X на Х2 и Х3 представляет собой функцию
g(x2, х3)=Е(Х | Х2—х2, Х3=х3).
Особое значение имеет линейная регрессия. С линейной регрессией мы встречаемся, например, когда распределение тройки (X, Х2, Х3) нормально.
Статистические проблемы регрессии связаны прежде всего с оцениванием неизвестных параметров регрессии и другими статистическими выводами (доверительное оценивание, проверка гипотез и т. п.). В типичной двумерной задаче оценивания регрессии, в частности в рассмотренном выше примере, где оценивалась регрессия роста сыновей на рост отцов, данные выборки могут быть записаны так, как представлено в табл. 6.5.1.
Таблица 6.5.1. Запись данных в векторной форме в задаче оценивания регрессии Y на X
Значение х
X, Хг хк
Значение у 7(1,1) 7(2,1) 7(^,1) 7(1,2) 7(2,2) 7(л2, 2) . . . У<Х,к) 7(2Л) У(пк,к)
Число наблюдений П\ пг . . пк п
Среднее 7~(1) Т"(2) . . . У (к) т"
322
(Значения х здесь, конечно, округлены. Например, до целого числа дюймов.)
Если значения у тоже округляются или группируются, то данные могут быть представлены в виде таблицы частот.
Таблица 6.5.2. Запись данных в виде таблицы частот в задаче оценивания регрессии Y на X
Значение х
Х1 Хг Хк
У1 л(1, 1) л(1, 2) л(1, к)
У1 и(2, 1) л(2, 2) п(2, к)
Значение у • . . •
Уа л(в, 1) л(а, 2) л(в, к)
Число наблюдений П\ пг пк л
Среднее F(I) Г(2) Ук У
(Числовые значения приведены в табл. 6.5.3, а их анализ — в примере 6.5.1.)
Название «регрессия» в дальнейшем было распространено на ситуации, в которых значения независимой переменной х обозначили заранее указанные уровни управляемой переменной. В подобных ситуациях значение у часто называют откликом системы на управление. Типичный пример такой регрессии: независимая переменная представляет собой количество удобрения, вносимого на поле (управление), а откликом (зависимая переменная) служит размер урожая, собранного на этом поле.
В обоих вариантах регрессионной модели обычно предполагают, что переменная у, соответствующая данному значению х (которое обозначим через xj), представляет собой реализацию нормальной случайной величины с параметрами (ду, оу), при этом ду является известной функцией от Xj.
Одна из распространенных форм регрессионных моделей — полиномиальная модель, для которой
ду = а0 + «1*/ + «2>у+ ••• + ар^>
где р задано (целое), а коэффициенты регрессии а0, ос\, ..., ар неизвестны и подлежат оцениванию на основе имеющихся данных. В частном случае, когда р=1, говорят о «линейной регрессии». Тогда
Hj = a + 0Xj.
323
Иногда предполагают, что
<ту = а= const,
т. е. дисперсия наблюдений yj постоянна и не зависит от xj. В этом случае говорят, что наблюдения гомоскедастичны. В гетероскеда-стичном случае (oy# const) среднеквадратическое отклонение необходимо представить в виде функции xj. Например, оу может быть пропорциональна квадрату хр т. е.
где параметр 7>0 неизвестен и подлежит оцениванию.
6.5.2. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ЛИНЕЙНОЙ РЕГРЕССИИ С ВЕСАМИ
Рассмотрим сначала ситуацию, когда для каждого значения х (=Xj) имеется единственное наблюдение у^ т. е. пх=п2 = ... = Пк = \ [см. табл. 6.5.1]. Тогда
ILj = a + ftxj, 7=1,2 к, (6.5.1)
где а,- предполагаются не обязательно равными, но известными. Напомним, что уравнения правдоподобия для а и /3 получают дифференцированием логарифма функции правдоподобия; их необходимо решить относительно а, /3- Итак, имеем
Z(a, 3) =Пег-1 ехр[-у (yj—a—$Xj)2/Оу ].
Логарифм функции правдоподобия равен:
log Z=—Е log ау—у Е (yj—а—0Xj)2/а2-.
Дифференцируем:
д log Z/ да = Е (yj—а—&Xj) / оу,
д log Z/ Э/3 = Е Xjfy—a—($xj) / Oj.
Приравнивая уравнения к нулю, приходим к системе уравнений:
а Е Wj + /? Е WjXj = Е wyjy,
(6.5.2)
а Е WjXj + /3 Е WjX^ = Е wjxjyj,
где wy = l/oy, 7=1»2..........................к.
Значения му называют весами.
324.
Уравнения (6.5.2), определяющие оценки максимального правдоподобия а и @ коэффициентов регрессии, совпадают с нормальными уравнениями взвешенного метода наименьших квадратов [см. гл. 8]. Напомним, что по этому методу необходимо минимизировать сумму квадратов отклонений
L(yj— a—Е Wjtyj— a—0Xj)2. (6.5.3)
6.5.3. ЛИНЕЙНАЯ РЕГРЕССИЯ С ОДИНАКОВЫМИ ВЕСАМИ
а) Оценки. Наиболее распространенные формы представления данных в задаче оценивания коэффициентов линейной регрессии показаны в табл. 6.5.1 и 6.5.2. Причем мы предполагаем, что
aj = a, j=\,2 k.
В целях удобства формулу для щ в (6.5.1) перепишем в несколько ином виде:
Hj = a + 0(xj—x), (6.5.4)
где
х ^'EnjXj/n, n=Lnj. (6.5.5)
Необходимо оценить три параметра а, 0 и а (заметим, что здесь а отлична от а в формуле (6.5.1)). Обозначая а из (6.5.1) через а', мы получаем
а = fix = а'.
В дальнейшем будем использовать запись (6.5.4). Функция правдоподобия, нетрудно видеть, пропорциональна
к
1(а, ft, а) = П/(/),
где, следуя обозначениям табл. 6.5.1,
/(/) = o~ni exp [—у Й [yij—a—&(xj—х )2] / а2],
где yij=y(i,J). Логарифм функции правдоподобия равен:
log/= —rtloga—у а—/?(х7—х)]2/<Л
2 i i
n=£rij — общий объем выборки. Дифференцируем:
31ogZ/3a= LL[yij—a—P(xj—х)]/о2 =
i J
= [ppyij—na—^'pij(xj—x)]/o2,
325
что приводит к
dlogZ/da = pp(yij—па) /а2, поскольку £nj(Xj—х)=0 по определению х. Аналогично
dlogl/dP = [W/- х)уу— ^nj(xj—х)2]/а2.
Приравнивая обе производные к нулю, приходим к оценкам максимального правдоподобия:
а = fpij/n = 'pijyj/n =у — (6.5.6)
общее среднее,
х )yij/J2nj(xj—х )2 =
=pnj(xj—х )yj + ptjtxj—x )2 = (6.5.7)
= (pijXjyj—nxy) / (E njxj— nx2),
где x определяется по формуле (6.5.5).
Если бы Hj задавались по формуле (6.5.1), а не по формуле (6.5.4), то мы бы имели недиагональную систему уравнений относительно а и 3, решить которую было бы сложнее; по этой причине более простой вид имеют и решения этой системы — (6.5.6) и (6.5.7). Еще одно положительное свойство записи (6.5.4) заключается в том, что оценки а и 0 распределены независимо друг от друга.
б) Выборочные свойства оценок. Чтобы получить представление о точности этих оценок, нет необходимости пользоваться приближенными формулами из раздела 6.2.5. Поскольку а и /3 — линейные функции yij, которые по условию нормально распределены, они также имеют нормальное распределение. Выборочные математические ожидания, дисперсия и ковариации будут следующими:
математическое ожидание а равно а,
(6.5.8)
« « 0 равно 0,
т. е. оценки не смещены:
дисперсия а равна аг /п,
« 0 равна х~)\ (6.5.9)
ковариация <5 и 0 равна нулю.
Таким образом, а и /3 независимо распределены [см. II, раздел 13.4.2]. 326
Теперь найдем оценку для а2. Уравнение dlogZ/d<r=0 приводит к следующей оценке:
о.м.п. a2 = pp[yij—а—(3(xj—х)]2/п =SS/n,
где SS обозначает сумму квадратов (Sum of Squared) отклонений:
SS=J2J2[yij-a-0(xj-x)}2 =
' (6.5.10)
= — na2—02Z(Xj—x)2.
i j J
С вычислительной точки зрения формула ЕлДху—х)2 лучше, чем StyxJ—лх2.
На практике пользуются не оценкой максимального правдоподобия для ст2, а некоторой ее модификацией:
a2 = SS/(n—2). (6.5.11)
Можно показать, что в отличие от первой оценки она является несмещенной. Однако не свойство несмещенности делает эту оценку предпочтительней. Более важно то, что оценка (6.5.11) согласована с существующими статистическими таблицами. (Несколько замечаний сделаем относительно последней формулы. Читателю может показаться странным, что в (6.5.11) делителем является значение п—2, а не более привычное п. Использование п вместо п—2 повлекло бы за собой лишь дополнительное видоизменение статистических таблиц, к тому же статистика (6.5.11) является несмещенной оценкой а2.)
в) Доверительные интервалы для а и (3. Как уже было отмечено, аир являются линейными комбинациями нормально распределенных случайных величин и имеют математические ожидания, равные а и 0 соответственно. Их дисперсии можно оценить как
уаг(а)=ст2/и, var(/?)=<r2/Enj(Xj—х)2, (6.5.12)
где а2 задается формулой (6.5.11), т. е.
o2 = SS/(n—2),
где SS определяется в (6.5.10). Можно показать (например, с помощью методов из раздела 2.5.8), что случайная величина
(л—2)^/ст2
имеет распределение х2 с п—2 степенями свободы [см. раздел 2.5.4, а)] и стохастически независима от а и /3. Отсюда следует, что
(а—а)/(а/4п)_ а—а а/а а/у/п
327
имеет распределение Стьюдента с п—2 степенями свободы [см. раздел 2.5.5]. Таким образом, центральным 95%-ным доверительным интервалом для а будет
d±Z97 5a/Vn (6.5.13)
[ср. с примером 4.5.2], где ?97>5 является 97,5 %-ной точкой распределения Стьюдента с п—2 степенями свободы.
Аналогично находят 95%-ный доверительный интервал для /3:
0±Г97>5<?/\/Ёл7(х7—х)2. (6.5.14)
г) Критерий значимости для а и Как следует из предыдущих рассуждений (односторонний) уровень значимости для разности а—ан, где — гипотетическое значение неизвестного коэффициента регрессии, может быть найден благодаря тому, что случайная величина t имеет распределение Стьюдента с п—2 степенями свободы, где
а—
''=777Г <6'5Л5>
Аналогичное утверждение справедливо и для 0—(1Н, в этом случае
S/y/Zn^x—x)2
При двухстороннем критерии уровень значимости удваивается.
Критерий, основанный на (6.5.16), — один из наиболее распространенных статистических критериев. Наиболее часто он применяется при условии 0Я=О; в этом случае на основе его проверяется, есть ли значимая (линейная) зависимость у от х.
д) Доверительный интервал для у(х). Линейная модель
ILj = a + $(Xj—x)
эквивалентна
=Ж),
или
Д У(х0)} = а + 3 (х0—х),
где Ё[У(х0)] обозначает оценку ожидаемого отклика при условии, что независимая переменная х примет значение х0, а х вычислено по формуле (6.5.5). Поскольку а и 0 нормально распределены с параметрами, задаваемыми выражениями (6.5.8) и (6.5.9), случайная величина _Р(х0) также будет иметь нормальное распределение с математическим
328
Рис. 6.5.1. Линия регрессии и 95%-ный доверительный интервал (коридор) для а + /3(х—х )
ожиданием, равным а 4- /3(х0—х), и дисперсией, оценку которой можно найти по формуле
уаг[Ях0)] + [^-+ R • <6-5-17)
Легко видеть, что минимальное значение этой величины достигается при х0=х (т. е. наименьшая дисперсия будет наблюдаться вблизи «середины» данных по х). Наоборот, при возрастании расстояния х0 от х дисперсия также будет возрастать. Этот эффект иллюстрируется на рис. 6.5.1, где показаны также линия регрессии у(х) и кривые у(х) ± 2Vvar , которые для каждого х задают приближенно 95%-ный доверительный интервал (коридор) для а + /3(х—х). Расчет данных показателей позволяет оценить качество экстраполяции у по х в зависимости от величины (х—х). Множитель 2 получен в результате округления, более точно интервальной оценкой значения а + + /?(х0—х) на основе а+(3(х0—х) служит 95%-ный доверительный интервал
7(xo)±r97>5Vvar№o)}’ (6.5.18)
где t91 <5 — 97,5%-ная точка распределения Стьюдента с п—2 степенями свободы (t915 «2).
Пример 6.5.1. Линейная регрессия. Методы, изложенные в разделе 6.5.3, проиллюстрируем на данных из табл. 6.5.3, где измерения зависимой переменной являются логарифмом числа фацет глаза насекомых семейства Drosophela Melanogaster при различных уровнях тем-
329
7
6
Рис. 6.5.2. Зависимость средних значений от температуры, данные см. в табл.
6.5.3 (наблюдения отмечены кружками). Оцененная линия регрессий Я*) =—1,536—0,7938(х—23,277)
пературы. Данные имеют вид таблицы частот типа табл. 5.8.4 (значения зависимой переменной обозначают Уг,...^25, тогда как в табл. 5.8.4 они обозначены как х2,...,ха; значения независимой переменной обозначены xit х2,...,х9 и соответствуют выбранным экспериментатором уровням температуры).
Данные из табл. 6.5.3 анализировались в примере 5.8.5, где было обнаружено влияние температуры. Даже визуальный анализ убеждает в том, что температура оказывает отрицательное воздействие на зависимую переменную; это и было подтверждено в примере 5.8.5. Цель данного примера — провести анализ данных в предположении, что исследуемая зависимость от температуры представляет собой линейную регрессию. Прежде чем приступать к соответствующим расчетам, необходимо убедиться в том, что гипотеза линейности в действительности справедлива. Для этого нанесем данные на график (рис. 6.5.2), по оси ординат отложим средние значения зависимой переменной, а по оси абсцисс — соответствующую температуру. Как следует из этого графика, за исключением скачка между 23° и 25°, который вполне мог произойти за счет случайных колебаний, средние действительно достаточно хорошо ложатся на прямую линию. Наклон этой прямой, оцененный на глаз, приблизительно равен —0,79.
Итак, будем считать, что линейная регрессия в данной задаче адекватна; для оценивания параметров а и /3 модели
Hj=a + fi(Xj—х)
ззо
воспользуемся методами из раздела 6.5.3. Оценкой отклика тогда будет служить выражение
fij = a+^(Xj—х). (6.5.19)
Для нашей выборки статистики принимают следующие значения:
х =23,2770, bnjXpj = —44482,23, пху =—29425,11
7 =—1,536,
разность = —15057,12,
Ел^=464,887, пх2 =445,917
разность = 18,969.
Как следует из (6.5.6) и (6.5.7), а =—1,536, £='—0,7938.
В табл. 6.5.4 приведены значения Д с наблюдаемыми значениями Jy.
Таблица 6.5.3. Зависимость числа фацет глаза от температуры
Отклик = In 1 (число) фацет глаза Контролируемая переменная температуры (С°)
J 1 2 3 4 5 6 7 8 9
/ Л X. J 15 17 19 21 23 / 25 27 29 31
1 8,07 3 1 1
2 7,07 5 2 5 1
3 6,07 13 7 3
4 5,07 25 9 2 1
5 4,07 22 10 16 2
6 3,07 12 10 12 6 1 3
7 2,09 7 5 14 16 2 2
8 1,09 3 4 14 21 8 9
9 0,07 3 7 26 7 19 1
10 —0,93 1 7 12 11 24 3 1
11 —1,93 1 9 14 22 8 6
12 —2,93 2 1 5 12 15 15 4
13 —3,93 2 19 18 44 10 1
14 —4,93 1 4 4 26 6 6
15 —5,93 1 2 2 19 14 13
16 —6,93 2 11 28 9
17 —7,93 3 1 8 8 8
18 —8,93 1 2 5 5
19 —9,93 4 4
20 —10,93 10 2
331
Продолжение табл. 6.5.3
Отклик» In (число) фацет глаза Контролируемая переменная температуры (С°)
J 1 2 3 4 5 6 7 8 9
/ Л XJ 15 17 19 21 23 25 27 29 31
21 22 23 24 25 —11,93 —12,93 —13,93 —14,93 —15,93 1 1 0,5 0,5 2 1,5 0,5 1
Число наблюдений Пу 90 «2 54 Из 83 100 «5 86 «6 122 «7 137 «» 98 «9 53 л = = 823
Среднее 4,548 У I 3,514 У 2 2,492 Уз 0,320 У 4 —2,420 Уз —1,627 Ув -4,623 У 7 —6,660 Уз —7,713 У 9 —1д536 У
Перепечатано с разрешения Macmillan Publishing Company [см. Fisher (1970) — С].
Таблица 6.5.4. Оцененные значения fij и их сравнения с наблюдаемыми величинами ц
J п J xj
1 90 15 5,034 4,548 —0,486
2 54 17 3,446 3,514 0,068
3 83 19 1,859 2,492 0,633
4 100 21 0,271 0,320 0,049
5 86 23 —1,316 —2,420 —1,104
6 122 25 —2,904 -1,627 1,277
7 137 27 —4,491 -4,623 —0,132
8 98 29 —6,078 —6,660 —0,582
9 53 31 —7,666 —7,713 —0,047
-Ду)2=395
При оценивании стандартных ошибок для а, $ и Ду необходимо вычислить сумму квадратов отклонений (т. е. сумму квадратов разности между наблюдаемыми значениями и значениями, полученными по модели) по формуле (6.5.10). В наших обозначениях эта величина равна:
55= ppijjy-—па1— Р2рп}{х—х)2.
332
Поскольку а=у, первые два члена равны что пред-
ставляет собой общую сумму квадратов см. (5.8.18), ее численное значение можно найти в табл. 5.8.5, оно равно 16,202. Таким образом, 55= 16,202—(0,7938)2 -18,969=4249.
Отсюда следует, что оценка дисперсии, определяемая по формуле (6.5.11), равна:
З2 =4249/821 =5,175, а соответствующие оценки выборочных дисперсий для а и 3, вычисляемые по формуле (6.5.12), равны:
var(a)=<?/ п=0,00629=(0,079)2, var(/3) = <?2/Г n^Xj—х )2=0,000273 = (0.0165)2.
95%-ные доверительные интервалы для а и 3 определяются в (6.5.13) и (6.5.14). Для параметра а:
—1,536± 1,96-0,079=—1,536 ±О,155 = (—1,691, —1,381), для параметра /3:
—0,794 ± 1,96-0,0165 = —0,794 ±0,032=(—0,826, —0,762).
Для проверки гипотезы 3=0 (зависимость от температуры отсутствует), как следует из (6.5.15) и (6.5.16), необходимо найти значение /-статистики
r = l§/Vv^=48.
Высокое значение этой статистики не вызывает сомнения в ошибочности гипотезы 3=0.
95%-ный доверительный коридор для значений регрессии, задаваемый формулой (6.5.18), требует знания величины var(P(x)), которая вычисляется по формуле (6.5.17); в нашем случае она равна: ™r^»=[ik+ni^a,]-5’1775=
=0,0063 + 0,00027 (х—23,277)2.
Подставляя это выражение в (6.5.18) и полагая /97>5 = 1,96, находим доверительный коридор для $(х). Для некоторых х он показан в табл. 6.5.5.
333
Таблица 6.5.5. Верхняя ^(х) +1,96Vvar(P(x)) и нижняя у(х)— 1,96Vvar СР(х)) 95%-ные доверительные границы для коридора значений регрессии Я*) -а + рх, где а=—1,536, £=—0,7938, Г = 23,277 и var(x)=var{j?(x)] = =0,0063 + 0,00027(х—23,277)2
X №) '/var(J>(x)j Верхняя граница J’(x)+l,96Vvar0>(x)) Нижняя граница 9М— l,96Vvar(5>(x))
15 5,034 0,157 5,342 4,726
17 3,446 0,130 3,702 3,192
19 1,859 0,106 2,067 1,651
21 0,271 0,088 0,443 0,099
23 —1,316 0,080 —1,159 —1,473
25 —2,904 0,084 —2,739 —3,069
27 —4,491 0,100 —4,295 —4,687
29 —6,078 0,123 —5,837 —6,319
31 —7,666 0,150 -7,372 —7,960
6.6. ОЦЕНИВАНИЕ ЗАВИСИМОСТИ ТОКСИЧНОСТИ ИНСЕКТИЦИДА ОТ УРОВНЯ ДОЗИРОВКИ
6.6.1. КВАНТИЛЬНЫЕ ОТКЛИКИ
В разделе 6.5 обсуждались способы оценивания отклика Я-*) в зависимости от управляемого фактора х, что было проиллюстрировано на примере оценивания зависимости числа фацет глаза насекомого от температуры. В качестве другого примера можно было бы рассмотреть зависимость «продолжительности жизни» у(х) электрической лампы от величины напряжения х, измеряемого в вольтах. Допустим, отбирается некоторое количество электрических ламп. Каждая лампа горит под напряжением х, измеряемым в вольтах до тех пор, пока не перегорит. Продолжительность горения (продолжительность жизни) обозначим через у(х), уровни напряжения выбираются исследователем заранее, т. е. х — контролируемая переменная.
Предположим теперь, что имеющееся оборудование не позволяет измерять продолжительность горения каждой лампы в отдельности (для малых х соответствующее время может быть чересчур велико). Вместо этого можно предложить следующую процедуру. Оставим все лампы включенными при напряжении х на некоторое фиксированное время (например, 2000 часов), по истечении которого будем регистрировать число перегоревших ламп. Эту процедуру необходимо повторить при разном напряжении.
При достаточно малых значениях контролируемой переменной все лампы будут оставаться зажженными. При высоком напряжении по истечении указанного срока все (или почти все) лампы перегорят. При средних уровнях значений контролируемой переменной показателем качества ламп будет служить число зажженных электрических ламп, причем при возрастании напряжения следует ожидать, что в среднем число потухших ламп будет увеличиваться.
334
Рис. 6.6.1. S-образная “кривая. По оси ординат — зависимая переменная (процент погибших насекомых), по оси абсцисс — доза яда
Рис. 6.6.2. Зависимость (процент погибших насекомых) от логарифма дозы
Рассмотренный пример иллюстрирует «количественные зависимости», чаще всего исследуемые в биологии. Например, в задаче исследования эффективности некоторого инсектицида мерой воздействия яда может служить* доля пораженных насекомых по истечении некоторого времени при разных уровнях дозировки. Доля пораженных насекомых будет высокой при очень больших дозах инсектицида. При средних уровнях дозировки каждое насекомое будет вести себя по-разному, в частности, некоторые насекомые погибнут, а некоторые нет. Данные опытов по исследованию зависимости доли пораженных насекомых от уровня дозировки инсектицида приведены в табл. 6.6.1. На рис. 6.6.1 они иллюстрируются графически.
Таблица 6.6.1. Результаты измерения токсичности ротенона для насекомых вида Macrosiphonlella Sanborn!
Номер опыта j Доза ротеиоиа (мг/л) logic (доза) X. j Общее число насекомых п j Число пораженных насекомых г Доля пораженных насекомых PJ
1 10,2 1,07 50 44 0,88
2 7,7 0,89 49 42 0,86
3 5,1 0,71 46 24 0,52
4 3,8 0,58 48 16 0,33
5 2,6 0,41 50 6 0,12
Перепечатано с разрешения правообладателя из книги (Finney (1971)].
6.6.2. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
Пороговым уровнем токсичности ротенона для насекомых Масго-siphoniella Sanborni удобно назвать тот уровень дозировки инсектицида, при котором погибает 50% всех насекомых. Грубо это значение можно определить графически из рис. 6.6.1. Приблизительно оно рав-
335
>Х
Рис. 6.6.3. Процент погибших насекомых на вероятностной бумаге, по оси абсцисс — логарифм дозы
но 4,8. Для получения более точной оценки необходимо обратиться к данным табл. 6.6.1. На основе этих данных можно не только построить оценку порогового уровня, но и найти точность (надежность) этой оценки. Для этого необходимо предложить соответствующую вероятностную модель и оценить ее параметры. Описание такой модели и ее анализ содержатся в оставшейся части раздела 6.6, при этом изложение следует книге [Finney (1971)].
Вероятностная модель состоит из двух гипотез (частей). Первая достаточ
но очевидна.
1. При данной дозе инсектицида поражается определенная доля тг всей совокупности насекомых; в выборке п насекомых реак
ция на инсектицид одних насекомых не зависит от реакции других. Та-
ким образом, можно считать, что число пораженных является случайной переменной и подчинено биномиальному закону с параметрами
(п, тг) [см. II, раздел 5.2.2].
Вторая часть модели менее очевидна. В ней задается формула зависимости вероятности тг от дозы д. Рассмотрим рис. 6.6.2, на котором по оси абсцисс откладываются значения не самих доз, а их логарифмы. Нарисованная кривая очень напоминает функцию нормального распределения. Это сходство может быть проверено нанесением данных на вероятностную бумагу [см. раздел 3.3.2, г)]. При этом масштаб выбирается таким образом, чтобы точки с нормальным распределением легли на прямую линию [см. раздел 2.7.4]. На рис. 6.6.3 видно, что наши данные действительно достаточно хорошо ло
жатся на прямую линию, проведенную «на глаз». Таким образом, вторая часть вероятностей модели выглядит следующим образом.
2. В терминах «измерителя» дозы
x=logio(no3a)
336
вероятность того, что случайно отобранное из совокупности насекомое погибнет за данное время, равна:
X
7г(х)= J [(27г)-1/2а-1ехр[— ~(у—д)2/ст2]]о(у=Ф(^) =
(6.6.1)
= Ф(а + /?х), v '
где ц и а — параметры нормального распределения [см. II, раздел 11.4.6]. В нашей задаче более удобно ввести другие параметры:
а ——д/ст и /3=1/ст.
В примере 7.4.2 гипотеза об адекватности описания данных моделью (6.6.1) проверяется по критерию х2.
Замечание к обозначениям. Значение а + /Зх определяется единственным образом по значению тг(х). Например, из таблиц нормального распределения находим, что Ф( 1,96)=0,975. Таким образом, значение а + /3(х)=1,96 соответствует Ф =0,975. Эта операция может быть записана с помощью обратной функции как 1,96 = Ф—40,975). Значение 1,96 называют квантилью уровня 0,975 стандартного нормального распределения. В последнее время исследователи, применяющие этот метод, предпочитают избегать отрицательных чисел, чего можно добиться, добавляя 5 к значению квантили, поскольку квантили меньше —5 почти никогда не встречаются на практике. Модифицированное таким образом значение называется пробитом. Следующие утверждения эквивалентны:
$O) = v,. >>=ф-1(у),
у + 5 есть пробит v.
(В последующем описании пробиты не используются.)
Можно было бы предложить и другие функции распределения в качестве 7г(х). Так, вполне подходящим было бы логистическое распределение вида
тг(х)= 1/{1+е—+
[см. II, раздел 11.10]. Величина а + /3х, определяемая значением функции тг(х), называется в этом случае логитом тг(х) (ср. с пробитом). Разумеется, можно предложить и другие распределения. В задаче исследования зависимости токсичности инсектицида от уровня дозировки число экспериментов не так велико, чтобы можно было обоснованно отличить выбор одного распределения от другого. Нормальное же распределение позволяет получить хорошие результаты подгонки. Кроме того, существуют таблицы нормального распределения. В этой связи достаточно ограничиться выбором одного подходящего распределения. Вот почему можно рассмотреть лишь модель (6.6.1).
337
6.6.3. ИССЛЕДОВАНИЕ ПОВЕРХНОСТИ ФУНКЦИИ ПРАВДОПОДОБИЯ
Энтомолога, как правило, интересует не только уровень дозировки яда, при котором погибает 50% (или, скажем, 90%) всей совокупности насекомых, но и значения параметров а и /3 вероятностей модели (6.6.1), отвечающие максимуму функции правдоподобия, а также характеристики точности их статистического определения. Пороговый уровень токсичности, соответствующий гибели 50% всей совокупности насекомых, выраженный в логарифмах дозы яда х (значение фактической дозы равно 10х), можно найти из уравнения тг(х)=0,5. Грубое приближение для х было получено из рис. 6.6.3 «на глаз». Оценкой д является значение х, соответствующее 50%, т. е. 0,68, а оценкой а является 0,23. Таким образом, как следует из графика, оценкой зависимости 7г(х) будет Ф((х—0,68)/0,23) = Ф(4,4х—3,0).
Для построения более точной оценки найдем функцию правдоподобия
/(д, <т)=П^(1-^-О,
где используются те же обозначения, что и в табл. 6.6.1. В терминах наблюдаемых значений долей Pj = Tj/rij [см. табл. 6.6.1]. Функция правдоподобия может быть переписана как
g(n, <r)=log/(/*, a)=Jlnj[pj\ogTrj + (i—p/)log(l—тгу)], (6.6.2)
где
^Гj=^г(Xj) = Ф [(Ху—fi)/а] = Ф(а + 0Xj) (6.6.3)
при замене параметров (ц, а) на (а, /3),
a = fi/(j, /3=1 /а. (6.6.4)
Стандартная процедура нахождения оценок максимального правдоподобия а и /3 (т. е. значений а и /3, максимизирующих (6.6.2)) заключается в решении системы уравнений правдоподобия и вычислении асимптотической ковариационной матрицы. Вместо этого исследуем сначала поверхность функции правдоподобия в окрестности максимума, за который приближенно можно взять а =—3,0, /3=4,4. Значения g легко вычисляются по формуле (6.6.2) или по формуле
g(a, /3) = Е[г ^Ф +(л —r )log^ ], (6.6.5)
j J1 J J J J
значения rj и nj приведены в табл. 6.6.1, Фу = Ф(а+/3xy) и ¥у=(1 —Фу). В табл. 6.6.2 показаны необходимые промежуточные результаты при а =—3,2 и /3 =4,4.
338
Таблица 6.6.2. Промежуточные результаты вычислений g(a, (3) для а = —3,2 и 3=4,4
XJ а + 0Х} rj * J nj rj
1,01 1,24 0,892 44 0,108 6
0,89 0,72 0,764 42 0,236 7
0,71 —G,08' 0,469 24 0,531 22
0,58 —0,65 0,258 16 0,742 32
0,41 —1,40 0,081 6 0,919 44
С помощью обычного калькулятора находим логарифм Фу=0,892, умножаем полученное значение на /у=44, повторяем то же самое для ¥у=0,108 и rij—rj-6, складываем результаты и эту процедуру выполняем еще четыре раза. Значение функции правдоподобия равно: g(—3,2, 4,4) =—121,92.
В табл 6.6.3 приведены значения функции g(a, 0), вычисленные для различных (а, 0) в окрестности точки максимума.
Таблица 6.6.3. Значения функции правдоподобия в окрестности максимума
а
—3,4 —3,2 —3,0 -2,8 —2,6 -2,4
4,8 —121 —122 —126 — 135
4,6 —123 —120 —122 — 128
4,4 —122 —120 — 123
3 4,2 —126 —121 —120 -125
4,0 —124 —121 —121
3,8 —123 —120 —123
3,6 —122 —121
Как следует из этой таблицы, приближенно можно считать а = = —3,0, 0=4,4, т. е. максимум, полученный из рис. 6.6.3, является достаточно хорошим приближением. Следует, однако, заметить, что для целого набора значений а и 0, удовлетворяющих (приближенно) условию
а+ 0 = 1,4,
339
значение функции правдоподобия практически не меняется: с точностью до трех значащих цифр g(—3,2, 4,6)=g(—3,0, 4,4)=g(—2,8, 4,2) =—120. Это означает, что максимум определяется недостаточно точно, а поверхность функции правдоподобия имеет почти горизонтальный хребет в направлении а+ /3=1,4. Максимум можно было бы определить с любой степенью точности, выполняя расчеты, как в табл. 6.6.3, но на более узком интервале. Однако и в этом случае можно было бы заметить, что величина а + (3 имеет малую степень изменчивости, в то время как /3 —а изменяется довольно сильно. Это означает, что оценки а и /3 имеют высокую отрицательную корреляцию.
6.6.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
По определению оценка максимального правдоподобия является решением системы уравнений правдоподобия, которая в нашем примере имеет вид
3g _ pj_______Zirk -п
да ’
(6.6.6)
3g
3/3
р, — Ф;
~ ^nJXJ ф.у. =0»
где
$j = Ф (а + /Зху), ¥у = 1 —Фу, а
Фу = (2тг)—1/2ехр(—уЛу) —
значение плотности стандартного нормального распределения в точке Xj. Для решения этой системы необходимо прежде всего найти первое приближение (аь 00 для (а, 0). В качестве такого приближения вполне подходит значение, полученное на основе рис. 6.6.3. Им является
«1=3,0, /31=4,4.
Для построения следующего, более точного приближения
а2 — «1 + Sai, 02 —0i + 50i
340
снова рассмотрим систему уравнений правдоподобия
dg/da2 = dg/3/32=0
и разложим dg/da2 и dg/dfi2 в ряд Тейлора в окрестности точки («!, /3|) для членов первого порядка. Тогда уравнения правдоподобия с некоторой степенью приближения перепишутся следующим образом:
+ За-Д- + 5/3 —Ц-
Эа, 3af doiidfii
=0,
(6.6.7)
Э31 да,Э/31
Здесь под записью dg/dax следует понимать значение dg/За, вычисленное в точке (аь j3i), и т. д. Выражения для dg/da и dg/dfd приводятся в (6.6.6). Как следует из (6.6.6), в системе (6.6.7) присутствуют также члены, содержащие d$/dot и ЭФ/3/3. Они равны:
Г = Аф(а + 0х)=ф(а + /Зх)
и
= 7;Ф(а + /Зх)=хф(а + /Зх).
Отсюда следует, что
dg = E/j Р/-Ф(а, + /3|ХУ)
Эа, j J Ф(а, + /3,Х;)^(а, + {3iXj)
0(Q1 + (3xXj)
И
dg _ - Ру —Ф(«|
Э01 j Ф(а, + /31Ху)Ф(а, +/3tXj)
Xj^(ax + fixXj),
где
ФО)=1-ФО)
для всех у. Найдем теперь вторую производную:
a2# v , т х а / Ф) ч v ф, эф,. тт = Ел,(р,-—Ф.) г- () — 22П; . i > da j J^J J' да v Фу*у' J
(6.6.8)
где
Фу = Ф(а, + /3]Ху), Фу = 1—Фу.
341
При условии, что «1 и 31 — хорошие приближения, значение Pj—Фу будут малы по абсолютной величине для каждого j [табл. 6.6.4], поэтому первый член в правой части (6.6.8) по сравнению со вторым будет ничтожно мал, причем ЭФу/Эа = фу.
Таблица 6.6.4. Значения | Pj—Фу |
X j pj Ф =ф(4,4г—3.0) 1 ₽-♦ 1
1,01 0,88 0,93 0,05
0,89 0,86 0,82 0,04
0,71 0,52 0,55 0,03
0,58 0,33 0,33 0,00
0,42 0,12 0,14 0,02
. Отсюда с оговоренной степенью приближения
* —р7уф2(а! + 0!Ху)/Ф(а1 + 31Xy)*(«l + 3,Ху) = —DlyWy, где
= + ^х^/Ф(ах + 0lXj)*(ai + 3i*y). (6.6.9)
Аналогично: поскольку дФу/дЗ=Хуфу, находим
Точно так же 32g v 2 ---------------------------------Znjwrf.
Таким образом, окончательно система (6.6.7) для да и 53 приближенно переписывается как
daErijW: + d^LrijWjXj = £П:М:(р:—Ф:)/ф:, J J J J J J J J J J
(6.6.10)
da'Ln.WjX; + дР'Е.пы-.х2- = Ел •и'.х.(р.~Ф,)/ф,-, J J J J J J J J J J J J
где веса Wy определяются по формуле (6.6.9).
Процедура сводится к итерации следующего вида. Решаем систему линейных уравнений (6.6.10) относительно да и 53 и полагаем
a2 = ai+Sa, Зг = 31+З3.
342
Затем вычисляем новые веса по формуле (6.6.9), подставляя вместо aj и 31 значения а2 и Зг- После некоторого числа итераций значения 6а и 63 станут близкими к нулю, описанная процедура представлена в табл. 6.6.5а и 6.6.56.
Прокомментируем расчеты, показанные в этих таблицах. В качестве первого приближения, как уже было предложено, берем ai = =—3,0, 3i=4,4 на основе рис. 6.6.3. Затем вычисляем значения столбцов
a,+3ix? Фу=Ф(а]+ /3!%;); фу = ф(а1+31Ху); njWj = nj(^/Фу).
Значение иу берем из табл. 6.6.1, Pj-rj/nj, (р}—Фу)/фу. Значения фу (функции плотности нормального распределения) Фу надо взять из стандартных таблиц [см. приложение 3]. Значение Wj может быть получено по формуле (6.6.9) или непосредственно из специальных таблиц (входом этих таблиц является пробит-значение 5 + а+(Зх, а не само значение а + (3х [см. Fisher and Yates (1957), табл. 1X2—G]. После этого вычисляются суммы произведений ^nw, Znwx и Ели*2, и система (6.6.10) решается относительно поправок ai и 3i- Нетрудно проверить, что 6a=0,121 и 63 = —0,231, что приводит к новым значениям а2 = = —2,879 и Зг=4,169. Следующий цикл итераций дает 6а=0,017 и 63=0,008, откуда а3 = —2,862 и Зз=4,175. Можно ожидать, что дальнейшие итерации не изменят первые три разряда значений а и 3, поэтому в качестве оценок берем
а = —2,862, 3 = 4,175, (6.6.11)
а оцененная кривая зависимости имеет вид
тг(х)= Ф(4,175х—2,862), (6.6.12)
где х равно логарифму по основанию 10 дозы яда. Оценка 50%-ного значения х50, для которого тг(х)=0,5, находится из уравнения
4,175х—2,862=0.
Отсюда
х5о=О,685, (6.6.13)
соответствующий пороговый уровень дозы яда равен:
й50 = 100.685 =4,84 мг/л. (6.6.14)
6.6.5. ТОЧНОСТЬ ОЦЕНОК
Как следует из раздела 6.2.5,в), стандартным приближением к ковариационной матрице оценок а и 3 служит матрица, обратная к
d2g/da2 d2g/dad(3~
_ d2g/dad(3 d2g/d&2 _
343
Таблица 6.6.5а. Вычисление поправок 8а и 80 на основе системы (6.6.10). Первая итерация, а, =—3,0, 8i=4,4
X a + 0x Ф Ф nw p (p—Ф)/ф
1,009 1,44 0,925 0,141 14,50 0,880 —0,319
0,886 0,90 0,816 0,266 23,68 0,857 0,154
0,708 0,12 0,548 0,396 29,12 0,522 —0,066
0,580 —0,45 0,327 0,361 28,32 0,333 0,017
0,415 —1,17 0,121 0,201 19,40 0,120 —0,005
Enw = Enwx = Enwx2 = 114,12, 80,05, 60,29, Enw(p—Ф)/ф= Lnwx(p—Ф)/ф = —2,42, = —2,64,
114,125a+80,05 80 = — 2,42,
80,05 5a+ 60,2015/3 = — 2,64,
5a = 0,121, 80 = —0,231.
Таблица 6.6.56. Вычисление поправок 8а и 80 на основе системы (6.6.10). Вторая итерация, а2 =—2,879, 81=4,169
X a + 0x Ф Ф nw p (p—Ф)/Ф
1,009 0,886 0,708 0,580 0,4 U 1,330 0,815 0,073 —0,461 —1,149 0,908 0,792 0,528 0,323 0,125 0,164 0,286 0,398 0,359 0,206 16,30 24,45 21,96 28,27 19,30 0,880 0,857 0,522 0,333 0,120 —0,171 0,227 —0,015 0,028 —0,024
Enw =117,48, Enw(p—Ф)/0 = 2,654, Enwx = 83,16, Enwx(p—Ф)/ 0=2,062, Enwx2 = 80,83,
117,485a+ 83,1658=2,654, 83,165a+ 80,8358 = 2,062, 5a=0,017, 58=0,008.
344
и вычисленная в точке (а, 0). Как следует из сказанного выше, удовлетворительной оценкой этой матрицы в нашем случае может служить
— 1
Enw LnWX
- Enwx Enwx2 -
Нетрудно видеть, что обращаемая матрица с определенной степенью точности есть не что иное, как матрица коэффициентов системы уравнений, соответствующей последней итерации. Она равна [см. табл.
6.6.56]
“ 117,48 83,16
9
83,16 80,83 _
а обратная к ней —
1 Г 80,83 —83,16“] Г 0,0313 —0,0322“
2580 =
—83,16 117,48 —0,0322 0,0455
Запишем ее в виде
v(a) с(а,
9
_ с(а, 0) v(0) _
где v(a) и v(/3) — выборочные дисперсии а и /3 соответственно, с(а, (3) — выборочная ковариация. Тогда
v(a)=0,0313 = (0,177)2, v(0) = 0,0455 = (0,213)2, с(а, (3) = —0,0322.
(6.6.15)
Коэффициент корреляции между а и /3 равен:
—0,0322/(0,177-0,213) = —0,85.
Корреляция, как видим, отрицательна и достаточно высока. Этот вывод согласуется с рассуждениями из раздела 6.6.3, основанными на геометрическом свойстве поверхности функции правдоподобия.
Доверительная полоса для тг(х). Оценкой максимального правдоподобия зависимости тг(х) является
7г(х)=Ф(а + Дх).
345
Таблица 6.6.6. Приближенная 95%-ная доверительная полоса для т(х)
X ад) ir(x)+ 2v'var(i(x)) «(*)—2Vvar(i(x-))
0,2 0,021 0,047 —
0,4 0,117 0,161 0,073
0,6 0,360 0,430 0,290
0,8 0,684 0,717 0,618
1,0 0,905 0,943 0,867
1,2 0,985 0,995 0,975
Рис. 6.6.4. Оцененная зависимость тг(х)=Ф(а+/Зх) с верхней и нижней 95%-ными границами, наблюдения обозначаются кружками
На основе (6.2.19) для каждого х может быть найдена выборочная дисперсия этой функции var(?r(x)) (естественно, с определенной степенью приближения), а именно
var[i(x)} =
= [ф(а + @x)]2{v(a) +
+ 2хс(а, ^)+x2v(0)}.
Грубой 95%-ной доверительной полосой для 7г(х) будет служить коридор, заключенный между кривыми
тг(х) ± 2Vvar (7г(х)]. (6.6.16)
Расчет доверительных границ для некоторых значений х дается в табл. 6.6.6. Графически это иллюстрируется на рис. 6.6.4.
346
6.6.6. ДОЗА, НЕОБХОДИМАЯ ДЛЯ ЗАДАННОГО ЗНАЧЕНИЯ ОТКЛИКА
а) Грубая оценка. Если функция вероятности тг(х) гибели одного насекомого при данной дозе яда х известна и равна:
ir(x)= Ф(а+ 0х),
то уровень дозы х50, при котором погибает 50% насекомых, находится из уравнения
0,50-Ф(« + 0х5о) или
а + 0х,5О = Ф—1(0,50)=0,
откуда х50 = —а/3- Оценкой максимального правдоподобия для х50 будет
х5о = —«/0= 0,685. (6.6.17)
Это логарифм дозы; фактическая доза равна:
й5о = 100,685 =4,84 (6.6.18)
[ср. с (6.6.13) и (6.6.14)]. С принятой степенью приближения выборочная дисперсия х5о равна [см. (6.2.19)]:
уаг(Д>)= [ ff)+ £ »(»] | (а>й=(0,022)2.
Достаточно точным 95%-ным доверительным интервалом для х50 будет
х50 ± 2<var(x50) =0,685 ± 0,044=(0,64, 0,73). (6.6.19)
Соответствующий интервал для фактической дозы м = 10х равен (4,36, 5,37). Аналогичные расчеты можно провести для Хю, х25 и т. д.
б) Более точная оценка. Альтернативная и более сложная (но и более точная) процедура определения точности оценки х50 основана на теореме Филлера [см. пример 4.5.8], в соответствии с которой 95 % -ные доверительные границы для х50 являются корнями Хн Х2 квадратного уравнения
(Х6+«)2 = Г97>5у
[см. (4.5.12) и (4.5.14)], где
«=«=—2,862, 6=0=4,175,
v=X2 v(0) + 2Хс(«, 0) + v(a)=0,31 ЗХ2—0.0644Х+0,0455;
347
значения v(0), v(a) и c(a, 0) приводятся в (6.6.15), а /97>5 обозначает 97,5%-ную точку /-распределения с соответствующей степенью свободы. Принимая во внимание способ приближения, использованный при получении оценок (6.6.15), можно грубо положить /=2,0 (значение, соответствующее нормальному распределению, равно 1,96). Таким образом, квадратное уравнение принимает вид
(4,175Х—2,862)2 = 4 • (0,0313Х2—0,0644Х + 0,0455)
или
17,30Х2—23,64Х +8,01=0,
откуда
X] =0,641, Х2 =0,729.
Как видно, для данного примера доверительные границы практически совпали с предыдущими (6.6.19).
Итак, заключаем, что 95%-ным доверительным интервалом для 50%-ного значения логарифма дозы яда является (0,641, 0,729) с о.м.п., равной 0,685. Соответствующие значения фактической дозы 10х равны (4,38, 5,36) и 4,84. Для более глубокого изучения этих вопросов читатель может обратиться к работе [Finney (1971)].
6.7. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПО ГРУППИРОВАННЫМ, ЦЕНЗУРИРОВАННЫМ И УСЕЧЕННЫМ ДАННЫМ
6.7.1. ДИСКРЕТНЫЕ ДАННЫЕ
Рассмотрим таблицу частот*:
Значения наблюдаемой величины 0 1 2 ... к
Частота «(0) л(1) л(2) п(к)
Наблюдения производятся над генеральной совокупностью с дискретной п.р.в. f(y, 0), _у=0,1,... . В нашей таблице к — наибольшее значение наблюдений. Данные наблюдений могут быть представлены не в такой полной форме. В частности, они могут быть: а) усечены, б) сгруппированы, в) цензурированы.
* Здесь под частотой понимают число элементов выборки, которые приняли данное значение. — Примеч. пер.
348
а) Усечение. В качестве примера рассмотрим таблицу частот:
Значения 0 1 2 3 к
Частота отсутствуют л(3) п(к)
Здесь данные усечены, т. е. частоты п(0), и(1) и /7(2) отсутствуют (это может быть, например, следствием ошибок регистрации измерительного прибора). Имеющиеся наблюдения тогда можно представить как выборку из некоторой гипотетической совокупности с п.р.в.
Ли 0)=ЛИ 0)/[/(О, 0)+/(1, 0)+/(2, 0)], J=3,4,...
Если исходная генеральная совокупность имеет пуассоновское распределение с параметром 0, то усеченное распределение (усеченное так, как сказано выше) имеет п.р.в., равную
Л(Л »)= [е-веУ/у1]/[е~е(,1 + е+ J02)J =
= + 3»=2,3..
при этом функция правдоподобия будет пропорциональна
к
П ли «Ж
У~3
Опуская неинформативные множители, за функцию правдоподобия в этом случае можно взять
/(0) = / (1 + 0 + 102) S «(У) = / (1 + 0 + 102)«,
где, как обычно, у обозначает среднее выборки, а п — объем выборки. Оценка максимального правдоподобия § есть подходящий корень уравнения правдоподобия cfln//dl9=O, которое в нашем примере соответствует квадратному уравнению
(1у_1)02 + Ог-1)0+7=о.
349
б) Группировка и цензурирование. В качестве другого примера записи данных рассмотрим следующую таблицу частот:
Значения 0 1 ZZ+1 z+2z+3 z+4 > z+5
Частота л(0) «(1) ... n'(z) n'(z+2) n'(z+5)
Здесь частоты n(z) и w(z+l) отдельно не фиксируются, они сгруппированы, известна лишь их сумма w/(z) = «(z)+w(z+1). Аналогично сгруппированы частоты n(z+2), n(z+3) и n(z+4). Что касается частот n(z+5), w(z+6) и т. д., то ни одна из них не фиксируется отдельно; известно лишь, что число элементов выборки со значением, которое больше или равно z+5, было л'(г+5). Последняя операция над данными называется цензурированием (аналогично можно было бы цензурировать левый конец, т. е. данные с наименьшими значениями, или цензурировать оба конца). В этом случае функция правдоподобия имеет вид
z—1
/(0)=П [f(y, 0) V(z+i,0)]"WU+2. 0)+
J=o
+/U+3, 0)+Лг+4, 0)]^+2)[G(z+5, 0)}'’(*+5>,
где G(u, 0)=g(u, 0)+g(u +1, 0) + ... — правый хвост ф.р. На практике данные могут быть сгруппированы, но не цензурированы, или цензурированы, но не сгруппированы, а также одновременно и сгруппированы, и цензурированы, с усечением или без усечения. Во всех подобных ситуациях можно быть уверенным, что с помощью численных методов уравнение правдоподобия будет решено.
Пример 6.7.1. Данные из пуассоновского распределения, сгруппированные по ячейкам. В качестве примера сгруппированных дискретных данных рассмотрим таблицу частот из раздела 3.2.2. При пуассоновском с параметром 0 исходным распределением функция правдоподобия имеет вид
ДО)=[П (е-«У/г!)Л] е-»( *- + + в- ) ,
r=0 1Z; 1J; 14
где значения /0./ь известны.
В этом примере эффект группировки (два наблюдения в классе «12, 13 или 14») незначителен, поэтому можно ожидать, что значение 0, максимизирующее функцию правдоподобия, будет близко к соответствующему значению при условии, что оба наблюдения будут принадлежать классу «13». Отсюда следует, что это значение 0] можно 350
принять в качестве первого приближения о.м.п. Оно равно средней модифицированных данных, т. е. 3,871. Истинная оценка максимального правдоподобия максимизирует функцию
log/ = E7rlog(e-’eVr!) + 21og(e-«(^ + £ + 9-‘)],
т. е. является корнем уравнения правдоподобия. Это уравнение, как нетрудно проверить, имеет вид
ЛГАО . 10070 , 24 1 + 0/12 + 09156 Л
—Zvvo “г --- Н----’ -------;------- — U.
0 0 1 + 0/13+09182
Подходящий корень 0* = 3,867, что достаточно близко к первому приближению 0=3,871.
6.7.2. НЕПРЕРЫВНЫЕ ДАННЫЕ И ГРУППИРОВКА. ПОПРАВКА ШЕППАРДА
Наблюдения непрерывных случайных величин могут быть представлены в естественном виде, т. е. так, «как они наблюдаются», или в виде таблицы частот. Итак, допустим, что п.р.в. генеральной совокупности, из которой происходит выборка, равна f(x, 0). Если наблюдения Xi, х2,...,хп фиксируются с достаточно высокой степенью точности, их можно считать реализацией непрерывной случайной величины. Их совместная выборочная плотность^в точке (х\, х2,...,хп) при условии независимости наблюдений равна П/(хг, 0). На практике же точность регистрации наблюдений всегда конечна, поэтому, например, выражение «значение наблюдения хг равно 1,02» в действительности соответствует неравенству 1,015 <хг< 1,025, а элемент функции правдоподобия 0, отвечающий этому наблюдению, будет равен не /(1,02; 0), а
1,025
J f(x, 0) dr=F( 1,025, 0)—F(l,015, 0),
1,015
где F(x) — ф.р. генеральной совокупности.
Допуская, что выборка из непрерывного распределения записывается в виде таблицы частот, обозначим частоту ячейки (хг—±-h, хг+ уй) через и(г), г=1,2,...,й. Обозначим п.р.в. случайной величины X в точке х через Дх, 0), а ее ф.р. — через F(x, 0).
351
Если предположить, что данные получены из дискретного распределения с частотой наблюдения хг, равной л(г), то функция правдоподобия будет
№)=ПДхг, 0)"W
а ее логарифм равен:
log/i(0) = En(r)log/(xr, 0).
Оценка максимального правдоподобия является корнем уравнения 3 log Л (0)/30=0.
Если же считать, что в действительности исходная совокупность непрерывна, то (правильная) функция правдоподобия имеет вид
/ОТ=ПИхг + уЛ, «)-Ях,-уЛ,
Она должна быть максимизирована с привлечением некоторого численного алгоритма. Однако если h достаточно мало, например h<s /2, то, опуская члены начиная с Л4 в разложении по Тейлору, получим
/(»)= ГЦЛ/Ц-, 0) + уЛ7(хг. «) +
где штрихи означают дифференцирование по хг. Тогда
log/W) = nlogft + logMO) + ± Л!Еп(г)^^
J\Xr*
и с той же степенью приближения
Slog _ Slog/) J_ ,2г- А ^Хг>
эе зе + 2Ah еу
Например, если исходное распределение является нормальным с параметрами (ц, а), то, рассматривая в качестве 0 параметр д, мы получим
31og/i / Эд=2(х—д).
Таким образом, группированной оценкой д будет
* ——
Д! =Х .
Уравнение правдоподобия, основанное на подправленной п.р.в., сведется к
по~2(х—ц)—h2n(x—ц)/ 12а4 =0, 352
откуда подправленная о.м.п. будет равна д =х. Как видим, здесь оценки совпали: /л=рц.
Теперь рассмотрим помимо параметра д группированную оценку для о. Имеем
dlog/]/до-—п/а+ Еп(г)(хг—д)2/а3.
Приравнивая это выражение к нулю и решая его в системе с уравнением для д, получаем
л (у2—о2)/о3=0, где
s2 = Е п(г) (хг—х)2/ п.
Отсюда следует, что группированной оценкой для а2 будет
(о2)Г=л
Подправленное уравнение правдоподобия сводится к а2=52+ —h2--------------------------h2q4/s4,
3 4 4
где q4 — группированный четвертый выборочный момент, равный Ел(г)(хг—х)4/п. Если мы далее аппроксимируем это уравнение, заменяя q4 и s4 на их соответствующие выборочные моменты, то при c/4/.s'4~ 3 с принятой степенью точности (с точностью до членов Л4) получаем
а2 = у2—-А2/12.
Таким образом, подправленная о.м.п. дисперсии исходной совокупности получается из оценки дисперсий по группированным данным с поправкой на А2/12, где h — ширина интервала группировки. (Это известно как поправка Шеппарда.)
6.8. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Метод максимального правдоподобия на практике в конечном счете сводится к таким численным процедурам, как обращение матриц и решение нелинейных уравнений. Чаще всего решению уравнений помогают существующие статистические таблицы. В других случаях, как в примере с 6.3.8 с оцениванием плотности распространения микроорганизмов методом разбавления, значения оценок и их точности можно найти в специальных таблицах [см. Fisher and Yates (1957), табл. VIII2—G]. Таблица оценок параметров логистического распределения приведена в [Berkson (I960)].
353
Ссылки на работы, где подробно описываются общие принципы метода максимального правдоподобия, можно найти в разделе 3.6. Можно добавить к ним также книгу (Fisher (1959)]. Полезное и короткое, впрочем, достаточное специальное исследование содержится в работе [Shenton and Bowman (1977)].
Широкое использование и популяризация метода максимального правдоподобия было начато Р. Фишером. По однотомнику его избранных статей, снабженных короткими примечаниями, можно судить о развитии и становлении в двадцатом веке статистики вообще и, в частности, метода максимального правдоподобия [см. Fisher (1950) — D]. Формальное и строгое математическое описание основных свойств метода максимального правдоподобия приведено в работе [Cramer (1946)]. Современное изложение с использованием почти исключительно метода максимального правдоподобия можно найти в написанной ясным языком книге [Kalbfleish (1979) — С]. Проблемы оценивания зависимости токсичности яда от уровня дозировки рассматриваются автором соответствующих моделей в работе [Finney (1971)].
Finney D. J. (1971). Probit Analysis, Cambridge University Press.
Berkson J. (1960). Nomogram for Fitting the Logistic Function by Maximum Likelihood, New Statistical Table No. XXIX (Biometrika), Cambridge University Press.
Shenton L. R. and Bowman K. L. (1977). Maximum Likelihood Estimation in Small Samples, Griffin.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Айвазян С. А., Енюков И. С., Мешал кин Л. Д. Прикладная статистика: Основы моделирования и обработка данных. — М.: Финансы и статистика, 1983. — 471 с.
Бикел П.,Доксам К. Математическая статистика. — М.: Финансы и статистика, 1983. Вып. 1. — 278 с.
Боровков А. А. Математическая статистика. — М.: Наука, 1984. — 472 с.
КлепиковН. П., Соколов С. Н. Анализ и планирование экспериментов методом максимума правдоподобия. — М.: Наука, 1964. — 184 с.
Р а о С. Р. Линейные статистические методы и их применение /Пер. с англ.; Под ред. Ю. В. Линника. — М.: Наука, 1968. — Гл. 5.
Уилкс С. Математическая статистика. — М.: Наука, 1967. — 632 с.
ГЛАВА 7
СТАТИСТИКА ХИ КВАДРАТ. КРИТЕРИИ СОГЛАСИЯ, НЕЗАВИСИМОСТИ И ОДНОРОДНОСТИ
7.1. АДЕКВАТНОСТЬ МОДЕЛИ
7.1.1. ВВЕДЕНИЕ
Говоря об основных задачах статистики, в гл. 1 мы включили (в раздел 1.1) такие понятия, как формирование вероятностной модели, получение оценок ее параметров, исследование надежности этих оценок и проверка адекватности.
Совсем простые процедуры обычно позволяют установить, что модель не является совершенно непригодной. Однако на вопрос, будет ли лучше некоторая альтернативная модель, ответить не так легко. В примере 6.5.1 данные табл. 6.5.3 анализировались в рамках гомоске-дастичной (однородной по дисперсии) нормальной линейной регрессионной модели. Предполагалось, что каждый столбец является таблицей частот для выборки из нормального распределения. Относительно этих девяти нормальных распределений предполагалось также, что они имеют равные дисперсии, а их математические ожидания представляют собой линейные функции температуры. Графики накопленных частот по некоторым столбцам, построенные на вероятностной бумаге [см. раздел 3.2.2,г)], показаны на рис. 7.1.1. Из графика видно, что точки лежат на (или около) системе параллельных прямых, т. е. допущение нормальности распределений и равенства дисперсий представляется приемлемым. Для объективной проверки допущения нормальности могут применяться более тонкие методы (такие, как описанные в разделе 5.9 и примере 5.9.1) с использованием третьих и четвертых моментов, критерия хи-квадрат [см. пример 7.4.1] или критерия равенства дисперсии [см. раздел 5.10.1].
Что касается допущения линейности, то и здесь на первом этапе надо использовать простейший способ проверки, а именно построить график средних по столбцам в зависимости от температуры и пос-
355
Рис. 7.1.1. Графический критерий гомоске-дастичности, состоящий в проверке на параллельность графиков эмпирических функций распределения на вероятностной бумаге. Графики накопленных Частот столбцов табл.6.5.3.
мотреть, в самом ли деле точки лежат на прямой линии или около нее [см. рис. 6.5.2]. С помощью такой графической процедуры, однако, невозможно обнаружить малые систематические отклонения от линейности. Для этого следует прибегнуть к более тонкой методике. Она описана ниже в разделе 7.1.2, содержащем пример применения критерия согласия. В разделе 6.6 также описывалась процедура для оценки токсичности инсектицида по данным типа база—эффект; анализ был выполнен в терминах кривой отклика специального («пробит») вида. То, что модель является достаточно правдоподобной, было установлено графическим способом по рис. 6.6.3, но такой способ проверки не дает возможности обнаружить малые отклонения от предполагаемой модели; возникает необходимость в объективном критерии согласия. Такой критерий описан в примере 7.4.2.
7.1.2. АДЕКВАТНОСТЬ ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ
В разделе 6.5.3 и примере 6.5.1 мы имели дело с подгонкой линейной регрессионной модели к данным, для которых, возможно, более подходит некоторая кривая линия регрессии. При принятых процедурах оценивания исходили из того, что линейная модель, указанная на рис. 6.5.2, была адекватной. Имея редкие и рассеянные данные, трудно идти дальше; очевидно, чтобы обнаруживать малые отклонения, нужны большие выборки. В рассмотренном примере массивы данных достаточно многочисленны, и можно использовать объективный критерий. Это связано с тем, что при справедливости основного допущения гомоскедастичности внутригрупповая сумма квадратов w в табл. 356
5.8.5 дает одну оценку дисперсии а2, а именно w/(n—к)=4,708, а выражение (6.5.11) — другую, независимую, оценку. Первая является состоятельной независимо от того, линейна регрессия или нет; состоятельность второй оценки зависит от наличия линейности. Поэтому если эти две оценки заметно различаются, то предположение линейности следует отвергнуть. Процедура состоит в разложении «межгрупповой» суммы квадратов Ь(= 12,370) в табл.5.8.5 на часть, объясняемую линейной регрессией, и часть, представляющую отклонения от регрессии. Последняя сразу получается из табл. 6.5.4; она равна:
(yj-^395.
Отсюда первая часть равна: 12370—395 = 11975. Мы получаем таблицу дисперсионного анализа:
Источник дисперсии Сумма квадратов Степени свободы Средний квадрат отклонения
Линейная регрессия 11975 1
Отклонения от линейной регрессии 395 7 56,4
Общая (=«межстолбцовая» сумма квадратов Ь) 12370 8
Если мы объединим эту таблицу с таблицей 5.8.5, то окончательно получим следующую таблицу данных:
Источник дисперсии Сумма квадратов Степени свободы Средний квадрат отклонения
Внутригрупповая
(=случайные флуктуации) 3832 814 4,708
Линейная регрессия 11975 1
Отклонения от линейной
регрессии 395 7 56,4
Общая = Е л„ (у,—у")2 !,У J * 16202 822
357
Если бы линейная гипотеза была справедлива» два «средних квадрата», представленных в таблице, были бы независимыми оценками одной и той же величины (ст2), а их отношение 56,4/4,708 («12) — реализацией случайной величины, имеющей F-распределение с числом степеней свободы 7 и 814. Математическое ожидание этой случайной величины очень близко к 1, и .такое большое значение, как 12, весьма маловероятно. Уровень значимости существенно меньше 0,1% (имеющиеся таблицы не позволяют сформулировать более точное утверждение), поэтому линейную гипотезу следует отвергнуть. Для удовлетворительного описания данных нужна более продуманная модель, может быть, такого типа:
Hj = ct0 + ci\{Xj — ~x)+a:(Xj — T)2 + (Xi(Xj — X-)3.
7.2. РАССТОЯНИЕ К. ПИРСОНА: КРИТЕРИЙ X2
В разделе 7.1 было сказано, что в подходящих случаях можно построить объективный критерий, позволяющий ответи г ь на вопрос: совместима ли с данными используемая при их анализе вероятностная модель. Можно было бы ожидать, что каждый такой критерий, если он существует, должен быть специально «сконструирован» для каждого вида данных. Однако большинство критериев согласия, применяемых на практике, не имеет такой специфики: они основаны на одной общей идее, принадлежащей Карлу Пирсону [см. Pearson (1900)]. Эта идея состоит в использовании в качестве статистики определенной меры расхождения между данными и моделью. Вектор данных (или таблица частот) определяег координаты точки в многомерном пространстве, и расхождение оценивается как обобщенное расстояние [см. раздел 7.2.2] между этой точкой и точкой, определяемой вектором ожидаемых частот, полученных с помощью модели. Основной характерной чертой этого метода является то, что выборочное распределение функции расстояния в большинстве случаев отлично аппроксимируется распределением хг [см. раздел 2.5.4,а)]. Это верно при любом распределении, лишь число степеней свободы зависит от более детального исследования модели и структуры данных.
Критерий можно пояснить с помощью модели, описывающей одномерное распределение вероятностей, где данные представлены в виде таблицы частот, как в следующих примерах.
Пример 7.2.1. Данные Уэлдона об игральных костях. Это данные о количестве очков, полученных в ставшем теперь уже классическим эксперименте с игральными костями. В повторных бросаниях двенадцати костей количество очков, превышающее 4 на какой-либо одной кости, рассматривалось как «успех», и число успехов 12 костей записывалось для 26306 повторных бросаний. Эти частоты фиксировались в табл. 7.2.1, приведенной из работы [Fisher (1970), табл. 10—С], и сравнивались с ожидаемыми частотами в предположении, что каждая кость идеальна. В последнем случае вероятность успеха для любой 358
кости была бы равна 0 = 1/3 и вероятность г успехов среди 12 костей (r=0,1,..., 12) вычислялась бы согласно биномиальному распределению [см. II, раздел 5.2.2]:
* = (/)(!
= (12!/г! (12—г)! ]2|2-'/312, r=0,1,..., 12,
а ожидаемая частота исхода «г успехов» была бы равна 26306 рг [см. II, табл. 6.4.2]. Расхождения оказываются весьма значительными. Это может быть следствием того, что кости на самом деле не являются идеальными. Так как количество очков, выпавшее на одной отдельно взятой кости, не идентифицировано, то лучшее, что мы можем сделать, это счесть, что все кости дают одинаковое смещение, и оценить его. Если мы обозначим эту общую вероятность успеха через 0, то по данным найдем оценку максимального правдоподобия для 0:
0*=Т = Ег/г /12Е/Г=0,33770
[см. пример 6.3.2]. Если мы пересчитаем ожидаемые частоты в предположении, что параметр 0 один и тот же для всех костей и равен 0*, то получим для ожидаемых частот
ег = 26306/?*,
где
р; = (12)(0*)г(1_0*)12-г г=0,1,...,12.
Таблица 7.2.1. Наблюденные и ожидаемые частоты г успехов
Число костей из 12, на которых выпало более 4 очков г Наблюденные частоты /г Ожидаемые частоты (с 9=1/3) ег Расхождение f— е.
0 185 202,75 — 17,75
1 1149 1216,50 —67,50
2 3265 3345,39 —80,37
3 5475 5575,61 —100,61
4 6114 6272,56 —158,56
5 5194 5018,05 170,05
6 3067 2927,20 139,80
7 1331 1254,51 76,49
8 403 392,04 10,96
9 105 87,12 17,88
10 14 13,07 0,83
11 4 1,19 2,81
12 0 0,05 0,05
Воспроизведено с разрешения Macmillan Publishing Company из [Fisher (1970) — С].
359
Численные значения представлены в табл. 7.2.2. Эта модель дает лучшее согласие, большинство расхождений по абсолютной величине меньше соответствующих величин из габл. 7.2.1.
Таблица 7.2.2. Наблюденные и ожидаемые частоты г успехов с костями, имеющими одинаковое смещение
г Наблюденные частоты fr Ожидаемые частоты в случае костей со смещением в* = 0,33770, ег =- 26306 р’ Расхождение 4 ~ ег
0 185 187,38 —2,38
1 1149 1146,51 2,49
2 3265 3215,24 49,76
3 5475 5464,70 10,30
4 6114 6269,35 — 155,35
5 5194 5114,65 79,35
6 3067 3042,54 24,46
7 1331 1329,73 1,27
8 403 423,76 —20,76
9 105 96,03 8,97
10 14 14,69 —0,69
11 4 1,36 2,64
12 0 0,06 —0,06
Воспроизведено с разрешения Macmillan Publishing Company из [Fisher (1970) — С].
Теперь, очевидно, нужен способ объединения индивидуальных расхождений в единую статистику, которую можно было бы взять как меру расстояния между вектором наблюденных частот и вектором ожидаемых частот. Именно это и дает статистика согласия х2 Карла Пирсона, определяемая как
х2 = Е (7.2.1)
где fr — наблюдаемая частота в ячейке с номером г и ег — соответствующая ожидаемая частота; сумма берется по всем наблюдениям (ячейкам).
В разделе 2.9.4 было показано, что совместное выборочное распределение fr является мультиномиальным (к), где к обозначает число ячеек (к = 13 в табл. 7.2.2), с индексом п = Lfr й с вероятностями
360
Рй,Р\, Рп, где рг — вероятность того, что наблюдение попадет в ячейку с номером г, г, = 0,1, ..., 12. Таким образом,
ег = прг.
Можно показать, что [см. Cramer (1946), разделы 30.1, 30.3 — С] выборочное распределение х2 приближается распределением суммы квадратов к —s стандартных нормальных случайных величин (где 5 — число оцениваемых параметров). Эта аппроксимация следует из того, что мультиномиальное распределение может быть аппроксимировано многомерным нормальным распределением, точно так же как биномиальное распределение при соответствующих условиях аппроксимируется нормальным распределением. Аппроксимации замечательно устойчивы, но в действительности предполагается, что ег должна быть не слишком малой (насколько малой — см. раздел 7.3). Когда ожидаемая частота в ячейке опускается ниже критического значения [см. раздел 7.3], эту ячейку приходится объединять с одной или более ее непосредственными соседями так, чтобы новая ожидаемая частота стала выше запрещенного уровня; при этом наблюденные частоты также должны быть соответствующим образом объединены.
Очевидно, что статистика по величине будет малой, когда согласие между наблюденной и ожидаемой частотой хорошее, и большой, когда согласие плохое. Вопрос, является ли данное значение статистики х2 достаточно малым для того, чтобы приписать его случайным флуктуациям, указывая тем самым на приемлемое согласие, должен обсуждаться в терминах выборочного распределения статистики х2 (7.2.1).
Выборочное распределение статистики К. Пирсона. Выборочное распределение х2 является (приблизительно) распределением хи-квадрат с числом степеней свободы и, которое вычисляется по следующему правилу:
v = а — b — 1, (7.2.2)
где а — число элементов в столбце «Наблюденные частоты» (считая каждую группу объединенных частот как один элемент) и Ъ — число параметров вероятностной модели, которые должны быть оценены по тем же данным. По этой причине критерий назван критерием согласия х2 (или критерием Пирсона). Из определения следует, и это иллюстрируется в последующих примерах, что для v > 1 х2 смешивает вместе все расхождения между наблюдением и ожиданием, какова бы ни была их природа. Отклонение от проверяемой гипотезы будет всегда приводить к увеличению* значения х2, и уровень значимости поэтому всегда вычисляется с помощью односторонней процедуры [см. раздел 5.2.3] следующим образом:
Уровень значимости = Р (х2^х2).
* При сохранении предположения о независимости наблюдений. При неумелой фальсификации и подгонке экспериментальных данных наблюденные значения х1 могут оказаться и неправдоподобно малыми. — Примеч. ред.
361
Случай, когда у = 1, является специальным, к нему неприменимо сказанное выше. Он обсуждается в разделе 7.4.1.
Терминология. Читателей следует предупредить, что статистика Пирсона, которую мы назвали х2, часто называется х2 Пирсона или просто х2. Мы, таким образом, сталкиваемся с запутанной ситуацией, когда статистика, называемая х2, имеет выборочное распределение, лишь приближенно совпадающее с распределением х2- В этой книге мы пытаемся избежать этой двусмысленности, сохраняя обозначение X2 для случайной величины, имеющей распределение хи-квадрат, или для названия этого распределения.
Пример 7.2.2. Статистика Пирсона для данных об игральных костях из примера 7.2.1. Рассмотрим вычисление х2 для данных о бросании игральных костей из примера 7.2.1 сначала при гипотезе, что кости идеальны, а затем при гипотезе, что игральные кости имеют одинаковое смещение с 0* = 0,33770.
При справедливости первой гипотезы ожидаемые частоты ец = 1,19 и ей = 0,05 [см. табл. 7.2.2] слишком малы, чтобы использовать распределение х2 как достаточно точное приближение к выборочному распределению х2. Какие ожидаемые частоты считать приемлемо малыми, сказано ниже. Сумма
£ю+£i1 + £12 — 13,07+1,19 + 0,05 = 14,31 является достаточно большой. Вот почему наблюденные частоты /ю+/и+/12 = 18 были объединены в табл. 7.2.3. Объединенная частота 18 сравнивалась с соответствующими объединенными ожидаемыми час-
.... 1Л с- ч Л (18—14,31Н
тотами £ю + £ц +£12 = 14,31. Их общий вклад был равен:—:-----’—-
14,31
= 0,952. Этот вклад в величину х2 представлен последним элементом в предпоследнем столбце табл. 7.2.3. Таким образом, хотя исходная таблица частот содержала 13 элементов в столбце частот (а именно Л, /ь •••./и)» операция объединения сократила их число до 11, а именно /0, ft, ..., /9 и (/10+/11+/12)- Величина х2 равна 35,491.
В случае, когда кости идеальны, величина в определяется этой гипотезой (0 - 1/3) и никакие параметры не следует оценивать по данным. Число степеней свободы равно, таким образом, р = 11 — 1 = 10.
Уровень значимости статистики х2 при гипотезе, что кости идеальны, равен приблизительно
Р(х?о > 34,491).
Эта величина меньше, чем 0,005 = 0,5%, что служит сильным аргументом против принятия этой гипотезы.
При гипотезе, что кости имеют одинаковое смещение, обращаясь к табл. 7.2.2, видим, что еи = 1,36 и е12 = 0,06 слишком малы для успешного использования х2-аппроксимации, и снова рекомендуется объединить последние три частоты. Величина х2 оказывается равной 8,179, и на этот раз число степеней свободы равно:
v = 11—1—1 = 9,
362
поскольку один параметр (0) должен быть оценен по данным. Уровень значимости статистики при справедливости гипотезы, что кости имеют одинаковое смещение, равен
P{xj > 8,179).
Это число равно примерно 0,5, что представляет собой довольно большую вероятность. Поэтому данные следует рассматривать как не противоречащие этой гипотезе*.
Таблица 7.2.3.
Число успехов г Наблюденные частоты f. Идеальные кости 3 Смещенные кости -• 0,33770
0 185 1,554 0,030
1 1149 3,745 0,005
2 3265 1,931 0,770
3 5475 1,815 0,019
4 6114 4,008 3,849
5 5194 6,169 1,231
6 3067 6,677 0,197
7 1331 4,664 0,001
8 403 0,306 1,017
9. 105 . 3,670 0,838
10 14
11 объединенные 4 10,9521 (0,222)
12' 0 ' л2 = 35,491 х2 = 8,179
v = 10 v = 9
* Утверждение о том, что при увеличении числа наблюдений (г. е. объема выборки) статистика хг при справедливости гипотезы сходится к у2, верно лишь в том случае, когда параметры модели оцениваются именно по тем частотам, которые в дальнейшем будут сопоставлены с их ожидаемыми значениями (ожидаемыми в условиях модели). К тому же способ оценивания должен быть в определенном смысле эффективным. Именно так была найдена выше величина в* (методом наибольшего правдоподобия). При объединении нескольких ячеек в одну, что делается ради удовлетворительной аппроксимации, наблюденные частоты меняются. Строго говоря, приближенное значение для 6 теперь надо искать, основываясь на этой новой таблице частот. К сожалению, формулу для новой оценки максимального правдоподобия получить довольно сложно; ею не пользуются. В данной ситуации новое значение оценки ft будет мало отличаться от найденного ранее д* = 0,33770. Поэтому указанное приближение хи-квадрат для выборочного распределения х2 оказывается удовлетворительным. Но надо помнить, что такой способ действия содержит еще одно (плохо контролируемое) приближение и при неосторожности может привести к ошибочному заключению (см., например: Рао С. Р. Линейные статистические методы и их применения. — М.: Наука, 1968. — С.363.). Сказанное относится и к следующим примерам. — Примеч. ред.
363
Пример 7.2.3. Проверка согласия для пуассоновского распределения. Данные в табл. 3.2.1 являются частотами, с которыми 0,1,2,... частиц испускались некоторым радиоактивным источником в течение интервалов в 7,5 секунд. Вероятностная модель, диктуемая физикой радиоактивных процессов, предполагает, что величина R — число частиц, испускаемых в случайно выбранный 7,5-секундный интервал — имеет пуассоновское распределение вероятностей
Р (R = г) =7гг(0) = е~вег/г !, г = 0,1,...
Таблица 7.2.4.
Число испускаемых частиц г Наблюденная частота 4 Оцененная ожидаемая частота е г (4 - еу/ег
0 57 54,56 0,109
1 203 210,99 0,303
2 383 407,95 1,526
3 525 525,85 0,001
4 532 508,37 1,099
5 408 393,17 0,560
6 273 253,40 1,516
7 139 139,98 0,007
8 45 67,66 7,589
9 27 29,07 0,148
10 10 11,24 0,137
11 4 3,95 0,001
12—14 2 1,76 0,001
Статистика Пирсона 15,355
(см. П, раздел 20.1), где в пропорциональна интенсивности радиоактивного излучения образца. Величина в может быть оценена по данным. Оценка максимального правдоподобия в равна: 6* = 3,867 [см. пример 6.7.1]. Оцененная ожидаемая частота наблюдения г (г = 0,1,2,...) будет равна тогда лтгг(0*), где л(= 2608) — объем выборки. Численные значения представлены в табл. 7.2.4, при записи результатов экспериментов частоты /12, /и и /14 были объединены в /ч+/1з+/м — 2.
В учебниках часто говорится, что наименьшая ожидаемая частота, при которой можно пользоваться аппроксимацией распределением х2» равна 5; если принять эту рекомендацию, то элементы последних двух строк таблицы должны быть объединены. В результате получим
Г fr er (f—erY/er
111 (6) (5,71) (0,015)
12—14 f объе-динен-J ные
364
что приводит к
х2 = 15,368
с числом степеней свободы
v = 12 — 1 — 1 = 10,
т. е. теперь имеется 12 эффективных частот, а именно /0, fi, ...» /ю и (/11 + /12 + /13 + /и)-
Уровень значимости этого значения х2 при гипотезе, что распределение величины R является распределением Пуассона, равен
Р(х?о > 15,368) » 0,11.
Это большая вероятность, и данные следует рассматривать как вполне согласующиеся с гипотезой о пуассоновском распределении.
Согласно обстоятельным исследованиям У. Кокрена рекомендация использовать ожидаемые частоты не меньше пяти является чрезмерно ограничительной, и для распределений типа тех, с которыми мы имеем дело, достаточно требовать, чтобы частоты были не меньше 1 [см. раздел 7.3]. В нашем примере поэтому никакого объединения производить не следует, кроме того, которое уже было сделано в табл. 7.2.4. Величина х2 тогда равна 15,355 с v = 13 — 1 — 1 = 11, а так как
Лх?1 > 15,355) > 0,1, данные совместимы с гипотезой о пуассоновском распределении: результат тот же, что и полученный ранее.
7.3. ОБЪЕДИНЕНИЕ ЯЧЕЕК С НИЗКИМИ ЧАСТОТАМИ. КРИТЕРИЙ У. КОКРЕНА
Статистика Пирсона привлекает пользователя тем, что ее выборочное распределение достаточно близко аппроксимируется распределением х2, для которого имеются подробные таблицы. Естественно, должны быть приняты некоторые меры предосторожности. Важнейшие из них следующие:
1) когда ожидаемые частоты основаны на оцененных значениях параметров, оценки должны быть получены с помощью эффективной процедуры, например методом максимума правдоподобия;
2) ожидаемые частоты не должны быть слишком малыми. Не так легко ответить на вопрос: насколько малы могут быть ожидаемые частоты, чтобы можно было пользоваться х2-аппроксимацией. Как было упомянуто, во многих учебниках названо число 5 (или даже 10) как наименьшее значение и рекомендовано объединять соседние ячейки для достижения этого минимума. Хотя такие консервативные действия, несомненно, уменьшают опасность обесценивания х2-аппрокси-мации, они, к несчастью, приводят к снижению чувствительности критерия: это может оказаться важным, если полученное эффективное число ячеек будет малым. Чтобы не снижать чувствительности критерия, следует избегать объединения ячеек, кроме тех случаев, когда это действительно необходимо.
365
По поводу объединения ячеек в таблице частот при использовании критерия х2 известный статистик У. Кокрен [см. Cochran (1952), (1954)] считает: при унимодальных распределениях, когда ожидаемые частоты будут малы только на «хвостах», спедует добиться того, чтобы минимальная ожидаемая частота на .каждом «хвосте» была не меньше 1.
7.4. КРИТЕРИЙ х2 ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
Принципы, используемые при работе с данными из непрерывного распределения, представленными в виде таблиц частот, идентичны применяемым в дискретном случае. Некоторые дополнительные вычислительные трудности, однако, могут возникнуть при крупных интервалах группирования.
Оценка параметров по таблице частот (округленных) непрерывных данных обсуждалась в разделе 6.7.2. Похожие рассмотрения возникают при вычислении ожидаемых частот. Если данные сгруппированы в ячейки хг ± у А, г - 1,2,..., к, и проверяемая гипотеза состоит в том, что плотность распределения рассматриваемой случайной величины в точке х равна f (х;0) с функцией распределения F (х,0), то ожидаемая частота (при этой гипотезе) в r-й ячейке оценивается величиной
п lF(xr + ±Л;
где в* — оценка максимального правдоподобия параметра 0 [см. раздел 6.7.2] ил — объем выборки. Если А невелико, го можно заменить это выражение более простой формулой nkf (хг\ 0*).
Что касается наименьших допустимых частот, то целесообразно придерживаться рекомендаций К. Кокрена для критериев х2 с непрерывными данными. А. именно объединять ячейки на «хвосте» (на «хвостах») таким образом, чтобы наименьшая ожидаемая частота была не меньше 1. Для максимизации чувствительности критерия размер интервалов группирования следует выбирать достаточно малым, чтобы ожидаемые частоты не превышали 12 в каждой ячейке для выборки объема л -- 200, 20 — для л = 400 и 30 — для л = 1000 [см. Cochran 0952), (1954)].
Пример 7.4.1. Критерий х2 для проверки нормальности. Данные о количестве осадков (воспроизведенные в табл. 7.4.1) обсуждались в примере 5.9.1 и проверялись на асимметрию и эксцесс. Коэффициенты асимметрии и эксцесса этой выборки незначительно отличались от соответствующих величин для нормального распределения. Мн теперь применим к тем же данным критерий х2, принимая в качестве рабочей гипотезы, что данные имеют нормальное распределение с параметрами (^,<т).
366
Среднее выборки было найдено в примере 5.9.1 и равнялось 28,62 дюймам; это — оценка максимального правдоподобия математического ожидания ц гипотетического нормального распределения. Был найден и второй момент выборки относительно среднего, он равнялся = 23,013 (дюйма)2. Используя поправку Шеппарда на группировку [см. раздел 6.7.2], найдем оценку а2:
23,013 — 1/12 = 22,930 « (4,788)2,
откуда следует, что оценка о равна 4,788. Ожидаемые частоты поэтому соответствуют нормальному распределению с параметрами (28,62;4,788). Ожидаемая частота в ячейке с центром хг дюймов будет равна, с достаточной точностью,
( /х + Ц_ 23,013\ /хгу-23,013\ ] пл /ХГ -23'°‘3 90 * —2_________- ) — Ф -1-2------------/ * 90 Ф (---------
X 4,788 ' X 4,788 ' > V 4,788
(7.4.1)
Таблица 7.4.1
Для того чтобы проиллюстрировать, как производятся вычисления с укрупненными ячейками (не обязательно постоянной ширины), мы объединим ячейки, как показано в табл. 7.4.1, и оценим ожидаемые частоты способом, указанным в табл. 7.4.2.
367
Таблица 7.4.2
Граничное значение х — 28,62 = и 4,788 Ф(и) Разность х 90
<16,5 0,513
16,5 —2,531 0,0057 0,0217 1,952
19,5 — 1,905 0,0284 0,0722 6,4®
22,5 —1,278 0,1006 0,0943 8,487
24,5 —0,860 0,1949 0,1340 12,060
26,5 —0,443 0,3289 0,1611 14,499
28,5 —0,025 0,4900 0,1628 14,652
30,5 +0,393 1—0,3472 0,1382 12,438
32,5 0,810 1—0,2090 0,0995 8,955
34,5 1,228 1—0,1095 0,0596 5,364
36,5 1,646 1—0,0499 0,0375 3,375
39,5 2,272 1—0,0114 0,0114 1,026
89,8
В табл. 7.4.3 приведены наблюденные частоты (в объединенных ячейках), соответствующие ожидаемые частоты (дальнейшие объединения требуются, чтобы избежать очень малых ожидаемых частот на «хвостах») и, наконец, величина х2.
Величина х2 равна 7,487. Число степеней свободы равно:
11 — 1—2 = 8.
Уровень значимости равен Р (xj 7,487) >0,40. Эта весьма большая вероятность показывает, что гипотеза о нормальности распределения не противоречит имеющимся данным*.
Таблица 7.4.3
Наблюденная частота п г Ожидаемая частота е г (nf — е^2 / ег
< 19,5 4 2,463 0,959
19,5—22,5 5 6,498 0,345
22,5—24,5 5 8,487 1,433
24,5—26,5 16 12,060 1,287
26,5—28,5 11 14,499 0,844
28,5—30,5 17 14,652 0,376
30,5—32,5 13 12,438 0,025
32,5—34,5 8 8,955 0,102
34,5—36,5 7 5,364 0,499
36,5—39,5 4 3,375 0,116
>39,5 0 1,026 1,026
7,487
* В рассмотренном примере отступление от условий применения х2-аппроксимации состоит еще и в том, что оценки математического ожидания и дисперсии получены по исходной выборке, а надо бы — по группированным данным (частотам). К настоящему времени разработаны более совершенные способы проверки нормальности. Применяют и обсуждаемый метод, несмотря на присущие ему недостатки. — Примеч. ред.
368
Пример 7.4.2. Критерий х2 для модели доза — эффект из раздела 6.6. Ранее мы имели дело с оценкой токсичности инсектицида методом, при котором предполагалось, что вероятность тг(х) гибели насекомого после обработки дозой инсектицида, измеренной в логарифмах, In (дозы) = х, задается формулой
7г(х) = Ф(а + @х), где Ф означает стандартный нормальный интеграл. Были найдены оценки максимального правдоподобия для а и /3:
а* = —2,862, (3* = 4,175
[см. (6.6.10)]. Число подвергнутых обработке насекомых и погибших при различных дозах инсектицида [см. табл. 6.6.1] вместе с оцененными вероятностями тг* (х) = Ф(а* + /3*х) представлено в следующей таблице:
5 Число насекомых И / Число погибших г / Верояп пость Iибели я, - * (х.) Ожидаемое число not ибших е -- пЛ(х.)
1,01 50 44 0,9123 45,62
0,89 49 42 0,8040 39,40
0,71 46 24 0,5488 25,25
0,58 48 16 0,3300 15,84
0,41 50 6 0,1251 6,26
В каждой строке записано число наблюденных успехов (/••) в биномиальной схеме с параметрами (л1у-,7Гу), для которой ожидаемое число успехов равно лу7г,; неявно здесь также записано число неудач (лу — /у) со средним rij (1—7Гу).
Вклад такой строки в общую величину пирсоновского х2 равен:
xi (Г1~П/1Ё + (ni ~ rJ ~~ nJ +
7 ЛУ7Г/ Лу(1 • Лу)
= {rj — n-Xj)l/njTj (1 — 7Гу ),
его выборочное распределение (приблизительно) х2- Если бы тгу были известны, т. е. не было бы параметров, которые надо оценивать, то число степеней свободы было бы равно 1 (2 ячейки, 0 параметров;
2 + 0— 1= 1). Таким образом^ для всего множества данных х2 = = £ {г. _ п^)2/п^ (1-7Гу),
выборочное распределение этой величины есть х2- Пять членов, дающих вклад, а именно х2,х2,... ,xj, составляют в сумме пять степеней свободы. Однако теперь мы должны сделать поправку на то, что два
369
параметра (а и /3) оценивались, поэтому в итоге число степеней свободы равно трем. Таким образом, уровень значимости данных при гипотезе
тг(х) = Ф(а + (Зх)
равен:
P(Xj х2) = Р(х32 1,68) > 0,50.
Эта очень большая величина указывает на то, что Ф-гипотеза совместима с данными.
7.5. ТАБЛИЦЫ ЧАСТОТ ПЕРЕКРЕСТНОЙ КЛАССИФИКАЦИИ (ТАБЛИЦЫ СОПРЯЖЕННОСТИ). КРИТЕРИИ НЕЗАВИСИМОСТИ
7.5.1. ТАБЛИЦЫ 2X2; СПЕЦИАЛЬНЫЙ СЛУЧАЙ ОДНОЙ СТЕПЕНИ СВОБОДЫ
Примером типичной таблицы 2x2 (два на два) [см. также 5.4.2] может служить табл. 7.5.1. В ней приведены сведения о числе людей в некоторой совокупности, заболевших и не заболевших холерой, с указанием, была ли им сделана противохолерная прививка.
Таблица 7.5.1. Влияние прививки иа холерную инфекцию
Незаболевшис Заболевшие Всего
Привитые 1625 5 1630
Непривитые 1022 11 1033
Всего 2647 16 2663
Воспроизведено с разрешения Macmillan Publishing Company из [Fisher (1970) — С].
Четыре элемента таблицы, а именно 1625, 5, 1022, 11, — это частоты; мы имеем, таким образом, таблицу в виде квадрата вместо более привычного ряда столбцов. Эта таблица частот в принципе пригодна для построения критерия согласия х2 с некоторой выдвинутой гипотезой.
Есть особенности таблиц 2x2, которые заслуживают специального упоминания:
1) в некоторых случаях необходимо делать «поправку на непрерывность», чтобы уменьшить погрешность, возникающую при аппроксимации непрерывным распределением х2 точного выборочного распределения, которое является дискретным;
370
2) для таблиц 2x2 односторонний критерий х2 для расхождений между наблюдаемыми и ожидаемыми частотами превращается в двусторонний.
Эти особенности рассмотрены ниже.
Нулевая гипотеза. В связи с табл. 7.5.1 возникает вопрос: значимо ли воздействие прививки на вероятность заболевания? Попробуем принять в качестве нулевой гипотезы, что прививка не оказывает действия и что видимый эффект от прививки есть результат случайных флуктуаций. Мы должны, следовательно, сравнить элементы в таблице с соответствующими ожидаемыми элементами в предположении справедливости гипотезы.
Ожидаемые частоты. Из гипотезы следует, что для 2663 человек, находящихся в группе риска, ожидаемая доля заболевших после прививки будет той же, что и ожидаемая доля заболевших среди тех, кому прививку не делали; общее значение этих долей совпадает с долей заболевших во всей выборке, а именно р = 16/2663. Эти ожидаемые доли представлены в табл. 7.5.2. Мы, естественно, отождествляем понятие независимости высказываний:
а) случайно выбранный представитель из группы людей с прививкой будет инфецирован и б) случайно выбранный представитель из группы непривитых людей будет инфецирован с понятием однородности для ожидаемых долей.
При нулевой гипотезе ожидаемая частота в любой ячейке может быть найдена умножением доли (р или 1 — р) на маргинальное общее число соответствующей строки (1630 для категории привитых, 1033 для остальных). Это приводит к таблице ожидаемых частот.
Таблица 7.5.2. Ожидаемые доли заболевших людей при гипотезе, что прививка неэффективна
Незаболевшие Заболевшие (Общие числа)
Привитые 1 — Р Р (1630)
Непривитые 1 -р Р (1033)
(Обшие числа) (2647) , 2647 1 ~ Р ~ 2663 (16) 16 Р “ 2663 (2663)
Таблица 7.5.3. Ожидаемые частоты, соответствующие табл. 7.5.2
1630 (1 —р) - 1620,21 5р = 9,79 1630
1033 (1 — р) = 1026,79 Ир = 6,21 1033
2647 16
371
Только один элемент следует вычислять умножением маргинальной частоты на ожидаемую долю; остальные элементы находятся вычитанием.
Значение хг (без поправки на непрерывность). Располагая вместе в виде таблицы наблюденные и ожидаемые частоты, запишем в каждую ячейку: наблюденную частоту, (ожидаемую частоту), [разность]. Таким образом, прямые вычисления позволяют получить следующую величину статистики Пирсона:
2 4,792 4,792 4,792 4,792
х “ 1620,21 + 9,79 + 1026,79 + 6,21 “ °’07,
(7.5.1)
Таблица 7.5.4. Наблюденные частоты, ожидаемые частоты и разности
1625 (1620,21) [4,79] 5 (9,79) [-4,79]
1022 11
(1026,79) (6,21)
[-4,79] [4,79]
Число степеней свободы v = 1. Вычисление ожидаемых частот неявно включало оценку двух параметров. Так, например, вероятность Ph того, что индивидуум с прививкой не заболеет, равна (при нулевой гипотезе) произведению где рх. — вероятность того, что случайно выбранный индивидуум будет иметь прививку (оцененная как р*. - 1630/2663), ар#1 — вероятность того, что случайно выбранный индивидуум не заболеет (оцененная как р*х = 2647/2663). Оцененная ожидаемая частота в ячейке «привитые и незаболевшие» будет тогда равна: 2663 р*.р*\ = 1630x2647/2663. Поскольку ожидаемые частоты в сумме дают соответствующие наблюденные значения маргинальных частот, этого одного вычисления достаточно для того, чтобы определить ожидаемые элементы во всех четырех ячейках, и никаких дополнительных параметров не требуется [см. раздел 5.4.2].
Число степеней свободы тогда равно:
( число \ . ( число \ .
V ~ ) - 1 - ( 1=4 — 1 — 2 - 1.
\ ячеек / \ параметров /
Поправка на непрерывность. В точном критерии для проверки гипотезы независимости, описанном в разделах 5.4.1 и 5.4.4, уровень значимости является суммой вероятностей (при нулевой гипотезе) получения ряда таблиц 2x2, а именно той таблицы, которая реально наблюдалась, плюс все таблицы с теми же маргинальными частотами, но еще более далекие от независимости. Поясним, что такое «бо
372
лее далекие» таблицы. В нашем примере ожидаемые частоты при нулевой гипотезе [см. табл. 7.5.3] равны:
1620,21 9,79
1026,79 6,21
а наблюденные частоты следующие:
1625 5
1022 11
5 случаев заболевания после прививки — это малая частота (меньше ожидаемой) и упомянутые выше более далекие случаи были бы представлены таблицами с 4, 3, 2, 1 и 0 заболевшими после прививки. Поскольку маргинальные числа должны остаться теми же, эти таблицы образуют следующее множество:
1625 5 1626 4 1627 3 1629 1 1630 0
1022 И 1021 12 1020 13 1018 15 1017 16 (7‘5,2)
Так как имеется только одна степень свободы, мы должны рассмотреть только один элемент в каждой таблице, скажем, элемент в верхнем правом углу, представляющий категорию «заболевших после прививки». Уровень значимости относительно гипотезы независимости тогда равен
Р(5) + р(4) + ... + р(0), где р(г) — вероятность того, что после прививки заболеют г человек, г = 0,1, ..., 5. В примере 5.4.4 получены вероятности р(г) и найдена их сумма. При х2-аппроксимации выборочное распределение непрерывно и сумму следует заменить интегралом. Мы можем изобразить отдельные вероятности р(г) ординатами, показанными на рис. 7.5.1, или же прямоугольниками, показанными на рис. 7.5.2. Эти прямоугольники имеют ширину, равную 1, и, следовательно, сумма р(г) численно равна общей площади прямоугольников, т. е. интегралу от соответствующей ступенчатой функции в пределах —0,5, +5,5. Прямоугольник, соответствующий р(0), имеет очень малую площадь, поэтому на практике не важно, берется ли интеграл от —0,5 до 5,5 или от 0 до 5,5. Важно то, что правая точка 5,5, а не 5. Ф. Йейтс [см. Yates (1934)] предложил в связи с этим заменять таблицу наблюденных частот
1625 5
1022 11
модифицированной таблицей
1624,5 5,5
1022,5 10,5 (7,5,3)
в которой число 5 увеличено до 5,5, а все другие элементы изменены так, чтобы сохранить общие маргинальные частоты. При такой модификации ожидаемые частоты остаются без изменения. Эта процедура
373
р (г)ф
L о
Рис. 7.5.1. Ординаты, представляющие р(0), р(1),...,р(5). Сумма этих ординат равна уровню значимости данных относительно гипотезы независимости
Рис. 7.5.2. Прямоугольники единичной ширины с высотами, равными ординатам р(0), д(1).р(5) на рис. 7.5.1. Сумма ординат численно равна сумме площа-
дей прямоугольников, т. е. интегралу от — 0,5 до 5,5 от ограничивающей ступенчатой функции
известна как поправка Йейтса на непрерывность для критерия х2 для таблиц 2x2. Перед вычислением х2 следует уменьшить на 0,5 абсолютную величину разности между каждой из наблюденных и ожидаемых частот. В нашем случае это приводит к уменьшению абсолютной величины (4,79) этих расхождений [см. табл. 7.5.4] до величины 4,29. Модифицированная таблица имеет вид:
4,29 —4,29
—4,29 4,29
Модифицированная величина х2 равна:
(4,29)2 (—5— + —JJ?—) = 4,873. (7.5.4)
4 1620,1 9,79 1026,79 6,21 '
374
Уровень значимости. Поскольку разности между ожидаемыми частотами и скорректированными на непрерывность наблюденными частотами при вычислении статистики Пирсона х2 возводятся в квадрат, величина х2 = 4,873, полученная в (7.5.4), могла также быть вычислена из таблицы
1615,42 14,48 (1630)
1031,58 1,42 (1033)
(2647) (16)
которая имеет те же маргинальные частоты и поэтому те же ожидаемые частоты, но в которой каждая разность имеет обратный знак. Например, — 4,79 превращается в +4,79 и наоборот. Следовательно, если мы возьмем в качестве нашего уровня значимости вероятность
Р(х? 4,873), то должны будем принять во внимание не только сумму вероятностей для таблицы наблюденных частот, но также и сумму Pi вероятностей «обращенной» таблицы и всех более крайних таблиц. Это изменит уровень значимости, так как нас интересует только сумма Р.
Чтобы выделить интересующую нас вероятность, заметим, что xi имеет то же распределение, что и квадрат стандартной нормальной случайной величины U [см. раздел 2.5.4, а)], откуда
Р (Х2 х2) = Р (U2 > х2) = P(U > I х I) + Р (—и — I х I) =
= Р (U | х |) + Р (U — | х |) = 2P(U > | х |), так как U имеет то же распределение, что и —U. Здесь слагаемое Р (U | х |) соответствует одному набору разностей, a P(U — | х |) — набору с обратными знаками. Таким образом, наш уровень значимости равен:
SL = Р (V > | х | ) = ip (х; > х2). (7-5.5)
В нашем примере х2 найдено в (7.5.4) и равно 4,873 = (2,207)2. Таким образом, уровень значимости = Р (U 2,207) = 0,014 (точная величина, найденная в примере 5.4.4, равна 0,015). Вывод состоит в том, что гипотезу независимости следует отвергнуть: прививка в действительности имеет некоторый предупредительный эффект.
Условия Кокрена применимости критерия х2 к таблицам 2x2. Рекомендация Кокрена для таблиц 2x2 состоит в следующем [см. Cochran (1952), (1954)]. Если сумма четырех частот меньше 20, то следует использовать точный критерий Фишера [см. раздел 5.4.2]. Если сумма между 20 и 40 и наименьшая ожидаемая частота меньше 5, то следует использовать точный критерий Фишера. Если сумма 40 или более, то можно применить критерий х2 при условии, что сделана поправка на непрерывность.
Следующий пример показывает, что даже эта рекомендация не универсальна. В примере сумма четырех частот равна лишь 30, но
375
в то же время процедура х2 (с коррекцией на непрерывность) дает приемлемую аппроксимацию к точному результату, полученному в примере 5.4.5.
Пример 7.5.1. Преступность и близнецы. Данные относятся к 30 преступникам мужского пола, каждый из которых имел брата близнеца. Тридцать человек были классифицированы: а) по природе родства (однояйцовые или разнояйцовые близнецы) и б) по виновности или невиновности брата. Результаты представлены в табл. 7.5.5.
Таблица 7.5.5
Брат виновен Браг не виновен
Однояйцовый близнец 10 3 13
Разнояйцевый близнец 2 15 17
12 18 30
Непосредственное вычисление ожидаемых частот в предположении отсутствия связи между природой родства и преступностью близнеца приводит к следующим ожидаемым частотам:
5,2 7,8 13
6,8 10,2 17
J2 18 30
Статистика Пирсона, вычисленная непосредственно по этим данным, равна
1 1
(4,8V (------+ —
5,2 7,
1 1
бУ + То, 2
Применение поправки на непрерывность, которая уменьшает абсолютную величину разности между наблюденной и ожидаемой частотой в ячейке на 0,5, приводит к скорректированной величине статистики:
1111
X2 = (4 3)2 (-+---+ - +-) = 10,46.
5,2 7,8 6,8 10,2
Ясно, что требуется односторонний критерий, и соответствующий уровень значимости поэтому равен:
Р (х2 Ю,46) = 0,0006.
376
Этот результат хорошо соотносится с величиной 0,0005, полученной по точному критерию. Он является высоко значимым и решительно отвергает нулевую гипотезу.
7.5.2. ТАБЛИЦЫ кхт
В разделе 7.4.1 мы обсуждали таблицы сопряженности, основанные на двойной дихотомии; каждый индивидуум в выборке классифицировался как: а) принадлежащий категории А или нет, а также как б) принадлежащий категории В или нет. Если первую дихотомию заменить разделением на к категорий, а вторую — на т (к, т 2), то мы получим так называемую таблицу сопряженности кхт:
я. в: В ! в >!l Всего
Л] «и Пц «|у Bill! r.
А2 «21 «22 "2./ П2т Г1
«Л "i2 "</ nim ri
Ак Пк\ "к2 nkj "km Гк
Всего <-'1 CJ cm t
В этом случае данные могут быть, например, выборкой из детей школьного возраста, классифицированных по цвету волос (категории Аь А2, ..., Afc) и качеству зубов (категории В,, В2, ..., Вт); тогда — число школьников с волосами категории А, и зубами категории Bj. В предположении справедливости нулевой гипотезы независимости (т. е. что цвет волос не влияет на качество зубов, и наоборот) ожидаемая частота, соответствующая наблюденной частоте п^, равна: etj - rjCj/t, а статистика Пирсона имеет вид
i / е J ij
Выборочное распределение этой статистики в предположении справедливости нулевой гипотезы представляет собой приблизительно распределение х2 с v степенями свободы, где
v - (к — 1)(т —1),
а уровень значимости х2 равен
Р1х2^*2}.
Таблица 2хк. В случае таблиц сопряженности 2хк или (кх2) неза
377
висимость эквивалентна однородности, как в случае таблицы 2x2, обсуждавшемся в разделе 7.4.1. Таким образом, для данных вида
Качество зубов Всего
I 2 к
Цвет светлый «II «12 nik Г\
волос темный «21 «22 пгк Г1
Всего С| С2 Ск t
независимость качества зубов и цвета волос эквивалентна однородности ожидаемых долей, как показано в следующей таблице:
1 2 к
Светлый Р Р Р
Темный \—р \—р 1—Р
где р = rjt. Соответствующие ожидаемые частоты будут равны:
rxcx/t rxC2/t rxck/t
ггсхН r2c2/t r2Ck/t
Итак, чтобы проверить гипотезу, что доля успехов одна и та же в каждой из к совокупностей, можно применить критерий х2, основанный на статистике
= Е(Я|;-Г|С7//)2 + Е j rtCj./t j r^j/t
считая это число реализацией случайной величины х2 с {к — 1) степенями свободы.
7.6. ИНДЕКС РАССЕЯНИЯ
7.6.1. ИНДЕКС РАССЕЯНИЯ ДЛЯ ВЫБОРКИ ИЗ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
В частном случае, когда все сг равны (скажем, с общим значением с), таблица может быть записана в виде
378
X! С — X! хг с —х2 1 о кх к (с - х )
с с ••
Оценка р равна х/с, а ожидаемые частоты равны:
х х ... X
С — Х~ С — X ... С — X
Отсюда
, _ (Xj - Г)2 I (с - х) - (с - Г)!2 _ j X j c — x~
= E (x; — x~y/cpq (p = x/c,q - 1 — p = 1 — x~/с) J J _
= E(x- — x )2/x q.
j J
Эта форма статистики x2 называется индексом рассеяния для биномиальных выборок. Его можно использовать для проверки того, являются ли частоты «успехов» х2,...,хк в к выборках одного и того же объема с совместимыми с гипотезой, что все они порождены схемой Бернулли с параметрами (с, р). Если это действительно так, то х2 есть реализация х2 с к — 1 степенями свободы.
Биномиальные данные. В выборках по 100 детей, взятых из пяти районов Англии, оказалось следующее число левшей:
Район 1 2 3 4 5 Среднее
Число левшей х> Хг Х3 х4 х. х”
Являются ли районы однородными в смысле частоты появления левшей? В предположении гипотезы однородности индекс рассеяния
5
х2 = Е (л\ — х )2/х(1 — х/100)
будет реализацией х\ и уровень значимости будет равен
Р(Х24>*2).
7.6.2. ИНДЕКС РАССЕЯНИЯ ДЛЯ ПУАССОНОВСКИХ ВЫБОРОК
Для выборок из пуассоновского распределения также существует индекс рассеяния, имеющий распределение х2. Хотя этот индекс и не соответствует частному случаю таблицы сопряженности, сходство с индексом рассеяния для выборок из биномиального распределения оправдывает его рассмотрение здесь.
379
Распределение частиц пыли в атмосфере при соответствующих допущениях и условиях можно считать пуассоновским. С помощью специального прибора стандартный объем воздуха затягивался в трубу и частицы пыли оседали на фильтровальную бумагу. Число частиц определялось по их общему весу. Если, скажем, в десяти таких пробах, взятых в различных районах Лондона, были получены числа частиц пыли х,, х2,..., Хю со средним то может представлять интерес вопрос, является ли средняя плотность частиц постоянной. При таком малом числе проб нецелесообразно формировать таблицу, по которой затем строить критерий согласия \г с предполагаемым пуассоновским распределением (как в примере 7.2.3); тем не менее критерий может быть построен. Соответствующий индекс рассеяния имеет вид
X2 = Е (X; — Х)2/Х .
j J
При справедливости нулевой гипотезы, что все ху- порождены одним и тем же пуассоновским распределением, выборочное распределение х2 есть х2 с 9 степенями свободы, а уровень значимости х2 по отношению к этой гипотезе равен
р (х29 X2).
7.7. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ Z
В тексте мы упоминали оригинальную статью К. Пирсона по критерию х2, а также исследования Кокрена о влиянии малых частот. Говорилось и о поправке на непрерывность Йейтса. Работы, посвященные этим проблемам, приведены ниже. Доказательство того, что асимптотическое выборочное распределение статистики Пирсона есть распределение х2 с соответствующим числом степеней свободы, можно найти в работе [Cramer (1946), гл. 30—С]. Много практических примеров приведено в книге [Fisher (1970) — С]. Наиболее общие учебники содержат примеры использования статистики х2» см., например, [Hald (1950) — С] или [Mood, Graybill and Boes (1974) — С].
Cochran W. G. (1952). The x2 Test of Goodness of Fit, Annals of Maths. Statistics, 23, 315.
Cochran W. G. (1954). Some Methods of Strengthening the Common x2 Tests, Biometrics (1954) 417.
Yates F. (1934). Contingency Tables Involving Small Numbers and the x2 Test, Supplement to Journal Royal Statist. Soc. i, 217.
Pearson K. (1900). On a Criterion that a System of Deviations from the Probable in the Case of a Correlated Systems of Variables is Such that it can be Reasonably Supposed to have Arisen in Random Sampling, Phil. Mag. 50, 157.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Аптон Г. Анализ таблиц сопряженности /Пер. с англ. — М.: Финансы и статистика, 1982. — 143 с.
Головач А. В., Ерина А. М., Трофимов В. П. Критерии математической статистики в экономических исследованиях. — М.: Статистика, 1973. — 136 с.
К о л к о т Э. Проверка значимости /Пер. с англ. — М.: Статистика, 1978. — 128 с.
380
Глава 8
ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ И ДИСПЕРСИОННЫЙ АНАЛИЗ
8.1. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ МОДЕЛЕЙ ОБЩЕГО ВИДА
Метод наименьших квадратов упоминался ранее в разделе 3.5.2. Теперь мы приступим к более подробному рассмотрению этого очень важного способа оценивания.
Пусть п наблюдений J,, / =* 1, 2, .... п, рассматриваются как результаты измерений п случайных величин У,-, / = 1, 2, ...» п, математические ожидания которых £'(У,) зависят от р неизвестных действительных параметров 0^ j = 1, 2, ..., р (р^.п), входящих в п известных функций fit i = 1, 2, ..., п, следующим образом:
Ж У,) 02, 0Р) =7,(0),
где в = (0Н в2, .... вру. Тогда У,= /,(0) + €(, где е, — случайная «ошибка» /-го наблюдения, причем предполагается, что е, независимы и равновелики, а их математические ожидания равны нулю. Обозначим их (неизвестные) реализации через е15 е2, ...» еп, тогда л = Л(0) +
Допустим, что u =(«,, и2, .... ирУ — некоторая вектор-функция от ji, у2, ...,уп — претендует на роль оценки для в [см. определение 3.1.1]. Рассмотрим сумму квадратов разностей между наблюдениями и их ожиданиями, оцениваемыми на основе и, т. е.
п
S(u) = Е[у,-Л(и)Р. (8.1.1)
Чем ближе эти ожидания к фактическим значениям наблюдений, тем меньше должно быть S. Следовательно, значение S может использоваться в качестве меры того, насколько хорошо наблюдения описываются моделью, в которой в оценивается с помощью U. Принцип наименьших квадратов, предложенный Гауссом, гласит, что в качестве оценки для в следует выбрать такую оценку в = (0i, 62, ..., др)', которая минимизирует эту сумму квадратов отклонений, т. е. минимальное значение Su при вариации U достигается для U = 0.
381
Оценки метода наименьших квадратов (МНК-оценки) при обычных условиях можно найти, решая «нормальные уравнения»:
ras(u)] _п _
I ди I О’ J ~ •••’ Р-
J u = w
Они сводятся к
I = 0, / = 1, 2, .... р. (8.1.2) 1-1 J U-?
Свойства оценок [см. определение 3.1.1], получаемых этим методом, зависят от распределения Ун Y2, ..., Yn. Если, например, е, — независимые и одинаково распределенные нормальные случайные величины, то МНК-оценка 0 совпадает с оценкой метода максимума правдоподобия [см. гл. 6]. Вообще говоря, МНК-оценки не несмещен-ны [см. раздел 3.3.2], однако в одном (важном) частном случае, который обсуждается ниже — при линейной модели, — они оказываются несмещенными, а также обладают оптимальным свойством, рассматриваемым в разделе 8.2.3.
8.2. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ЛИНЕЙНЫХ МОДЕЛЕЙ ПОЛНОГО РАНГА. НОРМАЛЬНЫЕ УРАВНЕНИЯ. ТЕОРЕМА ГАУССА—МАРКОВА
8.2.1. ПРИМЕРЫ ОЦЕНИВАНИЯ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
Пример 8.2.1. Повторные (параллельные) измерения в одной точке. Единственное численное значение 0t измеряется п раз при наличии ошибки. Наблюдения представлены в виде yz = 0t + ez, где ez — ошибка z-го наблюдения. В этом случае сумма квадратов (8.1.1) превращается в
S(u) = 5(U]) = £(yz. — их)\
а нормальное уравнение (8.1.2) — здесь оно только одно — сводится к £(yz-0i) = О,
поэтому МНК-оценка 01 равна: 01 = Еу,/л -= у .
Пример 8.2.2. Девять наблюдений пяти постоянных силы тяжести. Более интересный пример — определение физических постоянных на основе следующих данных:
382
g2=981,1880, g3 =981,2000, gj—#2=0,0140,
#4—g, =-0,0030, g4-g3= 0,0647, g4~gs= 0,1431,
g<-gs =0,1390, gt =981,2670, g, =981,2690,
где gi, g2, ..., g5 — значения ускорения силы тяжести для пяти различных мест. Попытка решить получающуюся систему математических уравнений здесь явно не состоятельна из-за экспериментальных ошибок. Фактически эти «уравнения» весьма приблизительны, и мы могли бы описать ситуацию точнее, если бы учли, что g2 + ei = 981,1880, g4 — gi + e2 = —0,0030 и т. д. В обозначениях раздела 8.1 (для параметров gt, g2...g5) имеем/i(gb g2, , gs) = g2,
f2(gi, g2....gs) = g4 — gi, ...» а сумма квадратов, которую надо ми-
нимизировать, равна:
S(u) = (981,188O — и2)г — (—0,0030 — w4 + u1)2+...4-(981,2690— и,)2.
Дифференцирование по и,, и2, ..., и5 и подстановка u, = g,, / = 1, 2, ..., 5 приводят к нормальным уравнениям:
3gi — g4 — 1962,5390 = 0,
2gi — gi — 981,1740 = 0,
—g2 + 3gi — g4 — 981,1493 = 0,
—g\ — gi + 4g4 — 2gs—0,3438 = 0,
—2g4 + 2g5 + 0,2821 = 0.
Это система (регулярная) неоднородных линейных уравнений полного ранга* с пятью неизвестными, имеющая (единственное) решение:
gi = 981,2681, gi = 981,1873, gi = 981,2006,
g4 = 981,2652, gs =981,1241
[продолжение см. в примере 8.2.4].
8.2.2. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ МОДЕЛЕЙ
В примерах 8.2.1 и 8.2.2 мы имели дело с линейными моделями, поскольку в обоих случаях каждое наблюдение выражается как линейная функция от параметров плюс ошибка. В терминах раздела 8.1 функция /, представляет собой линейную функцию вектора параметров в = (01, 02, •••» 0рУ, а У, можно записать в виде
* В данном случае речь идет о свойствах систем линейных уравнений. См., например: Мишина А.П., Проскуряков И.В. Высшая алгебра/Под. ред. П.К. Рашевского. — М.: Физматгиз, 1962. — С. 46—66. — Примеч. пер.
383
Yj = ahe} + ah62 +... + aip9/} + ez, i = 1, n,
или
~ j*~\a u® j + 6,1
где atj — известные константы. Запишем: Y = (У,, Y2, ...» Yn)', e = (ci, e2, e„)z и обозначим (n x р)-матрицу, составленную из констант \с1ц} через А (она известна как матрица плана)*. Тогда мы можем записать модель в сжатой форме: Y = А0 + е. А для экспериментальных значений у = А0 + е, где у Сн, у2, уп)' — наблюдаемые значения Y, а е = (е,, е2, ..., еп)' — вектор ошибок. Отсюда сумма квадратов, подлежащая минимизации, примет вид
5(u) = £ — £ а^и]1 = (у — Au)(y — Au).
/1 J - 1 J J
Нормальные уравнения (8.1.1) для оценок 0у в данном случае линейны и их можно записать так:
Е [j, - Е а,у0 ] = О, J = 1, 2, ..., р,
или в матричной форме:
А у — А'А0 - 0.
Для дальнейших ссылок мы перепишем его:
А'А0 = Ау. (8.2.1)
Мы предполагаем, что р столбцов матрицы А линейно независимы (это и есть случай полного ранга)**. Тогда ранг г(А) матрицы А будет равен р. Отсюда следует, что симметричная матрица А'А тоже имеет ранг г(АА)=р, а поскольку ее размер (р х р), то она не вырождена*** и имеет обратную (А'А)-1****. Вот единственное решение нормальных уравнений:
0 = (А'АГ’А'у, (8.2.2)
представляющее собой линейную функцию от результатов наблюдений ji, у2, ..., уп и служащее МНК-оценкой для 0. Случай, когда г(А) < р, обсуждается в гл. 10.
* О свойствах матриц см.: Мишина А. П., Проскуряков И. В. Высшая алгебра. — С. 67—174. — Примеч. пер.
“Там же. — С. 54—59. — Примеч. пер.
*** Т а м же. — С. 71. — Примеч. пер.
•’•‘Там же. — С. 71—75. — Примеч. пер.
384
Пример 8.2.3. Продолжение примера 8.2.1. Для модели измерений
ИЗ примера 8.2.1 матрица А — просто вектор из единиц размера
(п х 1), матрица АА = п , а А у = L у,-1 — 1 *
Пример 8.2.4. Продолжение примера 8.2.2. Для этого примера век-
тор параметров 9 = (glt g2, ..., g5)' и мы имеем:
’г.' 981,1880 0 1 0 0 о ei
y2 —0,0030 —10010 е2
Уз 0,1390 0001—1 ' gi~ е3
У4 981,2000 0 0 10 0 ёг е4
Уз — 0,0647 00—110 ёз + е> •
Уб 981,2670 1 0 0 0 0 ё4 е6
Уз 0,0140 0—1 10 0 ёз е2
уе 0,1431 0001—1 L> -1 е»
у. 981,2690 1 0 0 0 0 е9
Здесь " 3 0 0 —1 0 —1
0 2—100
АА = 0—1 3—1 0
— 1 0—1 4 —2
- 0 0.0—2 2 —
а поскольку 0 = (АА) ‘Ay, получаем
-0,4211 0,0526 0,1053 0,2632 0,2632“ “ 1962,5390“ - 981,2681“
0,0526 0,6316 0,2632 0,1579 0,1579 981,1740 981,1873
0,1053 0,2632 0,5263 0,3158 0,3158 981,1493 = 981,2006
0,2632 0,1579 0,3158 0,7895 0,7895 0,3438 981,2652
- 0,2632 0,1579 0,3158 0,7895 1,2895- 0,2821 - - 981,1241-
(продолжение в примере 8.2.8)
Пример 8.2.5. Регрессия. Часто зависимость между переменной У и несколькими «независимыми» переменными хь х2, ..., xs приближают «линейной моделью» вида
E{Y) = /Зо + 01Л1(Хь х2..х5) +
+ 02Ы*ь Х2....Х5) +...+ 0дЛд(хь Х2..Xs)
[ср. с разделом 3.5.5], где Л,, h2.. hq — заданные функции от
Xj, х2, ..., xs, а 0о, 01, •••, 0q — неизвестные параметры (заменившие 0,» 02, ..., 0р в общих формулировках, приведенных выше). Наблюдения У,, У2....Yn получаются при различных комбинациях известных
385
значений переменных х,,х2, ...,xs. Обычный случай — множественная линейная регрессия [ср. с примером 6.5.1], когда Лу(хь х2, • ••, х5) = Xj, a q = s, так что модель принимает вид
E(Y) = /30 + 31-Vi + ••• +
(В примере 6.5.1 обсуждается случай, когда есть только одна переменная-регрессор х,.) Используемая здесь терминология может ввести в заблуждение. Действительно, наша модель линейна, поскольку она представляет собой линейную функцию от параметров /30, /3,, ..., /35. Кроме того, регрессия называется линейной, поскольку линейны зависимости E(Y) от каждой независимой переменной хг. Вместе с тем следующая модель линейна по параметрам /30, Зь •••» 3$, и, следовательно, линейна:
£(У) = /Зо + /31Х + /32х2 +...+ /3$х5,
но она выражает нелинейную зависимость E(Y) от единственного регрессора х, а значит, это уже нелинейная регрессия. Такая регрессия называется полиномиальной. Нелинейную зависимость E(Y) от нескольких регрессоров можно явно представить в виде линейной модели
E(Y) = /30 + /З.ЛГ1 + /ЗцХ) + /32х2 + /322*22 +
+ /312Х,х2 + /3,23*1X2X3,
где для большей ясности переобозначены параметры.
Чтобы записать эту модель в матричной форме, предположим, что фактические значения переменных х,, х2, ..., xs для z-ro наблюдения Y равны хп, ..., xjs. В случае, например, множественной линейной регрессии имеем
У, = /Зо + /З.Хл + 32х/2 +...+ /3$x/s + eit
т. е.
у = А0 + е,
где
386
Следовательно,
АА = п Ex,- . Exj, . ^xis ^xi\xis , АУ = ^y,xh
^xis Lx- x-IS • ^xis £yjxis
Вовсе не обязательно, чтобы все наблюдаемые значения регрессоров различались, но мы предполагаем, что эти значения в общем и целом окажутся такими, что матрица А будет иметь полный ранг (в нашем примере равный s + 1). Совсем иная ситуация, например, если все п наблюдений сделать при одних и тех же значениях Х\.....xs. Для
отыскания МНК-оценок 0О, ..., /35, нам нужна матрица (А'А)-1, которая получается обычным численным обращением матрицы А'А на компьютере. А для однофакторной линейной регрессии, которая в наших обозначениях имеет вид
E(Y) — /30 + 13\Х],
можно получить простые явные формулы. Условимся в этом случае отбросить индекс при х и писать просто E(Y) = /Зо + ft\X. Обозначив фактические значения х через хь х2...хп, получим
(А А)"1 =
1
лЕ(х, — х-)2
- ех;
L —пх
—пх
п ’
где х = (Ех^/п. Воспользовавшись соотношением ft = (А'А) ‘Ау, найдем МНК-оценки:
в - v — Я y R - L(Xi ~ Х ~ РО У Р\Х , 0J Е(Х,- — х)2
где у = (Еу,)/п.
Для полиномиальной регрессии имеем
Л = 0о + + 02х?+...+ + е, ,
где X, — значение х, полученное в z-м наблюдении. Записав у = Aft + е, получим
' 1 X) X2, - $ 1 Xi n zxi Exj ... Ex]
1 X1 Хг •• ^xi Ex2 Ex! ... Ex*+1
A = 1 xn x2„ .. X5 , AA = Ex] Exs+1 I E/+2 ... 1 Ex? /
387
И в этом случае, как правило, требуется численное обращение матрицы А'А .
Наконец, рассмотрим еще один пример нелинейной модели:
E(Y) = /30 + 31-^1 + @21*2 + З0/З1Х3.
Хотя здесь и представлена линейная зависимость E(Y) от Xi, х2 и х3, модель нелинейна по параметрам, и мы не можем выразить ее в матричной форме E(Y) - А/3, а значит, все формулы, полученные ранее, не применимы.
Пример 8.2.6. Односторонняя классификация (однофакторная классификация, классификация с одним входом). Допустим, что данные разделены на I групп с Jt наблюдениями в /-й группе, i = 1, 2, .... I. Тогда результаты можно обозначить так: yj2, ..., уи при
z = 1, 2...I. Данные можно свести в таблицу:
Группа Наблюдения Среднее в группе
1 2 I Гн, Yl2, Yu< Y2i, Y22, .... У2А Уи, У12, .... YUi у,. y2. Y,.
Полагая, что наблюдения в z-й группе — это случайная выборка из
распределения с Уи = математическим ожиданием д,, получим модель P-i 4* Сц, i 1, 2, ..., I, j 1, 2, ..., Jj,
где е — фактические значения случайной величины с математичес-
ким ожиданием у = Ав + е или У1 _уп J нуль. Эт так: 'J11 1 У21 yu2 Уп Уи'\ у модель можно представить в виде 1 0 0 01 Г ен 1 0 0 0 0 10 0 Д] е21 ’ ’ ‘ ’ . (8.2.3) 0 10 0 [Д/] e2Ji 0001 еп 0 0 0 1 efJi
388
В этом случае АА — диагональная матрица* с диагональными элементами У1Э J2, •••» Jj- Запишем
А А = diag[jr1, J2, Jj, тогда
(АА)-1 = diagtl/Л, 1/Л, .... 1///]
и
АТ = -•
J.
Отсюда Д, = Zy-fj/J-, = yi+/ Ji = yt , т. е. среднему по z-й группе наблюдений (здесь и далее мы будем обозначать суммирование по данному индексу подстрочным знаком плюс (+), а усреднение — точкой (.)).
Модель односторонней классификации можно представить в регрессионной форме еще одним способом:
E(Y) = Д1Х, + ц2х2 + ...+ iijXj,
где регрессоры xt, х2, х1 выбраны так, что для i = 1, I мы имеем х,= 1, если данное наблюдение принадлежит z-й группе и xz=0 в противном случае. Соответствующие значения х; приводятся в z-m столбце матрицы плана А. В таком случае регрессор становится качественной переменной, обеспечивающей только указание структуры данных, тогда как переменные из примера 8.2.5 были количественными.
Пример 8.2.7. Односторонняя классификация с сопутствующей переменной. В дополнение к информации о разделении данных на I групп мы можем иметь дополнительные сведения о количественной переменной z, известной как сопутствующая переменная. В этом случае получается такая модель:
Уу = Д/ + + еи.
В регрессионной форме она точно соответствует виду
E(Y) = Д]Х1 +...+ д/х/ +
а ее вектор параметров 0' - (gu ..., ц{, ф), причем матрица плана А, приведенная в предыдущем примере [см. (8.2.3)], пополняется столбцом с элементами (zi.....z17, Z21, •••» z2J1..zn, ..., zuy.
* См.: Мишина А. П., Проскуряков И. В. Высшая алгебра. — С. 89. — Примеч. пер.
389
Эта идея естественно обобщается на модели с несколькими сопутствующими переменными. В таком случае матрица плана будет состоять из нескольких столбцов с элементами 0 или 1, указывающими структуру данных, а затем из нескольких столбцов, содержащих значения сопутствующих переменных.
8.2.3. СВОЙСТВА ОЦЕНОК МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
Насколько хороши МНК-оценки? Оценить метод можно, только рассматривая статистические свойства МНК-оценок [см. определение 3.1.1] 9= (91, Qz, ..., 9р)' = (А'А)-1 AY, получаемых на основе результатов наблюдений 0 = (A'A)-,A'Y. Ясно, что распределение Q зависит от распределения Y. В этом разделе рассматриваются только первые два момента* распределения 9 (другие свойства распределения обсуждаются в разделе 8.3.1). Кроме того, мы будем здесь предполагать, что случайные ошибки наблюдений имеют математические ожидания, равные нулю, и равные дисперсии, а некоррелированность, которая раньше предполагалась для независимых ошибок в разделе 8.1**, не необходима для непосредственного получения следующих результатов. Итак, вот наши постулаты:
Е(е) = О, £>(<) = а21„,
где £>(•) — дисперсионная матрица [см. II, определение 9.6.3)***. Отсюда следует, что
E(Y) = A0, Z>(Y) =
При этих условиях МНК-оценки имеют следующие свойства: Свойство 1. Несмещенность.
Е(9) = е
для j = 1, ..., р величины 0у без смещения оценивают 0у.
Свойство 2. Дисперсионная матрица. Дисперсионная матрица вектора О равна:
D(G) = ст2(А'А)-1.
Таким образом, дисперсией z-го коэффициента 0, служит z-й диагональный элемент этой матрицы, а ковариация cov(6z, 0у) равна (/, j)-элементу.
* Определение моментов см., например, в работе: Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. Основные понятия, предельные теоремы, случайные процессы. — М.: Наука, 1967. — С. 209—217. — Примеч. пер.
** См.: Там ж е. — С. 43—49. — Примеч. пер.
*** См. также работу: Ермаков С.М., Жиг лявский А.А. Математическая теория оптимального эксперимента. — М.: Наука, 1987. — С. 24—25. — Примеч. пер.
390
Свойство 3. Минимальная дисперсия (теорема Гаусса—Маркова). Формула для оценивания (й по 0у представляет собой линейную функцию от наблюдаемых значений Уь У2, • •., Yn, которая обладает тем свойством, что ее дисперсия меньше, чем дисперсия любой другой линейной функции от отклика Y, которая бы тоже оценивала 0, несмещенно, т. е. если Е(1, У) = 0у, где К= (/ь /2, 1пУ — заданный вектор, то _
var0y varГУ для любых [.
Другим^ словами, среди всех несмещенных линейных оценок 0у МНК-оценка 0у наилучшая в смысле минимума дисперсии. Она представляет собой линейную несмещенную оценку с минимальной дисперсией (ЛНОМД) [см. раздел 3.3.2].
В более общем виде: если мы рассмотрим оценивание любой известной линейной комбинации параметров, скажем Х'9 = Xi0i + + Х202 +•••+ Хр0р, где X = (Хь Х2, ..., \р)' задано, то мы можем сказать, что КО = Xt0i + Х202 +..+ Хр0р — несмещенно оценивается \'О, а дисперсия этой оценки не больше, чем у любой другой несмещенной оценки Х'в, которая тоже линейна относительно независимой переменной У, т. е. Х'О — ЛНОМД для Х'6; ее дисперсия есть
X'D(O)X = а2Х'(АА)~‘Х. р — р
В частности, E^Y^ = £д/:/0у есть ЛНОМД для Еа#0у-.
Свойство, выражаемое теоремой Гаусса—Маркова, не обязательно означает, что принцип наименьших квадратов всегда приводит к хорошим оценкам. Может случиться, что оценка окажется наилучшей в ограниченном классе, но при этом будет весьма «средненькой». Так, например, вполне возможно построить нелинейные функции от У,, У2, ..., Yn, которые будут несмещенными для 0Ь 02, ..., 0р, но окажутся лучше МНК-оценок, если ошибки еь е2, ..., еп получатся распределенными ненормально [см. ниже]. С другой стороны, если €i, ..., еп распределены нормально, можно показать, что МНК-оценки будут точно теми же, что и оценки метода максимума правдоподобия [см. раздел 3.5.5], так что в этом случае, в дополнение к тем свойствам, что были перечислены выше, они приобретают многочисленные новые свойства, делающие их более привлекательными, чем любые иные оценки, линейные или нелинейные. Для применения теоремы Гаусса—Маркова требуется лишь выполнение довольно слабых предположений, указанных выше, и можно быть уверенными в ее справедливости при применении метода наименьших квадратов в ситуациях, когда мы не можем или не хотим вводить более жесткие предположения относительно распределения ошибок. Если же распределение ошибок известно, то обычно более предпочтительны другие методы (например, метод максимума правдоподобия).
391
В случае модели измерения
Yi = el + €i
с некоррелированными ошибками и при Е(е) = 0, vare( = а2, ЛНОМД для 61 служит 0]=У, a var0, = а2(А'А)-1 = а2/п. Для различных симметричных, но не нормальных распределений ошибок медиана Yi, Y2, Yn (нелинейная функция от У,, У2, ..., Yn) имеет меньшую дисперсию, чем У.
Пример 8.2.8. Данные о силе тяжести [см. примеры 8.2.2 и 8.2.4], рассмотренные ранее. В этом примере мы находим, что
“ 0,4211 0,0526 0,1053 0,2632 0,2632 "I
0,0526 0,6316 0,2632 0,1579 0,1579
(А'А)-1 = 0,1053 0,2632 0,5263 0,3158 0,3158
0,2632 0,1579 0,3158 0,7895 0,7895
0,2632 0,1579 0,3158 0,7895 1,2895
Заметим, что, поскольку диагональные элементы матрицы (АА) 1 не равны между собой, различными будут и дисперсии МНК-оценок Gi, ..., G5, а значит, и константы gi, ..., g5 оцениваются с различной точностью, что обусловлено асимметрией, с которой эти параметры входят в уравнения модели. В частности, самая точная оценка — это gi (с дисперсией varG ] = 0,4211а2), а самая неточная — g5 (с дисперсией varG5 = 1,2895а2). Стоит также обратить внимание на некоторые другие свойства структуры уравнений модели, такие, как:
1) cov(G4, Gj) = cov(Gs, Gj), y’=l, ..., 4,
2) cov(G2, G3) = cov(G], G4).
После рассмотрения индивидуальных оценок ускорения силы тяжести в разных местах мы можем заинтересоваться средним значением g для всех пяти мест, т.е. оценкой g = (gt +g2 +g3 +^4+^5)/5. Для отмеченных условий ЛНОМД для этой линейной функции есть (Gi + G2 + G3 + G4-i-G5)/5, равное 981,2091. Ее дисперсия равна а2Х'(А'А)-1Х, где X = (1/5, 1/5, 1/5, 1/5, 1/5), а это как раз произведение дисперсии а2 на среднее арифметическое элементов матрицы (АА)-1, что в данном случае равно 0,3611а2 [продолжение см. в примере 8.2.12].
Пример 8.2.9. Линейная регрессия для одной переменной. Это случай, для которого E(Y) = /З0+/З1Х, и ЛНОМД для /?0 и /31 равны:
392
Bq — Y — В\Х , Bi —
Е(х; — х)(У. — У)
Е(х,-х)2
Заметим, что, поскольку регрессор х — не случайная величина, его заданные значения х}, ..., хп входят в эти формулы точно так же, как и в ранее рассмотренные выражения для fa, fa (из примера 8.2.5), которые мы уже получили.
В соответствии со свойством 1 Е(В0) - fa, E(Bt) = fa. Используя далее свойство 2 и матрицу (А'А)1, как и в примере 8.2.5, получим
a2Exj
var Во -0 — х)2
varBi =
а2
Ш,-*)2
Отметим также, что Во и В} коррелированы. Их ковариацию представляет внедиагональный элемент матрицы а2х(А'А)-1, равный а2х /Е(х(- — х )2.
Пример 8.2.10. Односторонний план (конфигурация). В этом случае [см. пример 8.2.6] ЛНОМД групповых средних ..., д7, равны У1, ..., Yj соответственно с дисперсиями а2/Л, ..., a2/ Jj. Внедиагональные элементы матрицы (А'А)-1 равны нулям, поэтому любые две из этих оценок некоррелированы. Для получения ЛНОМД линейных комбинаций Д1, ..., д7 строят такие же линейные комбинации Ун ..., Yj. Например, ЛНОМД для цг — ns равна Уг. — Ys. с дисперсией ст2{1//г + 1/JJ. ЛНОМД для J\Hi + J2n2 4-...+ Jjfij равна /]У1. + J2Y2. +... + JjYj., а ее дисперсия равна: Е/^уагУ,. = a2EJ, = = па2, где п — общее число наблюдений. Эту дисперсию тоже можно было получить непосредственно, если заметить, что Yt. = Е У(+ = = У++ — сумма всех наблюдений.
8.2.4. ОСТАТКИ
На практике дисперсия ошибки а2 не известна. Но поскольку а2 входит как общий множитель в дисперсии и ковариации Оь ..., Qp, а также и в дисперсии их линейных функций, нам приходится оценивать ст2 при оценке всех этих величин. Тогда оценки стандартных отклонений 0Ь ..., 0р будут давать некоторое представление о точности оценок 0i, ..., 0р и аналогично для линейных функций от этих параметров.
Для оценки а2 заметим, что если бы мы знали все 0t, то мы могли бы определить фактические ошибки из выражения
е = у — А0.
Оценивание а2 могло бы тогда опираться на величину
393
*е = (у - А0)(у — Ад), равную как раз Ее*. Это одно из значений случайной величины ее = Ее*, имеющей математическое ожидание, равное па2. Следовательно, оценкой для а2 должно быть (Ее*)/л. Но поскольку на самом деле 0,- не известны, мы модифицируем метод, используя вместо них их МНК-оценки. Тогда ЛНОМД для е равна: е = у — А0, и мы получаем оценку а2 на основе е?е = Ее*, где е, — /-й остаток, получаемый из р _
= Л-Еа,/у.
Заметим, что Ее* — это и есть то самое минимальное значение
5(и) = (у — Au)'(y — Au),
которое по определению должно получиться при и = 0. Величина Ее* — остаточная сумма квадратов (ОСК), которую мы обозначим через г. Тогда г = Ее* = 5(0). Оказывается, что случайная величина R, для которой г служит частной реализацией, больше не имеет математического ожидания па2. Вместо этого математическое ожидание сводится к (п — р)а2, так что оценка а2 равна:
Отсюда одна из формул для несмещенной оценки D(9) имеет вид (A'A)~'R/(n — р).
Мы оцениваем стандартное отклонение 0у из выражения а х [С/» 7) элемент матрицы (А'А)-1]12,
а стандартную ошибку линейной функции Х/0 - XjOi+ ... +ХрОр из выражения
ст[Х/(А'А)~1Х]1/*.
Можно заметить, что (8.2.4) «не срабатывает» при п = р, когда число наблюдений оказывается таким же, как и число параметров. В этом случае, хотя у нас и достаточно наблюдений для оценки 0Ь ..., 0р, нет никаких дополнительных данных, на основе которых можно было бы оценить а2 (на самом деле г = 0, так что наблюдения можно описать превосходно). Однако на практике, поскольку оценивание а2 существенно для суждения о точности оценок 0Ь ..., 0р, мы должны гарантировать, что п > р.
Далее (в уравнении (8.3.7)) будет показано, что для оценки г не обязательно находить индивидуальные остатки. Вместо этого можно воспользоваться формулой
394
r = (8.2.5)
т. e. мы вычитаем из Ly] — суммы квадратов всех наблюдений — произведение МНК-оценки 0 на правую часть системы нормальных уравнений, приведенной в уравнении (8.2.1).
Пример 8.2.11. Остатки в примерах 8.2.1 и 8.2.3. В модели измерений yt; = 0i + ejf i = 1, 2, ..., п, i-ti остаток получается из
= у. — 0 j = у. — у.
Остаточная сумма квадратов в этом случае равна: r= L(yj — у)2. Можно записать ее и иначе: г = Ly2 — пу2, причем эта формула получается непосредственно, если исходить из уравнения (8.2.5).
Для оценки а2 имеем
а2 = Е(у.-7)2/(и- 1).
Пример 8.2.12. Остатки в примере с ускорением силы тяжести. В этом случае [см. примеры 8.2.2, 8.2.4 и 8.2.8] остатки таковы: (981,1880 — g2), (—0,0030 — g4 + g >),..., (981,2690 — gi), т. e. 0,0007, —0,0001, —0,0021, —0,0006, 0,0001, —0,0011, 0,0007, 0,0020, 0,0009, откуда г = S(0) = Le2 = 0,00001179. А поскольку n - 9, p = 5, to ct 2 = r/4 = 0,00000295. Оценки дисперсий Gi, ..., G5 (с использованием элементов матрицы (АА)-1 из примера 8.2.8) таковы: 0,4211 ст2, 0,6316ст 2, 0,5263ст2, 0,7895 ст2, 1,2895ст2. Воспользовавшись оценками значений ст 2, получим соответствующие оценки стандартных отклонений: 0,0011, 0,0014, 0,0012, 0,0015 , 0,0017. Дисперсия, связанная с оценкой g = (gi +... +g5)/5, получена в примере 8.2.8 и равна 0,3611 ст2, следовательно, оценка стандартного отклонения есть (0,3611)1/2ст = 0,0010 (продолжение см. в примере 8.3.1).
Пример 8.2.13. Остатки в обычной линейной регрессии. В регрессионной модели yt = 0О + 0iXj + е, [ср. с примером 8.2.9] имеем г = .£(/,• — Зо — 3i*,-)2,
где 0О = У — 01*, 3'1 = Е(х( — х)(у(. — У)/Е(х, — х)2.
Подстановка вместо З'о того, что ему равно, и раскрытие скобок дает
r=L(yi — у)2 — 23'1Е(х/ — х)(у, — у) + 3" ?Е(х,- — х)2.
Среднее слагаемое равно —2^2L(Xj— х)2, отсюда г = 'Ey2 — пу2 — 3"2 Е(^ — X )2.
395
Достаточно просто показать, что это выражение равно тому, что было использовано в уравнении (8.2.5), а именно
г = Е/^ — ^Х1У1-
Пример 8.2.14. Остатки в односторонней конфигурации. В одно стороннем плане с моделью
(ij + в(у, i 1, 2, ..., I, J 1, 2, ..., Jj
[ср. с примером 8.2.6] имеем для (/, у) остаток
€ ij ~ У ij М / — У ij У i't
так что остаточная сумма квадратов равна:
г
Это сумма квадратов отклонений наблюдений в группе от группового среднего. Так как число параметров равно I, то о2 = г/(п—Г), где
А вот другое выражение для г, получаемое из уравнения (8.2.5): г = Е Е4-Ед/Л+ = EE^-EJ^-
8.2.5. ОРТОГОНАЛЬНЫЕ ПЛАНЫ И ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
Модель называется ортогональной, когда матрица плана А такова, что матрица А А имеет диагональный вид*, скажем diagG4n, ..., Арр). В этом случае обратная матрица тоже диагональна: (АА)-1 = = diag(>4“’ ..., А~р), а вектор решений допускает запись в простой скалярной форме:
= -Jr-^yflij’ J = •••’ р> jj
что легко проверяется нормальными уравнениями, которые в свою очередь становятся совсем простыми:
Zy,aij - - 0. j = 1....Р-
Односторонняя конфигурация из примера 8.2.6 представляет ортогональную модель. Та легкость, с которой могут решаться нормальные
* См., например: Мишина А.П., Проскуряков И.В. Высшая алгебра. — С. 122—129. — Примеч. пер.
396
уравнения, — одно из привлекательных вычислительных свойств ортогональных моделей. Мы еще покажем это, когда будем рассматривать ортогональные полиномы.
Допустим, что надо построить полиномиальную регрессионную модель в виде
у = |80 + (3iX + (32х2 + ... + 0sxs + е
по экспериментальным данным (у^ х(), / = 1, 2, ..., п.
Матрицы А и АА приведены в примере 8.2.5, откуда видно, что план не ортогонален. Но модель можно многими эквивалентными способами привести к следующему виду:
у = а0Р0(х) + aiPi(x) +...+ asPs(x) + е, (8.2.6)
где для г = 0, 1, ..., s, Рг(х) — полиномы степени г по х (Ро(х) = 1), коэффициенты которых (вместе с (30, ..., |8S) определяют а0, ..., as. Для этой новой модели матрица плана имеет вид
‘ Ро(х.) Ро(Хг) P^Xi) ... Р5(Х1) Pi(x2) ... Ps(x2)
А = • 9 9 9
• 9 9
9 9
Ро(Хп) Р.(^) ••• ps(xn)
так что (j, £)-й элемент AJk матрицы А А оказывается равным: п
Ajk = £Pj(x>)Pk<xi)-
Поскольку А'А должна быть диагональной матрицей, требуется, чтобы
= О, j = 0, 1, ..., s, к = 0, 1, ..., s, j # к.
Полиномы, удовлетворяющие этому условию, называются ортогональными и позволяют однозначно определить xif х2, ..., хп отдельно от их сомножителей. Диагональный элемент матрицы АА с номе-Л 2
ром j равен: А = ЕРдх,), откуда МНК-оценка для оказывается равной:
а, == E^P/x^/EP^x,), j = 0, 1, ..., s, л 2 а дисперсия, связанная с этой оценкой, равна ст2/ЕРдх). В частное-ти, поскольку Р0(х) = 1, получаем Ej/Po(x/) = Ej( и Ац=п, откуда ао = у, а МНК-оценка для а0 имеет дисперсию а2/п. Заметим, что, 397
поскольку А А — диагональная матрица, оценки параметров, полученные методом наименьших квадратов, в ортогональных планах всегда некоррелированы.
Из (8.2.5) видно, что остаточную сумму квадратов можно записать так:
г = Еу2 — аоу; — a^yjP^Xj) —...— а5Еу(Р5(х,),
или, учитывая, что Еу,Ру(х() = aJ'EP2j(xi), так:
г = Еу2 — — а^ЕР2(х,) —а2ЕР2(х().
Мы уже отмечали, что ортогональные полиномы определяются независимо от констант-сомножителей. Поэтому неважно, какие именно константы выбрать. Так, если мы рассмотрим
у = а0Р0(х) + а\Р\(х) + ...+ а'$Р;(х) + е,
где Р'(х) = CjPj(x), при у = 1, 2, ..., s (с7 — заданные константы), то сразу видно, что а' = а /с., и, следовательно, Еа'Ру(х) = Еа Р (х). Таким образом, остатки в обоих случаях одни и те же.
Пример 8.2.15. Ортогональные полиномы в обычной линейной регрессии. Раньше уже обсуждалась [см. пример 8.2.5] линейная регрессия для одной переменной (5=1) с использованием модели
У/ = 0о + 01Х(- + е(-, / = 1, 2, ..., п.
Эта модель неортогональна. В примере 8.2.5 для нее приведены А А, (А А)-1, 0о, 01- А вот альтернативная модель, которая оказывается ортогональной:
У, = 00 + 0i(x( —х) + ez, i = 1, 2, ..., п.
Здесь переменная х измеряется относительно среднего х наблюдаемых значений хь х2, ...»хл, а 0О удовлетворяет соотношению 0о = 0Ь — 01Х . Для такой новой модели имеем
/ п Е(х. — х) \ / п 0 \
А'А - / । = ( 1
\ Е(х( —х) Е(х, —х)2 / Е(х, —х)2 / ’
- ( Ъу‘ )
А'У - \ Е>((х ,-х) / ’
откуда 0Q = у, 0] = Еу((х( — x)/E(xz;j-х)2. Следовательно, 01 в обеих моделях одинаково, а 0О = 0Ь — Р\Х. Кроме того,
398
var/3'о = a2/n, var3i = a2/'L(xi— x)2
и 3 b, 3i некоррелированы (тогда как Зо, наоборот, коррели-рованы).
Для множественной линейной регрессии мы можем прибегнуть к тому же методу получения частичной ортогональности, переписывая модель
Л = Зо + + 02xi2 + ...+ 0,xis + е(
в альтернативной, «скорректированной на среднее» форме:
yt = 3b + 3i(^, — х i) + 02(xi2 — x,2) + ...+ 3$(хй — х.5) + e,-,
где x.j обозначает усреднение наблюдений xiy-, x2J, ..., xnj no Xj. В s
этом случае З'о удовлетворяет условию Зо = З'о — рЗу*у- Для второй модели первая строка матрицы АА такова:
[д, Е(х- — х.,), ..., Е(х,5 — xj],
т. е. (/?, 0, 0, ..., 0), отсюда следует, что первая строка матрицы (А'А)-1 будет: (л"1, 0, 0, ..., 0). Значит, МНК-оценка для З'о как раз и получается по формуле у = Еу,/и. Кроме того, каждая из МНК-оценок для 31, Зг, •••, 3$ не коррелирует с оценкой для З'о-
Возвращаясь к модели с ортогональными полиномами (8.2.6), отметим, что оказывается, когда значения х расположены произвольно, не на равных расстояниях друг от друга, ортогональные полиномы приходится строить специально для каждого конкретного набора данных, что в значительной степени снижает преимущество ортогональных моделей, обусловленное легкостью решения системы нормальных уравнений. Если же, однако, значения х расположены равномерно, на равных расстояниях друг от друга (как говорят, с равным шагом), да еще все различны, то мы можем воспользоваться стандартными полиномами, для которых существуют таблицы.
Возьмем стандартизованную переменную и = (х — х )/А, где х = = LXj/n, a h = х;+1 — х(, i = 1, 2, ..., п—1. Тогда значения и будет соответствовать значениям хн х2, ...» хп, а именно uIt и2, ..., ип (с очевидными перестановками):
0, ±1, ±3, ..., ±(п—1)/2, если п нечетно;
±(1/2), ±(3/2), ..., ±(л—1)/2, если п четно,
т. е. Uj — i — (л+1)/2, i = 1, 2, ..., п. Тогда фактически оцениваемая модель примет вид
У ~ То + TiQi(M) + ••• + TSQ/M) + е,
399
где Qt — ортогональные полиномы, выбранные из таблиц и вычисленные с тем расчетом, чтобы соответствовать каждому целому значению «1, и2, ..., ип. В Biometrika Tables [см. Pearson and Hartley (1966), табл. 47 — G], приводятся формулы для Q (м) при j = 1, 2,
J п
..., 6 и 3 п 52, а также численные значения Qy(wz) и SQ](wz)*. Проиллюстрируем этот метод на конкретном примере.
Пример 8.2.16. Подбор кубической кривой с помощью ортогональных полиномов. Были собраны следующие данные об осадках по месяцам:
Месяц Январь Февраль Март Апрель Май Июнь
Осадки 2,52 2,68 2,92 2,85 3,26 3,44
Месяц Июль Август Сентябрь Октябрь Ноябрь Декабрь
Осадки 3,01 2,51 2,54 2,17 2,07 2,35
Мы закодируем месяцы 1, 2, ..., 12 и возьмем эти значения в качестве х-ов. А данные об осадках будут служить соответствующими значениями У-ов. Будем подбирать по данным различные полиномиальные модели и для переменной и = х—(13/2) составим следующую таблицу:
и п — 2 9 — 2 7 “ 2 5 2 3 ~ 2 1 — 2 1 2 3 5 2 2 7 2 9 2 11 2
Осадки, у 2,52 2,68 2,92 2,85 3,26 3,44 3,01 2,51 2,54 2,17 2,07 2,35
е,(м) —11 —9 —7 —5 —3 —1 1 3 5 7 9 11
55 25 1 —17 -29 —35 -35 —29 —17 1 25 55
2з(м) —33 3 21 25 19 7 —7 —19 —25 —21 —3 33
Ее три последние строки получены из упомянутых выше таблиц, откуда мы еще и узнали, что
SQi(«i) = 572, EQ22(w,) = 12,012 и EQ^u,) = 5148.
Начнем с подбора модели
У - То + TiQi(M) + ed)-
* Таблицы ортогональных полиномов см., например, в работе: Большее Л.Н., Смирнов Н.В. Таблицы математической статистики. — 3-е изд. — М.: Наука, 1983. — С. 100—102, 376—385. — Примеч. пер.
400
По нашим данным подсчитаем
Е/,. = 32,32 и Ел01(«/) = -16,84.
Вот МНК-оценки для у0 и 71:
То = У — 2,693333,
Ii = ^ytQ^/^Q\(u^ = -0,029441.
Из таблиц для л =12 находим, что Qi(u) = 2и, откуда подобранный полином имеет вид
у = 2,6933 — 0,0589м.
Подставляя и = х— (13/2), получим
у = 3,0761 — 0,0589%.
Это тот же результат, какой мы получили бы, применив метод наименьших квадратов к неортогональной модели
у = fa + fax + е(1).
Теперь подберем квадратичную модель
У = То + TiQi(«) + 7262(1/) + е(2).
Оценки 7о и 71 не изменятся, поэтому остается только вычислить 72 с учетом того, что Ъуфг^и^ = —93,02:
Тг = ^/G2(«/)/SQ22(m/) = -0,007744.
Из таблиц (л = 12) имеем Q2(w) = Зм2 — (143/4), поэтому подобранный полином таков:
у = 2,6933 — 0,0589м — 0,0077(Зм2 — 35,75), или
у = 2,3714 + 0,2431% — 0,0232%2.
Это тот же результат, который мы получили бы, применив метод наименьших квадратов к обычной квадратичной модели
у = 0О + fax + fax2 + е(2).
Заметим, что в противоположность ортогональной модели здесь оценки 0о и 0] иные, чем в модели первого порядка.
Для кубической модели
У = То + TiQi(w) + 7262(1/) + 7з6з(м) + е(3)
нам остается только с учетом того, что Е//2з(м,-) равно 36,98, найти
Тз = Елвз^/Ебз^/) = 0,007183.
401
Таблицы показывают, что Qi(u) = (2/3) (и3 — 21,25м), поэтому кубическая модель будет следующей:
j=2,6933—0,0589м — 0,0077(3 и2—35,75)+0,0048 (м3—21,25м), или
у = 1,7177 + 0,2348* — 0,1166х2 + 0,0048*3,
и это снова тот же результат, что дает применение метода наименьших квадратов к модели
У = 0о + 01* + 02*2 + 0з*3 + е(3).
Вопрос о том, какая из этих моделей лучше соответствует данным, мы обсудим позже, в разделе 8.3.5. Этот метод предполагает последовательный подбор нескольких моделей повышающихся степеней. В таких случаях использование ортогональных полиномов имеет, в частности, то преимущество, что при переходе к каждой следующей степени требуется совсем немного дополнительных вычислений, в то время как для неортогональных моделей приходится на каждом этапе обращать матрицу (что, конечно, не проблема, когда вычисления проводятся на компьютере).
8.2.6. МОДИФИКАЦИИ ДЛЯ НЕРАВНОТОЧНЫХ НАБЛЮДЕНИЙ; ВЗВЕШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Мы по-прежнему предполагаем, что наблюдения yt.........уп равнонадежны, т. е. что случайные ошибки €i.................имеют равные дис-
персии. Но это не общий случай: матрица £>(<) может быть диагональной, но иметь на диагонали неодинаковые элементы а]......ст2.
Допустим, что эти дисперсии известны нам с точностью до постоянного множителя а2, который не известен, т. е. ст2 = v(ct2, где v,, i = 1, ..., п, известны. Имеем
У, + (j, /=1,2......п.
Меняя масштаб с помощью преобразования Z( = У(у71/2, получим новую модель:
Zz = ^bijej + 6,., i = 1, 2.п,
где by - ajjV~i/2, Теперь при i = 1, ..., п из
Е(е) = 0
следует
402
Е(6) = О,
а из
var cz = v(a2 следует
6- = а2.
Понятно, что если не коррелируют, то это верно и для 6Г Значит, к такой новой модели можно применять методы, которые мы уже обсуждали. Оценки метода наименьших квадратов для 02, •••> находятся из минимизации выражения
"Г п 12
S(u) = E[z, -2ЬЛ]2.
где Zj — эмпирические значения Z(. А для исходной модели имеем (подставляя zt = Z,v,’1/2»
п г п 1 -у
S(U) = Evt’^-E^uJ2.
Выходит, что вместо того, чтобы минимизировать сумму квадратов ошибок оценок, как мы делали раньше [см. раздел 8.2.2], теперь мы «взвешиваем» каждый член этой суммы, умножая его на величину, обратную дисперсии соответствующей случайной величины. Это придает больший вес тем наблюдениям, ошибки которых оказываются меньше, что интуитивно кажется вполне разумным. Такая процедура называется взвешенным методом наименьших квадратов.
Выраженная в матричных терминах новая модель имеет вид Z = В0 + 6 с матрицей плана В = W-1 А, где W = diag(V]l/2, v2l/2, ..., vj/2) и Z = (Z|, Z2, .... Zn)' получается из Z = W-1Y.
МНК-оценка для & следующая:
Q = (В ВГ'В z,
где z — конкретные значения Z.
Подставляя вместо В значение W~'A и замечая, что W — симметричная матрица, находим
е =
Но WW = diag(vj, v2, .... vn). Обозначая это через V, получим
& = (A'V’AF'A'V-’y, (8.2.7)
а это и есть то значение U, которое минимизирует сумму квадратов S(u) = (у — Au) V-1(y — Au).
Дисперсионная матрица вектора 0 равна:
D(0) = ct2(BzB)-1 = ст2 (AV”1 АГ1.
403
Пример 8.2.17. Повторные наблюдения. Пусть Yt — среднее из т, наблюдений, причем все они имеют одно и то же математическое ' р
ожидание Ед.Д. и общую дисперсию ст2, i = 1, 2.... п. Если все
наблюдения независимы, то У, имеет дисперсию ст2//и( и на основе полученных ранее результатов V = diagf/wi1, т2х.тп ’).
Пример 8.2.18. Линейный закон — прямая, проходящая через начало координат. Рассмотрим модель регрессии
£(У/) = 0х/, /=1, 2, .... п.
Здесь А = (Хь х2, ..., х„)'. Используя (8.2.7), найдем
а дисперсия 0 равна ct2/S(x]/v().
Положим для примера, что Y — доля потерь тепла в стандартном коттедже (одноквартирном с тремя ванными и общей стеной с соседним коттеджем), а х представляет собой разность между внутренней и наружной температурой. В таком случае дисперсия Y будет, скорее всего, возрастать с ростом х. Простейший вид такой зависимости — это Vj = cXj, т. е. дисперсия У( пропорциональна разности температур. Значит, мы найдем, что
д = = L
LXj X и
0 = ca2/Y,x( = cCT2/(nx”).
Наоборот, если стандартное отклонение У( пропорционально х(, т. е. Vj = сх], то
~ 1 п У; ~
0 = —Е — и var0 = ест2/п.
П,= \ Xj
8.2.7. МОДИФИКАЦИИ ДЛЯ НЕ НЕЗАВИСИМЫХ НАБЛЮДЕНИЙ
Метод, использованный в разделе 8.2.6, — это частный случай более общего подхода, который приводит нас к рассмотрению наблюдений, имеющих не только различную точность, но и не независимых. Теперь дисперсионная матрица ошибок, которая предполагается известной с точностью до постоянного множителя, т. е. относительно которой предполагается, что D(e) = ct2V, где V — известная, положительно определенная* симметричная матрица, но уже не обязательно диагонального вида.
* См.: Мишина А.П., Проскуряков И.В. Высшая алгебра. — С. 44. — Примеч. пер.
404
Для такой матрицы V можно показать, что существует (не обязательно единственная) невырожденная симметричная матрица W, такая, что W W = V. Ее можно получить, например, факторизацией по Холецкому*. Исходная модель имеет вид
Y = А0 + €, где £(«) = 0, D(e) = ct2V.
Умножая обе части на W~', получим новую модель:
Z = В0 + 8,
где Z = W-‘Y, В = W-'A, 8 = We.
Тецерь и
Е(8) = W-'£(e) = О
D($) = W-’DCeXW-') =
= o2W 'VW 1 (поскольку W симметрична) =
= ct2W-1WWW_| = ст21„.
Это новая модель в стандартной форме, и 0 = (В'В)"1 B'z доставляет минимум выражению S(u) = (z — Bu) (Z — Ви). Или в терминах исходной модели
S(u) = (у — Au)V'(y — Au).
Хотя W теперь недиагональна, она все еще симметрична, так что алгебра из раздела 8.2.6 остается в силе, поэтому
0 = (AV-1 Ар1 AVy,
D(G) = ct2(A'V-' А)"1.
Остаточная сумма квадратов равна:
г = S(S) = (у - A?) V“'(y - А?),
а дисперсия ошибки оценивается выражением ст2 = г/(л — р).
Пример 8.2.19. Анализ порядковых статистик методом наименьших квадратов. Положим, что yit у2, у„ — некоторая выборка независимых наблюдений из распределения, зависящего только от двух параметров ц и ст, о которых мы предполагаем, что это математическое ожидание и стандартное отклонение (можно, конечно, использовать и более общие, чем /х и ст, произвольные меры центральной тенденции и разброса). Мы будем оценивать /г и ст из упорядоченной выборки у(1), у(2),..., У(П), где у(1) < у(2} <...<у(п) [см. раздел 14.3].
* Обзор методов такого рода читатель найдет в работе: И к р а м о в Х.Д. Численные методы линейной алгебры. — М.: Знание, 1987. — 48 с. Еще см., например: Мэйндоналд Дж. Вычислительные алгоритмы в прикладной статистике /Пер. с англ. — М.: Финансы и статистика, 1988. — Примеч. пер.
405
Положим Sj = (уj — ц)/a, у=1, 2.....п. Это наблюдения из стан-
дартизованного распределения, которые не зависят ни от каких параметров. Упорядочивая их по возрастанию $(1), 5(2)..5(л) (так, чтобы
= (у^— ц)/а), мы получаем новые случайные величины:
= тр var(S0)) = Vjj, cov(S0)S(jt)) = vjk.
Эти величины можно находить непосредственно, поскольку их значения зависят от формы исходного распределения, но не зависят от его параметров. Для исходных случайных величин У(1), У(2), ..., У(л) имеем
Е(У0)) = д + omj, уаг(У0)) = a2vjJy соу(У0), У(Л)) = <j2vjk, следовательно, теперь мы можем воспользоваться нашими старыми результатами при
9 =
8.3. ДИСПЕРСИОННЫЙ АНАЛИЗ И ПРОВЕРКА ГИПОТЕЗ ДЛЯ ПЛАНОВ ПОЛНОГО РАНГА
8.3.1. НОРМАЛЬНАЯ ТЕОРИЯ
Приведенные выше методы и результаты не зависят от формы распределения ошибок. Однако в большинстве приложений важно не только получить оценки параметров и их стандартных ошибок, но нужно построить еще доверительные области [см. раздел 4.9] и найти методы для проверки гипотез [см. гл. 2], которые представляют интерес.
Имея в виду эти цели, мы теперь предположим, что ошибки имеют нормальное распределение, т. е. ~ N(0, а) при / = 1, 2, ..., п. Теперь из предположения, что е, и некоррелированы, следует их независимость*. При этом вектор ошибок е становится многомерным нормальным** MVN(0, ст21п). А с точки зрения самих наблюдений
У( независимо от Уу, i # j,
* См.: Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. Основные понятия, предельные теоремы, случайные процессы. — М.: Наука, 1967. — С. 48, а также Справочник по теории вероятностей и математической статистике /Под ред. В.С. Королюка. — Киев: Наукова думка, 1978. — С. 32—33. — Примеч. пер.
•* См.: Мэйндоналд Дж. Вычислительные алгоритмы в прикладной статистике. — С. 128—130. — Примеч. пер.
406
и Р
Yi - N(Sa/y, a), i = 1, п.
Вектор наблюдений Y — многомерный нормальный MVN(A0, ст21л). Отсюда следует, что оценка метода наименьших квадратов 0 = = (AZA)~*A'Y тоже имеет многомерное нормальное распределение с математическим ожиданием 0 и дисперсионной матрицей (AA)~‘AD (Y)A(A'A)-1 = (АА)-1 ст2. Остаточная сумма квадратов равна: р
i = (У - А? ) (у - лё) =
= У У — А у — у А0 + 0 A A0 .
А так как 0 = (AA)~‘A'Y, то все это сводится к YCY, где
С = I — А(АА) ‘А = С = С2.
Поскольку С = С2, из теоремы 2.5.1 следует, что R/а2 имеет распределение хи-квадрат с числом степеней свободы п — р. И линейная комбинация ХО тоже распределена нормально с математическим ожиданием Х0 и дисперсией Х(А'А)_|Хст2.
8.3.2. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
Доверительный интервал для отдельного параметра, скажем Oj, можно получить обычным способом, используя распределение Стьюдента [см. пример 4.5.3]. Воспользуемся следующим свойством:
(ёу — р)]|/2
имеет распределение Стьюдента с п—р степенями свободы [см. раздел 2.5.5], где (АА)'1 = [Л-0]- Отсюда центральный 100(1—а)%-ный доверительный интервал для Oj есть
(ё, ±
где !„-Р ~ t„_pU — (1/2)а) — верхняя 100(1 — (1/2)а)%-ная точка распределения Стьюдента с п—р степенями свободы. Для ортогонального плана получится как раз
где Ajj есть у-й диагональный элемент матрицы А'А. Аналогично центральный 100(1 — а)%-ный доверительный интервал для Х0 получается из выражения
(х-ё ±
407
Когда же два или несколько параметров рассматриваются вместе, мы должны помнить, что нельзя «перемножать» индивидуальные доверительные интервалы для построения доверительного «ящика», поскольку они не независимы (даже если независимы 0у), из-за того, что каждый использует одни и те же остатки [ср. с разделом 4.9]. Приемлемый доверительный интервал для нескольких параметров 0., 0у-2,..., 0у , (Q С Р) можно построить следующим^ образом. Пусть ф = ,
0у’..6j У. МНК-оценка для ф есть ф = (0у,..., 0 .)'. Дисперсионная
матрица’вектора Ф, которую мы обозначим a2Q, находится после вычеркивания из матрицы а2 (А А)-1 всех строк и столбцов, не включенных в ф, т. е. мы сохраняем строки (столбцы) .Л, У2..Jq- Тогда
можно показать, что
(Ф - ФУСГЧФ - 4)/[qR/(n - р)]
имеет распределение Fq>n_p [см. раздел 2.5.6]. Отсюда [ср. с разделом 4.9.2] 100(1 — а)%-ный доверительный интервал для ф равен:
[«:(?- ♦)'СГ‘(? - - «)],
где F9ZI_p(l — а)-верхняя 100(1 — а)%-ная точка jF-распределения.
В общем такое множество точек определяет (/-мерный эллипсдид с центром в ф . А для ортогонального плана это будет ^-мерная сфера.
Пример 8.3.1. Доверительный интервал для констант силы тяжести из примера 8.2.2. Для этого примера мы нашли:
gi = 981,2681 со стандартной ошибкой Ъ = 0,0011,
g5 = 981,1241 со стандартной ошибкой а = 0,0017,
g = 981,2091 со стандартной ошибкой 0,0010.
Поскольку в этом примере и=9, р=5, то, предполагая нормальное распределение ошибок, мы должны находить 95%-ный доверительный интервал для соответствующих параметров с использованием ?4(0,975) = 2,776. Получим:
g, : (981,2681 ± 0,0031) = (981,2650, 981,2712),
g5 : (981,1241 ± 0,0047) = (981,1194, 981,1288),
g : (981,2091 ± 0,0028) = (981,2063, 981,2119).
Соблазнительно воспользоваться прямоугольником, определяемым следующим образом:
[(g>, g5) : 981,2650 g, 981,2712, 981,1194 g5 981,1288]
как доверительным множеством для (gH g5). Однако такой подход состоятелен только для независимых индивидуальных интервалов
408
(когда доверительный коэффициент для них равен (0,95)2). Если же это не так, то мы должны действовать иначе [ср. с разделом 4.9.2]. Поскольку дисперсионная матрица вектора Ф = (GH G5) равна:
/ 0,4211 0,2632
а2 (
\ 0,2632 1,2895
100(1 — а)%-ный доверительный интервал для (gb g5) получается из
{(gi > g5):(g>— gi, gs—g5)
0,4211
0,2632
0,2632 \-i / g,—g,
1,2895 / \g5 —g5
€ 2a^Fz 4(1—a)} .
Он задает некоторую эллипсоидальную область в плоскости g5 с центром в точке (gi,~gs) = (981,2681, 981,1241), размер которой зависит от величины а (большие эллипсы соответствуют малым значениям а).
Пример 8.3.2. Доверительный интервал для регрессии. В предположении, что подобранная в примере 8.2.16 модель в виде полинома второго порядка корректна, можно построить доверительный интервал для истинных средних осадков в каком-нибудь месяце, скажем, в августе. Исходное уравнение таково:
У = 7о + 7iQi(u) + 7г6г(м) + е(2).
Теперь, поскольку августу соответствует и = (3/2), ожидаемые осадки в этом месяце равны:
Ms = 7о + 7iQi(3/2) + 7202(3/2).
МНК-оценка для щ равна: д8 = 70 + 7iQi(3/2) 4- 72<2г(3/2).
Вычислив это выражение, получим /Г8 = 2,83.
Далее, вследствие ортогональности МНК-оценки для у0, 7ь 7г некоррелированны, поэтому дисперсия МНК-оценки /х8 получается равной
аф/л + Q](3/2)/SQ2(w() + Q2(3/2)/EQ2(«,)] ,
что равно 0,1691a2. А так как в данном случае п = 12 и р = 3, то 95%-ным доверительным интервалом для будет
М8 ± Г9(0,975) (0,1691)|/2 а,
где а = г/(п — р), а г — фактическое значение ОСК для квадратичной модели. Для отыскания г воспользуемся соотношением
Г = — 7oSj, — 71^7,61(м() — 72^7,Q2(m,),
которое дает г - 0,706, откуда а2 = г/9 = 0,078. Тогда вычисленный интервал для /г8 есть (2,83 ± 0,26), т. е. (2,57, 3,09).
409
8.3 3. ПРОВЕРКА ГИПОТЕЗ
В дополнение к оцении.шию параметров модели E(Y) - АО и вычислению стандартных ошибок или доверительных интервалов мы ча сто хотим еще проверять различные гипотезы [см. гл. 5] относительно этих параметров. Типичная гипотеза Н налагает ограничения на вектор параметров 0, т. е. заранее фиксирует значения одного или нескольких компонентов 0, или, в более общей форме, задает значения одной или нескольких линейных комбинаций этих компонентов. Если теперь скажется, что Q не вполне соответствует условиям Н, то нам придется снова применить метод наименьших квадратов для оценки 0, но уже при ограничениях, налагаемых гипотезой Н. Это требует минимизации S(u) = (у — Аи)'(у — Аи) при условии Н, что приведет к МНК-оценке0*, которая будет удовлетворять Н, но, вообще говоря, не будет совпадать с 0.
Точно так же, как и в случае без ограничений, минимизируемая сумма квадратов, а именно 5(0*), служит мерой того, насколько хорошо модель (в данном случае модель с учетом Н) соответствует имеющимся данным, когда 0 оценивается с помощью 0*, a S(0*) — это остаточная сумма квадратов для нашей ограниченной модели (мы будем обозначать ее через гн). Очевидно, что ограниченный минимум S(0*) будет удовлетворять условию 5(0*) > 5(0), или, иными словами, гн г. Разность гн — г служит мерой способности к дополнительной подгонке модели, когда параметры не связаны ограничениями гипотезы Н. Если эта разность мала, т. е. если модель с ограничениями выглядит на фоне вариабильности данных почти так же хорошо, как и модель без ограничений, то гипотезу Н стоит воспринимать как разумную. Напротив, большая разница указывает, что если гипотезой Н пренебречь, то модель будет гораздо лучше соответствовать экспериментальным данным. Это должно привести к дискредитации гипотезы Н. Конечно, нужен критерий для определения, что значит «малая» или «большая» разница. Обычно он строится на сравнении (после выполнения стандартных преобразований) разности гн — г с г. Такие критерии можно построить в предположении нормальности ошибок. Как отмечалось ранее, в этом случае оценка метода наименьших квадратов есть фактическая оценка метода максимума правдоподобия, поэтому и критерии можно описать как критерии максимума правдоподобия [см. раздел 5.5]. В следующих разделах этот подход будет проиллюстрирован подробными примерами.
8.3.4. ОСНОВНЫЕ ТОЖДЕСТВА
Для исходной модели (без ограничений) есть следующее важное тождество относительно переменной и:
(у—Аи) (у—Аи) = (0—и) А А(0— и) + (у—A0) (y—А0), (8.3.1)
410
или, что короче,
5(u) = (6 — u)'A'A(fl — u) + S(0). (8.3.2)
Это можно показать, записав у—Au в виде (у — АС) 4- А(0 — и), откуда и следует (8.3.1), если заметить, что (Y — А0)А(0 — и) = О, поскольку в нормальных уравнениях Ау — А АО = 0.
Так как S(0) = г, подставляя в (8.3.2) частное значение и = 0, получим уравнение
S(0) = (0 — 0) А А(0 — 0) + г. (8.3.3)
Вспомнив, что S(0) = ее, мы можем записать соответствующее уравнение в терминах вторичных случайных величин:
€<Е = (б — 0) АА(б — 0) 4- R. (8.3.4)
При выполнении предпосылок из раздела 8.3.1 величина представляет собой сумму квадратов п независимых нормально распределенных случайных величин, каждая из которых имеет нулевое среднее и дисперсию а_2, значит ее распределена как а2х2„ [см. раздел 2.5.4, а)]. Поскольку О имеет распределение MVN(0, а2(АА)-1), распределение первого слагаемого в правой части (8.3.4) можно найти с помощью стандартной теоремы*. Это распределение имеет вид а2Хр- Более того, можно показать, что оба слагаемых в правой части этого выражения независимы. Как следует из теоремы 2.5.4, R — случайная величина с распределением а2х*_р. Следовательно, при наших жестких предположениях можно легко получить, что E(R) = (п—р)а2, как и было установлено в разделе 8.2.4.
Из приведенного выше уравнения (8.3.3) не удается вычислить значение г, поскольку оно содержит сумму квадратов относительно неизвестного ожидаемого значения. Однако, подставив в уравнение (8.3.2) и = 0, получим
5(0) = 0 А АО 4- S(0).
Учитывая, что 5(0) = у'у, можно переписать это выражение так:
у у = 0 А АО 4- г. (8.3.5)
Полученное соотношение известно как тождество дисперсионного анализа (ANOVA) [ср. с разделом 5.8.7]. Оно показывает, что общую сумму квадратов у'у = Ly2 можно разделить на две части: 0 А'А0 — сумму квадратов, обусловленную моделью, которая подогнана к
* См.: Ш е ф ф е Г. Дисперсионный анализ /Пер. с англ. — М.: Физматгиз, 1963. — С. 45. — Примеч. пер.
411
данным (СКМ), иг — остаточную сумму квадратов (ОСК), представляющую собой ту остаточную вариацию в данных, которая еще сохраняется после того, как модель подогнана к данным, т. е.
Общая СК = СКМ + ОСК.
Для проверки различных гипотез в последующих разделах мы будем пользоваться множеством других тождеств дисперсионного анализа при разбиении СКМ на компоненты, связанные с различными источниками вариации.
В выражении (8.3.5) нет неизвестных, и мы можем вычислить по нему г следующим образом:
Г=уу — 0AA0, (8.3.6)
что позволяет избежать возведения в квадрат и сложения отдельных остатков. Из системы нормальных уравнений видно, что, поскольку A y = А'А0, СКМ можно еще записать в виде 0 А'у, т. е. как произведение 0 на правую часть системы нормальных уравнений. Следовательно, г получается и из
Г = у у — 0 Ау. (8.3.7)
Эта формула использовалась раньше для вычисления г в примерах 8.2.11 и 8.2.14.
Выше мы отмечали, что общая сумма квадратов у7у равна 5(0), что представляет собой остаточную сумму квадратов при Н: 0 = 0, т. е. это сумма остатков, полученных при условии, что ни один параметр не подбирался по имеющимся данным. Тогда СКМ = 0 'А'А0 = = 5(0) — 5(0) — та величина, на которую уменьшаются остатки в результате построения модели E(Y) = А0. Чтобы подчеркнуть это, мы будем обозначать СКМ как г(0) и рассматривать эту величину как уменьшение общей суммы квадратов, обусловленное подбором 0.
Пусть теперь снова 0* обозначает МНК-оценку 0 при условии, что верна гипотеза Н. Подставив и = 0* в основное тождество (8.3.2), получим
5(0*) = (0 — 0*)'А'А(0 — 0*) + г.
Так как 5(0*) = (у — А0*) (у — А0*) = гн— остаточная сумма квадратов для модели, ограниченной согласно гипотезе Н, дополнительная подгонка (т. е. дополнительное уменьшение гн — г в общей сумме квадратов), когда подбирается модель без ограничений, получается из выражения
гн — г = (0 — 0*) А А(0 — 0*). (8.3.8)
412
С другой стороны, мы можем думать об этом увеличении в остатках как об отсутствии подгонки (т. е. соответствия между данными и моделью), когда на 0 наложены ограничения Н. Эту разность часто называют суммой квадратов, обусловленной гипотезой. Хотя (8.3.8) может пригодиться при поиске дополнительного уменьшения в некоторых простейших случаях, приведенных ниже, общий подход заключается в вычислении обоих остатков и вычитании.
8.3.5. ПРОВЕРКИ ГИПОТЕЗ В ОРТОГОНАЛЬНЫХ ПЛАНАХ
Рассмотрим ортогональную модель, в которой АА диагональна diag(Aи,...,Арр), с МНК-оценкой 0, j-я компонента которой получается из 0j = j = 1, ..., р. Такая диагональная структура
матрицы АА позволяет выразить сумму квадратов, обусловленную подбором модели, в явной форме:
р
СКМ = 0 А А0 = ЕЛ/?, (8.3.9)
а (8.3.6) превращается в р
г-Ъу'-ЪА^. (8.3.10)
Наиболее простая из представляющих интерес гипотез заключается в том, что некоторый параметр нашей модели, скажем 0t, равен нулю, т. е. он не нужен в модели, описывающей имеющиеся данные. Такая гипотеза в зависимости от контекста может интерпретироваться по-разному. Это, например, может означать а) отсутствие эффекта в односторонней классификации, в которой группы различаются получаемой обработкой, или б) что член степени t не нужен в полиномиальной регрессионной модели.
Для ортогональных моделей тот факт, что каждое из р нормальных уравнений содержит только один параметр, чрезвычайно упрощает многократное повторное вычисление оценок 0 при Н: 0t = 0. Мы просто пренебрегаем Z-м уравнением, поскольку оно уже не нужно, а все остальные оставляем без перемен. Следовательно, МНК-оценки всех компонентов вектора 0, кроме 0t, остаются неизменными независимо от того, истинна ли гипотеза Н, а значит, 0 и 0* отличаются только /-м компонентом, который согласно гипотезе равен нулю в 0*. Отсюда дополнительное уменьшение, обусловленное включением в модель 0t, равно согласно (8.3.8) rH— г = Att0 2Г Мы будем обозначать эту величину r(0t), или короче г,. Как упоминалось в разделе 8.3.3, проверка этой гипотезы сводится к сравнению rt с подходящим стандартом. Точный метод должен соответствовать предположениям, что
1) rt — реализация случайной величины Rt = AttQ2t',
413
2) 01 — нормально распределенная случайная величина с параметрами (0t, так что если Н верна = 0), то Rt — случайная
величина, распределенная как а2х2} с математическим ожиданием а2;
3) г — реализация R, представляющая собой случайную величину с распределением и математическим ожиданием (п — р)а2
[см. раздел 2.5.4].
Таким образом, мы сравниваем реализации (эмпирические значения) Rt и R/(n — р), поскольку обе эти величины имеют одно и то же математическое ожидание а2, когда гипотеза Н верна. Кроме того, можно показать, что Rt и R независимы, так что F = (п — p)Rt/R имеет F-распределение [см. раздел 2.5.6] со степенями свободы 1 и (л — р), когда гипотеза Н верна. Соответствующую критическую область можно отыскать, обнаружив, что когда Н ложна, E(Rt) > о2. Это свойство позволяет записать Rt так:
r,=a„(§, - «,+в,г=л„(ё,-е,)г+2л„(в,-е,)в,+л„^,
откуда E(R,) = а2 + Аг1в2.
Итак, хотя при ложной гипотезе Н малые значения F возможны, мы не должны рассматривать события, связанные с их появлением, как аргумент против Н. Просто доверительная область задается в виде / с, где с — константа, a f ~ (п — p)rt/г. Следовательно, критерий размера а отвергает гипотезу, что 0f=O, если f Fj>и_р(1—а). Заметим, что //2 = Ot/(aA((|/2), где а2 = г/(п-~р) [см. раздел 5.8.2], и мы видим, что это эквивалентно /-критерию, который отвергает гипотезу, что 0, = О, когда | 0, | >~5 Аа‘/21п_р(1— у а) .
Для проверки, не равны ли нулю одновременно несколько компонентов вектора 0, можно использовать простой подход. Пусть ф обозначает некоторое подмножество из (0j,..., 0р), включающее т членов, и пусть Н состоит в том, что ф = 0. Для оценки 0 при условии Н заметим, что нормальные уравнения модели с ограничениями в точности те же, что и для полной модели, и отличаются только тем, что исключены те т уравнений, что соответствуют параметрам из ф. Следовательно, 0 и 0* различаются только в тех компонентах, которые соответствуют параметрам из ф, причем в 0* на этих местах стоят нули. Отсюда, используя (8.3.8), найдем, что дополнительная подгонка, когда 0 не ограничена условием Н, есть
гн-г=ЬА/2, (8.3.11)
ф
414
где Е* обозначает суммирование по значениям, соответствующим параметрам из ф. Мы обозначим дополнительное уменьшение остаточной суммы, когда параметры ф включены в модель, через г(Ф). Отметим, что
г(Ф) = Е г„ (8.3.12)
в частности, р
СКМ = г(0) = Ег,.. (8.3.13)
Это важная формула. Она показывает, как можно разложить на р компонентов уменьшение общей суммы квадратов, обусловленное построением модели £(¥) = А0, причем так, чтобы j-й компонент соответствовал вкладу 0j в это уменьшение. Отметим, что вклад в г(ф) любого параметра, входящего в ф, всегда одинаков независимо от того, какие еще параметры входят в ф. Мы еще увидим, что это свойство оказывается несправедливым для неортогональных планов.
Поскольку г(ф) — это реализация Я(ф) = Е А^О], то если гипотеза Н верна, Я{ф) будет суммой квадратов т независимых нормально распределенных случайных величин, каждая из которых имеет среднее нуль и дисперсию а2. Поэтому Л(ф) имеет распределение а2х2т при верной Н. Следовательно, мы сравниваем г(ф)/ т с г/ (п — р), т. е. если Н верна, то критерий снова приводит к сравнению двух оценок дисперсии а2. Действительно, Я(ф) независимо от R, так что F = (л — р)К(ф)/mR распределено как Fmtv_p, когда гипотеза Н верна. Математическое ожидание Rty) возрастает, если гипотеза Н ложна, и критерий размера а отвергает 0 = 0, если f Fin n_p(l — а), где f = (п— р)г(ф)/тг.
Принято обобщать такие процедуры в таблицах дисперсионного анализа (ANOVA). Элементарный дисперсионный анализ Y Y = СКМ + г представляется в следующей форме:
Источник Сумма квадратов, SS Число степеней свободы, DF Средний квадрат, MS
Обусловленный моделью Остаток СКМ=0 А А0 = р ~ = > г=/у—СКМ Р п—р г/(п — р) = а2
Общий у у п
415
Можно сделать эту таблицу более наглядной и удобной для проверки гипотез при разбиении СКМ:
Источник SS DF MS f
Обусловленный rt=Aite । 1 - ft = rt/a2
Обусловленный в2 • Г2=А22в 2 1 <2 /2 = ггГо2
• • • • •
• • • • •
• • • • •
Обусловленный вр rp=Ap^р 1 ГР fp-rp/'o2
Остаток р ~,=/‘ п—р ~о2 = г/(п—р)
Общий У У п
В этой таблице «Обусловленный 0у» означает вклад А-6 2 коэффициента 0у- в СКМ. Это как раз та величина, на которую возросло бы г, если бы 6j было исключено из модели. Таким образом, проверяя Н: 01=0, мы получаем гн — г = гх и сравниваем fx с F^ . А для проверки Н: вх = 02=0, получаем гн— г = гх + гг и сравниваем (Г1 + + г2)/2а2 с F2n_p, и т. д.
Иногда интересно проверить, не отличается ли некоторый параметр от заданного ненулевого значения, причем это требует лишь незначительной модификации изложенного выше подхода. Пусть мы хотим проверить гипотезу Н: 0t = ct, где ct задано. Как и раньше, 6 и 6* отличаются только t-м компонентом, который теперь в 0* равен ct. Следовательно, дополнительное уменьшение в 5(0) = уу, обусловленное включением в модель свободной оценки 0, вместо 0t = ct, равно A tt(0\ — cty. Вся остальная аргументация та же, что и раньше, только с использованием этой величины вместо г,. Значит, когда Н верна, Я,=Л„(Э, — с,)2 распределено как а2х\ и проверка сводится к сравнению f = Att(6t — сууГо1 с FX n_p.
Аналогично, если надо проверить Н\ ф = с, где ф — множество из т значений 0у, а с —заданный вектор с т элементами, то возрастание остатков вычисляется так:
гя-г= Е (8.3.14)
ф
Когда гипотеза Н верна, это реализация случайной величины, распределенной как о2х2т, и мы сравниваем (г н — г)/та2 с ^„^-распределением.
416
Покажем теперь на примерах, как «работают» эти методы.
Пример 8.3.3. Односторонняя классификация: проверка гипотезы, что все средние имеют одно и то же общее значение. В таком случае с моделью
Уjj P-j i 1, 2, I, J 1, 2, Jj, связано уменьшение, обусловленное вычислением средних и равное rt-A^L]. Имеем (число наблюдений в /-й группе) и ~^i=yi
(среднее наблюдений в /-й группе), откуда Вот таблица дис-
персионного анализа:
Источник SS DF
Обусловленный g| г, = J>y\. 1
Обусловленный ц2 ri = Лт2. 1
• • •
• • •
• • •
Обусловленный gz ТЬУг1. 1
1
Остаток r=y'y = Er,- п — I
1
Общий УУ п = LJ,- 1 '
На самом деле эта таблица представляет ограниченный интерес, поскольку обычно проверка, имеет ли отдельная группа (или совокупность групп) нулевое среднее, не актуальна. Давайте вместо этого рассмотрим проверку гипотезы Но: gi =g2 = ... = gz=go, где g0 задано. В принятых нами обозначениях ф = (gb g2, • ••, g/У и с = (g0, go, ...» go), а используя (8.3.14), получим
гн0 - r
Когда гипотеза Но верна, это наблюдение из распределения а2х), и мы можем оценить свидетельства против Но непосредственно, сравнивая (п — 1Цгн —- г)/ 1Г с Fj^ ^Распределением.
Пример 8.3.4. Проверка индивидуальных коэффициентов полиномиальной регрессии, полученной с помощью ортогональных полиномов. По данным О',, х,), <=1,2, ..., п, с помощью ортогональных полиномов подобрана следующая модель:
У = а0 + aiPi(x) + а2Р2(х) +... + otsPs(x) + е.
417
МНК-оценка для ау равна:
5; =
а сумма квадратов (уменьшение), обусловленная а,, есть г(ау)=ЛЛа}=5}Е Pjfx,) = = [елрА)]!/[?^М.
что приводит к такой таблице дисперсионного анализа:
Источник SS DF MS
Обусловленный а0 Обусловленный • • • Обусловленный as Остаток г(а0) = п_Г2 ria^a^P^Xj) • • • <(а5) = а2ЕР2(х/) Г^У'у-Erfa,) 1=0 1 1 • • • 1 n—s—1 Го rt • 9 9 rs ~a2=r/(n—s—1)
Общий у/у = py2i n
Теперь, если известно (на основе опыта или из теории), что наша модель корректна, мы можем, как указано выше, проверить, не равен ли нулю любой из коэффициентов а,, сравнивая rfa^/h2 с
Пусть, например, мы хотим проверить, не окажется ли адекватным представление полиномом меньшей степени, скажем ($ — 1). Поскольку Р5(х) — единственный член в модели, содержащий Xs, такая проверка означает испытание гипотезы Н: а ее мы можем
проверить, сравнивая r(as)/a2 с Fj n_s_P Чаще, однако, экспериментатор просто хочет приблизить свои данные полиномом для аппроксимации точной зависимости, которая, увы, неизвестна. В частности, не известно, до какой степени надо наращивать аппроксимирующий полином. Конечно, всегда можно аппроксимировать данные точно, взяв полином степени (п—1). Но мы хотим добиться удовлетворительной аппроксимации полиномом низкой степени. Один из подходов к решению этой задачи заключается в том, чтобы строить последовательность полиномов возрастающих степеней и использовать соответствующий дис
418
персионный анализ и F-критерий для оценки вклада в модель того члена, который включен последним. Решение заканчивается, когда считается, что два последовательных члена полинома оказались равными нулю. Это необходимое условие, поскольку если подгонять к данным полином нечетной степени, то члены четных степеней (не считая свободного члена), скорее всего, будут вносить малый вклад, и наоборот. Проиллюстрируем этот метод на примере об осадках, который рассматривался ранее [см. пример 8.2.15]. График для этих данных показывает, что должна подойти квадратичная или, быть может, кубическая аппроксимация.
Начнем с модели первого порядка
У - 7о + 7iQi(w) +2(1)-
Получаются оценки 70 = 2,693333, 71 = —0,029441, и таблица дисперсионного анализа имеет вид:
Источник SS DF MS
Обусловленный 70 г(70)=и72=87,049 1
Обусловленный 7, r(yi)=V}£Q](Ui)=0,496 1 0,496
Остаток г\=у'у—г(у0) — ^7!)= 1,426 10 0,1426
Общий у"у = 88,971 12
Видно, что коэффициент 71 не слишком сильно снижает остатки по сравнению с моделью, которая включала бы только 70 и имела бы 1,922. Для более точной оценки сравним уменьшение, равное 0,496, с подходящим масштабом, а именно с оценкой дисперсии ошибки, равной 0,1426, что дает F-отношение, равное 3,48. Вероятность того, что случайная величина с распределением F, 10 превзойдет это значение, гораздо больше, чем 0,05(Fj 1О(О,95) = 4,96, F1>10(0,9) = 3,285), так что проверка не дает оснований для отбрасывания гипотезы 71 =0.
Если данные нанести на график, сразу ясно, что модель _у=7о + + е(0) не может дать удовлетворительного описания, откуда снова видна необходимость именно того правила остановки, которое было сформулировано ранее. Подберем теперь квадратичную модель:
У = 7о + 7121 (и) + 72Q2(m) + е(2) •
Оценки для 7о и 71 остаются теми же, что и в модели первого порядка, а 7 2 =—0,007744. Вот таблица дисперсионного анализа:
419
Источник SS DF MS
Обусловленный 70 г(7о)=87,049 1
Обусловленный 71 г(7,)=0,496 1
Обусловленный у2 <(72) = 722Ее22(«,) = 0.720 1 0,720
Остаток л2=у'у—=0,706 9 0,078
Общий уу = 88,971 12
В этом случае F-отношение равно 9,23, а поскольку Fi 9(0,975)=7,21 и Fx 9(0,99) = 10,56, налицо основания для отбрасывания гипотезы 7г=0-
Переходим к подбору кубической модели
^=7о + 7iQi(w) + VzQzCw) + 7з(?з(и) + £(зр
для которой 7з=0,007183 и таблица дисперсионного анализа такова:
Источник SS DF MS
Обусловленный 70 л(7о) = 87,049 1
Обусловленный 71 <(7i)=0,496 1
Обусловленный 72 <(72)=0,720 1
Обусловленный 73 <(7з) = 72Ее2(«,)=0,266 1 0,266
Остаток <з = У'у—Е<(7/)=0,440 8 0,055
Общий УУ = 88,971 12
На этот раз F-отношение равно 4,84. Поскольку Fx 8(0,95) = 5,32, а F, 8(0,9) = 3,46, мы приходим к заключению, что основания для отбрасывания гипотезы, что 73 =0, недостаточны.
Для модели четвертого порядка
У — 7о + Т1С1(«) + 7гСг(^) + 7з0з(м) + 7404(w) + е4
420
находим, что 74 = 0,005527 и таблица дисперсионного анализа такова:
Источник SS DF MS
Обусловленный 7о г(7о) = 87,049 1
Обусловленный 7| г(71) = 0,496 1
Обусловленный у2 г(72)=0,720 1
Обусловленный 7з л(7з)=0,266 1
Обусловленный у4 <(V4)=V24Se4(«,?=0,245 1 0,245
Остаток гл=у'у-^Г(у^0,195 7 0,028
Общий у'у = 88,971 12
F-отношение равно 8,66, а из таблиц находим F17(0,975) = 8,07 и Fx 7 (0,99) =12,25. Отбрасывать ли гипотезу, что 74=6? Прежде чем сделать это, стоит учесть следующие моменты.
а) Критерий F, скажем, для 7у=0 основан на предположении, что модель степени j верна, ошибки независимы и извлечено из N(0, а). Если же на самом деле нужна модель более высокой степени, то остатки гу в модели степени j не будут служить оценками для а2 (что предполагает критерий), поскольку они будут смещенными из-за вкладов ненулевых членов более высоких порядков. Появления вполне возможных здесь больших ошибок обычно удается избежать, если нанести на график данные и убедиться в том, что требование равенства нулю двух последовательных коэффициентов выполняется. В нашем примере уже первый критерий показал, что 71 может быть равно нулю. Однако возможны различные выводы. Так, если строить критерий с использованием остатков от последующей модели, т. е. если г2 служит подходящей оценкой для а2, то соответствующим значением F-отношения будет 6,36.
б) Относительную важность различных параметров можно оценить непосредственным сравнением их вкладов в снижение дисперсии. Выходит, что 7з и 74 имеют примерно одинаковые вклады в общую сумму квадратов, составляющие приблизительно половину от вклада 71. Отсюда следуют одинаковые представления о гипотезах Н3: 73=0 и Н4: 74 =0 — ни одну из них не стоит отвергать, если не отвергнута гипотеза Нх: 71=0.
Если принять во внимание эти замечания, то становится ясно, что для интерпретации F-критерия нужен гибкий подход и что вместо
421
автоматического отбрасывания Н4: у4=0 на основе того, что 8,66 лежит за верхней 2,5%-ной точкой распределения Fi 7, более целесообразно решить, что аргументы против 74=0 слабы. Таким образом, мы приходим к выводу, что имеющиеся данные вполне приемлемо аппроксимируются квадратичной моделью у = 2,3714 4- 0,2431х— — 0,0232х2.
8.3.6. ПРОВЕРКА ГИПОТЕЗ ДЛЯ НЕ ОРТОГОНАЛЬНЫХ ПЛАНОВ
При проверке гипотез Н для неортогональных планов используются те же подходы, что были описаны в разделе 8.3.3, т. е. дополнительное уменьшение (подгонка), получаемое при условии, что вектор в не ограничен гипотезой Н, а именно г(0) — r(0 | Н) сравнивается (после нормирования) с дисперсией ошибки, служащей оценкой для а 2=г/(л—к), где г = у'у — г(0) — остаток для полной модели. Из-за более сложной структуры нормальных уравнений конкретная реализация метода оказывается более сложной, чем в случае ортогонального плана, для которого, напомним, если Н не накладывает ограничений на 6t, то МНК-оценка 6t одинакова безотносительно к тому, верна ли гипотеза Н. Это очень удобное свойство в общем отсутствует у неортогональных планов (хотя в исключительных случаях и встречаются отдельные компоненты вектора 0, имеющие свои собственные изолированные нормальные уравнения).
Для демонстрации различий рассмотрим вопрос о проверке гипотезы Н: 6t=0, о том, нужен ли в модели параметр Дополнительная сумма квадратов при включенном в модель 6, в соответствии с (8.3.8) есть
гн — г = (0 — 0*)А'А(0 — 0*),
где 0* — МНК-оценка для 0 при условии Н, а гн — соответствующие остатки. В ортогональном случае такое выражение включает только Qt. В общем случае, однако, когда оценки остальных параметров не влияют на Н, оно тем не менее от них зависит. Обозначим такое уменьшение через r(6t | ф), где ф — остальные параметры, включенные в модель. Для ортогонального плана r(9t | ф) = Att6 2t, что не зависит от ф. Поэтому мы могли говорить однозначно об уменьшении r(0t) в общей сумме квадратов, обусловленном включением в модель данного параметра Qt, не обращая внимания на другие параметры (если они включены в модель). Это приводит к единственному разбиению (т. е. дисперсионному анализу) СКМ, приводящему, как мы видели раньше, к разделению на вклады, обусловленные включением в модель каждого из параметров, в виде
СКМ = г(0) = 0 А А0 = рАи021 = .Ег(0,).
422
В неортогональном случае r(6t | ф) зависит от каждого из параметров, входящих в модель 0, а СКМ можно разделить множеством разных способов в виде
скМ=г(»Г1)+г(0 | | е,,«,)+...+r(e, | е,. е...е, ).
1 41 J i 2 р 1 Z р—/
В этом выражении r(9t) обозначает уменьшение в общей сумме квадратов, обусловленное включением только параметра 0,; г(0,2 | 0,) — дополнительное снижение, полученное при включении в модель еще и параметра 0, . Когда же включены сразу оба параметра, уменьшение равно г(0,, 0,2); вычитание г(0,) дает г(0^ | 0, ), что в общем случае зависит от обоих параметров, а в случае ортогонального плана только от 0,. Аналогично г(0,з | 0,, 0, ) — это дополнительное уменьшение, проявившееся после включения 0,з в дополнение к 0, и 0,; оно равно г(0, , 0,, 0, ) — г(0,, 0,), и т. д. Последний член — дополнительное уменьшение при включении в модель 0, в дополнение ко всем остальным параметрам. Можно показать, что если 0, =0, это , р уменьшение распределено независимо от остатков как Следовательно, последний член годится для проверки гипотезы 0, =0 (относительно полной модели £(Y) = Ад) с помощью F-критерия.
Пример 8.3.5. Критерий для коэффициентов полиномиальной регрессии при неортогональном плане. Вернемся к вопросу о получении адекватной модели полиномиального вида для данных об осадках, на этот раз воспользовавшись обычными полиномиальными моделями. Напомним читателю, что описываемые здесь методы анализа без всяких изменений приложимы к построению полиномов по значениям х-переменных, расположенных не на равных расстояниях друг от друга (не с равным шагом). Начнем с построения полинома первого порядка:
у = 0о + 01* +
Обозначим матрицу плана для этой модели через А]. Тогда система нормальных уравнений примет вид A'lAJJ = A,Y или
Для данных об осадках она принимает вид
12 78\ /£0\ / 32,32'
78 650/ \ ^7 \201,66,
а решение таково: 0о=3,О761 и 0,= —0,0589. В соответствии с (8.3.6) уменьшение, обусловленное этой моделью, есть г(0о» 0i)=/TA'iAi/L Для его
423
вычисления воспользуемся эквивалентной, но более удобной формулой
г(3о, 31) = 3'Aly = + iSiSx/j,.
и получим г(3о, 31) = 87,545.
Представляет интерес гипотеза Н{: &i=0, при которой модель сводится к у = Зо + е(0). Нормальные уравнения этой модели получаются из предыдущих после вычеркивания последнего столбца и последней строки из матрицы и последних строк из векторов, поэтому Зо* = У =2,693333. Тогда легко найти дополнительное уменьшение без использования (8.3.8). Уменьшение для этой модели равно: г(3о) = Зо^Л = пу2 = 87,049, отсюда дополнительное уменьшение от включения в модель еще и 31 равно: r(3i | Зо) = ''(Зо, 31) — г(3о) = 0,496. Дисперсионный анализ для проверки гипотезы Нх'. fit- 0 сводится к
У У = '(Зо) + '(31 I Зо) + '1, а его таблица имеет вид:
Источник SS DF MS
Обусловленный Зо г(3о) = 87,049 1
Обусловленный 3i I Зо г(3. | /Зо) = 0,496 1 0,496
Остаток ''i =У/у—^Зо, 31)= 1,426 10 0,1426
Общий уу = 88,971 12
Рассуждения остаются теми же, что и раньше. Мы приходим к выводу, что существуют недостаточные основания для отбрасывания гипотезы Нх \ 31=0, и ясно, что нужен полином по меньшей мере второго порядка. Построим его: у = Зо + 31* + Зг*2 + е(2). Обозначим матрицу плана для этой модели через А2, тогда система нормальных уравнений будет выглядеть так: А2А23=А2у, и ее можно переписать
в явном виде:
424
Подставив значения для данных об осадках и обратив матрицу, получим
00 = 2,3714, 0! =0,2431, 02 = —0,0232.
Уменьшение общей суммы квадратов, обусловленное построением квадратичной модели, равно:
г(0о, 01, 02) = ?/А/2у = 0о2Л + 31Е*,// + PiZxfy .
Произведя вычисления, получим г(0о, 0Ь 02) = 88,265. В условиях гипотезы Н2: 02=О выполняется модель первого порядка, построенная ранее. Для нее мы находили r(0o, 0i) = 87,545. Дополнительная подгонка за счет включения еще и 02 равна: r(02 | 0О, 0i)=r(0o, , Зг)—',(0о,
0i)=0,720. Вот дисперсионный анализ:
УУ = '•(Зо, 31) + '•(Зг | Зо, 31) + Г2
и его таблица:
Источник SS DF MS
Обусловленный 0О, г(0о> /3,) = 87,545 2
Обусловленный 02 | 00» 01 r(02 I 0о, 0i) = O,72O 1 0,720
Остаток Г2 = У'У—'•бЗо. 0.. 02)=О,7О6 9 0,078
Общий у'у = 88,971 12
Интерпретация та же, что и раньше: мы заключаем, что Зг # 0.
Теперь построим кубическую модель у = 0О + 0i%+ (32х2+ Зз*3 + + е(3). Подставляя соответствующие значения в нормальные уравнения
и обращая матрицу, найдем
0О = 1,7177, 0! =0,2348, 02 = О,1166, 03 = О,ОО48.
425
Уменьшение, обусловленное этой моделью, равно
г(3о, 31, Зг, Зз)=ЗоЕу/ + 31ЕхАу/ + 32Ех^/ + ЗзЕх^/,
что после вычислений дает 88,531. Теперь мы хотим проверить гипотезу Н3: Зз=О- В условиях этой гипотезы «работает» уже полученная квадратичная модель, для которой уменьшение было г(3о, 31, Зг)=88,265. Дополнительное уменьшение из-за 3з равно:
г(3з | Зо, 31, Зг) — г(Ро> 31, Зг, Зз) — ''(Зо, 31, Зг) = 0,266.
Вот дисперсионный анализ:
УУ = '(Зо, 31, Зг) + '(Зз | Зо, 31, Зг) + fз
и его табличная форма:
Источник SS DF MS
Обусловленный /30, 3„ 02 '•(Зо, 3,. 32) = 88,265 3
Обусловленный 03 1 Зо, 01 , 02 г(0з I Зо, 3,, Зг)=0,266 1 0,266
Остаток О=У/У—г(0о, 0,, 02, Зз)=0,440 8 0,055
Общий у'у = 88,971 12
Заключение, как и ранее, состоит в том, что основания для отбрасывания гипотезы Н3 слишком слабы. Аналогично можно рассмотреть и модель четвертого порядка: у=Зо + 31Х+32Х2+ЗзХ3 + 34Х4+в(4). В этом случае надо обращать матрицу размера 5x5, после чего дисперсионный анализ примет вид
У/У = г(3о, 31, Зг, 3з)+'(34 | Зо, 31, Зг, Зз) + '4 с таблицей:
Источник SS DF MS
Обусловленный (30, 31, 02, 03 '(Зо, 31, 02, Зз) = 88,531 4
Обусловленный 04 | Зо, 01, 02, 03 r(04\0o, 0i, 02, Зз)=0,245 1 0,245
Остаток '^У'У-'ГЗо, 3., 02, 0з, 3<) = 0,195 7 0,028
Общий у'у = 88,971 12
426
Интерпретация F-критерия та же, что и раньше, при обсуждении ортогональной модели, и мы заключаем: квадратичная модель у = 2,3714 + 0,2431х— 0,0232х2 адекватно описывает наши данные.
Подчеркнем еще раз: для ортогональной модели надо проводить единственный дисперсионный анализ, выраженный соотношением (8.3.9), и уменьшение, с помощью которого мы судим о вкладе данного параметра в модель или в любую ее часть (подмодель), всегда одинаково. Для неортогональной модели дисперсионный анализ зависит от рассматриваемой гипотезы. Так, основное тождество дисперсионного анализа для модели первого порядка
УУ = г(/3о, /31) + г, в приведенном выше примере превращается в
У'У = r(/8o) + | /Зо) + Г1,
поскольку мы хотим проверить гипотезу, что /31=0, a r(/3i j /30) — представляет собой вклад /31, дополнительный к тому, что уже дал /30 в модели первого порядка. Поскольку это интересно не только для рассмотренного выше примера, можно оценить вклад /30 дополнительно к вкладу /31 с помощью
У У = г(/31) + г(/31 I /Во) + Г..
Такое разбиение относится к проверке гипотезы /Зо=О в модели первого порядка. Первый член в этом выражении не равен r(/3i | /30). В этом можно убедиться, подбирая модель у = /31X4- е, для которой нормальное уравнение есть
(BiEx,- = Еед и
г(01) =
Стоит отметить, что дополнительное уменьшение r(/3i | /30) соответствует проверке гипотезы /31=0 только в модели первого порядка. В нашем примере проверка /32=0 для квадратичной модели приводит к дисперсионному анализу
УУ = г(/30, /31) + г(/32 | /во, /81) + г2.
Теперь его можно разбить на
УУ = г((30) + г(/31 | /Зо) + г(^2 | /30, /31) + г2,
но второй член в этом разбиении не годится для проверки гипотезы /31=0 для данной модели. Если интересна именно эта гипотеза, то мы пользуемся разбиением
427
У'У = r(J30t Зг) + r(3i | Зо, 31) + r2,
где r(3i I Зо, Зг)=г(3о, 31, З2)—r(3o, З2). Получим г(3о, З2), подбирая квадратичную модель при условии /31=0, т. е. модель у=(30 + &2х2 + + е. Нормальные уравнения для этой модели таковы:
п
Для данных об осадках
/ 12
\ 650
/0О\ / ЕУ, \
Ex)/ \ 0*/ = \ Exh / ’
получаем
650 \ /0О*\ / 32,32 \
60710/ \ 02*/ = \ 1610,2/ ’
откуда находим 30*=2,991691, 3*=—0,005508. Уменьшение, обусловленное подбором этой модели, равно: г(/30, Зг) = Зо*^Л + 3*Е*/Л = 87,822, а таблица дисперсионного анализа имеет вид:
Источник SS DF MS
Обусловленный 0О, 02 /•(00, 02) = 87,822 2
Обусловленный 31 | 00, 02 /"(01 I 0о, 02)=0,443 1 0,443
Остаток гг = 0,706 9 0,078
Общий у'у = 88,971 12
F-отношение равно 5,68, и мы имеем Fx 9(0,95) = 5,12, Fx 9(0,975)=9,21. Из предыдущих таблиц и из этих данных видно, что:
а) квадратичная модель без линейного члена лучше, чем модель первого порядка;
б) в квадратичной модели член второго порядка (с дополнительным уменьшением, равным 0,720) более важен, чем. линейный член (с дополнительным уменьшением 0,443);
в) дополнительный вклад линейного члена меньше (хотя он и не очень мал) в квадратичной модели, а не в модели первого порядка. Однако F-критерий формально гораздо более значим именно для модели первого порядка. Это связано с тем, что сравнение происходит с различными остатками. Вклад таких членов низких порядков в полиномиальные модели практически не представляет интереса, поскольку общее решение касалось прежде всего степени полинома, подходящего для аппроксимации имеющихся данных.
428
Мы можем аналогично проверить гипотезу, не лишняя ли в модели группа параметров. Пусть ф — подмножество из 6 и пусть ф обозначает параметры, не включенные в ф. При гипотезе Н: ф=0 модель Y = А0 + е переходит в у = W^+ е, где матрица W получается из матрицы А после вычеркивания столбцов, соответствующих параметрам из ф. Тогда нормальные уравнения для гипотетической модели будут равны:
wwv* = Wy,
откуда получается оценка МНК для вектора ф при условии Н в виде ф* = (W W)-‘Wy. Это совсем не то же самое, что МНК-оценка ф в полной модели, содержащей соответствующие компоненты в = = (А'Ар’А'у.
Уменьшение для ограниченной модели равно: г(ф) = ^*'W'W^* = = ^'W'y, отсюда дополнительное уменьшение при подборе полной модели равно: г(0) — г(ф) = 6 'А у — ф* №у. Можно показать, что когда Н: ф=0 верна, это дополнительное уменьшение распределено независимо от остатков полной модели как о2х^, где т — число параметров в ф.
Вот таблица дисперсионного анализа:
Источник SS DF MS
Обусловленный г(Ф) р—т
Обусловленный ф | ф г(ф | ф) = Г(в) — г(ф) т г(Ф I ф)/т
Остаток г=У'У—г(0) п—р а2= ~ г/{п—р)
Общий УУ п
При гипотезе Н:ф=0 два средних квадрата служат независимыми оценками для о2, основанными на т и (п—р) степенях свободы соответственно, поэтому мы можем проверить Н, сравнивая (л— —Р)г(Ф I Ф)/тг с Fm „_p.
Пример 8.3.6. Продемонстрируем описанный выше метод при проверке гипотезы Н: /31 = /32=0 для квадратичной модели, построенной по данным об осадках, которая имеет вид у=2,3714 + 0,2431х— — 0,0232х2.
В принятых обозначениях ф = (/31, /32у, ф=Ро- Ранее мы нашли, что г(0) = г(/30, /31, /32) = 88,265. При условии Н модель у=/30 + е0, которую мы тоже рассматривали, дает г(/30) = 87,049.
429
Вот таблица дисперсионного анализа:
Источник SS DF MS
Обусловленный /30 г(80)=87,049 1
Обусловленный /3|» 02 I 0о г(0>, 02 1 0о)= 1,216 2 0,608
Остаток г2^у'у—г(0о, 0,, /32) = 0,706 9 0,078
Общий у'у = 88,971 12
Отношение средних квадратов равно 7,79, что весьма убедительно свидетельствует против Н (F2 9(0,975) = 5,71, F2 9 (0,99) = 8,025).
Точно так же, как мы решаем, можно ли исключить из модели некоторые параметры, мы можем поинтересоваться, удовлетворяют ли данные гипотезе, что различные параметры имеют определенные значения.
Пример 8.3.7. Проверка состоятельности данных об ускорении силы тяжести при определенных значениях параметров. Для этих данных из примеров 8.2.2, 8.2.4, 8.2.8 и 8.2.12 вопрос о проверке, требуются ли различные параметры, не возникает. Может представлять интерес другой тип гипотез вроде Нх\ gi=981, Н2. gi=g2=g3=g4=g5 = = 981,2 или Н3: gx =g4=981,26, g2=#3=981,2. Теперь мы проверим их при обычных предположениях, что ошибки независимы и распределены как N(0, ст2).
Поскольку Нх содержит всего лишь один параметр, для ее проверки можно ограничиться просто /-критерием. Тогда, если Нх верна, то (gi — 981) делится на оценку стандартного отклонения, в результате получается значение случайной величины, имеющей распределение Стьюдента с четырьмя степенями свободы (поскольку наша оценка ст2 базируется на остатках, имеющих 4 степени свободы).
Таким образом, приближенно
g - 981 = 0,2681 = 244 a VO,4211 0,0011
Теперь сравним эту величину с двусторонним критерием на 5 %-ном уровне, равным /4(0,975) = 2,78. Ясно, что гипотеза несостоятельна (на любом уровне!).
430
Эквивалентный метод заключается в проверке, попадает ли гипотетическое значение 981 в центральный 95%-ный доверительный интервал для gi, который мы нашли в примере 8.3.1, и он оказался равным (981,2650, 981,2712). Наше гипотетическое значение явно лежит вне указанного интервала. Преимущество такого подхода состоит, как мы можем заметить, в том, что сразу видно, какие значения gt не попадают в интервал от нижнего значения 981,2650 до верхнего 981,2712, и если они не попадают, то это непосредственно означает, что они не согласуются с экспериментальными данными, а это должно привести к отбрасыванию гипотезы Н\ с помощью /-критерия на 5%-ном уровне значимости.
Теперь мы проверим ту же гипотезу по F-критерию, а затем применим его к гипотезам Нг и Н3, для которых /-критерий не применим. При Hi уравнения модели из примера 8.2.2 приводят к
981,1880 = g2 + еь
981,2000 = g3 + е4,
0,0140 = g3 — g2 + е7,
—0,0030 = g4 — 981 + e2, 0,0647 = g4 — g3 + e5, 0,1431 = g4 — g5 + eg,
0,1390 = g4 — gs + e3,
981,2670 = 981 + e6,
981,2690 = 981 + e9.
Это можно записать и в матричной форме:
981,1880 1 0 0 0 £1
980,9970 0 0 1 0 е2
0,1390 0 0 1 —1 gl е3
+
981,2000 0 1 0 0 §3 е4
0,0647 0 —1 1 0 g* е5
0,2670 0 0 0 0 gi е6
0,0140 —1 1 0 0 е7
0,1431 0 0 1 —1
0,2690 0 L 0 0 0
z = Вф + е..
или
431
Заметим, что в матрице В есть две нулевых строки, которые соответствуют уравнениям 6 и 9 и в которых ошибки известны точно. Имеем
2 —1 0 0 981,1740
В В = —1 3 —1 0 , В z = 981,1493
0 —1 4 —2 981,3438
0 0 —2 2 —0,2821
МНК-оценки g2,..., gs при условии Нх обозначим через g2,..., g* и получим из решения системы нормальных уравнений ВВф* = Вг в виде
ф* = (981,1538, 981,1336, 981,0976, 980,9566)'.
Мы видим, что это совсем не те оценки g2,..., g5, которые были найдены в примере 8.2.2 для модели без ограничений, что является следствием неортогональности плана. Остаточная сумма квадратов при условии Hi равна: гн = Е(е,}2, где е* — МНК-оценка при остатка е,- (конечно, е*=е6 и е*=е9). Получим е*, подставив g2, g3, g4, g5 в уравнения для модели с ограничениями по их МНК-оценкам, отсюда:
е* = 0,0342, е* = —0,1006, е\ = —0,0020,
е* = 0,0664, е* = 0,1007, е6* = 0,2670,
е* = 0,0342, е* = 0,0021, е* = 0,2690.
Это дает гн =0,1706675, что можно также найти по формуле гн = = rz —Ф*ёг.
Полная модель имеет вид у = А0 + е, где в = (gH g2,..., g5), а у и А приведены в примере 8.2.4. Остаточная сумма для полной модели равна: г=Ев;, где ei — МНК-оценка для в модели без ограничений. Оценки €j были получены ранее в примере 8.2.12:
е, = 0,00071, е4 =—0,00058, е7 = 0,00071,
е2 = —0,00011,
е5 = 0,00011, ё8 = 0,00205,
ё3 = —0,00205, е6 = —0,00106, ё9 = 0,00094.
За исключением третьей и восьмой, все они меньше, чем в модели с ограничениями, что порождает сомнение в нашей гипотезе. Для формальной проверки мы возводим их в квадрат и складываем, получая г—0,00001178, откуда гн — г = 0,17065572. Можно показать, что если 432
эта гипотеза (т. е. g,=981) верна, то RH — R распределена как а2х] и независима от R, которое само распределено как а2х4. Следовательно, соответствующее F-отношение равно 4(гя — г)/г, что приблизительно составляет 58 х 103, так что может встретиться весьма мало еще больших значений F-отношений.
Обратимся теперь к гипотезе Н2: g\ =g2=-'g3=g4=g5 =;981,2. В суждениях о таких гипотезах индивидуальные доверительные интервалы для параметров могут вводить в заблуждение из-за пренебрежения корреляциями между оценками. Так, если воспользоваться индивидуальными интервалами, гипотетическое значение 981,2 будет казаться подходящим для g3, но не подходящим для остальных оценок. В общем случае окончательное суждение может оказаться различным в зависимости от структуры матрицы (А'А)-1, хотя и тогда мы можем ожидать отбрасывания Н2, когда гипотетическое значение оказывается отстоящим далее, чем на три интервала. Для выбранного уровня можно построить совместную доверительную область, на которой основан критерий. По определению пятимерный доверительный эллипсоид для (gb g2, g}, gi, g$) требует отбрасывания гипотезы Н2, если точка (981,2, 981,2, 981,2, 981,2, 981,2) ему не принадлежит. Действительно, можно построить F-критерий обыДным способом.
При условии Н2 нет параметров, подлежащих оценке, а ошибки известны точно, а именно:
6 г = —0,0120, б2+ = —0,0030, 63+ = 0,1390,
б4‘ = 0, б5+ = 0,0647, б6+ = 0,0670,
б7+ = 0,0140, е8+ = 0,1431, б9+ = 0,0690,
откуда гн = Е(б,+ )2=0,0535837. Если гипотеза Н2 верна, то RH распределено как а2х29 и можно показать, что RH — R распределено независимо от R как a2Xj. Следовательно, формула критерия такова:
— г)/5
774
= 3638.
Как и ожидалось, наша гипотеза, безусловно, отброшена. Рассмотрим, наконец, гипотезу Н3: gi =g4 = 981,26, g2=g3 = 981,2, для которой уравнения модели таковы:
—0,0120=6], —0,0030=б2, 0,1390=981,26—g5+б3, 0=б4, 0,0647 = 0,06 + 65, 0,0070=б6, 0,0140=б7, 0,1431 =981,26—g5 + 68, 0,0090 = б9.
433
В матричных обозначениях это выглядит так:
—0,0120 о1 £1
—0,0030 0 ei
—981,121 —1 е3
— (gs) +
0 0 ч е4
0,0047 0 е3
0,0070 0 е6
0,0140 0 ej
—981,1169 —1 е8
0,0090 0 е9
или
W = С#5 + е.
Поскольку С'С = 2, a Cw= 1962,2379, МНК-оценка для g5 при условии Н3 равна 981,11895. Все ошибки, кроме е3 и е», заданы, а для них мы получаем оценки ё3 =0,00205 и ё» =0,00205. Возводя в квадрат и складывая, найдем rHj =0,0005095, откуда гн* — г=0,00049772. Можно показать, что когда гипотеза Н3 верна, RH — R распределено независимо от R как а2х24. Значит, статистика, лежащая в основе критерия, есть (rHj — г)/г-42,25, и наша гипотеза, безусловно, должна быть отвергнута (F4 4 (0,995)=23,15, 4 (0,999)=53,44).
8.3.7 ГРУППОВАЯ ОРТОГОНАЛЬНОСТЬ
Иногда, хотя план и не ортогонален в рассматриваемом до сих пор смысле, частичная ортогональность все же наблюдается благодаря разбиению параметров на ортогональные группы. При этом мы полагаем, что ^ = (^1, 0р) можно (после переупорядочения, если это
надо) представить в виде
0 = (Ф\, Ф'г,--, 4>'s),
где при /=1, 2, ..., 5 величина ф, заключает в себе несколько компо-$
нентов 0, скажем р, штук, при условии, что Ер, = р, и где матрица ! — 1
434
плана А (соответствующим образом перестроенная, если это надо) такова, что А'А имеет блочно-диагональную форму, т. е.
где, кроме квадратов на диагонали, представляющих собой квадратные подматрицы А,, А2,..., А5 (размеров pt х pif ..., ps х ps соответственно), все остальные элементы — нули. Отсюда следует, что матрица, обратная к А А, имеет вид
Это говорит о том, что МНК-оценки элементов $ в разных ф; некоррелированны. Что же касается корреляции между элементами *0 в одной группе, скажем ф., то они находятся путем деления внедиагональ-ных элементов матрицы Az на корень квадратный из соответствующих диагональных элементов. А отсюда следует, что модель суммы квадратов г(0) = 0'(А'А)~*0 можно разложить следующим образом:
= Ыф.), <=1
где г(ф;) = фуА^’ф,- — уменьшение, обусловленное подбором модели для параметров, входящих в ф;. Более того, это уменьшение обусловлено ф; безотносительно к тому, входят ли в модель остальные параметры. Это видно из структуры матрицы А'А, которая показывает, что МНК-оценка для любого ф, не зависит от любых гипотез, использующих остальные параметры. В частности, для гипотезы Н: фу=О МНК-оценки всех остальных ф не изменятся, а дополнительное уменьшение, когда гипотеза Н не проходит, останется г(ф;). Следовательно, мы можем проверить гипотезу Н, рассматривая отношение
435
r/(n — p)
которое должно быть реализацией распределения Fpn_p^ если Н верна.
С другой стороны, для проверки почти того же самого для параметров внутри приходится обращаться к обычным процедурам для неортогонального случая, поскольку МНК-оценки остальных параметров 0Z, так же как и обусловленные ими уменьшения, меняются в зависимости от того, какие из остальных элементов включены в модель. Те же трудности будут возникать и в тех случаях, когда мы захотим проверить гипотезы для групп параметров, входящих в разные
Позже [см. гл. 10], при рассмотрении модели классификации данных, мы еще встретимся с различными примерами частичной ортогональности.
8.3.8. ОБЩИЕ ЛИНЕЙНЫЕ ГИПОТЕЗЫ
Все гипотезы, обсуждавшиеся до сих пор, были общими линейными гипотезами. Общие линейные гипотезы Н налагают на вектор параметров 0 линейные ограничения, т. е. приписывают некоторые определенные значения заданным линейным комбинациям параметров 01, 02,..., 0р в виде уравнений такого типа:
Йц01 4- Л1202 +...+ Ь\рОр — С1,
^2101 + ^22 0 2 + ••• + h^pOp = С2,
+•••+ hfnpQp — ст’
где и коэффициенты htp и константы Cj известны. В матричной форме эти уравнения можно записать так:
Н0 = с,
где Н — матрица размера т х р с элементами (Z, j) = h-, a cz = = (Cj, с2, ..., ст). Например,
а) На: 0( = 0, 02 = 0,..., 0р = О,
б) Н6: 0р = 0,
в) Нв: 0( = сь 02 = 0р = ср —
это все случаи, с которыми мы уже встречались. А вот важный пример системы общих линейных гипотез, с которыми мы еще не знакомы:
436
г) нг-. е{ - е2 = о, 02 - 03 = о,ер_х - ер = о,
что можно представить короче: Нг: 0! =02 = ... = 0р.
Отметим, что существует различие между Нг, когда общее значение не определено, и тем частным случаем Нв, когда оно задано, а именно ct =с2 = ...=ср.
Для проверки гипотез Н мы пользуемся тем же общим подходом, что и в уже рассмотренных частных случаях: берем в качестве исходных данных остатки для полной модели и оцениваем важность дополнительного уменьшения общей суммы квадратов, когда модель не ограничена условиями Н.
Как обычно, для полной модели F(Y) = Ав имеем
У'У = г(0) + г,
где г(0) — уменьшение, обусловленное вектором О с р степенями свободы, аг — остатки с («—р) степенями свободы.
Для модели с ограничениями E(Y) = А0 при условии Н обозначим уменьшение в у'у через r(9 | Н), так что
у у = г(6 | Н) + гн, где гн — остатки в модели с ограничениями.
Мы могли видеть, что предположение об ошибках как о независимых наблюдениях с распределением N(0, а) ведет к тому, что R оказывается распределенным как огх2п_р. На основании этого можно далее показать, что если гипотеза Н верна, то дополнительное уменьшение /?(0) — R(9 | Н) = RH— R имеет распределение независимое от распределения R, где h р — число математически независимых уравнений, определяемых Н. Величина h называется порядком системы Н и равна рангу матрицы Н.
В приведенных выше примерах мы заметили, что На и Нв содержат по р независимых условий, налагаемых на вектор 0 (в каждом из этих случаев матрицей системы гипотез служит единичная матрица 1р), поэтому каждая из них имеет порядок р. Для гипотезы Н6 поря-, док равен 1. А для Нг, содержащей (р— 1) независимых условий на 0, порядок равен (р — 1).
Как отмечалось, все эти гипотезы имеют полный ранг и не содержат избыточных условий. Для (а) и (в) h-m-p, для (б) h = m=\, наконец, для (г) h = m=p—1. Когда т > Л, некоторые из уравнений оказываются избыточными. Это показывает добавление к гипотезе Нг ограничений типа 0t=03, 20 2— 04— 05=0, которые не создают дополнительных связей, зато увеличивают т до (р + 1).
Основу полученных ранее результатов о распределениях прежде всего составляет то, что когда гипотеза Н верна, мы можем восполь-
437
зоваться уравнениями, определяемыми Н для исключения из 0 h параметров. А это позволяет выразить эти параметры (если какой-либо выбор возможен, то не важно, какие именно значения h выбраны) в терминах остальных (р — h) параметров. Обозначим оставшиеся параметры через а исключенные — через ф. Тогда решения для ф можно подставить обратно в исходную модель. Благодаря этому удается выразить модель с ограничениями через новую матрицу плана D относительно (р — h) параметров, которые теперь не связаны никакими ограничениями. Значит, при условии Н нашу модель можно записать так: E(Y) = D^, где ф содержит (р — h) компонент. А к такой модели приложима стандартная теория, поэтому МНК-оценка для ф при условии Н (в предположении, что матрица D D не особенная) есть ^* = (DD)-'D/y, а остатки равны: rH = у'у — ^*Dy. При обычных предположениях об ошибках RH распределена как а2 х л_(р—*)• Поскольку RH - (RH—R) + R, остается только установить независимость (RH — R) и R, чтобы доказать, что (RH — R) распределено как а2х2л. Гипотезу Н можно проверить с помощью обычной статистики , rSJh
f — r>'h J ~ r/(n—p) •
Если гипотеза H верна, то f — реализация случайной величины с распределением Гк'П—р' ВеРхний хвост этого распределения используется в качестве ожидаемого превышения, когда гипотеза Н ложна.
Все эти результаты можно суммировать в виде следующей таблицы дисперсионного анализа для проверки гипотез Н :
Источник SS DF MS
Обусловленный 6 Обусловленный 9\Н Дополнительное уменьшение Остаток /•(«)=в'А'у r(fi I H)=f'D'y г(9) - r(9,\ Н) г=фу—г(9) Р p — h h п—р {r(9) — r(fi\H)}/h ~ог = г/(п — р)
Общий п
В этой таблице г(0) — уменьшение, обусловленное подбором модели E(Y)=A0, делится на две части. Первая из них — величина r(9 | Н), на которую уменьшается уу, когда гипотеза Н верна, а вторая — г(0) — дополнительное уменьшение, когда 9 не связано ограничениями гипотезы Н.
438
Все предыдущие примеры — варианты этой таблицы. Если, например, Н соответствует ф=0, где ф содержит т параметров из в, то мы имеем h = т и г(6 | Н) = г(ф), где ф обозначает остальные параметры из в. Отсюда г(6) — г(0 | Н) = г(6) — г(ф) = г(ф | ф), и мы получаем дисперсионный анализ г(9) = г(ф) + г(ф | ф), использованный в предыдущих обсуждениях наших гипотез.
Рассмотрим теперь несколько новых примеров и покажем проверку более сложных гипотез с помощью изложенной выше теории.
Пример 8.3.8. Критерий равенства средних в односторонней классификации. В примере 8.3.3 было показано, как проверяется гипотеза Но, что все группы имеют известное общее среднее ц0. Теперь рассмотрим более общие гипотезы Н, что средние имеют общее, но не известное значение. Когда план Ортогонален, то дополнительное уменьшение легко отыскивается с помощью (8.3.8), что уже обсуждалось. Для иллюстрации общего метода найдем теперь гн непосредственно и для сравнения сначала проверим гипотезу Но таким способом.
Напомним из примера 8.2.14, что остатки для полной модели Уц = Д» + е,у равны:
где у,. — среднее из J, наблюдений в группе с номером i, а г — реализация R, распределенная как а2х2п_{.
При условии Но модель имеет вид у^ = цо + е^. Слева нет неизвестных параметров, поэтому
что равно j
+ где п
Следовательно,
ГЯ0 “ Г =£Jiy2i- “ 2^Jiyi- + ~ ^2'
Полная модель содержит / параметров, каждый из которых равен д0 по условию Но, и в силу этого она имеет порядок I. А вот статистика, лежащая в основе критерия:
“ Г)// — i- — 1
г/(П — I) I Ji
Е Е (Уа — УгУ/(п — /) /=0=1 у '
439
Когда гипотеза Но верна, это наблюдение из распределения Ff п_1. Однако в большинстве практических ситуаций гораздо интереснее проверить гипотезу, что все д, равны без указания их общего значения, поскольку Оно практически не бывает известно. Как уже отмечалось, когда мы хотим проверить гипотезу Н: р.} = ц2 = ... = ц(= ц, где д не известно, порядок оказывается равным (7— 1).
При условии Н модель имеет вид у^ = + еу, поэтому, рассматривая в данный момент д просто как алгебраическую переменную, мы должны минимизировать по ц такую сумму квадратов:
S(g) = .£ Д(Ау — д)2.
Дифференцируя по д и подставляя вместо д ее оценку д, получим нормальное уравнение
,5^-?) = о,
решением которого будет =У.., т. е. общее среднее по всем наблюдениям. Вот остатки для этой модели:
rH = SQF) = Ь^(Уи-у\.У,
и дополнительное уменьшение
что после упрощения дает
rH-r=hi(yi.~y.y.
Когда гипотеза Н верна, RH — R распределено как о2х{_1. Статистика, лежащая в основе критерия, такова:
(ГН -г)/(/-1) = г/(п — I) j Ji
££(у„-уУ)2/(п-Г) i=\j=\ IJ 1
Для верной гипотезы Н это наблюдение из распределения FI—X п_{.
Пример 8.3.9. Вернемся к данным об ускорении силы тяжести, для которых представляют интерес следующие гипотезы:
Я,: g,=g2=g3=g4=gs, T/2:g = 981,2, H3:g{ = g4.
Заметим, что Н, предполагает общее значение для всех параметров, которое, однако, не задано (допустим, g). Значит, Н\ — более общая
440
гипотеза, чем вторая гипотеза из примера 8.3.7, где утверждалось, что общее значение равно 981,2, и в данном случае мы можем ожидать лучшего соответствия. Для проверки Нх нам понадобится остаточная сумма квадратов для модели с ограничениями, которая устанавливается из соотношений:
981,1880 = g + eif
981,2000 = g + е4, 0,0140 = е7,
—0,0030 = е2,
0,0647 - е5,
0,1431 = е8,
0,1390 = е3,
981,2670 = g + е6,
981,2690 = g + е9,
или в матричной форме:
981,1880
—0,0030
0,1390
981,2000
0,0647
981,2670
0,0140
0,1431
981,2690
1
0
0
1
0
1
0 о
1
е9
£1
откуда g =(981,1880 + 981,2000 + 981,2670 + 981,2690)74 = 981,2310.
А вот и остатки: —0,0430, —0,0030, 0,1390, —0,0310, 0,0647, 0,0360, 0,0140, 0,1431, 0,0380, откуда гн =0,0497397. Это чуть-чуть меньше, чем остатки для гипотезы об общем значении, равном 981,2, которые были равны 0,0535837, так что мы снова можем ожидать большой величины критерия-отношения. В дальнейших вычислениях надо помнить, что наше общее значение не определено и порядок Нх равен 4. Имеем — г-0,04972792, а искомое значение критерия есть )(гя — г)/4]/[г/4] = 4221. Ясно, что мы не можем принять гипотезу о каком-либо общем значении.
Займемся теперь гипотезой Н2 : g = 981,2. Снова заметим, что это более общая гипотеза, чем гипотеза об общем значении 981,2, рассмотренная ранее в примере 8.3.7. Для модели, удовлетворяющей этой гипотезе, есть два способа нахождения остатков. Первый заключается в том, что мы можем воспользоваться ограничением для исключения одного параметра, скажем g2, решая относительно него
441
уравнение g, +g2+gi+g4+gs = 5 x 981,2 и записывая уравнения модели, пользуясь только переменными gi, gi, g4, gs. Тогда g2=4906 — — gi — gi — g4 — gs, значит, все уравнения модели не изменятся, за исключением первого и седьмого, которые примут вид
981,1880 = 4906 — g, — g3 — g4 — g5 + et
и
0,0140 = gt + 2g3 + g4 + gs — 4906 + e7.
В матричной форме имеем:
—3924,812 -1 —1 — 1 —1
—0,0030 —1 0 1 0
0,1390 0 0 1 —1 gl e.
981,2000 0 1 0 0 g3 •
0,0647 = 0 —1 1 0 g4 +
981,2670 1 0 0 0 gs
4906,0140 1 2 1 1
0,1431 0 0 1 —1 *
981,2690 1 0 0 0
Поскольку при таком подходе на gt, g3, g4, g5 не наложены никакие ограничения, теперь можно применить для нахождения гн стандартную теорию. Обозначив предыдущее соотношение через z = D^, получим
5 3 1 2 10793,365
D D = 3 7 2 3 , D z = 14717,975
1 2 6 0 8831,169
2 3 0 4 8830,544
МНК-оценка для равна: '=(£*» g*> 84, ^*) = (D/D) 1 D'Z, откуда g*=981,2625, g*=981,1929, g>981,2536, g5* = 981,l 101.
Теперь появились МНК-оцейки для g,, g3, g4, g5 при условии Т/2. А МНК-оценка для линейной функции 4906 — gi — g3 — g4 — g5, т. e. для g2, равна: g*=4906 — g* — g* — g* — g*=981,1809.
442
Отсюда можно найти сумму квадратов остатков гн либо из rH = Z'Z— либо вычисляя индивидуальные остатки, а затем
возводя их в квадрат и складывая. Мы нашли, что гн^ = 0,00023854.
Альтернативный подход заключается в сохранении всех пяти параметров и минимизации суммы:
S = (981,1880 — и2)г + (—0,0030 — и4 + m,)2+...+ (981,2690 — и,)2 при условии, что U\ + и2 + и3 + и4 + и5 = 4906.
Введя неопределенный множитель Лагранжа, получим безусловный минимум Т = S + \(ui + и2 + и3 + и4 + и5 —4906). Дифференцируя Т по «1, ..., и5 соответственно и подставляя w, = g*, i = 1, ..., 5, получим
3g? -g4 - 1962,5390 + X = 0,
2g2 — g* — 981,1740 + X = 0,
~g2 + 3g3* - g4* - 981,1493 + X = 0, ~g; - g' + 4g4* —2g* - 0,3438 + X = 0, —2g* + 2g* + 0,2821 + X = 0.
Ограничение означает, что оценки должны удовлетворять соотношению g* + g* + g* + g* + g* = 4906. Эти шесть уравнений можно решить относительно g*, ..., g* (на этом этапе X представляет собой мешающий параметр, который надо исключить). Мы получим те же МНК-оценки параметров g15 ..., g5 при условии Н2, что были получены ранее методом исключения одного параметра. Теперь можно определить остатки для модели с ограничениями, подставляя найденные оценки в уравнения исходной модели.
Для проверки гипотез нам нужно значение гн^ — г = 0,00022675. Заметим, что для гипотезы Н2 порядок равен 1, поэтому формула для критерия упрощается: (гн? — г)/(г/4) = 76,93. Представление о том, что среднее значение g для пяти мест измерения равно 981,2 крайне неправдоподобно.
В качестве последней иллюстрации на данных о силе тяжести возьмем гипотезу H3'.gx = g4, для которой уравнения примут вид
981,1880 = g2 + е,,
981,2000 = gi + е4,
0,0140 = g3 — g2 + е7,
—0,0030 = е2,
0,0647 = gt — gi + е5,
0,1431 = gi — g5 + е8,
0,1390 = g, — g5 + е3,
981,2670 = g, + e6, 981,2690 = g, + e9
443
или
981,1880 —0,0030 0 0 1 0 0 0 0 0
0,1390 1 0 0 —1 gi е.
981,2000 0,0647 — 0 1 0 0 1 —1 0 0 g2 g3 + • •
981,2670 0,0140 1 0 0 —1 0 1 0 0 gs
0,1431 1 0 0 —1
981,2690 1 0 0 0
Обозначив эти уравнения через Y = D^, получим
5 0 —1 —2 1962,8828
D D = 0 2 —1 0 , D'y = 981,1740
—1 — 1 3 0 981,1493
—2 0 0 2 —0,2821
МНК-оценка для gi, g2, g3, g5 при условии Н3 оказались равными:
£* = 981,26739, £* = 981,18774, £>981,20148, £>981,12634,
а остатки таковы: е* = 0,00026, е* = —0,0030, е* = —0,00205, е* = = —0,00148, е* = —0,00121, е* = —0,00039, е>0,00026, е>0,00205, е* = 0,00161, откуда гн = 0,00001503 и — г = 0,00000324. Поскольку порядок Н3 равен 1, вычисляем (rHi — г) (г/4) = 1,099. Тогда Fj 4(0,95)=7,71, так что аргументы против гипотезы £i = g4 слабоваты.
8.4. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Указания по дальнейшему чтению работ, посвященных методу наименьших квадратов и дисперсионному анализу, можно найти в конце гл. 10.
444
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Аренс X., Л ёй тер Ю. Многомерный дисперсионный анализ / Пер. с нем. — М.: Финансы и статистика, 1985. — 230 с.
Дрейпер Н., Смит Г. Прикладной регрессионный анализ. — 2-е изд., пере-раб. и доп. Кн. 1 / Пер. с англ. — М.: Финансы и статистика, 1986. — 366 с.
Дрейпер Н., Смит Г. Прикладной регрессионный анализ. — 2-е изд., пере-раб. и доп. Кн. 2 / Пер. с англ. — М.: Финансы и статистика, 1987. — 351 с.
Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. — 2-е изд., перераб. и доп. — М.: Физматгиз, 1962. — 352 с.
Ш е ф ф е Г. Дисперсионный анализ. — 2-изд./ Пер. с англ. — М.: Наука, 1982. —
628 с.
Глава 9
ПЛАНИРОВАНИЕ СРАВНИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
9.1. ИСТОРИЧЕСКОЕ ВВЕДЕНИЕ
В естествознании XIX века постановки задач и сложность лабораторных методик обеспечивали снижение ошибки эксперимента до такого уровня, при котором надлежащим образом организованные повторения эксперимента позволяли воспроизводить исходные наблюдения с точностью, достаточной для любых практических целей. В биологии же ситуация была совершенно иной. Фрэнк Йейтс [см. Yates (1937)] писал: «Большинству биологических объектов свойственна вариабельность, и прелесть простоты и воспроизводимости физических или химических экспериментов из-за этого утрачивается. А значит, на передний план начинают выдвигаться' статистические проблемы».
Статистические проблемы стали актуальны в связи с трудностями интерпретации невоспроизводимых результатов. Они привели к вопросу о том, как же надо расположить опыты, чтобы минимизировать влияния вариабельности, обусловленной конкретной задачей.
В агробиологии прежде, чем в других науках, началось систематическое изучение такого рода проблем. Особая роль принадлежит агробиологической станции в Ротамстеде (Англия), основанной в 1843 г. Здесь были начаты полевые опыты для оценки влияния удобрений на урожай и, для сравнения урожаев различных сортов зерновых. Занимавшиеся этим ученые должны были не только считаться с большой изменчивостью их материала — в плодородии делянок, качестве семян, количестве осадков и т. п., — но и с тем, что каждый из их опытов требовал для своего завершения приблизительно год.
В этих обстоятельствах не оставалось иного пути, как провести специальные исследования и создать продуманные планы экспериментов, обеспечивающих уменьшение негативных последствий внутренней вариабельности настолько, насколько это возможно, и позволяющих объективно оценивать точность окончательных выводов.
В качестве типичного можно было бы рассматривать эксперимент по сравнению урожаев (скажем, пшеницы), получаемых при отсутст-446
вии удобрений («контроль») и при внесении в почву определенного количества азотных удобрений. Или более реалистично: по множественному сравнению контрольного урожая и урожаев при различных уровнях азотных, фосфорных и калийных удобрений (для каждого вида удобрений в отдельности).
К концу прошлого столетия были разработаны некоторые общие принципы планирования и накоплен большой объем данных. Следующий шаг вперед в интерпретации этих данных и изобретение таких планов, снижающих ошибку, которые можно было усовершенствовать в процессе работы, связаны с деятельностью в Ротамстеде Р. А. Фишера. Он сразу же начал изучать вопрос, как лучше всего приспособить принципы современной статистики к исследовательской работе в агробиологии, что привело его к параллельной и взаимосвязанной с этим разработке собственных принципов теории статистического вывода. Подобные проблемы и методы относились не только к агробиологии; они положили начало новой науке о планировании и анализе сравнительных экспериментов в таких областях, как агробиология, биохимия, материаловедение, инженерная химия и т. д., т. е. там, где высока вариабельность результатов эксперимента. Теперь это отдельная область профессиональной деятельности со своими законами, известная как планирование и анализ экспериментов.
Цель данной главы состоит в том, чтобы кратко описать основные принципы планирования эксперимента, включая рандомизацию, разбиение на блоки, балансировку, взаимодействия, смешивание. Это в основном качественные принципы. Анализ экспериментальных данных включает оценивание методом наименьших квадратов параметров подходящей (часто линейной) модели в соответствии с планом и проверку гипотез (вроде гипотезы относительно равенства некоторого параметра нулю или равенства двух параметров) стандартными методами дисперсионного анализа.
В терминах гл. 8 модели, используемые в большинстве планов, окажутся «вырожденными», т. е. вследствие симметрии они содержат параметров больше, чем модель в состоянии оценить, да еще компенсирующие условия, элиминирующие избыток.
Соответствующая этому случаю модификация теории метода наименьших квадратов приведена в гл. 10.
9.2. ЛЕДИ, ДЕГУСТИРУЮЩАЯ ЧАЙ
Фишер дал знаменитое толкование принципов планирования эксперимента на примере (вероятно, придуманном) спланированного эксперимента для испытания способности некой леди различать, что было
447
раньше налито в чашку — чай или молоко, после того, как она попробует содержимое чашки с напитком неизвестного ей происхождения*. Построенный Фишером план обладал следующими свойствами [см. Fisher (1950)]:
повторяемость (дублирование): это обычно необходимый компонент. Ни один экспериментатор не должен делать каких бы то ни было выводов о верной или ошибочной идентификации порядка смешивания молока и чая по одной единственной чашке;
сбалансированность: наша леди должна попробовать равное число чашек с молоком, добавленным в чай, и с чаем, долитым в молоко, чтобы в ее суждении не возникло смещения;
рандомизация: этот существенный момент в планировании относится к тому, в каком порядке следует представлять чашки на дегустацию. Рандомизация их порядка есть на самом деле необходимое условие для того, чтобы стало возможным применение к анализу результатов статистических принципов;
чувствительность: Р. Фишер отмечал, что пока число чашек не превысит некоторый минимум, никаких разумных выводов сделать нельзя, т. е. эксперимент может оказаться совершенно нечувствительным, если выборка слишком мала. Причем после того, как этот минимум пройден, чувствительность эксперимента растет тем больше, чем больше (в пределах ограничений) число повторений;
однородность: изложенные выше соображения нельзя распространять слишком далеко. Когда число чашек превысит некоторый предел, утверждаемое леди различие в букете, обусловленное тем, что раньше было налито молоко или чай, может маскироваться разностью температур, эффектом настаивания, притуплением вкусовых рецепторов леди и т. п. А это нарушает однородность, что может затруднить анализ или даже сделать его невозможным.
* На первый взгляд такая задача кажется надуманной и практически неинтересной. Однако давайте послушаем, что говорит специалист по чаю: «Англичане — одна из самых любящих чай наций в мире ... Культ чая господствует почти в каждой английской семье, и до сих пор чаепитие составляет одну из характернейших национальных традиций англичан. Вот почему с полным правом можно говорить об английском способе чаепития ... Англичане пьют чай с молоком или со сливками. Предварительно подогревают сухой чайник. Затем в него насыпают чай из расчета 1 чайную ложку на чашку воды и 1 чайную ложку «на чайник». Чайник тотчас же заливают кипятком (дважды) и настаивают 5 минут. Пока чай настаивается, в сильно разогретые чашки разливают молоко — от 1/6 до 1/4 чашки (по вкусу) и затем в молоко наливают чай. Следует подчеркнуть, что англичане строго следуют правилу наливать чай в молоко, а ни в коем случае не наоборот. Замечено, что доливание молока в чай портит аромат и вкус напитка, и поэтому подобная ошибка рассматривается как невежество» (см.: ПохлебкинВ. В. Чай, его типы, свойства, употребление. — М.: Пищевая промышленность, 1968. — С.118—119).
Получается, что, как обычно у Фишера, пример достаточно актуален и интересен не только для статистиков. Что же касается последних, то они многократно описывали и обсуждали эту знаменитую задачу (см., например: Н е й м а н Ю. Вводный курс теории вероятностей и математической статистики /Пер. с англ.; Под ред. Ю. В. Линника. — М.: Наука, 1968. — С.344—373; М а р к о в а Е. В., М а с л а к А. А. Рандомизация и статистический вывод.— М.: Финансы и статистика, 1986. — С.83—87. — Примеч. пер. 448
Анализ проводится так. Сначала ясно определяется цель эксперимента, которая заключается в установлении того, способна ли наша леди различать ситуации. Это формулируется в виде нуль-гипотезы, что она на самом деле совершенно не способна различать порядок введения ингредиентов.
Допустим, что ей в случайном порядке предложены 2п чашек чая: п — молоко-чай и п — чай-молоко. Если верна нуль-гипотеза, то вероятность того, что она способна правильно идентифицировать г раз, равна*:
= г=о,1....
Так, например,
при л = 2: р0 = 1/6, pi = 2/3, р2 = 1/6;
при п-3: ро = 1/2О, pi =9/20, р2-9/20, р3 = 1/20;
при п = 4: ро = \/7О, pi = 16/70, р2 = 36/70, р3 = 16/70, р4 = 1/70.
Таким образом, если п = 2 (т. е. по две чашки каждого вида), то один шанс из семи определить все совершенно правильно, даже если на самом деле леди ничего не понимает. Это довольно большая вероятность, так что даже абсолютно правильная идентификация всех чашек не может служить аргументом против нуль-гипотезы. (Это как раз случай нулевой чувствительности, о котором говорилось выше.) При л=4 правильное определение всех четырех чашек, начинавшихся с чая (а значит, и всех четырех чашек, начинавшихся с молока), было бы невероятно, если бы леди не умела их различать. Такое событие имеет всего один шанс из семидесяти.
Однако вполне можно себе представить, что она допустила случайную ошибку. Требовать, чтобы она могла точно классифицировать каждую чашку, было бы слишком строго. Тогда для л=4 с правильным определением трех или более чашек чая из четырех связана вероятность 17/70, близкая к одной четвертой. А это слишком большое значение, чтобы дискредитировать нуль-гипотезу. Следовательно, если мы хотим отвергнуть ее претензии даже в том случае, когда допустима одна ошибка, чашек каждого вида потребуется больше, чем 4. Так, например, при л = 7 уровень значимости (см. раздел 5.2.2) для результата, когда из л выборов правильно сделаны л—1, составит 0,015, и большинство специалистов, по-видимому, его сочтут достаточно малым для дискредитации нуль-гипотезы (см. табл. 5.2.1), а значит, такое событие' будет рассматриваться как убедительное подтверждение претензий нашей леди.
* См., например: Прохоров Ю. В., Розанов Ю. А. Теория вероятностей. — С. 12—16.— Примеч. пер.
449
9.3. БОЛЕЕ СЛОЖНЫЙ ПРИМЕР: ЭКСПЕРИМЕНТ ДАРВИНА
Пример с леди, дегустирующей чай, хотя и дает повод поговорить об основных принципах планирования эксперимента, все же не является типичным. Во-первых, он направлен, скорее, на доказательство или опровержение способности леди к различению ситуаций, тогда как более общий план должен был бы оценивать величину этого эффекта. Во-вторых, более общие планы снабжены механизмом «блокирования», позволяющим продолжить эксперимент (т. е. включить больше наблюдений) без потери преимуществ из-за неоднородности экспериментального материала и подходящих условий малого эксперимента.
Эти дополнительные моменты были выявлены и обсуждены Р. Фишером [см. Fisher (1951)] при знаменитом эксперименте, выполненном Чарльзом Дарвином для установления того, способствует ли перекрестное опыление растений увеличению их роста по сравнению с самоопылением, и если да, то насколько*. Этот эксперимент и обсуждение его Фишером были описаны в примере 5.7.1. Использованные Дарвином классические принципы характеризуются следующими признаками:
1) блокированием: прямое сравнение можно было сделать только для пары растений, одно из которых подверглось перекрестному опылению, а Другое — самоопылению, причем оба растения выращивались в одном цветочном горшке, следовательно, в настолько близких внешних условиях, насколько это возможно. Такой прием снижает влияние неустранимых различий между внешними условиями выращивания одного и другого растения, плодородием почвы в одном горшке и в другом и т. д.;
2) повторяемостью: конечно же, использовались несколько цветочных горшков. В данном конкретном эксперименте на самом деле было 15 повторений (дублирований основного экспериментального модуля). Благодаря усреднению всех 15 повторений Дарвин смог минимизировать вклад ошибки эксперимента в исследуемый эффект высоты растений;
3) сбалансированностью: оба вида растений использовались равное число раз, так что ни один из них не получил преимущества.
Р. Фишер предложил еще один дополнительный признак:
4) рандомизацию: Дарвин фактически не воспользовался этим приемом, который был указан Фишером как необходимый для того, чтобы стал возможным состоятельный анализ эксперимента. В данном контексте термин «рандомизация» означает определение для каждого из 15 горшков с помощью физического процесса рандомизации (подобного подбрасыванию монеты), какое из двух семян, с каким способом опыления (самоопыление или перекрестное) должно за
*Этот пример Ч. Дарвина описан в его собрании сочинений, переведенных на русский язь/к, и неоднократно обсуждался в статистической литературе. См., например: Ю л Дж. Э., К е н д э л М. Дж. Теория статистики. — 14-е изд. / Пер. с англ.; Под ред. Ф. Д. Лившица. —М.: Госстатиздат. — 1960. — С. 73. — Примеч. пер.
450
нять, скажем, северную, а какое — южную сторону горшка. В поддержку своих представлений Фишер утверждал, что когда верна нуль-гипотеза, что отсутствует систематическое различие между перекрестным опылением и самоопылением, наблюдаемые различия в значительной степени могут объясняться условиями окружающей среды. Поэтому надо сравнивать фактически наблюдаемые различия с теми, что могли бы появиться при всех других перестановках мест закладки семян (равноправных с точки зрения нуль-гипотезы), которые могли бы возникнуть в процессе рандомизации. Действительно, с такой точки зрения только «оброк» рандомизации позволяет обратиться к вероятностному рассмотрению.
Анализ эксперимента основан на «модели рандомизации», т. е. на представлении о том, что имеющиеся данные образуют некоторую выборку из генеральной совокупности равновероятных потенциально возможных наборов данных, полученную в результате рандомизации, как показано в примере 5.7.1. Можно заметить, что даже в таком простом примере, как рассматриваемый, вычисления нетривиальны. А в более сложном эксперименте над вычислениями, связанными с анализом рандомизации, придется попотеть. Возможно, по этой причине в докомпьютерную эру обсуждались и альтернативные модели. Главная конкурирующая точка зрения состоит в том, что наши 15 пар семян фактически представляют собой случайную выборку из (двумерной) совокупности пар растений с некоторым значением математического ожидания разности Ь=Е(Х—У) между ростом растений с перекрестным опылением и самоопылением. Обычно в качестве оценки для 5 используется среднее 7Г из наблюдаемых разностей dr=xr—уг, на основании центральной предельной теоремы теории вероятностей рассматриваются как реализации независимых нормально распределенных случайных величин. Практически одинаковые вычисления определяют значимость наблюдаемых различий независимо от того, получены ли они с использованием модели рандомизации или с помощью этого варианта модели нормального распределения.
На первый взгляд кажется, что модель нормального распределения противоречит соображениям Фишера о необходимости рандомизации как существенной части планирования эксперимента. В действительности, однако, она вполне согласуется с тем, что рандомизация служит одним из ключевых моментов, пусть не из-за фишеровских соображений, приведенных выше, но в силу не менее веских причин: без рандомизации ошибки эксперимента нельзя рассматривать как взаимно независимые и одинаково распределенные случайные величины.
9.4. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЕ БЛОЧНЫЕ ПЛАНЫ
В эксперименте Дарвина сравнивались всего две «обработки», и в каждом повторении было два сеянца, естественно объединяемых в относительно малый «блок», образуемый обычным цветочным горш-
451
ком, в котором можно легко создать желаемую степень однородности плодородия почвы и окружающей среды. Однако в агробиологических (да и других) экспериментах обработки обычно более многочисленны, а кроме того, требуется больше пространства. Например, в опытах по выращиванию зерновых культур нужны делянки размером с поле. С другой стороны, время может оказаться лимитирующим фактором; скажем, в прикладной химии эксперимент часто требует нескольких часов, причем обработки, которые надо сравнивать, это различные растворители, и тогда в качестве «блока» может выступать рабочий день. Все эти факторы действуют в направлении «пересыщения» блоков: при таких условиях иногда невозможно согласовать имеющиеся обработки с блоком подходящего размера (например, в дне не будет хватать часов) или же если блок можно увеличить настолько, чтобы поместились все обработки, то он станет настолько большим, что исчезнет однородность. Значит, существует предел, за которым прямое обобщение плана Дарвина не практично.
Если же удается разместить все «обработки» в одном блоке (например, три сорта пшеницы на одном поле) так, чтобы не слишком сильно нарушалась однородность, принцип «полного блокирования» явно начинает играть роль «первой скрипки». Если каждый из трех сортов пшеницы удается разместить на одной из трех делянок опытного поля, то конечно, размещение сортов по делянкам внутри блока надо рандомизировать. Это приводит к плану (полностью) рандомизированных блоков. Отсюда, например, для четырех обработок А, В, С, D и пяти блоков «карты» пяти полей могут оказаться такими, как на рис. 9.4.1.
А В D
D D С
В С А
С А В
Блок 1 2 3
С А
А С
В D
D В
4 5
^ис. 9.4.1. Полностью рандомизированные блоки (4 обработки, 5 блоков) 452
Сравнения урожаев следует делать только внутри блоков, тогда элиминируются насколько возможно различия в плодородии и т. п. между блоками.
9.5. ОБРАБОТКИ НА ОДНОМ И НА НЕСКОЛЬКИХ УРОВНЯХ
В плане с пятью блоками, показанном на рис. 9.4.1, сравниваемыми растениями («обработками») могут быть четыре сорта пшеницы. Это могут быть также четыре различные обработки удобрениями (А — контроль, без удобрений, В, С, D — заданные количества азотных (7V), фосфорных (Р) и калийных (К) удобрений). Возможны и качественные различия уровней двух видов удобрений (А — поверхностное внесение N и поверхностное внесение Р удобрений, В — поверхностное для N и глубокое для Р, С — глубокое для N и поверхностное для Р, D — глубокое для N и глубокое для Р). Есть две «обработки» (N, Р) на двух уровнях каждая, причем каждый уровень N встречается с каждым уровнем Р. Это пример эксперимента с полным перебором комбинаций, содержащего информацию не только об отдельных эффектах азотных и фосфорных удобрений, но и об их совместном влиянии на урожаи.
Это понятие, называемое взаимодействием, явно не подходит к первой иллюстрации, когда мы сравнивали четыре сорта пшеницы. Каждая из четырех обработок (сортов) была представлена только одним уровнем. Дифференциальный эффект обработок, например дифференциальный урожай сорта А по сравнению с сортом В, можно оценить по разности а—b между урожаем а сорта А и урожаем b сорта В в некотором данном блоке. Любые влияния, характеризующие этот блок с точки зрения возможного урожая, должны рассматриваться как одинаковые для А и В. Кроме того, все влияния считаются аддитивными, так что разность а—b в любом блоке не зависит от характеристик этого блока. Следовательно, подходящей мерой дифференциального эффекта А относительно В может служить усредненная по всем блокам оценка разности а—Ь.
9.6. ПОТРЕБНОСТЬ В РАЗРАБОТКАХ ПО УМЕНЬШЕНИЮ РАЗМЕРОВ БЛОКОВ
Чтобы оценить по достоинству число обработок, которое может потребоваться даже в каком-либо небольшом исследовании, рассмотрим ситуацию, когда мы пытаемся оценить влияние двух различных удобрений, скажем, на урожай пшеницы. Мы хотели бы знать функцию z=f(x, у), выражающую зависимость урожая (z) на акр от х — количества фосфатов, а у — количества нитратов, внесенных на поле с обычным плодородием и при обычных климатических условиях. Перед нами стоит задача построения настолько точной, насколько это 453
возможно, поверхности отклика z=f(x, у) по конечному числу наблюдений (zi, Xi, yi), (z2, x2i Уг),..., (z^ xk, yk). Проблему больших ошибок эксперимента мы оставляем в стороне. Даже если каждое удобрение варьирует только на четырех уровнях (допустим, 0, поверхностное, среднее и глубокое внесение), то число комбинаций обработок фосфатом на уровне г с нитратом на уровне s(r, $=1, 2, 3, 4) должно достигнуть 16. А при более двух обработках, когда каждая на нескольких уровнях, число комбинаций может стать слишком большим для размещения в одном относительно однородном блоке.
Такие трудности характерны не только для экспериментов, где оцениваются эффекты разных комбинаций из различных уровней и интенсивности обработок. Они могут возникать в любом сравнительном эксперименте. Следовательно, планы должны строиться с учетом того, что понадобится обходить подобные затруднения с помощью различных изобретений, направленных на уменьшение объемов блоков без больших потерь информации.
9.7. СБАЛАНСИРОВАННЫЕ НЕПОЛНЫЕ БЛОКИ ДЛЯ СРАВНЕНИЯ ОДНОУРОВНЕВЫХ ОБРАБОТОК
В полностью рандомизированном блочном плане, представленном на рис. 9.4.1, каждый блок содержит все 4 обработки А, В, С и D. Допустим теперь, что по чисто практическим причинам в одном блоке удается разместить только три обработки. Такой блок окажется неполным (поскольку не будет содержать всех обработок). Для балансировки нужна некоторая симметрия между блоками. В сбалансированном неполноблочном плане требования «баланса» следующие:
каждая обработка должна встречаться в каждом блоке один и только один раз;
число блоков, содержащих данную обработку, должно быть одинаковым для всех обработок;
число блоков, содержащих данную пару обработок, должно быть одинаковым для всех пар.
Пример 9.7.1. Четыре обработки в шести блоках. Для примера с
четырьмя обработками и шестью блоками возьмем:
Блок 1: А, В л
Блок 2: В, С
Блок 3: С, D расположение обработок эксперименталь-
Блок 4: В, D [ ных единиц по блокам рандомизировано.
Блок 5: А, С
Блок 6: A, D j
Вот альтернативный способ представления этих данных:
Блок 1 2 3 4 5 6
А X X X
Обработки В X X X
С X X X
D X X X
454
Здесь дифференциальный эффект А и В можно оценить из а—b в блоке 1, для В и С — из b—с в блоке 2 и т. д. Это слишком простой пример, поскольку каждый блок содержит только одну пару обработок. Вот более интересный пример с четырьмя обработками по три в каждом из четырех блоков:
Блок 1 2 3 4
А X X X
Обработки В X X X
С X X X
D X X X
Здесь дифференциальный эффект АиВ можно оценить из а—b в блоке 1, а также из а—b в блоке 2. Их усреднение дает эффективную оценку. То же для А и С из блоков 1 и 3, и т. д.
Из сказанного ясно, что конструкция сбалансированного неполноблочного плана глубоко связана с комбинаторным анализом. Существуют соответствующие представления планов для различных чисел обработок, размеров блоков и чисел блоков (см. список литературы в конце главы).
9.8. ПОЛНЫЙ ФАКТОРНЫЙ ПЛАН
Когда мы сталкиваемся с обработками, которые можно прилагать к экспериментальным единицам одновременно и возможны несколько уровней воздействия, «полным» планом называют блоки, каждый из которых включает любую комбинацию уровней обработок. Такой план называют планом «полного перебора» или «полным факторным» планом. Например, для двух удобрений А и В эксперимент с полным перебором 2x3, где А варьирует на двух уровнях Ао и Ait а В — на трех уровнях Во, и В2, содержит всего 2x3 = 6 комбинаций Аг и Bs, и его можно представить в виде
Уровень фактора В
в. В\ В2
Уровень фактора А ^0 X X X
А ] X X X
При третьем факторе С на двух уровнях Со и Ci получится 2x3x2=12 комбинаций Ar Bs и Ct, которые имеют вид:
455
50 О «5 Вг в0 С, Вг
Ао X X X X X X
л, X X X X X X
9.8.1. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ: ДВА ФАКТОРА НА ДВУХ УРОВНЯХ
Рассмотрим сначала план 22, который представляет собой план для двух факторов А и В на двух уровнях: «нижнем» (Ао, Во) и «верхнем» (На практике «нижний» уровень фактора А может
означать полное отсутствие обработки А, аналогично и для В.) Наиболее простой метод для анализа состоит в следующем. Уровни обработки и соответствующие им отклики кодируются так:
Уровень А Код Уровень В Код Отклик
Ао х0 Во Уо Z(X0, У о)
Л, Xi Во Уо z(x(, Х0)
Ао Хо в. У1 z(x0, у,)
А, Х1 5, У1 z(x,, у,)
Этими данными можно воспользоваться (временно пренебрегая ошибками опыта) для построения некоторой обусловленной функции вида z=f(x, у), например
Z = 0О + 0Ю* + 0о1 У + 01 ixy.
Более реалистично, не пренебрегая ошибкой эксперимента, для подбора искомой функции применить какую-нибудь сглаживающую процедуру, вроде метода наименьших квадратов. Полученное уравнение в дальнейшем может быть использовано для построения линий равного отклика этой поверхности.
Методы такого рода обычны в современной практике. Например, в прикладной химии они предназначены для локализации максимума поверхности отклика. Это особенно удобно, когда можно относительно быстро проводить новые опыты с различными комбинациями уровней факторов, что позволяет работать с помощью методов «влезания на гору» для приближения к максимуму (эволюционное планирование*), и когда контуры линий равного отклика в окрестностях
* Упоминание автором в таком контексте метода эволюционного планирования, видимо, связано с оговоркой. Скорее всего речь идет о методе «крутого восхождения». — Примеч. пер.
456
максимума хорошо описываются эллипсами с одинаковыми фокусами. Однако долгое время этот подход не считался особенно продуктивным. В качестве первой цели такого эксперимента выдвигалось общее (эффективное) описание поверхности отклика, а не отыскание ее максимума. С учетом представлений о главных эффектах и взаимодействиях развитый метод можно непосредственно обобщить на любое число факторов и любое число уровней. Так, в плане 2x2 (два фактора на двух уровнях) эффект (или главный эффект) А пропорционален разности между:
1) средним по всем откликам из комбинаций обработок, включающих верхний уровень А, и
2) средним по всем откликам из комбинаций обработок, включающих нижний уровень А.
Главный эффект В определяется аналогично.
Взаимодействие между А и В пропорционально разности между:
1) эффектом увеличения А при В, зафиксированном на верхнем уровне, и
2) эффектом увеличения А при В, зафиксированном на нижнем уровне. (В последнем определении буквы А и В, конечно же, можно было бы поменять местами.) Таким образом, взаимодействие — это мера неаддитивности эффектов А и В относительно отклика. Например, увеличение концентрации углерода в стали без вольфрама может определенным образом повлиять на прочность, но этот эффект может оказаться совершенно другим после того, как в сплав будет введено определенное количество вольфрама [ср. с разделом 11.3.5].
Обозначение z=f(x, у) не вполне подходит к такому взгляду на вещи. Удобна и широко распространена следующая система обозначений:
Уровень А Уровень В Код
Ао в0 (1)
А 1 в» а
Ао В, b
А 1 В, ab
Здесь а указывает, что фактор А находится на верхнем уровне, Ъ — что фактор В находится на верхнем уровне, ab — что оба фактора на верхнем уровне, тогда как обозначение (1), не содержащее ни а, ни Ь, указывает на то, что оба фактора на нижних уровнях. Не возникнет никаких неоднозначностей, если мы воспользуемся теми же обозначениями не только для комбинаций уровней факторов, но и для соответствующих им откликов. Тогда главный эффект фактора А будет пропорционален
(a+ab) - ((1)+д).
Заметим, что это выражение можно было бы получить, раскрыв скобки в
457
(a-1) (d+1)
имея в виду, что обозначение 1 надо читать как (1), т. е. как обозначение отклика, полученного при обоих факторах на нижних уровнях.
Аналогично главный эффект В пропорционален
(b + ab)—((1)+а) = (а+1) (b— 1)
(с той же оговоркой относительно (1)), и взаимодействие А и В пропорционально
(ab-b)-(a-m
или, что эквивалентно,
(ab-a)-(b-(V)).
Помня о принятом ранее соглашении относительно 1 и (1), получим, что оба эти выражения можно представить в виде
Когда в блоке присутствует по одному представителю от каждой из четырех комбинаций обработок (1), a, b, ab, за неимением информации о вариабельности данных для четырех откликов можно выразить результаты в аналогичной, но интуитивно кажущейся более информативной форме, а именно в виде статистик, включающих: 1) три меры эффектов обработок — два главных эффекта и взаимодействие и 2) «эффект блока», измеряемый общим средним данного блока. При обычном предположении об аддитивности влияния всех откликов внутри блока равноценны (аддитивны). Значит, эффекты обработок, оцениваемые внутри блока, не оказывают влияния на эффект блока.
В жизни, конечно, нельзя игнорировать вариабельность откликов. Допустим, что есть всего к блоков, каждый из которых содержит (в случайном порядке) все четыре комбинации обработок. Тогда главные эффекты и эффект взаимодействия можно оценить, усредняя по всем блокам соответствующие статистики, полученные в каждом блоке. А средние по к индивидуальным блокам можно использовать для оценки эффектов блоков. Следовательно, из 4к отдельных наблюдений 3+к величин могут служить для оценивания, что оставляет 4к—(3 + +к)-3(к—1) наблюдений для получения оценки вариабельности, на которой можно построить проверку значимости оцененных эффектов.
9.8.2. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ: ТРИ ФАКТОРА НА ДВУХ УРОВНЯХ
Для плана 23, в котором три фактора А, В и С варьируют (каждый) на двух уровнях, кодирование выглядит так:
458
Уровень А Уровень В Уровень С Код
Ад Вд Со (1)
At Вд Со а
Ад В\ Со b
л, Bl Со ab
Ад Вд С, с
At Вд Cl ас
Ад Bl Cl Ьс
А. Bl Cl abc
Главный эффект А, как и раньше, пропорционален разности между:
1) средним по всем комбинациям обработок, включающим верхний уровень фактора А (сумма всех таких откликов равна a+ab+ac+abc) и
2) средним по всем комбинациям обработок, включающим нижний уровень фактора А (сумма всех таких откликов равна ((1)+£>+с+£>с).
Значит, главный эффект фактора А пропорционален (a+ab+ac+abc) — ((l)+a+b+c+bc),
и следовательно, с учетом соглашения, что 1 обозначает (1), это эквивалентно выражению
(a—1)(Z>+1)(с+1).
Аналогично для главных эффектов факторов В и С соответствующие комбинации откликов вычисляются по формулам:
(для В): (д+1) (b— 1) (с+1), (для С): (я+1) (£>+1) (с—1).
В этом случае существуют четыре взаимодействия: три взаимодействия второго порядка* Ас В, АсСиВсС плюс тройное взаимодействие А, В и С. Их определения аналогичны тем, что были использованы для эксперимента 22. Например, взаимодействие АВ определяется разностью между:
1) эффектом повышения А при условии, что В зафиксирован на верхнем уровне, а по всем уровням С проведено усреднение, и
2) соответствующим эффектом, полученным для В, зафиксированного на нижнем уровне.
* Здесь автор пользуется терминологией, которая противоречит общепринятой и может вызвать ошибочное понимание. О взаимодействиях двух факторов обычно говорят как о взаимодействиях первого порядка (а не второго, как у автора) или о парных взаимодействиях. Тогда соответственно три фактора будут давать взаимодействия второго порядка, или тройные взаимодействия, и т. д. Имея это в виду, мы всюду далее правим авторскую терминологию без специальных указаний. — Примеч. пер.
459
Здесь эффект 1 пропорционален
(ab+abc) — (b+bc),
а эффект 2 пропорционален
(а+ас) — ((1) + с).
Таким образом, взаимодействие факторов А и В (АВ - взаимодействие) в полученной комбинации откликов определяется из
(ab+abc) — (b+bc) — (д+ас) + ((1)+с).
Это выражение можно получить непосредственно из
(я—1) (6—1) (с+1).
Аналогично для взаимодействия АС имеем
(а-1) (6 + 1)(с-1),
а для взаимодействия ВС
(а+1) (6—1) (с—1).
Наконец, тройное взаимодействие АВС представляет собой разность между тем, что можно назвать частным взаимодействием Л В на верхнем уровне фактора С, а именно
(abc—Ьс) — (ас—с),
и соответствующей комбинацией на нижнем уровне С:
(ab-b) - (а-(1)), откуда тройное взаимодействие получается из формального выражения
(а-1) (6-1) (с-1).
В приведенных вычислениях все отклики относились к одному блоку. На практике может встретиться несколько блоков, скажем к. Тогда эффекты обработок надо оценивать, усредняя по всем блокам отдельные оценки, получаемые в каждом из них. Так, главный эффект фактора А надо будет оценивать, вычисляя статистику (а—1) (Ь+ + 1) (с+1) для каждого блока отдельно, а затем усредняя по всем блокам. И точно так же — по всем остальным главным эффектам и эффектам взаимодействия. Индивидуальные наблюдения, которых теперь 8к(23 = 8 в каждом из к блоков), можно использовать для оценки семи эффектов обработок (три главных эффекта, три взаимодействия второго порядка, одно тройное взаимодействие) и еще к блоковых средних, оставляющих 8к—7—к-1(к—1) эффективных наблюдений для оценивания вариабельности.
460
9.8.3. ГЛАВНЫЕ ЭФФЕКТЫ И ВЗАИМОДЕЙСТВИЯ В ПЛАНЕ 2'
В эксперименте с полными блоками, где каждый из t факторов представлен на двух уровнях в каждом блоке (на блок приходится 2‘ наблюдений), для анализа откликов внутри любого такого блока надо вычислить:
средний выход в данном блоке,
t главных эффектов, по одному для каждого фактора,
= —1) взаимодействий первого порядка,
= —1) (t—2) взаимодействий второго порядка,
• « •
взаимодействий порядка t—1 и
v 7 (единственное) взаимодействие порядка t.
В итоге это составит
({)++(;н_.
оценок эффектов обработок. На практике оценки должны усредняться по к блокам. В дополнение к к отдельным блоковым средним можно вычислить эффекты блоков. После вычисления этих 2'—1+А: статистик на основе 21к исходных наблюдений останется еще
2'£—(2'—1+£) = (2'—1) (Ar—1) эффективных наблюдений, которыми можно воспользоваться для вычисления вариабельности.
9.9. НЕПОЛНЫЕ БЛОКИ: СМЕШИВАНИЕ
Когда по экономическим или техническим соображениям, или просто по договоренности не все комбинации обработок могут быть представлены в каждом относительно однородном блоке факторного эксперимента, приходится применять различные стратегии для планирования неполных блоков. Один из главных критериев сравнения подходящих неполноблочных планов основан на представлении о смешивании.
Допустим, что в эксперименте 23 в один блок удается объединить только 4 комбинации обработок. А поскольку всего надо рассматривать 8 комбинаций обработок, то оказывается невозможным (рандомизированное) повторение всех обработок во всех блоках. Рассмотрим последствия такого разделения обработок по блокам:
блок 1: (1), a, b, ab, блок 2: с, ас, be, abc.
Отклики в этом случае можно представить так:
461
блок 1: (1), a, b, ab, блок 2: с+Х, ec+dc+X, abc+\,
где X представляет собой дифференциальный эффект блока, обусловленный, например, большей урожайностью блока 2 по сравнению с блоком 1. Блок 2 отличается от блока 1 тем, что в нем все отклики скомбинированы так (аддитивно); что
1) имеют фактор С на верхнем уровне и
2) включают отклики, относительно более высокие, чем в блоке 1, благодаря дополнению «эффекта блока» X.
В таком случае говорят: фактор С оказывается смешанным с блоками, что искажает некоторые (но не все) оценки эффектов обработок. Для облегчения вычислений эффектов взаимодействия удобно воспользоваться табл. 9.9.1, где символы в шапке соотносятся с соответствующими обозначениями строк, использованными ранее в экспериментах с полными блоками. Здесь главные эффекты обозначены А, В, С, взаимодействия А с В — АВ и т. д. Те комбинации обработок , которые относятся ко второму блоку и для которых отклики увеличены на величину X, отмечены звездочкой. В полном факторном плане взаимодействие АВ вычисляется по формуле
(1)—а—b+ab+c—ас—bc+abc.
Таблица 9.9.1.
А в АВ с АС ВС АВС
(1) — — + — + + —
х а + — — — — + +
*Ь — + — — + — +
ab + + + — — — —
х*с — — + + — — +
*дс + — — + + — —
*Ьс — + — + — + —
х *abc + + + + + + +
В смешанном плане при рассмотрении откликов (отмеченных звездочкой) с, ас, be, abc надо подставлять соответственно с+Х, ас+Х, bc+X, abc+X. Поскольку они используются в формуле для взаимодействия АВ, куда входят два положительных и два отрицательных значения, то суммарный вклад X в оценку равен нулю. Следовательно, взаимодействие АВ оценивается правильно. Из таблицы знаков сразу видно, что то же 462
относится и ко всем главным эффектам и взаимодействиям, за исключением главного эффекта фактора С, для которого расчет будет давать слишком большое значение, увеличенное на величину 4Х. Из-за того что эффект обработки С смешан с эффектом блоков именно таким образом, оказывается невозможным оценить главный эффект С. Искусство смешивания, а значит, и искусство планирования сравнительных экспериментов состоит в распределении комбинаций между неполными блоками таким образом, чтобы те эффекты обработок, которые не надо оценивать (или можно оценить с меньшей точностью, чем остальные), экспериментатор смог отнести к тем, чем надо пожертвовать. Обычно главные эффекты гораздо более интересны, чем эффекты взаимодействий высоких порядков. В рассмотренном эксперименте 23, когда в каждом блоке размещается только по 4 обработки, следующее расположение смешивает с блоками трехфакторное взаимодействие, но оставляет свободными главные эффекты и взаимодействия первого порядка:
блок 1: (1), ab, ас, Ьс,
блок 2: ab, с, abc.
Те комбинации обработок, которые относятся к блоку 2 по этой схеме, отмечены в табл. 9.9.1 знаком х. Если каждый из отмеченных крестиком откликов увеличивается на величину X благодаря эффекту блока, то можно показать, что в формуле, например, для эффекта АВ два отклика из блока 2 фигурируют со знаком плюс, а два — со знаком минус, так что итоговый вклад эффекта блока X равен нулю. Аналогично обстоит дело со всеми главными эффектами и парными взаимодействиями.
9.10. ЧАСТИЧНОЕ СМЕШИВАНИЕ
В обычном дробном эксперименте, допустим, с четырьмя повторениями, мы можем получить четыре варианта блока 1 и блока 2 с описанной выше структурой. Оценки трех главных эффектов и трех парных взаимодействий будут иметь точность, соответствующую числу повторений, но при этом не будет никакой информации о тройном взаимодействии.
Однако можно модифицировать эти реплики так, чтобы оказались смешанными различные взаимодействия. Например:
Вариант реплик 1 и ш IV
(1) а (1) а (1) а (1) ь
ab Ь ab Ь Ь с а ab
ас с с ас ас ab Ьс с
Ьс abc abc Ьс abc Ьс abc ас
Смешивание АВС АВ АС ВС
463
В данном случае из первой реплики нельзя определить трехфакторное взаимодействие, зато его можно оценить во всех остальных вариантах. Итог состоит в том, что по сравнению с экспериментом того же объема, но с такими репликами, в которых присутствуют все повторения, этот модифицированный план оценивает главные эффекты с той же точностью, парные взаимодействия с меньшей точностью, а, кроме того, еще и тройное взаимодействие (если удастся, то с той же точностью, что и парные взаимодействия).
Это называется частичным смешиванием.
9.11. ФАКТОРЫ НА ТРЕХ И БОЛЕЕ УРОВНЯХ
Ясно, что планы с полным перебором факторов на всех уровнях не ограничиваются двухуровневыми факторами. Представления о главных эффектах, взаимодействиях и смешивании можно распространить на планы, в которых факторы имеют три или более уровней. Однако мы ограничимся лишь простыми частными случаями.
9.11.1. ЛАТИНСКИЙ КВАДРАТ
Самый важный из частных случаев — это план латинского квадрата, когда рассматриваются три фактора, каждый на 5 уровнях, где s может быть равно 2, или 3, или 4, или ... Для каждого фактора можно оценить дифференциальный эффект уровней i и у, но нет информации о взаимодействии между факторами. Такой план, в частности, приемлем для экспериментов, где разумно считать, что три фактора будут независимыми (т. е. не будут иметь взаимодействий). В качестве примера можно рассмотреть эксперимент с исследованием зависимости ходимости автомобильных шин от давления в камере, положения колеса и скорости езды*. Прежде всего предположим, что между давлением, положением колеса и скоростью нет взаимодействий (для любой пары). Затем, поскольку у автомобиля 4 колеса, а значит, и 4 возможных положения, число уровней для давления и для скорости тоже надо положить равным 4. Тогда комбинации давления (Рь Р2, Р3, Р4), положений (Li, L2, L3, L4) и скоростей (SH S2, S3, S4) можно представить в квадратной таблице:
Pl p, P.
^1 Li 1-з Lt s2 Si St ^on on on on On On On On 1 - ю w *. On On On o.
* Аналогичный пример обсуждается в книге X и к с Ч. Основные принципы планирования эксперимента /Пер. с. англ.; Под ред. В. В. Налимова.— М.: Мир, 1967,— С.97—100.— Примеч. пер.
464
Здесь четыре уровня одного фактора (Рь Р2, Рз, Р4) задаются четырьмя столбцами, четыре уровня другого фактора L2, L3, L4) — четырьмя строками, а уровни Sx, S2, S3, S4 последнего фактора располагаются в квадратной решетке 4x4, задаваемой строками и столбцами, образующими как раз латинский квадрат, т. е. решетку, устроенную таким образом, что каждый из четырех символов Si, S2, S3, S4 встречается однажды в каждой строке и однажды в каждом столбце. (Латинские квадраты обычно описываются с помощью латинских букв А, В, С,... Вот примеры латинских квадратов в таких
обозначениях:
А В С D A D С В
В С D A D В А С
С D А В В С D А
D А В С С А В D
Существуют таблицы латинских квадратов различных размеров [см.,
например, Fisher and Yates (1957) — G]. В таблицах они представлены в стандартных формах. Одну из них можно выбрать случайно. Один квадрат из семейства можно получить с помощью рандомизации. Наконец, распределение факторов по строкам, столбцам и латинским буквам тоже проводится случайно.)
Полный факторный план для трех факторов на четырех уровнях требует 43=64 комбинаций обработок в каждой реплике-повтора. А латинский квадрат требует всего 16 таких комбинаций. Экономия достигается здесь, конечно, за счет потери информации относительно взаимодействий.
Если мы обозначим символом (г, с, t) результаты эксперимента, соответствующего r-й строке, с-му столбцу и t-му уровню St «латинской буквы», г, с, t= \, 2, 3, 4, то данные для квадрата с положением Lr, давлением Рс и скоростью S примут вид
(1, 1, 1) (1, 2, 3) (1, 3, 4) (1, 4, 2)
(2, 1, 2) (2, 2, 1) (2, 3, 3) (2, 4, 4)
(3, 1,3) (3, 2, 4) (3, 3, 2) (3, 4, 1)
(4, 1, 4) (4, 2, 2) (4, 3, 1) (4, 4, 3)
Отсутствие взаимодействий между факторами влечет за собой аддитивность их эффектов. Из представленного варианта таблицы хорошо видно, что сумма откликов в столбце с будет оценивать эффект Рс, усредненный по всем положениям и скоростям, с=1, 2, 3, 4. Значит, дифференциальный эффект увеличения давления от уровня 1 до уровня 2, усредненный по всем положениям и скоростям, можно оценить по разности между суммой столбца 2 и суммой столбца 1. Аналогично разность между итогами строк Г] и г2 оценивает дифференциальный эффект положения колеса в позициях гх и г2. Если, наконец, мы возьмем сумму четырех наблюдений (1,1, 1), (2, 2, 1), (4, 3, 1), (3, 4, 1), 465
соответствующих уровню 1 факторов скорости, и вычтем из нее сумму четырех измерений (2, 1, 2), (4, 2, 2), (3, 3, 2), (1, 4, 2), соответствующую S2, то получим оценку дифференциального эффекта от увеличения скорости испытания автомобиля при переходе от уровня 1 к уровню 2.
Модификация: фиктивные уровни. Отметим, что можно ослабить требование об одинаковом числе уровней для всех факторов. Положим, например, что испытания ходимости шин приходится проводить на машине, имеющей только три скорости, а именно S2, S3. Мы можем подогнать эту ситуацию под схему латинского квадрата, сохранив исходный план и приравняв S4 к одной из скоростей. Если, например, наивысшая скорость требует повышенного внимания, мы можем положить S4 = S3.
9.11.2. ГРЕКО ЛАТИНСКИЙ КВАДРАТ
План латинского квадрата (5x5), в котором сравниваются три фактора, каждый на 5 уровнях, можно обобщить для сравнения четырех факторов, снова каждый на 5 уровнях и снова с ограничением, связанным с тем, что нет информации о взаимодействиях между факторами. Следовательно, такой план приложим только в тех случаях, когда все четыре фактора независимы, т. е. аддитивны. В комбинаторном анализе греко-латинским квадратом называется расположение такого типа:
Аа By С0
Су А/3 Ва
ВЦ Са Ау
Здесь латинские буквы сами по себе образуют латинский квадрат. То же — и греческие буквы. Кроме того, греческая буква а встречается однажды с А, однажды с В и однажды с С. Аналогично и для у.
Говоря о приложениях планирования эксперимента, вернемся к примеру с ходимостью шин, но добавим еще качество дорожного покрытия как четвертый фактор. Как и раньше, выделим четыре столбца для уровней фактора давления Р,, строки для указания положения колеса Lt, а для скорости оставим латинские буквы S,-. Четыре уровня нового фактора Qt, Q2, Q3, (2 4 будем обозначать греческими буквами. Вот таким может быть греко-латинский квадрат:
Р, Р1 р> pt
S. Q, S2 Qi «3 2з S4 24
S2 2з S, 2д «4 21 s3 Qi
Сз «з 2д «4 2з Si Qi s2 2.
Lt S4 Q1 «з 2. s2 Q> S, 2з
466
Как и раньше, дифференциальный эффект увеличения давления с самого низкого уровня до второго, усредненный по всем положениям, скоростям и качествам дорожного покрытия, оценивается по разности между итогом столбца 1 и итогом столбца 2. То же для эффектов положения и т. д. Наконец, итог по всем наблюдениям, в которых встречается символ Q4, уменьшается на соответствующий итог для Q2, что приводит к оценке дифференциального эффекта качества дороги между уровнями 4 и 2.
Как и для латинских квадратов, составлены таблицы греко-латинских квадратов всех размеров, которые требуются чаше всего, за исключением квадрата 6x6.
9.12. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Рассмотренные в этой главе проблемы были изучены Р. Фишером и Ф. Йейтсом в тридцатые годы. Книга [Fisher (1951)] впервые опубликована в 1935 г., а классическая монография Йейтса о факторных экспериментах — в 1937 г. [см. Yates (1937)]. Широко известные статистические таблицы Фишера и Йейтса [Fisher ahd Yates (1967)—G] впервые появились в 1938 г. Этот объемистый том — не только собрание стандартных таблиц статистических функций. В нем содержатся также таблицы латинских квадратов и сбалансированных неполных блоков, сопровождающиеся подробными комментариями.
Ниже предложен список лучших работ других авторов.
F i s h е г R. А. (1951) The Design of Experiments (1950). Sixth edition, Oliver and Boyd.
F i n n e у D. J. (I960). An Introduction to the Theory of Experimental Design, University of Chicago Press.
Cochran W. G. and Cox G. M. (1957) Experimental Designs (Accord, ed.), Wiley.
С о x D. R. (1958). Planning of Experiments, Wiley.
D a v i e s O. L. (editor) (1954). The Design and Analysis of Industrial Experiments, Oliver and Boyd.
F i n n e у D. J. (1955). Experimental Design and its Statistical Basis, University of Chicago Press.
Kempthorne O. (1952). The Design and Analysis of Experiments, Wiley.
Y a t e s F. (1937). The Design and Analysis of Factorial Experiments, Imperial Bureau of the Soil Science.
V a j d a S. The Mathematics of Experimental Design: Incomplete Block Designs and Latin Squares, Griffin.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
МаркоцаЕ. В., Л исенковА.Н. Комбинаторные планы в задачах многофакторного эксперимента. — М.: Наука, 1979. — 345 с.
М а р к о в а Е. В., М а с л а к А. А. Рандомизация и статистический вывод. — М.: Финансы и статистика, 1986. — 208 с.
Глава 10
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И АНАЛИЗ СТАТИСТИЧЕСКИХ ЭКСПЕРИМЕНТОВ: ВЫРОЖДЕННЫЕ МОДЕЛИ, МНОЖЕСТВЕННЫЕ КРИТЕРИИ
10.1. ВЫРОЖДЕННЫЕ МОДЕЛИ
10.1.1 ВВЕДЕНИЕ
Во всех методах, обсуждавшихся в гл. 8, предполагалось, что основная модель E(Y) = A0 имеет полный ранг*, т. е. что матрица А имеет ранг р, равный числу подлежащих оценке параметров, или, что эквивалентно, матрица АА не вырождена**. Многие важные модели, в частности из области планирования эксперимента, — это вырожденные модели, в которых матрица А имеет ранг s<p. Следовательно, матрица А А размера (рхр) вырождена, поскольку ее ранг точно такой же, что и у матрицы А.
В некоторых примерах [см. примеры 8.2.6, 8.2.10, 8.2.14 и 8.3.8] мы рассматривали планы односторонней (однофакторной) классификации с моделью
yij = lii + eij, /=1,...,/; /=1,.(10.1.1) Такая параметризация приводит к модели полного ранга (здесь р=Г). Ее матрица плана А рассматривалась в примере 8.2.6, а матрица A A=diag(Ji, J2,.где Jz — число наблюдений в группе с номером Ясно, что такая параметризация чувствительна. Действительно, есть I групп наблюдений, которые соответствуют каждому из I условий (обработок), а модель выделяет по одному параметру на каждую обработку.
Существует, правда, заманчивая альтернатива: выражается как Hi=a + bj, /=1, 2,..., I,
т. е. щ рассматривается как заданная константа а, одинаковая для всех обработок, и некоторое отклонение от а, характеризующее ью обработку. Эта параметризация обладает симметрией, но здесь по-
* См., например: Мишина А. П., Проскуряков И. В. Высшая алгебра.—С. 54—62— Примеч. пер.
"Там ж е.—С. 71.—Примеч. пер.
468
являются 1+1 параметров, хотя понятно, что мы фактически можем оценить только I из них. У нас появился лишний параметр. Дело в том, что формула „.-ад-Ь.
явно не имеет смысла, поскольку она эквивалентна выражению
/х( = (а + а) + (bj—а) = а' + Ь-
при любом значении а. Правда, ей можно придать смысл, налагая на bj линейное ограничение. Наипростейшее из приемлемых ограничений заключается в том, чтобы для каждой группы, содержащей одинаковое число наблюдений, положить
LZ>, = 0.
Этим при желании можно было бы воспользоваться для выражения одного из bj через остальные и подстановки полученного значения в нашу формулу
fij = a+b.
На практике часто предпочитают сохранять «избыточную» форму с соответствующим дополнительным линейным ограничением в роде Y,bj = O. (Этот подход обсуждается более подробно в разделе 10.1.2.) Таким образом, наша модель принимает вид
(вместе с наложенным ричным обозначениям
yij=a + bi + eij (10.1.2)
на bj линейным ограничением). Переход к мат-дает
или более подробно:
1 1 0
_лл_ 1 1 0
^21 1 0 1
— 1 0 1
Л1 1 0 0
1 0 0
*п
*21
%
еп
(10.1.3)
где 6-[а, b\, b2...,bj\' включает (/+1) компонентов, а матрица А имеет порядок лх(/+1), n=Y.Jj — общее число наблюдений. Поскольку первый столбец матрицы А представляет собой сумму всех остальных столбцов, ранг (А)<(/+1) и, таким образом, мы имеем вырожденную модель (в данном случае р=/+1).
469
Имея вырожденную модель Е(У)-А6, для которой ранг матрицы A-s<p, мы всегда можем выбрать новые параметры так, чтобы для
<t>s получилась модель полного ранга E(Y) = B0. Эти новые параметры, которые можно выбрать различными способами, оказываются независимыми линейными функциями от Так, например,
начав с вырожденной формулировки для односторонней классификации, приведенной в (10.1.3), мы можем ввести новые параметры
PL\=a+b\, p1^a+b1,...,pI = a+bl
и пересчитать модель в невырожденную форму, приведенную в (10.1.1). Другая репараметризация рассматривается в (10.1.5). Тогда модель можно анализировать стандартными методами, обсуждавшимися в гл. 8.
Однако, как замечено ранее, иногда есть причины для того, чтобы предпочесть вырожденную модель модели полного ранга. Так, в ситуации планирования эксперимента модель обычно получается перепара-метризованной, поскольку это наиболее естественный способ описания задачи, и параметры, используемые в такой модели, допускают простую интерпретацию с точки зрения данного исследования. Отсюда проистекает интерес к приложению метода наименьших квадратов непосредственно к вырожденной модели.
10.1.2. ОЦЕНИВАНИЕ. ФУНКЦИИ, ДОПУСКАЮЩИЕ ОЦЕНКУ
Если для вырожденной модели E(Y) = A0 при rank (A)-s<p^n, мы попытаемся, как в разделах 8.1 и 8.2, минимизировать^форму S(u) = (y—Au) (у—Au), то снова обнаружим, что МНК-оценке 0 для 9 удовлетворяют нормальные уравнения (8.2.2), а именно
AA0 -AY.
Однако их решение теперь не удается представить в форме 6 -= (AA)-‘AY, поскольку матрица А А не имеет обратной. Фактически эти уравнения вообще не имеют единственного решения, а дают бесконечное множество их.
На первый взгляд этот результат кажется обескураживающим. Метод, который дает множество различных оценок одного и того же, вряд ли может оказаться полезным. Однако правильная интерпретация покажет, что определенные компоненты вектора 0 нецелесообразно оценивать количественно. Это можно легко заметить на примере однофакторного плана. Ожидаемый отклик для группы / равен Е(/,) = «+ + Ь/, и, как отмечалось ранее, он не изменится, если мы заменим а на (а+а) и bj на (Z?z—а) для произвольной константы а. Отсюда и возникает основа для неопределенности в модели (которая ведет и к соответствующей неопределенности в оценках параметров), обусловленная тем фактом, что в структуре модели больше параметров (р), чем это абсолютно необходимо (з). Вырожденность матрицы А'А оказывается просто алгебраическим следствием этой особенности модели.
470
Тем не менее существуют вещи, которые можно оценивать, а именно некоторые линейные функции от Они известны как
функции, допускающие оценку, и обладают следующими свойствами:
а) каждый элемент E(Y) = A0 допускает оценку;
б) если X'0=X,0i+... + Хр0р (где X задана) — функция, допускающая оценку^т. е. единственная оценка метода наименьших квадратов, а именно Х0 , которая не зависит от того, какое из решений 0 системы нормальных уравнений использовать. Более того, эта оценка Х9 доставляет минимум дисперсии для несмещенного линейного оценива-теля Х'0;
в) максимальное число линейно независимых функций, допускающих оценку, равно 5, следовательно, любые другие такие функции можно получить в виде линейных комбинаций исходных. Любые 5 линейно независимых функций, допускающих оценку, могут служить в качестве новых параметров в репараметризации модели, обладающей полным рангом.
Односторонняя классификация иллюстрирует эти моменты: (a + bj), — это независимые функции, допускающие оценку, а
их линейные комбинации есть ЛНОМД. Мы можем увидеть это уже в невырожденной формулировке задачи, когда Hj = a+bj.
Кроме того, из полученных выше результатов следует, что какое бы решение 0 нормальных уравнений мы~не использовали, все равно получатся одни и те же остатки е = (у—Ад ), а значит, и одна и та же остаточная сумма квадратов (ОСК), т. е. г=е'е. Более того, как и в случае полного ранга, мы можем получить
уу=0 АА0 +г, поскольку для получения этого результата достаточно воспользоваться нормальными уравнениями, а не непосредственно формулой 0 = = (А/А)-1А/у. Значит, мы получим еще и ту_же самую сумму квадратов, обусловленную моделью (СКМ), т. е. 0 'А' А0 , какая бы оценка 0 ни использовалась, причем ее тоже можно выразить в виде СКМ = 0 А'у, как и в том случае, когда г(А)=р. На самом деле эти значения ОСК и СКМ в точности такие же, как если бы мы репара-метризовали модель в модель полного ранга вида Е(У) = Вф, где СКМ = ф'В'у, а ОСК = у у—ф B y [см. раздел 8.3.4].
Выходит, мы можем выбрать любое частное решение системы нормальных уравнений, а затем наложить ограничения, которым будет удовлетворять только одно из этих решений. В частности, будем требовать, чтобы 0 удовлетворяло независимым линейным ограничениям, или дополнительным условиям. Число таких условий должно быть равно числу избыточных параметров в нашей модели, т. е. (р—s). Точнее, мы имеем: ~
gl|0| +0 1202 + •••+£1р0р =0, ^2101 +^2202 + • • • + §2р^р — 0, Sp—sJ01 + Sp—s,2@2 + ••• + Sp—s,p®p ~ 0,
471
где коэффициенты g,j известны и выбраны так, чтобы матрица G = \Sij} имела ранг, равный (р—s). Для матрицы G эти условия соответствуют просто равенству G0=O. Совершенно ясно, что такие ограничения приведут к неопределенности в модели, поскольку эти уравнения придется применить для элиминирования (р—s) параметров из модели (при решении их относительно остальных), что и приводит при другом выборе параметров к модели полного ранга.
Теперь можно оценить 9, выбирая 9 так, чтобы минимизировать (у—Au)(y—Аи) при условии Gu=0.
При этом оказывается, что вектор 9 должен удовлетворять не только нормальным ~у равнениям, но и естественным требованиям, чтобы G0 =0, т. е. 9 должен удовлетворять тем же условиям, что и вектор, выбранный для оценки. _
В итоге мы оцениваем 0 по единственному решению 9 системы нормальных уравнений __
А'АО =Ау, которое удовлетворяет условию __
G0 =0.
Можно показать, что 0 — это ЛНОМД для всех 9, удовлетворяющих условиям G0=O.
Мы уже отмечали, что остаточную сумму квадратов можно вычислить из выражения _
г=уу—бАу.
При обычных предположениях о распределении ошибок соответствующая случайная величина R будет распределена как a2x2„_s [см. раздел 2.5.4, а)], поскольку мы можем с помощью репараметризации получить модель которая будет невырожденной, с рангом s
и теми же остатками. Отсюда
E(R)-(n—s)o2 и о2 = г/(п—s).
Пример 10.1.1. Модель односторонней классификации в форме с «избыточными параметрами». Проиллюстрируем сказанное на примере односторонней классификации. В модели полного ранга (16.1.1) есть I параметров, а в вырожденном варианте (10.1.2) используется (/+1) параметров. В последнем случае получается, что р=1+\ и s=I, а это значит, что одного линейного соотношения между параметрами достаточно для устранения избыточности. Вот условие, которое обычно выбирается в таком случае:
£^,•=0. (10.1.4)
Его предпочитают отчасти из-за алгебраических удобств, а отчасти потому, что оно допускает простую интерпретацию в том контексте, в котором используется модель. Допустим, например, что сравниваются I антикоррозионных обработок, которым подвергаются изделий в /-й группе, а ун обозначает наблюдение над у-м изделием в •
J ! Ji
i-й группе, z=l,...,Z Тогда из (10.1.4) следует, что £{ Е Е У,,}=ид,
/=1у=1 V
472
так что в модели E{Yij} = a+bi параметр а можно интерпретировать как общее среднее для всех обработанных изделий, в то время как будет средней вариацией относительно этого значения, обусловленной обработкой с номером i. Здесь параметр b рассматривается как «эффект /’-й обработки». Более точно, это (средний) эффект обработки / относительно остальных рассматриваемых обработок. «Фактический» эффект обработки / по предположению относится к разности между ожидаемым откликом, когда используется i-я обработка, и ожидаемым откликом, когда не используются никакие обработки. Если мы хотим оценить такой эффект, то нам надо иметь контрольную группу, не подвергаемую никаким обработкам. Положим, что это могла бы быть группа с номером 1. Тогда естественным дополнительным условием было бы Ь\ =0, так что оценка а стала бы ожидаемым откликом для случая, когда обработки не применялись. Модель у^ — а + Ь^е^ при bi-О имеет полный ранг с I независимыми параметрами, где о, представляет «фактический» эффект обработки z.
/ Возвращаясь к модели y,j = a+ bj + ejj с дополнительным условием Ё /Д = 0, замечаем, что это дополнительное условие можно было бы использовать для получения иных репараметризаций, чем /tj-a+bj. Например, записывая Jjb^—YLJibl и применяя это соотношение для
исключения bt из исходной модели, мы могли бы иметь:
110 0
110 0
10 1 0
: : : : I
10 1 0
J\ строк
J2 строк
А =
(пх/)
1 о
1 ——J2/J^
1
1
i
•//_! строк
Jj строк,
1 —J2/Jl
0=
(Zxl)
a b} b2
bi-i
(10.1.5)
473
В этом случае матрица А имеет ранг I, и мы могли бы обратиться к теории из гл. 8, но тогда утратилась бы симметрия, и у нас не было бы простого параметра, представляющего эффект /-й обработки. Поэтому мы работаем с моделью
1
ytj = a+bj + бу, Jjbj—0.
Для этой модели матрица плана А приведена в (10.1.3), откуда
А'А = п J} J2 . . Л . 0 , 0 Л 5 Ау = п у.. Л У\ J1 У 2 •
Л Л 0 . . J2 . . 0 . .
Л Л 0 0
Л У1
Теперь можно найти вектор МНК-оценок в = (а Ь\,.. ;Ь{\ , решая
уравнения f
AA0 =А у и Е /Д. = 0.
Более подробно: нормальные уравнения имеют вид па + 'LJjbi=ny„, Jta +Jibj=Jjyi., /=1,...,/.
Используя ограничения, получим
а =х.» bj^yj—y.., /=1,...,/. (10.1.6)
Соответствующие оценки A -Y.., Bj = Yj—У.. — это ЛНОМД для а и bj, причем их дисперсии равны ст2и~‘ и <т2(^“ 1—п~1). К тому же они еще и некоррелированные Из этих результатов следует, что ЛНОМД для iij^a + bj будет A + Bj-Yj, с дисперсией ст2/1, которую мы получили бы из модели полного ранга, параметризованной для
Более того, остаточная сумма квадратов, равная:
г= Е ,Е (у tj~a -Ь,)2 = Ь (у у у (Ю.1.7)
/= 1 j= i ‘ i= i j= i ,J 1
снова та же, что и раньше. Используя соотношение г=уу—9 Ау, получим альтернативное выражение
г= ££у?- —па у..—£ bjJjyj., (10.1.8)
соответствующая случайная величина В распределена как a2x2_s, где s = ранг A.-I, а дисперсия ошибки оценивается из а2-г/(п—Г).
Делая обычные предположения об ошибках, можно непосредственно получить доверительные интервалы для групповых средних. Так gz, поскольку ct_|(^z.—М/)*Л 2РаспРеделено как 1 Стьюдента [см. раздел 2.5.5] с п—/степенями свободы, центральный 100(1—оО^о-ный доверительный интервал д, [см. раздел 4.5] равен
[Y'±aJT'%_^-a/2)].
474
10.1.3. ПРОВЕРКА ГИПОТЕЗ
Пусть мы хотим проверить общую линейную гипотезу Н, заданную в виде
Н0 = с, где Н — известная матрица размера тхр и ранга Л, а с — данный тх 1-вектор. Когда проверяются такие гипотезы для вырожденной модели с учетом дополнительных условий, мы действуем как и раньше, с той лишь оговоркой, что если какое-либо из ограничений, налагаемых на Н уже включено в дополнительные условия G₽-0, то порядок Н уменьшается на число дублированных среди независимых условий. Если это число окажется равным d, то порядок Н бу дез равен (Л—d}. Построим критерий отношения правдоподобия для Н обычным способом [см. раздел 5.5]:
1) Для полной модели
у=А0 + е при условии G0 = O
получить г (ОСК), которое минимизирует значение
S(u) = (y—Au) при условии Gu = 0.
Истинна ли Н или ложна, R распределено как o2x^_s, где 5=ранг А.
2) Для модели, ограниченной условием Н, а именно
у = А0 + е при условиях G0=O и Н0=с получить гн, ОСК при гипотезе Н, что достигается при минимуме значения S (u) при условиях Gu = 0 и Ни = с. Если гипотеза Н верна, то дополнительное уменьшение RH—R распределено независимо от R как o2x^_d, где (Л—d) — эффективный порядок матрицы Н (ранг Н = й, d — число ограничений, общих для Н и для дополнительных условий).
3) Вычислить [(гн—r)/(h—d)]/[r/(n—5)]. При условии Н это наблюдение из Fh_d „-^-распределения [см. раздел 2.5.6].
И снова, если Н верна, то мы сравниваем две независимых оценки для а2.
Пример 10.1.2. Анализ «внутри и между». Для иллюстрации воспользуемся односторонней классификацией и рассмотрим гипотезу, что все обработки дают один и тот же (неизвестный) эффект. В терминах параметров вырожденной модели это означает, что Н\ Ь]=Ьг = ... = bt = 0. На первый взгляд эта гипотеза выглядит так, как будто она имеет порядок I. На самом деле эта гипотеза относительно общего неизвестного эффекта уже проверялась раньше [см. пример 8.3.8] для модели полного ранга, где мы установили, что ее порядок был (/—1). В данном случае это можно увидеть непосредственно, поскольку дополнительное условие Е/Д=0 означает, что b\-b2 = ... = bf = O устанавливает только (Z—1) независимых ограничений. Точнее, если бы оказалось, что Ь,-Ь2 -...= b/_i =0, то из условия LJjbj = O мы получили бы, что и Ь{ = 0 [см. пример 8.3.3].
rH= S (Уу-у..)2^У-пу1
475
С помощью (10.1.8) получим: rH—r='LbiJi.yi. = 'LJ-yb(yL—y„)='LJfyi —
—у..)Е 2 * * * *. Если гипотеза //верна, то RH—R пропорционально случайной величине с распределением х2 и числом степеней свободы, равным порядку матрицы Н, т. е. I—1. Следовательно, статистика, лежащая в основе критерия L—R, равна:
(г„-г)/(/-1) _ £<(>,•-Л.)2/(/-1) г/(п—Г) ~ ^(уи—у-у/(п—Г)
IJ 7
[см. пример 8.3.3].
В обычной табличной форме получаем:
Источник Сумма квадратов SS Степени свободы DF Средний квадрат MS
Снижение, обусловленное вектором 9=(а, г(0) = в Ау I
Снижение, обусловленное 9\Н-снижению, обуслов- г(9\Н) = г(а) = пу\ 1
ленному а
Дополнительное сниже- r(fi)—r(9\H)=rH—r= Ц(угу.У /—1 ГН~Г
ние I—I
Остаток г=У У-9'а'(Уи -у^у Я—1 °2=Ti=J
Общий У У п
(10.1.9)
Те части этой таблицы, которые нужны для проверки гипотезы Н, можно быстро отыскать следующим образом. Рассмотрим тождество
y-ij—У..=(Уц~•.) + (>,•.—К.)- (10.1.10)
Это выражает отклонение наблюдения от общего среднего выборки через сумму его отклонения от группового среднего (по той группе, к которой оно принадлежит) и отклонения самого группового среднего от общего среднего. Возводя обе части выражения (10.1.10) в квадрат и суммируя по / и по j, получим
Е Е (Уу-у..)2 = Е Е Оу—jz.)2+ Е ЕО/. -У..У +
/ = ]У=1 V I J IJ
+ 2Е Е О,;—Л'.)О/.—.У ..)•
Член, содержащий произведение и представляющий собой
2?{О/.-Х.)2О,у-Л.)),
обращается в нуль, поскольку ^(у^—yz) = 0, z = l,...,/. Отсюда получается тождество 7
^Оу-лЭ^^Оу-л-.^+рЛО/.-з'..)2- (Ю.1.11)
476
Основная идея этого тождества, как и аналогичных ему, которые будут построены позже, заключается в том, чтобы разбить общую сумму квадратов отклонений некоторой случайной величины относительно ее среднего выборки на несколько отдельных сумм квадратов, каждая из которых относится к своему источнику вариации. В данном частном случае мы заметим, что:
а) величина Е(у,-.—у,)2 представляет собой меру вариабельности j ,J
внутри группы тогда как величина .—У/ )2 — мера обшей вари-
(• j и
абельности внутри групп. Она известна как внутригрупповая сумма квадратов (ВСК) и представлена как остаток в приведенной выше таблице дисперсионного анализа;
б) величина —J..)2 служит мерой вариабельности между
группами. Она называется межгрупповой суммой квадратов (МСК) и представлена членом, отражающим дополнительное снижение в таблице дисперсионного анализа.
Если не пользоваться методом наименьших квадратов, то с помощью выражения (10.1.10) можно проверить гипотезу относительно равенства групповых средних на основе следующих рассуждений. Когда групповые средние fij-a + bj различны, мы вправе ожидать, что МСК будет больше, чем если бы они были одинаковыми. С другой стороны, мы не ожидаем, что это обстоятельство каким-либо образом отразится на величинах ВСК. Следовательно, интуитивно разумный метод проверки, одинаковы ли групповые средние, заключается в том, чтобы рассмотреть отношение МСК/ВСК. Исследование распределений этих двух статистик, когда ошибки независимы, нормально распределены, имеют нулевое среднее и одинаковые дисперсии а2, показывает, что (как при подходе, основанном на методе наименьших квадратов):
а) ВСК распределена как случайная величина a2Xn—i [см. раздел 5.4, а)];
б) МСК распределена как случайная величина cf2xj—i независимо от ВСК, если математические ожидания для групп равны.
Следовательно, можно принять в качестве функции критерия выражение
МСК/(/—1)
ВСК/(и—1) ’
которое имеет распределение Fj_x х [см. раздел 2.5.6], когда ожидания равны.
477
С этой точки зрения естественно использовать таблицу дисперсионного анализа несколько иного вида:
Источник SS DF MS E(MS)
Между группами Внутри групп I—I n—I MCK/(/—1) ВСК/(я—Z) , LJibi °2+~r=r a2
Общий (относительно среднего) ^j-у..У n— 1
(10.1.12)
В последнем столбце приведены математические ожидания двух средних квадратов, подтверждающие, что математическое ожидание для МСК действительно возрастает, когда у групп оказываются неравные средние, что предполагает применение одностороннего критерия. Когда же групповые средние равны, эти два средних квадрата становятся независимыми оценками величины а2.
Хотя эта вырожденная модель неортогональна (на самом деле модель может оказаться и невырожденной, поскольку матрица А'А не диагональна), она обладает частичной ортогональностью, что было видно и раньше в разделе 8.3.7. В табл. (10.1.9) величина СКМ разбивается так:
r(6) = e 'Aty=ny2 + EJ.(>.-х.)2, /
где первый член в выражении, стоящем справа, есть г(а), а второй — сумма квадратов для проверки гипотезы, что b\ = ... = bj=O, так как это не что иное, как дополнительное уменьшение, когда гипотеза окажется «подорванной». Далее, МНК-оценка для а оставалась той же, как в модели полного ранга, так и в модели, ограниченной гипотезой, а именно а=у.. . Если же теперь мы рассмотрим вторую гипотезу (обычно не представляющую никакого интереса) й=0, то метод наименьших квадратов приведет к оценкам Z>;(z= 1,...,7), которые будут теми же, что и для полной модели, причем r(b) =r(bi,...,bf)= —у..)2
будет снижением, обусловленным данной гипотезой, а г(а) — дополнительным снижением, когда ограничение а-0 устранено. Получается, что в обеих гипотезах используется одно и то же разложение СКМ r(6) = r(a) +г(Ь), в котором члены в зависимости от ситуации меняются ролями. Вот как можно резюмировать наши рассуждения:
Гипотеза H a bi
ф=0 bl = ... = b, = o У.. y,-y.. £Jj(yi -У..У I ny\ r(a) = ny2 г(Ь)=Ы'(У'-у.У
478
Это позволяет говорить, что параметры a, bt, bz,...,bj распадаются на две ортогональные группы, причем в одну входит параметр я, а во вторую — (&п...,67). Действительно, ковариация cov (А ,Вj)=0, i Ортогональность этих двух групп параметров особенно хорошо видна в ранее рассмотренном варианте модели полного ранга, где для исключения Ь; использовались дополнительные условия. Из выражения (10.1.5), где приведена матрица плана, видно, что матрица А'А есть
п 1 0 ... 0
?: в
о 1
Для других гипотез, скажем, для гипотезы Z>i=0, эти особые свойства дисперсионного анализа вполне могут исчезнуть, так как оценки для a, b2,...,bI вовсе не обязательно будут одинаковыми для модели полного ранга и для модели, ограниченной данной гипотезой.
10.1.4. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ИЕРАРХИЧЕСКАЯ КЛАССИФИКАЦИЯ
В односторонней классификации данные разделяются на несколько групп с помощью некоторого группового фактора, такого, как получаемая обработка, и имеют такую структуру:
Группы i 2 /
Наблюдения X X X
X X X
X X
Здесь каждый крестик обозначает одно наблюдение.
Если второй фактор используется для разделения каждой группы, то мы имеем двустороннюю иерархическую, или гнездовую, классификацию, которая обладает следующей структурой:
Группы 1 2 /
Подгруппы 12 3 4 1 2 3 1 2
Наблюдения X X X X XX X X X X XXX X X X X X X X X X
479
Здесь группа 1 разбита на 4 подгруппы, каждая из которых содержит четыре, два, одно и три наблюдения, и т. д. Так, например, данные могут представлять собой результаты измерений загрязнения воздуха в различных городах нескольких стран; страны образуют группы, а города — подгруппы.
Обозначим к-е наблюдение в j-й подгруппе z-й группы через у^к и предположим, что z-я группа имеет Jz подгрупп, j-я из которых содержит Кц наблюдений. Так, группа 2 в примере, приведенном выше, имеет J2 = 3 подгруппы, а число наблюдений в первой из них равно: Кг. =3.
Модель полного ранга для этой ситуации такова:
Уук ^ц + ецк’
где /jLjj — неизвестные параметры, а е^к — независимые наблюдения со средним 0. Иначе говоря, наблюдения в j-й подгруппе z-й группы представляют собой случайную выборку из распределения со средним gzy. ^4исло параметров s равно, следовательно, числу подгрупп, т. е. 5- 2 J: .
/=1 '
Такая модель не вполне подходит. Она недостаточно хорошо отражает структуру данных. В ней нет простых параметров, связанных с теми эффектами, которые мы обычно хотим исследовать, а уточнение гипотез, рассмотренных ниже, получается громоздким. Вместо этого будем рассматривать вырожденную модель
У ij к ~ &i + sij + eijk»
где z= 1,...,/; у= 1,...,JZ; к=1,...,Кц. t
Эта новая модель имеет р=1+1+ Ё J, параметров и оказывается /= I '
перепараметризованной. Если вместо g подставить (р,—а), вместо gt—(gj—а, + а), а вместо sy—(Sy + az), то gy не изменится. Всего есть (/+1) избыточных параметров.
Мы приходим к этому, используя следующие дополнительные условия на gj и на Sjjt
i^KjjSjj = Q при
?«j+gj^
Ji
где К:, = Е К:: — число наблюдений
' у=1 lJ
в z-й группе. В результате этих
(/+1) дополнительных условий получаются единственные МНК-оценки для ц, gj и Sy, что позволяет нам следующим образом интерпретировать параметры:
д — математическое ожидание среднего по всем наблюдениям; g+gj — математическое ожидание среднего по наблюдениям в z-й
группе;
следовательно, gj — мера эффекта группы z;
480
ц+gj+Sjj — математическое ожидание среднего по наблюдениям в подгруппе j группы z; следовательно, stJ — мера эффекта j-й подгруппы в z-й группе.
МНК-оценки параметров находят, минимизируя сумму —
—М—Si—Sy}1 с учетом указанных выше дополнительных условий, причем параметры при поиске минимума рассматриваются как алгебраические переменные. Как можно предположить, мы найдем, что:
/Г =у..., среднее по всем наблюдениям,
ё,=У,. —К.., где у, — среднее в z-й группе, s^y^—у, , где у^ — среднее в у-й подгруппе z-й группы. Остаточная сумма квадратов равна:
Г= ^^ijk-yij)2
с числом степеней свободы, равным числу наблюдений минус число независимых параметров, т. е. ’L'LK-.-.——s, где п — число наблю-
/ j ‘J i
дений, as — число подгрупп. Представляют интерес, главным образом, две гипотезы:
1) Hg:gi=g2-...=gj=O, т. е. что между группами вообще нет никакой разницы;
2) Hs: все \;=0, т. е. что внутри каждой группы нет различий в подгруппах.
Для проверки этих гипотез нам надо снова оценить параметры с учетом каждой из них и найти соответствующие остаточные суммы квадратов. Детали такого подхода очевидны, и мы их опустим, а основные моменты обсудим. Параметры образуют три ортогональные группы, а именно д; g= {gz-}, содержащие I параметров, из которых только (7—1) независимы; s = {sjj}, содержащие s параметров, из которых только (s—Г) независимы. Следовательно, оценки значений g при гипотезе Hs и значений s при гипотезе Hg будут теми же, что и для модели полного ранга, а оценка д, равная у.., сохраняется во всех трех случаях. Величина, на которую у'у уменьшается благодаря подгонке значений g, останется той же независимо от того, включены ли в модель значения s, и наоборот. Таким образом, сумму квадратов, обусловленную подбором полной модели (СКМ), можно представить в виде
г(в)=у у—г=г(д) + r(g) + г (s), где r(g) — уменьшение, обусловленное подбором g,,...,gz, т. е. увеличение остатков при условии Н„ (так что r^ = r+r(g)), a r(S) — увеличение остатков при условии Н]. Такой дисперсионный анализ можно представить в обычной табличной форме:
Источник SS DF MS
Обусловленный средним Обусловленный группами Обусловленный подгруппами Остаток г(ц) г(д) r(s) r = y/y_r(/t)_r(g)_r(S) 1 I—I s—I n—s r(g)/(/-D r(S)/(s—/) 02 = r/(n—s)
Общий JUZ a
481
где и=££Ау, a s=EJz-. Для каждой группы число степеней свободы — это число независимо подбираемых параметров. Критерии строятся обычным образом с помощью сравнения каждого среднего квадрата с а2 и соотнесения полученного отношения с подходящим значением /^-распределения.
Непосредственные выражения различных сумм квадратов через наблюдения появляются как естественная составная часть анализа методом наименьших квадратов. Их можно отыскать и скорее с помощью простого приема, который применялся ранее при односторонней классификации. Представим отклонение произвольного наблюдения от общего среднего в виде суммы трех слагаемых:
Уук-У.. • = (Уцк-Уц)+(Уи ~У1.)+О'/. ~У-
Если теперь возвести обе части этого равенства в квадрат и просуммировать по i, j, к, то получим
+ Е?Xzy(yzy.-yz- )2 + (у(-у.. .)2, (10.1.13)
так как члены, содержащие перекрестные произведения, равны нулю. Члены, стоящие в правой части этого уравнения, не что иное, как г, r(s) и r(g). Левую сторону можно представить как
Это с учетом того, что ц=г(ц)-пу2,, позволяет при простом переобо-: значении получить основную формулу
yzy=r(g) + r(g) + r(S) + r.
Из выражения (10.1.13) можно увидеть, что уменьшение r(g), обусловленное подбором группы параметров, может служить некоторой мерой вариабельности между группами. В соответствии с этим выражением r(g)= E/Tz+(yz- —у...)2 называется межгрупповой суммой
квадратов.
Аналогично
величина Е/Г.-Ду.-,-—у...)2 служит некоторой
мерой вариабельности между подгруппами внутри z-й группы, а величина r(S)=EE/C(y(y,y—у,- )2 объединяет эти меры по всем группам и называется суммой квадратов между подгруппами внутри групп (МПВГСК). Математические ожидания средних квадратов для этих сумм можно найти с помощью элементарных методов:
E(MCK) = E[r(g)/(/-l)] = а2 + EXz+gz?/(/-l),
ДМПВГСК)=E[r(S)/(s—/)] = о2 + /(s—I),
а значит, снова критерий для сравнения с остатками будет односторонним. 482
10.1.5. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ПЕРЕКРЕСТНАЯ КЛАССИФИКАЦИЯ
В описанной выше иерархической классификации каждая группа была связана с различными множествами подгрупп. Так, в примере с загрязнением окружающей среды различные (по необходимости) множества городов выбирались в каждой стране. Когда же в каждую группу входят одни и те же подгруппы, получается иная структура (план). Например, для одного группового фактора (страна) мы могли бы интересоваться годовой Долей умерших за период в несколько лет от множества болезней, общих для всех рассматриваемых стран. Такие данные образуют перекрестную классификацию:
Страны
1 2 3
А X X X X X X X
Болезни В X XXX X X X X
С X X X X X X X X
Каждый крестик обозначает долю умерших в отдельном году. Может оказаться, что у нас нет одинакового числа данных во всех ячейках, т. е. для любых комбинаций стран и болезней. Мы будем говорить о факторе-строке и о факторе-столбце. В рассматриваемом примере это соответственно «болезни» и «страны». Если болезни не окажутся общими для всех стран (как могло бы случиться при включении тропических болезней и стран умеренного климата), то в представленном выше расположении появились бы пустые ячейки, а перекрестная классификация оказалась бы неполной. Тогда практически получился бы возврат к иерархической классификации, в которой отдельные подгруппы оказались бы общими для нескольких групп.
Мы обозначаем к-е наблюдение в /—у-й ячейке (строка i и столбец J) через yijk, где /=1,...,/; y=l,...,J; к- 1,...,Х;у. Следовательно, существует 1J ячеек и ячейка (z, J) содержит Кц наблюдений. Вот модель полного ранга:
yijk = P-ij + eijk>
в которой для каждой ячейки оценивается один параметр, представляющий собой теоретическое среднее этой ячейки. Как и в случае иерархической классификации, мы будем пользоваться вырожденной моделью, соответствующей структуре данных и содержащей ясные параметры для интересующих эффектов:
Уук — /*++ Cj + (RC)jj + ejjk,
где параметры Rt,...,Rf представляют эффекты строк, Ci,...,C7 — эффекты столбцов, a (RC)ti,...,(RC)Ij — взаимодействия [см. раздел 8.9.1] между строками и столбцами. Эти эффекты взаимодействия
483
мЕ(УЦк>
пиеча' -* 'X" Ячейка (1,2)
Ячейка (1,1) \ Параллельно
" Ячейка (2,2)
* Ячейка (2,1)
—,--•---------— « —........
Лекарство 1 Лекарство 2
Рис. 10.1.1. Эффект обработок, когда нет взаимодействий
AE(Yijk*
Диета 2 Диета 1 ^х'
<Z
------1----------1— Лекарство 1 Лекарство 2
e<Y)Jk>
* Диета 1
Диета 2
----1___________L
Лекарство 1 Лекарство 2
Рис. 10.1.2. Эффект обработок, когда есть взаимодействие
включаются в модель в обшей ситуации, когда эффекты строк и столбцов действуют не аддитивно. Если же мы исключим параметры взаимодействий, то останется такая модель: yljk-[i+Ri + Cj + eijk. Она является менее обшей, чем модель полного ранга, поскольку охватывает только U+J) параметров, а это значит, что
E(Yijk—Yijk) = Ri—Ri для всех/, Е(¥цк—-¥и k)~Cj—Cj для всех i.
Для рассмотренного выше примера это адекватно только в том случае, когда разность ожидаемых долей умерших для любых двух болезней одинакова во всех странах, а разность долей умерших в любых двух странах одинакова для всех болезней. (И конечно, никакая из этих моделей не годилась бы, если бы изучаемые доли менялись во времени.)
Для иллюстрации характерных особенностей взаимодействий рассмотрим пример с двумя лекарствами, каждое из которых может сочетаться с двумя режимами питания (диетами)
Ленаре 1 но
1 *»
Диета 1 J’i 11 • • "н •Г|'' У,2*л
Диета 2 ii,-
Когда взаимодействия отсутствуют, ситуация такая, как, на рис. 10.1.1. В этом случае ожидаемые разности между диетами одинаковы для обоих лекарств, а ожидаемые разности между лекарствами одни и те же для двух диет. Причем диета 1 всегда лучше, чем диета 2, а лекарство 2 всегда лучше, чем лекарство 1. Но если только есть взаимодействие, то это уже другой случай, что видно из рис. 10.1.2. В первом из представленных на этом рисунке варианте нет большой разницы как между диетами, так и между лекарствами, но для лекарства 1 лучше диета 2, тогда как для лекарства 2, наоборот, лучше
484
диета 1. Это означает, что лекарства и диеты взаимодействуют. Во втором варианте нет большой разницы между лекарствами, но диета 1 всегда лучше, чем диета 2, и это, в частности, верно для лекарства 1, что снова указывает на взаимодействие лекарства и диет. Короче говоря, взаимодействие означает, что различие между лекарствами зависит от диеты, и наоборот*.
Отклик Уук не изменится, если в модель вместо g подставить величину (/4—а), вместо R, — величину (/?,—а,), вместо Су — величину (Су—|3у), а вместо (/?С),у— [(ЛС^у + а+а,-»-^,], что указывает на присутствие в модели (/+J+1) избыточных параметров (и наоборот, мы можем просто вычесть это число параметров модели полного ранга, т. е. IJ, из соответствующей величины (/J+/+J+1) для получения вырожденной модели). Следовательно, (/+•/+1) линейно независимых дополнительных условий достаточны для получения единственного набора параметров методом наименьших квадратов. Вообще говоря, МНК-оценки не удается просто выразить через наблюдения. А их численные значения находят в результате решения обычных уравнений:
AA0 =Ау,
G0 =0,
где А — матрица, a G0 =0 — дополнительные условия. Правда, для пропорциональных частот можно найти явные выражения.
Пропорциональные частоты. О пропорциональных частотах говорят, когда Kjj/Ki+ не зависит от / и
Kjj/K+j не зависит от у, где Ki+ ~ LKjj — общее число наблюдений в ячейках /-й строки, а K^j = 'LKij — общее число наблюдений в ячейках J-го столбца. Другими словами, числа в ячейках в любой данной строке (столбце) пропорциональны общему числу наблюдений в данном столбце (строке). Точно так же мы имеем
Ку = К^Кч/п.
Это, в частности, справедливо, когда во всех ячейках одинаковое число наблюдений, т. е. когда = что известно как сбалансированный случай [см. раздел 9.7].
Когда же условие пропорциональности частот выполняется, мы выбираем следующие (I+J+1) независимых дополнительных условий: £*/+*<=0,
S*+yCy = O,
‘ К сожалению, дело обстоит не так просто, как здесь представлено. Более реалистичное описание ситуации можно найти, например, в книге Ф. Мостеллера и Дж. Тью-ки «Анализ данных и регрессия» (М.: Финансы и статистика, 1982.—Вып. 1), гл. 11 которой называется «Нормирование данных для сравнений».—Примеч. пер.
485
-1.
Из условий на параметры взаимодействия следует, что ЕуЛ,у(/?С),у = 0 и когда i-I. А в сбалансированном случае (К^=К) эти условия упрощаются:
ЕЯ, = ЕСу- = = Е(/?С),7 =0.
При подобных дополнительных ограничениях все параметры получают простую и удобную интерпретацию. Так д — это математическое ожидание среднего по всем наблюдениям, g+Z?z — математическое ожидание среднего наблюдений в z-й строке (так что /?, эффект z-й строки), а д+Су — математическое ожидание среднего наблюдений в j-м столбце (так что Cj — эффект /то столбца). Среднее наблюдений в ячейке (z, j) имеет ожидание д+/?, + Су + (/?С),у. Когда взаимодействия нет, мы видим, что оно отличается от ц просто суммой эффектов строки и столбца. Такую ситуацию для краткости называют аддитивной.
МНК-оценки параметров получают в результате минимизации (по g, Rj, Cj,(RC)jj) суммы квадратов
lyIJk-n-R r-Cj-iRCfu) ’
с учетом приведенных выше дополнительных условий. Это дает:
Д'
Cj=yj-J..., (RC^yij-y,. -уJ. +у...
Эти результаты отнюдь не удивительны с точки зрения тех интерпретаций параметров, которые приведены выше. Отсюда сумма квадратов остатков равна:
Общее число наблюдений равно: n=EEX,7, а число независимых па-i j J
раметров есть IJ. Следовательно, величина г пропорциональна переменной х2 с п—IJ степенями свободы, а а2=г/(л—IJ). Прежде всего представляют интерес три гипотезы:
HR:Ri=R2-...=R/=0 (нет эффектов строк),
Hc:Ci = C2-... = Cj=0 (нет эффектов столбцов), Hf.{RC)ij=Q для i= 1.../; j= 1...J (нет взаимодействия).
Параметры образуют четыре ортогональные группы:
д, R = {/?,}, С= {Cj}, (RC)= {(RC)ij).
Сумма квадратов, обусловленная построением данной модели, в таком случае имеет вид
rtf)=г(д) + z<R) + z<C) + zX(RC)),
486
и каждое из слагаемых вносит свой вклад в у'у (общую сумму квадратов СК), обусловленную подбором параметров данной группы, безотносительно к тому, включены ли другие параметры в модель. Значит, мы можем проверить три сформулированные выше гипотезы, сравнивая соответствующие члены средних квадратов с оценкой а2. Для каждого из этих членов число включенных независимых параметров дает соответствующее число степеней свободы (с учетом дополнительных условий). Выходит, что r(g) имеет 1 степень свободы, r(R)—(7—1) степеней свободы, r(C)—(J— 1) степеней свободы и r((RC))—(/+J—1) = (/— 1)(J— 1) степеней свободы.
Можно найти явные выражения для всех этих различных сумм квадратов, на которые раскладывается общая сумма квадратов модели, и без обращения к деталям метода наименьших квадратов. Достаточно воспользоваться следующим разбиением:
уик-у...=(yjjk-yu)+^i.-y-^+(yj—y--^+(yu—yi.—y.j. +У-^
Возводя обе части этого тождества в квадрат и суммируя по i, j, к, получим
^(yiJk-y.. .У=ЪЪК^-уц)2+
1 j к (10.1.14)
+ ^Ki+ (у,- -у,.,у + j —у,..У + ^К^-у^-у^у...)2,
поскольку все члены, содержащие парные произведения, равны нулю. Как и в примерах, рассмотренных выше, уменьшение, обусловленное величиной /4, а именно г(д) = лу.2.., можно присоединить к общей сумме квадратов относительного среднего, полученной методом наименьших квадратов, поскольку справа мы имеем г, r(R)» г(С) и r((RC)) соответственно. Три последние суммы квадратов известные как СК между строками, СК между столбцами и СК взаимодействия. Таблица дисперсионного анализа представлена табл. 10.1.1.
Таблица 10.1.1.
Источник SS DF £(MS)
Среднее г(д) = лу.2.. 1 а2+пц2
Между строками r(R)=EX,.+ (y,. —у...)2 7—1 02+£Ki+Ri/(I—\)
Между столбцами r(C} = jK+j(yj-у..У J—I a2 + £K+jC?/(J-V)
Взаимодействие r((RC))= -У,.. + +yj-y..y (Z-D(j-l) (Z-1XJ-1)
Остаток r=yzy-r(R)-r(C)-r((RC)) n—IJ a2
Общий У У n
487
Гипотезы проверяются сравнением каждого среднего квадрата с а2 = = г/(п—IJ), причем столбец ожидаемых средних квадратов показывает, что в каждом из этих случаев используется верхний хвост F-pacnpe-деления. Когда верна гипотеза HR (что нет эффектов строки), величина
r(R)/(/—1)
о1 имеет распределение Ft_{ п_и. Когда верна гипотеза Нс (что нет эффектов столбца), величина
г(С)/(У—1)
О 2
имеет распределение Fj_Kn_u. Когда верна гипотеза Ht (что нет эффектов взаимодействия), величина
r((RC))/(/—1)(У—1)
<7 2 имеет распределение F(/_1)(7_1( п_и.
Интерпретация этих проверок идет по следующим направлениям. Мы уже говорили, что отсутствие взаимодействия означает, что эффекты строк и столбцов проявляются аддитивно. Допустим, что строки соответствуют различным сортам пшеницы, а столбцы — различным удобрениям. Тогда если гипотеза Ht не отвергается, а гипотеза HR отвергается, мы заключаем, что существуют действительные различия между сортами и что различие между двумя заданными сортами должно быть одинаковым для всех удобрений. Иными словами, если сорт А лучше, чем сорт В, то это соотношение останется неизменным для всех удобрений. Если же, наоборот, взаимодействие существует, а гипотеза HR отбрасывается, то различие между сортами оказывается зависящим от рассматриваемого удобрения, а отбрасывание HR происходит потому, что существуют различия в эффектах сортов, усредненных по всем удобрениям. Вообще (т. е. после усреднениям по всем рассматриваемым удобрениям) сорт А может быть лучше, чем сорт В, хотя при некоторых удобрениях сорт В мог бы и превосходить сорт А. Понятно, что интерпретация таблицы дисперсионного анализа гораздо проще, когда нет взаимодействия. Если гипотеза Ht была отвергнута в отличие от гипотез HR и Нс, мы могли бы заключить, что существуют различия между средними ячеек, но не проявляются различия в сортах, усредненных по всем удобрениям, и наоборот, в удобрениях, усредненных по всем сортам.
При использовании выражения w=r(R) + r(C) + r((RC)) получается общий критерий для всех трех гипотез (т. е. для общего среднего в ячейке, fi). Когда верны все три гипотезы, величина w/o2 представляет собой наблюдение из распределения х2 с числом степеней свободы, равным (/—!)+ («/—!)+ (/—!)(./—!)=/./—1. Тогда функция этого критерия примет вид w/(IJ—1)а2, что, как известно, имеет распределение Fij—\, п—и-488
В частном случае, когда частоты ячеек равны (все Кц = К), таблица дисперсионного анализа упрощается и принимает вид:
Источник SS DF E(MS)
Среднее Между строками Между столбцами Взаимодействие Остаток г(д) = ЛУ;.. z-(R) = J/CLO-, /(С)=/лто'./-л...н J J r((RO)=/q:?(y,7-j', - -у.^у..У r=^ijk-yijy (по разности) 1 /—1 J— 1 (/-1)(•/-!) IJ (К— 1) о2 + МКУ o2 + JKZRr o'-ylKLCj /(У—1) а2 + ХТЕ(ЛС)г / (/—1)(J—1) о1
Обший У У ик
Если же в каждой ячейке содержится только по одному наблюдению (Х=1), то нельзя построить рассмотренные выше критерии, поскольку остаток теперь г-'£,Е(Уцк—Уц.)2, что равно нулю. Происходит это потому, что число наблюдений оказывается равным IJ, а это точно равно числу независимых параметров. Значит, данные можно подогнать точно, без остаточной вариации. Правда, если нет взаимодействий (все (7?С)/у=0), то модель принимает вид
Она содержит (/+J+1) параметров, из них (I+J—1) независимых, если учесть два дополнительных условия E/?z = ECj=O. Применение к этой модели метода наименьших квадратов позволяет получить оценки ~ ~
Д' =У.., Ri=yi.—y.., Cj=y.j—y..,
а остаточная сумма квадратов та же, что и СК для взаимодействия в более общей модели. Таблица дисперсионного анализа тогда принимает вид:
Источник SS DF £(MS)
Среднее Т(д) = п>'?. 1 о2 + Uy
Между строками r(R)=JEO'|.—у. У /—1 a2 + JL^2/(/—1)
Между столбцами r(C) = /L(.v —у..)2 J 7 J— 1 a2 + /L(y/(J—1)
Остаток Г=??0',у-у,-Ху+У..)2 (по разности) (/-!)(/-!) О2
Общий У У и
489
Следовательно, мы можем проверить эффекты строк и столбцов обычным путем, сравнивая средние квадраты и обращаясь к Г-крите-рию. Подчеркнем, что этот подход состоятелен лишь в том случае, когда верна аддитивная модель. Если же есть взаимодействия, их средний квадрат в качестве оценки а2 не годится и необходимо обеспечить, чтобы К>1, если мы хотим проверить эффекты строк и столбцов.
Вернемся теперь к общей модели с неравными частотами ячеек, когда не удовлетворяется условие пропорциональности частот и параметры не образуют ортогональных групп. В этой ситуации для проверки, скажем, гипотезы HR нам нужно знать дополнительное снижение в у'у, когда параметры строки подбираются в дополнение к остальным параметрам. Аналогично и для всех остальных гипотез, Из-за отсутствия ортогональности эти суммы квадратов не будут входить в сумму квадратов модели аддитивно. Метод наименьших квадратов не удается применить в полном объеме, так как процедура, основанная на (10.1.14), не приведет к нужным суммам квадратов, поскольку при отсутствии пропорциональности частот не пропадает член, содержащий парные произведения. В такой ситуации нет смысла сохранять те дополнительные условия, которые были в случае пропорциональных частот, и обычно (новое) численное решение системы нормальных уравнений получают при наипростейших ограничениях:
Е/?,.== Е(ЯС)/7 = URC)'J=0.
Более подробное обсуждение этих проблем содержится в работах [Kendall and Stuart (1966)] и [Scheffd (1959)].
10.1.6. КЛАССИФИКАЦИИ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
По. мере включения в классификацию новых факторов анализ быстро становится громоздким. Мы можем повторить иерархическую структуру для включения в классификацию третьего фактора, внутри которого наш предыдущий пример образует гнездо. Этот третий фактор мог бы быть, например, «континентом», а используемая модель приняла бы тогда вид
Уцк! ~ fl+Bi "* sij "* tijk + eijkb где главная группа параметров [g,] относится к континентам, подгруппа параметров Цу) — к странам, а подгруппа [Где] — к городам. Аналогично мы можем рассматривать перекрестную классификацию трех факторов, в которой каждая пара факторов образует перекрестную классификацию, как обсуждалось в разделе 10.1.5. Далее мы обсудим этот случай более подробно. Оба эти обобщения «чистые»: одно из них — чисто иерархическое, а второе — чисто гнездовое (перекрестное). Новое свойство, проявляющееся при трех и более факторах, — это наличие возможности получить смеси из иерархических и перекрестных классификаций. Чтобы проиллюстрировать сказанное, рассмотрим модель для исследования забастовок в международных промышленных компаниях:
Уцк! “ М+ С/+-Л4у + + Fjjk + eijkb
490
где в качестве факторов рассматриваются: а) страны (Cz); б) компании (Л/у) и в) предприятия (Fjjk/). А в качестве отклика уук1 можно было бы взять, например, (потери в человеко-днях из-за забастовок в год)/(число рабочих дней в году) за период lijk на предприятии (4 Л*).
Допустим, каждая компания имеет промышленное предприятие в каждой стране, тогда «страны» и «компании» образуют двустороннюю перекрестную классификацию, в которой каждая ячейка, т. е. комбинация страны и компании, образует основную группу в двусторонней иерархической классификации с предприятиями в качестве подгрупп. Подробности анализа смешанных классификаций, как, впрочем, и чисто иерархических, с тремя- факторами, приведены в книге [Scheffe (1959)].
Рассмотрим теперь более подробно трехстороннюю перекрестную классификацию. Данные, относящиеся к ожирению, могут быть представлены в виде перекрестной классификации в зависимости от действия лекарств, режима питания и типа личности. Вот соответствующая модель:
Уцк! = n+Dj + Fj + рк+ + (DP)ik + (FP)jk + (DFP)ijk + eijkh
где j=k=\,...,K; l=l,...,Ljjk. Здесь D, относятся к ле-
карствам, Fj представляют различные режимы питания (диеты), а Рк связаны с разными типами личностей. Отметим, что наряду с этими тремя наборами параметров надо учитывать взаимодействия первого порядка между каждой парой факторов, а также параметры {DFP)(jk, представляющие взаимодействие второго порядка между всеми тремя факторами, поскольку без них наша модель окажется не в состоянии описывать общий случай различий в математических ожиданиях для всех IJK ячеек. В частности, отсутствие взаимодействия второго порядка свидетельствует о том, что, например, взаимодействие первого порядка между лекарствами и диетами будет одинаковым для всех типов личности (т. е. для каждого к лекарства и диеты взаимодействуют одним и тем же способом, что выражается только через параметры (JDFjJ. Аналогично и для взаимодействий первого порядка между остальными парами факторов. Мы рассмотрим только сбалансированный случай, когда во всех ячейках представлено одинаковое число наблюдений (Ьцк = Ь). Число параметров такой модели равно
1 + Z+J+ К+IJ+IK+JK+IJK, а число ячеек равно IJK. Значит, число избыточных параметров — 1+I+J+K+IJ+IK+JK.
Воспользуемся следующими дополнительными условиями:
?dz=?f7 = lpa.=o, ?(DF)zy=5my=0, p(DP)z)t = E(DP)zJt = 0,
491
UFP)Jk=^P)jk^O, ^DFP)ijk - yDFP)ijk = V(PFP)ijk =0. Метод наименьших квадратов позволяет получить оценки параметров с помощью минимизации выражения
5 Е {Лу„-д-Р,.-Гу-Р^ } *
с учетом приведенных выше дополнительных условий. Причем параметры в этом выражении обрабатываются просто как алгебраические переменные. Вот МНК-оценки z- '
Д' -Л..., п^у^-у...., _ (^F),y =Лу -j. ~Jy +Л...,
=Уук-Уц. -yi.k~y.jk. +Л... +Х/. +У..к -У....-Для оценок остальных параметров тоже есть соответствующие выражения. А вот остаточная сумма квадратов:
r~ FJ?^^Уук—УцкУ-
Поскольку число наблюдений равно IJKL, а число независимых параметров равно IJK, остаточная сумма квадратов имеет IJK(L—1) степеней свободы.
Как и при двусторонней перекрестной классификации, здесь параметры образуют ортогональные группы лишь в том случае, если удовлетворяется условие «пропорциональности частот». Это применимо и к данному случаю с разными частотами в ячейках. Поэтому в обычных обозначениях мы имеем
CKM=r(^)+r(D)+r(F)+r(P)+r[(DF)]+r[(DP)]+r[(FP)]+r[(DFP)].
Различные суммы квадратов в этом выражении можно найти после повторной минимизации с учетом соответствующей гипотезы или воспользовавшись представлением выражения для отклонений (УцкГ~ —у....} в виде суммы различных компонентов. Соответствующая таблица дисперсионного анализа представлена в табл. 10.1.2.
Число степеней свободы в каждом случае (за исключением двух последних строк) определяется числом включенных независимых параметров, т. е. общим числом параметров, связанных с каждым эффектом без числа независимых наложенных ограничений.
В столбце средних квадратов использовалась следующая система обозначений: ,
492
Таблица 10.1.2
Источник SS DF £(MS)
Среднее г(д)=ду.2... 1
Между лекарствами (£>) r&)=JKLKD ?=JKL£tyL —у,,.? I— 1
Между диетами (F) r(F)=IKLLF^IKLL(y.f.-y....y J—\ д2+ агг
Между типами (Р) r(P)=IJLT.P l=IJL1L(y t—y У к к к "K' K— I a2+Op
Взаимодействие (DF) r[(DF)]=KLtt(DF)i u J (/-1XJ-1) <r2+alF
Взаимодействие (DP) r{(^P)]=JL^(DP)lk (/-1)(^-1) O2+ Opp
Взаимодействие (FP) r{{W)}=ILtt(FP)?k J к JK
Взаимодействие (DFP) r[(DFP)] = ЛЕЕЕ ^p)ijk (Z-1XJ-1XA--1) aZ+aDFP
Остаток r=V'y -SSM=^(yiJkr-yiJk.y a2
Общий УУ IJKL
Аналогично и для аР, ар, а^р, арр (заметьте, что это не дисперсии!).
При соответствующих гипотезах каждая сумма квадратов распределена независимо от остатка и пропорциональна случайной величине с распределением хи-квадрат. Критерий F строится как обычно. Например, для проверки различий между лекарствами мы пользуемся тем фактом, что при отсутствии таких различий (т. е. когда все Z), равны нулю) величина r(D)/ff®(Z— 1) распределена как где 5^ =
=r/IJK(L—1). Аналогично, чтобы проверить, что «нет взаимодействия между лекарствами и типами личностей», обращаемся к статистике r[(DP)]/ff2(7— 1)(Х— 1) с распределением F(/_^K_l)t ®т’
брасывание этой гипотезы означает, что одни лекарства оолее эффективны (по сравнению с другими) для некоторых типов личностей.
Если L = 1, остатки обращаются в нуль и все проверки оказываются невозможными. Если, однако, мы захотим при этом предположить, что' взаимодействие второго порядка равно нулю, то остальные гипотезы снова станут проверяемыми. Для них по предположению величина r[DFP)] будет играть роль остатка, что должно учитываться в соответствующих критериях. Так, например, для проверки возможного эффекта диеты мы воспользуемся величиной (/— 1)(А— l)r(F)/r[DFP)], которая имеет распределение F(J_^ когда различие между ди-
етами отсутствует.
10.1.7. КОВАРИАЦИОННЫЙ АНАЛИЗ
При сравнении эффектов групп при односторонней классификации часто удается получить дополнительную информацию об относящихся к делу переменных. В случае, например, упомянутых ранее I обработок антикоррозионными составами дополнительная информация, которая могла бы пригодиться при сравнении, включает температуру, время выдержки, влажность и т. п. Можно ожидать, что различия в значениях этих дополнительных факторов будут в определенной мере влиять на наблюдаемые различия между обработками. Ковариационный анализ (ANOCOVA) учитывает такие эффекты. Мы обсудим этот анализ для случая, когда есть результаты наблюдений над одной из таких сопутствующих переменных (или совместно изменяющихся случайных величин), скажем, временем выдержки, X. Тогда получим модель
y^a+bi+pxtj+etj, (10.1.15)
где Ху — время выдержки у-го образца из z-й группы. Дополнительное условие остается прежним, а именно
£ /Д=0.
/=1 1 1
Поскольку рассматривается набор гипотез о равенстве групповых эффектов (все bj=O), анализ этой модели методом наименьших квадратов в основном сводится к учету различий во времени выдержки, чтобы элиминировать эффекты таких различий при сравнении обработок. Матрица плана А получается в этом случае добавлением нового столбца к матрице плана односторонней классификации без ковариации, приведенной в (10.1.3). Вот этот новый столбец:
(*п.....XiJt> Х21.X2J2.Хд,...,Хуу) .
494
Для получения МНК-оценок параметров мы решаем уравнения
где 6= (a, bi9. :,Ь19 (3) Л 0 0 Лх1ф А'Ав = Ау, ,Е/Д-=0, '. В данном случае имеем: пу.. ЛУ\. ЗгУг, ^Xijyij
А'А = п J\ Ji Л пх.. Л ... Jj 0 ... 0 л ... о 0 ... Jj J2x2' . . . JjXt пх.. Лх2. г. fH , Ау =
откуда 1) а + (3х.
2) a + bj+(3 хь=уь, /=1...1,
3) nx..a + ^JjXjbj + fi LjLjX^'LjLjXjjyij.
Можно переписать выражение 1) в виде а =у„—(3 х... Подставив это в выражение 2), получим bj=yi—y.—P (х,.—х..), что можно было бы сравнить с соответствующими оценками в случае, когда нет ковариаций (10.1.6). Подстановка в выражение 3) дает уравнение для (3 , которое можно решить:
_ ЕЕЦу—-V/JOy—//.)
Вот остаточная сумма квадратов:
г= ^(Уу-а -Ь,—^ хф2.
В этой модели «работают» (1+2) параметров и одно дополнительное условие. Значит, число независимых параметров равно (Z+1) и остаток пропорционален случайной величине с распределением хи-квадрат с (п—7—1) степенями свободы. Следовательно, оценка дисперсии ошибки равна: о2=г/(п—7—1).
Оказывается, что все требуемые нам величины сводятся в таблицу:
Источник SS(№) SS(xj) SSO*)
Среднее Группы Остаток лхЛ Gxx=^nSxi- Х-У рр^</ Х‘ пх..У.. Gxy = ^ni<xi~х..)(Уг~У..) ^ху= Х1-УУц У/) пу Л G^F'’/07-л.)2 ^уу= Fp^y
Общий № ^>1
495
Последний столбец — обычный дисперсионный анализ, который проводится при отсутствии дополнительной информации об X. Остальные два столбца содержат соответствующие вычисления для х2 и ху. Отсюда и возник термин ковариационный анализ. Используя введенные обозначения, получим (3 =Rxy/Rxx. Далее, покажем, что
r=Ryy—(3 Rxy.
Это можно записать и в иной форме:
r=RYV—$2Rx=Rvv—R2/Rxx. jrJr АЛ Jr Jr лу ЛЛ
Давайте вспомним тождество, установленное ранее для классификации групп без учета сопутствующих переменных, а именно
Обозначив общую сумму квадратов относительно среднего через Туу и используя обозначения, введенные в таблице дисперсионного анализа, получим
7’ = R । уу уу • уу*
Обозначив
£Е(х/у—х..)2 и £Е(Ху—x.Jtfy—Л.)
через Тхх и Тху соответственно, можно вывести (тем же методом, что и для упомянутого выше тождества) аналогичные тождества:
Т = R 4-1 XX XX ~ ^ХХ’
Тху = *ху + @ху
Отсюда видно, что (поскольку ТЛЖ=£Ех?-— пх2 и Тху = SEx,ypzy—пх.у.,) в каждом столбце остаточный член можно получить, вычитая первые два члена из общего разброса.
Для проверки гипотезы Н, что все группы эффектов одинаковы, т. е. bi=b2 = ... = bl-0t рассмотрим следующую таблицу дисперсионного анализа.
Таблица 10.1.3. Ковариационный анализ
Источник SS DF 1
Уменьшение, обусловленное (а, Ь, /3) R(a, b, /3) /+1
Уменьшение, обусловленное а, 0 =уменьшение при Н: Ь=0 R{a, /3) 2
Дополнительное уменьшение /?(Ь|а, @)=гн—г 1—1
Остаток г=УУ —R(a, b, 0) п—1—1
Общий У У п
496
При гипотезе Н мы исследуем сокращенную модель
Теперь получилась модель, которая постулирует линейную регрессию У на/, а значит, как в примере 8.2.4, МНК-оценки для а и /3 при гипотезе Н (обозначенные через а* и /3*) получаются из:
а*=Л.—/3*х..
* .Ху,;—Л.) Л*= -_____— .
IJ J
В соответствии с примером 8.12.13 остаток равен:
Отсюда
и г —Т ___________________________Тг /Т
'Н уу ху' 1XX'
Следовательно, увеличение остатков, обусловленное гипотезой Н, равно:
г=Туу ?ху / Txx—(R „ „—R * /Rxxx= jj лу АЛ)
^У.
^хх
поэтому функция критерия
^ху + &ху) УУ~ ^хх^ =
Порядок для гипотезы Н равен (I—1), такова:
r/(n—I—l)
Если гипотеза Н верна, то F имеет распределение (n-i-iy
Основные результаты для проверки гипотезы Н: b\=b2 = ... = bj=G мы можем свести в следующую таблицу:
Источник SS DF MS F
Остаток при Н ГН=^уу Tiy / п—2
Остаток р р 2 / р г ^уу л\Ху' л\хх п—1—1 ^ = г/(л^/—1)
Дополнительное уменьшение без Н гн~г 1—1 W = (rH-r)/(I-l) w/a*
Хотя естественный интерес концентрируется на проверке групповых эффектов, отчасти интересно проверить и гипотезу Н':(3=0, поскольку ее отбрасывание означает, что в модели имеет смысл учитывать ковариацию.
497
При справедливости гипотезы Н' эта модель превращается просто в обычную модель односторонней классификации без всяких ковариаций, так что rH,=Ryy, откуда дополнительное уменьшение равно:
rH,—r = 02 Rxx=Rxy /Rxx.
Теперь, поскольку гипотеза Н' имеет порядок 1, ее проверка основывается на критерии F'-^R^ff2, который имеет распределение F, когда /3=0.
Аналогичные методы приложимы и к моделям, включающим дополнительные классифицирующие факторы и/или сопутствующие переменные. Так, например, при двусторонней перекрестной классификации с двумя сопутствующими факторами W и X и одинаковым числом наблюдений во всех ячейках мы могли бы воспользоваться моделью
Уijk ~ P+Rj + Cj + + aWijk ^ijk^^ijk’
с дополнительными условиями
ЕЛ. = ЕС,- = Е(ЛС) = Е(ЛС)..=0. i ' j J i lJ j *J
Пшотезы проверяются обычным путем. Так, проверяя гипотезу, что «нет эффекта строки», мы должны получить остаточную сумму для этой гипотезы и сравнить ее увеличение по отношению к остаточной сумме для полной модели. Основные вычисления можно представить в виде таблицы, где один столбец представляет собой обычный дисперсионный анализ для перекрестной классификации без учета ковариаций, а остальные столбцы соответствуют вычислениям w2, х2, wy, ху, wx.
10.2. МНОЖЕСТВЕННЫЕ КРИТЕРИИ И СРАВНЕНИЯ
10.2.1. ВВЕДЕНИЕ
Представленные примеры исследования экспериментальных данных методом наименьших квадратов показали, что при этом обычно приходится проверять некоторые гипотезы и строить доверительные границы. Мы можем провести различие между двумя типами задач статистического вывода, а именно:
а) указание на то, какие еще эксперименты следует выполнить, б) как строятся границы по имеющимся данным.
Таким образом, если мы располагаем данными, расклассифицированными по группам факторами, критерии дисперсионного анализа, основанные на F-распределении, применяются для установления наличия различных эффектов, ради чего и планировался этот эксперимент. Следовательно, формулировка соответствующих гипотез и их проверка согласуются с собранными данными. Например, если в полной двусторонней перекрестной классификации сравниваются четыре лекарства (скажем, А, В, С, D) для каждого из трех режимов питания (диет), то мы, конечно, должны проверять те гипотезы, которые связаны с приведенным ранее дисперсионным анализом, т. е.:
1) нет взаимодействия между лекарствами и диетами,
2) нет различия между лекарствами,
3) нет различия между диетами.
498
Еще нас могут заинтересовать доверительные интервалы для средних эффектов каждого лекарства и каждой диеты. Все это надо отнести к задаче типа а). Сверх того мы могли бы сформулировать и другие вопросы, подсказанные результатами. Так, если критерий указывает на различия между лекарствами (предположим, что они соответствуют строкам), отбрасывая гипотезу HR: Ri=R2=R3 = R4, мы можем выяснить далее, какие именно (если они есть) лекарства имеют одинаковые эффекты, а какие — разные. Пусть, например, из итогов по строке видно, что лекарства А, В и D дают примерно одинаковые результаты, в то время как лекарство С действует несколько лучше. Мы можем спросить: дают ли А, В и D одинаковые эффекты? И если да, то действительно ли С лучше, чем все они? Для ответа на первый вопрос мы могли бы рассмотреть гипотезу Н: /?1=/?2=/?4, что предполагает обычную процедуру переоценивания при условии Н, чтобы найти гн. Не столь важно, что это утомительно (то же можно сказать и о других задачах типа б)), важнее другое, номинальный уровень значимости, при котором проверяется Н (скажем, 5%), не совпадает с истинным уровнем значимости. А это может ввести в заблуждение. Почему это происходит? Главным образом, потому, что Н выдвигается на основе результатов, и проверка, следовательно, обусловлена данными наблюдений. Если бы гипотеза Н проверялась все время (в гипотетических повторных экспериментах), то уровень значимости был бы равен 5%, т. е. в длинном ряду проверок ошибочно отвергнутые гипотезы Н составили бы около 5%. В действительности мы можем проверить гипотезу Н лишь однажды, когда: 1) либо F-критерий отвергнет гипотезу Н, 2) либо он покажет, что не видно противоречий с этой гипотезой. Мы, например, совершенно не должны беспокоиться, если А, В и D дают сильно различающиеся результаты, но может случиться, что гипотеза Н на самом деле верна и явно приемлема, но 5% вероятности ее отбрасывания все-таки остаются. В результате фактическая доля отбрасываний гипотезы Н, когда она верна, сводится к неизвестному числу, меньшему, чем 5%, и это число зависит от субъективных решений экспериментатора при проверке гипотезы Н. В случае, относящемся ко второму вопросу, доверительный интервал для —(R\ +R2+R4)/3 удается построить. Но и здесь номинальный уровень значимости достигается лишь приближенно, если такой интервал строится независимо от конкретных результатов эксперимента, а не просто подгоняется к ситуации.
Следовательно, необходим такой метод, который допускает подобные проверки и построения доверительных интервалов, подходящих для анализа получаемых данных с общим уровнем значимости или доверия. Один из таких методов обсуждается в разделе 10.2.3.
10.2.2. КОМБИНАЦИИ ПРОВЕРОК И ОБЩИЙ РАЗМЕР КРИТЕРИЯ
Сначала обратимся к случаю нескольких гипотез Hit Н2...Нк,
сформулированных для проверок как часть плана эксперимента до того, как начался анализ данных (задача типа а)). Если гипотеза Ht проверяется на уровне значимости а,, то, даже если все а, малы, может оказаться, что будет заметная вероятность по крайней мере одной
499
ошибки первого рода, если только к не очень мало, т. е. если проверяются достаточно много гипотез, то мы, скорее всего, получим «значимые результаты» даже при отсутствии эффектов. Предполагая, что проверки гипотез назависимы, найдем вероятность того, что не будет отвергнута ни одна из истинных гипотез. Она равна к П(1-а,).
I® 1 ‘
А вероятность того, что по крайней мере одна гипотеза будет отверг-
нута, когда на самом деле все гипотезы верны, равна
к 1—,П(1—а,).
Рк(а) = !-(!-«)<
Если все <Х[=а, то
(10.2.1)
При условии, что Ка не слишком велико (скажем, каС (1/4)), это приблизительно равно kat что демонстрирует следующая таблица:
к /\(0,05) ^(0,01)
1 0,05 0,01
2 0,0975 0,0199
4 0,1855 0,0394
8 0,3366 0,0773
16 0,5599 0,1485
Ясно, что когда проверяются некоторые гипотезы, значение Р^(а) отвечает целям их интерпретации, и может оказаться удобнее зафиксировать общий размер критерия Р^(а) на подходящем уровне, соответствующем выбору а, чем использовать обычные уровни для индивидуальных критериев. Так, например, если надо проверить четыре гипотезы при требуемом общем размере 0,05, то мы должны решить уравнение 0,05=P4(a)= 1—(1— а)4* Его правая часть приблизительно равна 4a, так что as 0,05/4=0,0125 (точное значение равно 0,0127). Взяв это значение а для каждого критерия, мы гарантируем, что вероятность некорректного отбрасывания одной или более гипотез из четырех проверяемых (когда они все верны) равна 0,05.
Есть одна проблема, непосредственно связанная с применением этого метода к проверке гипотез в таблице дисперсионного анализа, поскольку все такие гипотезы проверяются с помощью одной и той же остаточной суммы квадратов, и, следовательно, оказываются не независимыми. К счастью, однако, можно показать, что (10.2.1) остается справедливым в качестве приближения и в этом случае, так что получается критерий с приближенным общим размером а', если каждый из критериев в таблице дисперсионного анализа имеет уровень значимости а, где а = 1—(1—а')1/* = а'^.
10.2.3. МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ
К задачам типа а) относится также сравнение заранее выбранных линейных комбинаций параметров (например, групповых средних или разностей между ними), для которых требуется установить довери-
500
тельные утверждения С\, С2...Ст. Проблема того же рода возника-
ет и тогда, когда доверительные границы устанавливаются в каждом конкретном случае отдельно, но мы хотим знать общий уровень значимости для них всех, т. е. вероятность того, что все утверждения корректны одновременно. И снова зависимость между ними может затруднить точный ответ на такой вопрос, но мы по крайней мере можем сказать, что
Р(все С, верны) >1—ЕР(С, — неверны).
Таким образом, если в каждом случае используется один и тот же доверительный коэффициент 1—а=Р(С, верны), мы имеем Р (все верно) =1—mot. Следовательно, мы располагаем нижней границей для требуемой вероятности и можем гарантировать величину доверительной вероятности 1—а при выборе а=а7т. Это известный метод Бонферрони для построения совместных доверительных интервалов, а установленное выше неравенство называется неравенством Бонферрони.
Для иллюстрации этого подхода рассмотрим односторонний план
с моделью
Уц I 1» 2,...,Z, j 1,
Если мы строим 100 (1—а)О7о-ные доверительные интервалы для каждого группового среднего, т.е. С\= {у,. ±а J, —а/2)}, где
a2=r/(n—/), то какой уровень доверия мы можем иметь для утверждения (д,€С,-, / = 1, 2,...,/)? В данном случае мы имеем т=1, так что это будет по меньшей мере 1—1а, и можно положить а^а/1 для получения общего уровня доверия, по меньшей мере равного 1—-а.
Когда F-критерий позволяет отбросить гипотезы Н: аи =/42 = ... = gi относительно равенства эффектов групп, обычно хотят знать, какие группы следует рассматривать как одинаковые, а какие — как разные. Доверительные интервалы для различия между двумя средними, скажем ^z—g, (/#/ )» с вероятностью 100(1—а)% (поскольку дисперсия var (Yb —Yj'.) = а2(Jj1 + J,71)) равны
Di, i'=
Мы считаем, что два средних различны, если А у не содержит нуля. Когда все группы имеют одинаковые объемы (7-=J), это просто сводится к сравнениям всех разностей у(—у^, с наименьшей значимой разностью, L = a (2/J)1/2?„_1(l—а/2), причем групповые средние признаются значимо различными, когда (у/.—У/'.) превосходит L. Если это выполняется для каждой пары, то для (/, г) при i*i' получается всего т=^1(1—1) интервалов, и мы можем гарантировать общее доверие на уровне по крайней мере 1— а при выборе а-а’/т. К сожалению, когда т велико, такие интервалы получаются очень широкими и поэтому имеют ограниченное применение. Более того, доверительный коэффициент 1—а' корректен только в том случае, когда эти интервалы строятся безотносительно к результатам применения F-критерия. Если же, что вполне разумно, мы заботимся только о том, чтобы F-критерий не отбрасывал Н, то истинный уровень доверия оказывается неизвестным.
501
Пример 10.2.1. Совместные доверительные интервалы. В следующей таблице приведены результаты измерений предела прочности на разрыв для шести сплавов:
1 2 3 4 5 б
15,1 15,1 14,9 15,3 15,2 15,2
15,0 15,3 15,4 14,9 14,8 15,1
15,4 15,5 15,2 15,0 15,4 15,3
15,0 15,6 15,1 15,5 14,9 15,2 14,9 15,0 15,0 15,1
Л 4 5 4 6 5 4
у,. 15,12 15,32 15,25 15,03 15,08 15,17
Вот таблица дисперсионного анализа:
Источник SS DF MS
Между группами 0,9143 5 0,1828
Внутри групп (остаток) 0,2942 22 0,0134= а2
Общий (относительно среднего) 1,2085 27
Отношение средних квадратов равно 13,6; a F522(0,99) = 3,99, следовательно, существуют сильные аргументы в пользу значительных различий между прочностями рассматриваемых сплавов. Взяв а =0,1156 в качестве стандартных ошибок средних получим: 0,058, 0,052, 0,058, 0,047, 0,052, 0,058. Отсюда (используя /22(О,975)=2,074) найдем следующие индивидуальные 95%-ные доверительные интервалы для МьМг.-.Мб: (15,12 ± 0,12), (15,32±0,11), (15,25±0,12), (15,03±0,10), (15,08 ± 0,11), (15,17 ± 0,12).
Если мы хотим иметь шесть доверительных интервалов с совместной доверительной вероятностью не меньше 95%, то нужно взять «=0,05/6=0,0083 и провести повторные вычисления, используя ^22(0,9958)=2,9 [см. приложение 5]. Тогда требуемые интервалы (каждый из которых остается отдельным, но с доверительным коэффициентом 0,9917) будут такими: (15,12±0,17), (15,32±0,15), (15,25 ±0,17), (15,03±0,14), (15,08 ± 0,15), (15,17±0,17).
Если же мы рассмотрим интервалы для разностей между всеми парами средних, то окажется, что ш=^-х6х5 = 15, так что общее доверие 1—а'>0,95 потребует выбора «=0,05/15=0,0033, и нам придется воспользоваться /2г(0,9983)=3,3. В результате доверительные интерва-502
лы довольно заметно расширятся. При сравнении первых двух групп, например, мы получим Т>ц2 = (—0,20±0,25), а для групп 2и4 — Z)2>4± (0,29 ±0,23).
Иногда заранее ясно, что предстоит рассмотреть заданное подмножество таких сравнений. Это уменьшает т и, как следствие, сужает интервалы. В нашем примере группа 4 относится к наблюдениям над стандартным сплавом, а остальные пять групп относятся к пяти новым разработкам. Если мы ограничим внимание только сравнениями каждого из новых сплавов со стандартным, то получим т = 5, а значит «=0,05/5=0,01 для достижения общего доверия, равного 0,95. Тогда получатся следующие интервалы:
Ml — М4:0,09 ± 0,21, М5—М4:0,05 ±0,20,
М2—М4:0,29 ±0,20, Мб—М4:0,14±0,21,
Мз—М4-’0,22 ±0,21,
Совместная доверительная вероятность для этих интервалов (т. е. вероятность того, что все пять разностей укладываются в интервал типа — 0,12^mi—М4^0,30) равна 0,95.
Как видно на примере интервала для мг—М4, при ограничении внимания только этими пятью сравнениями мы получаем более узкие интервалы для разностей в отличие от случая, кдгда рассматриваются все пары.
Когда заранее трудно определить, какие сравнения окажутся интересными, полезно иметь подходящие методы для получения интервалов, относящихся к вопросам, возникшим после того, как данные были исследованы. Одним из подходов к решению этой проблемы служит 5-метод Шеффе [см. Scheffe (1959)].
Мы ввели термин контраст для параметров мн М2,- -»М/ примени-/
тельно к любой линейной функции от скажем ф=Е обладающей тем свойством, что с(=0, где с, — известные константы.
Так, разность mi—М? между средними любых двух групп будет контрастом. Среднее одной группы минус среднее средних всех остальных групп, т.е. ри—(мг + мз + ... + д7) / (j— 1), — тоже контраст. И вообще, контрастом будет среднее средних некоторого числа групп минус среднее средних некоторых других групп. Можно показать, что гипотеза Н: = ц2 = • •• = эквивалентна Н': все возможные контрасты равны нулю. В основном метод Шеффе дает интервалы для всех возможных контрастов при заданном общем доверии. Тогда, какие бы контрасты мы ни выбрали (заранее или после изучения данных), они автоматически окажутся включенными в рассмотрение. __ __
Найдем теперь МНК-оценку для ф, равную ф ='Lcini ='Lciyi. Соответствующая формула Ф =Е ct Yi f что дает Е(Ф ) = ф и var Ф =Е с-varT, =Ё с-(ст2//,). Мы оцениваем эту дисперсию из
503
var Ф =_ст Е где °2 — обычная оценка а , основанная именно ст2 = г/(п—/).
Шеффе показал, что когда ф охватывает все возможные
сты, существует вероятность 1—а того, что все неравенства
< ф < Ф +S
ф
п-1
___i__i п—1
на г, а
контра-вида
(10.2.2)
удовлетворяются одновременно, где 5 получается из 52 = (/—„_/ (1—“), п — общее число наблюдений Заметим, что сомножитель (/—1) — это порядок гипотезы Н: = ц2 = ... -
Пусть для любого контраста ф Нф обозначает гипотезу, что ф=6. Мы отвергаем Нф на совместном уровне значимости а, если интервал, вычисленный для ф, а именно ф ±S Vvar Ф не включает значения ф-0. Можно показать, что F-критерий отвергает гипотезу Н, если и только если отвергается по меньшей мере одна из гипотез Нф. Значит, когда все контрасты фактически равны нулю, существует вероятность а того, что по меньшей мере одна из гипотез Нф будет отвергнута. Мы можем применить эти результаты к любым контрастам и выбрать то, что удалось выявить, что повлекло за собой отбрасывание гипотезы Н. Отметим, что если внимание концентрируется на отдельном контрасте ф, выбранном заранее, а не на пришедшем в голову под влиянием результатов, то выражение (10.2.2) дает обычный 100(1—а)°7о-ный доверительный интервал для ф после замены (I—1) на 1 в определении S2. Если же мы хотим построить совместные доверительные интервалы для всех линейных комбинаций gi, ц2...pt, (т. е. не только контрастов), то нам придется лишь заме-
нить в определении S2 (/—1) на I.
Пример 10.2.2. S-метод Шеффе. Применим S-метод Шеффе к данным, использованным ранее в примере 10.2.1. Имеем So = (5F522 (0,95)0,0134)12 = 0,4222.
В соответствии с (10.2.2) получим:
Контраст Ec’/J / / Интервал
1. д,—д4 0,42 0,09 ±0,27
2. А2~ А4 0,37 0,29 ±0,26
3. А3~ А4 0,42 0,22±0,27
4. As А4 0,37 0,05 ±0,26
5. Аб~ А4 0,42 0,14±0,27
6. А2~ Аб 0,45 0,15±0,28
7. Аг — As 0,40 0,24 ±0,27
8. 7- (Аг + Аз)— А4 0,3125 0,255 ±0,236
9. (А, + А$ + Аб)~А4 0,2444 0,123 ±0,209
10. 7- (Аг + Аз)—у (Ai+As + Ab) 0,1903 0,160±0,180
504
Оказывается, что группы 1, 5 и 6 относятся к разным сплавам с одной структурой (назовем их сплавами типа 1), а группы 2 и 3 — к разным сплавам с другой структурой (не с той же, что сплавы 1, 5 и 6). Назовем их сплавами типа 2. Все результаты можно суммировать следующим образом. При сравнениях пяти сплавов со стандартом (первые 5 контрастов) создается впечатление, что сплав 2 лучше, чем стандарт, а для всех остальных не выявлено очевидных преимуществ. Но если, например, сплав 1 лучше, чем стандарт, то различие, по-видимому, не превышает величины 0,36. Аналогично и для остальных сплавов, кроме шестого контраста, который показывает, что нет достаточных оснований для заключения, что лучший сплав типа 2 превосходит лучший сплав типа 1, хотя различие между ними и может быть — самое большее в 0,43 единицы разрывной прочности. Интервал для восьмого контраста показывает, что сплавы типа 2 лучше, чем стандарт. Девятый интервал указывает, что нет достаточных оснований для утверждения, что сплавы типа 1 в общем лучше, чем стандарт. Последний контраст сравнивает сплавы типа 1 со сплавами типа 2. Разница в пользу типа 2 могла бы быть самое большее порядка 0,34, так что даже превосходство типа 1 не исключается и нужны дальнейшие исследования. Всеобщая доверительная вероятность для всех этих утверждений (и для любых других контрастов, интервалы которых мы в состоянии вычислить) равна 95%.
Что же касается первых пяти контрастов, то можно было бы получить более короткие их интервалы методом Бонферрони, но за это пришлось бы заплатить невозможностью делать какие бы то ни было заключения относительно любых других контрастов.
Когда все группы имеют одинаковые объемы, можно воспользоваться для получения интервалов для всех контрастов другим методом (предложенным Дж. Ъ>юки). Он основан на стьюдентизированном размахе [см. раздел 2.5.9]. Эти интервалы получаются короче, чем при S-методе для контрастов вида pt,—но длиннее для других контрастов. Более подробное обсуждение этих вопросов можно найти в работе [Scheffe (1959)].
В общем S-метод можно применить к любому набору эффектов в линейной модели для получения совместных доверительных утверждений такого типа, как в (10.2.2). Общая теория изложена Шеффе [см. Scheffe (1959)]. В качестве заключительной иллюстрации рассмотрим сбалансированную перекрестную двустороннюю классификацию:
Уук = -fy + Cj + (R С)у 4-е^к; i= 1,2,...
./=1,2,...,/; Ar=l,2.К.
Если HR: все Rj=O отвергнута, мы можем воспользоваться S-методом для построения контрастов со средними по строкам fi+R, и найти интервалы вида
ф ± S Vvar Ф , где
505
Ф-L ci(i/.+Ri)='E CjRj, Ф =L cj(yL—y...)=L CjyLt var Ф — оцениваемая дисперсия E czj,, основанная на о* =r/IJ(K—l), a
S2 = (/-l)F/_U7(X_1)(l-a).
Если же отвергнута Hc: все Cj=0, то можно обратиться к контрастам для средних по столбцам ц+Cj, используя на этот раз
10.3. ПРЕДПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ОШИБОК
10.3.1. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ
Продолжим краткое рассмотрение предположений, лежащих в основе представленного выше анализа. Детальное обсуждение этих вопросов приведено в работах [Kendall and Stuart (1966)] и [Scheffe (1959)]. Напомним предположения, принимаемые относительно ошибок €i, е2.е„ в линейной модели Y=A0+«:
1) ошибки имеют нулевые математические ожидания,
2) ошибки независимы,
3) ошибки имеют одинаковые дисперсии (гомоскедастичность), 4) ошибки распределены по нормальному закону.
Напомним также, что последнее предположение требуется для проверок гипотез и построения доверительных интервалов, но не требуется для получения результатов, приведенных в разделе 8.2, где рассматриваются средние и свойства второго порядка оценивателей МНК.
Первое из предположений не создает проблем. Даже если ошибки и имеют ожидание ^#0, мы можем ввести его как дополнительный параметр в модель или, если он присутствует в модели, модифицировать. В первом случае это означает переход от (0Н 62,...,0р)' к
02,...,вр)' и исправление матрицы А введением нового первого столбца, состоящего из единиц. Во втором случае, полагая, что 01 есть тот самый компонент E(Y{) для всех /, мы должны заменить Oi на 01 + ц и рассматривать его далее как параметр, входящий в модель.
Второе предположение более важное Обычно считают само собой разумеющимся, что физическая установка или метод получения выборки делают это предположение разумным. Дисперсионный анализ, представленный ранее как чисто алгебраические тождества, свободен от предположений 1—4. Однако если мы хотим воспользоваться им для проверки гипотез, то нам потребуются предположения 3 и 4. Предположение о постоянстве ошибок тоже важно. Без него, когда ошибки гетероскедастичны, наши методы могут привести к глубоким заблуждениям в результате нарушения уровня значимости даже для сбалансированного плана (т. е. имеющего одинаковое число наблюдений в каж-
506
дой группе или ячейке). Если, как в разделе 8.2.6, заранее известно, что дисперсии отличаются постоянным множителем, то мы можем прибегнуть к описанному методу преобразований, дающему новую модель, к которой применимы наши методы. На практике такую исчерпывающую информацию часто просто неоткуда взять, но можно использовать различные преобразования, стабилизирующие дисперсию [см. раздел 2.7.3] для преодоления некоторых видов гетероскеда-стичности, обычно встречающихся в классифицированных данных. Если, например, дисперсия в группе пропорциональна групповому среднему, мы преобразуем наблюдения по закону а если
групповому среднему пропорциональна стандартная ошибка, то по закону y=log [см. Kendall and Stuart (1966); Scheffe (1959)].
Последнее предположение о нормальном законе распределения ошибок на практике выполняется лишь приближенно, но, к счастью, метод дисперсионного анализа устойчив к нарушениям нормальности, т. е. должны произойти значительные нарушения нормальности прежде, чем стандартные критерии дисперсионного анализа начнут существенно реагировать.
10.3.2. АНАЛИЗ ОСТАТКОВ
Анализ данных будет совершенно не полным и иметь предварительный характер до тех пор, пока не станет очевидным, что приведенные выше предположения могут считаться разумными. Это на практике означает отсутствие явных нарушений. Осуществить такую проверку проще всего с помощью наглядных графических методов с использованием остатков. Подробное обсуждение этого вопроса приведено в работе [Draper and Smith (1966)].
Предположения 1—4 можно суммировать так: eif е2,...,еп — случайная выборка из N(0, о2). Остатки ег , е2...еп как наилучшие
оценки для этих величин должны, следовательно, быть похожи на случайную выборку из N(0, а2), и мы можем нанести е, на нормальную вероятностную бумагу [см. раздел 3.2.2, cf)], чтобы увидеть, тот ли это случай. Некоторых отклонений вполне можно ожидать (даже если наши предположения выполняются совершенно точно), хотя бы потому, что остатки не могут быть случайной выборкой из N(0, а2), так как между ними есть зависимости, которые можно сразу увидеть, если записать нормальные уравнения так:
Ее/ аи=0, j=\,2,...,p.
Таким образом, для любой модели с аддитивной константой 01 остатки должны давать в сумме нуль.
507
Рис. 10.3.1. Примеры графических представлений
Возможны ^еще и другие графические построения с остатками:
1) график е/ в зависимости от оцениваемого среднего
2) график е, в зависимости от i, если известен порядок реализации наблюдений (тогда, если наблюдения упорядочены во времени, остатки на этом графике будут идти в хронологическом порядке);
3) в случае регрессионной модели с регрессорами Xif XZ,...,XS (положим) графики остатков в зависимости от каждого из регрессоров, т. е. в зависимости от Х^ при ./=1,2......5.
Зависимости [рис. 10.3.1] демонстрируют некоторые возможности (z обозначает ту переменную, которая выбрана для графика). Для классифицированных наблюдений можно разбить остатки на группы, 508
к которым они относятся, и исследовать каждую подгруппу рассмотренными выше методами. Мы можем также заметить различия в остатках между такими группами.
10.4. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Существует множество работ, посвященных вопросам, обсуждавшимся в данной главе. Они имеют такие названия, как «Дисперсионный анализ», «Анализ статистических экспериментов», «Регрессионный анализ», «Корреляционный анализ», «Линейная гипотеза» и т. д. Читатель найдет полезную информацию, например, в следующих работах, приведенных в разделе С списка литературы в томе 2 данного Справочника: [Davies (1957)], [ Graybill (1976)], [Hald (1957)], а также [Kendall and Stuart (1976), т.З]*.
Перечислим еще отличные работы:
Draper N. and Smith Н. (1966). Applied Regression Analysis, Wiley.
Edwards A. L. (1976). An Introduction to Linear Regression and Correlation, Freeman.
P 1 a c k e 11 R. L. (1960). Principles of Regression Analysis, Oxford, Clarendon Press.
S c h e f f ё H. (1959). The Analysis of Variance, Wiley.
S e b e r G. A. F. (1980). The Linear Hypothesis: A General Theory (Second eddition), Griffen.
См. также список дополнительной литературы к гл. 8. — Примеч. пер.
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию ............................ 5
Глава 1. Введение в статистику (перевод И. С. Енюкова) .. 9
Г л а в а 2. Выборочные распределения (перевод И. Г. Грицевич) 29
Г л а в а 3. Оценивание. Вводное обозрение (перевод Ю. Н. Тюрина) .................................................... 84
Г л а в а 4. Интервальное оценивание (перевод Ю. Н. Тюрина) 141
Г л а в а 5. Статистические критерии (перевод Ю. А. Кошевни-ка) ................................................... 211
Глава 6. Метод максимального правдоподобия (перевод Е. 3. Демиденко) ........................................ 281
Г л а в а 7. Статистика хи-квадрат. Критерии согласия, независимости и однородности (перевод В. Д. Конакова) 355
Г лава 8. Оценивание методом наименьших квадратов и дисперсионный анализ (перевод Ю.П. Адлера) ................. 381
Г л а в а 9. Планирование сравнительных экспериментов (перевод Ю.П. Адлера) ........................................ 446
Г л а в а 10. Метод наименьших квадратов и анализ статистических экспериментов: вырожденные модели, множественные критерии (перевод Ю. П. Адлера) ... 468
Научное издание
СПРАВОЧНИК ПО ПРИКЛАДНОЙ СТАТИСТИКЕ
Под редакцией Э. Ллойда, У. Ледермана
Том 1
Книга одобрена на заседании секции редсовета издательства 25. 03. 87
Зав. редакцией К. В. Коробов
Редактор Е. В. Крестьянинова
Мл. редакторы Н. Е. Мендрова, Т. Т. Гришкова
Худож. редактор Ю. И. Артюхов
Техн, редактор И. В. Завгородняя
Корректоры Г В. Хлопцева, С. Г Мазурина, ГА. Башарина, М. А. Суняговская, Т. Г Рослякова Переплет художника А. В. Овчарова
И Б № 2248
Сдано в набор 5.12.88. Подписано в печать 3.10.89.
Формат 60 x 90 1/16 Бум. кн.-журн. офс. Гарнитура «Литературная»
Печать офсетная Усл. п. л.31,36 Усл. кр.-отт.31,36 Уч.-изд. л.31,53
Тираж 20 000 экз. Заказ 112 3. Цена 2 р. 50 к.
Издательство «Финансы и статистика», 101000, Москва, ул. Чернышевского, 7. Набрано на ФКМП Госкомстата СССР Отпечатано в типографии им. Котлякова издательства «Финансы и статистика» Государственного комитета СССР по печати
195273. Ленинград, ул. Руставели, 13.