Российская академия наук
Институт проблем механики
КОМПЬЮТЕРНЫЕ МОДЕЛИ ФИЗИЧЕСКОЙ МЕХАНИКИ
Тепловое излучение
газов и плазмы
Редакционная коллегия:
академик Д.М. Климов
академик А.С. Коротеев
профессор С.А. Медин
профессор Г.Э. Норман
член-кор. РАН Ю.В. Полежаев
профессор СТ. Суржиков
член-кор. РАН И.Б. Федоров
академик В.Е. Фортов
академик Г.Г. Черный
Москва
Издательство МГТУ имени Н.Э. Баумана
2004

Российская академия наук
Институт проблем механики
СТ. Суржиков
Тепловое
излучение
газов и плазмы
Москва
Издательство МГТУ имени Н.Э. Баумана
2004

УДК 533
ББК 22.365
С 90
Отделение энергетики, машиностроения, механики
и процессов управления
Программа фундаментальных исследований
Рецензенты: д-рфиз.-мат. наук, проф. С.А.Лосев,
д-р физ.-мат. наук, проф. Ю.П. Райзер
Суржиков СТ.
С 90 Тепловое излучение газов и плазмы. -М.: Изд-во МГТУ
им. Н.Э. Баумана, -2004. -544 с: 120 ил. (Компьютерные
модели физической механики).
ISBN 5-7038-2605-5D.1)
ISBN 5-7038-2604-7
Введены основные понятия теории переноса лучистой энергии
в горячих газах и низкотемпературной плазме. Представлена
мулировка феноменологических коэффициентов и функций
рии переноса, а также их связь с квантовыми характеристиками.
Приведены основные законы теории переноса теплового
ния. Сформулировано уравнение переноса и даны наиболее часто
употребляемые его частные формы. Обсуждаются особенности
применения моделей элементарных радиационных процессов к
построению феноменологических моделей переноса излучения.
Представлены методы интегрирования уравнения переноса
чения по частоте и по пространственным переменным.
Для научных сотрудников и инженеров в области теплообмена
излучением, физической газовой динамики и физики
ратурной плазмы, а также для студентов и аспирантов физико-
технических специальностей университетов.
УДК 533
ББК 22.365
ISBN 5-7038-2605-5 D.1)
ISBN 5-7038-2604-7 © СТ. Суржиков, 2004

ОГЛАВЛЕНИЕ
Предисловие 14
Глава 1. Основные характеристики теории переноса теплового
излучения 17
1.1. Спектральная интенсивность излучения и основные
усредненные характеристики теплового излучения 17
1.2. Феноменологические коэффициенты теории переноса
теплового излучения 21
1.3. Радиационные характеристики поверхностей 24
1.4. Спектральные, групповые и интегральные характеристики
теории переноса теплового излучения 30
Глава 2. Фундаментальные законы теплового излучении.
Термодинамическая формулировка 33
2.1. Равновесное тепловое излучение 33
2.2. Принцип детального равновесия 34
2.3. Абсолютно черное тело. Закон Планка 34
2.4. Функции излучения абсолютно черного тела 37
2.5. Следствия из закона Планка 38
2.6. Закон Кирхгофа 40
2.7. Закон Ламберта 42
2.8. Закон Бугера 42
2.9. Термодинамика равновесного теплового излучения 43
2.10. Приближение локального термодинамического равновесия .. 47
Глава 3. Уравнение переноса селективного теплового излучения 48
3.1. Уравнение переноса теплового излучения.
Общие и частные формулировки 48
3.2. Формальное решение уравнения переноса 53

Оглавление
3.3. Формулировка уравнения переноса в различных
одномерных геометриях 62
3.3.1. Прямоугольная декартова система координат.
Одномерный случай (бесконечный плоский слой) 62
3.3.2. Сферическая система координат. Одномерный случай
(сферическая симметрия) 63
3.3.3. Цилиндрическая система координат. Одномерный случай
(цилиндрическая симметрия) 64
3.4. Уравнения переноса излучения в трехмерном случае 65
3.4.1. Прямоугольная декартова система координат 66
3.4.2. Сферическая система координат 66
3.4.3. Цилиндрическая система координат 67
3.5. Интегральная форма уравнения переноса излучения для
произвольной геометрии 68
3.6. Интегральная форма уравнения переноса излучения
для плоского слоя применительно к задачам физики
звездных фотосфер. Задача Милна 71
3.7. Феноменологический вывод уравнения переноса излучения... 73
3.8. Граничные условия, формулируемые для уравнения переноса
излучения 77
Глава 4. Основные понятия теории моделирования
радиационных процессов '. 82
4.1. Феноменологическое введение квантовых понятий в теорию
переноса излучения 82
4.1.1. Коэффициенты Эйнштейна 83
4.1.2. Связь между коэффициентами Эйнштейна 84
4.1.3. Скорости элементарных радиационных процессов 84
4.1.4. Связь феноменологических коэффициентов поглощения
и излучения с коэффициентами Эйнштейна 86
4.1.5. Приближение полного перераспределения по частотам .... 90
4.1.6. Спектральный объемный коэффициент поглощения с
поправкой на вынужденное излучение 90
4.1.7. Спектральная функция источников в линии 91
4.2. Общие сведения о способах расчета вероятностей квантовых
переходов 92

Оглавление 7
4.3. Иерархия моделей описания радиационных процессов 93
4.3.1. Модели элементарных радиационных процессов 96
4.3.2. Модели статистических радиационных процессов 99
4.3.3. Феноменологические модели радиационного переноса .... 101
Глава 5. Модели и методы переноса селективного теплового
излучения в условиях ЛТР 104
5.1. Приближения предельных оптических толщин 105
5.1.1. Приближение оптически тонкого слоя 106
5.1.2. Приближение оптически толстого слоя 107
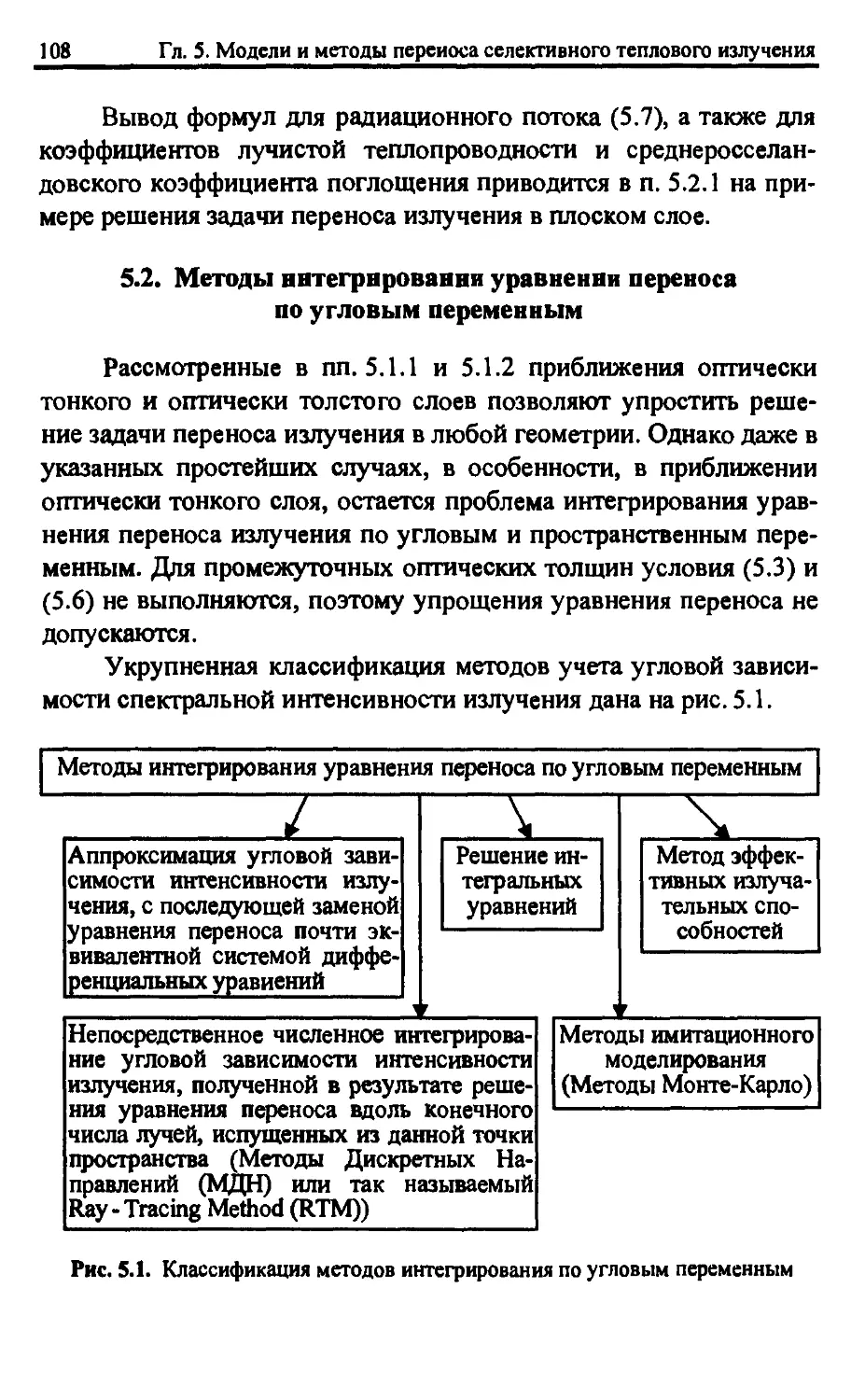
5.2. Методы интегрирования уравнения переноса по угловым
переменным 108
5.2.1. Модель плоского слоя 110
5.2.2. Метод Шварцшильда-Шустера 128
5.2.3. Диффузионное приближение 132
5.2.4. Метод Эддингтона 137
5.3. Метод моментов 140
5.4. Метод эффективных излучательных способностей 145
5.4.1. Метод эквивалентного излучающего объема 145
5.4.2. Метод произвольных от полусферических
испускательных способностей 146
Глава б. Методы сферических гармоник (Рм-метод) 147
6.1. Применение метода сферических гармоник к решению
задачи переноса излучения в плоском слое 148
6.2. Применение метода сферических гармоник к решению
задачи переноса излучения в осесимметричной слое 155
6.3. Конечно-разностные схемы численного интегрирования
двумерных уравнений Ргприближения метода сферических
гармоник 165
6.4. Особенности формулировки граничных условий для методов
сферических гармоник 180
6.4.1. Граничные условия Марка 180
6.4.2. Граничные условия Маршака 181
6.5. Формулировка уравнений Pi-приближения метода
сферических гармоник для произвольной геометрии 183

8 Оглавление
Глава 7. Метод конечного объема для решения задач теории
переноса теплового излучения 190
7.1. Общие понятия 190
7.2. Понятие о консервативных и неконсервативных численных
схемах 191
7.3. Формальное описание метода 193
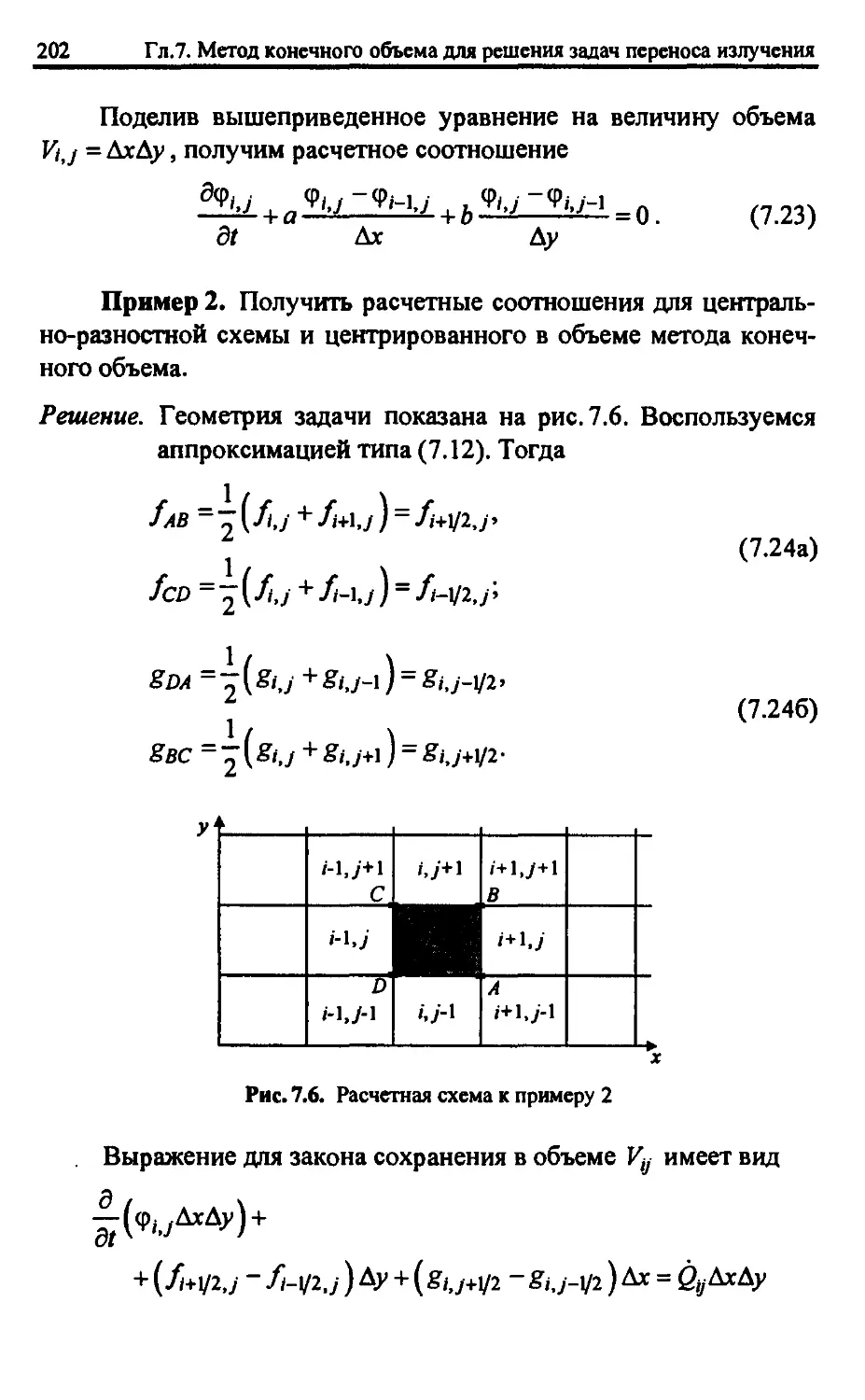
7.4. Расчетные соотношения метода конечного объема
в двумерной геометрии 194
7.4.1. Расчетные формулы для потоков при использовании
потоковой аппроксимации и центрированного в объеме
метода конечного объема 196
7.4.2. Расчетные формулы для потоков при использовании
потоковой аппроксимации и центрированного
в узлах метода конечного объема 197
7.4.3. Расчетные формулы для потоков при использовании
центрально-разностной аппроксимации и центриро-
ванного в объеме метода конечного объема 198
7.4.4. Расчетные формулы для потоков при использовании
центрально-разностной аппроксимации и центриро-
ванного в узлах метода конечного объема 200
7.4.5. Представление производных в методе конечного объема.. 203
7.5. Расчетные соотношения метода конечного объема
в трехмерной геометрии 206
7.5.1. Вводные замечания , 206
7.5.2. Расчет объема трехмерной ячейки 207
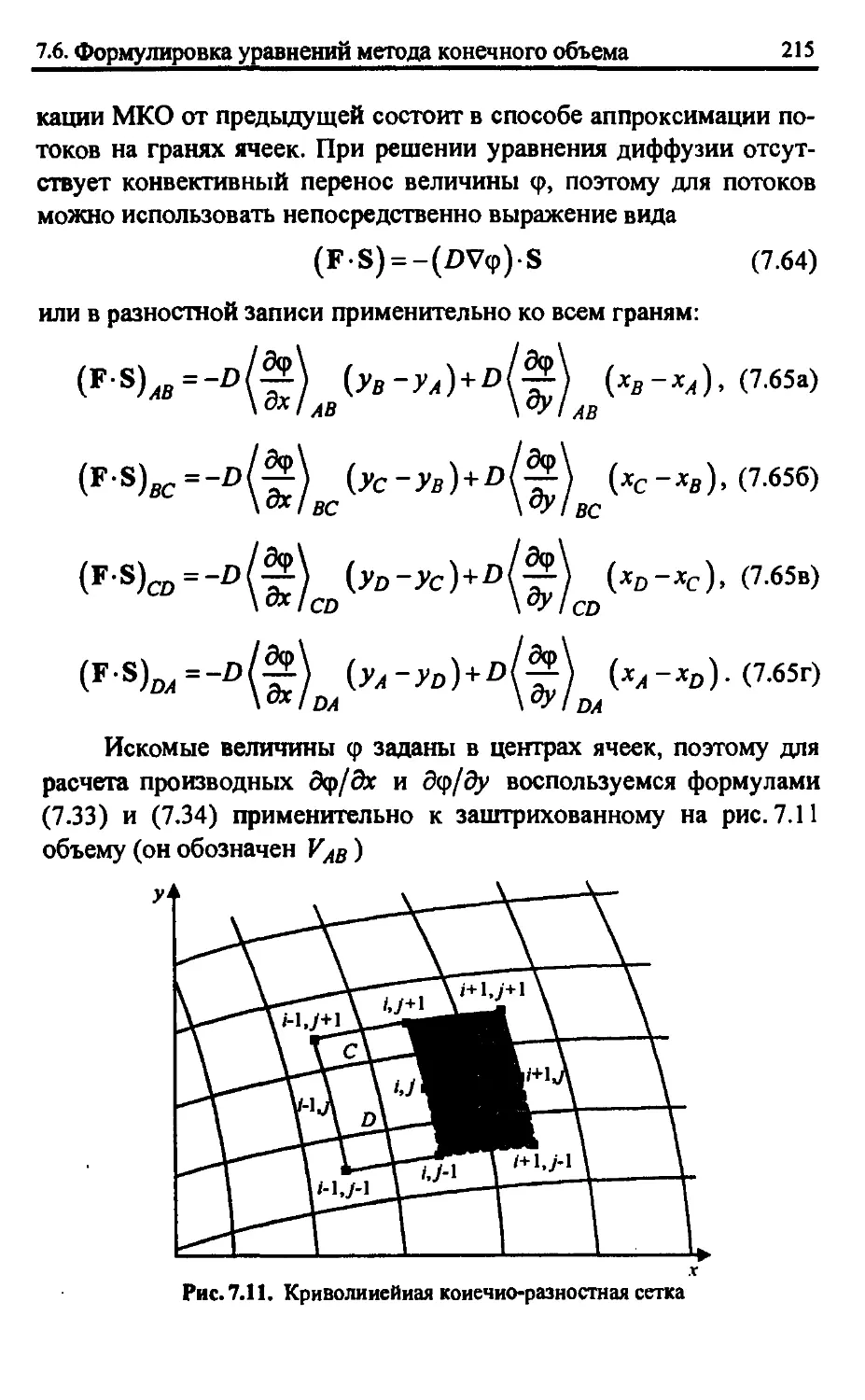
7.6. Формулировка уравнений метода конечного объема
применительно к двумерной задаче переноса теплового
излучения в области произвольной геометрии 209
7.6.1. Вариант центрированного в объеме метода конечного
объема, основанный на центрально-разностной
аппроксимации 209
7.6.2. Вариант центрированного в объеме метода конечного
объема (МКО), основанный на потоковой аппроксимации 214
Глава 8. Методы дискретных ординат, характеристик
и дискретных направлений 223
8.1. Одномерная формулировка 223

Оглавление 9
8.2. Трехмерная формулировка 227
8.3. Расчет переноса излучения без учета эффектов
светорассеяния 233
8.4. Метод характеристик 235
8.4.1. Метод характеристик для одномерной сферической
геометрии 235
8.4.2. Метод характеристик с интерполяцией 237
8.4.3. Консервативный метод характеристик с интерполяцией... 239
8.5. 5„ -метод 241
8.5.1. Применение Sn -метода для решения одномерных задач.. 242
8.5.2. Применение Sn -метода для решения двумерных задач 243
8.5.3. DSn -метод 245
8.6. Методы непосредственного численного интегрирования
угловой зависимости интенсивности излучения 246
Глава 9. Потоковые методы 258
9.1. Методы модифицированных сферических гармоник.
D?L -методы 259
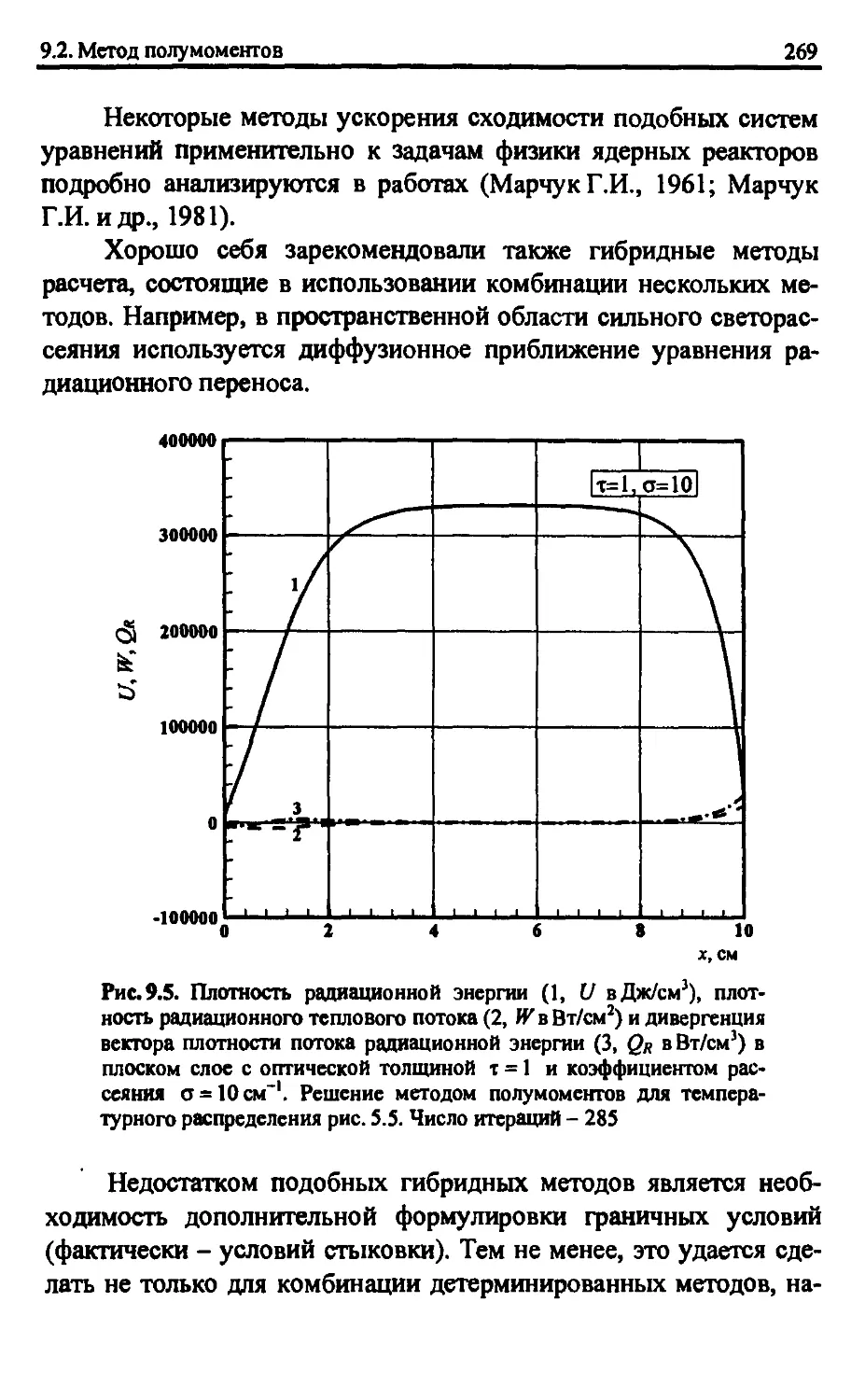
9.2. Метод полумоментов 260
9.3. Итерационные методы решения уравнения переноса 270
9.3.1. Метод последовательных приближений 270
9.3.2. Аналитические итерационные методы 271
9.3.3. Вариационные методы решения уравнения переноса
излучения 272
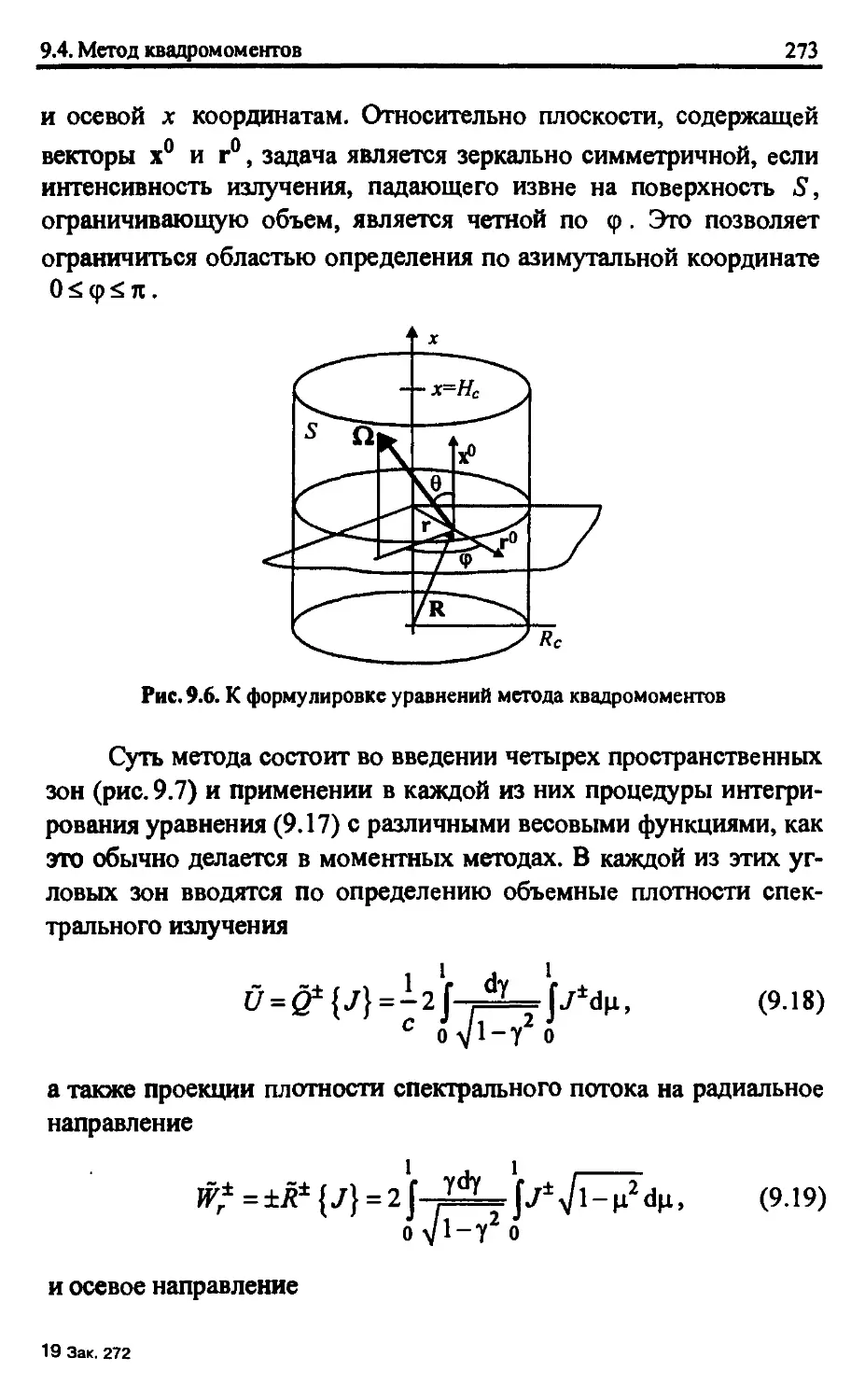
9.4. Метод квадромоментов 272
Глава 10. Статистическое моделирование переноса теплового
излучения в неоднородных объемах
светорассеивающих горячих газов 279
10.1. Общие понятия о принципах имитационного моделиро-
вания распространения излучения в рассеивающей среде 281
10.2. Исходная информация имитационного моделирования 284
10.3. Расчет случайных чисел распределенных по произвольным
законам 286

10 Оглавление
10.4. Моделирование изотропного случайного вектора 287
10.5. Дискретизация исследуемого объема 289
10.6. Определение начальных координат траекторий 291
10.7. Построение прямолинейного участка траектории
в замкнутой области 293
10.8. Моделирование длины свободного пробега 294
10.9. Розыгрыш столкновений 296
10.10. Моделирование процессов поглощения и рассеяния 296
10.11. Регистрация конца историй фотонов 301
10.12. Регистрация актов поглощения 301
10.12.1. Регистрация частиц, покидающих исследуемый
объем через цилиндрическую поверхность 302
10.12.2. Регистрация фотонов на плоскостях z = 0 и z = # 304
10.13. Определение спектральной силы излучения
по результатам моделирования 304
10.14. Определение плотностей радиационных потоков 305
10.15. Особенности имитационного моделирования в твердых
и жидких средах 305
10.16. Оценка достоверности имитации и некоторые другие
алгоритмы статистического моделирования 308
Глава 11. Методы учета спектральной зависимости
коэффициентов поглощения в теории
теплообмена излучением 315
11.1. Классификация спектральных оптических моделей 316
11.2. Среднеинтегральные коэффициенты поглощения 325
Глава 12. Методы интегрирования уравнения переноса
по частоте электромагнитного излучения 329
12.1. Обзор методов интегрирования уравнения переноса
по частоте в задачах теплообмена излучением
и радиационной газовой динамики 329
12.2. Модели разделения переменных интегрирования 338

Оглавление 11
12.2.1. Приближение Милна-Эддингтона 338
12.2.2. Модель разделяющихся переменных в коэффициенте
поглощения 339
12.2.3. Методы разделения переменных Шмыглевского 340
12.2.4. Моментный метод, использующий в качестве
независимой переменной коэффициент поглощения 341
12.2.5. Методы лебегова усреднения 341
12.3. Групповые модели 342
12.3.1. Основные типы групповых моделей 342
12.3.2. Метод группового усреднения 349
12.4. Line-by-line модели 349
12.4.1. Расчет параметров атомных линий 351
12.4.2. Расчет коэффициентов поглощения
в молекулярных линиях 355
Глава 13. Модели нелокального усреднения 358
13.1. Квазидиффузионный метод Гольдина 359
13.1.1. Уравнения метода квазидиффузии в случае одномерной
плоской геометрии 359
13.1.2. Уравнения метода квазидиффузии в случае двумерной
геометрии 362
13.1.3. Потоковый вариант метода квазидиффузии 364
13.2. Многогрупповой квазидиффузионный метод 366
13.3. Интегральное квазидиффузионное приближение 368
13.4. Метод усреднения уравнения переноса Анфимова и Шари... 370
13.5. Метод усредненных уравнений переноса Немчинова 374
13.6. Метод усредненных парциальных характеристик 378
13.7. Метод нелокальных интегральных характеристик для
больших градиентов температуры и химического состава .... 383
13.8. Метод эффективных сечений 386
13.9. Метод эффективных полумоментных характеристик 390
13.10.Метод эффективных квадромоментных характеристик 392
Глава 14. Модели полос. Статистические модели 394
14.1. Общие понятия 395

12 Оглавление
14.2. Статистический подход к расчету переноса
теплового излучения в спектральных линиях 400
14.3. Усреднение параметров спектральных линий
в неоднородных объемах сплошной среды.
Приближение Кертиса-Годсона 404
14.4. Эквивалентная ширина и средняя поглощательная
способность групп атомных линий в модельном
представлении 412
14.5. Эквивалентная ширина и поглощательная способность полос
вращательных линий при электронно-колебательно-
вращательных переходах 416
14.6. Применение статистических моделей к расчету переноса
селективного излучения в плоских слоях
низкотемпературной плазмы 420
14.7. Математическая технология обработки информации
по атомным линиям для расчета температурных
зависимостей групповых функций 427
14.8. Перенос излучения в объемах произвольной геометрии
с учетом спектральных линий 428
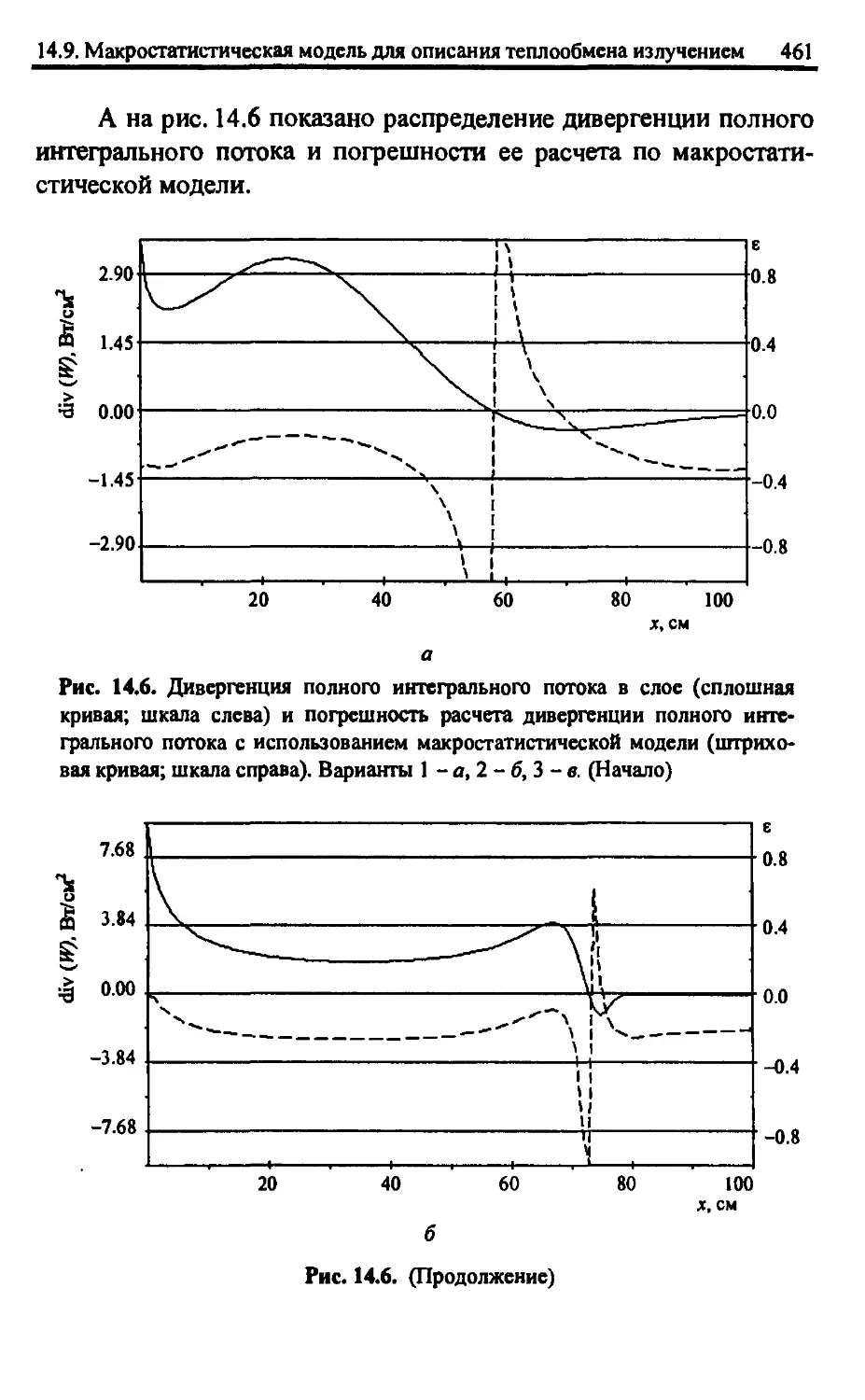
14.9. Макростатистическая модель для описания теплообмена
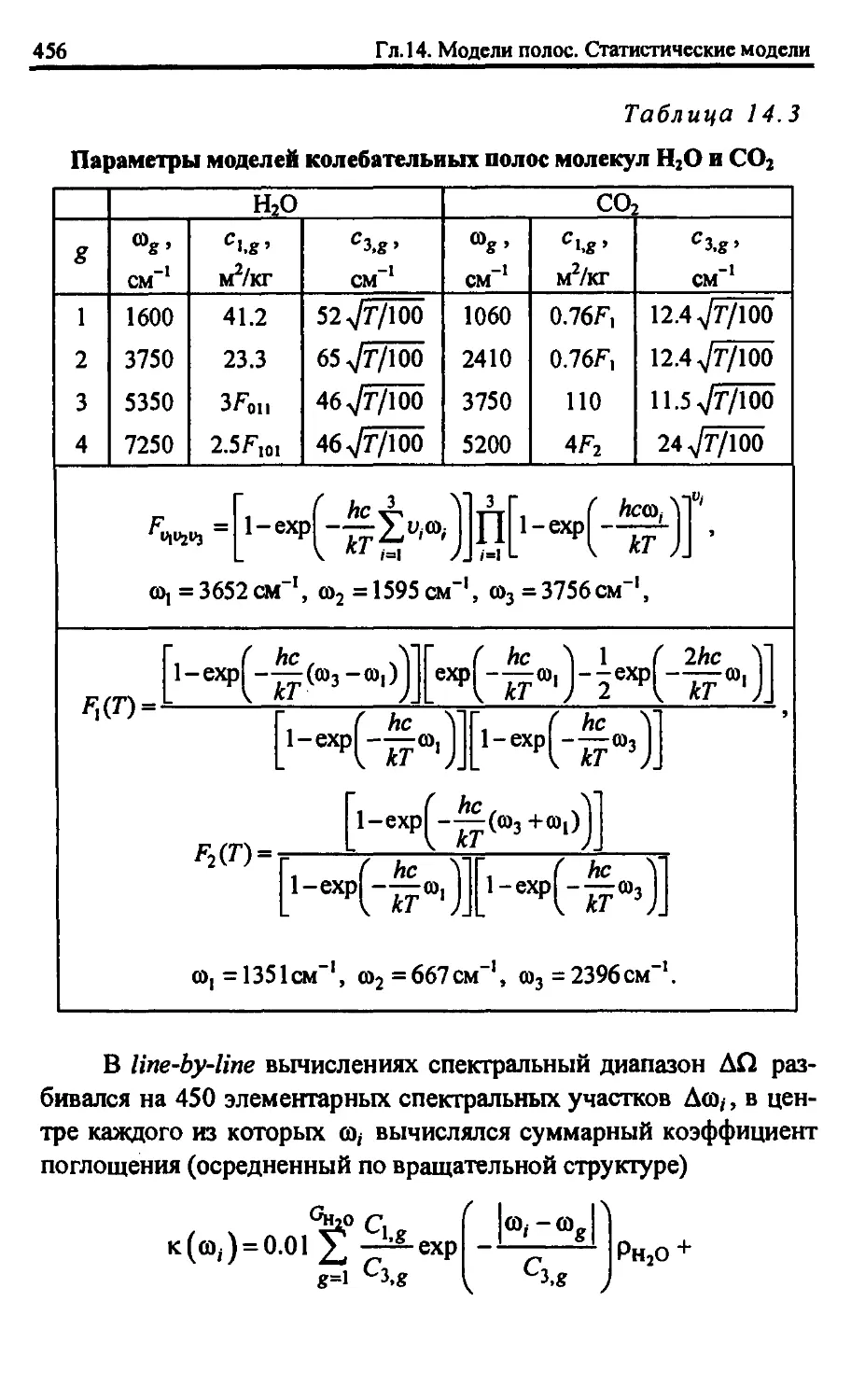
излучением с учетом спектра колебательных полос 432
14.9.1. Формулировка статистических модели молекулярных
линий применительно к одной линии 434
14.9.2. Формулировка макростатистической модели для
однородного оптического пути 440
14.9.3. Формулировка макростатистической модели для
неоднородного оптического пути 442
14.9.4. Расчет переноса излучения методом полумоментов
совместно с макростатистической моделью 446
14.9.5. Результаты расчетов интегральных радиационных потоков
в плоских неоднородных слоях газов, содержащих
молекулы Н2О и СО2 452
14.10. Расчет имитационными методами Монте-Карло переноса
излучения с учетом вращательных линий молекулярного
спектра 463

Оглавление 13
14.10.1. LBL-метод 466
14.10.2. Гибридный метод статистического моделирования 467
14.10.3. Метод усредненных коэффициентов линейчатого
поглощения 475
14.10.4. LBL-метод с малым числом моделируемых траекторий 476
14.10.5. Тестовые расчеты 478
14.10.6. Результаты расчетов спектральной направленной
излучательной способности 483
14.11. Пространственная модель излучения струй
продуктов сгорания 492
Список литературы 514
Предметный указатель 538

ПРЕДИСЛОВИЕ
Теория переноса теплового излучения своими корнями
дит в начало 20-го века, когда в эпоху революционных открытий в
теории атома, начала интенсивно развиваться теоретическая
рофизика.
Уже в первой половине прошлого века было известно, что
большинство задач теории переноса излучения сводится к
нию интегро-дифференциальных и интегральных уравнений и, в
наиболее простых случаях, к решению систем дифференциальных
уравнений в частных производных (как правило, эллиптического
типа). Математически задача оказалась чрезвычайно сложной и
основные усилия математиков, физиков и астрофизиков первой
половины прошлого века были сосредоточены на создании
дов их решения.
Теоретической основой проблемы переноса излучения
ется интегро-дифференциальное уравнение переноса излучения,
которое формулируется относительно спектральной
сти излучения - скалярной функции пространственных и угловых
переменных, частоты электромагнитного излучения и времени.
Два наиболее известных способа вывода уравнения переноса
лучения как феноменологического закона сохранения
магнитной энергии и как уравнения Больцмана для фотонного
газа, непосредственно связаны с корпускулярно-волновым
лизмом трактовки физической природы теплового излучения.
Анализ области применимости уравнения переноса дано в
альной литературе (Апресян Л.А. и др., 1983; ГудменДж., 1988;
ИсимаруА., 1981; Сэмпсон Д., 1969; Адзерихо К.С., 1975; Оци-
сикМ.Н., 1976). Принципиально важным результатом явилось
установление связи феноменологических коэффициентов погло-

Предисловие IS
щения и рассеяния, входящих в это уравнение, с квантовыми
нятиями, основанными на квантовых коэффициентах Эйнштейна.
В середине прошлого века совместными усилиями физиков
и математиков было показано, что уравнение переноса нейтронов
в ядерных реакторах является тем же самым уравнением, но с
особой ролью поведения энергии нейтронов при столкновении с
элементами среды. Такие уравнения были выведены в работах
(ГаланинА.Д., 1957; Murray R.L., 1957; WeinbergA.M. et al., 1958).
Книги, давно ставшие классическими для специалистов по
носу излучения (МарчукГ.И., 1961; ДэвисонБ., 1960;
лев В.В., 1967), не только подвели итог развитию теории переноса
излучения первой половины двадцатого века, но и во многом
ределили направления дальнейших исследований.
Параллельно с использованием в астрофизике и физике
ядерных реакторов теория переноса излучения получила развитие
применительно к задачам атмосферной оптики (Гуди Р., 1966;
Краснопольский В.А., 1987), физики атмосферы, водоемов и льда
(Кондратьев К.Я., 1977; МаровМ.Я. и др., 1987; Хргиан А.Х.,
1986; БояриновП.М. и др., 1991; Красе М.С. и др., 1990),
обмена и теплоэнергетики (Блох А.Г., 1984; Васильев А.П. и др.,
1967; Исаев С.А. и др., 1979; Жуков М.Ф. и др., 1987).
Особое место теория переноса излучения занимает в
плексе наук, основополагающих для аэрокосмической техники.
Излучение струй продуктов сгорания любых типов двигателей,
теплообмен в энергетических устройствах, тепловая защита
планетных и возвращаемых на Землю космических аппаратов -
это лишь малый перечень задач, остающихся до настоящего
мени одними из главных в проблеме создания образцов новой
техники.
Необходимо отметить еще одну принципиальную
ность современной теории переноса теплового излучения. Это
тесная связь с интенсивно развивающейся компьютерной
кой и разнообразными информационно-компьютерными
гиями. Основные проблемы сегодняшнего дня - это решение
гомерных задач переноса селективного теплового излучения с

16 Предисловие
произвольным соотношением элементарных процессов
ния, поглощения и рассеяния.
На содержание данной книги наложили отпечаток научные и
педагогические пристрастия автора, а именно многолетняя работа
в области физической механики и аэрокосмической техники, а
также опыт преподавания в Московском государственном
ческом университете им. Н.Э Баумана и в Московском физико-
техническом институте. Поэтому рассмотрение многих
ментальных вопросов теории переноса излучения, как правило,
завершается изложением способов решения практических задач.
По мнению автора, это должно представлять наибольший интерес
для широкого круга научных сотрудников и инженеров,
тающих в области теплообмена излучением, физической
ки и физики низкотемпературной плазмы, а также для студентов и
аспирантов физико-технических специальностей университетов.
Данная книга является далеко не первой по теории переноса
излучения, как среди отечественных, так и, в особенности, среди
зарубежных изданий (см. список литературы). Однако читатель
найдет в ней ряд новых методов и подходов к расчетно-теоре-
тическому решению задач теплообмена излучением, получивших
распространение в практике исследований.
Автор выражает глубокую благодарность академикам
Д.М. Климову, Г.Г. Черному и чл.-корр. РАН Ю.В. Полежаеву за
многолетнюю поддержку работ в области физической механики и
теплообмена излучением.
С благодарностью автор вспоминает совместную работу с
А.П. Будником, В.Я. Гольдиным, В.В. Горским, В.А. Гореловым,
В.Н. Елисеевым, А.Ю. Киреевым, С.А. Лосевым, В.М.
лаевым, Ю.А. Пластининым, Ю.П. Райзером, В.А. Товстоногом,
Б.А. Хмелининым и СВ. Резником.
Автор выражает признательность сотрудникам издательства
Ml ТУ им. Н.Э. Баумана: директору Т.И. Попенченко и Г.А. Нило-
вой, внесшим большой вклад в создании этой книги. Особенно,
автор благодарит Т.А. Суржикову, выполнившую компьютерную
верстку и макетирование книги.

Глава 1
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ТЕОРИИ
ПЕРЕНОСА ТЕПЛОВОГО ИЗЛУЧЕНИЯ
1.1. Спектральная интенсивность излучения и основные
усредненные характеристики теплового излучения
Основу определения всех характеристик теории переноса
излучения составляет фундаментальное понятие спектральной
интенсивности излучения.
Спектральная интенсивность излучения - количество
гии теплового излучения, проходящее в единицу времени через
единичную площадку, которая расположена перпендикулярно
правлению распространения излучения Q, внутри единичного
лесного угла с осью Q, в единичном интервале частот,
щем частоту v
Jv(r,n,t)= lim ^ , A.1)
v ' &F&nAvAt AFcosGAQAvA/
где A2?v - количество энергии теплового излучения,
го в спектральном диапазоне Av (количество спектральной
тромагнитной энергии); AF - элементарная площадка с вектором
нормали n; cos6 = (n-Q); AQ - элементарный телесный угол с
осью Q; Av - элементарный спектральный диапазон; А/ -
ментарный отрезок времени.
Термин «элементарный» используется здесь с целью
черкнуть, что в пределах элементарной площадки, телесного угла,
спектрального диапазона и отрезка времени - характеристики
лучения изменяются пренебрежимо мало, что допускает
ность вычисления предела в A.1).
3 Зак. 272

18 Гл. 1. Основные характеристики теории переноса излучения
В данном определении спектральной интенсивности
ния понятие энергии теплового излучения введено
чески. Физическая природа теплового излучения, как явления
распространения квантов электромагнитного излучения, была
тановлена классиками классической и квантовой физики на стыке
XIX и XX веков. Она подробно обсуждается в современных
сах общей физики (Сивухин Д.В., 1985; Савельев И.В., 1973;
Тамм И.Е., 1966; Матвеев А.Н., 1985; Фейнман Р. и др., 1972).
вестно, что явление распространения теплового излучения
вильно описываются в рамках волновой физической теории.
нако для изучения взаимодействия теплового излучения и
ва необходимы корпускулярные (квантовые) представления.
этому полная теория переноса теплового излучения является кор-
пускулярно-волновой. Это находит свое отражение в
тивных формулировках спектральной интенсивности излучения.
Связь спектральной интенсивности излучения с
стиками волновой теории устанавливается посредством
магнитной теории для плоской волны, характеризующейся
рами спектральной напряженности магнитного Hv и
ского Ev полей. Введено понятие вектора Умова-Пойнтинга
Sv=-MevxHv]/ A.2)
который определяет количество спектральной энергии,
щей в единицу времени через единичную площадку в
нии, перпендикулярном векторам Ev и Hv (в соответствии с
вилом правой руки). Поэтому
i 0-3)
Соотношения A.2) и A.3) связывают спектральную
сивность излучения с уравнениями Максвелла электромагнитной
теории.
* В Гауссовой системе единиц.

1.1. Спектральная интенсивность излучения 19
Связь спектральной интенсивности излучения с
стиками корпускулярной теории устанавливается посредством
функции распределения фотонного газа /v(r, П), которая
деляется из того, что величина
fv(r,n,t)dvdCldV A.4)
«сть число фотонов, в момент времени t внутри телесного угла
dil с осью П в объеме dV с координатой г в интервале частот
dv, включающем частоту v. Каждый фотон обладает энергией
Av и скоростью с, поэтому
Jv(r,n,t) = hvcfv(r,n,t) . A.5)
Соотношения A.4) и A.5) связывают спектральную
сивность излучения с уравнением Больцмана для фотонного газа.
Установление связи спектральной интенсивности излучения с
личеством энергии, переносимой фронтом электромагнитной вол-
ны, с одной стороны, и с функцией распределения фотонного газа,
с другой стороны, конечно, ни в коей мере не решает проблему
корпускулярно-волнового дуализма, а лишь позволяет
вить теорию переноса теплового излучения, с другими
тальными теориями в тех случаях, когда один из подходов
вится более адекватным. Поскольку главное уравнение теории
переноса теплового излучения (далее - уравнение переноса
чения или просто уравнение переноса) формулируется, как
ло, именно для спектральной интенсивности излучения (см. главу
3), то неудивительно, что для ряда решаемых задач остро встает
вопрос о справедливости этого уравнения (см., например, Адзери-
хо, К.С., 1972; Зигель Р. и др., 1975).
Как следует из определения A.1), спектральная
ность излучения есть скалярная функция трех пространственных
переменных (г), двух угловых переменных (О) и времени (/).
реднение или интегрирование этой функции по некоторым из
речисленных переменных приводит к появлению в теории
носа теплового излучения ряда интегралов, имеющих наглядное
физическое толкование и использование которых часто значи-

20 Гл. 1. Основные характеристики теории переноса излучения
тельно упрощает решение практически важных задач. Рассмотрим
некоторые из этих интегралов.
Спектральная объемная плотность энергии излучения - это
количество лучистой (электромагнитной) энергии, заключенное в
единице объема в единичном спектральном интервале частот
Uv{r,t) = - J 7v(r,Q,r)dQ. A.6)
° П=4я
Вектор плотности спектрального потока излучения
деляется интегралом
Wv(r,/) = J Jv(r,n,t)udCl. A.7)
Плотность полного спектрального потока излучения в
правлении п - это количество лучистой (электромагнитной)
гии, распространяющейся во всех направлениях в пределах
ного сферического телесного угла в единицу времени через
ничную площадку, перпендикулярную направлению п в
ном интервале частот
*FVjn(M) = (n.Wv(r,/))= J 7v(r,Q,/)(nQ)dQ. A.8)
П=4я
Плотность одностороннего спектрального потока
ния в направлении п - это количество лучистой
ной) энергии, которая распространяется в направлениях,
ризуемых знакопостоянством скалярного произведения (п • Q) , и
проходит в единицу времени через единичную площадку,
дикулярную направлению п, в единичном интервале частот
= J yv(r,fi,/)(
(nfl)iO
= J
()
Jv{r,Cl,t)(nCl)dQ.(\.\O)

1.2. Феноменологические коэффициенты теории переноса излучения 21
Давление излучения - это результирующая величина
са, действующего на единичную площадку произвольной
ности. Давление излучения определяется тензором давления,
поненты которого
PVJJ(r,t) = - J 7v(r>Q)/)^.QydQ, A.11)
П=4я
где Ц, Clj - единичные векторы, задающие направление
странения излучения и выделенной элементарной площадки.
В случае изотропного излучения
tf ('.О-Г J Л(¦%">/)dQ = ±t/v(r,/)- 0.12)
iC П=4я *
Другие характеристики переноса излучения,
щие, в частности, поляризацию излучения, представлены в
тах (Адзерихо К.С., 1975; ОцисикМ.Н., 1976; БлохА.Г. и др.,
1991).
1.2. Феноменологические коэффициенты теории
переноса теплового излучения
Для того чтобы описать процесс распространения теплового
излучения в среде, необходимо ввести в теорию ряд функций,
рактеризующих взаимодействие излучения с веществом.
стейшим способом введения таких функций является
логическое определение коэффициентов переноса излучения, не
избавляющим, однако, от необходимости квантового
ния процессов этого взаимодействия.
Рассмотрим феноменологические определения ряда
циентов теории переноса излучения.
Спектральный объемный коэффициент поглощения
ния kv (r) - это доля падающего на элементарный объем
ния, поглощенная веществом на единице длины пути
нения излучения внутри этого объема.

22 Гл. 1. Основные характеристики теории переноса излучения
Величина
задает количество поглощенного веществом падающего
ния
в единицу времени, в единичном объеме, в единичном интервале
частот в пределах телесного угла dfi с осью Q.
Величина
Kv
(r) J Jv(r,n,t)dQ A.13)
П=4*
задает количество поглощенного веществом излучения,
го на единичный объем со всех направлений в единицу времени, в
единичном интервале частот.
Спектральный объемный коэффищент рассеяния излучения
сту(г) - это доля падающего на элементарный объем излучения в
пределах телесного угла dO' с осью П', рассеянная веществом во
всех направлениях на единице длины пути распространения
чения.
Величина
CTv(r)yv(r,n\/)dn' A.14)
задает количество рассеянного веществом во всех направлениях
излучения, падающего на единичный объем в пределах телесного
угла dQ! с осью П', в единицу времени, в единичном
ном диапазоне.
Спектральный объемный коэффищент ослабления
ния Pv (r) определяется как сумма спектральных объемных
эффициентов поглощения и рассеяния:
Pv(r) = Kv(r) + av(r) • A.15)
Вероятность выживания кванта или альбедо однократного
рассеяния задает долю рассеяния в ослаблении среды:

1.2. Феноменологические коэффициенты теории переноса излучення 23
«
М-
Спектральная индикатриса рассеяния yv(r, ?У, Q) - это
функция, характеризующая вероятность рассеяния по разным
правлениям, такая, что величина
¦i-Y(r,Q',n)dQ A.17)
4я
определяет вероятность того, что излучение, падающее в
лении Q', будет рассеяно в пределах телесного угла сЮ с осью
П.
Отсюда следует условие нормировки индикатрисы
рассеяния
j- J у(г,Л\П)сЮ = 1, A.18)
которое утверждает, что с вероятностью, равной единице,
щее излучение будет рассеяно в телесном угле 4л .
С учетом выражений A.14) и A.17) определяется количество
излучения
рассеянного в пределах телесного угла dfi с осью П, в единицу
времени, в единичном спектральном диапазоне, при падении на
единичный объем среды излучения
в пределах телесного угла dQ.' с осью П'.
Количество излучения, рассеянного в единицу времени, в
единичном спектральном диапазоне в пределах телесного угла
dO с осью П при падении на единичный объем излучения со
веек направлений, определяется выражением
i-av(r)dn J yv(r,n',/)y(r,n',n)dnf.

24 Гл. 1. Основные характеристики теории переноса излучения
Среда, взаимодействующая с излучением, не только
щает или рассеивает его, но и испускает спектральное тепловое
излучение, что определяет необходимость введения в теорию
ственной спектральной излучательной способности единицы
объема J™ (r,Cl,t) - излучения, испускаемого единицей объема,
в единицу времени, в единичном спектральном диапазоне, в
ничном телесном угле, осью которого является П.
Собственная спектральная излучательная способность
ницы объема считается изотропной функцией У'1" (г,/) и часто
называется также спектральным объемным коэффищентом
чения.
Построение теории переноса теплового излучения в
ном приближении, когда пренебрегают зависимостью
ентов переноса от интенсивности излучения, позволяет
ждать, что спектральное излучение, испускаемое единицей
ма, в единицу времени, в единичном спектральном диапазоне, в
единичном телесном угле, осью которого является направление
П, состоит из собственного излучения и рассеянного излучения
^(г.О+Т-МО f Л(г,Л',;)у(г,П',П)сЮ',A.19)
4Я П'=4п
причем анизотропия спектрального излучения, испускаемого
ничным объемом, обусловлена процессами рассеяния излучения.
1.3. Радиационные характеристики поверхностей
Значительная часть задач теории переноса теплового
чения связана с проблемой обмена энергией между излучающими,
поглощающими и рассеивающими (отражающими)
ми, а также между средой и ограничивающими ее поверхностями.
Исключительно важна также математическая проблема
ровки граничных условий для уравнения переноса излучения.
Также как и для объема среды, взаимодействие
го излучения с поверхностью можно характеризовать как
нологическими, так и квантовыми коэффициентами и функциями.

1.3. Радиационные характеристики поверхностей 25
Рассмотрим определение наиболее важных феноменологических
коэффициентов.
Спектральная индикатриса отражения
A.20)
определяет долю излучения Jv (r,n',f)cos0'dQ', падающего под
углом 0' к нормали единичной площадки, принадлежащей
верхности, в пределах телесного угла dfi' с осью П',
ную в направлении Q. в единицу времени, в единичном
тральном диапазоне. В теории переноса теплового излучения
именно спектральная индикатриса отражения характеризует
ческие (электромагнитные) свойства поверхностей. Остальные
функции определяются с ее использованием.
Спектральная интенсивность излучения Уу(г,П,/),
женного в заданном направлении П от единичной площадки, в
единицу времени, в единичном телесном угле, определяется
ражением
Jv(r,n,t)= J J^(r,n\n)yv(r,n',f)cose'dn'. A.21)
Спектральная направленно-полусферическая
ная способность
J d/v(r,n,f)cos0dQ
J A.22)
П=2*
где 9 - угол между направлением отраженного луча и нормалью
к единичной площадке. Эта величина определяет отношение
гии излучения, отраженного во всех направлениях, к величине
энергии, падающей на поверхность в направлении П'.
Спектральная полусферически-направленная
ная способность
2 Зак. 272

26 Гл. 1. Основные характеристики теории переноса излучения
A.23)
Jv(r,n',t)cosQ'dn'
П'=2*
определяет отношение энергии излучения отраженного в
лении О. к энергии, падающей на поверхность во всех
ниях.
Спектральная полусферическая отражательная
ность
J pv (г; П' -> 2я) Jv (г, П') соэЭ'сЮ'
™ * AЛ4)
П'=2п
определяет отношение отраженной энергии к падающей энергии.
Особый практический интерес представляют три частных
случая, которые наиболее часто используются в практике
лировки граничных условий для задач переноса излучения.
Поверхность называется диффузно-отражающей, если
тенсивность отраженного излучения одинакова по всем углам
ражения в пределах полусферы и не зависит от угла падения.
Поверхность называется зеркально-отражающей, если
дающий и отражающий лучи симметричны по отношению к
мали в точке падения, а телесный угол, в котором
ся отраженное излучение, равен телесному углу, в пределах
рого распространялось падающее излучение.
Поверхность называется непрозрачной, если она только
щает и отражает излучение, но не пропускает его. Для
ной поверхности вводится также несколько феноменологических
характеристик.
Спектральная направленно-полусферическая поглощатель-
ная способность

1.3. Радиационные характеристики поверхностей 27
где dqv - количество энергии излучения, поглощенного единицей
площадки поверхности в единицу времени, в единичном
тральном диапазоне; Jv (r,n',/)cos9'dfi' - количество энергии
излучения, падающего на единицу площадки поверхности с
малью п в единицу времени, в единичном спектральном
не, в пределах телесного угла dQ.' с осью О', расположенной под
углом 6' к нормали п.
Очевидно, что для непрозрачной поверхности
dqv = Jv (г, П', t) cosG'dn' - pv (г, ?У -> 2л) Jv (г, П', t) cosG'dQ',
поэтому
<xv(r;n') = l-pv(r;n'-»27i). A.26)
По аналогии со спектральной полусферической
ной способностью A.24) определяется спектральная
ческая поглощателъная способность
av ( г; Л' ) Jv ( г, П') cosG'dn'
. A.27)
J
П'=2п
Для непрозрачной поверхности
av(r) = l-pv(r). A.28)
Так как при любой температуре поверхности всегда может
быть определена соответствующая этой температуре
ность излучения абсолютно черного тела, которая, к тому же,
ляется максимально возможной, представляется очень удобным
ввести нормировку излучательных способностей поверхностей.
Спектральной степенью черноты поверхности называется
отношение спектральной плотности потока энергии, испускаемого
данной поверхностью, к плотности потока энергии, испускаемого
абсолютно черным телом при той же температуре.
Спектральная направленная степень черноты - это
шение спектральной интенсивности излучения, испускаемого по-

28 Гл. 1. Основные характеристики теории переноса излучения
верхностью при температуре Т в направлении П при частоте v, к
спектральной интенсивности излучения абсолютно черного тела
«v(r.Q)= , Уг'/..;т 0-29)
По закону Кирхгофа для непрозрачной поверхности (см.
п.2.6) спектральная излучательная способность равна
ной поглощательной способности, поэтому
В большинстве практически важных случаев используется
спектральная полусферическая степень черноты, которая
деляется по формуле
J Jb>v[T(r)]cos9dn
!=2*
= л f JJV[Th)~\C°SQd*1 = 'n I ev(r,n)cos9dQ. A.31)
П=2*
По закону Кирхгофа для непрозрачной поверхности
ev(r) = av(r) = l-pv(r). A.32)
В общем случае испускающей, отражающей и
щей излучение поверхности интенсивность излучения,
страняющегося от этой поверхности, состоит из трех составных
частей: испущенного, отраженного и пропущенного (например, от
внутреннего источника) излучения. Если решается задача о
пространении излучения в объеме, ограниченном такой
стью, то пропущенное излучение добавляют к собственному
лучению, полагая поверхность как бы непрозрачной. В этом
чае спектральная интенсивность эффективного излучения (эй)
элемента непрозрачной поверхности в направлении D.
ется по формуле

1.3. Радиационные характеристики поверхностей 29
n', A.33)
П'=2п
где Л,си(г»^) - спектральная интенсивность собственного
лучения поверхности; Л,ои (r>^) ~ спектральная интенсивность
отраженного излучения поверхности.
Интегрируя спектральную интенсивность эффективного
лучения по всем направлениям, определяют плотность
трального потока эффективного излучения в направлении п
ницы площади поверхности
= f
?Ъ2
A.34)
где 0 - угол между направлениями Пип.
С учетом энергии излучения падающей на поверхность,
плотность спектрального потока результирующего излучения
данной поверхности определяется как энергия результирующего
излучения, распространяющегося в полусфере, характеризуемой
нормалью п, отнесенная к единице площади поверхности, к
нице спектрального диапазона и к единице времени
где
W~n{r)= f yv(r,n')cos9'dQ'.
П'=2п
Представленные формулы A.20)-A.35) позволяют решать
задачи переноса излучения в объемах, ограниченных
стями с практически произвольными оптическими свойствами.
Однако на практике, как правило, используют два типа
стей: зеркальную или диффузную (Оцисик М.Н., 1976).

30 Гл. 1. Основные характеристики теории переноса излучения
1.4. Спектральные, групповые и интегральные
характеристики теории переноса теплового излучения
Все характеристики переноса теплового излучения,
ленные выше, относятся к единичному спектральному диапазону
и называются спектральными характеристиками.
В качестве аргументов спектральной зависимости
циентов и функций в теории теплового излучения используются:
• частота колебаний v - число полных колебаний
нитных волн за единицу времени. Измеряется в с.
• длина волны X - расстояние, на которое смещается
ность одинаковой фазы волны за одно полное колебание,
гаясь со скоростью распространения электромагнитных волн в
среде. Измеряется в (мкм = 10~6 м), (А=1(Г8см) или
(нм=1(Г9м).
• волновое число со - величина, обратная длине волны, то есть
показывающая, сколько длин волн укладывается на единице
длины. Измеряется в см.
• циклическая частота щ = 2nv. Измеряется в рад/с.
Так как скорость света в вакууме со и в диэлектрической
среде с со спектральным показателем преломления nv различна,
при установлении связи между единицами измерения
ной зависимости необходимо конкретизировать условия
странения излучения.
При решении задач переноса теплового излучения в
ке сплошной среды для целей перехода от одних единиц
ния к другим используется предположение о независимости
зателя преломления п от частоты излучения, тогда связь между
единицами измерения выражаются следующими соотношениями
=T = -fi-, dv =
X Х
-fi-, dv = —f
пХ пХ2
v = cw = — w, dv = — do, dw = —-dX.
n n X2
Представленные дифференциальные соотношения между
спектральными переменными следует использовать во всех слу-

1.4. Спектральные, групповые и интегральные характеристики 31
чаях перехода от одних единиц измерения функций
го переноса к другим. Любое преобразование единиц измерения
должно удовлетворять закону сохранения энергии для
ного спектрального диапазона
где Jv,Jx,Jw - спектральные интенсивности излучения,
сенные к единичному диапазону частот, длин волн и волновых
чисел.
Интегральные характеристики теплового излучения
ляются по формуле
00
' А. A36)
где Fv - любая спектральная функция, введенная выше, а
лы интегрирования обычно заменяются границами спектрального
диапазона, в котором интегрируется уравнение переноса.
Интегральные характеристики теории переноса теплового
излучения в спектральных группах определяются по формуле
Fvdv, A.37)
vi
где Fv - любая спектральная функция; vi,v2 - наименьшая и
наибольшая границы спектрального диапазона Av = v2 - Vj. В
теории переноса теплового излучения часто используется термин
спектральная группа, являющийся синонимом понятия
тральный диапазон.
Усредненные по спектральным группам (диапазонам)
теристики теории переноса теплового излучения называются
групповыми функциями. Они рассчитываются по формуле
/Г — Av
Av
Традиционно весь спектральный диапазон, рассматриваемый
в теории переноса теплового излучения, разделяется на три под-

32
Гл. 1. Основные характеристики теории переноса излучения
диапазона: ультрафиолетовый, видимый и инфракрасный.
ные границы этих поддиапазонов даны в табл. 1.1.
Таблица 1.1
Физическая классификация по диапазонам длин волн
теплового излучения
Излучение
Инфракрасное
(ИК)
Видимое
Ультрафиолетовое
(УФ)
ДА., мкм
3.0хЮ2 +
7.6x10''
7.6x10"' +
4.0x10"'
4.0x10"' +
З.ОхЮ
ДА., нм
3.0хЮ5 +
7.6хЮ2
7.6хЮ2 +
4.0хЮ2
4.0х102 +
3.0x10°
ДА., А
3.0хЮ6 +
7.6х103
7.6хЮ3 +
4.0хЮ3
4.0x103 +
3.0x10'
До, см"'
3.3x10' +
1.32хЮ4
1.32хЮ4 +
2.5хЮ4
2.5хЮ4 +
З.ЗхЮ6
Ду, с"'
10'2 +
3.95хЮн
3.95хЮ'4 +
7.5хЮ14
7.5хЮ|4 +
10'7
Следует иметь в виду, что границы спектральных областей в
табл. 1.1 указаны приближенно. При этом весь диапазон
го излучения составляет лишь малую часть шкалы
нитных волн, представляющих практический интерес в различных
приближениях. Указанная шкала приведена в табл. 1.2.
Таблица 1.2
Шкала электромагнитных волн
Область спектра
Радиочастотная:
длинноволновая
коротковолновая
микроволновая
Теплового
излучения:
инфракрасная
видимая
ультрафиолетовая
Рентгеновская
Гамма-излучения
v.c-'
103+107
107+10»
10'+Ю'2
1012+3.95х1014
3.95х10|4 + 7.5хЮ'4
7.5хЮ'4+10п
107+ 1020
>1020
<D, СМ"'
З.ЗхНГ' + З.ЗхЮ
З.Зх10 + З.Зх10
З.ЗхЮ+З.Зх10'
3.3x10'+1.32хЮ4
1.32хЮ4 + 2.5х104
2.5хЮ4+ 3.3x10*
З.ЗхЮ6+З.Зх109
>З.ЗхЮ9
А., мкм
ЗхЮ" + З.ЗхЮ7
ЗхЮ7+З.Зх105
ЗхЮ5 + З.Зх102
3.0хЮ2+7.6х10"'
7.6x10"'+4.0x10"'
4.0хЮ"' + 3.0х10
3.0хЮ +3.0x10"*
< 3.0x10"*
Еще раз подчеркнем, что излагаемая ниже теория переноса
теплового излучения имеет под собой физическое обоснование
для спектрального диапазона теплового излучения.

Глава 2
ФУНДАМЕНТАЛЬНЫЕ ЗАКОНЫ ТЕПЛОВОГО
ИЗЛУЧЕНИЯ.
ТЕРМОДИНАМИЧЕСКАЯ ФОРМУЛИРОВКА
2.1. Равновесное тепловое излучение
Феноменологическая теория переноса теплового излучения
базируется на ряде фундаментальных законов, представленных в
данном разделе. Определим основные фундаментальные понятия
теории теплового излучения. Физическое обоснование
мых утверждений дано в ряде фундаментальных трудов
(ПланкМ., 1975; Шпольский Э.В., 1974; СпроулР., 1974;
Фриш С.Э., 1963) и в курсах общей физики.
Излучение, находящееся в некоторой области пространства в
равновесии с окружающими телами, называется равновесным.
Равновесным называется такое состояние области, адиабатически
изолированной от окружающей среды, при котором объемная
плотность энергии для любой точки области не меняется со
менем, а термодинамические параметры, определяющие
ние любых двух точек, равны между собой. Заметим, что область
может содержать среду, взаимодействующую с излучением.
При термодинамическом равновесии внутри области
ствует результирующий теплообмен между любыми ее
ментами.
¦ При термодинамическом равновесии тел их температуры Т
одинаковы. Поэтому и излучение, находясь в равновесии с
ми телами, имеет температуру Т этих тел.
Равновесное тепловое излучение изотропно.

34 Гл. 2. Фундаментальные законы теплового излучения
2.2. Принцип детального равновесия
Принцип детального равновесия формулируется следующим
образом: каждому микропроцессу, протекающему в некотором
направлении изменения термодинамических параметров в
скопической системе, с равной степенью вероятности
вует микропроцесс, идущий в обратном направлении.
2.3. Абсолютно черное тело. Закон Планка
Абсолютно черным называется тело, обладающее свойством
полностью поглощать все падающее на него излучение любой
частоты, не отражая и не пропуская его через себя.
Тело, находящееся в тепловом равновесии, испускает
ко же излучения, сколько поглощает, следовательно, абсолютно
черное тело при температуре Т испускает максимальное
ство энергии излучения на любой частоте.
Спектральная интенсивность излучения абсолютно черного
тела при температуре Т в вакууме определяется формулой
ном) Планка (рис. 2.1)
со2[ехр(*у/*Г)-1] expD.8xlO"v/r)-l '
где J° v (Г) - в эрг/(см2ср); Т- в К; v - в с;
j0 ггч 2he<i 119.25 хЮ9
"'ХЛ ] X50[exp{hc0/\0kT)-\] ^[exp(l.44xl04A07J-l]'
где J$i (Г) - в эрг/(см2-с-мкм-ср); Т- в К; Хо - в мкм;
$1 119. 74
ехр(АсошоДГ)-1 ехрA.44аH/Г)-Г
где J$^ (Т) - в эрг-см/(см2сср); Г- в К; ю0 - в см.

2.3. Абсолютно черное тело. Закон Планка
35
10
10° W1
Длина волны,мкм
а
10
10"
Волновое число, см"
б
Рис. 2.1. Спектральная зависимость функции Планка от длины
волны (а) и волнового числа (б) при разных температурах в
пичной области теплового излучения

36
Гл. 2. Фундаментальные законы теплового излучения
Интегральной интенсивностью излучения абсолютно
го тела называется интенсивность излучения, испускаемого
лютно черным телом на всех частотах
B.2)
о
п
где 5 = -^fT = 5.6699xl0 эрг/(с-см2-К4) =
= 5.6699 х 10"8 Вт/(м2-К*) =
= 4.96х10~8 ккал/(чм2К4).
Спектральная интенсивность излучения абсолютно черного
тела при температуре Т в диэлектрической среде с показателем
преломления п определяется с учетом того, что скорость света в
диэлектрической среде с связана со скоростью света в вакууме с0
соотношением с = со/п, где п - показатель преломления
трической среды (или просто показатель преломления), поэтому
2hcl
B.3)
21 I Av , ,
с \ ехр — -1
2hc2
ехр
1
Ыт)
п2 ехр
пкт)
¦ Следует иметь в виду, что в общем случае произвольных
сред показатель преломления может зависеть от частоты и быть
комплексной величиной. Применительно к теории теплообмена
излучением этот вопрос подробно обсуждается Р. Зигелем и
Дж. Хауэллом A975).

2.4. Функции излучения абсолютно черного тела 37
Интегральная интенсивность излучения абсолютно черного
тела при температуре Т в диэлектрической среде с показателем
преломления п определяется по интенсивности излучения
лютно черного тела в вакууме при той же температуре
Jb{T) = n2J°b(T). B.4)
Поверхностная плотность спектрального потока излучения
абсолютно черного тела
= \ ^v(r)(n-n)dQ = KJi>v(r). B.5)
П'=2*
где п - вектор нормали к элементарной площадке на поверхности
абсолютно черного тела.
По аналогии для других единиц спектральной зависимости
Поверхностная плотность интегрального потока излучения
абсолютно черного тела находится интегрированием по всему
спектральному диапазону:
v = n^r. B.6)
v=0
Формула B.6) является математическим выражением закона
Стефана -Больцмана.
2.4. Функции излучения абсолютно черного тела
Для удобства расчетов теплообмена излучением без
чения компьютеров удобно использовать некоторые интегралы от
функции Планка по частоте излучения, которые обычно
ляются в табулированном виде (Зигель Р., Хауэлл Дж., 1975; Оци-
сикМ.Н., 1976). На практике используются две из них: функции
излучения первого и второго рода.

38 Гл. 2. Фундаментальные законы теплового излучения
Функция излучения первого рода /о_х (Т) определяется как
доля интегральной интенсивности излучения абсолютно черного
тела в интервале длин волн от 0 до X :
"ь.о-х V )
—7SF~
-0
jb{T) - wb{T)
х
где Wbfi-\{T)=\wbtV{T)&k' и предполагается, что показатель
о
преломления п не зависит от частоты.
Функция излучения второго рода f^\ (T) определяется по
формуле
Связь между функциями излучения первого и второго рода
выражается зависимостью
Функции излучения B.7) и B.8) применяются для быстрого
расчета интегральных характеристик переноса излучением путем
замены интегралов на суммы. Примеры этого представлены в ряде
книг (Зигель Р. и др., 1975; Оцисик М.Н., 1976).
2.5. Следствия из закона Планка
Формулировка закона Планка в виде B.1), B.3) позволяет
получить ряд важных следствий из него в виде законов, которые
исторически были установлены ранее закона Планка. К ним
сятся законы смещения Вина, Рэлея-Джинса, Вина.
ские аспекты установления закона излучения абсолютно черного

2.5. Следствия из закона Планка 39
тела с наибольшей полнотой и достоверностью можно проследить
по трудам Планка (Планк М., 1975; Кляус Е.М., Франкфурт У.Н.,
1980).
Закон смещения Вина. Положение максимума
ной энергии излучения, испускаемой абсолютно черным телом
(или, что одно и тоже: спектрального потока излучения,
каемого поверхностью абсолютно черного тела, (^д)тах),
деляется законом смещения Вина
{nXT)(w ч = 2897.6,мкм-К. B.9)
Максимальная спектральная интенсивность излучения
лютно черного тела при заданной температуре равна
Д) = 4.083х 10"9Г5,эрг/(см2смкмср). B.10)
Закон Рэлея-Джинса. При X0T-»hc0/k из формулы
Планка получается предельное выражение для спектральной
тенсивности излучения абсолютно черного тела в вакууме (так
называемая длинноволновая аппроксимация функции Планка)
2с0кТ 8.28хЮ6Г ., 2 ч ,, ,1Ч
= -7Г~ = Л ' эрг/(см2смкм-ср). B.11)
Закон Вина. При \0T<t:hcQ/k из формулы Планка
чается предельное выражение (так называемая коротковолновая
аппроксимация функции Планка)
И) /„ч 2йс? 119.25 хЮ9 „ 2
B.12)
В пирометрии широко используется следующая форма
на Вина, которая получается отнесением функции Планка к
пературе излучающего тела в пятой степени:

40
Гл. 2. Фундаментальные законы теплового излучения
2hcl
т5
B.13)
Представление о длинноволновой и коротковолновой
проксимациях функции Планка дает рис. 2.2.
10°
? ю2
1
I 10°
-2
10
10"
2 /
/
/
/
» ч
\
*
/
^ \\
— ¦••• к
-- кмк
• - кмк
¦- IMMK
10
-1
10й
Длина волны, мкм
10'
102
Рис. 2.2. Сравнение спектральной зависимости функции Планка
(/, 2), функции Рэлея-Джинса E,4) и Вина E, 6) для двух
ратур абсолютно черного тела
2.6. Закон Кирхгофа
Этот закон является столь же основополагающим для теории
переноса теплового излучения, как и закон Планка, поскольку,
если последний определяет предельно большую энергию, которая
может быть испущена любым телом при фиксированной
туре и длине волны, то закон Кирхгофа определяет связь
сов испускания и поглощения. Закон Кирхгофа формулируется в
следующем виде.

2.6. Закон Кирхгофа 41
В условиях термодинамического равновесия отношение
ности спектрального (интегрального) потока испускаемого
лучения к спектральной (интегральной) полусферической по-
глощательной способности тела является одинаковым для всех
тел и равным спектральной (интегральной) плотности потока
излучения абсолютно черного тела при той же температуре:
B.14)
Следствия из закона Кирхгофа. Следствия из закона
Кирхгофа формулируются для условий, когда внутри
ной изотермической оболочки заключены различные тела.
гласно закону Кирхгофа при термодинамическом равновесии:
1) излучение в каждой отдельной однородной среде является
нородным, изотропным и неполяризованным;
2) спектральная и интегральная направленная поглощательная
способность поверхности равна спектральной и интегральной
направленной степени черноты
a(r,Q) = 6(r,n); B.15)
3) спектральная и интегральная полусферическая
ная способность поверхности равна спектральной и
гральной полусферической степени черноты
<х(г) = б(г); B.16)
4) собственная спектральная излучательная способность
цы объема (спектральный объемный коэффициент излучения)
равна
Г() ()[()] B.17)
где kv (r) - спектральный объемный коэффициент
ния. Феноменологическое определение спектрального
ного коэффициента поглощения дано в п. 1.2;

42 Гл. 2. Фундаментальные законы теплового излучения
5) если Jv - интенсивность излучения в произвольной точке
нородной среды с показателем преломления nv, то величина
Jv jrft одинакова для всех рассматриваемых сред.
2.7. Закон Ламберта
Интенсивность излучения единичной площадки на
ности абсолютно черного тела в каком-либо направлении Q
порциональна косинусу угла между этим направлением и
лью к поверхности п
Подчеркнем, что закон Ламберта формулируется для
гии излучения, испускаемого в данном направлении единичной
площадкой, расположенной на поверхности тела (а не ее
ей). Поэтому определение B.18) не вступает в противоречие с
ределением интенсивности излучения абсолютно черного тела
(см. B.1)) как функции, не зависящей от направления.
2.8. Закон Бугера
Интенсивность спектрального излучения вдоль некоторого
правления О экспоненциально уменьшается при
нении излучения в поглощающей среде, а показатель
ты равен интегралу от текущего объемного коэффициента
лабления по длине пути, пройденного излучением.
Это закон Бугера, математическое выражение которого
ет вид
B.19)
где s - физическая координата вдоль луча с направляющим
тором Q; Jv(s = 0) - спектральная интенсивность излучения,
падающего на элементарную площадку с координатой s = 0 в
правлении С1.

2.9. Термодинамика равновесного теплового излучения 43
Спектральной оптической толщиной отрезка луча s
вают интеграл
S
tv= JPv (*')*'• B-2°)
В теории переноса излучения используются понятия
тральных оптических толщин по отношению к отдельным
сам:
s
Tv а = J kv (s')ds' - спектральная оптическая толщина по по-
*=о глощению;
s
ty s = J Oy (.s')ds' - спектральная оптическая толщина по рас-
*=о сеянию.
Примечание. В различных литературных источниках закон
Бугера иногда называют законом Ламберта, законом Бугера-
Ламберта, законом Бера.
2.9. Термодинамика равновесного теплового излучения
Равновесное тепловое излучение может быть описано в
минах классической равновесной термодинамики (Базаров И.П.,
1983; Плате М., 1975; Кляус Е.М. и др., 1980).
Для того чтобы воспользоваться выводами термодинамики,
необходимо дать формулировку термического и калорического
уравнений состояния теплового излучения, что, как известно,
лать с использованием самой термодинамики невозможно
ев СИ., 2003; Базаров И.П., 1983). Напомним, что термическое
уравнение состояния идеального газа было установлено в
динамике на основе эмпирических законов Бойля - Мариотта и
Гей-Люссака. Указанные закономерности обобщены законом
Клайперона A834 г.), объединение которого с законом Авогадро
дано Д.И. Менделеевым в 1874 г.
Термическое уравнение состояния теплового излучения
зируется на опытных данных П.Н. Лебедева A901 г.) и на теоре-

44 Гл. 2. Фундаментальные законы теплового излучения
тическом предсказании А. Бартоли A876 г.) о существовании
тового давления, которое он сделал на основе второго начала
модинамики. Подчеркнем, что указанные экспериментальные и
теоретические данные не позволяют предсказать зависимость
ления излучения от его температуры, а лишь утверждают
вование давления теплового излучения. Такую зависимость
но определить, привлекая или электродинамическое или
кулярное представление о природе распространения излучения.
Например, феноменологическое введение основных понятий
рии переноса теплового излучения (фактически базирующееся на
корпускулярной модели) дает (см. п. 1.1)
{,t), B.21)
где U{r,t) - интегральная по спектру объемная плотность энер-
гии излучения; Р (г, /) - давление излучения.
В условиях термодинамического равновесия можно записать
следующую связь между полной энергией теплового излучения в
объеме К и объемной плотностью энергии:
B.22)
где U(T) - объемная плотность энергии излучения U(r,t),
торая зависит только от температуры (в равновесии температура
термодинамической системы не зависит от координат и времени).
Применим к равновесному излучению термодинамическое
соотношение, связывающее термическое и калорическое
ния состояния (Базаров И.П., 1983)
B.23)
Подставляя сюда B.21) и B.22), получаем

2.9. Термодинамика равновесного теплового излучения 45
или U = dTA, B.24)
что является законом Стефана-Больцмана. Постоянная
рования а называется константой Стефана-Больцмана.
чально эта постоянная была определена на основе анализа
риментальных данных. Позднее ее удалось рассчитать (см.,
пример, формулу B.2)).
Закон Стефана-Больцмана позволяет дать формулировку
термического и калорического уравнений состояния равновесного
теплового излучения
Р*=-дТ4, B.25)
B.26)
Воспользуемся дифференциальной записью первого начала
термодинамики применительно к тепловому излучению:
TdS = dU + PRdV. B.27)
Отсюда с учетом B.25) и B.26) получаем уравнение для
ления энтропии теплового излучения
B.28)
3
или с учетом третьего начала термодинамики (? = 0 при Т = 0)
S=-aVT\ B.29)
В адиабатическом процессе E = const) для теплового
чения получаем
УТг = const B.30)
или Г*уФ= const. B.31)
Опираясь на соотношение B.25), можно утверждать, что
изобарный процесс является одновременно изотермическим,
этому объемная теплоемкость теплового излучения при постоян-

46 Гл. 2. Фундаментальные законы теплового излучения
ном давлении равна бесконечности. Можно определить объемную
теплоемкость теплового излучения при постоянном объеме, т.е.
B.32)
Феноменологический подход классической термодинамики
позволяет получить ряд практически важных выводов для теории
переноса теплового излучения. Пусть величина C/v (r,f)dv задает
количество энергии излучения в спектральном диапазоне dv в
окрестности v в единице объема. Если на единицу площади
верхностного слоя среды падает энергия ¦ излучения Wvndv в
спектральном диапазоне dv, то можно предположить, что в
щем случае часть этой энергии отразится (Wvrdv), часть
тится (wvadv), а часть пройдет сквозь поверхностный слой
( Wv^dv ). Тогда закон сохранения энергии дает
Wv>rdv+ wvadv+ wvxdv = Wvndv
или pv+av+Tv=l, B.33)
WWW
где pv=-^, av=-^4 tv=-^l B.34)
W,,n' и\„' v W^
соответственно спектральные коэффициенты отражения,
щения и пропускания теплового излучения.
Очевидно, что введенные таким образом первые два
тральных коэффициента, характеризующие взаимодействие
чения с поверхностью, аналогичны спектральной
ской отражательной и поглощательной способностям,
ным в п. 1.3.
Если для любой частоты электромагнитного излучения
av = 1, а, следовательно, из B.33) pv = tv = 0, то такая
ность называется абсолютно черной. Если для любой частоты
pv = 1, то поверхность называется зеркальной или белой, а при
tv .= 1 - абсолютно прозрачной.
Приведенные здесь некоторые следствия термодинамики не
исчерпывают основных ее выводов относительно теплового
чения. Более подробно этот вопрос изложен в книге (Базаров И.П.,
1983).

2.10. Приближение локального термодинамического равновесия 47
2.10. Приближение локального термодинамического
равновесия
Классическая термодинамика постулирует условия полного
термодинамического равновесия (Базаров И.П., 1983; Ландау Л.Д.
и др., 1976), которые, как правило, нарушаются, если решаются
задачи переноса теплового излучения. Основными причинами
этого нарушения являются неоднородные распределения
динамических параметров в исследуемых объемах и не
тость этих объемов. Однако, если пространственные масштабы
достаточно велики, а физические процессы, приводящие к
новлению термодинамического равновесия в любом
ном физическом объеме интенсивны, то равновесие может
няться локально. В этом случае говорят о локальном
мическом равновесии (ЛТР).
Среди указанных физических процессов следует назвать,
прежде всего, столкновительные процессы между тяжелыми
тицами (атомами, молекулами и их ионами) и свободными
тронами. В результате этих столкновений происходит обмен
гией и импульсом между сталкивающимися частицами, а также
рождение и исчезновение новых частиц. В результате указанного
обмена в любом элементарном физическом объеме
ется максвелловское распределение по скоростям всех частиц и
больцмановское распределение по внутренним энергетическим
состояниям частиц, которые характеризуются единой
рой. Радиационные процессы чаще всего являются возмущающим
фактором, приводящим к отклонению от указанного равновесия.
Условия справедливости ЛТР в газах и плазме подробно
суждаются в работах (Биберман Л.М. и др., 1982; Грим Г., 1969;
Фортов В.Е. и др., 1984).
При решении задач астрофизики, физики ударных волн,
рофизики космических аппаратов достаточно часто наблюдается
отклонение не только от условий полного, но и локального
динамического равновесия. Излучение, испускаемое атомами и
молекулами с небольцмановским заселением возбужденных
гетических уровней, называется неравновесным.

Глава 3
УРАВНЕНИЕ ПЕРЕНОСА СЕЛЕКТИВНОГО
ТЕПЛОВОГО ИЗЛУЧЕНИЯ
3.1. Уравнение переноса теплового излучения.
Общие и частные формулировки
Уравнение переноса селективного теплового излучения
мулируется для спектральной интенсивности излучения
Jv(s,Cl,t), распространяющегося вдоль произвольного луча 5,
имеющего единичный вектор Q. В данном разделе уравнение
переноса излучения приводится сразу в наиболее общей форме.
Феноменологический вывод этого уравнения дан в п.3.7.
Пусть из некоторой точки пространства с радиус-вектором г
испускается тепловое излучение (см. рис.3.1). Тогда спектральная
интенсивность излучения может быть найдена из решения
дующего уравнения переноса
dt ds
/{s,t)+oy/{s,t)]jy/{s,Cl,t) = Jevm(s,t)+-±-ov(s,t)x
оо
х J J yE;Q',n;v',v)yv.E,O',/)dO'dv', C.1)
v'=0 ff=4n
где t - время; с - скорость света; Jv (s, О, i) - спектральная
сивность излучения; v - частота излучения; s - физическая
дината вдоль луча; Q - единичный вектор направлений; Ky(s,t)
- спектральный объемный коэффициент поглощения; oy(s,t) -

3.1. Уравнение переноса теплового излучения
49
спектральный объемный коэффициент рассеяния; Jevm(s,t) -
спектральная излучательная способность единицы объема;
y(s;Cl',Q;v',v) - спектральная индикатриса рассеяния по
правлениям и частоте излучения; СУ - единичный вектор,
теризующий направление распространения теплового излучения,
падающего на элементарный физический объем с координатой 5 и
рассеиваемого им с вероятностью y(s; СУ, С1; v', v).
Z ж
Рис. 3.1. К определению понятия спектральной интенсивности излучения
В приближении локального термодинамического равновесия
С3-2)
Уравнение C.1) описывает нестационарный процесс
странения теплового излучения в рассеивающей по направлениям
и частоте излучения среде. Подавляющее большинство задач
рии теплообмена излучением решается в приближении
вившегося во времени процесса переноса {квазистационарное
приближение). Это означает, что характерный временной масштаб
решаемых задач t* много больше времени распространения
тромагнитного излучения на характерном пространственном
штабе I*: f *» Vjc . Фактически это означает, что используется
приближение мгновенности переноса электромагнитной энергии в
исследуемом объеме. В квазистационарном приближении первым
слагаемым в левой части C.1) пренебрегают, а время t в списке
5 Зак. 272

50 Гл. 3. Уравнение переноса селективного теплового излучения
аргументов функций и коэффициентов означает изменение
тральной интенсивности излучения вследствие изменения во
мени свойств среды. В ряде физических задач нельзя использовать
приближение квазистационарности: астрофизика и космология
(Теория звездных спектров, 1966), взаимодействие
ких импульсов излучения с веществом (Хора X., 1986),
стская радиационная газовая динамика (Имшенник B.C. и др.,
1981) и т.п.
Еще одно упрощение, широко используемое в теории
обмена излучением, связано с пренебрежением рассеяния
ния по частоте электромагнитного излучения. Это так называемое
приближение когерентного рассеяния. В этом случае считается,
что фотоны падающего на элементарный физический объем
чения рассеиваются на той же самой частоте электромагнитного
излучения.
Стационарное уравнение переноса селективного излучения в
приближении когерентного рассеяния формулируется в виде
4Я П'=4я
где 7V(^;Q',O) - спектральная индикатриса рассеяния по
правлениям.
Стационарное уравнение переноса селективного излучения в
приближении нерассеивающей среды описывает распространение
излучения только в излучающей и поглощающей среде
C.4)
Стационарное уравнение переноса селективного излучения в
нерассеивающей среде, находящейся в состоянии локального
модинамического равновесия получается из C.4) с учетом C.2)
C.5)

3.1. Уравнение переноса теплового излучения 51
Спектральной функцией источника излучения называется
функция следующего вида
{){) C.6)
4Я П'=4*
Данная функция получается делением уравнения переноса C.3) на
спектральный коэффициент ослабления &v(s) и позволяет его
записать в следующей простой форме
где tv - спектральная оптическая толщина.
Следует обратить внимание на то, что уравнение C.4) имеет
вид обыкновенного дифференциального уравнения первого
рядка, где О служит параметром. Однако для решения задачи
теплообмена излучением в объеме даже самой простейшей
метрии (в плоском слое), это уравнение необходимо
ровать по всему пространству угловых направлений О.
том такого интегрирования будет расчет основных спектральных
характеристик теплообмена излучением. Соответствующие
гральные характеристики определяются интегрированием по
спектру. Приведем наиболее часто используемые функции.
а). Объемная плотность энергии излучения
c/v(r) = - f Jv(r,Cl)dn, C.8)
\ / _ J N /
С П=4я
0 0 П=4я
\ yv(r,O)dQ. C.9)
Физический смысл величины Uv (r) устанавливается
дующим образом. Пусть в элементарном цилиндрическом объеме
dV = dFdtc в единицу времени находится [Jv (r,O)]dFdQd/da)
5*

52 Гл. 3. Уравнение переноса селективного теплового излучения
энергии. Поэтому удельная монохроматическая энергия для
чения, распространяющегося в направлении О внутри dQ равна
c~lJv (r,O)dQ. Интегрируя по телесному углу dQ, находим
С/ДО-
б). Вектор радиационного теплового потока
Wv(r)= J yv(r,O)OdQ, C.10)
П=4я
00
W(r)=Jdv J Jv(r,Q)OdQ. C.11)
О П=4я
Обычно используется спектральная плотность потока
чения РГу.л в некотором фиксированном направлении п , в
стве которого, как правило, выступают координатные линии
пользуемых в расчетах систем координат. Величина
Wvn = nWv (r) = J Jv (г,Q)пШП
4я
представляет собой плотность потока мощности
ской энергии через единицу площади поверхности,
лярной к направлению и.
в). Функция источников тепловыделения в среде
J yv(r,Q)dO, C.12)
П=4я
v(r) J yv(r,O)dOdv.C.13)
0 0 П=4я
Формулы C.12) и C.13) получены как результат
вания по полному телесному углу уравнения переноса C.3).
нако в ряде вычислительных алгоритмов используется
ное применение оператора дивергенции
Заметим, что слагаемые в правой части C.12) не содержат
характеристик светорассеяния, поскольку акты рассеяния излуче-

3. 2. Формальное решение уравнения переноса
53
ния не приводят в явном виде к изменению внутренней энергии
вещества. Конечно, через интенсивность Jv (s,Cl') такое влияние
есть, поскольку падающая энергия формируется, в том числе и
процессами рассеяния.
Когда в отдельных спектральных диапазонах или в полной
спектральной области испускание существенно превосходит
глощение энергии (оптически тонкая среда), то выражение C.12)
становится особенно простым (так называемое приближение
емного высвечивания)
3.2. Формальное решение уравнения переноса
Запись уравнения переноса в форме C.7) позволяет получить
формальное решение уравнения переноса
L о
ds', C.14)
где Jv(s = 0,Q) - спектральная интенсивность излучения,
дающего на границу s = О .
Данное решение называется формальным, поскольку
тральная функция источников излучения Sv(s', Q) под
лом в C.14) содержит искомую интенсивность излучения
Jv(s,Cl), а следовательно, формула C.14) представляет собой
интегральное уравнение.
Если среда нерассеивающая и находится в состоянии
кального термодинамического равновесия, то формальное
ние уравнения переноса излучения заметно упрощается:
L о

54 Гл. 3. Уравнение переноса селективного теплового излучения
з
JKv(s')Jbv(s')exp
ds\ C.15)
или
,fi) = Jv°exp(-tv)+Jji>v(t'v)exp[-(Tv-T'v)]dT',C.16)
где
Физический смысл слагаемых в формальном решении
нения переноса C.15) следующий:
1-е слагаемое характеризует экспоненциальное ослабление
дающего на границу s = О излучения вдоль луча О до точки s;
2-е слагаемое характеризует вклад в функцию Jv(s, Q) излучения,
испущенного в точке s' и экспоненциально ослабленного на
участке [s', s].
Очевидно, что в данном случае можно говорить о точном
решении задачи переноса излучения вдоль луча, поскольку
тральная интенсивность излучения определяется из C.15) или
C.16) путем интегрирования известной функции координаты s. В
случае однородного оптического луча (излучательная способность
не зависит от координаты) эта задача имеет следующее
ческое решение
Jv(Tv,O) = yv°exp(-Tv) + yijV[l-exp(-Tv)]. C.17)
Рассмотрим две практически важные задачи, связанные с
использованием аналитических формул расчета переноса
ния вдоль луча.
Задача 1. Расчет полусферической излучателъной
ности нерассеивающей среды. Эта задача формулируется
дующим образом: определить спектральную плотность потока
излучения на элементарной единичной площадке, расположенной

3.2. Формальное решение уравнения переноса
55
в основании полусферического однородного объема раднусом R.
Расчетная схема задачи показана на рис. 3.2.
По определению плотности одностороннего спектрального
радиационного теплового потока A.9) и A.10)
Wv= \ Jv(R,Cl){Cin)dQ
П=2я
и с учетом геометрии задачи, получаем
2я я/2
WV(R)= Jdcp J Jv(/?,9,0)cos0sined0 =
о о
1
C.18)
Рис. 3.2. К расчету полусферической излучательной способности
Отношение полученной плотности спектрального потока
лучения к спектральной полусферической излучательной
ности абсолютно черного тела называется спектральной
нью черноты полусферического однородного объема раднусом R
Аналогично определяется интегральная степень черноты
полусферического однородного объема

56 Гл. 3. Уравнение переноса селективного теплового излучения
Задача 2. Численное интегрирование уравнения переноса
вдоль луча. Наиболее экономичные расчетные алгоритмы удается
построить для решения уравнения переноса в интегральной
ме, когда в качестве аргумента используется оптическая толщина
C.16). Для фиксированного направления О имеем
о
Вычислению интеграла в C.19) мешает сложный вид функции
за исключением, конечно, случая постоянства температуры вдоль
луча C.17), который ввиду тривиальности рассматривать не
дем. Наиболее очевидным и конструктивным представляется
ленное интегрирование на специально вводимой для этого
стной сетке w = {sj, j = \,2,...,N}. Будем считать, что функции
ту и JbiV (ту ) заданы в узлах этой сетки. Обозначим их
ственно (опустив для краткости индекс v) xj и Jbj. Тогда для
вычисления интеграла можно использовать традиционные методы
интегрирования (методы прямоугольников, трапеции, Симпсона и
др.) (Калиткин Н.Н., 1978). Укажем на трудности, с которыми
приходится при этом сталкиваться. Во-первых, сетка sj не всегда
построена настолько оптимально, что в полной мере отражает
ведение функции источников Jb,v(iv)- При решении сложных
сопряженных задач радиационного теплообмена часто сетка
циально не перестраивается для решения задач переноса
ния. В то же время функция J^v (ту) является чрезвычайно
ной функцией температуры, так что от узла к узлу она может
чительно изменяться. Во-вторых, следует учесть, что луч для
тегрирования может быть выбран так, что он не будет совпадать

3.2. Формальное решение уравнения переноса 57
ни с одной координатной линией, что в еще большей степени
ложнит ситуацию вследствие необходимости интерполяции.
Из сказанного следуют два вывода. Первый - о
сти предъявления высоких требований к разностной сетке для
расчета переноса излучения. Второй - об осторожности
вания традиционных методов интегрирования. Опыт численных
расчетов показьшает, что на грубых расчетных сетках
ние можно отдавать более простым методам интегрирования:
тоду трапеций или методу прямоугольников. В этих простейших
случаях расчетные формулы имеют следующий вид.
1. Расчет по формуле трапеций:
AM T*+i
J •/„(т')ехр(т'-тл,)с1т' =
ЛМ
м "!)-(** -1))]} > C-20)
- хк),
h = {JbM\ ~ Jb,k
Для пояснения алгоритма расчета по формуле C.20) на
рис. 3.3 представлена расчетная сетка
Jb,k\
~0 Tj V2 T/t ~i+l Xtf
Рис З.З. Схема переноса излучения в пределах расчетной ячейки
2. Расчет по формуле прямоугольников:
4 Зак. 272

58 Гл. 3. Уравнение переноса селективного теплового излучения
= ехр(-тА,)| Jo + X Jb,k ехр(тл)[(ехр(тл+1 -хк)-\) |, C.21)
I J
Величина Уд* может быть выбрана произвольно, например
Л,*=Л,*> C-22,а)
Л.*=Л.*+1» C-22,6)
C.22, в)
Однако при сильном изменении функции источников на
тервале [тьТ/t+il ее выбор делать формально нельзя. Например, в
случае, когда t*+i - т* »1, расчет интенсивности к правой
це ячейки [t*,t*+i] (см. рис.3.3) разумнее выполнять с
Jb.k = Л,*+1» а расчет интенсивности к левой границе ячейки - с
Jb,k =Jb,k ¦ Поэтому формула C.22, в) является предпочтительной.
Расчет по формулам C.20) и C.21) даже при разумном
боре аппроксимации Jb,k (x) не является экономичным.
ство экспонент, которые необходимо вычислить для расчета
У(т#), равно ~N . Существует алгоритм расчета
сти всего с -^-кратным расчетом экспонент. Для этого сначала
рассчитывают шкалу функций пропускания расчетных ячеек
((N-X) экспонента)
Т =ехрГ—(т —т I C 23)
. Вклад в интенсивность излучения на правой границе участка
[t.*>t.*+i] (при расчете излучения вдоль луча от ti до т#)
жается формулой
C.24)

3.2. Формальное решение уравнения переноса 59
где
~ хк
Очевидно, что до точки Т// дойдет лишь ослабленная доля
излучения от участка [т*,
т ГТ т _ / т е
¦"/*,*+1 11 4J+\-Jk,k+\lk+\,N -\
Использование формул C.23)-C.25) составляет основу
номичного алгоритма расчета переноса излучения вдоль луча.
чиная расчет с ячейки [т#-ь*//] и продвигаясь в сторону
уменьшения номера узлов сетки, достаточно рассчитать величину
Л,*+1 и умножить ее на суммарное пропускание слоя, которое
формируется шаг за шагом умножением предшествующей
чины пропускания (в первой ячейке [i/v-i, xN] она равна 1) на
множитель 7i+i,*+2 • Дойдя до первой точки луча, остается учесть
внешнее излучение, умножив его интенсивность Jo на
ванное суммарное пропускание слоя 7j,//.
Если при взятии интеграла применять метод
ков, то изменится лишь выражение для Л,*+1:
Изложенный экономичный алгоритм используется не только
для вычисления интенсивности излучения вдоль луча, но и в
гих расчетных методах. Вместе с этим, не всегда возможно
пользование экономичного алгоритма. В его основе лежит
цип аддитивности функции оптической толщины, когда
ская толщина всего отрезка \s\, % ] равна сумме оптических
щин участков, составляющих отрезок. Этот принцип нарушается
при анализе линейчатой структуры спектра (см. главу 11).
Возможен другой способ построения решения в точке Т//. За
основу берется уравнение C.5). Предполагается, что температура
(а значит, и функция источников Jb(T)) и коэффициент погло-

60 Гл. 3. Уравнение переноса селективного теплового излучения
щения k(s) являются кусочно-постоянными функциями на
тервалах (ty_i, sk ), к = 2,..., N. Тогда C.5) в конечно-разностном
виде примет вид
JJ Jk-\ + Jk _
sk~sk-l
K*-i/2 1 = к*-1/гЛ,*-1/2 > О -27)
где к^_]/2, Jb,k-i/2 ~ некоторые значения функций ки Jj внутри
отрезка [*jt-i»**] • Согласно оценкам (Четверушкин Б.Н., 1985)
схема C.27) устойчива с локальной погрешностью
ции, равной О ( As2 ) на гладких решениях.
Отметим, что выбор к*_|/2 = 0.5(ka_i +кк) будет
ски эквивалентен записи уравнения C.5) относительно
ских толщин т*:
+ 'i,jt-i/2> C.28)
2
Ч-Ч-Х
так как
Ч-Ч-\= J
а значения коэффициента известны только в граничных точках
интервала. Поэтому наиболее разумной аппроксимацией для
k(s) является линейная аппроксимация
следовательно,
Теперь рассмотрим оба вида аппроксимации C.24), C.25) и
C.28) в пределах одного отрезка [s*_i,s*]. Положим
ность излучения, падающего на его левую границу, равной нулю.
Тогда, в соответствие с C.28)

3.2. Формальное решение уравнения переноса 61
-V2'Лт= Н*')^'^*-^- C29)
Значение интенсивности в точке s^ no первой из
маций задается формулой C.24), где во всех индексах надо
честь единицу
C.30)
Значения интенсивностей J* и J*k* совпадают лишь при
ловии Дт •« 1 и Jb,k-i/2 = Л,*-1 > когда получается
J?=Jl*ATJbJcA. C.31)
Если же в качестве второго типа аппроксимации
вать соотношение C.26) для кусочно-постоянной зависимости
Jb,k внутри отрезка [s*_j, s* ], то получим
Если положить Дт •« 1, то
Jk=^bjt-i- C.33)
Таким образом, аппроксимации C.24), C.26) и C.28)
дают при малых оптических толщинах ячейки, если выбрать
наковыми ВеЛИЧИНЫ Jb,k-l/2 И Jb,k-l ¦
Если же условие Дт «с 1 не выполняется, т.е. Дт ? 1, то
грешности всех видов аппроксимации можно сравнить, положив
Л (s) = Jb,k = const, тогда
4~'М. C-34)
]-С*- C-35)
Точное решение уравнения переноса в этом простейшем
случае имеет вид, совпадающий с C.35). Значит, если Дт» 1, то

62 Гл. 3. Уравнение переноса селективного теплового излучения
аппроксимация C.34) может дать примерно двукратное
ние интенсивности. Поэтому использование аппроксимаций C.24)
и C.26) считается более обоснованным. Укажем также на работу
(Гольдин В.Я., 1960), в которой анализировался вопрос о типах
аппроксимации функции источников для правильного расчета
чистых потоков и их дивергенций. В этой работе (см. также (Чет-
верушкин Б.Н., 1985)) показано, что кусочно-линейная
мация обеспечивает переход уравнения переноса к виду
ния лучистой теплопроводности при Ах »1.
Заметим, что в двух предельных случаях малых ( Ах «1) и
больших ( Ах »1) оптических толщин уравнение переноса
кает простые решения, называемые приближениями оптически
тонкого и оптически толстого слоев:
при Ах «1: Jv (xv ) = Jv>0 + f Jb (x'v ) dxv,
о C-36)
при Ах»1: Jv(s) = Jbv(s).
Подробно указанные случаи предельных оптических толщин
рассмотрены в главе 5.
3.3. Формулировка уравнения переноса излучения
в различных одномерных геометриях
Рассмотрим запись уравнения переноса излучения в трех
ортогональных системах координат: прямоугольной декартовой,
сферической и цилиндрической. В данном разделе получим
занные уравнения для наиболее простых случаев изменения
ко одной пространственной переменной. После этого уравнение
переноса излучения будет представлено в общем трехмерном
чае (см. п.3.4).
3.3.1. Прямоугольная декартова система координат.
Одномерный случай (бесконечный плоский слой)
Геометрия данного случая показана на рис. 3.4. Полагая, что
рассматриваемый плоский слой бесконечен в направлении осей х

3.3. Формулировка уравнения переноса излучения
63
и у, что приводит к зависимости интенсивности спектрального
излучения лишь от двух координат: ги <в:= cos 9 = ц, получим
частную производную по направлению s в виде
a/v _ a/v
a/v
35 dz dbc
ds
Рис. З.4. Прямоугольная декартова система координат
Из рис. 3.4 очевидно, что
80 Ц,
ds ds
Тогда уравнение переноса излучения для бесконечного
плоского слоя имеет вид
C.37)
-1
З.ЗЛ. Сферическая система координат.
Одномерный случай (сферическая симметрия)
• В этом случае спектральная интенсивность излучения
сит от двух переменных: г и ц = cos 0 (рис. 3.5). Поэтому
a/v (r, ц) = a/v (r, ц) dr | a/v (r, ц) ац
3s 3r dj Эц ds

64
Гл. 3. Уравнение переноса селективного теплового излучения
ИЛИ
Рис. 3.5. Сферическая система координат
Из геометрических соображений следует, что
dr d0
— = cos0, sin0 = -r —
ds ds
dr= d|?=bV.
ds ds r
Поэтому уравнение переноса излучения в одномерной
рической системе координат имеет вид
C.38)
-1
3.3.3. Цилиндрическая система координат.
Одномерный случай (цилиндрическая симметрия)
В этом случае спектральная интенсивность излучения
сит от одной пространственной переменной г и двух угловых
ременных 9 и ф, показанных на рис. З.б. Поэтому
a/v(r,<p,8)_a/v(r,<p,8)dr | a/v(r,<p,e)d9 | а/у(г>ф>
ds 9r ds1 Э0 ds Эф ds1
Из геометрических соображений очевидно, что dф/d$ = 0 .

3.4. Уравнения переноса излучения в трехмерном случае 65
Рассмотрим треугольник аЪс со сторонами ab: - rd0,
ас: ds sin <p, be: d$ sin <p cos @ - d0) « d$ sin <pcos0 . Здесь знак
нус у d6 показывает, что при изменении физической координаты
s на ds угол 9 изменяется на величину -d9. Отсюда следует, что
Q dr . a rd0
cos9 = ;—, sin0 =
ds sin ф ds sin ф
и
dr . -
— = sin © cos 9,
ds
d9
1 . . .
= — sin 0 sin ф.
r
Рис. З.6. Цилиндрическая система координат
Уравнение переноса теплового излучения в одномерной
линдрической геометрии имеет вид
dr
1
— sin 9 sin ф
r
дв
-•CW + T-M'O J Yv(r,H',n)Jv(r,n')dn'.C.39)
Заметим, что в случае цилиндрической геометрии интеграл
по направлениям П' не может быть упрощен по аналогии со
чаями плоской и сферической геометрий.
3.4. Уравнения переноса излучения в трехмерном случае
Существует несколько форм записи уравнения переноса в
трехмерном случае. Здесь представлен вид, принятый в работах
(Гринспен X. (ред.) и др., 1972; Pomraning G.C., 1973).

66
Гл. 3. Уравнение переноса селективного теплового излучения
3.4.1. Прямоугольная декартова система координат
Интенсивность спектрального излучения зависит от
менных Jy = Jv (jc, у, z; ft) = J4 (jc, у, z; <p, 0), и уравнение
са формулируется в виде
оот
dJy
дх
ал,
ал.
ду dz
1
ZZ J IVVTI4- —— <Т I Y V Т I У
4я
х J Yv(^^z;Q',Q)yv(je,^z;Q')dQ',
C.40)
П'=4я
где направляющие косинусы (ux,G>y,(uz рассчитываются по
мулам (рис.3.7) ах = sin 0 cos<p, co^ = sin 0sin cp, coz = cos0.
Z. .
Рис. 3.7. Трехмерная прямоугольная декартова система координат
3.4.2. Сферическая система координат
Уравнения переноса излучения формулируется для
тральной интенсивности излучения Jy = Jv (г, Ф, ©, <р, 0) в виде
a/v
а/„
Ц_^ + ЛГ^ +
а/..
a/v
a/v
йг г 9© г sin© дФ
д\х
дер
(г,Ф,©) J
где направляющие косинусы вектора Q. определяются: по
лам (рис. 3.8) n = cos0, r| = sin0cos9, ^ = sin0sin(p.

3.4. Уравнения переноса излучения в трехмерном случае
67
Q
Рис. Э.8. Трехмерная сферическая система координат
3.4.3. Цилиндрическая система координат
Уравнения переноса излучения формулируется для
тральной интенсивности излучения Jv = Jw ( r, z, ©, <p, 0 ) в виде
д
дг г д® S dz г дер
+ ~av(r,z,&) J Yv(r,z,©;Q',Q)Jv(r,z,©;Q')dQ', C.42)
где направляющие косинусы вектора О. определяются по
лам (рис. 3.9) ^ = cos9, (i = sin0cos9, r) = sin 0 sin ф.
Большой практический интерес представляет формулировка
уравнения переноса излучения в осесимметричной
ской системе координат. В этом случае зависимость от угла ©
чезает, и уравнение переноса излучения принимает вид
_.дал
iav(r'z) J
C.43)
где Jv=Jv(r,z,9,0).

68
Гл. 3. Уравнение переноса селективного теплового излучения
Рис. Э.9. Трехмерная цилиндрическая геометрия
3.5. Интегральная форма уравнения переноса излучения
для произвольной геометрии
Интегральные уравнения теории переноса были впервые
следованы в работах (HilbertD., 1912, 1913) при решении задач о
переносе излучения в фотосферах звезд. Этот тип уравнений
роко используется при решении задач теплоэнергетики,
зики, физики плазмы, физики ядерных реакторов и атмосферной
оптики.
Получим уравнения для стационарного случая переноса
лового излучения. Уравнение переноса излучения C.3)
вим в следующем виде:
где
Qv(r,Cl)=J°m(r)+j-Gv(r) | Yv (г,П',П) Jy (r,Q')dQ' .C.45)
П'»4я
виде
Граничные условия для решения уравнения C.44) задаются в
l(rO)a) = rv(rolfl),(n.n)<0I C.46)
где п - единичный вектор внешней нормали к поверхности,
ничивающей объем, внутри которого распространяется
ние; г0 - радиус-вектор точки поверхности.

3.5. Интегральная форма уравнения переноса излучения
69
Рассмотрим процесс распространения излучения из
рой точки а внутри (или на границе объема) в направлении Q.
ли s - физическое расстояние от точки а, то вместо C.44) можно
записать (воспользовавшись определением производной по
правлению) следующее уравнение:
OS
= Gv (r_5Q,Q) .C.47)
Уравнение C.47) является дифференциальным уравнением
первого порядка, поэтому
C.48)
Интегрируя C.48), получаем
где Jy (r-saQ.,Cl) - постоянная интегрирования.
Поделив уравнение C.49) на экспоненту, получим
Jv (г - sCl, О.) = Jv (г - saCl, Q) ехр
_s
. C.50)

70
Гл. 3. Уравнение переноса селективного теплового излучения
В уравнении C.50) величина s используется как параметр.
Положив s = 0, определим зависимость спектральной
ности в точке г:
Jv (г,Q) = Jv (г-saQ, Q) ехр
-}pv(r-5"n)d*'
C.51)
Для определения постоянной интегрирования Jv (r-saQ,Q.)
положим (r-saQ, Q) = r0, т.е. сопоставим искомую постоянную
граничному значению интенсивности
Jv(r-san,n)\ =rv(r0,Q). C.52)
•V'T rol
С учетом C.52) уравнение C.51) приобретает вид
г-г„
ds'. C.53)
Уравнение C.53) называется интегральным уравнением
реноса теплового излучения. В частном случае отсутствие
ния излучения, ov =0, из C.53) получается так называемое
мальное решение уравнения переноса излучения
г-г„
- J ку
г-г„
-С (г) ехр
ds'.
C.54)
Сравнивая C.54) с C.15), несложно убедиться в их
венности в условиях ЛТР.

3.6. Интегральная форма уравнения переноса излучения 71
3.6. Интегральная форма уравнения переноса излучения
для плоского слоя применительно к задачам физики
звездных фотосфер. Задача Милна
Проблема расчета переноса излучения в плоском
родном светорассеиваюшем слое была сформулирована в работе
(Milne E.A., 1921) применительно к задаче определения излуча-
тельной способности звездных фотосфер.
Л* (т. |
<Гп
п.и)
Рис. 3.10. К постановке задачи Милна
Для изотропного рассеяния уравнение переноса излучения в
одномерной плоской геометрии (рис. 3.10) имеет вид (индекс
спектральной зависимости опущен)
^ J./(T,n')dn\ C.55)
где т= Jp(x')dbc', ц =
, co=
-1
а{х)
(т) ~ интенсивность собственного излучения среды.
Граничные условия для уравнения C.55) формулируются в
виде
= 0,
C.56)
C.57)

72 Гл. 3. Уравнение переноса селективного теплового излучения
Для сформулированной задачи несложно определить
чину интенсивности излучения, обусловленного внешними
никами, приходящего в любую точку х.
j
о
О г \
M^exp -^-^ U. C.58)
Вводится эффективная функция источников излучения:
C.59)
f
-1
Тогда в новой формулировке уравнение переноса излучения
имеет вид
^^ + -/(х.ц) = У„(х) C.60)
с граничными условиями
т = 0, ц>0: У@,ц) = 0, C.61)
т = тя, ц<0: У(тя,ц) = 0. C.62)
Формальное решение уравнения C.60) выглядит следующим
образом
—, Ц>0, C.63)
^. ц<0. C.64)
Подставляя C.63) и C.64) в C.59) находим интегральное
уравнение для эффективной функции источников

3.7. Феноменологический вывод уравнения переноса излучения 73
х -1
Уравнение C.65) можно представить в более компактной
форме:
~ J * VI I/ сш \ ~ / ~~ " Bill \ "/ • - V "/ ' \У-°°/
Z 0
где E\ - интегроэкспоненциальная функция первого порядка.
При J1^ (т) = 0, хн -»°о, @ = 1 получается частный вид
уравнения C.66):
Уравнение C.67), называемое уравнением Милна - одно из
основополагающих уравнений теории переноса излучения,
рающее чрезвычайно важную роль в ее развитии.
Интегральное уравнение переноса применительно к
новесной плазме независимо сформулировано в работах (Бибер-
манЛ.М., 1947, 1949; HolsteinT., 1947). Методы решения
гральных уравнений переноса излучения анализируются в работе
(МарчукГ.И., 1961; Соболев В.В., 1972).
3.7. Феноменологический вывод уравнения переноса
излучения
В настоящем разделе рассмотрен простейший
гический вывод уравнения лучистого переноса C.1) в
нии когерентного рассеяния. Указанный вывод состоит в
лении баланса лучистой энергии, пронизывающей некоторый
элементарный физический объем среды. Уравнение формулирует-

74 Гл. 3. Уравнение переноса селективного теплового излучения
ся относительно спектральной интенсивности излучения
Jy = Jy (s, О, t) в точке пространства с координатами s.
Рассмотрим распространение энергии излучения в пределах
элементарного телесного угла <Ю с осью Q., совпадающей с
правлением координаты s. Выделим элементарный физический
объем в форме усеченного конуса с осью s и площадью
ного сечения dF (рис. 3.11). С точностью до бесконечно малых
величин ds усеченный конус представим в виде цилиндра с
площадью основания dF = s2dQ..
OS
Рис. 3.11. К феноменологическому выводу уравнения переноса излучения
Пользуясь определением спектральной интенсивности
чения, найдем, что величина
QydFdQdvdtds =
U,t)-Jy(s,Cl,t)]dFdndvdtds =
Па/а/П (з.б8)
dFdQdvd/ ^
ds [с dt ds )
есть изменение лучистой энергии в элементарном физическом
объеме за время d/. Постулируется, что это изменение
дит вследствие поглощения или испускания излучения, а также
из-за его рассеяния. Причем рассеяние излучения может
дить как к потерям, так и восполнению энергии контрольного
ментарного физического объема.
Энергетический баланс объема запишем в интегральном виде

3.7. Феноменологический вывод уравнения переноса излучения 75
где Q°, Qyc~ характеризуют убыль энергии за счет поглощения
излучения и рассеяния в направлениях, не совпадающих с ?2; Qev ,
Q$c+ задают источники энергии, обусловленные испусканием и
светорассеянием в направлении О..
Введенные в п. 1.2 феноменологические коэффициенты
реноса позволяют описать слагаемые в C.69).
Коэффициент поглощения kv (s) определен как величина,
равная доле падающего излучения, поглощенного веществом на
единице длины пути, поэтому Q° = kv (s)Jv (s, Q,t) .
Мощность собственного излучения среды, отнесенная к
нице объема, единице телесного угла и единичному интервалу
волновых чисел, определяется спектральным объемным
циентом излучения (см. п. 1.2), который является искомым
гаемым Ql . В условиях локального термодинамического
весия справедлив закон Кирхгофа, связывающий испускание с
поглощением
Ослабление излучения за счет светорассеяния описывается
коэффициентом рассеяния ov(s) A.14), который определяется
как доля падающего излучения, рассеянного веществом во всех
направлениях. Та часть излучения, которая рассеивается в
лении О., не должна входить в стоки энергии, поэтому она
тывается отдельно. Таким образом, Q^~ =ay(s)Jv(s,Cl,t).
Для описания источников энергии, обусловленных
нием излучения, падающего на элементарный объем со
можных направлений, необходимо вводить интегральное
слагаемое
^ y^',Cl)Jy(s,Cl',t)dn', C.70)
4л
где Yv (?&'» Л) - спектральная индикатриса рассеяния.
Величина yv (^'.^) dCl/4n является вероятностью того, что
излучение, падающее в направлении О.', будет рассеяно в
ный угол <Ю с направлением Q.. Значит, если в некоторой точке
элементарного физического объема рассеивается доля

76 Гл. 3. Уравнение переноса селективного теплового излучения
ay(s)Jy(s,Cl',t)dCl' излучения, падающего в телесном угле
АО!, то в направлении Q. будет рассеяно количество энергии,
равное
yv(fl',fl)dflov (s)Jv (s,Cl',t)dQ.'
4я
Интегрирование по всему телесному углу направлений С1' и
отнесение к dQ дает искомую формулу C.70). Здесь, как уже
мечалось в п. 3.1, предполагается, что рассеяние происходит
ко по направлениям, а энергетическое взаимодействие фотонов с
рассеивающим центром, приводящее к изменению частоты
чения, отсутствует (приближение когерентного рассеяния).
Подставляя полученные соотношения в C.68), получаем
искомое уравнение переноса
1 dJy(s,Cl,t) | dJy(s,Cl,t)
с dt ds
(*.«'.')«Ю-
Пренебрегая нестационарностью процесса переноса лучистой
энергии, в дальнейшем первое слагаемое в левой части C.71)
опустим.
Несмотря на то что интегро-дифференциальное уравнение
C.71) имеет ясный физический смысл, оно является чрезвычайно
сложным для решения. Это уравнение обычно решают либо
ленными методами, либо вводят упрощающие допущения
тельно закономерностей изменения феноменологических
циентов переноса kv(s), av(s), yv(Q',Q). Широко использу-
ют следующие приближения:
изотропно рассеивающей среды - уУ(^'>^) = 1
дельта-рассеивающей среды - уу (Cl',Cl) =8(O',Q)
нерассеивающей среды - av(s) = 0

3.8. Граничные условия для уравнения переноса излучения 77
непоглощающей среды - kv (s) = О
неизлучающей среды - Jby(T) = 0.
3.8. Граничные условия, формулируемые для уравнения
переноса излучения
Для решения уравнения переноса селективного излучения
требуется сформулировать граничные условия. Различные виды
граничных условий применительно к задачам динамики
чающего газа рассмотрены в работах (Адрианов В.Н., 1972; Адзе-
рихоК.С, 1975; БайШи-и, 1968; ОцисикМ.Н., 1976; Четверуш-
кин Б.Н., 1985). Остановимся лишь на наиболее
ных случаях граничных условий.
Встречаются два основных типа моделей поверхностей,
раничивающих объем, внутри которого рассматривается перенос
лучистой энергии. Первый вид поверхности - свободная
ность, не вносящая каких-либо возмущений в процесс
странения энергии излучением (например, в задачах об излучении
струй продуктов сгорания). Второй вид поверхности - это
ца раздела фаз с относительным показателем преломления, не
равным единице. Поверхность второго вида может испускать
лучение, отражать и частично пропускать его.
Необходимости в определении вида граничных
стей нет только в одном случае, когда средняя длина свободного
пробега квантов излучения пренебрежимо мала по сравнению с
характерным размером (случай оптически толстой среды). В этом
случае граничное условие для излучения вообще можно не
мулировать, а воспользоваться приближением лучистой
проводности. Однако, в последнем случае необходимо
ровать граничное условие для температуры.
На свободной границе задается спектральная интенсивность
излучения, падающего на объем извне. Частным случаем
ных условий является отсутствие падающего на объем излучения.
Пусть (L4 - элемент свободной поверхности S с внешней
лью п (рис. 3.12). Граничное условие формулируется относитель-

78
Гл. 3. Уравнение переноса селективного теплового излучения
но спектральной интенсивности внешнего излучения, т.е. в виде
заданной функции J^ угловых и пространственных переменных
J~(s,n) = 7°E,ф,9), (Q,n)<0, C.72)
где ф, 9 - азимутальный и широтный углы в системе координат,
связанной с п. Верхний индекс минус у интенсивности излучения
напоминает о том, что излучение, входящее в объем, заполняет
нижнюю полусферу направлений относительно вектора п.
Рис. 3.12. К формулировке граничных условий на границе раздела двух сред
Частные виды граничного условия C.72):
1) Jv (s,(p, 9) = 0 - поток излучения от внешних источников
сутствует (со стороны среды 1 в направлении среды 2);
2) Jv (s, ф, 9) = JV6 (9-90) - плоскопараллельный поток
чения;
3) J° (s, ф, 9) = J° - диффузный поток излучения.
При решении задач динамики излучающего газа в
ной среде с асимптотическим стремлением температуры от
дуемого объекта к бесконечности {Т->ТХ) следует задавать
тенсивность фонового излучения в форме Jv E,ф,B)-Jj,v {Tx).
Граничные поверхности, вносящие возмущения в процесс
распространения излучения, подразделяют на гладкие и
ватые. В первом случае выполняются законы Френеля и Снелла
(Борн М. и др., 1973), при этом отраженные и преломленные лучи

3.8. Граничные условия для уравнения переноса излучения 79
лежат в одной плоскости с падающим и характеризуются одними
значениями углов падения и отражения. Во втором случае
женные и преломленные лучи могут лежать в различных
стях и характеризуются множеством широтных и азимутальных
углов.
Рассмотрим обобщенный вид граничного условия, не
лизируя специфические особенности поверхностей. Считается,
что интенсивность излучения, отходящего от границы раздела
сред 1 и 2, может состоять из трех составляющих (рис. 3.13):
2л л
Jdq>' J j;(s,9',
О л/2
{\-bn)sv{s,<?,Q)Jbv{Tw)
2л л/2
5„ Jdq>' J Jv°(s,9',e')Pv(.s
C.73)
•А
Рис. 3.13. Обобщенные граничные условия
. Функции Rv (s;<p',В';ф,9) и Pv (s;q>',В';ф,9) называются
индикатрисами отражения и пропускания, a ev E,9,9) - слек-
тральной направленной степенью черноты. Три слагаемых в
C.73) задают спектральную интенсивность отраженного
ния J^ , испущенного поверхностью с температурой Tw излуче-

80 Гл. 3. Уравнение переноса селективного теплового излучения
ния J"cn > а также спектральную интенсивность пропущенного
излучения ./"Р0". Спектральная индикатриса отражения Rv и
спектральная направленная степень черноты ev были определены
в п. 1.3.
При записи формулы C.73) предполагалось, что реализуется
только одна из двух взаимно исключающих ситуаций. Либо
ница является непрозрачной для излучения F„=0), либо
зрачной ( 8„ = 1 ). Очевидно, что использование такой гипотезы не
является принципиальным моментом теории, а отражает лишь
специфику решаемых задач. Поэтому если в силу конкретной
туации необходимо учесть как пропускание, так и испускание, то
в C.73) можно исключить сомножители 8„ иA-8„).
Из определения характеристик Ry (s;ср',0';ср, 0), ev (s, ср, 0),
Pv (s;(p',0';(p,0) ясно, что вся специфика граничных
стей заключена в соответствующих функциональных
стях. Как уже отмечалось, в работах по теории переноса теплового
излучения рассматривается ограниченное число моделей
ностей. Число этих моделей становится совсем малым при
нии задач динамики излучающего газа и плазмы. В самом деле, в
таких задачах редко проявляется тонкая специфика
вия излучения с поверхностями. Кроме этого, следует учесть
большую сложность определения оптических характеристик
верхностей при высоких температурах. Поэтому функции
Ry, Ey,Py упрощают. Обычно предполагают отсутствие их
симости от ф. В приближении гладкой, зеркально отражающей
поверхности
6@'-0)rv(*,0') 6@'-0)gvE,0',0)
2я ' C.74)
ev=Av(s,0).
р _ " V" "/'v V»" / р _
Зависимости от угла rv(s, 0',0) и gv (s,0',0) имеют
стой аналитический вид и следуют из законов зеркального
жения Френеля и Снелла. В приближении диффузной
сти Ry = Гу (s)/n , Ру = Гу {s)/n , Ну = hy E). В функции rv (s),
qv{s), ev(s) не входят угловые переменные. Это означает, что

3.8. Граничные условия для уравнения переноса излучения 81
при диффузном отражении, пропускании и испускании энергия
распределяется равномерно по всем направлениям.
Представленные граничные условия сформулированы
сительно спектральной интенсивности излучения. Однако
шое число расчетных методов теории переноса теплового
ния формулируется относительно интегралов от интенсивности
излучения по угловым переменным. В этом случае граничные
ловия вида C.73) должны быть также предварительно
рированы в соответствующих диапазонах изменения угловых
ременных. К сожалению, не всегда переход от интенсивности
лучения к усредненным по угловым переменным функциям
водит к точным граничным условиям. Подробно указанные
блемы обсуждаются, например, в главах 5, 6 и 9.
Имеется еще одна проблема формулировки граничных
вий на границах раздела сред. Речь идет о задании спектральных
оптических свойств реальных поверхностей. Сведения о
тральных излучательных и отражательных способностях
ных материалов, в том числе и полупрозрачных, т.е. частично
пропускающих излучение, можно почерпнуть из книг (Блох А.Г.,
1984; БлохА.Г. и др., 1991; КлименкоА.В. и др., 2001; Петров
В.А. и др., 1985). При необходимости выбора специальных
риалов для спектральных оптических приборов с целью подбора
спектральных диапазонов пропускания излучения следует
титься к специализированным каталогам, которые можно
скать в специальной литературе и Интернете.
7 Зак. 272

Глава 4
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МОДЕЛИРОВАНИЯ
РАДИАЦИОННЫХ ПРОЦЕССОВ
4.1. Феноменологическое введение квантовых понятий
в теорию переноса излучения
Основным противоречием теории радиационного переноса
является то, что она базируется как на классических
гических, так и на квантово-механических и квантово-электроди-
намических представлениях о характере взаимодействия
ния с частицами вещества.
Основное уравнение теории - уравнение переноса C.1)
ляется феноменологическим. Оно выражает в интегральном виде
баланс энергии излучения в элементарном физическом объеме.
Феноменологическими являются и коэффициенты, входящие в это
уравнение.
Если при описании поля спектрального излучения все
тральные коэффициенты в уравнении переноса (kv(s), av(s),
yv(s;Q',Q),J$m(s)) являются известными функциями
нат пространства, или используемые допущения о
ческой модели среды таковы, что указанные коэффициенты могут
бьпъ вычислены в любой наперед заданной точке пространства по
известным термодинамическим параметрам среды, то задача
реноса излучения может быть решена без привлечения каких-либо
дополнительных знаний о физических закономерностях процесса.
Например, в модели локального термодинамического равновесия
эти функции можно предварительно рассчитать и представить в
виде таблиц, входными параметрами которых является любая па-

4.1. Феноменологическое введение квантовых понятий 83
ра термодинамических параметров (давление и температура,
плотность и температура и т.п.).
В общем случае для определения указанных коэффициентов
в уравнении переноса необходимо привлекать квантово-механи-
ческие понятия о взаимодействии излучения с веществом и
рии квантовых переходов в частицах среды.
Переход от одного уровня описания к другому производится
посредством введения феноменологических квантовых
циентов Эйнштейна.
4.1.1. Коэффициенты Эйнштейна
Предполагается, что среда состоит из частиц (атомов,
кул, ионов), каждая из которых может находиться в различных
энергетических состояниях. Переход между энергетическими
стояниями сопровождается поглощением или испусканием
тов электромагнитного излучения.
Рассматривается изолированная частица, имеющая
тические состояния Еи и Еь (Ен < Еь). Эйнштейном определены
три феноменологических коэффициента, характеризующих
ментарные радиационные процессы с участием этих
ских состояний:
Л„н - вероятность спонтанного радиационного перехода из
него квантового состояния в нижнее, с. Это так
мый коэффициент Эйнштейна спонтанного излучения;
cBmU (vBH) - вероятность радиационного перехода из верхнего
квантового состояния (Еь) в нижнее (Е„) под действием
лучения с объемной плотностью f/(vBH) на частоте
vBH = (EB -EH)/h, с. Это так называемая вероятность
нужденного излучения;
c5HBf/(vHB) - вероятность радиационного перехода из нижнего
квантового состояния (Ен) в верхнее (?в) под действием
излучения с объемной плотностью C/(vHB) на частоте
vHB =vBH =(?„-EH)/h, с. Это так называемая
ность вынужденного поглощения.
7*

84 Гл. 4. Основные понятия теории моделирования радиационных процессов
Здесь U(y) - объемная плотность спектральной лучистой
гии, эргс/см3; Ввн (vBH), Bm (vHB) - коэффициенты Эйнштейна
вынужденного излучения (испускания) и вынужденного
ния соответственно, см2/эрг-с.
4.1.2. Связь между коэффициентами Эйнштейна
Между коэффициентами Эйнштейна установлена
щая связь
, D.1)
^ D.2)
гДе ?н> ёь - статистические веса нижнего и верхнего
ских уровней. Соотношение D.1) и D.2) являются следствием
термодинамического равновесия в двухуровневой квантовой
теме (Фриш С.Э., 1963; Блохинцев Д.И., 1976; Давыдов А.С.,
1973; Фок В.А., 1976; Шпольский Э.В., 1974).
4.1.3. Скорости элементарных радиационных процессов
Скорость квантовых переходов из нижнего состояния в
нее определяется по формуле
J Л=Унв(П)(Ю, D.3)
где ин - число частиц в 1 см3 на нижнем энергетическом уровне.
Скорость квантовых переходов из верхнего состояния в
нее определяется по формуле
I =
пь J yv=VBH(n)dQ, D.4)
где ив - число частиц в 1 см3 на верхнем энергетическом уровне.

4.1. Феноменологическое введение квантовых понятий 85
В условиях радиационного равновесия
D.5)
выполняется следующее соотношение детального баланса
cBmnHU ( vHB) = 4яивЛ„ + сВгЛи (vBH), D.6)
VHB ~ VBH •
Скорости квантовых переходов из нижнего энергетического
состояния в верхнее D.3) и из верхнего состояния в нижнее D.4)
сформулированы для случая квантовых переходов между
кретными энергетическими состояниями. Однако из-за
ний, вызываемых окружающими атомами и ионами, а также из-за
конечности времени жизни частицы на верхнем возбужденном
уровне существует некоторый разброс частот, в пределах
го возможен квантовый переход. Спектральная линия,
вующая квантовому переходу, не является бесконечно тонкой
(дельта-функцией частоты излучения). Распределение
сти поглощения (испускания) в пределах линии описывается
тральной функцией профиля поглощения (испускания) /(v). В
общем случае она различная для поглощения и испускания.
Если в пределах спектральной линии частотная зависимость
поля излучения 7V (С2) изменяется сильно, то вместо D.3) и D.4)
необходимо использовать
=]/(v)*HB»H^(v)dv, D.7)
в->н
J
dv. D.8)
В предположении о слабом изменении спектральной
мости интенсивности излучения в пределах спектральной линии
Av и при использовании условия нормировки

86 Гл. 4. Основные понятия теории моделирования радиационных процессов
со
J/(v)dv«J/(v)dv = l D.9)
Av О
получаются формулы D.3) и D.4).
4.1.4. Связь феноменологических коэффициентов
поглощения и излучения с коэффициентами Эйнштейна
Связь между феноменологическим спектральным
ентом объемного поглощения и коэффициентом Эйнштейна
нужденного поглощения Вт устанавливается из соотношения,
выражающего темп убывания спектральной энергии из падающей
на единичный объем лучистой энергии со всех направлений
J (v) D.10)
или kv = nHhvBmfm (v), D.11)
где /HB(v) - спектральная функция профиля поглощения,
деляющая долю частиц njj, способных поглощать энергию на
частоте v:
Спектральная функция профиля поглощения удовлетворяет
следующему очевидному условию нормировки:
D.13)
Собственная спектральная излучательная способность
ницы объема (спектральный объемный коэффициент излучения)
связана с коэффициентами Эйнштейна спонтанного и
ного излучения следующим образом:
J { D.14)

4.1. Феноменологическое введение квантовых понятий 87
где /Bh(v) ~ спектральная функция профиля излучения,
ляющая долю частиц nB, способных испускать энергию на
частоте v:
"в
D.15)
Спектральная функция профиля испускания удовлетворяет
следующему очевидному условию нормировки:
(v)dv = l. D.16)
о
В условиях термодинамического равновесия
/BH(v) = /HB(v),
поэтому Jlm = «„/„„ (v) /iv5HB7B v = kv>/b v. D.17)
Здесь при формулировке связи феноменологических
циентов переноса с коэффициентами Эйнштейна предполагалось,
что все поглощение и все испускание излучения на данной
те обусловлено только квантовыми переходами внутри частиц
одного сорта, число которых в нижнем и верхнем энергетических
состояниях в единице объема равно соответственно ин и ив.
Соотношения D.11) и D.14) служат для определения
нологических спектральных дифференциальных сечений
щения и испускания соответственно
<*= — = ^hb/hb(v), D.18)
"н
И»
-Av/i(v)
¦ D.19)

88 Гл. 4. Основные понятия теории моделирования радиационных процессов
Феноменологическое спектральное дифференциальное
ние поглощения av a определяется как спектральный
ент поглощения в расчете на одну частицу, находящуюся на
нем энергетическом уровне.
Феноменологическое спектральное дифференциальное сечение
излучения av e определяется как спектральный коэффициент
лучения в расчете на одну частицу, находящуюся на верхнем
энергетическом уровне.
Феноменологические объемные спектральные коэффициенты
поглощения и излучения для частиц k-ro сорта определяются по
формулам
ЙЙ *
X() . D2°)
NiNf k
•^*=??я*.*К.),. D-21)
e=l i=l
где Ng -число элементарных процессов поглощения,
кающих с участием частиц jfc-ro сорта; Nf - число
ских состояний у частиц к-го сорта, находясь на которых
ца может принять участие в квантовом радиационном переходе
а-го типа; / - индекс энергетического уровня;
(°у.Д =hv{B**,a )i [fm,a (v)],. " спектральное
ное сечение поглощения квантового перехода а-го типа с /-го
энергетического уровня для частиц к-го сорта;
1
спектральное дифференциальное сечение излучения для
вого перехода е-го типа с /-го энергетического уровня для частиц
Jt-ro сорта;
) (^) ~ коэффициенты Эйнштейна для квантового
(Ане) »
не)
перехода е-го типа с /-го энергетического уровня для частиц к-го
сорта;

4.1. Феноменологическое введение квантовых понятий 89
(^т,а ) ~ коэффициент Эйнштейна для квантового перехода о-го
типа с i-го энергетического уровня для частиц к-го сорта;
[/нв.в (v)], > [/вн,е (v)], - спектральные функции профиля
глощения и излучения для а-го (е-го) квантового перехода с /-го
энергетического уровня для частиц к-го сорта.
Феноменологические объемные спектральные
ты поглощения и излучения для смеси частиц, каждая из которых
может принимать участие в радиационных процессах посредством
разных квантовых переходов, определяются с использованием
принципа аддитивности
Nk Nka Nf k
Kv,* = ? S S "k,i (°v.e ), ' D-22)
k\ \ i\
N
7
J7 = I J% = ? 11 "k; {°*.e t. D-23)
где Nk - число сортов частиц, принимающих участие в
тарных радиационных процессах.
Феноменологическое спектральное полное сечение
щения (или просто спектральное сечение поглощения)
онного процесса о-го типа для частицы jfc-ro сорта определяется по
формуле
1 Nt
()K D24)
Феноменологическое спектральное полное сечение
ния (или просто спектральное сечение излучения) для частицы
к-го сорта определяется по формуле
D.25)
6 Зак. 272

90 Гл. 4. Основные понятия теории моделирования радиационных процессов
Установленные соотношения между феноменологическими
коэффициентами переноса излучения и коэффициентами
штейна справедливы для любых типов квантовых переходов
занно-связанных, связанно-свободных, свободно-связанных,
бодно-свободных).
4.1.5. Приближение полного перераспределения
по частотам
В приближении полного перераспределения по частотам,
справедливого при термодинамическом равновесии, спектральные
функции профилей поглощения и излучения тождественно равны
/HB(v)s/BH(v). D.26)
4.1.6. Спектральный объемный коэффициент поглощения
с поправкой на вынужденное излучение
С учетом коэффициентов Эйнштейна Ам,Ваи,Вт
ние переноса излучения может быть записано в общем случае
равновесных радиационных процессов в следующем виде (без
учета процессов светорассеяния):
a/v(*,o,r)
D.27)
ds
1
(v)
В предположении об изотропности поля излучения для
оценки интеграла в правой части, уравнение переноса
ется в виде
OS
D.28)
где k'v = nHhvBmfm (v)[ 1 -^M=-1, D.29)

4.1. Феноменологическое введение квантовых понятий 91
yvem(^0 = «B^v/BH(v)^H. D.30)
Коэффициент к'у называется спектральным объемным
эффициентом поглощения с поправкой на вынужденное
чение.
В условиях термодинамического равновесия
DJI)
поэтому спектральный объемный коэффициент поглощения с
правкой на вынужденное излучение D.29) имеет следующий вид:
инАуВнв/нв(у) 1-ехр -—
/IV
kT
D.32)
4.1.7. Спектральная функция источников в линии
Спектральная функция источников в линии определяется по
формуле (в отсутствии рассеяния)
bh
В приближении полного перераспределения по частотам, в
соответствии с тождеством D.26)
В приближении термодинамического равновесия
ная функция источников в линии совпадает со спектральной
тенсивностью излучения абсолютно черного тела
2Av3
-,. D.35)
Cn exp — -
и г im I
6*

92 Гл. 4. Основные понятия теории моделирования радиационных процессов
4.2. Общие сведения о способах расчета вероятностей
квантовых переходов
Между вероятностями квантовых переходов
тов Эйнштейна) существует связь вида D.1), D.2). Поэтому для
расчета той или иной вероятности обычно выбирают наиболее
простой способ расчета какого-либо из коэффициентов, а затем
используют формулы D.1), D.2).
Существуют три последовательно усложняющихся уровня
сложности расчета вероятностей квантовых переходов.
1-й уровень. Квантовый переход рассматривается в приближении
классического атома и классического электромагнитного
ля. Электрон в атоме считается затухающим гармоническим
осциллятором, возбуждаемым электромагнитным полем.
Для вероятности квантового перехода в поглощении
ется формула, в которую асимптотически переходит любая
другая формула, полученная при меньшем числе допущений.
Числовые значения, рассчитываемые по данной формуле,
имеют правильную размерность и для сильных линий
ваются достаточно точными.
2-й уровень. Квантовый переход рассматривается в приближении
квантово - механического атома и классического
нитного поля. Это приближение дает правильные выражения
для вероятностей вынужденного поглощения и
го излучения (Вт, Вт). Величина вероятности спонтанного
излучения (Д,н) в этой теории не появляется, поэтому ее
вычисляют с использованием формул D.1), D.2).
3-й уровень. Квантовый переход рассматривается в модели кван-
тово-механический атом и квантованное электромагнитное
поле. Эта теория является полной, и она дает правильные
зультаты для всех вероятностей квантовых переходов.
В работах по физической механике и теплообмену
ем для расчетов вероятностей квантовых переходов используются
теории 1-го и 2-го уровней. Полное изложение теории 3-го уровня
дано в работах (Дирак П., 1964; Гайтлер В., 1956).

4.3. Иерархия моделей описания радиационных процессов 93
4.3. Иерархия моделей описания радиационных
процессов
Попытка преодолеть основное противоречие теории
ционного переноса привела к тому, что в эту теорию было
но три уровня описания радиационных процессов.
1. Квантово-механический - для нахождения вероятностей
квантовых радиационных переходов в отдельно взятых
цах. Именно этот уровень описания квантовых переходов
жду энергетическими состояниями частиц был представлен в
виде трех подуровней, обсуждавшихся в п.4.2.
2. Статистический - для нахождения спектральных
циентов поглощения и испускания статистических ансамблей
частиц.
3. Феноменологический - для нахождения полей радиационных
характеристик в различных средах, для решения задач
венно радиационного переноса энергии.
Очевидно, что важным вопросом теории переноса излучения
является проблема согласования указанных уровней описания
процессов.
Для того чтобы перейти от квантово-механического уровня
описания к статистическому необходимо привлечь ту или иную
термодинамическую или квантово-статистическую модель
стояния среды, т.е. учесть специфику протекания радиационных
процессов в частицах, находящихся во взаимодействии с другими
частицами и электромагнитными полями.
Для того чтобы перейти к еще более высокому уровню
сания - феноменологическому, необходимо выбрать адекватный
изучаемому процессу способ описания радиационного переноса
(другими словами, метод решения уравнения переноса излучения)
и подготовить соответствующую этому способу оптическую
дель среды (об оптических моделях см. главу 11).
Каждому из перечисленных уровней описания поставлены в
соответствие следующие модели радиационных процессов,
рые реализуются в виде расчетных соотношений или компьютер-

94 Гл. 4. Основные понятия теории моделирования радиационных процессов
ных кодов, используемых при решении задач переноса теплового
излучения.
• Модели 1-го уровня описания (квантово-механические
ли) - это модели элементарных радиационных процессов,
зволяющие производить расчеты вероятностей элементарных
радиационных процессов, т.е. радиационных процессов,
провождающих переход изолированной частицы из одного
энергетического состояния в другое. Здесь же могут
тываться сечения отдельных элементарных радиационных
процессов для изолированной частицы.
• Модели 2-го уровня (статистические модели) - это модели
чений и коэффициентов поглощения частиц, принадлежащих
статистическому ансамблю, распределение которых по
гетическим состояниям в данном ансамбле определено
той моделью состояния среды. Следовательно, это модели
чений и коэффициентов, усредненных по распределению
тиц по возбужденным энергетическим состояниям.
В условиях локального термодинамического равновесия в
качестве такой функции распределения выбирается больцма-
новская функция заселенности энергетических состояний. В
моделях 2-го уровня могут также учитываться эффекты,
водящие к отклонению от условий равновесия физико-
химических процессов и идеальности среды.
• Модели 3-го уровня (феноменологические модели) - это
дели радиационного переноса и соответствующие им
ские модели среды.
В научной и учебной литературе по радиационному
су нет единообразия в определении понятия сечения
го процесса. Чаще всего под спектральным сечением поглощения
радиационного процесса понимается спектральный объемный
эффициент поглощения, отнесенный к одной частице (т.е.
ленный на объемную концентрацию частиц). Размерность такого
сечения поглощения равна см2. При этом подразумевается, что
спектральный коэффициент получен с использованием
жения о больцмановской заселенности возбужденных состояний
частиц в исследуемом ансамбле путем суммирования вкладов

4.3. Иерархия моделей описания радиационных процессов 95
элементарных радиационных процессов для всех уровней
гии, принимающих участие в данном радиационном процессе. В
данной книге используется понятие сечений элементарных
цессов, введенное в п. 4.1.4.
В рамках представленной трехуровневой классификации
чение поглощения, определенное таким образом, относится к
делям 2-го уровня - статистическим моделям. Однако если учесть
определения, данные в п. 4.1.4, то сечения радиационного
са могут быть отнесены одновременно и к классу моделей 1-го
уровня. Имеются следующие обоснования для использования
кой классификации:
• в отличие от коэффициентов поглощения (испускания) в
четных соотношениях для определения сечений отсутствуют
концентрации поглощающих (излучающих) частиц;
• возможно использование понятий сечений элементарных
диационных процессов, отнесенных как к двум уровням
гии, так и учитывающих вклад всех квантовых переходов.
Исходя из сказанного, далее будем придерживаться
щего соглашения:
1) для того чтобы различать понятия сечений, относящихся к
элементарному радиационному процессу и к сумме по этим
цессам, используются понятия дифференциального и полного
чений процесса соответственно, что имеет аналогию в
ской теоретической механики и теории столкновения заряженных
частиц (Ландау Л.Д. и др., 1974; Ольховский И.И., 1978; Смирнов
Б.М., 1968).
2) теория расчета полных сечений радиационных процессов
относится к моделям 1-го уровня описания, т.е. к моделям
тарных радиационных процессов. При описании моделей 2-го
уровня указывается способ пересчета от сечений к
там поглощения (излучения).
. Представленные уровни описания моделей элементарных
радиационных процессов и соответствующие им модели
онного переноса энергии оказываются весьма важными при
ре метода решения задачи о теплообмене излучением. Ниже эти
модели рассмотрены более подробно.

96 Гл. 4. Основные понятия теории моделирования радиационных процессов
4.3.1. Модели элементарных радиационных процессов
Моделирование элементарных радиационных процессов
зируется на рассмотрении процессов поглощения и испускания
излучения, как результата взаимодействия фотонов или
ванных электромагнитных волн с веществом (ФришС.Э., 1963;
Ельяшевич М.А., 2001; Никифоров А.Ф. и др., 2000).
К элементарным радиационным процессам относятся:
1. Квантовые переходы между дискретными («связанными»)
энергетическими состояниями атомов, молекул и их ионов,
провождаемые поглощением или испусканием квантов
магнитного излучения (фотонов). Такие переходы называются
связанно-связанными и обозначаются символом «b-b» (от
лийского термина «bound-bound» transition).
Коэффициенты поглощения или излучения при связанно-
связанных переходах представляют собой функции с очень
ной зависимостью от энергии фотона. Этим переходам
вуют линейчатые спектры испускания и поглощения. В
атомном газе связанно - связанные переходы происходят между
различными конфигурациями электронных орбит в поле ядра,
ладающими разной энергией. В молекулярных газах связанно-
связанные переходы могут сопровождаться изменением как
тронных, так и вращательных и колебательных квантовых
ний молекулы. В соответствии с этим могут наблюдаться
тельные, колебательно-вращательные и электроно-колебательно-
вращательные спектры поглощения и испускания.
Электронным переходам (точнее: электроннд-колебательно-
вращательным переходам, поскольку любой электронный
ход всегда сопровождается колебательно-вращательными квано-
тыми переходами) соответствуют электронные полосы
ния или испускания в ультрафиолетовой, видимой и
ной областях спектра. Колебательно-вращательные и
ные спектры молекул располагаются в инфракрасной и
тотной областях.
В задачах теплообмена излучением, физики
ной плазмы и аэрофизики наибольший интерес представляют

4.3. Иерархия моделей описания радиационных процессов 97
электронно-колебательные и колебательно-вращательные спектры
молекул.
2. Квантовые переходы между дискретными {«связанными»)
и непрерывными {«свободными») энергетическими состояниями
атомов, молекул и их ионов, сопровождаемые поглощением или
испусканием квантов электромагнитного излучения (фотонов).
Такие переходы называются связанно-свободными или свободно-
связанными и обозначаются символами «й-/» и «/-ft»
соответственно («bound-free», «free-bound» transition).
Коэффициенты поглощения при связанно-свободном переходе
и коэффициент излучения при свободно-связанном переходе
представляют собой непрерывную функцию энергии фотона hv,
ограниченную в области больших энергий. Такие спектры
щения и испускания называются сплошными.
При связанно-свободных переходах в атомах, молекулах и
нах, происходит поглощение фотона, приводящее к
ции или фотодиссоциации частиц вещества с образованием иона
более высокой кратности и свободного электрона или продуктов
деления молекулы на атомы или простые молекулы.
Процесс обратный фотоионизации называется
нацией и состоит в присоединении электрона к иону с
нием иона меньшей кратности или нейтральной частицы,
вождаемой испусканием фотона. Пороги связанно-свободных и
свободно-связанных процессов наблюдаются в ультрафиолетовой,
видимой и ближней инфракрасной областях спектра.
3. Квантовые переходы между непрерывными {«свободными»)
энергетическими состояниями атомов, молекул и их ионов,
провождаемые поглощением или испусканием квантов
магнитного излучения (фотонов). Такие переходы называются
свободно-свободными и обозначаются символами «/-/» («free -
free» transition).
Коэффициенты поглощения или излучения при свободно-
свободных переходах представляют собой непрерывные функции
энергии фотона hv. Такие спектры поглощения и испускания
зываются сплошными.

98 Гл. 4. Основные понятия теории моделирования радиационных процессов
При свободно-свободных квантовых переходах происходит
ускорение или торможение электронов в полях атомов, молекул и
их ионов, сопровождаемое поглощением или испусканием
нов. В частности, если при взаимодействии электрона с полем
ложительного иона или с нейтральной частицей, происходит его
торможение, сопровождаемое испусканием фотона, то такое
чение называют тормозным. Ускорение электронов в полях
тиц при поглощении фотонов называется процессом излучения,
обратным тормозному поглощению.
В основе классификации компьютерных моделей
ных радиационных процессов, которая используется для
тизации методов и компьютерных кодов, применяемых в теории
радиационного переноса, лежит разделение этих процессов на
связанно-связанные, связанно-свободные и свободно-свободные.
В пределах каждой группы моделей вводится дополнительное
разделение, отражающее специфику радиационных процессов в
частицах разного типа, а так же уровень подробности описания
характеристик процессов.
Пример классификации моделей элементарных
ных процессов, обычно принимаемых в учет в теории переноса
теплового излучения, представлен ниже. Отдельными пунктами
данного классификатора представлены разделы «Модели
вых функций» и «Модели потенциалов взаимодействия ядер
двухатомных молекул». Необходимость выделения раздела
та волновых функций диктуется тем, что основу многих моделей
элементарных радиационных процессов составляют именно
ли расчета волновых функций соответствующих энергетических
состояний. Причем, эффективность расчета последних, как
ло, определяет эффективность всей модели элементарных
ционных процессов.
Молекулярные постоянные, по-разному определяемые в
личных потенциалах межъядерного взаимодействия, также
ко используются в моделях расчета характеристик элементарных
радиационных процессов. Поэтому классификация описания
более часто используемых потенциалов межъядерного
ствия является необходимой.

4.3. Иерархия моделей описания радиационных процессов 99
Классификатор моделей элементарных радиационных процессов
1. Модели связанно-связанных (b-b) элементарных радиационных
процессов
1.1. Модели вероятностей связанно-связанных переходов в атомах и
ионах
1.2. Модели вероятностей связанно-связанных переходов в молекулах и
молекулярных ионах
1.2.1. Модели разделения различных типов переходов (электронных,
колебательных и вращательных)
1.2.2. Модели вероятностей электронных переходов
1.2.3. Модели вероятностей колебательных переходов
1.2.4. Модели вероятностей вращательных переходов
1.2.5. Модели вероятностей, учитывающие взаимные влияния
ных типов переходов
2. Модели связанно-свободных (b-f) и свободно-связанных {f-b)
элементарных радиационных процессов
2.1. Модели фотоионизации атомов и ионов с дискретных
ских состояний
2.1.1. Модели фотоионизации водородоподобных атомов и ионов
2.1.2. Модели фотоионизации неводородоподобных атомов и ионов
2.1.2.1. Модели фотоионизации с основных состояний
2.1.2.2. Модели фотоионизации с возбужденных состояний
2.1.3. Модели фотоотрыва от отрицательных ионов
2.1.4. Модели фотоионизации молекул
2.1.5. Модели фотодиссоциации молекул
3. Модели свободно-свободных переходов (/-/)
3.1. Модели тормозного излучения (поглощения) электронов в полях
нейтральных частиц
3.2. Модели тормозного излучения (поглощения) в полях ионов
4. Модели неидентифицированных радиационных процессов
5. Модели элементарных радиационных процессов при участии
сированной фазы газовых течений
6. Модели волновых функций дискретных и непрерывных
ских состояний атомов, молекул и их ионов
7. Модели потенциалов взаимодействия ядер двухатомных молекул
4.3.2. Модели статистических радиационных процессов
Статистические модели радиационных процессов
значены для расчета спектральных сечений и спектральных
емных коэффициентов поглощения и испускания атомов, молекул

100 Гл. 4. Основные понятия теории моделирования радиационных процессов
и ионов, принадлежащих статистическому ансамблю частиц, т.е.
как раз для расчета феноменологических коэффициентов
щения, испускания и рассеяния, входящих в уравнение переноса
излучения. Распределение частиц в ансамбле по возбужденным
энергетическим состояниям определяется принятой в каждом
конкретном случае термодинамической (статистической) моделью
среды. В подавляющем большинстве случаев, представляющих
интерес для практических приложений, используются модели,
основанные на равновесном (больцмановском) энергетическом
распределении частиц.
Пример классификации статистических моделей,
мых в теории радиационного переноса, представлен ниже. Основу
классификации составляют признаки разделения по типу спектра
поглощения и испускания (линейчатый и непрерывный).
Классификатор статистических моделей радиационного переноса
1. Модели спектральных сечений и коэффициентов поглощения
кания) в линейчатом спектре
1.1. Модели спектральных коэффициентов поглощения и испускания в
атомных линиях
1.2. Модели спектральных коэффициентов поглощения и испускания во
вращательных линиях молекулярного спектра
2. Модели спектральных сечений и коэффициентов поглощения
кания) в непрерывном спектре
2.1. Модели спектральных сечений и коэффициентов поглощения
пускания) при связанно-свободных и свободно-связанных
дах
2.2. Модели спектральных сечений и коэффициентов поглощения
пускания) при свободно-свободных переходах
2.3. Комбинированные модели спектральных сечений и коэффициентов
поглощения (испускания) при связанно-свободных (свободно-
связанных) и свободно-свободных переходах
3. Модели учета неидеальности плазмы в расчетах спектральных
фициентов поглощения в линейчатом и сплошном спектре
4. Модели спектральных сечений и коэффициентов поглощения
кания) усредненных на спектральных участках по линейчатой
туре (физическое усреднение)
4.1. Модели усредненных коэффициентов поглощения (испускания) в
полосах двухатомных молекул

4.3. Иерархия моделей описания радиационных процессов 101
4.1.1. Модели усреднения по вращательной структуре
4.1.2. Модели усреднения по колебательной структуре
4.2. Модели усредненных коэффициентов поглощения (испускания)
в полосах многоатомных молекул
4.2.1. Модели усреднения по вращательной структуре
4.2.2. Модели усреднения по колебательной структуре
S. Спектральные модели оптических коэффициентов конденсированной
фазы газовых течений
5.1. Модели расчета коэффициентов поглощения, рассеяния
и ослабления
5.1.1. Монодисперсные среды
5.1.2. Полидисперсные среды
5.2. Модели расчета индикатрис рассеяния
5.2.1. Монодисперсные среды
5.2.2. Полидисперсные среды
4.3.3. Феноменологические модели радиационного переноса
Конечной целью использования любой феноменологической
модели радиационных процессов является определение полей
диационных характеристик в объемах и (или) на поверхностях,
ограничивающих эти объемы.
Для решения этой задачи необходимо использовать два типа
феноменологических моделей: оптическую модель среды,
ционную модель среды.
Оптической моделью среды называется феноменологическая
модель коэффициентов поглощения, рассеяния и испускания,
кватная используемой форме уравнения переноса излучения и
следуемому физическому процессу.
Радиационной моделью среды называется совокупность
модинамической и оптической моделей, а также модели переноса
излучения, обеспечивающих адекватное описание исследуемого
физического процесса.
Моделью переноса излучения называется совокупность
бранной формы уравнения переноса и методов его
ния по частоте, пространственным переменным и направлениям
распространения излучения.
Пример классификации феноменологических моделей
диационного переноса представлен ниже.

102 Гл. 4. Основные понятия теории моделирования радиационных процессов
Классификатор феноменологических моделей
радиационного переноса
1. Оптические модели среды
1.1. Модели спектральных сечений и коэффициентов поглощения
(испускания) газов и плазмы сложного химического состава
1.2. Модели непрерывного спектра, основанные на аналитическом
представлении спектральной зависимости
1.3. Модели линейчатого спектра, основанные на аналитическом
ставлении спектральной зависимости
1.3.1. Регулярные и статистические модели спектра атомных линий
1.3.2. Регулярные и статистические модели спектра молекулярных
линий
1.4. Групповые модели коэффициентов поглощения (испускания)
1.4.1. Line-by-line модели
1.4.2. Многогрупповые модели (узкополосные модели)
1.4.3. Малогрупповые модели (широкополосные модели)
1.5. Гибридные модели
1.5.1. Атомные линии на фоне групповых моделей
1.5.2. Статистические модели атомных линий иа фоне групповых
моделей
1.6. Модели интегральных коэффициентов поглощения
1.6.1. Средние коэффициенты поглощения по Планку
1.6.2. Средние коэффициенты поглощения по Росселанду
1.6.3. Средние коэффициенты поглощения по Чандрасекхару
1.6.4. Коэффициенты квазидиффузии
1.6.5. Однонаправленные усредненные коэффициенты поглощения
(в методах полумоментов и квадромоментов)
1.7. Модели степеней черноты
1.7.1. Спектральные степени черноты
1.7.2. Групповые степени черноты
1.7.3. Интегральные степени черноты
2. Модели переноса излучения
2.1. Модели расчета усредненных и интегральных по спектру
онных характеристик
2.1.1. Line-by-line метод расчета
2.1.2. Групповой метод расчета
2.1.3. Статистические модели
2.1.3.1. Статистические модели атомных линий

4.3. Иерархия моделей описания радиационных процессов 103
2.1.3.2. Статистические модели вращательных линий электронно-
колебательных полос
2.1.3.3. Статистические модели вращательных линий колебательных
полос многоатомных молекул
2.1.3.4. Макростатистическая модель колебательных полос
многоатомных молекул
2.1.4. Модель Томаса - Пеннера
2.1.5. Метод эффективных сечений
2.1.6. Метод моментов Шмыглевского
2.1.7. Лебегово ускорение
2.1.8. Модели нелокального усреднения
2.2. Модели расчета усредненных по угловым переменным
радиационных характеристик
2.2.1. Методы сферических гармоник
2.2.2. Методы дискретных ординат
2.2.3. Методы моментов
2.2.4. DPn-методы
2.2.4.1. Методы половинных сферических гармоник
2.2.4.2. Методы полумоментов
2.2.4.3. Методы квадромоментов
2.2.5. Приближенные аналитические методы
2.3. Методы статистического моделирования (методы Монте-Карло)
В последующих главах все модели переноса излучения,
речисленные во втором разделе Классификатора
ческих моделей радиационного переноса, будут рассмотрены
робно. Связь со всеми моделями других представленных
фикаторов будет обсуждаться по мере необходимости в описании
отдельных моделей. Модели элементарных и статистических
диационных процессов рассмотрены в книге (Суржиков СТ., 2004
(в)).

Глава 5
МОДЕЛИ И МЕТОДЫ ПЕРЕНОСА СЕЛЕКТИВНОГО
ТЕПЛОВОГО ИЗЛУЧЕНИЯ В УСЛОВИЯХ ЛТР
Решение уравнения переноса излучения в одной из форм,
представленных в главе 3 подразумевает чаще всего определение
векторного поля плотности спектрального и интегрального потока
излучения, дивергенции этого поля, а также спектральной и
гральной объемной плотности энергии излучения. Реже требуется
определить поле спектральной интенсивности излучения на
торой поверхности или в некотором элементарном объеме. Как
правило, задачи первого типа характерны для проблем
мена излучением, радиационной газо- и плазмодинамики. Задачи
второго типа характерны для задач спектральной диагностики из-
лучательной способности горячих газов и плазмы.
Задача нахождения поля вектора интегрального потока
чения и его дивергенции, а также интегральной объемной
сти энергии излучения даже в случае нерассеивающей среды,
ходящейся в условиях ЛТР (см. п. 2.10), когда уравнение переноса
излучения имеет простейший вид
E-1)
оказывается весьма трудоемкой, поскольку подразумевает
ходимость интегрирования уравнения E.1) в каждой
ной точке по пространственной переменной s (первый этап
шения задачи) и по угловым переменным, т.е. вдоль лучей s,
имеющих разные направления Q, (второй этап). Найденное таким
образом поле спектральной интенсивности излучения еще необ-

5.1. Приближения предельных оптических толщин 105
ходимо проинтегрировать по частоте излучения (третий этап).
Очевидно, что при учете эффектов светорассеяния сложность
шения задачи возрастает во много раз, поскольку вместо (S.1)
обходимо решать интегро-дифференциальное уравнение C.3).
В соответствии с тремя указанными этапами решения задачи
различают группы методов, предназначенных для интегрирования
по пространственным переменным (далее совокупность
ственных переменных обозначается радиус-вектором текущей
точки пространства г в лабораторной системе координат),
вым переменным ( Q ) и частоте излучения ( v ).
В принципе, каждый из этих трех этапов является
мым. По крайней мере, всегда можно указать не связанные между
собой методы интегрирования по г, Q и v. Однако в наиболее
эффективных расчетных методиках существует взаимная
словленность методов, т.е. совместимой является лишь
ленная комбинация методов. Указанные методы рассматриваются
в главе 12.
В большинстве расчетных методик в качестве базового
тода выбирается метод интегрирования уравнения переноса
лективного излучения по угловым переменным. Затем решается
задача интегрирования по пространственным переменным и,
конец, найденные спектральные характеристики интегрируются
по частоте. Однако существует группа методов, в которых
численные проблемы решаются особенно просто, - эти методы
основаны на приближениях предельных оптических толщин.
5.1. Приближения предельных оптических толщин
Приближения оптически тонкого и оптически толстого
слоев являются, пожалуй, наиболее часто используемыми
ближениями теории радиационного переноса. Физический смысл
этих приближений состоит в том, что в первом случае вероятность
поглощения квантов электромагнитного излучения в исследуемом
объеме очень мала, а во втором случае - очень велика. Это
чает, что в случае справедливости приближения оптически
го слоя фотоны собственного излучения практически беспрепят-

106 Гл. 5. Модели и методы переноса селективного теплового излучения
ственно покидают объем, а фотоны внешнего излучения
чески беспрепятственно пронизывают его. В случае
сти приближения оптически толстого слоя, наоборот, фотоны
собственного излучения поглощаются самой средой вблизи места
своего рождения (в этом случае говорят о сильной реабсорбции,
т.е. о поглощении средой испущенного ею излучения), а фотоны
внешнего излучения поглощаются вблизи границы. Ниже дана
математическая формулировка этих приближений. Необходимо
подчеркнуть, что при решении задач радиационного переноса
то встречается ситуация, когда в одной спектральной области
справедливо одно из приближений предельных оптических
щин, а в другой спектральной области - противоположное
ближение.
5.1.1. Приближение оптически тонкого слоя
Пусть L - характерный размер исследуемой области. Тогда
L
4v = JKv (*')*' E-2)
о
- спектральная оптическая толщина слоя длиной L.
В приближении оптически тонкого слоя полагают, что
E.3)
Это позволяет существенно упростить все расчетные
ния теории переноса излучения. Например, формальное решение
уравнения переноса C.15) упрощается до следующего
шения:
°J6>v(T')dx', E.4)
поскольку для экспонент, входящих в C.15) справедливо
щее разложение:
ехр(-т)«1-т + 0(т2), E.5)

5.1. Приближения предельных оптических толщин 107
Это означает, что в случае оптически тонкого слоя
тральная интенсивность излучения в любой точке пространства
определяется суммой спектральной интенсивности излучения
внешнего источника (У°) и интеграла от интенсивности
венного излучения среды на отрезке луча s от границы
щей области до рассматриваемой точки пространства.
Приближение оптически тонкого слоя значительно упрощает
не только формальное решение уравнения переноса, но
ется весьма полезным для многих других расчетных методов.
Примеры использования этого приближения совместно с другими
методами будут рассмотрены в главе 6.
5.1.2. Приближение оптически толстого слоя
В приближении оптически толстого слоя полагают, что
Tiv»l. E.6)
Это приближение хорошо известно, как приближение Россе-
ланда (Rosseland S., 1936) или диффузионное приближение.
Последнее название проистекает из того, что в приближении
оптически толстого слоя вектор плотности радиационного
вого потока (в условиях ЛТР) может быть представлен в виде
¦W = -b*V7\ E.7)
где Хн=\6п2дТ3/Зкк - коэффициент лучистой
сти; K/j - среднеросселандовский коэффициент поглощения; д -
постоянная Стефана-Больцмана (см. формулу B.2)); п -
тель преломления.
При этом процесс распространения излучения можно
бить диффузионному процессу, поскольку поглощение любого
фотона вблизи места своего рождения приводит к
ному нагреву среды и, как следствие, увеличению вероятности
испускания здесь нового фотона, который, однако, испускается в
произвольном направлении, что как раз очень похоже на
зионный процесс.

108
Гл. 5. Модели и методы переноса селективного теплового излучения
Вывод формул для радиационного потока E.7), а также для
коэффициентов лучистой теплопроводности и среднеросселан-
довского коэффициента поглощения приводится в п. 5.2.1 на
мере решения задачи переноса излучения в плоском слое.
5.2. Методы интегрирования уравнения переноса
по угловым переменным
Рассмотренные в пп. 5.1.1 и 5.1.2 приближения оптически
тонкого и оптически толстого слоев позволяют упростить
ние задачи переноса излучения в любой геометрии. Однако даже в
указанных простейших случаях, в особенности, в приближении
оптически тонкого слоя, остается проблема интегрирования
нения переноса излучения по угловым и пространственным
менным. Для промежуточных оптических толщин условия E.3) и
E.6) не выполняются, поэтому упрощения уравнения переноса не
допускаются.
Укрупненная классификация методов учета угловой
мости спектральной интенсивности излучения дана на рис. 5.1.
Методы интегрирования уравнения переноса по угловым переменным
Z
Аппроксимация угловой
симости интенсивности
чения, с последующей заменой
уравнения переноса почти
вивалентной системой диффе-
ренциальных уравнений
Решение
тегральных
уравнений
Метод
тивных излуча-
тельных
собностей
Непосредственное численное
ние угловой зависимости интенсивности
излучения, полученной в результате
ния уравнения переноса вдоль конечного
числа лучей, испущенных из данной точки
пространства (Методы Дискретных
правлений (МДН) или так называемый
Ray - Tracing Method (RTM))
Методы имитационного
моделирования
(Методы Монте-Карло)
Рис. 5.1. Классификация методов интегрирования по угловым переменным

5.2. Методы интегрирования уравнения переноса по угловым переменным 109
Как уже отмечалось выше, методы интегрирования по
вым и пространственным переменным, а также по частоте
тромагнитного излучения тесно связаны между собой. Поэтому
следует иметь в виду, что любой из методов этой классификации
(рис. 5.1) не является завершенным методом теории переноса
лового излучения, а с неизбежностью должен быть дополнен
ним из методов интегрирования по пространству и частоте
тромагнитного излучения.
Среди методов интегрирования по угловым переменным,
представленным на рис. 5.1, исторически наиболее развитыми
оказались методы аппроксимации угловой зависимости
тральной интенсивности излучения. Это во многом связано с тем,
что наиболее интенсивно теория переноса излучения развивалась
применительно к задачам астрофизики (первая половина XX века)
и к задачам физики ядерных реакторов (вторая половина XX века)
в условиях отсутствия или слабого развития вычислительной
ники. Появление в 50 - 60-х годах компьютеров начало
но изменять соотношение в пользу альтернативных методов
шения уравнения переноса. Современная теория переноса
вого излучения во многом основана на использовании мощных
компьютеров и ориентирована на решение задач переноса
ния в любой геометрии с подробным учетом спектральной
симости оптических свойств среды. Однако методы, основанные
на аппроксимации угловой зависимости, остаются весьма
страненными и широко используемыми. Исключительная
ность этих методов для современной теории переноса теплового
излучения, базирующейся на последних достижениях
ной физики, состоит не только в их высокой экономичности, но, в
первую очередь, в возможности их использования в качестве
товых и асимптотических решений.
Указанные методы развиты применительно к объемам
стейших геометрий (плоский слой, сферические и
ские объемы), однако наиболее развитой является теория переноса
излучения в плоском слое. Это объясняется, с одной стороны, тем,
что плоский слой является простейшей моделью излучающего и
поглощающего объема, а с другой стороны, тем, что указанная
модель является чаще других наиболее обоснованной физической
моделью описания процесса переноса излучения.

по
Гл. 5. Модели и методы переноса селективного теплового излучения
Рассматриваемые далее методы интегрирования по угловым
переменным применяются для отыскания спектральной
ности излучения и моментов этой функции по угловым
ным. С целью упрощения записи индекс спектральной
сти далее опускается.
5.2.1. Модель плоского слоя
В данной модели излучающий и поглощающий объемы
меняются плоским слоем конечного размера (рис. 5.2) в
нии одной из пространственных переменных (х) и бесконечной
протяженности в направлении двух других переменных (у, z).
V i
/ .
/>¦¦«
/Л-(Т *,,.U!
/ /
Рис. 5.2. Модель плоского слоя для расчета переноса излучения
Во многих исследованиях показано, что модель плоского
слоя позволяет получить хорошую точность результатов
чески во всех случаях, когда одна из пространственных
ных много меньше двух других. Исключение составляет
шой круг специфических задач переноса излучения в волновод-
ных оптических системах. Эта модель наиболее широко
валась при решении задач астрофизики, физики ядерных
ров, теплообмена излучением и радиационной газовой
намики.
Интенсивность излучения в модели плоского нерассеиваю-
щего слоя удовлетворяет следующей краевой задаче:

5.2. Методы интегрирования уравнения переноса по угловым переменным 111
цау1ц) + у E8)
от
т = 0, 0<ц<1: У(х,ц) = У+(х = 0,ц), E.9)
х = хн, -1<ц<0: У(т,ц) = У"(т = тн,ц), E.10)
где 5(т, ц) = Jb \ Т[х)Л - функция источников излучения
сивность излучения абсолютно черного тела); ц = cos9 ;
х х=Н
х- |к(х')(Ьс' - оптическая толщина; хн - \ к(л:')с!х'.
о о
Следствием допущения о бесконечной протяженности и
нородности слоя в направлениях у и z (фактически это
лентно условию осевой симметрии для произвольной оси х)
ется неравенство нулю только одной составляющей вектора
ности спектрального потока излучения
1
() E.11)
Плотности односторонних спектральных потоков излучения
определяется по формулам
E.12)
E.13)
где верхними индексами «+» и «-» обозначены спектральные
тенсивности излучения, распространяющегося в положительном и
отрицательном направлениях оси х соответственно (в верхнюю и
нижнюю полусферы пространства угловых направлений).
ление потока излучения на две составляющие удобно при учете
внешнего по отношению к исследуемому объему излучения, т.е.

112 Гл. 5. Модели и методы переноса селективного теплового излучения
излучения, падающего на объем со стороны внешних источников.
Очевидно, что в рамках рассматриваемой модели интенсивности
падающего излучения У+(т = 0,ц) и ./~(т = тя,ц) должны
также удовлетворять условию осевой симметрии.
Интенсивность излучения в модели плоского рассеивающего
слоя удовлетворяет следующей краевой задаче:
т = 0, 0<ц?1: У(т,ц) = ./+(т = 0,ц), E.15)
У(т,ц) = ./-(т = тЯ)ц), E.16)
где S(m)= (l-&)Jb[T{t)] + ^
-i
5"(т,ц) - функция источников излучения;
T=J[K(x') + a(x')]dx'; тя = J [к(х')
о о
Введение двух составляющих интенсивности излучения в
плоском слое позволяет вместо краевой задачи E.14)—E.16)
сматривать две эквивалентные задачи:
^{) { E.17)
= 0, 0<ц*1: У(т,ц) = У+(т = 0,ц), E.18)
E.19)
^Kj(x,ii) S(x,ii),
ох
0: У(т,ц) = У~(т = тя,ц). E.20)
Формальное решение краевых задач E.17), E.18) и E.19),
E.20) имеет вид

5.2. Методы интегрирования уравнения переноса по угловым переменным 113
dt\
E.21)
Формальное решение краевых задач E.8)—E.10) и E.14)—
E.16) позволяет записать формулу для расчета спектральной
емной плотности энергии излучения и плотности спектрального
потока излучения
W(x) = W+(x)-W-(x), E.22)
где выделены потоки излучения в верхнюю ((x-il)^O) и
нюю ((!•(!)< 0) полусферы:
_0
о
О,»1
E.23)
1 т
JJs(x»exp -
Oo v
T-T'
E.24)
9 Зак. 272

114 Гл. 5. Модели и методы переноса селективного теплового излучения
.0
f js(T\-n)exp(-—Idi'
От ^ ^ '
E.25)
В следующих частных, но практически важных случаях
ное расчетное соотношение упрощается:
1) изотропное рассеяние
\J (т=0,ц)ехр — dp,-
Lo v Н/ 0
2я
с
2%
*н
Ю
E.26)
L0
-2%
+ (т=0,ц)ехр[--] Hd^+ )s(x')E2 (x-x')dx'
(т=тя,-ц)ехр -ifl-I
Lo
E.27)
2) изотропное рассеяние и изотропная интенсивность
него излучения
: = 0)E2{x)+)s{x')El{x-x')dx'
с
2%
,E.28)

5.2. Методы интегрирования уравнения переноса по угловым переменным 115
-2*
Js(T')?2(T-T')dT'
H-x)+ ]s(x')E2(x'-x)dx'
;E.29)
3) нерассеивающая среда и изотропная интенсивность
внешнего излучения
2я
с
2п
= 0)E2{x)+jJb[T{x')]E](x-x')dx'
(x = xH)E2{xH-x)+]jb[T{x')]E1(x'-x)dx'
.Г (т = 0) Я, (т) + \jb [Т (т')] Е2 (т - т') dx'
; E.30)
-2%
. E.31)
В формулах E.26)—E.31) введены интегро-экспоненциаль-
ные функции (Чандрасекхар С, 1953; Kourganoff V. et al., 1963)
-- U"~2dn, E.32)
связанные между собой рекуррентными соотношениями
Еп+1(х)=—\ехр(-х)-хЕп(хI, л?1. E.33)
п
Используют также следующие эквивалентные представления
интегро-экспоненциальных функций
E.34)

116 Гл. 5. Модели и методы переноса селективного теплового излучения
Еп+Х (*) = ~]«Р(-*)?(''"К <5-35>
ИЛИ
1
а также ряд соотношений, следующих из E.34) и E.35):
Г+оо, при п = \,
ст при
E-36)
\{) прии = 1
ViW» прии>1.
Асимптотические значения интегро-экспоненциальных
функций получаются из ее разложения в ряд
. E.38)
E.39)
С=0.577216... - постоянная Эйлера.
В частности,
1 E-40)
= 0) = 0.5, Е„(х)я—ехр(-х), при дг-»оо.
На рис. 5.3. показаны интегро-экспоненциальные функции,
наиболее широко применяемые в практике расчетов.
Подчеркнем, что из приведенных формул E.23)-E.31)
чет радиационных потоков может быть произведен
венно только для нерассеивающей среды, т.е. по формулам E.30),
E.31). В остальных случаях подынтегральные выражения содер-

5.2. Методы интегрирования уравнения переноса по угловым переменным 117
жат функцию источников излучения S, которая зависит от
сивности излучения в каждой точке пространства, т.е. расчетные
формулы E.23) -E.29) не являются замкнутыми, а требуют
циальных методов решения.
10"
,-2
ю
10"
10"
10
,-s
=¦¦¦
:
•
!
Е, , , ,
iiii
\
1 1 1 1
\
i i i i
i i i i
—— Е
••••••_• в
Е
ч
1 1 1 1
ч
1111
i
i
i
s
1 1 1 1
ч
iiii:
0 1
2 34S6 789 10
х,см
Рис.5.3. Интегро-экспонснциальнысфункции EVE2,?3
Как уже отмечалось выше, для расчета мощности
деления в среде Qr , обусловленного радиационными процессами,
необходимо определить дивергенцию вектора плотности
трального потока излучения. Очевидным, но не всегда
ным способом расчета этой функции, является применение
ференциального оператора div к найденному вектору. В модели
плоского слоя операция div сводится к дифференцированию по
пространственной переменной х
^=divW = ^ = —-^^- = (к + а)-— . E.41)
dx 9т dx 9т
Дивергенция вектора плотности потока излучения может
быть также рассчитана по формуле

118 Гл. 5. Модели и методы переноса селективного теплового излучения
K(s) jj(s,Q)dCi, E.42)
которая следует непосредственно из уравнения переноса
ния C.3) после его интегрирования по полному телесному углу.
Рассмотрим получение формулы E.42) более подробно.
полним интегрирование уравнения C.3) по полному телесному
углу Q = 4я (спектральный индекс опустим)
— a(s) | | y(s,Cl',Q)j(s,Cl')dCl'dCl.EA3)
П=4я П'=4я
Дальнейшее преобразование E.43) связано со следующими
свойствами слагаемых этого уравнения:
= f QgmdJ(s,Q)dCl = dWW, E.44)
поскольку физическая координата s отсчитывается вдоль вектора
2) — f Y(^Q',Q)dQ = l E.45)
4я •
в соответствии с условием нормировки A.18).
Учитывая E.44) и E.45) в E.43), получаем
J J(
П=4я
J(s,Sl')dQ'. E.46)
Из E.46) очевидно, что слагаемые, пропорциональные
эффициенту рассеяния а,, сокращаются и при Jem(s) = Jb (s)
получается уравнение E.42). Таким образом, формула для расчета
divW или, что одно и тоже, мощности тепловыделения, обуслов-

5.2. Методы интегрирования уравнения переноса по угловым переменным 119
ленного радиационными процессами, не содержит коэффициентов
и функций, характеризующих светорассеяние. Однако
ность излучения, находящаяся под интегралом в E.42) должна
быть вычислена с учетом всех особенностей переноса излучения,
в том числе и с учетом светорассеяния.
Для плоского слоя соотношение E.42) упрощается:
E.47)
или
1
= 4TtK(X)Jb[T(X)]-2nK(X) J
-1
1
о
Перейдем к оптической толщине
тогда вместо E.47) и E.48) получим
1
1
E.48)
. E.49)
о о
Подставив в E.49) формальные решения E.21), получим
т

120
Гл. 5. Модели и методы переноса селективного теплового излучения
J.T (т = тн,-ц)ехр -
хн-т
-A-шJя
гтг1
JJ-S(x»exp -
00^
1 т" 1
J J-5(T',-n)exp -
т-т
V М-
0 т
1
. E.50)
В простейшем случае нерассеивающей среды и изотропной
интенсивности внешних источников
-2л
J
где
= тн)Е2(тн -т)]-
E.51)
Напомним, что для определения скорости тепловыделения,
обусловленного радиационными процессами в формуле E.51)
обходимо перейти от оптической толщины к физическим
пространственным переменным, т.е. воспользоваться формулой
E.41). В качестве примера использования полученных
ний для основных характеристик переноса теплоты излучением в
плоском слое E.28), E.29) и E.49) рассмотрим задачу о переносе
теплового излучения в ударном слое, образующемся у
сти космического аппарата, входящего в плотные слои
сферы.

5.2. Методы интегрирования уравнения переноса по угловым переменным 121
Схема решаемой задачи дана на рис. 5.4, где показано
ратурное поле вблизи аэротермодинамического щита и в следе,
образующемся за космическим аппаратом (Surzhikov S.T., 2004
(а)). На рисунке приведена реальная форма и даны характерные
размеры российского сегментально-конического космического
аппарата.
600
S00 -
0 100 200 .100 400 v.)i!
Рнс. 5.4. Температурное поле вблизи поверхности спускаемого
космического аппарата, К
Результаты расчетов, приведенные на рис. 5.5, отвечают
ке траектории входа космического аппарата в атмосферу Марса со
скоростью 5.223 км/с. Термодинамические параметры на
риваемой высоте в атмосфере Марса задавались равными:
ние /7 = 78.7 эрг/см3, плотность р = 2.97x10 г/см3, температура
Т = 140 К.
Видно, что вблизи лобовой поверхности космического
рата толщина ударного слоя существенно меньше его
ных размеров, поэтому в этой области течения для решения
чи переноса излучения можно рассматривать плоский слой (см.
рис. 5.2). Пусть при х2.Н среда прозрачна и не излучает
мущенный поток газа), а при х = 0 находится непрозрачная, диф-
фузионно-отражающая поверхность тела. Учтем спектральную
зависимость излучения в явном виде. Тогда граничное условие на
фронте ударной волны (поверхность 2) формулируется в виде
8 Зак. 272

122
Гл. 5. Модели и методы переноса селективного теплового излучения
Wv (tv =ту,я) = ^у,2 =0, а поверхность космического аппарата
A) диффузно излучает с интенсивностью Jb,v,\ и диффузно
жает падающее излучение, так что спектральная плотность потока
излучения, покидающего поверхность, равна
К\ = К(% = 0) = *Jb.v.i*v + PvW; (tv = 0), E.52)
где sv, pv - полусферические излучательная и отражательная
собности поверхности 1. Из E.25) имеем выражение
J 76v(t'v)?2(t'v)dt'v, E.53)
подставляя которое в E.52) и затем в E.22), получим
Kvtt
.у (ту) Щ. (xv - <
VJ
- tv) d<
. E.54)
Из этой формулы при tv = 0 получим результирующий
чистый поток на поверхности тела
ЛлМ-2
E.55)
Для идеально отражающей поверхности ev = 0, pv = 1 и из
E.55) следует, что Wv (tv = 0) = 0. В частном случае при sv = 1,
из выражения E.55), изменяя знак, получим поток, падающий от
газа на поверхность
Wv(tv = 0) = 2% \ JbvE2{x'v)dt'v .
E.56)
Найдем скорость тепловыделения в единице объема газа за
счет теплообмена излучением

5.2. Методы интегрирования уравнения переноса по угловым переменным 123
fi,fV=-divWv=Kv
E.57)
Заметим, что Qr>v <0 означает потери энергии излучением,
Qr,v > 0 - нагрев вещества излучением.
Используя формальное решение краевых задач E.17), E.18)
и E.19), E.20) в виде E.21), учитывая при этом, что
Sy (t'v, ц) = Jb,v (t'v), получим для спектрального и интегрального
по спектру тепловыделения
E.58)
E.59)
В частном случае холодной, черной поверхности, когда
тенсивностью ее излучения можно пренебречь, Jb v j -> 0, pv -> 0,
получим
E.60)
Рассмотрим случай однородного слоя газа, в котором
ратура и химический состав постоянны по координате. Тогда,
тегрируя по оптической координате, из E.55) получим
Чя=куЯ. E.61)
Величину sv = 1 - 2?з (тУ)я) называют спектральной излу-
чательной способностью плоского слоя или спектральной
нью черноты плоского слоя (не путать со спектральной степенью
черноты поверхности).
8*

124 Гл. 5. Модели и методы переноса селективного теплового излучения
Интегрируя E.61) по частоте излучения, получают
ность интегрального радиационного потока на поверхности
о
Величину
^()[()]v E.63)
аТ 0
называют интегральной степенью черноты плоского слоя. Для
величин 8 и 8V как функций состава газа, давления, температуры
и толщины слоя Н для ряда смесей газов составлены подробные
таблицы (Авилова И.В. и др., 1970; Каменщиков В.А. и др., 1971).
Из формулы E.61) видно, что спектральный поток
ния слоя конечной толщины Н, или его яркость, всегда меньше
равновесного значения nJf,v. Наибольшее отличие спектра от
планковского должно наблюдаться в пределе оптически тонкого
слоя при куН «: 1 или
« \ ~ куЯ, Wv(x = 0) * 2жкуШЬу. E.64)
При tv i «: 1 оптический тонкий слой испускает как
ный излучатель. При этом кванты света, рожденные в любой
ке, выходят из слоя практически без поглощения по пути. В таком
слое нет «самопоглощения», и каждый элемент объема вносит
одинаковый вклад в излучение, выходящее с его поверхности. Это
и служит основанием называть такой слой объемным
телем.
Для оптически тонкого плоского слоя степень черноты
но выразить через средний коэффициент поглощения Планка
=^ = _|KW__da, „._. E.65)

5.2. Методы интегрирования уравнения переноса по угловым переменным 125
Тогда, интегрируя по частоте, из E.63) получим
8 = 2кРЯ. E.66)
Для оптически толстого слоя туЯ »1 и Wv(xv = 0)-»•nJb v,
т.е. среда светит как черный излучатель. Такой слой излучает с
«поверхности», так как кванты, рожденные в глубине, не выходят
через поверхность тела, поглощаясь по пути. Если kv# »1, то из
E.63) следует 8 = 1.
Для многих прикладных задач радиационной газовой
мики космических аппаратов важно оценить поток излучения к
поверхности обтекаемого тела в окрестности критической линии
тока с тем, чтобы ответить на вопрос, является ли существенным
радиационный нагрев тела или нет. Для приближенной верхней
оценки потока излучения в критическую точку тела можно
лать следующие предположения:
1. Сжатый ударный слой у поверхности затупленного тела
диусом R заменяется плоским слоем газа толщиной
Я = (рю/р,)Л с постоянной температурой Ts, давлением
р, и равновесным химическим составом при этих Ts и ps.
2. Ударная волна рассматривается как прозрачная поверхность
и на ней внешний поток излучения равен Wy(x = Н) = 0 .
3. Тело рассматривается как абсолютно черное, а его
ным излучением пренебрегают.
Тогда лучистый поток к телу рассчитывается по формуле
W = saTs\ 8 = ?(Г„р„Я). - E.67)
В случае равновесного ударного слоя степень черноты
кого слоя для рассматриваемой атмосферы может быть взята из
таблиц (Авилова И.В. и др., 1970; Каменщиков В.А. и др., 1971).
На рис. 5.5 и 5.6 показаны примеры результатов расчетов
радиационных характеристик U, W, Qr = divW в ударном слое.
Распределение температуры в слое дано на рис. 5.5. Объемная
плотность энергии излучения и плотность радиационного потока,
а также дивергенция вектора плотности радиационного потока в
плоском слое толщиной 10 см показаны на рис. 5.6. Предполага-

126
Гл. 5. Модели и методы переноса селективного теплового излучения
лось, что коэффициент поглощения в слое постоянен и равен
к = 0.1 см, так что оптическая толщина слоя равна т = 1, а на
прозрачные поверхности слоя слева и справа падает изотропное
излучение интенсивностью J+ (т = 0)= У~(т = т//) = 100 Вт/см2.
Интенсивность излучения абсолютно черного тела
лась для интегрального по спектру излучения
Объемная плотность энергии излучения достигает внутри
объема своего максимума. Снижение U(x) вблизи границ
четной области объясняется потерями энергии излучения,
щего на холодную поверхность и покидающего свободную
цу при х = Н.
10000
8000
6000
лплп
2000
п
\
10
ДГ.СМ
Рис. 5.5. Распределение температуры в плоском слое
Плотность полного потока излучения меняет знак внутри
объема. Это означает, что в части слоя (х ? 5.5 см) полный
ционный поток преимущественно направлен к поверхности, а в
другой части (х ? 5.5 см) - к свободной поверхности. Знак
ции Qr = divW позволяет сделать вывод, что при Qr < 0

5.2. Методы интегрирования уравнения переноса по угловым переменным 127
(дс^О.85 см) излучение нагревает среду, а при Qr >0 (х>0.85
см) - охлаждает ее. Заметим, что односторонние потоки
ния являются знакопостоянными функциями.
300000
200000
100000
-100000
-200000
i
1
3
ш..-""г
ED
0 -г»
Ю
X, СМ
Рис. 5.6. Плотность радиационной энергии A, U в Дж/см3),
ность радиационного теплового потока B, W в Вт/см2) и
генции вектора плотности потока радиационной энергии C,QR
в Вт/см3). Точное решение для плоского слоя с оптической
щиной т = 1
Распределение радиационных характеристик внутри
го слоя с тем же распределением температуры, но с увеличенным
на порядок коэффициентом поглощения, к = 1 см'1, показано на
рис.5.7. Качественные изменения в распределении плотности
диационного теплового потока и его дивергенции с изменением
оптической толщины хорошо видны при сравнении рис.5.6 и 5.7.
Внутри оптически толстого слоя D<дс<8 см) наблюдается
ласть, в которой плотность радиационного потока близка к нулю.
Это означает, что плотности односторонних полусферических
токов равны между собой. Близость нулю дивергенции вектора
плотности радиационного потока в этой же области означают
примерное равенство скорости потерь и поглощения излучения.

128
Гл. 5. Модели и методы переноса селективного теплового излучения
Указанная область оптически толстого плоского слоя является
хорошей моделью термодинамически равновесного состояния
среды.
400000
зооооо
200000
100000
-100000
-
7
- ~"з
^—
..•••
'lL=1OJ
^
/
/,
//
у/
о
10
х, см
Рис. 5.7. Плотность радиационной энергии A, (У в Дж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенции
вектора плотности потока радиационной энергии C,2/? в Вт/см3).
Точное решение для плоского слоя с оптической толщиной т = 10
Однако вблизи границ такого слоя равновесие нарушается,
поскольку излучение, уходящее за пределы плоского слоя, не
пенсируется внешним по отношению к нему излучением.
Примеры расчетов, представленные на рис. 5.6 и 5.7,
стрируют основные тенденции влияния оптической толщины на
распределение радиационных характеристик в слое.
ния функций, показанные на рис. 5.6 и 5.7, далее будут
ваны для сравнения с результатами расчетов по другим методам.
5.2.2. Метод Шварцшильда-Шустера
Метод разработан применительно к задачам, в которых
ется одно выделенное направление переноса лучистой энергии,

5.2. Методы интегрирования уравнения переноса по угловым переменным 129
например, для плоского бесконечного слоя (Schuster А., 1905;
Schwarzchild К., 1906).
Предполагается изотропность интенсивности излучения в
каждой из полусфер, совместной осью которых является
ное направление распространения излучения, в плоском слое -
ось х (рис. 5.8). Усредненная интенсивность излучения в каждой
из полусфер определяется по формулам (индекс частотной
симости опущен)
1
() E.68)
(л-cose. E.69)
•С (т.
.v-0
Рис. 5.8. Аппроксимация угловой зависимости интенсивности
излучения в методе Шварцшильда - Шустера
Тогда вместо уравнения переноса излучения E.8) следует
использовать два уравнения следующего вида (S (т, \х) - Jb):
~ = Jb-I+, E.70)
2 dt
±-«L = Jb-r, E.71)
2 at

130 Гл. 5. Модели и методы переноса селективного теплового излучения
о
Система уравнений E.70) и E.71) является линейной, ее
решение в интегральной форме имеет вид
т
Г = 2/+ (т = 0) ехр (-2т) + 2 \jb ехр[-2 (т - т*)] dx', E.72)
Г=2Г(т = <ся)ехр[-2(тя-т)] + 2 ] Jb exp[-2 (t'-t)]dt', E.73)
т
где /+(т = 0), /" (т = т// ) - усредненные интенсивности
ния, падающего на исследуемый слой при х = 0 и х = Н.
Плотности полного и односторонних спектральных потоков
излучения рассчитываются по формулам
) E.74)
() () E.75)
В соответствии с E.42)
[()]() E.76)
Распределение радиационных характеристик U, W,
Qr -K(dW(x)/dx) в плоском слое с распределением
ры, показанном на рис. 5.5, представлено на рис. 5.9 и 5.10.
Сравнение результатов расчетов по методу Шварцшильда -
Шустера с результатами точных расчетов (рис.5.6 и 5.7) позволяет
сделать вполне ожидаемый вывод о возрастании погрешности
указанного приближенного метода с уменьшением оптической
толщины излучающего слоя. Тем не менее, если интегро-экспо-
ненциальную функцию рассчитывать в процессе решения
ния переноса излучения (а не табулировать ее), то метод
шильда-Шустера является существенно более экономным.

5.2. Методы интегрирования уравиеиия переноса по угловым перемениым 131
C
300000
200000
100000
-100000
•200000
3
¦
^—
- —"¦
^
ш
0 —з
10
х, см
Рис. 5.9. Плотность радиационной энергии A, U в Дж/см1),
ность радиационного теплового потока B, W в Вт/см2) и дивергенции
вектора плотности потока радиационной энергии C,0д в Вт/см1).
Решение методом Шварцшильда - Шустера для плоского слоя с
тической толщиной т = 1
C
400000
300000
200000
100000
•100000
\
/'
. / .-'
>—-2
//
8 10
X, CM
Рис. 5.10. To же, что и на рис. 5.9, но т = 10

132 Гл. 5. Модели и методы переноса селективного теплового излучения
5.2.3. Диффузионное приближение
Расчетные соотношения, даваемые диффузионным
жением, являются тождественными Pi - приближению метода
рических гармоник (см. главу 6). Однако в литературе эти
ношения получили широкое распространение именно как
зионное приближение, поскольку могут быть получены из
глядных физических представлений о диффузии фотонов
ния в среде. Очевидно, что чем более рассеивающая среда (чем
ближе альбедо однократного рассеяния к единице), тем
онное приближение в большей степени отвечает физике процесса
переноса излучения. По этой причине это приближение особенно
эффективно применяется к расчету распространения излучения в
сильно-рассеивающих средах, где применение других методов
становится весьма затруднительным. Однако диффузионное
ближение применяется также в физике низкотемпературной
мы при отсутствии рассеяния. В этом случае этот метод дает
удовлетворительные результаты для оптически толстых слоев, а
для оптически тонких слоев погрешности могут быть
чительны.
Рассмотрим расчетные соотношения диффузионного
ближения при отсутствии светорассеяния.
В основе диффузионного приближения лежит процедура
тегрирования уравнения переноса E.8) по угловым переменным в
пределах полного телесного угла, результатом чего является
уравнение
V-W = ck(?/6-C/). E.77)
Второе уравнение постулируется исходя из предположения
об аналогии процесса распространения квантов излучения
цессу диффузии атомов и молекул в неоднородных средах
W = -DVC/, E.78)
где D = с/Зк - коэффициент диффузии излучения. Вывод
лы E.78) и выражения для коэффициента диффузии излучения
приведен в п. 6.5.

5.2. Методы интегрирования уравнения переноса по угловым переменным 133
Получить без каких-либо допущений уравнение вида E.78),
связывающее вектор плотности потока излучения с объемной
плотностью лучистой энергии в общем случае произвольной
ловой зависимости интенсивности, невозможно в принципе (см.
подробнее главу 6). Соотношение вида E.78) дает хорошие
зультаты только для слабоанизотропного поля интенсивности.
Важным достоинством диффузионного приближения
ется то, что уравнения E.77) и E.78) являются достаточно
стыми в численной реализации и, что особенно важно, позволяют
достаточно просто сформулировать задачу переноса излучения в
двумерной и трехмерной постановках для произвольной системы
координат. Подставив E.78) в E.77), получим
. E.79)
После определения поля плотности лучистой энергии вектор
плотности потока излучения определяется по формуле E.78).
Дивергенция вектора плотности спектрального потока
дится по формуле ~~
E.80)
Решение дифференциального уравнения E.79) производится
с привлечением граничных условий, формулировка которых дана
в п. 3.8. Для примера рассмотрим два типа граничных условий:
х = Н, -1<;ц<0: 7(л; = Я,ц) = 7я- E.81)
Граничные условия E.81) сформулированы относительно
интенсивности излучения, а дифференциальное уравнение
мулировано относительно плотности энергии излучения. Поэтому
сначала необходимо преобразовать условия E.81) таким образом,
чтобы они содержали только плотность лучистой энергии. С этой
целью предположим, что в диффузионном приближении угловая
зависимость интенсивности излучения может быть представлена в
виде

134 Гл. S. Модели и методы переноса селективного теплового излучения
E.82)
причем это представление единственно. В самом деле, в нашем
распоряжении имеются только два соотношения E.77) и E.78), на
которых базируется диффузионное приближение.
Воспользовавшись определениями плотности энергии
чения
и плотности потока излучения
1
-1
можно получить значения коэффициентов а и Ь в E.82):
а = — U, b = — W.
4я 4я
Поэтому вместо E.82) можно использовать
? 1 E.83)
Для того чтобы получить граничное условие при х = 0,
пишем выражение для плотности потока излучения
1
W(x = 0) = 2njj(x=:Q,\i)\id\i. E.84)
-1
Проводя интегрирование в E.84) с учетом того, что при ц е [0,1]
интенсивность излучения берется из E.81), а при це[-1,0] - из
(S.83), получаем
W(x = 0) = 2nJt ~-U(x = 0). E.85)
Но в диффузионном приближении постулируется связь E.78)
жду W» U, поэтому искомое граничное условие имеет вид

5.2. Методы интегрирования уравнения переноса по угловым переменным 135
jc_dt/
Зк dx
х=0
с
"г
По аналогии формулируется граничное условие на правой
це * = Н
Зк dx _
В итоге получаем замкнутую краевую задачу переноса излучения
в плоском слое в диффузионном приближении
dt'
с dU
Зк dx
ы>
где
х = Н:
Зк dx
_4тс
~TJb'
х=Я
с
E.86)
E.87)
E.88)
При произвольном распределении температуры и
ента поглощения в плоском слое задача E.86)—E.88) решается
численно методом прогонки (Самарский А.А., 1987). Введем
нечно-разностную сетку
=Xj-Xj_x = const; ; = 1,...,Л
на которой определим сеточную функцию С/у =t/(xy), для
чета которой воспользуемся каноническим видом
ностного уравнения прогонки:
AjUH-CjUj + BjUJ+l + Fj = 0, j = 2,...,NJ-\, E.89)
где Aj,Bj,Cj,Fj - прогоночные коэффициенты:

136
Гл. 5. Модели и методы переноса селективного теплового излучения
Конечно-разностное представление граничных условий
E.87) и E.88) имеет следующий вид:
?/.=¦
2тс
Vnj-\+-
E.90)
J-H.E.9\)
Результаты численного решения задачи E.89)-E.91)
ставлены на рис. 5.11 и 5.12 соответственно для хн = 1 и 10 и
пределения температуры, показанного на рис. 5.5. Сравнение этих
результатов с точным решением (см. рис. 5.6 и 5.7) подтверждает
высказанное ранее утверждение о том, что диффузионное
ближение обеспечивает удовлетворительные результаты расчетов
лишь при больших оптических толщинах.
300000
C
200000
100000
•100000
1
3
2
-
——
—
10
дг, см
Рис. 5.11. Плотность радиационной энергии A, U в Дж/см1),
ность радиационного теплового потока B, W в Вт/см2) и дивергенции
вектора плотности потока радиационной энергии Q,Qr в Вт/см1).
Решение диффузионным методом для плоского слоя с оптической
толщиной т = 1

5.2. Методы интегрирования уравнения переноса по угловым переменным 137
Заметим, что при численной реализации краевой задачи
E.89)-E.91) необходимо проводить дополнительное
ние получаемых результатов на разных расчетных сетках. В
бенности указанное требование необходимо выполнять при
чии областей сильного пространственного изменения
ента поглощения или наличия разрывов 1-го рода.
Дополнительные численные исследования рекомендуется
проводить также с целью изучения свойств численных решений
вблизи границ расчетной области. При этом сгущение расчетной
сетки вблизи границ не всегда является достаточным.
400000
зооооо
200000
100000
-100000
\/
1
{ 3
/—
ьи--
\
/¦
//
10
Х.СМ
Рис. 5.12. Плотность радиационной энергии A, V в Дж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенции
вектора плотности потока радиационной энергии (i,Qr в Вт/см1).
Решение диффузионным методом для плоского слоя с оптической
толщиной т = 10
5.2.4. Метод Эддингтона
Метод был разработан для решения задач о переносе
чения в фотосферах звезд (Eddington A.S., 1926). Расчетные соот-

138 Гл. 5. Модели и методы переноса селективного теплового излучения
ношения метода сформулируем применительно к уравнению
реноса в условиях ЛТР для изотропно рассеивающей среды
H^^ + ^(t.n) = (l-»)J»(t) + f J./(T,n')dn', E.92)
ОТ 2 _•
где с!т = (к + а)(к.
В идейном отношении методы Шустера-Шварцшильда,
Эддингтона и диффузионное приближение подобны между собой.
В их основе лежит процедура последовательного интегрирования
уравнения переноса по телесному углу с разными весовыми
циями. Методы отличает способ замыкания получающейся
бесконечной системы уравнений. В методе Эддингтона
щее соотношение формулируется для давления излучения.
Процедура получения расчетных соотношений состоит из
шести этапов.
1-й этап. Применение к уравнению (S.92) интегрального
оператора вида
i
Л{ }=2tiJ{ }<1ц, E.93)
-1
результатом чего является уравнение
dt
i
где G (т) = 2л
-1
2-й этап. Применение к уравнению E.92) интегрального
оператора вида
i
Л{ } = 2я f{ }^d^, E.95)
-i
результатом чего является уравнение
dx ;.;. E.96)

5.2. Методы интегрирования уравиения переиоса по угловым переменным 139
. 1
где PR (т)=—2я f J{x, ц) ц2с1ц - радиационное давление.
0 -1
3-й этап. Интенсивность излучения представляется в виде
двух составляющих:
E.97)
E.98)
х,\1), при ц>0;
7(т,ц) = 7~(т,ц), при ц<0;
С учетом такого разделения получается
о 1
L-i
о
(т,ц)цс!ц +
L-i о
L-i
E.99f
E.100)
E.101)
4-й этап. Делается допущение о независимости от
ления интенсивностей излучения в полусферах
7"(т,ц) =
, при 0
, при -
С учетом этого
E.102)
E.103)
E.104)
E.105)
E.106)

140 Гл. 5. Модели и методы переноса селективного теплового излучения
5-и этап. Исключение радиационного давления по
лам E.104), E.106)
РЛ(т) = A/Зс)С(т), E.107)
В результате вместо E.96) имеем
6-й этап. Система уравнений E.94) и E.108) заменяется
одним дифференциальным уравнением второго порядка
ах
E.109)
Уравнение E.109) называется приближением Эддингтона к
уравнению переноса излучения. Перейдем в уравнении E.109) к
плотности лучистой энергии
E.110)
Видно, что для нерассеивающей среды (о> = 0) уравнение
E.110) тождественно уравнению диффузионного приближения
E.86). В п. 6.1 будет показано, что полученное уравнение
ственно уравнению Р {-приближения для изотропно рассеивающей
среды F.25).
5.3. Метод моментов
Рассмотренные в предыдущих разделах методы основаны на
последовательном интегрировании уравнения переноса излучения
по угловым переменным с некоторыми весовыми функциями и
введении некоторых априорных предположений относительно
угловой зависимости интенсивности излучения. Указанный
ход обобщается в группе моментных методов.
Метод моментов предложен в работе (Krook M., 1955). Для
вывода расчетных соотношений воспользуемся уравнением
носа излучения в прямоугольной декартовой системе координат
(рис. 5.13) в приближении ЛТР:

S.3. Метод моментов
141
СО,
а/ а/ а/ =
2', E.111)
где оох =sin8cos9, а>у =sin8sin9, юг =cos8 - направляющие
синусы единичного вектора направления распространения
чения П.
Z'
к
Z'
j x*
71
\
/у
У
Рис. 5.13. К выводу уравнений метода моментов
Уравнение E.111) получено с использованием так
мого транспортного приближения светорассеяния, которое
зволяет существенно упростить расчет интеграла рассеяния.
занное приближение является одним из простейших и весьма
фективным.
В транспортном приближении индикатриса рассеяния
ставляется в следующем виде:
-1), E.112)
где 5 - дельта-функция Дирака; ц' - косинус угла рассеяния в
теме координат центра рассеяния; Д - средний косинус
ния:
_ I1
Д=1|у*(ц')с1ц,
1
E.113)
-I
где у* (ц') - реальная индикатриса рассеяния, аппроксимируемая
транспортным приближением E.112).

142 Гл. 5. Модели и методы переноса теплового излучения
Заметим, что предполагается азимутальная симметрия
сеяния, а соотношение E.112) удовлетворяет условию
ки A.18)
Подставим E.112) в интеграл рассеяния уравнения переноса
излучения в трехмерной геометрии C.3)
± J 7(G')Y(G',Q)dG«
471 П=4*
=— f 7(Q')[(l-P)+2p5(Q'-l)]dQ=— f 7(Q')dQ'+op7.
471 im, 47tn=4*
Тогда, вводя обозначение для эффективного коэффициента
ослабления J3 = к + а, а = A -р) о, получаем уравнение E.111).
Далее предполагается, что интенсивность излучения может
быть представлена рядом
j(r,n)=jo+2eX+Z*X+Zc^' <5Л14>
7-1 У-1 7=1
где Jo, dj, bj,Cj - искомые функции координат, а величина N
называется порядком приближения метода моментов. В частном
случае N = 1 получается первое приближение метода моментов
() E.115)
для которого и получим расчетные соотношения.
После подстановки E.115) в E.111) и интегрирования в
делах полного телесного угла, получается первое уравнение
темы моментных уравнений
Второе, третье и четвертое уравнения получают путем
становки E.115) в E.111), умножения соответственно на сох, со^,

S.3. Метод моментов
143
<ог и последующего интегрирования по полному телесному углу.
Итогом указанных действий являются уравнения
J3 дх '
ia/0
E.117)
E.118)
Э dz
E.119)
Подставляя E.117) - E.119) в E.116) получают
альное уравнение второго порядка относительно Jq
или
Учитывая, что
U=-
—J0, Ub=—Jb,
g% g%
уравнение E.121) можно переписать в виде
или
E.121)
E.122)
E.123)
E.124)
где <о =
Последнее уравнение позволяет перейти к новой переменной
- оптической толщине по ослаблению

144 Гл. 5. Модели и методы переноса теплового излучения
dT = J3dr, E.125)
что приводит к наиболее компактной записи уравнения переноса
излучения в первом приближении метода моментов
2 f/6). E.126)
Вектор плотности радиационного потока определяется по
формуле
W= JyQdQ=—(ai + bj + ck), E.127)
yQdQ=
4»
а дивергенция этого вектора
. E.128)
Граничные условия для решения уравнения E.126)
лируются с использованием задаваемой в исходных данных
тенсивности излучения внешних по отношению к объему
ников. Здесь, как и в других методах предварительного
рования уравнения переноса по угловым переменным,
ся основной недостаток метода моментов: на границе, как
ло, задается интенсивность излучения в полусфере, обращенной
вовнутрь исследуемого объема, а интегрирование производится
по полному телесному углу. Поэтому в задачах, где перенос
чения от поверхности, окружающей исследуемый объем, является
важной составной частью решения, необходимо проводить
альные исследования с целью более адекватной формулировки
граничных условий (см., в частности, п. 6.4). Развитие метода
ментов применительно к светорассеивающим средам со сложной
индикатрисой рассеяния представлено в работе (Горский В.В. и
др., 1976).

5.4. Методы эффективных излучательных способностей 145
5.4. Методы эффективных излучательных способностей
5.4.1. Метод эквивалентного излучающего объема
Этот простейший метод оценки интегральной излучательной
способности объема излучающего газа основан на использовании
понятия полусферической степени черноты
, E.129)
где R - радиус полусферического однородного объема горячего
газа, находящегося в термодинамическом равновесии с
турой Т и давлением р .
Из E.129) следует, что функция z(p,T,R) может быть за-
табулирована в виде функции трех аргументов для стандартных
газовых смесей (например: воздух, Нг, СОг, смесь CO2-N2, НгО и
т.п.). Примеры таких таблиц приведены в работе
ков В.А. и др., 1971). Имея в распоряжении подобные таблицы,
расчет плотности интегрального радиационного потока в
нии однородной полусферы выполняется по формуле
W = dT4s(p,T,R). E.130)
Однако, к сожалению, в большинстве практически
ных случаев излучающие объемы являются неоднородными и не
имеют форму полусферы.
В рамках обсуждаемого простейшего метода проблема
однородности излучающего объема решается приближенной
меной истинного неоднородного объема некоторым эффективным
однородным объемом. При этом алгоритм такой замены не
делен и во многом основан на опыте и интуиции специалиста,
шающего задачу.
. Проблема отличия формы исследуемого объема от
рического объема решается также путем введения эквивалентного
полусферического объема, имеющего радиус
Reff=0.9DV/F), E.131)
11 Зак. 272

146 Гл. 5. Модели и методы переноса теплового излучения
где V - объем излучающего газа; F - площадь его поверхности.
В этом случае оценка плотности интегрального
ного потока на поверхности F дается формулой
E.132)
5.4.2. Метод производных от полусферических
испускательных способностей
Метод предназначен для расчета переноса излучения в
нородных газовых объемах и подробно изложен в книге (Пен-
нер С.С., 1963), в которой дается ссылка на оригинальную работу,
выполненную Р.Томсоном и С.С.Пеннером в виде отчета в 1959
году.
Метод изложен применительно к решению задачи о
се излучения в плоском слое. Суть метода состоит в том, что
ность интегрального потока излучения может быть выражена
через производные от степеней черноты однородных
ческих объемов. Поскольку эти производные пропорциональны
среднепланковским коэффициентам поглощения, то при наличии
таблиц предварительно рассчитанных коэффициентов (для
дартных смесей горячих газов и низкотемпературной плазмы)
числительная процедура становится весьма эффективной. Однако
недостатком метода является его ориентация на плоские
чающие слои. Обобщение на случай других геометрий и
ностей проблематично.

Глава 6
МЕТОД СФЕРИЧЕСКИХ ГАРМОНИК (Pn-МЕТОД)
Метод сферических гармоник предложен в работе (Jeans
J.H., 1917) и подробно исследован в работах (ДэвисонБ., 1960;
МарчукГ.И., 1961; Чандрасекхар С, 1953; Султангазин У.М.,
1979). Этот один из наиболее широко распространенных методов
решения уравнения переноса излучения основан на
ции угловой зависимости интенсивности излучения и
сы рассеяния рядом по сферическим функциям. Сферические
функции являются ортогональными полиномами, возникающими
при решении уравнения Лапласа в сферических координатах
кифоров А.Ф. и др., 1984). Поскольку непрерывные решения
уравнения Лапласа называют гармоническими функциями, то
рические функции часто называют сферическими гармониками.
Отсюда и следует происхождение названия данного метода. Что
касается сокращенного обозначения метода сферических
ник (Pn), to его происхождение обязано полиномам Лежандра,
входящим в сферические функции и для которых обозначение Pn
является общепринятым.
Большая популярность метода сферических гармоник
словлена исключительно высокой эффективностью решения задач
переноса излучения в светорассеивающих средах в объемах
стейших и сложных геометрий. Указанная эффективность
няется тем, что, с одной стороны, представление угловой
мости интенсивности излучения и индикатрисы рассеяния рядом
по сферическим функциям вполне адекватно физике процесса
реноса излучения в большом числе практически важных случаев,
а, с другой стороны, ортогональность используемых для
ного разложения полиномов позволяет свести исходное интегро-
11*

148 Гл. 6. Метод сферических гармоник (Рц-метод)
дифференциальное уравнение переноса к системе
альных уравнений. Причем в отличие от других методов решения
исходного интегро-дифференциального уравнения точность
шения задач переноса излучения и вычислительная
ность соответствующих расчетных кодов возрастают с ростом
альбедо однократного рассеяния.
Ниже основная идея метода будет сначала изложена на
мере решения задачи переноса излучения в плоском слое, а затем
будет дано обобщение для других геометрий.
6.1. Применение метода сферических гармоник
к решению задачи переноса излучения в плоском слое
Рассматривается задача о переносе излучения в плоском слое
рассеивающей среды (см. рис. 5.2)
' F.1)
- _1
при граничных условиях
т = 0, ц>0: 7(О,ц) = 7о (ц), F.2)
x = Xff, ц<0: J(ifj,\i) = JJf (ц). F.3)
В основе метода сферических гармоник, применяемого к
решению задачи о плоском слое, лежит предположение о том, что
интенсивность излучения может быть представлена в виде ряда по
полиномам Лежандра
Предполагается, что индикатриса рассеяния может быть
также представлена в виде разложения
)=ЕBм + 0^М^(Ю> Yo=l- F-5)
т=0

6.1. Применение метода сферических гармоник в плоском слое 149
Полиномы Лежандра обладают важным^ свойствами орто-
нормированности (Никифоров А.Ф. и др., 1984)
0, тФп,
2 F.6)
» m ~ п
U/M +
и могут быть выражены друг через друга посредством следующей
рекуррентной формулы:
Полиномы Лежандра низких степеней имеют следующий
вид:
F.8)
Подставляя F.4) и F.5) в F.1), интегрируя полученное
нение по полному телесному углу, а также, учитывая F.6),
чают
I
2/w + l
„=o 4я — Ц'
M (t)
m=0
а с использованием F.7)
iil
где 60 m - дельта-функция Дирака.

150 Гл. 6. Метод сферических гармоник (Рц-метод)
Уравнение F.9) должно выполняться при любых ц, значит,
выражения в квадратных скобках при любом т должны равняться
нулю
= 4яA-шO6(тN0>т, т = 0,1,2,... F.10)
Однако система дифференциальных уравнений F.10) не
замкнута. Каждое из уравнений при фиксированном т содержит
три функции: <pm_i(T), фи(т), фи+1(т).
Для того чтобы ограничиться конечным числом уравнений,
необходимо допустить, что с некоторого номера m = N все
следующие производные равны нулю:
.. F.11)
dx
Число N называется порядком приближения, а система
ференциальных уравнений - Рм-приближением метода
ских гармоник.
Очевидно, что ограничение числа решаемых
альных уравнений эквивалентно ограничению членов ряда в
ложении интенсивности по компонентам Лежандра, т.е. введение
фиксированного числа т = N означает аппроксимацию угловой
зависимости интенсивности излучения конечным рядом по
рическим функциям.
Наиболее широкое распространение в практике расчетов
реноса излучения получило Pi-приближение, в котором т = 0,1 и
система дифференциальных уравнений выглядит следующим
разом:
й)У6(т), F.12)
o, F.13)
а коэффициенты уо и у\ задают индикатрису рассеяния в
дующем виде:

6.1. Применение метода сферических гармоник в плоском слое 151
'. F.14)
Это так называемое линейно анизотропное рассеяние. В
стном случае изотропного рассеяния (Yo=l;Ym=O при т>\)
система уравнений F.12) и F.13) еще более упрощается:
^1 + A-ш)Фо(т) = 4тгA-шO6(т), F.15)
;<c)=o. F.i6)
Система уравнений F.12) и F.13) приобретает более
ный вид, если учесть, что искомые функции имеют следующий
физический смысл:
1
фо(т) = 2я |J(x,\i)d\i = G(т) = cU(т), F.17)
-1
W(x), F.18)
-1
что легко установить, учитывая, что в первом приближении
да сферических гармоник
р,Ж(ц), F-19)
Поэтому система уравнений метода сферических гармоник
для плоского светорассеивающего слоя приобретает вид
= 4яA-шO6(т), F.20)
Г(х)~ "^ F.2.)
3A-соу) dx

152 Гл. 6. Метод сферических гармоник (Рц-метод)
или
3A-coy,) dx2
или
1 d2t7
3(l-coYl) dx2 V
где Ub(x) = — Jb.
с
Умножив последнее уравнение на знаменатель дроби при
второй производной, получим в окончательном виде уравнение
переноса излучения в Р|-приближении метода сферических
моник, которое при отсутствии рассеяния (со = 0 ) в точности
падает с уравнением диффузионного приближения E.86).
Формулировка граничных условий в методе сферических
гармоник обсуждается несколько позднее, в п. 6.4. Однако,
зуясь тем, что в Pi-приближении интенсивность излучения
ставляется в виде ряда F.4) и ограничивая его в соответствии с
выбранным приближением, получим
1 з , / \ с г v 3
т.е., граничные условия, также как в диффузионном приближении
(см. формулу E.83)), могут быть сформулированы по аналогии с
п. 5.2.3.
В итоге получаем краевую задачу Р|-приближения метода
сферических гармоник расчета переноса излучения в плоском све-
торассеивающем слое, обобщающую диффузионное приближение
в части учета светорассеяния
. с dU
= 0:
Зк дх
х=0
с
"г
F.26)

6.1. Применение метода сферических гармоник в плоском слое
153
х-Н- ° W
Зк дх
х=н
+-
2
F.27)
Еще раз напомним, что в данном случае оптическая толщина
определяется по коэффициенту ослабления
с1т=Р<к=(к+а)<к.
На рис. 6.1-6.3 показано распределение радиационных
рактеристик U, W, Qn в плоском изотропно рассеивающем слое
при температурном распределении, показанном на рис. 5.5,
фициенте поглощения к = 1 см и разных альбедо.
зооооо
200000
100000
-100000
1
¦
3
.—¦—
10
X, СМ
Рис 6.1. Плотность радиационной энергии A, U в Дж/см3), плотность
радиационного теплового потока B, W в Вт/см2) и дивергенции
тора плотности потока радиационной энергии C, Qr в Вт/cm3); в
плоском слое с оптической толщиной т = 1. Решение уравнения
реноса излучения с использованием Р|-при6лижения метода сфери-
' ческих гармоник
После расчета U(x) плотность потока излучения
лась по формуле F.21), а дивергенция вектора плотности
стого потока находится по одному из следующих соотношений:
ЮЗак.272

154
Гл. 6. Метод сферических гармоник (Рц-метод)
- формальное дифференцирование по т дает
3A-%,) dx2 '
- формула, следующая из F.20)
F.28)
F.29)
Здесь дивергенция рассчитана на шкале оптических толщин.
400000
зооооо
200000
100000
•100000
У
;/
Г з
Ц | 1 I
^—"~~
'•
1 1 I I
1 t I I
ш
<
/
10
X, СМ
Рис 6.2. Плотность радиационной энергии A, U в Дж/см3),
ность радиационного теплового потока B, ff в Вт/см2) и дивергенции
вектора плотности потока радиационной энергии C, Qr в Вт/cm3); в
плоском слое с оптической толщиной т -10. Решение уравнения
переноса излучения с использованием Р,-приближения метода
рических гармоник
На рис. 6.3 показано распределение тех же радиационных
характеристик, но для изотропно рассеивающего слоя толщиной
10 см, оптической толщины по поглощению т = 1 и с
ентом рассеяния а = 10 см, т.е. с альбедо однократного рассея-

6.2. Метод сферических гармоник в решении задачи переноса излучения 155
ния со = 0.99 . Сравнение данных на рис. 6.1 и 6.3 показывает, что
рассеяние в еще большей степени способствует установлению
равновесия внутри излучающего слоя.
400000
зооооо
200000
100000
-100000
3
1т=1,о=10|
о ¦=»
10
X, СМ
Рис. 6.3. Плотность радиационной энергии A, U в Дж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенции
вектора плотности потока радиационной энергии C, Qr в Вт/cm3); в
плоском слое с оптической толщиной т = 1,а = 10 см'1. Решение
уравнения переноса излучения с использованием Р,-приближения
метода сферических гармоник
6.2. Применение метода сферических гармоник
к решению задачи переноса излучения
в осесимметричной постановке
Рассматривается задача о переносе излучения в осесиммет-
ричном цилиндрическом объеме радиусом R и длиной Я (рис. 6.4).
Такая геометрия излучающей области широко используется в
ных технических приложениях: ракетные двигатели, плазменные
генераторы, электроразрядные устройства и т.п.
ю*

156
Гл.б. Метод сферических гармоник (Рм-метод)
Рис. 6.4. Расчетная схема переноса теплового излучения в
ном осесимметричном объеме
Уравнение переноса излучения в нерассеивающей среде в
цилиндрическом объеме имеет вид
dJ(r,z,\i,y) 1-y2 dJ(r,z,\i,y)
дг
OZ
при граничных условиях
z = 0, ц>0:
z = H, ц<0:
r = R, у<0:
F-30)
F.31)
F.32)
F.33)
где (i = cose,Y = cos9; функции ^(
J^ (z,(i, у) задают интенсивность внешних по отношению к
ему источников излучения.

6.2. Метод сферических гармоник в решении задачи переноса излучения 157
Предполагается, что интенсивность излучения J = J(R,z,n,y)
может быть разложена в ряд по сферическим функциям
щим образом (Никифоров А.Ф. и др., 1984):
00 Г1 ' 1
/=0 L2 м=1 ' ' J
где а/>Я) и р/)Я) - неизвестные функции пространственных
динат; Р™ (ц) - присоединенные полиномы Лежандра, для
рых справедливы следующие условия ортонормирования:
-1
где 5//' - дельта-функция Дирака; а также следующие
ные формулы
Q&m&l-l; F.37)
F.38)
/-1. F.39)
Другие свойства сферических функций можно найти в
вочниках (ЯнкеЕ., Эмде Ф. и др., 1968; АбрамовицМ. и Сти-
ганИ.(ред.), 1979).
Для получения системы уравнений метода сферических
моник используется так называемая моментная процедура, кото-

158
Гл.б. Метод сферических гармоник (Рц-метод)
рая состоит в применение к уравнению переноса F.30)
ного оператора следующего вида:
2л 1
Ai,m{ }= J J{ }^И1(ц)(а/)Я)со8/мф + C/я)8т/мф)AфAц. F.40)
0 -1
Так как задача сформулирована в осесимметричной
ке, то
() () F.41)
т.е. интенсивность является четной функцией по углу ф . Отсюда
следует, что
Р/.*=0 F.42)
и основной задачей является формулировка уравнений для
скания функций a/ m.
Применение интегрального оператора F.40) к уравнению
F.30) с учетом F.42) приводит к бесконечной системе
циальных уравнений, ограничение которой путем задания
мального числа l = N в разложении вида F.34) дает следующие
уравнения Рм-приближения метода сферических гармоник:
1+8,
Чо
2B/
7»I+1
7+1
дг
.m+1
1 + 6
т,0
2B/
pm+l
~дг~
?m+l
Г
2B/ + 1)
дг
2B/
2/ + 1
2/ + 1 dz
F.43)

6.2. Метод сферических гармоник в решении задачи переноса излучения 159
1 + 5«,о
2BN +
(JV + те -
N + m di
2N + 1
где
I)
ЯРЙ+1
9r
\)(N + m)(\-bm0
2BN + l)
Fin.
dz +K/>-°'
1 2k
-1 0
Fjri 1
Jcosw
Е'/Я—I
Г
F.44)
F.45)
Граничные условия для системы уравнений F.43), F.44)
формулируются в форме условий Марка или Маршака (см. п. 6.4).
Система F.43), F.44) позволяет получить расчетные
ния для плоской и осесимметричной постановки любого
жения. Ниже представлены уравнения наиболее часто
мых вычислительных моделей.
Л Частный случай задачи о переносе излучения в двумерном ifu-
линдрическом объеме: Рi-приближение для плоского слоя
В этом случае iV = 1 ив уравнениях F.43), F.44) должны
быть исключены все слагаемые, содержащие зависимость от
диальной переменной.
Указанная система сводится к следующей
/ = 0, т = 0
F.46)
OZ
=0;
F.47)

160 Гл.б. Метод сферических гармоник (Рм-метод)
+к/г1=0; F.48)
3 dz
Приближение одномерного плоского слоя подразумевает
выполнение условия осевой симметрии, поэтому
F.49)
как содержащие интегралы вида
2*
о
где J - четная функция по переменной ср.
Кроме этого
if (ц) = 0 при 1<т, F.50)
так как т й I, поэтому
^=/го2=О. F.51)
В результате получаем систему уравнений Pi-приближения
для плоского слоя
^ ^ F.52)
F-53)
Fo° = J J ЛЬ0 (Ц) <1цс1ф = 2izjJdix = cU, F.54)
1 2я
где
-1 о -1
1 2* 1
Ff = J J JP,° (ц)AцAф = 2я jJiid\i = W. F.55)
-1 0 -1
Полученные уравнения совпадают с F.20) и F.21).

6.2. Метод сферических гармоник в решении задачи переноса излучения 161
2. Частный случай задачи о переносе излучения в двумерном ifu-
линдрическом объеме: Рi-приближение в одномерной
рической геометрии
В этом случае iV = 1 ив уравнениях F.43), F.44) должны
быть исключены все слагаемые, содержащие зависимость от
вой переменной.
Указанная система уравнений сводится к следующей
/ = 0, w = 0
^ + + к^047ПС/6; F.56)
or г
2-3^ дг г ) 2-3
F.58)
Воспользовавшись условиями осевой симметрии и условием
F.58), получаем систему уравнений Pi-приближения метода
рических гармоник для одномерной цилиндрической геометрии
^ + F=4nKj F>59)
дг г
+ ^-0, F.60)
3 дг
1 2я
где Fo° = | J JPq (ц) Aцс1ф = 2я J 7с1ц = cU, F.61)
-1 0 -1
1 2*
F,1 = J | JPl (ц) созфAцAф=Ж. F.62)
-1 0

162 Гл.б. Метод сферических гармоник (Рц-метод)
Подставим F.61) и F.62) в систему уравнений F.59), F.60)
rer F63)
f^T-O. F.64)
Зк дг
Сформулируем краевую задачу для цилиндрической области
с абсолютно черными границами, с температурой Tw
F.65)
г = 0: — = 0; F.66)
дг
r = R: —— = Ub(Tw)-U. F.67)
Ък дг bKW}
Численный метод решения краевой задачи F.65)-F.67)
смотрен в п. 6.3.
3. Частный случай: Р/-приближение для двумерной гщлиндриче-
ской геометрии
В этом случае ^ = 1 и должны быть учтены условия осевой
симметрии.
Итоговая система уравнений имеет вид
1
я, я, -• "-•' F68)
Г ОТ 02
F'0=-f^' F-69)
Зк &
Л1 =—L^S_. F.70)
1 Зк дг '
Поскольку
1 2% 1
Fo°= f f 7/>оо(ц)AцAф = 2п f Jd\t, = cU, F.71)
-l о -l

6.2. Метод сферических гармоник в решении задачи переноса излучения 163
1 2*
F? = J J7/»10(ц)со8Фс1цс1ф = Ж2> F.72)
-1 О
1 2*
F,1 = J J JP,1 (ц) cos фёцскр = FP,, F.73)
-1 О
то вместо F.68)- F.70) можно записать
F.74)
Зк 02
¦»>-—¦ («-W)
Зк 9г
Для замкнутой цилиндрической области с абсолютно
ми поверхностями, температура которых Tw, имеем краевую
задачу
+— \ = K(U-Ub), F.77)
гдг{3к дг ) &Uk dz ) К Ь)
Щ 0, F.78)
or
ub-Ut F.79)
Зк дг
0: ±^U-Ubt F.80)
Зк &
z tf: ^^ Ub-U. F.81)
Зк &
4. Частный случай: Ргприближение для двумерной
ской геометрии
В этом случае N = 3 .

164 Гл.6. Метод сферических гармоник (Рм-метод)
/ = 0, ю = 0
^< F.82)
1 1 drFi 2
<683)
/ = 1, т = \
1 ( 8f} f2 ~\ 1 8Е? 1 ак° 1 ал1 •
61 or г \ Ъ or 3 дг 3 dz
1 = 2, тп = О
ilM_II^+2^?+2^+1cFo=0 f6g5,
Ьг дг Ьг дг 5 dz 5 dz 2 ' K ' '
= z, m=\
^=0,F.86)
+2 +++
10 [ ar r J 5 аг 5 дг 5 az 5 dz
1=2, т=2
10 [ аг г J 10 дг 5
.o. F.87)
lldrF} 3dF? 0_
I Г ОТ 1 OZ
dFi -F}} 12aF2 4 3F2 _, Л ,, om
—z_+2_z_ + z_+ L + k/t'o, F.89)
dr r ) \4 dr 1 dz 3

6.3. Конечно-разностные схемы численного интегрирования 165
20(dFi F}} 5dF? „2 n ^ ЛЛч
— -i—2- +-—2- + kF32=0, F.90)
14 ^ дг ?г J 1 oz
Дальнейшее упрощение данной системы уравнений связано
с использованием свойств симметрии, в частности F.49), F.50) и
т.п.
6.3. Конечно-разностные схемы численного
интегрирования двумерных уравнений
Pi-приближения метода сферических гармоник
Рассмотрим разностную аппроксимацию диффузионных
уравнений в плоском (р = 0) и цилиндрическом (р = 1) случаях.
Для сокращения записи не будем указывать индекс селективности
(или номер спектрального диапазона, в котором выполнено
реднение оптических свойств). Решаемая система имеет вид
1 drpW dW rr rr ^MS
— ¦—— + —- +KU = KUb, F.92)
rF or oz
LELL+Kwr=o, F.93)
3 dr
L<!LL+Kwz=o, F.94)
3 & K
где W и Wz суть проекции вектора плотности лучистого потока
на оси г и z соответственно, а скорость света с включена в U.
дет использовано также эквивалентное системе F.92)-F.94)
уравнение
1 д(г" ди) д(\ диЛ _. _. ,,-_.
—+ +— —+ \ + ки = киь. F.95)
гр дг{3к дг ) дг\Ък dz) "

166
Гл.6. Метод сферических гармоник (Рц-метод)
Граничные условия на оси симметрии задаются в обычном
виде:
ди_
дг
= 0,
F.96)
3 к дп
либо асимптотические граничные условия вида:
а на внешних границах, либо в виде соотношения, выражающего
отсутствие внешнего потока (см., например, E.88)):
F.97)
F.98)
При построении разностной схемы будем исходить из того,
что на двумерной сетке по переменным г и z заданы поля
ратур Tij, функции источников Jb,i,j, коэффициенты
ния Kij . При построении разностной схемы будем следовать
боте (Четверушкин Б.Н., 1985) и определим плотности лучистой
энергии и потоки так, как это показано на рис. 6.5.
Z*
ij
1
'////¦
t
Рис. 6.5. Радиационные потоки в расчетной ячейке
Плотность лучистой энергии определена в ячейке, а
ции потоков - на ее сторонах. Воспользуемся интегро-интерполя-
ционным методом (Самарский А.А., 1987). Проинтегрируем
ходное уравнение F.92) по объему заштрихованной на рис. 6.5
ячейки

6.3. Конечно-разностные схемы численного интегрирования 167
Если в пределах этой ячейки положить
к = к/7, F.100)
U = ?/,,, Vr е [г„ гы ], Vz е [г,, xJ+l ],
то получим
Р+1 _ р+1 .У р+1
1+1 Ч ГМ ~
+1К4^^/^0(
zJ+l~zJ zJ+l~zj
Замкнутое конечно-разностное уравнение удается получить,
если установить связь между плотностью энергии и плотностью
потока. Для этого рассмотрим сначала в тех же предположениях
F.100) одномерный случай, например, вдоль радиальной
менной (пренебрегая кривизной по г):
. -„, F.102)
dr
dU
—+3kW = 0. F.103)
dr
Из F.102), F.103) имеем уравнение
—-—XW = 0, F.104)
решение которого имеет вид
() ) F.105)
гдеЯ.2=Зк2, % = r-rt, г

168
Гл.б. Метод сферических гармоник (Рц-метод)
Подставив F.105) в F.102), получим уравнение
но U. Постоянные С] и С2 легко найти из условий
= WM.
В результате получим уравнения
F.106)
^f/^, F.107)
-1, F.108)
Но нам необходима связь между функциями U и W,
ными не в одних и тех же точках, а со смещением на половину
ячейки. Для того, чтобы получить формулу для плотности потока
излучения через разность объемных плотностей энергии
ния в соседних ячейках, уравнение F.108) записываем на отрезках
1+1/2 ] И \jUfr,
J F.109)
. F.110)
Складывая F.109) и F.110), получим
2V3
где допускается, что
, F.111)
F.112)

6.3. Конечно-разностные схемы численного интегрирования
169
Но, в соответствии с F.100) надо положить
После чего придем к окончательному выражению
2V3
F.113)
. F.114)
Формула F.114) с точностью до несущественного
циента совпадает с формулой, полученной в работе (Четверушкин
Б.Н., 1985). Однако при получении связи между потоками и
ностями энергии, можно не применять допущения F.112), а
пользоваться уравнением F.107) для тех же самых половинных
ячеек и, тем самым, получить более обоснованные уравнения:
th
ri-ri-\/2
-2/>Mthl
+ Щ = 2Wt + 2/» th
x 2 J ^
С использованием формул F.115) вместо F.114) имеем
-.F.115)
F.116)
где G,=2
' 2

170
Гл.6. Метод сферических гармоник (Рц-метод)
Теперь аналогичное соотношение запишем в двумерном
случае, используя в радиальном направлении те же самые
ненциальные функции, что и в осевом. Отметим, что при этом мы
получим правильную асимптотику решений, как в случае
ски тонкой, так и в случае оптически толстой среды
F.117)
щ
F.118)
где Я; =2^3

6.3. Конечно-разностные схемы численного интегрирования 171
С учетом полученных соотношений сформулируем
чечную разностную схему, аппроксимирующую уравнение
фузии излучения
, A/+i -сиии+fu=о,
F.119)
где 4, = , ^ ' , BtJ= . , \ ?,F.120)
g
ГМ ~П )пМ \rM ~ri
1
+
nz<+1 l' |Jg, 1
zy+i zj zj+\ zj
Можно показать, что полученная разностная схема для
ких функций к и Ub имеет второй порядок точности.
Несложно видеть, что полученная разностная схема весьма
трудоемка. Поэтому, когда нет необходимости, обычно
ют пятиточечную конечно-разностную схему F.119) схему,
чаемую из уравнения F.9S)
г" дг[ък дг у ьЪк dz Г { bh
при использовании интегро-интерполяционного метода

172 Гл.6. Метод сферических гармоник (Рм-метод)
г,-
4/= ==*= г, 4/= =F , F.121)
¦. в,, =—
* 1 r + '
У - ZJ~\
где
Примеры использования конечно-разностной схемы F.119),
F.121) для решения уравнения переноса излучения в двумерной
цилиндрической области показаны на рис. 6.6-6.16.
Для иллюстрации распределения полей радиационных
рактеристик в двумерной осесимметричной цилиндрической
четной области выбрано распределение температуры, показанное
на рис. 6.6. Это локализованная в пространстве
турная область сферической формы. Такое задание температуры,
с одной стороны, хорошо соответствует реальному
нию температуры в ряде реальных энергетических устройств,
пример, в лазерной плазме (Суржиков СТ., 2000), а с другой
роны представляется весьма перспективным для методических
исследований в теории переноса теплового излучения.
ванная сферическая излучающая область, помещенная в
рическую расчетную область, позволяет тестировать все расчет-

6.3. Конечно-разностные схемы численного интегрирования
173
ные методы, разрабатываемые как для цилиндрической, так и для
сферической геометрий. Но самое главное заключается в том, что
локализованность излучающей области является заведомо
нее благоприятным расчетным случаем для всех методов решения
уравнения переноса излучения, в том числе для метода
ских гармоник.
R, см
10
9
S
7
6
5
4
3
2
16391
11013
М04
«453
4729
ММ
2540
IU2
13*4
1000
0 12345678
Рис. 6.6. Распределение температуры (К) в цилиндрической области
9 10
X, СМ
Температурное поле, показанное на рис. 6.6, рассчитывалось
по формуле
Т {х, г) = Гт!п + G^ - Гт!п ) ехр (- J
где
rmin=300K, Гтах=18000К,
Xq = 5 см, r0 = 0, Rq = 1 см.
Поля радиационных функций, соответствующих
му коэффициенту поглощения к = 0.1 см, показаны на рис. 6.7 -
6.10.

174
Гл.6. Метод сферических гармоник (Рц-метод)
Л, см
10 13310
9 И(Э
« Т4М
Т 561*
« «1J
S JIM
4 1370
3 177»
2
1000
О 123456789 10
X, СМ
Рис. 6.7. Поле объемной плотности энергии излучения, Дж/см3; к -0Л см'
3
2
1
О
-1
-2
Л, см
, . 11
f Ч
/ \
(г—V, \
Ш)
10 31246
1 24302
I 1735»
1 IMIS
i 34T2
J -3472
• -1М15
> -1735»
1 -14352
-31146
I I I I I 1 1 ) I
1
89 10
д:, см
Распределение осевой проекции вектора плотности потока
излучения, Вт/см2; к = 0.1 см'1

6.3. Конечно-разностные схемы численного интегрирования
175
Л, см
Рис. 6.9. Изолинии модуля радиальной проекции вектора плотности
потока излучения, Вт/см2; к: - 0.1 см'1
R, см
3
2
1
0
-1
•2
10
»
«
7
«
S
4
1
г
i
115042
19115»
К7477
143**4
ИМИ
96135
71347
415*5
147*2
1000
Illltlllllltlltllllllll
10
х, см
Рис. 6.10. Изолинии функции тепловыделения QR, Вт/см3; /г = 0.1 см'1

176
Гл.6. Метод сферических гармоник (Рц-метод)
Конечно-разностная сетка, на которой проводился расчет
показана на рис. б. 11.
R, см
6 7 8 9 10
X, СМ
Рис. 6.11. Конечно-разностная сетка, используемая в расчетах по
Р,- приближению метода сферических гармоник
Как уже отмечалось, представленные здесь расчетные
ные могут быть использованы в качестве тестовых, которые для
более полного изучения свойств численных решений, должны
быть дополнены расчетными вариантами с переменными по
странству оптическими свойствами среды. Важное значение имеет
также выбор различных конечно-разностных сеток. Причем,
четные сетки могут быть не обязательно структурированными
(см., например, главу 7). Что касается расчетных данных,
занных на рис. 6.7-6.10, то следует помнить о приближенности
полученных решений, которые, тем не менее, дают общее
ставление о закономерностях радиационного переноса.
Серия расчетных данных, показанная на рис. 6.12 -6.15
ответствует температурному полю, показанному на рис. 6.16
где
rmin = 300 К,
= 18000 К, L = 7 см,

6.3. Конечно-разностные схемы численного интегрирования
177
о о, от = 4.
Такое распределение температуры может моделировать
плазменные конфигурации в плазменных генераторах различного
типа: высокочастотных индукционных плазмотронах, дуговых и
лазерно-плазменных генераторах.
Особо подчеркнем, что в отличие от предыдущего
го случая, здесь степень локализации горячей области
но ниже лишь в одном из пространственных направлений.
ко, локализация наиболее излучающей области вблизи оси
метрии часто приводит даже к большим погрешностям расчетов,
чем в случае сферической симметрии
Сравнение результатов расчетов плотности радиационного
потока на боковой поверхности цилиндрического канала для
представленных двух расчетных случаев с результатами,
зываемыми методом дискретных направлений, даны в п. 8.6.
Л, см
10
9
«
7
6
5
4
3
2
97*51
90 «47
S3U4
76901
69917
629L
55950
4S967
4I9U
35000
6 7 8 9 10
X, СМ
Рис. 6.12. Поле объемной плотности энергии излучения, Дж/см3; *г = 0.1см~
13 Зак. 272

178
Гл.6. Метод сферических гармоник (Рц-метод)
R, см
10 36К9
9 21676
20413
12290
4097
-409Т
-12290
-204*3
-2М76
-36М9
0123456789 10
X, СМ
Рис. 6.13. Распределение осевой проекции вектора плотности потока
излучения, Вт/см2; к = 0.1 см
R, см
2
1
О
-I
-2
1
10
9
*
7
6
5
4
3
г
i
92599
U42I
74243
65ОМ
55IM
46711
ЗТ533
2MS5
1917»
10000
8
9 10
X, СМ
Рнс.6.14. Изолинии модуля радиальной проекции вектора
сти потока излучения, Вт/см2; к = 0.1 см

6.3- Конечно-разностные схемы численного интегрирования
179
R, см
О 1
Рис. 6.15. Изолинии функции тепловыделения QR , Вт/см3; к = 0.1 см
R, см
Рис.б.16. Распределение температуры (К) в цилиндрической области
13*

180 Гл.6. Метод сферических гармоник (PN - метод)
6.4. Особенности формулировки граничных условий
для методов сферических гармоник
Проблема формулировки граничных условий для методов
сферических гармоник состоит в том, что в указанных методах
для нахождения объемной плотности лучистой энергии и
стей радиационных тепловых потоков используется
ние по полному телесному углу, в то время, как угловые
деления интенсивности внешних по отношению к объему
ников излучения известны лишь в половине телесного угла.
этому сформулировать точные граничные условия нельзя в
ципе и необходимо использовать какие-либо приближения или
предусматривать решение проблемы на алгоритмическом уровне,
например, организуя итерационный процесс последовательного
уточнения усредненной по угловым переменным интенсивности
излучения.
В практике расчетов широко применяются два типа
женных граничных условий, разработанных при решении задач
нейтронной физики.
6.4.1. Граничные условия Марка
Формулировка граничных условий данного типа подробно
обсуждается в работах (ДэвисонБ., 1964; МарчукГ.И., 1961;
ОцисикМ.Н., 1976). Оригинальная работа была опубликована в
форме отчета в 1945 г.
Марк предположил, что для Рм-приближения метода
ческих гармоник граничные условия должны выполняться при
значениях углов, отвечающих корням полинома Лежандра
0, F-121)
то есть, если, например, на поверхностях плоского слоя известно
распределение интенсивности внешних источников излучения
т = 0, ц>0: J@,\i) J(\i),
V ' V ' F.122)
т = хя, ц<0: 7() 7"()

6.4. Особенности формулировки граничных условий
181
то граничные условия должны формулироваться следующим
разом
х = 0, ц>0: •/@,ц/) = 7+(ц/),
F.123)
х = хя, ц<0: J(xH,-\ij) = J (-Hi),
где щ -положительные корни уравнения F.121).
При решении задачи в Ргприближении, граничные условия
F.123) должны выполняться при значениях ц,,
щих
то есть, при цф =
Если задача решается относительно объемной плотности
лучистой энергии, то
V ' dx
и граничные условия формулируются в виде
v 1
: = 0: 7+(цф) = —I
4я [_
у/3 dx
х = хя: 7 (цф) = — U/(x)+-Tr *-!¦
4n v3 dt
6.4.2. Граничные условия Маршака
F.124)
F.125)
Граничные условия данного типа предложены в работе
(Marshak R.E., 1947).
. Если в решаемой задаче заданы граничные условия вида
х = 0, ц>0:
= хя, ц<0:
F.126)
F.127)

182
Гл.6. Метод сферических гармоник (PN-метод)
то для решения уравнения переноса излучения в Рм-приближении
метода сферических гармоник находятся усредненные моменты
интенсивностей на границах по следующим формулам
1
, ц>0,
, ц<0,
F.128)
F.129)
-1
Например, в Pi-приближении метода сферических гармоник
для плоского слоя
«/(т)"
и граничные условия Маршака формулируются в виде
2 dx
1 <К/(т)
2 dx
т=0
F.130)
F.131)
F.132)
Для удобства построения численных схем представим
ношение F.131) и F.132) в конечно-разностном виде.
емся 1-м порядком аппроксимации и схематическим
ем расчетной области вблизи границ, показанных на рис. 6.17
= 0:
¦2(х2-т,)
1
¦2(х2-т,) с
F.I33)

6.5. Формулировка уравнений Ррприближения
183
U
Рис. 6.17. Конечно-разностная сетка вблизи границ расчетной области
6.5. Формулировка уравнений Р]-приближения метода
сферических гармоник для произвольной геометрии
Подводя итог рассмотрению метода сферических гармоник,
приведем несколько общих замечаний, которые окажутся
ными при формулировке задач переноса излучения в
ных геометриях.
В общем случае в методе сферических гармоник
ся разложение функции интенсивности излучения в ряд по
ческим функциям следующего вида, т.е. фактически применяется
метод разделения переменных
л=0
п
' F135)
где Y™ - сферические функции, определяемые через
ние функции Лежандра
, т>0,
, т7>0,
8о>от - символ Кронекера.

184 Гл.6. Метод сферических гармоник (PN - метод)
Теория сферических функций, присоединенных функций и
полиномов Лежандра изложена в работе (Никифоров А.Ф. и др.,
1984). Особенностью указанных функций является их
нальность, а также наличие удобных рекуррентных соотношений.
Это дает возможность достаточно просто реализовать
ское интегрирование уравнения переноса излучения по угловым
переменным, сводя, при этом, исходное интегро-дифференциаль-
ное уравнение переноса к системе дифференциальных уравнений
относительно функций ф^ (г).
Алгоритм формулировки дифференциальных уравнений
носительно фюя (г), называемый моментной процедурой, состоит
в следующем. Сначала интенсивность излучения в форме F.135)
подставляется в уравнение переноса C.3). При этом индикатриса
рассеяния также представляется в виде ряда по полиномам
жандра. Затем, поочередно умножая полученное уравнение на
ждую из сферических функций и интегрируя его по угловым
ременным, используя свойства ортогональности сферических
функций, приходим к бесконечной системе обыкновенных
ференциальных уравнений относительно ф„т (г) . Аналогичным
образом поступают с граничными условиями.
Если ограничить разложение F.135) конечным числом
гаемых, то придем к конечному числу уравнений, количество
торых (без единицы) и составит порядок приближения.
мое приближение называется Рм-приближением метода
ских гармоник (N - порядок приближения).
Одной из серьезных проблем метода сферических гармоник
является задача построения граничных условий. Особые
сти возникают, когда функция интенсивности излучения на
нице терпит разрыв (напомним, что при построении Рц-прибли-
жения используется интегрирование по всему телесному углу).
Как уже отмечалось в п. 6.4, для решения краевых задач Рц-
приближения обычно используют граничные условия Марка или
Маршака. Применяются также граничные условия Помранинга
(Pomraning G.C., 1964,1973).
В задачах динамики излучающего газа и плазмы наиболее
широкое распространение получило Pi-приближение метода сфе-

6.5. Формулировка уравнений Ргприближения 185
рических гармоник. Имея в виду, что его точность примерно
ответствует точности расчета оптических свойств горячих газов и
низкотемпературной плазмы, можно сказать, что этот метод (а
также эквивалентные по точности ему методы) в настоящее время
является оптимальным для задач рассматриваемого класса.
Система уравнений Pi-приближения практически совпадает
с системой диффузионных уравнений, которую получим в общем
виде, следуя работе (Четверушкин Б.Н., 1985). Наиболее просто
получить требуемые уравнения в произвольной системе
нат, исходя из уравнения переноса, записанного в виде
fi.VJv(r,fi)+Kv(r)^(r,fi) = Kv(r)y6iV(r). F.137)
Оставляя в разложении F.135) первые два члена, получим
, F.138)
где коэффициенты разложения (pijV(r) и ф2>У(г) подлежат
делению. Выражение F.138) позволяет сделать некоторые
орные выводы о применяемом приближении. Учитывая, что
вая зависимость интенсивности излучения содержит только два
слагаемых в разложении в ряд, от него можно ожидать хорошей
точности при исследовании радиационного поля с изотропной или
достаточно гладкой угловой зависимостью интенсивности
чения, и худшей точности, когда функция интенсивности терпит
разрыв или меняется резко.
Для выяснения физического смысла коэффициентов Ф1>у(г)
и ф2,у(г) достаточно левую и правую части формулы F.138)
интегрировать один раз по телесному углу с единичным весом, а
второй раз - с весом Q. Тогда, воспользовавшись определением
объемной плотности энергии и вектора плотности потока
ния, найдем
г), F.139)
4я
;r,Q)dn = 92v(r) = Wv(r). F.140)
4л
12 3ак. 272

186 Гл.6. Метод сферических гармоник (Рм - метод)
Таким образом, в диффузионном приближении используется
следующая аппроксимация интенсивности:
r)Q]/47t. F.141)
Первое уравнение диффузионного приближения не связано с
разложением интенсивности в ряд и получается при
нии F.137) по всему телесному углу:
M(r), F.142)
= Jj6>v(r)dQ
4л
Второе уравнение можно получить, проинтегрировав F.137)
свесом Q и с учетом F.141)
w'(r>=-i^)w-<r>- F-143)
Из F.143) становится понятным название полученного
ближения: поток излучения пропорционален градиенту объемной
плотности энергии с коэффициентом «диффузии» D = 1/3 кv (г).
Уравнения F.142) и F.143) можно также представить в виде
одного уравнения:
-V^-i—VC/v(r)+Kv(r)cC/v(r) = Kv(r)cC/6>v(r). F.144)
Однако при построении разностных схем часто удобнее
пользовать представление F.142), F.143).
Для получения граничных условий к диффузионному
ближению необходимо соответствующим образом преобразовать
соотношение для интенсивностей на границах (например,
ство нулю потока на оси симметрии). Укажем наиболее
тельные из них.
1. Внешнее излучение на границу s рассматриваемого объема не
падает, т.е.
Jv (r,Q) = 0 , при [Cl • п) < 0, где п - внешняя нормаль.

6.5. Формулировка уравнений Pi-приближения 187
В этом случае
^„(r) = (n-Wv(r)M=-|c/v(r) F.145)
или, в силу F.143)
= -C/v(r). F.146)
2. Осевая симметрия в цилиндрическом объеме или центральная
симметрия в сфере
rWv(r) = 0, F.147)
где г° - единичный вектор в радиальном направлении. Условие
F.147) можно записать в форме
^М 0. F.148)
дг
Представляет практический интерес рассмотреть следствия
из диффузионных уравнений в случаях оптически тонких и
чески толстых сред. Они будут позднее использоваться при
строении конечно-разностных схем.
/. Приближение оптически тонкой среды.
Уравнение F.142) перепишем в виде
V.Wv(r) = Kv(r)c[f/6>v(r)-f/v(r)]. F.149)
Из условия tv <к 1 следует, что в отсутствие внешних
ников излучения
Jv(xv)<*:Jiv(Tv),
а значит, и t/v (г) <*; Ubv (г).
Отсюда
VWv(r) = cKv(r)C/6>v(r). F.150)
12*

188 Гл.6. Метод сферических гармоник (PN - метод)
Интегрируя F.150) по волновому числу, приходим к
мости дивергенции плотности интегрального лучистого потока от
среднепланковского коэффициента
00
r) = 47UcP(r)a7'4(r), F.151)
о
00
с Jkv (r)C/6>v (r)dv Jkv (r)y6>v (r)dv
где кР(г) = -? = ^ . F.152)
0 4я О
При решении задач радиационной газовой динамики редко
удается использовать приближение оптически тонкого слоя во
всей спектральной области из-за больших коэффициентов
щения в ультрафиолетовой части спектра. Но использование этого
приближения в отдельных спектральных областях оказывается
весьма удобным и приводит к значительной экономии временных
ресурсов компьютера. Таким образом, в практике расчетов
но используется не F.152), а выражение
Rv(r)Kv(r)dv
Kp,Av(r) = ^ . F-153)
Rv(r)dv
о
где Av - спектральный диапазон, в котором справедливо
ближение оптически тонкой среды.
2. Приближение оптически толстой среды.
В этом случае
иЛг)*иь,Лг)- FЛ54)
. Численная оценка величины дивергенции плотности
стого потока по формуле F.149) может привести к неправильному
результату, поскольку в ее правой части стоит разность двух
близких чисел. Дивергенцию потока в этом случае вычисляют
посредственно по его величине:

6.5. Формулировка уравнений Ргприближения 189
Wv(r)=^)VC/M(r)' F>155)
Интегрирование F.155) по волновому числу дает
F.156)
где Kr(i") - средний коэффициент поглощения по Росселанду,
определяемый по формуле
\\/Kv(r)][dUbtV(T)/dT]dv
KR1(r) = -^ - . F.157)
J[«/4i?(r)/dr]dv
о
Так же как и в случае оптически тонкого слоя, в практике
расчетов используют среднеросселандовские коэффициенты не во
всей спектральной области, а только на отдельных участках
спектра.
В заключение следует подчеркнуть, что по мере
ния к границе расчетной области метод сферических гармоник
дает все большую погрешность, которая может достигать
ков процентов. Точность метода возрастает при увеличении
ческой толщины по поглощению или по рассеянию.
Снизить погрешность метода сферических гармоник вблизи
граничных поверхностей удается также при использовании более
высоких приближений, однако при этом возрастает сложность
системы решаемых уравнений. Тем не менее, кроме Ррприбли-
жения может быть рекомендовано Рз- и даже Р5-приближение
тода сферических гармоник. Установлено, что использование
четных приближений метода является предпочтительным.
робно с анализом высших приближений метода сферических
моник можно познакомиться в книгах (Марчук Г.И., 1961; Марчук
Г.И. идр., 1981; Смелов В.В., 1978; СултангазинУ.М., 1979).

Глава 7
МЕТОД КОНЕЧНОГО ОБЪЕМА ДЛЯ РЕШЕНИЯ
ЗАДАЧ ТЕОРИИ ПЕРЕНОСА ТЕПЛОВОГО
ИЗЛУЧЕНИЯ
7.1. Общие понятия
В предыдущих главах было показано, что уравнение
са излучения, формулируемое относительно моментов
ности излучения по угловым переменным, часто сводится к
ференциальным уравнениям в частных производных
ского типа. Получаемые уравнения имеют широкую область
менения в разных областях науки и техники и, в частности, в
ханике сплошной среды, где были разработаны эффективные
тоды их численного решения. В данной главе дано подробное
ложение одного из таких методов - метода конечного объема,
который целесообразно использовать для решения широкого
класса задач переноса теплового излучения в объемах
ной геометрии.
Метод конечного объема применительно к двумерным
чам механики сплошной среды предложен в работах (McDonald
P.W., 1971; MacCormack R.W. et al., 1972) и обобщен на
ную расчетную область в (Rizzi A.W. et al., 1973). Этот метод
рактеризуется следующими двумя свойствами.
1. Метод конечного объема формулируется для объектов
произвольной геометрии.
2. В основу построения метода положено дискретное
ставление законов сохранения массы, импульса и энергии в
нечных элементарных объемах, на которые делится вся расчетная
область.

7.2. Понятия о консервативных и неконсервативных численных схемах 191
Сначала рассмотрим теоретические основы метода, а затем
получим расчетные соотношения для уравнения переноса
ния в диффузионном приближении для произвольной геометрии.
7.2. Понятие о консервативных и неконсервативных
численных схемах
Законы сохранения механики сплошной среды (массы,
пульса и энергии) могут быть представлены в следующем виде:
— Jq>du + (jFdS= JQdv. G.1)
dt v s v
Уравнение G.1) формулирует условия изменения некоторой
скалярной величины ф с течением времени t в объеме V за счет
потоков F этой величины через поверхность S, ограничивающую
объем V, и производства (исчезновения) этой величины в объеме
V со скоростью Q. Элемент поверхности dS характеризуется не
только площадью, но и направлением нормали n: dS = ndS. Для
однозначности физической трактовки G.1) необходимо ввести
правило определения положительного направления п. Например,
положительным направлением вектора нормали к поверхности
является направление из объема наружу. Тогда втекающий в
ем V поток скалярной величины ф имеет к dS компоненту,
тивоположную п, а вытекающий - совпадающую с п.
Разобьем объем V произвольными криволинейными
ностями на меньшие не перекрывающиеся объемы, которые будем
именовать элементарными объемами. Пусть N - число
ных объемов и в сумме они составляют полный объем V. Запишем
для каждого к-го элементарного объема интегральный закон
хранения G.1)
— l^dv + JFdS= JQdv, k = \,2,-,N. G.2)
Если просуммировать все N интегральных законов
ния G.2), то в результате должен получиться общий закон сохра-

192 Гл.7. Метод конечного объема для решения задач переноса излучения
нения G.1). При этом легко убедиться, что интегралы по
ним поверхностям элементарных объемов Vk , не совпадающих с
поверхностью всего объема V, сократятся, поскольку при одном и
том же направлении потока F скалярной величины ф на любой
внутренней поверхности обязательно найдутся два одинаковых
интеграла с противоположными знаками (для одного и того же
участка внутренней поверхности в один из смежных
ных объемов скалярная величина ф втекает, а из другого -
кает).
Теперь представим, что разделение объема V на
ные объемы Vk было произведено посредством какой-либо
стной схемы, с использованием которой производится также
чет потоков F на их поверхностях. Очевидно, что условие
ного уничтожения потоков на смежных поверхностях может при
этом не выполняться. Результатом чего станет невыполнение
тегрального закона сохранения по объему V.
Далее будем использовать следующие определения.
1. Расчетная схема называется консервативной, если при
численной дискретизации объема выполняются интегральные
коны сохранения. Это значит, что при формальном суммировании
разностных соотношений в расчетной формуле должны остаться
потоки только через поверхность, охватывающую весь объем V.
2. Если в результате такого суммирования в итоговом
четном соотношении остаются потоки через внутренние
ности, то такая схема называется неконсервативной.
В качестве примера читателю предлагается убедиться в том,
что использование одной и той же конечно-разностной схемы с
центральными разностями для уравнения переноса
dt дх
ди . ди Л
и его аналога — + 2м — = 0
dt дх
приведет соответственно к консервативной и неконсервативной
расчетным схемам.

7-3, формальное описание метода 193
7.3. Формальное описание метода
В исследуемой расчетной области V введем N элементарных
объемов Vk, внутри каждого, из которых скалярная величина ц>к
распределена равномерно. Тогда закон сохранения G.1) для к-го
элементарного объема запишем в виде
=fitfk. G.3)
где V/c - объем к-го элементарного объема; g* - скорость
чения (уменьшения) величины ф* в объеме в единицу времени;
суммирование ведется no Nk поверхностям, ограничивающим
объем Vk.
Очевидно, что элементарные объемы можно ввести многими
способами. Необходимо следить лишь за тем, чтобы вводимые
объемы не перекрывались, и для каждой внутренней поверхности
любого элементарного объема можно было указать соседний
ем, имеющий с ним ту же самую граничную поверхность. Для
ресекающихся или находящихся на удалении друг от друга
ментарные объемы это условие не выполняется.
Расположение и координаты элементарных объемов
ляются используемой для этого разностной сеткой, покрывающей
исследуемое пространство.
Применяются два типа сеток:
- конечно-разностный тип сетки,
- конечно-элементный тип сетки.
В первом случае узлы сетки лежат на пересечениях
ва координатных линий (в общем случае - криволинейной
мы координат). Такие сетки называются структурированными.
Во втором случае сетка формируется с использованием
темы треугольных и четырехугольных ячеек в двумерной
рии (или пирамидальных и тетраэдральных - в трехмерной
метрии). При этом узел сетки не может быть ассоциирован с
кими-либо координатными линиями, и такая сетка называется
структурированной.

194
Гл.7. Метод конечного объема для решения задач переноса излучения
До сих пор ничего не говорилось о том, в какой точке
дого элементарного объема определяется искомая функция ф*.
Безотносительно к типу используемой сетки различают метод
нечного объема, центрированный в ячейке (в объеме) и метод
нечного объема, центрированный в узлах. В первом случае
мая величина ф* приписывается всему объему (в пределах
рого она считается постоянной). Во втором случае ф*
ется в узлах сетки. Пример указанных сеток показан на рис. 7.1.
Рис. 7.1. Пример центрированного в ячейке (а) и центрированного
в узлах (б) метода конечного объема
7.4. Расчетные соотношения метода конечного объема
в двумерной геометрии
Пусть в произвольной двумерной геометрии введена система
конечных объемов, для каждого из которых интегральный закон
сохранения может быть записан в следующем виде:
- Jfidu,
G.4)
где f, g - декартовы проекции вектора потока F в каждой точке
поверхности Sk, ограничивающей объем Vy.
Для объема Vy, показанного на рис. 7.2, из G.4) имеем
д f iv+ <J {fdy~gdx)= J?dv. G.5)
dt
ABCD

7.4. Расчетные соотношения метода конечного объема
195
Рис. 7.2. Пример двумерной расчетной сетки
Для каждой из сторон четырехугольника АВ, ВС, CD, DA
можно определить вектор, определяющий ориентацию
ности:
G.6а)
G.66)
G.6b)
G.6г)
тогда вместо G.5) получим
Числовая величина объема Vy (в двумерном случае -
щади поверхности) рассчитывается с использованием известного
из аналитической геометрии (Ильин В.А., ПознякЭ.П, 1981)
отношения
G'8>

196
Гл.7. Метод конечного объема для решения задач переноса излучения
Заметим, что если узлы ячейки (i,j) располагать в
вательности против часовой стрелки, то последние два выражения
под модулем в G.8) дадут положительную величину.
Ключевым моментом метода конечного объема является
ределение величин компонент векторов потоков через
сти, ограничивающие объем. Расчетные соотношения
ся в зависимости от способов аппроксимации потоков и способа
определения искомой величины ф на расчетной сетке.
7.4.1. Расчетные формулы для потоков при использовании
потоковой аппроксимации и центрированного в объеме
метода конечного объема
Компоненты скорости конвективного переноса для
вой схемы определяются следующей формулой:
G.9)
где а = <У/Эф, Ь - 9g/dq> - компоненты Якобиана.
В простейшей потоковой схеме принимается, что поток на
границе ячейки равен потоку, выходящему из данной ячейки или
входящему в нее из соседней ячейки, в зависимости от знака
лярного произведения скорости W на вектор ориентации
ности S.
Рис. 73. К использованию
токовой аппроксимации и
центрированного в ячейке
тода конечного объема

7.4. Расчетные соотношения метода конечного объема 197
Для геометрии показанной на рис. 7.3 используются
дующие расчетные соотношения:
Gioa)
<7-106)
f(F-S).., ()n
=Г J Г7 10г>
{ )<o GЛ0г)
7.4.2. Расчетные формулы для потоков при использовании
потоковой аппроксимации и центрированного в узлах
метода конечного объема
Для геометрии, показанной на рис. 7.4, используются
дующие соотношения:
(FS)_,, ecnH(WS)_>0,
V /DA V /ВС G.116)
(F'SL'

198
Гл.7. Метод конечного объема для решения задач переноса излучения
Рис. 7.4. К использованию потоковой аппроксимации и
ного в узлах метода конечного объема
7.43. Расчетные формулы для потоков при использовании
центрально-разностной аппроксимации и центрированного
в объеме метода конечного объема
Используются следующие альтернативные варианты (см.
рис. 7.3):
а)
G.12а)
G.12b)
б)
G.13а)
G.136)

7.4. Расчетные соотношения метода конечного объема 199
-\ G.13B)
); C7.13D
в) /ав=\[/а+/в], G.14а)
G146)
G.14в)
G.14г)
где
). /с=/(Фс).
.16а)
(,у и ии) G.16в)
г) для формул G.14) используется усреднение следующего вида:
*л -\[fi.j + Лу-i +/ы,п +/м

200 Гл.7. Метод конечного объема для решения задач переноса излучения
/с =j(/i.j +fM,j +//+1./Й +Aj+l)> G-17в>
/d =\(fi.j +Лу+1 +/м.у+1 +/-и)- G-17г)
7.4.4. Расчетные формулы для потоков при использовании
центральио-разиостной аппроксимации и центрированного
в узлах метода конечного объема
Используются следующие альтернативные варианты (см.
рис. 7.4)
й) JAB-J\ ^ ' (/.isa)
G.186)
G.18в)
G.18г)
б) /ав=\{/а+/в), G.19а)
G.196)
G.19b)
/оа=^{/о+/а)> G-19г)
где
К /с=/(Фс)> Л)=/(фО)-G-20)

7.4. Расчетные соотношения метода конечного объема
201
Рассмотрим примеры использования формул G.12)-G.20).
Пример 1. Получить расчетные соотношения для потоковой
схемы и центрированного в объеме метода конечного объема в
двумерной прямоугольной декартовой системе координат.
Решение. Расчетная схема будет получена на примере уравнения
G.21)
ot дх ду
для геометрии, показанной на рис. 7.5.
Рис. 7.5. Расчетная схема к примеру 1
Компоненты потока в данном случае определяются по
мулам
Воспользуемся формулами G.10):
(F• S)ab = -ft.y-i {*в-*л) = -*<P,,y-iА*.
(F • S)CD = +glJ {xc-xD) = +b^j Аде,
(F' S)da = -fi-U {Уо~Ул) = -оф<
В соответствии с формулой G.7) получаем
G.22а)
G.226)

202
Гл.7. Метод конечного объема для решения задач переноса излучения
Поделив вышеприведенное уравнение на величину объема
ij = Ах Ay, получим расчетное соотношение
dt
, д
Ах
1.У , b
Ау
G.23)
Пример 2. Получить расчетные соотношения для
но-разностной схемы и центрированного в объеме метода
ного объема.
Решение. Геометрия задачи показана на рис. 7.6. Воспользуемся
аппроксимацией типа G.12). Тогда
/ав - Г [fij + /m,j ) - fi+y2j>
SBC =^
/CD = j (Л/ + fl-l.J ) = f 1-У2./'
8DA = 2 (Sij + g/j-1) = Sij-l/2'
G.24a)
G.246)
Рис. 7.6. Расчетная схема к примеру 2
. Выражение для закона сохранения в объеме Vy имеет вид
~(ц>иАхАу) +
(//+1/2,7 " ft-1/2,j
= QyAxAy

7.4. Расчетные соотношения метода конечного объема 203
или, поделив на величину объема V, j = ДхДу и учитывая
ления потоков G.24), получим
dt 2Дх 2Ду
V '
7.4.5. Представление производных в методе конечного объема
Из теоремы Гаусса-Остроградского следует (Ильин В.А.,
Позняк Э.Г., 1980), что для функции, удовлетворяющей свойством
непрерывности вместе со своими частными производными
го порядка, справедливо следующее соотношение:
, G.26)
где .У- как и прежде, поверхность охватывающая объем V.
Определим понятие среднего градиента скалярной
ции ф в объеме К по формулам
Ut G.27)
j-ds- <7-28)
W/y Vydy V]
В случае двумерной геометрии i • dS = dy, j • dS = —dx, поэтому
- G-29)
) 6ц>дх 6хйц>. G.30)
ду/у vy v4
Формулы G.29) и G.30) имеют следующее
ностное представление:

204 Гл.7. Метод конечного объема для решения задач переноса излучения
G.31)
N
1Л / =-^2ЛФ*+Ф*+1
\ду/у 2V к
1
н) (Фаг+i -
G.32)
где N/c - число узлов (и граней) элементарного объема V; К -
декс (имя узла).
Рис. 7.7. К определению среднего градиента скалярной величины
Применительно к 4-угольному элементарному объему,
занному на рис. 7.7, эти формулы дают следующие соотношения:
+Ч>с){Ус-Ув)
+{Ус
G-33)

7.4. Расчетные соотношения метода конечного объема205
G-34)
Несложно убедиться в том, что имеется еще одна более
стая форма записи соотношений G.31) и G.32):
/ = ? Ф Ы" Ук-\ )к=—^ *
G.35)
G.36)
Используя определения G.29) и G.30) получим, что при ф = х
(Srty <7-37)
а при ф = у
что позволяет рассчитывать величину К по простым формулам
& 1 ^
1 &
" ^-i )*= т 5- ^ (х«+> ~ **-•) •G39)
В качестве примера рассмотрим получение формулы расчета
средних производных в двумерном четырехугольнике произволь-

206 Гл.7. Метод конечного объема для решения задач переноса излучения
ной формы. Для этого воспользуемся соотношениями G.35) и
G.36) совместно с G.39):
\дх/у
-Ус)
у (xA-xc)(yB-yD)-(xB-xD)(yA-yc)'
7.5. Расчетные соотношения метода конечного объема
в трехмерной геометрии
7.5.1. Вводные замечания
Использование интегральных соотношений G.1) и G.2),
ражающих один из законов сохранения, в принципе не
вает никаких ограничений на форму элементарных объемов.
нако очевидно, что здесь необходимо пытаться удовлетворить
двум противоречивым требованиям: с одной стороны, форма
ема должна быть насколько это возможно проста (что влечет за
собой простоту получаемых расчетных соотношений), а с другой
стороны, форма объема должна быть настолько сложной,
сколько это диктуется требованием описать сложную геометрию
исследуемой области.
С вычислительных позиций задача формулируется
щим образом: необходимо получить формализованные
ния, определяющие площади граней и их направляющие векторы,
а также величины объемов элементарных ячеек.
В практике расчетов наиболее широко распространены гек-
саэдральные и тетраэдральные конечные объемы. При этом
бенностью гексаэдральных конечных объемов является то, что в
общем случае любые четыре точки, формирующие одну из сторон
гексаэдра, не обязательно лежат в одной плоскости, так что грань
элементарного объема может практически состоять из двух
костей (рис. 7.8).

7.5. Соотношения метода конечного объема в трехмерной геометрии 207
Рис. 7.8. Грань ABCD гексаэдра состоит из двух плоскостей ABC
и ADC, каждая из которых имеет свою нормаль, в общем случае
не параллельных друг другу
В соответствии с этим можно дать два определения вектора
нормального поверхности ABCD:
a) S^cr)=0.5(ACxBD); G.42)
б) S^CZ)=0.5[(ABxBC) + (CDxDA)]. G.43)
Можно убедиться в том, что формулы G.42) и G.43)
дят к одному и тому же результату.
7.5.2. Расчет объема трехмерной ячейки
Для того чтобы рассчитать объем гексаэдра, его делят на
тетраэдры или пирамиды, для определения объемов которых
имеются достаточно простые формулы. Рассмотрим способ
та объема гексаэдра путем разбиения его на тетраэдры. Например,
на рис. 7.9 показан один из возможных таких способов.
. Каждый гексаэдр может быть представлен в виде суммы
шести пирамид: DABE, DEFB, DGCB, DBFG, DEHG, DEGF. При
составлении списка пирамид использовалось следующее правило:
а) выбирается одна из вершин (в данном случае D), относительно
которой выстраиваются пирамиды;

208 Гл.7. Метод конечного объема для решения задач переноса излучения
б) фиксируются три грани, на которые из точки D можно
тить перпендикуляр (AEFB, EFGH, BCGF);
в) через три вершины, не имеющие общих ребер с точкой Д
водится сечение (GEB). Это сечение делит каждую из граней на
два треугольника, каждый из которых и является основанием
искомых пирамид: ABE, EFB, GCB, BFG, EHG, EGF.
Е л
Рис. 7.9. Представление гексаэдра в виде суммы шести пирамид
Для того чтобы рассчитать объем любого из элементарных
тетраэдров, удобно воспользоваться формулой
градского (Ильин В.А., Позняк Э.Г., 1980)
G.44)
приняв в качестве вектора А - радиус-вектор г = х\ + у\ + гк, для
которого выполняется очевидное соотношение: (V • г) = 3.
Например, для тетраэдра DABE
Ъ\ G-45)
так как для вектора rDA выполняются условия
rDA # &ADE ~ rDA ' &ADB ~ ®
в силу того, что он принадлежит плоскостям ADE и ADB.

7.6. Формулировка уравнений метода конечного объема 209
Учитывая, что площадь SAbe может быть определена
средством векторного произведения
&АВЕ ="ZrEAx ГАВ = ГГАВ Х ГВЕ ~Т ГВЕ х ГЕА >
2 2 2
получаем для объема тетраэдра
У ABED =-7rDA-( *ЕА х *АВ ) G-46)
О
или VABED=-
*D Уй ZD
Ч Уе Ч
XA У А *А
Ч У В ZB
G.47)
7.6. Формулировка уравнений метода конечного объема
применительно к двумерной задаче переноса теплового
излучения в области произвольной геометрии
7.6.1. Вариант центрированного в объеме метода конечного
объема, основанный на центрально-разностной
аппроксимации
Рассмотрим уравнение диффузии излучения в двумерной
геометрии в прямоугольной декартовой системе координат:
Q- — (п^] + — I Г>Ю- UG Г748^
Ы дх{ 8х) ду{ ду)
где Z) = 1/Ck) - коэффициент диффузии, обратно
нальный коэффициенту поглощения к; G - функция источников
излучения. Будем считать коэффициент диффузии D постоянным
в пределах элементарных объемов, на которые будет разделена
вся исследуемая область. Нестационарное слагаемое в G.48)
жет, не иметь физического смысла. Включив его в уравнение,
дем подразумевать использование итерационной схемы
ления (Самарский А.А. и др., 1978; ОртегаДж. и др., 1975).
смотрим построение расчетной схемы для одного временного
шага.
15 3ак. 272

210
Гл.7. Метод конечного объема для решения задач переноса излучения
Рис. 7.10. Расчетная сетка для уравнения диффузии излучения
Дискретизацию уравнения G.48) выполним на произвольной
криволинейной сетке, показанной на рис. 7.10, аппроксимируя
расчетные ячейки четырехугольниками.
Компоненты диффузного потока имеют вид
ох
ду
Зададим следующую аппроксимацию потоков на
стях элементарного объема ABCD (для прямоугольной ячейки):
(/+
> /а>=т(/с+./Ь)>
G.49)
Искомая расчетная схема будет получена с использованием
балансового соотношения следующего вида (или, в общем случае
G.7)):
, G.50)
где SAB, SCd > Sbc > $da ~ длины сторон четырехугольника.
Сначала получим формулы для расчета потоков в узлах
ментарного объема. Для этого воспользуемся соотношениями,
определяющими среднюю величину производной. Так, например,

7.6. Формулировка уравнений метода конечного объема 2П
для того чтобы рассчитать компоненты потока в точке А,
димо воспользоваться этими формулами применительно к
рем объемам, окружающим эту точку: (/,/), (i,j-l), (i+l,j-l),
(/+1,у). В соответствии с G.33) имеем серию тождественных
отношений (местоположение точек (/,_/) внутри элементарных
объемов будет определено ниже):
м,н " Ду-0] =
= —^г|_Ф/+1,У-1 \yMJ ~ УМ,П + yM,j-\ ~ Ду-1
1.у - Л+Ly-i + У и
+%j (Ду - Ум,] + Уц-i ~ У и)+
+Ф/.У-1 (Ду-i " Уи +У»и-1 ~ Ду-i)] =
" Ду-i) + Ф|+1.у (Ду " Ину-1
+Ф',у (Ду-i ">'/+1,у)+Фи-1 U+i.y-i -Ду)]- G-5
Аналогично
/я = -^г[ф/+1,у (д+1.у+1" Ду) + Ф/+и+1 (Ду+i" Ум,]) +
+Ф/.У+1 (>u "^+i.y+i)+<Рлу (я+1,у " Ду+i
/с = - 2^"[я>1.у (Ду+i -У1-и)+Флу+1 [ум,м
+Фм,у+1 (Ум,] - Ду+1 ) + Ф*-1.у (Ду -Ум.У
15*

212 Гл.7. Метод конечного объема для решения задач переноса излучения
+Ф/-и (>Uy-i "Ду ) + Фм,у-1 (Лу-i ~У1-и)]> G-54)
8а = ^г[ф/+и-1 (xmj "xi,j-\) + Ф<+1,у (xtj ~xmj-\
J ) + Ф/,7-1 (XMJ~\ ~ XU
SB
=Г7г1 Ф'+W l^'+U+l -дсо
[ и "*м.у-1 ) + Ф/.у
+Ф/ЧУ (xW.y-i - */,у ) + Фм.у-1 (*/.у-
Потоки на правой и верхней гранях элементарного объема
(по формулам G.49)) равны соответственно:
/ав = -Т7Г
у+1 ~ Л+1.у)+ Ф*,у+1 (У и ~ Л+u
+Ф/.У (Ду-i" Ду+i)+ Ф/.У-1 (Л+1.У-1" Ду)]' G-59)

7.6. Формулировка уравнений метода конечного объема 213
i,j ~ xt-l,j+\
- хи
Потоки на левой и нижней гранях элементарного объема
можно определить по тем же формулам, если вычесть единицу из
всех z'-x индексов в G.S9) и из всеху-х индексов в G.60).
Длины граней рассчитываются по формулам
sab =у}{хв-хаJ +{Ув-УаJ* sbc =\j{xc~хвJ +(Ус-Ув?, , ч
('-61)
2 ?
+{Ус -УйJ. Sda =yj{xA -*dJ +(уа -
И, наконец, объем ячейки рассчитывается с использованием
формул G.39)
VU = 2^Xa +хв)(Ув ~Уа)+{хв +хс)(Ус ~Ув) +
G-62)
Неудобство использования формул G.51)—G.60) и G.61),
G.62) состоит в том, что в них входят координаты вершин ячеек и
их центров. Чаще расчетная сетка строится заданием координат
вершин ячеек, поэтому координаты центров целесообразнее
считывать. Здесь возникает вопрос, который ранее не обсуждался:
что принимать за центр ячейки?
В принципе метод конечного объема не дает каких-либо
ловий выбора центра ячейки, поэтому здесь остается
дствоваться некоторыми соображениями «разумности».
ним, что координаты центров расчетных ячеек появляются в
мулах для расчета потоков на гранях ячеек, в которые в свою
редь входят сеточные значения искомой функции во всех четырех
ячейках, окружающих узел. С узлом расчетной ячейки
ется значение искомой функции ф, приписываемой этой ячейке.
Используя механическую аналогию можно говорить о «центре
масс» однородной ячейки, а ее координаты (хо,уо) определять по
известным формулам

214 Гл.7. Метод конечного объема для решения задач переноса излучения
xo=\\xdS, yo = \\y<lS,
где интеграл берется по площади ячейки. При этом ясно, что на
сильно неоднородных ячейках следует ожидать появление
нительных погрешностей, связанных, например, с ситуацией,
гда вокруг узла располагаются ячейки с сильно различающимися
размерами. Впрочем, с этой проблемой приходится сталкиваться
во всех численных методах, и ее решение кроется в первую
редь в способах построения хороших расчетных сеток. В
стейшем случае однородной сетки в прямоугольной декартовой
системе координаты узлов и центров ячеек сдвинуты на половину
сеточного шага.
Далее будем считать, что координаты узлов и центров ячеек
нам известны по результатам численной процедуры построения
неоднородных сеток. Тогда искомое конечно-разностное
вое соотношение примет следующий вид:
=Ч»
w (HC
j +
\j,y ~<JCU +GUVU>
где коэффициенты {LL\., (LC)tJ, {LR\j ,(MR)UJ ,(HR)tj,
(HC)t j ,{HL). j,(ML)( j ,Ctj зависят только от координат
тров и узлов ячеек. Верхний индекс «.?» означает, что расчетное
соотношение G.63) можно реализовать по явной (s = p) или
явной ( s = р +1) схеме.
7.6.2. Вариант центрированного в объеме метода конечного
объема (МКО), основанный на потоковой
аппроксимации
За основу возьмем то же самое уравнение диффузии
ния G.48), которое будет представлено в разностном виде G.S0)
на сетке, показанной на рис. 7.10. Отличие обсуждаемой модифи-

7.6. Формулировка уравнений метода конечного объема 215
кации МКО от предыдущей состоит в способе аппроксимации
токов на гранях ячеек. При решении уравнения диффузии
ствует конвективный перенос величины <р, поэтому для потоков
можно использовать непосредственно выражение вида
(FS) = -(Z>Vq>)S G.64)
или в разностной записи применительно ко всем граням:
АВ
^) {хв-ха), G.65а)
\°У I AB
. G.65Г)
DA
DA
Искомые величины ф заданы в центрах ячеек, поэтому для
расчета производных дф/cbc и dq/ду воспользуемся формулами
G.33) и G.34) применительно к заштрихованному на рис. 7.11
объему (онобозначен
Рис. 7.11. Криволинейная конечно-разностная сетка

216 Гл.7. Метод конечного объема для решения задач переноса излучения
1 АВ 1УАВ
G-66)
С7'67)
Аналогично строятся расчетные соотношения для средних
производных, ассоциируемых с гранями CD, DA и СВ
Хь) =5?
OXICD lvC
(Ф/j-i + Ф/.y
(фг.у-1 + Ф*j+i) (xw - *t.j-\
м.у+1) (xi-hM - \
DA lYDA

7.6. Формулировка уравнений метода конечного объема 217
+ (фй-1 J-1 + Фн-и ) (Уми ~ Уьи-1
+ (фй-i j + Ф/-и ) (У1-и - Ум,]) +
-i,j ~ xmj
+ (ф/-и +4>/-U-i)(
ВС
(ф/-и + Ф/+и
/-1,у) ( xt-\,j - Л/-1,у+1
/-1,у + 4>mj )(xmj ~ xi-ij)] •
Итоговая формула получается подстановкой G.66)-G.73) в
G.65), а затем в G.50):
-9JL,,,-,
14 Зак. 272
UVU, G.74)

218 Гл.7. Метод конечного объема для решения задач переноса излучения
где коэффициенты (LL)tJ,(LC),,,{LR)tj,{MR)tj,(HR)tJ,{HC\.,
(HL)j >(Mtyt >Cij зависят только от координат центров и узлов
ячеек. Как и ранее (см. уравнение G.63)) верхний индекс «s»
начает возможность решения задачи в явной и неявной
постановках.
Производные G.66) - G.73) преобразуем к виду
\ду] =~2К
/+1.У+1 \xi,j+\ -JC/+i,y-i)+9/j+i \xij-\~xmj+i)J > G-76)
T
()()], G.77)
{ ) ( )]' G-78)
l DA
( ) {j-\ -Учи
l)+ФнJ (^

7.6. Формулировка уравнений метода конечного объема 219
вс ivb
-крм.л-1{yHj-yMj+i)+4>t-\j{yM,j-yi-i,j+\)]> G-81)
вс
( ) {xm,J ~xi-ij+i)] ¦ G-82)
Поток на грани АВ в соответствии с G.65а), G.75), G.76)
где
(АВ)м,П =ЯГ
AtS
Поток на грани CD в соответствии с G.65в), G.77), G.78)
(F-S)o> =-[ф.-и-1 {Щ,-и-х +Ф/,7-1 (CZ))u-i +
где
YCD
14*

220 Гл.7. Метод конечного объема для решения задач переноса излучения
hl J+, =—[(yD -Ус)(У1-х j-x -y
[(yD Ус)(У1-х j-x yw)(D c)(i-i j-i ~хш)] ¦
Поток на грани ВС в соответствии с G.656), G.81), G.82)
и (BC)MJ +Ф/+и+1 (BC)MJ+i+
1_1М + Ф/_1O. {ВС\_Х. ], G.85)
где
j+i ~х,-\ j)] ;
Поток на грани AD в соответствии с G.65г), G.79), G.80)
где
yDA

7.6. Формулировка уравнений метода конечного объема 221
(DA)mj =
Балансовое расчетное соотношение имеет вид
(CD)н ._, -Ф/,,ч (CZ)). у_,
+. -<Рм.;>1 (CZ))hJ+i]+
jrt +Фн j (ВС\-и
Ф'-W
>У., (LC)tj +9MJA (LR)tJ +
>1 («R)u +Ф*^1 (яс)о +
+ФН J (Ж)/ j -*UCU +G'JVU
где:

222 Гл.7. Метод конечного объема для решения задач переноса излучения
{HR).r(AB)MJ+i+(BC)MJ+i;
Заметим, что площади (протяженности) граней и величины
объемов (площадей) ячейки (/,/) вычисляются по формулам
+{Ув-Уа) > sbc4(xc-xb) +{Ус~Ув) >
G.89)
SCD = V(^C ~xdJ +{УС -УйI > SDA =
VU = 2
vcd ^
У da =-j
Расчетные формулы G.88), G.89) представляют собой
нутую двумерную вычислительную модель МКО в объеме
вольной геометрии.

Глава 8
МЕТОД ДИСКРЕТНЫХ ОРДИНАТ
Метод предложен Виком (WickG.C, 1943) и детально
следован Чадрасекхаром (Чандрасекхар С, 1953). Подробное
ложение метода дано в книге (Гринспен X. и др. (ред.), 1972).
же представлено краткое описание одномерной и трехмерной
формулировок, представляющие, по сути, различные методы, а
также даны примеры использования этих методов.
8.1. Одномерная формулировка
Сначала рассмотрим классическую простейшую
ровку метода дискретных ординат для неизлучающей среды,
ключенной в бесконечный плоский слой. Как уже неоднократно
отмечалось, эта модель широко применяется в астрофизике и в
задачах динамики излучающего газа.
За основу возьмем уравнение переноса для изотропно
сеивающего плоского слоя без собственного излучения (символ
частотной зависимости опущен)
Интегральное слагаемое в этом уравнении
ся квадратурной формулой, например, гауссовой квадратурой
(Корн Г. и др., 1974)
J 7(т, ц') ф' - ? ajj(т, n'j ) - ? ajJj (t), (8.2)
-1 М 7=1

224 Гл. 8. Метод дискретных ординат
где о, - квадратурные весовые коэффициенты; цу - корни
линомов Лежандра, определяемые из условия PN (ц) = 0.
Корни многочленов Лежандра и квадратурные весовые
эффициенты приведены в (Абрамович М. и др. (ред.), 1979)
вплоть до N= 96. Приведем для примера узлы и весовые
циенты гауссовой формулы для некоторых первых значений:
п — 1, тп — 1
ц+, =+0.5773503,
ц_, =-0.5773503,
а+1 = а_, = 1;
и = 2, m = 4
ц+, =+0.3399810,
ц_, =-0.3399810,
а+х=а_х =0.6521452;
ц+2=+0.8611363,
ц_2 =-0.8611363,
а+2=а_2 =0.3478548.
Подчеркнем, что значения коэффициентов а7 и ц7 не
сят от подынтегрального выражения. Уравнение (8.1) необходимо
решить для каждого ц7
^ §?,./,(г). (8.3)
Представим интенсивность •/, (т) в виде экспоненциальной
функции
() {) (8.4)
тогда (8.3) примет вид
>,.Л,^с (8.5)
1

8.1. Одномерная формулировка 225
(ш/2)с
или 4 = • (8-6)
Подставив (8.6) в сумму тождества (8.5), получим
ристическое уравнение
fSi- (8-7)
Уравнение (8.7) определяет набор чисел кт, при которых
экспоненциальное представление (8.4) будет удовлетворять
нению (8.3). Пусть число таких чисел М. Тогда решение (8.4)
представим в виде ряда
•М*)=2Х«ехр(-М' (8-8>
т=\
где коэффициенты Aim подлежат определению из граничных
ловий. Таким образом, фактически решение поставленной задачи
сводится к отысканию корней характеристического уравнения
(8.7). Исследование свойств корней характеристического
ния выполнено в (Дэвисон Б., I960). Предложен следующий
числительный алгоритм поиска корней.
Если предположить неограниченное увеличение порядка
приближения N, то вместо (8.7) можно записать
in.
^ ^ 2к \-к
Это означает, что при N-юо имеются два решения к+\ и к.\,
стремящиеся соответственно к х]} и -т^1. Поиск промежуточных
значений к упрощается при использовании особых свойств
ратурной формулы:
1) она симметрична относительно средней точки интервала, т.е.
; (8.10)

226 Гл. 8. Метод дискретных ординат
2) она дает точное значение интеграла, если подынтегральное
ражение является полиномом порядка, не превосходящего
Z (N) , т.е., если п - положительное целое число:
ууц»={2/(» + 1)> Для нечетных n^Z(AT), (gn)
j?x J J \ О, для четных и;
3) если подынтегральное выражение положительно в интервале
(-1,1), то интеграл (8.2) также положителен, а это означает, что
aj>0; (8.12)
4) все \ij различны;
5) используются только приближения с четным числом N, т.е.
цу.*0. (8.13)
Использование соотношений (8.10)-(8.13) позволяет
новить следующие свойства корней: между двумя
ными значениями ц}1 одного и того же знака лежит только один
корень, причем
|*±м|>1, для т7>2.
Вычислительная процедура становится замкнутой при
мулировке граничных условий: на свободных поверхностях дс = 0
и х = Н считается известной интенсивность падающего на слой
излучения
прих = 0, ц,>0: 7(т = 0,^) = У;, (8.14)
придс = Я, Ц;<0: j(x = xH,\ij) = J- , (8.15)
где положительные и отрицательные значения цу определяются
выбранной квадратурной формулой, а соответствующие значения
JjiJ] определяются по известному закону распределения
дающего на слой излучения.
Заметим, что недостатком приведенной формулировки
тода дискретных ординат является сложность учета собственного

8.2. Трехмерная формулировка
227
излучения среды. Развитие этого метода дано ниже
но к общему виду уравнения переноса. Сначала метод
руется для прямоугольной декартовой системы координат в
щем трехмерном случае. Затем будут рассмотрены некоторые
стные случаи.
8.2. Трехмерная формулировка
Рассматривается перенос излучения в трехмерной области,
показанной на рис. 8.1.
Рис. 8.1. Направления распространения излучения в трехмерной геометрии
Уравнение переноса излучения формулируется для
вольной индикатрисы рассеяния в приближении ЛТР (символ
тотной зависимости опущен)
4л
с граничными условиями следующего вида:
- Jy(r,O')y(r,O',O)dO' (8.16)
приг = 5:
? J |n-Q'|7(r,Q')dQ', (8.17)
71 (лП')<0
(л-П')<0

228 Гл. 8. Метод дискретных ординат
где е - полусферическая степень черноты поверхности; р -
лусферическая отражательная способность; п - вектор
ной нормали к поверхности (направленный вовнутрь объема).
В подавляющем большинстве расчетных случаев
са рассеяния может быть представлена в виде ряда по полиномам
Лежандра Р„, с добавлением слагаемого, описывающего
щественное рассеяние вперед (так называемое дельта-рассеяние)
(8.18)
где ц* =cos9* - косинус угла рассеяния в системе координат,
связанной с рассеивающим центром; Ц - средний косинус
сеяния; 5 - дельта-функция Дирака; й„=(а„-Д)/A-Д)
фициенты разложения индикатрисы по полиномам Лежандра с
учетом среднего косинуса рассеяния; а„ - коэффициент
ния индикатрисы без учета среднего косинуса рассеяния (р=0).
Поскольку угловые координаты произвольного вектора Q в
трехмерной лабораторной системе координат задаются
ляющими косинусами (см. рис. 8.1)
со =? = sin8sinq>,
у (8.19)
то следует иметь в виду связь между угловыми координатами в
лабораторной системе координат и в системе координат центра
рассеяния
ц'=Щ1' + %'+ЛЛ\ (8-20)
где штрихами помечены направляющие косинусы единичного
вектора, отвечающего падающему излучению на рассеивающий
центр.
С учетом разложения (8.18) уравнение переноса излучения
принимает вид

8.2. Трехмерная формулировка 229
М
I
I', (8.21)
' 4я л=0
где ст = A-ц)а, р
Пусть задан набор угловых направлений С1т={цт,?,т,т)т}
на основе выбранной квадратурной формулы.
Уравнение переноса для m-го направления формулируется в
виде
Я 7^ Я /"* Я 7^ гт
^^- + ^^- + n.^- + ^=^+f^, (8.22)
a 4я
где Jm = J{r, Qm ) ; зависимость от аргументов всех функций для
краткости опущена;
( ) ^y'(8-23)
т' л=0
где т' - индекс направления падающего излучения, wm -
мент телесного угла в направлении т.
Учитывая (8.20), сумму (8.23) перепишем в виде
JW(«'m)/, (8.24)
т1
М
где у (т\ т) = ? Bи +1) й„Р„ (цицда. + $„?и. + ЛИЛИ') • (8-25)
л=0
Граничные условия для прямоугольной расчетной области
формулируются на каждой грани:
при * = 0 Jm=sJb+- ? wm.\vm.\jm>, (8.26.1)
71 т\
при х = хн Г = ь/4 + - X iv |ци. | У1', (8.26.2)
71 т'

230
Гл. 8. Метод дискретных ординат
при ,=о
(8.26.3)
при у =
Jm=tJb+
(8.26.4)
при z = 0 Jm=eJb+- 2 *>m
71 _.
у1ли-17й',
(8.26.5)
при г =
Л
(8.26.6)
Конечно-разностная схема для решения уравнения (8.22)
лучается интегрированием по элементарному объему в
стве физических координат (рис. 8.2). Центр объема обозначен
точкой Р. В этой точке ищется решение уравнения переноса.
Шесть граней прямоугольника,
щего точку Р, обозначены индексами /
(ближняя), b (дальняя), w (левая), е
вая), п (верхняя) и s (нижняя). За
численными гранями находятся соседние
по отношению к точке Р узлы расчетной
ячейки (соответственно F, В, W, E, N, S).
Интегрирование (8.22) по объему
ячейки дает связь между интенсивностя-
ми на гранях
w
L
•p
Рис. 8.2. Объем ячейки
1 + KVPJ
PJbP
WY«rn) Jf , (8.27)
где Fey
сом Р.
- площади граней; Vp - объем ячейки с

8.2. Трехмерная формулировка 231
Для расчета интенсивности в центре ячейки используется
линейная интерполяция
+ (l-a)J^, (8-28)
где весовой коэффициент а, как правило, полагается равным 0.5.
Соотношения (8.28) позволяют исключить из (8.27) три
чения интенсивности. Исходя из структуры этого уравнения (в
нем присутствуют разности между интенсивностями на
положных гранях), вместо J",J" и J™ подставим (8.28)
- иА-С + ЕА-С + л,УГ + a (s,+s2) vP
Jp = , (о./У)
где
Расчетная формула (8.29) не может быть использована для
посредственного расчета интенсивности излучения по двум
чинам:
1) сумма S2 включает в себя искомую интенсивность,
этому необходимо реализовать итерационное решение задачи;
2) в случае появления в знаменателе отрицательных
ляющих косинусов, могут возникнуть проблемы вычислительного
характера.
Поэтому в целях обеспечения вычислительной реализуемости
формулы (8.29) ее преобразуют к следующему виду:
-
где У?=оС+A-а).С;
У?=о/?+A-а)./;; (8.31)

232 Гл. 8. Метод дискретных ординат
Здесь индексами е и г обозначены значения концевых и
ных граней вычислительной ячейки так, что в формулу для
сивности Jp входят значения интенсивностей на опорных гранях
( г). Для пояснения этого допустим, что все направляющие
нусы (цот>, ?,„', т|от') положительны, т.е. излучение входит в объем
через одну из граней w,s,b и выходит через одну из граней
e,n,f . Тогда опорные грани имеют индексы w,s,b,a концевые
- е, n,f.
Если направление С1т> имеет хотя бы один отрицательный
направляющий косинус, например г\т- < О, то опорными гранями
являются w, s,f, а концевыми - е,п,Ь.
Таким образом, для каждого ординатного направления С1т
интенсивность в точке Jp определяется по известным интенсив-
ностям на опорных гранях. После этого, с использованием (8.31)
находятся значения интенсивности на концевых гранях.
Итерационный процесс организуется следующим образом:
1) обход пространственных ячеек осуществляется в таком
порядке, чтобы можно было лучшим образом воспользоваться
заданными граничными условиями;
2) на первой итерации источниковые слагаемые S2
ется равными нулю;
3) фиксируется ординатное направление Пт ={цт,?,т,Цт},
и обходятся все пространственные ячейки;
4) затем обходятся все ординатные направления;
5) рассчитываются источниковые слагаемые S2',
6) вычисления повторяются, начиная с пункта 3.
В процессе вычислений могут возникнуть различные
ленные неустойчивости:
1)при экстраполяционном нахождении интенсивности на
концевых гранях по формулам (8.31) последняя может оказаться
отрицательной. В этом случае рекомендуется полагать ее равной
нулю;
2) установлено, что получаемые с помощью (8.30), (8.31)
интенсивности численно устойчивы, если выполняются
щие условия:

8.3. Расчет переноса излучения без учета эффектов рассеяния 233
' Ф **< 7гЦ(()'(8-32)
)
а3 +A- аJ B -5а)
где Ф = * — - .
а
Что касается выбора ординатных направлений, то здесь
комендуется использовать симметричную систему ординат, т.е.
желательно, чтобы квадратурные ряды были инвариантны
сительно любого поворота на 90°. Требуется также, чтобы они
давали правильные значения нескольких выделенных моментов
интенсивности излучения (Fiveland W.A., 1987):
1) нулевого момента по полной сфере @^ф^2я, О^Э^я);
2) первого момента по полусфере @ ? ф ? 2я, Ойдйя/2);
3) первого момента по полной сфере @ ? ф ? 2я, 0 ? 0 ^ я).
8.3. Расчет переноса излучения без учета эффектов
рассеяния
Расчетный алгоритм метода дискретных ординат
но упрощается при пренебрежении процессами рассеяния. В этом
случае требуется решить уравнение переноса следующего вида:
П) = к(гO4(г), (8.33)
при граничных условиях (8.17), или в ординатном представлении
fs jfn fs г/И *S г/И
Цот^- + ^^- + Ли^-+^'я=^, (8.34)
ox ay oz
с граничными условиями (8.26).
Рассмотрим частные случаи применения метода дискретных
ординат.
Задача 1. Дать формулировку уравнений первого
жения метода дискретных ординат для плоского светорассеиваю-
щего не поглощающего слоя.

234 Гл. 8. Метод дискретных ординат
В первом приближении и = 1, a+i - a_i = 1, Зц2 -1 = 0,
вательно, ц+1 = -ц_1 = 1/V3 . Тогда вместо уравнения
^2
получаем
Задача 2. Дать формулировку Л^-го приближение метода
дискретных ординат для плоского нерассеивающего слоя.
В работе (Четверушкин Б.Н., 1985) анализируется одна из
конечно-разностных схем, которую можно использовать при
тегрировании (8.34) в одномерном плоском случае. В
жении, что интенсивность собственного излучения J/, и
циент поглощения к являются кусочно-постоянными на
ле (Xi-i,Xi), Л=Л,ы/2> к = Кы/2, формулируется система
четных соотношений:
, Ji,mJl-\,m . „ Jj-\,m + Ji,m _ „ т
-m + К,_1/2 1 = К;-1/2Л,/-1/2 '
Xj - ДС,_, /
цт*0, / = 2,3,...,^.
~ Ki+V2 Jb,i+\/2

8.4. Метод характеристик
235
Цм<0, / = fy-l,...,l.
Данная конечно-разностная схема является устойчивой с
кальной погрешностью аппроксимации О (Ах2) на гладких
ниях и легко реализуется в виде явной расчетной схемы.
8.4. Метод характеристик
Метод характеристик (фактически семейство
стических методов) определен в книге (Четверушкин Б.Н., 1985)
как метод, в котором интегрирование уравнения переноса в орди-
натном представлении производится вдоль направлений полета
фотонов. Важным отличием конечно-разностных схем,
танных для характеристических методов, от дискретно-ординат-
ных схем является то, что в криволинейной геометрии (например,
цилиндрической и сферической) линия траектории фотона не
ляется прямой. Для плоского слоя методы характеристик и
кретных ординат идентичны.
8.4.1. Метод характеристик для одномерной сферической
геометрии
Рассмотрим решение уравнения переноса излучения в
мерном сферическом объеме нерассеивающей среды (рис. 8.3)
П
Рис. 83. Геометрия сферической области
а/ 1-ц2 а/
(8.37)

236 Гл. 8. Метод дискретных ординат
при заданной интенсивности излучения на внешней поверхности
сферы
r = R, ц<0, У(г = Л,ц) = /-(ц), (8.38)
воспользуемся конечно-разностной схемой Самарского
ский А.А., 1987)
rt~rM ri Vm-Vm-X
(8.39)
JUm~Ji-\,m ^-Цд, Ji,m-Ji,m-\ f _
+ + K/-l/2 Jt,m ~
»*
N, ; m = —^ ,—^r ,--->Nm; цт>0.
Данная конечно-разностная схема применяется
но к уравнению переноса в сферической системе координат на
следующих сетках:
по радиусу
wr-{rlt / = 1,2 ЛГ,;Д/;=/; -/;_,};
по углу (точнее, по косинусу угла)
Реализация схемы (8.39), (8.40) начинается от внешней
верхности сферы заданием граничных значений интенсивности:

8.4лМетод характеристик 237
и от луча цот=1 = -1, / = Nt -1, Nt¦,- 2,..., 1, на котором уравнение
переноса излучения для сферически симметричного случая имеет
вид
^ - -о (8-41)
и реализуется по схеме
(8.42)
1 1 ""* /+1 1
: !_
ч ~ гм
Затем расчет ведется по рекуррентным формулам (8.39) и (8.40).
8.4.2. Метод характеристик с интерполяцией
Данная схема предложена и подробно исследована в работе
(Гольдин В.Я., 1960). Решается уравнение переноса (8.37) в
рической системе координат (рис.8.3) на следующей сетке:
по радиусу
тэг = {/}, / = 1,2 Nt; Ar, =rt -/;_,};
по косинусу угла
Исходное расчетное соотношение записывается в
ристических координатах s (т.е. вдоль прямолинейной
рии полета фотона)
nc/ ic/4 (8.43)
as
на отрезке характеристики [sq,S\] , где коэффициенты
ния и интенсивность излучения абсолютно черного тела
маются постоянными. Значения интенсивности в точке S\
деляется по формуле
7, =У0 ехр[-к($, -sQ)] + KJb {l-exp[-ic(s, -sQ)]}. (8.44)

238
Гл. 8. Метод дискретных ординат
Далее эта формула применяется для интегрирования
ния переноса вдоль луча т = 1 (щ = -1)
x{l-exp[-Kj+1/2 (/-,+,-/;)]}, / = ^-1,^-2 1, (8.45)
Следующий шаг вычислительного алгоритма состоит в
ределении интенсивности в узлах сетки т = 2,3 причем
тается, что при расчете 7/>м значения функций Ji+\,m,Ji,m-i,
Jm,m-\ уже известны:
Ji,m =
(xi,m -¦*/,«.
= Ni-\,Nt-2 1,
где
(8.47)
xi,m ~
(8.48)
1+1
(8.49)
7A) _
, г
(8.50)
(8.51)
После достижения центральной точки необходимо
лить значение интенсивности J\(Nm+i)/2 ПРИ Ц = 0- Для этого

8.4. Метод характеристик 239
используется условие симметрии при г - 0: независимость
сивности от угла. Вычисления интенсивности в положительных
направлениях осуществляется по формулам:
{ [ (Xi,m ~K
где
Xi,m=Wm-> (8-53)
(8.55)
J - Ji-\,m-\ + Ji-\,m
rl~ri-\
Данная конечно-разностная схема имеет второй порядок точности
на гладких решениях, однако является неконсервативной.
8.4.3. Консервативный метод характеристик
с интерполяцией
Данный метод предложен и исследован в работе
ва А.В. и др., 1972).
В случае плоского слоя задача решается особенно просто,
поскольку нет необходимости в интерполяции. Для
ных и положительных значений цм на сетке <»ц соответственно
используются следующие формулы:

240
Гл. 8. Метод дискретных ординат
ri ~
J,
b,i+l/2
I
i,m -^i-\,m exP ~
1-exp -к
(8.58)
Г- —Г-
-
1-exp -кь1
- rl-\
, ци>0. (8.59)
Достоинства данного метода проявляются при решении
дач в криволинейных системах координат.
В случае одномерной цилиндрической геометрии решается
уравнение переноса вида
(8.60)
где y = coscp (рис. 8.4).
Расчетная сетка вводится не только по г и ц,но также и по у
Рис.8.4. Геометрия цилиндрической области
Конечно-разностная схема формулируется в виде
ном характеристической схеме с интерполяцией

8.5.5я-метод
241
1-exp
-к
¦/+1/2
xi,m xi,m
(8.61)
Jimk-J eXP
~K/-l/2
*f,w */,w
1-exp -к,-
, (8.62)
где величина J определяется по интерполяционным формулам,
аналогичным (8.50), (8.51) и (8.56), (8.57); координаты узловых
точек определяются по формулам (8.47), (8.48) и (8.53), (8.54).
Используется следующий алгоритм:
1) сначала уравнение (8.60) решается при цт=1 =-1. Расчет
для каждого узла сетки по радиусу проводится в порядке
шения индекса i-Nt-\,Ni-2 1;
2) производится последовательный расчет искомой функции
в порядке увеличения индекса т -1,2,3,...,[(Nm +1)/2]-1,
чем для каждого [хт последовательность расчетов по индексу i
сохраняется;
3)при достижении значения индекса m-{Nm+\)/2
ется уравнение переноса при Ц = 0 ;
4) расчеты интенсивности излучения при положительных
значениях косинуса щ, > 0 проводятся в порядке возрастания
декса /.
8.5. Sn -метод
Метод предложен в работе (Карлсон Б., БемД.Ж., 1958) и
подробно исследован в работах (Марчук Г.И., Лебедев В.И., 1981;
Трощев В.Е. и др., 1968; Четверушкин Б.Н., 1985).
17 Зак. 272

242
Гл. 8. Метод дискретных ординат
8.5.1. Применение Sn -метода для решения одномерных задач
Уравнение переноса излучения формулируется в форме,
предложенной Самарским А.А. и Гольдиным В.В. для
ски-симметричной одномерной задачи переноса
1 д
——
г2 дг
д Г 1-ц2
— —-
Зц I r
(8.63)
Для численного решения вводится конечно-разностная сетка
хзг = {/•, i = 1, N,; Art = rM -г,],
и,,/и = 1,Лгт;Ац = ^1=цИ1+1-цт;ц:А^11 =Q,Nm=2k + l I.
Разностная схема строится для расчетной ячейки Vim,
зованной соседними сеточными узлами (рис. 8.5). В диапазоне
свойства среды полагаются постоянными.
Рис. 8.5. Расчетная ячейка в области пространственно-угловых переменных
К уравнению (8.63) применим интегральный оператор
Л{ }= f dli]r2{ }dr, (8.64)
в результате чего получится следующее уравнение:
гм
ш+1
-'*2 J

8.5. Sn-метод 243
+ */,« J rdr J M^^Jb,A^mJiijJ~- (8.65)
Зависимость интенсивности излучения от угловой и
странственной переменным вводится следующим образом:
_ (r"r<)^/fi.» +{rM -r)Ji,m T _
- T » Ji,m ~)
При подстановке интерполяционной формулы (8.66) в (8.65)
получается четырехточечное конечно-разностное соотношение
вида
,mJi,m ~ Fi,m > (8.68)
- г,3
коэффициенты \т, Bim, Cim, Dim выражаются через
ты узлов конечно-разностной сетки и усредненный в ячейке
эффициент поглощения К/.
Алгоритм расчета с использованием формулы (8.68)
гичен методу характеристик с интерполяцией.
8.5.2. Применение Sn -метода для решения двумерных задач
В двумерный постановке в прямоугольной декартовой
теме координат уравнение переноса имеет вид (рис. 8.6)
где ц = cosG, у =
17*
+f^) + KJ «Jb, (8.69)
дх ду )

244
Гл. 8. Метод дискретных ординат
У
i
/
fa
i
у
У
У-1 J х
Рис. 8.6. Расчетная область в двумерной геометрии
Для конечно-разностного решения уравнения (8.69) вводятся
следующие разностные сетки:
При фиксированных значениях цот и ут уравнение (8.69)
интегрируется по объему элементарной расчетной ячейки (см.
рис. 8.6), в результате чего получается следующее разностное
отношение:
2
m (JU - Ji,j-\ + Jt-\,j ' Ji-\,j-\
-^ [Jij-\ ~ Ji-\,j-\ + Ji,j ~ Ji-\J
KU \Ji.j + JU-\ + Ji-\J-\ - Ji-U ) =
iU, (8.70)

8.5.5л-метод
245
Расчет по схеме (8.70) начинается от границ, на которых
дана интенсивность падающего на объем излучения. Например,
если граничное условие задано при х = у = 0, то из формулы
(8.70) по трем значениям функций можно найти величину Jij (на
рис. 8.6 узлы сетки, в которых известна интенсивность, помечены
квадратиками, а узел, в котором ищется интенсивность -
кружочком).
8.5.3. DSn -метод
Об алгоритме использования DSn -метода применительно к
двумерной геометрии сообщается в работах (Марчук Г.И.,
дев В.И., 1981; Четверушкин Б.Н., 1985). Отличие DSn -метода от
Sn -метода состоит в том, что интенсивность излучения
ется не в узлах расчетной сетки, а в серединах расчетных ячеек.
На рис. 8.7 изображена элементарная расчетная ячейка, на гранях
которой показаны известные значения интенсивности
ки) и обозначены определяемые значения интенсивности
(кружочки).
Ji-\n,j-\n
7-1 J x
Рис. 8.7. Интенсивности излучения на гранях и в центре ячейки
Уравнение переноса вида (8.69) также интегрируется по
ему ячейки, но конечно-разностное уравнение формулируется
сколько в ином виде, чем (8.70):

246 Гл. 8. Метод дискретных ординат
(8.71)
где •//-1/2.7-1/2 ~ интенсивность в центре расчетной ячейки.
Связывая интенсивность в центре расчетной ячейки с интен-
сивностями на гранях по интерполяционным формулам
щего вида:
Л-1/2.У-1/2 = aJi-yij + 0 " a)Jt-y2.j-\,
т ит /1 и\ т \9-и)
J2,j~i/2 ~ bJiJ-\l2 +\})^
где
xJ~xj-\ yt-Уьл
можно исключить из уравнения (8.71) неизвестные интенсивности
на верхней и правой гранях и сформулировать его относительно
•//-1/2.У-1/2 •
На заключительном этапе расчетов по найденной
ности в центре расчетной ячейки и известных значениях
сивности на левой и нижней гранях, с использованием (8.72)
ходятся интенсивности на правой и верхней гранях. Конечно-
разностная схема DSn -метода при а = 6 = 0.5 называется
ческой.
Расчеты по изложенному алгоритму проводятся для всех
ловых значений цот и у*, после чего определяется интегральные
по угловым переменным функции радиационного переноса.
8.6. Методы непосредственного численного
интегрирования угловой зависимости
интенсивности излучения
Суть этих методов состоит в том, что для отыскания
сивности излучения в любой наперед заданной точке расчетной
области, производится испускание из этой точки лучей, для каж-

8.6. Методы непосредственного численного интегрирования 247
дого из которых находится формальное решение уравнения
носа (см. п. 3.2). При отсутствии рассеяния это формальное
ние является точным решением уравнения переноса вдоль луча,
выраженном в интегральном виде. С использованием формул
ленного интегрирования искомое решение для интенсивности
лучения находится без принципиальных трудностей, хотя при
этом необходимо учитывать особенность интегрирования на
тически толстых расчетных интервалах (см. п. 3.2, задача 2; Лосев
С.А. и др., 1990; Чарахчьян А.А., 1976). Выбор пространственных
направлений, в которых испускаются лучи, производится с учетом
особенностей решаемой задачи. При этом, конечно, могут
няться и формализованные алгоритмы, например, использующие
гауссовы квадратуры (см. метод дискретных ординат).
При увеличении числа лучей, испускаемых из каждой
странственной расчетной точки, решение должно сходиться к
точному значению интеграла по угловым переменным. Указанный
метод получил название метода дискретных направлений (МДН)
или Ray - Tracing Method.
Подчеркнем, что отличительной чертой методов
венного численного интегрирования является использование
мул формального решения уравнения переноса вдоль луча. Этот
факт приобретает особое значение при решении уравнения
носа селективного теплового излучения с учетом спектральных
линий атомов и молекул. Вычислительный алгоритм, основанный
на совместном использовании метода дискретных направлений и
различных моделей полос атомных и молекулярных линий,
зывается весьма эффективным (Суржиков СТ., 1992, 1993).
робно этот алгоритм рассмотрен в главе 14.
Алгоритм метода дискретных направлений рассмотрим на
примере расчета радиационных потоков к поверхности
ского аппарата сложной формы, входящего в плотные слои
сферы (рис. 8.8). Для того чтобы рассчитать плотности
онного теплового потока, к элементу поверхности вводится
кальная сферическая система координат с нормалью п. В этой
системе координат каждый луч О. определяется двумя угловыми
координатами: углом широты 8 е [0, я/2] и азимутальным углом

248
Гл. 8. Метод дискретных ординат
<ре[0,2я]. Плотность спектрального радиационного потока на
поверхности определяется по формуле
2я я/2
W(г) = Jdq> J У(г,Cl)cos9sin 9d9, (8.73)
о о
где г - радиус-вектор точки на поверхности в лабораторной
теме координат; J(r,Q) - спектральная интенсивность
ния, соответствующая лучу ?1.
Направление потока
>
Рис. 8.8. Схема космического аппарата
Введение расчетной сетки угловых направлений позволяет
провести интегрирование спектральной интенсивности излучения
на поверхности по пространству угловых переменных и найти
спектральную плотность потока
или
/Я=1 /1=1
(sin е„+, cos ея+, - sin е„ cos е„) (е„+1 - е„) (8.74)
, (8-75)
/я=1
я=1

8.6. Методы непосредственного численного интегрирования 249
где Ny,Ne - числа дискретных угловых направлений.
Направляющие косинусы вектора
°*.п = К )„,„ * + К )т,п j + (ш*)«,« k
рассчитываются по следующим формулам:
где Ря=-(ц„+Ц„+1); Mw=cos9w,; Ф„ =-(ф„+Ф„+,) • (8.77)
Ось z системы координат угловых направлений совпадает с
локальной нормалью к поверхности.
Для того чтобы определить величину J (Q.m,n), необходимо
проинтегрировать уравнение переноса вдоль неоднородного
тического луча. Здесь целесообразно воспользоваться
ным решением уравнения переноса следующего вида:
У(т)= Jyi(x')exp[-(T-T')]dt', (8.78)
о
где s = 0 и s = L начальная (на поверхности) и конечная (на
внешней границе расчетной области) координаты отрезка луча
&т,л, вдоль которого проводится интегрирование уравнения
(8.78).
Конечно-разностная сетка по пространственной переменной
s, с использованием которой проводится численное
ние (8.78), находится для каэкдого луча С1туП. С этой целью
скиваются координаты пересечения в лабораторной системе
динат луча Clm.n со всеми встречающимися на его пути
ностями конечно-разностной сетки, начиная от первой точки (на
16 Зак. 272

250
Гл. 8. Метод дискретных ординат
поверхности, s = 0 ) и кончая последней точкой (на внешней
нице расчетной области или на сопряженной поверхности, s = L ).
Этот алгоритм иллюстрируется графически на рис. 8.9 (луч а).
Заметим, что для определения координат пересечения следует
пользовать соотношения аналитической геометрии. Однако такой
алгоритм оказывается неэкономичным применительно к
нейным (а особенно - неструктурированным) расчетным сеткам.
I X
Рис. 8.9. Два способа введения расчетной сетки вдоль луча
В работе (Surzhikov S.T., 2004 (а)) применен алгоритм
зислучайной выборки координат расчетной сетки. Этот алгоритм
состоит в следующем. Отрезок луча с направляющим вектором
П.т,п, заключенный между первой и последней точками, делится
на Ns -1 одинаковых участков, как это показано на рис. 8.9 (луч
Ь). Очевидно, что требование однородности расчетной сетки на
участке ле[0,1] необязательно для используемого алгоритма.
Хорошо работает также алгоритм случайной выборки координат
точек вдоль луча. Затем для каждого узла расчетной сетки вдоль
луча С1т,п отыскивается ближайший узел пространственной
четной сетки (или ячейка, которой принадлежит этот узел), на
торой заданы теплофизические и оптические свойства среды.
Температура и спектральный коэффициент поглощения
го узла (или ячейки) присваиваются текущему узлу расчетной
сетки вдоль луча. Таким образом, в каждом узле расчетной сетки
вдоль луча С1т,„ становятся известными температура и
ские свойства газа.
Численное интегрирование формального решения уравнения
переноса (8.78) производится по формуле

8.6. Методы непосредственного численного интегрирования 251
-sA, (8.79)
где У^,* - спектральная интенсивность излучения абсолютно
ного тела, рассчитанная по температуре отрезка [sA,s^].
В заключение подчеркнем, что метод дискретных
ний выгодно отличается от ранее рассмотренных методов
кретных ординат, характеристических методов, Sn и
дов возможностью численного интегрирования уравнения
са излучения в задачах с произвольной геометрией с учетом
нейчатой структуры спектра посредством статистических
лей. В последнем случае, уравнение переноса излучения
чески интегрируется по спектру электромагнитного излучения в
спектральных группах вдоль каждого из выделенных
ний. Дополнительные затраты компьютерного времени на расчеты
по несколько усложненным формулам (см. главу 14) многократно
окупаются тем, что вместо сотен и тысяч спектральных точек
внутри каждого спектрального диапазона, расчет производится
сразу для всего спектрального диапазона, то есть как бы для
ной спектральной точки.
Главным недостатком метода дискретных направлений, по
сравнению с упомянутыми методами, является его относительно
большая трудоемкость, обусловленная необходимостью введения
большого числа лучей, вдоль которых производится
ние уравнения переноса. Однако, с внедрением в практику
тов параллельных компьютерных технологий, этот недостаток
легко преодолевается распараллеливанием вычислительных
цессов не только по спектральным группам, но и по дискретным
направлениям. Обоснованием эффективности такого
ливания является независимость вычислительных процедур, как
16*

252
Гл. 8. Метод дискретных ординат
для отдельных спектральных диапазонов, так и отдельных
правлений.
Результаты расчетов плотности радиационных тепловых
токов вдоль поверхности космического аппарата (КА) MSRO
(Mars Sampler Return Orbiter) показаны на рис. 8.10 (Surzhikov
S.T., 2004 (а)). Решалась задача о входе КА MSRO в атмосферу
Марса со скоростью Vn = 5.223 км/с.
1.75
s
I
о
S
о
1.5
1.25
С 0-75
0.5
0.25
0L_u_i
20 40 60 80 100 120 140 160 180
Число расчетных точек
Рис.8.10. Распределение плотности интегрального радиационного
ка вдоль поверхности MSRO от передней до задней критической точки.
Параметры газа в набегающем потоке: р^ = 2.93 х 10" г/см3, pw = 78.7
эрг/см3, Кда = 5223 м/с, 7^ =140 К. Атмосфера Марса моделировалась
смесью газов 97%СО2 - 3%N2 (объемные доли). Число спектральных
групп Ng = 42 , число расчетных точек вдоль каждого луча Ns = 100 ,
число угловых направлений по широте и азимуту Nq =\\, Л^ф =11
Для получения указанных распределений использовался ра-
диационно-газодинамический программный код, разработанный в
работе (Surzhikov S.Т., 2004 (а)). Последовательно
лись системы двумерных нестационарных уравнений Навье-
Стокса, химической кинетики и радиационного переноса.
лась задача о входе КА MSRO в атмосферу Марса со скоростью

8.6. Методы непосредственного численного интегрирования
253
Vx =5.223 км/с. Рассчитанное температурное поле представлены
на рис. 8.11. Параметры выбранной точки траектории даны в под-
рисуночных подписях. Расчет производился на 42-х спектральных
участках (в 42-х спектральных группах).
Рис. 8.11. Распределение температуры (К) в ударном слое и следе за
ским аппаратом MSRO. Параметры газа в набегающем потоке: р^ = 2.93 х 10"'
г/см3, Ра, = 78.7 эрг/см3, Кда = 5223 м/с, 7^ =140 К. Атмосфера Марса
ровалась смесью газов 97%СОг - 3%Ыг (объемные доли)
На рис. 8.12 показано распределение номеров точек вдоль
поверхности MSRO, в которых производился расчет
ных радиационных потоков. Используя данный график легко
тановить, что плотность интегрального радиационного теплового
потока ~ 1.9 Вт/см2 отвечает 80-й точке (см. рис. 8.10) и осевой
координате лобовой поверхности ~70 см (см. рис. 8.11). Первая
точка соответствует передней критической точке, а 180-я точка -
задней критической точке.

254
Гл. 8. Метод дискретных ординат
I
220
210
200
190
160
170
160
150
140
130
120
110
100
90
во
70
60
50
40
30
20
10
1 /
I /
i /
i /
i/
= f , , i
f
1 I 1 1
¦'
, . , , :
50
100
150
200 250
x, см
Рис. 8.12. Соответствие номера расчетной токи ее продольной
координате иа поверхности космического аппарата
В качестве еще одного примера использования метода
кретных направлений рассмотрим задачу определения плотности
радиационных тепловых потоков на внутренней поверхности
нала цилиндрической геометрии, на оси симметрии которого
ется излучающая плазменная область. Эта задача рассматривалась
ранее (см. п. 6.3, рис. 6.5 и 6.15) и, как уже отмечалось, может
быть использована как тестовая.
Распределение плотностей радиационных тепловых потоков
вдоль внутренней поверхности цилиндрической камеры для
рической излучающей области показано на рис. 8.13
ент поглощения к = 0.1 см; NQ=NV = 11) и на рис. 8.14
( к = 1 см). На этих же рисунках приведены результаты расчетов
по Р)-приближению метода сферических гармоник.
ные данные иллюстрируют влияние оптической толщины на
плотность радиационных тепловых потоков и позволяют оценить
относительные погрешности используемых методов.

8.6. Методы непосредственного численного интегрирования 255
J5 2500
ю
2 2000
1500
3 1000
о.
а
I 500
I 0
0 123456789 10
х, см
Рис. 8.13. Распределение плотностей радиационных тепловых потоков
вдоль внутренней поверхности цилиндрического канала: к = 0.1 см*1;
пределение температуры показано на рис. 6.5; сплошная кривая - расчет
методом дискретных направлений, штриховая кривая - Ррприближение
метода сферических гармоник
У
7
7
1
/'
i
\
\
ч
>
\
ч
ч
2500
2000
//
1
\
\
1
й 1500
1000
500
0123456789 10
х, см
Рис. 8.14. Распределение плотностей радиационных тепловых потоков
вдоль внутренней поверхности цилиндрического канала: к = 1 см;
пределение температуры показано на рис. 6.5; сплошная кривая - расчет
методом дискретных направлений, штриховая кривая - Р,-приближеиие
метода сферических гармоник

256
Гл. 8. Метод дискретных ординат
Аналогичные результаты расчетов для эллипсоидального
распределения температуры в цилиндрическом канале показано
на рис. 8.15 и 8.16.
4s 40000
« 35000
| 30000
1 25000
х
§ 20000
| 15000
| 10000
| 5000
1 0
.-
/
¦/
7
/
j
/
,—
--
--
N
V
--
\
0 12 3
6 7
8 9
х, см
10
Рис. 8.15. Распределение плотностей радиационных тепловых потоков
вдоль внутренней поверхности цилиндрического канала: к = 0.1 см'1;
пределение температуры показано на рис. 6.IS; сплошная кривая - расчет
методом дискретных направлений, штриховая кривая - Р,-приближение
метода сферических гармоник
J 40000
& 35000
| 30000
/
f
\
\
0 12 3
5 6 7 8
9 10
х, см
Рис. 8.16. Распределение плотностей радиационных тепловых потоков
вдоль внутренней поверхности цилиндрического канала: к = 1 см*1;
пределение температуры показано на рис. 6.15; сплошная кривая - расчет
методом дискретных направлений, штриховая кривая - Р,-приближение
метода сферических гармоник

8.6. Методы непосредственного численного интегрирования 257
Следует иметь в виду, что использование метода дискретных
направлений для решения задач переноса теплового излучения в
областях с локализованными источниками излучения, необходимо
особенно тщательно выбирать сетки по угловым переменным и
вдоль каждого рассчитываемого луча. Здесь необходима
зация расчетных алгоритмов.
Эти алгоритмы должны, с одной стороны, учитывать
фику неоднородности расчетной области, а с другой стороны,
ляться как можно более экономичными. Конечно, простейшим
решением этой задачи является задание большого числа угловых
направлений и подробной расчетной сетки вдоль луча. Однако это
приведет к чрезмерным затратам расчетного компьютерного
мени. Весьма эффективными являются алгоритмы
ного анализа наиболее предпочтительных направлений расчета
распространения излучения и построения расчетной сетки вдоль
луча, основанной на поведении оптических толщин вдоль луча.
Например, шаг такой расчетной сетки может выбираться из
вия равенства оптической толщины каждой расчетной ячейки
фиксированной величине.

Глава 9
ПОТОКОВЫЕ МЕТОДЫ
К этой группе относятся методы аппроксимации угловой
зависимости интенсивности излучения не в полном телесном угле,
а в некоторой его части. Выбор диапазона изменения угловых
ременных, в котором производится указанная аппроксимация,
диктуется решаемой задачей. Наиболее наглядным является
пользование таких методов в задачах о плоском слое, где полный
телесный угол разделяется на сумму двух полусфер, в пределах
каждой из которых применяется своя аппроксимация угловой
висимости интенсивности. Простейшим из потоковых методов
применительно к плоскому слою является метод Шварцшильда-
Шустера (см. п. 5.2.2).
Обобщение потоковых методов в форме так называемого
тензорного приближения было выполнено в работе
нов В.Н., 1972). В этом методе используется тензорное
ление вектора плотности потока излучения, используемое в
чах астрофизики (Амбарцумян В.А., 1934; РосселандС, 1936).
Уравнения метода тензорного приближения получаются путем
интегрирования уравнения переноса излучения, предварительно
умноженного на некоторые весовые функции по всему телесному
углу. В качестве этих весовых функций выбираются
щие косинусы вектора С1. Так же как и в других подобных
дах, здесь возникает проблема замыкания получающейся
нечной системы дифференциальных уравнений. С этой целью
формулируются дополнительные условия, связывающие
ненты тензора теплового излучения. Метод оказывается весьма
удобным для прямоугольной декартовой системы координат. Од-

9.1. Методы модифицированных сферических гармоник 259
нако его использование в случае криволинейных геометрий
ставляется проблематичным и требует дальнейших исследований.
Потоковые методы обладают двумя важными
вами, отличающими их от других методов:
1) адекватностью описания граничных условий (внешнего по
отношению к исследуемому объему излучения);
2) удобством введения усредненных по спектру
ных коэффициентов поглощения.
9.1. Методы модифицированных сферических гармоник.
DPN-методы
Наиболее детально метод модифицированных сферических
гармоник (DPN-метод) исследован в работе (Галишев B.C., 1980).
Несмотря на то, что в 50-х годах этот метод был предложен и
следован рядом авторов (Gerstl S.A.W., 1969, 1971; MertensR.,
1954; Yvon J., 1957; Ziering S., Schiff D., 1958), в литературе часто
этот метод называется методом Ивона-Мертенсона (см.,
мер, работу (Николайшвили Ш.С., 1966)).
Методу модифицированных сферических гармоник присущи
две отличительные особенности:
1) интенсивность излучения в светорассеивающей среде
ставляется в виде суммы двух составляющих, одна из которых
отвечает нерассеянному излучению, а другая - рассеянному;
2) интегрирование по угловым переменным при отыскании
интенсивности, отвечающей рассеянному излучению,
ся с использованием ее аппроксимации в виде ряда по
рованным сферическим гармоникам. Другими словами,
ность рассеянного излучения разлагается в ряд по сферическим
функциям, ортогональным не на полном телесном угле 4я, а на
некоторой его части (в данном случае - в полусфере, т.е. на
вине телесного угла). Заметим, что при решении задачи о
се излучения в плоском слое модифицированные сферические
гармоники совпадают с модифицированными полиномами Ле-
жандра.

260 Гл. 9. Потоковые методы
В работе (Галишев B.C., 1980) приводятся данные,
тельствующие о более высокой точности DPN-метода по
нию с соответствующим Рм-методом для задачи о плоском слое
(по точности сопоставимы DPn- и Ргы-методы).
Обобщение DPN-метода на двумерную геометрию
но в работах (Галишев B.C., 1980; Gerstl S.A.W., 1969, 1971;
SchiffD. et al., 1960). Суть указанного обобщения состоит во
дении двух угловых зон аппроксимации вдоль каждой из
менных. Например, для двумерной цилиндрической геометрии
интенсивность излучения отдельно аппроксимируется в
рах, соответствующих положительному и отрицательному
правлениям осевой и радиальной переменных.
Применительно к решению задач переноса теплового
чения аналогичный метод рассмотрен в (MengucM.P., IyerR.K.,
1988).
9.2. Метод полумоментов
Метод полумоментов предложен в работах (Sherman M.P.,
1967; OzisikM.N. et al., 1975). В первой из них задача переноса
излучения решается в плоскопараллельной геометрии с
ной функцией источников, а во второй формулируются системы
уравнений (без их решения) в случаях плоской и сферической
геометрий и изотропного рассеяния. В настоящем разделе
смотрено получение полумоментных уравнений и численный
тод решения их первого приближения.
Исходное уравнение переноса излучения запишем в виде
(Ozisik M.N. et al., 197S), опустив индексы селективности
±ц—±а—?-—-
or r д\х.
-J-+| |у(ц')[у+(ц') + ^(ц')]^\ (9.1)
-1
где Р = а + к; к, а - коэффициенты поглощения и рассеяния,
у(ц') = у(ц',ц) - индикатриса рассеяния; Jem - излучательная
способность элементарного физического объема, равная в услови-

9.2. Метод полумоментов 261
ях ЛТР Jem -к-Jb', Jb - интенсивность излучения абсолютного
черного тела; У* - интенсивность излучения в положительном
Q+ и отрицательном СГ направлениях; а = 0 для плоского слоя
и а = 1 для сферы.
Граничные условия к (9.1) сформулируем в виде,
вующем горячему газовому облаку сферической формы со
бодной границей или плоскому излучающему слою вблизи
дой поверхности с обобщенными граничными условиями:
г = 0, У+(г = 0,ц)
r = R, J-(r = R,ii) = Jb(r = R), (9.2)
где ро - полусферическая направленная отражательная
ность, Jb - интенсивность внешнего по отношению к среде
чения.
При задании конкретного вида функции у(ц,ц')
емся транспортным приближением, когда реальная индикатриса
аппроксимируется изотропным и дельта-рассеянием
где Ц - средний косинус рассеяния, 5(ц'-1) - дельта-функция.
Получить расчетные соотношения можно и с другим видом
функции у(ц'), допускающим разложение в ряд по ц'. Однако
эти соотношения получаются более сложными и не вносят в
шение нового качества.
Применим к уравнению (9.1) интегральный оператор вида
1
Lm= mmd\i, m = 0,1,2,..., , в результате чего придем к беско-
о
нечной системе обыкновенных дифференциальных уравнений
(ц)]} , (9.3)

262Гл. 9. Потоковые методы
где
Система (9.3) незамкнута, и ее можно решить, лишь ограничив
число уравнений /я = 0,1,2,...,//. В этом случае говорят о JV-m
приближении метода полумоментов. Однако в уравнении любого
приближения N обязательно присутствуют полумоментные
рактеристики следующего (N + \)-ro приближения. Чтобы
ключить функции A/tf+i необходимо привлечь какое-либо
нительное условие, связывающее М#+1 со всеми предыдущими
характеристиками. Такое замыкающее условие представим в виде
8Х
л=0
что эквивалентно аппроксимации интенсивности излучения рядом
где С„ - коэффициенты, подлежащие определению; а* (г) -
известные функции координат.
Используя (9.4) в (9.3), можно получить систему уравнений
для определения коэффициентов С„
Г1 Г1 Г1 Г1
с& -l S +...+ ?к на
N.
Оценки, сделанные в работе (Лосев С.А. и др., 1990),
зывают, что N-e приближение метода полумоментов примерно
соответствует по точности 2iV-My приближению метода моментов
(и сферических гармоник). Поэтому для решения задач переноса
теплового излучения можно рекомендовать 1-е приближение
тода полумоментов
dr

92. Метод полумоментов
263
(9.6)
где
Рассмотрим итерационный метод решения уравнений (9.6).
В системе (9.6) перейдем к оптической толщине dx = Cdx и введем
эффективные функции источников
(9.7)
dx
dx
где
Решение данной системы для полумоментных характеристик
имеет вид
xexp[pw(x-T')]dx'-?:exp(pwx)}, /, = 0,1; (9.8)
xexp[pw(x'-x)]dx'-?;exp[pw(x5-x)]}, (9.9)

264 Гл. 9. Потоковые методы
где
+
El =
Отметим, что при а = 1 и г-»0 вследствие изотропности
излучения в центре сферы 2М* = A/q , поэтому слагаемые вида
12Mf - Mq JIг в i^ следует полагать равными нулю.
Алгоритм решения задачи теперь состоит в организации
следовательных итераций между функциями Л/+(х) и А/~(т).
Для рассматриваемых граничных условий вычислительный
цесс целесообразнее начинать с расчета функций А/~(т).
По результатам расчета функций Л/* определяются
ция плотности потока излучения на ось г
?-Mi), (9.10)
а также дивергенция вектора лучистого потока в прямоугольной
декартовой системе координат
()] (9.11)
и в сферической системе координат
)l ^(9.12)

9.2. Метод полумоментов
265
Следует иметь в виду, что введенные указанным образом
полумоментные функции знакопостоянны во всей области
деления
A/j^O, А/,+ ?0, А/о ^0, A/f ?0,
что является важным свойством рассматриваемого потокового
метода, специально используемым при решении задач переноса
селективного теплового излучения (см. главу 13).
Результаты тестовых расчетов переноса излучения методом
полумоментов для неоднородного плоского слоя, имитирующего
ударный слой у поверхности космического аппарата, входящего в
плотные слои атмосферы (см. рис. 5.5), представлены на рис. 9.1 -
9.5. Для сравнения с результатами расчетов по другим методам
граничные условия и коэффициенты поглощения выбраны такими
же, как в п.п. 5.2 и 6.1.
400000
300000
200000
100000
-100000
-
3
; _ JK. -
1 ¦ ¦ i
f * * '
.—i—
.. •" ""
—-—^
¦ ¦it
ш
о—,
10
х, см
Рис. 9.1. Плотность радиационной энергии A, U вДж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенция
весторв плотности потока радиационной энергии C, QR в Вт/см3) в
плоском слое с оптической толщиной т = 1. Решение методом
моментов для температурного распределения рис. 5.5

266
Гл. 9. Потоковые методы
400000
300000
200000
100000
-100000
V
;/
/
/
^—
„--3
;
J
10
х, см
Рис. 9.2. Плотность радиационной энергии A, U вДж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенция
вектора плотности потока радиационной энергии C, QR в Вт/см3) в
плоском слое с оптической толщиной т = 10. Решение методом
лумоментов для температурного распределения рис. S.S
Расчеты переноса излучения проводились для нерассеиваю-
щего и светорассеивающего слоев. При отсутствии рассеяния
лучения распределения радиационных характеристик в слое
ки с погрешностью не более 3% результатам точных расчетов
(п. S.2). При этом время, необходимое для расчета примерно в сто
раз меньше, чем при получении точного решения. Это различие в
основном определяется необходимостью расчета интегро-экспо-
ненциальных функций. Однако, если при точном решении
нения переноса излучения в бесконечном плоском слое
вать предварительную табуляцию интегро-экспоненциальных
функций, то времена расчета становятся сопоставимыми.
Расчетные данные, представленные на рис. 9.3-9.5,
ляют получить представление о влиянии процессов
ния на распределение радиационных характеристик. Общая
номерность заключается в том, что с увеличением коэффициента

9.2. Метод полумоментов
267
рассеяния плотность радиационной энергии в центральных
тях расчетной области повышается, а на границах - снижается.
Систематически снижаются также плотность полного
ного потока и его дивергенция (см. последовательно рис. 9.3-
9.5). Примечательно, что с увеличением коэффициента рассеяния
резко возрастает число итераций решения системы уравнений
(9.7). Указанные числа представлены в подрисуночных подписях.
Сравнивая полученные решения с результатами расчетов по
Pi-приближению метода сферических гармоник для светорассеи-
вающего слоя (см. п. 6.1), можно сделать заключение о близости
получаемых распределений радиационных характеристик (кроме
непосредственной близости от границ).
400000
зооооо
200000
100000
•100000
/
¦ JL..
—
^. ^ т
|т=1, о=0.11
^
N
о гг»
10
х, см
Рис 9.3. Плотность радиационной энергии A, U вДж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенция
вепора плотности потока радиационной энергии C, QK в Вт/см3) в
плоском слое с оптической толщиной т = 1 и коэффициентом
сеяния о = 0.1 см'1. Решение методом полумоментов для
турного распределения рис. 5.5. Число итераций - 8
Однако следует иметь в виду, что численное решение по
Pi-приближению метода сферических гармоник оказывается су-

268
Гл. 9. Потоковые методы
щественно более экономичным (в десятки раз). Это лишний раз
подтверждает эффективность указанного метода для расчета
реноса излучения в сильно рассеивающих средах, когда
ние угловой зависимости интенсивности излучения обусловлено
физическими причинами.
400000
300000
200000
100000
0 г
-100000
3
г--г'
, •*» ^ ^ —
^-—¦ ¦
|т=1,О=1|
\
\
10
х, см
Рис. 9.4. Плотность радиационной энергии A, U вДж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенция
вектора плотности потока радиационной энергии C, QR в Вт/см3) в
плоском слое с оптической толщиной т = 1 и коэффициентом
сеяния а=1см"'. Решение методом м полумоментов для
турного распределения рис. 5.5. Число итераций - 3S
Относительно итерационных методов решения задачи (9.8),
(9.9) следует заметить, что изложенный алгоритм является
лее простым, но, к сожалению, не самым эффективным. С
чением вероятности светорассеяния, т.е. при стремлении альбедо
однократного рассеяния ш = ст/р к единице, расчет по данному
алгоритму становится все более трудоемким. В этом случае
сообразно использовать иные алгоритмы и методы решения
темы уравнений (9.7).

9.2. Метод полумоментов
269
Некоторые методы ускорения сходимости подобных систем
уравнений применительно к задачам физики ядерных реакторов
подробно анализируются в работах (МарчукГ.И., 1961; Марчук
ГИ.идр., 1981).
Хорошо себя зарекомендовали также гибридные методы
расчета, состоящие в использовании комбинации нескольких
тодов. Например, в пространственной области сильного
сеяния используется диффузионное приближение уравнения
диационного переноса.
400000
300000
200000
100000
•100000
\
' 3
:—?¦
i i i i
1 ¦ i i
o=10|
\
10
х, см
Рис 9.5. Плотность радиационной энергии A, U вДж/см3),
ность радиационного теплового потока B, W в Вт/см2) и дивергенция
вестора плотности потока радиационной энергии C, QR в Вт/см3) в
плоском слое с оптической толщиной т = 1 и коэффициентом
сеяния о = 10 см'1. Решение методом полумоментов для
турного распределения рис. 5.5. Число итераций - 28S
Недостатком подобных гибридных методов является
ходимость дополнительной формулировки граничных условий
(фактически - условий стыковки). Тем не менее, это удается
лать не только для комбинации детерминированных методов, на-

270 Гл. 9. Потоковые методы
пример метода полумоментов и Pj-приближения, но также и для
комбинации методов статистического моделирования (методов
Монте-Карло) и детерминированных методов. По всей видимости,
впервые указанные гибридные методы были исследованы в
тах Дж. Хауэлла и его коллег (Howell J.R., 1998), где
ный метод Монте-Карло был объединен с диффузионным
ближением при решении трехмерной задачи о переносе излучения
в сильно рассеивающей среде.
9.3. Итерационные методы решения уравнения переноса
9.3.1. Метод последовательных приближений
Метод последовательных приближений применяется для
решения задач переноса излучения с учетом рассеяния и основан
на представлении искомой интенсивности излучения в виде ряда
Vn(r,Q), (9.13)
л=0
где ш - альбедо однократного рассеяния; Jn - интенсивность
излучения, отвечающая учету л-кратного рассеяния.
Рассмотрим получение системы уравнений метода
вательных приближений на примере задачи о рассеивающем
плоском слое, т.е. для уравнения
ц+у(ТрЦ)(,й)Л(х) +
ОХ I .
Подставив разложение (9.13) в уравнение (9.14) и приравняв
слагаемые в полученном соотношении при одинаковых степенях
ш, получаем
-1

9.3. Итерационные методы решения уравнения переноса 271
Система уравнений (9.15) решается при следующих
ных условиях:
х = 0, ц>0: Jo(O,n) = Jo»
У„@,ц)
х = х//, ц<0: 7()
Л(^»Ц) = О, л = 1,2,... (9.16)
Преимуществом метода последовательных приближений
является то, что здесь удается в явном виде учесть вклад
сивности л-кратного рассеяния. Кроме этого, система (9.15)
держит полностью подобные уравнения по своей структуре, что
облегчает компьютерную реализацию данного метода. Тем не
нее, как и прежде, с увеличением кратности рассеяния сходимость
данного метода ухудшается.
9.3.2. Аналитические итерационные методы
Суть аналитических итерационных методов, типа методов
Унзольда, Плачека, Унзольда-Майне (Чандрасекхар С, 1953;
Kourganoff V., Busbridge I.W., 1963), состоит в подборе
ных функциональных зависимостей для функции источников
лучения (функция первого приближения) и использовании их в
интегральных уравнениях типа уравнения Милна. При удачном
подборе функции первого приближения уже во втором
нии получается удовлетворительное решение.

272 Гл. 9. Потоковые методы
9.3.3. Вариационные методы решения уравнения
переноса излучения
Вариационные методы получили наибольшее развитие в
трофизике и физике ядерных реакторов в середине прошлого века
(Владимиров B.C., 1958, 1961; ДэвисонБ., 1960; МарчукГ.И.,
1961; Смелое В.В., 1978; MarshakR., 1947; PlaczekG., 1946; Kur-
ganoff V. et al., 1963). Главная идея вариационных методов
чается в подборе некоторой (пробной) функции, содержащей ряд
подлежащих определению постоянных и достаточно близкой к
искомому решению. Если такая функция задана и сформулирован
некоторый функционал от невязки (разницы между истинной и
пробной функцией), то из условия минимума этого функционала
удается получить уравнения для определения неизвестных
янных. Как правило, погрешность вариационных методов
шается при удачном выборе пробной функции.
Использование вариационных методов представляется
спективным совместно с широко применяемыми численными
тодами для получения асимптотически точных решений
мерных задач.
9.4. Метод квадромоментов
Этот метод предложен и реализован в работах (Суржиков
СТ., 1988; Surzhikov S.T., 1996), где рассмотрен перенос
ния в двумерной цилиндрической геометрии (рис. 9.6).
Спектральная интенсивность излучения в этом случае
сит от четырех координат Jv - Jv (jc, г, Cl) = Jv(x, r, <p, 0) ив
ловиях ЛТР в нерассеивающей среде удовлетворяет уравнению
(индекс спектральной зависимости опущен)
•) дх
где ц = cosG, у = cos<p, Q, = (шх, шг), шх = ц, шг = уф - ц2 -
правляющие косинусы вектора Л по отношению к радиальной г

9.4. Метод квадромоментов
273
и осевой jc координатам. Относительно плоскости, содержащей
векторы х° и г°, задача является зеркально симметричной, если
интенсивность излучения, падающего извне на поверхность S,
ограничивающую объем, является четной по ф. Это позволяет
ограничиться областью определения по азимутальной координате
¦х=Нс
Рис. 9.6. К формулировке уравнений метода квадромоментов
Суть метода состоит во введении четырех пространственных
зон (рис. 9.7) и применении в каждой из них процедуры
рования уравнения (9.17) с различными весовыми функциями, как
это обычно делается в моментных методах. В каждой из этих
ловых зон вводятся по определению объемные плотности
трального излучения
(9.18)
oVl-YZS
а также проекции плотности спектрального потока на радиальное
направление
^±=±F{J} = 2f-^=fj1Vl-^dn» (919)
и осевое направление
19 Зак. 272

274
Гл. 9. Потоковые методы
-у о
(9.20)
(9.21)
Рис. 9.7. Четыре квадранта расчетной области
В (9.18)-(9.21) использована система индексов {(~=*о, и),
+,-}, фиксирующих угловую зону: (о)-ц^О, (и)-ц<0,
(+) - у ? 0, (-)-у<0. Последовательное применение операторов
б*, Й*, X* к (9.17) дает следующую систему уравнений:
ас
—
= O, (9.24)

9.4. Метод квадромоментов 275
где Ц = 2 Г / f \Г J1 - ц2 dn; (9.25)
(9.26)
i i
yi-y2dyjj±(l-^2^d\i; (9.27)
о о
l
¦¦2JJ±(y = Q)\iyjl-n2d\i; (9.28)
О
E-29)
(9.30)
у > 0, w = 1; у < 0, w = -1; ц > 0, n = 1; ц < 0, n = -1.
Полученная система уравнений может являться исходной
для построения группы расчетных методов. Несмотря на то что
при ее выводе не делалось каких-либо упрощающих
ний, эту систему нельзя считать точным аналогом уравнения
реноса. Точной являлась бы бесконечная система
альных уравнений, получаемых последовательным применением к
уравнению (9.17) операторов вида
1= JoofdQ, * = 0,1,2,...,оо, i = r,x. (9.31)
дп
Ограничение числа дифференциальных уравнений
тельно моментов интенсивности излучения означает, что в
жении интенсивности в ряд по ортонормированным функциям
19*

276 Гл. 9. Потоковые методы
удержано конечное число слагаемых. В полном телесном угле 4л
удобным ортонормированным базисом является система
ских гармоник. Первые два слагаемых такого ряда (что
вует Pi-приближению метода сферических гармоник) с учетом
четности по ф,дают:
j(x,r,y,Q) = c(x,r) + a(x,r)\i + b(x,r)yyJ\-\i2 . (9.32)
Аппроксимация интенсивности излучения полиномом
гональным на половинных отрезках имеет вид
(9.33)
Заметим, что вопрос о правомерности ограничения
ным числом слагаемых разложения интенсивности в ряд по
рическим функциям до настоящего времени остается открытым и
обсуждаемым в специальной литературе. Вместе с тем, из теории
лучистого теплообмена известно, что в большинстве задач вид
задаваемой угловой зависимости J(?2) слабо сказывается на
лучаемых величинах плотностей лучистых потоков и объемной
плотности лучистой энергии. Поэтому для практики решения
дач теплообмена излучением и динамики излучающего газа
проксимация (9.32) считается удовлетворительной. Поскольку
разложение (9.33) определено только на четверти телесного угла,
от его использования можно ожидать большей точности.
Определим дальнейшие пути возможного решения задачи.
Если разложением (9.33) воспользоваться для расчета функций
U±, Wf, W*, Ц, М?, то вместо (9.22)-(9.24) получится
ма уравнений относительно коэффициентов а,Ь,с. Естественно
этот метод назвать методом квадромоментов, так как он имеет
аналогию с моментными методами, но отвечает четверти
го угла.
Разложение типа (9.33) можно использовать для расчета
эффициентов в (9.22), (9.23), предварительно преобразовав их так,
чтобы под дифференциальными операторами появились искомые

9.4. Метод квадромомснтов 277
функции. Если уравнения (9.22), (9.23) решать относительно
функций 0±, то приходим к аналогу метода квазидиффузии
(Гольдин В.Я., 1964). Если уравнения (9.22), (9.23) решать
сительно потоков Wp и W*, то получаются уравнения метода
потоковой релаксации (Суржиков СТ., 1987).
Рассмотрим простейший расчетный случай, когда все
занные методы тождественны (фактически это обобщение метода
Шварцшильда-Шустера на случай 4-х пространственных зон)
r,9,0) = c±(jc,r). (9.34)
С учетом (9.34) уравнение (9.24) приобретает вид
т дгс дс т _+_,-+-,, ,_ -,ч
— + п— с* + 2*е* = 2fc/ft, (9.35)
г or ox r
0±=ж±, W^ = W^=-c±. (9.36)
Граничные условия формулируются для каждого из четырех
направлений. Пусть на внешнюю поверхность цилиндра падает
изотропное излучение интенсивностью /°, тогда
при r = Rc, c~=c~=J°,
при jc = O, c~=c+=J°, (9.37)
при х = Нс, ?-=c+=J°.
На оси симметрии
с+(г = 0) = Г(г = 0), с> = 0) = Г(г = 0). (9.38)
Если внешнее излучение неизотропно, то его необходимо
усреднить.
Заметим, что в приведенной записи уравнение (9.3S)
ет нулевому приближению метода квадромоментов. С учетом
(9.36) его можно записать относительно функций 0± или W^ .
Выполненный в работе (Суржиков СТ., 1987) численный
анализ решений системы уравнений (9.35)-(9.38) на примере
шения задачи о переносе излучения в двумерной цилиндрической

278 Гл. 9. Потоковые методы
области с высокотемпературной излучающей областью
ской формы (постановку задачи см. в п. 6.3) показал на
творительное совпадение с результатами расчетов по
жению метода сферических гармоник. При этом были определены
основные недостатки и преимущества метода квадромоментов. К
первому недостатку следует отнести относительно большую
доемкость этого метода, что вполне очевидно, ибо метод требует,
по крайней мере, четырехкратного прохождения расчетной
ти. Вторым недостатком присущим, очевидно, всем потоковым
методам, применяемым для решения задачи переноса излучения в
нерассеивающих криволинейных объемах, является разрывность
решений на границах областей угловых направлений и
ние немонотонностей в пространственных распределениях
ности радиационной энергии, которые удается исключить лишь
при введении искусственного (численного) сглаживания.
Важным достоинством метода квадромоментов является
возможность введения неразрывных интегральных по спектру
электромагнитного излучения эффективных коэффициентов
глощения, типа интегральных по Чандрасекхару коэффициентов
поглощения, которые позволяют построить эффективный
ный алгоритм решения селективных задач теории радиационного
теплообмена. Наличие существенных недостатков и достоинств
метода квадромоментов диктуют необходимость дальнейшего его
исследования.
В заключение рассмотрения потоковых методов заметим,
что их применение к решению задач переноса излучения в
мах криволинейных геометрий является в настоящее время не до
конца решенной задачей.

Глава 10
СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПЕРЕНОСА
ТЕПЛОВОГО ИЗЛУЧЕНИЯ В НЕОДНОРОДНЫХ
ОБЪЕМАХ СВЕТОРАССЕИВАЮЩИХ ГОРЯЧИХ
ГАЗОВ
В данной главе рассматриваются методы численного расчета
направленных спектроэнергетических радиационных
стик излучения неоднородных светорассеивающих объемов, а
также радиационных тепловых потоков на границах этих объемов.
Под спектроэнергетическими радиационными характеристиками
будем понимать пространственное и спектральное распределения
основных радиационных характеристик.
Наиболее сложные математические модели, описывающие
процессы светорассеяния, составляют значительную часть задач
теплообмена излучением в многокомпонентных многофазных
зовых смесях и небольшую долю от общего числа моделей
ционного переноса в динамике низкотемпературной плазмы. В
самом деле, при относительно низкой температуре среды
(Г < 2000+3000 К), когда еще существуют твердые и жидкие
тицы, процессы взаимодействия излучения с веществом являются
низкоэнергетичными и не оказывают влияния на
скую структуру потока. Решение задач радиационной газовой
намики при этом существенно упрощается. Сначала решается
зодинамическая часть задачи. По найденным полям температуры
и концентраций газа и частиц производится однократный расчет
переноса излучения. Однако решение самой задачи о переносе
теплоты излучением является весьма сложным из-за наличия
торассеяния.

280 Гл. 10. Статистическое моделирование переноса теплового излучения
С ростом температуры среды начинают проявляться
сы взаимодействия излучения и вещества, но доля
ванных и твердых частиц резко падает. Вместе с этим исчезают и
светорассеивающие центры. Среда становится нерассеивающей.
Однако на первый план выходят проблемы взаимного влияния
излучения и динамики среды.
Взаимодействие излучения с веществом может оказаться
заметным при высоких плотностях последнего. Так, например,
скорость разрушения полупрозрачной теплозащиты космических
аппаратов в значительной степени может определяться радиаци-
онно-кондуктивным взаимодействием. Однако здесь имеются
рощающие обстоятельства: во-первых, задача движения
чающей среды является достаточно простой, а во-вторых, как
правило, в задачах теплообмена излучением можно пользоваться
упрощенными моделями светорассеяния.
При высоких температурах в радиационной плазмодинамике
может возникнуть необходимость учета эффектов светорассеяния,
обусловленных другими физическими механизмами, например,
комптоновским рассеянием (Имшенник B.C. и др., 1981; Грынь
В.И., 1981).
В предыдущих главах основное внимание уделялось
дам расчета переноса излучения, основанным на усреднении
ловой зависимости интенсивности излучения, т.е.
ным, в первую очередь, для нахождения таких характеристик
диационного переноса, как: объемной плотности радиационной
энергии, вектора плотности радиационного потока и его
генции. Однако в теории переноса излучения существует другой
весьма важный круг задач - расчет угловой зависимости
сивности излучения и, как частный случай, расчет направленной
излучательной способности горячих газовых объемов.
Методы расчета переноса излучения, ориентированные на
нахождение направленных излучательных характеристик, условно
разделим на три группы.
К первой группе относятся такие методы расчета, которые
позволяют получить точное решение уравнения переноса. Круг
задач, допускающих точное решение, чрезвычайно узок. При этом

10.1. Общие понятия о принципах имитационного моделирования 281
накладываются сильные ограничения на геометрию исследуемой
области, оптические свойства среды и граничные условия.
Ко второй группе относятся приближенные
ванные методы решения уравнения переноса: методы
ских гармоник, дискретных ординат, характеристик.
Третью группу составляют методы статистических
ний или методы Монте-Карло. Среди них выделим
ские методы моделирования процесса переноса излучения и
тистические методы решения интегральных уравнений переноса.
Остановимся на вычислительных моделях прямого
стического моделирования (имитации), нашедших широкое
менение в практике решения задач определения спектроэнергети-
ческих характеристик излучения газовых объемов. Теоретические
основы этого метода даны в работах (Соболь И.М., 1973; Ермаков
СМ. и др., 1982; Зигель Р. и др., 1975; Суржиков СТ., 1992).
10.1. Общие понятия о принципах имитационного
моделирования распространения излучения
в рассеивающей среде
Пусть в рассматриваемую замкнутую область G попадает
поток частиц (фотонов). При этом вопрос о причинах, вызвавших
появление этих частиц в области, пока обсуждать не будем.
смотрим одну из частиц. От точки своего рождения фотон будет
двигаться по прямой до тех пор, пока не пересечет границу
ти (поверхность S) или не столкнется с материальными частицами
вещества. Местоположение точки пересечения прямолинейного
участка траектории с границей может быть определено с
чением аппарата аналитической геометрии. Акт столкновения
тона с элементом вещества является существенно вероятностным
процессом.
Предполагая, что закон распределения длин свободного
пробега известен (эта величина определяется свойствами среды и
длиной волны излучения фотона), можно выбрать случайную
длину пробега. Эту процедуру называют розыгрышем длины
бодного пробега.
18 3ак. 272

282 Гл. 10. Статистическое моделирование переноса теплового излучения
Следующий этап рассмотрения истории движения частицы
состоит в розыгрыше (вероятностном оценивании) типа
вения. При этом определяется дальнейшая судьба частицы. Если
фотон поглощается атомом, молекулой или конденсированной
частицей вещества, то на этом его история заканчивается (в
виях локального термодинамического равновесия). Если фотон
испытывает рассеяние, в результате чего он продолжает движение
в новом направлении (в общем случае с новой энергией), то
цедура рассмотрения истории фотона является аналогичной
смотренной выше.
Важным моментом теории статистического моделирования
физического процесса распространения излучения в веществе
ляется использование расчетных и теоретических данных,
жающих количественную сторону моделируемых явлений. Речь
идет об интерпретации оптических сечений физических процессов
поглощения, испускания и рассеяния, вносящих основной вклад в
процесс распространения излучения.
При решении задачи моделирования здесь имеются два
ти. Первый из них заключается в том, что, основываясь на знании
оптических сечений реальных процессов взаимодействия фотонов
с атомами, молекулами и конденсированными частицами, можно
при каждом акте разыгрывать типы столкновения, не только
разделяя их на поглощение и рассеяние, но и вводя детализацию
по типам поглощения. Вероятность же того или иного типа
глощения определяется известными сечениями процессов и
чеством частиц, с которыми происходит взаимодействие фотонов.
Таким образом, в отличие от детерминированных методов расчета
переноса излучения, оптическим сечениям элементарных
ционных процессов здесь придается смысл вероятностных
теристик, каковыми они и являются по своей природе.
Второй путь состоит во введении некоторых эффективных
характеристик элементарного объема вещества: объемного
фициента поглощения, испускания и рассеяния, а также
ненной по элементарному физическому объему индикатрисы
сеяния. В предыдущих главах обсуждалось, что эти
ты являются макроскопическими характеристиками и присутст-

10.1. Общие понятия о принципах имитационного моделирования 283
вуют в интегро-дифференциальном уравнении переноса
ния. Однако при моделировании траекторий фотонов эти
ны носят также вероятностный характер, т.е. определяют
ность поглощения и рассеяния фотона элементарным объемом
вещества. При розыгрыше типа столкновения с учетом
ентов поглощения и рассеяния не только делается вывод о его
пе (дается ответ на вопрос: есть поглощение или нет), а также
ределяется относительная вероятность процессов поглощения и
рассеяния.
Указанные два способа моделирования типа взаимодействия
фотонов излучения с веществом равноправны не во всех случаях.
При наличии равновесия между термодинамическим состоянием
среды и излучением оба обсуждаемых способа эквивалентны. В
противном случае, вероятность рождения нового фотона в
тате элементарных радиационных процессов в веществе не
кова, что не позволяет использовать второй подход для
ша вероятности поглощения.
Остановимся на вопросах розыгрыша типа рассеяния. Когда
в гетерогенной смеси присутствуют частицы разных размеров,
характер рассеяния фотонов на них существенно различается. Тем
не менее, для того чтобы определить вероятность акта рассеяния,
можно ввести суммарную характеристику рассеяния
ного объема среды, проинтегрировав с некоторой весовой
цией сечения рассеяния всех частиц. Дальнейшим шагом
рования траектории является розыгрыш угла рассеяния или,
гими словами, определение нового направления, в котором фотон
продолжает свой путь. Здесь также можно использовать два
хода.
Первый, наиболее сложный, состоит в дифференциации
процессов рассеяния. Поскольку индикатриса рассеяния
ция, определяющая вероятность реализации произвольного угла
рассеяния) сильно зависит от размеров частиц, то для выполнения
процедуры моделирования надо сначала представить всю
генную смесь в виде совокупности групп частиц с близкими
раметрами. Затем следует разыграть номер группы частиц, на
торых происходит рассеяние, принимая во внимание, что вероят-
18*

284 Гл. 10. Статистическое моделирование переноса теплового излучения
ность рассеяния фотона фиксированной группой определяется
величиной сечения рассеяния частиц с данными размерами. Угол
рассеяния частицами данной группы определяется
щей индикатрисой рассеяния.
Второй способ моделирования углов рассеяния состоит в
определении индикатрисы рассеяния полидисперсного
тарного объема. Определение суммарной индикатрисы рассеяния
полидисперсного объема позволяет моделировать угол рассеяния
фотона без розыгрыша актов столкновения с отдельными
частицами.
История каждой вновь появившейся частицы
ся точно таким же образом. Анализируя большое количество
торий, можно сделать необходимые выводы (с определенной
пенью вероятности) относительно интересующих нас
теристик.
Подчеркнем, что основу применения метода Монте-Карло
составляют допущения об отсутствии взаимодействия фотонов
между собой и о линейности процессов переноса излучения
сительно механизмов взаимодействия квантов энергии с
вом, что позволяет моделировать реальные процессы
нения излучения поведением небольших модельных групп частиц
НО5).
10.2. Исходная информация имитационного
моделирования
В настоящем разделе излагается способ применения
ционного метода Монте-Карло на примере решения задачи
деления силы излучения от конечномерного осесимметричного
объема, расположенного в пространстве произвольным образом.
В такой постановке удается решить большой круг практически
важных задач, в частности о переносе излучения в светорассеи-
вающих объемах плоской, сферической и цилиндрической
метрии. Для решения этой задачи необходимо задать исходную
информацию, которую условно можно подразделить на четыре
группы.

10.2. Исходная информация имитационного моделирования
285
В 1-ю группу входят данные, задающие геометрию
чающей области. Это есть числовые массивы, содержащие
динаты цилиндрических поверхностей, охватывающих
мый объем, и плоскостей, перпендикулярных оси симметрии в
цилиндрической системе координат. На рис. 10.1 показана
пользуемая расчетная сетка и исследуемая область G .
о
Рис. 10.1. Расчетная область
Во 2-ю группу исходных данных входят числовые массивы
свойств среды в узлах расчетной г - z сетки. Здесь задаются
пературные поля газовой и конденсированной фазы,
ты поглощения газа и полидисперсных объемов частиц,
циенты рассеяния полидисперсных элементарных объемов и
ответствующие индикатрисы рассеяния. К этой же группе
ных данных относится шкала длин волн электромагнитного
чения, в которой требуется выполнить расчеты переноса
излучения.
3-ю группу исходных данных составляют массивы угловых
координат, предназначенных для дискретизации множества
правлений, в которых моделируемые фотоны покидают
ную область. Это необходимо для выполнения количественной
регистрации. Таким образом, фотоны «сортируются» по
ным направлениям, а в результате расчета получаются массивы

286 Гл. 10. Статистическое моделирование переноса теплового излучения
чисел фотонов, покинувших область в каждой из выделенных
ловых зон. Углы задаются в системе координат, связанной с
ной нормалью к элементарной площадке, принадлежащей
верхности, охватывающей исследуемый объем.
В 4-ю группу исходных данных входят характеристики
ленного моделирования: число серий фотонов и число фотонов в
каждой серии. Произведение числа серий и числа фотонов в серии
дает полное количество разыгрываемых историй. Введение серий
фотонов объясняется желанием снизить корреляцию данных,
словленную квазислучайным характером чисел, выдаваемых
граммным генератором случайных чисел. Кроме этого, анализ
зультатов расчетов после розыгрыша каждой серии фотонов
зволяет экспериментально установить степень сходимости
зультатов моделирования.
10.3. Расчет случайных чисел, распределенных
по произвольным законам
Для решения задач статистического моделирования
димо иметь генератор случайных чисел у, равномерно
ленных на участке [0,1]. Случайные числа, распределенные по
другим законам, также моделируются при помощи чисел,
мерно распределенных на [0,1]. Поясним, как это делается в
щем виде. Пусть р(х') - плотность вероятности распределения
случайной величины, тогда
F{x) = P{t><x}=)p(x')dx', A0.1)
-00
где F(x) - функция распределения случайной величины (так
зываемая кумулятивная функция), задающая вероятность
ции случайного события на интервале (-оо, х). Выборочное
ние случайной величины t, распределенной по закону с р(х),
ределяется по формуле
у= 1р{х')дх'. A0.2)

10.4. Моделирование изотропного случайного вектора 287
Известны три метода получения случайных чисел:
ный метод, метод датчика случайных чисел и метод
чайных чисел. Наибольшее распространение получил метод
дослучайных чисел, под которыми понимают набор чисел,
ляемых по заданной формуле, и которые могут быть
ны при решении задач статистического моделирования. Среди
этих методов отметим метод Неймана и метод вычетов
ния) (Соболь И.М., 1973). Отметим, что вопросам получения
псевдослучайных чисел посвящена обширная литература
ков СМ. и др., 1982; МарчукГ.И. и др., 1976; Франк-Каменец-
кий А.Д., 1978). Имеются тексты программ (Ермаков СМ. и др.,
1982; Франк-Каменецкий А.Д., 1978). Вместе с этим, следует
тывать, что все современные трансляторы программных языков
включают в себя генераторы псевдослучайных чисел, качество
работы которых вполне удовлетворяют требованиям прикладных
задач теории статистического моделирования.
10.4. Моделирование изотропного случайного вектора
Необходимость в численном моделировании угловых
теристик изотропного случайного вектора возникает при
лении направления движения частицы после акта изотропного
рассеяния или в акте испускания фотона элементарным объемом.
И в том, и в другом случае предполагается, что фотон может
гаться с равной степенью вероятности в любом из направлений
телесного угла 4л. Плотность реализации этого события
вается в виде 1/4я. Произведение плотности вероятности и
мента телесного угла равно р (С2) = sin8d8/4n. Поэтому функция
F(Q) имеет вид:
n
= \ Jdq>Jsin8d8 \/4n. A0.3)
Выбор граничных значений углов поясняется на рис. 10.2.
Отсюда следует, что cos9 равномерно распределен на [-1,1],

288
Гл. 10. Статистическое моделирование переноса теплового излучения
угол ф на отрезке [0,2л], а их моделирование можно производить
по формулам cos9 = 2уе -1, <р = 2яу<|>.
Рис. 10.2. К моделированию изотропного случайного вектора
В процессе численного моделирования необходимо иметь
значения не самих углов q>, а функций coscp и sirup, которые
можно вычислять с использованием программ расчета
метрических функций или моделировать по алгоритму Неймана
(Франк-Каменецкий А. Д., 1978):
1) рассчитываются два случайных числа у\ и уг, равномерно
распределенных на отрезке [0,1];
2) для указанных случайных чисел вычисляется величина
3) если D ? 1, то эта пара чисел отбрасывается и берется новая;
4) если Z)<1,to
у/), siiKp = 2By,-l)y2/Z>.
По вычисленным значениям тригонометрических функций
определяются направляющие косинусы траектории
<вх = sinG coscp, <Bj, = sinGsiiup, <вг = cosG. О 0.4)
Практическими вычислениями установлено, что алгоритм
на оказывается более экономичным.

10.S. Дискретизация исследуемого объема 289
10.5. Дискретизация исследуемого объема
Заданием узлов расчетной сетки фактически производится
дискретизация исследуемого объема на N, зон. В качестве
мера рассмотрим элементарный цилиндр с высотой h = zj+\ - zj ,
j = \,2,...,NJ-l, и ограниченный поверхностями rt и гм,
i -1,2,..., N1 -1, NJ, N1 - число узлов сетки вдоль осей гиг (см.
рис. 10.1).
В любом сечении этого элементарного цилиндра
стью, содержащей в себе ось 0z, получится прямоугольник,
браженный на том же рисунке. Координаты вершин этого
угольника известны, кроме того, в этих точках заданы все
димые свойства среды. Осредненные свойства в элементарном
цилиндре определяются по формуле
) )]. A0.5)
Степень приближенности такого задания свойств
тарных объемов существенно зависит от качества задания
ной сетки.
Важным моментом процедуры моделирования
нения фотонов в среде является способ расчета длины пробега
фотона. Как отмечается в работе (Франк-Каменецкий А.Д., 1978),
на вычисление этой величины при решении реакторных задач
тратится около половины всего расчетного времени.
кость решения этой задачи обусловлена тем, что траектория
тицы прослеживается отдельно в каждом элементарном объеме.
Существуют более экономичные приемы моделирования
рии в неоднородной среде, например, метод максимального
сечения.
Метод максимального сечения основан на том очевидном
положении, что добавление любого количества 5-рассеивателя в
исследуемый объем не изменит процесса распространения
нов E-рассеяние - это рассеяние без изменения направления).
Введем максимальный полный коэффициент ослабления
среды

290 Гл. 10. Статистическое моделирование переноса теплового излучения
P/.max = max {рЛ/}, P,,i = Kg>, + кЛ, + а,, A0.6)
где / - номер элементарного объема, определяемый четырьмя
дексами узлов расчетной сетки; Kgi,Kpj - коэффициенты
емного поглощения газа и частиц; а/ - коэффициент объемного
рассеяния.
Для каждого 1-го элементарного объема помимо истинного
коэффициента ослабления рЛ/ можно ввести коэффициент 5-
рассеяния
Использование характеристик P,,max> P;,/ и ps,/ позволяет
выполнять моделирование распространения фотонов в среде с
ременными свойствами так же, как и в однородной среде. При
этом считается, что при столкновении с вероятностью Ps,//P/,max
происходит 5-рассеяние, а с вероятностью (l-ps,//P/,max ) -
альное взаимодействие. Обоснование такого подхода дано в
тах (Ермаков СМ., Михайлов ГЛ., 1982). Приведем его здесь.
Уравнение для потока моделируемых частиц Ф(г,П)
летворяет интегро-дифференциальному уравнению переноса
лучения
+Ф0(г,П)+ \ф{г,С1')о(г)р{П',П,г)йП', A0.8)
где /?(Q',Q,г) - индикатриса рассеяния. Обратим внимание на
то, что в данной главе для обозначения индикатрисы рассеяния
используется не y(Q',Q,r), а р(С1',С1,г). Это сделано во
жание путаницы, поскольку общепринятым обозначением для
случайного числа является у.
Отметим, что в методах Монте-Карло более естественно
пользовать не интенсивность, а поток частиц, которые связаны
между собой энергией моделируемой частицы.
Запишем тождество
[А.™ - А (г)]ф (г> о) = 1Ф (г>«') [А,— - A W] 5 (о' - о) сю'

10.6. Определение начальных координат траекторий 291
и сложим его с A0.8):
|ф(г,П')о(г)/7(П',П,г)AП'
Отсюда видно, что уравнение A0.9) можно трактовать как
уравнение переноса в некоторой фиктивной среде, для которой
Р/,тах - полный коэффициент ослабления, сг(г) -коэффициент
рассеяния с индикатрисой р(С1',С1, г), и [р/>тах ~Р/ (г)] -
фициент рассеяния без изменения направления.
10.6. Определение начальных координат траекторий
Если на исследуемый объем падает излучение от внешних
источников, то начальные координаты траекторий всех фотонов
принадлежат поверхности, ограничивающей объем. При
рении актов испускания фотонов элементами самого объема,
ординаты соответствующих точек заранее неизвестны. Изложим
один из возможных алгоритмов их нахождения.
Для решения этой задачи требуется назначить число
лируемых фотонов N/, испускаемых во всем объеме, а затем
распределить эти фотоны по всем излучающим элементарным
линдрическим объемам. Число фотонов, излучаемых в каждом
таком объеме, пропорционально отношению энергии, излучаемой
этим объемом, к энергии, теряемой всей областью. Количество
лучистой энергии, теряемой элементарным цилиндрическим
емом в приближении объемного высвечивания, вычисляется
дующим образом:
il-^), A0.10)
где j?[ и Jf( - спектральные интенсивности излучения
лютно черного тела при температурах частиц и газа.
Суммированием величин Я/ по всем / определяется общая
энергия Ну, теряемая областью. Тогда вероятность испускания

292 Гл. 10. Статистическое моделирование переноса теплового излучения
квантов энергии в объеме с номером / можно представить в виде
Р,=Н,/НУ.
Распределение фотонов по излучающим зонам следует
изводить с учетом величин Р/, т.е. число фотонов, испускаемых в
/-й зоне N/j, равно целой части произведения [N/Pi]. Если
суммировать числа N/j по всем /, то, как правило, не получится
суммарное число фотонов N/. Оставшееся число фотонов N}
следует распределить по всем зонам опять с учетом величин Pt.
В работе (Франк-КаменецкиЙ А.Д., 1978) приводится несколько
способов такого распределения. Например, используется
ритм случайной выборки номера зоны: проводится Nj-
мых испытаний, в каждом из которых номер зоны разыгрывается
из условия
После того, как выполнено распределение общего числа
тонов по всем излучающим зонам, следует разыграть точные
ординаты рождения каждой частицы в пределах 1-го объема.
чем, если распределение числа фотонов по излучающим
тарным объемам производится до начала моделирования
рий, то определение координат рождения частиц целесообразно
делать последовательно при моделировании движения каждой
отдельной частицы. В этом случае в памяти ЭВМ необходимо
хранить лишь Ni чисел N/j.
Для вычисления координат рождения фотонов, как и при
распределении их по зонам, можно использовать как
ческую, так и случайную выборки (Франк-Каменецкий А.Д.,
1978). При случайной выборке можно использовать следующие
формулы для координат рождения частиц:
+ У (&-'?), Zm=ZJ+y(zJJ,l-zJ). A0.12)
Определив начальные координаты траектории фотона,
ется задать направляющие косинусы вектора скорости. Предпола-

10.7. Построение прямолинейного участка траектории 293
гая, что в актах испускания нет какого-либо выделенного
ления, для определения направляющих косинусов вектора
правления траектории испущенного фотона можно использовать
способ моделирования изотропного случайного вектора.
10.7. Построение прямолинейного участка траектории
в замкнутой области
Как уже отмечалось, предполагается, что от места своего
рождения фотон движется прямолинейно в заданном направлении
до тех пор, пока не произойдет его столкновение с частицей
ства, или же он не пересечет границу рассматриваемой области.
Рассмотрим способ нахождения величины пробега фотона до его
пересечения с поверхностью ограничивающей области.
В силу специального задания расчетной сетки (в
ваемом случае - цилиндрическая осесимметричная система
динат) можно считать, что фотон движется внутри кругового
линдра, ограниченного двумя плоскостями z = 0 и z = H,
мальными к оси цилиндра. Очевидно, что в замкнутой круговой
цилиндрической области фотон не может пройти расстояние
больше, чем L^^ = V.D2 + Я2 , где D и Н - диаметр и высота
линдра. Фотон может столкнуться с любой из плоскостей или с
цилиндрической поверхностью. Координаты столкновения
деляются с использованием аппарата аналитической геометрии.
Уравнения траектории фотона, цилиндрической поверхности и
плоскостей записываются в виде
A0.13)
A0.14)
D2
' 4
z = 0, z = H, A0.15)
где хс,ус, zc, азх, озу, аз2 - координаты и направляющие косинусы
вектора направления траектории.

294 Гл. 10. Статистическое моделирование переноса теплового излучения
Длина пути фотона до пересечения с цилиндрической
верхностью 1С найдется из A0.13) и A0.14)
lc=tl2=±±Jlf Е = Ь2-4ас, A0.16)
с = х2+у2-~. A0.17)
Но пересечение прямолинейного участка траектории фотона
с цилиндрической поверхностью возможно лишь при выполнении
следующих условий
а Ф 0, 0 ? -Ъ + у/е й laLnyx,
поэтому только положительное значение t\ > 0 соответствует
альному физическому процессу lc-t\-
Решая A0.13) и A0.15) при <вг <0, находим длину пути 1р
до точки пересечения траектории с плоскостью г = 0, а при
<вг > 0 - до точки пересечения траектории фотона с плоскостью
Заслуживает внимания случай <вг = 0 (с вычислительной
точки зрения <вг -> 0). Чтобы избежать аварийных остановок
компьютера при <вг -> 0, целесообразно использовать следующие
условия:
<вг<0, A0.18)
<вг<0. A0.19)
Если соотношения A0.18) и A0.19) не выполняются, то
ресечение траектории фотона с плоскостями невозможно.
10.8. Моделирование длины свободного пробега
Вероятность испытать столкновение в точке / для частицы,
летящей вдоль вектора направления Q от точки 1 = 0, равна
1 - F(l), где F(l) - функция распределения случайной величины
/. Поэтому вероятность столкновения в интервале (I+1+dI) равиа

10.8. Моделирование длины свободного пробега 295
A0.20)
где Р,Д/ характеризует вероятность столкновения на
ном отрезке луча Д/ (по определению коэффициента
ния). Разделив на Д/ и перейдя к пределу при Д/ -> 0, получим
[] A0.21)
Но F(/ = 0) = 0, откуда
) j A0.22)
Учитывая, что р, = const (вследствие использования метода
максимального сечения), получаем окончательно
Процедура моделирования длины свободного пробега
вывается на том, что величина F(/) является случайной и
мерно распределенной на [0,1], т.е. F(/) = y. Из формулы A0.22),
с учетом одинакового распределения у и A - у) получаем
/ = -р,-'1пу. A0.23)
Моделирование пробега связано с получением
ально распределенных случайных чисел, причем прямой расчет
по формуле A0.23) достаточно трудоемок. В связи с этим
ботаны специальные приемы сокращения времени расчетов.
пример, может быть рекомендован алгоритм Вотау-Рафферти,
который состоит в следующем. Вырабатываются уо и yi. Если
У1 <уо, то вырабатывается у 2, если yj+у2 <у<>, то
ся уз и т.д. Как только выполнено условие У| + У2+---+Уя^Уо>
анализируется число п. Если п - четное, то процесс повторяется
снова, начиная с выработки чисел у{> и yj. Если п - нечетное, то
- In (у) = (f -1) + уо, где t - полное число построенных
тельностей. Как утверждается в (Франк-Каменецкий А.Д., 1978),
для получения одного значения In у требуется примерно 4.3
ла у.

296 Гл. 10. Статистическое моделирование переноса теплового излучения
10.9. Розыгрыш столкновений
Если установлено, что фотон испытывает столкновение
внутри среды, т.е. / <{1с,1р ), то необходимо выяснить:
ло ложное или истинное столкновение. В первом случае в
лительной программе следует продолжить моделирование
тории без какого-либо изменения. При этом к счетчику ложных
столкновений следует добавить единицу.
Во втором случае следует разыграть тип этого столкновения:
• если это поглощение, то увеличить счетчик поглощений на
ницу и приступить к моделированию новой траектории фотона;
• если моделируется неравновесное излучение, то имеется
ятность переизлучения поглощенного фотона;
• если это рассеяние, то необходимо определить новое
ние движения и прибавить единицу к счетчику числа рассеяний.
Вопрос о выборе типа столкновения решается следующим
образом. Выше указывалось, что при использовании метода
симального сечения вероятность 5-рассеяния есть рь = Ps/P/.max >
а вероятность реального взаимодействия р5,к=^~Ръ- Поэтому
для моделирования типа столкновения следует проверить
нение условия р&>у, означающего, что произошло 5-рассеяние.
Иначе считается, что произошло истинное столкновение.
Истинное столкновение может быть как поглощением, так и
рассеянием. Генерируя новое случайное число и сравнивая его с
вероятностью рассеяния ps = сг/р4,, делаем вывод относительно
типа столкновения. Если y<ps, то произошло рассеяние, а при
y>ps, или, что одно и то же, у < рк = 1 - ps, считается, что
изошло поглощение.
10.10. Моделирование процессов поглощения
и рассеяния
Пусть в результате взаимодействия фотона с веществом он
поглощается. Если исследование процесса переноса излучения
проводится в предположении о существовании радиационного
равновесия, то поглощение частицы должно сопровождаться эк-

10.10. Моделирование процессов поглощения и рассеяния 297
вивалентным актом испускания частицы с той же энергией (на той
же частоте излучения), что и у поглощенной. Изучая эти явления
на макроскопическом уровне взаимодействия фотона с
тарным объемом вещества можно считать, что среда испустит
квант энергии в произвольном направлении.
Часто термодинамическое состояние среды определяется не
радиационными процессами, а столкновительными. В этом случае
на акте поглощения фотона его история должна заканчиваться,
иначе излучательная способность элементарных объемов не будет
соответствовать их термодинамически равновесному состоянию.
Сложность алгоритма моделирования рассеяния частицы
элементом объема зависит от типа рассеяния. Если рассеяние
тропное, то новое направление движения разыгрывается
ством моделирования изотропного случайного вектора и к
чику числа рассеяний прибавляется единица. Координаты начала
нового отрезка траектории фотона совпадают с координатами
столкновения.
Неизотропное рассеяние моделируется различными
бами. Наиболее простой из них - транспортное приближение,
описан в работе (МарчукГ.И. и др., 1976; Франк-Каменецкий
А.Д., 1978). Этот метод получил широкое распространение в
рии переноса излучения, в особенности в приближенных
тических методах. Суть метода состоит в следующем. Как
ло, рассеяние азимутально симметрично. Тогда коэффициент
дифференциального рассеяния может быть представлен в виде
A0.24)
где р(\х) - индикатриса рассеяния; ц = (С2'П) - косинус
сеяния по широтному углу. Аппроксимируя р(\х) соотношением
/з(ц) = A-Д) + 2Д5(ц-1), т.е. используя транспортное
жение, формулу A0.24) перепишем в виде
4л
где Ц - средний косинус рассеяния.

298 Гл. 10. Статистическое моделирование переноса теплового излучения
Дельта-рассеяние означает просто отсутствие рассеяния.
этому можно сделать важный практический вывод: рассеяние
делируется как изотропное, но с уменьшенным на Цст
коэффициентом
Остановимся на физическом смысле формулы A0.25), для
чего рассмотрим два крайних случая: а) />(ц) = 25(ц-1), при
ц = 1; б) /з(ц) = 1, при ц = 0. Отсюда следует, что если рассеяние
близко к изотропному (случай б), то a, (Q',f2)=a, а если
сеяние происходит в основном «вперед», то as (Q1, Q) <зс а.
Алгоритм моделирования рассеяния при использовании
транспортного приближения следующий:
при p&s = [о - о A - ?)]/<* = Ц > у - 5-рассеяние,
ПРИ P&.s < У ~ реальное рассеяние.
Когда применяется метод максимального сечения, алгоритм
расчета рассеяния в транспортном приближении еще более
щается. В качестве коэффициента суммарного 5-рассеяния
рается величина ре =Р/,тах-[к+A-Д)а] или, по-другому,
р8=Р/,тах~Р/+СУД • Следовательно, учет анизотропности
ния в транспортном приближении можно производить на уровне
моделирования типа столкновения (истинное столкновение или
нет).
Несмотря на кажущуюся простоту этого метода, он не
бавляет от необходимости знания вида функции индикатрисы
рассеяния, которая часто бывает очень сложной. В некоторых
случаях, представляющих практический интерес, приходится
казаться от приближенных методов и моделировать истинную
дикатрису рассеяния.
В общем случае индикатриса рассеяния р(С1',С1)
ется так, что вероятность ухода рассеянного фотона в
нии ft, лежащем в телесном угле с координатами (ф,6),
ваемыми от направления Q, может быть записана в следующем
виде (рис. 10.3):

10.10. Моделирование процессов поглощения и рассеяния
299
j X
Рис. 10.3. Схема рассеяния фотона
<U(ff.Q).
' 4я
Считая распределение по азимутальной координате ф
новероятным и независимым от распределения по широте 6,
лучаем
ф
о
A0.26)
При изотропном рассеянии по широтному углу р (9) = 1, поэтому
l-cos9
Уе="
A0.27)
Если же рассеяние анизотропное, то используется
щий алгоритм. На отрезке [0, л] строится функция
фF) = /j(9)sin6, после чего она аппроксимируется ломаной
сочно-линейной кривой. Очевидно, что аппроксимация должна
быть достаточно аккуратной, чтобы сумма площадей всех
угольников и трапеций была близка к полной площади Az под
истинной кривой ФF). В этом случае можно положить
А(9) = 4qAz . Это и есть уравнение для отыскания 9.

300 Гл. 10. Статистическое моделирование переноса теплового излучения
Пусть по углу 6 индикатриса задана в Nq точках. Тогда
площадь всей фигуры определяется по формуле
В процессе построения суммарной площади Аг
разно определить массив
-l. 00.29)
Тогда последовательность расчета такова:
1) находится число у, для которого Fj > А (9);
2) решается уравнение F* =А (9) - Fj, откуда находится
Независимо от способа моделирования рассеяния, после того
как определены координаты ф и 9, следует перейти от системы
координат, связанной с центром масс системы «фотон - частица
вещества» к лабораторной системе координат. Если в
ной системе координат вектор скорости до рассеяния
ft' = ico} + jo>2 + ^°>3 » а ft = ifi>i + jo>2 + kfi>3 ~ после рассеяния,
тогда
^j , A0.30)
1 — CO3
C03 = СО3Ц -(l -O>22 ) СО8ф 1-^- ,
v ' yl-<B3
где n =

10.11. Регистрация конца историй фотонов 301
10.11. Регистрация конца историй фотонов
В процессе моделирования траекторий фотонов в
щей и рассеивающей средах накапливается большое количество
информации, которая может быть использована для различных
целей. Рассмотрим, какая информация требуется для вычисления
направленной силы излучения и плотностей радиационных
ков. Для этого необходимо знать количество фотонов,
щих поверхность, которая ограничивает объем, а также их
вое распределение на произвольно выбранной элементарной
щадке. Для определения условного количества энергии,
симого одной частицей, необходимо знание общего числа частиц
испускаемых объемом (напомним, что речь идет о моделируемых
квазичастицах), количество актов поглощения и рассеяния,
ших место при имитации движения всех частиц вместе взятых.
Чтобы избежать в дальнейшем неясности в вопросе
дения энергии частиц, определим это понятие подробнее. Исходя
из физического смысла, энергия излучения определяется
турой среды (находящейся в локальном термодинамическом
новесии с излучением) и длиной волны излучения. Несмотря на
то, что при моделировании распространения излучения мы
пользуем термин частица или фотон, физически более обосновано
подразумевать под этим ансамбль невзаимодействующих частиц,
энергия которого определяется не только энергией, переносимой
одной частицей, но и числом этих частиц в ансамбле.
10.12. Регистрация актов поглощения
Эта регистрация состоит в подсчете общего числа
ний. Для этого в программу вводится специальный счетчик,
рый регистрирует каждое поглощение частицы. Существенным
моментом здесь является то, что неважно, в какой зоне
щего объема произошло поглощение.
Число поглощений, которое, если это диктуется физикой
процесса, определяет и число испусканий фотонов в актах
модействия с веществом, вместе с числом исходных частиц и
ставляет общее число фотонов, испущенных объемом.

302 Гл. 10. Статистическое моделирование переноса теплового излучения
10.12.1. Регистрация частиц, покидающих исследуемый объем
через цилиндрическую поверхность
Каждая частица, достигающая поверхности, является
телем информации, необходимой для расчета направленной излу-
чательной способности цилиндрической поверхности или
сти радиационного потока к ней. Регистрируются следующие
данные:
• номер зоны по высоте (вдоль оси z) цилиндрического объема;
• направление полета частицы в системе координат, связанной с
нормалью к элементарной площадке, принадлежащей
ности ограничивающей объем.
По оси z целесообразно использовать шкалу, введенную для
дискретизации всего объема. Если частица имеет координату
ресечения с цилиндрической поверхностью zc a[zj, zj+i], то в
дальнейшем координата zc не используется, а запоминается лишь
номер зоны у, т.е. все частицы, которые покидают у'-ю зону,
ждествляются между собой по значениям осевой координаты.
Аналогично вводится дискретизация угловых координат.
Поскольку исследуемый объем обладает осевой симметрией, то
достаточно ввести два массива дискретных значений широты
9от(ш = 1,2,...,Лге) и азимута %п{п = \,2,...,NX). На рис. 10.4
казаны соответствующие угловые координаты. На этом рисунке
O.s „ - проекция вектора Q на площадку Sn .
Рис. 10.4. Схема регистрации фотонов, покидающих расчетную область

10.12. Регистрация актов поглощения 303
Алгоритм регистрации частиц на цилиндрической
сти состоит в следующем. Для каждой вылетающей частицы
вестны координаты хс, ус, zc, со*, <йу, со2 . По направляющим
синусам вектора скорости частицы рассчитываются значения
синусов углов
= coscpcosp-sirup sinp, cos9 = co2,
где coscp = -=*=, sin(p = -7=4=, A0.31)
Ус
R '
«Г
мшр — ¦
хс
'" R '
2
Элементы массива чисел фотонов в дискретных зонах
деляются при анализе неравенств для каждого вылетающего
фотона
cos9OT < cos9 < cos9OT+,, т = 1,2,..., NQ -1,
cosxn ^cosx<cosxn+i , n = \,2,...,Nx-\,
Zj<,z<zj+X, j = \,2,...,NJ.
Формируются следующие массивы. В первом массиве
стрируются частицы, вектор скорости которых имеет
ную азимутальную угловую координату %, но фиксированный
правляющий косинус coz = cosG. Это позволяет получить силу га-
лучения цилиндра от участка длиной (z;+i-z7) в любом из
данных углов наблюдения 9. Расстояние наблюдения должно
быть много больше диаметра цилиндра.
Под силой излучения понимают интеграл от направленной
излучательной способности поверхности, испускающей
ние, по площади этой поверхности, видимой с большого
ния под заданным углом 9.
Второй массив нужен для регистрации фотонов,
щих с цилиндрической поверхности под заданными углами х и 9.

304 Гл. 10. Статистическое моделирование переноса теплового излучения
Направленная сила излучения, получающаяся при использовании
этого массива чисел, может быть интерпретирована как
ментально замеренная сила излучения объема, т.е. когда
ник излучения находится в непосредственной близости от
верхности.
10.12.2. Регистрация фотонов на плоскостях г = 0 и г-Н
Регистрация фотонов на любой плоскости, нормальной к оси
симметрии, производится одинаково, поэтому рассмотрим лишь
плоскость z = H. В описываемом варианте алгоритма
вания переноса излучения определяется общее количество
нов, покидающих кольцевые площадки с радиусами границ г, и
гм в выделенном направлении. В силу этого оказывается
точным регистрировать фотоны только по угловой координате 6
вектора скорости. Подчеркнем, что это справедливо лишь при
наличии осевой симметрии задачи.
По аналогии с регистрацией на цилиндрической
сти вводится дискретизация углов наблюдения Qm. Точно таким
же образом ищется и номер угловой зоны, соответствующей
сматриваемому вектору скорости.
10.13. Определение спектральной силы излучения
по результатам моделирования
Предположим, что термодинамическое состояние среды
ределяется условием локального термодинамического равновесия.
Тогда энергия одного фотона (ансамбля частиц) определяется из
условия
Зная общее число фотонов, двигающихся в заданном
правлении, можно вычислить спектральную силу излучения. Сила
излучения единичной площадки вычисляется с использованием
теоремы о среднем

10.14. Определение плотностей радиационных потоков 305
Т7 — 7 • (Ю.ЗЗ)
-xn)(cosem-cosem+1)
где % с[х„,Хп+\]> 6*c[em,em+,]; W/(AQ) - число фотонов,
покидающих элемент поверхности площадью А в пределах
ного угла AQ; х„» Хп+и вт> 0m+i ~ угловые координаты,
ляющие телесный угол AQ.
Спектральная интенсивность излучения определяется как
2Nf(An)e,
*-± ^ A0.34)
10.14. Определение плотностей радиационных потоков
Расчет плотностей спектральных потоков излучения к
верхности, ограничивающей исследуемую область, производится
также с использованием величины энергии одной частицы.
точно подсчитать общее количество фотонов NA, достигающих
выделенную площадку на поверхности под любыми углами.
Плотность одностороннего потока излучения найдется из
формулы
NAef
A0.35)
10.15. Особенности имитационного моделирования
в твердых и жидких средах
Изложенные алгоритмы прямого численного моделирования
при незначительной модификации могут применяться для расчета
радиационного теплообмена в твердых и жидких средах, а также
при решении сопряженных задач сложного
тивного и лучисто-кондуктивного) теплообмена, возникающих
при анализе тепловой защиты и различных технологических
процессов.
21 Зак. 272

306
Гл. 10. Статистическое моделирование переноса теплового излучения
При рассмотрении указанных задач необходимо учитывать
следующие особенности:
1) отражение и пропускание излучения поверхностями в случаях,
когда излучение падает на среду с относительным показателем
преломления (и), большим единицы;
2) отражение и пропускание излучения поверхностями в случаях,
когда излучение выходит из среды с п > 1.
Методы Монте-Карло предоставляют большие возможности
по учету оптических свойств границ раздела, частными случаями
которых являются диффузные и гладкие поверхности. Поясним
отмеченные особенности для случая преломления и отражения
плоской волны на гладкой границе раздела двух изотропных сред
(рис. 10.5).
¦ z
Рис. 10.5. Прохождение излучения через границу раздела сред
Рассмотрим неполяризованное излучение. Имитация
ждения фотонов через границу раздела сред I—II состоит в
делении вероятности каждому из моделируемых фотонов
зиться от поверхности или пройти через нее, изменив
чальное направление (преломление плоского фронта волны).
роятность отражения луча 1 отождествляется с коэффициентом
отражения, даваемым формулой Френеля (Борн М. и др., 1973)

10.15. Особенности имитационного моделирования 307
Л = 0.5
1/2
(п2 -1 + cos2qA -
(л -l + cos2^) +l-cos6i
In-1 + cosz QA -cosG,
-1 + cos 9,1 +cosG,
A0.36)
а направление вектора траектории после преломления
ется законом Снелла
A0.37)
sin62 = sin 0i/и .
Отражательная способность неполяризованного света,
дающего на границу раздела изнутри (луч 2), определяется по
формуле
R = 0.5
+ 1
: I I г ? \У2 '
п\х+у\-п +п ц 1
= cosG
A0.38)
При численном моделировании процессов отражения
нов от внутренней границы образца материала могут возникнуть
особенности, связанные с наличием угла полного внутреннего
отражения. Поэтому формулу A0.38) следует применять только
при
что эквивалентно условию положительности подкоренного
жения A0.38). В противном случае, R = 1.
Моделирование отражения фотонов от границы можно вести
по схеме, предложенной в работе (Франк-Каменецкий А.Д., 1978).
21*

308 Гл.10. Статистическое моделирование переноса теплового излучения
Поскольку отражательная способность меняется от 0 до 1, то ее
можно моделировать непосредственно случайным числом у,
номерно распределенным на отрезке [0,1]. Отражательная
собность рассчитывается для каждого фотона, достигшего
верхности, и сравнивается с величиной у. Если R > у, то фотон
пропускается поверхностью, иначе - фотон отражается.
Для фотона, вылетевшего из твердого диэлектрика, угол
лета Gj определяется по формуле
cosGi =[l-«2(l-cos2e2)] 2. A0.39)
Так как падающий, отраженный и преломленный лучи лежат
в одной плоскости, то азимутальный угол вылета равняется
мутальному углу падения.
Наличие угла полного внутреннего отражения необходимо
учитывать при численной имитации поведения фотонов
ного излучения. Если поглощательная способность материала
лика, то фактически никаких дополнительных мер
вать не следует, поскольку фотоны достаточно быстро
ются. Если же поглощательная способность мала, то во избежание
чрезмерных затрат машинного времени требуется использовать
специальные приемы. Например, если решается задача
ния испускательной способности нерассеивающего материала, то
фотоны, претерпевающие полное внутреннее отражение, можно
не моделировать.
В заключение отметим, что при моделировании излучатель-
ной способности материала с п > 1 необходимо учитывать
ношение между интенсивностями излучения абсолютно черного
тела в среде Jb (T) и в вакууме J° {T) = Jb {T)/n2 .
10.16. Оценка достоверности имитации и некоторые
другие алгоритмы статистического моделирования
Все методы Монте-Карло имеют своим преимуществом то,
что допускают оценку статистической ошибки в процессе
лирования. Пусть по результатам N независимых опытов получе-

10.16. Оценка достоверности имитации 309
на цепочка значений случайной величины (случайные
ции) Z,h / = 1,2,...,N. Наша задача состоит в определении не
только наиболее вероятного значения искомой величины %, но и в
получении количественных характеристик качества
ского моделирования.
Приближенное значение искомой величины, определяемое
по конечному числу испытаний, называется ее оценкой и
чается |. Очевидно, что оценка есть также случайная величина.
Наиболее вероятным значением искомой величины % является ее
математическое ожидание, оценка которого дается средним
арифметическим
N I
A0.40)
К оценке | случайной величины % предъявляется ряд
бований: она должна быть состоятельной, несмещенной и
фективной. Состоятельность оценки определяется как ее
ностная сходимость к искомой величине при бесконечном
чении N. Несмещенность оценки означает отсутствие
ческой ошибки, т.е. М[|] = ?. И, наконец, эффективность оценки
определяется условием минимальности ее дисперсии, D[%] = min .
Дисперсия случайной величины ?, определяется по формуле
A0.41)
поэтому ее оценка может быть представлена как
(Ю.42)
1=1
Однако оценка A0.42) хотя и состоятельная, но не является
несмещенной (Вентцель Е.С. и др., 1988). Несмещенная оценка
дисперсии получается при следующей коррекции
ной при больших значениях N):
N v- „^ ,,r iwr»n- i A0.4i)

310 Гл. 10. Статистическое моделирование переноса теплового излучения
Еще раз подчеркнем, что М и D - вероятностные величины.
дежность оценок числовых характеристик М и D позволяет
тановить центральная предельная теорема, которая гласит, что
сумма большого числа N независимых случайных величин имеет
распределение, близкое к нормальному, с математическим
нием М[М] = М и дисперсией D[M] = D[%]/N, а значит, и
ним квадратическим отклонением а[М] = y]D[M] =
Следовательно, вероятность отклонения оценки М[%] от своего
математического ожидания в пределах наперед заданного числа е
приближенно равна
л/-М|<Е} = 2ф(е/а[л/]), A0.44)
где Ф - функция Лапласа.
Рассмотрим оценку достоверности результатов
ния, когда наиболее вероятностные величины оцениваются по
частоте их реализации (Вентцель Е.С. и др., 1988), как это
ся, например, при расчете силы излучения поверхности. Пусть из
N опытов событие А, состоящее в вылете фотона в заданном
правлении, наступает в п случаях. Тогда частота события А
деляется по формуле р* = n/N. Так как опыты независимы,
чайная величина п распределена по биномиальному закону с
раметрами N и р (р - вероятность события А). Ее
ское ожидание равно Np, а дисперсия - Np A - р) .
Остается выяснить степень близости величин р* и р . Для
этого представим п в виде суммы случайных величин 8,
л = ?5,, A0.45)
/=1
где 8/ = 1, если событие А произошло, и 8, = 0 в противном
чае. Тогда, в соответствии с центральной предельной теоремой,
случайная величина п распределена нормально с M = pN и
o = -sjNp(\-p). Но величина р* есть линейная функция от п,
поэтому

10.1 б. Оценка достоверности имитации 311
Приближенно положив р = р* и задав произвольное число
е, получим искомую количественную характеристику
A0.47)
Более подробно с этими и другими оценками случайных
личин можно познакомиться в работах по приложениям теории
вероятностей и статистическому анализу, например (Вентцель
Е.С. и др., 1988; Ермаков СМ. и др., 1982; Соболь И.М., 1973).
Изложенный выше алгоритм расчета излучательной
ности светорассеивающих объемов является простейшим. Его
применение оправдано наглядностью и эффективностью
ния больших объемов информации в одном расчете. Однако он
обладает и серьезными недостатками, которые не позволяют
сматривать его как универсальный. Для примера достаточно
вести задачу нахождения мало-углового рассеяния направленного
пучка света, падающего на светорассеивающий слой (Домбров-
скийЛ.А. и др., 1990). Использование конечной величины
ного угла при регистрации вылетающих из объема фотонов
водит к очень большой погрешности в той угловой зоне, которой
будут принадлежать фотоны нерассеянного излучения. А
шение размеров этой угловой зоны приведет к потере точности
из-за того, что все меньшее число фотонов будут в нее попадать.
При решении задач, связанных с поиском узконаправленных
потоков излучения, а также задач определения энергии,
щаемой в объемах малых размеров (по сравнению с
мой областью), расчетом прохождения излучения через слои
очень больших оптических толщин и т.п., использование
женных алгоритмов без модификации является
образным.
Альтернативные алгоритмы статистического моделирования
процессов переноса излучения изложены в работах (Ермаков СМ.
и др., 1982; МарчукГ.И. и др., 1976; Мельниченко А.С и др.,
1977; Соболь И.М., 1973), поэтому здесь отметим лишь их
венные стороны.

312 Гл.10. Статистическое моделирование переноса теплового излучения
Собственно один из таких алгоритмов - метод
го сечения, уже был рассмотрен выше. Основное его
во состоит в том, что он позволяет избежать многократного
ния уравнений A0.13)—A0.15) в пределах каждой из
ранственных зон. Поскольку геометрический расчетный блок,
реализующий решение указанных уравнений, является самым
трудоемким в программе, то применение метода максимального
сечения дает экономию по времени расчета в десятки раз.
Метод максимального сечения не эффективен, по крайней
мере, в двух случаях. Во-первых, когда моделируемый объем
держит участки с сильно различающимися свойствами, и
ние максимального сечения является чрезмерной оценкой
ских свойств с реально малыми сечениями поглощения. Во-
вторых, при имитации переноса излучения в спектральных
зонах, содержащих атомные или молекулярные линии. Специфика
линейчатого спектра состоит в том, что пропускание всего
ка физического пути до столкновения фотона с частицей среды не
является аддитивной функцией пропускания отдельных его
ков. В указанных расчетных случаях более эффективным может
оказаться способ прямого моделирования траекторий фотонов
внутри каждой из пространственных зон.
Теоретической предпосылкой математически строгого
лиза методов статистического моделирования процессов переноса
является установление соответствия между двумя фактами. С
ной стороны, уравнение переноса излучения может быть
ставлено в виде интегрального уравнения Фретгольма 2-го рода, а
его решение представлено в виде ряда Неймана (Ермаков СМ. и
др., 1982). С другой стороны, по своему физическому смыслу
процесс блуждания фотонов по светорассеивающей,
щей и излучающей среде имеет своим математическим
зом однородные цепи Маркова, главной особенностью которых
является независимость вероятности перехода моделируемой
личины из одного состояния в другое от номера этого состояния.
В теории методов Монте-Карло разработаны способы
ния интегральных уравнений посредством моделирования цепей
Маркова. Так что процедура имитации движения фотона в среде

10.16. Оценка достоверности имитации 313
всегда может быть поставлена в прямое соответствие процедуре
решения интегрального уравнения переноса. Введение любой
дификации в алгоритм моделирования может анализироваться на
примере соответствующего изменения ядра интегрального
нения и следствий по сходимости ряда Неймана, к которым это
изменение приведет. Примером этому может служить
ние метода максимального сечения.
Введение модификаций в алгоритмы имитации всегда
водит к тому, что моделируется уже не реальный, а некоторый
фиктивный процесс (часто эти методы называют
ными). Задача теории при этом состоит в поиске наиболее
мального фиктивного процесса и в доказательстве сходимости его
результатов к истинным результатам. Среди наиболее развитых
модифицирующих алгоритмов выделим весовые методы и
кальные оценки. Если в этот перечень включить рассмотренный
выше алгоритм имитации, то по способу регистрации конца
екторий фотонов его следует отнести к методам нелокальных
нок (методы интегральной выборки).
Суть весового метода состоит в том, что вместо
ния имитации траектории фотона (при его поглощении или
те из расчетной области) ему приписывается некоторый вес,
чающий вероятности продолжать движение внутри среды, и
цесс имитации продолжается. В работе (Соболь И.М., 1973)
ложено интерпретировать весовой метод следующим наглядным
способом. Пусть в начальной точке траектории элементарным
объемом среды испущен не один фотон, а пакет, состоящий из
большого числа Wo. Тогда при столкновении фотона (пакета
тонов) с частицей среды поглощается kWq/$ фотонов, a oWq/$ -
рассеивается. Значит, следующий отрезок траектории проходят
уже W\ = oWq/$ фотонов и т.д. Таким образом, при каждом
столкновении нет необходимости разыгрывать вероятность
глощения, а следует лишь изменить его вес (количество фотонов в
пакете). Процесс моделирования можно закончить, когда вес
тона станет меньше наперед заданного числа, обусловленного
решаемой задачей. Отмечается, что дисперсия результатов
занного весового метода не хуже дисперсии результатов прямого
20 Зак. 272

314 Гл. 10. Статистическое моделирование переноса теплового излучения
имитационного моделирования. Оптимизация весовых методов
рассматривается в работах (Михайлов Г.А., 1974,1987).
Своеобразной разновидностью весовых методов являются:
метод подобных траекторий (зависимых испытаний), когда
зультаты одной серии моделирования применяются к нескольким
геометрически подобным задачам, а также метод аналитического
интегрирования части случайных переменных. Последний метод с
успехом используется при решении задач теплообмена
ем в полубесконечных объемах: бесконечный цилиндр
ется конечным цилиндром с зеркальными плоскостями z = 0 и
z = H, а бесконечный плоский слой - конечным цилиндром с
зеркальной цилиндрической границей.
При решении ряда задач весьма полезными могут оказаться
методы аналитического интегрирования (при разделении фотонов
на испытавшие и не испытавшие столкновения), а также метод
локальной выборки. Метод локальной выборки, применяемый для
нахождения направленной излучательной способности, состоит в
оценке вероятности для фотона вылететь из объема в заданном
направлении после каждого акта рассеяния. Очевидно, что этот
метод может использоваться совместно с другими весовыми
тодами. Кроме перечисленных методов, обратим внимание на
боту (Золотухин В.Г., Усиков Д.А., 1979), в которой изложена
рия возмущений применительно к методам имитационного
лирования, позволяющая путем модификации стандартных
ритмов учитывать эффекты, дающие относительно малый вклад в
итоговое решение.
В заключение рассмотрения особенностей статистического
моделирования переноса излучения в излучающих, поглощающих
и рассеивающих средах отметим, что во многих работах,
щенных аналогичным вопросам (Марчук Г.И. и др., 1976; Поля-
ченкоА.А., 1987; Франк-Каменецкий А.Д., 1978; Хисамутдинов
А.И. и др., 198S), уделяется внимание проблемам организации
вычислительного процесса и создания комплексов программ.

Глава 11
МЕТОДЫ УЧЕТА СПЕКТРАЛЬНОЙ ЗАВИСИМОСТИ
КОЭФФИЦИЕНТОВ ПОГЛОЩЕНИЯ В ТЕОРИИ
ТЕПЛООБМЕНА ИЗЛУЧЕНИЕМ
Интегрирование по частоте является одной из наиболее
сложных задач в проблеме интегрирования уравнения переноса
из-за сильной зависимости оптических свойств от частоты
чения. Развитие методов интегрирования уравнения переноса
лучения по спектру непосредственно связано с двумя факторами:
совершенствованием моделей и методов расчета спектральных
оптических свойств (создания так называемых спектральных
тических моделей) и увеличением производительности
ров.
Разнообразие спектральных оптических моделей порождает
большое число способов учета спектральной зависимости
фициентов и функций, входящих в уравнение переноса излучения.
Систематизация оптических моделей дана в следующем разделе.
Заметим, что спектральная зависимость коэффициентов и
функций далее будет обозначаться индексом со - волнового числа
излучения. Как отмечалось в главе 1, между единицами измерения
спектральной зависимости существуют взаимно однозначное
ответствие, поэтому в принципе нет разницы в том, какую
менную использовать. Тем не менее, такая запись часто
ляется более предпочтительной, поскольку в этом случае
странственные и частотные переменные имеют схожие
сти, (см и см'1), а местоположение спектральных линий
ния нагретых газов определяется простой разностью табличных
значений энергий квантовых состояний. Немаловажное значение
имеет также сложившаяся в литературе по теплообмену
ем традиция.
20*

31 б Гл. 11. Учет спектральной зависимости коэффициентов поглощения
11.1. Классификация спектральных оптических моделей
При решении задач радиационного и сложного теплообмена
в газах и низкотемпературной плазме всегда приходится
зовать те или иные модели переноса теплового излучения,
ными элементами которых являются модели оптических свойств
среды и радиационного переноса. Для того чтобы создать модель
оптических свойств смесей газов и низкотемпературной плазмы
сложного химического состава необходимо иметь возможность
определять состав смеси в каждой точке исследуемого объема,
установить закон распределения частиц по возбужденным
тическим состояниям (сформулировать термодинамическую
дель среды), принять во внимание многообразие элементарных
радиационных процессов, протекающих с участием каждой из
частиц смеси и определить вклад каждого из этих процессов в
суммарное поглощение или испускание данного элементарного
физического объема в выделенном спектральном диапазоне.
Столь большое разнообразие задач делает проблему построения
оптических моделей нагретых газов и низкотемпературной
мы сложной многофакторной задачей.
В настоящее время в мире особое внимание уделяется
блеме компьютерного построения оптических моделей смесей
газов и плазмы, предназначенных для решения задач сложного
теплообмена, и основанных на использовании квантово-механи-
ческих и квазиклассических моделей элементарных
ных процессов, учитываемых в таких моделях. Очевидно, что
здесь кроется основное противоречие обсуждаемой проблемы. С
одной стороны, расчетные модели должны быть универсальными
и теоретически обоснованными для того, чтобы можно было
давать оптические модели любой сложности для произвольных
смесей газов и плазмы. С другой стороны, подробность описания
спектральных оптических свойств должна быть адекватной
шаемой задаче радиационного и сложного теплообмена, где не
всегда требуется высокое спектральное разрешение.
Как уже отмечалось, основа теории и практики создания
^пектральных оптических моделей для радиационной газодина-

11.1. Классификация спектральных оптических моделей 317
мики была заложена более 40 лет назад (Armstrong B.H., et al.,
1961; Авилова И.В. и др., 1970; Каменщиков В.А. и др., 1971). Эти
модели широко используются в научных исследованиях (в первую
очередь в аэрофизике) до настоящего времени. Вместе с этим, в
последнее десятилетие наблюдается повышение интереса к
числительным технологиям создания оптических моделей сред в
связи с интенсивным развитием персональных ЭВМ (Романов
Г.С. и др., 1993; Суржиков СТ., 1992; ParkCh., 1990). В
щее время наблюдается качественный скачок в способах
ки обширной информации, что всегда являлось критическим для
обсуждаемой проблемы. Специалисты ведущих научных групп
мира в этой области знаний сходятся во мнении, что
ми проблемами сегодняшнего дня являются верификация и
мизация используемых вычислительных моделей элементарных
радиационных процессов, высококвалифицированная экспертная
оценка исходной спектроскопической информации, а также
тематизация компьютерных моделей, число которых быстро
личивается с каждым годом (Суржиков СТ., 2004 (а)).
Среди радиационных моделей простейшими являются
ближения оптически тонкой и оптически толстой сред. Однако
даже в этих случаях необходимо иметь в распоряжении
гральные по Планку или Росселанду коэффициенты поглощения,
что для смесей газов произвольного химического состава является
весьма трудоемкой задачей.
Если приближения оптически тонкой и оптически толстой
сред использовать нельзя, что бывает в большинстве случае*
представляющих практический интерес для теории сложного теп*»
лообмена, необходимо создавать адекватные исследуемому
нию оптические модели среды и соответствующие модели
носа теплового излучения. Разнообразие решаемых на практике
задач определяет разнообразие моделей, которые можно
лировать.
При построении компьютерных оптических моделей теории
радиационного и сложного теплообмена используются
щие основные понятия.

318 Гл. 11. Учет спектральной зависимости коэффициентов поглощения
Оптической моделью среды называется совокупность
тральных, квазиспектральных, групповых и (или)
ных моделей спектральной зависимости коэффициента
ния km (T,ф) (или коэффициента испускания), представленных в
графической, табличной, аналитической форме или в виде
ютерной программы, позволяющей получить требуемое число по
вводимым параметрам со, Т, <р. Здесь со - волновое число
лучения (используются также длина волны излучения X и частота
излучения v); T - температура; <р - набор параметров,
ляющих химический состав смеси газов (плотность или давление
при исходном элементном составе и температуре, набор
траций химических компонентов). При построении радиационных
моделей неравновесных сред под температурой Т следует
мать набор эффективных температур, а в набор параметров <р
гут входить заселенности отдельных энергетических состояний
атомных и молекулярных частиц.
Спектральная модель коэффициента поглощения -
ция, построенная с учетом непрерывной и линейчатой структуры
спектра без каких-либо усредняющих процедур. Часто эту модель
называют синтетическим или полинейчатым (line-by-line)
тром коэффициента поглощения. Пример спектральной модели
показан на рис. 11.1.
Групповая модель ?дшG\ф) - совокупность значений
эффициентов поглощения, усредненных в пределах спектральных
диапазонов (спектральных групп) Аю, где указанные функции
считаются независимыми от волнового числа. На рис. 11.2 показан
пример групповой модели коэффициентов поглощения смеси
зов, составляющих атмосферу Марса. В данном случае
ние спектральных коэффициентов поглощения производилось в
пределах 37 спектральных групп (Суржиков СТ., 2004 (в)).
При любом графическом или табличном представлении
спектральной модели всегда используется групповая модель или
дается процедура интерполяции по волновому числу между
выми значениями. В практике решения задач радиационного
реноса, как правило, используются групповые модели,
ные на квазиспектральных моделях.

11.1. Классификация спектральных оптических моделей 319
10"
50000 100000
Волновое число, 1/см
150000
7> = 10000К
р = 0
Ро=<
С
N
О
Е"
О2
N2
с2
NO
СО,
CN
СО
С+
N+
О+
OJ
Щ
NO+
СО+
100Е + 01ата
).168Е-01кг/м3
0.26357Е + 00
0.29532Е-01
0.60935Е + 00
0.47630Е-01
0.15934Е-04
0.4750Ш-05
0.29461Е-04
0.12040Е-04
0.19539Е-07
0.17257Е-04
0.22535Е-02
0.42263Е-01
0.35859Е-03
0.48974Е-05
0.12489Е-05
0.39070Е-07
0.56213Е-05
0.58285Е-04
Рис. 11.1. Спектральный коэффициент поглощения смеси газов СО2 (95.37%) и
N2 D.63%) при температуре 10000 К и давлении 1 атм. Указан объемный состав
7> = 10000К
50000 100000
Волновое число, 1/см
150000
Ро=О.
С
N
О
Б"
О2
N2
с2
N0
СО2
CN
СО
С+
N+
О+
о2
Щ
NO+
СО+
168Е-01кг/м3
0.26357Е+00
0.29532Е-01
0.60935Е + 00
0.47630Е-01
0.15934Е-04
0.47501Е-05
0.29461Е-04
0.12040Е-04
0.19539Е-07
0.17257Е-04
0.22535Е-02
0.42263E-0I
0.35859Е-03
0.48974Е-02
0.12489Е-05
0.39070Е-07
0.56213Е-05
0.58285Е-04
Рис 11.2. 37-ми групповой коэффициент поглощения смеси газов СО2 (95.37%)
и N2 D.63%) при температуре 10000 К и давлении 1 атм. Указан объемный
состав

320
Гл.11. Учет спектральной зависимости коэффициентов поглощения
Квазиспектральная модель - это такая модель, при
нии которой использовалась та или иная процедура усреднения по
тонкой (линейчатой) структуре спектра. Например, коэффициент
поглощения в электронных спектрах двухатомных молекул
но усредняют по вращательной структуре (рис. 11.3; здесь полный
спектральный диапазон ДП = 10000 + 30000 см, а диапазон
реднения Лоо = 50 см~').
15000 20000 25000
Волновое число, 1/см
Рис. 11.3. Спектральный коэффициент поглощения при разных
рах, усредненный по вращательной структуре. Молекула Q, переход
d3Tlg - а2Пи (система Свана)
Для сравнения на рис. 11.4 представлена вращательная
структура спектра поглощения узкого спектрального участка. В
этом случае полный спектральный диапазон ДП = 20100+ 20200
см, а диапазон усреднения Да> = 0.01см~'. Хорошо видно, что
при усреднении исчезает осцилляторная структура спектра на
масштабах, характерных для поперечных размеров вращательных

11.1. Классификация спектральных оптических моделей 321
линий, но зависимость от волнового числа на масштабах,
терных для колебательных полос спектра, остается.
20100
20125
201S0
Волновое число, 1/см
20175
Рис. 11.4. Вращательный спектр коэффициента поглощения при Т= 10000 К.
Молекула Сг, переход d3U - агТ\и (система Свана)
Очевидно, что шаг усреднения Асо в квазинепрерывной
дели должен заметно превосходить характерное значение
ширины линии у~0.01-«-0.1см~', что в задачах радиационной
зовой динамики обычно выполняется с большим запасом, так как
при числе участков усреднения от 2-10 (простейшая групповая
модель) до -1000 (многогрупповая модель) в полном
ном диапазоне АС2 = 1000* 250000 см средний размер
тральной группы составляет ~200 +10000 см.
Еще один пример квазиспектральной модели коэффициента
поглощения в инфракрасной области для высокотемпературных
паров Н2О показан на рис. 11.5.
Комбинированная оптическая модель - это модель
того поглощения (атомного или молекулярного спектра) на фоне

322
Гл.11. Учет спектральной зависимости коэффициентов поглощения
непрерывного или усредненного спектра (как правило, атомные
линии на фоне групповой модели). Спектральный коэффициент
поглощения, представленный на рис. 11.1, фактически показывает
комбинированную оптическую модель, поскольку спектр
тельных линий здесь не разрешен, и атомные линии показаны на
фоне квазинепрерывного спектра.
3 10
10°
10'
1-1
10"
,-2
10'
.-J
10'
.-7
1
- мЛ АЛ
——— T-SOO К
•"•"¦¦¦¦""» Т'вОО К
——— Т'ЮООК
T-UOOK
Т'2000К
——— Т«00 К
| V v \j
\ v x
Г
iiliiiiliitil L-—i—J—
1 1 1 t I I
2000 4000 6000 8000
Волновое число, 1/см
10000
Рис. 11.5. Усредненный по вращательной структуре коэффициент
щения Н2О при давлении 1 атм
Все перечисленные типы оптических моделей одинаково
формулируются как в отношении спектральных коэффициентов
поглощения, так и испускания. Связь между этими
тами проще всего устанавливается при локальном
ческом равновесии.
При построении спектральных оптических моделей среды
(коэффициентов поглощения и испускания) для неравновесных
условий в целом можно использовать аналогичную классифика-

11.1. Классификация спектральных ошических моделей 323
цию, однако следует иметь в виду, что неотъемлемой составной
частью таких моделей является кинетическая модель заселенно-
стей возбужденных состояний атомных и молекулярных частиц.
Проблемы, связанные с созданием оптических моделей
весных сред, обсуждаются в работе (Биберман Л.М. и др., 1982).
Среди универсальных компьютерных реализаций оптических
делей неравновесных сред можно отметить программу Ч. Парка
(Park Ch., 1990) NEQAIR.
При решении задач лучистого переноса проблема
ния оптической модели среды является лишь промежуточным
этапом. Далее эту модель необходимо использовать при решении
уравнения переноса с целью определения требуемых
ных характеристик (интенсивности излучения, плотностей
стых потоков и их дивергенций, излучательных и поглощатель-
ных способностей объемов и т.п.). При этом не всякая оптическая
модель является приемлемой или реализуемой, что вызывает
обходимость создания радиационной модели среды.
Радиационная модель среды - это совокупность оптической
модели среды и модели радиационного переноса, позволяющая
оптимальным образом решить задачу нахождения требуемых
диационных характеристик. Практическая трудность проблемы
создания радиационной модели среды состоит в том, что
можно формально сочетать любую оптическую модель с любым
методом расчета переноса излучения. Приходится согласовывать
эти модели со значительной вероятностью их модификации.
Наиболее простым способом компьютерного построения
радиационных моделей сред в настоящее время является алгоритм
пробных решений. Основу этого алгоритма составляет
тельная система построения оптических моделей сред
ная с программными модулями, реализующими различные
ды расчета переноса теплового излучения.
С использованием оптической модели можно рассчитать
тегральные характеристики радиационного переноса, которые
широко используются в задачах теплообмена излучением и
диационной газовой динамики. Среди них особое место занимают
следующие интегральные характеристики:

324 Гл. 11. Учет спектральной зависимости коэффициентов поглощения
1) среднепланковский коэффициент поглощения
«/>=<•, .— . 01-1)
где Jb ш - спектральная функция Планка;
2) среднеросселандовский коэффициент поглощения
3) среднеросселандовская длина свободного пробега фотонов
s=^fc~aF ; ( 3)
4) интегральная излучательная способность
0ет=4краТ4; A1.4)
5) коэффициент радиационной теплопроводности
XR=~5T\ kr=±. A1.5)
Используя аналогичные формулы, можно рассчитать
ветствующие групповые функции, например, групповые
планковский и среднеросселандовский коэффициенты
щения:
JKaJbt(ad(o JK-J-^-dw
кРЬ 7Z кЛД Т7 \110>
Вывод приведенных коэффициентов дан в следующем
деле.

11.2. Срсднеинтсгральные коэффициенты поглощения 325
11.2. Среднеинтегральные коэффициенты поглощения
В п. 11.1 было определено, что среднеинтегральные
циенты поглощения получаются при интегрировании
ентов поглощения по спектру с некоторыми весовыми
ми, выбор которых и определяет тип коэффициента. Наибольшее
распространение получили два среднеинтегральных
та. Если в качестве весовой функции взять интенсивность
ния абсолютно черного тела JbtW (T)tto получается среднеплан-
ковский коэффициент A1.1).
Среднеросселандовский коэффициент определяется по
муле A1.2). Среднепланковский и среднеросселандовский
фициенты поглощения в отдельных спектральных диапазонах
ределяются по формулам A1.6).
Если рассматривать квазинепрерывный спектр
та поглощения, то численный расчет коэффициентов кР и кл не
представляет трудностей, поскольку величины к<» « кдш/, где
A1.7)
являются постоянными в пределах участков усреднения
где Nun - число групп в модели; с - постоянная Стефана-
Больцмана.
При взятии интегралов вида A1.8), A1.9) удобно
вать квадратурные формулы Гаусса с небольшим числом узлов
(Бронштейн И.Н. и др., 1986).
Не представляет также особого труда и расчет среднеплан-
ковских коэффициентов с учетом линейчатой структуры. В этом

326 Гл.11. Учет спектральной зависимости коэффициентов поглощения
случае для квазинепрерывной составляющей спектра
ся формула A1.8), а интегрирование по линейчатой составляющей
сводится к суммированию интегральных коэффициентов
щения в линиях, так как спектральные размеры линий
зуемые их полуширинами) во много раз меньше размеров
ков усреднения Аш.
Сложнее обстоит дело с расчетом среднеросселандовских
коэффициентов поглощения в линейчатом спектре. Этот вопрос
был детально проанализирован в работах (Биберман Л.М., Ла-
гарьков А.Н., 1964, 1967), где предложено применение
ческих моделей. Однако следует иметь в виду, что все
ские модели имеют уровень погрешности ~30%, что не всегда
является удовлетворительным для расчета среднеинтегральных
коэффициентов.
Третий тип средних коэффициентов - средние по Чандра-
секхару, имеют в качестве весовой функции спектральную
сивность излучения Уш
*c=Jf ' • (НЛО)
На идее введения средних по Чандрасекхару основано
сколько высокоэффективных методов ускорения процедуры
ленного решения задачи переноса селективного излучения (Ан-
фимовН.А. и др., 1968; Гольдин В.Я., 1964; Горский В.В. и др.,
1982; Немчинов И.В., 1970). Поскольку интенсивность излучения
зависит от направления, то коэффициент кс также может
сеть от направления. Чтобы избежать этого, спектральную
сивность излучения усредняют по направлениям. Тип усреднения
зависит от используемого метода, поэтому можно определить
большое многообразие средних коэффициентов типа A1.10).
Рассмотрим физический смысл среднепланковского и сред-
неросселандовского коэффициентов поглощения. Как уже
чалось, среднепланковский и среднеросселандовский
енты характеризуют перенос лучистой энергии соответственно в
оптически тонких (k^L^I, L -характерный размер) и оптиче-

11.2. Среднеинтегральные коэффициенты поглощения 327
ски толстых (кш? »1) средах. Воспользуемся уравнением
носа селективного излучения без учета светорассеяния для
тральной интенсивности излучения Ja вдоль некоторого
ления ?
^ (ПИ)
и проинтегрируем его по волновому числу в диапазоне Лео
— J Jad(u = JK<n7i<ndco- Jic^d© =
Лю Дш Дш
= 1СЛДю J Ko^dco, A1.12)
где а - постоянная Стефана-Больцмана. Отсюда видно, что
вое слагаемое в A1.12), пропорциональное К/>>Дю, соответствует
энергии, которая излучается элементарным физическим объемом
в спектральном диапазоне Дш. Аналогично заданием величины
кР определяется энергия, излучаемая в полной спектральной
области.
С целью выяснения физического смысла среднеросселандов-
ского коэффициента необходимо рассмотреть выражение для
плотности спектрального лучистого потока в оптически толстой
среде. Воспользуемся соотношением для плотности
го потока в приближении плоского слоя (S.S4)
о
-2nfjbt<a(x')E2(x'-xo)dT'. A1.13)
При получении A1.13) пренебрегалось излучением,
щим на границы слоя при s = 0 и s = L. Разлагая функцию
ка в ряд в окрестности тш и удерживая только слагаемые первого
порядка по (тш - т'), получаем

328 Гл.11. Учет спектральной зависимости коэффициентов поглощения
A1.14)
Отсюда получается, что лучистый поток в спектральной
ласти Аш равен
Аналогично определяется лучистый поток в полной
тральной области. Таким образом, лучистый тепловой поток в
тически толстой среде описывается законом Фурье с
том теплопроводности
а величина LR = к^ характеризует расстояние эффективной
редачи теплоты посредством излучения. Эта величина называется
среднеросселандовской длиной свободного пробега фотонов.

Глава 12
МЕТОДЫ ИНТЕГРИРОВАНИЯ УРАВНЕНИЯ
ПЕРЕНОСА ПО ЧАСТОТЕ ЭЛЕКТРОМАГНИТНОГО
ИЗЛУЧЕНИЯ
Обзор спектральных оптических моделей коэффициентов
поглощения нагретых газов и низкотемпературной плазмы,
полненный в предыдущем разделе, позволяет сделать три
чески важных вывода:
1) спектральный коэффициент поглощения является очень
сильной функцией термодинамических параметров среды и
нового числа излучения;
2) в условиях локального термодинамического равновесия
спектральный коэффициент поглощения ка(р,Т) может быть
представлен в виде электронных таблиц;
3)в условиях отсутствия локального термодинамического
равновесия значения спектрального коэффициента поглощения
должны рассчитываться в каждой точке пространства с учетом
моделей физико-химической кинетики.
Далее будем полагать, что тем или иным способом
тральный коэффициент поглощения и испускания рассчитан.
смотрим способы интегрирования уравнения переноса излучения
по спектру с учетом сделанного предположения.
12.1. Обзор методов интегрирования уравнения переноса
. по частоте в задачах теплообмена излучением
и радиационной газовой динамики
Прямым способом учета селективности оптических
ристик является использование так называемых групповых (или

330 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
ступенчатых) моделей, в которых групповой коэффициент
глощения находится осреднением спектрального коэффициента.
Если количество спектральных групп становится настолько
шим (порядка ~106), что удается корректно описать контуры
атомных или вращательных линий атомных и молекулярных
понент нагретого газа, то вводится специальное наименование
такой модели - полинейчатая или line-by-line модель. Указанные
модели можно считать точными в том смысле, что если имеется
сколь угодно точная спектральная оптическая модель (задан
соб расчета, имеется электронная база данных и т.п.), то
рование уравнения переноса излучения по спектру производится
со сколь угодно малой погрешностью.
Простейшей групповой моделью является модель «серой»
среды (БайШи-и, 1968; ОцисикМ.Н., 1976). Решение большого
числа задач теплообмена излучением в аэрофизических
ниях (Андерсон Дж.Д., 1968, (а, б, в), 1969; Белоцерковский О.М.,
БиберманЛ.М. и др., 1969; Биберман Л.М., Бронин С.Я., Лагарь-
ков А.Н., 1972) показали удовлетворительную точность расчетов
по малогрупповым моделям. Оказалось, что часто достаточно
учесть хотя бы две энергетические группы фотонов. В
пенчатой модели Андерсона (Андерсон Дж.Д., 1968, (а, б, в), 1969)
коэффициент поглощения выражался через среднепланковский
коэффициент поглощения. Некоторый предварительный итог
следований по применению различных моделей в задачах
ционной газовой динамики был подведен в работе (Бронин С.Я.,
Брыкин М.В., 1977). В этой работе были сопоставлены результаты
расчетов радиационных потоков к поверхности затупленного тела
при его входе в плотные слои атмосферы с гиперзвуковой
стью. В качестве опорных значений брались результаты работ
(БиберманЛ.М., БронинС.Я., ЛагарьковА.Н., 1972;
ский О.М., Биберман Л.М., Бронин С.Я. и др., 1969). В работе
лоцерковский О.М., Биберман Л.М., Бронин С.Я. и др., 1969)
тывались сильные атомные линии. Отмечается, что модель
го» газа не только с самого начала исключает возможность
чения спектрального распределения, но дает также неверные
тегральные лучистые потоки.

12.1. Обзор методов интегрирования уравнения переноса по частоте 331
В работе (БронинС.Я., БрыкинМ.В., 1977) анализируется
также двухступенчатая модель Андерсона (Андерсон Дж.Д., 1968,
(а)), шести ступенчатая модель Чина (Чин Ж., 1969), восьми
пенчатая модель Олстеда (ОлстэдВ., 1971). Основные результаты
этого анализа сводятся к тому, что перенос излучения в
рывном спектре (включающем усредненное молекулярное
щение) удовлетворительно описывается ступенчатыми моделями
с числом ступеней с фиксированными границами от 2 до 8.
В более поздних работах, где этот вопрос анализировался с
точки зрения поиска оптимальных моделей (Суржиков СТ.,
1992), было установлено, что групповая модель получается более
экономичной, если рассматривать ее как некий функционал
шаемой задачи, т.е. оптимальные групповые модели должны
даваться для отдельных классов задач. Так, решение задачи о
прерывном оптическом разряде в воздухе атмосферного давления
показало слабую зависимость уровня температуры в плазме от
внешних условий. Такой консерватизм позволил подобрать путем
численных экспериментов весьма экономичную трехступенчатую
модель коэффициента поглощения. Численное исследование ра-
диационно-конвективного теплообмена при дозвуковом
нии поверхности низкотемпературной воздушной плазмой
шилось также подбором экономичной трехступенчатой модели.
Однако границы спектральных диапазонов в этой модели
сколько отличались от предыдущей. Расчет лучистого
на в окрестности точки торможения возвращаемого на Землю
космического аппарата проводился при давлениях, близких к
мосферному. Здесь использовалась семиступенчатая модель
эффициента поглощения. И, наконец, работа над построением
логрупповой модели, обеспечивающей удовлетворительный
вень точности при решении аналогичной задачи в широком
пазоне температур и давлений, привела к оптимальной 37-
групповой модели (Суржиков СТ., 2004 (в)).
Вывод о том, что для каждой решаемой задачи существует
своя оптимальная модель спектрального коэффициента
ния, представляется очевидным. Однако важно то, что
мость той или иной модели определяется не только разумным

332 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
способом осреднения сечений радиационных процессов, но также
типичным распределением поля функции источников в изучаемом
объеме среды (в условиях ЛТР - равновесной планковской
сивности) и характером конечных результатов, для получения
торых решается задача. Допустимость использования
повых спектральных моделей в задачах, перечисленных выше,
легко объясняется тем, что там рассматривалась воздушная
ма при температурах 2000+20000 К в диапазоне давлений
0.01 -4-50 атм. Характерные размеры излучающих объемов
лись от 0.1 до 10 см. Малогрупповые модели использовались либо
для нахождения плотности интегрального лучистого потока к
верхности тела, либо для расчета дивергенции вектора
ного лучистого потока в объеме, занимаемом плазмой.
мая точность результатов оказывалась достаточной. Напротив,
расчеты спектрального излучения, сопровождающего полет
каемого аппарата на участке торможения в атмосфере планеты
Венера (Анфимов Н.А., Демьянов Ю.А., Заверняев Ю.А. и др.,
1981; Surzhikov S.T., GorelovV.A., KireevA.Yu., 2003) или
мости ударных волн (Немчинов И.В., Светцов В.В., Шувалов В.В.,
1977), потребовали использования соответственно 55-, 100- и 456-
групповых моделей. Попытки применения здесь малогрупповых
моделей оказались безуспешными.
При обсуждении проблем построения оптимальных
тральных моделей следует иметь ввиду, что при нахождении
мосогласованных распределений полей температуры и
онных функций приходится пользоваться итерационными
ленными методами. Это значит, что решение уравнения переноса
в фиксированных спектральных участках проводится
но. Здесь весьма плодотворным оказался подход, при котором
тегрирование уравнения переноса по частоте выполняется не на
каждой итерации, а по мере необходимости, которая диктуется
ходом итерационного процесса. При этом расчет переноса
чения в фиксированном спектральном диапазоне может
няться одним из методов усреднения по пространству,
вавшихся в предыдущих главах.

12.1. Обзор методов интегрирования уравнения переноса по частоте 333
По-видимому, впервые такие способы решения задачи были
применены в работах (Анфимов Н.А., ШариВ.П., 1968; Голь-
дин В.Я., 1964; Гольдин В.Я., Четверушкин Б.Н., 1970, 1972;
чинов B.D., 1970). Уже в первоначальном виде эти подходы
зались приспособленными к учету атомных линий. Так, в работе
(Немчинов И.В., Светцов В.В., Шувалов В.В., 1977) выполнен
расчет интенсивно излучающих ударных волн в воздухе с учетом
наиболее полной на то время оптической модели (Авилова И.В. и
др., 1970), в том числе атомных линий. Дальнейшее развитие и
использование метода Немчинова представлено в работах
гельсон В.И. и др., 1974; МалявинаТ.Б., 1973; СветцовВ.В., 1980).
Квазидиффузионный метод Гольдина также получил свое
тие в работах (Волчинская М.И. и др., 1983; Гольдин В.Я.,
рев В.А., 1985; Гольдин В.Я., Кудинова Г.А., 1976; Репина Г.Е. и
др., 1979; Филиппычев Ю.С. и др., 1976). Модификация
тельного алгоритма Анфимова и Шари, выполненная в работе
(Горский В.В. и др., 1982), позволила не только улучшить
во итерационного процесса, но и построить достаточно простой
расчетный алгоритм учета атомных линий в явном виде. В этой
работе применен метод полумоментов для расчета осредненных
по пространству характеристик излучения и статистическая
дель спектра атомных линий для интегрирования по частоте.
В методах (Гольдин В.Я., Кудинова Г.А., 1976; Кривцов
В.М., 1968, 1974 (а, б); Кривцов В.М., Наумова И.Н. и др., 1975;
Шмыглевский Ю.Д., 1963, 1973, 1976, 1977) предусматривается
специальное представление функций, входящих в уравнение
реноса излучения. В моментном методе (Шмыглевский Ю.Д.,
1976) спектральная интенсивность излучения и спектральный
эффициент поглощения разлагаются в ряд по ортогональным
линомам от частоты. Использование обычной процедуры
ния моментных уравнений, т.е. умножение исходного уравнения
на v"(и = 0,1,2,...) с последующим интегрированием по частоте,
позволяет получить систему обыкновенных дифференциальных
уравнений относительно неизвестных коэффициентов в
нии функций по ортогональным полиномам. Применение этого
метода к расчету переноса излучения в непрерывном и линейча-

334 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
том спектрах требует специального подбора наиболее удобных
комбинаций функций, разлагаемых в ортогональные ряды.
В подходе (Кривцов В.М., 1974) предполагается возможным
представление функции спектрального коэффициента поглощения
в виде ряда, члены которого являются произведением функции от
частоты на функцию от температуры и давления. Здесь также
дится система ортогональных полиномов для аппроксимации
спектральной интенсивности излучения.
Была разработана серия методов, в которых выполняется
предварительное интегрирование по частоте с использованием
некоторых опорных распределений температуры (Головнев И.Ф.,
Замураев В.П. и др., 1984; Карасев А.Б., Кондранин Т.В.,
минский И.Н., 1979; Кондранин Т.В., Кузьминский И.Н., 1981;
Овсянников В.М., 1983; Севастьяненко В.Г., 1979). Среди
ных работ выделим (Головнев И.Ф., Замураев В.П. и др., 1984),
где представлены обширные данные для конкретных расчетов
реноса излучения в водороде, аргоне, воздухе и углекислом газе.
В работе (Овсянников В.М., 1983) выполнен подробный анализ
многих из упоминавшихся методов и приведено сравнение их
фективности.
Весьма эффективным оказался метод, предложенный в
те (Бронин С.Я., Лагарьков А.Н., 1970). В дальнейшем были
дены более простые расчетные соотношения, которые позволили
улучшить его экономичность (Бронин С.Я., БрыкинМ.В., 1977).
Основное содержание этого подхода заключается в
ном учете наиболее сильных атомных линий ударного профиля.
Использование предположения о малости изменения ударной
луширины на расстояниях пробега фотонов, равных обратной
личине коэффициента поглощения в центре линии, позволяет
полнить аналитическое интегрирование по частоте. Получаются
удобные расчетные соотношения для интегральных лучистых
токов и их дивергенции в плоскопараллельной и цилиидрической
геометрии. С использованием этого метода получены расчетные
данные по величинам лучистых потоков в высокотемпературных
ударных слоях (Биберман Л.М., Бронин С.Я., Лагарьков А.Н.,
1972).

12.1. Обзор методов интегрирования уравнения переноса по частоте 335
При расчетах переноса излучения в дуговых разрядах
менялся также подход (Онуфриев А.Т., Севастьяненко В.Г., 1966).
В этой работе предложен групповой способ построения
тральных моделей, учитывающих реабсорбируемые атомные
нии. Использовался как точный, так и диффузионный способ
сания переноса излучения. К наиболее плодотворным
ям методов группового интегрирования и введения специального
представления функции коэффициента поглощения следует
сти работы (Гольдин В.Я., Дегтярев В.А., 1985; Можейко СВ. и
др., 1992; Цветкова И.Л. и др., 1989; Шильков Е.В., 1991).
Выше, приступая к анализу работ, посвященных расчету
реноса селективного излучения, была введена их первичная
сификация по типу осреднения уравнения переноса:
венному или частотному. Когда речь идет об учете
ных линий, возникает еще проблема интегрирования уравнения
переноса вдоль неоднородной трассы распространения излучения.
С физической точки зрения трудность здесь состоит в том, что
вдоль выделенного в пространстве луча контуры линии могут
сильно изменятся. Поглощение (излучение) в узкой центральной
части линии может сменяться поглощением (излучением) в ее
леких крыльях. Возможно также смещение центра линии по
тоте. В таких случаях задачи интегрирования по пространству и
по частоте становятся взаимосвязанными. Подходы осреднения по
угловым переменным, изложенные в предыдущих главах, могут
оказаться неприемлемыми.
Анализируя методы расчета теплообмена излучением,
циально ориентированные на учет спектральных линий, будем
предполагать наличие в среде локального термодинамического
равновесия и считать известными характеристики атомных линий:
силу (интегральный коэффициент поглощения) и
ширину.
Простейшим примером учета атомных линий в расчетах
плообмена излучением является использование приближения
тически тонкого слоя (см. п. 5.1). Представим спектральный
эффициент поглощения в виде суммы

336 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
кш=4 + <, A2.1)
где Кщ и к? - коэффициенты поглощения в непрерывном
тре и в атомных линиях соответственно. Приближение оптически
тонкого слоя для спектрального диапазона Дш можно
вать, если для любой частоты излучения из диапазона Аю
няется условие
L
x<0{L)=JKa(x')dx'<s:\, УюеДю, A2.2)
о
где L - характерный линейный размер рассматриваемого объема.
В этом случае интегральная удельная мощность излучения
определяется формулой
о
A2.3)
Вычисление интеграла с детальным учетом спектральной
зависимости кш - является трудоемкой, но вполне решаемой
дачей. Такие расчеты выполнены, например, для равновесной
душной плазмы в работах (Авилова И.В. и др., 1970;
ков В.А. и др., 1971; КобзевГА., 1983, (а, б); КобзевГ.А.,
ный В.А., 1984, (а, б)). Часто с достаточной степенью точности
удается избежать полинейчатого интегрирования. Когда в
ных пределах линии функция Планка изменяется незначительно,
ее можно вынести за пределы интеграла, а последний заменить
величиной интегрального поглощения в линии
00
Q = 4n\jb<a*
о '=1

12.1. Обзор методов интегрирования уравнения переноса по частоте 337
где at - интегральный коэффициент поглощения i-й линии; Jb ю
- спектральная функция излучения абсолютно черного тела с
новым числом©,, соответствующим i-й атомной линии; N^ -
число атомных линий.
Именно этот прием позволяет считать приближение
ски тонкой среды наиболее простым с точки зрения учета
ных линий.
В другом крайнем случае - в приближении оптически
стой среды - должно выполняться условие
тшA)»1, УюеДю. A2.5)
Введение коэффициента лучистой теплопроводности
ляет достаточно просто учесть лучистый теплообмен в среде.
нако расчет среднего свободного пробега уже не допускает
щения аналогично случаю оптически тонкой среды для атомных
линий. Влияние спектральных линий на коэффициент лучистой
теплопроводности изучено в работах (Биберман Л.М., Лагарь-
ков А.Н., 1964, 1967). На примере атомных линий водорода
зано, что, пренебрегая ими, можно завысить средний пробег
чения на порядок. Для учета вращательной структуры
ного спектра при расчетах среднего пробега в указанных работах
предлагается использовать модель Эльзассера равностоящих
ний и статистическую модель (см. главу 13).
Таким образом, индивидуальный учет спектральных линий в
расчетах переноса излучения приводит к необходимости
вательно решать следующие задачи интегрирования: по частоте,
вдоль луча и по направлениям. Причем, в отличие от расчетов
реноса излучения в непрерывном спектре, далеко не любые
бинации методов интегрирования можно использовать.
Прежде чем приступить к анализу методов интегрирования
уравнения переноса по частоте излучения отметим, что
дительность компьютеров, используемых в настоящее время для
решения практически важных задач теории переноса излучения,
позволяет использовать для этих целей полинейчатые {line-by-line)
методы. Однако приближенные методы интегрирования по часто-
23 Зак. 272

338 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
те излучения остаются существенно более эффективными, в
бенности в тех случаях, когда решаются задачи сложного (радиа-
ционно-кондуктивного и радиационно-конвективного)
мена. Имеется также еще одна причина, сдерживающая широкое
применение полинейчатых методов. С увеличением подробности
описания спектральных оптических свойств повышенные
вания предъявляются к точности предсказания этих оптических
свойств, что является не менее сложной задачей из области
товой физики и химии.
12.2. Модели разделения переменных интегрирования
Эти модели объединяет допущение о возможности
ния функциональной зависимости спектральных коэффициентов
поглощения от частоты и пространственных переменных с целью
упрощения процедуры интегрирования. В различных вариациях
моделей разделения переменных предполагается также
мость разложения в ряд по ортогональным полиномам функции
частоты излучения. Это, в свою очередь, допускает применение
моментной процедуры, когда умножение уравнения переноса
лучения на специально подобранную функцию частоты с
дующим его интегрированием по частоте, приводит к заметному
упрощению проблемы селективности излучения.
12.2.1. Приближение Ми л на-Эддингтона
В модели разделения переменных (модель
тона) предполагается допустимость следующего представления
спектрального коэффициента поглощения
Kv=F(v)-SG\j7), A2.6)
где. F(v) - функция спектральной зависимости при некоторых
фиксированных температуре и давлении; S(T, p) - функция
пературы и давления в низкотемпературной плазме.
На основе этого приближения разработана целая серия
четных методов (Гольдин В.Я. и др., 1970,1972).

12.2. Модели разделения переменных интегрирования 339
12.2.2. Модель разделяющихся переменных
в коэффициенте поглощения
Модель предложена и исследована в работе (Гольдин В.Я. и
др., 1970).
Предполагается, что функциональная зависимость
трального коэффициента поглощения от частоты и
ческих параметров среды (( Т, р ), (Т, р ) и т.п.) допускает
ние переменных, т.е. спектральный коэффициент поглощения
жет быть представлен в виде
Тогда уравнение переноса излучения в плоском одномерном
случае нерассеивающей среды формулируется в виде
с граничными условиями
* = 0, ц>0:
х = Н, ц<0:
A2.9)
Умножая A2.8) на /2 (©) и интегрируя это уравнение по
волновому числу в совокупности тех спектральных диапазонов
Дюг, где
1
получаем
Л»)
A2.10)
A2.11)
-max
с граничными условиями
23*
Л*)}'

340 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
2*0: I{xo,z) =
Люх
^-r,« dm, A2.13)
I со I
где /= J/2(Q)Ow(x,n)dQ). A2.14)
Дт,
Особенностью данного метода разделения переменных
ется то, что при такой формулировке удается от трех независимых
переменных (х,оа,\х) перейти к двум переменным (x,z), что
метно упрощает проблему интегрирования. По найденной
фицированной интенсивности / интегральная плотность потока
излучения рассчитывается по формуле
+ ПИХ-
Дю)
W= j zldz. A2.15)
l
-max-
Л»)
12.2.3. Методы разделения переменных Шмыглевского
Основная идея метода, предложенного в работе (Шмыглев-
ский Ю.Д., 1973), состоит в применении моментной процедуры к
уравнению переноса излучением, в котором функциональная
висимость интенсивности от спектра излучения представлена в
виде ряда по ортогональным полиномам. В итоге применения
ментной процедуры (последовательное умножение уравнения на
v", п = 0,1,2,...) получается бесконечная система обыкновенных
дифференциальных уравнений первого порядка относительно
эффициентов указанного разложения и не содержащих частотной
зависимости. Метод применяется раздельно для учета спектра
прерывного излучения и линейчатого спектра (Шмыглев-
скийЮ.Д., 1969, 1977).

12.2. Модели разделения переменных интегрирования 341
12.2.4. Моментный метод, использующий в качестве
независимой переменной коэффициент поглощения
Идейной основой метода является использование для
рирования уравнения переноса по частоте понятия интеграла
бега. Метод предложен и подробно изложен в работах (Кривцов
В.М., 1974,1976).
Интегрирование по Лебегу дает основание построить
тивный метод расчета переноса селективного излучения,
вающий большое число спектральных линий. Если при
вании многогруппового (или line-by-line) метода расчетная сетка
вводится по шкале частот, при интегрировании по которой и
ходятся интегральные функции, то в случае лебеговского
рирования расчетная сетка вводится по шкале коэффициентов
глощения. Для реализации такого интегрирования удобно
ставить зависимость спектрального коэффициента поглощения в
виде
<ЛР'Т) = ЦъП^{р,Т)- 02.16)
Такая форма представления коэффициента поглощения
видным образом сопоставляется табличной форме задания
трального коэффициента поглощения, когда для каждого
рованного значения давления pt и температуры 7} дается
тральная зависимость коэффициента поглощения кУл (ph Tj).
В данном моментом методе также используется
ление спектральной зависимости интенсивности излучения в виде
ряда по ортогональным полиномам Лежандра.
12.2.5. Методы лебегова усреднения
Группа методов лебегова усреднения развита в работах
(МожейкоСВ. и др., 1992; ЦветковаИЛ. и др., 1989; Шиль-
ков А.В., 1991). Подробное описание этих методов представлено в
статье (Аристова Б.Н., Гольдин В.Я., 2002).

342 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
12.3. Групповые модели
12.3.1. Основные типы групповых моделей
Под групповой (ступенчатой) моделью коэффициента
глощения понимается такая зависимость коэффициента
ния от частоты, когда весь спектральный диапазон разбивается на
конечное число участков, в пределах каждого из которых
водится усреднение коэффициента поглощения. Внутри участков
усреднения коэффициент поглощения принимается равным
ему среднему значению и не зависит от частоты. Или, в случае
малогрупповых спектральных моделей, когда в пределах одной
спектральной группы коэффициент поглощения изменяется очень
сильно (на порядок величин), среднее значение определяется
средством интегрирования коэффициента поглощения по спектру
с последующим делением полученной величины на величину
ответствующего спектрального диапазона. Такое приближение
оказывается чрезвычайно удобным и широко используется при
расчетах переноса селективного излучения. Количество участков
спектра, в которых усредняют коэффициент поглощения,
ляется решаемой задачей. В задачах теплообмена излучением
зывается достаточным спектральную область теплового излучения
(в дальнейшем эту область будем называть полной спектральной
областью) разбить на небольшое число участков -10-20. В
дачах, связанных со спектральной диагностикой газовых потоков
и учетом тонких радиационно-газодинамических эффектов,
ходится вводить сотни и тысячи участков усреднения для того,
чтобы достаточно подробно описать спектр. Примером
групповых моделей коэффициента поглощения
турного воздуха служат табличные и графические данные
лова И.В. и др., 1970; Каменщиков В.А. и др., 1971;
ков СТ., 2004 (в)).
В литературе до сих пор нет общепринятого определения
понятия групповой модели. Часто групповая модель спектра (в
нашем определении) называется ступенчатой моделью или
лью «частокола» (с некоторыми вариациями: двух-, трех- и т.д.

12.3. Групповые модели 343
ступенчатые модели, модель «обобщенного частокола» и т.п.).
Используемое здесь понятие групповой модели усреднения
чает в себя все многообразие указанных моделей. Специфические
отличия одной модели от другой, путем указания количества
энергетических групп, в которых выполняется усреднение, для
определения групповой модели является столь же естественным,
как и для ступенчатой модели или модели частокола. В то же
мое время, понятие групповой модели является более физичным,
поскольку подразумевает усреднение свойств среды в пределах
заданной энергетической группы квантов электромагнитного
лучения.
Как уже отмечалось, простейшей групповой моделью
ется модель «серой» среды. В модели «серой» среды принимается,
что коэффициент поглощения и рассеяния, а так же индикатриса
рассеяния не зависят от частоты излучения
к.(г) = к(г), аф(г) = а(г), ув(г,П',П) = у(г,П',П). A2.17)
В этой модели уравнение переноса излучения в
нии локального термодинамического равновесия формулируется
относительно интегральной интенсивности излучения
.18)
ds
или без учета рассеяния
^''в^кЛ.-ПЬкЛЫ A2 19)
&
гдеУE,й)= |У0)E,Й)Aш.
До
Интегральные объемная плотность излучения и плотность
потока излучения определяются по интегральной интенсивности
?/(г) = - |у(г,Й)(Ю, W(r)=
4я

344 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
В задачах теплообмена излучением в горячих газах и в
котемпературной плазме в подавляющем большинстве случаев
нельзя использовать модель «серой» среды. Поэтому при
зовании группового приближения обычно применяется
щий алгоритм.
1. Задается спектральный диапазон [G>min»<°maxL в котором
будут проводиться расчеты переноса излучения. При
нии процессов переноса теплового излучения в газах и плазме
гретых до температур не более ~ 20000 К полная спектральная
область обычно полагается равной a>min =1000 см,
Ютах =500000 СМ'1.
2. Указанный спектральный диапазон разбивается на
ное число Ng спектральных интервалов [a>g,a>g+i], g = \,2,...,Ng
- число энергетических групп квантов электромагнитного
чения.
3. В пределах каждой спектральной группы находятся
ние коэффициенты поглощения и рассеяния, а также индикатриса
рассеяния:
K()d A220)
у,(г,П',П) = ~- Jye(r,n\n)<to, A2.22)
где Aa>g=oog+1-a>g; g = l,2 Ng .
4. Уравнение переноса интегрируется в пределах каждой
спектральной группы относительно интегральной групповой
интенсивности:
в()в() A2.23)
4я

12.3. Групповые модели 345
где Jg(r,Cl)= J Jm(r,Cl)dm; A2.24)
Jbgir)= f Ло.(г)<1о>; A2.25)
Дш«
A2.26)
Граничные условия аналогичным образом преобразуются от
спектральных к групповым.
5. Интегральная плотность потока излучения и плотность
лучистой энергии рассчитываются по формулам
Их
•¦ у d \ Jg {r,\l)\ld\l, A2.27)
g=l 4я
N.
A2.28)
Заметим, что при решении задач радиационной газо- и плаз-
модинамики, вместо функции источников собственного
ния (в уравнении A2.23)) в форме
более удобно использовать следующий вид этой функции:
Kp>g(r)Jb(r), A2.29)
J ка>(г)Л(Дг)<1<0
где кЛж(г)-^_; , A2.30)
о
pg - среднеппанковскии групповой коэффициент поглощения.
22 Зак. 272

346 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
Использование функции источников собственного
ния в форме A2.29) целесообразно при правильном выборе
ниц полного спектрального диапазона [G>mjn,G>max]> когда с
данной степенью точности выполняется условие
ш = ?1_ . A2.32)
л
"rain «
В этом случае уравнение переноса, записанное относительно
интегральной групповой интенсивности имеет следующий вид
A2.33)
Как уже отмечалось, в групповых моделях усреднение по
спектру производится по формуле
..
"д., -^- / *»¦ (.34)
Однако часто при построении многогрупповой модели нет
необходимости проводить интегрирование по спектру.
ется достаточным рассчитать коэффициент поглощения в любой
точке, принадлежащей интервалу. Такой подход основан на том,
что в пределах узкого спектрального диапазона коэффициент
глощения в непрерывном спектре меняется незначительно, а для
систем молекулярных полос используются сечения, усредненные
по вращательной структуре. Исключение здесь составляют
ные линии, для учета которых приходится разрабатывать
альные вычислительные модели.
. Сложность построения оптических групповых моделей
тра, в которых учитываются атомные линии, состоит в том, что
перенос излучения в атомных линиях на спектральных
зонах, превосходящих их характерные ширины, нельзя описать
локальными функциями поглощения и испускания. Поэтому соз-

12.3. Групповые модели 347
даются либо приближенные модели переноса излучения,
тивно учитывающие линии, либо учет атомных линий
дится на фоне групповых моделей непрерывного спектра.
вимся на втором подходе.
Квазинепрерывный спектр (включающий сечения
ных полос двухатомных молекул) и спектр атомных линий
ставляются в виде двух аддитивных составляющих. Групповая
модель квазинепрерывного спектра строится так, чтобы, во-
первых, отразить основные элементы структуры спектра, а во-
вторых, учесть практические потребности задачи. Границы
тральных диапазонов групповой модели выбираются так, чтобы
учесть пороги фотоионизации, сильные молекулярные полосы.
Определенная сложность возникает при выборе границ
тральных диапазонов осреднения, когда модель строится для
рокого диапазона температур. Как известно, в этом случае
дается смещение порогов фотоионизации. Если этот эффект
жет оказать заметное влияние на результаты решения задачи, то
приходится вводить дополнительные спектральные диапазоны.
Требования, предъявляемые к модели со стороны решаемой
чи, могут привести либо к увеличению числа участков
ния, либо наоборот, уменьшить их. Примером реализации такого
подхода может служить методика построения групповых моделей
квазинепрерывного спектра коэффициента поглощения
температурного воздуха и смесей CO2-N2, учитывающих не
только структурные особенности спектра, но и типовые
ния, предъявляемые к моделям при решении задач об излучении
высокотемпературных газовых объемов вблизи летательных
аппаратов (Суржиков СТ., 2004 (в)).
Если оптическая модель разрабатывается с целью ее
дующего использования в некотором классе задач теории
са теплового излучения или динамики излучающего газа, то
сообразно создать оптимальную для данного класса физических
задач оптическую модель (см. п.11.1).
Построение оптимальных групповых моделей состоит из
нескольких этапов. Например, при разработке оптической модели
оптимальной для данного класса задач теории переноса теплового
22*

348 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
излучения, на первом этапе выделяются границы спектральных
диапазонов на основе анализа спектральной зависимости
ного коэффициента поглощения от длины волны в широком
пазоне температур. На втором этапе выбранные границы
тральных диапазонов уточняются при решении задачи расчета
интегральных лучистых потоков в объеме плоской,
ской или сферической геометрий. При этом размеры расчетной
области и распределение температуры в таком объеме задаются
по возможности близкими к тому, что ожидается при решении
требуемой задачи. Решение этой задачи проводится дважды:
чала с использованием как можно более полной информации по
коэффициенту поглощения, а затем с использованием
мой групповой модели. Если точность расчета плотностей
гральных лучистых потоков по групповой модели оказывается
недостаточной, то выполняется коррекция границ спектральных
диапазонов.
Вдобавок к этому, при разработке оптической модели
мальной для некоторого класса задач радиационной газовой
намики, необходимо провести аналогичные расчеты на примере
модельной радиационно-газодинамической задачи. Одной из
можных модельных задач является расчет обтекания поверхности
затупленного тела в окрестности критической линии тока
звуковым потоком вязкого теплопроводного селективно
чающего и поглощающего газа. Здесь коррекцию границ
тральных диапазонов также приходится делать дважды. Первый
раз при построении модели спектра для заданных величин
ния /?5 и температуры Г5 за фронтом ударной волны. Второй - на
заключительном этапе решения задачи, когда групповые модели
построены при различных р5 и Г5, но они не совпадают между
собой. Таким образом, построенная групповая модель называется
оптимальной для класса задач внешнего обтекания.
Модель с учетом атомных линий поддается оптимизации
гораздо меньше. Рассмотрим два типа таких моделей. Первый тип
групповой модели с учетом атомных линий - это синтетический
спектр поглощения атомных линий на фоне квазинепрерывного
спектра. Использовать такую модель в расчетах переноса излуче-

12.4. Line-by-line модели 349
ния неудобно из-за большой трудоемкости, поскольку даже с
пользованием неоднородной расчетной сетки, на одну линию
приходится отводить 10-20 точек. Это позволяет использовать
такие типы моделей только в качестве эталонных. Второй тип
групповых моделей - это модели, в которые вводятся
ные групповые функции, позволяющие провести расчет переноса
излучения без увеличения числа групп. Их недостатком является
необходимость использования специализированных расчетных
алгоритмов. Однако с этим приходится мириться из-за их
тельной простоты и очень высокой эффективности.
12.3.2. Метод группового усреднения
Одну из разновидностей групповых моделей представляет
метод группового усреднения, предложенный в работе (Онуфриев
А.Т. и др., 1967). В указанном методе спектральные группы
дятся не по принципу деления шкалы волновых чисел, а по
ципу деления полного диапазона изменения коэффициента
глощения:
- задается диапазон изменения спектрального коэффициента
глощения [ Kmjn, ктах ] во всех внутренних точках
го объема;
- задается расчетная сетка в выделенном диапазоне [ кт;п, ктах ];
- к /-Й спектральной группе относится совокупность
ных диапазонов, в которых спектральный коэффициент
глощения удовлетворяет условию к, < kv < k,+i ;
- уравнение переноса излучения решается столько раз, сколько
выделено спектральных групп.
12.4. Line-by-line модели
Это наиболее точные модели учета спектральной
сти оптических свойств низкотемпературной плазмы. При
зовании line-by-line (LBL) моделей интегрирование уравнения
реноса по спектру производится в стольких спектральных точках,
сколько необходимо для подробного описания контуров атомных

350 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
линий и, если необходимо, вращательных линий молекулярного
спектра. Фактически, эти модели представляют собой
повые модели учета спектральной зависимости. Однако при столь
подробном учете спектральных оптических свойств отпадает
обходимость в нахождении среднего значения коэффициента
глощения (испускания) в каждом отдельном спектральном
зоне Дш* ¦ Оказывается достаточным рассчитать спектральные
оптические свойства в любой (например, центральной) точке
внутри До*.
Несложно сделать верхнюю и нижнюю оценки числа точек
по спектру, в которых необходимо проинтегрировать уравнение
переноса для решения задачи о теплообмене излучением в
чих газах и низкотемпературной плазме. Положим, что для
ния контура атомной (молекулярной) линии требуется
тельно десять точек по спектру. Тогда, при типичной полуширине
линии y~0.01-f-0.lcM для ее описания необходимо
дусмотреть спектральный диапазон ~ 1 см'1, в пределах которого
шаг интегрирования по спектру оценивается величиной
~ 0.1 -г- 0.01 см'1 (при этом, конечно, в реальных расчетах разумнее
использовать неоднородные сетки по волновому числу). Для задач
теплообмена излучением в горячих газах и в низкотемпературной
плазме типичные расчеты переноса излучения проводятся в
тральной области ~ 105 см, отсюда следует верхняя оценка
ходимого числа точек ~107. При более реалистической оценке,
когда принимается необходимость учета только атомных линий
(поглощение в молекулярном спектре усредняется по
ной структуре), оценка необходимого числа точек делается иначе.
Достаточно число учитываемых атомных линий умножить на 10.
Например, для воздушной плазмы, при учете по ~ 4000 атомных
линий атомов и ионов азота и кислорода получается нижняя
ка ~4х104 спектральных точек. При этом следует иметь в виду
необходимость разработки алгоритма построения неоднородной
шкалы по волновому числу.
Таким образом, если вычислительные мощности позволяют
проводить столь подробные расчеты, то, как таковая, проблема
интегрирования по спектру уравнения переноса отпадает. В край-

12.4. Line-by-line модели 351
нем случае, несколько подобных расчетов можно выполнить с
лью получения эталонных решений, с которыми затем будут
сравниваться результаты, полученные по приближенным
лям.
Гораздо чаще LBL-расчеты проводятся не в полной
тральной области, а в отдельных спектральных диапазонах,
держащих относительно небольшое число линий (например,
~ 100-5-200). Такие расчеты делаются также в основном для
чения эталонных решений.
В LBL-расчетах проблема выбора расчетной шкалы по
новому числу не является единственной. Необходимо выбрать
адекватные решаемой задаче способы расчета параметров
тральных линий. Задача расчета параметров атомных и
лярных линий выходит за рамки проблем, обсуждаемых в данной
книге.
Однако в следующих подразделах представлен краткий
зор методов решения этой задачи для того, чтобы дать
ление о том, как результаты квантовой механики по расчету
метров спектральных линий используются в феноменологической
теории радиационного переноса энергии.
12.4.1. Расчет параметров атомных линий
Проведению расчетов переноса излучения и спектральных
коэффициентов поглощения с учетом атомных линий всегда
предшествует подготовительная работа, связанная с выбором
менклатуры учитываемых линий и анализом условий в нагретых
газах и плазме для построения адекватного метода расчета
метров атомных линий. Этим вопросам посвящена специальная
литература по атомной спектроскопии (Грим Г., 1969; Грим Г.,
1978; КасабовГЛ. и др., 1979; КорлиссЧ. и др., 1968; Левин-
сон И.Б. и др., 1962; Собельман И.И., 1963). Применительно к
дачам теплообмена излучением рассматриваются более простые
методы, в которых вся сложность и многообразие квантовомеха-
нических процессов, протекающих при связанно-связанных
ходах в атомах и ионах, представляется в виде ряда феноменоло-

352 Гл.12. Методы интегрирования уравнения переноса по частоте излучения
гических констант, таких как интегральное поглощение в линии и
ее полуширина. Анализу некоторых методов расчета указанных
коэффициентов и используемых вычислительных алгоритмов
священ данный раздел.
Физические и математические модели, а также реализующие
их программные модули могут быть разбиты на две независимые
группы. Первая группа моделей и программ обеспечивает
товку параметров атомных линий к стандартизованному виду и
формирование базы данных. Обычно отдельно взятую атомную
линию характеризуют: волновое число центра линии озтп (для
квантового перехода из нижнего энергетического состояния т в
верхнее и), статистический вес нижнего состояния gm и его
гия Ет, сила осциллятора в поглощении fmn, атомная масса иона
или атома Ма, константа (или несколько констант),
щая уширение линии. В этот набор могут также входить
ры верхнего уровня квантового перехода тя —> и.
Все физические аспекты расчета параметров линейчатого
спектра включаются в эту первую группу. Здесь производится
расчет сил осцилляторов (если отсутствуют соответствующие
экспериментальные или расчетные данные) и постоянных ушире-
ния. Примером стандартного вида набора параметров атомных
линий могут служить таблицы (Авилова И.В. и др., 1970;
щиков В. А. и др., 1971; Грим Г., 1978; КасабовГЛ. и др., 1979;
WieseWX. et al, 1966, 1969; Wilson K.H., NicoletW.E., 1967;
Surzhikov ST., 2002 (a)).
Вторая группа моделей и программ практически не связана с
первой, а использует лишь информацию из базы данных атомных
линий. Основное назначение этой группы вычислительных
лей состоит в расчете синтетического спектра коэффициента
глощения и в подготовке информации по атомным линиям для
вычислительных моделей, реализующих расчет переноса
излучения.
Анализ линейчатого излучения в низкотемпературной
ме, выполненный в работах (Авилова И.В. и др., 1970;
ков В.А. и др., 1971; Коньков А-А. и др., 1969), показывает, что
основными механизмами уширения атомных и ионных линий в

12.4. Line-by-line модели 353
диапазоне температур ~5ООО-з-20000 К и давлениях порядка
сферного можно считать доплеровское и штарковское уширение
заряженными частицами. При этом форму линии следует
вать функцией Фойгта, обеспечивающей асимптотические
ходы к контурам линий, описываемых функциями Лоренца и
плера.
Для построения расчетной модели коэффициента
ния необходимо определить три функции: атп - интегральный
коэффициент поглощения линии, лоренцевскую полуширину yj^, и
доплеровскую полуширину утп (у - половина ширины линии на
половине высоты).
Анализ методов расчета указанных величин дан в работе
(Суржиков СТ., 2004, (а))
Спектральный коэффициент поглощения в атомной линии
рассчитывается с использованием функции Фойгта
О — , X —
Id Id
где а>о - волновое число центра линии; а = amn
Id -Imn • Вместо интеграла A2.35) оказывается удобным
зовать достаточно простую аппроксимацию фойгтовской
ции, предложенную в работе (Матвеев B.C., 1972). Если ввести
обозначения ii = (g>-(»o)/Yo , ? = Yi/Yu (Yu - полуширина линии
с фойгтовским контуром), то
/ -ч аа%
)A,5/1п 2 +1 + ^)| 0.66exp(-0.V)-D0-5.5л2 + Л4)"'

354 Гл. 12. Методы интегрирования уравнения переноса по частоте излучения
\У2
1-2v,
lU ¦ A2.36)
Использование формул A2.36) позволяет рассчитать
цию профиля фойгтовской линии с точностью 3%, чего вполне
достаточно для практических целей.
В расчетах контуров спектральных линий может возникнуть
проблема корректности определения коэффициента поглощения в
далеких крыльях. На больших расстояниях от центра линии
тур не описывается дисперсионной (лоренцевской) функцией.
При анализе этого вопроса следует выделить различные
ные случаи. Первый случай - это построение синтетического
профиля коэффициента поглощения применительно к задачам
спектроскопии. Здесь необходимо каждый раз задачу решать
дивидуально, исходя из конкретных условий в плазме. В случае
необходимости можно использовать иную зависимость для
фициента поглощения в крыльях линий (например, степенную).
При решении задач теплообмена излучением можно считать, что
контур линии на фоне квазинепрерывного спектра с достаточной
точностью находится по формулам A2.36).
Таким образом, для расчета синтетического спектра
фициента поглощения в атомных линиях необходимо
ваться одной из баз данных, упомянутых выше, выбрать
дящий способ расчета параметров атомных линий и выполнить
расчет контура каждой атомной линии по формуле A2.36).
Суммарный коэффициент поглощения в спектральном
пазоне Асо с атомными линиями определяется по формуле
N
=кД + 2>/(<°0/><»)> A2-37)
где Кди - фоновый коэффициент поглощения в
ном спектре; к,(соо;><л) - коэффициент поглощения на частоте со,
обусловленный i-й линией с центром а>0/; N - число линий,
павших в Асо.

12.4. Line-by-line модели 355
Формула A2.37) определяет спектральный коэффициент
глощения в фиксированной точке со шкалы волновых чисел. Эта
же формула используется для построения подробной
ной зависимости коэффициента поглощения в выделенном
тральном диапазоне Дсо (так называемого синтетического
ра спектра коэффициента поглощения). С этой целью в
тральном диапазоне Дсо вводится подробная расчетная сетка по
волновому числу, в каждой точке которой спектральный
циент поглощения находится по формуле A2.37). Расчетная сетка
должна быть настолько подробной, чтобы контур каждой линии
можно было описать без заметного искажения.
Пример расчета спектрального коэффициента поглощения с
подробным учетом контуров атомных линий в
турной смеси газов СОг и N2 при р = 1атм и Г = 10000 К
ставлен на рис.11.1.
12.4.2. Расчет коэффициентов поглощения
в молекулярных линиях
Задача вычисления контуров вращательных молекулярных
линий возникает при построении синтетического контура
фициентов поглощения и испускания, а также при проведении
эталонных расчетов переноса излучения в однородных и
родных слоях молекулярных газов. Под эталонными понимаются
наиболее точные и подробные расчеты, предназначенные для
сравнения с ними результатов, полученных по различного рода
приближенным моделям. В этом смысле соответствующие
ты можно было бы назвать «точными». В настоящее время
лее полная информация по вращательным линиям двух- и
атомных молекул, расположенных в инфракрасной области
тра, собрана в банке данных HITRAN (Rothman L.S. et al., 1992).
Здесь представлены все необходимые данные для расчета интен-
сивностей и полуширин линий при условиях в газе, близких к
нормальным.
Анализ механизмов уширения вращательных линий
лярного спектра показывает, что с достаточной точностью для

356 Гл.12. Методы интегрирования уравнения переноса по частоте излучения
задач переноса теплового излучения, можно принимать в учет
лишь два механизма уширения: ударный и доплеровский (Гуди Р.,
1966; ПеннерС.С, 1963).
Доплеровское уширение рассчитывается по формуле
У/* ( т у/*
"\ — \ <omn,cM-\(\23S)
у Mamac0 J ума
где та = 1.66x1027 г - атомная единица массы; Ма - атомный вес
в относительных атомных единицах; а>тп - волновое число
тра вращательной линии; Г- температура, К.
Ударное уширение вращательных линий, описываемое
туром Лоренца рассчитывается по соотношению,
рующему опытные данные (ПеннерС.С, 1963;LudwigCB., 1971):
yf =Z Vy B73/гУ2 +buPl B73/ЗГ), A2.39)
j
где индексами / и j помечены параметры поглощающей и
ряющих молекул; р - парциальное давление; by - эмпирическая
постоянная уширения; Ьи - эмпирическая константа резонансного
уширения. При получении указанной аппроксимации полагалось,
что составляющие уширения, обусловленные различными
ряющими молекулами, являются аддитивными. Зависимость
yL ~ рТ~У2 получается при использовании кинетической теории
газов. Константа уширения by оценивается по формуле
by = 2.2 х ЮD,Dj (\/Мш + \/М0 f2, A2.40)
где Dt,Dj - оптические диаметры, А. Выполненное в работе
(Кузнецова Л.А., Кузьменко Н.Е. и др., 1980) сопоставление
ческих диаметров с кинетическими диаметрами столкновения
казывает, что они достаточно близки. Однако, следует
нуть, что проблема расчета уширения вращательных линий
ется до настоящего времени актуальной проблемой молекулярной
спектроскопии высокого разрешения. Сложность данной
мы обусловлена во многом тем, что уширение линий является ха-

12.4. Line-by-line модели 357
рактеристикой не только самой молекулы, а во многом зависит от
условий в газе и плазме. Кроме этого, еще следует иметь в виду
возможность штарковского уширения вращательных линий
тронами, которое может оказаться существенным при Т ? 8000 К
(для атмосферных давлений) (Breene R.G., Jr., 1968).
Таким образом, для расчета синтетического спектра
щения во вращательных молекулярных линиях необходимо
пользоваться базой данных для задания местоположения (о>о/)>
интенсивности at и постоянных, характеризующих уширение
ждой вращательной линии, после чего воспользоваться
ми A2.36) и A2.37). Теоретические расчеты указанных
ров выполняются методами квантовой механики и квантовой
мии (Собельман И.И., 1963; Степанов Н.Ф., 2001).
Пример расчета спектрального коэффициента поглощения
во вращательных линиях молекулы Сг показан на рис. 11.4.
Исследование влияния учета вращательной структуры
тронно-колебательно-вращательных спектров на характеристики
радиационного нагрева элементов конструкций энергетических
устройств выполнено в работе (Kuznetsova L.A. et al., 1988).
зано, что в спектральных диапазонах Асо>5О-5-1ООсм
ние по вращательной структуре позволяет получить результаты с
достаточно высокой точностью. В меньших спектральных
зонах необходимо принимать в учет линейчатую структуру
тра. При этом большое значение имеет корректный учет
ры ветвей вращательных линий.

Глава 13
МОДЕЛИ НЕЛОКАЛЬНОГО УСРЕДНЕНИЯ
Модели нелокального усреднения составляют отдельную
группу методов интегрирования уравнения переноса по частоте
электромагнитного излучения, которые ориентированы на
ние задач радиационной газовой динамики, то есть в тех случаях,
когда уравнение переноса излучения интегрируется многократно
совместно с другими уравнениями динамики сплошной среды.
К этому классу моделей относятся:
• модели эффективных средних «серых» коэффициентов
son D.H., 1965; Sampson D.H. et al., 1972; Traugoff S.C., 1968),
где усредненный по спектру коэффициент поглощения
ся в виде функциональной зависимости типа
k = F(kp,kr),
где к> и Кд - среднепланковский и среднеросселандовский
коэффициенты поглощения;
• квазидиффузионный метод (Гольдин В.Я., 1964) и различные
варианты этого метода, представляющие собой его развитие
для различных конкретных ситуаций;
• метод введения усредненных по спектру коэффициентов
поглощения Анфимова и Шари (Анфимов Н.А. и др., 1968);
• метод нелокального усреднения (Немчинов И.В., 1970);
• метод парциальных характеристик (Севастьяненко В.Г., 1979,
1980);
• метод эффективных сечений (Овсянников В.М., 1982;
Овсянников В.М. и др., 1971);

13.1. Квазидиффузионный метод Гольдииа 359
• метод нелокальных интегральных характеристик (Гудзовский
А.В. и др., 1981; Карасев А.Б. и др., 1979);
• метод эффективных полумоментных коэффициентов
ский В.В. и др., 1982);
• метод эффективных квадромоментных коэффициентов
жиков СТ., 1992).
13.1. Квазидиффузионный метод Гольдина
Этот метод предложен в работе (Гольдин В.Я., 1964).
Суть квазидиффузионного метода состоит во введении
но-линейных функционалов решения уравнения переноса,
позволяющих существенно повысить эффективность
тельной процедуры. В данном разделе будет изложена общая идея
метода. Применение метода квазидиффузии к решению задач
тегрирования по частоте многими авторами показало
ность данного подхода.
13.1.1. Уравнения метода квазидиффузии в случае
одномерной плоской геометрии
Рассмотрим уравнение переноса для одномерной плоской
геометрии без учета рассеяния
с граничными условиями
т = 0, ц>0: У@,ц) = У0+, A3.2)
т = тя, ц<0: j(xH,\i) = rH. A3.3)
Применим к уравнению A3.1) последовательно следующие
два интегральных оператора
Ло{ }=J{ }Ф, A3.4)

360 Гл.13. Модели нелокального усреднения
1
Л,{ }= |ц{ }dn, A3.5)
-1
в результате чего получим
с) .
-L + KcU{x) = K.cUb{x), A3.6)
dx
гМх)
dx
где ^(^)=^1 — • A3.8)
-i
Функция D(x) называется коэффициентом квазидиффузии.
Граничные условия для системы A3.6), A3.7)
ся из соотношений
1
)= |у(ц)цёц = С01/(х = 0), A3.9)
-1
1
: \j(xH,\i)\id\i = CHU{x = xH), A3.10)
-1
1
где Cq=c=\ , A3.11)
A3.12)
-1

13.1. Квазидиффузиониый метод Гольдина 361
Соотношения A3.9) и A3.10) могут быть записаны с учетом
A3.7) только относительно объемной плотности лучистой
энергии
Отметим основные особенности сформулированной краевой
задачи A3.6), A3.7), A3.13), A3.14):
1) система уравнений не содержит в явном виде зависимости
от угловых переменных;
2) коэффициенты D(x),Cq и Си не могут быть найдены из
решения самой краевой задачи, то есть система уравнений
замкнута;
3) если угловая зависимость интенсивности известна точно,
то система уравнений A3.6), A3.7) дает также точное решение
относительно плотности потока излучения и объемной плотности
лучистой энергии.
Метод квазидиффузии оказывается весьма экономичным при
решении задач радиационной газо- и плазмодинамики.
рим типичный алгоритм использования метода квазидиффузии
при решении задачи радиационной газодинамики (РГД)
онным методом. Пусть на некоторой /7-ой итерации расчета всех
искомых функций задачи, производится точное решение
ния переноса A3.1), после чего рассчитываются функции
D{x),Cq и Си . В течение ряда последующих итераций решения
системы уравнений РГД используется только система уравнений
квазидиффузии с коэффициентами D(x),Cq и Си,
ными на р-й итерации. Очевидно, чем реже необходимо уточнять
указанные коэффициенты, тем более экономичным будет весь
горитм. Важной особенностью метода квазидиффузии является
то, что коэффициенты D(x),Cq и Си являются весьма
вативными функциями, требующими редкого уточнения. Именно
это и определяет высокую эффективность данного метода при

362
Гл.13. Модели нелокального усреднения
решении задач радиационной газовой динамики в условиях
ного радиационно-газодинамического взаимодействия.
13.1.2. Уравнения метода квазиднффузнн в случае
двумерной геометрии
Обобщение метода квазидиффузии на двумерный случай, и
пример его использования даны в работе (Аксенов Н.Н. и др.,
1979;ЧетверушкинБ.Н., 1985).
Их х
Рис. 13.1. Расчетная область для использования метода квазиднффузии
На примере двумерного уравнения переноса излучения в
прямоугольной декартовой системе координат (рис. 13.1)
со,
A3.15)
ox y by
с граничными условиями (oo^ = cos 8, co^ = cos (я/2 - 8) ):
y = 0, cosa>0: J(x,y = O,Cl) = Jx~, а = я/2-8, A3.16)
y = Hy, cosa<0: j(x,y = Hy,Cl) = J^, а = я/2-8,
x'=0, cos8>0: J(x = 0,y,Ci) = Jy,
= Нх, cos9<0:
J.
Действуя на уравнение A3.15) сначала интегральным оператором

13.1. Квазидиффузнонный метод Гольдина 363
Ao{}=J{}dn.
4я
а затем
A,{ }= J{ }fidfl,
4я
получим систему квазидиффузионных уравнений
дх оу
dD^U dDxyU
дх ду х~ '
dDJJ dDJU
дх dv
A3.17)
A3.18)
A3.19)
A3.20)
A3.21)
где
n =i« n =i« n =4* П3 22"»
" f JdQ ' ^ f JdQ ' ^ f Jd« • ( }
4я 4я 4я
Граничные условия формулируются в виде
(Wn)s=(CnU)s, A3.23)
где s - одна из четырех границ (поверхностей) расчетной
ти; п - внешняя нормаль к границе,
С„=4* . / . A3.24)
Jj(n)dn
4я
Алгоритм метода квазидиффузии такой же, как в случае
номерной задачи. На некотором /7-ом шаге решения задачи
рационного или истинно нестационарного процесса) решается
уравнение переноса излучения A3.15) относительно
сти J(r,Q). Затем рассчитываются коэффициенты квазидиффу-

364 Гл.13. Модели нелокального усреднения
зии A3.22) и коэффициенты граничных условий A3.24). На
тяжении ряда последующих итераций (временных шагов) эти
эффициенты считаются заданными функциями координат (иногда
используется термин «замораживание» коэффициентов). Затем
указанный вычислительный цикл повторяется.
В работе (Четверушкин Б.Н., 1985) изложен алгоритм,
зволяющий исключить процедуру решения исходного уравнения
переноса, что при допустимой потере точности, заметно
ет экономичность расчетного алгоритма. В этом методе при
чете коэффициентов квазидиффузии используется не исходное
уравнение переноса, а система одномерных уравнений,
тельно аппроксимирующая его
+ кГхъ!ь, A3.25)
r\—Z- + *Jy=KJb, A3.26)
йу
где n=cos8, ti=cos(rc/2-8).
Тогда коэффициенты квазидиффузии рассчитываются по
формулам
1 /1
/ A3.27)
-l / -l
A3.28)
13.13. Потоковый вариант метода квазиднффузин
Метод предложен и исследован в работах (Гермогенова Т.А.
и др., 1969; Николайшвили Ш.С., 1966) для плоского слоя,
нос излучения, в котором описывается уравнением

13.1. Квазидиффузионный метод Гольдина 365
с граничными условиями
х-0, Ц>0:
х = хя,
К уравнению A3.29) последовательно применяются
гральные операторы следующего вида
1
ло{ } = J{ }<*И, A3.31)
}=f{ }ёц, A3.32)
-l
в результате чего получается система двух уравнений
+U+=2nUb, A3.33)
У +U2nUb,
dx
dx
=2nUb , A3.34)
с соответствующими граничными условиями
1
?/+(x = O)=J./o+(n)dn, A3.35)
о
о
?Г(х = хя)= J./o(n)dn, A3.36)
—1
1 о
где D+=± , д-4
О -1
1 О
?Г =

366 Гл.13. Модели нелокального усреднения
13.2. Многогрупповой квазидиффузионный метод
Метод подробно изложен в работе (Четверушкин Б.Н., 1985).
За основу выбрано уравнение для плоского нерассеивающего слоя
в многогрупповом приближении
(x)Jg(x,\i) = Kg(x)Jb<g, g = l,2,...Ng, A3.37)
с граничными условиями
х = 0, ц>0: 7г(О,ц) = 4о(ц), A3.38)
х = Н, ц<0: 78(Я,ц) = 7-я(ц), A3.39)
где
Jg{x,\i)= f Ja(x,\i)d(Q, A3.40)
Применим к уравнению A3.37) сначала интегральный оператор
1
Л?{ } = J{ }ёц, A3.42)
о
о
азатем А~о{ }= J{ }<1ц, A3.43)
-1
в результате чего получим
A3.44)
, A3.45)

13.2. Многогрупповой квазидиффузнонный метод 367
где
0
0
Wg(x)= \\xJg(x,\i)d\i,
-1
l
TT 1 vl— 1 J IY 11 1 /4l 1
0
0
U~(x)= jjg(x,\i)d\i.
-l
A3.46)
A3.47)
A3.48)
A3.49)
Просуммировав A3.44) и A3.45) по всем спектральным группам,
получим
A3.50)
dx
где
&{x)W-{x) = S{x)t A3.51)
N,
A3.52)
N.
s{x) = LKg(x)Jb,gix)> A3-53)
N. N.
g=l g=l
Введение интегральных среднепланковских коэффициентов
позволяет дать окончательную формулировку

368 Гл.13. Модели нелокального усреднения
+ D4x)W+ix) = *P(*)дТ* » A355>
(х)^-(*) = кя(*)а74. A3.56)
dx
Граничные условия для системы A3.55), A3.56)
руются в следующем виде
N. N. 1
W* (х = 0) = 2^1?* (х = 0) = 2^ |м^о>8(и)Ф» A3.57)
g=i g=i о
N. N. 1
g=l g=l О
13.3. Интегральное квазидиффузионное приближение
Система интегральных квазидиффузионных уравнений
лучена в работе (Гольдин В.Я. и др., 1972; Четверушкин Б.Н.,
1985).
В качестве исходной рассмотрим систему
ных уравнений в групповом приближении
(x)Ug{x) = cKg(x)Ub,g, A3.59)
x)We(x) = 0, g = l,2,...NK A3.60)
с граничными условиями
( g = \,2,..-Ng, A3.61)
х = Н: Wg(H) = CH>gUg(H), g = \,2,-Ng. A3.62)
Суммируя по всем спектральным группам, получаем

13.3. Интегральное квазидиффузионное приближенне 369
*I/(*)-в5(*), A3.63)
dD^t/^) + K(x) [cU(x) + W(x)]-k(x)cU(x) = O,
с граничными условиями
W@) = C0U@), A3.65)
W(H) = CHU{H), A3.66)
где W{x) = ^Wg{x), U{x) = ^Ug(x). A3.67)
g=i g=i
N. 1
N. l
Л^ 1
r _ g=i -i r _ g=i
g=l -1 g=l -1
N. 1 N. 1
(x=x
L !JAx>№ L !
g=i -i g=i -i
Заметим, что введение коэффициента к(дг) вместо
25 Зак. 272

370 Гл.13. Модели нелокального усреднения
N.
N. 1
позволяет избежать неблагоприятного случая обращения в нуль
знаменателя последнего выражения.
13.4. Метод усреднения уравнения переноса
Анфимова и Шари
Метод разработан и применен для решения задачи
онной газодинамики в работе (Анфимов Н.А. и др., 1968).
В идейном отношении этот метод подобен методу
диффузии и состоит во введении усредненных по направлениям и
спектру коэффициентам поглощения. Однако для получения
фективных коэффициентов переноса используются не уравнения
квазидиффузии, а непосредственно уравнение переноса. Метод
применен к решению задачи о радиационно-конвективном
обмене в ударном слое у поверхности затупленного тела при
текании его гиперзвуковым потоком воздуха в окрестности
тической линии тока.
Излучающий' ударный слой представляется в виде плоского
неоднородного слоя, для которого решается следующая система
уравнений
^ VV *0 A3.68)
? JJ МО A3.69)
где ц = cos 8, 8 - угол между направлением распространения
излучения и осью х, нормальной к поверхности плоского слоя,
J? =/?(дс,|л), J^ =J?(x,'ti) - спектральная интенсивность излу-

13.4. Метод усреднения уравнения переноса Анфнмова и Шари 371
чения в верхнюю и нижнюю полусферы, кх = к\(х) -
ный коэффициент поглощения, Jb,x=Jb,x(x) - спектральная
функция излучения абсолютно черного тела.
Граничные условия формулируются следующим образом:
х = 0 (поверхность обтекаемого тела):
^, A370)
це[0,1];
х = Н (фронт ударной волны):
[]; A3.71)
где &х - спектральная степень черноты поверхности,
о
^-(дс = 0) = 2я|^(* = 0,ц)ЦAц A3.72)
-1
- плотность спектрального одностороннего потока излучения к
поверхности.
Уравнения A3.68), A3.69) с граничными условиями A3.70),
A3.71) интегрировались с использованием многогрупповой
ли коэффициента поглощения в Nx =128 спектральных группах
для различных угловых направлений. Число равновеликих
вых зон варьировалось в пределах Nq = 1 +10 . Дивергенция
грального радиационного потока рассчитывалась по формуле
где к{ - средний (групповой) коэффициент поглощения в /-м
спектральном диапазоне ДА./; Х{ - любая точка спектрального
диапазона ДХ, (например, центр этого диапазона).
Изложенная процедура расчета переноса теплового
ния является в особенности трудоемкой при решении радиацион-
ночгазодинамической задачи, когда вычисление интегральных ра-
25*

372 Гл. 13. Модели нелокального усреднения
диационных характеристик в слое приходится производить
гократно.
Предложен следующий алгоритм, позволяющий значительно
повысить экономичность расчетов.
1. Перенос селективного излучения в многогрупповом
ближении рассчитывается лишь на некоторых итерациях радиа-
ционно-газодинамической задачи. После этого в каждом узле
четной сетки по оси х вычисляются два средних коэффициента
поглощения:
00
(*)- ° со 0 ~' • <135>
0-1
2. Вводится предположение об угловой зависимости
сивности излучения:
1 , 1
Jjfrid|i = ±pjd|i. A3-76)
о zo
3. Уравнение переноса интегрального излучения
руется в виде двух уравнений для интегральных интенсивностей в
верхнюю (ц ? 0 ) и нижнюю (ц ^ 0 ) полусферы:
<13-78'

13.4. Метод усреднения уравнения переноса Анфнмова и Шари 373
где J+=^JJ^dndX, Jb = \jbx&\. A3.79)
2яоо о
Система уравнений A3.77), A3.78) с соответствующими
граничными условиями для интегральной по спектру
сти решается на протяжении большого числа итераций. При этом
дивергенция интегрального лучистого потока определяется по
формуле
*% [()()] A3.80)
2
Профили средних коэффициентов поглощения к* (*)
лись таким образом на протяжении ряда итераций по радиацион-
но-газодинамическому взаимодействию.
4. По заданному алгоритму (например, через 10+20
ций), производилось уточнение профилей средних
тов, с которыми уравнения A3.77), A3.78) решались на
нии последующих итераций.
Предложенный способ решения радиационно-газодинами-
ческой задачи оказался весьма эффективным. Однако данный
тод обладает двумя недостатками:
1) из соотношений A3.74) и A3.75) следует, что в некоторой
точке внутри ударного слоя средние коэффициенты терпят разрыв
второго рода, что может сказаться на вычислительной процедуре;
2) в спектральной и интегральной задачах переноса
ния используются различные методы интегрирования по угловым
переменным.
Указанные недостатки могут быть преодолены
нием специальной численной процедуры исключения разрывов
функций, например, введением локального усреднения или
терполирующих дробно-линейных функций. Значительно более
эффективным оказалось развитие метода Анфимова-Шари,
полненное в работе (Горский В.В. и др., 1982). Этот подход
стоит в использовании метода полумоментов, обеспечивающего
знакопостоянство и неразрывность всех функций (см. п. 13.9).

374 Гл.13. Модели нелокального усреднения
13.5. Метод усредненных уравнений переноса
Немчинова
Этот метод подробно изложен и исследован в работе
чинов И.В., 1970) применительно к одномерным плоским (v = 1)
и сферически симметричным (v = 3) задачам
,. A3.81)
Граничные условия для плоского слоя формулируются в виде
г = 0, ц>0: Ju@,v.) = J+fi,
г = Л, ц<0: Уш(/г,ц) = ^>Л.
Для сферически-симметричного случая граничные условия
формулируются в виде
r = R, ц<0: Л, (Л,ц) = •?.*, A3.83)
кроме этого следует использовать условие осевой симметрии.
Предположим, что с использованием какого-либо расчетного
метода найдена спектральная интенсивность излучения, тогда
можно определить полусферические радиационные
ки, усредненные по угловым переменным в верхней (ц > 0) и
нижней(ц<0 ) полусферах:
а) спектральные характеристики
1 о
; о1 <13-84>
о -1
б) групповые характеристики
WHr)= f »^(r)do», f/*(r)= ff/*(r)dco; A3.85)

13.5. Метод усредненных уравнений переноса Немчинова 375
причем в группу A(og могут входить также подгруппы,
женные в разных участках спектра;
в) интегральные характеристики
A3.86)
8=1
С использованием полусферических радиационных
ристик определяются следующие полные радиационные
ристики
g;, ug=u+g+u;, A3.87)
w=w++w-, и=и++и~.
Вводятся функции, характеризующие диаграмму
ности излучения
ч?=4" A388)
и спектральный состав в пределах каждой g-й группы
(Ф = ?/±' ШеЛсо«' A389)
а также спектральные односторонние средние косинусы
и<о\г) О
О г / \ О
^^d^ = 27tJv^dH A3.91)
f^r7T^d^ 27tJ
-1 U<oV) -I

376 Гл. 13. Модели нелокального усреднения
и групповые односторонние средние косинусы
4= f с»(ф») dw- о3-92)
С использованием введенных односторонних средних
нусов определяются полусферические плотности потоков
Если к уравнению A3.81) применить последовательно
гральные операторы
1
}=2я|{
°0 A3-94)
-1
то вместо A3.81) получим следующие два уравнения
G»±?/»±+K»?/»±=K»?/^' A3-95)
где С?*= + :Ц^, A3.96)
G* - спектральный односторонний коэффициент сферичности.
После интегрирования в пределах спектральной группы
лучаем групповые уравнения переноса
1 ^ CU V1
где
G*= J С?*(ф*) dco, A3.98)

13.5. Метод усредненных уравнений переноса Немчинова 377
4 = АЮ' ± , A3.99)
J
Am
Kd.=—*-. . A3.100)
Рл ff/dco
Предложен следующий алгоритм использования
рованных уравнений при решении задач радиационной газо- и
плазмо динамики.
1) Пусть в некоторый момент времени tp производится
чет спектральной интенсивности излучения Уш (г, ц) во всей
четной области.
2) Последовательно производится расчет функций:
и?(г) -по формуле A3.84),
- по формуле A3.88),
с* (г) -по формулам A3.90) и A3.91),
G* ( г ) - по формуле A3.96),
, g = 1, N. - по формуле A3.89),
с* , g=l,Ng - по формуле A3.92),
G* , g = \,Ng - по формуле A3.98),
к* , g = \,Ne - по формуле A3.99).
о о
3) Используя найденные усредненные коэффициенты,
шаются уравнения A3.97) на протяжении ряда последующих
гов по времени Гр+1, t^2,..., tp+s.
4) После завершения расчетов в момент времени tp+s опять
производится решение исходного уравнения относительно
сивности излучения и процедура повторяется снова.
24 Зак. 272

378
Гл.13. Модели нелокального усреднения
13.6. Метод усредненных парциальных характеристик
Метод разработан в работах (Севастьяненко В.Г., 1979,1980)
и подробно изложен в (Головнев И.Ф. и др., 1984). Основная идея
метода состоит в предварительном интегрировании уравнения
переноса по частоте и по направлениям распространения
ния для типичного набора температурных профилей, с целью
следующего использования полученных функционалов при
рийных расчетах.
Рис. 13.2. К использованию метода усредненных парциальных характеристик
Формула для расчета дивергенции интегрального
онного потока в объеме произвольной геометрии может быть
представлена в следующем виде (рис. 13.2)
VW(r)=JJ(QV)Ja)(r,Q)dQdco =
4я
¦dQdco,
A3.101)
0 4л
где подразумевается, что при взятии интеграла по угловым
менным Q необходимо найти интенсивность излучения вдоль
всех лучей s,s,s,... (в идеале - бесконечно большого, на
ке - достаточного для вычисления интеграла с заданной точно-

13.6. Метод усредненных парциальных характеристик
379
стью), пронизывающих элементарный физический объем с
ус-вектором г. Спектральная интенсивность излучения вдоль
деленного направления дается формальным решением уравнения
переноса
s
~JKa>
. 0
(s')ds'
S
+
ds'. A3.102)
Тогда с учетом A3.102), выражение для дивергенции
ности интегрального лучистого потока может быть записано
VW(r)= jVJ(s)dCl,
A3.103)
4я
где
00 00
. s
ds'dco =
JOO
0
xexp
. s'
Введем обозначения
00
deeds'.
A3.104)
h (*.*')= f K«
do, A3.106)
24*

380
Гл.13. Модели нелокального усреднения
с учетом которых
A3.107)
Автором работ (Севастьяненко В.Г., 1979, 1980) предложено
дополнительное преобразование, позволяющее сделать расчет по
формулам A3.103)-A3.107) более удобными. Это
ние состоит в том, что к правой части A3.104) добавляется и
читается следующее слагаемое
ds'dco,
00
что позволяет записать
-К ю^'
7, (s, s') = Jkw (sf) kw (s) [Jb>w (*') - JbtW (*)] exp
A3.108)
do, A3.109)
do.
A3.110)
До настоящего времени никаких допущений не делалось и
формулы A3.108)-A3.ПО) позволяют в принципе получить
шение задачи отыскания дивергенции плотности интегрального
радиационного потока с любой наперед заданной точностью.
Целью метода парциальных характеристик является
ботка способа экономичного расчета интегралов A3.109) и
A3.110). Видно, что основу расчетного алгоритма должна
лять процедура вычисления интеграла
s
J(s)= jJb(s')KP(s')e\p(-x)ds',
о

13.6. Метод усредненных парциальных характеристик 381
0 (*')./*,„ (У) d(D
где kp(s') =
_ о
К»
о
x = x(s,s') - средняя по спектру эффективная оптическая
толщина.
Главная идея метода состоит в том, что в качестве
го (эффективного) оптического пути, для которого и
ется среднее пропускание, и который должен быть эквивалентен
реальному оптическому пути, следует выбирать не однородный, а
некоторый неоднородный модельный путь, который может, в
принципе, сколь угодно точно аппроксимировать реальный путь
поглощения.
В качестве примера простейшего неоднородного пути
ложен луч с линейным распределением температуры между двумя
граничными точками. Причем, если значение T(s') берется по
точке s' (в этой же точке рассчитывается излучательная
ность к/> {s')Jb (•*'))> то значение температуры во второй точке
(s), где собственно и ищется решение, подбирается из условия
равенства интеграла по истинной температуре и по линейному
распределению
Предлагается заранее (до решения задачи) вычислять с
пользованием модельных распределений температуры функцию
AJ(s',s) = Jb(s')KP{st)exp[-x(s-s')],
которая является (по определению) интегральной по частоте па>;
циальной интенсивностью излучения, то есть интенсивностью
лучения, которое испускалось в точке s' и ослабилось на пути
s-s'

382 Гл.13. Модели нелокального усреднения
Если функции AJ(s',s) известны на заданной сетке вдоль
луча, то интенсивность излучения в точке s найдется по формуле
s ЛГ,-1
J(S)= \AJ(s',s)ds'* ? &J(s,,s)As,, A3.111)
О <=1
где As< = sl+\ -s{ - шаг расчетной сетки вдоль луча.
Очевидно, что если значения функционалов AJ(sj,s)
рать из заранее рассчитанной базы данных, то алгоритм расчета,
основанный на формуле A3.111) является очень экономным.
В целом алгоритм метода парциальных характеристик
мулируется следующим образом (для примера при постоянном
давлении).
1. Исходя из предварительного анализа решаемой задачи,
формулируется набор модельных профилей температуры,
рые будут использоваться для предварительного расчета
альных интенсивностей. Рекомендуется использовать в качестве
модельных профилей непрерывные кусочно-гладкие функции
(сплайны).
2. Для данного газа проводятся расчеты спектральных
фициентов поглощения в требуемом диапазоне температур.
3. Для выбранных модельных профилей рассчитываются
тегральные по спектру характеристики: средние оптические
ности пути поглощения, интегральные по частоте парциальные
интенсивности излучения. Рассчитанные парциальные
стики являются функционалами модельных температурных
филей (сплайнов). Например, парциальная интегральная
сивность есть функционал следующего вида
>w [Т (*')] кш [Т {*')] exp
о
[Г
о
4. С помощью заранее рассчитанных парциальных
ристик производится расчет интенсивности излучения по формуле
A3.111).

13.7. Метод нелокальных интегральных характеристик
383
В работе (Головнев И.Ф. и др., 1984) представлены
ные таблицы парциальных характеристик, предназначенные для
расчета полей интенсивностей, потоков и их дивергенций в
темах произвольной геометрии с характерными размерами до 1 м,
содержащих газы: водород, аргон, воздух с произвольным
делением температур от 300 до 20000 К и давлений от 0.3 до
30 атм. Там же представлены подробные инструкции для
вания этими таблицами.
3.7. Метод нелокальных интегральных характеристик
для больших градиентов температуры
и химического состава
Метод предложен и подробно изложен в работах (Гудзов-
ский А.В. и др., 1981; Карасев А.Б. и др., 1979). Метод
ван на расчет теплообмена излучением в неоднородных слоях
низкотемпературной плазмы с разделением интенсивности на две
части, отвечающие излучению, распространяющемуся в
тельном направлении оси х (рис. 13.3) и в отрицательном
лении
J*(x=0)
Рис. 13.3. К формулировке метода нелокальных интегральных характеристик
, A3.112)
. A3.113)
dx
dx

384
Гл.13. Модели нелокального усреднения
К уравнениям A3.112) и A3.113) формулируются граничные
условия для поверхностей, диффузно отражающих падающее
лучение.
С целью численного решения уравнений A3.112) и A3.113)
исследуемый плоский слой неоднородной плазмы разбивается на
N элементарных подслоев толщиной (ht = 1,2,..., N), в пределах
которых свойства плазмы полагаются однородными (температура
7} и концентрации компонент с*(<(Л = 1,2 N^) не изменяются
по толщине слоя).
Искомая интенсивность в каждой расчетной точке области
представляется в виде разложения в ряд в окрестности некоторых
базовых (опорных) температур и концентраций
dcki I 2
i N N
Ivy
dTp8Tq
*=I p=\ q=\
A3.114)
где 57I=7;-7;0,6cfti,=cftt,-cJ,.
Плотность одностороннего интегрального потока излучения
определяется с использованием разложения A3.114)
W±(xJ) = Jdv Jс!ф JJ*j F)cos6 sin 6d6 =
о о о
аи
=л Jdv J J* y F) sin 26d6 « qfc
о о
<=i
A3.115)
q=\
*=i p=i ?=i

13.7. Метод нелокальных интегральных характеристик
385
где
00
= яJdvJjJД6,Гу°,с?,) sin26de;
о е
4Й-*М
о е
дт,
<у(е)
о е
дтрдгч
sin26d6;
sin26d9;
sin26d6;
A3.116)
A3.117)
A3.118)
A3.119)
о е
sin26d6. A3.120)
Очевидно, что коэффициенты A3.116)-A3.120) могут быть
считаны заранее для фиксированного набора значений Tj и с? •.
После чего задача о распределении интегральных радиационных
потоков в неоднородном плоском слое сводится к вычислениям
по формуле A3.115).
Спектральная интенсивность излучения, определяемая для
опорных профилей температуры и концентраций, находится
средством рекуррентного соотношения
[()] .A3.121)
где в качестве J^ F) выбирается граничное значение
Kv,j+l\xJ+l~xj)
Дт.
COS 6
С использованием A3.121) находятся производные по
пературе и концентрациям, входящие в A3.117)-A3.120).
пример, для производных по температуре

386 Гл. 13. Модели нелокального усреднения
A3.122)
дт{ эг,+1
[1-ехр(-Дту,,+1)]
i> ;=U,...,tf. A3.123)
Формулы A3.122) и A3.123) являются рекуррентными,
скольку производные от интенсивности по температуре dTvj/dTi
известны из расчетов предыдущей ячейки.
Изложенный метод является весьма экономичным по
ни расчета и позволяет получить хорошую точность (в первом
приближении разложения в ряды) при условии задания опорных
профилей достаточно близких к исследуемым. Очевидным
татком метода является быстрый рост объемов предварительно
рассчитываемой информации при усложнении компонентного
става смеси и, особенно, при попытке учесть более высокие члены
в разложении.
13.8. Метод эффективных сечений
Метод разработан в работе (Овсянников В.М. и др., 1971).
Подробно изложен и исследован в работе (Овсянников В.М.,
1983).
Формулировка метода дана для излучающего объема
вольной геометрии (рис. 13.4). Вектор плотности интегрального
радиационного потока и его дивергенция записываются в виде
(без учета внешних источников излучения)
00
W(r)= Jcos6dQjdvx
4л О
х J J6>v[r(r')]iV(r')CTv(r')exp[-Axv(r,r')]dr',A3.124)

13.8. Метод эффективных сечений
387
V
divW(r)=Jicv(r)dv- JdQx
О 4л
x J J6v[r(r')]iV(r')CTv(r')exp[-Axv(r,r')]dr', A3.125)
г
r'
Дту(г,г')= \N(r')<jv(r')dr', A3.126)
где
N(r) - число поглощающих частиц в единице объема в
ности точки пространства с радиус-вектором г; г\ - радиус-
вектор произвольной граничной точки; п^ - нормаль к
ной площадке F.
Рис. 13.4. К формулировке метода эффективных сечений
В методе эффективных сечений вводятся три функции,
зываемые эффективными сечениями s,a и е, которые
ляются следующим образом:
хехр
-pV(r')av(r")dr"
. г
dv,
A3.127)

388
Гл.13. Модели нелокального усреднения
хехр
dv, A3.128)
х < 1 - ехр
. г
[dv, A3.129)
где
J*l/(r')]=Rv[>(r')]dv. A3.130)
о
Тогда вектор потока излучения и его дивергенция
ются через эффективные сечения следующим образом:
ч(
W(r)=Jcos6dQ J
A3.131)
JdQ J
г
-47cJ6[r(r)]a?(r)iV(r), A3.132)
4л
где
ст?(г)= Jav(r)J6[r(r)]dv. A3.133)
о
Из соотношений A3.131) и A3.132) следует, что вся
мация о спектральных свойствах среды содержится в
лах ст(г,г') и s(г,г'), между которыми имеется следующая
связь:

13.8. Метод эффективных сечений 389
A3.134)
При этом очевидно, что вся тяжесть проблем
ния по частоте приходится на задачу расчета и формирования
таблиц указанных функционалов. В частном случае разделения
переменных вида
)*(у) A3.135)
*=1
эта задача упрощается.
Если ввести функцию вида
A3.136)
г *=1
то выражение для вектора плотности лучистого потока и его
вергенции примут вид
W(r)= JcosedQX J
4я *=1 г
ха,[г(г'),п,(г,г') п^(г,г')]A«,(г'), A3.138)

390
Гл.13. Модели нелокального усреднения
J Л[^(г')]х
где
-4л/ь[71(г)]а4[71(г),0,0,...,0]},
di%(r>tf(r>4|Y(r')]dr';
A3.139)
oo r
nNЛ = f *'
о •
(v)Ф, (v)exp
v)rij
dv;
0 J>
dv;
>dv.
Порядком приближения метода эффективных сечений
вается число Nk. При Nk =1 получается метод Томсона-Пен-
нера (Пеннер С.С., 1963).
В работе (Овсянников В.М., 1983) приведены алгоритмы
пользования метода эффективных сечений, а также его
шее развитие, получившее название методов групповой
нальности.
13.9. Метод эффективных полумоментных
характеристик
В п. 13.4 отмечено, что главным недостатком метода
нения уравнения переноса излучения, который показал свою
сокую эффективность при решении задач радиационной газовой
динамики, является разрывной характер вводимых эффективных
коэффициентов переноса. При сохранении эффективности
четного алгоритма этот недостаток удается устранить в потоковых
методах.

13.9. Метод эффективных полумоментных характеристик 391
Введение эффективных интегральных коэффициентов в
тоде полумоментов первого порядка, применительно к расчету
переноса излучения в плоском слое выполнено в работе
ский В.В. и др., 1982). Расчет спектральной интенсивности
•Ло (*»ц) в этом случае сводится к решению системы
ных дифференциальных уравнений относительно полумоментных
характеристик (см. п. 9.2):
AA/f+
Ш'п
03-140)
где х - координата, отсчитываемая от нижнего основания по
нормали вглубь слоя.
Интегрируя A3.140) по волновому числу и определяя
гральные полумоментные характеристики по формуле
00
А/± = р<шА»>, и = 0,1,
о
приходим к следующей системе уравнений

392 Гл.13. Модели нелокального усреднения
A3.141)
00
где к* = J КщА/^щёш/Л/* - эффективные среднеинтегральные
о
коэффициенты; кР - среднепланковский коэффициент.
Процедура решения задачи в первом и втором случаях
наковая:
а) ищется решение спектральной задачи A3.140) в
повом приближении, то есть уравнение переноса интегрируется
по пространству на N^ спектральных участках;
б) определяется зависимость интегральных коэффициентов к%
и К/> от пространственной переменной х;
в) уравнения A3.141) решаются на протяжении ряда итераций.
При необходимости процедура повторяется с пункта а).
видно, что экономичность такого метода возрастает при
ном учете спектральной зависимости свойств среды.
13.10. Метод эффективных квадромоментных
характеристик
Метод разработан применительно к проблеме расчета
ционного теплообмена в двумерных осесимметричных объемах с
локальным энерговыделением на оси симметрии (Суржиков СТ.,
1987; Surzhikov S.T., 1996).
В нулевом приближении метода квадромоментов (см. п. 9.4)
относительно спектральных функций c? формулируется
щая система уравнений
<13Л42>
В групповом приближении (с числом групп N^) индекс со
следует заменить на целочисленный индекс k = \,2,...,Nk,
рый означает номер спектральной энергетической группы. Вместо

13.10. Метод эффективных квадромоментных характеристик 393
четырех уравнений вида A3.142) при этом образуется AN^
добных уравнений.
Проинтегрируем A3.142) по всей спектральной области
c± + »-—- + 2JKe)c*da) = 2riceJ4(Bda), A3.143)
г or г oz J J
N
где с± = [с* dco = Л с^ДшА , и введем эффективные интегральные
коэффициенты поглощения
К* --^ jK^dTDS-j^K^dlD» . A3.144)
С С *i
Тогда уравнение A3.143) примет вид
т дгс т ± дс „ + + 2 _4 ,,-, ,..,-ч
<г+ л +2к -с = —КпстГ , A3.145)
г дг г dz n
где К/> - среднепланковский коэффициент. Граничные условия
для уравнения A3.145) получаются интегрированием
вующих спектральных условий по волновому числу.
ство метода квадромоментов состоит в том, что в отличие от
тодов осреднения по полному телесному углу, где введенный по
формуле A3.144) среднеинтегральный коэффициент поглощения
может иметь разрывы 2-го рода, в данном случае - это гладкая
знакопостоянная функция, не имеющая никаких особенностей. В
остальном алгоритм интегрирования спектральных и
ных уравнений остается прежним.

Глава 14
МОДЕЛИ ПОЛОС. СТАТИСТИЧЕСКИЕ МОДЕЛИ
Значительная часть задач теории переноса теплового
чения связана с учетом линейчатой структуры спектра излучения
и поглощения атомов и молекул. При решении этих задач
кое распространение получили статистические модели атомных и
молекулярных линий.
Статистические модели могут быть характеризованы двумя
свойствами, одно из которых составляет несомненное их
ство, а второе - недостаток. Главным достоинством
ских моделей является возможность аналитического
ния уравнения переноса по частоте электромагнитного излучения.
Это практически означает возможность отказа от использования
многогрупповых и line-by-line моделей, что приводит в численных
расчетах к экономии компьютерного времени в десятки и сотни
тысяч раз. Недостатком статистических моделей является
ствие их асимптотической сходимости, т.е. в общем случае
межуточных оптических толщин данные модели всегда дают
грешность расчетов порядка 30%. В пределе оптически тонких
слоев статистические модели обеспечивают точность расчетов не
хуже нескольких процентов.
Несмотря на указанный недостаток развитие статистических
моделей составляет одно из перспективных направлений
менной теории переноса теплового излучения, поскольку, с одной
стороны, эти модели являются реальной альтернативой чрезмерно
трудоемких line-by-line расчетов, а, с другой стороны, их точность
соизмерима с требованиями, предъявляемыми к методам расчета
переноса теплового излучения в задачах астрофизики, атмосфер-

14.1. Общие понятия 395
ной оптики, радиационной газовой динамики и различных
нерных приложениях теории теплообмена.
14.1. Общие понятия
Среди первых попыток решения задачи о переносе
ния в совокупности спектральных линий без line-by-line
рования излучения по спектру электромагнитного излучения
метим метод, состоящий в представлении реального спектра в
де регулярного или хаотичного набора неперекрывающихся
ний. Этот подход имеет простое физическое обоснование.
сложно представить условия, при которых расстояния между
спектральными линиями существенно превосходят их
ны, а оптическая толщина излучающего объема мала даже в
трах спектральных линий. Модель неперекрывающихся
тральных линий оказалась достаточно удобной и получила
кое распространение. Поглощение в совокупности
вающихся линий пропорционально сумме поглощательных
собностей в отдельных линиях, так как каждая линия может
сматриваться как изолированная. Анализ подобных простейших
моделей дан в работе (Гуди Р., 1966).
Аналитическое представление интегральной поглощатель-
ной способности изолированной линии (или так называемой
валентной ширины) с ударным профилем впервые было получено
Р. Ладенбергом и Ф. Райхе (Ladenberg R., et al., 1913)
= 27ryi«exp(-«)[/0 («) + /,(«)], u = Sx/2kvl, A4.1)
где x - отрезок оптически однородного луча; у - лоренцевская
полуширина; S - интегральный коэффициент поглощения в линии
(сила линии). Заметим, что спектральная поглощателъная
собность 4e=l-exp(-Kffl;c) является безразмерной величиной и
обозначает долю излучения с фиксированным волновым числом,

396 Гл. 14. Модели полос. Статистические модели
поглощенным на длине х. Данное определение спектральной по-
глощательной способности справедливо для произвольного kw .
Важно также учесть, что при рассмотрении реального спектра
глощения в газах и плазме, когда атомные и молекулярные линии
наблюдаются на фоне непрерывного поглощения, бесконечные
пределы интегрирования в A4.1) можно приближенно заменить
конечными пределами
где к спектральному диапазону Дсо предъявляется требование
Напомним, что ударное уширение линии описывается
персионной (лоренцевскоЙ) функцией
где а>о ~ волновое число центра линии.
Функция L(u), выражающаяся через функции Бесселя
мого аргумента /о(«) и /(и), называется функцией Ладенбер-
га-Райхе, по имени авторов, получивших это решение.
тические соотношения для функции Дм) при и«1 и и»\
имеют простой вид
которые называют соответственно линейным законом и законом
квадратного корня. Поскольку величина и(х) пропорциональна
оптической толщине в центре линии, то соотношения A4.2)
обретают ясный физический смысл. При малых оптических
щинах поглощение в линии практически не зависит от ее формы и
прямо пропорционально физическому пути пробега излучения.
Когда «(*)» 1, то в центральной части линии происходит полное
поглощение излучения, а зависимость интегральной поглоща-

14.1. Общие понятия 397
тельной способности от х определяется крыльями линий. Исходя
из этого, в работе (Гуди Р., 1966) отмечается, что линейный закон
и закон квадратного корня предпочтительнее трактовать как
ближение слабой и сильной линий соответственно. Особо
черкнем большое значение для теории переноса излучения
дов, следующих из асимптотических соотношений A4.2):
поглощательная способность слоя газа на отрезке луча х в
тральном диапазоне, содержащем атомную или молекулярную
линию, в общем случае не является линейной функцией х. Это
означает, что интегральная на Дсо поглощательная способность
суммы двух отрезков (Д*1 + Дхг) не равна сумме поглощатель-
ных способностей каждого отрезка.
В работе (Тьен К.Л., 1975) приводятся различные
мации функции WL(x) , среди которых наиболее удобна при
расчетах следующая:
A4.3)
В случае, когда уширение линии определяется эффектом
Доплера, ее контур описывается формулой
2/A)J] A4.4)
где yD - доплеровская полуширина.
_, / \ Sx /InT
Если и 1 х) = —тг J оптическая толщина в центре доп-
У
леровской линии, то интеграл
можно представить в виде следующего разложения в ряд
(Тьен К.Л., 1975):

398 Гл. 14. Модели полос. Статистические модели
Аппроксимация эквивалентной ширины линий доплеровско-
го контура выполнена в работах (Huffaker R.M., 1968; Kavanagh
R.W.,etal., 1953):
12 _?0.7 + 0.3ехр[-и(;
_ A4.6)
WD(x) =—p1—A In 1+
V У 2Vnln2V I
В ограниченной области определения 0.1 ^и ^30 можно
использовать простую формулу (Пеннер С.С, 1963)
Наиболее сложным случаем для исследования является
чай лоренц-доплеровского контура линий. Такой контур
ется функцией Фойгта. Обзор работ по исследованию свойств
функции Фойгта содержится в монографии (Пеннер С.С, 1963).
Позднее появились достаточно удобные аппроксимации фойгтов-
ского контура и средней эквивалентной ширины такой линии. В
работе (Huffaker R.M., 1968) используется аппроксимация для
вивалентной ширины фойгтовского контура следующего вида:
AJ]+[l-(^>AJ]-l, A4.7)
, WD=WD/A®,
где Дсо - величина спектрального диапазона, см.
. В работе (Матвеев B.C., 1972) получена удобная
мация функции Фойгта и соответствующей эквивалентной
ны. Зависимость для коэффициента поглощения в линии
ского контура Ку =к(г),4) приведена в п. 12.4. Эквивалентная
ширина линии представляется в виде

14.1. Общие понятия
399
Wy=y
A4.8)
Wv=Wv/2yy =
«4>Hi)-«P -T7ZT
bD=a yj я!п2, Z>i = a • ?, a =
0.6 + 0.4T/. 0.2 + 0.4тд
Ti> TD ~ оптические толщины в центре лоренцевской и доплеров-
ской линий; уу - полуширина линий фойгтовского контура (см.
п. 12.4.1). Наиболее простая аппроксимация средней
ной ширины линии фойгтовского контура, обеспечивающая
ность порядка 8%, представлена в работе (Rodgers CD., et al.,
1974)
Wv
A4.9)
В работе (Гуди Р., 1966) упоминается ряд модификаций
дели неперекрывающихся линий, предназначенных для учета
тичного наложения их друг на друга. Однако эти методы
лись слишком трудоемкими и не получили распространения.
Значительным прогрессом в теории переноса излучения в
реальном линейчатом спектре явилась разработка принципов его

400 Гл. 14. Модели полос. Статистические модели
моделирования эквивалентными по некоторым критериям
купностями спектральных линий. Два основных подхода
ставляют, вообще говоря, два крайних случая: 1) замена реального
спектра линий некоторой эффективной регулярной моделью;
2) представление спектра в виде случайной совокупности линий.
Многолетний опыт использования и развития этих моделей
зал, с одной стороны, на их высокую эффективность, а с другой
стороны, на значительную гибкость этого подхода, т.е.
ность создания на базе регулярной и статистической моделей
большого разнообразия их комбинаций, которые хорошо
сабливаются к реальному линейчатому спектру.
14.2. Статистический подход к расчету переноса
теплового излучения в спектральных линиях
В работе (Гуди Р., 1966) отмечается, что сложно установить
авторский приоритет создания этих моделей, но с исчерпывающей
полнотой они описаны в работах (Гуди Р., 1966; Пеннер С.С.,
1963; PlassG., 1958, 1960, 1967). Отметим здесь также работу
(Смирнов Б.М. и др., 1976), в которой статистическая модель
сформулирована посредством введения характеристической
функции для плотности вероятности оптической толщины, а
же работы (Пеннер С.С., 1963; Сошников В.М., 1961), в которых
затронуты важные вопросы методики расчета. В работе (Пласти-
нинЮ.А. и др., 1981; Суржиков СТ., 1992) дано обобщение
тистических моделей на случай вероятностного описания не
ко распределения интенсивностей спектральных линий, но и их
полуширин, что приобретает особое значение для описания
носа излучения в спектре атомных линий. Этой работе будем
довать при изложении статистической модели.
Пусть в спектральный диапазон Дсо попадает ТУ линий с
личными интенсивностями и полуширинами. Введем функции
плотности вероятностей распределения интенсивностей p(S,S)
и полуширин р(у,у) линий, а также допустим равновероятное
распределение линий в Дсо. Математическое ожидание пропуска-

14.2. Статистический подход к расчету переноса излучения 401
ния газа Тф(х) вдоль некоторого выбранного направления х
но записать в следующем виде
ю о у у S S
N N
где S, Y - математические ожидания интенсивности и
рины линий в исследуемой полосе; кш- суммарный
ный коэффициент поглощения газа, при вычислении которого
учитываются все линии, присутствующие в Дю.
Если выбрать интервал Дсо достаточно большим по
нию с размерами линий, присутствующих в нем, а также учесть,
что все функции />(У/,7) и p{Si,S) взаимно независимы, то
выражение A4.10) можно преобразовать к виду
. A4.11)
Переход от многократного интеграла от произведения
ций к произведению интегралов от соответствующих функций
(см. более подробный вывод ниже, в п. 14.9) получил название
статистический принцип Гуди. Фактически указанный принцип
является гипотезой, в соответствии с которой среднее
ние группы линий равно произведению средних пропусканий
ждой линии в данной группе.
В заданном интервале Дсо могут быть линии с сильно
личающимися значениями интенсивностей и полуширин линий.
Разобьем N линий на К групп, чтобы в каждой отдельно взятой
группе присутствовало Nn линий с близкими параметрами. Тогда
формула A4.11) приобретает еще более простой вид
27 Зак. 272

402 Гл. 14. Модели полос. Статистические модели
Л=1
\
s J я=1
Полученная формула является наиболее общим выражением
статистической модели, в которой, в отличие от известных ранее
соотношений, учитывается плотность вероятности распределения
полуширин />(У/,7)- Существенно также введение групп линий,
объединяемых по определенным признакам.
При задании функций p(St,S), /?(у/,у) и функции
ров линий можно получить простые аппроксимационные
лы для Dn. Так, в случае молекулярных вращательных линий
наиболее яасто используется экспоненциальное распределение
линий по интенсивностям вида
= [exp(-S/s)]/s ,
что позволяет получить для интегральной поглощательной
собности формулу (при К = 1)
A4.13)
Условия К = 1 и /?(y,Yi) = 5(y-Y1) соответствуют
стой статистической модели Гуди (Гуди Р., 1966). В этом случае
D\ вычисляется с использованием параметров всех линий. Усло-
_ N _
вия K = N, р(у,у) = р(у,у„) и p(S,S) = j^b(S-S)/N дают
/=i
обобщенную статистическую модель Гуди (Гуди Р., 1966).
Более общее выражение обобщенной статистической модели
получается при введении двумерной плотности распределения
вероятностей

14.2. Статистический подход к расчету переноса излучения 403
()(Y/)- 04.14)
я ,=1
Очевидно, что обобщенная статистическая модель
ет индивидуальные параметры каждой линии точнее, чем простая
статистическая модель, но требует значительно больших затрат
компьютерного времени и оперативной памяти.
В случае, когда 1<K<N пропускание Д, вычисляется с
использованием параметров тех линий, которые принадлежат л-й
группе. В работе (Пластинин Ю.А. и др., 1981) такая модель
звана групповой обобщенной статистической моделью. Ее также
можно трактовать как одну из разновидностей моделей
ческого наложения регулярных и случайных моделей (Гуди Р.,
1966).
К вопросу о понимании сущности статистического
рования спектра следует добавить, что применение
ской модели к одной спектральной линии не противоречит
ным посылкам о множественности линий. Каждую линию можно
периодически продолжить за пределы рассматриваемого
трального диапазона, величина которого, таким образом, будет
отвечать среднему расстоянию между линиями в их бесконечной
последовательности. Бели поглощение в крыльях линий
ется существенным, т.е. учет линий вне диапазона дает заметный
вклад в поглощение, то, предполагая профиль линии в далеких
крыльях лоренцевым (или степенным), можно получить среднюю
«фоновую» добавку, например, в виде (для лоренцевских линий)
/-=Дсо~1 f Kmdco = f У
яДю /=0
Оценку необходимого числа слагаемых в этой формуле
сложно сделать в каждом конкретном случае.
27*

404 Гл. 14. Модели полос. Статистические модели
14.3. Усреднение параметров спектральных линий
в неоднородных объемах сплошной среды.
Приближение Кертиса - Годсона
До сих пор предполагалось, что объемы излучающей и
глощающей сплошной среды, в которой распространяется
ние, являются однородными. Это означает, что в любой точке
следуемого объема свойства среды остаются постоянными.
этому статистические модели спектральных линий были
рены для независящих от пространственных координат
гральных коэффициентов поглощения (сил линий) и полуширин
линий. Значительно больший практический интерес представляют
случаи неоднородной среды.
Основная сложность расчета переноса линейчатого
ния вдоль неоднородной трассы состоит в том, что параметры
спектральных линий могут сильно изменяться в зависимости от
положения рассматриваемой точки внутри неоднородного объема.
В условиях непрерывного спектра поглощения это создает
чительные трудности, связанные с заменой произведения на
грал в формуле расчета оптической толщины: в однородном
еме оптическая толщина участка nyraCxg -xq)рассчитывается как
произведение хт = kw(x^ -хо), а в неоднородном - в виде
грала
] A4.16)
Как в том, так и в другом случаях оптическая толщина всего
слоя является аддитивной по отношению к оптическим толщинам
своих частей. Следовательно, интеграл A4.16) может быть
ставлен в виде суммы
*«,=! ] Kw(x')dx'. A4.17)
'=0 х,
Поскольку в подавляющем числе практически важных
чаев спектральный коэффициент поглощения в непрерывном

14.3. Усреднение параметров спектральных линий 405
спектре мало меняется в пределах выделенных спектральных
пазонов (например, на участке, где есть несколько близко
ложенных спектральных линий), то свойство аддитивности
ведливо и для средней оптической толщины на участке
*д«, = 1 )'кДо, (*')<*'• A4.18)
'=о ,,
(х) = —
где кАв)(х)
Принципиально иная ситуация возникает при анализе
носа излучения вдоль неоднородной трассы в спектральных
ях атомов и молекул. Здесь средняя оптическая толщина на
тральном участке Асо не является аддитивной даже при
родном оптическом пути. Примером этому может служить закон
квадратного корня для изолированной линии лоренцевского
тура (см. п. 14.1). Когда же слой становится неоднородным, то
пользовать процедуру суммирования типа A4.18) невозможно.
Оптическую толщину приходится определять сразу между двумя
точками xq и *5 • Однако и эту процедуру не удается выполнить
просто, поскольку оптическая толщина нелинейно зависит от трех
независимо изменяющихся в пространстве параметров: ?(х),
yL (х), yD (x). Поэтому, прежде чем применить статистическую
модель спектральных линий, необходимо решить вопрос о
лемом способе интегрирования уравнения переноса вдоль
ски неоднородного луча. С математической точки зрения
ма состоит в нахождении удачной процедуры расщепления
грального оператора двойного интегрирования (по пространству и
по частоте электромагнитного излучения) на произведение двух
однократных интегралов по разделенным переменным. Более
глядно эту процедуру можно представить как поиск параметров
такого эффективного однородного слоя, излучение и поглощение
которого эквивалентно реальному неоднородному слою.
лее удачным методом решения этой проблемы является
жение Кертиса-Годсона (Curtis A.R., 1952; Godson W.L., 1953).

406
Гл. 14. Модели полос. Статистические модели
Идея данного метода была высказана также в других работах (van
de Hulst H.C., 1945; Plass G.N., 1956).
Основной смысл данного метода состоит в замене истинного
неоднородного пути некоторым эквивалентным однородным.
Эффективные параметры указанного однородного пути находятся
из условия равенства пропусканий эквивалентного и истинного
неоднородного слоев в предельных случаях сильных и слабых
ний. Очевидно, что при промежуточных значениях оптических
толщин возможно возникновение ошибок. Как показали
вания, точность приближения Кертиса-Годсона зависит не
ко от оптической толщины слоя, но и от степени неоднородности
слоя. Рассмотрим эти вопросы подробнее.
Эквивалентная ширина совокупности линий на
ном участке Асо для неоднородного отрезка пути (х§ -хо)
деляется по формуле
-Jkj
A4.19)
а для его части
= Н1-
Аш
L *\
A4.20)
Спектральная интенсивность излучения в точке х§, как это
следует из уравнения переноса, равна
dx', A4.21)
*0
где Jw(xq) - интенсивность излучения, падающего на
ваемый объем газа от внешнего источника. В дальнейшем
ся допущения физического характера относительно спектральной

14.3. Усреднение параметров спектральных линий 407
зависимости функций Jw(xq) и Jbm(x). Предполагается, что на
участке Асо эти функции изменяются незначительно, поэтому их
можно заменить средними величинами Jaw(xq) и Л.доЛ*) на
участке спектра Дсо. Это позволяет записать
Д(В - W (*
Из A4.22) следует решение для однородного пути
(хь) До) = УДв) (х0)[ао) - W* {хо,хь)] + Л*>Дш W* {х0, х&) .A4.23)
Звездочка в A4.23) означает, что соответствующие величины
определены для некоторого однородного слоя. Приравнивая
вые части соотношений A4.22) и A4.23), получаем исходное
уравнение для отыскания параметров эквивалентного
го слоя
'. A4.24)
Из этого соотношения нельзя получить однозначные
мые условия, поскольку зависимость Л.ДшОО может быть
извольной. Однако некоторые общие предварительные
ния высказать можно. Рассмотрим два случая. Первый состоит в
пренебрежении собственным излучением, тогда
*И*0>*8) = »Ч*0>*8)- О4-25)
Во втором случае, наоборот, пренебрежем внешним
нием Удд, (*о )
(x')dW{?Xs)<ix'. A4.26)
«о
= "

408 Гл. 14. Модели полос. Статистические модели
Отсюда очевидно, что если на трассе (*§ -*o) функция
лучения Jb,Aw(x') меняется незначительно, то ее можно вынести
из-под интеграла и в результате придем опять к формуле A4.25).
Следовательно, A4.25) можно использовать для определения
раметров эквивалентного слоя только при условии слабого
нения Jb,Aw(x') вдоль трассы. Однако при численных расчетах
переноса излучения формула A4.26) в непосредственном виде не
используется. Интеграл в правой части A4.26) преобразуют
к виду
АмИЬ)] (Н.27)
/=о
Здесь среднее значение функции Л,Да>,/ на участке [х,,х/+1]
выносится за пределы интеграла, поэтому качество такого
ближения уже существенно зависит от расчетной сетки.
лы типа W(xh xs) берутся по неоднородному оптическому пути и
именно их удобно заменить интегралами вида W* (х/, х§). В этом
случае снова применима формула A4.25), но следует иметь в
ду, что в A4.27) входит разность между двумя эквивалентными
ширинами, поэтому погрешность вычисления разности может
оказаться больше, чем погрешность вычисления отдельных
гаемых. На это было обращено внимание в работах (Lindquist
G.H., et al., 1972; Young ST., 1975), что, как будет показано ниже,
привело к созданию модификации метода Кертиса- Годсона.
Рассмотрим сначала получение основных соотношений Кер-
тиса-Годсона. Исходным является соотношение A4.25). Пусть в
спектральном диапазоне Асо есть N линий, тогда суммарный
спектральный коэффициент поглощения определяется по
формуле
к» (*') = ?*«>,,(*') A4-28)

14.3. Усреднение параметров спектральных линий
409
и соотношение A4.25) имеет вид
J ехр
Аш
N
N
~ехР ~
1=1
= 0.A4.29)
Рассмотрим модель неперекрывающихся линий для того,
чтобы соотношение A4.29) можно было применить к одной
нии. В этом случае спектральный диапазон Асе»;, принадлежащий
Асо и охватывающий мо линию, также оказывается много
ше, чем полуширина i-й линий
J ехр
Дш,
Ч N
]
= 0. A4.30)
В случае слабой линии вместо интеграла A4.30) получим условие
ч
fdx' | Kw>t(x')d<s> = (xb-x0) J K^da), A4.31)
x0 Дю,
Дш,
и, поскольку величина Асо/ предполагается много больше, чем
ширина линии, то
s;=-
A4.32)
Это первое из двух основных соотношений приближения
Кертиса-Годсона. Отметим, что функция контура линии не
валась, поэтому формула A4.32) может применяться как для ло-
ренцевских, так и для доплеровских линий.
В случае, когда выполняется «закон квадратного корня»,
линия поглощает как абсолютно черное тело во всей области,
кроме далеких крыльев. Второе условие приближения
са-Годсона получим исходя из того, чтобы в далеких крыльях
поглощение в однородном и неоднородном слоях было
вым. Рассмотрим линии лоренцевского контура. Главной
ной выбора лоренцевского контура является то, что в далеком
26 Зак. 272

410 Гл. 14. Модели полос. Статистические модели
крыле линия фойгтовского контура описывается дисперсионной
(лоренцевской) функцией. Кроме этого, уширение линии допле-
ровского контура пропорционально квадратному корню из
ратуры, так что в рассматриваемом диапазоне температур допле-
ровская полуширина может измениться не более чем в 3 раза (при
изменении температуры от 2000 до 20000 К). После получения
соотношения для эквивалентной полуширины лоренцевского
тура мы распространим его и для эквивалентной полуширины до-
плеровского контура, надеясь, что этим мы добьемся большей
точности. В формуле A4.30) введем новую шкалу волновых
сел, отсчитываемую от центра i-й линии, и интеграл по волновому
числу представим в виде
exp
о
d© - j ехр [-к^, (дс6 - ^)] da>+
+ Jexp
К,
00
da) - J exp [-к;, (x8 - xq)] da) = 0. A4.33)
@,
Выберем слой (xg -xq) настолько толстым, чтобы с любой
наперед заданной точностью первые два интеграла в A4.33)
ращались в нуль. При этом потребуем, чтобы coi»max|yf] .
Несложно показать (подынтегральные функции удовлетворяют
условию знакопостоянства их производных по частоте), что
тавшиеся два интеграла приводят к формуле
-, A4.34)
которая является вторым искомым соотношением приближения
Кертиса - Годсона.
Метод Кертиса-Годсона неоднократно применялся в
тах переноса излучения вдоль неоднородных трасс в
ных и атомных линиях. Исследование переноса излучения в
ных высокотемпературных слоях, образующихся у лобовой
верхности затупленного тела при его входе в плотные слои атмо-

14.3. Усреднение параметров спектральных линий 411
сферы с гиперзвуковой скоростью (Суржиков СТ., 1992),
ло на удовлетворительную точность аппроксимации Кертиса-
Годсона. Его использование совместно с обобщенно-групповыми
статистическими моделями спектра дало погрешность на уровне
30%. Хорошо зарекомендовало себя это приближение и в задачах
атмосферной оптики (Гуди Р., 1966). Исследование метода Керти-
са-Годсона проводилось в литературе по двум направлениям. Во-
первых, анализировались погрешности этого приближения в
симости от степени неоднородности слоя, во-вторых,
лись неизолированные линии и полосы, где, помимо всего
го, приходится вводить эффективные параметры линий, осред-
ненные по полосе. Пример интегрирования переноса излучения в
полосе приведен в (Krakov В., et al., 1966). В работах
(Simmons F.S., 1966, 1967) приведен анализ эквивалентной
ны линии лореицевского контура в двух предельных случаях
сильной и слабой линий. Исследованию переноса излучения в
изолированной линии лоренцевского контура посвящена также
работа (Gogley А.С., 1970). Расчеты, проведенные в этой работе,
показали, что уровень погрешности не превосходит 5% в
ком диапазоне оптических толщин. Сопоставление метода Керти-
са-Годсона с подходом учета неоднородности, в котором
фициент поглощения разлагается в ряд в окрестности конца
тервала интегрирования, выполнено в (Chan S.H., et al., 1969). В
работе (Simmons F.S., et al., 1970) показаны расчеты излучения от
пламен, содержащих СОг и НгО через холодные слои атмосферы.
В работе (Lindquist G.H., et al., 1972) выполнен анализ
чин больших погрешностей, возникающих при расчете переноса
излучения в неоднородных слоях. Показано, что точность расчета
разности между эквивалентными ширинами слоев различной
щины (производной от эквивалентной ширины) гораздо ниже, чем
точность расчета самих эквивалентных ширин. Развитие данной
работы выполнено в работе (Young S.J., 1975), где сформулирован
способ расчета производных от эквивалентных ширин и
лены результаты обширных расчетов для линий лореицевского и
доплеровского контуров. Получены также асимптотические
мулы для расчета производных от эквивалентных ширин.
26*

412 Гл. 14. Модели полос. Статистические модели
Основное отличие применения аппроксимации Кертиса-
Годсона к расчету переноса излучения в полосе линий от расчета
изолированной линии состоит в замене эффективной
сти средним коэффициентом поглощения, а эффективной
ширины средним отношением полуширины к расстоянию между
линиями (Young S.J., 1975).
Укажем также на работы (Киселев К.А., 1979, 1981), где
даны аналитические методы расчета среднего пропускания
нородных молекулярных слоев в линиях фойгтовского контура.
Этот подход основан на разложении контура оптической толщины
в спектральной линии в ряд Фурье.
В заключение заметим, что методы расчета переноса
ния в спектральных линиях, представленные в работах
mons F.S., 1967; БронинСЯ. и др., 1970, 1977; Wilson K.H., et al.,
1971; Кондранин Т.В. и др., 1981) также во многом базируются на
основной идее метода Кертиса-Годсона.
14.4. Эквивалентная ширина и средняя поглощательная
способность групп атомных линий в модельном
представлении
Оценка точности статистических моделей выполнена в
те (Суржиков СТ., 1992) по результатам численных расчетов по-
глощательной способности однородных и неоднородных газовых
слоев в различных группах линий атомов азота, кислорода и
рода. В качестве точных значений интегральной поглощательной
способности А принимались результаты полинейчатого
line) численного интегрирования поглощения вдоль луча.
Многочисленные расчеты показали, что применение простой
статистической модели к расчету переноса излучения в атомных
линиях приводит к погрешностям ~ 100% и более, а
ние групповых и обобщенных статистических моделей позволяет
производить вычисления с точностью порядка ~ 30%.
При вычислениях поглощательных способностей
родных слоев газов (исследовались высокотемпературные удар-

14.4. Эквивалентная ширина и средняя поглощательная способность групп 413
ные слои, образующиеся у лобовой поверхности затупленных тел,
входящих в плотные слои атмосферы с гиперзвуковыми
стями), статистические модели использовались совместно с
ближением Кертиса-Годсона, что вносило дополнительную
грешность в результаты расчетов. Применялась модификация
тода Кертиса-Годсона, которая заключается в том, что
тивные интенсивность и полуширина атомных линий в
лентном однородном слое рассчитываются не для каждой
тральной линии, а для группы линий.
При использовании модельного представления спектра
вместно с приближением Кертиса-Годсона, можно указать, по
крайней мере, два варианта усреднения по частоте и по
ству вдоль неоднородного луча: 1) для каждой из линий
тываются средние параметры вдоль луча, а затем статистическая
модель применяется к расчету переноса излучения в эффективном
однородном слое с постоянными параметрами линий; 2) в каждой
точке пространства на выделенном луче определяются средние
параметры для группы, а затем эти групповые параметры осред-
няются вдоль луча.
Заранее понятно, что первый из указанных путей является
более точным, поскольку поглощательные способности истинного
и эквивалентного однородного слоев согласуются для каждой
нии. Однако этот путь является и существенно более трудоемким
из-за необходимости расчета интегралов вдоль слоя для каждой
линии. Для удобства анализа различных моделей, целесообразно
разбить их на три группы. Введем также среднюю поглощателъ-
ную способность газа в спектральном диапазоне Дю: А = А/Аса и
среднюю эквивалентную ширину W = JF/Aco.
Ниже даны расчетные соотношения для каждой из групп
тодов. Главное отличие между этими расчетными методами
стоит в способе усреднения интенсивностей и полуширин в
купностях учитываемых линий. Что касается способа
мации эквивалентных ширин, то это не является принципиально
важным. Для примера здесь используется одна из аппроксимаций,
представленных в п. 14.1.

414 Гл. 14. Модели полос. Статистические модели
1-я группа: Простые статистические модели (т = 1,2).
Поглощательная способность N линий, присутствующих в
спектральном диапазоне волновых чисел Асо, определяется по
формулам
Здесь для расчета эквивалентной ширины Wv =Wy(x,aL,aD)
используется аппроксимация (Rodgers CD., et al., 1974)
Wv =^W? + W*+(wDWL/x2f , A4.36)
в которой
& \ A4.37)
A43S)
В зависимости от способа расчета функций Ys и Yl(D)
дем различать модели:
' «6 ' *b
т = 2
Х6 N
?/(Су/ JS, A4.40)
где S - интегральный коэффициент поглощения в линии (сила
нии); у - полуширина линии; индексы L и D означают тип уши-
рения - лоренцевский или доплеровский; / - индекс линии;
*о, *5 ~ границы отрезка неоднородного луча в пространстве.

14.4. Эквивалентная ширина и средняя поглощательная способность групп 415
Первая из приведенных моделей отвечает простой
ческой модели Гуди с параметрами эффективного однородного
слоя, определяемыми по методу Кертиса-Годсона. Недостаток
этой модели состоит в необходимости расчета двух интегралов по
пространству для каждой линии. Вторая модель строится на
положении о допустимости расчета интегралов от суммарных
функций, единственным обоснованием которой является
ложение о компенсации погрешностей средних величин
мых, распределенных случайным образом. Эта модель весьма
экономична, так как требует вычисления лишь двух интегралов
для спектрального диапазона Асо.
2-я группа: Обобщенная статистическая модель (т = 3).
Здесь поглощательная способность рассчитывается по
формулам
x,=YSJ/Am, aL{D%t=YL{D)i/A<i>, A4.41)
Ys>{ = Jfyfc, YL{D)>i = \styL{Dlidx
/
3-я группа: Обобщенно-групповые статистические модели
(т = 4,5).
Расчетные соотношения имеют следующий вид:
= 1 - exp
A4.42)
» aHD),k=YL(D),k/A(i>>
)dx, A4.43)

416
Гл. 14. Модели полос. Статистические модели
,d*. A4.44)
Видно, что модели 4 и 5 соответствуют моделям 1 и 2, но
строятся для отдельных групп линий. Заметим, что при расчете
эффективных полуширин Уцо) по формуле A4.43) можно
пользовать другие подынтегральные функции, например
I
однако численные эксперименты показали, что эта замена не дает
ощутимых положительных результатов.
14.5. Эквивалентная ширина и поглощательная
способность полос вращательных линий при
электронно-колебательно-вращательных переходах
Электронный спектр двухатомных молекул обладает
сительно хорошо идентифицируемой структурой, что делает
обоснованным использование для описания такого спектра
щенно-группового подхода.
Поглощательная способность молекулярного газа на отрезке
луча [jco.xg] для диапазона волновых чисел Асо определяется
формулой
1
Асо
J
1-ехр
х0 ее' ии' Jf
dco, A4.45)
где кш (х) - коэффициент поглощения во вращательной линии.
Здесь суммирование производится по электронным (ее'),
колебательным (vv')n вращательным {jf) переходам. Расчет
эффициента поглощения кш (х) состоит, как и прежде, в задании

14.S. Эквивалентная ширина и поглощательная способность полос
функции профиля линии и параметров, определяющих эту
цию: интегрального коэффициента поглощения S, полуширины у
и волнового числа со о центра этой линии. Коэффициент
щения, получаемый суммированием по всем вращательным
ям, определяет так называемый синтетический спектр
глощения.
Если не использовать статистические модели спектра, то при
проведении line-by-line расчетов поглощательной способности по
формуле A4.45) контур линии можно описывать функцией Фойг-
та. Интегральные коэффициенты поглощения вращательных
ний S вычисляются с использованием данных по электронным
силам переходов, факторам Хенля-Лондона и Франка-Кондона.
При выполнении line-by-line расчета минимальный шаг
четной сетки по волновому числу со следует выбирать таким,
бы описать половину контура линии с чисто доплеровским уши-
рением не менее чем в 10 точках. В каждой расчетной точке
лы со определялся суммарный коэффициент поглощения с
зованием аппроксимации фойгтовской функции. Ограничение на
наибольшее вращательное квантовое число вводится при расчете
синтетического спектра по рекомендациям (ГурвичЛ.В. и др.,
1978).
Именно большая трудоемкость расчетов по формуле A4.45)
объясняет необходимость использования статистических
делей.
Поглощательная способность слоя газа, при расчете по /я-й
модели, может быть записана в виде
4, =l-exp[-?S2X (w'J, A4.46)
L ее' vt/ л=1 J
где суммирование ведется по электронным (ее') и колебательным
(vv) переходам, а также по ветвям колебательных полос (п).
личина L отвечает числу учитываемых вращательных полос. Так,
при Ь = Ъ, когда учитывается вращательная структура спектра
(Р-, Q-, R- ветви), т.е. средняя эквивалентная ширина Wm (vv\ ri)
рассчитывается только для линий, принадлежащих л-й ветви, и

418 Гл.14. Модели полос. Статистические модели
L = 1, когда вращательная структура не учитывается, т.е. средняя
оптическая толщина определяется по линиям колебательного
рехода w', безотносительно к принадлежности той или иной
ви. Заметим, что число ветвей может значительно превышать
тываемые здесь три ветви.
Как и прежде (см. п. 14.4), исследуемые модели удобно
представить в виде двух групп. К первой группе (модели 1 и 2)
относятся модели, в которых контуры вращательных линий не
учитываются. Это наиболее грубые модели спектра. В них
пользуется средний коэффициент поглощения каждой линии,
лученный делением ее интегрального коэффициента поглощения
на величину некоторого спектрального диапазона.
ние по пространственной координате проводится по методу Кер-
тиса-Годсона.
Модель 1{L = 1).
Средняя эквивалентная ширина находится по формуле
, ^ A4.47)
Асо , л*
где Nv - число вращательных линий в колебательном переходе,
попавших в Лео* с Асо. Отметим, что величина спектрального
диапазона Асо*, в пределах которого ищется средняя оптическая
толщина, должна выбираться меньшей, чем Асо.
Модель 2 (L = 3).
Средняя эквивалентная ширина находится по формуле
W2(vv',n) = -^- f^Ji-dx, A4.48)
где Nv<n - число линий л-й ветви полосы uv', попавших в Асо*;
Асо i - расстояние между ближайшими линиями в ветви п.
Отличие этой модели от первой состоит в том, что здесь
средний коэффициент поглощения линии рассчитывается не в

14.5. Эквивалентная ширина и поглощательная способность полос
419
диапазоне Дсо*, а только в его части Дсо / с: Дсо*, т.е. лучше
тывается реальное расположение линий.
Ко второй группе анализируемых моделей (модели 3 и 4)
относятся статистические модели с экспоненциальной плотностью
вероятности распределения интенсивностей линий. В них
вается реальный контур вращательных линий. Отличие между
этими моделями состоит в способе разбиения всей совокупности
линий, попавших в Дсо, на группы. Отметим, что это оказывается
важным при расчете переноса излучения в неоднородных слоях
или при исследовании распространения излучения селективного
источника в селективно поглощающей среде.
Модель 3(L = 1).
Это статистическая модель, в которой линии группируются
по принадлежности к колебательной полосе, а для учета
тия групп используется статистический принцип Гуди. В данном
случае средняя эквивалентная ширина линий с фойгговским
туром аппроксимируется согласно (Huffaker R.M., 1968).
родность слоя учитывается в приближении Кертиса-Годсона. С
учетом сказанного
=](S)(l/d)
dx, A4.49)
-2
-2
-k-x]fL(x)*xt
*0
-1,
-V2
]/d{xNx,

420 Гл.14. Модели полос. Статистические модели
% ? d=A<o/Nv
Модель 4 (L = 3).
В этой модели линии группируются по принадлежности к Р-,
Q-, или /{-ветви каждой колебательной полосы, поэтому расчет
W4(vv',n) производится по формулам A4.49), в которых следует
заменить Nv на Nv>n. Следует также учесть, что количество
вей вращательных линий может быть значительно больше, чем
три. В этом случае суммирование необходимо проводить по всем
ветвям.
14.6. Применение статистических моделей к расчету
переноса селективного излучения в плоских слоях
низкотемпературной плазмы
В п. 14.1 было показано, что поглощательная способность
слоя газа на спектральном участке, содержащем атомные или
лекулярные линии, в общем случае не является линейной
ей физической длины отрезка луча, вдоль которого
ется излучение. Этот, на первый взгляд, не слишком
ный факт имеет своим следствием то, что большинство методов
интегрирования уравнения переноса излучения по угловым
менным несовместимы со статистическими моделями спектра
глощения, позволяющими проводить интегрирование уравнения
переноса излучения по волновому числу. В данном разделе
смотрен одни из методов интегрирования по угловым
ным - метод полумоментов, который допускает объединение со
статистическими моделями спектра.
Рассмотрим задачу интегрирования уравнения переноса
лучения в плоском неоднородном слое по спектру на отдельном
спектральном диапазоне, содержащем атомные линии.

14.6. Применение статистических моделей к расчету переноса излучения 421
Уравнение переноса селективного излучения применительно
к плоскопараллельной геометрии без учета светорассеяния в
ближении локального термодинамического равновесия запишем
относительно спектральной интенсивности излучения Jw
cLL
T -
A4.50)
где Jb,w - планковская спектральная интенсивность; ц = cosQ, 6
- угол между направлением распространения излучения и
жительным направлением оси х, нормальной к рассматриваемому
слою (Х\ = 0, хн = Н - границы плоского слоя, рис. 14.1)).
J+(x=0)
\
х=0
Л
Г{х
/
х=Н
=0)
/
X
Рнс. 14.1. Схема переноса излучения в плоской геометрии
Введем спектральную оптическую толщину скш = KfflcLt. В
соответствии с методом полумоментов (см. п. 9.2) подействуем на
A4.50) полумоментными операторами следующего вида:
Л+ = 2%
в результате чего получим
dM"+l.o>
•
и Л" = 2л
-l
2Л
'b,w>
п +
11 = 0,1,2,...
. « = 0,1,2,...
A4.51)

422 Гл.14. Модели полос. Статистические модели
1 О
где Л/;ш = 2яp>i, Л^>ш = 2тс \raV.nd)x, A4.52)
О -1
индексами «+» и «-» у спектральной интенсивности фиксирована
ее принадлежность областям 8 е [0, тс/2] и 8 е [тс/2, тс]
ственно.
Для замыкания бесконечной системы уравнений необходимо
постулировать вид угловой зависимости интенсивности
ния, в каждом из полупространств, например
^/^, A4.53)
где Р - порядок приближения. Далее рассмотрим приближение
второго порядка Р = 2, в котором имеется линейная зависимость
интенсивности от ц: У* =af\i+a2 , что дает однозначную связь
между полумоментными характеристиками
-А/п. A4-54)
Подставляя A4.54) в A4.51) при л = 0,1, получаем систему
уравнений
'
+ Af0(B =
ТШ (Н.55)
которая при граничных условиях вида
(х = Я) = 0, A4.56)

14.6. Применение статистических моделей к расчету переноса излучения 423
имеет следующее решение:
2
<<»(*«,) - 0.5 ? ЙГ J '*.. exp [-ft. (х. - х)] dx,
т=\ о
m=l
где
= 0,1; xffl =
Если в постановке задачи учитываются потоки излучения,
падающие на границы х = 0 и х = Н ,то соответствующие
ничные условия формулируются с использованием формул
A4.52) и подходящей аппроксимации угловой зависимости
тральной интенсивности излучения. Заметим, что, несмотря на
простоту соотношений A4.57), следует иметь в виду особенность
аппроксимации функции Планка на оптически толстых расчетных
ячейках (см. п. 3.2).
С целью применения статистического метода учета
той структуры, проинтегрируем по спектру соотношения A4.57) в
пределах спектрального диапазона Дсо
= О.5 (-1
m=l
m=\
где
0 Am
Н
Am
-ft./к. (*•)<!*•
A4.58)
dco,
ёш.
Дальнейший анализ достаточно выполнить для одного из
интегралов, например 1„{х)

424
Гл.14. Модели полос. Статистические модели
A4.59)
где Wm (х,х')= jJl-exp
Введем конечно-разностную сетку то = {xj¦¦, j = 1, 2, 3, ..., б
где xi = 0, дс8 = Я}. Тогда для любого фиксированного узла сетки
с индексом / имеем
8-1
j-f
-Vrm(xf>XjJ]- 04.60)
Считая поглощение в атомных линиях к^ (дс) аддитивным с
поглощением в непрерывном спектре к?, (х) = кс (х), т.е.
кш (*) = к^ (х)+ Kg, (x), получаем
где
A4.61)
>do, A4.62)
о
W*m{xf,Xj)= J 1-ехр
~ эквивалентная ширина линий, попавших в
тральный диапазон Дсо.

14.6. Применение статистических моделей к расчету переноса излучения 425
Для определения эквивалентной ширины FF?(jt/,jty)
пользуемся статистической моделью спектра
К (xf,Xj ) = ЛДи>от Дю = [l - ГД(М1Дю] До =
A4.63)
а среднее пропускание группы линий g, имеющих фойгтовский
контур, аппроксимируем следующей связью между пропусканием
групп линий с лоренцовским Df и доплеровским контуром
D%g (Rodgers CD., et al., 1974):
Функции Xm,g> aL,g> aS,g определяются в рамках
ния Кертиса-Годсона для каждой g-й группы линий
xj
\NaFg[T{x')]dx',(\4.6S)
от,г) \NaFg[T(x')]NeGLtg[T(x')]dx', A4.66)
= (рот/До,2Хот,,) ]"aFg[T(x')]"eGD,g[T(x')]dx'. A4.67)

426 Гл. 14. Модели полос. Статистические модели
Введенные групповые функции Fg,Gi,,g и Gu,g
нальны суммарному интегральному поглощению всех линий Ng
данной g-й группы, сумме лоренцевских yL и доплеровских yD
полуширин (Суржиков СТ., 2004 (а)):
N.
тс
N.
7=1
где Л/д,^е - концентрация поглощающих атомов и электронов;
//,g7 - сила осциллятора в поглощении и статистический вес
нижнего уровня с энергией Ej, при переходе с которого
ется атомная линия; C°j, C+j - константы квадратичного
та Штарка при уширении атомных (а) и ионных @ линий; со0>7 -
волновое число центра у'-й линии; Sj - интегральный
ент поглощения ву-й линии; Ма - атомный вес; Q -
ская сумма по состояниям:
где La - число энергетических состояний, учитываемых для
ного атома, к - постоянная Больцмана.
Обратим внимание на то, что в условиях локального
динамического равновесия групповые функции зависят только от
температуры и не зависят от заселенностей поглощающих
ней. Это означает, что при расчетах переноса излучения они могут
быть определены один раз заранее. При практической численной

14.7. Математическая технология обработки информации 427
реализации такого подхода температурные зависимости в круглых
скобках A4.69) можно включить в подынтегральные выражения
A4.66) и A4.67), тогда для каждой группы остается запомнить в
памяти компьютера лишь две постоянные, вычисляемые
рованием констант квадратичного эффекта Штарка и волновых
чисел центров линий.
14.7. Математическая технология обработки
информации по атомным линиям для расчета
температурных зависимостей групповых функций
В работе (Суржиков СТ., 1993 (б)) показано, что
вание метода полумоментов совместно со статистическими
лями групп атомных линий позволяет с высокой вычислительной
эффективностью решать задачи о переносе теплового излучения в
слоях низкотемпературной плазмы. Экономия расчетного времени
составляет порядка 104 раз, а ожидаемая точность предсказания
плотностей радиационных тепловых потоков оценивается в
20+30%. Для успешного использования данного метода
димо реализовать алгоритм построения групповых функций
ных линий. Алгоритм включает в себя следующие этапы.
1. Определение номенклатуры атомных линий.
2. Расчет параметров этих линий S, fj, gj, Ej ,C°j, C'4j-, oo0 j,
т.е. величин, позволяющих рассчитать функции A4.68)- A4.70).
3. Выбор спектральных групп, в пределах которых будет
пользоваться статистическая модель.
4. Расчет групповых функций A4.68)—A4.70) для каждой
группы.
Учитывая большое число атомных линий, целесообразно
компьютеризировать указанную процедуру. Пример базы данных
атомных линий элементов С, N, О, С+, NT, O+ приведен в работе
(Surzhikov S.T., 2002 (а)). Указанная база данных, в свою очередь,
была создана с использованием специально разработанных
матизированных процедур расчета параметров атомных линий на
основе компьютерного представления информации, содержащей-

428 Гл.14. Модели полос. Статистические модели
ся в электронной базе данных уровней энергии атомных частиц,
созданной на основе таблиц экспериментальных значений
ней энергии атомов и ионов (Moore C.E., 1949, 1952, 1958).
данная таким образом электронная база данных уровней энергии
представлена также в работе (Surzhikov ST., 2002 (а)).
14.8. Перенос излучения в объемах произвольной
геометрии с учетом спектральных линий
Среди рассмотренных методов интегрирования уравнения
переноса по угловым переменным особое место занимает метод
дискретных направлений (Ray-tracing method), поскольку только
этот метод наиболее гармонично сочетается со статистическими
моделями спектральных линий. В рамках указанного метода
чет плотности интегрального потока излучения путем
вания уравнения переноса излучения вдоль луча с применением
статистических моделей производится очевидным способом.
нако вычисление дивергенции плотности потока излучения с
пользованием этого метода является чрезмерно трудоемким.
Рассмотрим применение статистической модели спектра при
нахождении интегральной (или групповой) дивергенции
го потока в случаях, когда в выделенной точке пространства xq
известна спектральная интенсивность излучения Ja(xo)
ков СТ., 1993 (а)). В этом случае дивергенция группового
стого потока определяется по формуле
= 47Г J Kffl (*о ) Jba (ХО ) dO) -
Да
M*o) J^U.«)d«d(o, A4.72)
Да 4л
а данная формула применима к объемам произвольных геометрий.
Спектральный диапазон Лео включает в себя, в общем случае,
ультрафиолетовый, видимый и инфракрасный участки спектра.
Для того чтобы воспользоваться статистическим подходом к
чету 0ьш(xq) , делается ряд упрощающих допущений.

14.8. Перенос излучения в объемах произвольной геометрии
429
Допущение 1. Спектральный интервал по Дсо делится на
кие участки Дсо/ (общим числом #дщ), в пределах которых
функция Планка может быть с достаточной степенью точности
заменена средней величиной.
Тогда первое слагаемое в A4.72) можно представить в виде
'=1
A4.73)
Дсо,
где
Ла>/
Допущение 2. Объемный спектральный коэффициент
щения можно представить в виде суммы коэффициента
ния в непрерывном спектре к?, и коэффициента поглощения в
линиях Кщ. Считается, что в пределах любого участка Лш
фициент поглощения в непрерывном спектре не зависит от
ты: Кш(д;о)=К/(хо). Это допущение позволяет формально
должить запись формулы A4.73)
<t
A4.74)
где NLl - число линий, попавших в диапазон /.
Допущение 3. Диапазон Дсо/ должен быть достаточно
шим для того, чтобы выполнилось условие
J <,
Да,
где St - интегральный коэффициент поглощения /-й линии. Это
позволяет записать окончательное выражение для второго
мого в сумме A4.74)
A4.75)
ы

430
Гл.14. Модели полос. Статистические модели
Второе слагаемое в формуле A4.72) описывает удельную
объемную мощность поглощения лучистой энергии. Отметим, что
в первом слагаемом формулы A4.72) интегрирование по
му углу выполнялось тривиально, поскольку функции Уд „, и кш
являются изотропными. Спектральная интенсивность ^(хо,С1)
зависит от направления, поэтому представим искомое слагаемое в
виде
A4.76)
J ки
№ Дш,
где Jaj рассчитывается для одного из направлений,
жащего элементарному телесному углу ДОу, число которых
но Nn, и приписывается всему
X
dx'
Ключевым моментом излагаемого численного метода
ется способ взятия интеграла h,ij '.
Да,
*b
где
L «ь
dbc'.
, A4.77)
A4.78)
для чего вводится еще одно допущение.
Допущение 4. Пусть расчетная сетка построена настолько
хорошо, что
*b
*=1

14.8. Перенос излучения в объемах произвольной геометрии
431
где Jb,<o,k ~ средняя на шаге сетки планковская функция;
число точек координатной сетки.
Тогда, используя Допущение 1, получаем
В A4.80) входит интеграл вида
расчет которого, с учетом формул представленных выше, будет
означать решение задачи в целом. Учитывая разделение
ного коэффициента поглощения на непрерывную и линейчатую
составляющие, получаем
A4.81)
'Am,
При выводе этой формулы было использовано свойство
дифференцирования интеграла с переменными пределами
рирования.
Именно при расчете последнего интеграла возникает
ходимость использования статистического моделирования
тра линий. Этот интеграл можно представить в виде
где
L «ь
>**)= J
Да,
1-ехр -
A4.83)
Теперь остается рассмотреть производную

432Гл.14. Модели полос. Статистические модели
or (л.
*> ,.<
^Ш/expl
dx0
,yd"
д
dxo
A4.84)
где К- число групп атомных или молекулярных линий в До>/.
Формула A4.84) получена с использованием статистической
модели. Функции Wv n (xq, xk ) представляют собой
ные ширины групп атомных линий, выражения для которых
лучены в разделе 14.4. Суммируемые производные в A4.84)
дятся в аналитическом виде, для чего используются аппроксима-
ционные зависимости для эквивалентных ширин.
Таким образом, применение метода дискретных
ний (Ray-tracing method) совместно со статистическими
ми спектра вдоль каждого из моделируемого направления
странения излучения позволяет с высокой вычислительной
фективностью найти усредненные на спектральном диапазоне
тенсивность излучения и среднюю по спектру дивергенцию
тора лучистого потока, т.е. энерговыделения в среде,
ного радиационным теплообменом.
14.9. Макростатистическая модель для описания
теплообмена излучением с учетом спектра
колебательных полос
Выше были изложены вычислительные модели расчета
ности потока излучения в плоском слое с использованием метода
полумоментов и расчета дивергенции плотности потока излучения
с использованием метода дискретных направлений, в которых
интегрирование уравнения переноса по спектру излучения
производится с использованием статистических моделей

14.9. Макростатистическая модель для описания теплообмена излучением 433
спектральных линий. Эти методы применимы как к спектру
ных линий, так и к спектру вращательных линий молекулярного
спектра.
В каждой из этих моделей исследуемый спектральный
пазон Дсо разбивается на более мелкие спектральные участки
(спектральные группы), в пределах каждого из которых тем или
иным способом решается уравнение переноса излучения.
гральная поглощательная (излучательная) способность в
не Дсо определяется суммированием интегральных поглощатель-
ных (излучательных) способностей в отдельных диапазонах.
Средние характеристики находятся делением интегральных
рактеристик на величину До. Очевидно, что чем больше
тральных диапазонов вводится внутри До, тем расчеты
ся менее экономичными.
Существует дальнейшее обобщение статистических
лей, состоящее в их применение не к вращательным линиям, а к
совокупности колебательных полос молекулярного спектра. Такие
модели, получившие название макростатистических моделей,
отличаются еще большей экономичностью, чем обычные
стические модели.
Макростатистическая модель спектра, представленная в
боте (Суржиков СТ., 1998 (а)), предназначена для определения
интегральных (средних) радиационных характеристик в диапазоне
Дсо без его деления на более мелкие спектральные участки. С
этой целью статистическая модель молекулярных линий
ется на описание спектра колебательных полос. Особенностью
используемой статистической модели является то, что она
лируется применительно к одной линии, попавшей в
ный диапазон Дсо. При этом, как отмечалось выше, никакого
тиворечия с традиционной формулировкой статистических
лей нет, так как в данной статистической модели предполагается,
что в рассматриваемый спектральный диапазон Дсо попала только
одна спектральная линия из бесконечной совокупности, среднее
расстояние между линиями в которой равно Дсо. При этом
предполагается справедливость статистического принципа Гуди о
пропускательной способности совокупности линий.
29 Зак. 272

434 Гл.14. Модели полос. Статистические модели
В следующем разделе дана подробная формулировка
стической модели спектральных линий, обобщающая
ровку, данную в п. 14.2.
14.9.1. Формулировка статистической модели
молекулярных линий применительно к одной лнини
Статистическая модель молекулярных линий была
жена и первоначально исследовалась в работах (Гуди P.M., 1966;
PlassCM, 1958; WyettP.J., et al, 1962; Goody R.M., 1952; Пен-
нер C.C., 1963). В работе (Сошников В.М., 1961) дано уточнение
вывода основных соотношений, состоящее в учете линий,
ложенных за исследуемым спектральным диапазоном Дсо.
зано, что для расчета среднего пропускания в спектральном
пазоне Дсо необходимо провести дополнительное интегрирование
по ДО с последующим делением на АС1, где Ml - спектральный
диапазон, охватывающий Дсо. В работе (Пластинин Ю.А. и др.,
1981) выполнено обобщение статистических моделей
ного спектра на спектр атомных линий. Основываясь на
ных работах, получим расчетные соотношения, обобщающие
нее разработанные модели.
Пусть в спектральном диапазоне Дсо присутствует N
кулярных линий. Тогда спектральная пропускательная
ность в пренебрежении линиями, лежащими вне Дсо, вдоль
родного отрезка оптического пути L найдется по следующей
муле:
(>со<)> A4.85)
где Г(ш,ю/) = ехр[-к/(ш,ш<I], к,(со,со/)- спектральный
эффициент поглощения в /-ой линии; со, - волновое число центра
1-Й ЛИНИИ.
' Интегральное пропускание в спектральном диапазоне Дсо
определяется по формуле
Г= J7»dco, A4.86)
Am

14.9. Макростатистическая модель для описания теплообмена излучением 435
а среднее пропускание
Очевидно, что среднее пропускание A4.87) будет зависеть
от того, как линии располагаются внутри диапазона До>.
тивно также ясно, что при большом числе N эта зависимость будет
не сильной. Справедливость такого предположения легко
рить посредством line-by-line интегрирования для любой
ности линий.
Этот факт позволяет дать вероятностную трактовку
му пропусканию. Для этого необходимо сформулировать
ность реализации именно данной конфигурации спектра линий
внутри диапазона Дсо, а затем оценить математическое ожидание
среднего пропускания для всевозможных конфигураций.
Определим вероятность того, что /-я линия будет иметь
тенсивность в диапазоне dSt в окрестности St, полуширину - в
диапазоне dy/ в окрестности у,, и будет находиться в пределах
dco, вблизи со, следующим образом:
dP, = dPt (ш„ S,, у,) = р, (ш,) р, (S,) р, (у,) do>,dS,dy,., A4.88)
где предполагается статистическая независимость реализации
стоположения, интенсивности и полуширины линии; /?(©,),
p(Sj), p(yt) - плотности вероятностей распределения
ложения, интенсивности и полуширины линии.
ное доказательство справедливости принципа статистической
зависимости и подробное его обсуждение выполнено в работах
(Burch D.E, et al., 1956; Kaplan L.D., 1953; Godson W.L., 1955).
гда математическое ожидание интегрального пропускания
деляется следующим образом:
Аса [Дго, Д5, Ду, Дш^ &SN
A4.89)
29*

436
Гл.14. Модели полос. Статистические модели
Предположим, что вероятность реализации параметров /-й
линии (со,,S,,у,) не зависят от реализации параметров любой
другой линии. Это позволяет упростить соотношение A4.89)
f.J
Дсо
П
пи
1=1 Дш, ДУ, Ду,
dco.
A4.90)
Здесь для наглядности в список аргументов спектрального
пускания в явном виде введена зависимость от со,, ?, и у,.
Среди линий, попавших в спектральный диапазон Дсо, могут
находиться как сильно различающиеся линии, так и линии с
таточно близкими параметрами. Введем условное деление линий
на группы (общим числом G), в пределах которых вероятности
реализации параметров линий могут быть описаны единым
ном. При этом напомним, что в пределах любой выделенной
группы от перестановки линий ничего не меняется, т.е. линии
различимы (статистическая независимость параметров линий уже
использовалась при переходе от A4.89) и A4.90)). Тогда A4.90)
можно переписать в виде
т=\
Дш
G \
ПП J J f
dco,
i[_g=l 1=1 Дш, ДУ,^
A4.91)
где Ng - число линий в g-й группе.
Дальнейший анализ A4.91) будет связан с конкретизацией
вида плотностей вероятностей. Примем, что все спектральные
диапазоны Дсо, равны между собой Дсо, = Дсо, / = 1,2,..., Ng, при
этом Дсо й Дй. Предположим, что все линии внутри АО.
делены равновероятно, т.е. /?,(со,) = \/АС1, тогда
МП
dco,
A4.92)

14.9. Макростатистическая модель для описания теплообмена излучением 437
где ASg и Дуг - диапазоны изменения соответствующих G
метров в пределах g-й группы.
Далее рассмотрим преобразование выражения в квадратных
скобках
ДПДУ„
лг.
A4.93)
Введем новую шкалу волновых чисел, связанную с центром
спектрального диапазона Ail = fi^ - fimin
v = o-fi0> A4.94)
ГДе С10 = 0-5 (ftmin + ^max ) J ^min. ^max ~ Границы СПеКТраЛЬНОГО
диапазона.
Тогда vmin=-0.5Aa vmax=+0.5Afi. A4.95)
Если среднее расстояние между линиями в g-vi группе
делить как
5g=AQ/Ng, A4.96)
то v • =—Q5N 8 v = + Q5N 8
lu vmin u>JJYgug> vmax TU>JJYgug>
Теперь A4.93) можно переписать в следующем виде;
IF И IT I
A/
- 1 -Li-x
 "8
1- J lT(<s>,<s>',S',y')p(S')p(y')dS'<iy'
dv'
A4.97)

438
Гл. 14. Модели полос. Статистические модели
При достаточно большом числе Ng в соотношении A4.97)
можно перейти к экспоненте
wg
8
где
g(v'~ J
1- J J T(o,a>,S\yl)p{S>)p{yl)dS'dfl
1- J lT((o,(o',S',y')p(S')p(y')dS'dyl
ASg Ayg
dv'. A4.98)
Величина Wg называется эквивалентной шириной линий g-й
группы. Переход от конечных пределов интегрирования в A4.98)
к бесконечным можно осуществить, потребовав, чтобы Ng ->• да .
Однако достаточно, чтобы выполнялось условие
у «АО, A4.99)
поэтому такой переход справедлив даже при Ng = 1.
Выше уже говорилось о том, что все линии в диапазоне АО
можно разделить на ряд групп по некоторым признакам. В
стейшем случае предполагается близость полуширин линий в
пределах группы и одинаковый вероятностный закон
ния интенсивностей линий:
A4.100)
A4.101)
Соотношение A4.100) означает, что в пределах группы все
линии имеют одинаковую полуширину. Соотношение A4.101)
часто используется в теории статистического моделирования

14.9. Макростатистическая модель для описания теплообмена излучением 439
вращательных линий молекулярного спектра и физически
вано в (ПеннерС.С, 1963). С учетом A4.100) и A4.101) вместо
A4.98) имеем
dv'. A4.102)
По определению сила линии S' является интегральным
эффициентом поглощения в этой линии
A4.103)
где функция контура линии удовлетворяет следующему условию:
+00
J/(v.v',yf)«l,
-оо
поэтому, подставив A4.103) в A4.102), получим
г)
[l-exp(-Sy(v,v',yg)l)]dS'}dv\ A4.104)
Дальнейшее преобразование A4.104) возможно при
зации спектральной зависимости коэффициента поглощения в
лекулярных линиях. В теории статистического моделирования
спектральных линий (ГудиP.M., 1966; ПеннерС.С, 1963)
чены точные и аппроксимирующие выражения для эквивалентных
ширин линий лоренцевского, доплеровского и фойгтовского
туров (см. также п.14.1). Например, для линии лоренцевского
тура применительно к рассматриваемому случаю
K(v>v')= U S% 2 г A4105)
поэтому для эквивалентной ширины получается

440 Гл. 14. Модели полос. Статистические модели
A4.106)
Обратим внимание на важную особенность соотношения
A4.106): эквивалентная ширина линий g-й группы не зависит от v,
что является следствием использования бесконечных пределов
интегрирования в A4.104) (или, что одно и то же, следствием
пользования условия A4.99)), наряду с предложением о
роятности распределений линий в ДО.
Таким образом, математическое ожидание интегрального
пропускания в диапазоне Асо приобретает следующий вид:
G ( W Л
Г=ДсоПехр ?. . A4.107)
Следовательно, среднее пропускание в любом диапазоне
Дсо < ДО не зависит от волнового числа
( цг Л
HTI A4108)
В данной формулировке статистической модели содержится
большое разнообразие статистических моделей: от простой
стической модели (G = 1) до обобщенной статистической модели
(G = N) наложения линий различных серий (ГудиP.M., 1966).
Условие G = N означает, что статистическая модель используется
для одной линии в Дсо = ДО. Другими словами, удается
лить среднее пропускание в спектральном диапазоне, содержащем
всего одну линию, являющуюся членом спектральной серии со
средним расстоянием линий ДО.
14.9.2. Формулировка макростатистической модели
для однородного оптического пути
Основная идея макростатистической модели состоит в том,
что колебательная полоса (осредненная по вращательной
ре) рассматривается как изолированная линия поглощения. Для

14.9. Макростатистическая модель для описания теплообмена излучением 441
того чтобы можно было воспользоваться статистической
лью, изложенной в предыдущем пункте, необходимо задать
цию профиля полосы поглощения /(v, v', S', у'), где под
сивностью 5' и полушириной у' теперь следует понимать
метры, задающие интегральный коэффициент поглощения в
се и полуширину полосы. Необходимо также следить за
нием условия A4.99), т.е. полуширина полосы должна быть много
меньше, чем размер спектрального диапазона AQ.
В настоящей работе рассматривается аппроксимация
ции профиля колебательной полосы, предложенная Эдвардсом
(Edwards D.K., 1976):
K(v,v')=-Lexp
V-V'
A4.109)
где v' - центр полосы поглощения; С\ и Сз - параметры,
ляющие интенсивность и полуширину полосы. Положим v' = 0,
тогда
Вид аппроксимации A4.109) позволяет принять, что yg = С3,
тогда
S'
k(v,v')=-—ехр
2у_
v-v'
A4.110)
Если предположить, что плотность вероятности
ния интенсивностей колебательных полос имеет такой же вид, как
и для вращательных линий в колебательной полосе, т.е.
то для нахождения эквивалентной ширины остается вычислить
интеграл A4.104), подставив в него
?8 зэк. гтг

442 Гл. 14. Модели полос. Статистические модели
V-V'
В результате получается
Таким образом, среднее пропускание спектрального
зона Ago, содержащего колебательные молекулярные полосы,
может быть рассчитано по формуле
где эквивалентная ширина g-ой колебательной полосы Wg
считывается по формуле A4.111), а функции С\ и С3 из
мационных формул Эдвардса. Аналогичные расчетные
ния можно получить для других аппроксимационных формул
глощения в полосах молекул.
14.9.3. Формулировка макростатистической модели
для неоднородного оптического пути
Для расчета среднего в Лю пропускания неоднородного
тического пути используется метод Кертиса-Годсона. Суть этого
метода состоит во введении для каждой линии (или каждой
сы) осредненных по оптическому пути параметров: средней
тенсивности линии Sg и средней полуширины yg.
Введение осредненных параметров Sg и ~yg фактически
начает переход к рассмотрению некоторого эффективного
родного оптического пути. Для того чтобы найти осредненные
параметры необходимо, как это и было предложено Кертисом и
Годсоном, интегральное поглощение (или, что одно и то же,
валентную ширину) эффективного однородного оптического пути
приравнять интегральному поглощению истинного неоднородно-

14.9. Макростатистическая модель для описания теплообмена излучением 443
го пути в двух предельных случаях: в случае оптически тонкого и
оптически толстого слоя.
Повторим получение расчетных соотношений Кертиса-
Годсона, рассмотренных в п. 14.3, применительно к
ной колебательной полосе. Запишем точное выражение для
валентной ширины в следующем виде:
+00
WT= \ 1-ехр
—00
00
L L
= 2|]l-exp
-\K(v,S(x),y(x))dx
-\K(v,S{x),y(x))dx
L L
>dv. A4.113)
Тогда, для эффективного однородного слоя имеем
A4.114)
И в том, и в другом случае, волновое число отсчитывается от
центра полосы. _
Для нахождения осредненных величин S и у потребуем
выполнения условия WT =W, или
00 00
Jexp[-ic(v,5,y)z]dv= Jexp
dv.A4.115)
Очевидно, что из этого соотношения можно определить
комые величины лишь приближенно, для чего и рассматривается
два противоположных приближения: оптически тонкой
(k(v,.S',y)I«*:1) и оптически толстой (K(v,.S',y)l»l) среды.
Эквивалентная формулировка этих приближений выглядит
дующим образом:
Jic[v,,SX*),Y(*)]dx«*:l для любого v,
npnv<vj.
и
28*

444
Гл.14. Модели полос. Статистические модели
Смысл последнего неравенства состоит в том, что
тельно найдется волновое число vj » тах{у(дс)}, при котором
тическая толщина среды станет меньше единицы. В этом случае
перенос излучения будет иметь место только в далеких крыльях
полос (v>vi)-
Рассмотрим интеграл
U ехр [-к (v, S,y)LJ- exp
-Jic(v,S(x),y(x))dx
•dv = 0. A4.116)
В случае оптически тонкого оптического пути получаем
00 00
L /к (v, S, у ) dv = Jdx Jk (v, S{x), y(x)) dv
0 L 0
или по определению интенсивности
A4.117)
В случае оптически толстой среды при v < vj будет
даться полное поглощение излучения, а значит, обе экспоненты в
A4.116) практически равны нулю и приближенно можно записать
ехр [-к (v, S, у ) LJ - ехр
[dv = O.A4.118)
Для некоторых видов функции контура линии, вместо
A4.118) можно потребовать, чтобы подынтегральное выражение
равнялось нулю при любом волновом числе, а именно
exp[-ic(v, 5,7I] = ехр
или
-Jic(v,S(x),y(x))dx
,y) = -J-Jic(v,S(x),y(x))dx.
я -\ 1

14.9. Макростатистическая модель для описания теплообмена излучением 445
Например, для линии лоренцевского контура получается (с
учетом vj » тах{у(дс)}) хорошо известное соотношение
Sy = j\S{x)y(x)dx. A4.119)
Несколько сложнее обстоит дело с экспоненциальным
туром линии A4.110). Здесь не удается приравнять нулю
тегральную функцию. Поэтому при получении соотношения для
средней полуширины приходится использовать дополнительные
приближения.
Интеграл A4.118) можно представить в следующем виде:
Nexp[-K(v,5,y)l]-exp
-Jic(v,S(x),y(x))dx
L L
>dv = 0,A4.120)
где V2 - волновое число, при котором экспоненты в A4.120) при
расчетах на компьютере становятся равными «машинному» нулю
в силу экспоненциального уменьшения коэффициента
ния при больших v. Воспользовавшись теоремой о среднем,
но утверждать, что подынтегральное выражение будет равно
лю хотя бы в одной точке v* спектрального диапазона [ Vi,v2 ],т.е.
L
s f v') i гад ( v* V
или —exp =— I—^-exp obc.
2y V{ у ) L[2y(x) V{ y(x)J
Допустим, что функцию у(х) в показателе экспоненты
можно заменить средней величиной у, тогда получим
женное соотношение для средней полуширины
d,. A4.121)
у SL[y(x)
Соотношения A4.111),A4.112),A4.117),A4.121) составляют
макростатистическую модель поглощательной (пропускательной)
способности однородных и неоднородных слоев молекулярного

446 Гл.14. Модели полос. Статистические модели
газа, учитывающую колебательную структуру спектра. В
дующем разделе будет рассмотрен способ применения макроста-
тистической модели при расчете переноса излучения в плоских
неоднородных слоях газа и выполнена оценка точности этой
модели.
14.9.4. Расчет переноса излучения методом полумоментов
совместно с макростатистической моделью
Цель настоящего раздела - показать, как формулы
тистической модели можно применять в расчетах переноса
тивного теплового излучения в плоских неоднородных слоях
рячих газов. Для этого опять воспользуемся методом
тов (см. п. 14.6).
За основу возьмем уравнение переноса излучения
щего вида:
где Jw,Jbw ~ спектральная интенсивность излучения среды и
солютно черного тела; кш - спектральный объемный
ент поглощения; S - направление распределения излучения.
В п. 14.6 было показано, что уравнение A4.122) может быть
аппроксимировано приблизительно эквивалентной системой
дифференциальных уравнений относительно спектральных полу-
моментных характеристик М% ю
A4.123)
ахш п +1
где A/n+)(D=2Kjj»,A/-(D=27i(-l)'I|j;n'IdH, A4.125)

14.9. Макростатистичсская модель для описания теплообмена излучением 447
ц = cos9,
0 - угол между направлением распространения излучения и осью
х(см. рис. 14.1).
Допустим, что на внешние границы слоя падает излучение,
которое характеризуется спектральной интенсивностью ./„
* = О,./ш(ц,;с = О) = ./+(* = О), цс[0,1],
Для того чтобы ограничить число решаемых уравнений в
системе A4.123-14.124), необходимо использовать какое-либо
замыкающее условие, положив все полумоментные функции,
чиная с некоторого номера, равными нулю. Такое замыкающее
условие можно получить, аппроксимируя угловую зависимость
интенсивности конечным рядом по косинусам угла 0.
рировав этот ряд по двум полусферическим углам (в диапазоне
0^0 ? я/2 и я/2<0?я) с разными весовыми функциями ц",
можно получить следующие замыкающие соотношения:
> *У(Та) A4.126)
A4.127)
где aj (хш) и cTj{xw) коэффициенты разложения. Исключив их
из системы A4.123) - A4.124), можно найти связь между полумо-
ментными характеристиками
^ + M > Щ,<а = —g"
j=\ N-j + n + l
$K } J\m

448
Гл.14. Модели полос. Статистические модели
В первом приближении метода полумоментов (N = 2,
и = 0,1) система уравнений A4.123-14.124) имеет следующее
решение:
') ехр
A4.128)
т=\ О
2
1Я=1
где
m=lO
2
m=l
A4.129)
m=l
m=l x
2
Я
A4.130)
2 я
и=1 ж
2
m=\
H
A4.131)
+
fe-ft
' 2=
fe-ft '

14.9. Макростатистическая модель для описания теплообмена излучением 449
'"
' 2""
Fo~ =
Теперь найдем интегральные полумоментные
ки в спектральном диапазоне Ago . Вычисление для четырех полу-
моментных функций идентичны, поэтому получим требуемое
отношение для M\tW (x), т.е. для односторонней плотности
ка излучения.
Проинтегрируем A4.129) по со в пределах Доо
~ \К*(*)*<»=
Дю
2 *
т=Л 0 Дю
2
"X Г СтехР
/Я—1 До)
c'U (*'Ьх
ю хр
—6 [к (х'^Лх"
х'
—р_ (к», (x')dx'
0
dco.
A4.132)
Рассмотрим преобразование интеграла, отвечающего
венному излучению среды:
О Дю
04.133)
где Wm {х\ х) = | 1 - exp
I
Дм
-Ри|кш (*")<*"
do, A4.134)

450
Гл.14. Модели полос. Статистические модели
~
До)
При расчете интеграла 1\ на компьютере удобно
вать следующую формулу:
, A4.135)
где/- номер расчетной точки, в которой ищется решение.
Представим коэффициент поглощения к,» (х) в виде суммы
коэффициентов поглощения в линиях Кщ(дс) ив непрерывном
спектре к? (х), т.е. воспользуемся комбинированной моделью
«ш (*) = 4 (*) + *!»(*)•
Считается, что к? (дс) = кс (дс), т.е. не зависит от волнового
числа в пределах Дсо. Тогда выражение для эквивалентной
ны A4.134) можно представить в следующем виде:
+ехр
W^(xitxf), A4.136)
= Nl-exp
Доэ
>dco. A4.137)
Для расчета эквивалентной ширины линий 0^ (*/,*/•)
жет быть применена макростатистическая модель, построенная в
предыдущем разделе:
Х% () <14-138)

14.9. Макростатистическая модель для описания теплообмена излучением 451
где
SaL
A4.139)
G - число колебательных полос, учитываемых в расчете. Средние
для эффективного однородного слоя [*/,*/] интегральный
фициент поглощения Sg и полуширина yg находятся с
ванием метода Кертиса-Годсона.
Рассмотрим преобразование интеграла, отвечающего вкладу
внешнего излучения, падающего на плоский слой. Предположим,
что интенсивность внешнего излучения слабо изменяется по
тру в пределах Ago , так что коэффициенты с% считаем
щими от волнового числа. Тогда
/2= Jexp
Дю
-Ри|кш (*')<**'
о
da>.
Воспользовавшись комбинированной моделью спектра, получим
/2=ехр
Jexp
Дш
-ри| *'«>(*') <**'
dco.
В этой формуле интеграл по волновому числу представляет
собой интегральное пропускание спектрального диапазона Дю,
т.е. в соответствие с макростатистической моделью
тогда
/2=ехр
Дю
. A4.140)
Таким образом, расчетная формула для определения полу-
моментной характеристики М\^ (xf) имеет следующий вид:

452
Гл.14. Модели полос. Статистические модели
в=1 Pm /=1
G
,т (*!=<>,*/)
Да>
Доэ,
A4.141)
где эквивалентные ширины рассчитываются по формуле A4.139).
14.9.5. Результаты расчетов интегральных радиационных
потоков в плоских неоднородных слоях газов,
содержащих молекулы Н2О и СО2
Предварительная оценка точности приближенного метода
расчета осредненных радиационных характеристик была
нена при расчете полусферической излучательной способности
однородного плоского слоя, толщиной # = 1см, содержащего
среду, поглощающую и испускающую излучение в спектральных
линиях лоренцевского профиля при температуре Т = 5000 К.
эффициент поглощения в непрерывном спектре полагался равным
кс =0.0001 см. В спектральном диапазоне Да> = 3600 4-3620 см
располагалось 5 одинаковых линий, коэффициент поглощения в
центре которых, изменялся в диапазоне k'((d0) = 0.1 + 10cm~', т.е.
оптическая толщина слоя в центре линий составляла
х0 = к' (йо)^ = О.1+1О. Полуширина линий изменялась в
зоне у = 0.05-г 0.5 см. Результаты расчетов полусферической
лучательной способности
О —
nJb
A4.142)
представлены в табл. 14.1.
Расчеты выполнялись два раза при каждом значении
ской толщины to и полуширины линий. Результаты, полученные

14.9. Макростатистическая модель для описания теплообмена излучением 453
с использованием алгоритма line-by-line интегрирования, могут
быть приняты за точные (погрешность 1-го приближения метода
полумоментов по сравнению с точным решением в интегро-
экспоненциальных функциях не превосходит 2 %). Спектральный
диапазон Лсэ делился на 1000 элементарных спектральных
ков шириной Доэ, =0.02 см, в центре каждого из которых ю,
ределялся спектральный коэффициент поглощения
Sy
A4.143)
где 5 = 7гухо/Я; оо„ - волновое число центра «-линий, которое
определялось по следующей формуле:
=^Г' A4л44)
Nn - число линий в полосе (в данном случае Nn = 5); oomjn -
нижняя граница спектрального диапазона. В пределах Дю,
фициент поглощения к' (со,) полагался постоянным.
Таблица 14.1
Полусферическая излучательная способность плоского слоя
в пяти линиях лореицевского профиля
у, см
0.05
0.1
0.5
0.05
0.1
0.5
0.05
0.1
0.5
Line-by-line расчеты
0.0075
0.0146
0.0683
*o =
0.0487
0.0961
0.4140
0.1800
0.3436
0.9340
Статистическая модель
0.1
0.0073
0.0142
0.0677
¦1.0
0.0448
0.0870
0.3550
= 10
0.1650
0.3000
0.8120

454
Гл.14. Модели полос. Статистические модели
В расчетах использовалась простая статистическая модель,
согласно которой все линии в диапазоне Ago включались в одну
полосу, т.е. полагалось, что G = 1. Среднее расстояние между
ниями равно
/ A4.145)
Расчеты по методу полумоментов проводились с
ванием обоих алгоритмов на однородной сетке вдоль оси х с
лом узлов iVy = 100.
Сравнение результатов расчетов, представленных в табл.
14.1 показывает, что погрешность приближенного метода не
восходит ~15% в широком диапазоне изменения определяющих
параметров. Указанная погрешность является характерной для
статистической модели несильно различающихся линий при
четах поглощательной способности однородных слоев.
Макростатистическая модель колебательных полос молекул
НгО и СОг применялась при расчете переноса излучения в
ских неоднородных слоях. Распределение температуры и
тельных мольных концентраций указанных молекул по толщине
слоя задавалось в следующем виде:
х-хс
(*max-**,o)exP
х-хс
A4.146)
A4.147)
гле 7max>7b>**,max>x*,o ~ наибольшее и наименьшее значение
температуры и концентрации к-й компоненты; dx,n- параметры,
определяющие степень неоднородности исследуемого слоя.
На рис. 14.2 показано типичное распределение температуры
и концентраций в плоском слое (для 2-го варианта расчета из
табл. 14.2). Значения параметров, которые использовались в
четных вариантах приведены в табл. 14.2. Общими для всех
четов были следующие величины: Го = 300 К, Тп^ = 2500 К,
*н2о,о =0.01, *н2о,т« =0.7, jcfco^o =0.01, л^>тах =0.3.

14.9. Макростатистическая модель для описания теплообмена излучением 455
540
40
120
160 200
*,см
Рис. 14.2. Распределение температуры (сплошная кривая, шкала слева)
сительных мольных концентрации паров воды (штриховая линия; шкала
справа) и двуокиси углерода (пунктирная линия; шкала справа)
Расчеты каждого варианта проводились два раза: с
зованием алгоритма line-by-line интегрирования и макростатисти-
ческой модели. В спектральном диапазоне ДО = 1000+ 10000 см
учитывалось 4 колебательных полосы молекулы НгО и 4 полосы
молекулы СОг.
Таблица 14.2
Параметры, определяющие распределение температуры
н концентраций в плоском слое
Параметр
п
дсс,см
Я, см
«/д., СМ
Вариант 1
2
25
100
50
Вариант 2
20
25
100
50
Вариант 3
4
25
200
50
Использованные в расчетах параметры моделей
ных полос, соответствующих классу экспоненциальных
полосных моделей Эдвардса, были заимствованы из работы (Зи-
гель Р. и др., 1975). Они приведены в табл. 14.3.

456
Гл.14. Модели полос. Статистические модели
Таблица 14.3
Параметры моделей колебательных полос молекул Н2О н СО2
Н2О
со
g
«>*.
см

м'/кг
см

см

м2/кг
см

1600
3750
5350
7250
41.2
23.3
3F011
2.5F101
1060
2410
3750
5200
0.76F,
0.76F,
110
4F2
со, =3652 см, со2 = 1595 см, со3 =3756 см,
F,(r) =
- IN]
Г, Г
^1-ехр^
he
-
со,
[1-ехр("^ш'11"ехр(-#ш0]
©,= 1351см, ©2 =667 cm, ш3= 2396 cm.
В line-by-line вычислениях спектральный диапазон АП
бивался на 4S0 элементарных спектральных участков Асо,, в
тре каждого из которых щ вычислялся суммарный коэффициент
поглощения (осредненный по вращательной структуре)
-exp -
Рн2о

14.9. Макростатистическая модель для описания теплообмена излучением 457
+0.01
С,
—^
Рсо,
A4.148)
где GHjO, GCOj - число колебательных полос, учитываемых для
молекул НгО и СОг соответственно; рн о, рсо - плотность
лекул Н2О и СО2.
Давление в слое полагалось постоянным и равным р = \ атм,
поэтому плотность к-й молекулярной компоненты (с
ным весом Мк) рассчитывалась по формуле
рк =
, кг/м3.
A.149)
В пределах До, коэффициент поглощения полагался постоянным.
Спектральный коэффициент поглощения в двух точках
внутри плоского слоя (для варианта 1, см. табл. 14.2),
мый в line-by-line расчетах показан на рис. 14.3.
к, 1/см
ю°-
1800 2700 3800 4500 5400 8300 7200 8100 9000 9900
со, 1/см
Рис. 14.3. Спектральный коэффициент поглощения осредненный по
щательной структуре в точках слоя с координатами л = 0A)ил = ЯB)
Варианты расчетов различались степенью неоднородности
исследуемых слоев. Наименьшая неоднородность параметров газа
в расчетной области задавалась в первом варианте, наибольшая -

458
Гл.14. Модели полос. Статистические модели
во втором. В третьем варианте половина расчетной области занята
холодным газом, что моделирует сильно неоднородные
щие слои. В этом случае ширина колебательных полос в
ных слоях существенно ниже их ширины в горячих слоях.
венно, что это же наблюдается и для отдельных вращательных
линий. Распределения интегральных полумоментных функций в
плоском слое показаны на рис. 14.4 для каждого из вариантов. Как
и прежде, следует обратить внимание на знакопостоянство
моментных характеристик радиационного переноса, м*
12
140
70
-70
-140
Mt
щ
20
40
60
80
100
X, СМ
Рис. 14.4. Распределение интегральных полумоментных характеристик в
плоском слое для расчетных вариантов: \-а,2-б,Ъ-в. (Начало)
182
« 91
$" о
+^ -91
-182
20
40
60
80
100
б
*,см
Рис 14.4. (Продолжение)

14.9. Макростатистическая модель для описания теплообмена излучением 459
?
164
82
t§ -82
-164
40
80
120
160 200
X, СМ
Рис. 14.4. (Окончание)
На рис. 14.5 показано распределение полного интегрального
потока, полученного в line-by-line вычислении
A4.150)
4s
I
43.8
21.9
-21.9
-43.8
M
I
20
40
60
E
0.8
0.4
0.0
-0.4
-0.8
80 100
x, см
Рис. 14.5. Полный интегральный поток в слое (сплошная кривая; шкала
ва) и погрешность его расчета с использованием макростатистической модели
(штриховая кривая; шкала справа). Варианты 1 - а, 2 - б, 3 - в. (Начало)

460
Гл.14. Модели полос. Статистические модели
i
68
34
0
-34
-68
59.8
29.9
0
-29.9
-59.8
/
/
—>y
/
1
_
20
/
/
I
40
/
40 60
6
Рис. 14.5. (Продолжение)
/
——^
80 120
80 100
X, CM
160 200
X, CM
E
0.8
0.4
0.0
-0.4
-0.8
e
0.8
0.4
0.0
-0.4
-0.8
Рис. 14.5. (Окончание)
На этом же рисунке даны погрешности его расчета
*)) по макростатистической модели
. \WT{x)-WmM{x)\
A4.151)
Отсюда видно, что уровень погрешности можно оценить
личиной 30%.

14.9. Макростатистическая модель для описания теплообмена излучением 461
А на рис. 14.6 показано распределение дивергенции полного
интегрального потока и погрешности ее расчета по
стической модели.
Is
о
2.90
1.45
I 0.00
-1.45
-2.90
20
40
60
80
Е
0.8
0.4
0.0
-0.4
-0.8
100
X, СМ
Рис. 14.6. Дивергенция полного интегрального потока в слое (сплошная
кривая; шкала слева) и погрешность расчета дивергенции полного
грального потока с использованием макростатистической модели
вая кривая; шкала справа). Варианты I -а, 2-б, 3-е. (Начало)
Е
0.8
0.4
0.0
-0.4
-0.8
7.68
и
23 3.84
| 0.00
-3.84
-7.68
V i
\
\
1
\
\
\
20
40
60
80
100
*,см
Рис. 14.6. (Продолжение)

462
Гл. 14. Модели полос. Статистические модели
5.18
2.59
I
-2.59
-5.18
е
0.8
0.4
0.0
-0.4
-0.8
40
80
120
160
200
дс, см
Рис. 14.6. (Окончание)
Поскольку по своему физическому смыслу дивергенция
диационного потока определяет объемную мощность
ления, обусловленного переносом теплового излучения, то эта
величина в первую очередь необходима для решения задач
пряженного радиационно-конвективного теплообмена.
И, наконец, на рис. 14.7 показано распределение
ных радиационных потоков на границах плоского слоя, что
зволяет при сопоставлении со спектральной зависимостью
ного коэффициента поглощения получить представление о том, в
каких спектральных диапазонах слой излучает как абсолютно
черное тело, а в каких диапазонах - излучение доходит от
лее удаленных слоев объема.
Погрешность расчета полного интегрального потока и его
дивергенция практически во всей расчетной области и для всех
расчетных вариантов составляет величину ~30%, что является
вполне приемлемым для практики расчета теплообмена
ем. В отдельных очень узких участках эта погрешность может
ходить до нескольких сот процентов, однако это наблюдается
только в тех точках внутри слоя, где полный интегральный поток
или его дивергенция близка к нулю, поэтому указанные
ности не ухудшают в целом точность данного приближенного
метода.

14.10. Расчет имитационными методами Монте-Карло переноса излучения 463
10
1800 2700 3800 4500 5400 8300 7200 8100 9000 9900
со, 1/см
Рис. 14.7. Распределение спектральных односторонних радиационных
токов при хш0 (М\ , кривая /) и х = Н {М\ , кривая 2), а также
тральной плотности потока излучения абсолютно черного тела при
ратуре в точках х = 0 (кривая 3)их" Н (кривая 4)
Анализ расчетных данных позволяет сделать вывод об
летворительной точности макростатистической модели. Данная
модель может быть рекомендована для проведения инженерных
расчетов теплообмена излучения, а учитывая ее высокую
мичность - и для радиационно-газодинамических расчетов.
14.10. Расчет имитационными методами Монте-Карло
переноса излучения с учетом вращательных линий
молекулярного спектра
В предыдущих разделах рассмотрены способы применения
статистических моделей спектральных линий совместно с
дом дискретных направлений (Ray-tracing method) и методом
лумоментов.
Дальнейшее развитие статистических моделей спектра
стоит в их использовании совместно с имитационными методами
Монте-Карло. Указанная комбинация методов представляется
весьма перспективной, поскольку наиболее органично отражает
статистическую природу процесса распространения теплового
излучения.

464 Гл.14. Модели полос. Статистические модели
Задача расчета переноса селективного теплового излучения в
светорассеивающих средах с учетом линейчатой структуры
тра является одной из наиболее трудоемких в теории теплообмена
излучением и прикладной вычислительной физики. Проблема
лективности теплового излучения представляет значительный
терес не только для фундаментальных исследований, но и
чайно важна в различных приложениях, таких, как построение
вычислительных моделей теплообмена излучением в различных
энергетических устройствах, разработка тепловой защиты
каемых космических аппаратов, создание средств дистанционного
обнаружения старта ракет и дистанционных методов
ской безопасности (Simmons F.S., 2000; Surzhikov S.T., et al.,
2003).
Даже без учета светорассеяния задача расчета переноса
лективного теплового излучения состоит в интегрировании
нения переноса в десятках тысячах спектральных диапазонов, при
этом характерная оптическая толщина среды тт по спектру
жет меняться в миллионы раз от i^ <к 1 (оптически тонкий слой)
до тю »1 (оптически толстый слой). При расчете радиационного
переноса в инфракрасной (ИК) области спектра Дсо~5ОО-5-10000
см'1 оказываются важными следующие два масштаба
ных диапазонов: характерный масштаб колебательной полосы
Д<в„~200 + 500см"' и характерный размер вращательной линии,
который задается ее полушириной у ~ 0.01 + 1 см. При учете
вращательной структуры спектра необходимо проводить расчеты
с шагом по волновому числу Acor ~ O.ly. Такие вычисления
ваются line-by-line (LBL), т.е. расчетами переноса селективного
теплового излучения с учетом вращательной структуры спектра
молекулярных линий. Если, исходя из физической постановки
дачи, достаточно учесть лишь колебательную структуру спектра,
усреднив коэффициенты поглощения и испускания по
ной структуре, то спектральные расчеты можно проводить с
гом Acog -10+ 50 см. Это так называемые многогрупповые
спектральные расчеты без учета вращательной структуры.
чина Ago; должна бьпъ не слишком малой, чтобы в этот диапазон
попадало достаточное число вращательных линий, и не слишком

14.10. Расчет имитационными методами Монте-Карло переноса излучения 465
большой, чтобы при усреднении вращательной структуры спектра
не слишком искажался контур колебательной полосы.
Заметим, что в подавляющем большинстве задач,
щих при определении селективного теплового излучения в газах
атмосферного давления вполне достаточно учитывать лишь
бательную структуру ИК-спектра. С понижением давления до
сятых и тысячных долей атмосферы неучет вращательной
туры может привести к большим погрешностям. Итак, далее
дем различать два типа спектральных расчетов: с учетом и без
учета вращательной структуры.
Трудоемкость решения проблемы селективности
но возрастает, если необходимо учитывать светорассеяние
ных сред (например, в топках паровых котлов, в струях продуктов
сгорания ракетных двигателей твердого топлива - РДГТ) и
дить расчеты переноса излучения в объемах сложных геометрий.
Одним из возможных путей решения данной проблемы является
разработка приближенных методов, позволяющих с достаточной
для практики точностью учитывать основные закономерности
реноса теплового излучения с учетом линейчатой структуры
тра и процессов светорассеяния. Однако с каждым годом
тает также актуальность совершенствования LBL-методов
та, поскольку производительность современных вычислительных
комплексов уже позволяет решать этими методами задачи
тической важности.
В данном разделе проводится сравнительный анализ
рых алгоритмов статистического моделирования переноса
тивного теплового излучения, основанных на классе
ных методов Монте-Карло (Ермаков СМ., 1971; Соболь И.М.,
1973; Франк-Каменецкий А.Д., 1978; Ермаков СМ., Михайлов
Г.А., 1982), развитых в работах (Суржиков СТ., 1987, 1993, (в, г);
ДаладоваЛ.А. и др., 1990; Surzhikov S.T., et al, 1998)
тельно к проблеме расчета спектральной направленной излуча-
тельной способности струй продуктов сгорания ракетных
телей. Указанный анализ выполняется на примере определения
полусферической степени черноты плоского и цилиндрического
объемов, усредненной на спектральном диапазоне, содержащем
31 Зак. 272

466 Гл.14. Модели полос. Статистические модели
вращательные линии, а также на примере вычисления
ной направленной излучательной способности модельной струи
РДГТ с усреднением и без усреднения вращательной структуры.
Будет показано как использовать следующие методы расчета:
LBL-метод, гибридный метод статистического моделирования,
метод усредненных коэффициентов, LBL-метод с малым числом
моделируемых траекторий.
14.10.1. LBL-метод
Этот метод, является наиболее трудоемким, и его
разно применять, прежде всего, для получения эталонных
ний. При использовании LBL-метода спектральный диапазон
Доо;, в пределах которого рассчитываются усредненные
онные характеристики, делится, в свою очередь, на Nn
тральных диапазонов (групп) Д<в„, число которых должно быть
достаточно большим для того, чтобы рассчитать контур каждой из
учитываемых вращательных линий, по меньшей мере, в 10 точках.
В любой спектральной точке <x»o,n диапазона Дсо„ (как правило -
в его центре) рассчитывается спектральный коэффициент
щения к (со), составными частями которого являются:
ент поглощения в непрерывном спектре газообразных
тов смеси кс(со0„), коэффициент поглощения твердых и (или)
жидких частиц кр(щ„), присутствующих в исследуемом объеме
и спектральный коэффициент поглощения в спектре
ных линий к (соо.л)- При расчете коэффициента поглощения
к/(юо,л) необходимо учитывать все близлежащие вращательные
линии, поскольку поглощение в их крыльях может быть весьма
заметным
Ё'К) A4152>
Здесь К/(а)о>п,о)/) - коэффициент поглощения в спектральной
точке соо.л > обусловленный вращательной линией, расположенной
в точке со,. Число вращательных линий Ni, которые следует
учесть в сумме A4.152), определяется условиями в газе и
ром линий (уширением и интенсивностью).

14.10. Расчет имитационными методами Монте-Карло переноса излучения 467
Напомним, что для вращательной линии лоренцевского
тура имеем
где 5/,у/ - интенсивность и лоренцевская полуширина ;-й
тельной линии.
При вычислениях можно задать фиксированную величину
Аоо* -5-5-Юсм и в сумме A4.152) учитывать все линии,
шие в спектральный диапазон Гоо0 „ - О.5Аоо*, оэ0 „ + О.5Дсо* 1.
нако для получения эталонных решений такой алгоритм может
оказаться не достаточно точным, что потребует использования
более трудоемкого учета далеко лежащих от Аоо* линий.
В пределах каждой спектральной группы Асо„
ние траекторий фотонов выполняется с использованием
онного метода Монте-Карло, как это обычно делается для серого
газа (см. главу 10). Заметим, что использование вполне
ванного для рассматриваемого класса задач допущения о
ности процесса переноса по отношению к энергии фотонов
висимость свойств среды от интенсивности излучения) позволяет
моделировать относительно небольшое число траекторий
(#/~104-П05), применяя полученные результаты к полному
числу фотонов. Подчеркивая этот факт, далее будем использовать
термин имитация траекторий групп фотонов. В рассматриваемом
варианте LBL-метода общее число моделируемых траекторий для
одного спектрального диапазона A<og является весьма большим и
оценивается величиной Ntot = N/Nn ~ Ю7 -5-108.
14.10.2. Гибридный метод статистического моделирования
' В данном случае за основу выбирается обычный
ный метод Монте-Карло. Расчеты проводятся в пределах целого
спектрального диапазона Д<% без его деления на поддиапазоны.
Однако с использованием имитационного метода Монте-Карло
31*

468 Гл. 14. Модели полос. Статистические модели
проводится моделирование не монохроматических групп
нов, а имитация распространения групп фотонов, энергия которых
определяется усреднением на всем спектральном диапазоне Acog .
При этом усредненные энергетические характеристики групп
тонов для различных оптических путей находятся с
ем статистических моделей реальных линейчатых спектров и
тода Кертиса-Годсона, позволяющего учесть неоднородность
свойств среды вдоль траектории движения.
Отметим преимущества такого подхода: интегрирование по
волновому числу в этом методе производится аналитически, и для
выделенного спектрального диапазона Доо;, содержащего сотни
спектральных линий, достаточно решить практически
тическую задачу, т.е. один раз для всего спектрального диапазона.
Таким образом, расчетная эффективность метода возрастает в
~ Nn раз по сравнению с LBL-методом.
Для реализации этого метода на базе существующих
грамм расчета переноса излучения методом Монте-Карло
точно модифицировать подпрограмму расчета длины свободного
пробега фотонов и в очень незначительной степени
ский модуль.
Тип рассчитываемых спектральных линий (атомные или
лекулярные) не имеет принципиального значения, как и характер
их расположения (регулярное или хаотическое), а также тип их
контура (лоренцевский, доплеровский, фойгтовский). Все
ные особенности учитываются в рамках статистических моделей,
которые можно использовать без каких либо ограничений.
В случае необходимости учета очень резкого изменения
тических свойств среды вдоль траектории фотона, вместо
ближенной модели Кертиса-Годсона можно использовать любую
другую модель, более адекватно учитывающую неоднородность
среды.
Метод сохраняет главные преимущества имитационных
тодов Монте-Карло, связанные с возможностью решения задач
для объемов сложных геометрий и учета многообразия
ских процессов, в том числе неравновесности излучения.

14.10. Расчет имитационными методами Монте-Карло переноса излучения 469
В качестве основных недостатков следует отметить
нимую погрешность статистических моделей полос, что не
ляет выполнить асимптотический переход к LBL-интегриро-
ванию, и необходимость введения в модель эмпирических
метров, учитывающих вращательную структуру анализируемого
спектра.
Расчет по гибридному статистическому методу начинается с
момента формирования вектора координат lj, соответствующих
точкам пересечения анализируемого луча, направленного вдоль
предполагаемого движения фотона в неоднородной среде. При
этом учитываются встречающиеся на луча пути граничные
верхности элементарных объемов, на которые разделена
дуемая область введенной разностной сеткой; //, j = 1,2,3,..., N;
h = 0> In ~ координата пересечения луча с граничной
стью расчетной области. Геометрия исследуемого объема может
быть произвольной. Заметим, что в работе (Surzhikov S.T., 2003)
предложен имитационный алгоритм, свободный от
сти находить координаты точек пересечения каждого из
ных лучей с гранями элементарных физических объемов. Это
зволило заметно сократить расчетное время и реализовать
ционный алгоритм на произвольных неортогональных сетках.
Поскольку при нахождении координат lj обязательно
сируются элементарные расчетные объемы, то можно считать, что
помимо вектора // сформированы также векторы значений
вой температуры Tj, температуры частиц Tf, концентрации
тически активных компонент газовой смеси xf , (для
ленности будем считать, что xf , - молярные концентрации),
суммарного давления в смеси газов pj, концентрации оптически
активных жидких и твердых компонент смеси ng j. При этом и?у.
- число частиц заданного размера в единице объема; если смесь
полидисперсная, п% . - числовая концентрация частиц с
рым средним размером. Размерность всех перечисленных
ров равна (N-1), поскольку внутри каждой элементарной зоны
свойства предполагаются постоянными.

470 Гл. 14. Модели полос. Статистические модели
Это позволяет в пределах каждого отрезка вектора Ij
считать следующие оптические характеристики, определяющие
процесс переноса излучения вдоль луча:
1) коэффициенты поглощения к^ и рассеяния а?
сированной фазы (этот расчет производится обычно с
нием теории Ми (Борен К. и др., 1986)), а также индикатрису
сеяния или средний косинус рассеяния цу, характеризующий
пень асимметрии индикатрисы рассеяния (в дальнейшем
ные функции считаются независящими от волнового числа в
делах спектрального диапазона Дсо^ );
2) коэффициенты поглощения Ку в непрерывном спектре
газовой фазы;
3) средний коэффициент поглощения в спектральных линиях
Kk,bj ={S/d)k ь > паРаметР уширения спектральных линий
Р*АУ» эффективное давление (Pe)ft b . (Edwards D.K., et al., 1973;
Edwards D.K.,etaL, 1967).
Указанные усредненные функции рассчитываются для
дой молекулярной полосы (индекс «Ь») каждой компоненты
декс «А») , дающей вклад в поглощение излучения в диапазоне
Дс%, S,d - усредненная интенсивность вращательных линий и
среднее расстояние между ними.
Следующим этапом расчетного алгоритма является
ние вектора эффективных оптических толщин для каждой полосы
спектральных линий, для чего используется метод Кертиса-
Годсона. Пусть основным механизмом уширения является столк-
новительный, т.е. линии имеют лоренцевский профиль. Тогда
04-154)
P*('«-'«-i). 04.155)
k,b,m

14.10. Расчет имитационными методами Монте-Карло переноса излучения 471
iff] рИ
Pk{lm-lm-\)
, A4.156)
где р* - плотность Л:-й компоненты смеси; ф - эмпирический
эффициент, подбираемый для улучшения согласия с результатами
LBL-расчета и учитывающий вращательную структуру
руемого спектра. Заметим, что иногда усредненная интенсивность
линий относится не к единице массы, как в данном случае, а к
единице объема. В этом случае формулы A4.155) и A4.156) не
содержат плотности.
Предполагая справедливым принцип статистической
симости пропускания в полосах спектральных линий, а также
учитывая поглощение в непрерывном спектре, полную
скую толщину находим суммированием
4*,y+L<j+L<y> C14.157)
к b к к
где
>y <m(/m-/m_,). A4.158)
Заметим, что при учете доплеровского уширения
мо изменить способ расчета Xk,bj по формуле A4.154).
. Параллельно с расчетом оптической толщины по
нию производится расчет оптической толщины по рассеянию
<CT(^-^-i). 04-159)
к т-2

472 Гл. 14. Модели полос. Статистические модели
что позволяет впоследствии оценить вероятность рассеяния при
установлении факта столкновения моделируемого фотона с
тицей среды.
Длина свободного пробега фотонов в излагаемом алгоритме
находится обычным образом. Однако для нахождения физической
координаты точки столкновения фотонов с частицами среды
обходимо выполнить дополнительные расчеты. Главной причиной
этого является нелинейная зависимость пропускания на участке,
где есть спектральные линии, следствием чего является
ство пропускания всего участка сумме пропусканий отдельных
его составляющих.
Пусть после генерации очередного случайного числа
ческая толщина тс, отвечающая длине свободного пробега,
летворяет неравенству
ту?тс?ту+1, A4.160)
где Ту = Ту + Ту.
Отсюда необходимо найти координату Iе, соответствующую
величине хс. В общем случае следует организовать итерационный
процесс для поиска величины 1е. Однако приемлемым является и
следующий безытерационный метод. Если в диапазоне A4.160)
справедлива линейная зависимость оптической толщины от
ческой координаты, что хорошо выполняется при малой
ской толщине расчетных ячеек, тогда
(/у+1-/..)(тС-Ту)
Теперь осталось оценить вероятность поглощения
ния) в точке столкновения фотона с частицей среды. В отличие от
расчетов переноса монохроматического излучения методом
те-Карло, где вероятность поглощения (рассеяния) оценивается
отношением коэффициента поглощения (рассеяния) к полному
коэффициенту ослабления, здесь аналогичная процедура выпол-

14.10. Расчет имитационными методами Монте-Карло переноса излучения 473
няется применительно к соответствующим оптическим толщинам.
Например, вероятность рассеяния оценивается соотношением
где & - вероятность выживания кванта (альбедо однократного
рассеяния).
Весьма важным для излагаемого метода является расчет
редненной энергии е/ для каждой моделируемой группы
нов. Один из возможных методов состоит в следующем. Сначала
вычисляется вероятность испускания фотонов из и-й
венной зоны исследуемого объема. Для этого рассчитывается
энергия Е„, испускаемая в единицу времени и-й
ной зоной и полная энергия, испускаемая всем объемом
й. A4.163)
Здесь Ny - число ячеек (элементарных объемов) расчетной сетки.
Искомая вероятность рассчитывается по формуле
р„=^. A4.164)
Затем вычисляется число групп фотонов, испускаемых к-й
пространственной зоной
NLn=PnNf, A4.165)
где N/ - число моделируемых траекторий.
. И, наконец, энергия одной группы фотонов, испускаемых
и-й зоной, определяется по формуле
Nf,n
A4.166)
30 Зак. 272

474 Гл. 14. Модели полос. Статистические модели
Несмотря на ясный физический смысл изложенного
ритма, имеются значительные проблемы, связанные с расчетом
полной энергии, испускаемой отдельной пространственной зоной.
Величина Е„ обычно рассчитывается по формуле
Е„=4п\ I K((u)Jb<od(udV. A4.167)
Здесь Vn - объем и-й пространственной ячейки; J^ -
ная интенсивность излучения абсолютно черного тела (функция
Планка); к (со) - спектральный коэффициент поглощения. В
делах небольшого спектрального участка Аоо^ с хорошей
стью можно ввести среднюю функцию Планка
Wda). A4.168)
а интеграл от коэффициента поглощения представить в
щем виде:
N.
J ю,я ~ п g n g J 2Li i,n\ )"*
*KPA<og+KcnA<og+?sl>n, A4.169)
где использовано допущение yln <z Aoog, поэтому
oo
Si,» - Мя (»)de) * f к!)Я (a))doo. A4.170)
Тогда энергия, испускаемая и-й зоной, рассчитывается по
формуле
которая легко обобщается на случай различия температур газовой
и конденсированной фаз

14.10. Расчет имитационными методами Монте-Карло переноса излучения 475
или
.A4.172)
• ¦
1=1
Здесь Jb,n'^b,n ~ планковские интенсивности при температуре
частиц Тр и газа Tg соответственно; ic?, icf - средние
циенты поглощения частиц и газа.
Подробный анализ допустимости использования
ния A4.172) для расчета излучательной способности
го объема Vn выполнен в (Surzhikov S.T, et al., 1998). Главными
условиями справедливости A4.172) являются условия локального
термодинамического равновесия и малости оптической толщины
объема Vn. Именно последнее условие может нарушаться в
дельных участках диапазона Д<%, содержащих молекулярные
линии. В этом случае рассчитываемая излучательная способность
элементарной расчетной ячейки оказывается несколько
ной, что является причиной возрастания погрешности расчетов с
использованием указанного алгоритма. Несколько уменьшить
данную погрешность удается при учете самопоглощения (реаб-
сорбции) испущенного излучения в элементарном расчетном
еме или расчетом излучения только с его поверхности.
14.10.3. Метод усредненных коэффициентов
линейчатого поглощения
По сравнению с гибридным методом статистического
лирования здесь используется упрощающее допущение
Ч*.У=Х*а;, A4Л73>
которое справедливо при выполнении условия ——- <к 1.
Заметим, что A4.173) не обязательно отвечает условию
лой оптической толщины. Если уширение линий велико, так что
30*

476 Гл. 14. Модели полос. Статистические модели
они перекрываются, то приближение A4.173) может быть
лемым и для случая большой оптической толщины. Если же
тральные линии перекрыты слабо, то A4.173) будет приводить к
значительной погрешности при увеличении оптической толщины
слоя.
Достоинство данного метода по сравнению с гибридным
ключается в возможности существенного упрощения алгоритма
имитационного моделирования. Вследствие отсутствия
ного корня в знаменателе A4.154) оптическая толщина т*ду
бого составного отрезка становится аддитивной функцией
ческих толщин отрезков его составляющих. А это в свою очередь
позволяет использовать наиболее экономичный алгоритм
мального сечения для моделирования длины свободного пробега.
Напомним, что суть этого метода состоит в замене реальной
однородной среды некоторой фиктивной однородной средой с
модифицированными оптическими свойствами. В работе
ков СМ. и др., 1982) дано строгое обоснование этого метода и
доказывается эквивалентность прямого статистического
рования длины свободного пробега методу максимального
ния. Главным преимуществом метода максимального сечения
ляется радикальное упрощение геометрического модуля
ной программы, поскольку нет необходимости рассчитывать
ресечение луча каждого участка траектории с гранями
ных расчетных объемов конечно-разностной сетки.
14.10.4. LBL-метод с малым числом моделируемых
траекторий
Опыт решения задач теплообмена излучением в сером
ближении с использованием имитационного метода Монте-Карло
показывает, что для получения приемлемой точности необходимо
моделировать примерно N/ =104 -5-105 траекторий. Строгое
тистическое обоснование этой оценки дано в работе
ков СТ., 1993, (г)). Для случая малых альбедо однократного
сеяния (<5<0.9) и малых оптических толщин (т' <1) число N/
может быть уменьшено примерно на порядок. Однако для сильно

14.10. Расчет имитационными методами Монте-Карло переноса излучения 477
рассеивающих сред (<5>0.99) и при т'>1 величину N/
необходимо увеличивать с целью уменьшения погрешности
вычислений. Спецификой расчета переноса излучения в
спектральном диапазоне A<og, где присутствуют вращательные
линии молекул, является существенная зависимость оптической
толщины исследуемого объема от волнового числа со. Вот
почему, если использовать обычный метод LBL-интегрирования,
спектральный диапазон Д<%, как отмечалось выше, следует
разделить на Nn поддиапазонов Асо„, в пределах каждого из
которых решать задачу в «серой» постановке. При этом алгоритм
расчета числа моделируемых траекторий остается в силе для
каждого такого поддиапазона. Таким образом, если в интервале
Aoog присутствует N/ линий, то общее число моделируемых
траекторий оценивается величиной Ntot ~\0N/Nf.
При использовании предлагаемого здесь метода
ные в Acog радиационные характеристики рассчитываются только
для N/ моделируемых траекторий. Это достигается тем, что в
каждом спектральном диапазоне Асо„ моделируется не
N/ = 105 -МО6, а всего N*/ ~ 10-5-20 фотонов. Полное число
лируемых траекторий в этом случае определяется по формуле
Кроме возможной статистической компенсации
стей статистического моделирования на большом числе
тральных участков Доо„, такой подход имеет следующие
щества. Известно, что в имитационных методах Монте-Карло
бая радиационная характеристика (в нашем случае - излучатель-
ная и поглощательная способности) определяется усреднением
параметров моделируемых траекторий в заданной элементарной
ячейке или на заданной элементарной площадке, размеры которых
определяются используемой расчетной сеткой. Однако при
ших оптических толщинах лишь малая доля этих траекторий
канчивается на границах области, где и накапливается
ция, требуемая для расчета излучательной способности.
ляющее большинство групп фотонов поглощается внутри объема,
практически безвозвратно унося с собой накопленную
цию. В оптически толстой среде граничных поверхностей дости-

478 Гл. 14. Модели полос. Статистические модели
гают лишь группы фотонов, испущенные вблизи поверхности и
практически не несущие информацию о состоянии среды во
ренних слоях объема. Поэтому при больших оптических
нах нет необходимости в моделировании траекторий фотонов по
всей расчетной области, т.е. можно не рассчитывать большое
ло траекторий в оптически толстой среде, определяя
ски усредненные результаты именно для участков с большой
тической толщиной. Кроме этого, для участков с большой
ской толщиной целесообразно применять весовой алгоритм
лирования (Ермаков СМ. и др., 1982; Суржиков СТ., 1997). Для
участков с малой оптической толщиной ситуация гораздо проще,
так как небольшое число моделируемых траекторий в пределах
одной подгруппы Доо„, будучи умноженным на число этих
групп, дает вполне приемлемое общее число моделируемых
екторий. Результаты вычислительных экспериментов
ждают эти качественные соображения.
14.10.5. Тестовые расчеты
Представленные алгоритмы статистического моделирования
тестировались путем сравнения с расчетными и
ными данными других авторов. Программная реализация
танного метода ориентирована на решение широкого класса задач
в объемах различных геометрий: в плоских бесконечных слоях, в
сферических объемах, в бесконечных и конечных осесимметрич-
ных объемах произвольной геометрии.
В работе (TangK.C, et al., 1994) выполнены расчеты
ностей лучистых тепловых потоков в плоском слое поглощающей,
излучающей и рассеивающей среды, содержащей частицы
рода и смесь газов СОг, N2 с температурой 1000 К и полным
лением - 1 атм. Частицы углерода имели концентрацию
ис = 2х107,2х108,2х109м и представляли монодисперсную
смесь частиц радиусом 15 микрон. Мольная концентрация
окиси углерода принималась равной хсо2 =0.21.
щие объем поверхности считались холодными и абсолютно
черными.

14.10. Расчет имитационными методами Монте-Карло переноса излучения 479
Коэффициент поглощения в полосах СОг рассчитывался с
использованием модели равномерно распределенных линий Эль-
зассера (Гуди P.M., 1966). Учитывались следующие полосы
глощения СОг: 2.0, 2.7,4.3, 9.4, 10.4, 15 мкм. Радиационные
ства частиц углерода вычислялись с использованием теории Ми
(Борен К и др., 1986), а оптические константы заимствовались из
работы (Foster P.J., et al., 1962). Индикатриса рассеяния
лялась в транспортном приближении
/7(ц) = 2/8A-ц) + A-/)A + 3?Ц), A4.174)
где n = cos9, 9 - угол рассеяния фотона в системе координат,
связанной с рассеивающим центром; / = 0.111 и g = 0.215
эффициенты, определяющие характер рассеяния. Задание
катрисы рассеяния в таком виде позволяет использовать в
тах модифицированную величину коэффициента рассеяния
ст,=A-/)ст. Расстояние между вращательными линиями во
всех расчетах полагалось постоянным и равным 1 см'1.
Расчеты по гибридному методу статистического
вания проводились практически для тех же самых условий.
значительные отличия состояли в следующем. При расчетах
носа излучения в молекулярных полосах границы колебательно-
вращательных полос (cDmjn,<»max) выбирались в соответствии с
работой (Edwards D.K., et al., 1967), так как в работе (Tang K.C., et
al., 1994) они не указаны (табл. 14.4). Незначительная вариация
границ спектральных диапазонов не сказалась на результаты.
Таблица 14.4
Границы колебательных полос СО2
Имя полосы
15 мкм
10.4 мкм
9.4 мкм
4.3 мкм
2.7 мкм
1.9 мкм
«>min > СМ
565
955
1055
2150
3550
5196
<°тах . см~'
770
965
1065
2410
3770
5204

480 Гл. 14. Модели полос. Статистические модели
В пределах каждой полосы вводилось от одного до десяти
спектральных участков, в каждом из которых применялась
ридная статистическая модель. Параметры экспоненциальных
делей полос рассчитывались в соответствии с работой
wards D.K., et al., 1973), т.е. в данном случае использовалась так
называемая широкополосная модель спектра. Так же, как и в
боте (Tang K.C., et al., 1994), в расчетах рассеяния считалось
ведливым транспортное приближение, т.е. реальная индикатриса
рассеяния представлялась в виде суммы дельта рассеяния и
тропного рассеяния. Коэффициент рассеяния полагался равным
(l-jl)a, где средний косинус рассеяния соответствовал
циенту / в работе (Tang K.C., et al., 1994).
В табл. 14.S представлено сравнение результатов расчетов
плотности лучистого теплового потока к поверхности плоского
слоя. В целом отметим хорошее соответствие расчетных
тов: относительные погрешности не превосходят 10%. Гибридный
метод статистического моделирования показал, что для расчета
интегрального радиационного потока для наиболее трудоемкого
из представленных вариантов («с =2х109м~3) потребовалось 10 с
процессорного времени (Pentium-IV, тактовая частота процессора
-2.53 ГГц, Nf=\05).
В работе (Thynell S.T., 1990) проведено исследование
носа излучения в одномерной цилиндрической геометрии.
ты выполнены для колебательных полос двуокиси углерода с
трами в 15, 10.4, 9.4, 4.3, 2.7 и 2.0 мкм, а также для полос паров
воды с центрами в 6.3, 2.7, 1.87, 1.38 мкм. Проведено
ческое исследование полусферической излучательной
сти при различных значениях вероятности выживания кванта.
Вычислена также полусферическая излучательная способность
для условий экспериментов X. Хоттеля (Hottel Н.С., 1954) и
зано удовлетворительное согласие с экспериментальными
ми при различных температурах и парциальных давлениях
окиси углерода и паров воды. Кроме этого выполнено
ние влияния сажи и твердых частиц на полусферическую излуча-
тельную способность. Поверхность цилиндрической области
талась холодной и абсолютно черной.

14.10. Расчет имитационными методами Монте-Карло переноса излучения 481
Таблица 14.5
Интегральные радиационные потоки на границе плоского слоя
в полосах поглощения СО2
Имя
полосы
2.0 мкм
2.7 мкм
4.3 мкм
9.4 мкм
10.4 мкм
15.0 мкм
TangK.C,
et aL, 1994
1.902х10
3.298x10"'
5.218x10"'
б.ПЗхЮ
4.987xlO
1.846x10"'
10+7,м
Гибридный
метод
2.01хЮ
3.4хЮ
5.0x10"'
б.ЗхЮ
5.1хЮ
2.0x10"'
/t=2xl0+9,M
TangK.C,
etal., 1994
3.916xlO
3.916x10"'
5.729x10"'
9.846x10
8.826хЮ
2.119x10"'
Гибридный
метод
4.2хЮ
4.3x10"'
6.1x10"'
1.1x10"'
9.3хЮ
2.5x10"'
Для сравнения с результатами (Thynell S.T., 1990) и
(HottelH.C, 1954) методом гибридного имитационного
рования рассчитывалась полусферическая излучательная
ность на границе бесконечного цилиндрического объема,
ненного двуокисью углерода при температурах Т =833, 1111,
1389,1667,1944 К и парами воды при Г= 500,1000,1500, 2000 К.
Предполагалось, что цилиндрическая область радиусом Rq
нена прозрачным газом при давлении Pq=\ атм. Излучающие
зовые компоненты (СОг и НгО) составляли примесь, парциальное
давление которой рассчитывалось по формуле
A4.175)
где
(Рсо24фф) = 0.003; 0.0091; 0.0244; 0.0609; 0.1827; 0.609 и
фф 0.01; 0.02; 0.1; 0.2; 2.0, L^=\.9Ro.
Сравнение с расчетами (Thynell S.T., 1990) проводились на
примере двух серий вычислений. Сначала сопоставлялись
таты параметрических расчетов полусферической излучательной
способности однородного бесконечного цилиндрического объема
для серого излучения. Результаты расчетов представлены в
табл. 14.6. Здесь использованы обозначения
= ст/р.
A4.176)

482
Гл. 14. Модели полос. Статистические модели
В табл. 14.6 представлены результаты расчетов,
вующие случаю Ц = 1, jRo = 1 см при моделировании JV/=104
траекторий групп фотонов.
Таблица 14.6
Полусфернческая излучательная способность бесконечного цилиндра
с оптическим радиусом R = R$. Параметрическое исследование
R
0.1
1.0
10.0
к, см '
0.099
¦ 0.09
0.01
0.001
0.99
0.9
0.1
0.01
9.9
9.0
1.0
0.1
<т, см
0.001
0.01
0.09
0.099
0.01
0.1
0.9
0.99
0.1
1.0
9.0
9.9
со
0.01
0.1
0.9
0.99
0.01
0.1
0.9
0.99
0.01
0.1
0.9
0.99
Thynell S.T.,
1990
0.1754
0.1611
0.0197
0.0020
0.8108
0.7773
0.1736
0.0197
0.9959
0.9750
0.4872
0.1386
Гибридный
метод
0.1700
0.1560
0.0190
0.0019
0.7840
0.7610
0.1710
0.0190
0.9900
0.9800
0.4900
0.1510
Сравнение полусферической излучательной способности
цилиндрического объема, содержащего СО2 и Н2О, при разных
температурах и парциальных давлениях приведено в табл. 14.7 и
14.8.
Таблица 14.7
Интегральная полусфернческая способность бесконечного
цилиндра, заполненного двуокисью углерода
Г, К
833
1389
1944
РсО2^»фф»
атм-м
0.003
0.0244
0.1827
0.003
0.0244
0.1827
0.003
0.0244
0.1827
Thynell S.T.,
1990
0.0286
0.0669
0.1205
0.0187
0.0529
0.1094
0.0097
0.0331
0.0760
Hottel H.C.,
1954
0.03
0.072
0.115
0.02
0.057
0.11
0.0105
0.0340
0.078
Гибридный
метод
0.033
0.076
0.120
0.024
0.059
0.120
0.011
0.038
0.08

14.10. Расчет имитационными методами Монте-Карло переноса излучения 483
Таблица 14.8
Интегральная полусферическая способность бесконечного
цнлнндра, заполненного парами воды
Г, К
500
1000
1500
2000
Рн2О^»фф>
атм-м
0.01
0.1
2.0
0.01
0.1
2.0
0.01
0.1
2.0
0.01
0.1
2.0
Thynell S.T.,
1990
0.0623
0.1812
0.4689
0.0348
0.1307
0.4022
0.0201
0.946
0.3475
0.0114
0.0648
0.2916
Hottel H.C.,
1954
0.049
0.180
0.480
0.026
0.130
0.430
0.013
0.085
0.330
0.0065
0.046
0.230
Гибридный
метод
0.052
0.194
0.510
0.029
0.132
0.440
0.011
0.085
0.340
0.0068
0.049
0.240
Можно сделать вывод об удовлетворительной точности,
торую позволяет обеспечить предлагаемый гибридный метод
тистического моделирования в рассмотренных задачах
ния плотностей радиационных потоков. Однако выполненные
тестовые расчеты не могут служить обоснованием применимости
гибридного метода для других расчетных случаев, например, для
нахождения направленной излучательной способности.
14.10.6. Результаты расчетов спектральной направленной
излучательной способности
Имитационные алгоритмы Монте-Карло применялись для
расчета спектральной направленной излучательной способности
модельной струи РДТТ. Распределения температуры газа и
денсированной фазы, а также объемной концентрации частиц
АЬОз показаны на рис. 14.8 (давление в газовой фазе полагалось
равным 1 атм).
На рис. 14.9 представлены распределения относительных
мольных концентраций молекул ССЬ и Н2О.

484
Гл. 14. Модели полос. Статистические модели
х, см
*,см
х, см
20 40
Л, см
а б в
Рис. 14.8. Распределение температур газовой - (а) и конденсированной -
" " ~ " ' У кривых - Т в К; (в) - объемная
л, см
(б) фаз в модельной струе Р„
концентрация частиц А12О3 в см'3
л, см
R, см R, см
Рис 14.9. Распределение относительных мольных концентраций
Н2О и СОг в модельной струе РДТТ

14.10. Расчет имитационными методами Моите-Карло переноса излучения 485
Газодинамические параметры на срезе сопла полагались
близкими к исследованным в (Нельсон Х.Ф., 1986) при анализе
направленной излучательной способности (сигнатуры)
ного цилиндрического объема, аппроксимирующего струю
дуктов сгорания тактической ракеты на твердом
ном топливе. Частицы АЬОз полагались монодисперсными с
диусом г = 2мкм. Их оптические свойства рассчитывались по
теории Ми, а спектральные коэффициенты преломления и
щения заимствовались из (Plastinin Yu.A., et al., 2001).
Анализ различных оптических моделей излучающих газовых
компонент продуктов сгорания ракетных топлив был выполнен в
(Surzhikov S.T., 2002). Было показано, что использование базы
данных молекулярных линий HITRAN (Rothman L.S., et al., 1992)
для расчета сигнатур струй продуктов сгорания ограничено лишь
центрами колебательных полос поглощения. Поэтому для
тельного анализа представленных в данной работе алгоритмов
был выбран спектральный диапазон Д<% = 3600 -J-3620 см'1,
чающий центру полосы поглощения 2.7 мкм НгО. Параметры
вращательных линий рассчитывались по формулам
l-exp(-1.44<of/r)
1-ехр(-1.44ш,/Г0)
04.178)
A4.179)
Здесь То = 296 К, & = QrolQvlb,
2, m = 3(H2O),2(CO2),
О*,Н20={3657,1595,3756},см, QA,Co2 ={1388,2349,667,667},см'1,

486
Гл. 14. Модели полос. Статистические модели
Sj - интегральный коэффициент поглощения во вращательной
линии, cb^;yLhyDtl - лоренцевская и допплеровская
ны i-й линии; Ш/ - волновое число центра линии, см; S* -
тенсивность вращательной линии, приведенная в базе данных
HITRAN; Е{ - энергия нижнего уровня, см; Wm -
ный вес, г/моль; (у/,/J7з» Dt,j)m ~ полуширины,
ные резонансными и нерезонансными столкновениями при
мальных условиях; r\ij - эмпирический коэффициент
турной коррекции полуширин (г|/у= 0.5, г|,, = 1).
Результаты выполненных расчетов анализировались по
спектральной излучательной способности в двух направлениях
(углы наблюдения струи 8 = 90° и 150°, 6 - измеряется от оси
симметрии струи X) и по интегральной излучательной
сти в спектральном диапазоне А<% в нормальном к оси струи
правлении Si. Сравнение результатов по интегральной
тельной способности позволяет сделать вывод об эффективности
используемых имитационных алгоритмов (табл. 14.9).
Таблица 14.9
Интегральная направленная нзлучательная способность модельной
струи РДТТ в диапазоне Дсое - 3600 + 3620 см
-1
Метод
Nf
SL, Вт/ср
t,c
Нерассеивающая среда
LBL
LBL + метод максимального сечения
LBL с малым числом траекторий
Гибридный метод
Метод усредненных коэффициентов
104
104
ю2
10J
10J
276
277
282
336
327
226
197
17.4
10.1
9.20
Рассеивающая среда
LBL
LBL + метод максимального сечения
LBL с малым числом траекторий
Гибридный метод
Метод усредненных коэффициентов
ю4
ю4
102
10J
10J
313
304
283
303
271
705
689
187
11.5
8.9
Влияние светорассеяния изучалось путем увеличения
центрации частиц АЬОз в модельной струе (при неизменных кон-

14.10. Расчет имитационными методами Монте-Карло переноса излучения 487
центрациях газовых компонент). В табл. 14.9 представлены
зультаты расчетов для нерассеивающей и сильно рассеивающей
струи с объемной концентрацией частиц на срезе сопла
иаьОз =5х10б см.
При использовании LBL-метода диапазон А<% разбивался
на N„=1000 участков Дш„. Число моделируемых траекторий
фотонов N/ в каждом спектральном диапазоне Дсо„ указано в
табл. 14.9. Последняя колонка таблицы содержит время решения
задачи для каждого варианта (Pentium-IV, тактовая частота
цессора 2.53 ГГц).
В табл. 14.9 представлены расчетные данные, полученные с
использованием двух имитационных LBL-алгоритмов Монте-
Карло (метод максимального сечения и прямое моделирование
траекторий внутри каждой зоны), гибридного метода
ного моделирования и метода усредненных коэффициентов
нейчатого поглощения. Представлены также результаты LBL-
моделирования с малым числом траекторий.
Спектральный коэффициент поглощения в нерассеивающей
струе (в точке с координатами Х= 264 см и R = 0) и в
щем пространстве (Х= 264 см и R = 40 см) показан на рис. 14.10.
При расчете поглощения в окружающей среде полагалось
хц2о =ЗхЮ~5. Очевидно, что выбранный для анализа расчетный
случай обеспечивает широкий диапазон оптических толщин для
моделируемых участков траекторий. Рассчитанная с
нием LBL-метода спектральная направленная излучательная
собность модельной струи показана на рис. 14.11. Заметим, что
спектральные осцилляции величины 5(ш) в данном случае
словлены не только истинной спектральной зависимостью, но и
статистической погрешностью метода Монте-Карло, что легко
устраняется увеличением числа моделируемых траекторий
нов. Однако статистическая компенсация указанной погрешности
приводит к весьма стабильному результату для интегральной в
Д<% интенсивности излучения струи 5П = J 5п(ш)Aш, где ин-
деке Q означает зависимость от угла наблюдения.

488
Гл. 14. Модели полос. Статистические модели
#
й, СМ
Рис. 14.10. Спектральный коэффициент поглощения внутри
нерассеивающей струи 1 и в окружающей среде 2
3605
3610
3615
ю, см
Рис. 14.11. Спектральная направленная излучательная
ность нерассеивающей модельной струи РДТТ. Сплошная кривая
- угол наблюдения 90°, штриховая кривая - 150°

14.10. Расчет имитационными методами Монте-Карло переноса излучения 489
Нормальная компонента S± =?90° представлена в табл. 14.9.
Отсюда видно, что интеграл от сильно осциллирующей функции
5q(oo) предсказывается с хорошей точностью независимо от
горитма имитационного моделирования (первые две строки
лицы) и используемого числа N/ .
Определение величины S±, с использованием гибридных
методов позволяет сократить время расчетов примерно в 10 раз.
Эти вычисления проводились с применением подгоночного
фициента ф = 2 —10. При (р = 1 различие между результатами
LBL- и гибридных расчетов для некоторых вариантов достигало
100%. Это подтверждает выводы (Гуди P.M., 1966) о том, что
верный выбор параметров статистической модели спектра
тельных линий может привести к погрешности в 200^300%.
четы модельного спектра случайно расположенных вращательных
линий одинаковой интенсивности и полуширины дали типичную
погрешность 20 + 30 %. Таким образом, следует принимать в учет,
что в суммарной погрешности гибридного метода присутствуют
источники погрешности разной природы: погрешность
ческих моделей, погрешность статистического моделирования и
погрешность самого гибридного метода.
Различие между результатами, полученными по гибридному
методу и методу усредненных коэффициентов в данном случае
невелико, а экономия времени расчетов у менее точного метода
незначительна.
На рис. 14.12 показаны спектральный коэффициент
щения и альбедо однократного рассеяния для сильно
щей струи в той же пространственной точке, что и на рис. 14.10.
Спектральная направленная излучательная способность для
этого расчетного случая показана на рис. 14.13. Как и прежде,
ращает на себя внимание стабильность результатов расчета
гральной величины Si (см. табл. 14.9), что является
ным подтверждением принципа статистической компенсации
грешности. Гибридный метод имитационного моделирования
казал высокую эффективность и в данном случае, поскольку
зволил добиться приблизительно стократного сокращения
ни расчета при незначительной потере точности.

490
Гл. 14. Модели полос. Статистические модели
10
ю, см
Рис. 14.12. Спектральный коэффициент поглощения 1 и альбедо
однократного рассеяния 3 внутри рассеивающей струи, и
циент поглощения в окружающей среде 2
60000
ю, см
Рис. 14.13. Спектральная направленная излучательная
ность модельной рассеивающей струи РДТТ. Сплошная кривая -
угол наблюдения 90°, штриховая кривая - 150°

14.10. Расчет имитационными методами Монте-Карло переноса излучения 491
Таким образом, разработанные гибридные алгоритмы
тационного моделирования объединяют два метода:
ный метод Монте-Карло и метод статистических моделей полос
линий. Известно, что имитационный метод Монте-Карло имеет
большую дисперсию и низкую скорость сходимости результатов
при увеличении числа моделируемых фотонов. Несмотря на
занные недостатки, имеется широкий набор вычислительных
приемов (методов), позволяющих получить достаточную для
практических целей точность результатов за приемлемое
ное время. Применительно к задачам переноса теплового
ния, возникающими на практике, достаточной точностью для
имитационных расчетных методов можно считать величину
«3%. Подчеркнем, что имеются в виду методы расчета,
няемые при решении прикладных задач, и не затрагиваются
блемы получения эталонных решений.
На самом деле точность * 3 % является избыточной,
скольку используемые в расчетах радиационные свойства газов и
твердых (жидких) частиц известны с меньшей определенностью.
Для хорошо исследованных газов, таких, как НгО и СО2,
терна примерно 10%-ная достоверность знания усредненных во
вращательной структуре коэффициентов поглощения (или
метров, широкополосных моделей, позволяющих рассчитать
ренос излучения с учетом линейчатой структуры) при давлениях,
близких к атмосферному и температурах 500+3000 К.
тельная структура спектра (номенклатура вращательных линий,
их полуширина и интенсивность) известна при высоких
турах с меньшей точностью. Для менее изученных, чем НгО и
СОг, газовых смесей точность расчета коэффициентов
ния снижается до 30-J-50 и более процентов. Исходя из этого,
тается, что в инженерных приложениях суммарная погрешность
расчетов лучистого теплопереноса в пределах 30 % является
летворительной.
Второй из использованных методов - метод статистических
моделей спектральных линий, не обладает асимптотической
димостью. Детальное исследование точности методов
ских моделей полос, выполненное в работах (Гуди P.M., 1966;

492 Гл. 14. Модели полос. Статистические модели
Surzhikov S.T., 2002), показало, что специальный выбор модели
для описания конкретного спектра линий может позволить
тичь точности -10-*-20%. Наличие сильно неоднородных слоев
вдоль оптической трассы увеличивает эту погрешность примерно
до 30%. Подчеркнем, что необоснованный выбор модели полосы
приводит к погрешностям 100 -з- 300 %.
Таким образом, общую погрешность предложенного
ридного метода статистического моделирования можно оценить в
10+30% (при подходящем выборе эмпирического коэффициента).
Анализ имитационных алгоритмов Монте-Карло
тельно к проблеме расчета спектральной излучательной
сти продуктов сгорания РДТТ позволяет прогнозировать
нейшее развитие LBL-методов имитационного моделирования, в
особенности с использованием параллельных вычислений.
14.11. Пространственная модель излучения струй
продуктов сгорания
Развитие методов численного моделирования спектрального
направленного излучения струй продуктов сгорания жидкостных
ракетных двигателей (ЖРД) и ракетных двигателей твердого
лива (РДТТ) является одной из актуальных проблем спектральной
диагностики работы двигателей, а также раннего обнаружения
старта ракет и оптических методов сопровождения их полета по
траектории (Simmons F.S., 2000). При этом наиболее трудоемкими
задачами, требующими десятки и сотни часов расчетного
ютерного времени, являются задачи расчета направленной
чательной способности с высоким спектральным разрешением
светорассеивающих струй продуктов сгорания (см. предыдущий
раздел).
К проблемам физического характера следует отнести задачи
расчета спектральных оптических свойств продуктов сгорания и
окружающей атмосферы, включая возможность их
венного и временного изменения, а также проблемы выбора
ватных спектральных диапазонов, в которых производится расчет.
Размер спектральных диапазонов, в которых выполняется интег-

14.11. Пространственная модель излучения струй продуктов сгорания 493
рирование уравнения переноса, определяется в первую очередь
требованиями регистрирующей аппаратуры. Типичными
тральными диапазонами для регистрации теплового излучения
струй продуктов сгорания являются Доо= 10*30 см. В
красной области спектра AQ = 2000^-5000 см4 такие
ные диапазоны содержат сотни и тысячи вращательных линий
испускания излучения молекулярными газами. Это означает, что
расчеты переноса излучения проводятся с усреднением по
тельной структуре спектра. Повышение точности
ских и расчетных методов ведет к необходимости учета реальной
вращательной структуры спектра. Однако при этом возникают
новые проблемы физического характера: чем выше точность
чета спектра излучения, тем менее точными и более громоздкими
становятся расчетные методы определения параметров
тельных линий (интенсивности, полуширины, местоположения
линий). Кроме этого, здесь также имеются проблемы расчетно-
методического характера, связанные с тем, что подробные
тральные расчеты требуют исключительно больших затрат
пьютерного времени. Оценка необходимого количества
тральных диапазонов для подробного спектрального расчета (так
называемого line-by-line расчета) делается следующим образом:
если предположить, что на описание контура каждой
ной линии необходимо предусмотреть ~ 10 расчетных точек, то
общее число расчетных точек оценивается величиной ~10iV/, где
N/ - число вращательных молекулярных линий в исследуемой
спектральной области. Так как число вращательных линий,
рые необходимо учитывать во всем спектральном диапазоне,
тигает десятков и сотен тысяч, то полное число спектральных
чек для расчета может быть порядка 10 . Использование
мерных расчетных сеток по спектру и параллельных вычислений
позволяет заметно сократить трудоемкость расчетов (в десятки
раз), но принципиально решить проблему учета тонкой
тельной структуры спектра все же пока не удается.
В ряду перечисленных задач, проблема расчета
венного поля спектральной направленной излучательной
ности струй продуктов сгорания является не менее актуальной.

494
Гл. 14. Модели полос. Статистические модели
Имеется два класса задач, для решения которых необходимо
пользовать трехмерные расчетные методики. К первому классу
относятся задачи предсказания излучения многоблочных ракет-
носителей, имеющих расположение твердотопливных
лей в одной плоскости. Ко второму классу относятся задачи
сеяния солнечного излучения (или излучения другого источника)
на осесимметричной и многоблочной струе.
К пространственным моделям спектральной направленной
излучательной способности струй ракетных топлив
ся требования учета перечисленных выше особенностей расчетно-
методического и физического характера.
Рис. 14.14 и 14.15 иллюстрируют указанные два класса
задач. В первом случае рассматривается осесимметричная струя
продуктов сгорания, а во втором случае - блок трех струй
дуктов сгорания.
¦200
20Г
200
•200
Рис. 14.14. Температура газа в К (о) и концентрация частиц А12О3 в см~3 (б)
в осесимметричной струе. Пространственные координаты в см

14.11. Пространственная модель излучения струй продуктов сгорания 495
f
-20
о"-'
О1
0""
О'01
О'"'
О'01
0"
О'*'
О1
10""
10'°'
10""
1Q""
Ю'*1
ю
10""
10"
«¦*•¦
Ю"'
10"
1П'"
400
800
1200
N1600
2000
2400
2800
200
Рис. 14.15. Температура газа (о), частиц А12О3 (б) и концентрация частиц
А12Оз (в) в трехблочной струе

496 Гл. 14. Модели полос. Статистические модели
Для дальнейшего анализа выбраны две простейшие
гурации, одна из которых отвечает одиночной (осесимметричной)
струе продуктов сгорания, а вторая - трехблочной струе
тов сгорания, моделирующей газодинамическую конфигурацию
ракеты-носителя типа Ariane-V, у которой на центральном
рителе, работающем на криогенных компонентах топлива Ог и Нг,
подвешены два твердотопливных ускорителя, расположенные в
одной плоскости.
Рассмотрим представленные расчетные случаи более
робно, обращая особое внимание на особенности расчетно-
методической части задачи.
Расчет направленной излучательной способности одиночной
струи представляет большой интерес как для решения
ски важных задач, так и для сравнения результатов с данными
других авторов. Подавляющее большинство всех расчетно-
теоретических исследований основано именно на модели
метричной струи. На рис. 14.14 (а) показано распределение
ратуры газовой фазы, а на рис. 14.14 (б) - распределение
траций частиц А12Оз со средним радиусом 2 мкм. Здесь и далее
представлены параметры модельных струй, отражающие, тем не
менее, особенности газовой динамики реальных ракетных струй.
Обратим внимание, что в расчетной методике, основанной на
имитационных методах Монте-Карло, легко учитывается
чие температур газовой и конденсированной фаз.
Трехмерность проблемы переноса селективного теплового
излучения возникает при анализе рассеянного поля излучения на
одноблочной струе от произвольного источника внешнего
чения, например от Солнца. В этом случае считается, что на одну
из плоскостей расчетной области падает плоскопараллельный
ток излучения под произвольным углом атаки. Поскольку
ние Солнца можно сопоставить излучению абсолютно черного
тела при температуре ~ 6000 К, то спектральное распределение
этого излучения является достаточно гладким в диапазоне AQ, а
спектральная зависимость рассеянного солнечного излучения
дет определяться оптическими свойствами газовой и
ванной фаз продуктов сгорания.

14.11. Пространственная модель излучения струй продуктов сгорания 497
Трехмерность задачи расчета спектральной излучательной
способности многоблочных струй продуктов сгорания является
очевидной даже по отношению к собственному излучению.
лиз расчетных методик, разработанных для предсказания
тральной направленной излучательной способности осесиммет-
ричных струй на ортогональных и криволинейных сетках (Surzhi-
kov S.T., 2003) показал, что наибольшей простотой и
стью подобные методики обладают при решении трехмерных
дач теории переноса излучения именно в прямоугольной
вой системе координат. В этом случае легко реализуется
щий расчетный алгоритм.
1. В выбранной системе координат фиксируются
ния наблюдения, а конфигурация струи задается произвольным
образом.
2. Численное моделирование внутри светорассеивающей
ласти производится по расчетным алгоритмам (см. п. 14.10).
3. Результаты статистического моделирования
ся на всех поверхностях, ограничивающих расчетную область.
Выполняется анализ углового распределения групп фотонов,
кидающих поверхности, ограничивающие излучающий объем,
например, через поверхности в плоскостях X0Z и Y0Z,
женных при максимальных и минимальных значениях у и х.
тывая то, что направленная излучательная способность струй
дуктов сгорания формируется плоскопараллельными лучами,
ходящими от излучающей струи, на каждой из отмеченных
костей достаточно анализировать потоки групп моделируемых
фотонов в следующих угловых зонах (рис. 14.16):
9е
"min' "max J >
33 Зак. 272

498
Гл. 14. Модели полос. Статистические модели
* = *min> фе[я±Дф],
0e[0min»0max]'
где Д(р~5°,етт=1О°, 6^=170°.
Выбор значений Д<р, 8mjn, 8тах в значительной мере
волен. Однако чрезмерно большая величина Д<р приведет к
кой погрешности расчета угловой зависимости излучательной
способности, а маленькая величина - приведет к росту
ческой погрешности результатов моделирования. Диапазон
дельных значений Gmin, G^ ограничен реальной видимостью
излучающего объекта через ограничивающие расчетную область
поверхности.
8
С
I
Рис. 14.16. Система координат измерения угловых переменных
Изложенный алгоритм имитационного моделирования
носа селективного теплового излучения в трехмерном случае
пользовался в работе (Суржиков СТ., 2004 (б)) для анализа
тральной излучательной способности струй продуктов сгорания
для двух расчетных случаев, показанных на рис. 14.14 и 14.15. В
каждом из расчетных случаев анализировалась спектральная и
интегральная излучательная способность при слабом уровне
торассеяния в струях (концентрация частиц АЬОз на срезе сопел
РДТТ пр =103см~ ) и при сильном светорассеянии (концентрация
частиц АЬОз на срезе сопел РДТТ пр = 107 см" ). Радиус частиц во
всех расчетных случаях полагался равным 2 мкм. Анализ свето-

14.11. Пространственная модель излучения струй продуктов сгорания 499
рассеяния струями продуктов сгорания бокового излучения
водился на примере освещения этих струй солнечным светом под
углом 90° и 10°. Распределение температур газа и
ванной фазы задавались на основе приближенного аналитического
решения задачи о двухфазной струе, а распределение массовых
долей оптически активных компонент смеси задавалось с
зованием теории подобия между тепло- и массообменными
цессами. Спектральные оптические свойства продуктов сгорания
рассчитывались с использованием компьютерной системы (Surz-
hikov S.T., 2003 (а)), расчеты оптических свойств частиц А12Оз
проводилось с использованием теории Ми (Борен К. и др., 1986) и
оптических свойств частиц АЬОз, предложенных в (Plastinin
Yu.A., et al., 2001). Спектральные расчеты переноса излучения
выполнялись по 100-групповой модели оптических свойств с
реднением по вращательной структуре спектра. В каждой
тральной группе моделировались траектории 105ч-106 групп
тонов, так что общее число моделируемых частиц достигало 108.
Результаты расчетов интегральной и спектральной
ленной способности осесимметричной струи при двух значениях
концентраций частиц АЬОз на срезе сопла (пр =\6* ш~3 и
пр = 107 см) показаны на рис. 14.17.
Сравнение угловых зависимостей интегральной излучатель-
ной способности в двух плоскостях наблюдения позволяет
лать вывод о том, что разработанный алгоритм правильно
лирует условия симметрии излучения осесимметричной струи.
Наблюдаемые осцилляции угловой зависимости интегральной из-
лучательной способности являются типичными для
го метода имитационного моделирования и устраняются путем
увеличения числа моделируемых траекторий. Отметим также
вышение погрешностей расчета в направлениях сильно
щихся от нормальных по отношению к оси струи. Спектральная
направленная излучательная способность, представленная для
двух углов наблюдения (рис. 14.18 и 14.19), отражает
ные оптические свойства струй продуктов сгорания
ные полосы СОг, СО, Н2О) и конденсированной фазы.
33*

500
Гл. 14. Модели полос. Статистические модели
10'
8-
&
104
10'
•
¦
60 100 160
Угол наблюдения, град
а
10"
10'
_г!'-:
П
.
60 100
Угол наблюдения, град
б
160
Рис. 14.17. Интегральная направленная излучательная способность осе-
симметричной струи с низким (сплошная кривая) и высоким (пунктирная
кривая) уровнями светорассеяния. Поверхности наблюдения: х = хтах
(я). У = Ушах (^)- Число моделируемых групп фотонов в каждой
тральной группе Npi, = 105

14.11. Пространственная модель излучения струй продуктов сгорания
501
3000 4000
Волновое число, см
а
3000
4000
Волновое число, см"'
б
Рис. 14.18. Спектральная направленная излучательная способность осе-
симметричной струи с низким уровнем светорассеяния: сплошная кривая
-угол наблюдения 6 = 90°, пунктирная кривая - в = 41°. Поверхности
наблюдения: х = хтах (а), у = утхк (б). Число моделируемых групп
тонов в каждой спектральной группе Npf, = 105

502
Гл. 14. Модели полос. Статистические модели
3000 4000
Волновое число, см
а
3000
Волновое число, см"
б
Рис. 14.19. Спектральная направленная излучательная способность осе-
симметричной струи с высоким уровнем светорассеяиия: сплошная
вая - угол наблюдения в = 90°, пунктирная кривая - в = 41°.
сти наблюдения: х = хтах (а), у = утт F). Число моделируемых групп
фотонов в каждой спектральной группе Npi, = 105

14.11. Пространственная модель излучения струй продуктов сгорания
503
При увеличении концентрации твердых частиц в окнах
зрачности между колебательными полосами отчетливо видно
личение испускательной способности (сравнить рис. 14.18 и
14.19). Здесь и далее спектральная направленная излучательная
способность показана для двух углов наблюдения 8 = 90° и 41°.
Результаты расчетов излучательной способности такой же
осесимметричной струи, но с моделированием на порядок
шего числа траекторий групп фотонов в каждой спектральной
группе (NPh = 106), показаны на рис. 14.20, 14.21.
ю'
ю4
ю'
tJ ,-•
г*
¦г1
¦"¦-...
50 100
Угол наблюдения, град
150
Рис. 14.20. Интегральная направленная излучательная способность
метричной струи с низким (сплошная кривая) и высоким (пунктирная
вая) уровнями светорассеяния. Поверхности наблюдения: х = д:тах Число
моделируемых групп фотонов в каждой спектральной группе Л^ = 106
Сравнение результатов расчетов с разным числом
руемых фотонов позволяет сделать вывод об очевидном
шении стохастических пульсаций угловой и спектральной
симостей излучательной способности при увеличении Npf,. Тем
не менее, можно говорить и об удовлетворительной точности и
расчетных данных, получаемых при моделировании Nph = 105
групп фотонов в каждом спектральном диапазоне.

504
Гл. 14. Модели полос. Статистические модели
10'
«ю4
10' :
ю1
10'
:
1
ii
*
\%
V. ш
: J
* ' i
м
;'.У.'
1 • 1
* * 1
» 1 1
1 «1
1 М
• •
• •
1 •
3000 400.0
Волновое число, см"
а
6.
I
10'
10»
f
1
1
90
•.•••¦«'
1
[
1
r
w
*
3000 4000
Волновое число, см
Рис. 14.21. Спектральная направленная излучательная способность осе-
симметричной струи с низким (а) и высоким E) уровнями
ния: сплошная кривая - угол наблюдения в = 90°, пунктирная кривая -
6 = 41°. Поверхности наблюдения: х = хтах . Число моделируемых групп
фотонов в каждой спектральной группе Npi, = 10е

14.11. Пространственная модель излучения струй продуктов сгорания
505
Излучательная способность трехблочной струи с высоким
уровнем светорассеяния показана на рис. 14.22, 14.23.
ная излучательная способность в направлении перпендикулярном
плоскости расположения струй продуктов сгорания увеличивается
примерно в два раза по сравнению с направлением наблюдения,
совпадающим с плоскостью расположения струй.
ю'
ю4
¦
г-—"
I..
SO 100
Угол наблюдения, град
150
Рис. 14.22. Интегральная излучательная способность трехблочной струи
с высоким уровнем светорассеяния. Поверхности наблюдения: х = хтах
(сплошная кривая), у = утах (пунктирная кривая). Число моделируемых
групп фотонов в каждой спектральной группе N^ = 106
При компьютерной имитации радиационных процессов в
случае бокового освещения струй продуктов сгорания солнечным
светом собственное излучение обычно не рассчитывается. Тем не
менее допущение о линейности процессов переноса собственного
и рассеянного излучения позволяет учесть суммарный эффект
собственного излучения и светорассеяния путем простого
ния интегральных и спектральных излучательных способностей.
Статистическое моделирование указанных процессов
ся отдельно с использованием схожих расчетных алгоритмов.
32 Зак. 272

506
Гл. 14. Модели полос. Статистические модели
Ю'г
гЮ4
10'
10'
я
и
41
¦
- •
- I»
J
, J
I
:
J
i
i
!
i
•' i '\}\ I ?
* • ! *«
'* ••
*• »•
M
3000 4000
Волновое число, см
ю1
ПО4
10'
10»
1
-^^— to
щ
"is!
А. У
г-...»../-"-""
3000 4000
Волновое число, см'1
б
Рис. 14.23. Спектральная излучательная способность трехблочной струи
с высоким уровнями светорассеяния: сплошная кривая - угол
ния 6 = 90°, пунктирная кривая - 6 = 41°. Поверхности наблюдения:
х = Хпих (а), у = утжх (б). Число моделируемых групп фотонов в каждой
спектральной группе Npi, = 106

14.11. Пространственная модель излучения струй продуктов сгорания
507
На рис. 14.24 показаны угловые зависимости интегральной
излучательной способности в трех плоскостях наблюдения в тех
же плоскостях. В данном случае солнечный свет освещает осе-
симметричную струю под углом 0=10° к ее оси, а концентрация
частиц АЬОз радиусом 2 мкм на срезе сопла полагалась равной
пр = 107 см, т.е. предполагался высокий уровень светорассеяния.
Особенностью полученных результатов являются то, что излуча-
тельная способность, регистрируемая на плоскости XZ при
У ~ Утах. > содержит в себе незначительно ослабленное солнечное
излучение (локальный максимум излучательной способности) и
светорассеянное излучение с интенсивностью приблизительно
10 Вт/ср. В направлении нормали при х = хтгк наблюдается
таточно гладкое угловое распределение интегральной
ной способности, достигающей в максимуме величины 3 х 104 .
Наибольшая интенсивность рассеянного излучения наблюдается в
направлениях противоположных падению солнечного излучения.
Это связано с тем, что в других направлениях рассеяния
ется вероятность поглощения фотонов.
ю1
<S «'г-*
- 10'
10'
104
10'
SO 100
Угол наблюдения, град
а
Рис. 14.24. (Начало)
150
32*

508
Гл. 14. Модели полос. Статистические модели
10'
8"
m
104
10'
'. Г-'""
•••\-v..
••
\
150
SO 100
Угол наблюдения, град
б
Рис. 14.24. Интегральная направленная способность светорассеяния осесим-
метричной струи, освещенной солнечным светом под углом 6 = 10°. Высокий
уровень светорассеяния. Поверхности наблюдения: у = утах (а), х = хтю (б)
- сплошная кривая; у = ут[в (б) - пунктирная кривая. Число моделируемых
групп фотонов в каждой спектральной группе Л^Л = 105. (Окончание)
На рис. 14.25 представлены результаты расчетов рассеяния
солнечного излучения на одноблочной осесимметричной струе
продуктов сгорания при угле падения солнечного излучения
0 = 90°. Сравнение угловых зависимостей интегральных сигнатур
светорассеяния в двух рассмотренных выше случаях показывает,
что за исключением направления падения солнечного света, они
качественно подобны.
Спектральная направленная излучательная способность,
обусловленная рассеянным солнечным излучением, показана на
рис. 14.26. В рассматриваемых условиях высокой концентрации
частиц AI2O3 спектральная излучательная способность в окнах
прозрачности молекулярного поглощения близка излучательной
способности абсолютно черного тела, рассеянного
ванной фазой струи. Вблизи центров полос поглощения
лярных газов наблюдается сильное поглощение рассеянного
излучения.

14.11. Пространственная модель излучения струй продуктов сгорания
509
10*
10*
10'
10*
104
10'
50 100 150
Угол наблюдения, град
...
"¦¦¦-¦¦¦••-...
К.,
I
150
50 100
Угол наблюдения, град
б
Рис. 14.25. Интегральная направленная способность светорассеяния осе-
симметричной струи, освещенной солнечным светом под углом 6 = 90°.
Высокий уровень светорассеяния. Поверхности наблюдения: у = утт (а),
х = Хпих (б) — сплошная кривая; у = j>m;n (б) - пунктирная кривая. Число
моделируемых групп фотонов в каждой спектральной группе Nph = 105

510
Гл. 14. Модели полос. Статистические модели
10*
#
10'fe
ю' t
а
ю1
:
:
- 1 Ч ?•& Г. "
: *+{< '.' v;
! , , !
Л
. »
. »
* «в
3000
Волновое число, см
а
4000
Рис. 14.26. (Начало)
3000 4000
Волновое число, см
б
Рис. 14.26 (Продолжение)

14.11. Пространственная модель излучения струй продуктов сгорания
511
3000
Волновое число,см
в
4000
Рис. 14.26. Спектральная направленная способность светорассеяния осе-
симметричной струи, освещенной солнечным светом под углом в = 90°.
Сплошная кривая - угол наблюдения 6 = 90°, пунктирная кривая -
0 = 41° Высокий уровень светорассеяния. Поверхности наблюдения:
У = Утю. («). х = *max F)i У = Утт (»)• ЧИСЛО МОДвЛИруеМЫХ Групп фОТО-
нов в каждой спектральной группе Np/, = 10 . (Окончание)
Совместное моделирование фотонов собственного и
него излучения позволяет рассчитать полную интегральную и
спектральную излучательную способность струи, освещенную
солнечным светом. Результаты таких расчетов показаны на
рис. 14.27. В данном случае концентрация частиц А12Оз радиусом
2 мкм на срезе сопла полагалась равной пр = 107 см, т.е.
лагался высокий уровень светорассеяния. Сопоставляя рис. 14.27
(собственное + рассеянное излучение внешнего источника),
рис. 14.24 (собственное излучение), хорошо видно, что для всех
углов наблюдения, не совпадающих с направлением падения
нечного излучения, спектральная и интегральная излучательная
способность рассматриваемой струи определяется совместным
вкладом собственного и рассеянного солнечного излучения.

512
Гл. 14. Модели полос. Статистические модели
10"
10'
Lr1
SO 100
Угол наблюдения, град
а
150
10*
ю4
•
^—,
•¦¦¦¦-".. .,.,.,
¦
50 100
Угол наблюдения, град
б
150
Рис. 14.27. Интегральное собственное излучение и рассеяние солнечного
излучения, падающего на осесимметричную струю под углом в = 90°.
Высокий уровень светорассеяния. Поверхности наблюдения: у=утах (о),
х=хтах (б) - сплошная кривая; у=утт (б) - пунктирная кривая. Число
моделируемых групп фотонов в каждой спектральной группе Л^ = 105

14.11. Пространственная модель излучения струй продуктов сгорания 513
Таким образом, расчетная модель переноса селективного
теплового излучения основанная на имитационном методе Монте-
Карло, позволяет учесть основные особенности
го поля излучения светорассеивающих струй продуктов сгорания.
Заметим, что в расчетах использовалось умеренное число
руемых групп фотонов A05) в каждой их 100 спектральных групп,
что позволяло получить допустимый для данного исследования
уровень статистической погрешности (~ 5 %).
В заключение отметим, что изложенные методы расчета
пространственного поля излучения с учетом тонкой структуры
спектра посредством line-by-line интегрирования или с
ванием статистических моделей спектра, несомненно, найдут
дальнейшее развитие в будущем при решении задач переноса
лективного неравновесного излучения.

СПИСОК ЛИТЕРАТУРЫ*
Абрамовщ М., Стиган И. (ред) Справочник по специальным функциям.
М.: Наука. 1979. 832 с.
Авилова И.В., Биберман Л.М., Воробьев B.C. и др. Оптические свойства
горячего воздуха. М.: Наука. 1970. 320 с.
Адзерихо КС. Лекции по теории переноса лучистой энергии. Минск:
Изд-воБГУ. 1975. 192 с.
Адзерихо К.С., Анг&левич В.М., Некрасов В.П. и др. Моделирование
чистого теплообмена в средах неплоской геометрии // Инж.-физ. ж.
1979. Т. 36. № 2. С. 231-243.
Адзерихо КС, Ноготов Е.Ф., Трофимов В.П. Радиационный теплообмен
в двухфазных средах. Минск: Наука и техника. 1987. 166 с.
Адрианов В.Н. Основы радиационного и сложного теплообмена.
М.:Энергия. 1972.464 с.
Аксенов КН., Гольдин В.Я. Расчет двумерного стационарного уравнения
переноса нейтронов методом квазидиффузии//ЖВМ и МФ. 1979.
Т. 19. №5. С. 1341 -1343.
Алексеев Б.В., Гришин A.M. Физическая газодинамика реагирующих
сред. М.: Высшая школа. 1985.464 с.
Амбарцумян В.А. Курс астрофизики и звездной астрономии. 4.1. ОНТИ,
1934.
Амбарцумян В.А., Мустелъ Э.Р., Северный А.Б. Теоретическая
зика. М.: Гостехиздат. 1952.635 с.
Андерсон Дж.Д. Обзор исследований излучающего сжатого слоя с
женерной точки зрения // Ракетная техника и космонавтика. 1969. Т. 7.
№9. С. 3-17.
АндерсонДж.Д. Несерый лучистый теплообмен в точке торможения
// Ракетная техника и космонавтика. 1968 (а). Т.6. №4. С.242-243.
Андерсон ДжД. Тепловой поток от сжатого слоя вязкого излучающего
несерого газа//Ракетная техника и космонавтика. 1968 (б). Т. 6. №8.
С. 169-172.
* Список литературы оформлен не по ГОСТ 7.1-84, поскольку ссылки на
туру включают в себя фамилии авторов.

Список литературы 515
Андерсон Дж.Д. Уравнение для лучистого теплообмена в точке
жения // Ракетная техника и космонавтика. 1968 (в). Т. 6. № 11. С. 208 -
211.
АнистратовД.Ю., Гольдин В.Я. Сравнение нелинейных потоковых
тодов численного решения уравнения переноса//Препринт ИПМ им.
М.В. Келдыша АН СССР. № 130. М, 1989.36 с.
АнистратовД.Ю., Гольдин В.Я. Сравнение разностных схем
фузионной системы уравнения переноса//ВАНТ. Сер.: Методики и
программы численного решения задач математической физики. 1986.
Вып.2.С.17-23.
Анфимов Н.А., Демьянов Ю.А., Заверняев Ю.А. и др. Об измерении
торых параметров атмосфер планет по излучению, сопровождающему
полет спускаемых аппаратов на участке торможения // Изв. АН СССР.
МЖГ. 1981.№1.С.36-45.
Анфимов Н.А., Шари В.П. Решение системы уравнений движения
тивно излучающего газа в ударном слое// Изв. АН СССР. МЖГ. 1968.
№3. С. 18-25.
Апресян Л.А., Кравцов Ю.А. Теория переноса излучения: Статистические
и волновые аспекты. М.: Наука. 1983.216 с.
Аристова Е.Н., Гольдин В.Я. Эффективное понижение размерности
нения переноса излучения для задач радиационной газовой динамики.
Энциклопедии по низкотемпературной плазме. Вводный том // Под
ред. Фортова В.Е. -М: Наука. 2001.
Амосов О.В., Кудрявцев КН., Новиков С.С. и др. Диагностика
весных состояний в молекулярных лазерах. Минск: Наука и техника.
1985.208 с.
Базаров ИЛ. Термодинамика. М.: Высшая школа. 1983. 344 с.
Бай Ши-и. Динамика излучающего газа. М.: Мир. 1968. 323 с.
Баранов В.Б., Краснобаев КВ. Гидродинамическая теория космической
плазмы. М.: Наука. 1977.333 с.
БассЛ.П. Конечно-разностные методы решения уравнения переноса в
задачах со сложной геометрией // Препринт ИПМ им. М.В. Келдыша
АН СССР. № 14. М., 1974. 74 с.
Батенин В.М., Климовский И.М., Лысое Г.В., Троицкий В.Н. СВЧ-гене-
раторы плазмы: Физика, техника, применение. М.: Энергоатомиздат.
1988.224 с.
Батенин В.М., Минаев П.В. К вопросу об излучении плотной
пературной плазмы инертных газов//ТВТ. 1977. Т. 15. №3. С. 647-649.

516 Список литературы
Белоцерковский О.М., Биберман Л.М., БронинС.Я. и др. Обтекание и
нагрев затупленных тел гиперзвуковым потоком газа с учетом
са излучения // ТВТ. 1969. Т. 7. №3. С. 529-541.
Бергельсон В.И., Лосева Т.В., Немчинов И.В. Численный расчет задачи о
распространении дозвуковой радиационной волны навстречу потоку
излучения // Ж.прикл. мех. и техн. физ. 1974. №4. С. 22 - 34.
Биберман Л.М. К теории диффузии резонансного излучения // ЖЭТФ.
1947.Т. 17.С.416.
Биберман Л.М. Нарушение термодинамического равновесия в плазме,
вызванное выходом излучения // ЖЭТФ. 1949. Т. 19. С. 584.
Биберман Л.М., Бронин С.Я., Лагарьков А.Н. Радиационно-конвективный
теплообмен при гиперзвуковом обтекании затупленного тела //Изв.
АН СССР. МЖГ. 1972. №5. С. 112-123.
Биберман Л.М., Воробьев B.C., Лагарьков А.Н. и др. Течение воздуха за
фронтом сильной ударной волны с учетом неравновесной ионизации и
излучения // Изв. АН СССР. МЖГ. 1967. №6. С. 46 - 57.
БиберманЛ.М., Воробьев B.C., Якубов И.Т. Кинетика неравновесной
низкотемпературной плазмы. -М.: Наука. 1982.375 с.
Биберман Л.М., Лагарьков А.Н Влияние спектральных линий на
фициент лучистой теплопроводности // Оптика и спектроскопия. 1964.
Т. 16. Вып. 2. С. 320-324.
Биберман Л.М., Лагарьков А.Н. О вычислении коэффициента лучистой
теплопроводности при наличии молекулярного спектра//ТВТ. 1967.
Т.5.№5.С.924-926.
БлохА.Г. Теплообмен в топках паровых котлов. Л.: Энергоатомиздат.
1984.240 с.
Блох AT., Журавлев Ю.А., Рыжков Л.Н. Теплообмен излучением.
вочник. М: Энергоатомиздат. 1991.431 с.
Блохинцев Д.И. Основы квантовой механики. М.: Наука. 1976,664 с.
БобкоР.П. Направленные излучательные способности для двумерной
поглощающей рассеивающей среды (полубесконечный
слой) // Теплопередача. Сер. С. 1967. Т. 89. №4. С.38-46.
БоренК, ХафменД. Поглощение и рассеяние света малыми частицами.
М.: Мир. 1986.660 с.
Бори М., Вольф Э. Основы оптики. М.: Наука. 1973.719 с.
Бояринов П.М., Петров М.П. Процессы формирования термического
режима глубоких пресноводных водоемов. Л.: Наука. 1991. 174 с.
Бронин С.Я., Брыкин М.В. О применимости некоторых спектральных
моделей // ТВТ. 1977. Т. 15. № 1. С. 137 -142.

Список литературы 517
Бронин С.Я., Брыкин М.В. Приближенный метод расчета излучения
спектральных линий // ТВТ. 1976. Т. 14. №6. С. 1158 - 1165.
Бронин С.Я., Лагарьков А.Н. Перенос излучения в неоднородных слоях в
спектральной линии ударного профиля // ТВТ. 1970. Т. 8. №4. С.741 -
748.
Бронштейн КН., Семендяев К.А. Справочник по математике для
неров и учащихся втузов. М.: Наука. 1986. 544 с.
Васильев А.П., Кудрявцев В.М., Кузнецов В.А., Курпатенков В.Д. и др.
Основы теории и расчета жидкостных ракетных двигателей. М.:
шая школа. 1967.674 с.
Вентцель КС, ОвчаровЛ.А. Теория вероятностей и ее инженерные
ложения. М: Наука. 1988.480 с.
Визе В. Ширина спектральных линий. В кн.: Диагностика плазмы. М:
Мир. 1967. С. 218-262.
Висканта Р. Перенос тепла теплопроводностью и излучением в
щающих и рассеивающих средах // Теплопередача. 1965. № 1. С. 171 -
180.
Владимиров B.C. О некоторых вариационных методах приближенного
решения уравнения переноса // Вычислительная математика. М: Изд-
во ВЦ АН СССР. 1961. Т. 7. С. 95 -114.
Владимиров B.C. О некоторых вариационных методах приближенного
решения уравнения переноса. В сб.: «Вычислительная математика».
М.: Изд-во АН СССР. 1958. №7.
Войтишек А.В., Махоткин О.А. Решение задач радиационно-кондук-
тивного теплообмена методом Монте-Карло. В кн.: Теория и
мы статистического моделирования. Новосибирск: Изд-во ВЦ СО АН
СССР. 1984. С. 122-136.
Волчинская М.И., Маокукин В.И., Четверушкин Б.Н. и др. Решение
мерных нестационарных задач динамики излучающего газа // ЖВМ и
МФ. 1983. Т.23. №5. С. 1177-1185.
Гайтлер В. Квантовая теория излучения. -М: ИЛ. 1956.491 с.
ГаланинА.Д. Теория ядерных реакторов на тепловых нейтронах. М:
Атомиздат. 1957.
Галшиев B.C. Метод модифицированных сферических гармоник в
рии многократного рассеяния частиц. М: Атомиздат. 1980. 132 с.
Гермогенова Т.А., Сушкевич Т.А. Решение уравнения переноса методом
средних потоков. В кн.: Вопросы физики защиты реакторов. М.:
издат. 1969. Вып. 3. С. 34 - 43, С. 69 - 77.

518 Список литературы
Головнев И.Ф., Замураев В.П., Кацнеяьсон С.С. и др. Радиационный теп-
лоперенос в высокотемпературных газах: Справочник. М: Энерго-
атомиздат. 1984.256 с.
Головнев И.Ф., Севастьяненко В.Г., Солоухин Р.И. Математическое
делирование оптических характеристик углекислого газа//Инж.-физ.
ж. 1979. Т. 36. №2. С. 197-203.
Голубицкий Б.М., Закирова А.Р., Танташев М.В. Расчет переноса
ния в однородной рассеивающей среде с центральным точечным
точником методом Монте-Карло//Физ. атмосферы и океана. 1966.
Т.2.№11.С.1200-1201.
Голубь А. П. Численный метод решения уравнений переноса излучения в
одномерных задачах радиационной газовой динамики // ЖВМ и МФ.
1983.Т.23.№1.С.142-151.
Гольдин В.Я. Квазидиффузионный метод решения кинетического
нения //ЖВМ и МФ. 1964. Т.4. №6. С. 1078- 1087.
Гольдин В.Я. О математическом моделировании задач сплошной среды с
неравновесным переносом // Современные проблемы математической
физики и вычислительной математики. М: Наука. 1982. С. 113 -127.
Гольдин В.Я. Характеристическая разностная схема для нестационарного
кинетического уравнения. ДАН СССР. 1960. Т. 133. №4. С.748-751.
Гольдин ВЯ., Дегтярев В.А. Расчет переноса излучения в линии с фойг-
товским профилем // Препр. ИПМ им. М.В. Келдыша АН СССР. №35.
1985.17 с.
Гольдин В.Я., Калиткин Н.Н., Шитова Т.В. Нелинейные разностные
схемы гиперболических уравнений//ЖВМ и МФ. 1976. Т. 15. №5.
С. 938-944.
Гольдин В.Я., Колпаков А.В. Нелинейный метод потоковой прогонки для
решения многомерного диффузионного уравнения // Препр. ИПМ им.
М.В. Келдыша АН СССР. №22.1982.13 с.
Гольдин В.Я., Кудинова Г.А. Расчет потока энергии излучения в воздухе
// ЖВМ и МФ. 1976. Т. 16. № 3. С. 805 - 808.
Гольдин В.Я., Четверушкин Б.Н. Методы расчета переноса излучения в
одномерных задачах низкотемпературной плазмы // Препр. ИПМ им.
М.В. Келдыша АН СССР. № 12. 1970.49 с.
Гольдин В.Я., Четверушкин Б.Н. Методы решения одномерных задач
радиационной газовой динамики//ЖВМ и МФ. 1972. Т. 12. №4.
С. 990-1000.
Гольдин ВЯ., Четверушкин Б.Н. Эффективный метод решения
ния переноса излучения в низкотемпературной плазме//ДАН. 1970.
Т. 195.№2.С.315-317.

Список литературы 519
Горский В В., Суржиков СТ. О применении метода полумоментов к
шению задачи теплообмена излучением в ударном слое // ИФЖ. 1982.
Т.42.№ 1.С. 129-133.
Горский В.В., Товстоног В.А. О применении метода моментов к
нию уравнения лучистого переноса. В кн.: Тепловой режим
ций из полупрозрачных материалов. Сб. научн. трудов МВТУ. №205.
1976. С. 70-78.
Горский В.В., Штыря А.С Применение метода полумоментов к
ванию теплообмена излучением в поглощающих, излучающих и
сеивающих средах. В кн.: Вопросы теплообмена и тепловых
ний конструкций. Труды МВТУ. №495. М. 1988. С. 43 - 57.
Грим Г. Спектроскопия плазмы. М.: Атомиздат. 1969.452 с.
Грим Г. Уширение спектральных линий в плазме. М.: Мир. 1978.489 с.
ГринспенХ., КелберК., ОкрентД.-М. (ред) Вычислительные методы в
физике реакторов. М.: Атомиздат. 1972.370с.
Грудницкая Т.Я., Шипшин А. В. Дозвуковое течение излучающего
рода в канале с коаксиальными стенками. В кн.: Динамика
го газа. Вып. 1. М.: ВЦ АН СССР. 1974. С. 81 - 93.
ГрыньВ.И. О вариационных принципах для уравнения переноса и их
связи с Р„ - приближением метода сферических гармоник // ЖВМ и
МФ. 1984. Т. 24. № 1. С. 75 - 91.
ГрыньВ.И. Схемы расчета переноса излучения. В кн.: Динамика
чающего газа. М.: ВЦ АН СССР. 1981. С. 17-55.
Грязное В.К., Иосшевский И.Л., Красников Ю.Г и др. Теплофизические
свойства рабочих сред газофазного ядерного реактора. М: Атомиздат,
1980.303 с.
Гудзовский А.В., Кондранин Т.В., Кузьминский КН. Перенос излучения в
линейчатом спектре в неоднородных газовых слоях. В кн.: Труды 4
Всес. конф. по динамике излучающего газа. Т. 2. -М.: Изд-во МГУ.
1981. С. 61-67.
Гуди Р. Атмосферная радиация. М.: Мир. 1966. 522 с.
ГудменДж. Статистическая оптика. М.: Мир. 1988,527 с.
ГурвичЛ.В., Вещ КВ., Медведев В.А. и др. Термодинамические свойства
индивидуальных веществ. Т. 1,2. М.: Наука. 1978.
Давыдов А.С. Квантовая механика. М.: Наука. 1973.703 с.
ДаладоваЛ.А., МакиенкоА.К, Суржиков СТ. и др. Вычислительная
дель теплового излучения осесимметричных объемов рассеивающих
двухфазных сред // Математ. Моделирование. 1990. Т. 2. №4. С. 54.
Дейрменджан Д. Рассеяние электромагнитного излучения сферическими
полидисперсными частицами. М.: Мир. 1971.265 с.

520 Список литературы
Детков СП. Сопоставление простейших приближений в расчетах
чения неизотермического газа//ТВТ. 1972. Т. 10. №3. С.609-614.
Дирак П. Лекции по квантовой механике. М: ИЛ. 1964.
ДомбровскийЛ.А., Колпаков А.В., Суржиков СТ. Приближенный метод
расчета переноса направленного излучения в поглощающей и
тропно рассеивающей среде // ТВТ. 1990. № 5. С. 983 - 987.
Дорошенко В.М., Крючков СИ., Кудрявцев НИ. и др. Об ИК-излучении
СО и СО2 содержащих смесей колебательно-неравновесных газов
//ТВТ. 1981. Т. 19. №4. С. 735-745.
ДрагаловВ.В., Никифоров А.Ф., Новиков ВТ. и др. Статистический метод
учета спектральных линий при расчете коэффициентов поглощения
света в плазме//Препр. ИПМ им. М.В. Келдыша АН СССР. №157.
1987.12 с.
Дэвисон Б. Теория переноса нейтронов. М: Атомиздат. 1960. 520 с.
Ельяшевич М.А. Атомная и молекулярная спектроскопия. М: УРСС,
2001.894 с.
Ермаков СМ. Метод Монте-Карло и смежные вопросы. М.: Наука. 1971.
327 с.
Ермаков СМ., Михайлов Г.А. Статистическое моделирование. М: Наука.
1982.296 с.
Ершов Ю.И., ШиховСБ. Математические основы теории переноса. Т.1.
Основы теории. М.: Энергоатомиздат. 1985.232 с.
Жуков М.Ф., Девятое Б.Н, Новиков О.Я. и др. Теория термической
тродуговой плазмы. 4.2. Нестационарные процессы и радиационный
теплообмен в термической плазме. Новосибирск: Наука. 1987.287 с.
ЖуковМ.Ф., КоротееваА.С (ред.) Теория термической электродуговой
плазмы. Новосибирск: Наука. 1987. Т. 1,2.
ЖуковМ.Ф., Урюков Б.А., ЭнгельштВ.С и др. Теория термической
электродуговой плазмы. Новосибирск: Наука. 1987.288 с.
Зельдович Я.Б. и РайзерЮ.П. Физика ударных волн и
турных гидродинамических явлений. М.: Наука. 1966. 686 с.
Зигель Р., ХауэллДж. Теплообмен излучением. М.: Мир. 1975.934 с.
Золотухин ВТ., Усиков ДА. Оценка реакторных параметров методом
Монте-Карло. М.: Атомиздат. 1979. 93 с.
Ильин В.А., Позняк ЭТ. Аналитическая геометрия. М.: Наука. 1981.232 с.
Ильин В.А., Позняк ЭТ. Основы математического анализа. 4.2. М: Наука.
1980.447 с.
Имшенник B.C., Морозов Ю.И. Радиационная релятивистская
мика высокотемпературных явлений. М.: Атомиздат. 1981. 88 с.

Список литературы 521
Иолтуховский А.А., Стрелков С.А., Сушкевич Т.А. Тестовые модели
ленного решения уравнения переноса//Препр. ИПМ им.
ша АН СССР. № 150. -М, 1988. 25 с.
Исаев С.А.., Кожинов И.А., Кофанов В.И., Леонтьев А.К и др. Теория
тепломассообмена. М: Высшая школа. 1979.495 с.
Исаев С.Л..Термодинамика. М.: Изд-во МГТУ им. Н.Э.Баумана. 2000.
413 с.
Исимару А. Распространение и рассеяние волн в случайно-неоднородных
средах. Т. 1 и 2. М.: Мир. 1981.
Калиткин Н.Н. Численные методы. М.: Наука. 1978. 512 с.
Каменщиков В.А., Пластинин Ю.А., Николаев В.М. и др. Радиационные
свойства газов при высоких температурах. М.: Машиностроение. 1971.
440 с.
Карасев А.Б., Кондранин Т.В., Кузьминский ИН. К расчету переноса
лективного излучения в неоднородной плазме // Изв. АН СССР. МЖГ.
1979. №4. С. 129-136.
Карлсон Б., БемД.Ж. Решение транспортного уравнения Sn-методом. В
кн. Труды II международной конференции по мирному использованию
атомной энергии. Женева. 1958. Избранные доклады иностранных
ных. М.: 1959. Т. 3. С.408-432.
Касабов Г.А., Елисеев В.В. Спектроскопические таблицы для
пературной плазмы. М.: Атомиздат. 1979. 160 с.
КатковскийЛ.В., Ходыко Ю.В., ЛепарскаяЛ.В. Расчет методами Монте-
Карло выходящего излучения в колебательно-вращательной полосе
СО из цилиндрической сверхзвуковой струи молекулярного газа при
отсутствии локального термодинамического равновесия//Ж. прикл.
спектроскопии. 1983. Т.38. Вып.2. С.256-262.
Каули Ч. Теория звездных спектров. М.: Мир. 1974.255 с.
Кейз К, Цвайфель П. Линейная теория переноса. М.: Мир. 1972.384с.
Киселев КА. Аналитический метод расчета пропускания неоднородного
слоя газа для спектральной линии с фойгтовским контуром//Ж.
прикл. спектроскопии. 1979. Т. 30. Вып. 3. С. 397-404.
Киселев КА. О возможности аналитического расчета среднего
ния неоднородного слоя газа по параметрам тонкой структуры спектра
// Ж. прикл. спектроскопии. 1981. Т. 34. Вып. 6. С. 1071 -1077.
Клименко А.В. и Зорин В.М. (ред.). Теоретические основы теплотехники.
Теплотехнический эксперимент. Справочник, Книга вторая. М.: Изд-во
МЭИ, 2001, 561 с.
Кляус Е.М., Франкфурт У.И. Макс Планк. М.: Наука. 1980.391 с.

522 Список литературы
КобзевГ.А. Оптические свойства воздушной плазмы при высоких
пературах // Препр. ИВТ АН СССР. №1-112. М, 1983 (а). 73 с.
Кобзев ГА. Уширение спектральных линий положительных ионов азота
и кислорода// Препр. ИВТ АН СССР. №1-101. М, 1983 (б). 49 с.
КобзевГ.А., НужныйВ.А. Оптические свойства воздушной плазмы с
учетом спектральных линий, Т= 20000+300000 К //Препр. ИВТАН
СССР. № 1-134. М. 1984 (а). 56 с.
КобзевГ.А., Нужный В.А. Спектральные и интегральные оптические
характеристики непрерывного спектра воздушной плазмы при
ких температурах // Препр. ИВТ АН СССР. № 1-131. М. 1984 (б). 83 с.
Кольчужкин A.M., Учайкин В.В. Введение в теорию прохождения частиц
через вещество. М: Атомиздат. 1978. 255 с.
Компьютеры и нелинейные явления//Под.ред. А.А. Самарского. М:
Наука. 1988.192 с.
Кондранин Т.В., Кузьминский И.И. Влияние линейчатого спектра на
чистый теплообмен в ударном слое//ТВТ. 1981. Т. 19. №4. С. 777-
785.
Кондратьев К.Я. Метеорология планет. Л.: Изд-во ЛГУ. 1977.293 с.
Кондратьев К.Я., Биненко В.И. Влияние облачности на радиацию и
мат. Л.: Гидрометеоиздат. 1984.240 с.
Коньков А.А, Непланд В.Я., Николаев ВМ. и др. Проблемы лучистого
теплообмена в гиперзвуковой аэродинамике//ТВТ. 1969. Т. 7. №1.
С. 140-161.
Корлисс Ч, Бозман У. Вероятности переходов и силы осцилляторов 70
элементов. М: Мир. 1968. 562 с.
Корн Г., Корн Т. Справочник по математике для научных работников и
инженеров. М.: Наука. 1974. 831 с.
Komepoe B.H. Эквивалентность методов сферических гармоник,
кретных ординат и экспоненциальной аппроксимации для плоских
дач теории переноса. В кн.: Динамика излучающего газа. М.: Изд-во
ВЦ АН СССР. 1974. Вып. 1.С. 7-13.
Краснопольский В.А. Физика свечения атмосфер планет и комет. М.:
Наука. 1987. 304 с.
Красе М.С., Мерзликин ВТ. Радиационная теплофизика снега и льда. Л.:
Гидрометеоиздат. 1990.261 с.
Кривцов В.М. О расчете селективного излучения. В кн.: Динамика
чающего газа. М.: Изд-во ВЦ АН СССР. 1976. Вып. 2. С. 36 - 41.
Кривцов В.М. Об одном подходе к расчету селективного излучения //
ЖВМ и МФ. 1974 (а). Т. 14. №6. С. 1595-1599.

Список литературы 523
Кривцов В.М. Расчет течения селективно излучающего газа между
сиальными цилиндрами. В кн.: Динамика излучающего газа. М: Изд-
во ВЦ АН СССР. 1974 (б). Вып. 1. С. 94 -108.
Кривцов В.М., Наумова И.Н, Шмыглевский Ю.Д. и др. Сравнение
тов осесимметричных течений излучающего газа//ЖВМ и МФ. 1977.
Т. 17. №4. С. 1077- 1081.
Кривцов В.М., Наумова И.Н, Шулишнина Н.П., Шмыглевский Ю.Д.
ба двух методов расчета переноса излучения//ЖВМ и МФ. 1975. Т. 15.
№ 1.С. 163-171.
Кросби А. Излучательная способность изотермической изотропно
сеивающей среды // Ракетная техника и космонавтика. 1973. Т. 11. № 8.
С. 181-183.
КузнецоваЛ.А., Кузьменко НЕ., Кузяков Ю.Я. и др. Вероятности
ских переходов двухатомных молекул. М: Наука. 1980. 320с.
Куликов Ю.Н., Четверушкин Б.Н. Неявный разностный метод
ния температуры в задачах радиационной газовой динамики // ЖВМ и
МФ. 1973. Т. 13. №1. С. 136-146.
ЛандауЛ.Д., Лифшиц ЕМ. Гидродинамика. М.: Наука. 1986.
Ландау Л.Д., Лифшиц ЕМ. Квантовая механика. Нерелятивистская
рия. М.:Наука. 1974.752 с.
Ландау Л.Д., Лифшиц ЕМ. Статистическая физика. Часть 1. М: Наука.
1976, 583 С.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Физ-
матгиз, 1959.532 с.
Левинсон КБ., Никитин А.А. Руководство по теоретическому
нию интенсивностей линий в атомных спектрах. Л.: Изд-во ЛГУ. 1962.
359 с.
Лосев С.А., Пилюгин НН, Суржиков СТ. Моделирование радиационных
процессов в механике излучающего газа. М.: Изд-во МГУ. 1990. 190 С.
Мажорова О.С. Итерационный метод решения двумерных матричных
уравнений // Препр. ИПМ им. М.В. Келдыша. №22. М. 1982.28 с.
Мажорова О.С, Попов Ю.П. О методах численного решения уравнений
Навье-Стокса//ЖВМ и МФ. 1980. Т. 20. №4. С. 1005-1015.
Малявина Т.Б. Осреднение уравнений переноса по углам в двумерном
случае//Прикл. мат. и махан. 1973. Т.37. №2. С.355-368.
МаровМЯ., Колесниченко А.В. Введение в планетную аэрономию. М.:
Наука. 1987.456 с.
МарчукГ.И. Методы расчета ядерных реакторов. М.: Госатомиздат.
1961.667 с.
МарчукГ.И. Методы расщепления. М.: Наука. 1988.264 с.

524 Список литературы
МарчукГ.И., Лебедев В.И. Численные методы в теории переноса
тронов. М: Атомиздат. 1981.496 с.
Марчук Г.И., Михайлов Г.А., Назаралиев М.А. и др. Метод Монте-Карло в
атмосферной оптике. Новосибирск: Наука. 1976.216 с.
Матвеев АН. Оптика. М.: Высшая школа. 1985.351 с.
Матвеев B.C. Приближенные представления коэффициента поглощения
и эквивалентных ширин линий с фойгтовским контуром//Ж. прикл.
спектроскопии. 1972. Т. 16. Вып.2. С.228-233.
Махоткин О.А. Решение задач радиационно-кондуктивного теплообмена
методом Монте-Карло. 1 - общий алгоритм. В кн.: Численные методы
и статистическое моделирование в теории переноса. Новосибирск:
Изд-во ВЦ СО АН СССР. 1980. С. 119-130.
Мельниченко А.С, Огибин В.Н. Применение метода Монте-Карло к
шению спектральных задач лучистого теплообмена//ЖВМ и МФ.
1977. Т. 17. №4. С. 1068-1074.
Методы Монте-Карло в физике и геофизике. Уфа: Изд-во Башкирского
гос. университета. 1973.322 с.
Минин И.Н. Теория переноса излучения в атмосферах планет. М.: Наука.
1988.264с.
Михайлов Г.А. Некоторые вопросы теории методов Монте-Карло.
сибирск: Наука. 1974.141 с.
Михайлов Г.А. Оптимизация весовых методов Монте-Карло. М.: Наука.
1987.240 с.
Можейко СВ., Цветкова И.Л., Шильков А.В. Расчет переноса излучения
в горячем воздухе // Матем. моделирование. 1992. Т. 4. № 1. С. 65 - 82.
НельсонХ.Ф. Влияние частиц на ИК-излучение выхлопных струй
ческой ракеты // Аэрокосмическая техника. 1986. № 1. С. 119 -127.
Немчинов И.В. Об усредненных уравнениях переноса излучения и их
использовании при решении газодинамических задач // Прикл. мат. и
мех. 1970. Т. 34. №4. С. 706 -721.
Немчинов И.В., Светцов В.В., Шувалов В.В. О структуре прогревного
слоя перед фронтом сильной интенсивно-излучающей ударной волны
//Ж. прикл. мех. итехн. физ. 1978. №5. С.86-92.
Немчинов И.В., Светцов В.В., Шувалов В.В. Решение задачи о
странении сильных интенсивно излучающих ударных волн в воздухе
методом осреднения уравнения переноса. В кн.: Низкотемпературная
плазма в космосе и на Земле. М.: Изд-во ВАГО АН СССР. 1977.
С. 47-89.
Никифоров А.Ф., Новиков ВТ., Уваров В.Б. Квантово-статистические
дели высокотемпературной плазмы. М.: Физматлит. 2000. 399 с.

Список литературы 525
НикифоровА.Ф., Уваров В.Б. Специальные функции математической
физики. М.: Наука. 1984.343 с.
Никифорова А.В., Тарасов В.А., Трощиев В.Е. О решениях кинетических
уравнений дивергентным методом характеристик//ЖВМ и МФ. 1972.
Т. 12. №4. С. 1041 -1048.
Николайшвипи Ш.С. О решении односкоростного уравнения переноса с
использованием приближения Ивона-Мертенса// Атомная энергия.
1966. Т. 20. Вып. 4. С. 344-345.
Овсянников В.М. Учет селективности поглощения излучения в
ковом потоке газа. М: Наука. 1983. 152 с.
Овсянников В.М., ТирскийГ.А. Метод расчета радиационного потока и
его дивергенции в области со ступенчатым распределением
туры и состава// ПМТФ. 1971. №2. С. 54-62.
Олстэд В. Обтекание гладких симметричных тел потоком с селективным
излучением//Ракетная техника и космонавтика. 1971. Т. 9. №1.
С. 147-158.
Ольховский И.И. Курс теоретической механики для физиков. М: МГУ.
1978.574 с.
Онуфриев А.Т., Севастьяненко ВТ. О расчете переноса энергии
ния в спектральных линиях // ПМТФ. 1967. № 1. С. 125-128.
Онуфриев А. Т., Севастьяненко ВТ. Перенос лучистой энергии в
тральных линиях с учетом реабсорбции//ПМТФ. 1966. №2, С. 122 —
125.
ОртегаДж., Рейнболд В. Итерационные методы решения нелинейных
систем уравнений со многими неизвестными. М.: Мир. 1975. 558 с.
Оиисик М.Н. Сложный теплообмен. М.: Мир. 1976.616 с.
Пеннер С.С. Количественная молекулярная спектроскопия и излучатель-
ная способность газа. М.: Изд-во иностранной литературы. 1963.330 с.
Петров В.А., Марченко НВ. Перенос энергии в частично прозрачных
твердых телах. М.: Наука. 1985. 189 с.
Пилюгин Н.Н, ТирскийГ.А. Динамики ионизованного излучающего газа.
М.: Изд-во МГУ. 1989.309 с.
ПланкМ. Избранные труды. М.: Наука. 1975. 788 с.
Пластинин Ю.А., Суржиков СТ. Перенос излучения в неоднородных
слоях высокотемпературных газов в атомных линиях фойгтовского
контура //Труды 4 Всес. конф. "Динамика излучающего газа". Т.2. М.:
Изд-во МГУ. 1981. С. 35-45.
Полежаев Ю.В., Юревич Ф.Б. Тепловая защита. М.: Энергия. 1976.392 с.
Поляк Г.Л. Лучистый теплообмен при наличии лучепоглощающей и
сеивающей среды //Докл. АН СССР. 1940. Т. 27. Вып. 1.

526 Список литературы
Попяченко А.Л. Численные методы в ядерной геофизике. М: Энерго-
атомиздат. 1987. 150 с.
Попов Ю.А. Излучение рассеивающих объемов простейших
ских форм // ТВТ. 1980. Т. 18. №3. С.567-571.
Попов Ю.А. О приближении Куртиса-Годсона для расчета излучения
неизотермического газа // Инж.-физ. ж. 1977. Т. 32. №4. С. 743 - 745.
Попов Ю.А. Применение статистической модели полос к расчету
ционных характеристик неоднородного и неизотермического газов //
ТВТ. 1974. Т. 12. №4. С.790-796.
Репина Г.Е, Четверушкин Б.Н. Об одном методе решения уравнения
переноса излучения в двумерных задачах радиационной газовой
мики//ЖВМ и МФ. 1979. Т. 19. №6. С. 1513-1520.
РомановГ.С, Станкевич Ю.А., СтанчицЛ.К. и др. Термодинамические
свойства, спектральные и средние коэффициенты поглощения
компонентных газов в широком диапазоне параметров. Минск: АНК
ИТМО. Препринт № 2.1993.
Росселанд С. Астрофизика на основе теории атома. ОНТИ. 1936.
Рубцов И.А. Теплообмен излучением в сплошных средах. Новосибирск:
Наука. 1984.277 с.
РумынскийА.Н., Чуркин В.П. Обтекание затупленных тел
вым потоком вязкого излучающего газа//ЖВМ и МФ. 1974. Т. 14.
№6. С. 1553-1570.
Савельев И.В. Курс общей физики. Т. III. M.: Наука. 1973. 526 с.
Самарский А.А. Введение в численные методы. М.: Наука. 1987.286с.
Самарский А.А., Андреев В.Б. Разностные методы для эллиптических
уравнений. М.: Наука. 1976.352 с.
Самарский А.А., Николаев КС. Методы решения сеточных уравнений.
М.: Наука. 1978.591с.
Светцов В.В. Расчет сферически симметричной задачи о взрыве методом
осреднения уравнения переноса. В кн.: Динамика излучающего газа.
М.: Изд-во ВЦ АН СССР. 1980. Вып. 3. С. 46 - 57.
Севастьяненко ВТ. Перенос излучения в реальном спектре.
вание по частоте // Инж.-физ. журнал. 1979. Т. 36. №2. С.218-230.
Севастьяненко ВТ. Перенос излучения в реальном спектре.
вание по частоте и углам//Инж.-физ. журнал. 1980. Т. 38. №2.
С; 278-285.
СивухинД.В. Общий курс физики. Оптика. М.: Наука. 1985. 751 с.
Смелое В.В. Лекции по теории переноса нейтронов. М.: Атомиздат. 1978.
215 с.

Список литературы 527
Смирнов Б.М. Атомные столкновения и элементарные процессы в
ме. М.: Атомиздат. 1968. 363 с.
Смирнов КМ., Шляпников Г.В. Излучательные переходы в
ном газе//Химия плазмы. Вып.З. М: Атомиздат. 1976. С. 130-188.
Смокший О.И. Моделирование полей излучения в задачах космической
спектрофотометрии. Л.: Наука. 1986.352 с.
Собельман И.И. Введение в теорию атомных спектров. М: Наука. 1963.
640 с.
Соболев В.В. Курс теоретической астрофизики. М: Наука. 1967. 528 с.
Соболев В.В. Перенос лучистой энергии в атмосферах звезд и планет. М:
Гостехиздат. 1956.
Соболев В.В. Рассеяние света в атмосферах планет. М: Наука. 1972.335 с.
Соболь ИМ. Численные методы Монте-Карло. М.: Наука. 1973.311с.
Сошников В.М. Влияние вращательной структуры молекулярных полос
на поглощение света слоями конечной толщины // Оптика и
скопия. 1961. Т. 10. №4. С. 448-456.
Спроул Р. Современная физика. М.: Наука. 1974. 501 с.
Спэрроу ЕМ, Сесс Р.Д. Теплообмен излучением. Л.: Энергия. 1972.
Степанов Н.Ф. Квантовая механика и квантовая химия. М.: Мир. 2001.
519 с.
Стокхем Л, Лав Т. Лучистый перенос тепла от цилиндрического облака
частиц // Ракетная техника и космонавтика. 1968. Т. 6. №10.
С. 136-142.
Стокхем Л., Маклеялен К. Угловое распределение теплового излучения
от облака частиц цилиндрической формы // Ракетная техника и
навтика. 1971. Т. 9. №11. С. 5-6.
Султангазин УМ. Методы сферических гармоник и дискретных ординат
в задачах кинетической теории переноса. Алма-Ата: Наука. Каз. ССР.
1979.268 с.
Суржиков С. Т. Вычислительный эксперимент в построении
ных моделей механики излучающего газа. М.: Наука. 1992. 157 с.
Суржиков СТ. К расчету селективного радиационного теплообмена в
объемах произвольной геометрииIIТЫ. 1993 (а). Т. 31. №3.
С. 434-438.
Суржиков С. Т. Теплообмен излучением с учетом атомных линий в слоях
низкотемпературной лазерной плазмы // Матем. моделирование. 1993
(б). Т. 5. №10. С. И-31.
Суржиков СТ. Имитация распространения линейчатого излучения в
светорассеивающих объемах // ТВТ. 1993 (в). Т. 31. №4. С. 680.

528 Список литературы
Суржиков СТ. Статистическое моделирование переноса теплового
лучения. М. ИПМех РАН. Препринт №508. 1993 (г). 40 с.
Суржиков С. Т. Макростатистическая модель для описания теплообмена
излучением с учетом спектра колебательных полос. Формулировка
модели//ТВТ. 1998 (а). Т. 36. №2. С. 285-290.
Суржиков СТ. Макростатистическая модель для описания теплообмена
излучением с учетом спектра колебательных полос. Расчет переноса
излучения // ТВТ. 1998 (б). Т. 36. №3. С. 475 -481.
Суржиков С. Т. Методы потоковой квазидиффузии для расчета переноса
излучения в конечных цилиндрических объемах. В кн.: Тезисы
дов VI Всесоюзной конференции по динамике излучающего газа. М.:
ИПМ АН СССР. 1987. С. 51 - 52.
Суржиков С Т. О расчете направленного теплового излучения светорас-
сеивающих объемов методом Монте-Карло//ТВТ. 1987. Т.25. №4.
С. 691.
Суржиков СТ. Оптические свойства газов и плазмы. М.: Изд-во МГТУ
им. Н.Э. Баумана. 2004 (а). 557 с.
Суржиков СТ. Пространственная модель спектральной излучательной
способности светорассеивающих струй продуктов сгорания//ТВТ. 2004
(б). Т. 31. (в печати).
Суржиков СТ. Оптические свойства газов и плазмы. М.: МГТУ им.
Н.Э. Баумана. 2004 (в). 560 с.
Суржиков С. Т. Спектральные коэффициенты поглощения горячих
сферных газов. Атмосферы Земли и Марса. М.: ИПМех РАН. 2004 (в).
170 с.
Суржиков С. Т. Расчет имитационными методами Монте-Карло
ния струй продуктов сгорания с учетом вращательной структуры
тра // ТВТ. 2003. Т. 41. № 5. С. 785 - 799.
Суржиков С. Т. Расчет переноса селективного излучения в двумерной
цилиндрической геометрии. Нулевое приближение метода квадромо-
ментов. М.: ИПМех АН СССР. Препринт №352.1988.23 с.
Суржиков СТ. Тепловое излучение крупномасштабных кислородно-
водородных огневых шаров. Исследование вычислительных
лей // ТВТ. 1997. Т. 35, № 4, С. 584.
Суржиков С. Т. Численный анализ радиационных лазерных волн
ного горения// Квантовая электроника. 2000. Т.30. №5. С.416-420.
Сэмпсон Д. Уравнения переноса энергии и количества движения в газах
с учетом излучения. М.: Мир. 1969. 207 с.
Тамм И.Е. Основы теории электричества. М.: Наука. 1966. 624 с.
Теория звездных спектров. Сб. трудов. М.: Наука. 1966. 388 с.

Список литературы 529
ТрощиевВ.К, Юдинцев В.Ф., Федянин В.И. Об ускорении сходимости
итераций при решении кинетического уравнения //ЖВМ и МФ. 1968.
Т. 8. №2. С. 452-458.
Тьен К.Л. Радиационные свойства газов // Успехи теплопередачи. Т. 5.
М.:Мир. 1975. С.280-360.
Фспженд В.А. Решение трехмерного уравнения радиационного теплопе-
реноса методом дискретных ординат//АКТ. 1989. №9. С.79-88.
Фано У, Спенсер Л., Бергер М. Перенос гамма излучения. М: Госатом-
издат. 1963.284 с.
Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 3.
Излучение. Волны. Кванты. М: Наука. 1976.496 с.
Фшиппычев Ю.С., Четверугикин Б.Н. Об одном способе осреднения
уравнений диффузионного типа по энергиям фотонов // ЖВМ и МФ.
1976. Т. 16. №6. С. 1601 -1605.
Фок В.А. Начала квантовой механики. М.: Наука. 1976. 376 с.
ФортовВ.Е., ЯкубовИ.Т. Физика неидеальной плазмы. Черноголовка:
Институт химической физики АН СССР. 1984.263 с.
Франк-Каменецкгш А.Д. Моделирование траекторий нейтронов при
чете реакторов методом Монте-Карло. М.: Атомиздат. 1978. 94 с.
Фриш С.Э. Оптические спектры атомов. М., Л.: ГИФМЛ. 1963. 640 с.
Хисамутдинов А.И., Стариков В.Н., Морозов А.А. Алгоритмы Монте-
Карло в ядерной геофизике. Новосибирск: Наука. 1985. 158 с.
Холодов Н.М., ФломЗ.Г., Колтун П.С. Расчет радиационно-кондуктив-
ного теплообмена полупрозрачной пластины методом Монте-Карло
//Инж.-физ. ж. 1982. Т. 42. №3. С.455 -461.
ХораХ. Физика лазерной плазмы. М.: Энергоатомиздат. 1986.272 с.
Хошизаки Ш., Лэшер Л. Конвективный и лучистый теплообмен на
верхности тела с учетом массы // Ракетная техника и космонавтика.
1968. Т. 6. №8. С. 3-13.
Хошизаки Ш., УилсонЛ. Конвективный и лучистый теплообмен при
входе со сверхорбитальной скоростью//Ракетная техника и
космонавтика. 1967. Т. 5. № 1. С. 29 -42.
Цветкова И.Л., Шильков А.В. Осреднение уравнения переноса в
нансно поглощающей среде//Матем. моделирование. 1989. Т. 1. №1.
С. 92-100.
Чандрасекхар С. Перенос лучистой энергии. М.: Изд-во иностранной
литературы. 1953.432 с.
Чарахчьян А.А. Об одной численной схеме для уравнения переноса на
оптически грубой сетке // ЖВМ и МФ. 1975. Т. 15. №4. С. 999-1005.
34 Зак. 272

530 Список литературы
Чарахчьян А.А. Об одном подходе к расчету уравнения переноса для
дач динамики излучающего газа. В кн.: Динамика излучающего газа.
М: Изд-во ВЦ АН СССР. 1976. Вып.2. С. 16-35.
Чарахчьян А.А. Расчет нестационарных, сферически симметричных
чений излучающего серого газа. В кн.: Динамика излучающего газа.
М: Изд-во ВЦ АН СССР. 1974. Вып. 1. С. 54-74.
Чарахчьян А.А., Шмыглевский Ю.Д. Численные методы в динамике
лучающего газа//ЖВМ иМФ. 1980. Т.20. №5. С. 1249-1265.
Черный Г.Г. Газовая динамика. М: Наука. 1988.424 с.
Четверушкин Б.Н. Математическое моделирование задач динамики
лучающего газа. М.: Наука. 1985.304 с.
Четверушкин Б.Н. Численное решение спектральной задачи о прогреве
падающим извне излучением вещества//ЖВМ и МФ. 1971. №2.
С. 48-53.
Чин Ж. Перенос излучения при течении в окрестности передней
ческой точки с учетом влияния излучения в линиях и слоя продуктов
абляции//Ракетная техника и космонавтика. 1969. Т. 7. №7.
С. 117-128.
Шильков А. В. Методы осреднения сечений и энергетического спектра в
задачах переноса нейтронов//Матем. моделирование. 1991. Т.З. №2.
С. 63-80.
Шмыглевский Ю.Д. Вариант моментного метода расчета переноса
тивного излучения // ЖВМ и МФ. 1977. Т. 17. №3. С. 785-790.
Шмыглевский Ю.Д. Моментный метод расчета переноса селективного
излучения. В кн.: Динамика излучающего газа. М: Изд-во ВЦ АН
СССР. 1976. Вып.2. С.42-60.
Шмыглевский Ю.Д. О переносе энергии излучением в спектральных
ниях // Ж. прикл. мех. и техн. физ. 1969. №3. С. 12-20.
Шмыглевский Ю.Д. Расчет переноса лучистой энергии методом Галер-
кина//ЖВМ иМФ. 1973. Т. 13. №2. С.398-407.
Шпольский Э.В. Атомная физика. Т. 1 и 2. М.: Наука. 1974.
ЭдвардеДК. Излучательные характеристики
дача. Сер. С. 1969. Т.91. №2. С.96-113.
Эдварде ДК, ГлэссенЛ.К, ХаузерВ.К. и др. Лучистый теплообмен в
неизотермических несерых газах//Теплопередача. Сер.С. 1967. Т. 89.
№3. С.26-39.
Эдварде ДК, Нельсон КЕ. Ускоренный метод расчета лучистого
обмена между несерыми стенками и газами Н2О и СОг в
ских условиях // Теплопередача. Сер.С. 1962. Т. 84. №4. С. 3 - 9.

Список литературы 531
Эдварде Р., Бобко Р. Лучистая теплопередача от изотермической
персной среды с изотропным рассеянием // Теплопередача. Сер.С.
1967. Т. 89. №4. С. 23-33.
Янке К, Эмде Ф., Леш Ф. Специальные функции. М: Наука. 1968. 344 с.
Armstrong В. Н., SokoloffJ., Nichols R. W., et al. Radiative Properties of High
Temperature Air // JQSRT. 1961. V. 1. № 2. P. 143 -162.
Bougner R.E. An improved separability approximation for line radiative
transport in nonhomogeneous media//JQSRT. 1973. V. 13. №6.
P. 499-508.
BreeneR.G.,Jr. Stark broadening in air molecule system//JQSRT. 1968.
V.8.№3.P.1013-1017.
BurchD.E, Howard J.N., Williams D. Infrared Transmission of Synthetic
Atmospheres, V. Absorption Laws for Overlapping Bands // J. Opt. Soc.
Amer. 1956. V. 42. P. 452.
Cess R.D., WangLS. A band absorptance formulation for nonisothermal
gaseous radiation//Int. J. Heat Mass Transfer. 1970. V. 13. №3.
P. 545-555.
ChanS.H., Tien C.L A band absorptance of non-isotermal infrared radiating
gases // JQSRT. 1969. V. 9. №9. P. 1261 -1271.
ChuC.M., Churchill S.W. Representation of the angular distribution of
tion scattered by a spherical particle//J. Opt. Soc. Amer. 1955. V.45.
№11. P. 958-962.
Conrad R., Rater Yu.P., SurzhikovS.T. Continuous Optical Discharge
lized by Gas Flow in Weakly Focused Laser Beam // AIAA Journal. 1996.
V.34.№8.P.1584-1588.
Crosbie F.L., Viskanta R. The Exact Solution to a Simple Non-Grey Radiative
Transfer Problem // JQSRT. 1969. V. 9. № 5. P. 553 - 568.
Curtis A.R. Discussion of'A Statistical Model for Water-Vapour Absorption"
by R.M. Goody // Quart. J. Roy. Meteorol. Soc. 1952. V. 78. P. 638.
Dombrovsky LA. Radiation Heat Transfer in Disperse Systems. Begell House.
Inc., publishers. 1996.256 p.
Eddington A.S. The Internal Constitution of Stars. Cambridge University
Press, London. 1926.
Edwards D.K. Molecular Gas Band Radiation. Advances in Heat Transfer.
1976. V. 12. Ed. by Thomas F. Irvine, Jr., James P. Hartnett. Academic
Press, New York, San Francisco, London.
Edwards D.K., Balakrishnan A. Thermal radiation of combustion gases // Int.
J. Heat Mass Transfer. 1973. V. 16. № 1. P. 26-40.
34*

532 Список литературы
Edwards D.K., Glassen L.K., HauserW.C, Tuchscher J.S. Radiation Heat
Transfer in Nonisothermal Nongray Gases//Transactions of ASME. 1967.
V.89.№3.
Edwards D.K., Menard W.A. Comparison of models for correlation of total
band absorption // Appl. Optics. 1964. V. 3. №5. P. 621 -625.
Edwards D.K., Morizumi S.J. Scaling of vibrational-rotation gas radiation
//JQSRT. 1970. V. 10. №3. P. 175-188.
Federighi F.D. Vacuum boundary conditions for spherical harmonics methods
//Nucleonics. 1964. V.6. P.277-285.
FelskeJ.D., Tien C.L Infrared radiation from non-homogeneous gas mixtures
having overlapping bands // JQSRT. 1974. V. 14. № 1. P. 35-48.
FerrisoC.C, LudwigC.B. Spectral emissivities and integrated intensities of
the2.7 H2O band between 530 and 2200 deg K// JQSRT. 1964. V.4. № 1.
P. 215-227.
FerrisoC.C, LudwigC.B., ThompsonA.L Empirically determined infrared
absorption coefficients of H2O from 300 to 3000 К//JQSRT. 1966. V.6.
№3.P.241-275.
Fiveland W.A. Discrete-Ordinate Methods for Radiative Heat Transfer in Isot-
ropically and Anisotropically Scattering Media//J. of Heat Transfer, 1987.
V. 109. P. 809-812.
Fleck J.A., Cummings Jr. and J.D. An implicit Monte-Carlo scheme for
lating time and frequency dependent non-linear radiation transport // J. of
Comput. Phys. 1971. V. 8. P. 313 - 342.
Foster P. J., Howarth CR. Optical Constants of Carbons and Coals in the
frared // Carbon. 1962. V. 6. P. 719.
GerstlS.A.W. Trans. Amer.Nucl. Soc, 1969. V. 12. Nil. P.733; 1971. V. 14.
№ I. P.214; 1971. V. 14. №1. P.215.
Godson W.L The Computation of Infrared Transmission by Atmospheric
ter Vapour, I and II // J. Meteorol. 1955. V. 12. P. 272 and 533.
Godson W.L The Evaluation of Infra-Red Radiative Fluxes due to
pheric Water Vapour // Quqrt. J. Roy. Meteorol. Soc. 1953. V. 79. P. 367.
GogleyA.C Radiative transport of Lorentz lines in nonisothermal gases
//JQSRT. 1970. V. 10. №9. P. 1065-1075.
Golden S.A. The Dopier analog of the Elsasser band model//JQSRT. 1967.
V.7.№3. P. 483-494.
Golden S.A. The Voigt analog of an Elsasser band // JQSRT. 1969. V. 9. № 8.
P. 1067-1081.
Goody KM. A Statistical Model for Water-Vapour Absorption // Quart. J.
Roy. Meteorol. Soc. 1952. V.78. P. 165.

Список литературы 533
Goody R.M. Atmospheric Radiation. I. Theoretical Basis. Oxford at the Clare-
don Press, 1964.
HilbertD. Phys. Zeitschrift., 1912. Bd. 13. №5. s. 1056.
Hilbert D. Phys. Zeitschrift., 1913. Bd. 14. № 13. s. 592.
Hire C. Numerical Computation of Internal and External Flows. Volume 1.
Fundamentals of Numerical Discretization. 1994, A Wiley Interscience
Publication, John Wiley & Sons, Chichester, New York.
Hohtein T. Imprisonment of resonance radiation in gases//Phys. Rev., 1947.
V.72.№10.P.1212.
Hottel HC. Radiant Heat Transmission. Heat Transmission. 3rd ed. Edited by
McAdams W.H. McGraw-Hill. New York. 1954. Chapt. 4.
HowellJ.R. The Monte Carlo Method in Radiative Heat Transfer//ASME
Proceedings of the 7th AIAA/ASME Joint Thermophysics And Heat
fer Conference. Volume 1. HTD V. 357-1. 1998. P. 1 -19.
Huffaker R.M. Current research on infrared radiation from rocket exhaust //
JQSRT. 1968. V. 8. № 1. P. 87 -104.
Jeans J.H The Equations of Radiative Transfer of Energy. Monthly Notices
Roy. Astron. Soc, 1917. V.78. P. 28-36.
Kaplan L.D. A Quasi-Statistical Approach to the Calculation of Atmospheric
Transition//Proc. Toronto Meteorol. Conf. (Roy. Meteorol. Soc). 1953,
1954.
Kavanagh R.W., Bjornerud E.K., PennerS.S. Nomogram for the evaluation of
peak and total intensities for spectral lines with Doppler contour // J. Opt.
Soc. Amer. 1953. V.43. №5. P.380-382.
KowganoffV., BusbridgeI.W. Basic Methods in Transfer Problems. Dover
Publications, Inc., New York, 1963.281 p.
Krakov В., Babrov H.J., MaclayGJ. et all. Use of the Curtis-Godson
proximation in calculations of radiant heating by inhomogeneous hot gases
//Appl. Opt. 1966. V.5. № 11. P. 1791 - 1800.
KrookM. On the Solution of Equation of Transfer. 1 //Astrophys. J., 1955.
V. 122. P. 488-497.
Kuznetsova LA., Surzhikov S.T. Radiative Heat Transfer in Narrow Bands Of
Rotational Lines Of Diatomic Molecules Electronic Spectra // ASME
ceedings of the 7th AIAA/ASME Joint Thermophysics And Heat Transfer
Conference. V. 1. HTD-Vol.357-1. 1998. P.41 -49.
KyleT.G. Absorption of radiation by uniformly spaced Doppler lines //
phys. J. 1967. V. 148. №3. P. 845-848.
LadenbergR., Reiche F. Uber Selective Absorption // Ann. Phys. 1913. V.42.
P.181.

534 Список литературы
Lindquist G.H., Simmons F.S. A band model formulation for very nonuniform
paths // JQSRT. 1972. V. 12. №5. P. 807-820.
LudwigC.B. Measurement of the curves-of-growth of hot water vapor//
Applied Optics. 1971. V. 10. №5. P. 1057-1073.
LudwigC.B., Malcmus W., ReardonJ.E. et all. Handbook of infrared
tion from combastion gases//NASA SP-3080. Washington: Marshal Space
Flight Center, 1973.
LudwigC.B., Malkmus W., ReardonJ.E., ThomsonJ.A.L. Handbook Infrared
Radiation from Combustion Gases. NASA, Washington, D.C., 1973;
Ludwig C.B., Malkmus W., et al, The Standard Infrared Radiation Model //
AIAA 81-1051, 1981.
Lyons R.B.,Wormhoudt J., Gruninger J. Scattering of radiation by particles in
low altitude plumes // Journal of Spacecraft and Rockets. 1983. V. 20. №2.
P. 189-192.
MacCormack R. W., Paullay A.J. Computational efficiency achieved by time
splitting of finite difference operators//AIAA Paper 72-154, San Diego,
1972.
MarshakR.E. Note on the Spherical Harmoniks Method as Applied to the
Milne problem for a Spherical Harmonics Method //Phys. Rev., 1947.
V. 71. P. 443-446.
MarshakRE. Variation Method for Asymptotic Neutron Densities//Phys.
Rev. 1947. V. 71. P. 668.
McDonald P. W. The computation of transonic flow through two-dimensional
gas turbine cascade // ASME Paper 71-GT-89,1971.
Menguc M.P., lyerKK. Modeling of radiative transfer using multiple
cal harmonics approximations // JQSRT. 1988. №6. P. 445-461.
Mertens R Simon Stevin. Suppl., 1954. V. 30. P. 1.
Milne E.A. Radiative equilibrium in the outer layers of a star. Monthly
Not.Roy.Astron.Soc. 1921. V. 81. P. 361.
Moore CE Atomic energy levels. NBS Circular 467. Washington D.C. V. 1.-
1949; V. 2. 1952; V.3. 1958.
Murray RL Nuclear Reactor Physics. Prentice-Hall. Englewood Cliffs. N.J.
1957.
OzisikMM, MenningJ., Hald W. Half-range moment method for solution of
the transport equation in a spherically symmetric geometry // JQSRT. 1975.
V, 15. № 12. P. 1101-1106.
ParkCh. Nonequilibrium Hypersonic Aerothermodynamics. Wiley-Inter-
science Publication. J.Wiley & Sons. New York. 1990.
Placzek G. On the Theory of the Slowing Down of Neutrons in Heavy
stances // Phys.Rev. 1946. V. 69. P. 9 - 10, P. 423.

Список литературы 535
Plass G.N. The Influence of the 9.6 ц Ozone Band on the Atmospheric Infra-
Red Cooling Rate//Quart. J. Roy. Meteorol. Soc. 1956. Vol.82. P.30.
Plass G. Radiation from nonisothermal gases//Appl.Opt. 1967. V.6. №11.
P. 1995-1999.
Plass G. Useful representations for measurements of spectral band absorption
// J. of the Opt. Soc. of America. 1960. V. 50. №9. P. 868 - 875.
Plass G.N. Models for Spectral Band Absorption // J. Opt. Soc. Amer. 1958
V. 48. P. 690.
Plastinin Yu.A., Karabadzhak G., Khmelinin В., BaulaG, Rodionov A.
violet, Visible and Infrared Spectra Modeling for Solid and Liquid-fuel
Rocket Exhausts // AIAA Paper №2001-0660. 2001. P. 15.
Pomraning G.C. An Extension of the Eddington Approximation//JQSRT,
1969. V. 9. P. 407-422.
Pomraning G.C. An inproved tree-surface boundary condition for the P3
proximation //Nucl. Sci. Eng. 1964. V. 18. №4. P.528-530.
Pomraning G.C. The Equations of Radiation Hydrodynamics. Oxford, New
York: Pergamon Press, 1973.
ReardonJ.E. Prediction of radiation from rocket exaust gases//AIAA 5-th
Thermophysics Conference. Los Angeles. June 29, 1970. AIAA Paper 70-
841.
Rizzi A. W., Inouye, W. Time split finite volume method for three-dimensional
blunt-body flows // AIAA Journal. 1973. V. 11. P. 1478 -1485.
Rodgers CD., Williams W. Integrated absorption of a spectral line with the
Voigt profile//JQSRT. 1974. V. 14. №4. P.319-323.
RosselandS. Theoretical Astrophysics, Oxford University Press, London,
1936.
RothmanLS., GamacheKR., Tipping R.H. et al. The HITRAN Molecular
Database: Editions of 1991 and 1992//JQSRT. 1992. V.48. №5/6. P. 469.
Sampson D.H. Choice of an Appropriate Mean Absorption Coefficient for
Use in the General Grey Equations // JQSRT. 1965. V. 5. № 1. P. 211 -225.
Sampson D.H., Marlon R.T. On a Semi-Grey Approximation to Non-Grey
Radiative Transfer//JQSRT. 1972. V. 12. №10. P. 1389-1408.
SchiffD, ZieringS. //Nucl. Sci. Engng. 1960. V.7. №2. P. 172.
Schluter D. Die emissionskontinua thermischer edelgasplasmen // Zeitschrift
furPhysik. 1968. Band 210. Heft 1. P. 80-91.
Schuster A. Radiation Through a Foggy Atmosphere//Astrophys. J. 1905.
V.21.P.1-22.
Schwarzchild K. Uber das Gleichgewicht der Sonneatmosphere // Akad. Wiss.
GOttingen, Math.-Phys. Kl. Nachr. 1906. V. 1. P. 41 -53.

536 Список литературы
Sherman M.P. Moment methods in radiative transfer problem // JQSRT. 1967.
V.7. №1. P.89-109.
Simmons F.S. Band model for nonisothermal radiating gases // Appl. Opt.
1966. V. 5. № 11. P. 1801 -1811.
Simmons F.S. Radiances and equivalent widths of Lorentz line for nonisoter-
mal paths // JQSRT. 1967. V. 7. № 1. P. 111 -121.
Simmons F.S. Rocket Exhaust Plume Phenomenology. The Aerospace Press.
El Segundo, California. 2000.236 p.
Simmons F.S., Arnold C.B., Lindquist G.H. et all. Calculation of radiation
from hot H2O and CO2, viewed through a cool intervening atmosphere //
Appl. Opt. 1970. V.9. №12. P. 2792-2793.
Staylor W.F. Determination of stack plume properties from sattelite imagery
// J. Spacecraft. 1978. V. 15. №2. P. 92-99.
SwzhikovS.T. Calculation of the radiation flux divergence near the region of
local heat release by quadromoment method. Radiative Transfer - 1, Ed.
M. Pinar Menguc. Begell House, Inc., New York. 1996. P. 92 -106.
SwzhikovS.T. Computing System For Solving Radiative Gasdynamic
lems of Entry and Re-Entry Space Vehicles // Proc. Int. Workshop
tary Probe Atmospheric Entry and Descent Trajectory Analysis and
ence", Lisbon, Portugal, 6-9 October, 2003. ESA SP-544. 2004 с
P. Ill —117.
SurzhikovS.T. Database of Atomic Lines for Radiative Gas Dynamics//
AIAA Paper 2002-2898,2002 (a), 48 p.
Surzhikov S.T. Direct Simulation Monte-Carlo Algorithms for the Rocket
haust Plumes Emissivity Prediction//AIAA Paper 2002-0795.2002(b). 1 lp.
Surzhikov S.T. Spectral and Narrow Band Directional Emissivity of Light-
Scattering and Non-Scattering Volumes//AIAA Paper 2002-3324. 2002
(c).P.21.
Surzhikov S.T. Monte-Carlo Simulation of Plumes Spectral Emission//AIAA
Paper 2003-3895.2003. lip.
Surzhikov S.T. Numerical Simulation of Heat Radiation Generated by
ing Space Vehicle//AIAA Paper 2004-2379, Portland, Oregon, 2004 (a),
lip.
Surzhikov S.T. Prediction of 3D Rocket Exhaust Plume Signatures by the
Monte-Carlo Method // AIAA Paper 04-1354.2004 (b). 24 p.
Surzhikov S.T, GorelovV.A., KireevA.Yu. Determination of Trajectory
rameters and Some Parameters of Planetary Atmospheres by Means of
Spectral Heat Radiation Generated by Entering Space Vehicle // Proc. Int.
Workshop "Planetary Probe Atmospheric Entry and Descent Trajectory

Список литературы 537
Analysis and Science", Lisbon, Portugal, 6-9 October 2003. ESA SP-544.
2004. P. 93-100.
Surzhikov S.T., HowellJ.R. Monte-Carlo Simulation of Radiation in
ing Volumes with Line Structure // J. of Thermophysics and Heat Transfer.
1998. V. 12. №2. P. 278.
TangK.C, Brewster M.Q. K-Distribution Analysis of Gas Radiation with
Nongray, Emitting, Absorbing, and Anisotropic Scattering Particles//
Transactions of the ASME. 1994. V. 116. P. 980.
ThynellS.T. Radiation due to CO2 or H2O and Particles in Cylindrical
dia//J. Thermophysics. 1990. V.4. №4. P. 436.
Tien СL, Lewder J.E. A correlation for total band absorptance of radiating
gases // Int. J. Heat and Mass Transfer. 1966. V. 9. № 7. P. 698 - 701.
TraugoffS.C. On Grey Absorption Coefficient in Radiative Transfer//
JQSRT. 1968. V. 8. №3. P. 971 -999.
van de Hulst H.C. Theory of Absorption Lines in the Atmosphere of the Earth
//Ann. D'Astrophys. 1945. Vol. 8. P.21.
Weinberg A.M., Wigner EP. The Physical Theory of Neutron Chain
tions. The University of Chicago Press. Chicago. IL. 1958.
WeinerMM., Edwards D.K. Non-isothermal gas radiation in superposed
bration-rotation bands// JQSRT. 1968. V.8. №5. P. 1171 -1183.
Weiner M.M., Edwards D.K. Teoretical expression of Water vapor spectral
emissivity with allowance for line structure // Int. J. of Heat and Mass
Transfer. 1968. V. 11. №1. P.55-65.
Wick G.C. Uber Ebene Diffiisionsprobleme // Z. Phys. 1943. V. 121. P. 702.
Wiese W.L., Smith M. W., Glennon B.M. Atomic transition probabilities.
tional Standard Reference Data Series. National Bureau of Standards 4.
1966. V.I; 1969. V. 2.
Wilson K.H., GreifR. The separability approximation in non-homogeneous
gases // JQSRT. 1971. V. 11. №8. P. 1245 -1263.
Wilson K.H., Nicolet W.E. Spectral absorption coefficients of carbon, nitrogen
and oxygen atoms // JQSRT. 1967. V. 7. № 6. P. 891 - 941.
WyettPJ., StullV.R., PlassG.N. Quasi-Random Model of Band
tion // J. Opt. SocAmer. 1962 V. 52. P. 1209.
Yamamoto G., AidaM. Transmission in a non-homogeneous atmosphere with
an absorbing gas of constant mixing ratio//JQSRT. 1970. V. 10. №6.
P. 593-608.
YoungS.J. Band model formulation for inhomogeneous optical paths//
JQSRT. 1975. V. 15. №6. P.483-501.
Yvon J. II J. Nucl. Energy. 1957. V. 4. №3. P. 305.
ZieringS.. SchiffD. //Nucl. Sci. Engng. 1958. V.3. №6. P.635.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютно прозрачная поверхность 46
Абсолютно черное тело 34
Алгоритм квазислучайной выборки 250
Альбедо однократного рассеяния 22
Аналитические итерационные методы 271
Белая поверхность 46
Вектор плотности потока излучения 20
Вектор Умова - Пойнтинга 18
Вероятность выживания кванта 22
Вероятность вынужденного излучения 83
Вероятность вынужденного поглощения 83
Волновое число 30
Вращательные полосы 94
Гармонические функции 148
Гибридный метод статистического моделирования 467
Граничные условия Марка 180
Граничные условия Маршака 181
Групповая модель 329 , 342
Групповая обобщенная статистическая модель 403
Групповые функции 31
Давление излучения 21
Дельта-рассеяние 290
Дисперсионная форма линии 354
Диффузионное приближение 132
Диффузно-отражающая поверхность 26
Длина волны 30
Доплеровская полуширина 353
Задача Милна 71
Закон Бера 43
Закон Бугера 42
Закон Бугера - Ламберта 43
Закон Вина 39

Предметный указатель 539
Закон квадратного корня 396
Закон Кирхгофа 40
Закон Ламберта 42
Закон Рэлея - Джинса 39
Закон смещения Вина 39
Закон Стефана - Больцмана 37
Зеркально-отражающая поверхность 26
Изотропно рассеивающая среда 76
Индикатриса отражения 25
Индикатриса пропускания 79
Индикатриса рассеяния 23
Интегральная излучательная способность 324
Интегральное уравнение переноса излучения 70
Интегральные характеристики 31
Интенсивность излучения абсолютно черного тела 34
Интенсивность излучения 17
Интенсивность отраженного излучения 25
Интенсивность эффективного излучения 28
Квадратурные весовые коэффициенты 224
Квазидиффузионный метод Гольдина 359
Квазиспектральная модель 320
Квазистационарное приближение 49
Колебательно-вращательные полосы 94
Комбинированная оптическая модель 321
Конечно-разностная схема Самарского 236
Конечно-разностный тип сетки 193
Конечно-элементный тип сетки 193
Консервативная расчетная схема 192
Консервативный метод характеристик с интерполяцией 239
Коэффициент квазидиффузии 360
Коэффициент радиационной теплопроводности 324
Коэффициент Эйнштейна спонтанного излучения 83
Кумулятивная функция 286
Линейно-анизотропное рассеяние 151
Линейный закон поглощения 396
Линейчатый спектр 94
Локальное термодинамическое равновесие (ЛТР) 47
Лоренцевская полуширина 353
Макростатистическая модель 432
Метод Анфимова - Шари 370

340 Предметный указатель
Метод группового усреднения 349
Метод дискретных направлений (МДН) 247
Метод дискретных ординат (МДО) 223
Метод квадромоментов 272
Метод Кертиса - Годсона 404
Метод конечного объема центрированный в узлах 194
Метод конечного объема центрированный в ячейке 194
Метод конечного объема 190
Метод максимального сечения 89
Метод моментов 140
Метод нелокальных интегральных характеристик 383
Метод полумоментов 260
Метод последовательных приближений 264
Метод потоковой квазидиффузии 364
Метод разделения переменных Шмыглевского 340
Метод усредненных коэффициентов
линейчатого поглощения 475
Метод усредненных парциальных характеристик 378
Метод усредненных уравнений переноса Немчинова 374
Метод характеристик с интерполяцией 237
Метод характеристик 235
Метод Шварцшильда - Шустера 128
Метод Эддингтона 137
Метод эквивалентного излучающего объема 145
Метод эффективных квадромоментных характеристик 392
Метод эффективных полумоментных характеристик 390
Метод эффективных сечений 386
Методы Лебегова усреднения 341
Многогрупповой квазидиффузионный метод 366
Моделирование длины свободного пробега 294
Модель радиационного переноса 94
Модель разделяющихся переменных
в коэффициенте поглощения 339
Модель серой среды 343
Модель состояния среды 93
Модель частокола 342
Моментная процедура 157
Моментный метод Кривцова 341
Направленная степень черноты 27
Направленно-полусферическая отражательная способность 25
Направленно-полусферическая поглощательная способность 26

Предметный указатель 541
Неконсервативная расчетная схема 192
Непрозрачная поверхность 26
Неструктурированная сетка 193
Обобщенная статистическая модель Гуди 402
Объемная плотность энергии излучения 20
Объемный излучатель 124
Объемный коэффициент излучения 24
Объемный коэффициент ослабления 22
Объемный коэффициент поглощения 21
Объемный коэффициент рассеяния 22
Оптическая модель среды 93 , 318
Оптически толстый слой 105
Оптически тонкая среда 53
Оптически тонкий слой 105
Оценка случайной величины 309
Плотность одностороннего потока излучения 20
Плотность полного потока излучения 20
Плотность потока эффективного излучения 29
Поверхностная плотность потока излучения
абсолютно черного тела 37
Полинейчатая модель 330
Полиномы Лежандра 148
Полная спектральная область 342
Полусферическая отражательная способность 26
Полусферическая поглощательная способность 27
Полусферическая степень черноты 28
Полусферически-направленная отражательная способность 25
Приближение когерентного рассеяния 50
Приближение Милна - Эддингтона 338
Приближение объемного высвечивания 53
Приближение полного перераспределения по частотам 90
Приближение Росселанда 107
Приближение сильной линии 397
Приближение слабой линии 397
Приближения предельных оптических толщин 106
Принцип детального равновесия 34
Присоединенные полиномы Лежандра 157
Простая статистическая модель Гуди 402
Равновесное излучение 33
Радиационная модель среды 323

542 Предметный указатель
Реабсорбция 106
Розыгрыш длины свободного пробега 281
Розыгрыш столкновений 296
Свободно-свободные квантовые переходы 97
Свободно-связанные квантовые переходы 97
Связанно-свободные квантовые переходы 97
Связанно-связанные квантовые переходы 96
Синтетический спектр 417
Скорость квантовых переходов 84
Собственная излучательная способность единицы объема 24
Спектральная группа 31
Спектральная функция источников в линии 91
Спектральная функция источников излучения 51
Спектральная функция профиля испускания 86
Спектральная функция профиля поглощения 86
Спектральное сечение излучения 88
Спектральное сечение поглощения 88
Спектральные характеристики 30
Спектральный диапазон 31
Спектральный объемный коэффициент поглощения
с поправкой на вынужденное излучение 90
Спектроэнергетические характеристики 280
Сплошной спектр 97
Среднепланковский коэффициент поглощения 324
Среднеросселандовская длина свободного пробега фотонов 324
Среднеросселандовский коэффициент поглощения 324
Средний коэффициент по Чандрасекхару 326
Средняя поглощательная способность 412
Средняя эквивалентная ширина 417
Статистический принцип Гуди 401
Степень черноты поверхности 27
Степень черноты полусферического однородного объема 55
Структурированная сетка 193
Ступенчатая модель 330
Сферические гармоники 148
Тензорное приближение 259
Термодинамическое равновесие 33
Тормозное излучение 98
Транспортное приближение рассеяния 140 , 261
Уравнение Милна 73

Предметный указатель 543
Условие нормировки индикатрисы рассеяния 23
Феноменологический объемный
спектральный коэффициент излучения 89
Феноменологический объемный
спектральный коэффициент поглощения 89
Феноменологическое спектральное
дифференциальное сечение излучения 88
Феноменологическое спектральное
дифференциальное сечение поглощения 88
Феноменологическое уравнение переноса 76
Фойгтовская полуширина 353
Формальное решение уравнения переноса излучения 53
Функция излучения второго рода 38
Функция излучения первого рода 38
Функция источников тепловыделения в среде 52
Функция Планка 34
Функция распределения фотонного газа 18
Функции излучения абсолютно черного тела 37
Характеристические координаты 237
Циклическая частота 30
Частота колебаний электромагнитного излучения 30
Эквивалентная ширина 395
Электронные полосы 94
Яркость 124
DPn-метод 259
DSn-метод 245
LBL-метод с малым числом моделируемых траекторий 476
LBL-статистическое моделирование 466
Line by line (LBL) модель 330 , 349
Ray-Tracing метод 247
, Sn-метод 241

Научное издание
КОМПЬЮТЕРНЫЕ МОДЕЛИ ФИЗИЧЕСКОЙ МЕХАНИКИ
Суржиков Сергей Тимофеевич
Тепловое излучение
газов и плазмы
В авторской редакции
Художник Н.Г. Столярова
Компьютерная верстка Т.А. Суржиковой
Подписано в печать 30.12.2004.
Формат 60 х 90 /16. Печать офсетная. Бумага офсетная.
Усл. печ. л. 34. Уч.-изд. л. 33,5.
Тираж 300 экз. Заказ №272
Издательство МГТУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская, 5.
Отпечатано с оригинал-макета в типографин ГП «Облиздат».
248640, Калуга, пл. Старый торг, 5.