Автор: Nasritdinov G.N. Mirzaahmedov M.A. Usmonov F.R. Aripova SH.R. Rahimova F.S.
ISBN: 978-9943-28-650-4
Год: 2016
Текст
ALGEBRA 9
Aniq fanlarga ixtisoslashtirilgan umumiy o‘rta ta’lim
maktablarining 9-sinfi uchun darslik
O‘zbekiston Respublikasi
Xalq ta’limi vazjrligi tomonidan tasdiqlangan
Toshkent
«0‘zbekiston»
2016
мм
UO‘K 512 (075.3)
КВК 22.14 уа 72
А 45
мм
MUALLIFLAR:
G‘. N. NASRTTDINOV, М. A. MIRZAAHMEDOV,
F.R.USMONOV, SH.R. ARIPOVA, F. S. RAHIMOVA
мм
ММ
Maxsus muharrir — Z.N. Ten — RTM tabiiy va aniq fanlar bo'limi bosh metodisti.
Taqrizchilar — R.N. Dadajonov — O'zMU dotsenti, f.-m.f.n; J.Yu. Saparboyev —
TDPU katta o‘qituvchisi; Af.Af. Shoniyozova — Toshkent shahar
300-AFIDUMning oliy toifali matematika o'qituvchisi.
мм
Aziz o‘quvchi!
„Bizning eng ulug‘ maqsadimiz, eng ulug‘ g'oyamiz shuki, O'zbekistonning bitta yo‘li
bor: mustaqillikni mustahkamlab, mamlakatimizni har tomonlama yuksaltirib, yorug‘ va erkin
hayot sari olg'a yurish". — Prezidentimiz LA. Karimovning „Yuksak ma’naviyat — yengilmas
kuch‘ asarlarida alohida urgcu berib aytgan bu durdona fikrlari hammamiz uchun dasturilamal
bolishi zarur.
Shu ulug‘ maqsadga erishish uchun Siz bilim cho'qqilarini zabt etishingiz, bilimlami
hayot bilan boglay ohshingiz kerak. Matematika, xususan, algebra, bu sohada muhim ahamiyatga
ega. Uni o‘rganish qunt va izchillikni, ko‘plab hayotiy masala va misollami idrok etib yechishni
talab etadi. Matematikani yaxshi o'rganib olsangiz, u Sizga umrbod sadoqatli do‘st bo‘lib qoladi.
Xulq-u odobingiz barkamol, ilmingiz ziyoda bolishini tilaymiz.
ММ
Ьтаи
мм
Darslikdagi shartli belgilar
ММ
| | — masalani yechish yoki isbotlash boshlandi.
M — masalani yechish yoki isbotlash tugadi.
^5) — faollashtiruvchi savol va topshiriqlar.
* — rivojlantiruvchi, murakkabroq masala.
** — olimpiada masalalari.
| — asosiy ma’lumotni ajratish.
— olingan bilimni mustaqil tekshirish uchun test mashqlari.
(^) — tarixiy ma’lumotlar.
— manbalaming elektron manzili.
ISBN 978-9943-28-650-4
© G‘.Nasritdinov va boshqalar, 2016
© «0‘zbekiston» NMIU, 2016
1Ж
7—8-SINFLARDA O‘TILGANLARNI
TAKRORLASH
Aziz о ‘quvchi! Siz 7—8- sinflar „ Algebra “ darsligida: algebraik ifodalar,
birhadlar va ko‘phadlar, ko‘phadni ko'paytuvchilarga qjratish, algebraik
kasrlar, tengsizliklar, chiziqli funksiya va uning grafigi, ikki noma’lumli
ikkita chiziqli tenglama sistemasi, kvadrat ildizlar, kvadrat tenglamalar,
taqribiy hisoblashlarga doir misol va masalalami yechgansiz. 7—8-sinflarda
matematikadan olgan bilimlaringizni yodga solish maqsadida Sizga bir qator
mashqlar taklif etamiz.
жж
1. Soddalashtiring:
1) (Ja - 3b)-(b-3d);
2) (4a-56)-(-2a+3^);
Tenglamani yeching [2—3]:
2. 1) 10x-7 = 3x + 35;
2) 3x + 4 = 5x - 6;
3) 11a-(2a-76)-66;
4) 8a-(36-4a)-10a.
3) 7x-3 = 9 + 2x;
4) 2x — 5 = 8 + 28x.
8x 2x+l
15 4~’
4. Ko‘paytuvchilaiga ajrating:
1) 2a(3x + 4y) - 56(3x + 4j>);
2) 4a(2x - у) - 7(у - 2x);
3) 2x(a-4) + y(4-a) + 3(4-a);
4) p(a - b) + q(a - b) + n(b — a).
5. Ifodani soddalashtiiing:
1) (a + b)2-(a-b)2;
2) (a-b)2 + (a + b)2;
3) (2a + 3b)2-(2a-3b)2 ;
4) (4a-5b)2 +(4a + 5b)2.
6. Tenglamalar sistemasini yeching:
7x + 8y = 23,
3x - у = 1;
fx_4+z±3
3 6
x+1 _ 3-y _ _2
.52
жж
жж
3
IXXIZTXI
мм
мм
мм
7. Tijoratchi donasi 4500 so‘m bo‘lgan bir nechta buyum oldi. Warning -
qismining donasini 5400 so‘mdan, qismining donasini 5000 so'mdan,
о
| qismining donasini 4800 so‘mdan sotdi. Qolganini esa donasini, zarariga
bo‘lsa-da, 4000 so‘mdan sotib yubordi. Bu savdodan u 51000 so‘m foyda
qildi. Tijoratchi nechta buyum sotgan?
8. Aravaning oldingi g‘ildiragi radiusi keyingi g‘ildiragi radiusidan 0,5 m
qisqa. 90 m masofada oldingi g‘ildirak necha marta aylansa, 108 m masofada
keyingi g'ildirak shuncha marta aylanadi. Har bir g‘ildirak aylanasi radiusi
uzunligini toping.
мм
9. Bir son ikkinchisidan 7 taga ko‘p. Agar sonlardan kichigini 4 ga, kattasini
5 ga bo'lsak, birinchi bo‘linma ikkinchisidan 2 taga ortiq bo‘ladi. Shu
sonlami toping.
10. Tengsizlikni yeching:
1) 23-4(5x + 0,75)>0; 3) 4(x-2)-5(x-3)<0;
2) |(4x+7)<9; 4) 5(4x + 3) <7(3x-4)+10.
мм
11. Tengsizliklar sistemasini yeching:
мм
7x-3>ll,
5 + 2x> 4;
Зч-2х>7,
' 3 + 2x£13;
3)
2x > -3,
x _ x 1_
8 4 2'
12. Tenglamani yeching:
1) |2x+3| = |2x-3|;
2) |2-x| = |4x+l|;
13. Hisoblang:
1) 8-Лб9-7-лЯ21;
2) 5 V225 + 4 V144;
14. Tenglamani yeching:
1) x2-8x+15 = 0;
2) x2-5x+4 = 0;
3) 2x2-5x+3 = 0;
3) |x + 7| = |x-5|;
4) |3x + 5| = |x-9|.
3) V652 - 632;
4) 7502 - 482;
5) 7з+>/36;
6) V154 V100
4) 3x2+2x-l = 0;
5) х24-7хч-8 = 0;
6) 8x2 + 6x +1 = 0.
15. Ikki sonning o‘rta arifmetigi 22,5 ga, ulaming o‘rta geometrigi esa
18 ga teng. Shu sonlami toping.
Ж
16. 9-sinfni bitiruvchi o‘quvchilar bir-birlari bilan rasmlarini almashtirdilar.
Agar 1190 ta rasm almashtirilgan bo'lsa, sinfda necha nafar o‘quvchi bor?
17. Buyumning narxi 12000 so‘m edi. Bu narx ketma-ket ikki marta bir xil
foizga arzonlashtirilgandan so‘ng buyumning narxi 9720 so‘m bo'ldi.
Har gal buyumning narxi necha foizga arzonlashgan?
18. Qavariq ko‘pburchakning tomonlari soni bilan diagonallari sonining
yig‘indisi 36 ga teng. Shu ko‘pburchak tomonlari sonini toping.
19. Idishda ma’lum miqdor suv bor. Agar idishga a litr suv quyilsa,
idishning 0,25 qismi to'ladi. Agar idishdagi dastlabki suvdan a litr olib
tashlansa, idishning 0,15 qismi to‘la bo'ladi. Dastlab idishning qancha
qismi to‘la bo'lgan?
20. Qavariq ko‘pburchakning tomonlari soni bilan diagonallari sonining
yig'indisi 190 ga teng. Ko‘pburchakning tomonlari sonini toping.
21. Poyezd A va В shaharlar orasidagi yo‘l o‘rtasida 20 minut to‘xtab qoldi.
Haydovchi В ga jadvalga muvofiq yetib kelish uchun poyezdning dast-
labki tezligini 12 km/soatga oshirdi. A va В shaharlar orasidagi masofa 240
km bo‘lsa, poyezdning dastlabki tezligini toping.
1 1 1
22. hw? ТсйтГ’ эпйп oddiy kasrlarnin8 nechtasini: 1) chekli o‘nli
kasrga; 2) sof davriy kasrga; 3) aralash davriy kasrga aylantirish
mum kin? Javobingizni asoslang.
жж
23. 2,5 kg olma va 3,5 kg nok uchun 11 100 so‘m to‘landi. Olmaning narxi
10% oshib, nokning narxi 20% arzonlashgach, 3 kg olma va 2 kg nok
uchun 8 310 so‘m to‘landi. Dastlab olmaning 1 kilogrammi va nokning
1 kilogrammi necha so‘mdan bo‘lgan?
24. „Bolalar dunyosi" do‘konida 1-xil o'yinchoqlaming 6 tasi, 2-xil
o‘yinchoqlarning 9 tasi, 3-xil o‘yinchoqlaming 18 tasi 50 000 so‘mdan
ekan. Ona farzandiga har bir o‘yinchoq xilidan teng miqdorda sotib olib,
50 000 so‘m to‘ladi. Ona har bir o'yinchoq xilidan nechtadan olgan?
25. Uchta sonning yig‘indisi 208 ga teng. 1-sonning 2-siga nisbati 3:4; 2-
sonning 3-siga nisbati esa 2:3 kabi. Bu sonlaming kichigi x?—16x+64=0
tenglama ildizidan necha marta katta?
жж
26. a sonning qanday qiymatlarida
|12x + 2a + 6| = 3y,
|3y + a + 6| = 12x
tenglamalar sistemasi cheksiz ko‘p yechimga ega bo‘ladi?
5
IXXIZTXI
ЖЖ
жж
жж
I ВОВ
KVADRAT FUNKSIYA
жж
жж
жж
№ж
жж
1- §. Kvadrat funksiyaning ta’rifi
8- sinfda у = kx + b chiziqli funksiya, uning xossalari o‘iganilgan, к va
b ning turli qiymatlarida bu funksiya grafigi chizilgan edi. Matematikada,
fizikaning turli sohalarida chiziqli funksiyalar bilan bir qatorda kvadrat
funksiyalar ham uchraydi. Misollarga murojaat qilaylik.
1-misol. Tomoni x bo‘lgan kvadratning yuzi y = x2;
2-misol. Radiusi x bo‘lgan doiraning yuzi у = лх2;
3- misol. Qirrasining uzunligi x bo'lgan kub sirtining yuzi у = 6x2 formula
bo‘yicha hisoblanadi.
4-misol. Fizika kursidan Sizga s = -^- + vf + s0 formula tanish;
g= 9,8 m/s2 — erkin tushish tezlanishi. Bu formula yuqoriga v tezlik bilan
otilgan jismdan Yer sirtigacha bo‘lgan masofa t vaqtda qancha bo‘lishini
hisoblash imkonini beradi, bunda — vaqtning /=0 boshlang‘ich paytida
jism Yer sirtidan qancha masofada ekanini bildiradi.
Qaralgan bu misoliar y = ax2 + &c+ c ko‘rinishdagi funksiyaning xu-
susiy hollaridir.
Chindan ham: 1- misolda a = 1, b = c = 0; 2- misolda a = я, b = c = 0;
3- misolda esa a = 6, b = c = 0. 1-3- misollarda o£zgaruvchilar x va у harflari
g
bilan belgilangan. 4-misolda a = b=v, c = sQ bo'lib, t va s -
o‘zgaruvchilardir.
Ta’rif. y=ax?+bx+e funksiya kvadrat funksiya deyiladi, bunda a,
b va c — berilgan haqiqiy sonlar, a^O, x — haqiqiy o‘zgaruvchi.
Quyidagi funksiyalar kvadrat funksiyaga misol bo£la oladi:
1) У = х2; 5) y = x2-4x;
2) у = 3x2; 6) у =—2x2 + x;
3) y = |x2; 7) y = 6^ + 5x-2;
4) У =—4x2; 8) у = 6x2 + x - 2.
Argument x ixtiyoriy qiymatni qabul qilishi mumkin. Demak, kvadrat
funksiyaning aniqlanish sohasi barcha haqiqiy sonlar to‘plami /?=(—«>, «>)
dan iborat.
1- masala, x = —1, x = 0, x = 2 bo‘lganda y(x) = x2 + x - 6 funksiyaning
qiymatini toping.
□ ?(-!) = (-1)2 +(-l)-6 = -6;
жж
6
1Ж
у(0) = 02 + 0-6 = -6;
у(2) = 22+2-6 = 6-6 = 0.
2- masala, х ning qanday qiymatlarida у = x2-5x+6 kvadrat funksiya:
1) 2 ga; 2) 12 ga; 3) 20 ga; 4) 0 ga teng bo‘ladi?
□ 1) Masala shartiga ko'ra, x2-5x + 6 = 2, bundan x2-5x + 4 = 0.
Bunday tenglamani yechib, uning ildizlarini topishni 8- sinfdan bilasiz.
xt = 1 va Xj = 4 sonlar bu tenglamaning ildizlaridir. Shunday qilib, y(l) = 2
va y(4) = 2.
2) Shartga ko‘ra x2 - 5x+6 = 12, bundan x2 - 5x - 6 = 0. Tenglamaning
ildizlari Xj = — 1, = 6 ekanini mustaqil toping.
Demak, у (-1) = y(6) = 12.
3) x2-5x+6 = 20, x2-5x-14 = 0, Xj=-2,x2=7. y(-2) = y(7) = 20.
4) x2-5x+6 = 0, bundan xt = 2, Xj = 3. Q
Demak, y(2) = 0, y(3) = 0. x ning x = 2 va x = 3 qiymatlarida kvadrat
funksiyaning qiymati 0 bo'ldi. x ning kvadrat funksiyani nolga aylantiradigan
qiymatlari kvadrat funksiyaning nollari deyiladi.
3-masala. y = 3x2-15x kvadrat funksiyaning nollarini toping.
□ 3x2 — 15x=0 tenglamani yechib, xx = 0, x2 = 5 ekanini topa-
miz. Ц
1. Savollarga javob bering. Topshiriqlami bajaring:
__ 1) Kvadrat funksiya deb qanday funksiyaga aytiladi?
Misoliar keltiring.
2) Kvadrat funksiyaning aniqlanish sohasi qanday to‘plam boladi?
3) Kvadrat funksiyaning nollari nima? Misoliar keltiring.
4) Kvadrat funksiya bilan kvadrat tenglamaning qanday farqi bor?
5) Funksiyalardan qaysilari kvadrat funksiya:
a) у = x2 -12x + 35;
b) у = 2x2 + 3x + l;
жж
d) у = x3 - 4x2 + x;
e) y = 5x+7?
Javobingizni izohlang.
1
2. x = 2; x = 0; x=—1; x = -;
1) y(x) = 6x2 + x - 2;
3) y(x) = 3x2 - 4x - 4;
funksiyaning qiymatini toping.
2
x = --; x = 3 bo'lganda:
2) y(x) = -x2 + 2x + 3;
4) y(x) = -3x2 + 7x + 6
IXXIZTXI
жж
жж
3. х ning qanday qiymatlarida:
9 1
у(х) = 6х -5x + l kvadrat funksiya: 1) 1 ga; 2) 0 ga; 3) 2 ga; 4) 3-ga;
5) -^-ga; 6) 41 ga teng qiymatni qabul qiladi?
4. -1;-V7; 0; 1; 72; 75; 2^;
4
6; 10 sonlardan qaysilari qaysi kvadrat
жж
жж
funksiyaning nollari bo‘ladi:
1) у = x2 + x;
2) у = -x2 + x;
3) у = x2 — 16x + 60;
4) y = 6x2-llx + 4;
5) y = x2-2;
6) у = x2 - 5;
7) у = x2 + V7x;
8) у = x2-(V2+V5)x + ViO;
9) у = 12x2-29x-11;
10) у =-12x2+29x +11;
11) y = x2-7x + 6;
12) y = x2-9x-10?
жж
5. Kvadrat funksiyaning nollarini toping:
1) у = 2x2 - 3x; 6) у = 3x2 - x -10;
2) у = 3x2 + 4x; 7) у = -2x2 + 3x + 5 =
3) у = -4x2 + 5; 8) у = -x2 - 4x - 3;
4) у = -6x2 + 5x -1; 9) у = -x2 + 3x;
5) у = 12x2 + 7x +1; 10) у = -2x2 - 5x.
6. Agar у = x2 + px + q kvadrat funksiyaning xt va Xj nollari ma’lum bo‘lsa, p
va q koeffitsiyentlami (xt + x^ = —p\ xi'x1 = q) toping:
1) Xj= 4, X2= 6; 5) Xj=-2, xj =|;
2) Xj=—2, x^=—4; 6) Xj= 1, Xj= -1;
3) x1=2,5, x^—1,5; 7) Xj= 0, X2= 2;
4) xx= 4, Xj= 4; 8) Xj= —2, x^= —2.
7. x ning berilgan funksiyalar teng qiymatlar qabul qiladigan qiymatlarini toping:
1) у = x2 - 5x + 6 va у = 2x;
2) у = 6x2 - 5x +1 va у = —3x +1;
3) у = -2x2 + 5x + 3 va у = 1;
4) у = -x2 + 4x + 5 va у = — x +5;
5) У = x2 - 7x +12 va у = x2 - 3x + 2;
жж
1Ж
6) у = 2х2 + Зх - 2 va у = х2 - 2х - 4;
7) у = 6х2 + х — 2 va у = (2х-1)(х-1);
8) у = Зх2 - 5х - 2 va у = 4х2 - 5х - 6.
2-§. у = х2 funksiya
кЯЯкЯ^
у = ах2 +Ьх +с kvadrat funksiyada
а= 1, b = с = 0 deyilsa, у = х2 funksi-
yani hosil qilamiz. у=x2 funksiya grafigini
yasaylik. Koordinata tekisligida funksiya
grafigiga tegishli bir nechta (x0, Xq)
nuqtalami yasab, ulami silliq egri chiziq
bilan tutashtiramiz. Natijada y = x2
funksiya grafigini olamiz. 1- rasmdagi
grafik ushbu jadval bo‘yicha yasalgan:
x -3 -2 -1 0 1 2 3
y = x2 9 4 1 0 1 4 9
kS^kS^
|| y = x2 funksiyaning grafigi parabola deyiladi.
y = x2 funksiya xossalarini jadval ko'rinishida beraylik.
Grafikning xossalari Funksiyaning xossalari
Grafik koordinata boshida Ox o‘qqa urmadi. 0(0; 0) nuqta grafikning eng pastki nuqtasidir. a) x = 0 da y = 0 ga teng. b) x^O bo'lganda, y>0. d) x=0 da fiinksiya eng kichik qiymatiga erishadi.
Parabolaning tarmoqlari yuqoriga yo‘nalgan va cheksiz davom etadi. Pa- rabola Ox o‘qdan yuqorida joylashgan va Ox ga parallel ixtiyoriy to‘g‘ri chiziqni kesadi. Ixtiyoriy nomanfiy son funksiyaning qiymati bo‘la oladi. Funksiyaning qiy- matlar sohasi у > 0, ya’ni [0; oo) to‘plamdan iborat.
Grafik Oy o‘qqa nisbatan simmetrik. Ordinata o‘qi parabolaning simmetri- ya o‘qi. Parabolaning o‘z simmetriya o‘qi bilan kesishish nuqtasi parabo- laning uchi deyiladi. 0(0; 0) nuqta у = x2 funksiya grafigi — parabolaning uchidir. Argumentning qarama-qarshi qiymat- lariga у = x2 funksiyaning teng qiymat- lari mos keladi: (—x)2 = x2.
мм
мм
мм
Grafikning xossalari Funksiyaning xossalari
a) Grafik x < 0 oraliqda ,,tepa“dan pastga ketadi Grafikda yurayotgan jism grafik bo'ylab pastga tusha boradi; b) x>0 oraliqda grafik yuqoriga ko‘tariladi. Grafikda yurayotgan jism grafik bo‘ylab yuqoriga ko‘tariladi. a) x > 0 bo‘lsa, x ning katta qiymatiga funksiyaning katta qiymati mos keladi. Masalan, 4 > 3 dan y(4) > y(3) kelib chiqadi. у = x2 funksiya x > 0 ora- liqda o‘suvchi deyiladi. b) x < 0 da esa x ning katta qiymatiga funksiyaning kichik qiymati mos keladi: —5 <—3, y(~3) < y(“5). у = x2 funksiya x < 0 oraliqda kamayuvchi deyiladi.
Masala. у = х2 parabolaning: 1) у = 4, 2) у = 5х-6 to^ri chiziq
bilan kesishish nuqtalarining koordinatalarini toping.
мм
2
□ 1) Kesishish nuqtalari <7
Ь = 4
мм
sistemaning yechimlari bocladi. x2 = 4 tenglamani yechib topamiz:
x1 = —2, X2 = 2. Demak, у = x2 parabola va у = 4 to‘g‘ri chiziq (—2; 4) hamda
(2; 4) nuqtalarda kesishadi.
Javob: (-2; 4) va (2; 4).
мм
2)
< y x sistemani yechamiz. Bundan x2 = 5x - 6, ya’ni
у = 5x-6
x2 - 5x + 6 = 0 tenglamaga kelamiz. Uni yechib, Xj = 2, Xj = 3 ekanini topamiz.
Demak, parabola va y = 5x~6 to^ri chiziq (2; 4), (3; 9) nuqtalarda
kesishadi.
Javob: (2; 4) va (3; 9). О
8. Savollarga javob bering. Topshiriqlami bajaring:
1) У = x2 funksiyaning grafigi nima deb ataladi?
2) Parabola qanday chiziq? Uni chizish bosqichlarini ayting. Parabolani
chizib ko'rsating.
3) У = x2 funksiya xossalarini uning grafigiga qarab ayting.
4) Parabolaning simmetriya o‘qi nima? Uchi nima? у = x2 parabola
misolida tushuntiring.
5) Qaysi oraliqda у = x2 funksiya o‘suvchi? Qaysi oraliqda kama- yuvchi?
9. (Og'zaki.) Nuqtalardan qaysilari y = x2 parabola grafigiga tegishli? Qay-
silari tegishli emas? Nima uchun?
10
Л(-3; 9); Д-2; 4); С(10; 100); Z>(10; -100); Д-2; -4); Д1; -1);
Д4; 16), Д-4; 16); <2; 8).
10. у = funksiya grafigida А(—2; 4); В(—3; 9); С(>/2; 2); D(— 1; 1)
nuqtalarga Оу o‘qiga nisbatan simmetrik bo‘lgan nuqtalami toping.
11. 1) x = 2 va x= 1; 3) x = — 1 va x=2;
2) x = -3 va x = 3; 4) x = -3,5 va x = 3
bo'lsa, у = х* funksiyaning ularga mos qiymatlarini taqqoslang.
12. у = x2 parabolaning:
1) у = 16; 5) у = 4х; 9) у = -у;
2) J- = 8; 6) у = —2х; Ю) у = 0;
3) у = 9; X 7) У = ^ И) у = л/2х;
4) У = 36; 8) У = ^ 12) у = —73х
to‘g‘ri chiziq bilan kesishish nuqtalarining koordinatalarini toping.
13. у = x2 parabola bilan tocg‘ri chiziqning kesishish nuqtalan koordinatalarini
toping:
1) у = 4х + 5; 5) у = 2х + 3; 9) у = 6х - 9;
2) у = -Зх - 2; 6) У = -Зх + 2; Ю) у = -6х-9;
3) у = -2х +15; 7) у = -5х - 6; И) у = х - 0,25;
4) у = 4х - 4; 8) у = 2х -1; 12) 2х 1 л 3 9
14. Bitta koordinata tekisligida у = x2 parabola bilan: 1) у = 1; 2) у = 5 to‘g‘ri
chiziqni yasang. x ning qanday qiymatlarida parabolaning nuqtalari to‘g‘ri
chiziqdan yuqorida bo‘ladi? Qanday qiymatlarida pastda bo‘ladi?
15. x ning qanday qiymatlarida у = x2 funksiyaning qiymati: 1) 4 dan kichik;
2) 8 dan katta; 3) 16 dan katta emas; 4) 25 dan kichik emas; 5) 0 dan
katta, ammo 1 dan kichik emas; 6) 4 dan kichik emas, ammo 9 dan katta
emas?
16. Nima uchun y = x2 parabola: 1) y = ~ 1; 2) y=~3; 3) y=—4;
4) у = -2;
5) y=~0,25; 6) y=
to‘g‘ri chiziq bilan kesishmaydi?
17. у = x2 funksiya quyida berilgan oraliqda o‘sadi, degan tasdiq to‘g‘rimi?
Sababini tushuntiring.
1) [0;12];
5)
9) x < 2;
Ж
ЖЖ
ЖЖ
кЯЯкЯ^
ЖЖ
ЖЖ
ЖЖ
№•3
жж
ЖЖ
ЖЖ
11
жж
жж
2) (0; 3); 6) [-1;2]; 10) x > -4;
3) x>5; 7) (-10; 0); 11) (-6; 3];
4) x > 0; 8) x<l; 12) -4 < x < 5.
жж
18. у = х2 funksiya quyida berilgan oraliqda kamayadi, degan tasdiq to‘g‘rimi?
Sababini tushuntiring.
1) [-8;-3]; 4) x<0; 7) (-3;-2);
2) [-5;0]; 5) [-2; 2]; 8) (-1;1);
3) x<-l; 6) [1;3); 9) x>-2.
19*. у = x2 parabola va у = kx + b to‘g‘ri chiziq кчъЬ ning qanday qiymatlarida
(1; 1) va (-2, 4) nuqtalarda kesishadi?
ЖЖ
YechilishL Parabola va to‘g‘ri chiziq ikkita umumiy nuqtaga ega bo'lsa, bu
nuqtalarning koordinatalari parabola va to‘g‘ri chiziq tenglamalarini
qanoatlantirishi lozim. Bundan к va b parametrlami topish uchun ushbu
tenglamalar sistemasiga kelamiz:
k + b = l,
-2k + b = 4 Sistemani yechib, k= — 1,
b = 2 ekanini topamiz. Javob: k=—1, b = 2.
жж
жж
20*. к ning qanday qiymatlarida у = kx - 6 to‘g‘ri chiziq va у = x2 parabola
(2; 4) umumiy nuqtaga ega bo‘ladi? Boshqa kesishish nuqtasi ham bormi?
21*. b ning qanday qiymatlarida у = 5x + b to‘g‘ri chiziq va у = x2 parabola
(—3; 9) umumiy nuqtaga ega bo'ladi? Boshqa kesishish nuqtalari ham bormi?
22*. к ning qanday qiymatlarida у = x2 parabola va у = kx - 3 to‘g‘ri chiziq
abssissasi: 1) x = 4; 2) x= — 1; 3) x=3; 4) x = V3 bo‘lgan umumiy
nuqtaga ega bo‘ladi? Boshqa kesishish nuqtalari ham bormi?
23. b ning qanday qiymatlarida у = x2 va у = Зх — b chiziqlar abssissasi:
3 г
1) x= 2) x = — 1; 3) x=V5; 4) x = 2 boMgan umumiy nuqtaga ega
bo‘ladi? Boshqa kesishish nuqtalari ham bormi?
3-§. y=axi funksiya
Koeffitsiyent a bilan у = ax2 funksiya grafigining xususiyatlari orasida
qanday bog'lanish bor? Awal a > 0 holni qaraylik. a = 1 bo‘lganda 2- § da
o‘rganilgan y = x2 funksiyani hosil qilamiz.
1 2
1-masala. y=2x2 va y = -x funksiyalar grafiklarini yasang.
1 2
0 у = 2л? va У = fimksiyalaming qiymatlar jadvalini у = x2 funksiyaga
ЖЖ
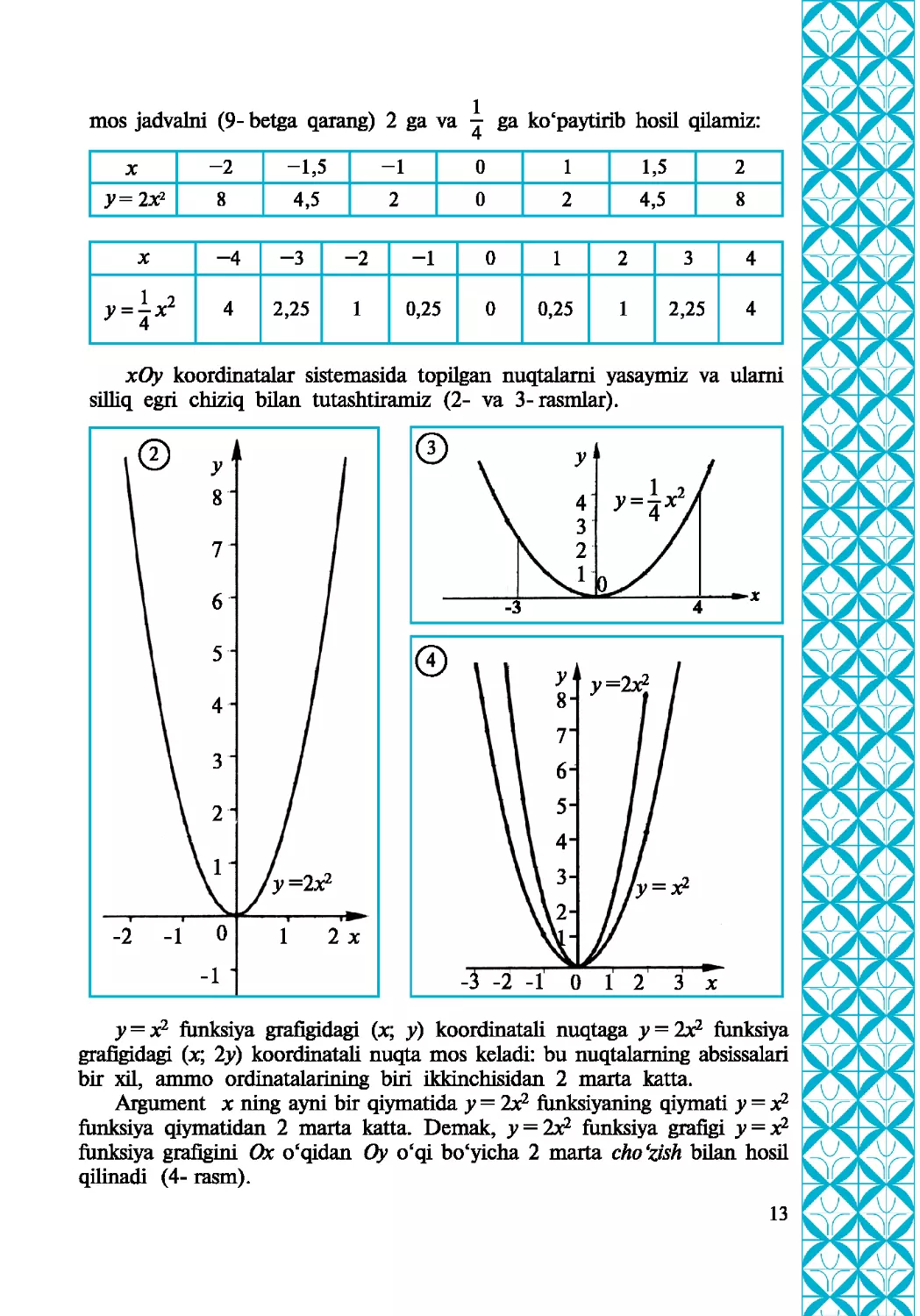
mos jadvalni (9- betga qarang) 2 ga va - ga ko‘paytirib hosil qilamiz:
X -2 -1,5 -1 0 1 1,5 2
y= lx2 8 4,5 2 0 2 4,5 8
X -4 -3 -2 -1 0 1 2 3 4
1 2 y = -^x 4 2,25 1 0,25 0 0,25 1 2,25 4
xOy koordinatalar sistemasida topilgan nuqtalami yasaymiz va ulami
silliq egri chiziq bilan tutashtiramiz (2- va 3-rasmlar).
ЖЖ
ЖЖ
ЖЖ
жж
ЖЖ
у = x2 funksiya grafigidagi (x; y) koordinatali nuqtaga у = 2x2 funksiya
grafigidagi (x; 2y) koordinatali nuqta mos keladi: bu nuqtalaming absissalari
bir xil, ammo ordinatalarining bin ikkinchisidan 2 marta katta.
Argument x ning ayni bir qiymatida у = 2x2 funksiyaning qiymati у = x2
funksiya qiymatidan 2 marta katta. Demak, y = 2x2 funksiya grafigi y = x2
funksiya grafigini Ox ocqidan Oy ocqi bo'yicha 2 marta cho‘zish bilan hosil
qilinadi (4- rasm).
13
ЖЖ
IXXIZTXI
мм
мм
мм
мм
мм
мм
1 2
Endi у = х2 va у = - х funksiyalar grafiklarini taqqoslaylik. у = х2 funk-
siya grafigidagi (x; у) koordinatali nuqtaga y = -^x2 funksiya grafigidagi
(x;iy) koordinatali nuqta mos keladi: bu nuqtalaming absissalari bir xil,
ammo ordinatalarining bin ikkinchisidan 4 marta kichik.
1 2
Argument x ning ayni bir qiymatida у = - x funksiyaning qiymati у = x2
funksiya qiymatidan 4 marta kichik. Demak, у = - x funksiya grafigi у = x2
funksiya grafigini Ox o‘qiga Oy o‘qi bo‘yicha 4 marta siqish yo'li bilan hosil
qilinadi (5-rasm). |
1 2
2- masala. 1) у = x2 va у = Zx2; 2) у = x2 va у = - x funksiyalar grafik-
larini bitta koordinatalar sistemasida chizing.
Endi a < 0 bo‘lgan holni qaraymiz.
1 2
3- masala у = - - x funksiya grafigini yasang.
□ у = - x va у = - - x funksiyalar x ning ayni bir qiymatida modullari
1 2
teng va qarama-qarshi ishorali qiymatlar qabul qiladi. Demak, У-~~^х
1 2
funksiya grafigini У = ^х funksiya grafigidan uni Ox o'qqa nisbatan sim-
metrik aks ettirish (ko'chirish) bilan hosil qilish mumkin (6-rasm). |
1 2
У = - - x va у = —x2 funksiyalaming grafiklari Ox o‘qqa nisbatan, mos
ravishda, у = | x2 va у = x2 funksiya grafiklariga simmetrikdir (7, 8-rasmlar).
1Ж
у = ox2 funksiyaning grafigi istalgan a*0 da ham parabola deb
ataladi.
Parabolaning tarmoqlari: a>0 bo‘lganda yuqoriga, a<0 bo4ganda
esa pastga yo‘nalgan.
жж
y=ax2 funksiyaning asosiy xossalari
1- xossa. a>0 va x*Q bo'lganda у = ax2 funksiyaning qiymatlari mus-
bat;
a<Q va x#0 bo‘lganda y = ax2 funksiyaning qiymatlari manfiy.
Faqat x = 0 bo'lganda y=ax2 funksiyaning qiymati 0 ga teng bo‘ladi.
2-xossa. y = ax2 funksiyaning grafigi — parabola Oy o‘qqa nisbatan
simmetrik joylashgan (9-rasm).
3- xossa. a > 0 bo‘lsa, у = ax2 funksiya x > 0 oraliqda o‘sadi, x < 0
oraliqda esa kamayadi;
a < 0 bo‘lsa, у = ax1 funksiya x > 0 oraliqda kamayadi, x < 0 oraliqda
esa o'sadi.
y=ax2 funksiyaning bu xossalari grafikdan yaqqol ko‘rinib turibdi.
жж
кЯЯкЖ
жж
15
мм
мм
мм
мм
мм
мм
мм
24. Savollarga javob bering:
1) у = лх2 funksiyaning grafigi nima deb ataladi?
(У) 2) a ning qanday qiymatlarida parabolaning tarmoqlari yuqoriga (pastga)
yo‘nalgan?
3) Funksiya grafigini Ox o'qidan Oy o‘qi bo£ylab (bo£yicha) к marta
cho‘zish deganda nimani tushunasiz? у =3xi funksiya grafigi y = x2
funksiya grafigidan qanday qilib hosil qilinadi?
4) Funksiya grafigini Ox o‘qiga Oy o£qi bo'ylab (bo£yicha) к marta
1 2
si qish deganda nimani tushunasiz? У=^х funksiyaning grafigi y = x2
funksiyaning grafigidan qanday hosil qilinadi?
25. 1) y = x2 va y = —x2 funksiyalar grafiklari Ox oeqqa nisbatan qanday
joylashgan? Ulardan birining grafigi berilsa, ikkinchisining grafigi qanday
hosil qilinadi?
2) у = cd? funksiya a va x ning qanday qiymatlarida o'suvchi (kamayuvchi)
bo‘ladi?
3) у = cd? funksiya a va x ning qanday qiymatlarida musbat (manfiy)
qiymatlar qabul qiladi?
26. (Og‘zaki.) Parabola tarmoqlarining yo'nalishini ayting:
1) y = 2xt; 2) y = ±x2; 3) y = -3x2; 4) y = -^x2; 5) y = 0,4x2.
27. Funksiyalaming grafiklarini bitta koordinata tekisligida chizing:
1) y = —x2 va y=— 2л2; 3) y = x2 va y = ^x2;
2) y = ±x2 va y = -|x2; 4) У = -^х2 va У = ^х2-
Grafikdan foydalanib bu funksiyalaming ocsish va kamayish oraliqlarini
aniqlang.
28. Funksiyalar grafiklari kesishish nuqtalarining koordinatalarini toping:
1) y=3x2 va y=x+2; 2) y = 5x2 va y=— 33x+14;
3) y = — 2x2 va y = x~6; 4) y = 2j? va y = — 5x~ 2.
29*. a ning qanday qiymatida у = ax2 parabola va to‘g£ri chiziq faqat bitta
umumiy nuqtaga ega bo'ladi?
1) y = 4x + 2; 2) y = — 4x + 2; 3) y=~6x— 1; 4) y = 6x— 1.
Ko frsatma\ 8-sinf „Algebra“ darsligidan ma’lumki, ax2+lfx+c = 0
tenglama: D = &—4ac>0 bo£lsa, ikkita; D = 0 bo£lsa, bitta ildizga ega.
D < 0 bo'lganda tenglama ildizga ega ernas. Shu xossadan foydalaning.
30*. a ning qanday qiymatida у = cd? parabola va to£g£ri chiziq ikkita nuqtada
kesishadi?
16
1Ж
1) у = х+3; 2) у=— х + 4; 3) у=5х~ 2; 4) у=~5х — 2.
31*. a ning qanday qiymatida у= ах? funksiya va to‘g£ri chiziq kesishmaydi?
1) y=3x + 2; 2) y=3x— 2; 3)y = -3x + 2; 4) y=—3x —2.
at2
32. Tekis tezlanuvchan harakatda jism bosib o‘tgan yo‘l s=~ formula
bo‘yicha hisoblanadi, bunda s — yo‘I (metrlarda); a — tezlanish
(m/s2 larda); t—vaqt (sekundlarda) o‘lchanadi. Jadvalni to'ldiiing:
t 4 6 5 10 60
a 4,5 9 2 4
48 144 36 120 1800
33**. (Tadqiqot uchun.) a, k, b parametrlar orasida qanday bog‘lanish
(mimosabat) bo'lganda у = дх2 va у = kx + b chiziqlar: 1) ikkita nuqtada
kesishadi; 2) kesishmaydi; 3) faqat bitta nuqtada kesishadi? a, k, b
parametrlarga mos sonlar topib, har bir hoi uchun uchtadan misol
tuzing.
34*. (Tadqiqot uchun.)
1 2
1) У = ^Х parabolani yasang.
2) Shu koordinatalar sistemasida y = — 1 to£g‘ri chiziqni o‘tkazing va
ДО; 1) nuqtani belgilang.
3) Parabolada koordinatalari (qulaylik uchun) butun sonlardan iborat
bir nechta nuqtani belgilang. Shu nuqtalardan F nuqta va у = — 1 to‘g‘ri
chiziqqacha bo'lgan masofalami hisoblang.
4) Xulosa chiqaring va uni daftaringizga yozib qo'ying.
1 2
5) у = x parabolaning barcha nuqtalari F nuqtadan va у = -1 to‘g‘ri
chiziqdan teng uzoqlikda yotishini isbotlang.
кЯЯкЖ
жж
Ko 'rsatma. Parabolaning ixtiyoriy (x; | x2)
nuqtasidan ДО, 1) nuqtagacha va у = — 1 to‘g‘ri
chiziqqacha bo‘lgan masofani hisoblang va taqqoslang.
1 2
ДО, 1) nuqta у = x parabolaning /otezdir.
Umuman, у = ax1 parabolaning fokusi uning
simmetriya o'qida joylashgan va koordinatasi
(0; ) bo‘lgan nuqtadir. Parabola va uni Oy o‘qi
2—Algebra, 9
17
жж
жж
жж
жж
жж
atrofida aylantirishdan hosil bo‘lgan jism — paraboloid texnikada keng tatbiqlaiga
ega. Paraboloid fokusida joylashtirilgan yorug‘lik manbayi taratgan nurlar
paraboladan akslanib, parallel bo‘ladi. Projektorlar, parabolik antennalar,
lokatorlar va turli texnik asboblar tayyorlashda parabola fokusining bu xossasidan
foydalaniladi (11-rasm).
4- §. у = ox2 + bx + c funksiya
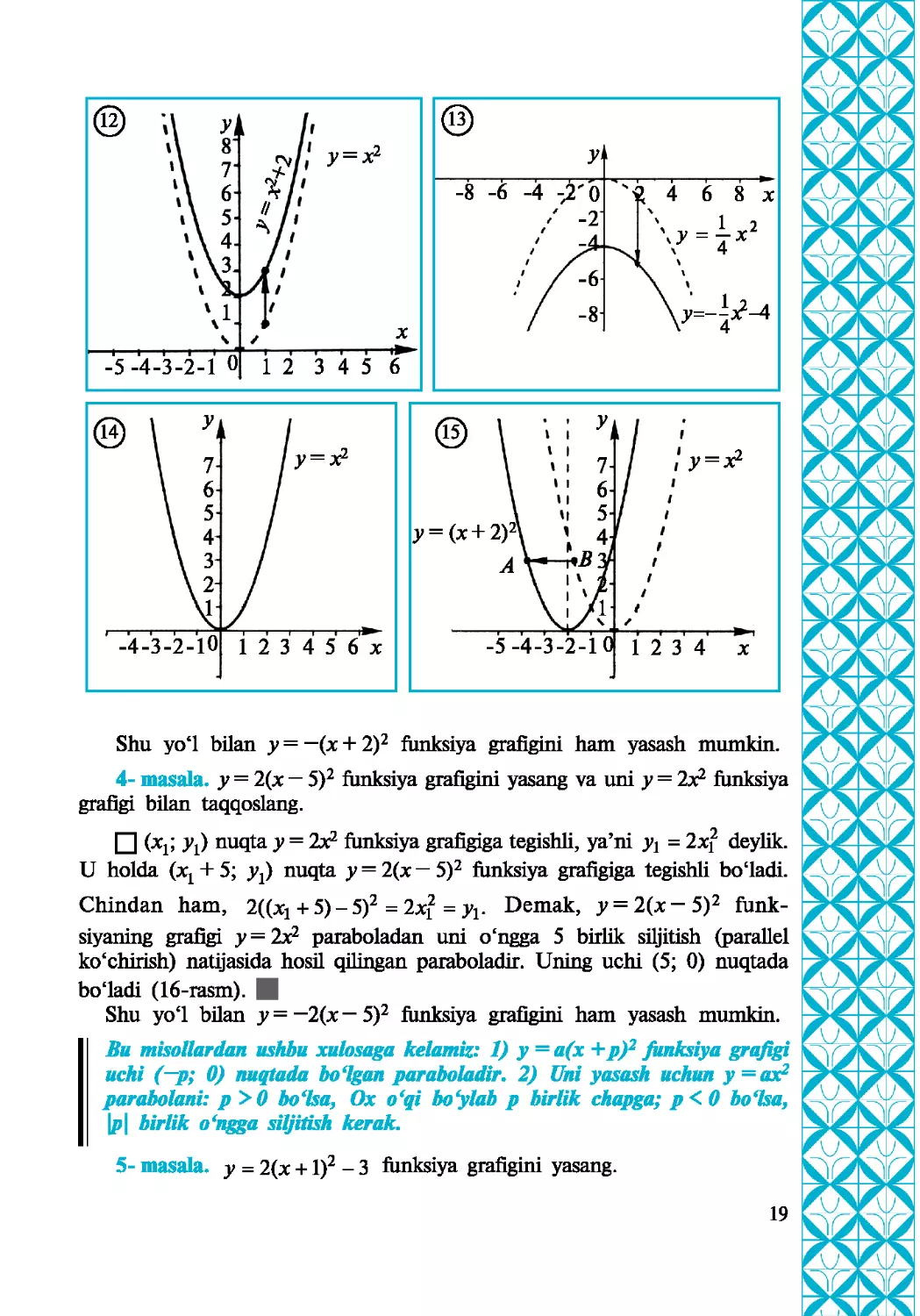
1-masala. y = x2 + 2 funksiya grafigini yasang va uni y = xi funksiya
grafigi bilan taqqoslang.
П Argument x ning har bir qiymatida у = x2 + 2 funksiyaning qiymati
у = jr funksiyaning mos qiymatidan 2 birlikka ortiq. Demak, y = x2 + 2
funksiyaning grafigi y = x2 parabolani 2 birlik yuqoriga siljitish bilan hosil
qilingan paraboladir. Uning uchi (0; 2) nuqtada bofiadi (12- rasm). |
Shunday mulohaza bilan у = x2 — 2 funksiya grafigini ham yasash mumkin.
1 2 12
2-masala. y = --x -4 funksiya grafigini yasang va uni У = ~^х
funksiya grafigi bilan taqqoslang.
I—I 1 9
LJ Argument x ning har bir qiymatida y = --x -4 funksiyaning
1 2
qiymati y = -^x funksiyaning mos qiymatidan 4 birlikka kam. Demak,
у = -|x2 -4 funksiya grafigi у = ~x2 parabolani 4 birlik pastga siljitish
bilan hosil qilingan paraboladir. Uning uchi (0; —4) nuqtada bo‘ladi
(13-rasm). |
1 9
Shunday yo‘1 bilan у = - -x + 4 funksiya grafigini ham yasash mumkin.
Bu misollardan ushbu xulosaga kelamiz: 1) у = ar2 + q funksiya grafigi
uchi (0; q) nuqtada bo‘lgan paraboladir, 2) Uni yasash uchun y=ax?
parabolani: q>0 bo‘lsa, q birlik yuqoriga; q<0 bo‘lsa, |?| birlik pastga
Oy o‘qi bo У lab siljitish kerak,
3- masala, у = (x + 2)2 funksiya grafigini yasang va uni у = x2 funksiya
grafigi bilan taqqoslang.
□ У1) nuqta у = x2 funksiya grafigiga tegishli, ya’ni = x2 deylik.
U holda (Xj - 2; nuqta у = (x + 2)2 funksiya grafigiga tegishli bo‘ladi.
Chindan ham, ((xt - 2) + 2)2 = x2 = yP Demak, у = (x + 2)2 funksiyaning
grafigi у = x2 paraboladan uni chapga 2 birlik siljitish (parallel ko‘chi- rish)
natijasida hosil qilingan paraboladir. Uning uchi (—2; 0) nuqtada bo£ladi
(14— 15-rasmlar). |
18
жж
1Ж
Shu yo‘l bilan у — — (x + 2)2 funksiya grafigini ham yasash mumkin.
4- masala. y = 2(x~ 5)2 funksiya grafigini yasang va uni y = 2x2 funksiya
grafigi bilan taqqoslang.
□ (xp ^i) nuqta у = 2x2 funksiya grafigiga tegishli, ya’ni = 2x2 deylik.
U holda (jq + 5; nuqta y = 2(x~ 5)2 funksiya grafigiga tegishli bo‘ladi.
Chindan ham, 2((x1 + 5) - 5)2 = 2x2 = Demak, у = 2(x - 5)2 funk-
siyaning grafigi y=2x2 paraboladan uni o‘ngga 5 birlik siljitish (parallel
ko‘chirish) natijasida hosil qilingan paraboladir. Uning uchi (5; 0) nuqtada
bo‘ladi (16-rasm). I
Shu yo‘l bilan y=~ 2(x— 5)2 funksiya grafigini ham yasash mumkin.
Bu misollardan ushbu xulosaga kelamiz: 1) у = a(x + p)2 funksiya grafigi
uchi (~^p; 0) nuqtada bo‘lgan paraboladir. 2) Uni yasash uchun y=ax?
parabolani: p>0 bo‘lsa, Ox o(qi bo*ylab p birlik chapga; p<0 bo(lsa,
|p | birlik o(ngga siljitish kerak.
5- masala, у = 2(x +1)2 - 3 funksiya grafigini yasang.
19
жж
IXXIZTXI
жж
жж
жж
йтаи
жж
жж
стаяя
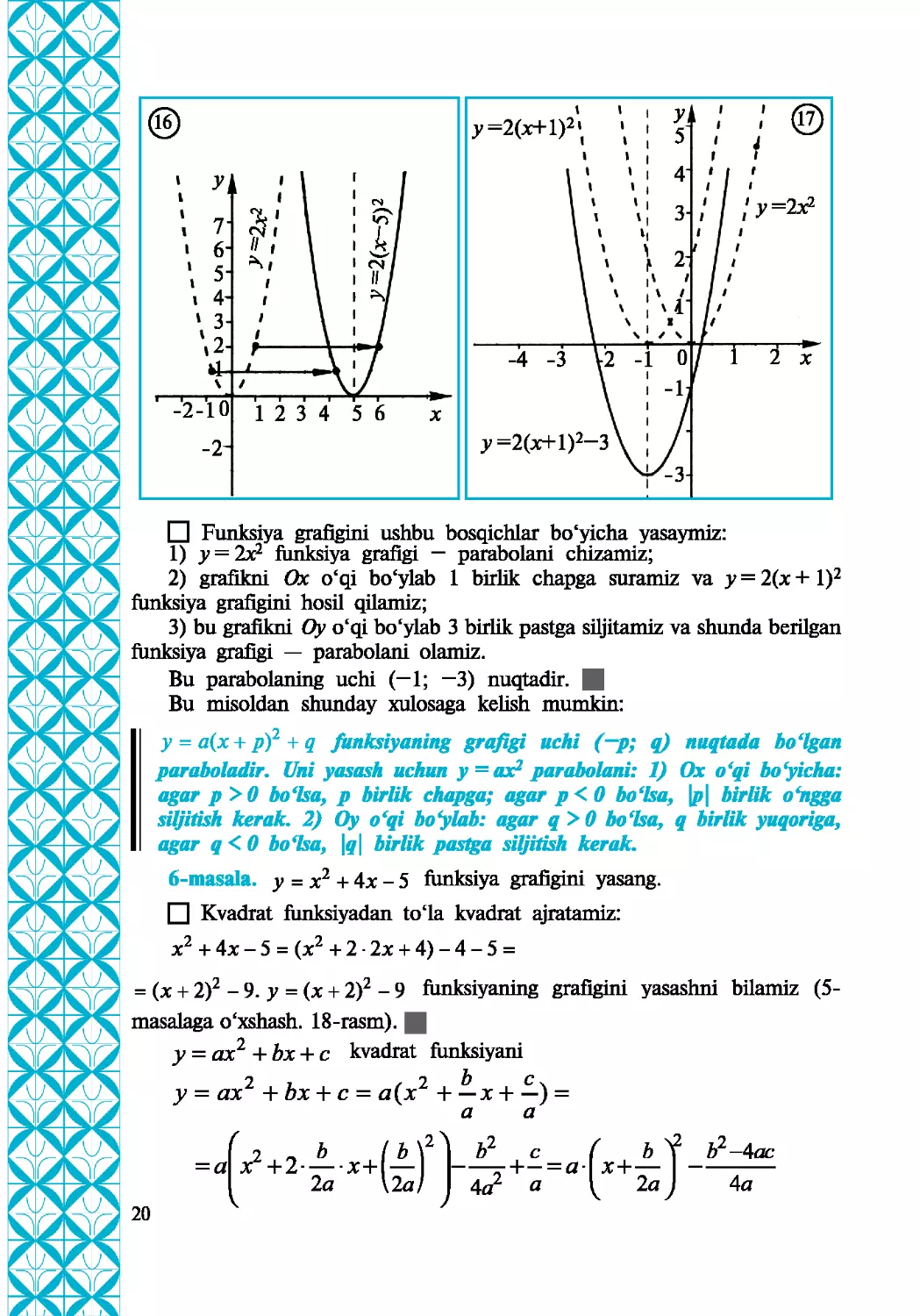
П Funksiya grafigini ushbu bosqichlar bo‘yicha yasaymiz:
1) y = 2x2 funksiya grafigi — parabolani chizamiz;
2) grafikni Ox o£qi bo‘ylab 1 birlik chapga suramiz va у = 2(x + I)2
funksiya grafigini hosil qilamiz;
3) bu grafikni Oy o£qi bo'ylab 3 birlik pastga siljitamiz va shunda berilgan
funksiya grafigi — parabolani olamiz.
Bu parabolaning uchi (—1; —3) nuqtadir. |
Bu misoldan shunday xulosaga kelish mumkin:
у = a(x + p)2 + q funksiyaning grafigi uchi (—p; q) nuqtada bo‘lgan
paraboladir. Uni yasash uchun у—ax? parabolani: 1) Ox o‘qi bo^icha:
agar p>0 bo‘lsa, p birlik chapga; agar p<0 bo‘lsa, |p| birlik o*ngga
silfitish kerak. 2) Oy o‘qi bo^lab: agar q>0 bo‘Isa, q birlik yuqoriga,
agar q<0 bo‘lsa, |g| birlik pastga silfitish kerak.
6-masala. у = x2 + 4x - 5 funksiya grafigini yasang.
О Kvadrat funksiyadan to£la kvadrat ajratamiz:
x2 + 4x - 5 = (x2 + 2-2x + 4)-4-5 =
= (x + 2)2 - 9. у = (x + 2)2 - 9 funksiyaning grafigini yasashni bilamiz (5-
masalaga o'xshash. 18-rasm). |
у = ax2 + bx + c kvadrat funksiyani
2i / 2 b cx
у = ax + bx + с = a(x H—x H—) =
a a
7 _ b (b \ b e ( b \ b -4ac
= a лг+2-----x+ —-----------4— = a хч—--------------
2a \2a 4сг a к 2a J 4a
к J v 7
жж
IXTXIXXI
1Ж
ko‘rinishda yozib olish mumkin. (8- sinf „Al-
gebra “ kursida ax2 + bx + c = 0 kvadrat
tenglama ildizlarini topish formulasini
chiqarishda bu usuldan foydalangansiz.) Uni
kvadrat funksiyadan to 4a kvadrat ajratish usuli
deyiladi.
Demak, у = a.
tenglik o‘rinlidir.
b V Z>2-4ac
4a
2а
A b -(b2-4ac) , , .
Agar xq=-—, y0=-^------------belgi-
2a 4a
lashlar kiritsak, u holda у = a(x -x0)2 + y0
bo'ladi. yQ = у(х^) ekanini osongina ko‘isatish
mumkin. Demak,
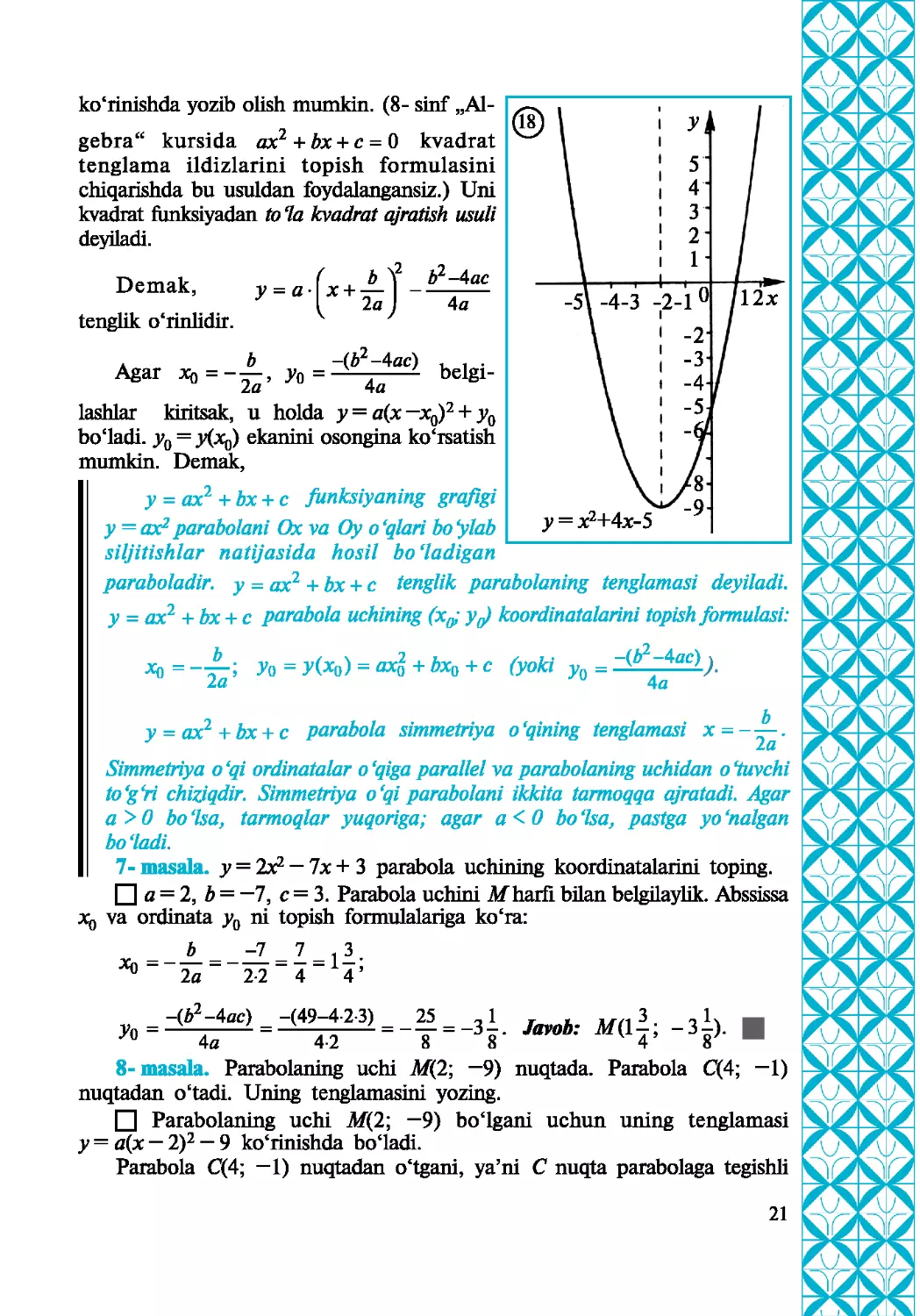
y = ax2+bx + c funksiyaning grafigi
у = ax2 parabolani Ox va Оу о ‘qlari bo "ylab
siljitishlar natijasida hosil bo‘ladigan
paraboladir. у = ax2 +bx + c tenglik parabolaning tenglamasi deyiladi.
у = ax2 +bx + c parabola uchining (х& у J koordinatalarini topish formulasi:
хй=~', Уо = y(xa) = «о + Ъхй + c (yoki y0 =
2a v 4a
у = ax2 + bx + c parabola simmetriya о ‘qining tenglamasi x = -—.
2a
Simmetriya о ‘qi ordinatalar о ‘qiga parallel va parabolaning uchidan о ‘tuvchi
to‘g‘ri chiziqdir. Simmetriya o‘qi parabolani ikkita tarmoqqa ajratadi. Agar
a >0 bo ‘Isa, tarmoqlar yuqoriga; agar a<0 bo ‘Isa, pastga yo ‘nalgan
bo‘ladi.
7- masala, у = 2x* — lx + 3 parabola uchining koordinatalarini toping.
□ a = 2, b = —7, c = 3. Parabola uchini Mhart! bilan belgilaylik. Abssissa
Xq va ordinata yQ ni topish formulalariga ko‘ra:
_ 7 _1 3.
2a 2-2 4 14 ’
жж
жж
-(У-4ас) -(49-4-2-3) 25 ,1 T . 3. Q к _
ye=A_2 = ^__^ = __ = _3_. Jmob: M(l-; -3-).
8-masala. Parabolaning uchi —9) nuqtada. Parabola C(4; — 1)
nuqtadan octadi. Uning tenglamasini yozing.
□ Parabolaning uchi M(2; —9) bo£lgani uchun uning tenglamasi
у = a(x — 2)2 — 9 ko‘rinishda bo‘ladi.
Parabola C(4; —1) nuqtadan o‘tgani, ya’ni C nuqta parabolaga tegishli
21
IXXIZTXI
жж
жж
bo'lgani uchun С nuqtaning koordinatalari parabola tenglamasini
qanoatlantiradi: —1 = a (4 — 2)2 — 9, bundan 4o = 8, a = 2. Demak, pa-
rabola tenglamasi у = 2(x — 2)2 — 9 yoki у = 2x2 — 8x — 1 bo‘ladi.
Javob: у = 2x2 — 8x — 1. |
35. Savollarga javob bering. Topshiriqlami bajaring:
1) у = ax2 + bx + c kvadrat funksiya grafigi nima deb ataladi?
2) y = ax2 + bx+ c kvadrat funksiya grafigi y=x2 funksiya grafigidan
qanday hosil qilinadi? Misollarda tushuntiring.
©3) у = ax2 + bx+ c parabola uchining koordinatalarini yozing; у = 6x2 —
— 5x +1; у = —2x2 + 6x - 3 parabola uchining koordinatalarini toping.
4) у = ax2 + bx + c parabolaning simmetriya o‘qi qaysi o‘qqa parallel va
qaysi nuqtadan oetadi? Parabola o‘qining tenglamasini yozing. Misoliar
keltiring.
5) у = дх2 + bx 4- c funksiya xossalarini ayting.
жж
жж
36. y = x2 parabola grafigini:
1) o'ngga ikki birlik, yuqoriga uch birlik;
2) chapga bir birlik, pastga ikki birlik;
3) o'ngga uch birlik, pastga to‘rt birlik;
4) chapga ikki birlik, yuqoriga bir birlik siljitish (parallel ko‘chirish)
natijasida hosil bo'lgan parabola tenglamasini yozing.
37. (Og'zakL) Parabola uchining koordinatalarini ayting:
жж
1) y=(x-2)2-7; 2) у = (x + I)2 + 3; 3) y=-4(x-3)2-2; 4) у = 3(x - 4)2 + 5; 5) y = 2(x—l)2 + 3; 6) у = —5(x + 2)2 + 6.
38. Parabola uchining koordinatalarini toping: 1) y = x2— 6x4-7; 4) y = x2 — 4x + 4; 2) у = -4x2 4- 8x4- 1; 5) y = x2 + 2x+7; 3) у = — Зх2— 12x— 10; 6) y = —x24-2x —2.
39. Parabolaning simmetriya o‘qi 1) y = x2 — 4; 2) y = x2 + 7; 3) у = —x2 — 3; 4) у = -x2 4- 1; 5) y = 2x24-5; 6) у = Зх2 — 4; Ox o‘qidagi qaysi nuqtadan o'tadi? 7) у = x2 - 5x + 6; 8) y=lxj 4- 6x4- 1; 9) у = —x2 — x + 12; 10) у = —4x2 4-3x4-1; 11) y=-5x2 + 7x-2; 12) у = 4x2 — 9x 4- 5.
40. Parabolaning koordinatalar koordinatalarini toping: 1) у = 12X2 4- 7x4- 1; 2) у = 12x2 - 7x4- 3; o‘qlari bilan kesishish nuqtalarining 5) у = 4X2 4- 7x— 11; 6) у = 7x2 4- 8x— 15;
22
1Ж
3) у = 4х2 — Зх; 7) у = Зх2 — 4х + 4;
4) у = х2 + Зх — 2; 8) у = —х2 + 2х + 7.
41. Parabola N(x^, у0) nuqta orqali o'tishi va uning uchi M(x^ nuqta
ekani ma’lum bo‘lsa, parabola tenglamasini yozing:
1) М2; -2), Ml; -3); 4) MO; 1), М3; -8);
2) М3; -7), Ml; -3); 5) MO; 0), M~2; -4);
3) MO; 5), M-2; 1); 6) M-l; 2), MO; 3).
42*. b ning qiymatiga bog‘liq ravishda parabola va to‘g‘ri chiziq nechta
umumiy nuqtaga ega bo‘ladi:
1) y = 2x2 —8x+5, y = 4x+Z>;
2) у = — Зх2 — 12x+ 6, y = — 2x + A;
3) y = 4x2 + 4x+l, x + y=b;
4) у = 9x2 — 6x +1, 2x + 3y = 6?
43*. Bo‘yi a sm, eni b sm bo‘lgan to‘g‘ri to‘rtburchak shaklidagi tunukadan
yuzi S boclgan to‘geri to‘rtburchak shaklidagi teshik ochishmoqchi.
Teshikning tomonlari berilgan to‘g‘ri toertburchak tomonlaridan bir
xil x masofada bo'lishi kerak (19-c rasm). S yuzni x ning funksiyasi
sifatida ifodalang.
44*. ABC ko‘prik parabolaning yoyi shaklida bo‘lib, OB ustun 6 m ga,
ЛЛС yoyga mos AC «vatar» 24 m ga teng. Ko‘prik 5 ta vertikal ustunga
ega boelib, ular AC ga perpendikular va uni teng qismlarga ajratadi (19-
b rasm). Ustunlaming uzunliklarini toping.
45. Agar: 1) A(— 1; 10) nuqta y=ax2 — 3x+2; 2) 2?(2; —5) nuqta
у = ax2 + 7x — 3 parabolaga tegishli bo‘lsa, a ning qiymatini toping.
3 о
46. Agar: 1) C(—1; —5) nuqta y=-x +£x-4,5; 2) D(— 1; 4) nuqta
5 2 2
y=--x +bx+3- parabolaga tegishli bo‘lsa, b ning qiymatini aniqlang.
жж
47. у = x2 + px + q parabolaning uchi: 1) М3; 1); 2)
( 7 25 A ( 3 7 A
; 4) nuqtada bo‘lsa, p va q ni toping.
48. у = ax2 + bx + c parabolaning uchi M(x; y) va parabola bilan Oy
23
IXXIZTXI
жж
жж
жж
жж
жж
o'qining kesishish nuqtasi V(0; у) berilgan bo‘lsa, л, b, c sonlami
toping:
1) MO; 3); 3) ЛгГ|;-Ц\ MO; -1);
2) Ml; I), MO; -3); 4) Affeyl, MO; 7).
49*. yT = mx2 — 3 va y2 = 4x + 1 funksiyalaming grafiklari parametr m
ning qanday qiymatlarida: 1) kesishmaydi; 2) bitta nuqtada kesishadi;
3) ikkita nuqtada kesishadi?
50*. a ning qanday qiymatida:
1) у = ax2 - 4x + parabolaning uchi I chorakda;
2) у = ax2 — lx + 4a parabolaning uchi II chorakda;
3) у = ax2 + 6x + parabolaning uchi III chorakda;
4) у = ax2 -5x + y parabolaning uchi IV chorakda yotadi?
51. 1) c ning qanday qiymatlarida у = х2 + 6x + c parabola uchi bilan
koordinata boshi orasidagi masofa 5 ga teng bo‘ladi?
2) b ning qanday qiymatlarida у = x2 + 2bx + 13 parabola uchi bilan
koordinata boshi orasidagi masofa 5 ga teng bo'ladi?
3) a ning qanday qiymatlarida у = ax2 + 2x + 1 parabolaning uchi
J(l; 2) nuqtadan 2^/2 masofada boladi?
52**. (Tadqiqot uchun.) To‘g‘ri to‘rtburchakning perimetri /> = 36 sm
bo‘lsin. Uning asosini x sm desak, 5 yuzi x ning funksiyasi bo‘ladi.
1) x ning funksiyasi sifatida S yuzni hisoblash formulalarini toping.
2) Bu funksiya kvadrat funksiya boladimi? a, b, c parametrlaming
qiymatlari nechaga teng?
3) Topilgan funksiyaning grafigini chizing.
4) S(x) funksiyaning aniqlanish sohasini toping.
5) Asos uzunligi x qanday boHganda to‘g‘ri to‘rtburchakning yuzi eng
katta bo'ladi? Bunda qanday shakl hosil bo‘ladi?
5-§. Kvadrat funksiyaning grafigini yasash
Bitta kvadrat funksiya grafigini yasab ko‘raylik.
1- masala, у = x2 - 2x - 8 funksiya grafigini yasang.
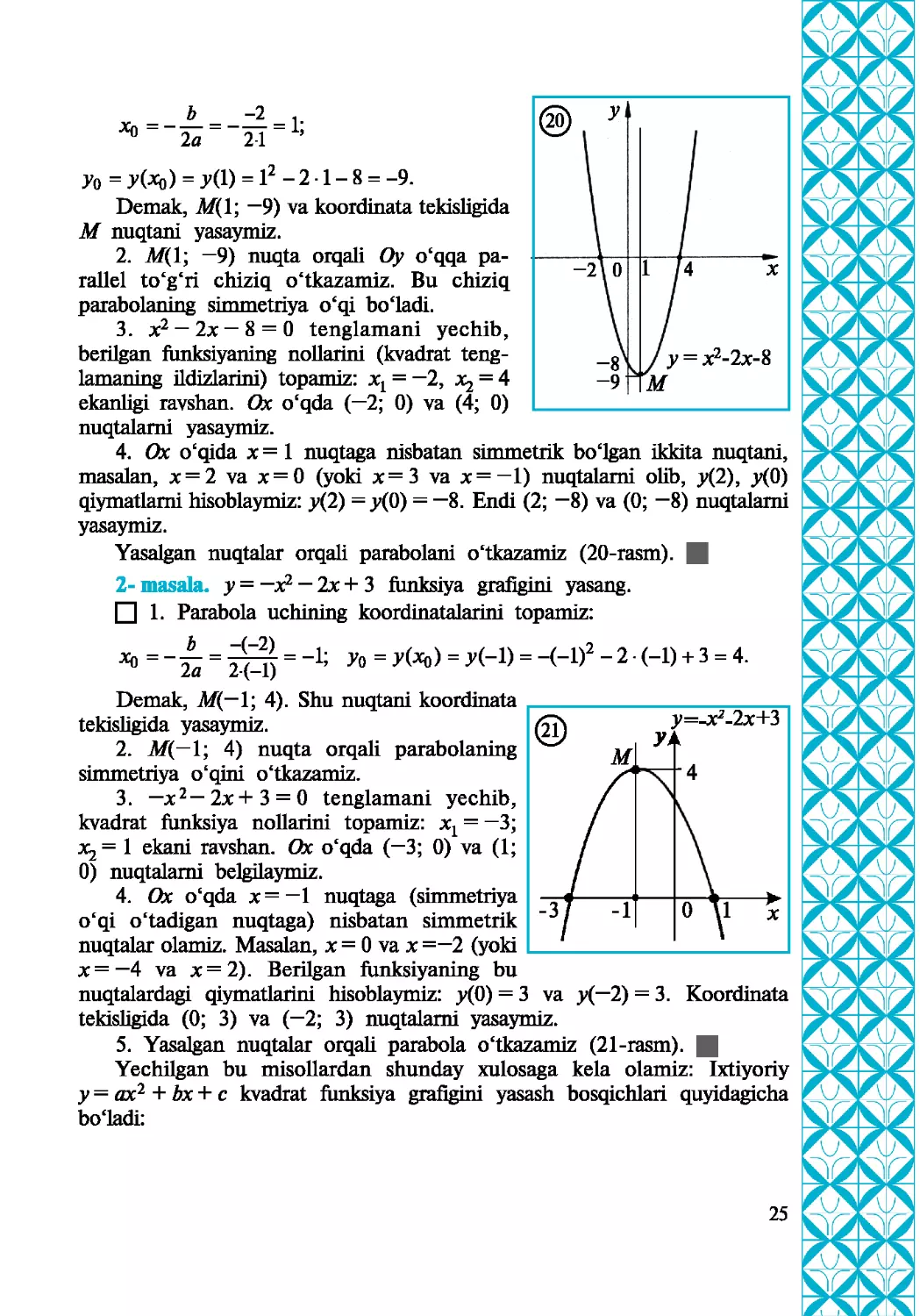
□ 1. Bu funksiyaning grafigi parabola ekanini ko'rdik. Parabola uchining
koordinatalarini topamiz:
жж
24
Ж
-8
-9
X
у = х2-2х-8
М
b _ -2 _,
** 2а 21 х’
Уо=У(ло) = у(1) = 12-2-1-8 = -9.
Demak, М(1; —9) va koordinata tekisligida
M nuqtani yasaymiz.
2. Af(l; —9) nuqta orqali Oy o‘qqa pa-
rallel to‘g‘ri chiziq o'tkazamiz. Bu chiziq
parabolaning simmetriya o‘qi boladi.
3. x2 — 2x~ 8 = 0 tenglamani yechib,
berilgan funksiyaning nollarini (kvadrat teng-
lamaning ildizlarini) topamiz: xt = -2, = 4
ekanligi ravshan. Ox oeqda (—2; 0) va (4; 0)
nuqtalami yasaymiz.
4. Ox o‘qida x = 1 nuqtaga nisbatan simmetrik bo‘lgan ikkita nuqtani,
masalan, x = 2 va x=0 (yoki x=3 va x= — 1) nuqtalami olib, y(2), j(0)
qiymatlami hisoblaymiz: y(2) =y(0) = “8. Endi (2; —8) va (0; —8) nuqtalami
yasaymiz.
Yasalgan nuqtalar orqali parabolani o‘tkazamiz (20-rasm). |
2- masala, у = —x2 — 2x + 3 funksiya grafigini yasang.
□ 1. Parabola uchining koordinatalarini topamiz:
*>=-£ = -1; = y(*b) = И-D = -(-I)2 - 2 • (-1) + 3 = 4.
la 2-(-l)
Demak, M(— 1; 4). Shu nuqtani koordinata
tekisligida yasaymiz.
2. M(— 1; 4) nuqta orqali parabolaning
simmetriya o'qini olkazamiz.
3. —x2-2x+3 = 0 tenglamani yechib,
kvadrat funksiya nollarini topamiz: xt = —3;
Xj = 1 ekani ravshan. Ox o‘qda (—3; 0) va (1;
0) nuqtalami belgilaymiz.
4. Ox o'qda x= — 1 nuqtaga (simmetriya
o‘qi o‘tadigan nuqtaga) nisbatan simmetrik
nuqtalar olamiz. Masalan, x = 0 va x =—2 (yoki
x=— 4 va x=2). Berilgan funksiyaning bu
nuqtalardagi qiymatlarini hisoblaymiz: y(0) = 3 va y(~2) = 3. Koordinata
tekisligida (0; 3) va (—2; 3) nuqtalami yasaymiz.
5. Yasalgan nuqtalar orqali parabola o'tkazamiz (21-rasm). |
Yechilgan bu misollardan shunday xulosaga kela olamiz: Ixtiyoriy
у = ax2 + bx + c kvadrat funksiya grafigini yasash bosqichlari quyidagicha
bo‘ladi:
жж
жж
ЛИЙ
жж
жж
ЖЖ
жж
№•3
жж
1ЖЖ
жж
25
жж
жж
жж
йтаи
жж
№ж
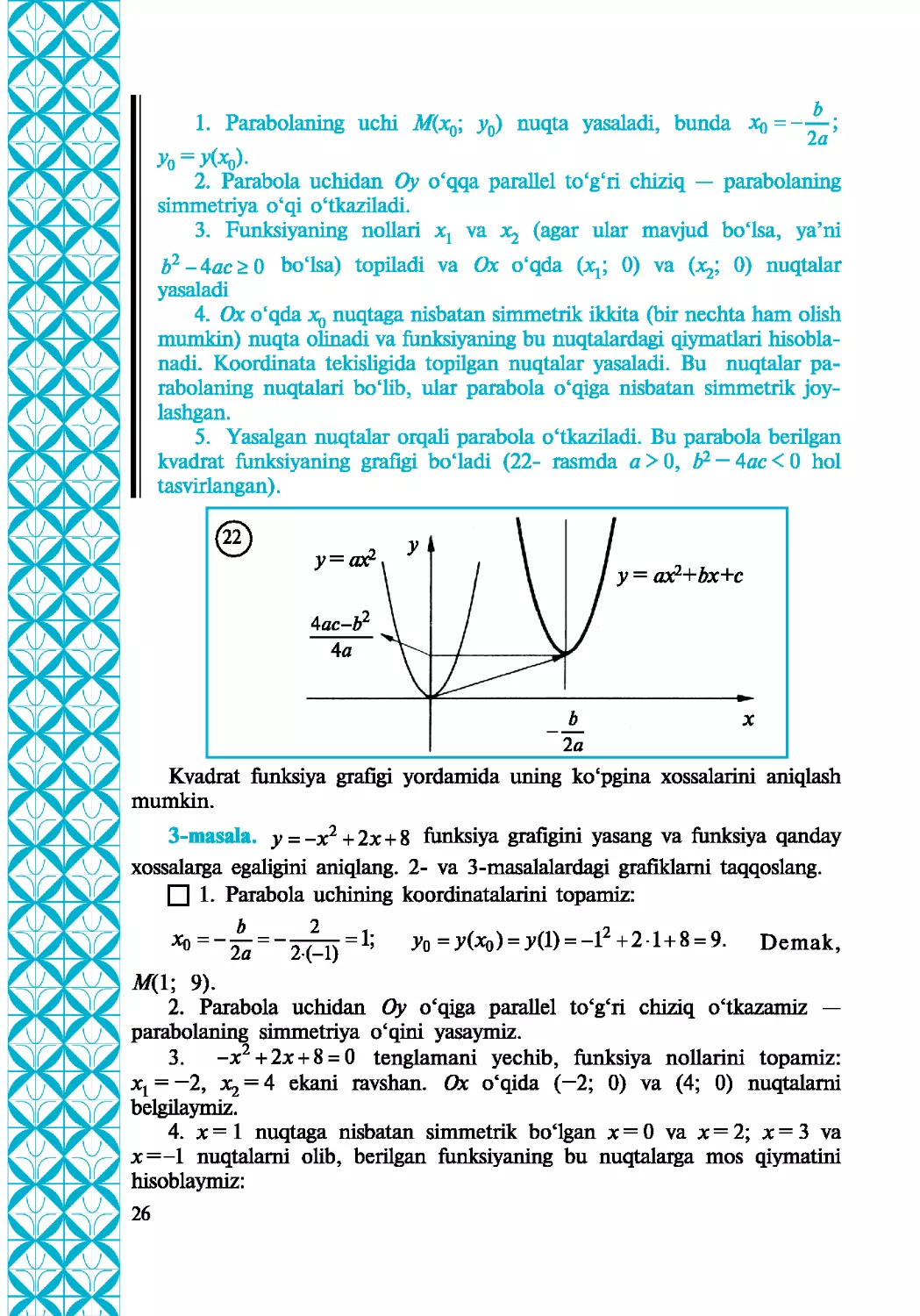
1. Parabolaning uchi М(х^ у0) nuqta yasaladi, bunda *b=——;
2a
y^yi^Y
2. Parabola uchidan Oy o‘qqa parallel to‘gcri chiziq — parabolaning
simmetriya o‘qi o‘tkaziladi.
3. Funksiyaning nollari va x^ (agar ular mavjud bo‘lsa, ya’ni
й2-4дс^0 bo‘lsa) topiladi va Ox o‘qda (xt; 0) va (x^, 0) nuqtalar
yasaladi
4. Ox o‘qda nuqtaga nisbatan simmetrik ikkita (bir nechta ham olish
mumkin) nuqta olinadi va funksiyaning bu nuqtalardagi qiymatlari hisobla-
nadi. Koordinata tekisligida topilgan nuqtalar yasaladi. Bu nuqtalar pa-
rabolaning nuqtalari bo‘lib, ular parabola o‘qiga nisbatan simmetrik joy-
lashgan.
5. Yasalgan nuqtalar orqali parabola o‘tkaziladi. Bu parabola berilgan
kvadrat funksiyaning grafigi bo'ladi (22- rasmda a > 0, & — 4ac < 0 hoi
tasvirlangan).
жж
Kvadrat funksiya grafigi yordamida uning ko'pgina xossalarini aniqlash
mumkin.
3-masala. y = -x2+2x + 8 funksiya grafigini yasang va funksiya qanday
xossalarga egaligini aniqlang. 2- va 3-masalalardagi grafiklami taqqoslang.
□ 1. Parabola uchining koordinatalarini topamiz:
x«=_^ = _2^4j = 1; Jo =y(-*o) = J'(l) = -l2+21 + 8 = 9. Demak,
Ml; 9).
2. Parabola uchidan Oy o‘qiga parallel to‘g‘ri chiziq o‘tkazamiz —
parabolaning simmetriya o‘qmi yasaymiz.
3. -x2+2x + 8 = 0 tenglamani yechib, funksiya nollarini topamiz:
Xj = —2, X2 = 4 ekani ravshan. Ox o‘qida (—2; 0) va (4; 0) nuqtalami
belgilaymiz.
4. x = 1 nuqtaga nisbatan simmetrik bo‘lgan x = 0 va x = 2; x = 3 va
x=-l nuqtalami olib, berilgan funksiyaning bu nuqtalarga mos qiymatini
hisoblaymiz:
26
жж
у(0) = у(2) = 8; у(-1) = у(3) = 5.
Koordinata tekisligida hosil qilingan (0; 8)
va (2; 8), (—1; 5) va (3; 5) nuqtalami
yasaymiz.
5. Yasalgan nuqtalar orqali parabolani
o‘tkazamiz. Bu parabola у = -x2 + 2x + 8
funksiyaning grafigi bo'ladi.
Grafikka qarab, funksiyaning quyida-
gi xossalarini bilib olamiz:
1) a=— 1 bo'lgani uchun parabola
tarmoqlari pastga yo‘nalgan;
2) grafik x= 1 to‘g‘ri chiziqqa nisbatan
simmetrik;
3) x ning istalgan qiymatida funksiyaning qiymatlari 9 dan katta emas;
4) funksiya x= 1 da eng katta qiymatni qabul qiladi: y(l) = 9;
5) x < 1 oraliqda funksiya o‘sadi; x > 1 oraliqda esa kamayadi;
6) —2<x<4 oraliqda funksiya musbat qiymatlami,
x < —2 va x > 4 oraliqlarda esa manfiy qiymatlami qabul qiladi.
x = -2 va x = 4 da funksiya nolga teng. y(—2) = y(4) = 0. Grafikdan yana
funksiyaning qiymatlar sohasi у <9 oraliq (ya’ni ye (-«>,9]) ekanini ham
bilib olamiz (23- rasm). |
Bu misoldan shunday xulosa cbiqarisb mumkin: у = ax2 +bx + c funk-
siya: a>0 bo‘lsa, eng kichik; a<0 bo‘lganda esa eng katta qiymatga
ega bo‘ladi. Bu qiymatga funksiya nuqtada erishadi. Bu
qiymatning o‘zi esa у(х0) songa teng.
20- rasmdagi у = x2 -2x- 8 funksiya x = 1 bo'lganda —9 ga teng bo‘lgan
eng kichik qiymatga erishadi. 21-rasmdagi у = —x2 — 2x + 3 funksiya x = —1
nuqtada 4 ga teng bo'lgan eng katta qiymatni qabul qiladi.
4-masala. Ikki sonning yig'indisi a ga teng (a>0). Bu sonlar qanday
bo‘lganda ulaming kublari yig‘indisi eng kichik bo‘ladi?
Q Sonlardan birini x desak, u holda ikkinchisi a — x boladi. Ushbu
у = x3 + (a-x)3 funksiyani tuzamiz va bu funksiya x qanday bo‘lganda eng
kichik qiymatni qabul qilishini topamiz. Funksiyani shunday yozib olaylik:
у = х3 + а3-За2х+Зах2-х3 =3ax2-3a2x+a3. Demak, masala y=3ax2-
—За2х+д3 kvadrat funksiyaning eng kichik qiymatini topishga keldi, biz esa
bunday masalani yecha olamiz.
-3c2 a
Chindan ham, x0 = - ——— = - va a > 0 bo‘lgani uchun funksiya eng
2-3c 2
жж
27
fj Q
kichik qiymatga Xq = - da erishadi. U holda ikkinchi son ham — ga teng
z
жж
жж
жж
жж
жж
bo‘ladi: a-Xo = a-| = ^. Shunday qilib, qo'shiluvchilar o‘zaro teng bo‘lganda
ular kublarining yig'indisi eng kichik boladi. Bu eng kichik qiymat —
/ \ a3 , f «V a3 a3 a3 a3 л H
yo = yv*b)=-8-+ «--J = y lborat-
53. Topshiriqlami bajaring. Savolga javob bering:
1) y = ax2 + bx + c kvadrat funksiyaning grafigini yasash bosqichlarini
ayting. Shu bosqichlar bo'yicha:
©a) у = x2 — 5x + 4; b) у = —Зх2 + 4x — 1 funksiyaning grafiklarini
yasang.
2) у = 4x2 — 5x + 1 va у = —x? + 7x — 6 funksiyalar grafiklarini yasang
va bu funksiyalar qanday xossalaiga ega ekanliklarini grafikka qarab
ayting.
3) у = ax2 + bx + c funksiya qanday x va qanday a da eng katta (eng
kichik) qiymatga ega bo‘ladi? Misollarda tushuntiring.
54. у = ax2 + bx + c funksiyaning: 1) nollari Xj = 2 va x^ = 3; eng kichik
qiymati ~ boTsa;
2) nollari Xj = 2 va x^ = 4, eng katta qiymati 1 bo‘lsa, у = ax2 + bx + c
parabolani yasang.
55. Funksiyaning grafigini yasang va grafik bo‘yicha:
1) x ning funksiya qiymatlari musbat, manfiy bo‘ladigan qiymatlarini
toping; 2) funksiyaning o'sish va kamayish oraliqlarini toping;
3) x ning qanday qiymatlarida funksiya eng katta yoki eng kichik qiymatlar
qabul qilishini aniqlang va ulami toping:
1) у = 4x? + 4x + 2; 6) y = 2x2 —x;
2) у = 9x2 + 6x + 1; 7) у = 4x2 + x;
3) у = 9x2 —6x— 5; 8) у = —Зх2 + x;
4) у = -x2 - 4x - 8; 9) у = —x2 + Зх;
5) у = —x2 + 6x — 13; 10) у = 16х2 - 8х + 2.
56*. 1) y=ax2 + bx+c funksiya grafigi bitta chorakda yotishi mumkinmi?
Nega? Sababini tushuntiring.
2) у = ax2 + bx+ c funksiya grafigi: a) 2 ta chorakda; b) 3 ta
chorakda; d) to‘rttala chorakda yotadigan hollaiga 3 tadan misol keltiring.
57. Tocg‘ri to‘rtburchakning qo‘shni tomonlari yig‘indisi 40 sm ga teng.
Tomonlar qanday bo‘lganda bu to‘g‘ri to‘rtburchakning yuzi eng katta
bo‘ladi?
28
1Ж
58. To‘g‘ri tohtburchak shaklidagi dala hovlining ,,etagi“dan soy oqib o‘tadi.
Hovlining uchta tomonini 72 m h panjara bilan o‘rashmoqchi. Maydon-
ning bo‘yi va eni qanday bo‘lganda uning yuzi eng katta boladi? (Soy
qirg‘og‘ini to‘g‘ri chiziqli deb oling.)
59**. y — ax2 + &c + c parabola uchining koordinatalari M(x; y) va a>0
deylik. Agar 1) x>0, y>0; 2) x>0, y<0; 3) x<0, y<0; 4) x<0,
y>0 bo'lsa, b va c ning ishorasini aniqlang. Mos shakllar chizing.
60**. у = ax2 + bx + c parabola uchining koordinatalari M(x; y) va a < 0
deylik. Agar 1) x>0, y>0; 2) x>0, y<0; 3) x<0, y<0; 4) x<0,
y>0 bo‘lsa, b va c ning ishorasini aniqlang. Mos shakllar chizing.
61. O‘t o‘chiruvchi nasosidan otHib chiqayotgan suv y = — 0,2& + 3x para-
bolani „chizadi". Bu parabolaning — otilib chiqayotgan suvning —eng
katta balandligi va eng uzoq deganda qayerga „tushishini“ toping.
ri to‘rtburchak qanday qilib
62. Perhnetrlari o‘zaro teng, chegaradosh to‘g‘ri to‘rtburchak shaklidagi
ikkita maydormi o‘rab olish uchun 240 m sim panjara (to‘r) zarur.
Maydonlaming yuzi eng katta bo‘lishi uchun ulaming bo‘yi va eni
qanday uzunlikda bo‘lishi kerak?
63. 1) Diagonal! 10^2 bo'lgan barcha to‘g‘ri
to‘rtburchaklar ichida yuzi eng kattasi
topilsin.
64*. O‘tkir burchakli ABC uchburchakda
BDLAC, AC=4Q sm, £D = 20 sm. Shu
uchburchakka EFKL to‘g‘ri to'rtburchak
ichki chizilgan (to‘gcri to‘rtburchakning EL
tomoni AC tomonda yotadi, F uchi AB
tomonda, К uchi esa BC tomonda). To‘g‘
chizilganda uning yuzi eng katta bo‘ladi?
□ EF=x, EL = y deylik. U holda SEFKL = xy. ЖЦ AC bo'lgani uchun
OFBK" OABC. Bundan = ya’ni £ = y = 2-(20-x).
AL dJJ W Zu
U holda SEFKL = x (4O-2x) = -2x2 +40x = -2(x-10)2 + 200.
Shunday qilib, EFKL toeg‘ri to‘rtburchakning yuzi x ning kvadrat
iunksiyasi sifatida tafsiflandi. Bu kvadrat funksiya x= 10 da eng katta
qiymatga erishadi va bu eng katta qiymat 200(sm2) ga teng. Demak, FK
tomon BD balandlikning o‘rtasidan asos AC ga parallel qilib o'kazilishi
kerak ekan.
Javob: x=10 sm, у = 20 sm, eng katta yuz 200 sm2. Tocg‘ri to‘rtburchak
tomoni uchbuichak asosiga parallel qilib, berilgan balandlik o'rtasidan
o‘tkazilishi kerak (24- rasm). |
жж
29
мм
мм
65. 5 m balandlikda kamondan 50 m/s tezlik bilan yuqoriga vertikal ravishda
nayza otildi. Nayzaning t sekunddan keyin ko£tarilgan balandligi metrlarda
h = h(f) = 5 + 50? — formula bilan hisoblanadi, bunda g « 10 m/s2.
Nayza necha sekunddan keyin: 1) Eng katta baLandlikka erishadi va u
qanday balandlik bo‘ladi? 2) Yeiga tushadi?
6-§. I bobga doir mashqlar
66. Jadvalni toldiring:
мм
мм
у =x2-sx+6 0 2 6 12 20 30 42 56
X 2;3
у =2x2-7x+3 0 3 7 12 25 33 42 52
X 0,5; 3
67. Parabolaning koordinata o'qlari bilan kesishish nuqtalari koordinata-
larini toping:
1) у = x2 - lx + 6; 5) у = 2х2 + 5х + 3;
2) у = x2 - 9x + 8; б) у = Зх2 - х - 4;
3) у = x2 -5x-6; 7) у = -2х2 +Зх+5;
4) у = x2 + Зх - 4; 8) у = -7х2 -Зх+4.
мм
мм
68. у = ax2 + bx + c parabola ko‘rsatilgan nuqtalardan o‘tsa, a, b, c
sonlami toping.
1) Д0; 6), 5(1; 2), C(4; 2);
2) Д0; -2), 5(1; 0), C(3; -2);
3) Д0; 3), 5(3; 0), C(l; -2);
4) Д1; 2), 5(3; -8), C(2; 0).
69. 1) у = £ — 8x + c funksiyaning eng kichik qiymati 1 ga teng. Shu
funksiyaning grafigini chizing.
2) у = —x2 + 6x + c funksiyaning eng katta qiymati 4 ga teng. Shu
funksiyaning grafigini chizing.
70** (Tadqiqot uchun).
1) b ning qanday qiymatida у = -Зх2 + bx - 2b - 12 kvadrat uchhad
(funksiya)ning ildizi 6 ga teng bo'ladi?
2) b ning topilgan shu qiymatida uchhadning ikkinchi ildizini toping;
3) у funksiyaning grafigini chizing;
4) grafikdan у funksiyaning o‘sish va kamayish oraliqlarini aniqlang;
5) x ning qanday qiymatlaTida: a) у < 0; b) у > 0 bo‘ladi?
** (Tadqiqot uchun).
1) c ning qanday qiymatida у = x2 — 12x + c kvadrat uchhad (funksiya)ning
ildizi 9 ga teng bo‘ladi?
30
Ж
2) c ning topilgan shu qiymatida uchhadning ikkinchi ildizini toping;
3) у funksiyaning grafigini chizing;
4) grafikdan у funksiyaning o‘sish va kamayish oraliqlarini aniqlang;
5) x ning qanday qiymatlarida: a) у < 0; b) у > 0 bo‘ladi?
72**. a ning qanday qiymatida у = 2ax2 + 2x + 1 va у = 5л? + 2ax — 2
funksiyalaming grafiklari bitta nuqtada kesishadi?
73. x ning qanday qiymatlarida funksiyalar teng qiymatlar qabul qiladi? Mos
grafiklami chizing:
1) у = л? —5x+6 va y=|x —4|;
2) у = 4x2 — 5x + 1 va у = |x + 1|;
3) y = x2-3x+2 va y=|x-2|;
4) у = л? — 8x+15 va y=|x—4|.
74. Funksiyaning eng katta yoki eng kichik qiymatini toping (grafigini yasash
shart emas).
1) y = x2-4x; 4) y = -x2+7x+8;
2) y = -x2+6x; 5) y = 2x2-7x+9;
3) y = x2+9x-10; 6) y = -3x2+5x + 8.
ЖЖ
ЖЖ
ЖЖ
ЖЖ
75**. a ning qanday qiymatlarida tenglamaning ildizlari kvadratlari yig‘indisi
eng kichik bo‘ladi:
1) x2 + (2 — a)x — a— 3 = 0;
2) x2 + (3 + 2a)x + 2a + 1 = 0;
3) x2 + (2a — l)x+3a + 2 = 0;
4) x2 + (2a+l)x + a2-1 = 0?
76**. Uzunligi a sm И simni ikkiga bo'Hb, biridan kvadrat, ikkinchisidan
muntazam uchburchak yasashmoqchi. Hosil bo'ladigan shakllar
yuzlarining yig‘indisi eng kichik bo'lishi uchun simni qanday kesish
kerak?
77. To‘g‘ri to'rtburchakning perimetri p sm ga teng. Uning asosi bilan
balandligi qanday bo‘lganda yuzi eng katta bo‘ladi?
78. у = x2 + px + q kvadrat funksiya uchun:
1) y(0) = 12, y(l) = —12 bo'lsa;
2) y(0) = 10, y(2) = 0 bo‘lsa, p va q koeffitsiyentlami toping.
79. Agar у = x2 + px + q parabola:
1) abssissalar ocqini x = 1 va x = 5 nuqtalarda kessa;
2) abssissalar o‘qini x = —3 nuqtada va ordinatalar o'qini у = — 6 nuq-
tada kessa;
3) abssissalar o'qiga x=—1 nuqtada urinsa, p va q lami toping.
80. Agar у = x2 + px + q parabolaning:
31
ЖЖ
жж
ЖЖ
ЖЖ
IXXIZTXI
жж
1) (0; —7) va (—1; 0) nuqtalardan o'tishi;
2) (1; 3) nuqtadan o‘tsa va uchi (2; 4) nuqtada boclsa, shu parabolani
yasang.
жж
I bobga doir sinov (test) mashqlari
жж
1. a ning shunday qiymatini topingki, у = ar2 parabola bilan у = 5x + 1
to‘g‘ri chiziqning kesishish nuqtalaridan binning absissasi x = 1 bo'lsin:
A) a = 6; B) a = —6;
C) a = 4; D) a = -4.
2. к ning shunday qiymatini topingki, у = —x2 parabola bilan y=kx~ 6
to‘g‘ri chiziqning kesishish nuqtalaridan birining absissasi x = 2 bo‘lsin:
A) к = -1; В) к = 1; С) к = 2; D) к = -2.
3. b ning shunday qiymatini topingki, у = Зх2 parabola bilan у = 2x + b
toeg‘ri chiziqning kesishish nuqtalaridan birining absissasi x = 1 bo‘lsin:
A) b = 2; B) b = -1; C) b = 1; D) b = -2.
жж
4. Parabola uchining koordinatalarini toping: у = -x2 + 2x.
A) (-1; -1); В) (1; -2); C) (0; 2); D) (1; 1).
жж
жж
5. Absissalar o'qini x = 1 va x = 2 nuqtalarda, ordinatalar o‘qini esa (0; 2)
nuqtada kesib 0‘tuvchi parabolaning tenglamasini yozing:
A) y = + B) y = +
С) у = x2 — Зх + 2; D) у = x2 -1 x + i.
6. Parabola qaysi choraklarda joylashgan? у = Зх2 + 5x — 2.
A) I, II, III; В) II, III, IV; С) I, III, IV; D) I, II, III, IV.
7. Ox o‘qini x^l,5 va x=0,25 nuqtalarda, Oy o‘qlari esa (0: 0,75) nuqtada
kesib o'tuvchi parabolaning tenglamasini yozing:
A) y=2x2—3,5x+0,75; B) y=x2-3,5x-0,75;
C) y=—2x2+3,5x+0,5; D) y=l,5x?—0,25x+l,75.
8. Parabola uchining koordinatalarini toping: y=—x2—6x—5
A) (-3; 4); B) (3; -4); C) (3; 4); D) (-3; -4).
9. a ning qanday qiymatida x2+(a~4)x—(a+l)=0 tenglama ildizlari
kvadratlarining yig‘indisi eng kichik bo'ladi?
A) 1; B) -1 C) 3; D) -2.
10. Parabola uchining koordinatalarini toping: y=—j^+Sx—18
A) (4; -2); B) (-4; 2); C) (4; 2); D) (-4; -2).
32
1Ж
11. Parabola uchining koordinatalarini toping: y=4x2+12x+ll
A) (-1,5; 2); | B) (1,5; -2); | C) (-1,5; -2); | D) (4; 11).
12. A (—1; 0), В (1; 0), C (0; 1) nuqtalardan o‘tuvchi parabola tenglamasini
yozing:
A) y=-x2+l; В) y=x2-l; C) y=x2+l; D) j=-x2-l.
13. y=-x2+4x4-l parabola qaysi choraklarda joylashgan?
A) III, IV В) I, II, III; С) II, I; D) I, II, III, IV.
14. y=6x2+x—4 kvadrat funksiya grafigi qaysi choraklarda joylashgan?
A) II, III, IV, I; В) I, II; C) III, IV; D) II, III, IV.
15. p ning qanday qiymatlarida л2+/?х+15=0 tenglamaning ildizlari orasidagi
masofa 2 ga teng bo‘ladi?
A) ±8; B) ±15; C) ±5; D) 12.
16. Agar x2—3x4-^=0 tenglamaning x{ va x^ ildizlari uchun x13+x23=63
tenglik o'rinli bo'lsa, q ning qiymatlarini toping.
A) -4; B) 4; C) 63; D) 8.
17. x2—Ipx+p2 —9=0 tenglamaning ikkala ildizi (—3: 5) oraliqda joylashgan
bo'lsa, p ning qiymati qaysi oraliqda oczgaradi?
A) (0; 2); В) (1; 2); C) (2; -9); D) (1; -2).
18. x2—4x+^=0 tenglama ildizlari Xj va uchun x14+x24=82 tenglik o‘rinli
bo‘lsa, q ni toping.
A) 3; B) 4; C) -4; D) -3.
Olimpiada masalalari
1. Tomoni a ga teng bo'lgan kvadratning diagonaliga parallel va kvadratni
kesuvchi I to‘g‘ri chiziq o'tkazilgan. Bu to‘g‘ri chiziq kvadratdan yuzi 5
bo‘lgan uchburchakni ajratadi. Kvadratning A uchidan I gacha bo‘lgan
masofa x deylik. s va x orasidagi bog‘lanishni toping.
2. Teng yonli ABCD trapetsiyaning asoslari AD = a, BC=b (a> b)
balandligi BL = h bo'lib, A uchidan AD bo‘yicha AF= x masofa naridan
£jF|| BL to‘g‘ri chiziq o'tkazilgan. ABEFLA shakl yuzini x ning funksiyasi
sifatida ifodalang.
3. p haqiqiy qiymatlar qabul qilsa, у = x2 + 2px + p2 + p parabolaning uchi
qanday chiziqni chizadi?
3—Algebra, 9
33
жж
жж
IXXIZTXI
ЖЖ
жж
жж
жж
жж
жж
№ж
жж
4. р haqiqiy qiymatlar qabul qilsa, у = x2 — 2px + Ip1 parabolaning uchi
qanday chiziqni chizadi?
5. у = kx + I to‘g‘ri chiziq va у = ax2 + bx+ c parabolaning: 1) kesishishi; 2)
urinishi; 3) kesishmasligi shartlarini toping.
6. 1) yj = Зх2 — 1 va y2 = 5x + b; 2) yt = 2л2 + 1 va y2 = -x + b funksiyalar
grafiklarining o‘zaro joylanishini parametr b ga bog'liq holda tadqiq qiling.
7. у = —x2 + 2x va у = x2 — lOx + 24 funksiyalar grafiklari у = a to‘g‘ri chiziq
bilan kesilgan. Parametr a ning qiymatlariga bogfiiq holda kesishish nuqtalari
sonini toping.
8. 1) b ning qanday qiymatlarida y = a? + 2fex+13 parabola uchi bilan
koordinata boshi orasidagi masofa 5 ga teng bo'ladi?
2) a ning qanday qiymatlarida A(l; 2) nuqta bilan y = ax2 + 2x+l
parabolaning uchi orasidagi masofa 2л/2 ga teng bo'ladi?
9. y = 2x~ 5 to‘g‘ri chiziqda shunday C nuqtani topingki, undan A(—7; 1)
va B(—5; 0) nuqtalargacha bo‘lgan masofalar yig‘indisi eng kichik bo‘lsin.
10. у = x2 + px + q parabola у = 2x — 3 to‘g‘ri chiziqni absissasi Xq = 1 bo'lgan
nuqtada kesib o‘tadi. pN&q ning qanday qiymatlarida parabolaning uchidan
Ox o‘qqacha bo'lgan masofa eng kichik bo'ladi? Shu masofani toping.
11. 1) x3 — y3 = xy + 61; 2) x2 — y2 = 2012; 3) x2 — y2 = 799 tenglamalami
natural sonlarda yeching.
12. Katetlari a va b bo‘lgan (a>b) to‘g‘ri burchakli uchburchakka to‘g‘ri
to‘rtburchak ichki chizilgan. Uning uzunligi x bo‘lgan tomoni kichik katetga
parallel. 1) Shu to‘g‘ri to‘rtburchak yuzini x ning 5(x) funksiyasi sifatida
ifodalang; 2) S(x) funksiyaning aniqlanish sohasi va qiymatlar sohasini
toping; 3) S(x) funksiya grafigini chizing; 4) x ning qanday qiymatida
S(x) funksiya o‘zining eng katta qiymatiga erishishini aniqlang.
13. Hisoblang: l2-22+32-42+...+20142-20152+20162.
14. a = 1 • 2+2 • 3+3 - 4+...+98 *99, b = l2+22+32+...+972+982 bo‘lsa, a+b
yig‘indini toping.
3 3 3 3
15. Hisoblang: т + -—- + -—-—- + — + -—-— -------------------—.
1 1 + 2 1 + 2 + 3 1 + 2 + 3 + ... + 100
16. Katta shaming massasi kichik shar massasidan
1 - marta ko‘p. Tarozi muvozanatda bo‘lishi uchun
3
uning o‘ng pallasiga eng kamida nechta shar qo'shish
kerak? Sharlami olib tashlash mumkin emas,
ammo o‘ng pallaga kichik yoki katta sharlami
qo'shish mumkin.
жж
34
1Ж
17. Ikkita uchxonali abc va cba sonlar (a>c) ko‘paytmasi 396396 ga teng.
abc sormi toping, bunda a, b, c — raqamlar.
18. Natural sonlar uchburchak shaklida quyidagicha joylashtirilgan:
a (m; n) orqali m-qatordagi n—o‘rinda turgan sonni belgilaymiz. Masalan,
a (4; 1)=7, a (4, 3)=9.
Agar a (m; я)=2016 bo‘lsa, (m+«)ni toping.
19. Natural sonlar uchburchak shaklida quyidagicha joylashtirilgan:
Toq nomerli qatorlarda toq sonlar, juft nomerli qatorlarda juft sonlar
yozilgan.
1-qatorda 1 ta, 2-qatorda 3 ta, 3-qatorda 5 ta, 4-qatorda 7 ta, 5-qatorda
9 ta va hokazo. 2016 soni nechanchi nomerli qatorda joylashgan?
20. x+y=x2—лу+у2 tenglamaning butun sonlardan iborat ildizlami toping.
□ Berilgan tenglamani у ga nisbatan kvadrat tenglama deb qaraymiz:
y2—(x+l)y+x2—Bu tenglamadan у ni topamiz:
(x +1) ± J(x +1)2 - 4(x^ - j) (x +1) ± 3x^ + +1
У =------------2------------=----------2---------• О
2 2
Masala mazmunidan —Зл?+6лН-1>0, bundan 1 —— < x < 1 +
7з V5
Bu qo‘sh tengsizlikning butun yechimlari x=0, x=l, x=2. x ning bu
qiymatlariga mos у ning qiymatlarini (*) tenglikdan topamiz.
Javob: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
35
жж
жж
IXXIZTXI
мм
II ВОВ
KVADRAT TENGSIZLIKLAR
мм
мм
мм
мм
7-§. Kvadrat tengsizlik va uning yechimi
Kvadrat tengsizlik tushunchasiga olib keluvchi bitta masalani ko‘-
raylik.
1- masala. Tomorqa to‘g‘ri to‘rtburchak shaklida boclib, uning eni
23 m, bo‘yi 26 m ga teng. Uning tomonlari qanday bir xil songa orttirilsa,
tomorqaning yuzi 810 m2 dan ortiq bo‘ladi?
□ Tomorqaning har bir tomoni x metiga orttirilgan, deylik. U holda
kengaytirilgan tomorqaning eni (23 + x) m, bo‘yi (26 + x) m, yuzi esa
(23 + x)(26 + x) m2 bo'ladi. Masala shartiga ko‘ra, (23 +x)(26+ x) > 810
bo‘lishi kerak, bundan x2 + 49x+598 > 810 yoki x2 + 49x~ 212 > 0 teng-
sizlikka kelamiz. Uning chap qismini ko‘paytuvchilarga ajratamiz: (x + 53) -
(x — 4) > 0. Mazmuniga ko‘ra x > 0, demak, x + 53 > 0. Tengsizlikning
ikkala qismini x + 53 musbat songa bo'lib, x — 4 > 0, ya’ni x > 4 ni hosil
qilamiz.
Javob: tomorqaning har bir tomonini 4 m dan ko‘proqqa orttirish kerak.
x2 + 49x — 212 > 0 tengsizlik kvadrat tengsizlikka misol boTa oladi, bunda
x — noma’lum son.
мм
Ta’rif. Agar tengsizlikning chap qismida kvadrat funksiya, о‘ng qis-
mida nol tursa, bunday tengsizlik kvadrat tengsizlik deyiladi.
Tengsizlikning yechimi deb, noma’lumning shu tengsizlikni to‘gcri
sonli tengsizlikka aylantiruvchi qiymatlariga aytiladi.
Tengsizlikni yechish deganda uning barcha yechimlarini topish yoki
ulaming yo'qligini ko'rsatish tushuniladi.
2- masala, x2 — 5x + 4 > 0 tengsizlikni yeching.
□ x2 - 5x + 4 = 0 tenglamaning ildizlari xt = 1, x2 = 4. x2 — 5x + 4 kvadrat
uchhadni ko‘paytuvchilaiga ajratamiz: x2 — 5x + 4 = (x — l)(x — 4).
U holda berilgan tengsizlik (x—l)(x —4)>0 kabi yoziladi. Ikkita
ko‘paytuvchi bir xil ishoraga ega bo'lsa, ko'paytma musbat bo'ladi. Ikki holni
qaraymiz:
1- hoi. x — 1 > 0 va x — 4 > 0 bo‘lsin. Bu ikki tengsizlik, ravshanki,
Jx-l>0 ,
tengsizliklaming ushbu ' x_4 > q
sistemasini tashkil qiladi. Uni yechib,
x > 1 ,
x>4
tengsizliklami olamiz, bundan x > 4 yoki (4; °®).
36
Shunday qilib, barcha х>4 sonlar (х—1)(х —4)>0 tengsizlikning
yechimi bo‘ladi.
2- hot x—l<Ovax~4<0 bo'lsin. Bu ikki tengsizlik ushbu
х-1< 0 >
х-4< О
л tengsizliklami olamiz, bundan
x<4
Ж
жж
sistemani tashkil qiladi. Uni yechib,
x< 1 yoki (—°°; 1).
Shunday qilib, barcha x<l sonlar (x—l)(x —4)>0 tengsizlikning
yechimi bo‘ladi. Demak, x2 — 5x + 4 > 0 tengsizlikning yechimlari barcha
x < 1 va x > 4 sonlardan iborat boladi.
Javob: x< 1, x>4. Uni (—00; 1) u (4, °°) kabi yozish ham mumkin.
3-masala. 2x2 + 7x-4<0 tengsizlikni yeching.
П 1) 2x2 + 7x - 4 = 0 tengsizlikning ildizlari i va x, = ~4 sonlardan
2 z
iborat. Kvadrat uchhadni ko‘paytuvchilaiga ajratamiz:
жж
ЛИЙ
1ЖЖ
1ЖЖ
2x2 + 7x + 4 = 21 x
жж
U holda berilgan tengsizlikni 2 (x - i )(x - 4) < 0 kabi yozib olamiz. Ikkita
ko‘paytuvchi har xil ishoraga ega bo4lsa, ko‘paytma manfiy bo‘ladi.
Ikki holni qaraymiz:
x-|>0,
x+4<0.
1-hol.
1- holda
1
X> 2’
ega emasligi ravshan.
1
X<2’
x>-4
2- holda
жж
жж
x-i<0
2-hoL 2 ’
x+4>0.
sistemani hosil qilamiz, ammo bu sistemaning yechimga
sistemani olamiz. Uning yechimi -4 < x < -| boladi.
жж
Demak, berilgan
oraliqdagi barcha nuqtalardir.
г г Л 1 —
Javob: -4 < x < -. И
2х2 + 7х + 4 < 0 tengsizlikning yechimlari -4 < х < i
жж
37
мм
мм
Eslatma: 1) -4<х<| javobni f-4;i | kabi yozish ham mumkin.
2) Agar 2x2 + 7x-4^0 tengsizlikni yechish talab qilinganda edi, u
1 Г 11
holda javob -4 < x < - bo‘lar edi. Uni |_-4; kabi yozsa ham boladi.
мм
мм
3) -x2 + 10x-9>0 tengsizlikni yechishda, qulay bo‘lishi uchun,
uning har ikkala qismini (—1) ga ko‘paytirib, x2-10x+9<0 tengsizlikka
keltiriladi va bu tengsizlik yechiladi. Masalalami yechishdan shunday xulosaga
kelish mumkin:
a£+bx+c=§ kvadrat tenglama ikkita turli xt va x2 ildizga ega
bo‘lsin, deylik. U holda аэ?+Ьх+с>§ yoki axl+bx+c<(/ kvadrat teng-
sizlikni yechish uchun:
1) kvadrat tengsizlikning chap qismi ko‘paytuvchilarga ajratiladi.
ax1 +bx+c=a(x—x])(x—xj >0, (<0);
2) birinchi darajali tengsizliklar sistemasi tuziladi va ikkita hoi
qaraladi:
мм
a)
x-Xj > 0,
x-^>0 У°ы
x-xj < 0,
x-x2 <0.
мм
b)
<[x-xi>Q,
[x-X2 < 0
yoki
x - Xj < 0,
X-X2 > 0.,
3) hosil qilingan tengsizliklar sistemasi yechiladi va javoblar
olinadi.
81. Savollarga javob bering. Topshiriqlami bajaring:
1) Kvadrat tengsizlik deb nimaga aytiladi? Misollar keltiring.
©2) Tengsizlikning yechimi nima? Misollarda tushuntiring.
3) Tengsizlikni yechish deganda nimani tushunasiz?
4) ax2 +bx + c = 0 tenglama ikkita ildizga ega bo^a, ax2 + bx + c > 0
(yoki ax2 + £x + c < 0) tengsizlik qanday yechiladi? Misollarda
tushuntiring.
82. (Og‘zaki.) Tengsizliklardan qaysilari kvadrat tengsizlik ekanini ayting:
1) x2 - 9 > 0; 2) 2x2 - 7 < 0; 3) Зх3 + 5x> 0;
4)-7x+l<0; 5) —x2 + 6x—1 <0; 6)x2-16<0.
83. (Og‘zaki.) —1; 0; 1 sonlardan qaysilari:
1) x2 —3x + 2>0; 2) 3x2-5x-8<0;
3) -x2+x-l<0; 4) —2x2+x+l>0
tengsizlikning yechimlari bo‘ladi?
38
Ж
84. —3, —2, —1, О, 1, 2, J’ 3 sonlardan qaysilari tengsizlikning yechimi
bo'ladi?
1) 2x2 - 5x + 2 < 0; 5) x2 -1 > 0;
2) 5x2 + 3x - 2 £ 0; 6) x2 - 3x + 2 £ 0;
3) x2 - 5x + 6 > 0; 7) 10x2 - 9x + 2 < 0;
4) x(x + 2) > 0; 8) Sx2 +8x-4 > 0?
85. Tengsizlikni yeching. Javobni tengsizlik (oraliq) ko‘rinishida yozing (85—87):
1) (x — 3)(x — 7) > 0;
3) (5-x)(x- 1) > 0;
86. l)x2 —5x>0;
4) x2-49^0;
87. 1) x2 —7x+6>0;
3) —x2 + 4x + 5 > 0;
5) 3x2—4x—7>0;
88. Tengsizlikni yeching:
2) (x+3)(x +7) < 0;
4) (2 — x)(x — 3) < 0.
2)x2 + 3x<0; 3) x2 — 25 2 0;
5) —x2 + 4x > 0; 6) —x2 + 6x < 0.
2) x2 + 5x+4<0;
4) —x2 — 7x + 8 < 0;
6) -2x2 + 9x+ 1K0.
П f
(x-3)220; 3) ^-x s°;
4x2 + 2 < x2 -5x; | 6) (2x- l)(x-4) > -3.
89. Tengsizlikning butun yechimlari ko'paytmasini toping:
1) x2-6x + 5<0;
3) (2x-l)(x-4)< 0;
5) x2 - 8x + 6 < 0;
<0;
2)
5)
2) x2 - 6x + 4 < 0;
4) 15x2 - 38x +16 <. 0;
6) -x2-10x-21 > 0.
90. Tengsizlikning butun yechimlari yig‘indisini toping:
1) (2x + 3)(x-3) < 0; 2) 3x2 - 17x - 28 < 0;
3) 6x2 + 29x-5<0; 4) x2-10x + 23<0;
5) 3x2-26x-9^0; 6) 2x2 + llx-6<0.
91. Kvadrat funksiya grafigini chizing. Grafik boeyicha x ning qanday qiymatlarida
funksiya: musbat; manfiy; nolga teng bo'lishini aniqlang:
1) y = (x-2)2; 2) y = -(x + l)2;
3) у = x2 + x +1; 4) у = x2 - 2x + 3;
5) У = 2x2 - 5x + 3; 6) у = -x2 + 8x + 9.
92**. Xj va Xj sonlar (bunda xY < x^) у = ax2 + bx + c funksiyaning nollari
ekani ma’lum. Agar Xq sonXj vax2 orasidayotsa, ya’nixl<xQ<x2bo'lsa,
u holda a(axQ + bx$ + c) < 0 tengsizlik bajarilishini isbotlang.
жж
39
мм
8- §. Kvadrat tengsizlikni kvadrat funksiya grafigi
yordamida yechish
мм
мм
1- masala, x2 4- x — 6 < 0 tengsizlikni grafik yordamida yeching.
□ a = 1 > 0 bo‘lgani uchun у = x2 + x — 6 kvadrat funksiyaning
grafigi — tarmoqlari yuqoriga yo‘nalgan paraboladir. x2 + x — 6 = 0 tengla-
mani yechib, parabolaning Ox o‘qi bilan kesishish nuqtalarini topamiz.
x2 + x — 6 = 0 tenglamaning ildizlari x1 = —3, Xj = 2 ekani ravshan. Parabola
Ox o‘qini x = — 3 va x = 2 nuqtalarda kesadi. x2 + x - 6 < 0 tengsizlikni
qanoatlantiruvchi x larda parabolaning nuqtalari Ox o‘qida yoki shu o'qdan
pastda yotadi. 25- rasmdan bunday nuqtalar [—3; 2] kesmadagi barcha nuqtalar
ekani koermib turipdi.
Javob: —3 < x < 2. И
мм
ММ
«Ж
у = x2 + x — 6 kvadrat funksiya grafigidan berilgan tengsizlikdan boshqa
tengsizliklami yechishda ham foydalanish mumkin:
1) x2 + x — 6 < 0 tengsizlikning yechimlari —3 < x < 2 bo‘ladi;
2) x2 + x — 6 > 0 tengsizlikning yechimlari x < —3 va x > 2 oraliqdagi barcha
sonlardan iborat;
3) x2 4- x — 6 > 0 tengsizlikning yechimlari esa x < —3 va x > 2 oraliqlardagi
barcha sonlardir.
2- masala, x2 + 6x + 9 > 0 tengsizlikni yeching.
□ a = 1 > 0 boclgani uchun parabola tarmoqlari yuqoriga yo‘nalgan.
x2 4- 6x 4- 9 = 0 tenglama bitta x = —3 ildizga ega — parabola (—3; 0) nuqtada Ox
o‘qiga urinadi. у = x2 + 6x 4- 9 kvadrat uchhad grafigi 26- rasmda tasvirlangan.
x2 4- 6x 4- 9 > 0 tengsizlikni yechish — x ning qanday qiymatlarida parabola
Ox o'qidan yuqorida yotishini aniqlash demakdir. 26- rasmdan ravshanki, son
o‘qining x = —3 dan boshqa barcha nuqtalari berilgan tengsizlikni qanoatlantiradi.
Javob:хф —3.1
мм
IXTXIXXI
40
1Ж
Javobni x<— 3, x> — 3 yoki
-3) ц (-3;+°°) kabi yozish mumkin.
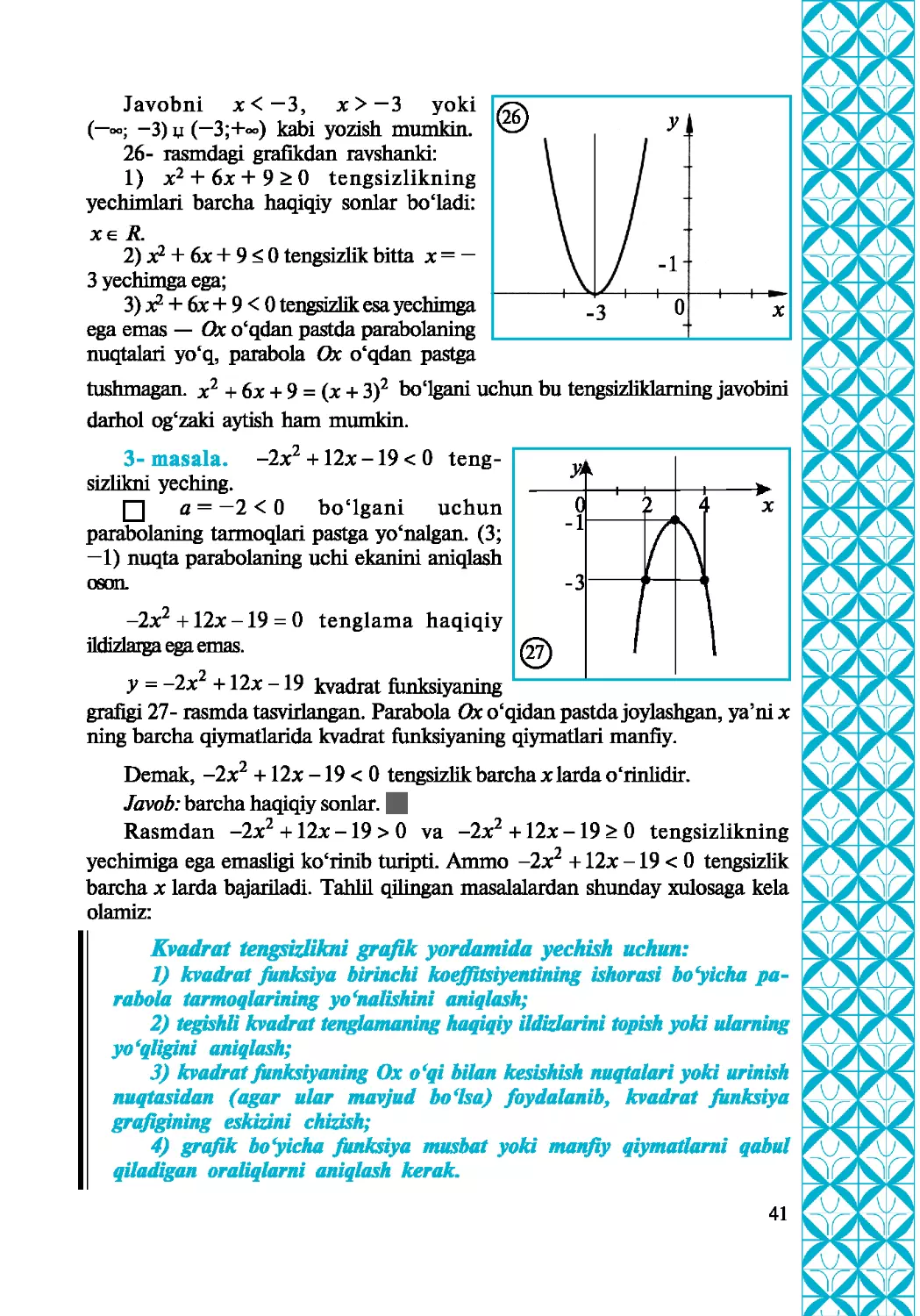
26- rasmdagi grafikdan ravshanki:
1) x2 + 6x + 9 0 tengsizlikning
yechimlari barcha haqiqiy sonlar bo‘ladi:
X£ R.
2) x2 + 6x + 9 < 0 tengsizlik bitta x = —
3 yechimga ega;
3) x2 + 6x + 9 < 0 tengsizlik esa yechimga
ega emas — Ox o‘qdan pastda parabolaning
nuqtalari yo‘q, parabola Ox o‘qdan pastga
tushmagan. x2 + 6x + 9 = (x + 3)2 bo'lgani uchun bu tengsizliklaming javobini
darhol og‘zaki aytish ham mumkin.
3- masala. -2x2 + 12x -19 < 0 teng-
sizlikni yeching.
Q] a = —2 < 0 bo'lgani uchun
parabolaning tarmoqlari pastga yo‘nalgan. (3;
—1) nuqta parabolaning uchi ekanini aniqlash
□SOIL
-2x2 + 12x -19 = 0 tenglama haqiqiy
ildizlarga ega emas.
У = -2x2 + 12x -19 kvadrat funksiyaning
grafigi 27- rasmda tasvirlangan. Parabola Ox o'qidan pastda joylashgan, ya’ni x
ning barcha qiymatlarida kvadrat funksiyaning qiymatlari manfiy.
Demak, -2x2 + 12x -19 < 0 tengsizlik barcha xlardaohinlidir.
Javob: barcha haqiqiy sonlar. |
Rasmdan -2x2 + 12x-19>0 va -2x2 +12x-19>0 tengsizlikning
yechimiga ega emasligi ko‘rinib turipti. Ammo -2x2 + 12x -19 < 0 tengsizlik
barcha x larda bajariladi. Tahlil qilingan masalalardan shunday xulosaga kela
olamiz:
Kvadrat tengsizlikni grafik yordamida yechish uchun:
1) kvadrat funksiya birinchi koeffitsiyentining ishorasi bo’yicha pa-
rabola tarmoqlarining yo(nalishini aniqlash;
2) tegishli kvadrat tenglamaning haqiqiy ildizlarini topish yoki ularning
yo‘qligini aniqlash;
3) kvadrat funksiyaning Ox o‘qi bilan kesishish nuqtalari yoki urinish
nuqtasidan (agar ular mavjud bo4sa) foydalanib, kvadrat funksiya
grafigining eskizini chizish;
4) grafik bo^yicha funksiya musbat yoki manfiy qiymatlami qabul
qiladigan oraliqlarni aniqlash kerak.
жж
жж
41
IXXIZTXI
мм
мм
мм
93. Savollarga javob bering. Topshiriqlami bajarmg:
©1) Kvadrat tengsizlik mos kvadrat funksiyaning grafigi yordamida qanday
yechiladi? Misolda tushuntiring.
2) Kvadrat tengsizlikni grafik yordamida yechish bosqichlarini ayting
va a) 2x2 — 3x + 1 > 0; b) 6x2 — 17x + 12 < 0 tengsizliklami bosqichma-
bosqich yeching.
3) Funksiya grafigi yordamida berilgan tengsizlikdan boshqa yana qanday
tengsizliklami yechish mumkin? Misollarda ko'rsating.
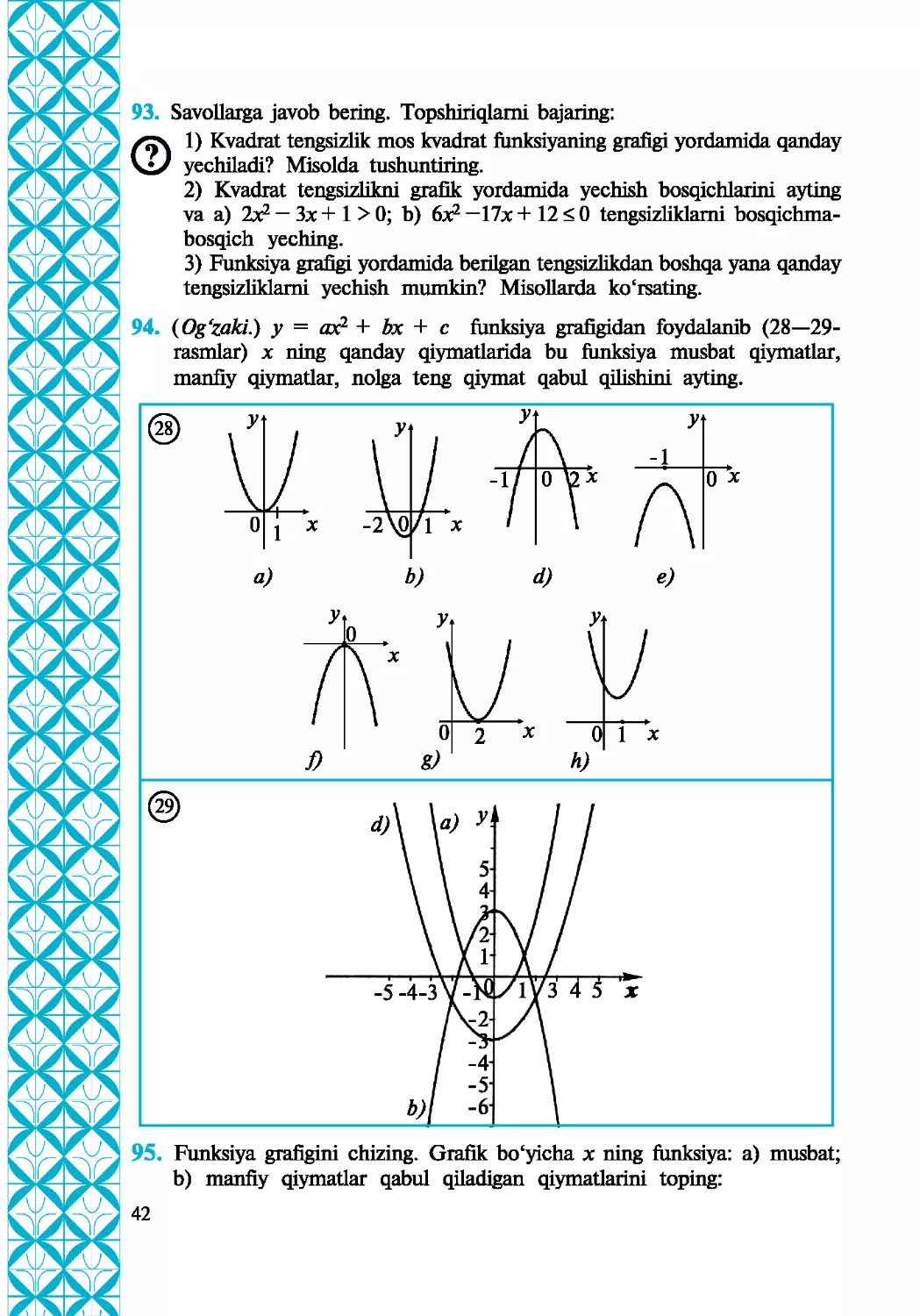
94. (Og'zakL) у = ax2 + bx + c funksiya grafigidan foydalanib (28-29-
rasmlar) x ning qanday qiymatlarida bu funksiya musbat qiymatlar,
manfiy qiymatlar, nolga teng qiymat qabul qilishini ayting.
йтаи
мм
мм
мм
95. Funksiya grafigini chizing. Grafik bo‘yicha x ning funksiya: a) musbat;
b) manfiy qiymatlar qabul qiladigan qiymatlarini toping:
42
Ж
1) у = 2x2 + 7x - 4; 6) у = 4х2 + 12х + 9;
2) у = Зх2 - 34x+ 11; 7) у = 9х2 - 12х + 4;
3) у = —4x2 - x + 3; 8) у = —16х2 + 24х - 9;
4) у = —Зх2 + 7x + 6; 9) у = 9х2 — 6х + 9;
5) у = —x2 + Зх + 4; Ю) у = 4х2 + 4х+ 3.
ЖЖ
ЖЖ
Kvadrat funksiya grafigi yordamida kvadrat tengsizlikni yeching (96—99):
96. 1) x2-Sx~9<0-, 3) —x2 + 9x+10 < 0; 2) x2 + 5x — 6 i 0; 4) —x2 — 7x + 8 > 0.
97. 1) 2X2—llx—13^0; 3) -4x2-5x + 9>0; 2) 3x2 + 10x+7<0; 4) -Зх2 + 7x + 10 < 0.
98. 1) 4x2 + 4x+l>0; 3) x2 —4x+4<0; 2) x2 + 4x + 4 S 0; 4) —4x? + 4x — 1 > 0.
99. l)x2 + 4x+9>0; 3) —x2 + 5x — 7 < 0; 2) x2-3x+8<0; 4) 2x2-4x+l<0.
ЖЖ
ЖЖ
100. (Og‘zaki.) Tengsizlikni yeching:
1) x2 + 1 > 0; 3) —(x —4)2 —l<0;
2) (x-3)2 + 1 > 0; 4) —(x—l)2 —2>0.
101*. к ning qanday eng kichik butun qiymatida:
1) x2 - 2{k + 4)x + k2 -15 = 0; 2) x2 + 2(k + 5)x + k2 + 40 = 0
tenglama ikkita turli haqiqiy ildizga ega bo'ladi?
Ko^rsatma: 1) Diskriminant D=b2—4ac=4((£+4)2—(k2—15))=4(8£+31).
41 7
8£+31>0 bo‘lishi kerak. Bundan к >---= -3-. Demak, к ning eng
8 8
kichik butun qiymati —3 ga teng: k=—3.
ЖЖ
ЖЖ
жж
102. Kvadrat tengsizlikni yeching:
1) 9x2-16a0;
2) 4x2 - 25 £ 0;
3)
4) 0,5x2 > 0,125.
9-§. Intervallar usuli
ЖЖ
Tengsizliklami yechishning intervallar usuli mohiyatini masalalar yechish
jarayonida tushuntiramiz.
1- masala, x ning qanday qiymatlarida:
У = x2 - 5x + 6 kvadrat uchhad musbat qiymatlami; manfiy qiymatlami
qabul qiladi?
43
ЖЖ
IXXIZTXI
мм
мм
□ х2 - 5х + 6 = 0 tenglamaning ildizlari xt = 2 va = 3 ekani ravshan.
Demak, x2 — 5x + 6 = (x — 2)(x — 3). Son o‘qida 2 va 3 nuqtalami belgilaymiz.
Son o‘qi uchta oraliqqa bo‘linadi: x<2, 2<x<3, x>3 (30-rasm).
Y Y
J! „
2 3 x
мм
мм
мм
мм
x< 2 va x> 3 oraliqlar ham 2 < x< 3 oraliq kabi interval deyiladi. x> 3
intervalda x — 2 > 0 va x — 3 > 0, ya’ni (x — 2)(x — 3) ko‘paytma musbat
bo'ladi. 2 < x< 3 oraliqda esa x~ 2 > 0, ammo x~ 3 < 0, ya’ni (x~ 2)(x— 3)
ko‘paytma manfiy bo‘ladi.
Aigument x son o‘qi bo'yicha harakat qilib x = 3 nuqtadan chapga
o‘tganda (x — 2)(x — 3) ko‘paytma oez ishorasini „+“ dan “ ga o'zgartiradi.
x<2 bo‘lganda, ravshanki, x — 2<0 va x — 3<0, ya’ni (x—2)(x—3)
ko‘paytma musbat qiymatlar qabul qiladi: argument x son o‘qi bo‘yicha
harakat qilib, x=2 nuqtadan chapga o‘tganda (x —2)(x~ 3) ko‘paytma o‘z
ishorasini endi “ dan „+“ ga o‘zgartiradi.
Demak, aigument x son o‘qi bo‘yicha o‘ngdan chapga harakat qilib bir
intervaldan qo'shni intervalga o‘tganda (x — 2)(x~3) ko‘paytmaning ishorasi
almasha boradi.
Shunday qilib, x2 — 5x + 6 kvadrat uchhadning ishorasi qaysi x larda
qanday bo'lishi masalasini ushbu usul bilan hal qilish mumkin:
1) x2 — 5x + 6 = 0 tenglamaning xt = 2 va x^ = 3 ildizlarini son o‘qida
belgilaymiz. Ildizlar son o‘qini 3 ta intervalga ajratadi.
2) x > 3 intervalda (x - 2)(x - 3) ko‘paytma, ya’ni x2 - 5x + 6 kvadrat
uchhad musbat qiymatlar qabul qiladi.
3) Qolgan intervallarga o‘tishda uchhadning ishorasi almasha boradi
(31- rasm).
+ X — ¥ +
2 3 ► X
Javob: x < 2 va x > 3 bo‘lganda x2 — 5x + 6 > 0; 2<x<3 intervalda esa
x2 - 5x + 6 < 0. |
Kvadrat uchhad ishorasini aniqlashning bu usuli intervallar usuli deyi-
ladi.
Biz yuqorida x2 - 5x + 6 > 0 va x2 - 5x + 6 < 0 tengsizliklami interval-
lar usulidan foydalanib yechdik.
2- masala. Tengsizlikni yeching: (x + 5)(x — 2)3 • (x — 3) > 0.
□ (x—2)3 va x—2 ifoda x Ф 2 bo‘lsa, bir xil ishoraga ega bo'ladi. Binobarin,
berilgan tengsizlik (x+ 5)(x — 2) • (x — 3) > 0 tengsizlikka teng kuchlidir. Bu
tengsizlikni esa intervallar usuli bilan yechish oson.
44
Ж
Javob: —5<x<2, x>3. О
3- masala. Tengsizlikni yeching: (x + 7)(x — l)2(x — 4) < 0.
□ x*l bo‘lsa, (x~1)2>0. Demak, berilgan tengsizlik
(x + 7)(x-4) < 0,
x Ф 1
sistemaga teng kuchli (32-rasm).
ЖЖ
ЖЖ
Javob: — 7 < x< 1, 1 <x< 4. |
i 15
4*-masala. —-----------^0 tengsizlikni yeching.
x -6x+8
□ Kasming surat va maxrajini ko‘paytuvchilarga ajratamiz:
(x-3)(x-51 л
----—------<0 m
(x-2)(x-4) ‘ ш
P(x}
—^<0 tengsizlikning yechimlari to‘plami P(x) • Q(x) < 0 tengsizlikning
Q(x)
yechimlari to'plami bilan ustma-ust tushishini, ya’ni bu tengsizliklar teng
kuchli ekanini bilasiz, bunda P(x) va Q(x) ko‘phadlar, Q(x)*Q.
Demak, (1) tengsizlik
(x - 2)(x - 3)(x - 4)(x - 5) < 0 (2)
tengsizlikka tengkuchli. Son o‘qida (1) ning surat va maxrajini nolga
aylantiradigan 2, 3, 4, 5 nuqtalami belgilaymiz (33-a rasm).
ЖЖ
ЖЖ
a) 0 2 3 4 5
b) Z t
0 2 3 4 5
жж
Bu nuqtalar son o‘qini 5 ta oraliqqa ajratadi. x > 5 oraliqda kasming surat
va maxraji musbat. Bu oraliqdan awalgisiga, (4; 5] oraliqqa o'tishda (2) ifoda
((1) kasr ham) o‘z ishorasini o‘zgartiradi. Ishoralaming qanday o‘zgarishi
33 -b rasmda tasvirlangan.
x=3, x=5 sonlar (1) tengsizlikni qanoatlantiradi (bu qiymatlarda (1)
da tenglikka — „=“ ga erishiladi), ammo x = 2 va x = 4 sonlar uchun maxraj
nolga teng, ya’ni kasr ma’noga ega emas: x = 2 va x = 4 sonlar tengsizlikning
yechimi bo‘la olmaydi (bu nuqtalar a), b) rasmdagi ,,oq“ nuqtalardir; x = 3,
x = 5 „qora“ nuqtalar esa tengsizlikni qanoatlantiradi).
45
ЖЖ
ЖЖ
IXXIZTXI
жж
Bizga х ning kasr manfiy bo‘ladigan qiymatlari kerak. Ular (2; 3] va
(4; 5] oraliqlardan iborat.
Javob: 2<x<3, 4<x<5 yoki (2;3] и (4;5]. О
жж
x2—8x+15
Agar —-----------> 0 tengsizlikni yechish talab qilinganda edi, u holda
x-6x+8
javob x < 2, 3<x<4, x > 5 bo‘lardi.
103. Savollarga javob bering. Topshiriqlami bajaring:
1) Kvadrat tengsizlikni yechishning qanday usullarini bilasiz?
vxz 2) Intervallar usuli nima? Misollarda tushuntiring.
3) Tengsizlikni yechish jarayonida intervallar usulidan qanday
foydalaniladi? Misollarda tushuntiring.
4) Intervallar usuli kvadrat tengsizlikdan boshqa yana qanday
tengsizliklami yechishda qo‘l keladi? Misoliar keltiring.
жж
жж
жж
104. (Og‘zaki.) x=2 son tengsizlikning yechimi bo‘lishini ko'rsating:
1) 2 (x—l)(x+1) > 0; 3) (x-4)(x-5) > 0;
(x - 3)(x + 4) < 0; 4) (x+ 2)(x - 7) < 0.
105. Tengsizlikni intervallar usuli yordamida yeching (105—109): 1) (x + 3)(x + 4) > 0; 4) (x—5)(x+6) >0; 2) (x—3)(x —4) < 0; 5) (x-4) (x+|)>0; 3) (x+ 5)(x —6) < 0; 6) (x+ l)(x-|)<0.
106. 1) x2 + 4x < 0; 2) x2 — 4x > 0; 3) x2 — 5x > 0;
4) x2 + 6x < 0; 5) 3x2 - 4x > 0; 6) 5x2 - 7x < 0.
107. 1) 2) 3) x3 — x<0; 4) 16x3 — x>0; x3—4x>0; 5) (x2 —4)(x+ 1) > 0; 9x3—x<0; 6) (x2 — 9)(x — 2) > 0.
108. 1) (x — 3)2 • (x2 — 9) > 0; 4) (x — 7)(x2 — 49) > 0;
2) 3) (x+4)2• (x2 — 16)<0; 5) (x —2)(x—5)(x2 — 25)<0; (x—l)(x2 — 1) < 0; 6) (x+6)(x2 — 36)(x —4) < 0.
109. 1) ^4>0; 3) ^^>0; 5) (я+2)(^~1) < o; x-4 5-x x+4
2) т|<0; 4> l45+x*0; 6> - ? 2X+5) a °-
110*. Tengsizlikni yeching:
x(x+l)
(x-2)(4-x) “°’ 7> X3-6x2+llx-6< 0;
46
2) x2-4x+4 n. l-xz 8) (x -1)3 (x - 2)2 < 0;
3) -x2+4x-3 > x(4-x) " ’ 9) (x-l)(x-2)(x + 3)2 <0;
4) x2-6x-l6 „ (x-l)(x-ll) " ’ 10) (x+3)3 < 0: (x+4)(x-2)(x-3)
5) -x2+7x-!0 x -7x+l2 11) . о 54 x + 8>-—; 7-x
6) ^-^+g.SQ; x-7 12) 1 о —- < x - 3. x+2
111*. Tenzsizlikning barcha butun yechimlari yig‘indisini toping:
1) (x-l)(x+l)4(x-3)5 (x-4)2S0; 2) f^^O;
3) x + 2 л —7<°; x + 6 4) 2(x2-6)<5x.
112. Tengsizlikning natural yechimlari ko‘paytmasini toping:
1) Зх2 - 19x + 20 < 0; 3) x2-x-12<0;
2) 4X2- 13x + 3£0; 4) 3x2 — 4x — 55 < 0.
113. Tengsizlikni yeching:
1) x2-7 x-8 . n . x2-64 3) 5x2-3x-2 > л. l-x2 ’ ’
2) x2+7x+l0. n. 2 л 4 ’ X -4 4) X2-16- >0. 2x2+5x-12
10- §. II bobga doir mashqlar
Tengsizlikni yeching (114—116):
114. 1) (x - 3)(x + 5) > 0; 4)
2) (x + 2)(x — 1) > 0; 5)
3) (x+l)(x + 4)<0; 6)
115. 1) 4x2>x; 3) 16 <x2;
2) 9x2<49; 4) 49>4x2;
116. 1) 4-9x2<0; 4)
(x + 2)(x - 4) > 0;
(x + l,5)(x —3,5) > 0;
( iY 2V n
x-- x+- <0.
3 3
5>
6>
4x + 5x2 > 0;
47
жж
жж
жж
жж
жж
жж
2) - 16 + 9х2>0; 5) х(3-5х)>0;
3) 2х —Зх2<0; 6) х(2х+1)<0.
Kvadrat uchhad grafigini chizing. Grafik bo‘yicha x ning qanday qiymatlarida
funksiya musbat, manfiy qiymatlar qabul qilishini aniqlang:
117. 1) у = з?-6х, 4) у = -x2 + 1; 5) у = x2 - 4x + 5; 6) у = —x2 + 6x + 7.
2) у = -x2 + Зх;
3) y = x2-4;
Tengsizlikni yeching (118—122)
118. 1) (x — 3)(2x — 5)>0; 3) (3x+ l)(2-x)<0;
2) (5- 2x)(x- 6)< 0; 4) (x- l)(4x+ 3)>0.
119. 1) (x1 - 9)(2x - 3) < 0; 3) ’J.O;
2) (1 - x?)(3 - 5x) S 0; 4) ^7 so. ' 9-x2
120. 1) ^=^<0; 3) x-9 (x? - 9)(25x2 - 1) > 0;
2) ^<0; 4) 4-x2 (x2 - 36)(25 - 16X2) г 0.
7x x2 121. 1) 4£-^->l; 7 10 10 <44 x2 1 2 10 3) —--x >-X- —; ’ 9 3 3 9
2) |x2-|x^x-l; гм н еч |m 1 VI н |m 1
122. 1) x2+7x+8 <0; x2-49 <44 2x2+5x-3>n. ’ 4x2-1 " ’
<44 x2-5x+6 л. ’ x?-4 4) о*2-16 ^0. 3x2+4x-32
123*. a ning qanday qiymatlarida tenglama ikkita turli ildizga ega:
1) 3x2 - 2ax + 12 = 0; 2) x2 + (1 - d)x + 1 = 0;
3) (2a - l)x2 + 2x - 1 = 0; 4) ax2 - (2a - l)x + a + 2 = 0?
124*. a ning qanday qiymatlarida x2 — (2 + a)x + 4 > 0 tengsizlik x ning
barcha qiymatiari uchun o‘rinli bo‘ladi?
Ko‘rsatma\ 2>=^-4ас=(2+д)2-4 1 4=a2+4a-12=(a+6)(a-2) < 0
bo‘lishi kerak. Bundan: — 6<« < 2.
125*. a ning qanday qiymatlarida x2 + 2(a — l)x + 2 > 0 tengsizlik x ning
barcha qiymatiari uchun o‘rinli boTadi?
48
1Ж
126*. 1) a < b bo'lganda ushbu (x — a)(x — b) < 0, < 0, < 0
x-b x-a
tengsizliklaming har bin a < x < b qo‘sh tengsizlikka teng kuchli
ekanini isbotlang.
2) Yuqoridagi tasdiqdan foydalanib tengsizlikni yeching:
1) (x - 3)(x - 7) < 0; 4) ^4<o;
x-7
2) (x - 5)(x + 2) < 0; 5) (x + 7)(x + 1) < 0;
3) ^4<0; 6) ^±|<0.
x-1 x+5
127*. 1) a < b bo‘lganda ushbu (x — a)(x — b) > 0, > 0, —- > 0
x-b x-a
tengsizliklaming har biri x < a yoki x > b ga teng kuchli ekanini
isbotlang.
2) Yuqoridagi natijadan foydalanib tengsizlikni yeching:
1) (x - 4)(x - 11) : > 0; 4) X-2 Л . ^5>0’
2) (x - 8)(x + 7) > 0; 5) ^4^0; x-1
3) (x + l)(x + 3) > 0; 6) ^0. x+3
128. Funksiyalar grafiklarini bitta koordinata sistemasida chizing va x ning
qanday qiymatlarida bir funksiyaning qiymati ikkinchisinikidan katta
(kichik) bo‘lishini aniqlang. Natijani mos tengsizlikni yechib tekshiring.
1) y = x2, y = x+2; 4) y = —x2 + 2x+3, y=3x+l;
2) y = x2— 4, y = 2x~ 5; 5) y = x2 — Зх, y = ~2x2 + x — 1;
3) y = x2-3x-4, y = x —4; 6) y=3x2 + 4x-7, y = x2 + 5x-6.
11-§. Kvadrat funksiya va kvadrat tengsizliklarga
olib keluvchi masalalar
жж
Kvadrat funksiyaning eng katta (eng kichik) qiymatini topishga, kvadrat
tengsizliklarga olib keluvchi masalalar bilan tanishamiz.
129. Kema 8 soatdan ko‘p bo‘lmagan vaqt davomida daryo oqimi bo'yicha
45 km yurishi va orqasiga qaytishi kerak. Agar daryo oqimining tezligi
3 km/soat bo'lsa, kemaning tuig'un suvdagi tezligi qanday bo‘lishi
kerak?
□ Kemaning turg‘un suvdagi tezligini x km/soat deylik. U holda:
жж
4—Algebra, 9
49
IXXIZTXI
жж
(х + 3) km/soat — kemaning daryo oqimi bo'yicha yurish tezligi,
(x—3) km/soat — oqimga qarshi yurish tezligi bo'ladi, ya’ni x—3>0,
45
x > 3 bo'lishi kerak. soat — kemaning oqim bo'yicha berilgan masofaga
45
borish vaqti; soat — kemaning oqimga qarshi berilgan masofaga kelish
vaqti.
Masala mazmuniga mos tengsizlik ushbu ko'rinishda bo'lishi ravshan:
жж
45 | 45
x+3 x-3
45(x—3+x+3) Q
-----5------- °
x2-9
Bundan: 45(x - 3 + x + 3) < 8 - (x2 - 9), chunk! x2 — 9>0.
8x2 - 90x~ 72 > 0, ya’ni 4x2 - 45x - 36 > 0, (x - 12)(4x + 3) > 0
жж
tengsizlikka kelamiz. Uning yechimlari x^ 12 va x < - -. Ammo, ma’nosiga
ko'ra x>3. Demak, x£12 (km/soat).
Javob: kemaning turg'un suvdagi tezligi 12 km/soatdan kam bo'lmasligi
kerak. I
жж
жж
130** (Tadqiqot uchun). Daryoning A va В bekatlari orasidagi masofa s km.
Kemaning A dan В ga borishi va orqaga qaytishi uchun t soatdan ko'p
bo'lmagan vaqti bor. Agar daryo oqimining tezligi v km/soat bo'lsa,
kemaning turg'un suvdagi tezligi x qanday bo'lishi kerak?
5, t, v parametrlarga turli son qiymatlari berishingiz mumkin.
Masala javobini tahlil qiling.
131*. Bog' to'g'ri to'rtburchak shaklida bo'lib, uning bir tomonidan kanal
oqib o'tadi (qirg'oqni to'g'ri chiziqli deb faraz qilamiz). Bog' uch
tomondan jami 80 metr uzunlikdagi devor bilan o'ralgan. Bog'ning
bo'yi va eni qanday bo'lganda uning yuzi 8 sotix (800 m2) dan kam
bo'lmaydi?
132. 131- masalada devoming jami uzunligi p metr, bog'ning yuzi 5 m2 dan
kam bo'lmasligi uchun bog'ning bo'yi va eni qanday bo'lishini toping.
133. Uzunligi Z metr sim panjara bilan to'g'ri to'rtburchak shaklidagi yer
maydonini o'rab olishmoqchi. Maydonning bo'yi va eni qanday bo'lganda
uning yuzi eng katta bo'ladi?
134**. ABC uchburchakka bir tomoni uch-
burchakning AC asosida, ikkita uchi esa
AB nsl BC tomonlarida bo'lgan to'g'ri
to'rtburchak ichki chizilgan. AC= I m,
BD = h m, ACL BD (34-rasm).
1) To'g'ri to'rtburchakning yuzi eng katta
bo'lishi uchun uning bo'yi va eni qanday
bo'lishi kerak?
50
1Ж
2) FK tomon BD ning qayeridan o‘tish! kerak?
3) I va h ga tayin qiymatlar berib ko'ring. Javobni tahlil qiling.
135**. Teng yonli ABC uchburchak be-
rilgan, AC = BC. Uning AB tomonida shunday
ABDK to‘g‘ri toertburchakni chizingki, uning
KD tomoni DABC ning BC va AC tomonlarini,
mos ravishda, F va E nuqtalarda kesib o‘tsin
hamda AKE, DBF, FCE uchburchaklar yuzla-
rining yighndisi eng kichik bo'lsin (35-rasm).
Kofaatmcr. AB=l, CP=h deylik. Aytilgan
uchburchaklar yuzlari yig'indisini tuzing.
ПАВС co DCEF ekanidan foydalaning.
I va h ga tayin qiymatlar berishingiz mumkin.
134—135 kabi masalalar uchburchak
shaklidagi: yer maydonidan, fanerdan,
tunukadan, matodan yuzi eng katta bo'lgan (kam chiqindi chiqadigan)
to‘g‘ri to‘rtburchakni ajratib (kesib) olishda qocl keladi va amaliyotda ko‘p
uchraydi.
136. 1) Ko‘ndalang kesimi to‘g‘ri to‘rtburchak shaklida bo‘lgan ariq qazilmoqchi.
Ariq ko'ndalang kesimining perimetri 6 metrga teng bo‘lishi kerak.
Ariqning chuqurligi qanday bo‘lganda undan eng ko‘p suv oqib o‘tadi?
2) Perimetr p metr bo‘lgan holni tahlil qiling.
137*. Kanalning ko‘ndalang kesimi to‘g‘ri to'rtburchak shaklida bo‘lib,
perimetri 12 m ga teng.
Kanalning uzunligi 250 m. Kanaldagi suvning hajmi 4500 m3 dan kam
bo‘lmasligi uchun uning chuqurligi va asosi (tubi)ning uzunligi qanday
bo‘lishi kerak?
KcErsatma: 250x(12 — 2x) >4500, bundan esa —x2 + 6x> 9 tengsizlikni
hosil qiling.
138*. ABCD to^ri to'rtburchakda AS =10 sm, BC= 25 sm. AB tomon
2 sm/s tezlikda uzayadi, BC tomon esa 1 sm/s tezlikda qisqaradi.
1) To‘g‘ri to‘rtburchakning yuzi t vaqtga nisbatan qanday o‘zgara
boradi?
2) Qanday t da yuz eng katta qiymatga erishadi?
3) Qanday t da yuz 400 sm2 dan kam bo‘lmaydi?
139. Diagonal! d bo‘lgan barcha to‘g‘ri to‘rtburchaklar ichida yuzi eng
kattasini toping.
140. Radius! R bo'lgan yarimdoiraga to‘g‘ri to'rtburchak ichki chizilgan.
Uning bir tomoni diametrda yotadi. Bunday to‘g‘ri to£rtburchaklar
ichida yuzi eng kattasini toping.
жж
51
жж
Ко ‘rsatma: SMCD = 2х л/л2 -х2 = J-(2x? -R2)2 +Л4 < R2.
жж
141. ABC uchburchakning АВ asosida F nuqta olingan. АВ ga parallel qilib
DE tocg‘ri chiziq o'tkazilgan, u AC va BC tomonni, mos ravishda,
D va E nuqtalarda kesib o‘tadi. Parallel chiziqni AB asosdan qanday
masofada o'tkazilsa, HDEF ning yuzi eng katta bo'ladi?
142**. ABC uchburchakning A va В uchlari qo‘zg‘almas bo‘lib, C uchi AB
жж
ga parallel bo‘lgan I to‘g‘ri chiziq bo‘ylab harakat qiladi. Bunda ABC
uchburchakning ortomarkazi (balandliklari kesishgan nuqta) qanday
chiziqni chizadi?
Ko'rsatma: Koordinata sistemasi kiriting. AB=2a, CD — balandlik h
bo'lsin. Ortomarkaz koordinatalari
(x; y) deyilsa, u harakat davomida
x2 a2
у = -- + — parabolam chizadi.
h h
ЖЖ
143*. To‘g‘ri to‘rtburchak shaklidagi yer maydonini o‘rash uchun har
birining uzunligi 2,5 m bo‘lgan 78 dona sim-panjara tayyorlandi.
Maydonning bo‘yi va eni qanday bo‘lganda uning yuzi eng katta bo‘ladi?
Bunda bo'yiga va eniga nechtadan sim-panjara ketadi?
О Bo‘yiga x dona, eniga у dona sim-panjara joylashadi deylik. U holda
2x + 2y = 78 yoki x + у = 39, bundan у = 39 - x. Maydonning yuzi
S= xy = x(39 — x) = —x2 + 39x = —(x — 19,5)2 + (19,5)2. Demak, bo‘yiga
x=19, eniga у = 20 (yoki x = 20, у = 19) dona sim-panjara joylansa,
maydonning yuzi eng katta bo‘ladi. U holda maydonning 0‘lchamlari:
20 • 2,5 = 50(m), 19 • 2,5 = 47,5(m), yuzi esa 2375 m2 ga teng bo'ladi. |
144*. 2 metr balandlikdan gorizontga ma’lum bir burchak ostida mushak
(xabar beruvchi raketa) otildi. Vaqt o'tishi bilan uning balandligi h = —
5t2 + 2U+ 2 formulaga ko‘ra o'zgara boradi.
1) Qancha vaqtdan so‘ng raketa 20 m balandlikka ko‘tariladi? Pastga
tushishda u bu balandlikda yana qachon bo‘ladi?
2) Raketa 1,5 sekunddan so'ng qanday balandlikda bo'ladi? Bu
balandlikda u awal ham bo‘lganmi?
3) Qancha vaqtdan so‘ng raketa uchishining eng baland nuqtasiga
ko‘tariladi?
52
II bobga doir sinov (test) mashqlari
Tengsizlikni yeching (1—2):
1. —^0. A) -1 <x<0, 2 < x < 4;
-£+6x-b 2 5 ’
C) 0<x<l;
B) -2 < x < 4;
D) -l<x<4.
жж
Ж
2. > 0.
х-х-6
А) -2 <х< 3; В) х< -2, —1 <х< 1, х> 3;
С) —1 <х<3; D) х*~2, х*3.
3. х2 + 6х + 5 < О tengsizlikning barcha butun yechimlari yig'indisini toping.
A) 10; B) 9; C) -9; D) -10.
x2-6x-7
4. 0 tengsizlikning barcha natural yechimlari yig'indisini toping.
x +4x+4
A) 29; B) 24; C) 25; D) 28.
5*. a ning qanday qiymatlarida ox2 + 4x + 9a < 0 tengsizlik x ning barcha
qiymatlarida o'rinli bo'ladi?
A) a < B) a > |; C) a < -1; D) a > 1.
Namuna'. a ning qanday qiymatlarida ox2+6x+25a < 0 tengsizlik x ning
barcha qiymatlarida o'rinli bo'ladi? Kvadrat uchhad barcha x larda manfiy
qiymatlar qabul qilyapti, demak, a < 0 bo'lishi kerak. Shu bilan birga
diskriminant ZHZ?2—4ac=36—4a • 25a < 0 bo'lishi kerak. Bundan, a >—.
3 3
Parametr a < 0 bo'lgani uchun -a > -, demak, a
6. к ning qanday eng kichik butun qiymatida x2 — 2(£+3)x + 20 + A? = 0 teng-
lama ikkita turli haqiqiy ildizlarga ega bo'ladi?
A)£=3; В) k=2; C) k=l; D)k=~2.
4jc~3
7. к ning qanday qiymatlarida = к +1 tenglama manfiy ildizga ega?
A)|<*<2; B)|<*<3; C)<t <-|, Jt > 3; D)jt>3.
8. a ning qanday qiymatida ax2 — 8x — 2 < 0 tengsizlik x ning barcha qiymat-
larida o'rinli bo'ladi?
A) — 8 < a < 8; B) a > 8; C) a < 8; D) a < —8.
9. Tengsizlikni yeching: - x.
A) x^-1, 0<x£l; | B)xS-l; | C) 0<x< 1; | D) -l£x£l.
10. Tengsizlikni yeching: < 2.
ЖЖ
ЖЖ
ЖЖ
жж
ЖЖ
ЖЖ
53
IXXIZTXI
мм
мм
мм
мм
A)x<0; В)х>0; С) i<x<2; D)x<2.
х - 8 к
11. к ning _|q = ~ tenglama ildizga ega bo‘lmaydigan barcha natural
qiymatiari yig£indisini toping.
A) 35; B) 36; C) 22; D) 32.
1 —Ax
12. к ning qanday qiymatlarida -----k+3 tenglama manfiy yechimga ega
1-x
bo‘ladi?
A) -2<Jt<l; B) —1<£<4; C) 0<£<2; D) k<2.
Зх "Ь1
13. к ning qanday qiymatlarida-----= it - 2 tenglama manfiy yechimga ega
x + 1
bo‘ladi?
A) £<3, £<5; B) 3<iK4; C) -2<it<3; D) 2<£<5.
14. к ning qanday qiymatlarida 1 < 3g+1° < 2 tengsizlik o£rinli bo'ladi?
a + 4
A) -3<a<-2; В) -2<л<3; C) -5<a<2;
D) to‘g‘ri javob berilmagan.
мм
мм
15. к ning Ax24-4x4-^+l>0 tengsizlik yechimga ega bo‘lmaydigan butun qiymatiari
мм
orasidan eng kattasini toping.
A) -3; B) 3;
C) -2;
D) -4.
143x 1001 , . ... . . .
16. -------->--------- tengsizlikni yeching.
x-2016 %-2016
A) 11] u (2016; ~); В) 11); C) (2016; ~)
D) Tengsizlikning yechimi yo‘q.
17. x2—4x+l<0 tengsizlikning tub sonlardan iborat yechimlari yig'indisini
toping.
A) 5; B) 7; C) 13; D) 4.
18. q ning qanday qiymatlarida x2—2x+#=0 tenglamaning bitta ildizi q dan
katta, bitta ildizi esa q dan kichik bo'ladi?
A) 0<$<l; B) -l<q<l\ C) -l<$<0; D) q<l.
19. p ning qanday qiymatlarida x2-px+p—1=0 tenglama bittagina musbat
ildizga ega bo‘ladi?
A) p=2, psi; В) p=l; C) p=3; D) p=4; 0<p<l.
54
Ж
20. у - ^Д),5х2 -5x4-13 funksiyaning [3; 6] kesmadagi eng katta va eng kichik
qiymatlarini toping.
A) Eng katta qiymati ^2^5 ; eng kichik qiymati ^/o^5 ga teng;
B) Eng katta qiymati 6; eng kichik qiymati 3 ga teng;
C) Eng katta qiymati 2,5; eng kichik qiymati 1 ga teng;
D) Eng katta qiymati л/б ; eng kichik qiymati Л ga teng.
ЖЖ
ЖЖ
Olimpiada masalalari
1. a ning barcha shunday qiymatlarini topingki, ulaming har bin uchun
25У2 4- 0,01 > x — axy 4- у — 25x2 tengsizlik |x| = |y| shartni qanoatlantiruv-
chi ixtiyoriy (x; y) sonlar juftligida o‘rinli bo‘lsin.
ЖЖ
ЖЖ
2. Л(0; —2) nuqtadan у = — - 2 funksiya grafigining (x; y) nuqtasigacha
x
boclgan masofalar ichida eng kichigi topilsin.
3. у = —x? 4- Юх — 15 va у = —(x — 5)2 4- 7 funksiyalar grafiklari x = a to‘g‘ri
chiziq bilan kesilgan. Kesishish nuqtalari orasidagi masofani toping.
ЖЖ
16x2
(x2 4-l)(9x2 4-1)
ifodaning eng katta qiymatini toping.
5. к ning qanday eng katta butun manfiy qiymatida x2 — 2(k + 4)x 4- £2 —
— 15 = 0 tenglama ikkita turli haqiqiy ildizga ega bo‘ladi?
6. Raketadagi kuzatuvchi uchun gorizontning „ko‘rinadigan“ uzoqligi
2000 km dan kam bo'lmasligi uchun raketa qanday balandlikka ko'tarilishi
lozim? (Yer radiusini 6370 km deb oling.)
3 1 n
7. Tengsizlikni yeching: . 2 _----- - ——-------- > u.
3x - 7x + 4 x + 3x + 2
8. Tengsizlikning barcha butun yechimlari yig'indisini toping:
(x - l)(x + I)4 (x- 3)5 • (x - 4)2 < 0.
9. Kvadrat uchhadning ildizlarini bevosita topmasdan c ning shunday qiymat-
larini topingki, bunda uchhadning x1 va x^ ildizlari ushbu tengsizlikni
qanoatlantirsin:
у = 4x2 — 12x 4- 2c 4-1; Xj3 + XjX2 + xf >3.
жж
ЖЖ
10. у = ax2 + bx + c kvadrat uchhadning ildizlari xL va x^ ga teng. Agar kvadrat
uchhad x= 0,5 da o‘zining eng katta qiymati 25 ga erishsa va xf + xf = 19
bo‘lsa, a, b, c koeffitsiyentlami toping.
ЖЖ
55
IXXIZTXI
жж
яки
жж
мм
жж
яти
жж
«тая
жж
жж
«гая
11. я ning barcha shunday natural qiymatlarini topingki, ularda 7 kasr
natural son bo'lsin.
12. Ixtiyoriy haqiqiy sonlar ay a2, ..., an uchun
(^+^2+ ... +ай)2 < n (flj2+a22+ — +«й2) tengsizlik o'rinli ekanini isbotlang.
О Quyidagi ayniyatdan foydalanamiz:
(^+02+03+ — "*"ля)2 = Л12+а22+«з2+. ..+ай2+2а1 a2+2a^a3+. ..+2ай_1 ап (1)
Ravshanki, (ап—ат)2> 0 (2)
tengsizlikdan 2алаи<аи2+аст2 (3)
tengsizlik kelib chiqadi.
(1) tenglikda 2ara2, 2ara3, 2an_y an qo'shiluvchilami, mos ravishda,
Л12+а22, ai2+a32’ an-i2+an yig£hidilar bilan, (3) tengsizlikni hisobga olib
almashtiramiz va berilgan tengsizlikning to'g'riligiga ishonch hosil qilamiz.
Tenglik belgisiga a1=a2=...=on bo'lganda va faqat shu holda erishiladi. |
13. Ushbu +1 + 42a - 30 + V50 - 3a < 12 tengsizlikning chap qism a ning
qanday qiymatlarida aniqlangan bo'lsa, shu qiymatlaming barchasida
bajarilishini isbotlang.
О Awalo, manfiy bo'lmagan x, y, z, sonlar uchun
x + у + Z <73C*2 +У2 +z2) (*)
tengsizlik o'rinli ekanini ta’kidlaymiz. (12-masalaga qarang). (*) tengsizlikda
x = Ja+l, y=42a-3, z=4^-3a deylik. U holda
4a+\ + V2a-3 + л/50-3a <^3[(a+1) + (2a-3) + (50-3a)] = 7^48 =12.
14. a, b, c —uchburchak tomonlarming uzunliklari, l=a+b+c, d=ab+bc+ac
bo'lsa, 3d < I2 < 4d ekanini isbotlang.
О 12-3d=(a+b+c)2-3(ab+bc+ac)=a2'+b2+c2-ab-ac-bc=
= | -l(a-b)2 + (a-c)2+(Z>-c)2]>0; a, b, c sonlar uchburchakning tomonlari
bo'lgani uchun a—b<c<a+b tengsizliklar bajariladi. U holda
l2—4d=(a+b+c)2—4(ab+ac+bc)=a2+b2+c2—2ab—2ac—2bc=
= (a-b)2+c2-2ac-2bc<2c2-2ac-2bc=2c- [с-(а+ВД<0.И
15. a ning barcha shunday qiymatlarini topingki, bu qiymatlarda
y=x2+2(a+l)x+l va y=ax2~x+a parabolalaming uchlari y=0,75 to'g'ri
56
Ж
chiziqdan turli tomonlarda bo‘lsin.
Ko ‘rsatma: 1-parabola uchining ordinatasi (—a2—2a) ga, 2-parabola
4a2 -1
uchining ordinatasi esa —-—ga teng. Demak, masalani hal qilish
4a
жж
4a2 -1 1
--------0,75 <0 tengsizlikni yechishga keltiriladiki,
4a
uni intervallar metodi bilan yechish mumkin.
r 3 11 n
Javob: — -< a , - - < a < 0, a > 1.
2 2 4
(—a2—2a —0,75)
16. a ning barcha shunday qiymatlarini topingki, bu qiymatlarda
y=4x2+8ax-a va y=4ax2—8x+a—2 parabolalaming uchlari y=—5 to‘g‘ri
chiziqdan bir tomonda bo‘lsin.
Ko "rsatma: Masala (—4a2—a+5) •
> 0 tengsizlikni yechishga
ЖЖ
кЯЯкЯ^
ЖЖ
ЖЖ
keltiriladi. Javob: a < -4, - у < a < 0.
4
17. A shahardan В shaharga qarab ertalab soat 8 da tezyurar poyezd yo‘lga
chiqdi. Xuddi shu vaqtda В dan A ga qarab yolovchi va yuk poyezdlari ham
yo'lga chiqdi. Yoelovchi poyezdining tezligi yuk poyezdining tezligidan 2
marta katta. Tezyurar poyezd В ga o‘sha kuniyoq soat 13 dan 50 minut
o‘tganda yetib keldi va yolovchi poyezdini uchratganda soat 1030 dan oldin
ЖЖ
№•3
жж
emas edi. Tezyurar poyezdning yolovchi poyezdi bilan va tezyurar
poyezdning yuk poyezdi bilan uchrashish vaqtlari orasidagi farq 1 soatdan
kam emasligi malum. Yuk poyezdining A shaharga kelish vaqtini toping.
О A va В shaharlar orasidagi masofani s, tezyurar poyezdning tezligini
yuk poyezdining tezligini v2 deylik. U holda yolovchi poyezdining tezligi
shartga ko‘ra 2v2 boladi.
Poyezdlar harakatini chizmada (ramziy ravishda) tasvirlaylik.
ЖЖ
8oo4
vi
^V2
V2
4—0
-----i\B
l350
ЖЖ
57
IXXIZTXI
^k^^lll!^
жж
жж
жж
жж
sm®
жж
жж
Ushbu jadvalni tuzamiz:
Masala sharti Unga mos tenglama, tengsizlik
Tezyurar poyezd В ga soat 1350 da ya’ni yo'lga chiqqanidan 5 soat-u 50 minut o‘tganda yetib keladi. c ™ < 5 + 35 + 5 soat-u 50 minut = 5—soat = — soat 0 0 s 35 vT = -6 W
Tezyurar poyezd yo‘lovchi poyezdi bilan IO30 dan awal uchrashmaydi, ya’ni harakat boshlanganidan 2 soat-u 30 minutdan oldin uchratmaydi. 5 2 soat-u 30 minut = —soat s . 5 V!+2V2_2
Tezyurar poyezdning yoTovchi poyezdi bilan, tezyurar poyezdning yuk poyezdi bilan uchrashish vaqtlari orasidagi farq 1 soatdan kam emas. — (3) vi+v2 П+2у2
жж
(2) va (3) tengsizliklami quyidagicha o‘zgaitirish mumkin:
5 ± £.
———7---------------------~~-1- Bu tengsizliklarga (1) dan —ning
1 + 2^ 2 1 + ^2. 1 + 2^2. Vi
vj vj vj
qiymatini qo‘yib va o‘zgartirishlar bajarib, quyidagi tengsizliklarga kelamiz:
v? . 2 2 v2 3 A v2 2 . . . , . ttvu
— < - va — < — < — . Bundan — = - ekanini topamiz. U holda,
vj 3 3 vj 4 V1 3
c 5 vn 35 3 35 3
— =-------~ = ~r^ = ~r = ^~7 (soat). Shunday qilib, yuk poyezdi yo‘lga 8
V2 V1 V1 6 2 4 4
soat-u 45 minut sarflaydi va A shahriga soat 16 dan 45 minut o‘tganda yetib
keladi. |
H http://www.mathtype.narod.ru/manbadan mazkur bobga oid
ma’lumotlami toping va o‘iganing.
58
жж
IZTXJZTXI
жж
HI BOB RATSIONAL KO'RSATKICHLI DARAJA
12-§. Butun ko'rsatkichli daraja va uning xossalari
Awal natural ko‘rsatkichli daraja tushunchasini eslab o'tamiz. Ma’lumki,
bir xil qo'shiluvchilar yig'indisini ko'paytma shaklida qisqacha yozish mumkin:
9+9+9+9+9 = 5 9, m+m+m+m = 4-m.
Bir xil sonlaming ko'paytmasi ham qisqacha quyidagicha yoziladi:
9.9.9.9.9 = 95 m’m'm - m = m4
va uni daraja deb ataladi. Bunday 0‘qiladi: „To'qqiz darajasi besh“ yoki
„to'qqiz beshinchi darajada''; „m darajasi tocrt“ yoki „m to'rtinchi darajada".
I a sonning natural ko(rsatkichli n- darajasi deb har biri a ga teng
bo‘lgan n ta sonning ko(paytmasiga aytiladi:
а” =4’4*2>43a’ bunda n > 1.
n ta
Agar n = 1 bo'lsa, a1 = a, 21 = 2, 101 = 10, ya’ni ixtiyoriy sonning
birinchi darajasi shu sonning o'ziga teng. Shunga o'xshash, 32 — uchning
kvadrati, a2 — a ning kvadrati; 53 — bestirring kubi, a3 — a ning kubi deb
o'qiladi.
Natural ko'rsatkichli darajalar uchun ko'paytirishga oid
aP • aq = aP+q,
bo'lishga oid
cP : cfl= aP~q, p> q, (1)
xossalar o'rinli ekani ma’lum.
Agar (1) tenglikda p<q bo'lsa, u holda p — q<0 bo'ladi. Bunda biz
manfiy yoki nol ko'rsatkichga egamiz. Shu holda ham (1) tenglik o'rinli
bo'laveradi. Masalan, p= 3, q= 5 bo'lganda (1) formula bo'yicha quyidagini
hosil qilamiz:
жж
жж
жж
жж
Ikkinchi tomondan
1
Bundan a - deb yozish mumkinligi kelib chiqadi.
59
IXTXIXTXI
Ж
жж
жж
жж
1-ta’rif. Agar а*0 va п — natural son bo‘lsa,
a~" = —
an
bo‘ladi.
Misollar. 1) 3-2=-l = l; 2) (-2)-’= 1 =-|.
J ' \ *>)
Agar (1) tenglikda p — q bo‘lsa,
ap :ap =ap~p = a°
tenglik o‘rinli. Ikkinchi tomondan, ap :ap = ^- = 1. Shuning uchun o° = 1
deb hisoblanadi.
ж
ж
жж
ЖЖ
| 2-ta’rif. Agar a*0 bo‘lsa, a° = l bo‘ladi.
Masalan, 5° = 1, =1.
O‘nli kasrlami standart shaklda yozish uchun manfiy ko‘rsatkichli
darajadan foydalanish mumkin. Masalan,
0,38 = 3,8 10-1; 0,047 = 4,7 10"2; 2011=2,011-103.
Natural ko(rsatkichli darajalarning barcha xossalari istalgan butun
ko‘rsatkichli darajalar uchun ham o‘rinli.
Istalgan a*0, b*0 va istalgan butun p va q lar uchun quyidagi
tengliklar to‘g‘ridir:
1. ap aq = ap+q .
2. (ap)q = apq.
3.
4. ap : aq = ap~q. 5. (ab)p =ap bp.
1Ж
1ВИ
Bu tengliklaming har birini isbot qilish mumkin. Masalan, p — q < 0
bo‘lganda cf: cfl = 9 tenglikning toeg‘ri]igini isbot qilamiz. p — q — butun
son bo‘lsin, uni p — q = —r (r — natural son) deb belgilaymiz. Manfiy
ko‘rsatkichli daraja ta’rifidan va natural ko‘rsatkichli darajaning xossalaridan
foydalanib quyidagini hosil qilamiz:
„ a ap a1 at a?-9 ap-9 ap~9 B-a
n? n" — —_ = = ____= _____= ______= qP 9
<fl cfl.a9 cfl-i a° 1
ж
60
Misollar.
1) 3"4 • 313 3"7 = З-4*13-7 = 32 = 9;
2)
p2
2«3
_ У-2Х-3) _ 23y
2-3.?3-(-3) ?-9 P « '
жж
Masala. a6(a~2 -e"4)(e2 +e3)-1 ifodani soddalashtiring:
О e6 (e-2 - °-4) (°2 + e3 )-1 = e6 j-4-----j
6 a2-l 1 (o+l)(o-l) .
= a —4~' 2/, =a~L Javob: a-1.
a4 a1 (l+o) l+a
145. Savollarga javob bering. Topshiriqlami bajaring:
©1) Butun ko'rsatkichli daraja nima? Misollarda tushuntiring.
2) Butun ko'rsatkichli darajaning xossalarini ayting.
3) Butun ko'rsatkichli darajaning xossalarini qo'Uanishga doir misollar
tuzing.
4) Manfiy ko'rsatkichli darajadan sonni
qanday foydalaniladi?
Bir bilan taqqoslang (146—147):
1) (0,3)-2;
standart shaklda yozishda
146.
2) 2015°;
3) (1,2)—3;
.-3
,-2
147.
1) ir3;
2) 32°;
3) (o,4)“3;
4)
7
13
.-1
148.
Hisoblang:
1) (-3)-2 + 2-3;
3)
149.
150.
151.
2) (0,3)-2 + (0,5)-3;
Hisoblang (149-151):
1)
2)
32 + (-2)3 - (-3)2 + (-1)3;
(-5)2 + (-2)3 + 32;
4)
3)
4)
1)
3)
0,5s • 0,5-7;
/ i \ / 1 \-2
2)
4)
13-3 . 132.13;
1)
98:9’;
3)
3 f
И
3
11
2)
(0,3)2: (0,3)-2;
4)
(-0,2)-l — (—0,2)-3;
(Я’-з-2.
11 33 - 9 - 33 + 32;
7 -32 +4 (-3)2 -(-3)2.
5) 0,63 0,6~4;
6) 18-2 92 - 4.
,3
.5
15 Y2
17 J
.-7
8
9
152. Ifodani natural ko'rsatkichli daraja shaklida yozing:
61
жж
жж
жж
жж
IXTXIXTXI
жж
жж
жж
жж
жж
sm®
жж
жж
жж
153.
154.
155.
156.
157.
158.
159.
160.
161.
162.
163.
62
43-49 62-68-63 e3a7Z>4 c4rf4e8
1) 410 ’ гЗ г7 ’ 3) 8~Тз ’ 4) и ,3 •
41 6-6' а b ста
Manfiy ko'rsatkichli daraja shaklida yozing:
1 11111
1) TP 2) 772’ 3) -p 4) 7; 5) 6) -y-
J JL wJ At L4 W J
Ifodani musbat ko‘rsatkichli daraja shaklida yozing (154—155):
(x + y) 3; 4) 16a4 b-3; 7) 25b2 c“3;
(x - y)~2; 5) a-2*-1^; 8) 0,09a-4 b~2;
4-2 c6; 6) a"3*"1?; 9) 0,001a8 i-4 ?.
(x + y)-1; 2) (x-у)’2; 3) 9a3*-4; 4) a~2bc~3.
Darajani darajaga ko‘taring:
1) (a-2)4; 2) (*-3)-2; 3) (a4)-3; 4) (b5)~3.
Ko'paytmani darajaga ko'taring:
1) (л2*-1)3; 2) (a3*-2)3; 3) (3a3) 2; 4) (2a-3)4.
Amallami bajaring (158—159):
1)
2)
P
1)
1) x = 5, у = 6,7 bo‘lganda
toping;
ning qiymatini
Л 3 . 44
2) a = 2, b = 1 bo‘lganda \crb 1 j
ing.
жж
j i )
-Эх-4?2 |
? J '
f-2x-3y?
U3 г
ning qiymatini top-
Sonni standart shaklda yozing:
1) 20003; 2) 0,0043; 3) 3000(T3; 4) 0,004~2.
Oynani silliqlash jarayoni uning sirtidagi o‘yiqlar chuqurligi 3 • 10-3 mm
dan ortmaydigan bo'lganda to'xtatiladi. Shu sonni o'nli kasr shaklida
yozing.
Gripp virusining olchamlari taqriban 10~4 mm ni tashkil etadi. Shu
sonni o'nli kasr shaklida yozing.
ZTXIZTXI
жж
164. Kasmi daraja shaklida tasvirlang va uning qiymatini a ning berilgan qiy-
matida hisoblang:
165*. Soddalashtiring:
1) (a"3 - b~3) (a~2 -b~2)- (a~2 + a"1/?"1 + b~2 )-1;
2) (a~2b + ab~2): (a~2 - a~lb~l + b~2).
жж
166. Darajalami taqqoslang:
D3-2va2-3; 2) gf va g; 3) (| j’ va
4) 4 3 va 3^4.
ЖЖ
13- §. Natural koTsatkichli darajaning arifmetik ildizi
Quyidagi masalani kocramiz:
1- masala. Tenglamani yeching: x2 = 9.
□ Tenglamani x2 — 9 = 0 yoki (x + 3)(x — 3) = 0 kabi yozib olamiz.
Bundan xr = —3, X} = 3. Demak, tenglama 2 ta haqiqiy ildizga ega. |
Ular 9 ning kvadrat ildizlari, musbat = 3 ildiz esa 9 ning arifmetik ildizi
deyiladi. 9 ning kvadrat ildizlari V9 = ±3 kabi, 9 ning arifmetik ildizi esa
V9 = 3 kabi belgilanadi.
Matematikada arifmetik ildiz bilan ish ko‘riladi. Ravshanki, 32 = 9.
Ta’rif. a nomanfiy sonning n=2 natural ko(rsatkichli arifmetik ildizi
deb, 2- darajasi a ga teng bo‘lgan nomanfiy songa aytiladi va 4a kabi
belgilanadi.
Arifmetik ildizning ta’rifini bundan umumiyroq ko‘rinishda ham bayon
etish mumkin.
Ta’rif. a nomanfiy sonning n22 natural ko(rsatkichli arifmetik ildizi
deb, n- darajasi a ga teng bo‘lgan nomanfiy songa aytiladi va 4a kabi
belgilanadi.
4a ifoda a dan olingan и-darajali ildiz deb o'qiladi.
Ta’riiga ko‘ra a > 0 bo‘lsa,
жж
жж
жж
жж
(44} = a, = a
tengliklar 0‘rinli. n = 2 bo‘lsa, u holda 4a o'miga 4a yoziladi.
Masalan, (Иб)3 = 6; ^17* =17; ^16 = Лб = 4.
жж
63
IXTXIXTXI
Ж
Ж
Biror nomanfiy sonning n-darajali ildizini izlash amali n-darajali ildiz
chiqarish deyiladi va u n-darajaga ko'tarish amaliga teskari amal bo‘ladi.
ж
ж
Umuman, 4a2 =\a\,2\la2n = |a|. tfa ning b ga tengligini ko‘rsatish
uchun 1) £>0; 2) & = a ekanini ko‘rsatish kerak.
ж
1Ж
жж
зтая
ж
от
жж
ЖЖ
жж
ж
2- masala, x3 = -27 tenglamani yeching.
П Tenglamani —x3 = 27 yoki (—x)3 = 27 kabi yozamiz, so‘ngra -x = у
deb almashtirish bajaramiz: y3 = 27. Bu tenglamaning faqat bitta ildizi bor:
у = 3. Bundan —x = 3 yoki x = —3 kelib chiqadi. Berilgan x3 = -27 tenglaman-
ing yechimini qisqacha x = -^27 = -3 deb yozish mumkin.
Javob: x=~ 3. |
Bu masaladan shunday xulosaga kelish mumkin:
I Istalgan toq 2k+ 1 natural son uchun a<0 boHganda x2k+1 =a teng-
lama faqat bitta, manfiy ildizga ega va и x = 2k+¥a kabi belgilanadi.
Masalan, = -2; 3/-1 = -1, лД32 = -2.
Agar a < 0 bo'lsa, quyidagi tenglik ocrinli:
2k+\la = -2k+iPa = -2Л+^/|л[.
Masalan, ^/—64 = -л/64 = — ^/|—64| = -4.
Sonning arifmetik kvadrat, arifmetik kub, n-darajali ariftnetik ildizi deyish
o‘rniga, qisqacha, sonning kvadrat, kub, n-darajali ildizi deb aytamiz.
167. Savollarga javob bering:
1) Natural ko‘rsatkichli darajaning arifmetik ildizi deb nimaga
(?) aytiladi?
2) Kvadrat ildiz nima?
3) n-darajali arifinetik ildiz chiqarish amali nima?
4) a < 0 bo‘lganda x2i+1 = a tenglama nechta manfiy ildizga ega (2£+l —
toq son)?
5) y[a = b tenglikni isbotlash uchun nimalami tekshirib ko‘rish kerak?
168. (Og'zakL) Sonning kvadrat ildizini ayting:
1; 0; 9; 0,64; 144; ±; jL; ±.
169. (Og'zakL) Sonning kvadrat ildizini ayting:
4; 9; 0,49; 1,69; 225; ±
oZj ol luU
170. Sonning kub ildizini toping:
1) 1; 0; 8; 0,027; 64; —, —,
64
жж
2) 8; 27; 125; |; 0,064; 0,125;
о 2/ 210
171. Sonning 4- darajali ildizini toping:
1; 0; 81; 0,0016; 0,0081.
ol ozj
Hisoblang (172-175):
172. 1) 2) ^4 ; 3) j ; 4) 4/2252
173. 1) 2) 3) </о, 58; 4) .
174. 1) ^27; 2) О; 3) j]—; 4) ^5_
175. 1) 2) ^44 - 42 ; 3) ; 4) ^2258.
Tenglamani yeching (176—177):
176. 1)^ = 64; 2) х5 = -243; 3)2^ = -64; 4)2х7 = 256.
177. 1) 3x4 = 243; 2>х3=-2^64; 3)3х« = -96; 4)4x4 = 256.
Hisoblang (178-179):
178.1)^64+|^64; 3) ^16-|WI; 5) ^/=27 + ^64;
2) 3/32-1^-216; 4) </-1000 +1^256 ; 6) Ш-^27 О 4 v v
жж
ЖЖ
жж
жж
жж
179. 1) 77 + ЛЗ л/7-ЛЗ; 3) ^3 + V5-л/З - V5;
! 12--/х 12----/т\2 ('Л+'Л у/З-у/2 А 1
2) (>/2 + >/3-72->/з) ; 4) ^1+л/2 /Тб'
180*. 1) %j(x + 2)3 ifodani soddalashtiring.
жж
2) a) x < 3; b) x > 3 bo‘lganda - x)2 ni soddalashtiring.
181. Hisoblang:
>/3+1 >/3-1.
3) >/3-1 Л+1’
ЖЖ
5—Algebra, 9
65
IXTXIXTXI
жж
жж
жж
жж
2) p4 + V7-V4-V7)2; 4)
\ / Vfl-1 Vfl+1
182*. 17 < 4п < 18 tengsizlikni qanoatlantiradigan nechta natural son n bor?
x ning qanday qiymatlarida ifoda ma’noga ega (183—184):
183. 1)727=3; 2) 7Г7; 3) ^-2x-l; 4)
184.1)4/537=5; 2) 77=5; 3) ^7+x + l; 4)
14- §. Arifmetik ildizning xossalari
1. Kvadrat ildizning xossalari. Kvadrat ildiz quyidagi xossalarga ega:
agar a^O, b>0 bo‘lsa, и holda ushbu tengliklar o‘rinli:
жж
жж
жж
жж
жж
Kvadrat ildizning xossalarini isbot etish mumkin. Biz 1-xossani, ya’ni
a>0, Z>>0 bo'lganda
ab = чачЬ
yoki 4a-4b = 4ab
tenglik to'g'ri ekanini isbot qilamiz. Buning uchun arifinetik kvadrat ildizning
ta’rifidan foydalanamiz:
1) 4a-y/b>Q, chunki a>0, £>0;
2) ab = (4a 4b^ , chunki ab = (4a • >lb^ = (4a^ (4b^ .
Bundan 1- xossaning isboti kelib chiqadi.
жж
жж
Misoliar:
1) V9 a/4 = 79^4 = V36 =6;
-,4
2) \81 Jsi 9’
3) Va/256 = 4/256 = = 4;
4) (Л)2=^ = 3.
Hisoblang (185-187):
185. 1) 716 0,25 ; 2) 764 0,49 ; 3) 7225 100;
4) 71,44 256.
жж
66
186. 1) д/22 -З2; 2) л/72 -42;
187. 1) 7з4 • 52 ; 2) V25 -24;
188. Ildiz chiqaring:
1) \{36хлу2 ; I 2) у]а4Ь6;
3) 7(0,3)2 -42;
3)
3) ^77;
4) ТЖ
4) >77.
189. Ifodani soddalashtirmg («X), b>0):
1) 2) 71777; 3)
V8 V b V16£z
Hisoblang (190-191):
190. 1) 74 0,09 ; 2) ,/0,36-9; 3) >/1,21-100; 4) 716 1,69.
191. 1) V42 32 ; 2) 7б2 52 ; 3) >/(l,l)2 (1,2)2 ; |4) 7o,252-42.
192. Ildiz chiqaring (x>0,y<0, <z>0):
1) 716x2y4; | 2) 777; 3) 74xs -y4; 4) 797-7.
193. Ifodani soddalashtirmg (aX), #X)):
жж
ЖЖ
2. л-darajali arifmetik ildizning xossalari.
n-darajali arifmetik ildiz quyidagi xossalaiga ega:
Agar a £0, b >0vap, qnaturalsonlar uchunp22, q22bo‘lsa, quyidagi
tengliklar o‘rinli bo‘ladi:
Bu xossalaming har birini arifmetik ildizning ta’rifiga asoslanib isbot qilish
mumkin. Biz 1-xossaning isbotini keltiramiz. Ta’rifga ko‘ra,
□ 1) Ца-у[Ь>§, chunki a > 0, b > 0.
2) ^[a = ab, chunki ^[a ^[b^ = ~ a^'
67
жж
жж
Bundan 1-xossaning to‘g‘riligi kelib chiqadi.
Misollar: 1)
W Лз = 3/9~3 = 3/27 = $? = 3;
жж
Ж • JI = 4^0 = = = JF = 2
V243 V3 4243'3 4243 4 \81 ^З4 3'
жж
жж
жж
sm®
W T
Masala. Ifodani soddalashtiring (a > 0, b > 0): X , ' .
З/Ж^
□ Arifmetik ildizning xossalariga ko£ra
= aW = a2^ =^L=b_ Javob. b_
^/Л12 #(o4)6 (i2)6 ^(o4)6-^(i2)6 в4*2 a2 aV° '
жж
жж
жж
194. Topshiriqlamibajaring. Savolga javob bering.
®1) Arifinetik ildizning xossalarini ayting. Misollar keltiring.
2) Arifinetik ildizning xossalaridan misollar yechishda qanday foydala-
nasiz?
Hisoblang (195-198):
195. 1) 3/125 0,125; 2) з/Що27; 3) ^16-0,0016; 4) ^32 100000.
196. 1) V43 53 ; 2) 3/94 - 74 ; 3) V(0,3)5 -65; 4) 126-
197.1)3/2-3/4; 2)3/O3-3/M9; 3)^16-^; 4)^.
198. 1) Ум : Ш; 2) 3) {fl»)2 ; 4) : 3/^05-
199. Ildiz chiqaring (o>0, b>0):
жж
68
ZTXIZTXI
Hisoblang (200-204):
20 0.1)^; 2)g; 3)Д; 4) 5) g
201. 1)3/128 :№; 2) №1: №000; 3) 4) (V125 - V45): №.
202. 1) ^216-0,064; 2) №375-343;
3) №56 0,0064; 4) №43 100000.
203. 1) №10-215; 2) №3 -46; 3) ^28 J; 4) (1J° .
204. 1) 3) (№0-V45):№;
2) 3/128:3/2000; 4) (№25 - 3/5): 3/5.
жж
жж
жж
Ifodani soddalashtiring, bunda a>0, Л>0, х>0, y>0 (205—206):
205. 1) : з^; 5) ^‘^6445’
2) $24х4/ : 3 4) JZ 4^- Ш3 V’ 6>
206. 1) 3/За263 Ъа ; 3) Ja2b3 Ja4c N c 'b ’
2) $2a3b3 ffiab; 4) 4/g^ ^b L2 L2' ‘>
Hisoblang (207- -210):
207. 1) ; 2) (№б)’3; 3) (1№43)2; 4)
208. 1) ЗА/б4; 2) >АЖ; 3) ^№ -№1; 4) V№5 -№5.
209. 1) (Vx)4; 2) (^7)2; 3) (№-№)6; 4) (^27a3 1
жж
жж
жж
жж
69
ж^бш
жж
210.1) $ ^|Ц;
»f <•
3*) 717-ТЗЗ-717 + ТЗЗ;
211. Ifodani soddalashtirmg («>0, b>0, с>0, х>0, у>0):
жж
1) У abc • tfa3b2c tfb5c2 ;
ЛИЯ
жж
лгай
212*. Isbot qiling:
1) (72 + 73 - 72 - 73? =2;
2) (74 + 77+74-77) =14;
3) ^7*6/2 -(^у2) ;
$8x2y5 $4x3y
3) (710 + 751 - V10 - V51)2 = 6;
4) (719 + 737-719-737) = 2.
жж
жж
15- §. Ratsional ko‘rsatkichli daraja
Yuqorida natural ko‘rsatkichli daraja va uning arifmetik ildizi tushunchalari
bilan tanishdik. Endi ratsional ko‘rsatkichli daraja va uning xossalarini bayon
etamiz. Awal bitta masala ko‘raylik:
Masala. ^312" ni hisoblang.
□ 312 = (33)4 bo‘lgani uchun л/з^ = >/(33 )4 = З3 = 27. Demak,
жж
12
= 31 =33. Javob: 21. ш
Shunga o‘xshash, 74~10 = 4 5 = 4“2 = -j = tenglikni ham isbot
qilish mumkin. |
Endi umumiy holni ko‘ramiz.
Agar q^2, p — butun son va — butun son bo‘lsa, a>0 bo‘lganda
q
quyidagi tenglik to^ri bo‘ladi:
(1>
___ p p
О — — butun son, uni к deb belgilaymiz: — = k, bundan p — kq kelib
q q
chiqadi. Daraja va arifmetik ildiz xossalaridan foydalanib topamiz:
70
жж
лгая
I— I— I----- 2.
№ = № = tf(ak )q = ak = aq .
p
Agar — butun son bo'hnasa, a9 (a > 0) daraja uchun (1) formula o‘rinli
deb hisoblanadi. Shunday qilib, (1) formula istalgan butun p, istalgan natural
q>2 va a > 0 uchun to‘g‘ri boladi. Masalan,
6
22 = =23 =8,
1 2
22 = 72, 27 з
71 1 1
Endi r — ratsional son boHsin. Uni r = —, bunda p — butun son, q —
p
natural son, deb yozish mumkin. (1) formula bo^yicha ar = a9 = \[a^ deb
yozamiz. Shunday qilib, daraja istalgan ratsional ko(rsatldch va istalgan
musbatasosuchun aniqlanadi. Shu bilan birga, (1) formula a =0bo‘lganda
ham o‘rinli: = 0. Shuning uchun r>0 bolganda 0r = 0 tenglik to‘g‘ri
жж
deb hisoblanadi.
(1) formula va ildizning xossalaridan
p pk
a9 = aqk
tenglik kelib chiqadi, bunda a > 0, p — butun son, к va q lar natural sonlar.
ЖЖ
Ratsional ko(rsatkichli va musbat asosli darajalar uchun quyidagi teng-
liklar o‘rinli (p, q — ratsional sonlar; a > 0, b> 0):
1) ap-aq=ap+q; 4) (ab)p = ap bp;
2) ao-.aq=ao-q- 5) g J = <
3) (ap)q=apq;
Ildizlaming xossalaridan foydalanib bu tengliklami isbot qilish mumkin.
Masalan, 1-xossani isbot qilamiz.
□ P = —,q = y (n, I — natural sonlar, m va к — butun sonlar) deb
n I
belgilaylik. Unda:
? 4 f+7 (2)
an a1 = an 1 k'
tenglikni isbotlash lozim.
жж
71
т к . . . . , . ml кп
— va у kasrlarm umumiy maxrajga keltiramiz: — va —.
n l nl nl
Ratsional ko‘rsatkichli daiajaning ta’rifidan, ildizning va butun ko‘rsatkichli
daiajaning xossalaridan foydalanib, quyidagmi hosil qilamiz:
m к ml kn _________________ _______ .__________
. a7 = a7i . аы = ^«1 . = чЦа”'. akn = 4^^+*» =
ml+kn m к
— —+ —
= a = an 1.
Daiajaning xossalarini qo'llanishga oid misollar:
1212 21 21 4-1 1
1) S’ 5’ = 5’+з = 5; 2) 43;4«=4з‘=46 =4з=л/4=2;
3) 243 =(23 -3)з =23 з зз =4$»; 4) = =
V ' I 27 J 1 3.1
273 3 3
- - -+^ - 2 1 2_1 1 3 1
5) 76-76 =76 6 =76 =7; 6) 83 : 83 = 83 3 = 83 = 2 3 = 2.
Irratsional ko‘rsatkichli daraja haqida tushuncha
Siz natural, butun va ratsional ko'isatkichli daraja bilan tanishdingiz.
Musbat sonning daraja ko'rsatkichi irratsional son bo'lsa, u irratsional
ko'isatkichli daraja deb atalaveradi. Aniqlik uchun 2^ bo'lgan holni ko'raylik.
Awal ni 0,1; 0,01; 0,001; ... aniqlikda hisoblab olamiz:
1,7; 1,72; 1,732; 1,7320; 1,73205, ...
Shu ketma-ketlikdan foydalanib, 2 sonining daraja ko'rsatkichlari ket-
ma-ketligini yozamiz:
71,7. 71,72. 71,732. 71,7320 . 71,73205.
Ketma-ketlikning har bir hadi ratsional ko‘rsatkichli daraja bo‘lib,
biror haqiqiy sonning taqribiy qiymatidan iborat. 10-9 aniqlikda quyidagilami
yoza olamiz:
21-7 = 3,249009585,
21-72 « 3,317278183,
21732 =3,321880096,
21,7320 „ 3,321880096,
21,73205 = 3,321995226,
2^ =3,321997086.
Aniqlikni qancha oshirsak, ketma-ketlikning tegishli hadi 2^ ning
qiymatiga shuncha yaqin bo'ladi. Demak, talab etilgan aniqlikka qarab, 2^
72
ni mos ratsional ko‘rsatkichli darajaga almashtirish mumkin. Shu sababli 2^
ni irratsional ko‘rsatkichli daraja deb atasa bo‘ladi. Buni biz bitta misolda
tushuntirdik. Agar asos a musbat bo‘lsa, ixtiyoriy irratsional ko‘rsatkichli ab
daraja shunga o'xshash aniqlanadi.
Irratsional ko‘rsatkichli darajaning xossalariga to‘xtalmaymiz, chunki bu
xossalar ratsional ko‘rsatkichli darajaning xossalari kabi ta’riQanadi.
213.
©
Savollarga javob bering. Topshiriqni bajaring:
1) Ratsional ko‘rsatkichli daraja qanday ta’riflanadi?
2) Ratsional ko'rsatkichli darajaning xossalarini ayting. 2—3 ta misolda
bu xossalaming to‘g‘riligini tekshiring.
3) Irratsional ko‘rsatkichli daraja tushunchasi qanday kiritiladi?
ЖЖ
214. (Og'zaki.) Ratsional ko‘rsatkichli daraja shaklida yozing (xX), a>0, 6X)):
жж
1) I 2) ^2; |
3) I 4) | 5) | 6)
215. (Og‘zaki.) Ratsional ko'rsatkichli daraja shaklida yozing (л^О, b>Q):
1) 2) 77; | 3) | 4) | 5) 6) ^4.
Hisoblang (216—220):
1 1 2 3
216. 1) 162; 2) 643; 3) 273 ; 4)164; 5) 16-0’75; 6) Г1-5.
4 11 1 2 2 1 2
217. 1) 35 -35 ; 2) 43 .43; З)93:96; 4) (8~3) з .
1 1 2 3
218. 1) 92; | 2) L I5; 1 3) 8’3; | 4) (jij4 ; | 5) 16-».5; | 6) 81-3.5.
3 2 8 2 5 4 1
219. 1) 24 -21; 2) 35 -35 ; 3) 73 : 4 3; 4) 53 :5’.
220. 1) Г1Г0’75 ( (1б) +1 |оо 4 2) 15 2 (0,04)-1'3 -(0,125) з .
жж
Я0И05
жж
таи
ЖЖ
ЖЖ
221. Hisoblang:
1) a = 0,04 bo‘lganda 4a-4a ning qiymatini;
2) b = 8 bo‘lganda 4b : 4b ning qiymatini.
жж
73
Ratsional ko'rsatkichli daraja shaklida yozing (fl>0, £>0, y>0) (222—223):
жж
222.
2
1) a3 4a\
1 1
| 2) Z>2 -*3;
| 3) :b*; | 4) у 3,8 : у2,3 TP"-
2 11 1
223. 1) у/a; I 2) b^b^1^; I 3) $b :b» ; I 4) y3’8 :/* • V/•
жж
224. Hisoblang:
1) a = 0,09 bo'lganda 4a 4a ning qiymatini;
2) a = 64 bo'lganda 4a : 4a ning qiymatini.
225*. Ifodani soddalashtiring (a>0, £>0):
яии
жж
4 ( 3 \4
1) (a3) 3 /> 2
< j
1 1
a3 4b+b3 4a
4а+4ь
жж
жж
226*. Ifodani soddalashtiring (д>0, £>0):
227. Hisoblang:
2) (a3*"4)2
1)
fl 3 1 3
2) 5* :24 -24 :54 J/1000.
228*. Ifodani soddalashtiring (x>0, y>0,
x^y, a>0, £>0, a^b):
1)
Зху-у2 _ у4у _ y4x .
X-y 4x-y/y 4x+yjy ’
жж
a+b
2) tfo-llb I I ‘
a3 -4ab+b3
f 5 1 5 _1 >
23 . з з _ 33 .2 з
16- §. Sonli tengsizUklarni darajaga ko‘tarish
8- sinf „Algebra" kursida sonli tengsizliklar va ulaming asosiy xossalari,
tengsizliklami qo‘shish va ko'paytirish kabi mavzular bayon etilgan edi. Endi
sonli tengsizliklami darajaga ko‘tarish amaliga to‘xtalamiz.
I Agar a>b>0 va n natural son bo(lsa, >lf tengsizlik to(g(ri bo‘ladi.
14
жж
жж
О л > О, Ь > О va а> b bo'lgani uchun п ta bir xil a > b tengsizliklami
hadma-had ko'paytirib, an > У1 ni hosil qilamiz. |
/6 у
1- masala. (0,35)7 * va I — I sonlami taqqoslang.
О 0,001 aniqlik bilan « 0,316. Shuning uchun 0,35 > 0,316. Bundan
7 г 6 Y
(0,35) >1—1 tengsizlik kelib chiqadi. Endi quyidagi xossani bayon etish
mumkin:
жж
Agar sonli tengsizlikning chap va о‘ng qismlari musbat bo‘lsa, teng-
sizlikni istalgan ratsional darajaga ko'tarish mumkin:
1. a>b>®, r>0 boelsa,
ar>& (1)
bo'ladi;
2. a>b>Q, r<0 bo'lsa,
аГ<ЬГ
(2)
bo'ladi.
□ (1) xossani isbotlaymiz. Dastlab r = - (n — natural son) bo'lsin.
n > 1, a> 0, b>0 va shartga ko'ra a> b; an> if ekanini isbot qilamiz. Faraz
1 1
qilaylik, bu tengsizlik bajarilmaydi va an < bn bo'lsin. U holda shu tengsizlikni
n natural darajaga ko'tarib, a < b ni hosil qilamiz, bu esa a > b shartga zid.
i i
Demak, a > b dan an > bn kelib chiqadi.
жж
жж
Endi (1) ni umumiy, r = — bo'lgan holda isbotlaymiz, bunda m va n
— natural sonlar. a > b > 0 shartdan аУп > Л1/" kelib chiqadi. Buni m natural
darajaga ko'tansak, quyidagi tengsizlik hosil bo'ladi:
( i Vя f i
> bn
an
m m
ya’ni an >bn .
4 4 _9_ 9
Masalan, 39 > 29 , chunki 3>2; 410 < 510 , chunki 4 <5.
(2) xossa ham shunga o'xshash isbotlanadi. Shu xossaga ko'ra
(0,4)-7 < (0,3)-7, chunki 0,4 > 0,3; 14-0’4 5 * > 15-0’5, chunki 14 < 15.
Aslida (1) xossa istalgan musbat r haqiqiy son uchun, (2) xossa esa
istalgan manfiy haqiqiy son uchun to'g'ri. Buning isboti oliy matematika
kursida beriladi. Masalan,
75
IXTXIXTXI
и-
Ta’kidlab o'tamizki, (1) va (2) xossalar noqat’iy tengsizliklar a>b>$,
r>0 va a>&>0, r<0 uchun ham tocg‘ri.
Endi quyidagi umumiy xossani keltiramiz:
I Agar tengsizlikning ikkala qismi musbat bo *Isa, uni musbat dara-
jaga ko‘targanda tengsizlik belgisi saqlanadi, manfly darajaga
ko‘targanda esa tengsizlik belgjsi qarama-qarshisiga o*zgaradi.
2-masala. Sonlami taqqoslang:
d (Upva (if Г: 2) (ifva (o,86)'6 •
16 . . ,
—, shuning uchun
15 Yi
16 I
16 A 2
15 I
6 6
2) Ravshanki, у = 0,857... bo£lgani uchun у <0,86. Bundan
<(0,86/* kelib chiqadi. И
3-masala. Tenglamani yeching: 5х =1.
□ Agar x = 0 bo‘lsa, tenglama to'g'ri tenglikka aylanadi. Agar x < 0
bo‘lsa, 5х<1; x>0 bo‘lsa, 5х>1 bo‘ladi. Demak, x = 0 yagona yechim
bo‘ladi. |
лх= l(a>0, atl) tenglama ham yagona x = 0 yechimga ega.
Shuningdek,
0* = ^ (3)
tenglama yagona x = у yechimga ega, bunda a > 0, at 1. Isbotlash uchun (3)
tenglikni cTy ga ko'paytiramiz: a^y = 1, bundan x —y=0, ya’ni x = y kelib
chiqadi.
4- masala. 42r^1 = 16 tenglamani yeching.
П 42x+1 = 42, bundan 2x + 1 = 2,
Endi & = a > 0, a* 1, £ > 0 tenglamani qaraymiz. Tenglama yagona
x^ yechimga ega. Uni topish jarayoni logarifm tushunchasiga olib keladi.
son a asos bo‘yicha b sonning logarifmi deyiladi va logaZ> kabi belgilanadi.
Masalan, 2X=5 tenglamaning ildizi x = log25 bo‘ladi. Shu bilan birga,
logj 27 = -3, chunki || j =27.
76
жж
жж
Agar a = 10 bo‘lsa, log10 b ni lgZ> (0‘nli logarifm), a = e (irratsional
son e = 2,718281828459045...) bo‘lsa, loge b (natural logarifm) lnZ> deb
belgilanadi va „natural logarifin b“ deb o‘qiladi.
Logarifmlar va ulaming xossalarini akademik litsey va kollejlaming
matematika kursida bilib olasiz.
229. Topshiriqlami bajaring:
©
1) Sonli tengsizliklami darajaga ko‘tarish qoidalarini ayting.
2) Tengsizlikni r ratsional darajaga, keyin ixtiyoriy haqiqiy musbat
darajaga ko‘tarish amallariga 2—3 tadan misol tuzing.
3) Qat’iy tengsizliklami darajaga koctarishning xossalari noqat’iy teng-
sizliklar uchun ham o‘rinli bo‘lishini misollarda ko‘rsating.
жж
жж
230. (Og‘zaki.) Sonlami taqqoslang:
ii r
1) 42 va 52; 3) 3®va5®; 5) 8® va (7,9)V3;
2) 3"5 va 5'5; 4) 15"Л va 19"Л; 6) 2^ ya 2^.
231. Sonlami taqqoslang:
1 Г1ЛЧ7 за ( i №
1) (0,76)5 vaIJ; 3) (3,09f4 va(3±j ;
2) Щ'4 va (0,41/5; 4) vag) .
232. (Og'zaki.) Sonlami taqqoslang:
1 1 4 4
1) 43 va 53; 12) з’з va О ; 13) 473 va 5Л ; 14) 1Г® va 15“®.
жж
жж
233. Sonlami taqqoslang:
1 z , d „ z , 4?2
1) (0,88)4 va ^f; 3) (3,05)® va 3±
I 1JL j 1 j
va(0,41)-6 ; 4)(^ va(g) .
234. Tenglamani yeching (234—235):
1) 52x=55 ; 3) 63x-1 = 6"10; 5) 72“x=l;
Zl\4x-3
2) 3* = 27; 4) 22x+1 = 32; 6) | =5.
235. 1) 62х=3б5; 2) 7*=49; 3) 3*+1 = 27; 4) 53+*=5°;
77
жж
жж
жж
жж
IXTXIXTX
Ж
жж
жж
7) 4х+2 = 16;
1
5) 22х =83; 6) 82х = 26;
236. Sonlami taqqoslang (236—237):
4-И™
4-П
ж
жж
жж
жж
ЗОКЯЗ
ЖЖ
жж
245. 1)
ж
2)
238. 1) 2>"-2 = 8; 1 2) 35’ -2x= 1; 1 3) 42х 1 = 2; 1
/. \x+4
239. 1) (3) 3) 2X+^ = — •
2) 4) ufl 1 bl b- II Тл| h-2 V o>
240. i) 24x-’ =f|T4; 241. Sonlami taqqoslang: 2) 25x~2 = (Г J“7’5 .
Tenglamani yeching (238—240):
3--U
4) 27 3 -81 = 0.
5) у-1.^+2=^.
б)
3) ^ = з~’.
>/3
_ _ г ( 44 Г
1) a = n^ va 6 = (3,14)'fi; 2) а = (1,75)’^ va b = 11 — .
242. 3 > 2 tengsizlikni:
1) 2; 2) -2; 3) 4) 5) Л; 6) -A
darajaga ko‘taring. Qaysi hollarda tengsizlik belgisi qarama-qarshi belgiga
almashadi? Nima uchun?
243. Tenglamani yeching:
Hisoblang (244-249):
244. 1) (0,5)-2 + (0,l)-i-(0,2)-3;
(0,6)~2+(1,5)~2 .
(0,6+l,5)-2
2)
= 43*-2 • л/2
(^Г
2) (0,7)-1 + (0,3)-i
2>mir
4Г1
78
жж
246.
1)
247.
1)
(0,4)-2-(0,1)-2 + (0,2)-3;
(0,5)-2+4 .
(0,4+1,6)-2 ’
2)
6”1
2) (—0,1)-3 + (0,2)2 — (—0,2)-2.
(0,2)"2+5
(1,7-0,2)
3)
248.
1)
4
(0,75)° +(0,49)’2 -V;
-2
1
Р + 2-967°;
249.
2)
1
Г0,34 -(0,027)3 +(19,34)°;
4)
(0,216)3 +Г1? -(193,4)°.
жж
1)
36 10’5 :(3,2 -10-4);
. / . М-1 /, \-1
3)
4)
2 IO'1
0,23 10“6 • 3 105;
НГ (1Г Ш
2)
\3
ЖЖ
6,4 • IO5: (1,6 -107);
5) 21,6 - 104 : (3,6 10’)
IO'2.
250*. Ifodaning qiymatini toping:
1)
1 5 \ 2
т.
, bunda х = |; 2)
f 2 1
а3
~2~
а'9
, bunda
1
а'Г
251.
252.
253.
254.
17-§. Ill bobga doir mashqlar
Hisoblang (251-252):
1) (tV + 4-379°;
1) 8,1 • 1016 - 2 * 10-14;
/ 1 \-1 '
3) 3-10"1- 8°--
Ifodaning qiymatini toping:
f 1 5 у2
X2 X®
1)
1
2) (0,125)3 +
-(1,85)°.
if (ОШ-
2) 3,2 -105: (0,8 -107);
-,-1
7
5 bunda х = -; 2)
f 1 1
а~^
Ifodani soddalashtirmg (x>0, yX), x>y):
> bunda a— 0,1.
жж
жж
жж
жж
ЖЖ
79
LZTXJXTXI
2)
а^ж
j x
255. Ifodani soddalashtiring, bunda —l<a<l:
1)
12= + yfi^a
l+«
l+«
2) (3/216х-3/27х)-(3/125х-$Йх).
256. Tenglamani yeching:
1) 8bt-3 = 64;
2) (0,2)-2-* = 0,04;
257. Tenglamani yeching:
1) 93x-2 = 81;
2) (0,5)’-* = 1;
Hisoblang (258-259
258*. 1) 27’-(-2)’2+f:
259*.
1)
+ 1OOOO0-25
(-0,5)4 -225
260. x ning qanday qiymatida ifoda ma’noga ega bo'ladi (260—261):
1) 7x2 -4; 2) Их2 -3x + 2;
4) Их2 -3x+2?
261. 1) 7x2 -9; | 2) tlx2 -15x + 26; | 3) V+x-2;
262*. Ifodani soddalashtiring (a>0, />>0, a*b):
4 2
1 2 ’
a^-a^
2)
1 _3
b*-b * .
3 1 ’
b*-b *
| 4) V-l.
80
5 1 _3
.. М+2М+**
3 1
b4 +b4
3 1 13
a4b 4+a 4b4
4) i _i _i _i '
a4b 4-a 4b 4
263. Ifodaning qiymatini a = 5, b = 4 boclganda hisoblang:
Vg+^+16+л/д2-^2 . л/д2 +b2 +40+л/д2 -b2 +40
) yla+b-5 -л/a2 -b2 л/д3 +1? +100-л/д3 -I? +20
HI bobga doir sinov (test) mashqlari
2. Ifodani soddalashtiring: ^[a+lfb^
1. Hisoblang: lll + y/3 -^/7-4>/3.
A) 1; В) -1; С) 3 + 2л/3; D) 3-2л/3.
<2 2 л
а3 - tfab + Ь3 .
< J
А) а + b; В) a~b; С) д3 + b\ D) (« + />)!.
3. Soddalashtiring: 27д7
<-*r13 OP*6t
,(a > 0,£ > 0).
10a. p\ 10a. 9a.
A) B) b > b f
4. Tenglamani yeching: 3х = 27 • (л/3)*+2
A) 8; В) 4; С) 6;
2 _
5. Tenglamani yeching: x3 = v4.
A) 4; B) 2; C) 8;
5 1
Д6 +Д3
6. Ifodaning son qiymatini toping: ——p, bunda
a^-a3
A) 14,4; B) 12; C) 11;
D) 4-
D) 5.
D) 3.
a=l,44.
D) 1,2.
7. Hisoblang:
(V7+ л/2-1) (л/7-^ч-l).
A) 4 + 2^; B)4-2>/2; C) J-y/2;
2 2
8. Hisoblang: (^3-Л) -(V3 + V2)
А) -4л/б; B)3>/6; C) 275;
6—Algebra, 9
D) y/5 + 1.
D) 472.
81
1 1
л/7-л/24 +1 V7 + V24-1
10. Hisoblang:
A) 0; B) 1; C) 47; D) 246.
4
11. Hisoblang: + 46 + 442 '
A) 242-2; B) 246 ; C) 46 + 4 2; D) 242+1.
4a 4b 24ab f 4ab + b У
12. Soddalashtirmg: —= — + —— — + 4a+4b 4a-4b a + b I 4^+4b)
A) 4a + 4b ; B) 24a -4b ; C) 4a- 24b ; D) 5 lab — 4a.
Tarixiy ma’lumotlar
Ratsional ko‘rsatkichli daraja Isaak Nyuton (1643—1727) tomonidan
kiritilgan. Ixtiyoriy a haqiqiy son uchun. a?, a > 0 daraja tushunchasi Le-
onard Eyler (1707—1783) tomonidan uning „Analizga kirish“ asarida bayon
qilingan.
Abu Rayhon Beruniy (973—1048) o'zining mashhur „Qonuni
Ma’sudiy" asarida „aylana uzunligining uning diametriga nisbati irratsional
son" ekanligini aytadi. G‘iyosiddin Jamshid al-Koshiyning (1385—1429)
„Arifmetika kaliti" asarida natural sondan kvadrat ildiz chiqarishning umumiy
usuli keltiriladi. Shuningdek, al-Koshiy ildizni aniqroq hisoblash usulini,
ildizlar ko‘paytmasini umumiy ko‘rsatkichga keltirish qoidasini ham bayon
etgan:
Qiziqarli masalalar
1. n ning nechta natural qiymatida 2011 < 4n < 2012 qo£sh tengsizlik o'rinli
bo‘ladi?
Sonlami taqqoslang (2—3):
2. 1) л/2011 + 5/2013 va 2 -5/2012;
2) 5/12 + 1 + 4a + 4a + l va 4a + 4a + l + 4a, a > 0.
11 1 1 2012
3. 1) --------+ -J------+ ------ va 2-——;
7 71-2012 72’2011 7*-(2012-* + !) 72012 1 2013
82
2) 1 + 4= + -т= + - + -j==— va л/2012.
72 7з 72012
4. Yig'indini hisoblang: ^ + -^ + ...+ 7^^.
Hisoblang (5—6):
5. 1) 720 + 14-^+720-145^; 2) J|40^-57| - ^40^2 + 57.
6. 1) ^ + ^52-л/5+ 2-713- ^^52-75;
2) 7>/2-712-72 + 2-73-7712+Л.
7. (Qadimgi hind masalasi). Tenglikni isbotlang:
5/10 + 5/24 + >/40 + 760 = ^ + >/3+>/5-
Kofaatmcr. tenglikning ikkala qismini kvadratga oshirib taqqoslang.
8. Ifodani soddalashtiring:
1) 4 c? - £3 + a2b - ab2 , bunda д>й>0;
a2 . 11 4(l-a)
2) 2-a \«+ a3 , bunda a>2.
9. Ifodani soddalashtiring:
1) 710a + 23 + 5/a4 + 4a2 + 4 ;
2) 710a+ 92 +7a4 + 16a2 + 64 .
10. Qaysi son katta: 71001 + 71003 mi yoki 7999 + 71005 mi?
□ 71001 +71003 - 7999 - 71005 =(71001-7999)-(71005 - 71003) =
, ------—, ---, > 0, chunki 1-kasr maxraji 2-kasr
71001+7999 71665 + 71003
maxrajidan kichik. Demak, 71001 + 71003 > 7999 + 71005
11. Hisoblang: 5/З6-25/З2З - 5/36 + 2^23 .
□ 1-usul: 36=19+17 va 323=19- 17 ekanidan foydalanamiz. U holda
5/З6- 25/323 = 7(5/19 )2 — 2л/19 -л/17 + (л/17)2 = 7(5/19-Л7)2 = 5/I9 - л/17.
ЖЖ
жж
W3W5
жж
жж
жж
жж
жж
83
жж
жж
ЖЖ
жж
Shunga o'xshash 736 + 2>/323 = 719 + 717. Demak, berilgan ifoda quyidagiga
teng: 719-717 - (719 + 717 ) =-2717. Javob: -2717 .
2-usul: Berilgan ifodani a bilan belgilaylik. U holda
a* 1 2 3 4 5 6 7 = 36 - 2л/323 - 27362 - 4 • 323 + 36 + 2>/323 = 72 - 2V1296 -1292 =
=72—4=68. Shunday qilib, л2=68. Ammo «<0 bo'lgani uchun
a = -V68 = -V4-17 = -2-717. Javob: -2717 .
12. Hisoblang: (5 - л/зТ) - 756 +10731.
Q 1-usul: Ildiz ostiga kiritish. 5 - 731 < 0 ekanini hisobga olib (5 - 731)
sonni kvadrat ildiz ostiga kiritamiz. Berilgan ifodani a deb belgilaylik. U holda
a = -7(5 - TIT)2 (56 + 10л/зТ) = -7(56 - 10Т31)(56 +Ю731) =
= -73136-3100 = -736 = -6. Javob: -6.
2-usul: Ildiz ostidan chiqarish. a = (5 —731) • 7(5 +'/Й)2 =
= (5 —ТЙ)-(5 + ТЙ) = 25-31 =-6. Javob: -6.
жж
жж
жж
жж
жж
жж
Mantiqiy masalalar
1. Tomoni 1 bo'lgan kvadratga 126 ta nuqta ixtiyoriy ravishda joylashtirilgan.
Radius! у bo'lgan doirada ulardan oltitasining yotishini isbotlang.
2. n + 1 ta natural son ichidan ayirmasi n ga bo'linadigan 2 ta son tanlab olish
mumkinligini isbotlang.
3. 2 012 bilan tugaydigan va oxirgi 4 ta raqamini o'chirganda butun son marta
kamayadigan natural sonlami toping.
4. 1 dan n gacha bo'lgan sonlami yozib chiqish uchun 2 893 ta raqam kerak
bo'ladi. n ni toping.
5. 1331 sonining qo'shni raqamlari orasiga к tadan nol qo'yilsa, hosil bo'lgan
son biror sonning kubi bo'lishini isbotlang.
6. Massalari 1 gr, 2 gr, ..., 2 010 gr bo'lgan 2 010 ta tarozi toshlari bor.
Ulami har birida toshlar soni va umumiy massasi bir xil bo'lgan beshta
guruhga ajratish mumkinmi?
7. p, />+10, />+14 tub sonlar bo'lsa, /> ni toping.
QJ P sonning 3 ga bo'linishini (ya’ni />=3) ekanini isbotlaymiz. Agar
p ni 3 ga bo'lganda 1 qoldiq chiqsa, u holda />+14=(p—1)+15 son 3 ga
bo'linadi, bu esa shartga zid. Agar p ni 3 ga bo'lganda 2 qoldiq chiqsa,
84
жж
u holda />+10=(р—2)+12 son 3 ga bo‘linadi, bu ham shartga zid. Demak,
p son 3 ga bo‘linadi. p tub son bo'lgani uchun p=3. Javob: p=3. |
8. p — tub son, p>3. Biror natural son n da pF soni 20 ta raqamdan iborat
bo‘lsa, bu raqamlar ichida kamida 3 tasi bir xil ekanini isbotlang.
□ Agar 20 ta raqam ichida 3 ta bir xili bo'lmaganda edi, pF sonning
yozuvida 10 ta: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 raqamlaming har bin
roppa-rosa 2 martadan uchrar, aks holda, pF ning raqamlari soni 20
tadan kam bo‘lar edi. U holda pF sonning raqamlari yig‘indisi
2- (0+l+2+...+9)=90 ga teng bo‘ladi, ya’ni pF son 3 ga bo'linadi.
p — tub son, p>3, bo‘lgani uchun pF va 3 soni o'zaro tub sonlardir.
Zidlikka keldik. Demak, pF sonning raqamlari ichida kamida 3 ta bir xil
raqam bor. |
жж
9. Kub 27 ta bir xil kubchalarda ajratilgan. Markaziy
kubchada chumoli bor. U har bir kubchadan shu
kubcha bilan umumiy yoqqa ega boclgan 6 ta “qo‘shni”
kubchalarga o‘tishi mumkin. Chumoli har bir
kubchada bir martadan bo‘lib, jami (27 ta)
kubchalami aylanib chiqishi mumkinmi?
□ Chumoli hamma kubchalami har birida bir
martadan bo'lib, aylanib chiqa olmasligini isbotlaymiz.
жж
Kubchalami, masalan, oq va qora rangga bo‘yaymiz. Kubning uchlaridagi
kubchalami qora rangga, ular bilan umumiy yoqqa ega bo'lganlarini oq
rangga bo'yaymiz. Oq rangli kubchalarga “qo'shni” kubchalami qora rangga
bo‘yaymiz va hokazo. Natijada 13 ta kubcha oq rangga, 14 ta kubcha esa
qora rangga bo‘yaladi. Markaziy kubcha — oq rangda. Chumolining har bir
yurishida kubchaning rangi o‘zgaradi: oq — qora — oq — qora — ... Oq
kubchalar 13 ta bo‘lgani uchun, 27 ta yurishda chumoli aqalli bitta oq
ЖЖ
жж
kubchadan ikki marta o‘tadi. |
10. 2 ta yashil, 2 ta ko‘k, 2 ta oq va 2 ta qizil rangli doirachalami kubning
uchlariga ikki nafar bola navbatma-navbat yopishtirmoqda. Hamma
doirachalar kubning uchlariga yopishtirildi deylik. Agar kubning biror
qirrasining ikkala uchidagi doiracha rangi bir xil bo‘lsa, 1-bola (o‘yinni
boshlovchi) yutqazadi, aks holda 2-bola yutadi. Bu o'yinda yutishning
yo‘rig‘i qanday bo‘ladi?
Ko'rsatma: 2-bola hamma vaqt yutishi mumkin. Kub markaziy—simmetrik
jism ekanidan foydalananing. 1-o‘yinchi qaysi doirachani qaysi uchda
yopishtirsa, 2-o‘yinchi o'sha rangdagi doirachani o‘sha uchga markaziy—
simmetrik bo‘lgan uchga yopishtirishi kerak. O‘yin tugaganda qo‘shni
uchlaming hech birida bir xil rangli doirachalar bo'lmaydi.
11. Bitta ikki o‘rinli motosikl bor, uning tezligi 50 km/soat. Uch nafar kishi
3 soatda 60 km naridagi qishloqqa borishi zarur. Piyoda kishming tezligi
5 km/soat. Manzilga vaqtida yetib borishlari uchun qanday tavsiya berasiz?
жж
жж
ЖЖ
85
ГЛкЧГЖЧ
жж
жж
«ИИ
жж
жж
жж
жж
рия
жж
жж
12. O‘lchamlari 2016x2017 bo‘lgan ikki jadvalning kataklari yashil va ko‘k
ranglarda shunday bocyalganki, bunda har bir qator va har bir ustunda
juft sondagi ko‘k kataklar bor. Jadvallardan birini ikkinchisining ustiga
qo‘yishdi, shunda kock kataklardan biri qizil katak bilan ustma-ust tushdi.
Hech bo‘lmaganda yana 3 ta katak topiladiki, ular boshqa rangdagi kataklar
bilan ustma-ust tushadi. Shu da’voni isbotlang.
13. x-2016 xonali son bo‘lsin, у son x dagi raqamlar o‘mini almashtirish
natijasida hosil bo‘lgan son, deylik. x+y=99 ... 9 (2016 ta 9) tenglik o‘rinli
bo‘lishi mumkinmi? Agar x 2017 xonali son bo‘lsa-chi?
Q Masala shartini qanoatlantiradigan 2016 xonali son mavjud. Masalan,
x=8787...87, y=1212...12, x+y=99...9, bunda x, у va x+y sonlaming har
biri 2016 xonali. Ammo, masala shartini qanoatlantiradigan 2017 xonali
son mavjud emas. Chindan ham x=ata2...an 2017 xonali son deylik, bunda
«=2017, ak — 0, 1, ..., 9 raqamlardan biri, son x sonning
raqamlari o‘mini ahnashtirmasdan hosil bo‘lgan son.
x+y=99...9 tenglikdan («=2017 ta 9) ал+£л=9, a1+^1=9
ekani kelib chiqadi (isbotlang!). Ushbu yig'indini hisoblaymiz:
S=(a}+b^+(a2+b^...+(an+br)=9+9+...+9=9• n — toq son. Shu bilan
birga д1+а2+...+дл=&1+£2+...+£л.
U holda S=(al+a2+...+ai)+(b1+b2+...+bn)=2(a1+a2+...+an) — juft son.
Zidlikka keldik. Demak, x+y=99...9 («ta xona) tenglik «toq son bo‘lganda
bajarilmaydi. |
14. Xaltada 2020 dona yong‘oq bor. Ikki nafar bola galma-galda yong‘oq
olishadi. Har bir olishda har bir bola 1 ta yoki 2 ta yong‘oq olishi mumkin.
Oxirgi yong‘oqni olgan (xaltani bo‘shatgan) bola o‘yinda yutgan hisoblanadi.
O‘yinda yutish uchun bola qanday yo‘l tutishi kerak?
□ 1-chi bo‘lib yong‘oq olgan bola (o‘yinni boshlovchi) yutadi. Buning
uchun u o‘zining har galgi yurishidan keyin xaltada qoladigan yong'oqlar
sonining 3 ga bo'linishiga erishishi kerak. 1-yurushda boshlovchi 1 dona
yong‘oq oladi (2020—1=2019 soni 3 ga bo'linadi.). Agar 2-bola 2 ta
yong‘oq olsa, 3-yurishda boshlovchi 1 ta, mabodo, 2-bola 1 ta yong'oq
olsa, 1-bola 2 ta yong‘oq olishi lozim. Shunda 1-bolaning istalgan yurishidan
so‘ng xaltada qolgan yong'oqlar soni 3 ga bolinadi, 2-bolaning ixtiyoriy
yurishidan so‘ng xaltadagi yong‘oqlar soni 3 ga bo‘linmaydi.
2019-3
1 + 2 —-— = 1347 yurishdan so‘ng xaltada 3 ta yong‘oq qoladi va gal
2-bolaniki bo'ladi. Demak, shunday yocl tutilsa, 1-bola o'yinda yutadi. Agar
yong‘oqlaming dastlabki soni 3 ga bo‘linsa (masalan, xaltada dastlab 2022
dona yong‘oq bo‘lsa), 2-bola o‘yinni yutadi. Buni o‘zingiz isbotlang. |
htt://www.matematikl.narod.ru/manbadan mazkur bobga oid
ma’lumotlami toping va o‘iganing.
86
ЖЖ
ZTXIXXI
IV BOB
DARAJALI FUNKSIYA
18-§. Funksiyaning aniqlanish sohasi
8- sinfda funksiya tushunchasi, uning berilish usullari, chiziqli funksiya
mavzulari bayon etilgan. Funksiya ta’rifmi eslatamiz:
X va Y sonli oraliqlar bo‘lsin.
Ta’rif. Agar X oraliqdan olingan har bir x songa Y dan olingan bitta
у son mos keltirilgan bo‘lsa, X oraliqda у =y(x) funksiya berilgan
deyiladi. Bunda x erkli o‘zgaruvchi yoki argument, у esa erksiz
o‘zgaruvchi yoki x ning funksiyasi deyiladi.
Shu у = y(x) funksiya chiziqli yoki chiziqsiz bo'lishi mumkin. Jumladan,
у = kx + b — chiziqli, у = ax2 + bx + c (a * 0) — kvadrat fimksiyadir. Yana
bo‘la oladi.
Siz natural ko'isatkichli, butun ko'isatkichli, ratsional ko'isatkichli
darajalar bilan tanishgansiz. Agar aP darajada a o'mida o'zgaruvchi x turgan
bo'lsa, darajali funksiya xP hosil bo'ladi. Ba’zi funksiyalar x? ko'rinishida
yoki shunga o'xshash darajali funksiyalar (yig'indisi, ko'paytmasi va nisbatijdan
tuzilgan bo'lishi mumkin. Masalan, у = Ax da p = 1, y = ax2 + bx + c kvadrat
funksiya uchta darajali funksiya yig'indisidan tashkil topgan: y1 = ax2, y2 = bx,
y3 = c. Ularda, mos ravishda, p = 2, p=l, p = 0 ekani ravshan.
Funksiya argumentining joiz qiymatlari to^lami (funksiyaning
aniqlanish sohasi)ni topish deyilganda argumentning funksiya ma9noga
ega bo(ladigan barcha qiymatlarini topish tushuniladi.
Masalan, у = kx + b (chiziqli), у = ax2 + bx + c (kvadrat) funksiyaning
aniqlanish sohasi son o'qi R = (-°°; °°) dan iborat; shunga o'xshash, у-4x
funksiya uchun x£0, ya’ni [0; «>) oraliq; у = funksiya uchun esa
ya’ni noldan farqli barcha haqiqiy sonlar to'plami aniqlanish sohasi bo'ladi.
1-masala. Funksiyaning aniqlanish sohasini toping:
0 /W = x2 -3x + 7;
2) /W = V3-x;
IZTXIXXl
О Ravshanki, 1) funksiya х ning istalgan qiymatida ma’noga ega.
Javob: x — istalgan son.
2) /(x) = V3 - x funksiya x< 3 bo‘lganda ma’noga ega. Javob: x< 3.
3) f(x) = -J— funksiya x* — 1 da ma’noga ega. Javob: x/~ 1.
л+1
jp_1
4) funksiya —j- 0 bo‘lganda ma’noga ega. Shu tengsizlikni yechib
жж
topamiz: Javob: x< — 1 va x> 1. |
Berilgan funksiyaning aniqlanish sohasi ma’lum bo'lsa, uning grafigini
chizish masalasini qo‘yish mumkin.
Funksiyaning grafigi deb shunday nuqtalar to‘plamiga (geometrik
o(miga) aytiladiki, bu nuqtalarning abssissalari funksiyaning aniqlanish
sohasidan olingan bo‘lib, ordinatalari esa funksiyaning mos qiymatlaridan
iborat bo‘ladi.
2- masala, у = |x| funksiyaning aniqlanish sohasini toping va uning grafigini
О Ma’lumki,
x, agar x > 0 bo‘lsa,
-x, agar x < 0 bo‘lsa.
жж
ЖЖ
у = |x| funksiya x ning istalgan haqiqiy qiymatida ma’noga ega. Demak, bu
funksiyaning aniqlanish sohasi barcha haqiqiy sonlar to‘plamidan iborat.
Endi uning grafigini chizaylik.
Agar x>0 bo‘lsa, y = x bo‘lib, uning grafigi I chorak bissektrisasi, agar
x<0 bo‘lsa, y = ~x bo£lib, grafigi II chorak bissektrisasi bo'ladi.
(36-rasm).
|—x| = x tenglik ixtiyoriy x da 0‘rinli bo'lgani uchun у = |x| funksiyaning
grafigi Oy o‘qqa nisbatan simmetrikdir. I
жж
жж
3- masala, у = |x — 2| — 1 funksiyaning grafigini chizing.
□ Bu funksiyaning grafigini chizish uchun y = |x| funksiya grafigini
o‘ngga 2 birlik siljitib, so‘ngra pastga 1 birlik tushirish lozim (37- rasm).
88
Umuman, agar у =f(x) funksiyaning grafigi chizilgan bo ‘Isa,
у —f(x — a) +b funksiyaning grafigini chizish uchun у =f(x) funksiya grafigini
avval a>0 bo‘lganda o‘ngga (a<0 da chapga) a birlikka siljitish kerak;
so‘ngra hosil bo‘lgan grafikni b birlikka b>0 bo‘lganda yuqoriga, b<0
bo‘lganda pastga surish kerak.
264. Savollarga javob bering. Topshiriqlami bajaring:
1) Funksiya deganda nimani tushunasiz?
2) Funksiyaning aniqlanish sohasi deb nimaga aytiladi?
3) Formula bilan berilgan funksiyaning aniqlanish sohasi qanday
topiladi?
4) Funksiyaning grafigi nima?
5) у = Зх + 2; у = —Зх —1; у = 2х — 5; у = —х + 2 chiziqli funksiyalar
grafigini chizing.
6) у = 6x2 + 5x + 1 va у = x2 — 5x + 6 kvadrat funksiyalar grafigini
chizing.
265. Funksiya /(x) = x2 — 3x + 2 formula bilan berilgan:
1) /(1); /(2); /(-1); /(-2); /(3) ni;
1
2) agar /(x) = 0; /(x) = 2; /(x) = 12; /(x) = - ^ bo‘lsa, x ning qiyma-
tini toping.
266. Funksiya y(x) = 3x2 — x — 2 formula bilan berilgan:
1) y(l); Я-l); J(0); y(2) ni;
2) agar y(x) = 0; y(x) = 8; y(x) = 12 bo‘lsa, x ning qiymatini toping.
267. Funksiya y(x) = x + i formula bilan berilgan:
1) y(l); y(”l); X2); y(”2) ni hisoblang;
2) XX) = 2; y(x) = -2; y(x) = 2,5 bo‘lsa, x ni toping.
Funksiyaning aniqlanish sohasini toping (268—270):
268. 1) у = 4x2; 2) y = |; =
4) y = 5) у = 4^2; 6) y = V81-x2.
9-x
ЖЖ
269.
270.
ЖЖ
жж
жж
271.
1)
2)
1)
3)
_ x
У x2-2x+l
_ x-3
x2-3x+2’
_ 3x
x2 +2x+l’
у = л/4х2 -Зх-5;
3)
4)
2)
4)
у = ух -5x + 6;
У =
x+2
4-x
у = yx2 - 7x + 6;
x-2.
x+5’
Л|Л
у = 61----
5)
6)
5)
У x2-6x+9
_ y/x-2
У ~ x2-7x+12 ‘
|3x-7
3-2x
272.
273.
жж
274.
жж
жж
x—1
Funksiya у = formula bilan berilgan bo'lsa, y(l)5 X”l)> X3),
j(10) ni toping.
Agar у = |3 — x| + 2 bo'lsa,
1) y(3); y(4); y(0); X”3) ni toping;
2) у = 5; у = 2; у = 3; у = 4 bo'lsa, х ni toping.
Funksiya у = |x 4- 2| — 3 formula bilan berilgan:
1) J>(3); y(-l); y(0) ni toping;
2) agar y(*)= “3; y(x) = 0; y(x)= “1 bo'lsa, x ni toping.
Quyidagi nuqtalardan qaysi biri у = x2 — 5x + 4 funksiya grafigiga tegishli
bo'ladi: 1) (1; 0); 2) (2; -2); 3) (-1; 0); 4) (-2; 18)?
жж
Funksiyaning aniqlanish sohasini toping (275—276):
1) 3’ = |(x-l)2; 2) у = ^-, 3) y =
—• 4) y =
х+2*
х-3
х+2*
275.
1) У =
Jx2+5x-6
V x2+5
жж
жж
(—2; 1) nuqta quyidagi funksiya grafigiga tegishlimi:
1) у = 3x2 + 2x + 29; 2) y=|4-3x|-9;
3) y = ^; 4) у=|ЛТ^-2|-
(1; -2) nuqta quyidagi funksiya grafigiga tegishlimi:
1)
3)
у — 5x2 — 3x — 4;
x2-5
y =—Г’
x+l
2) у = |3 - 2х| - 3;
5)у = |х—3| —4?
Ж
Funksiya grafigini chizing (279—280):
279*. 1) y = |x + 2| + 3; 2) У = - M + 2;
3) j>=l-|3-2x|; 4) y=k+ i|-|x|.
280*. 1) y = |x —2| + 3; 2) з' = -^И;
3) y=3|x|-2; 4) y = |x+ l| + |x|.
ЖЖ
ЖЖ
281. y = ax2 + bx + c funksiya (0; 3), (2; 9), (—1; 6) nuqtalardan o‘tadi.
1) a, b, c sonlarni toping; 2) x ning qanday qiymatlarida у = 4 bo‘ladi?
3) funksiya grafigini chizing.
19- §. Funksiyaning o‘sishi va kamayishi
Ma’lumki, у = x va у = x2 darajali funksiyalar
У = аГ (1)
(bunda r — berilgan son) funksiyaning xususiy hollaridir, ya’ni r= 1 va r= 2
bo‘lgan natural ko‘rsatkichli darajali funksiyalar. Endi r — istalgan natural
son bofisin, ya’ni r=n, n= 1, 2, 3, ... deylik. Bunda hosil bo'lgan y = x”
funksiya natural ko‘rsatkichli darajali funksiya bo'ladi. Bu funksiya son o‘qining
hamma yerida aniqlangan. Barcha haqiqiy sonlar to‘plami, odatda, R harfi
bilan belgilanadi. Shunga ko'ra у = x” funksiya x e R uchun aniqlangan.
-2k 1
Agar r — —2k, kcN bo‘lsa, У - x —funksiya x ning noldan
farqli barcha qiymatlarida aniqlangan. Uning grafigi Oy o‘qqa nisbatan sim-
metrik (38-a rasm). Agar г = ~(2k — 1), kcN bofisa, у = x ^2k .
Bu funksiya ham x ning noldan farqli barcha qiymatlarida aniqlangan. Uning
grafigi koordinata boshiga nisbatan simmetrik (38-Z> rasm).
ЖЖ
ЖЖ
ЖЖ
ЖЖ
Л2Я5
жж
ЖЖ
ЖЖ
IXXIZTXI
91
жж
жж
жж
НЮТ
жж
жж
жж
жж
ЖЖ
р
Endi ratsional ko'rsatkichli у = xq darajali funksiyani olaylik, unda p,
p
q — natural sonlar, ~ — qisqarmas kasr bo'lsin. Agar q = 1 bo'lsa, natural
ko'rsatkichli darajali funksiyaga ega bo'lamiz. q = 2, 3, ... bo'lsin. Funksiyani
ko'rinishda yozib olamiz. Uning aniqlanish sohasi pva. q ning juft yoki
toqligiga bog'liq. Masalan, у = у = tfx funksiyalar ixtiyoriy x e R da
aniqlangan, у = ifx, у = funksiyalar esa x ning nomanfiy (x> 0) qiy-
matlarida aniqlangan.
Ill bobning 4- § ida sizni irratsional ko'rsatkichli daraja bilan tanishtirgan
edik. (1) da r irratsional son bo'lsa, irratsional ko'rsatkichli darajali funksiya
hosil bo'ladi. r irratsional sonni r2, ..., rk, ... ratsional sonlar bilan ketma-
ket yaqinlashtirish mumkin. x> 0 da aniqlangan xn , x*2 ,..., x^ ,... sonlar
xf darajaning yaqinlashishlari bo'ladi. Bunday aniqlangan daraja irratsional
ko'rsatkichli daraja deyiladi. Demak, x > 0 bo'lganda daraja ko'rsatkichi ixtiy-
oriy r bo'lgan у = xf funksiyani aniqlash mumkin.
Ta’rif. Agar у =y(x) funksiya argumentining biror oraliqdan olin-
gan katta qiymatiga funksiyaning katta qiymati mos kelsa, ya’ni shu
oraliqqa tegishli istalgan xp x2 uchun x2 >xt tengsizlikdan y(x^ >y(xj)
tengsizlik kelib chiqsa, у =y(x) funksiya shu oraliqda о'save hi deyiladi.
Ta’rif. Agar biror oraliqqa tegishli istalgan xp x2 uchun x2 >xt
tengsizlikdan y(xj <y(xf) tengsizlik kelib chiqsa, у =y(x) funksiya shu
oraliqda kamayuvchi deyiladi.
Masalan, y = x, y = 2x~ 3 funksiyalar sonlar o'qida o'sadi, у = Зх2 funk-
siya esa x> 0 oraliqda o'sadi, x< 0 oraliqda kamayadi. Umumiy holda y = xf
darajali funksiyaning o'sishi yoki kamayishi daraja ko'rsatkich r ning isho-
rasiga bog'liq.
I Agar r>0 balsa, y=xr darajali funksiya x20 oraliqda o‘sadi,
r<0 bolganda esa x> 0 oraliqda kamayadi.
П 1) > xt > 0 va r > 0 bo'lsin. Bundan x2 > xf, ya’ni y[xf) >
kelib chiqadi; 2) x^ > x1 > 0 bo'lsin. > xx ni manfiy r darajaga ko'taramiz. U
holda x2 < x[. Bundan y(xj) < y{x^) ni hosil qilamiz. |
Masalan, у = 4x funksiya x> 0 oraliqda o'sadi, chunki r = ^ > 0, ixtiyoriy
1
Xj < x2 uchun Vxi < vx2 bo'ladi (39-a rasm). y = x^, ya’ni
92
1-masala. %4 = 64 tenglamani yeching.
жж
з
О У = x4 funksiya x>0 oraliqda aniqlangan. Shu sababli tenglama faqat
4 ,
nomanfiy ildizlarga ega bo'lishi mumkin. Ulardan bin x = (64)3 = Iv43 j =
= 44 = 256. Tenglamaning boshqa ildizlari yo'q, chunki x > 256 bo'lsa, x4 > 64;
з
x < 256 bo'lganda esa, x4 < 64 bo'ladi (40- rasm). Javob: x = 256. |
j.
xf= b (bunda гф 0, b > 0) tenglama har doim musbat x = br ildizga ega.
r > 0, x > 0 bo'lganda у = xf funksiya barcha musbat qiymatlami qabul qiladi.
Ravshanki, bu holda y(0) = 0r = 0 bo'lib, x? — o'suvchi. Shuning uchun у = xf
va у = b funksiya grafiklari albatta kesishadi (40- rasm).
жж
жж
64 у =64
з
0 256 х
жж
жж
2- masala, у = x + — funksiyaning x > 1 oraliqda o'sishini isbotlang.
П %2 >xt > 1 bo'lsa, Xx?) > Xxj) ni ko'rsatamiz. y(x^) — y(xt) ayirmani
tuzamiz:
93
жж
, , , . 1 г 1
y(Xi) - Х*1) = х2 +------*1 + —
х2 I Х1
Qfr-xiHxpfr-l)
*1*2
Shartga ко‘га xt > 1, х2 > 1, xY • х2 > 1. Shuning uchun х2 — хг > О,
*1 • X} - 1 > 0, xpCj > 0. Demak, ytxj - ytxj > 0, ya’ni y(x2) > у(х{). □
жж
жж
НЮТ
жж
жж
282. Topshiriqnibajaring. Savolga javob bering:
1) O'suvchi va kamayuvchi funksiyalar ta’rifini ayting.
2) Darajali funksiya y = xf ning r= 1; 2; —1; | hollarda aniqlanish
sohasini ayting.
3) у = xT darajali funksiya x > 0 bo‘lganda r ning qanday qiymatlarida
o'suvchi, qanday qiymatlarida kamayuvchi bo'ladi?
з
4) у = x, у = 4x va у = x2 funksiyalaming grafigini bitta koordinata
sistemasida chizing.
(Og'zaki.) Funksiya x>0 bo'lganda o‘sadimi yoki kamayadimi?
(283-284):
3_2
283.1)j> = x4; 2)j = %3; 3)j = x’V3; 4)y = xV2.
284. 1) у =x$; 2) у = x *; 3) у = x~^; 4) у = x®.
жж
Funksiyaning grafigini chizing, o‘sish va kamayish oraliqlarini toping
(285—286):
285. 1) y=3x+2; 2)y=3-2x; 3)y = x* + l; 4)y = 3-x2.
286. 1) y = 2x+7; 2)y = -x+3; 3)y = |x2-l; 4)y=(2-x)2.
x > 0 bo‘lganda funksiya grafigi eskizini chizing (287—288):
2 3 2 з
287. 1) у = x3; 2) y = x2; 3) У = X 3; 4) у = x 2.
2 5 2 _5
288. 1) y = x5; 2) y = x2; 3) у = X 5; 4) у = x 2.
жж
ЖЖ
Tenglamaning musbat ildizini toping (289—290):
11 1 --
289. 1) x3 = 2; 2) x* = 3; 3) x"2 =3; 4) x 4 = 3.
1 1 _i _i
290. 1) X5 = 4; 2) x4 = 2; 3) x ’ = 8’1; 4) x 4 = 1 •
94
Funksiyalar grafiklari kesishish nuqtalarining koordinatalarini toping
(291-292):
5 291. 1) у = хз va у = 32; 5 2) у = х6 va у = 243;
3) у = хз va у = 16; 4) У = х 3 4 va у = 125.
2 292. 1) у = хз vay = 2; 2) у = х4 va у = >/х;
1 3) у = хз va у = х; 3 4) у = хI 2 va у = х2.
293. Quyidagi funksiyalar grafiklari kesishadimi:
1) у = x2 + 5 va у = —2; 2) у = x2 - 3 va у = —x;
3) У = x3 va у = —x + 1; 4) у = x2 va у = x + 2?
294. Quyidagi funksiyalaming o‘sish va kamayish
©1) J' = x2-1; 2) y = y?+ 1;
4) y = x~4', 5)y=(x-l)3;
oraliqlarmi toping:
3) y = x*-2;
6) у = (x + 2)2.
ЖЖ
нтаи
жж
ЖЖ
ЖЖ
ЖЖ
295. Tenglamaning manfiy ildizinitoping:
1) хз = -2; 2) 3x5 = -96;
i i
3) xS = (-3)5 ;
1 2
4) 2x’=-16; 5) 2^x + (^x) =0; 6) -4x5 = 128.
296. Funksiyalar grafiklari kesishgan nuqtalari koordinatalarini toping:
1) у = x2 va у = —x2 +1; 2) у = x2 va у = ;
1
3) у = —x2 va у = —; 4) у = x2 — 2 va у = —x2 + 6.
ЖЖ
ЖЖ
297. у = x + i funksiyaning 0 < x < 1 oraliqda kamayishini va x — 1 oraliqda
o'sishini isbotlang.
20- §. Funksiyaning juft va toqligi
I Agar y(x) funksiyaning aniqlanish sohasidan olingan istalgan x uchun
y(—x) =y(x) tenglik o‘rinli bo‘lsa, bu funksiya juft funksiya deyiladi,
Masalan, у = x2 va у = |x| funksiyalar juft funksiyalardir. Juft funksiya-
laming grafigi ordinatalar o‘qiga nisbatan simmetrik bo'ladi (41- rasm).
I Agar y(x) funksiyaning aniqlanish sohasidan olingan istalgan x uchun
y(—x) = ~y(x) tenglik o‘rinli bo‘lsa, bu funksiya toq funksiya deyiladi.
ЖЖ
жж
95
жж
жж
жж
зяте
жж
жж
жж
@ y‘ 8- 1- -2 -1 — y = x3
2 3 x -8
жж
1 1
Masalan, у = х\ у = х, у = -—, У = —
-* х
funksiyalar toq funksiyalardir. Ulaming grafigi koor-
dinata boshiga nisbatan simmetrikdir.
1-masala. y = x3 funksiyaning grafigi koordi-
nata boshiga nisbatan simmetrikligini isbotlang
(42-rasm).
□ 1) y=x3 uchun R to'plam aniqlanish sohasi.
2) y = x3 ning qiymatlari to'plami ham R
bo'ladi; bu qiymatlar x > 0 bo'lganda musbat, x < 0
bo'lganda manfiy va x = 0 da nolga teng.
Aytaylik, (Xq; y0) nuqta у = x3 ning grafigida yo-
tadi, ya’ni y0 = xo • (xo’ Уо> nuqtaga koordinata
boshiga nisbatan simmetrik bo'lgan nuqta
(—,Xq; —yQ) bo'ladi va u ham у = x3 ning grafigida
yotadi, chunki yQ = Xq dan -y0 = -Xq yoki
-y0 = (-До )3 helib chiqadi. О
2- masala, у = \[x funksiyaning grafigi koordinata boshi О (0;0)ga nisba-
tan simmetrik ekanini isbotlang (43-rasm).
жж
(x^, nuqtaga О (O;O)ga nisbatan simmetrik nuqta (——y0) boladi. Shu
nuqta у = tfx funksiya grafigidayotadi:-y0 = yoki -y0 = $-Xq . I
Juft va toq funksiyalaming aniqlanish sohasi koordinata boshiga nisbatan
simmetrik bocladi.
Juft ham, toq ham bo‘lmagan funksiyalar mavjud.
1
Masalan, у = 2x + 1, y = x + x2, —j- funksiyalar shular jumlasidandir.
Buni y=2x+ 1 funksiya uchun isbotlaylik: у(-x) = 2 • (-x)+1 = -2x+1,
ammo x > 0 bo‘lganda —2x + 1 2x + 1.
ЖЖ
жж
жж
298. Topshiriqlarni bajaring. Savollarga javob bering:
1) Juft funksiya ta’rifini ayting. Misollar keltiring.
(?) 2) Toq funksiya ta’rifini ayting. Misollar keltiring.
3) Qanday funksiyalaming grafigi ordinatalar o‘qiga nisbatan simmetrik
bo‘ladi?
4) Qanday funksiyalaming grafigi koordinata boshiga nisbatan simmetrik
bo'ladi?
5) Toq funksiyalar uchun koordinata boshiga nisbatan simmetrik nuq-
talaming koordinatalari qanday yoziladi?
6) Toq ham, juft ham bo‘lmagan funksiyalarga 1—2 ta misol keltiring.
жж
Funksiyaning juft yoki toqligini aniqlang (299—300):
299. 1) y = x\ 2)y = -x;
3)y=—x3;
ex 1
5) y = x + -.
300. 1) у = 2x + Зх3;
4) у = —x2 + 2;
2) У = Л;
x
5) У = $к| + 1-
3) у = х*;
Funksiya juft ham, toq ham emasligini ko‘rsating (301—302):
301. 1) у = x + x2; 2)y = x3-l; 3) y = Vx + x; 4)y = -^-j.
jc+2
302. 1) у = — 2x + x2; 2) у = x3 4- 2; 3) у = x 4- |x|; 4) у = .
x -1
Funksiyaning juft yoki toq bo‘lishini aniqlang (303—305):
303. 1) y = x24-3;
304. 1) y=—3x;
305. l)y = -5x;
2) y = x+^/x;
2) y = 5x2;
2) у = —2X3 — x;
3) j> = |x|+x4;
3)y = x3 + x;
3)y=3x2 + 2;
4) y = &.
4)у = 2хг— 3.
4)y=3|x| —4.
7—Algebra, 9
жж
97
жж
306*. 1) у = л?-3;
x2 x < 0*
4) y = f \X- ’
-x , x £ 0;
307*. 1) y = x2-2|x| + 1;
3) у = x2 + 2|x| + 1;
жж
жж
НЮТ
жж
жж
жж
жж
ЖЖ
Sinunetriyadan foydalanib juft funksiyaning grafigini chizing (306—307):
2) У = (И + 1)2;
3)y = (|x|-l)2;
x4 x < 0’
6)y= ’ ’
—x4, x £ 0.
2) у = x2 — 2|x|;
4) y = x2 + 2|x|.
308. Simmetriyadan foydalanib toq funksiyaning grafigini chizing:
1) y = x3 + x\ 2)y = ~2r, 3)y = 4x;
Funksiya grafigi eskizini chizing (309—310):
.. X
4) = ы
309. 1) y = -|x| + 3; 2)y=2x—3; 3)y = j2^x; 4)y = llx+4.
310. 1) y = 2|x| —1; 2)y = 2-3r, 3) y = V^2; 4)
311. Quyidagi toq ham emas, juft ham emas funksiyaning grafigini chizing:
1) y = |x| + x; 2)y = x2 — 2x; 3)y = x} — 2; 4)y = x2 + 2x.
к
21- §. y = - funksiya
Agar k=Q bo'lsa, y = 0, ya’ni absissa o'qining tenglamasi hosil bo'ladi.
Ko'rinadiki, к parametr noldan farqli bo'lgan hollami o'rganish lozim. Awal
1=1 bo'lganda У = “ funksiyani o'rganamiz.
1
1- masala, у = — funksiyaning grafigini chizing.
□ 1) Aniqlanish sohasi x^0, ya'ni noldan farqli barcha haqiqiy sonlar
to'plami;
2) у = — funksiya toq, chunki x Ф 0 da ~ _ “ 5
X —X X
3) funksiya x>0 bo'lganda kamayuvchi, chunki i = x"1, r =—1<0;
4) x > 0 bo'lganda — > 0 bo'ladi.
5) Funksiya grafigiga tegishli bir necha nuqtalami topamiz:
Shu nuqtalar yordamida grafikning eskizini chizamiz (44-a rasm.) So'ngra
x < 0 bo'lganda unga koordinata boshiga nisbatan simmetrik bo'lgan egri chi-
ziqni chizamiz. k=—1 bo'lgan hoi 44-b rasmda ko'rsatilgan. |
98
Ж
ЖЖ
ЖЖ
1
у - — funksiyaning grafigi giperbola deyiladi. U ikki qismdan iborat.
Ular giperbolaning tarmoqlari deb ataladi. Bittasi I chorakda, ikkinchisi
esa III chorakda joylashgan.
2 2
2- masala. У ~~ va У ~~~ funksiyalaming grafigini chizing.
□ у = i funksiya grafigini absissalar o‘qidan ordinatalar o‘qi bo‘ylab 2
2 2
baravar cho‘zish bilan у = — funksiya grafigi hosil qilinadi. у = - — funksiya
ЖЖ
grafigi esa у = — funksiya grafigiga Ox o‘qqa nisbatan simmetrikdir. H
ЖЖ
Л2Я5
жж
Umuman, к * 0 bo'lganda у = — funksiyaning grafigi ham giperbola deyi-
ladi. Giperbola 2 ta tarmoqqa ega. к > 0 da tarmoqlar I va III choraklarda,
к < 0 da —II va IV choraklarda joylashgan.
к
Endi к > 0 bo‘lganda у = — funksiyaning xossalarini keltiramiz:
к .
у = — fimksiya:
1) x^O da aniqlangan;
2) noldan boshqa barcha haqiqiy qiymatlami qabul qiladi;
3) toq;
4) x > 0 da musbat, x < 0 da manfiy;
5)x<0vax>0da kamayuvchi.
к
Agar к < 0 bo‘lsa, у = — funksiyaning xossalari quyidagicha bo‘ladi:
1, 2, 3- xossalar o'rinli, k>§ holdagi kabi; 4) xossa: x<0 da musbat,
x > 0 da manfiy; 5) xossa: x < 0 va x > 0 da o'suvchi.
ЖЖ
ЖЖ
IXXIZTXI
99
у - — funksiya к > 0 boclganda teskari
proporsional bog'lanishni ifoda etadi,
deyiladi. Bunday boglanish turli fanlarda
uchraydi. Fizikada v=y, bunda 5 —
berilgan musbat son (bosib o'tilgan
masofa), t — vaqt, v — tezlik;
iqtisodiyotda talab bilan narx orasida chiziqli
va chiziqsiz bog‘lanishlar bor. Agar x deb
narxni, у deb talabni belgilasak, ular
orasidagi bog‘lanishni у = +b kabi yozi-
lishi mumkin, bunda a > 0, b > 0. Agar
narx istalgancha ortib borsa, talab kama-
yib b ga yaqinlashadi. Inson uchun talab hamma vaqt bor va eng kam talab b
dan kam bo‘lmaydi.
3- masala, у = - 3 funksiya grafigini chizing.
□ у = i funksiya grafigini Ox o‘qi bo'ylab o'ngga 2 birlik, socngra Oy o‘qi
bo'ylab 3 birlik pastga suramiz. Natijada у =
(44-fif rasm). I
1
x-2
-3 funksiya grafigi hosil
bo'ladi
312. Topshiriqlarni bajaring. Savollarga javob bering:
1) To‘g‘ri proporsional, teskari proporsional miqdorlarga misollar kel-
tiring.
®2) у = i funksiya xossalarini ayting.
к
3) у = — {к < 0) funksiya xossalarini ayting.
4) у = i, у = ^(k*Q) funksiyalaming grafigi nima deb ataladi?
5) Giperbola nechta tarmoqqa ega?
к
6) у = —, к > 0 bo‘lganda tarmoqlar qaysi choraklarda yotadi?
к
7) у = —, к < 0 bo‘lganda tarmoqlar qaysi choraklarda yotadi?
3
313. у = — funksiya grafigini chizing. x ning qanday qiymatlarida:
100
1) у(х) = 6; 2) у(х) = --; 3)у(х) = 2; 4) у(х) = 4 bo'ladi?
4
314. у = — funksiya grafigini chizing. x ning qanday qiymatlarida 1) y(x) = 2;
2) y(x) = 4; 3) y(x) = 1; 4) y(x) = -2 bo'ladi?
2
315. У = ~— funksiya grafigini chizing. Agar: 1) x=l; 2) x=—1;
1 1
3) x = - -; 4) x = - bo'lsa, у ni toping.
4 1
316. У~~~ uiug grafigini chizing. Agar: 1) x=l; 2) x=2; 3) x = —;
4) x = —1 bo'lsa, у ni toping.
317. Funksiyalaming grafiklarini chizing. Kesishish nuqtalari koordinatalarini
toping:
2 3
1) у = - — va у = x — 3; 2) у = - va у = 4 - x;
2 12
3)y = — vay = x—1; 4) у = — va y=-x +7.
318. Funksiyalaming grafiklari kesishish nuqtalarini toping:
7 1
1) у = — va у = —x2 + 7x+1; 2)y = x2va y = -;
1 к
3) у = —x2 va у = -; 4) у = — va у = —x2 + kx + 1.
319. Funksiyaning grafigini chizing:
I) y = j-3; 2) y = f+2; I 3)y = -^-2; 4)y = ^-+l.
Л Л Л । J J Л
3
320. У = - bo'lsa, 1) x>l; 2) x>3; 3) x<—1; 4) x<—3 bo'lganda у
qanday tengsizlikni qanoatlantiradi?
4
321. y(x) = — funksiya uchun x ning qanday qiymatlarida quyidagi tengsiz-
liklar to‘g‘ri bo'ladi:
l)y(x)>2; 2)y(x)^-l; 3)y(x)^4; 4) y(x) > 5?
322. Funksiyalaming grafiklarini chizing. Kesishish nuqtalari koordinata-
larini toping:
3 -2
1) y = — vay=-x + 2; 2) у = — va y = x~3;
101
жж
жж
жж
жж
жж
кал
жж
жж
жж
жж
3) у = х~ 3 va у = 2х + 3; 4) y = 2xvay = — х + 3.
к
323. к ning qanday qiymatlarida у = — va у = kx chiziqlar o'zaro kesishadi?
Nechta nuqtada?
324*. a va A; ning qanday qiymatlarida у = vay = Ax chiziqlar kesishadi? Qanday
qiymatlarida o'zaro kesishmaydi?
4
*. a ning qanday qiymatlarida У = ~ va у = — x+ a chiziqlar o'zaro urinadi
(ya’ni bitta umumiy nuqtaga ega bo'ladi)?
326*. a va b ning qanday qiymatlarida y=ax2 — 1 va у = dx2, atb, parabolalar
o'zaro kesishmaydi?
22- §. Daraja qatnashgan tengsizlik va tenglamalar
Siz chiziqli va kvadrat tenglamalami, tengsizliklami yechishni bilasiz. Hozir
ratsional ko'rsatkichli daraja va darajali funksiya xossalaridan foydalanib, ba’zi
chiziqsiz tengsizliklar, tenglamalar va irratsional tenglamalami yechish
usullarini keltiramiz.
1- masala, x3 > 8 tengsizlikni yeching.
□ у = x? funksiya x ning barcha haqiqiy qiymatlarida aniqlangan va o'suvchL
y(2) = 8 bo'lgani uchun x > 2 bo'lganda y(x) >8 va x < 2 bo'lganda y(x) < 8.
Bundan x > 2 ekani kelib chiqadi.
Javob: x> 2.1
2- masala. x4 < 16 tengsizlikni yeching.
Пу “ / funksiyax< 0 bo'lganda kamayadi, x> 0 bo'lganda o'sadi. x4 = 16
tenglama 2 ta haqiqiy ildizga ega: xx = —2; x^ = 2. x4 < 16 tengsizlik x< 0 da
2<x<0 yechimlarga, x> 0 da 0 <x<2 yechimlarga ega.
Javob: —2<x<2. И
2 2 1
3- masala. Funksiyalaming grafiklari yordamida — = x +1 tenglamani
yeching.
2
□ Koordinatalar tekisligida У = ~ va у = x2 + 1 funksiyalaming grafigini
2 о
chizamiz (45- rasm). Chizmadan ko'rinadiki, x < 0 bo'lganda — = x +1 teng-
x
lama yechimga ega emas. x > 0 bo'lganda esa, u butta yechimga ega. Bu yechim
у = % va у = x2 + 1 funksiyalaming yagona kesishish nuqtasining absissasidan
iborat. Rasmdan ko'rinib turibdiki, x = 1. Tenglama boshqa musbat yechimlarga
102
жж
Ж
жж
жж
2
ega emas, chunki x > 1 bo‘lganda у = —
x
kamayadi, у = x2 + 1 esa o‘sadi.
Demak, grafiklar x > 1 da kesishmay-
di.
Javob: x = 1.1
Endi daraja qatnashgan irratsional
tenglamalami yechish usullarini kel-
tiramiz.
4- masala, л/8-х2 = x (1) tengla-
mani yeching.
□ 1- usul. Awal tenglamaning
aniqlanish sohasini (x ning tenglama
ma’noga ega bo‘ladigan qiymatlarini)
topamiz. Ravshanki, 8 — x2 > 0 yoki
8 > x2; |x| < 2y/2 , ya’ni -2V2 < x < 2V2. Ikkinchi tomondan, 7s-x2 ning
arifmetik qiymati nomanfiy bo‘lgani uchun tenglamaning o‘ng tomoni x uchun
x>0 tengsizlik o‘rinli boTishi kerak. Demak, tenglamaning aniqlanish sohasi
0 < x 2V2 bo‘ladi. Endi tenglamaning ikkala tomonini kvadratga oshiramiz:
8 — x2 = x2, ya’ni x2 = 4. Bundan Xj 2 = ±2 kelib chiqadi. Ammo x^ = —2 son
[0; 2V2 ] ga tegishli emas. Demak, javob*, x = 2 bo‘ladi. |
2- usul (ildizlami tekshirish usuli). (1) ning ikkala qismini kvadratga os-
hirib, yana Xj 2 = ±2 ni hosil qilamiz. Har bir Xj = 2; x^ = —2 sonlami (1) ga
qo‘yib chiqamiz. Xj = 2 da >/8 -22 = >/4=2; o‘ng tomon ham 2 ga teng. De-
mak, xt = 2 yechim. Endi x2 = —2 ni qo£yamiz: - (-2)2 = >/8-4 =
= \/4 = 2, ammo o‘ng tomon —2 ga teng. Demak, Xj = -2 yechim emas. Shu
х^ = —2 son tenglamaning ikkala tomonini kvadratga oshirish natijasida paydo
bo‘lgan ,,chet“ (,,yot“) ildiz deb ataladi. Javob: x = 2.
Shunday qilib, 1- usulni qo‘llaganda awal tenglamaning aniqlanish sohasi
topiladi, socngra tenglamaning ikkala tomonini kvadratga oshirib, uni yechiladi.
Topilgan yechimlar ichidan aniqlanish sohaga tegishli bo'lgani olinadi.
2- usulda tenglamaning ikkala tomonini kvadratga ko‘tarish bilan hosil bo'lgan
tenglama yechilsa, berilgan tenglamaning chet ildizlari paydo bo'lishi mumkin.
Shuning uchun tekshirish o‘tkazish lozim bo‘ladi.
5- masala. V2 -x = 4 + x tenglamani yeching.
□ Tenglamaning ikkala tomonini kvadratga ko‘taramiz: 2 - x = 16 + 8x + x2
103
жж
жж
жж
жж
жж
yoki х2 + 9х +14 = 0, bundan xt = —2; = —7. xr = —2 soni tenglamani to‘g‘ri
tenglikka aylantiradi: >/2 - (-2) = \/4 = 2; 4 + (—2) = 2. = —7 esa chet ildiz,
chunk! y/2 - (-7) = V2 + 7 = 5/9 = 3; 4 + (-7) = —3. Javob: x = —2.0
6- masala. V2x-3 > 7x + 6 tengsizlikni yeching.
П Tengsizlikning aniqlanish sohasi x > 1,5. Tengsizlikning ikkala qismini
kvadratga oshiramiz: 2x—3>x+6, bundan x>9. Javob: x>9.1
7- masala. x/2x + l < x/Зх-б tengsizlikni yeching.
П Tengsizlikning ikkala qismini kubga oshiramiz: 2x+l<3x-6, bundan
x>7. Javob: x>7.1
жж
327. Topshiriqlami bajaring. Savollaiga javob bering:
1) Daraja qatnashgan tengsizlikka misollar keltiring va ulami yeching.
2) Daraja qatnashgan tenglamaga misollar keltiring va ulami yeching.
3) Chet (yot) ildiz nima? Uning paydo bo'lishiga sabab nima?
4) Irratsional tenglamalami yechishning qanday usullarini bilasiz? Mi-
sollar keltiring.
Tengsizlikni yeching (328—330):
328. 1) r® < 16; 2) x5 > 1;
4) 4x > x; 5) Vx + 1 >2;
329. 1) x2>9; 2) x3 > 8;
4) 4x < x; 5) Vx-1<2;
330. 1) 7x^2 < 3;
3) ^<16;
6) V2x + 3<7.
3) x*<64;
6) \/3xT7>4.
3) >/3x + 4 < >/x +13;
2) л/Зх-2 >5;
4) V3x -1 £ у)х - 7.
331. 1) Agar to‘g‘ri to‘rtburchakning yuzi 40 sm2, bo‘yi a < 10 sm bo‘lsa,
eni b qanday bo'lishi mumkin?
2) Agar kubning hajmi 216 sm3 dan kichik bo'lsa, uning qirrasi a qan-
day bo‘lishi mumkin?
332. 1) Agar kvadratning yuzi 16 sm2 dan kam bo'lsa, uning tomoni qanday
bo'lishi mumkin?
2) Agar kubning qirrasi 4 sm dan katta bo'lsa, uning hajmi qanday
boclishi mumkin?
333. (Og'zaki.) 5 soni tenglamaning ildizi ekanini ko'rsating.
1) 7x^1 = 2; 2) -7x+"4 - V3x -14 = 2.
334. (Og‘zakL) 7 soni tenglamaning ildizi ekanini ko'rsating:
1) Vx + 9=4; 2) 4х^3-4х^1 = 2-
104
335. (Og‘zaki.) 3 soni tenglamaning ildizi ekanini ko‘rsating:
1) Vx + 6 =3; 2) Vx-2 + Vx + l = 3.
Tenglamani yeching (336—339):
ЖЖ
жж
336. 1) Vx = 4; 2) 4x = 5; 3) Vx-2 =0; 4) V2x + 1 =0.
337. 1) -Ух-1=3; 2) \lx +1 = 4; 3) V2-3x = 4; 4) V2x + 1 =3.
338. 1) 7х + 1 =2; 2) 7x-1=4; 3) 73x - 5 = 4; 4) 72x-3 =3.
339. 1) Vx-l = V2x -6; 2) y/x + 2 = V3x - 2;
3) у/х2 +1 = V3x; 4) 7x2+16 =V7x + 4.
Tenglamani yeching (340—342):
340. 1) Vx + 7 = \/2х + 5; 2) Vx-2=V10-.
3) Vx2 + 4 = л/5х; 4) Jx2-8 = y/2x.
341. 1) V-x + 6 = x; 2) y/5x - 4 = x;
3) 725-X2 =2x; 4) ф)}4-х2 =3x.
342*. 1) 7x2+2x-6 = 6 - x; 2) Vx2 + x - 6 = x -i.
Tengsizlikni yeching (343—345):
343. 1) (x+ I)3 > 1; 2) (x- I)3 <8;
3) y/2 — x < x; 4) Vx + 3 < x + 1.
344. 1) (x-1)3 >±; | 2) (2x +1)3 > 8; 1 3) Vx + 2 <2; | 4) V3 - x < 4.
2) y/x + 1 < >/2x-l;
жж
ЖЖ
жж
ЖЖ
ЖЖ
345. 1) л/х + 2 < $3x -4;
3) >/3x -2 > \/2x + 3;
4) л/2х-1 > у/5 + х.
ЖЖ
23- §. IV bobga doir mashqlar
346. Funksiyaning aniqlanish sohasini toping:
1)
3
У ~ 2x+l
2) y = (2-5x)~2;
жж
105
IZTXIZTXI
3) y = Vx2-4; 4) у = Ц5^.
347. Funksiyaning aniqlanish sohasini toping:
1) y = 3T4; 2) y = (3x + 2)-2;
3) у = V(x + 2)(x-3); 4) у = \'3-2x.
348. у = Vx va у = х3 funksiyalaming ocsish yoki kamayish xossalaridan
foydalanib sonlami taqqoslang:
1) дДЛ va V3/7;
3) (—3)3 va (—5)3;
2)
4)
349. Funksiyaning o‘sish yoki kamayishi oraliqlarini toping:
i) y = 4; 2) у = 4; з) y=^/2T3; 4)y=-j=
x x Vx+1
350. Funksiyaning xossalarini aniqlang va uning grafigi eskizini chizing:
1) y = -|x4; 2) y = |x5; 3) y = 3№; 4) y=5ilx.
351. (Og‘zaki.) Agar: £=3; k= — 4 bo'lsa, у = — gipefbolaning tarmoqlari
x
qaysi choraklarda joylashgan?
352. Bitta koordinatalar sistemasida у = x va у = x3 funksiyalaming grafiklarmi
chizing. Shu grafiklar kesishish nuqtalarining koordinatalarini toping.
353. Funksiyalar kesishish nuqtalarining koordinatalarini toping:
1) У = х2; y = 5x3; 2) y = |;y = 2x;
3) y = |x|, y = x2-2; 4) y = $x,y = |.
354. Tengsizlikni yeching:
1) x3 < 27; 2) x4 > 16; 3) x6 > 64; 4) x5 < -243.
355. Tenglamani yeching:
1) V2^ = 3; 2) J4x + 4=6; 3)7зЛБ = 2х;
4) 73x2 + 5x-1 = Зх; | 5) V2x-3 =x-9; 6) V3 + x = x-9.
356. Tenglamani yeching:
1) V2 + x=l; 2) л/2х^1=3;
106
3) V2 - 7x = 2 - x;
4) 7x2 + x + 4 = 7 - x.
357. Funksiyaning juft yoki toqligini tekshiring:
1) y = 2x + 3x3; 2) y = x2+3|x|;
|x|+x4 . 9
3) У=х~’ 4) y = x'(x + 1>-
358. Funksiyaning o‘sish va kamayish oraliqlarini toping:
i)y = 4: 2)> = тЛз-; з)> = ^+2; 4)y=v=.
xz (x-2) \/x+l
359. Funksiyaning xossalarini aniqlang va uning grafigini chizing:
ill 1
1) У = т^'’ 2)y = 4; 3) y = —+ 1; 4) y = 2—L.
(x-3)z xJ x3 xL
жж
360. Tenglamani yeching:
1) V2x2+х-3 = Vx-1; 2) \llx2 - 4x + 2 = x + 4;
3) Vx + 19 = 1 + Vx; 4) \/7 - x + V3x -5=4.
361*. Tengsizlikni yeching:
1) Vx2 -8x < 3; 2) Vx2 -3x > 2;
3) >/3x-2 > x - 2; 4) V2x +1 > x -1.
Bu kabi tengsizliklami yechishda ushbu qoidalaiga rioya qilish tavsiya etiladi:
1. > a tengsizlik:
a) a > 0 bo‘lsa, /(x) > a2n ;
b) a < 0 boTsa, /(x) > 0 tengsizlikka teng kuchlidir.
2. < a tenglizlik:
/(x) > 0,
a) a>0bo‘lsa, < v \
l/(x) <
tengsizliklar sistemasiga teng kuchlidir.
жж
b) a < 0 bo‘lsa, berilgan tengsizlik yechimga ega emas (yechim. bo‘sh
tocplamdan iborat).
3. 2rtff(x) > <p(x) tengsizlik ushbu
<p(x)>0,
/(x)><f?”(x)
<p(x) < 0
_/(x)>0
ikkita
tengsizliklar sistemasining to‘plamiga teng kuchlidir.
жж
107
IZTXIZTXI
4. 2\lf(x) < <p(x) tengsizlik quyidagi
<p(x) > 0,
< f(x) Z 0,
/(x) < <р2й(х)
uchta tengsizlikdan tuzilgan sistemaga teng kuchlidir.
5. 2\lf(x) > 24jv(x) tengsizlik
/(x) > <p(x),
tp(x) > 0
tengsizliklar sistemasiga teng kuchlidir.
6. Tengsizliklaming ikkala qismini tengsizlik ishorasini o'zgartirmay, toq
darajaga ko'targanda hosil bo'lgan tengsizlik berilgan tengsizlikka teng kuchli
bo'ladi
1-misoL Tengsizlikni yeching: V7—2x > x - 2.
□ Bu xildagi tengsizliklaming yechimi tengsizlik о'ng qismidagi
<p(x) = x — 2 funksiya ishorasiga bog'liq. Shuning uchun ikkita holni qaraymiz:
1) x — 2^0;x — 2 < 0.
1-hol x - 2 > 0 bo'lsin. Agar 7 - 2x > 0 bo'lsa, berilgan tengsizlikning ikkala
qismi manfiy emas. Tengsizlik ikkala qismini kvadratga oshiramiz:
7—2x>(x-2)2
x-2>0
3-qoidaga ko'ra berilgan tengsizlik shu sistemaga teng kuchli.
Sistemaning 1-tengsizligidan (x - 3)(x +1)<0 tengsizlikni hosil qilamiz.
Demak, yuqoridagi sistema
(x-3)(x + l)<0
x 2
sistemaga keladi. 1 -holda javob: [2; 3) oraliqdan iborat.
2-hol. x - 2<0 bo'lsin. Bu holda berilgan tengsizlik x ning V7—2x ifoda
ma’noga ega bo'ladigan barcha qiymatlarida o'rinlidir. Demak, berilgan tengsizlik
ushbu
x-2<0,
‘ 7-2x>0
tengsizliklar sistemasiga teng kuchli. Bu sistemaning yechimi (—°°, 2)
oraliq ekani ravshan.
Ikkala javobning birlashmasi (-°°J 2) U [2; 3) ? ya’ni (—«©, 3) oraliq bo'ladi.
Javob: (—oo, 3). |
108
2-misol. л]х2 -Зх + 2 < 5-х tengsizlikni yeching.
Q 1-hoL 5—x > Obo‘lsin. Agar x2 - 3x + 2 > 0 bo‘lsa, tengsizlikning ikkala
qismi manfiy emas. U holda 4-qoidaga ko£ra, berilgan tengsizlik ushbu
жж
жж
5—x > 0,
- x2 - 3x + 2 > 0,
x2 - 3x + 2 < (5—x)2
жж
sistemaga teng kuchlidir.
Bundan
x < 5,
« (x — l)(x — 2) 0,
7x — 23 > 0
sistemaga kelamiz. Uning yechimi (-<»; 1) U [2; —).
2-hol. 5—x < 0 bo‘lsin. Kvadrat ildiz ostidagi ifoda manfiy bo‘lmasligi lozim.
Demak, bu holda yechim yo‘q. 1-holda olingan javob berilgan tengsizlikning
javobi bo‘laveradi.
23
Javob: (^o;l)U[2;y). |
3-misoL <j2x2 - 3x - 5 < ^x—1 tengsizlikni yeching.
Q 5-qoidaga muvofiq bu tengsizlik ushbu
2x2 - 3x - 5 < x -1,
2x2 - 3x - 5 0
tengsizliklar sistemasiga teng kuchli.
Bundan
(х-(1-Л))(х-(1+Л))<0,
(x + l)(x-2,5) > 0
sistemaga kelamiz. Uning yechimi [2,5; >/3 +1) oraliqdan iborat.
Javob: [2,5; V3 + 1) В
4-misol. 2л/2х + 1 > Зл/-х2-х + 6 tengsizlikni yeching.
□ 5-qoidaga muvofiq bu tengsizlik ushbu
жж
жж
жж
109
жж
ЖЖ
4(2х +1) > 9(-х2 - х + 6),
—х2 - х + 6 2 О
tengsizliklar sistemasiga teng kuchli.
Bundan
9л2 +17x-50>0,
,
x2 + x - 6 < 0,
жж
ya’ni
sistemaga kelamiz.
Л^(-17+^;2].
18
17+V 2089., -17+V 2089
+ —18—)(X-----18— >
(x + 3)(x - 2) <; 0
IV bobga doir sinov (test) mashqlari
1. Funksiyaning aniqlanish sohasini toping: у =
>/x2 - 3x + 2 .
жж
A) l<x<2;
C) x< — 1, x>2;
В) x< 1, x> 2;
D) -2<x<-l.
жж
жж
жж
жж
ЖДИ
2x-l
2. Funksiyaning aniqlanish sohasini toping: у = 4-.
v x+2
1 1
A) x<-2, x£^; B) x<-l,x>-;
z
C) -2<X<1; D)x>3;x<—3.
3. Quyidagi funksiyalaming qaysilari o‘suvchi?
1) у = -lx, l)y = --', 3) $c; 4) У = Vx-64.
A) Hanunasi; B) 1, 1, 4; С) 1, 3, 4; D) 2, 3, 4.
4. Quyidagi funksiyalaming qaysilari kamayuvchi?
1) У = -“т> 2)y = —4x+3; 3) y = x3-16; 4) у =
x
A) 2, 4; В) 1, 2; С) 3, 4; D) 2, 3.
5. Funksiyalaming qaysilari juft?
l)y = 2x + -; 2) у = x2 +3-|x|; 3)y = -2 + ^; 4)y = x2
x x
A) 2, 3; B)2, 4; C)l,4; D) 3, 4.
110
x.
X I NJ
6. Funksiyalaming qaysilari toq?
Y)y = kx\ 2)y = 3/x; 3)y=3x+5; 4)y = 2x?-7.
A) 1, 2; В) 1, 3; C) 2, 3; D) 3,4.
к
*. у = ax2 va у = — chiziqlar a va к ning qanday qiymatlarida (3; 2) nuqtada
x
kesishadi?
А) а = |,Л = 6;|В) в = -|,Л = 6;|С) a = 6; * = |;|D) a = 6,k = -j.
к
8 *. к ning qanday qiymatlarida у = — giperbola bilan у = 2x + 5 to'g'ri chiziq
ikkita nuqtada kesishadi?
A) k<- 3,125; | B) k< 3,125; |C) £>-3,125; | D) k= 3,125.
к
9. к ning qanday qiymatlarida у = — giperbola bilan у = 6 — x to'g'ri chiziq
bitta umumiy nuqtaga ega bo'ladi?
A) 10; B) -9; C) 8; D) 9.
к
10. Qanday к larda у = — giperbola va у = 3 — 2x to'g'ri chiziq kesishmaydi?
x
A) k = 9-- В) k<9--, C) k>-9--, D) k>9-.
_______о о о о
11. а/х2 - 8х + 5 = —х + 2 tenglamani yeching.
А) В) |; С) D) -1.
Т1
агав
жж
йети
жж
жж
жж
оо
жж
ретП
ЖЖ
12*. л/5 - х - а/х2 - 8х +15 0 tengsizlikning natural yechimlari yig'indisini
toping. A) 10; B) 11; C) 12; D) 13.
13.Tenglamaniyeching: a/x + -Jx - a/1 - x =1. A) 0,64; B) 0,5; C) 1,5; D) 0,36.
14.Tenglamaniyeching: y/x+Jx + ll +Jx-ylx-l =4. A) 5; B) 4; C) 6; D) 11.
15. Tengsizlikni yeching: 'llx - Зх2 < 5 — x. A) [0; 2]; B) (0; 2]; C) [0; 1); D) (1; 2).
16. Tengsizlikni yeching: Vx2 + 7x +12 > 6 — x.
111
ЖЖ1
5 12
А) х>1 —; В) х<-; С) х>1;
17. Tengsizlikni yeching:
Зх —1
2 — х
А) (0,75; 2) В) (1; 2);
С) (0; 2);
жж
жж
18. Tenglamani yeching: >/б-4х-х2 = х + 4.
А) -1 В) 1; С) 2;
D) yechimi yo‘q.
D) to‘g‘ri javob yo‘q.
D) -2.
19. Tenglamani yeching: J5 - 1 - х2 - 2.
жж
жж
A) 0; ±V2; B) 1; C) 2; D) 7з.
Ko ‘rsatma: 11 - x2| = 1 tenglamaga keling.
20. Tenglamani yeching: ^/5 + |x—2| = 1 - x.
A) -2; B) 2; C) -3; D) 1.
Ko "rsatma: Tenglamaning o‘ng qismi 1—x > 0, x < 1 ekanini hisobga oling.
жж
жж
жж
жж
Tarixiy ma’lumotlar
жж
жж
ЖЖ1
жж!
Abu Rayhon
Beruniy
(973-1048)
Yurtboshimiz LA. Karimov „Yuksak ma’naviyat—
yengilmas kuch“ asarlarida shunday yozadilar: „Milliy
tariximizning yana bir yorqin yulduzi Abu Rayhon Beruniy
faoliyatiga haqqoniy baho berar ekan, amerikalik fan
tarixchisi Sarton XI asmi „Beruniy asri“ deb ta’riflaydi.
Bunday yuksak va haqli baho awalo qomusiy tafakkur sohibi
bo‘lmish buyuk vatandoshimizning ilm-fan taraqqiyotiga
qo‘shgan beqiyos hissasi bilan izohlanadi“.
Buyuk qomusiy olim Abu Rayhon Beruniy ham ocz
asarlarida funksiya tushunchasidan, uning xossalaridan foy-
dalangan. Abu Rayhon Beruniy mashhur «Qonuni Ma’su-
diy» asarining 6-maqolasida aigument va funksiyaning
o'zgarish oraliqlari, funksiyaning ishoralari va eng katta,
eng kichik qiymatlarini ta’riflaydi.
«Funksiya» so‘zi lotincha «functio» so‘zidan olingan boflib, u «sodir
bo'lish», «bajarish» degan ma’noni bildiradi. Funksiyaning dastlabki ta’riflari
G.Leybnis (1646-1716), I.BemuHi (1667-1748), N.LLobachevskiy (1792-
1856) asarlarida berilgan.
Funksiyaning hoziigi ta’rifini bilishmasa-da, qadimgi olimlar o‘zgaruvchi
miqdoriar orasida funksional bog'lanish boelishi lozimligini tushunishgan.
112
To‘rt ming yildan awalroq Bobil olimlari radiusi r bo‘lgan doira yuzi
uchun — xatoligi sezilarli bo‘lsa-da — S = 3r* formulani chiqarishgan.
Sonning darajasi haqidagi ilk ma’lumotlar qadimgi bobilliklardan bizgacha yetib
kelgan bitiklarda mavjud. Xususan, ularda natural sonlaming kvadratlari, kublari
jadvallari berilgan.
Sonlaming kvadratlari, kublari jadvali, trigonometrikjadvallar, kvadrat ildizlar
jadvali miqdorlar orasidagi bog‘lanishning jadval usulida berilishi, xolos.
Murakkabroq masalalar
Funksiyaning aniqlanish sohasini toping (1—3):
1. 1) У =
x2 -7x +10
2. 1) У =
x -7
x2 - x + 20
2) У =
—x2 - 5x + 6
x2 + 7x +10
x2 + Их + 24*
2) У = л/Зх + 4 -
L(2x2 + 5x + 2) ’
4. Parametr a ning kvadrat funksiya ko‘rsatilgan oraliqning birinchisida
kamayuvchi, ikkinchisida o‘suvchi boladigan qiymati mavjudmi:
1) у = (a + l)x2 + ax + 3, -«><x^2, x 2;
2) y = (a + l)x2 + (a-2)x + l, -oo<x^2, x^2?
2
5. Parametr a ning qanday qiymatlarida giperbola у = - va у = ax — 1
X
(a>—1) to‘g‘ri chiziq: 1) ikkita nuqtada kesishadi? 2) to‘g‘ri chiziq
giperbolaga urinadi; 3) kesishmaydi?
6. к va b ning qanday qiymatlarida у = kx + b to£g‘ri chiziq у = x2 parabolaga
ham, у = — giperbolaga ham urinadi?
x
7. Tengsizlikning butun yechimlari sonini va ulaming yig'indisini toping:
1) Vx-50 V100-x >0; 2) $3-x \l-2x2, +9x+5 >0.
Tenglamani yeching (8—9):
8. 1) 2a/x + 75-x = Vx + 21; 2) 2>/x + л/61-х = V8x + 1;
3) >/x2 - 9x + 24 - \/вх2 - 59x +149 = 5 - x.
9. 1) V4x2 + 9x + 5 - V2x2 + x -1 = Vx2 -1;
2) \l2x2 +2x + 3 - л/2х2 - 4x + 3 = x.
8—Algebra, 9 11 a
IZTXIXXl
V BOB TRIGONOMETRIYA ELEMENTLARI
24-§. Burchaklaming radian o'lchovi
Trigonometriya atamasi yunoncha „trigonos"— uchburchak, „metriya"—
o'lchash so'zlaridan tuzilgan bo‘lib, uchburchakni o‘lchash degan ma’noni
anglatadi. Burchak, markaziy burchak tushunchalari sizlarga geometriya
darslaridan ma’lum.
Tekislikda О nuqta va undan chiqqan OA hamda OB nurlami chizaylik.
Bu nurlar tekislikni 2 bolakka ajratadi (46-д rasm). AOB burchak deyilganda
tekislikning OA numi soat milining yo'nalishiga qarshi yo'nalishda (musbat
yo'nalishda) to OB nur bilan ustma-ust tushguncha burganimizda hosil
qilingan bo'lagini tushunamiz (46-£ rasm). Shu burchakni graduslarda yoki
radianlarda o'lchash mumkin. OP radius (46-J rasm) musbat yo'nalishda
burilib yana OP holatga kelsa, u 360° li burchakni chizgan bo'ladi.
I Uzunligi aylana radiusiga teng bo‘lgan yoyga tiralgan markaziy burchak
miqdori 1 radian deyiladi.
U holda 1 radian burchak uzunligi R ga teng yoyni tortib turadi, deymiz.
Radian so'zini, qisqacha, rad kabi yozamiz. 1 rad burchakning gradus
o£lchovini topaylik. Ravshanki, 90° li markaziy burchak uzunligi (chorak
aylana) bo'lgan yoyni tortib turadi. Demak, uzunligi R bo'lgan yoyni
90°: burchak tortib turadi, ya’ni 1 rad burchakka yoy mos keladi.
2 7Г
Buni quyidagicha yozamiz:
i л 180°
Irad---------
7Г
я « 3,14 bo'lgani uchun 1 rad burchakning gradus o'lchovi taqriban
57,3° ga mos keladi, ya’ni 1 rad - 57,3°. Endi a rad ga teng yoyni tortib turgan
burchakning gradus o'lchovini topish oson:
180°
a rad ~-----a.
n
(1)
114
1-masala. 1) л rad; 2) jtad; 3) ^rad; 4) -^rad ga mos burchakning
gradus o'lchovini toping.
180?
□ (1) formula bo'yicha л rad-----л = 180°, demak, л rad-180°. Shunga
л
o'xshash, yrad~90°, rad-45°, ^rad~135° boTadi. M
л rad -180° dan 1°~-^—rad
lol)
munosabat kelib chiqadi. Demak,
жж
<x°~ • a rad (2)
180
formulani yoza olamiz.
2-masala. 1) 45° ga teng burchakning; 2) 15° ga teng burchakning
radian o'lchovini toping.
О (2) formula bo'yicha:
1) 45°- ——• - 45 rad = —rad, ya ni 45 ~ .
180 4 4
2) 15°~ -15 rad = -^-rad. О
7 180 12 “
Quyidagi jadvalda tez-tez uchraydigan burchaklaming gradus o‘lchovlariga
mos radian olchovlari berilgan:
жж
жж
жж
жж
0° 30° 45° 60° 90’ 120° 135е 180°
0 л 6 л 4 л 3 л 2 2л т Зл т л
ЖЖ
Burchak radian o‘lchovi bilan berilsa, sonning o‘zi yoziladi, rad belgisi
yozilmaydi.
1 radian burchak uzunligi R radiusga teng yoyni tortib turgani uchun
a radian burchak
l=uR (3)
uzunlikdagi yoyni tortib turadi. Masalan, a = bo‘lsa, I = R, a =
bo‘lsa, I = у R va a = 2л bo‘lsa, I = 2nR, ya’ni 2л rad burchakka butun
aylana uzunligi mos keladl
3-masala. Shahar kurantlari minut milining uchi radiusi l?=0,8 m
bo‘lgan aylana bo‘ylab harakat qiladi. Bu milning uchi 20 minut davomida
qancha yo‘lni (yoyni) bosib o‘tadi?
жж
жж
115
1ХГХ1ХХ1
Ж
ж
ж
ж
ЕИ
жж
ж
от
жж
ЗИЕИ
ЖЖ
О Soat mill 20 minut davomida -у radianga teng burchakka buriladi. (3)
2tc
formula bo'yicha a = — bo'lganda I ni hisoblaymiz:
2л 2-3,14
I = —R « —-—0,8m ~ 1,7m.
3 3
Javob: 1,7 m. H
(3) formulada R = 1 bo'lsa, yoy uzunligi shu yoyga tiralgan markaziy
burchak kattaligiga teng bo'ladi, ya’ni 1= a. / = у bo'lsa, markaziy burchak
to'g'ri burchak bo'ladi.
4-masala. Agar radiusi R bo'lgan doiraviy sektor a radian burchakka ega
bo'lsa, shu sektoming yuzi
c r2
formula bilan hisoblanishini isbotlang, bunda 0 < a < n.
i—i
□ Ravshanki, л rad li doiraviy sektor (yarim doira) yuzi ga teng.
R^
1 rad li sektoming yuzi esa -y— : n = — bo'ladi. Bundan a rad li sektoming
yuzi ekani kelib chiqadi. И
362. Savollaiga javob bering. Topshiriqlami bajaring:
1) Burchak deb nimaga aytiladi?
2) Burchakning gradus o'lchovi nima?
3) Markaziy burchak deb nimaga aytiladi?
4) 1 rad burchak nima?
5) a rad burchakning gradus o'lchovi uchun formulani yozing.
6) a burchakning radian o'lchovi uchun formulani keltiring.
жж
ж
363. Graduslarda ifodalangan burchakning radian o'lchovini toping:
1) 50°; 2) 70°; 3) 100°; 4) 120°; 5) 15°; 6) 35°.
364. Graduslarda ifodalangan burchakning radian o'lchovini toping.
1) 60°; 2) 80”; 3) 95’; 4) 115°; 5) 25°; 6) 55°.
365. Radianlarda ifodalangan burchakning gradus o'lchovini toping:
1) P 2) 3) y; 4) 4; 5) 2,5; 6) 0,49.
116
ИЖ
гаи
366. Radianlarda ifodalangan burchakning gradus o'lchovini toping:
1) 2) y; 3) y; 4) 3; 5) 2; 6) 0,5.
367. Sonni 0,01 gacha aniqlikda yozing:
1) f; 2) 3) y; 4) 3л; 5) у; 6) у.
368. Sonlami taqqoslang:
1) у va 1,5; 2) у va 1,3; 3) я va з|; 4) -у va-1,6.
369. (Og‘zaki.) 1) Teng tomonli uchburchak; 2) teng yonli to'g'ri burchakli
uchburchak; 3) kvadrat; 4) muntazam oltiburchak burchaklarining
gradus va radian o'lchovlarini aniqlang.
370. Aylananing 0,9 rad ga teng markaziy burchak tiralgan yoyining uzunligi
0,49 m bo‘lsa, aylana radiusini toping.
371. Agar (3) formulada:
1) J? =1,5; Z=3; 2) Я = 3,2; Z=4 bo'lsa, a ni toping.
Зтс
372. Agar: 1) a = —, 7?=1; 2) а = я, 2?=1 bo'lsa, mos doiraviy sektor
yuzi S ni toping.
жж
жж
жж
жж
жж
373. Agar: 1) a = -^, A=l;2)a=^, R=1 bo'lsa, mos doiraviy sektor
о 2
yuzi S ni toping.
374. Agar: 1) J? = 2,5; 5=6,25; 2) /? = 3; 5=18 bo'lsa, doiraviy sektor
yoyi tortib turgan burchakni toping.
375. Agar: 1) jR = 3,5; 5=7,4; 2) U = 4; 5=8 bo'lsa, doiraviy sektor
yoyi tortib turgan burchakni toping.
25-§. Nuqtani koordinatalar boshi atrofida burish
жж
Koordinatalar tekisligida radiusi 1 ga teng va markazi koordinata boshida
bo'lgan aylana chizamiz. Aylananing nuqtasini koordinata boshi atrofida а
radian burchakka burish tushuncbasi quyidagicha kiritiladi.
1. Awal a>0 bo'lsin. Bu holda P (l;0) nuqta birlik aylana bo'ylab
musbat yo'nalishda (soat mili yo'nalishiga qarama-qarshi) harakat qilib, а
uzunlikdagi yoyni bosib o'tadi va biror M nuqtaga keladi. Bu jarayon nuqtani
koordinata boshi atrofida а > 0 radian burchakka burish deb ataladi (47-a
rasm).
117
жж
жж
1ХГХ1ХХ1
жж
жж
ЖЖ
жж
2. Agar а<0 bo'lsa, Р (1;0) nuqta birlik aylana bo‘ylab manfiy
yo‘nalishda harakat qiladi va |oc| uzunlikdagi yoyni bosib o'tadi hamda biror
N nuqtaga keladi (47-й rasm).
жж
жж
жж
жж
жж
жж
жж
ЖЖ
Misollar:
1) Д1;0) nuqta rad burchakka burilsa,
u (0; 1) nuqtaga keladi (48-1 rasm).
2) Д1;0) nuqta -y rad burchakka burilsa,
u (0; —1) nuqtaga o‘tadi (48-2 rasm).
3) Д1; 0) nuqta у rad yoki rad
burchakka burilsa, u har ikki holda ham (0;
—1) nuqtaga o‘tadi (48-3 rasm).
Geometriyada, asosan 0° dan 180° gacha
bo‘lgan burchaklar qaralgan. Birlik aylana
nuqtalarini koordinatalar boshi atrofida
burishdan foydalanib, 180° dan katta
burchaklarni, shuningdek, manfiy bur-
chaklami ham qarash mumkin. Burish bur-
chagini graduslarda ham, radianlarda ham bersa
bo'ladi. Masalan, P (1; 0) nuqtani bur-
chakka burish uni 270° ga burishni bildi-
radi; burchakka burish —90° ga bu-
rishdir.
Ba’zi burchaklarni burishning radian va
gradus o‘lchovlari jadvalini keltiramiz (48-
rasm).
118
ЯМ
Д1; 0) nuqtani 2л ga, ya’ni 360° ga
burishda nuqta dastlabki holatiga qaytishini
ta’kidlab o'tamiz (jadvalga qarang). Shu nuqtani
—2л ga, ya’ni —360° ga burishda u yana
dastlabki holatiga qaytadi.
Nuqtani 2л dan katta burchakka va —2л dan
kichik burchakka burishga oid misollar
qaraymiz. Masalan, P(l;0) nuqtani
= 2 • 2я + у burchakka burishda nuqta soat
MM
mill harakatiga qarama-qarshi ikkita to'la aylanadi va yana yo'lni bosib
o'tadi, natijada (0;l) nuqta hosil bo'ladi (49-a rasm).
P(l;0) nuqtani-Д^ =-2-2лburchakka burishda nuqta soat mili
harakati yo'nalishida ikkita to'la aylanadi va yana shu yo'nalishda yo'lni
bosadi, natijada (0;—1) nuqta hosil bo'ladi (49-Z> rasm).
P(l; 0) nuqtani burchakka burishda j burchakka burishdagi nuq-
taning ayni o‘zi hosil bo'lishini ta’kidlaymiz (49-a rasm). burchakka
burishda esa - j burchakka burishdagi nuqtaning ayni o'zi hosil bo'ladi (49-
b rasm).
Umuman, agar а = а0 + 2л£ (bunda к — butun son) bo'lsa, u holda
a burchakka burishda cc0 burchakka burishdagi nuqtaning ayni o'zi hosil
bo'ladi (50-a rasm).
Shunday qilib, har bir haqiqiy a songa birlik aylananing (1; 0) nuq-
tasini a rad burchakka burish bilan hosil qilinadigan birgina nuqtasi mos
keladi.
Biroq, birlik aylananing ayni bir M nuqtasiga (P(l; 0) nuqtani burishda
M nuqta hosil bo'ladigan) cheksiz ko‘p а + 2лк haqiqiy sonlar mos
keladi, к — butun son (5Q-b rasm).
1-masala. P (1; 0) nuqtani: 1) 7л; 2) burchakka burishdan hosil
bo'lgan nuqtaning koordinatalarini toping.
□ 1) 7л = л + 2л • 3 bo'lgani uchun 7л ga burishda л ga burishdagi
nuqtaning o'zi, ya’ni (—1; 0) nuqta hosil bo'ladi. 2) = -^-2л bo'lgani
5л
uchun ga burishda ga burishdagi nuqtaning o'zi, ya’ni (0; -1)
nuqta hosil bo'ladi. |
119
MM
MM
MM
яии
MM
MM
MM
MM
2-masala. M
nuqtani hosil
P(l; Q) r
Ж
ж
ВИ
Ж
жж
впвп
ж
ВИ
жж
ВИВИ
ж
Ж
ВИ
2’ 2
qilish uchun Д1; 0) nuqtani burish kerak
bo‘lgan barcha burchaklarni yozing.
□ 51-rasmdaANOM — to‘g‘ri burchakli
nzlaNOM = j. Д1; 0) nuqtani burishda M
nuqta hosil bo‘ladigan barcha burchaklar
j + 2ti;£ kabi yoziladi, bunda istalgan
376.
butun son. Javob: у + 2л£. Q
Savollarga javob bering:
1) Aylana va birlik aylana deb nimaga aytiladi?
2) Birlik aylanadagi nuqtani koordinata boshi atrofida a radian burchakka
burish deganda nimani tushunasiz?
3) <x>0 bo‘lganda burish qanday bajariladi?
4) a<0 bo‘lganda burish qanday bajariladi?
120
ЖЖ
жж
377. Birlik aylananing Д1; 0) nuqtasini:
1) 45’; 2) yj 3) 60’; 4) -л; 5) 240’; 6) y; 7) -y
burchakka burish natijasida hosil bo'lgan nuqta koordinatalarini toping.
378. Birlik aylananing Д1; 0) nuqtasini:
1) 30";|2)—y|3) -60’; |4) у; 15)-135"; |б) Зл; | 7) -у
burchakka burish natijasida hosil bo'lgan nuqta koordinatalarini toping.
379. Birlik aylanada Д1; 0) nuqtani:
1) у 2) -y 3) y; 4) -y; 5) у + я; 6) -|+4я
burchakka burish natijasida hosil bo'lgan nuqta koordinatalarini toping.
380. Birlik aylanada P(l; 0) nuqtani:
1 X ZXX *XX . JX 2Л —. Л x’» ЗЛ q
I) 4’ 2) — —, 3) 4) - —, $) 2~Л’ 4+8^
burchakka burish natijasida hosil bo'lgan nuqta koordinatalarini toping.
381. Д1; 0) nuqtani:
1) 2,Зя; 2) 2-|л; 3) -у! 4) -yS 5) 730’; 6) 400’
burchakka burish natijasida hosil bo'lgan nuqta qaysi chorakda joylash-
gan bo'ladi?
382. Д1; 0) nuqtani:
1) 3,6л; 12) 1,6л; |3) -у; |4) -yy; 15) 700’;|б) 500’;|7) 840"
burchakka burish natijasida hosil bo'lgan nuqta qaysi chorakda joylashgan
bo'ladi?
383. Д1; 0) nuqtani berilgan:
1) 2;|2) 1,5;|3) 3,07;|4) 4,56;15) -1;16) я-1;|7) 3,14
radian burchakka burish natijasida hosil bo'lgan nuqta joylashgan koordina-
talar choragini ko'rsating.
384. Birlik aylanada P(l; 0) nuqtani:
1) 5±2л; 2) ^±2я; 3) у±4я; 4) -у + 6я;
5) 3,5я; 6) 4,5л; 7) -4л; 8) -9л
burchakka burish natijasida hosil bo'lgan nuqtani belgilang.
121
ЖЖ
ЛЕИ
жж
жж
жж
жж
жж
жж
жж
зек
жж
жж
жж
жж
1ХТХ1ХтЧ1
385. Д1; 0) nuqtani:
1) -y + 2rat; 2) у + 2л*г; 3) у + 2лЛ; 4) -у + 2лЛ
burchakka (bunda £—butun son) burishdan hosil boclgan nuqtaning
koordinatalarini toping.
386. Д1; 0) nuqtani:
1) у + 2лк; 2) -у + 2л£; 3) -у + 2лк; 4) --^ + 2тск
burchakka (bunda butun son) burishdan hosil bo'lgan nuqtaning
koordinatalarini toping.
387. 1) (—1; 0); 2) (1; 0); 3) (0; 1); 4) (0; —1) nuqtalami hosil qilish
uchun Д1; 0) nuqtani burish kerak boclgan barcha burchaklarni
yozing.
hosil qilish uchun P(l; 0) nuqtani burish kerak bo‘lgan barcha
burchaklarni yozing.
26-§. Burchakning sinusi, kosinusi, tangensi va
kotangensi ta’riflari
Burchakning sinusi, kosinusi, tangensi va kotangensi ta’riflarini
nuqtani koordinatalar boshi atrofida burish tushunchasi yordamida ki-
ritamiz
1-ta’rif. a burchakning sinusi deb
P(l; 0) nuqtani koordinatalar boshi
atrofida a burchakka burish natija-
sida hosil bo‘lgan nuqtaning or-
dinatasiga aytiladi va sina kabi bel-
gilanadi (52-rasm),
P(1; 0)
2-ta’rif. a burchakning kosinusi deb
P(l; 0) nuqtani koordinatalar boshi
atrofida a burchakka burish natijasida
hosil boHgan nuqtaning abssissasiga --------------------------------
aytiladi va cosa kabi belgilanadi (52-rasm).
a burchak graduslarda ham, radianlarda ham ofichanishi mumkin.
Agar a°—burchakning gradus olchovi, a — shu burchakning radian
o'lchovi bo‘lsa,
sina0 = sin a, cosa0 = cos a
tengliklar o'rinli bofiadi.
122
жж
жж
тс
Agar Д1; 0) nuqta - burchakka, ya’ni 90° ga buiilsa, u nuqta (0; 1)
nuqtaga o'tadi. (0; 1) nuqtaning ordinatasi 1 ga teng. Shuning uchun
sin | = sin 90° = 1,
bu nuqtaning abssissasi esa 0 ga teng, shuning uchun cos^ = cos 90° = 0.
• 7Г ♦ 1
Shunga o'xshash sin - = sin 30° = -, cos л - cos 180° = -1
о 2
tengliklami ham isbotlash mumkin.
1-masala. sin (-л) va cos (-л) ni toping.
О (1; 0) nuqtani -it burchakka buiganda u (—1; 0) nuqtaga o'tadi.
Shuning uchun sin(-n)=0, cos(-n)=-l. О
2-masala. sin 270° va cos 270° ni toping.
О (1; 0) nuqtani 270° ga buiganda u (0; —1) nuqtaga o'tadi. Shuning
uchun cos 270” = 0, sin 270’ = —1. О
3-masala. sin x = 0 tenglamani yeching.
□ Bu tenglamani yechish sinusi nolga teng bo'lgan barcha burchaklami
topish demakdir. Birlik aylanada ordinatasi nolga teng bo'lgan nuqtalar
2 ta: (1; 0) va (-1; 0). Bu nuqtalar (1; 0) nuqtani 0, л, 2л, 3л va hokazo,
shuningdek, -л, -2л, -3л va hokazo burchaklarga burish natijasida hosil
qilinadi. Bundan x= kit (fc—istalgan butun son) bo'lganda sinx = 0 bo'lishi
kelib chiqadi, ya’ni sin(£u)=0, keZ, Z bilan butun sonlar to'plami
belgilangan. Demak, x = kn, keZ |
4-masala. cosx = 0 tenglamani yeching.
□ Birlik aylanada abssissasi nolga teng bo'lgan 2 ta nuqta bor: (0; 1) va
(0; -1). Bu nuqtalar (0; 1) nuqtani у’у + я>у + 2я, ... shuningdek,
| - л, | - 2л, ... burchaklarga, ya’ni + kit, к g Z burchaklarga burish
natijasida hosil qilinadi. Demak, x = + kit, к e Z. Ц
5-masala. Tenglamani yeching: 1) sinx= 1; 2) cosx=l.
□ 1) Birlik aylanada ordinatasi 1 ga teng bo'lgan yagona (0; 1) nuqta
bor. Bu nuqta (1; 0) nuqtani ^ + 2л£, keR burchakka burish bilan hosil
qilinadi. Demak, x = j + 2яА;, kt Z.
2) Birlik aylanada abssissasi 1 ga teng bo'lgan yagona (1; 0) nuqta bor.
Demak, x = 2л£, к e Z. О
123
ЖЖ
ЛИИ
жж
жж
жж
жж
жж
жж
жж
жж
жж
жж
жж
жж
жж
1ХТХ1ХтЧ1
Ж
жж
жж
жж
Javob', 1) х = у + 2лЯ; 2) х = 2пк, ке Z.
3-ta’rif. a burchakning tangensi deb a burchak sinusining uning
kosinusiga nisbatiga aytiladi va tga kabi belgilanadi:
. sin a
tga =------.
cos a
жж
я V2
- n sm— —
,, , smO О л . л 4 2 1
Masalan, tgO° = —— = - = 0; tg- = —- = —= 1;
cosO° I 4 я V2
l/Uo“ —
4 2
• я Л
sm- _
, Л 3 2
tg- = —i = 4- = V3.
cos-
3
• Я 1
sm ± .
л = £ = _2_ = X
6 n Л л/з
cos- — v
6 2
£
2
жж
жж
жж
ЖЖ
жж
жж
жж
жж
XXIZTXI
4-ta’rif. a burchakning kotangensi deb
cosot
ga aytiladi va ctga kabi
belgilanadi.
Masalan
я
cos 1
, Л 4 1
etg- = —- = —
4 я .я
sin— tg
4 4
. cosa
ctga = ——.
sma
ctg9o° = = т = o;
sin 90° 1
ctg270° = C0S^°° = 4 = °;
sin 270’ -1
я 1
< „ cos- -
1 = 1- Ctg—=____3. = i = _ = _.
1 ’ 3 я Л Лз 3
1 J Sln_ 2_ MJ J
3 2
i V3
Sinus, kosinus, tangens, kotangenslaming 0° dan 360° gacha (0 dan
2л gacha) tez-tez uchrab turadigan qiymatlari jadvalini keltiramiz:
a 0 (0*) ж 6 <30‘) n 4 (45*) 3 (60*) 2 (90*) (18(f) Зя "5" (270') 2л (360*)
sina 0 £ dv •^5 ~2~ ^*3 "2" 1 0 — 1 0
cosa I 75 T 4i 2 2 0 -1 0 1
Iga 0 i “W» V3 1 mavjud emas 0 mavjud emas 0
ctga mavjud emas i 1 3 0 mavjud emas 0 mavjud etnas
124
6-masala. Hisoblang:
жж
жж
жж
жж
жж
О Jadvaldan foydalanamiz:
ry Л Л J Л ry try 1 try
2 • sin- + V3 cos - - tg - = 2 — + V3 - - V3 = —.
3 3 3 2 2 2
Agar har bir haqiqiy x songa sinx son mos keltirilsa, u holda haqiqiy
sonlar to‘plami R da у = sinx funksiya berilgan deyiladi. у = cosx, у = tgx
va у = ctgx funksiyalar ham shu kabi aniqlanadi. у = cosx funksiya R
to‘plamda aniqlangan, у = tgx funksiya x Ф + лк, к e Z, у = ctgx funksiya
esa x # nk, ke Z bo'lganda aniqlangan. у = sinx va у = cosx funksiyalaming
grafiklari 53- va 54-rasmlarda tasvirlangan.
у = sinx, у = cosx, y = tgx, у = ctgx funksiyalar asosiy trigonometrik
funksiyalar deyiladi.
Ulaming xossalari bilan litsey, kollejlaming matematika kursida tanishasiz.
389. Topshiriqni bajaring:
Ixtiyoriy a burchak uchun sina va cosa, tga va ctga ta’riflarini ayting.
Hisoblang (390-391):
390. 1) stay; 2) cos у; 3) tgy; 4) sta(-60°);
ЖЖ
жж
жж
125
1ХГХ1ХХ1
5)
cos
л ь
6 ’
6)
7)
cos(—225°);
ox 5л
8) sm—.
4
жж
391. 1)
. 4л
smT’
2)
4л
COST’
3)
. 4л
1-S ’
4)
sin(—135°);
ЖЖ
5)
cos(-150°);
6)
7)
cos210°;
8)
sin210°.
392. Agar:
ЖЖ
14 • V3
1) sma = —;
-Л
5) sm a =
2)
6)
1
sma = --;
-y/2
cos a = ;
3)
cos a = 1;
~ V2
7) cosa = —;
V3
4) cosa= —;
8) sina = —•
bo'lsa, birlik aylanada a burchakka mos keluvchi nuqtalami belgilang.
393. Agar:
жж
1)
4)
m 1
2) cosa = --;
.. 1
5) cosa = -;
y/2
3) since = —;
6) cosa = -l
жж
жж
1
sma = -;
7з
cos a = —
2
bo'lsa, birlik aylanada a burchakka mos keluvchi nuqtalami belgilang.
394. 1)
395. 1)
3)
396. 1)
Hisoblang (394-396):
. л . л
sm- + sm-;
3 4
4)
sin2rc-cos0;
2)
5)
. ( л
sm —
I 3
л
+ cos-;
sin я + sin 1,5гц
3) cos л-sin л;
6) cosO-cos^.
ЖЖ
tgn + sin л;
tg3rc + sin 5л;
2sm- + V2 cos--tg-;
6 6 3
л.
6’
. Л ] л
-tg- cos-;
3 J г
2)
tg0°-tg360°;
4)
2)
3)
Tenglamani yeching (397—398):
1) |sinx = 0; 2) 2cosx = 0;
4)
3)
cos Зл - tg 2 л.
4sin£ + 2tg£ + sin£-6tgb
6 4 4 4
Л л 1 , л
sm — cos--tg —.
6 3 4 4
2 — 2sinx = 0; 4) 2cosx —2 = 0.
1) sinx = -l; 2) cosx = -l; 3)sin2x = 0; 4) cos|x = l.
a ning berilgan qiymatida ifodaning qiymatini toping (399—400):
1) 2 cos a + VI sin a, bunda a = p
ИЖ
гаи
2) 2 sin a + л/2 cos a, bunda a = ?.
4
400. 1) cos3a-sin2a, bunda a = ^; 2) cos^ + sin^, a = л;
6 2 2
3) cos4a + sin2a, a = 4) sin3a-cosa, a =
4 4
401. Tenglamani yeching:
1) cos(x + rc) = -1; 2) sin|(x-l) = 0; 3) sin(x + u) = l.
жж
27-§. Masalalar yechish
402. 1) 0°, 15°, 30°, 45°, 54°, 60°, 90°, 135°, 180°, 270°, 330°, 360° li
burchaklaiga mos radian o‘lchovni toping va jadval tuzing.
2) 0, yL yL y, ?, я, y, у, 2л radian burchaklaiga
12 13 D 4 3 3 2 4 2
mos gradus o'lchovni toping. Mos jadval tuzing.
403. 1) Burchakning radian o'lchovini toping:
a) 72°; b) 153°; d) 198°; e) 207°; f) 89Г; j) 396°.
2) Burchakning gradus o'lchovini toping:
a) b) 0,45л; d) 0,65л; e) 0 v? j) 0,3л.
О о 5
404. 1) Aylana radiusi R bo'lsin. a radian burchak qanday uzunlikdagi yoyni
tortib turadi?
2) a radian burchak I uzunlikdagi yoyni tortib turadi. Aylana radiusini
toping.
3) Aylana radiusi R ga teng. I uzunlikdagi yoyni tortib turuvchi radian
burchakni toping.
жж
жж
жж
жж
жж
405. 1) Doiraning radiusi 4,5 sm ga teng, doiraviy sektoming yuzi esa 20,25 sm2 ga
teng. Shu doiraviy sektor yoyini tortib tuigan burchakni toping.
2) Doiraning radiusi 5 sm ga teng. Doiraviy sektor yoyini tortib tuigan
burchak 2 radianga teng. Doiraviy sektor yoyini toping.
3) Doiraviy sektor yoyini tortib tuigan burchak a radianga, sektor yuzi
esa 5 ga teng. Shu doira radiusini toping.
406. Sonlami taqqoslang:
1) л va a/10;
5) у va 1,6;
2) луа —;
6) у va 4,9;
3) 2л va 6,3;
7) -луа -3-;
7
4) луа 3 —;
7 50’
8)—у va—1,57.
жж
жж
127
1ХГХ1ХХ1
ж^бш
жж
407*. Tishli g‘ildirak bir marta tola aylanganda ikkinchi tishli g‘ildirak qarama-
qarshi yo'nalishda ikki marta tola aylanadi. Agar birmchi g‘ildirak:
1) 320°; 2) 700°; 3) 1800°; 4) 100°; 5) 180°; 6) 90° ga burilsa, ikkinchi
g‘ildirak necha gradusga buriladi?
408*. Tishli g‘ildirakda 90 ta tish bor. Bu g‘ildirak: 1) 15 ta; 2) 30 ta; 3) 60 ta;
4) 90 ta; 5) 270 ta „tishga burilsa", u necha radian burchakka burilgan
boladi?
жж
ЛИЯ
жж
жж
жж
409. G‘ildirak rad/s burchak tezlik bilan aylanyapti. Gcildirak: 1) 15 s;
6
2) 20 s; 3) 45 s; 4) 1 minutda qanday burchakka buriladi?
410. 1) Teng yonli tocg‘ri burchakli uchburchakning; 2) kvadratning; 3)
octkir burchagi 24° bo'lgan rombning; 4) muntazam oltiburchakning;
6) muntazam n-burchakning barcha burchaklarini radianlarda ifodalang.
411*. 1) Toshkent shahri 4Г32' shimoliy kenglikda joylashgan. Yer radiusi
o'rtacha 6375 km bolsa (5-sinf „Tabiiy geografiya" darsligiga qarang),
Toshkent ekvatordan qancha masofada
boladi?
(ZTO£=41O32', OT= OE= 6375 km
bolsa, ТЕ yoy uzunligini toping.)
(55-rasm).
2) Yer radiusi 6375 km bolsa, 1° И
markaziy burchakka mos keluvchi ekvator
yoyi uzunligini; 3) Yer ekvatori
uzunligini hisoblang. Natijalami 1 km aniqligida yaxlitlang.
412*. Mirzo Ulugcbek nomidagi Kitob Xalqaro kenglik stansiyasi 39° parallel-
da, Toshkent shahri esa 4Г32' shimoliy kenglikda joylashgan. Toshkent
va Kitob orasidagi masofani toping.
жж
413*. Soat mayatnigi („kapgiri") ning uzunligi 1 metr bo‘lib, u vertikal ho-
latdan 1 sekundda eng ko‘pi bilan 24° o‘ngga va
chapga „borib keladi". Mayatnik uchi bir sutkada
qancha masofani ,,bosib“ olarkin (56-rasm)?
□ ZAOC= ZBOC =24\ ХАОВ = 4Г,
cz4LB = Z deylik. 48° И burchakning radian
olchovi yy gateng.
4л 4 3,14 12,56 n ол/ jx
H=-ir=nr“0’84(rad)-
Darslikdagi 1= aR formulaga muvofiq, AB yoyning
uzunligi 1= 1-0,84 = 0,84 (m). Demak, soat
жж
128
ИЖ
гаи
,,kapgiri“ning uchi bir sekundda 0,84 metr masofani o'tadi. (0,42 m o'ngga,
0,42 m chapga, uAB = \jAC + uCB .)
1 sutka= 86400 sekund bo'lgani uchun:
86 400 0,84 = 72 576 (m) = 72,576 (km).
Javob: soat mayatnigining uchi 1 sutkada 72,576 km masofani o'tadi. |
жж
28-§. Sinus, kosinus, tangens va kotangensning ishoralari
1. Sinus va kosinusning ishoralari
жж
жж
Birinchi chorakda joylashgan nuqtalaming absissalari va ordinatalari
musbat. Shuning uchun 0 < a < j bo'lganda since > 0 va cosa > 0 bo'ladi
(57- a, b rasmlar). Ikkinchi chorakda joylashgan nuqtalar uchun ordinatalar
musbat, absissalar manfiy.
n
Shuning uchun - < a < л bo'lganda sina > 0, cosa < 0. Shunga o'xshash
жж
жж
л < a < — da sina < 0, cosa < 0 hamda — < a < 2л da sina < 0, cosa > 0
bo'ladi.
Agar (1; 0) nuqta birlik aylana bo'ylab manfiy yo'nalishda harakat qilsa,
sina va cosa laming ishoralari nuqta qaysi chorakda joylashganiga qarab
aniqlanadi.
ЖЖ
1-masala. Quyidagi: 1) —; 2) 410°; 3) ——
burchaklar uchun sinus va kosinuslaming ishoralarini aniqlang.
__। 2л
□ 1) P (l;0) nuqtani — burchakka burganda unga aylananing ikkinchi
2л 2л
choragida joylashgan nuqta mos keladi. Demak, sin — > 0, cos — < 0 bo'ladi.
2) 410° = 360° + 50° bo'lgani uchun (1; 0) nuqtani 410° ga burganda
birinchi chorakda joylashadigan nuqta hosil bo'ladi. Shuning uchun
sin 410° > 0, cos 410° > 0 bo'ladi.
9—Algebra, 9 129
жж
жж
1ХГХ1ХХ1
—4л п 4л
3) -л<^—<-j bo‘lgani uchun (1; 0) nuqtani burchakka
burganda uchinchi chorakda joylashadigan nuqta hosil qilinadi. Shuning uchun
( 4лЛ л ( 4tcA n м
sin < 0, cos <0.1
I 7 J I 7 J
4n
7
2. Tangens va kotangensning ishoralari
_ , . sin a . cosa , „ . , ,
Ta rifga ко ra tga =----, ctga = —— bo Igani uchun tga va ctga laming
cos ot sin Ct
ishoralari bir xil bo‘ladi va sina hamda cosa laming ishoralari orqali aniqla-
nadi. Agar sina va cosa bir xil ishoraga ega bo'lsa, tga > 0 bo'ladi. Bu hoi
birinchi va uchinchi choraklarda joylashgan nuqtalar uchun sodir bo'ladi.
ctga ning ishoralari tga ning ishoralari bilan bir xil. Shunday qilib,
tga > 0, ctga > 0— birinchi va uchinchi choraklarda;
tga < 0, ctga < 0 — ikkinchi va to'rtinchi choraklarda (57-d rasm).
2-masala. Burchak tangensi va kotangensi ishoralarini aniqlang:
1) 200°; 2) 150°; 3) 4; 4) 3.
□ 1) 180° < 200° < 270° bo'lgani uchun tg200°>0, ctg 200° >0;
2) 90° < 150° < 180° bo'lgani uchun tg 150° < 0, ctg 150° < 0;
3) tc<4<^- bo'lgani uchun tg4>0, ctg4>0;
4) у < 3 < л bo'lgani uchun tg 3 < 0, ctg 3 < 0. О
414. Savollarga javob bering. Topshiriqni bajaring:
1. Tekislikdagi nuqta koordinatalarining ishoralari qanday aniqlanadi?
2. Sinus va kosinusning ishoralari qanday aniqlanadi?
3. Tangens (kotangens) ishoralari qanday aniqlanadi?
4. Matndagi 3 ta 57- a, b, d rasmlami daftaringizga chizib oling.
415. Agar:
1) a-f; 2) a = y! 3) a = 205’; 4) a = -210’
bo'lsa, (1; 0) nuqtani a burchakka burganda hosil bo'lgan nuqta qaysi
chorakda yotishini aniqlang.
416. Agar:
1) a = y 2) a = y; 3) a=-260’; 4) a = 250’
bo'lsa, (1; 0) nuqtani a burchakka burganda hosil bo'lgan nuqta qaysi
chorakda joylashgan bo'ladi?
130
417. Agar: 1) a = y; 2) а = у5 3) а = -у;
bo'lsa, sina ning ishorasini aniqlang.
л. — ± .. 2 7л Зл
418. Agar: 1) a = 2) a = y; 3) a = y;
bo‘lsa, sina ning ishorasini aniqlang.
419. Agar: bo^sa, .. 4л 4л 4л 1) а = у; 2) а = у; 3) а = -у; cosa ning ishorasini aniqlang. 4) 5л “__т
420. Agar: .. Зл 6л 4л 1) а = у; 2) а = у; 3) а = —у 4) 6л 7
bo‘lsa, cosa ning ishorasini aniqlang.
\ 5 12л Зл
421. Agar: 1) « = 7^; 2) а = —; 3) а = ——;
О J J
.. 5л
4) « = -у
bo‘lsa, tga ning ishorasini aniqlang.
sina, cosa, tga, ctga laming ishoralarini aniqlang.
425. Sonning ishorasini aniqlang:
.v 2 л . 3л v 2 л л
1) sin— sm —; 2) cos— cos-;
'34 '36
.. v • 2 л Зл л v . 5 л . л
3) sin— :cos —; 4) tg — + sm-.
3 4 4 4
131
29-§. Ayni bir burchakning sinusi, kosinusi, tangensi va
kotangensi orasidagi munosabatlar
гак
Awal sinus va kosinus orasidagi bog'lanishni topamiz. Aytaylik, M(x, y)
nuqta Д1; 0) nuqtani birlik aylana bo'ylab a burchakka burishdan hosil
bo'lgan (59-rasm). U holda sinus va kosinusning ta’rifiga ko'ra x = cosa,
у = sina bo'ladi. M(x; y) nuqta birlik aylanada yotadi, shuning uchun uning
koordinatalari x2+y2=l tenglamani qanoatlantiradi. Demak,
sin2a + cos2a = 1. (1)
Bu yer da a&R (1) tenglik asosiy trigonometrik ayniyat deyiladi,
Undan
sina = ±71 - cos2 a, (2)
cosa = ±71 - sin2 a
formulalar kelib chiqadi. Ildizlar oldidagi
ishora sina va cosa ishorasi bilan
aniqlanadi.
1-masala. Agar
cosa = -| va ^<а<л bo'lsa,
sina ni hisoblang.
(2) formuladagi
□ sina son у < a < n oraliqda musbat bo'lgani uchun
ildiz oldida musbat ishora olinishi kerak:
sina = Jl-
25 5
1 3л
2-masala. Agar sina = - - va л < а < — bo'lsa, cosa ni hisoblang.
Зтс
□ cosa son л< a < — oraliqda manfiy bo'lgani uchun (3) formuladagi
ildiz oldida minus ishora olinishi kerak:
cosa =
V3
2 ’ И
Endi tg a va ctg a orasidagi bog'lanishni aniqlaymiz. Ta’rifga ko'ra
. sina . cosa
tga =----------------------------, ctga = -—.
cosa sin a
Bu tengliklami ko'paytirib,
tga • ctga = 1 I
tenglikni hosil qilamiz. Bundan yana
132
(4)
жж
жж
+ 1 4 1
tga = —-, ctga = —- (5)
ctga tga 4 7
tengliklarni chiqarish mumkin. (4)—(5) tengliklar, mos ravishda,
a * k, a * nk, к e Z bo'lganda o'rinlidir.
3-masala. Agar tga = 34 bo'lsa, ctga ni hisoblang.
□ (5) formulaga ko'ra ctga = = Tv О
tga 34
ЖЖ
ЛЕИ
жж
жж
4-masala. Agar sina = 0,6 va < a < л bo'lsa, tga ni hisoblang.
□ Awal cosa ni topib olamiz. у < a < л oraliqda cosa < 0 bo'lgani
uchun (3) formuladagi ildiz oldida minus ishorasini olamiz:
-71-sin2 a = -71-0,36 = -76^64 = -0,8.
ЖЖ
cosa =
Shuning uchun
ЖЖ
ЖЖ
ЖЖ
0,6 _ 3
4
tg“ =-0,8
Endi tga va cosa orasidagi munosabatni chiqaramiz. Faraz etaylik, cos a # 0
bo'lsin. sin2 a + cos2 a = 1 tenglikning ikkala qismini cos2a ga bo'lamiz:
cos a+sin a _—1 Bundan quyidagi ayniyat kelib chiqadi:
cos2 a cos2 a
1 + tg2a =
cos a
Bunda cosa # 0, a * - + itk, кe Z. (6) formuladan
(6)
жж
жж
1
cosa = ±
tga
+tg2a
, ; sina = ±
71+tg2a
formulalami keltirib chiqarish mumkin.
3 Л
5-masala. Agar cosa = --va-<a<u bo'lsa, tga ni hisoblang.
5 2
О (6) formulaga ko'ra
tg2a = —— 1 =
cos a
(7)
1 1 = 16
ЗА2 9
5
жж
жж
133
ЖЖ
ЖЖ
1ХТХ1ХтЧ1
— < а < п oraliqda tga < 0 bo‘lgani uchun tga = - - bo‘ladi.
2 3
жж
жж
3it
6-masala. Agar tga = 3 va л < а < — bo‘lsa, cosa ni hisoblang.
7 1 1
□ (7) formulaga ko‘ra cos а =----------.
l+tgza iv
жж
жж
Зл 1
л < а < -^- oraliqda cosa manfiy bo'lgani uchun cosa = bo'ladi.
ЖЖ
жж
жж
ЖЖ
426. Savollarga javob bering. Topshiriqlarni bajaring:
1) Ayniyat deganda nimani tushunasiz? Misollar keltiring.
2) Asosiy trigonometrik ayniyatni yozing.
C?) 3) sina ning cosa orqali, cosa ning sina orqali ifodasini yozing.
4) tga va ctga orasida qanday bog'lanish bor?
5) tga va cosa orasida, tga va sina orasida qanday munosabat bor?
6) cosa va sina ni tga orqali ifodalang.
427. Agar:
12 3л o , £1 x
1) cosa = — va — < а < 2л bo Isa, sina va tga ni;
• 5 л - .
2) sm a = — va - < a < n bo Isa, cosa va tga m;
3 л
3) cosa = -- va -<а<я bo‘lsa, sina, tga va ctga ni;
. \ . 15 3л . r. . . . . ..
4) tga = — va л < a < — bo Isa, sina va cosa m hisoblang.
О Z
428. Asosiy trigonometrik ayniyat yordamida tengliklar bir vaqtda bajarilishi
yoki bajarilmasligini aniqlang:
1) sina = 1 va cosa = l; 2) sina = 1 va cosa = 0;
4 3
3) sina = 0 va cosa = -l; 4) sma = - va cosa = --.
429. To‘g‘ri burchakli uchburchakning burchaklaridan biri a bo‘lsin.
Agar cosa = у bo‘lsa, sina va tga ni toping.
430*. Agar cos4 а - sin4 а = | bo'lsa : 1) cosa ni; 2) sina ni toping.
О
134
ИЖ
гаи
431. 1) sina = ^- bo'lsa, cosa ni;
2) cosa = --$- bo'lsa, sina ni toping.
432*. Agar sina + cosa = i ekani ma’lum bo'lsa: 1) sina cosa;
2) sin3 a + cos3 a ifodalaming son qiymatlari hisoblansin.
433. Tenglamani yeching:
1) 2 sin x - sin2 x - cos2 x = 1; 2) 12 sin x = sin2 x + cos2 x;
3) 1-2sin2x = 2cos2x-cosx; 4) 4-cosx = 4cos2x + 4sin2x.
434. Tenglamani yeching:
1) sin3(x-l) = l; 2) cos2(x-2) = 0; 3) cosi(x-l) = l;
4) sin(x + 9^) = 0; 5)cos(x + lbr) = 0; 6) sin(x + 7^) = l.
жж
жж
жж
жж
жж
30-§. Trigonometrik ayniyatlar
Ayniyatlami isbotlashda uchta usuldan foydalaniladi: 1) O'ng qismining
shaklini o'zgartirib, uning chap qismiga tengligini ko'rsatish; 2) ayniyat-
ning o'ng va chap qismlari ayirmasi nolga tengligini ko'rsatish; 3) ayniyat-
ning har ikki qismi shaklini o'zgartirib bir xil ifodaga keltirish.
Berilgan ayniyatni isbotlash uchun shu uch usuldan eng qulayi tanlab
olinadi.
1-masala. a nk, ke Z bo'lganda
1x2 I
I + ctga = —x—
sin2 a
ayniyatning o'rinli ekanini isbotlang (sina 0, a ф тик, keZ).
О l-usulni qo'llanamiz:
2 -2 2 1
ix2 1 cos a sm a+cos a 1
1 + ctgza = 1 + —z— =-------z-----= —z—. I
sin a sin a sin a "
2-masala. cos2 a = (l-sina)(l+sina) ekanini isbotlang (aeR).
□ l-usulni qo'llanamiz. Ayniyatning o'ng qismini o'zgartiramiz:
(1-sin a) (1+sin a) = 1 - sin2 a = cos2 a. I
135
жж
жж
жж
1ХГХ1ХХ1
жж
„ , ж . . , cosa 1+sina
3-masala. Ayniyatni isbotlang: ;—:— =------------•
1-srna cosa
жж
□ Avvalo 1-sina 5* 0, ya’ni а * j + 2^, ke Z; cosa * 0, ya’ni
a * у + it к, ke Z. Ayniyatni isbotlash uchun 2-usulni qo‘llaymiz:
жж
cosa 1+sina _ cos2a-(l+sina)(l-sina) _ cos2 a-(l-sin2 a
1-sina cosa (l-sina)cosa (l-sina)cosa
2 2
_ cos a-cos a _
(1-sina) cos a
4-masala. Ayniyatni isbotlang:
жж
жж
sm®
l-tg2a 4 . 4
—-^z— = cos a - sin a.
l+tg2a
О Bu ayniyatni 3-usul bilan isbotlaymiz. Uning uchun ayniyatning
ikkala qismini alohida-alohida o'zgartiramiz:
жж
жж
, sin2 a
1x2 5 2 • 2
1-tg a cos2« cos a-sm a 2 -2
— = — 3 a = —z---------------z— = cos2 a - sm2 a,
l+tg2a sin2 a cos2 a + sin2 a
1 + ~
cos a
4 - 4
cos a - sm a =
’ 2 • 2
cos a - sm a
' 2 • 2
cos a + sin a
2 • 2
= cos a - sm a.
Ayniyat isbotlandi, chunki uning ikkala qismi ham cos2 a - sin2 a ga
teng chiqdi. I
жж
1
5-masala. Ifodani soddalashtiring: tga+ctga •
О tga, ctga ning ta’rifidan va (1) ayniyatdan foydalanamiz:
1 1 sin a cos a
---------= —------------= —z---------z— = sin a cos a.
tga+ctga sina cosa sjn2 a + cos2 a
cos a sin a
Trigonometrik ifodalami soddalashtirishda masalaning shartida talab
qilinmagan bo‘lsa, burchaklaming joiz qiymatlarini topib o‘tirmaymiz. Ba’zi
hollarda ifoda soddalashtirilgandan keyin a ning biror qiymatida uning
son qiymatini topish masalasi ham qaraladi.
n
6-masala. Ifodani soddalashtiring va a = j bo'lganda uning qiymatini
hisoblang: (sina + cosa)2: sin2a— (1 + ctg2a).
136
жж
ZTXIZTXI
□
(sin a+cosa)2
Г~2
sm a
- (1 + ctg2a) =
sin a+cosa
sina
-1 - ctg2a =
= (1 + ctga)2 -1 - ctg2a = 1 + 2ctga + ctg2a -1 - ctg2a = 2ctga;
2ctga = 2ctg| = 2-^ = ^.
1 и
Javob\ —j-.
435. Savollarga javob bering. Topshiriqni bajaring:
1) Ayniyat deganda nimani tushunasiz?
ИР) 2) Qanday trigonometrik ayniyatlami bilasiz? Ularni yozing.
3) Ayniyatlami isbotlashning qanday usullarini bilasiz?
4) Trigonometrik ifodaning berilgan a da qiymatini hisoblash uchun
nima qilish kerak?
Ayniyatni isbotlang (436—437):
436. 1) (l-cosa)(l + cosa) = sin2 a;
3) cos2 a - sin2 a = 1 - 2sin2a;
2) cos2 a - sin2 a = 2cos2a -1;
4) 3-sin2 a-cos2 a = 2.
437. 1) ——=—= 1 — sin2 a;
l+tg2a
3) cosa tga = sina;
438. Ifodani soddalashtirmg:
1) cosa tga - 3 sin a;
. 2
3) 4)
l+cosa
439. Ifodani soddalashtirmg:
tgq+tgjS .
ctga+ctgj8 ’
_ 1 1
3 ) 7“-----+ j;
' l+cosa 1-cosa
2) ------5— = 1 - cos2 a;
l+ctg2a
4) sina ctga = cosa.
2) 3 cos a - sina - ctga;
2 2
cos a . cos a
1-sina’ 1+sina
4)
cos2a-cos2j3
cosa+cosjS
+ cosjS;
l-sin2a
1-sina
+ tga • ctga.
440. Ifodani soddalashtirmg va uning son qiymatini toping:
1) 1~* 5 *У1 a , bunda a = ^; 2) —~5—1» bunda a
cos2a-l 3 7 cos a
137
Ж
жж
мм
жж
жж
жж
ж
жж
жж
ж
1ВИ
3) cos2 а - ctg2a + sin2 a, bunda а = ;
6
4) cos2 а - tg2a + sin2 a, bunda а = j.
441. Ifodani soddalashtiring va uning son qiymatini toping:
1) (cosa+8ina) - h + ctg2a), bunda a = у;
sin2a v 7 4
2) (i + tg2a)-(sing-C2OSg)2, bunda a = *
' ' cos2a 6
442. 1) sina + cosa = m bo'lsa, sina cosa ni toping;
2) tga + ctga = m bo'lsa, tg2a + ctg2a ni toping.
Tenglamani yeching (443—445):
443. 1) 2cos2x-2 = 2sinx-2sin2л;
2) cos2 x - sin2 x = 2sinx + l- 2 sin2 x.
444. 1) sin2 x = 1 + cos2 x; 2) sin3 x - 2 sin x = 0.
445. 1) sin2 x - 2 sin x = 0; 2) tg2x = tgx; 3) cos3x - cos x = 0.
31-§. a va —a burchaklaming sinusi, kosinusi, tangensi va
kotangensi
IV bobda juft va toq funksiyalar tushunchasi kiritilgan bo'lib, ular
darajali funksiyalar misolida tushuntirilgan edi. Endi shu tushunchani asosiy
trigonometrik funksiyalar uchun keltiramiz.
Aytaylik, birlik aylana chizilgan va Д1; 0) uning nuqtasi. Shu nuqtani,
mos ravishda, a va —a burchaklarga burish natijasida va M2 nuqtalarga
o'tildi, deylik (60-rasm). Bunda Ox o'q MtOM2 burchakni teng ikkiga bo'ladi
va shuning uchun va M2 nuqtalar Ox o'qqa nisbatan simmetrik joylashgan.
Shunday qilib, ulaming abssissalari bir xil bo'ladi, ordinatalari esa faqat
ishoralari bilan farq qiladi. nuqta (cosa, sina) koordinatalarga, M2
nuqta (cos(—a), sin(—a)) koordinatalarga ega. Bundan
sin (-a) = - sin a, cos (-a) = cos a (1)
munosabatlar kelib chiqadi. Shunga o'xshash, tangensning ta’rifidan foydalanib
hosil qilamiz:
ж
138
tg(-a) =
sin(-a) -sina ,
—7-4 =----------= -tga.
cos(-a) cosa
Demak,
tg(-a) = -tga.
Kotangensning ta’rifiga ko‘ra
ctg (-a) = -ctga
(2)
munosabat kelib chiqadi.
К
(1) formula a ning istalgan qiymatida o‘rinli, (2) formula а Ф — + nk,
кь Z bo£lganda, (3) formula esa, а * як, keZ bo‘lganda o‘rmli bo‘ladi.
(1), (2), (3) formulalardan sinx, tgx, ctgx funksiyalar toq, cosx
funksiya esa juft ekanligi kelib chiqadi.
Misollar:
(3)
COS
. л 1
= -tg- = -l;
. / я
sm 3
л v3
_cos_ ;
. л v3
= -sin- = - —;
3 2
ctgl -
446. Savollarga javob bering:
1) P (1; 0) nuqtani —a burchakka burish deganda nimani tushunasiz?
©2) P (1; 0) nuqtani a burchakka burish bilan bu nuqtani —a burchakka
burish orasida qanday farq bor?
3) P (1; 0) nuqtani a va —a burchaklaiga burganda hosil bo‘ladigan
Ma va M_a nuqtalaming abssissa va ordinatalari qanday bo‘ladi?
Hisoblang (447-448):
447. 1)
. I /Cr
sin - —
I 6
f n 1 x ( Я
• cos —— + tg -- ;
3 I 4 J
я
3
l+tg2(-60°)
1+ctg2 (-60°)
448. 1)
sin^-+ sin^ + sin^-sin
6 3 2
_K
6
+ COS
I-
I ’
2)
• 2 A 7C . 7C
sinz - - tg- -4cos- - 2ctg-.
4 4 4 2
WOT
139
456. Sonlami taqqoslang:
1) sin 0,8 va sin 3,2;
3) cos 1 va cos 1 °;
5) cos— va cos —;
2) cos 1,5 va cos 1,6;
4) sin 1 va sin Г;
6) sm— va sin-.
/ 7 7
ЖЖ
457*. Tengliklar bir vaqtda bajarilishi mumkinmi:
2>/б n /7 3>/7 3 o
I) cosa = —— va ctga = 2v6; 2) tga = cosa = -?
458. tga = 2 bo'lsa, ifodaning son qiymatini toping:
2sin2a-sin a cos a
/ 4 i '
3 sin a+2 cos a
I) 3sina-5cosa.
4sina+cosa ’
ЖЖ
Ж
459. ctga = —2 bo'lsa, ifodaning son qiymatini toping:
2) 2cos2a-7 sin2 a
3 cos2 a+4 sin a cos a
2sina+3cosa
5sina-cosa
ЖЖ
Л2Я5
жж
460. sin a + cosa = a bo'lsa:
sinacosa; 2) sm a + cos a; 3) sin a + cos a m toping.
, 1 , £, cos4 a-2sinacosa
tga = - bo'lsa, ———------------- iu;
2 sin a-2sinacosa
1)
461. 1)
2)
x 1 „ z„ 2 sin4 a+2 sina cosa
ctga = - bo Isa, -—з-------—---------- m toping.
2 2cos a+2 sina cosa
462. Ayniyatni isbotlang:
1 + tga . I
1) 7—f- = tga;
1+ctga
2)
1-ctga . I
=-ctga; 3)
l-1ga |
1 + tg2a ,2
—-2-z—= tg a.
1 + ctgza
ЖЖ
463*. tga + ctga = a bo'lsa:
1) tg2a + ctg2a ni;
464. Funksiyaning
funksiyalaming
2) tg3a + ctg3a ni toping.
qiymatlariga ko'ra, qolgan trigonometrik
1) sin a = 0,8;
ax 15
3) cosa = —,
17
berilgan
qiymatlarini toping:
Л
- < a < л;
2
Зя п
— < a < 2л;
2
ox • 5
2) sm a =--------,
13
.. . 3 -
3л
T
4) tga = -, 0<a<-.
4 2
4
465*. 61-rasmdan foydalanib ayniyatlami isbotlang:
ЖЖ
жж
ЕЮ»
141
Ж
жж
1)
sin20 = 2sin0cos0;
3)
-2л 1 - cos20
smz0 =--------
2
ж
да
жж
жж
ЖЖ
дада
жж
дада
ж
ж
да
2)
, „ sin20
tg0 =-----z-;
l+cos2G
4)
(birlik
2„ l + cos20
cos 0 =
aylana);
ZZO5 = 20,
(1).
□ 1) 0C= OP= 1
AACB = Q deylik,
ZABP=Q ekani ravshan.
□ AOB dan:
. AB AB An
sin20 = — = — = AB
OB 1
ПАВР dan: AP=BP sinG; ПАСВ dan:
AC=BCcos6. DPBC dan:
AB2 = AC • AP = BP' BC' sinGcosG, ammo
BP-BC= 2 • Sn= 2 \pc AB = 2 AB,
2
2
bundan AB2 = 2AB * sinOcosO;
AB = 2sinGcos0; (1) ga ko‘ra, sin2G = 2sinGcos0. |
2) Druce dan: tg9 = —; rUOS dan: cos26 = —, sin29 = —,
AC OB OB
OB= 1 boHgam uchun AB=sin20, OA = cos20.
Ammo, AC= 1 + OA = 1 + cos20. U holda tg0 = sjn2Q . м
1 + cos 20
3) П AP— 1 — OA= 1 — cos20 (1); \APB dan: AP = 5P-sin0, shu
bilan birga, ЯРСВ dan: BF = PC AP= = 2 • AP=2' BP sin0; BP= 2
sin0. U holda, AP= = 2sin20 (2)-(l) va (2) dan: 2sin2G =
=1 — cos20, bundan sin20 = -—cos 28.
2 “
4) □ AC= 0C+ 0A= 1 +cos20;
OACB dan: AC = BC' cosG, bundan: AC2 = BC2 • cos20, APBC dan:
Demak,
BO = PC AC = 2 AC, A О = 2 • A C • cos20, AC = 2cos20.
1 + cos 20
2cos20 = 1 + cos20, ya’ni cos20 = ---------•
Isbotlangan formulalardan foydalanib tgl5°; sinl5°, cosl5°
topish mumkin.
33-§. Qo‘shish formulalari
sonlami
Qo‘shish formulalari deb cos(a±/3) va sin(a±j8) lami
burchaklaming sinus va kosinuslari orqali ifodalovchi formulalaiga aytiladi.
a va p
142
ЖЖ
жж
ЖЖ
ЛЕИ
жж
Teorema. Ixtiyoriy a va p uchun quyidagi
tenglik o‘rinli:
cos(a +Д) = cosacos/3-sinasinjS (1)
О (1) formulaning isboti Af(l; 0) nuqtani
birlik aylana bo‘ylab koordinatalar boshi atrofida
burish g‘oyasiga asoslangan. J^(l; 0) nuqtani
a, — p va a+p radian burchaklarga burish
natijasida mos ravishda va J/a+p
nuqtalar hosil bo‘ladi (62-rasm). Sinus va
kosinuslar ta’rufiga ko‘ra bu nuqtalar quyidagi
koordinatalaiga ega:
Ma(cosa; sina), M_p(cos(—p); sin(—P)), Ma+p (cos(a + /3); sin(a + /3)).
Yasashga ko‘ra ХМ0ОМа+р = Z.M_^0Ma. Shuning uchun nif0OJ/a+p=
=nif_pOAfa, demak, uchburchak asoslari ham teng, ya’ni Af0Afa+p= =M_
pMa yoki ^MQMa+^ = . Bundan koordinatalar! berilgan ikki
nuqta orasidagi masofa formulasiga ko‘ra (1—cos(a+p))2 + (sin(a+p))2=
=(cos(—p) —cosa)2 + (sin(—p) — sin a)2 tenglik kelib chiqadi. Qavslami
ochib chiqib, 29-§ dagi (1) formuladan foydalanamiz:
1-2 cos (a + p) + cos2 (a + p) + sin2 (a + p) =
жж
жж
жж
жж
жж
= cos2 p - 2 cos p • cos a + cos2 a + sin2 p + 2 sin p sin a + sin2 a,
2-2 cos (a + p) = 2 - 2 (cos a cos p - sin a sin p).
Bundan cos (a + p) = cos a cos p - sin a sin p formula kelib chiqadi. |
1-masala. cos75° ni hisoblang.
□ (1) formula bo'yicha topamiz:
cos 75° = cos (45° + 30°) = cos 45° - cos 30° - sin 45° • sin 30° =
= >/2 73 V2 1 = л/б->Й H
"22 2 ’2“ 4 ‘ И
(1) formulada p ni —P ga almashtirsak, yana bitta
cos (a - p) = cos a cos p + sin a sin p (2)
formulaga ega bolamiz.
2-masala. cos 15° ni hisoblang.
□ (2) formulaga ko‘ra cos 15° = cos (45° - 30°) = cos 45° cos 30° +
• ЛСО ’ “5ЛО л/2 '^2 1 у[б+у/2
4-sin 45° sin 30° = — ~ + — - = ———.
2 2 2 2 4 “
жж
жж
жж
жж
жж
жж
143
1ХТХ1ХтЧ1
3-masala. Quyidagi formulalami isbotlang:
cos?-a I = sin a, sin I ^-a I = cos a.
I 2 J 12 I
__ 7Г
□ (2) formulada a = ~^ deb, 0 ni a ga almashtirsak,
= cos 5- cos a + sin sin a = sin a, ya’ni
2 2
cosf ? - a | = sin a kelib
2 J
chiqadi. Agar (2) formulada p = --a deb almashtirsak, cos I у -
2 к 2
144
= s'n^T”aJ’ cosa = _aj’ ya’ni sin^-aj=cosa formulaga
kelamiz. I
Yuqorida isbotlangan formulalardan foydalanib topamiz:
sin p = sina cos p + cosa sin p.
+sin
Shunday qilib, sin (a+p) = sin a cos p + cos a sin p. (3)
(3) formulada p ni —p ga almashtirsak, yana bitta formula olamiz:
sin(a-j3) = sin a cos p -cos a sin j8. (4)
Misollar: 1) sin 240° hisoblansin. Ravshanki,
sin 240° = sin (270° - 30°) = sin 270° cos 30° - cos 270° sin 30° =
V ’ 2 2 2
2) Hisoblang:
. 7i 8тг . 8тг n . (ж &Й - / \ л
Sin— COS— -Sin— COS— = Sin —-— =Sin(-ff) = (k
7 7 7 7 ^7 7 J k 7
4-masala. Tenglikni isbotlang:
tg(a + p) =
tga + tgp
1 - tgatgp
(5)
□ Ta’rif bo'yicha tg(a + p) = • Bunda (1) va (3) formulalarga
asosan
tg(a + j8) =
sin (a+p) _ sin a cos p + cosa sin p
cos(a+j8) cos a cos p -sin a sin p
жж
жж
Kasming surat va maxrajini cosacosp ga bo‘lsak, (5) formula kelib
chiqadi.
Misol: tg210° = tg(180° + 30°) = tgl80°+ tg30° = 3 .
' ’ l-tgl80“ tg30” Л
. x / л\ cosfa+S) cos a cos j3 - sin a sin Й ._ . .
Agar ctg (a + p) = —7—=--------------------------— ifodanmg surat va
sin (a+p) sin a cos p + cos a sin p
maxrajini since sinp ga bo‘lsak,
(6)
etga + ctg/3
formulani hosil qilamiz.
Misol: ctg 315° = ctg (270° + 45”) = ctg270°' ctg4s° ~1 = -1.
v ' c1g270° + ctg45°
466. Savollarga javob bering. Topshiriqni bajaring:
1) Qo‘shish formulalari deganda nimani tushunasiz?
ИА 2) (1) va (2) formulalami isbotlang.
3) (3) va (4) formulalami isbotlang.
4) (5) va (6) formulalami isbotlang.
Qo‘shish formulalari yordamida hisoblang (467—471):
ЖЖ
ЛЕИ
жж
ЖЖ
ЖЖ
ЖЖ
ЖЖ
467. 1) cosl50°; 2) cosl35°; 3) cos 210°; 4) cos 225°.
468. 1) cos 240°; 2) cos 270°; 3) cos 300”; 4) cos 330”.
469. 1) sml35’; 2) sinl50e; 3) sin 180°; 4) sin 225°.
470. 1) sin 240”; 2) sin 270°; 3) sin 300°; 4) sin 330°.
471. 1) cos 48°30' • cos 18’30' + sin 48’30' • sin 18’30';
2) cos 21° • cos24° — sin 2Г sin 24;
3) 6я . 6w . 8w cos — cos — - sin — sin —; 7 7 7 7
4) Ия 2я . Ия . 2я cos—- • cos— + sm —- - sm —. 9 9 9 9
л/з 472. Agar sina = — va 0 < а < — bo'lsa, cos (j+“j ni toping.
473. Agar cosa = -|vay<a<^ bo‘lsa, cos fa - у 1 Z Z I j 1 ni toping.
10—Algebra, 9
145
жж
жж
жж
жж
ЖЖ
ЖЖ
1ХТХ1ХтЧ1
ЖЖ
жж
жж
жж
474*. Agar sina = -|, < а < 2я va sin# = —, 0 < р < - bo‘lsa,
j z 17 2
cos (a + p) va cos (a - p) ni hisoblang.
475*. Agar cosa = -0,8, < a < n va sinfl = -—, n < в < — bo‘lsa,
2 13 2
sin (a + p) va sin (a - p) ni hisoblang.
Ifodani soddalashtiring (476—477):
476. 1) cos 4a cos a -sin 4a sin a;
2) cos 3a cos a+sin 3a sin a.
жж
жж
477. 1) cos (a + p) + cos —a sin I ~p ; 2) sin 2a • cos a + cos 2a • sin a;
I t ЯГ
-a -sin —-B
J 2 r
cos(a+/3); 4) cos 2a cos a-sin 2a sin a.
жж
жж
жж
Qo‘shish formulalari yordamida hisoblang (478—479):
жж
жж
478. 1) sin 71° cosl9” + cos 71° sin 19°;
2) sin 71° cosir — cos 71° sin 11°;
3) sm—cos—+ sin —cos—; 4) sin36°• cos54°+cos54° sm36°;
J.Xr J.Xr
5) sincossin-Д-cos6) cos75° cos 15°-sin75° sin 15°.
7 12 12 12 12 7
(7Г A 3 Зтг
a + j , bunda cosa = -- va^<a<—;
2) sinf^-a\ bunda sina = ^y- vay<a<?r.
ЖЖ
Ifodani soddalashtiring (480—481):
480. 1) sin(a+j8) + sin(-a)cos(-j8);
3) cos(-a)sin(-j8)-sin(a-j3);
2) cos (a~P) - cos (-a) cos p;
4) cos(a+j8) + sm(-a)sm(-j8).
146
481. 1) sin ——a +sin а+-
I 3 J I 3
2)
cos
lit
“+ 3
+ COS
1t
3 “
жж
482*. Ayniyatni isbotlang:
I) sin(a + £)sin(a- j3) = sin2 a-sin2 Д;
2) cos (a - $)cos(a + P) = cos2 a - sin2 fl.
Ifodani soddalashtiring (483-484):
tg27° + tg33°
483’ l-tg27” tg33°’
ctg29° • ctg31°-l
ctg29° + ctg31Q
2)
A 9it it
tg—-tg-
8 8
- . 9it . it'
1 + tg— tg-
8 8
жж
жж
ctgl5° • ctg45° -1
ctgl5° + ctg45°
жж
жж
34-§. Ikkilangan burchakning sinusi va kosinusi
Qo'shish formulalaridan foydalanib sin2a va cos2a ni sina va cosa lar
orqali ifodalash mumkin.
1) sin 2а = sin (a + a) = sina cosa + cosa sina = 2 sin a cos a.
Shunday qilib,
sin2a = 2sinacosa. (1)
2) cos2a = cos(a + a) = cosacosa - sina sina = cos2 a - sin2 a.
Demak,
cos2a = cos2a — sin2a. (2)
жж
Misollar:
-ft 1 Ji
1) sin 120° = sin 2 60° = 2 sin 60° cos 60° = 2 — - = —
' 2 2 2
2)
cos 120° = cos 2 - 60° = cos2 60° - sin2 60°
1
2'
1-masala. Agar sina = -0,8 va it < а < — bo'lsa, sin2а ni hisoblang.
□ (1) formula bo'yicha topamiz:
sin2a = 2 sin a cos a = 2 (-0,8) cos a = -l,6cosa.
жж
жж
147
1ХГХ1ХХ1
Ж
жж
мм
жж
ж
1Ж
жж
ж
к < а < (HI chorak) da cos а < 0 bo‘lgani uchun
cos а = —л/1 - sin2 а = —71 - 0,64 = -0,6.
Demak, sin 2а = -1,6 (-0,6) = 0,96. □
2-masala. Agar cosa = 0,6 bo‘lsa, cos 2а ni hisoblang.
□ (2) formula bo‘yicha va asosiy trigonometrik ayniyatdan foydalanib
topamiz:
cos2а = cos2 а - sin2 а = cos2 а - (1 - cos2 a) = 2cos2 a-l =
= 2 0,62 -1 = 2 • 0,36 -1 = 0,72 -1 = -0,28.
3-masala. Ifodani soddalashtiring: sinacosa
1-2 sin2 а
_ sin a cos а _ 2 sin a cos а _ sin 2а _
1-2 sin2 a 2(sin2 а+cos2 a-2 sin2 a) 2(cos2 a-sin2 a)
жж
жж
sin 2a 1 , ~
-----— -tg2a.
2 cos 2a 2
4-masala. Agar tga = V3 bo‘lsa, tg2a ni hisoblang.
□ tg(a + /3) =
tga+tgj3
l-tgatgj3
formulada 0 = a desak, tg2a uchun formulaga
ega bo'lamiz:
ж
1ВИ
tg2a =
2tga
l-tg2a ’
ctg2a =
ctg2a—1
2ctga
(3)
Shu formulaga asosan tga = V3 bo'lganda
. 0 2-ТЗ 273 к
tg2a =--------T = —- = -V3.
1 / П г 1—j
485. Topshiriqlami bajaring:
1) Sinus, kosinus uchun qo‘shish formulalarini yozing.
2) Ikkilangan burchakning sinusi, kosinusi, tangensi va kotangensi
formulalarini chiqaring.
Hisoblang (486-488):
486. 1) 2sin 22’30'• cos 22’30'; 2) cos2 30’- sin230’;
3) (cos 22’30'-sin 22’30')2; 4) (cos 75° + sin 75’)2.
148
ж
ИЖ
гаи
А ОЯТ 1 \ \ 2 2 TC
487. I) 2sm — cos —; 2) cos — -sm —;
4 4 4 4
_ _ * я я ^2 л. л/2 ( Я • Я A
3) sin-cos-- — ; 4) — - cos- + sin-I .
488. 1) 2cos215°-l; 2) 1 -2sin222°30'; 3) 2cos2 22’30'-1;
4) 2cos2|-l; 5) l-2sm2^; 6) 2cos2^-1.
489*. Agar:
4 ж 3 Зтг
1) sina = у va — < a < 2) cosa = -- va n < a < —
bo‘lsa, sin2a ni hisoblang.
3 Зтг 4 Зя
490*. Agar: 1) sina = -- va n < a < —; 2) cosa = -va — <а<2я
bo‘lsa, cos2a ni hisoblang.
жж
жж
жж
жж
жж
Ifodani soddalashtiring (491—492):
491. 1) sin^j-ajcosa;
492. 1) cos 4a + sin2 2a;
2) cosa cos^j-aj.
2) sin2a -(sina + cosa)2.
Ayniyatni isbotlang (493—494):
493. 1) sin2a + l = (sina + cosa)2;
494. 1) cos4 a - sin4 a = cos 2a;
2) (sin a - cos a)2 = 1 - sin 2a.
2) 1-2 sin2 a = cos2a.
жж
Hisoblang (495—496):
495* 1) 2cos2 75°-1; 4) 2cos2£-l; О 2) l-2sin215°; 5) l-2sin2£. О 3) 1 —2sin275°; 6) 2cos2^-1. 6 Ctg 1 Л\ 3
jnr 1 \ ___ 2я 2tg т 6tgl5° . . 2 n 1 Ctg 1 6 .
1) l-tg215°’ 3) s ’ 2Ctg- ctg- 3
жж
жж
149
1ХГХ1ХХ1
Ж
Ж
ж
Ж
жж
зтая
ж
35-§. Keltirish formulalari
Istalgan burchakning sinusi, kosinusi, tangensi va kotangensini hisoblashm
o‘tkir burchakning sinusi, kosinusi, tangensi va kotangensi qiymatlarini
hisoblashga keltiradigan formulalar keltirish formulalari deyiladi,
1-masala, sin 840° va cos 840° ni hisoblang.
О 840’= 2 • 360” + 120°. Shuning uchun Д1; 0) nuqtani koordinata
boshi atrofida 840’ ga buiganda nuqta 2 marta tola aylanadi va 120’ ga buriladi,
ya’ni nuqtani 120° ga buigandagi M nuqtaning xuddi o'zi hosil boladi (63-
a rasm). Shuning uchun sin 840° = sinl20°, cos 840° = cosl20° bo'ladi.
M nuqtaga ordinata o'qiga nisbatan simmetrik bo'lgan Mr nuqtani
topamiz. Ulaming ordinatalari bir xil, absissalari esa faqat ishoralari bilan
farq qiladi (63rasm). Shuning uchun
Ji 1
sin 120° = sin 60° = —; cos 120° = - cos 60° = - -.
2 2
жж
жж
Javob*, sin 840° = ; cos 840° - - -.
Ж
1ВИ
Masalani yechishda, aslida,
sin 840° = sin (2 360° +120°) = sin 120°, (1)
cos 840° = cos (2 360° +120°) = cos 120°, (2)
sin 120° = sin (180° - 60°) = sin 60°, (la)
cos 120° = cos (180° - 60°) = cos 60° (2d)
tengliklardan foydalanildi.
(1) va (2) tengliklami umumiy ko'rinishda yozish mumkin:
sin (a + 2як) = sin a, cos (a + 2nk) = cos a, к e Z. (3)
Xususan, к = 1 bo'lganda
sin (2я + a) = sin a, cos (2я + a) = cos a (3a)
tengliklar o'rinli. (la), (2a) tengliklar
150
ж
sin (я - a) = sin ct, cos (я:-ct) =-cos ct (4)
tengliklaming xususiy holidir. Ulardan birinchisini isbotlaymiz.
sin (я -ct) = sin я cos a-cos я sin a = 0 -cos a- (-1) sin a = sin a.
(3) va (4) formulalar yordamida sinus va kosinusni hisoblashni o‘tkir
burchakning sinusi va kosinusi qiymatlarini hisoblashga keltirilishi munikin.
2-masala. sin 975° ni hisoblang.
О (3) va 33-§ dagi (3) formulalardan foydalanamiz:
sin 975° = sin (2 • 360° + 255°) = sin 255° = sin (360° -105°) = sin (-105°) =
= - sin 105° = - sin (90° +15°) = - cos 15° = - (cosl5° ning qiymati 149-
betda hisoblangan). Javob: sin 975° = -
1 1
3-masala. cos------ ni hisoblang.
4
□ 11я (a 'I
cos —- = cos 4тг— = cos
3 I 3 J
жж
ЖЖ
я
3
я 1 T . 11я 1
= cos - = -. Javob. cos—= -
(3) formuladan va tangensning ta’rifidan
3
tg (a + 2nk) = tga, keZ
tenglik kelib chiqadi. Shu tenglik va (4) formuladan foydalanib quyidagini
topamiz:
tg (a + яг) = tg (ct - я + 2я) = tg (ct - яг) = -tg (я - a) =
sin(tf-a) sin ct
=------------ =---------= tga.
cos(tf-a) -cos a
Umuman, ushbu formula o‘rinli:
tg (a + як) = tga, к e Z. (5)
ж
4-masala. Hisoblang: 1) 2) tg —.
□ 1) tg^ = tg(4^]=tgf-^ = -tg| = ->/3;
2) (5) ga ko‘ra tg^ = tgpr+^1=tg^ = l.
жж
жж
151
ЖЖ
Ж
ЗЯ
33-§ da isbotlangan formula (3-masala) va (3)—(5) formulalar keltirish
formulalari deyiladi. Quyida sinus, kosinus, tangens va kotangens uchun
keltirish formulalari jadvalini beramiz: 1-jadval
ЖЖ
зязи
жж
зязи
жж
звзи
жж
Keltirish formulalari
sina cosa
1 sin ' л A <2 = cosa 1 cos 'л = sin a
2 sin <2 J = = COSa 2 cos 'л 'I J+“J = - sina
3 sin ju - a ) = sina 3 cos Jtu — a) = -cosa
4 sin p +a) = -sina 4 cos [л + a ) = -cosa
5 sin ^Зл A <T-aJ = - cosa 5 cos '3л л = -sina
6 sin 3 л A <T+aJ = - cosa 6 cos '3л = sina
7 sin (2л - a) = - sina 7 cos '2л -a) = cosa
8 sin (2л +a) = sina 8 cos ^2л +a) = cosa
2-jadval
жж
звт
tga ctga
1 tg| "a | = clga \ z / 1 Ctg| y-a = tga
2 1л . i cgl 7 । * 2 cig | 7 +u । = -tga
3 lg(x - a )= -tga 3 ctg (я - a ) = -ctga
4 tg(ft + a)~ Iga 4 Cig (ft + a ) = ctga
5 ( Зя 1 (g | — - a - ctga 5 Cig -z--a = tga
6 tg I + a 1 = Ctga 6 clg| — ’♦•a |» -tga
7 tg(2ir -a )= -Igu 7 ctg (2я - a )= -ctga
8 tg(2n 4a)- (ga 8 ctg (2л ♦ a ) - ctga
ЖЖ
152
ИЖ
гаи
Eslatma. Jadvalda keltirilgan formulalar istalgan a lar uchun to‘g‘ri.
Masalan,
(Зтг A
— - 25л = -cos 25л = -cos(12 - In + я) = -cosя = - (-1) = 1 yOfcj
sin f— -2 5л 1 = -sin (2 5л- — 1=-зтГ12-2л + л- — =
I2 J I 2 J 2 )
= -sin(-^=-(-l) = l.
(3) formulalardan ma’lum bo'ldiki, argument 2л ga (yoki, baribir, —
2л ga) o‘zgarganda sinus va kosinuslaming qiymatiari takrorlanadi, ya’ni
sin (x + 2л) = sin x, cos (x + 2л) = cos x.
Bunday funksiyalar davriy funksiyalar deyiladi. у = sinx va у = cosx
funksiyalaming eng kichik musbat davri 2л ga teng.
2л soni у = cosx funksiyaning eng kichik musbat davridir.
□ T>0 son kosinusning davri bo‘lsin, ya’ni istalgan x uchun
cos(x+ 7) = cosx tenglik bajarilsin. x = 0 bo‘lsa, cos 7"= 1 boladi. Bundan
T = 2лк, ke Z bo‘lganda cos 2nk= 1 ni hosil qilamiz. Demak, T quyidagi
2л, 4л, 6л, ... qiymatlami qabul qila oladi, degan natijaga kelamiz. U holda,
T ning qiymati 2л dan kichik bo'lishi mumkin emasligi, T= 2л eng kichik
musbat davr ekani kelib chiqadi. |
IShunga o‘xshash, у = sinx funksiyaning eng kichik musbat davri 2n
ga teng ekanini isbotlash mumkin.
жж
жж
жж
жж
жж
497. Savolga javob bering. Topshiriqlarni bajaring:
®1) Keltirish formulalari deganda nimani tushunasiz? Bu formulalaming
mohiyati nimadan iborat?
2) Sinus, kosinus, tangens uchun keltirish formulalaridan birini
yozing va isbotlang.
3) Keltirish formulalari jadvalini o'rganib chiqing; jadvaldagi har bir
formula nimaga asoslanib yozilganini aytib bering.
жж
Hisoblang (498-502):
498. 1) . 15л sm—; 2) sin 13 л; 3) cos 9л; 4) 13л COS——. 2
499. 1) sin 360°; 2) cos 720°; 3) sin 540°; 4) cos 270°.
500. 1) cos 390°; 2) tg210°; 3) sin 3750°; 4) cos 3750°.
жж
жж
153
1ХГХ1ХХ1
л/2 73
510. [0; 2л] oraliqda sinuslari
bo'lgan burchaklarni toping.
1 73 _J2
511*. [0; 2л] oraliqda kosinuslari -1; - -; —; bo'lgan burchaklarni
toping.
-72 л/з
512*. [0; 2л] oraliqda sinuslari -1; ; 0 bo'lgan burchaklarni
toping.
36-§. V bobga doir mashqlar
513. Burchak sinusi va kosinusining qiymatini toping:
1) 3л; 2) 4л; 3) 3,5л; 4) |л; 5) лк, ке Z; 6) (2£ + 1)л, ке Z.
514. Toping (514-515):
1) Agar sina = va < а < л bo'lsa, cosa ni;
2) agar cosa=-^ va л < а < bo'lsa, tga ni.
515. 1) Agar tg а=2л/2 va 0 < а < bo'lsa, sina ni;
2) agar tga=^2 va л<а< у bo'lsa, cosa ni.
516. Ayniyatni isbotlang:
1) 5sin2a + tgacosa + 5cos2a = 5 + sina;
2) ctga sina - 2cos2a - 2sin2a = cosa— 2;
жж
жж
жж
ЛИИ
жж
ЖЖ
ЖЖ
ЖЖ
жж
жж
жж
3) —^- = 3cos2a;
l+tg2a
4) —— = 5sin2a.
l+ctg2a
517. Ifodani soddalashtiring:
1) 2sin(-a)cos (y - a j- 2cos(-a)sin^y - a
2) 3sin(ft-a)cos^-a) + 3sin2 .
518. Ifodani soddalashtiring va uning son qiymatini toping:
1) gifl(|i - а}+ sinlln + а
7 \2 J \2
bunda cosa = -7;
4
жж
жж
жж
жж
155
1ХТХ1ХтЧ1
2) cosf-J + aJ + cosl^^-a
’ \2 J к2
bunda sina = 4-.
6
жж
жж
519. Hisoblang:
1) 2sin75°cos750;
4)sin75o;
2) cos275° - sin275°;
5) cosl5°;
3) sinl5°;
6) 2sinl5°cosl5°.
ЖЖ
жж
520. Ifodani soddalashtiring:
1) cos2 (я-a)-cos21 у-a
Hisoblang (521-522):
521. 1) sin-^—;
D
. 25я
2) tg—;
3)
2)
2sin --a cos --a
l 2 I 2
, .. 2br
ctg—; 4) cos—.
жж
жж
522. 1)
23я . 15лг
cos —— sin ——;
4 4
3) 3 cos 3660° + sin (-1560°);
2)
. 25я . Юя
sm— -tg —;
4) cos (—945°) + tg 1035°.
жж
жж
жж
523. Sonlami taqqoslang:
1) sin3 va cos4; 2) cosO va sin5; 3) sinl7 va cos2.
Hisoblang (524-525):
524.1) sin£cos^-+sin^-cos£ ; 2)sinl65°; 3) sinl05°.
8 8 8 8
525. 1) sin£; 2) 1 - 2sin2195”; 3) 2cos2^-l.
1Z О
жж
жж
526. Ifodani soddalashtiring:
1) (l + tg(-a))(l-ctg(-a))-sm(~a). ; 2)------ . z v, .
/v // cos(-q) ’ ' cosa+sm(-a) sina
527*. Agar sina = ^ va £<а<я bo‘lsa, cosa, tga, ctga, sin2a, cos2a
laming qiymatlarini hisoblang.
ctgq+tg(-q) , tg(-q)
ЖЖ
Ifodani soddalashtiring (528—530):
528. 1) cos3asina - sin3acosa; 2) sma+sm2a
l+cosa+cos2a
529 1) sin 2a—sin 2a cos 2a . 2) _____2 cos2 2a___
7 4cosa ’ ' sin4acos4a+sin4a ‘
156
530. 1) cos.2* -sm(Tt-x); 2) cos.2 x + cos(l, 5n + x).
1-sinx 7 1+sinx v 7
531. Agar tg a = - va tgp = 2,4 bo‘lsa, tg(a + P) ni hisoblang.
532. Ifodani soddalashtiring:
1) 2sin(^- +2a)sm(^--2a^; 2) 2sin(4" 2a)cosf^--2a
V bobga doir sinov (test) mashqlari
1. Sonlami o‘sish tartibida yozing: a = sinl, 57; b = cosl, 58; c = sin3.
A) a < c < b; B) b < с < a\ С) c < a < b; D) b<a<c.
2. Kamayish tartibida yozing: a = cos2; b = cos2°; c = sin2; d - sin2°.
A) a > c > d > b\
C) b > c > d > a;
B) d> c> b > a;
D) c > d > b > a.
sinl360 cos460-sin460 cos2240
3. Hisoblang: sinll0o.cos40°-sm20o cos50D '
A) cos40°; B)0,5; C)sin44°; D) 2.
!*. sina = 0,6 bo‘lsa, tg2a ni toping (o < a <
A) 3,42; B)3|; C)^; Г>)
5*. tga = V5 bo‘lsa, sin2a ni toping.
A) B)-^; C)^; D) -Л.
(*. tga = л/7 bo'lsa, cos2a ni toping.
A) 5; B)-< C)|; D)
7*. tga = >/7 bo‘lsa, -4sin a hisoblang.
5 sin a+15cos a
A) 0,59; B) 0,49; C) -0,49; D) 0,2.
8*. cosa + sina = | bo‘lsa, sin4a+cos4a ni toping.
A>^ »< C>g; D>-|.
157
9. Agar sin x - —— = -3 bo'lsa, sin2 x + —ning qiymati qanchaga
sinx sin2 x
teng bo'ladi?
A) 7 B) 8 C) 9 D) 11.
10. Agar tgx=3 bo'lsa, -3sina—ning qiymati qanchaga teng
5 sin3 ot+10 cos3 a
bo'ladi?
It m -• сч A- m
A) 39’ B) 9’ C) 15’ D> 29
11. Agar 2sin* cos* = з bo'lsa, tgx ni hisoblang.
2cosx+sinx
A) 7; B) -3; C) 3; D) -7.
r 9
12. Agar ctg a = V3 bo'lsa, —j---------r— ni hisoblang.
sin4 a+cos4 a
A) 5; B) 4,5; C) 81; D) 14,4.
13. Agar sin a - — va
2
7C
— < a < л bo'lsa,
2
|—1+cos a|+2 cos a
^-0,5
л/З
ni hisoblang.
A) B) 1; C) 3; D) -1.
... A . 13 u ci 2cosa + sina . . . .
14. Agar ctga = — bo Isa, ------------ kasming qiymatini toping.
4 cosa-2sina
A) 6 B) 5; C) 6,2; D) 4,8.
ts a ________ ci 1 — sin2a + cos2a• sina -гл- • •
15. Agar cosa = — bo Isa, ---------—-------—------— ifodaning qiymatini
2 1 + sin a
toping.
3 1
A) B) 1,5; C) 15; D) 1.
5 sin2 a + 4 cos2 a
16. —-----5—-----. 7 ifodaning eng katta qiymatini toping.
4 cos p + 5sin p
A) 1,25; B) 1,5; C) 2,25; D) 2,5.
158
17. Agar ctga = 2 bo‘lsa, -------------------=— ifodaning
3 sin a-cos a + cos a
toping.
A) -0,375; B) -0,5; C) 1,5; D) -1,3.
qiymatini
ЖЖ
18. tg sin ctg ni hisoblang.
6 3 4
1 л/2
A) 1,5; B) 0,5; C) D)
19. sin - • cos3 - — sin3 - • cos - ni hisoblang.
8 8 8 8
A)0; B) 1; C) 2; D)
20. cos—+ cos—+ cos— ni hisoblang.
7 7 7
A) B)i; C) D)
Hisoblang (21-23):
21. 16sinl0’sin30esin50’sin70°sin90’.
A) 1; B) 0,5; C) 1,2; D) 0,125.
22. sinl0°sin200sin300sin40°cos 10°cos200cos300cos40°.
ЖЖ
Ж
жж
ВИЯ
ЖЖ
А) 256’ В> 128’ С) 250’ D> £•
23. cos550cos65°cosl75°. _ 1+^ 1 . 8л/2 ’ В) 8л/2 ’ с> D> 4^-
ЖЖ
ЖЖ
ЖЖ
Л2Я5
159
ж
жж
Tarixiy ma’lumotlar
жж
жж
жж
Mirzo Ulug‘bek
(1394-1449)
жж
жж
жж
жж
жж
Matematikaning, xususan, trigonometriyaning rivo-
jiga buyuk allomalar — Muhammad al-Xorazmiy, Ahmad
Farg‘oniy, Abu Rayhon Beruniy, Mirzo Ulug‘bek, AU
Qushchi, G‘iyosiddin Jamshid al-Koshiy katta hissa
qo‘shganlar. Yulduzlaming osmon sferasidagi koordina-
talarmi aniqlash, sayyoralarning harakatlaiini kuzatish,
Oy va Quyosh tutihshini oldindan aytib berish va boshqa
ilmiy, amaliy ahamiyatga molik masalalar aniq hisob-
lami, bu hisoblarga asoslangan jadvallar tuzishni taqozo
etar edi. Ana shwiday astronomik (trigonometrik) jad-
vallar Sharqda «Zij»lar deb atalgan.
Muhammad al-Xorazmiy, Abu Rayhon Beruniy,
Mirzo Ulug'bek kabi olimlarimizning matematik asarlari bilan birga «Zij»lari
ham mashhur bo‘lgan, ular lotin va boshqa tiUaiga taijima qilingan, Yevropada
matematikaning, astronomiyaning taraqqiyotiga sahnoqU ta’sir o'tkazgan.
Prezidentimiz LA. Karimov «Yuksak ma’naviyat—yengilmas kuch» asar-
larida Mirzo Ulug‘bek haqida shunday durdona fikrlami aytganlar: «Bu benazir
alloma o‘zida minglab yulduzlar harakatini jamlagan mukammal astronomik
jadvalni yaratdi. Ushbu jadvalda zikr etilgan ilmiy ma’lumotlaming naqadar
aniq va to‘g‘ri ekanini bugungi eng zamonaviy asboblar ham tasdiqlaydi.
Ulug‘bekning hayoti va ilmiy faoHyati xalqimiz ma’naviyatining poydevoriga
qo‘yilgan tamal toshlaridan biri bo‘lib, yurtimizda bundan necha zamonlar
oldin fundamental fanlami rivojlantirishga qanchalik katta ahamiyat berilganini
ko‘rsatadi».
Beruniyning «Qonuni Ma’sudiy» asarida sinuslar jadvaU 15 minut oraliq
bilan, tangenslar jadvaU Г oraliq bilan 10-8 gacha aniqlikdaberilgan. Nihoyatda
aniq «Zij»lardan biri Mirzo Ulug‘bekning «Zij»i — «Ziji Ko‘ragoniy» asaridir.
Bunda sinuslar jadvali 1 minut oraUq bilan, tangenslar jadvali 0° dan 45° gacha
1 minut oraliq bilan, 46° dan 90° gacha esa 5 minut oraliq bilan IO-10 gacha
aniqlikda berilgan.
Mantiqiy masalalar
жж
жж
1. To‘g‘ri burchakli ПАВС da AB = c, BC=a, AC=b, ZA=a deylik. U
holda a = c • cosa, b = c- sina. Oxirgi ikki tengtikni kvadratga oshirib,
hadma-had qo‘shayUk: a2 + & = c2 • cos2a + c2 sin2a. Asosiy trigonometrik
ayniyat sin2a + cos2a = 1 dan foydalanib, a2 + £2=c2x
x(cos2a + sin2a) = c2 1 = c2 tengliklami yoza olamiz.
Shunday qiUb, a1 + й2 = c2. Bu bilan Pifagor teoremasining yana bir
isbotini oldik, deya olamizmi? Keltirilgan ,,isbot“ mantiqan noto‘g‘ri
ekanini ko'rsating.
160
жж
XXIZTXI
2. cos I — (зх + л/9х2
I 8 \
+ 160x + 800 =1 tenglamaning butun yechimlarini toping.
3. cos2 a + cos2 (120° - a) + cos a • cos(120° - a) ifodaning son qiymatini toping.
. . я . 5я . 7л ж . ,n
4. sin — sin — sin— son ratsionalmi?
18 18 18
5. Jadvaldan foydalanmay hisoblang:
. . 4 л .4 3 л . 4 5л . 4 7л л 2л Зл
1 ) sm — + sin — + sin — + sin —; 2) tg- tg—tg —.
7 16 16 16 16 7 *7 7 7
6. 9 dan boshlab 49 gacha bo'lgan barcha toq sonlar bitta son kabi yozildi:
«=911131517...4749. Shu n soni 3 ga bo'linadimi? 9 ga-chi?
7. x? — 6x2 + 1 = 0 tenglamaning ildizlari tg^, tg^, tg^, tg^ bo'lishini
О о о о
isbotlang.
о „ sinl sinl sinl sinl . c. .. . x .
8. Sn = — ------ + — ------ + — ------ +... + ———-------yig rndini toping.
cosOcosl cosl-cos2 cos2cos3 cos(«-l)cosn
9. tg20° tg40° • tg80° = >/з ekanini isbotlang.
10. Burchaklari a, p, у bo'lgan uchburchak to'g'ri burchakli bo'lishi uchun
cos 2a + cos 2p + cos 2y = -1 tenglikning bajarilishi zarur va yetarli ekanini
isbotlang.
11. Ikkita varaqqa 9876 son bilan tugaydigan ayni bir yetti xonali son n
yozilgan. 1-qog‘ozni kesib ikkiga bo'lishdi, bunda kesish chizig'i 3- va 4-
raqamlar orasidan o'tdi. 2-qog‘ozni ham kesib ikkiga bo'lishdi, bunda
kesish chizig'i 4- va 5-raqamlar orasidan o'tdi. 1-qog‘ozning ikkala qismidagi
sonlar yig'indisi 2-qog‘ozning ikkala qismidagi sonlar yig'indisiga teng
bo'ladigan biror yetti xonali n songa misol keltiring.
| | Masalani yechish uchun ushbu
a£c+9876=a£c9+876
rebusni yechish kifoya, bunda turli harflarga bitta raqam to'g'ri kelishi
ham mumkin. Ravshanki, a, b, c — raqamlar, abc — uch xonali, abc9
— to'rt xonali son. Tenglikning ikkala qismidan 876 sonini ayiramiz. U
holda,
aZ>c+9OOO=aZ>cO+9,
bundan esa, 9 • abc=9QQQ—9, ya’ni abc=999 tenglikka kelamiz.
9 999 876 son masala shartini qanoatlantiradi. Chindan ham,
999 + 9876 = 9999+876=10 875.
Javob: 9 999 876. |
11—Algebra, 9 161
ЖЖ
ЖЖ
ЖЖ
жж
ЗИЯ
ЖЖ
ж
ж
жж
ЕЮ»
IXXIXTXI
жж
Murakkabroq masalalar
жж
жж
Ayniyatlami isbotlang (1—13):
j 1-2 sin2 a _ 1-tga
l+sin2a 1+tga
2 1^ i - 2 I I •
2. cos - - a - sin - - a = sin 2a.
И J И J
3. cos5 ot = —— cos 5a + Д cos 3a + - cos a.
16 16 8
жж
жж
sm®
4. sin5 a =—sin 5a- — sin 3a +-sina.
16 16 8
— 2 2 (2tl । 2 (2л | 3
5. cos a + cos — + a + cos — - a = -.
I 3 I | 3 2
6. Agar tga=|;sinp = jL
bo‘lsa, a+2p=45° (a va p — o'tkir burchaklar)
жж
жж
ekanini isbotlang.
p burchak octkir bo‘lgani uchun
smp
1 1
®R’3
tg2p=
2tgP
l-tg2p
2 3
( 0 4
3 1-i
9
жж
J_+3
tg(a + 2p)=^-j-iT = ^ = l.
1 — —
"7'4
Bundan a +2p=45°+180° • k, bunda &=0, ±1, ±2, ... . 0<а<45\ 0<p<45° ekanini
ko‘rsatish mumkin. U holda, 0<a+2p<135° bundan, £=0 va a+2p=45Q kelib
chiqadi. Ц
жж
162
ZTXIZTXI
„ sinv + smxcos(x + у) . , , .
7. -------- z , ( = <s(* + y)
cos у - sm x • sin(x + y)
8. cos2a+cos2p—2cosacospcos(a+p)=sm2(a+p).
9. cos2(a+p)+cos2(a—p)~cos2a • cos2p=l.
10. tg2(T+tg4(T~V3 tg20° • tg40° = Л .
j 1 + sma _ j_
1 + cos a 2
1 * a
1 + tg-
1Ж
cos a _ 1 (. 2 a
1 + cos a 2 2
-----+ tga
cosa
1
------tga
cosa
14. Agar uchburchakning burchaklari a, p va у lar uchun
3
cosa+cosp—cos(a+p)= - munosabat o‘rinli bo‘lsa, uchburchak muntazam
(teng tomonli) bo'lishini isbotlang.
o « a + P a-p z оч ,, 2« + P i
cosa + cosp = 2cos——- cos——- va cosia + P) = 2 cos ——- -1
2 2 v 7 2
ayniyatlardan foydalanib, berilgan munosabatni bunday yozamiz:
n a + P a-p « 2 a + P 1 n
2cos- „ cos „ - 2cos ——--- = 0.
2 2 2 2
2 a + p a-p a + p 1 n
cos - cos - • cos + - = 0,
2 2 2 4
( a + p 1 a-pV 1 1 2 a-p n
cos - —cos + - - — cos ~ = 0,
[ 22 2 J 4 4 2
163
( а + р 1 a-pV 1 .2 a-p л
cos --cos- „ r + -• sin „ = 0.
2 2 2 J 4 2
Ammo ikkita haqiqiy sonlar kvadratlari yig‘indisi 0 ga teng bo‘lishi uchun
shu sonlaming o‘zi 0 ga teng bo‘lishi kerak, ya’ni
a + p 1 а-p n . a-p n
cos ~ -cos - 0 va sin - 0.
2 2 2 2
Ikkinchi tenglikdan a va p uchburchak burchaklari bo‘lgani uchun o=p bo‘ladi.
1 1л
Birinchi tenglikka cc=p qo‘ysak, cos a — = 0, cos a = —, a = — kelib chiqadi.
7U 7U
Demak, a = p = — Bunda uchinchi burchak ham — ga teng bo'ladi.
Shunday qilib, uchburchak teng tomonli ekan. Ц
15. Agar 5smp=sin2a+p bo‘lsa, tg (a + = — ekanini isbotlang.
tga 2
16. Ayniyatni isbotlang: 4sina • sin(60e—a)sin(60'’+a)=sin3a.
17. Hisoblang: cos— cos------cos—
7 7 7
| | Ifodani quyidagicha almashtiramiz:
п . л л 4я f 2л
, 2sin -COS -COS COS Л- —
л 4л 5л 7 7 7 7
cos - • cos — cos — =
7 7 7
2sin-
7
164
2л
7
. 2л 4л 2л
sm — • cos — cos—
7 7 7
. 4л 4л
sin— cos—
7 7 _
2sin^
4 stay
8л
Sin —-
7
о л
8 sm —
7
O • Л
8 sm —
7
л
Sln 7 1
8 sin — 8
7
18. Ayniyatni isbotlang: 16sinl0',sin30esin50’sin70',sin90e=l.
19. Agar sina+sinp=p va cosa+cosp=?
bo'lsa, cos(a+p) va sin(a+p) lami hisoblang.
sin a + sin p = 2 sin
+ p a-p
—-cos—-— = p,
2 2
o n a + B a-p
cos a + cos В = 2 cos cos - r = q.
2 2
« л + P P • n 2tgr - l-tg2x * , , ,
Bundan tg —-— — —. Endi sin2x = -------va cos2x =------=— formulalardan
2 q 1+tgx 1 + tg2x
foydalanib, topamiz:
sin (a + p) = va cos (a + p) = —%-
p2+q2 P +q
20. Ayniyatni isbotlang:
tg2a tg(30°—a)+tg2a tg(60’—a)+tg(60’—a) tg(30’—a)=l.
21. Л+1?+С=л, a = n = C tengliklar berilgan bo'lsa,
8тЯ sin 2? smC
д2=й2+с2—2^c‘co&4 tenglik isbotlansin. (Ya'ni sinuslar teoremasidan
kosinuslar teoremasini keltirib chiqaring.)
Ifodani soddalashtiring (22—25):
cos2a cos4 a + sin4a
22. cos4 a-sin4 a 1_lsjn22a
2
жж
cos 2a
Malum formuladan foydalanamiz: (cos2 a + sin2 ч /со§2 a _ sin2 a
cos4 a + 2sin2 acos2 a + sin4 a - 2sin2 acos2 a
1 - i sin2 2a
2
cos 2a 1^
lcos2a
2
жж
165
жж
м 1 +sin 4а-cos 4а
23.---------------
l + cos4a + sin4a ’
жж
«ИИ
24. 4cos4a — 2cos2a—-cos4a.
n л 2л Зя 4л 5л 6л
25. cosO + cos — + cos-hcos — + cos— + cos — + cos—.
7 7 7 7 7 7
жж
жж
26. Agar a+p+y=n bo‘lsa, cos2a+cos2p+cos2yi-2cosacospcosy=l tenglikni
isbotlang.
| | Mazkur tenglik uning chap tomonini ketma-ket almashtirish yordamida
isbotlanadi:
жж
жж
рия
жж
жж
2 2n 2 n n l + cos2a l + cos2B
cos a + cos p + cos у + 2 cos a cos p cos у =------+------—- +
+ cos2 у + (cos(a - P) + cos(a + p)) cos у = 1 + cos(a + p) cos(a - p) +
+ cos(a + p) cos у + (cos(a - p) cos у + cos2 y) =
= 1 + cos(a + p) (cos(a - p) + cos y) + cos у (cos(a - p) + cos y) =
= 1 + (cos(a - p) + cos y) (сов(л - у) + cos у) =
= 1 + (cos(a-p) + cosy) (-cosy + cosy) = 1. И
27. Isbotlang: cos24°4-cos480—cos84°—cosl2°= j.
i4=cos240+cos480-cos840-cosl20=2cos36° cosl2°-2cos48° cos36°=
= 2cos36°(cosl20-cos480)=4cos36° sinl8° sin30°=
_2cos 18°• sin 18°-cos36° _ sin36°• cos36° _ 2sin36°-cos36° _ sin72° _1
cos 18° cosl8° 2 cos 18° 2sin72o 2
Demak tenglik isbotlandi. Ц
http://www.matematikl.narod.ru/manbadan mazkur bobga oid
ma’lumotlami toping va o‘iganing.
ЖЖ
166
ZTXIXXI
ЖЖ1
VI BOB PROGRESSIYALAR
37- §. Ariftnetik progressiya
Progressiya tushunchasiga olib keluvchi misol kocraylik.
Jamg‘arma bankida omonatchiga shaxsiy varaq ochiladi, unda omonatchining
qancha puli borligi qayd qilinadi. Omonatchilaming varaqlari nomerlab chiqiladi.
Aytaylik, 1- nomerli varaqda ax so‘m, 2- nomerli varaqda 02 so‘m va hokazo, n-
nomerli varaqda an so‘m va hokazo... turgan bo‘lsin. Natijada
^1’ ^2’ *•* (1)
sonlar ketma-ketligi hosil bo‘ladi. (1) ni sonli ketma-ketlik deyiladi. Unda
a2, ... lar ketma-ketlikning hadlari, an esa uning n- hadi deyiladi.
Misollar: 1) Toq sonlar ketma-ketligi: 1, 3, 5, 7, ..., 2n~ 1, ...;
2) juft sonlar ketma-ketligi: 2, 4, 6, 2n, ...; bunda n= 1,2, ... . Bular
ketma-ketlikka misol bo‘la oladi.
Ketma-ketlik hadlari orasida turli munosabatlar bo‘lishi mumkin. Masa-
lan, 1, 2, 3, 4, ... natural sonlar ketma-ketligida har bir had oczidan oldingi
hadga 1 ni qo‘shishdan; 5, 8, 11, 14, ... ketma-ketlikda har bir had o‘zidan
awalgi hadga 3 ni qo‘shishdan; 4, 2, 0, —2, —4, ... ketma-ketlikda esa har bir
had o‘zidan awalgi haddan 2 ni ayirishdan hosil bo‘ladi. Shunday xossaga ega
bo‘lgan ketma-ketliklar ariftnetik progressiya deyiladi.
Ta’rif. Agar a19 a29 ..., a„> ... sonli ketma-ketlikda barcha natural
n lar uchun
a„+i=a„+d (2)
tenglik bajarilsa, bunday ketma-ketlik ariftnetik progressiya deyiladi, d —
0 dan farqli biror son.
Agar (2) formulada d= 0 bo‘lsa, an+l = an, ya’ni hanuna hadlari o‘zaro
teng bo‘lgan ketma-ketlikka ega bo‘lamiz. Bu holda ham ketma-ketlik arifmetik
progressiya deb atalaveradi.
(2) dan d = an+x~an, d son n ga bog‘liq emas. d — ariftnetik progres-
siyaning ayirmasi deyiladi.
Misollar:
1) Natural sonlar qatori 1, 2, 3, n, ... ariftnetik progressiyani tashkil
etadi, unda d= 1.
2) 4, 2, 0, —2, —4, ...sonli ketma-ketlik ham ariftnetik progressiya tashkil
etadi, unda d= —2.
1- masala. an = 2,4 + 5n formula bilan berilgan ketma-ketlik ariftnetik
progressiya bo'lishini isbotlang.
167
жж
жж
жж
□ ап + J — ап ayirma o'zgarmas son ekanini isbotlash talab etiladi. Ketma-
ketlikning ай+1 hadini yozamiz va ай+1 — an ayirmani tuzamiz:
«л+1 =2,4 + 5(я+1) = 7,4 + 5я;
лй+1 -an = (7,4 + 5л)-(2,4 + 5л) = 5.
Demak, a„+1 — an ayirma n ga bog'liq emas, ya'ni berilgan. ketma-ketlik
arifmetik progressiya ekan. H
Arifmetik progressiyaning ta’rifiga ko'ra
an+l =an an-l ~an
Bundan
жж
жж
жж
жж
жж
жж
жж
tenglik kelib chiqadi.
Agar (2) formuladan
@n+k = * an-k = ~
kelib chiqishini e’tiborga olsak (buni mustaqil isbotlang!)
an = a^k+2an-t>n>k>k = l>2,...
formula hosil boladi.
Shunday qilib, arifinetik progressiyaning ikkinchi hadidan boshlab har
bir hadi undan teng uzoqlikda joylashgan ikkita hadining o‘rta arifmetigiga
teng. ,faiftnetik“progressiya degan atama shundan kelib chiqqan.
Agar аг va d berilgan bo'lsa, (2) formula yordamida qolgan a2, a3,... hadlarini
hisoblash mumkin. Agar аг va d bo'yicha biror ak hadni hisoblash talab etilsa, ak
ni hisoblash uchun formula chiqarib, undan foydalanish mumkin.
Arifmetik progressiyaning ta’rifiga ko'ra
02 = ax + d,
a3 = 02 + d= 0^ + 2d,
a4 = a3 + d = at + 3rfva h. k.
Bu munosabatlarga asoslanib
an = ax + (n — l)d (3)
formulani yozish mumkin.
(3) formula arifmetik progressiyaning n- hadi formulas! deyiladi.
2- masala. Agar ax = — 5 va d= 3 bo'lsa, a100 topilsin.
Q (3) formula bo'yicha: д100 = —5 + (100 — 1) • 3 = 292. Q
3-masala. 179 soni 2, 5, 8, 11, ... arifmetik progressiyaning hadi. Shu
hadning nomerini toping.
□ Aytaylik, n izlangan nomer bo'lsin. al = 2, d=3 bo'lgan! uchun
an = + (n — 1)</ formulaga ko'ra: 179 = 2 + (n - 1) 3. Shuning uchun
179 = 2 + 3«-3; 179 = Зл-1; Зя=180, я = 60. Javob: w = 60.
168
жж
ЖЖ1
4-masala. Arifmetik progressiyada = 111, д13 = 139. n- hadning for-
mulasini toping.
QJ (3) formuladan foydalanib topamiz:
a9 = <?i + 8J, д13 = ar + 12J.
Berilgan a$ va a13 ga ko'ra va d ga nisbatan tenglamalar sistemasini hosil
qilamiz:
Oy +%d = 111,
\+12 d = 139.
Ikkinchi tenglamadan birinchi tenglamani ayirib topamiz:
4J=28, d=7.
Shunga ko‘ra ax = 111 — 8 7 = 111 — 56 = 55, = 55.
Endi n- had formulasini yozamiz:
an = 55 + (n — 1)7 = 48 + 7n.
Javob: an = 48 4- 7л. И
5- masala. Burchakning bir tomonida
uning uchidan boshlab teng kesmalar ajratildi.
Ulaming oxirlaridan burchakning ikkinchi
tomonini kesib o'tadigan parallel to'g'ri
chiziqlar o'tkazildi (64-rasm). Kesuvchilaming
burchak tomonlari orasida joylashgan kesma-
lari ^2,an,... arifmetik progressiya tashkil
etishi isbotlansin.
□ Chizmadan ko'rinadiki, asoslari ab , an-i> an> bo'lgan
qator trapetsiyalarga egamiz. an kesma va an+i asoslarga ega bo'lgan trapetsi-
yaning o'rta chizig'idir.
Shuning uchun
n _an-\+an+\
°n~ 2
Bundan 2a„ = an^l + дй+1 yoki an+l — an = an — an-V Bu ayirma arifmetik
progressiyaning ayirmasidan iborat. Shunday qilib, ab a2, .an, ... ketma-
ketlik arifmetik progressiya bo'ladi. I
533. Savolgajavob bering. Topshiriqlami bajaring:
©1) Qanday sonli ketma-ketlik arifmetik progressiya deb ataladi?
2) Arifmetik progressiya degan atama nima bilan izohlanadi?
3) Arifmetik progressiyaning n- hadi formulasini keltirib chiqaring.
534. (Og'zaki.) Arifmetik progressiyaning birinchi hadi va ayirmasini
ayting:
1) 3, 5, 7, ...; 2) 2, 5, 8, 11,
3) 19, 15, 11, ...; 4) -13, -10, -7, ....
жж
169
ИТЧ1ХТХ1
535. Agar: 1) aY = 3, d=2; 2)^ = —4, rf = 3; 3)^ = 5, d = — 2
bo‘lsa, ariftnetik progressiyaning dastlabki 5 ta hadini yozing.
536. n- hadining formulas! bilan berilgan ketma-ketlik ariftnetik progressiya
bo‘lishini isbotlang:
1) ал = 4 + 3л; 2) an = — 2 + 3л; 3) an = 7 — 5n;
4)а„ = 2(л + 3); 5) ал = 3(2-л); 6)лл = 4(л-1).
537. Ariftnetik progressiyada:
1) = 3, d= 2 bo‘lsa, a13 ni;
2) ^ = 2, d=3 bo‘lsa, д20 ni;
3) = -3, d = — 2 bo‘lsa, a18 ni;
4) aY = —2, d= — 4 bo‘lsa, a13 ni toping.
538. Ariftnetik progressiyaning n- hadi formulasini yozing:
1) 1, 5, 9, 13, ...; 2) 23, 19, 15, 11,
3) -3, -5, -7, -9, ...; 4) 2, -1, -4, -7, ... .
539. Ariftnetik progressiyada:
1) aY = — 3 va d= 0,7 bo‘lsa, an ni;
2) aY = 18 va d= —0,6 bo'lsa, ni toping.
540. Agar: 1) ^ = 10, <Z=4; 2) ^ = 1,7, d =—0,2; 3) aY = — 3,5,
d = 0,6 bo‘lsa, ariftnetik progressiyaning dastlabki 5 ta hadini toping.
541. Agar: 1) -1; ; 2) 2,3; 1; ... ; 3) 8, 11, 14, ... .
bo‘lsa, ariftnetik progressiyaning o‘ninchi va n- hadini toping.
542. —10 son 44, 38, 32, ... ariftnetik progressiyaning hadi. Shu sonning
nomerini toping.
543. 12 son —18, —15, —12, ... ariftnetik progressiyaning hadi bo‘la oladimi?
544. Agar ariftnetik progressiyada: 1) ^ = 6, a15 = 48; 2) a1 = ~5,
я10 = 17 bo‘lsa, uning ayirmasini toping.
545. Agar ariftnetik progressiyada: 1) d=— 3, 0^ = 20; 2) a21 = —10,
д22 = —5,5 bo‘lsa, uning birinchi hadini toping.
546. Agar ariftnetik progressiyada: 1) a3 = 13, a6 = 22; 2) a2 = —7, ay = 18
bo‘lsa, uning л- hadi formulasini yozing.
547. Agar ariftnetik progressiyada: 1) a2 = 4; a5 = 10; 2) a3 = —9, a10 = 12
bo‘lsa, uning n- hadi formulasini toping.
548. n ning qanday qiymatidan boshlab 19, 16, 13, ... ariftnetik progressiya-
ning hadlari manfiy bo‘la boshlaydi?
170
1ЖЖ
549. n ning qanday qiymatidan boshlab —29, —25, —21, ... arifinetik prog-
ressiyaning hadlari musbat bo'ladi?
550. Jism o'z harakatining birinchi sekundida 7 m masofani o'tdi, keyingi
har bir sekundda esa awalgisidan 3 m ortiq yo'l o'tadi. Jism sakkizinchi
sekundda qancha masofani o'tgan?
551*. Siniq chiziqning birinchi bo'g'ini 5 sm ga teng. Keyingi har bir bo'g'in
awalgisidan 2 sm uzun. Siniq chiziqning 10- bo'g'ini uzunligini toping.
n- bo'g'irmi hisoblash formulasini chiqaring.
552. Havo vannasini olish yo'li bilan davolanishda birinchi kuni davolanish
15 minut davom etadi, keyingi har bir kunda uni 10 min dan orttirib
boriladi. Varina olish ko'pi bilan 1 soat 45 min davom etishi uchun
ko'rsatilgan tartibda havo vannasini olish necha kun davom etishi kerak?
553*. Qavariq ko'pburchaklar (uchburchak, to'rtburchak, beshburchak va h.
k.) ichki burchaklari yig'indisi arifmetik progressiya bo'lishini isbotlang.
Uning ayirmasini toping.
554*. —14 va 1 sonlar orasiga 4 ta son shunday qo'yilganki, natijada u sonlar
berilgan sonlar bilan birgalikda arifmetik progressiya tashkil qiladi. Qo'yilgan
sonlami toping.
555*. —23 va —8 sonlari orasiga 4 ta sonni shunday qo'yilganki, natijada u
sonlar berilgan sonlar bilan birgalikda arifmetik progressiya tashkil qiladi.
Qo'yilgan sonlami toping.
38- §. Arifinetik progressiya dastlabki n ta hadining yig'indisi
Arifmetik progressiyaning, masalan, dastlabki 100 ta hadi yig'indisini
hadma-had qo'shib hisoblash ancha vaqtni oladi va talaygina hisoblashlami
bajarishga to'g'ri keladi. Shu sababli tegishli yig'indi uchun formula topilsa maqsadga
muvofiq bo'ladi.
1- masala. 1 dan 100 gacha bo'lgan barcha natural sonlar yig'indisini
toping.
□ 1 + 2 + 3 +... + 99 + 100 yig'indini, ravshanki, yana 100 4- 99 + 98 4-... + 2 + 1
ko'rinishda yozib olsa ham bo'ladi. Agar yig'indini 5 deb belgilasak, u holda
5 = 1 + 2 + . ..+99+100,
5 = 100+99 + . ..+2 + 1.
Bu tengliklami hadma-had qo'shib topamiz:
25= 101 + 101+101+...+101+101
100 ta qo'shihivchi
Bundan 25= 101 • 100, 5= 101 • 50 = 5050 kelib chiqadi.
Javob: S= 5050.
жж
ЖЖ
жж
жж
таи
ЖЖ
ЖЖ
ЖЖ
171
ж
зкж
зкж
жии
1- masalada qo'llanilgan usul arifmetik progressiya dastlabki n ta hadining
yig'indisi uchun umumiy formula chiqarish imkonini beradi.
Ixtiyoriy
^1’ fl2’ •5 ^л’ ••
arifmetik progressiya berilgan bo'lsin. Sn — uning dastlabki n ta hadining yig'indisi
deylik:
Sn = ai + 02 + ...+ an.
Teorema. Arifmetik progressiya dastlabki n ta hadining yig‘indisi uchun
ushbu
S„=^-n (1)
formula o‘rinlidir.
□ Sn ni ikki usul bilan yozib olamiz:
= ai + 02 +... + an_i + an,
= an + дя_1 +... + 02 + di.
Arifmetik progressiyaning ta’rifiga ko'ra, bu tengliklami quyidagicha
yozish mumkin:
= +(A[ + d) + (^ +2rf) +...+(O\ + (w—l)t/),
Sn -an +(an -d)+(an -2d) + ...+(an -(n-l)d).
Endi (2) va (3) tengliklami hadma-had qo'shamiz:
25« = V*4+^ 4 a4
n ta qo‘shiluvchi
Demak, 2Sn = (ax + a^ • n, bundan (1) formula kelib chiqadi: Sn = Д1*а” • n
2- masala. Dastlabki n ta natural sonlar yig'indisini toping.
□ Natural sonlar qatori
1, 2, 3, ..., n, ...
ayirmasi d=l bo'lgan arifmetik progressiya tashkil qiladi, unda ar = 1, an = n.
(1) formulaga ko'ra topamiz:
Sn =l + 2 + ... + w = i^«.
n 2
Shunday qilib,
1 + 2 + 3+... + » = ^.
2 "
3- masala. Agar 43 + 39 + 35 + ... +(—9) yig'indining qo'shiluvchilari
arifmetik progressiyaning ketma-ket hadlari bo'lsa, shu yig'indini toping.
172
□ Shartga kocra a1 = 43, d= — 4, an = — 9. Qo‘shiluvchilar sonini
an = ai + (n ~ 1)^ formuladan foydalanib topamiz: —9 = 43 + (« — 1) • (—4),
bundan n = 14. Endi 514 ni (1) formula bo‘yicha hisoblaymiz:
514 =^ 14 = 238.
Javob: S14 = 238. |
4*- masala. Yigeindi 110 ga teng bo‘lishi uchun 2, 4, 6, ... ketma-ketlik-
ning dastlabki nechta hadini qo‘shish kerak?
□ 2, 4, 6, ... sonlar qatori av = 2, d=2 bo'lgan ariftnetik progressiyadir.
Unda 5„=110. Qo'shiluvchilar sonini topamiz. Uning uchun
« ai+an ai+a^+^n-lld 2al+(n-l')d , , r
Sn = n = ——----------n = —i—z------« deb yozib olamiz. Bu formu-
n 2 2 2 J
laga berilganlami qo'yamiz:
11Л 2-2+(«-1)-2 .. 9 11л n
110 =-----------n yoki n2 + n — 110 = 0.
Kvadrat tenglamani yechamiz:
«12=-^±Л + 110=-^±
1,2 2 V4 2
1
1 .>441 =_1 +21
2” 2 ~ 2“2
ЖЖ
жж
ТСЖ
жж
ТСЖ
жж
Bundan qo‘shiluvchilar soni, ma’nosiga коета, musbat bo‘lgani uchun
n = 10 kelib chiqadi. Javob: и = 10.
556. Topshiriqlarni bajaring:
1) Ariftnetik progressiya dastlabki n ta hadi yig'indisi formulasini
ЖЖ
тстс
2) Ariftnetik progressiya dastlabki n ta hadi yig'indisi formulasini chiqarishda
qanday usuldan foydalanilganini ayting va misol keltiring.
557. Agar ariftnetik progressiyada:
1) аг=1, a„= 19, n = 60; 2) a{ = l, an= 199,
3) в1 = -1, e„ = -41, « = 40; 4) a, = 2, a„=102,
bo‘lsa, uning dastlabki n ta hadining yig‘indisini toping.
558. Agar ariftnetik progressiyada:
1) Д! = 3, ал = 47, «=12; 2) ar = 2, дй=118,
3) at = —1, «„ = 41, « = 20; 4) ^ = —2, a„ = 44, « = 21
bo‘lsa, uning dastlabki n ta hadi yig'indisini toping.
559. 3 dan 99 gacha (99 ham kiradi) bo‘lgan barcha natural sonlar yig‘indisini
toping.
560. 1 dan 99 gacha (99 ham kiradi) bo'lgan barcha toq sonlar yig‘indisini
toping.
п = 15;
жж
л = 99;
л = 50
жж
жж
ТСЖ
173
Ж
жж
ж
ИИ
ж
1ПП
жж
ж
пи
561*. 1 dan In — 1 (л= 1, 2, ...) gacha bo'lgan barcha toq sonlar yig'indisi
uchun formula chiqaring.
562. 2 dan 100 gacha (100 ham kiradi) bo'lgan barcha juft sonlar yig'indisini
toping.
563*. 2 dan 2 л gacha (л= 1, 2, ...) bo'lgan barcha juft sonlar yig'indisi
uchun formula chiqaring.
564. Agar arifinetik progressiyada
1) в1 = -5, rf=0,5; 2)fli=i,d = -3; 3)a, = 7, d=3
bo'lsa, uning dastlabki 12 ta hadi yig'indisini toping.
565. Agar
1) 3+7+11+15+...+163; 2) 110+ 105+ 100+ ... + (-40)
yig'indining qo'shiluvchilari arifinetik progressiyaning ketma-ket hadlari
bo'lsa, shu yig'indini toping.
566. Barcha: 1) ikki xonali; 2) uch xonali natural sonlar yig'indisini toping.
567. Arifmetik progressiya n- hadining formulas! bilan berilgan.
Agar: 1) an = 3n + 4; 2) a„ = 2n + 5 bo'lsa, S40 ni toping.
жж
жж
568. Agar arifinetik progressiyada:
1) at = 9, n = 15, £15 = 600;
bo'lsa, an va d ni toping.
569. Agar arifinetik progressiyada
1) «7 = 21, £7 = 205;
bo'lsa, ax va d ni toping.
жж
ж
570*. Sharlar uchburchak shaklida
shunday terilganki, birinchi qator-
da 1 ta, ikkinchi qatorda 2 ta,
uchinchisida 3 ta va hokazo shar bor.
Agar hamma sharlar 120 ta bo'lsa,
ular nechta qatorga terilgan? 30 ta
„qatorli" uchburchak yasash
uchun shu sharlardan nechta kerak
bo'ladi (65-rasm)?
571. Arifmetik progressiya uchun
a3 + 69 = 8. 5И ni toping.
2 33
2) fll=l|,л = 11,£п=-у
2) an = 92, £n = 22
572. Arifinetik progressiyada л4 = 40,
aj = 52, Sn = 460 bo'lsa, n ni toping.
174
1ЖЖ
573*. Arifmetik progressiya a18 = 0, Sn = 0 bo'lsa, n ni toping.
574. Arifmetik progressiya an = 15 — 2л formula bilan berilgan. 521 ni toping.
575. 1+2 + 3 + ... + л = 4950 bo'lsa, n ni toping.
39- §. Geometrik progressiya
2, 4, 8,16,... ketma-ketlikning har bir hadi oldingisini 2 ga ko'paytirishdan
hosil bo'lgan. Agar muntazam uchburchakning tomonlari o'rtalarini
tutashtirsak, yana muntazam uchburchak hosil bo'ladi; kichik uchburchak bilan
Зо 3d
ham shunday amalni bajaraversak, uchburchaklar perimetrlari 3a, —, —, —
(bunda a — dastlabki uchburchak tomoni) ketma-ketlikni tashkil etadi. Unda
ikkinchisidan boshlab har bir hadi awalgisini 2 ga bo'lishdan hosil bo'ladi.
Bunday ketma-ketliklar geometrik progressiya deyiladi.
жж
ЖЖ
Ta’rif. 4gor
bi, ^2, bj,..., b„,... (1)
sonli ketma-ketlikda barcha natural n uchun
bn+i ~ 9b„, (2)
tenglik bajarilsa, bunday ketma-ketlik geometrik progressiya deyiladi,
bunda bn*0, q — nolga teng bo4magan biror son.
(2) formuladan = q kelib chiqadi. q son geometrik progressiyaning
bn
maxraji deyiladi.
ЖЖ
жж
сети
Misollar:
1) 3, 12, 48, 192, ... — maxraji 4 ga teng bo'lgan geometrik progressiya;
2) I ’ К ’ — maxraji ga teng bo'lgan geometrik progressiya;
5 9 27 3
3) - |1,1, - 3,... — maxraji -3 ga teng bo'lgan geometrik prog-
ressiya;
4) 6, 6, 6, 6, ... — maxraji 1 ga teng bo'lgan geometrik progressiya.
(1) dagi bb b2, ... sonlar geometrik progressiyaning hadlari, bn esa uning
л-hadi deyiladi.
ЖЖ
ЖЖ
Geometrik progressiya uchun b„ berilgan bo'lsa, unda n = 1, 2, ..., к deb
geometrik progressiya hadlarini yozib chiqish mumkin.
1- masala. bn = 32” formula bilan berilgan ketma-ketlik geometrik prog-
ressiya bo'lishini isbotlang.
жж
яки
175
жж
жж
жж
жж
жж
sm®
жж
жж
жж
Yechish. Agar -7^ nisbat barcha n = 1, 2,... lar uchun bir xil son bo'lsa,
bn
masala yechilgan bo'ladi. Chindan ham, 32” 0 bo'lgani uchun
bn+l _ 32(л+1) _ 32”+2 _ ,2 «
bn 32n 32n
ya’ni nisbat n ga bog'liq emas.
bn
Geometrik progressiyaning muhim xossasini chiqaraylik.
Ta’rifga ko'ra
^n+1 = Я bn, bn = qbn_i.
Bundan
Й = 4-А+1> »>1- (3)
Umuman,
bn = An-k ' Дч+Jtj = 1,2,... (4)
Agar progressiyaning barcha hadlari musbat bo‘Isa, и holda
bn = \lbn-ibn+i bo ‘ladi, ya 'ni geometrik progressiyaning ikkinchisidan
boshlab har bir hadi undan teng uzoqlikda turgan ikkita hadining o‘rta
geometrigiga teng. „Geometrik"progressiya degan atama shundan kelib chiqqan.
Agar bv va# berilganbo'lsa, b2, b3,...hadlamib^ = bn* qformulabo'yicha
hisoblash mumkin. Biroq, n katta natural son bo‘lsa, hadlami ketma-ket
hisoblab borish ko'p vaqtni oladi va ko'plab hisoblashlami bajarish kerak
bo'ladi. Shuning uchun bn ni hisoblash formulasini chiqarish va undan
hisoblashlarda foydalanish maqsadga muvofiq.
Ta’rifga ko'ra
bi - b^q,
b3=b2q = b{q2,
b^ =b3q = b^q3 va h.k.
Umuman,
bn=bl-g”-1. (5)
(5) formula geometrik progressiyaning n- hadi formulasi deyiladi.
2- masala. Agar b^ = 256 va q = i bo'lsa, geometrik progressiyaning 8-
hadini toping.
□ (5) formulaga ko'ra
176
жж
XTXIXTXI
b& =h V"1 =256
256 _ 1
64 • 256 " 64' ।
3- masala. 768 son 3, 6, 12, 24, ... geometrik progressiyaning hadi. Shu
hadning nomerini toping.
□ n izlangan nomer bo‘lsin. = 3, q = 2 bo‘lgani uchun bn = • ^"-1 for-
mulaga ko‘ra
768 = 3 • 2й-1 yoki 2й-1 = 256,2n-1= 28, bundan, «—1 = 8, n=9.
ЖЖ1
Javob: n = 9.1
4- masala. Geometrik progressiyada b5 = 48, b2 = 384. Shu progressiya n-
hadining formulasini yozing.
П (5) formulaga kocra Z>5 = b±(f, Z>8 = • q1 formulalaiga egamiz. Bundan
48 = bx - tf4, 384 = b^. Bu tengliklaming ikkinchisini birinchisiga bo'lamiz:
384 _ b^q1
48 W ’
Bundan 53 = 8 yoki q = 2; 48 = bx • 24 dan bx = 3 kelib chiqadi.
Natijada bn = 3'2й-1 formula hosil bo‘ladi. И
5*- masala. Radiusi 1 bo‘lgan aylanaga kvadrat ichki chizilgan. Bu ichki
chizilgan kvadratga yana aylana ichki chizilgan. Bu aylanaga yana kvadrat ichki
chizilgan. Hosil bo‘lgan aylanalar radiuslari va kvadratlaming perimetrlari
geometrik progressiya tashkil etishini isbotlang.
□ Awal aylanalar radiuslari geometrik progressiya tashkil etishini isbot-
laylik. n- marta chizilgan aylananing radiusi rn bo'lsin. Pifagor teoremasiga
ko‘ra (66-rasm)
2 2 2
tf+l + tf+l =6T-
12—Algebra, 9
Bundan r„2+1 = 1^, ya’ni r„+1 = -Lr„.
Demak, r15 r2, ..., rn, ... radiuslar
ketma-ketligi maxraji bo‘lgan geometrik
progressiyani tashkil etadi.
Shunga o'xshash, аг deb birinchi ichki
chizilgan kvadrat tomonini belgilasak, 2-,
_ Oi Oi
3-,... kvadrat tomonlan c3 = —
y/2 z
... uchun ham maxraji bo‘lgan geometrik
177
жж
ж
4ai
progressiyaga kelamiz. Kvadratlaming perimetrlari pr = 4ait Pi - J — uchun
ham maxraji -^= ga teng bo'lgan geometrik progressiya hosil bo'ladi.
зкж
зкж
жии
576. Topshiriqni bajaring. Savollaiga javob Bering:
1) Qanday sonli ketma-ketlik geometrik progressiya deb ataladi?
(?) 2) Geometrik progressiya degan atama qayerdan kelib chiqqan?
3) Geometrik progressiyaning n- hadi uchun formulani keltirib chiqa-
ring.
577. (Og'zaki.) Geometrik progressiyaning birinchi hadi va maxraji nimaga
teng:
1) 2, 6, 18, 54, ...; 2) -5, +10, -20, 40, ...;
2 1
3) 18, 6, 2, I 4) -25, -5, -1,
578. Agar geometrik progressiyada:
1) ^ = 7; ? = 3; 2) ^ = -5, q = -3
bo'lsa, uning dastlabki 6 ta hadini yozing.
579. Agar geometrik progressiyada:
1) ^ = 9, ?=3; 2) ^ = —4, g = —5; 3)^ = 2, ^=-2
bo'lsa, uning dastlabki 4 ta hadini yozing.
Ketma-ketlik n- hadining formulas! bilan berilgan. Shu ketma-ketlik
geometrik progressiya bo'lishini isbotlang (580—581):
580.1)4^=3-2”; 2)ЛЛ=4”+3; 3)йл=(1Г3; 4)Д,=^.
581.1)^ = 23”; 2)Z>„=6”+1; 3)6И=Г|Г1; 4)
Geometrik progressiyada (582—583):
582. 1) bi = 2 va q = 8 bo'lsa, bs ni;
2) bx = 3 va q = у bo'lsa, b6 ni;
3) bi = 1 va q = — 3 bo'lsa, b7 ni;
1
4) bi = — 2 va q = - - bo'lsa, b7 ni hisoblang.
583. 1) bi = 3 va q = 5 bo'lsa, b5 ni;
2) bi = — 3 va q = | bo'lsa, b6 ni;
178
1ЖЖ
3) bx = — 1 va q = 3 bo'lsa, b7 ni;
4) bx = 4 va q = -i bo'lsa, b6 ni hisoblang.
Geometrik progressiya n- hadining formulasini yozing (584—585):
584. 1) 3,12,48,...; 2)4, 1,1,...; 3)3, -1,1....
4 3
1 1
585. 1) 2,8,32,...; 2)1,11...; 3)-4, 8,-16, ... .
J 9
Geometrik progressiyada tagiga chizilgan hadning nomerini toping (586—
587):
586. 1) 2, 6, 18, ... ; 2) 4, 12, 36, 324, ...;
3) 625, 125, 25, 4) 1, -2, 4, -8, -128, ... .
587. 1) 2, 4, 8, ..., 512, ...; 2) 3, 6, 12, ..., 384, ...;
3) -2, 1, -1,1,...; 4) 1, 3, 9, 27, ..., 2Ш.
588. Agar geometrik progressiyada:
1) br = 2, b5= 162; 2) = -128, b7 = -2;
3) bi = 3, />4 = 81; 4) *j = 250, *4 = -2
bo'lsa, uning maxrajini toping.
589. 3, 6, 12,... geometrik progressiya berilgan:
1) shu progressiyaning 7- hadini hisoblang;
2) ketma-ketlikning 192 ga teng hadining nomerini toping.
590. Agar musbat hadli geometrik progressiyada:
1) a5 = 32, *7= 128; 2) *3 = 27, *5 = 243; 3) *6= 160, *8 = 640
bo'lsa, uning 6- hadini va maxrajini toping.
591. Agar geometrik progressiyada:
1) *4 = 9, *6 = 20; 2) *4 = 9, *6 = 4; 3) *4 = 24, *6 = 96
bo'lsa, uning birinchi va beshinchi hadlarini toping.
592*. Tomoni 4 sm bo'lgan kvadrat berilgan. Uning tomonlarining o'rtalari
ikkinchi kvadratning uchlari bo'ladi. Ikkinchi kvadrat tomonlarining
o'rtalari uchinchi kvadratning uchlari bo'ladi va hokazo. Shu kvadratlar
yuzlarining ketma-ketligi geometrik progressiya tashkil qilishini isbotlang.
Yettinchi kvadratning yuzini toping.
593*. 4 va 324 sonlar orasiga uchta musbat son shunday qo'yilganki, natijada
u sonlar berilgan sonlar bilan birgalikda geometrik progressiya tashkil
qiladi. Qo'yilgan sonlami va ulaming yig'indisini toping.
179
ЖЖ
дам
жж
ЖЖ
жж
ЖЖ
ЖЖ
ЖЖ
S/V/ 594*. 2 va 162 sonlar orasiga uchta musbat son shunday qo‘yilganki, natijada
u sonlar berilgan sonlar bilan birgalikda geometrik progressiya tashkil
qiladi. Qo‘yilgan sonlami va ulaming yig‘indisini toping.
40- §. Geometrik progressiya dastlabki n ta hadining yig‘indisi
Geometrik progressiyaning dastlabki bir necha hadlarini hadma-had qo‘shib
chiqish anchagina mehnat talab qiladi. Shu sababli hadlar yig‘indisi uchun
formula chiqarib, shu formula bo'yicha hisoblashlami bajarish qulay.
1- masala. Ushbu yig‘indini toping:
5 = 1+ 2 + 22 + 23 + 24 + 25.
О Tenglikning ikkala qismini 2 ga ko'paytiramiz:
25 = 2 + 22 + 23 + 24 + 25 + 26.
(1) va (2) tengliklami quyidagicha yozib olamiz:
5 = l + (2 + 22+23+24+25),
25 = (2+ 22 +23+24+25)+26.
Ikkinchi tenglikdan birmchi tenglikni ayirib chiqamiz:
2S- S= 26 - 1, 5= 26 - 1 = 64 - 1 = 63.
Javob: S= 63.
Endi q*l bo'lgan ixtiyoriy bb bxq, ..., b^cf, ... geometrik progressiyaning
dastlabki n ta hadi yig'indisi uchun formula chiqaramiz.
□ Sn = + b^q + biq2 + ... + (3)
deb belgilaymiz.
(3) tenglikning ikkala qismini q ga ko‘paytiramiz:
qSn = ^q + biq2 + ^q3 +... + biqn.
(3) va (4) tengliklami quyidagicha yozib olamiz:
Sn = by + (Ъм + byq1 +... + *),
= (byq + byq2 +... + + byq".
Qavslar ichida turgan ifodalar teng. Shuning uchun
‘S'n ~ A = \ - biqn.
Bundan (1 - q)Sn = ^(1 - qn) yoki
„ _ (!-<?") —
" l-« ’"
q = 1 bo'lgan hoi alohida qaraladi.
Agar q = 1 bo'lsa, ravshanki, Sn = bY * n bo'ladi.
Demak, quyidagi natijaga keldik:
©Teorema. Maxraji q^l bo‘lgan geometrik progressiyaning dastlab-
ki n ta hadi yig‘indisi (5) formulaga ko‘ra hisoblanadi.
Yuqoridagi (1) yig'indini (5) formulaga ko'ra hisoblaymiz. Unda br = 1,
q = 2, n = 6 bo'ladi. Shuning uchun 56 = 1 > = 26 -1 = 63. Yig'indi (5)
formula bo'yicha osongina topildi.
3
2- masala. 6,3, -,... geometrikprogressiya dastlabki 5 ta hadining yig'indisini
toping.
□ Shu progressiyada bx = 6, q = 2-1. (5) formula bo'yicha topamiz:
(5)
ЖЖ
жж
ТСЖ
жж
ТСЖ
= 12(1-^-
I 32
31-3 93
8 " 8 ’
3- masala. Maxraji q = | bo'lgan geometrik progressiyaning dastlabki
364
6 ta hadining yig'indisi —- bo'lsa, progressiyaning birinchi hadini toping.
81
О Hisoblashlami (5) formula bo'yicha olib boramiz:
h 1
364
жж
ТСЖ
жж
ТСЖ
J , . 364 2 , 728
81 !_1 yokl 81 3 ^ 729’
3
729 _ 819 _ -
81-3 813 ’ 01
жж
жж
Javob: bY = 3.1
4- masala. Geometrik progressiyaning dastlabki n ta hadining yig'indisi
364 . .. - .. 1
— ga teng. Bu progressiyaning birmchi hadi 3 ga, maxraji esa - ga teng. n ni
ol 3
toping.
□ Masalani yechish uchun (5) formuladan foydalanamiz:
жж
181
Ж
жж
жж
364
81
ч
2-364 . 1 1 81-9—728
у°И -81у = 1-уГ, УОМ 7 = -8iy
J_ = J_
3й з6 ’
ж
1Ж
жж
яняи
ж
жж
ЖЖ
жж
ж
Bundan п = 6 kelib chiqadi. Javob: п = 6. |
5- masala. 4, 12, 36, 72, ... geometrik progressiya. 4 + 12 + 36 + ... + 918
yig'indini toping.
□ Berilgan progressiyada ^ = 4, g=3, Ай = 918. (5) formuladan foy-
dalanamiz. Awal (5) ni quyidagicha yozib olamiz:
о _ ^(l-/1) _ fr-frg”"1 g _ b^-bn-q
n 1-q 1-g 1-g *
Masalada berilganlarni o'miga qo'yamiz:
c 4-918-3 4-2754 2750 1T7<
n 1-3 -2 2
Javob: Sn= 1375.
595. Savolga javob bering.
©1) Geometrik progressiya dastlabki n ta hadi yig'indisi nimaga teng?
2) Geometrik progressiya dastlabki n ta hadi yig'indisi formulasini
chiqarishda qanday usul qo'llanildi?
596. Agar geometrik progressiyada:
1)
=|,д = 3,л = 6;
=1, g = -|,« = 4;
bt = 5, q = 1, n = 200;
2) =-|,g = 3, л = 5;
4) =-4, q = ~,n = 5;
6) b{ = — 3, g=l, я =100
3)
5)
bo'lsa, uning dastlabki n ta hadining yig'indisini toping.
597. Geometrik progressiya dastlabki yettita hadining yig'indisini toping:
1) 5, 15, 45, 2) 2, 8, 32, ... ; 3) 8, 12, 18, ... .
598. Agar geometrik progressiya uchun:
1) q = 2, S1 = 635 bo'lsa, bx va ni;
2) q= -2, *У8 = 85 bo'lsa, bx va b% ni toping.
599. Agar geometrik progressiya uchun:
1) *$'„ = 242, ^ = 2, g=3; 2) 5„=189, ^ = 3, g = 2;
3) 4-170, *1 = 256, « = -|; 4) s„ = -189, *j = 9, ?=-2
bo'lsa, n ni toping.
182
1ЖЖ
600. Agar geometrik progressiya uchun:
1) 5„ = 363, ^ = 3, $=3; 2) 5„ = 341, ^ = 1, q = 4;
3) 5^ = 567, ^ = 27, q = 4; 4) 5n=189, ^ = -9, q=~2
bo'lsa, n ni toping.
601*. Agar geometrik progressiya uchun:
1) br = 7, q = 3, Sn = 847 bo'lsa, n no. bn ni;
2) bv = 8, q = 2, Sn = 4088 bo‘lsa, n va bn ni;
3) bi = 2, bn = 1458, S„ = 2186 bo'lsa, n va q ni;
4) bi = 1, Sn= 2801, £„ = 2401 bo'lsa, n va q ni toping.
602. Agar qo'shiluvchilar geometrik progressiyaning ketma-ket kelgan had-
lari bo'lsa, yig'indini toping:
1) 1 + 3 + 9 + ... + 243; 2) 2 + 6 + 18 + 54 + ... + 486;
3) -1 + 3-9 + 27 + ... + 2187; 4) 2-6 +18-54 +... +1458.
603. Agar qo'shiluvchilar geometrik progressiyaning ketma-ket kelgan had-
lari bo'lsa, yig'indini toping:
1) 2 + 4 + 8 + ... + 512; 2) 3 + 9 + 27 + ... + 729;
3) 2-4 + 8-16 + ... + 512; 4) 3-9+ 27+ ... + 729.
604. Agar geometrik progressiya uchun:
1) b2=X5, ^3 = 25; 2) b2 = 14, &4 = 56, q>§ bo'lsa, S9 ni toping.
605. Agar geometrik progressiya uchun:
1) bi = 5; b3 = 45; 2) bY = 12, Z>4 = 96, q>0 bo'lsa, bs va S5 ni toping.
606. Geometrik progressiya n- hadi formulas! bilan berilgan:
1) bn = 2- 3й"1 bo'lsa, Sj ni;
2) A„=-4 (i) bo'lsa, *У6 ni toping.
607. Geometrik progressiya n- hadi formulasi bilan berilgan:
1) bn = 4 • 3й"1 bo'lsa, *S5 ni toping;
2) = bo'lsa, S10 ni toping.
608. Geometrik progressiyaning maxraji 3 ga, dastlabki to'rtta hadi yig'indisi
80 ga teng. Uning to'rtinchi hadini toping.
609. Geometrik progressiyaning birinchi hadi 486 ga, maxraji | ga teng. Shu
progressiyaning dastlabki to'rtta hadi yig'indisini toping.
610. Geometrikprogressiyada \ = - - va # = 2bo'lsa, 514 — 513ayirmani toping.
183
ЖЖ
дам
жж
ЖЖ
жж
ЖЖ
ЖЖ
жж
ЖЖ
жж
жж
жж
жж
жж
жж
жж
611. —0,25; 0,5; ... geometrik progressiyaning hadlari 10 ta. Shu progres-
siyaning oxirgi 7 ta hadi yig'indisini toping.
41- §. Masalalar yechish
612. (Og'zaki.) Arifmetik progressiyaning birinchi hadini va ayirmasini ayting:
1) 3, 8, 13, ... ; I 2) 5, 9, 13, ... ; I 3) 7, 10, 13, ...;
4) 19, 15, 11, ... ; | 5) -22, -19, -16, ... ; | 6) 49, 45, 41, ...
613. Agar:
1) ax = 3, rf=5; I 2) ax = 5, rf=4; I 3) ax = 19, rf=-4;
4) ax = —3, d=—T, | 5) ax = — 22, d= 3; I 6) ax = —5, d= — 2
bo'lsa, arifmetik progressiyaning dastlabki to'rtta hadini yozing.
614. Ketma-ketlik o'zining n- hadi formulas! bilan berilgan. Bunday ketma-
ketlik ariftnetik progressiya bo'lishini isbotlang:
1) an = 2 — Зя; 2) an = — 3 + 4я; 3) an = 2(n — 1);
4) an = 4(я - 5); 5) an = -3(5-я); 6) an = -2(8 +«).
615. Arifmetik progressiyada:
1) agar a1 = — 1; d= — 3 bo'lsa, д13 ni;
2) agar = 1, d= 4 bo'lsa, alg ni toping.
616. Arifmetik progressiyaning n- hadi formulasini yozing:
1) 1, 5, 9, 13, ... ; 2) 20, 17, 14, 11, ...;
3) -4, -7, -10, ...; 4) 3, -2, -7, -12, ... .
617. —54 soni 41, 36, 31, ... ariftnetik progressiyaning hadi.
Shu hadning nomerini toping.
618. Agar ariftnetik progressiyada:
1) ax = 2, an = 18, n = 50; 2) дх = 2; an = 40; n = 100;
3) ax = —2, ап = —ЗЪ, я = 50; 4) ax = — 1, лл = 51, я =100
bo'lsa, uning dastlabki n ta hadining yig'indisini toping.
619. 2 + 4 + ...4-108 yig'indini hisoblang.
620. 1 4- 34-54- ...4- 99 4- 101 yig'indini hisoblang.
621. 1) Agar n = 10 bo'lsa, 5; 9; 13, ... ;
2) agar n = 12 bo'lsa, -14; —11; —8, ...
ariftnetik progressiyaning dastlabki я ta hadi yig'indisini toping.
622. Arifmetik progressiya n- hadining formulas! bilan berilgan.
Agar: 1) an = 4я 4- 3; 2) an = 5 4- 2я bo'lsa, 550 ni toping.
623. Agar arifmetik progressiyada:
1) a4=16, 520 = 710; 2) аъ = 26, 512 = 606
bo'lsa, ax va d ni toping.
184
1ЖЖ
624. (Og‘zaki.) Ushbu geometrik progressiyaning birinchi hadi va maxraji
nimagateng:
1) 4, 12, 36, 2) -7, 14, -28, 3) 2, 6, 12,
4) 24, 12, 6, ...; 5) -64, 16, -4, ... ; 6) -4, 8, -16, ...?
625. Agar geometrik progressiyada:
1) ^ = 4, q=3; 2) ^ = -3, <? = 2; 3) ^ = 2, q=-2
bo'lsa, uning dastlabki beshta hadini yozing.
626*. Ketma-ketlik n- hadining formulas! bilan berilgan. U geometrik
progressiya boclishini isbotlang:
l)i„ = 2-3»; 2)Z>„ = 4"-2; 3)*.=(|J’3; 4)4,=^.
627. Geometrik progressiyada:
1) bY = 2, q=5 bo'lsa, b4 ni; 2) b{ = 4, q = | bo'lsa, b5 ni;
3) ^ = 1, q=~3 bo'lsa, b5 ni; 4) ^ = —2, # = bo'lsa,
b6 ni hisoblang.
628. Geometrik progressiya n- hadining formulasini toping:
1) 3, 12, 48, 2) 4, 1, |, 3) 3, -1,
4)3,14,28,...; 5) 5, 2, |,... . 6) 9, 3, 1, ... .
629. Agar geometrik progressiyada:
1) bY = 2, b8 = 256; 2) = -128; b6 = 4;
3) bt = 3, b5 = 243; 4) = 5, b4 = 625
bo'lsa, uning maxrajini toping.
630. Agar geometrik progressiyada:
1) A =|> 4=2, n = 5; 2) dt = -2; 4 = |, л = 6;
3) ^ = 3, = n = 4; 4) ^ = -5; <? = -|, « = 5
bo'lsa, uning dastlabki n ta hadining yig'indisini toping.
631. Geometrik progressiyaning dastlabki beshta hadining yig'indisini toping:
1) 3, 6, 12, 24, ...; 2) 81, 27, 9, 3, ... .
632. Agar geometrik progressiyada:
1) q = 2, S7 = 635 bo'lsa, bt va b6 ni;
2) q = —2, 58 = 85 bo'lsa, bx va b8 ni toping.
ЖЖ
дам
жж
ЖЖ
жж
ЖЖ
ЖЖ
ЖЖ
185
633. Agar geometrik progressiyada:
1) 5„=120, 61 = 3, «=3;
3) 5^=170, />, = 256, ? = -l;
bo'lsa, n ni toping.
2) 5„ = 315, ^ = 5, g = 2;
4) 5Й = —77, ^ = -7, q = -2
634. Geometrik progressiya n- hadining formulasi bilan berilgan:
1) bn = 2 3й 1 bo'lsa, Ss ni; 2) b„ = -Q) bo'lsa, S6 ni toping.
635. Geometrik progressiyada:
1) ^2 = 3 va b4 + b6 = 60 bo'lsa, q ni;
2) b3 — bx = 24 va bs — bY = 624 bo'lsa, Ss ni toping.
636. Geometrik progressiya n- hadi formulasini yozing:
1) 32, 16, 8, 4, 2) 27, 9, 3, 1, |,
3) -25, -5, -1, -i, 4) -64, 32, -16, 8, ... .
637. Geometrik progressiya dastlabki 10 ta hadi yig'indisini toping:
1) 8, 4, 2, 1, 1, ...; 2) 1, ±,...;
3) -25, -5, -1, ...; 4) -64, 32, -16, ... .
Geometrik progressiya n- hadi formulasini yozing (638—639):
638. 1) 9 = 1, = 2; 2) 4 = -|, ^ = 6; 3) 9 = |. ^ = 8.
639. 1) 9 = |, 65=±; 2) 9 = -j, *4=-|; 3)9 = т,
J 01 о
640. n- hadining formulasi bilan berilgan geometrik progressiya dastlabki 5 ta
hadi yig'indisini toping:
l)^ = 2(-3)«; 2)Z>„ = -2-4"; 3)/>Й = 3-2Й;
-1) ; 5) *»=7-(-l) ; 6)4=4-(-l] .
42- §. Cheksiz kamayuvchi geometrik progressiya
ПАВС ning asosi AC=a, balandligi h deylik. U holda uning yuzi
5i = ^ah- DABC ning АгСг o'rta chizig'ini o'tkazamiz. da asos
4G = f, balandlik у, yuz S2 = - - - = -ah. Endi da o'rta chi-
2 2 2 2 2 8
ziq A2C2 ni o'tkazamiz. ПА2ВС2 da A2C2 = balandlik ga teng, yuzi esa
186
1ЖЖ1
c 1 a h 1 , , . „
o3 = - - - • - = — ah va hokazo. Bu
jarayonni davom ettiraversak, natijada
maxraji 4 ga teng bo'lgan geometrik
4
progressiya hosil bo'ladi (67-rasm):
111
— ah, —ah, —ah,...
2 ’ 8““’ 32
(1)
ЖЖ
67- rasmdan ko'rinadiki, ketma-ket hosil qilingan uchburchaklaming
yuzlari borgan sari kamayib, nolga yaqinlasha boradi. Shuning uchun (1) prog-
ressiya cheksiz kamayuvchi geometrik progressiya deyiladi. Bu progressiyaning
maxraji birdan kichikligini aytib o'tamiz: q = < 1.
Yana bitta misol ko'raylik. Tomoni uzunligi a bo'lgan kvadrat tomonlari
a
o'rtalarini ketma-ket tutashtiramiz. Hosil bo'lgan kvadratning tomoni ga
teng. U kvadratning tomonlari o'rtalarini yana ketma-ket tutashtiramiz, key-
ingi kvadratning tomoni | ga teng bo'ladi. Shu jarayonni davom ettiraversak,
a
Ja
a , a
2’
- . 1
(2)
cheksiz kamayuvchi geometrik progressiya hosil bo'ladi. Unda q = < 1.
IMaxrajining moduli birdan kichik bo4gan geometrik progressiya cheksiz
kamayuvchi geometrik progressiya deyiladi.
2
1- masala n- hadi bn = — formula bilan berilgan geometrik progressiya
cheksiz kamayuvchi bo'lishini isbotlang.
□ Shartga ko'ra = 5U bundan q = |$| < 1
3 У 2/ D[ 3
bo'lgani uchun berilgan progressiya cheksiz kamayuvchi bo'ladi. |
(1) va (2) progressiyalar cheksiz kamayuvchi. (1) ning n- hadini topamiz:
If1"1 ah , . , ah
| = ^P yarn bn=^.
sonlar nolga istalgancha yaqinlashib
bn = blqn 1 =^ah
Agar n cheksiz o'sib borsa,
boradi, bu holni shunday yozishadi:
22B-1 U
жж
ЖЖ
ЖЖ
ЖЖ
ЖЖ
жж
187
Ж
(0‘qilishi: n cheksizlikka intilganda sonlar ketma-ketligi nolga intiladi)
yoki
Bin ~^r = °.
«->«> 22"-1
(0‘qilishi: n cheksizlikka intilganda . ketma-ketlikning limiti nolga teng).
Endi ixtiyoriy cheksiz kamayuvchi geometrik progressiyani qaraymiz:
bfa l\q\..., \q\ < 1.
Ta’rif. Cheksiz kamayuvchi geometrik progressiyaning barcha hadlari
yig‘indisi deb da uning dastlabki n ta hadi yig(indisi intiladigan
songa aytiladi,
Progressiyaning dastlabki n ta hadi yig'indisi formulasini yozamiz:
c _ h(l-qn) ,. „ by b[ n
s„------------------------— yoki s„- — q.
1-г
(3)
к
Agar п cheksizlikka intilsa, |^ < 1 ekanidan lim --3- qn = 0 bo'ladi.
л-»** 1—q
bt
Demak, lim Sn = .
i-q
<411^^11^
(4)
Cheksiz kamayuvchi geometrik progressiya barcha hadlari yigfindisi S
quyidagi formula bilan topiladi:
S = -h~.
l-(?
Xususan, agar = 1 bo'lsa, S = bo'ladi. U bunday yoziladi:
l-(?
1 + # + +... + qn~x
1Й’ l?l<1-
зияя
2-masala. —, —, —,... cheksiz kamayuvchi geometrik progressiya
2 8 32
barcha hadlari yig'indisini toping ((1) ga qarang).
□ Ravshanki, , q = -. (4) formulaga ko'ra topamiz:
ah
о 2 A ah 1 2 , „ 2 ,
5вД-4ТГ»* 5=звй Н
4
3- masala, a, ...cheksiz kamayuvchi geometrik progressiya
188
1ЖЖ1
barcha hadlari yig‘indisini toping ((2) ga qarang).
□ Shu progressiyada = a, q = ~^=. (4) formulaga ko‘ra topamiz:
5, = -V = -^-« = (2 + ^)a, S = (2 + -j2)a.
V2-1
^2
4- masala. (4) formuladan foydalanib, a = 0, (7) = 0,777... davriy o‘nli
kasmi oddiy kasr shaklida yozing.
□ Agar «1 = 0,7 = ^; ^ = 0,07 = ^; a3 =0,007 = —^; ... deyilsa,
berilgan davriy ocnli kasmi 0,7 + 0,07 + 0,007 +... ko‘rmishda yozish mumkin
7 7 7 1
boiadi, yighndi a = — + — + + ... maxraji — ga teng bo'lgan cheksiz
kamayuvchi geometrik progressiya barcha hadlari yig‘indisini ifodalaydi. Shun-
7
, 10 7 м
ing uchun a = —= -. I
1-J- 9
10
641. Savollarga javob bering. Topshiriqlami bajaring:
1) Qanday ketma-ketlik cheksiz kamayuvchi geometrik progressiya deyi-
ladi?
©2) Cheksiz kamayuvchi geometrik progressiya barcha hadlari yig‘indisi
formulasini yozing.
3) Davriy o£nli kasmi oddiy kasrga aylantirish uchun uni cheksiz ka-
mayuvchi geometrik progressiya barcha yig'indisi shaklida qanday ifoda-
lanishini tushuntirib bering.
4) Geometrik progressiya cheksiz kamayuvchi bo‘lishi uchun qanday
shart bajarilishi kerak?
Geometrik progressiya cheksiz kamayuvchi ekanini isbotlang (642—643):
ЖЖ
жж
ЖЖ
ЖЖ
642. 1) 2, 1, 1, 1 ... •» 2) 3, 1, | 1 5 95
3) -36,-6,-1, 1 _6’"; 4) -8,-4, -2,-1,-i
1 1 1 643. 1) 32 > 64 > 128, "3 2) -5,-1, 1 5’"’’
~ _1 1 __L A X 1 1 1
3’9’ 27 ’ "••5 4) 16 ’ 64 ’ 256 ’ " ‘
644. Agar geometrik progressiyada:
1) ^ = 30, *2 = -15; 2) *7=12,
ЖЖ
ЖЖ
жж
189
жж
жж
ЖЖ
3) а7 = -20, Ь6= 10; 4) Z«5=-3,
bo'lsa, u cheksiz kamayuvchi bo'ladimi? Shuni aniqlang.
645. Agar geometrik progressiyada:
1) *i=20, 62 = -10; 2) Zfe = 6, Аю = |;
3)^ = |, *7 = 1; 4) *i = -6, *ю = -А
bo'lsa, u cheksiz kamayuvchi bo'ladimi? Shuni aniqlang.
Cheksiz kamayuvchi geometrik progressiya barcha hadlari yig'indisini toping
ЖЖ
жж
жж
ЖЖ
(646-648):
646.i) <? = |, *i=|;
4) ? = |, *4 = ^;
647. i) i,
' ’3’9’ ’
4) —25, -5, -1, ...
648. 1) ? = |, 6l=1;
A 1 I. 1
4) ’=3’ ^ = 81;
7) q = — —, *i — 5;
2) = *1=3;
5) ? = -2> = i6;
2) 6,1,|,...;
5) -7,-l,-|,...;
2) q = ~\, *1=12;
5) ? = -|, *t=-|;
Z О
ox 1 A 11 .
8) « 5> 625*
3) 4 = \, *1=4;
6) <7 = y, *1=25.
3) 49, 7, 1, ...;
6) -16, -4, -1, ... .
3) q = ~, *1 = 36;
О
6) q = *! = 25;
9) q = *1 =64.
О
649. Ketma-ketlik o'zining n- hadi formulas! bilan berilgan. U cheksiz kama-
yuvchi geometrik progressiya bo'ladimi:
1) ^ = 2-(-3)«; 2) йй = -3-2«;
(i f i
-|j ; 4)*„ = 54-lj ?
650. Cheksiz kamayuvchi geometrik progressiya hadlari yig'indisini toping:
1) 12,6,3,|,...; 2) 50,-10,2,
651. Cheksiz kamayuvchi geometrik progressiya hadlari yig'indisini toping:
жж
жж
190
1ЖЖ
652. Cheksiz kamayuvchi geometrik progressiyaning barcha hadlari yig'indisi
150 ga teng. Agar:
1) q = | bo'lsa, bx ni; 2) bx = 75 bo'lsa, q ni toping.
653. Cheksiz kamayuvchi geometrik progressiyaning hadlari yig'indisi
270 ga teng. Agar:
1) q = | bo'lsa, bx ni; 2) br = 180 bo'lsa, q ni toping.
Cheksiz kamayuvchi geometrik progressiyaning hadlari yig'indisini toping
(654—657):
654*. 1) 1 + sin 30° + sin2 30° + sin3 30° + ...;
2) 1 - cos 30° + cos2 30° - cos3 30° +....
655*. sin60° + sin260° + sin360° + .... 656*. tg30° + tg230° + tg330° + ....
657*. cos45° + cos245° + cos345q + ....
658*. 60” li burchakka bir-biriga va burchak tomonlariga urinuvchi aylanalar
ketma-ket ichki chizilgan (68- rasm). Birinchi aylananing radiusi ga
teng. Qolgan aylanalaming R2, R3, ..., Rn ... radiuslarini toping, ular
cheksiz kamayuvchi geometrik progressiya tashkil qilishini ko'rsating va
uning hadlari yig'indisini toping.
659*. Qirrasi a bo'lgan kubning ustiga qirrasi bo'lgan kubni qo'yishdi,
uning ustiga qirrasi bo'lgan kubni qo'yishdi, so'ngra uning ustiga qir-
rasi bo'lgan kubni qo'yishdi va hokazo. Hosil bo'lgan shaklning baland-
ligini va barcha kublar hajmlari yig'indisini toping (69- rasm).
ЖЖ
дам
жж
ЖЖ
жж
ЖЖ
ЖЖ
ЖЖ
191
43- §. Progressiyaning tatbig‘iga oid masalalar
1- masala. Omonatchi yil boshida jamg‘arma bankiga к so‘mni yiliga p%
ortishi sharti bilan n yil muddatga qo‘ydi. n- yil oxirida omonatchining puli
necha so‘mga yetadi?
□ Bunda ikki hoi bo‘lishi mumkin.
1- hoi. Har yili к so‘m hisobidan foiz hisoblanadi. Bunda bir yilda к so'mga
к
qo'shiladigan pul p so'mni tashkil qiladi. n yil davomida har yili к so'mga
к
— - p so‘m pul qo'shilib boraveradi va pul qo'ygan kishi bankdan n- yil
oxirida
к +-!¥- n = к (1 +—
K loo n K ( loo,
100
socm pul oladi. Bankka bunday shart bilan pul qo'yish nddiy foiz (protsent)
boyicha to‘lash deyiladi.
Hosil qilingan an, ... sonlar ayirmasi d = bo‘lgan o'suvchi
ariftnetik progressiya tashkil qiladi.
2- hoi. Har yilgi oshadigan pul miqdori (foyda) oldingi yilgi pulga qo'shiladi
va hosil bo‘lgan yig'indidan p% foyda hisoblanadi. Omonatchining puli 1- yil
oxiriga kelib so‘mga ortadi va uning puli 1 - yil oxirida h = £^1+) so‘m
bo'ladi. 2- yil oxiriga kelib omonatchining puli b} so‘mning p% iga ortadi va
b\ d ( d A ( d V
^=^+ioo = M1+loo Гд1+1оо J ga yetadi‘ 3" yil oxirida esa
/ \3
omonatchining bankdagi puli b2 so'mning p% iga ortadi va jami = к 1 + —
so‘mni tashkil etadi.
1+ioo
so'mga yetadi. |
Bankka bunday shart bilan pul qo'yish murakkab foiz (protsent) bo yicha
to‘lash deyiladi. Hosil qilingan b„ b^, .... b, ... sonlar maxraji q = l + т^г ga
i z « uju
teng o‘suvchi geometrik progressiyadan iborat.
ar= Ьг hamda b{> at {1= 2, 3, ...) ekaniga e’tibor bering. Demak, bankka
murakkab foiz bocyicha mablagc qo‘yish maqsadga muvofiq ekan.
Misol uchun />=10%, k= 1 000 000 so‘m, n = 3 bo'lsa,
192
1ЖЖ
(10-3 A
l + -^£ = 1000000-1,3=1300000
1000 J
so'm bo‘ladi.
bi = 1000000fl+-^J =1000000 (1,l)3 =1331000 so'm bo'ladi.
b3 - a3 = 31 000 so'm.
660. Bankka murakkab protsent hisobida qo'yilgan 1 000 000 so'm pul 3 yil
o'tgach 1 331 000 so'm bo'ldi. Pul yiliga necha protsent hisobidan
qo'yilgan?
661. Bankka murakkab protsent hisobida qo'yilgan 1 000 000 so'm pul ma’lum
muddat o'tgach 1 210 000 so‘m bo'ldi. Agar pul yiliga 10% hisobidan
qo'yilgan bo'lsa, u necha yilga qo'yilgan edi?
662. 800 000 so'm pul murakkab protsent hisobida 2 yil muddatga qo'yildi.
Agar pul yiliga 20% hisobidan qo‘yilgan bo'lsa, 2- yil oxirida u necha
so'm bo'ladi?
ЖЖ
дам
жж
663*. Firma har yili 10 000 dona mahsulot ishlab chiqarar edi. Agar u yangi
texnologiyani joriy etib, ishlab chiqarishni har yili awalgi yilga nisbatan
20% oshirishga erishsa, firma: 1) ikkinchi yilning; 2) uchinchi yilning;
3) to'rtinchi yilning oxiriga kelib necha dona mahsulot ishlab chiqaradigan
bo'ladi?
ЖЖ
664*. Bank qo'yilgan jamg'armaning 2% i miqdorida oyiga daromad to'laydi.
Hisob raqamiga 1000 000 so‘m qo'yilgan va har oyda daromad jamg'armaga
qo'shib borilayotgan bo'lsin. 1 oydan; 2 oydan; 3 oydan so'ng jamg'arma
miqdori qancha bo'ladi?
жж
2- masala. 0,(5) davriy kasmi oddiy kasr ko'rinishida ifodalang.
О 0,(5) = 0,555... bo'lgani uchun 0,(5) sof davriy kasmi 0,(5) = 0,5 +
+0,05 + 0,005 +... kabi yozib olamiz. 0,5 + 0,05 + 0,005 + ... yig'indi birinchi
hadi b{ = 0,5, maxraji q = 0,1 bo'lgan cheksiz kamayuvchi geometrik progressiya
barcha hadlarining
yig'indisidir.
5 = ^-
formulaga muvofiq,
ЖЖ
ЖЖ
Demak’ °’(5)4Javob: I-
Shunga o'xshash, 0,(7)Ц; 0,(3) = | = |; 0,(83) = ||;
“ У □ УУ
qi q Ind
0,(81) = — = —; 0,(124) = —. Bu misoldan shunday xulosaga kelamiz:
99 11 999
13—Algebra, 9
193
ЖЖ
Ж
Ж
ж
ж
1Ж
жж
яняи
ж
жж
ЖЖ
Sof davriy kasmi oddiy kasrga aylantirish uchun uning davridagi sonni
oddly kasming surati deb, davrida nechta raqam bo‘lsa, shuncha 9 ni oddiy
kasming maxraji deb olish kifoya.
3- masala. 0,3(4) aralash davriy kasmi oddiy kasr ko'rinishida yozing.
О 0,3(4) ni 0,3 + 0,0(4) ko'rinishda yozib olamiz. So'ngra 0,0(4) ni
0,04 + 0,004 + 0,0004 + yig'indi kabi yozamiz. Bu yig'indi maxraji 0,1 bo'lgan
cheksiz kamayuvchi geometrik progressiya barcha hadlari yig'indisini ifodalaydi.
Uni hisoblash uchun b. = 0,04; q = 0,1 ekanini e’tiboiga olib, 5 = formula
1-?
bo'yicha hisoblaymiz:
n ил\ f\ a 0,04 3 0,04 3 4 31 л 34-3 31
5 ~ 5 +1-0,1 ” 10 + 0,9 10 + 90 90* Demak, 0,3(4) = ^- = — .
31
Shunga o‘xshash: 1) 0,5(8) = ^ = §; 2) 0,2(3) = 2g2 =g = 1;
3) 4^W = 4^ = 4S; 4> 2’9(2)=2¥ = 2§;
5) 0>3(24) = ^ = g = lg; 6) 1,69(36) = 1^ = 1Ц1 = 1^.
Bu misollardan shunday xulosaga kelamiz:
жж
ж
Aralash davriy o‘nli kasmi oddiy kasrga aylantirish uchun: 1) vergulga
e’tibor bermay, ikkinchi davrgacha bo‘lgan sondan birinchi davr-
gacha bo(lgan sonni ayirish; 2) ayirmani oddiy kasrning surati qilib
yozish; 3) maxrajiga esa davrda nechta raqam bo‘lsa, shuncha 9 yozish; 4)
uning yoniga (ketidan) verguldan birinchi davrgacha nechta raqam
bo‘lsa, shuncha nol yozish kifoya.
Quyidagi davriy o'nli kasrlami oddiy kasr shaklida yozing (665—667):
665. 1) 0,(1); 2) 0,(5); 3) 0,(16); 4) 0,2(3); 5) 2,5(2); 6) 0,2(35).
666. 1) 0,(8); 2) 0,(6); 3) 1,4(7); 4) 0,(59); 5) 0,4(5); 6) 0,43(75).
667. 1) 3,(4); 2) 2,3(8); 3) 4,7(5); 4) 0,7(19); 5) 0,9(3); 6) 0,74(3).
668. Tomoni uzunligi V2 m bo'lgan kvadrat berilgan. Uning tomonlari o'rtalari
ikkinchi kvadratning uchlari bo'ladi. Ikkinchi kvadrat tomonlari o'rtalari
uchinchi kvadratning uchlari bo'ladi va hokazo. Shu kvadratlar tomon-
larining va yuzlarining ketma-ketligi cheksiz kamayuvchi geometrik prog-
ressiya bo'lishini isbotlang. Kvadratlar tomonlarining va yuzlarining
yig'indisini toping.
194
1ЖЖ
669*. Bir xil radiusli sharlami awal muntazam uchburchak shaklida, keyin
o‘sha sharlami to‘g‘ri to£rtburchak shaklida taxlashdi. Uchburchakning
tomonidagi va to‘g‘ri tocrtburchakning katta tomonidagi sharlar soni to‘g‘ri
tocrtburchakning kichik tomonidagi sharlar sonidan 2 taga ko‘p bo‘lsa,
jami sharlar nechta?
670. 1) To‘g‘ri burchakli trapetsiyaning balandligi 15 sm, asoslarining uzun-
liklari 10 sm va 25 sm ga teng. Balandlik 10 ta teng kesmalarga ajratildi va
bo'linish nuqtalaridan asoslarga parallel kesmalar o‘tkazildi. Hosil bo'lgan
trapetsiyalar yuqori (kichik) asosidan boshlab nomerlandi. 8-trapetsiya
yuzi bilan 3-trapetsiya yuzi orasidagi farqni toping.
2) To‘g‘ri burchakli trapetsiya asoslarining uzunliklari 5 sm va 25 sm ga,
balandligi esa 20 sm ga teng. Balandlik 10 ta teng kesmalarga ajratildi va
bo‘linish nuqtalaridan asoslarga parallel kesmalar o‘tkazildi. Hosil bo‘lgan
trapetsiyalar yuqori (kichik) asosidan boshlab nomerlandi.
7-trapetsiya yuzini toping.
671**. 1) Fenner bog'idan olma terib, ulami yashiklarga joylashdi va yo‘l yoqa-
siga olib chiqishdi. Yashiklar soni toq bo‘lib, ular yo‘l yoqasida bir-biridan
10 metr masofada turardi. Bir ishchi yashiklami o‘rtadagi yashik turgan
joyga to‘playdigan bo‘ldi. U yashiklami ketma-ket, bittadan va biror chek-
kadagisidan tashishni boshladi. Hamma yashiklami tashib boTganda, uning
840 m yo‘l bosgani ma’lum boldi. Yashiklar nechta edi?
2) Yo‘l yoqasida bir-biridan 8 metr masofada olma solingan 11 ta yashik
turardi. Ishchi ulami o‘rtadagi yashik turgan joyga to‘playdigan bo‘ldi. U
yashiklami ketma-ket, bittadan va biror chekkadagisidan tashishni
boshladi. Hamma yashiklami tashish uchun u necha metr yocl bosadi?
жж
жж
672**. Uchta eritmadagi tuzning tarkibi (massa bo‘yicha) geometrik progres-
siya tashkil etadi. Agar I, II va III eritmalami 2:3:4 nisbatda (massalar
bo‘yicha) aralashtirilsa, u holda tarkibida 32% tuz bo‘lgan eritma hosil
bo‘ladi. Agar I, II va III eritmalami 3:2:1 nisbatda (massalar bo'yicha)
aralashtirilsa, tarkibida 22% tuz bo‘lgan eritma hosil bo‘ladi. Har bir
eritma tarkibida necha protsent tuz bor?
44- §. VI bobga doir mashqlar
Arifmetik progressiyaning ayirmasini toping, uning to‘rtinchi va oltinchi
hadlarini yozing (673—674):
1 2
673. 1) 2, 2|, 2|
3) 2,2 + ^2,2 + 2-Л,...;
674. 1) 1, 1|, 1|,
3) 3 + y/3, 3 + 2-J3, З + Зу/З,...;
1 1
2) 2|, 2, 1|
4) Л Л-2,
?3-4.
2) 6, 4|, 3,
4) y/2, y/2-4, y/2-8,....
жж
195
675. Ketma-ketlikning n- hadi an = 2n + 9 formula bilan berilgan. Uning ar-
ifmetik progressiya bo'lishini isbotlang.
676. n- hadi an = 2n — 3 formula bilan berilgan ketma-ketlik ariftnetik prog-
ressiya bo'lishini isbotlang.
677. Agar arifmetik progressiyada:
1
1) aY = 3, d = - bo'lsa, a5 ni; 2) = 2,5 , d= 4 bo'lsa, an ni;
1
3) «1 = -2 -, d = -3 bo'lsa, Oq ni hisoblang.
Agar ariftnetik progressiyada (678—680):
678. 1) = —2; a2 = 2; 2) ar = 3, a2 = — 3;
3) ai = 5, «2 = 9
bo'lsa, 510 ni hisoblang.
679. 1) «1=-1, «2=1; 2) «1 = “3, «2 = 3; 3) «1 = -4, «2=1
bo'lsa, 52o hisoblang.
680. 1) «! = —4, «2 = 4; 2) = 4; a2 = —4; 3) = 0, a2 = —2
bo'lsa, 516 ni hisoblang.
Agar ariftnetik progressiyada (681—682):
681. 1) at = -2, a„ = -60, л=10; 2) a„ = 25± n = 11
bo'lsa, uning dastlabki n ta hadining yig'indisini toping.
682. 1) «i = 3, an = 2n + 1, n = 10; 2) «1 = - , an = 3, n = 12
bo'lsa, uning dastlabki n ta hadining yig'indisini toping.
683. Agar:
1) -40 + (-36) + (-32) + ... + 4 + 8; 2) -29 + (-26) + ...+ 4 + 7+ 10
yig'indining qo'shiluvchilari ariftnetik progressiyaning ketma-ket kelgan
hadlari bo'lsa, shu yig'indini toping.
684. Agar:
1) —10 + (—5) + 0 + 5 + ... + 85;2) -33 - 29 - 25 - ... + 11 + 15
yig'indining qo'shiluvchilari ariftnetik progressiyaning ketma-ket kelgan
hadlari bo'lsa, shu yig'indini toping.
Geometrik progressiyaning maxrajini hamda uning 7- hadini toping
(685-686):
685. 1) 4, 2, 1, 1
4) 5, -5^2, 1(1
жж
тете
686. 1) 1, 7з 3, з7з,.„; Г- J?. J2 2) 72, %,
3) 3, 1, 1, 4) 2, 72, 1,....
687. Agar geometrik progressiyada:
1 1 1) h = -, =-4, n = 5; 2) b[ =-, q = 5, «-4 z о bo'lsa, b„ ni toping. Geometrik progressiyaning n- hadi formulasini yozing (688—689):
688. 1) -3; 6, —12, 2) -i - 2’ 2’ 2’""
689. 1) 1, 73, 3, ЗТЗ,...; 2) 5, -5-J2, 10,...;
3) 3, 1, |,...; 690. Agar geometrik progressiyada: 4) 2, 72, 1,....
1 1) — 2 ’ ~ ~4’ ft ~ 2) ^=2, q = ~, n = 10;
3) bY = 10, q=l, n = 6; bo'lsa, Sn ni toping. 4) ^ = 5, 9 = -l, » = 9
691. Geometrik progressiya uchun Sn ni toping: 1) 128, 64, 32, ..., w = 6; 2) 162, 54, 18, ..., n = 5;
2 1 3 3) 3, 2, g, И-5, 3 1 1 л 4) 4, 2> 3, -,«-4-
692. Berilgan geometrik progressiya cheksiz kamayuvchi bo'lishini isbotlang va uning barcha hadlari yig'indisini toping: n _1 _1 __L • 2) -2 — ' 3’ 9’ 27’"'’ ’ ’ 5’ 25’" "
693. Agar arifmetik progressiyada q = 2^ va Og = 23- bo'lsa, uning ayir- 2 2
masini toping.
ЖЖ
тем
ЖЖ
тете
жж
тете
жж
тете
жж
тете
694. Agar arifinetik progressiyada:
1) = 4, a4 = 13; 2) a3 = 12, a5 = 2; 3) a4 = 36, = 57
bo'lsa, uning dastlabki 5 ta hadini yozing.
695. —23 va —8 sonlar orasiga 4 ta son shunday qo'yilganki, natijada u sonlar
berilgan sonlar bilan birgalikda arifinetik progressiya hosil qilgan. Shu
sonlami toping.
696. 16 va 6 sonlar orasiga 4 ta son shunday qo'yilganki, natijada u sonlar
berilgan sonlar bilan birgalikda arifinetik progressiya hosil qilgan. Shu
sonlami toping.
197
жж
тете
жж
тете
жж
жж
ЖЖ
697*. а19 02, ..., ап, ... arifmetik progressiya bo'lsa, a„+ajk=an4+ajH.z tenglik;
Ьъ b2, ..., bn, ... geometrik progressiya bo'lsa, bn-bk= b^-b^ tenglik
o'rinli bo'lishini isbotlang. Awal misollarda sinab ko'ring.
698. x ning qanday qiymatlarida:
1) 3x, 2x-l; 2) Зх2, 2, llx
sonlar arifmetik progressiyaning ketma-ket kelgan hadlari bo'ladi?
699*. Quyidagi sonlar arifmetik progressiya tashkil etishini isbotlang:
1) sin(a + p), sin a cos p, sin(a-p);
2) cos(a + p), cos a cos p, cos(a-p);
3) cos2a, cos2a, 1; 4) —cos2a, sin2a, 1;
5) sin5a, sin3acos2a, sina.
жж
жж
жж
жж
жж
жж
жж
жж
700. (Og'zakL) —12 va 4 sonlari orasiga bitta sonni shunday qo'yingki, natijada u
son berilgan sonlar bilan birgalikda arifmetik progressiya tashkil qilsin.
701. (Og‘zaki.) 9 bilan 16 sonlari orasiga bitta sonni shunday qo'yingki, na-
tijada u son berilgan sonlar bilan birgalikda geometrik progressiya tashkil
qilsin.
702. 6 va 96 sonlari orasiga 3 ta musbat son shunday qo'yilganki, natijada u
sonlar berilgan sonlar bilan birgalikda geometrik progressiya hosil qilgan.
Qo'yilgan sonlaming yig'indisini toping.
703. Agar ketma-ketlik n- hadining formulas! bilan berilgan bo'lsa, u chek-
siz kamayuvchi geometrik progressiya bo'ladimi?
H=4«+1; 2)iB = (-5)»+2; 3)*„=^; 4)Й„ = -Д.
У 4
704*. Agar arifmetik progressiyada ax + 02 + «3= 15 va • a2 * a3 = 80 bo'lsa,
uning birinchi hadi va ayirmasini toping.
VI bobga doir sinov (test) mashqlari
1. 701 soni 1, 8, 15, 22, ... progressiyaning nechanchi nomerli hadi?
A) 101; B) 100; C) 102; D) 99.
2. 1 001, 999, 997, ... progressiyaning nechanchi nomerli hadidan boshlab
uning hadlari manfiy sonlar bo'ladi?
A) 500; B) 502; C) 503; D) 504.
3. Arifmetik progressiyada = 7, d = 5, Sn = 25450 bo'lsa, n ni toping.
A) 99; B) 101; C) 10; D) 100.
198
1ЖЖ
4. 1 va 11 sonlar! orasida 99 ta shunday sonni joylashtiringki, ular bu sonlar
bilan birgalikda ariftnetik progressiya tashkil qilsin. Shu progressiya uchun
550 ni toping.
A) 172,5; B) 495; C) 300; D) 178.
5. Geometrik progressiyada *У4= 10,625, S5 = 42,625, 2^ = 0,125 bo'lsa, q=l
A) 4; B) 2; C) 8; D) 0,5.
Geometrik progressiyada 6 ta had bor. Dastlabki 3 ta hadining yig'indisi
26 ga, keying! 3 ta hadining yig'indisi esa 702 ga teng. q ni toping.
A) 4; В) 3; C) 0,(3); D) 2-Л-
Cheksiz kamayuvchi geometrik progressiyada Zj = 1, S = 16. q ni toping.
6.
7.
A) 2 ’ 65 ’ 64 ’
8.
a/3 r~
Geometrik progressiyada q — -y , bY = 2 - V3 bo'lsa, S ni toping.
A) 2 + V3; В) 3; C)
D) 2.
Ariftnetik progerssiyaga oid masalalar
9. Agar a2, .... an sonlar ariftnetik progressiya tashkil qilsa,
1.1.1, 1
anan
«1«2 fl2fl3 a3fl4
yig'indini toping.
B)«rw C)
10. m ning V/w-1; V5m-1; >/12m4-l;... lar ko'rsatilgan tartibda ariftnetik
progressiya tashkil qiladigan qiymatlari yig'indisini toping.
A) 12; B) 13; C) 8; D) 5.
A) 1;
D) —.
’ alan
11. Uchta sonning o'rta arifmetigi 2,6 ga, birinchi son esa 2,4 ga teng. Agar
keying! son awalgisidan ayni bir songa farq qilsa, keying! sondan oldingisining
ayirmasini toping.
A) B) 0,1;
C)
D) 0,2.
12. 7, 10,13,... ariftnetik progressiyaning nechta hadining har birining qiymati
100 dan katta, 200 dan kichik bo'ladi?
A) 33; B) 34; C) 35;
D) 32.
ЖЖ
ЖЖ
ЖЖ
жж
ЖЖ
ЖЖ
жж
ж
зкж
зкж
жии
1 2 N
13. 100 + 100 + " + 100 = 100j^ tenglikni qanoatlantiruvchi son N ni toping.
A) 19 999; B) 9 999; C) 21 999; D) 1 999.
14. y; 3y+5; 5y+10; ... ariftneyik progressiyaning dastlabki 8 ta hadi yig'indisi
396 ga teng. у ning qiymatini toping.
A) 2; В) 3; C) 4; D) 5.
15. 2 va 65 sonlari orasiga 20 ta shunday sonlar qo'yilganki, natijada hosil
bo'lgan ketma-ketlik arifmetik progressiyani tashlik etgan. Shu progressiya
hadlarining o'rta arifmetigini toping.
A) 27,5; B) 32; C) 44; D) 33,5.
16. д+2д+3д+..я-яд _ 2(3*3) ifodani soddalashtiring.
A) B) C) D) T-
17. 1 dan 75 gacha bo'lgan natural sonlardan kvadratini 3 ga bo'lganda 1 qoldiq
qoladigan sonlar yig'indisini toping.
A) 1 875; B) 925; С) 1 900; D) 2 850.
18. Sakkista ketma-ket kelgan natural sonlaming yig'indisi 700 ga teng. Shu
sonlaming eng kichigini toping.
A) 78; B) 84; C) 82; D) 80.
1
19. O'zidan oldingi toq natural sonlar yig'indisining - qismiga teng bo'lgan
natural sonni toping.
A) 16; B) 24; C) 32; D) 64.
Geometrik progressiyaga oid masalalar
20. x ning qanday qiymatlarida 0,(36); x; 0,(49) sonlar ishoralari almashi-
nuvchi geometrik progressiyaning ketma-ket keluvchi hadlari bo'ladi?
14 14 13 15
A) -Тз, В) C) D)
21. 5; 5>/2; 10;... progressiyaning nechanchi hadi 5 120 ga teng bo'ladi?
A) 20; B) 21; C) 19; D) 22.
22. Geometrik progressiyaning dastlabki 6 ta hadi 3; b2, b3, b4, b5, bo'lsa,
bisoblang.
200
ИТЧ1ХТХ1
1ЖЖ
A) 1g; В) 1||; С) 1g; D) 1g.
23. 32; 16; 8; ... geometrik progressiyaning 9-hadi bilan 6-hadi ayirmasini
toping.
7 5 3 9
A) В) -f; C) -f; D)
О ООО
24. 2, 6, 18, 54, ... geometrik progressiyaning b5 va b7 hadlarining o'rta
geometirigini toping.
A) 486; B) 485; C) 480; D) 490.
25. Yig'indisi 35 ga teng bo'lgan uchta son o'suvchi geometrik progressiyaning
dastlabki uchta hadlaridir. Agar shu sonlardan, mos ravishda, 2; 2 va 7 sonlar
ayrilsa, hosil bo'lgan sonlar ariftnetik progressiyaning ketma-ket hadlari bo'ladi.
Ariftnetik progressiyaning dastlabki 10 ta hadining yig'indisini toping.
A) 245; B) 275; C) 255; D) 265.
26. Geometrik progressiyaning maxraji 3 ga, dastlabki to'rtta hadi yig'indisi 80
ga teng. Uning to'rtinchi hadini toping.
A) 24; B) 32; C) 54; D) 27.
27. Geometrik progressiyaning birinchi hadi 486 ga, maxraji | ga teng. Shu
progressiyaning dastlabki to'rtta hadi yig'indisini toping.
A) 680; B) 840; C) 720; D) 760.
28. x ning qanday qiymatlarida 2x4-4, 4x+8, 11x4-4 o'suvchi geometrik
progressiyaning ketma-ket kelgan hadlari bo'ladi?
A) 4; В) 3; C) 5; D) 3,5.
29. cosa; 2sinacos2a; 4sin2acos3a sonlar geometrik progressiya tashkil qiladi.
Uning maxrajini toping.
A) sin2a; B) sin2a; C) cos2a; D) 2sina.
30. 5 va 1 280 sonlar orasiga 3 ta musbat son shunday qo'yilganki, u berilgan
sonlar bilan birgalikda geometrik progressiya hosil qilgan. Qo'yilgan sonlaming
yig'indisini toping.
A) 420; B) 410; C) 430; D) 408.
ЖЖ
дам
жж
мм
мм
ЖЖ
Маи
ЖЖ
ЖЖ
MM
ЖЖ
ЖЖ
„,111111 К 1 1 К- x 1 • •
31. 2*3 + 4*9 + 8'27 + ‘“ c^le^slz kamayuvchi geometrik progressiyaning
hadlari yig'indisini toping.
A) 0,2; B)
C) D) 1,2.
201
жж
ММ
жж
жж
111 1 .
32. ^з-9+27-81+ ” ni hisoblang.
А) 0,3; В) 0,4;
С) 0,5;
D) 0,6.
Tarixiy ma’lumotlar
Abu Rayhon Beruniy «Qadimgi xalqlardan qolgan yodgorliklar» asarida
shaxmatning kashf etilishi haqidagi rivoyat bilan bog'liq birmchi hadi = 1 va
maxraji q = 2 bo‘lgan geometrik progressiyaning birinchi 64 ta hadining yig‘indisini
hisoblaydi; shaxmat taxtasidagi k- katakka mos sondan 1 soni ayirilsa, ayirma
k- katakdan oldingi barcha kataklarga mos sonlar yig'indisiga teng bo'lishini
ko'rsatadi, ya’ni ф— l = 14-^+^2 + ... 4- ekanini isbotlaydi.
ЖЖ
жж
Olimpiada masalalari
1. 1, 7,7,sonlar ichidan arifmetik progressiya tashkil qiluvchi 2012
2 3 n
ta sonni ajratib olish mumkinmi?
2. 1 + 2\/2 + 3(\l2)2 +... + n yig'indini hisoblang.
жж
ЖЖ
3. 7 + 77 + 777 +... + 777.3? yig'indini hisoblang.
n ta
4. Uchta kesmaning uzunliklari geometrik progressiya tashkil qiladi. Maxraj q
ning qanday qiymatlarida bu kesmalardan uchburchak yasash mumkin?
5. —19,88 va 19,91 sonlari orasiga shunday n ta son qo'yilganki, ular berilgan
sonlar bilan birgalikda arifmetik progressiya tashkil qiladi. n ning qanday
qiymatlarida bu progressiya ayirmasi у = ^7|x|-x2 -12 fiinksiyaning
aniqlanish sohasiga tegishli bo'ladi?
6. by b2, ...» bn sonlar geometrik progressiya tashkil qilishi uchun
(i? + + ••• + +*) + ••• + #) = +... + b„_ib„)2 tenglikning
bajarilishi zarur va yetarli ekanini isbotlang.
7. Agar + px1 + 2=0 tenglamaning ildizlari arifmetik progressiya tashkil
etsa, 9/x2 = 100# tenglik o'rinli ekanini isbotlang.
8. Sn — ariftnetik progressiya dastlabki n ta hadining yig'indisi. Isbotlang:
1) 3 • (S2„ - $пУ’ 2) *5Я+3 - 3*Уя+2 + 3*Уя+1 - Sn = 0;
3) Sm~Sn т~п
S +п т + п
Turli darajadagl matematik otimpiaddlar, musobaqalarda taklif etilgan
masalalardan namunalar
жж
жж
202
жж
9. Chizmadagi jadval birlik kubchalardan tashkil topgan fazoviy jismni ifodalaydi.
Katakda yozilgan son shu katak ustida turgan parallelipiped nechta
kubchalardan tashkil topganligini ko'rsatmoqda.
Masalan, 8 raqamli katak ustida turgan
parallelepiped 8 ta kubchalardan tashkil topgan
va h.k. Kubchalar ustma-ust zich joylashgan.
Jismning to'la sirti (pastki 9 ta kubchalaming
asoslari bilan birga) bo'yalgan. Kubchalaming
bo'yalgan yoqlari sonini toping.
2 8 6
3 9 7 5
ЖЖ
10. Uchta natural son berilgan. Ulaming birinchisi
ikkita bir xil raqamdan tuzilgan ikki xonali sondir. Ikkinchi son ikkita har
xil raqamdan tuzilgan ikki xonali son, bunda shu sondagi birliklar xonasidagi
raqam birinchi sondagi o'nliklar xonasidagi raqamga teng. Uchinchi son
ikkinchi sonning o'nliklar xonasidagi raqamiga teng. Ma’lumki, shu uchta
sondan faqat ikkitasi tub sonlardir. Shu uchta natural sonlami nechta usul
bilan tanlash mumkin?
11. Natural A sonni 5 ga bo'lganda hosil bo'ladigan to'liqsiz bo'linma shu A
sonni 3 ga bo'lgandagi qoldiqqa teng. A sonni 3 ga bo'lganda hosil bo'ladigan
to'liqsiz bo'linma shu A sonni 5 ga bo'lgandagi qoldiqqa teng. A sonning
barcha mumkin bo‘lgan qiymatlar ko'paytmasini toping.
12. 100 xonadonli uy qurildi. Undagi xonadon nomerining raqamlari yug'indisi
o'zaro teng bo'lgan xonadonlar soni eng ko'pi bilan nechta bo'lishi
mumkin?
13. (Masalani O(zbekiston jamoasi taqdim etgari). Ashula aytayotgan guruhda
2
o'g'il bolalar soni barcha guruh a’zolarining qismidan ko'p, ammo
2 qismidan kam. Guruhda eng kamida nechta a’zo bo'lishi mumkin?
Javob: 1.
14. (Kanadd). Agar Minining yoshiga 1 yil qo'shib Maksning yoshiga ko'paytirsak
kvadrat son hosil bo'ladi. Maksning yoshiga 1 yil qo'shib Minining yoshiga
ko'paytirsak unda ham kvadrat son hosil bo'ladi. Ma’lumki, Minining
yoshi 8 ga teng, Maksning yoshi esa 1 dan katta va 100 dan kichik.
Maksning yoshi nechada? Javob: 49.
15. (Xitoy). Kontsertga chiptaning narxi kattalar uchun 26000 so'm, o'smirlar
uchun 18000 so'm va bolalar uchun 10000 so'm deb belgilandi. 131 ta
a’zodan iborat bo'lgan guruh chiptalargajami bo'lib 2014000 so'm pul
sarfladi. Guruhdagi bolalar soni kattalar sonidan qancha ko'p? Javob: 43.
203
ЖЖ
жж
жж
жж
жж
ЖЖ
ж
16. (Xitoy). Osmondagi yulduzlar soni
8 • 12 + 98 • 102 + 998 • 1002 +... + 99... 98 • 100... 02 ga teng. (Bu yerda
oxiigi hadning 99 ... 98 ko'paytivchisida 9 raqam 2014 marta, 100 ... 02
ko'paytuvchisida 0 raqam 2014 marta yozilgan. Yulduzchalar sonining
o'nli yozuvida raqamlar yig'indisi nechaga teng?) Javob: 2019.
17. (Bolgariyd). 18 ta 1, 2, ..., 18 sonlami shunday 9 ta jufliklarga yozingki,
har bir juftlikdagi sonlar yig'indisi kvadrat son bo'lsin. Javob: (18, 7),
(17, 8), (16, 9), (2, 14), (11, 5), (4, 12), (13, 3), (6, 10),
(15, 1)
18. (Bolgariyd). 19 yoki 23 ga karrali 2014
ta ikki xonali sonlar ketma-ketligi
berilgan. Ikkinchi sondan boshlab har
bir sonning o'nlik xonasidagi raqami
oldingi sonning birlik xonasidagi
raqamga teng. Ketma-ketlikdagi oxirgi
son 23 ga teng bo'lsa, birinchi sonni
toping. Javob: 95.
19. 1, 2, 3, ..., 10”—2, 10”—1 sonlar
yozuvidagi barcha raqamlar yig'indisi
toping.
Q к va (10” — 1 — k} sonlar juftliklarini qaraymiz. Har bir juftlikdagi
зкж
raqamlar yig'indisi 9w ga teng, juftliklar soni esa —-— ga teng.
Juftliklarga kirmagan (10й—1) son bor, uning raqamlari yig'indisi
9w ga teng. Demak, berilgan sonlaming raqamlari yig'indisi:
9"‘^T“^ + 9”= j'10”’9"' Javob: I'lo” ' 9"
20. (Singapur) Har bir qiz otga yakka o'zi minib olishni xohlamoqa, ammo
зкж
зияя
otlar qizlaming faqat qismi uchun yetarli. Agar barcha qizlar va otlar
oyoqlari soni jarni 990 ga teng bo'lsa, necha nafar qiz otga minish uchun
o'z navbatini kutmoqda. Javob: 45.
21. Uch xonali sonning raqamlari arifmetik progressiya tashkil qiladi. Agar bu
songa 101 qo'shilsa, hosil bo'lgan sonning raqamlari geometrik prograssiya
tashkil qiladi. Shunday xossaga ega bo'lgan uch xonali sonni toping.
204
RIVOJLANTIRUVCHIMASHQLAR
Masalalami murakkabroq masala, qiziqarli masala, noan’anaviy masala,
mantiqiy masala, olimpiada masalalari, matematik boshqotirmalar kabi
guruhlarga (sinflarga) ajratish shartlidir. Matematikaning har bir
masalasini yechish ma’lum bir mantiqni talab etadi, albatta. Olimpiada
masalalari ko‘p hollarda qiziqarli, shu bilan birga, noan’anaviy bo'ladi.
Ayni bir masalaning o'zi yuqorida sanalgan turli guruhlarga tegishli
bo'lishi mumkin. Biz bunday masalalami rivojlantiruvchi mashqlar deb
atadik.
1. (Proffessor N.G'anixojayev masalas!) e15 a2, a3, д4 va b19 b2, b3, b4 —
raqamlar ar a2 a3 a4 va bx b2 b3 b4 — tocrt xonali sonlar, deylik. Bu sonlar
uchun “ko'paytirish” amalini shunday aniqlaymiz:
flj ^3 ^4 X b-^ Ь2 b3 b4~ Cj C2 Cj ^4?
bunda: 1) agar at * bt (odatdagi ko'paytma) bir xonali son bo'lsa, u holda
c1=a1 ‘ 2) agar at • bt — ikki xonali son bo'lsa, u holda son
a1 • bt ko'paytmaning oxirgi raqamiga teng. c2, c3, c4 raqamlar kabi
aniqlanadi.
Ushbu
a^ a2 a3 a4 x a^ a2 a3 a4 1998,
bY b2 b3 b4 X 1998 = 1998,
a1 02 a3 a4 x 1998 = a2 a3 a4
tengliklami qanoatlantiruvchi barcha to'rt xonali sonlami toping.
2. Quyidagi jadvalda barcha toq sonlar yozilgan:
1
3 5 7
9 11 13 15 17
19 21 23 25 27 29 31
жж
жж
жж
жж
Jadvalning birmchi n ta qatoridagi barcha sonlaming yig'indisi natural
sonning to'rtinchi darajasiga teng ekanini isbotlang.
Isboti: Birinchi n ta qatordagi sonlar yig'indisini topaylik:
1 + 3 + 5 + ... + (2и-1) = l + 1) 'n=n2. n-chi qatordagi oxirgi son
(2Л2 - 1) ga teng. U holda 5-l+3+5+...+(2^-l)=l^
Da’vo isbotlandi.
3. xp x2, ..., xn, ... ketma-ketlik х,=0, хи+1 = 5хй +^24x^ + 1, «=1, 2, ...
formula yordamida aniqlangan. Ketma-ketlikning barcha hadlari butun
son ekanini isbotlang.
205
жж
жж
жж
ЖЖ
жж
4. Ixtiyoriy tub son р > 3 ning kvadratini 24 ga bo'lganda 1 qoldiq qolishini
isbotlang.
2 . p(p-l)(p + V)
Jsboti, p2 =24m+l bo'lsin, deylik. p2 — 1 = 24m, P 1 “ “ >
p * 2, p * 3, bundan p2 - 1 ning 2 ga bo'linishini ko'ramiz. p2 -1 = 2k
bo'lsa, p + 1 = 2(£+l), demak, p2 - 1 = 4k(k + 1), ammo к • {к + 1) son
2 ga bo'linadi, u holda (p2 — 1) son 8 ga bo'linadi. Bundan esa,
p2 — 1 ning 3 * 8 = 24 ga bo'linishi kelib chiqadi. Shunday qilib, p2 - 1 =
=24m, ya’ni p2 = 24m + 1 deyishimiz to'g'ri ekan. Da’vo isbotlandi.
жж
жж
жж
жж
жж
5. Agar 111... 11 sonning 41 ga bo'linishi ma’lum bo'lsa, bu sondagi 1 raqamlar
nechta?
Ko^satma: 11111 son 41 ga bo'linadi. 5 к ta 1 lardan tuzilgan son 41 ga
bo'linadi, к — natural son.
6. Ixtiyoriy olingan, barchasi 15 ga karrali 135 ta natural son orasida ayirmasi
2010 ga bo'linadigan 2 tasi topilishini isbotlang.
Isboti. a=i5bv a=\5b2,..., я135=15#135- ixtiyoriy 135 ta natural son bo'lsin.
2010 = 10 3 • 67 = 15 134 bo'lgani uchun alf av ..., a135 sonlami 134
ga bo'lsak, u holda ulaming kamida ikkitasida bir xil qoldiq chiqadi. Bir xil
qoldiqqa ega bo'lgan ana shu 2 sonning ayirmasi 134 ga bo'linadi. Agar a va
sonlami 134 ga bo'lganda bir xil qoldiq chiqsa, u holda af — a. ayirma
134ga bo'linadi. a( — a. =15 * (b( — ty. Agar a. — a. 134 ga bo'linsa, b. — b.
ham 134gabo'linadi.Demak, a.—a. ayirma2010 = =15 134gabo'linadi.
Da’vo isbotlandi.
жж
жж
ЖЖ
л 2л Зл 1
7. cos у - cos -y- + cos — = - ekanini isbotlang.
Ko‘rsatma: Tenglikning chap qismini 2cos-^- (yoki 2sin-^-) ga
14 14
ko'paytiring va bo'ling, so'ngra 2cosacosp=cos(a+p)+cos(a—0) formulani
qo'llang.
8. x, y, z ~ raqamlar, xonali, — n xonali sonlar.
2«ta «ta «ta
zz-..z
tenglik n ning kamida ikkita turli qiymatiari uchun
o'rinli ekanini ma’lum. n ning bu tenglik to'g'ri bo'ladigan barcha
qiymatlarini toping.
Yechilishi. n — masala shartini qanoatlantiradigan ixtiyoriy natural son bo'lsin.
Quyidagilami hosil qilamiz:
2«ta
«ta
206
х- Щ...Ц-y Щ...Ц = ?- (111...11)2, (1)
2/ita nta '
Shu bilan birga, ixtiyoriy natural son £ uchun
10s-1 +IO*’2 +... +10+1 = .
10-1
тть ы 102л-1 10й-1 2 I10”-1)
U holda x—----------У—= 92
Bu tenglikni (10я — 1) ga qisqartirib, umumiy maxrajga keltirib, so'ng
quyidagicha yozib olamiz:
(9x-z2)10«=9y-9x-z2 (2)
Shartga ko‘ra, n ning shunday 2 ta turli n} * n2 qiymatlari borki, ular uchun
(1) va (2) o'rinli bo'ladi:
(9x-z2)10^ = 9y-9x-z2, (9x-z2)-10^ =9y-9x-9z.
Bu tengliklami birini ikkinchisidan ayirib,
9x~ z2=0 (3)
tenglikka kelamiz. - Ю^2 * o) (2) va (3) dan
9y - 9x - z2 = 0 (4)
tenglamani olamiz. (3) va (4) dan: x = к2, у = 2k2, z = 3k(k — butun son)
ekani kelib chiqadi.
0 < x, y, z < 9 ekanidan shunday ikkita yechimni olamiz:
x = 1; 4; у =2; 8; z =3; 6.
(x, y, z) ixtiyoriy yechim bo'lsa, har bir n uchun (2) va demak, (1) ham
o'rinli.
Javob. Berilgan tenglik barcha n lar uchun o'rinli.
9. tg7Q30'= \/б + >11 - у/З - 2 ekanini isbotlang.
Ko‘rsatma: tgl5°=<2-V3 tenglikni ko'rsating;
. 0 - 2tga
rS2a । tg2a formuladan foydalaning;
а/з—л/З = (>/6 - yjl) tenglikni isbotlang.
ЖЖ
жж
жж
жж
10. a, p, у — biror uchburchakning burchaklari (a + p + у = я) bo'lsa, u
holda cos2a + cos2p + cos^ + 2cosacospcosy = 1 bo'lishini isbotlang.
11. Idishda 9 ta shar bor. Har bir sharga bitta raqam yozilgan: 1, 2, 3, 9. 9
nafar o'quvchi shunday o'yin o'ynamoqda: O'quvchilaming har biri
207
жж
IZTXIXXI
жж
жж
ЖЖ
жж
navbatma-navbat idishdan 1 dona shar oiadi va shaming nomermi (sharga
yozilgan raqamni) qog'ozga yozib qo'yadi. 9 ta shar olib bo'lingach, ulaming
hammasi idishga qaytariladi va o‘yin yangidan boshlanadi. Endi chiqqan
sharlaming nomen awalgi songa (qog'ozga yozib qo'yilgan songa) qo'shiladi.
O'yin shu tarzda davom etaveradi. Quyidagi savollarga javob toping: 1)
o'yin 3 marta takrorlanganda 9 ta o'quvchining har birida bir xil (o'zaro
teng) ochko (uchta o'yinda chiqqan shar nomerlarming yig'indisi) bo'lishi
mumknuni? 4 marta takrorlanganda-chi? 2) o'yin bir necha marta
takrorlangandan so'ng har bir o'quvchi to'plagan ochkolari yig'indisi
2010 ga teng bo'lishi mumkinmi? 2011 ga -chi?
12. 1, 2, 13 sonlarini doirachalarga shunday joylashtiringki, qo'shni sonlar
bir-biridan kamida 3 ga farq qilsin.
Masalan, 7 raqami 5, 6, 8, 9 raqamlari bilan qo'shni bo'la olmaydi.
жж
жж
жж
ЖЖ
13. д-rasmdagi doirachalarga 1, 2,8 raqamlami; 6-rasmdagi doirachalarga
esa 1, 2, 9 raqamlami shunday joylashtiringki, har bir qora nuqtaga
keluvchi strelkadagi raqamlar yig'indisi shu nuqtadan chiquvchi
strelkalardagi raqamlar yig'indisiga teng bo'lsin.
14. Faraz qilaylik, o'lchamlari 9 * 9 bo'lgan shaxmat taxtasi va bitta shaxmat
donasi — ot berilgan. Ot bu taxta ustida, otning yurish qoidasiga muvofiq,
13 ta yurish qiladi. Ot bo'lgan kataklaiga 1,2,14 sonlami yozib chiqildi.
Har bir qatordagi va har bir ustundagi sonlar yig'indisi mos qator va
208
mos ustun yoniga yozildi (rasmlarga qarang). Ot qaysi kataklarda bo'lgan,
ya’ni 1, 2, ..., 14 sonlari taxtaning qaysi kataklariga yozilgan?
ЖЖ
ЖЖ
ЖЖ
ЖЖ
15. Bir xil doirachalar bir xil kvadratchalarga ichki chizilgan. Doirachalar
orasidagi masofa deganda ulaming markazlari orasidagi masofani
tushunamiz.
Doirachalarga 1, 2, 12 sonlarini shunday joylashtiringki, ketma-ket
kelgan sonlar yozilgan doirachalar orasidagi masofa ortib borsin. Ya’ni
2 va 3 sonlar yozilgan doirachalar orasidagi d{2\ 3) masofa 1 va 2 sonlar
yozilgan doirachalar orasidagi d(l, 2) masofadan katta bo'lsin: </(1,2)
< </(2,3). Shu kabi </(2,3) <</(3,4)< ... < d (11,12) bo'lsin.
ЖЖ
ЖЖ
СЛОТ
ЖЖ
ЖЖ
16. Qanday eng kichik natural son a uchun x2 oldidagi koeffitsiyenti a, qolgan
koeffitsiyentlari butun sonlardan iborat, ildizlari turli va musbat hamda 1
dan kichik bo'lgan kvadrat uchhad topiladi?
Kf/rsatma: Izlanayotgan kvadrat uchhad y=ax2+&c+c ning ildizlari xr va
14—Algebra, 9
209
жж
IZTXIXXl
жж
жж
жж
жж
жж
sm®
жж
жж
bo'lsin. a2xl(l—xl)(l—x2) £ 1 va ildizlaridan bittasi, masalan, * 0,5
ekanini ko'rsating.
Javob: a= 5. Masalan, y=5x2—5x + 1.
17. To'rtburchakning qarama-qarshi burchaklari kosinuslarining ko'paytmasi
o'zaro teng. Shu to'rtburchakning trapetsiya ekanini isbotlang.
Ko‘rsatma: To'rtburchakning qarama-qarshi burchaklari a va 8 hamda p va
у deylik. Shartga ko'ra, cosacos8=cospcosy. 2cosmcosv=cos(w+v)+
+cos(m~v) va a+p+8+y=360o ekanidan cos(a—8)=cos(p—7) tenglikka keling.
Bundan berilgan to'rtburchakning burchaklari quyidagi tenglamalar
sistemasining kamida bittasini qanoatlantirishi kelib chiqadi:
a + P+ 8+у=360о a+ p +3 + y = 360d
a + 7-(p + S) = 0° ’ a + p-(8+7) = 0°.
Endi a+y=p+8 yoki a+p=8+y ekanidan foydalaning.
18. Qanday natural n uchun 19 ifoda eng katta qiymatga ega bo'ladi?
n!
(n\ = 1 2 ‘3 • ... • n ekanini eslatib o'tamiz).
Ko‘rsatma: an-an-i=——(19~”>+69—(69-n) ayjnnaning 1< n <68 uchun
n\
musbatligini va 1 < n < 68 orasidagi barcha n lar uchun л68>Д„ hamda
n > 69 bo' Iganda an~ал4<0 bo'lishini ko'rsating.
Javob: n=68.
19. Dala hovlini shunday 7 ta teng qismga ajratingki, ulaming har birida bittadan
daraxt bo'lsin (a-rasm).
20. Dala hovlini shunday 8 ta teng qismga ajratingki, ulaming har birida ikkitadan
daraxt bo'lsin (й-rasm).
жж
И
4 » *
4 $$
M <1
4___J________
й-rasm.
21. Д ABC ning burchaklari А, В, C va ular qarshisidagi tomonlar uzunliklari,
mos ravishda, a, b, c bo'lsin. Ushbu (sirL4+sirLS-i-sinC)(ctg24+ctgB+ctgC)=
210
жж
ZTXIZTXI
= (д + ^ + сХд^+^ +с ) tenglikni isbotlang.
KoFsatma: sinuslar va kosinuslar teoremalaridan foydalaning.
22. A ABC ning burchaklari a, ft, у bo'lsin. Ushbu tg2 у + tg2 у + tg2 > 1
tengsizlikni isbotlang.
23. a, b, c, d~ musbat sonlar bo'lsin. kasming qiymati va у sonlar
orasida yotishini isbotlang.
KoFsatma: 1) т < 4 > 2) т - "S hollami qarang.
ba ba
n,k— natural sonlar bo'lsa, + kasming ham qiymati 7 va sonlar
nb+kd b d
orasida yotadimi? Shu holni tatqiq qiling.
24. Buyuk ingliz olimi Isaak Nyuton masalalari.
1) Geometrik progressiyaning 3 ta ketma-ket hadi berilgan. Ulaming yig'indisi
19 ga, ular kvadratlarming yig'indisi esa 133 ga teng. Shu hadlami toping.
2) Geometrik progressiyaning 4 ta ketma-ket hadi berilgan. Ikkita chetki
hadlar yig'indisi 13 ga, ikkita o'rta hadlar yig'indisi esa 4 ga teng. Shu
hadlami toping.
25. 1, 2, 15 sonlami doirachalarga shunday
joylashtiringki, 7 ta uchburchakning har /j \
biridagi doirachalarga yozilgan sonlar yig'indisi f \ Т/ x
24 ga, 2 ta aylanadagi doirachalarga yozilgan /
sonlar yig'indisi esa 48 ga teng bo'lsin. i /
26. «Fizika, matematika va informatika» jumalidan \
olingan masala.
Awal futbol musobaqasida shunday qoida bor “T
edi: g'alabaga 2 ochko, durangga 1 ochko / \
mag'lubiyatga 0 ochko berilar edi. «Burgut» / \
jamoasi chempionatda oxirgi o'rinni egalladi. О-----О
Endi futbol musobaqasida yangi qoida amal
qiladi: g'alaba 3 ochko, durang va mag'lubiyat awalgidek baholanadigan
bo'ldi. Yangi qoidaga muvofiq ochkolar boshqatdan hisoblab chiqilgandi,
«Buigut» jamoasi birinchi o'rinni egallashi ayon bo'libdi. Shunday bo'lishi
mumkinmi?
KoFsatma: Musobaqada 13 ta jamoa qatnashgan. «Burgut» jamoasi 5 ta
o'yinni yutib, 7 tasini yutqazgan, qolgan barcha o'yinlar durang natija
bilan tugagan bo'lsin. Shu holni tahlil qilib ko'ring.
211
IZTXIXXI
ЖЖ
жж
жж
жж
27. (10”+10й х+... +10+1) • (10й+1+35)+36 soni biror natural sonning kvadrati
ekanini isbotlang.
28. Ketma ket kelgan bir nechta natural sonlar yig'indisi 100 ga teng bo'lishi
mumkinmi?
29. Rasmda radiusi 2 ga teng va o'zaro urinuvchi ikkita
doira tasvirlangan. Chumoli yurishni A nuqtadan
boshladi va ABCDEFCGA yo'lni bosib o'tdi. U
2005 л sm masofa yurgach charchadi va to'xtadi. U
qaysi nuqtada to'xtagan? Agar chumoli 2016 л sm
yurib to'xtasa, qaysi nuqtada to'xtagan bo'lar edi?
30. Agar ap a2, a3, a4, a5 — musbat sonlar va
д1+л2+л3+а4+а5=1 bo'lsa,
жж
жж
ekanini isbotlang.
жж
жж
жж
31. Tenglamani yeching:
(x + 2003)(x + 2004) + (x + 2004)(x + 2005) + (x + 2005)(x + 2006) +
_________1_________ 1
+ (x + 2006)(x + 2007) 999999
1 1 1
Ko^atma: 1) “ 7ГП
tenglikdan foydalaning; 2) tenglamani
soddalashtirgach t = x + 2005 belgilash kiriting.
жж
жж
ЖЖ
32. O'rtadagi raqamini o'chirganda 13 marta kamayadigan 3 xonali sonlami
toping.
33. Yig'indisi 2015 ga teng bo'lgan to'rtta turli uch xonali son berilgan.
Bu sonlardan har binning raqamlari yigindisi bitta S soniga teng. S ning
barcha mumkin bo'lgan qiymatiari yigindisini toping.
34. Berilgan oltita 1, 2, 3, 4, 5 va 6 raqamlardan bitta bir xonali, bitta ikki
xonali va bitta uch xonali son tuzilmoqda. Bunda har bir raqam faqat bir
marta qatnashadi. Bir xonali va ikki xonali sonlaming yig'indisi 47 ga,
ikki xonali va uch xonali sonlarining yig'indisi esa 358 ga teng. Tuzilgan
uchta sonning yig'indisini toping.
212
IX SINF „ALGEBRA" KURSINI TAKRORLASH UCHUN MASHQLAR
ЖЖ
1. Kvadrat funksiya
1. Funksiyaning grafigini yasang:
1) 1) у = х2 + 3; 4) у = -х2 - 3; 7) у=(х —2)2;
2) у = х2 — 4; 5) у = (х + I)2; 8) у=-(х-2)2;
3) у = -х2 + 1; 6) у=—(х+1)2; 9) у = —0,5(х+4)2.
2. Parabola uchining koordinatalarini toping:
1) y=(x-2)2 + 3; 4) y=-(x + 2)2 + 5;
2) y=—(x—l)2 + 4; 5) y=-(x-3)2-l;
3) y=(x+3)2+l; 6) y=-(x-2)2-3.
3. Funksiyaning grafigini yasang va xossalarini ayting:
1) у = x2 — 8x + 7; 4) у = —2x2 + 5x +7;
2) у = —x2 + 7x — 6; 5) у = x2 + 2x + 3;
3) у = 2x2 - 5x + 3; 6) у = —x2 - 2x - 2.
ЖЖ
ЖЖ
4. Funksiyaning grafigini bitta koordinata tekisligida yasang:
1) У = y*2 va У = _4*2; 3)y = 2x2-3vay = 2x2 + 3;
2) у = -^x2-l va у = ^x2 +1; 4) у = x2 va у = (x — I)2 + 3.
5. Agar x2 + px + q kvadrat uchhad x = 0 bo'lganda 3 ga teng qiymatni, x = 1
bo'lganda esa 8 ga teng qiymatni qabul qilsa, shu kvadrat uchhadning pva.q
koeffitsiyentlarini toping.
ЖЖ
жж
6. Parabola absissalar o'qini x = 3 nuqtada kesadi. Uning uchi (2; —1) nuq-
tada. Shu parabolaning tenglamasini yozing.
Teleskopning (reflektorning) qaytaruvchi
ko'zgusi o'q kesimi bo'yicha parabola shakliga
ega (70-rasm). Shu parabolaning tenglamasini
yozing.
8. Agar у = ax2 + bx + c kvadrat funksiyaning
grafigi:
1) A(— 1; 0), B(3; 0) va C(0; —6) nuqta-
lardan o'tsa;
2) Д-2;0), £(l;0), 2) nuqtalardan
o'tsa, uning koeffitsiyentlarini toping.
1ЖЖ1
9. x ning qanday qiymatlarida kvadrat funksiya: 1) musbat; manfiy qiymat-
lami qabul qiladi? 2) Eng katta (eng kichik) qiymatiga erishadi?
1) у = x2 — 2x — 15; 4) у = —x2 — 3x + 4;
213
ЖЖ
жж
IZTXIXXI
2) y = x2—12x—13;
3) у = -x2 + 4x + 5;
2. Kvadrat tengsizliklar
Tengsizlikni yeching (10
10. 1) (x- 3)(x + 7) >0;
2) (x + 8)(x + 5) < 0;
3) (x- 6)(x+ 9) < 0;
11. 1) x2 + 9x>0; 3
2) x2 - V3x £ 0; 4
12. 1) x2—10x+25^0;
2) x2 + 8x + 16 < 0;
3) x2—14x+49>0;
13. 1) x2- 9x- 10 >0;
2) x2—llx+ 10<0;
3) 2x2 — 7x + 6 0;
14. 1) (x + 6)(x — 5) > 0;
2) (x — 3)(x + 6) < 0;
3) (x + 0,5)(x — 0,7) >0;
Tengsizlikni untervallar usuli bilan yeching (14—15):
15.1) 3)
x+3 ' x + 1
2)
^<0;
x-1
16. Trapetsiyaning yuzi 33,62 dm2 dan ortiq. Uning o'rta chizigl balandli-
gidan ikki marta uzun. Trapetsiyaning o'rta chizig'i va balandligi qanday
bo'lishi mumkin?
17. Parallelogrammning tomoni shu tomonga tushirilgan balandlikdan
3 sm ortiq. Agar parallelogrammning yuzi 40 sm2 dan ortiq bo'lsa, shu
tomonning uzunligi qanday bo'lishi mumkin?
18. Tengsizlikni intervallar usuli bilan yeching:
1) (x + 6)(x + 4)(x-l)(x-3)>0;
2) (x + 2)(x2 + l)(x + l)(x - 3) < 0;
2x -1 x - 2
-----+-----> 0;
2x+l x+2
3x4-1 3x-l<f^
x-2 x+2"
214
5) у = x2 + 6x + 10;
6) у = -x2- 2x— 3.
13):
4) (x + 5)(x + 3) Z 0;
5) (3 - x)(x + 5) > 0;
6) (2 —x)(x~ 7) <0.
2x2-3x<0; 5) x2 —25<0;
3x2 + 4x>0; 6) x2—10>0.
4) x2- 12x+ 36 <0;
5) -x2 + 6x - 9 < 0;
6) —x2 + 16x — 64 > 0.
4) 3x2 + 8x-3>0;
5) 16x2 + 4x+0,25 > 0;
6) —9x2 + 2x <0.
4) (x —0,9)(x —0,1) < 0;
5) (x—I)2 • (x +7) >0;
6) (x + 3)2 • (x~ 4) < 0.
x + 3 0
4) x(x + l)(x + 4)<
IZTXIXX
3. Ratsional ko‘rsatkichli daraja
Ildizdan chiqaring (19—20):
19- 1)
3> Й
I 25
5> F§-
20. 1)
/4а2
W5
I16a4b6
Ъ5а2!>2’
3)
W. J16-x4-/
27£6 ’
21. Hisoblang:
1) (8$20+7$80-2$5): $5;
3) $16+3$15-л/16-3$15;
4) </б-2лУ17 ^/б + 2>/17.
22. Sonlami taqqoslang:
1) $26 va $5; 4) -МУЙ) va-$$99;
2) $7 va $47; 5) $2 va $3;
3) 43 va $5; 6) -ТгЖ va $5$2;
7) $30 va ЦУ901;
8) $5 va $4;
9) -$2$^ va-$2$3.
23. Ifodani soddalashtiring:
\lx3l/x з 2 i
1) .2 ; 2) ---------3) (16a-4)’4; 4) (27£-6р; 5) (8a’3) 3.
a 5 x3
24*. Ildiz belgisi ostidan ko‘paytuvchini chiqaring:
1 ) $9o2^, bunda a < 0, b > 0; 2) $25a2Z>3, bunda a > 0, b > 0;
3 ) $8a3Z>3, bunda a < 0, b < 0; 4) y/12a3b3, bunda a < 0, b < 0.
25. Ko‘paytuvchini ildiz belgisi ostiga kiriting:
1) x45, bunda x > 0; 2) x$3, bunda x < 0;
3 ) -a$3, bunda a £ 0; 4) -a$5, bunda a < 0.
26*. Ifodaning qiymatini toping:
1)
1 1 1
a1a2b2
1 1 a-b
a2 -b2
i i
a-lc^V2 ^b
a
bunda a = 3, b = 12.
2)
m-2-Jmn + n 4mn + n
n m-n
4m
4m+4n
, bunda m = 5, n = 20.
215
жж
жж
жж
жж
жж
жж
27*. Ildiz belgisi ostidan ko‘paytuvchini chiqaring:
1) bunda a < О, b > 0; 2) ^So3#4, bunda a < 0, b > 0;
3) д/(а-1)2, bunda a< 1; 4) ^(3+a)z, bunda a >-3.
28. Berilgan son qanday ikkita ketma-ket butun sonlar orasida yotadi?
1) $36; 2) $68; 3) $-460; 4) ^1112;
5) $100; 6) $64; 7) ^29; K) ^4098.
29. Tenglamani yeching:
1 1 1) x’=4; 3) x’=2; 5) 2 x* =4; i 7) (l-2x)i=3;
1 1 2) x‘2=5; 4) x‘5=2; 6) i x*=2; 2 8) (5-3x)s=l.
4. Darajali funksiya 30. Funksiyaning grafigini yasang:
1) y = y/x; 4) y = Vx2-2x+l; 7) y = |x-l|+2;
2) y=y/x?; 5) y=V4x2+4x+l; 8) y = |x+l|-2;
3) y=Vx4; 6) у=Vx2 +6x+9; 9) у = 7x2+2x+1+|x-1|.
31. y=V2x-l funksiya grafigiga: 1) A (1; 1); 2) В (5; 3); 3) C
4) D (0; —1); 5) E (3; 5) nuqta tegishli bo‘lish yoki bo‘lmasligini aniqlang.
жж
32. У=-~ funksiya grafigiga: 1) Л(3; -4); 2) Б(-4; 3), 3) С (л/б;->/2);
4)(-л/2;л/б); 5) Е(—5; 2); 6) Д—8; 4) nuqtaning tegishli bo'lishi yoki
bo‘hnasligini aniqlang.
Funksiyaning aniqlanish sohasini toping (33—34):
жж
33. 1) y = 6) y = Vx2+2x+2;
2) y=V5-2x; 7) y=7(2-x)(x+3);
3) y=$16-x; 8) y=7(l-x)(4+x);
4) у = Vx2-5x-6; 9) y=7(x-5)(2+x);
5)* 1 у = V-x2-7x + 8; 10) y^-tx-lfoc-fy
жж
216
83К
I x-5
34- О y~y4^3x’
5) У =
6-x
2) У=ФШ; 3) y=H
x-3
9-x
4) У =
x2 -1.
x + 2 ’
ЖЖ
л/x-l Vx + 3
6) У-^l 7) У = ^ 8) У =
। x + 2
4-x2
35. Funksiyaning grafigini yasang va grafik bo'yicha uning asosiy xossalarini
aniqlang:
5 1) У=?; 4) у = л/=3х; 7) у = д/х+1;
2) у=— ' x-l 5) у = у/5-х; 8) у = Й-х;
4-х 3) У= 2х ; 6) у = >/2х-1; 9) у = ^4-3х;
36. Tenglamani yeching: 1) Л-5 =2; 4) л/2-х = V2+3x; 7) Vx-4=7;
2) >/x + l = 6; 5) >/8+x=V5x+4; 8) Jx+3=x+5
3) Vl-2x=3; 6) л/х+7 = 72(х-1); 9) V5-x=Vx+3.
ЖЖ
ЖЖ
ЖЖ
Л2Я5
жж
37. Quyidagi funksiyalaming qaysi bin juft, qaysi bin toq? Ulami ajratib
yozing. Javobingizni asoslang:
i 5
l)y = x3 + x; 2)y=|x| + x2; 3) y~ 1+^+’
4) y = x+x3 + x5; 5) у = x2 +X4 + x*; 6) J=p’;
7) 8) y=^ 9)
ЖЖ
5. Trigonometriya elementlari
38. Hisoblang:
1) 3lg^ + 2cos^-sin j; 2) 2cos ^ + 6 sin у - tgK.
39. Ko'paytmaning ishorasini aniqlang:
1) sin 240° cos 301°;
3) tg 227° - cos 350°;
5) cos 314° • sin 147°;
7) cos 505° • cos 655°;
2) sin 171° • ctg 242°;
4) cos 163° • cos 295°;
6) tg 200° ctg 201°;
8) tg 380° ctg 620°.
ЖЖ
жж
ЕЮ»
IXXIZTXI
217
жж
жж
жж
жж
жж
жж
. _ 1 К - 2*у10 1 £1 . Л
40. 1) sm а = -^— bo Isa, cosa, tga ш toping, 0 < a < —;
2) tga = 2y/2 bo'lsa, cosa, sina ni toping, 0 < a < j;
3) sin a = bo'lsa, cosa, tga, ctga ni hisoblang;
1
4) cosa =--/j bo'lsa, sina, tga, ctga ni hisoblang.
41. Hisoblang:
1) sin 225° • cos 120° • tg 330° ctg240°;
2) sin 300"-cos 135° tg 120° ctg 120°; 3) sin^-cos^-tg^ ctg^;
4 6 3 3
.. . 11тс 7л 5л x 5л 13л . Пл 7л 9л
4) sm-^cos— tg— ctg —; 5) cos-^ sin-— tg— ctg —;
' 6 6 4 3 ' 6 6 4 4
. 9я Ил . 13я , 15л .9л 7л , 7л , 5л
6) sm— cos— tg—°ctg—; 7) sin —-cos —-tg —-ctg —.
7 4 6 4 4 7 4 4 3 3
42. tga = 3 bo'lsa, ifodaning son qiymatini toping:
3tgq + 4ctgq
' 6ctgq-tga ’
4sina+7cosa
4) - . Z 5
2sina-3cosa
3sina-2cosa
7 4sina+cosa
5 sin2 q+2cos2q.
4sin2q-cos2 a
5tg2a+3tga .
7 9ctg2q-4tgq’
7sina+8cosa
7 4sina-5cosa
жж
43*. Ayniyatni isbotlang:
1) (sina+tga) (ctga-cosa)=( 1+cosa)( 1 -sina);
2) 1+cosp-sinp—ctgp=( 1 —ctgp) (1 -sinp);
3) sin6a+cos6a+3sin2acos2a=l;
1-cos4 a-sin4 a „ 4
----------------= 2 cos a;
tg2
5)
1 - cos 4a
1+cos4a
= tg22a.
жж
Hisoblang (44—45):
3 5 3~д
44*. 1) cosa = -, cosp = — va-^-<a, р<2л bo'lsa,
sin(a+p), sin(a—p), cos(a+p), cos(a—p) ni;
2) sina = -j^, sinp = -0,8 уал<а, P<^ bo'lsa,
sin(a—P), cos(a+P) ni.
жж
WKS5
218
5 7Г
45*. 1) cosa = -—, cosp = -0,6 va-<a, р<л bo'lsa,
cos(a—p), sin(a+p) ni;
2) sma = -0,6, sinp = ^-, у <а<2л, 0<p<^ bo'lsa,
cos(a—p), sin(a+p), tg(a+p) ni.
46*. 1) Ях2 — 6x + 1 = 0 tenglamaning ildizlari sina va sinp bo'lsa, sin(a + p) ni;
2) 6x2 — 5x + 1 = 0 tenglamaning ildizlari cosa va cosp bo'lsa, cos(a + p),
sin(a — p) ni hisoblang (a va p burchaklar I chorakda, deb faraz
qilinadi).
6. Progressiyalar
Agar arifinetik progressiyada (47—48):
47. 1) д10 = 25, a30 = 95 bo'lsa, ni;
2) д18 = 42, a34 = 170 bo'lsa, a7 ni;
3) a5 + a6 = 18 bo'lsa, a2 + a9 ni;
4) a2 + c4 = 7, a6 + ag = 23 bo'lsa, аъ + ni toping.
48. 1) — a30 = 180, a10 = 35 bo'lsa, an ni;
2) а100 —a49 = 204 bo'lsa, d ni;
3) д14 = 46; а7 + а33 = 200 bo'lsa, an ni;
4) «2 + a6 = 26, аг • a3 = 40 bo'lsa, an ni toping.
49*. 1) 701 soni 1, 8, 15, 22, ... progressiyaning nechanchi nomerli hadi?
2) 1002, 999, 996, ... progressiyaning nechanchi nomerli hadidan
boshlab uning hadlari manfiy sonlar bo'ladi?
3) <?! = — 31,5; J =2,1 bo'lsa, progressiyaning eng katta manfiy hadi
nechaga teng?
4) ax = —25,3; d = 1,9 bo'lsa, progressiyaning eng kichik musbat hadi
nechaga teng?
50. 1) at = l, 5101 = 15251 bo'lsa, d ni;
2) й?=4, *S100 = 20000 bo'lsa, д201 ni;
3) д2 + ag = 29, д10 — a14 = 18 bo'lsa, 5100 ni;
4) 4- д7 =—14, ax + a4 = 1 bo'lsa, *S40 ni toping.
51. 1) Mashina 6 soat yo'l yurdi. Birinchi soatda u 40 km, keyingi har bir
soatda awalgisidan 10 km ortiq yo'l bosdi. Mashina hammasi bo'lib necha
kilometr yo'l yurgan?
219
ЖЖ
ЖЖ
ЖЖ
ЖЖ
жж
ЖЖ
ЖЖ
жж
IZTXIXXI
ж
1ВП
жж
жж
Ж
ж
ВИ
ж
2) Soat 1 dan 12 gacha (12 ham kiradi) har soatda soat mill nechani
ko'rsatsa, shuncha marta bong uradi. Soatlar orasida esa har 15 minutda
1 marta bong uradi. Soat 1 sutkada necha marta bong uradi?
52. Geometrik progressiyada:
1) ^ = 2, q=3 bo'lsa, S6 ni;
2) q=3, S5 = 363 bo'lsa, S3 ni;
3) q = 2, S7 — 56 = 32 bo'lsa, b3 ni;
4) q = ~4, S6 = — 819 bo'lsa, b4 ni toping.
53. 1) Geometrik progressiyada: bx + b3 = 10, b2 + b4 =—30 bo'lsa, br va q ni;
2) b4 = 8, b% = 128 bo'lsa, bv q va Sn ni;
3) &3 = 9, b7 = 729 bo'lsa, bv q va Sn ni;
4) b2 = 2, bs = 384 bo'lsa, bx, q va Sn ni toping.
54. Cheksiz kamayuvchi geometrik progressiyada:
2) = ^=2(>/2-l) bo'lsa, 5 ni;
3) ?=“|’ ^5=| bo'lsa, S ni;
4) £ = 7, bo'lsa, & ni toping.
4 32 J
жж
55*. Yig'indini hisoblang:
3 2 8 ^4,3 c 1 1 1
7 2 3 27 7 3 4 7 2 20 200
4) 5> Л+1+^+1+ "
56. Davriy kasmi oddiy kasr ko'rinishida ifodalang:
1) 0,3(47); 4) 7,2(3); 7) 3,21(345);
2) 0,19(38); 5) 2,1(35); 8) 0,308(38);
3) 0,23(345); 6) 1,2(34); 9) 0,432(18).
57*. Har bir hadi o'zidan keyin keluvchi barcha hadlar yig'indisidan:
a) 10 marta; b) 100 marta katta bo'lgan cheksiz kamayuvchi geometrik
progressiyani toping.
ж
1ВИ
жж
220
KXIZTXI
0‘ZINGIZNI TEKSHIRIB KO'XING!
9-SINF “ALGEBRA” KURSINI TAKRORLASH BO'YICHA SINOV
MASHQLARI (TESTLAR)
I bob. 1. y=-x2+x+2 parabolaning uchi koordinatalar tekisligining
qayerida joylashgan?
A) I chorakda B) Ox o'qida С) IV chorakda D) III chorakda
2. y=x2—4x+5 parabolaning uchi koordinatalar tekisligining qayerida
joylashgan?
A) Ox o'qida В) IV chorakda С) I chorakda D) II chorakda
3. Parabolalardan qaysi biri Ox o'qi bilan kesishadi:
1) y=x2+x+l 2) y=2x2+3x+4
3) y=x2—llx+10 4) y=llx2—10x+9?
A) 1; 2 B) 2; 4 C) 3 D) hech biri
4. y= — 6x2+5x—1 kvadrat ftmksiya nollarining vig'indisini toping:
A) 1 B) J C) 4 D) |
5. Parabola A (0; 6), В (2; 0), C (3; 0) nuqtalardan o'tadi. lining
tenglamasini toping:
A) y=x2—5x+6 В) y=2x2—Зх+6 C) y=x2—3x+6
D) aniqlab bo'lmaydi.
6. c ning qanday qiymatida y=x2—6x+7+c parabolaning uchi M (3; 2)
nuqtada bo'ladi?
A) c=5 В) c=4 C) c=-2 D) c=3
7. y=axz—13x+17 parabola vay=Ax—7 to'g'ri chiziq absissalari 4 va 2 bo'lgan
nuqtalarga kesishadi. к — a ayirma nechaga teng?
A) -5 B) -3 C) 2 D) 1
8. y=ax2—5x+6 parabolani a{—2; 3) vektor yordamida parallel
ko'chirishdan hosil bo'lgan kvadrat funksiyani yozing:
A) y=2x2-5x+9 В) y=x2+2x+6 C) y=-2x2+5x+9
D) y=x2-x+3
Ko‘rsatma: y=f(x) funksiyani a(c; d) vektorga parallel ko'chirsak,
y=f(x~c)+d ftmksiya hosil bo'ladi.
9. y=x2—6x—7 parabolaning simmetriya o'qidan koordinatalar boshigacha
bo'lgan masofani toping:
A) 3 B) 4 C) 3,5 D) 4,5
10. y=£—px+q parabola x=—3 nuqtada Ox o'qiga urinadi. nisbatini
3 2 3 5
toping. A) В) C) D) |
221
^«•5
жж
жж
жж
жж
IZTXIXXI
Ж
жж
жж
жж
жж
II bob. 1. у = Jlx-x3 funksiyaning aniqlanish sohasini toping:
A) (-o,-J7]U[0;>/3) B) (->/75 5/7) C) [0;>/7)
D) (-oo-^U^oo)
2. (x~4)(x+2) < 0 tengsizlikning eng katta va eng kichik butun yechimlari
(x-1)
ayirmasini toping:
A) 3 B) 4 C) 1 D) 6
3. Tengsizlikning butun yechimlarini sonini toping:
(—x2 + x - l)(x2 +x — 2) q
x2 -7x + 12
жж
жж
A) 3 B) 2 C) 4 D) topib bo‘lmaydi.
Xr^ _ 20x + 64
4.-----x------<0 tengsizlikni eng katta va eng kichik yechimlari ayirmasini
x2+9
toping:
A) 44 B) 20 C) 11 D) 12
y2 _7у_1 о
5. -—\ <0 tengsizlikni qanoatlantiruvchi natural sonlar nechta?
x+5
A) 9 B) 10 C) 8 D) 7
жж
x2 -9
6. ————tengsizlikning butun sonlardan iborat yechimlaridan
nechtasi [—5; 6] kesmada joylashgan?
A) 5 B) 4 C) 7 D) 3
7. Agar xe(-2;0) bo‘lsa, ushbu lx+3l+^x ~8x+16 ifodani
|l-x| + x
soddalashtiring:
жж
A) 2x+l B) 8 C) 7 D)
4x2 — x + 4
8. 1< —— < 3,75 tengsizlikning tub sonlardan iborat yechimlari
nechta?
A) 1 B) 5 C) 4 D) 2
жж
222
Ж
_ x2-12x + 23 2 . ... . к t. i л u * .. . •
9. —5— -----—z tengsizlikning butun sonlardan iborat yechimlari
x -3x-4 4-x
nechta?
A) 5 B) 6 C) 7 D) 3
10. x2+px+^=Q (q ?*0) tenglama ning qanday qiymatlarida haqiqiy
жж
ildizlaiga ega emas?
A) (0; 2) B) (-2; 2) C) (-2; 0)
D) to‘g£ri javob berilmagan
11. х?—20л? +64 < 0 tengsizlikning butun yechimlari nechta?
A) 3 В) 4 С) 6 D) 5
жж
ж
12. n ning qanday eng katta butun qiymatida nxz+2(«—12)л+12=0 tenglama
A) 13
B) 16
C) 18
D) 17
жж
ЗИЯ
жж
III bob. 1. Funksiyaning aniqlanish sohasini toping: у = л/20х-х2-96.
A) 8<x<12 В) 8<x C) x>12 D) -12<x<8.
жж
2. x ning qanday qiymatida ifoda ma’noga ega emas?
A) x * ±5
B) -5 < x < 5
C)
Ух2-25
1-x2 '
D) M<
жж
Hisoblang (3—6):
C) 3
D)
A) 3^2
^Т34+3>/2.
C)
-2
D)
5. ^5л/3-7П-^5л/з+>/11.
A) 4
B) -4
C) 5^/3
D)
5 + 1
-3
жж
2
IZ^IXTXI
жж
жж
\О,6
А) 1+Лз В) 713-1 С) зЛз
D) л/13-8
7. -__3/4 ifodaning х = V3 - ^2 bo‘lgandagi qiymatini toping.
х-л/З
жж
«гая
жж
А) -у/2 В) г/з С) О D) 1
8. Ko'rsatkichi kichikroq bo‘lgan ildiz ko‘rinishida tasvirlang: ^(2-V5)2.
А) у/5-у/2 B) yll+y/5 C) ^2-y/5 D) у1у/5-2
Hisoblang (9-10):
9. ^7+4^'^2
A) -1 B) 2 С) a/3 D) 3
10. $3+2yl2-tf^2
A) 2 B) -1 C) 3 D) >/3
11. Daraja ko‘rinishida ifodalang: Г 1 X3‘X к C) i. № 1 — * 4 O> | 1 D) X3
A) x2 B) x~3
12. Daraja kocrinishida ifodalang: ii i br°b 1 4 5 :b 15 i 23
А) Л15 B) Hisoblang (13-15): ( 81a°’4 13, 1 IOOOOjc08/2 224 d15 -0,75 C) b3 D) £30
lOOOx06/ 1Ох/ 100х6
A) 27a03 B) 9a C) 81a3/
IQOOx^-j7 8 9
81a3
IV bob, Funksiyaning aniqlanish sohasini toping (1—4):
1. j> = ^(x+7)(x-7)(x-8).
A) -7<,xi7,xk8 B) xs8 C) -7<xs7 D) x>7
2. У = 7(x+5)(x-7)(x-4)
A) xS7 В) -5<x<4,x>7 C) 4<x<7 D) xa4
3. у = №x2-5x+1 .
A) -l<xs| В)х<1 C) x<i,x<A D)x^|
A) x*5 B) x>-4 C) x<5 D) —4^x<5
5. Funksiya qaysi oraliqda o‘sadi: y=4-x2.
A) -«> < x < 0
B) x>4
C) -2<x<2
D) 4<x<~?
6. Funksiya qaysi oraliqda kamayadi: y=x2+6x+9?
A) x^3
B) x<-3
C) -3<x<3 D) x>0
7. Funksiyalaming qaysilari o‘suvchi:
l)y = ^x; 2)у = $х?; 3)y = -x+l; 4)y = -V5-x; 5)y=x2+5?
A) 2), 4) В) 1), 2) C) 3), 4) D) 1), 5)
8. Funksiyaning qaysilari kamayuvchi:
l)y = —2)y = -2x+3; 3)y = x’-20; 4)y = ^27^; 5)y = -x2?
x
A) 1), 5) B) 2), 4) C) 2), 3) D) 3), 5)
9. к ning qanday qiymatlarida у=-giperbolabilan y=3x—4 to‘gcri chiziq
ikkita nuqtada kesishadi?
15—Algebra, 9
225
ж
жж
А) Л = у В) Л<| С) к>~ D) к>~
жж
жж
ЖЖ
жж
к
10. к ning qanday qiymatlarida у = - giperbolabilan у=16—х to'g'ri chiziq
bitta umumiy nuqtaga ega bo'ladi?
A) £=16 В) £=8 C) £=256 D) £=64
к
11. £ ning qanday qiymatlarida у = - giperbolabilan y=5~3x to'g'ri chiziq
kesishmaydi?
25 12 25
A) k>£ B) k<™ C) * = §
12. Tenglamani yeching: у/9-х + y/x+4 = 5.
A) x=-16 В) x=0, x2=5 C) x=21
13. Tenglamani yeching: 2^3+ x - л/8 + х = 1
A) x=6 В) x=y Q x=l
V bob. 1. 216’ ning radian o'lchovini toping:
A) у в) у c) 5
2. 0,64 n ning gradus o'lchovini toping:
A) (103,4)° B) (113,4)° C) (115,2)°
it
3. (1, 0) nuqtani z + 2rc£, £eZburchakka burishdan hosil bo'ladigan
о
nuqtaning koordinatalarini toping:
D) k>~Tf
D) x=0
тлч 25
D) *—y
D) 1*
о
D) (117)°
жж
A)
г_а г
2’ 2
I J
B)
C)
Д 1
2 ’ 2
D)
r 1,л/з'
2’ 2
к 7
2 ’ 2
I )
nuqtaga tushish uchun (1, 0) nuqtani burish kerak bo'lagan
barcha burchaklami toping:
жж
А) 135°+180°Л, k&Z B) ^+2nk,keZ C) ~^+nk
3it
D) ^ + 2itk,keZ
4
жж
Ж2Я5
226
5. Sonlami o‘sish tartibida yozing: fl—sin 1,57; £=cos 1,6; c=sin 3.
A) b<c<a B) a<c<b
Hisoblang (6-11):
6. ctgl35° • sm210° cos225° • ctg675°.
72 72
A) -T В) T
C) c<a<b
D)
b<a<c
7. sin2225’ - ctg330” • tg405°
2
2
„ 4 7 71 . a 5n 4 Зя . 4Л .71
8. COS -5- +Sin -5- + COS -5- + Sin 3 + Sin7
о О ООО
A) 1,5
73
C) T
2
D)
D)
_1
2
B) 1,35
Э 3
9. sin32°cos2° + sin2 28° - -?
4
A) 0 B) 2
10. cosl50-(sinl50 + cosl5°)-0,75
C) 1,25
D)
2
C)
-0,25
D) 0,5
MM
A) V3+2
B) £
C)
73
2
D)
11. Hisoblang:
1 2 ® 2 -2
1 -sin - cos a -sin a
о
MM
ргаи
MM
4sin4^
lo
A) sin2^
B) ctg2|
C) -ctg^
D) tg2£
12. Agar sina +2cosa =—2 bo'lsa, tg у ni hisoblang.
C) -1
A) 4
B) 3,5
D) -2
VI bob. Ketma-ketlikning л-hadi
formulasini yozing
(1-2):
t 1 3 5 7 9 11
* 3’ 5’ 7’ 9’ IF 13
Ач 2л-1 л-1
A) xn=^—r B) xn = —т
7 n 2л+1 7 n л+1
2я-3 n-3
Q 7 D) xn=—г
7 n 2n+4 7 n n+3
1ЖЖ
№2
IXTXIXXI
2. -1; 2; -4; 8; -16; 32; ...
A) -2«+1 В) —(—2)"-1 С) -2я-1 D) (—2)2"-1
3. Qavariq to'rtburchakning burchaklari ayirmasi 42° bo'lgan ariftnetik
progressiya tashkil etadi. Shu to'rtburchak burchaklarini toping.
A) bunday to'rtburchak mavjud emas
C) 27°, 69’, 111’, 153’
B) 25’, 47°, 89’, 131’
D) 50’, 92’, 134’, 176’
4. Qavariq to'rtburchakning burchaklari maxraji 2 bo'lgan geometik
progressiya tashkil etadi. Shu to'rtburchak burchaklarini toping.
A) 24’, 48’, 96’, 192’ I B) 30’, 60’, 120’, 240’
C) 20’, 40’, 80’, 160’ D) bunday qavariq to'rtburchak mavjud emas
5. To'g'ri burchakli uchburchakning gipotenuzasi 2 ga teng.
Uchburchakning burchaklari ariftnetik progressiya tashkil qilsa, uning
katetlarini toping.
A) | va В) 1 va 1 C) | va | D) topib bo'hnaydi
5 5 8 6
6. To'g'ri burchakli uchburchakning gipotenuzasi 2 ga teng.
Uchburchakning katetlari geometik progressiya tashkil etsa, uning
maxrajini toping.
C) л/5 + l D) 1,3
7. Ariftnetik progressiyaning birinchi hadi a= —130, d=4 bo'lsa, a. ni
toping.
B) -300
C) -300
D) -340
Ariftnetik progressiyaning birinchi hadi аг va ayirmasi d ni toping (8—9):
4 8
A) 0=40, J=14
C) 0=46, d=5
9, < д12 д14 = _200,
а13 +Д14 + fl15 “15-
A) 0 =-287,5, rf=22,5
С) л=-280, zZ=20
В) a= -46, d=7
D) a = —46, dM4
B) 0=287, d=~22
D) 0=287,5, dT=—12,5
10. Geometrik progressiyaning birinchi hadi va maxraji q ni toping:
£.-&,+ Д. = 21,
b\ + b\=l5.
A) bt=3, q=2
C) b= -3, q= -2
B) ^=3, q= -2 yoki i =12, q= -0,5
D) b = -12, q=2
JAVOBLAR
7-8-sinflarda o‘tilganlarni takrorlash. 3. 3) 1,6; 4) 2,4. 6. 1) (1; 2); 2) (4; -
3). 7. 180 ta. 8. 2,5 m; 3 m. 9. 75 va 68. 10.4) x>33.12. 2) x=-l, x=0,2; 4) x=-
7, x=l. 14. 2) x = 1; x = 4, 4) x=—1, x=|. 15. 9 va 36. 16. 35 nafar. 17. 10% ga.
18.9.19.0,2 qismi. 20.20.21.60 km/soat. 24.3 tadan. 25.6 marta. 26. a=—4.
I bob. 5. 2) x = 0; 4) x=|; x = |- 6. 2) /> = 6, q = 8. 7. 2) x = 0;
x = |. 4)x = 0;x=5. 13.2) (-1; l)va(-2;4). 19. к = -1, b = 2. 20. k= 5; yana
bir umumiy nuqta bor: (3; 9). 21. b = 24. Yana bir umumiy nuqta bor: (8; 64). 22.
2) k=—4. Yana bir umumiy nuqta bor: (-3; 9); 4) k=2\[3 . 28. 2) (—7; 245) va
(|;|). 29. 2) a = —2; 4) a = 9. 30. 2) a>~fc 4) a<y. 31. 2) o>|. 33.
1) # + 4oi>0; 2) A? + 4e6<0; 3) # + 4ai = 0. 38. 2) (1; 5); 4) (2; 0); 6)
(l;0). 39. 2) (0; 0); 7) (2,5; 0); 8)
3 1 /31
--;0 ; 9) (-0,5; 0); 10) -;0 ; 11) (0,7; 0);
/ J l о J
12) - ;0 . 40. 2) 1X0 bo'lgani uchun Ox o‘qi bilan kesishmaydi; Oy o'qini
l О J
(0; 3) nuqtada kesadi. 6) (1; 0), (-И; o), (0, -15). 41. 2) у=-2,5х2+5х+Ъ,5: 4)
y=x2—6x+l. 42. 1) b< —13 bo'lsa, umumiy nuqta yo‘q; b = —13 bo'lsa, bittagina
umumiy nuqta; b>—13 bo'lsa, ikkita umumiy nuqta. 43. 5,(x) = 4x2 —
- 2(a + b)x+ab. 44. 31m,5|m,6m. 47. 2)p = -5, q = 6. 48. 2) a = -4, й=8,
жж
жж
c = —3. 49. 1) /я<—1; 2) m = -l; 3) m>-l, (m*0). 50. 2) -2<a<0. 51. 2)
b = ±3; b = ±4. 57. Bo‘yi va eni 20 sm dan bo'lsa. 58. Bo'yi 36 m, eni 18 m. 62.
Bo'yi 60 m, eni 40 m bo'hshi kerak. Eng katta yuz 2400 m2 ga teng. 68. 2)
« = -1, b = 3, c = -2; 4) a=~3, b = 7, c = ~2. 72. a = 4; a = 2,5. 73. 2)
4>/3a
x=0; x= 1,5. 75. 2) a = —l; 4) a = — 1. 76. Uzunligi 9+4л^ simdan kvadrat,
uzunligi simdan muntazam uchburchak yasash kerak. 77. sm. 78. 2)
p = ~7, $=10. 79. 2) p=l, ? = -6.
a^j2
Olimpiada masalalari, 1. Agar 0<x<—bo'lsa, 5(x)=a2—x2; agar
^^-<х£л\/2, S'(x) = (eV2-x)2. 2. Agar 0^x<^—bo'lsa, S(x)=—-—x2;
2 2 a-b
a—b a+b a—b a+b
agar -^—<x<—- bo'lsa, 5(х)=Л-(х——); agar ------^x^a bo'lsa,
2 2 4 2
a-b (a-b)2'
2 a-b
7. a>l, a<—2 bo'lsa, 2 ta nuqtada kesishadi; a=l,
a=—2 bo'lsa, kesishish nuqtalari soni 3 ta; —2<«<1 bo'lsa, 4 ta nuqtada kesishadi.
8. 1) Z>=±3; b=±4; 2) a=l. 10. p=—2, 0=0; eng kichik masofa d=l.
IIbob. 85. 2) -7 <x< - 3; 4) x< 2, x> 3. 86. 2) (-3; 0); 4) [-7; 7]. 87.
2) —4<x< —1; 4) x< —8, x> 1. 88. 2) x — ixtiyoriy son. 89. 2) 120; 4) 2. 90.
2) 20. 101. 1) Jt= —3; 2) k=1. 102. 2) -|<x<|. 105- 2) 3 <x<4; 4) x<-6,
x > 5. 106. 2) x < 0; x > 4; 4) — 6 < x < 0. 107. 2) — 2 < x < 0; x > 2. 6) — 3 < x < 2,
x>3. 109. 2) —2<x<2. 110. 2) —l<x<l; x = 2; 6) x>7; 8) x<l; x = 2.
10) 2 <x< 3; -4 <x< -3. 111. 2) 7; 4) 9. 112. 2) 6; 4) 24. 113. 2) x< -5, x> 2.
4) x<—4, -4<x<|, x>4. 114. 2) x<~ 2, x>l; 4) x<—2, x>4. 115.
Ж
2) x<—2, x>3. 123. 2) a<-1, a> 3; 4) a^0, a<± 124. -6<a<2. 130.
x > s+^s ** . 131. Bo'yi 40 m dan, eni 20 m dan kam bo'hnasligi kerak. 133.
a = b = ^. 134. EFEng katta yuz |m2. FK tomon BD ning
o'rtasidan o'tishi kerak, FKLBD. 136. Chuqurligi 1,5 m, asosi (tubi) 3 m. 137.
Chuqurligi 3m, asosi (tubi) 6m. 138. 1) s(t) = —2f2+40H-250; 2) 1= 10 sek. 139.
Tomoni 7= bo'lgan kvadrat. 140. 2? VI; &R. 141. Cuchidantushirilganbalandlik
o'rtasidan. 144. 1) t— 1,2 sekund va t- 3 sekunddan so'ng. 2) 22,25 m; ha, t— 2,7
sekundda; 3) t = 2,1 sekunddan so'ng. Otimpiada masalalari. 2. 4^2 . 3. 3. 4.1. 5.
fc=-l. 9. c<4.10. a=-4, Z>=4, c=24.
/ \—3 / 4
ШЬЛ. 146. 2) 1; 4) (Al >1. 147. 2) 1; 4) [-L >1. 148. 2) 191; 4) A.
I 11 ) I 13 J 7
149. 2) 26; 4) 90.150. 2) -3; 4) 1. 151. 2) 0,0081; 4) 152. 2) 63; 4) c - d. 153.
2) 15- 4) a*. 154. 2) 4) 6) 155. 2) 4)
156. 2) Ifi; 4) Г15. 157. 2) 4) 16a~12. 158. 2) 4) 159. 2) m"3;
q * г
4) --^9- 160.1) 140,7. 161. 2) 6,4 • 10“s; 4) 6,25 • 104.162. 0,003. 163.0,0001.
164. 2) a5; 3"5.165. 2) a + b. 166. 2) >W"2; 4) 4~3 > 3"4.170. 2) 2; 3; 5;
i; 0,4; 0,5; |; 171. 1; 0; 3; j; |; 0,2; 0,3. 172. 2) 2; 4) 15; 173. 2) 81; 4)
JO J J
174. 2) -1; 4) -2. 175. 2) 2; 4) 225. 176. 2) x=-3; 4) x=2. 177.
2) x = --L; 4) x=2. 178. 2) 3; 4) -9. 179. 2) 2; 4) 4. 180. 2) a) 3-x;
ЖЖ
b) -3 + x. 181. 2) 2; 4) ±^. 182. 34. 183. 2) istalgan x uchun; 4) [|; 2). 184.
2) istalgan x uchun; 4) [|;|). 185. 2) 5,6; 4) 19,2. 186. 2) 28; 4) 3. 187. 2) 20;
4) 2.188. 2) a2*3; 4) <z4|Z>|. 189. 2) 9a3*2; 190. 2) 1,8; 4) 5,2.191.2) 30; 4) 1.192.
2) a*2; 4) За6*4. 193. 2) 195. 2) 0,3; 4) 20. 196. 2) 63; 4) 6. 197. 2) 0,3; 4)
21г
ЖЖ
ЖЖ
3. 198. 2) 2; 4) 5. 199. 2) 2ab; 4) 200. 2) |; 4) 201. 2) i; 4) 2. 202.
2) 105; 4) 30. 203. 2) 48; 4) 2. 204. 2) |; 4) 4. 205. 2) 2xf; 4) 206. 2) 2a*;
4) 207. 2) 4) 208. 2) 3; 4) 5. 209. 2) 4) 3a. 210. 2) 1^.; 4)
211. 2) 3x; 4) 2xy. 216. 2) 4; 4) 8; 6) 57. 217. 2) 4; 4) 64; 218. 2) 2; 4)
6) 219. 2) 9; 4) 5. 220. 1) 24; 2) 121. 221. 2) 2. 222. 2) b6; 4) у 5.223.
5 1,14
2) *; 4) -2 225. 2) a2*; 4) %*. 226. 2) -Ц-- 227. 2) 3; 228. 2) 0. 231.
z 3a
2)йг<(о,41)^; 4) 2эз-2) (Я‘<(°’41)‘:
4) ГнГ5 >Г1|Т'5 234. 2) x=3; 4) x = 2; 6) x = |. 235. 2) x = 2;
4) x = —3. 238. 2) x = |; 4) y=5. 239. 2) x = -|; 4) x=|. 240. 2) x = 4.
-1-1 г г
241. 2) a>b. 242. 2) 3“2<2-2; 4) 3 2 <2 2; 6) 3~V3 <2~'/3. 243. 2) x= 1. 245.
2) 1681. 246. 2) -1024,96. 247. 2) 30. 248. 2) 1,7; 4) -0,15. 249. 2) 0,069;
4) 0,04. 250. 2) 8. 251. 2) 252. 2) 253. 2) 1000. 254. 2) lj_y2 ' 255.
2) 21/x. 256. 2) x=-4; 4)x = 2. 257. 2) x=|; 4) x = |. 258. 2) -609i. 259.
2) -225260. 2) istalgan x da; 4) x< 1; x> 2. 261. 2) x< 2; x> 13; 4) x> 1.
262. 3) 4) 7=5-263. 1) -8; 2) 2.
жж
жж
231
IXTXIXXI
IV bob. 267. 2) 1; -1; 2 va |. 269. 2) x* 1; x*2. 4) [-2; 4). 270. 2)
x< 1; x^6. 4) x< -5; x^2. 273. 2) —2; -5 va 1; —4 va 0. 274. 2) tegishli; 4)
tegishli. 275. 2) x*3; 4) x^-2. 276. 2) x*4; 4) x^-6; x£ 1. 277. 2) Ha; 4)
Ha. 278. 2) Ha; 4) Ha. 281. 1) a = 2, b = -1, c = 3; 2) x = 1. 283. 2) kamayadi;
4) o'sadi. 284. 2) kamayadi; 4) o'sadi. 285. 2) xeJSda kamayadi; 4) x<0 da
o‘sadi, x>0 da kamayadi. 286. 2) istalgan x da kamayadi; 4) x<2 da kamayadi,
x>2 da o‘sadi. 289. 2) 81; 4) 290. 2) 16; 4) 1. 291. 2) (729; 243); 4)
(^;125). 292. 2) (0; 0), (1;1); 4) (1; 1), (0;0). 293. 2) Ha; 4) Ha. 294. 2)
xeAda o‘sadi; 4) xetfda o£sadi. 295. 5) -8. 296. 2) (1; 1); 4) (-2; 2), (2; 2).
299. 2) toq; 4) toq. 300. 2) toq; 4) juft. 303. 2) toq; 4) toq. 304. 2) juft; 4) juft.
305. 2) toq; 4) juft. 313. 2) -9; 4) 314. 2) 1; 4) -2; 315. 2) 2; 4) -4. 316.
2) -2; 4) 4. 317. 2) (1; 3); (3; 1); 4) (3; 4), (4; 3). 318. 2) (1; 1), 4) (1; fc), (fc;
1), (-1; -k). 320. 2) 0 < у < 1; 4) -1 < у < 0. 321. 2) [-4; 0); 4) (0; 322.2) (1;
—2); (2; —1). 323. M) ning istalgan qiymatida 2 ta nuqtada kesishadi. 324.1) a > 0,
к > 0 da 2 ta nuqtada kesishadi; 2) a < 0, к > 0 da kesishmaydi; 3) a < 0, к < 0 da
2 ta nuqtada kesishadi; 4) к < 0, a > 0 da kesishmaydi. 325. a=+4. 328. 2) x > 1;
4) 0<x< 1; 6) -|<x<23. 329- 2> x>2’ 4) °’ x~ 6> x-3- 33°- 2> x -9’ 4>
x > 7. 331. 2) 0<a < 6. 332. 2) V> 64. 336. 2) x = 25; 4) x=-|; 337. 2) x = 15; 4)
x = 4. 338. 2) x = 17; 4) x = 6. 339.2) x = 2; 4) j^3, x= 4. 340. 2) x= 6; 4) x = 4.
341. 2) x= 1; x=4; 4) x = 0,2. 342. 2) x = 343. 2) x< 3; 4) x> 1. 344. 2)
x>|; 4) -13 < x< 3. 345. 2) x> 2; 4) x> 6. 346. 2) x*|; 4) x — istalgan son.
348. 2) $ > • 349. 2) x > 0 da kamayadi, x < 0 da o‘sadi. 351. к = 3 da I va III
da, £=-4 da II va IV da. 352. (0; 0), (-1;-1), (1; 1). 353. 2) (1; 2), (-1;-2).
354. 2) x< —2, x>2; 4) x< -3. 355. 2) x=8; 4)x= x=|- 356. 2) x=5; 4) x=3.
360. 2) x=—l;x= 7; 4) x=3; x=7. 361. 2) x< -1; x> 4; 4) [-|; 4]. Murakkabroq
4 2 1
masalalar. 4. 1) c=--; 2) a = ~~$- 1* 1) 49 ta; 3675. 8. 3) x=5;
V bob. 363. 2) 4) 6) 364. 2) 4) 6) 365. 2)
22,5°; 4) [Z2of. 6) (»^3 f 366 2) f25^f; 4) ; 6) (sf. 367. 2)
£ = 0,79; 4) 9,42. 370. ^-o,54m. 371. 2) 1,25; 372. 2) f; 373. 2) £; 374. 2) 4.
375. 2) 1. 377. 2)f-l;f 1; 4) (-1; 0); 6) (0; -1). 378. 4) 6) (-1; 0).
\ 2 2 7 I 2 2 J
379. 2)fA-^'l; 4) 6) te-ll 380. 2) 4) (4^)
1^2 2 J {22 J I2 2) I22/ I22/
6) (zTLzT2). 381. 2) I chorakda; 4) IV chorakda; 6) I chorakda. 382.
2) IV; 4) IV; 6) II. 383. 2) I; 4) III. 385. 2) (0; -1). 386. 2) f|; -у 1 4) (0; 1).
387.2) 2ick;keZ; 4) -1 + 2nk, кe Z. 388.2) l£ + 2itk,keZ. 4)$ + 2itk, ke Z.
390. 2) 4) -4', 6) Л; 8) -#• 391. 4) 6) 0; 8) i. 392. 2)
‘ —1 — ‘ ——V 4Л f— (——‘ ) ЧОЧ (——* ——) f— — 4Л
\ 2 ’ 2/Ц 2 ’ 2)’^) 2 ’ 2/’ \ 2’2/* L> \ 2’ 2 /Ц 2’ 2 /’
(yi l); (yi _1)- 394. 2) 4) -1; 6) 1. 395. 2) 0; 4) -1; 396. 2) 4)
0. 397. 2) f+fat,fceZ. 416. 2) II; 4) III. 417. 2) musbat; 4) musbat. 418. 2)
manfiy; 4) manfiy. 419. 2) manfiy; 4) manfiy. 420. 2) manfiy; 4) manfiy. 421. 2)
musbat; 4) manfiy. 422. 2) manfiy; 4) musbat. 425. 2) manfiy; 4) musbat. 427.
2) cosa=—; tga = -^; 4) sina = -||; cosa = -^. 428. 2) ha; 4) ha. 429.
1J -1Z 1 f 1 /
sina = 4^; <ga = nr- <30. cosa = |; sina = 4- 431.2) sina = ±^L 433.2)
х = як, keZ- 4) x=^+kn, fa=Z. 434. 4) x=-9n+nk, k&Z. 438. 2) 2 cosa; 4)
1 + sina. 440. 2) 3; 4) -2. 441. 2) 2^; 442. 2) и2 - 2; 443. 2) x = кк, к e Z.
444. 2) х = яА, *e Z. 445. 2) x = nk, ke Z; | + Z. 447. 2) 3. 448. 2)
-1—2-72; 449. 2) 2sina; 4) 2. 452. 3) 1. 453. 3) X. 454. 2) 2. 455. 2) +; +; 4)
+; -; 6) -; +. 8) +; -. 456. 2) cos 1,5 >cosl,6; 4) sinl >sinl". 467. 2) 4)
468. 2) 0; 4) 4- 469. 2) X; 4) 470. 2) -1; 4) -i. 471. 2)
4) -1. 474. cos(a + 3) = И; cos(a-₽) = Й- 475. й-’й- 476. 2) cos2a. 477. 3)
sina sinp. 478. 2) 4) 1. 479. 2) -1.480. 3) -sinacosp. 481. 2) 0. 483. 2) 0.
486. 2) 5-; 4) 487. 2) 0; 4) -1. 488. 2) 5) 489. 2) 490. 2)
2 z 2 2 25
491. 2) cosasina. 492. 2) -1. 495. 2) 5) 496. 2) 4) 498.
233
жж
жж
жж
жж
жж
жж
жж
жж
жж
IZTXIZTXI
2) 0; 4) 0. 499. 2) 1; 4) 0. 500. 2) -ji 4) 501. 2) 4) 502. 2)
4) . 503. 2) 1; 4) -1. 504. 3) cos2a. 505. 2) 1.506.2) 507.2) 2cosa.
510. I, f, Ц-. 513. 2) 0; 1; 4) 1; 0. 514. 2) 515. 2) ' 517. 2) 3.
518. 2) 519. 2) -ф 4) . 520. 2) sin2a; 521. 2) 1; 4) -JL. 522.
2) -2®.; 4) -1-Ц=- 523. 2) cos0>sin5. 524. 2) . 525. 2) 526. 2)
gL- 528. 2) tga. 529. 2) 530. 2) 1. 531. ||. 532. 2) cos4a. Mantiqiy
masalalar. 2. l)x=—31;x=—7.3. |. 4. Berilgan ko'paytma | gateng. 5.1) |;2)
ko'rsating.
VI bob. 535. 2) -4, -1,2, 5,8. 537. 2) 59; 4) -50. 538. 2) 27-4и; 4) 5-Зл.
539. 2) 3. 540. 2) 1,7; 1,5; 1,3; 1,1; 0,9. 541. 2) -9,4; -1,3и + 3,6. 542. n = 10.
543. На. 544.2) . 545.2) -100.546.2) 5л -17.547.2) 3л - 18.548.8. 549.9.
550. 28 metr. 551. 23 sm; an = 2n + 3. 552. 10 kun. 553. d = n. 554. —11, —8, —5,
-2. 555. -20, -17, -14, -11. 557. 2) 9 900; 4) 2 600. 558. 2) 900; 4) 441. 559.
4 947.560.2 500.561. я2.562.2 550.563. n(n + 1). 564.2) -192.565.2) 1 085.566.
1) 4 905; 2) 494 550. 567. 2) 1 840. 568. 2) an = -4,4; d = -0,58. 569. 2) ar = -
88; d= 18.570. 15; 465. 571. = 44. 572. n = 10. 573. n = 35. 574. 52i = “147.
575. и = 99. 579. 2) -4; 20, -100, 500. 582. 2) 4) 583. 2) 4)
585. 2) -L.. 586. 2) л = 5; 4) л = 8. 587. 2) л = 8; 4) л = 8. 588. 2)
« = 4; 4) « = -1. 589.2) л = 7. 590. 2) q = 3; 729. 591. 2) b, = 2£; ^ = 6.592.
э б
593.12, 36, 108; 156. 594. 6, 18,54; 78. 596. 2) 4) 597. 2) 10922.
598. 2) -1; 128. 599. 2) л = 6; 4) л = 6. 600. 2) л = 5; 4) л = 6. 601. 2) л = 9;
2048.4) q = 7; п = 5.602. 2) 728. 4) 1094. 604 2) 3577. 606.2) - g. 608. 54. 609.
720. 610. -4096. 611. 86. 613. 2) 5, 9, 13, 17; 5) -22, -19, -16, -13. 615. 2)
69. 616.2) -Зл + 23; 4) -5л + 8. 617. п = 20.618.2) 2100; 4) 2500.622.2) 2800.
623. 2) а, = 12, d= 1. 625. 2) -3; -6; -12; -24; -48. 627. 2) 4) 628.
2)4(1] ; 5) 5-(|) . 629. 2) q = ^. 630. 2) -f|. 631. 2) 121. 632. 2)
234
Ьг =-1 A = 128. 633. 2) n = 6; 4) n = 5.634.2) - g. 635.2) = 781; S\ = 521.
644. 2) bo'ladi; 4) bo'ladi. 645. 2) bo'ladi; 4) bo'ladi. 646. 2) |; 5) 647. 2)
y! 5) -y- 648. 2) 9; 5) 649. 2) bo'lmaydi; 4) bo'ladi. 650. 2) If.
652. 2) q = \. 653. 2) ? = {. 654. 2) 7^-655. >/з<2 + 7з). 656. ^.657.
V2 +1.659.2a; |a3.. 660.10%. 661.2 yilga. 662.1152 000.663.14 400,17 280,20
736. 664. 1 020 000, 1 040 400, 1 061 208. 665. 2) j. 666. 2) j; 4) ||. 667. 2)
2^. 669. 15 ta. 670. 1) ll|sm2. 2) 36 sm2. 673. 2) d = ±\ a4= 1, <% = 0; 4)
d= —2; «4 = -^-6; <% = >/3-10. 674. 2) d = -|; a4 =y qj = -|; 4)d = —
4; «4 =>/2-12; ag =>/2-20. 677. 3) -20 J. 678. 2) 5lo = -24O. 681. 2) 143.
682. 2) 15. 683. 2) -133. 685 2)^; 4) 40. 687. 2) if. 688. 2) -|(-3)”’1.
690.4) 5. 691.2) 242; 4) g. 692.2)-j. 693. d= 3.694.2) 22,17,12,7,2. 695.
-20, -17, -14, -11. 696. 14, 12, 10, 8. 698. 2) -4; |. 702. 84. 704. at = 8,
fi?=—3 yoki ai = 2, zZ=3.
IX sinf „ Algebra" kursini takrorlash mashqlariga javoblar
2. 2) (1; 4); 4) (-2; 5). 5.p = 4, o=3. 6. x?-4x + 3. 7. У = 4 x1. 8. 2) a =
r
= — 1, b = — 1, c = 2.9.2) x < — 1 va x > 13 oraliqlarda musbat; — 1 < x < 13 oraliqda
manfiy; x = 6 da eng kichik qiymatga erishadi; y(6) = —49.10.2) — 8 < x < —5.11.
2) OSxsVI 12. 2)x=—4. 13. 2) 1SXS10. 14. 2) -6<x<3. 15. 2) -5sx<l.
16. O‘rta chiziq 8,2 dm dan ortiq, balandlik 4,1 dm dan ortiq. 17. 8 sm dan ortiq.
18. 2)x<—2, —l<x<3. 19.2) j; 4) |. 20.2) ||a|62; 4) у-д- 21.4)-2.22.
2) ^7 >>/47. 23. 2) >/x; 4) 9J"4. 24. 2) 5abjb. 25. 2) -л/зх2. 26. 2) -|. 27.
2) 2ab>lb; 4) a+ 3. 28. 2) 2<Ш<3. 29. 2) x = ^. 32. 2) Вnuqta tegishli. 33.
2) x<|; 4) x< — 1, x^6. 34. 2) —4<x^6. 36. 2) x = 35; 4) x=0. 37. 2) juft
funksiya; 4) toq funksiya. 38. 2) -Л+Зл/З. 41. 2) J*. 42. 2) 5) 47. 2) -
46.48.2) 4.49.2) 336; 4) 1,3. 50.1) 3; 4) -3580.51. 1) 390 km; 2) 228 marta. 52.
2) 39; 4) -64. 54. 2) 2>/2; 4) 421. 55. 2) у A y=-p 57. a) b; П’ -
235
Ж
жж
ж
ж
ВИ
жж
жж
ВИВИ
Ж
жж
жж
MUNDARIJA
7—8-sinflarda o'tilganlami takrorlash-------------------------------------------- 3
I bob. Kvadrat funksiya
1- §. Kvadrat funksiyaning ta’rifi----------------------------------------------- 6
2-§. у = x? funksiya------------------------------------------------------------- 9
3- §. у = ax* funksiya---------------------------------------------------------- 12
4- §. y = ox? + bx+ e funksiya-------------------------------------------------- 18
5- §. Kvadrat funksiyaning grafigini yasash-------------------------------------24
6- §. I bobga doir mashqlar-----------------------------------------------------30
I bobga doir sinov (test) mashqlari---------------------------------------------32
II bob. Kvadrat tengsizliklar
7- §. Kvadrat tengsizlik va uning yechimi---------------------------------------36
8- §. Kvadrat tengsizlikni kvadrat funksiya grafigi yordamida yechish-----------40
9- §. Intervallar usuli---------------------------------------------------------43
10- §. II bobga doir mashqlar---------------------------------------------------47
11 - §. Kvadrat funksiya va kvadrat tengsizliklarga olib keluvchi masalalar-----49
II bobga doir sinov (test) mashqlari--------------------------------------------52
Olimpiada masalalari------------------------------------------------------------55
III bob. Ratsional ko'rsatkichli daraja
12- §. Butun ko'rsatkichli daraja va uning xossalari-----------------------------59
13- §. Natural ko'rsatkichli darajaning ariftnetik ildizi------------------------63
14- §. Ariftnetik ildizning xossalari--------------------------------------------66
15- §. Ratsional ko'rsatkichli daraja. Irratsional ko'rsatkichli daraja
haqida tushuncha-----------------------------------------------------------------70
16- §. SonH tengsizliklami darajaga ko'tarish------------------------------------74
17- §. Ill bobga doir mashqlar---------------------------------------------------79
III bobga doir sinov (test) mashqlari--------------------------------------------81
Tarixiy ma’lumotlar--------------------------------------------------------------82
Mantiqiy masalalar---------------------------------------------------------------84
IV bob. Darajali funksiya
18- §. Funksiyaning aniqlanish sohasi-------------------------------------------87
19- §. Funksiyaning o'sishi vakamayishi-----------------------------------------91
20- §. Funksiyaning juft vatoqligi----------------------------------------------95
21- § у = funksiya-------------------------------------------------------------98
22- §. Daraja qatnashgan tengsizlik va tenglamalar-----------------------------102
23- §. IV bobga doir mashqlar--------------------------------------------------105
236
жж
ВИВИ
IV bobga doir sinov (test) mashqlari----------------------------------------110
Tarixiy ma’lumotlar---------------------------------------------------------112
Murakkabroq masalalar-------------------------------------------------------113
V bob. Trigonometriya elementlari
24- §. Burchaklaming radian o'lchovi---------------------------------------114
25- §. Nuqtani koordinatalar boshi atrofida burish-------------------------117
26- §. Burchakning sinusi, kosinusi, tangensi va kotangensi ta’riflari-----122
27- §. Masalalar yechish---------------------------------------------------127
28- §. Sinus, kosinus, tangens va kotangensning ishoralari-----------------129
29- §. Ayni bir burchakning sinusi, kosinusi, tangensi va
kotangensi orasidagi munosabatlar--------------------------------------132
30- §. Trigonometrik ayniyatlar--------------------------------------------135
31- §. a va —a burchaklaming sinusi, kosinusi, tangensi va kotangensi------138
32- §. Masalalar yechish---------------------------------------------------140
33- §. Qo'shish formulalari------------------------------------------------142
34- §. Ikkilangan burchakning sinusi va kosinusi---------------------------147
35- §. Keltirish formulalari-----------------------------------------------150
36- §. V bobga doir mashqlar-----------------------------------------------155
V bobga doir sinov (test) mashqlari------------------------------------------157
Tarixiy ma’lumotlar---------------------------------------------------------160
Murakkabroq masalalar--------------------------------------------------------162
VI bob. Progressiyalar
37- §. Ariftnetik progressiya----------------------------------------------167
38- §. Ariftnetik progressiya dastlabki n ta hadining yig'indisi-----------171
39- §. Geometrik progressiya-----------------------------------------------175
40- §. Geometrik progressiya dastlabki n ta hadining yig'indisi------------180
41- §. Masalalar yechish---------------------------------------------------184
42- §. Cheksiz kamayuvchi geometrik progressiya----------------------------186
43- §. Progressiyaning tatbig'iga oid masalalar----------------------------192
44- §. VI bobga doir mashqlar----------------------------------------------195
VI bobga doir sinov (test) mashqlari----------------------------------------198
Tarixiy ma’lumotlar---------------------------------------------------------202
Olimpiada masalalari--------------------------------------------------------202
Rivojlantiruvchi mashqlar---------------------------------------------------205
IX sinf „Algebra" kursini takrorlash uchun mashqlar-------------------------213
O'zingizni tekshirib ko'ring------------------------------------------------221
Javoblar--------------------------------------------------------------------229
237
O‘quv nashri
Gappar Nasritdinovich Nasritdinov
Mirfazil Abdilxakovich Mirzaxmedov
Faridon Raximovich Usmanov
Shohida Raxmatovna Aripova
Feruza Saidovna Rahimova
ALGEBRA
Aniq fanlarga ixtisoslashtirilgan umumiy o‘rta ta’lim
maktablarining 9-sinfi uchun darslik
Muharrir N. G'oyipov
Rassom-dizayner A Sulaymonov
Texnik muharrir T. Smirnova
Musahhih D. Husanova
Kompyuterda sahifalovchi A. Sulaymonov
Nashriyot litsenziya raqami № 158, 14.08.09.
Bosishga 2016-yil 9-iyunda ruxsat etildi. Bichimi 70x 100*/16.
Kegli 12 shponli. Times gamiturasi. Ofset qog'ozi. Ofset bosma usulida bosildi.
Shartlib.t. 19,5. Nashrt. 19,78. Adadi 7072 nusxa.
Buyurtma № 16—408.
(Tzbekiston Matbuot va axborot agentligining
«O‘zbekiston» nashriyot-matbaa ijodiy uyi.
100011, Toshkent, Navoiy ko‘chasi, 30
Telefon: (371) 244-87-55, 244-87-20
Faks: (371) 244-37-81, 244-38-10.
Algebra: Aniq fanlarga ixtisoslashtirilgan umumiy o‘rta ta’lim maktablarining
M31 9-sinfi uchun darslikI G‘.N.Nasritdinov [vaboshq.]. — Toshkent: «0‘zbekiston»
nomidagi nashriyot-matbaa ijodiy uyi, 2016. — 240 b.
ISBN 978-9943-28-650-4
UO‘K 512 (075.3)
KBK 22.14 ya 72
ЖЖ
ЖЖ
ЖЖ
жж
жж
жж
жж
жж
жж
жж
ЖЖ
r\j\ у у ж ж те ж те Ijaraga beriladigan darslik holatini ko‘rsatuvchi jadval
Ж те Зй ж те ж те §й F^LT’i № 0‘quvchining ismi, familiyasi О ‘quv yili Darslikning olingandagi holati Sinf rahbarining imzosi Darslikning topshirilgan- dagi holati Sinf rahbarining imzosi
1.
ylhk те 2.
5К 3.
4.
ж ж
те ж те те ж те 5.
6.
ж те ж те Darslik ijaraga berilib, o‘quv yili yakunida qaytarib olinganda yuqoridagi jadval sinf rahbari tomonidan quyidagi baholash mezonlariga asosan to‘ldiriladi:
>< >< те Yangi Darslikning birinchi marotabafoydalanishgaberilgandagi holati.
Yaxshi Muqovabutun, darslikning asosiy qismidan ajralmagan. Barchavaraqlari mavjud, yirtilmagan, ko'chmagan, betlaridayozuv vachiziqlar yoeq.
ж те Qoniqarli Muqovaezilgan, birmunchachizilib chetlari yedirilgan, dars- likning asosiy qismidan ajralish holati bor, foydalanuvchi tomonidan qoniqarli ta’mirlangan.Ko‘chgan varaqlari qayta ta’mirlangan, ayrimbetlargachizilgan.
1 :<й а §й Зй ж те Зй ж те г^ьл
ж 1 Qoniqarsiz Muqovachizilgan, yirtilgan, asosiy qismidan ajralgan yoki butunlay yo‘q, qoniqarsiz ta’mirlangan.Betlari yirtilgan, varaqlari yetishmaydi, chizib, bo‘yab tashlangan.Darslikni tiklab bo‘lmaydi.