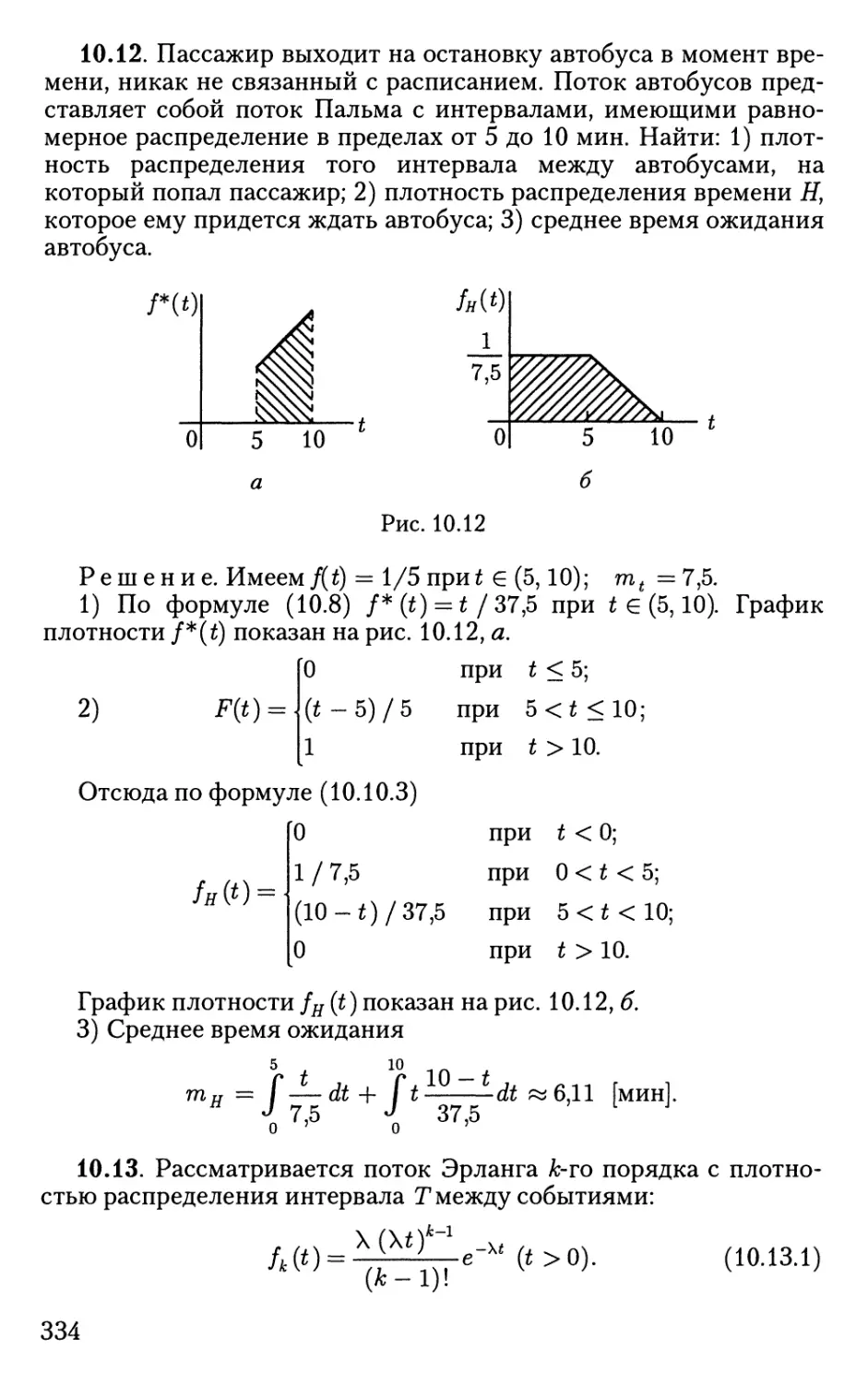
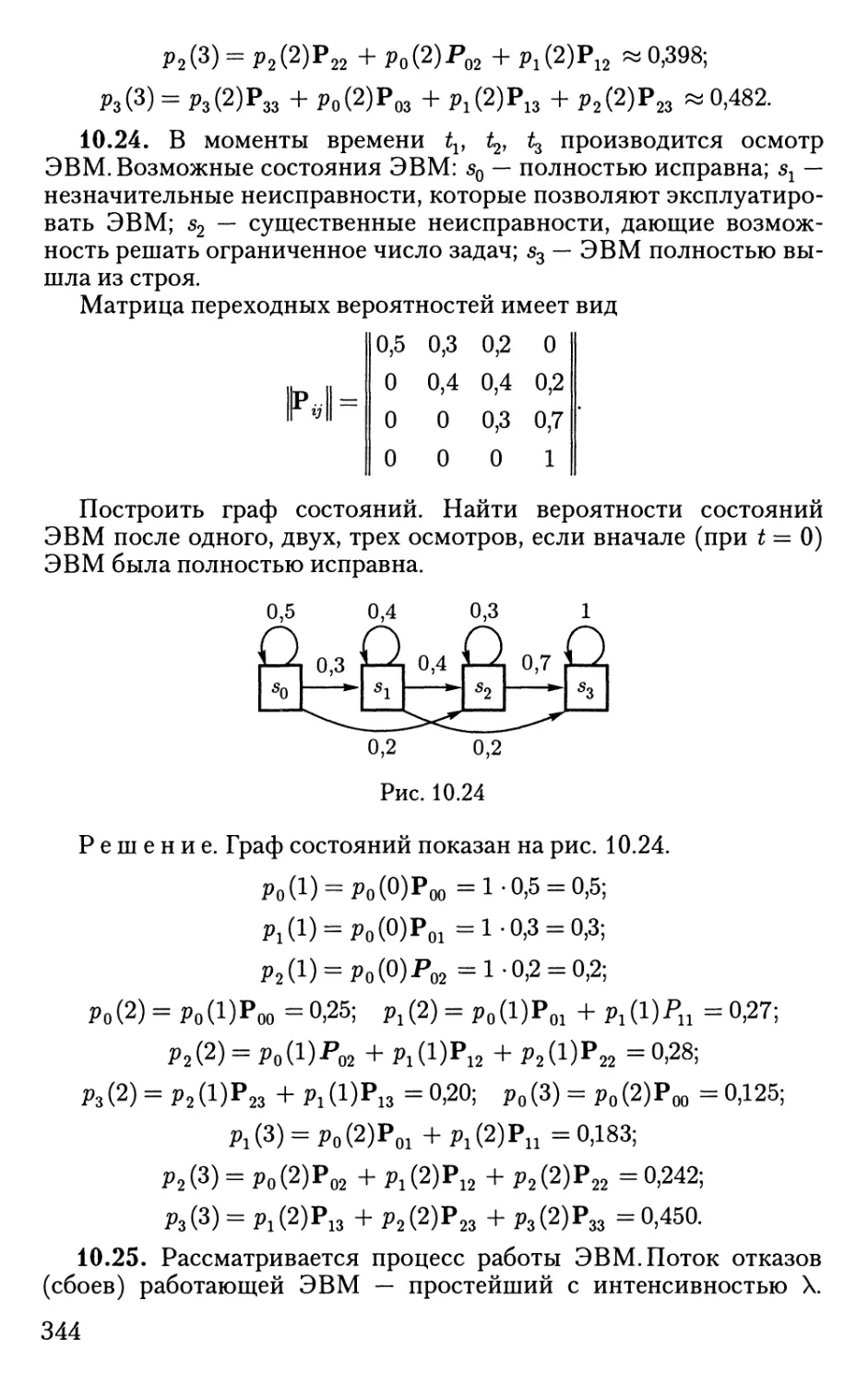
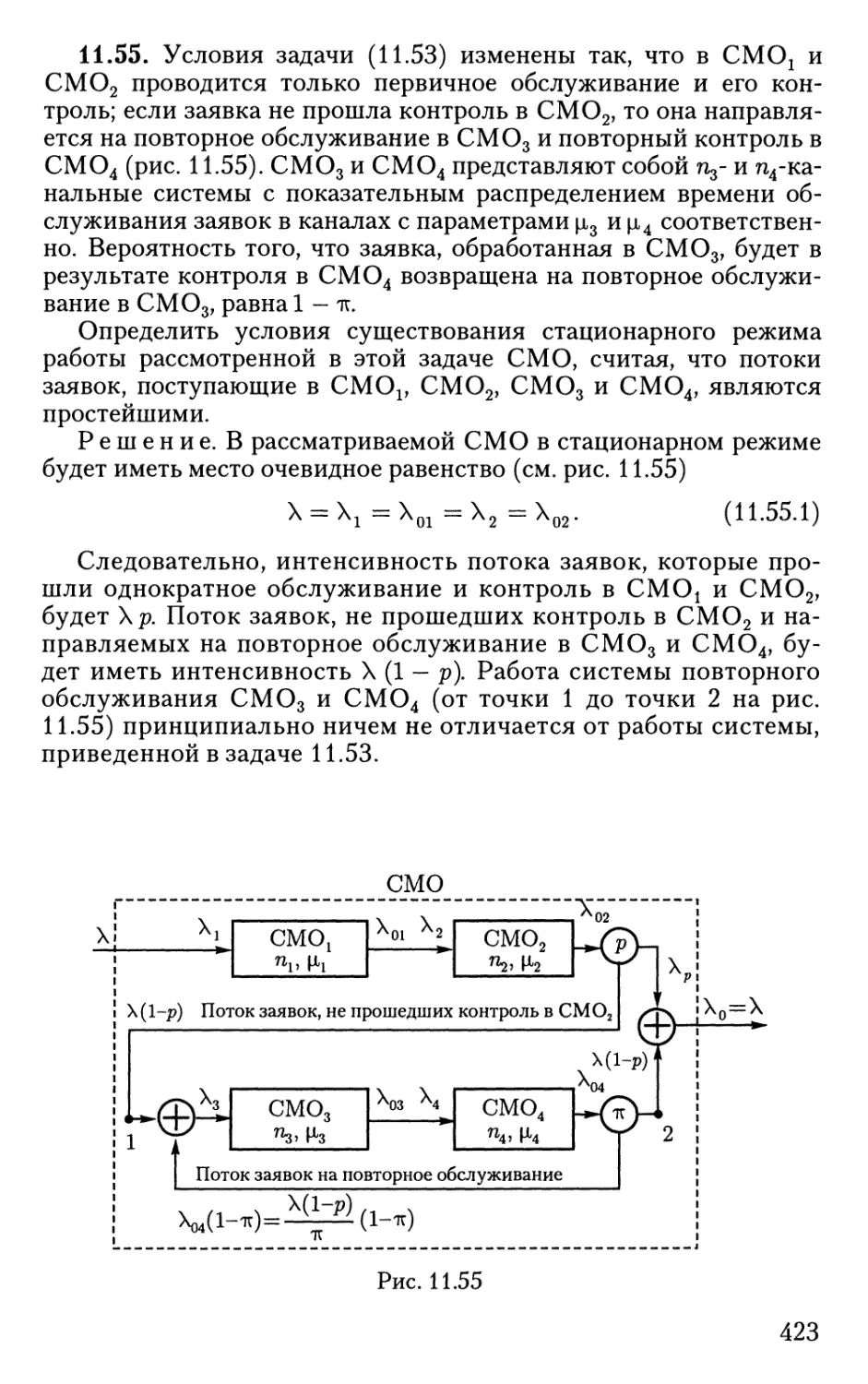
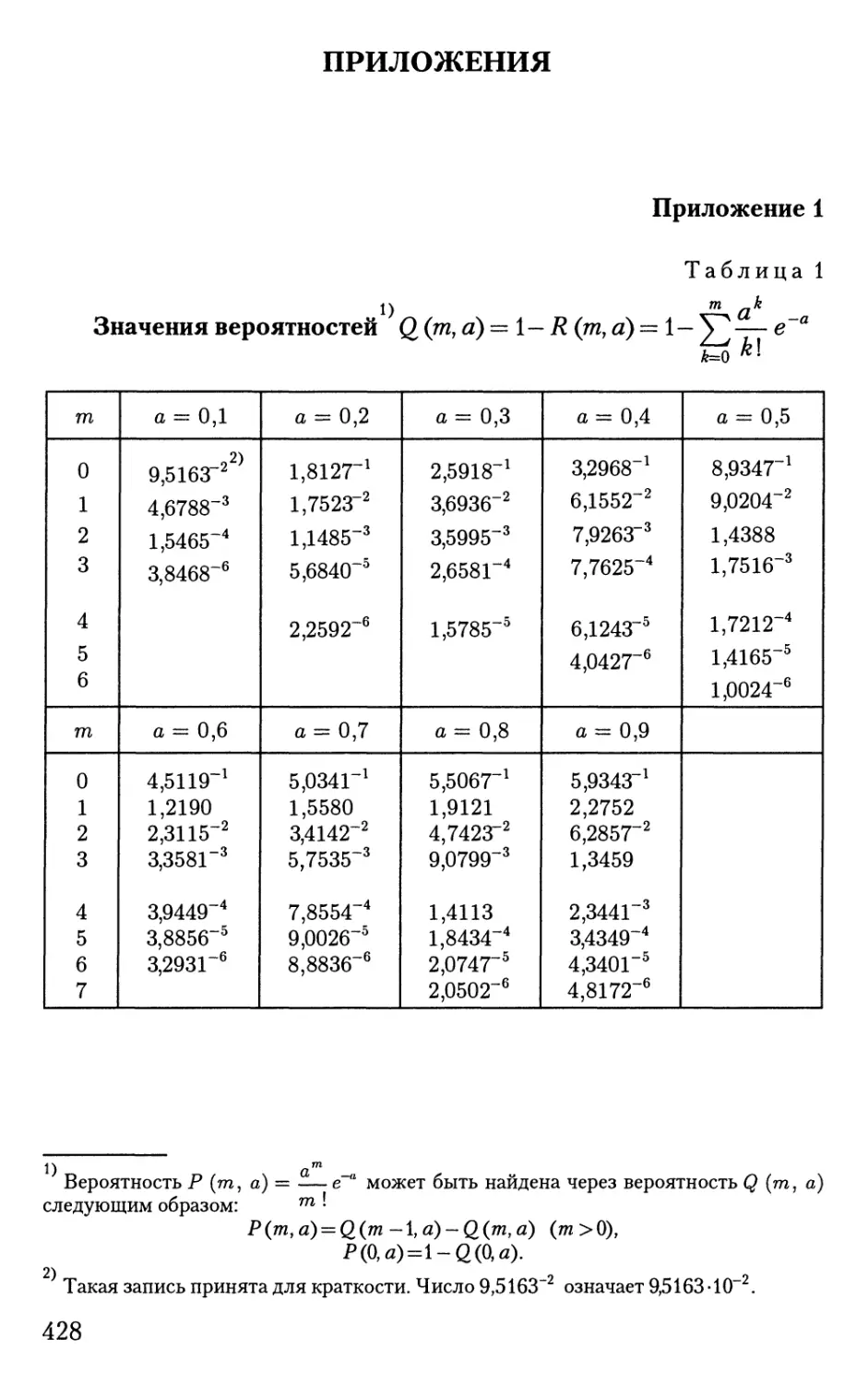
Автор: Овчаров Л.А. Вентцель Б.С.
Теги: теория вероятностей и математическая статистика задачи по математике высшая математика задачи по теории вероятностей
ISBN: 5-7695-1054-4
Год: 2003
Текст
Б. С. Вентцель
Л. А. Овчаров
ЗАДАЧИ
И УПРАЖНЕНИЯ
ПО ТЕОРИИ
ВЕРОЯТНОСТЕЙ
ВЫСШЕЕ ОБРАЗОВАНИЕ
Е. С. ВЕНТЦЕЛ Ь, Л. А. ОВЧАРОВ
ЗАДАЧИ И УПРАЖНЕНИЯ
ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Рекомендовано
Министерством образования Российской Федерации
в качестве учебного пособия для студентов высших технических
учебных заведений
5-е издание, исправленное
Москва
ACADEMA
2003
УДК 519.21(075.8)
ББК22.171я73
В 29
Рецензент —
директор Института проблем передачи информации РАН академик Н.А.Кузнецов
Вентцель Е. С.
В 29 Задачи и упражнения по теории вероятностей: Учеб.
пособие для студ. втузов / Е. С. Вентцель, Л. А. Овчаров. — 5-е изд.,
испр. — М.: Издательский центр «Академия», 2003. — 448 с.
ISBN 5-7695-1054-4
Настоящее пособие представляет собой систематизированную
подборку задач и упражнений по теории вероятностей. Все задачи снабжены
ответами, а большинство — и решениями. В начале каждой главы приведена
сводка основных теоретических положений и формул, необходимых для решения
задач.
Для студентов высших технических учебных заведений. Может быть
использовано преподавателями, инженерами и научными работниками,
заинтересованными в освоении вероятностных методов для решения практических
задач.
УДК 519.21(075.8)
ББК22.171я73
© Вентцель Е.С., Овчаров Л. А., 2003
ISBN 5-7695-1054-4 © Издательский центр «Академия», 2003
ПРЕДИСЛОВИЕ
Настоящее учебное пособие написано на основе многолетнего
опыта преподавания теории вероятностей в высшем техническом
учебном заведении, а также опыта применения вероятностных
методов для решения практических задач. В начале каждой главы
книги дана краткая сводка теоретических сведений и формул,
необходимых для решения задач, помещенных в главе.
Задачи, имеющиеся в пособии, весьма различны по трудности:
одни предназначены для приобретения навыков применения
готовых формул и теорем, другие требуют некоторой
изобретательности. При этом простые задачи снабжены только ответами, более
сложные — развернутыми решениями. В ряде случаев решения
содержат оригинальные методические приемы, которые могут
пригодиться при решении встречающихся на практике задач, так как
являются достаточно общими. Задачи повышенной трудности
отмечены звездочкой. Номера рисунков и формул к задачам
соответствуют номерам задач.
Особенностью, отличающей данную книгу от аналогичных
изданий, является больший объем решений и разборов задач по
сравнению с текстами самих задач. В связи с этим пособие
занимает своеобразное промежуточное положение между обычным
задачником и учебником. Для удобства чтения авторы отступили от
традиционного разделения текста на «задачи» и «ответы» к ним, а
предпочли давать ответ или решение каждой задачи
непосредственно за ее формулировкой. Добросовестному читателю это не
помешает самостоятельно решить каждую из предложенных
задач, обращаясь к решению только в случае неудачи.
Пособие предназначено для лиц, знакомых с теорией
вероятностей в объеме, например, учебника Е.С. Вентцель «Теория
вероятностей», а также учебных пособий Е.С.Вентцель, Л.А.Овча-
рова «Теория вероятностей и ее инженерные приложения» и
«Теория случайных процессов и ее инженерные приложения».
Некоторые дополнительные сведения, необходимые для решения
отдельных задач, приводятся в тексте.
Авторы выражают искреннюю благодарность рецензенту
первого издания книги профессору Б. В. Гнеденко, сделавшему ряд
полезных замечаний, а также научному редактору книги доценту
Л.З.Румшискому, который взял на себя нелегкий труд проверки
решений всех задач и этим помог устранить некоторые ошибки.
Книга впервые вышла в свет в 1969 г. и переиздана в 1973 г.,
2000 г. и 2002 г. В четвертом издании переработана гл. 10 и
введена новая гл. И, выполненная на основе книги авторов [4].
В общей сложности книга издана 10 раз, включая издания на
английском, французском и дважды на немецком и испанском языках.
ГЛАВА 1
ОСНОВНЫЕ понятия.
НЕПОСРЕДСТВЕННЫЙ ПОДСЧЕТ
ВЕРОЯТНОСТЕЙ
Событием (или «случайным событием») называется всякий факт,
который в результате опыта может произойти или не произойти.
Вероятностью события называется численная мера степени
объективной возможности этого события.
Вероятность события А обозначается Р(Л), Рили р.
Достоверным называется событие U, которое в результате опыта
непременно должно произойти.
P(U) = 1.
Невозможным называется событие V, которое в результате опыта не
может произойти.
P(V) = 0.
Вероятность любого события А заключена между нулем и единицей:
0 < Р(А) < 1.
Полной группой событий называется несколько событий таких, что в
результате опыта непременно должно произойти хотя бы одно из них.
Несколько событий в данном опыте называются несовместными, если
никакие два из них не могут появиться вместе.
Несколько событий в данном опыте называются равновозможными,
если по условиям симметрии опыта нет оснований считать какое-либо из
них более возможным, чем любое другое.
Если несколько событий: 1) образуют полную группу; 2) несовместны;
3) равновозможны, то они называются случаями («шансами»).
Случай называется благоприятным событию, если появление этого
случая влечет за собой появление события.
Если результаты опыта сводятся к схеме случаев, то вероятность
события А вычисляется по формуле
Р(Л)=™,
п
где п — общее число случаев; га — число случаев, благоприятных
событию А.
4
1.1. Образуют ли полную группу следующие группы событий:
а) опыт — бросание монеты; события: Ах — появление герба;
А2 — появление цифры;
б) опыт — бросание двух монет; события: Вх — появление двух
гербов; В2 — появление двух цифр;
в) опыт — два выстрела по мишени; события: А0 — ни одного
попадания; Ах — одно попадание; А2 — два попадания;
г) опыт — два выстрела по мишени; события: Сх — хотя бы одно
попадание; С2 — хотя бы один промах;
д) опыт — вынимание карты из колоды; события: Dx —
появление карты червонной масти; D2 — появление карты бубновой
масти; D3 — появление карты трефовой масти?
О т в е т: а) да; б) нет; в) да; г) да; д) нет.
1.2. Являются ли несовместными следующие события:
а) опыт — бросание монеты; события: Ах — появление герба;
А2 — появление цифры;
б) опыт — бросание двух монет; события: Вх — появление герба
на первой монете; В2 — появление цифры на второй монете;
в) опыт — два выстрела по мишени; события: С0 — ни одного
попадания; Сх — одно попадание; С2 — два попадания;
г) опыт — два выстрела по мишени; события: Dx — хотя бы
одно попадание; D2 — хотя бы один промах;
д) опыт — вынимание двух карт из колоды; события: Ех —
появление двух черных карт; Е2 — появление туза; Е3 — появление
дамы?
О т в е т: а) да; б) нет; в) да; г) нет; д) нет.
1.3. Являются ли равновозможными следующие события:
а) опыт — бросание симметричной монеты; события: Ах —
появление герба; А2 — появление цифры;
б) опыт — бросание неправильной (погнутой) монеты;
события: Вх — появление герба; В2 — появление цифры;
в) опыт — выстрел по мишени; события: Сх — попадание; С2 —
промах;
г) опыт — бросание двух монет; события: Dx — появление двух
гербов; D2 — появление двух цифр; D3 — появление одного герба и
одной цифры;
д) опыт — вынимание одной карты из колоды; события: Ех —
появление карты червонной масти; Е2 — появление карты
бубновой масти; Е3 — появление карты трефовой масти;
е) опыт — бросание игральной кости; события: Fx — появление
не менее трех очков; F2 — появление не более четырех очков?
О т в е т: а) да; б) нет; в) общем случае нет; г) нет; д) да; е) да.
5
1.4. Являются ли случаями следующие группы событий:
а) опыт — бросание монеты; события: Ах — появление герба;
А2 — появление цифры;
б) опыт — бросание двух монет; события: Вх — появление двух
гербов; В2 — появление двух цифр; В3 — появление одного герба и
одной цифры;
в) опыт — бросание игральной кости; события: Сх — появление
не более двух очков; С2 — появление трех или четырех очков; Съ —
появление не менее пяти очков;
г) опыт — выстрел по мишени; события: Dx — попадание; D2 —
промах;
д) опыт — два выстрела по мишени; события: Е0 — ни одного
попадания; Ех — одно попадание; Е2 — два попадания;
е) опыт — вынимание двух карт из колоды; события: Fx —
появление двух красных карт; F2 — появление двух черных карт?
О т в е т: а) да; б) нет; в) да; г) нет; д) нет; е) нет.
1.5. Приведите примеры:
а) трех событий, образующих группу случаев;
б) трех событий, равновозможных и несовместных, но не
образующих полной группы;
в) двух событий, несовместных и образующих полную группу,
но не равновозможных;
г) двух событий, равновозможных и образующих полную
группу, но совместных.
О т в е т: а) см. 1.4 в); б) см. 1.3 д); в) см. 1.3 в); г) см. 1.3 е).
1.6. В урне а белых и b черных шаров. Из урны вынимают
наугад один шар. Найти вероятность того, что этот шар — белый.
Ответ.
а + Ь
1.7. В урне а белых и Ь черных шаров. Из урны вынимают один
шар и откладывают в сторону. Этот шар оказался белым. После
этого из урны берут еще один шар. Найти вероятность того, что
этот шар тоже будет белым.
r\ а -1
Ответ. .
а + Ъ- 1
1.8. В урне а белых и Ь черных шаров. Из урны вынули один
шар и, не глядя, отложили в сторону. После этого из урны взяли
еще один шар. Он оказался белым. Найти вероятность того, что
первый шар, отложенный в сторону, — тоже белый.
г\ а -1
Ответ. .
а + Ъ- 1
1.9. Из урны, содержащей а белых и Ъ черных шаров,
вынимают один за другим все шары, кроме одного. Найти вероятность
того, что последний оставшийся в урне шар будет белым.
6
Ответ.
a + b
i.iO. Из урны, в которой а белых шаров и 6 черных, вынимают
подряд все находящиеся в ней шары. Найти вероятность того, что
вторым по порядку будет вынут белый шар.
Ответ. .
а + Ь
1.11. В урне а белых и b черных шаров (а > 2). Из урны
вынимают сразу два шара. Найти вероятность того, что оба шара будут
белыми.
Решение. Общее число случаев
2 (fl + ft)(fl + ft-i)
n = Ca+b= — .
Число благоприятных случаев
а(а — 1)
т =С
1-2
Вероятность события А — два белых шара — равна
Р(Л) = — - <а~1)
п (а +6) (о +6- 1)
1.12. В урне а белых и b черных шаров (а > 2, b > 3). Из урны
вынимают сразу пять шаров. Найти вероятность р того, что два из
них будут белыми, а три черными.
Решение.
_ 5 _ (а + Ь)(а + Ь - 1)(о + Ь - 2)(о + Ь - 3)(о + 6-4)
П ~ °а+ь 1.2-3.4.5 ;
Г2Гз а(а-1)6(6-1)(6-2),
1-2 1-2-3
__ т 10а (а-1)6(6-1)(6-2)
Р ~~ 7Г " (а + 6)(а + 6 - 1)(а + 6 - 2)(а + 6 - 3)(а + 6 - 4)'
1.13. В партии, состоящей из А; изделий, имеется I дефектных.
Из партии выбирается для контроля г изделий. Найти
вероятность р того, что из них ровно s изделий будут дефектными.
0/ПГ5/ПГ7 S
т в е т. р = l К 1
С
1.14. Игральная кость бросается один раз. Найти вероятность
следующих событий: А — появление четного числа очков; В —
появление не менее 5 очков; С — появление не более 5 очков.
Ответ. Р(А) = -] Р(В) = -- Р(С) = -.
2 3 6
1.15. Игральная кость бросается два раза. Найти вероятность р
того, что оба раза появится одинаковое число очков.
Решение. n = 6 ; m = 6; р = — = -.
п 6
(Другое решение. Искомая вероятность есть вероятность
того, что при втором бросании выпадет то же число очков,
которое выпало при первом бросании: n = 6, m = 1, р = -.)
6
1.16. Бросаются одновременно две игральные кости. Найти
вероятности следующих событий:
А — сумма выпавших очков равна 8;
В — произведение выпавших очков равно 8;
С— сумма выпавших очков больше, чем их произведение.
Ответ.Р(Л) = —; Р(В) = — = —; Р(С) = —.
36 36 18 36
1.17. Бросаются две монеты. Какое из событий является более
вероятным:
А — монеты лягут одинаковыми сторонами;
В — монеты лягут разными сторонами?
Ответ. Р(А) = Р(В).
1.18. В урне а белых и b черных шаров (а > 2; b > 2). Из урны
вынимают одновременно два шара. Какое событие более вероятно:
А — шары одного цвета;
В — шары разных цветов?
Cl + Cf а(а-1) + 6(Ь-1)
Решение. Р{А)
Р(В)
С2а+Ь (а + Ъ)(а + Ь-1) '
С\ С\ 2аЬ
С2а+Ь (а + Ь)(а + Ь-1)
Сравнивая числители этих дробей, находим
Р(А) < Р(5) при а (а - 1) + Ь(Ь - 1) < 2аЪ,
т.е. (а — Ь)2 <а + Ь;
Р(А) = Р(В) при (а - б)2 = о + Ь;
Р(А) > Р(В) при (а - Ь)2 > а + Ь.
8
1.19. Трое игроков играют в карты. Каждому из них сдано по
10 карт и две карты оставлены в прикупе. Один из игроков видит,
что у него на руках 6 карт бубновой масти и 4 — не бубновой. Он
сбрасывает две карты из этих четырех и берет себе прикуп. Найти
вероятность того, что он прикупит две бубновые карты.
Решение. Из 32 карт игроку известно 10, а остальные 22 —
нет. Взять 2 карты из прикупа это все равно, что взять их из 22. В
числе 22 карт две бубновых. Вероятность события равна
С222 231
1.20. Из урны, содержащей п перенумерованных шаров, наугад
вынимают один за другим все находящиеся в ней шары. Найти
вероятность того, что номера вынутых шаров будут идти по
порядку: 1, 2,..., п.
Ответ. —.
п!
1.21. Та же урна, что и в предыдущей задаче, но каждый шар
после вынимания вкладывается обратно и перемешивается с
другими, а его номер записывается. Найти вероятность того, что
будет записана естественная последовательность номеров: 1, 2,..., п.
Ответ. .
пп
1.22. Полная колода карт (52 листа) делится наугад на две
равные пачки по 26 листов. Найти вероятности следующих событий:
А — в каждой из пачек окажется по два туза;
В — в одной из пачек не будет ни одного туза, а в другой — все
четыре;
С— в одной из пачек будет один туз, а в другой — три.
Решение. Общее число случаев п — С™. Число
благоприятных событию А случаев т = С\С2^.
С* С24
Р(А)
4^48
26
^52
Событие В может осуществиться двумя способами: либо в
первой пачке будут все четыре туза, а во второй — ни одного, либо
наоборот:
Р(В)= 4 48
Г, 26
°52
Аналогично
9
9/°^/° 23
V ' yo26
°52
Интересно сравнить эти вероятности:
Р(А) : Р(5) : Р(С) = —^_:-J_:_?_ -3,5:1: 4,5.
23-24 25-26 23-25
1.23. В розыгрыше первенства по баскетболу участвуют 18
команд, из которых случайным образом формируются две группы по
9 команд в каждой. Среди участников соревнований имеется 5
команд экстракласса. Найти вероятности следующих событий: А —
все команды экстракласса попадут в одну и ту же группу; В — две
команды экстракласса попадут в одну из групп, а три — в другую.
Ответ. Р(А)
Р(В)
С» 34'
С91& 17
1.24. На девяти карточках написаны цифры: 0, 1,2, 3, 4, 5, 6, 7,
8. Две из них вынимаются наугад и укладываются на стол в
порядке появления, затем читается полученное число, например 07
(семь), 14 (четырнадцать) и т. п. Найти вероятность того, что
число будет четным.
Решение. Четность числа определяется его последней
цифрой, которая должна быть четной (нуль — тоже четное число).
Искомая вероятность есть вероятность того, что на втором месте
появится одно из чисел 0, 2, 4, 6, 8, т. е. -.
9
1.25. На пяти карточках написаны цифры: 1, 2, 3, 4, 5. Две из
них, одна за другой, вынимаются. Найти вероятность того, что
число на второй карточке будет больше, чем на первой.
Решение. Опыт имеет два возможных исхода: А — второе
число больше первого, В — второе число меньше первого.
Так как условия опыта симметричны относительно А и Ву то
Р(4) = Р(Я) = ±.
1.26. Тот же вопрос, что в задаче 1.25, но первая карточка после
вынимания кладется обратно и перемешивается с остальными, а
стоящее на ней число записывается.
Решение. Возможны три исхода опыта: А — второе число
больше первого; В — второе число меньше первого; С — второе
число равно первому.
10
Всего возможно 5 = 25 случаев; из них пять:
1, 1; 2, 2; 3, 3; 4, 4; 5, 5
благоприятны событию С, а остальные 20 случаев поровну делятся
на благоприятные событиям А и В. Следовательно,
10 2
р(Л) = Р(В) = ±Н = |.
1.27. В урне а белых, 6 черных и с красных шаров. Из урны
вынимают один за другим все находящиеся в ней шары и
записывают их цвета. Найти вероятность того, что в этом списке белый
цвет появится раньше черного.
Решение. Так как в условиях задачи наличие или отсутствие
красных шаров роли не играет, то искомая вероятность равна
вероятности вынуть первым белый шар из урны, в которой имеется
а белых и b черных шаров, т. е. равна
а + Ъ
1.28. Имеется две урны: в первой а белых и Ь черных шаров; во
второй с белых и d черных. Из каждой урны вынимается по шару.
Найти вероятность того, что оба шара будут бедыми.
Решение. Каждый шар из первой урны может
комбинироваться с каждым шаром из второй; число случаев п = (а + Ь)х
х(с + d). Число благоприятных случаев т = ас; вероятность собы-
ас
тия .
(a + 6)(c + d)
1.29. В условиях задачи 1.28 найти вероятность того, что
вынутые шары будут разных цветов.
~ ad + be
Ответ. .
1.30. В барабане револьвера семь гнезд, из них в пяти заложены
патроны, а два оставлены пустыми. Барабан приводится во
вращение, в результате чего против ствола случайным образом
оказывается одно из гнезд. После этого нажимается спусковой крючок;
если ячейка была пустая, выстрела не происходит. Найти
вероятность р того, что, повторив такой опыт два раза подряд, мы оба
раза не выстрелим.
Решение. Так как любое гнездо при первом выстреле может
сочетаться с любым при втором, число случаев п = 7 • 7 = 49.
Число благоприятных случаев равно числу комбинаций пустых гнезд:
т = 2 • 2 = 4; р = — = —.
п 49
1.31. В тех же условиях найти вероятность того, что оба раза
выстрел произойдет.
11
Решение. По-прежнему п = 49. Число благоприятных
случаев га — 5 • 4 = 20, так как при первом выстреле гнездо с патроном
можно выбрать пятью способами, а при втором выстреле — че-
га 20
тырьмя; р — — = —.
п 49
1.32. В урне имеется & шаров, помеченных номерами 1, 2, ..., к.
Из урны I раз вынимается по одному шару (I < &), номер шара
записывается и шар кладется обратно в урну. Найти вероятность р
того, что все записанные номера будут различны.
Решение. Число случаев п = к1. Число благоприятных
случаев равно числу размещений из к элементов по I, т.е. га =
= к (к — 1)...(к — I + 1). Вероятность события
_ га _
*;(&-!)...(&-/ + !) к\
i iJ
п к1 к1(к-1)\
1.33. Из пяти букв разрезной азбуки составлено слово «книга».
Ребенок, не умеющий читать, рассыпал эти буквы и затем собрал в
произвольном порядке. Найти вероятность р того, что у него снова
получилось слово «книга».
Ответ. р = 1/5! = 1/120.
1.34. Тот же вопрос, если было составлено слово «ананас».
Решение. Число случаев п = 6!; число благоприятных
случаев уже не один, как в задаче 1.33, а т = 3!2!, так как
повторяющиеся буквы «а» и «н» можно произвольным образом
переставлять между собой; р = —— = —.
J 6! 60
1.35. Из полной колоды карт (52 листа, 4 масти) вынимается
сразу несколько карт. Сколько карт нужно вынуть для того, чтобы
с вероятностью, большей чем 0,50, утверждать, что среди них
будут карты одной и той же масти?
Решение. Обозначим Ак наличие среди к вынутых карт не
менее двух одной масти.
'2 . _ л2
12
При к = 2: п = С5у, га = С/3 • 4; Р(А2) = — < 0,50.
51
При fc=3:n = Cjj2;m = C?3 -4 + ¾¾ -4; Р(Л3) = 0,602 > 0,50.
Итак, нужно вынуть к > 3 карт.
1.36. N человек случайным образом рассаживаются за круглым
столом (N > 2). Найти вероятность р того, что два фиксированных
лица А и В окажутся рядом.
Решение. Общее число случаев п = N\; подсчитываем число
благоприятных случаев га. Двух лиц А и В можно посадить рядом
12
двумя способами; остальных (N — 2)! способами; т = 2N(N — 2)!;
p = 2N(N - 2)\/N\ = 2/ (N - 1). Эту же задачу можно решить
проще: пусть лицо А садится куда угодно, тогда для В остается
N— 1 место, из них 2 благоприятных; р = 2 / (N — 1).
1.37. Та же задача, но стол прямоугольный, и N человек
рассаживаются случайно вдоль одной из его сторон.
Решение. п= N1; благоприятные случаи делятся на две
группы: 1) А сидит с краю, 2) А сидит не с краю. Число первых
т1 = 2(iV - 2)!,число вторых m2 = 2(N - 2)(N - 2)!;
р = (тг + т 2) / п = 2(N - 1)(N - 2)!/ N! = 2 / N.
1.38. На бочонках лото написаны числа от 1 до N. Из этих N
бочонков случайно выбираются два. Найти вероятности
следующих событий:
А — на обоих бочонках написаны числа, меньшие чем к
(2<k<N);
В — на одном из бочонков написано число, большее чем к, а на
другом — меньшее чем к.
Решение. Число случаев п = С^ .Для события А получим:
к~1 У ' С$ N(N-1)
Имея в виду, что к — 1 бочонков имеют номера меньше чем к,
N— к бочонков — номера больше чем к и один бочонок — номер к,
получим для события В:
m=cucw, P(B)=2(*-1)(*-*',
l'1 N N(N-1)
1.39. Батарея из М орудий ведет огонь по группе, состоящей из
N целей (М < N). Орудия выбирают себе цели последовательно,
случайным образом, при условии, что никакие два орудия
стрелять по одной цели не могут. Найти вероятность р того, что будут
обстреляны цели с номерами 1, 2, ..., М.
Решение. Число способов, которыми можно распределить М
орудий по N целям, равно п = N(N -l)...(iV-M + l) (число
размещений из N элементов по М). Число благоприятных случаев
(при которых обстреливаются только первые Мцелей) т = М!;
М! 1
Р ЛГ(ЛГ_1)...(ЛГ-М + 1) С# "
13
1.40. В урне имеется К шаров; из них:
Кг шаров 1-го цвета;
К{ шаров г-го цвета;
Кт шаров га-го цвета
т
£*.- =к
i=i
Из урны вынимают одновременно к шаров. Найти вероятность
того, что среди них будет:
кг шаров 1-го цвета;
к{ шаров г-го цвета;
кт шаров m-го цвета
т
u=i
Решение. Общее число случаев п равно числу способов,
какими можно вынуть А; шаров из К: п = СкК. Число благоприятных
случаев:
т
^=^^-^:=11¾.
г=1
так как группу шаров первого цвета можно выбрать С^ способами,
группу шаров второго цвета — С* способами и т. д. Вероятность со-
бытия
т
11¾
Р =
г=1
С
к
1.41. Батарея, состоящая из А; орудий, ведет огонь по группе,
состоящей из I самолетов (к < I). Каждое орудие выбирает себе цель
случайно и независимо от других. Найти вероятность того, что все
А; орудий будут стрелять по одной и той же цели.
n l 1
Ответ, -г =
Г /
к-1
14
1.42. В условиях предыдущей задачи найти вероятность того,
что все орудия будут стрелять по разным целям.
Решение. Группу из к обстрелянных целей можно выбрать
Cf способами, а в пределах группы распределить орудия А;!
способами: т =Cfk\] общее число случаев п = 1к; искомая вероятность
Cfkl (1-1)(1-2)...(1-к+ 1)
события -~— = — -—± •
1.43. Четыре шарика случайным образом разбрасываются по
четырем лункам; каждый шарик попадает в ту или другую лунку с
одинаковой вероятностью и независимо от других (препятствий к
попаданию в одну и ту же лунку нескольких шариков нет). Найти
вероятность того, что в одной из лунок окажется три шарика, в
другой — один, а в двух остальных лунках шариков не будет.
Решение. Общее число случаев п = 44. Число способов,
которыми можно выбрать одну лунку, где будут три шарика, С\ — 4.
Число способов, которыми можно выбрать лунку, где будет один
шарик, С\ = 3. Число способов, которыми можно выбрать из
четырех шариков три, чтобы положить их в первую лунку, С\ = 4.
Общее число благоприятных случаев т = 4 • 3 • 4. Вероятность собы-
т 4-3-4 3
тия: р — — = — = —.
п 44 16
1.44. Имеются М шариков, которые случайным образом
разбрасываются по N лункам (N> М). Определить вероятность того,
что в первых М лунках будет ровно по одному шарику.
Ответ.—— .
NM
1.45*. Имеется М шариков, которые случайным образом
разбрасываются по N лункам. Найти вероятность того, что в первую
лунку попадет ровно кх шариков, во вторую — /¾ шариков и т.д., в
N-ю — kN шариков,
К + k2+...+kN = М.
Решение. Число случаев п — NM. Число благоприятных
случаев подсчитывается следующим образом. Число способов, какими
можно выбрать из М шариков kv равно Cfy; число способов,
какими можно из оставшихся М— кх шариков выбрать А^, равно С^_к и
т.д.; число способов, какими можно из М — (кх + А;2+...+^^ ) = kN
выбрать kN, равно CtN = 1. Все эти числа нужно перемножить:
N
15
М\ (М-кг)1 [М-(кг + k2+...+kN_2)]\
кг \(М -кг)\к2 \[М - (кг + к2)]! kN_x \kN I
Ml Ml
к \h I к I N
„ ,, га M!
Вероятность события р = — = .
1.46*. В условиях задачи 1.45 найти вероятность того, что в
одной из лунок (все равно, в какой) будет кх шариков, в другой — /¾ и
т.д., в N-и — А;^ шариков (числа kv к^,..., kN предполагаются
различными).
Решение. По сравнению с задачей 1.45 число благоприятных
случаев увеличится в N1 раз (это число способов, каким можно
переставить между собой N чисел: кг, А^, ... kN). Вероятность
события
MINI
Р = n '
1.47*. В условиях задачи 1.45 найти вероятность того, что из N
лунок будет Iq таких, в которые не попадет ни одного шарика; 1Х
таких, в которые попадет ровно один шарик, и т.д.; 1Мтаких, в
которые попадут все М шариков:
10 +1г+.тя+1м =N;0-l0 + l'l1+...+M -1м = М.
Решение. Общее число случаев п = NM . Чтобы найти число
благоприятных случаев га, нужно перемножить число способов,
какими можно выбрать лунки, и число способов, какими мож-
, N1 N1
но выбрать шарики. Лунки можно выбрать — = -^
способами.
Найдем число способов, какими можно выбрать шарики.
Шарики распадаются на группы: начальная группа (по 0 шариков)
пустая; первая содержит 1Х шариков; вообще к-я — klk шариков
(к = 1, 2,..., М). Группы шариков можно выбрать
16
M! М\
{щу^у^у.-Щ^уГ м
к=\
Г№)!
способами. Теперь определим, сколькими способами можно
выбрать шарики внутри к-тк группы так, чтобы в каждой из 1к лунок
лежало по к шариков. Это число способов равно
(Ык)\ {Ык)\
к\к\...к\ (к\)1к '
а число способов, какими можно выбрать все шарики для всех групп,
равно произведению таких чисел для разных к: ГТ -—^-~.
Перемножая, получим число способов, какими можно выбрать шарики:
и
WI Г№)!
М! f^ М!
мм м
И(к1ку.ц(к\)1к п (*'•)'*
к=1 к=\ к=\
Умножая это на число способов, какими можно выбрать
лунки, находим число благоприятных случаев:
N\ М\
т =
м м
№!П(*!)(
г=0 к=1
откуда вероятность события
N\M\
Р мм'
ммЦ1{\Ц(к\)1*
i =0 к=\
1.48. В лифт семиэтажного дома на первом этаже вошли три
человека. Каждый из них с одинаковой вероятностью выходит на
любом из этажей, начиная со второго. Найти вероятности
следующих событий: А — все пассажиры выйдут на четвертом этаже; В —
все пассажиры выйдут одновременно (на одном и том же этаже);
С— все пассажиры выйдут на разных этажах.
Решение. Задача того же типа, что и задачи о разбрасывании
шариков по лункам. Этажи играют роль «лунок» (N= 6), пассажи-
17
3 ~ x 1
ры—«шариков» (М= 3). Число случаев п =6 = 216, Р(А) =
216
Вероятность события В вшестеро больше вероятности события А
(так как этажей, на которых можно выйти, шесть); т = 6 и
Р(В) = = —.Для события С число способов, которыми можно
216 36
распределить трех пассажиров по шести этажам: га = С\ = 20;
20 5
Р(С) = = —. Те же вероятности Р(В) и Р(С) можно найти и по
216 54
общей формуле решения задачи 1.47, полагая
/0 = 5; 1г =l2 = 0; 13 =1 для события В,
10 =3]1г = 3; 12 =13 =0 для события С.
ГЛАВА 2
ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ
ВЕРОЯТНОСТЕЙ
Суммой двух событий Аи В называется событие С, состоящее в
появлении хотя бы одного из событий А или В.
Суммой нескольких событий называется событие, состоящее в
появлении хотя бы одного из этих событий.
Произведением двух событий Аи В называется событие С, состоящее в
совместном появлении события А и события В.
Произведением нескольких событий называется событие, состоящее в
совместном появлении всех этих событий.
Теорема сложения вероятностей
Вероятность суммы двух несовместных событий равна сумме
вероятностей этих событий:
Р(А + В) = Р(А) + Р(В).
В случае, когда события А и В совместны, вероятность их суммы
выражается формулой
Р(Л + В) = Р(Л) + Р(В) - Р(АВ), (*)
где А В — произведение событий А и В.
Теорема сложения вероятностей для нескольких событий
Вероятность суммы нескольких несовместных событий равна сумме
их вероятностей:
/
п
Vi=l
п
£4 =£Р(л4).
г=1
В случае, когда события Л г совместны, вероятность их суммы
выражается формулой
19
n
p
\i=l ) i i , j
+ ^(^^)-...+ (-1)--^(4^3---^,),
», i, *
где суммы распространяются на все возможные комбинации различных
индексов г, j, к,..., взятых по одному, по два, по три и т. д.
Если события Av А2,..., Ап несовместны и образуют полную группу, то
сумма их вероятностей равна единице:
п
ТР(А{) = 1.
г=1
Событие А называется противоположным событию А, если оно
состоит в непоявлении события А.
Сумма вероятностей противоположных событий равна единице:
р(л) + р(1) = 1.
Условной вероятностью события А при наличии В называется
вероятность события А, вычисленная при условии, что событие В произошло.
Эта вероятность обозначается Р (А \ В).
События А и В называются независимыми, если появление одного из
них не меняет вероятности появления другого. Для независимых событий
Р(А\В) = Р(А); Р(Д|Л) = Р(Д).
Теорема умножения вероятностей
Вероятность произведения двух событий равна вероятности одного из
них, умноженной на условную вероятность другого при наличии первого:
Р(АВ) = Р(А)Р(В\А)
или
Р(АВ) = Р(В)Р(А\В).
Для независимых событий А и В
Р(АВ) = Р(А)Р(В).
Теорема умножения вероятностей для нескольких событий
Р(А1А2...Ап) = Р(А1)Р(А2\А1)Р(А3\А1А2)...Р(Ап\А1А2...Ап_1).
В случае, когда события независимы, т.е. появление любого числа из
них не меняет вероятностей появления остальных,
20
(n 1
^=1 ,
n
2.1. Может ли сумма двух событий А к В совпадать с их
произведением?
Решение. Да, может, если события эквивалентны
(равнозначны), т.е. если из события А вытекает В и, наоборот, из В вытекает
А. Например, пусть производится один выстрел по мишени.
Предположим, что попадание в мишень непременно приводит к
ее разрушению и никаким другим способом мишень разрушена
быть не может.
Тогда два события:
А — попадание в мишень,
В — разрушение мишени — эквивалентны (А = В) и для них
А + В = А = В; АВ = А = В.
2.2. Доказать, что вероятность суммы двух событий не больше,
чем сумма вероятностей этих событий:
Р(А + В)<Р(А) + Р(В).
Решение. Это неравенство вытекает из формулы (*), так как
Р(АВ) > 0.
2.3. Опыт состоит в бросании двух монет. Рассматриваются
следующие события:
А — появление герба на первой монете;
В — появление цифры на первой монете;
С— появление герба на второй монете;
D — появление цифры на второй монете;
Е — появление хотя бы одного герба;
F— появление хотя бы одной цифры;
G — появление одного герба и одной цифры;
Н — непоявление ни одного герба;
К— появление двух гербов.
Определить, каким событиям этого списка равносильны
следующие события: 1) А + С; 2) А С; 3) EF; 4) G+ Е\ 5) GE; 6) BD;
7)Е+К.
Ответ. 1) А+С=Е; 2) АС=К; 3) EF=G; 4) G+E=E;
5) GE= G) 6) BD = Я; 7) E+ K= E.
2.4. По мишени производится три выстрела. Рассматриваются
события А{ — попадание при г-м выстреле (г = 1, 2, 3).
21
Представить в^иде сумм, произведений или сумм
произведений событий А{иА{ следующие события:
А — все три попадания;
В — все три промаха;
С — хотя бы одно попадание;
D — хотя бы один промах;
Е — не меньше двух попаданий;
F — не больше одного попадания;
G — попадание в мишень не раньше, чем при третьем выстреле.
Ответ. 1) А = А1А2Аг; 2) В = А1А2А3; 3) С = Аг + А2 + А3 или
С=Аг + АгА2 +A1A2AZ или С=А1А2А3 + АгА2А3 + АгА2А3 +
+ АгА2А3 + АгА2А3 Ч-^Л^з + АгА2А3; 4) D = AX +А2+А3]5) Е =
= А,А2А3 + А,А2А3 +АгА2; 6) F = \А2А3 + AYA2A3 + А,А2; 7) G =
= АгА2.
2.5. Производится наблюдение за группой, состоящей из
четырех однородных объектов. Каждый из них за время
наблюдения может быть обнаружен или не обнаружен. Рассматриваются
события:
А — обнаружен ровно один из четырех объектов;
В — обнаружен хотя бы один объект;
С — обнаружено не менее двух объектов;
D — обнаружено ровно два объекта;
Е — обнаружено ровно три объекта;
F— обнаружены все четыре объекта.
Указать, в чем состоят события:
1)А + В; 2) АВ; 3) В + С; 4) ВС; 5) D + Е + F; 6) BF.
Совпадают ли события BF и CF? Совпадают ли события ВС
и№
Ответ. 1)А + В=В; 2) АВ = А; 3)В+С=В; А)ВС=С;
5)D + E + F= C;6)BF = F.
BFn CF совпадают; ВС и D не совпадают.
2.6. Событие В является частным
случаем события Ау т.е. из появления события В с
достоверностью вытекает появление
события А (рис. 2.6). Чему равны: 1) их сумма;
2) их произведние?
ОтветЛ)А + В = А;2)АВ=В.
2.7. Назвать противоположные для
следующих событий:
А — выпадение двух гербов при бросании
Рис. 2.6 двух монет;
22
В — появление белого шара при вынимании одного шара
из урны, в которой 2 белых, 3 черных и 4 красных шара;
С — три попадания при трех выстрелах;
D — хотя бы одно попадание при пяти выстрелах;
Е— не более двух попаданий при пяти выстрелах;
F — выигрыш первого игрока при игре в шахматы.
Ответы. А — выпадение хотя бы одной цифры;
В — появление черного или красного шара;
С — хотя бы один промах;
D — все пять промахов;
Е — более двух попаданий;
F — выигрыш второго или ничья.
2.8. Событие В есть частный случай события А} т.е. из
появления события В следует, что событие А произошло. Следует ли из
В, что А произошло?
Ответ. Нет, не следует! Например: опыт состоит из двух
выстрелов; А — хотя бы одно попадание; В — два попадания. Если
произошло В, из этого следует, что А произошло. Если же
произошло В (менее двух попаданий), из этого еще не следует,_что
произошло А (ни одного попадания). Наоборот, из А следует В.
2.9. Если событие В представляет собой частный случай
события А} зависимы эти события или нет?
Ответ. Зависимы, если Р(А) ^ 1, так как Р (А \В) = 1.
2.10. Зависимы или независимы:
1) несовместные события;
2) события, образующие полную группу;
3) равновозможные события?
Ответ. 1) Зависимы, так как появление любого из них
обращает в нуль вероятности всех остальных; 2) зависимы, так как
непоявление всех, кроме одного, обращает в единицу вероятность
последнего; 3) могут быть как зависимы, так и независимы.
2.11. Опыт состоит в последовательном бросании двух монет.
Рассматриваются события:
А — выпадение герба на первой монете;
D — выпадение хотя бы одного герба;
Е — выпадение хотя бы одной цифры;
F — выпадение герба на второй монете.
Определить, зависимы или независимы пары событий:
1) А и Е; 2) А и F; 3) D и Е; 4) D и F.
Определить условные и безусловные вероятности событий в
каждой паре.
23
Ответ.
3 1
l)P(E) = —; Р(Е\А) = -; события зависимы.
1 1
2) Р (А) = -; Р (A \F) = -; события независимы.
3 2
3) P(D) = —; Р (Z? IjB) = -; события зависимы.
4 3
3
4) Р (D) = —; Р (D |F) = 1; события зависимы.
4
2.12. Из полной колоды карт (52 листа) вынимается одна
карта. Рассматриваются события:
А — появление туза;
В — появление карты красной масти;
С — появление бубнового туза;
D — появление десятки.
Зависимы или независимы следующие пары событий:
1) А и В; 2) А и Q 3) Ви С; 4) Ви D; 5) С и ZJ?
Ответ:
1) независимы, так как Р (Л) = — = —; Р (А \В) = — = —;
4 52 13 26 13
2) зависимы, так как Р(А) = —; Р(А\С) = 1;
13
3) зависимы, так как Р (В) = -; Р (В | С) = 1;
4) независимы, так как Р (В) = -; Р (51D) = -;
5) зависимы, так как несовместны.
2.13. В урне а белых (б) и Ъ черных (ч) шаров. Из урны
вынимают (одновременно или последовательно) два шара. Найти
вероятность того, что оба шара будут белыми1^
Ответ. По теореме умножения вероятностей
р(бб)=_5—а~ь .
а+Ьа+Ь—1
2.14. В урне а белых и Ъ черных шаров. Из урны вынимается
один шар, отмечается его цвет и шар возвращается в урну. После
этого из урны берется еще один шар. Найти вероятность того, что
оба вынутые шара будут белыми.
Ответ.
' а А
,а + 6,
Данная задача, как и ряд других в гл. 2, может быть решена и с помощью
непосредственного подсчета числа случаев; здесь требуется решить их с помощью
теорем сложения или умножения.
24
2.15. В урне а белых и Ь черных шаров. Из урны вынимаются
сразу два шара. Найти вероятность того, что эти шары будут
разных цветов.
Решение. Событие может появиться в двух несовместных
вариантах: бч или чб; по теоремам сложения и умножения
г>/£ , *\ а Ь Ъ а 2аЪ
Р(бч + чб) = Ь
а+Ъ а+Ъ-1 а + Ьа + Ь-1 (а + Ъ)(а+Ъ-1)
2.16. Та же задача, но шары вынимаются последовательно и
после вынимания первый шар возвращается в урну.
Ответ. 2 .
(а+Ь)2
2.17. В урне а белых и Ъ черных шаров. Из урны в случайном
порядке, один за другим, вынимают все находящиеся в ней шары.
Найти вероятность того, что вторым по порядку будет вынут
белый шар.
Решение. Вероятность события может быть найдена
непосредственно (см. задачу 1.10). Тот же результат может быть
получен и по теоремам сложения и умножения:
Р (об + чб) = Ь
а +Ъ а +Ъ — 1 а + Ъ а +Ъ — 1 а+Ъ
2.18. В урне а белых, Ь черных и с красных (к) шаров. Три из
них вынимаются наугад. Найти вероятность того, что по крайней
мере два из них будут одноцветными.
Решение. Чтобы найти вероятность события А — по крайней
мере два шара будут одноцветными, — перейдем к
противоположному А — все шары разных цветов:
Р(Л) = Р(бчк -f бкч-f кчб 4-...) =
———v
6 комбинаций
= 6 а
а -\-b-\- с а + Ъ + с — 1 а +Ъ + с — 2
Отсюда
P(4) = l-P(4) = l- ^°
(а+Ь + с)(а + Ь + с- 1)(а + Ь + с - 2)
2.19. Имеется коробка с девятью новыми теннисными мячами.
Для игры берут три мяча; после игры их кладут обратно. При
выборе мячей игранные от неигранных не отличают. Какова вероят-
25
ность того, что после трех игр в коробке не останется неигранных
мячей?
Решение. Событие А может произойти единственным
способом: первый раз, второй и третий из коробки будут вынуты не-
игранные мячи. Первый раз это обеспечено; поэтому
Р(Л)-1 6 5 4 3 2 1_ 5
9 8 7 9 8 7 1764
2.20. В коробке N= 1М новых теннисных мячей; для одной
игры из коробки вынимают М мячей; после игры их возвращают в
коробку. Найти вероятность того, что после I игр в коробке не
останется неигранных мячей.
ъ,лъ (N-M)l
Ответ. Р(Л) = - - —.
[N(N-1)...(N-M + 1)]м
2.21. В ящике лежат п новых теннисных мячей; к из них
вынимаются и ими играют
'к<^
. После игры мячи возвращаются в
^ >
ящик. Следующий раз из ящика снова берут наугад к мячей.
Найти вероятность того, что все эти к мячей будут новыми (неигран-
ными).
~ п-к п-к-1 п-2к + 1 [{п-к)1}2
О т в е т. р = ... = — —— .
п п — 1 п — к + \ п\{п — 2к)!
2.22. Уходя из квартиры, TV гостей, имеющих одинаковые
размеры обуви, надевают калоши в темноте. Каждый из них может
отличить правую калошу от левой, но не может отличить свою от
чужой. Найти вероятности следующих событий:
А — каждый гость наденет свои калоши;
В — каждый гость, наденет калоши, относящиеся к одной паре
(может быть и не свои).
Решение. Каждый гость выбирает одну правую калошу и
одну левую; правых калош TV и левых N. По теореме умножения
Р(А) = ±-—±— -1 1- 1 -
ЛГ2 (ЛГ-1)2 "*22 (ЛП)2'
11 1
Р(£) = — —— ...1 = —.
v } N N-1 N1
2.23. В условиях предыдущей задачи найти вероятности
событий А и By если гости не могут отличить правой калоши от левой и
просто берут первые попавшиеся две калоши.
Решение. По теореме умножения
РШ = _2 1 2 1_ _ 2N .
2N 2N-12N -2 2N -З'" (2N)\'
26
p (5) = 1 - 1 - 1 - = -
2N -I 2N -Ъ 2N -Ь '" (2N-l)ti
где (2N - 1)!! = 1 • 3 • 5... (2N - 1).
2.24. Бросаются две монеты. Рассматриваются события:
А — выпадение герба на первой монете;
В — выпадение герба на второй монете.
Найти вероятность события С = А + В.
Решение. Р(С) = Р(А) + Р(В) - Р(АВ) = - + - - - = -
2244
или, через противоположное событие, Р (С) = 1 — Р (С) = 1 —
_1 = 3
4~ 4*
2.25. Ведется стрельба по самолету, уязвимыми частями
которого являются два двигателя и кабина пилота. Для того чтобы
поразить (вывести из строя) самолет, достаточно поразить оба
двигателя вместе или кабину пилота. При данных условиях стрельбы
вероятность поражения первого двигателя равна pv второго
двигателя р2у кабины пилота р3. Части самолета поражаются
независимо друг от друга. Найти вероятность того, что самолет будет
поражен.
Решение. Событие А — поражение самолета есть сумма двух
совместных событий:
D — поражение обоих двигателей;
К— поражение кабины.
P(A) = P(D) + P(K)-P(DK) = Plp2+p3-Plp2p3.
2.26. Два стрелка, независимо один от другого, делают по два
выстрела (каждый по своей мишени). Вероятность попадания в
мишень при одном выстреле для первого стрелка pv для второго
р2. Выигравшим соревнование считается тот стрелок, в мишени
которого будет больше пробоин. Найти вероятность Рх того, что
выиграет первый стрелок.
Ответ. ^=^2(1-^2^ + 2^^(1-^) + 2^(1-^)(1-^)2.
2.27. В урне а белых и Ъ черных шаров. Из урны вынимаются 2к
шаров (2к < а; 2к < Ь). Найти вероятность того, что среди них
будет больше белых, чем черных.
Решение. Данную задачу проще решить, комбинируя методы
непосредственного подсчета вероятностей с теоремой сложения.
Событие А — больше белых шаров, чем черных — можно
представить в виде суммы
А — 4ь+1 + 4ь+2 + ••• + ^ik — Z^^i 1
2к
L
г=к+1
27
где А{ — появление г белых шаров (г = к + 1,..., 2к).
2.28. В партии, состоящей из TV изделий, имеется М дефектных.
Из партии выбирается для контроля п изделий. Если среди
контрольных окажется более т дефектных, бракуется вся партия.
Найти вероятность того, что партия будет забракована.
Решение. Событие А — партия забракована — можно
представить в виде суммы
А — Ат+1 + Ат+2 + ... + Ап — у А
п
г J
i=m + 1
где А{ — событие, состоящее в том, что среди контрольных изделий г
дефектных.
Р(Л<)= M°f-M ; Р(А)= £ п ■
^N z=m+l ^N
2.29. Из полной колоды карт (52 карты) вынимают
одновременно четыре карты. Рассматриваются события:
А — среди вынутых карт будет хотя бы одна бубновой масти;
В — среди вынутых карт будет хотя бы одна червонной масти.
Найти вероятность события С = А + В. __
Решение. Переходя к противоположному событию С — нет
карты ни бубновой, ни червонной масти, имеем
та/77ч 26 25 24 23
Jr(G ) = — ,
52 51 50 49
откуда
Р(С) = 1-Р(С7) «0,945.
2.30. При одном цикле обзора радиолокационной станции,
следящей за космическим объектом, объект обнаруживается с
вероятностью р. Обнаружение объекта в каждом цикле происходит
независимо от других. Найти вероятность того, что при п циклах
объект будет обнаружен.
Ответ.1-(1-р)п.
2.31. Имеется т радиолокационных станций, каждая из
которых за один цикл обзора обнаруживает объект с вероятностью р
(независимо от других циклов и от других станций). За время Т
каждая станция успевает сделать п циклов.
28
Найти вероятности следующих событий:
А — объект будет обнаружен хотя бы одной из станций;
В — объект будет обнаружен каждой из станций.
Ответ. Р(А) -1-(1- р)тп ; Р(Я) = [1 - (1 - р)п }т .
2.32. Имеется группа из к космических объектов, каждый из
которых независимо от других обнаруживается радиолокационной
станцией с вероятностью р. За группой объектов ведут наблюдение
независимо друг от друга т радиолокационных станций. Найти
вероятность того, что не все объекты, входящие в группу, будут обнаружены.
Решение. Переходим к противоположному событию А — все
объекты будут обнаружены:
P(J) = [1 -(1- р)т}к; Р(Л) = 1 -[1 - (1 - р)т]к.
2.33. Над изготовлением изделия работают последовательно к
рабочих; качество изделия при передаче следующему рабочему не
проверяется. Первый рабочий допускает брак с вероятностью pv
второй — р2 и т.д. Найти вероятность того, что при изготовлении
изделия будет допущен брак.
к
Ответ. 1 — J][(l — р{).
t=i
2.34. 32 буквы русского алфавита написаны на карточках
разрезной азбуки. Пять карточек вынимаются наугад одна за другой
и укладываются на стол в порядке появления. Найти вероятность
того, что получится слово «конец».
~ 1 1 1 1 1 27!
Ответ — • — • — • — • — = —
'32 31 30 29 28 32!"
2.35. Те же условия, но вынутые пять карточек можно менять
местами произвольным образом. Какова вероятность того, что из
вынутых пяти карточек можно сложить слово «конец».
Решение. Существует 5! перестановок из 5 букв;
вероятность каждой из них вычисляется, как в предыдущей задаче; ис-
5!27! 1
комая вероятность равна = ——.
32! С!2
2.36. В лотерее п билетов, из которых I выигрышных. Некто
покупает к билетов. Определить вероятность того, что он выиграет
хотя бы на один билет.
Ответ.
п -I п -I - 1 п - / - к + 1 _ (п - 1)\(п - к)\
п п — 1 п — к + 1 п\ (п — I — к)\
2.37. Два шарика разбрасываются случайно и независимо друг
от друга по четырем ячейкам, расположенным одна за другой по
прямой линии. Каждый шарик с одинаковой вероятностью 1/4 по-
29
падает в каждую ячейку. Найти вероятность того, что шарики
попадут в соседние ячейки.
Решение. Событие А — шарики попали в соседние ячейки —
разобьем на столько вариантов, сколько можно образовать пар
соседних ячеек; получим
А = Ах + А2 + А3,
где Аг — шарики попали в первую и вторую ячейки;
А2 — шарики попали во вторую и третью ячейки;
А3 — шарики попали в третью и четвертую ячейки.
Вероятность каждого из вариантов одна и та же и равна
1.1.2 = 1; Р(4) = -.
4 4 8 8
2.38. Пусть к шариков разбрасываются случайным образом и
независимо друг от друга по п ячейкам, расположенным одна за
другой по прямой линии (к < п). Найти вероятность того, что они
займут к соседних ячеек.
Решение, к соседних ячеек из п можно выбрать п — к + 1
способами. Вероятность попадания к шариков в каждую из групп
соседних ячеек равна
г .. \к
П
к\ (так как их можно разбросать по
этим ячейкам А;! способами). Вероятность события А — шарики
попали в А:соседних ячеек — равна Р(А) = — к\(п — к + 1).
п
2.39. Производится стрельба по самолету зажигательными
снарядами. Горючее на самолете сосредоточено в четырех баках,
расположенных в фюзеляже один за другим. Площади баков
одинаковы. Для того чтобы зажечь самолет, достаточно попасть двумя
снарядами либо в один и тот же бак, либо в соседние баки.
Известно, что в область баков попало два снаряда. Найти вероятность
того, что самолет загорится.
Решение. Событие А — воспламенение самолета — есть
сумма двух несовместных вариантов:
А = А, + А
2'
где Аг — оба снаряда попали в один и тот же бак; А2 — снаряды
попали в соседние баки.
Р(Л) = 4
I)2 = I
А) 4
30
Вероятность события А2 находим согласно задаче 2.37:
Р(А0) = -; отсюда Р(А) = — + - = -.
2/ 8 4 8 8
2.40. Из полной колоды карт (52 листа) вынимаются сразу
четыре карты. Найти вероятность того, что все эти четыре карты
будут разных мастей.
Решение. Первая карта может быть какой угодно масти;
вторая должна быть не такой, как первая; третья — не такой, как
первая и вторая; четвертая — не такой, как три первые. Искомая ве-
., 39 26 13 Л. Л_
роятность равна р = 1 «0,106.
51 50 49
2.41. Та же задача, но каждая карта после вынимания
возвращается в колоду.
~ . 39 26 13 ппп.
Ответ. р = 1 » 0,094.
52 52 52
2.42. Вычислительная машина состоит из п блоков.
Надежность (вероятность безотказной работы) в течение времени Т
первого блока равна pv второго — р2 и т. д. Блоки отказывают
независимо друг от друга. При отказе любого блока отказывает машина.
Найти вероятность того, что машина откажет за время Г.
п
Ответ. 1 — ГТр» •
2.43. При включении зажигания двигатель начинает работать с
вероятностью р. 1) Найти вероятность того, что двигатель начнет
работать при втором включении зажигания; 2) найти вероятность
того, что для ввода двигателя в работу придется включить
зажигание не более двух раз.
Ответ. 1) (1 - р)р\ 2) 1 - (1 - р)2 = (2 - р)р.
2.44. Производится обстрел некоторой цели с к позиций; с г-й
позиции производится щ выстрелов; каждый выстрел независимо
от других попадает в цель с вероятностью pi (г = 1, 2,..., к). Найти
вероятности следующих событий:
А — хотя бы один выстрел попадет в цель;
В — не все выстрелы попадут в цель.
Ответ. Р(А) = 1 - f[(l - р. Г" р(5) = 1 - ПрГ'■
2.45. По некоторой цели одновременно производится п
выстрелов. Каждый выстрел независимо от других поражает цель
(выводит ее из строя) с вероятностью р. Найти вероятность того, что
после п выстрелов цель будет поражена. Изменится ли эта
вероятность, если выстрелы производятся последовательно, результат
каждого выстрела наблюдается и после поражения цели стрельба
31
немедленно прекращается? Сколько надо произвести выстрелов,
чтобы поразить цель с вероятностью не менее Р(Р > р)?
Решение. Обозначим А поражение цели; переходя к
событию Д получим Р(А) = 1 - Р(А) = 1 - (1 - р)п ; при наблюдении
вероятность не изменится.
Полагая 1 — (1 — р)п > Р и решая это неравенство относитель-
lg (1 _ р)
но п, получим п > —- -. в качестве решения задачи берется
lg (1 ~ р)
наименьшее целое число п, удовлетворяющее этому условию.
2.46. Истребитель, вооруженный двумя ракетами, посылается
на перехват воздушной цели. Вероятность вывода истребителя в
такое положение, из которого возможна атака цели, равна pv Если
истребитель выведен в такое положение, он выпускает по цели обе
ракеты, каждая из которых независимо от другой выводится в
окрестность цели с вероятностью р2. Если ракета выведена в
окрестность цели, она поражает ее с вероятностью ръ. Найти
вероятность того, что цель будет поражена.
Очвъч. p^l - (I - р2ръ)2\.
2.47. Производится стрельба одним осколочным снарядом по
беспилотному самолету-разведчику. Уязвимыми частями
самолета являются: двигатель и отсек с аппаратурой. Поражение любой
части приводит к выходу самолета из строя. При данном
положении точки разрыва снаряда в двигатель попадает т1 осколков, а в
отсек аппаратуры т2 осколков. Каждый осколок, попавший в
двигатель, поражает его независимо от других с вероятностью pv а
попавший в отсек аппаратуры — с вероятностью р2. Найти
вероятность вывода из строя самолета при данном положении точки
разрыва.
Ответ. 1 - (1 - рг)П1(1 - Р2Г2-
2.48. Производится стрельба двумя снарядами по fc бакам с
горючим (к > 2), расположенным рядом друг с другом в одну линию
(рис. 2.48).
Каждый снаряд независимо от других попадает в первый бак с
вероятностью pv во второй — с вероятностью р2 и т.д. Для
воспламенения баков требуется два попадания в один и тот же бак или
два попадания в соседние баки. Найти вероятность
воспламенения баков.
Решение. Событие А — воспламенение баков — распадается
на сумму двух вариантов:
A = Al + А2,
Pi
Р2
• • •
• • •
• • •
Рис. 2.48
32
где Аг — оба снаряда попали в один бак;
А2 — снаряды попали в соседние баки.
Р(Аг) = р\ + р\ +... + pi = £>;
i=i
Р(^2 ) = PlP2 +^2^1 +
г=1
к к-1
2 — ""^+1
»=1 г =1
р(л)=х)р.?+2х;р*р1
2.49. Завод выпускает определенного вида изделия; каждое
изделие может иметь дефект; вероятность дефекта р. После
изготовления изделие осматривается последовательно к контролерами;
г-й контролер обнаруживает дефект, если он имеется, с
вероятностью р{ (г = 1,2, ...,&). В случае обнаружения дефекта изделие
бракуется. Определить вероятности событий:
А — изделие будет забраковано;
В — изделие будет забраковано вторым контролером;
С — изделие будет забраковано всеми контролерами.
к
Ответ. P(j4) = р
1-11(1 -Рг)
1=1
Р(В) = р(1 - рг )р
2>
р(С) = рПр.--
г=1
2.50. Завод изготовляет определенного типа изделия; каждое
изделие имеет дефект с вероятностью р. Изделие осматривается
одним контролером; он обнаруживает имеющийся дефект с
вероятностью pv а если дефект не обнаружен, пропускает изделие в
готовую продукцию. Кроме того, контролер может по ошибке
забраковать изделие, не имеющее дефекта; вероятность этого равна а.
Найти вероятности следующих событий:
А — изделие будет забраковано;
В — изделие будет забраковано, но ошибочно;
С — изделие будет пропущено в готовую продукцию с
дефектом.
Ответ.Р(А) = рр1 +(1- p)ot] Р(£) = (1 - р)ъ; Р(С) = р(1 - рг).
2.51. В условиях предыдущей задачи изделие осматривается не
одним контролером, а двумя. Вероятности забраковать дефектное
изделие для первого и второго контролера равны соответственно
pv р2, вероятности по ошибке забраковать изделие, не имеющее де-
33
p
p
p
• • •
p
n
Рис. 2.52
фекта, равны соответственно а г, а 2. Если хотя бы один контролер
бракует изделие, оно идет в брак. Найти вероятности событий А,
В, С.
Ответ. Р(А) = р[1- (1 - Pl)(i-p2)] + (1- р)[1 - (1 - аг) х
х(1 - а2)]; Р(5) - (1 - р)[1 - (1 - а,)(1 - а2)]; Р(С) = р(1 - А) х
х(1-р2).
2.52. Прибор состоит из п блоков (рис. 2.52); выход из строя
каждого блока означает выход из строя прибора в целом. Блоки
выходят из строя независимо
друг от друга. Надежность
(вероятность безотказной работы)
каждого блока равна р. Найти
надежность Р прибора в целом.
Какова должна быть
надежность рх каждого блока для
обеспечения заданной надежности
Рх системы?
Примечание. Здесь и в дальнейшем на схемах элементы, без
которых работа системы невозможна, изображаются как звенья, соединенные
«последовательно»; дублирующие друг друга элементы изображаются
соединенными «параллельно». Надежность каждого элемента
записывается в соответствующем прямоугольнике.
Ответ.Р = рп ; Px=4jP[-
2.53. Для повышения надежности прибора он дублируется
другим точно таким же прибором (рис. 2.53); надежность
(вероятность безотказной работы) каждого прибора равна р. При
выходе из строя первого прибора происходит
мгновенное переключение на второй
(надежность переключающего устройства
равна единице). Определить надежность
системы двух дублирующих друг друга
приборов.
Решение. Отказ системы требует
совместного отказа обоих приборов;
надежность системы равна 1 — (1 — р) .
2.54. Та же задача, но надежность
переключающего устройства П,
обеспечивающего переключение с отказавшего первого
прибора на второй, равна рх (рис. 2.54).
Ответ. Надежность системы 1 — (1 — р) х
x(l-PiP)-
2.55. Для повышения надежности прибо-
П ра он дублируется (п — 1) другими такими
Рис. 2.54 же приборами (рис. 2.55); надежность каж-
Рис. 2.53
Pi
р
р
34
дого прибора равна р. Найти надежность
Р системы. Сколько надо взять приборов,
чтобы повысить надежность до заданной
?1?
Ответ. P=l-(l-p)";n>lg^~Pll
-lg(l-p)
2.56. Та же задача, но для включения
каждого дублирующего прибора применяется
устройство с надежностью рг (рис. 2.56).
Ответ. Р = 1 - (1 - р)(1 - ргр)п~{;
lgfl-PJ-lgfl-p)
п>
+ 1.
р
р
*
*
*
р
Рис. 2.55
lg(l — PiP)
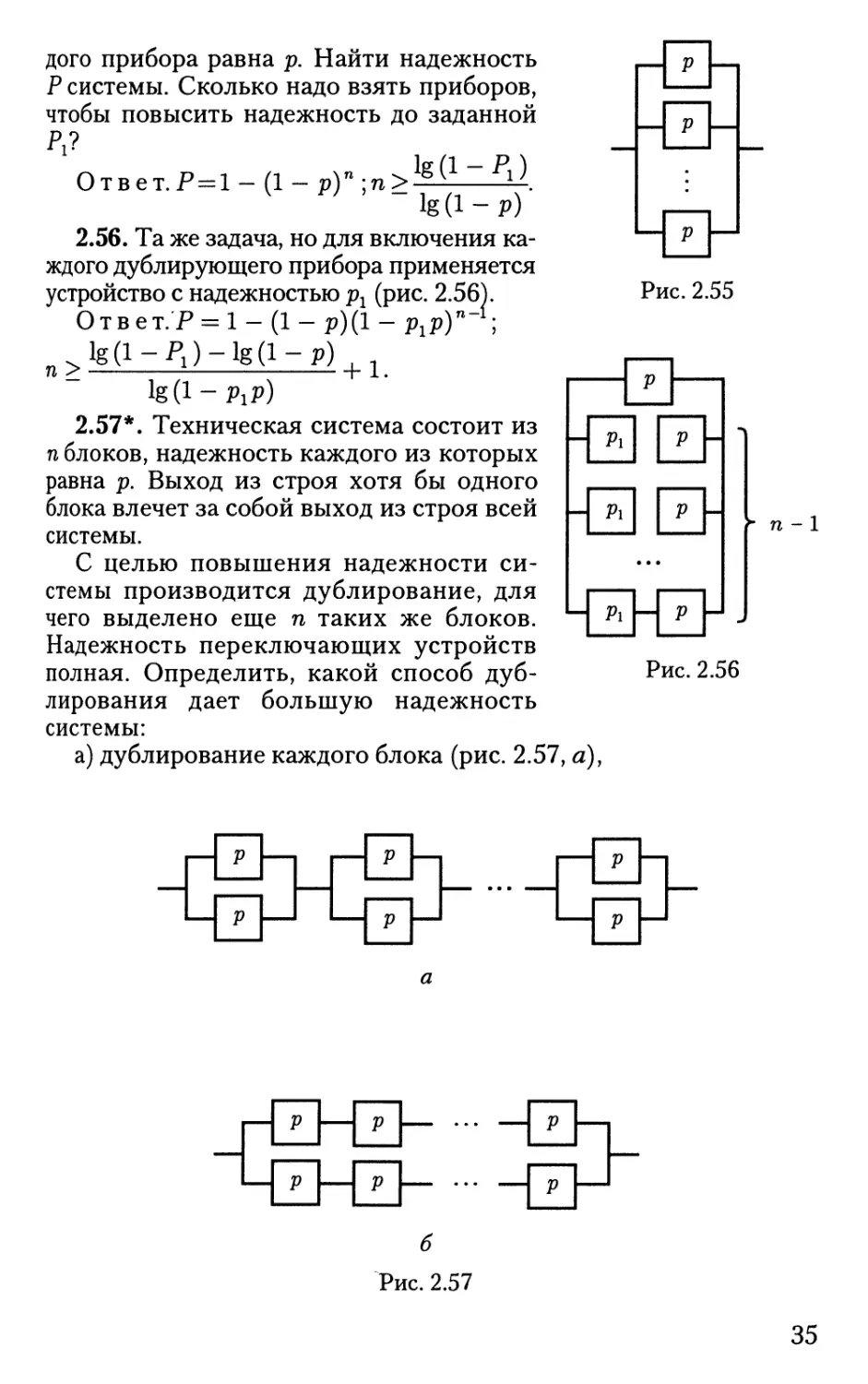
2.57*. Техническая система состоит из
п блоков, надежность каждого из которых
равна р. Выход из строя хотя бы одного
блока влечет за собой выход из строя всей
системы.
С целью повышения надежности
системы производится дублирование, для
чего выделено еще п таких же блоков.
Надежность переключающих устройств
полная. Определить, какой способ
дублирования дает большую надежность
системы:
а) дублирование каждого блока (рис. 2.57, я),
Рис. 2.56
а
р
р
р
р
р
р
б
Рис. 2.57
б) дублирование всей системы (рис. 2.57, б).
Решение. Надежность системы, дублированной по способу
а), будет ра = [1 - (1 - р)2]п ,по способу б): рб = 1 - (1 - рп )2.
Покажем, что ра > рб при любом п>1и0<р<1.
Так как
V,
2лп
[l-(l-p')]» = [1-1 + 2р-рЧ» = рп(2-р)п
п \2
2п
рб=1-(1-р"Г=1-1 + 2рп -Pin =р"(2-рп)
то достаточно доказать неравенство: (2 — р)п >2 — рп .
Положим q = 1 — р (q > 0); неравенство примет вид
(2-l + g)» >2-(l-g)n
или
(l + g)n + (l-ff)n >2.
Применяя формулу бинома, замечаем, что все отрицательные
члены уничтожаются:
+
(1 + ff)" + (l-ff)n =
П(П - 1) 2
П(П - 1) 2
1 + ng +— -q2 + ...
+
2 + n(n - 1)#2 +... >2,
что и доказывает требуемое неравенство.
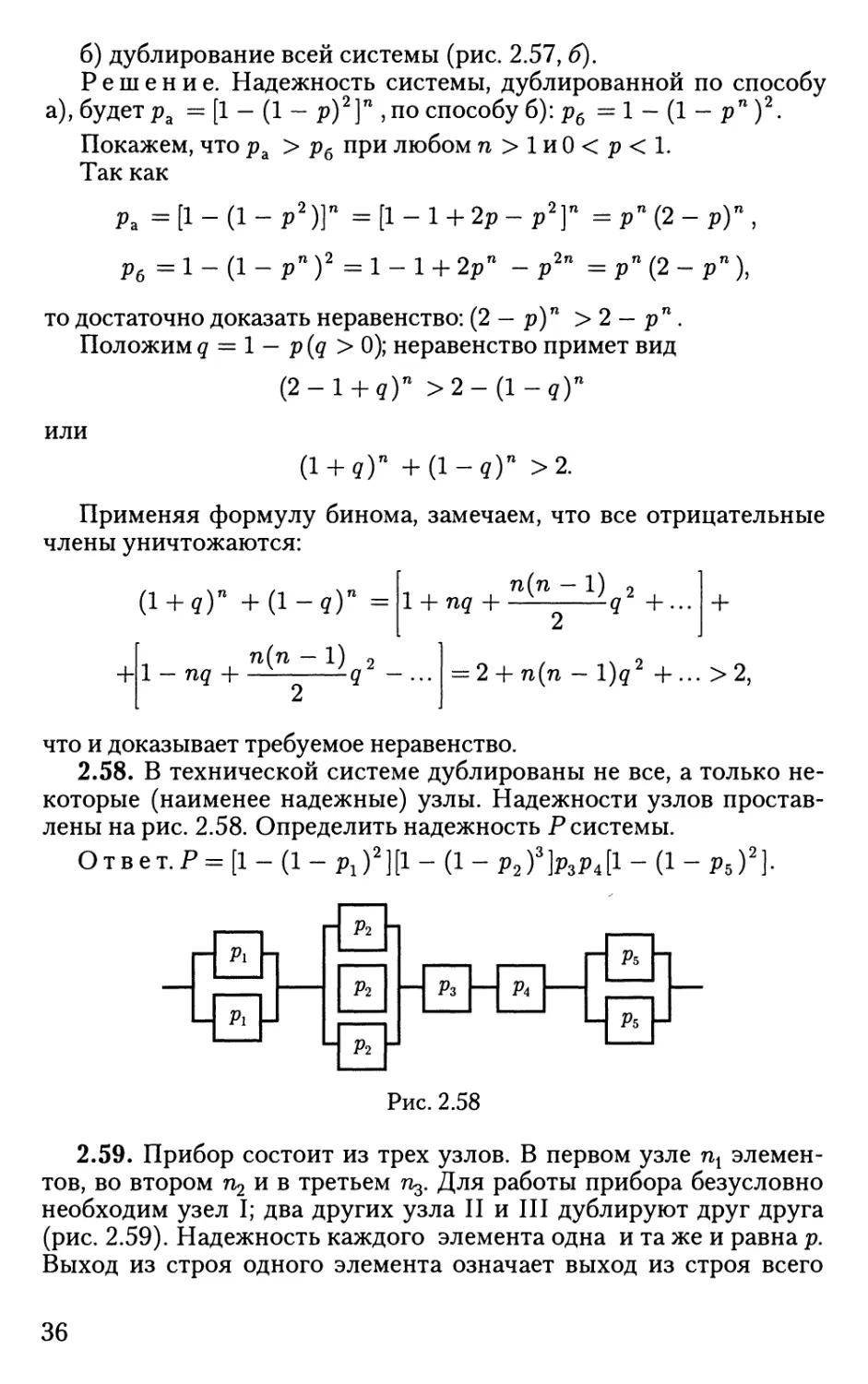
2.58. В технической системе дублированы не все, а только
некоторые (наименее надежные) узлы. Надежности узлов
проставлены на рис. 2.58. Определить надежность Р системы.
Ответ.Р = [1-(1- р1)2][1-(1- p2f]p,p,[l-(l- ръ)2).
Рис. 2.58
2.59. Прибор состоит из трех узлов. В первом узле пх
элементов, во втором п2 и в третьем щ. Для работы прибора безусловно
необходим узел I; два других узла II и III дублируют друг друга
(рис. 2.59). Надежность каждого элемента одна и та же и равна р.
Выход из строя одного элемента означает выход из строя всего
36
узла. Элементы выходят из строя независимо друг от друга. Най
ти надежность прибора Р.
Решение. Надежность узла \\р1=рПх.
Надежность узла II: рп = р7"2.
Надежность узла III: рш = рПз.
Надежность дублированного узла (II и III):
1-(1-рп>)(1-рп*\
v F n F J Рис. 2.59
Надежность прибора
Р = рп*[1 - (1 - рп*)(1 - рп*)}.
2.60. Производится стрельба ракетами по некоторой
наблюдаемой цели. Вероятность попадания каждой ракеты в цель равна р\
попадания отдельных ракет независимы. Каждая попавшая ракета
поражает цель с вероятностью pv Стрельба ведется до поражения
цели или до израсходования всего боезапаса; на базе имеется
боезапас п ракет (п > 2). Найти вероятность того, что не весь этот
боезапас будет израсходован. __
Решение. Переходим к противоположному событию А —
весь боезапас израсходован. Чтобы произошло событие А, первые
п - 1 ракет не должны поразить цель:
Р(Л) = (1-рр1)п"1; отсюда Р(А) = 1 - (1 - ррг )n~l.
2.61. В условиях предыдущей задачи найти вероятность того,
что после поражения цели в запасе останутся
неизрасходованными не менее двух ракет. __
Решение. Противоположное событие А — останется менее
двух ракет — равносильно тому, что первые п-2 ракет не
поразили цели:
Р(1) - (1 - PPl )-2; Р(А) -1-(1- т )п-2.
2.62. В условиях задачи 2.60 найти вероятность того, что будет
израсходовано не более двух ракет.
Решение. Чтобы было израсходовано не более двух ракет,
достаточно, чтобы при первых двух выстрелах цель была
поражена; вероятность этого Р(А) = 1 — (1 — ррх )2.
2.63. Производится стрельба двумя ракетами по самолету.
Самолет имеет оборонительное вооружение, позволяющее ему
произвести по каждой ракете два независимых выстрела. Каждым из
этих выстрелов ракета поражается с вероятностью р. Если ракета
не поражена, то она независимо от другой поражает самолет с
вероятностью Р. Найти вероятность того, что самолет будет поражен.
Решение. Чтобы поразить самолет, ракета должна быть не
поражена. Вероятность поражения самолета одной ракетой с уче-
37
том противодействия будет (1 — р)2Р, а двумя ракетами 1 —
-[i-(i-p)2p]2.
2.64. Радиолокационная станция ведет наблюдение за к
объектами. За время наблюдения г-й объект может быть потерян с
вероятностью pi (г = 1, 2,..., к). Найти вероятности следующих
событий:
А — ни один объект не будет потерян;
В — будет потеряно не менее одного объекта;
С — будет потеряно не более одного объекта.
Ответ. Р(Л) - П(1 - Pt); Р(В) = 1 - П(1 - р. );
к
г'=1
Р(С) = Ц(1 - Pi) + Pl(i - р2)... (1 - Рк) +
i=i
+0- - Pi)pzO- - р3) ■■■ (1 - Рк) +
+... + {1 - рг)(1 - р2)... (1 - рк_г)рк.
Последнюю вероятность можно записать в виде
р(0=па-л)+Ет^-П(1-л)-
г=1 7=1 L Pj i=l
2.65. Техническое устройство, состоящее из к узлов, работало в
течение некоторого времени t За это время первый узел
оказывается неисправным с вероятностью qv второй — с вероятностью q2 и
т.д. Наладчик, вызванный для осмотра устройства, обнаруживает
и устраняет неисправность каждого узла, если она имеется, с
вероятностью р, а с вероятностью q = 1 — р объявляет узел исправным.
Найти вероятность того, что после осмотра наладчиком хотя бы
один узел устройства будет неисправным.
Решение. Вероятность г-му узлу быть неисправным после
осмотра равна вероятности того, что он стал неисправным за
время £, умноженной на вероятность того, что наладчик не
обнаружит этой неисправности: q{q. Вероятность того, что это событие
к
случится хотя бы с одним из узлов, равна 1 — ГТ (1 — q i q).
i=l
2.66. К условиям предыдущей задачи добавляется новое: по
истечении времени t с вероятностью Q наладчика не оказывается на
месте, и устройство пускается в ход без профилактического
осмотра. Найти вероятность того, что после пуска хотя бы один узел
устройства будет неисправным.
Ответ. (1-0)
х-Ш1-^)
г=1
+ Q
i-Ш1-^)
i=i
38
2.67. N стрелков независимо один от другого ведут стрельбу
каждый по своей мишени. Каждый из них имеет боезапас к
патронов. Вероятность попадания в мишень при одном выстреле для
г-го стрелка равна pi (г = 1, 2,..., N). При первом же попадании в
свою мишень стрелок прекращает стрельбу. Найти вероятности
следующих событий:
А — у всех стрелков вместе останется неизрасходованным хотя
бы один патрон;
В — ни у кого из стрелков не будет израсходован весь боезапас;
С — какой-либо один из стрелков израсходует весь боезапас, а
все остальные — не весь. __
Решение. Событие А — весь боезапас израсходован —
требует, чтобы у всех N стрелков первые к - 1 выстрелов дали промах:
Р(1) = П(1 - Vi f'1; P(A) = i- П(1 - Pi )к~\
г =1 г =1
Событие В требует, чтобы у каждого стрелка хотя бы один из
первых к — 1 выстрелов дал попадание:
Р(5) = ^(1-(1-^,)^1].
г=1
Событие С может осуществиться в N вариантах: С = Сг +
где С{ — г-й стрелок израсходовал весь боезапас, а
остальные — не весь (г = 1,..., N).
P(C) = P(C1) + ... + P(CJV) =
= (1 - pj'-^l -(1- pj-1}... [1-(1- pN)k-1}+... +
+(1 - ^)^[1 -(1- ft)*-1]... [1-(1- pJV_1)'-1]=
N
E
П - T) ^-1 N
г -гГО-а-*,-)*"1]
1-(1-P,.)* J=!
2.68. Для стрельбы по некоторой цели выделено п снарядов.
Каждый снаряд попадает в цель независимо от других с
вероятностью р. Сразу же после попадания дается команда о прекращении
стрельбы, но за время передачи команды установка успевает
произвести еще s выстрелов (s< п- 1). Найти вероятности
следующих событий:
А — в запасе останется не менее т неизрасходованных
снарядов (1 <m<n — s)\
39
В — fc-й по порядку выстрел не будет осуществлен (s + 1 <
<к<п). _
Решение. Событие А означает, что при первых п — s — т
выстрелах попадание не произойдет; поэтому
р(А) = (1-р)п-*-т; Р(А) = 1-(1-р)п
—s—m
Событие В означает, что не позже, чем за s выстрелов до
(к- 1)-го, произошло попадание в цель; вероятность события В
равна вероятности хотя бы одного попадания при первых
(к - 1) - s = к - (s + 1) выстрелах. Р(В) = 1 - (1 - p)k^s+1^.
2.69*. N стрелков стреляют поочередно по одной мишени.
Стрельба ведется до первого попадания. Вероятность попасть в
мишень для каждого стрелка равна р{ (г =1,2,..., N). Выигравшим
считается тот стрелок, который первым попадет в мишень. У
каждого стрелка в запасе имеется п патронов. Определить
вероятность того, что выиграет г-й стрелок.
Решение. Рассмотрим событие Д-,, состоящее в том, что г-й
стрелок выиграет соревнование, израсходовав j патронов.
г-1
р(^)=лП«к ш*
к=1
N \
\к=1
3-1
PiQi-iQS
i-i
где
Чк =1~Рк, Qi =Ylqk
к=1
Вероятность выиграть г-му стрелку равна
р(^)=£р(^. )=^^^-1=^^-17-^-
2.70*. По некоторому объекту ведется стрельба п
независимыми выстрелами. Объект состоит из Участей (элементов).
Вероятность попадания в г-й элемент при одном выстреле равна
р. (г = 1,..., к). Найти вероятность Р{ ? l ? 1 того, что в
результате стрельбы будет 10 промахов, 1Х попаданий в первый элемент и
к
т.д., вообще ^попаданий в г-й элемент (г = 1, 2,..., к),V^Z,- = гг.
Решение. Число способов, какими можно из п снарядов
выбрать Iq таких, которые дадут промахи; 1Х таких, которые попадут в
1-й элемент, и т.д., равно ——— (см. задачу 1.45).
i=0
40
Вероятность каждого конкретного варианта расположения по-
паданий равна р1°, р1^ ,..., р£, где р0 = 1 — У^рг (вероятность
г=1
промаха). Умножая эту вероятность на число вариантов, получим
d п! Л I. iAp!'
*и,.»Л =Пь П^=п!Пг?
2.71*. В условиях предыдущей задачи найти вероятность
поражения (вывода из строя) объекта, если для этого требуется
поразить не менее двух элементов, а для поражения элемента
достаточно одного попадания.
Решение. Обозначим А — поражение объекта.
Противоположное событие А может осуществиться в (к + 1) вариантах:
А =В0 +ВХ +... + £• +... + Вк,
где В0 — ни один элемент не поражен;
В{ — поражен только г-й элемент, остальные не поражены
Р(В0) = Pq (все выстрелы дали промах).
Вероятность события В{ подсчитаем, разложив его на ряд
слагаемых: В- = В{Р + BJ2) +... + В[.5) +... + В1п),гдеВИ -элемент
поражен ровно sснарядами (s = 1, 2,..., п).
P(BW) = CipJPo—;
5=1
откуда
г=1 5=1
р(Л) = 1-к -^2Т,с°пР1рГ°.
г=1 s=l
2.72. Из полной колоды карт (52 листа) вынимают сразу две
карты. Одну из них смотрят — она оказалась дамой; после этого
две вынутые карты перемешивают, и одну из них берут наугад.
Найти вероятность того, что она окажется тузом.
41
Решение. Чтобы событие А — появление туза при втором
вынимании — имело место, нужно прежде всего, чтобы мы
вынули не ту карту, которую вынули первый раз (вероятность этого
14 2
1/2 ); затем, чтобы вторая карта была тузом. Р(^4) = = —.
Z 01 01
2.73. Условия опыта те же, что в предыдущей задаче, но первая
(посмотренная) карта оказалась тузом; найти вероятность того,
что при втором вынимании мы получим тоже туз.
Решение. Событие А — туз при втором вынимании — может
произойти в двух вариантах:
Ах — второй раз появился тот же туз, что первый раз;
А2 — второй раз появился не тот, а другой туз.
Р(А) = Р(А1) + Р(А2);
Р(А) = 1; Р(Л2) = ±4'- Р(Л) = 7?
I z 51 51
2.74. Из полной колоды карт (52 листа) вынимают сразу пкарт
(п< 52); одну из них смотрят; она оказывается тузом, после чего
ее перемешивают с остальными вынутыми. Найти вероятность
того, что при втором вынимании карты из этих п снова получим
ТУЗ- 1 _i <*
Ответ. Р(Л) = - + -—-• —.
п п 51
2.75. Происходит воздушный бой между двумя самолетами:
истребителем и бомбардировщиком. Стрельбу начинает
истребитель: он дает по бомбардировщику один выстрел и сбивает его с
вероятностью рх. Если бомбардировщик этим выстрелом не сбит,
он стреляет по истребителю и сбивает его с вероятностью р2. Если
истребитель этим выстрелом не сбит, он еще раз стреляет по
бомбардировщику и сбивает его с вероятностью р3. Найти
вероятности следующих исходов боя:
А — сбит бомбардировщик;
В — сбит истребитель;
С — сбит хотя бы один из самолетов.
Ответ.Р(Л) =Pl+ (1 - Pl)(l - p2)pz;P(B) = (l-Pl)p2;P(C) =
= Р(А) + Р(В).
2.76. Происходит воздушный бой между бомбардировщиком и
двумя атакующими его истребителями. Стрельбу начинает
бомбардировщик; он дает по каждому истребителю один выстрел и
сбивает его с вероятностью pv Если данный истребитель не сбит,
то он независимо от судьбы другого стреляет по
бомбардировщику и сбивает его с вероятностью р2.
42
Определить вероятности следующих исходов боя:
А — сбит бомбардировщик;
В — сбиты оба истребителя;
С— сбит хотя бы один истребитель;
D — сбит хотя бы один самолет;
Е — сбит ровно один истребитель;
F — сбит ровно один самолет.
Решение. Вероятность того, что один истребитель собьет
бомбардировщик, равна (1 — рг )р2; вероятность того, что хотя бы
один из них собьет бомбардировщика:
P(A) = l-[l-(l-Pl)p2}2; Р(Б) = р2;
P(C) = l-(l-Pl)2; P(D) = l-(l-Pl)2(l-p2)2;
P(E) = 2Pl(l-Pl).
Событие F представляется в виде
где F{ — сбит бомбардировщик, а оба истребителя целы;
F2 — первый истребитель сбит, а второй истребитель и
бомбардировщик целы;
F3 — второй истребитель сбит, а первый истребитель и
бомбардировщик целы.
Р(*1) = (1-Р1)2[1-(1-р2)а];
P(F2) = P(F3) = p1(l-ft)(l-p2);
P(F) -(1- Plf[l -(1- p2)2} + 2Pl(l - Pl)(l - p2).
2.77. Условия и вопросы те же, что в задаче 2.76, но с тем
изменением, что истребители идут в атаку только попарно: если сбит
один из них, то другой выходит из боя.
Ответ. P(A) = (l-Pl)2[l-(l-p2)2l Р(В) = Р2; Р(С) =
= 1-(1-р1)2;Р(2?) = 1-(1-Л)2(1-р2)2;Р(Е) = 2р1(1-р1);
P(F) = (1 - рх)2[1 - (1 - Р2)2] + 2Pl(l - Pl).
2.78. Прибор состоит из трех узлов; один из них безусловно
необходим для работы прибора; два других дублируют друг друга.
В результате работы устройства в нем появляются неисправности;
каждая неисправность с одной и той же вероятностью появляется
в любом из элементов, составляющих узлы. Первый узел состоит
из щ элементов; второй — из п2 элементов, третий — из щ элемен-
43
тов (nl + n2 + n3 = n). При неисправности хотя бы одного
элемента узел выходит из строя.
Известно, что в приборе имеется четыре неисправности (в
четырех разных элементах). Найти вероятность того, что наличие
этих неисправностей делает невозможной работу прибора.
Решение. Событие А — невозможность работы прибора —
распадается на два варианта:
А = А1 + л2,
где Ах — вышел из строя первый узел;
А2 — первый узел не вышел из строя, но второй и третий —
вышли.
Чтобы произошло событие Av нужно, чтобы хотя бы одна из
четырех неисправностей пришлась на первый узел:
Р(А1) = 1-Р(А1) = 1-П-П>П-П>-1П-П>-2П-П>-3.
п п — 1 п — 2 п — 3
Для определения вероятности события А2 надо вероятность
события Ах — первый узел не вышел из строя — умножить на
вероятность того, что второй и третий узлы вышли из строя (с
учетом того, что все четыре неисправности приходятся на второй и
третий узлы). Последнее событие может осуществиться в трех
вариантах: или одна неисправность будет во втором, а три других —
в третьем узле, или наоборот: три во втором и одна в третьем; или
же во втором и третьем узлах будет по две неисправности.
Вероятность первого варианта:
с\ п2 ^з п3-1 п3-2
п2 + п3 п2 + п3 — 1 п2 + п3 — 2 п2 + п3
Вероятность второго варианта:
с\ пз ^2 гс2 - 1 п2 -2
п2 + п3 п2 + п3 — 1 п2 + п3 — 2 п2 + п3 — 3
Вероятность третьего варианта:
Пп По — 1 По По — 1
ql '"2 '"2 ■"■ '"3 '"3
п2 + п3 п2 + п3 — 1 п2 + п3 —2п2+п3
Отсюда
44
P(A2) = Р(Аг) x
vn2n3[C\(n3- l)(n3- 2)+ C\(n2- l)(n2 - 2)+ g42(n2- l)(n3- 1)]_
д ^__^_________^^_—_____________________________
(n2 + n3)(n2 + n3 - l)(n2 + n3 - 2)(n2 + n3 - 3)
_ 2n2n3[2(n3 - l)(n3 -2) + 2(n2 - l)(n2 -2) + 3(n2 - l)(n3 - 1)]
n(n - l)(n-2)(n-3)
Р(Л) = Р(Л1) + Р(Л2).
2.79. Имеется электроприбор, который может выходить из
строя (перегорать) только в момент включения. Если прибор
включался до сих пор к — 1 раз и еще не перегорел, то условная
вероятность ему перегореть при к-м включении равна Qk. Найти
вероятности следующих событий:
А — прибор выдержит не менее п включений;
В — прибор выдержит не более п включений;
С — прибор перегорит точно при п-м включении.
Решение. Вероятность события А равна вероятности того,
что при первых п включениях он не перегорит:
п
Р(Л) = П(1-<?*)•
i=\
Чтобы найти вероятность события Д переходим к
противоположному:
В — прибор выдержит более п включений.
Для этого достаточно, чтобы при первых (п+1) включениях
прибор не перегорел:
п+1
п+1
р(я)=П(1-&); P(B) = i-i[(i-Qk).
к=1
к=1
Чтобы прибор перегорел точно при n-м включении, надо,
чтобы он не перегорел при первых (п - 1) включениях, а при n-м
перегорел^) = $п П(1 - ¢,).
г=1
2.80. Прибор состоит из четырех узлов; два из них (I и II)
безусловно необходимы для исправной работы прибора, а два
(III и IV) дублируют друг друга (рис. 2.80). Узлы могут
выходить из строя только при
включении. При к-м включении исправный
узел I (независимо от других)
выходит из строя с вероятностью q[k^;
узел II — с вероятностью qffl; узлы
III и IV — с одинаковой вероятно- Рис. 2.80
45
стью q[$ = q\ty = qk. Найти вероятности тех же событий А, В, С,
что в задаче 2.79.
Решение. Задача сводится к предыдущей, но здесь находим
условную вероятность Qk выхода из строя исправного прибора
при к-м включении:
(к)
(к)
й=1-(1-0(1-?Г )(!-«)•
2.81. В урне а белых и Ь черных шаров. Два игрока поочередно
вынимают из урны по одному шару, каждый раз вкладывая его
обратно и перемешивая шары. Выигравшим считается тот, кто
раньше вынет белый шар. Найти вероятность Р(1) того, что
выиграет первый игрок (тот, кто вынимал шар первым).
Решение. Выигрыш первого игрока может осуществиться
или при первом же вынимании, или при третьем (для чего первые
два вынимания должны дать черные шары, а третье — белый), и
т.д.
Р(1)
а
а + Ь
+
оо
1
i
Ка
Ь )
+ Ь)
Ь )
+ Ь)
а
а + 6
+ ... +
Ъ
2к
а
1
2к
а
+
а + 6
1-
а + 6
_ а + 6
' Ь \2 а + 26
<а + Ъ
(очевидно, Р(1) > при любых а и Ъ).
2.82. В урне два белых и три черных шара. Два игрока
поочередно вынимают из урны по шару, не вкладывая их обратно.
Выигрывает тот, кто раньше получит белый шар. Найти вероятность
Р(1) того, что выиграет первый игрок.
Решение. Р(1) = -Н = -.
5 5 4 3 5
2.83. Производятся испытания прибора. При каждом
испытании прибор выходит из строя с вероятностью р. После первого
выхода из строя прибор ремонтируется; после второго — признается
негодным. Найти вероятность того, что прибор окончательно
выйдет из строя в точности при к-м испытании.
Решение. Для того чтобы произошло данное событие,
нужно, во-первых, чтобы прибор вышел из строя при к-м испытании —
вероятность этого р. Кроме того, нужно, чтобы за предыдущие
к - 1 испытаний прибор вышел из строя ровно один раз;
вероятность этого равна (к — 1)р(1 — р)к~2. Искомая вероятность равна
(к - 1)Р2 (1 - Р)к-2.
46
2.84. Самолет, по которому ведется стрельба, состоит из трех
различных по уязвимости частей: 1) кабина летчика и двигатель,
2) топливные баки и 3) планер. Для поражения самолета
достаточно одного попадания в первую часть или двух попаданий во
вторую, или трех попаданий в третью. При попадании в самолет
одного снаряда он с вероятностью рх попадает в первую часть, с
вероятностью р2 — во вторую и с вероятностью р3 — в третью.
Попавшие снаряды распределяются по частям независимо друг от
друга. Известно, что в самолет попало га снарядов. Найти
условную вероятность поражения самолета Р(А |га) при этом условии
для га = 1, 2, 3, 4
Решение. Чтобы самолет оказался пораженным при одном
попадании, нужно, чтобы снаряд попал в первую часты
?(A\l) = Pl.
Для того чтобы найти_Р(Л |га) при га > 1, перейдем к
противоположному событию Р(А |га) — непоражение самолета при га
попаданиях.
Чтобы самолет не был поражен при двух попаданиях, надо,
чтобы оба снаряда попали в планер или один — в баки, а другой —
в планер:
V(A\2) = pl+2p2p,-
Р(4|2) = 1-(р32+2р2р3)-
Аналогично получаем
Р(Л|з) = 1-Зр2р32; Р(4|4) = 1.
2.85. Те же условия, что в предыдущей задаче, но первая часть
забронирована и сделана неуязвимой для попадающих в нее
снарядов. Найти P(j4|1), Р(4|2)и Р(Л|га)прига > 2.
Ответ. Р(Л|1) = 0; Р(Л|2) = р22; Р(А|га) = 1 - [р™ +тр™'1 х
х(Р2 + ft) + С1рГ2(Рз + 2р2Р3) + С3тр^3р2р23].
2.86. Прибор состоит из трех узлов. При включении прибора с
вероятностью рх появляется неисправность в первом узле, с
вероятностью р2 — во втором узле, с вероятностью р3 — в третьем узле.
Неисправности в узлах возникают независимо друг от друга.
Каждый из трех узлов безусловно необходим для работы прибора. Для
того чтобы узел отказал, необходимо, чтобы в нем было не менее
двух неисправностей. Найти вероятность того, что прибор
благополучно выдержит п включений.
Решение. Чтобы прибор работал (событие А), нужно,
чтобы работали все три узла. Вероятность того, что первый узел
выдержит п включений, равна вероятности того, что при п вклю-
47
чениях в нем окажется не более одной неисправности (0 или 1):
(1-PX)" +71^(1-^)-1.
Вероятность того, что все три узла выдержат п включений,
равна
Р(Л) = П [(1-^)- +npl(i-Pi)n-1i
2.87. Лвиабомба, предназначенная для бомбометания по
наземной цели, снабжена радиовзрывателем, работающим по сигналу от
поверхности земли. Взрыватель срабатывает на высоте h.
Эффективное действие бомбы по наземной цели имеет место тогда, когда
hx < h <h2. При h > h2 наблюдается преждевременный разрыв;
при h < /i2 — запоздалый разрыв; оба неэффективны. Вероятность
нормального разрыва равна р, преждевременного — pv
запоздалого - р2; рг+р2+р = 1.
С целью повысить вероятность нормального разрыва на бомбе
устанавливается второй взрыватель, имеющий те же
характеристики, что и первый, но работающий независимо от него.
При каком условии эта мера повысит вероятность
нормального разрыва бомбы?
Решение. При одном взрывателе вероятность нормального
разрыва р = 1 — рг — р2. При двух взрывателях вероятность
нормального разрыва равна р' = р2 + 2рр2 (либо оба взрывателя
сработают нормально, либо один нормально, другой запоздает).
Решая неравенство р' = р2 + 2рр2 > р, получаем требуемое условие
для У > р:
р + 2р2 >1, т.е. р2 > рг.
ГЛАВА 3
ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ
И ФОРМУЛА БЕЙЕСА
Если об обстановке опыта можно сделать п исключающих друг друга
предположений (гипотез)
-"I» -"2> •••' "п
и если событие А может появиться только при одной из этих гипотез, то
вероятность события А вычисляется по формуле полной вероятности:
Р(А) = Р(Н1)Р(А\Н1) + Р(Я2)Р(Л|Я2)+...+Р(Яп)Р(Л|Яп)
или
Р(А) = £Р(Я,.)Р(А|Я,.),
гдеР(Я2) — вероятность гипотезы Щ; Р(А\Н{) — условная вероятность
события А при этой гипотезе.
Если до опыта вероятности гипотез были P(^), Р(Я2), ...,Р(ЯП), а
в результате опыта появилось событие Л, то с учетом этого события
«новые», т.е. условные, вероятности гипотез вычисляются по формуле
Бейеса:
Рда и) = ^&ЕИШ_ « _,,, „,.
£Р(Я,)Р(Л|Я,)
1=1
Формула Бейеса дает возможность «пересмотреть» вероятности
гипотез с учетом наблюденного результата опыта.
Если после опыта, закончившегося появлением события А}
производится еще один опыт, в котором может появиться или не появиться
событие Д то вероятность (условная) этого последнего события вычисляется
по формуле полной вероятности, в которую подставлены не прежние
вероятности гипотез Р(Я2), а новые Р(Яг-1 А):
р(яИ) = £р(Я;|а)Р(Я|я;л).
1=1
49
3.1. Имеются три одинаковые с виду урны. В первой а белых
шаров и Ъ черных; во второй с белых и d черных; в третьей только
белые шары. Некто подходит наугад к одной из урн и вынимает из
нее один шар. Найти вероятность того, что этот шар белый.
Решение. Пусть событие А — появление белого шара.
Формулируем гипотезы:
Н{ — выбор первой урны;
Н2 — выбор второй урны;
Н3 — выбор третьей урны.
Р(Я1) = Р(Я2) = Р(Я3) = ^;
Р(А\Н1) = -?-; Р(Л|Я2) = -^-; Р{А\Н3) = 1.
а + о с + а
По формуле полной вероятности
тл/ л\ 1 а, 1 с 1 ., 1
Р(Л) = - + - + -.1 = -
3 а + о Зс+а 3 3
t а - ^
+ —+ 1
,а + Ь с + d
3.2. Прибор может работать в двух режимах: 1) нормальном и
2) ненормальном. Нормальный режим наблюдается в 80 % всех
случаев работы прибора; ненормальный — в 20 %. Вероятность
выхода прибора из строя за время t в нормальном режиме равна
0,1; в ненормальном — 0,7. Найти полную вероятность р выхода
прибора из строя за время t
Р е ш е н и е. р = 0,8 • ОД + 0,2 • 0,7 = 0,22.
3.3. Группа самолетов в составе: один ведущий и два ведомых,
направляется на бомбометание по объекту. Каждый из них несет
по одной бомбе. Ведущий самолет имеет прицел, ведомые — не
имеют и производят бомбометание по сигналу ведущего. По пути
к объекту группа проходит зону противовоздушной обороны, в
которой каждый из самолетов, независимо от других, сбивается с
вероятностью р. Если к цели подойдет ведущий самолет с обоими
ведомыми, они поразят объект с вероятностью Рг „. Ведущий
самолет, сопровождаемый одним ведомым, поразит объект с
вероятностью Рг г. Один ведущий самолет, без ведомых, поразит объект с
вероятностью Рг 0. Если ведущий самолет сбит, то каждый из
ведомых, если он сохранился, выходит к объекту и поражает его с
вероятностью Р0 г.
Найти полную вероятность поражения объекта с учетом
противодействия.
Решение. Формулируем гипотезы:
Нх — к объекту вышли все три самолета;
Н2 — к объекту вышел ведущий с одним ведомым;
50
#з — к объекту вышел один ведущий;
#4 — к объекту вышли два ведомых (без ведущего);
#5 — к объекту вышел один ведомый.
Вероятности этих гипотез: Р(Нг) = (1 — р)3;
Р(Я2) = 2р(1-р)2; Р(Я3) = р2(1-р);
Р(Я4) = р(1-р)2; Р(Я5) = 2р2(1-р).
Обозначим А — поражение объекта.
P(yl|^) = Pli2; Р(Л|Я2) = Р1Д; Р(Л|Яз) = Рм;
Р(Л|Я4) = 1-(1-Р0д)2; Р(Л|Я5) = Р0Д.
Р(А) = (1 - р)3Рм + 2р(1 - р)2Р1Д + /(1- p)Pli0 +
+р(1 - р)2[1 - (1 - Р0Д)2] + 2р2(1 - р)Р0Д.
3.4. Радиолокационная станция ведет наблюдение за объектом,
который может применять или не применять помехи. Если объект
не применяет помех, то за один цикл обзора станция
обнаруживает его с вероятностью р0; если применяет — с вероятностью рх < р0.
Вероятность того, что во время цикла будут применены помехи,
равна р и не зависит от того, как и когда применялись помехи в
остальных циклах. Найти вероятность того, что объект будет
обнаружен хотя бы один раз за п циклов обзора.
Решение. Полная вероятность обнаружения за один цикл
(1 - р)р0 + рр1; вероятность хотя бы одного обнаружения за п
циклов равна! — [1 — (1 — р)р0 — рр^71.
3.5. Завод изготовляет изделия, каждое из которых с
вероятностью р имеет дефект. В цехе работают три контролера; изделие
осматривается только одним контролером, с одинаковой
вероятностью первым, вторым или третьим. Вероятность обнаружения
дефекта (если он имеется) для г-го контролера равна р - (г = 1, 2, 3).
Если изделие не было забраковано в цехе, то оно попадет в ОТК
завода, где дефект, если он имеется, обнаруживается с
вероятностью Pq.
Определить вероятности следующих событий:
А — изделие будет забраковано;
В — изделие будет забраковано в цехе;
С— изделие будет забраковано в ОТК завода.
Решение. Так как события В и С несовместны и А = В + С,
тоР(Л) = Р(£) + Р(С).
Находим Р(В). Для того чтобы изделие было забраковано в
цехе, нужно, чтобы оно, во-первых, имело дефект, и, во-вторых, этот
дефект был обнаружен. Вероятность обнаружения имеющегося
51
дефекта по формуле полной вероятности равна -(рг + р2 + Р$)\
о
отсюда Р(В) = р Pl + Р2 + Рз.
Аналогично
Ро
3.6. Группа, состоящая из трех самолетов-разведчиков,
высылается в район противника с целью уточнить координаты объекта,
который предполагается подвергнуть обстрелу ракетами. Для
поражения объекта выделено п ракет. При уточненных координатах
объекта вероятность его поражения одной ракетой равна рь при
неуточненных — р2. Каждый разведчик перед выходом в район
объекта может быть сбит противовоздушными средствами
противника; вероятность этого р3. Если разведчик не сбит, он
сообщает координаты объекта по радио. Радиоаппаратура разведчика
имеет надежность р4. Для уточнения координат достаточно
приема сообщения от одного разведчика. Найти вероятность
поражения объекта с учетом деятельности разведки.
Решение. Гипотезы:
#l — координаты объекта уточнены;
#2 — координаты не уточнены.
р(я,) = 1 - [1 - (1 - рзЫ3; Р(я2) = [1 - (1 - у,)р4]3;
^4^) = 1-(1-Pl)"; Р(Л|Я2) = 1-(1-р2)".
Полная вероятность события А — поражение объекта:
Р(А) = {1 - [1 - (1 - Рз )р4 f }[1 - (1 - Pl Г ] +
+ [1-(1-Рз)р4]3[1-(1-р2Г].
3.7. Имеются две урны: в первой а белых шаров и Ь черных; во
второй с белых и с? черных. Из первой урны во вторую
перекладывают, не глядя, один шар. После этого из второй урны берут один
шар. Найти вероятность того, что этот шар будет белым.
Решение. Событие А — появление белого шара; гипотезы:
#l — переложен белый шар;
#2 — переложен черный шар.
Р(Я1) = -^-;Р(Я2)= Ь
а + о а + о
Р(А\Н1)= С + 1 ; Р(А\Н2) = ;
1 с+d+l К ' 2 c+d+1
52
Р(Л)- а c + 1 I b c
а+Ьс+d+l a + bc + d + l'
3.8. В условиях предыдущей задачи из первой урны во вторую
перекладывают не один, а три шара (предполагается, что а > 3;
6 > 3). Найти вероятность того, что из второй урны появится
белый шар.
Решение. Можно было бы выдвинуть четыре гипотезы:
#t — переложены 3 белых шара;
#2 — переложены 2 белых шара и 1 черный;
#з — переложены 1 белый шар и 2 черных;
#4 — переложены 3 черных шара,
но проще решить задачу, имея всего две гипотезы:
Нх — вынутый из 2-й урны шар принадлежит 1-й урне;
#2 — вынутый из 2-й урны шар принадлежит 2-й урне. Так как
во второй урне три шара принадлежат первой урне, а с + d —
второй, то
Р(# ) = 1 ; P(g2)= CJrd .
V 1J c + d + 3 V 2J c + d + 3
Вероятность появления белого шара из первой урны не
зависит от того, вынимается ли этот шар непосредственно из первой
урны или после перекладывания во вторую:
РОад^-^-; Р(А\Н2) = -^-,
а + о с + а
откуда
Р{А) = § а_+ c + d с
с + d + 3 а + Ъ с + d + 3 с + d
3.9. Имеется п урн, в каждой из которых а белых шаров и Ь
черных. Из первой урны во вторую перекладывается один шар; затем
из второй в третью один шар и т.д. Затем из последней урны
извлекается один шар. Найти вероятность того, что он белый.
Решение. Вероятность события А2 — извлечения белого
шара из второй урны после перекладывания — найдем так же, как в
задаче 3.7 (при c = a,d = Ь):
ш л \ — а о. -\-\ Ь а а
a + ba + b+l a + ba + b+l a + b
Таким образом, вероятность извлечения белого шара из второй
урны после перекладывания будет такой же, как и до переклады-
53
вания. Следовательно, такой же будет и вероятность вынуть
белый шар из третьей, четвертой и т.д., п-й урны:
Р(Ап)= а
а + Ъ
3.10. Приборы одного наименования изготовляются двумя
заводами; первый завод поставляет 2/3 всех изделий, поступающих
на производство; второй 1/3 . Надежность (вероятность
безотказной работы) прибора, изготовленного первым заводом, равна рх;
второго — р2. Определить полную (среднюю) надежность р
прибора, поступившего на производство.
Ответ.р = -р1 Н— р0.
3 3
3.11. Производится стрельба по цели одним снарядом. Цель
состоит из трех частей, площади которых равны Sv S2, S3
(Sx + S2 + Ss = S). Для попавшего в цель снаряда вероятность
попасть в ту или другую часть пропорциональна площади части.
При попадании в первую часть цель поражается с вероятностью
рх; во вторую часть — с вероятностью р2; в третью — р3. Найти
вероятность поражения цели, если известно, что в нее попал один
снаряд.
Ответ. р = —±-рл + —-р9 Н—-р%.
S г S 2 S 3
3.12. Имеется две партии однородных изделий; первая партия
состоит из TV изделий, среди которых п дефектных; вторая партия
состоит из М изделий, среди которых т дефектных. Из первой
партии берется случайным образом if изделий, а из второй L
изделий (К < N; L < М); эти К + L изделий смешиваются и образуется
новая партия. Из новой смешанной партии берется наугад одно
изделие. Найти вероятность того, что изделие будет дефектным.
Решение. Событие А — изделие будет дефектным. Гипотезы:
Нх — изделие принадлежит первой партии;
#2 — изделие принадлежит второй партии.
р(Я1 ) = _*_; Р(Я2) = —L—; Р(Л) = -^-^ + —L— ™.
l K+L v 2 K+L K+LN K+LM
3.13. В условиях предыдущей задачи из новой, смешанной,
партии берется не одно изделие, а три. Найти вероятность того,
что хотя бы одно изделие из трех окажется дефектным.
Решение. Гипотезы:
#0 — все три изделия принадлежат первой партии;
Нх — два изделия принадлежат первой партии, а одно — второй;
#2 — одно изделие принадлежит первой партии, а два — второй;
#з — все три изделия принадлежат второй партии.
54
Р(# 0 ) =
P(#! ) =
Р(Я2) =
Р(Я3 ) =
Р(Л|Я0) =
Р(Л|ЯХ):
Р(А\Н2) =
Ч A\U \ — Л
К{К -1)(К-2)
(К + L){K + L-1)(K + L-
ZK(K - l)L
(K + L)(K + L-1){K + L-
3KL(L - 1)
{K + L){K + L-l){K + L-
L(L-l)(L-2)
(K + L)(K + L-1)(K + L-
(N - n)(N - n - 1)(N -
N(N -l)(JV-2)
(N -n)(N -n-l)(M ■
N(N - l)M
(N - n)(M - m)(M - rr,
NM{M - 1)
(M - m)(M - m -1)(M -
•
-2)'
•
-2)'
•
-2)'
я
-2)'
»-2).
J
- m)
* •
i
'-!).
J
m -2)
3
M{M -1)(M -2)
Р(Л) = Р(Я0)Р(Л|Я0) + Р(Я1)Р(Л|Я1) +
+ Р(Я2)Р(Л|Я2) + Р(Я3)Р(Л|Я3).
3.14. Имеются две урны: в первой а белых шаров и Ъ черных; во
второй с белых и с! черных. Из первой урны во вторую
перекладывается один шар; шары перемешиваются и затем из второй урны в
первую перекладывается один шар. После этого из первой урны
берут наугад один шар. Найти вероятность того, что он будет
белым.
Решение. Гипотезы:
#l — состав шаров в первой урне не изменился;
Я2 — в первой урне один черный шар заменен белым;
Я3 — в первой урне один белый шар заменен черным.
Р(Я1)^—i±i_+ b d + 1
a + bc + d + l a + bc + d + l'
Р(Я2)= b , С, ,; Р(Я3)= й d
a + bc + d + l' a + bc + d + l'
55
P(A) =
( a c + 1 b d+1 ) a
,a + bc + d + l a + bc + d + 1,
a + b
b с a + 1 a d a — 1
а + Ъ с + d + 1 a + b a + b с + d + 1 a + b
a(a + b)(c + d + 1) + be — ad a be — ad
(a + b)\c + d + 1) a + & (a + b)2(c + d + 1)
Полученное решение показывает, что вероятность вынуть
белый шар не изменится, если доли белых и черных шаров в обеих
с d
урнах одинаковы: — = — (be — ad = 0).
а Ъ
3.15. Из чисел 1, 2, ... , га одно за другим выбирают наугад два
числа. Какова вероятность того, что разность между первым
выбранным числом и вторым будет не меньше т (т > 0).
Решение. Событие А состоит в том, что разность между
первым выбранным числом к и вторым выбранным числом I будет не
меньше т (т.е. к — I > т).
Гипотезы Нк — первым вынуто число A; (A; = m + 1,..., га);
Р(Я*) = -; P(A\Hk) = ±Zll;
га га — 1
it=m+1 п(п-1) га (га - 1) к±^+1
1 г ч, (га — т)(п — т +1)
[1 + 2+...+ (га -т)}= v А ;
га (га — 1) 2га (га — 1)
3.16*. Из N стрелков можно выделить четыре группы: ах
отличных стрелков, (¾ хороших, % посредственных и а4 плохих.
Вероятность попадания в мишень при одном выстреле для стрелка г-й
группы равна р{ (г = 1, 2, 3, 4). Вызываются наугад два стрелка и
стреляют по одной и той же мишени. Найти вероятность хотя бы
одного попадания в мишень.
Решение. Событие А — хотя бы одно попадание в мишень.
Гипотезы Я{ — первым вызван стрелок г-й группы (г = 1, 2, 3, 4).
Р(Я4) = ^-; Р(Л) = £^-Р(Л|Я<),
где Р (А | Н ■ ) снова находим по формуле полной вероятности при
четырех гипотезах о том, какой стрелок был вызван вторым:
p(^iFj=^^[i-(i-^)2]+x:-^-[i-(i-pl.)(i-pi)]-
N-l UN-1
56
3.17. Производится п независимых выстрелов зажигательными
снарядами по резервуару с горючим. Каждый снаряд попадает в
резервуар с вероятностью р. Если в резервуар попал один снаряд,
горючее воспламеняется с вероятностью рх\ если два снаряда — с
полной достоверностью. Найти вероятность того, что при п
выстрелах горючее воспламенится.
Решение. Гипотезы:
fft — в резервуар попал один снаряд;
Я2 — в резервуар попало два или более снарядов.
Р(Я1) = пр(1-р)"-1; Р(Я2) = 1-(1-р)" -пр(1-Ру-\
Искомая вероятность равна
Р(Л) = Р(Я1)р1+Р(Я2)1 =
= пр(1-р)п~1р1 + 1 - (1 - р)п -пр(1-р)п-1 =
= 1-(1-р)» -np{\-py-l{l-Pl).
3.18. Группа студентов состоит из а отличников, Ь хорошо
успевающих и с занимающихся слабо. Отличники на предстоящем
экзамене могут получить только отличные оценки. Хорошо
успевающие студенты могут получить с равной вероятностью хорошие
и отличные оценки. Слабо занимающиеся могут получить с
равной вероятностью хорошие, удовлетворительные и
неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один
студент. Найти вероятность того, что он получит хорошую или
отличную оценку.
Решение. Гипотезы:
Нх — вызван отличный студент;
#2 — вызван хороший студент;
#з — вызван слабый студент.
р^) = -тт—; р(я*) = -^—; р(яз) = —т—•
а+о+с а + о + с а + о + с
Искомая вероятность равна
Р(Л) = Р(Я1)Ц-Р(Я2)1 + Р(Я3)^ =
I к 1 а + Ь+ -
— а + 1 с з
а + Ь + с 3а+Ь+с а + Ь + с
3.19. В условиях предыдущей задачи вызываются наугад три
студента. Найти вероятность того, что они получат отметки:
отлично, хорошо и удовлетворительно (в любом порядке).
57
Решение. Событие А — получение отличной, хорошей и
удовлетворительной отметок — возможно только при одной из
следующих гипотез:
Нх — вызваны один слабый студент, один хороший и один
отличник;
#2 — вызваны один слабый студент и два хороших;
#з — вызваны два слабых студента и один хороший;
#4 — вызваны два слабых студента и один отличник.
Р(ЯХ) = 6^--^ —; Р(Я2)=:ЗА6-1 С ;
х NN-1N-2 2 NN-1N-2
Р(Н3) = 3— С °~1;Р(Я4) = 3— С с-1
NN-1N-2 * NN-1N-2
P(A) = P(^)l.i.I + P(Fa)|.| + P(F,)i.| + P(F4)l.|.
3.20. В автобусе едут п пассажиров. На очередной остановке
каждый из них выходит с вероятностью р; кроме того, в автобус с
вероятностью р0 не входит ни один новый пассажир; с
вероятностью 1 - р0 — один новый пассажир. Найти вероятность того, что
когда автобус снова тронется в путь после очередной остановки, в
нем будет по-прежнему п пассажиров.
Решение. Событие А — после остановки снова п
пассажиров. Гипотезы:
#0 — не вошел никто;
#l — вошел один пассажир.
Р(Я0) = р0;Р(Я1) = 1-р0;
Р(А\Н0) = (1-Р)п;Р(А\Н1) = пр(1-Р)а-1;
Р(А) = Ро(1 - р)п + (1 - Ро )пр(1 - р)"-1.
3.21*. Условия предыдущей задачи сохраняются, но надо
найти вероятность того, что после двух остановок в автобусе будет
по-прежнему п пассажиров (при расчете учесть, что новый
пассажир также выходит с вероятностью р на последующей остановке).
Решение. Гипотезы:
#0 0 — за две остановки не вошел никто;
Нг 0 — на первой остановке вошел один пассажир, а на
второй — ни одного;
Н0 г — на первой остановке не вошел ни один пассажир, а на
второй — один;
Нг г — на каждой остановке вошло по пассажиру.
58
р(я0,о) = ро2; p№,o) = (i-Po)Po;
Р(Ям) = р0(1-р0); Р(Яг11) = (1-р0)2.
Чтобы при гипотезе Н0 0 число пассажиров осталось га, нужно,
чтобы ни один из га пассажиров не вышел ни на первой, ни на
второй остановках:
Р(Л|Я010) = [(1-р)"]2=(1-р)2\
Чтобы при гипотезе Нг 0 число пассажиров осталось прежним,
нужно, чтобы или на первой остановке вышел один пассажир, а на
второй — никто, или на первой остановке не вышел никто, а на
второй — один пассажир:
Р(А|Я110) = пр(1-р)"-1(1-р)п + (1-р)"(п + 1)р(1-р)" =
= р(1-р)2п-1[п + (п + 1)(1-р)}.
Аналогично, но учитывая, что вошедший на второй остановке
пассажир не выходит:
P(y4|ff0il)=np(l-p)"-1(l-p)" + (l-p)"np(l-p)"-1=2np(l-p)2-1.
Чтобы при двух вошедших пассажирах число их после двух
остановок оставалось неизменным, нужно или чтобы на первой
остановке вышли два пассажира, а на второй — никто; или на
первой — никто, а на второй — два; или чтобы вышло по пассажиру
на каждой остановке:
Р(Л|Я11) = С2р2(1-р)"-2(1-р)"-1 +
+ (1 - рГ с2п+У(1 - р)-1 + c\p{i - рГ-'с* p(i - р)-1 =
p2(i-p)
2п-3
га (га - 1) о/-. \ п(п + 1) /-1 \
-^ '- + га2(1 - р) + —^ i(l - р)
2
Р(Л) = Р(Я010)Р(Л|Я010) + Р(Я110)Р(Л|Я110) +
+ Р(Я011)Р(Л|Я011) + Р(Я111)Р(Л|Я111).
3.22. Три орудия производят стрельбу по трем целям. Каждое
орудие выбирает себе цель случайным образом и независимо от
других. Цель, обстрелянная одним орудием, поражается с
вероятностью р. Найти вероятность того, что из трех целей две будут
поражены, а третья нет.
Решение. Гипотезы:
Нх — обстреляны все три цели;
#2 ~ все орудия стреляют по одной цели;
59
Я3 — Две цели из трех обстреляны, а третья нет.
2 1 2
Р(Я:) = 1
3 3 9
111 2 1
Р(Я2) = 1 • - ■ - = -; Р(Я,) = 1 - - - - =
3 3 9 9 9
P(^|^) = 3p2(l-p);PH|F2) = 0;
Р(Л|Я3) = [1-(1-р)2Ь = р2(2-р);
2
3
Р(А) = 2р
-!'
II
Рис. 3.23
3.23. Прибор состоит из двух дублирующих друг друга узлов I
и II (рис. 3.23) и может случайным образом работать в одном из
двух режимов: благоприятном и
неблагоприятном. В благоприятном режиме надежность каж-
— дого из узлов равна pv в неблагоприятном р2.
Вероятность того, что прибор будет работать в
благоприятном режиме, равна Pv в
неблагоприятном 1 — Рх. Найти полную (среднюю)
надежность прибора р.
Ответ, р = Рг[1 - (I - рг)2}+ (I - Рг)[1 - (I - р2)2}.
3.24. На телефонную станцию поступает случайный поток
вызовов; вероятность приема к вызовов за время t равнаpk(t)
(к = 0,1, 2, ...). Число вызовов, принятых за промежуток времени
t, не зависит от того, сколько вызовов поступило до или после
этого промежутка. Найти вероятность того, что за промежуток
времени 2t будет 5 вызовов.
Решение. Разделим промежуток 2t на две части: первую и
вторую, каждая длительности t Гипотезы Нк — на первый участок
попало А;вызовов (к= 0, 1, ..., s).
P(Hk) = pk(t) (к = 0,1,...,8).
Для того чтобы при гипотезе Нк на промежуток 2t попало 5
вызовов, нужно, чтобы на второй участок поступило s— к вызовов.
Условная вероятность этого равна ps_k (t). Полная вероятность
события А — за время 2 £ поступит 5 вызовов — равна
Р(Л) = £р(Я4)Р(Л|Я*) = £Л(0р^(*)-
*=0
*=0
3.25. В ящике находится а новых теннисных мячей и Ь
игранных. Из ящика наугад вынимается два мяча, которыми играют.
После этого мячи возвращают в ящик. Через некоторое время из
60
ящика снова берут наугад два мяча. Найти вероятность того, что
они будут новыми (а > 2; b > 2).
Решение. Гипотезы:
Нх — оба вынутых первый раз мяча были новыми;
#2 — оба вынутых первый раз мяча были игранными;
#з — один из мячей был новым, а другой — игранным.
(а + Ь)(а + Ь-1)' 2 (а + Ь)(а + Ь-1)'
2аЬ
Р(#з)
(а+ Ь)(а+ 6-1)'
а(а-1)(а-2)(а-3) + Ь(Ь-1)а(а-1) + 2аЬ(а-1)(а-2)
(а + Ь)2(а + Ь-1)2 "
3.26. Имеется п экзаменационных билетов, каждый из которых
содержит два вопроса. Экзаменующийся знает ответ не на все 2п
вопросов, а только на к< 2п. Определить вероятность р того, что
экзамен будет сдан, если для этого достаточно ответить на оба
вопроса своего билета или на один вопрос из своего билета и на один
(по выбору преподавателя) вопрос из дополнительного билета.
Решение. Гипотезы:
Нх — экзаменующийся знает оба вопроса своего билета;
#2 — экзаменующийся из двух вопросов своего билета знает
один.
fc(fc-l) . 2А;(2п -к) к-1
р = — -1 +
2п (2п - 1) 2п (2п - 1) 2п - 2
3.27*. Цель, по которой ведется стрельба, с вероятностью рх
находится в пункте I, а с вероятностью р2 = 1 — рх в пункте II рг > - .
V 2,
В нашем распоряжении имеется п снарядов, каждый из
которых может быть направлен в пункт I или в пункт II. Каждый
снаряд поражает цель независимо от других с вероятностью р. Какое
число снарядов п1 следует направить в пункт I для того, чтобы
поразить цель с максимальной вероятностью?
Решение. Событие А — поражение цели при направлении щ
снарядов в пункт I. Гипотезы:
Ht — цель в пункте I;
#2 — цель в пункте II.
Р(Я1) = р1; Р(Я2) = 1-Р1;
61
P(A) = Pl[l -(1- p)-]+ (1 - Pi)[l -(1- P)"""1]-
Рассматривая P(A) как функцию непрерывного аргумента п{у
находим
dP(A)
dnl
[-Pi(l - Р)"1 + (1 - Pl)(l - P)n_ni]ln(l - p),
^11 = -^(1 -p)"'+(l-Pl)(l-p)—■]ln2(l-P)<0)
откуда видно, что эта функция имеет единственный максимум в
точке
п рг dP(A) п
пг = - + — , где ^ = 0.
2 21n(l-p) А^
Заметим, что пл > — при о, > -.
1 2 1 2
Если полученное число п{ целое и < п, то это и есть искомое
число; если оно не целое (но < п), то нужно вычислить Р(Л) для
двух ближайших целых значений и выбрать то из них, для
которого Р (А) больше; если полученное число окажется больше п, то
следует направить все п снарядов в пункт I (это случится при
1 — р 1
In < nln(l — р),т.е. при рг > ).
Pi 1 + (1-р)п
3.28. Рассматривается посадка самолета на ВПП аэродрома.
Если позволяет погода, летчик сажает самолет, наблюдая за
состоянием ВПП визуально. В этом случае вероятность
благополучной посадки равна р{. Если аэродром затянут низкой облачностью,
летчик сажает самолет вслепую по приборам. Надежность
(вероятность безотказной работы) приборов во втором случае Р. Если
приборы «слепой» посадки сработали нормально, то самолет
садится благополучно с той же вероятностью ри что и при
«визуальной» посадке. Если же приборы «слепой» посадки не сработали,
то летчик может благополучно посадить самолет только с очень
малой вероятностью р[.
Найти полную вероятность благополучной посадки самолета,
если известно, что в к % всех случаев посадки аэродром затянут
низкой облачностью.
Решение. Гипотезы:
Н{ — низкой облачности нет;
62
ff2 — низкая облачность есть.
Р(Я1) = 1- —; Р(Я2) = —; Р(Л|Я1) = р1;
1 100 100
Р(А|Я2) находим снова по формуле полной вероятности:
Р(Л|Я2) = РР1+(1-Р)р1;
А; 1
100 J
А;
Р(Л) - 1 - -=L- Pl + -2-[PPl +(1- P)pJ].
100
3.29. Цель, по которой ведется стрельба, состоит из двух
различных по уязвимости частей. Для поражения цели достаточно
одного попадания в первую часть или двух попаданий во вторую.
Для каждого попавшего в цель снаряда вероятность попадания в
первую часть равна pv во вторую р2 = 1 — рг. По цели
производится три выстрела; вероятность попадания при каждом выстреле
равна р. Найти вероятность того, что данными тремя выстрелами
цель будет поражена.
Решение. Гипотезы:
Н{ — в цель попал один снаряд;
Н2 — в цель попало два снаряда;
#з — в цель попало три снаряда.
Р(Я1) = Зр(1-р)2; Р(Н2) = Зр2(1-р)] Р(Н3) = р\
Р(Л|Я1) = р1; P(A\H2) = l-(l-Pl)2+p22] Р(А\Н,) = 1;
Р(А) = Зр(1 - p)2Pl + Зр2(1 - р)[1 - (1 - Pl )2 + р\\ + рг • 1.
3.30. Группа из трех самолетов совершает налет на объект.
Объект защищен четырьмя батареями зенитных ракет. Каждая
батарея простреливает угловой сектор размерами 60°, так что из
полного угла 360° вокруг объекта оказываются защищенными
240°. Если самолет пролетает через защищенный сектор, его
обстреливают и поражают с вероятностью р; через незащищенный
сектор самолет проходит беспрепятственно. Каждый самолет,
прошедший к объекту, сбрасывает бомбу и поражает объект с
вероятностью Р. Экипажи самолетов не знают, где расположены
батареи. Найти вероятность поражения объекта для двух
способов организации налета:
1) все три самолета летят по одному и тому же направлению,
выбираемому случайно;
2) каждый из самолетов выбирает себе направление случайно
независимо от других.
Решение. 1) Гипотезы:
Нх — самолеты выбрали незащищенное направление;
63
H2 — самолеты выбрали защищенное направление.
Р(Яг) = 1; Р(Яа) = |;
Р(А\Н1) = 1- (1 - Р)3; Р(Л|Я2) = 1 - [1-(1- p)Pf;
Р(Л) = i[l -(1- Р)3] + |{1 - [1 - (1 - p)Pf}.
2) Находим для каждого самолета полную вероятность рх пора-
1 2
зить объект: рг = -Р + -(1 — р)Р.
Для трех самолетов вероятность поражения объекта будет
P(A) = 1-(1-Piy=l
1-±Р--(1-р)Р
3 3
Можно показать, что полученная вероятность больше, чем для
способа 1).
3.31. Имеются три урны: в первой из них а белых шаров и Ъ
черных; во второй с белых шаров и d черных; в третьей — к белых
шаров (черных нет). Некто выбирает наугад одну из урн и
вынимает из нее шар. Этот шар оказался белым. Найти вероятность
того, что шар вынут из первой, второй или третьей урны.
Решение. Решаем задачу по формуле Бейеса.
Гипотезы:
Нх — выбор первой урны;
Н2 — выбор второй урны;
Н3 — выбор третьей урны.
Априори (до опыта) все гипотезы равновероятны:
Р(Яг) = Р(Я2) = Р(Я8) = 1.
Наблюдалось событие А — появление белого шара. Находим
условные вероятности:
Р(А\Н1) = -?-; Р(А\Нг) = -^-; Р(Л|Я8) = 1.
а + о с + а
По формуле Бейеса вероятность того, что шар был вынут из
первой урны:
Р(ЯХ|Л)= 3 - а + Ь
1 Д-. а с
-УР(А\НЛ г + Т + 1
г =1
64
Аналогично
P(HJA) = _ c + d ; Р(Я3|Л) =
а с л а с
+ - + 1 + + 1
а + Ъ с + d a + b с + d
3.32. Прибор состоит из двух узлов: работа каждого узла
безусловно необходима для работы прибора в целом. Надежность
(вероятность безотказной работы в течение времени t) первого узла
равна ри второго р2. Прибор испытывал ся в течение времени t, в
результате чего обнаружено, что он вышел из строя (отказал).
Найти вероятность того, что отказал только первый узел, а второй
исправен.
Р е ш е н и е. До опыта возможны четыре гипотезы:
#0 — оба узла исправны;
Н{ — первый узел отказал, а второй исправен;
#2 — первый узел исправен, а второй отказал;
#з — оба узла отказали.
Вероятности гипотез:
P(#0) = ftP2; Р(Я1) = (1-р1)р2; Р(Я2) = Р1(1-р2);
Р(Я3) = (1-Р1)(1-р2).
Наблюдалось событие А — прибор отказал.
Р(Л|Я0) = 0; Р(Л|Я1) = Р(Л|Я2) = Р(Л|Я3) = 1.
По формуле Бейеса
Щ |Л) _ (1 - Pi )Р2 _ (1 ~ Pi )Р2
(1 - Рг)р2 + рг(1 ~ Р2)+ (1 - рг)(1 ~ Р2) 1 ~ РгР2
3.33. В условиях задачи 3.28 известно, что самолет
приземлился благополучно. Найти вероятность того, что летчик пользовался
приборами «слепой» посадки.
Решение. Если летчик пользовался приборами «слепой»
посадки, то, значит, облачность была (гипотеза Н2). По данным
задачи 3.28 находим
Р(Я2|Л) =
* [PPl + (1 - P)pi]
100
( к
100 J
Pi + ~^{РРг + (1 - P)Pl]
3.34. У рыбака имеется три излюбленных места для ловли
рыбы, которые он посещает с равной вероятностью. Если он заки-
65
дывает удочку на первом месте, рыба клюет с вероятностью р{; на
втором — с вероятностью р2] на третьем — с вероятностью р3.
Известно, что рыбак, выйдя на ловлю рыбы, три раза закинул удочку
и рыба клюнула только один раз. Найти вероятность того, что он
удил рыбу на первом месте.
Ответ. Р(Н1\А) = ^(1-1^ .
3.35. Завод изготовляет изделия, каждое из которых с
вероятностью р имеет дефект. В цехе изделие с равной вероятностью
осматривается одним из двух контролеров. Первый контролер
обнаруживает имеющийся дефект с вероятностью pv второй — с
вероятностью р2. Если в цехе изделие не забраковано, оно поступает
на ОТК завода, где дефект, если он имеется, обнаруживается с
вероятностью р0. Известно, что изделие забраковано. Найти
вероятность того, что оно забраковано: 1) первым контролером; 2)
вторым контролером; 3) ОТК завода.
Решение. Априори возможны четыре гипотезы:
Н0 — изделие не забраковано;
Щ — изделие забраковано 1-м контролером;
Н2 — изделие забраковано 2-м контролером;
Я3 — изделие забраковано ОТК завода.
Событие А — изделие забраковано. Гипотеза Н0 нам не нужна,
так как Р(А\Н0) = 0;
Р(ЯХ)
РР\
Р(Я2)
pp.
Р(Я3) = Р
\ Pl + Pl'
2 ,
Ро
Вероятности гипотез после опыта:
2)Р(Я2|Л)
з)Р(ЯзИ)
Р(#х)
Pi
P(^)+P(ff2) + P(ff3)
: Рг
2р0 +(Pi +Р2)(1- Ро)
Р№-{Рг+Рг))
2p0 + (Pi+ Р2)(1-Ро)'
2р0 + (Pi +^2)(1-^)
3.36. В группе из 10 студентов, пришедших на экзамен, 3
подготовленных отлично, 4 — хорошо, 2 — посредственно и 1 — плохо.
В экзаменационных билетах имеется 20 вопросов. Отлично
подготовленный студент может ответить на все 20 вопросов, хорошо
подготовленный — на 16, посредственно — на 10, плохо — на 5.
Вызванный наугад студент ответил на три произвольно заданных
66
вопроса. Найти вероятность того, что этот студент подготовлен:
а) отлично; б) плохо.
Решение. Гипотезы:
Н{ — студент подготовлен отлично;
#2 — студент подготовлен хорошо;
#з — студент подготовлен посредственно;
#4 — студент подготовлен плохо.
До опыта:
Р(ЯХ) = 0,3; Р(Я2) = 0,4; Р(Я3) = 0,2; Р(Я4) = 0,1;
Р(Л|Я,) = 1; Р(А\Н2) = — • — • — « 0,491;
1 2 20 19 18
РМ1Я,) = — • — • — « 0,105; Р(Л|Я4) - — • — • — « 0,009.
20 19 18 20 19 18
После опыта
а) Р(Я, | А) = <^1± и 0,58;
0,3-1 + 0,4-0,491 + 0,2-0,105 + 0,1-0,009
б)Р(Я4|Л) = 2^^« 0,002.
0,518
3.37. На вход радиолокационного устройства с вероятностью р
поступает полезный сигнал с помехой, а с вероятностью (1 — р) —
только одна помеха. Если поступает полезный сигнал с помехой,
то устройство регистрирует наличие какого-то сигнала с
вероятностью р{; если только помеха — с вероятностью р2- Известно, что
устройство зарегистрировало наличие какого-то сигнала. Найти
вероятность того, что в его составе имеется полезный сигнал.
Ответ. х
ррг + (1 - р)р2
3.38. Пассажир может обратиться за получением билета в одну
из трех касс. Вероятности обращения в каждую кассу зависят от
их местоположения и равны соответственно р{, р2, ръ. Вероятности
того, что к моменту прихода пассажира имеющиеся в кассе билеты
будут распроданы, равны: для первой кассы Ри для второй Р2, для
третьей Р3. Пассажир направился за билетом в одну из касс и
приобрел билет. Найти вероятность того, что это была первая касса.
Решение. Р(ЯХ) = рх; Р(Я2) = р2; Р(Я3) = р3-
Р(Л|Я1) = 1-Р1; Р(Л|Я2) = 1-Р2; Р(Л|Я3) = 1 - Р3.
Pi(l-Pi)
Р(Нг\А)
Л(1-Р1) + р2(1-Р2) + р3(1-Р3)
67
3.39. Производится один выстрел по плоскости, на которой
расположены две цели: I и II (рис. 3.39). Вероятность попадания в
цель I равна ри в цель II — р2. После выстрела получено известие,
что попадания в цель I не произошло. Какова
теперь вероятность того, что произошло
попадание в цель II?
Решение. Гипотезы:
Н{ — попадание в цель I;
Н2 — попадание в цель II;
Н3 — непопадание ни в одну из целей.
Рис. 3.39
Событие А — непопадание в цель I.
Р(Я1) = р1;Р(Я2) = р2;Р(Я3) = 1-(р1+р2)
Р(А\Н1) = 0;Р(А\Н2) = 1;Р(А\Н3) = 1.
Р(Н2\А)
Р:
Р:
Р2 + 1 - (Pi + Р2 ) 1~Pl
Эту задачу можно решить и без формулы Бейеса:
Р(Я2Л) Р(Я2) р2
Р(Н2\А)
Р(А) Р(А) 1 - Pl
3.40. Имеются две урны: в первой а белых шаров и Ь черных, во
второй — с белых и d черных. Выбирается наугад одна из урн и из
нее вынимается один шар. Этот шар оказался белым. Найти
вероятность того, что следующий шар, который вынут из той же урны,
будет тоже белым.
Решение. Н{ — выбрана первая урна;
Я2 — выбрана вторая урна.
А — появление белого шара при первом вынимании.
а
Р(Я1) = Р(Я2) = ^; Р(Нг\А)
а + Ь
а
+
а + Ь с + d
Р(#2|Л) =
c + d
а
+
a+b c+d
В — появление второго белого шара.
Р(Я|Л) = Р(Я1|Л)Р(5|Я1Л) + Р(Я2|Л)Р(Я|Я2Л)
68
Условная вероятность появления второго белого шара при
условии, что была выбрана первая урна и из нее вынут белый
шар:
Р(В\НгА): а~1
а + Ь-1
аналогично
Р(В|Я2Л)
c + d
Р(В\А)
а
+
а (а — 1) с (с — 1)
(а + 6) (а + 6-1) (с + d)(c + d - 1)
a + b c + d
3.41. Имеется группа в составе N стрелков. При одном
выстреле в мишень г-й стрелок попадает в нее с вероятностью р{
(г = 1, 2, ..., N). Вызывается наугад один из стрелков. Произведя
один выстрел по мишени, он попал в нее. Найти вероятность
того, что при следующих двух выстрелах того же самого стрелка
будет одно попадание и один промах.
Решение. Л — попадание при первом выстреле;
В — одно попадание и один промах при двух последующих
выстрелах.
Гипотезы Н{ — вызван г-й стрелок (г = 1, 2, ..., N).
Р(Я,|Л) = ^-,гдер = ^>,;
Р Ы1
Р(В\Н{А) = 2р,(1-р{);
Р(В\А) = £р(Я, |Л)Р(ВДЛ)=Л][>?(1 - Pi ).
i=\ Р i=l
ГЛАВА 4
ПОВТОРЕНИЕ ОПЫТОВ
Опыты называются независимыми, если вероятность того или иного
исхода каждого опыта не зависит от того, какие исходы имели другие
опыты.
Независимые опыты могут производиться как в одинаковых
условиях, так и в различных. В первом случае вероятность появления какого-то
события А во всех опытах одна и та же, во втором случае она меняется от
опыта к опыту.
Частная теорема о повторении опытов
Если производится п независимых опытов в одинаковых условиях,
причем в каждом из них с вероятностью р появляется событие А, то
вероятность Рт п того, что событие А произойдет в этих п опытах ровно га раз,
выражается формулой
Рт,п =С:Ртдп~т (m =0,1,...,n), (4.0.1)
где q = 1 - p.
Формула (4.0.1) выражает так называемое биномиальное
распределение вероятностей.
Вероятность хотя бы одного появления события А при п независимых
опытах в одинаковых условиях равна
Общая теорема о повторении опытов
Если производится п независимых опытов в различных условиях,
причем вероятность события А в г-м опыте равна p{(i — 1, 2,..., п),то
вероятность Рт п того, что событие А появится в этих опытах ровно га раз,
равна коэффициенту при zm в разложении по степеням z производящей
функции:
п
4>n(z) = Yl^i +piz),Ymqi =1-р,-.
г=1
Вероятность хотя бы одного появления события А при п независимых
опытах в различных условиях равна
70
n
1=1
Для любых условий (как одинаковых, так и различных)
п
Z_j*m,n 1'
m=0
Вероятность Rk п того, что при п опытах событие А появится не менее
&раз, выражается формулой
п к—1
Rk,n = 52Рт,п ^111 Rk.fi =1~ Y^Pm,n-
т=к ш=0
Теоремы о повторении опытов, как частная, так и общая, допускают
обобщение на tojt случай, когда в результате каждого опыта возможны не
два исхода (А и А), а несколько исходов.
Если производится п независимых опытов в одинаковых условиях,
причем каждый опыт может иметь А; исключающих друг друга исходов Av
А2,..., Ак с вероятностями pv р2,..., рк
к
, то вероятность того, что в
т{ опытах появится событие Av в тщ опытах — событие А2 и т.д., в тпк
опытах — событие А,.
£
га.
п
i =1
выражается формулой
Р
п\
m j, m«,..., тп j(.; п
m1 \m2!... mk !
mk
p™>pp... p™* (4.0.2)
или
* p J
x ml,m2, ..., mk;n " *J[ 1
#msl
Если условия опытов различны, т.е. в г'-м опыте событие Aj имеет
вероятность p{j(г =1,2, ...,n;j = l,2, ..., *), то вероятность Pmi,m2,...,mjfc;n
вычисляется как коэффициент при члене, содержащем z^lz™2 ...z™* в
разложении по степеням z^, z2,..., zk производящей функции:
п
4>n(Zl,Z2> '->Zk) = Yl(PliZl + P2iZ2+~'+Pbzk)-
i=l
4.1. Прибор состоит из 10 узлов. Надежность (вероятность
безотказной работы в течение времени t) для каждого узла равна р.
Узлы выходят из строя независимо один от другого. Найти
вероятность того, что за время t а) откажет хотя бы один узел; б) отка-
71
жет ровно один узел; в) откажут ровно два узла; г) откажет не
менее двух узлов.
Ответ, а) Д110=1-д10, где q = 1 - р\ б) Plflo=cioW9 =
= 10М9; в) P2A0 = C?0p2q8=45p2q8; г) Д2|10 = 1-д10-10ОТ9 =
= l-q9(q-Wp).
4.2. Производится четыре независимых выстрела по некоторой
цели. Вероятности попадания при разных выстрелах различны и
равны: рг — 0,1; р2 = 0,2; ръ — 0,3; р4 = 0,4 Найти вероятности Р0 4;
Рх 4; Р2 4; Р3 4^ -^4,4 ни одного, одного, двух, трех, четырех
попаданий; вероятность Rx 4 хотя бы одного попадания; вероятность R2 4
не менее двух попаданий.
Решение. Производящая функция
<p4(z) = (0,9 + ОД* )(0,8 + 0,2z)(0,7 + 0,3z)(0,6 + 0,4z).
Раскрывая скобки и приводя подобные члены, имеем
Ф4(г) « 0,302 + 0,460z + 0,205z2 + 0,031z3 + 0,002z4;
откуда
P0>4 - 0,302; P1>4 - 0,460; P2 4 - 0,205;
P34 =0,031; P4 4=0,002.
*i,4 = 1 ~ Po,4 = 0,698; Д2 4 = 1 - P0>4 - P1>4 = 0,238.
4.3. Производится четыре независимых выстрела в
одинаковых условиях, причем вероятность попадания при одном выстреле
р есть средняя из четырех вероятностей предыдущей задачи:
4
Найти вероятности
р . р . р . р . р . и . и
^0,4? М,4> ^2,4' ^3,4? ^4,4? 1Ъ1,4> 1Ъ2,4*
Ответ. Pi>4 = С'р'в4"*; Р0 4 = 0,314; Рх 4 = 0,422; Р2 4 =0,212;
Р3 4 = 0,048; Р44 = 0,004; Д14 = 0,686; Д24 = 0,'264.
' 4.4*. По некоторой цели производится п независимых
выстрелов. Вероятность попадания при i-м выстреле равна р{
{г — 1, 2,..., п). При вычислении вероятности хотя бы одного
попадания различные вероятности р{ заменяют их средней
арифметической:
п
Р
п
72
Увеличится или уменьшится от такого осреднения
вероятность хотя бы одного попадания?
Решение. Точное значение R, п :
1, п
п
г=1
Приближенное (по осредненной вероятности):
/£„=1-<1-рТ=1-
п
n~J2Pi
i=l
П
п
= 1-
п
Е«
п
п
Требуется сравнить величины
п
' п
Е«<
i=l
п
п
П««и
»=1
Известно, что среднее геометрическое не равных между собой
положительных величин меньше, чем их среднее
арифметическое, следовательно,
п
п
Е«.
п
№'<±t-Iin«i<
V *=i п *=1
п
Е«.
г=1
П
n
значит, Дх 4 > Д* n ; от примененного осреднения вероятность хотя
бы одного попадания уменьшится.
4.5. Завод изготовляет изделия, каждое из которых должно
подвергаться четырем видам испытаний. Первое испытание
изделие проходит благополучно с вероятностью 0,9; второе — с
вероятностью 0,95; третье — с вероятностью 0,8 и четвертое — с
вероятностью 0,85. Найти вероятность того, что изделие пройдет
благополучно:
А — все четыре испытания;
В — ровно два испытания (из четырех);
С— не менее двух испытаний (из четырех).
Решение.
Ф4(г) = 0,00015 + 0,00565z + 0,06965z2 +
+ 0,34315z3 +0,58140z4;
73
P(A) = P4,4 = 0,58140; P(B) = P2 4 = 0,06965;
P(C) = Да> 4 = 1 - P0i 4 - Plf 4 = 0,99420.
4.6. Завод изготовляет изделия, каждое из которых с
вероятностью г (независимо от других) оказывается дефектным. При
осмотре дефект, если он имеется, обнаруживается с вероятностью р. Для
контроля из продукции завода выбирается п изделий. Найти
вероятность следующих событий:
А — ни в одном из изделий не будет обнаружено дефекта;
В — среди п изделий ровно в двух будет обнаружен дефект;
С — среди п изделий не менее чем в двух будет обнаружен
дефект.
Решение. Вероятность того, что в одном наугад взятом
изделии будет обнаружен дефект, равна рг.
Р(Л) = Р0,„ =(1-рг)»;
Р(£) = Р2,„ =Cl(pr)\l-pry-2;
Р(С) = 1 - Р0> „ - Рх „ = 1 - (1 - рг)""1 [(1 - рг) + прт].
4.7. При въезде в новую квартиру в осветительную сеть было
включено 2к новых электролампочек. Каждая электролампочка в
течение года перегорает с вероятностью г. Найти вероятность
того, что в течение года не менее половины первоначально
включенных лампочек придется заменить новыми.
Ответ.Р(Л) = 1-£рт1Й=1-2с5г"(1-г)«--.
т=0 т=0
4.8. Система противовоздушной обороны охраняет
территорию от воздушного налета, в котором принимает участие N
самолетов. Для поражения каждого из самолетов выделяется два
истребителя-перехватчика; каждый истребитель поражает цель
независимо от другого с вероятностью р. Найти вероятность того,
что во время воздушного налета будет поражено: А — ровно три
самолета; В — не менее двух самолетов.
Ответ.Р(Л)- С%[1 - (1 - p)2f(l - p)2{N~3);
Р(В) -1-(1- p)2N - N(1 - p)2{N-l)[l -(1- р)2).
4.9. По самолету производится п независимых выстрелов;
каждый из выстрелов с вероятностью рх попадает в зону, где он
поражает самолет немедленно; с вероятностью р2 попадает в
топливный бак и с вероятностью р3 не попадает в самолет вообще.
Снаряд, поразивший топливный бак, оставляет в нем пробоину, через
74
которую вытекает к литров горючего в час. Потеряв М литров
горючего, самолет становится небоеспособным. Найти вероятность
того, что через час после обстрела самолет не будет боеспособен.
Решение. В результате каждого выстрела может
произойти одно из трех событий:
Ах — самолет поражен;
А2 — пробоина в баке;
А3 — нет попадания.
Вероятности этих событий pv р2, р3. Вероятность того, что в
результате п выстрелов событие А{ произойдет т{ раз, А2 — т2 раз и
А3 — щ раз, равна
р = п]Т1
mi, ш2' Ш3> П JL JL
3 Pi
быть тп2к > М). Обозначая
Самолет может быть поражен двумя способами: или
произошло хотя бы одно попадание в зону безусловного поражения, или
не произошло ни одного попадания в эту зону, но зато самолет
выведен из строя за счет вытекания горючего (для чего должно
— = I наибольшее целое число, со-
к \
держащееся в М/к («целая часть» от числа М/к), находим
вероятность поражения самолета:
р(А) = 1-(1-Р1)"+ £ ——i!—-р^р;-».
т^й-1™2!(™-™2)!
4.10. Производится три опыта, каждый из которых
заканчивается результатом Ах с вероятностью ри, А2 — с вероятностью p2i,
А3 — с вероятностью p3i и АА — с вероятностью pAi (г = 1, 2, 3 — но-
4
мер опыта; Y^Pji — 1)- Требуется найти вероятность р того, что в
м
результате этих трех опытов событие Ах произойдет один раз,
А2 — два раза, а А3 и АА не произойдут совсем.
Написать производящую функцию и указать, коэффициент
при каком члене ее разложения будет равен искомой вероятности.
Ответ. р = рпр22р2г+ р21 р12 р2Ъ + р21 р22 рп. Производящая
функция
3
Ч>з(*1>*21^|0 = ШРЬ-*1 +PHZ2 +PziZZ +Plizi)\
»=1
75
вероятность р представляет собой коэффициент при zxz2b
разложении ф3 (z\ ? z2> zz» z4)по степеням аргументов.
4.11. Первый прибор состоит из щ узлов, второй из п2 узлов.
Каждый из приборов работал в течение времени t За это время
каждый из узлов первого прибора выходит из строя, независимо от
других, с вероятностью qv второго — с вероятностью q2. Найти
вероятность р того, что за время t в первом приборе выйдет из строя
тх узлов, а во втором — 77¾ узлов.
Ответ. p = C^q™i(l-qi)n*-miC™>q™>(l-q2)n*-m*.
4.12*. В условиях задачи 4.11 найти вероятность того, что в
первом приборе выйдет из строя больше узлов, чем во втором.
Решение. Вероятность события В — в первом приборе вышло
из строя больше узлов, чем во втором — находим по формуле
полной вероятности с гипотезами Hi — в первом приборе вышло из
строя г узлов (г = 1, 2, ...,пг).
P(Hi) = Pl%i=Ciiqi(l-qir-i;
i -1 г -1
P(B\Ht ) = £PJ2>2 = £^2(1 - в.)"1"' (i<n2+ 1),
Р(ВД) = 1(»>п2+1).
Еслип1 < п2 + 1,то
t =1 j=0
еслип1 > п2 + 1,то
п 0+1
2tx . г-1
г =1 j=0
п !
+ Е^^1-^)"1"'-
г=п2+2
4.13. Монета бросается m раз. Найти вероятность р того, что
герб появится не менее к раз и не более Z раз (к <1 <т).
[2)
[2)
i=k
г=к г=к
АЛА. Прибор, состоящий из А: узлов, работал в течение времени
t Надежность (вероятность безотказной работы) каждого узла за
время t равна р. По истечении времени t прибор выключается,
техник осматривает его и заменяет узлы, вышедшие из строя. На
замену одного узла ему требуется время т. Найти вероятность Р
76
того, что через время 2т после выключения прибор будет готов для
нормальной работы.
Решение. Для этого нужно, чтобы за время t вышло из строя
не более двух узлов:
Р = р* + jfc(i _ р)р*-' +
.-1 , *(*-!)
(1-рУр
2 к-2
4.15. Что вероятнее, выиграть у равносильного противника:
1) три партии из четырех или пять из восьми? 2) не менее трех
партий из четырех или не менее пяти партий из восьми?
Решение.
1) р»а = с\
,v*
\2)
-; ^5,8-с
(л \
8
8
[2
— —• Р > Р
Три партии из четырех выиграть более вероятно.
2) Дз>4 = С\
/r2^4 иИ
[2)
+
1
12J
_5_
16
^5,8 — ^8
(Л \
[2
8
+ с
'1\* . „7(V
8
l2j
+ cl
8
8
[2)
+
93
256
5 ^5,8 > "^3,4-
Не менее пяти партий из восьми выиграть более вероятно.
4.16. Человек, принадлежащий к определенной группе
населения, с вероятностью 0,2 оказывается брюнетом, с вероятностью
0,3 — шатеном, с вероятностью 0,4 — блондином и с вероятностью
0,1 — рыжим. Выбирается наугад группа из шести человек. Найти
вероятности следующих событий:
А — в составе группы не меньше четырех блондинов;
В — в составе группы хотя бы один рыжий;
С— в составе группы равное число блондинов и шатенов.
Решение.
Р(Л) = 1 - [0,66 + 6 • 0,4 • 0,65 + 15 • 0,42 • 0,64 ] « 0,455;
Р(В) = 1 - (1 - ОД)6 « 0,468; С = С0 + Сг + С2 + С3,
где С0 — в группе нет ни блондинов, ни шатенов;
Сх — в группе по одному блондину и шатену, а остальные — ни
то, ни другое;
С2 — в группе по два блондина и шатена, а остальные — ни то,
ни другое;
С3 — в группе по три блондина и шатена.
Р(С0) = (1-0,7)6 « 0,0007;
77
pm.) = —^—0,3 • 0,4(1 - 0,7)4 « 0,0292;
1!1!4! v '
P(C, ) =-^-0,32 -0,42(1-0,7)2 «0,1166;
2!2!2!
P(C3 ) = —0,33 -0,43 «0,0346; P(C)« 0,181.
4.17. Мишень состоит из яблока и двух колец. При одном
выстреле вероятность попадания в яблоко равна р0, в первое
кольцо — pv во второе — р2] вероятность непопадания в мишень р3. По
мишени произведено пять выстрелов. Найти вероятность того,
что они дадут два попадания в яблоко и одно — во второе кольцо.
Ответ. Р2012;5 = 2lolll2]PoPiPiP* = 30PoP2ft2-
4.18. Производится стрельба по цели тремя снарядами.
Снаряды попадают в цель независимо друг от друга. Для каждого
снаряда вероятность попадания в цель равна 0,4. Если в цель попал
один снаряд, он поражает цель (выводит ее из строя) с
вероятностью 0,3; если два снаряда — с вероятностью 0,7; если три
снаряда—с вероятностью 0,9. Найти полную вероятность поражения
цели.
Решение. ГипотезыЯ^ — в цель попало г снарядов (г = 1, 2, 3);
Р(#х) = 3-0,4-0,62 =0,432;
Р(Я2) = 3-0,42 -0,6 = 0,288;
Р(Я3 ) = 0,43 =0,064.
Событие А — поражение цели,
Р(Л) = 0,432 • 0,3 + 0,288 • 0,7 + 0,064 - 0,9 « 0,389.
4.19. Производится стрельба по цели п независимыми
выстрелами. При одном выстреле попадание в цель происходит с
вероятностью р. Если в цель попало т снарядов (ш = 1, 2,..., п), то
условная вероятность поражения цели выражается формулой
Р(А\т) = 1 - 5т , где 0 < 5 < 1.
Определить полную вероятность поражения цели.
Решение. Гипотезы Нт — попало т снарядов (т = 1, ..., n).
п п
р(а)=£р(ят )р(л\т)=52е: рт (1 - р)п~т (1 - *т )•
771=1 т=1
Упростим это выражение; так как 1 — 5° = 0, то
78
n
р(А)=^2спРт(1-рУ~т(1-$т>>
m=0
n
n
£c;rPm (l - P)n-m - J2C» (p*)m (1 - p)n~m>
T71=0
T71=0
HO
n
^C„mpm(l-p)"-m =1;
T71=0
далее, по формуле бинома
n
J2C: (ps)m (1 - p)n-m = [ps + 1 - p]n = [1 - p (1 - 5)]" ;
m=0
поэтому
P(A) = l-[l-p(l-8)]"
Этот же результат получается проще, если заметить, что
р(1- s) есть вероятность поражения цели при одном выстреле и
что из формулы Р(А\т) = 1 — $ш следует независимость
поражений цели при любом заданном числе попаданий.
4.20. Подводная лодка атакует корабль, выпуская по нему
последовательно и независимо одна от другой п торпед. Каждая
торпеда попадает в корабль с вероятностью р. Каждая попавшая в
корабль торпеда с одинаковой вероятностью попадает в любой из к
отсеков, на которые разделена подводная часть корабля. Торпеда,
попавшая в отсек, приводит к его заполнению водой. Корабль идет
ко дну, если водой заполнено не менее двух отсеков. Найти
вероятность того, что корабль будет затоплен.
Решение. Эту задачу удобно решать по формуле полной
вероятности с гипотезами Нт — в корабль попало т торпед
(т = 1,2, ..., п).
?{нт)=рт,п =с:Рт(1-Ру
■т
Найдем Р(А\Нт ). По условию Р(А\Н1) = 0. При т > 2
попавших торпедах корабль не затопляется, только если все торпеды
попали в один отсек; следовательно,
Р(А\Нт ) = 1-к
= i
к
т—1
[гп >2).
Полная вероятность потопления корабля:
п
\>{A)=Y,c:pm(\-py
m
m=2
m—1
79
4.21. В течение времени t эксплуатируется iV приборов.
Каждый из приборов имеет надежность р и выходит из строя
независимо от других. Найти вероятность Р(А) того, что мастер,
вызванный по окончании времени t для ремонта неисправных приборов,
не справится со своей задачей за время т, если на ремонт каждого
из неисправных приборов ему требуется время т0.
Решение. Событие А равносильно тому, что число
вышедших из строя приборов больше чем I -
наибольшее целое число, заключенное в
Р(А)
т=1+\
р)
Т
то.
, где
т
то.
обозначает
т
то'
т
Р
-771
•
4.22. Имеется iVнеисправных приборов, которые подвергаются
испытаниям (тестам) с целью локализации неисправности.
Каждый тест независимо от других с вероятностью р приводит к
локализации неисправности. Если неисправность локализована,
прибор передается на ремонтную станцию, а обследованию
подвергаются другие приборы. Если во всех N приборах неисправность
локализована, то тесты прекращаются. Всего имеется
возможность произвести п тестов {п > N). Найти вероятность того, что
неисправности во всех JV приборах будут локализованы.
Решение. А — все неисправности локализованы.
Противоположное событие А означает, что при п опытах (тестах) событие,
состоящее в том, что неисправность локализована, появилось
менее iVpa3.
Р(А) = 1
N-1
171=0
трт(1-р)П
■т
п
ИЛИ
п
р(а)= yc:Pm(i-p)n
m=N
■т
4.23. В условиях предыдущей задачи найти вероятность того,
что в результате п тестов среди N неисправных приборов
останется не менее к приборов с нелокализованными неисправностями
(* < N).
80
Решение. Задача равносильна следующей: найти
вероятность того, что при п тестах будут локализованы неисправности
не больше чем в N— к приборах.
p(A)=j2c:Pm(i-Py-m.
m=0
4.24*. Происходит соревнование между к стрелками; каждый
из них делает п выстрелов по своей мишени. Вероятность
попадания в мишень при одном выстреле для г-го стрелка равна
pt (г = 1, ..., п). Выигрывает соревнование тот из стрелков,
который будет иметь больше попаданий, чем остальные. Найти
вероятность того, что среди соревнующихся стрелков будет один
(только один), выигравший соревнование.
Решение. Таким одним может быть любой из к стрелков.
Найдем вероятность того, что г-й стрелок выиграет соревнование
(событие Аг). Это событие может произойти следующими
способами:
А\т^ — г-й стрелок получил ровно га попаданий, а каждый из
остальных — не более чем пот -1 (га = 1,..., п).
Вероятность того, что г-й стрелок получил га попаданий, равна
^т,п(0 = СГ PTQi~m > ГДе Qi =^-Pi- Обозначим вероятность
того, что j-й стрелок получил не более га — 1 попаданий, через
т—1
Tm{j) = Y,cnPsflr (™>!)-
5=0
Тогда вероятность того, что все остальные стрелки, кроме г-го,
получили не более га — 1 попаданий, равна
Тт (1)Гт (2)... Тт (i - 1)Тт (i + 1)... Тт (к) = ЦТт (j).
Суммируя полученные вероятности для всех Значений т,
получим вероятность того, что г-й стрелок в единственном числе
выигрывает соревнование:
Р(Л,)=£Рга1„(0ПГт(Ж<= 1.2, -..,*).
га=1 у*г
Суммируя эти вероятности для всех стрелков, получим
г=1 i=l m=l j^i
4.25. В урне имеется к шаров; каждый из них с вероятностью
1/2 (независимо от других) может оказаться белым или черным.
Из урны вынимается п раз по одному шару, причем вынутый шар
81
каждый раз возвращается обратно, и шары перемешиваются.
Среди вынутых п шаров га оказались белыми (0 < га < п). Определить
вероятность того, что среди к шаров урны ровно / белых.
Решение. Решаем задачу по формуле Бейеса. Гипотезы: Н1 —
в урне / белых шаров и к — I черных (/ = 1, ..., к — 1). До опыта
Р(Я;) = с[
V
[2,
к
Событие А — среди п вынутых шаров оказалось ровно те
белых.
p(a\h1)=c: i
m
<к,
т
(
1 -
v
п
к)
п —т
После опыта вероятность гипотезы Н{.
P(Ht\A)
С[
(Г
к,
m , 7\
1--
к)
П —171
к-\
Т. с!
(i \m (
i=\
<к j
п—тп
1-
к)
С[Г{к-1)п
•тп
j2ciim(k-i)n-m
4.26. Производится стрельба пятью снарядами по группе,
состоящей из трех целей. Обстрел ведется в следующем порядке:
сначала обстреливается первая цель и огонь по ней ведется до тех
пор, пока она не будет поражена или не кончатся все пять
снарядов. Если первая цель поражена, огонь переносится на вторую, и
т.д. Вероятность поражения цели после одного выстрела равна р.
Найти вероятности: Р0, Рх, Р2, Р3 того, что будет поражено 0
целей, 1 цель, 2 цели, 3 цели в составе группы.
Решение. Для того чтобы не было поражено ни одной цели,
нужно, чтобы ни один снаряд не поразил цели, по которой он
направлен: Р0 = (1 — р)ъ.
Чтобы была поражена ровно одна цель, нужно, чтобы из пяти
выстрелов только один поразил цель, по которой он направлен, а
остальные — не поразили: Рг = С\р1 (1 — р)4 = Ър (1 — р)4.
Аналогично Р2 = C5V(1 - pf = 10р2(1 - pf.
Так как события, вероятности которых обозначены Р0, Рг, Р2,
Р3, несовместны и образуют полную группу, то
Р3 = 1 - (Р0 + Рг + Р2) = 1 - (1 - pf (1 + Зр + 6р2).
4.27. Та же задача, но число целей N, число выстрелов;
п (п > N) найти вероятности Р0, Рг,..., PN того, что будут
поражены 0 целей, 1 цель, ..., Уцелей.
82
Ответ. Р0 =(1-р)п;Рг = пр(1- р)
п-\.
, ... ,
Рк=Скпрк(1-р)п-* (k<N); iV=l-2c*p*(l-p)"-*.
к=0
4.28. В условиях предыдущей задачи обстрел целей ведется не
в порядке номеров, а в случайном порядке, причем каждый
выстрел случайным образом направляется на любую до сих пор не
пораженную цель. Найти Р0, Рг,..., PN.
Ответ. Тот же, что и в задаче 4.27.
4.29*. Производится стрельба п снарядами по группе из N
целей (N < п). Каждый выстрел с одинаковой вероятностью
направляется на любую из N целей (безотносительно к тому, поражена
она предыдущими выстрелами или нет). Каждый выстрел сражает
непораженную цель, по которой он направлен, с вероятностью р.
Снаряд, выпущенный по уже пораженной цели, не меняет ее
состояния. Найти вероятность того, что в составе группы будет
поражено к целей (к = О,1,..., N).
Решение. Вероятность Рк поражения к целей из N найдем по
формуле полной вероятности. Введем гипотезу (nl,n2l ...,nN):
по первой цели пришлось nt выстрелов, по второй п2, ..., по ЛГ-й —
N
%,причем У2п1 —п-
i=i
При этой гипотезе условная вероятность Рк,п п п
поражения Уцелей из N равна коэффициенту при z в разложении по
степеням z производящей функции
N
ФЛГ(г;п15п25...,пя) = Y[(<li + Piz)>
i=i
где Pi = 1 — (1 — pYl есть вероятность поражения /-Й цели за щ
выстрелов, qx — 1 — рх = (1 — р)щ •
Вероятность гипотезы (пг, п2, ..., nN) находим тем же
способом, каким находили вероятность того, что п шариков
распределяется определенным образом по N лункам (см. задачу 1.45):
Р\п1 )^2' *•• ' nN ) ''
п^.п^.... nN\ Nn
Вероятность Рк по формуле полной вероятности равна
ni\n2l..nN\Nn fcl"i- "2,- »jv '
где сумма распространяется на все возможные способы разбиения
числа пна./Vслагаемых: пх, п2, ..., nN (О < п1 < га; I = 1, ..., N).
83
4.30. В условиях задачи 4.29 написать формулы для Рк при
n=5,N = 2.
OTBeT.P0=qs;P1=l[(l-q)*+5q(l-2qt+q3) +
+10g2(l - 2g3 + ?)] = ^[(1 + 9)5 - 32g5];
16
P2=^-[5(l-q)(l-q4) + 10(l-q2)(l-q3)};q = l-P.
25
4.31. Имеется TV лунок, по которым случайным образом
разбрасываются М шариков. Найти вероятность р того, что в данную
(вполне определенную, например, первую) лунку попадет ровно к
шариков.
Решение. Рассмотрим М бросаний шариков как М
независимых опытов, каждый из которых с вероятностью 1/N
заканчивается попаданием в данную лунку; тогда
V
с
м
Я,
к
{ N )
ГЛАВА 5
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ.
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ВЕЛИЧИН
Случайной величиной называется величина, которая в результате
опыта может принять то или иное значение, неизвестно заранее, какое
именно.
Дискретной (прерывной) случайной величиной называется случайная
величина, принимающая отделенные друг от друга значения, которые
можно перенумеровать.
Непрерывной случайной величиной (в широком смысле слова)
называется случайная величина, возможные значения которой непрерывно
заполняют какой-то промежуток.
Законом распределения случайной величины называется всякое
соотношение, устанавливающее связь между возможными значениями
случайной величины и соответствующими им вероятностями. Закон
распределения может иметь разные формы.
Ряд распределения
Рядом распределения дискретной случайной величины X называется
таблица, где перечислены возможные (различные) значения этой
случайной величины Xj, ж2,..., жп с соответствующими им вероятностями
Р\) Vl ч •••Рп'
п
, где Pi = Р(Х = х{); ]П р. = 1.
i =1
Графическое изображение ряда распределения (рис. 5.0.1) называется
многоугольником распределения.
Функция распределения
Функцией распределения случайной величины X называется функция
F (х), выражающая вероятность того, что X примет значение, меньшее
чем х:
F(x) = P(X <х).
Xi
Pi
Xi
Pi
Xi
Pi
• • •
• • •
xn
Pn
85
Рис. 5.0.1
Функция F (х) есть неубывающая
функция; F(-oo) = 0,F(+oo) = 1.
Для дискретных случайных величин
функция распределения есть
разрывная ступенчатая функция, непрерывная
слева.
Если функция распределения F (х)
везде непрерывна и имеет производную,
случайная величина называется
непрерывной в узком смысле слова или просто
непрерывной.
Если функция распределения F (х) на некоторых участках
непрерывна, а в отдельных точках имеет разрывы, случайная величина называется
смешанной.
Плотность распределения
Плотностью распределения непрерывной (в узком смысле слова)
случайной величины называется функция f(x) — F'(x).
Плотность распределения любой случайной величины
неотрицательна, f(x) > 0, и обладает свойством
оо
/ f(x) dx = 1.
—оо
График плотности f(x) называется кривой распределения.
Элементом вероятности для случайной величины X называется
величина f(x) dx, приближенно выражающая вероятность попадания
случайной точки X в элементарный отрезок dx, примыкающий к точке х.
Функция распределения F (х) выражается через плотность
распределения формулой
F(x) = -J f{x) dx.
—оо
Вероятность попадания случайной величины X на участок от а до (3
(включая а) выражается формулой
Р(а <Х <(3) = F((3)-F(a).
Если случайная величина :г непрерывна, то Р(Х = а) = 0 и
Р(а <X<(3) = F((3)-F(a).
Вероятность попадания на участок от а до (3 для непрерывной
случайной величины выражается формулой
Р(а <Х < (3) = f f{x) dx.
о.
86
Математическим ожиданием случайной величины X называется ее
среднее значение, вычисляемое по формулам:
п
М [X] = ^ х{ р{ — для дискретной случайной величины;
i =1
оо
М [X] = I xf(x) dx — для непрерывной случайной величины.
— 00
Для смешанной случайной величины математическое ожидание
выражается суммой двух слагаемых:
М[Х] = 5>,.р,. + fxF'(x)dx,
(н)
где сумма распространяется на все точки разрыва функции
распределения, а интеграл — на все участки ее непрерывности.
В некоторых случаях М[Х] будем обозначать строчной буквой с
индексом
М[Х] = тх.
- Центрированной случайной величиной называется разность между
случайной величиной Хи ее математическим ожиданием:
о
X = X — т
X'
Дисперсией случайной величины X называется математическое
ожидание квадрата соответствующей центрированной случайной величины:
В[Х]=М[Х2].
Дисперсия вычисляется по формулам:
п
D [X] = ]Р (х{ — тх)2 pt — для дискретной случайной величины;
00
D[X] = I (х — mx)2f(x) dx — для непрерывной случайной величины;
— 00
D[X] = ^2 (xi ~ mx)2Pi + / (х ~~ mx)2F'(x) dx — для смешанной
(н)
случайной величины.
Дисперсия D [X] кратко обозначается Dx.
Средним квадратическим отклонением случайной величины X
называется корень квадратный из дисперсии
Начальным моментом k-го порядка случайной величины X называется
математическое ожидание к-й степени этой случайной величины:
*к[Х] = М[Хк].
87
Для дискретной, непрерывной и смешанной случайной величины
а к[Х] вычисляется соответственно по формулам
cck[X] = J2x*Pi, сск[Х]= fxkf(x)dx,
»' =1 -00
ak[X] = ^xkPi + JxkF'{x)dx.
(н)
Центральным моментом к-го порядка случайной величины X
называется математическое ожидание к-й степени центрированной случайной
о
величины X:
»к{Х} = М[Хк].
Вычислительные формулы дляц^Х]:
п
1=1
00
Мч-РП =/(^- mi)VW dx,
— 00
(н)
Математическое ожидание случайной величины X есть ее первый
начальный момент, а дисперсия — второй центральный:
М[Х]^а1[Х}] D[X] = v.2[X].
Второй и третий центральные моменты выражаются через начальные
формулами
щЭД = a3[Jf] - 3raxa2[X] + 2га*.
Дискретная случайная величина X называется распределенной по
биномиальному закону, если ее возможные значения 0,1,..., п, а вероятность
того, что X = т, выражается формулой
■т
?{Х = т) = Рт,п =С?ртдп-
где
О < р < 1; g = 1 — р.
Математическое ожидание случайной величины Х} распределенной
по биномиальному закону, равно тх — пр, а дисперсия Dx — npq.
88
Дискретная случайная величина X называется распределенной по
закону Пуассона, если ее возможные значения 0,1,2,..., т, ..., а вероятность
того, что X = т, выражается формулой
т
Р(Х = т) = Рт = 2-е-,
т !
где а > О — параметр закона Пуассона.
Математическое ожидание и дисперсия случайной величины X,
распределенной по закону Пуассона, равны параметру закона а: тх = а;
Dx = a.
Потоком событий называется последовательность событий,
наступающих одно за другим в случайные моменты времени.
Плотностью (интенсивностью) потока называется среднее число
событий в единицу времени.
Поток событий называется потоком без последействия, если
вероятность появления на любом участке времени того или иного числа
событий не зависит от того, какое число событий попало на другие, не
пересекающиеся с данным участки.
Поток событий называется ординарным, если вероятность появления
на элементарном участке Лt двух или более событий пренебрежимо мала
по сравнению с вероятностью появления одного события.
Ординарный поток событий без последействия называется пуассонов-
ским.
Если события образуют пуассоновский поток, то число событий,
попадающих на любой участок времени (¾, ^ 4- т), распределено по закону
Пуассона:
711 ■ '
т !
где а — математическое ожидание числа точек, попадающих на участок:
а = I \(t) dt, \(t) — плотность потока.
to
Если \(t) = const, пуассоновский поток называется «стационарным
пуассоновским» или простейшим потоком.
Для простейшего потока число событий, попадающих на любой
участок длины т, распределено по закону Пуассона с параметром а = \т.
Расстояние Т между двумя соседними событиями в простейшем
потоке есть непрерывная случайная величина, распределенная по
показательному закону, с плотностью
О при t < О,
Xe"Xi при t > 0.
Л*) =
89
Для случайной величины Т, распределенной по показательному зако-
1 п 1
ну,™* = ^ A =-^-.
Случайным полем точек называется совокупность точек, случайным
образом распределенных на плоскости (в пространстве).
Плотностью поля называется среднее число точек, попадающих на
единицу площади (объема).
Если плотность поля постоянна, оно называется равномерным.
Поле точек называется пуассоновским, если оно обладает свойствами:
1. Вероятность появления того или другого числа точек в любой
области плоскости (пространства) не зависит от того, сколько точек попало
в любые области, не пересекающиеся с данной;
2. Вероятность попадания в элементарную область двух или более
точек пренебрежимо мала по сравнению с вероятностью попадания одной
точки.
Число точек пуассоновского поля, попадающих в любую область S
плоскости (пространства), распределено по закону Пуассона:
т
Р =— е-
т !
где а — математическое ожидание числа точек, попадающих в область S.
Если поле равномерно и имеет плотность X, то а — sX, где s — площадь
(объем) области S.
Если поле неравномерно, то
а — II \ (х, у) dx dy (для плоскости),
(S)
а = 11 I X (#, у, z) dx dy dz (для пространства).
(S)
Для вычислений, связанных с распределением Пуассона, применяют-
т т к
ся таблицы функций Р(т, а) = —е~а и R(m, а) = V] — е~а. Таблица
т i
1 ;—п п> -
к=0
функции Q (т, а) — 1 — R (т, а) дана в прил. 1 (табл. 1).
Непрерывная случайная величина X называется равномерно
распределенной в интервале (а, (3), если ее плотность распределения в этом
интервале постоянна:
/(*) =
при а?€(а,р),
р — а
О при х ¢ (а, (3),
где запись х е (а, (3) означает: «х лежит на участке от а до (3», а х ¢ (а, (3)
означает: «хне лежит на участке от а до (3».
Математическое ожидание и дисперсия случайной величины, распре-
деленноиравномернонаучастке (а, Нравны™, = —;D, = -^-.
90
Непрерывная случайная величина X называется распределенной по
нормальному закону, если ее плотность распределения равна
(х—т)
ау2тс
2а'
Математическое ожидание случайной величины X, распределенной
по нормальному закону, равно тх = т, а дисперсия Dx = or2.
Вероятность попадания случайной величины X, распределенной по
нормальному закону, в интервал (а, (3) выражается формулой
(п \ (
р — т '
Р(а <Х<(3) = Ф5
а
Ф:
а — т
а
X
гдеФ* (х) — —== I е 2 <ft— табулированная функция (см. прил. 1 табл. 2).
V2ir J
—оо
5.1. Может ли при каком-либо значении аргумента быть:
1) Функция распределения больше единицы?
2) Плотность распределения больше единицы?
3) Функция распределения отрицательной?
4) Плотность распределения отрицательной?
Ответ: 1) нет; 2) да; 3) нет; 4) нет.
5.2. Какова размерность: 1) функции распределения; 2)
плотности распределения; 3) математического ожидания; 4)
дисперсии; 5) среднего квадратического отклонения; 6) третьего
начального момента?
Ответ. 1) Безразмерна; 2) обратная размерности случайной
величины; 3) размерность случайной величины; 4) размерность
квадрата случайной величины; 5) размерность случайной
величины; 6) размерность куба случайной величины.
5.3. Рассматривая неслучайную величину а как частный вид
случайной, построить для нее функцию распределения, найти для
нее математическое ожидание, дисперсию и третий начальный
момент.
0 при х < а, з
1 гт™ ^ Ma =а; Da =0; а3[а] = а .
1 при х > а.
Ответ. F(x) =
5.4. Дан график плотности
распределения f(x) случайной величины X
(рис. 5.4). Как изменится этот график,
если: а) прибавить к случайной
величине 1; б) вычесть из случайной
величины 2; в) умножить случайную величину
на 2; г) изменить знак величины на
обратный?
х
Рис. 5.4
91
Рис. 5.5
Ответ, а) Сдвинется влево на 1; б) сдвинется вправо на 2;
в) масштаб по оси абсцисс удвоится, а по оси ординат уменьшится
вдвое; г) график переменится на свое зеркальное отражение
относительно оси ординат.
5.5. Дан график функции
распределения F(x) случайной величины X (рис. 5.5).
Как изменится этот график, если: а)
прибавить к случайной величине 1; б) вычесть
из случайной величины 2; в) умножить
случайную величину на 2; г) изменить
знак случайной величины на обратный?
Ответ, а) Сдвинется влево на 1;
б) сдвинется вправо на 2; в) масштаб по
оси абсцисс удвоится; г) график нужно
зеркально отразить относительно оси
ординат и каждую ординату вычесть из единицы.
5.6. К случайной величине X прибавили постоянную,
неслучайную величину а. Как от этого изменятся ее характеристики:
1) математическое ожидание; 2) дисперсия; 3) среднее
квадратическое отклонение; 4) второй начальный момент?
Ответ. 1) Прибавится слагаемое а; 2) не изменится; 3) не
изменится; 4) прибавится слагаемое а2 +2атх (так как а2[Х] =
= Dx+m2x).
5.7. Случайную величину Xумножили на а. Как от этого
изменятся ее характеристики: 1) математическое ожидание; 2)
дисперсия; 3) среднее квадратическое отклонение; 4) второй начальный
момент?
Ответ. 1) Умножится на а; 2) умножится на а ; 3) умножится
на \а\; 4) умножится на а .
5.8. Производится один опыт, в результате которого может
появиться или не появиться событие А; вероятность события А
равна р. Рассматривается случайная величина Х7 равная единице,
если событие А произошло, и нулю, если не произошло (число
появлений события А в данном опыте). Построить ряд
распределения случайной величины Хи ее функцию распределения, найти ее
м. о., дисперсию, второй начальный момент, третий центральный
момент.
Ответ. Ряд распределения:
, где q = 1 - р.
xi
Pi
0
ч
1
р
Функция распределения F(x) представлена на рис. 5.8.
92
а2[Х] = 02.<? + 12.р = р;
Dx=oi2[X]-mx =р- р =p(l-p) = pg;
■Р).
|i3[^] = (0-рГ9 + (1-рГр = Р9 (9
5.9. Производится три независимых опыта, в
каждом из которых событие А появляется с
вероятностью 0,4. Рассматривается случайная
величина X — число появлений
события А в трех опытах.
Построить ряд распределения и
функцию распределения случайной
величины X. Найти ее
математическое ожидание тх, дисперсию Dx>
среднее квадратическое отклонение
1
я
0
F(x)
т
1
,. А
V
l
l
l
1
Рис. 5.8
0,936
0,648
0,216
их и третий центральный момент
Ответ. Ряд распределения:
xi
Pi
0
0,216
1
0,432
2
0,288
3
0,064
X
X
Функция распределения показана на рис. 5.9; т^ = 1,2;
Л, = 0,72; а, =0,85; ii3[X] = 0,144
5.10. Монета подбрасывается п раз; рассматривается
случайная величина X — число выпавших гербов. Построить ряд
распределения этой случайной величины и найти ее характеристики:
™x,Dx,ox,[i3[X}.
Ответ.
х.
т
Р
т
о
1
с\
т
С
т
п
(л \
v2,
П
П
(t\n
v2,
71 п п
m« = -; A* =-7; G
x
4n
; ^з [X] = 0 (так как распределение
симметрично относительно га
п
х
)■
5.11. Производится п независимых опытов, в каждом из
которых с вероятностью р появляется событие А. Написать ряд
распределения случайной величины X — числа появлений противо-
93
положного А события А в п опытах — и найти ее математическое
ожидание и дисперсию.
Ответ.
%т
Рт
0
п
Р
1
СпЯР
• • •
771
>ог m^TTin— m
49^
• * •
n
n
9
гдед = 1 - p; шг = nq\ Dx = npq.
5.12. Производится n независимых опытов, в каждом из
которых с вероятностью р появляется событие А. Рассматривается
случайная величина R — частота появления события А в п опытах,
т.е. отношение числа появления события А в п опытах к общему
числу произведенных опытов п. Написать ряд распределения этой
случайной величины; найти ее математическое ожидание и
дисперсию.
Ответ.
%т
Рт
0
qn
1
п
Lnpq
• • •
т
п
/~1ТП „77* П— ТП
СпР Я
• • •
• • #
1
р
гдед
р; ™* = р; А* =
Р9
п
5.13*. Производится п независимых выстрелов по мишени.
Вероятность попадания при каждом выстреле равна р. Определить
наивероятнейшее число попаданий в мишень га*.
Решение. Рассмотрим, при каком условии га* = 0. Если
т*=:0,тодп > C\pq
п 1 или q > пр, откуда р <
п + 1
п-\
П
Еслига* = п,торп > Clnqp" А или р > nq, откуда— р >
п + 1
Рассмотрим случай, когда 0 < т* < п; в этом случае должны
выполняться совместно два неравенства
тп* „ га* га—га*
п Р Q
\ /im*+l ,^га*+1 га — га*— 1
>W Р 9
i * <т *
Cm" „т* „ п—т* \ /-* т*— 1 ^ т*— 1 _ га — т*+1
n Р Q >Спр q
Эти два неравенства эквивалентны следующим:
(га * + 1)# > (п — га*)р, (п — т * + 1)р > га * #,
94
откуда га* должно быть целым числом, удовлетворяющим
неравенству
(п + 1)р - 1 < га* < (n + 1)р.
Можно убедиться в том, что это неравенство выполняется и в
1 п
случае р < (га* = 0) и в другом крайнем случае: р >
га + 1 я+1
{т*=п).
Поскольку правая часть неравенства на единицу больше левой,
то между ними лежит только одно целое число га*; исключение
составляет только случай, когда (га + 1)р — целое. В этом случае
имеется два наивероятнейших числа попаданий: (n + 1)р и
(п 4- 1)р — 1. Если пр — целое число, то га* = пр, т.е. наивероят-
нейшее значение числа попаданий в мишень равно его
математическому ожиданию.
5.14. Два стрелка стреляют каждый по своей мишени, делая
независимо друг от друга по одному выстрелу. Вероятность
попадания в мишень для первого стрелка pv для второго р2.
Рассматриваются две случайные величины:
Х{ — число попаданий первого стрелка;
Х2 — число попаданий второго стрелка
и их разность
Z/ — Л. л — л. 2 •
Построить ряд распределения случайной величины Z и найти
ее характеристики т2 и Dz.
Решение. Случайная величина Z имеет три возможных
значения: -1, 0 и +1.
P(Z = -l) = P(X1=0)P(X2=+l) = g1p2;
P(Z = 0) = Р(Х, = 0) Р(Х2 = 0) + Р(Х, = 1) Р(Х2
= 9i92 + PiP2;
P(Z = l) = P(X1=l)P(X2=0) = p1q2>
meq1 =1 -рх; q2 =l-p2.
Ряд распределения величины Z имеет вид
1)
zi
Pi
-1
Q1P2
0
QiQ2 + P1P2
1
Р\Ь
^1 = (-1)9^2 +%i92 +PiP2) + 1Pi92 =-?iP2 + Pi?2 =Pi ~ P2-
95
Дисперсию находим через второй начальный момент:
<*2[Z} = (-1)2 •qlV2 +02 -(qiq2 +^^) + 12 'pxq2 =
= QiP2 + P1Q2 = Pi + P2 ~ 2PiP2\
Dz =а2^]-тг =Pi + P2 ~2PlP2 ~ (Pi -P2)2 =Pl«l +^2^2-
5.15. Производится ряд независимых опытов, в каждом из
которых может появиться некоторое событие А. Вероятность
события А в каждом опыте равна р. Опыты производятся до первого
появления события А, после чего они прекращаются. Случайная
величина X — число произведенных опытов. Построить ряд
распределения этой случайной величины и найти ее
характеристики — математическое ожидание и дисперсию.
Решение. Ряд распределения имеет вид
xi
Pi
1
р
2
qp
3
q2p
* • •
• • •
г
дг~1р
т 9 •
где q = 1 - р.
оо
га
\р + 2qp + 3g2p +..• iql lp + ... = рУ^гд
г-1
t=l
00
Замечаем, что ряд V^ гдг г представляет собой результат диф-
9 .
г=0
ференцирования геометрической прогрессии V\г = —
г=1 1
оо
г=1
г-1
dg
f 00 l
U=i J
_ d
dq
q
Л-я,
(1-9)
2 ^2
P
,(1)
P 1
^=-7 = -
P P
Дисперсию определяем через второй начальный момент:
оо
оо
оо
а2[^1=1^ Pi = Х/ 9* 1Р = рХ]<29
2_ г-1
г=1
г=1
г=1
96
mj
Для вычисления суммы ряда Y^i qг 1 умножим ряд (1) на q и
г=1
продифференцируем по q:
00
г 9 -
г=1
d_
dq
а-?)'
(1-9)1
Умножая на р = 1 — g, получим
<*2(*)
1 + g
(1-9)"
Dx = <*-2{X)-m
2
1 + g 1_
{l-qf (1-q)
P
Полученное распределение можно связать с распределением
Паскаля:
P(Y = k) = qkp (к = 0,1,2,...)
с характеристиками: га = —; Dy = —. Легко видеть, что случайная
Р р2
величина X выражается через Y следующим образом: X = Y + 1.
Распределение случайной величины X можно назвать «сдвинутым
на 1 распределением Паскаля».
5.16. Производится два независимых выстрела по мишени.
Вероятность попадания при каждом выстреле равна р.
Рассматриваются случайные величины:
X — разность между числом попаданий и числом промахов;
Y— сумма числа попаданий и числа промахов.
Построить для каждой из случайных величин X, Уряд
распределения. Найти их характеристики: тх, Dx,my , Dy.
Решение. Ряд распределения величины X имеет вид
Хг
Pi
-2
t
0
2pq
2
Р2
meq = 1- р.
т
<2q2+2p2=2(p-q); а2[Х] = 4(q2 + р2);
Dx =a2[^]- Ш
2
х
Spq.
Случайная величина Y фактически не случайна и имеет одно
значение 2; ее ряд распределения:
97
Vi
Pi
•my =2; Dy = 0.
5.17. В нашем распоряжении имеется п лампочек; каждая из
них с вероятностью р имеет дефект. Лампочку ввинчивают в
патрон и подают напряжение; после чего дефектная лампочка сразу
же перегорает и заменяется другой.
Рассматривается случайная величина X — число лампочек,
которое будет испробовано. Построить ее ряд распределения и
найти математическое ожидание тх.
Решение. Ряд распределения величины X
Хг
Pi
1
q
2
pq
3
p2q
* • •
г
p'-'q
• • •
• • w
n
P
гдед
P-
d
n-\
Е- г —1 i n —1
ip q + np =q —
i-i dP
P
П
P J
+ np
n-\
P
n
P
5.18. Случайная величина X подчинена закону Пуассона с
математическим ожиданием а = 3. Построить многоугольник
распределения и функцию распределения случайной величины X.
Найти: а) вероятность того, что случайная величина X примет
значение меньшее, чем ее математическое ожидание; б) вероятность
того, что величина X примет положительное значение.
Ответ: а) 0,423; б) 0,950.
5.19. Поток заявок, поступающих на телефонную станцию,
представляет собой простейший (стационарный пуассоновский)
поток. Математическое ожидание числа вызовов за час равно 30.
Найти вероятность того, что за минуту поступит не менее двух
вызовов.
Ответ: 0,0902.
5.20. При работе электронной вычислительной машины время
от времени возникают неисправности (сбои). Поток сбоев можно
считать простейшим. Среднее число сбоев за сутки равно 1,5.
Найти вероятности следующих событий:
А — за двое суток не будет ни одного сбоя;
В — в течение суток произойдет хотя бы один сбой;
С— за неделю работы машины произойдет не менее трех сбоев.
Ответ. Р(Л) = 0,050; Р(5) = 0,777; Р(С) = 0,998.
98
5.21. При заданном положении точки разрыва снаряда цель
оказывается накрыта пуассоновским полем осколков с
плотностью X = 2,5 [оск./м ]. Площадь проекции цели на плоскость, на
которой наблюдается осколочное поле, равна 5=0,8 [м ]. Каждый
осколок, попавший в цель, поражает ее с полной достоверностью.
Найти вероятность того, что цель будет поражена.
Ответ. 0,865.
5.22. Та же задача, но каждый осколок, попавший в цель,
поражает ее не с полной достоверностью, а с вероятностью 0,6.
Решение. Рассмотрим вместо заданного поля осколков «поле
поражающих осколков» с плотностью Х*=Х -0,6 = 1,5 [пор. оск./м ].
Математическое ожидание числа поражающих осколков, попавших
в цель, будет а* = X* s = 1,2 [пор. оск.]; отсюда вероятность
поражения
Rx = 1 - е"а* = 1 - 0,301 = 0,699.
Другое решение: по формуле полной вероятности с гипотезами Нт — в
m
цель попало т осколков (т = 1,2, ...). Р(#т) = Рт = —е~а, а = \s = 2.
т !
А - поражение цели,Р(Л|#т) = 1 - (1 - 0,6)т;
р(А)=f2Pm [i-(i- о?б)- ]=1 - р0 - х:[fl(1 °;6)Г е-° =
= 1 - е-аеа(1-°'6) = 1 - е"1'2 = 0,699.
5.23. Электронная лампа работает исправно в течение случай
ного времени Г, распределенного по показательному закону:
/(О
0 при t < 0,
р,е~м при t > 0.
По истечении времени Г лампа выходит из строя, после чего ее
немедленно заменяют новой. Найти вероятность того, что за
время т: а) лампу не придется заменять; б) лампу придется заменять
ровно три раза; в) лампу придется заменять не менее трех раз.
Решение. Отказы ламп образуют простейший поток с
плотностью [L. Математическое ожидание числа отказов X за время т
равно а = [iT.
а)Р0=е-^; б)Р3=^-е^т;
в) А, = 1 - [Р0 + Рг + Р2] = 1 - е~^ [1 - цт - ±(рт)2].
99
5.24. Техническое устройство состоит из трех узлов; в первом
узле щ элементов, во втором п2 элементов, в третьем щ элементов.
Первый узел безусловно необходим для работы устройства;
второй и третий дублируют друг друга. Время исправной работы
каждого элемента распределено по показательному закону; среднее
время работы элемента, входящего в первый узел, равно t[lJ, во
ср
второй или третий узлы — t[*K Первый узел выходит из строя,
если в нем отказало не менее двух элементов; второй узел (так же,
как и дублирующий его третий) выходит из строя при отказе хотя
бы одного элемента. Для выхода из строя устройства в целом
достаточно, чтобы отказал первый узел или второй и третий вместе.
Найти вероятность того, что за время т устройство выйдет из
строя.
Решение. Вероятность выхода из строя одного элемента
первого, второго или третьего узлов за время т равна
соответственно
Pi
ехр
t
(1)
ср
р>
Рз
ехр
t
(2)
ср
гдеехрх = е .
Вероятность выхода из строя первого узла за время т:
Рг = Д2, „, = 1 - (1 - Pi Г' - »iPi(l - Pi)"1"1-
Вероятности выхода из строя второго и третьего узлов:
Р2=1-(1-р2)"*; Р3=1-(1-РзГ3-
Вероятность выхода из строя всего устройства:
Р = ^+(1-^)^3-
5.25. Искусственный спутник земли, движущийся по своей
орбите в течение п суток, может случайным образом сталкиваться с
метеоритами. Метеориты, пересекающие орбиту и
сталкивающиеся со спутником, образуют пуассоновский поток с плотностью х
(метеоритов в сутки). Метеорит, попавший в спутник, пробивает
его оболочку с вероятностью р0. Метеорит, пробивший оболочку, с
вероятностью р1 выводит из строя аппаратуру спутника. Найти
вероятности следующих событий:
А — за время полета спутника его оболочка будет пробита;
В — за время полета спутника его аппаратура будет выведена
из строя;
С — за время полета спутника будет пробита только оболочка
спутника, а аппаратура будет действовать.
100
Решение. Математическое ожидание числа метеоритов,
пробивающих оболочку: а0 = хпРо- Математическое ожидание числа
метеоритов, пробивающих оболочку и поражающих аппаратуру:
a^xnPiPo-
Р(Л) = 1-е~а° =1-е-хпр0]
Р(5) = 1-е"а1 = 1 - e"XWl;
Р(С) = Р(Л) - Р(В) = е-хпр°р* - е-хпр°.
5.26. Число атак истребителей, которым может подвергнуться
бомбардировщик над территорией противника, есть случайная
величина, распределенная по закону Пуассона с математическим
ожиданием а = 3. Каждая атака с вероятностью 0,4 заканчивается
поражением бомбардировщика. Определить: а) вероятность
поражения бомбардировщика; б) ту же вероятность, если число атак
истребителей — не случайная величина и в точности равна трем.
О т в е т. а) 0,699; б) 0,784.
5.27. При работе некоторого прибора в случайные моменты
времени возникают неисправности. Время Т работы прибора от
его включения до возникновения неисправности распределено по
показательному закону с параметром у:
/(*)=
ve vt при t > 0,
0 при t < 0.
При возникновении неисправности она мгновенно
обнаруживается, и прибор поступает в ремонт. Ремонт продолжается время
<q, после чего прибор снова включается в работу.
Найти плотность распределения / * (t) и функцию
распределения F* (t) промежутка времени Т* между двумя соседними
неисправностями. Найти его математическое ожидание и дисперсию.
Найти вероятность того, что время Т* будет больше 2t0.
Решение. T* = T + t0,
/*(*) =
F*(t) =
ve-v(t-t0) при t>tQ,
0 при t < t0.
l_e-<t-t0) при t>tQi
0 при t <tQ.
M[T*] = i + *0; D[T*]= X
2 '
P(T* > 2*0) = 1 - F*(2i0) = e~vt°
101
5.28. Время Т между двумя сбоями вычислительной машины
распределено по показательному закону с параметром X:
/(О
О
при
при
t >0,
t <0.
Решение определенной задачи требует безотказной работы
машины в течение времени т. Если за время т произошел сбой,
то задачу приходится решать заново. Сбой обнаруживается
только через время т после начала решения задачи.
Рассматривается случайная величина 0 — время, за которое задача будет
решена. Найти ее закон распределения и математическое
ожидание (среднее время решения задачи).
Ответ. Случайная величина 0 дискретна и имеет ряд
распределения
е,
Pi
т
р
2т
pq
m m ш
• • •
it
pq''1
...
• • •
-Хт
где р = е ; q = 1 - р = 1
-Хт
т
V
Шл = — = —
tt -Хт
5.29. В условиях предыдущей задачи найти вероятность того,
что за данное время t = кт будет решено не менее тп задач (тп < к).
Решение. Обозначим Pm к вероятность того, что за время
t = кг будет решено ровно т задач. Pm к есть вероятность того,
что из к промежутков времени т ровно т будет таких, в которых
не будет сбоев. Вероятность того, что за время т не будет сбоя:
р = Р(Т > т) = е~Хт. По теореме о повторении опытов
Pm,k=C?pmq
к-
= Ск е
тп _ — гаХт
(1
—Хт \к—т
У
Вероятность того, что будет решено не менее т задач:
к к
= VP, и = ГЙе-Лт(1-е-Хт)м
тп , к / у г , к ^ _j
г =га г =т
или, если это удобнее,
тп— 1
Дт,*=1-£^е -*Т(1-е -Хт)
-Хт \к—г
г=0
5.30. Охотники, собравшиеся для охоты на волка,
выстраиваются в цепь случайным образом так, что расстояние между двумя
соседними охотниками D не зависит от других расстояний и рас-
102
пределено по показательному закону с параметром X. Волк бежит
перпендикулярно цепи. Любой охотник стреляет по волку только
в случае, если волк пробегает от него не дальше чем на расстоянии
Д0, и, выстрелив, убивает его с вероятностью р. Определить
вероятность того, что волк будет убит, если он не знает, где
расположены охотники, и цепь достаточно длинна для того, чтобы волк с
достоверностью не пробежал за пределами цепи.
Решение. Цепь охотников (рис. 5.30) может рассматриваться
как пуассоновская последовательность точек на оси Ох. Волк,
бегущий по направлению, указанному стрелкой, обстреливается в
случае, если в полосу шириной 2Д0, связанную с его траекторией,
попадает хотя бы один охотник. Каждый охотник, если ему придется
стрелять по волку, с вероятностью р оказывается «удачливым», т.е.
убивает волка. Перейдем от «цепочки охотников» на оси Ох к
«цепочке удачливых охотников», имеющей плотность X* = \р.
X
Рис. 5.30
Волк будет убит в случае, если в отрезок длиной 2 Д0, случайно
брошенный на ось абсцисс, попадет хотя бы один «удачливый»
охотник; вероятность этого:
Р(А) = 1 - е"2ЛоХ* = 1 -
■2R0\p
5.31. Рассматривается равномерное пуассоновское поле точек
на плоскости с плотностью X. Найти закон распределения и
числовые характеристики mr, Dr расстояния R от любой точки поля
до ближайшей к ней соседней точки.
Решение. Найдем функцию распределения F(r) величины
R. Для этого проведем вокруг точки поля ок- #
ружность радиуса г (рис. 5.31). Для того чтобы # • • #
расстояние R от этой точки до ближайшей к •
ней соседней было меньше г, надо, чтобы в круг #
попала хотя бы одна точка (кроме данной). По
свойствам пуассоновского поля вероятность • • •
этого события не зависит от того, есть ли уже в #
центре круга точка или ее нет. Поэтому
Рис. 5.31
103
-ттг^Х
F(r) = l-e"Kr А при г>0,
откуда
f(r) =
2ттХге_1;Хг2 при г>0,
О при г < 0.
Такой закон распределения называется законом Рэлея.
00
-ivXr2 1 1 .
шг
= [г2ъ\г е-*^dr = _
сю
а2[Д] = Гг22кХге-,Хг^г = —;
Д.=а2[Д]-тг' =
О
2 1 1 4-ТТ
ттХ 4Х 4ттХ
5.32. Деревья в лесу растут в случайных точках, которые
образуют пуассоновское поле с плотностью X (среднее число деревьев
на единицу площади). Выбирается произвольная точка О в этом
лесу. Рассматриваются случайные величины:
Rx — расстояние от точки О до ближайшего к ней дерева;
R2 — расстояние от точки О до следующего по порядку
(второго по удаленности) дерева;
Rn— расстояние от точки О до n-го по удаленности дерева.
Найти закон распределения каждой из этих случайных
величин.
Решение. Функция распределения случайной величины R{
найдена в предыдущей задаче:
F^r) = 1 - е-"2* (г>0).
Функция распределения F2(r) = P(R2 < г) равна вероятности
того, что в круг радиуса г попадет не менее двух деревьев:
F2(r) = 1 - е"*г2х - -кг2Хе-*г2х (г > 0).
Аналогичными рассуждениями получим
Fn(r) = P(Rn <r) = l-g^j-e-" (г>0, п>1),
гдеа = irr2X.
104
Плотность распределения получим дифференцированием
Fn (г) по г:
fn{r)=dFn(r)da ' -1 -*-1 -1^
da dr
а
(
Yk — e~a + У — е~а 2ттХг =
n-1
е"а2тт\г (r>0).
(n-1)!
5.33. В пространстве трех измерений случайным образом
расположены точки. Число точек в некотором объеме пространства v
есть случайная величина, подчиненная закону Пуассона с
математическим ожиданием a = Xv, где X — среднее число точек,
находящихся в единичном объеме. Требуется найти закон распределения
расстояния R от любой точки пространства до ближайшей к ней
случайной точки.
Решение. Функция распределения F(r) есть вероятность
того, что в сферу радиуса г попадет хотя бы одна точка:
F(r) = Р(Д < г) = 1 - e"Xv(r)
4 з
где v (г) = — -кг — объем сферы радиуса г. Отсюда
ч4 з
/(г) = 4ттг2\е 3 (г>0).
5.34. В некотором звездном скоплении звезды образуют
трехмерное пуассоновское поле точек с плотностью X (среднее
количество звезд в единице объема). Фиксируется одна (произвольная)
звезда и рассматриваются: ближайшая от нее звезда, следующая
(вторая) по удаленности, третья и т.д. Найти закон распределения
расстояния R от данной звезды до n-й в этом ряду.
Ответ. Функция распределения Fn(r) имеет вид
Fn(r) = l-J2?-e-a,mea = ^r3\ (г>0);
плотность распределения
/ (Г) = ^EiL^l = °>П~1 е- 4irXr2 (г > 0).
пК J dr (n-1)! V J
5.35*. Предыдущие задачи можно обобщить на произвольное
число измерений N: в ЛГ-мерном пространстве случайным образом
расположены точки. Число точек, попадающих в некоторую
замкнутую область V этого пространства, есть случайная величина X,
105
подчиненная закону Пуассона. «Объем» г; этой области
Vопределяется так:
v — I ... I CLX-I сиХп... ах at .
J (V)J l L
(V)
Математическое ожидание случайной величины X будет равно
Хг;, где X — среднее число точек, находящихся в единичном объеме.
Требуется найти закон распределения «расстояния» R от
любой точки этого пространства до ближайшей случайной точки.
Под «расстоянием» R между двумя точками х (хг, х2, ..., xN ) и
у (у 1? у 2, ..., yN ) понимается величина
Решение. Известно, что объем vN (г) гиперсферы радиуса г в
ЛГ-мерном пространстве равен
%(г) = -
N+l N-1
2 2 тт 2
ЛП!
2тт2
.#
при N — нечетном,
.N
N
(N-2]
при N — четном,
!
при ЛП! = 1 -3 5 -7 -... - N (при нечетном N). Заметим, что
«площадь» поверхности гиперсферы SN(r) радиуса г в ЛГ-мерном
пространстве определяется так:
d N
SN И = у VN И = — VN (г).
dr г
Функция распределения случайной величины R будет равна
вероятности того, что в гиперсферу радиуса г попадает хотя бы
одна случайная точка:
F(r) = Р(Д < г) = 1 - e"Xv"(r) (г > 0),
откуда
/(г) = Х5^(г)е"х^(г) (г>0).
5.36*. Рассматривается ЛГ-мерное пространство, в котором
задано пуассоновское поле точек с плотностью X (среднее число
точек в единице TV-мерного объема). Найти закон распределения
расстояния от произвольной точки поля до п-й от нее в порядке
возрастания расстояния.
106
Ответ. Функция распределения
^(г) = 1-ЕтГе"° <г>0)'
к=0
к\
где а = Хг;^ (г); плотность распределения
п-1
/» (г) =
а
(п-1)!
e~a\SN(r) (г>0)
(см. задачу 5.35).
5.37. Автомобиль проходит технический осмотр и
обслуживание. Число неисправностей, обнаруженных во время техосмотра,
распределяется по закону Пуассона с параметром а. Если
неисправностей не обнаружено, техническое обслуживание
автомобиля продолжается в среднем 2 ч. Если обнаружены одна или две
неисправности, то на устранение каждой из них тратится в среднем
еще полчаса. Если обнаружено больше двух неисправностей, то
автомобиль ставится на профилактический ремонт, где он
находится в среднем 4 ч.
Определить закон распределения среднего времени Т
обслуживания и ремонта автомобиля и его математическое ожидание М[Т].
Решение.
*,■
Pi
2
е~а
2,5
ае~а
3
2
1-е-
6
( „21
а
1 + а+ —
2
k )
М[Т] = е-"
3 ^
2 + 2,5а + -а
2
+ 6
1-е
—а
1 + а +
а
= 6-е_а(4 + 3,5а + 1,5а2).
5.38. Производится вынужденная посадка самолета на мелкий
кустарник. Точки, в которых растут кусты, представляют собой
равномерное пуассоновское поле точек с параметром X. Размах
крыльев самолета равен г, а длина пробега L. Благополучная
посадка возможна, если самолет не заденет ни одного куста
(размерами кроны куста можно пренебречь). Определить вероятность р
того, что самолет произведет благополучную посадку.
Ответ, р = e~Lr .
5.39*. Обследуется группа животных; каждое из них с
вероятностью р является больным. Обследование производится путем
анализа крови. Если смешать кровь п животных, то анализ этой
107
смеси будет положительным, если среди п животных будет хотя
бы одно больное. Требуется обследовать большое число 7V
животных. Предлагается два способа обследования:
1) обследовать всех N животных; в этом случае нужно
провести панализов;
2) вести обследование по группам, смешав сначала кровь
группы из п животных; если анализ отрицательный, считать, что
все животные группы здоровы, и переходить к следующей
группе из п животных; если анализ положительный, обследовать
каждое из п животных и после этого переходить к следующей
группе (п> 1).
Определить, какой способ обследования выгоднее — первый
или второй — в смысле минимального среднего числа анализов.
Определить, при каком п= п* для обследования группы
животных потребуется в среднем наименьшее число анализов.
Решение. Случайная величина Хп — число анализов на
группу из п животных при втором способе — имеет ряд распределения
Х{
Pi
1
n
q
n+ l , где q = 1 - p.
i n
1 - q
Среднее число анализов на группу из п животных при втором
способе будет
M[Xn] = g" +(n + l)(l-qn) = n-(nqn - 1).
При первом способе на группу из п животных приходится п
анализов. Очевидно, при nq п < 1 первый способ выгоднее
второго, а при nq п > 1 второй способ выгоднее первого.
Установим, при каком q второй способ становится выгоднее и
каково при этом будет оптимальное значение п = п*. Из
неравенства nq п > 1 вытекает q > —==, а из последнего q > 0,694, так как
1 Q
минимум -т= для целых п достигается при п = 3.
Предположим, чтод > 0,694, и найдем то значение п = п*,
которое обращает в минимум среднее количество анализов,
приходящееся на одно животное:
п п
Для этого надо найти наименьший положительный корень
уравнения
108
—^ = -q Inq - = 0,
an n
взять ближайшие к нему два целых числа и прямой подстановкой
их в Rn выбрать оптимальное п*. Уравнение — qn \nq = —
п
.2-х
подстановкой — Inq = a; an = х приводится к х е = а х
а = — \nq < = 0,366 . Последнее уравнение при малых а (и,
значит, малых р = 1 — q) имеет решение х « л/а, откуда п*
л/а
При немалых а непосредственное сравнение величин R2, Д3 и -¾ по~
зволяет сделать вывод о том, что Д3 < ^2 всегДа и что -&$ < Д4 ПРИ
0,694 < q < 0,876; следовательно, при 0,694 < q < 0,876 оптимальное
п* = 3. Можно показать, что при q > 0,889 (р < 0,111) хорошее
приближение дает формула п* « -= + 0,5.
5.40. Случайная величина X распределена
по «закону прямоугольного треугольника» в
интервале (0, а) (рис. 5.40).
а) Написать выражение плотности
распределения.
б) Найти функцию распределения F(x).
в) Найти вероятность попадания
случайной величины X на участок от а/2 до а.
г) Найти характеристики величины X тх,
Dx,ox,\i3[X}.
Рис. 5.40
Ответ.
а) /(*) =
2 Г
1_£
а
б) F(x) =
0
х
а
1
2--
а
при
при
при
при
х € (0, а),
х£ (0, а).
0 < х < а,
х> 0.
B)F(a)-F
V
,2,
_1
4
г)тх =-; ^х = —
3 18
<** =
а
Зл/2'
ц3[Х] = а3[Х]-Зт1а2[Х] + 2то^ =
а
135
109
Рис. 5.41
5.41. Функция распределения случайной
величины X задана графиком (рис. 5.41).
Найти математическое ожидание и
дисперсию величины X.
Ответ, тп =
а + 6
D„ =
(а-Ъ)
2 12
5.42. Случайная величина X подчинена
закону Симпсона («закону равнобедренного
треугольника») на участке от —а до + а
(рис. 5.42, а).
а) Написать выражение плотности распределения.
б) Построить график функции распределения.
х
х
а
Рис. 5.42
в) Найти числовые характеристики случайной величины X
™>x,Dx,ox,\iz[X].
г) Найти вероятность попадания случайной величины X в ин-
а
2;й
тервал
Ответ.
у
а) /(х) = . а
О
|£|
а
при х Е (—а, а),
при #¢(-а, а).
б) График функции распределения при х € (—а, а) составлен из
двух участков парабол (рис. 5.42, б).
2
ъ)тх =0; Dx =^-; стх =-^; м.3[*] = 0.
г)Р
а
2
-,а
/у
7
8
110
5.43. Случайная величина X распределена по закону Коши:
а
/(*)
1 + х
а) Найти коэффициент а; б) найти функцию распределения
F(x); в) найти вероятность попадания величины X на участок
(-1, +1); г) существуют ли для случайной величины X числовые
характеристики: математическое ожидание и дисперсия?
111 1
Ответ, а) а = —; б) F(x) = — arctgx + -; в) Р(-1 < X < 1) = -;
тг -к 2 2
г) характеристики тх и Dx не существуют, так как выражающие их
интегралы расходятся.
5.44. Случайная величина X подчинена
показательному закону распределения с
параметром |i:
я*)
lie
О
*х при х > О,
при х < 0.
Рис. 5.44
а) Построить кривую распределения;
б) найти функцию распределения F(x);
в) найти вероятность того, что случайная
величина X примет значение меньшее, чем ее математическое
ожидание.
О т в е т. а) См. рис. 5.44;
б) F(x)
в)тх =
М-
0
при
1 - е-^ при
•>
; Р
X <-
= F
V
IX
х<0,
х>0;
= 1-е"1
0,632.
5.45. Случайная величина X подчинена закону Лапласа:
f(x) = ae-W (Х>0).
а) Найти коэффициент а; б) построить графики плотности
распределения и функции распределения; в) найти тхи Dx.
Ответ. а)а = —;
2
— е
2
б) F(x) -.
при х < 0,
1 - Vх*
2
при х > 0.
111
X
б
Рис. 5.45
Графики плотности распределения и функции распределения
даны на рис. 5.45, я, б.
2
в)тх =0; Dx =—.
У
5.46. Случайная величина R — расстояние от точки попадания
до центра мишени — распределена по закону Рэлея (рис. 5.46):
т
2_2
Are~h г
0
при
при
г >0,
г <0.
; в)тг =
Рис. 5.46
= М
hj2
тс ..о 4 — it
Найти: а) коэффициент А) б) моду М случайной величины Д,
т.е. точку максимума ее плотности распределения; в) тг и Д.;
г) вероятность того, что в результате
выстрела расстояние от точки попадания
до центра мишени окажется меньше, чем
мода.
Ответ.а)Л = 2/12;6)Л?
(тс _ vtc . п _ 4 —
2~2р Г~~4Л'2 2 '
г) Р(Д < Ж) = 0,393.
5.47. Случайная величина X с вероятностью рх имеет
плотность распределения Д (х), а с вероятностью р2 — плотность
распределения f2(x) (рг + р2 = 1). Написать выражение для
плотности распределения и функции распределения величины X. Найти
ее математическое ожидание и дисперсию.
Решение. По формуле полной вероятности (с гипотезами
Я{ — величина X имеет плотность распределения f{ (х), i= 1, 2)
получаем
X
F{x) = Р(Х < х) = PlFx(х) + p2F2(x), где ^ (х) = J f{ (х) dx;
f(x) = pj^x) + p2f2(x);
112
oo
oo
mx — V\ I xfl{x)dx + p2 j xf2(x) dx — p^m^ + p2m
(2)
x >
-oo
—oo
где m^\rn^ — математические ожидания для распределений
Ь(х),/2(х)]
00 00
Ае = Pi j x2f\ (х) dx + р2 I x2f2 (х) dx — т
2
х
— 00
= рго.^ + Р2а^ — т2
— 00
2
a; J
где а 2^, а (22) — вторые начальные моменты для распределений Д (х)
и/2(х).
5.48. Браковка шариков для подшипников производится
следующим образом: если шарик не проходит через отверстие
диаметром dv но проходит через отверстие диаметром d2 > dl, то его
размер считается приемлемым. Если какое-нибудь из этих
условий не выполняется, то шарик бракуется. Известно, что диаметр
шарика D есть нормально распределенная случайная величина с
cL + d0 d0 — d,
характеристиками md = — и od = -½
ятность p того, что шарик будет забракован.
Решение.
. Определить веро-
p = l-P(d1 <d<d2) = l-
ф*
(d2 -md
_ф=
ф'
(A — A \ (A — A \
a2 ai лч* ai a2
2a
d )
- ф*
2a
d )
так как Ф* (—x) = 1 — Ф* (ж), то
p = l
2Ф*
d2 -dxy
2a
d )
= 2 - 2Ф*
(d2 - dx
2a
d J
и по таблицам функции Ф* (ж) (см. прил. 1 табл. 2) находим
р = 2 - 2Ф* (2) = 0,0456.
5.49. Известно, что размер D шарика для подшипников
является случайной величиной, распределенной по нормальному
закону. Браковка шарика производится так же, как указано в
задаче 5.48. При этом известно, что средний размер шарика равен
113
m
dx + d2
, а брак составляет 10 % всего выпуска. Определить
среднее квадратическое отклонение диаметра шарика od.
Решение. Вероятность брака
Р = 2 - 2Ф:
fd2 - dl У
2а
0,1,
откуда Ф*
fd2 - dl У
2а.
табл. 2) находим
d,
0,95. По таблицам функции Ф* (х) (см. прил. 1
ч
2а
-^ = 1,25;а, =-¾
2,5
t
5.50. Ha перекрестке стоит автоматический светофор, в
котором 1 мин горит зеленый свет и 0,5 мин — красный, затем опять
1 мин горит зеленый свет, 0,5 мин — красный и т.д. Некто
подъезжает к перекрестку на автомобиле в
случайный момент, не связанный с работой
светофора. Найти: а) вероятность того,
что он проедет перекресток, не
останавливаясь; б) закон распределения и
числовые характеристики времени
ожидания у перекрестка.
Решение. Момент проезда
автомобиля через перекресток распределен
равномерно в интервале, равном периоду
смены цветов в светофоре. Этот период равен 1 + 0,5 = 1,5 [мин]
(рис. 5.50).
Для того чтобы автомобиль проехал через перекресток, не
останавливаясь, достаточно, чтобы момент проезда перекрестка
пришелся на интервал времени (0; 1). Для случайной величины,
подчиненной закону постоянной плотности в интервале (0; 1,5),
вероятность того, что она попадет на интервал (0; 1) равна
- • 1 = -.Время ожидания Тож есть смешанная случайная величи-
3 3
2 1
на; с вероятностью - она равна нулю, а с вероятностью -
принимает с одинаковой плотностью вероятности любое значение
между 0 и 0,5 мин.
Среднее время ожидания у перекрестка
ЩТож ] = 0-- + 0,25 • - « 0,083 [мин].
3 3
Дисперсия времени ожидания
114
0,=*2[Тож}-(М[Тож})
0,5
О2 • - + i ft2 • —eft - (0,083)2 « 0,0208 [мин2];
о
0,5
а, «0,144 [мин].
5.51. Кривая распределения случайной величины X
представляет собой полуэллипс с полуосями а и Ь (рис. 5.51, а).
X
■а 0
х
а
б
Рис. 5.51
Величина а известна. Требуется определить величину Ь,
найти mx, Dx, найти и построить функцию распределения F(x).
Решение. Величина Ь находится из условия равенства
единице площади, ограниченной кривой распределения:
nab .. 7 2
= 1; о = —.
тш
Плотность распределения
ь [7*
— у/а —
№
X
а
0
при х G (—а; а),
при х^(—а;а).
Математическое ожидание mx = 0. Дисперсия
2
4
оо
D, = fx2f(x)dx = ?-;
— ОО
х
F(x)= Jf(x)dx
— ОО
о
тш
при х < —а,
хуа
2-х'
2 . х а -к
+ a arcsm—I
а 2
при — а < х < а,
при х > а.
График функции F(x) приведен на рис. 5.51, б.
115
5.52*. Показать, что функция вида
ш
2 2
л«.5л_а х
ах е
О
при
при
х>0,
х<0,
где а > 0 и а > 0 — некоторые постоянные и s — натуральное число
(5=1,2,3,...) обладает свойствами плотности распределения.
Определить параметры а и а, исходя из заданного математического
ожидания тх, и найти Д..
Решение. Параметры а и а находятся из условий
оо
оо
faxse-{«x)2dx = 1, faxs+1e-{«x)2dx = rnx.
о
о
Данные интегралы заменой (ах)2 =t приводятся к
гамма-функции Эйлера:
ОО ОО S—1
[xse-{«x)2dx = —— {e-lt~dt
0 za 0
s + V
I 2 ,
2a
5 + 1
OO
гдеГ(га) = I e Чт ldt (m > 0), причем Г(га + 1) = га Г (га) и для це-
o
лых п = 1, 2, ... получаем Г(п + 1) = п!, Г
' Ц (2п-1)!!
п + - —
2J
2П
-/к,
(2п - 1)!!=1 -3-5...(2п -1).
Из заданных условий находим
a
Гз + Г
, 2 ,
2a
5 + 1
1; а
fs + T
, 2 ,
2a
5+2
™>x,
откуда
a
2a
5 + 1
(s + 1
\ »
a
ra
{ 2 J
Второй начальный момент
г
J.
г
J.
fs + 2]
I 2 J
[s + 1]
I 2 J
(s + 3) s + 1.
OO
a 2[X] = Jaxs+2e-(ai)2£fe = a
I 2 J
о
2a
s+3
a
's + V
, 2 ,
2a a
s + 1
2a2
116
откуда
D.
Q.2[X]
TO. =
8 + 1
2a2
m
m
(s + l)t
's + V
, 2 ,
2Г
's + T
, 2 ,
Некоторые из законов вида fs(x) имеют определенные
названия: Д (х) называется законом Рэлея, а /2 (х) — законом Максвелла.
Для закона Рэлея (s= 1)
/i(*)
axe
О
^22
—а а;
при х > О,
при х < О
имеем соотношения
1 л/тг
a
a = 2a
тс
m
2m
Dx=ml
Для закона Максвелла (s = 2)
/20O
ax e
0
О ^.2 2
2 _— a a;
-1
IT
при x > 0,
при x < 0
имеем соотношения
а
m
л/тт
а
4оГ
л/тт
2„3 ' *
т
тс m
(3-гс
[8
\
- 1
у
Замечание. Все законы вида
/.(*) =
2 2
з —ах
ах е
0
при х > 0,
при х < 0
при заданном 5 являются однопараметричными, т. е. зависят только от
одного параметра, в качестве которого можно задать, например,
математическое ожидание (или дисперсию).
5.53*. Имеется случайная величина X, распределенная по
нормальному закону с параметрами т и а. Найти выражение для
величины a s [X] — начального момента 5-го порядка.
Решение. Выразим начальные моменты a s [X] = M[XS ] через
центральные моменты\ia[X] = М[(Х — га)5]:
а.[Х] = М[(Х-т + тУ] = £ск.\1к[Х]т»*, V-0[X] = 1.
k=o
117
Для центральных моментов при нечетном s = 2п + 1
оо l(x-m)
^[Х} = —j= J{x-m)se 2 °2 dx =
crV^rc
—ОО
ОО
hrrr J
1 2
У
ал/^к
?/5е 2а' dj/ = o,
— ОО
а при четном 5 = 2п — по формулам предыдущей задачи
М*] = -4=]Уе
ojzit
— ОО
00
Г 1
ал/^к
/
о
У
2 г • ^ > rfj,
У е
а* 2а2 ^ dy =
,[2п + 1
' , 2
(1-7¾ 2
(2п-1)!!а2п.
(а^)
2п+1
Например,
а2[Х] = га2 + а2;
2_.
а3[^] = т + За га;
2_ 2
М.4[*] = 3а4; а4[Х] = га4 +6а2га' +3а4;
а5[Х] = га5 +10ozm6 + 5-15а4га;
[i6[X] = 15o6; a6[X] = m6 + 15а2га4 + 15-За4га2 =15а6.
5.54. Случайная величина X подчинена нормальному закону с
математическим ожиданием тх = 0. Вероятность попадания этой
случайной величины на участок от -а до а равна 0,5. Найти ох и
написать выражение нормального закона.
Решение.
Р(-а<Х<а) = 2Ф*
'а^
о)
1 = 0,5; Ф*
'а"
о)
0,75.
а
По таблицам функции Ф* (х) имеем — « 0,675, откуда а = 1,48а,
а
118
№
1,48ал/2тт
4,4a
5.55*. Функция распределения
F(x) неотрицательной случайной
величины Xзадана графиком (рис. 5.55).
Математическое ожидание случайной
величины X равно тх. Показать, что тх
геометрически может быть
представлено площадью фигуры, заштрихованной
на рисунке (ограниченной кривой
у = F(x), прямой у = 1 и осью ординат).
Решение. Имеем
Рис. 5.55
оо
оо
оо
тх = / xf(x) dx= I xF'(x) dx—— I x[l — F{x)}'dx.
0
0
0
Применяя интегрирование по частям, получим
тх = -х[1 - F(x)}
оо
О
оо
+ Г [1 - F{x)]dx.
о
Докажем, что первое слагаемое равно нулю:
оо
х[1 - F(x)} = lim х[1 - F(x)} = 0.
о
оо
Действительно, для случайной величины X > 0, имеющей
конечное математическое ожидание, из сходимости интеграла
00
оо
I xf (х) dx следует, что / xf (х) dx —> О (М —> оо), и так как
м
оо
оо
М Г f(x)dx< fxf(x)dx,
м
м
получаем
M[l-F(M)]-+0 (М-+оо)
Следовательно,
lim х[1 - F{x)} = 0.
оо
119
Отсюда
00
т
J* [1 - F(x)} dx,
О
а это есть площадь, заштрихованная на рисунке.
5.56. Случайная величина X распределена по нормальному
закону с математическим ожиданием т и средним квадратическим
отклонением а. Определить абсциссы хи :¾ и ординату у точек
перегиба кривой распределения у = f(x) (рис. 5.56).
О т в е т. хг = т — а; х2 = т + а; у =
0,24
ал/2-гс сг
5.57. Случайная величина X подчинена нормальному закону с
математическим ожиданием тх = 0 (рис. 5.57).
Jb* lib Jin
Рис. 5.56
X
а (3
Рис. 5.57
Задан интервал (а, (3), не включающий начало координат. При
каком значении среднего квадратического отклонения а
вероятность попадания случайной величины X в интервал (а, (3)
достигает максимума?
Решение. Значение а найдем, дифференцируя по а
вероятность попадания в интервал (а, (3) и приравнивая производную
нулю. Имеем
Р(а <Х<(3) = Ф*
ф*
а
IP
V2*
3 а
~~ ,2 "~ ,2
Ге Tcft - Te~dt
—оо
—00
J-P(«<*<B] = ^L
f 32
е 2°2
( Э]
1 а2 J
с.2
-е 2°2
{ о2)'
0;
отсюда
120
(Зе
Л
2а'
ае
а
2а'
и следовательно,
а
р:
а
2(1п(3-1па)
(3 + а (3
а
2 1п(3-1па
Для малого интервала (а — е, а + е)
а
а
1 -
1
6
[6]
la J
2
а.
Например, при — < 0,24 формула а « а имеет погрешность ме-
а
нее 1 %.
5.58. Имеется случайная величина X, подчиненная
нормальному закону с математическим ожиданием тх и средним
квадратичным отклонением ох. Требуется приближенно заменить
нормальный закон законом постоянной плотности в интервале (а, (3);
границы а,(3 подобрать так, чтобы сохранить неизмененными
основные характеристики случайной величины Х\ математическое
ожидание и дисперсию.
Решение. Для закона постоянной плотности на участке (а, (3)
га
а + (3
X
; °х =
(3-а
2V3
Решая эти уравнения относительно а и (3, имеем
а = гах -сг^л/З; (3 = гах
5.59. Производится стрельба по наземной цели снарядами,
снабженными радиовзрывателями. Номинальная высота подрыва
снаряда, на которую рассчитан взрыватель, равна а, но
фактически имеют место ошибки в высоте, распределенные по нормально-
а ,
му закону со средним квадратическим отклонением а = — (систе-
матической ошибки нет). Если взрыватель не сработает над
землей, взрыва снаряда вообще не происходит. Найти вероятности
следующих событий:
А — при стрельбе одним снарядом точка разрыва окажется на
высоте, превышающей 1,2 а;
В — при стрельбе тремя снарядами ни один снаряд не
разорвется на высоте более чем 1,2 а;
121
С— хотя бы один из трех снарядов не разорвется;
D — один из трех снарядов не разорвется, а два другие
разорвутся.
Решение.
Р(Л) = Р(Х>1,2а) = 1-Ф
1,2а
а
2
= 1 - Ф * (2,4) = 0,0082;
Р(5) = 0,976.
Вероятность того, что один отдельный снаряд не разорвется:
р0=Р(Х<0) = Ф
■а
а
I 2 )
0,023;
Р(С) = 1 - (1 - Ро )3 = 0,068;
P(D) = Cl • 0,023 • 0,9772 = 0,066.
5.60. Производится стрельба тремя независимыми выстрелами
по цели, имеющей вид полосы (мост, автомобильная дорога,
взлетно-посадочная полоса). Ширина полосы 20 м. Прицеливание
производится по средней линии полосы; систематическая ошибка
отсутствует; среднее квадратическое отклонение точки попадания
в направлении, перпендикулярном полосе, 16 м. Найти
вероятность р попадания в полосу при одном выстреле, а также
вероятности следующих событий при трех выстрелах:
А — хотя бы одно попадание в полосу;
В — не менее двух попаданий в полосу;
С — один снаряд попадет в полосу, один ляжет с недолетом и
один с перелетом.
(1(Л
■ 1 = 0,468;
Решение. р = 2Ф*
U6J
Р(А) = 1-(1- pf =0,849;
Р(5) = 1-(1- pf - Зр(1 - pf = 0,452;
т2
Р(С) = 3\р
(1-р)
0,199.
122
5.61. Завод изготовляет шарики для подшипников.
Номинальный диаметр шариков d0 = 5 мм. Вследствие неточности
изготовления шарика фактический его диаметр — случайная величина,
распределенная по нормальному закону со средним значением
do и средним квадратическим отклонением ad = 0,05 мм. При
контроле бракуются все шарики, диаметр которых отличается от
номинального больше чем на 0,1 мм. Определить, какой процент
шариков в среднем будет отбраковываться.
Решение. Вероятность того, что шарик не будет забракован:
( 01 )
р = 2Ф* —^— — 1 = 0,954. Вероятность того, что он будет забрако-
(0,05 J
ван: q = 1 — р = 0,046. Следовательно, около 4,6 % шариков будет
браковаться.
ГЛАВА 6
СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН
(СЛУЧАЙНЫЕ ВЕКТОРЫ)
Совокупность двух случайных величин (Х} У), рассматриваемых
совместно, называется системой двух случайных величин. Система двух
случайных величин (X, У) геометрически интерпретируется как
случайная точка с координатами (X, У) на плоскости хОу (рис. 6.0.1, а) или как
случайный вектор, направленный из начала координат в точку (X, Y),
составляющие которого представляют собой случайные величины Хи Y
(рис. 6.0.1, б).
Y
О
У
{X,Y)
Y
X
х
О
У
(х,У)
X
х
а
Рис. 6.0.1
Система трех случайных величин (X, У, Z) изображается случайной
точкой или случайным вектором в трехмерном пространстве] система п
случайных величин (Хг, Х2,..., Хп) — случайной точкой или случайным
вектором в пространстве п измерений.
Функцией распределения F (х, у) системы двух случайных величин (X,
У) называется вероятность совместного выполнения двух неравенств:
X < х nY <у:
F(x,y) = P((X<x)(Y<y)).
Геометрически F(x, у) интерпретируется как вероятность попадания
случайной точки (X, У) в квадрант с вершиной (х, у), заштрихованный на
рис. 6.0.2, а. Функция распределения F (х} у) обладает свойствами:
1) F(-oo, - оо) = F(-oo, у) = F(av-oo) = 0;
2)F(+oo,+ oo) = l;
124
3) F(x, + oo) = F^x); F(+oo, y) = F2(y), где F^x), F2(y) - функции
распределения случайных величин Хи Y;
4) F (х, у) — неубывающая функция хиу.
Вероятность попадания случайной точки (X, У) в прямоугольник R со
сторонами, параллельными осям координат, включающий свою нижнюю
и левую границы, но не включающий верхнюю и правую (рис. 6.0.2, б),
выражается через функцию распределения формулой
Р ((X, Y) € R) = F ((3, 6) - F (а, 6) - F ((3, ч) + F (а, ч).
У
Ч
О
а
р
х
а
Рис. 6.0.2
Плотностью распределения /(х, ?/) системы двух случайных величин
(X, У) называется предел отношения вероятности попадания случайной
точки в элементарный участок плоскости, примыкающий к точке (х, у), к
площади этого участка, когда его размеры стремятся к нулю. Плотность
распределения выражается через функцию распределения формулой
/(*, у)
d2F(x, у)
дх ду
К^у)
ху
Поверхность, изображающая функцию /(х, у), называется
поверхностью распределения.
Элементом вероятности для системы двух случайных величин
называется величина /(х, у) dx dy, приближенно выражающая вероятность
попадания случайной точки (X, Y) в элементарный прямоугольник со
сторонами dx, dy, примыкающий к точке (х, у).
Вероятность попадания случайной точки (X, У) в произвольную
область D выражается формулой
P((X,Y)€D) = fff(x,y)dxdy.
Свойства плотности распределения
1)/(*,») >0;
00
2) J J /(х, у) dx dy = 1.
-00
125
Функция распределения системы выражается через плотность
распределения формулой
х У
F{x, У)= f J /(*, У) dx dV
-00-00
(интегрирование производится сначала по у, а потом по х).
Плотности распределения отдельных величин, входящих в систему,
выражаются через плотность распределения системы формулами
ОО 00
1Лх) = f f(x> у) ^2/; /2(2/) = f f(x,y) dx.
—00 —00
Условным законом распределения случайной величины, входящей в
систему, называется ее закон распределения, вычисленный при условии,
что другая случайная величина приняла определенное значение.
Условные функции распределения случайных величин X и У,
входящих в систему, обозначаются F2 (х\у) и F2(y\x), а условные плотности
распределения - fx (х\ у) и /2 (у | х).
Теорема умножения плотностей распределения
f(x, у) = МХ) f2(y\x) или f(x, у) = f2(y) &(х\у).
Выражения для условных плотностей
распределения через безусловные
Л(у1*) = :^пг при Л(*)*<*
fl(x)
j-(x\y) = i&2l при f2(y) *0.
Л(2/)
Случайные величины (X, Y) называются независимыми, если
условный закон распределения одной из них не зависит от того, какое значение
примет другая:
Мх\у) = fi(x) или }2{у\х) = f2(y).
Начальным моментом порядка k+ s системы (X, У) называется
величина
atit[X,Y] = M[XkY'].
Центральным моментом порядка к+ s системы (X, Y) называется
величина
]xkJX,Y} = M[XkYs].
126
Расчетные формулы для определения моментов
а) Для дискретных случайных величин
* з
^,.[^У] = ЕЕ^-т.)'(»;-т»)Ч-.
* 3
где р#=Р((Х = х£)(У = »,-));
б) для непрерывных случайных величин
оо
ам = [X, У] = Jjxkysf{x, у) dx dy;
— ОО
ОО
1чЛ*>у] =//(*-т*)*(г/ -my)sf(x>y) dx dv>
—ОО
где/(ж, ?/) — плотность распределения системы.
Корреляционным моментом К'^двухслучайных величин (X, Y)
называется центральный момент порядка 1+1, т.е.[\>U(X, Y) (второй смешанный
центральный момент):
Кщ = цп[Х,У]=М[ХУ].
Для независимых случайных величин корреляционный момент равен
нулю.
Коэффициентом корреляции г• двух случайных величин (X, У)
называется безразмерная величина
Кху
г = —
' хи »
гдеа, = JD~X = ^2<0[X,Y);ay = Д" = >0,2[*,П
Коэффициент корреляции характеризует степень тесноты линейной
зависимости между случайными величинами.
Случайные величины {X, Y) называются некоррелированными, если их
корреляционный момент (или, что равносильно, коэффициент
корреляции) равен нулю.
Из независимости случайных величин следует их
некоррелированность; напротив, из некоррелированности случайных величин еще не
следует их независимость.
Если случайные величины (X, Y) связаны линейной функциональной
зависимостью вида У = аХ + Ь, то их коэффициент корреляции г = ±1,
где знак + или — берется в соответствии со знаком коэффициента а.
Для любых двух случайных величин | г | < 1.
127
Функцией распределения системы п случайных величин {Хх, Х2,...,
Хп) называется вероятность совместного выполнения п неравенств вида
Х{ < х{ :
F(xux2,..., хп) = Р((Хг < х1){Х2 < х2)... (Хп < хп)).
Плотностью распределения системы п случайных величин называется
смешанная частная производная n-го порядка функции распределения:
дп
/(3¾, х2, ..., хп) = — - - г (2¾, х2, ..., хп).
охг ох2 ... охп
Функция распределения F{ (х{) одной из величин Х{, входящих в
систему, получается из F(x1, х2,..., хп), если положить в ней все аргументы,
кроме xit равными +оо:
Р{(х{) = F (+00, + 00,..., х{,..., + оо).
Плотность распределения отдельной величины Xif входящей в
систему {Хх, Х2,..., Хп), выражается формулой
оо оо
Ji \Xi ) — J •" J J \X1 » X2 » *''» Xn ) ®&\ ''' ^Xi -1 ^Xi +1 ' *' **Хп *
— 00 —00
Плотность распределения отдельной подсистемы (Х{, Х2,..., Xk),
входящей в систему (Хх, Х2,..., Хк, Хк+1,..., Хп), выражается формулой
оо оо
Л ' •''' к \Х1 > • • • > Хк) — I '" \ JV^l ' " *' Хк' " '' Хп) ^Хк+1 ' *' ^Хп
—00 —00
Условная плотность распределения подсистемы Хг,..., Хк при
фиксированных значениях всех остальных случайных величин выражается
формулой
Хп)
Л+1» • • •» п\Хк+1> ' * *' Хп)
Если случайные величины (^, Х2,..., Хп) независимы, то
/(2¾ , Х2, ..., Хп) = M^iMjV^) '•• 1п\Хп)-
Вероятность попадания случайной точки {Хх,..., Хп) в пределы п-мер-
ной области D выражается n-кратным интегралом
P((^i» •••, ^п) € D) = J ... J /(2¾,..., xn) сЦ ... dxn.
128
Корреляционной матрицей системы п случайных величин {Хх, Х2,...,
Хп) называется таблица, составленная из корреляционных моментов всех
этих величин, взятых попарно
*М1 *Ч2 ••' ^1п
к,
Л21 Л22 ••• Л2п
■**nl ^п2 •*• ^пп
о о
где К{- — Кхх. = М[Х{ Xj] — корреляционный момент случайных
величин Х{, Xj.
Корреляционная матрица симметрична: K{j = Kj{, поэтому обычно
заполняется лишь половина таблицы,
*Ч1 *Ч2 ••' ^1п
^22 * * * ^2 п
#
nn
По главной диагонали корреляционной матрицы стоят дисперсии
случайных величин{Хх, Х2,..., Хп):
К и = D[X,. ].
Нормированной корреляционной матрицей системы п случайных
величин называется таблица, составленная из коэффициентов корреляции
всех этих величин, взятых попарно,
Ы\
1 Г12 Г13 •** Г\п
1 г23 ... г2п
1 ... Г.
Зп
К,
где r{j = —- коэффициент корреляции величин Х{, Xj,
G{Gj
Нормальный закон распределения для двух случайных величин (X, Y)
(нормальный закон на плоскости) имеет плотность вида
/(я, у)
1 |(x-mx)2 2г(х-тх)(у-ту) (у-ту) ]
__. _ 1 _ .
2(1-г2)| о\ охоу а\ ]
2-kojj^^I — г2
х У
где Шр ту — математические ожидания случайных величин X, Y;ox,oy —
их средние квадратические отклонения; i— их коэффициент корреляции.
129
Для случайных величин, распределенных по нормальному закону,
некоррелированность равносильна независимости. Если случайные
величины (X, У) некоррелированы (независимы), то г = 0 и
/(*, у)
2-ксгхау
(х-тх)2 (У-Тпу У
В этом случае оси Ох, Оу называются главными осями рассеивания, а
сг , сг — главными средними квадратпическими отклонениями.
Если при этом тх = ту = 0, то нормальный закон принимает
канонический вид:
у
/(*, У)
2тшхсгу
2(7* 2aJ
Вероятность попадания случайной точки, распределенной по
нормальному закону, в прямоугольник R (см. рис. 6.0.2, 6) с осями,
параллельными главным осям рассеивания, выражается формулой
ЩХ, Y) б R)
ф*
, °х ,
- ф*
f у
а-тх
< °* У
ф*
6-ту
1 °У J
_ ф*
Ч-т„
1 °У J.
Эллипсом равной плотности (эллипсом рассеивания) называется
эллипс, во всех точках которого плотность распределения /(х, у)
нормального закона постоянна: /(х, у) = const.
Полуоси эллипса рассеивания пропорциональны главным средним
квадратическим отклонениям:
a = kox;b= koy.
Вероятность попадания случайной точки, распределенной по
нормальному закону, в область Eh ограниченную эллипсом рассеивания,
равна
ЩХ, Y) б Ек) = 1 - е » ,
где А;— размеры полуосей эллипса в средних квадратических отклонениях.
Если ох = оу = а, рассеивание по нормальному закону называется
круговым.
При круговом нормальном рассеивании с тх — ту = 0 расстояние R
от точки (X, У) до начала координат (центра рассеивания)
распределяется по закону Рэлея:
130
/(r) =
г2
Г 9a2
-ire 2a
a2
0
при
при
г >0,
г <0
Нормальный закон в пространстве трех измерений для независимых
случайных величин (X, У, Z) выражается формулой
Дя, у, ^)
(х-тх)2 ^(y-гпу)2 ^z-mj2
(¾)
3/2
ах°уаг
Вероятность попадания случайной точки (X, Y, Z) в область Ек,
ограниченную эллипсоидом равной плотности с полуосями
а = fccr,6 = fccr,c = fca
2 >
равна
Р((Х, У, Z) е St) = 2Ф* (*) -1 - J-ke * .
6.1. Два стрелка независимо один от другого производят по
одному выстрелу, каждый по своей мишени. Случайная величина
X— число попаданий первого стрелка; Y — второго стрелка.
Вероятность попадания в мишень для первого стрелка рг, для второго
р2. Построить функцию распределения F(x,y) системы случайных
величин (X, У).
Решение. Составим таблицу значений функции F(x,y) для
различных значений аргументов. Так как случайные величины
(X, У) независимы, то
F(x, у) = Р(Х < х) Р(У <у) = F^F^y).
Построим функцию распределения Fx(x):
Fx(x) =
0 при х < О,
qx при 0 < х <1,
1 при х > 1,
гдед1 = 1 — рг. Аналогично
ш
0
92
1
= 1-
-Р*
при
при
при
У<0,
0<у<1,
у>1.
131
Значения функции F(x, у) даны в таблице
У
У<0
0 < у < 1
х> 1
X
х <0
0
0
0
0 <х < 1
0
?1?2
¢1
X > 1
0
Q2
1
6.2. По мишени производится один выстрел. Вероятность
попадания равна р. Рассматриваются две случайные величины: X —
число попаданий; Y — число промахов. Построить функцию
распределения F(x, у)системы (X, У).
Решение. Случайные величины (X, У) зависимы, причем
жестко (функционально):
X + Y = l.
Таблица возможных значений X, Y с соответствующими
вероятностями будет
Х{
0
1
Уз
0
0
Р
1
q
0
Значения функции F(x, у) даны в таблице
У
у <о
0 < у < 1
х> 1
X
х <0
0
0
0
0 <х < 1
0
0
q
х> 1
0
р
1
6.3. Функция распределения системы двух случайных величин
(X, Y) равна F(x, у). Найти вероятность попадания случайной
точки (X, Y) в область D (рис. 6.3), ограниченную справа абсциссой а,
снизу и сверху ординатами % 6.
132
Ответ.Р((Х, Y) е D) = F(a, 6) - F(a, 4).
6.4. Дана поверхность z = f(x,y)y изображающая плотность
распределения системы (X, Y) (рис. 6.4). Задано некоторое
значение х. Дать геометрическую интерпретацию:
fo, у)
Рис. 6.3
Рис. 6.4
а) значению fx (х) в точке х;
б) условной плотности распределения /2 (у\х).
Решение. Для данного х:
а) /j (х) изображается площадью сечения, заштрихованного на
рисунке;
б) условная плотность распределения изображается кривой,
каждая ордината которой равна ординате сечения, деленной на
6.5. Имеются две независимые случайные величины (X, У),
подчиненные каждая показательному закону:
Л(*) =
О при х < О,
Хе
при х > О,
О
-и/
при 2/ < О,
при у > 0.
Написать выражения: а) плотности распределения системы;
б) функции распределения системы (X, У).
Ответ.
f(x,y) =
0 при а; < 0 или у < 0,
\м,е-(Хх+и/) при яг > 0 и у > 0,
F(s,y) =
0
(1
—Хх
)(1
при х < 0 или 2/ < 0,
"^ ) при а: > 0 и у > 0.
6.6. Система случайных величин (X, У) распределена с
постоянной плотностью внутри квадрата R со стороной 1 (рис. 6.6 а).
133
X
a
Рис. 6.6
Написать выражение плотности распределения /(#, у). Построить
функцию распределения системы.
Написать выражения fi(x), f2(y)- Определить, являются ли
случайные величины (X, Y) независимыми или зависимыми.
1 при (x,y)eR,
О при (x,y)£R.
Ответ, /(#, у) =
F(x, у) =
О
ху
X
У
1
при х < О
при 0 < х < 1
при 0 < х < 1
при х > 1
при х > 1
или у < О,
и 0<2/<1,
и у >1,
и 0< у < 1,
и у > 1.
Поверхность ^(#, у) представлена на рис. 6.6, 6.
1 при #€(0,1),
Л (*) =
Л (2/) =
0 при #¢(0,1),
1 при у € (0,1),
0 при ^ (0,1).
Случайные величины (X, Y) независимы, так как
/(^у) = Л(^)/2Ы-
6.7. Поверхность распределения системы случайных величин
(Х7 Y) представляет собой прямой круговой конус (рис. 6.7, а);
основанием конуса служит круг К с центром в начале координат и с
радиусом г0. Вне этого круга плотность распределения равна
нулю.
134
Ах> у)
a
Рис. 6.7
а) Написать выражение /(я, у), б) Найти ^(х); f2(y); f2(y\x)]
fx(x\y).B) Определить, являются ли случайные величины X, У
зависимыми, г) Определить, являются ли случайные величины X, Y
коррелированными.
Решение.
а) /(ж, У)
го ~ V
2 , 2
r07TV
О
при х2+2/2<г02,
при х2 + у2 > г02;
б) Л (х) =
г0-к
Wro2 -
а;
х21п
r0 + ^
о
а;
ж
О
при я<г0,
при |ж|> г0,
Ш =
Г07Т
о
Vro2 - У2 -2/21п
го +лК
2 2
-2/
2/
о
при |у|<г0,
при М>г0.
Далее, при |ж|< г0
Л(»1ж) =
о
Л
гс2 +у2
W
Гпл/Г0 - X
О
х21п
го +лЙ
2 2
- X
Я
при \у\< Jr[-x2
при у >
V^T1
X
135
и при \у\< г0
Л И у)
п> -4х2 + ^2
r0h2-y2-y2^
0
ro +Vro2 -У2
м
^ /
■\<4'
при \х\< Vo2 - у2
4<
при |я|> л/г02 - у2.
в) Так как /2 (гг|г/) v± Д (#), то случайные величины X, F зависимы.
г) Находим корреляционный момент К^ так как rnx = my = О, то
Кху = JJxyf(x^y)dxdy =JJ xyf(x,y)dxdy + JJxyf(x, y)dxdy,
(К)
(*i)
(*2)
где ^ — правая половина круга К; К2 — левая половина (рис. 6.7, б).
Функцияxyf(x, у) нечетна относительно аргумента х7 поэтому
интегралы по Кх и К2 отличаются только знаком; в сумме интегралы
взаимно уничтожаются, значит, К = 0, и случайные величины X, Уне
коррелированы.
6.8. Система случайных величин (X, Y) распределена по
закону:
f(x,y) =
а
\ + х2 +х2у2 Л-у2
а) Найти коэффициент а. б) Установить,
являются ли величины X, Y зависимыми;
найти /г(х)] f2(y). в) Найти вероятность
попадания случайной точки (X, Y) в пределы
квадрата Л, центр которого совпадает с началом
координат, а стороны параллельны осям
координат и имеют длину 6 = 2 (рис. 6.8).
Р е ш е н и е. а) Из условия
оо
J J f(x> y)dxdv = 1
•oo
находим a =
1
7Г
б) Случайные величины X, Yнезависимы:
л oo=
i
■к(1 + х2)
; ЛЫ =
1
it (l + j/2)
;/(z, 2/) = /10*0/2 Ы
136
1 1
B)P((X,Y)€R) = ff
dx dy
1
:^^(1 + ^)(1 + 2,2) 4
6.9. Имеются независимые случайные величины X, Y.
Случайная величина X распределена по нормальному закону с
параметрами: тх = 0; а.
1
л/2
. Случайная величина Y распределена
равномерно на интервале (0, 1). Написать выражения для плотности
распределения f(x,y) и функции распределения F(x, у) системы
(X, У). ^
е-*2 при у €(0,1),
Ответ. /(#, у)
л/тг
0
F(x,y) = Fl(x)F2(y)
при у ¢(0,1).
0 при у < 0,
уФ*(хл/2) при 0<у<1,
Ф * (W2) при у > 1.
6.10. Поверхность распределения /(#, у) системы случайных
величин (X, У) представляет прямой круговой цилиндр, центр
основания которого совпадает с началом координат (рис. 6.10, а)у а
высота равна к Определить радиус цилиндра г, найти fx (х); f2(y)\
Лх, у)
а
Рис. 6.10
Решение. Радиус цилиндра г определяется из условия:
объем цилиндра равен единице, откуда г = /—. Плотность
распределения f(x,y) имеет вид
h, если
0, если
ir/i
2 , 2^2
Х +у < Г ,
х2 + у2 > г2.
137
Следовательно,
00
/i(z)= jf(x,y)dy =
■OO
Ъ&~*К при H<rf
О при |rr| > r.
Аналогично,
ш=
2д/г2 - y2h при \y\< г,
при | у\ > г.
О
График функции fx (х) показан на рис. 6.10, б. При \у\< г
Л(%)
/fo г/)
Л (у)
2V
2 2
Г -у
при Ж <
у2,
о
при |Х|> л/Г2 - у2.
7.
Аналогично, при Ы< г
/2(2/к) =
!>/i
2Vr2 - х2
О
при
|y|<V
2 2
Г — Ж ,
при |у| > Vr2 — ж2.
Математические ожидания равны нулю:
Шх = ™>у =0,
так как функция /(ж, у) четна как по ж, так и по у;
£>х = 2hjx2jr2 -
x2dx= hrA — =
;°* =
Г- /Г
2' *
= 0.
6.11. Система случайных величин (X, Y) распределена по
круговому нормальному закону со средним квадратическим
отклонением а:
/(#,</) =
1
1 <х2 + У2)
2ткг
2а'
а) Заменить приближенно этот закон распределения законом
постоянной плотности в круге; радиус круга г0 подобрать так,
чтобы сохранились неизменными дисперсии величин Хи Y.
б) Заменить приближенно этот закон распределения законом с
поверхностью, изображаемой прямым круговым конусом с
центром основания в начале координат; радиус гх основания также
подобрать из условия равенства дисперсий.
138
Решение.
а) Сравнивая с задачей 6.10, из соотношения Dx = — = а на-
4
ходим r0 = 2а.
б) Сравнивая с задачей 6.7, из соотношения
D,=
Ях2\х2 — Jx2 + у2 dxdy = —г2 =а
I J 20 *
1 'V (K\
находим r.
V20
V3
(*)
a = 2,58 a.
6.12. Случайная точка (X, Y) распределена с постоянной
плотностью внутри квадрата Л, заштрихованного на рис. 6.12, а.
Написать выражение плотности распределения /(а;, у). Найти
выражения плотностей распределения f1(x), f2(y) отдельных величин Ху
Y, входящих в систему. Написать выражения условных
плотностей fx (х\у)и /2(у\х). Зависимы или независимы случайные
величины Ху Y? Коррелированы они или нет?
Решение. Площадь квадрата равна 2, поэтому
/(*> У)
- при (х, у) е Л,
О при (х, у) ¢ R.
Л (*) =
1 1_х
~ I dy = 1 — х при 0 < а; < 1,
-(1-х)
1+х
1 г
- I dy = 1 + х при — 1 < х < О,
-(1+х)
О
при х < — 1 или а; > 1
или, короче,
Л (*) =
1
о
N
при
при
#|< 1,
х\> 1.
График закона /Да;) показан на рис. 6.12, б (закон Симпсона).
Аналогично,
h (у) =
1-\у\ при \у\<1,
0 при | у\ > 1.
139
Далее, при \у\< 1
Л (*1у) =
/(д. у)
Л(У)
1
— при Id < 1 — \у\,
2(Ну1)
О при \х\ > 1 — |у|.
График плотности /х (а:|?/) показан на рис. 6.12, в. Аналогично,
при х\ < 1
1
ЛЫ^Н-
— при Ы<1 —Ы,
2(1-|х|)
О при |у| > 1 — |ж|.
Случайные величины X, ^зависимы, но не коррелированы.
/.(*)
L
/Ш
~^ш
-1
У
*1
X
а
А
-1 0
\
1
6
Р]
дс. 6.12
х
Ы-1 о
1-12/1
X
в
6.13. Плотность распределения системы случайных величин
(X, Y) задана формулой
Дя,у) =
1
1,61с
1,28
[(х-2)2-1,2(х-2)( у +3)+( у +3)2]
Найти коэффициент корреляции величин X, Y.
Ответ.г^ = 0,6.
6.14. Независимые случайные величины X, Yраспределены по
нормальным законам с параметрами
га
2\ту =-3;ах =1;сг
у
2.
Вычислить вероятности следующих событий:
a) (X<mx)(Y<mV б) X < 3; в) Y < X - 5; г) \Х\<1;
д)(|Х|<1)(|У|<2).
Решение.
a)P((X<mx)(r<m„)) = P(X<ms)P(r<m„) = i.i = 7-
б)Р(Х<3) = Ф*
3-2'
I 1 ,
2 2 4
= Ф* (1) = 0,8413.
140
в) Искомая вероятность равна интегралу
пп 1 (*-2)2 (у+3)2
8
(D)
2тгл/2
dx dy,
взятому по области Д где у < х — 5. Область Z) заштрихована на
рис. 6.14; она лежит правее и ниже
прямой у = х — 5. Эта прямая проходит
через точку с координатами тх =2;
ту =— 3 (центр рассеивания). В силу
симметричности нормального законаъе-
роятность попадания случайной точки
по одну сторону от прямой, проходящей
через центр рассеивания, равна
вероятности попадания по другую сторону от
этой прямой, поэтому P(Y < X — 5) = -.
у—х-Б
х
Рис. 6.14
г)Р(|Х|<1)=Р(-КХ<1) = Ф
1-21
Ф
-1-21
= 0,1573.
д) Р((|Х|< 1)(|У|< 2)) = Р(|Х|< 1)Р(|У|< 2) =
= 0,1573
Ф
(2-31 * (-2-31
= 0,0476.
6.15. Система случайных величин (X, У) имеет распределение
с плотностью /(х, у). Выразить через плотность распределения
вероятности событий: а) X > Y; б) X >|У|; в) \Х\> У; г) Y - X > 1.
Решение. На рис. 6.15, а, б, в, г заштрихованы области
jDe, D6 , De, Dz, попадания в которые соответствуют событиям а),
б), в), г). Вероятности попадания в них:
-оо X
ОО X
а)Р(Х > Y) = J ff(x, у) dx dy; б) Р(Х >\Y\) = J J f(x, у) dx dy;
-oo—oo
0 -x
oo x
oo oo
b)P(\X\>Y)=J ff(x,y)dxdy; r)P(Y-X>l)=J J f(x,y)dxdy.
-oo—OO
-oo *+l
6.16. Система двух случайных величин X, У распределена по
нормальному закону с параметрами тх =гпу =0; ах =ау = а;
г^ =0. Определить вероятности следующих событий: a) \Y\< X;
6)Y<X;b)Y<\X\.
141
a
б
в
Рис. 6.15
Решение. На рис. 6.16, а, б, в показаны области,
соответствующие событиям а), б) и в). При круговом рассеивании
вероятности событий будут: а) 0,25; б) 0,5; в) 0,75.
х
а
б
Рис. 6.16
в
6.17. Случайная величина X имеет плотность распределения
f(x); случайная величина Y связана с ней функциональной
зависимостью
Y = X\
Найти функцию распределения F(x, у) системы (X, Y).
Решение. Исходим из того, что значение случайной
величины Y полностью определяется значением случайной величины X.
Случайная точка (X, Y) может находиться только на кривой
у = х2. Вероятность попадания ее в квадрант с вершиной в точке
(х, у) равна вероятности попадания случайной точки Хна проек-
142
цию на ось Ох участка кривой у =х2, попадающей в квадрант
(рис. 6.17). Пользуясь этой интерпретацией, имеем
О при у < 0 или у > 0 и х < -yfy,
F{x, у)
Я
ff(x)dx при у>0 и x>Jy,
■Л"
ff(x)dx при у>0 и - Jy <х<4у-
HV
6.18. Случайная точка (X, У) распределена по нормальному
закону на плоскости:
1 -V+y2)
f(x,y) = —е 2
Найти вероятность р попадания точки (X, 7) в квадрат R
(заштрихованный на рис. 6.18), сторона которого равна двум.
Решение. Так как рассеивание круговое (ах =оу = 1), то
координаты точки (X, Y) остаются независимыми при любом
повороте координатных осей, и поэтому при повороте на 45° получаем
a ^2
р=
2Ф
--1
U
= 0,467.
6.19. Случайная точка (X, Y) распределена по нормальному
закону на плоскости с параметрами
тх =1;ту =-1;а, = 1;сту = 2; г„ =0.
Найти вероятность того, что случайная точка попадет внутрь
области D, ограниченной эллипсом
(х-1У +
2 , (У + 1)2
= 1.
у=хл
X
Рис. 6.17
143
Решение. Область D ограничена эллипсом рассеивания Ev с
полуосями а = ах =\1Ъ = оу = 2; вероятность попадания в эту
область р = 1 — е 2 « 0,393.
6.20. Производится стрельба по точечной (малоразмерной)
цели снарядом, зона разрушительного действия которого
представляет собой круг радиуса г. Рассеивание точки попадания
снаряда круговое, с параметрами тх =ту =0^^ =ау = 2г (центр
рассеивания совпадает с целью). Сколько выстрелов нужно
произвести для того, чтобы разрушить цель с вероятностью Р = 0,9?
Решение. Вероятность разрушения цели при одном BblCTpe-
ле р = 1 — е 2 «0,118. Потребное число выстрелов
n>lg(1-P)=-ML«18,4,T.e.n=19.
Ig(l-P) lg 0,882
6.21. Система трех случайных величин (X, Y, Z) имеет
плотность распределения f(x,y,z). Написать выражения:
1) плотности распределения /г (х) случайной величины X;
2) плотности распределения /2 z(y,z) системы случайных
величин (У, Z);
3) условной плотности распределения/2 3(у, z\x);
4) условной плотности распределения /2\у|х, z);
5) функции распределения F(x, y,z);
6) функции распределения Fx (х) случайной величины X;
7) функции распределения Fx 2(х, у) системы (X, Y).
Ответ.1)/1(х) = ///( х, у, z) dy dz;
—оо
оо
2)/2,s(»i«)= ff(x,y,z)dx;
-ОО
3)/,,,(,,,1,)- . /(w)
f f f(x,y,z)dydz
—oo
4)«»|V) = ^
Jf(x,y,z)dy
-OO
x 2/ г
5)F(x,y,z)=ffff(x, y,z)dxdy dz\
-oo—oo—oo
144
X oo oo
6) Fx (x) = F(x, oo, oo) =111 /(x, y, z) dx dy dz\
-oo—oo—oo
I у oo
7) Fi, 2(^ 2/) = F(^ 2/, 00) = / / /Ях' 2/? *) <& <fy dz.
-00—00—00
6.22. Производится стрельба одним снарядом по точечной
(малоразмерной) воздушной цели. Рассеивание точки разрыва
снаряда происходит по нормальному закону; центр рассеивания
совпадает с целью; средние квадратические отклонения ах=оу =
= az —о. Цель поражается, если расстояние между ней и точкой
разрыва снаряда не превышает г0 = 2а. Найти вероятность р того,
что при одном выстреле цель будет поражена.
Решение. По формуле для вероятности попадания в
эллипсоид равной плотности имеем
/9
р = Р((Х, У, Z) е Е2) = 2Ф * (2) - 1 - lf=.2e~2 « 0,739.
6.23. Система трех случайных величин (X, Y, Z) распределена
равномерно внутри шара S радиуса г. Написать выражение
плотности распределения системы /(х, у, z\ плотностей
распределения fx(x), Д(у) и f3(z) отдельных величин, входящих в систему, а
также условной плотности распределения fx (х|у, z).
Решение.
/(*,»,*) =
с при х2 + у2 + z2 < г2,
0 при х2 + у2 + z2 > г2.
Постоянную с находим из условия, что объем шара 5, умно-
4 з -, 3
женныи на с, равен единице: —-кг с = 1, откуда с = -.
3 4гкг
Плотность /j (ж) определяется выражением
оо
fi(x) = f f f(x, У, *) dy dz.
-00
При|х|> г, очевидно,/j (x) = 0.При|х|< г имеем
[с при (y,x)eDs,
f(x, у, z) = -■
0 при (y,z)£DxJ
где Dx — круг радиуса л/г2 — х2 (рис. 6.23, а, б). Следовательно,
145
V г2— х2
У
а
б
Рис. 6.23
в
fx(x)= I I с dy dz = ск (г2 — х2) (\х\< г)
(Dx)
Таким образом,
Л (х) =
3 г2 - х
4 г3
О
при |х|< г,
при |х|> г.
Кривая распределения представлена на рис. 6.23 в. Числовые
г2
характеристики этого закона следующие: тх = 0; Dx = —. Плот-
5
ноеги распределения /2 (у)af3(z) имеют ©ид
ш=
/,(*)=
Зг2 -у2
4 г3
0
Зг2-*2
4 г3
0
при \у\< г,
при |у|> г,
при \z\< г,
при Ы> г.
Плотность распределения подсистемы (Y, Z)
оо
/2,з(У^)= Jf(x,y,z)dx =
-оо
Г~2 2 2
-у/Г -7/ -2
1 с dx = 2c ф
[~2 2 2
—у/Г -7/ -Z
о
у2 — z2 при
при
2 . 2 ^ 2
2 + у < Г ,
2 . 2^2
г + У > Г .
146
Отсюда при z + у < г находим условную плотность
распределения
1
Ux\y,z) = .2jr2-y2-z
2
i i I 2 2 2~
при \х\< д/г ~У -Z 1
О при |ж|> д/г2 — у2 — z2.
Y = *
6.24. Система трех случайных величин (X, Y, Z) распределена с
постоянной плотностью внутри шара радиуса г. Найти
вероятность попадания случайной точки (X, F, Z) внутрь шара,
концентричного данному, с радиусом г/2.
Ответ. р = —.
8
6.25. Из урны, в которой а белых, Ь черных и с красных шаров,
вынимается один шар. Случайные величины X, Y, Z определяются
следующими условиями:
[1, если появится белый шар,
[О, если появится черный или красный шар.
1, если появится черный шар,
О, если появится белый или красный шар.
[1, если появится красный шар,
[О, если появится белый или черный шар.
Построить корреляционную матрицу и нормированную
корреляционную матрицу системы случайных величин (X, Y, Z).
Решение. Корреляционные моменты определим из таблицы
вероятностей отдельных значений X, Yn Z.
Обозначим
pXti ,it ,k=-p((x = Xi W = Vj){z = zk)).
Имеем
P0i о, о =P((* = 0)(7 = 0)(2 = 0)) = 0;
PW=P((J = 1)(7 = 0)(Z = 0))= a ;
a + b + с
Р„,1,о=Р((* = 0)(Г = 1)(3 = 0))= Ь ;
a + 0 + с
f>=P((X = 0)(K = 0)(3 = 1)) = c
a + b + с
P — P — P — P — П
-M, l, о — ri, o, 1 "~r0,l,l — ^1, 1,1 ~~ u*
147
га
а
а + Ь + с
5ту
а + Ъ+ с
; га
а + Ъ + с
К*у = Х>< ~т*)(»j- ту)Рж, у,,
**
г , ;, А;
1-
а
+
+
0-
0-
а
а + Ъ + с,
а +6+ С;
а
а + 6 + с
у
0
vo- " *
а
а + Ъ + с)а + Ъ + с
Ь \ Ь
+
а + Ъ+ с,
Ь N
а + Ъ + с
+
а + Ъ + с
аЪ
а + Ъ + с (а + Ъ + с)
Аналогично
К
ас
XZ
(а + Ъ + с)
\К
-be
у*
(а + Ъ + с)
Далее находим дисперсии
Dx = <*2[*]-т* =
а а2 _ а(Ь + с)
а + Ъ + с (а + Ъ + с)2 (а + Ъ + с)
аналогично
D Ъ(а + с) D с(а + Ъ)
У (а + Ъ + с)2' 2 (а + Ъ + с)2'
Отсюда находим коэффициенты корреляции
Кл
Г™ =
ху
ху
•ab
аЪ
jDxDy Jab(a + c)(b + c) Ч(а + с)(Ь + с)
Аналогично
ас
г =
XZ
(а + Ъ)(с + Ъ)
v =
> ' уг
Ъс
(Ъ + а)(с + а)
6.26. Имеется система случайных величин X и Y. Случайная
величина X распределена по показательному закону с
параметром X:
Л со =
Xe-Xl
0
при х > 0,
при х < 0.
148
Случайная величина Y при заданном значении X = х > 0
распределена также по показательному закону, но с параметром х:
Л (у к)
хе
О
-ту
при у > О,
при у < 0.
Написать плотность распределения f(x,y) системы (X, Y) и
найти плотность распределения /2(у) случайной величины Y;
найти условную плотность Д (х|у).
Решение.
f{x,y) = -
0 при х < 0 или у < 0,
Xxe"(x+y)l при х>0 и у>0.
оо
/2(2/)= Jf(x,y)dx =
■ОО
X
при г/ > о,
(Х + 2/)2
0 при у < 0.
Далее, при у > 0
Л(%) =
/foy)
/2(2/)
x(X + y)2e"(x+y)l при х>0,
0 при х < 0.
6.27. Даны две независимые случайные величины:
непрерывная X с плотностью /г(х) и дискретная Y со значениями
ух,у2» • • •' Уп > имеющими вероятности рг, р2, ..., рп. Найти
функцию распределения системы (X, Y).
X
Ответ. F(x, y) = Fx (х) F2 (у), где Fx (х) = J fx (х) dx\
-00
Чу) =
0
к-1
Ел
при
при
при
У < Vi,
У! <У <У2,
УЛ:-1 <У<Ук,
[К — Zi. Oj ... j ТЬ ) 7
г=1
при
У >Уп-
6.28. Случайная величина X— дискретная величина с двумя
значениями х1 и х2 (х2 > хг), имеющими вероятности рг и р2.
Случайная величина Y — непрерывная величина; ее условным
распределением при X = х{ служит нормальный закон с
математическим ожиданием, равным х-, и средним квадратическим
отклонением, равным а.
149
Найти функцию распределения F(x, у) системы случайных
величин (X, Y). Найти плотность распределения /2(у) случайной
величины у.
Решение.^, у) = Р(Х <x)P(Y <у\Х <х).
Пусть х < хг; тогда Р(Х < х) = 0 и F(x, у) = 0; пусть хг < х < х«;
(у — х
тогда Р(Х < х) = рх и F(x, у) = pxP(Y < у\Х = хх) = ргФ* 1
При х > х2 по формуле полной вероятности имеем
Р(х,у) = ргФ
'У-*,'
+ р2Ф:
а
Следовательно,
F(x,</) =
0
^ф*
РХФ*
к.
+ р2Ф*
'у-х2у
при х < хх,
при X, < X < X
2'
при х > х2
Далее, полагая х = оо и дифференцируя по у, получаем
ау ал/2-к
(У-Х!)2 (У"Х2)2
рхе 2ст2 + р2е 2ст"
6.29*. Звезды на небесной сфере рассматриваются как пуассонов-
ское поле точек. Число звезд, попадающих в объектив телескопа,
является случайной величиной, распределенной по закону Пуассона с
параметром Х5, где S — площадь участка, вырезаемого на поверхно-
а
Рис. 6.29
150
сти сферы полем зрения телескопа (в радианах) (рис. 6.29, а). Поле
зрения телескопа имеет координатную сетку (рис. 6.29, б) (отсчет
ведется в радианах). Показать, что при любом положении телескопа
координаты (X, У) ближайшей к перекрестию звезды распределены
по нормальному закону с параметрами
Решение. В задаче 5.31 было показано, что расстояние R от
центра перекрестия до ближайшей к нему точки пуассоновского
поля подчиняется закону Рэлея. Но R = VX2 + У2,
следовательно, вероятность попадания точки (X, У) в круг D (х2 + у2 < г2)
может быть записана в двух формах:
г
Р(Д<г)= f 2ъ\ге-«Хг2 dr (г>0),
о
PUX,Y)eD) = fff(x,y)dxdy, (1)
где f{x,y) — плотность распределения системы (X, У). В силу
симметрии надо считать, что f(x,y) зависит только от расстояния:
/(ж, у) = д(г), где г = ^х2 + у2. Переходя к полярным координатам
(г, ip), получаем
Р((Х, Y)£D) = fd4> Jg(r) rdr = totf g(r) r dr. (2)
0 0 0
_ ч 2
Сравнивая выражения (1) и (2), находим: g(r) = \е * г и,
значит, f(x, у) = \е~^х +у \что и требовалось доказать.
ГЛАВА 7
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН
Если X — дискретная случайная величина с рядом распределения
Х{
Pi
Х\
Р\
Х2
Т>1
...
...
Хп
Рп
а величина У связана с X функциональной зависимостью У
тематическое ожидание величины У равно
Ч>(Х), то ма-
п
тпу =М[ч>(Х)] = ^2ч>Мр{,
i =1
а дисперсия выражается любой из двух формул
Dy = D[«p (X)} = J2 [«Р (*<) - mv ?Pi = X> (*i )fPi - ml ■
i =1
i =1
Если (X, Y) — система дискретных случайных величин,
распределение которой характеризуется вероятностями
Pij=P((X = *,)(У = „,)),
a Z = ф (X, У), то математическое ожидание величины Нравно
ш2 = М [Ф (X, У)] = £ J2 Ч> (¾ • **) *«.
а дисперсия выражается любой из двух формул
D2 = D[<p (X, У)] =
2^ 2-Дч> (xi'2/i)-mJ р* = 2^2-Дч> (x*'2/i)] р*-™*-
* j
» ^
Если X — непрерывная случайная величина с плотностью
распределения /(я), а У = ср (X), то математическое ожидание величины У равно
00
га
у
М [«р (X)] = J 4,(¾) /(*) dr,
-00
а дисперсия выражается любой из двух формул
152
00 00
Dy = D [<p (X)} = f [9 (x) - my ff(x) dx = f [<p (z)]2/ (s) <ir - m 2
■OO —OO
Если (X, У) — система непрерывных случайных величин с плотностью
/(х, у), a Z = ср (X, У), то математическое ожидание величины Нравно
оо
т2 = М[ф (Х,У)] = JJtp (х,у) f(x,y) dx dy,
-00
а дисперсия выражается любой из двух формул
оо
Я = D[9 (X, У)] = JJ [Ф (*, у) - т2] /(*, у) dx dy
— ОО
ОО
Ц [ф (^, 2/)f/ (^, У) dx dy - т].
—ОО
Если (Х1? ...,ХП) — система п непрерывных случайных величин с
плотностью f(a\, ..., хп\ а У = Ч>(ХХ, • • •, Хп), то математическое ожидание
величины У равно
оо
т
М[ф (Х15 ...,Хп)] = JJ ... J ф (^,...,2^)/(^,..., xj сЦ ...cbn,
—оо
а дисперсия выражается любой из двух формул
D,=D[f>(Xu...,Xn))-
ОО
JJ '" I ^ (^'•••'^n)-771^]2/ (^, —I &«) ^1 '•• ^п
■оо
оо
Ц '" l [ф fo''"' Х")]2/ (Xl'---'Xn) ^1 -"^п - ту
-оо
Если с — не случайная величина, то
М[с] = с; D[c] = 0.
Если с — не случайная величина, г X — случайная, то
М = [сХ] = сМ[Х}; D[cX] = c2D[X].
Теорема сложения математических ожиданий
Математическое ожидание суммы случайных величин равно сумме их
математических ожиданий:
М[Х + У] = М[Х]+М\У];
и вообще
153
n
n
M
E*
EM№1-
i=i
i=i
Математическое ожидание линейной функции нескольких случайных
величин
п
y = £>,.xj+b,
i=l
где а{ и Ь — не случайные коэффициенты, равно той же линейной
функции от их математических ожиданий:
ту = М
п
£«Д<+ь
i=l
п
Ylaim*i +6'
i=l
гдешХ1- = MfX,] (г = 1, ..., п).
Короче это правило можно записать так:
M[L(XUX2, ,..,Хп)] = Цтх. , тХ2, ..., тХп),
где L — линейная функция.
Математическое ожидание произведения двух случайных величин X,
У выражается формулой
M[XY] = M[X]M[Y] + Kxy,
где Кщ — корреляционный момент величин X, У Эту формулу в другом
виде можно записать так:
K„ = M[XY] - тхту
или, имея в виду, чтоМ[ЛТ] = аг г[Х, У],
Теорема умножения математических ожиданий
Математическое ожидание произведения двух некоррелированных
случайных величин X, У равно произведению их математических
ожиданий
M[XY] = М[Х] М[У].
Если Хг, Х2, ..., Хп — независимые случайные величины, то
математическое ожидание их произведения равно произведению
математических ожиданий
М
п
п*.
1=1
п
ПМ[Х,].
i=i
Дисперсия суммы двух случайных величин выражается формулой
D[X + Y] = D[X] + D[Y] + 2KV.
154
Дисперсия суммы нескольких случайных величин выражается
формулой
D
п
Е*.
i=i
п
Е^( +2Е^<х,.>
i=l i<7
где КХш х — корреляционный момент случайных величин Хь X.
i j J
Теорема сложения дисперсий
Дисперсия суммы двух некоррелированных случайных величин Xf Y
равна сумме их дисперсий
D[X + Y] = n[X] + D[Y],
и вообще, для некоррелированных случайных величин Хх, Х2, ..., Хп
D
п
£*
1=1
п
ЕВД1-
i=i
Дисперсия линейной функции нескольких случайных величин
1=1
где aif b — не случайные величины, выражается формулой
A. =D
у
п
ЕаЛ + 6
i=i
п
i=l i<j
В случае, когда величины Хх, Х2, ..., Хп не коррелированы,
п
Еа^+6
i=i
п
= £a*D[X,.].
1=1
При сложении некоррелированных случайных векторов их
корреляционные моменты складываются, т. е. если
Х = Х1 + Х2; Y = Y1 + Y2, К
К,
х1х2 х1у2
К Z=2 К = Г)
У\У2 У\х2 '
ТО
к
ху
К Л- К
Х\У\ х2у2 *
Функция у> (Хг, Х2, .-., Хп) нескольких случайных аргументов
Хг, Х2, ..., Хп называется «почти линейной», если во всем диапазоне
практически возможных значений аргументов она может быть с
достаточной для практики точностью линеаризована (приближенно заменена
линейной). Это означает, что
155
n
Ф (Х19Х2,...,Хп) « ip (тЖ1, тЖ2,..., тЖя)+ ^
i =1
$ Ж-
№ -™*,).
т
где
dtp
дч>(™>х.тх. ...,тх )
т
ЭХ;
— — частная производная функции
ср (дг17 х2,..., х„) по аргументу xi7 в которую вместо каждого аргумента
подставлено его математическое ожидание.
Математическое ожидание почти линейной функции Y =
= ср (Х1, Xj,..., Хп) приближенно вычисляется по формуле
га
у
<Р (таг1 ,™>хч, '-.,ГПХ )•
Дисперсия почти линейной функции приближенно вычисляется по
формуле
D = У *£- D + 2 V
i =1
дх
Кг )
т
КЗ
Kdxi J
т
( \
dtp
дх.
is
xixj
т
гдеDx — дисперсия случайной величины Х-;Кхх — корреляционный
момент величин Xit Xj.
В случае, когда случайные аргументы Х1, Х2,..., Хп не коррелированы,
dtp I
i =1
^.,
D.
т
7.1. Дискретная случайная величина X имеет ряд
распределения
Хг
Pi
-1
0,2
0
0,1
1
0,3
2
0,4
Найти математическое ожидание и дисперсию случайной
величины У = 2х.
Решение.т„ = 2"1 • 0,2 + 2° • ОД + 21 • 0,3 + 22 • 0,4 = 2,4.
у
-1\2
,0\2
Dy =0^-^=(2-^-0,2+(2^.0,1 +
Л \2
,2\2
+(21 у • 0,3 + (2' У • 0,4 - 2,4' = 1,99.
7.2. Непрерывная случайная величина X
распределена в интервале (0, 1) по закону с
плотностью
/00 =
X
2х при же (0,1),
0 при х £ (0,1)
Рис. 7.2
(рис. 7.2). Найти математическое ожидание и
дисперсию квадрата случайной величины Y = X2.
156
Г 2 1
Решение. ту —а2[Х)= I х 2xdx = -;
о
X
Dy =a2[K]-mJ = f(x2)22xdx-
о
/i\2
[2)
1 _ 1 __1_
3 4~12
7.3. Непрерывная случайная величина X распределена по
показательному закону:
Хе"Хх
/(*) =
О
при х > О,
при х < О
(Х>0).
Найти математическое ожидание и дисперсию случайной
величины У = е~х.
00
Решение. гат, = Ге х\е Xxdx =
У J X 4-1.
о
00
Dy = а2\У]-т2у =fe-2x\e-Xxdx-
X
о
IX + 1J
X
(Х + 2)(Х + 1):
7.4. Непрерывная случайная величина X распределена по
показательному закону:
Хе"Хх
/(*) =
О
при х > О,
при х < О
(Х>0).
Установить, при каких условиях существуют и чему равны
математическое ожидание и дисперсия случайной величины Y — ех.
оо
Решение. my = Jex\e~Xxdx = X fe~{x~l)xdx]
о
о
при X — 1 > 0, т.е. при X > 1, этот интеграл существует и равен
т.. = ; при X < 1 он расходится.
у
Х-1
00
00
а2Р1 = fe2x\e-Xx<b = X fe-{X-2)xdx.
о
о
X
При X > 2 этот интеграл существует и равен а 2 [Y] = , а
дисперсия равна Dv =
X
Х-2
Л-1,
X
(Х-2)(Х-1)
Х-2
; при
X < 2 интеграл расходится, и дисперсии D не существует.
157
7.5. Непрерывная случайная величина Xраспределена по закону:
1
/(*)
2
О
cos х при х €
при х £
f 7Г тО
2 2J
2' 2J
Найти математическое ожидание и дисперсию случайной
величины Y = sinX.
1 ^
Решение, га„ =- / sinxcosx dx = 0;
у 2J
it
~~2
it
*2
Z)y = а 2 [F] = - / sin2 xcos х dx
it
1
3
7.6. Случайная величина X распределена по тому же закону,
что и в предыдущей задаче. Найти математическое ожидание и
дисперсию случайной величины Y =|sinX|.
Решение.
it
га
у
= — \ \smx\cosxdx= I sinxcosx dx =
it
1
о
It
*2
1
2
a2[F] = - / |sinx|2 cosxcte = / (smx)2 cosx dx =
it
~2
0
1
3
Л,=<*2р1
my =
4 12
7.7. Случайная величина Xраспределена с постоянной
плотностью в интервале (1; 2):
/(*)=
1 при £€(1,2),
0 при х £ (1, 2).
Найти математическое ожидание и дисперсию случайной
величины Y = —.
X
158
Решение, т
у
2П
/ —dx = 1п2;
J х
Dy =a2\Y}- т2у = j±dx - (Ы2)2 =±- (Ы2)\
X &
7.8. Случайная точка (X, Y) распределена равномерно внутри
круга if радиуса г— 1 (рис. 7.8). Найти математическое ожидание
и дисперсию случайной величины Z= XY.
Решение.
f(x,y) =
1
- при (х,у)еК,
О при (х,у)£К.
т
= — 11 ху dxdy = 0 (см. задачу 6.7).
тс ~°\
1 - 2« 1 -
D2 = — J I x2y2dx dy = — J d у I гъ cos2 у dr = —.
{К) о о
7.9. Случайная точка (X, Y) распределена равномерно внутри
квадрата R (рис. 7.9). Найти математическое ожидание и
дисперсию случайной величины Z= XY.
Рис. 7.8
Рис. 7.9
Решение. Так как случайные величины X, Y независимы, то
1 1 1
m=mTmv = = —
у 2 2 4
D,=OL2[z]-mi = Щ(ХУУ]-т'я =М[Х']М\У<]-
М[Х2} = а2[Х} = ±- M[72]=i; D2 = 1-
i j 2i 3» L J з 144
га
г )
159
7.10. Имеются две случайные величины Хи У, связанные
соотношением Y = 2 — ЗХ. Числовые характеристики величины X
заданы: тх = -1]DX = 4.
Определить: а) математическое ожидание и дисперсию
величины Y; б) корреляционный момент и коэффициент корреляции
величин X, Y.
Решение, а) ту = 2-3mx = b\Dy =(-3)2 -4 = 36.
б)^ = ЩХУ]-тхту = М[Х(2 - ЗХ)} + 1-5 = 2М[Х]- ЗМ[Х2]+ 5,
иоМ[Х2] = а2[Х] = Dx + тх = 4+ 1 = 5; отсюда
ДГ = -2 -3-5 + 5= -12; г =
12
ху
ху
«Vy
-12
л/4-36
= -1,
что и естественно, так как Хи Усвязаны линейной функциональной
зависимостью.
7.11. Имеется случайная величина Хс математическим
ожиданием тх и дисперсией Dx. Найти математическое ожидание и
дисперсию следующих случайных величин:
Y = -X] Z = X + 2Y-1; U = ЗХ - Y + 2Z - 3.
Ответ.ту =-mx\Dy =Dx;mz =-mx -\\DX = Dx;
mu = 2mx -5;£u = 4DX.
7.12. Имеется система случайных величин (X, У, Z) с
заданными характеристиками: математическими ожиданиями тх,ту, т2
и корреляционной матрицей
Dx Кху Kxz
Dy Kyz
Найти математическое ожидание и дисперсию случайной
величины U = аХ — Ь Y + cZ — d.
Ответ, т.. =ат„ —ЬтЧ1 -f cm — d;
U X 1]
u
X
2а&АГ + 2асАГ2 -26cAT .
ху ' х.г уг
7.13. Имеется n-мерный случайный вектор Х= (Х1?Х2, ...,
Хп), составляющими которого являются п случайных величин
Х{ с математическими ожиданиями тх_ (г = 1, 2,..., п),
дисперсиями Dx (г = 1, 2,..., п)и нормированной корреляционной матрицей
(г =1,2,..., п; г <.;').
х^-
160
Случайный вектор X преобразуется в m-мерный случайный
вектор Y = (Ух, У2,..., Ут ), причем составляющие вектора Y
получены из составляющих вектора X линейными преобразованиями
п
Yk = J2a*X* + Ь* (* = 1, 2,..., та).
г=1
Найти характеристики случайного вектора Y: математические
ожидания m (к = 1, 2,..., га), дисперсии Dy (к = 1, 2,..., т) и
элементы нормированной корреляционной матрицы
УАгУ/
(/ = 1, 2,..., га; А; < Z).
п
Ответ, га^ =^ai/tmIj. +¾ (Л = 1, 2,..., га);
г=1
г=1 г<.7
УАгУ/
УАгУ/
л/^Х"
где
п
7.14. Имеются две независимые случайные величины X и У
Величина X распределена по нормальному закону:
Л (*) =
2л/2гс
8
Величина У распределена равномерно в интервале (0; 2).
Определить: а) М[Х + У];б) М[ХУ];в) М[Х2];г) М[Х - У2]; д)
D[X + y];e)D[X-y].
Решение.
а) М[Х + У] = M[Jf ] + М[У] = 1 + 1 = 2;
б) М[ХУ] = М[Х] М[У] = 1-1 = 1;
в) М[Х2] = а2[Х] = D[X] + ml = 4 + 1 = 5;
г) М[Х - У2 ] = М[Х] - М[У2 ] = 1 - а 2 [У] = 1 -
fl)D[X + y] = D[X] + D[y]=4 + i = 4;
e)D[X-y] = D[X] + (-l)2D[y] = 4i.
О
'_4
Л2
+ 1
1
3
161
7.15. Случайная величина X распределена равномерно в
интервале (0, а). Определить: а) М[2Х + 3]; б) М[ЗХ2-2Х + 1];
b)D[2X + 3]; r)D[X2 + 1].
2 2
Решение.mT=-; Д. = —; a.JX} = —.
2 12 3
а) М[2Х + 3] = 2М[Х] + 3 = а + 3;
б)М[ЗХ2 -2Х + 1] = Зес2[Х}-Ш[Х}+1 = а2 - а + 1;
а2
в) D[2X + 3] = 4Д =
r)D[X2+l] = D[X2] = a2[X2]-(M[X2])2=a2[X2]-
-(а2[Х])2; a2[X2] = ±/V<£r = ^-;
отсюда
a
о
4 L2^2
D[X2+1] = ^-
a
= — a4
45 a
7.16. Случайная величина X подчинена нормальному закону:
X
/(*)=
ал/2тг
2а
Найти математическое ожидание случайной величины
Y = 1-3X2 + 4Х3.
Решение.
ту =М[1-ЗХ2 + 4Х3] = 1-ЗМ[Х2] + 4М[Х3].
Так как тх = 0,тоМ[Х2] = Dx =a2; М[Х3] = 0; ту = l-3a2.
7.17. Независимые случайные величины Хи У распределены
по законам /Дя),/2(у)> графики плотностей которых
представлены на рис.7.17, ау б.
а
Рис. 7.17
162
Определить: а) М[Х+ Y]; б) D[3X-67 + l]; в) М[ЯУ];
г) M[2XY-3X2 + Y2 -1].
Решение.
М[Х] = ±а; М[У]=Лб; ЩХ} = ^-; D\Y}=b-.
о о 1о 1о
а)М[Х + У] = -(2а + Ь);
О
6)D[3X-&T + 1] = 9D, +36Dy = — + 2b2;
B)M[XY] = -ab;
О
г) M[2XY - ЪХ2 + Y2 - 1] = 2M[XY] - За2[X] + а2[F] -
-1 = -аб а2 Н 1.
9 2 6
7.18. Ответить на вопросы а), б), в) предыдущей задачи, если
величины X, Y зависимы и их коэффициент корреляции равен
rv = -ОД
Решение.
a)M[X + Y} = ±-(2a + b);
О
а
б) D[3X - 6У + 1] = — + Ъ1 + 36
аЬ
л/18 • 18
•0,9 =
а
в) МГЛУ] = -аЬ - 0,9— = — аЬ.
9 18 180
= — + 2bz + 1,8 аЬ;
2
7.19. По сторонам прямого угла хОу концами скользит линейка
АВ длины /, занимая случайное положение (рис. 7.19), причем все
значения абсциссы X ее конца А на оси Ох в пределах от 0 до /
одинаково вероятны.
Найти математическое ожидание
расстояния R от начала координат до линейки.
Решение. Случайная величина X рас- g
пределена равномерно в интервале (0, /):
/(*)=
- при хе (о,/),
V
0 при х ¢(0,/).
в
0
2/
/S*
/■К <^ч
т
4 /
т
Рис. 7.19
163
Случайная величина R выражается через X формулой (см.
рис. 7.19)
Ее математическое ожидание равно
7.20. Случайные величины V, Uсвязаны линейно со
случайными величинами Ху Y:
V = aX + bY + c; U = dX + fY + g.
Известны числовые характеристики системы случайных
величин (Х7 Y): тх1 ту, Д., D , Кху. Требуется найти числовые
характеристики системы случайных величин (V, U): mv, ти, Dv, Du, Kvu,
т
Решение.
mv=amx + bmy + с; Dv = a2Dx + b2Dy +2abKxy]
mu=dmx+fmy+g; Du = d2Dx + f2D v +2dfKxy.
Далее
о о о о о о
V = aX+bY; U = dX+fY;
Km= M[VU] = adDx +bfDy+ (af + bd)^ ; rm = K' "
7.21. Производится стрельба независимыми выстрелами по
некоторой цели; вероятность попадания в цель для каждого
выстрела равна р. Запас снарядов неограничен; стрельба ведется до к-то
попадания, после чего прекращается. Найти математическое
ожидание числа израсходованных снарядов.
Решение. Обозначим X — число израсходованных снарядов.
Имеем
Х = Хг +Х2+...+Х
fc>
где Хх — число выстрелов до первого попадания (включая первое);
Х2 — число выстрелов от первого до второго попадания
(включая второе);
164
Xk — число выстрелов от (к- 1)-го до к-то попадания (включая
к-е).
По теореме сложения математических ожиданий
М[Х] = £м[Х<].
Так как выстрелы независимы и вероятность р одинакова для
всех выстрелов, можно вычислять М[Х{ ] как математическое
ожидание числа выстрелов до первого попадания (см. задачу
5.15): М[Х± ] = —, откуда
Р
М[Х]=£М[Хг]=Л
Ы v
7.22. Тело взвешивается на аналитических весах. Истинное
(неизвестное нам) значение массы тела равно а. Вследствие
наличия ошибок результат каждого взвешивания случаен и
распределяется по нормальному закону с параметрами а и а.
Для уменьшения ошибок взвешивания пользуются
следующим приемом: взвешивают тело п раз и в качестве
приближенного значения массы берут среднее арифметическое результатов п
взвешиваний
у(») =LyXi.
а) Найти характеристики случайной величины У'п' —
математическое ожидание и среднее квадратическое отклонение.
б) Сколько нужно сделать взвешиваний для того, чтобы
уменьшить в десять раз среднюю квадратическую ошибку массы?
Решение.
а)М[У<")] = 1£м[Х;].
nTU.
Так как все взвешивания производятся в одинаковых
условиях, то M[Xt} — а при любом i;
М[У(я)] = 1^о= — = а.
n—i п
Считая ошибки отдельных взвешиваний независимыми,
находим дисперсию У* .
D[r(n)] = _l_£D[Xi] = J_£CT2 =
2 2
па а
п" ~\ п" ~\ п2 п
165
б) Число взвешиваний п находим из условия
п л]п 10
■(n)i \G О О
7.23*. По некоторой цели производится п независимых
выстрелов; вероятности попадания в цель для этих выстрелов равны
Pv Piy —у Рп- Для упрощения вычислений эти вероятности осредня-
ют, заменяя одной постоянной
_ 1 п
p = -J2Pi-
По этой средней вероятности приближенно определяются
математическое ожидание fhx и среднее квадратическое отклонение
дх числа попаданий X. Будут ли эти характеристики вычислены
верно? Если нет, то в какую сторону будет ошибка?
Решение. Математическое ожидание будет вычислено верно:
_ п п
ГПХ=П p = -yPi =mx-
- П у-^
= п p = -^Pi =
Что касается среднего квадратического отклонения ах, то оно
будет завышено: дх >ох. Для доказательства сравним
приближенное выражение дисперсии
Dx=npq,rneq=l-p = -]Г^ =-^(1 ~ Pi )
n~i nT=i
с ее точным значением
п
Аг =YlV^i'
Преобразуем двумя способами сумму
п п п п
Х)(Р» ~ШЧг ~g) = YlPiqi ~12РЛ ~J2Pqi + ПРЯ =
г=1 1=1 г=1 i=l
п
= YlPiqi -ПРЧ'
г=1
Х>< - Шяг - Q)=Y2(Pi - pX1- р* -1+ p)=-J2(Pi - pf ^ °-
г =1 г =1 г =1
166
Отсюда
n
2^PiQi - npq = Dx - Dx <0, DX>DX,
1=1
что и требовалось доказать. Заметим, что знак равенства в
Dx > Dx достигается только при рг = р2 = ... = рп = р.
7.24. Светящаяся точка, изображающая наблюдаемый объект
на круглом экране радиолокатора, может случайным образом
занимать любое положение на экране (плотность вероятности
постоянна). Диаметр экрана равен D. Найти математическое
ожидание расстояния R от светящейся точки до центра экрана.
Решение. R = sjX2 + Y2, где (X, Y) — система случайных
величин, распределенная равномерно в круге KD диаметра D:
/(^2/) =
ir£>2
О
при (x,y)eKD,
при (x,y)£KD.
тг =М[Д]= ffjx2 +у2 -^-dxdy
(Kd)
или, переходя к полярной системе координат (г, у),
2* D/2
I d^p J r2dr = —.
rnr =
4 "г , "г 9, D
-kD2 j. Ч 3
о
о
7.25. Две точки Хи Y, независимо друг от друга, занимают
случайное положение на отрезке (0; 1) оси абсцисс (рис. 7.25, а),
причем плотность вероятности на этом отрезке постоянна для обеих
случайных величин. Найти математическое ожидание расстояния
R между этими точками и квадрата расстояния между этими
точками.
X
Г"
о
R
Y
О
н—X
а
Рис. 7.25
167
Решение. Имеем
R=\Y-X\- mr = M[\Y-X\].
Изобразим систему (X, Y) как случайную точку на плоскости
хОу (рис. 7.25, б), распределенную с постоянной плотностью
f(x,y) = l в квадрате со стороной 1. В области Dx\ X > Y\
\Y - Х\= X - Y. В области D2: Y > X; \Y - X\= Y - X.
mr = jj(x-y)dxdy + J J (y - x) dx dy =
(A)
X
(D2)
У
= jdxj (x- y)dy + jdyj (y - x)dx = -.
0 0 0 0
2i AJNTZ vi2
М[ДЧ = М[|У-*П = а2[К] + а2[Х]-2тхт,
6
2{Dx+ml)-2m
X
X.
R
Y
—«—
0
x
7.26. Ha оси абсцисс имеются два соседних отрезка (рис. 7.26)
длиной по единице; в пределы одного из них случайным образом
попадает точка X; в пределы другого —
точка У, причем координаты точек X и
Y независимы. Плотность
распределения каждой из случайных величин X,
Y в пределах соответствующего
отрезка постоянна. Найти математическое
ожидание, дисперсию и второй начальный момент расстояния R
между ними.
1 2
Рис. 7.26
Решение.
R = Y-X:
mr =M[Y]-M[X]
1; Д.
Dy+D
Oi2[R] = M[R2] = Dr +m
2
г
х
7
6
1
6
7.27. Имеется квадрат К со стороной,
равной 1 (рис. 7.27). На смежные стороны квадрата
случайным образом и независимо друг от друга
падают точки Хи Y; каждая из них имеет в
пределах соответствующей стороны равномерное
распределение. Найти математическое
ожидание квадрата расстояния между ними.
Решение.
R2=X2+Y2; т
= M[R2} = *2[X} + *2[Y} = ±.
168
7.28. Условия предыдущей задачи
изменены так, что точки X, Упадают не на смежные,
а на противоположные стороны квадрата
(рис. 7.28). Найти математическое ожидание
квадрата расстояния между точками Хи Y.
Решение.
R2 =1 + (у_Х)2;
X
К
1
•* ►
1
•Y
Рис. 7.28
М[Д2] = 1 + а2[У] + а2[Х]-2М[Х]М[У] = 1 + ^-А = 1.
о Z о
7.29. Условия предыдущих задач (7.27 и 7.28) изменены так,
что точки X и Y случайным образом и независимо друг от друга
занимают с постоянной плотностью любое положение на
периметре квадрата К. Найти математическое ожидание квадрата
расстояния между ними.
Решение. Выберем три гипотезы:
#t — точки X, У легли на одну и ту же сторону квадрата;
#2 — точки X, У легли на смежные стороны квадрата;
#з — точки X, У легли на противоположные стороны квадрата.
Математическое ожидание величины R2 найдем по формуле
полной вероятности:
М[Л2] = Р(Я1)М[Д2|Я1] + Р(Я2)М[Д2|Я2] + Р(Я3)М[Д2|Я3])
гдеМ[Я2 \Нг ] ,М[Д2 |Я2 ],М[Д2 |Я3 ] — условные математические
ожидания величины R2 при соответствующих гипотезах.
Из ранее решенных задач 7.25, 7.27, 7.28 имеем
M^2|^] = i; М[Д2|Я2]=Л; М[Д2|Я3] = ^.
6 3 6
Находим вероятности гипотез:
Отсюда
Р(Я1) = ^; Р(Я2)
4
М[Л2] = ±-- + ±
4 6 2
-; Р(Н3) = -
2 4
2 1 7 = 2
3 4 6~3'
7.30*. Задача Бюффона. Игла длиной /бросается на
плоскость, разграфленную параллельными прямыми, разделенными
расстояниями L(L> I) (рис. 7.30, а). Все положения центра иглы и
все ее направления одинаково вероятны.
Найти вероятность р того, что игла пересечет какую-нибудь из
линий.
169
V
a
6
Рис. 7.30
в
*~x
Решение. Положение и ориентация иглы определяются
двумя случайными величинами: Хи9, где X — расстояние от центра
иглы до ближайшей к нему линии ив — угол, образованный
иглой с направлением перпендикуляра к параллельным линиям
(рис. 7.30, б). Эти случайные величины распределены
равномерно:
X — на участке от 0 до —;
Поэтому /(ж, 0) = — при х е
в — на участке от до —.
' L)
°''2)
и9е
2' 2 J
; f(x, 9) = 0 при
х ¢
£)
или9¢
2 2 J
Рассмотрим на плоскости хОу прямоугольник возможных
значений величин X и G (рис. 7.30, в). Пересечение иглы с линией
происходит, если выполняется условие
X < -cosО,
2
т. е. если случайная точка X, О попадает в область Д
заштрихованную на см. рис. в; отсюда
р= II—dxdQ = —SD)
JJ Lis Ьъ
(D)
где SD — площадь области D:
*/2
SD = I -cosQdQ
—к/2
%
-к/2
/JTcos9d9 = /,
о
откуда р =
Ы
170
7.31. В условия предыдущей задачи внесено изменение,
состоящее в том, что ограничение / < L снимается. Найти
математическое ожидание числа пересечений иглы с параллельными
линиями, которыми разграфлена плоскость.
Решение. Разделим иглу на п элементарных участков
Al = -<L.
п
Рассмотрим случайную величину Y— число пересечений иглы
с линиями; она равна сумме п случайных величин:
IV
п
г •>
г'=1
где Y{ — число пересечений с линиями для г-го участка иглы. Так как
Д/ < L, то случайная величина Y{ может иметь только два значения:
1 и 0 с вероятностями и 1 . Математическое ожидание
L'K L'k
этой величины равно
2ДП
L'K ;
■ 0 = ^
L'K
По теореме сложения математических ожиданий
M\Y]-^h2Al 2nAl 2
fr^ L'k L'k Lit
7.32. На плоскость, разграфленную параллельными прямыми,
фигурирующую в предшествующих задачах, бросается случайным
образом любой контур (выпуклый или невыпуклый, замкнутый
или незамкнутый) длиной /. Определить математическое
ожидание числа пересечений этого контура с прямыми.
Решение. Как и в предыдущей задаче,
21
L-k
Чтобы доказать это, нужно разделить контур на п
элементарных, практически прямолинейных участков длины Д/; для каждо-
. . 2Д/
го из них математическое ожидание числа пересечении будет ,
L -к
2/
а для всего контура .
L тг
7.33. На плоскость, разграфленную параллельными прямыми
на расстоянии L, бросается случайным образом выпуклый замк-
171
нутый контур длиной /, наибольший размер которого а не
превосходит L (рис. 7.33).
Найти вероятность того, что он пересечется
с какой-либо из прямых.
Решение. Обозначим р — искомую
вероятность, Y — число точек пересечения контура
с прямыми. Так как контур выпуклый и
замкнутый, а его наибольший размер меньше L, то
контур может иметь либо две точки
пересечения с прямыми, либо ни одной. Ряд
распределения случайной величины У имеет вид
Рис. 7.33
Уг
Pi
0
1-P
2
V
На основании задачи 7.32
М[У] = 0 (1 - р) + 2р = 2р =
2/
Lit
откуда
Р
Lit
7.34. Плоскость разграфлена на прямоугольники со сторонами
Ьи М (рис. 7.34). На плоскость случайным образом бросается игла
длиной I (I < L, 1<М). Найти вероятность того, что игла
пересечется хотя бы с одной из линий.
Решение. Рассмотрим прямые, ограничивающие
прямоугольники, как две системы линий — горизонтальных и вертикальных.
Рассмотрим события:
А — игла пересечется с одной из вер-
- тикальных прямых;
В — игла пересечется с одной из гори-
- зонтальных прямых.
Так как положение иглы относительно
вертикальных прямых никак не влияет на
ее положение относительно
горизонтальных, события А и В независимы; поэтому
искомая вероятность
МЛ
М
\
Ml
I
—у
L
Рис. 7.34
Р(Л + В) - Р(А) + Р(Б) - Р(А) Р(В).
172
На основании задачи 7.30
Р(Л)
; Р(Д)
2/
тгМ
откуда
Р(А + Б)
%
+
2/
4/
irL тгМ it2LM
7.35. Игла длиной / случайным образом
бросается на плоскость, так что все
значения угла в (рис. 7.35), составленного
иглой с фиксированной осью 7—7, одинаково
вероятны.
Найти математическое ожидание
длины X проекции иглы на ось 7—7.
Решение. Имеем X — Icos6. Угол в
распределен равномерно; поскольку речь
идет о длине проекции, можно задать этот
угол в интервале от 0 до —:
у
X
Рис. 7.35
/(б) =
2
при 0е
0 при 0 ^
Ч)
т:
М[Х] = - flcosQdQ = -
0
7.36. Прямоугольник размерами 1г х /2 случайным образом
бросается на плоскость (рис. 7.36); все
значения угла в равновероятны. Найти
математическое ожидание длины X его
проекции на ось 7—7.
Решение. Представим Хкак сумму
X = Хг + X
2'
7
где Х{ — проекция отрезка 1{,Х2 — проекция
отрезка ^-
Y
X
Рис. 7.36
7
173
Искомое математическое ожидание равно
м[х\ = м[хг ] + м[х2} = Ъ, + h, = Щ±Ы г
т.е. равно периметру прямоугольника, деленному на тт.
7.37. Выпуклый замкнутый контур длиной /бросается
случайным образом на плоскость, причем все его ориентации одинаково
вероятны (рис. 7.37). Найти
математическое ожидание длины Хего проекции на
ось.
Решение. Так как контур
выпуклый, то каждый элемент проекции Ах
получается проектированием двух и
только двух противолежащих
элементов контура: А1г и А12 (см. рис. 7.37);
значит, средняя длина проекции
контура вдвое меньше, чем сумма средних
длин проекций элементарных отрезков
Д/, на которые можно разбить контур:
I
—»—
х
Рис. 7.37
Z тт
-к
7.38. Имеется случайная величина Хс плотностью
распределения f(x). Найти математическое ожидание и дисперсию
случайной величины Y =\Х\.
Решение. Запись Y =\Х\ означает, что
У = -
-X при X < О,
X при 1> 0.
т
у
00
сю
М[7] - J\x\ f(x) dx = -Jxf(x) dx
+
-oo
-oo
сю
00
+ J xf(x) dx = J x [f(x) - f(-x)} dx.
-oo
0
oo
Dy =a2\Y]-m
2
У
— I \x\2 f(x)dx — rriy =a2[X]
-00
Dx + К
m
У '
m
у
7.39. Найти математическое ожидание и дисперсию модуля
случайной величины X, распределенной по нормальному закону с
параметрами тх, ах.
174
Р е ш е н и е. Из предыдущей задачи
(х-тх)2
га
2а Г
У
-== [ хе 2<Jx dx-\ ■== \ хе
o^JZk
X
-co
Делая замену переменных
х — га
X
^^ О
2, получим
X
т
га
у
1 °г ~-'2
= J (t<jx+mx)e 2 dt +
J%k
-oo
+-= j{tox+mx)e 2 dt =
2(7
V5ir
m
7¾
X о 2
e
cfcc.
, a*,
2
+ ms
1
-2Ф*
/ v
™x
, ax J
n 2.2 2
#y =ox +rnx -my.
В частности, при га = О
га
у
-<тх «0,80 a,; Dy = о2х--о2х
IT IT
'l-i)
a? «0,36 a*
X
7.40*. Независимые случайные величины Хи У имеют
плотности распределения /г(х) и /2(у). Найти математическое ожидание
и дисперсию модуля их разности Z =
У
\X-Y
Решение. Имеем
со
mz = JJ\х - y\fx(x) f2(y) dxdy.
—со
Прямая у = оделит плоскость хОу на
две области (I) и (И) (рис. 7.40). В об-
=Ь
ласти (I) х > у,
(II) у > s,|s- у
х — 2/|= а; — у. В области
= у — х. Отсюда
mz = ff (х - у) /г(х) f2(y) dx dy +
(i)
Рис. 7.40
00
+JJ(У - х) /j(х) f2(y)dxdy = J xfx(х)
(П)
—со
X
ff2(y)dy
L-co
■ £&£ —
175
со
fyf2(y)
—со
00
J fx (х) dx
У
оо у
dy + Jyf2(y)\ J/iW dx
-co
-00
dy
CO
-co
CO
Jxfx{x)- J f2(y) dy
X
► dx.
Введем в рассмотрение функции распределения
х у
Fx{x) = j fx{x) dx; F2(y)=ff2(y)dy.
—00
-со
Тогда
00
оо
т* = f xfi(x) F2(x) dx - Jyf2(y)[l-F1(y)}dy
+
-co
-co
CO
CO
+ Jyf2{y)Fl{y)dy- f xfl(x) [1 - F2(¢)]dr.
— CO
—CO
Объединяя первый интеграл с четвертым, а второй с третьим,
получим
со оо
т
f {2xf1 (x)F2(x)- xfx(x)} dx + J{2yf2(y) F^y) - yf2(y)} dy
—CO
CO
-co
CO
= 2Jxfx{x) F2{x) dx-mx + 2 f yf2(y) Fx(y) dy - m
у
-co
— CO
Так как X, У независимы, то
a2[Z] = M[\X -Y\2} =
= M[X2) + M[Y2}-
-M[(X-Y)2}
ЩХ] M[Y] =
= a 2[X] + a 2[Y] -2mxmy = DX +Dy +(mx -my)
Отсюда находим
D2 =a2[Z]-m2z.
7.41. Независимые случайные величины Хи У имеют
плотности распределения /г(х) и /2(у). Найти математическое ожидание
и дисперсию минимальной из этих двух величин
Z = min{-Y,r},
176
т.е. случайной величины Z, определяемой следующим образом:
X, при X < У,
У, при X > Y.
Решение. Прямая у = х делит плоскость хОу на две области
(см. рис. 7.40): (I), где Z— У, и (II), где Z— X (случай не
рассматриваем, как имеющий нулевую вероятность).
т2 = M[Z] = ffzfxix) /2(у) dxdy + fj*у/г(х) /2(у) <fcdy =
(И) (I)
оо
•оо
оо
I х
оо
JVi (*> /Л(2/) dydx-\- Jyf2(j/> J/i (^) dz
00
-00
00
00
У
rfy
- ^^(^[1-^(^^+ /и^(у)[1-ад]<*у,
-оо
-оо
где Fv F2 — функции распределения случайных величин Хи Y.
оо
00
a2[Z]= /z2/i(*)[l - F2(a;)]<fe+ /у2/2(у)[1 - *1(У )]<*»;
—00
-00
7.42. Случайное напряжение [/распределено по нормальному
закону с параметрами ти и ou . Напряжение [/поступает на
ограничитель, который оставляет его равным [/, если U < и0 и делает
равным щ, если U > и0:
Z = min{[/, гг0}
[/ при U < и0,
и0 при U > и0.
Найти математическое ожидание и дисперсию случайной
величины Z.
Решение.
оо
и
гаг = M[Z] = / min {u, u0} f(u) du = I uf (u) du +
-00
-00
00
u
(u-mu)'
«n -OO
2a
u du +
u
177
со
+u0J f(u)du =тиФ:
"о
u0 -mu
и J
■fa
- e 2
w0-^«
V "u )
+
+ U
0
1-Ф
u0 -mu
и )
0 u
1 -Ji
*0Ф*(*0) + -_е
л/27Г
где*
о
и0 -ти
и
и,
со
<x2[Z]= ju2f(u)du-\- \ulf(u)du
-со
w0
2 j. 1.2
(m2 +а2и)Ф*(^о)-2СТ"ТО^(Ти'0е"^0 + и\\\ - Ф* (t0)];
£>г=а2[^]-тг2^(72|(1 + *02)Ф*(*0) + <0-=е
•J2-K
2*в
*0Ф*(*0) + -=е
л/2тг
1 t2
Заметим, что при и0 = ти ,^ = 0 будет
т r = т
и -fa
2-тг
7.43. Случайная величина X распределена по нормальному
закону:
ш=Ше
8
Независимая от нее случайная величина Y распределена
равномерно в интервале (0, 2). Найти: а) М[Х + У]; б) D[X + Y\
B)M[XY};T)D[XY};z)M[X-Y2};e)M[X-Y+X2Y2}^)D[X-Y].
Решение-m, =-1; ту = 1; Dx = 4; Dy = -.
а)ЩХ + Y] = mx +my = 0:
6)D[X + r] = Z?x+Z?v=4i;
в)М[ДУ] = т,т
у
178
r)D[XY}=oc2[XY}-m2xm2y =(Dx+m2x)(Dx+m2y)-m2xm2y =
= DxDy +m2xDy + m2y Dx =б|;
r)M[X - Y2} = mx - а2[У] = mx - Dy - m\ = -2±;
e)M[X-Y + X2Y2] = mx -my + M[X2]M\Y2} = mx -my +
+ (Dx+m2)(Dy+m2y) = 4l;
M)V[X-Y] = Dx+Dy=l\.
7.44. Случайная величина X распределена по нормальному
закону с параметрами тх — —1; ох = 3; случайная величина Y—
равномерно в интервале (0, 3); случайная величина Z — равномерно в
интервале (-3, 0). Нормированная корреляционная матрица
случайных величин X, Y, Z имеет вид
1 0,5 - 0,2
1 0,4 .
1
Найти математическое ожидание и дисперсию случайной
величины U = 1 - 2Х + 37 - Z.
Решение. ти = 1 — 2тх +Ъту — mz =9.
Du = 4DX +9Dy+D2+2 [(-2) 3 охауГху +
+(-2)(-1) охаггХ2 + 3 (-1) оуаггуг] = 41,7 - 10,2 7з « 24,0.
7.45. Система случайных величин (X, У) распределена
равномерно в прямоугольнике R (рис. 7.45). Определить: а) М[Х + У]; б)
M[X-Y}; в) M[XY}; г) D[X+ Y]; д) D[X-Y]; е) М[(Х-Y)2];
ж) М[2Х3 +ЗУ2 +1].
Решение. гпх —1, my = -;
Zj
a)M[X + Y} = mx+my =l\;
Zi
6)М[Х-Y] = mx-m, = ±;
в) M[XY] = mxmy =i;
Z
r)D[X+ Y] = DX+Dy =-^-
Z)D[X-Y)=;DX+Dy=^;
179
; Dx=±; Dv =i-; Kr. = 0.
12
12
ij/
2 *
Рис. 7.45
e)M[(X-Y)2] = M[X2] + M[Y2}-2M[X}M[Y] = Dx + m2 +
о
+Dy +ml -2m*my =-;
ж) M[2X3 + ЗУ2 + 1] = 2M[Z3 ] + 3M[72 ] + 1 = 6, так как М[Х3} =
= — / х dx = 2.
2^
о
7.46. При работе прибора возникают случайные
неисправности; среднее число неисправностей, возникающих за единицу
времени работы прибора, равно X; число неисправностей за время т
работы прибора — случайная величина, распределенная по закону
Пуассона с параметром а = Хт. Для ликвидации неисправности
(ремонта) требуется случайное время Грем; это время
распределено по показательному закону:
ДО
|ле ^ * при t > О,
О при t < 0.
Времена ликвидации неисправностей независимы.
Найти: а) среднюю долю времени, которую прибор будет
исправно работать и среднюю долю времени, которую он будет
находиться в ремонте; б) средний интервал времени между двумя
последовательными неисправностями.
Решение, а) Среднее время исправной работы прибора
(математическое ожидание времени, которое проработает прибор
после пуска до остановки для ремонта)
испр
_1_
X
Среднее время ремонта
срем
1_
М-
Средняя доля времени а, которую прибор будет исправно
работать:
*испр X М*
а
*испр+*рем ±_ + 1 Х + ^
X [L
180
Аналогично средняя доля времени (3, которую прибор будет
находиться в ремонте:
X
р=1-а =
\ + [i
б) Средний интервал времени It между двумя
последовательными неисправностями
it=i
испр
1 1 X + LL
+ U = — +- = —-^
X \х, \\х,
рем
7.47. В пределы прямоугольника R со сторонами аи Ъ (рис.7.47)
случайным образом бросается точка (X, У), все положения
которой в прямоугольнике R равновероятны.
Строится прямоугольник R' с вершиной в
точке (Х7 Y). Найти математическое
ожидание и дисперсию площади S R, этого
прямоугольника.
Решение. Выберем за начало
координат левый нижний угол
прямоугольника, а за оси координат — его нижнюю
и левую стороны; тогда случайные
величины Х7 У независимы, и S R, = XY.
Поэтому
Рис. 7.47
M[SR,] = M[XY] = mxmy =^
ab
4
D[SR,] = D[XY] = DXDV +mlDy + m\D,
2l2
azb
a^bl b2 a2 _ 7a2b2
12-12 4 12 4 12 144
7.48. Случайная точка (X7 Y) распределена на плоскости по
нормальному закону с круговым рассеиванием:
тх =ту =0 И °х
а = а.
у
Случайная величина R — расстояние от точки (Х7 Y) до центра
рассеивания. Найти математическое ожидание и дисперсию
величины R.
Решение.Д = ^Х2 + Г2.
оо
mr=M[R] = ffylx2+y
1
—ОО
2а'it
х +у
2ст аз; ш/.
181
Переходим к полярной системе координат (г, ф):
т
сю Т 2тт I—
= I г2 е 2°2dr I dф = a,/— 5¾ 1,25а
Д. = D[i2] = а 2 [Л] - m
2 . 2
Я +У
СЮ ^ 1-у
= ff(x2+y2)-^-e 2°2dxdy-m2r =
— СЮ
2ст'тг
сю __£ 2тт
/г3 е 2°2dr I cfф — а2 — =
О
2аЧ
о
сю
с> 2 Г. -t 1. 2^ о 2 2 ^
= 2а / £ е at — о — = 2а —а — = ст
J 9 9
4 — тт
о
2 2 2
7.49. Событие А состоит в выпадении ровно двух гербов при
бросании трех монет. Опыт, заключающийся в бросании трех
монет, повторяется п раз. Найти математическое ожидание и
дисперсию следующих случайных величин:
X — число появлений события А при п опытах;
Y — частота события А при п опытах.
Решение. Вероятность события А в одном опыте:
р = 3 •
/1 \2
12J
1 = 3
2~~8
М[Х] = пр = —; П[Х] = пр(1-р)=15п
8
64
У = —; М[Г] = ^И = -; D[T] =-V DpT] = 15
гг
гг
8
гг
64гг
7.50. Из урны, в которой находятся два белых шара и три
черных, вынимается сразу два шара. Найти м.о. и дисперсию числа
появившихся при этом белых шаров а) непосредственно; б)
пользуясь теоремами о математических ожиданиях и дисперсиях.
Решение, а) Обозначим X — число появившихся белых
шаров. Ряд распределения величины X будет
Х{
Pi
0
0,3
1
0,6
2
0,1
182
Математическое ожидание величины X
m = 0 ■ 0,3 + 1 ■ 0,6 + 2 • 0,1 = 0,8
Дисперсия величины X
Dx =а2[Х}-т2х =12 -0,6 + 22 -0,1-0,82 =0,36-—.
25
б) Разделим мысленно опыт на два вынимания шара: первое и
второе. Обозначим
X — число белых шаров при двух выниманиях;
Хх — число белых шаров при первом вынимании;
Х2 — число белых шаров при втором вынимании;
2 4
Х = Хг+Х2; mXi=mX2=-] mx=mXi +тХ2=-]
Находим Кхх через начальный момент аг г[Хг, Х2]=^М[ХгХ2].
Построим таблицу распределения вероятностей для системы
величин (Xv Х2)
х2
0
1
Хг
0
3
10
3
10
1
3
10
1
10
alil[X1IA-2] = M[X1A-2]
Я Q Q 11
0-0—+ 0-1 • — + 1-0-- + 1-1-- = -
10 10 10 10 10
К*Ъ =(*l,l[Xl>X2]-mxim:
50;
D. = В„ + Р,,+2К„,= ±.
183
7.51. В урне а белых и Ь черных шаров. Из урны вынимают
сразу к шаров (к < а + Ъ). Найти математическое ожидание и
дисперсию числа вынутых белых шаров.
Решение. Обозначим X число вынутых белых шаров;
* = £*<•
г=1
где Х{ — число белых шаров, появившихся при г-м вынимании;
Р(Х{ =0) = -^-^(^ =1): а
а + Ъ
а + Ъ
т
к к
ка
i=l
r^a + Ъ а + Ъ
'Г" J
Для нахождения дисперсии Dx подсчитаем D и KXiXi.
п _ а b _ а^
Xi ~ а + Ъа + Ь~ (а + Ъ)2 '
Находим Кхх .Для этого, как и в предыдущей задаче, строим
таблицу распределения вероятностей для пары случайных
величин
Xj
0
1
Xi
0
6(6-1)
(a+b)(a+ 6-1)
ab
(a+b)(a+ 6-1)
1
ab
(a+ 6)(a+6-l)
a (a — 1)
(a+ 6)(a+6-l)
Имеем
#*,*, =M[A'<A'>]-mSim ;
М[Х,Х,] = 1-Р((Х, = !)(*, =1))
a
a-1
a + b a + b — 1
и
#
a (a — 1)
a
ab
*i*j-
(a + b)(a + b - 1) (a + b)2 (a + b)2(a + 6 - 1)
184
Далее находим дисперсию случайной величины X
к
X / j Х± / j xixj
г=1
i<j
Так как дисперсии Dx. и корреляционные моменты Кх„ все
одинаковы, то
X{Xj
Dx = fcD + 4C\KstLi =
kab a + b — k
'V"J
(a + bf a + b - 1
В частном случае, когда вынимаются все шары (А;
лучаем естественный результат:
а + Ь), по-
т
к
а
а +Ъ
= а, Д
0.
7.52. Через произвольную точку А на окружности радиуса г
случайным образом проводится хорда АВ (рис. 7.52), так что все ее
направления одинаково вероятны. Найти среднее значение длины
хорды.
Решение. Выразим длину хорды Y в
зависимости от угла Ф, который составляет хорда с
направлением радиуса в точке А. Из рис. 7.52
имеем
Y = 2 г соэФ,
гдеФ — случайная величина, которую будем
считать распределенной равномерно в интервале
Рис. 7.52
0;
тт
2J
. Тогда
IV
т
4г
у
= I 2r cos ф — d ф = — « 1,
J IT ТТ
о
27r.
7.53*. Через произвольную точку А внутри круга радиуса г
проводится хорда ВС (рис. 7.53). Все положения точки А в пределах
круга одинаково вероятны. Все направления
хорды В Су характеризуемые углом Ф между нею и
радиусом, направленным в точку А7 также
одинаково вероятны. Найти среднюю длину хорды ВС
Решение. Длину хорды D выразим через
координаты точки А (X, У) и угол Ф:
D
2л/г2-Я2 = 27г2-(Х2+У2)81п2Ф,
Рис. 7.53
185
где Н = yjX2 + Y2 этФ — перпендикуляр, опущенный из центра
круга на хорду ВС. Так как точка (Х7 Y) равномерно распределена в
круге ^радиуса г, а угол Ф можно считать равномерно распределен-
, причем точка (Х7 Y) и угол Ф независимы, то
ным в интервале
( ^
°'2)
\ £ )
плотность распределения системы (Х7 Y7 Ф) есть
/(я, 3/, ф)
2 1 2 2 2
при х +у < г ,
О при х2 + у2 > г2
IT
0< ф <-,
2
ИЛИ ф ¢
V 4 )
Поэтому
га
2 2
тт г
I dp J I 2-yjr2 — (х2 + y2)sm2 ф drcdy.
О А-
Переходим к полярным координатам (р, *ф):
2* 2тт
m
rf 2 2
IT Г
I dp I (Ц) I -y/r2 — p2 sin2 фр dp
0 0 0
IT
8
ТТГ
r3(l — cos3 ф) 16r
0
о • 2
osin ф
Зтт
1,70 r.
7.54*. Найти среднее значение длины хорды БС(рис. 7.54),
проведенной через точку А внутри круга, находящуюся на расстоянии
L от центра круга радиуса г, причем все
направления этой хорды одинаково вероятны.
Решение. Хорда ВС выражается следую-
С щим образом через величины L7 ф, г:
ВС = 2rJl-4- sin2 ф.
Рис. 7.54
~2
т
= Г—2гЛ
Если длину хордыjE? С считать случайной
величиной Х7 то
*2
0
sin2 ф йф = — I <s]l — k2 sin2 ф dp,
тг
о
и L
где к = —.
г
186
Полученный интеграл представляет собой полный
эллиптический интеграл Е
к -
'2)
с модулем А;; его значения можно найти в
1
справочниках. Например, при к = - интеграл Е
'1 ТГ
,2'2j
= 1,4675 и
тх и
1,87г.
Так как полный эллиптический интеграл Е
к,
IT
2)
изменяется
тт
от — (при к = 0) до 1 (при к- 1), то средняя длина хорды тхбудет
Li
принимать значения от 2г (при & = 0, т.е. для точки А в центре
4
круга) до — г (при L = г, т.е. для точек А на окружности).
тт
7.55*. Техническое устройство состоит из п узлов. Каждый
узел может выходить из строя независимо от других. Время
исправной работы i-ro узла распределено по показательному закону
с параметром Х-:
Л (О
Х-е~х,< при t>0,
0 при t < 0.
Каждый узел, оказавшийся неисправным, немедленно
заменяется новым и поступает в ремонт. Ремонт i-ro узла продолжается
случайное время, распределенное по показательному закону с
параметром jo, {:
Ф.-(0
0
-м
при t > 0,
при t < 0.
Устройство работает в течение времени т. Определить: а)
математическое ожидание и дисперсию числа узлов, которые
придется заменить; б) математическое ожидание суммарного времени Г,
которое будет затрачено на ремонт вышедших из строя узлов.
Р е ш е н и е. а) Обозначим Х{ число узлов г-го типа, вышедших
из строя за время т. Эта случайная величина распределена по
закону Пуассона и имеет математическое ожидание тХш =Хг-т и
дисперсию Dx. = \{ т.
Обозначим X общее число узлов, вышедших из строя за время
т. Имеем
п
п
п
Х = ЕХ*'>
т
i=i
Е
т
х,-
Ev
г=1
187
Так как величины Х- независимы, то
п п
X / j X,- / J
г =1 г =1
б) Обозначим Т{ общее время, затраченное на ремонт всех
вышедших из строя за время т узлов i-ro типа. Оно представляет
собой сумму времен, затраченных на ремонт каждого из узлов. Так
как число этих узлов равно Х{, то
т{ =тр +тм+...+т$х'> =J2t?\
к=1
где Г/*) — случайная величина, распределенная по показательному
закону с параметром^; величины Т\1^, Т/2),... независимы.
Найдем математическое ожидание случайной величины Т-у для
этого сначала предположим, что случайная величина Х{ приняла
определенное значение га. При этом условии математическое
ожидание величины Т{ будет
тп тп
mtj(m) = £Mpf>] =
1 га
2^— = —
Умножив это условное математическое ожидание на
вероятность Рт того, что случайная величина Х{ приняла значение га, и
просуммировав все эти произведения, найдем полное
(безусловное) математическое ожидание величины Т-.
00
т 1 А „ 1 жжгт, , Х,т
*ч, = Ер- —=—Е™ р™ = — MfXi 1=^--
m=l И* г ri m=l И* г Ич'
Применяя далее теорему сложения математических ожиданий,
получим
м[г] = т£^-.
Заметим, что тот же результат можно получить путем
следующих (не вполне строгих) рассуждений. Среднее число выходов из
строя узла i-ro типа за время т равно \{ т; среднее время ремонта
одного такого узла равно 1 / \х •; среднее время, которое будет
затрачено на ремонт всех вышедших из строя за время т узлов г-го
типа равно Xi т / |л^; среднее время, которое будет затрачено на
^Х
ремонт узлов всех типов, равно т л
Ь>г
188
7.56*. Условия задачи 7.55 изменены таким образом, что
каждый вышедший из строя узел отправляется в ремонт, а
техническое устройство на это время прекращает работу; при
неработающем (выключенном) устройстве узлы выходить из строя не могут.
Найти: а) математическое ожидание числа остановок устройства
за время т; б) математическое ожидание той части времени т, в
течение которой устройство будет простаивать (оно же среднее
время, затраченное на ремонт).
Решение, а) Обозначим X — число остановок за время т и
найдем его математическое ожидание гаг Задачу будем решать с
помощью следующих не совсем строгих (но тем не менее верных)
рассуждений. Рассмотрим неограниченный во времени процесс
работы устройства в виде последовательности «циклов» (рис. 7.56),
)( )( )( )( )( к
О v v v
1-й цикл 2-й цикл 3-й цикл
Рис. 7.56
каждый из которых состоит из периода работы системы (отмечен
жирной линией) и периода ремонта. Длительность каждого цикла
представляет собой сумму двух случайных величин: Граб (времени
работы устройства) и Грем (времени ремонта). Средняя
длительность времени работы устройства mt ^ вычисляется как среднее
время между двумя последовательными отказами в потоке отказов
п 11
плотности X = У2 X { ; это среднее время равно га t = — = .
х Ех<
г=1
Находим среднее время ремонта mt . Будем его искать по
формуле полного математического ожидания при гипотезах Я- —
ремонтируется узел г-го типа (г = 1, 2,..., п).
Вероятность каждой гипотезы пропорциональна параметру Хг
р(я< ) = -^- = х-
г=1
X
Условное математическое ожидание времени ремонта при этой
гипотезе равно 1/\1{; отсюда
га, =
срем
п \ 1 п \
k^i ^k»i
189
Среднее время цикла
mt
ц X Xfr^ X ^-
ЗМ
V i=l Г i )
Теперь представим себе последовательность остановок
устройства как последовательность случайных точек на оси Ot,
разделенных интервалами, в среднем равными mt . Среднее число
остановок за время т будет равно среднему числу таких точек на отрезке
длиной т:
т Хт
тх — — :—•
1 + 2,-^-
г=1 Мг
б) За каждый цикл устройство будет простаивать
(ремонтироваться) в среднем время mt = —V^ —-; за тх циклов среднее
X i=1 \i{
время простоя будет равно
Хт 1 ^Хг- ^|1г.
1 .х- Y^—-г- i=l ^1 l + v^ *
г=1 М'г г=1 Мг
7.57. Случайная величина X распределена по нормальному
закону с характеристиками тхиох. Случайные величины У и Z
связаны с Xзависимостями Y — У2; Z — X3. Найти корреляционные
моменты К^, Кхги Kyz.
Решение. Для упрощения вычислений перейдем к
центрированным величинам и воспользуемся тем, что для центрирован-
о
ной нормальной величины X — X — тх все моменты нечетных
о О
порядков равны нулю, а М[Х2] = а2, М[Л"4] = За* (см. задачу
5.53). Так как
у=(Х+тх)2 -М[Х2} = Х2 +2Хтх + т2 - Dx -т
х х
= Х'+2Хтх-о'х;
ТО
Кщ = М[ХY] = М[Х(Х2+ 2Хтх -а2х)] = 2о2хтх
190
Далее
О О о
,3 »»rv3i v3 , о v2 „ , o\r„2 , _3
Z = (X+mxy -М[Хл] = Хл+ЗХ'т, + 3Xmlx+m
X
(Зтхи2х + т3х) = Х*+ЗХ2тх + ЗХт2 -Зтхи,
и поэтому
Кхг = ЩХУ\ = М[Х4] + 3mxM[Xz] + Зт2М[Х2]
2»*rv-l о_4 , о_ 2_2
-Зтхо2хМ[Х] = За4 + Зт>
Наконец,
К„=М[(Х2+2Хтх-о2 ){Х3+ЗХ2тх + 3Xт2 - Зтхо2х)] =
°4i , /* /2 _2\ii>rrv-2i , о™ _4 1Л _4 , /-3 2
= 5roxM[X4] + 6ms(< -^)M[X^ + 3mlCTl4 = 12тха4 + 6т'хо
XX
7.58. Воздушная цель перемещается над обороняемой
территорией со скоростью v. В течение времени т цель находится в зоне
действия средств противовоздушной обороны. Число обстрелов,
которому может подвергнуться цель, находясь над территорией,
есть случайная величина, распределенная по закону Пуассона с
параметром а = Хт. В результате каждого обстрела цель
поражается с вероятностью р. Пораженная цель немедленно прекращает
полет, а) Найти вероятность Pt того, что к моменту t0 < т цель
будет поражена, б) Найти среднюю глубину проникания цели на
обороняемую территорию.
Решение.а) Выделим из пуассоновского «потока обстрелов»
цели с плотностью X поток «поражающих обстрелов» с
плотностью \р. Вероятность того, что за время t0 цель будет поражена,
равна вероятности того, что за время t0 произойдет хотя бы один
поражающий обстрел: Pt = 1 — e~Xpt°.
б) Введем гипотезу: цель поражена в интервале времени
(t,t + dt). Вероятность этой гипотезы будет \pe~Xptdt (0 < t < т).
В предположении, что указанная гипотеза имела место, дальность
Д на которой самолет будет поражен, равна vt. Следовательно,
средняя глубина проникания цели на обороняемую территорию
будет:
т
mD= fvte-tXp\p dt=—[l- е"Хрт (Хрт + 1)].
\р
о г
191
Заметим, что т D —» — при т —» оо.
\р
7.59. Тело, масса которого равна а [г], взвешивается на
аналитических весах четыре раза; получаются результаты Xv Х2У Х3, ХА.
В качестве измеренного значения массы принимается их среднее
арифметическое: Y — — {Хх + Х2 + Х3 + Х4). Результаты
взвешиваний независимы. Весы дают систематическую ошибку
тх = 0,001 [г]. Среднее квадратическое отклонение каждого
взвешивания ох = 0,002 [г]. Найти параметры: математическое
ожидание и среднее квадратическое отклонение случайной величины Y.
Решение. ту = — -4 (тх + а) = а + 0,001 [г].
D,=±.AD,=±D,; ау =^ = 0,001 [г].
7.60. Производятся четыре независимых измерения одной и
той же величины X. Каждое измерение характеризуется одним и
тем же математическим ожиданием тх и средним квадратическим
отклонением ох. Результаты измерений: Xt, Х2, X3J ХА.
Рассматриваются разности между соседними измерениями: Yl —Х2 — Хг\
Найти характеристики системы этих случайных величин:
математические ожидания т , га у , га у ; средние квадратические
отклонения а , а , а ; нормированную корреляционную матри-
цу
Г- •
Р е ш е н и е. га „ = га„ = га„ =0.
2 2 2 2 2 "з I—
°у1 =°у2 =°у3 =2^ СТУ1 = сту2 = сту3 = CTW2-
V V \J V
В силу независимости величин А"х, А"2, А"3»-X"
4
tfmi=M[(*2- ^)(^3- Х2)] = -М[Х22] = -с^;
*Г^ =М[(Х3-Х2)(Х4-Х3)} = -М[Х^-а1;
КУ1У=М[(Х2- ^)(^-^)1 = 0.
ГУ1»2 r»2V3 2 2 2' Гу'Уз
•С/
192
1 --
* 3
1
2
О
1
2
1
7.61. Стрельба по некоторой цели Ц начинается в момент ее
обнаружения и продолжается вплоть до некоторого момента £*, в
который цель покидает зону обстрела и становится уже
недоступной. Момент Т, в который обнаруживается цель, представляет
собой случайную величину, распределенную с постоянной
плотностью в промежутке от 0 до £*. Число выстрелов, которое
может быть осуществлено по цели за время ее обстрела £*— Т, есть
случайная величина, распределенная по закону Пуассона с
математическим ожиданием а = \(£* —Г). При каждом выстреле цель
поражается с вероятностью р. Найти полную вероятность
поражения цели с учетом случайности момента обнаружения.
Решение. Вероятность поражения цели есть функция
момента обнаружения р (Т). Рассматривая пуассоновский поток
«поражающих» выстрелов с плотностью \р7 имеем р(Т) = 1 -
_е-рЧ**-т) Полная вероятность поражения
t*
p = M\p(T)] = ±f[l-e-*^]dt = l--±;[l
-p\t*
}■
Отметим, что при малых p\t* будет р « - p\t*.
Li
7.62. Имеется кубический бак с горючим, на одной из шести
стенок которого случайным образом появляется пробоина от
осколка; пробоина оказывается с равной вероятностью на любой из
шести стенок бака и в любой точке каждой из шести стенок.
Вследствие наличия пробоины из бака вытекает все горючее,
находящееся выше пробоины. В неповрежденном состоянии бак
заполнен на 3/4 своего объема. Определить среднее количество
горючего, которое сохранится в баке после пробития его осколком.
Решение. Для простоты будем считать ребро бака равным
единице. Высоту пробоины обозначим через Х7 количество
оставшегося горючего через Y. Так как площадь основания равна
единице, то
Y
X при X < 0,75,
0,75 при 0,75 < X < 1.
193
Если пробоина окажется выше чем на 0,75 от дна бака
(X > 0,75), то горючее вытекать не будет, и в баке останется, как и
было, количество горючего У = 0,75; вероятность этого равна
доле площади поверхности бака, находящейся выше уровня 0,75:
Р(У = 0,75) = Р(Х > 0,75) = 1 + 4--. 0,25 = -.
6 6 3
Если пробоина окажется в дне бака (Х= 0), то вытечет все
горючее; вероятность этого равна доле площади, приходящейся на
дно бака:
P(F = 0) = P(* =0) = 1.
6
Если пробоина окажется в одной из боковых стенок бака на
расстоянии Х< 0,75 от дна, то в баке останется количество
горючего У = X. Плотность вероятности в интервале 0 < х < 0,75 посто-
янна и равна —— = -. Среднее количество оставшегося в ба-
0,75 3
ке горючего будет равно
0,75
m =0,75-- + 0--4- Гх.-<& = - + — = — = 0,44.
у 3 6 J 3 4 16 16
о
7.63. В интервале (0, 1) зафиксирована точка а (рис. 7.63).
Случайная точка X распределена равномерно в том же интервале.
Найти коэффициент корреляции между случайной величиной Хи
расстоянием R от точки а до X (расстояние R всегда считается
положительным). Определить, при каком значении а величины Хи
R будут не коррелированы.
X
я к.—1 х
о ^р« 1
Рис. 7.63
Решение. Определим К„ по формуле
Кхг=М[ХЩ-тхтг.
1
M[XR] = М[Х\а -Х\} = Jx\a-x\ f(x) dx =
о
1 а 1 3
= / х\а — х\ dx = / х (а — х) dx — I х (а — х) dx = 1—;
а 1
2 3
0 0 а
194
1 l a
mx = —; mr — I \a — x\ dx = I (a — x)dx
о о
Г 1
— / (a — x) dx = a — a -\—.
a
Отсюда
a3 a 1 If о 1) a3 a2 1
#= — -- + ---
xr
3 2 3 2
Находим
a — a -\—
2)
3 2 12
1 1
a2[R]= I (a — x)2dx = a2 -aH—;
о 3
DT = 2o3 - a4 - a2 + —; стг = .ЖГ.
12 y
Отсюда
3 2 i
a a 1
r = 3 2 12
XT
4 .2-11
I2a° -а'-аЧ
12 2V3
,, a a 1 .
Уравнение 1 = 0 имеет только один корень в интер-
3 2 12
вале (0, 1): о = -. Поэтому случайные величины X, R становятся
Li
1
некоррелированными только при о = -.
Li
7.64. Автомобиль может двигаться по шоссе с произвольной
скоростью v(0 < v < vmax ).Чем быстрее движется автомобиль, тем
больше вероятность того, что он будет задержан автоинспектором.
Каждая задержка длится в среднем время t3. Инспекторы на пути
следования стоят случайным образом; при этом на единицу длины
пути приходится случайное число инспекторов, распределенное
195
по закону Пуассона с параметром X. Зависимость вероятности
задержки от скорости автомобиля линейная:
где А; =
p(v) = kv (0< v <vmax),
1
v
max
Определить рациональную скорость движения vp автомобиля,
при которой он пройдет путь s в среднем за минимальное время.
Решение. Среднее время прохождения пути s будет
t = —Ь X sp (v) t3 = —h X skvt3.
v v
Если минимум этой функции лежит внутри интервала
(О, vmax ), то его можно найти из уравнения
— = - — + \skt3 = О,
dv у2
откуда
у = уп = i_L_ = pSSL
з I ' %"3
Эта формула справедлива при г; < vmax, т.е. при vmax >
1
Так, например, при vmax = 100 [км/ч], X =
20
X*
1 '
км
и t3 =20 мин
имеем
vp = /-^у «77,5 [км/ч].
20 3
1 5
Если vmax < , то минимум функции £ = — + X sp (у) t3 ле-
Х*3 V
жит вне интервала (0, vmax ), и наивыгоднейшей является скорость
vp — vmax- Например, если при указанных выше данных время
задержки уменьшить до 10 мин, то vp = vmax = 100 [км/ч].
7.65. Описывается окружность с помощью циркуля,
расстояние между ножками которого номинально равно 5 см, но
фактически устанавливается с ошибкой, математическое ожидание
которой равно нулю, а среднее квадратическое отклонение 0,1 см.
Ошибка распределена по нормальному закону. Найти
математическое ожидание и среднее квадратическое отклонение площади
описанной окружности S двумя способами: а) точным и б)
приближенным, пользуясь методом линеаризации.
196
Решение.
a)S =ъ(5 + Х)2,
где X— ошибка в установке радиуса, тх =0,ах = 0,1.
ms = M[S] = it М[(5 + X)2] = it (25 + 10М[Х] + М[Х2}) =
= it (25 + ст2) = -к • 25,01;
D[5] = a2[5]-m
2.
s J
a2[5] = M[Tt2(5 + X)4] = Tt2{625 + 500m:E + 150a2[X] +
+20a3[X] + a4[X]} = Tt2(625 + 150a2 + 3ст*),
так как при тх = 0 начальные моменты совпадают с центральными
(см. задачу 5.53);
D[5] = Tt2[625 + 150a2 + 3a*] - -к2[625 + 50ст2 +ст*] = -к2 -1,0002;
ст, = 1,0001-it;
б) mf = 25it; Ds
Os
\2
.dxt
D
X
(2--K-5)2 -0,01 = it2;
m
IT.
Таким образом, разница при вычислении точным и
приближенным методами мала (0,04 % по га5 и 0,01 % по os).
7.66. Для построения равностороннего треугольника со
стороной а = 3 см пользуются следующим способом: из произвольной
точки О откладывают отрезок длиной а;
при нем строят угол а, равный 60°; затем на
стороне этого угла снова откладывают
отрезок длиной а и полученную точку
соединяют с точкой О (рис. 7.66). Отрезки длиной а
откладываются с помощью линейки с
делениями по 1 мм; максимально возможная
при этом ошибка равна 0,5 мм. Угол
откладывается с помощью транспортира с
максимально возможной ошибкой 1°. Пользуясь
методом линеаризации, найти
математическое ожидание и среднее квадратическое отклонение третьей
стороны X.
Решение. Обозначим фактическую длину первой стороны
Х{у второй Х2у фактическое значение угла 0. Эти случайные
величины можно считать независимыми. Имеем
Рис. 7.66
X = ^Xl + Х\ - 2ХгХ2 cosG.
197
Пользуясь методом линеаризации, найдем
га
X
= ^т1 +т*2 - 2тXimъ cosть,
тд,етпх = mx = 30 [мм], cosme =-, откуда
Li
mx = V900 + 900 - 900 = 30 [мм].
Далее
дх
дхл
1 /
тп
2хх — 2х2 cos 0
y^i + х\ — 2хгх2 cos 0
тп
дх
кдх2)
тп
2х2 — 2xl cos 0
VX12 ~*~ Х2 ~ 2ххХ2 COS0
тп
2^^2 sin 9
-Jz2 + ij — 2^^2 c°s9
30л/3
= 15л/3 [мм]
m
Вычисляем
D.
дх
К +
m
дх
Кдх2)
D..+
тп
'дх?
,30,
D
е
тп
Дисперсии аргументов не заданы, заданы лишь максимальные
практически возможные отклонения их от математических
ожиданий:
Ахг = Ах2 = 0,5 [мм]; Л0 = 1°= 0,01745 [рад].
Полагая приближенно
<тЯ1 = о = \Ахг = 0,167 [мм]; DXi = D = 0,0278 [мм2],
о
сте = -Д0 = 0,00582 [рад]; Д, = 3,39 • 10"5 [рад],
О
получим
Dx=~- 0,0278 • 2 + 675 • 3,39 • Ю-5 и 0,0139 + 0,0229 = 0,0368 [мм2];
ах = 0,192 [мм]
198
7.67. Расстояние Dot некоторой точки О до объекта К
определяется следующим образом: измеряется угол а, под которым
виден объект из точки О (рис. 7.67); далее, зная линейный размер
объекта Ху определяют расстояние по приближенной формуле:
X X
D =
2 sin —
а
Рис. 7.67
Линейный размер объекта X в зависимости от случайного
положения объекта может изменяться в пределах от 8 до 12 м; угол
а определяется с точностью до 0,1 тысячной радиана. Расстояние
D велико по сравнению с размером объекта X. Найти
приближенно среднее квадратическое отклонение о D ошибки в определении
расстояния Д если измеренное значение угла а равно одной
тысячной радиана.
Решение. Применяя метод линеаризации, имеем
oD =
д1У
°1 +
т
ЭР'
а. '
т
Линейный размер X считаем равномерно распределенным в
интервале (8, 12):
*х =
#2 х\
12 — 8 2Г1 о 4Г2т 1лгт
= -= м ; ol = - М; тх = 10 [м].
2л/3 2V3 л/3
Далее
а
0,0001 2
'а
ю
-8
9
; rn а =o,ool
откуда
oD =
X '
va
т
X
К OL J
°l =
( l
т
ш
4
- +
3
+
1 10 ? 10~8 4 _6 , 1 ,лв 13 1л6 г..2
Uo-
- = Z . юь + - • 10" = — • 10" [м1;
9 3 9 9
QD =
Vi3
103 =1,20-103 [м].
199
7.68. Имеются две почти линейные функции га случайных
аргументов:
Y — Фу 0^1 > ^2> "-ч^пУ % — У г(Хг) Х2, ...,Хп).
Даны характеристики системы тх , Dx (г =1,2, ..., га) и
корреляционная матрица КФ .
Найти приближенно корреляционный момент К .
Решение. Линеаризуя функцииф иф2)получим
п (&Р„ 1
г=1
У
п
2«фг(тХ1,тХ2, ...,mxJ + ]^
г=1
х>\
*i\
отсюда
п
Y = E
t=i
Г?р,1
П
*<; * = Е
m
i=l
ар/
*<;
m
^,, - M[TZ] = M
n
E
(ЯФ„1
г=1
У
дх.
п
г /
т
п
Е
{дЧ>Л
У
дх-
г I
т
'Эф/
дх
^ + Е
*. Е
3=1
9ф
9х
j J
X
т
i^j
У
, дх
т
дх- ,
з )
*7
т
Последняя сумма содержит га (га — 1) членов; каждому КФ
соответствуют два члена суммы:
(АР,)
т
дхп
К& и
'<Эф„ '
т
дх
у
3 )
т
а:
(*)
У
7.69*. Летательный аппарат, находящийся над плоскостью хОу в
точке А (рис. 7.69), определяет свои координаты (Ху Y) с помощью
двух наземных радиолокационных
станций О и О', измеряя углы а и (3,
составленные направлениями на эти станции с
фиксированным направлением АВ±Ох.
Размеры базы Б (расстояние между
станциями) известны со средней квадрати-
х ческой ошибкой а Б; углы а и (3
определяются с одной и той же средней квадрати-
X ВО'
Рис. 7.69
ческой ошибкой аа =сг3. Известны:
200
номинальное значение базы m Б и измеренные значения углов а и (3,
равные та и т0. Ошибки в определении всех параметров
независимы. Пользуясь методом линеаризации, определить приближенно
математические ожидания случайных величин X и У, их средние квад-
ратические отклонения и коэффициент корреляции.
Решение. В соответствии с рис. 7.69 находим
X
Б tg а
tg а + tg (3
; У =
tg а + tg (3
ЭХ „ sec2 а tg Р
= Ь-
ЭХ -Btgasec2(3
да "(tga + tg (3)2 ' 9(3 (tg а + tg (З)2
ах
tg a
<9Б tg a + tg (3
97
9a
sec a
dY
Bsec2(3 97
(tg a + tg (3)2 ' 9(3 (tg a + tg (3)2 ' дБ tg a + tg (3'
m
X
гаБ tgma
tg ma + tg m3
m
; my =
tg ma + tg m3
Л
m
+
sec m a tg m 3
(tgraa +tgm3)2>
tg^a
+
m
tg m a sec m 3
(tgma +tgm3)
** +
tgma +tgm3>
аБ = тБ
2 sin 2m a + sin 2m 0 2
i: —°* +
+
sin m a cos m 0
sin (m a + m 3)
4 sin (ma + ra0)
£
у
sec m
m
a
(tgma + tgm0) ;
( \2
+
+
sec m
m
3
(tgma + tgm0)2;
°l +
[tgma + tgm0J
аБ =тБ
2 cos4 ma + cos4 m0 2
i: : —G<* +
sin (ma + ra0)
+
i2
cos m a cos m 0
sin (ma + m0)
ав; s = 7^7-
201
Корреляционный момент Кщ подсчитаем по формуле,
полученной в предыдущей задаче. В силу независимости величин а, (3,
Б эта формула принимает вид
К—, —
ху
эх
т
ЗУ
а? +
а
т
'дГ
т
4
'дГ
°1 +
т
'дХу
т
dY)
[дБ)
стБ =
т
= 7П
2 tg га а sec га 0 - tg га 0 sec га а 2
(tgraa + tgra3)
*а +
tg^Q
(tgraa +tgra3)
°2Б =
.3 „_ • 3
2 sin га a cos~ raa — sin rapcos~ rap tg га 2
ШБ ГТ^ : aa +" 7^°Ъ
sin (raa + ra0)
(tgraa + tgm3)
Отсюда
#
Zy
zy
°х°У
При raa — ra3 это выражение можно упростить:
Щ)
2a Б sin гаа cos2 гаа
(2а| sin2 га а cos гаа +а2гаБ)
7.70. Для определения расстояния R от точки К до начала
координат можно применить два способа:
1) определить расстояния ХиУдо осей координат и затем
найти R по формуле R —
2) измерить только расстояние Y до оси абсцисс и угол a
(рис. 7.70), затем найти R по формуле R = .
cos a
Какой способ приведет к меньшей
погрешности, если расстояния X и Y и угол а
определяются с независимыми друг от друга
ошибками, причем средние квадратические
отклонения ошибок X, Y равны ох—оу, а
ошибки в угле — aa ?
Привести численный расчет для значений
средних квадратических ошибок ох — оу =1 [м],
aa = 1°= 0,0174 [рад] при средних значениях
параметров, равных тх—100 [м]; гау=60 [м];
га„ г
Рис. 7.70
га
a
Решение.
dR
X
arctg
dR
<»>-»
<»>-»
га
1,03 [рад].
у
У
дх
4
2 , 2
X +у
9У л[хТТ7
202
2)
ад
dR
х
2 , 2
(Z + j/ J
ol +
m
У
2 , 2
<*г/ = ^ СГ
У
У
m
1 dR у sin a
dj/ cos a da cos2 a
1=СТУ
В2[Д]
Icos a )
< +
m
У tg2a
cos a
2^2
CTa >CTJ,;
m
a2 >ст!
Первый способ дает большую точность.
Для числовых данных задачи:
1 +
'1001
,60
I2 +60
1001
,60
• 0,0174:
3,90 [м].
7.71. Система трех случайных величин X, Y, Z имеет
математические ожидания тпх=Щ тпу — 5; тпг=3, средние квадратиче-
ские отклонения ах = 0,1; ст — 0,06; стг — 0,08 и нормированную
корреляционную матрицу
0,7
1
0,3
0,6
1
Пользуясь методом линеаризации, найти математическое
ожидание и среднее квадратическое отклонение случайной величины
ЗХ2 +1
и=
Y2 + 2Z2
п 3-100 + 1 301 _
Решение. т„ — — — 7.
v 25 + 2-9 43
ди
6х
ди
(Зх2 +1)2у д
и
2\2
дх у2+2z2 ду (у2+2z2)
dz
(Зх2 +1)4г
(y2+2z2)2''
'dvr
кдх,
6 10
43
= 1,40;
fa \
ди
,9у
301•10
(43)2
1,63;
'диГ
,dz,
301•12
(43)2
= -1,95;
203
D[C/] = 1,402 -ОД2 + 1,632 -0,062 + 1,952 -0,082 +
+2[-l,40 • 1,63 • 0,7 • 0,1 • 0,06 + 1,40 • 1,95 • 0,3 • 0,1 • 0,08 +
+1,63 -1,95 • 0,6 • 0,06 • 0,08] « 0,066;
ou «0,26.
7.72. Производится параллельное соединение двух выбранных
наугад сопротивлений Rx и R2. Номинальное значение каждого
сопротивления одинаково и равно rari = гаг =900 [Ом].
Максимальная ошибка в R при изготовлении сопротивлений равна 1 %
номинального значения. Определить методом линеаризации
номинальное значение сопротивления такого соединения и его
среднее квадратическое отклонение.
Решение. i? = -—-— = ср (i?x, R2);
Rl + R2
, v 900-900 ._пГГ| ,
rar = cp (га , mr ) = = 450 [Ом].
ri
900 + 900
1 900 Q rri ,
a_ =a_ = = 3 Ом.
1 2 3 100
<9cp
An
m
(Г1 + ^)
<9ф
<9r
m
2;
m
<9ф
[&ril
m
п[Л] = Е
«=1
9ф
a„- =
ri
m
^[Om2]; a,
О
<»>-»
<»>-»
1,06 [Ом]
При этом максимальная ошибка будет 3,2 Ом, что составляет
0,7 % (а не 1 %, как было первоначально) от номинала.
7.73. Резонансная частота колебательного контура /
определяется из выражения
/р 2tzJLC'
где L — индуктивность контура; С— емкость контура.
Определить приближенно среднее значение резонансной
частоты контура и ее среднее квадратическое отклонение, если
га, = 50 [мкГн]; гас =200 [пФ]; а, = 0,5 [мкГн] иас = 1,5 [пФ].
Решение, гаг =
2кфп1
= 1,59 [МГц].
га
204
(dL)
di
' m
2т: ^Jm c д/m f -2
== m
/o
2ra z
2ъ^т~^^т3с 2
m
h
2m
Df =
Jo
di
of +
M-
9c
2 1
4
f -2
m r • —
■'p
2 ^
+
ra, m
с )
— m
/o
(0,012 +0,0075)2 =m
/«,
'5}2
i,
•10
-4
/n
m, ---10-2 «1,0-Ю"2 [МГц],
/p
8
что составляет 0,62 % от номинальной частоты.
7.74*. Доказать, что если Хг,Х2, ..., Хп независимы, положи
тельны и одинаково распределены, то
М
п
Я=1
1=1
к_
п
Решение. Так как все величиныХг,Х2, ..., Хп
положительны, то в знаменателе никогда не стоит нуль. По теореме сложения
математических ожиданий имеем
М
п
£*./ХХ
i=i
j=i
Ем
i=i
п
*«/£*.
Я=1
Так как все величины Хг, Х2,..., Хп распределены
одинакового
М
п
*</£*.
М-
м
п
хт/Ех.
j=l
при любых гит. Обозначим а их общее значение:
М
п
*« /£*.
j=i
а (г = 1, 2, ..., п)
205
n
Вместе с тем ясно, что сумма всех величин вида Х{ /У2,Х ■ рав-
м
на единице, следовательно, и математическое ожидание ее тоже
равно единице:
М
п
п
£*./£*;
i=i
п
= ЕМ
г=1
п
*< /Е*
М
= 1.
Заменяя выражение, стоящее под знаком математического
х^ - 1
ожидания, через а, имеем /а = па = 1, откуда а = —. Следова-
тельно,
п
М
п
Е*«/Е*.
t=i
М
Jfc
Ем
i=i
п
*«/Е*.
М
-£±4.
1=1
П П
что и требовалось доказать.
ГЛАВА 8
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ
СЛУЧАЙНЫХ ВЕЛИЧИН. ПРЕДЕЛЬНЫЕ
ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Если X — непрерывная случайная величина с плотностью
распределения f(x), а случайная величина У связана с нею функциональной
зависимостью
где у — дифференцируемая функция, монотонная на всем участке
возможных значений аргумента X, то плотность распределения случайной
величины У выражается формулой
9(у) = №(уШ'(у)\,
где ф — функция, обратная по отношению к ф.
Если ф — функция немонотонная, то обратная функция неоднозначна,
и плотность распределения случайной величины определяется в виде
суммы стольких слагаемых, сколько значений (при данном у) имеет
обратная функция:
д(у) = ЕЛ*.- (»))№(у)I.
г=1
гдео^(у), 0^2(у), ..., т\>к(у) — значения обратной функции для данного у.
Для функции нескольких случайных величин удобнее искать не
плотность распределения, а функцию распределения. В частности, для
функции двух аргументов
£ = ф(*,У)
функция распределения вычисляется по формуле
О = (z)fff(x> v)dx dVi
D(z)
где/(я, у) — плотность распределения системы (X, У); D(z) — область на
плоскости хОу, для которой ф(я, у) < z.
207
Плотность распределения д (z) определяется дифференцированием
G{z):
g(z) = G'{z).
Плотность распределения суммы двух случайных величин
Z = X + Y
выражается любой из формул
00 00
9{z)= Jf(x,z-x)dx, g{z)= J f(z-y,y)dy,
— CO —00
где f(x,y) — плотность распределения системы (X, Y).
В частности, когда случайные величины X, Y независимы,
/(z>2/) = /i(z)/2(2/)>TO
00
9{z)= J fi(x)f2(z-x)dx
—со
или
со
—со
В этом случае закон распределения суммы д{х) называется
композицией законов распределения слагаемых }х (я), /2{у).
Если случайные величины, подчиненные нормальному закону,
подвергать любому линейному преобразованию, то будут получаться снова
случайные величины, распределенные нормально.
В частности, если случайная величина X распределена нормально с
параметрами тх, ох, то случайная величина
Y = aX+b
(где а, Ь — неслучайны) распределена нормально с параметрами ту =
= атх + Ь; оу =\а\ах.
При композиции двух нормальных законов: £(х) с параметрами
тх,ох и f2(y)c параметрами ту,оу получается снова нормальный закон
с параметрами
тг = тх + тУ; ° = vCT*+ °1 '
При сложении двух нормально распределенных случайных величин
X, Yc параметрами тх, ох, ту,оуп коэффициентом корреляции г^ полу-
208
чается случайная величина Z, также распределенная нормально, с
параметрами
т
z=mx + ту; о = ^Jo2x + о] + 2гщ<зхоу .
Линейная функция от нескольких независимых нормально
распределенных случайных величин Хг, Х3, ..., Хп
п
z = j2aixi + b>
i=i
где aiy Ь — неслучайные коэффициенты, также имеет нормальный закон
распределения с параметрами
п \ п
т
с
i =1 V i =i
гдеm^ , a^ — параметры случайной величиныX{(i = 1, ..., n).
В случае, когда аргументыХ1У Х2 -.., Хп коррелированы, закон
распределения линейной функции остается нормальным, но с параметрами
п
т
i =1
п
где гх.Хш — коэффициент корреляции величинХ{, ХАъ = 1, ..., п; j ^i).
Композицией двух нормальных законов на плоскости называют закон
распределения случайного вектора с составляющими
X = Xl + X2; Y = Yl + Y2,
где {Хъ Yx), {Х2, Y2) — случайные векторы, не коррелированные между
собой {rXxX2 = rXiV2 = ryiX2 = гу1У2 = 0).
При композиции двух нормальных законов на плоскости получают
снова нормальный закон с параметрами
тх = шхх + т*2; тУ = тУ1 + тУ2\
К = К А- к
откуда
Т* /Т /Т I 1У» /Т /Т
— Д1У1 х1 У 1 Х2У2 х2 У2
' XV
При проектировании случайной точки (X, У), распределенной на
плоскости по нормальному закону, на ось Oz, проходящую через центр
209
рассеивания и составляющую угол а с осью Ох, получается случайная
точка Z, распределенная по нормальному закону с параметрами
mz = тх cos a + ту sin а;
о2 = ^а2 cos2 а + а2 sin2 а + r^oхоу sin 2а .
Характеристической функцией случайной величины X называется
функция
g(t) = M[eitX],
где г = V—1 — мнимая единица.
Для дискретной случайной величины X
п
k=l
тдерк = Р(Х=хк)(к = 1,..., п).
Для непрерывной случайной величины
оо
5(t)=Je-'7(x)rfx,
—ОО
где /(я) — плотность распределения случайной величины X.
Отметим,чтод (0) = 1 и\д (t)\< 1 для любого t
Плотность распределения f(x) выражается через g{t) формулой
f(x) = ^te-itxg{t)dt
Если случайные величины X и У связаны соотношением У = аХ, где
а — неслучайный множитель, то их характеристические функции связаны
соотношением
Если случайная величина У представляет собой сумму независимых
случайных величин
то
п
Jfc=l
т.е. характеристическая функция суммы независимых случайных
величин равна произведению характеристических функций слагаемых.
210
вале
8.1. Случайная величина X распределена равномерно в интер-
. Найти закон распределения случайной величины
тг тг
I 2 2)
Y = sinX.
' it ^
монотонна,
Решение. Функция у = sinx в интервале
поэтому плотность распределения величины У может быть
найдена по формуле
р(у) = /(-Ф(у))|ФЧу)1-
Решение задачи располагаем в виде двух столбцов; слева будем
писать обозначения функций, принятые в общем случае; справа —
конкретные функции, соответствующие данному примеру:
/(*)
У = 4>(х)
х = ^(у)
W(y)\
9(У) = №(УШ'(У)
1
— при х е
7Г
0 при х ¢
7Г 7г'
Г 2' 2,
( \
"2* 2
у = sin X
х = arcsin у
1
VT
2/
рЫ
^v^-
2/
О
при 2/ G (-1, 1),
при 2/ £ (-1, 1).
Интервал (—1, 1), в котором лежат значения случайной
величины Yy определяется областью значений функции у = sinx для
1Г 1Г | 1)
, 2 2J
8.2. Случайная величина X распределена равномерно в интер-
вале , — . Найти плотность распределения случайной величи-
ны Y — cos X.
В дальнейшем при решении аналогичных задач для сокращения будем
записывать выражение плотности распределения только на участке, где она отлична от
нуля, подразумевая при этом, что вне этого участка она равна нулю.
211
Решение. Функция у = cos х немонотонна в интервале
—, — . Решение будем составлять аналогично предыдущему с
той разницей, что в данном случае для любого у обратная
функция будет иметь два значения. Решение снова оформляем в виде
двух столбцов
Л*)
У =
х = •
М(у)\
■■4>(х)
4»i(2/)
$2 (У)
=\Шу)
к
*(v) = £/H>i(v)MM
г =1
— при х е
7Г
9(У)
t \
7Г 7Г
2'2
у = COS X
0¾ = —arccos у
х2 = arccos у
jn
У
+
ъф^
Тсд/1 ~ У ^>/1 - У
9
при 2/ G (0, 1)
У
8.3. Случайная величина X распределена равномерно в интер-
вале , — . Найти плотность распределения случайной величи-
^ 2, 2 j
ныУ =|sinX|.
Ответ. д(у) =
*<Jl
при у е (0,1).
2/
8.4. Случайная величина X имеет плотность распределения
f(x). Найти плотность распределения случайной величины
Y= 1-Х\.
Решение. Функция у = |1 — х\ немонотонна. Решение будем
составлять так же, как в задаче 8.2.
X
№
У = ф(я)
ЛЫ
$2 (У)
№
У =|1 -х
хх =1-2/
х2=1 + у
212
№MI=U>i(v)l
9(у) = Ц2№((у)Ж(у)
i =1
g (у) = /(1 -2/)+ /(1 + у) при 2/ > 0.
Рис. 8.5
8.5. Круглое колесо, закрепленное в центре О (рис. 8.5),
приводится во вращение, которое затухает вследствие трения. В
результате фиксированная точка А на ободе колеса
останавливается на некоторой высоте Н
(положительной или отрицательной)
относительно горизонтальной линии I -1, проходя- j
щей через центр колеса; высота Н зависит от
случайного угла в, при котором
остановилось вращение.
Найти: а) закон распределения высоты Я;
б) закон распределения расстояния D от
точки А до прямой I -1 (считая это расстояние
всегда положительным).
Р е ш е н и е. Н = г sin в, где угол в — случайная величина,
распределенная равномерно в интервале (0, 2тг). Очевидно, решение
задачи не изменится, если считать случайную величину в распре-
_2'2
нотонной функцией в.
Плотность распределения величины Н:
деленной равномерно в интервале
; тогда Н является мо-
9(h) =
( U \2
при
г < h < г.
irrjl
h
г)
Плотность распределения величины D = \Н |:
*(<*)=
irrjl
fd]2
при 0 < d < г.
8.6. Случайная величина X распределена по закону Рэлея с
плотностью
/со=
1_е 2о>
а2
0
при
при
х>0,
х<0.
213
-X2
Найти закон распределения величины Y = е
Решение. На участке возможных значений аргумента X
2
функция у = е~х монотонна. Применяя общее правило, получим
У = 4>(х)
х = *ф ¢2/)
№v)\
9(у) = №(уШЬ)
JLP 2а2
а2
(гг > 0)
— х
X
у = е
2у^Ы
У
9{У)
1 «,2
2a2j/
,2а
1-2ст
1 -тгг
2а
2/
2ст
при 0 < у < 1,
рЫ
Графики д(у) при разных а
приведены на рис. 8.6.
8.7. Случайная величина X
распределена по закону Коши с плотностью
f(x) = — 7: (-оо <х<+оо).
тг(1 + х2)
Найти плотность распределения
у обратной величины Y = —.
X
Решение. Учитывая, что,
несмотря на разрывный характер функции
у = ~ обратная функция х = —
одного у
значна, и решая задачу по правилам для монотонной функции,
получим
д(у) =
Рис. 8.6
•гс
1
[ М2!
1 +
—
Ы
У
или
214
s(y) =
ъ(1 + У2)
(-oo < у < +оо)
т.е. величина, обратная величине, распределенной по закону Коши,
также имеет распределение Коши.
8.8. Через точку Л, лежащую на оси Оу на
расстоянии 1 от начала координат, проводится
прямая АВ под углом а к оси Оу (рис. 8.8). Все
значения угла а от до — равновероятны.
Найти плотность распределения абсциссы X
точки В пересечения прямой с осью абсцисс.
Решение. X = tg а; функция монотонна
на участке
— < а < —. Имеем
2 2
9(х) =
тг(1 + х2)
(—оо < х < +оо),
т.е. случайная величина Xраспределена по закону Коши.
8.9. Дискретная случайная величина X характеризуется рядом
распределения
Х{
Pi
-2
0,1
-1
0,2
0
0,3
1
0,3
2
0,1
Найти законы распределения случайных величин
У = Х2+1; Z=\X\.
Решение. Определяя для каждого х{ соответствующие
значения величин Y и Z и располагая их в возрастающем порядке,
получим ряды распределения
Vi
Pi
Zi
Р?
1
0,3
1
0,3
2
0,5
2
0,5
5
. 0,2
2
0,2
215
8.10. Через точку А с координатами (0, 1) проводится прямая
АВ под случайным углом G к оси ординат (рис. 8.10). Закон
распределения угла G имеет вид
1
У
<1
1'
О
л
е\
у\
в\
Рис. 8.10
/(в) = -COS в
при
ТС л ТС
— < 0< —
X
Z = | sin 61 на интервале
схему записи, имеем
л*)
Найти закон распределения расстояния
L от прямой А В до начала координат.
Решение. Имеем L = | sin 01. Функция
2 ' 2,
не монотонна. Применяя обычную
У =
х = ■
М(у)\
: Ч>(Х)
Му)
$2 (у)
= 1Ф£М
g(x) = J2№i (У)Ш(У)
i=l
1 Л 7Г л 7Г
— cos 0 при < 0 < —
2 2 2
/ = | sin 0|
—arcsin /
arcsin I
4\^i'
9(L)
л[Г^Т2
при 0 < I < 1,
cos (arcsin /) = 1
т.е. расстояние L распределено равномерно в интервале (0, 1), как
это можно видеть и из геометрических соображений.
8.11. Радиус круга R — случайная величина, распределенная по
закону Рэлея:
/(г) = ~Те 2ст ПРИ г > 0.
а2
Найти закон распределения площади круга 5.
Решение. Функция 5 ==тгД2 на участке возможных
значений R (0, оо) монотонна, следовательно,
216
9(*) =
2kg'
e 2lTa2 при s > О,
т.е. закон распределения площади круга есть показательный закон с
1
параметром .
2тш2
8.12. Маятник совершает свободные незатухающие колебания,
причем угол ф (рис. 8.12) изменяется в зависимости от времени t
по гармоническому закону:
Ф = asin(uj£ + 0),
где а — амплитуда; и — частота; 0 — фаза
колебания. В некоторый момент t = О, совершенно
не связанный с положением маятника,
производится его фотографирование. Так как
положение маятника в момент фотографирования
неопределенно, то фаза 0 есть случайная
величина, распределенная равномерно в
интервале (0, 2тг). Найти закон распределения угла Ф, который будет
составлять маятник с вертикалью в момент фотографирования,
найти его математическое ожидание и дисперсию.
Решение. Ф = a sin0, где фаза 0 распределена равномерно в
интервале (0, 27г), на котором функция ф =asin0 не монотонна.
Очевидно, решение задачи не изменится, если считать фазу 0 рас-
пределеннои равномерно в интервале , — , где функция
Ф = a sin 6 монотонна. Плотность распределения величины Ф будет
Рис. 8.12
'1-
[2)
2 а
Ъл]а
при |ф|<а.
Ф
Так как закон #(ф) симметричен, то его математическое
ожидание тф = 0. Дисперсия угла Ф равна
а
Д. =
Ф
-a Va
Ф
= dp = —
2 ТГ
2 v
2.0, . ф
Ф -\ arcsm—
2 а
а
0
а
8.13. Завод изготовляет шарики для подшипников,
номинальный диаметр которых d0, а фактический диаметр L — случайная
величина, распределенная по нормальному закону, с математиче-
217
ским ожиданием d^ и средним квадратическим отклонением az.
После изготовления каждый шарик проходит контроль, причем
бракуются все шарики, проходящие сквозь отверстие диаметром
d0 — 2az, и все шарики, не проходящие сквозь отверстие
диаметром d0 + 2az.
Найти закон распределения диаметра шариков, прошедших
контроль (незабракованных).
Решение. В этой задаче нужно найти плотность
распределения некоторой случайной величины £*, которая равна L только в
случае, когда L приняло значение между d0 — 2az и d0 + 2az; вне
интервала (d0 — 2az, d0 + 2ol) плотность распределения должна
быть равна нулю (рис. 8.13), а внутри
интервала — пропорциональна /(/),
причем
d0 + 2ai
d0-2at d0 d0+2o[
Рис. 8.13
I
ff*(l)dl =
d.Q—2ai
Из этого соотношения можно найти
коэффициент пропорциональности а:
J f*(l)dl=a f /(0<й = о[2Ф*(2)-1] = 1,
dQ—2oi
do~2ai
откуда
a ==
2Ф* (2)
0,9544
1.05.
Таким образом,
/*(0 =
1,05
a/V^K
0
(l-^o):
2a?
при \l — d0 |< 2a/5
при \l — d0\> 2az.
8.14. Имеется случайная величина Xc плотностью
распределения f(x). Случайная величина У определяется через X
соотношением
Y = min{X, 1},
т.е. У=ХириХ< 1, У=1приХ>1.
218
Найти закон распределения случайной величины Y и
определить ее математическое ожидание и дисперсию.
Решение. Случайная величина Y будет величиной
смешанного типа. При у = 1 ее функция распределения имеет скачок
рх, равный вероятности того, что величина X примет значение,
большее единицы:
оо
Pi
= ff(x)dx=l-F(l).
При у < 1 функция распределения Fx (у) случайной величины
Y будет совпадать с функцией распределения F(x) случайной
величины Хпри х — у:
F1(y) = F(y)= Jf(x)dx.
—ОО
При у > 1 Fx (у) = 1 (рис. 8.14).
Математическое ожидание
смешанной случайной величины Y
равно
Ш
Рис. 8.14
оо
ту =1-Pl + JyF'(y)dy = Jf(x)dx+ fyf(y)dy.
-ОО
—ОО
Дисперсия случайной величины Уравна
ОО
Dy =a2[Y]-ml = f f(x)dx+ Jy2f(y)dy - m
—OO
8.15. Имеется непрерывная случайная величина X с
плотностью распределения f(x). Найти закон распределения случайной
величины
Y = sgnX =
+1 при X > О,
О при X = О,
-1 при Х<0
и ее числовые характеристики.
219
Решение. Дискретная случайная величина У имеет всего два
значения: минус единица и плюс единица (вероятность того, что
У = 0, равна нулю).
о
Р(У = -1) == Р(Х < 0) = ff(x)dx = F(0);
—оо
оо
Р(У = +1) = Р(Х > 0) = ff(x)dx = 1 - F(0);
о
my = -1 . F(0) + 1 • [1 - F(0)] = 1 - 2F(0);
a2[y] = bF(0) + l-[l-F(0)] = l;
Dy =a2[Y] - m\ = 1 - 1 + 4F(0) - 4[F(0)]2 - 4F(0)[1 - F(0)].
8.16. Имеется непрерывная случайная величина X с
плотностью распределения f(x). Найти закон распределения случайной
величины
У = гшп{Х,Х2},
т.е. величины, которая равна Х7 если
X <Х\иХ\еслиХ2 <Х.
Решение. Функция у = ф(х)
монотонна (рис. 8.16)
У
\ 1
\
ч
^
• у~х'
' /У=х
ф(х)
х2 при х € (0,1),
х при х ¢ (0, 1).
О 1
Рис. 8.16
Так как интервал (0, 1) оси Ох
отображается на интервал (0, 1) оси Оу7 то
по общему правилу
д(у)
f{4v)A= ПРИ У €(0,1),
ъ4у
т
при у ¢(0,1).
Рис. 8.17
8.17. Случайная величина X имеет
плотность распределения f(x)7 заданную
графиком (рис. 8.17). Случайная
величина У связана с X зависимостью
У = 1 — X2. Найти плотность
распределения случайной величины У.
Решение. Плотность f(x) дается
функцией
220
f{x)=l-{x + l)
при
X£ (-1, + 1).
Функция 2/ = 1 — x2 на этом участке не монотонна; обратная
функция имеет два значения:
х1 = -д/1 " У> Х2 = +V1 ~ У-
Отсюда
д(у) = i [(1 - VW) + (1 + VW)]
4V1-»
или
д(у) = —===== при 0 < х/ < 1-
2д/1 - 2/
8.18. Случайная величина X распределена по закону с
плотностью/(ж). Найти плотность распределения обратной ей случайной
величины Y = —.
X
Решение. Функция у = — хотя и не монотонна в обычном
х
смысле слова (при х = 0 она скачком возрастает от -оо до оо), но
обратная функция однозначна, значит, задача может быть решена
так, как она решается для монотонных функций:
9(У) = /
V
kVj
у2
при тех значениях у, которые могут быть обратными заданной
совокупности возможных значений х.
8.19. Натуральный логарифм некоторой случайной величины
J распределен по нормальному закону с центром рассеивания т и
средним квадратическим отклонением а. Найти плотность
распределения величины X.
Решение. Обозначим нормально распределенную величину
через U. Имеем
(и—т )
£/ = 1пХ; Х = еи; f(u) = -^=e *°*~.
Функция е" монотонна;
221
9(x)
стл/2тг
—(Ini—m )'
2a2
X
XG
V^K
—(Ini—m )'
2a2
при x > 0.
Такое распределение величины X называется логнормалъным.
8.20. Пятно П, изображающее объект на круглом экране
радиолокатора, может занимать на нем произвольное положение
(рис. 8.20), причем плотность распределения
координат (X, Y) пятна в пределах экрана
постоянна. Радиус экрана равен г0. Найти
плотность распределения расстояния R от пятна до
центра экрана.
Решение. Найдем функцию
распределения
Рис*8'20 G{r) = Р(Д < г) = Р((Х, Y)e Кг),
где К— круг радиуса г с центром в точке О. Так как в пределах экрана
плотность распределения постоянна, то вероятность попадания в
круг равна его относительной площади
о
G(r) =
-кг
ТС Г,
0
КГ0>
откуда
9{r) = G'{r)
2г
при 0 < г < r0.
о
8.21. Случайная величина Xраспределена равномерно в
интервале (0, 1). Случайная величина У связана с X монотонно
возрастающей функциональной зависимостью Y = ф(Х).
Найти функцию распределения G(y) и плотность
распределения д(у) случайной величины Y.
Решение. Имеем f(x) = 1 при х £ (0,1).
Обозначим т\)(у) функцию, обратную по отношению к функции
у = ф(#). Так как ф(х) монотонно возрастает, то
откуда G(y) = ty(y), т. е. искомая функция распределения есть
обратная по отношению к функции ф (в области возможных значений
величины Y).
8.22. Какому функциональному преобразованию надо
подвергнуть случайную величину Х} распределенную равномерно в
интервале (0, 1), чтобы получить случайную величину У,
распределенную по показательному закону
д(у) = \е-Ху (приу>0)?
222
Решение. На основании решения предыдущей задачи мы
должны положить У = ф(Х), где ф — функция, обратная
требуемой функции распределения G(y) случайной величины У Имеем
у
G(y) = J\e~Xy dy=l-e'Xy.
о
Полагая в этом уравнении 1-е Ху — х и разрешая его
относительно у, получим
» = -—ln(l-x),
откуда искомая зависимость будет
У = --1п(1-Х), 0<Х<1.
8.23*. Имеются две случайные величины; Хс плотностью fx (х)
и Ус плотностью /2 (у). Известно, что величина У представляет
собой монотонно возрастающую функцию величины X: У = ц>(Х).
Найти вид функции ф.
Решение. Введем в рассмотрение, кроме плотностей /х (х)у
f2(y)y функции распределения
х у
Fi(*)= J7i (*)<&; F2(y)= ff2(y)dy.
-oo —oo
Представим случайную величину X как функцию от У:
X = ф-1(У), где ф — функция, обратная по отношению к
искомой ф.
Применяя обычный способ нахождения функции
распределения монотонной функции, находим
*!(*) = ff2(y)dy = F2(v(x)).
-oo
Разрешая это уравнение относительно ф(х) и вводя функцию
F^1 у обратную функции F2, получим
<p(x) = F2-1(F1(x))
или, возвращаясь к случайным величинам,
Y = F2-1(F1(X)).
Полученная формула определяет функцию ф(х) только в тех
интервалах, где плотность /г (х) отлична от нуля.
223
8.24. Случайная величина X распределена по показательному
закону:
/1(x) = Xe-Xl (х>0)
Каким функциональным преобразованием можно превратить
ее в случайную величину Y, распределенную по закону Коши:
ш= 1Л1 2 ?
Решение.^(г) = 1 - е~Хх (х>0);
Р2(У)
-к
arctg у +
-к
Полагая во втором уравнении
-к
arctg у +
-к
м и разрешая его
относительно у, найдем обратную функцию F2 1 (и):
y = F-\u) = tg
тш —
-к
2)
—ctg-KU
По решению предыдущей задачи получим
Y = F'^F^X)) = -ctgir(l - е'хх) = ctgire"xx (X > 0).
8.25*. Решить ту же задачу, что и 8.23, но при условии, что
связывающая две случайные величины функция ф должна быть не
монотонно возрастающей, а монотонно убывающей.
Решение. В тех же обозначениях, что в задаче 8.23, имеем
оо
откуда
Х = Ф-1(П> *l(s)= ff2(y)dy = l-F2[4>(x)]
<р(х)
4>(x) = F2-1[l-F(x)} и У = ^1-*!(*)].
8.26. Двое условились встретиться в определенном месте в
промежутке времени от 12.00 до 13.00. Каждый из них приходит
на место встречи независимо от другого и с постоянной
плотностью вероятности в любой момент назначенного промежутка.
Пришедший раньше ожидает другого. Найти распределение
вероятностей времени ожидания и вероятность того, что ожидание
продлится не менее получаса.
Решение. Обозначим моменты прихода двух лиц Тг иГ2; за
начало отсчета времени примем 12 ч. Тогда каждая из независи-
224
мых случайных величин Tv Т2 распределена с постоянной
плотностью в промежутке (0, 1). Случайная величина Т— время
ожидания Т=\Тг - Т21.
Найдем функцию распределения G(t)
этой величины. Выделим на плоскости Ьг0Ь2
область D(t), в которой |^ — t2\<t
(заштрихованная область на рис. 8.26).
Функция распределения G(t) в данном t
случае равна площади этой области:
G(t) = 1-(1 -t)2 =*(2 —*),
откуда g(t) = 1 - (2 - t) при 0 < t < 1.
С 11
т>-
{ 2)
= 1-
-а
m
I2J
= 0,25.
8.27. Случайная точка {X, Y) распределена равномерно в
квадрате К со стороной 1 (рис. 8.27, а). Найти закон распределения
площади S прямоугольника R со сторонами X, Y.
Решение. Выделим на плоскости хОу область D(s), в
пределах которой ху < s (рис. 8.27, б).
xy=s
х
а
б
Рис. 8.27
Функция распределения в данном случае равна площади
области D(s)
1 1
G(s) = 1—1 I dxdy = 1 — I dx I dy = s(l — his).
D(s) s ±
x
Отсюдаg(s) = G'(s) = —Ins при 0 < s < 1.
8.28. Система случайных величин (X, Y) имеет плотность
распределения f(x, у). Найти плотность распределения g(z) их от-
7 Y
ношения Z = —.
X
225
Решение. Зададимся некоторым
значением z и построим на плоскости
хОу область D(x\ где — < х (рис.8.28, за-
х
Рис. 8.28
штрихованная область). Функция
распределения G(z) имеет вид
G(z) = J J f(x,y)dxdy =
D(z)
0
oo
oo zx
jdxjf(x, y) dy + Jdxjf(x, y)dy.
—oo zx
0 -oo
Дифференцируя no z} имеем
0 oo
g(z) = — / xf(x, zx) dx + / xf(x, zx)dx.
-oo
0
Если случайные величины^, У независимы, то
О оо
g(z) = - J xfx (x)f2 (zx)dx + J xfx (x)f2 (zx)dx.
-oo
0
У
8.29. Найти закон распределения отношения Z — — двух
независимых нормально распределенных случайных величин Х> Ус
характеристиками тх = т = О, ахиа .
Решение. Рассмотрим сначала частный случай ох =о =
= 1. На основании предыдущей задачи
о
*(*) = -/
2 , .2 2
I -Цх' + z'x*)
00
х—е
2-гс
dx+ f
2 , _2„2
X
-ОО
О
1 -Цх' + хЪ*)
— е 2
2тг
da; =
о
00 X " ,„ . 2'
-(!+*')
ГГс£г
-к(1 + ^2)
(закон Коши).
У
В общем случае отношение Z = — можно представить в ви-
о У X У
де Z = ———, где величины Хх = — и Ух = — имеют уже нор-
°х Х1 °х °у
мальные распределения с дисперсией, равной 1; поэтому в общем
случае
226
fa)
It
1 +
V°V I
У
В частном случае, если ох = о , получим
fa) =
тг(1 + г2)
8.30. Случайная точка (X, Y) распределена равномерно в круге
К радиуса 1. Найти закон распределения случайной величины
X
Решение. В данном случае G(z) есть
относительная площадь области D(z)
(рис. 8.30):
G(z) =
-к
arctg z +
-к
2J
откуда
9{*) = G'{z)
it(1 + ^2)
(закон Коши).
Рис. 8.30
8.31. Составить композицию двух показательных законов
Х^""*1*1 при хг > 0,
при хг < 0,
Л (¾)
о
Л (Х2 )
Х2е ^2 при х2 > 0,
при х2 < 0.
0
Решение. Обозначим X = Хг + Х2, где Хх, Х2
распределены по законам /х (^), /2 (х2).
Согласно общей формуле для композиции законов
распределения
со
fa) = J Л («1 )/2 (х - xi )dxi •
—со
Но в нашем случае оба закона отличны от нуля только при
положительном значении аргумента; значит, fx (хг) = 0 при хг < 0 и при
/2(я — з^) = 0при хг > х.
227
При х > О получим
д[х) = J \ге-х^ \2e-^{x'Xl) dx,
о
XlV V [e(X2"Xi)s _Ц= \МС Xl" "е V)
х2 - хх
Х2 - \
(обобщенный закон Эрланга 1-го порядка).
При \г = Х2 = X, раскрыв неопределенность, получим закон
Эрланга 1 -го порядка:
2 -Хх
р(х) = Х^хе при х > 0.
Примечание. Методом математической индукции можно
доказать, что закон распределения суммы п независимых случайных величин,
Хг,..., Хп, подчиненных показательным законам распределения с
различными параметрами \,..., Хп, т. е. обобщенный закон распределения
Эрланга (п-1)-го порядка, имеет плотность
0»-iW = '
п п
(-D-'II^E-
■\jX
при х > 0,
i=1 ^П(\--х*)
о
при х < 0.
п
(Запись J~J означает, что берется произведение всех биномов вида
\j — \k при k = 1, 2,..., j - 1, j + 1,..., rc, т.е. кроме X^ - X ..)
В частном случае, когда Xt = г X:
n
Функция распределения обобщенного закона Эрланга (п — 1)-го
порядка имеет вид
п п -I _ p-Xjx
^-,(^) = (-1)-41^2-4-^ при *>°-
•■-1 ^\^(X;-\fc)
Ы1
Если X, = г X, то
п
^,(3) = 2(-^^11-^] при *>0.
228
Если \ = Х2 =...= \п = X, то получаем закон Эрланга (п — 1)-го
порядка:
(п -1)!
х
G„-i (*) = Г хр(п - 1, Xz) cfc =
о
00
= 1 - Г ХР(п - 1, Xz) cb = 1 - Д(п - 1, \х) (х > 0),
где
Р(ту а) = — е а\ R{m9 ^) = ^-е а
Jb=0 *!
m !
8.32. Имеется система двух случайных величин (X, Y) с
плотностью распределения Дх, у). Найти функцию распределения
G(z) и плотность распределения g(z) максимальной из этих двух
величины: Z = max{Xy Y}.
Решение. Будем искать функцию распределения случайной
величины Z: G{x) = P(Z < z).
Для того чтобы максимальная из величин X, Y была меньше z,
нужно, чтобы каждая из этих величин была меньше z:
G(z) = T>((X<z)(Y<z)) = F(z,z),
где
х у
F(x, У)= J f f(x> У)^ dV
— 00—00
Таким образом,
Z Z
G(x) = J J /(ж, y)dx dy.
-oo—oo
Чтобы найти плотность распределения g(z)}
продифференцируем G(z) по величине z, входящей в пределы двойного интеграла.
Дифференцировать будем как сложную функцию двух
переменных zx и г2, из которых каждая зависит от z(zx = z,z2 = z):
9(z)
dG{z) d
dz
dz
i
-oo
~2
ff(x,y)dy
dx
—oo
229
= dC^d^ + dGMd^ = -jf{Zt y)dy + 'rm z)d%
dz. dz az0 dz J u
В частном случае, если величины X, У независимы, /(ж, j/) =
= /i(^)/2(»)»TO
Z х
9{z) = Л(«) J f2(v)dy + /2(г) J fi(x)dx,
-OO
—OO
или, более компактно,
g{z) = f1{z)F2(z) + f2{z)F1(z).
Если случайные величины Хи У независимы и одинаково
распределены [Д (ж) = /2 (я:) = /(ж)], то р(г) = 2f(z)F(z).
8.33. Система двух случайных величин (X, У) имеет плотность
распределения /(ж, у). Найти функцию распределения G(u) и
плотность распределения р(гх) минимальной
из этих двух величин: U = min{X, У}.
Решение. Будем искать дополнение до
единицы функции распределения:
1 - G{u) = P(J7>tx) = Р((Л>и)(У > и)).
Это есть вероятность попадания
случайной точки (X, У) в область D(u),
заштрихованную на рис. 8.33. Очевидно,
Рис. 8.33 1 - G(u) = 1 - F(u, oo) - F(oo, w) + F(u, u),
откуда
G(tx) = F(ti, oo) + F(oo, ix) - F(tx, и) = Fx{u) + F2(tx) - F(u, u).
Дифференцируя по и, имеем (см. задачу 8.32)
и
и
0(u) = ./i(tO + /2(u)- ff(u,y)dy- ff(x,u)dx.
—OO
—OO
В случае, когда величины Хи У независимы,
U
U
g{u) = fx{u) + /2(u) - /x(u) - Jf2(y)dy - f2(u)ff1(x)dx =
-OO
-OO
= />)[1-ад]+/2н[1-ад]-
Если случайные величины Хи У независимы и одинаково
распределены [/j (ж) = /2 (ж) = /(ж)], то
p(«) = 2/(«)[l-F(«)].
230
8.34. Имеется п независимых случайных величинХг, Х2,...,
Хп, распределенных по законам с плотностями Д^), /2(х2),...,
Найти плотность распределения максимальной из них:
Z = max{X1?X2, ...,ХП}
и минимальной:
и = тт{Хг,Х2, ...,ХП},
т.е. той из случайных величин, которая в результате опыта примет
максимальное (минимальное) значение.
Решение. Обозначим Gz (z) функцию распределения
величины Z. Имеем
Gz{z) = V{Z<z) = f[Fi{z\
где
Z
Fi(*)= ffi(*i)<bi (<=l,2,...,n).
—OO
Дифференцируя, получим сумму произведений производных
отдельных функций распределения Fl(xl),F2(x2), ...,Fn(xn) на
произведения всех остальных функций, кроме той, которая
продифференцирована. Результат можно записать в виде
п f(z) п
Аналогично, обозначая Gu(u) функцию распределения
величины U, получим
gu оо = 1-П[1-*;(«)]•
Дифференцируя, получим
п f (и) п
8.35. Имеется п независимых случайных величин Хг,Х2,...,
Хп, распределенных одинаково с плотностью /(х). Найти закон
распределения максимальной из них:
Z = т&х{Х1,Х2, ...,ХП}
231
и минимальной:
и = тт{Хг,Х2, ..., Хп}.
Решение. На основании решения предыдущей задачи
G,{z) = F»{z); gz{z) = nFn-\z)f{z);
Gu («) = 1 - [1 - F(u)}n ; gu (и) = n[l - F(u)]"-'f(u).
8.36. Производится три независимых выстрела по плоскости
хОу; центр рассеивания совпадает с началом координат,
рассеивание нормальное, круговое, ах =ау =а. Из трех точек попадания
выбирается та, которая оказалась ближе всех к центру
рассеивания. Найти закон распределения расстояния Rmin от точки
попадания до центра.
Решение. Имеем Rmin = min^, R2, R^}.
Из решения предыдущей задачи имеем
S*mi>) = 3[l-F(r)]2/(r),
mm
где F(r), /(г) — функция распределения и плотность распределения
расстояния R от точки попадания любого выстрела до центра
рассеивания,
г2
F(r) = P(/J<r) = l-e 2а ,
г2
/(r) = -Le 2ff2 (r>0).
а2
Отсюда
5дш1„ (г) =
Зг "
— е
а2
Зг2
о 2
2а
/
т.е. плотность распределения расстояния от ближайшей из трех
точек до центра рассеивания имеет тот же вид, что и для каждой из
них, но при условии, что параметр а уменьшен в ->/3 раз, т. е. заменен
значением а = ——.
л/3
8.37. Найти закон распределения минимальной из двух
независимых случайных величин Ти Т2, распределенных по
показательным законам:
Л (*i) = VX|t| при 'i >°;
/2(*2) = VXA ПРИ *2 >0'
232
Решение. На основании решения задачи 8.33
РЛ^) = /1(^)[1-^(^)] + /2(т|)[1-^(11)]==
= X1e-Xltte"x*tt +X2e"X2Ue-XlU - (\ + Х2) e"(Xl+X2)u (тх >0),
т.е. закон распределения минимальной из двух независимых
случайных величин, распределенных по показательным законам, есть
тоже показательный закон, параметр которого равен сумме
параметров исходных законов.
Вывод нетрудно обобщить на любое число показательных
законов.
8.38. В условиях предыдущей задачи найти закон
распределения gz(z)максимальной из величин Ть Т2.
Решение.
5Л*)=л(*)ад+/2(*)зд=
= X^-^l -е~х*г] + \2е~х*г[1 -е-х,*] =
= \e~^z + \2е~х*г - (\ + Х2) e-(Xl+x^ (z > 0).
Этот закон показательным не является. При \1 — \2 ~ ^
5Дг) = 2\е-Хг(1-е-Хг) (z>0).
8.39*. Над случайной величиной X, имеющей плотность
распределения /(х), производится п независимых опытов;
наблюденные значения располагаются в порядке возрастания; получается
ряд случайных величин Zx, Z2, ..., Zk, ..., Zn.
Рассматривается к-я из них Zk Найти ее функцию
распределения Gk (z) и плотность распределения дк (z).
Решение. Gk(z) = P(Zk < z). Для того чтобы к-я (в порядке
возрастания) из случайных величин £,, Z2, ..., Zk, Zn была
меньше z, нужно, чтобы не менее к из них оыли меньше z:
тп=к
где Рт — вероятность того, что ровно га из наблюденных в п опытах
значений случайной величины X будут меньше z. По теореме о
повторении опытов
откуда
Gk{z)=Y,C:[F{z)Yn[l-F{z)}n-m1
т=к
233
где
F{z) = Jf(x)dx.
—OO
Плотность распределения gk(z) можно найти, дифференцируя
это выражение и учитывая, что
Оп т = = пСп_1 ;
(т — 1)!(п — га)!
С™ (п - га) = пС™^ (га < п).
После простых преобразований получим
9Л*) = nCkn^f(z) [^)]^[1 - F(z)]n'k.
Однако гораздо проще получить gk(z) непосредственно, с
помощью следующего простого рассуждения.
Элемент вероятности gk(z)dz приближенно представляет
собой вероятность попадания случайной величины Zk (к-то в
порядке возрастания значения случайной величины X) на участок
(z, z + dz). Для того чтобы это произошло, нужно, чтобы
совместились следующие события:
1) какое-то из значений случайной величины X попало на
интервал (z, z + dz);
2) (к — 1) других каких-то значений оказались меньше z;
3) (п — к) остальных значений оказались больше z
(вероятностью попадания более чем одного значения на элементарный
участок (z, z + dz) пренебрегаем).
Вероятность каждой такой комбинации событий равна
f(z) dz [F(z)]k~l[l — F(z)]n~k. Число комбинаций равно
произведению числа п способов, какими можно выбрать одно значение из п,
чтобы поместить его на интервал {z,z + dz), на число Ск~\
способов, какими из оставшихся п — 1 значений можно выбрать к — 1,
чтобы поместить их левее z. Следовательно,
дк (z) dz = nC^fWiFWt^ ~ Пг)Гк<1г,
откуда
5* (*) = nCk-\f{z)[F{z)}k-l[l - F{z)]n-k.
8.40. В электропечи установлено четыре регулятора
(термопары), каждый из которых показывает температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым
математическим ожиданием и средним квадратическим
отклонением at. Происходит нагревание печи. В момент, когда две из четы-
234
рех термопар покажут температуру не ниже критической т0, печь
автоматически отключается. Найти плотность распределения
температуры Z, при которой будет происходить отключение печи.
Решение. Температура Z, при которой происходит
отключение печи, представляет собой второе в порядке убывания (т.е.
третье в порядке возрастания) из четырех значений случайной
величины Т, распределенной по нормальному закону с центром
рассеивания т0 и средним квадратическим отклонением ot:
/(О
1
(*-т0):
2а?
а, л/2тс
Соответствующая функция распределения
F(t) = $*
V Gt J
Пользуясь результатами предыдущей задачи при п — 4, к = 3,
получим
Рз(') =
12
2а?
о+ V2tc
ф*
fj. \
t - т0
1 Gt J
2
1-Ф*
t - т0
I °t J]
8.41. Имеется n независимых случайных величин Хг, Х2, ...,
Xn, функции распределения которых имеют вид степенной
зависимости:
Fi (*•• ) =
О
х
1
Ь
при
при
при
*i <0,
0 < х< < 1,
х4 >1
(г = 1, 2,.
••,»)
Наблюдается значение каждой из случайных величин и из них
выбирается максимальное Z. Найти функцию распределения G(z)
этой случайной величины.
Решение. На основании решения задачи 8.34
п
п
G(z) = HFi(z) = '[lzki при 0<z<l
i-l
i=\
235
n
или, если обозначить к = У~]к{,
i=l
ОД =
0 при z < О,
z* при 0 < z < 1,
1 при z > 1,
т. е. максимум нескольких случайных величин, распределенных по
степенному закону в интервале (0,1), также распределен по
степенному закону с показателем степени, равным сумме показателей
степеней отдельных законов.
8.42. Дискретные случайные величины Хг, Х2, ...,Хп
независимы и распределены по законам Пуассона с параметрами
п
Показать, что их сумма Y = ^Х{ также подчинена
п
закону Пуассона с параметром а = У~]а>г.
i=i
Решение. Докажем сначала, что сумма двух случайных
величин Х1 и Х2 подчинена закону Пуассона, для чего найдем
вероятность того, что Хг + Х2 = m (m = 0,1, 2, ... ):
т
Р(Хг + Х2 = т) = X]P(Xi = *) Р(Х2 = т - Л) =
fc=0
т пк пт~^
_ ул «i_ ^_ai a2 c-a2 .
К *! (m-t)! '
^jb т!
учитывая, что Ст = , представим это выражение в виде
к\(т — к)\
* -ус1акгаГк -(Ql+fl2) е^'+Ч
га! ££ га!
а это есть распределение Пуассона с параметром al + а2.
Таким образом доказано, что сумма двух независимых
случайных величин, подчиненных законам Пуассона, тоже подчиняется
закону Пуассона. Распространение этого результата на любое
число слагаемых производится по индукции.
8.43. Система случайных величин (X, Y) распределена по
нормальному закону с характеристиками тх, ту,ох,оу иг^.
Случайные величины (U, V) связаны с (X, Y) зависимостью
U = aX + bY + c; V = kX + lY + m.
236
Найти закон распределения системы случайных величин (U, V).
Ответ. Система (£/, V) распределена нормально с характери
стиками
ти = атх + Ъту + с;
т v = ктх +lmy + га;
°и =^а2°2х + Ъ2о\ + ^Ьахаугяву\
ov = Jk2o2x+l2o2y -h2kloxoyrxy;
ак о2х +Ыо2у + (Ък + al) о^уГ^
UV
°u°v
8.44. Самолет-бомбардировщик
производит бомбометание по полосовой цели ширины
b = 40 м, заходя на нее под углом 30° по
отношению к направлению полосы (рис. 8.44).
Координаты точки попадания распределены по
нормальному закону; главные оси
рассеивания — направление полета и
перпендикулярное к нему; начало координат на средней
линии полосы. В этой системе координат хОу
параметры нормального закона 77^.= 10 [м];
ту = 0; °х = 50 м]; оу = 25 [м].
Найти вероятность р попадания в полосу
при сбрасывании одной бомбы.
Решение. Проецируем рассеивание на
ось Oz, перпендикулярную к полосе:
Рис. 8.44
тz = 10 -cos60°= 5 [м];
gz = Ja2 sin2 60°Wy sin2 60° = yjbO2 -0,25 + 252 -0,75 « 33,1 [м];
_ <т>*
р = Ф
(20-5]
I 33,1 j
_ ф*
[-20-5)
I 33,1 J
0,450.
8.45. Цех завода выпускает шарики для подшипников. За
смену производится п = 10 000 шариков. Вероятность того, что один
шарик окажется дефектным, равна 0,05. Причины дефектов для
отдельных шариков независимы. Продукция проходит контроль
сразу после изготовления, причем дефектные шарики бракуются
и ссыпаются в бункер, а небракованные отправляются в цех
сборки. Определить, на какое количество шариков должен быть
рассчитан бункер, чтобы с вероятностью 0,99 после смены он не
оказался переполненным.
237
Решение. Число забракованных шариков X имеет
биномиальное распределение; так как п велико, то на основании
центральной предельной теоремы можно считать распределение
приблизительно нормальным с характеристиками:
тх =пр = 10 000 • 0,05 = 500;
Dx = npq = 500 • 0,95 = 475; ах «21,8.
Находим такое значение /, для которого Р(Х < /) = 0,99, или
ф=
(I
т
\
°х
= ф*
(I - 500
21,8
= 0,99.
По таблицам функции Ф* (х) находим
2 — 500
21,8
2,33, откуда / «551,
т.е. бункер, рассчитанный примерно на 550 шариков, с
вероятностью 0,99 за смену переполняться не будет.
8.46. Условия задачи 8.45 изменены в том отношении, что
причины брака являются в значительной степени общими для
различных шариков, так что вероятность одному шарику,
изготовленному в течение данной смены, быть дефектным, при условии,
что другой (любой) шарик уже был дефектным, равна 0,08.
Примечание. Число опытов (тг = 10000) считать достаточно
большим для того, чтобы, несмотря на зависимость опытов, закон
распределения суммарного числа дефектных шариков был приближенно
нормальным.
Решение. Рассмотрим случайную величину X — общее
число забракованных (дефектных) шариков — как сумму п= 10 000
слагаемых:
10 000
i=l
где величина Xi принимает значение 1, если шарик дефектный, и 0 —
если не дефектный. Имеем
тх=пр = 10 000 • 0,05 = 500;
10 000
D = Y^D +2 V# =
X / _j Ij / _j xixj
i=l i<j
= 475 + 2C2W ШКХ(С. = 475 + 10 000 • 9999 KX(C.,
где Kx<e. — корреляционный момент случайных величин Х{, X.
238
Найдем
Так как произведение Х{ X • принимает только два значения: 1
(при Х{ = 1, Х^•= 1) и 0 (в остальных случаях), то
М[Х{Х;] = 1 -Р((Х, = l)(Xj = 1) = 0,05-0,08 = 0,004
и
КХХт = 0,004 - 0,05 • 0,05 = 0,0015,
XtXj
откуда
Dx « 475 + 15 • 104 « 15,05 .104, <т « 388.
Далее находим /из условия
Г/-5001
Ф
*
I 388 )
= 0,99; -—— = 2,33; / = 1404,
388
т.е. бункера, рассчитанного примерно на 1400 шариков, будет
достаточно (с вероятностью 0,99) для бракованной продукции за смену.
8.47*. Лотерея организована следующим образом. Участникам
продаются билеты, на каждом из которых имеется таблица с
номерами: 1, 2,..., 90. Участник должен выбрать произвольным образом
пять различных номеров, отметить эти номера и послать билет
организаторам лотереи, которые хранят все присланные билеты в
запечатанном виде до дня розыгрыша. Розыгрыш лотереи состоит в
том, что случайным образом выбираются (разыгрываются) пять
различных номеров из девяноста; выпавшие номера сообщаются
участникам. Если у игрока совпали с объявленными менее двух
номеров (0 или 1), он никакого выигрыша не получает. Если
совпали с объявленными два номера, он выигрывает 1 руб.; если три
номера — 100 руб.; если четыре номера —10 000 руб.; если все пять
номеров - 1 000 000 руб.
1) Определить нижнюю границу цены билета, при котором
лотерея в среднем еще не приносит убытка ее организаторам;
2) определить средний доход М, который приносит лотерея
организаторам, если в ней участвуют 1 000 000 человек,
назначающих свои номера независимо один от другого, каждый покупает
один билет, а цена билета 30 коп.;
3) пользуясь «правилом трех сигма», найти границы
практически возможных выплат по лотерее; можно ли считать суммарную
выплату по лотерее распределенной по нормальному закону?
239
Решение. 1) Обозначим р{вероятность того, что из пяти
названных игроком номеров ровно г совпадут с выпавшими.
Находим
р2 = ^1-2,25- Ю-2; ft =-¾^ « 8,12 • 10"
-^- « 2,25 • Ю-2; р. = -^85
90 w90
р = 5 85 ^9,67-10"6; р5 =-4-«2,28-Ю-8.
°90 °90
Минимальная цена билета должна быть равна
математическому ожиданию выигрыша игрока, купившего этот билет:
т = 2,25 • 10~2 • 1 + 8,12 • 10~4 • 102 + 9,67 • 10~6 • 104 +
+ 2,28 • 10"8 • 106 = 22,3 • 10"2 [руб.],
т.е. минимальная цена билета — около 23 коп.
2) М = (0,30 - 0,223) • 106 = 77 • 103 [руб.].
3) Общая сумма выигрышей X, которая подлежит выплате по
лотерее, представляет собой сумму выигрышей отдельных
игроков:
1000000
х= Е*«.
i=\
где Х{ — выигрыш г-го игрока.
Считается, что игроки называют свои номера независимо друг
от друга, так что величины Х{ (г = 1, 2,..., 1 000 000) независимы.
Из центральной предельной теоремы известно, что сумма
достаточно большого числа независимых одинаково распределенных
случайных величин приближенно распределена по нормальному
закону. Требуется выяснить, достаточно ли в данном случае числа
слагаемых п = 1 000 000 для того, чтобы величину X можно было
считать распределенной нормально?
Находим математическое ожидание тх и среднее квадратиче-
ское отклонение ох случайной величины X. Для любого г = 1, ...,
1 000 000
тХ{ =22,3-10"' =0,223;
а2[Х{] = 2,25 • 10~2 + 8,12 + 9,67 • 102 + 2,28 • 104 = 2,38 • 104;
Dx. = 2,38 • 104 - 0,222 = 2,38 • 104.
Отсюда
т =106 -rn =2,23-105;
240
а-+оо л—* rn f
га=0 "b '
a _ m
Dx = 106 Д^ =2,38-1010; ox = 105 7^38 « 1,54 -105.
Известно, что для случайной величины X, распределенной по
нормальному закону, границы практически возможных значений
заключены между тх ±Зох («правило трех сигма»).
В нашем случае нижняя граница возможных значений
случайной величины X, если бы она была распределена по нормальному
закону, была бы тх - 2>ох = (2,23 - 3 • 1,54) • 105 = -2,39 • 105.
Отрицательное значение этой границы указывает на то, что
случайная величина X не может считаться распределенной
нормально.
а ат
8.48*. Найти предел lim У^ е а, где а — целое положитель-
ное число.
Решение. Выражение У^ е~а есть вероятность того, что
случайная величина X, распределенная по закону Пуассона, не
превзойдет своего математического ожидания а. Но при
неограниченном увеличении параметра а закон Пуассона
приближается к нормальному. Для нормального закона вероятность того,
что случайная величина не превзойдет своего математического
а т -1
ожидания, равна 1/2, значит, lim У^ е~а =-.
a-*oo ^-< 771 ! 2
га=0
8.49. Доказать, что показательный закон распределения
является устойчивым по отношению к операции нахождения
минимума, т.е. если случайные величины Хг,Х2, ..., Хп независимы
и подчинены показательным законам распределения с
параметрами Х15 Х2,..., Хп соответственно, то случайная величина Z =
= 111111(^, Х2,..., Хп } также подчинена показательному закону,
п
причем параметр этого закона X = У^Х^.
г=1
Решение. На основании решения задачи 8.34 функция
распределения случайной величины Z:
G(z) = l-Y[e iZ =1
п -2X»Z
г=1
а это есть функция распределения показательного закона с парамет-
п
Р0М\ = VX;.
1=1
241
8.50. Независимые случайные величины Хг,Х2, ...
распределены одинаково по показательному закону с параметром X:
—\х
/(х) = Хе"Л1 (х > 0).
Рассматривается сумма случайного числа таких величин:
г=1
где случайная величина Y распределена по сдвинутому на единицу
закону Паскаля (см. задачу 5.15):
Рп =V(Y = n) = Vqn-1 (0<р<1; п = 1,2, ...).
Найти закон распределения и числовые характеристики
случайной величины Z.
Решение. Сумма фиксированного числа п случайных вели-
п
чин У^Х{ подчинена закону Эрланга (п— 1)-го порядка (см. за-
t=i
дачу 8.31) с плотностью
f^(x)=X{Xx)n~1 е^х (*>0).
V ; (n-1)! V
Плотность распределения случайной величины Z находим по
формуле полной вероятности с гипотезами Нп (Y = п):
п=1 п=1 V72, ■*•/•
= p\e~Xzf2^^- = pXe"XzeX9Z = pXe"X|tt (z > 0),
n=l *'
т. е. случайная величина Z будет также подчинена показательному
закону, но с параметром \р. Следовательно,
1
™*=—> D2 =
2 2
\Р * \2Р
8.51*. Рассматривается сумма случайного числа случайных
слагаемых
*=i
где Xv Х2,... — последовательность независимых одинаково
распределенных случайных величин с плотностью f(x), Y— положитель-
242
ная, не зависящая от них целочисленная случайная величина с
законом распределения P(Y = п) = Рп (п = 1, 2, ..., N).
Требуется найти закон распределения и числовые
характеристики случайной величины Z.
Решение. Допустим, что случайная величина Y приняла
значение п (п = 1, 2, ..., N). Вероятность этого равна Рп. При этой
гипотезе
п
z = zn=^x{.
t=l
Обозначим плотность распределения суммы п независимых
одинаково распределенных величин Xv Х2, ..., Хп через /^п)(х).
Эти плотности можно найти последовательно: сначала f^(x) —
композицию двух одинаковых знаков f(x) и /(ж), затем f^{x) —
композицию /(2)(х) и f(x) и т.д.
По формуле полной вероятности плотность распределения
случайной величины Сбудет
<p(*) = £/(n)(*)iV
Для нахождения числовых характеристик воспользуемся тем
же приемом. Допустим, что Y= п. В этом случае условное
математическое ожидание будет
M[Zn} = м
п
£*
i=i
птх,
где
оо
тх = М.[Х{ ]= I xf (х) dx.
—оо
Тогда полное математическое ожидание найдем из выражения
N
mz = M[Z] = ]pnmxPn =™>хту1
n=l
где
N
mv
Е-?*
71=1
243
Таким же образом найдем и условный второй начальный
момент при условии, что У= п:
M[Zl} = м
п
Ех
W=l
= м
п
52Х>+2^Х{Х
г=1
п
= Е^+2Е
2
2„ 2
ШхШх ~Па2х + П(П ~~ 1) mx ~ ПЦр + П тх 5
г=1
«<j
где
оо
D,=D[^]= J(x-mx)2f(x)dx.
-оо
Второй начальный момент случайной величины Z
N N
а
1z
м[я2] = 5>[я2]Р„ =2(^,+п2»»|)Л -
га =1 П =1
= Dxmy +т*а2у
N
ГДеа2у = Х> Pn =^у +
га
у '
п=1
Дисперсия случайной величины Z
ха2у
D. = ои. — га? = Д.ти + т^а9„ — mlml = Drm„ + m*Du .
2z
x'" у
x ••" у
х"" у
я У
8.52. Независимые случайные величины Х15Х2, ...,ХП, ...
распределены одинаково по показательному закону с параметром
X. Случайная величина Y = Ух + 1, где случайная величина yt
распределена по закону Пуассона с параметром а. Найти закон
распределения и числовые характеристики случайной величины
г=1
п
Решение. Закон распределения суммы У^^г представляет
г=1
собой закон Эрланга (п— 1)-го порядка (см. задачу 8.31) с
параметром X:
(п)Л^- Ч^ХУ г
f{n)(x)
■\х
(п-1)!
(я>0).
По формуле полной вероятности плотность распределения
случайной величины Z будет
244
00
00
Ф) = Т,гп)мрп=Е
\(\z)
П-l лП-1
•a
n=l
= \e
■\z—a
^ (n-l)! (n-1)!
v^ (Xza)*
V- — приг>0.
4* (k\)2
e =
к
Эту плотность можно выразить через модифицированную ци-
\ 2л
X
линдрическую функцию /0(х) = У^
ср(г) = \e~Xz~aIQ(2yf\za) при z > 0.
Далее на основании решения предыдущей задачи
а + 1
M[Z] = тхт
у
X
D[Z] = Dxmy +m2xDy =
а + 1
+
а
х;
2a + l
X2
8.53. Рассматривается система случайных величин Х{ {% = 1,
2, ..., п), которая связана с дискретной случайной величиной Y
следующим образом:
1, если i <Y,
О, если i > Y.
X, =-
Известна функция распределения F(y) случайной величины Y.
Требуется найти закон распределения каждой случайной
величины Х{ и числовые характеристики системы случайных величин
Решение. Ряд распределения случайной величины Х{ имеет
вид
О
Р(У < г)
Р(У >t)
Так как Р(У < г) = F(i), то ряд распределения имеет вид
О
Яг)
F(i)
откудатЯ| = 1 - F(»),ЛЯ| = ВД[1 - F(t)].
245
Найдем корреляционные моменты случайных величин Х{ и Xjy
для чего определим М[Х {Х j]. Произведение ХгХ при г< j может
принимать только два значения: 1, если X = 1, и 0, если X j = 0.
Следовательно,М[Хг XЛ = тх_ = 1 — F^') (г < j), откуда
K{j = М[Х{Х^ - mxmXj = 1 - F(j) - [1 - F(i)][l - F(j)} =
= F(i)[l - F(j)} (i<j),
а коэффициент корреляции
К,
г-
У
F(i)[l-F(j)}
°i°i
F(i)[l-F(j)\
jF(i)F(j)[l-F(i))(l-F(j)] iFU)[1 - F(i)]
(1 < i < j < n).
8.54. Найти характеристическую функцию случайной
величины, равномерно распределенной в интервале (о, Ь).
Решение. g(t)= Г e'txdx —
J b-a
1 Л itb Л ita
1 е — е
Ь — а
it
. Если а — —Ъ
а
(Ь>0),то
1 е — е
26 й
lea-e_ffl sintf»
ib
2г
it
8.55. Найти характеристическую функцию случайной
величины X, распределенной по показательному закону:
—Ха:
/(a;) = Xe"AI, х > 0.
ОО
Решение.р(£)= f Хе'^ eitx dx
X
о
X2 + Хй
X - it X2 + t
8.56. Найти характеристическую функцию для случайной
величины Ху распределенной по закону Лапласа:
х— т\
/(*)=!*-
Решение. Заменой х — т = у получим
ОО
g(t)=feit^e-a
х—т\
dx
-00
О^ л itm
— е
2
— е
о
ОО
feityeavdy + Jeitve-a4y
\ — 00
1
О
+
0£ i£m
е
2 ia+й a — it) a2 +t2
246
a2
При га = 0 получим g(t) =
^2,.2
a -\-ъ
8.57. Найти характеристическую функцию случайной
величины X, распределенной по биномиальному закону с параметрами р
и п:
P(X = m) = C:Pmqn
■т
5
гдед = 1 — р\ 0 < р < 1; т = 0,1, ..., п.
Решение. Представим величину X как сумму п независимых
случайных величин:
x = J2x
п
где Х{ — случайная величина с рядом распределения
О
Р
Характеристическая функция величины Хк равна
gk(t) = M[e*x*] = qe°+pe* = q + ре*.
Так как характеристическая функция суммы независимых
случайных величин равна произведению их характеристических
функций, то
$(*) = ГЫ*) = (« + Рей)в.
к=1
8.58. Найти характеристическую функцию случайной
величины, распределенной по закону Пуассона с параметром а:
т
Р(Х = т) = —е-а (а>0; га = 0,1, 2,...).
га!
оо m оо Л,рй \т
Решение. <?(*)= У" — e^e*" =e-flY"1 ; =
^га' ^n ml
т=0 ''6 ' т=0 ''6 '
= е е = е v .
8.59. Характеристическая функция случайной величины X
равна gx(t). Случайная величина У получается из X прибавлением
постоянной величины a: Y = X + а. Найти характеристическую
функцию ду (t)случайной величины Y.
247
Решение. Рассматривая неслучайную величину а как
частный случай случайной, находим ее характеристическую функцию
да (t) — exia .Так как случайная величина Хне может зависеть (в
вероятностном смысле) от неслучайной а, получаем
»*(*) = 5.(0 5.(0 = 5.(0^
ita
8.60. Найти характеристическую функцию ду (t) случайной
величины У, распределенной по закону Паскаля:
P(Y = k) = pqk (к = 0,1, 2,...),
а также характеристическую функцию случайной величины X,
распределенной по «сдвинутому на единицу» закону Паскаля:
X = Y + 1\ Р(Х = к) = рдк-г (к = 1,2,...)-
Решение.
00 00
к=о к=о L — qe
Применяя правило, выведенное в предыдущей задаче, получим
it
9Л*) =
ре
1 ЛЛ и
1 — qe
8.61. Производится ряд независимых опытов, в каждом из
которых событие А появляется с вероятностью р. Опыты
прекращаются, как только событие А появилось п раз (п >1). Найти закон
распределения, числовые характеристики и характеристическую
функцию числа X «неудачных» опытов, в которых событие А не
произошло.
Решение. Найдем вероятность того, что случайная величина
X примет значение к. Для этого нужно, чтобы общее число
произведенных опытов было равно п + к (к опытов кончились
«неудачно», an— «удачно»). Последний опыт по условию должен быть
«удачным», а в предыдущих п — к + 1 опытах должны
произвольным образом распределиться п - 1 «удачных» и к «неудачных»
опытов. Вероятность этого равна
P(X = k) = Ckn+k_lPnqk (к = 0,1,...)-
Полученный закон распределения является естественным
обобщением закона Паскаля. Мы будем его называть «обобщен-
248
ным законом Паскаля п-го порядка». Случайную величину X
можно представить в виде суммы п независимых случайных величин:
п
X
£*..
5=1
где каждая случайная величина Xs распределена по закону Паскаля:
P(Xs=k) = pqk (fc = 0,1,...)-
Действительно, общее число «неудачных» опытов
складывается из: 1) числа «неудачных» опытов до первого появления
события А; 2) числа «неудачных» опытов от первого до второго
появления события А и т. д.
Отсюда получаем числовые характеристики величины X
т
Щ .
V
i D,
nq
7
и характеристическую функцию
я Л)
V
\П
it
l-ge"J
8.62. Условия задачи те же, что и в задаче 8.61, но случайная
величина У представляет собой общее число опытов,
произведенных до n-кратного появления события А. Найти закон
распределения, числовые характеристики и характеристическую функцию
случайной величины Y.
Решение. Y = X + п, где X — случайная величина,
фигурирующая в предыдущей задаче. Отсюда
p(Y = k) = P(X = k-n)
k—n „ п _&—п
ck-i Р я
п—1 „п _к—
C£-iPng п (к = n, n + i,...)
Числовые характеристики величины Y
т
у
nq п ъ
тх + п — + п — —> d
v
v
y=D*
nq
V
Характеристическая функция
9v(t) = 9x(t)e
itn
ре
it
1 ЛЛ "и
[l-qe j
n
249
8.63. Найти характеристическую функцию случайной
величины Ху распределенной по обобщенному закону Эрланга (п — 1)-го
порядка (см. задачу 8.31):
п
п
■\;Х
Л-1 (*) = (-1)-1Пх^ Ет-2
i=1 МШХ;-Х*)
при х > 0.
k*j
Решение. Обобщенный закон Эрланга (n-l)-ro порядка
получается как результат сложения п независимых случайных
величин, распределенных по показательным законам с различными
параметрами Х15 Х2, ...,ХП.
Следовательно, характеристическая функция будет равна
произведению п характеристических функций показательных
законов (см. задачу 8.55):
п
*„-!(*) = П
X,
л х* + \и
jt'=i *к ~ М k=i Xt +1
Если все п случайных величин распределены одинаково, то
получаем закон Эрланга (п — 1)-го порядка:
/»-i(*)
\{\х)
п-1
—Ха:
(п-1)!
(«>0),
с характеристической функцией
ff»-i(*) =
Г X
га
А — it ,
X2 + \it
[\2+t2
га
8.64. Имеется случайная величина Y, распределенная по
показательному закону с параметром X:
f(y) = \e-Xv (у>0).
Случайная величина X при заданном значении случайной
величины Y— у распределена по закону Пуассона с параметром у:
к\
(fc = 0,1, 2, ...).
Найти безусловный закон распределения случайной величи
ны X
250
Решение. Полная вероятность события X = к будет
P(X = k) = JZ-e-y\e-yydy = —Jyke-(1+x)ydy--
= Лш1 + \)-(*+1) = ?Ц— (А = 0,1, 2, ...)
A! (1 + X)t+1 ^ '
Если ввести обозначения
X 1
Р; : г = 9 = 1 - Р,
1 + Х 1+Х
получим
P(X = fc) = M* (fc = 0,1,2,...),
т.е. случайная величина Xподчинена закону Паскаля с параметром
X
р = .
1 + Х
8.65. На космическом корабле установлен счетчик Гейгера для
определения числа космических частиц, попадающих в него за
некоторый случайный интервал времени Г. Поток космических
частиц — пуассоновский с плотностью X; каждая частица
регистрируется счетчиком с вероятностью р. Счетчик включается на время Г,
распределенное по показательному закону с параметром \л.
Случайная величина X — число зарегистрированных частиц. Найти
закон распределения и характеристики тх, Dx случайной
величины X.
Решение. Предположим, что Т = t, и найдем условную
вероятность того, что X— га (га = 0,1, 2,...):
771
га!
Тогда полная вероятность события X = га будет
00 /\ „i\Wl
^ га!
о
00 /\„\т
(\р)т Пте-(Хр+,1)(<Й=^
Xp + jj,
Xff
(га =0,1,2,...).
251
А это и есть распределение Паскаля с параметром —-— (см.
Хр + р,
предыдущую задачу), поэтому (см. задачу 5.15)
га
\Р
м-
хр.
\р + \l \р + \l \1
д
\р
Хр + р,
М-
Лр + м<,
\р (Хр + м-)
м-
— + ^ = mx(mx+l).
I М- J М-
8.66. Решить задачу 8.65 при условии, что счетчик включается
на случайное время Тс плотностью распределения f(t) (t > 0).
Решение. Так же, как и в предыдущей задаче, условный
закон распределения величины Хпри T—t:
P(X = m\t)
(\pt)
т
~\pt
га!
(га =0,1,2,...).
Безусловный закон распределения будет
00
Р(Х = т) = J
(\pt)
т
~\pt
О
ТП I
/(О*
(га =0,1,2,...).
Находим числовые характеристики случайной величины X.
Условное математическое ожидание m.t = Хр£; безусловное
математическое ожидание
00
оо
га
J \ptf(t)dt = \р Jtf(t) dt = \pmt,
о
о
где mf = М[Г]. Аналогично находим второй начальный момент
случайной величины X (заметим, что так можно находить только
начальные безусловные моменты, а не центральные):
a 2[X\t}= \pt + (\pt)2 ]
оо
оо
a2[X]=\pflf(t)dt + (\p)2ft2f(t)dt = \pmt + (Хр)2а2[Г]
о
о
\pmt +(Хр)а(Д +m(2),
где Д — дисперсия случайной величины Т. Отсюда имеем
Dx=a2[X]-mZ = \pmt + (\p)2Dt.
252
8.67. Решить предыдущую задачу для конкретного случая,
когда f(t) есть закон Эрланга fc-ro порядка с параметром \i:
/(*)=и (t)
—\lt
(t >0).
Решение.
00
P(X = m) = f
Mle-V tMle-^A
0
m!
fc!
m jt oo
m! fc!
Ctm+ke-{\p+v)tdt
0
^x(Xp)m p,* (m + fc)!
m! fc! (Xp + M-)
m+fc+l
С
771
771 +k
M-
Лр + м->
ifc+i
' Xp
Итак, величина X распределена по «обобщенному закону
Паскаля (fc + 1)-го порядка» (см. задачу 8.61) с параметром рх —
М-
Хр + р,
Лр + ц-
i-Pi
Математическое ожидание случайной величины Г,
распределенной по закону Эрланга fc-ro порядка, будет га
Персия Dt —
fc + 1
Ц2
fc + 1
М-
, а дис-
. Следовательно, по формулам, полученным в
предыдущей задаче,
тпх=±1(к + 1); Dx=±P(k + l)
fl + ^1
V- )
что, как и в задаче 8.61, можно представить в виде
_ _ (fc +1) gx п _(* + 1)«г
Рх
, D =
Pi
8.68. Найти характеристическую функцию гамма-распределе-
ния
а _ а — 1
/(я) = е
^ --31 (ж>0;Р>0;а > 1).
Г(а)
Решение. g(t)= f^l—e-^eibxdx
J0 Ца)
Ра
(Р-«Г
253
Примечание. При целом а гамма-распределение превращается в
распределение Эрланга (а - 1)-го порядка, так как
Г(а) = (а-1)!и/(х)=Р(Рх)й" е^ (х > 0),
(а -1)!
и характеристическая функция распределения Эрланга имеет такой
же вид, как и для гамма-распределения (см. задачу 8.63).
8.69*. Случайная величина Z представляет собой сумму
случайного числа случайных слагаемых
k=i
где Хк — одинаково распределенные случайные величины с
плотностью f(x) и характеристической функциейgx(t),a. случайная
величина У распределена по сдвинутому на единицу закону Паскаля:
Р(У = т) = рдЯ1"1 (т=1,2,...).
Случайные величины Хк (к = 1, 2,...) и У независимы между
собой. Требуется найти характеристическую функцию случайной
величины Zn ее числовые характеристики.
Решение. Допустим, что случайная величина Y приняла
значение га. При этой гипотезе
т
z = zm=Y;xk-
k=i
Характеристическая функция случайной величины Zm будет
равна
следовательно, характеристическая функция случайной величины
Z будет
оо оо
т=1 У т=1
ТаккакО < g < 1 и 0 < |<7Х(£)1 ^ 1>то
(*) = £ "*№ - P9*W
Q ! -<19Л) 1~Q9x(t)
254
Отсюда
M[Z) = *U =
dgy(t)
d{it)
(=0
пд9 ,(t)
a (u)
prry
P
2: V '
1 у
t=0
так как га = —. Далее имеем
Р
а
d29At)
2z
d{it)
>=0 = Р
^хО- -9) + 2^mx а2хР + 2^m
2
x
P*
P
откуда
D
ol2z -mz
a2xp + 2qmx m
2
X
— Dm + m2D ,
XV ' XV'
p
p
x у
где£>
У 2
p
Получили тот же результат, что и в задаче 8.51, но другим
методом.
8.70. Найти
характеристическую функцию случайной
величины X, подчиненной закону Симп-
сона (закону равнобедренного
треугольника) в интервале (а, Ь)
(рис. 8.70).
Решение.
Рис. 8.70
/(*) =
0
4 (х — а)
4 (Ь - х)
(Ъ-а)2
0
при х < а,
при а < х <
а + Ь
а +b ,
при < х < о,
при х > Ь.
255
a+b
oo
g(t)= feitxf(x)dx = J e
itx
b
a+b
—oo
to 4 (b - x) , 4
a
4 (x — a)
[b-af
dx +
., a+6
rt
г£ h 1
(6-a)
dx =
ita
(b-a)
t
+
..a+6 / Lv
lt-z-L ., a -b\
+ ■
1-й
2 J
— e
i*6
(b-a)
t
Итак,
9(t) =
t2(b-a)
ita
itb
it
a+b
-elw -euo +2e 2
t (b-a)
it— it —
e 2 — e 2
При a = —b (b>0) имеем
f2 . *M
— sin—
[tb 2)
Сравнивая полученные результаты с решением задачи 8.54,
заключаем, что распределение Симпсона можно рассматривать как
(а Ь'
композицию двух равномерных распределении на интервале —, - .
\2 2,
8.71. При измерении физических величин результат
измерения неизбежно округляется в соответствии с минимальной ценой
деления прибора. При этом непрерывная случайная величина
превращается в дискретную, возможные значения которой отделены
друг от друга интервалами, равными цене деления. В связи с этим
возникает следующая задача. Непрерывная случайная величина
X, распределенная по закону с плотностью /(х), округляется до
ближайшего целого числа; получается дискретная случайная
величина У = Ц(Х), где под Ц(Х) подразумевается целое число,
ближайшее к X.
Найти ряд распределения случайной величины Y и ее
числовые характеристики: ту, Dy.
Решение. График функции Ц(х) представлен на рис. 8.71
Правило округления в случае, когда расстояния от значения х до
256
двух соседних целых значении
равны, несущественно, так как для
непрерывной случайной величины
вероятность попадания в любую точку
равна нулю.
Вероятность того, что случайная
величина Y примет целое значение
к, равна
*+0,5
Р(7 = к)= J f(x) dx
Jfc-0,5
Щх)
-2,5 -1,5 -0,5
—т г г
0,5 1,5
-2
Рис. 8.71
(fc = 0,±l,±2,...),
2,5
х
откуда
£ + 0,5
fc + 0,5
т
У
£ к J f{x)dx- Dy=Y,k J f(x>>dx
=—oo l n к k—— oo ;-_n *
m
2 1)
У '
k=-oo k_05
00 Л;—0,5
8.72. Случайные величины Хи Y независимы и распределены
по законам Пуассона с параметрами а и Ъ. Найти закон
распределения их разности Z = X— Yn модуля их разности U = \Х — Y[
Решение. Случайная величина Z может принимать как
положительные, так и отрицательные значения. Вероятность того,
что Z примет значение к > 0, равна сумме вероятностей того, что X
и Y примут два значения, различающиеся на к (причем X —
больше или равно Y):
т +к
P(Z = к) =
оо ьт
Е
а
,-(«+&)
т
=0т ! (га + к)\
(*>0).
Вероятность того, что Z примет отрицательное значение -ку
будет
оо т im +к
P(Z = -k)=Y- е~(а+Ь) (к>0).
^0т\ (т + к)\
Для случайной величины U получим
00
P(tf = 0)=£
(ab)
т
,-(«+&).
т
=о("г!)
ОО
P(U = k)=J2
(ab)
т
т
Г^га ! (га + к)\
е"<в+6)(а* +Ьк) (к>0).
1)
Если единица измерения (цена деления прибора) мала по сравнению с
диапазоном возможных значений случайной величины X, то т и rnx]Dy « Dx.
257
Эти вероятности могут быть записаны с помощью
модифицированных цилиндрических функций 1-го рода:
Х (£ = 0,1,2,...)-°
00
Ik(x) = I_k(x)=Yl
т
-^0т ! (к + га)!
2)
При этом
P(Z = *) = /,
(2VSb) (-
UJ
2 „-(«+&)
(fc = o,±i,±2,...);
P([/ = 0) = /0(2V^)e-(fl+6);
P(U = k) = Ik(2jab)
V
+
'a^
b
1N
2
\u J
,"(«+6)
(fc>0)
8.73. Грибник вышел собирать грибы в лесу. Радиус обзора его
равен R. Перемещаясь по лесу, он обнаруживает каждый гриб,
находящийся в пределах круга обзора, с вероятностью p(v), которая
зависит от скорости v передвижения грибника по лесу. Считается,
что грибы в лесу образуют пуассоновское поле точек с плотностью
X (X — среднее число грибов на единицу площади).
Определить оптимальную скорость движения грибника по
лесу, при которой он за время t обнаружит в среднем наибольшее
количество грибов, если вероятность p(v) задана формулой
р{у)
—оси
(a >0, v >0),
и грибник не возвращается на уже пройденные им места.
Решение. За время t грибник просмотрит полосу, площадь
которой S= 2vtR, и обнаружит в среднем количество грибов,
равное га = S X р{у) = 2vt R\e~av.
Для нахождения оптимальной скорости движения
продифференцируем величину га по v и приравняем производную нулю:
dm --2tR\e-™ (l-tx3t) = 0,
dv
откуда оптимальное значение скорости будет v*
1
a
8.74. В условиях задачи 8.73 грибник идет со скоростью v и
собирает все обнаруженные им грибы. Массы отдельных грибов
представляют собой независимые случайные величины Yi9
распределенные по одному и тому же закону с математическим ожи-
1)
Таблицы цилиндрических функций можно найти в справочниках.
258
данием ту и дисперсией Dy. Найти математическое ожидание
общей массы Z всех собранных грибов за время t и (приближенно,
считая число грибов большим) вероятность того, что эта величина
превзойдет заданную вместимость корзинки z0.
Решение. Число собранных грибов X будет случайной
величиной, распределенной по закону Пуассона с параметром
тх = 2vtR \е~™. Общая масса всех собранных грибов будет
В соответствии с решением, изложенным в задаче 8.51 или
8.69, имеем га = гахга . Далее
D2 =mxDy +m2yDx = mx(Dy + m2y) = mx -a2y,
так как для распределения Пуассона Dx = тх. Считая приближенно
случайную величину Z распределенной нормально, получим
/
Р(£>г0) = 1-^(г0)«1-Ф
z0 -т2
*z
гдеа2 =V^7-
8.75. Известна плотность распределения /(х, у) системы
случайных величин (X, Y). Найти закон распределения их разности:
Z=X- Y.
Решение. Для системы (X, —Y) плотность распределения
есть/(х, — у)> поэтому из X — Y — X + (—К) находим
00
g(z) = G\z) = J /(х, x - z) dx.
— 00
Если случайные величины (X, Y) независимы, то
оо оо
9{?)= J' fi(x) f3(x - z) dx = Jf1(y-z)f2(y)dy.
—OO —OO
8.76. Найти плотность распределения разности двух
независимых показательно распределенных случайных величин с
параметрами \H[i;Z = X - YJx(x) = \e~XxJ2(y) = p,e"w (я > 0, у > 0).
оо
Решение. g(z)= I fx(x) f2(x — z) dx; /г(х) отлично от нуля
—оо
при х > 0; /2 (х — z) отлично от нуля при х — z > 0.
259
t*J
a) z > 0; g(z) - J Xe"x V^(x~2)^
Xp,e
-Xz
X + jj, '
00
6)г<0; g(z) = j\e~Xx[ie-ii{x-z)dx =
\\ie
\IZ
0
X + JJ,
Следовательно,
9(z)
\\ie
-\z
X + jj,
X -h |л
При 2? > 0,
при 2 < 0.
Параметры этого закона:
m
1 1_ц-Х.
X jj, Xjj,
; А
1 1
+
х2 ' ^2
\2+ii:
(Х^х)2
\[i \9{z)
Рис. 8.76
Кривая распределения будет иметь вид, изображенный на
рис. 8.76, а.
При Х = р, получаем g(z) = — е~х'2' (рис. 8.76, 5). Такой закон
АЛ
распределения называется законом Лапласа.
ГЛАВА 9
СЛУЧАЙНЫЕ ФУНКЦИИ
Случайной функцией X(t) называется функция, которая в результате
опыта может принять тот или иной конкретный вид, неизвестно заранее,
какой именно.
Конкретный вид, принимаемый случайной функцией в результате
опыта, называется реализацией случайной функции.
При фиксированном t случайная функция X(t) обращается в
случайную величину X(t), называемую сечением случайной функции.
Одномерным законом распределения случайной функции X(t)
называется закон распределения f(x, t) сечения X(t) случайной функции.
Двумерным законом распределения случайной функции X(t)
называется закон распределения системы двух ее сечений: X(tt), Х(^),
представляющий собой функцию четырех аргументов: f(xv а^, tv ^).
Случайная функция X(t) называется нормальной, если закон
распределения системы любого числа п ее сечений представляет собой п-мер-
ный нормальный закон.
Математическим ожиданием случайной функции X(t) называется
неслучайная функция mx(t), которая при каждом t представляет собой
математическое ожидание соответствующего сечения случайной функции:
mt{t) = М [X (*)].
Корреляционной функцией случайной функции X(t) называется
неслучайная функция двух аргументов Kx(t, t'), которая при каждой паре
значений аргументов t, t' равна корреляционному моменту соответствующих
сечений случайной функции:
Kx(t,t') = M[X(t)X(t%
о
гдеХ(г) = X(t) — mx(t) — центрированная случайная функция.
При t' = t корреляционная функция превращается в дисперсию
случайной функции:
Kx(t,t) = Dx(t) = D{X(t)] = [ox(t)f.
Основные свойства корреляционной функции:
1) Kx(t, t') = Kx(tf, t), т.е. функция Kx(t, t') не меняется при замене t на
t (симметричность).
261
2)\Kx(t,t')\<ax(t)ax(t').
3) Функция Kx(t, t') — положительно определенная, т.е.
J jKx(t,tf)^(t)^(tf)dtdtf>0,
(В) (В)
где tp (t) — любая функция; (В) — любая область интегрирования,
одинаковая для обоих аргументов.
Для нормальной случайной функции характеристики mx(t), Kx(t, t')
являются исчерпывающими и определяют собой закон распределения
любого числа сечений.
Нормированной корреляционной функцией случайной функции X(t)
называется функция
r a t>) = *«(*» V = К*У> **>
Л' ' ox(t)ox(t') jDx(t) Dx(t')'
т.е. коэффициент корреляции сечений X(t) и X (tf); при t = t' функция
rx(t, t') равна единице: rx(t, t) = 1.
При прибавлении к случайной функции X(t) неслучайного слагаемого
tp (t) к ее математическому ожиданию прибавляется то же неслучайное
слагаемое, а корреляционная функция не меняется.
При умножении случайной функции X(t) на неслучайный множитель
tp (t) ее математическое ожидание умножается на тот же множитель tp (t),
а корреляционная функция — на tp (t) tp (tf).
Если случайную функцию X(t) подвергают некоторому
преобразованию A t, то получается другая случайная функция
Y(t) = MX (<)}•
Преобразование l\ ^ называется линейным однородным, если
1)4
(0)
£ВД
к=\
= £40) №.(*)}
(т.е. преобразование к сумме может применяться почленно);
2) 40){сХ (t)} = с1\°\Х (*)}
(т. е. множитель с, не зависящий от аргумента t, по которому
производится преобразование, можно выносить за знак преобразования).
Преобразование Lt называется линейным неоднородным, если
mX(t)} = ^{X(t)} + 4>(t),
где tp (t) — любая функция, никак не связанная с X(t).
Если случайная функция Y(t) связана со случайной функцией X(t)
линейным преобразованием
Y(t) = Ц{Х (*)},
то ее математическое ожидание ту (t) получается из mx(t) тем же
линейным преобразованием
262
а для нахождения корреляционной функции Ку (t, t') нужно дважды
подвергнуть функцию Kx(t, t') соответствующему линейному однородному
преобразованию, один раз по t, другой раз по t':
Ky(t,t') = ^{^{Kz(t,t')}}.
Взаимной корреляционной функцией R^ (t, t') двух случайных функций
X(t) и Y(t) называется функция
R^ (t, t') = М [X (t) Y (?)}.
Из определения взаимной корреляционной функции вытекает, что
R*y (t, f) = Ryx(t', t).
Нормированной взаимной корреляционной функцией двух случайных
функций X(t), Y(t) называется функция
Ъ С О =
К (МО R4{t,t')
ox{t)°y(t') px(t) Dy(?) '
Случайные функции X(t) и Y(t) называются некоррелированными,
если R^ (t, t') = 0.
EcjinZ{t) = X{t) + Y(t),To
Кz{t, О = Kx(t, t') + Ky (t, О + R^ (t, 0 + i^ (f, t).
Для некоррелированных случайных функций X(t) и У(£)
^(^0 = ^0 + ^(^0-
Если
п
где Xl (t),..., Хп(t) — некоррелированные случайные функции, то
(*) = X>It(<)' Kz{t,t') = Y,KXk{t,t').
z
При выполнении различных преобразований со случайными
функциями часто бывает удобно записывать их в комплексном виде.
Комплексной случайной функцией называется случайная функция вида
Z(t) = X(t) + iY(t),
г
где X(t), Y(t) — действительные случайные функции.
263
Математическое ожидание, корреляционная функция и дисперсия
комплексной случайной функции определяются следующим образом:
™2{t) = mx(t) + гту (i); Kz(t, t') = М [X(t) X(t%
где чертой вверху обозначена комплексная сопряженная величина;
Dz(t) = Kz(t,t) = M[\X(t)\2}.
При переходе к комплексным случайным величинам и функциям
необходимо определять дисперсию как математическое ожидание
квадрата модуля, а корреляционный момент — как математическое ожидание
произведения центрированной одной случайной величины на комплексную
сопряженную центрированной другой.
Каноническим разложением случайной функции X(t) называется ее
представление в виде
т
X(t) = mx(t)+^2Vk4>k(t), (9.0.1)
Jt=l
где Vk (k = 1,..., m) — центрированные, некоррелированные случайные
величины с дисперсиями Dk (к = 1,..., m); 4>k(t) (к = 1,..., т) —
неслучайные функции \
Случайные величины Vk (к = 1,..., т) называются коэффициентами,
а функции 1рЛ(£)(А; = 1,...,т) — координатными функциями
канонического разложения.
Если случайная функция X(t) допускает каноническое разложение
(9.0.1) в действительной форме, то корреляционная функция Kx(t, t')
выражается суммой вида
т
ЗД О = 2^(3^. (9.0.2)
Jk=l
которая называется каноническим разложением корреляционной функции.
Если случайная функция X(t) допускает каноническое разложение
(9.0.1) в комплексной форме, то каноническое разложение
корреляционной функции имеет вид
т
^,(«.О = ЕАч»*(*)ч»*(*0. (9-0.3)
где чертой вверху обозначена комплексная сопряженная величина.
Из возможности канонического разложения вида (9.0.2) или (9.0.3)
корреляционной функции вытекает представимость случайной функции
X(t) в виде канонического разложения (9.0.1), где случайные величины
Vk (£ = 1,..., т) имеют дисперсии Dk (k = 1,..., т).
В частности, может быть т = оо.
264
При линейном преобразовании случайной функции X(t), заданной
каноническим разложением (9.0.1), получается случайная функция
Y(t) = Ц {X(t)} в виде канонического разложения
m
Y(t) = my(t)+^V^k(t),
k=l
где
",№ = №,(*)}; Ф*(*) = 40){ч>*(*)},
т.е. при линейном преобразовании случайной функции, заданной
каноническим разложением, ее математическое ожидание подвергается тому
же линейному преобразованию, а координатные функции —
соответствующему линейному однородному преобразованию.
Стационарной случайной функцией X(t)1^ называется случайная
функция, математическое ожидание которой постоянно, mx(t) = тх = const, а
корреляционная функция зависит только от разности между своими
аргументами Kx(t, t') = кх(т), где т = t' — L
Из симметричности корреляционной функции Kx(t, t') следует, что
кх[т) = кх(—т), т.е. корреляционная функция стационарной случайной
функции есть четная функция аргумента т.
Дисперсия стационарной случайной функции постоянна:
Аг = #*(', *) = *,(0) = const.
Корреляционная функция стационарной случайной функции
обладает свойством:
1*,(т)|<Л,.
Нормированная корреляционная функция р1(т) стационарной
случайной функции X(t) равна
/ л *«(т) *,(т)
р*(т) = "Ш'
Каноническое разложение стационарной случайной функции имеет
вид
оо
*(*) = ™* + Е Фкcos <*>** + Vk sin w4t), (9.0.4)
Jk=0
где Uk, Vk (k = 0, 1,...) — центрированные, некоррелированные
случайные величины с попарно равными дисперсиями
Щик] = D[Vk] = Dk.
Разложение (9.0.4) называется спектральным. Спектральному
разложению стационарной случайной функции соответствует разложение в
ряд ее корреляционной функции
Точнее, стационарной в широком смысле.
265
00
kx(T) = ^2^008 UfcT,
k=0
откуда
00
Спектральное разложение (9.0.4) стационарной случайной функции
при ш0 = 0 можно переписать в комплексной форме:
оо
/:=—оо
где
u>_t = -u>t> W0=U0, Wk = UkZiV",
2
W_k = "k ' "* (к = 1,2,...)-
Uk + iVk
Спектральной плотностью стационарной случайной функции X(t)
называется предел отношения дисперсии, приходящейся на данный
интервал частот, к длине этого интервала, когда последняя стремится к нулю.
Спектральная плотность Sx(u) и корреляционная функция кх(т) связаны
преобразованиями Фурье. В действительной форме они имеют вид
су °° °°
^х(Ш) = "~ I ^х(Т) C0S ^Т^Т, К(Т) = / &х(и) C0S ^T^UT,
о о
из последнего соотношения вытекает, что
оо
Dx = kx(0) = fSx(u)du.
В комплексной форме преобразования Фурье, связывающие
спектральную плотность S*x(ш) и корреляционную функцию, имеют вид
оо оо
S;(u) = -L j*,(T)e-*'UTc*r, *,(т)= /^Не'-^ы,
—00 —00
где£(и)=Л5».
Как Sx(u), так и 5^(ш), — действительные, неотрицательные четные
функции, но Sx(w) рассматривается только в интервале (0, оо).
Нормированной спектральной плотностью sx(uj), s*(u) называется
спектральная плотность, деленная на дисперсию случайной функции
266
*«0*>) = —-—; ««(«) = ——•
Белым шумом называется случайная функция X(t), любые два
различные (сколь угодно близкие) сечения которой некоррелированы и
корреляционная функция которой пропорциональна дельта-функции:
Kz(t, о = G(t) 6 (t - О-
Величина G(t) называется интенсивностью белого шума.
Стационарным белым шумом называется белый шум с постоянной
интенсивностью G(t) = G = const.
Корреляционная функция стационарного белого шума имеет вид
*я(т) = С6(т),
откуда его спектральная плотность постоянна и равна
£М = — •
Дисперсия стационарного белого шума равна Dx = G 6(0), т.е.
бесконечна.
Если на вход стационарной линейной системы L поступает
стационарная случайная функция X(t), то спустя некоторое время, достаточное для
затухания переходного процесса, случайная функция Y(t) на выходе
линейной системы также будет стационарной. Спектральные плотности
входного и выходного сигналов связаны соотношением
S» = S»|#(iw)|,
гдеФ (г и) — амплитудно-частотная характеристика линейной системы.
Говорят, что стационарная функция X(t) обладает эргодическим
свойством, если ее характеристики (mx, kx(r)) могут быть определены как
соответствующие средние по времени для одной реализации достаточно
большой продолжительности. Достаточным условием эргодичности
стационарной случайной функции (по математическому ожиданию)
является стремление к нулю ее корреляционной функции при т —> оо:
lim *,(т) = 0.
Т-+00
Для того чтобы случайная функция X(t) была эргодична по дисперсии
о
Dx, достаточно, чтобы случайная функция Y(t) = {X(t)}2 обладала
аналогичным свойством, т.е. при т —> оо:
lim k (^ = 0^
Т-+00 у
Для того чтобы случайная функция была эргодична по корреляционной функции,
нужно, чтобы аналогичным свойством обладала функция Z (t, т) = X (t) X (t + т).
267
При решении задач, связанных со случайными функциями, часто
бывает удобно выполнять преобразования с помощью различных
скачкообразных функций, а также обобщенных функций типа дельта-функции.
Приведем определения и основные свойства таких функций от
действительного аргумента т.
1.1 т | — модуль (абсолютная величина):
т при т > О,
■
—т при т < 0.
2.1(т) — единичная функция (единичный скачок):
1 при т > 0,
1(т) =
— при т = 0,
2
0 при т < 0.
3. sgn т —
знак величины т (сигнум):
sgn т =
1
0
-1
при
при
при
т>0,
т = 0,
т<0.
4. б (т) — дельта-функция:'
б(т) = ^1(т).
ат
Дельта-функция — четная функция т.
Основные свойства дельта-функции:
а) тб (т) = 0 и вообще tp (т) б (т) = 0, если ip (т) — нечетная функция,
непрерывная при т = 0.
0+е
б) J4(t)6(t) Лт = ^(0), если функция *ф (*) непрерывна в точке
0-е
0+е
т = 0 (е > 0), / г[) (т) б (т) d т = / г[) (т) б (т) d т = - г[) (0), если функция
0-е 0
г[) (т) непрерывна в точке т = 0.
Из этих определений вытекают следующие свойства, имеющие место
для любых действительных т и нечетной функции ip (t):
l.|T|=TSgnr, 2.т=|т| sgn г, 3. ф(т) = ф(|т|) sgn т;
4.ip(|T|) = ip(T)sgnT; 5.ф2(|т|) = ф2(т); 6.sgnr = 2 -1 (т) - 1;
71(т)=ЭДп(т)+1. 8.|Т|=Т[2.1(Т)_1]; 9d\T\
dT
sgn т ;
10^ = ^sgn_T = 26(T);
d-r dr
268
11.1 (т)= J,6(T)dT = ij*d(sgnT);
— 00
— 00
12. Для нечетных положительных A;(sgn т) * = sgn т. Для четных
положительных к
1 при т ^ О,
О при т = 0;
(sgn-r)'
13.|тГ
d\T
dT
,\*
М|т|]
dr
k+s
т5
т5
|т|т'
S-1
при 5 нечетном и А; четном,
при 5 нечетном и А; нечетном,
при s четном и А; четном,
при s четном и А; нечетном;
14. г
(d\r\)
dT
к
| т | ts при к нечетном,
15V(M)
т
при к четном;
ip'(T)
М|т|1
*+*
г^з *
4>'(т)|
<р'(т)
ip'(r)
при 5 нечетном и А; четном,
при 5 нечетном и А; нечетном,
при s четном и А; четном,
ф(1т1)фв (т) пРи s четном и к нечетном;
16V(t)
fell
dT
Ф5(т)
при А; четном,
Ф (1т1)фв (т) ПРИ & нечетном.
9.1. Случайная функция X(t) в каждом сечении представляет
собой непрерывную случайную величину с плотностью
распределения f(x, t). Написать выражения для математического ожидания
тх (t) и дисперсии Dx (t) случайной функции X(t).
Ответ.
оо
тх(*)= fxf(x,t)dx;
—оо
оо
Dx(t)= f[x-mx(t)}2f(x,t)dx.
—ОО
9.2. Случайная функция X(t) представляет собой случайную
величину X(t) = V, где V— непрерывная случайная величина с
плотностью распределения ф(г;). а) Написать выражение одномер-
269
ного закона (плотности) распределения f(xy t) случайной функции
X(t). б) Найти математическое ожидание mx(t)n дисперсию Dx(t)
случайной функции X(t). в) Написать выражение двумерной
функции распределения Р(хг,x2,t1,t2) двух сечений X{tx)^X{t2)
случайной функции X(t).
оо
Ответ, а) /(я, t) = ф(я); 6)771^(^)= I хц> (х) dx = т v,
—оо
оо
Dx(t) = j(х- т v)2Ч> (x)dx = Dv; в) F(x1,x2,t1,t2)
-ОО
= P((X(tl)<x1)(X(ti)<xi)) = P((V<x1)(V<xi)).
Еслия^ < х2,то mV < хх следуете < х2,иР((7<а;1)(7<х2)) =
P(V < хх) = I ф (х) dx. Следовательно,
—оо
Г (Х^ , 3?2> ^1 > ^2 /
I ф (я) dx = Р(хг) при хх < х2,
—оо
/ ф (я) eta; = F(x2) при я2 < хг,
L-oo
где F(x) = I y>(v)dv — функция распределения величины V.
—оо
9.3. Случайная функция X{t) задана в виде X(t) = Vt + Ь, где
V — случайная величина, распределенная по нормальному закону
с параметрами mvfo v,b — неслучайная величина. Найти плотность
распределения f(x, t) сечения случайной функции X(t) и ее
характеристики mx(t), Dx(t), Kx(t,tf).
Ответ. /(х, t) — нормальный закон с параметрами
т vt + Ь\ \t \av:
/(М)
1
[x-(mvt+b))'
t\o„<>/2to
2t2a2v
v
mx(t) = mvt + b- Dx(t) = t2a2v; Kx(t,t') = o2vtt'.
9.4. Показать, что любая функция двух аргументов вида
п
£^Ф,(*)фЖ),
(9.4)
»=i
270
где Д — неотрицательные числа; ф^ (t) — любые действительные
функции (г = 1,..., п), обладает всеми свойствами корреляционной
функции.
Решение. Достаточно показать, что существует случайная
функция X(t), имеющая корреляционную функцию (9.4).
Рассмотрим действительную случайную функцию X(t)t заданную в
виде канонического разложения
п
X(t) = mx(t) + J2Vi4>i{t),
t=l
гдеВ^НД.
Корреляционная функции этой случайной функции имеет вид
п
Kx(t,t') = J2Di4>i(t)4>i(t'),
t=l
что и требовалось доказать.
9.5. Случайная функция X(t) имеет характеристики тх (t) = 1 и
Kx{t^t') = eCLi't+t\ Определить характеристики случайной функ-
dX(t) л ^
ции Y(t) = t — +1. Определить, являются ли стационарными
dt
случайные функции X(t) и Y(t).
Решение. В силу линейности преобразования t Ь 1
dt
my(t) = t~mx(t) + l = l.
at
K(t,t') = U'-^Kx(t,t') = tt'a2e^t+t'K
y dtdt'
Ни одна из случайных функций X(t) и Y(t) не является
стационарной, так как их корреляционные функции зависят не
только от т = t' — t} но от каждого из аргументов t} t'.
9.6. Случайная функция X(t) имеет характеристики:
mx(t) = 0, Kx(t,t>) = -—± -.
1+ (*'-«)
Найти характеристики случайной функции
t
Y(t)= fX(t)dt.
о
Определить, стационарны ли случайные функции X(t) и Y(t).
271
Решение. В силу линейности преобразования I X(t)dt
о
my(t) = fmx(t)dt=0,
о
t t'
t (tf
K,(t,t') = fdtfKx(t,t')dt' = f f-
0 0 0 I 0
о 0
t
dt'
lJo 1 + (*;-0:
dt =
= f [arctg (tf -t)- arctg(-t)] dt =
о
= t arctg t +t' arctg t' -{t-t') arctg (i - t') - - In (1+* )(! + * )
2 1 + (^-^)2
Случайная функция X(t) стационарна [Kx (t, t') = kx (t' — t))
случайная функция У (О = / X(0 dt нестационарна. Действитель-
o
но, дисперсия случайной функции Dy (t) равна
Dv (t) = Кч (t, t) = 2t arctg t - In (1 +12),
т.е. зависит от £
9.7. Найти математическое ожидание и корреляционную
функцию суммы двух некоррелированных случайных функций
X(t) и Y(t) с характеристиками
т, (<) = *; Kx(t,t') = tt'-
m(t) = -t; *(М') = й'еа('+0-
Ответ. 2(0 = ^(0 + ^(0; тх(0 = тх(0 + ту (0 = * - * = 0;
^(*i*,) = ^,(*i*,) + ^(«»«,) = tt/[l + ea(t+t,)].
9.8. Имеется комплексная случайная функция Z(t) = X(t) +
+ г У(0,где X(t), Y(t) — некоррелированные случайные функции
с характеристиками
mx(t) = t2; *,(М') = е-в1('-0,!
га
,(0 = 1; tfy(M') = e2^'+''>.
Найти характеристики случайной функции Z(t): mz(t),
Kz(t,t')nDz(t).
272
Ответ. m2(t)=t2+i; Kx(t, t')=e"ai("')2 +e2a*(t+t'); Dx(t)=
=Kx(t,t) = l + e***.
9.9. Траектория космического летательного аппарата в
вертикальной плоскости изображается двумя уравнениями:
X{t) = At2 +Bt + C, Y(t) = Et2 +Ft + H.
Коэффициенты А, Д С, Et Ft Я являются случайными, так как
определяются из опыта с ошибками; номинальные значения
величин Ау Д ..., Я равны а, Ь, ..., h соответственно; ошибки ДА,
ДБ,..., ДЯ представляют собой случайные величины с
математическими ожиданиями, равными нулю, и дисперсиями DA, DB,
..., DH. Нормированная корреляционная матрица этих ошибок
имеет вид
1 0,4
0,2
0,3
1
0
0
0
1
0
0
0
0,7
1
0
0
0
-0,2
0,5
Определить математическое ожидание, корреляционную
функцию и дисперсию случайных функций V(t) и U(t)t
представляющих собой горизонтальную и вертикальную составляющие
скорости снаряда.
Решение.Из условий задачи следует, что
V(t) = ^l = 2At + B; U(t) = ^l = 2Et + F.
dt
dt
Таким образом, случайные функции V(t) и U(t) представлены
в виде разложений (не канонических, так как их коэффициенты
зависимы). Имеем
mv(t) = 2at + b; mu(t) = 2et + /;
Kv(t,t') = 4DAtt' + DB + 0,4757¾¾ + а');
Ku(t,t') = 4DEtt' + DF +0,7jD^(2t + 2t');
Dv(t) = 4DAt2+DB + lfijDADBt;
Du (t) = 4DEt2 +DF+ 2,8jDE~DF~t.
9.10. Случайная функция X(t) имеет характеристики
273
' ^2
mx(t) = t2-l; Кх(Ь,Ь') = 2е-а«-{У.
Определить характеристики случайных функций
Y(t) = tX(t) + t2 +1; Z(t) = 2t^^- + (l-t)2;
dt
dt2
Решение.
my(t) = tm%(t) + t2 + 1 = t (t2 - 1) + t2 + 1 = t3 + t2 - t + 1;
Ky(t,t') = tt'2e-a{t'-t)2;
mz(t) = 2t ^^1 + (l-t)2=l-2t + 5t2;
dt
zK ' dtdt'
= -a • 16tt'[(t' - t) е~а« "'> 2a (t'-t)- e-tt<''-0' ] =
- 16a«'e-a(t'-t)2 [-2a (t' - t)2 + 1];
mu{4 = —71— + 1 = 3; л.(М ) = —-j——-•
Л2 dt2(dt')2
тт ^ /, ,л 92Kx(t,t')
При вычислении Kz(t,t ) мы уже нашли , следова-
dt dt
тельно,
^,(^) = ^4^ e-^'-^[l-2o.(t'-t)2} =
at at
J *\2
= 8aVa« -*r [3 + 4a2(^ - 04 - 12a («' - t)2].
9.11. Случайная функция X(t) задана выражением
X(t) = V cos u£,
где V — случайная величина с характеристиками т v — 2; a v = 3.
Найти характеристики случайной функции X(t): mx(t); Kx(t,t');
Dx (t). Определить, является ли случайная функция X(t)
стационарной. Найти характеристики случайной функции
274
at
где а — неслучайная величина.
Является ли стационарной случайная функция Y(t)?
Решение.
Tnx(t) = т v cos (jjt = 2cosu£;
Kxttit') = Dv cos и t cos и £' = 9 cos и £ cos u^;
Ц,(0 = 9cos2 ui.
Случайную функцию Y(t) можно представить в виде
лг/ \ т/ dVcOS ld£ _. , ч
j (О = к cos ш£ Н- а = К (cos ш^ -аш sin ш£);
eft
отсюда
my(t) = т v(cosu£ — а и sin ш£) = 2(cosu£ — а и smut);
^у (£, £') = 9(cosu£ — а и sin u£)(cosu£' — а и sinutf');
^y (0 = 9(cosu£ — а и sin ш£)2-
Случайные функции X(t) и У(£) нестационарны.
9.12. Задана случайная функция
X{t) = Vle-a* +^2е"а^
2Ь
где Vi и V2 — некоррелированные случайные величины с
характеристиками т v = т v =0; Dv , Dv . Найти характеристики
случайной функции X(t).
Решение. Случайная функция X(t) представлена
каноническим разложением, следовательно,
тх
(0 = 0; K,(t,t') = DVle-*«+t'> + D е"^^;
-2а ЛЬ , тл --2<*2*
D,(t) = DVie-<a*+Dve
9.13. Случайная функция X(t) задана своим каноническим
разложением
п
X(t) = J2Vie-*'+a,
i=l
где Vi — центрированные случайные величины с дисперсиями
D (г = 1, 2,..., п);М[У; V ] = 0приг ^ j; а— неслучайная величи-
на.
275
Найти характеристики случайной функции X(t).
Ответ. mx(t) = a; ^,(^0=^,,^^:
1=1
9.14. Случайная функция X(t) задана каноническим
разложением
X(t) = t + V{ cos иt + V2 sin и£,
где Vj и V2 — некоррелированные случайные величины с
математическими ожиданиями, равными нулю, и с дисперсиями Dx = D2 = 2.
Определить, является ли стационарной случайная функция X(t).
Решение. mx(t) = t\ Kx(t,t') — 2 (cos ut cos ш<4
+ sin и t sin и £') = 2 cos и (£' — £).
Корреляционная функция случайной функции X(t)
удовлетворяет условию стационарности, однако математическое ожидание
mx(t) зависит от времени. Случайная функция X(t) нестационар-
о
на, но центрированная случайная функция X(t) стационарна.
9.15. Заданы две случайные функции:
X(t) — Vx cos ujjtf + V2 sin uxt, Y(t) = Ux cos u2t + U2 sin u2£.
Математические ожидания всех случайных величин Vu V2, Ut
и U2 равны нулю, дисперсии равны D v = Dv =1;DU = Du = 4;
нормированная корреляционная матрица системы (Vj, V2, uv U2)
имеет вид
1 0 0,5 0
1 0 -0,5
1 0
1
Определить взаимную корреляционную функцию R^it^t') и
найти значение этой функции при t = 0, £' = 1. Определить
Ryx (t,t')n найти значение этой функции при t = 0; t' = 1.
Решение.
яч(*>*') = м[аду'(*/)] =
= М[(КХ cos иxt + V2 sin их£)(Ux cos w2t' + U2 sin и2£')] =
= cos ijjxt cos ш2£' MfV^Z/jH- cos ujxt sin ш2£' M[V1/72] +
+ sin и xt cos и 2t' M[V2U1 ] + sin и xt sin и 2£' M|V2/72 ] =
= cos Ujtf cos (jJ2t; — sin u^ sin w2t' = cos (cj^ + и2£').
276
Rxy (о, i) =cos w 2;
Л^М') = ^ (*', t) = cos (u^' + w20; Л^(0,1) - cos иг.
9.16. Имеются две некоррелированные случайные функции
X(t) и У(£) с характеристиками
(t) = t2; ^х(*,<') = вв1('+°;
т*
i/ *л2
Найти характеристики случайной функции Z(t) = X(t)+tY(t) +
+t2. Решить ту же задачу, если случайные функции X(t), Y(t) кор-
релированы и их взаимная корреляционная функция равна
Rxy(t,t') = ae-^t'-tK
Решение. В случае, еслиR (t,t') = 0,
т 2(t) = mx(t) + tm y(t) + t2 = 2t2 +t.
if *\2
K2(t,t') = Kx{t,t') + tt'Ky(t,t') = e«i{t+t,) +tt'ea*lt~i) .
В случае, когда Л (t,t,) = ae"0L^t ~^,т z(t) не меняется;
Kz(t,t') = Kx(t,t') + tt'Ky(t,t') + t%(t,t') + tRxy(t',t) =
9.17. Случайная функция Х(£) имеет характеристики тх (t) = 0;
Лх(т) = Ц,.е""а'т'.Найти ее спектральную плотность*?* (и).
Решение.
ОО ОО y-v
—oo 0
где Re — действительная часть.
9.18. Найти спектральную плотность случайной функции X(t),
если ее корреляционная функция
&ж(т) = £хе-а|т|со8(Зт.
Решение.
°° г (Зт , -г (Зт
/0е-а|т|-
2я
5;(ш) = — Г Л,е-а|т|- — е~^<к =
D
—ОО
ОО
= i^Re JVaT(e*3T + е"*'Зт ) е-' ^dr
о
277
Dx
2к
a
a2 + ((3-
a
a
1
-u)2 a2 + ((3 + qj)2
л 2 , q2 ,,,2
it [а2+(Э-ш)2][а2+(Э + Ш)2]'
где Re — действительная часть.
9.19. Комплексная случайная функция Z(t) задана в виде
Z(t) = X(t) + iY(t),
где
X{t) = j^{ak+Vk)e-^, У(*) = 1>* +Uk)e-^.
ы\
k=l
Математические ожидания всех случайных величин Vk и Uk
(к— 1, 2, 3) равны нулю, а корреляционная матрица системы
случайных величин (Vi, V2y V3j Uv U2j U3) имеет вид
10 0 10 0
2 0 0-10
3 0 0 3
10 0
2 0
3
Найти характеристики случайной функции Z(t).
Ы\ к=1
Kz(t,t') = Kx(t,t') + Ky(t,t') + i[Rxy(t',t)-Rxy(t,t%
где
Kx(t,t') = J2ke-«^; Ky(t,t') = J2ke-^t+t,);
it=l
к=1
/ ^ _ ^-а^'-З^ _ e-CL2t'-$2t _^_ 2е-а3^-Р3* .
9.20. Рассматривается случайная функция X(t),
представляющая собой число заявок, поступивших на телефонную станцию за
время t Одна из реализаций случайной функции X(t) показана на
рис. 9.20, а. Поток заявок простейший с плотностью X.
278
X(t)
5
4
3
2
1
О
,j i
, i i
1-1 I • •
-6-6——6-o-l>—&-o— t
0
a
t W-t
б
V
rxm
KJ&f)
t=tf
t = tf
в
Рис. 9.20
Найти закон распределения сечения случайной функции X(t)
и ее характеристики тх(t), Dx(t),Kx(t,t'),rx(t,t').
Решение. Закон распределения сечения X(t) есть закон
Пуассона с параметром a = \t, значит, вероятность того, что
случайная величина X(t) примет значение га, выражается формулой
рт =
(X*)
т
■\t
га!
(га = 0,1, 2,...).
Математическое ожидание и дисперсия случайной функции
X(t) будут
mx(t) = \t; Dx(t) = \t.
Найдем корреляционную функцию Kx(t,tf). Пусть tf >t.
Рассмотрим интервал времени (0, £') (рис. 9.20, б). Разобьем этот
интервал на два участка: от 0 до t и от t до t'. Число вызовов на всем
интервале (0, t') равно сумме чисел вызовов на интервалах (0, t) и
X(t') = X(t) + Y{t' -t),
где Y(t' — t) — число вызовов, пришедших на интервале (t ,tf);
вследствие стационарности процесса случайная функция Y(t) имеет то же
1)
Возможностью появления вызова в точности в момент t пренебрегаем.
279
распределение, что и X(t); кроме того, согласно свойствам пуассо-
новского потока событий, случайные величины X(t) и Y(t' — t) не-
коррелированы.
Имеем
Kx(t,t') = M{X(t)X(t')} =
= M[X(t)(X(t) + Y(t'-t))} = M[(X(t))2] = Dx(t) = \t.
Аналогично при t > t' получаем
*,(М') = Х*'-
Таким образом,
Kx(t9t') = \mm{t,t'}9
где min {£, t'} — минимальная из величин t, t' (при t = t' в качестве
минимальной можно взять любую из величин t, t').
Пользуясь символом единичной функции 1(я), можно
записать корреляционную функцию в виде
Кх(t, t') = \t l(t' - t) + \t' l(t - t').
На рис. 9.20, в показана поверхность Kx(t,t'). В квадранте
t> 0 и t' > 0 поверхность Kx(t,t') состоит из двух плоскостей,
проходящих соответственно через оси Ot и Ot' и
пересекающихся по линии ODx, аппликаты точек которой равны
дисперсии \t.
Нормированная корреляционная функция равна
Поверхность тх (t, t') показана на рис. 9.20, г.
9.21. Случайный процесс X(t) возникает следующим образом.
На оси времени Ot имеется стационарный пуассоновский
(простейший) поток событий с плотностью X. Случайная функция X(t)
попеременно принимает значения +1 и -1; при наступлении каждого
события она скачком меняет свое значение с +1 на -1 или
наоборот (рис. 9.21, а).
Найти характеристики mx(t), Dx(t) и Kx(t,t') случайной
функции X(t).
280
Решение. Сечение случайной функции X(t) имеет закон
распределения, представленный рядом
Хг(Ь)
Pi(t)
-1
1
2
+1
1
2
Действительно, так как моменты перемен знака никак не
связаны со значением случайной функции, нет никаких
оснований считать какое-либо из значений +1, -1 вероятнее другого.
Отсюда
тМ)
i + 1-OS
2 2
D,(t) = (-1)2 -^ + 12 -i = l.
Чтобы найти корреляционную функцию Kx(t,t'), рассмотрим
какие-то два сечения случайной функции: X(t) и X(t') (t* >t) и
найдем математическое ожидание их произведения:
Kx(t,t') = M[X(t)X(t')) = M[X(t)X(t')).
Произведение X(t) X(t') равно -1, если между точками t и t'
произошло нечетное число событий (перемен знака), и равно +1,
если произошло четное число перемен знака (включая нуль).
X(t)
1
О
1
"Г*
I
I
+
t
"1 Г
l l
Т\
+
rr^rt,
I I
I I
\t
I I
I
t
4W1)
a
t
Рис. 9.21
в
281
Вероятность того, что за время т = t' — t произойдет четное
число перемен знака, равна
(Хт)2т
V
чет
оо
£
=о (2т)!
_Хт _хт е + е
е = е
т=0
аналогично вероятность того, что за время т произойдет нечетное
число перемен знака, будет
Рнеч ~ е
Хт -Хт
-Хт е - е
Отсюда
*,(*,*')= (+1)Рчег +(-1)Рнеч=^
-2Хт
где т = t' — t.
Аналогично при t' < t найдем
где т = t' — t.
Объединяя эти две формулы, получим
*х(М') = *,(т) = е-2Х|т|.
График этой функции показан на рис. 9.21, б. Поверхность
Kx(t,t') = е-2Х|*-^т показана на рис. 9.21, в.
Случайная функция X(t) стационарна. Ее спектральная
плотность равна
1 °°
2Х
—ОО
тг(4Х2+и;2)
9.22. Случайный процесс X(t) возникает следующим образом.
На оси Ot имеется стационарный пуассоновский поток событий с
плотностью X (рис. 9.22). При наступлении каждого события
случайная функция X(t) скачком
меняет свое значение, принимая,
независимо от предыстории
процесса, случайное значение V и
сохраняя его до момента
появления следующего события. Слу-
X(t)
о
t
X(t)
X(tf)
i—6^_|_^--4-~H*--j»—j—t чайная величина V непрерывна и
1—' имеет плотность распределения
ф(и). Найти характеристики
тя(0, Ds(t) и Kx(t,t') случайной
функции X(t).
Рис. 9.22
282
Решение. Любое сечение случайной функции X(t)
распределено по закону ф (х); отсюда
оо оо
™*(0 = т,/ = fx4>(x) dx; Dx(t) = Dv = J (x - m v )2ф (x) dx.
—OO — OO
Корреляционную функцию Kx(t,t') находим с помощью того
же приема, что и в задаче 9.21. Рассмотрим два сечения X(t) и
X(t') (t1 >t), разделенные интервалом т = t' — t.Имеем
Kx(t,t') = M[X(t)X(t')}.
Если между точками t, t' не появилось ни одного события, то
X(t') = X(t) и Kx(t,t') = M[(X(t))2] = Dx(t) = Dv. Если между
о о
точками t, t появилось хотя бы одно событие, то M[X(t) X(t )] = 0.
Отсюда
Аналогично при t' < t Kx(t,t') = Dve~x^~T), откуда
корреляционная функция стационарного случайного процесса X(t) равна
*,(т) = Д„е-хМ.
Эта корреляционная функция не зависит от вида закона
распределения ф(и), а зависит только от его дисперсии Dv.
9.23. Случайный входной сигнал X(t) преобразуется с
помощью реле в случайный выходной сигнал Y(t), связанный с X(t)
нелинейной зависимостью Y(t) = sgn X(t), т. е.
Г(0 = -
1 при X(t)>0,
0 при X(t) = 0,
-1 при X(t)<0.
Входной сигнал представляет собой случайную функцию X(t),
рассмотренную в предыдущей задаче 9.22. Найти закон
распределения сечения случайной функции Y(t) и ее характеристики
my(t),Ky(t,t').
Решение. Случайная функция Y(t) может принимать
только два значения: +1 и -1 (значением 0 можно пренебречь,
так как P(X(t) = 0) = 0). Вероятность того, что X(t) > 0, равна р =
оо
= / ф (х) dx. Ряд распределения случайной величины Y(t) имеет
о
вид
283
ф)
Pit)
-l
i-p
l
p
Отсюда my = 2p — 1; Dy = 1 - (2p - 1)2 = 4p (1 — p). Пусть
t' >t nt' — t = т. Если за время т в пуассоновском потоке не
появилось ни одного события (а вероятность этого равна е~Хт), то
значения случайной функции Y{t) и Y(t') равны друг другу и
условная корреляционная функция Ky(t,t') = Dy{t) = Ар (1 — р).
Если же за время т появилось хотя бы одно событие, то Y{t) и
Y(t') между собой не коррелированы и условная корреляционная
функция Ky(t,t') равна нулю. Отсюда при t' > t
Ky(t,t') = e-^Ap(l-p),
а в общем случае (при любых t, t')
A-,(t><') = *,(T) = e-xlTl4p(l-p).
9.24. Случайный входной сигнал X(t), рассмотренный в задаче
9.22, преобразуется в случайный выходной сигнал Y(t) с помощью
реле с зоной нечувствительности:
Y(t) =
sgnX(t)
О
при \X(t) |> е,
при \X(t) |< е,
где е — зона нечувствительности реле.
Требуется найти закон распределения сечения случайной
функции Y(t) и ее характеристики: математическое ожидание и
корреляционную функцию.
Решение. Случайная величина Y(t) при любом t может
принимать одно из трех значений: —1,0, 1 и имеет ряд распределения
где
Vi{t)
Vi{t)
-1
Pi
0
pi
1
Рз
—е
Pi
= Р(ВД<-е)= f4>(x)dx;
—оо
Vi
с
P(-e<X(t)< е) = Гtp (ж) сЬг;
284
oo
Рз
= P(X(t)>e) = Jy(x)dx.
Отсюда
m
v = Рз ~ Pi; Dy = Pi + Рз ~ (Рз - Pi)
Рассуждая аналогично тому, как это делалось в предыдущей
задаче, определяем корреляционную функцию
9.25. Случайная функция X(t) преобразуется в случайную
функцию Y(t) с помощью нелинейного элемента, работа которого
описывается формулами
Y(t) =
—be при X(t) < —е,
bX(t) при |-Y(OI<e,
be при X(t) > е.
График зависимости у(х) показан на рис. 9.25, а.
Пу)
1
-бе О
i
Vi
т
fee
У
а
Рис. 9.25
На вход такого элемента поступает случайная функция X(t),
рассмотренная в задаче 9.22. Найти одномерный закон
распределения случайной функции Y(t) и ее характеристики:
математическое ожидание и корреляционную функцию.
Решение. Случайная величина Y(t) — сечение случайной
функции Y{t) — имеет непрерывное распределение в открытом
интервале (—fee, fee) и, кроме того, дискретные возможные значения
-Ье и Ье с отличной от нуля вероятностью; таким образом, сечение
Y(t) представляет собой смешанную случайную величину,
функция распределения которой F(y) непрерывна на участке (—be, be),
а на концах участка — в точках (—fee) и (fee) — терпит разрыв.
Скачки F(y) в точках разрыва равны
285
—e
P(Y(t) = -be) = P(X(t) < -e) = f у (x)dx = Pl,
-OO
OO
P(Y(t) = be) = P(X(t) > e) = f ip (x) dx =
Pi
Найдем функцию распределения случайной величины Y(t) в
промежутке (—be, be):
F(y) = P(Y(t)<y) = pix(t)<^\= J^(x)dx =
— OO
У_
b
= Pi + / Ф (x) dx (—be < у < be).
—e
График функции распределения F(y) показан на рис. 9.25, б.
Плотность распределения смешанной случайной величины Y(t) в
интервале (—be, be) равна производной от F(y) на этом интервале:
Я») = *"(») =4 ч>
О
(JL)
при — be < у <be.
Характеристики случайной функции Y(t) равны
™>y(t) = my =-Ьерг + Ъер2 +~/г/Ф Т dV =
-be
Kb)
= be (р2 — рг) + Ь I яф (x) dx]
—e
Dy(t) = Dy=OL2[Y(t)}-[my(t)}2 =
= (be)2(Pl +p2) + ijy2Jl dy-m2y =
—be
e
= b2e2(px + p2) + b2 I x2y(x) dx — m2.
—e
Аналогично предыдущим задачам находим корреляционную
функцию
ky(T) = Dye-x^.
286
9.26*. Рассматривается случайная функция Y(t) = Wcos х
х (u;^ — 9), где W — центрированная случайная величина с
дисперсией Dw, 9 — случайная величина, распределенная с
постоянной плотностью в интервале (0,2тт), аш1 - неслучайный параметр
(и;1 > 0). Случайные величины W и 9 независимы. Определить
характеристики случайной функции Y(t): математическое
ожидание, корреляционную функцию. Определить, является ли
случайная функция Y(t) стационарной и эргодической. Если она
стационарна, найти ее спектральную плотность S (и;).
Решение. Представим случайную функцию Y(t) в виде
Y(t) = H^cos (u;^ — Q) = W cos 9 cosu;^ + W sin 9 sin u;^.
Обозначим
W cos 9 = U, W sin G = V.
Найдем сначала основные характеристики системы случайных
величин U и V:
M[U] = M[W cos 9] = M[W] M[cos 9] = 0;
M[7] = M[W sin 9] = M[W] M[sin 9] = 0;
D[U] = M[(W cos 9)2] = M[W2] M[cos2 9] = £ JM[cos2 9];
D[V] = M[(W sin 9)2] = £ JM[sin2 9];
Kuv = M[W cos 9 W sin9] = DJVf[sin9cos 9].
Так как величина 9 распределена равномерно в интервале
(0,2тт), то
M[sin2 9] = M[cos2 9] = J cos2 G — dG = ±;
о
2тт
M[sin9cos9]= I sinGcosG—dG = 0.
о
Итак, имеем
M[U] = M[V) = 0, D[U) = D\V] = ^, Kuv=0.
Следовательно, выражение
Y(t) = W cosiuj — 9) = U cos u;^ + V sin u;^
287
-2-rc -3-Tf
Шх 2(jJi
2tJ! ^1
-7Г
Рис. 9.26
представляет собой спектральное разложение стационарной
случайной функции, корреляционная функция которой имеет вид
ку (т) = —— cosu^t, а ту =0.
График этой функции показан на рис. 9.26.
Функция Y(t) эргодичной не является, так как характеристики,
найденные по одной реализации, не совпадают с
характеристиками, определенными по множеству реализации. Действительно,
каждая реализация случайной функции Y(t) есть гармоническое
колебание, амплитуда которого представляет собой значение,
случайно принятое величиной W. Среднее по времени для каждой
такой реализации будет равно нулю и совпадает с математическим
ожиданием случайной функции Y(t), но дисперсия и
корреляционная функция, найденные как средние по времени для одной
реализации, уже не будут совпадать с соответствующими
характеристиками случайной функции Y(t). Например,
1 Т
lim — [Y2(t)dt =
-т
т
= lim — fw2-[l + cos2(uA -Q)]dt =-W2.
-T
Найдем спектральную плотность случайной функции Y(t).
Покажем, что она пропорциональна дельта-функции:
svH
D
w
■6 (w — U)j ) (0 < U) < оо).
Действительно, при такой спектральной плотности
корреляционная функция будет равна
00
00
D
D.
/си и
Sу (u;)cos и;т du; = I —— 6 (и; — и;2) cosurr du; = —— cos и^т,
о
о
288
что совпадает с корреляционной функцией для Y(t). А так как
прямое и обратное преобразования Фурье определяют спектральную
плотность и корреляционную функцию взаимно однозначно, то
написанное выше выражение для Sy (ы) дает спектральную плотность
случайной функции Y(t).
Если воспользоваться не действительной, а комплексной
формой преобразований Фурье, получим спектральную плотность
5* (и) в виде
5* (ш) = —— [6 (u; + wJ + 8 (w - wj] (-оо < uj < с»).
Заметим, что в аналогичном виде можно было бы записать и
5, (ы) = ^ [б (ы + ых) + б (ы - Ш1)],
но для положительных w (так как и^ > 0) 8 (w + u^) = 0.
9.27. Случайная функция Х(£) представляет собой случайную
величину U: X(t) = U с заданными числовыми характеристиками
Найти характеристики случайной функции X(t):
математическое ожидание, корреляционную функцию и дисперсию.
Определить, является ли случайная функция X(t) а) стационарной,
б) эргодичной. Если она стационарна, найти ее спектральную
плотность.
Решение.
mx(t) = M[X(t)} = M[U} = mu;
Kx(t,t') = M[X(t)X(t')) = M[UU)^Du;
Dx(t) = Kx(t,t) = Du.
Так как mx(t) = const и Кх (t, t') = const, то случайная функция
X(t) стационарна. Так как среднее по времени для каждой
реализации равно значению, принятому случайной величиной U в этой
реализации, и различно для разных реализаций, то случайная
функция X(t) неэргодична.
Рассматривая случайную функцию X(t) как частный вид при
и1 = 0 случайной функции Y(t) = U cos u;^ + V sinw^,
приведенной в предыдущей задаче, получим для нее спектральную
плотность вида
5» = Дц6(ш); 5,И = 25;И = 20„6(ы).
289
9.28. Случайная функция X(t) строится следующим образом.
В точке t = О она случайным образом и с одинаковой
вероятностью принимает одно из значений: +1 или -1 и остается
постоянной до t= 1. В точке t= 1 она снова, с одинаковой вероятностью
1/2 и независимо от того, какое значение она имела на
предыдущем участке, принимает одно из значений +1 или -1 и сохраняет
его до следующей целочисленной точки t = 2, и т. д. Вообще
функция X(t) постоянна на любом участке от га до га + 1, где га —
натуральное число, а на границе каждого нового участка независимо от
предыдущих принимает одно из значений +1 или -1с
вероятностью 1/2. Одна из возможных реализаций случайной функции
О
1+
1; 2 3| * 4 *';5 j6
*
t = t'
а
Рис. 9.28
X(t) показана на рис. 9.28, а. Требуется определить
характеристики случайной функции X(t): математическое ожидание,
дисперсию и корреляционную функцию. Определить, является ли
случайная функция X(t) стационарной.
Решение. Имеем
mx(t) = mx =(-1).1 + 1-1 = 0;
Dx(t) = Dx =(-1)2 -^ + (1)2 -1 = 1.
i
Найдем корреляционную функцию Кх (£,*')•
Если точки t и t' относятся к одному и тому же интервалу (га,
га+ 1), где га — целое, то Kx(t,t') = Dx = 1, в противном случае
Кх (t, t') = 0. Этот результат можно записать в более компактной
форме, если обозначить через b(t) целую часть числа t (см.
рис. 9.28, а). Тогда получаем
Kx(t,t') = -
1 при |т|< 1 — Ь (min{£, t'}),
0 при |т|>1-6(min {*,*'}).
290
Эта функция зависит не только от т = t' — t, но также и от того,
где на оси Ot находится участок (t, t'); следовательно, случайная
функция X(t) стационарной не является.
Поверхность Kx(t,t') выглядит как ряд кубов с ребром,
равным 1, поставленных на плоскости tOt' вдоль биссектрисы
первого координатного угла, на которой t =t\ так что диагонали
оснований совпадают с биссектрисой (рис. 9.28, б).
9.29. Случайная функция X(t) формируется так же, как и в
предыдущей задаче, с той разницей, что точки, в которых происходит
«розыгрыш» нового значения случайной функции, не закреплены
на оси Ot, а занимают на ней случайное положение, сохраняя между
собой постоянное расстояние, равное единице (рис. 9.29, а). Все
положения начала отсчета относительно последовательности
моментов «розыгрыша» одинаково вероятны.
а
Рис. 9.29
Найти характеристики случайной функции X(t) —
математическое ожидание, дисперсию и корреляционную функцию;
определить, является ли случайная функция X{t) стационарной.
Решение. Как и в предыдущем случае,
mx{t) = ™>x =0;
Dx(t) = Dx=l.
Найдем корреляционную функцию. Зафиксируем момент t
(рис. 9.29, а). Этот момент случаен относительно точек, в которых
случайная функция X{t) принимает новые значения. Обозначим
Г промежуток времени, отделяющий точку £от ближайшей точки,
в которой будет «разыгрываться» новое значение X(t). Случайная
величина Т будет распределена равномерно на участке от 0 до 1.
Пусть *'>*;т = *'-* >0. Если т < Г, то Kx(t,t') = l; если т > Г,
то Кх (t, t') = 0. Поэтому
^(^^) = Р(71>т)-1 + Р(Т<т).0 =
= Р(Г>т) = 1-т при 0<т<1.
Аналогично при т < 0 получим
Kx{t,t') = l + T при -1<т<0;
291
отсюда
tfx(M') = *,(T) = -
1-|т
О
при
при
т
т
<1
>1
(9.29)
X(t)
График этой функции представлен на рис. 9.29, б. Так как
Кх (t, t') = kx (т), то случайная функция X(t) стационарна.
Корреляционную функцию (9.29) можно записать в более
компактном виде с помощью единичной функции 1(х):
*.(т) = (1-|т|)1(1-|т|).
9.30. Условия предыдущей задачи изменены в том отношении,
что в каждый из случайных моментов t{, разделенных единичными
интервалами, случайная функция X{t) принимает (независимо от
других) значение Uiy являющееся случайной величиной с
математическим ожиданием т„ и дис-
Ля
Персией Du, и сохраняет его до
1 следующей точки. Одна из реали-
; зации такой случайной функции
' t показана на рис. 9.30. Найти ха-
1 рактеристики этой случайной
функции: математическое
ожидание, дисперсию и
корреляционную функцию и определить,
является ли случайная функция стационарной, а если стационарна,
то какова ее спектральная плотность.
Решение. Рассуждая точно так же, как и в предыдущей
задаче, найдем
mx(t) = M[X(t)} = mu; Dx{t) = D[X(t)} = Du ;
Du(1-\t\) ПРИ lTl<!.
0
Рис. 9.30
*,(<) =
0
при
>1,
или, в другой записи,
Мт) = £и(Чт|)1(1-|т|),
где 1(х) — единичная функция.
Случайная функция X(t) стационарна. Ее спектральная
плотность
5;И = ^.(1-С08Ы).
TV(jJ
9.31. Случайная функция X(t) представляет собой
ступенчатую знакопеременную функцию (рис. 9.31, <я), которая через еди-
292
X(t)
1-
0
1-
—I I 1 J 1
Г I I I I I
I I I I L
t
+
о
T
\—h
1 2
A 1 1—£
3 4 5 6
a
1 ,
-3/
Л ХУ
/ ' \ ' /
-2 V-l/O
\ i
V/
/1 \
2
i
\3
T
e
Рис. 9.31
ничные интервалы принимает попеременно значения: +1 и — 1.
Положение ступенчатой функции относительно начала отсчета
случайно; случайная величина Т, характеризующая сдвиг первой
точки перемены знака относительно начала координат, есть
случайная величина, распределенная равномерно в интервале (0, 1).
Найти характеристики случайной функции Х\ математическое
ожидание тхУ дисперсию Dx и корреляционную функцию.
Решение. Рассмотрим сечение случайной функции X(t); оно
с равной вероятностью может попасть как на участок, где
случайная функция равна единице, так и на участок, где она равна минус
единице.
Следовательно, ряд распределения любого сечения имеет вид
Х{
Pi
-1
1
2
1
1
2
откуда
тж = -1 • - + 1 ■ - = О, Dx= (-1)2 • - + I2 • - = 1.
1
2
1
2
Найдем корреляционную функцию
Kx(t,t + r) = M[X(t)X(t + T)] = M[X(t) X(t + т)].
Так как произведение может принимать только два значения
+ 1 или —1, то
M[X(t) X{t + т)] = 1 • Pl + (-1) • (1 - Pl) = 2Pl - 1,
293
где рх — вероятность того, что точки t и t 4- т попадут на участки, в
которых X(t) и X(t 4- т) имеют один и тот же знак. В силу
равномерности распределения сдвига Тна рис. 9.31, а можно перенести
начало отсчета в левый конец того участка, на котором находится точка t>
и считать, что точка t равномерно распределена в интервале (0, 1)
(рис. 9.31, б). При таком толковании рх есть вероятность того, что
точка (t 4- т) попадает в какой-либо из интервалов вида (2п, 2п 4-1),
п = 0, ± 1, ± 2,... (эти интервалы отмечены жирными линиями на
рис. 9.31, б). Подсчитаем эту вероятность для разных значений т.
При 0 < т < 1 точка (t 4- т) может попасть либо в интервал (0, 1),
либо в интервал (1,2), поэтому
Pl = Р (t 4- т < 1) = Р (t < 1 - т) = 1 - т.
При 1 < т < 2 точкам 4- т может попасть либо в интервал (1, 2),
либо в интервал (2, 3), поэтому
Pl = Р (t 4- т > 2) = Р (t > 2 - т) = 1 - (2 - т) = т - 1.
Продолжая эти рассуждения, получим
1 - (т - 2п) при 2п < т < 2п 4-1,
(т - 2п) - 1 при 2п 4- 1 < т < 2п 4- 2.
Рл =
Отсюда видно, что pv а значит и Кх (t, t 4- т) = 2рг — 1, зависит
только от т и является четной функцией т. Следовательно,
*.(*,* +т) = Мт) =
4п 4-1 - 2т при 2п < т < 2п 4- 1,
2т - {An 4- 3) при 2п 4-1 < т < 2п 4- 2.
График корреляционной функции представлен на рис. 9.31, в.
9.32. Случайная функция X(t) представляет собой
последовательность равноотстоящих положительных импульсов, имеющих
одинаковую ширину ^ < - Начало каждого импульса отделено от
начала каждого следующего единичным интервалом (рис. 9.32, а).
Последовательность импульсов занимает относительно оси 0£
случайное положение (см. условия предыдущей задачи).
Величина г-го импульса U{ случайна, распределена по одному и тому же
закону с математическим ожиданием ти и дисперсией Du и не
зависит от величин остальных импульсов. Найти характеристики
случайной функции X(t): математическое ожидание mx(t),
дисперсию Dx(t)n корреляционную функцию.
Решение. Математическое ожидание случайной функции
X(t) по формуле полного математического ожидания равно
294
Дисперсию найдем через второй начальный момент:
с*2[ВД] = с*2[£/Ь+ 0-(1-ч) = чфи +ml),
откуда
Dx = <x2[X(t)]-m2s=4(Du +т2и)-12т2и = чД, + ч(1-ч)т*.
В данном случае случайная функция X(t) нецентрирована. Ее
корреляционную функцию будем искать через второй
смешанный начальный момент:
Kx(t, t + т) = M[X(t) X(t + т)] - ml.
Найдем M[X(t) X(t + т)] по формуле полного математического
ожидания. Как и в предыдущей задаче, представим ось 0t
покрытой перемежающимися участками: зачерненные соответствуют
импульсам, а светлые — промежуткам между ними. Обозначим
Т — случайное значение левой границы участка (Т, Т + т).
Возможны три гипотезы:
Нх — обе точки ГиГ + т попали на участок одного и того же
импульса;
#2 — одна из точек Т, Т + т попала на участок одного из
импульсов, а другая — другого;
#з — хотя бы одна из точек Т, Т + т попала вне участков
каких-либо импульсов.
а
Ыт)
Ar=-A+i(i-i)™w
nf(l-nf)mtt
2 2
1™>и
б
Рис. 9.32
295
При первой гипотезе величины Х(Т) иХ(Т+ т)совпадают и
M[X(T)X(T+r)] = M[U2] = Du +ml.
При второй гипотезе величины Х(Т) и Х(Т + т) представляют
собой независимые случайные величины с одинаковыми
математическими ожиданиями тпи; по теореме умножения
математических ожиданий М[Х(Т) Х{Т + т)] = m \ .
При третьей гипотезе
М[Х(Т)Х(Т+т)] = 0.
Полное математическое ожидание будет
М[Х(*)Х(« + т)] = Р(Я1)(1)|, + т*) + Р(Я2)т*.
Вероятности Р(Н{) и Р(Я2), а значит, и корреляционная
функция зависят только от т.
1) при 0 < т < ч
Р(Я1) = Т-т> Р(Я2) = 0;
М[*(0 *(* + т)] = (ч - т) (Д, + т*).
Корреляционная функция на этом интервале
2) при ч < т < 1 — ^
Р(Я1) = 0; Р(Я2) = 0; М[Х(*) Х(* + т)] - 0;
3) при 1 — ч < т < 1
Р(Я1) = 0; Р(Я2) = т(1-т);
М[Х(0Х(^ + т)]=И-(1-т)]т^.
Дальнейшие интервалы значений т исследуются аналогичным
образом.
1
График функции кх(т) представлен на рис. 9.32, б. При |т|> -
кривая кх (т) периодически повторяется, достигая в целых точках
местных максимумов, равных ^ (1 — ^)m \ .
9.33*. Рассматривается стационарная случайная функция X{t),
представляющая собой пилообразное напряжение (рис. 9.33, а).
Начало отсчета занимает по отношению к зубцам случайное
положение, как в задаче 9.31. Найти математическое ожидание тпхУ
дисперсию Dx и корреляционную функцию.
296
Решение. Математическое ожидание тх легко найти, если
учесть, что распределение X(t) при любом t — равномерное на
интервале (0, 1). Отсюда тх = -.
Для отыскания корреляционной функции поступим
следующим образом: свяжем последовательность зубцов жестко с осью
0£, но зато будем случайным образом бросать на эту ось начало t
отрезка (t, t 4- т) (рис. 9.33, б). Так как зубцы периодичны,
достаточно случайным образом бросить точку t на первый интервал
(О, 1), распределяя ее с постоянной плотностью.
о t 1г+т2
к k + l
а
Рис. 9.33
При этом, как видно из рис. 9.33, б, значение X(t) = t, а
значение X(t 4- т) равно дробной части числам 4- т, т.е.
Х(*4-т) = *4-т-£(*4-т),
где Е (t 4- т) — целая часть числа (t 4- т). Если целая часть числа т
равна п, п < т < п 4-1, то
'п при t 4- т < п 4- 1,
п 4- 1 при t 4- т > п 4- 1,
Д(*4-т) =
и, значит,
X{t + T)
t 4- т — п при £ < п 4- 1 — т,
t 4- т — (п 4- 1) при t > п + 1 - т.
По формуле для математического ожидания функции от
случайной величины t имеем при п < т < п 4-1:
X
M[X(t) X{t 4- т)] = JX(t) X{t 4- т) • 1 • dt =
о
72 +1—Т
= J t{t + r-n)dt+ f t (t 4- т - n - 1) dt =
0
(n 4-1 - t)
4-
n +1—т
T — П 1
-- (n = 0,±l,±2,...).
z b
297
Отсюда следует, что корреляционная функция зависит только
от т и при п<т<п + 1(п — 0, ± 1, ±2, ...) имеет вид
Kx(t,t + T) = kx(T) = M[X(t)X(t + T)]-7n2x =
(n + 1-т)2 т-п 5
+
12
Это периодическая функция с периодом 1, график которой
состоит из периодически повторяющихся отрезков парабол,
обращенных выпуклостью вниз.
В интервале 0 < т < 1 это парабола
, , ч (!-т)2 т 5
2 2 12
(1 1 )
с вершиной в точке -, . Полагая т — 0, получим Dx — кх (0) =
12 24J
_ _1_
~~ 12'
9.34. Рассматриваются две некоррелированные
центрированные случайные функции X(t), Y(t) и их произведение
Z(t) = X(t) Y(t). Доказать, что корреляционная функция
произведения равна произведению корреляционных функций
сомножителей:
Kz(t,t') = Kx(t,t')Ky(t,t').
Решение. Kz(t,t') = M[Z(t) Z(t% Z(t) = Z (t) - m,(*). Так
как случайные функции X(t) и Y(t) некоррелированны и центри-
рованны, то
mz(t) = mx(t)my(t) = 0;
отсюда
Z(t) = X(t)Y(t) = X(t)Y(t)
и
Kz(t,t') = M[X(t)Y(t)X(t')Y(t')} =
= M[X(t)X(t')]M[Y(t)Y(t')} = Kx(t,t')Ky(t,t').
Отсюда, в частности, при t — t'
Dz{t) = Dx{t)Dy{t).
298
9.35. Доказать, что корреляционная функция произведения п
независимых центрированных случайных функций
п
z(t) = Y[xi(t)
i=l
равна произведению корреляционных функций сомножителей
Kz(t,t') = f[KXi(t,t').
i=l
Решение. Доказательство аналогично предыдущему, с той
разницей, что для применения теоремы умножения
математических ожиданий в этом случае недостаточно некоррелированности
сомножителей, а независимости — достаточно.
9.36. Рассматривается произведение двух некоррелированных
случайных функций
Z(t) = X(t)Y(t),
причем случайная функция X(t) такая, как в задаче 9.21 (случайное
чередование значений +1 и -1 с простейшим потоком перемен
знаков), а случайная функция Y(t) — такая, как в задаче 9.26. Найти
характеристики случайной функции Z(t).
-1
Z(t)=X(t) Y(t)
Рис. 9.36
Решение. Имеем:
™*(0 = ™у(0 = о; ™*(0 = о;
299
#ЛМ') = е-2Х|т|; /^(MO^cos^t (r = t'-t)
На основании задачи 9.34 имеем
D.
Kz(t,t') = Kx(t,t')Ky(t,t') = -^-e-2X^ cos u,r.
На рис. 9.36 показана одна из возможных реализаций
случайной функции Z(t), полученная перемножением соответствующих
ординат реализации случайных функций X(t) и Y(t).
9.37. На телефонную станцию поступает простейший поток
заявок с плотностью X. Случайная функция X(t) — число заявок,
поступившее за время t (см. задачу 9.20). Найти характеристики ее
dX(t)
производной Y(t) = —.
dt
Решение. В обычном смысле разрывная случайная функция
X(t) недифференцируема, однако, пользуясь обобщенной
дельта-функцией, можно записать характеристики производной.
Преобразование Y{t) = ——, связывающее случайную функцию Y{t)
dt
с X(t), является линейным однородным. Поэтому на основе
задачи 9.20
771 у (*) = 37т*(0 = Т7Х* = х>*
at at
д2 „ ,. .„ д
( д
dtdf ч ' dt
КуМ = 1^КЛ^') = ^ -^{\tl{t> -t) + \t>l{t-t>)]\ =
(dt
= ^[\(t-t')b(t-t') + \l(t-t')],
но(t -t')b(t -t') = 0,откуда
Ky(t,t') = -^(\l(t-t')) = \b(t-t') = \b(T).
Таким образом, корреляционная функция случайной функции
Y(t) пропорциональна дельта-функции, т.е. функция Y(t)
представляет собой стационарный белый шум с интенсивностью G = X
и средним уровнем т = X. Спектральная плотность такого
белого шума будет
X
5;И = ^-/х8(т)е-'итйт =
2ir J 2tv
—ОО
300
9.38*. Имеется функция кх(т\ обладающая следующими
свойствами:
1)М-т) = М-0;
2) к, (0) > 0;
3)|*,(т)|<*,(0).
Требуется выяснить, может ли функция кх (т) быть
корреляционной функцией стационарной случайной функции, т.е. обладает
ли она свойством положительной определенности. Показать, что
достаточным условием положительной определенности является
условие, чтобы функция
5я(ш) = - / kx(r)cosurdr (9.38а)
о
была неотрицательна при любом значении их
5,И>0, (9.386)
т.е. чтобы, вычисляя спектральную плотность по формуле 9.38а,
мы ни при каких w не получали отрицательных значений этой
плотности.
Решение. Предположим, что Sx (uj) > 0, и докажем, что при
этом функция кх(т) = kx(tf — t) будет положительно
определенной. Имеем
00
кх(т) = / Sx(u>) cos urr (Lj =
о
со со
/ Sx(uj) cos ujt cos u^7 (Lj + I Sx(u>) sin ut sin ujtf cL). (9.38b)
о о
Положительная определенность функции kx(t' — t) состоит в
том, что для любой функции ср(£) и любой области
интегрирования В должно выполняться условие
J J'М*''-*)ф (Оф (t')dtdt' >0.
Проверим это неравенство по отношению к функции (9.38в):
Г 00
/ I' I &х(и)cos ^cos ^^; ф (0 ф (^0^° +
(5)(5)1 О
оо
+ / ^Л^) sin ^ sin w£;tp (t) у (tf) cL) dt dtf =
о
301
00
fsxM
О
/ cos <jj£ ip (£) d£ I cos wt' y> (t') tit' +
[(B) (B)
+ / sin u£ ip (£) dt / sin (jJ^; ip (tf) dt'
(B) (B)
- (Lj.
Обозначая
/ cos u;^ ip (£) d£ = 'ФхСД и;), I sin u;^ ip (t) dt = il>2(5, u;)
(5) (5)
имеем
Г [К(* -*')ф (ОФ (t')dtdt' =
(В)(В)
СО
о
так как по условию 5Х (ш) > 0.
Можно доказать, что условие (9.386) является не только
достаточным, но и необходимым для того, чтобы корреляционная
функция была положительно определенной.
9.39. Имеется стационарная случайная функция с
характеристиками
т« (*) = "»«; #.(*>*') = **(т)> гДе т = *'-*.
Найти характеристики ее производной Y(t) = —X(t) и пока-
dt
зать, что она также стационарна.
Решение. Так как Y(t) связана с X(t) линейным однородным
преобразованием, то
d
т (t) = —т (t) = 0 = const;
dt
Ky(t,t') =
d2 d2
dtdt
д_
at
dtdt
-*,(т)*
dt at'
d_
dt
d
dt
7*.(т)
302
„ дт дт
Но —- = 1 и — = —1, поэтому
dt dt
K,(t,t') =
д_
dt
d
dr
Мт)
d
dr
dt
dr
M-0
Так как правая часть равенства зависит только от т, то
Ky(t,t') = ky(r) =
d
dr
Kb)
и случайная функция Y(t) стационарна.
9.40. Стационарная случайная функция X(t) имеет
корреляционную функцию кх (т). Случайная функция Y(t) получается из нее
дифференцированием: Y(t) = ——. Найти корреляционную
dt
функцию к (т), если:
а)Л,(т) = е-а'т|; б) кх(т) = е-а^(1 + а |т|);
в)^(т) = е"а|т|
а
cos Вт Н sin ВI т
з
(а >0).
Решение. При решении задачи будем применять аппарат
обобщенных функций, правила пользования которым приведены
в начале данной главы.
а)
d
Мт) = -тте
—а т
d
dr
= а
—ае
—а т
(d_\r\)
~dV
+
dT
d2\r
—ае
—а т
dfr
dr
—а т
dT
= ае-а|т|[26(т)-а (sgnr)2].
Наличие слагаемого 26 (т) показывает, что в составе случайной
функции Y(t) есть белый шум.
б) Мт) = --^[е-*М(1 + а|т|)] =
d_
'dr
= а
—ае
d
—а т
dr
d\r
~dr
(1 + а|т|) + а
d
d\r
1r~
-а т
[e-a|T|sgnT.|T|]-a2—[е"а|т|т]
dr dr
= a
—а т Л Л-а т1
1 ' — ae ' 't
d\r
dr
Л 2 -а|т
= a e '
(l-a|x|).
303
в)
Мт)
d
-а т
dT
а
cos В т Н sin В т
3
А
dT
-ае
—а т
а
cos 3 т Н sin 31т
dlT
dT
+
+е
-а т
— 3 sin 3 т + а cos 31 т
dHl
dr
— sin |3те
dT
-а It I Ot2 + Р2
3
а2 + (3:
(3
—а т
(3cos(3Te-a|T| -asinpTe-01
dlT
dT
2 \ -a It
= (<* +P )e_a
cos Зт sin 31 т
3
9.41. Найти спектральную плотность стационарной случайной
функции с корреляционной функцией:
L(T) = ae-a|T| [28(т)-а (sgnT)2].
if
Решение.
1 оо оо
5;(ы) = 1/^(т)е-'-<1|т| = 1/ае-(''т126(т)е-иЧт-
-ОО
— 00
1 °°
__L fa2(sgnT)2e-a|T|e-iuTdT.
2-kJ
— 00
Так как
(sgn т)2 =
1 при т 5й О,
О при т = О
и подынтегральная функция второго интеграла в точке т = Оне
имеет особенностей, во втором интеграле можно пренебречь точкой
т = 0. Получим
<?» =
a a
2a
a u;
те 2тг a2 + w
тс a2 +w2
График спектральной плотности представлен на рис. 9.41.
Спектральную плотность S* (и) можно было получить проще
следующими рассуждениями. Представим случайную функцию Y(t) как
производную случайной функции X(t) из задачи 9.40 (пункт а). Имеем
304
1 а
s*M
s:m =
2 . 2 '
-к а + иг
амплитудно-частотная характеристика
оператора дифференцирования равна Ф (г и) =
= «ы, следовательно,
а
-к
О
Рис. 9.41
и
s» = s;h^(»w)i2=-
а
2 . 2
-к а + иг
. ,2 а и
1Ш = —
2 . 2
-к а + иг
9.42. Спектральная плотность стационарной случайной
функции X(t) на участке от —ujx до +иг постоянна, а вне его равна
нулю, т.е. имеет вид, показанный на рис. 9.42 а:
s»
1
1
1
1
•
-wi о
а
i
i
i
i
U>!
а
вд
2а smu^T
U)
т
2аи1/
" \У 0
^ч.
Шх
У2тг Зтг
UJx UJx
Рис. 9.42
S» =
а при J uj |< uj15
О при |uj |> ujx
или, в другой записи,
S*x(bj) = aA
1
UJ
и
i ;
Найти корреляционную функцию кх(т) случайной функции
X(t).
Решение.
оо
Ui
кх(т)= I Si (и) ег WTduj =2а I cos ujt а\о —
2а sin ujxt
■00
О
£,=^(0) = 201^.
График корреляционной функции показан на рис. 9.42, б.
305
9.43. Показать, что не существует никакой стационарной
случайной функции X(t)y корреляционная функция которой кх (т)
постоянна в каком-то интервале (—тг, тг) и равна нулю вне его.
Решение. Предположим противное, т.е. что существует
случайная функция X(t)f для которой корреляционная функция
равна Ь ^ 0при |т|< Tj и равна 0 при |т|> тх.
Попробуем найти спектральную плотность случайной
функции X(t):
1 °° 1 Tl h
Sx (<jj) = — I kx (t) cos u;t dr =— lb cos u;t dr = -.
TV J TV ^ TV (jJ
о о
Из этого выражения видно, что функция Sx (и;) для некоторых
значений w отрицательна, что противоречит свойствам
спектральной плотности, и следовательно, корреляционной функции
указанного выше вида существовать не может.
9.44. Найти спектральную плотность стационарной
случайной функции, у которой корреляционная функция задана
выражением
-Х2т2
kx(r) = Dxe
Решение. Имеем
5* (ш) = 2. fDxe-x2r2e-ibiTdT = ^ fe-xV-' "Чт.
2tv j 2tv j
—00 —00
Пользуясь известной формулой
оо i— АС-В2
fe-Ax2±2Bx-°dx = J-e~ л (Л>0)
J V А
— 00
и имея в виду, что г2 = — 1, получим
2 2
2
5:(u;) = ^JiLe"4X2=A-e4X
2tv VX2 2\Vt7
График этой функции подобен кривой нормального закона.
9.45. Показать, что взаимная корреляционная функция
&ту (МО стационарной случайной функции X(t) и ее производной
Y(t) = —Х(£) удовлетворяет условию
т. е. при перемене местами аргументов меняет знак.
306
Решение. ПустьКх(£, t') = А:а.(т),гдет — t' — t,
Rv(t,t') = M
X(t)±X(t')
at
d
dt'
M
X(t)X(t')
dt' dt'
Но т = t' — t, следовательно,
R (t,t') = — кх(т) —f
^ dr dt'
ат
С другой стороны,
Rjv(t',t) = -^Kx(t,t') = ±kx(r)^
at от at
что и требовалось доказать.
9.46*. Определить, обладает ли функция
-а т
Мт) = е-а
а
ch рт Ч sh (3|т
р
(а > О, р > 0)
свойствами корреляционной функции.
Решение. Нужно проверить выполнение следующих
свойств:
1)к,(0) >0; 2)ЛЛ-т) = *,(т); 3) |Л,(т)|< кх(0); 4) S» =
1 °°
= — / Al (т) е~г WT dr > 0 при любом и.
2тг ^ ~
— 00
Свойства 1) и 2) очевидны. Проверим остальные.
3) Так как функция кх(т) четная, достаточно исследовать ее
при т > 0:
v ' 2
IP
_ 1е-(а+3)
IP
Так как кх (0) = 1, нужно, чтобы это выражение по модулю не
превосходило единицы. Можно доказать, что при а < Р это
условие не выполняется, так как при т —> оо выражение е~^~^т будет
неограниченно возрастать. В случае а. = $ кх(т) = 1; при а > Р
кх(т)<1. Таким образом, свойство 3) выполняется только при
а > р.
307
1 °°
2тт J
-iwtdT=—Re\
2тс
—00
1 + ^
PJ
00
Ге-(а-|3+;Ш)т^т +
0
+
1-*
I PJ
00
JVa+3+iw>TrfT
0
a
= — Re J
2тф
P + a (3-a
P:
2тф
a — p
a —P+iu; a + P+iw
1
(a -p)2 + w2 (a + P)2 + и
2a
* [(a_p)2+u;2][(a + P)2+u;2]
при a > P (Re — действительная часть).
>0
При a = P имеем Sx(w) = 6(w)
Таким образом, функция kx{r) = e"QL
-а т
a
chpT + -shp|T
р
при
a > Р обладает всеми свойствами корреляционной функции.
Графики кх(т) и 5* (и) при a > (3 показаны на рис. 9.46, а и б.
*(т)
ir(a-(32)
LJ
<2
б
Рис. 9.46
9.47. Случайная функция X(t) имеет корреляционную функцию
(а > Р > 0). Случайная функция
-опт
кх(т) = е-а
d
ch ВтН—shSk
(3
Y(t) = —X(t). Найти ее корреляционную функцию А; (т) и
спекай
тральную плотность S * (u).
Решение. При нахождении ку (т) применяем свойства 3, 4 и
9 обобщенных функций (см. с. 270):
d\r\
MT) = --^T*.(T) = -d
dr
dr
-e ' 'a
dr
x
X
a
chpTH shp It
P
+ e
—a т
3 sh (Зт + a ch (31 т
d\T\)
~dV
308
d_
(32-a
l 0
+(3e-a|T|ch(3r
e-a|T| sh^T
,-.2 o2
a — p
(3
-ae~a|T| shPr^ +
<h
= (a'-3')e
2 \ -a It
a
chpT shpk
* , v «*, v .. ,2 2au;
5 j, (w) = Sx(l;) |iw| =
^2 q2
a — p
•к [(a-p)2+u;2][(a + P)2+u;2]
Так как предел lim A:w (т) существует (он равен к (0) = а2 — (З2),
то случайная функция X(t) дифференцируема.
9.48. Случайная функция X(t) с характеристиками mx(t) =
= t2 +3nKx(t:t') = 5ttf подвергается линейному преобразованию
вида
t
Y(t) = fTX(T)dT + t*.
о
Определить характеристики случайной функции Y(t): т (t) и
KAt,t').
Решение. my(t)= I т(т2 + 3) dr + t
о
4
+
4 2
3 **+3<2 se
Однородная часть рассматриваемого линейного преобразова-
ния будет L[°^{X(t)} = I тХ(т) ^.Следовательно,
о
* f
(V
Ky(t,t') = fdr Jtt'Kx(t, rf) drf =5 J тт fr^'dr'
о 0
0
0
5 .3,/3
9
9.49. Случайная функция X(t) с характеристиками
mx(t) = 0- Kx(t,t')
подвергается линейному неоднородному преобразованию:
к(0 = 40){ВД} + «р(*),
где4>(t) — неслучайная функция. Найти взаимную корреляционную
функцию ^(М О-
Решение. Имеем
X = X(t); Y(t) = L[V{X(t)},
309
так как при центрировании случайной функции Y(t) неслучайное
слагаемое ср (t) уничтожается.
Отсюда
Rxy(t,t') = M[X(t)Y(t')} = M[X(t) L[V {X'(t')}\^
= L[VM[X(t)X(t')} = L[VKx(t,t').
9.50. Случайная функция X(t), имеющая характеристики
mx(t) = 0 и Kx(t, t') — 3e~(t+t \ подвергается линейному
преобразованию вида
dX(t)
Y(t) = -t ^^ + JtX(t) dr + sin ut.
0
Найти корреляционный момент случайных величин Х(0) и
У(1) (т.е. двух сечений случайных функций: X(t) при t = 0 и Y(tf)
при£; = 1).
Решение. На основании решения предыдущей задачи
R^ (t,t') = L[?{Kx(t,t')},
где Ь[У — однородная часть линейного преобразования, применен-
ная по аргументу t'. В нашем случае
Rxv(t,t') = -3t'de~it+,t) +з[т'е-<*+т"><к' =
ч,ч / д, j
о
= 3i'e-((+t,) + Зе-( [е~1' (-*' - 1) + 1] = Зе~1 (1 - е-*').
Полагая < = 0; i' = 1, получаем
^х(о), к(1) = ^ (0.1) = 3 (1 - е-1) « 1,90.
9.51. В различных технических задачах, относящихся к
стационарным случайным процессам, часто пользуются в виде
характеристики так называемым «временем корреляции»
оо
тк =/|p(T)|dT>
0
где р(т) — нормированная корреляционная функция случайного
процесса.
На рис. 9.51, а время корреляции геометрически
интерпретируется заштрихованной площадью.
310
Найти время корреляции тк для стационарного случайного
процесса с нормированной корреляционной функцией вида
Р(т) =
1-а
О
т
при т G
при т ^
1 1)
а а)
а а)
где а > 0.
Решение. Изобразим на рис. 9.51, б график зависимости р (т).
Величина тк численно равна заштрихованной на рис. 9.51, б пло-
1 1 1
щади: тк = =
2 а 2а
t
а
Рис. 9.51
9.52. Найти время корреляции тк для стационарной случайной
функции X(t), нормированная корреляционная функция которой
имеет вид
р(т) = е-а|т| (а>0).
Как будет вести себя время корреляции при а —> 0 и а —> оо?
00
Решение. тк = / e~ardr = —.
J а
о
При а —> 0 случайная функция вырождается в случайную
величину и ее время корреляции тк —> оо. При а —> оо случайная
функция превращается в стационарный белый шум, а тк —> 0.
9.53. Найти время корреляции для стационарной случайной
функции X(t) с нормированной корреляционной функцией вида
р(т) = е-(ат)2.
Ответ. тк =
2а
311
9.54. В радиотехнике в качестве характеристики случайного
процесса иногда пользуются величиной А/э — «энергетической
шириной спектра» стационарной случайной функции:
1 °°
D
ш
х
^тах^^ 0
^тах^ 5тах2^
где Smax — максимальное значение спектральной плотности,
достигаемое в точке ш max: S тах = S(wmax );smax = -¾ Найти энергети-
^ X
ческую ширину спектра стационарной случайной функции,
нормированная корреляционная функция которой имеет вид
рЛт)
1 — а |т| при т €
v
о
при т ^
1 1
1
а а)
1 п
а а
где а > 0.
Решение. Нормированная спектральная плотность случай
ной функции X(t) имеет вид
00
5*(w) = - fp2:(T)cosu;TdT =
О
2a
тги;
1 — cos
Id
Oi)
Эта функция достигает своего максимума при ш = ш тах =0:
1
5х(шт) + 5
тах
ira
Имеем
Д/э =
а
5 max2'* 2
9.55. Показать, что для стационарной случайной функции с
нормированной корреляционной функцией
р(т) = е—'т',
независимо от значения а, произведение тк А/э равно 1/4.
Решение. Из задачи 9.52 имеем тк=—. Нормированная
a
спектральная плотность равна
312
8Ли) = ——2 27;
it (al + ш )
2
ее максимальное значение smax = —, откуда
тга
д, _ 1 it a _ 1
Тк э ~a 2-2тг~4'
9.56*. Показать, что для любой стационарной случайной
функции X(t), корреляционная функция которой неотрицательна
(К(т) ^ 0), произведение времени корреляции тк на
энергетическую ширину спектра Д/э равно 1/4.
Решение. В данном случае рх (т) > 0, поэтому
00 00
тк =/|p*(T)l*" = /p*(T)*"-
о о
Нормированная спектральная плотность выражается через
р2Г(т) интегралом
2°°
sx(u) = - [рх(т) cos ит dr.
о
Полагая в этой формуле w = О, имеем
2 ? , ч , 2
>Л°) = - ГрЛт)^т = -тк-
о
Покажем, что если р2Г(т) > 0, то максимум спектральной
плотности достигается в точке w = 0:
5 max =^(0).
Это непосредственно вытекает из оценки интеграла:
2 г 2 г
(ш) = - I рж(т)совшт <*г<- / рж(т)-1А- = 5ж(0).
о о
Таким образом, при р^. (т) > О
2
5 max =^(0) = -
откуда
Sx
тк; АД
ткА/э =
^^3
1
•
4
1
с
max
■2-к
1
4т '
313
9.57. На вход колебательного звена системы автоматического
регулирования, передаточная функция которой имеет вид
Тр2 +Ь + к
подается белый шум, спектральная плотность которого равна
5*(ш) = N. Определить дисперсию выходного сигнала \
Решение.
Nk
5;(ы) = 5-;(ы)|фоы)|' =
T(ju)2 +U« + *
откуда
00
".=/
Nktb
JjTUuY + iJbi + k
-KkN
Заметим, что дисперсия выходного сигнала не зависит от
постоянной времени колебательного звена Г, а зависит лишь от
коэффициента усиления к, коэффициента демпфирования £ и
мощности сигнала N
9.58. Передаточная функция системы, на которую подается
сигнал X(t), имеет вид
Ф(р) =
2 2
T{V +Р+к
где к = 25
; Тг = 0,05 [с].
Спектральная плотность входного сигнала
1 + ш2Г2 '
град
гдеГ=1[с],8ж=4
Требуется найти дисперсию выходного сигнала.
Решение.
5;(ы) = 5-:(ы)|Ф0ш)|2 =
-26
-^(ju^+l
а:
ГГ^ы)3 + (Г + Гх) О'ш)2 + (1 + *Г) ju + к
Подразумевается, что речь идет о достаточно удаленных участках времени, после
окончания переходных процессов.
314
0„ = b»,to=Af цм'+^см'+ц
а0агЬ2
-a2b0 +а0Ьг
a3
2a0(a0a3 -a^)
2
в нашем случае b0 = О, Ьх = — Гх , Ь2 = 1, а0 = ГГХ, аг = Т + Тг,
а2 = 1 + кТ, а3 = А;.
h - aib2
£у = 4тгГ6 — ^ -^0,0428 [град2].
2(a0a3 -ага2)
9.59. Случайная функция X(i) имеет математическое ожидание
mx(t) = 5n спектральную плотность
тг(1 + и;2)
Найти корреляционную функцию случайной функции X(i).
Решение. В задаче 9.17 было показано, что для
корреляционной функции вида Кх(т) = JDrz.e_a'T' спектральная плотность
имеет вид
тг (а2 + и;2)
- т
Следовательно, в нашем случае a = 1; Dx = 8; А^ (т) = 8е
9.60. Случайная функция X(t) имеет математическое ожидание
mx(t) = 8и спектральную плотность
„*, ч 20 5 + ш2
it 25 + 6ш2 + ш 4
Найти корреляционную функцию случайной функции Х(£).
Решение. В задаче 9.18 было показано, что для
корреляционной функции вида
М-О^е-^'созрт
спектральная плотность имеет вид
315
*;и=
Dxa а2 + f32 + ш
тг [а2+((3-и;)2][а2+((3+и;)2]
_ Дда а2 +Р2 +и;2
тг (a2 + f32)2+2(a2-f32)u;2+u;4'
Следовательно, а2 + |32 =5, а2 — |32 =3, откуда аг 2 = V4 = ±2.
Нас удовлетворяет только положительное значение корня: a = 2;
тогда (3 = ±1 (оба корня отвечают условиям задачи), а^ = — = 10.
a
Таким образом, кх (т) = 10е"2|т| cos т.
ГЛАВА 10
ПОТОКИ СОБЫТИЙ.
МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Потоком событий называется последовательность однородных
событий, появляющихся одно за другим в случайные моменты времени.
Примеры: поток вызовов на телефонной станции; поток забитых шайб при
игре в хоккей; поток сбоев ЭВМ; поток заявок на проведение регламентных
работ в вычислительном центре и т.п.
Поток событий наглядно изображается рядом точек с абсциссами
6l7 G2,..., Gn,... (рис. 10.0.1) с интервалами между ними: Тх = G2 — 017
Т2 = G3 — G2, ..., Тп = Gn+1 — 0п.При его вероятностном описании поток
событий может быть представлен как последовательность случайных
величин: Gj; G2 = Gj + Тг; G3 = Gj + 7} + T2; ... .
Заметим, что термин «событие» в понятии «поток событий»
совершенно отличен по смыслу от ранее введенного термина «случайное
событие». В частности, не имеет смысла говорить о вероятностях «событий»,
образующих поток (например, о «вероятности вызова» на телефонной
станции; ясно, что рано или поздно вызов придет, и не один). С «потоком
событий» можно связывать различные случайные события, например:
А = {в течение времени от t0 до ^ 4- т придет хотя бы один вызов}
или
В = {в течение того же времени придут ровно два вызова}.
Вероятности таких событий можно вычислять.
Заметим также, что на рисунке в виде ряда точек можно изобразить не
сам поток событий (он случаен), а только какую-то его конкретную
реализацию.
В гл. 5 упоминалось о потоках событий и некоторых их свойствах;
здесь осветим их более подробно. Поток событий называется
стационарным, если его вероятностные характеристики не зависят от выбора начала
отсчета или, более конкретно, если вероятность попадания того или дру-
Тх Т2 Т3 Z
4
о Gj е2 е3 е4*°
т„
*1 ©„ ©
t
п+1
Рис. 10.0.1
317
X(t)
0
1
©1
1 '
1—»
1 «
1 '
©2@3
1
1—1
» » L
L.
@n
Рис. 10.0.2
гого числа событий на любой интервал времени зависит только от длины т
этого интервала и не зависит от того, где именно на оси 0^ он расположен.
Поток событий называется ординарным, если вероятность попадания
на элементарный интервал времени Л t двух или более событий
пренебрежимо мала по сравнению с вероятностью попадания одного события.
Практически ординарность потока означает, что события в нем
появляются «поодиночке», а не группами по два, по три и т.д. (точное совпадение
моментов появления двух событий теоретически возможно, но имеет
нулевую вероятность).
Ординарный поток событий можно интерпретировать как случайный
процесс X{t) — число событий, появившихся до момента t (рис. 10.0.2).
Случайный процесс X{t) скачкообразно возрастает на одну единицу в
точках Gj, G2,..., Gn.
Поток событий называется потоком без последствия, если число
событий, попадающих на любой интервал времени т, не зависит от того,
сколько событий попало на любой другой не пересекающийся с ним интервал.
Практически отсутствие последствия в потоке означает, что события,
образующие поток, появляются в те или другие моменты времени
независимо друг от друга.
Поток событий называется простейшим, если он стационарен,
ординарен и не имеет последействия.
Интервал времени Г между двумя соседними событиями простейшего
потока имеет показательное распределение
f(t) = \e~xt (при t>0), (10.0.1)
где X = 1 / М[Т] — величина, обратная среднему значению интервала Т.
Ординарный поток событий без последствия называется пуассонов-
ским. Простейший поток есть частный случай пуассоновского (а именно
стационарный пуассоновский поток).
Интенсивностью X потока событий называется среднее число
(математическое ожидание числа) событий, приходящееся на единицу времен-
ни. Для стационарного потока X = const; для нестационарного потока
интенсивность в общем случае зависит от времени: \ = \(t).
Мгновенная интенсивность потока \(t) определяется как предел
отношения среднего числа событий, которые произошли за элементарный
интервал времени (t,t+At),K длине Д £ этого интервала, когда она
стремится к нулю. Среднее число событий, наступающих на интервале времени т,
следующем непосредственно за моментом t0 (см. рис. 10.0.1), равно
318
t0+r
a (^, т) = j \(t) dt Если поток событий стационарный, то a (^, т) =
— а (т) = Хт.
Ординарный поток событий называется потоком Пальма (или
рекуррентным потоком, или потоком с ограниченным последствием), если
интервалы времени Т\, Т2,... между последовательными событиями (см. рис.
10.0.1) представляют собой независимые, одинаково распределенные
случайные величины. В связи с одинаковостью распределений Т\, Т2,...
поток Пальма всегда стационарен. Простейший поток является частным
случаем потока Пальма; в нем интервалы между событиями
распределены по показательному закону (10.0.1), где X — интенсивность потока.
Потоком Эрланга k-го порядка называется поток событий,
получающийся «прореживанием» простейшего потока, когда сохраняется каждая
к-я точка (событие) в потоке, а все промежуточные выбрасываются (на
рис. 10.0.3 показано получение потока Эрланга 4-го порядка из
простейшего потока).
Интервал времени между двумя соседними событиями в потоке
Эрланга к-то порядка представляет собой сумму & независимых случайных
величин Tj, Т2,..., Тк, имеющих показательное распределение с
параметром X:
к
T = Y,Ti- (10.0.2)
г =1
Закон распределения случайной величины Тназывается законом
Эрланга k-го порядка (см. задачу 8.3) и имеет плотность
(fc-1)!
Математическое ожидание, дисперсия и среднее квадратическое
отклонение случайной величины Т (10.0.2) соответственно равны:
mt=k/\ Dt=k/\2- <jt=jkj\. (10.0.4)
Коэффициент вариации случайной величины (10.0.2) равен
vt =ot /mt =1 / 4k] (10.0.5)
vt —> 0 при k —> oo, т.е. при увеличении порядка потока Эрланга «степень
случайности» интервала между событиями стремится к нулю.
Если одновременно с «прореживанием» простейшего потока
изменять масштаб по оси 0t (делением на к), получится нормированный поток
Т
i * 1
-I—© •—• •—© •—• • ©—• t
r\ у у—л-у-л—у—л*-у"м г . г v у ;
г, т2 т3 т4
Рис. 10.0.3
319
*<t
?fa
Wo
Ч
fiuee)
■*/
о.
°J \>Z
к
^(настоящее)
Рис. 10.0.4
Эрланга fc-го порядка,
интенсивность которого не зависит от к.
Интервал времени Т между
соседними событиями в нормированном
потоке Эрланга к-то порядка имеет
плотность
Ш) =
к\ (Ш)
(*-1)
к-\
-Ш
(при f>0),
(10.0.6)
Числовые характеристики случайной величины
1 к
равны:
M\f\=l/\ D\f\=l/k\2; 5t=l/(\y[k); vt=l/y[k. (10.0.7)
При увеличении & нормированный поток Эрланга неограниченно
приближается к регулярному потоку с постоянным интервалом / = 1 / X
между событиями.
Случайный процесс, протекающий в какой-либо физической системе 5,
называется марковским (или процессом без последствия), если он обладает
следующим свойством: для любого момента времени ^ (рис. 10.0.4)
вероятность любого состояния системы в будущем (при t > ^) зависит только от ее
состояния в настоящем (при t=t^)une зависит от того, когда и каким
образом система S пришла в это состояние (иначе: при фиксированном
настоящем будущее не зависит от предыстории процесса — от прошлого).
В данной главе будем рассматривать только марковские процессы с
дискретными состояниями sly s2, ...s„. Такие процессы удобно
иллюстрировать с помощью графа состояний (рис. 10.0.5), где
прямоугольниками (или кружками) обозначены
состояния slf л,, .-• системы 5, а
стрелками — возможные переходы из
состояния в состояние (на графе
отмечаются только непосредственные
переходы, а не переходы через другие
состояния). Иногда на графе состояний
отмечают не только возможные
переходы из состояния в состояние, но и
возможные задержки в прежнем
состоянии; это изображается стрелкой
(«петлей»), направленной из данного
состояния в него же (рис. 10.0.6), но
можно обходиться и без этого. Число
состояний системы может быть как
конечным, так и бесконечным (но
счетным).
й
Рис. 10.0.5
Рис. 10.0.6
320
X(t)
6
5
4
3
2
1
О
-
-
...
1
1
1
—4
1
i
i
1
f
i
i
i
i
1
—*
i
1
i
1
'l
Рис. 10.0.7
Марковский случайный процесс с дискретными состояниями и
дискретным временем обычно называют марковской цепью. Для такого
процесса моменты tv t2, ..., когда система 5 может менять свое состояние,
удобно рассматривать как последовательные шаги процесса, а в качестве
аргумента, от которого зависит процесс, рассматривать не время t, а
номер шага: 1,2,..,¾... . Случайный процесс в этом случае характеризуется
последовательностью состояний
5(0), 5(1), 5(2),..., 5(*),...,
(10.0.8)
если 5(0) — начальное состояние системы (перед первым шагом); 5(1) —
состояние системы непосредственно после первого шага; ...; S(k) —
состояние системы непосредственно после fc-го шага ....
Событие {S(k) = s{ } = {сразу после k-го шага система находится в
состоянии st) (г = 1,2,...) является случайным событием, поэтому
последовательность состояний (10.0.8) можно рассматривать как
последовательность случайных событий. Начальное состояние 5(0) может быть как
заданным заранее, так и случайным. О событиях последовательности
(10.0.8) говорят,что они образуют марковскую цепь.
Рассмотрим процесс с п возможными состояниями s1? s2,..., sn. Если
обозначить X{t) номер состояния, в котором находится система 5 в
момент t, то процесс (марковская цепь) описывается целочисленной
случайной функцией X(t) > 0, возможные значения которой равны 1,2,..., п. Эта
функция совершает скачки от одного целочисленного значения к другому
в заданные моменты tv Ц,... (рис. 10.0.7) и является непрерывной слева,
что отмечено точками на рис. 10.0.7.
Рассмотрим одномерный закон распределения случайной функции
X(t). Обозначим через р{(к) вероятность того, что после А:-го шага
[и до (&+ 1)-го] система 5будет в состоянии sz = (г = 1, 2,..., п).
Вероятности р{(к) называются вероятностями состояний цепи Маркова.
Очевидно, для любого к
п
Е Pi w =L
(10.0.9)
i =1
321
Распределение вероятностей состояний в начале процесса
д(0), р2(0),.... Pi (0),..., р„(0) (10.0.10)
называется начальным распределением вероятностей марковской цепи.
В частности, если начальное состояние 5(0) системы 5 в точности
известно, например 5(0) = s{, начальная вероятность р{ (0) = 1, а все остальные
равны нулю.
Вероятностью перехода на к-и шаге из состояния s{ в состояние Sj
называется условная вероятность того, что система 5 после к-то шага
окажется в состоянии sjf при условии, что непосредственно перед этим (после
к — 1 шагов) она находилась в состоянии s{. Вероятности перехода иногда
называются также «переходными вероятностями».
Марковская цепь называется однородной, если переходные
вероятности не зависят от номера шага, а зависят только от того, из какого
состояния и в какое осуществляется переход:
Р {S(k) = Sj\S (к-1) = 5- } = P{j. (10.0.11)
Переходные вероятности однородной марковской цепи P{j образуют
квадратную таблицу (матрицу) размером п х n:
(10.0.12)
£Рд- = 1 (г =1, ...,п). (10.0.13)
■3=1
Матрицу, обладающую таким свойством, называют стохастической.
Вероятность Ри есть не что иное, как вероятность того, что система,
пришедшая к данному шагу в состояние s{, в нем же и задержится на
очередном шаге.
Если для однородной цепи Маркова заданы начальное распределение
вероятностей (10.0.10) и матрица переходных вероятностей (10.0.12), то
вероятности состояний системы pi (к) (г = 1, 2,..., п) могут быть
определены по рекуррентной формуле
Pi (*) = J2 Pj(k - 1) P{j (i = 1, ..., n; j = 1,..., n). (10.0.14)
3=1
Для неоднородной цепи Маркова вероятности перехода в матрице
(10.0.12) и формуле (10.0.14) зависят от номера шага к.
Для однородной цепи Маркова, если все состояния являются
существенными, а число состояний конечно, существует предел lim Р{ (и) = Р{|,
Ml М2-" MJ-" Мп
Р Р Р Р
V
Р Р Р Р
1 п\ л п2"' х nj"' х пп
322
определяемый из системы уравнений
п п
Р{ = ^2 PjPji и Y2 ^ = *• Сумма переход-
з=\ i =1
ных вероятностей в любой строке
матрицы равна единице.
При фактических вычислениях по
формуле (10.0.14) надо в ней учитывать не все
состояния sjf а только те, для которых пе- рис 10.0.8
реходные вероятности отличны от нуля,
т.е. те, из которых на графе состояний ведут стрелки в состояние s{.
Марковский случайный процесс с дискретными состояниями и
непрерывным временем иногда называют «непрерывной цепью Маркова». Для
такого процесса вероятность перехода из состояния sz в s ■ для любого
момента времени равна нулю. Вместо вероятности перехода P{j
рассматривают плотность вероятности перехода \ijf которая определяется как
предел отношения вероятности перехода из состояния s{ в состояние s- за
малый промежуток времени At, примыкающий к моменту t, к длине этого
промежутка, когда она стремится к нулю. Плотность вероятности
перехода может быть как постоянной (\{j = const), так и зависящей от времени
[\„ = \у(£)]. В первом случае марковский случайный процесс с
дискретными состояниями и непрерывным временем называется однородным.
Типичный пример такого процесса — случайный процесс X(t),
представляющий собой число появившихся до момента t событий в простейшем
потоке (см. рис. 10.0.2).
При рассмотрении случайных процессов с дискретными состояниями
и непрерывным временем удобно представлять себе переходы системы S
из состояния в состояние как происходящие под влиянием некоторых
потоков событий; при этом плотности вероятностей перехода получают
смысл интенсивностей \{j соответствующих потоков событий (как только
происходит первое событие в потоке с интенсивностью Xi;, система из
состояния s{ скачком переходит в s-). Если все эти потоки пуассоновские
(т. е. ординарные и без последствия, с постоянной или зависящей от
времени интенсивностью), то процесс, протекающий в системе 5, будет
марковским.
Рассматривая марковские случайные процессы с дискретными
состояниями и непрерывным временем, очень удобно пользоваться
графом состояний, на котором против каждой стрелки, ведущей из
состояния 5^в 5;, проставлена интенсивность Х^ потока событий, переводящего
систему по данной стрелке (рис. 10.0.8). Такой граф состояний
называют размеченным^.
Вероятность того, что система S, находящаяся в состоянии sif за
элементарный промежуток времени (£, t+ dt) перейдет в состояние 5;
(элемент вероятности перехода из s{ в s), есть вероятность того, что за это вре-
' На графе состояний системы с непрерывным временем мы не будем проставлять
петли, соответствующие задержке системы в данном состоянии, так как такая
задержка всегда возможна.
323
мя ^появится хотя бы одно событие потока, переводящего систему 5из sz
в Sj. С точностью до бесконечно малых высших порядков эта вероятность
равна \{jdt.
Потоком вероятности перехода из состояния s{ в s- называется
величина \ijPi (t) (здесь интенсивность Х^ может быть как зависящей, так и
независящей от времени).
Рассмотрим случай, когда система 5 имеет конечное число состояний
s1? 52,..., sn. Для описания случайного процесса, протекающего в этой
системе, применяются вероятности состояний
ft(*)>ft(*),->P„(*), (10.0.15)
где Pi (t) — вероятность того, что система 5в момент t находится в
состоянии s{.
p.(i) = p{S(i) = *.}. (10.0.16)
Очевидно, для любого t
£>(*) = 1- (10.0.17)
г =1
Для нахождения вероятностей (10.0.15) нужно решить систему
дифференциальных уравнений (уравнений Колмогорова), имеющих вид
dPi (t)
п п
dt j=1 ,-_!
или, опуская аргумент t у переменных р{,
dPi
Е W) - Pi (*)Ех* (* = *>2- •••> п)>
п п
м =ЕХЛ-^ЕЧ- (t=l,2,...,n). (10.0.18)
Напомним, что интенсивности потоков X» могут зависеть от времени t
(аргумент t для краткости написания опущен).
Уравнения (10.0.18) удобно составлять, пользуясь размеченным
графом состояний системы и следующим мнемоническим правилом:
производная вероятности каждого состояния равна сумме всех потоков
вероятности, переводящих из других состояний в данное, минус сумма всех
потоков вероятности, переводящих из данного состояния в другие.
Например, для системы 5, размеченный граф состояний которой дан на
рис. 10.0.8, система уравнений Колмогорова имеет вид
dpi I dt= Х31р3 + \iP4 ~ (\2 + \а) Pv
dp2 / dt = \12рг - X23p2;
dp3 J dt = X23p2 - (X31 + X34 + X35) p3; (10.0.19)
dpA I dt= \upx + X34p3 + X51p5 - X41p4;
dpb I dt= \3bPl -X54p5.
324
Так как для любого t выполняется условие (10.0.17), можно любую из
вероятностей (10.0.15) выразить через остальные и таким образом
уменьшить число уравнений на одно.
Чтобы решить систему дифференциальных уравнений (10.0.18) для
вероятностей состояний pl(t), p2{t), •••» рп(0>нУжнозаДатьначальноеРас"
пределение вероятностей
Pi(0),P2(0),...,pz(0),...,pn(0),
(10.0.20)
сумма которых равна единице:
п
Е р* (°)
i =1
Если, в частности, в начальный момент t = 0 состояние системы S в
точности известно, например, 5(0) = s{, то р{ (0) = 1, а остальные веротно-
сти (10.0.20) равны нулю.
Во многих случаях, когда процесс, протекающий в системе, длится
достаточно долго, возникает вопрос о предельном поведении
вероятностей р{ (t) при t —► оо. Если все потоки событий, переводящие
систему из состояния в состояние, являются простейшими (т.е.
стационарными пуассоновскими с постоянными интенсивностями Ху), в
некоторых случаях существуют финальные (или предельные) вероятности
состояний
р{ = lim р{(Ь) (i =1,..., n),
(10.0.21)
•oo
не зависящие от того, в каком состоянии система S находилась в
начальный момент. Это означает, что с течением времени в системе 5
устанавливается предельный стационарный режим, в ходе которого она переходит
из состояния в состояние, но вероятности состояний уже не меняются.
В этом предельном режиме каждая финальная вероятность может быть
истолкована как среднее относительное время пребывания системы в
данном состоянии.
Система, для которой существуют финальные вероятности,
называется эргодической и соответствующий случайный процесс — эргодическим.
Для существования финальных вероятностей состояний одного
условия \у = const недостаточно, требуется выполнение еще
некоторых условий, проверить которые можно по графу состояний, выделив
на нем «существенные» и
«несущественные» состояния. Состояние s{
называется существенным, если нет другого
состояния Sj такого, что, перейдя однажды
каким-то способом из szb sjt система уже
не может вернуться в sz. Все состояния,
не обладающие таким свойством,
называются несущественными.
Например, для системы S, граф
состояний которой дан на рис. 10.0.9, со- рис wqq
325
sl
/ "
5з *_
S2
>YJ^
54 „ 5,
Рис. 10.0.10
стояния sv s2 несущественны (из вг можно
уйти, например, в s2 и не вернуться, а из s2 в s4
или 55 и не вернуться), а состояния s4, s5, s3, s6,
57 — существенны (существенные состояния
обведены жирными линиями).
При конечном числе состояний п для
существования финальных вероятностей
необходимо и достаточно, чтобы из каждого
существенного состояния можно было (за какое-то число шагов) перейти в
каждое другое существенное. Граф, представленный на рис. 10.0.9, этому
условию не удовлетворяет (например, из существенного состояния s4
нельзя перейти в существенное состояние s6); для графа, показанного на
рис. 10.0.10, финальные вероятности существуют (из каждого
существенного состояния возможен переход в каждое другое существенное).
Несущественные состояния потому так и называются, что из каждого
такого состояния система рано или поздно уйдет в какое-то из
существенных и больше не вернется. Естественно, финальные вероятности для
несущественных состояний равны нулю.
Если система Sимеет конечное число состояний s^, s2,..., sn, то для
существования финальных вероятностей достаточно, чтобы из любого
состояния системы можно было (за какое-то число шагов) перейти в любое
другое. Если число состояний sx, s2,..., sn,... бесконечно, то это условие
перестает быть достаточным, и существование финальных вероятностей
зависит не только от графа состояний, но и от интенсивностей \{j.
Финальные вероятности состояний (если они существуют) могут
быть получены решением системы линейных алгебраических уравнений,
они получаются из дифференциальных уравнений Колмогорова, если
положить в них левые части (производные) равными нулю. Однако удобнее
составлять эти уравнения непосредственно по графу состояний,
пользуясь мнемоническим правилом: для каждого состояния суммарный
выходящий поток вероятности равен суммарному входящему. Например, для
системы S, размеченный граф состояний которой дан на рис. 10.0.11,
уравнения для финальных вероятностей состояний имеют вид
(Х12 + \г)Р\ = X2lP25
(\21 + Х24)р2 = Х12Р! + Х42Р4;
(\34 4- Х35)р3 = \zPv
Х42 Р\ = Х24Р2 + ^34^3 + ^54^
(10.0.22)
Рис. 10.0.11
Х54 Pb = Х35РЗ'
Таким образом, получается (для системы 5
с п состояниями) система п линейных
однородных алгебраических уравнений с п
неизвестными р1? р2,..., рп. Из этой системы можно
найти неизвестные рг, р2,..., рп с точностью до
произвольного множителя. Чтобы найти точ-
326
X
о
\
*Ь
М-1
1^
\i2
X
X
>к-1
Мз
к-1
M-jfe
X
X
А:»
М*+1
'п-1
п-1
М-п
п
Рис. 10.0.12
ные значения рг,..., рп, к уравнениям добавляют нормировочное условие
Рх + р2+ ■•• 4- pn = 1, пользуясь которым можно выразить любую из
вероятностей р{ через другие (и соответственно отбросить одно из
уравнений).
На практике очень часто приходится встречаться с системами, граф
состояний которых имеет вид, показанный на рис. 10.0.12 (все
состояния можно вытянуть в цепь, причем каждое из них связано прямой и
обратной связью с двумя соседними, кроме двух крайних, каждое из
которых связано только с одним соседним). Схема, изображенная на
рис. 10.0.12, называется схемой гибели и размножения. Это название
заимствовано из биологических задач, где состояние популяции sk Ьзнача-
ет наличие в ней к единиц. Переход вправо связан с «размножением»
единиц, а влево — с их «гибелью». На рис. 10.0.12 «интенсивности
размножения» (Х0, Х1?..., Xn_j) проставлены у стрелок, ведущих слева
направо, «интенсивности гибели» (м-и Ц2» •••> M-n-i) — У стрелок, ведущих
справа налево; каждая из них отмечена индексом того состояния, из
которого исходит соответствующая стрелка.
Для схемы гибели и размножения финальные вероятности состояний
выражаются формулами:
Pi
X
о
M-i
р0; Vi
W
H<lH<2
р0;
•»
Л п A-i . .. Л i, 1
Рк = -2-1 — Ро
И-гйг—И1*
I Л/ ~~ \J . .... II/ j .....
рп = -iLJ—— р0; Ро
1 + -½° + XnX
o/xi , , X0X1...Xn_1
M-l H<lH<2
1^1^2- * •№n
(10.0.23)
Обратим внимание на правило вычисления любой вероятности
состояния (при/г = 1, 2,..., п)
Рк
\Q\l...\k_l
\Xl\X2"-\Xk
Ро
которое можно сформулировать так: вероятность любого состояния в
схеме гибели и размножения (см. рис. 10.0.12) равна дроби, в числителе
которой стоит произведение всех интенсивностей размножения, стоящих
левее s^ а в знаменателе — всех интенсивностей гибели, стоящих левее sk,
умноженной на вероятность крайнего левого состояния pQ.
Если процесс описывается схемой гибели и размножения, то можно
записать дифференциальные уравнения для математического ожидания
327
и дисперсии случайной функции X(t) — числа единиц в системе в момент
времени t
dmx(t)
dt
£(^-^)^(^
(10.0.24)
k=0
dt
П
£ [К + »к + Ы (\k - щ) - 2mz(t) (\k - pk)] Pk(t).(10.0.25)
k=0
В этих формулах нужно полагать \n = \i0 =0. Интенсивности
ХЛ(0 < к < п — 1)и|х^ (1 < к < п) могут быть любыми неотрицательными
функциями времени.
При достаточно больших значениях mx(t) (> 20) и выполнении
условия 0 < mx(t)± &yJDx(t) < п можно приближенно полагать, что сечение
случайной функции X(t) представляет собой нормальную случайную
величину с параметрами mx{t), y/Dx(t)f полученными решением уравнений
(10.0.24), (10.0.25). Формулы (10.0.24) и (10.0.25) остаются
справедливыми при п —> оо, если верхний предел в суммах заменить на оо.
10.1. Производится наложение («суперпозиция») двух
простейших потоков: 1) потока I с интенсивностью \г и 2) потока II с
интенсивностью Х2 (рис. 10.1). Будет ли поток III, получившийся
в результате суперпозиции, простейшим, и если да, то с какой
интенсивностью?
т
тт
110
ттт
1110
'■'"?
i
i
i
i
Т Т '
1 Т 1 Т
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
кк кк
Т
1
1
1
1
д
Т
• Т
i i
i i
i i
i i
к л
Т
i
i
i
i
▲
т
?■
i i
i >
i i
i i
*1
Т
| Т ТТ
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
к к кЛ
Т
• т
1 1
1 1
> 1
> 1
к А
t
Рис. 10.1
Решение. Да, будет, так как свойства стационарности,
ординарности и отсутствия последействия сохраняются;
интенсивность потока III равна \г + Х2.
10.2. Производится случайное прореживание простейшего
потока событий с интенсивностью X; каждое событие, независимо от
других, с вероятностью р сохраняется в потоке, а с вероятностью
1 — р выбрасывается (в дальнейшем такую операцию будем
называть ^-преобразованием потока). Каким будет поток,
получающийся в результате р-преобразования простейшего потока?
Решение. Поток будет простейшим с интенсивностью \р.
Действительно, все свойства простейшего потока
(стационарность, ординарность, отсутствие последействия) при р-преобразо-
вании сохраняются, а интенсивность умножается на р.
328
10.3. Интервал времени Т между событиями в ординарном
потоке имеет плотность
/(*)
Хе-М'-'о) при t>t0;
0 при t < t0.
(10.3)
Интервалы между событиями независимы. 1) Построить
график плотности f(t). 2) Является ли данный поток простейшим?
3) Является ли он потоком
Пальма? 4) Какова его интенсивность X?
5) Каков коэффициент вариации vt
интервала между событиями?
Решение. 1) См. рис. 10.3;
распределение такого вида назовем
«сдвинутым на t0 показательным».
2) Нет, не является, так как
распределение (10.3) непоказательное.
3) Да, является в силу ординарности
потока, независимости интервалов и
одинакового их распределения.
Рис. 10.3
4)Х = 1/М[Г]; М[Г] = 1/\ + *0; Х=(1 / X + *0) = Х/(1 + Х*0).
5)D[r] = i; crf=±;
cr,
V,
1/Х
М[Г] 1 / X + t0 1 + X*
о
10.4. На оси 0t имеется простейший поток событий с
интенсивностью X. Из этого потока формируется другой следующим
образом: интервал между каждыми двумя соседними событиями
делится пополам и в точку деления вставляется еще одно событие
(на рис. 10.4 где кружками обозначены основные, крестиками —
вставленные события). Найти плотность распределения f(t)
интервала Т между соседними событиями в новом потоке. Будет ли
этот поток простейшим? Будет ли он потоком Пальма? Каков
коэффициент вариации интервала Т между событиями?
Решение. Т = X /2, где X имеет показательное
распределение с параметром \:/г(х) — \е~Хх(х > 0). Пользуясь решением
задачи 8.1 и полагая в формуле (8.1) а = 1/2; 6 = 0, получаем
-2\*
f(t) = 2\e-lM{t>0).
(10.4)
Это есть показательное распределение с коэффициентом
вариации vt = 1. Тем не менее новый поток не будет ни простейшим,
ни даже потоком Пальма. Докажем сначала, что он не будет
потоком Пальма. Хотя интервалы между событиями распределены
одинаково по закону (10.4), они не являются независимыми. Рас-
329
нэ-х© х ©х©—х-©—х-<*>© х ©—х—©—г
о
Рис. 10.4
смотрим два соседних интервала между событиями потока. С
вероятностью 1/2 они независимы, с вероятностью 1/2 равны друг
другу, следовательно, зависимы. Таким образом, новый поток
событий — не пальмовский. Естественно, он не будет и простейшим,
так как простейший поток — частный случай пальмовского.
Таким образом, показательное распределение интервала
между событиями — недостаточное условие для того, чтобы поток
был простейшим.
10.5. Условия те же, что и в предыдущей задаче, с той
разницей, что преобразованный поток состоит только из «крестиков»
(середин интервалов). Ответить на те же вопросы, что и в
предыдущей задаче.
Решение. Очевидно, что интенсивность нового потока по
сравнению с интенсивностью исходного не изменится и останется равной
X. Интервал между двумя соседними крестиками (рис. 10.5) равен
Т = (Х{ +Х1+1)/2, (10.5)
где Х{, Х{ +1 — два соседних интервала исходного потока. Величины
Xi9 Xi+l распределены обе по показательному закону с параметром
X, а их полусумма (10.5) — по нормирован-
X Х- ному закону Эрланга 2-го порядка, так как
' *' —* —fr~fo t интервал Гравен сумме двух независимых
' i—' показательно распределенных случайных
величин, деленной на два. Таким образом,
Рис. 10.5 интервал Т между двумя крестиками
имеет плотность/(0 = 4\Че~2™ (* > 0).
В преобразованном потоке все соседние интервалы времени
будут зависимы, так как в состав этих интервалов входят одни и
те же случайные величины. Однако эта зависимость
распространяется только на соседние интервалы времени. Такие потоки
иногда называют потоками со слабым последействием.
Коэффициент вариации vt для случайной величины Т будет
равен [см. формулу (10.0.7)] vt = 1 / V2 < 1.
10.6. Поток автомобилей, движущихся по шоссе в одном
направлении, представляет собой простейший поток с
интенсивностью X. Человек выходит на шоссе, чтобы остановить первый
попавшийся автомобиль, движущийся в данном направлении.
Найти закон распределения времени Т, которое ему придется ждать;
определить его математическое ожидание mt и среднее квадрати-
ческое отклонение ot.
330
Решение. Так как простейший поток не обладает
последействием, то «будущее» не зависит от «прошлого», в частности, от
того, сколько времени тому назад прошел последний автомобиль.
Распределение времени Т точно такое же, как и распределение
промежутка времени между появлением соседних автомобилей,
т.е. показательное с параметром \:f(t) = \е~и (t < 0); отсюда
Примечание. Если поток автомобилей, идущих по шоссе, является
многорядным, то его можно рассматривать как суперпозицию нескольких
потоков, соответствующих каждому ряду. Если каждый поток —
простейший, то результат суперпозиции также является простейшим потоком,
так как свойства стационарности, ординарности и отсутствия
последействия при суперпозиции сохраняются (см. задачу 10.1).
10.7. Пассажир выходит на остановку автобуса в некоторый
момент времени, никак не связанный с расписанием движения.
Автобусы следуют друг за другом регулярно с интервалом
времени длины I Найти закон распределения времени Г, которое
придется пассажиру ждать автобуса, и выразить его характеристики
mt, ot через интенсивность потока автобусов X.
Решение. Момент прихода пассажира распределен с
постоянной плотностью на интервале длины I между двумя автобусами;
плотность распределения времени ожидания Т будет также
постоянная равномерное распределение на интервале (0, 1)]:
f(t) = 1/1 (0 < t < I) или, обозначая 1/1 = X, f(t) = X (0 < t < 1/Х).
Для равномерного распределения на участке длины 1/Х имеем
mt=l/(2X); Д=1/(12Х2); а, = 1 / (2л/ЗХ); vt = 1 / л/3.
10.8*. На оси 0£ имеется пальмовский поток событий,
интервалы между которыми распределены с плотностью /(£). На ось 0£
случайным образом бросается точка £* (например, прибывает
«инспектор», наблюдающий за появлением событий, или же
«пассажир» появляется на остановке автобуса), причем момент t* никак
не связан с моментами появления событий потока (рис. 10.8).
Найти плотность распределения того интервала Г*, на который
попала точка £*, его математическое ожидание, дисперсию и
среднее квадратическое отклонение.
Решение. С первого взгляда может показаться, что эта
плотность — такая же, как плотность распределения f(t) любого
интервала Т между событиями, однако это не так. Тот факт, что на
участок Г* попала случайно брошенная точка £*, меняет его
-к-
о "—^ ^ г*
Рис. 10.8
331
распределение; действительно, если на оси (И есть разные участки
(большие и маленькие), то с большей вероятностью точка £*
попадет на один из больших участков.
Найдем плотность распределения f*(t) того участка Т*, на
который попала точка £*. Для этого найдем элемент вероятности
/* (t) dt, равный вероятности того, что точка £* попадет на
промежуток, длина которого заключена в пределах (t,t + dt). Эта
вероятность приближенно равна отношению суммарной длины всех
таких промежутков на очень большом интервале времени Q к
полной длине этого интервала.
Пусть на очень большом интервале Q уложилось большое
число N промежутков между событиями. Среднее число
промежутков, длина которых лежит в пределах (t,t + dt), равна Nf(t)dt\
средняя суммарная длина всех таких промежутков приближенно
равнаtNf{t) dt. Средняя же общая продолжительность всех
7Vпромежутков на участке Q будет (приближенно) равна Nmp где
оо
mt — М[Т] = / tf(t) dt. Разделив одно на другое, получим
о
Nmt mt
Это равенство выполняется тем точнее, чем более длительный
интервал времени Q будет рассматриваться (чем больше N). В
пределе закон распределения случайной величины Т* будет
/*(*) = —/(*)(*><>)• (10.8)
1 °° 1 1
M[T*] = -Lf*2/(0<ft = — а2(*) = — (А+го,2);
D[T*] = a2[T*] - (M[T*])2 - — /V/(0 dt - (M[T*])2.
1 о
10.9. В условиях задачи 10.8 поток Пальма представляет собой
простейший поток с интенсивностью X, т.е. f(t) = \e~xt (t>0).
Найти плотность /* (t) того интервала Т*, на который попадает
точка t*.
Решение. С учетом того что mt = 1 / X, формула (10.8) дает
/* (t) = \2te~u (t > 0), что представляет собой не что иное, как
закон Эрланга 2-го порядка [см. формулу (10.0.3) при к= 2].
10.10*. На оси 0t имеется пальмовский поток событий с
плотностью f(t) интервала Т между соседними событиями. Случайная
точка £*(«инспектор») попадает куда-то на интервал Т* (рис. 10.10).
332
Она делит его на два промежутка: Q — £_
от ближайшего предыдущего события —• х ■•— t
до t* и Я — от t* до ближайшего после- Q ** Н
дующего события. Найти
распределение обоих этих промежутков. ^ис- Ю.10
Решение. Предположим, что
случайная величина Т* приняла значение s: Т* — 5, и найдем
условное распределение промежутка Q при этом условии. Обозначим
его плотность fQ(t \s). Так как точка t* бросается на ось Ot
совершенно случайно (безотносительно к событиям потока), очевидно,
она будет иметь равномерное распределение в пределах
промежутка Т* = s:
fq(t\s) = l/s при 0<t<s. (10.10.1)
Чтобы найти безусловное распределение fq(t), надо осреднить
плотность (10.10.1) с «весом» /*(s). Пользуясь формулой (10.8),
получаем
со
f*(s) = —f(s); fQ(t)= f fQ(t\s) f* (s) ds.
Учитывая, что fq(t\s) отлично от нуля только при s > t, можно
написать
со 1 со
/«(*)= [—f{s)ds = -L[№dt = -L-[i-F(t)],
J sm+ т+ J га,
о t t о t
где F(t) — функция распределения интервала Тмежду событиями в
потоке Пальма.
Итак,
/g(0 = —[1-F(*)]. (Ю.10.2)
mt
Очевидно, то же распределение будет иметь и промежуток
времени Я = Г*~ Q:
/я(0 = — [1-^(0]. (10.10.3)
10.11. Пользуясь результатами предыдущей задачи, проверить
решение задачи 10.6, полученное из других соображений.
Решение. Имеем f(t) = \e~U] F(t) = l-e~™ (t >0);mt=l/\.
По формуле (10.10.3)
/я (0 = X [1 - 1 + e~xt} = \е~и (t > 0),
т.е. задача 10.6 решена верно.
333
10.12. Пассажир выходит на остановку автобуса в момент
времени, никак не связанный с расписанием. Поток автобусов
представляет собой поток Пальма с интервалами, имеющими
равномерное распределение в пределах от 5 до 10 мин. Найти: 1)
плотность распределения того интервала между автобусами, на
который попал пассажир; 2) плотность распределения времени Я,
которое ему придется ждать автобуса; 3) среднее время ожидания
автобуса.
/*(0
о
10
а
Рис. 10.12
2)
F(t) = -
Решение. Имеем/(^) = 1/5 при£ е (5,10); mt =7,5.
1) По формуле (10.8) /*(*) = */37,5 при £ е (5,10). График
плотности f*(t) показан на рис. 10.12, а.
0 при t < 5;
(£-5)/5 при 5<£<10;
1 при t > 10.
Отсюда по формуле (10.10.3)
г0 при
1 / 7,5 при
(10-0/37,5 при
0 при
/я(0 =
t <0;
0 < t < 5;
5 < t < 10;
t >10.
График плотности /я (t) показан на рис. 10.12, б.
3) Среднее время ожидания
га
н — I —dt + / t—^-^-dt «6,11 [мин],
n ' j5
37,5
10.13. Рассматривается поток Эрланга А;-го порядка с
плотностью распределения интервала Т между событиями:
/*(*)=
х {\tf-
(А-1)
■XI!
е~м (*>0).
(10.13.1)
334
Найти функцию распределения Fk( t) этого интервала.
Решение. Можно было бы найти функцию распределения
по обычной формуле
t
Fk(t) = Jfk(t)dt,
О
но проще найти ее исходя непосредственно из определения
Fk(t) = P{T<t}.
Перейдем к противоположному событию и найдем Р{Т > t}.
Свяжем начало отсчета 0 с одним из событий потока Эрланга и
отложим от него вправо два участка: Т
(расстояние до следующего события потока Эр- t Т
ланга) и t<T (рис. 10.13).
Для выполнения неравенства Т > t
нужно, чтобы на участок t попало меньше чем к
событий простейшего потока с
интенсивностью X (либо 0, либо 1,..., либо к— 1).
Вероятность того, что на участок t попадет га событий, равна
га!
По правилу сложения вероятностей
га
е
га=0
*-* {\t)m
Р{г>*} = Е1-т-в'
Т^ ml
откуда
*-г (х*г __xt
Fn (t) = l- ЕМ" е = 1 - Д (* - 1, X*), (10.13.2)
га-0
га!
где 1 — R (га, а) — табулированная таблица (см. табл. 1 прил. 1).
10.14*. Поток отказов ЭВМ представляет собой поток Эрланга
А;-го порядка с плотностью (10.13.1) интервала между отказами
(восстановление машины после отказа происходит мгновенно).
«Инспектор» прибывает в случайный момент времени £* и
ожидает первого отказа. Найти плотность распределения времени Я, в
течение которого ему придется ждать отказа, и его
математическое ожидание гая.
Решение. По формуле (10.10.3)
/я(<) = — [1-**(<)],
mt
где Fk(t) дается формулой (10.13.2), a mt — к / X. Отсюда
335
Ш = ±Е^е^ =lgM^T e-x< (i>0). (10.14.1)
Перепишем формулу (10.14.1) в виде
к^ (г-1)!
Из (10.14.2) видно, что случайная величина Я имеет
распределение, «смешанное» из к эрланговских распределений разных
порядков; с одинаковой вероятностью \/к она имеет эрланговское
распределение го порядков. Математическое ожидание
такой случайной величины найдем по формуле полного
математического ожидания:
тн = М[#] - - VM[#|r], (10.14.3)
к г=1
где М[#| г] — условное математическое ожидание случайной
величины Я при условии, что она распределена по закону Эрланга r-го
порядка.
Находим по первой формуле (10.0.4) М[Н\г) = г / X, откуда
1 * (* + 1)* к + l ,лп4/ ,\
гпи = — Vr — — = . (10.14.4)
к\^ 2к\ 2Х }
10.15*. Пальмовский поток событий с плотностью
распределения /*(£) интервала между событиями подвергается р-преобразо-
ванию (см. задачу 10.2). Случайная величина V— интервал между
событиями в преобразованном потоке. Найти математическое
ожидание и дисперсию случайной величины V.
Решение. Случайная величина V представляет собой сумму
случайного числа независимых случайных величин (см. задачу
8.63): V = У2Тк1 где Y — дискретная случайная величина, имею-
к=\
щая геометрическое распределение Р {Y = га} = pq m_1 (га = 1,
2,... ),q = 1 — р, а каждая из случайных величин Тк имеет
распределение f(t).
Тогда последовательные интервалы между событиями в р-пре-
образованном потоке будут
Ух Y2
к=1 г =1
где случайные величины Vv V2,... независимы, и преобразованный
поток есть поток Пальма. В соответствии с задачей 8.63
336
га
rnv =
P
Dv =
D
1 +™\\
V
V
где
00
00
mt=Jtf(t)dt; Dt=f(t-mt)2f(t)dt.
0
0
Примечание. Можно доказать, что при многократном р-преобра-
зовании потока Пальма получается поток, близкий к простейшему.
10.16. Найти закон распределения интервала Т между
событиями в потоке Пальма, если случайная величина Т определяется из
выражения Т = V^Tj., т.е. представляет собой сумму случайного
числа случайных слагаемых, где случайные величины Тк
независимы и подчинены показательному закону с параметром X, а
случайная величина Y не зависит от них и имеет геометрическое
распределение, начинающееся с единицы: рп = Р {Y = п} = pq п~1 х
х (0< р< 1; п = 1,2,3,...).
Решение. В задаче 8.62 было показано, что случайная
величина Т подчинена показательному закону с параметром Хр,
следовательно, рассматриваемый поток Пальма является простейшим с
интенсивностью Хр, который получается путем р-преобразования
простейшего потока с интенсивностью X. Это подтверждает
правильность решения задачи 10.2.
10.17. Поток автобусов, приходящих на остановку,
представляет собой поток Пальма; интервал Т между ними имеет плотность
распределения fT (t). Автобус находится на остановке в течение
неслучайного времени т. Пассажир, подойдя к остановке в
случайный момент t* (рис. 10.17, а), садится в автобус, если тот находит-
Тх
"Л г
-X-
t* т'
Зона
захвата
а
Зона
захвата
Зона
захвата
е?^ ^^ vtm vm^—^^m
np*
Г*-(т-т')
-X-
V
t
-"-г-'
т т
в
Рис. 10.17
337
ся на остановке; если же автобуса нет, то ждет его в течение
времени т' и, если за это время автобус не подойдет, покидает остановку
и идет пешком. Закон распределения fT(t) таков, что случайная
величина Тне может быть меньше, чем т + т' (рис. 10,17, б).
Найти вероятность того, что пассажир сядет в автобус. __
Решение. Переходим к противоположному событию А —
= {пассажир не сядет в автобус}. Это означает, что пассажир
прибудет на остановку в момент £*, когда на ней нет автобуса, и за
время ожидания следующий автобус не придет. Каждое событие
«подход автобуса к остановке» сопровождается «зоной захвата»
пассажира; ширина этой зоны т' + т (рис. 10.17, в).
Событие А = {пассажир не сел в автобус} соответствует
попаданию точки t* вне пределов зоны захвата (рис. 10.17, г). Точка £*
распределена равномерно по всей длине интервала Т*.
Вероятность того, что она попадет на участок Т* — (т + т'), не вошедший
в зону захвата, равна (по интегральной формуле полной
вероятности)
00
^)= Е
*-(т+т')
00
т + т'
t
/*(*)*= /
*-(т + т') t
оо
га
J if(t)dt-
т-f т
т-f т
т + т7
га.
t
га
■f(t)dt =
оо
f f(t)dt,
т + т
где mt — средний интервал между автобусами.
Вероятность того, что пассажир сядет в автобус, равна
Р(А) = 1-Р(А).
10.18. Происходит преобразование простейшего потока с
интенсивностью X, состоящее в следующем. Если расстояние между
соседними событиями Т{ оказывается меньше какого-то
допустимого предела ^ («интервала безопасности»), то событие
отодвигается от предыдущего на интервал ^; если же Т{ > t0l то событие
остается на своем месте (рис. 10.18). Является ли
преобразованный поток, образованный точками &[, Qf2,... на оси 6V,
простейшим? Является ли он потоком Пальма?
Решение. Ни тем, ни другим преобразованный поток не
является, так как в нем имеется сколь угодно далеко идущее после-
0
г\1
О'
©.
т
о\
©2 ©3
т •
i *>
, , , А.
V* ' "■■"—^
©'2 ©'з
©4 ©5 ©6
f ^ ^
I Zg Zg
1 L *
0'4 0'5
—Л
0'
Рис. 10.18
©7 08©9 е10
т • • •
| Ч) Ч)
' Qf 0' 0'
6 KJ 7 w8 w9
'
©п
Т 1
А ,
\ 1
• * t
©'.о©'..
338
действие. Например, «теснящиеся» на оси 0V точки
97,08,09,01О отодвигают каждую последующую точку на оси
0V на отрезок времени, зависящий от моментов прихода событий
и интервалов между ними в прошлом. Если t0 много меньше
среднего расстояния между событиями в исходном потоке: t0 « 1 / X,
то последействием в преобразованном потоке можно пренебречь.
10.19. Происходит наложение (суперпозиция) двух
независимых потоков Пальма с плотностями распределения интервала
между событиями /х(0 и Л (0- Будет ли результирующий поток
потоком Пальма?
Решение. Суперпозиция двух потоков Пальма выглядит,
как показано на рис. 10.19. Ясно, что интервалы Tv Т2,...
результирующего потока III не будет независимыми, так как их размеры
могут быть обусловлены размерами одного и того же интервала
на оси I или II. Например, Тг и Т2 в сумме дают Тп и, значит, не
являются независимыми. Однако эта зависимость быстро
затухает по мере увеличения расстояния по времени между началами
интервалов.
Примечание. Можно доказать, что при суперпозиции достаточно
большого числа независимых потоков Пальма со сравнимыми интенсив-
ностями получается поток, близкий к простейшему.
10.20. В процессе эксплуатации ЭВМ может
рассматриваться как физическая система 5, которая в результате проверки
может оказаться в одном из следующих состояний: sx — ЭВМ
полностью исправна; s2 — ЭВМ имеет незначительные
неисправности в оперативной памяти, при которых она может решать
задачи; s3 — ЭВМ имеет существенные неисправности и может
решать ограниченный класс задач; s4 — ЭВМ полностью вышла
из строя.
В начальный момент времени ЭВМ полностью исправна
(состояние 5Х). Проверка ЭВМ производится в фиксированные
моменты времени tv t2, t3. Процесс, протекающий в системе 5, может
рассматриваться как однородная марковская цепь с тремя шагами
(первая, вторая, третья проверки ЭВМ). Матрица переходных
вероятностей имеет вид
339
*7
0,3
0
0
0
0,4
0,2
0
0
од
0,5
0,4
0
0,2
0,3
0,6
1,0
Определить вероятности состояний
Рис.10.20 ЭВМ после трех проверок.
Решение. Граф состояний ЭВМ
имеет вид, показанный на рис. 10.20.
Против каждой стрелки проставлена соответствующая
вероятность перехода. Начальные вероятности состояний рх (0)=1; р2 (0) =
= Рз (0) = Р4 (0) = 0.
По формуле (10.0.14), учитывая в сумме вероятностей только
те состояния, из которых возможен непосредственный переход в
данное, находим:
^(1) = ^(0)^=1-0,3 = 0,3:
P2(l) = Pi(0)Pi2 =1-0,4 = 0,4;
Рг (1) = Рг (0)Р13= 1-0,1 = 0,1;
^(1) = ^(0)^=1-0,2 = 0,25
^(2) = ^(1)^=0,3-0,3 = 0,09:
р2(2) = р,(1) Р12 + Р2(1)Р22 =0,3-0,4 + 0,4-0,2 = 0,20;
р3(2) = р,(1) Р13 + Р2(1)Р23 + Р3(1)Рзз = 0,27;
р4(2) = Pl(l)PM + р2(1)Р24 + Р3(1)^з4 + Р4(1)Р44 =0,44;
Pl (3) = Pl (2) Рп = 0,09 • 0,3 = 0,027;
Pi (3) = Pi (2) Р12 + р2 (2)Р22 = 0,09 • 0,4 + 0,20 • 0,2 = 0,076;
Рз (3) = Pi (2) Р„ +Р2(2)Р23 +Рз(2)рзз =0,217;
P4(3) = Pi(2)P14 +Р2(2)РМ + р3(2)Рм +р4(2)Р44 =0,680.
Итак, вероятности состояний ЭВМ после трех проверок:
Pj (3) = 0,027; р2 (3) = 0,076; р3(3) = °>217; р4 (3)-0,680.
10.21. Точка S «блуждает» по оси абсцисс Ох (рис. 10.21, а) по
следующему закону: на каждом шаге она с вероятностью 0,5
остается на месте, с вероятностью 0,3 перескакивает на единицу
вправо и с вероятностью 0,2 — влево. Состояние системы S после А;
шагов определяется одной координатой (абсциссой) точки S.
Начальное положение точки — начало координат. Рассматривая
последовательность положений точки S как цепь Маркова, найти
340
-2
О
х
0,2
а
0,5 0,5 0,5 0,5 0,5
0,3 ^0,3^0,3,11,0,3^0,3^1
'-2
0,2
0,2
'о
0,2
0,2
Рис. 10.21
вероятность того, что она после четырех шагов окажется от начала
координат не дальше, чем на расстоянии, равном единице.
Решение. Обозначим состояние системы (точки S) через siy
где i — координата S на оси абсцисс. Размеченный граф
состояний показан на рис. 10.21, б. (Здесь для наглядности проставлены
«петли», соответствующие задержке S в прежнем положении.)
Последовательность состояний образует цепь Маркова с
бесконечным числом состояний. Переходные вероятности Р£.
отличны от нуля только в случае j = г; j = г — 1; j = г + 1; Рг г = 0,5;
Р. .+1 =0,3; Pi ._х =0,2. Все остальные переходные вероятности
равны нулю. Искомая вероятность Р равна сумме вероятностей:
р0(4) + рх(4) + р_х(4). Найдем их, пользуясь рекуррентными
соотношениями (10.0.14).
Имеем р0 (0) = 1; рг (0) = р_г (0) =... = 0. Далее,
"о(1) = Ро(0)Р0,о =0,5; р1(1)=Ро(0)Р0,1
p_1(l) = p0(l)P0j_1=0,2;
0,3;
р0(2) = р0(1)Ро,о + Pi(l)Pi,o + P-i(l)P-i,o =0,5 -0,5 +
+0,2 • 0,3 + 0,3 • 0,2 = 0,37;
,^ 1,
P1(2) = Po(l)P0,i + Pi(1)pi,i =0,5-0,3 + 0,3-0,5 = 0,30;
p2(2) = p1(l)P12=0,3-0,3 = 0,09;
P_1(2) = p0(l)P0,_1 +P_1(1)P_1,_1 =0,5-0,2 + 0,2-0,5 = 0,20;
P_2(2) = p_! (1)P_X,_2 = 0,2 • 0,2 = 0,04;
Po(3) = Po(2)P0,o + px(2)Pli0 +p_1(2)P_li0 =0,305;
Pl(3) = p0(2)P0il + Р!(2)Р1Д + P2(2)P2,2 = 0,279;
p2(3) = Pl(2)P12 + p2(2)P2]2 =0,135;
Рз(3) = Р2(2)Р2,= 0,027;
341
P_1(3) = p_2(2)P_2_1 + p.^P.,.., + р0(2)Р0_г =0,186;
p_2(3) = p_2(2)P_2_2 + p.^P^ t =0,060;
P_s(3) = p_2(2)P.
■2,-3
0,008;
Po(4) = Px(3)Pli0 + Po(3)P0,o + P-i(3)P_ll0 «0,264;
Pl(4) = р2(3)Р2д + рг(3)Р1Д + p0(3)POil «0,257;
p_i(4) = Po(3)P0,-i + P-iCSJP-!,-! + P-2(3)P_2,-i «0,172.
Искомая вероятность
p=p0(4)+Pi(4)+P-i(4)«0,693.
Итак, вероятность события А, состоящего в том, что за четыре
шага точка S окажется от начала координат на расстоянии, не
большем единицы, равна 0,693.
10.22. В условиях предыдущей задачи найти вероятности того,
что за четыре шага точка S ни разу не удалится от начала
координат дальше, чем на единицу.
Решение. Обозначим р0 (к), рг (к), р_г (к) вероятности
состояний Sq, sv s_x при условии, что до fc-го шага включительно точка S
ни разу не удалялась от начала координат больше, чем на единицу.
С первого взгляда здесь процесс не является цепью Маркова
(так как вероятности будущих состояний зависят от
«предыстории» — была ли точка S хотя бы один раз дальше, чем на одну
единицу, от начала координат), но его можно свести к цепи
Маркова, если ввести еще одно состояние s* — точка хотя бы один раз
была от начала координат на расстоянии, большем, чем единица.
Граф состояний показан на рис. 10.22. Из состояния s* нет
перехода ни в какое другое, такое состояние называется в
теории марковских цепей
«поглощающим». Вероятность события А =
{точка S за четыре шага ни разу не
отойдет от начала координат на
расстояние, большее, чем единица} вы-
числится как сумма вероятностей
р0 (4) + р_г (4) + рг (4) для системы с
графом состояний, соответствующим
рис. 10.22. Предоставляем читателю
вычислить эти вероятности
самостоятельно.
10.23. Система S — техническое устройство, состоящее из т
узлов и время от времени (в моменты tv ^,..., tk), подвергающееся
профилактическому осмотру и ремонту. После каждого шага
(момента осмотра и ремонта) система может оказаться в одном из
следующих состояний: s0 — все узлы исправны (ни один не заме-
0,5
о
'5-i -
0^"
0,5
0,3 Д_1 о,з
► ~ —*-
5о
L—
0,2 ' ' 0,2
5*
0,5
0
5i s
0,3
Рис. 10.22
342
нялся новым); sx — один узел заменен новым, остальные
исправны; 52 — два узла заменены новыми, остальные исправны;...; s{ — г
узлов (г < т заменены новыми, остальные исправны;...; sm — все т
узлов заменены новыми.
Вероятность того, что в момент профилактики узел придется
заменить новым, равна р (независимо от состояния других узлов).
Рассматривая состояния системы S как марковскую цепь, найти
переходные вероятности и для т = 3, р = 0,4 вычислить
вероятности состояний системы S после трех шагов (в начальный момент
все узлы исправны).
Решение. Обозначая q = 1 — р, запишем переходные
вероятности цепи. Для любого состояния системы s{ вероятность P{j равна
нулю при j < г\ вероятность Рй
равна вероятности того, что на данном
шаге ни один узел не придется
заменить новым, т.е. т — г еще не
замененных узлов остаются в соста-
ве устройства: Рй =q . При г < j
вероятность перехода Pi{ равна
вероятности того, что на данном
шаге из т — г еще не замененных
узлов j — i придется заменить
новыми. Пользуясь биноминальным
0,216 0,36
1Хо.432Д-1
0,6
а
а
Рис. 10.23
распределением, находимP{j = С3т1{ р3 гдт
ляется поглощающим. Для т = 3, р
имеет вид, показанный на рис. 10.23:
3+г. Состояние sm яв-
0,4 граф состояний системы
*7
216
0
0
0
0,432
0,36
0
0
0,288
0,48
0,6
0
0,064
0,16
0,4
1,0
Имеем р0(0) — 1; р1 (0) = р2(0) = Р3(0)= 0. Находим
вероятности состояний после одного, двух, трех шагов:
р0(1) = 0,216; Pl(l) = 0,432;
р2(1) = 0,288; р3(1) = 0,064;
р1(2) = р1(1)р„ + ро(1)р0,1 ~0-249;
р2(2) = p2(i)p22 + Ро(1)Р02 + Pi(i)Pi2 «0>442;
Рз(2) = Рз(1)Рзз + Р2(!)р2з + Pi(l)Pi3 + Ро(1)^оз -0-26¾
р0(3) = р0(2)Р00 «0,010;
Р1(3) = р1(2)Р11 +р0(2)Р01 «0,110;
343
p2(3) = p2(2)P22 + P0(2)P02 + ^(2)P12 «0,398;
Рз(3) = Рз(2)Р3з + Ро(2)Роз + Pi(2)P13 + Р2(2)Р2з ~ 0.482.
10.24. В моменты времени tv tv tz производится осмотр
ЭВМ. Возможные состояния ЭВМ: s0 — полностью исправна; sx —
незначительные неисправности, которые позволяют
эксплуатировать ЭВМ; s2 — существенные неисправности, дающие
возможность решать ограниченное число задач; s3 — ЭВМ полностью
вышла из строя.
Матрица переходных вероятностей имеет вид
0,5 0,3 0,2 0
N
0 0,4 0,4 0,2
0 0 0,3 0,7
0 0 0 1
Построить граф состояний. Найти вероятности состояний
ЭВМ после одного, двух, трех осмотров, если вначале (при t = 0)
ЭВМ была полностью исправна.
0,5 0,4 0,3 1
Q„,Q„4Q0,rQ
>0
0,3
0,4
0,2
0,2
Рис. 10.24
Решение. Граф состояний показан на рис. 10.24.
р0(1) = р0(0)Р00= 1-0,5 = 0,5;
Ро(2)
Рз(2)
рх(1) = Ро(0)Р01 =1-0,3 = 0,3;
р2(1) = р0(0)Р02 = 1-0,2 = 0,2;
= р0(1)Роо =0,25; рх(2) = р0(1)Р01 + Pl(l)Pn =0,27;
р2(2) = р0(1)Р02 + рх(1)Р12 +Р2(1)Р22 =0,28;
р2(1)Р23 + рх(1)Р13 =0,20; р0(3) = Ро(2)Роо =0,125;
Рг (3) = Р0 (2)Р01 + рх (2) Pn = 0,183;
р2(3) = Ро(2)Р02 + Pi(2)P12 + Р2(2)Р22 =0,242;
р,(3) = рх(2)Рх8 + р2(2)Р23 + р3(2)Р33 = 0,450.
10.25. Рассматривается процесс работы ЭВМ. Поток отказов
(сбоев) работающей ЭВМ
344
простейший с интенсивностью X.
Если ЭВМ дает сбой, то он немедленно обнаруживается, и
обслуживающий персонал приступает к устранению неисправности
(ремонту). Закон распределения времени ремонта —
показательный с параметром |л: ф (t) = |ле~^ (t > 0). В начальный момент (t —
= 0) ЭВМ исправна. Найти: 1) вероятность того, что в момент t
ЭВМ будет работать; 2) вероятность того, что за время (0, t) ЭВМ
дает хотя бы один сбой; 3) финальные вероятности состояний
ЭВМ.
Решение. 1) Состояния системы S (ЭВМ) следующие: s0 —
исправна, работает; sx — неисправна, ремонтируется.
Размеченный граф состояний дан на рис. 10.25, а.
X
М-
X
Рис. 10.25
а
Уравнения Колмогорова для вероятностей состояний p0(t) и
p^t)имеют вид
dt
dt
(10.25.1)
Из этих уравнений одно (любое) может быть отброшено, так
как для любого момента t имеем р0 + р1 = 1. Подставляя в
первое из уравнений (10.25.1) рх = 1 — р0, получаем одно
дифференциальное уравнение относительно р0:
dp0
dt
= \i- (\ + \i)p0.
Решая это уравнение при начальном условии р0(0) = 1,
получаем
Ро(')
М-
Х + |л
1 + -е
М-
Х ~(\ + \L)t
(10.25.2)
откуда
л (О
х
Х + |л
[1
_ „-(Ь+М.)*
]•
(10.25.3)
2) Для нахождения вероятности p(t) того, что за время t ЭВМ
дает хотя бы один сбой, введем новые состояния системы S: s0 —
ЭВМ ни разу не давала сбоя; s2 — ЭВМ хотя бы один раз дала
сбой. Состояние^ будет «поглощающим» (рис. 10.25, б).
Решая уравнение Колмогорова dp* I dt = —\р0 при начальном
условии р0(0) = 1, получаем p0(t) = e , откуда px(t) = 1 — p0(t) =
1-е . Итак, вероятность того, что за время t ЭВМ даст хотя
345
бы один сбой, равна px(t) = \ — e~yt. Эту вероятность в данном
случае можно было бы вычислить и проще, как вероятность того,
что за время t появится хотя бы одно событие (сбой) в
простейшем потоке сбоев с интенсивностью X.
3) Из уравнений (10.25.2), (10.25.3) при t —> оо получим
финальные вероятности состояний: р0 = |л / (X + |л); рг = X / (X + м0>
которые, впрочем, можно было бы получить непосредственно из
графа состояний, пользуясь схемой гибели и размножения
(предоставим читателю сделать это самостоятельно).
10.26. В условиях предыдущей задачи 10.25 неисправность
ЭВМ обнаруживается не сразу, а по прошествии некоторого
времени, имеющего показательное распределение с параметром v.
Написать и решить уравнения Колмогорова для вероятностей
состояний. Найти финальные вероятности состояний
(непосредственно по графу состояний).
Решение. Состояния системы: s0 — ЭВМ исправна, работает;
sx — ЭВМ неисправна, но это
не обнаружено; s2 — ЭВМ
ремонтируется. Граф состояний
дан на рис. 10.26.
Уравнения Колмогорова
для вероятностей состояний
будут:
dv
^Ро -vpx; —^ = vpl -\ip2. (10.26.1)
at
dp0
dt
Рис. 10.26
\ip2 - \p0;
dpx
dt
Решать эту систему будем с помощью преобразования
Лапласа. Тогда уравнения (10.26.1) с учетом начальных условий для
изображений tv { вероятностей р{ примут вид:
s-k
о
|лтг2 — Xtv0 + 1; srv-
Хтт0 -укг;
srv2 = wkx — |лтг2.
Решая эту систему алгебраических уравнений, получаем
следующие уравнения для изображений:
tv.
X
S + У
tv0; tv2
у
TV.
уХ
TV,
S + |A (s + v)(s + p.)
TV
(s + v)(s + \l)
0
S (s2 + S(|I + У + X) + У\ + V|JL + X|l)
Обозначим
a = —
|j, + v + X mi + v + X)
+
— уХ — У|л — Xjjl;
346
Тогда выражения для вероятностей примут вид:
at
-bt
„„ai L„-ot „at „bt
, v ae - be . , e - e
Po(0 = ; + (v + |i) ;— + \lv
a — b
a — b
at _ bt
Pi(0 = ^4 ; Ь V
a — b
p2(t) = v\
1_ beat - ae
ab ab (a — 6)
i L at ^ bt
I be — ae
ab ab (a — b)
bt
1 U „at ~ „bt
1 be — ae
ab ab (a — b)
Для нахождения финальных вероятностей можно
воспользоваться как изображениями, так и самими вероятностями:
р0 = lim p0(t) = \imsb0(s) = - ^
г—>оо
Pi
Х|л
Х|л + Ху + У|л
; р2 =г - Ро - Pi
Ху
Х|л Н- Ху + У|л
(10.26.2)
Финальные вероятности состояний можно найти и
непосредственно по графу рис. 10.26 : \ip2 = Хр0; ^Ро = VV\\ VV\ — №2- Из
этих уравнений любое (например, последнее) можно отбросить.
Выражая р2 через р0 и рг: р2 = 1 — р0 — рг, получаем два
уравнения:
М- (1 ~ Ро ~ Pi) = хРо5 хРо = yPi •
Решение этих уравнений даст те же результаты (10.26.2).
10.27. Электронное техническое устройство (ЭТУ) состоит из
двух одинаковых взаимозаменяемых узлов. Для работы ЭТУ
достаточно, чтобы работал хотя бы один узел. При выходе из строя
одного из узлов ЭТУ продолжает нормально функционировать за
счет работы другого узла. Поток отказов каждого узла —
простейший с параметром X. При выходе из строя узла он сразу начинает
ремонтироваться. Время ремонта узла — показательное с
параметром |л. В начальный момент (при t = 0) оба узла работают. Найти
следующие характеристики работы ЭТУ:
1) вероятности состояний как функции времени: s0 —
исправны оба узла; sx — исправен один узел, другой ремонтируется; s2 —
ремонтируются оба узла (ЭТУ не работает);
2) вероятность p(t) того, что за время t ЭТУ ни разу не
прекратит работу;
347
3) финальные вероятности состояний ЭТУ;
4) для предельного (стационарного) режима ЭТУ среднее
относительное время, в течение которого ЭТУ будет работать;
5) для того же предельного режима среднее время tp
бесперебойной работы ЭТУ (от включения после восстановления до
очередного выхода из строя).
Решение. Граф состояний ЭТУ дан на рис. 10.27, а (у левой
верхней стрелки стоит 2Х, так как работают и могут выходить из
строя два узла; по аналогичной причине стоит 2|л у правой нижней
стрелки, так как оба узла ремонтируются).
1) Уравнения Колмогорова имеют вид:
dpn х dp*
- \ьрг - 2\р0; —± = 2\p0+2\ip2-(\ + \i)pl;
dt dt
dp2
dt
\рг -2\ip2. (10.27.1)
При этом должно выполняться условие р0 + рг + р2 = 1.
Решая эту систему уравнений при начальных условиях
Ро (°) = 1; Рг (0) = Р2 (0) = 0, получаем
~„at U^bt at bt
f v ae -be ,x . e — e
Po(0 = 7 + (^ + Зр.) — +
a — о a + о
1 be — ae /x ч , _ /x ч
где а = -(Х + |л); b = -2(\ + \i);
+2|л2
+
ab аЬ {а — Ь)
а — Ь = X + |л; аЬ = 2 (X + |л)2;
п и,_а2е« -бУ , (Х + 3^)(аеа< -6е"> , 2»{eat -е") , 2Х ...
|л (а — Ь) |л (а — Ь) а — b |л
Из полученных выражений находим:
p2(t) = l-p0(t)-p1(t)] р2 (0) = 0.
2) Чтобы найти вероятность j5(£), сделаем состояние s2 (ЭТУ
прекратило работу) поглощающим (s2) (рис. 10.27, б). Уравнения
Колмогорова для вероятностей состояний ЭТУ будут
dр0/dt =\1рг — 2\p0\dpl/dt =2\р0 — (X + |л)рх; dр2/dt = 2\рг.
Решая первые два уравнения при начальных условиях
р0 (0) = 1, рг (0) = 0, получаем
Ро(0 = £— + (Х + М-)
а — (3 а — (3
348
где
а
-(3\ + |л) + л/\2 +б\|л + |л2 п -(ЗХ + |л)-л/х2+6Х|л + |л:
- ; р =
(величины аир отрицательны при любых положительных
значениях X и |л). Далее
, ч 1 dpQ 2Х
|л dt
М-
1
М-
_ + (Х + ^)-
a - р
a - р
2Х , ч
+ —Ро(0-
М-
Искомая вероятность p(t) = p0(t) + px(t). Заметим, что
функция p(t) является монотонной убывающей, при этом р(0) = ];
р(оо) = 0.
3) Финальные вероятности состояний найдем по графу
(рис. 10.27, а) и общим формулам (10.0.23) для схемы гибели и
размножения
Рг
2Х
М-
р0; р2
2V
2р/
Ро
'\"
iMj
Ръ', Ро + Рг+ Р2=1'>
p0=[l + 2\/[i+(\/[iY}-1 =^/(Х + |1Г.
4) Среднее относительное время, которое ЭТУ будет работать,
равно
i-p:
1-
V
2
М-
> + м->
2
Г х ]
5) Величина t? есть математическое ожидание времени Гр,
проходящего между моментом включения ЭТУ в работу и
моментом ее следующего выхода из строя.
50
2Х
И-
5i
X
* 2у,
5?
*0
2Х
•%
5i
X
52
г
—е-
а
Работает
Не
работает Работает
Не
работает
~"»Г
—» Г"
-V Г
■<•>—
в
Рис. 10.27
349
Представим работу ЭТУ в стационарном режиме как
состоящую из ряда циклов: «работает» и «не работает» (на рис. 10.27, в
участки работы показаны утолщенной линией). Среднее время tnp,
в течение которого ЭТУ не работает (математическое ожидание
длительности нерабочего периода), очевидно равно 1 / (2|л) (так как
на ЭТУ, находящееся в состояние «не работает», действует поток
переходов в «рабочее» состояние с интенсивностью 2|л).
Далее, отношение среднего времени бесперебойной работы tp к
среднему времени простоя t равно отношению финальной
вероятности 1 — р2 того, что ЭТУ работает, к вероятности р2 того, что
оно не работает: tp /tnp = (1 — р2) / р2. Отсюда, учитывая, что
*пр =l/(2|i),
t
- 1-р2 1 1-р,
t
пр
Р:
2р, р.
10.28. Условия и вопросы те же, что и в задаче 10.27, с той
разницей, что пока один из узлов работает, другой находится в
«холодном резерве» и выходить из строя не может. При включении
резервного узла он немедленно начинает работать и подвергается
потоку отказов с интенсивностью X.
Решение. Граф состояний ЭТУ будет иметь вид,
показанный на рис. 10.28, а, граф с «поглощающим состоянием» — на
рис. 10.28, б.
5П
X
м<
*1
X
' 2р.
5?
50
X
' М-
5i
X
52
а
Рис. 10.28
Ответы на вопросы:
at
bt
at l
. ч , ч ае — be ,. л ч е
1) Ро(0 = г— + (^ + 3|i) -
а
а —Ь
at bt
а
-Ъ
1 be — ае
ab ab (a — b)
a V 4? , (X + Зц.), at
Pi(*) = : +
/ at , 7 bt \ , ^M* r oi bt i , X ( v
(ae + be )4 [e -e J4—Po(*)5
\i(a — b) |л(а—6) N ' a — b
p2(t) = l- p0(t)~ Pl(t)]
-(2Х + 3|л) + л/4|лХ + |л2 , -(2Х + 3|л) + л/4|лХ + |л2
ai _ о fit at _ 3t
2) ?„(*) = — ^- + (X + ^)e
a -(3
a -(3
350
Pl(t)=-
~ 2„at
a e
a -B
B2e3' aeQ' - Be3'
a -B
+ -Po(t);
p2(*) = i-Po(*)-Pi(*); a
-(2X + |x) + >/4Xm, + |j,2
в
-(2X + |x)-V4X|x + ^2 _ _
= ! ; v(t) = l-v
p2(0;
3)Px
X 1
-Po; p2=-
|x 2
'X^2
IH
p0; Po
, x 1
ц 2
'X4
l И
i-i
4)1-p2; 5)t
1 l-p2
2|x p.
50
x+y
И-
51
X
^2^
5?
10.29. Условия задачи 10.27 изменены таким образом, что
неработающий узел находится в «облегченном резерве» и выходит
из строя с интенсивностью X7 < X. 1)
Построить граф состояний ЭТУ, написать
уравнения Колмогорова для
вероятностей состояний. 2) Не решая этих
уравнений, найти финальные вероятности
состояний; вычислить их для Х = 1;Х' =
= 0,5, [I = 2. 3) Для этих же численных данных найти среднее время
t? бесперебойной работы ЭТУ.
Решение. 1) Граф состояний показан на рис. 10.29.
Уравнения Колмогорова:
dp0
Рис. 10.29
dt
-(Х+ХОРо +M>i5
dpx
dt
-(Х + М,)р1 + (\ + \')p0+2\Lp2;
Po + Pi + Р2 = L
2) Финальные вероятности состояний найдем, пользуясь
общими формулами (10.0.23) для схемы гибели и размножения:
Х + Х' (Х + Х')Х
Pi = р0; р2 =——о—Ро;
м-
2|i
Ро
1 | Х + Х' (X + XQX
м-
2|i
351
Подставляя сюда X = 1, X' = 0,5, [i = 2, получаем
-1
Ро
1 + М+1'5*1
3)1
1 1-Р2
4 р2
8
2,32.
0,516; рх « 0,387; р2 « 0,097.
10.30. В состав ЭВМ входят четыре накопителя на магнитных
дисках (НМД). Бригада в составе четырех человек
обслуживающего персонала проводит профилактический ремонт каждого
диска. Суммарный поток моментов окончания ремонтов для всей
бригады — пуассоновский с интенсивностью \(t). После
окончания ремонта диск проверяется; с вероятностью р он оказывается
работоспособным (время проверки мало, и им можно пренебречь
по сравнению со временем профилактики). Если диск оказался
неработоспособным, то вновь проводится его профилактика
(время, потребное на нее, не зависит от того, проводилась ли ранее
профилактика) и т.д. В начальный момент все НМД нуждаются в
профилактическом ремонте.
Построить граф состояний для системы S (четыре НМД),
написать дифференциальные уравнения для вероятностей
состояний. Найти Мт — математическое ожидание числа дисков,
успешно прошедших профилактику к моменту т.
Решение. s0 — все четыре НМД нуждаются в
профилактическом ремонте; sx — один НМД успешно прошел профилактику, а
три НМД нуждаются в профилактическом ремонте; s2 — два
НМД успешно прошли профилактику, а два нуждаются в
профилактическом ремонте; s3 ~ ТРИ НМД успешно прошли
профилактику, один нуждается в профилактическом ремонте; s4 — все
четыре НМД успешно прошли профилактику.
То, что каждый профилактический ремонт заканчивается
успешно с вероятностью р, равносильно р-преобразованию потока
окончаний ремонтов, после которого он остается пуассоновским,
но с интенсивностью рХ (t).
Граф состояний показан на рис. 10.30. Уравнения Колмогорова:
Фо I dt = -рЧ0р0; dP\ /dt = p\(t)(p0 -рх);
dp2 / dt = p\(t)(p1 - p2); ф3 J dt = p\(t)(p2 - p3);
dpA / dt = p\(t)p3.
(10.30.1)
»0
p\(t)
^
*1
*"
s2
?4t)
S3
pM*)
54
Рис. 10.30
352
Начальные условия р0 (0) = 1; рг (0) = ... = р4 (0) = 0.
Математическое ожидание числа дисков, успешно прошедших
профилактику к моменту т, равно
Мт=£>Лт)
(10.30.2)
i=i
При постоянной интенсивности X решениями уравнений
(10.30.1) будут:
Ро(*) = е"М; Pitt) = \pte~* ; p2(t) =
(\pt)
,-ър*.
Рз(*) =
(Хр*)!
3!
-Хр*.
p4(*)=i-£"*(*)•
г=0
10.31. В условиях предыдущей задачи за каждым членом
бригады закрепляется свой НМД, который он ремонтирует. Поток
окончаний профилактики, приходящийся на одного члена
бригады, имеет интенсивность \(t) / 4 Ответить на вопросы
предыдущей задачи.
Решение. Граф состояний дан на рис. 10.31. Уравнения
Колмогорова:
Фо /dt = -p\(t)p0\ dpx /dt = p\(t)(p0 -(3/4)^);
dp2 / dt = p\(t)((3 / 4)Pl - (1 / 2)р2);
Фз/л = рМ0((1/2)р2-(1/4)Рз); dp, / dt = (1 / 4)p\(t) p3.
Выражение (10.30.2) дляМт сохраняется.
sn
°0
pX(t)
s*
°1
|pM«)
Ри
»
Sr.
°2
с 10
|pM*)
.31
So
°3
|pM«)
5^
^4
10.32. Техническое устройство (ТУ) подвергается простейшему
потоку отказов с интенсивностью X. Отказ обнаруживается не
сразу, а через случайное время, распределенное показательно с
параметром у. Как только отказ обнаружен, производится осмотр ТУ, в
результате которого оно либо направляется в ремонт (вероятность
этого р), либо списывается и заменяется новым. Время осмотра —
показательное с параметром % время ремонта — показательное с
параметром |i, время замены списанного ТУ новым —
показательное с параметром \- Найти финальные вероятности состояний
ТУ. Определить: 1) какую долю времени в среднем ТУ будет рабо-
353
so
X
sl
V
S2
(i-p)ii
X
Рис. 10.32
X тать нормально; 2) какую долю
времени ТУ будет работать с
необнаруженным отказом (давать брак);
3) какова средняя стоимость
ремонтов ТУ и его замен за единицу
времени, если средняя стоимость
ремонта равна г, а нового ТУ равна с;
4) какова средняя величина потерь
за единицу времени от ТУ,
работающего иногда с необнаруженным
отказом, если такое ТУ приносит в единицу времени убыток /.
Решение. Состояния ТУ: s0 — исправно, работает; sx —
неисправно, но отказ не обнаружен, дает брак; s2 — неисправность
обнаружена, ведется осмотр; s3 ~~ ремонтируется; s4 — заменяется
новым. Граф состояний дан на рис. 10.32.
Линейные алгебраические уравнения для финальных
вероятностей состояний:
Хро = м-Рз + хра; ^Ро = уР\; vP\ = чр2; р чр2 = №;
(1-р)ЧР2 = ХРа-
Нормировочное условие р0 + рг + р2 + р3 + Ра = 1- Решая эти
уравнения, получаем:
Ро =
, X X р\ (1-р)Х
1 + - + - + —+ - -1—
у 4
М-
X
-1
X X
Рг =— Ро5 Р2 =— Ро5
у Ч
р\ (1-р)Х
Рз =—Ро5 Ра = Ро-
М- X
1) Доля времени нормальной работы ТУ равна р0; 2) рг; 3) ТУ
проводит в среднем долю времени р3 в состоянии ремонта;
каждый ремонт длится в среднем 1 / |л; поток отремонтированных ТУ,
выходящих из состояния 53, имеет интенсивность |ip3>* средняя
стоимость ремонтов в единицу времени r[ip3. Аналогично
средняя стоимость новых ТУ в единицу времени с \ Ра 5 общая средняя
стоимость того и другого равна r\ipz + с\Р^ 4) средние потери
от работы ТУ в неисправном состоянии за единицу времени
равны / у рг.
10.33. Рассматривается процесс накопления информации в
базах данных, хранимых в ЭВМ. Интенсивность поступления
единиц информации в базы данных равна \(t) и не зависит от того,
сколько их накоплено. Каждая единица информации, поступив-
354
шая в базы данных, хранится в них бессрочно. Найти
характеристики mx(t), Dx (t) случайной функции X(t) — числа накопленных
единиц информации в базах данных в предположении, что поток
поступлений единиц информации пуассоновский с
интенсивностью X(t) и в начальный момент времени t = 0 случайная функция
Х(0)=.0.
Решение. В этой задаче мы имеем дело с процессом «чистого
размножения» без ограничения числа состояний (га —> оо). Все
интенсивности «размножения» Х^. = \(t) (рис. 10.33) и
интенсивности «гибели» [ik = [ik (t)~0.
\(t)
\(t)
\(t) \(t)
\(t)
Рис. 10.33
Дифференциальные уравнения (10.0.24) и (10.0.25) для этого
случая примут вид
dmx(t)
оо
dt
= £М')л(') = М0;
к=0
dDx(t)
dt
ОО
= "£\\(t) + 2k\(t)-2mx(t)\(t)]pk(t) = \(t),
к=0
так как
оо
оо
£р*(*) = 1, £*Р*(*) = "»,(*)•
к=0
к=0
Решая эти уравнения для начальных условий тх (0) = Dx (0) =
0, получаем
mx(t) = Dx(t) = f\(T)dr.
о
Этот результат можно было ожидать; его можно найти
непосредственно из теории потоков. Можно доказать, что случайная
величина X(t) для любого момента времени t будет подчинена
закону Пуассона с найденными характеристиками mx(t) = Dx(t).
10.34. Условия те же, что и в предыдущей задаче, за
исключением того, что принятая на хранение в базах данных единица
информации хранится некоторое время, после чего по
определенному признаку исключается из баз данных. Поток исключений
для каждой единицы информации — пуассоновский с
интенсивностью [i(t).
355
Решение. В этой задаче имеет место процесс «гибели и
размножения» числа единиц информации, хранимых в базах данных
ЭВМ.Интенсивность гибели [ik (t) = k[i(t), так как в состоянии sk
в базах данных накоплено к единиц информации и на каждую из
них действует поток исключений с интенсивностью [i (t).
Дифференциальные уравнения для функций
mx(t)nDx(t)имеют вид
dmx(t)
dt
ОС
= £(X(i) - kp(t)) Pk(t) = \(t) -\i(t) mx(*);(10.34.1)
k=0
+2mx(t)k[L(t)]pk(t) = \(t) + [L(t)mx(t)-2[L(t)Dx(t), (10.34.2)
так как
00
00
£>*(*) = !; J2kPk(*) = "»,(*);
k=Q
k=0
oo
J2k2pk (t) = a2l(0 = Я (*) + mx2(*)-
Jfc=0
Для начальных условий mx(0) = m0, Dx(0) = D0 постоянных
интенсивностей пополнения и исключения единиц информации
X(t) = X; [l(t) = |iрешения этих уравнений будут иметь вид
тх(t) = т0е-*г + -(1 - е"^ ) = - + е~»ь
/
то -
<
м
— —
м-J
Dx(t) = \
1 е
- + -
М-
-2^
2е
—\it
М-
+ (X + |л^о +М-то)
е~^ — е~2^
+
М-
+£0 (2в~2^ - е-* ) = т,(0 + (А) ~ ™о)е
-2^
Для начальных условий т0 — D0 = О получим mx(t) = Dx(t) =
= — (l — e-Mi ). Можно доказать, что для этих начальных условий
процесс накопления информации X(t) будет распределен по
закону Пуассона для любого момента времени t и для любого вида
функции \(t) (интенсивности поступления информации), но для
этого интенсивность исключения единиц информации \х должна
быть постоянной.
При постоянных Хи|1и£—> оо в системе будет
устанавливаться стационарный режим накопления информации, который, есте-
356
ственно, не будет зависеть от начальных условий: тх = Dx =
10.35. Рассматривается процесс производства ЭВМ
определенного вида. Интенсивность производства ЭВМ \(t) представлена
на графике рис. 10.35, а. Эта интенсивность линейно возрастает в
течение первого года производства от 0 до 1000 ЭВМ в год, затем
три года производство сохраняется на уровне 1000 ЭВМ в год,
после чего ЭВМ снимается с производства. Средний срок
эксплуатации ЭВМ 5 лет. Считая все потоки событий простейшими,
определить математическое ожидание и дисперсию числа ЭВМ,
находящихся в эксплуатации в любой момент времени t
Решение. Интенсивность производства ЭВМ
Mt)
0
kt
X
0
при
при
при
при
t <0;
0 < t < 1;
1 < t < 4;
t > 4,
где к = 1000 1/год2; X = 10001/год.
Найдем решения уравнений (10.34.1) и (10.34.2) для участка
времени 0 < t < 1 и при условии, что [i = 0,2 1/год для любых
участков t> 0. Уравнение (10.34.1) при этих условиях имеет вид
—f±l = kt-\Lms(t).
at
Решая это уравнение для начального условия тх (0) = 0,
получаем
mx(t) = JL(e-^ - l + \it) - 25000 ( -*/R - П
:"'/5 - 1 + -
По истечении одного года в эксплуатации будет в среднем
mjl) = 25 000(е~1/5 - 1 + 0,2) = 468 ЭВМ. Заметим, что если бы
ЭВМ имели неограниченный срок службы, то их к концу года
было бы в эксплуатации 500 ЭВМ.
Уравнение (10.34.2) при тех же условиях имеет вид
dDx (t)/dt= 100« + 0,2тх (t) - 0,4¾ (t).
Решая это уравнение для начального условия Dx (0) = 0,
получаем Dx(t) = тх(t) = 25000 (e~t,b -1+t /5). По истечении
одного года дисперсия числа ЭВМ, находящихся в эксплуатации,
будет равна Dx = 468; ах = 21,6. Число ЭВМ, находящихся в
эксплуатации по истечении года, будет приближенно подчинено
нормальному закону с характеристиками тх = 468; ах =21,6.
357
На участке времени 1 < t < 4 соответствующие уравнения
будут иметь вид
dt
dt
Их нужно решать при начальных условиях:
mx(l) = Dx(l) = 468. Решение этих уравнений было найдено в
задаче 10.34, откуда
т
X
(О = тх(1) е-^-1} + -(1 - е-^-1}) (1 < t < 4);
М-
Л.(0 = ™.(0-
Найдем значение тх (0 Для * = 4:
mx(4) = mx(l)e-3^ +-(l-e~3^ ) = 2513.
М-
Таким образом, среднее число ЭВМ, находящихся в
эксплуатации к концу четвертого года выпуска, будет равно 2513. Обратим
внимание на то обстоятельство, что к этому времени было выпу-
а
\*>з(*)
M*+i(*)
3500
3000
2500
2000
1500
1000
500
3500
/ 12513
468./ |
/i II i i i i
4^920
1 1 1
123 456789 10 t, годы
в
Рис. 10.35
358
щено в среднем 3500 ЭВМ. Следовательно, в среднем за четыре
года было исключено из эксплуатации 987 ЭВМ.
На участке времени t > 4 будет иметь место процесс «чистой
гибели», граф состояний которого показан на рис. 10.35, б.
Дифференциальные уравнения для математического
ожидания и дисперсии процесса чистой гибели в общем случае имеют
вид
—т— = ~X,M*) a (*);
dt k=0
dD (t) °°
-^ = ^[*^(0-2*V,(0 + 2m,(0*^(0]P*(0-
dt k=0
Для нашего случая jj^ (t) = k[i, следовательно, получим
уравнение
dm At) ~ ,
dt k=0
которое нужно решать при начальном условии тх (4) = 2513.
Решение этого уравнения будет иметь вид
т
X
(t)^mM)e-^-^(t>A).
Так как Dx(4) = тх(4) и [i = const, то Dx(t) = тх(t) на участке
времени £ > 4.
На рис. 10.35, в показана зависимость mx(t) — среднего числа
ЭВМ, находящихся в эксплуатации от времени t На этом же
графике пунктирной линией показана зависимость от t среднего
числа выпущенных ЭВМ к моменту времени t
10.36. Рассматривается процесс накопления терминов в
динамическом словаре (тезаурусе) при функционировании
автоматизированного банка данных (АБД). Сущность процесса в том, что
термины заносятся в словарь по мере их появления в той
информации, которая вводится в АБД. Например, в АБД
автоматизированной системы управления производством (АСУП) могут в
качестве терминов заноситься наименования организаций, с которыми
данное предприятие поддерживает производственные отношения.
Динамический словарь наименований таких организаций будет
накапливаться в АБД АСУП по мере появления этих
наименований в единицах информации, вводимых в АБД.
В каждой единице информации, поступающей в АБД, в
среднем встречается х терминов словаря, а интенсивность
поступления единиц информации в АБД \(t). Следовательно,
интенсивность потока терминов словаря в информации, поступающей в
359
АБД, будет \(t) = х.Х(£). Предполагается, что поток терминов
словаря является пуассоновским. Число терминов словаря п
является конечным и неслучайным, хотя, возможно, и неизвестным
заранее. Все термины словаря могут находиться в единице
информации с одинаковой вероятностью, а в словарь заносятся
естественно лишь те термины, которые до сих пор еще не
встречались в единицах информации. Требуется найти математическое
ожидание и дисперсию числа терминов, накопленных в
динамическом словаре.
Решение. Обозначим X(t) число терминов, накопленных в
динамическом словаре. Очевидно, что случайный процесс X(t)
есть процесс «чистого размножения» с конечным числом
состояний п, граф состояний которого представлен на рис. 10.36. Для
нахождения интенсивности \k(t) (к = 0,1,... ,га — 1) введем в
рассмотрение гипотезу о том, что процесс находится в состоянии skJ
>0
\>(*)
\(t) \кл(*)
-► . •
'*
М*)
-^- •
Vi
Vi(«)
»п
Рис. 10.36
вероятность этой гипотезы по определению равна рк (t). В
предположении, что эта гипотеза имеет место, интенсивность потока
новых (еще не занесенных в динамический словарь) терминов будет
xt(t) = x(t)—- = х(*)
п
( к\
1--
п)
Дифференциальные уравнения (10.0.24) и (10.0.25) примут
вид:
dmx(t)
п
dt
= £М0
Ь=0
dDx{t)
1-
к)
п
А(0 = Х(0-^^; (Ю.36.1)
п
dt
-2mx(t)\(t)
= Е
к=0
( к\
1--
п)
МО
1-
к)
п
+ 2k\(t)
п
1--
П
Pk(t) = \(t)-\(t)^l-2\(t)
- (10.36.2)
л, (О
п
п
Найдем решение этих уравнений для простейшего случая,
когда
X (t) = X = const; п = const; тх (0) = Dx (0) = 0,
mx(t) = n
-V
1 - е п
; }immx(t) = n]
/—►ОС
(10.36.3)
360
Dx(t) = n
' -^
1
п
-Л -Л
е » =mx(t)e
П -
limD,(t) = 0. (10.36.4)
Обратим внимание на то, что функция тх (t) монотонно
увеличивается, стремясь в пределе к гг, в то время как функция Dx{t)
равна нулю при £=0и£—>оои достигает своего максимума при
некотором значении tm, которое можно найти из условия
dDx(t)/dt=0(t>0).
Отсюда
0,5 = е """* -*tm ttOJn /X.
При этом значении tm максимальная дисперсия max Dx(t) «
г
« и (1 — е-0'7) е-0'7 = гг 0,25; (т^ (*ш ) = 0,5л/гг~, а максимальное
значение коэффициента вариации ox{tm) / mx{tm) = l / 4п.
Если известна интенсивность X потока терминов словаря в
единицах информации, поступающих в АБД, и общее число
терминов гг, то можно с достаточной точностью определить среднее
время £н, потребное для накопления 95 % объема динамического
словаря: 1 — е п = 0,95, откуда tH « Зтг / X.
Если п неизвестно (что чаще всего на практике имеет место),
то можно найти оценку п величины п следующим образом. Для
моментов времени т2, т2, т3,..., т^т,- <тг+1) определяют
фактические количества накопленных терминов в словаре mv т2,...,
га,-. Полагаем эти величины приближенно равными средним
количествам накопленных терминов: mi —п (1 — е~Хт,/п )(г = 1, 2,...,/).
Решая это уравнение относительно гг, находим / значений nv гг2,
..., гг/для соответствующих пар значений: (т^т^; (га2, т2);...;
(га z, т /). Оценку п находим по формуле
п =
ni
/I.
10.37. Для условий предыдущей задачи найти время tH запол-
ления словаря на 95 % и вероятность того, что через два года после
начала накопления словаря он будет содержать не менее 90 % всех
терминов, если общее число терминов п = 100 000, в год в АБД
вводится 100 000 документов и каждый документ содержит в
среднем 1,5 термина.
Решение. Найдем интенсивность потока терминов словаря в
единицах информации, вводимых в АБД:
361
X = 100000 .1,5 = 150000 1/год.
Величина tu определяется из выражения tn=3n/\ =
= 3 • 100 000:150 000 = 2 года. Для определения вероятности того,
что через два года после начала наполнения словарь будет
содержать не менее 90 % всех терминов, нужно прежде всего найти
тх(2) и Dx{2) [см. формулы (10.36.3) и (10.36.4)]: тх(2) =
= 100 000 х (1-е-1'5"2) = 0,95 • 100 000=95 000; Dx(2) = 95 000-0,05 =
= 4750^(2) = 68,9.
Заметим, что максимальная дисперсия Dx(tm) = 0,25тг = 25 000;
<тя(*т ) = 158.
Число терминов в словаре в момент времени t = 2 года есть
случайная величина Х(2), приближенно распределенная по
нормальному закону с найденными выше характеристиками; поэтому
Р{Х(2)>0,9тг}«1,таккактд. -За,. > 0,9гг.
10.38. Рассматривается более общий случай
функционирования динамического словаря АБД. Первое усложнение по
сравнению с условиями задачи 10.36 состоит в том, что максимальное
число терминов словаря п не является постоянным, а зависит от
времени t n(t) (в случае с динамическим словарем названий
организаций это означает, что общее число организаций со временем
изменяется: увеличивается или уменьшается).
Кроме того, введенные в динамический словарь термины по
истечении некоторого случайного времени исключаются из словаря в
связи с тем, что сам термин устаревает. Предполагается, что поток
исключений термина в динамическом словаре — пуассоновский с
интенсивностью|i (t), одинаковой для всех терминов словаря.
В этом случае интенсивности потоков «размножения» и
«гибели» будут иметь вид
х*(*) = М0
1-
к
n(t)j
М0 = и(*)*> (10.38.1)
а уравнения (10.0.24) и (10.0.25) примут вид (зависимости от времени t
функций т х (t), Dx(t), n{t), Х(£), \i(t), pk(t) для краткости опущены):
dmx J dt = X - mx(\ / n 4- |л);
dDx I dt = X - mx (X I n - \i) - 2 (X / n + \i) Dx. (10.38.2)
Если величины X, n, |i постоянны (не зависят от времени), то
при t —► сю существует стационарный режим работы, для которого
dmx J dt— dDx / dt = 0, откуда
mx=n
\
i +
-i
Dx=mx
( \ 1
1 + —
[in)
-l
ГЛАВА И
ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
Системой массового обслуживания (СМО) называется любая система,
предназначенная для обслуживания каких-либо заявок (требований),
поступающих на нее в случайные моменты времени. Примеры СМО:
телефонная станция; бюро ремонта; билетная касса; парикмахерская;
ЭВМ. Теория массового обслуживания изучает случайные процессы,
протекающие в системах массового обслуживания.
Любое устройство, непосредственно занимающееся обслуживанием
заявок, называется каналом обслуживания (или «прибором»). СМО
бывают как одно-, так и многоканальными. Пример одноканальной СМО —
билетная касса с одним кассиром; пример многоканальной — та же касса с
несколькими кассирами.
Различают СМО с отказами и СМО с очередью. В СМО с отказами
заявка, пришедшая в момент, когда все каналы заняты, получает отказ,
покидает СМО и в дальнейшем в процессе ее работы не участвует. В СМО с
очередью заявка, пришедшая в момент занятости всех каналов, не
покидает СМО, а становится в очередь и ждет, пока не освободится
какой-нибудь канал. Число мест в очереди т может быть как ограниченным, так и
неограниченным. При т = О СМО с очередью превращается в СМО с
отказами. Очередь может иметь ограничения не только по количеству
стоящих в ней заявок (длине очереди), но и по времени ожидания (такие СМО
называются «системами с нетерпеливыми клиентами»).
СМО с очередью различаются не только по ограничениям очереди, но
и по дисциплине обслуживания: обслуживаются ли заявки в порядке
поступления, или в случайном порядке, или же некоторые заявки
обслуживаются вне очереди (так называемые «СМО с приоритетом»). Приоритет
может иметь несколько градаций или рангов.
Аналитическое исследование СМО является наиболее простым, если
все потоки событий, переводящие ее из состояния в состояние, —
простейшие (стационарные пуассоновские). Это значит, что интервалы времени
между событиями в потоках имеют показательное распределение с
параметром, равным интенсивности соответствующего потока. Для СМО это
допущение означает, что как поток заявок, так и поток обслуживании —
простейшие. Под потоком обслуживании понимается поток заявок,
обслуживаемых одна за другой одним непрерывно занятым каналом. Этот поток
363
оказывается простейшим, только если время обслуживания заявки Тобсл
представляет собой случайную величину, имеющую показательное
распределение. Параметр этого распределения \л есть величина, обратная
среднему времени обслуживания: \l = 1 / to6cjl, где £обсл = М [7^ ]. Вместо «поток
обслуживании — простейший» часто говорят «время обслуживания
показательное». Условимся в дальнейшем для краткости всякую СМО, в
которой все потоки простейшие, называть простейшей СМО. В этой главе
будем рассматривать главным образом простейшие СМО.
Если все потоки событий простейшие, то процесс, протекающий в
СМО, представляет собой марковский случайный процесс с
дискретными состояниями и непрерывным временем. При выполнении некоторых
условий для этого процесса существует финальный стационарный
режим, при котором как вероятности состояний, так и другие
характеристики процесса не зависят от времени.
Задачи теории массового обслуживания — нахождение вероятностей
различных состояний СМО, а также установление зависимости между
заданными параметрами (числом каналов п, интенсивностью потока заявок
X, распределением времени обслуживания и т.д.) и характеристиками
эффективности работы СМО. В качестве таких характеристик могут
рассматриваться, например, следующие:
среднее число заявок А, обслуживаемое СМО в единицу времени, или
абсолютная пропускная способность СМО;
вероятность обслуживания поступившей заявки Q или
относительная пропускная способность СМО; (J = А / X;
вероятность отказа РОТК, т.е. вероятность того, что поступившая заявка
не будет обслужена, получит отказ; РОТК = 1 — Q;
среднее число заявок в СМО (обслуживаемых или ожидающих в
очереди) I;
среднее число заявок в очереди г;
среднее время пребывания заявки в СМО (в очереди или под
обслуживанием) tcliCT;
среднее время пребывания заявки в очереди tQ4;
среднее число занятых каналов k.
В общем случае все эти характеристики зависят от времени. Но многие
СМО работают в неизменных условиях достаточно долгое время, и поэтому
для них успевает установиться режим, близкий к стационарному. Мы здесь
повсюду, не оговаривая этого каждый раз специально, будем вычислять
финальные вероятности состояний и финальные характеристики
эффективности СМО, относящиеся к предельному, стационарному режиму ее работы.
Для любой открытой СМ01} в предельном стационарном режиме
среднее время пребывания заявки в системе tcilCT выражается через
среднее число заявок в системе с помощью формулы Литтла:
Wt =г/\ (11.0.1)
где X — интенсивность потока заявок.
СМО называется открытой, если интенсивность поступающего на нее потока
заявок не зависит от состояния самой СМО.
364
so
sl
52
• • •
4½ м*
Рис. 11.01
5*
• • •
^+1 \
sn
Аналогичная формула (называемая также формулой Литтла)
связывает среднее время пребывания заявки в очереди tQ4 и среднее число г
заявок в очереди:
:г/Х. ч (11.0.2)
оч
Формулы Литтла очень полезны, так как позволяют вычислять не обе
характеристики эффективности (среднее время пребывания и среднее
число заявок), а только какую-нибудь одну из них.
Специально подчеркнем, что формулы (11.0.1) и (11.0.2) справедливы
для любой открытой СМО (одноканальной, многоканальной, при любых
видах потоков заявок и обслуживании); единственное требование к
потокам заявок и обслуживании — чтобы они были стационарными.
Аналогично универсальное значение для открытых СМО имеет
формула, выражающая среднее число занятых каналов к через абсолютную
пропускную способность А:
к=А/\х, (11.0.3)
где \i = 1 / to6cn — интенсивность потока обслуживании.
Очень многие задачи теории массового обслуживания, касающиеся
простейших СМО, решаются с помощью схемы гибели и размножения
(см. гл. 10). Если граф состояний СМО может быть представлен в виде,
показанном на рис. 11.0.1, то финальные вероятности состояний
выражаются формулами (10.0.23):
-1
Ро
X,
1 + -^.
, W , , Vi-Vi , , \Ai---^n-i
M-i
H-lH-2
M-iM-2- • -M-^
H-iH^-'-M-n
Pi =—p0; P2
_ W
M-lM-2
Po5
Pk
fc = Xo\-Vipo(0<t<w);_.
M-iM-2- ••М'Л
X0Xi... A ,
Pn =-2-J — P0
M'lM'2---M'n
(11.0.4)
При выводе формул для среднего числа заявок (в очереди или в
системе) широко используется прием дифференцирования рядов, состоящий в
следующем. Если х < 1, то
ОО 00
к=1
и окончательно
ьа dx
х
J ОО
х — у. х =
dx к=1
00 , т
X
X
X
dx 1 — х (1 — х)2
(11.0.5)
365
Ниже приведем без вывода ряд формул, выражающих финальные
вероятности состояний и характеристики эффективности для некоторых
часто встречающихся типов СМО. Другие примеры СМО будут
разобраны далее в виде задач.
1. Простейшая СМО с отказами (задача Эрланга). На п-канальную
СМО с отказами поступает простейший поток заявок с интенсивностью
X, время обслуживания — показательное с параметром \л = 1 / Ьо6сл.
Состояния СМО нумеруются по числу заявок, находящихся в СМО (в силу
отсутствия очереди, оно совпадает с числом занятых каналов):
50 — СМО свободна;
sa — занят один канал, остальные свободны; ...;
sk— занято А;каналов, остальные свободны (1 < к < п);...;
sn — заняты все п каналов.
Финальные вероятности состояний выражаются формулами Эрланга
■1
Р
2 п
1+v V-^
1! 21 п!
к
Рк=^Р0(к = 1,2,...,п), (11.0.6)
гдер= \/\i.
Характеристики эффективности:
А = X (1 - рп); Q = l-pn; Ротк = рп; к = р (1 - рп). (Ц>0.7)
При больших значениях п вероятности состояний (11.0.8) удобно
вычислять через табулированные функции:
а
Р (т, а) = —е а ^распределение Пуассона,) (11.0.8)
m !
и
т „к
а
R(m,a) = ^—e-a (11.0.9)
к=о к\
(см. прил. 1), из которого первую можно выразить через вторую:
Р (m, a) = R (т, а) - R (т - 1, а). (11.0.10)
Пользуясь этими функциями, формулы Эрланга (11.0.6) можно
переписать в виде
pk = P(k,p)/R(n,p) (к = 0,1,..., п). (11.0.11)
2. Простейшая одноканальная СМО с неограниченной очередью. На
одноканальную СМО поступает простейший поток заявок с
интенсивностью X. Время обслуживания — показательное с параметром \i = 1 / to6cJl.
Длина очереди не ограничена. Финальные вероятности существуют
только при р = X / (л < 1 (при р > 1 очередь растет неограниченно). Состояния
СМО нумеруются по числу заявок в СМО, находящихся в очереди или
обслуживамых:
50 — СМО свободна;
sa — канал занят, очереди нет;
366
52 — канал занят, заявка стоит в очереди;...;
sk — канал занят, к — 1 заявок стоят в очереди;....
Финальные вероятности состояний выражаются формулами:
р0=1-р, р* = р*(1-р) (^ = 1,2,.-.), (И.0.12)
гдер = X / (л < 1.
Характеристики эффективности СМО:
Л = \ Q=l; Ротк=0; (11.0.13)
* = ~^; г = -В—; Гт = £ ; L = В ; (11.0.14)
1-р 1-р сист Х(1-р)' оч Х(1-р)
среднее число занятых каналов (или вероятность того, что канал занят)
fc =Х/р, = р. (11.0.15)
3. Простейшая одноканальная СМО с ограничением по длине
очереди. На одноканальную СМО поступает простейший поток заявок с
интенсивностью X; время обслуживания — показательное с параметром
|i = l/ ^5^. В очереди тп мест. Если заявка приходит в момент, когда все
эти места заняты, она получает отказ и покидает СМО. Состояния СМО:
50 — СМО свободна;
sa — канал занят, очереди нет;
52 — канал занят, одна заявка стоит в очереди;...;
sk — канал занят, к — 1 заявок стоят в очереди;...;
5т+1 — канал занят, тп заявок стоят в очереди.
Финальные вероятности состояний существуют при любом р = X / \i и
равны:
Ро = : £&\ Рк = РкРо (к = *> •••> m + !)• (И.0.16)
1-р
Характеристики эффективности СМО:
A = \(l-pm+l); Q = l-pm+1; Ротк = pm+1.
Среднее число занятых каналов (вероятность того, что канал занят)
к=1-р0. (11.0.17)
Среднее число заявок в очереди
, = р2 [1 - рт (т + 1 - Щ>)]
(1-Pm+2)(1-P)
Среднее число заявок в СМО
z=r + k. (11.0.19)
По формуле Литтла
*сист=^/^; 4)4 =г/\. (11.0.20)
367
(11.0.18)
4. Простейшая многоканальная СМО с неограниченной очередью.
На n-канальную СМО поступает простейший поток заявок с
интенсивностью X; время обслуживания одной заявки — показательное с
параметром [L = 1 / tb6cn. Финальные вероятности существуют только при
Р / п = X < 1) гДе 9 = ^/^- Состояния СМО нумеруются по числу заявок
в СМО:
50 — СМО свободна;
sa — занят один канал; ...;
очереди нет;
sk— занято к каналов (1 < к < п); ...;
sn — заняты все п каналов;
5п+1 — заняты все п каналов, одна заявка стоит в очереди; ...;
sn+r— заняты все п каналов, г заявок стоят в очереди; ....
Финальные вероятности состояний выражаются формулами:
L . р . . pn . pn+1 1 Г
Ро
, р pn pn+1
! + ■£-+...+ £- + р
1!
п ! п • п ! 1 — х
п+г
Р*=7тРо (!<*<"); Pn+r=-7 ;Ро(г>1). (11.0.21)
А;! п. -п !
С помощью функций Р(т, а) и Д(т, а) формулы (11.0.21) могут быть
приведены к виду
Р(*,р)
Рк =
Д(п,р) + Р(п,р)
X
(А; = 0,..., п);
(11.0.22)
1-Х
Pn+r = XrPn (г = 1,2,...).
Характеристики эффективности СМО:
г = рп+Ч / [п ■ п! (1 - х)2] = х рп I (1 - х)2;
z = г + к = r-f р;
^сост = ^ / *> ЧЭЧ = ^ / *•
(11.0.23)
(11.0.24)
(11.0.25)
5. Простейшая многоканальная СМО с ограничением по длине
очереди. Условия и нумерация состояний те же, что в п. 4, с той разницей,
что число т мест в очереди ограничено. Финальные вероятности
состояний существуют при любых X и \i и выражаются формулами:
n+l 1-х ^1
1! n ! п • п ! 1
X
Р* = Т.Ро (1 - *- п);
А;!
368
0П+Г
Pn+r = -7 \Po (1 < r < m), (11.0.26)
n • n !
гдех = p/n = X/(np).
Характеристики эффективности СМО:
А = \ (1 - Рп+т); Q = l-Pn+m; Р0гК=Рп+т; к=р(1-Рп+т); (11.0.27)
п-п! (1-Х)
J = F+^; (11.0.29)
£оч — г / л; £сист — z / л.
(11.0.30)
6. Многоканальная СМО с отказами при простейшем потоке заявок
и произвольном времени обслуживания. Формулы Эрланга (11.0.6)
остаются справедливыми и тогда, когда поток заявок — простейший, а
время обслуживания_ Тобсл имеет произвольное распределение с
математическим ожиданием t^^ = 1 / р.
7. Одноканальная СМО с неограниченной очередью при простейшем
потоке заявок и произвольном времени обслуживания. Если на однока-
нальную СМО поступает простейший поток заявок с интенсивностью X, а
время обслуживания Тобсл распределяется по произвольному закону с
математическим ожиданием 1 / р и коэффициентом вариации v , то среднее
число заявок в очереди выражается формулой Полячека—Хитина
г = р2(1+^)2/[2(1-р)], (П.0.31)
где р = X / р, а среднее число заявок в СМО
z = {р2 (1 + *v)2 / [2 (1 - р)]} + р. (11.0.32)
Из (11.0.31) и (11.0.32) по формуле Литтла получим
^р2(1+^)2; LT=P2(1+^- (И.0.33)
оч 2Х(1-р) сист 2Х(1-р) (л V ;
8. Одноканальная СМО при произвольном (пальмовском) потоке
заявок и произвольном времени обслуживания. Точных формул для
этого случая не существует, приближенная оценка длины очереди может
быть произведена по формуле
г «Р2К2+<)/[2(1-р)], (11.0.34)
где i\ — коэффициент вариации интервала между событиями во входном
потоке; р = X / р; X — величина, обратная математическому ожиданию
этого интервала; р = 1 / Ьобсл — величина, обратная среднему времени
обслуживания; v — коэффициент вариации времени обслуживания.
Среднее число заявок, связанных с СМО,
z « {р2К2 + vl)/ [2 (1 - р)]} + р, (11.0.35)
а средние времена пребывания заявки в очереди и в СМО соответственно
равны:
369
L «p2(^ + *v2)/[2X(i-p)]; (11-0.36)
Lx « {P2(^ + t£) I [2 X (1 - p)]} + 1 / ц. (11.0.37)
9. Простейшая многофазовая СМО с очередью. Анализ
многофазовых СМО в общем случае затруднен тем, что входящий поток каждой
последующей фазы является выходным потоком предыдущей и в общем
случае имеет последействие. Однако если на вход СМО с неограниченной
очередью поступает простейший поток заявок, а время обслуживания
показательное, то выходной поток этой СМО — простейший, с той же
интенсивностью X, что и входящий. Из этого следует, что многофазовую
СМО с неограниченной очередью перед каждой фазой, простейшим
входящим потоком заявок и показательным временем обслуживания на
каждой фазе можно анализировать как простую последовательность
простейших СМО.
Если очередь к фазе ограничена, то выходной поток этой фазы
перестает быть простейшим и вышеуказанный прием может применяться
только в качестве приближенного.
Далее будем пользоваться обозначениями для характеристик
эффективности СМО, приведенными на с. 364, и по мере необходимости
вводить некоторые другие обозначения.
В дальнейшем, задавая плотность f(x) различными формулами на
разных участках оси Ох, мы также не будем указывать значения f(x) на
границах участков.
Если единица измерения времени не фиксирована, будем для
краткости обозначать интенсивности потоков событий просто буквами X, (л,...
(без указаний размерностей). То же относится и ко времени tcliCT, Ьоч. Если
же единица времени фиксирована (час, минута, год и т.д.), то мы будем
указывать единицы измерения.
В данной главе нам удобно будет записывать закон распределения
смешанной случайной величины Т не в форме функции распределения
F(t), з.в форме «обобщенной» плотности f(t), которая определяется
следующим образом:
/(*) = *#)+1>6 (*-*),
где F^(t) — производная функции распределения на участках ее
непрерывности: р{ = Р{Т = £,-); б(х) — дельта-функция, свойства которой
даны в прил. 2.
11.1. На вход одноканальной СМО с отказами поступает
простейший поток заявок с интенсивностью X; время
обслуживания — показательное с параметром ц. В начальный момент
времени t = 0 канал свободен. Построить размеченный граф состояний
СМО. Написать и решить дифференциальные
уравнения Колмогорова для вероятностей состояний
СМО. Найти финальные вероятности состояний и
(для установившегося режима) характеристики эф-
Рис. 11.1 фективности СМО: A, Q, Ротк, к.
э0
370
Решение. Состояния СМО: sQ — свободна; ^ — канал занят.
Граф состояний показан на рис. 11.1. Уравнения Колмогорова:
dp0 /dt = — \р0 +|л Pi 5 dpx /dt = \pQ—\ipl. (11.1.1)
Так как pQ + px = 1 для любого t, можно выразить рг через р0:
р — 1 — р0 и получить одно уравнение для р0:
dp0 j dt = -(X + |л) р0 + |л. (11.1.2)
Решая это уравнение, получаем р0 как функцию t
Ро(<) =
М-
Х + |л
отсюда
1 + -е-(х+^)4
М-
л(0 = 1-^(0 = 7^-11-6^^1-
X + |л
При t —> оо получим финальные вероятности
р0=|л/(Х + |л); рг=\/(\ + \1), (11.1.3)
которые можно было бы найти и гораздо проще, решая линейные
алгебраические уравнения для финальных вероятностей состояний:
>ф0 = м>1; Ро + Pi = 1-
Формулы (11.1.3) можно записать компактнее, если ввести
обозначение р = X / |л:
р0=1/(1 + р); Pi = р / (1 + р).
Характеристики эффективности СМО:
i4 = Xp0=- ; <2 = - ; Ротк = рх
1 + р 1 + р 1 + р
*=1-р0=_В_. (11.1.4)
1 + Р
11.2. Одноканальная СМО с отказами представляет собой
одну телефонную линию, на вход которой поступает простейший
поток вызовов с интенсивностью X = 0,4 вызов/мин. Средняя
продолжительность разговора £обсл =3 мин; время разговора имеет
показательное распределение. Найти финальные вероятности
состояний СМО: р0 и pv а также A, Q, Ротк, к. Сравнить пропускную
способность СМО с номинальной, которая была бы, если бы
разговор длился в точности 3 мин, а заявки шли одна за другой
регулярно, без перерывов.
371
Решение. X = 0,4; |л = 1 / to6cjl =1/3;р = Х/р, = 1,2. По
формулам (11.1.3) р0 «1/2,2« 0,455; ^ «0,545; Q« 0,455; Л = Х<2«
«0,182; к = рг «0,545.
Таким образом, линия в среднем будет обслуживать 0,455
поступающих на нее заявок, т.е. 0,182 разговора в минуту. Номинальная
пропускная способность канала была бы (при регулярно
приходящих и регулярно обслуживаемых заявках) Аном — 1 /to6cjl —
— 1/3 « 0,333 разг/мин, что почти вдвое больше, чем действительная
пропускная способность А.
11.3. Имеется одноканальная СМО с отказами. Поток заявок —
простейший с интенсивностью X . Время обслуживания — не
случайное и в точности равно to6cjl — 1 / |л. Найти относительную и
абсолютную пропускную способность СМО в предельном
стационарном режиме.
Решение. Рассмотрим на оси 0t простейший поток заявок с
интенсивностью X (рис. 11.3). Будем отмечать кружками все
заявки, которые приняты к обслуживанию. Пусть какая-то заявка,
^обсл
<£=^= 1
Рис. 11.3
пришедшая в момент tv принята к обслуживанию. Тогда все
заявки, пришедшие после нее за время to6cjl, получат отказ; следующей
будет принята к обслуживанию заявка, пришедшая в момент ^
такой, что t2 — tx > to6cjl. Рассмотрим интервал Г между концом
обслуживания первой заявки и моментом t2 прихода ближайшей
следующей, которая будет принята к обслуживанию. Из-за
отсутствия последействия в простейшем потоке распределение
интервала Т совершенно такое же, как и в вообще интервала между
заявками, т.е. показательное с параметром X. Средняя длина
интервала Т равна mt = 1/Х.
Итак, на оси 0t будут чередоваться неслучайные интервалы
занятости канала длины to6cjl — 1/|л и случайные свободные
интервалы со средней длиной 1/Х. На первые попадет доля всех заявок,
равная
I/H _ X
1/|л + 1/Х Х + |л'
а на вторые — доля, равная
|л(Х + |л) = 1/(1 + р), где р = Х/|л.
0
t
обсл
Jk
t
%
обсл
л
372
Эта величина и есть относительная пропускная способность
СМО
Q = l/(1 + P), (П.3.1)
откуда
Л = \д = Х/(1 + р). (11.3.2)
Отметим, что формулы (11.3.1), (11.3.2) совпадают с (11.1.4),
соответствующими показательному распределению времени
обслуживания. Это и естественно, так как формулы Эрланга
остаются справедливыми при любом распределении времени
обслуживания со средним значением, равным 1Дх.
11.4. Доказать, пользуясь формулой (11.0.5), что для
простейшей одноканальной СМО с неограниченной очередью среднее
число заявок, находящихся в СМО, равно z — р / (1 — р), где
р = \Дц а среднее число заявок в очереди г = р2/(1 — р).
Решение. По формулам (11.0.12) р0 = 1 — р; pk = р*(1— р)
1/С — ij Zij ... J.
Обозначим Zфактическое (случайное) число заявок в СМО:
оо оо оо
z = M[Z} = -£kpk=-£kpk(l-p) = (l-p)J2kPk.
к=0 /:=1 к=1
По формуле (11.0.5) для р < 1
y-fcpA=—р—,
к а-?)2
откуда^ = р / (1 — р). Среднее числскзаявок в очереди равноz минус
среднее число занятых каналов к=А/\х = \/\х = р, т.е. г =
= [p/(i-p)]-p=p2/(i-p)-
11.5. Железнодорожная сортировочная горка, на которую
подается простейший поток составов с интенсивностью X = 2
состава в час, представляет собой одноканальную СМО с
неограниченной очередью. Время обслуживания (роспуска) состава на горке
имеет показательное распределение со средним значением
^обсл = 20 мин. Найти финальные вероятности состояний СМО,
среднее число z составов, связанных с горкой, среднее число г
составов в очереди, среднее время £сост пребывания состава в СМО,
среднее время tQ4 пребывания состава в очереди.
Решение. X = 2 состава/ч; Гобсл =1/3 ч; (л = 3 состава/ч;
р = Х/|л = 2/3. По формулам (11.0.12) р0 = 1-2/3=1/3; рг=(2/3)х
х(1/3) = 2/9; р2 =(2/3)2(1/3) = 4/27;... ft =(2/3)*(1/3);... По
формулам^ 1.0.13), (11.0.14) z — р / (1 - р) = 2 состава; г = 4/Зсо-
става; £сист = 1 ч; tm = 2 / 3 ч.
373
11.6. Условия предыдущей задачи усложняются тем, что в
парке прибытия железнодорожной сортировочной горки могут
находиться одновременно не более трех составов (включая
обслуживаемый). Если состав прибывает в момент, когда в парке
прибытия уже находится три состава, он вынужден ожидать своей
очереди на внешних путях. За один час пребывания состава на
внешних путях станция платит штраф а руб. Определить средний
суточный штраф, который придется уплатить за ожидание
составов на внешних путях.
Решение. Вычислим среднее число zB — составов,
находящихся на внешних путях:
оо
в
1 'Ра +2Р5+---=У]кР
fc=4
оо
£*Р*Ро
А: =4
оо
РоХ^Р ;
А: =4
оо
£*р
к
оо
А: =4
Ed k
*=4«Р
ОО
d
P4(4-3p). y
oo
dp 1- p (1- p)
PoY,kp
A: =4
к
d ^ k
_P4(4-3P)
1-p
1,18.
По формуле Литтла среднее время, проводимое одним
составом на внешних путях, tB « 1,18 / X = 1,18 / 2 = 0,59 ч. За сутки
(24 ч) на станцию приходит в среднем 24Х = 48 составов. Средний
суточный штраф составляет 48 • 0,59 • а « 28,3а.
11.7. Вычислить непосредственно по графу состояний,
пользуясь схемой гибели и размножения, финальные вероятности
состояний для простейшей двухканальной СМО (n = 2) с тремя местами
в очереди (га = 3) при X = 0,6; |л = 0,2; р = X / |л = 3. Найти для этой
СМО характеристики z, f, tcllCT, ^оч, не пользуясь формулами
(11.0.26), а непосредственно через финальные вероятности, и
сравнить с теми, которые получаются по формулам (11.0.26).
*0
X
М-
*1
X
"" 2|i
*2
X
~" 2|i
*з
X
2|i
*4
X
' 2|л
55
а
Рис. 11.7
Решение. Граф состояний СМО показан на рис. 11.7. По схе
ме гибели и размножения, обозначая X / |л = р, получаем:
Ро
1 + Р + ^г + ^ + *V +
-1
.-1
(40,58)-1 » 0,025;
374
Px =
40,58
0,074; p.
4,5
40,58
10Д5
40,58
0,111; p3
15,18
40,58
6,75
40,58
0,165;
0,375;
z = 1 • 0,074 + 2 • 0,111 + 3 • 0,165 + 4 • 0,250 + 5 • 0,375 « 3,67;
f = 1 • 0,165 + 2 • 0,250 + 3 • 0,375 « 1,79;
*"сист = */ 0,6 « 6,11; tm = r I 0,6 « 2,98.
11.8. Формула для f (11.0.28) справедлива для любого х < 1
или х > 1- При х = 1 °на перестает работать (дает
неопределенность вида 0/0). Пользуясь непосредственно схемой гибели и
размножения, вывести для этого случая вероятности состояний
Ро, Рг >•••*> Рп+т и найти характеристики эффективности СМО: А,
V> *■ОТК' "*> ^5 Z 1 ^ОЧ ' ^СИСТ '
»0
X
м-
X
2|i
X
k\i
X
7111
п
X
71|1 П|1
Рис. 11.8
Решение. Граф состояний СМО имеет вид, показанный на
рис. 11.8. Пользуясь общими формулами для схемы гибели и
размножения и обозначая X / |л = р, имеем
Ро
2 п nn+l
1 + -^- + —+...+ — + ^ +...+ —
п +т
1! 2!
п
\
П • П!
пт -П\
-1
2 п
U + -P. + — +...+ —
1! 2!
П!
р +
[р]
2
+..
П (nJ
.+
[p]
m
In; j
-1
При x = P I n = 1
Po
l + £ + £_+...+£
n
1! 2!
n!
+
mp
n
n!
-l
(11.8.1)
Pk = ТГPo (1 < * < »); Pn+r = ^Po (1 < г < m); (11.8.2)
A;! n!
n
-* oth Pn+m i V ■*■ Pn+m ■*■
n!
p0;
375
n
n
A = \Q = \
1-
P
n\
0
к = Л / |i = p
1-
n!
Po
m
m »
Mb
n
p - 9n m (m+1) ...
Po X/ = . — -—-p0;(H-8.3)
г + fc; £
n
СИСТ
I
r=l
П!
/\ *оч = Г / X«
11.9. Автозаправочная станция (АЗС) имеет две колонки (п =
= 2); площадка возле нее допускает одновременное ожидание не
более четырех автомобилей (га — 4). Поток автомобилей,
прибывающих на станцию, простейший с интенсивностью X = 1
авт/мин. Время обслуживания автомобиля — показательное со
средним значением to6cjl = 2 мин. Найти финальные вероятности
состояний АЗС и ее характеристики: A, Q, РОТК, k,z,r, iCiiCT , iOH.
Решение. Х = 1, |х = 1/2 = 0,5; р = 2; х = Р /^ = 1. По
формулам (11.8.1)-(11.8.3) имеем:
•1
1 2
— 5 Рг =Р2=Рг
Ро
су 2 су 2
1+2+1-+1-4
2! 2!
13
Pi =Р>
Ре==Тз;
POTK=2/13; Q = l-POTK -11/13;
A = \Q = ll/13m 0,85 авт/мин;
к — Л / ^ = 22 / 13 « 1,69 колонки;
22 4(4+1) 1
2!
— «1,54 автомобиля;
13
z — г + к и 3,23 автомобиля.
11.10. Имеется двухканальная простейшая СМО с отказами.
На ее вход поступает поток заявок с интенсивностью X = 4
заявки/ч. Среднее время обслуживания одной заявки i - = 0,8 ч.
Каждая обслуженная заявка приносит доход с = 4 рубУ Содержание
каждого канала обходится 2 руб/ч. Решить: выгодно или
невыгодно в экономическом отношении увеличить число каналов СМО до
трех?
Р е ш е н и е. По формулам Эрланга (11.0.6)
Ро
1 + 3,2 +
3,2'
2!
(9,32)
-1
0,107; р.
5,12
9,32
0,550;
Q = 1 — р2 « 0,450; А = 4Q & 1,8 заявки/ч.
376
Доход от заявок, приносимый СМО в данном варианте, равен
D = A-c « 7,2руб/ч.
Подсчитаем те же характеристики для трехканальной СМО
(отмечая их штрихом вверху):
Р'о
,2 ооЗ
, 00 3,2z 3,2*
1 + 3,2 + -^- + '
2! 3!
0,0677; рз7 ~ 5'48 • °>0677 ~ °>3715
Q' = 1 - р3; « 0,629; Л' = 4(5' ~ 2,52; Df = Af-c& 10,08руб/ч.
Увеличение дохода равно D' — D = 2,88 руб/ч; увеличение
расхода равно 2 руб/ч; из этого видно, что переход отп = 2кп = 3
экономически выгоден.
11.11. Рассматривается простейшая СМО с практически
неограниченным числом каналов (п —> оо). На вход СМО поступает
поток заявок с интенсивностью X; интенсивность потока
обслуживании (для одного канала) равна |л. Найти финальные вероятности
состояний СМО и среднее число занятых каналов к.
Решение. Данная СМО не дает ни отказов, ни очередей; ее
можно рассматривать как предельный случай СМО с отказами
прип —> оо. Формулы Эрланга (11.0.6) дают
Ро
ос *-1
у
к
= е_р, где р = X / [I] рк = 4-е"р = Р (к, р)
А;!
(см. прил. 1). При неограниченном числе каналовЛ = Х; к =
= Х/^ = р.
11.12. Рассматривается одноканальная СМО с отказами; на ее
вход поступает простейший поток заявок с интенсивностью X.
Время обслуживания — показательное с параметром |л = 1 / t^CR.
Работающий канал может время от времени выходить из строя
(отказывать); поток отказов канала — простейший с
интенсивностью v. Восстановление (ремонт) вышедшего из строя канала
начинается мгновенно после его отказа; время ремонта Тр —
показательное с параметром ч = 1 / tp. Заявка, которая обслуживалась в
момент выхода канала из строя, покидает СМО необслуженной.
Найти финальные вероятности состояний СМО: s0 — канал
свободен; sx — канал занят, исправен; s2 — канал ремонтируется и
характеристики СМО: А и Q.
Решение. Граф состояний СМО дан на рис. 11.12, а.
Алгебраические уравнения для финальных вероятностей состояний:
ХРо =M-Pi +ЧР2; (v> + v)pl=\p0; vpx=~ip2; (11.12.1)
к ним прибавляется нормировочное условие
377
Po + Pi + P2 = L
(11.12.2)
Выразим вероятности pv p2 из (11.12.1) через pQ:
X у
Pi = Po\ P2 =-Pi
|л + v 4
m (м- + ^)
Po
Подставляя рхи р2в (11.12.2), получаем
р0 = {1 + X / (JJL + у) + \у / ft (ц + у)]}"1. (11.12.3)
Чтобы найти относительную пропускную способность ф,
нужно вероятность р0 того, что заявка будет принята к обслуживанию,
умножить на условную вероятность р1 того, что заявка, принятая
к обслуживанию, фактически будет обслужена (канал не откажет
за время обслуживания заявки). Найдем эту условную
вероятность по интегральной формуле полной вероятности. Сделаем
гипотезу, состоящую в том, что время обслуживания заявки попало
на участок от t до t + dt; вероятность этой гипотезы приближенно
равна f(t) dt, где f(t) — плотность распределения времени
обслуживания: f(t) = [ie~[Lt (t > 0). Условная вероятность того, что
канал не выйдет из строя за время t, равна e~vt; отсюда
оо
оо
р
J [1е~^ e~vt dt
J[ie-{[i+v)tdt
М-
о
о
|Л + V
Эту условную вероятность можно найти и проще: она равна
вероятности того, что начатое обслуживание закончится раньше,
чем канал выйдет из строя. Представим на оси 0t (рис. 11.12, б)
совмещение (суперпозицию) двух потоков: потока
обслуживании с интенсивностью |л (обозначен крестиками) и потока
отказов канала с интенсивностью v (обозначен кружками).
Зафиксируем любую точку t на оси 0t и найдем вероятность того, что
Ч—<•>
0
а
-*-©—I—X X ©—*-* *-<•>-<•>-*■
С/
X - поток обслуживании |i
© - поток отказов и
б
Рис. 11.12
t
378
первый после нее крестик придет раньше, чем кружок.
Очевидно, она равна отношению интенсивности потока крестиков к
суммарной интенсивности потока крестиков и кружков;
|jl / (jjl Ч- у).Таким образом,
Q=p0pf
м-
{\i + v)
I
1+
X
+
Ху
М-
A = \Q.
|л + v + 4 (1 + v/ч)
(11.12.4)
11.13. Условия задачи 11.12 повторяются, но с той разницей,
что канал может выходить из строя и в неработающем состоянии
(с интенсивностью у' < у).
Решение. Граф состояний СМО дан на рис. 11.13. Из
уравнений
Ро + Pi + Рг = 1
найдем финальные вероятности
Ро
X Ху + |л v' + уу '
|л + у
1 (М- + v)
Pi
X Ху + |лу ' + уу '
Ро; ^2= Г"—;—Ро\
|л + у
Ч (р, + у)
О
|л+ у
; Л = Х<2 = р0
X|JL
|Л + У
11.14. Рассматривается простейшая одноканальная СМО с
ограниченной очередью т — 2; работающий канал может иногда
выходить из строя (отказывать). Заявка, которая обслуживается в
момент отказа канала, становится в очередь, если в ней еще есть
свободные места; если нет, она покидает СМО необслуженной.
Интенсивность потока заявок X, потока обслуживании |л, потока
отказов канала у, потока восстановлений (ремонтов) ^.
Перечислить состояния СМО и найти для них финальные вероятности, а
*п
X ,
Ц
*1
У
S2
Рис. 11.13
Рис. 11.14
379
также характеристики эффективности СМО: A, k,r,z,tcllCT,t04
при X = 2, |л = 1, v — 0,5, ч = 1.
Решение. Состояния СМО:
500 — СМО свободна, канал исправен;
510 — канал занят и исправен, очереди нет;
sn — канал вышел из строя, ремонтируется; в СМО имеется
одна заявка, ждущая очереди;
520 — канал занят и исправен; одна заявка обслуживается,
другая ждет очереди;
521 — канал вышел из строя, ремонтируется; в очереди ждут две
заявки;
530 — канал занят и исправен; две заявки ждут очереди, одна
обслуживается.
Граф состояний СМО показан на рис. 11.14. Уравнения для
финальных вероятностей состояний:
М-Рю = ХРоо 5 W>20 + ЧРи + ХРоо = (М- + 1 + v) Ры;
М>зо + IP21 + ХРю = (М- + Ч + v) Р20;
ХР2о = (И« + v) Рго 5 VP20 =Ф + ^) Рзо;
VPlO = Ь + Х) Р\\ 5 XPll + ^20 + УР30 = 1 Р21 i
Р00 + Рю + Pll + Р20 + Р21 + РЗО = L
Решая эти уравнения при X = 2, |л = 1, v = 0,5, 4 = 1> получаем:
р00 = 3/61 « 0,049; р10 = 6/61 « 0,098; р20 = 14/61 « 0,230;
р30 = 56/183 « 0,306; рх = 1/61 w 0,016; р21 = 5/183 « 0,301.
Отсюда
z = 1 (р10 + рп ) + 2 (р20 + р21) + 3 р30 = 383/183 « 2,09;
г - 1 (р20 + рп ) + 2 (р21 + рзо) = 89/6* ~ Мб-
* = 1 (р10 + р20 + Рзо) = 116/183 « 0,63.
Абсолютная пропускная способность А для СМО с неотказы-
вающими каналами могла бы быть найдена умножением к на |л; в
нашем случае производительность одного канала (среднее число
заявок, фактически обслуживаемых в единицу времени) можно
найти, умножая к на вероятность |л / (|л + v) тогс^ что начатое
обслуживание будет доведено до конца: А = к\ь-\ь / (\l + v) =
= &|л2/(|л + у) «0,42.
11.15. В стоматологическом кабинете три кресла (n = 3), а в
коридоре имеются три стула (га — 3) для ожидающих приема. Поток
клиентов — простейший с интенсивностью X = 12 клиент/ч.
Время обслуживания (приема клиента) — показательное со средним
380
значением to6cjl = 20 мин. Если все три стула в коридоре заняты,
клиент в очередь не становится. Определить среднее число
клиентов, обслуживаемых за час, среднюю долю обслуженных клиентов
из числа пришедших, среднее число занятых стульев в коридоре,
среднее время £сист, которое клиент проведет в коридоре и в
кабинете; то же самое среднее время при условии, что клиент будет
обслужен.
Решение. р = 12/3=4; х = р/3 = 4/3; п = 3; га=3. По
формулам (11.0.26)-(11.0.30) находим:
42 43 44 1-(4/3)3^1
Ро =•
1 + 4+ — + —+
6 3-6 1-4/3
0,01218 « 0,012;
рг = 4 • 0,01218 « 0,049; р2 = 8 • 0,01218 « 0,097;
Я2 44
р3 = _ . 0,01218 « 0,130; p3+i = 0,01218 « 0,173;
3 36
4 _ 4
Рз+2 =~%+i ~ 0,231; Рз+з ~~%+2 ~ 0,307.
Средняя доля обслуживаемых клиентов Q = 1 — Ротн =
= 1 - Рз+з «1- °>307 = °>693-
Среднее число клиентов, обслуживаемых за час, равно А =
= \Q ^12-0,683^8,32.
Среднее число занятых каналов (кресел) [по формуле (11.0.27)]
к = 4 (1 - р3+з) ~ 2,78.
Среднее число клиентов в очереди [по формуле (11.0.28)]
f_44 -0,01218 1-4-(4/3)3+3(4/3)4 ^ ± ^
3-6 (1-4/3)2 ~ ' '
z = r + k = 4,34; i04 = г I X « 0,13 ч; £сист = J / X « 0,362 ч.
Такие малые значения fCHCT и £оч связаны с тем, что некоторые
клиенты уходят, не становясь в очередь. Условное среднее время,
проведенное клиентом в системе, при условии, что он был
обслужен, равно tciiCT = tcmT I Q « 0,52 ч, а условное среднее время
пребывания в очереди (при том же условии) t04 =t04 / Q ~ 0,19ч.
11.16. Формулы (11.0.26), (11.0.28) при х = 1 дают
неопределенность вида 0/0. Раскрыть эту неопределенность и написать
формулы, справедливые при х = 1-
Решение. При правилу Лопиталя
1га „_ га —1
- х -™>х
lim — = = га;
x=i 1 _ х -х
381
Po =■
! + £+...+£_+ P
1! n! n -n\
к
P
(11.16.1)
Л =T7?o (!<*<*); (11.16.2)
A:!
n
P„+l =Pn+2 =--=P»+m =—ГР0> (11.16.3)
n!
т.е. все вероятности, начиная с рп и заканчивая pn+m, равны друг
другу.
Формулы для A, Q, Р0ТК, достаются прежними.
Раскрывая неопределенность в формуле (1.1.0.28), получаем
. l-(m + l)xm +rnXm+1 m(m + l)
lim - = ;
(1-Х)'
___ pn+1p0m (га +1)
" 2n • n!
(11.16.4)
Формулы (11.0.29), (11.0.30) остаются прежними.
Формулы (11.16.1)-(11.16.3) можно было бы вывести и не
раскрывая неопределенность, а непосредственно из схемы гибели и
размножения.
11.17. 1) Подсчитать характеристики эффективности A, Q,
Ротк> ^> ^ ^ ^оч' ^сист Для простейшей одноканальной СМ О с тремя
местами в очереди (га = 3) при условиях: \ = 4 заявки/ч;
to6cji = 1 / jx = 0,5.2) Выяснить, как эти характеристики
изменяются, если увеличить число мест в очереди до га = 4.
Решение. |л=2; р = Х/|л = 2; по формулам (11.0.12)-(11.0.16)
при га = 3 имеем: р0 = 1/31; р4 = 16/31; Q « 0,484; Л = XQ « 1,93
заявки/ч; k = pQ « 0,968; г « 2,19 заявки; J « 3,16 заявки; £оч « 0,55
ч;*сист «0,79 ч.
2) При га = 4 имеем р0 = 1/63 « 0,0158; р5 = 32/63 « 0,507;
<2 ~ 0,493; Л « 1,96 заявки/ч; г « 3,11 заявки; z = 4,09 заявки;
*от «0,78ч;*сист «1,02 ч.
Таким образом, увеличение числа мест s с трех до четырех
приводит к незначительному увеличению абсолютной (и
относительной) пропускной способности, сопровождаясь при этом
некоторым увеличением среднего числа заявок в очереди и в системе, а
также соответствующих средних времен. Это и естественно, так
как некоторые заявки, получающие отказ в первом варианте, все
же становятся в очередь во втором.
382
11.18. Как изменятся характеристики эффективности СМО
предыдущей задачи, если X и [i остаются прежними, га = 3, но
число каналов обслуживания увеличится до п = 2?
Решение, х = 1; по формулам (11.16.1), (11.16.2) имеем
р0 =1 / 11] рг =...= рь =2 / 11] 0 = 1-2/11 « 0,818; А « 3,27
заявки/ч; г = 12 / 11 « 1,09 заявки; fc = Л / ц, « 1,64; z = г + fc « 2,73
заявки; £оч « 0,27 ч; гсист « 0,68 ч.
11.19. Система массового обслуживания — билетная касса с
одним окошком (гг = 1) и неограниченной очередью. В кассе
продаются билеты в пункты А и В; пассажиров, желающих купить билет
в пункт А, приходит в среднем трое за 20 мин, в пункт В — двое за
20 мин. Поток пассажиров можно считать простейшим. Кассир в
среднем обслуживает трех пассажиров за 10 мин. Время
обслуживания — показательное. Установить, существуют ли финальные
вероятности состояний СМО и если да — вычислить первые три
из них: р0, pv р2. Найти характеристики эффективности СМО:
Z4 Г' ^СИСТ И^ОЧ *
Р е ш е н и е. XА = 3 / 20 = 0,15 заявки/мин; X в = 2 / 20 = 0,10
заявки/мин. Общая интенсивность потока заявок X = \А +
+ \в = 0,25 заявки/мин; \l = 3 / 10 = 0,3 заявки/мин; р = X / \l «
« 0,833 < 1, финальные вероятности существуют. По формулам
(11.0.12)-(11.0.14): р0 «0,167; р1 «0,139; р2 «0,116; z«^^«
0,167
« 4,99 заявки; г = 0,8332 / 0,167 « 4,16 заявки; 1СШТ « 4,99 / 0,25 «
« 20,0 мин; t04 « 4,16 / 0,25 « 16,7 мин.
11.20. Одноканальная СМО — ЭВМ, на которую поступают
заявки (требования на расчеты). Поток заявок — простейший со
средним интервалом между заявками t = 10 мин. Время
обслуживания Тобсл распределено по закону Эрланга 3-го порядка с
математическим ожиданием to6cJl = 8 мин. Определить среднее число z
заявок в СМО и среднее число т заявок в очереди, а также средние
времена пребывания заявки в системе £сист и в очереди t04.
Решение. Характеристики СМО могут быть найдены по
формуле Полячека — Хинчина (11.0.31), (11.0.32). Имеем: X = 0,1
заявки/мин; \i = 0,125 заявки/мин; р = ХДх = 0,8.
Коэффициент вариации времени обслуживания для закона
Эрланга 3-го порядка равен 1/V3. По формуле (11.0.31)
г=0,64(1 + 1/3):(2-0,2)«2,13. По формуле (11.0.32) z = г + 0,8 «
« 2,93. По формуле Литтла£оч « 21,3 мин, £сист « 29,3 мин.
11.21. Условия предыдущей задачи изменены: поток заявок
уже не простейший, а пальмовский, причем интервал между
событиями в потоке распределен по обобщенному закону Эрланга 2-го
порядка (см. задачу 8.31) с параметрами Хх = 1/2; Х2 = 1/8. Найти
383
приближенно, по формулам (11.0.34)-(11.0.37), характеристики
эффективности СМО.
Решение. Случайная величина Т, распределенная по
обобщенному закону Эрланга 2-го порядка, есть сумма двух
случайных величин Тг и Т2, распределенных по показательным законам
с параметрами: 1г =1/2;Х2 =1/8. ОтсюдаМГГ] = 1 / Хх + 1/Х„ =
= 10 мин; D[T) = В[Тг) + D[T2] = 22 + 82 =68; v{ =68/102 = 0,68; v\ =
= 1/3. Следовательно, г = 1,62 заявки; ^=2,42 заявки; t04 =16,2 мин;
*сист= 24,2 мин.
11.22. Техническое устройство (ТУ) может время от времени
выходить из строя (отказывать). Поток отказов ТУ — простейший
с интенсивностью X = 1,6 отказа в сутки. Время Тв восстановления
(ремонта) ТУ имеет равномерное распределение на участке от 0 до
1 сут. Найти (для предельного стационарного режима) среднюю
долю R времени, в течение которого ТУ работает.
Решение. Состояния ТУ: sQ — работает; sx — ремонтируется.
Граф состояний ТУ показан на рис. 11.22, где \l = 1 /М[ТВ] =
= 1/0,5 = 2. Этот граф в точности совпадает с графом состояний
одноканальной СМО с отказами. Мы знаем, что если поток
заявок, поступающих на СМО, — простейший, а время
обслуживания имеет произвольное распределение, то справедливы
формулы Эрланга (11.0.6); в данном случае р = Х/|л = 0,8; pQ =
= {1 + р / 11}"1 = 1/1,8 « 0,556; рг = 1 - 0,556 « 0,444. Итак, R
« 0,556, т.е. ТУ будет работать немногим более половины всего
времени, а остальное время ремонтироваться.
11.23. В условиях предыдущей задачи ТУ дублировано точно
таким же ТУ, которое может выходить из строя только в
работающем состоянии; X, [i — такие_же, как в задаче 11.22. Найти
величину Д, а также среднее число к неисправных ТУ.
50
X 1
Г |i
5i
X I
1 2ll
5?
Рис. 11.22
Рис. 11.23
Решение. Состояния системы S: sQ — оба ТУ исправны (одно
из них работает, другое нет); sx — одно ТУ работает, другое
ремонтируется; 52 — оба ТУ ремонтируются. Граф состояний дан на рис.
11.23. Граф в точности совпадает с графом состояний двухканаль-
ной СМО с отказами. По формулам Эрланга (11.0.6)
-1
Ро =
1 + -^ +
1!
2!
{1 + 0,8 + 0,64/2}-1 ^0,472;
рг « 0,8 • 0,472 = 0,378; R = р0 + рг « 0,850; р2 = 0,150;
384
к = 1 • рг + 2р2 = 0,678.
Очевидно, тот же прием (сведения к СМО с отказами) может
быть применен и в случае, когда число дублирующих ТУ более
одного.
11.24. Система массового обслуживания — обувной магазин, в
котором каждый покупатель проходит три фазы обслуживания:
1) примерка и выбор обуви; 2) уплата денег в кассу и 3) получение
покупки на контроле. В магазин прибывает простейший поток
покупателей с интенсивностью X = 45 чел/ч.
В отделе примерки имеются четыре стула, занимая которые,
покупатели могут самостоятельно выбирать и примерять обувь.
Среднее время примерки и выбора обуви tl = 5 мин. Выбравший
обувь покупатель направляется в кассу, где вторично становится
в очередь (касса в магазине одна). Среднее время оплаты товара в
кассе t2 = 1 мин. После оплаты покупатель идет на контроль, где
становится в новую очередь и получает покупку. На контроле
работают три продавца; среднее время выдачи покупки t = 2 мин.
Все потоки событий — простейшие.
Рассматривая магазин как трехфазовую СМО, найти
характеристики ее эффективности:
^1 (^2>^з) ~~ среднее число покупателей в очереди к первой
(второй, третьей) фазе обслуживания;
zl (z2, z3) — среднее число покупателей, связанных с первой
(второй, третьей) фазой обслуживания;
^оч(1)5 (^оч(2)5 ^оч(3)) ~ среднее время ожидания покупателя в
очереди к первой (второй, третьей) фазе;
^сист(1)? (^сист(2)) ^сист(3)) ~ среднее время пребывания
покупателя в первой (второй, третьей) фазе обслуживания;
г — общее среднее число покупателей во всех трех очередях;
z — общее среднее число покупателей в магазине;
t_04 — общее среднее время, проводимое покупателем в очередях;
£сист — общее среднее время, затрачиваемое покупателем на
приобретение обуви в магазине.
Дополнительно ответить на следующие вопросы: 1) В каком
звене и как нужно улучшить обслуживание для того, чтобы
сократить затраты времени покупателей? 2) Как можно было бы учесть
тот факт, что не все покупатели находят себе подходящую обувь,
и какая-то доля а из них (0 < а < 1) уходит из магазина, не сделав
покупки?
Решение. Так как все потоки событий простейшие, то
выходные потоки всех трех фаз тоже будут простейшими, и можно
рассматривать три последовательные фазы как три отдельные
СМО со своими характеристиками.
385
1.Первая фаза. Так как в отделе примерки четыре стула, то
число каналов пх = 4. Далее, имеем tt = 1/[1г = 5 мин = 1/12 ч;
р2 = 45/12 = 15/4 « 3,75; Xi = Pi ln\ = 15/16 < 1- По формулам
(11.0.21)-(11.0.25) находим:
рР
л owr (3,75)2 (3,75)3 (3,75)4
1 + 3,75 + v ' у + v ' у + v ' у +
2 2-3 234
+ (3,75)
-1-1
-1
2-3-4-4(1-15/16)
= (3,75)5 р?)
(151,58)-1 « 0,0066; ^ = 3,75;
13,01; zx = 16,76;
1 4-4! (1-Xl)2 '
*W =гг /X «0,289 ч «17,3 мин; i$CT = ^ /X « 0,372 ч « 22,3 мин.
2. Вторая фаза. X = 45; п2 = 1; р2 = 0,75 < 1. По формулам
(11.0.12)-(11.0.14) получаем:
г2 = р*/(1 - р2) = 9/4 = 2,25; z2 = р2/(1 - р2) = 3;
^оч} = г2 Дх = °,°5 ч = 3 мин; t£lT = 1/15 ч = 4 мин.
3. Третья фаза. тг3 = 3; Х = 45; р3 =3/2; Хз = 0,5< 1 • По
формулам (11.0.21)-(11.0.25) находим: р{*] «0,210; г3 «0,237;
г3 « 1,737; 1$ « 0,316 мин; 1{СЦТ « 2,316 мин.
Складывая средние численности трех очередей, получаем
общую среднюю численность очереди:
г = rx + f2 + г3 « 15,5.
Аналогично находим среднее число покупателей в магазине
Z ~==- Z-j -}- Zn -}- Zn « ^Л,Э.
Среднее время пребывания покупателя в очереди
*оч = *от + *п + *п ~ 2°,6 МИН'
Среднее время пребывания покупателя в магазине
^сист = ^сист "I" ^сист "I" ^сист ~ 28,6 МИН.
1) Улучшить обслуживание можно, уменьшая время пребывания
покупателя в первой фазе, которая представляет собой наиболее
слабое звено СМО. Всего проще достигнуть этого, увеличив число
щ стульев в отделе примерки, т.е. число каналов обслуживания в
первой фазе. Например, простое увеличение числа стульев на еди-
386
ницу (т.е. переход от щ = 4 к щ = 5) дает существенный выигрыш
во времени. Действительно, при ггх = 5 для первой фазы получим:
Pl =3,75; xi =3,75/5 = 0,75; j#> = {59,71}-1; гг ^2,08;
zx « 5,13; * ^ « 1,84 мин; £^т « 6,84 мин.
2) Учесть наличие доли покупателей а, уходящих из магазина
без покупки, можно, умножив интенсивность входного потока
второй и третьей фаз на (1 — а).
11.25. На железнодорожную сортировочную станцию
поступает эрланговский 10-го порядка поток составов с
интенсивностью X = ^2 состава/ч. ' Время обслуживания
состава Тобсл распределено в интервале от 0 до 1 ч
по закону с плотностью tp(£), показанной на
рис. 11.25. Оценить приближенно [по формулам
(11.0.34)-(11.0.37)] характеристики
эффективности станции — среднее число z составов на
станции, в очереди г, среднее время £сист
пребывания состава на станции, среднее время t04
ожидания составом очереди на обслуживание.
Решение. Для закона ip (t) имеем
to6cjl = 1 / 3; р = X / [l = 0,8 < 1. Для потока Эрланга 10-го порядка
vl =(1 /л/к)2 =0,1; v* определяем, разделив дисперсию D[To6cjI]
на квадрат математического ожидания: v* = 1 / 2 = 0,5.
Находим характеристики СМ О:
^ = Р2(^х+^)/[2(1-р)] = 0,82(0,1 + 0,5)/(2.0,2) = 0,96;
z = г + р « 0,96 + 0,8 = 1,76;
i04 = г I X « 0,8 ч; tCIICT = im + 1 / [i « 1,13 ч.
11.26. Показать, что для простейшей гг-канальной СМО с
неограниченным числом мест в очереди среднее число заявок,
находящихся в очереди, заключено в пределах
Х"+1 п _ Xn+1
л. < г < л.
1-х х"(»-1) + 1 1-х
Решение. Запишем выражение для г в следующем виде [см.
формулы (11.0.23), (11.0.21)]:
- Pn+1 Ро X Р"
п-п\(1-ху (1-х) "!
Подчеркнем, что здесь X — интенсивность именно эрланговского потока, а не того
простейшего потока, прореживанием которого получен эрланговский.
387
Следовательно,
п
Рп
п\
п
1 + Р + —+...+^-+ р
п
-1
X
П\
п п (п - 1) п\
1 + - + —^—г -+...+ +
п\ 1 - х,
\-1
п
>
1 О *п
п п п х
1-х
\-1
>
п
X
xn(i - х)
С другой стороны,
Рп <
п-\
-1
In п
1 + - + —+...+—
Л 2 п
Р Р Р
+
X
XJ
xn(i-x)rc
х»(п-1) + 1
Так как [Хп (1 - х) "] / [Хп (п - 1) + 1] < Рп <Хп(1-х), то
указанное в задаче неравенство также выполняется. Заметим, что
последнее неравенство может быть использовано для
приближенного определения всех характеристик рассматриваемой СМО.
11.27. Железнодорожная касса имеет два окошка, в каждом из
которых продаются билеты в два пункта: Ленинград и Киев.
Потоки пассажиров, приобретающих билеты в Ленинград и в Киев,
одинаковы по интенсивности, которая равна Х0 = 0,45 пасс/мин.
Среднее время обслуживания пассажира (продажи ему билета)
*"обсл = 2 мин-
Поступило рационализаторское предложение: для
уменьшения очередей (в интересах пассажиров) сделать обе кассы
специализированными: в первой продавать билеты только в Ленинград,
а во второй — только в Киев. Считая в первом приближении все
потоки событий простейшими, проверить разумность этого
предложения.
Решение. 1) Вычислим характеристики очереди для двухка-
нальной СМО (существующий вариант). Интенсивность потока
заявок X = 2Х0 =0,9 пасс/мин; \i = 1 / to6cJl = 0,5 пасс/мин;
р = X / \i = 1,8; х = Р / 2 = 0,9 < 1, финальные вероятности
существуют. По формуле (11.0.21)
Ро
1,82 , 1,81
1 + 1,8 + -2Г_ +
4 1-0,9
-1
0,0525;
по формуле (11.0.23)
__ 1,83 -0,0525
2-2-0,01
7,7 пасс; i
04
0,9
8,56 мин.
388
2) Во втором варианте (предлагаемом) имеем две одноканаль-
ные СМО: р = Х0 / \х, = 0,45 / 0,5 = 0,9 < 1.
Средняя длина очереди у одной кассы [по формуле (11.0.13)]
равна г = р2/(1 — р) = 0,92 / 0,1 = 8,1 пасс. Суммарная длина
очереди к обеим кассам будет 2r = 16,2 пасс.
Время пребывания пассажира в очереди (11.0.14) t04 = г / X =
= 8,1 / 4,5 = 18 мин, что почти вдвое превосходит время стояния в
очереди в существующем варианте: 8,6 мин.
Вывод: «рационализаторское» предложение нужно отвергнуть,
как резко снижающее эффективность СМО. Резкое ухудшение
характеристик СМО при переходе от двухканальной СМО
(существующий вариант) к двум одноканальным СМО (предлагаемый вариант)
объясняется тем, что, разделив кассу на две специализированные,
мы лишили кассиров возможности подменять друг друга.
11.28*. Простейшая многоканальная СМО с «нетерпеливыми»
заявками и с неограниченным числом мест в очереди. Имеется
простейшая гг-канальная СМО с очередью; интенсивность потока
заявок X, потока обслуживании \i = 1 / to6cjI. Время пребывания
заявки в очереди ограничено некоторым случайным сроком Т,
распределенным по показательному закону с параметром у (на каждую
заявку, стоящую в очереди, действует «поток уходов» с
интенсивностью у).
Написать формулы для финальных вероятностей состояний,
найти относительную пропускную способность СМО Q, среднюю
длину очереди г, среднее время t04 пребывания заявки в очереди,
среднее число z заявок в СМО и среднее время £сист пребывания
заявки в СМО.
>о
X
М-
X
2\i
X
X
3|Х A:|jl
X
n\i
п
Рис. 11.28
П\Ь+У
n\L+rV
Решение. Состояния системы по-прежнему будем
нумеровать соответственно числу заявок, находящихся в СМО. Граф
состояний показан на рис. 11.28. Пользуясь общими формулами для
схемы гибели и размножения и вводя обозначения р = X / [i;
(3 = у / [i, получаем:
Ро =
2 п п
1 + JUL.+...+ P-+P
1! 2!
+
711
71
I
+
(n + (3)(n + 2(3)...(n + rf3)
n + (3 (n + j3)(n+2P)
il_1
+ ...
+ ...+
389
к п
Pi =7ТРо; —; Ра =ТТРо (1<*< л);...; рп = ^— р0;
1! А;! гг!
п
_р_ р
Рп+1 ~ , , о ^0 5 '•• 5
гг! гг + р
р =£1 В1 р (г >1);... .(11.28.1)
Уп+Г п\ (n + (3)(n+2(3)...(n + rf3) °V - >> \ )
В первую формулу (11.28.1) входит бесконечная сумма, не
являющаяся геометрической прогрессией, но члены которой
убывают быстрее, чем члены геометрической прогрессии. Можно
доказать, что ошибка, возникающая от отбрасывания всех членов
бесконечной суммы, начиная с r-го, меньше, чем -— -—-——е~9^.
п\ г!
Предположим, что вероятности р0, рх,..., рп ,..., pn+r, ...
вычислены, и покажем, как можно найти характеристики данной
СМ О: относительную пропускную способность Q, среднее число
заявок в очереди т и др. Найдем прежде всего Q. Обслужены
будут все заявки, кроме тех, которые уйдут из очереди досрочно.
Подсчитаем, сколько заявок в среднем уходит из очереди
досрочно в единицу времени. Интенсивность потока уходов,
приходящаяся на одну заявку, стоящую в очереди, равна у, а суммарная
средняя интенсивность потока уходов, приходящаяся на все
заявки, стоящие в очереди, равна у г. Значит, абсолютная пропускная
способность СМО
A = \-vr, (11.28.2)
а относительная
Q = A/\ = l-vr/\. (11.28.3)
Таким образом, для того чтобы найти Q, нужно прежде всего
знать г, которую непосредственно можно было бы найти по
формуле r = lpn+1 + 2рп+2 +...+ грп+г +... . Но эта формула плоха
тем, что содержит бесконечное число слагаемых. Этого можно
избежать, если воспользоваться выражением для среднего числа
занятых каналов к через А: к = A / \i или, учитывая (11.28.2),
к = (X - у г) / \l = р - (Зг. (11.28.4)
Из (11.28.4) получим
f = (p-Jfe)/P, (11.28.5)
а среднее число занятых каналов А; можно подсчитать как
математическое ожидание случайной величины К (число занятых каналов) с
возможными значениями 0, 1, 2, ..., п и соответствующими
вероятностями р0, pv р2, ...,Р„-1,[1- (Ро +Pl+-~Pn-l)]:
390
к = 1рг+2р2+... + (п-1) рп_г +
+ ^1-(^ + ^+... + ^)]. (11.28.6)
Далее по формуле (11.28.5) вычисляем г. Величину £оч
находим по формуле Литтла:
Кч =г /\. (11.28.7)
Среднее число заявок в СМО
I = f + fc' (11.28.8)
а среднее время пребывания заявки в СМО
*~сист = */Х. (11.28.9)
Примечание. Можно доказать, что для рассмотренной СМО с
«нетерпеливыми» заявками финальные вероятности существуют всегда,
если только (3 > 0. Это подтверждается тем, что ряд в первой формуле
(11.28.1) сходится при любых положительных р и (3. По существу это
означает, что очередь не может расти неограниченно: чем больше длина
очереди, тем интенсивнее уходят из нее заявки.
11.29. Рассматривается простейшая двухканальная СМО с
«нетерпеливыми» заявками (см. задачу 11.28). Интенсивность потока
заявок X = 3 заявки/ч; среднее время обслуживания одной заявки
to6cjl = 1 / \i = 1 ч; средний срок, в течение которого заявка
«терпеливо» стоит в очереди, равен 0,5 ч. Подсчитать финальные
вероятности состояний, ограничиваясь теми, которые не_меньше_0,001.
Найти характеристики эффективности СМО: Q, A,k,r,tQ4, tcllcT.
Решение. Имеем X = 3, р, = 1, у = 2; р = 3, (3 = 2, п =2. По
формулам задачи 11.28 получаем:
Ро
о 2 о 2
1 + 3 + —+ —
2 2
3 З2 З3 З4
- +— + + ь
4 4-6 4-6-8 4-6-8-10
I За | Зб | 3?
4-6-8-10-12 4-6-8-10-12-14 4-6-8-10-12-14-16
0,0692;
откуда
Pl = Зр0 » 0,208; р2 = |Pl « 0,311; р3 = -р2 « 0,234;
3 3 3
Pi = - Рз ~ °.117; Рь = - Pi ~ °.°44; р6 = — р5 « 0,013;
6 8 10
391
Pi = — Ре ~ °,°°3; p8 = — Pi
0,001.
Среднее число занятых каналов согласно (11.28.6):^ = 1^ +
+ 2 (1 - ^о - рг) « 1,654; средняя длина очереди согласно (11.28.5)
г = (р — A; )/(3 = (3 — 1,654)/2 « 0,673; абсолютная пропускная
способность A = fc[x « 1,654 заявки/ч; относительная пропускная
способность Q — А [К ~ 0,551 и далее: tOH = f/X « 0,224 ч; z =
= г + А; « 2,327; *сист = г/Х и 0,776 ч.
11.30. Простейшая СМО с «ошибками». Имеется п-канальная
СМО с неограниченной очередью. На ее вход поступает
простейший поток заявок с интенсивностью X; время обслуживания —
показательное с параметром \i. Обслуживание происходит без
гарантии качества; с вероятностью р оно удовлетворяет заявку, а с
вероятностью q = 1 — р — не удовлетворяет, и заявка обращается в
СМО вторично и либо сразу обслуживается, если нет очереди,
либо становится в очередь, если она есть. Ввести состояния СМО
(нумеруя их по числу заявок в СМО); найти финальные
вероятности состояний и характеристики эффективности СМО. Найти
среднее число рекламаций, поданных в единицу времени, если
каждая неудачно обслуженная заявка подает рекламацию с
вероятностью R.
Решение. Состояния СМО:
5,
0
Sl
Sk
СМО свободна;
занят один канал;...;
занято к каналов (1 < к < n);.
- заняты все п каналов
очереди нет;
}п+г
заняты все п каналов, а г заявок стоят в очереди
(г=1,2, ...)•
>о
X
X
X
X
X
м-
п
X
Рис. 11.30
Граф состояний приведен на рис. 11.30, где \L = p\i. Из этого
графа видно, что данная СМО эквивалентна другой СМО с
полной гарантией качества обслуживания, но с интенсивностью
потока обслуживании, равной ft = p\i; для этой СМО
p = X/fC = X/ (р|л). Формулы (11.0.21)-(11.0.25) остаются
справедливыми, но при замене р на р, \i на ft.
11.31. Простейшая одноканальная замкнутая СМО. Один
рабочий обслуживает т станков, которые время от времени отказы-
392
вают (требуют наладки). Интенсивность потока отказов одного
станка равна X. Если в момент отказа станка рабочий свободен, он
немедленно приступает к наладке; если нет — станок становится в
очередь на наладку, поток отказов станка простейший, время
наладки — показательное с параметром \i = 1 / to6cn. Ввести
состояния СМ О, нумеруя их по числу неисправных станков; найти
финальные вероятности состояний СМО и следующие
характеристики ее эффективности: А — среднее количество станков,
ремонтируемое рабочим в единицу времени; w — среднее число
неисправных станков; г — среднее число станков, ожидающих
ремонта в очереди; Рзан — вероятность того, что рабочий будет занят.
Решение. Состояния СМО:
s0 — все станки исправны (рабочий свободен);
Sj — один станок неисправен (рабочий занят его наладкой); ...;
sk — к станков неисправны, один налаживается, к — 1 ждут
очереди;
sm — все га станков неисправны, один налаживается, га — 1
ждут очереди.
Граф состояний показан на рис. 11.31.
>о
га\
М-
(т-1)Х (т-к+1)\{т_к)х х
М-
sk ^
М-
Рис. 11.31
М-
м-
т
Р =
По общим формулам схемы гибели и размножения, обозначая
- ХДх, получаем
р0 — {1 + rap + т (га - 1) р2+...+
+га (га - 1)...(га - к +1) рк+...+т !рт_1;
Pi = Щ>Ро', Р2 = т (т - 1) р2р0;...;
к
Рк ~ш (т —!)••• (т — & + 1) р Ро (1 < к < п);...;
Рт =т}-9тРо
(11.31.1)
Чтобы определить абсолютную пропускную способность А,
найдем сначала вероятность того, что рабочий занят:
* зан """ 1 п0-
(11.31.2)
Если рабочий занят, он налаживает \i станков в единицу
времени; значит,
A = (1-Po)\l. (11.31.3)
393
Среднее число неисправных станков w можно выразить через
А с помощью следующих рассуждений. Каждый работающий
станок порождает поток отказов с интенсивностью X; в среднем
работает т — w станков; порождаемый ими поток отказов имеет
интенсивность (га — гй) X; все эти неисправности ликвидируются
рабочим, значит, (1 — р0)\i — (га — w)\ откуда
w = m -(i-Po)/p. (11.31.4)
Среднее число г станков в очереди найдем следующим путем:
w = r + jfc, (11.31.5)
где к — среднее число обслуживаемых станков (или, иначе, среднее
число занятых каналов обслуживания). В нашем случае число
занятых каналов равно 0, если рабочий свободен, и 1, если он занят:
к = 0 • р0 + 1 (1 — р0) = 1 — р0. Следовательно,
г = т - (I - р0) / р - (1-Ро)
или
г = т -(1-р0)(1 + 1/р). (11.31.6)
11.32*. В условиях задачи 11.31 найти среднее время tQ4,
которое будет ожидать наладки произвольно выбранный вышедший из
строя станок.
Решение. Формула Литтла, которой мы пользовались ранее,
пригодна только для открытых СМО, где интенсивность потока
заявок не зависит от состояния СМО.Для замкнутых СМО она
непригодна. Время fOH найдем с помощью следующих
рассуждений. Пусть в какой-то момент t появилась заявка (отказал
станок). Найдем вероятность того, что в этот момент СМО
находилась в состоянии sk (к — 0, ..., т — 1) (ясно, что в состоянии sm она
находиться не могла). Рассмотрим т гипотез:
Н0 — в момент появления заявки СМО находилась в состоянии
Нг — в момент появления заявки СМО находилась в состоянии
Нк — в момент появления заявки СМО находилась в состоянии
^л? • • • i
Нт_ j — в момент появления заявки СМО находилась в
состоянии sm_v
Априорные вероятности этих гипотез равны р0, pv ..., рк, ...,
Теперь найдем апостериорные вероятности гипотез при
условии, что наблюдено событие А = {на элементарном участке време-
394
ни {t, t 4- dt) появился отказ станка}. Условные вероятности
этого события при гипотезах Я0, Hv ..., Нт_ 1 равны:
Р (А\Н0) = m\dt] Р (А\Н1) = (га - 1) \<ft;...;
Р (А\Нк) = (т - *) ХЛ;...; Р (А|Ят_1) = ХЛ.
По формулам Бейеса найдем апостериорные вероятности
гипотез (при условии, что событие А произошло). Обозначая эти
вероятности Po,pl,---,Pk,-.-,pm_l, получаем:
Ро =
тр0
т—1
J2(m ~к)Рк
Pi
(т - 1) рх
т—1
^2{т -к)рк
, . . . ,
к=0
к=0
Рк =
(га - к) рк
т—1
^(ш -к)рк
, ... ,
к=0
Рт-1 =
Ут —
т—1
т—1
.(11.32.1)
Y^(m -к)рк
к=о
Зная эти вероятности, найдем полное математическое
ожидание времени пребывания отказавшего станка в очереди. Если
станок отказал в момент, когда система находится в состоянии s0, он
не будет стоять в очереди; если в состоянии sv то будет
находиться в ней в среднем время 1 / \i9 если в состоянии s2 — время 2 / \i и
т.д. Умножая вероятности (11.32.1) на эти числа и складывая,
получаем
t
-| m—1
оч = ~~ /, *Рк '
М- к^1
(11.32.2)
Проводя аналогичные рассуждения, можно получить
выражения для плотностей распределения случайных величин:
Точ — времени нахождения в очереди и
Тпр — времени простоя станка:
Jb-1
Uik-iy.
e '"A;
Jfc=0
*!
(11.32.3)
При этом будет иметь место равенство:
М[Гпр ] = М[Т0Ч} + М[Т^ ] = t02 + -,
и-
395
где
00 - m-1
к'
Находим рк
«02= J #02(0 = -2
0 ^ *=1
= Р(т - А:, х). = \±
Д(т,х) ' X
~ _ (т - fc)P(m - k2,\)/R (™>,Х) _
^(т - А;) Р(т -к,х)/Р (т, х)
(га — к) Р(т — А;, х) (т — к) Р(т — А;, х)
т т
Y2(m-k)P(m-k,X) J2P(k,X)
к=0 к=0
(га — к) Р(т — к,\) Р (т ~ к ~ 1» х)
xR(m - 1, х) Д (™ -1, х)
Следовательно,
(А; = 0,..., га — 1).
/ww=E^'V)' *~-х--.-«
^ fc! (т-1-k)\R(m-1,\)
^е-^х—ie-x -=i(^/х)* (m-l)!
Е
R (т - 1, х)(тп - 1)! й) А!(т — 1 — fc)!
R (m - 1, х)
Таким образом, мы показали, что fOH(t) и /пр(£) представляют
собой вероятностную смесь законов распределения.
11.33. Рабочий обслуживает четыре станка (га = 4); каждый
станок отказывает с интенсивностью X = 0,5 отказа/ч; среднее время
ремонта tp = 1 / \i = 0,8 ч. Все потоки событий — простейшие.
Пользуясь формулами задач 11.31, 11.32, найти: 1) финальные
вероятности состояний; 2) пропускную способность А; 3) среднее
относительное время простоя рабочего Рпр; 4) среднее число станков в очереди
г; 5) среднее число неисправных станков щ 6) среднее время
пребывания в очереди tQ4 одного отказавшего станка; 7) среднюю
производительность группы станков с учетом их неполной надежности, если
в работающем состоянии один станок дает / единиц продукции.
Решение.\i = l /1 = 1,25; р = X / \i = 0,4.
1) По формулам (11.31.1) имеем:р0 = {1 + 1,6 + 1,92 + 1,53+
+ 0,61}-1 = 6fi6~x « 0,150; рг = 1,6р0 « 0,240; р2 = 1,92р0 « 0,288;
р3 = 1,53р0 « 0,230; р4 = 0,061р0 « 0,092;
396
2) A = 0,850м, w 1,06 станка/ч;
3) Рп? =Ро= 0,150;
4) г « 4 - 0,850 (1 + 2,5) » 1,03;
5) й7 « 1,03 + к « 1,03 + 0,85 = 1,88;
26) по формулам (11.32.1) и (11.32.2) |>0 =
4р0
4p0+3Pi+2p2+ft
« 0,283; рг и 0,340; р2 = 0,270; р3 = 0,108; *оч = 0,8 (рг + 2р2 + 3¾) «
« 0,964 ч;
7) производительность группы станков равна (т — w) I ж 2,12/.
11.34. Простейшая многоканальная замкнутая СМО. Бригада
из п рабочих обслуживает га станков (п < га). Поток отказов
каждого станка имеет интенсивность X; среднее время наладки станка
Ьо6сл — 1 / \i. Все потоки событий — простейшие. Найти финальные
вероятности состояний СМО; абсолютную пропускную
способность А; среднее число неисправных станков w.
Решение. Состояния СМО нумеруем по числу неисправных
станков:
s0 — все станки исправны, рабочие не заняты;
sx — один станок неисправен, один рабочий занят, остальные
свободны; ...;
sk — к станков неисправны, к рабочих заняты, остальные
свободны (к< га); ...;
sn— п станков неисправны, все рабочие заняты;
sn+\ ~~ п + 1 станков неисправны, из них п налаживаются, один
стоит в очереди; ...;
sn+r — п + г станков неисправны, из них п налаживаются, г в
очереди (п + г < га);...;
sm — все га станков неисправны, из них п налаживаются, га - п
ждут очереди.
Предоставляя читателю самостоятельно построить граф
состояний СМО, приведем только окончательные формулы для
вероятностей состояний:
Ро
га га (га - 1) 2 га (га - 1)... (га - к + 1) к
1-\ р -\ р +...Н р 4-
1! 2! fc!
га (га — 1)... (га — п) п+1 га (га — 1)... [га — (n -f г — 1)]
-j-. т г -| р -J-. ш # -| х
п\п п\пг
xpw+r+...+ m! pm
п\пт~п
-1
га га (га - 1) 2
Pi = jjPPo'> Pi = ~ Р Ро', — )
397
ra (га — 1)... (ra — к + 1) k . . ч
Pa =-51 ^y Vpo (1 < * < n)i
ra (ra - 1).,. (m - n + 1) . .
Pn = ; P Po;---;
ra (ra — 1)... [ra — (ra + r — 1)] n
Pn+r = — , r ~Pn+rPo (1 < r < m - 1);
Pm = tmw.w ртр0,гдер^Х/^. (11.34.1)
ra!ram n
Через эти вероятности выражается среднее число занятых
рабочих:
к = 0-р0+1рг + 2р2+...+(га — 1) р^^ +п (рп + pn+l +...+рот) =
= Pi + 2р2+...+(га - 1)рп_! + га (1- р0 - Vi-----Pn-i)- (Н.34.2)
Абсолютная пропускная способность
A = k\i, (11.34,3)
а среднее число неисправных станков
w = т — k\i / \ = т — к / р. (11.34.4)
11.35. Двое рабочих (га = 2) обслуживают шесть станков (га = 6).
Станок требует наладки в среднем через каждые полчаса. Наладка
занимает у рабочего в среднем 10 мин. Все потоки событий —
простейшие. 1) Определить характеристики СМО: среднее число
занятых рабочих к; абсолютную пропускную способность А; среднее
число неисправных станков w; 2) Установить, улучшатся ли
характеристики СМО, если рабочие будут налаживать станки совместно,
тратя вдвоем на наладку одного станка в среднем 5 мин.
Решение. 1) Решаем задачу в первом варианте (рабочие
налаживают станки порознь). Имеем га = 6; га = 2; X = 2;
|л, = б;р = Х/|л = 1/3. По формулам (11.34.1)
Ро
14--14---4- 6'5'4 J_ .1- 6'5'4'3 _! 4-
13 1-2 З2 1-2-2 З3 1-2-22 З4
6-5-4-3-2 1 6-5-4-3-2-1 1 ' 1
1-2-23 З5 1-2-24 З6
рг =6/1-1/3- р0 и 0,306.
0,153;
_ Среднее число занятых рабочих находим по формуле (11.34.2);
к = 1 • рг 4- 2 (1 — pQ — рг) « 1,235. Абсолютная пропускная спо-
398
собность A = k\i «7,41. Среднее число неисправных станков
w = б - 7,41 / 2 « 2,30.
2) Если рабочие налаживают станки вместе, то СМО
превращается в одноканальную (га — 6; п = 1) при \i = 12. Расчеты
произведем для р = Х/|1 = 1/б. По формулам (11.31.1)
Ро =
\ , , 6-5 , 6-5-4 , 6-5-4-3 , 6-5-4-3-2 ,
1 Н- 1 И—I 1 1 1 : г
6-5-4-3-2-Г 1
б6
63 64 65
0,264; рг «0,264; р2 «0,220; р3 «0,147;
р4 « 0,076; р5 « 0,024; р6 « 0,004; й7 = 6 - ^ « 1,59.
1/6
Среднее число занятых каналов к = 1 — р0 = 0,736. Однако,
учитывая, что «канал» обслуживания состоит в данном случае из
двух рабочих, среднее число занятых рабочих будет
V = 2- 0,736 « 1,47; A = k\i = 0,736 • 12 « 8,8.
Таким образом, взаимопомощь между рабочими (каналами
обслуживания) в данном случае повысила среднюю занятость с 1,23
до 1,47, снизила среднее число неисправных станков с 2,30 до 1,59
и повысила пропускную способность с 7,4 до 8,8.
11.36. Имеется простейшая трехканальная СМО с отказами; на
нее поступает поток заявок с интенсивностью X = 4 заявки/мин;
время обслуживания заявки одним каналом to6cjl = 1 / \i = 0,5 мин.
Спрашивается, выгодно ли с точки зрения пропускной
способности СМО заставить все три канала обслуживать заявки сразу?
Причем в этом случае среднее время обслуживания уменьшается
втрое? Как это скажется на среднем времени пребывания заявки в
СМО?
Решение. 1) Находим вероятности состояний СМО без
взаимопомощи между каналами по формулам Эрланга (11.0.6):
Ро
2 22 23
1 + — + — +
1! 2! 3!
23
0,158; РОШ=Р3=—Р0 ~0,21;
о.
Q = 1 - Ротн « 0,79; A = \Q и 3,16.
Среднее время пребывания заявки в СМО вычислим как
вероятность Q того, что заявка будет принята к обслуживанию,
умноженную на среднее время обслуживания: гсист « 0,79 • 0,5 « 0,395 мин.
2) Объединяем все три канала в один с параметром \i = 3 • 2 = 6;
получаем
399
p0 = 1—— = 0,6; Pl = (2 / 3) 0,6 = 0,4;
(1 + 2/3)-1
^otk=Pi=0,4; Q = l-PojK=0fr A = \Q = 4.0,6 = 2,4.
Сравнив эту пропускную способность с пропускной
способностью СМО в первоначальном варианте, видим, что она не
увеличилась (как это было в предыдущей задаче), а уменьшилась! Легко
понять, почему это произошло: благодаря объединению двух
каналов в один увеличилась вероятность отказа (того, что пришедшая
заявка застанет оба канала занятыми и уйдет необслуженной).
Среднее время пребывания заявки в СМО во втором варианте
будет меньше, чем в первом: tcliCT = Q (1/6) = 0,1 мин. Однако это
уменьшение куплено «дорогой ценой» — тем, что ряд заявок
вовсе не обслуживаются и, значит, проводят в СМО нулевое время.
Почему же в предыдущей задаче объединение двух каналов в
один повысило эффективность обслуживания? Предлагаем
читателю подумать над этим вопросом и объяснить кажущееся
противоречие. Не потому ли, что в СМО с отказами заявки не
становятся в очередь?
11.37. Имеется простейшая трехканальная СМО с
неограниченной очередью. Интенсивность потока заявок X = 4 заявки/ч;
среднее время обслуживания^^ = 1 / \i = 0,5ч. Выгодно ли, имея
в виду: 1) среднюю длину очереди, 2) среднее время пребывания
заявки в очереди, 3) среднее время пребывания заявки в СМО,
объединить все три канала в один, с втрое меньшим средним
временем обслуживания?
Решение. 21) В первоначальном варианте (трехканальная
СМО): п = 3, Х = 4,м. = 1/0,5=2;р = Х/м. = 2;х = р/п=2/3<1.
Финальные вероятности существуют. Вычисляем р0 по формулам
(11.0.21):
2 22 23 24 -(1/3) W
Ро
1 + — + — + — +
1
9
0,889; tQ4 = - = - « 0,222 ч;
1! 2! 3! 3!(1-2/3)
3-31(1/3)2 9 X 9
^сист — ^оч +*об ~ 0,722.
2) При объединении трех каналов в один: п = 1; X = 4; ц, = 6;
р = 2/3. По формулам (11.0.12)-(11.0.14) имеем
г = V-LzL ~ 1333; im = - « 0,333 ч;
1/3 оч X
*СИСТ = *"„, + trf = 1 / 3 + 1 / 6 = 0,500.
400
Таким образом, объединение трех каналов в один, несколько
снизив среднее время пребывания заявки в СМО (с 0,722 до
0,500), повысило среднюю длину очереди и среднее время
пребывания заявки в ней. Это произошло потому, что, пока три канала
совместно обслуживают одну заявку, другим (вновь пришедшим)
заявкам приходится ждать в очереди.
Повышение эффективности обслуживания, наблюдаемое при
объединении каналов в замкнутой СМО, связано с тем, что
интенсивность потока заявок при выходе из строя их источников
(станков) уменьшается.
11.38. Рассматривается система массового обслуживания —
стоянка такси, на которую поступают простейший поток
пассажиров с интенсивностью X и простейший поток автомобилей с
интенсивностью [I. Пассажиры образуют очередь, которая
уменьшается на единицу, когда к стоянке подходит автомобиль (берется
«идеальный» случай, когда водитель безропотно везет каждого
пассажира туда, куда ему требуется). В случае, если на стоянке нет
пассажиров, в очередь становятся автомобили. Число мест для
автомобилей на стоянке ограничено (равно га); число мест в очереди
для пассажиров также ограничено (равно /). Все потоки
событий — простейшие. Посадка производится мгновенно. Построить
граф состояний СМО, найти финальные вероятности состояний,
среднюю длину гп очереди пассажиров, среднюю длину гт очереди
автомобилей, среднее время tQ4n пребывания в очереди
пассажира, среднее время tQ4T пребывания в очереди такси и посмотреть,
как эти характеристики изменятся при га —> оо, / —> оо.
ч,о
X
М-
X
м-
Чо
X
м-
»1,0
X
М-
>о,о
X
м-
>од
X
м-
ьо:к
X
м-
'0,771
Рис. 11.38
Решение. Состояния СМО будем нумеровать
соответственно числу пассажиров и автомобилей на стоянке двумя индексами:
первый — число пассажиров, второй — число автомобилей.
Состояние 50 0 означает, что на стоянке нет ни пассажиров, ни
автомобилей; состояние sok — нет автомобилей, к пассажиров;
состояние 5С|0 — с автомобилей, ни одного пассажира. Граф состояний
СМО показан на рис. 11.38. Граф соответствует схеме гибели и
размножения. Применяя общие формулы (11.0.4) для этой схемы
и обозначая X / \l = р, получаем:
2 1-е
Р/-1,0 — РР/,0 J Р/-2,0 = Р Р/,0)-") Рс,0 = Р Р/,0)"-)
I 1+к 1+т
Ро,о — Р Р/,о5 ••• 5 Ро,к — Р Pl,0> — > Ро,т — Р Р/,о5
401
l + тп л -1
Л,о={1 + Р + р'+-+Р1+т}_1 (11.38.1)
или, суммируя геометрическую прогрессию со знаменателем р,
p;>0=(l-p)/(l-p'+m+1). (11.38.2)
Вероятности (11.38.1) образуют геометрическую прогрессию с
первым членом р1 0 и знаменателем р. Если р > 1, наивероятнеишее
состояние системы будет s0 т — автомобилей нет, все места в
очереди пассажиров заняты; если р < 1 — наивероятнеишее состояние
st 0 — пассажиров нет, все места в очереди автомобилей заняты.
При т —> оо, I —> оо финальные вероятности не существуют;
при р > 1 очередь пассажиров, а при р < 1 очередь автомобилей
имеют тенденцию возрастать неограниченно (эта тенденция
сдерживается тем, что как число пассажиров, так и число такси в
городе бесконечными быть не могут).
11.39*. В столовой самообслуживания имеется один
раздаточный пункт, на котором отпускаются как первые, так и вторые
блюда. Поток посетителей столовой — простейший с интенсивностью
X; на отпуск как первого, так и второго блюда идет случайное
время, распределенное по показательному закону с одним и тем же
параметром \l Некоторые посетители берут и первое, и второе
(доля таких посетителей равна q), другие — только второе (доля
1--(/). Найти: 1) условия, при которых существует устойчивый,
стационарный режим работы столовой; 2) среднюю длину очереди
и среднее время пребывания посетителей в столовой, если
посетитель съедает одно блюдо в среднем за время т, а два блюда — за
время 2т.
Решение. Время, идущее на обслуживание одного
посетителя, представляет собой случайную величину Г, распределенную с
вероятностью q по закону Эрланга 2-го порядка, со средним
значением to6cJl = 2 / \l, а с вероятностью (1 - q) — по показательному
закону с параметром \l. Найдем математическое ожидание
случайной величины Г. Для этого воспользуемся формулой полного
математического ожидания с двумя гипотезами: Нг = {посетитель
берет только второе блюдо}; Н2 = {посетитель берет оба блюда}.
Вероятности этих гипотез: Р (Нг) = 1 — q\ Р (Н2) = д.
Полное математическое ожидание случайной величины Г равно
М[Г] = Р(Я1)М[Г|Я1] + Р(Я2)М[Г|Я2] = (1-д)(1/ц) +
+?(2/и.) = (? + 1)/н.;
значит, столовая может обслуживать в среднем |л / (g + 1)
посетителей в единицу времени; если X > [i / (д + 1), то СМ О перегружена, и
финальные вероятности не существуют, если же X < [i / (q + 1), то
они существуют. Предположим, что X < [i / (q + 1).
402
Для нахождения средней длины очереди г, средних времен
пребывания заявки в очереди t04 и в системе (столовой) £сист
воспользуемся формулой Полячека — Хинчина (11.0.31). Для этого
надо знать коэффициент вариации случайной величины Т —
времени обслуживания. Найдем сначала второй начальный момент
этой величины М[Г2]. По формуле полного математического
ожидания (с теми же гипотезами Нх и Я2) получим
М[Г2] = (1-д)М[Г2|Я1] + дМ[Г2|Я2]. (11.39.1)
При гипотезе Ях случайная величина Г распределена
показательно с параметром [l:
M[r2|^] = D[r|^]+(M[r|^])2 = 1/^2+(1/^)2 =2/ц2.
При гипотезе Я2 вычислим второй начальный момент
величины Г по формуле
М[Г2|Я2] = В[Г|Я2]+(М[Г|Я2])2.
Но М[Г|Я2] = 2/^(М[Г|Я2])2 =4/^2; дисперсия В[Г|Я2]
вдвое больше, чем В[Г|ЯХ], как дисперсия суммы двух
независимых одинаково распределенных случайных величин 7\ и Г2, т.е.
D[T|#2] = 2 / \i2. Следовательно,
М[Т2|Я2] = 2/1х2+4/1х2 =6/^,
откуда по (11.39.1)
М[Т2] = (1 - д) 2 / [i2 + ¢6 / ц2 = 2 (1 + 2д) / [х2.
Дисперсия случайной величины Т
D[T] = M[T2]- (М[Г])2 = (1 + 2д - д2)/м-2;
отсюда коэффициент вариации случайной величины Г
^ =Jl + 2q-q2 /(q + 1).
Подставляя это выражение ир = \(д + 1)/р,в формулу Поля-
чека—Хинчина (11.0.31), получаем
(Х2/^2 )(q + l)
г =
1+l + 2q-q2
(¢+1)
(X2 /^)(1 + ¾)
2[1-(Х/^)(в+1)] l-(X/|i)(g+l)
Далее
*"оч = *УХ; *"сист =*«« +(g + l)/|A + (Q + 1) Т = tm + (q + 1) (Т + 1/ц).
403
11.40. Пример простейшей СМО с отказами и с приоритетом.
Имеется двухканальная СМО с отказами, на которую поступают
два простейших потока заявок: I с интенсивностью \г и II с
интенсивностью Х2 (будем кратко называть их «заявки I» и «заявки
II»). Заявки I имеют перед заявками II приоритет, состоящий в
следующем: если заявка I приходит в момент, когда все каналы
заняты и хотя бы один из них обслуживает заявку II, то пришедшая
заявка I «вытесняет» из обслуживания заявку II, становится на ее
место, а та покидает СМО необслуженной. Если заявка I
приходит в момент, когда все каналы заняты обслуживанием заявок I, то
она получает отказ и покидает СМО. Заявка II получает отказ,
если она приходит в момент, когда заняты оба канала
(безразлично какими заявками).
Построить размеченный граф состояний СМО, нумеруя
состояния двумя индексами (г, j); первый указывает число заявок I,
второй — число заявок II, находящихся в СМО. Написать
уравнения для финальных вероятностей состояний. Решить их при
\г = Х2 = \х,г = [i2 = 1. Выразить через p{j (г + j < 2) следующие
характеристики эффективности СМО:
^отк (^отк ) ~~ вероятность отказа в момент поступления для
заявки I (II);
Аг (А2) — среднее число заявок I (II), обслуживаемое СМО в
единицу времени;
К (&2) ~~ среднее число каналов, занятых обслуживанием
заявок I (II);
Ротк, А, к — те же характеристики для СМО в целом,
безотносительно к виду заявок.
Решение. Состояния СМО: s00 — в СМО нет заявок; s10 — в
СМО одна заявка I и ни одной заявки II; s01 — в СМО ни одной
заявки I и одна заявка II; s20 — в СМО две заявки I и ни одной
заявки II; 5И — в СМО по одной заявке I и II; s02 — в СМО ни одной
заявки I и две заявки II. Размеченный граф состояний СМО дан
на рис. 11.40.
Уравнения для финальных вероятностей состояний:
(\ + \2)р00 = ^1^10 + ^2^01 J (Xl +Х2 +M<i)PlO =XlP00 +2M<1 X
хр2о + ^2Рп5 2^р20 =Х1р10 +\рп\
(\ +\2 +^х2)хр01 =Х2Роо +HiPn +2^2Ро2;
(\ +м-1 +M<2)Pn=x2Pio + xiPoi + xiPo2; (xi + 2m<2)po2 = x2Poi;
Poo + Рю + P20 + P01 + P11 + P02 = L
Решая их при \г = Х2 = \х,г = \l2 = 1, получаем
404
Рис. 11.40
Poo =0,20; р10 -0,25; р20 =0,20;
р01 =0,15; рг =0,15; р02 =0,005;
pW =71 =0 2-
^отк ^20 и'^'
^i™ = р20 + Рп + Р02 = °>4°;
Аг = \ (1 - Р^) = 0,8.
Величину А2 вычислим, учитывая то,
что некоторые заявки II, принятые к
обслуживанию, вытесняются заявками I и
покидают СМО необслуженными.
Среднее число таких заявок в единицу времени равно
Хп(рп + р02), следовательно,
А2 = Х2 [1 ~ (?20 + Рп + Р02 )] ~ Х1 (Рп + Р02 ) = °^4;
*i = Ах J \1г; я2 = А2 / \ъ2.
Вероятность Ротк того, что произвольно выбранная заявка,
поступившая в СМО, получит отказ, найдем по формуле полной
вероятности с гипотезами: Нг = {пришла заявка I}; Н2 = {пришла
заявка II}. Вероятности этих гипотез
Р(Я1) = Х1/(Х1+Х2); Р(Я2) = Х2/(Х1+Х2).
Следовательно,
Р„™ =
X
отк
хх + х
р(1) +
•* ПТУ I
X
отк
(Х1+Х2)
р(2) _оз
Заметим, что все характеристики для заявок I можно было бы
получить, совершенно игнорируя заявки II и рассматривая задачу
так, как если бы на двухканальную СМО с отказами поступали
только заявки I. Предоставляем читателю убедиться в этом,
подсчитав все характеристики для двухканальной СМО с отказами,
на которую поступает только поток заявок I.
11.41. Условия предыдущей задачи изменены так, что
количество каналов СМО с отказами равно п = 3. Построить граф
состояний СМО. Написать уравнения для финальных вероятностей
Pij (¾ + J < 3), где i — число заявок I, j — число заявок II,
находящихся в СМО. Считая эти уравнения уже решенными, выразить
через р{- те же характеристики эффективности, что и в
предыдущей задаче.
Решение. Граф состояний показан на рис. 11.41.
Уравнения для финальных вероятностей состояний:
(\ + ^2)^00 =M-iPio +M<2P
01'
405
Рис. 11.41
+2^iP2o + м-2Рп;
(Xj+X2 + 2^l)P20 =
= \PW +З^Рзо +^2^21^
(\ + х2 +[i,2)p01 =
= Х2р00 +\i,2pn +2[i,2p02;
(\ +\2 + щ +[i2)pn =Х1р01 +
+ Х2р10 + 2^¾ +2^2р12;
(Х1+[х2 + 2[х1)р21=Х1(р11 +
+ р12) + Х2р20;
(Xj +Х2 +2ц2)р02 =
= Х2р01+[х1р12+Зц2р03;(Х1+ц1+2ц2)р12=Х1(р02+р03) + Х2р11;
(Xj + Зц,2) р03 = Х2р02;
Роо + Рю + Рго + Рзо + Рог + Рп + Рп + Ро2 + Ра + Роз = 1;
•* отк = РзО' "отк = РзО ' Р21 "■" Pl2 "■" РОЗ >
А =
Х1 (1 ~ РЗО ); А2 = Х2 I1 ~ (РЗО + Рп + Pl2 + РОЗ )1
-МРоз +Pi2 +Роз);
/C-i == У1-| / |JL-| j /Cn — -**9 / И19 ) — 1 ' 9 )
Р™ =
X
отк
хх+х
р(1) +
X
отк
хх+х
Pi2'.
отк
11.42. Пример СМО с очередью и с абсолютным приоритетом.
Имеется одноканальная СМО с двумя местами в очереди (га = 2).
На вход СМО поступают два простейших потока заявок I и II с
интенсивностями Х1,Х2. Времена обслуживания —
показательные с параметрами \1г, р,2. Заявка I, прибывшая в СМО,
«вытесняет» заявку II, если она обслуживается, и занимает место в очереди
перед ней, если она стоит в очереди. «Вытесненная» заявка II
покидает СМО необслуженной, если в очереди уже нет мест, и
становится в очередь, если места есть. Нумеруя состояния СМО
двумя индексами г, j соответственно числу заявок I и II, находящихся
в СМО, построить размеченный граф состояний СМО и написать
уравнения для финальных вероятностей состояний. Считая этим
уравнения уже решенными, выразить через p{j (i + j < 3)
следующие характеристики эффективности СМО:
■Ротк (^отк ) ~ вероятность того, что заявка I (II) получит отказ
немедленно после прибытия;
406
Q\ (Q2) ~ вероятность того, что заявка I (II) будет обслужена;
zx (z2) — среднее число заявок I (II), связанных с СМО;
г, (г2)_— среднее число заявок I (II), находящихся в очереди;
Чист (*сист) ~ среднее время пребывания в системе заявки I
(п)_;
t$ (t^ ) — среднее время пребывания в очереди заявки I (II);
^сист ~~ среднее время пребывания в системе любой
(произвольной) заявки;
t04 — среднее время пребывания в очереди любой заявки.
Решение. Состояние СМО: s- — в СМО находится г заявок I
J
и j заявок II (г + j < 3). Размеченный граф состояний показан на
рис. 11.42.
Уравнения для финальных вероятностей состояний:
(\ +\2)р00 =^гР10 +^2Poi5 (\ + х2 +11г)р10 =\Роо +
+M<iP20 + ^1^ (Х1^Х2 +M-i)P20 = XlPlO +VlP30 + ^2^
VlP30 =Xl(P20 + ^21 ); (X1^X2 + M-2)Poi =Х2^00 +M<iPi +H<2P02;
(Xl + X2 + И-i + V2)Pll = X2PlO+ X1^01 + VlP21 + ^2^125 (Xl + X2 +
+ M-2)P02 =X2P01 +VlPl2 +^2^03 5 (Xl + M<1 +H-2)Pl2 = XlP()2 +
+X2^11 + XlP03 5 (Xi + ^2) РОЗ = X2^02'
Poo + P10 + P20 + Рзо + P01 + P11 + P21 + P02 + P12 + Роз = 1;
■* отк = РзО' 'otk = РзО ■" ^21 ■" ^12 ■" ^03 ) Vi — 1 ~~ -Гotk = ^ ~~ РзО *
Рис. 11.42
407
Чтобы найти Q2l найдем сначала А2 — среднее число
обслуженных заявок II в единицу времени:
А2 = М1 ~ Ро(т2к) ~ \(Р03 + Pl2 + ?2l)= М1 - (Рад + Р21 +
+ Pl2 + РОЗ )] ~ Х1 (РОЗ + Pl2 + Р21 )•
Разделив это выражение на Х2, находим среднюю долю
обслуживаемых заявок II (вероятность того, что заявка II будет
обслужена): Q2 = А2 J Х2. Тогда
fl =1 (PlO + Pll + Pl2 ) + 2 (^20 + Р21 ) + 3%0 5 *2 = * (Poi + Pll +
+ Р21 ) + 2 (^02 + Pl2 ) + 3Р035 Г1 = ! (Р20 + Р21 ) + 2Р305 *2 = * (Pll +
+P2l) + 2Pl2-
По формулам Литтла
7(1) _ =■ / \ . 7(2) _ - / \ . /(1) _ г I \ . 7(2) _ = / \ .
^сист ~~ ^1 / л1 ) ^сист _^2 / А2' ^оч ~~ 'l / А1 ' ^оч ~ '2 / л2'
7 = Х1 7(1) , Х2 1(2) . 7 Х1 7(1) , Х2 7(2)
^сист ^ ^ ^СИСТ ' ^ х ^СИСТ 1 ЬОЧ х . ^04 ' ^ х Ь0Ч '
\г + А2 \г + А2 \г + А2 Aj + А2
Все характеристики, относящиеся к заявкам I, можно
вычислить и не решая уравнений (11.42), а просто игнорируя наличие
заявок II, рассматривая СМО с ограниченным числом мест в
очереди (га =2) и находя ее характеристики по формулам п. 3 (см.
с. 379, 380).
11.43. Простейшая: СМО без очереди и с «разогревом» каналов.
На вход n-канальной СМО поступает простейший поток заявок с
интенсивностью X. Время обслуживания — показательное с
параметром \l. Перед тем как начать обслуживание заявки, канал
должен подготовиться («разогреться»). Время «разогрева» Граз имеет
показательное распределение с параметром у и не зависит от того,
как давно канал прекратил работу. Заявка, заставшая канал
свободным, «занимает» его и ждет, пока он разогреется, после чего
поступает на обслуживание. Заявка, заставшая все каналы
занятыми (обслуживаемой или ожидающей заявкой), покидает СМО
и остается необслуженной. Найти финальные вероятности СМО
и характеристики ее эффективности: вероятность отказа Ротк,
относительную пропускную способность Q, абсолютную
пропускную способность А, среднее число занятых каналов к.
Решение. Будем считать, что обслуживание заявки состоит
из двух фаз: ожидания разогрева и самого обслуживания:
^обсл = тРаз + ^обсл • Случайная величина ?обсл распределена по
обобщенному закону Эрланга 2-го порядка (см. задачу 8.39) с
параметрами \i, у. Мы знаем, что формулы Эрланга (11.0.6)
справедливы не только для показательного, но и для любого распределе-
408
ния времени обслуживания. Найдем величину р = 1 / М[Тобсл ]
Имеем
MCZU* ] = М[Граз ] + М[Тобсл ] = 1 / ,1 + 1 / v = (\i + у) / (ил/),
откуда р = (pv) / (р + v). Вычислив р = X / р и подставив это
значение р в формулы Эрланга (11.0.6), получим:
Ро =
~П
1+ £+...+£-+...+£-
1! А;! п!
Рк =Т\Ро U^*^»);
п
Г? П
Ротк =Рп =^-гРо'^ ¢ = 1--^4^05 A = \Q = \
ты
ты
( ~п ^
1-£-о
п!
Чтобы найти среднее число занятых каналов к, нужно
разделить А на р:
* = *
f
п
1-
п!
Ро =Р
п
1-
п!
Ро
11.44. Простейшая одноканалъная СМО с очередью и
«разогревом» канала. На одноканальную СМО с неограниченной очередью
поступает простейший поток заявок с интенсивностью X. Время
обслуживания — показательное с параметром р (р > X). Перед тем
как приступить к обслуживанию заявки, свободный до того канал
должен «разогреться». Время «разогрева» — показательное с
параметром у и не зависит от того, как давно канал закончил работу.
Если обслуживание начинается сразу же после окончания
обслуживания предыдущей заявки, «разогрева» не нужно. Составить
граф состояний СМО и написать уравнения для финальных
вероятностей состояний; выразить через эти вероятности
характеристики эффективности СМО: средние числа заявок в системе z и в
очереди F, средние времена пребывания заявок в системе tr„„ и в
очереди t04.
Решение. Состояния СМО (рис. 11.44):
500 — канал свободен, не разогрет;
501 — пришла одна заявка и ждет, канал разогревается;
сист
Si
°0l
'
V
511
X
X
м*
s
°\У1
'
V
512
X
X
м*
Si
°0б
1
V
513
X
X
м*
Рис. 11.44
409
sn — канал разогрет, одна заявка обслуживается, очереди нет;
502 — канал разогревается, в очереди две заявки; ...;
50/ — канал разогревается, в очереди / заявок;
$и — канал обслуживает одну заявку, / — 1 заявка стоит в
очереди; ....
Уравнения для финальных вероятностей:
>Фоо = м>ц; (х + у) Рог = хРоо; (х + мО Рп = yPoi + M-Pi2;
(\ + v)p02 = \р01; (\ + il)p12 =vp02 + \рп +m>i3;---;
(\ + \i)phl =vp0j + \р1М +m«Pii/+i;-;
00 оо
*=^(Po,/ +Pl,/); f = ^(^0,/ +Plf/+l)-
t =0 /=1
По формуле Литтла
^сист — ^ / Х') ^оч — ^ / Х'
11.45*. Имеется одноканальная СМО с очередью,
ограниченной числом мест га = 2. На вход СМО поступает простейший
поток заявок с интенсивностью X. Время обслуживания
распределено по обобщенному закону Эрланга с параметрами \х,г, \l2 (см.
задачу 8.31). Найти вероятности состояний СМО:
50 — в СМО нет заявок;
s1 — b СМО одна заявка (очереди нет);
s2 — в СМО две заявки (одна обслуживается, одна в очереди);
53 — в СМО три заявки (одна обслуживается, две в очереди).
1)_ Найти характеристики эффективности СМО: Ротк, Q, А,
z,r,tcvlCTitm. Вычислить их для значений X = 2, р^ =6;р,2 =12.
2) Сравнить их с теми, которые получились бы для простейшей
СМО с таким же значением X и значением \l, равным 1 / £обсл, где
^обсл ~~ сРеДнее время обслуживания заявки в данной СМО.
Решение. Поток обслуживании — не пуассоновский, значит,
система не марковская, и найти вероятности состояний СМО по
обычной методике, которую мы применяем для марковских
процессов с дискретными состояниями и непрерывным временем,
нельзя. Однако процесс, протекающий в СМО, можно
искусственно свести к марковскому с помощью так называемого «метода
фаз».
Представим обслуживание состоящим из двух фаз (I и II),
продолжающихся соответственно время 7\ и Г2; полное время
обслуживания Тобсл = Тг + Г2, где Тх имеет показательное
распределение с параметром \х,г; Т2 — показательное распределение с
параметром \l2. Тогда Го6сл будет иметь обобщенное
распределение Эрланга с параметрами \ix и \х,2 (см. задачу 8.39).
410
so
X
A.
°11
X
S2\
X
51
M-i
4
M-i
\(4
1*1,
.4
°12
X
522
X
i>l
Рис. 11.45
Введем следующие состояния СМО:
50 — СМО свободна;
5И — в СМО одна заявка,
обслуживание в первой фазе;
512 — в СМО одна заявка,
обслуживание во второй фазе;
521 — в СМО две заявки (одна
обслуживается и одна в очереди);
обслуживание в первой фазе;
522 — в СМО две заявки, обслуживание
во второй фазе;
531 — в СМО три заявки, обслуживание
в первой фазе;
532 — в СМО три заявки, обслуживание во второй фазе.
Дальнейших состояний нет, так как (по условию т = 2)
больше трех заявок в СМО быть не может. Размеченный граф
состояний СМО показан на рис. 11.45. При таком подходе состояние sx
расчленяем на два: su и s12 (или, короче, sx = su + s12);
аналогично 5 2 = s21 + 522, 53 = 531 + 532. Уравнения для финальных
вероятностей, соответствующих графу рис. 11.45, будут:
ХР0 = ^¾ 5 (Х + М-1 ) Рц = ХРо + ^2^22 ; (Х + ^2 ) Pl2 = ^11 5
(Х + ^)^21 =М-2Р32 + XPll'> (Х + ^)^22 =M-iP2l +Х^12 5
м-ifti = x^2i; hft2 =M-ifti + х^22;
нормировочное условие р0 + ри + р12 + р21 + р22 + р31 + р32 = 1-
Решая эти уравнения, получаем:
Ро =
1 +
(Х + р,2)Х X Х3(Х + |хх +[i2) + \2ii2(\ + ii2)
+ — +
[1г[12 \i2
2/\ , . , .. \ \4/\ ... , .. \ , \3
2 2
M-lM-2
+
| Х'(Х + ц,х + [i2) | Х4(Х + 1хх +ц2) + ХУ2(Х + ц2) |
M-lM-2
2 3
M-lM-2
| Х3(Х + ц,х+ц2) X4(X + |i1 +|л2) + xV2(x + м-2)
(JqM-2
3 2
M-lM-2
-1
(Х+р,2)Х X Х3(Х+ |л1 + |л2) + Х2|а2(Х+|л2)
Рп=- -—р0; Рп=—Ро; р21 = —Vi— ^°;
V>\V>2 ^2 V>\V>2
_Х2(^ +^t2 + X) _Х4(Х + ^ +м,2) + ХУ2(Х + м,2)
Pll ~~ 2 ^0' ^31 ~~ ~ Р°'
M-iM-
1^2
3 2
1*11*2
411
^32 =
X4(X+^ + ^2) + \V2(X+^2)+ Х3(Х+^+^х2)
M-lM-2 M-iM-2
p0. (11.45.1)
Далее находим финальные вероятности состояний sv s2, s3:
Pi =Рп + Р12 = (x + M-i +M-2)Po;
X2
p2 =p21 + p22 = —2-[(X + |i1)(X + |i1 +^2) + ^2(X + ^2)]p0;
M-iM-2
X3
Ps =Psi + ¾ =-77^2 +xM-i +^i)(x + ^i +^2) +
+ M.2(M-i +^2)(X + ^2)]^o5 (11.45.2)
где p0 определяется первой из формул (11.45.1).
Характеристики эффективности СМО могут быть найдены
через вероятности р0, pv р2, р3 по формулам:
^отк = %; Q = 1 - р3; А = х (1 - я*); * = i?i + 2^2 + з^3;
f = lp2 + 2¾; ^"сист = * / х; ^оч = г I X. (11.45.3)
Подставляя в формулы (11.45.1) численные данные
X — 2, \1г = 6, \i2 = 12, получаем: р0 = 0,540; рп = 0,182; pl2 = 0,090;
р21 = 0,087; р22 = 0,050; р31 = 0,029; р32 = 0,022. Отсюда,
возвращаясь к исходной (немарковской) СМО, имеем: р0 = 0,540; рг = 0,272;
р2 = 0,137; р3 = 0,051.
Далее, по формулам (11.45.3):
Ротк = 0,051; Q = 0,949; А = 1,89; z = 0,705; г = 0,243; £сист = 0,352;
^„ =0,122.
оч
2) Подсчитаем те же характеристики для простейшей СМО с теми
же Х = 2, \l = (1 / \1г+1 / \12)~г = 4. По формулам (11.0.12)-(11.0.15)
имеем:
р = 0,5; р0 « 0,533; к = 1- р0 « 0,467; рх = рр0 « 0,267;
р2 = р2р0 « 0,133; р3 = рЧ « 0.067; Ротк = р3 « 0,067;
Q = 1 - р3 « 0,933; Л « 1,866; z « 0,733; г « 0,267; fCHCT = 0,367;
*„„ «ОД33.
оч
Видим, что наша немарковская СМО имеет над простейшей
СМО некоторое преимущество по пропускной способности и
очень мало отличается от нее (в лучшую сторону) по времени
пребывания заявки в СМО и по длине очереди.
11.46*. Имеется одноканальная СМО с двумя местами в
очереди. На ее вход поступает пальмовскии поток заявок с интервалом
Г, распределенным по обобщенному закону Эрланга с параметрами
412
X.
Рис. 11.46
Х15Х2; время обслуживания — показательное с
параметром jjl. 1) Применяя метод фаз, написать
уравнения для финальных вероятностей
состояний р0, pv р2, р3. Выразить через эти вероятности
характеристики СМО: Ротк, Q, A,z, f, £сист ,tm.
2) Вычислить финальные вероятности и
характеристики эффективности для следующих
исходных данных: Х1=3, Х2=6; [i = 4и сравнить их с
теми, которые соответствуют простейшей СМО с
параметрами X = (1 / Хх + 1 / Х2 )-1 = 2, [i = 4,
рассмотренной в задаче 11.45.
Решение. 1) Если рассматривать, как мы
делаем обычно, состояния СМО, нумеруя их
соответственно числу заявок в СМО: s0, sv s2, s3, то
система не будет марковской. Чтобы ее марко-
визировать, разделим на две фазы (I и II) не
время обслуживания, а интервал Г между заявками: Т = Тг + Г2, где
случайные величины Тг и Т2 имеют показательное распределение
с параметрами \ и Х2 соответственно.
Состояния СМО будем нумеровать по числу заявок в СМО и
номеру фазы между заявками:
501 — заявок в СМО нет; интервал между заявками в первой фазе;
502 — заявок в СМО нет; интервал между заявками во второй
фазе;
5И — в СМО одна заявка (обслуживается); интервал между
заявками в первой фазе;
512 — в СМО одна заявка (обслуживается); интервал между
заявками во второй фазе;
521 — в СМО две заявки (одна обслуживается, другая в
очереди); интервал между заявками в первой фазе;
522 — в СМО две заявки (одна обслуживается, другая в
очереди), интервал между заявками во второй фазе;
531 — в СМО три заявки (одна обслуживается, две в очереди);
интервал между заявками в первой фазе;
532 — в СМО три заявки (одна обслуживается, две в очереди),
интервал между заявками во второй фазе.
Граф состояний СМО дан на рис. 11.46.
Уравнения для финальных вероятностей:
\Р01 =М>ц; Х2^02 =\Р01 +№25 (Х1 +М0Рц = \Рю +м#
(Х2 +[l)pu =\РП + №22; (\ +V>)P21 =Х2^12 +№l5
(Х2 +[l) Р22 =\Р21 +М-Р32 5 (Х1 +М-)Р31 =Х2^22 +Х2^32;
(Х2 +[i)p32 =\р31.
21'
413
Нормировочное условие р01 + р02 + рп + р12 + р21 + р22 +
Эти уравнения удобнее всего решать, выражая вероятности p{j
через последнюю, р32- Выражения для вероятностей р{- (г = 0, 1,2,
3; j = 1,2) имеют вид:
Ръ2 = '
1 ( М" + Х2 , М" О* + Х1 + Х2 ) , И» (^2 + Х1^ + 2Х2^ + Х2 ) ,
X
Х1Х2
Х1Х2
2/2
[ \lz(\lz +2Х1м, + 2Х2м, + Х"1 +Х,Х2 +Х^2) [
2\2
ЧА2
2л.3 , ох ..2 , ох ..2 , х2.. , ох х . , о\2.. , хЗ
Х1Х2
+
|^(|Г +2\[iz +3X2|i + Х^ + 2X^2^ + ЗХз|л + Х2)
Х1Х2
+
+
p,J(p,J+3X1M,J+3X2p,J+3Xip,+4X1X2p,+3X2p,+Xi+XiX2+X1X2+\2)
Х1Х2
Зл.З
+
|Г(|Г + 2ХХ^Г +3X2|i + Х^ + 2Х1Х2ц + ЗХ2р,+ Х2)
Х1Х2
-1
Р31 =
Ц.+ X
~~хГ
Рз2 ' ^22 ~~
_|i(|i + X1 +х2)
ххх
Р32
_ [i ([i2 + \[i + 2X2|jl + Х22)
Р21 ~ ГоТ %2>
Х1Х2
_ м* (м* + 2\\l + 2\2\l + X; + ХгХ2 +\2)
Р\2 — % ох о %2 '
2x2
1Л2
2л 3 , ох ..2 , ох ..2 , х2.. , ох х .. , о\2.. , хЗ
Х1Х2
Pll =
_ \iz(\i6 +2X1|i^ +зх2|1 + х^ + гх^^ + зх^ч- х2)
Х1Х2
^32'
ро2 = 7Г72-^3 + ЗХ^2 + ЗХ2^2 + Х2^ + 4ХХХ2^ +
Х2Х2
+ зх22|л + \\ + х2х2 + ххх2 + х32)р32;
_ |i (|Г +2X1|iJ +3X2|i + \\\л, + 2X^2^1 + 3X2|jl + Х2)
Poi — TjTi P32 •
X1X2
Переходя обратно к исходной (немарковской) СМ О, получаем:
Ро = Рог + Ро2; Рг = Рп + Ры ?2 = Рт\ + Рц\Ръ = fti + ft2-
414
Далее, Pm=Pj\ (2 = 1-^ A = Q\;z = lp1+2p2+3р3; r =
= lp2 +2p3;tcmT =z /\;tm=r /\.
Финальные вероятности состояний: p0l «0,308; p02 «0,208; pu «
« 0,231; pl2 « 0,082; p21 « 0,091; p22 « 0,032; p31 « 0,037; p32 и 0,011.
Для исходной (немарковской) СМО р0 «0,616; рх «0,313;
р2 « 0,123; Ротк « 0,048; Q « 0,952; Л « 1,904; J « 0,703; г « 0,219;
*сист ^ 0,352; t оч «0,110.
Из сравнения этих данных с результатами предыдущей задачи
11.45 делаем вывод, что СМО задачи 11.46 имеет незначительное
преимущество перед СМО задачи 11.45 по всем характеристикам
эффективности и несколько большее преимущество перед
простейшей СМО с теми же X, [i.
11.47. Простейшая СМО без очереди с неограниченной
взаимопомощью между каналами. На n-канальную СМО с отказами
поступает простейший поток заявок с интенсивностью X. Каналы работают
со «взаимопомощью» — если в момент обслуживания очередной
заявки в СМО есть свободные каналы, то все они подключаются к
обслуживанию данной заявки. Интенсивность простейшего потока
обслуживании заявки есть некоторая функция \х, — ф (к) числа А;
каналов, одновременно обслуживающих ее. Построить граф
состояний СМО и найти финальные вероятности состояний. Выразить
через них характеристики эффективности СМО: вероятность
отказа Ротк, относительную пропускную способность Q, среднее число
занятых каналов к. Подсчитать эти характеристики при п = 4,
X = 1, [L (к) = k\i, [i = 0,5 и сравнить их с теми же характеристиками
в случае отсутствия взаимопомощи между каналами.
Решение. Так как в момент прихода первой же заявки все п
каналов подключаются к ее обслуживанию, то это означает, что
все каналы вместе всегда работают как один.
СМО превращается в одноканальную СМО с
отказами; ее состояния: s0 — ни один канал не
занят; sn — все п каналов заняты. Размеченный
граф состояний показан на рис. 11.47. Пользуясь
этим графом, получаем финальные вероятности
состояний:
>0
X
ф(я)
Рис. 11.47
Ро= 1 +
X
ф(п)
-1
ф(п)
Pi =
X
ф(п)
Ро =
ф(п) + X
X
ф(п) + X
Приф(п) = поимеем pQ = (n\i) / (n\i + X); pl — X / (пр, + X).
При п = 4, X = 1, [I = 0,5 имеем р0 = 2 / 3; Ротк = рг =1/3;
p1=l/3;Q = l-рг =2/3; A = \Q = 2/3& 0,667.
415
Среднее число занятых каналов к = 4 • 1/3 + 0 • 2/3 =
= 4/3«1,333. Этот же результат получим, разделив А на \l:
к = (2/3) / 0,5 = 4/3.
Для сравнения рассчитаем характеристики эффективности че-
тырехканальной СМО без взаимопомощи между каналами [см.
формулы Эрланга (11.0.6) и (11.0.7)]; при р = X / |л = 2
р0 ={1 + р + р2 /2 + р3 /6 + р4 /24)^=1/75
Рот=р4=(2/3)(1/7) = 2/21;
А = X (1 - 2 / 21) « 0,905; <2 = Л;А; = Л/|1^ 1,81.
Сравнивая эти характеристики с ранее полученными для СМО
со взаимопомощью между каналами, приходим к выводу, что в
наших условиях взаимопомощь невыгодна. Это на самом деле
так — для СМО с отказами неограниченная взаимопомощь (когда
все каналы сразу «набрасываются» на одну заявку, а тем
временем вновь приходящие заявки получают отказ) всегда невыгодна.
11.48. Простейшая СМО без очереди с равномерной
взаимопомощью между каналами. Имеется простейшая n-канальная СМО с
отказами, на которую поступает поток заявок с интенсивностью X.
Между каналами осуществляется взаимопомощь, но не объединением
всех каналов в один, как в предыдущем примере, а так называемая
«равномерная» организованная следующим образом. Если заявка
приходит в момент, когда все п каналов свободны, то все каналы
принимаются за ее обслуживание; если в момент обслуживания
заявки приходит еще одна, часть каналов переключается на ее
обслуживание; если, пока обслуживаются эти две заявки, приходит еще
заявка, часть каналов переключается на ее обслуживание и т.д., пока
не окажутся занятыми все п каналов; если они все заняты, вновь
пришедшая заявка получает отказ. Функция ф (k) = k\i, т.е.
обслуживание к каналами в к раз быстрее обслуживания одним каналом.
Составить размеченный граф состояний СМО, определить
финальные вероятности состояний и характеристики эффективности:
Q,A,k. Подсчитать их при п = 4, X = 1, \х, = 0,5, т. е. в условиях
задачи 11.47, и сравнить с тем, что получается без взаимопомощи.
Решение. Состояния СМО нумеруются по числу заявок,
находящихся в ней. Граф состояний (11.48) — тот же, что для простейшей
одноканальной СМО с производительностью (j,* = гг. (л и
ограниченной очередью, имеющей п — 1 мест. Для определения
характеристик можно воспользоваться формулами (11.0.16) — (11.0.19);
полагая р = р* = X / |i* = X / (п \i) = 0,5; имеем при т = 3:
При нашей постановке задачи все равно, какая часть каналов переключается на
обслуживание вновь прибывшей заявки; важно, что все время работают все п
каналов и ни одна вновь пришедшая заявка не получает отказа, пока в СМО не окажется
п заявок и все п каналов будут по одному их обслуживать.
416
so
\
51
X
•
• •
sk
X
•
• •
s„
П[Л
7l\X 7l[l
Рис. 11.48
n\x
n\i
Po
0,5
1- p*
1 - (p*)5 ~ 1 - 0,5
/л*\4
0,514; p4=(p*yPo « 0,032;
A = X (1 - p4) « 0,968; Q = 1 - p4 « 0,968; A; = Л / \l* « 1,936.
В условиях задачи 11.47 при отсутствии взаимопомощи А « 0,905;
Q ~ 0,905; А; « 1,81, т.е. взаимопомощь несколько увеличивает
пропускную способность СМО.В данном случае это увеличение
незначительно, так как СМО сравнительно мало нагружена.
11.49. Для простейшей трехканальной СМО с отказами и
параметрами: X = 4 заявки/мин, среднее время обслуживания заявки
одним каналом 1 / [i = 0,5 мин, интенсивность обслуживания
заявки к каналами ф_(А;) = к [i определить характеристики
эффективности СМО Q, А, к для трех вариантов использования СМО: 1) при
отсутствии взаимопомощи; 2) при неограниченной
взаимопомощи; 3) при равномерной взаимопомощи между каналами. _
Ответ. 1)Q«0,79; А«ЗД6; Jfc «1,58; 2)Q = 0,6; А=2,4; fc=l,2;
3) Q « 0,887; А « 3,51; jfc « 1,76.
11.50. Простейшая СМО с неограниченной очередью и со
взаимопомощью между каналами. Имеется простейшая п-канальная
СМО, на которую поступает поток заявок с интенсивностью X;
время обслуживания заявки одним каналом — показательное с
параметром \L. Интенсивность потока обслуживании заявки к
каналами пропорциональна их числу: ф (к) = к ^.Каналы
распределяются по заявкам, находящимся в СМО, произвольным образом, но
при условии, что если в СМО находится хотя бы одна заявка, все п
каналов заняты обслуживанием.
Построить граф состояний, найти финальные вероятности
состояний и характеристики эффективности: k, z, r,fCHCT , £оч.
Решение. Граф состояний этой СМО совпадает с графом
состояний простейшей одноканальной СМО с неограниченной
очередью, с интенсивностью потока заявок X и потока обслуживании
n\i (см. * 2, с. 366, 367). Полагая в формулах (11.0.12)-(11.0.15)
Р = Х= - ДпрЛ получаем р0=1- х',Рк = Х*(! ~ х) (* = 1, 2,...);
X
5^04
X
* = х/(1-х);г-х7(1-х);*сист = -,, v u, Wl ,
Х(1-х) Х(1-х)
Характеристики эффективности СМО в данном случае
совершенно не зависят от топ)* обслуживают ли каналы заявки «все
как один» или «равномерное так как заявки не получают отказов
417
(заметим, что не меняются от этого только средние значения
случайных величин Д R, Тсист, Точ, а не их распределения).
11.51. Простейшая СМО с ограниченной очередью и равномерной
взаимопомощью между каналами. Рассматривается простейшая
СМО с п каналами и равномерной взаимной помощью между
каналами. На СМО поступает простейший поток заявок с
интенсивностью X; поток обслуживании одного канала — простейший с
интенсивностью jj,; к каналов, обслуживающих одну заявку, дают
суммарный поток обслуживании с интенсивностью w(k) = k[i. Каналы
распределяются между заявками «равномерно» в том смысле, что
каждая вновь пришедшая заявка начинает обслуживаться, если
только есть возможность выделить для этого канал. Заявка,
пришедшая в момент, когда все п каналов заняты, становится в очередь.
Число мест в очереди т; если они все заняты, заявка получает отказ.
Нумеруя состояния СМО по числу заявок, находящихся в ней,
составить размеченный граф состояний СМО и найти финальные
вероятности состояний. Найти характеристики эффективности
СМО: Ротк, Q, Л, я, г, г~ , t
сист t 04
Решение. Состояния СМО:
50 — система свободна;
5а — одна заявка обслуживается всеми п каналами; ...;
sk— А;заявок обслуживаются всеми пканалами (1< к< п)\ ...;
sn— п заявок обслуживаются п каналами, одна заявка стоит в
очереди; ...;
— п заявок обслуживаются п каналами, га заявок стоят в
п +т
очереди.
50
iAj
51
iAj
5?
,х
X ,
...
sk
• • •
Sn
\
X
• • •
Sn+m
П[Л
П[1
П[Л П[Л
П[Л
П[Л П[1
Рис. 11.51
Граф состояний СМО дан на рис. 11.51. Этот граф состояний
СМО совпадает с графом состояний простейшей одноканальной
СМО с ограниченным числом га мест в очереди, интенсивностью
потока заявок X и интенсивностью потока обслуживании n\i
(см. п. 3, с. 367). Подставляя в формулы (11.0.16)-(11.0.20)
X = X / (п \l) вместо рип+m вместо га, получаем:
Po=(l-x)/(l-Xn+m+2); ft=X*Po(* = l..:.,nVm);
* отк = Рп+т » Ч =z ■*• ~ Рп+т ) А ~— \Q.
X2[l-Xn+m(n + m + l-
Г =
n+m+2
(i-xn+m+')(i-x)
£±*Ш; -Z = f + h
418
^сист — z I \ ^оч — r I ^-
11.52. На вход автоматизированного банка данных (АБД)
подается в среднем X = 335 статей/ч. Первая операция по обработке
входного потока первичных информационных документов (ПИД)
состоит в отборе тех статей, которые должны вводиться в АБД.
В отборе участвует 6 чел. (отборщиков); средняя
производительность каждого отборщика |л = 60 статей/ч. Известно, что в среднем
из входного потока отбирается для ввода в АБД 61,3 % ПИД.Все
потоки событий — простейшие. Рассматривая систему отбора
ПИД для ввода в АБД как шестиканальную (п = 6) СМО с неогра-
ниченной_очередью, определить ее характеристики
эффективности: Л, Q, к, z, г, ьсист , ъоч .
Решение. Так как очередь неограниченна, Q = 1; А = X.
Интенсивность потока ПИД, отобранных для ввода в АБД, Х0 = Хр,
где р « 0,613, т.е. Х0 = 335 • 0,613 « 205статей/ч.
Интенсивность потока ненужных для ввода в АБД ПИД будет
Хн = X (1 — р) « 130 статей/ч. _
Среднее число человек, занятых отбором ПИД, k = \/[i =
= р = 5,58 и не зависит от числа каналов (отборщиков).
Стационарный режим в СМО существует, если выполнено условие
X = X / (п |х) < 1; в нашем случае оно выполнено (х = 0,93).
Вероятность того, что в СМО будут заняты работой все п
отборщиков [см. формулу (11.0.22)], определяем по формуле:
рп = Р(п,р)/ Д(п,р) + Р(п,р)-*-
Пользуясь таблицами, данными в приложениях 1, 2, получаем:
0,93>
р6 =0,1584/
0,7603 + 0,1584
0,07 J
0,0569.
Среднее число ПИД в очереди [см. (11.0.23)] т —
= Рп X I (1 — х)2 ~ 10,8. Среднее время пребывания ПИД в
очереди^ = г J X « 1,87 мин. Среднее число ПИД, находящихся в
системе (в очереди и на обработке), z = r + p« 15,38. Среднее время
пребывания ПИД в системе tcliCT = £оч + 1 / р, « 2,87 мин.
11.53. На вход СМО (рис. 11.53) подается простейший поток
заявок с интенсивностью X. Обслуживание состоит из двух
последовательных фаз, выполняемых в СМОх и СМ02. В СМОх
проводится обслуживание заявки, а в СМ02 контролируется
качество проведенного в СМОх обслуживания. Если в СМ02 не
обнаружено недостатков в обслуживании, то заявка считается
обслуженной в СМО; если в СМ02 обнаружены недостатки в
обслуживании, то заявка возвращается на повторное обслуживание
419
в СМОх (см. рис. 11.53). Вероятность того, что заявка,
обработанная в СМОх, будет в результате контроля в СМ02 возвращена на
повторное обслуживание в СМ02, равна 1 — р и не зависит от
того, сколько раз она была обработана в СМОг
СМО
X
■е
L
Поток заявок на повторное обслуживание в СМО,
х02(1^р)
Рис. 11.53
СМОх и СМ02 представляют собой щ- и п2-канальные
системы с неограниченной очередью и интенсивностью потоков
обслуживании в каждом канале (ij и|12 соответственно. Время
повторного обслуживания заявки в канале в СМОх и повторного
контроля качества обслуживания заявки в канале в СМ02
распределено (так же, как и при проведении этих операций впервые) по
показательному закону с параметрами ^ и |i2 соответственно.
Определить условия существования стационарного режима
работы рассмотренной СМО, считая, что потоки заявок, поступающие
в СМОх и СМ02, простейшие.
Решение. Обозначим \ интенсивность потока заявок,
подаваемых на вход СМОх. Очевидно, что Хх > X, так как на вход
СМОх будет поступать поток заявок, направляемых на
обслуживание в СМОх впервые (интенсивность потока X), плюс поток заявок,
направляемых на повторное обслуживание (см. рис. 11.53). Если
стационарный режим существует, то интенсивность потока
обслуженных в СМОх заявок Х01 будет равна интенсивности \. Поток
обслуженных в СМОх заявок поступает в СМ02, следовательно, на
вход СМ02 поступает поток заявок с интенсивностью Х2 =Xt =
= Х01. В силу наличия стационарного режима в СМ02
интенсивность потока заявок на выходе СМ02 (Х02) будет также равна Х2.
Таким образом,
\ — ^01 — ^2 — ^02*
(11.53.1)
Очевидно, что интенсивность потока обслуженных заявок Х0
на выходе СМО в стационарном режиме будет равна
интенсивности входного потока X.
Интенсивность потока обслуженных в СМО заявок Х0 будет
равна интенсивности потока заявок на выходе СМ02 (Х02), умно-
420
женной на вероятность р того, что заявка не будет возвращена в
СМОх на повторное обслуживание:
^02^ ~" ^0 — \
(11.53.2)
откуда
Х02 =\/ р. (11.53.3)
Таким образом [см. формулы (11.53.1)—(11.53.3)],
\, =\2 =\ / р.
(11.53.4)
Для того чтобы существовал стационарный режим работы в
СМО, необходимо, чтобы как СМОх, так и СМ02 «справлялись»
с потоком поступающих на них заявок; следовательно, должны
выполняться два условия:
Xi = \ /(гсщ) = V (рп1|х1)<1; (11.53.5)
Х2 = х2 /(п2^2) = ^/(Рп2^2)<1- (Н.53.6)
Они вытекают из того, что как СМОх, так и СМ02
представляют собой пх- и ^-канальные системы с интенсивностью
обслуживания в каналах \хг и \х2 соответственно, с неограниченными
очередями (см. п. 4, с. 368).
11.54. Для условий предыдущей задачи определить среднее
время пребывания заявки в СМО и среднее число заявок,
находящихся в СМО.
Решение. Среднее время однократного пребывания заявки в
СМОх tx (см. рис. 11.53) будет определяться из условия, что на
вход этой системы поступает простейший поток заявок с
интенсивностью \г — X / р, число каналов обслуживания nv
интенсивность обслуживания \хг, число мест в очереди не ограничено. Для
этих условий в соответствии с (11.0.21)-(11.0.25) имеем
U =(Pi +ri)\
-i
Mi
+
p;i+4i
пг .^1(1- Xi) \
(11.54.1)
где
X . _Pi_. . _X
7 Xl '1 '
p\x.
n
p
Poi
2 Лп,
1! 2!
+
Pi
nl+\
1-1
n1\ n1 •n1!1 - Xi
Аналогично рассчитываем величину t2 — среднее время
однократного пребывания заявки в СМ02 для условий X2=X/p;n2;|i2:
421
Ч = (р2 + Г2)Х
-1
2
п2+1
М-2
+
Р
02
*2 -П2]Л1~ Х2)*Х2
, (11.54.2)
где
Р2 =
X
РМ-
х2
гг
—; Х2 —
X
Р
Р02 =
гс,
1! 2! ti.i
n2 + l
+
П
2 '
П
•п2!1- х
-1
Следовательно, среднее время однократной обработки заявки
CMC*! и СМ02 будет
Т12 ~ ^1 "Ь ^2*
(11.54.3)
Из условия задачи 11.53 следует, что случайная величина X —
число циклов обработки одной заявки в СМОх и СМ02 будет
иметь геометрическое распределение, начинающееся с единицы, с
параметром р:
X:
1
р
2
pq
3
pq2
к
pq
(11.54.4)
Обозначим Tv Т2, ..., Th ... — время первого, второго, ..., к-то
цикла обработки заявки в СМОх и СМ02. По условиям задачи
случайные величины Tv ..., Th ... независимы, одинаково
распределены и имеют математическое ожидание т12.
Время пребывания заявки в СМО ^с учетом возможных
возвратов заявки на повторное обслуживание' можно записать в ви-
X
де Т = У^Тк,т.е. оно представляет собой сумму случайного числа
к=\
случайных слагаемых, где число слагаемых X не зависит от
случайных величин Tv Г2, Т3, ... В соответствии с решением задачи
7.64 находим математическое ожидание величины Т:
i = м[г] = м[тк} м[Х] = т12 / р.
(11.54.5)
Для рассмотренной СМО формула Литтла также справедлива,
поэтому среднее число заявок, находящихся в СМО, будет
определяться по формуле
t X,
Н +Z2 =Pl +P2 + Г1 + V
(11.54.6)
422
11.55. Условия задачи (11.53) изменены так, что в СМС^ и
СМ02 проводится только первичное обслуживание и его
контроль; если заявка не прошла контроль в СМ02, то она
направляется на повторное обслуживание в СМОэ и повторный контроль в
СМ04 (рис. 11.55). СМОэ и СМ04 представляют собой п3- и п4-ка-
нальные системы с показательным распределением времени
обслуживания заявок в каналах с параметрами \хг и \х4
соответственно. Вероятность того, что заявка, обработанная в СМОэ, будет в
результате контроля в СМ04 возвращена на повторное
обслуживание в СМОэ, равна 1 — -к.
Определить условия существования стационарного режима
работы рассмотренной в этой задаче СМ О, считая, что потоки
заявок, поступающие в СМОх, СМ02, СМОэ и СМ04, являются
простейшими.
Решение. В рассматриваемой СМО в стационарном режиме
будет иметь место очевидное равенство (см. рис. 11.55)
Х = ХХ
^01 — ^2 — ^
02
(11.55.1)
Следовательно, интенсивность потока заявок, которые
прошли однократное обслуживание и контроль в CMOj и СМ02,
будет \р. Поток заявок, не прошедших контроль в СМ02 и
направляемых на повторное обслуживание в СМОэ и СМ04,
будет иметь интенсивность X (1 — р). Работа системы повторного
обслуживания СМОэ и СМ04 (от точки 1 до точки 2 на рис.
11.55) принципиально ничем не отличается от работы системы,
приведенной в задаче 11.53.
X
\
-►
СМО!
СМО
Х01 х2
».
смо2
У
02
р
\ (1-р) Поток заявок, не прошедших контроль в СМ02
ф
X,
11
СМ03
™3,М<3
Х0з \
■*-
смо4
Поток заявок на повторное обслуживание
^(1-,)=^)(1-,)
-к
X
X
Х(1-р)"
х„=
04
тг
\
Рис. 11.55
423
Из всего сказанного следует, что для стационарной работы
рассматриваемой в этой задаче СМО должны выполняться
совместно следующие условия:
X
<1; X
X , Х(1-р) 1
— <i; хз=—-—— <i;
ттгг3^з
X
X (1 - P)
<1.
(11.55.2)
Кроме того, будут иметь место равенства (см. рис. 11.55)
-1 (11.55.3)
Х3 = Х03 = Х4 = Х04 = Х (1 ~ Р)Ъ •
11.56. Для условий предыдущей задачи определить среднее
время t пребывания заявки в СМО и среднее число заявок J,
находящихся в СМО.
Решение. Среднее время пребывания заявки в СМОх будет
определяться из условия, что на вход этой системы поступает
простейший поток заявок с интенсивностью \г — X [см. рис. 11.55
и формулу (11.55.1)], число каналов обслуживания nv
интенсивность обслуживания в канале \x,v число мест в очереди не
ограничено. Для этих условий в соответствии с (11.0.21)-(11.0.25)
*i =(Pi +ri)x
-i
+
РГ1+1 Poi
M-i nl-nl\{l~Xi) ^
(11.56.1)
где
X
Pi =—;
x
i.
п.
V
01
J. —г" —Г~ Г~. • • -1 —г~
п1+1
1! 2!
пг\ пг -п^Л-Хг
-1
Аналогично рассчитываем величину t2 для СМ02 при
Х2 — X, n2, [i2:
ii = (р2 + Г2)Х
-1 1
+
я9+1
Р2 Р02
2 VK2 ' '2/ .,.. ч2
^2 п2 -ЛаК1-Х2) Х
(11.56.2)
где
__Х_. _Р2_.
Рг > Хг '
М-
п
424
l+p* + p*+..
1! 2!
П0 П0+1
1 Рг 1 p2 l
• \ \
-1
P02
Среднее время пребывания заявки в СМС^ и СМ02 равно
т
12
*!+*;
(11.56.3)
Среднее время tz однократного пребывания заявки в СМОэ
будет определяться из следующих условий: на вход этой системы
поступает простейший поток заявок с интенсивностью
\3 = \ (1 — р) I -к [см. рис . 11.55 и формулу (11.55.3)], число
каналов обслуживания п3, интенсивность обслуживания в канале \izy
число мест в очереди не ограничено. Тогда в соответствии с
(11.0.21)-(11.0.25)
raQ-fl
*з=(Рз+гз)хз ^/^з + Рз"3 Poz /inz'nzl(1-Xz) ХзЬ (П.56.4)
где
Роз
Рз
_ \ _ X (1 - р)
М-з
-к
М-з
Хз ~~
п.
i + £i+ £l+...+
1! 2!
Р«
п3!
По+1
з+_Рз
п.
™3! 1-Х:
-1
Аналогично рассчитываем величину £4 для СМ04 при
Х4 = Х(1- р)/-к,п4,|х4:
^4=(p4+r4)X-21=l/}i4 + p4t4
л4+1
Р04 /К •^4!(1-Х4)2Х4]Д11-56'5)
где
Р4 = — =
М-4
Х4 X (1 - р)
-к
М-з
Х4
Р4 .
п
Р04
о о2 о"4 о"4"1"1
1! 2!
п4 ! п4 -п4 !1 - х4
-1
Следовательно, среднее время однократной обработки заявки
в СМ03 и СМ04 будет
(11.56.6)
т
(1)
34
*q ~Г t л •
В соответствии с формулой (11.54.6) математическое
ожидание времени пребывания заявки в СМОэ и СМ04 (см. рис. 11.55)
с учетом возможной повторной обработки равно
(11.56.7)
т
34
т(1)/тг
34 ' '
425
Для определения среднего времени пребывания заявки в СМО
рассмотрим две гипотезы: 1) Нг — заявка подвергалась только
однократной обработке; Р{Н1) = р; 2) Н2 — заявка подвергалась
многократной обработке; Р(Н2)) = 1 — р.
При гипотезе Ях математическое ожидание времени
пребывания заявки в СМО будет определяться по формуле (11.56.3), при
гипотезе Н2 — по формулам (11.56.7) и (11.56.3). Полное
математическое ожидание времени пребывания заявки в СМО будет
*" = т12 + т£ (1 - р) / *. (11.56.8)
Среднее число заявок, находящихся в СМО, определяется по
формуле Литтла:
z=t\. (11.56.9)
11.57. Рассмотрим условия задачи 11.53 применительно к
многократной обработке информации в двух фазах. С целью контроля
правильности перфорации она осуществляется дважды: на
перфораторе и на «контрольнике», с помощью которого обнаруживают
ошибку. Перфораторщица осуществляет в среднем одну ошибку
на 1000 знаков (букв, цифр и т.п.). Каждая перфокарта содержит в
среднем 80 знаков. Если во время контроля на перфокарте
обнаружена хотя бы одна ошибка, то эта перфокарта возвращается снова
на перфорацию. За год необходимо обработать 50 000 документов,
каждый из которых содержит в среднем 400 знаков.
Найти минимально необходимое число перфораторщиц,
работающих на перфораторах и контрольниках, если одна
перфораторщица в год перфорирует 4,2 • 106 знаков, и определить
характеристики такой системы.
Р е ш е н и е. Из условий задачи следует, что в год необходимо в
среднем отперфорировать и проконтролировать 50 000 • 400 / 80 =
= 250 000 перфокарт. Следовательно, X = 250 000 перфокарт/год =
125 перфокарт/ч = 2,083 перфокарт/мин. Производительность
перфораторщицы, работающей за перфоратором или на
«контрольнике», составляет [хг =\х2 = 4,2 • 106 / 80 = 52 500
перфокарт/год = 26,25 перфокарт/ч = 0,438 перфокарт/мин.
Вероятность необнаружения ни одной ошибки на перфокарте равна
р = 0,99980 « 0,9. При этом мы пренебрегаем вероятностью того,
что и перфораторщица и контролер ошибутся одинаково в одном
и том же знаке. Эта вероятность намного меньше, чем
(0,001)2 = 10~6, так как клавиатура перфоратора и «контрольника»
имеет около 50 различных знаков. Если считать, что ошибочно
может быть нажат на клавиатуре любой знак из 50, то получим
вероятность одинаковой ошибки, равную 10~6 / 2500. Если считать,
что ошибочно может быть нажат на клавиатуре только ближай-
426
ший к нужному знаё (а их от 5 до 8), то эта вероятность будет
1(Г6 / 25 - Ю-6 / 64.
Условие стационарной работы перфораторщиц будет [см.
формулы (11.53.5), (11.53.6)]
х / Km-ip) = Xi < 1; V (^2^2^) = х2 <!)
откуда п1 > X / (\хгр) = 250 000 / (52 500 • 0,9) = 5,29; п2 > 5,29.
Таким образом, нужно иметь шесть перфораторщиц и шесть
контролеров.
Характеристики работы перфораторщиц: Хвх1 = X / р =
= 250 000 :0,9 = 278 000 перфокарт/год; пг = 6; \хг = 52 500
перфокарт/год; Xi = X /(пгр\1) = 0,882; рг = X / (р|л1) = 5,29.
По формуле (11.0.22) находим вероятность того, что все шесть
перфораторщиц будут заняты и «очереди» документов,
подлежащих перфорации, нет:
Рп = IS-llhl = 9Д52 =0>107.
1 v 0882
fl(n1>Pl)+P(n1>Pl)^— 0,282+0,152 '
Xl 1 - 0,882
Среднее число перфокарт, ожидающих перфорации, гг =
= РяХ1/(1-\1)2=6,78.
Среднее время ожидания перфокарты в очереди: t04l =
— ггр X"1 = 2,92 мин; tx = t04i + 1 / \хг = 5,21 мин.
Общее число перфокарт в первой фазе zx = гг + kx =
= гг+рг= 12,07.
Так как характеристики второй фазы (контроля) такие же, как
и первой, то можно выписать общие характеристики работы
системы с учетом возврата перфокарт на новую обработку. Общее
среднее число перфокарт, находящихся в системе, z = 2zx = 24,14;
из них в очереди будет г = 2гг = 13,56. Общее среднее время
обработки одной перфокарты с учетом ее возможного возврата на
повторную обработку равно t = т12 / р = (tt -\-t2)/p = 2t1 / р =
= 11,57 мин.
ПРИЛОЖЕНИЯ
Приложение 1
о1)
Таблица 1
Значения вероятностей Q (т, а) = 1 — R (т, а) = 1 — V) — в а
*=0
k\
т
0
1
2
3
4
5
6
т
0
1
2
3
4
5
6
7
а = 0,1
9,5163~2
4,6788-3
1,5465-4
3,8468-6
а = 0,6
4,5119-1
1,2190
2,3115-2
3,3581-3
3,9449-4
3,8856-5
3,2931-6
а = 0,2
1,8127-1
1,7523-2
1,1485-3
5,6840-5
2,2592-6
а = 0,7
5,0341-1
1,5580
3,4142-2
5,7535-3
7,8554-4
9,0026-5
8,8836-6
а= 0,3
2,5918-1
3,6936-2
3,5995-3
2,6581-4
1,5785-5
а = 0,8
5,5067-1
1,9121
4,7423-2
9,0799-3
1,4113
1,8434-4
2,0747-5
2,0502-6
а = 0,4
3,2968-1
6Д552-2
7,9263-3
7,7625-4
6Д243-5
4,0427-6
а = 0,9
5,9343-1
2,2752
6,2857-2
1,3459
2,3441-3
3,4349-4
4,3401-5
4,8172-6
а = 0,5
8,9347-1
9,0204-2
1,4388
1,7516-3
1,7212-4
1,4165-5
1,0024-6
т
Вероятность Р (га, а) = — е а может быть найдена через вероятность Q (га, а)
га !
следующим образом:
2)
P(Tn,a) = Q(m-l,a)-Q(m,a) (m>0),
Р(0,я)=1-(2(0, я).
-2
Такая запись принята для краткости. Число 9,5163 означает 9,5163-10
\-2
428
Продолжение табл. 1
т
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
га
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
а= 1
6,3212-1
2,6424
8,0301-2
1,8988
3,6598-3
5,9418-4
8,3241-5
1,0249
1Д252-6
а = 6
9,9752-1
9,8265
9,3803
8,4880
7,1494
5,5432
3,9370
2,5602
1,5276
8,3924-2
4,2621
2,0092
8,8275-3
3,6285
1,404
5,0910-4
1,7488
5,6917-5
1,7597
а= 2
8,6466-1
5,9399
3,2332
1,4288
5,2653-2
1,6564
4,5338-3
1,0967
* А
2,3745-4
4,6498-5
8,3082-6
1,3646
а= 7
9,9909-1
9,9270
9,7036
9,1823
8,2701
6,9929
5,5029
4,0129
2,7091
1,6950-1
9,8521-2
5,3350
2,7000
1,2811
5,7172-3
2,4066
* А
9,5818-4
3,6178
1,2985
а = 3
9,5021-1
8,0085
5,7681
3,5277
1,8474
8,3918-2
3,3509
1,1905
3,8030-3
1,1025
* А
2,9234-4
7,1387-5
1,6149
3,4019-6
а = 8
9,9966-1
9,9698
9,8625
9,5762
9,0037
8,0876
6,8663
5,4704
4,0745
2,8338-1
1,8411
1,1192
6,3797-2
3,4181
1,7257
8,2310-3
3,7180
1,5943
6,5037-4
а= 4
9,8168-1
9,0842
7,6190
5,6653
3,7116
2,1487
1,1067
5,1134-2
2,1363
8,1322-3
2,8398
9Д523"4
2,7372
7,6328-5
1,9932
4,8926-6
1,1328
а = 9
9,9988-1
9,9877
9,9377
9,7877
9,4504
8,8431
7,9322
6,7610
5,4435
4,1259-1
2,9401
1,9699
1,2423
7,3851-2
4,1466
2,2036
1,1106
5,3196-3
2,4264
а = 5
9,9326-1
9,5957
8,7535
7,3497
5,5951
3,8404
2,3782
1,3337
6,8094-2
3,1828
1,3695
5,4531-3
2,0189
6,9799-4
2,2625
6,9008-5
1,9869
5,4163-6
1,4017
а= 10
9,9995-1
9,9950
9,9723
9,8966
9,7075
9,3291
8,6986
7,7978
6,6718
5,4207-1
4,1696
3,0322
2,0844
1,3554
8,3458-2
4,8740
2,7042
1,4278
7Д865-3
Продолжение табл. 1
т
19
20
21
22
23
24
25
26
27
га
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
а = 6
5,1802-6
1,4551
а= 11
9,9998-1
9,9980
9,9879
9,9508
9,8490
9,6248
9,2139
8,5681
7,6801
6,5949
5,4011
4,2073
3,1130
2,1871
1,4596
9,2604-2
5,5924
3,2191
1,7687
9,2895-3
4,6711
2,2519
1,0423
4,6386-4
1,9871
8,2050-5
3,2693
1,2584
4,6847-6
а= 7
4,4402-5
1,4495
4,5263Г6
1,3543
а= 12
9,9999-1
9,9992
9,9948
9,9771
9,9240
9,7966
9,5418
9,1015
8,4497
7,5761
6,5277
5,3840
4,2403
3,1846
2,2798
1,5558
1,0129
6,2966-2
3,7416
2,1280
1,1598
6,0651-3
3,0474
1,4729
6,8563-4
3,0776
1,3335
5,5836-5
2,2616
а = 8
2,5294
9,3968-5
3,3407
1,1385
3,7255-6
1,1722
а= 13
9,9997-1
9,9978
9,9895
9,9626
9,8927
9,7411
9,4597
9,0024
8,3419
7,4832
6,4684
5,3690
4,2696
3,2487
2,3639
1,6451
1,0954
6,9833Г2
4,2669
2,5012
1,4081
7,6225-3
3,9718
1,9943
9,6603Г4
4,5190
2,0435
8,9416-5
а = 9
1,0560
4,3925-4
1,7495
6,6828-5
2,4519
8,6531-6
2,9414
а= 14
9,9999-1
9,9991
9,9953
9,9819
9,9447
9,8577
9,6838
9,3794
8,9060
8,2432
7,3996
6,4154
5,3555
4,2956
3,3064
2,4408
1,7280
1,1736
7,6505-2
4,7908
2,8844
1,6712
9,3276-3
5,0199
2,6076
1,3087
6,3513-4
2,9837
а= 10
3,4543
1,5883
6,9965-4
2,9574
1,2012
4,6949-5
1,7680
6,4229-6
2,2535
а= 15
9,9996-1
9,9979
9,9914
9,9721
9,9237
9,8200
9,6255
9,3015
8,8154
8,1525
7,3239
6,3678
5,3435
4,3191
3,3588
2,5114
1,8053
1,2478
8,2972-3
5,3106
3,2744
1,9465
1,1165
6Д849"3
3,3119
1,7158
8,6072'4
430
Продолжение табл. 1
т
29
30
31
32
33
34
35
36
т
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
о= 11
1,6882
о= 16
9,9998-1
9,9991
9,9960
9,9862
9,9599
9,9000
9,7801
9,5670
9,2260
8,7301
8,0688
7,2545
6,3247
5,3326
4,3404
3,4066
2,5765
1,8775
1,3183
8,9227-2
5,8241
3,6686
2,2315
1,3119
7,4589-3
4,1051
2,1886
1,1312
о= 12
8,8701-6
3,3716
1,2432
а =17
9,9999-1
9,9996
9,9982
9,9933
9,9794
9,9457
9,8740
9,7388
9,5088
9,1533
8,6498
7,9913
7,1917
6,2855
5,3226
4,3598
3,4504
2,6368
1,9452
1,3853
9,5272-2
6,3296
4,0646
2,5245
1,5174
8,8335-3
4,9838
2,7272
о= 13
3,7894
1,5568
6,2052-6
2,4017
о= 18
9,9998-1
9,9992
9,9968
9,9896
9,9711
9,9294
9,8462
9,6963
9,4511
9,0833
8,5740
7,9192
7,1335
6,2495
5,3135
4,3776
3,4908
2,6928
2,0088
1,4491
1,0111
6,8260-2
4,4608
2,8234
1,7318
1,0300
5,944Г3
о= 14
1,3580
5,9928-5
2,5665
1,0675
4,3154-6
1,6968
о= 19
9,9999-1
9,9996
9,9985
9,9948
9,9849
9,9613
9,9114
9,8168
9,6533
9,3944
9,0160
8,5025
7,8521
7,0797
6,2164
5,3052
4,3939
3,5283
2,7450
2,0687
1,5098
1,0675
7,3126-2
4,8557
3,1268
1,9536
1,1850
о= 15
4,1845
1,9731
9,0312-5
4,0155
1,7356
7,2978-6
2,9871
1,1910
о = 20
9,9998-1
9,9993
9,9974
9,9922
9,9791
9,9500
9,8919
9,7861
9,6099
9,3387
8,9514
8,4349
7,7893
7,0297
6,1858
5,2974
4,4091
3,5630
2,7939
2,1251
1,5677
1,1218
7,788Г2
5,2481
3,4334
2,1818
431
Окончание табл. 1
т
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
а= 16
5,6726-4
2,7620
1,3067
6,0108-5
2,6903
1,1724
4,9772-6
2,0599
а =11
1,4484
7,4708-4
3,7453
1,8260
8,6644-5
4,0035
1,8025
7,9123-6
3,3882
1,4162
а= 18
3,3308
1,8133
9,5975-4
4,9416
2,4767
1,2090
5,7519-5
2,6684
1,2078
5,3365-6
2,3030
а= 19
6,9819-3
3,9982
2,2267
1,2067
6,3674-4
3,2732
1,6401
8,0154-5
3,8224
1,7797
8,0940-6
3,5975
1,5634
а= 20
1,3475
8,0918-3
4,7274
2,6884
1,4890
8,0366-4
4,2290
2,1708
1,0875
5,3202-5
2,5426
1,1877
5,4252-6
2,4243
1,0603
Пример. Требуется определить вероятность того, что
событие А появится не более двух раз, если а = 7.
Имеем
-1
R (2, 7) = 1 - Q (2, 7) = 1 - 9,7036-1 = 1 - 0,97036 = 0,02964.
Примечания: 1. Если у числа в таблице показатель степени
отсутствует, то им будет показатель степени ближайшего
вышестоящего числа, у которого есть покзатель степени. Например,
Q(33; 19)= 12067-10"3. 2. При а > 20 вероятность Q (га, а) можно
рассчитывать по приближенной формуле
Q(m,a)r^ -** '
1-Ф
R (т,а) «Ф:
л/а
f т + 0,5 — а'
л/а
a
S
с
^3
H
4—'
*
Ф
H
H
4—'
*
ф
н
н
4—'
*
ф
н
t-
см
CO
см
CO
t*
о
1
I>-
IlO
IlO
CO
t*
CO
о
1
о
о
о
ю
о
о
о
о
1
I>- CD
о> со
см см
см см
ч* Ю
I>- t*
о о
1 1
о со
СМ 00
ю ^
со со
00 05
со со
о о
1 1
о о
CD СМ
05 05
Tf Tf
1-1 CM
о о
о о
1 1
CD CD
со о
см см
см см
CD t-
I>- t*
o о
1 1
CD
I>- 00
I>- ^
1—1 1—1
CM CM
00 05
I>- t*
o о
1 1
О) CM
4tf О t*
Tf
CO
о
о
Tf
о
1
о о
00 Tf
00 00
Tf Tf
CO 4tf
о о
о о
1 1
4tf CO
CO CO
i-l CM
Tf Tf
о о
1 1
1—1 1—1
О CD
00 t*
Tf Tf
Ю CD
о о
о о
1 1
Oi О
1—1 05
i-i о
см СМ
о
О i-i
00 00
о о
1 1
CD О ^
СО О CD
СО СО СМ
со со со
со ^ ю
1—1
CD
О
СМ
см
00
о
1
00
см
см
со
CD
^ ^ ^ ^
о о о
1 1 1
1—1 1—1 1—1
СМ 00 ^
I>- CD CD
^ ^ ^
1>- 00 05
О О О
о о о
1 1 1
о
1
со ю
со о
о о
см см
СО т*
00 00
о о
1 1
CM CD
о ю
1—1 1—1
со со
1> 00
1>- 05
см ^
t- ^ СМ 05
О О)
Ю CD
00 00
О О
1 1
i-i
СМ
1—1
со
О
^ ^ ^
о о
1 1
см СМ
О CD
CD IlO
О
1
СМ со
СМ 00
ю ^
О 00
1>- 00
00 00
о о
1 1
ю о
00 ю
о о
со СО
о
О i-i
ю ю
о о
1 1
СО ч*
rf О
Tf Tf
t*
CD
00
0>
00
о
1
IlO
1—1
о
со
см
IlO
О
1
Tf
CD
СО
i-i
Tf
00
о
о
О
О
1
i-i CD
00 т*
О) О)
СМ см
СО т*
IlO IlO
О О
1 1
IlO CD
CM 00
СО CM
Tf
1—1
00
1—1
О)
О
1
CM
1—1
О)
CM
IlO
IlO
О
1
t*
Tf
CM
^^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^ ^^
о
О 1-й
о о
1 1
см со
о о
1 1
^ IlO
о о
1 1
CD
О
1
I>- 00
О О
1 1
0>
О
1
00
00
I>-
CM
CM CD
CD CO
I>- t*
CO Tf
ObObO)
о
1
t*
о о
1 1
со о
t* 4tf i-i
00
CM
CD
IlO
О
1
00 00
CM CM
I>- 00
IlO IlO
О О
1 1
i—l IlO
i—l 00
t- cd
IlO CD
О) O)
О О
1 1
CD
I>-
I>-
CM
o>
IlO
О
1
t* 00 О) о
О CD
CM i-l
CM O)
i-i О
О IlO
CD CO
CD CD
I> 00
О) O)
О О
1 1
CO О)
rf О
J> I>-
CM CM
о
О i-i
CD CD
О О
1 1
1—1
1—1
CD
О)
О)
О
1
CD СО
Г- rf
CD CD
CM CM
CM CO
CD CD
О О
1 1
CM CO ^ CD
IlO i—l
О О
I>- CO
О) O)
I>-
00
IlO
О
о
о
1
1—1
1—1
CD
CM
Tf
CD
О
1
CO
CD
IlO
i—l
О
1
00
О)
со
IlO
CM
IlO
i—l
IlO
СМ О)
О) CD
Tf Tf
CO ч* Ю
о о
1
1
CD ч*
I>- ^
IlO
CM
IlO
CD
О
1
I>- O)
O)
00
IlO
00
■^•^•^•^•^•^cocococo
о
О i-i
CM CM
о о
1 1
CM CO ^ IlO
CM CM
о о
1 1
CM CM
о о
1 1
CD t-
CM CM
о о
1 1
00
CM
о
1
o>
CM
о
1
IlO
CM
CD
CD
О
1
i—l
о о
1 1
СО i—l
00 IlO
IlO ^ ^
CM
t*
CD
О
1
i—l
CM
00
CO
о
о
со
о
1
CM CM
00 О)
CD CD
О О
1 1
CO IlO
00 Tf
I>- I>-
CO CO
i-l CM
CO CO
о о
1 1
CD CO
^ CM
Tf Tf
CD t*
o О
1 1
о
CM
Tf
CM
о
о
t*
о
1
I>- О)
О CD
I>- CD
CO CO
CO Tf
CO CO
о о
1 1
r-i О)
о t*
^ со
00 О)
о о
1 1
О) 00
00 IlO
со со
см см
гН СМ
I>- t-
о о
1 1
СМ ч*
СО О)
CD IlO
со со
IlO CD
СО со
о о
1 1
s
§
о
H
4—^
*
ф
н
н
4—^
*
ф
н
н
^—y
*
ф
н
00
00
см
о
о
о
О
1
00
CD
CD
О
О
О
1
IV
ю
со
о
о
1
1—1
00
см
о
1—1
О
1
ю
ю
CD
О
1—1
1
ю
со
со
1—1
1
^f
IV
см
о
см
05
1
со
Tf
CD
О
СМ
1
Tf
1—1
со
см
1
00
CD
СМ
о
со
О
1
О
СО
CD
О
СО
1
СМ
О
СМ
со
1
см
CD
СМ
о
Tf
О
1
00
1—1
CD
О
Tf
1
1—1
IV
см
Tf
1
CD
Ю
СМ
о
ю
О
1
CD
О
CD
О
Ю
1
1—1
ю
см
ю
1
о
ю
см
о
CD
О
1
Tf
О
Ю
О
CD
1
О
СО
СМ
CD
1
Tf
Tf
CM
о
IV
05
1
CM
00
ю
о
IV
1
о
1—1
CM
IV
1
О
со
CM
о
00
О
1
i—l
IV
ю
о
00
1
о
О
i—l
00
1
со
со
см
о
О
О
1
О
Ю
Ю
О
О
1
О
IV
1—1
О
1
00
СМ
см
о
о
о
о
см
1
00
Tf
ю
о
о
о
CD
1
1—1
ю
1—1
о
о
см
1
О
IV
1—1
о
о
1—1
см
1
IV
со
ю
о
1—1
CD
1
1—1
со
1—1
1—1
см
1
О
СО
i—l
О
о
см
см
1
CD
СМ
ю
о
см
CD
1
СМ
1—1
1—1
см
см
1
IV
о
1—1
о
о
со
см
1
CD
1—1
ю
о
со
CD
1
СО
О
О
СО
СМ
1
см
00
о
о
о
^f
см
1
ю
о
ю
о
^f
CD
1
ю
IV
о
^f
см
1
см
CD
о
о
о
ю
см
1
ю
О
Tf
О
ю
CD
1
CD
Ю
О
Ю
СМ
1
IV
Tf
о
о
о
CD
СМ
1
ю
00
Tf
о
CD
CD
1
00
СО
О
CD
СМ
1
ю
со
о
о
о
IV
см
1
ю
IV
Tf
о
IV
CD
1
о
см
о
IV
см
1
CD
СМ
о
о
о
00
см
1
ю
CD
Tf
О
00
CD
I
СО
О
о
00
см
1
О
i—l
О
о
о
О
СМ
1
ю
ю
Tf
о
О
CD
1
Ю
00
О
О
О
СМ
1
Tf
1—1
о
о
о
о
о
со
1
CD
Tf
Tf
О
О
о
IV
1
00
CD
О
О
О
О
СО
1
О
1—1
о
о
о
1—1
со
1
CD
СО
Tf
О
i—l
IV
1
i—l
ю
О
О
i—l
СО
1
IV
о
о
о
о
см
со
1
IV
см
Tf
о
см
IV
1
Tf
со
О
о
см
со
1
ю
о
о
о
о
со
со
1
00
1—1
Tf
о
со
IV
1
00
1—1
О
о
со
со
1
со
о
о
о
о
Tf
со
1
О
о
Tf
о
Tf
IV
1
1—1
о
О
о
Tf
со
1
см
о
о
о
о
ю
со
1
1—1
о
Tf
о
ю
IV
1
ю
00
00
о
ю
со
1
см
о
о
о
о
CD
со
1
см
О
со
о
CD
IV
1
О
CD
00
о
CD
со
1
1—1
о
о
о
о
IV
со
1
Tf
00
со
о
IV
IV
1
со
ю
00
о
IV
со
1
1—1
о
о
о
о
00
со
1
ю
IV
со
о
00
IV
1
00
со
00
о
00
со
1
о
о
о
о
о
О
со
1
IV
CD
со
о
О
IV
1
со
см
00
о
О
со
1
о
о
о
ю
о
о
о
о
О
ю
со
о
о
о
00
1
00
о
00
о
о
о
1
о
Tf
о
ю
1—1
о
о"
1—1
ю
со
о
1—1
00
1
со
О
IV
о
1—1
1
о
00
о
ю
см
о
о
Tf
Tf
со
о
см
00
1
00
IV
IV
о
см
1
о
см
1—1
ю
со
о
о
CD
со
со
о
со
00
1
Tf
CD
IV
о
со
1
о
CD
1—1
ю
о
о
05
см
со
о
Tf
00
1
05
^
IV
о
Tf
1
05
05
1—1
ю
о
о
см
см
со
о
ю
00
1
ю
со
IV
о
ю
1
о>
со
см
ю
CD
о
о
Tf
1—1
со
о
CD
00
1
1—1
см
IV
о
CD
1
О) О) О)
t~- 1—1 ю
см со со
ю ю ю
IV 00 05
о о о
г» »■» с*
о о о
IV 1-1 ^
О О 05
со со см
о о о
IV 00 05
00 00 00
1 1 1
00 ^ 1-й
О 05 СО
IV CD CD
о о о
IV 00 05
^ ^ ^
1 1 1
00
а
x
§
о
а-
_
н
4—^
*
ф
н
н
4—^
*
ф
н
н
4—^
*
ф
н
О
Ю
1—1
00
О
О
О
ю
1—1
05
CD
О
О
Ю
О
00
05
СО
Ю
О
О
О
СО
00
т—t
00
1—4
о
о
ю
о
со
1—1
ю
о
00
со
Tf
ю
т—t
о
см
1—1
см
00
см
о
ю
00
О
со
см
ю
о
00
t*
Tf
ю
см
о
00
со
см
00
со
о
05
1—1
о
1>
со
ю
о
1>
1—1
ю
ю
со
о
Tf
со
см
00
Tf
о
Tf
ю
о
t*
Tf
ю
о
1>-
ю
ю
ю
Tf
о
О
00
см
00
ю
о
00
00
о
1>-
ю
ю
о
со
О
ю
ю
ю
о
ю
1—1
со
00
со
о
со
см
1—1
t*
со
ю
о
со
со
со
ю
со
о
о
Tf
со
00
t*
о
1>-
ю
1—1
1>-
1>-
ю
о
ю
t*
со
ю
t*
о
ю
со
со
00
00
о
о
О
1—1
1>-
00
ю
о
Tf
1—1
1>-
ю
00
о
О
00
со
00
О
о
Tf
см
см
t*
О
ю
о
со
ю
1>-
ю
О
о
со
1—1
Tf
00
о
о
о
1>-
ю
см
1>-
о
о
со
о
со
О
is
ю
о
о
см
о
t*
со
Tf
00
1—1
о
1—1
О
см
1>-
1—1
со
о
см
со
00
ю
1—1
см
о
1—1
со
Tf
00
см
о
Tf
см
со
1>-
см
со
о
1—1
|>-
00
ю
см
см
о
Ю 00
00 о
^ ю
00 00
СО ч*
о о
1> О
Ю 00
со со
l>- t*
со ^
со со
о о
о оо
1—1 Tf
О О
ю ю
СО ч*
см см
о о
1—t
со
ю
00
ю
о
см
см
^
1>-
ю
со
о
1>-
00
О
ю
ю
см
о
Tf
ю
ю
00
СО
о
Tf
ю
Tf
t*
СО
со
о
со
см
о
со
со
см
о
Г- О 1—1
t- О СМ
ю ю со
00 00 00
1>- 00 О
о о о
»■» »■» »■»
СО IS О
00 н ^
^ ю ю
b- b- t-
lS 00 О
со со со
о о о
rf СО Н
со о ^
О г-1 1—1
со со со
1>- 00 О
см см см
о о о
со
Tf
СО
00
о
о
»■»
о
00
ю
1>-
о
о
IS-
о
05
t-
1—1
со
о
о
со
о
ю
СО
со
00
1—1
»■»
т-Ч
1—1
со
1>-
т—t
t*
о
1>-
1—1
см
со
1—1
со
о
СО 00
оо о
СО Ь-
00 00
см со
»■» »^
см со
^ г*-
со со
1>- ь-
см со
1>- ь-
о о
ю со
Ю 05
см см
со со
см со
со со
о о
Oi Oi о
см ^ t-
I>- I>- 1>-
00 00 00
^ ю со
»"» »■» »■»
со ^ ^
о со со
1>- 1>- 1>-
I>- t- 1>-
^ ю со
t- t~ t~
о о о
1-й 00 СО
со со о
со со ^
со со со
^ ю со
со со со
о о о
о о о
05 1—1 СО
t- 00 оо
00 00 00
t- 00 05
»■» »^ »^
^ со см
Oi CN Ю
1>- 00 00
1>- 1>- 1>-
t^ 00 05
t* t* t*
о о о
coo ь
^ СО н
ч* ^ ю
со со со
1>- 00 05
со со со
о о о
о
4tf
00
00
о
о
см
г-Н
00
00
1>-
о
о
00
о
Tf
ю
ю
со
о
о
Tf
о
05
со
00
00
1—1
см
о
1—1
05
1>-
т—1
00
о
1—1
05
ю
со
1—1
Tf
о
00
00
00
00
см
см
05
со
05
1>-
см
00
о
00
см
со
со
см
Tf
о
t-
о
С5
00
со
см
1>
СО
05
1>
со
00
о
Tf
СО
СО
СО
со
Tf
о
ю ^
см ^
С5 05
00 00
^ ю
см см
ю со
05 СМ
05 О
1>- 00
т^ ю
00 00
о о
о со
о со
I>- t*
СО со
^ ю
Tf Tf
о о
см о is ю
СО 00 05 1—1
05 Oi 05 О
00 00 00 05
СО Is- 00 05
см см см см
»■» »■» »^ »■»
1—1 00 со со
ЮЬ О СО
О О 1-й 1-й
00 00 00 00
СО N 00 05
00 00 00 00
о о о о
СМ 00 ч* 05
t* о ^ **-
t- 00 00 00
со со со со
СО Is- 00 05
^ ^* ^ ^
о о о о
00
Окончание табл. 2
X
1,30
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
Ф*(я)
0,9032
9049
9066
9082
9099
9115
9131
9147
9162
9177
0,9192
9207
9222
9236
9251
9265
9279
9292
9306
9319
0,9332
9345
9357
9370
9382
9394
9406
9418
9429
9441
X
1,60
1,61
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
1,70
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,80
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
Ф*(я)
0,9452
9463
9474
9484
9495
9505
9515
9525
9535
9545
0,9554
9564
9573
9582
9591
9599
9608
9616
9625
9633
0,9641
9649
9656
9664
9671
9678
9686
9693
9699
9706
X
1,90
1,91
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
Ф*(я)
0,9713
9719
9726
9732
9738
9744
9750
9756
9761
9767
0,9772
9821
9861
9893
9918
9938
9953
9965
9974
9981
0,9986
9990
9993
9995
9997
9998
9998
9999
9999
1,0000
Приложение 2
Некоторые свойства обобщенных функций
При решении задач, связанных со случайными функциями,
часто бывает удобно выполнять преобразования с помощью
различных скачкообразных функций, а также обобщенных функций
типа дельта-функции.
Приводим определения и основные свойства таких функций
от действительного агрумента т.
1
т
— модуль (абсолютная величина):
т при т > 0;
-т при < 0.
т(1(т)-1(-т)).
2.1 (т) — единичная функция (единичный скачок):
1 при т > 0;
1(т)
- при т = 0;
2
0 при т < 0.
3. sgn т — знак величины т (сигнум):
1 при т > 0
0 при т = 0
— 1 при т < 0
sgn т
= 1(т)-1(-т)
4.6 (т) — дельта-функция:
8(т)
d
dr
1(т).
Дельта-функция — четная функция т. Основные свойства
дельта-функции:
а) тб (т) = 0 и вообще ср (т) 6 (т) = 0, если ср (т) — нечетная
функция, непрерывная при т = 0;
0 + Е
б) Г-ф (т) 8 (т) <Й = -ф (0), если функция г|; (т) непрерывна в
0-Е
точке т = 0 (е > 0);
0 0+Е
Г-ф (т) 6 (т) dt= J4 (т) 6 (т) dr = ±г|> (0),
0-Е
о
если функция г|; (т) непрерывна в точке т = 0.
437
Из этих определений вытекают следующие свойства, имеющие
место для любых действительных т и нечетной функции ф (т):
l)|T|=TSgnT; 2)T=|T|sgnT;
3) ф (т) = ф (|т|) sgn т; 4) ф (|т|) = ф (т) sgn г,
5)ф2(|т|) = ф2(т); 6)sgnT = 2.1(T)-l;
7)l(r)=Sgn^ + 1; 8)|т|=т[2.1(т)-1];
^ ^|т| ч с12\т\ d sgn т „ , ч
9)-^ = sgnT, ю)—Li = -2- = 28 (т);
ат а т а т
11)1(т)=/б(т)ЙТ=1/й(5ёПт).
2
— ОО —ОО
Приложение 3
Таблица соответствий корреляционных функций кх(т)
и спектральных плотностей Sx(u)
К(т)
s;m
1. Db (т), где б (т) — дельта-функция
2. D
3. Z>cos(3t
п
^2 A cos (3,.т
г=1
5.
6.
De~a
-а т
п
-а .• т
ЕА*-
i=i
Z?e-a|T|cos (Зт
Z> / (2*)
Д8(и)
(Z?/2)|6(u+p) + 6(u-3)|
Цд[8(и+р()] + 8(и,-р,.)]
^ i=i
(Лх/иХа'+ш2)-1
1 - _Да^
Л 2 , о2 , , ,2
а + р + и
£а
8. £е
-а т
а
cos (3 т Н sin (3 | т |
-а т
9. De~a
а
cos 6 т sin 8 I т
(3
10. Z>e
■а т
а
ch(3T + -sh(3|-n
(3
(а>Э)
iv [а2 + ((3-ш)2][а2 + (|3+ы)2]
Да 2 (а2 + (З2)
tv [ы2 + а2 - (З2)2] + 4а2(32
Да 2jJ_
тс [ы2 + а2 + (32)2]-4(32ы2
Да 2 (а2 - (З2)
тс [(а-(3)2 + ш2][(а + (3)2+ш2]
11. Д(1-|т|)1(1-|т|),
где 1(х) — единичная функция
12. Z?c"a|т,(1 +а |т|)
2-тс
sin (w / 2)
I w/2 J
фа/тг)[2а3/(^2 + а2)2]
13. Z)e-a|T|
1 + a I т 1+ - sin а2т2
1 ' 3
Da
a
14. £e
-a т
ii I I e~\ 22i 21 |3
1+a т-2а т + —a т
15. 2 a sin (Зт /t
16. 2a2(2cos (Зт-1)
sin (Зт
17.
£>е~(ат)2
18. i>e-u|T|[26(T)-a(sgnT)2]
-к 3(w2 + a2)3
£>a 16 a V
* (w2 + a2)4
al(l->|/(3)
0 при0<|и|< (3,
a2 при (3<|uj|< 2(3,
0 при2(3<|и|
Z?
2алггс
(Да/тс)[ы2/(а2 + ы2)1
exp
.
[2a J
2'
439
СПИСОК ЛИТЕРАТУРЫ
1. В е н т ц е л ь Е. С. Теория вероятностей. — М.: Издательский
центр «Академия», 2003.
2. ВентцельЕ.С, Овчаров Л.А. Теория вероятностей и
ее инженерные приложения. — М.: Издательский центр
«Академия», 2003.
3. ВетцельЕ.С, Овчаров Л.А. Теория случайных
процессов и ее инженерные приложения. — М.: Издательский центр
«Академия», 2003.
4. Ветцель Е.С., Овчаров Л.А. Прикладные задачи
теории вероятностей. — М.: Радио и связь, 1983.
5. Г н е д е н к о Б. В. Курс теории вероятностей. — М.: Физмат-
гиз, 1961.
6. Сборник задач по теории вероятностей, математической
статистике и теории случайных функций. / Под ред. А. А.
Свешникова. — М.: Наука, 1965.
7. Пугачев B.C. Введение в теорию вероятностей. — М.:
Наука, 1988.
8. X анч и н А.Я. Работы по математической теории массового
обслуживания. — М.: Физматгиз, 1963.
9. Ф е л л е р В. Введение в теорию вероятностей и ее
приложения. — М.: Наука, 1964.
10. Смирнов Н.В., Дунин-Барковский И.В. Теория
вероятностей и математическая статистика в технике. — М.:
Физматгиз, 1965.
11. Овчаров Л.А. Прикладные задачи теории массового
обслуживания. — М.: Машиностроение, 1969.
12. Тараканов КВ., Овчаров Л.А, Тырышкин А.Н.
Аналитические методы исследования систем. — М: Сов. радио, 1974.
ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. Основные понятия. Непосредственный подсчет
вероятностей 4
Глава 2. Теоремы сложения и умножения вероятностей 19
Глава 3. Формула полной вероятности и формула Бейеса 49
Глава 4. Повторение опытов 70
Глава 5. Случайные величины. Законы распределения.
Числовые характеристики случайных величин 85
Глава 6. Системы случайных величин
(случайные векторы) 124
Глава 7. Числовые характеристики функций случайных
величин 152
Глава 8. Законы распределения функций случайных величин.
Предельные теоремы теории вероятностей 207
Глава 9. Случайные функции 261
Глава 10. Потоки событий. Марковские случайные процессы 317
Глава 11. Теория массового обслуживания 363
Приложения 428
Список литературы 440
Учебное издание
Вентцель Елена Сергеевна,
Овчаров Лев Александрович
Задачи и упражнения по теории вероятностей
Учебное пособие
Редактор Л. В. Честная
Художественный редактор Ю. Э. Иванова
Технический редактор О.С.Александрова
Компьютерная верстка: В. Н. Канивец
Корректор Г. Н. Петрова
Изд. № А-442. Подписано в печать 20.03.2003. Формат 60 х 90/16.
Гарнитура «Петербург». Бумага тип. № 2. Печать офсетная. Усл. печ. л. 28,0.
Тираж 10000 экз. (1-й завод 1 — 5100 экз.) Заказ №2827.
Лицензия ИД № 02025 от 13.06.2000. Издательский центр «Академия».
Санитарно-эпидемиологическое заключение № 77.99.02.953.Д.002682.05.01 от 18.05.2001.
117342, Москва, ул. Бутлерова, 17-Б, к. 223. Тел./факс: (095)330-1092, 334-8337.
Отпечатано на Саратовском полиграфическом комбинате.
410004, г. Саратов, ул. Чернышевского, 59.